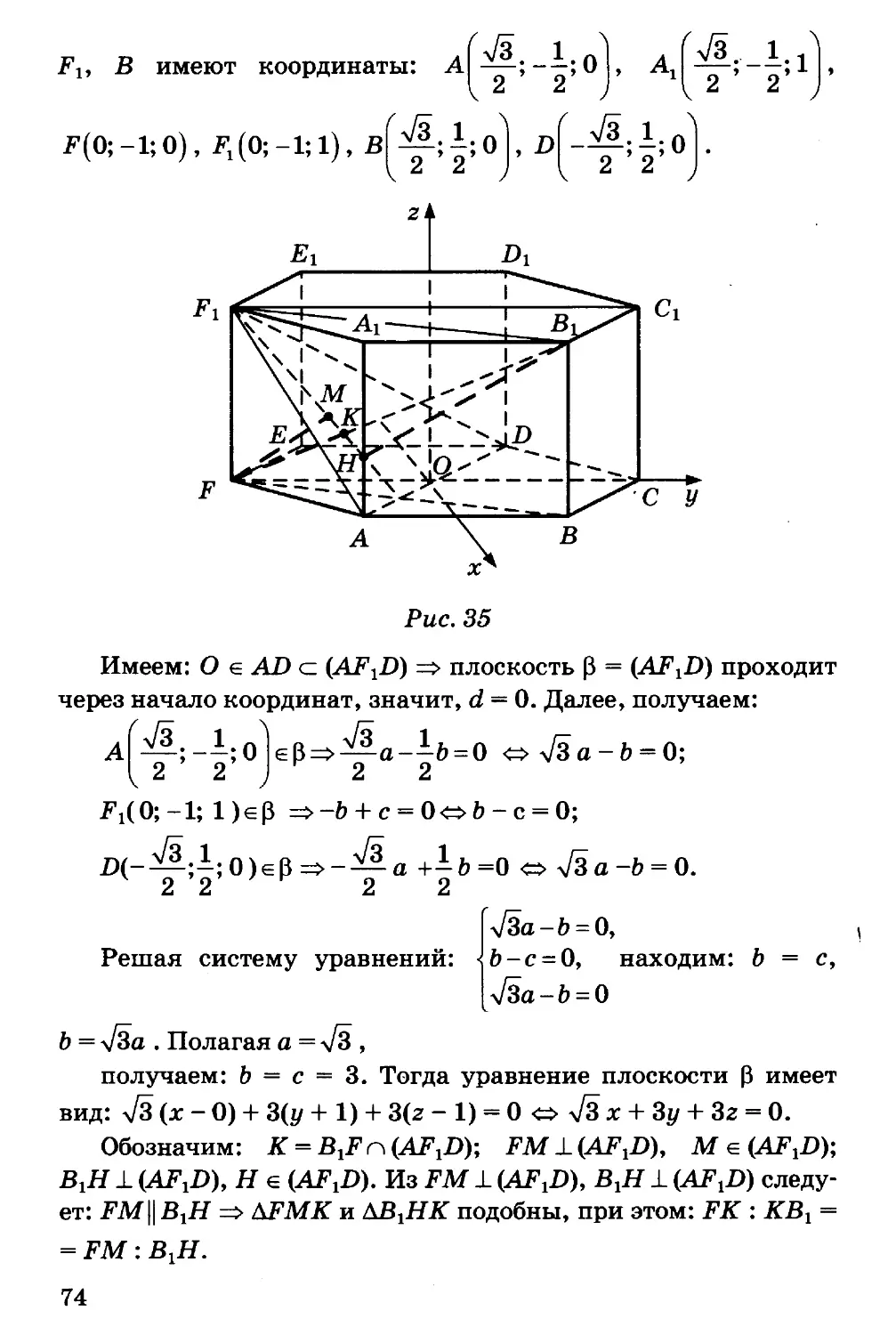
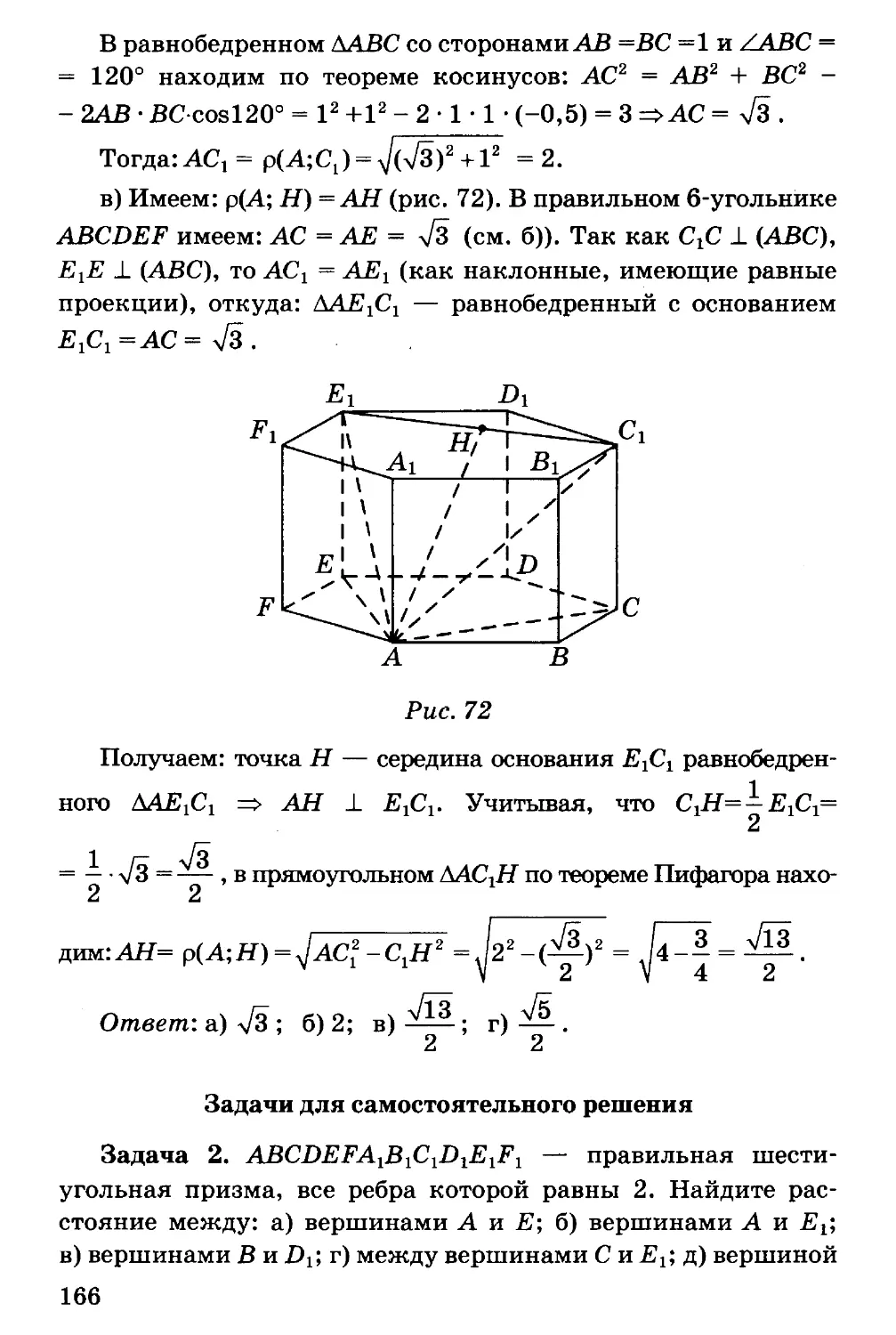
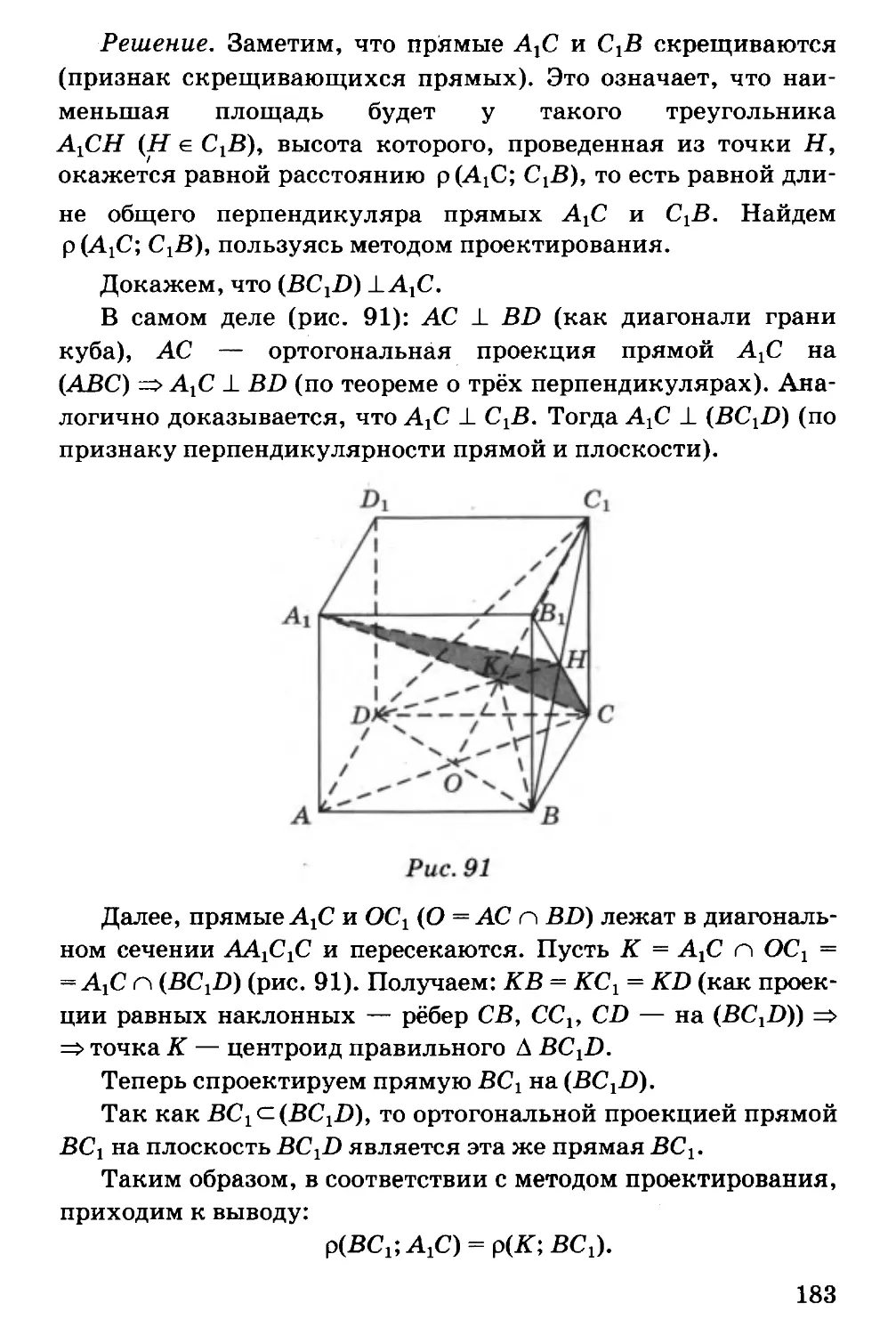
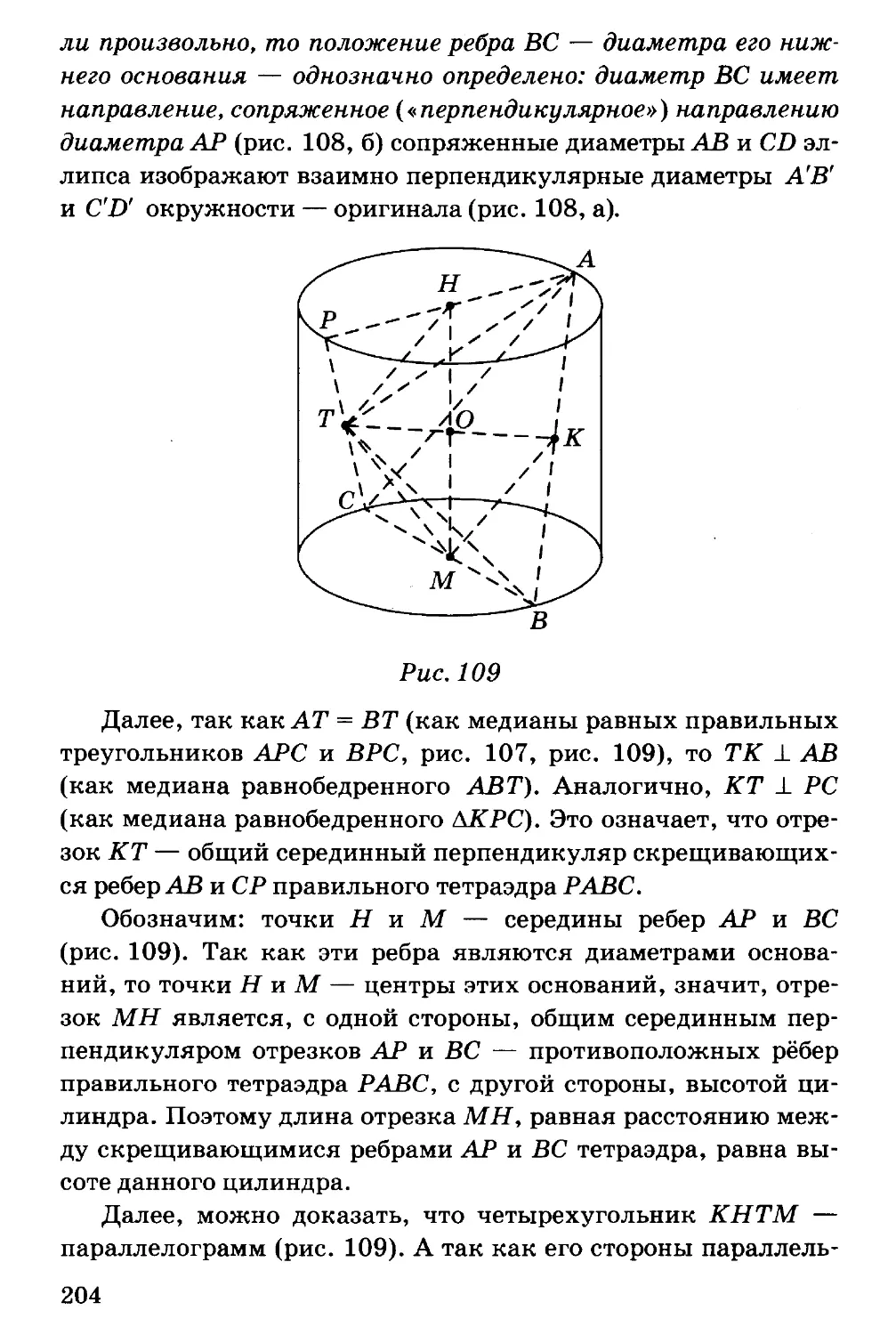
Автор: Потоскуев Е.В.
Теги: общее школьное образование общеобразовательная школа геометрия топология математика задачи по математике
ISBN: 978-5-377-13239-4
Год: 2019
Текст
ПРЕДПРОФИЛЬНАЯ
ЭКЗАМЕН
Предпрофильная и профильная подготовка
Е. В. Потоскуев
Векторно-
координатный метод
решения задач
стереометрии
• Скалярное, векторное и смешанное
произведения векторов в координатах
• Расстояния и углы в пространстве
• Сфера и многогранники в координатах
• Комбинации фигур вращения
и многогранников
• Вычисление площадей и объёмов.
Определители
• Задачи для самостоятельного решения
• Ответы
Издательство
«ЭКЗАМЕН»
МОСКВА • 2019
УДК 373:514
ББК 22.151я72
П64
Потоскуев Е. В.
П64 Векторно-координатный метод решения задач стереометрии. ФГОС / Е. В. По-
тоскуев. — М. : Издательство «Экзамен», 2019. — 223, [1] с. (Серия «Предпрофиль-
ная и профильная подготовка»)
ISBN 978-5-377-13239-4
Данное пособие полностью соответствует федеральному государственному образо-
вательному стандарту (второго поколения).
Выработка навыков и умений решать геометрические задачи векторно-координатным
методом развивает и повышает математическую культуру учащихся — будущих студентов •
вузов физико-математической и естественно-научной направленности.
В этой книге ведется разговор о применении векторов и координат при решении за-
дач позиционного и метрического характера в процессе изучения таких разделов стерео-
метрии в 10-11 классах, как геометрия прямых и плоскостей, геометрия многогранников
и фигур вращения. При этом большое внимание уделено вопросам верного, наглядного
изображения пространственных фигур на плоскости и корректной аргументации утвер-
ждений — проблем, возникающих при изучении стереометрии в 10-11 общеобразова-
тельных классах, классах с углубленным и профильным изучением математики: эти про-
блемы носят общий характер, вне зависимости от профиля и использования того или
иного учебника.
Используя изображения правильного тетраэдра, куба и правильной шестиугольной
призмы, фигур вращения, предлагаются методические рекомендации решения опорных
задач, задач повышенного уровня сложности о нахождении расстояний и углов между
прямыми и плоскостями, вычислении площадей и объемов геометрических фигур.
Заданный материал подобран с соблюдением принципа «от простого — к сложно-
му», что позволяет методически обоснованно реализовывать дифференциацию обучения
решению геометрических задач различного уровня сложности. Тематический набор за-
дач каждого раздела предваряется аргументированным решением их подготовительного
набора. Ко всем задачам указаны ответы.
Наряду с векторно-координатным методом, в данной книге предлагаются решения
задач геометрии многогранников и фигур вращения синтетическим методом.
В пособии имеются списки основных теорем, формул планиметрии и стереометрии.
Учебное пособие адресовано учащимся и учителям математики школ, лицеев, гимна-
зий, колледжей, а также студентам бакалавриата и магистратуры, аспирантам, препода-
вателям педвузов.
Приказом № 699 Министерства образования и науки Российской Федерации учеб-
ные пособия издательства «Экзамен» допущены к использованию в общеобразователь-
ных организациях.
УДО 373:514
ББК 22.151я72
Подписано в печать 24.12.2018.
Формат 60x90/16. Гарнитура «Школьная». Бумага газетная.
Уч.-изд. л. 8,24. Усл. печ. л. 14. Тираж 3000 экз. Заказ № 3255.
ISBN 978-5-377-13239-4
© Потоскуев Е. В., 2019
© Издательство «ЭКЗАМЕН», 2019
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ..........................................6
ГЛАВА 1. ВЕКТОРНАЯ АЛГЕБРА
И НАЧАЛА АФФИННОЙ СТЕРЕОМЕТРИИ...................11
1 Л. Линейные операции над векторами
в пространстве.................................13
Подготовительный набор задач................18
1.2. Разложение вектора
по трем некомпланарным векторам................22
Подготовительный набор задач................24
1.3. Содержательные аффинные задачи стереометрии...26
Задачи для самостоятельного решения.........35
ГЛАВА 2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
МЕТРИЧЕСКИЕ ЗАДАЧИ СТЕРЕОМЕТРИИ..................36
2.1. Начала метрической стереометрии...........36
Подготовительный набор задач................38
2.2. Содержательные метрические
задачи стереометрии............................41
Задачи для самостоятельного решения.........44
Задачи для самостоятельного решения.........53
Задачи для самостоятельного решения.........56
ГЛАВА 3. ГЕОМЕТРИЯ ПРЯМЫХ, ПЛОСКОСТЕЙ
И ФИГУР ВРАЩЕНИЯ В КООРДИНАТАХ...................57
3.1. Линейные операции над векторами в координатах ...58
3.2. Скалярное произведение векторов в координатах.60
3.3. Подготовительный набор задач..............62
3.4. Содержательные метрические
задачи стереометрии............................65
3.4.1. Расстояния в пространстве............67
а) Расстояние от точки до прямой. Задачи...67
Задачи для самостоятельного решения.........71
б) Расстояние от точки до плоскости. Задачи....71
Задачи для самостоятельного решения.........75
в) Расстояние между скрещивающимися
прямыми. Задачи...........................76
Задачи для самостоятельного решения.........84
3.4.2. Углы в пространстве..................85
а) Угол между двумя прямыми. Задачи.......85
Задачи для самостоятельного решения.........87
б) Угол между прямой и плоскостью. Задачи.88
Задачи для самостоятельного решения.........92
в) Угол между плоскостями. Задачи.........93
Задачи для самостоятельного решения.........97
ГЛАВА 4. СФЕРА И МНОГОГРАННИКИ
В КООРДИНАТАХ...................................98
Подготовительные задачи....................101
Задачи для самостоятельного решения........111
ГЛАВА 5. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
И ПЛОЩАДИ МНОГОУГОЛЬНИКОВ......................112
1. Определители второго и третьего порядка...112
Задачи...................................122
2. Векторное произведение двух векторов.... 123
2.1. Ориентация троек некомпланарных векторов.... 123
2.2. Определение векторного
произведения векторов......................125
2.3. Свойства векторного произведения векторов.
Векторное произведение векторов в координатах.125
Задачи...................................132
ГЛАВА 6. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
ТРЕХ ВЕКТОРОВ И МЕТРИЧЕСКИЕ
ЗАДАЧИ СТЕРЕОМЕТРИИ............................137
Определение смешанного произведения
трех векторов и его свойства.................137
Алгебраические свойства смешанного
произведения трех векторов...................138
Геометрические свойства смешанного
произведения трех векторов...................140
Задачи.....................................144
4
ГЛАВА 7. СИНТЕТИЧЕСКАЯ
ГЕОМЕТРИЯ МНОГОГРАННИКОВ
И ФИГУР ВРАЩЕНИЯ В ЗАДАЧАХ....................164
Правильная шестиугольная призма
как модель геометрии прямых и плоскостей......164
1. Расстояние между точками. Задачи.........164
Задачи для самостоятельного решения.......166
2. Расстояние от точки до прямой. Задачи....167
Задачи для самостоятельного решения.......169
3. Расстояние от точки до плоскости. Задачи.170
Задачи для самостоятельного решения.......173
4. Расстояние между скрещивающимися
прямыми. Задачи.............................173
Задачи для самостоятельного решения.......178
О наименьших значениях площадей в геометрии...179
Задачи......................................179
Задачи для самостоятельного решения.........196
Комбинации фигур вращения и многогранников....197
ПРИЛОЖЕНИЕ......................................210
ОТВЕТЫ..........................................218
ЛИТЕРАТУРА......................................223
ПРЕДИСЛОВИЕ
«О сколько нам открытий чудных
Готовит просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг, ...»
Александр Сергеевич Пушкин
(1799-1837)
В данной книге речь идет о динамике развития геометри-
ческой культуры учащихся, о выработке у них (при решении
задач любого уровня сложности) умений аргументированно
обосновывать логические утверждения, геометрические по-
строения и вычислительные операции, необходимые для ус-
пешной сдачи ОГЭ и ЕГЭ по математике.
Требования корректно обосновывать любое геометриче-
ское утверждение способствуют развитию логического мыш-
ления, пространственного воображения и повышению мате-
матической культуры учащихся. Поэтому обучение языку
геометрии является одной из важнейших целей математиче-
ского образования, интеллектуального развития творческой
личности. Заметим при этом, что хорошее геометрическое об-
разование, пространственное воображение и логическое
мышление необходимо не только математику, но и инженеру,
и экономисту, и дизайнеру, и юристу, и программисту, а так-
же специалистам многих и многих других профессий.
Опыт работы свидетельствует, что осознанное решение гео-
метрических задач (планиметрических и стереометрических)
достигается учащимися, если изучение геометрического мате-
риала согласуется с наглядно-модельным принципом его изложе-
ния: решение геометрической задачи начинается с аргументи-
рованного построения рисунка, обладающего наглядностью и
простотой, и сопровождается аргументированными обоснова-
ниями возникающих логических утверждений, дополнительных
геометрических построений и вычислительных операций. С са-
мых первых уроков изучения геометрии необходимо выработать
понимание учащимися, что аргументация шагов построения
изображений фигур, соответствующих условию геометрической
задачи, составляет своеобразный анализ пути её решения.
6
Объектами изучения в школьном курсе геометрии являют-
ся плоские и неплоские (пространственные) геометрические
фигуры, их аффинные и метрические свойства. Изучение этого
материала и его закрепление реализуется решением многих за-
дач, при этом все обоснования (логические, конструктивные,
вычислительные) с необходимостью аргументируются.
Постепенно в геометрических знаниях учащихся увеличи-
вается багаж теоретического материала, что естественным об-
разом позволяет расширять тематическую разновидность гео-
метрических задач: для решения задачи требуются не только
знания материала одной отдельной темы; необходимым ста-
новится умение интегративно использовать фактический ма-
териал различных тем. Это умение изучающего геометрию
вырабатывается посредством самостоятельного решения мно-
гих и многих задач различного уровня сложности, методом
необходимых проб и полезных ошибок.
Любой решающий стереометрическую задачу, ссылаясь на
наглядности и «очевидности» рассматриваемой геометриче-
ской «картинки», может высказывать основанные на интуи-
ции утверждения. Но даже в том случае, когда эти утвержде-
ния являются верными, каждое из них нуждается в логически
корректном обосновании. Логически необоснованное решение
геометрической задачи раздела «С» Единого государственного
экзамена, даже при безошибочных вычислениях и получении
верного ответа, влечет за собой снижение оценочного балла,
который достигает своего максимума лишь тогда, когда это
решение является верным и наполненным всеми необходимы-
ми корректными аргументациями каждого «шага» решения —
графического, логического, вычислительного.
Известно, что полезнее решить несколькими способами
одну и ту же задачу (творчество, креативность мышления),
чем несколько задач решать одним и тем же способом (на-
таскивание). При этом у учащихся вырабатывается вариа-
тивность мышления, закрепляются навыки и умения в при-
менении известных теорем (для обоснования необходимого
утверждения) и формул (для вычисления той или иной ком-
поненты геометрической фигуры).
7
Наряду с синтетическим (геометрическим) методом необ-
ходимо выработать владение также векторным, координат-
ным и векторно-координатным методами решения стерео-
метрических задач. Уровень сложности решаемых при этом
задач необходимо варьировать, соблюдая принцип «от базо-
вого — к повышенному», предварительно рассмотрев решения
опорных тематических задач.
Аффинные задачи стереометрии — это задачи, в которых
исследуются вопросы взаимного расположения прямых и
плоскостей в пространстве. Задачи, в которых находят рас-
стояния, углы, площади, объемы геометрических фигур, на-
зывают метрическими задачами стереометрии. Изучение ма-
териала о векторах и координатах в пространстве позволяет
решать векторным, координатным и векторно-координатным
методом многие аффинные и метрические задачи стереомет-
рии.
В главе 1 настоящей книги в заданном геометрическом ма-
териале различного уровня сложности закрепляется материал
векторной алгебры: операции сложения и вычитания векто-
ров, умножения вектора на число. Кроме того, здесь решают-
ся позиционные (аффинные) задачи геометрии прямых и
плоскостей, используя условия коллинеарности и компла-
нарности векторов.
В главах 2 и 3 данной книги с помощью скалярного произ-
ведения векторов решаются метрические задачи геометрии
прямых и плоскостей в пространстве. Сначала, используя мо-
дели и изображения куба, правильного тетраэдра, правильной
шестиугольной призмы, с помощью скалярного произведения
геометрических векторов решаются задачи о вычислении рас-
стояний и углов, затем решаются аналогичные задачи геомет-
рии прямых и плоскостей с помощью скалярного произведе-
ния векторов в координатном виде.
Глава 4 посвящена решению задач, в которых рассматри-
ваются различные комбинации многогранников и сфер, за-
данных в координатном виде. Кроме того, предлагаются
(с указанием ответов) задачи различного уровня сложности
для самостоятельного решения.
8
В главе 5 рассматриваются векторное произведение двух
векторов, его свойства, выражение в координатной форме, по-
сле чего векторное произведение используется как аппарат
решения задач на вычисление площадей многоугольников.
В главе 6 рассматриваются смешанное произведение трех
векторов, его свойства, выражение в координатной форме и
применение при решении задач на вычисление объемов мно-
гоугольников. Используя свойства скалярного, векторного и
смешанного произведений векторов в координатном виде, ре-
шаются многие задачи стереометрии на взаимное расположе-
ние в пространстве прямых и плоскостей, нахождение площа-
дей и объемов геометрических фигур.
Наряду с векторно-координатным методом решения задач
стереометрии в главе 7 данной книги предлагается дидактиче-
ский материал по решению содержательных задач стереомет-
рии геометрическим (синтетическим) методом. Эти задачи
посвящены геометрии прямых и плоскостей, комбинациям
многогранников и фигур вращения — материалу, изучаемому
в 10-11 классах (углубленный уровень) и включаемому в ЕГЭ.
На моделях и изображениях куба, правильного тетраэдра,
правильной шестиугольной призмы и их комбинациях с ша-
ром (сферой), цилиндром, конусом рассматриваются решения
задач различного уровня сложности. При этом наряду с гра-
фической, логической и вычислительной аргументацией ре-
шения этих задач предлагаются также «проверочные» задачи
(с указанием ответов) для самостоятельного решения.
При решении задач векторным методом «рабочими» явля-
ются: векторная «формула для середины отрезка», для точки
пересечения медиан (центроида) треугольника; условия кол-
линеарности двух векторов и компланарности трех векторов;
условия перпендикулярности двух векторов.
Сначала решаются стереометрические задачи, используя
операции сложения и вычитания векторов, умножения вектора
на число. Кроме того, рассматривается заданный материал о
коллинеарных, компланарных и некомпланарных векторах.
Изучение этого материала позволяет решать векторным методом
аффинные задачи стереометрии — задачи, в которых изучаются
вопросы взаимного расположения прямых и плоскостей.
9
Далее предлагаются метрические задачи стереометрии,
решение которых реализуется векторно-координатным мето-
дом, используя скалярное произведение векторов. Находят
расстояния, углы, площади, объемы геометрических фигур:
сначала решаются задачи курса стереометрии, используя гео-
метрические векторы, затем при их решении используется
скалярное произведение векторов в координатах.
Чтобы координаты и векторы стали эффективным аппара-
том решения геометрических задач, необходимо, прежде все-
го, научиться переводить условие геометрической задачи в
векторно-координатную символику и терминологию (на «ко-
ординатный язык»), затем грамотно выполнять соответст-
вующие алгебраические операции над координатами и векто-
рами, после чего полученный_в векторно-координатной форме
результат переводить вновь на язык элементарной (синтети-
ческой) геометрии. При этом, соблюдая принцип «от просто-
го — к сложному», следует рассматривать решения задач раз-
личного уровня сложности каждым из упомянутых методов.
Прежде чем приступать к решению стереометрической
задачи координатным методом, необходимо сначала соста-
вить «геометрический алгоритм» ее решения, что естествен-
ным образом связано с повторением и углублением всего ма-
териала школьной геометрии.
Теоретический материал каждой главы дополняется доста-
точным количеством тренировочных, опорных задач. В книге
приводятся подробные решения ряда задач из каждой главы.
Некоторые задачи решены различными способами. Почти ко
всем задачам даны ответы или указания к их решению.
Автор
10
ГЛАВА 1.
ВЕКТОРНАЯ АЛГЕБРА
И НАЧАЛА АФФИННОЙ СТЕРЕОМЕТРИИ
Следует заметить: векторное решение многих стерео-
метрических задач значительно проще их решения средства-
ми элементарной геометрии («чисто геометрически»). Причи-
на этого «упрощения» заключается в том, что при векторном
методе решения стереометрической задачи можно обойтись
без тех дополнительных построений, которые иногда затруд-
няют поиск решения даже некоторых простых геометриче-
ских задач.
Аппарат векторной алгебры находит свое широкое приме-
нение в геометрии, теории линейного программирования, в
курсах физики, теоретической механики и многих других ес-
тественно-научных теориях. Наряду с геометрией и физикой
векторный метод находит широкое применение также в дру-
гих науках, например в алгебре. Рассмотрим пример.
Решить уравнение: 2>Jx-l + 5x = ^xz + 4)(х + 24). (1)
Решение. Предварительно напомним, что если <р - Z(p, g), то
pq Л
coscp - ,5| Л., 1, при этом
р-д<|р|-|д| и |j5-g|<|p|-|g|. (*)
Причем \р • q\ = |р|• |g|« р || q .
Введем векторы р(2; х) и q(\lx-l; б) и используем соот-
ношение (*). Получаем:
pq =2-Jx-l + 5-x , |р|-|д|щ4 + х2 j-7x + 24 .
На основании соотношения p-g<|p|-|g| имеем:
2^х-1 + 5х < J(4 + x2)(x + 24) . (2)
Замечаем, что левые и, соответственно, правые части дан-
ного уравнения (1) и полученного неравенства (2) совпадают.
Но, согласно уравнению (1), левая часть неравенства (2) долж-
11
на быть равна его правой части, т.е. должно выполняться ус-
ловие: р • q = |р| • |д|. Это возможно тогда и только тогда, когда:
p(2;x)||g(V^Zl;5)o^J= = f. (3)
v ’ Vx-1 о
Таким образом, данное уравнение (1) равносильно урав-
нению (3), которое, в свою очередь, равносильно уравнению
х3 - х2 - 100 = 0.
Имеем: х3 - х2 - 100 = 0 <=> х3 + 4х2 - 5х2 - 100 = 0 о
(х3 - 5х2) + (4х2 - 100) = 0 о х2(х - 5) + 4(х2 - 25) = 0 о
о (х - 5)(х2 + 4х + 20) = 0.
Решением этого уравнения является единственное значе-
ние х = 5.
Ответ: х = 5.
В данной книге ведется разговор о применении векторов
при изучении стереометрии в 10-11 классах, о роли векторно-
го аппарата в повышении и развитии математической культу-
ры учащихся профильной школы — будущих студентов вузов
физико-математической и естественно-научной ориентаций.
Чтобы векторы стали аппаратом решения геометриче-
ских задач, необходимо, прежде всего, уметь переводить ус-
ловие геометрической задачи в векторную терминологию и
символику (на «векторный язык»), затем грамотно (безоши-
бочно) выполнять соответствующие алгебраические опера-
ции над векторами и, наконец, результат, полученный в век-
торной форме, верно переводить «обратно», на «язык чисто
геометрический».
Знание условия коллинеарности двух векторов и компла-
нарности трех векторов позволяет в векторной форме решать
аффинные задачи стереометрии — задачи, в которых изуча-
ются вопросы взаимного расположения прямых и плоскостей.
Знание свойств скалярного произведения двух векторов, ус-
ловия их перпендикулярности позволяет легко перевести в
векторную форму отношения перпендикулярности прямых и
плоскостей и с помощью векторов решать метрические зада-
чи, в которых находят расстояния, углы, площади, объемы
геометрических фигур. Одним словом, векторы — мощный
аппарат решения стереометрических задач.
12
1.1. Линейные операции над векторами
в пространстве
Отрезок АВ, у которого указан порядок концов, называет-
ся направленным отрезком: точка А называется «началом», а
точка В— «концом» направленного отрезка АВ.
Ненулевым вектором в пространстве называется мно-
жество всех равных между собой направленных отрезков
пространства.
Векторы обозначают обычно строчными буквами латин-
ского алфавита со стрелкой сверху: а , b , с , ... и изображают
направленными отрезками АВ , CD, EF, ... При этом если
направленный отрезок АВ изображает вектор а , то записы-
вают: АВ = а (рис. 1).
Длиной ненулевого вектора АВ = а называется длина от-
резка АВ. Длина вектора АВ = а обозначается: |ав| = |л| . На-
правлением ненулевого вектора АВ называется направление
луча АВ.
Вектор, длина которого равна нулю, называется нулевым
вектором (или нулъ-вектором). Нулевой вектор обозначает-
ся 0 и изображается точкой.
Векторы а и Ъ называются одинаково направленными
(сонаправленными) (обозначают а. ТТ Ъ ), если одинаково на-
правлены изображающие их направленные отрезки, и проти-
воположно направленными (обозначают а ТФ Ь ), если проти-
воположно направлены изображающие их отрезки.
Два ненулевых вектора называются коллинеарными, если
они сонаправлены или противоположно направлены. Нулевой
вектор коллинеарен любому вектору. Коллинеарность векто-
ров а и Ь обозначают: а\\Ь . На рис. 2 изображены попарно
13
коллинеарные векторы а, Ь и с: a\\b , а || с , Ъ || с . При этом:
a ttb,a tic.
Два вектора АВ = а и CD = Ъ называются равными, если
они сонаправлены и имеют равные длины, при этом записы-
вают: а = b или АВ - CD .
Рис. 2
На множестве всех векторов пространства вводят линей-
ные операции сложения, вычитания, умножения вектора на
число (на скаляр).
а) Сложение векторов. В стереометрии сумму двух векто-
ров можно найти, как и в планиметрии, по правилу треуголь-
ника (рис. 3) или по правилу параллелограмма (рис. 4).
Операция сложения векторов в пространстве обладает сле-
дующими свойствами.
— Коммутативность сложения (переместительное свой-
ство): для любых векторов а и Ъ имеет место равенство
а + Ъ — Ъ +а (рис. 4).
14
— Ассоциативность сложения (сочетательное свойство)’.
для любых векторов а, Ъ , с справедливо: (а+&)+с =a + (b +с)
(рис. 5).
— Свойство нуль-вектора: а+6=0+а=а для любого век-
тора а .
— Существование и единственность противоположного
вектора: для любого вектора а пространства существует
противоположный вектор -а, и притом единственный, та-
кой, что а + (-а) = 0.
Рис. 7
При сложении трех и более векторов применяется правило
многоугольника (или правило ломаной линии). На рис. 6 ил-
люстрируется нахождение суммы векторов а1, а2, а3, а4.
15
Если три вектора а - ОА , b - ОВ , с = ОС отложены от од-
ной точки и не лежат в одной плоскости (не параллельны од-
ной плоскости), то их сумма находится по правилу паралле-
лепипеда: построим параллелепипед на отрезках О А, ОВ и ОС
как на ребрах, выходящих из одной вершины (рис. 7). Тогда
вектор ODi - ОА + ОВ + ОС - ОА + AD + DDi — искомая сумма.
б) Вычитание векторов. Вычитание векторов — это опера-
ция, обратная сложению векторов. Разностью векторов а и
Ъ называется такой вектор с , который в сумме с вектором
Ъ дает вектор а , т. е. а-b =с =>Ь +с =а .
Если ОА-а , ОВ-b (рис. 8), то ОА-ОВ-ВА , так как по
правилу треугольника ОВ + ВА = ОА .
Отсюда: ВА = ОА-ОВ = с =а-Ь.
Вычитание векторов можно свести к сложению векторов:
а-Ь=а+(-&). (*)
Заметим, что АВ - СВ = АВ + ВС = АС.
в) Умножение вектора на число. Пусть даны вектор а и
действительное число X.
Определение. Произведением вектора а на число X
называется такой вектор Ъ (обозначается Ь = Ха), который
удовлетворяет условиям:
а ) если X = 0 или а = 0 , то X 0 - 0 • а = 0 ;
б) длина вектора b равна произведению длины вектора а
и модуля числа X, т. е. 6 =|Ха|-|Х|-|а|;
16
в) вектор Ъ сонаправлен с вектором а, если к > 0, и про-
тивонаправлен вектору а, если X < О, т. е. Ха Tt а , если
X > 0; Ха 14 а , если X < О.
Операция умножения вектора на число обладает свойст-
вами:
1. х (у а ) = (ху)а для любых чисел х, у и любого вектора а ;
2. (х + у) а = ха + у а для любых чисел х, у и любого век-
тора а;
3. х (а + Ь) = ха + хо для любых векторов а и Ь и любо-
го числа х (рис. 9).
Рис. 9
В пространстве имеет место признак коллинеарности двух
ненулевых векторов.
Ненулевые векторы а и Ь коллинеарны тогда и только
тогда, когда найдется такое число х, что выполняется ра-
венство b =ха . При этом число х является единственным.
Из этого следует: точка М лежит на прямой АВ тогда и
только тогда, когда выполняется условие AM = хАВ .
17
Рис. 11
♦ Рабочими» при векторном способе решения аффинных
задач стереометрии являются: «векторная формула»
OAf =—(ОА + Ов) для середины М отрезка АВ (рис. 10) и про-
извольной точки О пространства, а также «векторная форму-
ла»: ОМ =—(ОА + ОВ + ОС) —для центроида М треугольника
3' '
АВС (рис. 11) и произвольной точки О пространства.
В результате изучения этой темы необходимо
уметь:
• формулировать определение: коллинеарных векторов;
суммы, разности двух векторов; произведения вектора на
число;
• формулировать свойства линейных операций над векто-
рами и иллюстрировать их, используя изображения много-
гранников;
• формулировать признаки коллинеарности двух векторов
в пространстве, иллюстрируя их на изображениях многогран-
ников;
• на изображениях куба, пирамиды, параллелепипеда оп-
ределять векторным методом взаимное расположение точек,
прямых и плоскостей.
Подготовительный набор задач
Задача 1. В параллелепипеде ABCDA^^iDi обозначьте:
AtB = d, CD = Ь, AD = с . Изобразите на рисунке векторы:
а) а-b ; б) Ь-а; в) а-с ; г) а + с-Ъ ; д) с+b-а ; е) -а-b .
18
Задача 2. Упростите выражение:
а) АВ + РЕ-НМ + ВС + НМ-АС;
б) СЕ-МЕ-ЁР + МР + ЁЕ + ЁС;
в) АВ + СЕ + МЯ + ВА + ЁС + НМ.
Задача 3. Даны точки А, В, С, К. Представьте вектор АВ в
виде линейной комбинации следующих векторов: а) АС, КС ,
ВК; б) КА, КС, СВ; в) КА, СК , ВС; г) АС, ВК , КС,
СВ, ВА.
Задача 4. Дан параллелепипед ABCDA^yCyD^ М — произ-
вольная точка пространства. Докажите, что:
a) MA + MCi=MC-AE4i;6) MP + MBi-MB + MBi.
Задача 5. Пусть О — точка пересечения диагоналей куба
ABCDA^B^C^Dy.
Найдите число х, такое, что выполняется: a) AB = xCD;
б) AO = xACi;
в) DBr = xOBi; г) DB1 - xBrO ; д) СО = xAtC .
Задача 6. Векторы р = а + Ь и q = a-b коллинеарны. Кол-
линеарны ли векторы а и b ?
Задача 7. Докажите, что если точка М — середина от-
резка АВ, а К — произвольная точка пространства, то
КМ--(КА + КВ
2\
Рис. 12
19
Задача 8. Докажите, что если точка М — центроид тре-
угольника АВС, то МА + МВ + МС = б .
Решение. Пусть точка К — середина ВС (рис. 12). Тогда
мк=-(мв+мс}.
2\ )
С другой стороны, МК = -—МА (центроид М треугольни-
2
ка АВС делит его медиану АКТ в отношении 2:1, считая от вер-
шины, то есть AM : МК = 2:1). Тогда получаем:
-(мв+мс
2'
= -—МА, откуда МА + МВ + МС = б .
Что и требовалось доказать.
Задача 9. Докажите, что если точка К — центроид треуголь-
ника АВС (рис. 13), М — произвольная точка пространства, то
выполняется векторное равенство: МК = ( МА + МВ + МС j.
Решение. Сумму векторов будем находить по правилу
треугольника. Имеем (рис. 13): в ААКМ-. МА + АК-МК;
вКВКМ: МВ + ВК = МК ;в&СКМ: МС + СК = МК.
Рис. 13
После сложения всех этих равенств получаем:
ЗМК = (МА + МВ + МС) + (АК + ВК + СК} .
Так как АК + ВК + СК ^-^КА + КВ + КС^О , то:
ЗМК = МА + МВ + МС=>МК=—(МА + МВ + МС
3V
Что и требовалось доказать.
20
Задача 10. PABCD — правильная четырехугольная пира-
мида с вершиной Р и центром О основания. Докажите, что
АО+РВ + РС+ОР + ВР + ВА + ВС =
= АР + ВА + ВС + ВС + ВА + РС.
Задача 11. ABCBA^C^ — куб.
Начертите вектор АК, если: а) АК - АВ+ВС + СС1;
б) АК = АВ+ ВС+ СВ ; в) АК^АВ + АС + ВС.
Задача 12. Начертите тетраэдр РАВС и постройте на-
правленный отрезок, задающий вектор: а) АВ + ВС;
б) АС + АР; в) РВ + РС; г) АС-АВ; д) АВ-СР; е) -ВР+ВС;
ж) -ВР-РС + ВС.
Задача 13. АВСВА^ВуС^В^ — параллелепипед. Укажите
такую точку М, что справедливо равенство:
МА + МВ + МС + МВ + MAi + MBi + MCi + MBi = б.
Задача 14. Дан тетраэдр РАВС. Постройте такую точку М,
что справедливо равенство РА + РВ + PC - РМ = б .
Рис. 14
Решение. Имеем:
РА + РВ+РСРМ = 0 РА + РВ+РС = РМ .
21
Пусть точка К — центроид ДАВС. Тогда для этого тре-
угольника, его центроида К и точки Р имеет место
РК^^РА + РВ + РС^ или РА + РВ + РС = ЗРК. Таким обра-
зом, получили: PM = ЗРК , откуда следует, что векторы РМ
и РК , отложенные от точки Р, сонаправлены. Следовательно,
точки Р, К и М лежат на одной прямой (рис. 14), при этом ис-
комая точка М лежит на луче РК и \РМ\ = 3|Р.К|, где К — цен-
троид ДАВС.
Задача 15. Построены два треугольника, вершинами каж-
дого из которых служат середины несмежных звеньев данной
неплоской замкнутой ломаной, состоящей из шести звеньев.
Докажите, что центроиды этих треугольников совпадают.
1.2. Разложение вектора
по трем некомпланарным векторам
Определение. Базисом на плоскости называется любая
упорядоченная пара неколлинеарных векторов а и Ь . Векто-
ры а и Ъ называются базисными векторами. Базис из векто-
ров а и Ь обозначают (а; Ъ).
Если на плоскости дан базис (а; Ь), то для любого вектора
р этой плоскости существует единственная упорядоченная
пара чисел (х; у), такая, что выполняется векторное равенст-
во: p = xa + yb . При этом равенство p = xa + yb называется
разложением вектора р по базису (а; & а числа х и у — ко-
ординатами вектора р в этом базисе.
Три вектора а , Ь и с пространства компланарны тогда и
только тогда, когда существуют числа х и у, такие, что вы-
полняется равенство:
с -ха + уЪ .
В общем виде критерий компланарности трех ненулевых
векторов а, b и с выражает равенство: xa + yb+zc=O (при
условии, что не все коэффициенты одновременно равны нулю).
22
Если векторы ар а2, ак умножить соответственно на
числа Хр Х2,...»Хд , а затем полученные векторы
Х^р У.2а2,.\kak сложить, то получим некоторый вектор
с =Х1а1+ Х2а2+ ...Xtat, который называется линейной комби-
нацией векторов 5р а2, ..., ак; числа Хр Х2,...»Хй называют-
ся коэффициентами линейной комбинации.
Например, вектор с = 2а + ЗЬ является линейной комбина-
цией векторов а и Ъ с коэффициентами соответственно 2 и 3,
а вектор р = -2а + 0,5Ь -с —линейной комбинацией векторов
а , Ь и с с коэффициентами соответственно (-2), 0,5 и (-1).
Три вектора называются некомпланарными, если изо-
бражающие их направленные отрезки не лежат в одной
плоскости и не параллельны одной плоскости.
Базисом векторов в пространстве называется любая упо-
рядоченная тройка некомпланарных векторов. Векторы, об-
разующие базис, называются базисными векторами. Базис,
составленный из векторов а , b , с , обозначают (a; b; с j, при
этом всякий вектор р пространства можно представить в ви-
де: p = xa + yb+zc. Равенство p = xa + yb+zc называется
разложением вектора р по базису (а; 5; с) или разложением
вектора р по базисным векторам а , b и с; числа х, у, z на-
зываются координатами вектора р в базисе (а; Ь; с). Любой
вектор пространства можно единственным образом разложить
по векторам данного базиса.
Если в задаче требуется доказать, что три данные прямые
параллельны некоторой плоскости, то достаточно на каждой
из этих прямых выбрать вектор и, используя признак ком-
планарности трех векторов, доказать, что выбранные векторы
компланарны.
В результате изучения этой темы необходимо
знать/понимать:
• свойства линейных операций над векторами;
• определение: а) компланарных векторов; б) векторного
базиса на плоскости и в пространстве;
23
• признак компланарности трех ненулевых векторов;
• для доказательства параллельности трех прямых некото-
рой одной плоскости достаточно на каждой из этих прямых
выбрать вектор и, используя признак компланарности трех
векторов, доказать, что выбранные векторы компланарны.
Уметь:
• грамотно (безошибочно) выполнять алгебраические опе-
рации над векторами;
• производить разложение вектора в данном базисе;
• формулировать признаки коллинеарности двух и ком-
планарности трех векторов в пространстве, иллюстрируя их
на изображениях многогранников;
• на данном изображении многогранника задавать вектор-
ный базис, после чего правильно записывать разложение век-
тора по базису;
• доказывать векторным методом параллельность трех
прямых некоторой одной плоскости;
• на изображениях куба, пирамиды, параллелепипеда век-
торным методом определять взаимное расположение точек,
прямых и плоскостей;
• решать геометрические задачи векторным методом, для
чего переводить условие геометрической задачи в векторную
терминологию и символику (на «векторный язык»), затем
грамотно (безошибочно) выполнять соответствующие алгеб-
раические операции над векторами- и, наконец, результат,
полученный в векторной форме, верно переводить «обратно»,
на «язык геометрический».
Подготовительный набор задач
З адача 16. Дан правильный шестиугольник ABCDEF.
Пусть АС = а, АЕ-Ъ . Разложите по базису (a;b} векторы:
a) AD ; б) AF ; в) ED .
Задача 17. В тетраэдре РАВС точка М — центроид (точка
пересечения медиан) треугольника РВС, точка Н — середина
ребра PC, точка Е взята на ребре АР так, что АЕ : ЕР = 2:1.
24
Разложите вектор ЕМ по базису если а = ВА,
b =ВС , с =ВР (рис. 15).
Рис. 15
Решение. По правилу ломаной имеем: ЕМ = ЕА + АВ + ВМ .
Находим:
АЕ : ЕР = 2 : 3 ЁА ^-РА^-(вА-ВР\^-(а-с\;
3 3V / 3V ’
АВ - -ВА = -а.;
М — центроидЬРВС => ВМ = ^ВН = |• + ВР^ = + с).
Тогда ЕМ = —(a-c}-a + —(b+c] = -—a+—b-—c .
3V ' 3' ' 3 3 3
Ответ: ЕМ = --а+-Ь--с.
3 3 3
Задача 18. Основанием пирамиды с вершиной М является
параллелограмм ABCD, диагонали которого пересекаются в
точке О; точка К — середина ребра МС. Разложите векторы
MD и АК по векторам а = МА, b = МВ , с = МС .
Задача 19. ABCDAlBlClDl — параллелепипед; точка М —
точка пересечения диагоналей основания ABCD. Обозначим
AjA-a, АгВ = Ь , AxD = c . В базисе разложите сле-
дующие векторы: а) АХМ ; б) DXB; в) СХВ .
25
Задача 20. Точки К и Кг — центроиды треугольников со-
ответственно АВС и AjBjCp
Докажите, что AAt + BBi + CCi = ЗКК i.
Задача 21. Дан параллелепипед ABCDA^B^C^D^. Точки Р,
Н и К — середины ребер соответственно А^, ССг и АВ. До-
кажите, что плоскость НРК проходит через точку О пересече-
ния диагоналей параллелепипеда.
Задача 22. Векторы РА, РВ и PC некомпланарны. Из-
вестно, что PH = З^РА + РВ + РС^. В каком отношении плос-
кость АВС делит отрезок PH, считая от точки Р?
Задача 23. Точки К и Т — середины ребер соответственно
АВ и СР тетраэдра РАВС.
Докажите, что 2КТ = АС + ВР = АР + ВС .
Задача 24. Дана треугольная призма АВСЛ^С Нарисуй-
те вектор AM, если:
а) AM = АВ+ ВС+ А^А; б) АМ=-ААл + AB + BC-BJ3 .
Задача 25. Точки К и Е — середины ребер соответственно
АВ и СР тетраэдра РАВС. Докажите, что прямые АР, ВС и КЕ
параллельны некоторой плоскости.
1.3. Содержательные
аффинные задачи стереометрии
Задача 26. Докажите, что диагональ BrD куба
ABCDAiB^iDi делится плоскостью ADjC в отношении 2:1,
считая от вершины В^
Решение. Сначала докажем, что Bj-Dl (ADrC) (рис. 16).
Имеем: BjB±(ABC) =>BD — ортогональная проекция на-
клонной BXD на (АВС). Учитывая BDLAC (как диагонали
квадрата ABCD), заключаем: B^DLAC (по теореме о трёх пер-
пендикулярах).
26
Рис. 16
Аналогично, AjB, (A]AD)=>AXD — ортогональная проек-
ция наклонной BXD на (A^AD). Учитывая AjDIADj (как диа-
гонали квадрата AAXDXD), заключаем: BjDIADj (по теореме о
трёх перпендикулярах). Так как прямые АС и AZ)j пересека-
ются, то B1D±(AD1C) (по признаку перпендикулярности пря-
мой и плоскости).
Обозначим: М = BjDn (ADXC).
Так как наклонные DA, DC, DD} к (AD}C) равны (как ребра
куба) и BlDL(ADlC), при этом М = B1Dr\(AD1C), то равны и
их проекции AM, СМ и D^M на (ADjC).
Учитывая АС = AD1= DXC (как диагонали равных квадра-
тов — граней данного куба), приходим к выводу: точка М —
центроид правильного AADjC.
Теперь обозначим: DA-a , DC = b, DD^-c и примем
тройку некомпланарных векторов (a; b; с j в качестве базиса в
пространстве.
Имеем (по правилу параллелепипеда):
DB{ = DA + DC + DDi -a + b + с . (*)
Далее, так как точка М — центроид AACDj, то:
Дм = |(вА + ВС + 551) = |(а + Ь+с). (**)
Из (*) и (**) следует: DBr-3DM => векторы DM и DB}
коллинеарны и сонаправлены (3 > 0). Это означает: точка М
принадлежит диагонали В-J), при этом BrD : MD = 3:1, отку-
да В,М : MD = 2:1, что и требовалось доказать.
27
Задача 27. Отрезок, соединяющий, вершину тетраэдра с
центроидом противолежащей грани, называется медианой
этого тетраэдра; отрезок, соединяющий середины противо-
положных ребер тетраэдра, называется его бимедианой. До-
кажите, что: а) все медианы тетраэдра пересекаются в одной
точке и эта точка делит каждую из медиан в отношении 3:1,
считая от вершины; б) все бимедианы тетраэдра пересекаются
в одной точке и делятся ею пополам; в) точка пересечения би-
медиан тетраэдра совпадает с точкой пересечения его медиан.
Решение, а) Пусть Ht, Н2, Н3, Н4 — центроиды граней со-
ответственно АВС, АВР, ВСР, АСР; М — точка, делящая ме-
диану PHj тетраэдра РАВС в отношении РМ : MHt =3:1
(рис. 17). Тогда РМ : РНХ = 3 : 4, откуда РМ =—РНХ.
4
Для любой точки О пространства и центроида Нг грани
АВС выполняется: ОН\ = — (ОА + ОВ+Ос).
3\ '
Тогда ОМ = ОР + РМ = OP+-PHi
4
ОР + -(ОН1 -ОР} = ОР + -ОН1 --ОР =
4' /44
=1ор+^.1(од+дв+оск-(дА+дв+ос+ор).
443' / 4* /
Рис. 17
28
Аналогично можно доказать, что для точек Мг, М2 и М3,
делящих медианы соответственно СН2, АН3, ВН4 тетраэдра в
отношении 3:1, считая соответственно от вершин С, А и В,
выполняется:
ом}=ом2=омя=ом-^(оа+ов+ос+ор^ .
Это означает, что точки М, Мг, М2 и М3 совпадают, то есть
все четыре медианы РНГ, СН2, АН3 и ВНА тетраэдра пересека-
ются в одной точке М и делятся этой точкой в отношении
3:1, считая от соответствующей вершины, что и требовалось
доказать.
Точка пересечения медиан тетраэдра называется цен-
троидом этого тетраэдра.
б) Пусть точки К и Е — середины ребер соответственно ВС
и АР (рис. 17), то есть отрезок КЕ — бимедиана тетраэдра
РАВС. Если точка Q — середина бимедианы КЕ, то для любой
точки О пространства выполняется:
dQ = |(d^ + OE).
Так как К и Е — середины ребер соответственно ВС и АР,
то справедливо:
(Ж = -(ОВ + Оск ОЕ = -(ОА + ОР'). Тогда
2V > 2' '
oq=-(qk4oeU-( -(ов+ос)+-(оа+орп=
2' I 2<2' > 2V I)
= -(ОА + ОВ + ОС + ОР].
4' /
получаем:
Аналогично можно доказать, что для середины Q} биме-
дианы TF (рис. 17) имеет место: OQ} = — (ОА + ОВ + ОС + ОР).
4' '
Можно убедиться, что такое же равенство выполняется и для
середины Q2 третьей бимедианы данного тетраэдра. Это озна-
чает: OQj = OQ2 = OQ , откуда следует, что точки Q, Q} и Q2
совпадают, то есть все три бимедианы тетраэдра пересекаются
в одной точке Q и делятся этой точкой пополам.
29
в) Таким образом, для точек М и Q справедливы соот-
ветственно равенства: OM = ^OA + OB + OC-i-Op) и
OQ =—(ОА + ОВ + ОС + ОР\, из которых следует OM = OQ, от-
4\ /
куда: точка Q пересечения бимедиан тетраэдра РАВС совпа-
дает с его центроидом М, что и требовалось доказать.
Теперь рассмотрим решение этих задач синтетическим
методом.
Задача 28. Докажите, что все четыре медианы тетраэдра
пересекаются в одной точке и делятся этой точкой в отно-
шении 3:1, считая от вершины.
Пусть точки О и Т — центроиды граней соответственно
АВС и АРВ тетраэдра РАВС (рис. 18); РО, СТ — его медианы,
М = РО п СТ — точка пересечения этих медиан (РО и СТ ле-
жат в одной плоскости СРК). По свойству центроида тре-
угольника имеем PT : ТК = СО : ОК = 2 : 1 => ОТЦСР (поче-
му?), РК : ТК = СК : ОК = 3 : 1, откуда СР : ОТ = 3 : 1. Тогда
из подобия треугольников СРМ и ТОМ следует РМ : МО =
= СМ: МТ = СР : ОТ = 3:1. (Предлагается самостоятельно дока-
зать, что медианы тетраэдра, проведенные из вершин А и В,
также проходят через точку М и делятся этой точкой в отноше-
нии 3 : 1, считая от вершины.) Точка М пересечения всех четы-
рехмедиан тетраэдра называется центроидом тетраэдра.
Заметим, что доказанное свойство справедливо для любого
тетраэдра.
30
Это замечательное свойство тетраэдра следует помнить при
решении задач. Воспользуемся и мы этим свойством.
Задача 29. Докажите, что все бимедианы тетраэдра пере-
секаются в одной точке и делятся ею пополам.
Решение. Пусть точки Т, К, L, F, N, Н — середины ребер
соответственно АВ, ВС, СА, РА, РВ, PC тетраэдра РАВС
(рис. 19). Тогда отрезки FK, TH и NL — бимедианы данного
тетраэдра. Докажем, что середины всех этих трех отрезков
совпадают.
Так как FH и ТК — средние линии треугольников соответ-
ственно АРС и АВС, то FH\\AC, FH = -AC и ТХ||АС,
2
ТК -—АС, откуда FH = ТК и FH\\TK. Это означает, что четы-
2
рехугольник TKHF — параллелограмм, а бимедианы FK и
TH данного тетраэдра являются диагоналями этого паралле-
лограмма, поэтому они точкой М их пересечения делятся по-
полам.
Рис. 19
Аналогично, FN = KL и FN\\KL (как средние линии тре-
угольников РАВ и САВ). Значит, четырехугольник LKNF —
параллелограмм, и его диагонали, которыми являются биме-
дианы FK и LN данного тетраэдра, делятся точкой их пересе-
чения пополам. Пусть Мх = FKn LN. Так как серединой от-
31
резка FK является точка М и любой отрезок имеет лишь одну
середину, то точка Мj совпадает с точкой М. Это означает, что
точка М является серединой и отрезка LN. Таким образом, в
точке М пересекаются все три бимедианы тетраэдра РАВС и
делятся этой точкой пополам. Задача решена.
Задача 30. Докажите, что точка пересечения медиан тет-
раэдра совпадает с точкой пересечения его бимедиан.
Решение. Пусть отрезок KF — бимедиана тетраэдра РАВС',
Нг, Н2 — центроиды его граней соответственно АВС и РВС’,
М — точка пересечения его медиан АН2 и PHi (рис. 20).
Так как АН1: НГК= РН2: Н2К = 2 : 1, то в плоскости АРК
по теореме Фалеса НгН2 || АР. Значит, АРН2Н1 — трапеция,
диагоналями которой служат медианы АН2 и РНг данного
тетраэдра. По теореме о четырех точках трапеции точка К пе-
ресечения продолжений боковых сторон АН! и РН2 трапеции
АРН2НХ, точка М пересечения ее диагоналей АН2 и PHlt сере-
дины О и F ее оснований HtH2 и АР лежат на одной прямой.
Это означает, что точка М пересечения медиан тетраэдра
РАВС лежит на его бимедиане KF.
Рис. 20
Далее, так как Н1Н2 || АР и
АНг : НГК = PH2 : Н2К = 2 : 1, то треугольники KHiH2 и
КАР гомотетичны (К — центр гомотетии), при этом КН2: КР -
= 1 : 3 => КО : KF= 1 : 3 => КО =—KF. Гомотетичными явля-
3
ются и треугольники MHtH2 и MPA (М — центр гомотетии),
32
при этом МН2 : МА = 1 : 3 => Н2М : Н^А =1:4. Значит,
ОМ : OF =1:4 => MO = -^OF. Поэтому КМ = КО + ОМ =
1 1 я 9
=±OF+±OF=-OF. А так как АН. = -АК и Н,Н2 II АР, то
2 4 4 1 3
OF =—KF. Тогда КМ =— OF- — — KF = —KF. Это означает,
3 4 4 3 2
что точка М — середина бимедианы KF тетраэдра. Вследствие
того что середины всех трех бимедиан тетраэдра совпадают,
приходим к выводу: точка М пересечения всех медиан тетраэд-
ра РАВС (центроид тетраэдра РАВС) является общей серединой
всех бимедиан этого тетраэдра, что и требовалось доказать.
Далее продолжим решение геометрических задач вектор-
ным методом.
Задача 31. В параллелепипеде ABCDA^B^C^D^ точка М —
середина диагонали грани A2B2C2D2, точка К — середина
ребра ВВ2. Докажите, что прямые АХВХ, КМ и ВСХ параллель-
ны некоторой плоскости.
Решение. Введем векторы: В1А1=а, B1C1=b, В1В = с
(рис. 21). Тройку (а, Ъ, с j некомпланарных векторов а,Ь,с
примем в качестве базиса. Разложим векторы КМи BCi по
векторам этого базиса.
Рис. 21
Имеем: BCi =ВгС1 -В2В = Ъ -с ;
КМ = В.М - В^К = 0,5(а + Ь )-0,5с - 0,5а + 0,5b - 0,5с ;
33
BpAj 4-BCj =a + (b-cj = d+& -c=>0,5^B1A1+BC1) =
= 0,5a+0,5&-0,5c.
Тогда И = 0,5рЙ + ^) = 0,5вХ + 0,5ВС^.
Это означает, что векторы В1А1 , BCi и КМ компланарны,
следовательно, они параллельны некоторой плоскости, тогда
этой плоскости параллельны и прямые А^В^ КМ и ВСН для ко-
торых векторы BiA1 , КМ иВС1 являются направляющими.
Задача 32. На диагоналях АВг и ВСг параллелепипеда
ABCDA1B1C1D1 взяты точки соответственноНи.М так, что от-
резки МН и АгС параллельны. Найдите отношение длин этих
отрезков.
Решение. Введём векторы: ВА = а, ВС = b , BBi = с
(рис. 22). Тройку (а, Ь, с) некомпланарных векторов а, & и с
примем в качестве базиса и разложим векторы ABi, BCi и
CAi по векторам этого базиса. Имеем:
ABi=BBi-BA = c-a; BCi-BC + BBi=b + c;
CAi=CB + BA + AAi = -ВС + ВА + BBi =a-b +с .
Так как точка Н лежит на диагонали АВ1г то векторы
АН и ABi коллинеарны, поэтому существует такое число х,
34
что АН = х - ABi=x(c-а). Аналогично, в силу коллинеарно-
сти векторов ВМ и BCi, существует такое число у, что
ВМ = yBCi = y(b + с).
По правилу ломаной находим:
МН = МВ + ВА + АН = -ВМ + ВА + АН =
= -i/(b-t-c)-t-a + x(c-<i) = (l-x)a-i/6+(x-i/)c .
По условию MH\\AiC, значит, существует такое число t,
что МН = tCAi, то есть выполняется:
(l-x)a-yb +(х-у)с =t^a-b + с)<=>
<=>(l-x-£)a + (£-i/)d +(x-i/-z)c = б.
Вследствие некомпланарности векторов а,Ь,с и единст-
венности разложения вектора по базису приходим к выводу:
1 - х - i = 0, t - у = О, х - у - t = 0. Решением этой системы
1 2 ---* 1 —’
уравнений является: y = t = —, х = —. Тогда МН-— CAi, зна-
чит, МН : CAj = 1 : 3.
Ответ: 1: 3.
Задачи для самостоятельного решения
Задача 33. На диагоналях АВХ и AXD параллелепипеда
ABCDA^ByC^D^
взяты точки соответственно К и Т так, что отрезки КТ и
BDX параллельны. Векторным методом найдите отношение
длин этих отрезков.
Задача 34. Диагонали оснований параллелепипеда
ABCDAiB^iDi пересекаются в точках О и ОР Векторным ме-
тодом найдите отношение длин отрезков, на которые диаго-
наль BDj параллелепипеда делится пересекающими её пря-
мыми ВхО и OjD.
Задача 35. Векторным методом докажите, что плоскости
A}BD и BxCDx делят диагональ АСг куба ABCDAxB^C^x на три
равные части.
35
ГЛАВА 2.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
МЕТРИЧЕСКИЕ ЗАДАЧИ СТЕРЕОМЕТРИИ
2.1. Начала метрической стереометрии
Углом между двумя ненулевыми векторами а и b называ-
ется угол между равными им векторами ОА = а и ОВ = Ъ , от-
ложенными от одной точки (рис. 23).
Рис. 23
Определение. Скалярным произведением двух ненулевых
векторов называется произведение модулей этих векторов и
косинуса угла между ними.
Если из двух данных векторов хотя бы один нулевой, то
скалярное произведение двух таких векторов считается рав-
ным нулю.
Скалярное произведение векторов а. и Ь обозначают a b
или а Ъ . Таким образом, по определению:
а-Ъ = |а|• |b|• coscp , где ф = ^а, b) , 0 <ф < 180°. (*)
Если а = Ь , то скалярное произведение а-b принимает
вид а а, называется скалярным квадратом вектора а и
обозначается а2 . Так как Z(a; а) = 0° , cos 0° = 1, то из (*) по-
лучаем а2=|а|2, т. е. скалярный квадрат вектора равен
квадрату его модуля. Отсюда |а| = у/д2 . Если вектор а еди-
ничныи, то а = 1.
36
Для любых векторов а , b , с пространства и любого дей-
ствительного числа k выполняются следующие свойства:
1) а2 > 0, причем а2 > 0 , если а * 0 ;
2)а Ь -Ь а (коммутативный закон);
3)a(kb}=k[a-b j (ассоциативный закон);
4)(a + bjc=ac + bc (дистрибутивный закон умножения
по отношению к сложению векторов).
Два ненулевых вектора перпендикулярны тогда и только
тогда, когда их скалярное произведение равно нулю',
a Lb c>d‘b =0.
Для решения многих задач с применением векторов по-
лезны следующие формулы: |а| = х/й^; cosZ^a, fe j- .
В результате изучения этой темы необходимо
знать/понимать:
• определение скалярного произведения двух векторов и
его свойства;
• определение базиса в пространстве базисных векторов
(в качестве базисных выбирают такие векторы, длины кото-
рых и углы между которыми уже известны);
• признак перпендикулярности векторов (используется
для доказательства перпендикулярности прямых, прямой и
плоскости);
уметь:
• формулировать определение: а) угла между двумя нену-
левыми векторами; б) скалярного произведения двух ненуле-
вых векторов;
• используя свойства скалярного произведения векторов,
находить длину вектора, угол между векторами;
• формулировать и доказывать признак перпендикулярно-
сти двух векторов;
• доказывать векторным методом: а) признак перпендику-
лярности прямой и плоскости; б) теоремы о трех перпендику-
лярах;
37
• на данном изображении многогранника задавать вектор-
ный базис, после чего записывать разложение вектора по ба-
зису и векторным методом находить длины отрезков, углы
между ребрами;
• используя изображения куба, правильного тетраэдра,
прямоугольного параллелепипеда, векторным методом дока-
зывать параллельность и перпендикулярность прямых и плос-
костей, содержащих ребра, грани и сечения этих многогран-
ников;
• с помощью скалярного произведения находить величины
углов между прямыми и плоскостями, вычислять длины от-
резков, расстояния от точки до прямой и плоскости, исполь-
зуя модели и изображения куба, правильного тетраэдра;
• все геометрические задачи, решаемые векторным мето-
дом, сопровождать аргументированными объяснениями.
Подготовительный набор задач
Задача 1. (Устно.) В кубе ABCDA1B1ClD1 найдите угол
между векторами: а) ААГ и СГС ; б) AD и СВГ ; в) DA и СВг ;
г) DC, и ВА, .
Задача 2. (Устно.) Основанием четырехугольной пирами-
ды с вершиной М служит квадрат ABCD. Каждое боковое реб-
ро пирамиды равно стороне квадрата. Найдите угол между
векторами: а) МА и МВ ; б) МА и ВА; в) МА и МС; г) АВ
и АС.
Задача 3. Вычислите скалярное произведение векторов а
и b , если их модули и угол между ними равны соответствен-
но: а) 4; 5; 60°; б) 2; 7; 45°; в) 4; 5; 120°; г) 7; 9; 90°.
Задача 4. Для данных ненулевых векторов а и Ь извест-
но: ^а + Ь^^а-Ъ^-О. Докажите, что |а|= &|, и выясните гео-
метрический смысл данного равенства.
38
Задача 5. Векторы а, Ъ, с — единичные; Х(а, bj = 3O°,
X(b, сj = 60°, Х(а, с) - 45°. Вычислите скалярное произведение:
1)(а - Ь + с)-(Ь - с); 2) (а + Ь - с)-(а - Ь - с).
Задача 6. Найдите скалярное произведение векторов а и
Ь, если: а)|а| = 1, & =3, а + Ь =4; б) а + 2Ь = а-2Ь =тп .
Решение. Учитывая, что а2 = |а|2, получаем:
а)|а + Ъ| - ^a + bj = \la2 +2ab +b2 = \ll + 2ab+9 = 4 =>
=> 1 + 2аЬ + 9 = 16 => 2аЬ = 6=5>аЬ =3.
б)|а + 2bI = |а-2bI = т => 7а2 +4а& +462 -7а2 -4аЬ + 462 =
а2 +4аЬ +4&2 =тп2
а2 -4ab + 4b2 = т2
=> 8аЬ - 0 => ab = 0.
Ответ: а) 3; б) 0.
Задача 7. Дано: векторы а, b, с — единичные;
х(а, b j = X(a, с) = 90°, x(b, с) = 120°. Вычислите длины век-
торов: а) а + Ь ; б) а + Ь-2с .
Решение, б) Имеем: а2=|а|2; х{а, b) = 90°=t>a±b =>ab =0;
Х(а, ?) = 90°=>(2 с =0. При |а| -|b| = |с| = 1 находим: |а + Ь-2с| =
= (а+b -2с)2 = а2 + b2 + (-2с)2 + 2а • b + 2а(-2с) + 2Ь (-2с) =
= а2 +b2 +4с2-4b с=а2 +b2 +4с2-4-|b|-|c|-cosl20° =
= 1+1+4-1-44-1|-0,5| = 8=>|а+Ь-2с| = 2>/2 .
Ответ: а) -72 ; б) 2-72 .
Задача 8. В правильном тетраэдре РАВС с ребром, равным
2, точки М и К — середины ребер соответственно РА и PC.
Вычислите скалярные произведения векторов: a.) AB AC;
б) РА ВР;в) МК АВ; г) КМ ВС.
39
Задача 9. В тетраэдре МАВС взаимно перпендикулярны
рёбра МА и ВС, а также — рёбра МВ и АС. С помощью векто-
ров докажите перпендикулярность ребер АВ и МС.
Рис. 24
Решение. Пусть АВ = а , AC-b , AM -с (рис. 24). Исходя
из условия задачи, имеем:
маа.вс=> ма1вс^ма вс=ма(ас-ав)=о^
=><?(&-aj = O=>c-Ъ— с а=О^>ас =b с . (1)
М В1 АС =$ МВ 1 АС => МВ • АС = 0 => (АВ - AM) • АС = 0 =>
^ab-cb =0^>а Ь-Ь с . (2)
Из(1) и (2) следует: а с = a b => а с - a b = 0=>а (с - b = 0j=>
=> АВ • СМ - 0 => АВ ± СМ => АВ ± МС, что и требовалось дока-
зать.
Задача 10. В правильном тетраэдре МАВС точки Н и К —
середины рёбер соответственно АВ и МС. Векторным методом
докажите, что отрезок НК перпендикулярен каждому из этих
рёбер.
Задача 11. МАВС — правильный тетраэдр с ребром 1. Точ-
ка О — центроид основания АВС; точки Н, Т и К — середины
ребер соответственно ВС, СМ и АВ. С помощью векторов най-
дите: 1) длину отрезка: а) МО; б) КТ; 2) угол между прямыми:
а) МА и МН; б) МА и ВТ; в) НМ и СК.
40
Задача 12. С помощью векторов докажите, что сумма
квадратов длин диагоналей параллелограмма равна сумме
квадратов длин всех его сторон.
Задача 13. С помощью векторов докажите, что в прямо-
угольном параллелепипеде ABCDA1BiC1D1 квадрат длины диа-
гонали BDV равен сумме квадратов длин его ребер ВА, ВС и BBr.
2.2. Содержательные метрические
задачи стереометрии
В качестве базиса в пространстве можно выбрать любую
упорядоченную тройку некомпланарных векторов а , Ь и с .
Тогда всякий вектор р пространства единственным образом
можно разложить по векторам этого базиса:
р = ха + yb + zc .
В общем виде критерий компланарности трех ненулевых
векторов а , Ъ и с выражает равенство: ха + yb + zc = 0 (при
условии, что не все коэффициенты одновременно равны ну-
лю). Если в задаче требуется доказать, что три данные прямые
параллельны некоторой плоскости (её положение определять
не нужно), то достаточно на каждой из этих прямых выбрать
вектор и, используя признак компланарности трех векторов,
доказать, что выбранные векторы компланарны.
С помощью скалярного произведения двух векторов мож-
но находить длину отрезка, величину угла, следовательно,
находить расстояния, площади и другие метрические харак-
теристики геометрических фигур. Для доказательства пер-
пендикулярности прямых и плоскостей удобно пользоваться
признаком перпендикулярности двух ненулевых векторов.
Для нахождения длины отрезка АВ векторным способом в
качестве базисных выбирают такие векторы, длины которых
и углы между которыми уже известны. Затем записывают
разложение вектора АВ по базисным векторам и находят:
|АВ|= АВ =7аВ2 .
Если в задаче требуется найти величину угла <р между пря-
мыми и плоскостями, 70 в качестве базисных принимают
41
(«вводят») векторы с известными отношениями их длин и уг-
лами между ними. Затем выбирают векторы а и b на сторо-
нах данного угла с началом в его вершине и раскладывают их
ab
по базису, после чего находят: cos ср = —рг.
14 И
Рассмотрим векторные решения следующих задач.
Задача 14. В кубе АВСЛА1В1С1В1, ребро которого равно 6,
найдите:
а) расстояние от вершины до плоскости BC\D; б) угол
между диагональю ВАг грани АА^В^В и плоскостью BCAD.
Решение, а) Пусть отрезок АХМ — перпендикуляр из вер-
шины Ai на (BC^D) (рис. 25), М е (ВС^). Тогда p4.xAr| =
= р(Ах; (ВС^-О)). Найдем длину отрезка АХМ.
По правилу треугольника имеем: АХМ = ВМ - BAi.
Обозначим: ВА} = р, а в плоскости BCrD введем базис
(a, b), где a = BD, Ь = ВС\, и запишем разложение вектора
ВМ по векторам этого базиса в виде: ВМ = xa + yb . Тогда
ArM = xa + yb-р и (BCjD))= AjM |.
Рис. 25
Так как АХМ ± (ВС^-О), то АХМ ± ВС15 АаМ ± BD (по опреде-
лению прямой, перпендикулярной плоскости), значит,
АуМ la, AjM lb.
42
Коэффициенты х и у в разложении АХМ =xd+ybp век-
тора АгМ найдем, пользуясь условием: AjM±a, ArMLb ,
которое равносильно системе уравнений:
(xa + yb-p)a = O,
(xa + yb-р)-Ь = О.
Прежде чем решать эту систему уравнений, предваритель-
но найдем скалярные произведения векторов: а-а=а2, a b ,
ар, b-b~b2, bp, рр^р2.
Так как BC\D, А^ЗС^, А^В D — правильные и равные, а
длины их сторон равны 6л/2 , то Z^a,&j = Z(a, p) = Z^p, bj = 60°
и |a| = |& | = |р| = 6л/2 .
Тогда а • а = а2 = |а|• |а|• cosO° = 6\2 • 6д/2 • 1 = 72 = ft2 = р2; (**)
а &=|а| |&|-со8б0° = б72-бл/2 0,5 = 36 = а р = & р. (***)
Теперь вернемся к решению системы уравнений (*).
На основании свойств скалярного произведения векторов,
учитывая соотношения (**) и (***), получаем:
ха2 +yab-ра-О, (72x + 36i/-36 = 0, 12х + у = 1,
xa-b + yb2 -p-b = O [36x + 721/- 36 = 0 [x + 2y = l
Тогда
A,M = — a + — b -p =>|a.m| = Ja.M2 = . (-a + —b-p
1 з з I 1 I N 1 у1з 3
—a2 +—b +p2 + 2 — — (a&)-2— (ap)-2— (bp] =
9 9 3 3\ / 3k ’ 3V /
= 1.72 + 1.72 + 72 + 2 —•-•36-2 --36-2 --36 =
V9 9 3 3 3 3
= V8 + 8 + 72 + 8-24-24= 4^3.
43
Таким образом, P(Aj; (BCpD)) =| АХМ | = 4л/з .
б) Обозначим: Z(BAn (BCXD)) = <р. Так как АХМ ± (BQ-D), то
ВМ — ортогональная проекция ВСг на (BQ-D), значит, Z(BAlt
(BCiD)) = Z(BAlf ВМ) = ZAtBM = <р. Используя
соотношения (**) и (***) и учитывая, что вектор ВМ = xa + yb
при х = у = — имеет вид: ВМ =—а + —Ь, находим:
24 <3 л/3
= —т=---= — => ф = arccos— .
6V2-2V6 3 3
Ответ: а) 4л/з ; б) arccos^^ .
3
Задачи для самостоятельного решения
Задача 15. В кубе ABCDA^B^D', ребро которого равно 12,
векторным методом найдите расстояние между его диагона-
лью АгС и скрещивающейся с ней диагональю ВСг грани
BCCjBp
Задача 16. Которая из вершин, А или Alt куба
ABCDA^C^Di расположена дальше от прямой BDJ
Задача 17. В кубе ABCDA1B1C1D1, ребро которого равно 12,
векторным методом найдите расстояние между скрещиваю-
щимися диагоналями ABY и BCY граней АВВ}а и BCCjBj.
Задача 18. Основанием прямого параллелепипеда служит
параллелограмм с острым углом в 60°, а его стороны равны 18
44
и 32. Высота параллелепипеда равна 24. Найдите угол между
неравными диагоналями боковых граней.
Решение. Пусть ABCDA^B-fi^D^ — прямой параллелепи-
пед, в котором АВ = 32 м, AD = 18 м, АА, = 24 м, Z.BAD = 60°
(рис. 26).
Рис. 26
Так как противоположные боковые грани нашего парал-
лелепипеда — попарно равные прямоугольники, лежащие в
параллельных плоскостях, то достаточно найти углы, кото-
рые одна из диагоналей любой его боковой грани образует с
двумя диагоналями смежной с ней грани. Найдем, например,
углы, которые диагональ АВХ грани АВВГАХ образует с диаго-
налями AD} и DAT грани ADD 1А1 (так как ADJlBCj, Aj-ОЦВ^, то
Z(AB17 ADJ = ДАВи ВС J, AAB^AJ)) = Z(ABj, BjC)).
Решим задачу векторным методом.
Обозначим: AB = a,AD = b, АА} =с; Z^AB,, АО,) а,
zfABj, DA1) = P . Тогда ABi = a + c,
ADt = b + c, DAr =c — b ; cosa =
a + c
COSp =
ABt-DA,
abIIda^
ABj-ADj
a+c•c-b
45
Так как параллелепипед — прямой, тоа±с, Ь1с, значит,
ас=Ьс = 0; кроме того, a-b = |a|-|S|-cos60° = 32-18-^ = 288.
Учитывая это, получаем:
(a + c)-(&+c) = a-& + a-c + ft-c+c2 =288 + 576 = 864 ;
(a + c)-(c-b)=ac-a-b +сг-b с =576-288 = 288 ;
| ABj | = J AB. = ^(a + c)2 = -7a2 +2ac + c2 =
= V322+242 = ^82(42+32) = 40;
= j(b + c)2 =>lb2+ 2b-c+c2 =
= V182 + 242 = 7б2(32+42) = 30;
АЁ\| = DA. =30.
Тогда cos a = = 0,72 => a = arccos 0,72;
40 30
cosp= 288 =0,24 => P = arccos0,24.
40-30
Так как cos a = 0,72 > 0, cos p = 0,24 > 0,
то углы Z(AB., AD.) = a и ZI AB., DA. I = P между вектора-
ми, являющимися направляющими для соответствующих
прямых, равны углам между этими прямыми.
Ответ: arccos 0,24; arccos 0,72.
Задача 19. Около правильной четырехугольной пирамиды,
каждое ребро которой равно 10, описан цилиндр так, что все
вершины пирамиды находятся на окружностях оснований
цилиндра. Найдите объем и площадь боковой поверхности
цилиндра.
Сначала рассмотрим решение этой задачи геометрическим
(синтетическим) методом.
Решение. Пусть вершина Р данной пирамиды PABCD ле-
жит на окружности нижнего основания описанного около
этой пирамиды цилиндра, центрами оснований которого слу-
жат точки О и С>1 (рис. 27).
46
D
В
Рис. 27
Так как каждое ребро пирамиды равно 10, то в правильном
ДАВР находим: PH = = 5^/з , значит, ОН =—РН =
2 3 3
2 2 /— 1 Ол/з
ОР =—PH -—5уЗ---------. Тогда радиус R основания цилинд-
3 3 3
D юТз
ра равен ОР, т. е. R - —.
Если точки Н и М — середины противоположных сторон
соответственно АВ и CD квадрата ABCD (основания данной
пирамиды), то МН = 10, причем середина К отрезка НМ яв-
ляется серединой высоты ООг цилиндра. А так как плоскость
МРН перпендикулярна плоскости основания цилиндра и про-
ходит через центр О его основания, то высота OOj цилиндра
лежит в этой плоскости, и OOr = 2ОК. Находим ОК.
В прямоугольном ДНО К имеем: ОК = у/нкг -ОНг =
= 52_ 5уЗ = 25-—= 50 -.-5 2
\ t з J V з V з \з з ’
ТТ ПЛ О 5-Тб 10>/б m -
Поэтому OOj = 2 —— = —— . Тогда площадь боковой по-
3 3
верхности 5боК и объем Уцил цилиндра равны соответственно:
47
с оолл о юТз 10>/б 2я 102V2 2OOV2-71
бок 1 3 3 3 3
(кв. ед.),
Т7 О2 (Юл/З? 10 Уб тг103л/б 1000л/б я
цил 1 ( 3 J 3 9 9
(куб. ед.).
„ 200л/2-тг ЮООУб-л -
Ответ:------------кв. ед.;-----------куб. ед.
3 9
Теперь рассмотрим решение этой задачи векторным ме-
тодом.
Задача 20*. Около правильной четырехугольной пирами-
ды, каждое ребро которой равно 10, описан цилиндр так, что
все вершины пирамиды находятся на окружностях оснований
цилиндра. Найдите объем и площадь боковой поверхности
цилиндра.
Рис. 28
Решение. Пусть вершина Р данной пирамиды PABCD ле-
жит на окружности с центром О нижнего основания цилинд-
ра, описанного около этой пирамиды (рис. 28).
Так как каждое ребро пирамиды равно 10, то радиус R ок-
ружности основания цилиндра, описанной около правильного
ДРАВ со стороной 10, равен: R = ^^ .
48
Пусть точка М — середина ребра CD, МК — перпендикуляр
из М на плоскость АВР основания цилиндра, Ке(АВР). Тогда
МК ± ВА, МК 1ВР (по определению прямой, перпендикуляр-
ной плоскости), при этом высота h цилиндра равна |м^г|.
Найдем |мтс|, для этого введем в качестве базисных не-
компланарные векторы ВА = а , BP = Ь , ВС = с , разложим век-
тор МК в базисе (а, Ь, с) и найдем МК -\МК = МК = h .
Имеем: МК -РК-РМ; РК = хРА + уРВ = х[вА-ВР^-
-yBP = x(a-b}-yb = ха-(х + у)Ь ;
РМ = РС + СМ = ВС-ВР+0,5ВА = с-Ь +0,5а = 0,5а-Ь +с .
Тогда
МК = ха-(х + у)Ь -(o,5a-b + cj = (x-O,5)a + (l-x-y)b-c .
Числовые значения х и у найдем из условия:
WBA-0,
Й-ВР-0.
Система (2) равносильна системе уравнений:
нх-0,5)а+(1-х-г/)д-с )а = 0,
(2)
((х-0,5)а+(1-х-у)&-с)-& = 0.
Прежде чем решать эту систему уравнений, предваритель-
но найдем скалярные произведения векторов: аа = а2,
Ъ Ь = Ь2 ,с с = с2, ab, ас, Ьс .
Имеем: АВР, РВС — правильные и равные, а длины их
сторон равны 10,
поэтому Z^a,&) = z(&, с) = 60° и |a| = |d| = |c| = 10; ABCD —
квадрат со стороной 10, поэтому Z(a, с) = 90° и |с| = 10 . Тогда
ас =0;
аа = а2
= |а| • |а| cosO° = 10 10-1 = 100 = Ь2 = с2;
(3)
(4)
49
a b = |a|-|&|cos60° = 10 10 0,5 = 50 = fe -c . (5)
Продолжим решение системы уравнений (2). На основании
свойств скалярного произведения векторов, учитывая (3)-(5),
получаем:
(x-0,5)ii2 + (l-x-i/)(a-6 ) = 0,
(х-0,5)(а-& j+(l-x-i/)&2 -be =0
100(x-0,5) + 50(l-x-i/) = 0,
‘ 50(x-0,5)+100(l-x-j/)-50 = 0
x-i/ = 0,
x + 2i/ = 0,5
Тогда
МК = (x-0,5)a+(l-x-i/)& -с = f—+ ^Ь-с =
V.6 2) \ 6 6/
= ~а + -Ь-с^|мА:|-л/м№ = J(--a + -b-c
33 II VI 3 3
/1-2 Д-2 -2 19__ 9 - -
— .[—a +-b +с -2 - -(a b) + 2 -(a c)-2 -(b c) =
у9 9 3 3 3 3
=.100 Д 100 + 100-2 - - 50-2 - 50 = = h.
N9 9 3 3 3 3
Значит, площадь боковой поверхности цилиндра равна:
о т> ь о юТз Юх/б 200лл/2 , . я
2n-Rh = 2n—---------—---- (кв. ед.), а его объем равен:
о2 ь f 10л/3 Y 10х/б 1000лх/б . - ч
n-R h = n- ——- —— =--------------(куб. ед.),
о у О У
. 200л>/2 ЮООлл/б R
Ответ: ---------кв. ед.;-------куб. ед.
3 9
Если даны длины трех ребер РА, РВ и PC тетраэдра РАВС,
исходящих из его вершины Р, а также известны величины
плоских углов при этой вершине, то с помощью векторов мож-
50
но найти радиус, а следовательно, и площадь сферы (объем
шара), описанной (описанного) около этого тетраэдра.
Рассмотрим решение следующей задачи.
Задача 21*. В треугольной пирамиде РАВС все плоские уг-
лы при вершине Р прямые. Найдите площадь сферы, описан-
ной около этой пирамиды, если РА = 2, РВ = 3, PC = 4.
Рис. 29
Решение. Пусть точка О — центр сферы, описанной около
тетраэдра РАВС, R — радиус этой сферы. Тогда ОА = ОВ =
= ОС = OP = R.
Введем некомпланарные векторы РА - а , РВ = b , PC = с
(рис. 29) и примем их в качестве базисных в пространстве. То-
гда РО = p=xa + yb + 2c, при этом Ро| = R. Найдем коэффици-
енты х, у и z в этом разложении вектора РО.
По правилу треугольника имеем:
p-a+OA-b+ВО=с+СО , откуда АО=р-а, ВО = р-Ъ ,
СО = р-с . Из равенств ОА — ОВ = ОС — ОР (как радиусы
сферы, описанной около тетраэдра РАВС) следует
| РО |=| АО |=| ВО |=| СО |, значит, АО -ВО -СО -РО .Тогда
получаем:
51
р* 2-АО*=0, (p-Ao)(p + Ao) = 0,
<p2-BO = 0, < (p-BO^p +BO^ = 0,
p2-CO =0 (p-Co)(p + Co) = 0
(p - (p - a))(p + (p + a)) = o,
< (p-(p-b))(p + (p + b))-0,
(p-(p-c))(p+(p + c)) = 0
-» -» — 2
ap = -0,5a ,
_ _ -.2
b- p = -0,5b ,
-> — -.2
c-p = -0,5c .
Заметим: так как базисные векторы а , Ъ и с попарно пер-
пендикулярны и длины их равны соответственно 2, 3 и 4, то:
a b =а с =Ь с-0, а2=4, Ь2=9, с2=16. (*)
Заменяя р выражением (xa + yb+zc^ в последней системе
уравнений и учитывая (*), получаем:
_ _ _ —2
a(xa + yb + zc) = -0,5a ,
-2
b(xa + yb + zc) = -0,5b ,
_ _ _ _2
с • (ха + yb + zc) = -0,5с
— 2 —2
ха = -0,5а ,
yb = -0,5Ь , о
-.2 -2
zc --0,5с
х = -0,5,
' У = -®,5,
г = -0,5.
Тогда
РО = -0,5a -0,5b- 0,5с => |ро| = R = ^(-0,5а-0,5& -0,5с)2 =
= 7о,25а2 +0,2562 +0,25с2 = ^/0,25 4 + 0,25 9 + 0,25 16 =
= 71 + 2,25 + 4 .
2
Значит, площадь сферы равна:
Ясферы = 4яЯ2 = 4л
к 2 /
= 29л (кв. ед.)
Ответ' 29л кв. ед.
52
Задачи для самостоятельного решения
Задача 22. В тетраэдре РАВС два плоских угла при верши-
не Р прямые, а величина третьего плоского угла равна 60°.
Найдите радиус сферы, описанной около этой пирамиды, если
РА = РВ = PC = 12.
Задача 23. В тетраэдре РАВС все плоские углы при верши-
не Р прямые. Найдите радиус сферы, описанной около этой
пирамиды, если РА = РВ = PC = 6.
Если известны величины плоских углов при вершине Р
трехгранного угла РАВС и дано расстояние РО от этой верши-
ны до центра О сферы, касающейся всех трех ребер РА, РВ и
PC этого угла, то также можно найти радиус, а значит, и пло-
щадь этой сферы.
Рассмотрим следующие задачи.
Задача 24*. В трехгранном угле РАВС известны величины
плоских углов при вершине Р: ААРВ = АВРС = ААРС = 60°.
Сфера, центр которой удален от вершины Р на расстояние,
равное 3^6 , касается всех ребер этого угла. Найдите радиус
данной сферы.
Решение. Пусть сфера касается ребер РА, РВ и PC в точках
соответственно К, Н и М. Тогда РК = PH = РМ (как отрезки
касательных, проведенных к сфере из точки Р), при этом
ОК — ОН = ОМ= R (R — радиус сферы), ОК АРА, ОНАРВ,
ОМ ± PC (как радиусы сферы, проведенные в точки касания ее
с ребрами угла).
Введем некомпланарные векторы
РК - а, PH - Ь , РМ = с (рис. 30) и
примем их в качестве базисных в про-
странстве. Тогда РО-p-xa + yb+zc,
причем |РО = Зл/б .
Так как РК = PH = РМ,
Пусть |а| = |&| = |с| =
= т .
53
Сначала найдем значения коэффициентов х, у, z разложе-
ния вектора PO = p = xa + yb+zc , используя: OKI РА,
ОН1РВ,ОМ1РС =>КО 1 а , НО 1 b ,МО 1 с.
Имеем: КО = р-а , НО = р-b , МО-р-с . При этом:
КО1а^КО-а = 0^>[р-а)а = 0^ра-а2;
НО lb ^HO-b =O^(p-b).b =0^ p b ^b2;
MOic =>MO c = 0=>(p-c)d = 0=>p c = c2.
Заменив в трех последних равенствах вектор р выражени-
ем I ха + yb + zc I, получаем:
_ _ - - _2
a(xa + yb + zc) = a ,
- — _ _ _2
b(xa + yb + zc) = b ,
- — - - -2
с (ха + yb + zc) - с
-г - _ - - —2
ха + y(ab) + z(ac) = a ,
- - -2 - - -2
< x(a-b) + yb + z(bc) = b ,
— - - - -2-2
x(a-c) + y(bc) + zc =с .
(1)
Прежде чем решать эту систему уравнений, предваритель-
но найдем скалярные произведения векторов: аа = а2,
b b-Ь2 ,с с — с2, a b, а с,Ь с .
Имеем: ZAP В = ZBPC — ZAPC = 60°; |а| = Id I = |с| = т .
Тогда аа = а2 = |а|• |а|• cosO° = т2 =Ь2 = с2; (2)
а-b = |а|• Id!• cos60° = 0,5т2 =Ь -с =а-с . (3)
Продолжим решение системы уравнений (1).
После деления на т2 обеих частей каждого уравнения сис-
темы (8), учитывая (2), (3), получаем:
х 4-0,51/4-0,52 = 1, [2x + y + z-2,
0,5х + i/ + 0,52 = 1, <=> « х 4- 2у 4- г = 2,
0,5x4-0,5i/4- z = l х + у + 2г-2.
После сложения всех уравнений последней системы полу-
чаем х + у + 2 = 1,5. Тогда из первого уравнения 2х + у + 2 = 2
получаем: х + 1,5 = 2, откуда х = 0,5. Аналогично, из второго
и третьего уравнений системы находим: у = 0,5, z = 0,5.
54
Таким образом, р = 0,55+ 0,56 + 0,5с . (Равенство коэффи-
циентов разложения вектора РО = 0,55 + 0,56 + 0,5с означает,
что центр О сферы, касающейся всех ребер.трехгранного угла
с плоскими углами в 60°, лежит на прямой пересечения бис-
секторных плоскостей двугранных углов при ребрах этого
трехгранного угла.)
Далее найдем длины базисных векторов а, Ь и с , учиты-
вая условие:
РО =3>/б и соотношения (2), (3).
Получаем:
| РО =
= 7о,2552+ 0,2562+0,25с2+2-0,5 0,5(5-6) + 2 0,5-0,5(5-с) +
7+2 0,5 0,5(6 с) =
= 7о,25т2 + 0,25т2 + 0,25т2 + 2-0,5-0,5-0,5т2 +
7+2 0,5 0,5 0,5m2 +2 0,5 0,5 0,5m2 = ^^.
Тогда имеем: |ро| = З-Уб - т'^> =>т = 6.
Теперь найдем радиус R сферы, учитывая, что R = KO,
а2 =Ь2 = с2 = т2 =36 ; а Ъ =Ъ с = а с -0,5т2 =18 .
Имеем: КО = р-5-0,55 + 0,56 + 0,5с-а = -0,55+0,56 + 0,5с .
Тогда
R= КО =
'0,25а2 +0,2562 +0,25с2 -2 0,5 0,5(5-б)-
= 7о,25 36 + 0,25-36 + 0,25-36-2 0,5 0,5 18-
V-2 0,5 18+2 0,5 0,5 18 = 3>/2 .
Ответ: Зд/2 .
55
Задачи для самостоятельного решения
Задача 25. В трехгранном угле РАВС известны величины
плоских углов при вершине Р: ZAPB = ZBPC = ЛАРС = 90°.
Сфера, центр которой удален от вершины Р на расстояние
4>?3 , касается всех ребер этого угла. Найдите радиус данной
сферы.
Задача 26. В трехгранном угле РАВС известны величины
плоских углов при вершине Р: ZAPB = ЛВРС = 90°, ЛАРС = 60°.
Сфера, центр которой удален от вершины Р на расстояние
4х/3 , касается всех ребер этого угла. Найдите радиус данной
сферы.
Задача 27. Трехгранный угол называется прямым, если
все его плоские углы прямые. Ребра прямого трехгранного угла
с вершиной О пересечены плоскостью в точках А, В а С. До-
кажите, что треугольник АВС остроугольный.
Задача 28*. Докажите, что учетверенная сумма квадратов
расстояний от центроида тетраэдра до вершин этого тетраэдра
равна сумме квадратов длин его ребер.
Задача 29*. Противоположные ребра тетраэдра попарно
взаимно перпендикулярны. Докажите, что суммы квадратов
длин его трех пар противоположных ребер равны. Сформули-
руйте обратную теорему и докажите ее справедливость.
Задача 30*. Докажите, что если прямые, соединяющие се-
редины противоположных ребер тетраэдра, перпендикуляр-
ны, то противоположные ребра равны. Сформулируйте и до-
кажите обратную теорему.
Задача 31*. На ребрах прямого трехгранного угла с вер-
шиной О отложены равные отрезки ОА, ОВ и ОС. Из точки О
на плоскость АВС опущен перпендикуляр ОН. Докажите, что
если точка К симметрична точке Н относительно вершины О,
то тетраэдр К АВС правильный.
56
ГЛАВА 3.
ГЕОМЕТРИЯ ПРЯМЫХ, ПЛОСКОСТЕЙ
И ФИГУР ВРАЩЕНИЯ В КООРДИНАТАХ
' Решение многих стереометрических задач координатным
методом значительно проще их решения средствами элемен-
тарной геометрии, при этом можно обойтись без дополнитель-
ных построений, которые становятся необходимыми при
иных методах решения. Кроме того, применение координат-
ного метода при решении геометрических задач способствует
поиску интересных обобщений, которые могут возникнуть
при анализе полученных решений.
Задачи, в которых находят расстояния, углы, площади,
объемы, называют метрическими задачами стереометрии.
Чтобы координатный метод стал аппаратом решения метри-
ческих задач, необходимо, прежде всего, научиться перево-
дить условие геометрической задачи в координатную терми-
нологию и символику (на «координатный язык»), затем
грамотно оперировать формулами и уравнениями, наконец,
полученный в координатной форме результат переводить
вновь на язык геометрии.
При решении задач координатным методом «рабочими»
являются уравнения прямых и плоскостей. Знание условия
коллинеарности двух векторов и компланарности трех векто-
ров позволяет в координатном виде решать вопросы о взаим-
ном расположении точек, прямых и плоскостей. Выражение
через координаты расстояния между двумя точками, от точки
до плоскости, скалярного произведения двух векторов и углов
между ними, условия их коллинеарности и перпендикуляр-
ности позволяет легко перевести в координатную форму от-
ношения параллельности и перпендикулярности прямых и
плоскостей, находить углы и расстояния между ними, изу-
чать геометрию прямых и плоскостей в пространстве, а зна-
чит, геометрию многогранников. Одним словом, координат-
ный метод — мощный аппарат изучения пространственной
геометрии.
57
3.1. Линейные операции над векторами
в координатах
Упорядоченная тройка векторов (i ;j;k), таких, что i ± j ,
j 1 k , kli , | i | = |/| = |Л | = 1, называется декартовым прямо-
угольным (ортонормированным) базисом векторов в про-
странстве, а векторы i , j , k называются базисными (коор-
динатными ) векторами.
Рис. 31
Базисными векторами i , j , k , отложенными от точки О,
определяются три взаимно перпендикулярные направленные
прямые, которые называются координатными осями и обо-
значаются соответственно Ох, Оу и О г (рис. 31). При этом го-
ворят, что в пространстве задана прямоугольная декартова
система координат, которую обозначают Oxyz. Точка О на-
зывается началом системы координат; направленные пря-
мые Ох, Оу л Ог называются соответственно осью абсцисс,
осью ординат и осью аппликат. Плоскости, проходящие че-
рез каждые две координатные оси, называются координат-
ными плоскостями и обозначаются: (Оху) — проходит через
оси Ох и Оу; (Оуг) — проходит через оси Оу и Ог; (Охг) — про-
ходит через оси Ох и Ог.
58
Рене Декарт (1596-1650)
Такую систему координат называют декартовой по имени
всемирно известного французского ученого Рене Декарта
(1596-1650), который впервые ввел координаты в геометрии
(на плоскости).
Любому вектору р пространства в ортонормированном ба-
зисе (i ;j;k) соответствует единственная упорядоченная
тройка чисел (х; у; z), такая, что выполняется равенство:
p-xi+yj+zk. (*)
Если в пространстве дан прямоугольный базис (i ; j ; k ), то
между множеством всех векторов пространства и множеством
всех упорядоченных троек действительных чисел (х; р; г) ус-
танавливается взаимно-однозначное соответствие, при кото-
ром для каждого вектора р и соответствующей ему упорядо-
ченной тройки чисел (х; у; г) выполняется равенство (*).
Числа х, у и z в этом равенстве называются декартовыми пря-
моугольными координатами вектора р в базисе (i ; j ; k ). При
этом символически обозначают р (х; у; г) и говорят: «Вектор
р с координатами х, у, г», или «Вектор р имеет координаты
х, у, zв базисе(i ; j ; k )».
В частности, базисные векторы i ,j ,k и вектор 0 имеют
координаты:
i (1; 0; 0), 7(0; 1; 0), k (0; 0; 1)и б (0; 0; 0).
На основании свойств операции сложения векторов и ум-
ножения вектора на число справедливо:
59
^(XpZ/pZj)
&(x2;z/2;z2)
a + b = (x1+x2;yl+y2;z1+z2),
^а-Ь = (хг -x2;y1-y2;zl -z2),
Xa =(Xxt; Xz/jj XzJ.
Для ненулевых векторов a (alt’ а2; а3) и Ъ (Ьг; Ь2; Ь3) имеет
место:
а||д
flj = t-&j,
а2 = t-b2, где t е R.
a2 — t- bs.
Если векторы а}, а2, ak заданы своими координатами:
аДхй уь, zj, а2(х2; у2; г2), ak(xk; yk; zk), то, учитывая
правила нахождения координат суммы, разности векторов и
произведения вектора на число, вектор с = Xjdj + Х2а2 +... + ХАаА,
являющийся линейной комбинацией векторов ах, а2, ..., ак,
имеет координаты:
c(XiXj +Х2х2 + ...ХАхА; Xji/j + X2i/2 + ...Хкук', ^.1z1 +Х2г2 +.. .Хкгк^.
3.2. Скалярное произведение векторов
в координатах
Скалярное произведение векторов а и b равно:
а-Ъ = |а| р|• costp , где (р = /(а, . При этом:
а) а а = а2; б) а ± & <=> ab =0,
б) i •/'=/•£ = fe i =0, (1)
в) i i =|i| =1, j-j =|y| =1, fe-fe = |fe| =1, (2)
г) скалярное произведение векторов а (хг; у^, гг) и b (х2; у2; г2)
равно:
ab = x1x2 + У1У2 + г1г2, (3)
д) признак перпендикулярности векторов a(Xj; i/jj 2i) и
b (х2; у2; z2) в координатах выражается условием:
а 1 b <=> XjX2 + уху2 + zxz2 = 0, (4)
е) длина вектора р (х; у, г) находится по формуле:
|р| = 7хг + 1/2+22, (5)
60
ж) угол <р между векторами а и Ь находится с помощью
формулы:
а-Ъ
cos а-—г-
*l*2+W+^2
(6)
I4|6 ylxi+yi+z^xl+yl+zl
з) каждая координата вектора р (г; у; z) равна ортогональ-
ной проекции этого вектора на направление соответствующего
базисного вектора:
х = ПрЛ р; y = IIpJ р , z-IIp.kp . (7)
В результате изучения этой темы необходимо
знать/понимать:
• определение декартова прямоугольного базиса в про-
странстве;
• определение декартовых прямоугольных координат век-
тора в пространстве;
• в координатной форме:
а) выражение скалярного произведения и условие перпен-
дикулярности двух векторов;
б) признак коллинеарности двух векторов, условие ком-
планарности трех векторов;
в) формулу для вычисления длины вектора и угла между
двумя векторами;
• определение линейной комбинации векторов с заданны-
ми коэффициентами;
• свойства линейных операций над векторами, заданными
своими координатами;
• геометрический смысл декартовых прямоугольных ко-
ординат вектора;
уметь:
• изображать вектор по его координатам в декартовом
прямоугольном базисе в пространстве;
• грамотно (безошибочно) выполнять алгебраические опе-
рации над векторами, заданными своими координатами;
• в координатной форме:
а) вычислять скалярное произведение двух векторов и оп-
ределять, перпендикулярны ли они;
61
б) определять, коллинеарны (компланарны) ли данные
векторы;
в) находить длину вектора;
г) находить величину угла между двумя векторами;
• на данном изображении многогранника задавать вектор-
ный базис, после чего правильно записывать разложение век-
тора по базису;
• на изображениях куба, пирамиды, параллелепипеда век-
торно-координатным методом определять взаимное располо-
жение точек, прямых и плоскостей;
• решать геометрические задачи координатным методом,
для чего переводить условие геометрической задачи в коорди-
натную терминологию и символику, затем грамотно (безоши-
бочно) выполнять соответствующие алгебраические операции
над координатами векторов и, наконец, полученный в коор-
динатной форме результат верно переводить «обратно», на
«язык чисто геометрический».
3.3. Подготовительный набор задач
Задача 1. (Устно.) Запишите координаты векторов:
a = 2i -3] +5k; b--i +4j -6k; c = -3i +2j + 6k;
p = i -k; m- j + 2i; n = -k .
Задача 2. (Устно.) Даны векторы: а (3; -7; -2), Ъ (0; +5; -2),
с (1; -2; 0), р (-2; 0; 3), q (0; 0; -5). Запишите их разложения
в базисе (i ; j ; k ).
Задача 3. Даны векторы а (1; 2; 0), b (0; -5; -2), с (2; 1; -3).
Найдите координаты векторов р - -а + 2Ъ - Зе и q = -с + 2а - ЗЬ .
Задача 4. Коллинеарны ли векторы: а) а (-3; -4; 5) и
b (6; 8; -10); б) р (2; 3; 3) и q (4; -6; 2)?
Решение, а) Векторы а и Ъ коллинеарны, так как -3:6 =
= -4:8 = 5: -10; б) координаты вектора q не пропорциональ-
ны одноименным координатам вектора р , например, —2:4 =
= 3 : -6 * 3 : 2. Поэтому векторы р и q не коллинеарны.
Ответ: а) коллинеарны; б) не коллинеарны.
62
Задача 5. При каких значениях тип вектор a = 3 i + 2j-mk
коллинеарен вектору b = ni + j -2k ?
Задача 6. Компланарны ли векторы: а) 5(1; 2;-1),
Ъ (3; -1; 2), с (7; 0; 3); б) т (2; 0; 3), i , k ; в) а (1; 1; 2), Ь (5; -1; 0),
с(3; -3; -4); г) 5(0; 5; 2), Ь (3; 2; 3), с(6; -1; 4); д) 5(0; 5; 3),
6 (3; 3; 3), с (1; 1; 4)?
Решение. 1) Векторы а (1; 2; -1) и b (3; -1; 2) не коллине-
арны, так как 1 : 3 # 2 : -1 (их одноименные координаты не
пропорциональны).
Если существуют числа х и у, такие, что вектор с можно
представить в виде с = х а +у Ъ , то векторы а , Ь и с — компла-
нарны. В этом случае также говорят, что вектор с можно раз-
ложить по неколлинеарным векторам а и Ъ , он является ли-
нейной комбинацией векторов а и Ь с коэффициентами х и у.
Если вектор с (7; 0; 3) можно разложить по векторам а и Ь ,
то векторы а , Ъ и с компланарны; в противном случае векто-
ры а , Ь и с не компланарны. Таким образом, для решения за-
дачи достаточно установить, существуют ли числа х и у, такие,
что с — х а + y b . В координатах это означает, имеет ли реше-
ние относительно х и у следующая система уравнений:
x + 3i/ = 7,
« 2х - у - 0,
-х + 2у = 3.
Складывая первое и третье уравнения этой системы, полу-
чаем: 5у = 10=>у = 2. Тогда: 2х-2 = 0=>х = 1. Поэтому с =
= а + 2Ь . Это означает, что вектор с является линейной ком-
бинацией векторов а и b , следовательно, векторы а , Ъ и с
компланарны.
Ответ: а) да; б) да; в) да; г) да; д) не компланарны.
Задача 7. (Устно) Найдите длины векторов: а) а (5; 1; -7);
б) Ъ (-6; -2 >/з ;-1); в) с = i - j - k ; г) т = 3 i ; д) р = i - 3 j .
Задача 8. (Устно) Даны векторы: 5(1; -1; 2), Ь (-1; 1; 1),
с (-5; 6; 2). Найдите: 1) а • с ; 2)а • Ъ ; 3) а2; 4) >/£* .
63
Задача 9. Найдите угол между векторами р =2 а +3 b и
q =2а - 3Ь , если а = i - j + 2k , b = 2i + 2 j .
Решение. Найдем координаты векторов р и q в базисе
(Г; /; k).
Имеем: а (1; -1; 2) => 2d = (2; -2; 4),
& (2; 2; 0) => 36 = (6;6;0).
Тогда 2 а + 3 Ь = р (8; 4; 4), 2 а - 3 b - q (-4; -8; 4). Значит,
|р| = >/82+42+42 = 4л/б ; \q\ = 7(-4)2+(-8)2+42 = 4n/6 ;
р • q = 8 • (-4) 4- 4- (-8) + 4 • 4 = -48. Находим:
costp- ^ У =— = ~—=><p = z(p, g) = 120° .
|p|-|g| 4>/б-4л/б 2 Ч'
Ответ: 120°.
Задача 10. (Устно) Проекции вектора р на оси координат
равны соответственно: 3; -8; 5. Найдите координаты вектора р .
Задача 11. (Устно) Острый, прямой или тупой угол образу-
ет вектор b (-6; 0; 4) с базисными векторами: a) i ; б) j ; в) k ?
Задача 12. Даны векторы а (3; 1; -1), Ъ (6; 1; 0), с (-1; 2; -1).
Выясните, какой угол (острый, прямой или тупой) между век-
торами: 1) а и b ; 2) b и с ; 3) а и с .
Задача 13. Найдите угол между векторами: 1) а (2; -2; 2) и
Ь (3; 0; -3); 2) а (0; -5; 0) и b ( 0; ->/з ; -1).
Задача 14. Известно, что Z(a ,с) = Z(6 ,с) = 60°; |а| = 1,
| b | = | с | = 4. Найдите (а + b ) • с .
Задача 15. При каких значениях п векторы а (-3; п; -3) и
Ь (4; -3; п) перпендикулярны?
Задача 16. Дан куб ABCDA^B^C^D^. Найдите угол между
векторами: 1) ВВ1 и ВСг; 2) Z>1A1 и BD; 3) AjB иА^;
4) ВС и АС; 5) В£ и АС .
64
3.4. Содержательные метрические
задачи стереометрии
С помощью координатного метода можно эффективно
решать многие метрические задачи стереометрии, в том
числе задачи, которые предлагаются и, по всей вероятности,
будут предлагаться в ЕГЭ.
Для решения задач на взаимное расположение прямых и
плоскостей в пространстве, на вычисление расстояний и углов
между ними используется следующий учебный материал:
Ах + By + Сz + D = 0 — общее уравнение плоскости, где вектор
п (А; В; С) является вектором её нормали; А(х - х0) + В(у - у0) +
+ С(з - 20) = 0 — уравнение плоскости, проходящей через точ-
ку (х0; у0; 20) перпендикулярно вектору п (А; В; С); х = х0 + a^t,
у = у0 + а,2^ 2 = 2о + a-J — параметрические уравнения прямой,
проходящей через точку (х0; у{}', z0) параллельно вектору
Pi (Oi. ^2» а3).
Используются также формулы:
АВ - ^(х2 -хх)2 +(р2 -pj2 +(з2 - 2j)2 — расстояние между
точками A (xt; yt; 2t) и В (х2; у2; z2);
|Axn + Вуп + Czn +D\
р(М; р) = J—" —У-—1 — расстояние от точки
у/а2+В2 + С2
М(х0; у0; 20) до плоскости 0:
Ах + By + Cz + D = 0; |р| = ^х2 + у2 + z2 — длина вектора
p(x;y;z);
АВ = ^(х2 ~*i)2 +(у2 ~У1)2 +(22 -2i)2 — длина вектора АВ ,
заданного координатами его начала A(x1;y1;z1) и конца
В (х2; у2; г2);
хтх2 + угу2 + zxz2 -ab — скалярное произведение векторов
a (Xii yr, zO, b(x2; у2; z2);
а ± Ь <=> XjX2 + уху2 + zxz2 =0 — признак перпендикулярно-
сти векторов а (хг; yt; zj и b ( х2; у2; z2).
65
Угол ср между векторами а(хг; уг; zx) и Ь (х2; уг', z2) нахо-
дится с помощью формулы:
cos а = = xix2 +У1Уг + ziz2
|а| • |& 7Х2+У2+22
В результате изучения этой темы необходимо
знать/понимать в координатной форме:
— формулу для вычисления длины вектора и угла между
двумя векторами;
— формулу расстояния между двумя точками, деления от-
резка в данном отношении;
— различные уравнения плоскости, сферы;
— формулу для вычисления угла между двумя плоскостя-
ми, условия их параллельности и перпендикулярности;
— формулу для вычисления расстояния от данной точки
до данной плоскости; уравнения координатных плоскостей;
— для составления уравнения сферы достаточно знать или
найти координаты её центра и радиус. Для составления обще-
го уравнения плоскости достаточно знать или найти коорди-
наты любой ее точки и координаты любого вектора п, перпен-
дикулярного этой плоскости (вектора нормали к плоскости);
— различные уравнения прямой;
— формулу для вычисления угла между: двумя прямыми;
прямой и плоскостью; условия их параллельности и перпен-
дикулярности ;
— уравнения координатных осей;
— формулу для вычисления расстояния от данной точки
до данной плоскости.
Уметь в координатной форме решать аффинные и мет-
рические задачи:
— на составление уравнений плоскости, прямой, сферы;
— на вычисление расстояния: от данной точки до данной
плоскости (данной прямой); между параллельными плоско-
стями (параллельными прямыми; скрещивающимися пря-
мыми);
— на построение, доказательство и вычисление, используя
в качестве объектов изучения куб, прямоугольный паралле-
66
лепипед, правильный тетраэдр, правильную пирамиду, пра-
вильную призму, сферу;
— на вычисление угла между двумя плоскостями, двумя
прямыми, между прямой и плоскостью, заданными уравне-
ниями, определяя при этом, параллельны (перпендикулярны)
ли они;
— на нахождение точки пересечения прямой и плоскости;
— с помощью уравнений прямых и плоскостей решать мет-
рические задачи стереометрии на построение, доказательство
и вычисление, используя в качестве объектов изучения куб,
прямоугольный параллелепипед, правильный тетраэдр, пра-
вильную пирамиду, правильную призму, сферу, при этом вер-
но и наглядно выполняя рисунки и корректно аргументируя
утверждения логического, конструктивного и вычислитель-
ного характера.
3.4.1. Расстояния в пространстве
а) Расстояние от точки до прямой. Задачи
Расстояние от точки М до прямой а, расположенных в
пространстве, равно расстоянию между данной точкой М и
точкой К = р п а, где р — плоскость, проходящая через точку
М перпендикулярно прямой а.
Координатным методом эту задачу можно решать следую-
щим образом. Составить уравнение плоскости р, проходящей
через точку М перпендикулярно данной прямой а. Затем ре-
шить систему, состоящую из этого уравнения и уравнений
прямой а. Решением этой системы являются координаты точ-
ки К = рп а. Тогда расстояние между точками М и К равно
искомому расстоянию от точки М до прямой а. Продемонст-
рируем сказанное на решении следующей задачи.
Задача 17. Найдите расстояние от точки М(7; 9; 7) до пря-
мой а, заданной уравнениями: х = 2 + 4£, I/ = 1 + 3£, z = 2t.
Решение. Так как р ± а, то направляющий вектор р (4; 3; 2)
прямой а принимаем в качестве вектора нормали для плоско-
сти р, проходящей через точку М(7; 9; 7). Значит, уравнение
этой плоскости имеет вид:
67
4(х - 7) + 3(i/ - 9) + 2(z - 7) = 0 <=> 4х + Зу + 2z - 69 = 0. Да-
лее находим координаты точки К = 0па, для чего решаем
систему уравнений:
4x+3y + 2z-69,
x = 2 + 4t,
у-1 + 3/,
z-2t.
После подстановки в первое уравнение системы вместо
х, у, z их выражения через t получаем: 4(2 + 4t) + 3(1 + 3t) +
58
+ 2 • 2t = 69, откуда t = — = 2 . Тогда точка К имеет координаты:
х = 2 + 4 • 2 = 10; i/ = 1 + 3 • 2 = 7; z = 2 • 2 = 4, т. е. К(10; 7; 4).
Значит, МК = +(9-7)2 +(7-4)2 = V22 — искомое рас-
стояние от точки М до прямой а.
Ответ: V22 .
Задача 18. ABCDAlBiCiDl — единичный куб. Найдите рас-
стояние: а) от точки А1 до прямой BXD: б) от точки В до прямой
AjC; в) от точки А, до прямой D^B: г) от точки С до прямой
DXB.
Решение, а) Введем прямоугольную декартову систему коор-
динат Oxyz так, что : В(1; 1; 0), Ах(1; 0; 1), Сх(0; 1; 1), D(9: 0; 0),
Вх(1; 1; 1) (рис. 32).
Для решения задачи достаточно найти расстояние от точки
Аг до точки пересечения прямой BXD и плоскости 0, проходя-
Рис. 32
щей через точку Аг перпенди-
кулярно этой прямой. Дока-
жем, что (AjBCJ ± ВрО.
Имеем: В1В±(А1В1С1) в
данном кубе => прямая
B1D1 — ортогональная про-
екция наклонной BXD на
(AjBjCj). А так как B1D11A1C1
(как диагонали квадрата
AjBjCiBj), то B1Z)± AjCj (по
теореме о трех перпендику-
лярах).
68
Аналогично: CD ± (BBjCj) в данном кубе => прямая BiC —
ортогональная проекция наклонной ВХВ на (BBjCj). А так как
BjCXBCj (как диагонали квадрата BBjCjC), то BjDXBCj
(по теореме о трех перпендикулярах).
Учитывая, что прямые А^ и ВСГ пересекаются, приходим
к выводу: ВрОХСАхВСд) (по признаку перпендикулярности
прямой и плоскости).
Обозначим: Т = B^D^ (AjBCJ, тогдаАгТ = р(Ах; В^О).
Найдем координаты точки Т.
Вектор DBj(l; 1; 1) является направляющим для прямой
BrD и вектором нормали для плоскости AjBCp Поэтому пря-
мая B}D может быть задана системой параметрических урав-
нений: х = t, у = t, z = t, а плоскость AjBCj — уравнением:
(х - 1) + (у - 1) 4- (z - 0) =0 о х + у + г - 2 = 0.
Решая систему из уравнения плоскости A^BCi и уравнений
прямой BXD
х + у+ z-2 = 0,
x = t,
' y = t,
z = t,
находим: £ + / + £- 2 = 0 => t = — , откуда следует, что точка
3
<2 2 2^
Т имеет координаты: Т —; —; — .
\ 3 3 3)
/7 р 7 р 7 р
Тогда А,Т = .1— + 0— + 1— = . Это означает,
1 VI sJ I з) I з; 3
что р (А^, B}D) = ——. Аналогично решаются задачи: б); в); г).
3
Ответ: а) —; б) —; в) —; г) —.
3 3 3 3
Задача 19. ACDEFA&QD^Fx — правильная шести-
угольная призма, все ребра которой равны 1. Найдите рас-
стояние от точки В до прямой C-Dp
69
Решение. Введем прямоугольную декартову систему ко
ординат Охуz так, как показано на рисунке 33. Тогда
;--;Л в(—;о\ С(0;1;0), .
\ 2 2 ) [2 2 ) V \ 2 2 )
Для решения задачи достаточно найти расстояние от точки
В до точки пересечения прямой CD} и плоскости а, проходя-
щей через точку В перпендикулярно этой прямой.
Так как CZ^la, то вектор DYC
Составим уравнение плоскости а.
Уз. 1
2 ’ 2
является на-
правляющим для прямой CZ>i и служит вектором нормали
плоскости а. Для упрощения вычислительных операций в ка-
честве вектора нормали плоскости а примем п(л/3;1;-2),
коллинеарный
D.C . Тогда
I Z Z
прямая D}C задается
системой параметрических уравнений: х = yfst, у = 1 + t, г =
= -2t, (*), а плоскость a — уравнением:
/ч ( 1 А г~
л/3 х——— + 1 у—— l-2(z-0) = 0<=>>/3x + y-22-2 = 0. (**)
I 2 J V 2J
Обозначим: Т = ar'\CD1, тогда ВТ = р(В; D^C). Для нахож-
дения координат точки Т достаточно решить систему
70
л/Зх + y-2z-2 = 0,
х~teR ,
i/ = l + t,
z = -2t,
составленную из уравнений плоскости а и прямой CDX.
После подстановки в уравнение (**) вместо х, у и z их вы-
ражений (*) через параметр t получаем:
5/3V3t + l + t-2(-2t)-2 = 0<»8f-l = 0«>£ = —. Значит, точ-
8
л/3 9 1
ка Т имеет координаты: х =—; у = —', z-— .Тогда
8 8 4
Ответ'.
р(В;Р1С)=ВТ =
Задачи для самостоятельного решения
Задача 20. В системе координат Oxyz расположен куб
ABCDAXBXCXDX так, что В(0; 1; 0), 2>х(1; 0; 1), С^О; 0; 1),
С(0; 0; 0). Постройте этот куб. Координатным методом найди-
те расстояние до прямой ВС} от точки: а)^; б) Bt; в) С; г) D.
Задача 21. Правильная шестиугольная призма
ACDEFA^B^CiD^iF^, все ребра которой равны 1, расположена в
системе координат Oxyz так, что центр ее основания совпадает
с началом координат, а вершины А, В, F, F{ имеют координаты:
Постройте эту призму и координатным методом
найдите расстояние от вершины В до прямой: а) EXF; б)
в) C^Dy', г) AD,.
б) Расстояние от точки до плоскости. Задачи
Расстояние от точки М до плоскости а равно длине пер-
пендикуляра МК (Кеа ), проведенного из точки М на. плос-
кость а.
71
Расстояние от точки М(х0; у0; z0) до плоскости р:
Ах + By + Cz + D — О находится по формуле:
р(М; р) = 1Ахо +В^+Сго + 2)1.
V ’ у1а2+В2+С2
Задача 22. Куб ABCDA1B1C1D1 в системе координат Oxyz
расположен так, что Aj(l; 0; 1), В(1; 1; 0), Ci(0; 1; 1), Р(0; 0; 0).
Постройте изображение этого куба и координатным методом
найдите отношение, в котором плоскость АХВ(\ делит диаго-
наль BXD куба, считая от вершины ВР
Рис. 34
Решение. Из построенного по условию задачи изображения
куба ABCDAyB^iDy относительно системы координат Oxyz
(рис. 34) следует, что точка Z>(0; 0; 0) — начало координат,
точки А(1; 0; 0) и С(0; 1; 0) — единичные на осях Ох и Оу соот-
ветственно. Кроме того, в этой системе координат точки В, Въ
Аи С15 Z>i приобретают координаты: Bj(l; 1; 1), А(1; 0; 0),
С(0; 1; 0), Z>i(0; 0; 1). Теперь рассмотрим решение задачи.
Обозначим: а = (ApBCj). Плоскость а задается уравнением
х + у + г- 2 = 0 (см. задачу 1).
т (п \ |0 + 0+0 - 2| 2-Тз
Тогда р(В;а) = ' =~Ч~? р(Д;а) =
V1+1+1 з
Значит, р(В^ а):р(В; а)= — 1:2.
3 3
V1+1+1 3
72
Можно иначе решить эту задачу. Пусть Т = ar, BJ). Решая
систему
x = t,
<^~t' teR,
Z — t,
x + y + 2-2 = 0,
составленную из уравнений прямой B^D: x = t,y = t,z = tn
плоскости а:
2 (2 2 2^
x + u + z- 2 = 0, находим: t = — , значит, Т —; —; — .
3 V3 3 3)
Тогда
ВгТ =
DT= l(o--] +fo--1 +fo--l = ^,
VI 3j I 3) I 3) 3
поэтому BiT: DT = =1:2.
Ответ: 1: 2.
Задача 23. Правильная шестиугольная призма
АСВЕЕА&С^Е^, все ребра которой равны 1, расположена
в системе координат Oxyz так, что центр ее основания совпа-
дает с началом координат, а вершины С, D, Сг имеют коор-
/З. 1
2 ’ 2
динаты: Bx
1 , C(0; 1; 0), DT
1 , C^O; 1; 1).
2 2
Постройте эту призму и координатным методом найдите от-
ношение, в котором плоскость AF^D делит диагональ BrF
призмы, считая от вершины Вг.
Решение, а) Если плоскость р: ах -I- by -I- cz + d = 0 прохо-
дит через данную точку М(х0; у0: г0), то координаты этой точ-
ки удовлетворяют уравнению плоскости р, то есть имеет ме-
сто: ах0 + by0 + cz0 + d = 0. Воспользуемся этим утверждением
при составлении уравнения плоскости р = (AF^D).
Пусть ах + by + cz 4- d = 0 — уравнение плоскости р. На
рис. 35 изображено расположение данной призмы относи-
тельно системы координат Oxyz. В этой системе точки A, F,
73
Рис. 35
Имеем: О е AD a (AFrD) => плоскость р = (AFXD) проходит
через начало координат, значит, d = 0. Далее, получаем:
1 ,/ч 1 г-
—;0 ер=>— а--6 = 0 <=>V3a-d = 0;
2)2 2
Л(0;-1; 1 )е0 =>-Ь 4- с = 0<=> b - с = 0;
Р(-—
2 2
Решая систему уравнений:
V3a-d = 0,
•Ь-с = О, находим: b = с,
у/За-Ь-0
b = у[3а . Полагая а = д/З ,
получаем: b = с = 3. Тогда уравнение плоскости р имеет
вид: у/з (х - 0) + 3(у + 1) + 3(z - 1) = 0 <=> л/з х + Зу + За = 0.
Обозначим: К = BlFc\(AF1D); FM 1(AFXD), Me(AF1D);
ВгН 1 (AFJ)), Н е (AF^). Из FM ± (AFjZ»), BXH1 (AF^D) следу-
ет: FMWBiH => &FMK к. АВ^НК подобны, при этом: FK : КВг =
= FM: ВХЯ.
74
Теперь находим расстояния p(F; р) = FM и р(Вх; р) =
FM = p(F;P) =
|7з о+з (-1)+з о|
л/3 + 9 + 9 - 7
В1Н = р(В1;Р) =
§ .хЗ+з.1 + з.1
2 2
л/3 + 9 + 9
2^21
7
Тогда B1^:A'F = ^i:^ = 2:l.
1 7 7
Замечание. При нахождении расстояния от точки до плос-
кости координатным методом во многих случаях не требуются
аргументированные обоснования построения перпендикуляра
из данной точки на данную плоскость. Но если FM 1 (AFtD)
(«виртуально»), MefAFpD) (рис. 35), то FM = p(F; р).
Ответ: 2:1.
Задачи для самостоятельного решения
Задача 24. В системе координат Oxyz расположен куб
ABCDA^CJ^ так, что 0(1; 0; 0), В^О; 0; 1), А(0; 1; 0), В(0; 0; 0).
Постройте этот куб. Координатным методом найдите: 1) рас-
стояние до плоскости AiBCj от точки: а) Вг; б) С; в) Dr; 2) от-
ношение, в котором плоскость А, ВС! делит диагональ B}D ку-
ба, считая от вершины ВР
Задача 25. Правильная шестиугольная призма
ACDEFA1B1C1D1E1F1, все ребра которой равны 1, расположена
в системе координат Oxyz так, что центр ее основания совпа-
дает с началом координат, а вершины В, С, D, Сг имеют коор-
7 J3 ।
динаты: В — ; —
2 2
./Q 1
0 , С(0;1;0), D , С^О; 1; 1). По-
. {221
стройте эту призму и координатным методом найдите:
1. а) расстояние от вершины Aj до плоскости BCCj б) расстоя-
ния от вершин А: и до плоскости АС^; 2. отношение, в ко-
тором плоскость AB^D делит диагональ F^B призмы, считая от
вершины Вр
75
в) Расстояние между скрещивающимися прямыми.
Задачи
Используем следующий факт: расстояние между двумя
скрещивающимися прямыми равно расстоянию от любой
точки одной прямой до плоскости, проходящей через вторую
прямую параллельно первой прямой.
Задача 26. В системе координат Oxyz расположен куб
ABCDAtB&Di так, что С(0; 0; 0), А(1; 1; 0), Р(1; 0; 0), С^О; 0; 1),
Bj(O; 1; 1). Постройте этот куб. Координатным методом най-
дите расстояние между прямыми AjCj и АВг.
Решение. На рис. 36 изображено расположение данного
куба относительно системы координат Oxyz. Началом систе-
мы координат является точка С(0; 0; 0), при этом имеем:
А(1; 1; 1), ВД1; 0; 1), С^О; 0; 1), В(0; 1; 0).
Найдем расстояние p(ABj; А^).
Рис. 36
Первый метод. Для этого составим уравнение единствен-
ной плоскости а , проходящей через прямую АВг параллельно
прямой AjCp
Векторы ДАЦ; 0;-1) и CjAj (1; 1; 0) принимаем в качестве
направляющих для прямых соответственно ABj и AjCj. Тогда
эти прямые могут быть заданы уравнениями соответственно:
X = l + f, \x-t,
у = 1, ieB = tefl.
z — —t, 2 = 1,
к к
76
В качестве вектора нормали плоскости а примем вектор
п(а;&;с), перпендикулярный векторам BjA(1;0;-1)h
CjAj (1; 1; О). Найдем координаты этого вектора. Имеем:
п±В.А, пВ,А = О, \a-c-O, (а-с, ,
< _ ___, => , => { , _ => { ’ => а = —Ь = с.
nVCxAx [n-CjA^O 1а + Ь = О ^а = -&
Пусть, не нарушая общности, а = 1, тогда: b = -1, с = 1.
Имеем: n(l; -1; 1) — вектор нормали плоскости а. Исполь-
зуя принадлежность точки А(1; 1; 0) плоскости а(Ае а), полу-
чаем следующее уравнение этой плоскости:
1 • (х - 1) -1 • (у - 1) + 1 • (z - 0) = 0 <=> х - у + z = 0.
Теперь находим:
р(АВх; АХСХ) = р(Ах; а) = . 1 1 = 4= = .
712+(-1)2+12 7з 3
Второй метод. Обозначим: р = (АВХС). Так как АХСХ || АС, то
АХСХ ||Р (Почему?). Тогда учитывая инцидентность АВхс:0,
приходим к выводу: р(АВх; АХСХ) = р(Ах; Р).
Составим уравнение плоскости 0. Пусть ах -I- by + cz + d = 0 —
уравнение этой плоскости. Так как С(0; 0; 0)е р , то d = 0. Далее:
А(1;1;О)е0 => 1а +1Ь +0-с= 0 => а +6 = 0 =>а = -Ь;
Вх(0;1;1)ер => 0 а +1Ь +1-с= 0 => & + с = 0=> —Ь = с.
Таким образом, получаем: а = -b = с, d = 0. Значит, иско-
мое уравнение плоскости 0 имеет вид: х - у + z = 0. Тогда
|о-о+1|
р(АВх; АХСХ) = р(С; 0) = 2 2=^-
VI +(-1) +1 3
Третий метод. Из АХСХ||АС и AXD ||ВХС следует
(АВХС)|| (АХСХВ) (Почему?). Кроме того, направляющий вектор
р (-1; 1; -1) прямой BDX коллинеарен вектору n(l; -1; 1) нор-
мали плоскости АВХС, откуда следует: ВХР± (АВХС).
А так как расстояние между скрещивающимися прямы-
ми равно расстоянию между параллельными плоскостями,
проходящими через эти прямые, то для определения искомо-
го расстояния р(АВх;АхСх) достаточно найти расстояние
р((АВхС); (АХСХВ)).
77
Имеем: АВ-ЦА^С), (АВ^С) || (A^D) => рЦАВ^; (A^D)) =
= р (К', М), где К = АВ n (AiCjD), М = D.B о{АВгС).
Плоскость АВ}С проходит через точку А(1; 1; 0), её векто-
ром нормали служит вектор n(l; -1; 1). Поэтому уравнение
этой плоскости имеет вид:
1 • (х - 1) • - 1 • (у - 1) + 1 • (г - 0) = 0<=> х— у + z - 0 (*)
Плоскость AiA-D проходит через точку В(1; 0; 0), а её век-
тором нормали служит также вектор n(l; -1; 1). Поэтому
уравнение этой плоскости имеет вид:
1 • (х - 1) -1 • (у - 0) + 1 • (z - 0) = 0 о х- у + z - 1 = 0 (**)
Для нахождения координат точек К и М достаточно ре-
шить системы, уравнениями которых являются параметриче-
ские уравнения прямой BDX и общие уравнения плоскостей
ABiCnA^D.
Находим координаты точки К = D}B п (ДС’Д), которые
являются решением системы уравнений:
х - у + 2 = 0,
х-1 t, + = . Этоозначает:
y = t, v v ’ 3
2 = l-t
21 2 .21
— ----- ;y=— ;г=1 — =—,т. e. К —
3 3 У 3 3 3 l Г
i. 2.1
3’3’3
Аналогично, находим координаты точки М = DXB п (АВХС),
для чего решаем систему уравнений:
х-у + г-1 = 0,
<X = 1? =>t-(l-f) + t-l = O=>t = ^.
y=i-t, V ’ 3
2-t
rv 2 1 2 1 2 л/2 1 2>l
Тогда x =— ; у = 1 — = — ; 2 = — , т. е. М — —; — .
3 33 3 <33 3J
Следовательно, р(Х'; Af)-p((AB1); (A1C1Z>)) = p(AB1; AjCjj^
^2 _ 1Y +Г1 _ 2? +f 2 _ 1Y = Л
1з 3) 1з 3J 1з з) 3 ‘
Ответ: -— .
3
78
Задача 27. Дан куб ABCDA^B^C^D^ с ребром 2. Расположи-
те этот куб в системе координат Oxyz и координатным мето-
дом найдите расстояние между прямыми: а) АВГ и А&; б) ВОг
и ВгС; в) BD и В\М, где М — середина ребра АВ.
Задача 28. Правильная шестиугольная призма
ACDEFA-lBiC-lD-lEyFx, все ребра которой равны 1, изображена в
системе координат Oxyz (рис.37). Найдите расстояние между
прямыми: а) ВХС и АГВ; б) ВХС и ВЕГ.
Решение, а) Найдем расстояние между прямыми ВгС и AjB.
Введем систему координат Oxyz так, что вершины В, С,
Bi
и Aj данной призмы имеют координаты:
в[—;0|;
2 2
С(0; 1; 0); Вг
\/3.1
.2’2
1
7
-~;1
2
(рис. 37).
Так как расстояние между двумя скрещивающимися пря-
мыми равно расстоянию от любой точки одной прямой до
плоскости, проходящей через вторую прямую параллельно
первой прямой, то для нахождения искомого расстояния
p(BjC; AjB) составим уравнение плоскости а, проходящей че-
рез прямую В}С параллельно прямой А}В.
79
Пусть вектор п (а; Ъ; с) нормали плоскости а перпендику-
лярен направляющим векторам
и AjB(O; 1;-1)
прямых ВгС и АХВ. Найдем координаты вектора п(а; &; с).
Имеем:
п ± СВ,,
_ ____L =>
nl АгВ
п-СВ^О, ~^-а—Ь~с = О,
Тр о I 2 2
n-AjB-0 b-c = Q
[у/За-Ъ + 2с = 0, [с = -л/3а,
[& = с [& = с.
Полагая а = л/з, получаем: b = с = -3. Таким образом,
п (л/з ; -3; -3). Тогда плоскость а (С е а) имеет уравнение:
7з • (х - 0) - 3 • (у - 1) - 3(z - 0) = \/Зх - Зу - 3z + 3 = 0.
Теперь находим:
р( AjB; BjC) = р(В; а) =
л/3 + 9 + 9
б) Для нахождения расстояния pCBE^BjC) составим урав-
нение плоскости (обозначим ее Р), проходящей через прямую
ВгС параллельно прямой ВЕ^
Точка Ej во введенной системе координат (рис. 37) имеет
координаты:
/з. 1
2 ’ 2
координаты:
—; 1 , значит, вектор ЕХВ
В качестве вектора нормали плоскости р примем вектор
п(а; Ь; с), перпендикулярный направляющим векторам
СВг
/3 1 J
-—; —; 1 и
2 2
Е^В^у/З; 1; -1) прямых соответственно ВгС и
ВЕг. Найдем координаты этого вектора. Имеем:
80
nXCBj,^ n-CBl=O,
П-LEyB nEtB-Q
^-a-—b + c = O,
2 2
\T3a+b-c~0
y/3a-b + 2c = 0,
y[3a + b - c - 0
y/3a-b + 2c = 0,
2b = 3c
c = -2y/3a,
. 3
b-—c.
2
Jc = -2>/За,
[& = -3y/3a.
Полагая a = у/3 , получаем: b = -9, с = -6. Таким образом,
п(у/3; -9; -6). Тогда плоскость 0, проходящая через точку
С (0; 1; 0) перпендикулярно вектору п(л/3; -9; -6), имеет
уравнение:
л/з (x-0)-9-(z/-1)-6(2-0) = 0<=>>/3x-9i/-6z + 9 = 0.
Теперь находим:
р(ВЕ.; В.С) = р(В; р) =----. --------------= -^= =
V 7 7 7 >/3 + 81 + 36 л/120 Ю
Ответ: а) gj V30
7 10
В заключение этого раздела рассмотрим решение следую-
щей задачи геометрическим (синтетическим) методом и ме-
тодом координат.
Задача 29. Точка К — середина ребра ВС куба
ABCDAiB^^i, ребро которого равно 8. Какую наименьшую
площадь может иметь треугольник АСМ, где М — точка пря-
мой Cjjfii?
Решение, а) Геометрический метод. Принимая отрезок АС
за основание искомого треугольника АСМ с наименьшей пло-
щадью и вершиной М на КСг, приходим к выводу: площадь
треугольника АСМ с постоянным основанием АС достигает
минимального значения при минимальной высоте МР
(РеАС), проведенной из точки МеКСг на АС. Это означает,
81
что отрезок МР — кратчайшее расстояние между прямыми
АС и С]К, то есть МР — общий перпендикуляр скрещиваю-
щихся прямых АС и СгК (рис. 38).
Найдем длину МР. Для этого проведем плоскость а =
= (BDDi). Она перпендикулярна прямой АС (почему?) и плос-
кости АСС} (почему?), причем (BDD^ryAC = О =ACrBD,
(BDDy)n (ACCJ = OOi, где OOX (ABC) (почему?).
Спроектируем на плоскость а прямую САК, для чего че-
рез К проведем прямую КТЦАС, TeBD. Получаем: OjT —
ортогональная проекция прямой САК на плоскость а. Тогда
р(АС; СХК) = р(О; О^Т) = ОН, где ОН — высота М)ОХТ, при
этом ОН ± АС, так как AC ± (BDPJ. Найдем ОН.
ОТ ОО
В прямоугольном AOOjT имеем: ОН - . А= . Так как
JOT2+OO2
.КТ || АС, К — середина ВС, то Т — середина ОВ (по теореме Фа-
леса), откуда ОТ -—ОВ = 2>/2 .
2
Учитывая, что OOi = АА^ 8, находим:
пи — 2\/2-8 _ 8
Значит, ОН = р(С1К'; АС) = .
82
Проведем НМ\\АС, Me КСги МР\\ОН, Р&АС. Тогда МР =
= ОН, МР1АС, значит, МР — высота ЛАСМ. Тогда мини-
мальная площадь треугольника АСМ равна — АС МР =
2
= - 8>/2 - = 32^ .
2 3 3
~ 32^2
Ответ'. ——.
3
б)Координатный метод. Пусть ААСМ (МеСгК) — иско-
мый, то есть имеет наименьшую площадь; длина его высоты
МР равна длине общего перпендикуляра скрещивающихся
прямых АС и С}К и равна расстоянию от любой точки прямой
АС до плоскости (обозначим ее а), проходящей через прямую
СХК параллельно прямой АС. Для нахождения этого расстоя-
ния составим уравнение плоскости а.
Рис. 39
Во введенной системе координат (рис. 39) точки А, С, К, С{
имеют координаты: А(8; О; 0), С( 0; 8; 0), К( 4; 8; 0), С! (0; 8; 8).
В качестве вектора нормали плоскости а примем вектор
п(а; Ь; с), перпендикулярный направляющим векторам
г(-1;1;0) и q(-l; 0; 2) прямых соответственно АС и СгК,
г(-1;1;0) коллинеарен АС(-8;8;0), £(-1; 0; 2) коллинеарен
Щ*(-4; 0;8).
83
Найдем координаты вектора п (а; Ь; с). Имеем:
п ± г, п г-0, \-а + Ь = 0, (а -Ь,
nLq nq = O |-а + 2с = 0 |а = 2с.
Полагая с = 1, получаем а = Ь = 2; п (2; 2; 1). Тогда плоскость
а определяется своим вектором нормали Я (2; 2; 1) и точкой
СР Её уравнение имеет вид: 2(х - 0) + 2(у - 8) + (з - 8) = 0 <=>
<=> 2х + 2у + z - 24 = 0.
Значит, МР = р(АС; С1ЛГ) = р(А; а) =
|2-8-24| 8 v
-------L =—. Учиты-
3-------3
вая, что АС = 8^2 , находим:
8иис=-АС-МрЛ.^/2^=^. (кв. ед.).
лал/С 2 2 3 3
Ответ: Кв. ед.
3
Замечание. Анализируя сравнительные решения этой задачи
синтетическим (геометрическим) и координатным методами,
можно увидеть простоту ее решения координатным методом.
Задачи для самостоятельного решения
Задача 30. В системе координат Oxyz расположен куб
ABCDA1B1C1D1 так, чтоВ(1; 0; 0), С(1; 1; 1), D(0; 1; 0), А(0; 0; 0).
Постройте этот куб. Координатным методом найдите расстоя-
ние между прямыми: a) AjCj и ВХС; б)АС1 и BjC; в) BD иА-^М,
где М — середина ребра АО.
Задача 31. Правильная шестиугольная призма
ABCBA^jCjBjEjF!, все ребра которой равны 1, расположена в
системе координат Oxyz так, что центр ее основания совпадает
с началом координат, а вершины А15 В, С, Вг имеют координа-
ты: A,f—;11, sf—;i;ol, С(0;1;0), В, f 11. По-
l 2 2 J I 2 2 J ’ I 2 2 J
стройте эту призму и координатным методом найдите рас-
стояние между прямыми: а) АХВ и CrD; б) АХВ и EXF\ в) АХВ и
AF-p, г)АхВ и BXD.
84
3.4.2. Углы в пространстве
а) Угол между двумя прямыми. Задачи
Если прямые а и Ь, имеющие направляющие векторы соот-
ветственно рДсц; а2; а3) и р2(Ьг; Ь2; Ь3), проходят соответст-
венно через точки М^х^, уг; zj и М2(х2; у2; г2), то эти прямые
задаются параметрическими уравнениями соответственно:
а: х = хг + axt, у = ух + a2t, z = zt + a3t, teR.
b: x = x2 + b^, у = y2 + b2t, z — z2 + b3t.
Если <p = Z(a, b), \|/ = Z(p1,p2), то либо <p = у, либо ф + ф =
= 180° (рис. 40). Учитывая, что cos ср > 0 при ф е [0°; 90°], по-
лучаем cos ф = |cos ф|. Это означает, что косинус угла между
прямыми может быть найден с помощью формулы:
I I |Pi ' Рг |
соэф - cosy =или, в координатном виде:
|Р1|* |Р2|
СОвф =
la.b, +a,b, +а„Ь„|
| 1 1 Ci о О I
+ а2 + аз2 • 7&12 + Ь2 + 632
Задача 32. В системе координат Oxyz расположен куб
АВСВА^С^ так, что В(0; 0; 1), А(1; 0; 1), С(0; 1; 1), D^l; 1; 0).
Постройте этот куб. Координатным методом найдите угол ме-
жду прямыми: aJA^B и АС; б)ВгВ и ВгС; b)ACj nDiB.
а) Решение. На рис. 41 изображено расположение данного
куба относительно системы координат Oxyz: точка Bj(O; 0; 0) —
85
начало координат, точки At(l; 0; 0) и Сх(0; 1; 0) — на осях Ох
и Оу соответственно. Точки Alt D, Clf Вх имеют координаты:
АД1; 0; 0), Р(1; 1; 1), Ci(0; 1; 0), Вх(0; 0; 0). Найдем угол
(p = Z(A!B,AC).
Рис. 41
Направляющими векторами прямых АгВ и АС будем счи-
тать векторы соответственно AjB(-l; 0; 1)и АС(-1; 1; 0).
AB-Acl |-1(-1) + 01 + 10| 1
Тогда cos ср =— . . ,= J----=—=------1 = — => со =60°.
Ахв|-|ас| 42-^2 2
в) Обозначим: а = Z(ACX, ВХВ). Направляющими вектора-
ми прямых АС} и DjB будем считать векторы соответствен-
но АС^(-1;1;-1) и (1; 1; -1).
1-1-1 + 1-1 + (-1)-(-1)| 1
Тогда cos а = ------L J— Д i =>
acJ-bdJ х/З-л/З 3
_ 1
=> а = arccos—.
3
Аналогично находится угол между прямыми DrB и ВТС.
Ответ: 1. а) 60°; б) 90°; в) arccos^.
Задача 33. ABCDEFA1B1C1D1ElF1 — правильная шести-
угольная призма, все ребра которой равны 1. Найдите вели-
чину угла между прямыми А±В и ВХС.
86
Рис. 42
Alf В, Bit С имеют координаты: А.
Решение. HaftfleMZ(AiB, ВХС) = <р.
Введем систему координат Oxyz (рис. 42) так, что точки
(1
В —;-;0 ,
2 2
—;-А;1
2 2
С(0; 1; 0), Bt 1 . Тогда СВг
и ВАДО;-!;!).
Находим: cos<p = cos
з
Ответ: arccos—.
4
2 2
Задачи для самостоятельного решения
Задача 34. В системе координат Oxyz расположен куб
ABCPAiBjCiA так, что Р(1; 0; 0), С^О; 0; 1), В(0; 1; 0), С(0; 0; 0).
Постройте этот куб. Координатным методом найдите угол ме-
жду прямыми: a) AjB и АС; б) DXB и ВХС', в) АСХ и DXB.
Задача 35. Правильная шестиугольная призма
ACDEFA1B1C1D1E1P1, все ребра которой равны 1, расположена в
87
системе координат Oxyz так, что центр ее основания совпадает
с началом координат, а вершины A, F, Fu В} имеют координа-
х/ч 1 П 1
ты: А —;--;0 , F(0;-l;0), Ft(0;-1;1), Вг —;-;1 . По-
< 2 2 ) [ 2 2 у
стройте эту призму и координатным методом найдите: величи-
ну угла между прямыми: a) ABi и CF^ б) АВ и CD,; в) AFV пАгВ.
б) Угол между прямой и плоскостью. Задачи
Угол между прямой Z:
х = х0 +1 а,
' y = y0+tb, и плоскостью а:
z = г0 +1 с
Ах + By + Cz + D = О
можно найти, используя угол между направляющим век-
тором р (а; Ь; с) прямой I и вектором п(А; В; С) нормали
плоскости а (рис. 43, 44):
sinZ(Z; a) = sin(p = cosi|/ = |
| аА + &В + сС |_________
аг +b2 +сг у/а2 + В2 + С2
Задача 36. Куб ABCDA^BiCxD^ расположен в системе коор-
динат Oxyz так, что его вершины D, Аь С\, Dr имеют коорди-
наты: £)(0; 0; 0), A^l; 0; 1), С^О; 1; 1), Z>i(0; 0; 1). Постройте
изображение этого куба и координатным методом найдите си-
нус угла между прямой и плоскостью: a) D]CX и (АГВР); б) А}В
и (ABiC); в) BpDj и (АВгСу, г) АХВ и (BC^D).
88
Решение, а) Найдем sirup, где <р =Z(Z>1C1; (AjBD)).
В системе координат Oxyz (рис. 45) вершины куба име-
ют координаты: А(1; 0; 0), Bt(l; 1; 1), С(0; 1; 0), В(1; 1; 0).
В качестве направляющего вектора прямой примем
вектор D1Cl(0; 1; 0), в качестве вектора нормали плоскости
а = (AjBjD) — вектор п(а; Ь; с), перпендикулярный векторам
£4^(1; 0; 1) и ВВ(1; 1; 0).
Рис. 45
Найдем координаты вектора п (а; Ъ; с).
Имеем:
I п IBAp
nlDB
п DAV = 0,
п DB = 0
а + с = 0,
а + Ь = 0
=> а = -Ь = -с .
Полагая а - 1, получим: Ь = с--1, то есть n(l; -1; -1). Это
означает, что уравнение плоскости а (А.! е а ) имеет вид:
l(x-l)-l(y-0)-l(z-l) = 0<=>x-i/-2 = 0,
и sintp =
-DiCj • n
Z>iCi -|n|
|oi+i(-i)+o(-i)|
Ji з '
Замечание. Можно доказать, что АС\ 1 (AjBB). Тогда в ка-
честве вектора нормали для (AjBB) можно принять вектор
АС\(-1; 1; 1).
89
Аналогично находится синус угла между прямой и плос-
костью: б) АХВ и (ABjC); в) BXDX и (АВХС); г) АгВ и (BCjP).
Ответ: а) — ; б) —; в) —; г) — .
3 3 3 3
Задача 37. В правильной шестиугольной призме
ABCDEFA^iC^DiEiF!, все ребра которой равны 1, найдите
синус угла между прямой BD} и плоскостью BFjC.
Сначала рассмотрим решение этой задачи геометрическим
методом, аргументируя шаги построений и доказательства ут-
верждений, возникающих в процессе её решения.
Решение. Геометрический метод. Обозначим:
/(B-Dj, (BFjC)) = а. На рис. 46 построены точки Q = BCr\ED,
К = E^F^CiP!, принадлежащие плоскости BFjC, и точка
R = DD{ п -EjQ = (BFjC) n ВЛр AE^DjK — правильный, так как
Z.KEXDX = ZKD1E1 = 60° (почему?); стороны АЕгВхК равны 1
(почему?).
Рис. 46
Пусть точка Т — середина ЕХК, тогда DXTLEXK (как ме-
диана правильного AEXDXK => RT ±Е}К (по теореме о трех пер-
пендикулярах)^ E1KE(RD1 Т) (по признаку перпендикуляр-
ности прямой и плоскости) => (В7?1С)±(ЯВ]71) (по признаку
перпендикулярности двух плоскостей). Это означает, что пер-
пендикуляр DXO, проведенный из Dt на (BFXC), (Ое(ВРгС)),
расположен в (RDXT), причем OeRT = (BF1C)r^(RD1T).
90
Поэтому прямая ОВ — проекция BD, на (BF,C) и ZOBD^ =
= Z(BDi, ((ВРгС)) = а. Найдем величину этого угла.
Отрезок DtO — высота прямоугольного ЛВВУТ с катетами
ВгТ = = — и RD! = О.бЛрО = 0,5 (точка R — середина
ребра -D-Dj).
Значит, D.O = -TP1T D1R = 0,5^3 0,5 = 0 25 ^/з .
^D1T2 + DlR2 VO,75 + 0,25
В прямоугольном ABDjP находим:
Тогда в прямоугольном AOBDj с катетом В}0 = 0,25 v3 и
гипотенузой ВВ^ = 2 находим: sina = 0,125 >/з .
Теперь рассмотрим решение этой задачи координатным
методом.
Рис. 47
Координатный метод. Обозначим: Z(BDi, (BFjC)) = a.
Во введенной системе координат (рис. 47) точки В, С,
( /о 1 А
Вр Вг имеют координаты: В —;0 , С(0;1;0), 7^(0;-1;1),
I 2 2
Ч 2 2
91
Для прямой DXB направляющим является вектор
В£\(-л/3;0; 1).
Найдем координаты вектора нормали плоскости
Р = (BFjC), для чего составим ее общее уравнение.
Пусть ах + by + cz 4- d = 0 — искомое уравнение плоскости
р = (ВЛС).
Имеем: В
2 2
Gp=>^-a + -6 + d = O
2 2
С(0; 1; О)ер=>b + d = 0 ;
F1(O;-l;l)eP^-b + c+d = O.
Решением системы, состоящей из уравнений:
J^-a + -b + d = G, b+d=O,
2 2
—b + с + d = 0 является: а —\[3 , b = 3, с = 6, d =3. Значит,
вектор нормали плоскости р имеет координаты: п (>/з ; 3; 6).
Тогда sina= cosZ(BB1; п)
_|-УЗ;.Уз+03±.1^|= д
V3+O+1V3+9+36
Ответ: 0,125 л/з .
Задачи для самостоятельного решения
Задача 38. В системе координат Oxyz расположен куб
ABCDAXBXCXDX так, что 0(1; 0; 0), В^О; 0; 1), А(0; 1; 0), В(0; 0; 0).
Постройте этот куб. Координатным методом найдите синус
угла между прямой и плоскостью: а) ВС и б) АгВ и
(ABtC); в) BiPi и (ABiC); г) АХВ и (BCjP).
Задача 39. Правильная шестиугольная призма
ACDEFA1B1C1D1ElF1, все ребра которой равны 1, расположена
в системе координат Oxyz так, что центр ее основания совпа-
дает с началом координат, а вершины В, С, D, Dx имеют коор-
динаты: В
Постройте эту призму и координатным методом найдите си-
нус угла между: а) прямой ВХЕ и плоскостью ВСХС: б) прямой
/3.1
2 ’2
0 , С(0;1;0), D -
/3.1
2 ’ 2
—; —; 0 , D
2 2 1
92
АВ и плоскостью BFXC’, в) прямой BD{ и плоскостью BFrC-,
г) прямой АХВ и плоскостью ВВ]С.
в) Угол между плоскостями. Задачи
Угол между двумя плоскостями аир, заданными уравне-
ниями соответственно Агх + Вгу + (\z + = 0 и А2х + В2у +
+ C2z + D2 = 0, удобно связать с углом между их нормальными
векторами п^А^ Вг; Сх) и п2(А2; В2; С2) (рис. 48). Именно,
cos Z(а; р) = |cos Z(nx; п2 )| =
I ^1'^2 ^1^2 I
Ja, + в?+с.2 • Ja2 + в2 + с2
У/ L 1 X у 2 2 2
Задача 40. В системе координат Oxyz куб ABCDA^B^C^D^
расположен так, что А(1; 0; 0), В(0; 0; 0), С(0; 1; 0), 1; 1).
Постройте этот куб. Найдите угол между плоскостями:
а)АВхС иАВСх; б)АВхС и AjBCj; в) _ОХАС иВхАС.
93
Решение, а) Из условия следует, что точка В(0; 0; 0) — на-
чало координат, точки А(1; 0; 0) и С(0; 1; 0) — на осях Ох и Оу
соответственно. Тогда точки Вг, А1? Clf D приобретают коор-
динаты: В^О; 0; 1), Ai(l; 0; 1), С^О; 1; 1), D(l; 1; 0). На рис. 49
изображено расположение куба относительно системы коор-
динат Oxyz. Найдем угол \|/ между плоскостями а = (АВ}С) и
Р = (ABCJ. Пусть плоскость а = (АВГС) имеет уравнение: ах +
4- by + cz + d = 0. Так как плоскость а проходит через точки А,
В и СА, то координаты этих точек должны удовлетворять урав-
нению этой плоскости, значит, четверка чисел a, b, с nd явля-
ется решением системы уравнений:
а-d
а 4- d = 0, [ а = -d,
c + d = Q, <=> <! с = -d, о a-bc-~d.
&4-d = 0 b = -d
b = -d
Полагая d = -1, получаем уравнение плоскости а == (ABtC):
x + y + z~l = G. Значит, вектор п нормали этой плоскости
имеет координаты: п(1; 1; 1).
В качестве вектора нормали плоскости р = (АВС\) примем
вектор п1(а1; Ьг; cj, перпендикулярный векторам ВА(1; 0; 0) и
ВС\ (0;1;1).
Найдем координаты вектора пх.
Имеем:
п. ± ВА, п. ВА = 0, fa. = 0, _ .
---»=>1------- =>11? Л => а. =О,Ь.=-с..
п1±ВС1 [п.-ВС^О f&i+ci=0
Полагая (\ = -1, получаем: пх (0; 1; -1).
Тогда: n nl = 104-11 + 1(-1) = 0=> n±n, =>а±р=>\|/ = 90°.
Аналогично находятся углы между плоскостями: б) АВГС и
А^ВС^, в) D}AC и ВХАС.
1 2 \/2
Ответ: а) 90°; б) arccos —; в) arcsin-—.
3 3
Задача 41. В правильной шестиугольной призме
ABCDEFA1BiC1Z)1£1F1, все ребра которой равны 1, найдите
синус угла между плоскостями А^ВС и ABXF.
94
Сначала рассмотрим решение этой задачи геометрическим
методом, аргументируя шаги построений и доказательства ут-
верждений, возникающих в процессе её решения.
Решение. Обозначим: ZCCAjBC); (ABjP)) = 0; Р = BpEj °
К = ABj '"'i AjB. Тогда (АгВС) (ABjP) = КР — ребро двугран-
ного угла, образованного плоскостями АХВС и AB^F (рис. 50).
Найдем sin0.
Имеем: точка Р — середина диагоналей В^ и AtDi, рав-
ных 2, поэтому АГР = ВХР = 1.
Аналогично, точка К — середина диагоналей AjB и АВ15 рав-
ных V2 , поэтому А^-Bj^K = 0,5л/2 . Тогда ЛАгРК = ^ВгРК=^
=>А^Т = BjT, где АХТ и ВгТ — высоты этих треугольников,
проведенные к их общей стороне РК. Это означает, что
/((АрВС); (ABpF)) =ZA1TB1 = 0. Найдем sin 0.
Замечаем, что отрезок РК — средняя линия ЬАВ^, по-
этому РК = O.SAEj.
В прямоугольном ЛАЕ^Е с катетами АЕ-ТЗи ЕХЕ = 1 на-
ходим: AEj = у]АЕ2 +Е1Ег = +12 = 2, значит, РК = 1.
Если КТ = х, то РТ =1 - х, тогда на основании АХК2 - КТ2 =
= А,Р2 - РТ2 получаем: 0,5 - х2 = 1 - (1 - 2х + х2), откуда х =
= 0,25 = ТК. Значит, А,Т = ^А,К2-КТ2 = ^0,572^ =0,252 =
Далее, пусть точка Н — середина А^В^ Тогда в равнобед-
ренном AAjBjT:
95
z, Trr р . 0 Агн 1 v? 2^7 0 V21
ZA.TH = —, при этом sin— - —s— = —: — -, cos— =--.
1 2 2 AtT 2 4 7 27
m • о о • 0 P o2\/7 721 4ч/3
Тогда sinP = 2sin—cos— = 2—-—-—- .
2 2 7 7 7
Теперь рассмотрим решение этой же задачи координатным
способом.
Обозначим: Z(a; Р) = <р. Найдем координаты векторов нор-
малей плоскостей a = (А} ВС) и р = (ABjF).
Во введенной системе координат Оху г (рис. 51) точки Ait
В, С, А, В15 F имеют координаты: Аг
/О 1
С( 0; 1; 0 ), А —;0 , В,
2 2
/3.1
2 ’ 2
1 , В(0;-1;0).
1
Рис. 51
Вектор п(а; Ь; с) нормали плоскости а перпендикулярен
векторам AjB(O; 1; -1) и ВС
7з. 1
2 ’ 2
О . Координаты вектора
п(а; Ь; с) найдем из условия его перпендикулярности векто-
рам AjB(O; 1;-1)и ВС
/3.1
2 ’ 2
Имеем:
п- AjB = O
п ВС - О
b - с = О,
Ж+1(,=о
I. 2 2
(b = c,
(b = V3a.
О
96
Полагая a = V3, получим: b = с = 3. Таким образом,
^(л/З; 3; з).
Аналогично, вектор b^, cj нормали плоскости 0 пер-
пендикулярен векторам АВ} (0; 1; 1) и FA
/Ч 1
—;0 . Поэтому
2 2
&1=-Ci,
\ =-V3ar
координаты а1,Ь1и с} найдем, решая систему уравнений:
&! + Cj = О,
^-al+—bl=0
I 2 1 2 1
Полагая at =л/3 , получим: Ь{ = -3, с, = 3. Таким образом,
(л/3; - 3; 3j. Тогда:
cos ср = |cos Z(n; nl )| =
|л/3 л/3 + 3 (-3) + 3 3| 1 . 4^3
J—. ,— ----= — => sin (p =----.
V3 + 9 + 9J3 + 9 + 9 7 7
Ответ:
7
Задачи для самостоятельного решения
Задача 42. В системе координат Oxyz расположен куб
ABCDAjBAA так, что At(l; 0; 0), В(1; 1; 1), D(0; 1; 0), В^О; 0; 0).
Постройте этот куб. Координатным методом найдите угол ме-
жду плоскостями: а) АВгС и АВС^ б) АВХС и АхВС^, в) DYAC и
BjAC.
Задача 43. Правильная шестиугольная призма
ACBE.FA1B1C1B1.E1.F1, все ребра которой равны 1, расположена в
системе координат Oxyz так, что центр ее основания совпадает
с началом координат, а вершины А15 В, С, D имеют координа-
/3.1
2’2
• Л 1 1 I г>| Vo
ты: А. —; —; 1 , В —
42 2 2
0 , С(0;1;0), D -
/3.1
2 ’2
0 . По-
стройте эту призму и координатным методом найдите синус
угла между плоскостями: а) АВС и BC^F; б) FB,D, и АВС;
в) BCjB и АВС; г) А1СЕ1 и АВС; д) АВС и BFD1.
97
ГЛАВА 4.
СФЕРА И МНОГОГРАННИКИ
В КООРДИНАТАХ
При решении как планиметрических, так и стереометриче-
ских задач возникает необходимость выполнять: а) рисунки,
поясняющие (отражающие) геометрическую суть по условию
данной задачи; б) вычислительные операции; в) аргументации
логического, графического и вычислительного характера. При
этом последовательность (очерёдность) выполнения операций
логического, графического и вычислительного характера при
решении различных задач различна — она зависит от условия
решаемой в данный момент задачи.
Во многих случаях встречаются задачи, решение которых
необходимо начинать с выполнения рисунка по их условию,
после чего следует очерёдность неоднократно сменяющих одна
другую операций логического и вычислительного характера,
при этом в процессе этой очерёдности возможны дополнитель-
ные геометрические построения, необходимые для дальнейших
логических и вычислительных операций.
Таким образом, качественное, аргументированно обосно-
ванное решение геометрической задачи представляет собой ло-
гическую последовательность неоднократно повторяющихся,
чередующихся обоснований (действий) графического, логиче-
ского и вычислительного характера. И эта последовательность
выстраивается в зависимости от условия каждой решаемой за-
дачи. Важным является именно своевременное (в процессе ре-
шения) выполнение этих сменяющих одна другую необходи-
мых аргументированных операций, в результате чего и
достигается полноценное решение геометрической задачи —
планиметрической или стереометрической.
В результате изучения этой темы на профильном и углуб-
ленном уровне необходимо
знать/понимать:
— определение сферы и шара, их радиуса и диаметра;
— определение касательной плоскости к сфере;
— уравнение сферы и неравенство шара;
98
— определение сферы, вписанной в двугранный и много-
гранный угол;
— определение сферы и шара, вписанных в многогранник
и описанных около него;
— формулы для вычисления:
а) площадей сферы, сегментной поверхности, шарового
пояса, поверхности шарового сектора;
б) объемов шара, шарового сегмента, шарового сектора,
шарового слоя;
• если сечение сферы диаметральной плоскостью изобра-
жено в виде эллипса, то концы диаметра сферы, перпендику-
лярного этой плоскости, находятся не на окружности (абри-
се), «изображающей» сферу, а внутри круга этой окружности;
• плоскость, касательная к сфере, перпендикулярна ра-
диусу, проведенному в точку их касания;
• если прямая а касается сферы в точке М, то эта прямая
касается в точке М той окружности большого круга, которая
является сечением сферы и диаметральной плоскости, прохо-
дящей через прямую а;
• если расстояние d от центра шара (сферы) до данной плос-
кости меньше радиуса R шара (сферы), то пересечением шара
(сферы) с плоскостью является круг (окружность). Центром
этого круга (этой окружности) является основание перпенди-
куляра, проведенного из центра шара (сферы) на данную плос-
кость, или сам центр шара (сферы), если плоскость проходит
через этот центр. Радиус г сечения равен г = ^R2 -d2 ;
• если расстояние от центра шара (сферы) до данной плос-
кости равно радиусу шара (сферы), то плоскость касается ша-
ра (сферы);
• диаметр шара (сферы), делящий его хорду пополам, пер-
пендикулярен этой хорде;
• отрезки всех касательных прямых, проведенных к шару
из одной расположенной вне шара точки, равны между собой;
• произведение длин отрезков хорд шара, проходящих че-
рез одну и ту же внутреннюю точку шара, есть величина по-
стоянная (равная R2 - а2, где R — радиус шара, а — расстоя-
ние от центра шара до данной точки);
99
• если из одной и той же точки вне шара проведены к нему
секущая и касательная, то произведение длины отрезка всей
секущей на длину отрезка её внешней части равно квадрату
длины отрезка касательной (и равно а2 - R2, где R — радиус
шара, а — расстояние от центра шара до данной точки);
• множество всех точек двугранного угла, равноудаленных
от его граней, есть «биссекторная» полуплоскость этого угла;
в ней лежат центры всех сфер, вписанных в этот угол;
• множество всех точек пространства, лежащих внутри
трехгранного угла и равноудаленных от его граней, есть луч
прямой пересечения биссекторных полуплоскостей двугран-
ных углов этого трехгранного угла. На этом луче лежат цен-
тры всех сфер, вписанных в трехгранный угол;
• если сфера радиуса г вписана в трехгранный угол, все
плоские углы которого прямые, то для расстояния т от цен-
тра сферы до ребра трехгранного угла справедливо: т = г\!2 ,
а для расстояния d от центра этой сферы до вершины трех-
гранного угла выполняется: d = гл/з ;
• чтобы около многогранника можно было описать сферу
(шар), необходимо, чтобы около любой его грани можно было
описать окружность (круг). При этом центр описанной сферы
(описанного шара) проектируется в центр описанной около
любой грани окружности (описанного круга); перпендикуляр,
опущенный из центра описанной около многогранника сферы
(описанного шара) на ребро многогранника, делит это ребро,
как хорду сферы (шара), пополам;
• нельзя описать сферу около любой наклонной призмы;
• радиус сферы, вписанной в призму, равен радиусу ок-
ружности, вписанной в основание призмы;
• все высоты правильного тетраэдра проходят через центр
описанной около него (вписанной в него) сферы;
• в цилиндр можно вписать сферу тогда и только тогда, ко-
гда он равносторонний;
• при решении задачи на комбинацию сферы и цилиндра
(конуса) удобно использовать сечения комбинации сферы и
конуса (цилиндра) диаметральной плоскостью сферы, содер-
жащей ось конуса (цилиндра);
100
• при решении задачи, в которой даны две, три и более по-
парно касающиеся сферы, удобно «привлекать на помощь»
треугольник или тетраэдр с вершинами в центрах соответст-
венно данных сфер;
уметь:
— верно и наглядно изображать сферу в комбинациях с мно-
гогранниками, цилиндром и конусом и другими сферами, кор-
ректно аргументируя каждый шаг построения изображения;
— решать задачи:
а) на взаимное расположение сферы и плоскости; сферы и
двугранного угла;
б) на комбинации сферы с многогранниками и фигурами
вращения, корректно аргументируя утверждения, возни-
кающие по ходу решения задачи;
в) на вычисление;
— площади сферы, сегментной поверхности, шарового
пояса, поверхности шарового сектора;
— объёма шара, шарового сегмента, шарового сектора,
шарового слоя, корректно аргументируя возникающие ут-
верждения.
Сфера может быть описана около многогранника, вписана
в него, может проходить через некоторые вершины много-
гранника, пересекая при этом некоторые его грани.
Рассмотрим примеры аргументированных решений ряда
задач на комбинации сферы и многогранника.
Прежде чем приступать к решению стереометрической за-
дачи координатным методом, необходимо сначала решить эту
задачу конструктивно, геометрически. Иначе говоря, необхо-
димо составить «геометрический алгоритм» ее решения, что
естественным образом связано с повторением и углублением
материала школьной геометрии.
Подготовительные задачи
Задача 1. Найдите длину линии, состоящей из всех общих
точек двух сфер (х - I)2 + (у + З)2 + (г - 5)2 = 196 и (х + З)2 +
+ (у + 6)2 +(г+ 7)2 = 225.
101
Решение. Из данных уравнений следует, что первое из них
задает сферу радиуса Rx = 14 с центром А(1; -3; 5), а второе —
сферу радиуса R2 = 15 с центром В(-3; -6; -7).
На рис. 52 изображены окружности coj и ®2 — сечения этих
сфер плоскостью, проходящей через их центры А и В (центры
данных сфер являются центрами окружностей о»! и со2).
Так как расстояние
АВ = 7(1+ 3)2 +(-3 + 6)2 +(5 + 7)2 =13 между центрами дан-
ных сфер меньше суммы R} + R2 = 29 их радиусов, то эти сфе-
ры пересекаются, поэтому их диаметральные сечения — ок-
ружности со! и со2 пересекаются.
Пусть С — одна из точек пересечения данных сфер (одна из
точек пересечения окружностей <Oj и <о2). Тогда получаем
ААВС (рис. 52), в котором АВ = 13, АС = 14, ВС = 15.
Вращая окружности со t и <о2 вокруг прямой их центров А и
В, получаем данные сферы, при этом вращении точка С «про-
бежит» окружность пересечения данных сфер, радиус которой
равен высоте СН треугольника АВС.
тт пи 28ддвс 2V21-6-7-8 168 1О12 m
Находим: СН = _ддвс _ ?--------= ----= 12—. Таким
АВ 13 13 13
образом, длина окружности пересечения данных сфер равна
2я.1*8=2511^
13 13
Ответ: 25— тс.
13
Задача 2. Найдите площадь фигуры, состоящей из всех
общих точек двух шаров (х - З)2 + (у + 4)2 + з2 = 64 и (х - З)2 +
+ (у - 2)2 + (z - 8)2 = 36.
102
Решение. Из уравнений данных шаров следует, что цен-
тром первого шара является некоторая точка А(3; -4; 0), а его
радиус rj равен 8; центром второго шара — точка В(3; 2; 8),
его радиус г2 равен 6.
Так как расстояние АВ между центрами данных шаров, рав-
ное ^/(З-З)2 +(2-(-4))2 +(8-0)2 = 10, меньше суммы + г2 =
= 8 + 6 = 14 их радиусов, то эти шары пересекаются. Их пере-
сечение — круг с центром на прямой АВ.
На рис. 53 изображено сечение комбинации данных шаров
плоскостью, проходящей через их центры — точки А и В.
В сечении этой комбинации шаров получается два круга с пе-
ресекающимися в точках К и М окружностями (Oj и со2.
Треугольник АВК, стороны АК, ВК и АВ которого равны со-
ответственно 8, 6 и 10, является прямоугольным (АК2 + ВК2 =
= АВ2). Его высота КН А. АВ равна радиусу г3 круга пересече-
ния данных шаров. Найдем КН.
2 — АК ВК
Так как КН LAB, то КН - - —§---------=
АВ АВ
-АК ВК 8 6 л Q
--------— ---= 4, о.
АВ 10
Таким образом, радиус г3 круга пересечения данных шаров
равен КН = 4,8, значит, его площадь равна: л (4,8)2 =
= 23,04л (кв. ед.).
Ответ’. 23,04 л кв. ед.
Задача 3. Найдите все точки на оси Oz, через которые про-
ходит хотя бы одна прямая, касающаяся сферы (х - I)2 +
+ (у + 2)2 + (г + 2)2 = в точке Р(3; -1; -4).
103
Решение. Все прямые пространства, касающиеся в точке Р
данной сферы с центром А, расположены в плоскости а, каса-
тельной к этой сфере в точке Р. Плоскость а перпендикулярна
радиусу АР сферы, проведенному в точку касания (рис. 54).
На оси Oz точками, через которые может проходить иско-
мая касательная к сфере прямая, служат лишь точки, общие
для плоскости а и оси Oz. Число искомых точек зависит от
взаимного расположения плоскости а и оси Ог.
Найдем общие точки плоскости а и оси Oz.
Центром данной сферы является точка А(1; -2; -2); точка
Р(3; -1; -4) — точка касания этой сферы с прямой, проходя-
щей через некоторую точку оси Oz. Так как касательная в
точке Р плоскость к сфере перпендикулярна её радиусу АР, то
АР(2; 1;-2) — вектор нормали плоскости а. Значит, уравнение
этой плоскости имеет вид: 2(х - 3) + {у + 1) - 2(z + 4) = 0<->
<=> 2х + у - 2г - 13 = 0.
Точки оси Oz, через которые проходят касательные к дан-
ной сфере прямые, находятся в касательной к сфере плоско-
сти а. Поэтому их координаты являются решением системы,
составленной из уравнений плоскости а и оси Oz, т. е. системы
уравнений:
104
г = -6,5.
х = 0,
У = 0-
2х + г/-2г-13 = 0.
х = 0,
,У = 0
Эту задачу можно решить иначе, используя векторно-
координатный метод.
Действительно, так как касательная к сфере в точке
Р(3; -1; -4) прямая КР, проведенная через точку К(0; 0; z) е Ог,
перпендикулярна радиусу АР сферы, проведенному в точку ка-
сания, то векторы АР(2;1;-2) и КР(3; -1; - 4 - z) ортогональ-
ны. Это означает: АР КР =0 =>2-3 + 1 (-1) + (-2) (-4 - г) =
= 0=>2z + 13 = 0=>z = -6,5, откуда следует: точка К имеет ко-
ординаты (0; 0; -6,5).
Таким образом, на оси Oz существует единственная точка
Щ0; 0; -6,5), через которую проходит единственная прямая,
касательная к данной сфере в точке Р. На рис. 54 прямая КР
касается диаметральной окружности со данной сферы — ок-
ружности пересечения сферы с плоскостью АРК.
Ответ'. Единственная точка (0; 0; -6,5).
Задача 4. Найдите уравнения всех сфер с центром в начале
x = 3-2i,
У = 1 + *,
2=5.
координат, касающихся прямой
Решение. Обозначим: т — прямая, заданная уравнения-
х = 3-2£,
ми< y = l + i,
Из этих уравнений следует, что А(3; 1; 5) — точ-
2 = 5.
ка прямой т, р (-2; 1; 0) — её направляющий вектор.
Сфера с центром в начале координат 0(0; 0; 0) задается
уравнением: х2 + у2 + z2 = R2.
Так как касательная к сфере прямая т перпендикулярна
её радиусу, проведенному в точку К касания, то этой точкой
касания является точка пересечения прямой т и плоскости а,
проходящей через центр О сферы перпендикулярно прямой
т. Тогда длина радиуса R этой сферы равна длине отрезка ОК.
Найдем эту длину.
Составим уравнение плоскости а.
105
Так как а±ти, то вектор р(-2; 1; 0) служит вектором нор-
мали плоскости а, проходящей через начало координат —
точку 0(0; 0; 0). Поэтому уравнейие этой плоскости имеет вид:
-2х + у = 0=>2х-у = 0.
Координаты точки К = а п т находим, решая систему, со-
ставленную из уравнений прямой т и плоскости а:
х = 3-2£, х = 3-2£,
Л = 1 + *’ =>< г/=1+г,
2 = 5, =* 2 = 5,
2х-г/ = 0 2(3-20-(1 + 0 = 0
x = 3-2i,
2 = 5,
f=l
Таким образом, точка К касания сферы с данной прямой
т имеет координаты: ЛГ(1; 2; 5). Значит, длина радиуса этой
сферы равна длине отрезка ОК, т. е. равна
>/(1- О)2 +(2-0)2 + (5 - О)2 = л/30 . Тогда искомое уравнение
сферы имеет вид: х2 + у2 + г2 = 30.
Так как прямая и перпендикулярная ей плоскость имеют
единственную общую точку — центр сферы, касающейся дан-
ной прямой, то существует единственная сфера с заданным
центром, касающаяся этой прямой.
Ответ.'. Единственная сфера х2 + у2 + г2 = 30.
Задача 5. Найдите площадь сферы, описанной около тет-
раэдра РАВС, если: Р(0; 0; -6), А(0; 0; 0), В(8; 0; 0), С(0; -2; 0).
Решение. Площадь сферы находится по формуле: Всфер =
= 4 itR2, где R — радиус сферы. Так как радиус сферы равен
расстоянию от любой точки сферы до ее центра, то для реше-
ния задачи достаточно найти координаты центра Т сферы,
описанной около заданного координатами своих вершин тет-
раэдра РАВС.
Известно, что множеством всех точек пространства, равно-
удаленных от данных точек Е и F, является плоскость сере-
динных перпендикуляров отрезка EF. Поэтому центром сфе-
ры, описанной около тетраэдра, является точка пересечения
плоскостей серединных перпендикуляров трех любых не ле-
жащих в одной плоскости ребер этого тетраэдра.
106
Пусть а, р, у — плоскости серединных перпендикуляров
ребер соответственно АВ, ВС, АР тетраэдра РАВС; К, Н, М —
середины соответственно этих ребер.
Находим: Щ4; 0; 0), Н(4; -1; 0), М(0; 0; -3); АВ (8; 0; 0),
СВ (8; 2; 0) и РА(0; 0; 6) — векторы, перпендикулярные соот-
ветственно плоскостям а, Р и у.
Для составления уравнений плоскостей а, р и у в качестве
векторов нормалей стоит взять векторы tz^IjOjO) || АВ,
п2 (4; 1;0) || СВ и п3(0;0;1) || РА . Тогда уравнения плоскостей а =
= (К; ), Р = (Н; п2 ) и у = (М; п3 ) имеют вид соответственно:
х - 4 = 0, 4х 4- у - 15 = 0, z + 3 = 0.
Координаты точки Т = (ап р)пу являются решением сис-
х-4 = 0,
темы, <4x + i/-15 = 0, составленной из уравнений плоскостей
£ + 3 = 0,
а, р и у. Решением ее является тройка: х =4, у = -1, z = -3.
Значит, равноудаленной от всех вершин тетраэдра РАВС яв-
ляется точка Т(4; -1; -3) — искомый центр сферы, описанной
около этого тетраэдра. Причем удалена эта точка от вершин на
расстояние, равное ТА = >/16 + 1 + 9 = >/26 = R. Тогда Всфер =
= 4 л(Т26)2 = 104л (кв. ед.).
Ответ: 104л кв. ед.
Прежде чем приступать к решению стереометрической за-
дачи координатным методом, необходимо сначала решить эту
задачу конструктивно, геометрически. Иначе говоря, необхо-
димо составить «геометрический алгоритм» ее решения, что
естественным образом связано с повторением и углублением
материала школьной геометрии.
Рассмотрим, например, решение следующих задач.
Задача 6. Напишите уравнение плоскости, касающейся
поверхности х2 + 2х + у2 + 2у + z2 - 4г = 0 в точке М(-2; -2; 4).
Решение. Исходное уравнение преобразуется к виду
(х + I)2 + (у + I)2 + (2 - 2)2 = 6,
из которого следует, что данная поверхность является сфе-
рой с центром в точке А(-1; —1; 2) и радиусом >/б .
107
Убеждаемся, что точка М(-2; -2; 4) расположена на дан-
ной сфере (координаты точки М удовлетворяют уравнению
сферы). Далее учитываем, что касательная плоскость к сфере
перпендикулярна ее радиусу, проведенному в точку касания
(школьная стереометрия). Поэтому в качестве вектора норма-
ли плоскости, касательной к данной сфере в точке М, можно
принять вектор МА (1; 1; -2). Тогда искомое уравнение этой
плоскости имеет вид:
(х 4- 2) 4- (у 4- 2) - 2(з - 4) = 0 ox + i/ -2г 4-12 = 0.
Ответ: х 4- у - 2г 4-12 = 0.
Задача 7. Напишите уравнение сферы с центром А(1; 1; 2),
касающейся сферы х2 4- у2 4- г2 = 54.
Решение. Уравнение х2 4- у2 4- г2 = 54 задает сферу S с цен-
тром 0(0; 0; 0) и радиусом R = Зд/б . Расстояние ОА между
центром этой сферы и центром А касающейся ее сферы равно
л/1 + 1 + 4 = >/б < Зл/б = R. Это означает, что центр А располо-
жен внутри шара, поверхностью которого служит данная сфе-
ра S, поэтому эти сферы могут иметь только внутреннее каса-
ние.
Пусть линия центров ОА касающихся сфер пересекает данную
сферу S в точках В и С. Если АВ = ОВ - ОА = Зл/б - >/б = 2>/б ,
то АС = ОС 4- ОА =3^6 4->/б = 4>/б . Значит, существует две сфе-
ры с центром А, касающиеся сферы S: одна из них касается дан-
ной сферы в точке В, её радиус равен 2>/б , а уравнение имеет вид
(х - I)2 +(у - I)2 4- (z - 2)2 = 24; другая сфера касается сферы S в
точке С, её радиус равен 4^6 , она задается уравнением:
(х - I)2 + (у - I)2 + (z - 2)2 = 96.
Ответ: (х - I)2 4- (у - I)2 + (г - 2)2 = 24; (х - I)2 4- (у - I)2 4-
4-(з - 2)2 = 96.
Задача 8. Напишите уравнение множества точек простран-
ства, образованного центрами всех сфер радиуса 5, касающих-
ся сферы х2 4- у2 4- z2 = 4.
Решение. Прежде чем приступить к выводу искомого урав-
нения, необходимо представить предложенную в задаче «гео-
108
метрическую картинку»: «увидеть», кроме данной сферы S с
центром 0(0; 0; 0) радиуса 2, касающиеся её в некоторой точке
С сферы Si и S2; сфера S', с центром А радиуса 5 касается сфе-
ры S внешним образом, а сфера S2 с центром В радиуса 5 —
внутренним образом.
Теперь необходимо вообразить, что когда точка С касания
всех трех сфер «заметает» сферу S, вместе с ней перемещают-
ся сферы Sj и S2, а значит, и их центры А и В. При этом центр
А «заметает» множество Мх всех точек пространства, равно-
удаленных от точки О на расстояние ОА — ОС + СА = 2 + 5 = 7,
а центр В — множество М2 всех точек пространства, равно-
удаленных от точки О на расстояние ОВ = ВС - ОС = 5-2 = 3.
Это означает, что множество Мг — сфера с центром О и радиу-
сом 7, а множество М2 — сфера с центром О и радиусом 3. А
так как точка О — начало координат, то эти сферы имеют
уравнения соответственно х2 + у2 + г2 = 49 и х2 + у2+ z2 = 9. То-
гда искомое множество точек, являющееся объединением
этих сфер, задается уравнением:
(х2 + уЧ г2 - 49)(х2 + у2+ г2 - 9) = 0.
Ответ', (х2 + у2+ г2 - 49)(х2 + у2+ г2 - 9) = 0.
Целесообразно предлагать для решения содержательные
задачи более высокого уровня сложности. Например, такие.
Задача 9*. Найдите множество центров всех шаров, кото-
рым принадлежат все точки прямых
x = 4 + t, [х = 2-2и,
l:-ly = 2 — t, tefi и s: < у = 1 + 2и, и еВ
z-3-2t, z = -2 + u,
лишь при Ze[0;4] и ize[—2; 2] , а все остальные точки дан-
ных прямых этим шарам не принадлежат.
Решение. Промежуток t е [0; 4] на прямой I задает отрезок с
концами А(4; 2; 3) и В(8; -2; -5), а промежуток пе[-2;2] на
прямой s — отрезок с концами Н(6; -3; -4) и К(-2; 5; 0).
Отрезки АВ и НК являются хордами сфер, ограничиваю-
щих шары, множество центров которых требуется определить.
109
Множеством центров всех сфер, проходящих через точки А
и В, является плоскость а серединных перпендикуляров от-
резка АВ. Все точки отрезка АВ прямой I являются внутрен-
ними точками для всех шаров, определяемых этими сферами.
Аналогично, множеством центров всех сфер, проходящих че-
рез точки Н и К, является плоскость р серединных перпенди-
куляров отрезка КН. Для всех шаров, ограниченных этими
сферами, все точки отрезка КН являются внутренними.
Из уравнений данных прямых следует, что они не парал-
лельны (их направляющие векторы р (1; -1; -2) и q (-2; 2; 1)
не коллинеарны), поэтому плоскости аир, перпендикуляр-
ные этим прямым, также не параллельны, значит, пересека-
ются. Тогда прямая т = а п р содержит центры всех тех шаров
этих семейств, для каждого из которых являются внутренни-
ми все точки отрезков АВ и КН’, остальные точки прямых I и s
не принадлежат шарам этих семейств.
Найдем уравнения прямой т.
Имеем: a±l al р(1; -1; -2), значит, плоскость а опре-
деляется точкой С(6; 0; -1) — серединой отрезка АВ и векто-
ром р (1; -1; -2) нормали, поэтому имеет уравнение:
(х - 6) - (г/ - 0) - 2(z 4-1) = 0 <^>x-y-2z-8 = Q.
Аналогично, плоскость р определяется точкой Т(2; 1; -2) —
серединой отрезка КН и вектором q (-2; 2; 1), поэтому имеет
уравнение:
-2(х - 2) + 2(у - 1) + (г + 2) = 0 о 2х - 2у - z + 4 = 0.
Тогда прямая т пересечения этих плоскостей может быть
задана системой общих уравнений:
(х-у-2г-8 = 0,
(2х - 2у - z + 4 = 0
или параметрическими уравнениями:
х------+1
3
y = t,
20
Z =----,
3
teR,
110
в которых координаты (1; 1; 0) направляющего вектора
г (а; Ь; с) прямой т являются решением системы уравнений:
(а-Ь-2с = 0,
[2а-2Ь-с = 0,
выражающих условия перпендикулярности направляю-
щего вектора д (а; Ь; с) относительно векторов р(1; -1; -2) и
Таким образом, искомое множество центров всех шаров
есть прямая
16 , +
х =-----+ t.
3
y = t,
20
2 =-----,
3
t&R.
Ответ: Прямая
з
y = t,
20
2 =-----
3
t &R.
Задачи для самостоятельного решения
Задача 10. Напишите уравнение сферы с центром в точке
Л£(-1; 3; 5) и радиусом 3.
Задача 11. Напишите уравнение сферы с центром в точке
М(-2; 0; 3), проходящей через начало координат.
Задача 12. Напишите уравнение сферы с диаметром АВ,
если А(-3; 5; 0) и В(1; -7; 2).
Задача 13. Найдите множество точек, расстояние от кото-
рых до сферы (х - I)2 + у2 + (г + 2)2 = 16 равно 3.
Задача 14. Для каждого т определите множество точек
пространства, координаты которых удовлетворяют уравне-
нию х2 + 2 тх + у2 + г2 - 42 + 8 = 0.
Задача 15. Напишите уравнение сферы с центром (5; 1; 1),
касающейся сферы х2 + у2 + г2 = 3.
111
ГЛАВА 5.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
И ПЛОЩАДИ МНОГОУГОЛЬНИКОВ
Прежде чем приступить к изучению свойств векторного
произведения двух векторов и смешанного произведения трех
векторов, познакомимся с некоторыми вопросами нового для
вас раздела алгебры — теорией определителей. Мы ограни-
чимся рассмотрением лишь тех свойств определителей второ-
го и третьего порядка, которые необходимы для аргументиро-
ванного использования каждого из этих произведений при
решении геометрических задач.
1. ОПРЕДЕЛИТЕЛИ ВТОРОГО
И ТРЕТЬЕГО ПОРЯДКА
а Ь
с d
Таблица
, составленная из четырех чисел а, Ь, с и d,
называется квадратной матрицей второго порядка. Числа а, Ь,
end называются элементами матрицы, при этом числа а и b
называются элементами первой строки, числа с и d — элемен-
тами второй строки; числа а и с — элементами первого
столбца, числа Ь и d — элементами второго столбца; числа а
nd — элементами главной диагднали определителя, с и Ь —
элементами его побочной диагонали.
Определение. Число а • d - Ъ • с называется определителем
(или детерминантом) квадратной матрицы
а Ъ
с d
и обо-
значается так: А =
fl b
с d
Из этого определения следует, что
а b
с d
определитель матрицы
равен разности произведений
чисел а и d главной диагонали и чисел b и с побочной диагона-
а Ъ
с d
ли определителя, т. е. А =
= а • d - b • с. Например, опре-
112
делитель второго порядка
3 -4
1 -2
равен: Д =
-4
-2
= 3(- 2)-
3
1
- 1 (-4) = -6 + 4 = -2.
Поменяем местами столбцы в определителе Д и найдем
численное значение полученного определителя =
Имеем: Дг = (-4) • 1 - • (-2) • 3 = -4 + 6 = 2. Получаем:
3
1
-4
-2
, т. е. Aj = -Д.
-4 3
-2 1
Теперь поменяем местами строки данного определителя Д
и найдем численное значение определителя Д2 =
-2
-4
. Име-
1
3
ем^ 1 • (-4) -3 (-2) = -4 + 6 = 2.
Получаем:
1 -2
3 -4
3 -4
1 -2
т. е. Д 2 = _ Д.
Таким образом: если в определителе второго порядка по-
менять местами две строки (два столбца), то его значение
изменится на противоположное.
Далее введем понятия определителя третьего порядка,
рассмотрим правила его вычисления и свойства, которые при
этом используются.
а1 С1
Таблица а2 Ь2 с2 , составленная из девяти чисел
чаз Ьз сз>
Ор&рСр а2,62,с2, а3,&3, с3, называется квадратной матрицей
третьего порядка. Числа ар &р ср а2, Ь2, с2, а3,Ь3, с3 называ-
ются элементами матрицы, при этом числа ар br, сг называ-
ются элементами первой строки, числа а2,Ъ2,с2 — элемента-
ми второй строки, числа а3,Ь3,с3— элементами третьей
строки', числа ар а2, а3— элементами первого столбца, числа
&р Ъ2,Ь3 — элементами второго столбца, числа с1,с2,с3 — эле-
ментами третьего столбца. Будем говорить, что числа
113
at,b2, c3 образуют главную диагональ данной матрицы, а чис-
ла а3,Ь2,сх — ее побочную диагональ.
Ч
«2
Операция, при которой в матрице
\аз
&1 с/
^2 С2
^3 С3>
вместо первой
строки записывают ее первый столбец,
ки — её второй столбец и вместо третьей строки — её третий
столбец, т. е. меняют ролями ее одноименные строки и столб-
цы, называется транспонированием этой матрицы. В резуль-
вместо второй стро-
тате получается транспонированная матрица
а1
Квадратной матрице третьего порядка а2
,аз
«1 а2
Ь2
С2
Ь1
^2 ^2
Ь3 %
аз
Ь3
сз,
соответ-
ствует определитель этой матрицы — число, по определению
равное: а.-Ь9сч + ачЬ,с9 + а9 Ь9 с, -а9 Ъ9 с. - а9 Ь, с9~
Lio О 1 Z i О 1 О i L i 1 О
- • b3 • С2 •
Определитель третьего порядка будем обозначать симво-
лом « Д » и записывать: Д=
ai
а2
аз
Ъ. сх
^2
^3 С3
Таким образом,
д= OJ ГО С, .£> "О -н CSJ со Q Q Q = а, • Ь9 • сч + ач-Ь.с9 + LiO О 1 i
а„Ь.,с- а9Ь9с,—
i О 1 О i L
- ^2^1-С3-а1Ь3 С2-(*)
Обратите внимание: первые три слагаемые^ Ь2-с3 +
+ а3-Ъ1с2+ а2 Ъ3 сх, стоящие в (*) со знаком «+» (плюс),
представляют собой произведения элементов определителя,
взятых по три так, как указано пунктирными линиями на
рис. 55, а):
114
Рис. 55, а)
Следующие три слагаемые (-а3 • Ь2 q- a2-bl-cz- at-bz-c2),
стоящие в (*) со знаком «-» (минус), представляют собой про-
изведения элементов определителя, взятых по три так, как
указано пунктирными линиями на рис. 55, б):
cti bi fii
^2 \ Д с2
Хз 6з с3
Рис. 55, б)
Правило, по которому составлены шесть слагаемых в вы-
ражении (*) для вычисления определителя третьего порядка
по указанным схемам, называется правилом треугольников и
диагоналей.
Определители играют важную роль при исследованиях в
различных разделах математики, физики, экономики и мно-
гих других наук.
Рассмотрим свойства определителей третьего порядка,
которые используются при изучении некоторых разделов век-
торной алгебры и геометрии.
Свойство 1. Если в определителе 3-го порядка поменять
ролями строки и столбцы (транспонировать матрицу опре-
делителя), то значение определителя не изменится.
Доказательство. Имеем:
115
Я1
a2
«3
*>2
Ь3
Cl
C2
C3
di -t>2-c3 + d3‘&1-c2+ a2-b3-c1 a3-b2c1
- a9b.c4-a.b„-c9.
4 10 10 4
После транспонирования матрицы определителя получаем:
ai a2 аз
Ai= bx b2 b3
C1 C2 C3
— a2 • &i • c3 — dj • b3 c2.
Сравнивая правые части этих равенств, приходим к выводу:
a. • b„ • c, + dQ • • c, + a9 b4 • c, - d, • b9 c, -
14 0 О 1 4 4 0 1 0 4 1
dj &j с,
d2 b2 с2
а3 Ь3 с3
а1 а2 a3
Ь1 Ь2 Ь3
С1 С2 С3
Свойство 2. Если поменять местами две строки (два
столбца) определителя, то его значение изменится на про-
тивоположное.
Доказательство. Поменяв местами две первые строки
данного определителя А =
di bx с,
Ь2 ^2
d3 Ь3 с3
, получим определитель
d2 b2 с2
bl Cj
d3 b3 с3
Найдем его значение:
а2
di
аз
Ь2 С2
Ь1 С1
Ь9
о о
= а9 -Ь, -с9+ ач-Ь9-с,+ а.-Ь9-с9 — а9-Ь.-с9 —
410 041 104 014
— а. • Ь9 • с, — о, ft, • с. .
1 4 0 4 0 1
Теперь, сравнивая значения
Д, и А =а, Ь9 сч + d2 b, с,+ d, b9 с, - d, b9 с, - а9 Ь, - с, -
140 014 401 041 410
- ах-Ь3 с2, приходим к выводу: Aj = -Д, что и требовалось
доказать.
116
Свойство 3. Если две строки (два столбца) определителя
равны, то этот определитель равен нулю.
Доказательство. Пусть в определителе Д равны две пер-
вые строки.
Тогда
&1 Cj
bi Cj
Ь3 сз
= a1b1c3+a3b1c1 +
+ al b3 cl- a3b1c1-a1b3c1-a1b1c3= 0, что и требовалось
доказать.
Свойство 4. Общий множитель всех элементов какой-либо
строки (какого-либо столбца) можно вынести за знак опре-
делителя.
Доказательство. Пусть все элементы второй строки опре
делителя Д2 имеют общий множитель k, т. е.
«1 ci
Дй — йа2 kb2 Ас2 . Найдем его значение.
аз ь3 сз
«1 С1
Имеем: Ла2 feb2 йс2 = а, • kb9 • с, + a9-b,kc9 + ka9b4c. - 14 0 О 1 4 Z О 1
аз &з сз
- a4kb9c, - ka9b,c^ -a,b9-kc9 = k(a,-b9-c9 + a9-b,-c9 +
О Z 1 4 10 1 О Z v 1 Z О О 1 Z
«1 Ь1 С1
+ а2'^3'С1 «3^2^ ^2'^>1'('3 ^1'^з'^г) о2 Ь2 с2 = k-A,
&3 ^3 С3
т. e. Д2 = k-/\.
Это свойство определителя можно сформулировать и так:
если все элементы какой-либо строки (какого-либо столбца)
определителя умножить на одно и то же число, то опреде-
литель умножится на это число.
Из сказанного следует: если все элементы какой-либо
строки (какого-либо столбца) определителя равны нулю, то
и сам определитель равен нулю.
Свойство 5. Определитель, имеющий две пропорциональ-
ные строки (два пропорциональных столбца), равен нулю.
117
Доказательство. Пусть в определителе пропорциональны
вторая и третья строки и он имеет вид:
ai ci
ka, kb, kc,
ООО
аз 63 сз
. Найдем
значение этого определителя.
O' 1—• Ci
Имеем: ka3 kb3 kc3 = a, kb, c, + a, b, kc, + ka, b, c, loo О 1 О О О 1
^3 ^3 ^3
- a, kb, с, - ka, b, c, - a.b,kc, = k(a,b,c, + a, b, c, +
О О 1 О 1 О 1 О О v 1 О О О 1 о
+ а, Ь, с. - а,Ь,с. - а,Ь,с, - а. Ъ, с,) = 0, что и требова-
О О 1 О О 1 О 1 О 1 О О ' '
лось доказать.
Из сказанного следует: определитель с двумя равными
строками (столбцами) равен нулю.
Свойство 6. Если каждый элемент одной (данной) строки
определителя представлен в виде суммы двух слагаемых, то
этот определитель равен сумме двух определителей, у кото-
рых все строки, кроме данной, прежние, а в данной строке
первого определителя стоят первые, а во второй — вторые
слагаемые (то же верно и для столбцов).
Доказательство.
ar bY Cj
^2 “* ^4 ^2 + ^4
аз ^3 С3
Пусть имеем определитель
каждый элемент второй строки которо-
го является суммой двух слагаемых.
Пользуясь формулой (*), находим:
а2 + а4
аз
bi ci
^2 “* ^4 ^2 ^4
&3 ^3
‘ (^2 ^4 ) ’^3 "I" «3 ‘ &Г ^2 “* С 4 ) "^ ( ®2 ®4 ) ' ^3 ' ®3 ‘ (^2 ^4 ) ’^1
~(a2+ai)b1c3 - a1b3 (c2 + ci) =(a1b2 c3 + a3 b1c2 + a2 &3 c1 -
-a3b2c1 -a2b1c3 - a1b3c2) + (a1bic3 + a3b1c4 +a4-d3c1-
«1 ci Я1 Ьг С1
1 й W Й 1 > 1 й •-* сг W rfP 11 Д2 ъ2 С2 + «4 ^4 , ЧТО
аз ь3 С3 аз ^3 С3
и требовалось доказать.
118
Свойство 7. Если к элементам одной строки определите-
ля прибавить соответствующие элементы другой строки,
умноженные на одно и то же число, то значение определите-
ля не изменится (то же верно и для столбцов).
Доказательство. Прибавим к элементам второй строки
определителя Д=
01
о2
di С1
^2
Ь3 С3
соответствующие элементы его
аз
третьей строки, умноженные на одно и то же число k. Найдем
значение полученного определителя:
«1 «2 аз bi ci + ka3 b2 + kb3 с2 + kc3 &3 сз = а1 а2 «3 с- О' О' «ям ~ CS О о оо СО + «1 Ла3 «3 &1 Cj /гд3 kc3 &3 сз =
«1 а2 bi Ь2 С2 (определитель «1 /га3 ^i С1 равен нулю, так
аз Ьз С3 аз Ьз сз
как
вторая и третья его строки пропорциональны).
Замечание. Говорят, что одна строка определителя третье-
го порядка является линейной комбинацией остальных его
строк, если каждый элемент этой строки равен сумме произ-
ведений соответствующих элементов остальных строк на не-
которые числа, постоянные для каждой строки. (Аналогично
определяется линейная комбинация столбцов.)
«1 \
та, +ka„ mb,+kb„
i oio
аз fe3
вторая строка является линейной комбинацией
третьей строк: все элементы первой строки умножаются на
число т, а все элементы третьей строки — на число k, после
тсх + kc3
сз
первой и
Например, в определителе
чего полученные произведения, стоящие в одном и том же
столбце, складываются. Иначе говоря, вторая строка опреде-
лителя является линейной комбинацией первой и третьей
строк с коэффициентами, равными соответственно muk. I
С линейными комбинациями строк (столбцов) определите-
ля взаимосвязано следующее свойство определителей.
119
Свойство 8. Если одна строка (один столбец) определите-
ля 3-го порядка является линейной комбинацией остальных
его строк (столбцов), то определитель равен нулю.
Действительно,
mar + ka3 mb} + kb3
^3
ci
тсх + kc3
сз
если к определителю
применить свойство 6, а затем
к двум полученным определителям применить свойство 5,
то можно убедиться, что данный определитель равен нулю.
Свойство 9. Если в определителе
ai ci
^2 ^2 ^2
аз ^3 С3
вычеркнуть
строку и столбец, содержащие элемент а} (т. е. вычеркнуть
первую строку и первый столбец определителя), то получим
определитель второго порядка
^2 С2
Ь,л Ьа
, который
называется
алгебраическим дополнением элемента аи Аналогично, ал-
гебраическим дополнением элемента Ьг называют определи-
тель
а2
«3
С2
С3
, «взятый» со знаком «минус» (т. е. «
®2 *"2
«3 <-з
»),
который получается из данного определителя вычеркиванием
в нем первой строки и второго столбца; алгебраическое допол-
нение элемента Cj — определитель
а2
«3
Ь2
Ьз
, который получает-
ся из данного определителя вычеркиванием в нем первой
строки и третьего столбца.
«Раскроем» определитель
a, br с,
^2 ^2 <-2
«3 ^3 <-з
по правилу тре-
угольников и разобьем все шесть произведений на три пары
так, чтобы одна пара содержала общий множитель аг, вторая
пара — общий множитель Ьи а третья пара — общий множи-
тель Cj. После вынесения этих общих множителей за скобки
получим:
120
“1
А = а2
аз
а2'Ь\'Сз
а2Ъхс3) + (а2Ь3сх
Ь2
Ьз
С1
С2
С3
а, Ь„-с, = (а.-Ь~-сч
I о i ' 1 4 о
аз ’ Ьг ’ ci) —
^,1'Ь2'С3 + а3 • bj с 2 + а2 Ь3 • Cj а3 • Ь2 • с^
' ( а2 ’ С3 a3 ' С2 ) +
Cj • (а2 • &3 а3 b2 ) Oj •
— Я] • Ь3 • с2) + (а3 Ь, с2 —
(Ь2 с3 — Ь3 • с2) —
Ь2 с2
ьз ьз
а2 с.
«з ^з
+ сг-
а2 Ь2
а3 Ь3
= а,
ъ2
Ьз
а2
аз
С2
сз
а2
«з
ь2
Ь3
ь +ь‘-' -
Таким образом, получаем:
а2
аз
&1 q
^2 *"2
&з С3
= а,
^2 ^2 I Ь
'’ь\ ъ3 +ь<-
«2
аз
С2
С3
СГ
а2
аз
ь2
Ь3
а
откуда следует, что определитель третьего порядка равен
сумме произведений элементов первой строки на их алгеб-
раические дополнения. При этом выражение
. Ь2 С.
1 Ь3 Ь3
а.
2 +ь,-
^2
«3 сз
а2 Ь2
«3 ^3
называют разложением данного определителя по элемен-
там первой строки.
Аналогично можно разложить данный определитель по
элементам любой строки и любого столбца.
2
Найдем, например, значение определителя
3
-2
6
с по-
0
4
5
мощью разложения его по элементам первой строки. Имеем:
2
0
4
5
3
-2
7
-1 -2
5 7
+ 2-
0 -2
4 7
0 -1
4 5
+ 3 •
= -7 - (-10) -2 • (0 - (-8)) + 3 • (0- (-4)) = -7 + 10 - 16 + 12 = -1.
Вычислим значение этого же определителя, разложив его
по элементам третьей строки. Получаем:
121
12 3
О -1 -2
4 5 7
2 3
1 -2
1 3 "l
О -2 J
1 2
О -1
+ 7
= 4(- 4 - (-3)) -5 (-2 - 0) + 7(—1 - 0) = -4 + 10 - 7 = -1.
В итоге приходим к выводу: определитель третьего по-
рядка можно разложить по элементам любой строки (любого
столбца), при этом значение определителя не зависит от
номера строки (столбца), по элементам которой (которого)
такое разложение осуществляется.
Замечание. Мы остановились, в силу необходимости, на
разложении определителя лишь по элементам первой строки.
Приведенной информации о свойствах определителей вполне
достаточно для изучения дальнейшего геометрического мате-
риала. В данной по объему маленькой книге не представляет-
ся возможным подробно и достаточно корректно изложить
материал об алгебраических дополнениях, о разложениях оп-
ределителя по элементам какой-либо строки или столбца. В
высшей школе вы подробнее познакомитесь с теорией матриц,
определителей и ее приложениями в естественных науках.
Задачи
Задача 1. Вычислите определители 3-го порядка:
2 1 3 3 2 1 3 1 2 3 4 -5
а) 5 3 2 9 б) 2 5 3 ; в) 2 3 5 г) 8 7-2;
1 4 3 3 4 2 3 4 1 2-18
4 -3 5 0 а 0 а Ь с а b с
д) 3 -2 8 ; е) b с d ; ж) Ъ с а ; з) с а b •
1 -7 -5 0 п 0 cab b с а
Задача 2. Пользуясь свойствами определителей 3-го по-
рядка, вычислите следующие определители:
1 sin2 a cos2 а cos 2a sin2 a cos2 a
1) 1 sin2 р cos2 р 9 2) cos2p sin2 p cos2p
1 sin2 у cos2 у cos 2' r sin2 y 2 cos у
X ~Х1 ах - bxx (a + &)2 a2 +b‘ ab a+b c 1
3) У У1 ay + by1 ;4) (c + d)2 c2+d2 cd 9 5) b + c a 1
Z ~г1 az -bzx (&-c)2 b2 +c2 -be c+a b 1
122
2. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
2.1. Ориентация троек некомпланарных векторов
Три различных вектора будем называть упорядоченной
тройкой, если указан порядок их следования. Так, за-
пись ab с означает, что первым элементом этой тройки явля-
ется вектор а , вторым — вектор b и третьим — вектор с . Та-
ким образом, abc и Ь а с — две различные упорядоченные
тройки векторов.
В дальнейшем мы будем рассматривать только упорядо-
ченные тройки векторов, поэтому будем говорить просто
«тройка векторов».
Определение. Тройка некомпланарных векторов ab с на-
зывается правой, если выполнено одно из следующих трех
условий'.
1. После приведения всех трех векторов к общему началу
кратчайший поворот от а к Ь видится из конца вектора с со-
вершающимся против часовой стрелки (рис. 56, а);
2. Находясь внутри трехгранного угла, определяемого при-
веденными к общему началу векторами а , Ь , с , видим пово-
рот от а к & и от него к с совершающимся против часовой
стрелки (рис. 56, б);
3. Будучи приведенными к общему началу, векторы а , b и
с располагаются так, как могут быть расположены большой
(а), указательный (5) и средний (с) пальцы правой руки
(рис. 56, в).
123
Вы можете проверить эквивалентность условий 1, 2 и 3.
Если кратчайший поворот от а к b, упомянутый в усло-
виях 1 и 2, мы видим из конца вектора с совершающимся по
часовой стрелке (рис. 57, а, б), то тройка некомпланарных
векторов ab с называется левой; также тройка некомпла-
нарных векторов а b с называется левой, если, будучи приве-
денными к общему началу, векторы а, Ъ и с располагаются
так, как могут быть расположены большой (а), указательный
(6) и средний (с ) пальцы левой руки (рис. 57, в). Вы можете
легко убедиться в эквивалентности всех трех определений ле-
вой тройки некомпланарных векторов.
Если две тройки векторов обе правые (обе левые), то гово-
рят, что эти тройки одной ориентации. Если же из двух троек
векторов одна — правая, а другая — левая, то говорят, что эти
тройки противоположной ориентации. Например, тройки
векторов аЬсаЬса имеют одинаковую ориентацию, тройки
сЪа и аЪс — противоположную ориентацию (убедитесь в этом
с помощью рисунка).
Из трех векторов а , Ъ , с можно составить лишь следую-
щие шесть троек: abc , Ьса , cab, Ьас , acb , cba . Вы можете убе-
диться, что если первые три тройки правые, то остальные три
тройки левые.
В нашей книге тройка векторов i,j,k декартова прямо-
угольного базиса (ортонормированного репера) трехмерного
векторного пространства предполагается правой.
124
2.2. Определение векторного
произведения векторов
Определение. Если ненулевые векторы а и b неколлине-
арны, то векторным произведением вектора а на вектор b на-
зывается третий вектор с, обозначаемый символом а х b и
определяемый следующими тремя условиями:
1) модуль вектора с равен произведению модулей векторов
а и b на синус угла <р между ними, т. е.
|c| = |axb| = |a|-|fe|-sin<p; (*)
2) вектор с перпендикулярен каждому из векторов а и b ;
3) вектор с направлен так, что тройка векторов abc явля-
ется правой (рис. 58).
Рис. 58
Если векторы а и Ь коллинеарны, то по определению их
векторное произведение полагают равным б (нуль-вектору).
2.3. Свойства векторного произведения векторов.
Векторное произведение векторов в координатах
1. Длина векторного произведения неколлинеарных век-
торов а и b численно равна площади параллелограмма, по-
строенного на приведенных к общему началу векторах а и b
как на сторонах (рис. 52).
125
Справедливость этого утверждения следует непосредст-
венно из условия
•sintp в определении вектор
ного произведения векторов а и b .
2. (т • а )х Ъ = т • (а х Ь) (сочетательное свойство отно-
сительно числового (скалярного) множителя).
Для доказательства этого свойства обозначим:
р = (т- а)х Ъ и q = т-(а х Ь)
и рассмотрим случаи.
а) Если векторы а и b коллинеарны, то р = q = О .
б) Если т= 0, то т а = 0 и тогда р - 0 х Ь = 0 (вектор О
коллинеарен любому вектору). Если а х Ь= с, то т (а х Ь) =
= 0 с = 0 . Таким образом, вновь получили:
р- (т- а)х Ь = т-(а х b) = q .
в) Если векторы а и Ь неколлинеарны и т * 0, то некол-
линеарны и векторы та и Ь. Обозначим: а = Z(a ,b),
Р -Л(та ,Ь). Тогда |р | = |(та )| • |b | sinp = |(тиа )| • |Ь| sinp =
= |тп| • |а| • |&| sinP; |g| = | тп| • |а х &|=| т| • |а| • |&|sina. Учиты-
вая, что a = р при т > 0 (рис. 59, а) и a + р = п при т < О
(рис. 59, б), приходим к выводу, что sinp = sina. Это означает,
что и при т > 0, и при т < 0 длины векторов р и q равны, т. е.
|р 1=Iq I-
Осталось доказать, что векторы р и q коллинеарны и со-
направлены.
Коллинеарность этих векторов следует из того, что если
вектор q перпендикулярен плоскости, которой компланарны
векторы а и b (рис. 59, в), то этот вектор перпендикулярен и
плоскости, которой компланарны векторы та и Ь, так как
т а || а . Но этой плоскости перпендикулярен и вектор р . Зна-
чит, р || q .
126
Рис. 59
Далее, имеем:
тп > 0 => тп • aV\ а=> (axb)TT(zn
=> тп • (а х & )tT(zn- а) х b , т.е. р ТТ q .
а )х b > 0 =>
тп < О => тп • а 14 а=> т.е, (а х b) 14 (т • а )х Ь . А так как
тп • (а х Ь)14(а х Ь) при пг < О, то тп • (а х Ь)ТТ(тп • а)х Ъ,
т. е. р Т? q .
Таким образом, получили: |р|=|д| и р ТТ q, то есть
(тп - а) х Ь = тп- (а х Ь), что и требовалось доказать.
3. Векторное произведение а х Ъ векторов а и Ь есть век-
тор, координаты которого нужно уметь находить, если из-
вестны координаты векторов а и b .
Предварительно найдем всевозможные векторные произ-
ведения пар базисных векторов i, j, k. ,
I
Из определения векторного произведения, учитывая, что
векторы i, j, k попарно взаимно перпендикулярны (рис. 60) и
являются единичными, имеем:
127
i x j = k, j x k = i , k x i = j, j x i - -k, i x k = - j,
kx . (**)
Теперь найдем координаты векторного произведения а х b
векторов a = xCi + У1 / + zxk и fe = x2/ + у2 ] + z2k).
Принимая во внимание уже известные свойства векторно-
го произведения векторов, используя соотношения (**) и учи-
тывая, что тройка базисных векторов i, j, k является пра-
вой, находим:
а х Ь = (х^ +y1~j +2^) х (x2i +г/г J + 22k) = x1x2(i x i ) +
+ х1Уг (i X j) + X1z2 (ixk) + угх2 ( j X i ) + угу2 ( j x J ) +
+ У122 ( J x k) + z^x2 (kx i) + Z1y2 (kx j) + zTz2 (k-x k) = xrx2 0 +
+ хгу2 k+ Хг22(- j) + yrx2(-k) + yry2 0+ yxz2 i+ zrx2 i +
+ zxy2 (- i)+ zxz2 6 = (yxz2 - y2zr) i + (zTx2 - X1z2) j + (X1y2 -
-х2^1) k = * i tQ N to >— к H to j+ X1 X2 Vi Уг k = i j k xi У1 2i хг Уг ^г
Таким образом, получаем: a x b = с (X; У; Z) =
где X = ytz2 - y2zr, У = 2jX2 - хгг2, Z = хху2 - х2уг.
i j k
xi У1 2i »
x2 Уг %г
4. axb = -(b x а) (свойство антиперестановочности
сомножителей).
Докажем это свойство координатным методом. Пусть век-
торы а и & имеют координаты: а (х^ уг; zr), b(x2; у2, z2):
Имеем: а х b =
i j k
*1 У1 2!
*2 У2 Z2
Ь х
j k
Уг 2г •
У1 Z1
Замечаем, что вторая и третья строки одного из этих опре-
делителей являются соответственно третьей и второй строка-
ми другого определителя. На основании свойств определите-
лей это означает:
128
i
2
j *
Уу Zl
Уг z2
i j
X2 У 2
k
Z2
2l
=> b x a = -(a x b) (рис. 61).
Другое доказательство этого свойства. Обозначим:
p=a*b,q=b*a.
Если а || b , то р= <7=0 и свойство доказано. Если векторы
а и b неколлинеарны (рис. 61), то: 1) |р| = |<?|; 2) векторы
р- а х b и q = b х а коллинеарны, так как каждый из них
перпендикулярен плоскости, параллельной векторам а и Ь.
Учитывая при этом противоположную ориентацию троек
векторов abp и bap , приходим к выведу: а х Ь = -(о х а ), что
и требовалось доказать.
5. (a + Ь ) х с = а х с + Ь х с (распределительное свойство
векторного произведения относительно сложения векторов).
Используя свойства определителей третьего порядка, полу-
чаем доказательство этого свойства для векторов а (х^ ух-, zj,
b(x2,y2, z2), с (х3; у3; z3).
Пусть a + b = р (ху+ х2; ух + у2, zx + z2). Тогда, используя
свойства определителей третьего порядка, получаем:
129
р х с
j k
У1+У2 Zl+Z2
Уз Z3
i j k
*1 Vi zi
•£3 Уз Z3
j k
У2 Z2
Уз Z3
= a x с + b хе, что и требовалось доказать.
6. Для любого вектора а справедливо: а х а = 0, так как
любой вектор коллинеарен сам с собой.
Координаты X = yYz2 - y2zlf Y — z^ - хгг2, Z = хгу2 - х^ век-
торного произведения а х b = с (X; Y; Z) векторов a (xt; yt; z^ и
b(x2; у2; z2) являются определителями второго порядка, со-
ставленными из координат векторов — сомножителей. Дейст-
вительно, X = угг2 - y2z{ =
У1
У2
zi
Z2
Y = ZjX2 - xxz2 =
2i xi
22 X2
= Х1У2 - X2yx =
Xi У1
X2 У2
Таким образом, имеем: a
У1 Z1 .
ч У2 Z2
1
Z2
X1 . Х1 У1
X2
X2 У2
или
x b = c
; z =
в виде разложения по базису (i ; j ; k):
Уг Z1
У2 Z2
Z1 X1
Z2 X2
XX
X2
У1 .b
У2
Х1 У1 Z1
Х2 У2 Z2
называется прямоугольной матрицей (в прямоугольной
рице число строк не равно числу столбцов).
= У1 2i
У2 Z2
Таблица
Мы
Х1
Х2
, в которой две строки и три столбца,
видим, что координаты X
Уг
У2
мат-
zi
Z2
Х1
Х2
векторного произведения а х b векторов а (х^, уг; z})
a x b = c =
k.
и
Z =
и b (х2; у2‘, z2) составлены из элементов матрицы
Х1 У1 21
Х2 У2 Z2
, в
первой строке которой записаны координаты первого, во вто-
рой — второго из перемножаемых векторов. Причем абсцисса
X векторного произведения двух векторов равна определите-
лю, составленному из второго и третьего столбцов данной мат-
130
рицы; ордината Y — определителю, составленному из третье-
го и первого столбцов этой матрицы; аппликата Z — опреде-
лителю, составленному из первого и второго столбцов этой
матрицы, т. е. наблюдается круговая перестановка
1->2->3;2->3->1;3->1->2.
Рассмотрим пример нахождения координат вектора, рав-
ного векторному произведению двух Данных векторов.
Задача 3. Найдите векторное произведение а х Ь векторов
а = 4 i + 3 j и & = 2 i + j + 2k.
Решение. Выписываем матрицу
4 3 (П
2 1 2)
, в первой строке
которой — координаты
вектора b. Находим:
3 0
1 2
вектора а, во второй — координаты
= р(3-2-1-0; 0-2-2-4;
4-1-2-3;) = (6;-8;-2) = 6 i - 8 j-2k.
Ответ: р = 6i - 8 j- 2k.
Теперь рассмотрим пример нахождения площади паралле-
лограмма.
Задача 4. Найдите площадь параллелограмма, построенного
на приведенных к общему началу векторах а = 2 i + 3 j - 5k и
b = i -2 j + 4 fe как на сторонах.
Решение. Площадь S параллелограмма, построенного на
векторах а и b как на сторонах, равна модулю векторного
произведения этих векторов. Поэтому находим координаты
2 3 -5
1-2 4
вектора р = а х Ъ , для чего выписываем матрицу
а х & = р
0
2
4
2
4 3
2 1
и
составляем определители
3 -5
-2 4
-5 2
4 1
2 3
1 -2
= Z,
которые и являются соответственно абсциссой, ординатой и
аппликатой векторного произведения а х Ь, то есть:
131
k = (3 • 4 — (—2) • (—5)) ♦
• 1 + ((-5) • 1 - 4 • 2) • j + (2 • (-2) - 1 • 3) -A = 2i - 13 7 -Ik,
откуда S = |a x &| = ^22 + (-13)2 +(-7)2 = 7222.
Ответ: 7222 .
Задачи
Задача 5. Чему равно векторное произведение двух колли-
неарных векторов?
Задача 6. Используя определение векторного произведе-
ния, найдите векторы: а)гху; б) Ах/; в) 2г х ЗА; г) ЗАх2/;
д) гх(/ + А); е) 2/х(-2г+5А); ж) (-2г+5А)хЗг .
Задача 7. Докажите, что точки А, В и С лежат на одной
прямой тогда и только тогда, когда АВ х АС = 0 .
Задача 8. Докажите, что если для ненулевых векторов а, Ъ
и с выполняется условие а+Ъ + с = б, то ах6=Ьхс= сха.
Задача 9. Векторы а и с направлены по диагоналям двух
смежных граней куба, выходящим из одной вершины. Правда
ли, что вектор а х с параллелен одной из диагоналей этого куба?
Задача 10. Преобразуйте выражения: а) (a-b)x(a + b);
б)(а + 26-с)х(а-26); в) ах(Ь+с- а).
Задача 11. Даны векторы: а(0;1;0), А(2;-1;3), с(0;5;-2),
d(l;2;-3). Найдите координаты и модуль векторов: а)ах&;
б) ах с ; B)bxd ; г) dxa ; д) axd;e) Ъхс .
Задача12. Пользуясь векторным произведением векторов,
найдите площадь параллелограмма, построенного на векторах
а + ЗА и За + b как на сторонах, если |а | = |&| = 1, Z(a,&) = 30°.
132
Задача 13. Найдите векторное произведение векторов а =
= 2 i + 3 у +5 k и b = i +2 j + k.
Задача 14. Даны векторы а (1; -2; 5) и & (4; -2; 4). Найди-
те: а) а*Ь ; б) (Ь + 2а)х(Ь-2а) ; в) 7Ь х 2а ; г) |ахд |.
Задача 15. Найдите площадь параллелограмма, построен-
ного на векторах а (3; 2; 6) и b (2; 12).
Задача 16. Найдите площадь параллелограмма, построен-
ного на векторах a = 6 i + 3 j -2 k и b = 3 i -2 j + 6 k.
Задача 17. На векторах a (4; 6; 2) и (-2; 2; 4) как на сто-
ронах, построен треугольник. Пользуясь векторным произве-
дением векторов, найдите площадь и высоты этого треуголь-
ника.
Задача 18. Пользуясь векторным произведением векторов,
найдите площадь треугольника АВС, если: а)А(2;1;0),
В(-3; -6; 4), С(-2; 4; 1); б) А(4; 2; 3), В(5; 7; 0), С(2; 8; -1);
в)А(6; 5; -1), В(12; 1; 0), С(1; 4; -5); г) А(1; 1; 1), В(2; 3; 4),
0(4; 3; 2).
Задача 19. Докажите, что площадь параллелограмма, по-
строенного на диагоналях данного параллелограмма, вдвое
больше площади этого параллелограмма.
Задача 20. Дана трапеция АВСК (ВС || AK), АК — большее
основание. Докажите, что площадь данной трапеции равна
|ВАхВС| + 0,5|ВАхСК|.
Задача 21. Дан треугольник АВС площади S. Пользуясь
векторным произведением векторов, докажите, что площадь
треугольника, сторонами которого являются медианы данно-
Зс
го треугольника, равна — S.
4
Задача 22. Дана прямая треугольная призма АВСАгВ1С1,
основанием которой служит равнобедренный треугольник
133
АВС (АВ = АС = 5, ВС = 6). На ребрах AAlt ВВг и ССг выбраны
соответственно точки Р, К и М так, что АР : РАХ = 1:2,
ВК : КВХ = 2:1, СМ : МСг = 3:1 (рис. 62). Пользуясь вектор-
ным произведением векторов, найдите площадь треугольника
МРК — сечения данной призмы плоскостью МРК, если высо-
та призмы равна 12.
Решение. Прямоугольную декартову систему координат
Oxyz выберем так, как показано на рисунке 62 (точка О — се-
редина стороны ВС). В такой системе координат вершины приз-
мы и вершины сечения РКМ имеют координаты: А(4; 0; 0),
В(0; 3; 0), С(0; -3; 0), Ai(4; 0; 12), Вх(0; 3; 12), С^О; -3; 12),
Р(4; 0; 4), К(0-, 3; 8), М(0; -3; 9).
Площадь S^KM треугольника РКМ равна половине площа-
ди параллелограмма, сторонами которого служат отрезки РК
= 0,5 • РКхРм|. Найдем РКхРМ .
и РМ, т. е. S^KM
Рис. 62
Векторы РК и РМ имеют координаты: РК (-4; 3; 4),
РМ (-4; -3; 5). Тогда вектор q , равный векторному произведе-
-* Г 3 4 4 -4 -4 3
нию РК х РМ , имеет координаты: о _ _ ; _ _ =
1—3 О О —4 —4 —3 J
= (27; 4; 24). Значит, \~РК х рм\ = ^272+42+242 = V1321 . Зна-
чит, S^KM = 0,5 -V1321 (кв. ед.).
Ответ: 0,5- V1321 кв. ед.
134
Задача 23. Стороны основания ABCD прямоугольного па-
раллелепипеда ABCDAiBiCiDi равны соответственно: АВ = 4,
ВС = 3. На ребрах ААг, ВВг и CCj выбраны соответственно
точки Р, К и М так, что АР : PAt = 2:3, ВК : КВ} = 1:4,
СМ : МС} = 3:2. Пользуясь произведением векторов, найдите
площадь сечения данного параллелепипеда плоскостью РКМ,
если высота призмы равна 20.
Задача 24. Найдите единичный вектор, перпендикуляр-
ный векторам a = i + j + 2Л и Ь= 2 i + j + k.
Задача 25. К каждой грани произвольного тетраэдра вос-
ставлен перпендикулярный вектор, направленный во внеш-
нюю сторону тетраэдра и имеющий модуль, равный площади
соответствующей грани. Докажите, что сумма всех построен-
ных векторов есть нуль-вектор.
Решение. Введем векторы: РА = р , РВ = q , PC = г ; п1 ,
п2 , п3 , п4 — векторы, перпендикулярные граням соответст-
венно АВС, РАВ, РВС, РАС и направленные вне тетраэдра
(рис. 63).
Так как <8ДЛВС = 0.5-|ВАх ВС|, а модуль вектора пг равен
^давс’ т0 l^il = 0,5- ВА х ВС . Далее, по условию вектор пх
перпендикулярен грани АВС и направлен во внешнюю сторо-
135
ну тетраэдра. Это означает, что вектор пх сонаправлен с век-
торным произведением ВА х ВС. Таким образом,
пу = 0,5-(ВА х ВС). Учитывая, что ВА = РА-РВ = р - q ,
ВС = PC - РВ = г-q , получаем: пх = 0,5-((р - g )х(г-q)) =
= 0,5((/? *r)-(pxq)-(qxr) + (qxq)) = 0,5((р х г) -
~(р х q)-(q * г)).
Аналогично рассуждая, получим:
п2 = 0,5-( р х q ); п3 = 0,5 • (q х г);п4 = 0,5-( г х р ).
Тогда: пх+ пг+ п3+ ni = 0,5-((pxr)-(pxq)-(qxr)) +
+ 0,5*( р х q ) + 0,5- (q х г) + 0,5-( г х р) = 0, что и требова-
лось доказать.
Задача 26. К каждой грани произвольного тетраэдра вос-
ставлен перпендикулярный вектор, направленный в сторону
вершины, противолежащей соответствующей грани, и имею-
щий модуль, равный площади этой грани. Докажите, что
сумма всех построенных векторов есть нуль-вектор.
Задача 27. К каждой грани треугольной призмы восстав-
лен перпендикулярный вектор, направленный во внешнюю
сторону призмы и имеющий модуль, равный площади соот-
ветствующей грани. Докажите, что сумма всех построенных
векторов есть нуль-вектор.
Векторное произведение векторов может быть использова-
но при решении различных стереометрических задач позици-
онного и метрического характера при вычислении различных
расстояний, площадей и объемов геометрических фигур в тех
случаях, когда эти фигуры заданы координатным методом. Об
этом мы поведем разговор в главе 6, где точки заданы коорди-
натами, а прямые и плоскости — своими уравнениями в пря-
моугольной декартовой системе координат.
136
ГЛАВА 6.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
ТРЕХ ВЕКТОРОВ И МЕТРИЧЕСКИЕ
ЗАДАЧИ СТЕРЕОМЕТРИИ
Определение смешанного произведения трех векторов
и его свойства
Смешанным произведением трех векторов а, Ъ, с называ-
ется число, равное скалярному произведению вектора р = ах b
на вектор с . Смешанное произведение трех векторов называют
также векторно-скалярным произведением этих векторов.
Смешанное произведение векторов а, Ь, с обозначается
(а х Ъ )• с или (а; Ь\ с ). Таким образом, (a; b; с)- (a xb)- с .
Так как скалярное произведение векторов коммутативно,
то (а; Ь; с) = (а х b )• с = с • (а х Ь).
Найдем численное значение смешанного произведения
трех векторов а, b , с , если эти векторы заданы своими коор-
динатами в декартовом прямоугольном базисе (i ; j ; k).
Пусть: а (х^ у^, zt), b (х2; у2; z2), с (х3; у3; z3).
Разложения векторов р=ах Ъ и с (х3; у3; z3) по базису
(i ; j ; k) имеют соответственно вид:
р = а х Ъ =
У1 2х
У2 Z2
•7 +
xi У1
хг Уг
k; с= x3i + у3 j +
' i +
+ ZSk-
Тогда скалярное произведение (а х Ь )• с векторов (а х b) и
с равно:
(а х b )-с =
У1 zx
У2 Z2
•х3 +
Уз +
xi У1
Х2 У2
У1 zi
У 2 Z2
'Х3 + (“
Уз) +
Х1 У1
Х2 У2
Х1 Ух
Уз Z2
хз Уз 23
137
У1 2i
Это означает, что (a; b; с) = х2 у2 г2
Х3 Уз 23
Таким образом, смешанное произведение трех векторов
а,Ь ,с, заданных своими координатами в декартовом прямо-
угольном базисе (i; j; k), есть число, равное определителю
третьего порядка, в первой строке которого записаны коор-
динаты первого вектора (вектора а), во второй строке —
координаты второго вектора (вектора Ь), в третьей стро-
ке — координаты третьего вектора (вектора с).
Этот факт позволяет алгебраические и геометрические
свойства смешанного произведения векторов доказывать, ис-
пользуя известные свойства определителей третьего порядка
(см. гл. 5).
Алгебраические свойства смешанного произведения
трех векторов
Будем полагать векторы а у^, zj, Ъ (х2; у2; z2), с (х3;у3; г3)
данными.
1. Если поменять местами два любые вектора, то значе-
ние смешанного произведения изменится на противополож-
ное, т.е.(Ь; а; с) = -(а; Ь; с).
В самом деле, имеем:
*1 У1 21
Х2 Уз Z2
(а; Ь; с) = Д = х2 у2 z2 ; (Ь; а; с ) = Д j = хг ух zx
х3 Уз 23
*3 Уз 23
Если поменять местами две первые строки определителя
Д, то получим определитель ДР На основании свойства 2 оп-
ределителей (см. главу 5) при такой перестановке строк опре-
делителя его значение изменится на противоположное, т. е.
получаем Д! = -Д. Это, в свою очередь, означает:
(Ь; а; с)= - (а; Ь; с ), что и требовалось доказать.
2. Смешанное произведение векторов а,Ь и с не изменя-
ется, если переставлять перемножаемые векторы в круго-
вом порядке, то есть:
138
(a; b; c) = (b: c; а)Дс; a; b).
Действительно, на основании (**) имеем:
(а; Ь; с) = Д = НИН СО СО I-1 СО СО н-Г* N N tQ СО СО h- , (Ь; с; а ) = Дх = н н н м «о to S'2= У •!*
хз Уз Z3
(с; а; Ъ) = Д2 = X] У1 zi •
Х2 У2 Z2
Если в определителе Д сначала поменять местами первые
две строки, затем поменять местами третью строку с новой
второй строкой, то получим определитель ДР На основании
свойства 2 определителей значения данного и полученного
определителей окажутся равными: Д = Д1? значит, (а; Ь; с) =
= (Ь; с; а).
Аналогично доказывается, что (а; Ь; с) = (с; а; b). В итоге
получаем: (a; b; c) = (b; с; а) = (с; а; b).
3. Для любого скалярного множителя teR справедливо
равенство: (t a; b; с) = t • (а; Ь: с).
Так как вектор t а имеет координаты : t • а (txx; tyr\ tzj,
то на основании (**) имеем: (t а; Ь; с) =
txx tyx tzr
Х2 У2 Z2
Х3 Уз Z3
После вынесения общего множителя t элементов первой
строки за знак определителя получаем
iXj tyr tzr Xj У1 Z1
(t • а; &; с) = Х2 У 2 Z2 = t- X2 У2 Z2 = t' (а; &; c).
Х3 Уз Z3 X3 Уз Z3
4. ((<31 +а2): Ь: с) = (ai; b: с) + (аг; Ь; с).
Используя свойство (а + &) х с = а х с + Ъ х с векторного
произведения двух векторов и такое же свойство
(а + & ) • с = а с + b с скалярного произведения двух векто-
ров, получаем:
139
((ai +аг); b; с ) = ((ai + аг)* b )-c = ((ai x&) + (a2 x&) )*c =
= (ai xfe)- c + (a2 xb) • c = (ai; b; с) + (аг; b; с), что и требова-
лось доказать.
5. ((£jai + t,a2); b; c ) = (ai; b; c) + t2(aa; c )•
Докажите это свойство, используя предыдущие свойства 3 и 4.
Геометрические свойства смешанного произведения
трех векторов
Свойство 1. Интересным и замечательным является тот
факт, что модуль смешанного произведения трех некомпла-
нарных векторов а,Ь и с равен объему параллелепипеда, по-
строенного на этих векторах как на ребрах. Докажем это ут-
верждение.
А
Рис. 64
Пусть тройка векторов а, Ь, с — правая. Отложим от точ-
ки О векторы ОА = а , ОВ = b , ОС = с и построим на отрезках
ОА, ОВ и ОС как на ребрах параллелепипед (рис. 64).
Обозначим: a = Z(OC ;ОР), где ОР~р—а х b; (р =Z(a;&).
Так как тройки векторов а, Ъ, с и а, Ь, р — правые, то 0° < a < 90°,
значит, cosa > 0.
Найдем модуль смешанного произведения (а; Ь; с).
Ранее было доказано, что скалярное произведение двух
векторов равно длине одного из них, умноженной на проек-
цию второго на направление первого. Поэтому скалярное про-
140
изведение (а х Ь) • с = р с равно произведению длины вектора
р и проекции вектора с на направление вектора р .
Так как вектор р перпендикулярен плоскости основания
параллелепипеда, то проекция вектора с = ОС на направление
вектора р равна высоте ОК этого параллелепипеда (рис. 64).
Принимая во внимание, что модуль векторного произведе-
ния векторов а и b равен площади параллелограмма, лежа-
щего в основании параллелепипеда, приходим к выводу: мо-
дуль смешанного произведения (а; Ь; с) векторов а, Ь, с равен
объему параллелепипеда, ребрами которого являются на-
правленные отрезки ОА, О В и ОС, изображающие векторы
а, b, с , т. е.
|(ах&)-с| = || а х b Hc|-cosa| = (| а |’| Ь |-sin ф )-(| с pcosa) =
= Socn.'OK = ^па₽.» где: Iа 1'1 b I’sinq) = Sqch.; | с |-cosa = ОК — высота
параллелепипеда.
Это означает, что если векторы a(xj; y±, 24), &(х2; у2; 2г)>
с (хз? Уз1 гз) заданы своими координатами, то объем паралле-
лепипеда, построенного на этих векторах как на ребрах, мо-
жет быть найден по формуле:
Х1 У! 21 *1 У1
v г пар. = Хг Уг 22 или Fnap = mod Х2 У 2
Х3 Уз 23 хз Уз
zi
Z2
23
— модуль (абсо-
лютная величина) определителя
Xj
Х2
Х3
У1 21
Уг 2з
Уз 2з
Если тройка векторов а, Ь, с — левая, то угол a =
- Z.(OC ;ОР) — тупой, поэтому cosa < 0, значит, (а х b )*с =
= (|а х b Hcpcosa) < 0. И все-таки:
|(дх&)-с| = || а х b Нсрсоза! = (| а |*| b |-sincp)-(| с |-|cosa|) =
= SOCH.-OK = Vnap,
141
Таким образом, Упар_. = |( a; t>; с )| = mod
xi
х2
хз
У! 21
У2 22
Уз 23
Отрезки ОА, ОВ и ОС являются ребрами как параллелепи-
педа, так и тетраэдра СО АВ (рис. 64). Так как объем Утет тет-
раэдра СОАВ равен — объема параллелепипеда, построенного
6
на отрезках ОА, ОВ и ОС как на ребрах, то
VTeT = — Кар - — |( а.\ Ь; с )| = — mod
6 пар- 6 14 ’ " 6
Х1
х2
х3
У1 2i
У 2 22
Уз 23
Тройка базисных векторов i ,j ,k — правая и определи-
1
О
1
О
О
О
1
тель О
, составленный из координат этих векторов, по-
О
ложителен (он равен 1). Из вышесказанного также следует:
если тройка некомпланарных векторов а, Ь, с — правая, то
смешанное произведение этих векторов положительно, а если
эта тройка векторов — левая, то их смешанное произведение
отрицательно. Таким образом, для установления ориентации
тройки векторов (правая или левая тройка), заданных своими
декартовыми прямоугольными координатами, достаточно оп-
ределить знак определителя, составленного из координат этих
векторов.
Свойство 2. Для того чтобы векторы а, Ь, с были компла-
нарны, необходимо и достаточно, чтобы их смешанное про-
изведение было равно нулю.
Необходимость. Если векторы а, Ь, с компланарны, то
один из них является линейной комбинацией двух других.
Пусть вектор b (х2; у2; ?2) является линейной комбинацией век-
торов a(xj; уг; zj и с(х3; у3; г3). Тогда координаты (х2; у2; z2)
вектора Ь являются линейными комбинациями одноименных
координат (хх; уг; zt) и (х3; у3; z3) этих векторов. Поэтому вто-
142
рая строка определителя Д=
*i J/i *i
*2 У2 Z2
*3 У3 23
является линейной
комбинацией его первой и третьей строк. На основании свой-
ства 8 определителей получаем: Д = 0 => (а; Ь; с) = 0.
Достаточность, Пусть (а; Ь; с) = 0. Допустим, что векто-
ры а, Ь, с некомпланарны.
Отложим векторы а, Ъ от одной точки. Тогда параллеле-
пипед, построенный на этих векторах как на ребрах, имеет
объем, равный модулю смешанного произведения векторов
а, Ь, с , не равен нулю. Значит, (а; Ь; с) ф 0, что противоречит
условию (а; Ь; с ) = 0. Это противоречие свидетельствует о том,
что векторы а, Ь, с — компланарны.
Из сказанного следует, что смешанное произведение трех
векторов равно нулю, если:
а) хоть один из перемножаемых векторов есть нуль-вектор;
б) два вектора из перемножаемых — коллинеарны.
Любой вектор в базисе трехмерного пространства имеет
три координаты. Поэтому каждая строка определителя 3-го
порядка может быть принята в качестве декартовых коорди-
нат некоторого вектора.
Условие равенства нулю смешанного произведения трех
векторов
а(хг; У\-> 21), b(x2; у2; г2) и с(х3; у3; z3) равносильно усло-
вию компланарности этих векторов. А условие компланарно-
сти векторов а, Ъ, с равносильно тому, что один из них, на-
пример, вектор Ъ, является линейной комбинацией двух
других векторов — векторов а и с , что, в свою очередь, рав-
носильно равенству нулю определителя 3-го порядка, в стро-
ках которого записаны координаты данных компланарных
векторов (вторая строка определителя является линейной
комбинацией его первой и третьей строк).
143
Таким образом, векторы a (xt; уг; zt), b (х2; у2, 22), с (х3; у3; z3)
компланарны <=>
xi Уу 2i
*2 У1 22
Х3 у3 23
= 0.
Этот важный факт полезно помнить и использовать при
определении взаимного расположения прямых и плоскостей в
пространстве, когда прямые и плоскости заданы своими урав-
нениями. Об этом речь пойдет в нашей книжке.
Задачи
Задача 1. Найдите смешанное произведение (а; Ъ; с) век-
торов а = 2 i-j-k,b = i + 3 j-k, c = -i-j-4 .
Решение. Смешанное определение трех векторов, заданных
своими декартовыми координатами, равно определителю
третьего порядка, составленному из координат этих векторов.
Найдем значение определителя с помощью разложения его по
элементам первой строки. Имеем:
2 -1 -1 ,.3-1 , Г 1 -1
(а; Ь; с) = 13-1 -1 -1 -4 = 2‘ Л -4 + С’1) • -1 -4 + /
1 3
-1 -1
= 2 • (-13)-1 • 5-1 2 =-33.
+ (-!)•
Ответ.: -33.
Задача 2. С помощью смешанного произведения векторов
определите, компланарны ли векторы а = 2 i + 5 j +7 k, b =
= - i - j +k, c = - i -2 j - 2k .
Решение. Для того чтобы векторы а, b и с были компла-
нарны, необходимо и достаточно равенство нулю их смешан-
ного произведения. Так как векторы а,Ь м. с заданы своими
координатами, то для равенства нулю их смешанного произ-
ведения необходимо и достаточно равенство нулю определи-
теля третьего порядка, составленного из координат этих век-
торов.
144
Поэтому находим: (а; Ь; с) =
+ 5-
-1 1
-1 -2
+ 7-
2 5 7
-1 -1 1
-1 -2 -2
= 2-
-1 1
-2 -2
= 2- 4 + 5-(-3) +7-1=0.
Получили: (а; Ь; с) = 0, откуда следует, что векторы а, b и
с компланарны.
Ответ: Векторы а, Ъ и с компланарны.
Задача 3. Найдите объем тетраэдра РАВС, если Р(2; 2; 2),
А(4; 3; 3), В(4; 5; 4), С(5; 5; 6).
Решение. Объем тетраэдра РАВС равен — объема паралле-
6
лепипеда, построенного на отрезках РА, РВ и PC как на реб-
рах, т. е. Утет = - Упар = -1( РА; РВ; PC )|.
О о
Находим координаты векторов: РА (2; 1; 1), РВ(2; 3; 2),
PC (3; 3; 4). Далее вычисляем смешанное произведение
(РА; РВ; PC), которое равно определителю третьего порядка,
составленному из координат векторов РА, РВ и PC. Получаем:
(РА; РВ; PC) = 2 11 = 2- 3 2 3 4 + 1 ' 2 2 3 4 +
2 3 2
3 3 4
= 2 • 6 + 1 • (-2) + 1 • (-3) = 7. Тогда Утет.= | -7 = 1~.
о о
7
Ответ: — (куб. ед.).
6
Задача 4. Вычислите смешанное произведение векторов
(b-а), (а - с), (с - Ь).
Решение. Найдем сумму данных векторов. Имеем:
(b-а) + (а-с) + (с- Ь) = b-а + а-с + с- Ь= б =>
=> (с — Ъ) = ~(Ь - а) - (а - с) => вектор (с - b) является линей-
ной комбинацией векторов (Ь - а) и (а-с) => векторы (b - а ),
(а-с), (с - Ь) компланарны => их смешанное произведение,
145
по признаку компланарности трех векторов, равно нулю:
(Ь-аУ(а-с)-(с-Ь) = 0.
Ответ: 0.
Задача 5. Найдите смешанные произведения векторов
а, b, с, если:
а) а = 2 i + j + 3 k, b = 5 i +3 j + 2 k , c = i + 4 j +3k;
6) a = -3 i - 2 j - k, b = 2 i + 5 j + 3 k , c = 3 i + 4 j + 2 k;
в) a —3i - j -2k, b = 2 i - 3 j - 5k, c=3i- 4 j-k;
r) a = 3 i + 4 j + 5 k, b ~~ 8 i +7 j + 2k, c = 2 i-j-8k.
Задача 6. Компланарны ли векторы а, b и с , если:
а) а = 3 i + 4 j — 5k, b = 8i +7 j - 2 k, c = 2i - j + 8k;
6) a = 3 i + j + 2k, b = 5 i - 7 j + 5k, c = -i -9 j +k;
в) a = 7 i + j -k, b= i -j + 2k,c = 8i + j - 3k.
Задача 7. Дан куб АВСВА^В^СхВ^. Точки Р, К и Н — цен-
тры граней соответственно АВВХА, СВВХСХ и А^В^С^В^
(рис. 65). Используя свойства смешанного произведения век-
торов, определите, какую часть объема данного куба состав-
ляет объем тетраэдра АР КН.
Решение. Введем некомпланарные векторы а = АВ , b = АВ ,
с = ААг и примем их в качестве базисных в пространстве.
Если на векторах АК , АР и АН как на ребрах построить
параллелепипед, то его объем Vnap. будет равен модулю сме-
шанного произведения этих векторов: Упар = |( АК ; АР; АН )|.
Тогда объем Утет тетраэдра АРКН, для которого отрезки АК,
АР, АН служат ребрами, равен — Vnap_. Значит,
6
Найдем смешанное произведение (АК; АР; АН), предва-
рительно разложив векторы АК , АР и АН по базисным век-
торам а , b и с .
146
Так как точка Р — середина отрезка ВА}, то АР = — (АВ +
+ ААг) =— а + — с . По правилу ломаной находим: АК = AD +
2 2
+ DK = AD + АР = — а + b + — с; АН = АА. + А, Я =
2 2 11
- AAt + -(АВ + AD) =- а
2 2
+ — b + с . Тогда, используя
2
свойства а х a =b х b =0 и b х а = -(а х Ь) векторного про-
изведения, получаем: (АК АР АН) = ((— а + Ъ + — с) х
2 2
х (— а + — с ))•( — а + — 5 + с ) = (— аха+—ахс+ — b х
2 2 2 2 4 4 2
х а + —Ь х с + — с х а +— с х с )•( — а + — b + с) =
2 4 4 2 2
= (— b х а + — Ь х с)-(— а + — b + с)=— (6аа)+- (Ь а Ь) +
2 2 2 2 ' 4 4 '
+ |(Ьас) + |(&са) + + |(6сс) = |(6ас) +
+ — (Ь с а) = -—(a b с) + —(abc) = - — (abc), так как
4 2 4 4
(с a b) = (а b с )=-(с b а).
Таким образом, VTeT = —1( АК ; АР; АН )| = — — ( а Ь с )| =
6 6 4
- Ь гл - ^1(ЛВ AD ЛА,
Ответ: —.
24
147
Задача 8. Дан параллелепипед ABCDA^^CxDx, построен-
ный на векторах АВ(4; 3; 0), AD(2; 1; 2) и ААД-З; -2; 5).
Пользуясь скалярным, векторным и смешанным произведе-
ниями, найдите: а) объем параллелепипеда; б) площади гра-
ней; в) длину высоты, проведенной из вершины Aj на грань
ABCD; г) косинус угла между ребром АВ и диагональю В^Л;
д) косинус угла <р2 между гранями ABCD и ADD{A}.
Решение. Рисунок предлагается читателю сделать само-
стоятельно. При этом изображают параллелепипед любой
формы. А так как в нашей задаче не говорится, что данный
параллелепипед является прямым, то его следует изображать
«наклонным» (см. рис. 64).
0
2
5
а) Рпар. = | (АВ ; AD ; AAt) | = mod
4 3
2 1
-3-2
= 120-18 + 0-
-0-30 + 16| = |-12 | = 12.
б) ‘S’ABCD = I АВ х AD |.
Находим АВ х АЛ = р
4 з А ---------------.
= (6;—8; —2).
сл А 1
0 4
2 2
Тогда SACDB = ^36+64+4 = 2^26 ;
^ABB,At = | АВ х AAj |.
Находим
ТЗ л л' (3 0 0 4 4 3 Л|
АВхАА,-р^_26 ; 5 3;_3 2J=(15;-20;l).
Тогда В„„ А = V225 +400 + 1 = V626.
/if) D j /I ।
Аналогично находится площадь грани ADD1A1.
в) Длина высоты, проведенной из вершины Aj на грань
ABCD, равна частному от деления объема параллелепипеда на
V 12 6
площадь параллелограмма АВС Л: h = —= —у= -- .—.
&ABCD 2\26 л/26
г) Косинус угла между ребром АВ и диагональю BjB равен
косинусу угла между векторами АВ и ВХЛ, где
BXD = BjB+ ВЛ = -AAt - АВ + АЛ = (1;0; -3). Получаем:
148
cosip t - 4-1 + 3 0+0-(-3) 4
АВ| В,/J 74! + 3! + О2 ф2 + О2 + (-3)2 5л/10‘
д) Косинус угла ф2 между гранями ABCD и ADD1A1 равен
модулю косинуса угла между векторами, перпендикулярны-
ми этим граням. Такими векторами могут служить векторы
— (АВх AD ) = р (3; -4; -1) и AD х ААг = q (9; -16; -1). Тогда:
2
СО6ф2 =
|_ |3-9-4 (-16)-1(-1)| 92 46
Р q /16 + 9 + 1 /81 + 256 + 1 /26 /338 13V13
626,
Ответ-, а) 12; б) = 2^26 ,
= /j38;B) 6 }4 }46
л/26 5V10 13 у13
Задача 9. Лежат ли точки А, В, С и Е в одной плоскости,
если: А (2; 13; 3), В (1; 4; 1), С ( 1; 1; 4 ), Е ( 0; 0; 0 )?
Решение, а) Первый способ (с помощью системы уравне-
ний). Точки А, В, С и Е лежат в одной плоскости, если векто-
ры А_В(3; 17; -2), АС(1; 12; -7) и АЕ(2; 13; -3) компланар-
ны, т. е. если для этих векторов существуют такие
(одновременно не равные нулю) числа х и у, что АС = хАВ +
+ у АЕ . Это означает, что должна иметь ненулевое решение
3x + 2z/ = l,
система уравнений <17х + 13г/ = 12,
-2x-3j/ = -7.
Так как уравнение 17х + 13у = 12 является алгебраиче-
ской суммой уравнения Зх + 2у =1, умноженного на 5, и урав-
нения 2х + Зу = 7, то эта система равносильна системе уравне-
(Зх + 2и = 1,
(2x + 3i/-7 Решением которой является пара чисел:
11 19 —* —-
х =----, у = —. Таким образом, получаем 5АС+ ПАВ -
5 5
- 19АЕ = 0. Значит, векторы АС, АВиАЕ компланарны,
поэтому точки А, В, С и Е лежат в одной плоскости.
НИЙ
149
б) Второй способ (с помощью смешанного произведения
векторов).
Для компланарности векторов АВ (3; 17; -2), АС (1; 12; -7)
и АЕ (2; 13; -3) необходимо и достаточно, чтобы определитель
третьего порядка, составленный из координат этих векторов,
был равен нулю. Поэтому находим значение определителя
3 17 -2
1 12 -7
2 13 -3
Замечаем, что если первый столбец определите-
ля, умноженный на 5, сложить с третьим его столбцом, умно-
женным на (-1), то получим второй столбец. Это означает, что
второй столбец этого определителя является линейной комби-
нацией его первого и третьего столбцов. Такой определитель
равен нулю. Поэтому векторы АС, АВиАЕ компланарны, а
точки А, В, С и Е лежат в одной плоскости.
Ответ: Да, лежат в одной плоскости.
Задача 10. Составьте уравнение плоскости, проходящей
через точки М (2; -1; 2), К (1; -2; 3), Н (-1; 2; 0).
Решение, а) Первый способ (с помощью системы уравне-
ний). Пусть плоскость а = (МКН) имеет уравнение
Ax + By + Cz + D = 0. (1)
Составить уравнение вида (1) плоскости а означает — най-
ти коэффициенты А, В, С и свободный член D. Эти коэффици-
енты будем находить, используя условие принадлежности то-
чек М, К и Н плоскости а. Именно, если точки М, К и Н
принадлежат плоскости а, то их координаты должны удовле-
творять уравнению (1), т. е. должны выполняться условия:
М (2;-1;2)еа=> А-2 + В(-1) + С-2 + В = 0,
К (1;-2; 3)е а=> А 1 + В(-2)+ С-3 +В = 0,
Н(-1; 2;0)ба^А(-1) + В2 + С0 + Л = 0.
2A-B + 2C + D = 0,
=> A-2B + 3C + D = 0, >
-A +2B + D = 0.
(*)
После сложения второго и третьего уравнения этой систе-
2D
мы получаем: ЗС + 2D = 0, откуда С =-. После подстановки
3
п 2D
значения С =--- в первое уравнение системы получаем:
150
(6A-3B-D = 0, _ |-A + 2B + Z) = 0 ” (6A-3B-D = 0, * (-6A + 12B + 6D = 0 ‘ [b=-^, 9 -A + 2B + D = 0
[b=-^, 9 =>. B = 5D 9 ’
-A- — = 0 A = D
I 9 9 ’
гг й л D „ 5D „ 2D т-г
Таким образом, имеем: А = -—, В = —, С = ---------------. Пола-
9 9 3
гая D = -9, находим: А= 1, В = 5, С = 6. Подставив найденные
значения А, В, С и D в уравнение (1), получаем искомое урав-
нение плоскости МКН'.
х + Бу + 6г - 9 = 0.
б) Второй способ (с помощью смешанного произведения
векторов).
Принадлежность точки Т(х; у; z) плоскости МКН равносиль-
на компланарности векторов МК(-1; -1; 1), МН(-3; 3; - 2),
MT(x-2;y+l;z-2). Условие же компланарности векторов
РК , PH , РМ равносильно равенству нулю определителя
третьего порядка, элементами которого являются координаты
этих векторов, т. е.
х-2
-1
-3
z/H-1 z-2
-1 1
3 -2
= 0 или
2(х - 2) - 3 (у + 1) - 3 (г - 2) - 3 (z - 2) - 3 (х - 2) - 2 (у + 1) =
= 0ox + 5i/-I-62 9 = 0.
Таким образом, координаты х, у, z любой точки Т(х; у; г)
плоскости МКН удовлетворяют уравнению х + Бу + 6г - 9 = 0,
значит, это уравнение является искомым уравнением плоско-
сти МКН.
Ответ: x + 5y + 6z~9 = 0.
Замечание. Параметрические уравнения прямой т, прохо-
дящей через точку А(1; -2; 3) параллельно вектору р(-Б; 4; 2),
имеют вид:
х = 1 - 5t,
< y = -2 + 4t, teR.
z = 3 + 2t;
151
При каждом значении параметра t получается некоторая
(единственная) точка прямой т. В частности, при t = 2 полу-
чаем точку В(-9; 6; 7) этой прямой. Тогда данную прямую
можно задать и такими параметрическими уравнениями:
х = -9-5#,
< y = 6 + 4t, t&R.
2 = 7 + 2#;
Заметим, что параметр в уравнениях прямой можно обо-
значать любой буквой. Например, #, и или v. Кроме того, если
в качестве направляющего вектора прямой т принять вектор
q = 2 р , коллинеарный вектору р(-5; 4; 2), т. е. вектор
q (-10; 8; 4), то параметрические уравнения этой прямой
можно записать в виде:
х = 1-10и,
• у = -2 + 8и, veR.
z = 3 + 4v;
Если же в одной задаче заданы две различные прямые, то в
их параметрических уравнениях параметры обозначают раз-
личными буквами.
Например, если
нужно исследовать взаимное расположе-
х = -1 + 2#,
У = 2-t,
z = 3-2#;
ние двух прямых Г.
t&R и т:
х = -2 + Зи,
у = 4 - Зи, и е R ,
2 = 3-2и;
то решается система уравнений:
—1 + 2# — — 2 + Зи,
2-# = 4-Зи, решением
3-2#= 3-2и,
которой являются # = 1, и = 1. При этих значениях парамет-
ров на каждой из данных прямых получается одна и та же
точка (1; 1; 1). Следовательно, эти прямые пересекаются в
точке (1; 1; 1).
Но если в этих уравнениях параметр обозначить одной и
той же буквой, то данную задачу с помощью системы уравне-
ний решить не удастся.
Вместе с тем вопрос о взаимном расположении заданных
прямых разрешается другими методами, например, с помо-
щью смешанного произведения векторов и определителей
третьего порядка.
152
Задача 11. Определите взаимное расположение прямых
x = 5 + 7i, х = 3-2и,
l',<y = 2-t, teR и т: • у = 5 + 3u , ueR.
z = 9, z = 8-u,
Решение, а) Первый способ (с помощью смешанного произ-
ведения векторов).
Прямая I задана точкой А(5; 2; 9) и направляющим векто-
ром р (7; -1; 0), а прямая т — точкой В(3; 5; 8) и направляю-
щим вектором q (-2; 3; -1). Так как координаты векторов р и
q не пропорциональны, то эти векторы не коллинеарны, по-
этому прямые I и т не параллельны. Значит, эти прямые либо
пересекаются, либо скрещиваются.
Прямые I и т скрещиваются тогда и только тогда, когда
векторы р, q и АВ некомпланарны. Компланарность же
векторов р , q и АВ означает, что прямые I и т пересекаются.
Проверим, компланарны ли векторы р , q и АВ, для чего
найдем значение определителя, составленного из координат
7-10
этих векторов. Имеем: -2
-2
3 -1
3 -1
= 0 (две строки определите-
ля равны).
Равенство нулю этого определителя говорит о том, что
смешанное произведение векторов р , q и АВ равно нулю,
значит, эти векторы компланарны, а прямые I и т пересека
ются.
б) Второй способ (с помощью системы уравнений}.
Направляющие векторы р (7; -1; 0) и q (-2; 3; -1) данных
прямых I и т не коллинеарны, так как их одноименные коор-
динаты не пропорциональны. Поэтому эти прямые либо пере-
секаются, либо скрещиваются.
Для ответа на вопрос, имеют ли данные прямые общую
точку, достаточно выяснить, имеет ли решение система
153
5 + 7f = 3-2u,
2 -1 = 5 + 3u,
9 = 8-u,
составленная из уравнений этих прямых. Из уравнения
9 = 8 - и находим значение и = -1, которому соответствует точ-
ка (5; 2; 9) прямой т, являющаяся точкой прямой I при t = 0.
Это означает, что данные прямые пересекаются в точке (5; 2; 9).
Ответ: Прямые пересекаются.
Задача 12. Плоскости а и Р заданы уравнениями соответ-
ственно 2х + Зу-2 = 6их + у + 2 = 1. Определите взаимное
расположение этих плоскостей. Если эти плоскости пересека-
ются, то напишите параметрические уравнения прямой их
пересечения.
Решение, а) Первый способ (с помощью системы уравне-
ний).
Векторы пг (2; 3; -1) и пг(1; 1; 1) нормалей данных плос-
костей а (2х + Зу - z = 6) и р (х + у + z = 1) не коллинеарны (их
координаты не пропорциональны), поэтому данные плоскости
пересекаются по некоторой прямой т. Пусть р (а; &; с) — на-
правляющий вектор прямой т (рис. 66).
Заметим, что для составления параметрических уравне-
ний прямой необходимо знать координаты направляющего
вектора этой прямой и координаты любой её точки.
Координаты вектора р найдем из условий его перпенди-
кулярности каждому из векторов пх (2; 3; -1) и пг(1; 1; 1)
нормалей соответственно плоскостей аир. Имеем:
р±П1, р-П1=0, (2а + ЗЬ-с = 0,
р±Пг р-Пг=0 \а + Ь + с = О.
„ . (2а + 3& = -1, . , о г»
Если с = -1, то { , , откуда а = 4, о = -3. Значит,
[а + & = 1,
вектор р имеет координаты: р (4; -3; 1).
154
Осталось найти хотя бы одну точку прямой т. Можно рас-
суждать таким образом.
Так как плоскости а и ₽ не параллельны плоскости Оху
(почему?), то в уравнениях этих плоскостей для переменной г
выполняется: z е R . Пусть (для определенности) z = -1. Тогда
координаты х = 1 и у = 1 искомой точки прямой т являются
решением системы уравнений:
(2х + 3у = 5,
\х + у = 2.
Вычтя из первого уравнения этой системы удвоенное её вто-
рое уравнение, получаем: у = 1, после подстановки которого во
второе уравнение получаем: х = 1. Таким образом, (1; 1; -1) —
точка прямой т = ап р.
Найдя точку (1; 1; -1) и направляющий вектор р (4; -3; -1)
прямой т, записываем её параметрические уравнения в виде:
x = l + 4t,
< y = l-3t,
z = —l—t.
б) Второй способ (с помощью векторного произведения
векторов).
Координаты направляющего вектора р (а; Ь; с) прямой т =
= апр найдем, пользуясь определением векторного произве-
дения двух векторов.
155
Так как прямая т 1/ц (2; 3; -1), m±n2(l; 1; 1), то в качест-
ве направляющего вектора р этой прямой можно взять век-
тор, равный вектору д=пг х пг (рис. 66). Поэтому находим
ставляем матрицу
координаты векторного произведения пг х п2, для чего со-
2 3 -1
111
, в строках которой — координа-
ты векторов п, и п2 .Тогда: пх х n2 = q
3-1 -12
2
1 1 ’ 11’1
3
1
каж-
= (4;-3;-1).
Далее убеждаемся, что точка (1; 1; -1) принадлежит
дой из плоскостей а и р, т. е. принадлежит прямой т, затем
получаем параметрические уравнения этой прямой в виде:
x = l + 4t,
y = l-3t, t&R.
z = -\-t,
x = l + 4f,
Ответ: у = 1-31,
z = —l — t,
teR.
Замечание. Так как точка (-3; 4; 0) также принадлежит
прямой т, то параметрические уравнения этой прямой можно
записать иначе:
х - -3 + 4t,
t/ = 4-3f, teR.
z = -t,
Задача 13. Найдите расстояние от точки А(7; 9; 7) до
„ „ х-2 у-1 z
прямой т, заданной уравнениями = —.
Решение. Решим эту задачу несколькими способами.
а) Первый способ (с помощью системы уравнений). Можно
эту задачу решать таким образом. Составить уравнение плос-
кости а, проходящей через точку А перпендикулярно данной
прямой т . Затем решить систему, состоящую из этого урав-
нения и уравнений прямой т . Решением этой системы явля-
ются координаты точки К = а т . Тогда расстояние между
156
точками An К равно искомому расстоянию от точки А до пря-
мой т.
После такого «планирования» приступаем к решению за-
дачи.
Так как а± т , то направляющий вектор р (4; 3; 2) прямой
т принимаем в качестве вектора нормали плоскости а, про-
ходящей через точку А(7; 9; 7). Значит, уравнение этой плос-
кости имеет вид: 4(х - 7) + 3(у - 9) + 2(z - 7) = 0 <=> 4х + 3у +
+ 2г - 69 = 0.
Далее находим координаты точки К = а п т, для чего ре-
шаем систему уравнений:
4x + 3y + 2z = 69,
x = 2 + 4t,
y = l + 3t,
z = 2t.
После подстановки в первое уравнение системы вместо х, у, z
их выражения через t получаем: 4(2 + 4i) + 3(1 + 3t) +2 • 2t = 69,
58
откуда t = — = 2. Тогда точка К имеет координаты: х = 2 + 4 • 2 =
= 10; у = 1 + 3- 2 = 7;2 = 2- 2 = 4,т. е. Л'(10; 7; 4). Значит, АК =
= ^(7-10)2 +(9-7)2 +(7-4)2 = д/22 — искомое расстояние от
точки А до прямой т .
б) Второй способ (с помощью векторного произведения
векторов). Проверкой убеждаемся, что Ai т . Тогда через точ-
ку А и прямую т проводим плоскость и в ней строим парал-
157
лелограмм АВМС на векторах q - СА и р как на сторонах
(рис. 67). Из уравнений прямой следует, что С(2; 1; 0) — дан-
ная точка прямой т и р (4; 3; 2) — направляющий вектор
этой прямой. Тогда вектор СА имеет координаты: СА(5; 8; 7).
Расстояние от точки А до прямой т равно длине перпен-
дикуляра, опущенного из А на прямую т . На рис. 67 этим
перпендикуляром является высота АК параллелограмма
АВМС. Поэтому искомое расстояние от точки А до прямой т
равно частному от деления площади параллелограмма АВМС
на длину вектора р , т. е. АК =
q
^АВМС
I?
. А так как SABMC = q*p
то АК =
qxp
. Находим q х р и р .
Имеем: |р| = V16 + 9 + 4 = л/29 ; q х р - г =
-5;18;-17) => |$ хр\ = V25 + 324+289 = Тб38
Тогда = = V22.
V29
87.75.58
32’24’43
в) Третий способ (с помощью скалярного произведения).
Отрезок АК — перпендикуляр из точки А на данную пря-
мую — является катетом прямоугольного треугольника АСК
(рис. 67) и равен q ’sintp, где <р = Z(p,q).
Находим: costp =
4-5 + 38 + 2-7
V29-V138
58
V29-138
=> sincp =
L 582
V 29138
58 (69-58) _ ITT
58-69 V69 ’
Тогда АК = h =л/138 •
Ответ’. 422.
158
ли тп:
Задача 14. Найдите расстояние между прямыми тип, ес-
у-1 z — 2 х у-2 z
= ----=----- и п: = ----- = “ .
-12 -13 3
Решение. 1) Прямая т задана точкой А(3; 1; 2) и направ-
ляющим вектором р(1;-1;2); прямая п — точкой В(0; 2; 0) и
направляющим вектором q(-l; 3; 3).
Так как одноименные координаты направляющих векто-
ров р(1;-1; 2) и д(-1; 3; 3) не пропорциональны, то эти векто-
ры не коллинеарны, а прямые тп и п не параллельны. Тогда
эти прямые или пересекаются, или скрещиваются.
Если прямые тп и п скрещиваются, то они не лежат в одной
плоскости.
Поэтому векторы р, q и АВ не компланарны. Это озна-
чает, что их смешанное произведение не равно нулю, откуда
не равен нулю определитель, составленный из координат этих
векторов. Справедливо и обратное: если определитель, состав-
ленный из координат этих векторов р , q и АВ , не равен ну-
лю, то прямые тп и п скрещиваются.
Найдем значение этого определителя, учитывая, что
АВ(-3; 1;-2).
Получаем:
-3 1
-1 3
-2
2
3
= -3-
= 27-5-4=18*0.
-1 2
3 3
1 2
-1 3
) + (-2)*
3
Это означает, что прямые тп и п скрещиваются.
Рис. 68
159
Отложим от точек АиВ векторы р и q , затем на векторах
р , q и АВ как на ребрах построим параллелепипед (рис. 68).
При этом прямые тип лежат в плоскостях верхнего и ниж-
него оснований построенного параллелепипеда. А так как рас-
стояние между двумя скрещивающимися прямыми равно рас-
стоянию между параллельными плоскостями, проходящими
через эти прямые, то расстояние d между прямыми тип рав-
но высоте h построенного параллелепипеда. Если V— объем
параллелепипеда, S — площадь параллелограмма АСКМ, то
d-k-v.
S
Так как объем V параллелепипеда, построенного на векто-
рах р , q и АВ , равен модулю смешанного произведения этих
векторов, которое, в свою очередь, равно определителю
третьего порядка, составленному из координат этих векторов,
тоК = 18.
Площадь S параллелограмма АСКМ, построенного на век-
торах ри q , равна
модулю
смешанного произведения этих
векторов: S = pxd .
Находим:
2
2
3 ’ 3
1 . 1
-1 ’ -1
р х q = г
3
-1
3
|pxg| = 781+25+4 =
гг . V 18
Тогда h = — = -f—
S 7116
110 .
, значит, искомое расстояние d между
данными скрещивающимися прямыми тип равно
18
110
п 18
Ответ: ,
Тиб
Задача 15. Найдите расстояние между прямыми
x = 2 + 3t, х — 7 + 3?,
' y--l + 4t, teR и ’ y = l + 4t, teR.
z = 2t, 2 = 3 + 2?,
160
Задача 16. Составьте уравнение плоскости, проходящей
через точку М(1; 1; -3) параллельно прямым I и т, если
, (2x-2z/ + 3z-4 = 0, (3x-i/-z = 0,
’ |х + 2у - 4г +1 = О И т" [х + у - 3z +1 - 0.
Задача 17. Составьте уравнение прямой, проходящей через
точку М(1; 1; -3) перпендикулярно прямым I и т, если
, (2х-у + Зг + 4 = 0, (х —у —2 + 1 = 0,
' [-х + 2у + 22-2 = 0 ит' [2х + у + 4г = 0.
Задача 18. Найдите расстояние между прямыми I и т, если
, х-2 г/н-1 г-1 х + 4 у-2 г + 2
г.---= -— =----- и т: ----= ---=-----.
4 1-1 2-2-3
Задача 19. Даны две прямые
, х-2 г/4-1 2-1 х + 4 у-2 2 + 2
г.---= -— =----- и т: ----= --=-----.
4 1-1 2-2-3
а) Докажите, что они скрещиваются; б) составьте уравне-
ния плрскостей, проходящих через каждую из них парал-
лельно другой прямой; в) найдите расстояние между этими
плоскостями и сравните его с расстоянием между данными
прямыми.
Задача 20. Из вершины А наклонного параллелепипеда
ABCDAjBjCjDi провели три диагонали прилежащих к этой
вершине граней. Используя свойства смешанного произведе-
ния векторов, определите, какую часть объема данного па-
раллелепипеда составляет объем тетраэдра, тремя ребрами
которого служат проведенные диагонали.
Задача 21. Пусть а и с — произвольные векторы. Дока-
жите тождества: а) (а х с)2 + (а • с )2 = (а )2-( с )2; б) (а - с) х
х (а + с ) = 2.
Задача 22. Найдите объем тетраэдра РАВС, если:
а) Р(6; 0; -1),А(3; 0; -3), В(2; -1; -1), С(5; -1; 2);
б) Р(0; 0; 0), А(6; 0;-3), В(3; 4;-1), С(2; 3; 5).
161
Задача 23. Тетраэдр РАВС построен на векторах АВ(-1; 1; 0),
АС(-1;0;1), АР(-1;0;0), причем А(1; 0; 0). Пользуясь скаляр-
ным, векторным и смешанным произведениями, найдите:
а) длину высоты PH этого тетраэдра; б) величину угла ф меж-
ду гранями АВС и АРС.
Задача 24. Тетраэдр РАВС построен на векторах АВ(-2; 2; 0),
АС(-2;0;2), АР(-2;0;0), причем С(0; 0; 2). Пользуясь ска-
лярным, векторным и смешанным произведениями, найдите:
а) длину высоты PH этого тетраэдра; б) величину угла ф меж-
ду гранями АВС и АРС.
Задача 25. Тетраэдр РАВС задан координатами своих вер-
шин: А(5; 3; 3), В(3; 5; 3), С(3; 3; 5), Р(3; 3; 3). Пользуясь ска-
лярным, векторным и смешанным произведениями, найдите:
а) длину высоты PH этого тетраэдра; б) величину угла <р меж-
ду гранями АВС и ВРС.
Задача 26. Тетраэдр РАВС задан координатами своих вер-
шин: А(6; 4; 4), В(4; 6; 4), С(4; 4; 6), Р(4; 4; 4). Пользуясь ска-
лярным, векторным и смешанным произведениями, найдите:
а) длину высоты PH этого тетраэдра; б) величину угла ф меж-
ду гранями АВС и ВРС.
Задача 27. Тетраэдр РАВС задан координатами своих вер-
шин: А(7; 5; 5), В(5; 7; 5), С(5; 5; 7), Р(5; 5; 5). Пользуясь ска-
лярным, векторным и смешанным произведениями, найдите:
а) длину высоты PH этого тетраэдра; б) величину угла ф меж-
ду гранями ВСР и АРС.
Задача 28. В треугольной призме ABCA1B1Ci векторы
АВ(0; 1; -1) и АС (2; -1; 4) определяют основание, а вектор
АА, (-3; 2; 2) направлен по боковому ребру. Пользуясь ска-
лярным, векторным и смешанным произведениями, найдите:
а) объем призмы; б) площади граней; в) высоту призмы;
г) угол ф между ребрами В^ и ААр
162
Задача 29. Найдите длину высоты АН тетраэдра РАВС, ес-
ли А(2; -4; 5), В(-1; -3; 4), С(5; 5; -1), Р(1; -2; 2).
Задача 30. Тетраэдр построен на векторах АВ (2; 0; 0),
АС (3; 4; 0), AD(3; 4; 2). Пользуясь скалярным, векторным и
смешанным произведениями, найдите: а) объем тетраэдра;
б) площади граней; в) длину высоты й, проведенной из верши-
ны D; г) косинус угла а между ребрами АВ и ВС; д) косинус
угла р между гранями АВС и ADC.
Задача 31. Найдите смешанное произведение и определите
ориентацию тройки векторов а,Ъ,с в каждом из следующих
случаев: а) а(2;-3;1), Ь(1; 1;2), с(3; 1;-1); б) а(-2; 1;5), &(3;0;2),
с(-1;4;2); в) а(1;-1;1), &(5;2;-3), с(1;4;-2).
163
ГЛАВА 7.
СИНТЕТИЧЕСКАЯ
ГЕОМЕТРИЯ МНОГОГРАННИКОВ
И ФИГУР ВРАЩЕНИЯ В ЗАДАЧАХ
ПРАВИЛЬНАЯ ШЕСТИУГОЛЬНАЯ ПРИЗМА
КАК МОДЕЛЬ ГЕОМЕТРИИ ПРЯМЫХ И ПЛОСКОСТЕЙ
Каждому изучающему стереометрию необходимо овладеть
умениями «видеть» и вычислять различные расстояния в про-
странстве, так как эти умения являются фундаментом успеш-
ного изучения всей метрической стереометрии в 10-11 клас-
сах. Необходимо выработать умение верно и наглядно
строить, аргументированно обосновывать изображения вза-
имно перпендикулярных прямых и плоскостей, углов между
ними на уже изображенных многогранниках и их моделях.
Эти умения учащиеся приобретают, когда в заданном мате-
риале в качестве многогранника — тренажёра, наряду с пра-
вильной шестиугольной призмой предлагаются задачи раз-
личного уровня сложности на вычисление расстояний в
пространстве между точками, от точки до прямой и плоско-
сти, между скрещивающимися прямыми.
В данной статье предлагаются задачи, подобранные при
соблюдении принципов «наглядности», «доступности», «от
простого — к сложному». Их решения сопровождаются необ-
ходимыми аргументациями логического, графического и вы-
числительного характера.
1. Расстояние между точками. Задачи
Задача 1. ABCDEFAxB]CxDxExFr — правильная шести-
угольная призма, все ребра которой равны 1. Найдите рас-
стояние: а) между вершинами А и С; б) между вершинами А и
Ci; в) между вершиной А и серединой Н отрезка СХЕХ; г) между
вершиной А и серединой К отрезка BXFX.
Для решения задач на нахождение расстояний в простран-
стве, используя модель-изображение правильной шести-
угольной призмы (рис. 69), полезно иметь «перед глазами»
164
изображение основания этой призмы — оригинал правильно-
го шестиугольника (рис. 70), на котором «видна картина» вза-
имного расположения диагоналей и сторон этого многоуголь-
ника; их длины и величины углов между ними известны из
планиметрии.
Сочетая изображения правильной шестиугольной призмы
и правильного шестиугольника, будем решать эту задачу и все
задачи, следующие за ней в данной статье.
Решение, б) Расстояние между точками А и В обознача-
ют р( А; В); это расстояние равно длине отрезка АВ.
Имеем: р(А; CJ = ACt (рис. 71). Найдем длину отрезка АСР
Боковые ребра правильной призмы ABCDEFA^B^C^D^EiFi
перпендикулярны плоскости её основания. Тогда имеем:
^СДАВС), AC cz (АВС) => СгС ± АС (по определению прямой,
перпендикулярной плоскости) => ААСгС — прямоугольный =>
=> ACj = д/AC2 +С1С2 (по теореме Пифагора).
165
В равнобедренном ДАВС со сторонами АВ =ВС =1 и ZABC =
= 120° находим по теореме косинусов: АС1 2 = АВ2 + ВС2 -
- 2АВ • BC cosl20° = I2 +12 - 2 • 1 • 1 • (-0,5) = 3 => АС = 7з .
Тогда: ACi = р(А;С1) = 7(^)2+ 12 = 2.
в) Имеем: р(А; Н)=АН (рис. 72). В правильном 6-угольнике
ABCDEF имеем: АС = АЕ = V3 (см. б)). Так как СгС ± (АВС),
ЕгЕ ± (АВС), то АС\ = АЕХ (как наклонные, имеющие равные
проекции), откуда: ЛАЕ, С, — равнобедренный с основанием
е1с1=ас=7з.
Рис. 72
Получаем: точка Н — середина основания ЕАСА равнобедрен-
ного AAEjCj => АН ± -EiCp Учитывая, что С,Н= — E-iC^
2
1 г \/з
= — • л/З = — , в прямоугольном \АС}Н по теореме Пифагора нахо-
дим: АН= р( А; Н) = ^АС^-С.Н2
Ответ: a) v'3 ; б) 2; в) ; г) .
Задачи для самостоятельного решения
Задача 2. ABCDEFAlB1ClD1E1F1 — правильная шести-
угольная призма, все ребра которой равны 2. Найдите рас-
стояние между: а) вершинами А и Е; б) вершинами А и Ег;
в) вершинами В и D^, г) между вершинами С и Ег; д) вершиной
166
В и серединой Р отрезка D^F^, е) вершиной В и серединой М
отрезка AjCp
Задача 3. ABCDEFAtBiCiDtEiFi — правильная шести-
угольная призма, все ребра которой равны 1. Найдите рас-
стояние: а) между вершинами А и С; б) между вершинами А и
Сг; в) между вершиной А и серединой Н отрезка С^Е^, г) между
вершиной А и серединой К отрезка В^.
2. Расстояние от точки до прямой. Задачи
Расстояние от точки М до прямой а обозначают: р(М;а).
Расстояние от точки М до прямой а, расположенных в
пространстве, равно расстоянию от точки М до точки К пере-
сечения прямой а и плоскости 0, проходящей через точку М
перпендикулярно прямой а, т. е. р(М;а) = р(М;К) = МК, где ,
М е 0, р ± а, К = а п 0.
Задача 4. В правильной шестиугольной призме
ABCDEFA^B^C^D^E^F^ (рис. 73), все ребра которой равны 1,
найдите расстояние: а) от вершины F до прямой СгВ; б) от
вершины А до прямой в) от вершины А до прямой
г) от вершины А до прямой BFj.
Рис. 73
Решение, а) Имеем: ВгВ ± (ABC), BF с (АВС) (рис. 73) =>
=> ВгВ ± BF (по определению прямой, перпендикулярной плос-
кости). Учитывая BF ± ВС (рис. 70), получаем BF ± (ВгВС) (по
признаку перпендикулярности прямой и плоскости), откуда
167
BF ± BC} (по определению прямой, перпендикулярной плос-
кости). Это означает:р(Е; BCJ = BF = л/з .
б) Имеем: AD 1 ЕС (рис. 70); С, С ± (АВС), ЕС с (АВС) (рис. 73) ->
=> CrC 1 ЕС (по определению прямой, перпендикулярной плос-
кости). А так как СгС || D^D, то DXD ± ЕС. Таким образом,
J ЕС ± AD, „ „ । .
1 m । n п => ЕСДАО^О) (по признаку перпендикулярно-
I ЛС _L L)jL)
сти прямой и плоскости).
Учитывая, ECllEjCj (в данной призме), получаем:
EjCj 1 (ADXD). А так как AM с (ADrD), (М = EyC^ D^), то
Е^ ± AM (по определению прямой, перпендикулярной плос-
кости). Это означает, что АМ= р(А; Е]СГ).
В прямоугольном AAAjM по теореме Пифагора находим:
am=Ja1a2+a1m2 = = —.
v 1 1 V I2J 2
л/13
Таким образом, р(А; EjCJ = .
в) Имеем: AD\\EF, EFWE^i => AD\\E1F1 (рис. 73). Учиты-
вая, К е AD, заключаем: р(А; -Ei-Fj) = р(Е; EXFX), где К =
BEnAD.
Из (BiBFJlKCjCB) (Почему?) и (С]СЕ) ± AD следует
(BjBF) 1 AD. А так как АОЦЕЕЦЕ^, то (BrBF) 1
((рис. 73). Получаем: E1Fl 1 (BjBE), FXK с (BrBF) ЕгРг ± FrK
(по определению прямой, перпендикулярной плоскости). Это
означает: FrK = р(К; EjEJ = р(А; Е^). Теперь в прямоуголь-
ном AEjEE находим:
FrK = yjFlF2+FKz =
V7
2
г) Пусть AD n BF = P; AN 1 BEj, NeBF\ (рис. 74), значит,
AN = p(A; BEJ. Найдем длину отрезка AN.
Имеем: AD 1 BF (рис. 74), AD 1 FXF (FXF 1 (ABC)) =>
=> AD 1 (BEjE). Тогда (AND) ± (BF}F) (по признаку перпенди-
кулярности двух плоскостей), следовательно, PN — проекция
отрезка AN на (BFXF), поэтому PN ± BFr (по теореме о трех пер-
пендикулярах). Это означает, что прямоугольные треугольни-
168
ки BFrF и BPN подобны, откуда: BFr : BP = F\F : PN —>
Рис. 74
Далее, в прямоугольном AAPN (AAPN = 90°, АР = 0,5) на-
ходим: AN =у/аР2 +PN2 — = • Таким образом,
р(А;ВВ1)=^.
4
Эту задачу можно решить иначе (значительно проще) сле-
дующим образом. Отрезок AN (AN 1 BFr, NeBFr) является
высотой треугольника ABFr со сторонами АВ = 1, AF{ — 42 ,
BF} = 2. Если обозначить F^ = х, то BN = 2 - х. Из соотноше-
ния FrA2 - FYN2 = АВ2 - BN2 или 2 - х2 = 1 - (2 - х)2 получаем:
х = -. Тогда AN2 = FrA2 - FrN2 = 2 - — = — => AN= ^- =
4 16 16 4
= p(A; BF,).
Ответ: а) л/з ; 6) ; B) 2/Z; rj .
Задачи для самостоятельного решения
Задача 5. ABCBE.F’A1B1C1.D1.E1.F’1 — правильная шести-
угольная призма, все ребра которой равны 2. Найдите рас-
стояние от: а) вершины А до прямой CD; б) вершины А до пря-
мой C]DX; в) вершины В до прямой CjEj; г) вершины В до
169
прямой АС{; д) вершины В до прямой Dfi; е) вершины В до
прямой AXD.
Задача 6. ABCDEFA^B^C^D^E^F^ — правильная шести-
угольная призма, все ребра которой равны 1. Найдите рас-
стояние от: а) вершины А до прямой С^; б) вершины В до
прямой С^Е^, в) вершины А до прямой CD; г) вершины В до
прямой ACt; д) вершины В до прямой АгС; е) вершины С до
прямой АСР
3. Расстояние от точки до плоскости. Задачи
Расстояние от точки М до плоскости a (Af ё а) равно
длине перпендикуляра МК, Кеа, проведенного из точки М к
плоскости а. При этом обозначают: р (М;а) = МК, МК 1 а.
При построении прямой, перпендикулярной данной плос-
кости, при доказательстве перпендикулярности данной (по-
строенной) прямой и данной (построенной) плоскости, исполь-
зуются: а) признак перпендикулярности прямой и плоскости;
б) теорема: «если прямая лежит в одной из двух взаимно пер-
пендикулярных плоскостей и перпендикулярна линии их пе-
ресечения, то эта прямая перпендикулярна другой плоскости»;
в) теорема: «если две плоскости пересекаются по прямой, пер-
пендикулярной третьей плоскости, то каждая из них перпен-
дикулярна этой третьей плоскости».
Задача 7. В правильной шестиугольной призме
ABCDEFA^BiCiD^F!, все ребра которой равны 1, найдите:
а) расстояние от вершины В до плоскости АСгС; б) от вершин Вг и
Ег до плоскости BF}D}; в) от вершин Е и Сх до плоскости E^AD.
Рис. 75
170
Решение, а) Обозначим: Р = BE о АС (рис. 75). Так как бо-
ковые ребра правильной призмы перпендикулярны плоскости
её основания, то АгА ± (АВС). Тогда AjA ± BE (BE с (АВС)) (по
определению прямой, перпендикулярной плоскости). Кроме
того, BE ± АС (рис. 70), причем Р — середина АС. Получаем:
BElAjA,
< BE ± АС, => BE ± (AAjC) (Почему?) => ВР = р(В; (АСХС)).
ВЕпАС = Р
Найдем длину отрезка ВР.
В равнобедренном ААВС имеем: ZABC = 120°, ВР — медиана
и высота => АВРС — прямоугольный, в котором ZBCP = 30° =>
=> ВР = 0,5ВС = 0,5 • 1= 0,5 (как катет, лежащий против угла
в 30°). Таким образом, р (В; (ACjC)) = 0,5.
б) Имеем: FDVBE (рис. 70), FDVFXF, ВгВ (рис. 76) =>
=> FD ± (BjBE) (по признаку перпендикулярности прямой и
плоскости). Из FD || FXDX и FD1. (В^ВЕ) следует: FlDl 1 (ВрВЕ) =>
=> (B-Fi-DJ 1 (BjBE) (по признаку перпендикулярности двух
плоскостей).
Обозначим: К = Т^-О^ВрЕр Тогда (BFJ)^ п (ВгВЕ) = ВК,
и вследствие (BEjUJ ± (В^ВЕ) приходим к выводу: перпенди-
куляр из точки Bj на (BF^-Dj) расположен в (ВгВЕ), поэтому
р(Вр (BFiDj)) = р(Вр ВК) = ВгР, где ВгР — высота прямо-
угольного \В}ВК.
1 1,5 ЗУ13
В Д ВВгК находим: ВгР =
Vb^ + B^2 >/1 + 2,25 13
Рис. 76
171
зЛз
13
Таким образом, р(Вх; (BFjDi)) =
Так как BlE1 n (BFjDJ = К,
ЕгК : ВГК =1:3, то р(£15 (BFM) =| р(В1? (BFM) = .
в) Имеем: AD ± СЕ, М = ADr.CE (рис. 77); AD ± DDl9
DDr || CCj => AD ± CCj, тогда AD ± (С^СЕ) (по признаку перпен-
дикулярности прямой и плоскости) => (EyAD) ± (С-£Е) (по
признаку перпендикулярности двух плоскостей). Это означа-
ет: прямая, проведённая через точку Е перпендикулярно
(BjAD), лежит в (С\СЕ), перпендикулярна прямой ЕгМ =
= (E.AD) n (CjCE) и пересекает её в некоторой точке К
(рис. 78). Тогда ЕК = р(Е; (EjAD)). Найдем длину ЕК.
1 ./q
В прямоугольном АЕуЕМ: ЕМ = — ЕС =-*—, EtE = 1. Зна-
2 2
„„ Е^-ЕМ 10,5^3 V21 m Л
чит, ЕК = 1 = . = -—. Таким образом,
Je^ + EM2 ^1 + (о,5^)2 7
p(E;(E1AD))=^.
Далее, перпендикуляр СХР из вершины Сх на (E^AD) распо-
ложен в (СХСЕ), параллелен ЕК (ЕК ± (ЕХАО)) и перпендику-
лярен прямой ЕГМ, при этом Р е Е^М.
Рис. 78
Так как ЕХМ || СН (в прямоугольнике ЕЕ}САС точки Н и М —
середины противоположных сторон), то точка Т = СгР п СН яв-
172
ляется серединой перпендикуляра СгР (по теореме Фалеса).
Учитывая, что ЕК = СгТ, приходим к выводу:
С.Р = 2 С\Т = 2 EK = . Значит, р(Сх; CE^AZ»)) = .
г» ч п к «ч Зл/13 713 . V21 2V21
Ответ: а) 0,5; б) —— и -—; в)----и------.
13 13 77
Навыки и умения нахождения расстояний от точки до
плоскости (до прямой) вырабатываются и закрепляются, ко-
гда эти расстояния можно «увидеть», конструктивно постро-
ить соответствующие «отрезки перпендикуляров». Динамика
выработки таких навыков успешно осуществляется с помо-
щью решения задач с использованием моделей и изображений
куба, правильного тетраэдра, других правильных многогран-
ников.
Задачи для самостоятельного решения
Задача 8. В правильной шестиугольной призме
ABCDEFA^^DyE^!, все ребра которой равны 2, найдите
расстояние от:
а) точки В до плоскости A^EF: б) точки В до плоскости АВХС:
в) точки В р,о плоскости BXDF: г) точки В до плоскости DjAC;
д) точки В до плоскости EXDF: е) точки В до плоскости E^AD:
ж) точки В до плоскости A.DF: 3) точки В до плоскости EVCF.
Задача 9. В правильной шестиугольной призме
ABCDEFAyB^CyD^E^F^, все ребра которой равны 1, найдите
расстояние от:
а) точки В до плоскости ApE-F; б) точки В до плоскости Af^C;
в) точки В до плоскости BiFD: г) точки А до плоскости A1BF;
д) точки В до плоскости EXFD\ е) точки В до плоскости A^C^D:
ж) точки С до плоскости FjAD; з) точки А до плоскости CXBD.
4. Расстояние между скрещивающимися прямыми.
Задачи
Расстояние между двумя скрещивающимися прямыми
равно длине их общего перпендикуляра. Однако при решении
многих задач построение этого перпендикуляра затрудни-
173
тельно, поэтому вычисление расстояния между двумя скре-
щивающимися прямыми осуществляется иначе, другими ме-
тодами.
Именно, если anb — данные скрещивающиеся прямые, то
возможен один из трех следующих методов нахождения рас-
стояния между ними.
а) Провести (или «увидеть» уже построенные) через пря-
мые а и Ь параллельные плоскости. Тогда расстояние от любой
точки одной из этих плоскостей до другой плоскости равно
расстоянию между прямыми а и Ь (метод параллельных
плоскостей).
б) Провести (или «увидеть» уже проведенную), например,
через прямую а плоскость а, параллельную прямой Ь. Тогда
расстояние от любой точки прямой b до плоскости а равно рас-
стоянию между прямыми а и Ь.
в) Провести плоскость а, перпендикулярную прямой а и пе-
ресекающую ее в некоторой точке А; затем построить прямую
bi — ортогональную проекцию прямой Ь на эту плоскость. То-
гда расстояние от точки А до прямой Ь, равно расстоянию меж-
ду прямыми а и Ь (рис. 79) (метод проектирования).
Рис. 79
Необходимо научиться применять все три метода. Полезно
решать одну и ту же задачу различными методами.
Рассмотрим решения следующих задач.
Задача 10. В правильной шестиугольной призме
ABCDEFAXBXCXDXEXFX, все ребра которой равны 1. 1) Найдите
расстояние между прямыми: а) ВХВ и ЕХС\ б) Л}А и ЕХС; в) BXF
и ЕХС; г) АХВ и AFX. 2) Какую наименьшую площадь может
174
иметь треугольник АгВР с основанием А}В, если Р — точка
прямой FjA?
Решение. 1). а) В данной призме имеем: ВС ± В}В (как
смежные стороны квадрата ВВХСХС (рис. 80); Е}Е ± (АВС) =>
ЕС — ортогональная проекция наклонной Е^С на плоскость
АВС. Так как ВС ± ЕС (рис. 77), то ВС ± ЕгС (по теореме о трёх
перпендикулярах). Получаем:
BC L BtB,
BCVE^C
ВС — общий пер-
пендикуляр прямых ВгВ и Е^С, значит, p(BjB; ЕгС) = ВС = 1.
б) Так как АгА cz (AjAD), ЕгС n (AlAD) = Р «£ AjA (рис. 80),
то прямые AjA и ВгС скрещиваются (по признаку скрещиваю-
щихся прямых).
Далее, АХА ± (ABC), AD cz (АВС) АгА ± AD (по определе-
нию прямой, перпендикулярной плоскости). Учитывая, что
ЕС — ортогональная проекция наклонной ЕГС на плоскость
АВС, при этом ЕС ± АЕ> и АГА п (АВС) = А, заключаем (по ме-
тоду проектирования): p(AjA; ЕгС) = р (А; ЕС) =АК = 1,5, где
K = ECoAD.
Рис. 80
в) Имеем: В^ЕрЕ и BF\\EC (рис. 80) => (E1CE)\\(B1BF)
(по признаку параллельности двух плоскостей). А так как
АЕ> ± ЕС, AD ± СгС, где CjCHAjA, то AD ± (ЕХСЕ). Тогда, при-
нимая во внимание (E1CE)\\(B1BF), получаем: AD ± (BjBF).
Учитывая ЕгС cz (ЕХСЕ) и BXF cz (BXBF), приходим к выводу:
p(EjC; BtF) = p^EiCE); (BrBF)) (no методу параллельных
175
плоскостей). А так как pCCEjCE); (B^BF)) — р(ЕС; BF) =
= ТК (рис. 80), то p(EjC; BXF) -ТК-1.
г) Имеем: А}В с (AjAB), AFt п (А}АВ) = А^АгВ (рис. 81) =>
=> прямые АуВ и AFj скрещиваются (по признаку скрещиваю-
щихся прямых). Найдем расстояние между этими прямыми.
Рис. 81
Замечаем (рис. 81): BC||AD; АС|| FD и АС = FD. Учитывая
FD = FXDX, получаем: АС = F1D1, =>
ACDlF1 — параллелограмм => AFr = CDr, AFl\\CD1. Тогда из
параллельностей ВС ||AD, AFJICPi следует: (B'1AZ))|j (AjBC)
(Почему1?).
Точки Т = AD n BF и Т} = A1Dl гу В^ являются середина-
ми противоположных сторон прямоугольника BBxF^F =>
=> FiTHTjB, FXT = TjB, где FXT = (BXBF) n (FXAD), T\B =
= (BjBF) n (AjBC).
Далее, имеем: BF 1 AB, BrB ± AD (рис. 81) => (BrBF) 1 AD
(no признаку перпендикулярности прямой и плоскости) =>
=> (B.BF) ± (F]AD) (по признаку перпендикулярности двух
плоскостей). Значит, прямая, проведенная через точку F пер-
пендикулярно (В]АВ), расположена в (BXBF) и пересекает па-
раллельные прямые FVT и TjB в некоторых точках соответст-
венно М и К.
Тогда FT = ТВ => FM = МК (по теореме Фалеса), при этом
МК = ((FjAD); (AjBC)). А так как: AjB с (А^ВС); FXA с (F^AD)-,
МК 1 (FjAD), то р ((FiAD); (AjBC)) = р ((FjA); (ArB)) = МК.
176
Рис. 82
Найдем длину отрезка МК.
В прямоугольном i\F}FT, с катетами F\F = 1 и FT = 0,5BF =
к F.F FT 105.V3
= 0,5 у 3, находим: FM = , .....- = -7====== =
712+(°-5^з)* 2
7
V 4
л/йТ
Таким образом, р ((AFJ; (AjB)) = МК = —— .
2) Теперь найдем наименьшую площадь, которую может
иметь треугольник А^ВР, где Р — точка прямой Ь\А.
Площадь треугольника АХВР с данным основанием АХВ и
вершиной Р е FrA принимает наименьшее значение при наи-
меньшем удалении вершины PqF^A от прямой АгВ, то есть
при условии равенства высоты треугольника АгВР кратчай-
шему расстоянию между скрещивающимися прямыми АгВ и
FiA, которое, в свою очередь, равно длине их общего перпен-
дикуляра.
Проведем РН\\МК, PH = МК (P^F^A, Н^А^В) (рис. 82).
Тогда PH ± АгВ => PH — наименьшая высота ЬА^ВР. Наи-
меньшая площадь этого треугольника равна:
Saa вр = -АХВРН = 1-72-^=
AA;BP 2 2 7 14
Ответ'. 1). а) 1; 6)1,5; в) 1; г) . 2) .
177
Задачи для самостоятельного решения
Задача 11. ABCDEFArBx(\DiEJ<\ — правильная шести-
угольная призма, все ребра которой равны 2. Найдите рас-
стояние между прямыми: а) ВВХ и Е^С", б) FrB и EF; в) А}В и
CiD; г) AiB nAF^, д)АрВ и ЕгР; е) BJi и DXA.
Задача 12. ABCDEFA^BiCiD^EyF^ — правильная шести-
угольная призма, все ребра которой равны 2. Какую наи-
меньшую площадь может иметь: а) ДАВ^, где К — точка' пря-
мой В(\; б) ABjCM, где М — точка прямой AjB; в) ДА^М, где
М — точка прямой АВХ; г) \ВСХК, где К — точка прямой DXC.
Задача 13. ABCDEFA^B^C^D^E^F^ — правильная шести-
угольная призма, все ребра которой равны 1. Найдите рас-
стояние между прямыми: а) ВВХ и ЕгС (рис. 83); б) Р\В и EF
(рис. 84); в) AjB и C\D (рис. 85); г) АгВ и AF} (рис. 86).
178
О НАИМЕНЬШИХ ЗНАЧЕНИЯХ ПЛОЩАДЕЙ
В ГЕОМЕТРИИ
Вопросы об общем перпендикуляре двух скрещивающихся
прямых, о кратчайшем расстоянии между ними относятся к од-
ному из наиболее сложных в изучении взаимного расположения
прямых и плоскостей в пространстве. Вместе с тем с вычислени-
ем расстояния между двумя скрещивающимися прямыми свя-
заны решения многих задач на нахождение наибольшего и наи-
меньших значений площадей и объемов геометрических фигур,
поэтому этот вопрос заслуживает серьёзного изучения на приме-
рах решения задач различного уровня сложности.
Расстояние между двумя скрещивающимися прямыми
равно длине их общего перпендикуляра. Однако построение
этого перпендикуляра при решении многих задач является
затруднительным. Поэтому необходимо научиться применять
различные методы вычисления расстояния между двумя
скрещивающимися прямыми. Полезно решать одну и ту же
задачу различными методами.
Задачи
Задача 14. ABCDEFA1B1C1D1E1F1 — правильная шести-
угольная призма, все ребра которой равны 1. Какую наи-
меньшую площадь может иметь треугольник, основанием ко-
торого является диагональ AD} этой призмы, а его третья
вершина К расположена на прямой, содержащей диагональ
AXF грани AA^F^F?
Комментарий. Прямые ADi и AtF (рис. 87) скрещиваются
(Почему?).
в А
Рис. 87
179
Треугольник ADXK с данным основанием AJDX будет обладать
наименьшей площадью, если он будет иметь наименьшую высо-
ту КР (P^ADj), проведённую из вершины К ^AXF. То есть длина
высоты КР треугольника ADXK должна быть равна кратчайше-
му расстоянию между скрещивающимися прямыми ADj и AXF.
Это, в свою очередь, означает, что отрезок КР должен быть об-
щим перпендикуляром скрещивающихся прямых ADj и AXF.
Таким образом, для решения данной задачи необходимо
найти кратчайшее расстояние между скрещивающимися
прямыми ADX и AXF или, если возможно, построить их общий
перпендикуляр скрещивающихся прямых, найти его длину и
искомую площадь треугольника ADXK.
К завершению решения этой задачи мы вернемся после
некоторой пропедевтики.
Решение этой задачи и аналогичных ей задач, в условиях
которых необходимо вычислять кратчайшее расстояние меж-
ду скрещивающимися прямыми, обычно вызывает опреде-
ленные затруднения. Эти затруднения могут быть успешно
преодолены, если предварительно решать аналогичные зада-
чи, первоначально используя многогранники более простого
«устройства», например, правильный тетраэдр, куб. Приме-
ром может служить решение следующей задачи.
Задача 15. Дан правильный тетраэдр РАВС с ребром, рав-
ным 12. Какую наименьшую площадь имеет треугольник, ос-
нованием которого служит ребро АВ, а его третья вершина
принадлежит прямой СР?
Решение. Прямая PC пересекает плоскость АВС в точке
С € АВ (рис. 88), значит, прямые PC и АВ скрещиваются
(по признаку скрещивающихся прямых).
р
Рис. 88
180
Заметим, что &АВН с данным основанием АВ и переменной
вершиной Н на прямой СР (рис. 88) будет иметь наименьшую
площадь, если будет наименьшей его высота НК, проведенная
из вершины Н е СР, то есть когда точка Н прямой СР будет
ближайшей к прямой АВ. Это возможно, когда длина отрезка
КН будет равна кратчайшему расстоянию р(РС; АВ) между
скрещивающимися прямыми СР и АВ — длине их общего
перпендикуляра.
Таким образом, для решения данной задачи необходимо
построить этот перпендикуляр и найти его длину.
Будем, логически рассуждая, строить этот перпендикуляр.
Пусть точки М и К — середины рёбер соответственно PC и
АВ данного тетраэдра РАВС', (АВМ) = а.
Так как все грани данного тетраэдра являются равными пра-
вильными треугольниками, то AM = ВМ, AM ± СР, ВМ ± СР
(как медианы и высоты равных правильных треугольников
соответственно АРС и ВРС). Тогда по признаку перпендику-
лярности прямой и плоскости имеем: СР ± а => СР (Почему?).
А так как точка К — середина АВ в равнобедренном ДАВМ, то
МК 1 АВ. Таким образом, отрезок МК — общий перпендику-
ляр скрещивающихся прямых PC я. АВ. Найдём его длину.
В правильном ААСР со стороной АС =12 имеем:
2 2
Тогда в прямоугольном ,\АМК по теореме Пифагора нахо-
дим: МК = ^АМ2 * * * * * В-АК2 = 7(6>/3)2-62 = 6^2 = р(РС; АВ). Зна-
чит, искомая (наименьшая) площадь ХАВМ равна:
S^abm= -АВ МК= -12-672= 36^2 (кв. ед.).
2 2
Ответ: 36\/2 кв. ед.
В некоторых случаях для нахождения расстояния между
скрещивающимися прямыми а иЬ удобно использовать ме-
тод проектирования.
Построим плоскость а, перпендикулярную прямой а, и ор-
тогонально спроектируем прямую Ъ на эту плоскость (рис. 89).
Пусть прямая Ьх — проекция прямой Ь на плоскость а;
181
Р — плоскость, проектирующая прямую Ь на плоскость а, т. е.
= р п а. Так как а 1 а и р ± а, то а || р. Это означает, что если
А — точка пересечения прямой а с плоскостью а, то расстоя-
ние от точки А до прямой Ь} равно расстоянию между прямой а
и параллельной ей плоскостью р, содержащей прямую Ь, зна-
чит, равно расстоянию между данными скрещивающимися
прямыми а и b: р(а; b) = р(А; bj.
Рис. 89
Замечание. В решении неявно используется метод проек-
тирования. Действительно, мы имеем: а 1 СР; АВ с (АВМ) =>
=> ортогональной проекцией прямой АВ на а является эта же
прямая АВ. А так как a СР = М, то р(РС; АВ) = р(М; АВ) =
= МК — высота треугольника АВМ.
Используя метод проектирования, рассмотрим решение
некоторых аналогичных задач, постепенно повышая уровень
их сложности.
Задача 16. а) Найдите наименьшую площадь треугольни-
ка, основанием которого является диагональ AjC куба A...Dl
(рис. 90), а его третья вершина расположена на прямой
ВС} с (BBiC), если ребро куба равно 12.
Рис. 90
182
Решение. Заметим, что прямые АгС и СгВ скрещиваются
(признак скрещивающихся прямых). Это означает, что наи-
меньшая площадь будет у такого треугольника
АгСН (Н е CjB), высота которого, проведенная из точки Н,
окажется равной расстоянию p(AjC; CjB), то есть равной дли-
не общего перпендикуляра прямых АГС и CjB. Найдем
р (AjC; CjB), пользуясь методом проектирования.
Докажем, что (BCjD) ± АХС.
В самом деле (рис. 91): AC ± BD (как диагонали грани
куба), АС — ортогональная проекция прямой АгС на
(АВС) => А}С ± BD (по теореме о трёх перпендикулярах). Ана-
логично доказывается, что А}С ± С\В. Тогда А^ ± (BCjD) (по
признаку перпендикулярности прямой и плоскости).
Рис. 91
Далее, прямые АгС и ОС\ (О = AC n BD) лежат в диагональ-
ном сечении AAjCjC и пересекаются. Пусть К = АгС п ОСг =
= AjC n (BCjD) (рис. 91). Получаем: КВ = КС} = KD (как проек-
ции равных наклонных — рёбер СВ, СС1? CD — на (ВС^)) =>
=> точка К — центроид правильного A BC^D.
Теперь спроектируем прямую ВСГ на (BCjD).
Так как ВС1с(ВС1В), то ортогональной проекцией прямой
ВСг на плоскость BCrD является эта же прямая BCj.
Таким образом, в соответствии с методом проектирования,
приходим к выводу:
р(ВС1;А1С) = р(ЛГ; BCJ.
183
Учитывая, что DH 1 ВС\ (DH — медиана правильного
ABCXD), заключаем: КН = р(А,С; CjB) = р(ВГ; BCJ, следова-
тельно, КН — общий перпендикуляр скрещивающихся пря-
мых А}С и СгВ, значит, Л АХСН с основанием АХС и высотой
НК является искомым с наименьшей площадью. Найдем эту
площадь.
Имеем: СХВ = 12 >/2 (как диагональ квадрата ВВХСХС со
стороной 12), поэтому в правильном Л BCXD находим:
DH = =12^'^ = бл/б,
2 2
тогда КН ~ - DH= ~-6 V6 -2 V6 .
3 3
Следовательно, SV1(.„ = —А,С-КН = — • 12-Уз-2>/б = 36>/2 .
2 2
Ответ: а) 36%/2 кв. ед.
Задача 16. б) Теперь в этом же кубе найдем наименьшую
площадь треугольника, стороной которого является диаго-
наль ВС] грани ВВ}СХС, а его третья вершина расположена на
прямой АВ,.
Рис. 92
Заметим, что треугольник ВСХК с основанием ВС, и вер-
шиной К е ABj (рис. 92) будет иметь наименьшую площадь
при наименьшей его высоте КТ, проведенной из вершины К.
184
Прямые АВ{ и ВСг скрещиваются (почему?), поэтому
третьей вершиной искомого треугольника с данной стороной
ВСг является точка прямой АВГ, ближайшая к прямой ВСХ.
Это означает, что высота искомого треугольника ВСГК с наи-
меньшей площадью должна быть равна длине общего перпен-
дикуляра скрещивающихся прямых АВг и ВСг.
Найдем длину этого перпендикуляра методом проектиро-
вания.
Имеем (рис. 93): В(\ ± В^С (как диагонали квадрата);
ВС ± CD (в квадрате ABCD), ВС — ортогональная проекция
В]С на (АВС), следовательно, ВСХ ± CD (по теореме о трех пер-
пендикулярах). Получили: BCi ± CD, ВСг ± ВГС, следователь-
но, BCi ± (B^D) (по признаку перпендикулярности прямой и
плоскости), при этом BCi ° (BiCD) = М.
Далее, ADjIlBCi, ВСг ± (BiCD) => AD} ± (BiCD). Ортого-
нальной проекцией прямой АВг на (BiCD) является прямая
BiP, где Р = ADX гу A^D = ADj n (BiCD). Поэтому на основании
метода проектирования имеем: p(ABi; ВСг) = р(М; BjP).
Теперь пусть МН ± ВГР, Н^ВГР, тогда МН — высота пря-
моугольного A PMBV (ZBTMP = 90°, так как РМ || АВ). По-
ВгМ МР 6^212 . к iAO
этому: МН = . 1 = . = 4<3 = p(ABj; ВСЛ
7в,М2 + МРг 7(б72)2+12г
185
Рис. 94
Таким образом, высота искомого треугольника с наи-
меньшей площадью равна 4\/з .
Так как вершина К искомого треугольника BCjK должна
быть расположена на прямой АВХ, ортогональной проекцией
которой на плоскость BXCD в направлении прямой является
прямая BjP (рис. 94), то К является точкой пересечения пря-
мой АВ{ и прямой, проходящей через точку Н параллельно
прямой ВСг (BCi ± (В^В)).
Найдем искомую площадь треугольника BCiK, для чего
проведем НК || ADf, К е АВг, КТ = НМ. Тогда получаем:
к = -ВС. КТ = - 12V2-4>/3= 24>/б.
j л 2 1 2
Ответ: б) 24л/б кв. ед.
На рис. 95 изображен куб ABCDAiBiCiDi, в котором
МН 1 BiP, где М = ВгС п ВСИ Р = D{A п АгВ. Докажите, что
МН = (АВ1;ВС1).
Рис. 95
186
При решении этих задач важным является нахождение
расстояния между прямыми, содержащими скрещивающиеся
диагонали ВСг и АВг смежных граней куба. Практика свиде-
тельствует, что векторный метод решения многих стереомет-
рических задач, в том числе на вычисление расстояний между
скрещивающимися прямыми, значительно проще их решения
средствами элементарной геометрии («чисто геометрически»).
Причиной тому служит следующий факт: решение стерео-
метрической задачи векторным методом можно успешно
реализовать, не прибегая к дополнительным геометрическим
построениям.
Рассмотрим решение задачи векторным методом.
Решение. Введем векторы: ВА=а, ВС -Ь, BBi=c
(рис. 96). Тройку (а ,Ь, с) некомпланарных векторов а, & и
с примем в качестве базиса и разложим векторы ABi, BCi по
векторам этого базиса.
Имеем: ABi = BBi -ВА = с -а ; BCi = BC + BBi = b + c .
Пусть отрезок МН — общий перпендикуляр прямых АВ! и
ВСг (М g BClf Н е ABi). Его длина равна расстоянию между
этими прямыми: р(АВг; ВСг) = |МН|.
Так как точка Н лежит на диагонали АВг, то векторы
АН и ABi коллинеарны, поэтому существует такое число х,
что АН — х- ABi = х-( с - а ).
187
Аналогично, в силу коллинеарности векторов ВМ и BCi,
существует такое число у, что ВМ = у BCi = y(b + c).
По правилу ломаной находим: МН = МВ + ВА + АН =
= - ВМ + ВА + АН = -у(Ь + с) + а + х-(с~а ) = (1 - х) а -
-yb + (x-y) с.
Значения х и у найдем из условия:
[MHVAB,, [mHI-AB,, [мНАВ^-О,
(МН1ВС, [мн±вс} ^[МН-ВС^О.
Учитывая, что базисные векторы а , b и с попарно взаим-
но перпендикулярны и длина каждого из них равна 12, име-
ем: а'Ъ = а-с = Ь-с =0; а2 = Ь2 = с2 =144 .
Получаем: МН • ABi = 0 <=> ((1 - х)а - у b + (х - у) с )•( с -
- а) = 0 <=> (х - 1)а2 + (х - у) с2 = 0 <=> 2х - у - 1 = 0 <=> 2х - у = 1;
МН BCi= 0 <=> ((1 - х)а - yb+ (х - у)с)-(Ь + с) = 0 <=>
-у Ь2 + (х - у) с2 = 0 <=> х - 2у = 0.
Таким образом, система векторных равенств (1) равно-
сильна системе уравнений
(2х — г/ = 1,
[х-2у = 0,
решением которой яв-
2 1
ляется: х = —, у = — .
3 3
Тогда: МН = fl-— la- — b+ (—- —)с = — a- — S+ — с .
I 3J 3 3 3 3 3 3
I / \ 2 / z \
Значит, p(ABj; ВС\) = I МН I = .(-а-—Ь + — с | = а f — + — + — ] =
1 1 \кЗ 3 3 ) N <9 9 9J
.12^=473.
3
Тогда получаем: 8^^= — BCt МН = — 12\/2-4>/3= 24>/б .
2 2
Замечание. Векторное решение этой задачи вносит опре-
делённую ясность в построение высоты искомого треугольни-
ка, следовательно, и в построение самого этого треугольника.
---------------------• —> 2
Действительно, из АН = х- АВ\ при х = — следует:
188
2 --•
AH =-ABr ^АН:АВ~ 2 : 3 -АН : НВХ = 2 : 1; из ВМ =
3
= yBCi при у = —следует: ВМ = —ВСг => ВМ : ВС\ = 1 : 3 =>
3 3
=> ВМ: BCi = 1 : 2.
Таким образом, концы отрезка МН (рис. 97), являющегося
общим перпендикуляром скрещивающихся диагоналей ABt и
ВС\ смежных граней куба, делят эти диагонали в отношениях
АН : НВ} = 2 : 1 и ВМ : МСГ = 1:2. При этом отрезок МН
служит высотой искомого треугольника ВСгН с наименьшей
площадью.
После такой «пропедевтики» целесообразно рассматривать
различные методы решения аналогичных задач, используя
многогранники более сложного устройства, например, пра-
вильную шестиугольную призму. При этом расстояние между
двумя скрещивающимися прямыми находят методом парал-
лельных плоскостей, вытекающим из утверждения: расстоя-
ние между двумя скрещивающимися прямыми равно рас-
стоянию между параллельными плоскостями, проходящими
через эти прямые ([1], с. 84). Рассмотрим, например, решение
такой задачи.
Задача 17. АВСВЕВА1В1С1В1.Е1В1 (рис. 98) — правильная шес-
тиугольная призма, все ребра которой равны 12. Найдите наи-
меньшую площадь треугольника АВХМ с основанием АВ15 если
вершина М этого треугольника расположена на прямой ВСР
189
Рис. 98
Решение. Прямые АВ1 и BCj скрещиваются (по признаку
скрещивающихся прямых). Так как ААВХМ должен иметь
наименьшую площадь, то должна быть наименьшей его высо-
та, проведенная из вершины М на прямую АВХ, то есть точка
М должна быть ближайшей к прямой АВХ. Это означает, что
длина высоты искомого треугольника, проведенная из вер-
шины М, должна быть равна длине общего перпендикуляра
скрещивающихся прямых АВ! и ВСХ. Найдем длину этого пер-
пендикуляра.
Обозначим: О = AD n CF; Ох = AjDj п С^; Н = АС п ВО;
Н1=А1С1г\В1О1.
В прямом параллелепипеде АВСОА1В1С1О1, все ребра кото-
рого равны 12, а его основанием является ромб ОАВС, имеем:
АОХ || ВСХ, АВХ || ОСХ (как диагонали противоположных гра-
ней параллелепипеда) => (CjOBJlKAOpBj) (по признаку парал-
лельности плоскостей). Тогда из АВ1<^(АО1В), ВСХ<^(ВОСХ)
следует: p(ABt; ВСХ) = р((АОхВ); (ВОСХ)).
Найдем это расстояние.
Так как боковые грани этого параллелепипеда — равные
квадраты, то треугольники AOjBj и СХОВ являются равнобед-
ренными и равны (Почему?). Поэтому АНХ ± ВХОХ, СХН ± ОВ.
Учитывая ОВ ± АС, приходим к выводу: О В ± (АХАС)
(по признаку перпендикулярности прямой и плоскости), от-
куда (AjAC) ± (CjOB) (по признаку перпендикулярности двух
плоскостей). А так как, кроме того, (СХОВ) || (AOjBi),
190
то (АХАС) ± (AC^BJ. Это означает, что прямая, проведенная
через точку А! перпендикулярно плоскостям AOjBj и САОВ,
расположена в плоскости AtAC и пересекает плоскости AC^Bj
и С]ОВ в точках К и Т, принадлежащих прямым соответст-
венно АНг и СгН. Тогда р(АВх; BCJ = р( (АО^); (СХОВ)) = КТ.
Так как AHX|| СХН и АГНХ = HiCu то АгК = КТ (по теореме
Фалеса). Таким образом, р(АВх; ВСХ) = АХК. Найдем длину АгК.
В правильном ДАОВ со стороной, равной 12, имеем:
АН = бТз = АХНХ.
2 2
В прямоугольном ААА1Н1 с катетами АХА =12, А}Н} = бТз
находим его высоту АгК:
АК= А1А А1Н1 = 12-бТз _ 12 бТз = 12721
1 7A1A2+A1H12 ^^^(бУз)2 7144 + 108 7
Таким образом, р(АВх; ВСХ) = 12721
Расстояние между скрещивающимися прямыми АВг и BCi
равно длине их общего перпендикуляра, который служит вы-
сотой искомого треугольника АВ гМ с наименьшей площадью.
Пусть отрезок МР — общий перпендикуляр скрещиваю-
щихся прямых АВХ и ВСХ (МеВСх, Рё ABJ.
1 9 /91
Тогда МР = —-— — высота искомого ЛАВ}М с наимень-
шей площадью, которая равна:
S„, 1 АВ.-МР-1.1272.1^1=^.
2 1 2 7 7
~ 72742
Ответ: —-—кв. ед.
7
Полезно решать стереометрические задачи и координат-
ным методом, который, наряду с векторным, является мощ-
ным аппаратом изучения пространственной геометрии, а его
использование при решении стереометрических задач не тре-
бует дополнительных геометрических построений, в резуль-
тате чего процесс решения упрощается.
Рассмотрим решение данной задачи координатным мето-
дом.
191
Введем прямоугольную декартову систему координат Oxyz
так, чтобы вершины А, В, С, А1г Вг данной призмы имели ко-
ординаты (рис. 99):
А(бТз ; -6; 0), В(б/3 ; 6; 0), С(0; 12; 0), А^б^З ; -6; 12),
Bt(6>/3 ; 6; 12).
Используем следующий факт: расстояние между двумя
скрещивающимися прямыми равно расстоянию от любой
точки одной прямой до плоскости, проходящей через вторую
прямую параллельно первой прямой.
Рис. 99
Для нахождения искомого расстояния составим уравнение
плоскости (обозначим ее а), проходящей через прямую А^В
параллельно прямой ВгС.
В качестве вектора нормали плоскости а примем век-
тор п(а;Ь;с), перпендикулярный направляющим векторам
CBi(6\/3 ; -6; 12) и AjB(0; 12; -12) прямых В,С и АХВ. Най-
дем координаты вектора п, пользуясь условием перпендику-
лярности двух векторов в координатной форме.
Для упрощения вычислений будем использовать, не нару-
шая общности рассуждений, вместо векторов СВ} (б-Тз ; -6; 12)
и AjB(0; 12; -12) им коллинеарные векторы соответственно
р(л/3;-1; 2) и <7(0; 1;—1). Тогда имеем:
192
nip, |n-p = O, fV3a-& + 2c = 0, [л/За-& + 2с = 0,
nlq [n-g = O |b-c = O [b = c
\c = -yf3a,
|b = c.
Полагая a = ->/з, получаем: b = с = 3. Таким образом,
n (- л/з ; 3; 3). Тогда плоскость а = (В; п) имеет уравнение:
->/3 (х - 6V3) + 3 (z/-6) + 3(z-0) = 0o-V3x + 3i/ + 32 = 0.
|-л/30 + 312 + 3 о|
Теперь находим: р(А,В;В.С) = р(С;а) = ----------, ------ =
х/3 + 9 + 9
= 36 = 12л/21
л/21 7
Учитывая, что длина вектора АХВ равна длине изобра-
жающего его отрезка, находим:
pv?| =л/о2 +122 + (-12)2 =12л/2.
Получаем искомую (наименьшую) площадь треугольника
AjBM:
р(А1В;В,С) -1.1272-1^ - .
72>/42
Ответ: ------
7
кв.
ед.
После такой пропедевтики вернемся к задаче 14 на с. 179и
рассмотрим её решение сначала методом проектирования.
Найдем расстояние между прямыми AD^ nAxF.
Пусть: К = AjF n AFj (AFjC) = а.
Рис. 100
193
Имеем: AjFIAFj (как диагонали квадрата) (рис. 100);
AF ± АС (основание призмы — правильный шестиугольник)
(рис. 101) => AXF ± АС (по теореме о трех перпендикулярах).
Получаем: AXF 1 AFlf AXF 1 AC => AXF 1 а (по признаку пер-
пендикулярности прямой и плоскости).
Таким образом, в качестве плоскости, перпендикулярной
прямой AXF, выберем плоскость а, которая пересекает эту
прямую в точке К.
Прямая ADi лежит в плоскости а, поэтому ее проекцией на
а является эта же прямая ADp Значит, p(AD1; AtF) = ADJ.
Пусть: КР ± ADp P^ADlf тогда р(Х"; ADJ = КР. Найдем
длину КР.
Если FrM — высота прямоугольного AAFJ^ (AFt ± F^J,
то FXM || КР, откуда КР — средняя треугольника AAfFp Зна-
чит, КР =- FtM. В прямоугольном AAFiDj с катетами FxDi -
2
= 12 73и AFi = 12\2 и гипотенузой ADX • j D}F2 + AF2 =
= 7U2\/3)2 +(12x/2)2 =12^5 находим: «
ADt
= 12^3 12V2 = 12ч/30
12^5 5
Puc. 102
Тогда KP = . Таким образом, p(AZ>1; AXF) = ,
5 5
194
Поэтому наименьшая площадь треугольника с основанием
AD} и вершиной К на прямой АгР равна площади треугольни-
ка А1)ХК (рис. 102), то есть равна:
S^AD К= -AD.KP = -- 12^5 = 36\/б.
2 2 5
Теперь рассмотрим решение этой задачи координатным
методом.
Решение, а) Найдите расстояние между прямыми AD j и AXF.
Введем систему координат Oxyz так, чтобы вершины А, В,
F, Ar, D данной призмы имели координаты: вершины В, С, Вг и
Aj имеют координаты: А(6\/з ; 6; 0), В(6л/з ; -6; 0), F(0; 12; 0),
Aj( бл/3 ; 6; 12), В(-6л/з ; -6; 0) (рис. 103).
Рис. 103
Для нахождения искомого расстояния р(АОр ArF) соста-
вим уравнение плоскости 0, проходящей через прямую АгГ
параллельно прямой ADp
Во введенной системе координат точка и вектор DjА
имеют координаты: В^-бл/з ;-6; 12) и 2)^(1273; 12;-12).
В качестве вектора нормали плоскости 0 примем вектор
п(а;Ь;с), перпендикулярный направляющим векторам
FAX (6\3 ; -6; 12) и DXA (12>/з ; 12; -12) прямыхAYF иADX.
195
Для упрощения вычислений, не нарушая общности рассуж-
дений, будем использовать вместо векторов FA{ (6ч/3 ; -6; 12) и
DXA (12л/з ; 12; -12) им коллинеарные векторы соответствен-
но р(у/3;-1; 2) и q(y/3; 1;—1). Найдем координаты вектора п .
ч/За-д+2с = 0,
\у/За + Ь-с = 0
с - -2>/За,
b - -Зч/За.
тт п 1Р, пр = О,
Имеем: < _ f. .
[п±д [n-g = O
[ч/За-& + 2с = О, Гс = -2ч/3а,
2&-Зс = О |& = 1,5с.
Полагая а = ч/з , получаем: b = -9, с = -6. Таким образом,
п (ч/З ; -9; -6), поэтому плоскость (3, проходящая через точку
F(0; 12; 0), имеет уравнение:
ч/з (х - 0) - 9(г/ - 12) - 6(2 - 0) = ч/з х - 9у - 6z + 108 = 0.
Теперь находим: р(А1В;В1С) = р(А;а) =
|ч/3 • бч/З — 9-6 — 6-0 + 10з| у2 6ч/30
ч/З + 81 + Зб 7120 5
Находим искомую площадь треугольника ADrK:
S^ad -•|aa|-p(A1F;AD1) = -- 12^5 =зб7б
Ответ: 36 ч/б кв. ед.
Задачи для самостоятельного решения
Задача 18. Расстояние между скрещивающимися диаго-
налями смежных граней куба равно т. Найдите длину ребра
этого куба.
Задача 19. Расстояние между скрещивающимися диаго-
налями АВ} и BCY двух смежных граней куба A...Dl равно 8.
Какую наименьшую площадь может иметь треугольник
АВгМ, где М — точка прямой ВСг?
Задача 20. АВСВЕЕА^С^Е^ — правильная шести-
угольная призма, все ребра которой равны 7. Какую наи-
меньшую площадь может иметь треугольник AFгМ, где М —
точка прямой AjB?
196
КОМБИНАЦИИ ФИГУР ВРАЩЕНИЯ
И МНОГОГРАННИКОВ
При решении задач на комбинации сферы и многогранни-
ка необходимо, прежде всего, вырабатывать умение анализи-
ровать геометрическую ситуацию, в которой находятся дан-
ные многогранник и сфера. При этом решение задачи должно
начинаться с рисунка, на котором необходимо верно, нагляд-
но и лаконично изобразить фигуры, заданные её условием.
Далее, после установления логических взаимосвязей между
данными и искомыми элементами изображенных фигур ста-
новится возможным производить аргументированные обосно-
вания возникающих умозаключений и необходимые вычис-
лительные операции, безошибочное завершение которых
приводит к нужному и верному ответу к задаче.
Рассмотрим, например, решение следующей задачи, в
процессе которого сочетаются логические обоснования утвер-
ждений синтетического (геометрического) характера, аргу-
ментированные построения необходимых геометрических фи-
гур и мотивированные вычислительные операции.
Задача 21. Дан куб ABCDA1B1C1D1 с ребром 1. Найдите ради-
ус сферы, проходящей через три его вершины одной грани, если
центр этой сферы лежит на сфере, вписанной в данный куб.
Указание. Пусть — сфера, вписанная в данный куб;
со2 — сфера с центром на сфере о\, проходящая через его
вершины А, В и С. Найдем радиус R сферы <в2.
Обозначим: О — центр данного куба, К — центр его грани
ABCD (рис. 104).
197
Сфера со2 проходит через вершины А, В и С, поэтому она
проходит и через вершину D (почему?), значит, ее центр М
принадлежит прямой ОК (почему?). А так как центр сферы со2,
кроме того, лежит на сфере Юр то искомый центр сферы со2
является точкой пересечения прямой ОК и сферы а>г Таких
точек две — точка К и точка Р — центр грани А&С^.
Это означает, что одна из сфер имеет своим центром точку
Р, а ее радиус равен РВ = \РКг +АК2 = Jl2+(^-)2 = 0,5\/б .
у 2
Вторая сфера имеет своим центром точку К, а ее радиус равен
КА = 0,5>/2 .
Ответ: 0,5\/2 или 0,5>/б .
Сочетание графической логики и логики последователь-
ных аргументаций, основанных на свойствах геометрических
фигур, нередко позволяет находить оригинальные пути реше-
ния достаточно сложных стереометрических задач. Во многих
случаях необходимо произвести подробный анализ «картин-
ки», на которой верно, наглядно и просто (по условию данной
задачи) изображены геометрические фигуры, в результате че-
го «обнаруживается» достаточно красивое её решение с ми-
нимальными вычислительными операциями.
Рассмотрим, к примеру, решение следующей задачи.
Задача 22. Ромб со стороной а и острым углом в 30° враща-
ется вокруг одной из своих сторон. Найдите объем тела вра-
щения.
Решение. Пусть ромб ABCD с острым углом в 30° при вер-
шине В вращается вокруг прямой т, содержащей сторону АВ
(рис. 105). Тогда сторона CD данного ромба параллельна оси
вращения и при этом вращении заполняет боковую поверх-
ность цилиндра, образующая которого равна длине стороны
ромба и равна а.
Вершина С ромба вращается по окружности со, располо-
женной в плоскости, перпендикулярной оси вращения т; цен-
тром этой окружности является точка Н = т п ССР где точка
— образ точки С при повороте вокруг оси т на угол 180° —
диаметрально противоположна точке С этой окружности.
198
Так как плоскость окружности со перпендикулярна оси т
вращения, то Z.CHB — прямой (почему?). Тогда в прямо-
угольном ДВСН, в котором Z.CHB = 30°, имеем: СН = 0,5ВС =
= — (как катет, лежащий против угла в 30°). Это означает,
2
а
что радиус окружности со равен — .
2
Так как CD\\m, то совершенно аналогичная картина на-
блюдается при вращении вершины D вокруг оси т: точка D
описывает окружность cOj с центром К и радиусом — , где К —
2
точка пересечения оси т с плоскостью вращения точки D.
Таким образом, при вращении ромба ABCD вокруг прямой
т имеем: сторона ВС описывает боковую поверхность конуса
К1г радиус СН которого равен —; диагональ АС — боковую
2
поверхность конуса К2, радиус которого также равен — ; сто-
2
рона CD — боковую поверхность цилиндра К3 радиуса — ; сто-
2
рона AD — боковую поверхность конуса Kt, радиус DK кото-
вс
рого равен —.
199
На рис. 105 видно, что ромб ABCD представляет собой объ-
единение непересекающихся треугольников: ЬВСН, ААСН,
&ACD. При вращении вокруг прямой т имеем: ЛВСН описы-
вает конус К4 радиуса СН = — и высотой ВН; ААСН описыва-
2
ет конус К2 радиуса СН = — и высотой АН; AACD описывает
2
фигуру, которая является разностью цилиндра К3 и объеди-
нения конусов К2 и К4. Значит, объём тела, которое получает-
ся при вращении ромба ABCD, равен сумме объёмов конуса
и объема цилиндра К3, из которого удалены конусы К2 и К4.
Но конусы Кх и К4 равны, поэтому равны и их объёмы. Это оз-
начает, что искомый объем тела, полученного при вращении
ромба ABCD вокруг прямой т, равен объёму цилиндра К3. Так
а
как радиус основания этого цилиндра равен —, а его высо-
2
з
та — а, то его объём равен л а = -^—(куб. ед.).
з
Ответ'. куб. ед.
4
При решении геометрических задач осуществление алгеб-
раических операций реализуется на основе логики вычислений:
при вычислении длин, расстояний, площадей и объёмов геомет-
рических фигур возникает необходимость в решении различных
уравнений и их систем. При этом во многих случаях бывает
удобным введение буквенных обозначений, выражающих дли-
ны: сторон многоугольника и рёбер многогранника, высот тре-
угольника и многогранника, радиусов окружностей и сфер, о
которых идёт речь в условии задачи. Умение и навык введения
таких буквенных обозначений и оперирования с ними выраба-
тываются при решении достаточно большого количества задач
различного уровня сложности и различной тематики.
Рассмотрим, например, решение следующей интересной
задачи.
Задача 23. В основании тетраэдра ABCD лежит треуголь-
ник АВС со сторонами АВ = 9, АС = 7 и ВС = 8. Вершины тет-
раэдра являются центрами сфер. Сферы с центрами в верши-
200
нах основания тетраэдра касаются друг друга внешним обра-
зом, а сфера с центром в точке D касается всех остальных сфер
внутренним образом и её радиус равен 20. Найдите длины бо-
ковых рёбер тетраэдра.
Решение. Обозначим: г2, г3 — радиусы сфер соответст-
венно с центрами А, В, С, попарно касающихся внешним об-
разом; R — радиус сферы с центром в вершине D, касающейся
внешним образом сфер с центрами А, В и С; Е — точка внеш-
него касания сфер с центрами А и В; Н — точка внешнего ка-
сания сфер с центрами В и С; М — точка внешнего касания
сфер с центрами А и В; Alf Вг, С} — точка внутреннего касания
сферы с центром D со сферами, центрами которых являются
соответственно точки А, В и С (рис. 106).
Пусть: AD = a, BD = b, CD = с. Так как АС = гг-1- г3 ВС = г2 +
+ г3 АВ = гх+ г2, то имеем:
г1+г3=7,
< г2 + г3=8, (1)
Tj + г2 =9.
Так как AjD = BXD = CrD = R = 20, то получаем (рис. 106):
а + Г; = 20, т\ = 20 - а,
- & + г2 = 20, => г2=20-Ь, (2)
с + г3=20 г3=20-с.
201
В системе уравнений (1) вместо г1? г2, г3 запишем их выра-
жения через а , b и с из (2). Получаем:
20-а + 20-с = 7, а+с = 33,
20-Ь + 20-с = 8, => <Ь + с = 32, (3)
20-а + 20-& = 9, а + Ь = 31.
После сложения уравнений системы (3) получаем:
а 4- Ь + с = 48. (4)
Тогда, решая систему уравнений
а + с = 33,
Ь + с = 32,
а + Ь = 31,
а + Ь + с = 48,
находим: а = 16, b = 15, с = 17. Таким образом, боковые
ребра тетраэдра имеют следующие длины: AD =16; BD = 15;
CD= 17.
Ответ: AD = 16; BD = 15; CD = 17.
Чертеж, на котором изображена комбинация нескольких
фигур, может оказаться достаточно сложным, в результате
чего затрудняется процесс решения задачи. В таком случае
полезно пользоваться выносными рисунками, на которых
изображают отдельные фрагменты исходного «сборочного»
чертежа.
Рассмотрим решение следующей задачи на комбинацию,
например, цилиндра и тетраэдра.
Задача 24. Внутри цилиндра расположен правильный тет-
раэдр РАВС, скрещивающиеся ребра АР и ВС которого явля-
ются диаметрами соответственно верхнего и нижнего основа-
ний цилиндра. Найдите объем цилиндра, если расстояние
между осью цилиндра и скрещивающимся с ней ребром АВ
равно 8 см.
Решение. Сначала докажем, что скрещивающиеся ребра
правильного тетраэдра взаимно перпендикулярны. (Полезно
сделать отдельный рисунок с тетраэдром.)
Пусть точки К и Т — середины ребер соответственно АВ и
PC правильного тетраэдра РАВС (рис. 107). Тогда из перпен-
дикулярностей AT ± PC и ВТ ± PC (АТ и ВТ — медианы пра-
вильных треугольников АРС и ВРС) следует PC ± (АВТ) (по
признаку перпендикулярности прямой и плоскости), откуда:
202
PC 1 AB (по определению прямой, перпендикулярной плос-
кости).
Рис. 107
Рис. 108
Аналогично, можно доказать, что АР ± ВС иАС ± РВ.
Таким образом, скрещивающиеся (противоположные) реб-
ра АР и ВС правильного тетраэдра РАВС взаимно перпендику-
лярны и являются диаметрами соответственно верхнего и
нижнего оснований цилиндра. Но перпендикулярные диамет-
ры окружности обладают тем замечательным свойством, что
каждый из них делит хорды, параллельные другому, пополам.
Такие диаметры окружности называют её сопряжёнными диа-
метрами. Так их называют и в эллипсе — параллельной про-
екции окружности. А так как при параллельном проектирова-
нии параллельные отрезки изображаются параллельными
отрезками, а середина данного отрезка проектируется в сере-
дину его проекции, то для изображения в эллипсе перпендику-
лярных (сопряжённых) диаметров АВ' и CD' (рис. 108, а) ок-
ружности поступают следующим образом. Проводят
произвольный диаметр АВ эллипса с центром О (рис. 108, б) и
любую его хорду МАЦАВ. Тогда хорда CD эллипса, проходя-
щая через его центр О и середину хорды АВ, изображает диа-
метр этого эллипса, сопряженный диаметру АВ. Таким обра-
зом, диаметры АВ и CD эллипса изображают перпендикулярные
диаметры А'В' и CD' окружности.
Сказанное означает, что если ребро АР правильного тетра-
эдра РАВС — диаметр верхнего основания цилиндра — выбра-
203
ли произвольно, то положение ребра ВС — диаметра его ниж-
него основания — однозначно определено: диаметр ВС имеет
направление, сопряженное («перпендикулярное») направлению
диаметра АР (рис. 108, б) сопряженные диаметры АВ и CD эл-
липса изображают взаимно перпендикулярные диаметры А’В'
и CD' окружности — оригинала (рис. 108, а).
Рис. 109
Далее, так как АТ = ВТ (как медианы равных правильных
треугольников АРС и ВРС, рис. 107, рис. 109), то ТК ± АВ
(как медиана равнобедренного АВТ). Аналогично, КТ ± PC
(как медиана равнобедренного АКР С). Это означает, что отре-
зок КТ — общий серединный перпендикуляр скрещивающих-
ся ребер АВ и СР правильного тетраэдра РАВС.
Обозначим: точки Н и М — середины ребер АР и ВС
(рис. 109). Так как эти ребра являются диаметрами основа-
ний, то точки Н и М — центры этих оснований, значит, отре-
зок МН является, с одной стороны, общим серединным пер-
пендикуляром отрезков АР и ВС — противоположных рёбер
правильного тетраэдра РАВС, с другой стороны, высотой ци-
линдра. Поэтому длина отрезка МН, равная расстоянию меж-
ду скрещивающимися ребрами АР и ВС тетраэдра, равна вы-
соте данного цилиндра.
Далее, можно доказать, что четырехугольник КНТМ —
параллелограмм (рис. 109). А так как его стороны параллель-
204
ны (почему?) взаимно перпендикулярным ребрам АС и ВР
тетраэдра и равны их половинам (почему?), то четырехуголь-
ник КНТМ — квадрат. Значит, МН = КТ, МН ± КТ, при
этом ОК = ОТ = ОН = ОМ, где О = МН о КТ.
Теперь через скрещивающиеся прямые АВ и PC проведем
параллельные плоскости соответственно а и 0, а через точку
О — плоскость у серединных перпендикуляров отрезка КТ,
которая содержит прямую МН (МН ± КТ)\ у 1 КТ. Так как
отрезок КТ — общий серединный перпендикуляр скрещи-
вающихся ребер АВ и PC, то этот отрезок перпендикулярен
плоскостям а, 0, поэтому а||Р||у. Тогда расстояние между
АВ и PC равно расстоянию между а и 0 и равно длине КТ, а
длина отрезка ОК равна расстоянию между АВ и МН, значит,
ОК = 8. Тогда МН = КТ = 2ОК = 16.
Далее можно приступить к нахождению длины радиуса R
основания цилиндра.
Пусть АВ = ВС = СР = т. Тогда: СТ = —, СК = (в пра-
2 2
вильном АВС). В прямоугольном КТС (рис. 87, рис. 89, ЛКТС —
прямой): КТ = -JCK2-СТ2
2
Из КТ = 16 получаем: m = 16 —> т = 16 \/2 . Таким образом,
2
ВС = 16 л/2 . Значит, R = 0,5ВС = 0,5 • 16 л/2 = 8^2 . Теперь нахо-
дим объем цилиндра: Уцил = п R2h =п • R2 • МН = л (8 V2 )216 =
= 2048 л (куб. ед.).
Ответ: 2048 л куб. ед.
Задача 25. Основанием треугольной пирамиды РАВС яв-
ляется равносторонний треугольник АВС, сторона которого
равна 12. Грань РАВ — равнобедренный треугольник, в кото-
ром РА = РВ = 10. Найдите площадь сферы, описанной около
этой пирамиды, если высота пирамиды пересекает её основа-
ние и равна 4.
Решение. Пусть РК — высота данной пирамиды, точка
Н — середина ребра АВ. Так как РА = РВ, то АК = ВК (как
205
проекции равных наклонных). Значит, точка К — основание
высоты РК — принадлежит серединному перпендикуляру от-
резка АВ, то есть — медиане СН правильного АВС (рис. 110).
Из РК 1 (АВС) по признаку перпендикулярности двух плоско-
стей следует (СРН) ± (АВС).
Рис. 110
Обозначим: со — окружность, по которой плоскость АВС
основания пирамиды РАВС пересекает описанную около неё
сферу; точка Е — центр этой окружности. Так как прямая т,
проходящая через центр О сферы и центр Е окружности <о,
перпендикулярна плоскости АВС, Е&СН = (СРН) п (АВС),
при этом (СРН) ± (АВС), то плоскость СРН проходит через
центр О сферы (является её диаметральной плоскостью) и пе-
ресекает эту сферу по окружности которая проходит через
точки Р, С, М = СН п со, а ее радиус равен радиусу сферы.
Таким образом, радиус R сферы, описанной около пирами-
ды РАВС, равен радиусу окружности со,, описанной около
\СРМ. По теореме синусов в треугольнике СРМ имеем:
РМ
R ----------. Найдем длину РМ и sincp, где ср = ZMCP.
2 sin АМСР
В правильном ДАВС: СН = = бл/з; ВН =
2 2
АВ
= --- = 6. По теореме Пифагора в прямоугольных треуголь-
2
никах НВР и НРК соответственно имеем: HP = \[ВР2 - ВН2 =
206
= V102-62 = 8; НК = у1нР2-РК2 = л/82-42 = 4>/з . Тогда СК =
= СН - НК = 6>/3 - 4>/з = 2л/3 .
Теперь в прямоугольном СР К получаем: PC = \]РК2 +СК2 =
- j42+(2j3)2 - 2; sin<p - - -fi. - А .
Так как правильный &АВС вписан в окружность со, то КМ =
= СН = 6>/3 . Тогда в прямоугольном МРК: РМ = \1РК2 +МК2 =
= д/42 + (6д/3)2 = 2>/31. Наконец, в АСРМ по теореме синусов
D РМ 2^31 /217 Q о л „г
получаем: R = —— = v . Значит, S сфе = 4 л Rr =
2sin<p 2«— 2
’>/7
Г /91 7 Y
= 4л-Р^- = 217л (кв. ед.).
I 2 J
Ответ: 217 л кв. ед.
При решении задачи, в которой даны две, три и более по-
парно касающиеся сферы, бывает удобно воспользоваться се-
чением этих сфер плоскостью, проходящей через их центры
(диаметральной плоскостью). Тогда данная задача сводится к
планиметрической задаче на взаимное расположение двух,
трех и более попарно касающихся окружностей.
Иногда бывает удобно «привлечь на помощь» треугольник
или тетраэдр с вершинами в центрах соответственно трех или
четырех попарно касающихся данных сфер; при этом стороны
треугольника и ребра тетраэдра равны суммам радиусов дан-
ных сфер.
Рассмотрим, например, решение следующей задачи.
Задача 26. Четыре равные сферы радиуса 8 попарно каса-
ются друг друга. Найдите радиус сферы, которая касается
всех этих сфер.
Решение. Пусть центрами данных сфер являются точки Р,
А, В и С, а центром сферы, касающейся всех этих сфер, слу-
жит точка М.
Точка касания двух сфер принадлежит линии их центров,
и расстояние между центрами данных сфер равно сумме длин
207
их радиусов (сферы касаются внешним образом). Поэтому:
а) центры Р, А, В и С сфер являются вершинами правильного
тетраэдра с ребром, равным 16; б) МА = МВ = МС = МР = 8 + R
(R — искомый радиус сферы, касающейся данных сфер), то
есть точка М равноудалена от всех вершин данного правиль-
ного тетраэдра.
Известно, что в правильном тетраэдре РАВС точкой, рав-
ноудаленной от всех его вершин, является центроид этого тет-
раэдра — точка, в которой пересекаются все его высоты и де-
лятся ею в отношении 3:1, считая от вершин. Это означает,
что точка М совпадает с центроидом тетраэдра РАВС, причем
3
РМ = — ОР, где О — центроид правильного треугольника АВС.
4
Рис. 111
На рис. 111 изображено сечение данной комбинации тел
плоскостью АРН (Н — середина ВС), где (АРН) ± ВС (почему?),
(АРН) ± (АВС) (почему?). Сечением тетраэдра этой плоскостью
является Д АРН, а сечением двух данных сфер с центрами А и
Р — две равные касающиеся окружности (ot и ю2 с теми же
центрами и радиусом 8.
Так как центр М сферы, касающейся всех четырех данных
сфер, принадлежит секущей плоскости АРН, то ее сечением
208
является окружность со3 радиуса R, касающаяся окружностей
(Oj и со2. Найдем Я.
АвУз
2
В правильном Л АВС со стороной 16 имеем: АН =
= -УЬ/З = 8>/з ; АО = —АН = — 8л/з = ДД. Тогда в прямо-
2 3 3 Уз
угольном А АОР (ОР ± АО): ОР = -JAP2 - ОА2
'162-(1Д)2
Уз
1бУб 3 1бУб л К
= —-—. Теперь находим: РМ = — ОР = — —-— = 4 <6 .
Обозначим через Т и К — точки пересечения прямой МР с
окружностью <в2 (Т и К — диаметрально противоположные
точки сферы с центром Р). Тогда отрезки МТ и МК равны ра-
диусам концентрических окружностей со3 и со4 с центром М,
одна из которых касается окружностей w, и со2 внешним обра-
зом, другая — внутренним. Так как МТ = РМ - РТ, МК =
= РМ + РК, то МТ = 4Уб-8,МХ' = 4Уб +8.
Таким образом, существуют две концентрические сферы с
центром М, касающиеся всех данных четырех сфер: радиус од-
ной сферы равен 4 Уб - 8, а радиус другой — (4 Уб + 8).
Ответ: 4 Уб - 8; 4 Уб +8.
Замечание. При оформлении решения данной задачи и за-
дач, ей предшествующих, достаточно подробно продемонст-
рирована аргументация логических шагов конструктивного,
вычислительного и чисто геометрического (синтетического)
характера. Таким, наполненным аргументированными обос-
нованиями различного характера, и должно быть решение лю-
бой геометрической задачи (планиметрической или стерео-
метрической) при выполнении заданий ОГЭ и ЕГЭ.
209
ПРИЛОЖЕНИЕ
ФОРМУЛЫ СТЕРЕОМЕТРИИ
Векторы и координаты
Содержание формулы Формула Символы (обозначения)
Правило треугольника АВ + ВС = АС А, В, С — произ- вольные точки
Правило параллело- грамма ОА + ОВ = ОС О АС В — паралле- лограмм
Правило многоуголь- ника AyA2 + А2А3 + ... + + Ап ,А = А. А п-1 п In А1,А2,...,Ап_1, Ап — произволь- ные точки
Правило параллелепи- педа OA + OB + OC = OCi ОА, ОВ, ОС — ребра параллелепипеда ОС} — диагональ параллелепипеда
Формула вычитания OB - ОА = АВ А, В, 0 — произ- вольные точки
Признак кол- линеарности двух ненуле- вых векторов Ь = k- а |5-b| = |5|-|b| k — число, отличное от нуля, 5*6,Ь*б
Признак компланар- ности трех векторов р = ха + уЪ х, у — числа
Середина отрезка ОМ^-(ОА + ОВ\ 2' ' М — середина отрезка АВ О — произвольная точка
210
Содержание формулы Формула Символы (обозначе- ния)
Точка пересече- ния медиан (центроид) ОМ = = -(ОА + ОВ + ОС) 3 М — цен- троид тре- угольника АВС, О — произволь- ная точка
Скалярное произведе- ние векто- ров = la а • Ь = • | b | cos Z( а , b ) а, Ь — ненулевые векторы
Сложение и вычита- ние векто- ров в коор- динатах а ± Ъ = = (Xi ± х2; i/i ± у2; гг ± z2) a(Xi; b (х2; у2; z2)
Умножение вектора на число k a (kx; ky; кг) k — число а (х; у; г)
Скалярное произведе- ние а • b = =Xi х2 + y1y2 + z1z2 a (Xu yr, zj b (х2; у2; г2) Ф — вели- чина угла между век- торами
Косинус уг- ла между векторами COS ф = х,х2 +yly2+z1z2
yfxt + yt+ztjxl+yt+zl
Длина вектора а -V хг + у2 + г2 а (х; у; г)
Расстояние между точ- ками А и В АВ = (x2-x1)2+(y2-i/1)2 + ^+(У2-У1)2 А(Хи уг; Zi) В (х2; у2; г2)
211
Содержа- ние формулы Формула Символы (обозначения)
Уравнение плоскости по точке и вектору нормали А (х - х0) + В (у - у0) + + С (z - z0) = 0 n (А; В; C) — вектор, перпен- дикулярный плоскости; Mo (х0; у0; г0) — точка, принад- лежащая плос- кости
Общее уравнение плоскости Ax+By+Cz+D=O М (х; у; г) — произвольная точка плоско- сти
Косинус угла меж- ду двумя плоско- стями Условие перпенди- кулярно- сти двух плоско- стей Условие парал- лельности двух плоско- стей cos ср = lyL A2 + B.B2 +CCJ | 1 Z 14 I Z j Агх + В^ + + CjZ + £>! = 0 А2х + В2у + + C2z + D2 = = 0 — плоско- сти; ф — вели- чина угла меж- ду этими плоскостями
7 Af+в2+c; 7 a22+b22 + c2 AjA2 + -B1-B2 CiC2 — 0 A2 B2 C2
Расстоя- ние от точки до плоскости (d) d _\Ax0+By0+Cz0 + D /a2+b2+c2 1 мо (х0; у0; z0) — точка Ах + By + + Cz + D = 0 — плоскость
212
Содержание формулы Формула Символы (обозначения)
Парамет- рические уравнения прямой r=ra+kp x = x0+ka1, \у = У0+ка2, [ z = z0+ka3 г — радиус- вектор произ- вольной точки прямой, г0 — радиус-вектор данной точки прямой, р — направляющий вектор прямой, k — параметр, Мо (х0; у0; г0) — данная точка прямой, М (х; у; г) — произвольная точка прямой, p(aj;a2; a3) — направляющий вектор прямой
Уравнения прямой по двум ее точкам Косинус угла между двумя прямыми Условие перпенди- кулярности двух прямых Условие параллель- ности двух прямых X-Xx _ y-yx _ z-zl x2—xx y2-yx z2 — zx COS ф = la. b. +a9b, +аД _ (11 £ с. о о | Mi (хг; уг; zj, М2 (х2; у2; z2) — данные точки Pi (®15 я3), Рг (^1» ^2» Ьз) направляющие векторы прямых Ф — величина угла между ними
Taf + a22 + a32 ^b\ + &2+d2 Clxb^ "h a2&2 a3fe3 0 at _ a2 _ a3 &i b2 b3
213
Синус угла между пря- мой и плос- костью Условие перпенди- кулярности прямой и плоскости Условие па- раллельно- сти прямой и плоскости sin ср = l-Adj +Ва2 + Саэ| Ах + By + Cz + + n = o — плоскость pia^a^a^) — направляю- щий вектор прямой <р — величина угла между прямой и плоскостью
VA2 + B2 + C27af + a22+a3 А=А= с. Oj a2 a3 Ааг + Ва2 + Са3 = 0
Многогранники
Содержание формулы Формула Символы (обозначения)
Площадь поверхности куба(S) S = 6 а2 а — длина р ебра куба
Площадь боковой поверхности пря- мой призмы (Вбок) 8бок = Р ' h Р — периметр основания h — высота (длина бокового ребра)
Площадь боковой поверхности наклонной призмы (Вбок) ^к = Р-1 Р — периметр перпендикулярного сечения 1 — длина бокового ребра
Площадь боковой поверхности прямого параллелепипеда (S6ok) 8бок = Р ’ 1 Р — периметр основания 1 — длина бокового ребра
214
Содержание формулы Формула Символы (обозначения)
Площадь боковой поверхности правильной пирамиды (5бок) я * II II о ьэ|н- ° <© Чэ * В Р — периметр осно- вания а — апофема Q — площадь основания ср — величина дву- гранного угла при стороне основания
Площадь боковой поверхности пра- вильной усеченной пирамиды (5бок) ®бок Р + р 2 Р, Рг — периметры оснований h — апофема
Объем куба (V) V = а3 а — длина ребра куба
Объем прямоуголь- ного параллелепи- педа (V) V=abc а, Ь, с — измерения параллелен ипеда
Объем призмы (параллелепипеда) (Ю £ со II II 8ЖН — площадь основания h — высота Q — площадь перпендикулярного сечения 1 — длина бокового ребра
Объем пирамиды (Ю II W | М со 8 ЕС 53- <8осН — площадь основания, h — высота
Объем усеченной пирамиды (V) 7 = = j*(Qi + Qi, Q2 — площади оснований, h — высота
215
Фигуры вращения
Содержание формулы Формула Символы (обозначения)
Площадь боковой поверхности цилиндра (86ок) S6oK= 2л R-h R — радиус основания h — высота
Площадь полной поверхности цилиндра (впалн) 8П0ЛН = 2л R(h + R) R — радиус основания h — высота
Площадь боковой поверхности конуса (S6oK) *^бок И 1 R — радиус основания 1 —длина образующей
Площадь полной поверхности конуса (8ПОЛН) 8П0лн = л R (1 + R) R — радиус основания 1 — длина образующей
Площадь боковой поверхности усеченного конуса (S6oK) S60K = л 1 (R + г) R, 1— радиусы оснований 1 — длина образующей
Площадь сферы (8) 8 = 4л R2 R — радиус сферы
Площадь сегментной поверхности (8) S = 2tiR-H R — радиус сферы Н — высота сегментной поверхности
Площадь шарового пояса(S) S 2nR-H R — радиус шара Н — высота шарового пояса
216
Содержание формулы Формула Символы (обозначения)
Площадь поверхности шарового сектора (S) S = nR-(2h + + j2Rh-h! ) R — радиус шара h — высота шарового сегмента
Объем цилиндра(V) V=nR2-H R — радиус основания Н — высота
Объем конуса (V) у= lnR2-H 3 R — радиус основания Н — высота
Объем усеченно- го конуса (V) V= -nH(r2 + 3 + R r + R2) R, 1— радиусы оснований Н — высота
Объем шара (V) V= -jtfi3; 3 1 л d3 6 R — радиус шара d — диаметр шара
Объем шарового слоя (V) F = — (Зп2 + 6 + 3r22 + H2) Гр г2 — радиусы оснований шарового слоя Н — высота
Объем шарового сегмента (V) V=nH2 (R-—) 3 v = (Зг2 + я2) R — радиус шара Н — высота 1— радиус осно- вания шарового сегмента
Объем шарового сектора (V) V= - xR2-H 3 R — радиус шара Н — высота
217
ОТВЕТЫ
Глава 1. Векторная алгебра
и начала аффинной стереометрии
2. а)РЕ; 6)0; в) 0. 3. Указание: а) По правилу лома-
ной: АВ = AC + СК + КВ = АС-КС-ВК . 5. а) -1; б) 0,5; в) 2;
г) -2; д) -0,5. 6. Да. 11. а) АК = АС[; б) АК = AD ; в)АК~
— 2АС . 13. М — точка пересечения диагоналей АСг и АХС па-
раллелепипеда. 15. Указание. Достаточно доказать, что если
точки и М2 — центроиды этих треугольников, то для лю-
бой точки О пространства выполняется равенство:
ОЛГ = ОМ16. а) -а + -Ь; б) -~а + -Ь; в) -а--Ъ . 18. MD =
1 2 33 33 33
= a-b+с; АК = -а+ 0,5с. 19. а) 0 • а + 0,55 + 0,5с;
б) а + Ь - с ; в)2 а + 0 • Ь - с . 20. Указание. Воспользуйтесь соот-
ношением ОК = — (ОА + ОВ + ОС ), где О — произвольная точ-
3
ка пространства. 21. Указание. Найдите ОР + ОН + ОК и вос-
пользуйтесь условием компланарности трех векторов. 22.1:8.
23. Указание. Воспользуйтесь формулой: ОМ = — (ОА + ОВ)
2
для середины М отрезка АВ и произвольной точки О про-
странства. 24. а) АС .6) АС. 25. Указание. Достаточно доказать
компланарность векторов АР, ВС и КЕ . 33.1:3. 34.1:1:1.
Глава 2. Скалярное произведение векторов.
Метрические задачи стереометрии
1. а) 180°; г) 90°. 2. а) 60°; г) 45°. 3. а) 10; б) 7V2 ; в) -10;
г) 0. 4. Указание. Четырёхугольник, построенный на векторах
л/З-а/2-2
а п b как на сторонах, является ромбом. 5. 1) -------;
Л
2)1-72. 8. а) 2; б)-2; в)1; г)-1. 11.1)а)^; б) ;
3 &
218
2) a) arccos . 15. 2л/б . 16. Вершины Aj и А равноудалены от
О
прямой BDp 17. 4-Тз . 22. 2 л/21 . Указание. См. задачу 6. В каче-
стве базисных принять векторы РА = а , РВ = b , PC = с .
23.3 л/з . Указание. См. задачу 6. В качестве базисных принять
векторы РА=а, РВ = Ь, РС = с. 25. Ответ: 4\/2.26. .
27. Указание. Введите базис, состоящий из векторов ОА = а ,
ОВ = Ь, ОС=с. Тогда АВ=Ъ-а, АС=с-а. Получим:
АВ-АС > 0 => ABAC — острый. Аналогично определяются
величины двух других углов треугольника АВС. 28. Указание.
Воспользуйтесь: если точка М — центроид тетраэдра РАВС, то
МР + МА + МВ + МС = б => МР2 + МА2 + МВ2 + МС2 =
= 2 (МР • МА + МР • МВ + МР • МС + МА • МВ +
+ МА • МС + МВ • МС). 29. Указание. Воспользуйтесь: ес-
ли в тетраэдре РАВС ребра АР и ВС перпендикулярны, то
АР • ВС = 0 => АР • АС = АР • АВ. Аналогично для других
пар противоположных ребер. 30. Указание. В тетраэдре РАВС
введите векторы АВ = а , АС = Ъ , АР = с . Если при этом точки
М, Н, К и Т — середины ребер соответственно АВ, АР, СР и
ВС, то из НТ ± МК следует | b | = | а - с |. Аналогично для других
пар противоположных ребер. 31. Указание. Введите векторы
ОА = а, ОВ = Ь,ОС=с . Тогда ОН = -(а+Ь + с) ^КО , КА =
3
= —( 4 а+ Ь +с). Далее найдите разложение вектора КВ в ба-
3
зисе (а ,Ъ , с) и докажите, что треугольник АВК — правиль-
ный. Аналогично, докажите, что треугольники ВСК и АСК —
правильные.
Глава 3. Геометрия прямых, плоскостей
и фигур вращения в координатах
3. р(-5; -15; 5); g (-4; 18; 9). 5. т = 4, п = 1,5. 7. а)5ч/3 ;
б) 7; в)73 ; г)3; д) V10.8.1) -7; 2) 0; 3) 6; 4)л/з . 10. х = 3; у = -8;
219
z = 5. 11. а) Тупой; б) Прямой; в) Острый. 12. 1) Острый; 2) Ту-
пой; 3) Прямой. 13.1)0; 2)—. 14.10. 15. При п = -2.
6
16.1)45°; 2)135°; 3)60°; 4)45°; 5)60°. 20. а) ; б)^-;
3 3
в) 21. а) л/З; б) в) ; г) . 24. 1. а) ; б) ;
о Л Л О о о
ъ}—. 2.1:2. 25.1. а)^; б) и V13 2.2:1.
3 2 13 13
27. а) ; б) —; в) —. 30. а) — ; б) —; в) — . 31. а) —;
3 3 3 3 6 3 5
б) ; в) ; г) "^21 ' 34. a) 60q б) 90q B)arcsin^^-.
5 7 7 3
35. a) arccos^^; б) arccos^-; в) arccos— . 38 а) —; б) —;
10 4 4 3 3
в) Г)^. 39. а) 0,2>/15 ; б)0,25>/3; в)0,125>/3;
3 3
г) 0,25 <6. 42. a)90q б) arccos—;
3
6 2ЛЗ 2^ 2ЛЗ 2ЛЗ
13 5 13 13
в) arcsin
2V2
3
43. а) ;
2
Глава 4. Сфера и многогранники
в координатах
10. (х + I)2 + (у - З)2 + (2 - 5)2 =9. 11. (х + 2)2 + у2 + (2 - З)2 =
= 13. 12. (х + I)2 + (у + I)2 + (2 - I)2 = 41. 13. Две сферы:
(х - I)2 + у2 + (2 + 2)2 = 1 и (х - I)2 + у2 + (г + 2)2 = 49. 14. Если
те(-2; 2) — пустое множество; если т = -2 — точка (2; 0; 2);
если т = 2 — точка (-2; 0; 2); если т е (-ос; -2)и (2; + ) — сфе-
ра радиуса >Ап2 -4 с центром (~т; 0; 2). 15. (х - 5)2 + (у - I)2 +
+ (2 - I)2 = 12 или (х - 5)2 + (у - I)2 + (г- I)2 = 48. 25. б)
13
V13
и----
13
220
Глава 5. Векторное произведение векторов
и площади многоугольников
1. а) 40;.б) -3; в) -40; г) 0; д) 100; е) 0; р) ЗаЬс - а3 - &3 - с3;
q) а3 + Ь3 + с3 - 3abc.2. 1) 0; 2) 0; 3) 0; 4) 0; 5) 0. 3. р = 6 7 - 8 ) -
- 2 k. 4. 7222 . 5. 0. 6. a) k; б) - i ; в) - j ; г) -6 i ; д) k - j ;
е) 4fe+10 i . 9. Да. 10. а) 2 (ах 5); б) ахс + 4( Ьха ) + 2(сх& );
в) axb + ахс .11. а) (3; 0; 2), хТз ; б) (-2; 0; 0), 2; в) (-3; 9; 5),
7115 ; г) (3; 0; 1), 710 ; д) (-3; 0; -1), 710 ; е) (-13; 4; 10), 7285 .
12. 4. 13. -7 г +3 j + k. 14. а) 2 i +16 j +6k; б) 8 i + 64 j +24 ;
в)-28i-224y-84й; r) 2774.15. 5717.16. 49. 17.8 = юТЗ;
, . 5742 , tz [о ч a \ 72331 q /777 4 71326
h1=h2=—----; Л3=5л/2. 18. a) 21--; 6) 3<10 ; в) ---;
7 2 2
г) 724. 22. 0,571321 кв. ед. 23. 4782. 24. -/=(7- 3/ + fe);
-Д= (- i + 3 j - k). 26. Указание. См. 25. 27. Указание. См. 25.
Глава 6. Смешанное произведение трех векторов
и метрические задачи стереометрии
5. а) 40; б) 3; в) -40; г) 0. 6. а) Компланарны; б) Компла-
нарны; в) Некомпланарны. 15. 3. 16. х - 4г/ + 7г + 24 = 0.
17. £zl = £±3 =£+1 18 6 19 б) х _ 2у + 22 - 6 = 0 и х - 2у +
—1 5 9
+ 2г + 12 = 0; в) расстояния равны 6. 20. —. 21. а) Указание.
Воспользоваться: {а х с )2 = |а х с |2; б) Указание. Воспользо-
— -> Jq
ваться: а х с = -(с х а). 22. а) 0,5; б) 22.5. 23. а) — — длина
3
длина высоты;
высоты; б) arccos22^ . 24. а)
3 3
7з 2Тз л/з
б) arccos —. 25. а)------ — длина высоты; б) arccos^—.
3 3 3
221
26. а)
3
/д 2\/3
длина высоты; б) arccos — . 27. а) —— — длина
3 3
высоты; б) 90°. 28. а) 8,5; б) SABC^ ——, Л
2
Sacda=V357, Sbccb =7561; в) V17; г) 90°.
Т§4 ,
29.3.
30. a)—; 6)4; 5; 2^5; Vl¥; в)2;
3
г) д) 90°. 31. a) -29,
V17
левая тройка; б) 68, правая тройка; в) 19, правая тройка.
Глава 7. Синтетическая геометрия многогранников
и фигур вращения в задачах
2. а)2>/3; 6)4; в) 4; г) 4; д) Т13 ; е) Тб . 3. а) Тз ; 6)2;
В)4^; Г)^' S.a)2V3; 6)4; в)2Т2; г) ; д) ;
\ 25/30 с \ о /о ч /о \ Т7 \ Т7 \ ТЗ
е) -у- . 6. а) 2; 6) V2 ; в) V3 ; г) — ; д) — ; е) — .
а ч 4л/21 2^5 ч бТ13 х V7 ч бТб ч 2>/21 ч
8. а)---; 6) ——; в) —— ; г) — ; д) ——; е)---; ж)
7 7 5 13 4 5 7
3>/2 .
2 ’
3 2V2I e 2J2I зЛз V5 д) 3VL е) 3V2;
7 7 5 13 5 5 4
ч V21 . 2^5 .. ч . 6>/5 ч 2V2I . бл/б
ж)—-; з) —. 11. а) 2; 6) >/3 ; в)^-; г)——; д) -2-;
7 5 5 7 5
е) л/з . 12. а)^^; б) ; в)^^); г) . 13. а) 1;
б) ; в) ; г) . 14.36Тб кв. ед. 18. тТз . 19.32Тб кв. ед.
on
20. кв. ед.
2
222
ЛИТЕРАТУРА
1. Потоскуев Е. В., Звавич Л. И. Геометрия. 10 кл.: Учеб-
ник для общеобразовательных учреждений с углубленным и
профильным изучением математики. — М.: Дрофа, 2013.
2. Потоскуев Е. В., Звавич Л. И. Геометрия. 10 кл.: Задач-
ник для общеобразовательных учреждений с углубленным и
профильным изучением математики. — М.: Дрофа, 2013.
3. Потоскуев Е. В., Звавич Л. И. Геометрия. 11 кл.: Учеб-
ник для общеобразовательных учреждений с углубленным и
профильным изучением математики. — М.: Дрофа, 2012.
4. Потоскуев Е. В., Звавич Л. И. Геометрия. 11 кл.: Задач-
ник для общеобразовательных учреждений с углубленным и
профильным изучением математики. — М.: Дрофа, 2012.
5. Е. В. Потоскуев, Л. И. Звавич. Математика. Алгебра и
начала математического анализа, геометрия. Геометрия.
10 кл. Углублённый уровень. Учебник. — М.: Дрофа, 2016.
6. Е. В. Потоскуев, Л. И. Звавич. Математика. Алгебра и
начала математического анализа, геометрия. Геометрия.
10 кл. Углублённый уровень. Задачник. — М.: Дрофа, 2016.
7. Потоскуев Е. В., Звавич Л. И. Геометрия. 11 кл.: Учеб-
ник для общеобразовательных учреждений с углубленным и
профильным изучением математики. — М.: Дрофа, 2016.
8. Потоскуев Е. В., Звавич Л. И. Геометрия. 11 кл.: Задач-
ник для общеобразовательных учреждений с углубленным и
профильным изучением математики. — М.: Дрофа, 2016.
223
Учебное издание
Потоскуев Евгений Викторович
Векторно-координатный метод
решения задач стереометрии
Издательство «ЭКЗАМЕН»
Гигиенический сертификат
№ РОСС RU.HA34.H08638 с 07.08.2018 г.
Главный редактор Л. Д. Лаппо
Редактор И. М. Бокова
Технический редактор Л. В. Павлова
Корректоры О. Ю. Казанаева, А. В. Полякова
Дизайн обложки Л. В. Демьянова
Компьютерная верстка А. С. Федотова
Россия, 107045, Москва, Луков пер., д. 8.
www.examen.biz
E-mail: по общим вопросам: info@examen.biz;
по вопросам реализации: sale@examen.biz
тел./факс 8(495)641-00-30 (многоканальный)
Общероссийский классификатор продукции
ОК 005-93, том 2; 953005 — книги, брошюры, литература учебная
Отпечатано в соответствии с предоставленными материалами
в ООО “Красногорская типография”. 143405, Московская область,
г. Красногорск, Коммунальный квартал, дом 2. www.ktprint.ru
По вопросам реализации обращаться по тел.:
8(495)641-00-30 (многоканальный).