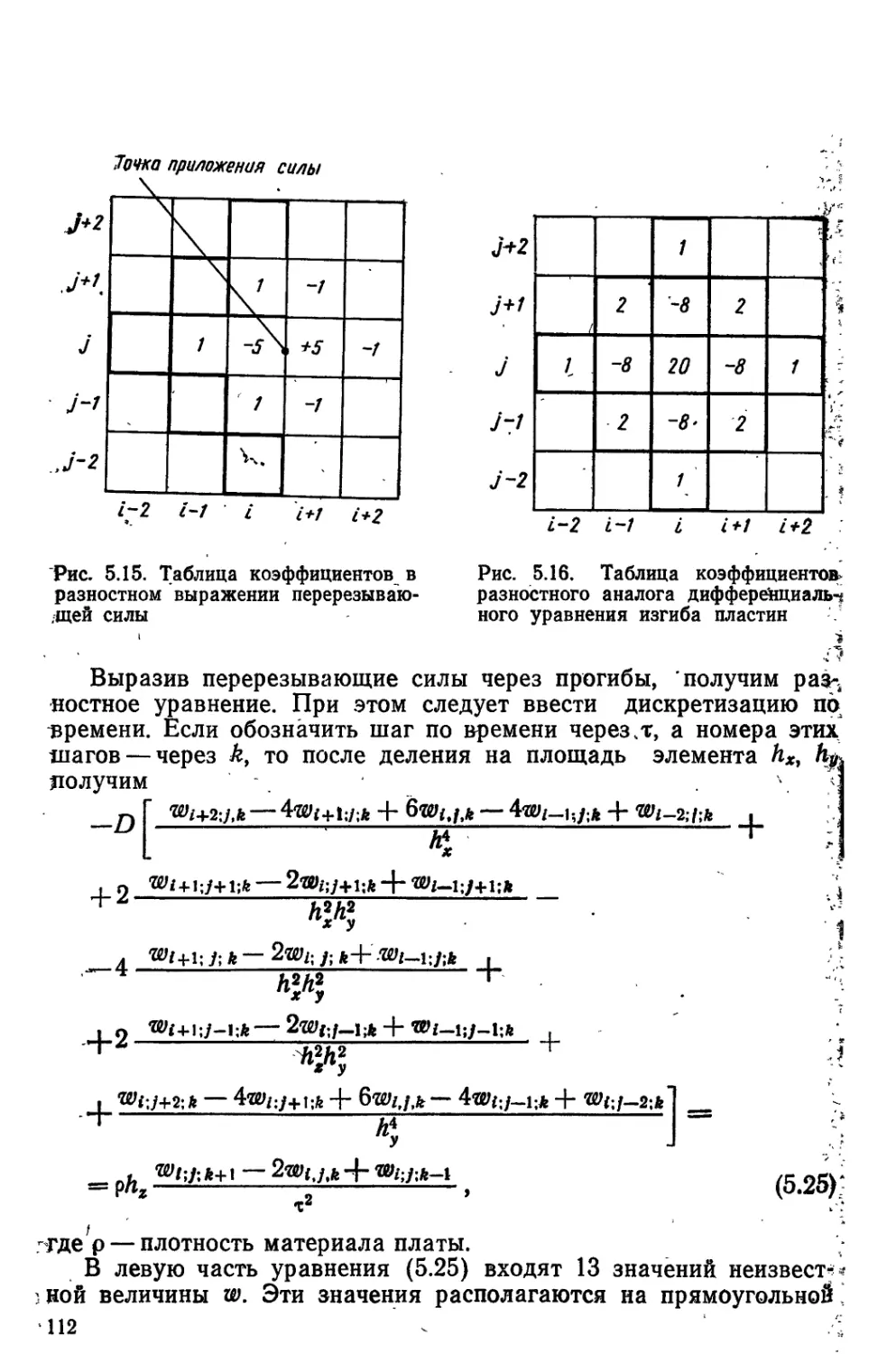
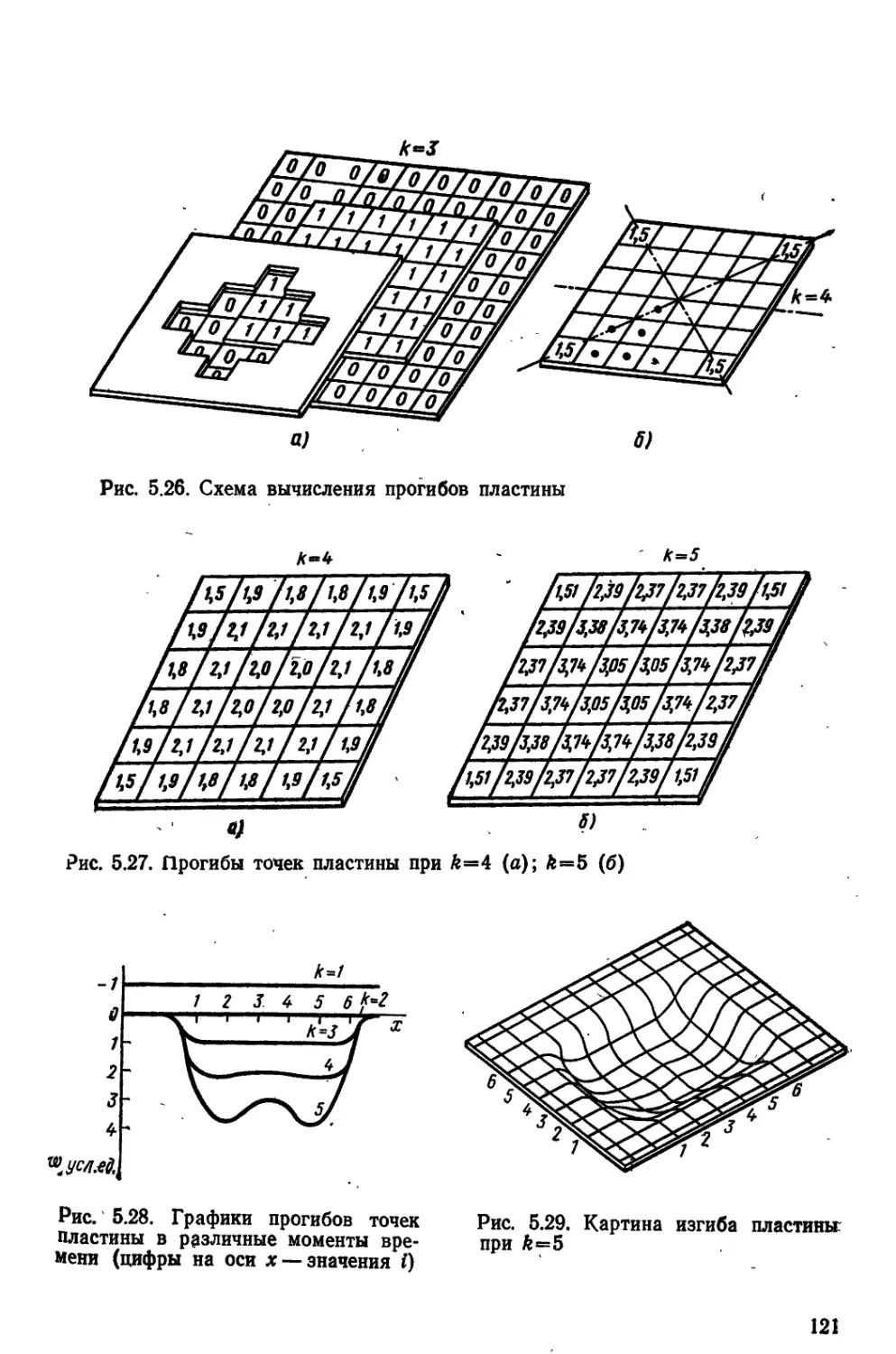
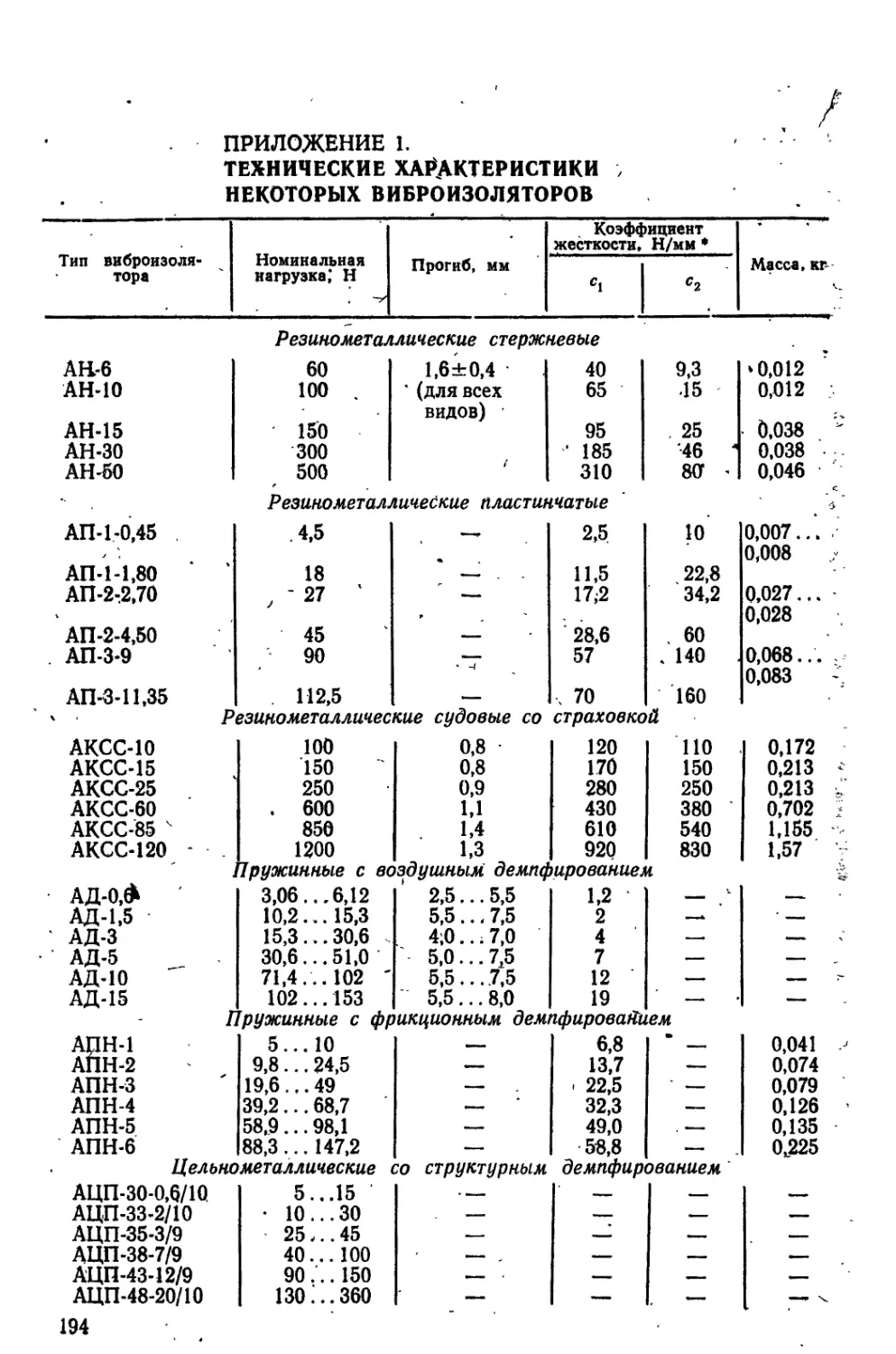
Автор: Маквецов Ё. Н. Тартаковский А.М.
Теги: электротехника радиоаппаратура (радиоэлектронная аппаратура) радиоэлектронная аппаратура учебник для вузов
ISBN: 5-256-01I13-8
Год: 1993
Текст
ЕНМаквецов
А. М. Тартаковский
МЕХАНИЧЕСКИЕ
ВОЗДЕЙСТВИЯ
И ЗАЩИТА
РАДИОЭЛЕКТРОННОЙ
АППАРАТУРЫ
Рекомендовано Комитетом по высшей
школе Министерства науки, высшей школы и
технической политики Российской Федерации
в качестве учебника для студентов,
обучающихся по специальностям: «Конструирование
и технология радиоэлектронных средств» и
«Конструирование и технология электронных
вычислительных средств».
Москва
«Радио и связь»
1993
Б 32.844
М15 - .
УДК 621.396.6-752
Рецензенты: Б/Ф. Высоцкий, А. С. Назаров, В. А. Волков, М. Ф. Токаре^
Редакция литературы по электронике i
Маквецов Ё. Н., Тартаковский А. М.
М15 Механические воздействия и защита радиоэлектронной*
аппаратуры: Учебник для вузов. ---М.: Радио и связь, 1993.—
200 с: ил.
ISBN 5-256-01I13-8.
Излагаются вопросы анализа и расчета механических процессов —
-ударов и вибраций — в типовых конструкциях радиоэлектронной
аппаратуры. Особое внимание' уделяется численным методам .расчета ' на ЭВМ
деформаций, напряжений, ускорений (перегрузок), возникающих в эле-
ментах конструкций в процессе ударов и вибраций. Приведенные методы
расчета на ЭВМ для различных вариантов конструкций позволяют
проектировать конструкции радиоэлектронной аппаратуры, устойчивые к
внешним механическим воздействиям. г' * - .
Для студентов вузов, специализирующихся в области конструировав
ния и технологии производства радиоэлектронной аппаратуры.
¦ "Г . -.: .
Учебное издание
Маквецов Евгений Николаевич, Тартаковский Александр Моисеевич -
МЕХАНИЧЕСКИЕ ВОЗДЕЙСТВИЯ И ЗАЩИТА
РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ . :-
Учебник • ' .
Заведующей редакцией Ю. Н. Рысев. Редактор Я. Е. Кочарьянц.
Обложка художника В. fi Виганта. Художественный редактор Н. С. Шеи-н.
Технический редактор А. *Н. Золотарева. Корректор Н. В. Козлова.
И Б № 956
Сдано в набор 12.10.92 Подписано в печать 09.12.92
, Формат 60X84/16 Бумага газетная Гарнитура литературная Печать высока*
Усл. печ. л. 11,63 ' г Усл. кр.-отт. 11,97 Уч.-изд. л. 12,80 - Тираж 2000 зкс
Изд. № 21637 л Зак. № 1216 С-020
Издательство «Радио и связь». 101000 Москва, Почтамт, а/%693 .
Типография издательства «Радио и связь». 101000 Москва, Почтамт, а/я 693
ISBN 5-256-01113-8 © Маквецов Е. В., Тартаковекий А. М., 199Г
ПРЕДИСЛОВИЕ
Конструктор радиоэлектронной аппаратуры (РЭА) или
электронно-вычислительной аппаратуры (ЭВА) часто выполняет работы,
связанные с анализом и устранением вредных влияний на
аппаратуру механических процессов, возникающих при ее
транспортировке или эксплуатации на автомобилях, кораблях., самолетах,
ракетах. Такой анализ приходится проводить при проектировании
новой аппаратуры, испытании опытных образцов., изучении резуль- *
татов испытаний и Дальнейшем улучшении конструкций.
Развитие методов расчета, как и методов совершенствования
конструкций, является основной задачей развития конструирования
вибропрочной и виброустойчивой нестационарной апйаратуры.
К сожалению, ^расчеты механических процессов в РЭА'и'ЭВА*
например ударов и вибраций, как правило, весьма сложны;
Расчеты достаточно сложных конструкций в радиоэлектронике начали
применяться только в 70-х годах.
Возникающие здесь трудности определяются следующими
факторами:
1. Сложностью конфигурации деталей РЭА и ЭВА и их
большим количеством. ^Учесть все эти особенности конфигурации и
структуры» конструкции в расчете обычно не удается* а введение
различных упрощений не позволяет оценивать появляющейся при
этом погрешности расчета. . .
2. Неприспособленностью конструкций РЭА и ЭВА к
выдерживанию механических нагрузок. Конструкции самолетов или
кораблей, например, могут быть сложнее, чем конструкции
радиоэлектронной аппаратуры, но кораблям и самолетам придаются
специальные формы, позволяющие выдерживать сопротивление
воды и встречного воздуха. А. конструкций РЭА и ЭВА прежде
всего должны выполнять свои основные функции —обработку
информации, Их формы определяются в первую очередь удобством
крепления, соединения и охлаждения радиоэлементов,
герметичностью аппарата и затем уже — устойчивостью к механическим
воздействиям.
3. Наличием в конструкции большого числа различных
материалов, часто имеющих нелинейные механические
характеристики, большие потери энергии на внутреннее трение, анизотропию
упругих свойств.
. 4
4. Необходимостью решать нестационарные задачи. Корабл|
и самолеты рассчитывают на стационарное нагружение, а радйф
конструкторов интересуют в первую очередь переходные процёф
сы, например удары. . : -.
Все это затрудняет решение механических задач применителЬ
но к радиоконструкциям. Поэтому, до настоящего времени оценк
вибропрочности и виброустойчивости проектируемой аппаратур*
осуществляется в основном экспериментально. Это требует изгс
товления опытных образцов, макетов, проведения дорогостоящи!
испытаний, .сложного анализа результатов эксперимента. Стон
мость проведения экспериментальных работ составляет,- как пра
вило, более половины стоимости'проекта. Но уже теперь приме
нение вычислительной техники позволяет сокращать число такщ
экспериментов^ и заменять их расчетами на ЭВМ. Такая замен/
дает огромный экономический эффект за счет сокращения натур
ных испытаний и связанного с этим сокращения сроков
проектирования. Поэтому в книге большое внимание уделяется расчета*
ударов и вибраций в типовых конструкциях. -
К сожалению, только в случае простейших конструкций удает-j
ей получить точное решение в аналитической форме. Такие реше-*
ния модельных задач очень ценны, так как позволяют производит^
всесторонний анализ процессов в конструкциях и получэть анализ
тические оценки. В отдельных случаях целесообразно йспользо
вать приближенные аналитические решения. Для расчетов реаль*
ных сложных конструкции приходится применять численные мето-|
ды. Наиболее приемлемыми численными методами расчета явля^
ются методы конечных элементов и конечных разностей. Для рас-*
чета'стационарных процессов рационально использовать метод
конечных элементов. Для расчета нестационарных переходных про-7
цессов (например, при ударах) приемлем метод кбнечных
разностей. Поэтому в книге рассматривается применение этих
дискретных методов для решения ряда задач. -
В настоящее время разработаны программы для расчета на
ЭВМ ударов и вибраций некоторых наиболее распространенных,
типовых конструкций, например печатных плат с навесными, эле-j
ментами. Этими программами можно пользоваться, не вникая в
сущность используемых в них теорий. Разработка новых программ
для расчета более сложных конструкций требует глубокого знания
теории. Поэтому она должна выполняться
инженерами-конструкторами радиоэлектронной аппаратуры с привлечением
программистов только как исполнителей. При этом инженер должен до
конца понимать теорию, иначе неизбежны грубые ошибки. В связи,
с этим при численном решении задач в тексте дается подробный
вывод всех формул, необходимых для выполняемый расчетов.
Для убедительности изложения и упрощения, где это
возможно, в тексте приводятся простые расчеты, которые можщувыпол-
4 • .
нить с помощью карманного микрокалькулятора. В. более
сложных случаях приходится использовать высокопроизводительные
ЭВМ. При этом подготовка входной информации и решейие
задачи производятся с помощью специализированных программных
комплексов, которые отаосят к имитационным системам. Основу
таких систем составляет имитационная модель рассчитываемой
конструкции.
По классификации, приведенной в [1], имитационные модели
объектов, например раДйоконструкций, представляют собой
описание поведения объекта при различных внешних воздействиях. Эти
модели позволяют, например, воспроизводить механические
процессы в конструкциях РЭА при ударах и вибрациях.
Автоматизированная система дает возможность автоматически строить
имитационные расчетные модели проектируемых конструкций,
производить многовариантные расчеты (численные эксперименты) и
анализировать результаты вычислений. В учебнике
рассматривается подход к построению таких моделей.
Глава 1. " МЕХАНИЧЕСКИЕ ВОЗДЕЙСТВИЯ
НА АППАРАТУРУ
Радиоаппаратура, устанавливаемая на подвижных объектах -г автомобилях, ко
граблях, самолетах и ракетах, подвергается действию интенсивных механически*
нагрузок. Внешние механические воздействия на. стационарную аппаратур)?
устанавливаемую в лабораториях^ менее интенсивны, но и их отрицательно!
влияние на работу точной аппаратуры может быть недопустимо большим. На|
пример, при разметке магнитных дисков-запоминающих устройств на специалы
ных машинах — серворайторах — допустимая амплитуда вибрации составляе
всего 1 мкм. А такие колебания легко возникают в самой машине при работ?
моторов^или передаются от фундамента через амортизаторы.; *
Различают три вида механических процессов, -возникающих в конструкций
ях при внешних, и внутренних воздействиях: вибрации, . удары и линейны!
ускорения. . х**
Вибрацией называют достаточно длительный (более одного периода) про*-
. цёсс распространения по конструкций упругих волн. . \
Говоря о длительности механического процесса, обычно сравнивают ее с це4
риодом собственных колебаний конструкции. Конструкция обладает спектрру
собственных частот. Если нег специальной оговорки, то под периодом
собственных колебаний понимают период колебаний на низшей частоте (первой
гармонике). ,
В процессе вибрации волны многократно отражаются от краев конструкции,
мест сочленения деталей и мест крепления, образуя сложную волновую
картину, В простейшем случа§ вибраций распространение волн в пространстве не
рассматривается и процесс колебаний происходит только во времени. , I
Ударом называется кратковременный переходный процесс движения точек
конструкции вследствие внезапного приложения или устранения внешних
воздействий. После удара может возникнуть процесс, затухающей вибрации.
Линейным ускорением называется достаточно длительное изменение ско-*
рости конструкции, например при взлете и посадке летательного аппарата.
Детали конструкции восприйимают э*го воздействие как силу инерции, равную
произведению массы на ускорение. Могут встречаться внешние воздействия в виде
угловых ускорений. Однако обычно радиус кривизны траектории намного
превышает размеры конструкции, и такое ускорение можно рассматривать как
линейное.
Заметим, что универсальных средств защиты аппаратуры, от механических
воздействий нет. Никакие амортизаторы и демпферы не защищают от
длительных; линейных ускорений. Пассивные амортизаторы, т. е. упругие элементы,
уменьшают колебания на высоких- частотах вибрации, а на низких не только
уменьшают, но и иногда даже усиливают. .
Весьма перспективным средством защиты от' вибраций являются так
называемые активные средства. В гл. .7 будут рассмотрены принципы работы актив- •
ных амортизаторов. Но и активные средства защить? не всегда помогают. При
больших амплитудах колебаний, превышающих ход якоря вибратора, защиты
не будет и могут возникнуть удары. Кроме того, активная защита
увеличивает габариты и массу аппаратуры.
Таким образом, полностью защитить аппаратуру от^ударов и вибраций
невозможно. Конструкция должна сама по себе выдерживать, некоторые,
механические воздействия, т. е. должна, обладать ¦ вибропрочностыо и виброуетойчи-
востью. ' г * .
Механические воздействия могут передаваться на аппаратуру различными
путями. При проектировании аппаратуры чаще всего приходится учитывать
внешние воздействия, передаваемые на аппарат со стороны движущегося объ-.
екта через места крепления аппарата к объекту. Эти воздействия обьгчно
известны. Они замеряются на движущемся объекте с помощью датчиков в тех '
местах, в которых должен быть установлен проектируемый аппарат.-
•Механические воздействия могут передаваться непосредственно на стенки
аппарата в виде изменения давления окружающего воздуха и воздуха внутри
аппарата. Например, звуковые и ультразвуковые колебания воздуха могут
вызвать сложные колебания. Говорят, что эти колебания* возникают в результате,
акустических воздействий. ¦ « '
В любом случае при проектировании вибропрочной и виброустойчивой
аппаратуры эти внешние механические воздействия должны быть заданы. Трудность
состоит в том, что внешние воздействия известны всегда только приближенно,
поскольку никто не может точно сказать, каким именно воздействиям будет
подвергаться проектируемая аппаратура в будущем. Поэтому в техническом
задании указываются заведомо завышенные требования вибропрочности и вибро-
устойчивости^ которые необходимо выполнять для обеспечения' запаса
прочности.
Изготовленные макеты или опытные образцы конструкции подвергаются
'испытаниям на- специальном оборудовании, на котором воспроизводятся
внешние воздействия в ^соответствии с требованиями технического задания и ацали-
зируются результаты испытаний. *
Не будем останавливаться на описании всего многообразия различных
внешних воздействий, встречающихся при эксплуатации аппаратуры.
Рассмотрим ее испытания на испытательном оборудовании.
В [2] подробно рассматриваются режимы проведения механических
испытаний и характеристики испытательного оборудования. Мы же остановимся
только на некоторых физических процессах при испытаниях, которые" позволят
определить характер внешних воздействий на аппаратуру.
1.1. ВИБРАЦИИ /
Причиной возникновения вибраций аппаратуры обычно
бывают колебания точек крепления аппарата к борту хранспортного
средства. Различают моногармонические, полигармо^ическне и слу-
* чайные колебания. Различные транспортные средства возбуждают^
колебания различной частоты [3J. На рис. 1.1 показаны диапазону
частот колебаний на борту различных транспортных средств. Ди*
апазоны частот достаточно* широки, поскольку двигатели транс*,
портных средств работают на разных оборотах, кроме того, могуг
быть и другие причины вибрации, например неровности дороги|
(для колесных транспортных средств) или волны (для кораблей).\
Амплитуды колебаний обычно измеряются с помощью датчи-j
ков ускорения. Это самый простой способ.- Его достоинства будут |
описаны в разд. .1.4, .. ' 1
Ускорение принято измерять коэффициентом перегрузки л, а= ]
= я#, где g —ускорение свободного падения, равное 9,81 м/с2. На!
рие. 1.1 показаны перегрузки, возникающие на* разных.транспорт-;
ных средствах.
Амплитуда колебаний А связана с амплитудой ускорения про- •
стым соотношением а=Л<о2, где со — круговая частота колебаний.^
Если перейти к линейной частоте f (в горцах), и измерить ампли- \
туду А (в миллиметрах), то зависимость между амплитудой и пе-^
регрузкой будет иметь вид А=250л//2. ]
Для возбуждения в испытуемой - конструкции периодических
колебаний заданной частоты и амплитуды применяются вибро-
стенды. Измерительные комплексы с использованием вибростендов
пт/ гвч **-
1...3
I
2 3 т - 20 зо ьо :so во wo 200 300 400 sop
Рис. 1.1'. Диапазоны частот вибраций транспортных средств
Измерительные
Датчики
*
V
Усилители w™
<}—
^Аппарат
шры
B)
Возбуди-
тель
колебаний
блок
питания
А}мм
700
Ю
1
V
0,01
0,001
¦J
"V
2
N
[\\
\
f\
\
1
л
\
1
0,7 1 W 100 1000 10000 fju;
Рис. 1.2. Схема измерения
параметров вибраций
Рис. 1.3. Области режимов
испытаний для различных возбудителей
колебаний вибростендов:
1 — магнитогидравлические возбудители;
2 — механические; 3 — эл&стродинамиче-
. ские; 4 — магнитострикционные
позволяют производить контроль и измерение параметров
вибрации в доступных точках конструкции (рис. 1.2). Возбудитель
колебаний, потребляя мощность от блока питания, приводит в
движение стол, который и совершает колебания. К столу крепится
испытуемый аппарат. На аппарате в нужных местах
устанавливаются датчики; Сигналы с датчиков усиливаются и фиксируются
измерительными приборами.
Вибростенд характеризуется тремя основными
эксплуатационными показателями:
диапазоном возбуждаемых частот /в... /н; - ч . .
диапазоном амплитуд колебаний Лт1п...Лтах;
допустимой массой испытуемых аппаратов.
Стремление расширить эксплуатационные возможности
вибростендов, т. е. повысить верхние пределы указанных показателей,
привело к необходимости решения целого ряда противоречивых
конструкторских задач. В результате было разработано много
совершенна различных принципов работы вибростендов,,
охватывающих довольно широкую область режимов испытаний. ,
На рис. 1.3 показаны области режимов испытаний,
определяемые различными принципами действия возбудителей колебаний
вибростендов. В радиоэлектронике применяются в основном
электродинамические возбудители. G их помощью можно испытать
аппаратуру в диапазоне частот от инфранизких (f>0,01 кГц) да
верхних* звуковых (,/>10 кГц) и диапазоне амплитуд 0... 10 мм,
Различные электродинамические возбудители колебаний позволя-
Рис., 1.4. Устройртво
электродинамически возбудителей .
ют испытывать блоки РЭА
массой от нескольких граммов до
десятков килограммов.
Действие электродинамиче:
ских возбудителей (рис.
1.4)^основано на возбуждении
колебаний катушки с переменным
током 1 в электростатическом поле.
Катушка соединяется со столом 2
вибростенда. И стол, и катушка
подвешиваются на эластичной
подвеске 3, Частота и амплитуда
переменного тока регулируются
Плавно (в нескольких
диапазонах) и определяют* частоту и
амплитуду колебаний стола.:
Для испытания более
тяжелой аппаратуры применяв
механические возбудители
колебаний. В них используется кривошипно-шатунный или кривошипно-
кулисный механизм. . .
Для возбуждения колебаний в области звуковых и
ультразвуковых частот применяются магнитострикционные возбудители
колебаний. *"¦'-•
1.2. УДАРЫ -
Удары могут возникать в аппаратуре по разным причинам.
Например, в.аппаратур^, устанавливаемой на летательных
аппаратах, удары возникают при приземлении, резком изменении
скорости, столкновении с преградой (стыковке).
Для возбуждения в аппаратуре вибраций кратковременными
ударными импульсами применяются ударные стенды. На рис. 1.5
показаны стенды, в которых платформа с аппаратом разгоняется
под действием силы тяжести и*ударяется о неподвижный демпфер.
В стендах, изображенных на рис. 1.6, используются
дополнительные массы и демпферы (устройства для гашения вибрации).
Движение такой двухмассовой системы с двумя демпферами
получается более сложным и позволяет в более широких пределах
регулировать длительность и фор*яу ударного импульса.
После того как платформа приходит в соприкосновение с
демпфером, закон ее движения целиком определяется конструкцией и
параметрами демпфера. Применяют самые различные
конструкции демпферов (рис. 1.7):
1. Демпферы с вязким трением, в которых поршень с малыми
отверстиями движется в цилиндре с вязкой -жидкостью (см.
10 • . ".
IL
-3
JL
Рис. 1.5. Ударные стенды, с. подвижной платформой:
/.— платформы; 2. — испытуемые аппараты
F /
S
ь
\ [tl
у _L
Рис. 1.6. Ударные стенды с дополнительными массами
11
. 6)
Рис. 1.7. Демпферы ударных стендов
рис. 1.7,а). Такой демпфер создает силу сопротивления F,
пропорциональную скорости движения платформы,
где 1UL — коэффициент вязкости.
Подобные демпферы устанавливаются на автомобилях .и
мотоциклах и называются амортизаторами.
2. Демпферы с гияравилической пружиной (см. рис. 1.7,6).
В этих демпферах используется сила сжимаемой жидкости,
которая пропорциональна перемещению платформы и. Если
перемещение отсчитывать от момента касания платформы и штока
гидропружины, то '
где с — жесткость гидравлической пружины.
3. Демпферы из твердых пластических материалов. В качестве
такого материала используют, например, свинец. Пирамида из
свинца устанавливается на пути платформы и при ударе
сминается (см. рис. 1.7, в). Сила сопротивления, воздействующая на
платформу, сложным образом зависит от перемещения. Если,
например, предположить, что сила пропорциональна объему смятой
части пирамиды, то
У=4-5(и), или l/ = 4-SOCH-^-: F = Bu\
где Soch — площадь основания пирамиды; h — ее высота; В —
коэффициент пропорциональности.
.12
Применяются и другие различные демпферы. Например, для
имитации падения летательного аппарата на грунт в ударном
стенде в качестве демпфера используют мешок с песком. В [2]
приводятся примеры конструкций демпферов.
Описать движение платформы, с аппаратом ударного стенда
гораздо труднее, чем движение стола вибростенда. Время
ударного импульса, его форма и амплитудное значение зависят от
конструкции демпфера и его параметров.. Эти характеристики можно
лолучить расчетным путем. Для этого рассмотрим примеры.
Пример 1. Платформа с аппаратом падает на демлфер с вязкостью (см.
рис. 1.7,а). В момент касания штока демпфера скорость платформы v= 10 м/с.
Определить характеристики движения при торможении в зависимости от
коэффициента вязкости демпфера р, и массы движущихся частей т.
Решение. Уравнение движения запишем в виде
^F = m— или .»_+>_- =0, A.1)
Это —линейное однородное дифференциальное уравнение второго порядка
с постоянными коэффициентами. Общее решение таких уравнений имеет вид
M=Ciexpaif+C2expc«2^ A.2)
где cti и ой — корни характеристического уравнения
Подставляя в A.2) значения корней
ai=0, a2=
получаем .
т
Постоянные С\ и Сг определяются из Начальных условий
Отсюда
C2= — Cit Ct^=v и Ct=
т {а '
Таким образом, платформа будет двигаться с замедлением по
экспоненциальному закону
Дифференцируя его выражение два раза, получаем скорость и ускорение
.движения:
da I* u. \ d2u a / [i -Л,
— = t>exp —— t), - = —^-s—exp —E— / :
dt \ m ) dt* m -\ m h
Если, например, масса платформы и аппарата равна 10 кг, а максимальное
ускорение должно быть при испытаниях 100g~981 м/с2; то коэффициент
вязкости демпфера должен быть равен
|А = 981 нс/м.
Для этих значений на рис. 1.8 показаны'графики перемещения, скорости и
ускорения платформы' при торможении. Максимальный ход штока равен
т
= 0,1019 м,
а максимальное значение-ускорения появляется в начале торможения и равна
v JL- = 981 —
т с2
Поскольку экспоненты приближаются к своим асимптотическим* значениям;
при '*=оо, то процесс торможения теоретически никогда не закончится. Такое
несоответствие практике — результат неточностей нашей расчетной мод ел*.
В частности,, мы не учитываем. потерь энергии на сухое трение поршня о ци
линдр и других трущихся деталей? В этом случае за длительность импульса
принимают значение Зти, где ти — постоянная времени, равная /п/|л=0,0102. Таким
образом, длительность импульса можно считать равной Зти=30,6 мс.
400-
Рис. 1.8. Графики перемещения,
скорости, ускорения платформы . при
вязком демпфировании -
14
\
Рис. 1.9. Графики перемещения,
скорости, "ускорения платформы при
падении на гидравлическую
Пример 2. Произвести те же вычисления, что и в примере 1, только при
условии, что платформа падает на гидравлическую пружину (см. рис. 1.7,6).
Решение. Уравнение, движения-в этом-случае будет иметь вид,
аналогичный A.1): '
d2u - /t ov
— си = т — . A.3>
at2 .
Так же, как и для уравнения A.1), решение можно найти в виде двух
экспонент A.2), у которых показатели будут равны
Переходя от экспонент к тригонометрическим функциям с 'помощью
формул Эйлера, окончательно получаем
W = WmaxSin(Ooif. * . A.5)
Это решение удовлетворяет уравнению A.3), в чем легко убедиться
подстановкой, и начальным условиям : . •
U @) = О, -JLL/ == йшах(»0=^.
at
Графики перемещения, скорости и ускорения показаны на рис. 1,9.
Максимальные .значения-этих величин соответственно равны и/<о0, v и va>o.
Чтобы платформа не поднималась, вверх, в нижнем положении штока
открывается вентиль, давление падает и платформа останавливается. Время
импульса (в секундах) равно одной четвертой периода колебаний:
t — — — — = JL
и~ 4 ~ 4/ ~2ш0 * ,
Если, например, жесткость гидравлической пружины' составляет С=
=25 т/м, то
а длительность импульса ?н—20 мс. ¦
• Пример 3. Произвести те же вычисления, что и в примере 1, толькб при
условий, что платформа падает на свинцовую пирамиду (см. рис. 1.7,в).
Решение. Уравнение движения платформы будет иметь вид
—Bu?=md2u/dt2. (Г.6)
Это уравнение — нелинейно. Единственным способом решения нелинейных
уравнений является линеаризация. В данном случае она сводится к тому, что
решение уравнения A.6) на достаточно большом интервале времени заменяется
последовательным решением ряда частных линейных уравнений на малых ин:
тервалах времени. Если интервалы времени взять одинаковыми, то из
уравнения A.6) можно получить частные уравнения в разностной форме.
. 15
Введем дискретизацию по времени. Для этого выберем некоторый шаг по
времени т и будем измерять перемещения только в моменты времени 0, т,
2т, ..., it, где 0, 1, 2, ..., i — номер шага по времени. Значения перемещений в'
эти Моменты времени обозначим через щ. х
- Скорость платформы в момент it может быть определена в виде разности
«вперед» Хщ+\—щ) /т или разности «назад» -(Ui—Ui-i)fxt а ускорение —в виде
разности от указанных разностей (или второй разности):
Заменив дифференциальное выражение ускорения в уравнении A.6)
приближенным разностным выражением, получим разностное .уравнение
- Поскольку теперь щ на каждом шаге по времени — постоянная
величина, щг выступает в роли постоянного коэффициент и нелинейность
исчезает. ' ,.
Вычислим ряд значений Мг,. которые удовлетворяли бы уравнению A.8).
¦Они и будут приближенным решением уравнения A.6). .Значения т
вычисляется последовательно, начиная с некоторых начальных условий. В начальных*
условиях нужно задать начальные значения щ и мь По этим значениям
вычисляется и2 и т. д. у
v Следовательно, с помощью формулы A.8) можно будет вычислять щ+i по
значениям щ и т~\. Для удобства вычислений решим уравнение A.8) относи-
-тельно щ+i:
и1^ = - — и\ + 2щ~ыа-л. • . A.9)
т
Это и есть нужная нам рекуррентная формула для последовательных зо
времени вычислений. % .
Теперь зададим начальные условия. Предположим, что за начало отсчета
перемещения и мы выберем момент *=т, когда происходит касание платформы,
•и пирамиды, т. е. «i=0. *
Если платформа в этот момент двигалась со скоростью я, то в момент f*0
-она находилась на расстоянии Uo=—vl% от платформы. Таким образом, с
помощью величин Ц\ и по мы задаем перемещение и скорость в начале расчета.
Ятобы получить численное значение Ыо, нужно знать шаг по времени т. Мы
должны задать шаг по времени, исходя из требований точности pac4efa. Для
получения малой погрешности расчета необходимо, чтобы шаг по времени был
небольшим. .
Выбор шага по времени — это очень сложный вопрос, особенно при
решении нелинейных уравнений. Нужный шаг мбжно выбрать при сравнении расчё- '
тов с разными шагами. Если, например, при уменьшении шагов по времени по-
следующие решения отличаются от предыдущих на значения, лежащие в
допустимых пределах, то шаги по времени приемлемы. *
16
Но с каких значений т нужно начинать пробные расчеты? Максимально
допустимое значение шага по времени выбирается из условия устойчивости
вычислительного процесса. Дело в том, что уравнение A.9) вместе с начальными
условиями для щ и и\ образует так называемую явную схему. Вычисления по
этой схеме являются условно устойчивыми. Если условие устойчивости не.вы-
лолняется, то погрешности расчета от шага к шагу по времени очень быстро
возрастают л\ ничего похожего на действительное решение задачи не
получается. Решение должно быть обязательно устойчивым.. Для этого шаг по
времени должен быть не больше, некоторого критического значения tKP. В .противном
случае решение будет неустойчивым.
В линейных задачах тКр — величина постоянная. В нелинейных задачах /tvp
само зависит от полученных решений. Поэтому при решении нелинейных задач
шаг по времени обычно выбирают заведомо меньше ткр.
В нашем случае значение т можно выбрать из следующих соображений.
Есть некоторое перемещение' платформы wkp, при котором торможение плат-4
формы должно обязательно закончиться. Предположим, что это значение
равно «кр=0,02 м. Выделим теперь в уравнении A.9) безразмерный коэффициент
(Вт*1т)щ2. Для того чтобы решение было устойчивым, нужно, чтобы при
w/=wxp этот коэффициент был меньше единицы. Возьмем (Вт/т) 0,0004=0,1,
тогда х2—250т/В. Подставим это значение в уравнение
Теперь, начиная с начальных'условий Uq^—v/t и щ—ч0, можно начать
вычисления. ;
Если т=1 мс, а у~10 м/с, то ио=0,001. Результаты вычислений
приведены ниже: . , , '
Номер шага
* 0
1
2
3
9
10
11
Л2
13
14
15
по времени ¦ щу м
—0,0010
0,0000 ¦'
0,0010
0,0020 - .
0,0080
0,0090
0,0100
.0,0107
0,0112
.0,0113
0,0110
После 14-го шага по времени перемещения начинают уменьшаться. Это
значит, что платформа пойдет обратно вверх, если будет продолжать
действовать сила ?=Виъ. Но в нашем случае форма свинцовой пирамиды после
смятия не восстанавливается, и как только платформа приходит в крайне нижнее
положение, сила торможения становится равной нулю. Платформа
останавливается. Таким образом, тормозящее действие, пирамиды сказывается практиче-
ски в течение 13 шагов по времени (рис. 1.10).
2—1215 " . 17
du м
Максимальный ход платформы
получается меньше критического, он
равен 0,0113 м. Максимальное ускорение
можно получить по разностной
формуле A.2) при i=13:
Рис. 1.10. Графики перемещения,
скорости, ускорения платформы при
падении на свинцовую пирамиду
=,_400— =-40 fig.
с
Таким образом," максимальное
ускорение получается равным примерно
41 g, а длительность импульса — пор яд-
ка 4 мс. При этом пирамида сминается
на 0,0133 м.
Подбирая различные демпферы, можно воспроизводить на ударных стент
дах испытания радиоаппаратуры в широком диапазоне ударных нагрузок.
Длительность ударных импульсов может колебаться от 20 до 0,2 мс, а
максимальное* ускорение — от 15 до 3500 g,
*' 13. ЛИНЕЙНЫЕ УСКОРЕНИЯ
Линейные ускорения обычно возникают в аппаратуре при
разгоне и торможении транспортных средств, например при взлете
и посадке летательных аппаратов.
Для испытания аппаратов на действие длительных постоянных
перегрузок применяют центрифуги, наподобие тех, с помощью
которых проводят тренировки космонавтов (рис. 1.11). Платформа
с аппаратом, проходящим испытания, движется по кругу с радиусом
R.> При этом центробежная сила создает ускорение, равное
а~Д<Л "- A.10)
Если, например, нужно получить ускорение в 1000?, то при
радиусе 7?, равном 2 м, платформа должна вращаться с частотой
, При этом то^ки крепления аппарата к платформе будут
испытывать центробежную силу, равную F=m-1000-9,81 «10* Н при мае-
Рис. 1Л1. Схема испытания
аппарата на центрифуге:
-/ — противовес; 2 — аппарат
18
се аппарата m=10 кг. Такие большие силы при поломке
центрифуги могут привести к большим разрушениям. Поэтому прочности
центрифуги и качеству крепления аппарата к платформе нужно
уделять большое внимание.
Мы рассмотрели испытательную аппаратуру
для,воспроизведения процессов ударов, вибраций и стационарных нагружений
радиоаппаратуры: Не менее важной является проблема измерений
механических характеристик нагружения, т. е. деформаций,
напряжений'и ускорений, возникающих в процессе испытаний.
Рассмотрим принципы таких измерений. ... " -
1.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК •
ВИБРАЦИИ .
Задача измерения характеристик вибрации постоянно
возникает в практике проектирования нестационарной аппаратуры. Чтобы
определить условия работы аппаратуры на борту транспортного
средства, необходимо произвести измерения в предполагаемом
месте установки аппаратуры. Для определения характеристик вибро-
дрочности и виброустойчивости аппаратуры необходимо измерить
характеристики движения в,разных точках конструкции при
испытаниях макетов и опытных образцов.
Измерения обычно производятся в нескольких точках
конструкции. Чем больше таких точек, тем полнее картина
деформированного состояния и тем легче выявить причины отказов и сбоев.
Одновременно измеряют характеристики движения стола зибростен-
да или ударного стенда; Па отношению к амплитуде колебаний
стола вибростенда измеряются коэффициенты усиления
колебаний конструкции на резонансных частотах,- например
'коэффициенты динамичности. . . "
Основными механическими величинами, представляющими ин^-
терее для радиоконструктора, являются перемещения, скорости и
ускорения точек конструкции. Могут представлять ийтёрес также
деформации и механические напряжения, возникающие
при,действии внешних возмущений.
При вибрациях точки конструкции совершают обычно
моногармонические колебания. Только при очень больших амплитудах
начинают сказываться различные нелинейные явления и помимо
колебаний основного тона появляются колебания высших тонов.
Если колебания моногармонические, то в принципе
безразлично, какую характеристику вибрации измерять — перемещение,
скорость или ускорение. Зная частоту вибрации со, легко перейти от
амплитуды перемещений к амплитуде скорости и ускорения с
помощью простых соотношений: если Л —амплитуда перемещений,
то Лео— амплитуда скорости и Лео2 — амплитуда ускорения.
Однако техническая реализация различных измерений —
задали различной сложности. Дело в том, что всякое движение отно-
2 ¦ • - - 19
сительно. Перемещение и скорость необходимо измерять относит;;
тельно неподвижных точек, например точек, находящихся на зем- J
ле. Точка отсчета может быть связана и с корпусом транспортно-/
го. средства, но она не должна двигаться с ускорением.. Создать /;
такие системы отсчета еложно. Другое дело ускорение. Оно вое-.
принимается частями конструкции как инерционная сила. А из-'
мерить силу гораздо проще. . ',
Существует большое количество различных принципов измере- ¦
ния механических величин и еще большее количество конструкций \
датчиков. Но в большинстве случаев механшеские величины пре- ?
образуются в электрические и затем измеряются электрическими
измерительными устройствами.
Широкое применение получили акселерометры — датчики для"
измерения ускорений вибраций и удара. Работа акселерометров \
основана на различных способах преобразования механической
энергии в электрическую.
Наиболее распространенными являются пьезоэлектрические
. датчики. Эти датчики обладают высокой чувствительностью [4], J
достаточной механической прочностью, имеют сравнительно малые
габариты и массу, линейную характеристику .преобразования в
широком диапазоне частот, слабо чувствительны к электрическим •
и магнитным полям. Различные типы пьезоэлектрических
датчиков, выпускаемых отечественной промышленностью,
предназначены для измерения ускорений, до lOOOg* на частотах до 20000 Гц.
Недостатком пьезоэлектрических датчиков является нестабиль-
. ность коэффициента преобразования.
. Для измерения, ускорений используются и потенциометриче-
ские датчики, обладающие высокой помехоустойчивостью. Однако
они имеют ряд недостатков . (невысокие динамические свойства,
низкая устойчивость выходного сигнала*к ударам и вибрациям
из-за наличия скользящих контактов), поэтому применяются для
измерения ускорений вибрации до 6g на низких (до 30 Гц)
частотах, а также для измерения Линейных ускорений до IQg.
'/ * *
L •¦ -
Рис. 1.12. Простейшая конструкция
пьезоэлектрического акселерометра
20
Рис. 1.13. Проволочный тензодатчнк-
Индуктивные датчики обладают достаточно высокой
надежностью и помехоустойчивостью. Они имек/т больший по сравнению
с предыдущим типом датчиков диапазон частот (до 500 Гц) и
больший предел измерения ускорений (до' 50 Гц). Кроме того,
индуктивные датчики позволяют измерять постоянную
составляющую ускорения.
' Конструкция пьезоэлектрического aкceлepoмefpa для
измерения ускорений в сравнительно широком диапазоне частот
изображена на рис, 1.12.
К основанию /крепится пьезоэлемент 2 и инерционная масса 3.
Между массой и кожухом 4 установлена пружина 5, создающая
предварительное поджатие пьезоэлемента. При ускоренном
движении на пьезоэлемент действует инерционная сила F=* та, где
т — инерционная масса; а —ускорение. Под действием этой силы
на обкладках пьезоэлемента возникает заряд, величина которого
пропорциональна силэ. Заряд измеряется по значению
напряжения на обкладках пьезоэлемента.
Для крепления к объекту измерения в конструкции датчика
предусматривается резьбовой наконечник или фланец» При малых
размерах датчиков они могут приклеиваться к объекту с помощью
гермозамазки.
Измерение деформации в элементах конструкций производится
проще и выполняется с помощью тензометрических и резиещвных
датчиков [4]. Проволочный тензодатчик (рис. 1.13) представляет
собой плоскую спираль из тонкой (несколько десятков микрон)
проволоки, наклеенную на бумажную или плёночнукэ подложку.
Фольговые тензорезисторы получают фо?отравлением, что
позволяет изготавливать датчики любой формы.
Тензодатчики наклеиваются на исследуемый элемент
конструкции с помощью прочного и эластичного, клея и покрывается
герметизирующим покрытием. При деформации конструкции
происходит изменение омического сопротивления датчика в результате
удлинения чувствительного элемента и уменьшения его
поперечного сечения. Зависимость омического сопротивления проводника
от деформаций удлинения приведена в разд. 2.1.
Полупроводниковые тензорезисторы имеют более высокую пб
сравнению с металлическими чувствительность. Однако они
чувствительны и к изменению теплового режима, а также имеют
значительный разброс параметров.
Рассмотренные чтипы датчиков устанавливаются на объектах
измерения, что искащаёт динамические свойства исследуемой
конструкции. Поэтому-датчики должны иметь малую массу по
сравнению с массой деталей конструкций. Стремление вообще
избавиться от этого влияния привело к разработке бесконтактных
датчиков— емкостных, оптических, электронных. Однако они
отличаются высокой сложностью и стоимостью. v
21
;
Современные испытательные установки позволяют 'получать
информацию с сотен вибродатчиков, которые устанавливаются в
различных точках объектов. Обработка информации ведется с
помощью ЭВМ. •
1.5. СЛОЖНЫЕ
МЕХАНИЧЕСКИЕ ВОЗДЕЙСТВИЯ
В практике эксплуатации радиоэлектронной аппаратуры гарг
монические вибрационные возмущения встречаются относительно
редко. Значительно чаще возмущения имеют-характер полигар*
монической или случайной функции. Источниками полйгармони-
ческих возмущений являются, например, силовые установки nor
движных объектов, на которые устанавливается аппаратура.
Случайные воздействия обычно являются результатом неровностей
дороги, турбулентных потоков воздуха и т. д.
* Полигармоническое возмущение в виде силы P(t) или
перемещения u(t) основания, на котором установлен* аппарат, обычно
представляется в виде суперпозиции гармонических составляющих.
Для колебательных систем, описываемых системрй линейных
дифференциальных уравнений, справедлив принцип суперпозиции^
т. е> реакция на воздействие P(t) представляет собой сумму
реакций на каждую гармоническую составляющую. Таким образом,
в этом случае рассматривается решение нескольких задач расчета
колебаний при заданных гармонических возмущениях.
Для расчета вибраций конструкций при случайных
воздействиях (в виде силы или перемещения в точках крепления аппарата
к транспортному средству или к вибростенду) необходимо
воспроизвести в расчете характер этих воздействий. Случайные
процессы, обладаьрт рядом статистических характеристик. Нужно,
чтобы в расчете внешние возмущения соответствовали этим
характеристикам. При этом можно подобрать некоторые
детерминированные функции с такими же. характеристикам!! и использовать
эти функции при задании внешних воздействий.
Таким образом, при расчете колебаний системы при случайных
воздействиях должны быть заданы вполне определенные
возмущения, полученные либо в результате преобразований, либо в
результате экспериментов. Если воздействия удается представить в
виде суперпозиции каких-либо простых функций, например
гармонических, то возможнб* получить точное аналитическое решение
задачи. В общем случае применяются численные методы, так как
они позволяют решать задачу при произвольном возмущении.
Такое возмущение может быть получено с помощью записи
реального процесса. . .' \ . .
Приведенные рассуждения' показывают, что аналитические или
численные расчеты полигармонйческих или случайных колебаний
. 22
конструкций строятся на тех же принципах, что и расчеты при
гармонических вибрациях и ударах.: ' .
Заметим также, чтог метод конечных разностей дает
возможность рассчитывать конструкцию пр» произвольной форме
внешних воздействий, в том числе и некотором детерминированном
процессе, построенном по вероятностным характеристикам
заданного случайного процесса. Специального рассмотрения такие
методы расчета вибраций не требуют. Другое дело — расчет
режимов испытаний аппаратуры при полйгармонических и случайных
воздействиях. Здесь открываются большие возможности
сокращения-объема испытаний за счет задания определенных
детерминированных режимов работы вибраторов. . - '
КОНТРОЛЬНЫЕ ВОПРОСЫ,
1. Указать причины возникновения в- аппаратуре ударов, вибраций, линей-
корений. .
Перечислить основные характеристики указанных механических, про-
ных ускорений.
цессов.
3. Каковы , особенности вычисления перемещений точек конструкций при
разностном расчете с помощью явной схемы? -
4. Что нужно предпринять, если решение задачи по явной схеме получилось
неустойчивым? •
5; Каким образом работают датчики деформаций, ускорений?
Г л а в а 2. ОТКАЗЫ И СБОИ В РАБОТЕ
АППАРАТУРЫ, ВОЗНИКАЮЩИЕ Ъ
РЕЗУЛЬТАТЕ УДАРОВ И ВИБРАЦИЙ
Все конструкционные материалы обладают упругими свойствами. Под
действием сил детали, изготовленные из упругих материалов, меняют свою форму, а
если силы снять, то форма частично или полностью восстановится. При ударах
и вибрациях изменяющиеся во времени формы деталей образуют сложную
картину деформации конструкции, в которой упругие волны, отражаясь и
преломляясь на наружных поверхностях деталей, местах' соединений и других неод-
нородностях, неоднократно накладываются друг на друга наподобие морских-
волн у изрезанных скалистых берегов. Чем тверже материал, тем меньше
изменяются размеры деталей конструкций. Например, стальной стержейь длиною
в 1 м и сечением в 1 см2 под' действием растягивающей силы в 105 Н
растягивается на 0,5. мм, а деформации растяжения составляют всего
e=AL = _0:5_= 0 .
I . 1000
где I — длина стержня; А? — приращение длины эследствие растяжения.
4 ' ' 23
Поскольку конструкции РЭА и ЭВА имеют обычно меньшие размеры, то w
перемещения в них меньше, обычно порядка нескольких десятков микрон.
Такие малые деформации, распространяясь по конструкции в виде упругих *волн„
вызывают появление больших сил. Не только непосредственно силы, но и сам»
малые деформации, а также скорости, ускорения (перегрузки) могут привести
к отказам и сбоям в работе аппаратуры. Поэтому малыми деформациями в
общем случае пренебрегать не следует. При анализе работоспособности
конструкций их необходимо учитывать. > „
В результате механических воздействий (вибраций, ударов) при испытание
ях или в эксплуатации в радиоаппаратуре могут возникнуть отказы и сбои [5].
Отказом считается такое повреждение, которое вызывает ^восстанавливаемое*
нарушение в работе аппаратуры. При этом отклонения выходных характерна
стик аппарата от их номинальных значений превышают допустимую величину.
Для восстановления после отказа аппаратуры требуется ее ремонт.
Сбоем считается временное нарушение в работе аппарата. Функции
аппарата сами восстанавливается после окончания действия внешних механических:
нагрузок.
Аппаратура, выдерживающая внешние механические нагрузки без отказов,
называется вибропрочной, а аппаратура, выдерживающая нагрузки без сбоев, —
виброустойчивой. ' ^
Требование виброустойчивости является*более" жестким, чем вибропрочно-,
сти. Внбр'оустойчивую аппаратуру разрабатывать труднее.
Нестационарные процессы деформаций в каждой точке конструкции в
каждый момент времени можно определить с помощью различных характеристик
движения: деремещений, деформаций, напряжений, скоростей и ускорений.
Перемещения, скорости |н ускорения являются векторами, т. е. определяются
в. общем случае тремя компонентами, а деформации и напряжения — тензорами
и имеют по 9 компонентов, записываемых в виде матриц 3X3. , -
Одни характеристики легко выражаются через другие с помощью простых
дифференциальных соотношений и закона Гука. Например, можно выразить
все характеристики движения через перемещения. Тогда деформации и
напряжения определяются через производные, от перемещений4 по координатам, а ско:
рости и ускорения — как производные от перемещений по времени.
Соответствующие математические выражения мы приведем ниже, когда в этом возникнет
необходимость. А пока заметим, что выражение всех характеристик движения
через какую-либо одну рационально при производстве расчетов. Делается это *с
целью сокращения числа неизвестных. Чаще всего в качестве единственной
неизвестной выбирают именно перемещение. При этом говорят, чтч> задачу
решают в перемещениях. - - . * •
Однако при анализе влияния механических процессов на работу
аппаратуры использовать в качестве характеристик движения только перемещения
нерационально. Дело в том, что отказы и сбои в работе аппаратуры
фиксируются как нарушения в работе электрической схемы или нарушения в работе
преобразователей электрических сигналов в сигнал другой физической природы,
например в звук или изображение на экране (табло). Так или иначе при таком?
анализе приходится рассматривать взаимодействие электрических и механиче-
24 '
ских процессов. В- общем случае электромагнитного поля в каждой точке
такого поля можно измерить потенциал, напряженность поля* плотность тока,
напряженность магнитного поля, магнитную индукцию и т. д. Все эти величины
также взаимосвязаны и могут выражаться через одну какую-либо величину
с помощью законов электродинамики.
Когда речь заходит о« взаимовлиянии электрических и механических вели-
чин, далеко не безразлично, какие механические и какие электрические
величины сравниваются. Например, закон электромагнитной индукции связывает
напряженность электрического поля в проводнике с магнитной индукцией поля
и скоростью движения проводника в магнитном поле. Эта зависимость
записывается в виде векторного произведения
E=VXB, • '
где Е — вектор напряженности электрического поля в проводнике; v — скорость
движения проводника; В — вектор электромагнитной индукции.
Можно, конечно, выразить эту взаимосвязь и через другие характеристики
механического движения и электромагнитного -поля. Но выражение получится.
/Шд7
/ донных о I
I конструкции/
Построение
? дискретной
модели
Расчет
перемещений
1 *
1 Расчет
1 деформаций
4
Задание первых
данных о
конструкции
L
Печать
„аварийная
ситуацияД "
печать
аварийная
ситуация А"
Печать
„аварийная
ситуация Л"
Рис. 2.1. Алгоритм анализа ре- -
зультатов расчета
25»
<>олее сложным, и,х главное» эти характеристики не так четко будут отражать
<^уть явления и окажутся менее пригодными для анализа. Поэтому при
рассмотрении различных причин возникновения отказов я сбоев используются
различные характеристики движения и электромагнитного поля.
При проектировании новой аппаратуры"* расчеты движения разных точек
будущей конструкции, если такие расчеты удается произвести, дают
возможность оценить влияние этого движения на работоспйсобдоеть различных
элементов электросхем. Такой подход используется, например, в разрабатываемых
имитационных системах проектирования вибропрочных и виброустойчивых
конструкций. В этих системах производится моделирование .процессор ударов и
вибраций в проектируемой аппаратуре. Вопросы построения расчетной модели и
проведения расчетов изложены в гл. 6. Здесь же кратко опишем алгоритм
-анализа работоспособности конструкций, представленный на рис. 2.1. -
По вычисленным в процессе решения значениям перемещений различных
точек конструкции определяют деформации, напряжения, скорости, ускорения
(перегрузки). Сравнение этих характеристик с предельно допустимыми
величинами позволит оцедгать работоспособность конструкций. Если все определяемые
характеристики в контрольных точках конструкции не превышают предельных
.значений, считается» что конструкция «испытания» прошла. Если же хотя бы в
«одной.точке вычисляемые величины превысят предельное значение, то
производится анализ причин возникновения недопустимых значений, вводятся
изменения в конструкцию и весь процесс— "от построения модели до анализа —
повторяется. . * ;
Допустимые величины деформаций, напряжений, скоростей и ускорений
определяются заранее при совместном рассмотрении механических и
электродинамических процессов и могут быть приведены в справочниках.
Рассмотрим процессы, происходящие в электрорадиоэлементах (ЭРЗ) при
тх деформации.
. 2.1. ИЗМЕНЕНИЕ ХАРАКТЕРИСТИК
ЭЛЕКТРОРАДИОЭЛЕМЕНТОВ
ПРИ ИХ ДЕФОРМАЦИИ
Деформация растяжения (сжатия)* и деформация сдвига опре- ,
деляются изменением формы деталей. Если эти детали .являются
ЭРЭ, то при деформациях изменяются их электрические
характеристики: сопротивления, емкости, индуктивности,. коэффициенты °
усиления транзисторов. , ч
Наиболее просто определить связь деформаций с омическим ;
сопротивлением проводников. Сопротивление R проводника связа- !
но с его геометрическими размерами (длиной L и сечением S) *
«известным соотношением * л
¦*-'¦§•'• ¦ ; '
26 -|
где р — удельное сопротивление материалов проводника. При
растяжении проводника, показанном на рис. 2.2, длина его
увеличивается на AL = eL, где в — относительное удлинение, а сечение
уменьшается на величину S[l—A—evJ], где v — коэффициент
Пуассона.
Таким образом, величина сопротивления с учетом
относительного удлинения составит
а относительное изменение сопротивления будет равно . .
^=_L+i 1. ' B.1)
R (l-ve)« '
Если, например, анализ работы, электросхемы показал, что
относительное изменение сопротивления при ,его деформации не
должно превышать одного процента Д/?/#0<0,01, то из уравнения
B.1) можно . найти .допустимую величину деформации еДоп =
=; 0,00665=0,665%. Это значение, получено при коэффициенте
Пуассона у = 0,25. ¦ ' * . ¦ •
При однородном растяжении металлических материалов такие
большие значения <8 встречаться практически не могут. Для этого
нужны слишком большие силы, которые вызовут разрушение
материала. Но при неоднородных деформациях, например при
изгибе пластин или стержней,-на их поверхности деформации
растяжения (сжатия) могут достигать указанного значения. Поэтому
наиболее опасны деформации проводников и резисторов на
поверхности плат, подложек, микросхем, мембран и других плоских
деталей, подверженных изгибным колебаниям.
В меньшей мер^ зависят от деформаций емкости и
индуктивности ЭРЭ, но и они могут привести к возникновению сбоев,
особенно йри вибрациях на высоких частотах, что может вызвать
появление резонансных явлений в колебательных контурах или
автоколебаний. Вычисление допустимых значений деформаций в этом
случае возможно по той же методике, что и для проводников, но
является несколько более сложным.
Ut+€)
Рис. 2.2. К определению зависимости сопротивления проводника от деформация
растяжения
27
3:2. РАЯРУШЕНИЕ ВЫВОДОВ •
ЭЛЕКТРОРАДИОЭЛЕМЕНТОВ
Электрорадиоэлементы, устанавливаемые на печатных плата:"
и других несущих конструкциях, обычно соединяются с остальной
злектросхемой с помощью* гибких выводов, которые припаиваются
или привариваются $ контактным площадкам на печатных
платах. Например, на рис. 2.3 показана компоновочная схема
функциональной ячейки IV поколения бортовой аппаратуры [6]. В этоь
ячейке используются навесные элементы /, у которых выводы
являются одновременно креплением элемента к плате, и
электрическим соединением. У гибридных интегральных . схем 29 которые
приклеиваются к печатной плате 3* соединительные золотые
проводники 4 выполняют только функции электрического соединения.
Выводы ЭРЭ имеют малую жедткость и поэтому при
вибрациях аппаратуры испытывают большие деформации и могуту-сло-
маться. Разрушение выводов ЭРЭ является частой причиной
отказов аппаратуры, поэтому расчет прочности выводов очень важек
при проектировании бортовой аппаратуры.
Если выводы ЭРЭ являются его креплением, провести расчет
прочности гораздо проще, поскольку массой выводов по
сравнению с массой навесного элемента можно пренебречь и расчетная
модель получается с одной * степенью свободы. Такие модели мы
будем рассматривать в тл. 3. В результате расчета вычисляются
Рис. 2Л. Компоновочная схема
функциональной ячейки
28
50 100 200 SO0 400 500 1000 2ШЮ
Рис. 2.4. Номограмма для
определения допустимых перегрузок
напряжения в выводах. Эти.напряжения сравниваются с
предельно допустимыми напряжениями для материала выводов. Если они
превышают предельно допустимые напряжения, то считают, что
выводы разрушатся. В противном случае определяют запас
прочности конструкции выводов как отношение предельно допустимых
напряжений к реальным напряжениям, полученным
экспериментальным или -расчетным путем. Поскольку напряжения в разных
местах выводов будут различными, нужно, взять амплитудные
значения в наиболее опасном месте, в котором напряжения
максимальны. О выборе максимально допустимых напряжений сказано
в следующем разделе, где рассматривается общий случай
разрушения деталей несущих конструкций.
Если выводы гибридной интегральной схемы служат только
для электрического соединения и не поддерживают интегральную
схему, расчет деформации их значительно сложнее. Массой
выводов пренебречь нельзя, и расчетная модель получается с
распределенными параметрами. Кроме того, большие различия могут
быть в форме выводов и их креплений к микросхеме и плате. По-
этомУ производить расчеты деформаций таких выводов 'нерацио- \
нально. Гораздо проще изучить прочность выводов
экспериментально. '
Эксперименты показали, что причиной разрушения выводов
могут быть слишком большие деформации, возникающее в
результате больших скоростей вибрации. Предельное^ значение
деформаций определяется амплитудой изгибных колебаний. Для
золотых выводов диаметром 0,05 мм и длиной не более 5 м амплитуда
колебаний А не должна превышать 0,3 мм.
Большие скорости могут привести к разрушению выводов
вследствие усталости материала выводов при вибрации. Скороетъ
, v не должна превышать 800 мм/с. . , '
Опасными для выводов являются резонансные колебания. В ре*
зонансе точки поверхности платы совершают гармонические во
времени колебания по закону
u=Asm(dOt, ф - • . " . B.2)
где шо=2jt/q — резонансная частота.
Значение скорости и ускорения получаются
дифференцированием B.2) по времени:
v *=А(йо cos 0M?, п=—Л too2 sin <юо?
При экспериментальных исследованиях проще всего
измеряется амплитуда ускорения, которая определяется как
где р — коэффициент динамичности конструкции, в данном
случае — платы; п — коэффициент * перегрузки f источника вибрации;
8~ускорение свободного падения .(#=9,81 м/с2).
/ 29
Коэффициент перегрузки п показывает, во сколько раз
амплитуда ускорения в местах крепления платы больше, чем ускорени.
свободного падения. А коэффициент динамичности показывает, в
сколько раз амплитуда ускорения в опасном месте платы
превышает амплитуду ускорения в местах крепления..
Если учитывается ограничение' по амплитуде колебаний А^
<0,3 мм,.то коэффициент перегрузки не должен превышать веди-
чины .
0,00121
B.3
Если же учитывается ограничение по скорости,/то коэффициент
перегрузки не должен превышать ~
,_=*¦<«!&.¦ - " ' ' ,2.4
В неравенство B.3) резонансная частота /0 входит в квадрате.
а в неравенство B.4)—в первой степени. Поэтому требование
B.3) является более жестким на низких частотах, а требование
B.4)—на высоких. На частоте f0 -0,512/0,00121 =423 Гц-оба
выражения дают одинаковое значение коэффициента перегрузок.
На рис. 2.4, взятом из [6], показана томограмма для
определения допустимых перегрузок аппаратуры с указанйыми золоты-
?апп
аап
DDDD
6)
в)
Рис. 2.5. Основные типы ячеек с различными коэффициентами динамичности,
зависящими от метода крепления:
а—ТИС приклеены к металлической рамке клеем КВК-68, Э=40; б — ГИС приклеены к
печатной плате клеем КВК-68, 3^25; в — ГИС приклеены к металлической рамке клеем
КВК-68, а печатная плата приклеена к ней компаундом КТ-102, Р=10; г — ГИС приклеенк
к металлической рамке компаундом КТ-102 с двух сторон, р=3; д — ГИС приклеены
к многослойной печатной плате клеем. КВК-68, а сама плата склеена компаундом гКТ-102..
р«з
30
ми выводами гибридных интегральных схем для разных
коэффициентов динамичности этой аппаратуры в зависимости от их
резонансной частоты. Если известна резонансная частота
конструкции fo и ее коэффициент динамичности р, то по номограмме
можно определить допустимый для данной аппаратуры коэффициент
перегрузок. Если действительный коэффициент превышает
допустимый, то выводы микросхем могут не выдержать вибрации..
В этом случае необходимо выбрать другую конструкцию с
меньшим коэффициентрм р или большей резонансной частотой.
В распоряжении конструктора может быть несколько извест- ,
ных конструкций с различными определенными коэффициентами,
динамичности. Тогда задача сводится к выбору конструкции с
подходящим коэффициентом динамичности. На рис. 2J5 показаны,
основные типы конструкций ячеек с различными коэффициентами:
динамичности, • . '
Пусть; к 'примеру, необходимо выбрать конструкцию ячейки,,
„которая должна работать в условиях заданных внешних
воздействий. Воздействия определяются как величины перегрузок в
зависимости от частоты вибрации. Эту зависимость' можно нанести)
на номограмму (см. рис. 2.4) в виде штриховой ломаной линии.
Далее выбирается подходящая, конструкция ячейки и
определяется ее резонансная частота. Пусть, например, она равна 400 Гц».
Соответственно этой частоте проводят на номограмме
вертикальную линию. Находят точки пересечения этой вертикали с линией,,
соответствующей коэффициенту динамичности р выбранной
конструкции (точка допустимых перегрузокI и do ступенчатой ли-*
нией внешних воздействий (точка действительных перегрузок)-
Если точка 1 находится выше точки 2, та это означает, что
нагрузки допустимы. Если же точка 1 ниже точки 2, то нужно выбрать
другую конструкцию — с меньшим коэффициентом динамичности.
Можно построить подобные номограммы и для других
конструкций, в которых предельные перегрузки определяются не
прочностью выводов- ГИС, а другими причинами. Важно только знать,
зависимость этих перегрузок от частоты вибрации.
2.3. РАЗРУШЕНИЕ ДЕТАЛЕЙ
НЕСУЩИХ КОНСТРУКЦИИ
Напряжение в курсе «Сопротивление материалов» [7]
связывают с прочностью деталей конструкций. Если напряжения превы-.
.шают допустимое для данного материала значение, то происходит
разрушение материала и, как правило, отказ аппаратуры.
Поэтому допустимые напряжения определяются значениями напряжений
в материале, при которых начинается разрушение.
Однако механизм разрушения в различных материалах
различен. По-разному разрушаются твердые и* мягкие материалы; крис-
3f"
тйллические и аморфные вещества. Механизм разрушения
различен при медленном и быстром нагружении, одиночных * импульс*,
яых, длительных периодических или случайных нагрузках. В
любом из этих случаев должны быть определены значения
допустимых напряжений. Для этих целей используются справочные
данные или данные,, полученные экспериментально, -'
Например/для конструкционных сталей, цветных.металлов и
сплавов, некоторых пластмасс, которые могут подвергаться
пластическим деформациям, в качестве предельно допустимого значе-1
ния напряжений выбирают предел пропорциональности. У низко-
углер9Дистых сталей он равен примерно 2-Ю8 Н/м2. При более
высоких напряжениях в материале деформации не
пропорциональны нанряже„ниям. Нарушаетея^закон Гука, который положен в
основу расчета упругих • деформаций. Картина деформаций,
полуденная расчетным путем, не соответствует действительной карти*
:не деформаций в конструкции. Расчет становится неправильным,
до главное состоит в том, что далее начинаются пластические
деформации и конструкция теряет первоначальную форму. При
конструировании это считают недопустимым. „
Если допустимые значения напряжений известны, то в
результате расчета необходимо убедиться, что во всех деталях конструк-'
ции действительные напряжения не превышают допустимые:
Однако при анализе прочности конструкций нужно учитывать
два обстоятельства*
1. В каждой точке конструкции ;
тензор . напряжений содержит
девять компонентов, по три на каж:
дой грани элементарного
прямоугольника в толщине материала
(рис. 2.6), Может случиться так,
что каждый' из этих компонентов *
не превышает допустимых значений t
соответственно нормальных или *
касательных напряжений, а
разрушение все-таки происходит. Это
бывает тогда, когда материал
разрушается* по поверхности,
наклонной к граням элемента. Чтобы из-:;
бежать таких ошибок, в расчёт вво-t
дят контроль прочности по главным ;
напряжениям в наиболее опасном^
направлении. Компоненты напря^/
жений позволят вычислить это глав- ]'
ное напряжение и определить его С
направление. Данный подход при расчетах прочности радиоконст-.
рукций представляет лишь теоретический интерес, поскольку
производить такие вычисления во всех точках конструкции в каждый
момент исследуемого процесса практически невозможно. Проще
и эффективнее другой подход, основанный на предварительном
анализе рассчитываемой конструкции и выявлении мест
возможного разрушения.
Наиболее часто разрушаются разъемные и неразъемные
соединения и места крепления, сечения, ослабленные отверстиями, места
гибки, места, в которых происходит трение и удар соседних
деталей, и т. п. Именно в этих местах, и производится контроль по
допустимым значениям напряжений.
2. Расчеты упругих деформаций в. сложных конструкциях
имеют весьма ограниченную точность. Основные источники
погрешностей расчета следующие:
отсутствие надежной информации о характеристиках
материала; например, модуль Юнга у разных образцов одного и того' же
материала имеет разброс tfc20% и более;
погрешности дискретизации, связанные с заменой непрерывной
среды дискретной моделью;
невозможность учета точной конфигурации всех деталей,
например мелких отверстий;
невозможность.прямого учета различных мелких
концентраторов напряжений, например рисок на поверхности деталей,
микротрещин, раковин и т. п. , .
Для косвенного учета этих погрешностей с целью обеспечения
прочнбсти конструкции приходится занижать значения
допустимых напряжений, как это делается в строительной механике
сооружений, кораблей, летательных аппаратов. Коэффициент запаса
берется порядка 2... 3.
2.4. ВИБРОШУМЫ И НАВОДКИ
Скорости относительного перемещения отдельных частей
конструкции могут явиться непосредственной причиной отказов и
сбоев в работе аппаратуры вследствие взаимосвязи процессов
различной физической природы [8].
Например, Относительное движение ЭРЭ приводит к
взаимодействию их электромагнитных полей. В результате появляются
Дополнительные* как правило, нежелательные электрические сиг*
налы, называемые наводками или виброшумами. Если наводки
превышают некоторое допустимое для данного аппарата
значение, то в работе аппарата происходят сбои, а иногда и отказы.
Таким образом, можно установить связь допустимых скоростей
относительного движения и допустимых наводок. . .
3-1215 ~- ". .' 33
Наиболее опасны вибрации электрических схем в сильных
нитных полях трансформаторов, дросселей, реле и магнитных ;j
пускателей. Эти элементы конструкций будут интересовать нас как. j
источники' по л я.ч Мы будем считать их неподвижными, а всю схему 1
или часть ее — движущейся в этом поле. -Для простоты^
будем считать ноле однородным, т. ?. вектор магнитной индукций i
во всех точках поля будет одинаковым и равным В. &
. Наибольшие наводки получаются на длинных деталях, т. е- j
*на соединительных проводах. Зависимость ЭДС наводки от ско- *
рости движения v и магнитной индукции поля В дается законом.2
электромагнитной индукции E=vXB. Но проводники, например j
печатные на плате, обычно образуют замкнутые контуры (рис. 2.7). 5
Поэтому при плоскопараллельном движении платы электродви-и
жущиеся силы взаимно уничтожаются. . ¦ . •
Для движущегося замкнутого контура закон электромагнит-.!
ной индукции можно записать в виде' . j
B.5К
dt
at
где ех — электродвижущая сила^ появляющаяся в контуре вслед-1
ствие изменения проекции магнитного потока Фх через контур. '\
Магйитный поток, связанный с магнитной. индукцией ВХу щЛ
меняется как за счет изменения проекции площади контура Sxs
(первый член), так и за счет изменения самой магнитной индук-}
ции Вх (второй член). Дополнительные составляющие наводки в,*
других направлениях еу и ег появляются в результате изменения j
. проекций Sy, By и Sz, Bz соответственно/В контуре эти электро-;?
движущие силы складываются:
y
Предположим, что магнртный поток направлен вдоль оси х и по-,
стоянен во времени (рис. 2.8). Если плата неподвижна и недефор-;
Рис. 2.7. Замкнутый контур
.34
Рис. 2.8. К определению наводок
колебаниях платы
мированна, то вектор площади платы S нормален к плоскости ху
Во время изгибных колебаний платы в направлении z контур
вместе с платой наклоняется на угол а@ и проекция^ $,на ось х
становится равной $x*=Ssina. Для расчета допустимого'значения
скорости эту проекцию выразим через прогибы платы.
Предположим,' что плата совершает гармонические во времени
колебания с амплитудой W(x,у), различной в разных точках
платы.1 В точках А и С на контуре эти прогибы будут равны WAX
X$in<o? и We sin Ы соответственно. Тогда проекцию площади
контура на ось х можно представить в виде
SX=(WA—WC)LS sin at, ,
где L — продольный размер контура. ЭДС навоДки на -контуре
равна \;
e=—Bx(WA~Wc)L«) cos at. n B.6)
4 Наводка имеет ту же частоту ш, что и вибрация* а ее
амплитудное значение зависит от магнитной индукции, размеров
контура и амплитуды скорости. Если ЭДС наводка не превышает
заданной величины еДол, то допустимое значение скорости определяют из
уравнения
? B.7)
Таким образом, допустимые значения *ск6ростей B.7) будут
различными в разных точках конструвдии. Они будут зависеть от
интенсивности электромагнитного излучения, размеров контуров,
образуемых проводниками, ориентации этих контуров
относительно вектора В, картины деформирования и. допустимых значений
ЭДС наводки на контуре. Не зная полной картины деформиррва:
ния конструкции, можно вычислятьл допустимые скорости только
приближенно, используя различные упрощения/ Если же задачу
нужно решить точнее, то необходимо рассматривать совместно
картину электромагнитного поля и картину поля деформаций, что
значительно сложнее.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какой порядок величины имеют деформации и напряжения в
металлических конструкциях при ударах и' вибрациях?
2. Каково влияние деформаций на электрические характеристики
резисторов?
3. Как оценить запас прочности конструкции по результатам расчета?
пл 4' ^аким обРазом вычисляется ЭДС в печатном контуре дои вибрации
5. Что такое резонанс?
6. Что такое коэффициент перегрузки, коэффициент динамичности?
3*
Глава 3. КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ 'J
БЛОКОВ РЭА НА АМОРТИЗАТОРАХ '1
Любой расчет физических процессов в конструкциях* (механических, электриче-|
ских, тепловых) или процессов другой физической природы всегда сопровожу
дается рядом упрощений действительной картины. При расчетах процессов .в*
сложных конструкциях РЭА эти упрощения прежде всего касаются формы кон*
струкций. - • * . ,
Б расчете, как правило, не учитываются мелкие детали конструкции, отдель-,;
ные массивные детали или узлы рассматриваются как недеформируемые эле- <
менты конструкций; т. е. сосредоточенные массы, а детали типа пружин счи-j
таются упругими безынерционными элементами и т. п. В результате получает-^
ся упрощённая расчетная модель конструкции. Упрощения всегда вносят в .рас- ¦
чет неконтролируемые погрешности, которые можно оценить лишь приближенно.. •
С другой стороны, чем .проще расчетная модель, тем проще сам расчет. ]
Для простых расчетных* моделей можно получить аналитическое решение за- :
дачи. Для более сложных моделей можно получить только численное' решение,
что, конечно, гораздо менее ценно, чем аналитическое. " •.
В самом простом для расчета случае конструкцию удается представить в
виде модели с одной степенью /свободы, . '
3.1. СОБСТВЕННЫЕ И ВЫНУЖДЕННЫЕ
КОЛЕБАНИЯ БЛОКА ЙА АМОРТИЗАТОРАХ
Для защиты аппаратуры от ударов и вибраций применяют раз- ¦
личные амортизаторы, например чашечные (рис. 3:1). Резиновая
втулка амортизатора играет роль упругого звена. Рассмотрим
процесс колебаний блока РЭА, установленного на амортизаторах-
(рис. 3.2). f :
Если считать блок абсолютно жестким, а амортизаторы — не*
имеющими массы и если учитывать только вертикальное движение *
блока, то мы приходим к системе с одной степенью свободы,
(рис. 3.3). '.-._" ?
Запишем уравнение динамического равновесия массы т под|
действием силы упругости, амортизаторов F\ силы тяжести Р и сил *
инерции: - - ' J
или - ' ¦ I
. \
— л
где « — перемещение массы туик — перемещение точек крёпления|
36 ' ' ' I
у Корпус
Рис. 3.1. Чашечный амортизатор типа Рис. 8.2. Блок на амортизаторах
АЧ
У/////////у
*'/////?/////,
"с* 3'3- Система с одной степенью
свободы
Рис. 3.4. Пружинный майтник
37
амортизатора к источнику рибрации, например корпусу автомох
биля, самолета или ракеты; с — жесткость амортизатора. <>
Предположим, что корпус движется по синусоидальному зако-;?
йу во времени, т. е. ' ' ф " %
где UK — Амплитуда колебаний корпуса, тогда . "
где <о — частота колебаний корпуса. Решение неоднородного урав-'f
нения C.1) складывается из общего решения однородного урав-^
нения и частного решения неоднородного уравнения. Однородное?
уравнение имеет вид :
си^пг—— =0.
~ dt* • • . \
4 Общее его решение ищется в виде \
где ai и «2 — корни характеристического уравнения
c + a2m—Qt . -
откуда .
Тогда __
. иоб = Сг ехр (у j/-^- *j + С2 ехр (-/
Пбстоянные Ci и С2 определяются из начальных условий зада-}
чи. Прежде чем продолжить решение этой задачи, рассмотрим^;
упрощенную задачу о собственных колебаниях блока, на аморти-J
заторах. }
Предположим, что ок-0и Р=0, тогда получим, уравнение,.,
аналогичное уравнению свободных колебаний пружинного маят-|
ника (рис. 3.4). Предположим далее, что в начальный момент *=01
маятник был отклонен от положения равновесия на величину tto,f
а скорость его была равна нулю. Тогда при ?=0 из C.2) следуету
откуда
Ci-Ci
Решение однородного уравнения будет иметь вид
38
Используя формулы Эйлера, переходим к тригонометрическим
функциям
Uo6—Uosini(o0tt C.5)
где юо=Ус/т —собственная частота колебаний блока на
амортизаторах. '
Таким образом,.блок на амортизаторах, отклоненный от
положения равновесия, будете колебаться с собственной частотой оH и
постоянной амплитудой щ. В нашей расчетной, модели, не^учиты-
ваются потери энергии на трение, поэтому в решении колебания
будут незатухающими.
Теперь вернемся к исходной задаче. Мы нашли общее решение
однородного уравнения C.1) в форме C.2). Далее нужно найти
какое-то частное решение неоднородного уравнения C.1).
Рекомендуется попытаться найти это частное решение в том же виде,
что и правая часть неоднородного уравнения C.1), т. е.
u4=;AUzf>mtot—ВР, .. - ^ C.6)
где А и В — неопределенные, коэффициенты. Подставим
предполагаемое решение C.6) в уравнение C.1):
сАUK sin(x>t—cBP—mAUK(x>2 sin <ut=CUK sin со/—Р.
Очевидно, что выражение C.6) будет решением уравнения
C.1) в том случае, если . ~ * " . .
В — 1/с, А = с/(с — /тоJ. .
Таким образом: -. ^ *
/ C.7)
с
а общее решение уравнения C.1) будет складываться из:
и = ио6 + ич = Сх ехр </юоО + Q ехр (—;V) +
+ Ulfi anmt--?-. ' " " C.8)
с—ты2 с
Перейдем к определению постоянных С\ и С2 при других
начальных условиях. Выберем в качестве начального момента
времени тот, в который корпус начинает движение. Тогда при *=0
и^—Р/с,с1и/Ш=0, и из C.8) следует —Р/с=Ci + C2—Р/с, или
€v=- С2, - _ .
—/ПОJ) аH^
39
Теперь общее, решение нашего уравнения приобретает оконча4
тельный вид
и = 4
4 Л 2ч
2 ©0(?—/пю)
sin «<- — •« U^c sin <o0* + U* slnvt —
B) 2
с—ты2 ' с щ(с—пк»2)
(sin(at -sin< йХ
с—mm2 \ ш,
4 - —•• C.9>
I Таким образом, блок на амортизаторах совершает сложное
движение. Он колеблется с частотой собственных колебаний шо и
с частотой^ колебаний корпуса -о, которую называют частотой
вынужденных колебаний. ' * ¦
Предположим, что блок проходит испытания на вибростенде^
тогда <о — частота колебаний виброетенда, которая может плавна
меняться в заданных пределах. *
•> Возможны три режима колебаний: , / .
1. Область низких частот со<<оо, в которой
a«?/Ksino)*~ ^_t . C.10)
с
т. е. амплитуда колебаний будет примерно равна амплитуде
корпуса (вибростенда) и никакой защиты от вибраций нет.
2. Область высоких частот ш>шо, в которой
«^?/K-^sin(o0<-—, • C.11)
(О С -
амплитуда колебаний уменьшается в .соо/1© раз. Колебания
происходят на частоте собственных колебаний. Коэффициент усиления'
(ослабления) определяется как отношение '
. % ~И™* = J^L . - C.12)
.Рассмотрим отношение амплитуд ^ускорений. Из C,9) получаем
При <о>©о - ". " ,
а ~ ^!— sin erf = i/KoJ sin Ы., C-13>
1 — UJ/«) I
40 . -
Ускорение колебаний корпуса
Отношение/амплитуды ускорения блока к амплитуде
ускорения корпуса, называемое коэффициентом Динамичности, здесь
меньше единицы: . -
. р=коо2М .-¦'."¦ . .C.14)
3. Область средних частот. Если частота внешних возмущений
со приближается к частоте собственных колебаний ш0, то
наступает явление резонанса. Рассмотрим предельный случай, когда 0H=*
=<о. Из формулы C.9) следует, что ё этом случае числитель и
знаменатель в первом члене равны нулю. Получается
неопределенность типа «нуль на нуль». Не будем Пытаться раскрыть эту
неопределенность известными методами, например по правилу Ло-
питаля. Проще взять не предельный случай (о = (йо, а близкий к.
нему, например . ^ *
ю.=4),9<о<ь *
тогда - ч -
и == —^_ (Sin о,9шо/ - 0,9 sin (DqO — — .
1—0,81 ^ с .
Синусоиды в скобках получаются с разными.периодами. В
определенные моменты амплитудные значения этих синусоид будут,
складываться. Это произойдет, когда их аргументы будут
отличаться на я, Зя, 5я и т. д*, т. е.
toot—0y9(dot=nl Зя, 5я,..., Bп—1)я.
Отсюда - v
/ о.
0,Ь>0 0,
где То — период собственных кол.ебанйй.
Через пять периодов амплитуда колебаний возрастет в
1,9/0,19=10 раз. Дальше колебания продолжаются в форме биё-
' ний с амплитудой 10С/к. . .
Если, лапример,' взять со=0,99соо, то амплитуда возрастет в
100 раз, но произойдет это не сразу, а через 50 периодов
колебаний. ..
Таким образом, при резонансе амплитуда колебаний возрастет
ДО бесконечности, но произойдет это в пределе (t-±oo). Чтобы
определить, как развивается резонанс, решим задачу численно.
Возьмем исходное уравнение C/1). Введем дискретизацию по времени, как.
Зто делали в разд. 1.2. Пренебрегая силой тяжести, получаем
с
sin wnx <—
m
41
Тис. 3.5. Нарастание амплитуды колебаний в процессе развития резонанса: ,?
Ж — вынужденные колебания; 2 — результирующие колебания / У:
где
0,1,2,
т
•Пусть резонансная частота равна ' ' i
/о=Ю Гц, (oo=2jt/o=-62,8318 1/с. v . .;
Выберем т=Г/12, где T=*lff — период колебаний. Тогда для /=f0;
= A/120) с,и г }
.c0gt2=397,8351/14l00«0,27il5 1/с2. ^
Таблица ЗЛ
I S
i
2
3
4
5
6
7
8
2,74 sin (dot
1,37
2,37
2,75
2,37
1,37 е
0
—1,37
—2,37
0
1,37
4,74
9,55
14,12
16,18
13,82
6,29
l
9
10
И .
12
IS
. 14
15
16
17
18
2,74 sin idot
-2,75
—2,37
• —1,37
0
1,37
2,37
2,75
2,37
• 1,37
0
—5,34
—18,24 r
-28,52
—29,61
-22,58 ',
—7,99
11,16
30,00 ;
42,98 e
45,55
Пусть ?/к = 10 см, тогда
.= 1,72585^— M,_i+2,7415 sin /aw.
C.15)
Для. начальных условий «0=0 и Wi=0 будем вести^вычисления по
рекуррентной формуле C.15). " •
Результаты расчетов приведены в табл. 3.1. На рис. 3.5 показан график
движения блока на амортизаторах при резонансе. Таким образом, амплитуда
колебаний нарастает но. линейному закону и достигает бесконечности за
бесконечное время. Поскольку внешние возмущения-действуют в течение
ограниченного времени, амплитуда колебаний остается ограниченной. При учете
потерь энергии ограничение амплитуды колебаний при резонансе происходит уже
^ерез несколько периодов колебании.
3.2. УДАР БЛОКА НА АМОРТИЗАТОРАХ
Рассмотренное в предыдущем разделе аналитическое решение
для движения блока на амортизаторах позволяет* достаточно
просто перейти к задаче о движении блока при ударе.
Предположим, что блок на амортизаторах установлен на плат-
рорме ударного стенда. Платформа падает вниз и в начальный
момент * касается демпфера (рис. 3.6). Демпфер воздействует на
ллатформу с силой торможения F, которая изменяется по синусо-
7/2 ,
-
'ис. 3.6. Испытание -блока на удар-
лбм стенде:
— блок; 2 — платформа; 3 —• демпфер
0 5 10 151,,
6).
Рис. 3.7. Графики ускорения (а) и
скорости (б) блока при ударе
43
идальному закону. Эта сила вызывает появление ускорения, кото&
рое также изменяется по синусоидальному закону (рис. 3.7): ^
где <о—условная- частота ударного импульса; Я—амплитуда*
ускорения. Действие этого ускорения длится в течение половины!
периода 7/2, а дальше действие демпфера прекращается, На прак?|
тике такое торможение встречается тогда, иногда транспортное^
средство преодолевает некоторую преграду. Вначале сопротивле-J
ние преграды растет, а затем, когда преграда .разрушается, сояро-;
тивление падает. Такое препятствие создается внутри демпфера..,;
Последовательно интегрируя C.16) 2 раза, получаем* выражение^
для скорости v (см. рис. 3.7, б) и перемещения ик: • . . >
Н
Из начальных условий (при ?=0) * -
duK л -
at: i
получаем
О)
Важно по4обрать начальную скорость vKo таким образом, чтобы
после преодоления преграды движение закончилось и платформа
остановилась.
Чтобы в нижней точке (^=Г/2) движение закончилось (о=0),
должно выполняться соотношение
2Н НТ .
VkO —' : ' ' '
О) П. ' * ¦
где Г — полный период ударного импульса.
Таким образом, уравнение движения бдока на амортизаторах
при ударе платформы будет иметь вид
—cIJL sin со/ + —t\ (ЗЛ7)
\ 0J О) / Ч
Общее решение однородного уравнения имеет, как (прежде, вид
C;2), а частное решение неоднородного уравнения, полу чается, в -.
том же виде, что и правая часть C.17):
*. = ' НС ,. ч sincof + JL и C.1JB)
ш2 (с — <!J/га) (о . . ¦. ?
44 • - ^
Тогда общее решение C.17) запишется в биде
и=Сх exp 04*)+C2 ехр (—j\t)+
77 *+
— /ПОJ) (о
Постоянные интегрирования определяют из начальных условий:
при *=0 w=0, duldt^Vxb тогда Ci = — C2 и ,
1 Г яс -Я]
2/ш0 [ ш (с — /ж»2) ' - о) J
% Используя уравнения Эйлера, получаем
[м и \ м
77— ТГ2Г Н 8|Пш0г+ —YTi 57-sr Sin (о/
4— ^ . (ЗЛ9)
ш . • " .
Таким образом, блок на амортизаторах после удара
платформы о демпфер совершает сложное движение: движение с
постоянной скоростью Я/ш и два колебательных процесса с собственной
частотой <«>о и условной частотой ударного импульса'©. Поскольку
ударный импульс короткий, а условная частота ш высокая, то ю/
1- Учитывая это, можно уравнение C.19) упростить:
N Яш* ' Н
<^rf"t.
& 0?4
0H)q м ОL (I)
К концу ударного импульса (/=Т/2г=л:/о)), перемещение
блока имеет вид .
sin щ — 4г = -— sin -S- it-f//— C.20)
2 * @-2 шш0 а) • оо2
и отличается от перемещения платформы на величину сжатия,
амортизаторов. '
Скорость блока в конце удара равна
l ^+. . C.21)
(О Ш . О>° Ш
Нас интересует в первую очередь защитное действие аморти-.
заторов. Для этого нужно проанализировать движение блока на
амортизаторах после удара. Поскольку платформа.при этом
будет стоять на месте, то. это будут собственные колебаниия C.2).
Можно просто найти постоянные интегрирования из условий C.20)
и C.21). Но еще проще выбрать новую систему отчета, в которой
за начало отсчета времени выбирается момент окончания движе-
ния платформы, и новое начало отсчета перемещения — нижнее
-положение блока. Для новой переменной и, описывающей
движение блока в новой системе отсчета, начальные условия будут иметь
45
следующий вид: при 4=0 w=0, а скорость останется в виде C.21)^
При этих начальных условиях решение для собственных колебав
ний в новой системе отсчета представляется выражением *:
n«0*f. - C.22^
О)
а ускорение имеет
dt*
L <°
ш°
cos
Ш(ОЛ
О),
ОK
О)
Сравнивая амплитуду ускорения блока с амплитудой ускоре^
ния платформы, получаем, что амплитуда блока будет меньше^
Их отношение с учетом того, что озо<|ш и cos(o)o/co)n^l получав
ется равным . - ' 1
Н
ш
C.24|
Рассмотрим в качестве примера результат решения описанной^
задачи для #=100 м/с2, соо^62,81/с, 7/2=10 мс. При этом <о=^
=2й/Г=314 1/с, и отношение C.24) не превышает 0,4. На рис. ЗЩ
приведены кривые движения платформы (кривая 1) и блока (кри*у
вая 2). Цъ рис. 3.9 изображены графики ускорений платформы?:
(кривая/) и-блока (кривая 2). . ¦ %
Таким образом, амортизаторы являются эффективным средств
вом защиты аппаратуры от ударов. При этом нужно следить,, что-у
бы амортизатор не препятствовал собственным колебаниям блокад
т. е. хюд амортизатора должен быть больше амплитуды собствен-!
ных колебаний: . . v *?
tr Г 1 (S>V , (о0 , 1 I ' 2Я • I
// I cos —^ к -\ ^ Н « . . :.
[|>0 ш оK ^ . о)ОH J ¦ о)Шо ' s
0 10 20 30 40 50 60 /7OtMC*j
\0 W 20 30 40 У
20 30 40 50t/tc
Рис. 3.8. Графики перемещения
блока и платформы
46
Рис. 3.9. Графики ускорений блокад
и платформы ?«
В противном случае возникают вторичные удары деталей,, огра-
ничивающиХуДвиже.ние, что недопустимо.
Мы не рассматривали затухания колебаний блока на\
амортизаторах. Между тем затухание колебаний имеет принципиальное
значение. Если бы колебания возникали,, но не затухали, то
энергия колебаний постоянно накапливалась бы, что привело бы к
'катастрофе. Затухание колебаний происходит вследствие потерь
механической энергии и перехода ее в тепловую. Эти потери
обусловлены различными видами трения. Например, при колебаниях
пружинного маятника в вакууме затухаиие колебаний происходит
только за счет потерь энергии в материале пружщш на
внутреннее трение. При движении в воздухе к этим потерям прибавляются:
потери на трение о воздух. .
Внутреннее трение и трение о воздух являются сложными
физическими явлениями, происходящими на молекулярном уровне.
Точное отображение этих явлений в наших расчетах колебаний
невозможно. Поэтому применяют различные простые гипотезы о
характере тормозящего действия этих сил трения.
Одной из наиболее простых гипотез является гипотеза Фохта.
JB соответствии. с этой гипотезой силы внутреннего трения в
материалах конструкций пропорциональны скорости изменения
деформаций во времени. Аналогичные потери возникают в вязких
жидкостях при движении в них твердых тел. Поэтому потери на
внутреннее трение в упругих материалах называют потерями на вязкое
трение. В "нашем случае .будем считать, что сила сопротивления
пропорциональна скорости движения блока.
3.3. КОЛЕБАНИЯ БЛОКА -. . '
НА АМОРТИЗАТОРАХ С ДЕМПФИРОВАНИЕМ
Гашение колебаний с помощью вязкого трения называют
демпфированием, а устройства для гашения вибрации — демпферами.
Хорошо известны демпферы с вязкой жидкостью — обычно маслом
(рис. ЗЛО). Такие демпферы часто применяются в транспортных
средствах, где они неточно называются амбртизаторами. При
движении поршня в них вязкая жидкость перетекает из одной части
Цилиндра в другую через отверстие в поршне и тормозит
движение поршня. Действие таких демпферов приходится учитывать при
расчетах вибраций радиоаппаратуры, устанавливаемой на
.автомобилях. . .
Непосредственно в радиоаппаратуре применяются воздушные
Демпферы, в которых используется тормозящее действие воздуха.
На рис. 3.11 показан амортизатор с воздушным демпфером. Роль
Демпфера выполняет резиновая полость, наполненная воздухом.
При колебаниях объем полости изменяется. Воздух частично
сживается и расширяется, а частично перетекает в верхнюю часть по-
47
•и
к
Рис. 3:10. Демпфер: . '
*$ — поршень; 2 — цилиндр; 3 — масло.
Рис. 3.1Ь Амортизатор с воздушным^
демпфером , ;
\
и обратно. В.результате создается сопротивление движению,^
пропорциональное Скорости движения. j
При графическом изображении расчетных моделей с вязким.;
трениедГ (рис. 3.12) демпфер изображается в виде цилиндра ci
цоршнем \i. Сила сопротивления пропорциональна скорости: I
„ du ^
48
У/////////////////////А
и
Fc Ffi
рис. 3.12. Модель с вязким трением
Рис. 3.13. График затухающих
колебаний при действии вязкого трения
где \х — коэффициент вязкости демйфера. В частном случае
пружинного маятника при использовании модели Фохта ji —
коэффициент вязкости материала пружины. , • ¦ . ,
Рассмотрим задачу о .собственных колебаниях пружинного
маятника с потерями Энергии в дружине в виде вязкрсти. Уравнение
колебания примет вид . .
du d2u * /о ооч
— си —и. — = т . C.26)
" • Р dt dP , . * f
Попытаемся найти решение уравнения в виде синусоиды,
амплитуда которой,экспоненциально убывает во времени
и=ехр (—•г)/) (A sin ®?+B cos ш/).. . . C.27)
Подставим решение C.2) ? уравнение C.27); После
сокращения на ехр (—i\t) получим ,
с (A sin Ы+В cps <ti?) —\щ (A sin a>t+B cos Ы) +
A + [ко (A cos со*—В sin со/) +mr\2(A sin ®t+B cqsio/) —
—2mr\G>(A cos Ы—В sin at) —mco2(A sin wt+B cos ®t) = 0. C.28)
Чтобы удовлетворялось равенство C.28), необходимо
выполнить два условия:
с—щ + тц2—тоJ=О,
C.29)
\х—2/пг|=0. . '
Иё второго уравнения C.29) следует
г\ = фт. . • * . C.30)
Подставим C.30) в первое уравцецие C.29):
4-1215
Отсюда - ' • • . -'='¦
¦ . с «*¦*'_, f~o ~7*~ ¦ ^
или • ' ',}
где шо — частота собственных колебаний при т)=0. Таким образом|;
при наличии вязкости частота собственных колебаний нескольку:
уменьшается. Общее решение C.26) будет иметь вид ~ .• %
и = ехр (- ^- ) (Asint j/wo_-4* + В cos t V®1 — ? ). C.3^;
\ 2m) 4 :;]
Постоянные Л и В определяются из начальных условий. ^;
Для нас важнр, что амплитуда колебаний экспоненциально^
убывает. Через период колебаний Т амплитуда уменьшается в|
ехр(|ия//л>со) раз. Эта величина не зависит от времени, т. е. во всеы^
процессе колебаний отношение двух соседних амплитуд есть ве4
личина постоянная. Натуральный логарифм этой величйнй назы*|
вается логарифмическим декрементом затухания колебаний^
. (рис. 3.13): {
^ U.1C ' U1C U.7T • .
Q — ¦ ¦ ^^у I
Обычно tJ<(u0. Однако если коэффициент вязкости jjt настоль^'
ко велик, что под корнем в выражении C.31) получается мнимая*
величина, т. е. ч i
4m2 щ :
то колебания «срываются» и блок из начального положения по*
экспоненте приближается к положению равновесия с одной сто-;*
роны, не переходя через него.
Потери энергии на внутреннее трение приводят к тому, чта*
при резонансе амплитуда колебаний не возрастает до
бесконечности, а стабилизируется на каком-то уровне. ^
В, общем виде уравнение, описывающее колебания системы с
одной степенью свободы с учетом вязкого трения (см. рис. 3.12)!*
при заданном возмущении ик корпуса (вибростенда), записывает^:
ся следующим образом: ' . ;
/ Ч dll CPU /О Ъл?
с(ик-и)-р—- = л ——>- . C.34)
at at1 ^ .
SO {'
Рассмотрим решение уравнения C.34) для случая, когда
возмущение задано синусоидальным законом. В этом случае
уравнение имеет вид
т J-!L +р ЁЕ + си = сик sin фг. C.35)
dt2 dt
Общее решение неоднородного уравнения C.35), как упоми*
налось выше, складывается из общего решения однородного
уравнения и частного решения неоднородного уравнения. Общее
решение будем искать в виде
* «об =d exp avt+С2 ехр и^7 C;36)
где аь аг — корни ¦характеристического уравнения
'ma2+jia + c=0; . C.37)
Си С% — постоянные интегрирования, определяемые из начадьных
условий.
Из C.37) следует
cxi =—р + &о, аг^—ftr-/со,
где p = jx/2mj со=У(Оо2—Р2 — частота собственных колебаний с
учетом вязкости. Тогда *
«об=ехр (—fU) (Cj ехр (/ко/) + С2 ехр (—/©*)).. . ' . C.38>
Частное решение неоднородного уравнения ищем в виде
ич=А sin <oKt+^B cos<uKt. * C.39)
Постоянные А и В определяем, подставляя C.39) в C.35),
после чего получаем два уравнения:?
4 .' ' C.40)
—П№>\ В + \хА сок 4- сВ=0,
решая которые, находим #
В конечном счете получаем общее решение в виде
или 1юсле преобразования,
w - ехр (—fit) (& ехр (/со/) + С2 ехр (—/©/)) +
f/ / C.42)
Где q>=-arctg — = arctg(—^<oK/(m((o2~aJ)) - C.43)
Угол сдвига фазы ' ,
• . . .51
•србственная частота колебаний без учета вязкости.' й$
Величина . ' ' ¦ Ш
U
* = 77Г =
характеризует зависимость амплитуды* вынужденных колёба*
массы от соотношения частот. Эта зависимость для различны!
значений р/соо приведена на рис. 3.14. Для определения С\ и
зададим конкретные начальные условия. Пусть, например, в
мент ?=0 корпус начинает движение, т.- е.
и@)=о, — ' =0. . C.4§
at
Тогда из C.42) и C.45) следует
С СгУО
2
C.4Я
|
ъ
—р (Ci + С2) +/о) (С}—С2) + С/к^к cos ф =Т), . C.4%
откуда • * . --?
с/.
Со"«= ^ sin ф -4 ^-(g sin 9 + <*>к cos <р) *• %
Для рассматриваемой задачи C.35), C.45) 'с учетом C.42)'щ
C.47) имеем ' , . к
f sin cp cos atf + -f^- (p sin <p + о>к cos
>ш
C'49^
f4 s
Q 0,5.
Рис. ЗЛ4. График зависимости
амплитуды вынужденных колебаний от
соотношения частот
52 \' ' ¦
Рис. 3.15; Модель с сухим трением^
/ — элемент жесткости; 2 — элемент
хого трения • * '
Первое слагаемое решения C.49) описывает собственные зй*
тухающие колебания. Второе — вынужденные колебания на
частоте колебаний корупса. .-. -., . '" [
- Определим частоту, при которой установившиеся колебания
имеют максимальную амплитуду. Из C.44) ясно, что амплитуда
будет наибольшей при минимальном значении выражения
Тогда из условия
получаем ~
«у-У^ —2р.. . . C.50)
Таким образом, с увеличением . коэффициента р.,
пропорционального коэффициенту вязкости [г,, величины юк и Щ
уменьшаются (см. рис. 3.14).
3.4. КОЛЕБАНИЯ БЛОКА
НА АМОРТИЗАТОРАХ С СУХИМ ТРЕНИЕМ
Другой вид потерь энергии при колебаниях конструкций
возникает при сухом трении, которое также приводит к затуханию
свободных колебаний. Однако характер затухания будет иным;
чем при вязком трении. Если трущиеся детали соединены с
корпусом и блоком, т. е. «параллельно» амортизатору, то силы
упругости и силы сухого трения будут складываться (рис. 3.15):
. .". ' C.51)
Сила трения всегда направлена против движения. Если блок
на рис. 3,17 движется вниз, то сила трения направлена вверх,
и наоборот. Поэтому в уравнении C.51) перед силой трения с;гоят
Два знака: «+» и .«—». Это уравнение — нелинейно* Чтобы его
Решить, нужно провезти его линеаризацию. Для этого нужно все
Движение разбить на участки тац, чтобы на каждом участке знак
в Уравнении оставался достоянным.
Пусть в начальный момент (*=0) блок находится в верхнем
положении и на первом участке движется вниз, тогда сила трения
направлена вверх. Уравнение будет иметь вид
* C;52)
S3
Общее решение, как ив разд. 3.2, ищем в виде
u = Ct exp (j<o0t) -f С2exp (
Начальные условия:
при /=0
-Ц
Отсюда
и решение уравнения C.52) на первом участке будет иметь
и _ 2 tp (ехр ОоО + ехр (—гАЧ ' ТР л*
Применяя формулу Эйлера, получаем
F \ F
1 тр \ • ¦ л t Гтр
I ^'IcOSCBn" '
~ ~T)щsln
В конце цервого участка скорость должна быть равна у?
т. е. (Oot=7t. Поскольку со6=2я/Г, то /=fГ/2..Таким образом,,пер4
вый участок заканчивается в конце первого полупериода свобод^
ных колебаний. В конце первого участка, как видно из C.53L
/c. ; C.54)^
Перенесем начало координат (/=0) в конец первого полупе-?
риода и решим задачу с новыми начальными условиями C.54) Л
В уравнении движения C.51) для второго участка сила
трения будет со знаком «•—»,.и решение примет вид
и = Ct exp (faot) + С2 ехр (— /шо<) — — . ' • -
Новые начальные условиям
при f=0 w= 2F/ d
откуда
54
Тогда
В конце второго участка
LlL
с
=—1 и
Таким образом, в каждом полупериодё колебаний амплитуда
уменьшается на величину 2Frp/c (рис. 3.16-, а).
Огибающая графика и будет прямой линией (рис. 3.16,6).
Когда в конце очередного участка и становится меньше цо
абсолютной величине, чем 2FTp/c, то движение прекращается^ Блок не
приходит в нейтральное положение и=0* поскольку силы
пружины не хватает, чтобы преодолеть силу трения. Сухое трение
эффективно используется дЛ"я гашения вибраций. Применяются, напри-
'мер, амортизаторы (рис. 3.17) с трением «сухарей» о корпус
амортизатора.
б)
Рис. 3.16. График затухающих
колебаний при действии сухого трения
Рис; 3.17. Амортизатор с сухим
трением:
* — «сухари»
55
Мы рассмотрели колебания блока на амортизаторах как
стемы с одной степенью свободы. К такой системе приводятся
личные-конструкции в радиоэлектронике, не только блоки на р^
тизаторах. Например, плавающие магнитные головки запоминаю-;
щих устройств крепятся на плоской пружине. Если считать, что;
сама магнитная головка не деформируется, а пружина не имеет"
массы, то получается расчетная модель- в виде колебательной сп-!
стемы с одной степенью свободы. . ' I
?5. КОЛЕБАНИЯ КОНСТРУКЦИЙ РЭА
ПРИ ДВОЙНОЙ СИСТЕМЕ АМОРТИЗАЦИИ "<
В некоторых случаях для получения более точных расчетов^
приходится учитывать деформации двух упругих звеньев и дви-^
жение двух сосредоточенных масс. Если при этом * учитывается \
движение каждой массы только в одном направлении, то расчет-*<
ная модель будет иметь две степени свободы. Примером такой ;
конструкции может служить шкаф, установленный на платформе <
транспортного средства (р^е. 3.18), например в кузове автомобиля
или на железйодорожной платформе. ,
Масса платформы Ш\ и масса шкафа т% представляются в.
расчетной схеме (рис. 3.19) сосредоточенными массами, а рессоры
и пружины амортизаторов — сосредоточенными жесткостями С\ и
с2. Если учитывать только вертикальные колебания системы, как
в случае испытания ее на вибростенде, то нетрудно записать урав-;,
нения колебаний масс т\ и /п2: • , ;
щ\т2\ .
с2 {щ — их) — сг (иг — ик) = тг —^-. C.55>
at2
Однако решить систему дифференциальных уравнений C.55)
в общем случае аналитическими методами непросто.
Аналитическое решение получается достаточно лросто только щ случае
свободных (собственных) колебаний (ик=>0) системы, причем
колебаний синхронных и синфазных. Иными словами — когда массы
колеблются с одинаковой частотой и фазой, например:
Ui***A\-sin®t.9 ^—Azsm&t. C.56)
Подставив решение C.50) в уравнения C.55), после
сокращения на sin tut получим ч
?2(^2—A\)— C\Ai=—mi<o2i4i,
C.57>
—с2(Л2—i4i).==— т&?Аъ . . . ¦ '
56 ¦
' Платформа
Iff
Рис. 3.1 &
Рис. ЗЛ8. Блок на платформе транспортного средства:
i — рессоры; 2 — пружинные амортизаторы^
Рис. 3.J9. Расчетная схема системы с двумя степенями свободы
Уравнения C.57) должны удовлетворяться при. любых
значениях амплитуд А\ и А2. Исключяв эти амплитуды из уравнений
из C.57), получим биквадратное относительно со уравнение
= 0. ' C.58)
Уравнение C.58) называют частотным уравнением. Решение
это дает два положительных значения частоты: ' ^
Высокая частота получается при положительном
знаке перед корнем, а низкая — при отрицательном. Это'
и есть собственные частоты колебаний системы. У
системы с двумя степенями свободы их две. Эти же
частоты будут и резонансными частотами системы.
Амплитуды колебаний Аг и А2 определяются из начальных
условий задачи.
Аналогично можно получить решение для
собственных колебаний системы с большим числом степеней
свободы (рис. 3.20). В результате'подстановки в уравнения,
подобные уравнениям C.55), решений в виде C.56) для
системы с п степенями свободы получается частотное
Уравнение порядка 2л. Решить такое уравйение анали-
Рис. 3.20: Система с несколькими степенями свободы
тически нельзя. Мож^о только подобрать подходящие частоты/!
подставляя различные их значения в уравнение частот. Они и бу^:
дут собственными частотами системы. В общем случае может быть
л различных частот. *
3.6. ПРОСТРАНСТВЕННЫЕ КОЛЕБАНИЯ '
БЛОКА РЭА НА АМОРТИЗАТОРАХ
Мы рассмотрели колебания блока на амортизаторах в одном^
направлении. Амортизаторы, как правило, допускают движение,,
точки крепления блока к амортизатору в трех направлениях, КрР|1,
ме того, возможны повороты вокруг трех взаимно перпендикуляра
ных осей. В. результате блок на амортизаторах как недеформи**
руемое тело имеет шесть степеней свободы (рис. 3.21)..Переме-;;
зцения и углы поворота, определяющие в каждый момент поло?*
жение блока, измеряются как перемещения центра О массы блокад
При конструировании амортизационной системы амортизаторь?<
стремятся расположить так, чтобы, движения в направлении всех]
шести степеней свободы были независимыми. Иными словами^
перемещение корпуса в направлении оси х не должно вызыват^
движения в направлении у и z и поворотов относительно любой
оси. То же самое "можно сказать о движении корпуса в направо
лении. оставшихся степеней свободы:
Для того чтобы все шесть движений были независимыми, долж*'
яы выполняться условия симметрии относительно трех ортогональ^
ных плоскостей, проходящих через центр массы (рис. 3,22). Ми-*
нимальное число амортизаторов, при котором выполняется услоч'
вие симметрии, равно шести, и. они должны быть расположен^:
так/как показано на рис. 3.23, а. Однако такую конструкцию
*гизационной системы нельзя считать удачной. Дело^ в том,
Рис. 3.21. Блок на амортизаторах
(система с шестью степенями
свободы) •
?8
Рис. 3.22. К. определению условий
симметрии * * г^
•h
\
'SSSS.
1
У/У//
1
'////'
а) ^
* Рйс. 3.23. Схема расположения амортизаторов
:ерийные амортизаторы предназначены для гашения вибраций в
направлении оси амортизатора. Движения и поворбты в двух дру^
лнх направлениях являются для амортизаторов
неблагоприятными. В этих направлениях либо амортизаторы обладают малой
жесткостью и амплитуды колебаний слишком большие (например,.
7 тросовых амортизаторов и амортизационных прокладок),.либо
конструкции амортизаторов не допускают больших* относительных
перемещений в поперечных направлениях, как у амортизаторов
типа АПН, либо, при, поперечном движении появляется большой
чзнос, как и у большинства других амортизаторов. В системе обя- .
зательно должны быть амортизаторы, которые деформируются в
1родольном направлении не только при поступательных
движениях блока, но и при поворотах.
В системе, показанной на рис. 3.23, а, при поворотах блока
тносительно любой оси ни один из амортизаторов не работает в
лродольном направлении. Поэтому вращательные движения блока
>удут сопровождаться вредными или опасными явлениями в амор-г
^изационной системе. Чтобы избежать таких неблагоприятных
явлений, достаточно взять восемь амортизаторов и, расположить их
"а.к, как показано на рис'. 3.23, б.
Все три условия симметрии при этом выполняются. Единствен-
шм неблагоприятным движением, является вращение „блока
вокруг вертикальной оси, когда все амортизаторы работают на сдвиг.
Однако возбуждение таких колебаний на всех известных транс?
1ортных средствах маловероятно.
Если все шесть движений независимы, то уравнения движения
чикак не связаны между собой:
'хх У
cyy(v-vK)=m
dt*
Сгг (W—WK) = md2Wfdt2, Dxx (<?x — <ржд) «5s ,
dt*
где ы, и, до— линейные перемещения^блока вдоль координатный
осей; ер*, фу, фг — угловые перемещения вокруг координатных осей;|
индексом «к» отмечены "перемещения источника возмущений. "•
Если же указанные условия симметрии не выполняются, той.
различные движения блока связаны между собой. • •. -
' Мы рассмотрели простейшие расчетные модели конструкций^
РЭА с упругими звеньями —амортизаторами, пружинами,
рессорами и т. п. Для таких простых моделей удается получить анали-,
тическое решение. Несмотря на то что такие случаи встречаются -s
редко, ценность этих решений очень велика. Они позволяют про^
изводить анализ влияния параметров конструкций на ход процес*-»
са вибраций, вычислить низшие резонансные частоты конструк-^
ций, перегрузки (ускорения) блоков, выбирать жесткость амор-'*
тизаторов так, чтобы прц заданных внешних воздействиях резр-.
нансов не возникало. . • |
В других случаях, когда аналитические решения получить не';
удается или они очень сложны, мы использовали численные ре-4;,
шения. Алгоритмы приведенных численных решений очень просты
и физически «прозрачны». Вычисления на несколько шагов по
времени можно произвести «вручную». Если же в расчете число шагов *
по времени превышает 8—10, то следует* воспользоваться простей- ¦
шими средствами вычислительной техники. Все приведенные выше \
расчеты выполнялись на программируемых микрокалькуляторах.^
В дальнейшем мы будем рассматривать более сложные задачи* \
и для их численного решения потребуется более совершенная
^вычислительная техника. - • -
Основной недостаток численных решений состоит в том,- что \
даже цри небольшом изменении условий задачи все вычисления \
приходится производив заново. Создается такая же ситуация, как .
при испытаниях макетов конструкций: даже при небольших изме-1
нениях конструкции испытания приходитсй производить заново» \
Но аналогия не только в этом. Конструктор с помощью численных i
решений получает ответы на те же вопросы, что и при проведении 1
экспериментов. Поэтому такие* расчеты стали называть числен- ?
ными экспериментами. - ' • |
КОНТРОЛЬНЫЕ ВОПРОСЫ %
1. Как получаются уравнения движения блоков на амортизаторах? *
2. Опишите способ решения дифференциального уравнения второго поряд- |
ка с постоянными, коэффициентами. . ^
60 . - : ч
3. Как определяется частота собственных н вынужденных колебаний
блока нд амортизаторах?
4. Каков характер возрастания амплитуды колебаний во времени при
резонансе?
\ 5. Каков характер колебаний блока на амортизаторах при ударном
воздействии? 7 . -
. 6. Как учитывается влияние демпфера при расчете колебаний блока на
.амортизаторах? . . - .
7.' Что такое логарифмический декремент колебаний?
8. Опишите учет потерь энергии в амортизаторах с помощью вязкого
трения. „
9., Каков характер затухания колебаний блока на амортизаторах при
наличии сухого трения? '. • '
10. Как строится система уравнений динамического равновесия для системы
с двумя и более степенями свободы? -
11. В каких случаях можно получить аналитическое решение задачи о
колебаниях системы с двумя и^более степенями свободы?
12. Как должны быть расположены амортизаторы, чтобы поступательные и-
вращательные движения блока в различных направлениях были взаимно
независимыми? .
Глава 4, ВИБРАЦИИ СТЕРЖНЕВЫХ
КОНСТРУКЦИЙ
Стержневые конструкции широко распространены в радиоаппаратостроении
как несущие конструкции — каркасы, рамы, фермы, кронштейны, корпуса
блоков, стоек и т. п. J9]. Деформации этих конструкций при ударах и вибрациях
и определяют в основном вибропрочность и виброустойчивость аппаратуры.
Поэтому в процессе проектирования конструкций РЗА расчеты стержневых
конструкций занимают важное место. •
Стержневые конструкции обычно представляют собой сложные трехмерные
пространственные тела. Задачи расчета вибраций таких тел достаточно сложны.
Поэтому мы начнем с* расчетов отдельных стержней. „
Рис. 4.1. Профили стержней
61
1
б).
Амортизатор
Рис. 4.2. Залитый блок РЭД (а) и
его расчетная модель (б)
О 0
О О О
О М О
о о
о о о #
о Ы о
0 О
О 0 О
о TLJT о
0 О
обо
о ТЫГ о
о о
о' о о
о--' И^Г о
10 ч О|
i, тыг ol
Л
7777%
(рутильныё.
у колебания ._
Изгибные
колебаний
а)
б)
Рис. 4.3. Стойка (а) и ее расчетная
модель (б)
В конструкциях РЭА применяют стержни различного сечения (рис. 4.1):
уголки (а), шнеллеры (б), двутавры (в), коробки. (г). Но для всех стержней
характерно.то, что их длина во много раз (в 10 и более) превышает
поперечные размеры. Благодаря этому при расчетах вибраций* стержней можно строить
простые гипотезы о распределении деформаций и напряжений по сечению
стержня. А такие гипотезы, в свою очередь, дают возможность свести сложную
трехмерную задачу - о деформировании стержней к нескольким одномерным
задачам. Это позволяет, в частности, рассматривать независимо друг от друга
продольные, крутильные и изгибные колебания стержней. Необходимость в
расчетах продольных и крутильных колебаний стержней при проектировании
радиоаппаратуры . встречается редко. Тем не менее ценность таких расчетов состоит
в том, что многие конструкции РЭА, например залитые блоки (рис. 4.2),
стойки (рис. 4.3), представляют собой конструкции, достаточно вытянутые в одном
направлении. Простыми одномерными моделями таких конструкций могут
служить однородные или неоднородные стержни. Расчеты продольных и
крутильных колебаний с помощью одномерных моделей позволяют достаточно просто
оценивать динамические характеристики * сложных конструкций.
62
4.1.. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ
ПРЯМЫХ УПРУГИХ СТЕРЖНЕЙ
Представим себе резиновый стержень прямоугольного сечения*
приклеенный по торцам к металлической скобе (рис. 4.4). На
боковой поверхности стержня нанесены риски с шагом А. Если скоба
совершает колебания в направлении оси стержня, • то сечения?
стержня также перемещаются параллельно самим еебе в
направлении оси, дричем расстояния между рисками не остаются
постоянными и равными А, а изменяются. В одних местах риски
сгущаются, в других, наоборот, становятся реже. Вдоль стержня
распространяются упругие1 волны. . . :
При остановке скобы колебательный процесс в стержне
постепенно затухает. В. конечном счете все риски приходят в исходное
состояние, т. е. в положение равновесия. Это и есть одна из картин
продольных' колебании упругого стержня. Нам важно^ что при
Любых продольных колебаниях -сечения стержня остаются плоскими и
перпендикуля'рными его оси. Иными словами, перемещения всех
точек стержня зависят только от одеой координаты х,
направленной вдоль оси стержня.
Такая же картина и в стержнях из более твердых материалов,
например в металлических стержнях. Однако там деформаций
меньше, зато напряжения могут достигать очень больших
значений. . ' . /
Как же движутся сечения стержня и как рассчитать это
движение? В общем случае можно сказать: движение происходит
таким образом, что все элементы стержня в каждый момент
находятся в динамическом равновесии. . "
Рис, 4.4. Возбуждение колебаний ре- . *. -
зинового стержня с помощью
металлической скобы
Рис. 4.5. К построению уравнения
продольных колебаний стержня
Рассмотрим математическую постановку задачи. Разобье*|:
стержень на прямоугольные элементы одинаковой длины г%
(рис. 4.5) и пронумеруем их. Выберем произвольный элемент <|
номером i и запишем уравнения его динамического равновесия!
При выводе уравнения и при дальнейших расчетах удобно вс^
рассматриваемые величины относить к определенным точкам, На*
пример* номера относятся к центрам элементов — узловым точкам^
совокупность которых образует так называемую сеточную область^
Тогда грани элементов будут иметь дробные номера. [
На элемент по его боковым граням действуют нормальные на{
лряжения, образующие' равнодействующие силы А+о,5 и Ft-o^k
Если деформации и напряжении в этой части стержня в. данный?
момент положительны^ т. е. элемент растягивается, то силы на-$
правлены так; как показано на рис. 4.5. _•;*
В соответствии с принципом Даламбера сумма проекций еил?
действующих на элемент, на ось координат равна соответствую-:^
щей проекции силы инерции. В данном случае |
тде гп — масса элемента; и, —перемещение центр а. элемента (узла|
-сетки) в направлении оси х. ./к , ' ' . *
Обычно/в расчетах упругих деформаций искомыми величина-)
ми являются перемещения щ. Поэтому силы F необходимо выра-|
зить через перемещения и. В соответствии с принятой гипотезой^
напряжения во всех точках одного сечения одинаковы, поэтому!
силы выражаются через напряжения простыми формулами: -
, ' • -7
D.2)!
. • %
где Ну и hz — размеры сечения стержня. |
Теперь необходимо выразить, напряжения через деформации.!
Для этого воспользуемся законом Гука для упругого стержня: |
тде Е — модуль Юнга материала стержня; е —деформации, кото-f
рые в данном случае являются относительными удлинениями^
стержня на участках с центрами в точках. . .5
Относительные удлинения легко выразить в виде отношения!
приращения длины элементов к их первоначальной длине k: *
А
П ш ft .. • ' :Щ
где и/+ь ЩуЩ-\ — перемещения соседних узлов. |
«4 . ¦ • %
После последовательной подстановки D.4) в D.3), D.2) и
далее в D,1) получаем
«1+1-2*,, +«i-i h^m?*L . - D.5)
а* - у z at* v
Это и есть искомое уравнение продольных колебаний упругого
стержня. Левая его часть представлена в разностной форме, а
правая— в дифференциальной. Если ввести дискретизацию не только
по координате х, но и по времени 4; то ^получится уравнение в
разностной форме * .
EZ J2 P ¦
где p=mfhhyhz — плотность материала,стержня; / — номер шага
по времени; т — шаг по времени. Если в уравнении D.6)
устремить шаги по координатам и времени к нулю, то вторые разности
по координатам и времени превратятся во вторые производные:
„ д2и д2и л +
Е*?-*!* • v - D-7)
v
Мы получили дифференциальное уравнение в частных
производных. Заметим, что от уравнения D.7) можно Перейти к
разностному уравнению D^.6) заменой производных их
конечно-разностными аналогами, как это обычно делается в методе конечных
разностей [9}.
Следует отметить, что уравнения вида D.6) можно составлять
лишь для внутренних узлов модели, которые связаны с соседними
узлами справа и слева. Для крайних узлов уравнения
составляются на основании граничных условий. При расчете
нестационарных процессов необходимо задать и начальные условия —
перемещения всех узлов для двух, начальных моментов времени.
Уравнения D.6) вместе с граничными условиями полностью
определяют задачу и образуют систему алгебраических уравнений,
число которых равно произведению числа шагов по,координате на
число шагов по времени. Это произведение может достигать
нескольких тысяч.
Интересно рассмотреть приведенные выше уравнения для
задачи в дифференциальной форме. Число элементов и число шагов
по времени возрастает до бесконечности. Бесконечно и числр
уравнений D.7) i если их 'записывать для каждой точки и в каждый
момент; но этого делать не надо, поскольку все уравнения
одинаковы. Решение ищется в аналитической форме, в виде
некоторой функции, которая должна удовлетворять уравнению D.7) в
любой точке стержня и в любой момент. Кроме того, она должна
Удовлетворять начальным и граничным условиям задачи. В этом.,
случае аналитическое решение дифференциальной задачи счита-
5-1215 * . 65*'
ется точным. Оно не содержит погрешностей дискретизации.
Разностное решение, которое получается в виде таблицы чисел,
содержит погрешности дискретизации и является приближенным.
При решении задачи нужно эти погрешности оценить, что далеко-
не всегда удается. Это один из основных недостатков разностных
решений.
Несмотря на то что задача о продольных колебаниях упругого
стержня является двухмерной, для отдельных простых случаев
удается найти аналитическое решение. Это решение получается в
виде стоячих или бегущих волн. Стоячие эолны получаются в
случае резонансов, что особенно важно при расчетах резонансных
явлений в радиоаппаратуре. . *
4.2. ВИБРАЦИИ В ВИДЕ СТОЯЧИХ ВОЛН
Рассмотрим случай, когда концы стержня длиной L
закреплены неподвижно. Граничные условия в этом случае наиболее
просты:
t/((U)=0, и(М)=0.
Пусть стержень выведен из состояния равновесия и совершает
свободные колебания. Нужно найти формулу, описывающую эти;
колебания.
Уравнение стоячих волн для нашего случая имеет вид
где Um — амплитуда колебаний; k — волновое число; со —
частота. ' .
Волновое число k равно числу длин волн %, которое
размещается на 2л метрах: . -
к=2л/%. . - D.9)
В этом смысле волновое число аналогично круговой частоте
ю=2л/Т, которая также определяемся числом периодов колебаний
Т на протяжении 2л;.- ' - . '
' Чтобы убедиться в том, что функция D.8) является решёниемг
уравнения D.7), подставим ее в.это уравнение. После сокращения
на синусы и на Um получим • , '
Действительно, в стержне возможны колебания D.8) при."
условии, что между частотой колебаний и волновым числом су-*
ществует соотношение D.10). Кроме того, должны
удовлетворяться граничные условия. При х=0 решение D.8) всегда равно нулю-
А при x*=L оно равно нулю только при
kLr*n, 2л>..., ля, :
где /1=1,2,...; k^nn/L. ^
ее , i
Таким образом:, в стержне возможны только такие стоячие
вОлны, при которьщ по длине стержня откладывается целое число
полуволн. Например, при /г=1 это Зудет одна полуволна
(рис. 4.6)- При /=774 и со*=90° в центре стержня сечения будут
отклоняться от нейтрального положения на максимальную
величину Um. . .
Наконец, для возникновения таких колебаний необходимо,
чтобы в начальный момент выполнялись условия
/ m л
и (х, 0) = 0,
dt
. = итш sin kx.
Таким образом, мы получили решение д^я свободных
колебаний в виде стоячих волн. В этом случае собственные частоты
колебаний определяются из D.9) и D.10):
¦-, я=1, 2,... - D.11)
Соответствующие этим частотам собственные формы
описываются функцией ' '
В частности, первая собственная частота (л=1) будет равна
первая собственная форма колебаний имеет вид
1С
I—'X.
I
I
I
<->
J%MM
I
л,
*-^
f "
•
*
W
Рис. 4.6. Стоячая волна при продольных колебаниях стержня
67
В тех случаях, когда начальные условия не заданы, определи!
величину Um невозможно и функция D.12) описывает л^
«носи'тельные значения амплитуд колебаний в точках стержня/.;]
Большой практический интерес представляет задача рас*з
перемещений, напряжений, ускорений (перегрузок) в режиме $
зонанса, когда частота внешних возмущений совпадает с собствё|
ными частотами. В рассматриваемом случае резонанс на^т
при вынужденных колебаниях концов стержня с частотой, ог
деляемой формулой D.11) .^ Для расчета указанных выше велич
необходимо решить более сложную задачу с учетом потерь энс
гии на внутреннее трение в материале стержня. Ниже мы рассмс
рим подход к решению подобных задач, а пока перейдем к иЩ
дольным колебаниям в виде бегущих волн. -^
4.а. ВИБРАЦИИ В ВИДЕ БЕГУЩИХ ВОЛН i
В простейшем случае бегущая волна описывается формулой
u=iUmsin(kx—©*).' . . D.Й)
Действительно, в момент ?=0 максимумы этой функции буДут
при - * ¦ ч
о ъ
1С ОТС . %
Через некоторое время М максимумы функции будут смещевы
Синусы имеют максимумы при условии ?
(**»!-«АО«у» -у » . :;
откуда . ' • ¦ А
тс , <о А ' Згс , со А, s
Максимумы будут сдвинуты на ^
k t _ *.
Таким образом, максимумы перемещаются • по направлению рс
со скоростью ч - • " *
Ад: ¦ ц> ' v ,л 4*ъ
М к ...
Если в формуле D.14) изменить зйак «—>> на знак « + », то
волна «побежит» влфотивбположную сторону,
Подставив решение D.14) в уравнение D.7), получим соотнр
шение между яастрхалли» и -длинами .вода .DЛШ. Таким образом,
68 * . , ^
"nag
«пр
Рис. 4.7. К распространению волн в неоднородном стержне
при соответствующих граничных и начальных условиях бегущая
волна будет решением уравнения продольных колебаний. Такие
решения позволяют рассматривать отражение и прохождение
упругих продольных волн на границе двух различных материалов.
Предположим, что в плоскости дс=О (рис. 4.7) стержень из
одного материала (риЕ\) «склеен» со стержнем из другого
материала (рг, ?2). Предположим далее, что к границе раздела
подходит «падающая волна»
Мпад = t/пад Sin (k\X—(d). " ,
От границы отражается волна
а через границу проходит волна
Все три волны имеют одинаковую частоту ю, но различные.длины
волн, определяемые во'лновыми числами k\ и /ь.".На границе
должны выполняться условия неразрывности: перемещения и
напряжения по обе стороны вблизи «границы должны бить одинаковыми:
Мпад + Wotp = Мпр,
Ег ад 1 Ег
откуда при .v=0
^пР. D.17)
Из выражений D.17) легко получить коэффициент отражения
** коэффициент прохождения волн:-
Uup
Для практики более подходящую форму записи коэффицшш
тов можно получить из D:18), если учесть D.10): * ^
I
¦f
В акустике выражение fEp называют акустической плотностью
среды. В случае E\pi=E2p2 отражения не будет, а коэф.фици|нт
прохождения будет равным единице. Если же E^p2>Eipt (ём
рис. 4.7), то проходящие волны будут иметь амплитуду значитесь
но меньшую, а длину волны значительно большую, чем у падйю
щих волн. На рис. 4.7 показана картина прохождения и отраже
ния упругих* волн при условии, что правая часть - стержня бо$ёе
тяжелая (p2=2pi) и более жесткая (Е2=8Е\). Коэффициенты. nfp
хождения и отражения в соответствии с D.19) получаются р$в
ными 2/5 j 3/5, соответственно волновое число в правой чайи
стержня в соответствии с D.10) получается вдвое меньшим, а дда
на волны — вдвое большей. %\
С увеличением, отношения Е2р21Е\р\ проходящие волны ncfte
зают, а коэффициент отражения приближается к единице. Моз&ет
показаться, что этот коэффициент должен быть равен — 1, ф
скольку закрепленная граница не должна двигаться. Однако это
не так. Если ?/Отр = ^пад, то это значит, что падающая и отражен
пая волны будут иметь одинаковую амплитуду. Но падающая
волна будет двигаться в сторону границы, а отраженная^в п^о
тивоположную, и волны будут взаимно уничтожаться. Наконец,
если Е2р2<^Е\р\1 то коэффициент отражения приближается к ~^1,
а коэффициент прохождения — к 2. Падающая и отраженная в^л
ны будут на границе складываться, и в среде с малой акустике
ской плотностью амплитуда волны будет вдвое больше, чем ai$n
литуда падающей волны. jj
Полученные соотношения дают представления о том, что п$ю
цессы вибраций можно представить как сложную картину падаю
щих, отраженных и проходящих волн. Однако при наличии ije
скольких границ раздела между средами производить каки^то
70 ' ' Й
'•Г
расчеты на основании этой картины чрезвычайно сложно, особен-
ло если это не только продольные волны в стержнях, но и
произвольно ориентированные волны в более ..сложных конструкциях.
Были рассмотрены практически установившиеся процессы, для
которых волны представляют собой гармонические колебания с
не изменяющимися во времени формой, амплитудой и частотой. Но
для конструктора часто представляют интерес переходные
нестационарные процессы* при которых возможны резкие изменения
напряжений и деформаций и достижение недопустимо больших их
зеличин. Такие процессы могут возникать, например, при ударах
лли при резком изменении режима вибрации.
Аналитические расчеты переходных процессов, как правило,
невозможны. В этих случаях используются численные методы.
Яиже рассмотрен пример решения задачи о продольном ударе
/пругого стержня.
4.4. УДАР
Упругий стержень падает на жесткую поверхность со скоростью
v (рис. 4.8) и в начальный .момент (/=0) касается этой поверхно-
:ти нижним торцом. Нижние точки стержня останавливаются, а
верхние продолжают по инерции двигаться. Нужно рассчитать
Таблица 4.1
/
2
5
7
8 -
9
10
11
12
13
14
15
16
1
-1
0
0^
0
0
0
0
0
0
0
0
—1
—2
—3
—4
—5
2
; ,
-1
0
1
1
1
1
1
1
1
1
0
—1
. 2
—3
—4
-5
3
-1
0
' 1
2
2
2
2
2 ..¦
2
I
0
—1
2
-3
—4
¦—5
i .
4
— 1
0
1
2
3
- 3
3
3
2
1
0
—1
-2
—3
—4
^5
5
1 '
0
• 1
2
3
4
'4/
3
2
1
0
-^1
-2
-3
—4
—5
6
—i
0
\
2
3
4
4
3
2
1
0
—1
—2
—3
__4
Рис. 4.8. Падение
упругого стержня на
жесткую поверхность
71
этот процесс^ т. е. вычислить перемещения во времени во всех/
точках стержня. . ¦ h
Введем дискретизацию по координате и зремени, т. е. выберем?
шаги сетки Лит, разобьем область решения на дискретные
элементы ЛХт и пронумеруем их. Тогда для дискретной области
уравнение движения примет вид D.6). Предположим, что по
координате выбрано шесть узлов, i= 1, ..., 6. -
Начальные условия представлены в виде перемещений и
скоростей всех точек стержня при ?=0. В разностной постановке эти
начальные условия вводим следующим ^образом: в первом шаге
по времени /=1 все центры элементов помещаем на одинаковом
расстоянии от начального положения, т. е*
Мм=_ит=_1, D.20)
тогда в следующем шаге, когда стержень касается твердой
поверхности (*—0), все точки приходят в начальное состояние*
Таким образом, мы задаем начальные перемещения всех точек
равными нулю (зададим систему отсчета), а скорости всех точек
равными хк
Результаты расчета будем записывать в табл. 4.1. Первые две
строки этой таблицы -и есть начальные условия, задали. Теперь-
определим граничные условия*. Нижний конец стержня не
перемещается, во всяком случае, пока он прижат к жесткой
поверхности. Поэтому fc левом столбце записываются нули. На верхнем,,
свободном, конце стержня отсутствуют напряжения, а значит,;
равны нулю и деформации растяжения: "^
h
т. е. перемещения в пятом и шестом элементах должны быть
одинаковыми:
«5,/, D.22)
Теперь можно произвести вычисления перемещений средних
точек стержня с помощью, разностной формулы D.6). В нее
входят пять значений перемещений (i, /), (t+1; /), (I—1; /), (t";/+l),«
(i; (j—1), которые должны быть записаны в.пяти соседних клетках
табл. 4.1. Если, например, 1=2 и /=2, то пять клеток будут
расположены в верхнем левом углу тгаблицы. Они образуют так
называемый пятиточечный шаблон. В четырех клетках шаблона
перемещения известны. Остается неизвестной только одна величина
w/,/+i. Ее можно легко вычислить по формуле D.6).
, Для удобства вычислений уравнение D.6) следует решать
относительно неизвестной м/,/+г.
Я*;У+1 = A (Ui+vj — 2Uij + Ut+w) + 2uitI
72
' . D.23)
. Эта формула, в которой значение неизвестной функции на
следующем временном слое /+1 явным образом выражено через
значения функции на предыдущих слоях~ совместно с начальными и
граничными условиями называется явной разностной схемой:
Величина безразмерного коэффициента А зависит от выбранных шагов h
и т. Самые простые вычисления получаются при А = 1. При этом разностная
формула приобретает простой вид:
. D.24>
Подставив в D.24) значения
#3,2 = О, Й1|2 = О, Й2.1 == — Ь
получим м2,з = 1.
Запишем это значение в табл.. 4.1, переставим шаблон на одну клетку
вправо и вычислим «3,3=1. Аналогично вычисляя и в последующих узлах,
заполняем строку /=3. Значение щ$ берется таким же, как и «5,$, в соответствие
с D.22). Переставим шаблон на одну строку вниз и произведем вычисления &
строке /=4. Продолжим вычисления последовательно по временным слоям / на
требуемое число шагов.
Остановимся пока на слое /=11, на котором все точки «вновь оказались i*
положении равновесия. Дальнейший расчет зависит от характера граничных
условий. Если торец стержня «прилипает» к Преграде, to «i/=0 и в столбце f«f
нужно продолжать записывать нули. Если же нижний конец свободно
отрывается от жесткой поверхности, то после того- как деформации на 'этом конце
становятся равными нулю (/=11), нижний конец также нужно считать
свободным и записывать Wi,/=w2,/-
На рис. 4.9 показаны положения центров элементов в каждом шаге по
времени. После касания поверхности при /=2 нижний узел (*=1) останавливается,
а дерхние продолжают движение. Затем при /=~3 останавливается второй узел
и т. д. В'шестом шаге по времени все узлы останавливаются. При этом весь
стержень равномерно сжат. Деформации во всех элементах межйу узлами
одинаковы, кроме верхнего элемента между узлами /=5 и *=6, в котором они
остаются равными нулю. Таким образом, весь процесс сжатия длится четыре
Шага. Это объясняется тем, что в модели стержня пять шагов по координате
н за каждый шаг по времени сжимается один элемент длиной Л, причем
верхний элемент не сжимается. Если бы мы взяли шаги поменьше, то количество
Шагов п по времени при сжатии приближалось бы к количеству шагов по
координате, укладывающихся по длине стержня, и тогда время сжатия
определялось бы по формуле
Гсж = лт = 4-,. - D.25)
п .
7S
¦4
/
I, 2 3 * 4
//,
7 8\ 9 10 . ft П 13 Ъ~.15 16j,
Рис. 4.9. Картина удара стержня о жесткую поверхность
Ио всоответствии с выражением А=Ет2/рй2=1 шаг по времени
тогда
Щ
Известно, что скорость распространения механических колебаний, наприм|
ультразвуковых волн, в твердых телах определяется соотношением ?
|
шоэтому время сжатия представляет собой отношение ?
- . 7СЖ=1/У, , D;2в'
¦которое определяет время прохода ультразвуковой волны по длине стержн*
Это время не зависит от скорости, падения стержня v и, конечно,. 6т выбра*
пых шагов h д т. ~ ' s
Начиная с восьмого шага по времени, стержень начинает разжиматься и за
то же время приходит в исходное недеформированное - состояние. Далее сте^
жень отрывается от твердой поверхности и «отскакивает» от препятствия. При
этом он остается недеформированным. ^ у
Максимальные деформации во „всех элементах получаются одинаковыми
равными
D.2S
74
а напряжения
о = Ее = V VW= Е —. ' _ D.30)
Чтобы определить, в. каком масштабе измеряется перемещение, нужно
воспользоваться принятым выше равенством ат=1. Если, например, материал
стержня имеет характеристики ?=1010 н/м2; р=5-103 кг/м3, а шаг сетки h
выбран равным 10 см, то в соответствии с D.26) juar по времени получается
равным
^О/п мс. . #
Если стержень падает со скоростью а=10 м/с, то г>т=0,71 мм и каждая
единица в табл. 4.1 равна 0,71 мм. Таким образом, перемещения получаются
малыми. / -
Были использованы разностные методы решения задач. В связи с этим
необходимо ознакомиться с основными положениями теории разностных*схем [6].
4.5. АППРОКСИМАЦИЯ, УСТОЙЧИВОСТЬ И
ПОГРЕШНОСТИ РАЗНОСТНЫХ РЕШЕНИЙ
Чтобы разностное решение не очень отличалось от точного аналитического
решения, необходимо прежде всего обеспечить аппроксимацию
дифференциальной задачи разностной. Это значит, что разностное уравнение D.6) при устрем*
лении шагов h и т к нулю должно переходить в дифференциальное
уравнение D.7). Аналогично должны переходить в дифференциальные соотношения
начальные и граничные условия. При этом важной характеристикой разностных
соотношений является порядок аппроксимации дифференциальных уравнений
разностными. Рассмотрим вычисление порядка аппроксимации на примере
уравнений D.6) и D.7). Порядок аппроксимации определяется для каждой
производной отдельно.
Найдем разность между вторыми производными, выраженными в
разностной и дифференциальной форме:.
д = uM— 2^-f-^__i _ дЧ
Применим формулу Тейлора t \
+ _. — + — -55Г + "Г
h дщ ' h2 d2ut h* dzut ¦ tA Q14
A L + •.. D.31)
1! dx T 2! dx* 3! rfx3 V ;
4! rf* /'
75
Таким образом» разность между точными и приближенным выражениями,
вторых" производных пропорциональна квадрату шага сетки h. В этом случае
говорят, что разностный аиало'г производной обладает вторым порядком
аппроксимации относительного шага h. Правая часть уравнения D.6) также
""обладает вторым порядком аппроксимации относительно шага т, поэтому
разностное^ уравнение обладает вторым порядком аппроксимации. Это означает,,
что если все шаги сетки h и т уменьшить вдвое, то погрешность дискретизации
уменьшится в четыре раза.
Аппроксимация разностной задачи дифференциальной. еще не гарантирует.
малой погрешности расчета, Дело в том, что сам процесс вычислений с
помощью разностных уравнений часто является рекуррентным процессом,
состоящим из множества шаго& или этапов вычислений. В каждом- следукйцем шаге
используются результаты предыдущего шага. Над этими результатами
производятся различные математические действия, одинаковые во всех шагах.
Если рекуррентный процесс построен неправильно, то некоторые малые
погрешности, всегда имеющие, в расчете, в последующих шагах вычислений
постоянно усиливаются и возрастают по закону геометрической прогрессий. Говорят*
что решение неустойчиво по отношению к малым возмущениям в виде
погрешностей. Если решение неустойчиво, то через несколько шагов вычислений
разностное решение будет'резко отличаться от точного решения.
Выполнение условия устойчивости при решении^ обязательно, • поэтому
анализу устойчивости уделяется большое • внимание [10]; В нашем случае условие
устойчивости запишется очень просто: ^
А<\. - ч D.32)
Таким образом, мы производили расчеты с помощью рекуррентной
формулы D.23) на грани устойчивости. Если взять коэффициент больше единицы, то
процесс будет неустойчивым, в чем легко убедиться, выполнив вычисления на
несколько шагов по времени.
В случае более сложных разностных уравнений, например, таких, которые
встретятся ниже, условия устойчивости получаются более сложными. Часта
пользуются при анализе устойчивости критерием Фридрихса, Куранта и Леви:
[10]. Суть этого-критерия состоит в следующем. В правую часть рекуррентной
формулы, записанной в таком же виде, как D.23), вместо переменных и
записываются единицы с различными знаками. Если в результате в левой части
получится число, большее, чем единица, по абсолютной величине, то решение
будет неустойчивым. Причем это условие должно выполняться # при любом
сочетании знаков перед единицами.
На' практике все возможные сочетания знаков перебирать, как правило, не
нужно, поскольку легко просматриваются наиболее неблагоприятные сочетания.
Чаще* всего это чередование знаков происходит по координатам и времени па
«правилу шахматной доски» [11].
Условия устойчивости накладывают жесткие ограничения на выбор шага
по. времени при решении нестационарных задач. Например, в нашей задаче об
ударе стержня о жестокую поверхность шаг по времени получается равным.
0,71 мс, т. е. порядка одной миллисекунды.
76
При расчетах более* мелких деталей из более твердых, материалов шаги
по времени получаются порядка десятков микросекунд. Это означает, что "при
необходимости расчета процесса длительностью 1 с вычисления следует
проводить на 100 000 шагов по времени. Однако при ударах и вибрациях"
переходные процессы, как правило, протекают довольно* быстро и расчеты обычно
производятся на меньшее число шагов.
Заметим, что всякие попытки как-то обойти эту трудность и увеличить шаги
по времени оканчиваются неудачей. Известно [10], что применение неявных
схем вместо явных снимает ограничения на выбор шага по времени т.
Решение при этом получается абсолютно устойчивым. Однако при больших т оно
настолько отличается от точного решения, что теряет всякий смысл.
Выполнение условий аппроксимации и устойчивости обеспечивает малые
погрешности. Однако значение их, как правило, неизвестно. Только в
отдельных простых случаях путем сравнения точного и приближенного решений
удается проанализировать кархину возникновения и развития погрешностей и
получить оценку «сверху». Например, для продольных колебаний упругого стержня
в виде бегущих или стоячих волн получена оценка [11] относительной пргреш-
ности амплитуды , . '
Д=±A-Л)^<7, ¦'' . , D.33)
ч
^где q — число полу периодов, колебаний, воспроизводимых в расчете.
Таким образом, при расчетах продольных колебаний с помощью явной
схемы погрешность амплитуды с течением времени возрастает. Амплитуды
колебаний в расчете выше, чем в точном решении.
Относительная погрешность фазы также возрастает', но - не превышает
величины ¦ ^
24! *
а погрешность в определении периода колебаний не превышает величины
Интересно, что при Л = 1 все погрешности в разностном расчете
отсутствуют. Разностное решение не содержит погрешностей дискретизации. Поэтому
полученные выше оценки D.28), D.29) и D.30) являются точными.
К сожалению, что исключительный случай. При решении двумерных и
трехмерных задач невозможно исключать погрешности дискретизации, и нужно их
определять.
Рассмотрим теперь другой вид упругих , колебаний стержней — крутильные
колебания.
77
4.6. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
Крутильные колебания возникают при вращении
стержня вокруг центральной оси (рис. 4.10) ./Простейшая
о распределении деформаций по сечению стержня состой:
положении, что форма сечения не меняется и происходи"
поворот сечения на угел <р*. Таким образом, функция <г
только от координаты х и не зависит от у и z.
/ Крутильные колебания * происходят под действием
моментов Мх. Эти моменты создаются упругими напр.._
моментами »инерционных сил или. моментами внешних г-
нию к стержню сил. . •'
Для вывода, уравнения крутильных колебаний пос~
же, как и при выводе уравнения продольных колебаний
стержень на элементы длины h и пронумеруем их. Вь
извольный элемент с номером i и запишем уравнение
в виде
где Jm — момент инерционных сил элемента (момент
мента).
ч
s
Ч dS
г
Рис. 4.10. Крутильные колебания
стержня
Рис. 4.11. К определению
щего момента
78
Крутящие моменты следует выразить через касательные
напряжения а (рис. 4.11):
где г —расстояние элемента площади до центра сечения.
Касательные напряжения <у изменяются по поверхности S как:
по значению, так и по направлению. Значение этих напряжений
можно определить через углы поворота сечений <p*. Для этого
рассмотрим кручение цилиндра, вырезанного из.элемента стержня:
(рис. 4.12). ~
Деформации сдвига определяются как tga '
tg,
а касательные напряжения пропорциональны tg оь
где jii — модуль сдвига материала стержня.
Теперь выражение для ^крутящего момента можно записать в
виде
h
Интервал в выражении D.36) называют полярным моментом
инерции сечения стержня. У стержня постоянного сечения
полярный момент инерции сечения постоянен по длине стержня и не
зависит от х:
f
В
Аналогично можно записать выражение для крутящего
момента Мх~. В НеГО ВОЙДУТ УГЛЫ ф*,; И фх;/-Ь
В результате уравнение равновесия примет вид
Т^-2?,,;+ ?*u-i 1±
А2 т dt2
Момент инерционных сил пропорционален полярному моменту
инерции сечения:
где р _ плотность материала стержня,
Разделив левую и правую части уравнения D.37) на 1У по-
D.38>
Рис. 4.12. Представление
касательных напряжений через угч
лы поворота сечений
Уравнение D.38) аналогий
уравнению продольных коцебащ
D.5). Его можно представить в,
разностной форме, аналогична
D.6), или в дифференциальна!
форме, аналогичной ,D.7). •<$
Дифференциальное уравнен»;
крутильных колебаний позволяй
дх2
получать аналитическое решение t
виде стоячих или бегущих воли:
Это решение совпадает с D.8)ifi
D.14) с точностью до рбозначен№&;
С помощью, разностного уравн^нй|
и v соответствующих начальных if
граничных условий можно получитК
численное решение для переходньй
процессов при крутильных колебз?
ниях. * ' Щ,
?При расчетах крутильных колебаний могут встречаться стержни перемер
«ого сечения. Например, в' различных приборах используются валы перемени^
го сечения. Чаще всего сечение изменяется *устУП0М» переходя от одного ди^
метра D\ к другому D2 (рис. 4.13).
При аналитическом решении возникает трудность в подборе формул дл$
«писания колебаний валов, которые помимо общих требований удовлетворений
уравнениям и начальным и граничным условиям должны еще удовлетворят^
промежуточным граничным условиям на стыке валов. Формулы для толстого |
тонкого валов на стыке должны давать одно и то же значение углов поворот^
ц крутящих моментов. Эти требования называют «сшиванием» решения по пр#"
межуточным граничным условиям. При поиске аналитических решений тако|
«сшивание» представляет собой существенную трудность. * v 3
При разностном решении задачи-такая трудность не,возникает, но появля*'
ется необходимость в дополнительном- уравнении движения, для элемента стьр*
• ка валов. Для толстого и тонкого валов записывают уравнения D.39) в раз*;
ностно.й форме,^а для стыка в уравнении D.34)./ нужно учесть, что моменты^
МJ и М~ относятся к валам разного диаметра. Проще всего поместить центр|
промежуточного элемента¦— узел сетки —на, границе раздела, тогда вм
уравнения D.37) нужно записать
;i;j-l« — 2<pxjj 4"
D.40)
Произвести сокращение в данном случае не удается и нужно вычислить
оба центральных момента инерции и момент инерционных сил: /тер.
Например:
у J |
.*' * D.41)
В случае валов круглого сечения вычисление интегралов в формулах
D.41) не представляет труда, если воспользоваться цилиндрической системой
координат (рис. 4.14). Например, dS-rdadr и
2*
в Г
Подставив численные значения в уравнения D.40), получим явную
формулу наподобие D.2^).
Не вызывает принципиальных трудностей при расчетах крутильных
колебаний и наличие в конструкции сосредоточенных масс, например укрепленных на
валах шкивов, шестерен, рычагов. Для соответствующих узлов сетки
записывают уравнения D.40), в правой части которых учитывают моменты этих до-,
полнительных деталей. • , . • _
¦
\
h
—
i-t
Рис. 4.13. Крутильные колебания
вала переменного сечения
Рис. 4.14. К вычислению момента
янерции круглого сечения
6—1215
81
Были рассмотрены продольные и крутильные колебания стержне* при «g
более сложный случай - изгибные колебания стержня.
4.7. ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ ^ g
Нянйопрр поостаж гипотеза о распределении деформаций пШ
сече^ю ГрХ^и и^бяых колебаниях-это гяпотеза. „рям.«|
^ST!T^al^ сержня, S
p яе »С"«™вает
ортольяой' формы разобьем по дливе.еа дискрет-»
"Знаковой длЬвы ft. Пр.сво™ этим элементам яо|
элемент с яомером i
правлении заменим касательными напряжениями *гх и __
сравнению с продольными и крутильными колебаниями задач%
с?ано!и??я более сложной. Приходится вводить и более сложныц
обозная. Перейдем к общей индексации, принятой в теорий-
и деформации будут иметь два индекса. Первый|
т на направление действия напряжения. Второй -4
нормали к площадке, по которой эти напряжение
индекс
^3
I
Рис. 4.15. К пояснению гипотезы прямых нормалей
I
Рис. 4.16. Дискретизация в задаче
об изгибных колебаниях стержня
Рис. 4.17. Дискретный элемент
стержня
действуют. Теперь нормальные напряжения будут иметь два оди-
1аковых индекса, например <уХх, а касательные напряжения — раз-
лые индексы, например ?сг^.
Считая касательные напряжения постоянными по сечению
:тержня,* можно записать уравнение проекций сил на ось z в виде
в с ™ dwi
^ 1+0,5 — /4-0,5 = ^
Л2
^де F;+o,5=<*+: 'db; ^-0,6=qZr ^2вЬ;- в ^-полутолщина стержня;-
Ь — ширина стержня.
Касательные напряжения, или перерезывающие силы Ft выра-
шм через прогибы w в соседних узлах сетки. Эти преобразования
зыполняем последовательно. Вначале углы поворота сечений
выражаем через прогибы (рис. 4.18). Далее деформации растяжения
лоев стержня выражаем через углы поворота сечений (рис.4Л8)".
Лри этом верхние слои стержня сжимаются и деформации
получаются отрицательными. Теперь изгибающие моменты М выража-
^ис. 4.18. К определению
зависимости углов поворота сечений *от про-
ибов ' /
Рис. 4.19. К определению
зависимости деформаций растяжения от
углов поворота сечений
83
D.42)
Рис. 4.20! К определению зависимости изгибающих моментов от углов
поворотов сечений " " J
ются через углы поворота сечений (рис. 4.20). Для .удобства изсй
бражения изгибающих, моментов на рисунке 4.20 элементы «ра$*
двинуты». . ' Ч
, Нормальные напряжения в сечении стержня выражаются- чере#
углы поворота а сечений: ~" '
Эти напряжения изменяются по сечению по линейному закону^
что позволяет легко вычислять изгибающий момент: \
где Jy = b l'z*dz — момент инерции сечения стержня относительней;
оси у.
-5
Если стержень имеет прямоугольное сечение, то
= 28.
Тогда' перерезывающие силь|
можно выразить через изгибающие^
моменты (рис. 4.21). Для этого pac-t
смотрим равновесие дискретный-
элементов под действием изгибаю-^
щих моментов и перерезывающих^
, сил F: . '*
* Mt+\-Mt + Ft+l ^-
Рис. 4.21. К определению,
зависимости перерезывающих сил *
от изгибающих моментов
D.44X
Если считать, что
то из D.44) получаем ., . -
^+о,5 = — . . D.45)
h* '
Остается только подставить D.45) в уравнение D.42) и
выразить изгибающие моменты через углы поворота, а углы
поворота— через прогибы. После деления левой и правой частей
уравнения на h получаем
где trio— масса одного метра стержня.
. Уравнение D,46) и является уравнением изгибныхЛ колебаний
стержня. В правой части у него, находятся инерционные силы,
представленные в дифференциальной форме. Е&пи задача решаетг
ся аналитическим методом, то разностный оператор в левой части
D.46) нужно заменить дифференциальным оператором. После'
этого получаем .
0- "¦ •. <4-47)
В практике конструирования радиоаппаратуры иногда прихб-
дится решать стационарные задачи об изгибных деформациях
стержней под действием внешних сил. Такую задачу приходится,
например, решать при определении жесткости плоских прулсин и
других деталей. Если инерционные силы равны нулю, но. на
стержень действуют внешние силы, уравнение принимает вид
_ :• D.48)
гДе /^ — внешняя распределенная нагрузка, приходящаяся на
единицу длины стержня.
4.8. ИЗГИБ КОНСОЛЬНО
ЗАКРЕПЛЕННОГО СТЕРЖНЯ
Решим аналитически задачу об изгибе консольно
закрепленного стержня, нагруженного силой Fz на свободном конце
(рис. 4.22).
По длине стержня внешние силы отсутствуют, поэтому
D.49)
85
Интегрируя D.49), получаеЦ
решение в виде степенного „пола*
нома • *
. Поскольку уравнение D.45
т, „««/*'•'• имело четвертый порядок прок»
Рис, 4.22. Стержень, жестко закреп- « кооплинате в оеш??
ленный на одном конце водной по координате, в реше*
нии D.50) появились четыре па*
стоянные интегрирования. Для н^
определения необходимо задать четыре граничных условия—щ
два на каждом конце стержня. . . Щ
На левом конце стержня прогиб равен нулю и угол поворой
сечения также равен нулю, f. e.
Первое условие D.51) дает Со—О. Второе условие D.51)
зволяет определять вторую постоянную Ci=0. *'?
На правом конце стержня задана перерезывающая сила и hj|
левой изгибающий момент. Выражение для изгибающего моментц
в дифференциальной форме можно получить с прмощью D.43)^
d(& d^*w ч /л -^
/VI ess CJ у ' - suss ?2,J , # уЧс*&Ж.
dx - dx2 . ^
Вырджение для перерезывающей силы получается из D.44L
На правом конце стержня изгибающий момент равен нулк%
M(L)= 0, откуда • » . ¦%
.2С2+ЗСз1=0. |
Перерезывающая сила на правом4 конце равна внешней силе|
т.'е. ' - §
—EJy6Cs=F. 1
Отсюда, , . \
F % ' • ' I
Г* * ¦ *
И
3 лг FA
86
—' CaL = - • , - ' - >?
2 e 4EJy
а
Таким образом, прогиб стержня определяется выражением
у
При x^L прогиб составляет
D.54)
Жесткость стержня в рассмотренном примере определяется
отношением
Flw(L)=l2EJylL*. Г D.65)
Выражения для изгибающего момента D.52) и
перерезывающей силы D.53) используются для задания граничных условий и
при решении нестационарных задач. Для отдельного стержня
можно получить аналитическое решение в виде стоячих или бегущих
волн.
1 - 4.9. УСТАНОВИВШИЕСЯ
ИЗГИБНЫЕ КОЛЕБАНИЯ
Рассмотрим стержень длиной L, шарнирно закрепленный по
краям (рис. 4.23). Предположим* что в начальный момент ось
стержня прямая, начальные прогибы равны нулю, ге/(д:, Q)f=G,
а начальные скорости dw(x,P)/dt не равны нулю. Необходимо
найти аналитическое выражение для функции w{x, t).
Будем, как и в случае продольных колебаний стержня D.8),
искать решение в виде стоячих волн .
w=*Wm sin kx sin Ш. N D.56)
Подставив это решение в уравнение изгибных колебаний
«D.47), после сокращений получим
?/^4=то(о2. * . D.57)
Следовательно, стержень может совершать установившиеся
свободные колебания, если между волновым числом- k и круговой
частотой о) существует зависимость D.57) ц выполняются
начальные, и граничные условия. '
L у///}/.
Рис. 4.23. Стержень, шарнирно
закрепленный по краям
Рйс. 4.24. Собственные формы из-
тибных колебаний стержня при
резонансе
87
, Граничные условия на концах стержня при шарнирных опорах
записываются в виде
0. \ D.58>
Вторые производные на концах стержня равны нулю, так как.
шарниры не препятствуют повороту стержня, и изгибающие мо-^
менты D.58) получаются равными нулю. Условия на левом краю i
удовлетворяются формулой D.52) автоматически. Для удовлетво*
рения условий на правом краю необходимо, чтобы при х—
—Lsin?L = 0, т. е. .
kL=nn, n=l,2,... ^ . D.59)
Таким образом, по длине стержня должно укладываться целое;
число I полуволн: . ¦
k n ,
В начальный момент скорости определяются из D.52): •
dw/dt= Wm® sin kx.
Частоты и формы свободных колебаний будут- такими же, как
и при резонансе. Поэтому уравнение ?4.57) определяет спектр ре*
зонансных частот *
i EJy
Собственные формы колебаний при резонансе являются
синусоидами с разной длиной волны (рис. 4.24). Стержень •
представляет собой систему с распределенными параметрами, которая
имеет бесконечное число степеней свободы и бесконечное
множество резонайсов.
Таким образом, каждая гармоника в 'отдельности является
решением поставленной задачи. Но решением будет также, и любая
линейная комбинация гармоник .
Это позволяет в некоторых случаях свободных колебаний
получать решение в виде суперпозиции D.61) собственных форм..
При этом учитывают, что собственные формы обладают двумя ин-
тересными свойствами: - • ч
88 .
1. Из, собственных форм можно'составить любую начальную
"форму колебаний, заданную,в виде перемещений или скоростей,
если соответствующим образом выбрать амплитуды гармоник Wi
в выражении D.61). Это свойство собственных форм называют
свойством полноты. Говорят, что ряд собственных форм является:
полным. Свойство полноты легко доказывается простым
рассуждением: в реальной задаче можно задать любую начальную
форму колебанийг и конструкция после этого начнет совершать
какие-то свободные колебания, представляющие собой суперпозицию
собственных колебаний. Значит, из собственных форм можно со^
ставить любую- начальную форму. •
2. Собственные формы колебаний являются ортогональными
по отношению друг к другу. Свойство ортогональности состоит в
том, что интеграл от произведения двух различных собственных
форм по,длине стержня всегда равен нулю:
' sin —р- 1с sin -~ xdx = 0 при nt Ф л2- D.62)
!•
Это утверждение можно доказать, вычислив интеграл D.62):
1С ' 1С ~\L *
sin — (пг — п2) х sin — (nt + п2) х
1 L =а
Поскольку П\ и t%2 являются целыми числами, аргументы обоих
синусов при x=L оказываются кратными я.
При Л1=л2 интеграл D.62) не равен нулю:
Ь /не - /не
sin^-p Xd*=_ . .
Свойства полноты и ортогональности собственных форм
используются при аналитических методах расчета собственных ко*
лебаний не только стержней, но и в отдельных случаях пластин.
В других, более сложных случаях нахождение собственных форм
аналитическими методами затруднительно и представление
решения в виде суперпозиции собственных форм теряет смысл.
Аналитическое решение в случае изгибных колебаний стержня
Можно получить и в виде бегущих волн, как это было сделаню
при рассмотрении продольных колебаний D.14). При этом также
Должно выполняться условие D.57). Рассмотрение продольных
бегущих волн.определило фазовую скорость бегущей волны в виде
D.15). В случае изгибных бегущих волн из D.57) можно
получить величину фазовой скорости в виде
D.63)
где /в—длина волны. „ ^Щ
Равенство D.63) говорит о том, что при изгибных колебани|р
скорость распространения волн обратно пропорциональна ш
волны, т. е; короткие волны бегут по длине стержня быстрее,
длинные. В пределе бесконечно короткие волны имеют бесконечЩ
высокую скорость. Это противоречит эксперименту, Результ&й
расчета отличаются от действительной картины изгибных волн,
грешность получается тем большей, чем короче волны. Поэто$
рассмотренные расчетные модели оказываются пригодными
расчета низших гармоник изгибных .колебаний и дают тем бо4|
щую погрешность, чем выше номер гармоники, т. е. чем короч
волны. > S
В случае расчета вибраций радиоаппаратуры конструктора щ
тересуют, как правило, низшие гармоники. Резонансы на низ
частотах наиболее опасны, поскольку имеют большие амплитуд
перемещений и ускорений (перегрузок) и медленнее затуха
Поэтому изложенные выше методы оказываются пригодными дщ
расчета изгибных колебаний. Щ
*' " ¦ ' . • ¦ ¦ а
4.10. РАСПРОСТРАНЕНИЕ Ц
УДАРНОГО ИМПУЛЬСА , %
Рассмотрим численный расчет распространения ударного импульса вдой
оси стержня. Пусть стержень жестко закреплен на левом конце и шарнирцщ
закреплен на правом (рис. 4.25). Ударный импульс воспринимается левой onj|j
рой. В результате она вместе с левым концом стержня поднимается на неко|
торую малую высоту, которую для упрощения примем равной единице. ¦$;
Таким образом, начальные условия задачи можно записать в виде 5
Представим правую часть в- уравнении D.46) в разностной форме:
<4Л4)
J I 5 6 7 в 9 ~W~KX Рис< 4-2B- K Расчету процесс||
" 77777 распространения ударного им&
пульса в стержне ' ^ :\
Решая уравнение D.64) относительно ю^ж, получаем явное уравнение
¦А\
—Wi;/-i, где
D.65 )
Коэффициент А выбирается из условия устойчивости. В правой части D.65)
разностного уравнения семь значений прогибов чад. Эти значения
располагаются на семиточечном шаблоне (рис. 4.26).
Для анализа устойчивости вычислительного процесса дадим этим семи
величинам единичные значения со знаками, чередующимися по правилу
шахматной доски (рис 4.27) :
. Л[1+4 + 6+4+1]—2— l=W(/;/+u<l.
Возьмем, как и раньше, предельное значение
16Л=4, Л=0,25.
* Если взять коэффициент А хоть немного большим, то решение с помощью
явной схемы будет неустойчивым. Тогда формула D.65) примет вид
У ' D.66)
• В табл. 4.2 приведены результаты расчета процесса распространения
ударного импульса по длине стер.жня на 6 шагов по времени. В каждом шаге по
времени во всех узлах стержня Определены перемещения ад.
Запишем начальные условия задачи так, как они записаны в первых двух
строках табл. 4.2. Граничные условия заданы в узлах i=0; 1; 10; 11.
Поскольку, левый конец стержня в начальный момент ?=0 поднимается
и остается перпендикулярным плоскости заделки, единичное перемещение
задается в узлах /=1; 2. В дальнейшем левый край остается неподвижным,
поэтому значение единиц в этих узлах сохраняется. Таким образом, задано
левое граничное условие-в виде единичного перемещения и нулевого угла
поворота. На правом конце стержня, закрепленном шарнирно, граничные условия
будут иными: -
dx*
= 0.
D.67)
1-2J i-U
ij-l
. и
1+1 J
i+2J
1-2
-hi
/-/
-t
- I
-/
+7
-/
i+1
-/
i+2
j
Рис. 4.26.Хемиточечный шаблон*
Рис. 4.27. К анализу устойчивости
вычислений
91
1
2
3
4
5
6
0
0
1
1
1
i
l
1
0
l
l
l
l
i
2
0
0
0,75
0,875
0;922
0,945
3
•
0
0
-0,25
-0,375
0,609
0,726
4
0
0
0
—0,438
—0,000
0,359
5
0
0
0
0,0625
-0,5
—0,633
i
e
0
0
0
0 .
—Ъ,172
—0,602
7
0
0
о
0
0,027
-0,55
Таблиц*
Ь
0
0
0
0
0
0,0002
0
0 '
0
0
0
—0,0004
у А
\
10
0
0
0
0
0
0
щ
it
:i
•ft
ft
ft
Второе равенство D.67) следует из равенства нулю изгибающего момент*"
D.52). Эти граничные услоря запишем в разностной форме: ~
. Л -V
t-2wl0 + w9 _,n D.68J
= 0,
*;
.п
Второе условие D.63) означает, что правый конец стержня не изогнут, т. ev|
что все три значения ш9, wtd, Wn лежат на одной прямой. Поэтому
^Ю-
Вычибления начинаются с третьего временного слоя, когда /=Д и произво- -
дятся последовательно по временным слоям. В каждом следующем шаге по вре-"
мени ударный импульс распрострацяется по. длине стержня вправо (рис. 4.28).
С правой стороны от основного' «гребня» волны появляется отрицательная".
волна, а затем еще правее — поло- «
жительная волна. Появление этих
дополнительных гребней согласуется
с физическими представлениями,
используемыми при выводе уравнений ¦"
изгибных колебаний.
/ Действительно, если в расчетной ;
модели какая-либо точка «резко под-'
нялась, то • соседние точки должны \
опуститься ниже первоначального по- *
^_^ ложения за счет действия перерезы-
j=S\ . ."Ч. вающих сил.
Рис. 4.28. Распространение ударного
импульса по длине стержня при
изгибных колебаниях
Основной гребень Ьопны
Положительная волна
Отрицательная волна
1 2 ¦ 3 4
8 9 10 11 х
Ударный импульс по мере продвижения по длине стержня «расплывается»,
становится более плавным. Поэтому деформации и напряжения будут
максимальными в каждой точке 'стержня в момент прохождения основного гребня
волны, и для контроля прочности нет надобности производить расчет на боль-
дгое число шагов по времени.
Численными методами приходится пользоваться не только при расчетах
переходных процессов. Ласто не имеют аналитического решения и задачи по
расчету стационарных процессов, например резонансных колебаний.
Тогда-применяют разностное решение задачи на собственные значения,
4.11. РЕЗОНАНСНЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ
Упругий стержень прямоугольного сечения, закрепленный шар-
нирно в трех местах (рис. 4.29), совершает резонансные изгйбные
колебания. Нужно определить нижнюю резонансную частоту и
форму колебаний.
Разностное уравнение движения произвольного элемента
запишем, как и прежде, в виде D.46). Поскольку при резонансе все
точки конструкции движутся синхронно по гармоническому
закону, прогиб в любой точке в любой момент можно представить в
виде
Witt=*Wi sin at, - ' • D.69)
"где со — резонансная частота.
Подставив решение D.69) в уравнение D.46), получим .
А*
• Уравнения D.70), записанные для всех внутренних элементов,
вместе с граничными условиями образуют следующую систему
уравнений: •
А
А (Wl—4W2+6W3—4WA+Wb) -
А (W2—4WS+6W4—4 W5+W6) =<
A(W3—4W4+6Ws—4We+W7)
W0 D.71)
.A (W6—4W7+6Ws—4W9+Wl0)
*Рис. 4.29. Стержень,
закрепленный шарнирно по
краям и в середине
,
где A=EJfh*m0.
Зададим числовые значения: ?=6-1010, /=1,5 м, Л=0,1 м,
10*"8 5»Ш3 ^
10
=5- Ю-1 кг/м.
Введем частотный параметр „ < '^
Я='*>2А4, D.72р
тогда система D.71) может быть записана в матричной форм^
CW-KW, . ' D.73§
где С — матрица, вид которой представлен на рис. 4,30. Ц
Полученная система уравнений не является замкнутой. В не||
число неизвестных на единицу больше числа уравнений. Ненз§^
левое решение системы D,73) получается только при определе^|
ных значениях частотного параметра X. Эти значения называю*!!
собственными числами матрицы С, а задачу отыскания собствей§|
ных чисел — задачей на собственные значения. ^
Собственных значений частотного параметра будет столько!
сколько степеней свободы имеет система,-т.. е. столько, скольк%
уравнений D.71) имеют в правой части частотный параметр йЦ
В нашем примере таких уравнений —девять. Собственные ф^
матрицы и определяют резонансные частоты конструкций.
5
-4
;
~4.
6
-4
1 ;
/
-4
6
-4
1
5
1
1
6
-4
/ .
-
-4
6
-4 •
;
/
-4
6
-4
/
/
-4
6
-4
;
-
;
-4
-4
;
7
-4
6
-4
'7
/
-4
б
-4
;
"/
-4
v 6
-4
/
-4
5
Рис. 4.30. Вид матрицы С
94
1
¦I
i
f
й
I
Существует много различных методов решения задачи на собг
.^венные значения". Однако большинство из них пригодно толька
для матриц ограниченной размерности. При расчетах конструкций
рЭА расчетные модели могут иметь тысячи и десятки тысяч стет
1вней свободы. Для таких громоздких задач наиболее
применяемым является, по-видимому, только один метод, представляющий,
обой итерационный процесс вычисления собственных чисел. Ок
юзволяет определять одну или две низшие резонансные частоты
и формы колебаний.
Итерационный процесс состоит в следующем. Вначале задает-
я приближенная форма колебаний, которая может быть выбрана
лроизвольно, поскольку описываемый итерационный процесс в.
дабом случае приводит к вычислению низшей резонансной часто-
гы и формы. Однако удачное первое приближение уменьшает чис~
ю итераций. , ,
Зададим первое приближение в виде треугольника, (рис. 4.31). Начальные
лшчения Wt для i=l,..., 15 приведены ниже:
i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0—1—2—2—1 0 1 2 3 4 4 3 2 1 О
Теперь из уравнений D.71) вычислим значение частотного параметра:
-5 + 8-2 ч1 .
—1 .
W,-4W2
-^ 4 Wt + W6
-2
1+8-12 + 4-0 1
0-4-4—12+- 8—I _ 1
, -2 2
-2+8-6+0+1 1
A, = —— — I,
ДГ // ]2 13 /« 15 X
Рис. 4.31. Приближения
(/, 2) формы в задаче*
на собственные значения
95
0-4+12-12 + 4 ft
_ 1-8+18-16 + 4 1 ' ~
9 ' з з ' '. м
. 2-12 + 24-16 + 4- 1 У
3-16 + 24 — 12 + 3 1 Т
Л„ = _ _ = —. ,
4 4 ¦ ,;'
4-16+18-8+1 1 4?
4-1^+12-4+0
Хь- _ .
.3-8+5
* " *
Далее вычислим некоторое среднее значение tap. В простейшем случае
вычисляется как среднее арифметическое значение Я|. Более эффективные
собы будут рассмотрены в следующей главе. Здесь же остановимся на
простейшем способе, наиболее^ удобном при ручных расчетах.
, При осреднении отрицательные значения h можно не учитывать,
шроцесс сходится быстрее: ' . * "
Хср i_^0,4. ~. f . j*
Теперь представим разностную формулу D.70) в виде . $
По формуле D.74) находим прогибы во втором приближении: D
• l =1>96> ' ?
5,6 . ¦ ¦ ц
— 5,6 .
-0.89,
г8=.-г,н, »:
—5,6 . •?
вб ' ¦ $
^
—5,6
4-16-8+1 _oon
—— = О,ОУ,
4-12-
—5,6
Прогибы в точках t=l,7 и 14 определяем по формулам D.71):
Г2=— 0,98; Г7=0,89; №14=1,07.
Таким образом, во втором приближении форма изогнутого стержня имеет
вид, представленный на рис. 4.30 (см. кривую 2). .
Первый итерационный цикл закончен. Далее, используя полученные
результаты, снова подсчитаем значения собственного параметра, произведем его
осреднение и т. д. — до тех пор пока итерационный процесс не сойдется. Если
последующие значения частотного параметра отличаются менее чем на заданную
величину, итерационный процесс заканчивается.
Частотный параметр определяет первую резонансную частоту, а полученные
значения прогибов — первую собственную форму.
Рассмотренный итерационный процесс всегда сходится к первому
собственному числу и первому собственному вектору матрицы, т. е. к первой
резонансной частоте и первой форме. Однако если такая возможность исключается, то
он сходится ко второй форме. Например, если первая резонансная частота и
первая форма уже вычислены,, то можно в каждом итерационном цикле вычитать
эту форму из формы очередного приближения, тогда процесс сходится ко второй
форме.
Рассмотренные алгоритмы применимы не только для расчета отдельных
стержней, но и для расчетов более сложных конструкций, например стержневых
конструкций, широко применяемых в практике конструирования РЭА,
4.12. РАСЧЕТЫ ВИБРАЦИИ
СТЕРЖНЕВЫХ КОНСТРУКЦИИ
Получить аналитические решения при расчетах вибраций
достаточно сложных стержневых конструкций не удается. В то же
время численные методы позволяют производить расчеты очень
сложных конструкций, содержащих сотни стержней. Здесь мы
ограничимся только конструкциями прямоугольных форм, в
которых стержни соединены под прямым углом. Распространение
излагаемой методики на стержневые конструкции, в которых
стержни соединяются под произвольным углом, не встречает принци-
7-1215 97
¦ш
zk,
Рис. 4.32. К построению расчетной
модели стойки
Рис. 4.33. Система с сосредоточений"
ми массами %
пиальнщ трудностей, хотя формулы становятся более громозд|
КИМИ. i
Типичной прямоугольной конструкцией является стойк^
(рис. 4.32). Сразу же заметим, что стержневые конструкции P9J|
выполняются из стержней непрямоугольного сечения, обычно и*
уголков. В приведенных ниже расчетных моделях используютс
стержни прямоугольного сечения. Если необходимо перейти
стержням другого профиля, нужно в соответствующих формула*
учесть характеристики сечения (площади, моменты инерции) эти
стержней. \
Стойки применяются для установки в них блоков РЭА. Эт
блоки могут быть достаточно легкими, когда их масса меньше ил*
равна массе стержневой конструкции. Тогда распределенной мае^
сой стержней в расчете пренебречь нельзя. В этом случае расчет^
ная модель получается в виде, показанном на рис. 4.32. Масс&
блоков добавляется (размазывается) к массе элементов стержней:.
Это — первый предельный случай. Он средней сложности. Второй
предельный случай — когда -масса блоков велика и значительно!
превышает массу стержней. Тогда масса стержней в расчете нё|
учитывается и модель представляет собой, систему с сосредото^
ченными массами (рис. 4.33). Данный случай наиболее простоШ
Промежуточный случай — когда прииходится учитывать ка#
распределенную массу стержней, так и сосредоточенную (или рас^;
пределенную)* массу блоков. Этот случай наиболее сложный. Его?
мы рассмотрим ниже в разделе расчета вибраций пластинчатое
стержневых конструкций. Л
98
1л
rf
WW
Рис. 4.34. Упрощение задачи расчета вибраций стержневых
конструкций ?
Случай сосредоточенных масс, соединенных упругими
элементами, масса которых не учитывается, принципиально ничем не
этличается от систем с сосредоточенными параметрами,
рассмотренными выше. На этом случае мы останавливаться не будем.
Рассмотрим первый предельный случай. Каждый стержень
конструкции может испытывать четыре вида деформаций: растя-
кение, два изгиба в разных плоскостях и кручение. Рассмотренные
зыше гипотезы.позволяют учитывать эти деформации в отдельном
стержне независимо друг от друга. Если же стержни соединяются
з единую конструкцию, то в местах соединения одни виды
деформаций переходят в другие и картина усложняется. Приходится
/читывать одновременно все виды деформаций, поскольку в этом
•лучае нельзя представить сложную задачу в виде нескольких
эолее простых задач.
Но не все виды деформаций одинаково опасны для
конструкции. Наиболее опасными являются деформации изгиба. При
изгибе амплитуды колебаний напряжения и ускорения достигают
наибольшей величины. Поэтому в отдельных случаях возникает
возможность вообще не учитывать деформации растяжения и
кручения и ограничиваться только деформацией изгиба. Это намного
упрощает расчет. Конструкцию можно будет представить в виде
нескольких отдельных частей.
Действительно, если деформации растяжения отсутствуют, т. е.
стержни в продольном направлении не растягиваются и не
перемещаются вообще, то все перекрестия будут неподвижными. При
этом изгибные колебания отдельного стержня в одной плоскости
7* 99
m
/is-
4
YSSS* 'S/SS.
m пг
6
ПЗ
6)
m
-
П5 Л6 П\
-
/74 / /16
Рис. 4.35. Приведение рамы (а) к модели стержня (б) ?
никак не будут связаны с его изгибными колебаниями в другойг.
ПЛСЕслй далее считать, что деформации кручения не препятствуют;
поворотам перекрестий стержней, то конструкция распадается на
несколько рам (рис, 4.34), процессы в которых можно рассчит^
вать независимо друг от друга. Такую раму можно разрезать щ
«развернуть» в виде одного стержня (рис. 4.35). Задача
приведена к расчету одного стержня на нескольких опорах. Ока аналоги^
на задаче об изгибных колебаниях одного стержня на двух опора&|
рассмотренной выше. Алгоритмы решения аналогичны, только не,
обходимо учитывать условие «разрезания». Например, в пер<^
крестиях Ш и П4 углы поворота сечений всех трех стержне^
должны быть одинаковы. { -j
Такой прием упрощения задачи очень привлекателен, но н?
позволяет оценивать погрешности от всех сделанных допущении*
Чтобы не вносить в расчет неконтролируемых погрешностей, нужно
Рис 4.36. К пострбению уравнений
равновесия сил для перекрестия
стержней
100
Рис. 4.37. К построению уравнений
равновесия моментов для nektf
стия стержня
учитывать все виды деформаций. Здесь открываются широкие
возможности для построения различных алгоритмов расчета.
В любом алгоритме основную проблему составляет описание
движения перекрестий стержней. Наиболее общий подход,
по-видимому, изложен в [11]. Он состоит в том, что для каждого
перекрестия стержней записываются свои уравнения движения. В
каждом сечении стержня у перекрестия действуют три силы и три
момента. Проектируя эти силы и моменты на координатные оси и
приравнивая их силам (моментам) инерции, получают шесть
уравнений движения. Например, проекции сил на ось х (рис. 4.36)
дают уравнение
?^ DJ5)
где т — масса элемента перекрестия; и — перемещение
перекрестия в направлении х\ j — номер шага по времени.
В уравнение моментов войдут проекции моментов на ось х
(рис. 4.37), а также моменты сил (см. рис. 4.36):
Мх1 - Му2 + MzZ — Мг4 - Qz2hzl
где Jx — момент чшерции элемента перекрестия относительно х\
*ф — угол поворота перекрестия вокруг оси х.
Если в перекрестии по сравнению с рис. 4.36 и 4.37 какие-то
стержни отсутствуют, то соответствующие силы и моменты в D.75)
и D.76) приравниваются нулю. Из них, например, можно
получить уравнения для элементов отдельных стержней.
Далее в уравнениях движения необходимо выразить силы и
моменты через искомые функции — перемещения и углы поворота
сечений в центре перекрестия и соседних с перекрестием узлах
стержней. Все необходимые выражения приведены выше при
рассмотрении продольных крутильных и изгибных деформаций.
Уравнения движения перекрестий вместе с уравнениями
движения элементов стержней образуют замкнутую систему
алгебраических уравнений. Ее можно решать различными методами. В
случае расчетов резонансных частот и форм колебаний время из этих
уравнений исключается и получается задача на собственные
значения.
В случае расчета нестационарных — переходных — процессов
конструируется явная разностная схема, которая и используется
в рекуррентном по времени вычислительном процессе. В
результате такого решения получаются таблицы чисел, определяющие
перемещение и углы поворота сечений во всех элементах модели
в каждый момент. Эти громоздкие таблицы непосредственно ма-
101
лопригодны для анализа механических процессов в конструкц»
Для оценки вибропрочности и виброустойчивости констру*
нужно произвести следующие операции:
перейти от перемещений й углов поворота сечений к
циям, напряжениям и ускорениям (перегрузкам);
выявить места конструкции, в которых эти величины достигав
максимального значения; ^
сравнить эти максимальные значения с допустимыми. Та*
образом выявляются аварийные ситуации, запасы прочности koJ^I
струкций. Эти операции легко автоматизируются с помощью ЭВД|^
Следовательно, конструктор априорно получает всю необх^|
димую ему информацию о виброирочности и виброустойчивосй!'
проектируемой конструкции. v|
щ
КОНТРОЛЬНЫЕ ВОПРОСЫ . $
1. Какие конструкции радиоаппаратуры относятся к стержневым консШ;
рукциям? ff
2. Какие гипотезы позволяют рассматривать независимо друг от друга ирф&
дольные, крутильные и изгибкые деформации? |f
3. Почему в уравнение продольных колебаний входят производные второго?
порядка? . %
4. Как движутся частицы материала при продольных стоячих волнах? ?'*
5. Как по форме стоячей волны узнать номер гармоники свободных проН
дольных колебаний стержня, закрепленного по концам? . Jf
6. От чего зависит фазовая скорость продольной бегущей волны в стержне^?
7. Чем отличается отражение продольных упругих волн в стержне на сво-у*
бодном конце от отражения на жестко закрепленном конце? ??
8: Каким образом можно аппроксимировать первую и вторую производный
разностным выражением? $t
9. Что такое явная разностная схема? 4*
10. Какие вычислительные процессы называются рекуррентными? с,;
11. Почему в результате неустойчивого вычислительного процесса погрешно-;^
стй расчета бесконечно возрастают? ' %
12. Как проверить, будет ли устойчивой явная разностная схема? *$
13. Чем отличается момент инерции сечения стержня от момента инерци%
элемента стержня? v " :J
14. Почему при изгйбных деформациях углы поворота сечений выражаются'!
через первые производные, крутящие моменты — через вторые производные, а>
перерезывающие силы — через третьи производные от прогибов по координате?^
15. Как построить разностный оператор для четвертой производной? J?
16. Что называют собственной формой колебаний? ) f
17. Как формулируется задача на собственные значения? Т;
Глава 5. ВИБРАЦИИ ПЛАСТИНЧАТЫХ
КОНСТРУКЦИЙ
Отдельные пластины и различные конструкции из пластин широко
применяются в конструировании радиоаппаратуры. Прежде всего это печатные
платы и различные микросхемы. Плоская форма плат и подложек удобна для
расположения на ней электро- и радиоэлементов, получения печатного монтажа,
закрепления самих пластин и т. д.
Различные соединения пластин (рис. 5.1) в виде щитков (а), кожухов (б),
шасси (в) и других деталей применяется в качестве несущих конструкций и
для защиты аппаратуры от случайных повреждений, а также климатическим,
тепловых, электромагнитных и других воздействий.
Малая толщина пластины по сравнению с другими ее размерами
приводит к тому, что жесткость пластины в этом направлении получается небольшой.
Прогибы при ударах и вибрациях в поперечном направлении пластины могут
достигать больших значений и приводить к отказам и сбоям в работе РЭА.
С другой стороны, та же малая толщина пластины позволяет строить
различные простые гипотезы о распределении напряжений и деформаций по ее
толщине и, таким образом, исключая одну координату, переходить от
трехмерной задачи к двухмерной. В качестве такой гипотезы можно, например, принять
гипотезу прямых нормалей, которая использовалась выше при расчетах
колебаний стержней! В случае пластин эта гипотеза будет применяться при
рассмотрении сечений в двух взаимно перпендикулярных направлениях. На гипотезе
лрямых нормалей основана техническая теория изгиба тонких пластин [12].
5.1, УРАВНЕНИЯ
ИЗГИБНЫХ КОЛЕБАНИЙ ПЛАСТИН
Прежде чем перейти к уравнению изгибных колебаний,
рассмотрим некоторые положения теории упругости применительно
к пластинам. Прямоугольный элемент пластины (рис. 5.2), имею-
в)
Рис. 5.1. Примеры пластинчатых конструкций
103
щий первоначальные размерь
1Х и 1у, растянут * в направлен»
х на величину Д/*, при этом ol
сжимается в направлении у на
величину ddy. Отношение отщ
сительного поперечного сжатая Щ
относительному продольно»
растяжению определяется коэ<[
фициентом Пуассона материал?
пластины
Му1х
Рис. 5.2. К определению
коэффициента Пуассона
который у большинства материалов колеблется в пределах
,=0,25... ОД J
Бели к элементу пластины в направлении х приложить нору
малыше напряжения оХх, то он растянется в направлении х н$й
величину A/*,: /i
"XXI
Г4*
Если вместо напряжений ахх приложить нормальные напряжен!
ния Оуу, то элемент сожмется в направлении х на величину А/жа»1
При одновременном приложении напряжений (рис. 5.3) в
обоих направлениях суммарное удлинение в направлении х соста- '
вит
Аналогично в направлении у
E.3)
Можно решить систему уравнений E.2) и E.3) относительна
нормальных напряжений. В результате получим
( + )
1-V*
1-V2
E.4)
104
}хх
Рис. 5.3. К определению деформации
пластины <
Уравнения E.4) описывают
закон Гука для пластин.
Рассмотрим основные
положения вывода уравнения из-
гйбных колебаний пластин,,
применяемого в технической
теории изгиба [14].
Ниже мы приведем решение
нескольких задач
аналитическим и разностным методами:
Для этого потребуется
уравнение в дифференциальной и
разностной формах. Можно
формально перейти-от известного дифференциального уравнения
изгиба тонких пластин к разностным уравнениям. Но представляется
более эффективным вывод в разностной форме с последующим
переходом к дифференциальным выражениям, как было сделана
в предыдущей главе применительно к стерйшям. При этом полнее
раскрывается физический смысл всех промежуточных
преобразований и определяются правила задания граничных условий при:
различных способах крепления пластин.
Вывод уравнения изгибных колебаний состоит из нескольких
этапов:
1. Построение уравнения динамического равновесия
произвольного дискретного элемента плагины размерами hXt hy, hz. По
граням элемента расположены четыре перерезывающие силы Q,
которые являются равнодействующими касательных напряжений
Рис. 5.4. Дискретный элемент плас-
тины
Рис. 5.5. К определению зависимости?
перерезывающих сил от изгибающих;
и крутящих моментов
(рис. 5.4). Если в центре элемента находится узел сетки с индексами
1, /, то перерезывающие силы будут приложены в точках (/+0,5; /);
(i—0,5; /);' (I; /+0,5); (i; /—0,5). Проецируя эти силы на ось г g
приравнивая их силам инерции, получаем уравнение равновесия
Поскольку в уравнение входит разности сил, в левой части полук
чаются разности первого порядка.
2. Представление перерезывающих сил через изгибающие ц
крутящие моменты. Для этого рассматриваем равновесие четыре|
дискретных элементов с центрами(i+0,5;/); (/—0,5;/); (/;/+0,5|
и (/;/—0,5). Один из них показан на рис. 5.5. Каждая перерезы*
вающая сила выражается через первые разности от этих моментов^;
и моментов получается в 4 раза больше, чем сил. Но точки прий
ложения некоторых моментов совпадают, поэтому получается ш^
16 точек, а только 9: 5 для изгибающих моментов (/,/), (*+1;Щ
(/—!;/), (*;/+!) и (/;/—1),4 для крутящих (/+0,5;/+0,5)§
(/—0,5; /+0,5), (/+0,5;/—0,5) и (/—0,5;/—0,5). Теперь ураввднви^
равновесия будет иметь второй порядок разностей от изгибзкшцщ?
моментов по координатам. -:*
3. Представление изгибающих и крутящих моментов черва
углы поворота сечений. Каждый изгибающий момент (рис. 5,6) и
каждый крутящий момент (рис. 5.7) выражаются через 4 угла
Всего прлучается 16 точек, в которых вычисляются углы поворотам
сечений. Они показаны на рис. 5.8. После подстановки значений
моментов в уравнение равновесия получаем уравнение в конечный
разностях третьего порядка относительно углов поворота.
4. Представление углов поворота сечений через прогибы пдас*
таны (рис. 5.9). Каждый угол выражается через два значения1
прогиба. Для этого требуется 13 точек, в которых измеряются про-
Рис. 5.6 К определению
изгибающего момента
106
Рис. 5.7. К определению крутящих
моментов
_+2-
j -
i-2-
i-?,5 L-0t5 i+0,5 i+?,5
i I I I
14 ! I
-H-H-f+4-H
+
+
—r-j+Ofi
j+tJS
иис. 5.8. Точки, в которых опреде- Рис. 5.9. Вычисление углов поворо-
ляются углы поворота сечений та сечений через прогибы
^ибы (рис. 5.10). Эти точки образуют 13-титочечный шаблон. Урав-
яение равновесия имеет четвертый порядок разностей относитель-
ло прогибов.
Вывод необходимых уравнений приводится в обратном
порядке. С учетом малых перемещений углы поворота выражаются че-
оез разности прогибов (см. рис. 5.9), например:
E.5)
flr
hy
Эти выражения являются следствием гипотезы прямых
нормалей, в соответствии с которой углы поворота сечений равны углам
товорота серединной поверхности.
Если устремить шаги сетки hx и hy к нулю, то получим
выражения для углов в дифференциальной форме:
« — = _ (*0L . E 6)
Чтобы выразить изгибающие моменты через углы поворота,
необходимо вначале вычислить деформации растяжения.
Например, в точке (*,/) деформации растяжения на верхней
поверхности пластины (рис. 5.11) определяются отношением^
^4l, F.7)
107
J+2
J+t
J
j-l
•
•
•
•
•
•
•
•
i-Z i-t i i+f
-Hi
1+2
Pi
Рис. 5Л0. Тринадцатиточечный шаб- Рис. 5.11. К определению деформа^
лон ций растяжения
Аналогично
,5;/— ?y;*-0,5;/) hz
2hx
Нормальные напряжения на верхней поверхности пластины pi
соответствии с законом Гука E.4) зависят от деформаций в двух?
направлениях (рис. 5.12), поэтому *
Ё
°xxtitl — f Г (sxx,i.j "Т" vsyy»^/) • E.9J
1—v2
Рис. 5.12. Нормальные напряжения
и деформации растяжения на
поверхности деформированного
элемента пластины
108
Рис. 5.13. К определению зависимо»
сти изгибающих моментов от
нормальных напряжений
Поскольку напряжения изменяются по толщине по линейному
закону (рис. 5.13) и при переходе через серединную поверхность
изменяют знак, то создается изгибающий момент ч
2С
h
hz
Выражая нормальные напряжения через деформации в виде
E$), деформации — через углы поворота сечений E.6), E.7) й
E8), а углы поворота — через перемещения E*5), получаем
+
12A —v2
тъ»у EЛ1)
От выражения EЛ0) перейти непосредственно к
дифференциальному нельзя, поскольку в числителе коэффициента имеется шар
по координате hy. Поэтому нужно разделить E.10) на fiy k
устремить шаги hx и hy к нулю. В результате получаетсй
дифференциальное выражение для изгибающего момента
. <5Л2>
где Мух ж—^—^ момент на единицу длины в направлении оси
Ау
момента у.
Для вывода уравнения крутящего момента необходимо
рассмотреть кручение элемента и появление на его гранях
касательных напряжений (см. рис. 5.7). Касательные напряжения
выражаются через деформации сдвига, которые на поверхности
пластины определяются суммой углов tyi и $2-
В свою очередь, углы t|?i и \р2 определяются углами поворота
сечений:
^^ EЛ4)
^ i EЛ5)
hx
ф2^
hy
Таким образом, касательные напряжения в центре элемента на
рис. 5.7 определяются выражением
109
°у*;*+0,5;/+0,5 :
+
да
где jbi=?/2(l+v)—модуль сдвига материала пластины.
Интегрируя касательные напряжения по* толщине пластиш|
(рис. 5.14), получаем выражение для крутящего момента •'
Щ
Если углы поворота сечений <р выразить через прогиб пласта^
ны, то получим выражение крутящего момента в общепринятой^
форме
Для того чтобы получить дифференциальное выражение ^
крутящего момента, нужно от значения Муу перейти к удельному;
моменту, приходящемуся на единицу длины в направлении х, т. ei$
выражение E.18) нужно разделить на hx и устремить hx и hy уф
нулю. После этого получим Ш
d2 Ч
EЛЩ
Mv
Eh\
12A+v) dxdy'
где М«
к
Рис. 5.14. К определению зависимо^
сти крутящего момента от
касательных напряжений
ПО
Теперь приступим к выводу уравнений перерезывающих сил„
связанных с изгибающими и крутящими моментами. Эту
зависимость можно получить при рассмотрении равновесия элемента на
рис. 5.5. Спроектировав моменты на ось х и приравняв сумму
проекций к нулю, получим
Qzx;i+VJ+ Qr
,5 • E.20>
Требуется значение перерезывающей силы, взятой в точке
/+0,5;/. Это значение можно выразить через значения сил в
точках i+l; \ и ?, и входящих в уравнение E.20):
Qzx;l+ij + Q
Если теперь перейти от выражения перерезывающих сил через
моменты E.20) к выражению через их прогибы, то получим.
Г + 3 & +
д§
Щ
— цилиндрическая жесткость пластины.
Разностное выражение в скобках можно изобразить в виде
шаблона коэффициентов при неизвестных прогибах. При hx=hy
коэффициенты будут иметь вид, представленный на рис. 5.15.
Чтобы получить дифференциальное выражение для
перерезывающей силы, нужно вначале разделить E.21) йа площадь
дискретного элемента, а затем устремить шаги по координатам х и у
к нулю. В результате получим
f4'/?). - E.23)
где г-ъх^Цгх/пхПу — перерезывающая сила, приходящаяся на
единицу поверхности пластины, т. е. распределенная нагрузка,
измеряемая в ньютонах на квадратный метр.
Перейдем к уравнению колебаний пластин. Для этого
рассмотрим динамическое равновесие дискретного элемента на рис. 5.4.
Спроектировав перерезывающие силы на ось z и приравняв
сумму проекций силам инерции, получим
/ + Qzy;iJ+Q,5 — Q*y;/;/-0,5 *
E.24)
at2
где т — масса элемента с размерами hxXhyXhz.
ill
j+2
¦ J+}.
j
j-1
J-2
7очка
\
приложения силы
\;
-Л
;
-/
-/
i-2 14
L+1
"Рис. 5.15. Таблица коэффициентов в
разностном выражении перерезываю-
дцей силы
jr.
j+t
J
J-1
j-2
/
2
-8
2
1
-8
20
-8<
1
2
-8
2
1
1-2 ?-7
i+1 1+2
Рис. 5.16. Таблица коэффициентов
разностного аналога дифферёнциаль-?
ного уравнения изгиба пластин
Выразив перерезывающие силы через прогибы, получим рК
ностное уравнение. При этом следует ввести дискретизацию па
времени. Если обозначить шаг по времени через л, а номера этих
шагов — через к, то после деления на площадь элемента hXy fe
получим
гл Г
L
2
Щ
Щ
2;fe1
E.25);
p — плотность материала платы.
В левую часть уравнения E.25) входят 13 значений нензвест^
ной величины w. Эти значения располагаются на прямоугольной;
112 ^ /;
сетке в виде 13-то^ечного шаблона (см. рис. 5.10). Если выбрать
шаги сетки по координатам одинаковыми, hx=hyi и привести в
левой части подобные члены, то коэффициенты при неизвестных
прогибах будут иметь значения, представленные на рис. 5.16.
Устремив шаги сетки по^ координатам и времени к нулю,
получим дифференциальное уравнение в частных производных
+ 2
E.26)
Таким образом, получены все необходимые уравнения для
решения задач по расчету изгибных колебаний тонких пластин.
В некоторых простых случаях можно получить аналитическое
решение задачи, например при стационарных свободных
колебаниях и однородном закреплении каждого края, когда вдоль
каждого края граничные условия не меняются, а на разных краях
могут быть и различными.
5.2. СВОБОДНЫЕ КОЛЕБАНИЯ ПЛАСТИНЫ
Рассмотрим свободные колебания прямоугольной пластины,
шарнирно закрепленной по контуру. Такой вид закрепления
широко используется в строительной механике сооружений.
Например, стационарное нагружение бетонной плиты, опирающейся по
контуру на твердое основание, хорошо описывается моделью
шарнирного закрепления. Действительно, такое закрепление
препятствует перемещению краев пластины, но не препятствуют их
повороту относительно края основания.
В реальных конструкциях радиоаппаратуры, подверженных
вибрациям, шарнирное закрепление реализовать сложно, поскольку
опора должна препятствовать прогибу граничных точек в обоих
направлениях и не должна
препятствовать повороту
пластины относительно краев.
Шарнирное закрепление не
препятствует повороту и,
следовательно, не создает
на.краях изгибающих моментов
E.12). Соответствующие
нормальные напряжения E.9) на
краю поверхности пластины
также будут отсутствовать. Не
будет опасности разрушения
пластины в самом
ответственном месте-в месте крепле- РйС. 6.17. Схема шарнирного крепления
Н"Я. пластины по контуру
8-1215 ' ИЗ
Близкое к шарнирному дает крепление, показанное на рис. 5.17
Но на практике гораздо легче осуществить закрепление краев че
рез эластичные прокладки из резины, поролона или пенопласта
Такое закрепление менее похоже на шарнирное, но дает xopoifljf
результат. ;• S
Тем не менее для получения аналитического решения будем
считать, что по краям пластины заданы следующие граничные
условия для шарнирного закрепления: 4;#
Л Lv L*
w=*0, Mvx = 0 при лг«= —?- и х— -; E
ух * 2 2
w = 0% ЛГжу = О при у = -^- и j/s= y ,
где L*, Ly —линейные размеры пластин.
Решение для свободных колебаний имеет вид
w = Wm cos Л^л: cos kyy cos cof,
где Wm — амплитуда колебаний.
Подставив это решение в уравнение E.26), получим
*
Это условие определяет частоты свободных колебаний в завд
симости от волновых чисел кх и ky. !ф
Чтобы удовлетворить на краях граничным условиям ш=0, не^
обходимо выбрать такие kx и ky, при которых соответствующей
косинусы обращаются в нуль, т. е.
и Lx
х 2
где пх и пу — целые нечетные числа.
Таким образом:
Теперь остается проверить, удовлетворяются ли но краям в1
рые граничные условия — равенство нулю изгибающих момен1
В соответствии с E.12)
) Wm &* C0S k*X C0S ky C°S Ш' +
-f- vft^ cos А^л: cos kyy cos <o<).
114
Выражение E.31) обращается в нуль при тех же условиях
E.30) и при x=±Lx/2. На двух других краях обращается в нуль
другой изгибающий момент Mxs. При я*=%=1 изгибные волны
будут иметь наибольшую длину, а волновые числа E.30) будут
наименьшими:
кх=— и йу=— .
Подставив эти значения в уравнение частот E.29), получим
низшую частоту собственных колебаний
12
ИЛИ
Для практических расчетов более удобна формула [9}
где т0 — удельная масса пластины, т. е. масса, приходящаяся на
квадратный метр поверхности.
Заметим, что решением поставленной задачи будет и другое
выражение
w — Wm sin kxx sin куу cos go*. EЛЗ)
В этом случае волновые числа будут определяться теми же
равенствами E.30), только пх и пу в них будут четными числами.
Таким образом, в общем случае решение задачи
представляется в виде стоячих волн, и в каждом направлении хи у по длине
пластины укладывается целое число полуволн. В начальный
момент (/=0) пластина должна иметь форму, соответствующую
выражению E.28) или E.33), а скорость всех точек может быть
равна нулю.
Если начальная форма не соответствует рассмотренной
волновой картине, а является более сложной, то аналитическое решение
может быть получено в виде суперпозиции волн различной длины,
удовлетворяющих условиям E.30).
При резонансах возникают те же самые картины колебаний,
что и при свободйых колебаниях.. Поэтому выражение E.32)
определяет резонансные частоты пластины, шарнирно закрепленной по
контуру, а выражения E.28) и E.33) —формы колебания.
Резонансные частоты нумеруются, начиная с самой низшей и далее в
порядке их возрастания. Собственные формы колебаний на трех
низших резонансных частотах показаны на рис. 5.18.
8* - 115
Рис. 5.18. Собственные формы?
колебаний пластины (шарнира
ны закрепленной ло KOHTypy)J
которые соответствуют первоШ
(а), второй (б), третьей (в)'
резонансным частотам *
Заметим, что не при всяком соотношении сторон пластины
рисунок 5.18, в соответствует третьей форме колебаний. Например*
если пластина слишком вытянута, то может случиться, что инаш
форма будет соответствовать более низкой частоте. Может быть ж
так, что одной и той же резонансной частоте сортветствуют две,
или более собственные формы. .1
При испытаниях конструкций на вибростендах обычно получав
ют резонансную кривую (рис. 5.19). Всплески этой кривой нумег:
руют по порядку и считают, что они соответствуют номерам гар#-
моник. Однако это не всегда соответствует реальной картине. Во*?
первых, при данном способе возбуждения резонансов не все гар?*
моники могут проявляться. Во-вторых, датчик перемещения ил^
ускорения может быть неудачно ^расположен и место, в котором-
он находится, на некоторых частотах практически не колеблется.)
Мы рассмотрели случай шарнирного закрепления краев пла^
стины. В теории колебаний [13] рассматриваются случаи жесткого
закрепления и различных комбинаций, когда разные края закреп*\
лены по-разному: шарнирно, жестко или находятся в свободном;
состоянии.
Приведенными решениями, собственно, и исчерпываются воз:
можности точных аналитических методов расчета колебаний тон?
ких пластин. В более сложных случаях —при сложной форме пла?;
стин, сложных граничных условиях, при нестационарных процесу.
сах — приходится решать задачу численным методом. Наиболее!
116
-'ис. 5.19. Резонансная кривая
универсальным среди
численных методов является уже
встречавшийся выше метод
конечных разностей.
В разд. 5.3 и 5.4 будут
приведены два примера
разностного решения задач. Первый
пример выбран предельно
простым, вычисления не требуют
применения вычислительной
техники или, в крайнем
случае, могут быть выполнены с
помощью карманного
микрокалькулятора.
Второй пример, наоборот, достаточно сложен и позволяет
иллюстрировать расчет реальных, плат с навесными элементами с
7роизвольным закреплением, например с помощью винтов.
Рассмотрим решение методом конечных разностей простой
нестационарной задачи.
5.3. УДАР ПЛАСТИНЫ
Наиболее опасными являются ударные нагрузки в направлении нормали к
носкости пластины. Если сама конструкция является достаточно жесткой н
ударяется о жесткую поверхность, то можно рассматривать процесс падения
тластины на жесткую поверхность (рис. 5.20). Пластина закреплена по контуру
эис. 5.20. Падение пластины (/) на
кесткую поверхность B)
fnfnfn п 0F70 0 о/о
/п/л/л/Л nfoJOJO/О/О
/оШШШШШШ
Рис. 5.21. Задание граничных
условий при закрепленных краях
пластины
117
жестко с помощью двух рамок. Вместе с рамками она падает на жесткую Щ$:
верхность со скоростью v. В момент f=0 нижняя рамка касается поверхнф-г^;
и останавливается. Это — начальные условия задачи. Вместе с ней останйв^-"
ваются края пластины и в дальнейшем остаются неподвижными. Это — гравд^'
ные условия задачи. Будем иллюстрировать алгоритмы вычислений с
трафаретов и шаблонов. Они не только очень наглядны, но и позволяют
производить вычисления, избегая ошибок.
Введем дискретизацию по координатам и времени. Выберем шаги по
динатам одинаковыми, hx=hy. В граничных условиях для защемленного
необходимо задать нулевые значения прогибов и углов поворота сечений.
разностном решении зададим нулевые прогибы в двух соседних точках по
(рис. 5,21).
Начальные условия задаются в виде двух таблиц (рис. 5.22), соответствуфг-f
щих моментам времени 6=1 и ?=2. Будем считать, что за шаг т до уда]^|
F=1) пластина летела вниз со скоростью t/. До момента удара все точки n«$Jf
стииы пролетают расстояние vx. Для простоты, расчетов будем считать э^|
расстояние, равным —1. Эти значения записаны в таблице, соответствуй
&— 1. В момент удара F=2) пластина еще не деформирована, поэтому в та
лице 6=2 все прогибы равны нулю.
При заполнении последующих таблиц прогибов необходимо удовлетворит^
разностному уравнению E.25). Если шаги сетки в обоих направлениях !
ковы, hx=hy=ht то уравнение E.25) несколько упрощается: ~
D — (
E.Щ
т2
В выражение в скобках входят 13 значений прогиба в 13 точках сетки
Для расчета можно построить соответствующий трафарет (рис. 5.23). Коэф-=
фициенты при неизвестных прогибах показаны на рис. 5.24.
к-1
5ЫНШШ
'J4r/7T74
y'/t//////
/о/oh/of о/о///
/О/0/о/О/О/pi/1
/ о/о/о /о/о /о
/о/ о /о /а /о /о
(о/о/о/о/о/о-
Рис. 5.22. Начальные условия в задаче об ударе пластины
118
рис. 5.23. Трафарет для расчета
изгиба пластины
Рис. 5.24. Коэффициенты при
неизвестных прогибах в шаблоне
Уравнение E.34) решают относительно неизвестного прогиба на верхнем
©рененнбм слое (k+l):
E.35)
где
Для того чтобы процесс вычислений с помощью явного уравнения E.35)
был устойчивым, нужно выбрать коэффициент А достаточно малым. „Условие
устойчивости можно проверить, если подставить в уравнение E.35) прогибы,
равные единице, со знаками, расположенными по правилу «шахматной доски»
(рис 5.25). В уравнение E.35) входят прогибы на трех временных слоях: k-~\;
к и &+1. Разностная схема с таким уравнением называется трехслойной. На
двух слоях к и 6—1 задаются единицы с соответствующими знаками, а на
третьем слое вычисляется '
ttH;/s*+i = 64A—2— 1.
Решение будет неустойчивым, если до*; /; k+i будет по модулю больше
единицы. Отсюда — условие устойчивости
А <4/64=0,0625.
Если взять предельное значение А=0,0625, при котором решение будет еще
устойчивым, то уравнение E.35) примет вид
- 0,
-l;/; k
- 6f
E.36)
119
PpEBu
Н+1Ч Н(Ч]1 it
/ / H ш
Предположим, что величины,
входящие в выражение для А,
имеют следующие значения: ?*•"'
= 1010 Н/м2; Лг-2.10-,5 м; v=0,2S;
А=10 м; pft*=10 кг/м2; цилиндрик
ческая жесткость ?>=7,11 Н/м; при-
Л=0,0625 шаг по времени т~7
=29,6 мкс.
Если, например, необходимо
рассчитать процесс длительностью в 1с,
то приходится производить
вычисления примерно на 34 тысячи шагфг!
по времени. Это, конечно, много-
особенно если учесть, что для каж*
дого шага по времени делается;
большой объем вычислений, пропори
циональный числу дискретных эле-.
ментов в модели. -
Благоприятным обстоятельством "
здесь является то, что переходные
/ / /р / / /. /L+\ процессы протекают быстро, при ;
/ / Iff / / ff этом наиболее опасным для конст-
/ /—/ /—/—J—J // рукпии является начало переходного^
процесса. ^:
Остановимся на процессе
вычислений. Начинать вычисления мож-^ а
но с любой точки таблицы про»;
Рис. 5.25. К проверке устойчивости раз- гибов- Порядок вычислений в од^ ^
ностной схемы ном шаге по времени роли не ;
играет. Установим на таблицу на-?-]
чальных условий таблицу прогибов М
k—2t а сверху положим 13-точечный шаблон. В отверстии шаблона видны зна-:
чения прогибов в 13 точках. В данном случае все эти значения равны нулюу
поэтому формула E.36) дает значение wi-,j; *+i=l за счет члена w*:/;*->. Ег^
значение берется из таблицы-^ =1. Обойдя все точки таблицы k=2, получим
всюду ДО/,/,з=1. Эти значения запишем в таблицу А~3.
Поменяем таблицу ?=2 на ?=3 и снова поставим шаблон на угловую точ--
ку, как на рис. 5.26, а. Теперь в шести точках до=1. Подставив значения проги- *1
бов в формулу E.36), получим wttf. *+1™1Д Запишем это значение в угловую-
точку таблицы k «4. Наша пластина обладает свойством симметрии относитель- :
но четырех осей, показанных на рис. 5.26,6. Симметричны также начальные ?
граничные условия. Поэтому нет надобности производить расчеты во всех
36 точках таблицы прогибов. Достаточно вычислить прогибы, кроме угловой .
точки, еще в пяти точках, отмеченных на рис. 5.26,6. В остальных клетках
таблицы прогибы записываются симметрично.
После вычисления и записи прогибов во всех точках таблицы ?=4 полу-
120
а) б)
Рис. 5.26. Схема вычисления прогибов пластины
t,shs/1,8/1,8/1,9/1,5 Л " /уя/&for/упрю/уя
b/v/ifl/1,0/1,1/1,8
4tsth,a/t,e/tjt/1,9/1,5
Рис. 5.27. Прогибы точек пластины при ft=4 (a); ft=5 (б)
1 2 3 4 5 6 Ы
Рис. 5.28. Графики прогибов точек
пластины в различные моменты
времени (цифры на оси х —значения О
Рис. 5.29. Картина изгиба пластины
при fc=5
121
*шм значения, указанные на рис. 5.27, а. Теперь таблицу 6=3 заменим табляЫ
дей /г=4 и продолжим вычисления прогибов на следующем временном слое|
?=5 (рис. 5.27,6). Так продолжаются вычисления на нужное число шагов.
Графики в поперечном сечении пластины показаны на рис. 5.28, а общиЩ
вид в момент ?=5 — на рис. 5.29. .
Теперь нужно решить, в каких единицах мы измеряем прогиб. В на
?ных условиях было задано 1>т=1. Пусть и «34 м/с. Тогда при т—29,6-10
получаем tnr=l мм. •' >
Решение задачи в прогибах wy как правило, еще не дает достаточной
формации о качестве конструкции. Для этого нужно от прогибов перейти к
гибающим и крутящим моментам, перерезывающим силам и нормальным и
сательным напряжениям. Но это уже более простая задача, чем вычислени
прогибов. Нужно только воспользоваться соответствующими разностными фор||
мулами, полученными выше. , *|
5.4. РЕЗОНАНС ПЛАТ Я
С НАВЕСНЫМИ ЭЛЕМЕНТАМИ \А
щ
В общем случае при произвольном способе закрепления плай
и произвольном способе закрепления плат и произвольном распар
ложении на них навесных элементов задачу расчета частот и форщ;|
колебаний при резонансах решить аналитически невозможно. ПаЩ
этому применяют численное решение задачи, используя метод ко^
нечных разностей. В разд. 4.9 было рассмотрено вычисление резо^
нансной частоты и формы колебаний первой гармоники при изгибе!
ных колебаниях стержней. Та же методика будет и при расчетах^
резонансов пластин. 'j
Сначала сформулируем задачу на собственные значения. Щ
этого запишем разностное уравнение E.25). В правой части уравй
нения вместо разностного уравнения запишем .вторую производи
ную по времени. Затем искомую функцию прогиба представим Цц
виде гармонической функции по времени D.54). Подставим эта;
выражение в уравнение E.25) и сократим на синус. v
В результате разностное. уравнение E.25) представляется ml
виде ' ^
JL E.37Й
где Lh — разностный оператор, соответствующий дифференциаль#;
ному оператору в левой части уравнения E.26); тц — масса пла-rjl
стины и навесного элемента, приходящаяся на единицу площади/
Эту величину получают в виде суммы pft*+A, где А —дополни-"
тельная масса (прикрепленная к данному элементу сетки),
ная на площадь элемента hxXhy.
Уравнения E.37) записываются для тех узлов модели, д€|
которых можно построить полный 13-точечный шаблон. Уравне^И
122
i
У,
X
Ряс. 5.30. Законтурные узлы в
. модели пластины
ния для остальных узлов
определяются граничными условиями,
зависящими от способа
закрепления пластины.
Рассмотрим различные
варианты закреплений и
соответствующие им граничные условия.
Если пластина имеет крепления
в виде винтов в определенных
точках, то, в соответствующих
узлах модели перемещения
полагаются равными нулю, адг-,/=0.
При расчете реальных
конструкций часто площадь области
винтового крепления (головки
винта, шайбы) оказывается
соизмеримой с площадью дискретного
элемента сетки. В этих случаях нулю приравниваются
перемещения, четырех узлов модели в окрестности винтового крепления.
Сложнее задать граничные условия на краю платы. Если
граничные условия заданы правильно, то после решения задачи при
жестком защемлении края должны оказаться равными нулю переме-.
щения граничных узлов и углы поворота, определенные
формулами E.5). В случае шарнирного закрепления должны быть равны:
ми нулю перемещения граничных узлов и изгибающие моменты
E.10).
Для свободного (незакрепленного) края пластины равными
нулю будут изгибающие моменты E.10) и перерезывающие
силы E.21).
Граничные условия можно задать двумя способами: с
помощью дополнительных «законтурных» узлов и без них {14].
В первом случае в расчетную модель платы вводятся два
ряда дополнительных узлов сетки с каждой стороны платы
(рис. 5.30). В этих узлах вычисляются фиктивные прогибы,
поэтому количество неизвестных прогибов в задаче увеличивается. Для
вычисления этих неизвестных нужны дополнительные уравнения.
В качестве таких дополнительных уравнений и используются
указанные выше значения прогибов, углов поворота сечений,
изгибающих и крутящих моментов и перерезывающих „сил. Например,
при жестком закреплении краев, чтобы прогибы и углы поворота
были равны нулю, нужно в законтурных узлах записать нулевые
значения прогибов.
В других, более сложных случаях эти значения -заранее
неизвестны. Они зависят от значений прогибов в граничных узлах и.
должны вычисляться с помощью общей системы уравнений для
внутренних узлов E.25) или E.37) и уравнений соответствующих
123
граничных условий. Для самих граничных узлов платы можно
пользовать те же разностные уравнения, записанные на 13-ти
чечном шаблоне, что и для внутренних узлов.
Во втором случае расчетной модели без «законтурных у
непосредственно использовать обычные уравнения, записанные
13-точечном шаблоне, в двух рядах граничных узлов нельзя, nowi
скольку шаблон выходит за пределы сетки платы. Поэтому дли]
граничных узлов записывают свои «усеченные» уравнения с «усеЦ
ченными» шаблонами. В этих уравнениях и шаблонах отсутствуй
ют как раз те члены, которые «выходят» за пределы границ шцм
ты. Например, в случае жесткого закрепления краев платы вофЦ
члены в уравнении E.25) за пределами платы приравниваются;!
нулю и из уравнения E.25) исключаются. В других», более слож~;
ных случаях «усеченные» уравнения получаются при совместном!
решении основного уравнения E.25) и соответствующих уравне~|
ний граничных условий. В результате получаются уравнения, ш
которых отсутствуют члены, относящиеся к «законтурным»
и «законтурные» узлы становятся ненужными [14].
Оба способа дают совершенно одинаковые результаты ^
лений, поскольку в них удовлетворяются одни и те же уравнения)!
для внутренних и граничных узлов. Но в первом случае этога|
добиваются в каждом шаге вычислений или итерационном цикли
при решении задачи в числах, а во втором случае это получается?:
заранее, путем алгебраических преобразований. Поэтому первый?*
способ более прост и понятен; в нем используется меньшее числвУ
формул. Но во втором способе значительно меньше объем вычис^ц
лений и необходимая емкость памяти ЭВМ, поскольку в этом спо-
собе нет вычислений, относящихся к «законтурным» узлам. ?.
Заметим, что при обоих способах уравнения, определяющие гра<
ничные условия, записываются с учетом ориентации границ. На-
пример, для границы, нормальной оси х, рассматриваются мо^
мент Мух, сила QZXy угол ср^, а для границы, нормальной оси у.,—
момент МХу, сила Q**-, угол ф*. к\
Таким образом, уравнения вида E.37) и граничные условия:^
или «усеченные» уравнения образуют систему алгебраических»!
уравнений, в которых неизвестными величинами являются узло-/]
вые прогибы Wtj, определяющие форму колебаний и собственную*; |
частоту ©. j
Остановимся на процедуре вычисления собственной частоты к-^
формы колебаний платы с навесными элементами. Исходными?!?
данными для расчета являются значения шагов сетки по коорди-г'1
натам hx и hy, число узлов модели в направлении х и у9 значе- ^
ния коэффициентов плотности тц в узлах, цилиндрическая жест* ~ \
кость D и способ крепления. -л
Для определения собственного параметра и собственной фор- 1
мы строится итерационный процесс, суть которого состоит в после- 1
124 J
довательном уточнении собственной частоты и формы.
Минимальное значение собственной частоты о2 определяется на основании
известного соотношения Рэлея [15]. В рассматриваемом случае
итерационную формулу для определения со2 можно представить
2 виде
S
(«>2)<«+1> - ¦=!_% , E.38)
(Щт)J
2
/2=1
где N— число разностных уравнений в системе, в которые входит
частотный параметр Я (см. гл. 4); т — номер итерационного
цикла. При работе без «законтурных» узлоэ оператор La будет
различным у полных и «усеченных» уравнений.
В свою очередь, уточненные значения перемещений в каждом
итерационном цикле определяются из уравнения E.25), которое
решается относительно Wij. Запишем итерационную формулу для
Wt,j в компактной форме с учетом E.37):
D
где
— коэффициент при Wij в левой части E.25).
Сформулируем теперь алгоритм решения задачи вычисления
лервой собственной частоты и формы колебаний пластин.
1. Задание начального приближения собственной формы. Как
м в случае стержня (см, гл. 4), начальное приближение может
быть задано произвольно; однако если удается задать исходную
форму, близкую к истинной, то итерационный процесс сходится
быстрее. В целях автоматизации задания исходной формы при
решении задачи на ЭВМ удобно задать во все «незакрепленные»
узлы модели единичные перемещения.
2. Вычисление перемещений в «законтурных» узлах в
соответствии с заданными граничными условиями, если «законтурные»
узлы имеются.
3. Определение со2 по формуле E.38).
4. Определение узловых перемещений IP,,/, т. е. следующего
приближения собственной формы, по формуле E.39).
5. Переход к п. 2 и т. д.
125
Процесс вычислений продолжается до тех пор, пока итерац$|
онный процесс не сходится. В простейшем случае условие в^
мости можно задать в виде
где е — заданная малая величина.
Полученное в процессе решения значение ю2 соответствует йщ
шей (первой) резонансной частоте колебаний платы, а вычислен^
ные значения Wi,j определяют первую собственную форму коле!
баний.
5.5. .РАСЧЕТЫ ВИБРАЦИИ
НЕСУЩИХ ПЛАСТИНЧАТЫХ
КОНСТРУКЦИИ РЭА
В качестве примера пластинчатой конструкции можно рассмо|^
реть кожух., изображенный на рис. 5.31. При расчетах вибраций
таких конструкций можно использовать различные предположу
ния, упрощающие задачу. Самое простое предположение — это '
что пластины, входящие в конструкцию, колеблются независи
друг от друга. Далее, используя гипотезу прямых нормалей, мол&
но произвести расчет изгибных колебаний каждой пластины в oig
дельности. Естественно, такое упрощение внесет погрешности. Б^
дут ли эти погрешности большими? Дать точный ответ на э
вопрос невозможно, поскольку мы не знаем точного решения.
То, что такие погрешности будут, можно понять, например, и;
следующего рассуждения. Каждая пластина будет иметь собой
венные частоты и формы колебав
ний. А какие частоты и формьг
будут у всей конструкции
единого целого? Например,
кадкой будет нижняя резонансна^/
частота? Любое предположение?
на этот счет нельзя обосноватвй
поэтому погрешности неизбежный
Гипотеза прямых нормалей]
позволяет довольно просто рас*Ц
сматривать изгибные колебаний^
всей пластинчатой конструкций^
в целом. Если учитывать переЧ|
мещения пластины только в
W
правлении нормали к ее поверх^
ности и не учитывать перемещен
ния в двух других направлениях,^
Рис. 5.31. Пластинчатая.конструкция то все ребра конструкции следу*
126 Й
Рис. 5.32. Развертка пластинчатой конструкции
ет считать неподвижными. Однако пластины могут поворачиваться:
относительно линии ребра. Прямой угол между двумя
пластинами, примыкающими к одному ребру, должен сохраняться.
Такие предположения позволят свести решение объемной
задачи к решению плоской задачи. Для этого выполняется
следующая подготовительная работа.
1. Намечают положительное направление прогибов всех
пластин. Можно за положительное направление выбрать направление
нормали к наружной поверхности пластины (см. рис. 5.31).
2 Выбирают шаги сетки по координатам и намечают на
поверхности пластин сетку. При этом стремятся к тому, чтобы на
ребра конструкции попали узлы сетки. Это облегчает расчет.
3. Представляют конструкцию в виде ее развертки (рис. d.<wj~
При этом узлы на гранях разрезаются и относятся к разным щю-
СТИНЙМ л
4 Производят расчет конструкции как одной пластины
сложной конфигурации. При этом нужно правильно задать граничные
условия На рис. 5.33 показан вид таблицы для вычисления
прогибов в' каждом шаге по времени. Форма таблицы соответствует
форме развертки конструкции, только каждому узлу сетки на
развертке соответствует клетка таблицы. Для узлов на ребрах,
которые относятся к обоим граням, имеется по две клетки —по од-
v 127
ной у каждой грани. Но щ
этих клетках записываются
прогибы в различных направ-1
лениях — по нормали к раз-|
иым поверхностям. В наших-;
предположениях оба прогиба^
равны нулю, поэтому по лини**!
граней в таблице на рис. 6.33*
проставлены нули. ;
5. В процессе вычислений^
учитывают, что развертка име-|
ет линии разреза. В свйзи с!
этим при расчетах прогибов в^
точках вблизи ребер берут!
значения прогибов из клето!с|
соседней грани. Именно бла-|
Таблица для расчета плас-годаря этому 0СУЩе™я^|
/л закреплениеСВЯзь между соседними гра*|
нями и конструкция представ-J
ляется как единое целое. ?
Рассмотренный прием приведения объемной конструкции^ st
0
0
0
0
0
0
0
0
0
г
0
0
\
0
0
S
_
г-
0
0
0
0
0
в
0
0
0
0
0
0
0
0
о
о
0
0
0
0
0
а
0
0
0
0
0
0
д
0
0
0
0
0
0
0
а
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
\
0
0
к
0
0
0
0
б
0
0
0
0
Рис. 5.33. Таблица для
гинчатой конструкции @
ребер)
Рассмотренный прием приведения о
плоской расчетной модели, разумеется, не
дает хорошее приближение при расчетах а^°^
оезонансных характеристик на низких частотах. Однако он не щ
ISS например при расчетах некоторых переходных процессов,
S'/yS учитывать перемещения ребер. Кроме того, он вдмв*
работает на высоких частотах вследствие применения гипотез»
i-iWM Mu»B1BW. от этих недостатков, необходимо решит*^
трехмерную задачу, что разумеется, значительно сложнее
КОНТРОЛЬНЫЕ ВОПРОСЫ >|
1. Каким образом представляются изгибные колебания пластин с использо,|
ванием ^^^P^X^^S закона Гука для пластин от аналогичного^
выражения^для стержней? ^ нении изгибных колебаний пластид!
даые от прогибов по координатам имеют четвертый
» времени — второй порядок?
_ ± яям должно удовлетворять решение
колебаниях платы? «лни*» ** к-пжт ппи жестко1** ^
5 Чем характеризуется форма изгиба платы вблизи ее края при жесткие
о. чем xdPd^icpnoy j /лжм%л„плт1Ц нли на свободном краю? , %
волн и частотами при изгибных ко-; |
7 Какие частоты и формы колебаний возможны нри свободных колеба: |
яиях прямоугольной платы, шарнирно закрепленной по контуру? :|
128 i
8. От чего зависят резонансные частоты пластин?
9. Как проверить, будет ли устойчивым разностное решение с помощью
явной схемы?
10. Как учитывается влияние навесных радиоэлементов на изгибные
колебания плат? ,
П. Чем отличается процедура задания граничных условий при разностном
решении с помощью «Законтурных» узлов от процедуры, в которой
«законтурные» узлы не используются?
12. Каким образом формулируется задача на собственные значения?
13. В чем состоит итерационная процедура вычисления резонансной
частоты и первой формы колебаний? ¦
14. Какие предположения позволяют использовать для объемной,
пластинчатой конструкции плоскую расчетную модель?
Глава 6. АВТОМАТИЗИРОВАННЫЙ РАСЧЕТ
ВИБРАЦИЙ И УДАРОВ СЛОЖНЫХ
КОНСТРУКЦИЙ РЭА И ЭВА
В большинстве случаев конструкции РЭА и ЭВА очень .сложны для расчетов
вибраций. Этим,во многом объясняется ограниченное применение расчетов при
проектировании вибро- и ударопрочной аппаратуры, недоверие к таким
расчетам, предпочтение экспериментальным методам оценки вибропрочности и
виброустойчивости конструкций.
Но за расчетами — будущее. Они дают большой экономический эффект, и
современная вычислительная техника открывает здесь, огромные перспективы.
В настоящее время вопросы создания подсистем и пакетов прикладных
-программ для автоматизации анализа вибррударопрочности конструкций РЭА
приобретают все большую.актуальность.
.... В разработке. математического обеспечения подсистем и программных
комплексов активную роль должны играть конструкторы, которые, с одной
стороны, хорошо представляют суть проблем, с другой ~-выступают кйк
пользователи. Поэтому рассмотрим принципы построения прикладных программ на
уровне описания алгоритмов.,
Программные .комплексы совместно с ЭВМ образуют некоторую систему,
предназначенную для моделирования механических процессов в
проектируемой конструкции, возникающих при ударах и вибрациях. Такие системы.стали
называть имитационными [1]. Имитационная система включает в себя
следующие основные блоки (рис. 6Л): ^
1. Блок построения расчетной модели конструкции. Входной информацией
здесь служит описание конфигурации конструкции и материалов ее деталей,
описание способа их соединения. На выходе блока получается расчетная. мо-
Дель конструкции в виде системы разрешающих уравнений, описывающих
.динамическое равновесие дискретных элементов модели. ¦ -, -.
9-1215 Ш
Данные о
конструкции^
Описание
внешних
воздействий I
Задание
блок
построения
расчетной
модели
и
блок
проведения
численных
экспериментов
\
блок
анализа
результатов
вычислений
Оценки v ?¦
бибропрочности 1
Рис. 6.1. Блок-схема имитационной системы
2, Блок проведения численных экспериментов. На вход этого блока
пает система разрешающих уравнений, а также описание внешних воздействий!'
на конструкцию. В блоке эта система уравнений решается, и результаты реиЙ-|
ния передаются в блок анализа результатов. . - . JJ
3. Блок анализа результатов вычислений. Здесь происходит преобразование
результатов расчета к форме, удобной для. конструктора, в соответствии с eloi
заданием, ?; i
. Рассмотрим работу этих блоков. , " '?
6.1. БЛОК ПОСТРОЕНИЯ ?!
РАСЧЕТНОЙ МОДЕЛИ j?
Разработаны и находятся в эксплуатации несколько програмййр
но-методических комплексов, предназначенных для расчетов типЙ
вых конструкций РЭА и ЭВА: стержневых конструкций, плат if
навесными элементами, пакетов плат и пластйнчато-стержневь1%
конструкций. Эти комплексы непрерывно совершенствуются: pagi;
ширяются их эксплуатационные возможности, сокращается объЩ
«ручных» работ, появляются новые сервисные программы, которые
облегчают работу пользователя-конструктора, повышают надеж*
ность вычислений. Совершенствуются и средства вычислительно*
техники. Все эти изменения происходят довольйо быстро, и н©?
смысла в рамках настоящей книги останавливаться на каком-трс
конкретном варианте системы. Поэтому мы рассмотрим некотора??
общие принципы построения таких систем и их реализацию. ^:f
Система должна быть достаточно универсальной и пригодноШ
для расчетов широкого круга различных конструкций. Но, ка$
обычно, повышение универсальности достигается за счет у^
нения системы, увеличения объема вычислений, применения бол^е
мощной вычислительной техники. ;^
Поэтому применение универсальных программных комплексе^
оправдано при необходимости анализа большого многообразий
сложных конструкций. В случае расчета однотипных конструкт*^
целесообразно использовать специализированные программное!
комплексы. Такие комплексы разработаны, например, для печа$
ных плат, стержневых конструкций.
130
Однако даже универсальные системы имеют ряд ограничений,
которые сужают круг решаемых задач. Для рассматриваемой
системы эти ограничения обусловлены следующими факторами:
1. Bee физические представления, используемые при
разработке системы, основаны на положения^ линейной теории упругости
при малых перемещениях. При выводе уравнений равновесия
напряжения в этой теории считаются пропорциональными
соответствующим деформациям, перемещения полагаются достаточно
малыми и вследствие этого синусы и тангенсы углов поворота
сечений деталей при деформациях — равными самим углам и, главное,
перемещения, в различных точках конструкции рассматриваются
как некоторые функции в этих точках,, а сами точки считаются
неподвижными* Если в конструкции возникают большие
перемещения, не укладывающиеся в рамки линейной теории упругости, то
результаты вычислений будут иметь погрешности, которые трудно
оценить. . ... .
2. Все расчетные соотношения получены с использованием
прямоугольной ортогональной системы координат, Поэтому система
предназначена для расчетов прямоугольных конструкций. Если в
конструкции встречаются детали непрямоугольной формы, то они
приближенно заменяются прямоугольниками. Это также вызывает
появление погрешностей расчета.
3. Некоторые ограничения связаны с ограниченными
возможностями современных вычислительных машин. И хоть эти
возможности . очень велики, для расчетов сложных конструкций они
могут оказаться недостаточными. Дело в том, что с усложнением
конструкций объем вычислений очень быстро возрастает. Поясним
это на примере. Предположим, что для воспроизведения в
расчетной модели конфигурации сложной конструкции необходимо в
каждом из трех направлений взять по 20 шагов, тогда в модели
будет 203 = 8000 дискретных элементов. Предположим далее, что
каждый дискретный элемент имеет б степеней свободы, т. е. вся
модель имеет.48000 степеней свободы. Необходимо,
таким-образом, решить систему алгебраических уравнений, матрица
коэффициентов которой имеет размерность 48 000X48000. И хотя эта
Матрица получается слабо заполненной, объем вычислений,
особенно при расчетах нестационарных процессов, когда эту систему
Уравнений преходится решать на каждом шаге по времени (а
шагов, в расчете может быть несколько тысяч), огромный.
.Применение специальных итерационных методов при решении
стационарных задач и явных разностных схем при решении нестационарных
задач в какой-то степени позволяет преодолевать эту трудность.
Тем не менее рассматриваемой системе, если даже она строится
На базе суперЭВМ, под силу решение задачи, если в расчетной мо-
Дели не более нескольких тысяч элементов.
Рассмотренные ограничения являются общими для всех подоб-
> 131
ных имитационных систем. Их преодоление связано с развитие!
теории упругости, методов вычислительной математики и co^bj
шевствованием вычислительной техники.
Говоря о йрименяемом математическом аппарате, заметЦ
что в рассматриваемом варианте системы используются идеи jijj
тода конечных разностей. И хотя при построении разностных ур"
нений не применяются явным образом дифференциальные coot
шения, тем не менее полученные уравнения обладают аппро?
мацией и сходимостью, а алгоритмы — устойчивостью вычислен
Большинство несущих конструкций аппаратуры имеет рщщ
угольную форму, т. е. мажет бшъ представлено композицией йа
некоторого количества компонентой конструкции ввиде пря$#
угольных параллелепипедов. Поэтому проще всего задать ков$|
рукцию в блоке построения расчетной модели в виде таблицы! в
которой для каждого параллелепипеда . указывается положение
шести ограничивающих его плоскостей, и характеристики
риала, из которого он сделан. ...... -
Далее нужно описать способ разбиения конструкции на
кретные элементы! Как правило, все элементы выбираются од$
ковых размеров (мы ограничимся здесь этим случаем). Поскор*!
ку сетка в этом случае регулярная, то достаточно указать чи&но
шагов сетки конструкции, укладывающихся по длине в каждом иа
трех направлений, или размеры Этих шагов hx, НУу Л*. На э1 ^
«ручная» подготовка входной информации заканчивается. Да
нейшее построение расчетной модели происходит в автомата
ском режиме. - . .. ' :
В блоке построения модели нд основе таблицы размеров и
рактеристик материалов конструкции, формируется матрица коз_
фициентов системы разрешающих, уравнений. Это преобразовав
осуществляется в несколько зталов. Каждый этап имеет йф8
зический смысл. . ;
Первый этап — разбиение (рис. 6.2). Конструкция раз<
вается на дискретные элементы плоскостями, параллельными "
ординатным плоскостям. При разбиении следует стремиться к
му, чтобы эти плоскости не совпадали с гранями параллелешйй
дов^ Внутрь каждого дискретного элемента (рис. 6.3) может й<
пасть несколько частей компонентов конструкции. Эти части
гут быть выполнены иа разных материалов. Кроме того, мог
быть и «пустые» элементы, в которые не попадает ни один к$
понент. •-.;,; -, - .
Если в таблице компонентов имеюгся малые детали, размер
которых меньше шагов сетки, то они могут целиком разместитье|
внутри дискретного: элемента. В дальнейшем такие детали буд^Г
автоматически учитываться в расчете лишь в инерционных
теристиках элементов. \
и
Рис. 6.2. Расположение конст-
рукции внутри сеточной обла-
сти .
Рис. 6.3. Дискретные элементы
модели
3 результате разбиения получаются неоднородные по своей
структуре дискретные элементы. Каждая грань элемента может
зключать в себя различные области (см. рис. 6.3), образованные
лересечением координатных плоскостей с компонентами конст-'
эукций.
Второй этап — осреднение. На этом этапе упругие свойст-
за каждого дискретного элемента рсредняются
(«размазываются») по всему дискретному элементу. Иными словами,
неоднородные, элементы, как на рис. 6.3, заменяются однородными, которые
з среднем деформируются так же, как и исходные неоднородные
элементы. Осреднение должно производиться отдельно по
каждому- виду деформаций элемента. В расчетной модели дискретные
элементы могут подвергаться следующим деформациям: растяже-
шю (сжатию) в трех направлениях; сдвигу в трех плоскостях:
изгибу в трех плоскостях; кручению в трех плоскостях.
Для каждого из этих 12 видов деформаций получается свое
вреднее значение жесткости- элемента. Формулы для вычисления
кесткостей дискретных элементов получаются при рассмотрении
взаимодействия дискретных элементов в модели.
Третий этап — выражение деформаций через обобщенные
еремещения. Состояние дискретного элемента в каждый момент
определяется шестью переменными (рис. 6.4): тремя линейными
перемещениями a, v и w в направлении соответствующих
координатных осей и тремя. углами поворота <р*, щ и «ф2 относительно
-тих осей. Перемещения и углы поворота называют обобщенными
перемещениями и относят к центру дискретного, элемента (узлу
133
Элемент связи
(
V
* \
1ц$
с
\
« "у >
\
(lij+f;k)
г
Рис. 6.4. Обобщенные перемещения
элемента
Рис. 6.5. Деформации растяжения
сетки с координатами t, /, к). Каждый дискретный элемент в
щем случае взаимодействует с шестью ближайшими соседями?
Это взаимодействие рассматривается как действие упругих сил -щ
моментов, * приложенных к каждой грани, которая находите^
между центрами двух соседних элементов. Элемент пространств^
между двумя соседними узлами называют элементом связи
(рис. 6.5). Элемент связи может испытывать вышеуказанные js&
формации. Каждый вид деформаций выражается через обобщай^
вы? перемещения в двух соседних узлах сетки. Рассмотрим эта?
деформации применительно к примеру, приведенному на рис. 6Щ
Различают однородные и неоднородные деформации. Одноро^
ные деформации одинаковы по объему элемента связи. Например^
растяжение в направлении оси у (см. рис. €.5) определяется
приращение длины элемента связи к первоначальной его
. Сдвиг, показанный на рис. 6.6, а, определяется отклонением
прямого угла элемента связи за счет сдвига противоположць^
Рис. 6.6. Деформации сдвига
134
Рис. 6.7. Деформации изгиба
раней, а сдвиг на рис. 6.6,6 — отклонением от прямого угла за
:чет поворота граней:
L . F.2)
Другие деформации элемента связи будут неоднородными, т. е.
^постоянными по объему элемента. Деформации изгиба (рис. 6.7)
определяются поворотами противоположных граней в различные
тороны относительно одной из осей этих граней. При этом верх-
ляя часть элемента связи растягивается, а нижняя —сжимается
или наоборот). Эти деформации определяются относительным
удлинением на расстоянии z от серединной поверхности элемента:
Z.
F.3)
Деформации кручения (рис. 6.8) вызываются поворотом про-
-ивоположных граней элемента связи в разные стороны
относительно центральной оси, нормальной к поверхности этих граней.
Эти деформации определяются отклонением от прямого угла на
эасстояние z от центральной оси:
$*U[Z) =5
К
Z.
F.4)
Четвертый этап — выражение сил и моментов через
деформации. Деформации растяжения определяют нормальные* на-
6.8. Деформации кручения
Рис. 6.9. Нормальныесилы
Рис. 6.10. Касательные силы
Рис. 6.11. Изгибающие
моменты
пряжения (рис. 6.9). Равнодействующая этих напряжений —
мальная сила, приложенная к грани дискретного элемента:
!
где
Индексы «+», «—» на рис. 6.9 указывают на то, что силы при*'
ложены к передней и задней (по отношению к узлу) граням
элемента соответственно. . -
Деформации сдвига определяют касательные напряжения и ка-
сательные силы. На каждой грани дискретного элемента таких:
касательных сил будет две —в направлениях осей х и z. На;
рис. 6.10 показана одна из них — F+, . /
где c.v —
пу '' %l
Неоднородные деформации определяют моменты. Деформации .
изгиба определяют изгибающие моменты (рис. 6.11), а деформа-;;
ции кручения — крутящие моменты (рис. 6.12): . .
F.7)"
^/2
= f
-ftJ
136
-'ис. 6.12. Крутящие МОМеН-
Рис. 6.13. К выводу уравнений
динамического равновесия
где
F.8)
где.
yy, /^ ' yy
Приведенные формулы для сил и моментов, изображенных на
эис. 6.9-г6Л2, относятся к одной грани дискретного элемента. Для
хъух других граней формулы получаются перестановкой символов.
Гакие же Силы и моменты, но противоположного направления
приложены к соответствующим граням соседних элементов. Для
неоднородных элементов связей в выражения сил и моментов должны
^ходить средние значения коэффициентов жесткости с и k.
Пятый э т а п — уравнения равновесия. К каждой грани дис-
<оетного элемента приложено по три силы и по три момента
рис. 6.13). Суммируя проекции сил и моментов на координатные
}си, получают шесть уравнений динамического равновесия.
Уравнения моментов получаются более сложными, поскольку в них
<ооме изгибающих и крутящих моментов входят еще и моменты
^т касательных сил. В качестве примера приведем уравнение
проекций моментов, на. ось х:.
т
__ /
dfi -
Все входящие в последнее уравнение моменты условно пока-;
заны на рис. 6.14. Каждому из моментов соответствуют опредй
ленные члены уравнения. ^. "*
Первые два слагаемых в левой части уравнения относятся к
моментам Мхх, следующие два слагаемых — к моментам Мху, д*у
лее — к моментам Мхг. Последующие члены соответствуют момеяй-f
там сил Ftyy FyZ. Правая часть уравнения содержит инерционный
член — произведение момента инерции на угловое ускорение.
В уравнениях сил суммируются соответственно силы, и их
гебраическая сумма приравнивается силам инерции.
При решении нестационарной задачи разностным методов
м,
'хг
Рис. 6.14. К выводу уравнения проекций моментов на ось-
138
ускорения в правой части представляются в разностной форме.
Это позволяет, например, конструировать явную разностную
схему и производить расчет последовательно по временным слоям.
В задаче на собственные значения (вычисление резонансных
частот ц форм колебаний) в правую часть уравнений входит ш2.
Аналогичное выражение рассматривалось в разд. 5.4. Там же
приведен итерационный процесс для вычисления частот и форм низ^
шихтармоник. Этот итерационный процесс применяется и для
расчетов с помощью рассматриваемой расчетной модели.
При решении стационарной задачи инерционные члены в
правых частях уравнений полагаются равными нулю или заданной
внешней нагрузке. Чаще всего для решения стационарной задачи
применяют итерационный процесс, построенный по методу Зей-
деля. Заслуживает внимания замена стационарной задачи
нестационарной задачей, в которой рассматривается процесс
успокоения системы после прекращения действия внешних нагрузок. Этот
способ называется способом релаксации. Но для использования
этого способа необходимо в левую часть уравнения равновесия
ввести дополнительные релаксационные члены.
Важно то, что при решении всех указанных задач левые части
в уравнениях равновесия остаются в основном неизменными.
Модель конструкции разрабатывается один раз,и используется для
различных расчетов без существенных изменений.
Важным обстоятельством для удобства программирования
является также то, что вид уравнений для дискретных элементов, в
том числе и граничных элементов, одинаков. Поэтому, во-первых,
не нужно принимать никаких специальных мер для
удовлетворения граничных условий задачи. В частности, в уравнения для
граничных элементов не входят члены, соответствующие силам и
моментам на свободных краях, т. е. выполняются граничные
условия для свободных краев. Эта процедура производится
автоматически, на основе анализа наличия или отсутствия связей с
соседними элементами. Граничные условия на свободных краях
выполняются автоматически. В точках, в которых задаются внешние
воздействия, в уравнения вводятся дополнительные члены, о чем
будет ниже сказано подробнее. Во-вторых, для задания
уравнений равновесия достаточно задать пять коэффициентов в
уравнении сил или семь коэффициентов в уравнении моментов.
Следовательно, для задания расчетной модели конструкции достаточно
вычислить для каждого дискретного элемента 36 коэффициентов
жесткости. Заметим, что коэффициенты в уравнении F.9),
отмеченные сверху знаком «—», относятся к соседним элементам, а
знаком « + » к данному элементу.
Кроме коэффициентов жесткости для каждого дискретного
элемента нужно вычислить его массу и три момента инерции.
139
Таким образом, в процессе пос?роений расчётной" модели: нуЩ
но для каждого дискретного элемента вычислить 40 величин. МсК
дель конструкции, в которую входит 8000 элементов, будет
содержать 320000 коэффициентов. . Щ
При заданных внешних механических воздействиях вбзцикаю^
щие в конструкции вибрации во многом зависят от- способа Kpenlf
ления конструкции к подвижному объекту. Этот способ креплений
должен быть отражен в расчетной модели, " «*
Отдельные элементы модели могут крепиться к объекту жесЩ}
ко или шарнирно. Кроме того, между элементами модели и обът:.
ектом могут быть установлены различные шарниры, амортизатор^
и демпферы. Через эти элементы передаются внешцие :воздейст%
вия. В частности, элементы крепления могут, быть неподвижными^*
Тогда при жестком закреплении у таких элементов, исключаются-
все шесть степеней свободы, т. е. приравниваются нулю все шеетьр
обобщенных перемещений. При шарнирном закреплении у эле&
ментов сокращается часть степеней свободы. Например, шаровой^
шарнир препятствует только линейным перемещениям, а цилин^;
дрический шарнир (петля) препятствует линейным перемещениям^
и поворотам в двух направлениях. . . . / 'Г
Могут также применяться для крепления различные комбинат*
ции шарниров и направляющих. Все они исключают у соответст^
вующих дискретных элементов какие-то степени свободы. Поэтому"-
в модели должны быть указаны номера закрепленных элементов^
и способ крепления. Это описание и гёозволяет задавать внешние^
воздействия в процессе расчетов: в блоке численных экспери-;;^
ментов. '-"- - ~ - ?
n .¦ - - - - • -• - ¦»,
6.2. БЛОК ПРОВЕДЕНИЯ ^
ЧИСЛЕННЫХ; ЭКСПЕРИМЕНТОВ' : -• .4
С помощью рассматриваемМ имитационной системы могут;про:;
изводиться- расчеты дёформироинного состояния7 проектируёмойЧ
конструкции. Рассматриваются следующие, случаи: ".,;'-. " \.. \
- 1. Статическое нагружёние силами и моментами: На конструк-- '\
цию могут-действовать-внешние ейлы и комёйты, передаваемые;-!:
через точки крепления (например^ от-" двигателе!); внутренние си-';
лы и моменты, возникающие" при движении объекта с" ускорений'
ем—линейным или угловым (например, при испытаний annapatai^
в центрифуге). Важно, что эти силы и моменты избеетны и по-;^
стоянны во времени" и необходимо решать статическую задачу, й;5
которой все величины he Зависят от времени, "'/'"'" ''".' '"
В этом случае левая часть системы уравнений расчётной мо-'/'
дели формируется обычным порядком, в правой час?и соответст- •[
вующих уравнений появляются постоянные величины-*-инерцйон- :
ные члены или внешние силы и (или) мом§шък ._• .".. . .. )..»..-.*
140 ;
Заметим, что решение таких систем большой размерности
связано с определенными трудностями. В частности, объем
вычислений при решении системы уравнений каким-либо прямым методом,
например методом Гауса, растет пропорционально кубу числа
уравнений. Кррме того, быстро нарастает погрешности
округления, и никакое увеличение разрядности чисел здесь не помогает4.
Наиболее эффектив«ьщ методом решения статической задачи,
потвадимому, является итерационный -.метод;- Однако выбор из
множества различных итерационных методов наиболее
рационального требует специальных исследований.
Заметим, что простейший итерационный метод — метод Зейде-
ля^- требует выполнения значительно меньшего объема
вычисления, чем прямые методы, например метод Гауса.
Другой подход — перевести задачу в разряд динамических и
решать ее, как указывалось выше, методом релаксации. Решение
•нестационарной, динамической задачи может- оказаться здесь
более экономичным,; чем решение стационарной задачи. Но в этом
случае нужно ввести в уравнение равновесия релаксационные
чл_еньь / ^ . „ .
2, Стадшнарное (установившееся) движение, до известному
закону:по времени. В некоторых редких, но важных для практики
случаях закон; изменения во времени обобщенных перемещений
всех незакрепленных элементов модели-заранее известен.
Например, в случае резонанса ?се: точки конструкций колеблются по
гармоническому закону во времени с одинаковой частотой и
ф
В этом случае вр.емя иа расчетных соотношений можно
исключить.. Получается стационарная - -задача — задача на собственные
значения. В матричной форме система алгебраических решений в
задачу на собственные значения записывается очень компактно:
где А -г* матрица коэффициентов (в наших задачах это
коэффициенты жесткости расчетной модели); х — вектор неизвестных
обобщенных перемещений; © — собственные частоты конструкции.
Существует-довольно, много различных методов решения
задачи на собственные значения. Например, в [16] описано 18
различных процедур (алгоритмов), которые применяются в зависимости
от вида матрицы А и от того, какие из собственных значений
(резонансных частот) и собственных векторов (собственных форм
колебаний) нужно определять.
В наших задачах матрица Л является квадратной,
действительной, симметричной и очень разреженной. Из общего числа N
неизвестных в одном уравнении не более 72 могут иметь коэффцт
циенты, отличные от нуля. И нам нужно вычислить всего
несколько резонансных частот и форм колебаний. Часто достаточно вы-
141
числить частоту и форму одной низшей гармоники колебаний при
резонансе.
Особенность наших задач — большое число N. Выше мы при-:
водили пример расчетной модели, в которой #=48000. При таких
больших N большинство из описанных алгоритмов оказывается
малоэффективным или непригодным и приходится использоваФь
алгоритм, приведенный в предыдущей главе.
ч 3. Нестационарные переходные процессы деформирования.
В практике конструирования нестационарной аппаратуры наибб-
лее часто возникают именно нестационарные задачи, в который
закон движения по времени частей конструкции заранее
неизвестен. Зависимость от времени исключить из уравнений не удаетсяг
Искомые функции, например обобщенные перемещения, стано*
вятся функциями трех координат и времени.
Нестационарные процессы конструкций могут- вызываться кай
внешними, так и внутренними факторами. При численном решений/
задачи и внутреннее, и внешнее воздействия задаются аналогично,
В теории упругости различают кинематическое и силовое
воздействия на конструкцию. При кинематическом воздействии счиг-
таются известными в некоторых точках обобщенные перемещений.;
При силовом воздействии считаются известными силы и (или);
моменты, приложенные в определенных точках. Можно задавать;
также различные распределенные нагрузки. Наконец, не исклюю
чен случай задания в одних точках кинематических, а в других —;
силовых воздействий. ?
Бывают в конструкциях особые точки, в которых внешняя сила;
зависит от перемещений этой и соседних точек конструкции. Та-
кими точками, например, могут быть точки соединения с аморти-^
заторами и демпферами. Если эта зависимость известна, то такие
внешние воздействия также можно вводить в блок проведения
численных экспериментов в качестве исходных данных.
Таким образом, в блок проведения численных экспериментов'
необходимо ввести список дискретных элементов, для которых
задаются внешние воздействия, а также задать вид этих
воздействий, например закон изменения обобщенных перемещений во *
времени или закон изменения сил и моментов. Этот закон может
быть дан в виде аппроксимирующих формул или в виде таблиц..
Следует заметить, что при задании внешних воздействий необ- .
ходимо исключить свободное движение конструкции как единого \
целого. В противном случае она может перемещаться или
поворачиваться и отдельные обобщенные перемещения будут неограни-,
ченно возрастать. Для исключения такого движения достаточна ,
задать шесть различных обобщенных перемещений в произволь-v,
ных точках, например для одного элемента — три перемещения й
три угла поворота либо для шести элементов — по одному пере- ^
мещению или углу поворота для каждого.
142
Нестационарные задачи называют также задачами с
начальными условиями. В начальных условиях нужно задать начальное
состояние конструкции, т. е. обобщенные перемещения и
обобщенные скорости всех дискретных элементов конструкции в
начальный момент. При разностном решении скорость представляется
как, первая разность от перемещений по времени. Поэтому
начальное состояние задается в виде двух значений перемещений
в два момента, разделенных шагом по времени т.
Начальное состояние конструкции выбирают таким, чтобы мож •
но было легко задать начальные условия задачи. Чаще всего
считают, что конструкция в начальный момент не деформирована,
т. е. обобщенные перемещения во всех точках конструкции при
t = 0 одинаковы. При этом конструкция может быть неподвижной,
тогда все перемещения в два начальных момента принимаются
равными нулю. Если же конструкция в начальный момент
движется как единое целое с заданной скоростью, то при
поступательном движении углы поворота всех элементов полагаются
равными нулю, а перемещения в направлениях координатных осей в
два начальных момента выбираются такими, чтобы они
соответствовали компонентам скорости. Можно, конечно, задать и
начальное вращательное движение конструкции, но это' несколько
сложнее, поскольку нужно согласовать величины углов и
перемещений так, чтобы конструкция была не деформирована.
В отдельных случаях задача легче формулируется, если в
начальных условиях задать некоторое деформированное состояние
конструкции. Например, для плоских конструкций типа пластин
или коробок, которые представляются в виде развертки (см.
рис. 5.32), часто можно приближенно определить первую
собственную форму колебаний. Если такую форму задать в начальных
условиях при нулевой скорости элементов и решать
нестационарную задачу на половину периода колебаний основного тона
(половине периода будет соответствовать положение, приближенно
совпадающее с исходной формой, но только с обратным знаком),
то по величине половины периода Г/2 = пт, я — число шагов
расчета, можно получить значение первой резонансной частоты fi =
= 1/2ят. Это — пример возможного перехода от стационарной
задачи на собственные значения к нестационарной задаче.
Так или иначе в блоках численных экспериментов должны
быть заданы две таблицы начальных значений обобщенных
перемещений всех дискретных элементов модели. Кроме того, должны
быть заданы матрица коэффициентов системы уравнений
равновесия и внешние воздействия. Эта информация служит исходными
данными для решения нестационарной задачи.
Всякое механическое движение в природе происходит так, что
состояние системы в каждый следующий момент определяется
только состоянием в предыдущий момент и внешними воздейст-
143
виями между этими моментами, Иными словами, чтобы опредЦ
лить состояние, системы в следующий момент, не нужно знать йц*
предыстории движения. Достаточно знать перемещения и скор
всех точек в предыдущий момент времени и внешние силы на
шедшем отрезке времени. .
Эти физические представления отражены в уравнении
весия вида F.9). Они позволяют строить рекуррентный
тельный процесс решения нестационарной задачи. Этот ру
ный процесс можно представить себе следующим образом;
положим, что имеются значения обобщенных перемещений-
дискретных элементов модели в момент т. Тогда, зная коэ
циенты в уравнениях равновесия, можно вычислить проекции
и моментов, действующих на каждый элемент в момент /п*
будут левые части в уравнении равновесия F.9). Разделив этрй
силы и моменты соответственно на массы и моменты йнерцщ||
элементов, получим линейные или угловые, ускорения всех
ментов в.настоящий момент времени т. • - .. -i ......
Теперь запишем ускорения в разностной фЪрме, например:
Ш
Выбрав соответствующие значения шага по времени т tf взяв
два значения угла ух,т n-q^m-i в два момента т.и (м— 1),"ьш
сможем вычислить обобщенные перемещения в следующий й
мент (т+Л), ...
Теперь нужно вычислить силы и ускорения в момент (
и затем перемещения в момент (m-h2). Так двигаясь по
временным слоям, можно продолжить расчет на необходимое число Щ
гов по времени. Это и будет решение с помощью явной разнйс$|'1|
ной схемы. Щ
Основное достоинство описанной вычислительной процедуры^;
состоит в том,, что фактически не нужно решать совместно системой
уравнений. Йа каждом временном шаге решаются отдельные урав^д
нения сродним неизвестным на верхнем временном слое (т+1)|;|;
Объем вычислений получается пропорциональным числу N. У^
щается также программирование задачи.
Однако явные схемы имеют весьма серьезные недостатки^ •
шаги т следует выбирать очень малыми, как правило поряд;;
ка нескольких микросекунд. В противном случае процесс вычис!^
лений может быть неустойчивым. Поэтому приходится производи
дить расчеты на большое число шагов по времени; '^
очень трудно судить о погрешностях дискретизации, появляю*^
щихся в расчете. Щ
Первый недостаток преодолеть пока не удается. Попытки уве3$
личения т, например переходом к абсолютно устойчивым неявньш^
разностным схемам, результата ае дают. Приходится с этим й
144 " f
«статком мириться и производить расчеты на большое числа шагов
по времени, часто на несколько тысяч, пока не будет определен
ход переходного процесса в конструкции. Упрощает задачу то
обстоятельство, что время переходных процессов в конструкциях,
как правило, невелико и соизмеримо с временем распространения
по конструкции упругих волн. J
Второй недостаток, на наш взгляд, является более
существенным. Дело в том, что погрешности дискретизации могут быть
настолько большими, что процесс деформирования в расчете
становится совершенно непохожим на действительный процесс в
конструкции. ' " '
Как оценить эти погрешности, теория ответа пока не дает. Мы
можем дать только некоторые рекомендации: . -
1. Для простых конструкций типа пластин и стержней можно
воспользоваться точными оценками погрешностей, полученными
в [11]. Основной характеристикой модели, определяющей величину
погрешностей, является число шагов сетки, приходящихся на
половину длины волны. Если это число превышает 10; то больших
погрешностей опасаться не следует, {(-''сожалению, мы не всегда
* знаем, какие длины волн могут получиться в расчете- В сложных
конструкциях могут возникнуть колебания с очень короткими
волнами, которые и будут, даже при малых амплитудах, определять
в модели значения деформаций и напряжений. * .
2. Задачу можно решать двумя различными методами.
Например, задачу на собственные значения решать как стационарную
(итерационным методом) и как нестационарную. Если результаты
двух решений не очень сильно отличаются друг от друга, то с
достаточной долей уверенности можно утверждать, что погрешности
не очень большие. >
Менее надежным, по нашему мнению, является сравнение двух
или большего числа решений с разными шагами сетки. Причем
изменять надо шаги по всем координатам и времени. В этом
случае можно ожидать, что решение с более мелкими шагами будет
более точным, и пытаться экстраполировать точное решение как
предел, к которому стремится приближенное решение при
уменьшении шагов сетки. Но здесь еще нет достаточного опыта и не
набрана статистика.
3. Наиболее надежным способом оценки всех видов
погрешностей расчета является экспериментальная проверка. Однако и
здесь возникают немалые трудности. Помимо того что. надо
сделать опытный образец и провести испытания, нужно еще
обеспечить повторяемость результатов испытаний в-различных
условиях. Например если -сравнить две осциллограммы движения какой-
то точки конструкции в двух последующих опытах на одном удар- '
ном стенде, то эти осциллограммы будут в любом случае
отличаться друг от друга (здесь можно говорить о плохо обусловлен-
Ю—1215 * 145
ном эксперименте). Но у этих двух осциллограмм будут близки^;
ми некоторые интегральные характеристики движения, напрвще^
периоды колебаний основного тона, максимальные амплитуды даЦс
формации и напряжений, максимальные значения перегрузив;
Именно по этим интегральным характеристикам ич следует сравщ.?
вать результаты расчета и эксперимента. Но здесь пока также <Щк
набрана достаточная статистика. Определенно можно сказатй
только то, что расчет низших резонансный частот дает хорошей
совпадение с экспериментом. Расхождение по первой резонансной^
частоте составляет всего несколько п^оц^йтов. . ¦ - ч:. дA
Не имея возможности получать точные оценки погрешностей!*
при численных экспериментах, все авторы уделяют много внишйг
ния улучшению расчетных моделей путем учета в них различных:
дополнительных физических факторов. Представляется целесооб^
разным* прежде всего, учитывать в модели потери энергии в мш|
/териалах конструкции на внутреннее трение.
Наиболее простой способ, не требурщйй переработки
денной выше модели и увеличения объема вычислений, основан
следующих соображениях. В реальных конструкциях высоко**^
статные составляющие колебаний затухают быстрее, чем низко-?
стотные. Затухание колебаний с течением времени происходит mi
закону, близкому к экспонекциальному. Аналогичные результа!й|
в расчете получаются в тех случаях, когда ^внутренние силы, взИ|
званные потерями энергии, берутся пропорциональными скорос№
изменения деформаций по времени. Такой прием называют ##
том лотерь на внутреннее трение в виде вязкости твердых
териалов. , ,, v
Например, если сумму проекций упругих сил на ось х,
вующих на какой-то дискретный элемент, обозначить через Qx/
проекцию сил вязкого трения на ту же ось можно представить
виде
(б.и!
где (Qx,m—Qx;m-.\)h — скорость изменения упругих сил во рЦ
ниг взятая как разность «назад»; Лп — коэффициент пропорцией
нальности между силами вязкости и упругими силам*}.
Теперь уравнение равновесия запишется в виде
Qx,m + An (Qx,m - QX;m^)= Ш
ИЛИ
346
Таким образом, если учитывать силы вязкости, то вместо
вычисления величины QXtm нужно теперь вычислять разность в левой
части уравнения F.11). Но величина Qx,m-i уже вычислялась на
предыдущем шаге по времени т—1. Поэтому вычисление левой
части в F.12) не представляет труда,* если известен коэффициент
Лч*. Этот коэффициент для каждого дискретного элемента
определяется выражением
Л„ = 4-' F.13)
где *) — коэффициент вязкости упругого материала.
Коэффициент вязкости ц можно в принципе определить
экспериментально. Напомним, что модуль Юнга определяется как
отношение нормальных упругих напряжений к деформациям
растяжения призматического стержня. По аналогий коэффициент
вязкости определяется как отношение нормальных вязких
напряжений к первой производной от деформаций по времени. Таким
образом,, при экспериментально^ определении коэффициента
вязкости возникают две трудности:
напряжение нужно определять не в статике, а в динамике}
когда деформации меняются во времени; ч
нужно отделять упругие напряжения от вязких. т
Обе-эти трудности преодолеть сложно, поэтому коэффициент
вязкости определяют косвенно, 'например по логарифмическому
декременту затухания материала:. •
иущг&
где б — логарифмический декремент затухания колебаний; L —
половина длины волны в эксперименте по определению
логарифмического декремента; v — коэффициент Пуассона.
Но и по логарифмическому декременту различных материалов
справочных данных, как правило, нет, и приходится его
определять экспериментально. Следует заметить, что данные по модулю
Юнга многих материалов в литературе также отсутствуют.
Поэтому в организациях, в которых внедряются имитационные
системы, необходимо создавать лаборатории по экспериментальному
определению коэффициентов упругости и вязкости материалов,
применяемых в конструкциях.
Численные эксперименты дозволяют подбирать значения
коэффициентов вязкости различных материалов путем повторных
расчетов вибраций простых конструкций* например стержней или
пластин. Расчеты производятся с разными коэффициентами Л% и
выбирается тот расчет,, который совпадает с экспериментом.
Так или иначе развитие* имитационных систем приводит к
пополнению статистики и составлению таблиц козффицентов вязко-
Ю* 147
сти для различных материалов, а может быть, и для
типовых конструкций. Если коэффициенты вязкости
определены, то несложно вычислить коэффициенты Ац для
го уравнения равновесия, а затем и проекции сил и моментов^
левой части уравнений динамического равновесия. «^
В результате выполнения численных экспериментов появляк#^
ся многочисленные таблицы чисел, в которых для каждого яЩЩ.
кретного элемента модели в каждом шаге по времени определей||
шесть обобщенных перемещений. Как правило, числовые массйй|
вы очень большие. Проанализировать их «вручную» невозможней
Для этого в имитационной системе имеется блок анализа резудйй|
татов вычислений. * ?М
6.3. БЛОК АНАЛИЗА '
РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИИ
При цифровом Моделировании механических процессов,
ходящих в конструкциях при их статическом и динамическом |
гружении, конструктора могут интересовать различные вопраа$||
1. Выдержит ли конструкция статические или динамические!
нагрузки в процессе эксплуатации при заданных внешних возде^
ствиях? Не произойдет или авария? * " ^
. 2. Если конструкция выдерживает внешние воздействия, то ka&f
кими запасами црочности она обладает? - ^ . Щ
3. Какими будут максимальные деформации в определенныр
местах конструкции, например на поверхности печатных плат? ^
-4. Какими будут ускорения (перегрузки) в местах крепления;;
элементов схем, чувствительных к перегрузкам? ' у<
5. Какими будут амплитуды и частоты колебаний различных;*
частей конструкции? ч *^ Щ
Ответы на эти и на многие другие вопросы содержатся в ре#|
зультатах вычислений, полученных в блоке численных эксперй^
ментов. Нужно только соответствующим образом обработать эущ]
результаты. При решении нестационарных задач* эту обработку^
нужно производить параллельно с вычислениями по временны^
слоям. При этом не нужно хранить в памяти машины значения^
обобщенных перемещений на всех временных слоях. В памяти^
хранят только перемещения на трех очередных временных слоях^ц
Затем они будут заменяться последующими значениями ^З
мещений. ч . '
Анализ результатов начинается с вычисления величин; р
водных of обобщенных перемещений: деформаций; напряжений
ускорений. В отдельных случаях могут потребоваться значения сш|д
и моментов. Эти величины вычисляются либо для всех элемента^
модели конструкции, либо только в отдельных, наиболее ^
местах, которые укажет конструктор.
148 '
Для вычисления деформаций служат формулы F.1)—F,4),
Нормальные и касательные^ напряжения, а также силы и моменты
можно вычислить по формулам F.5) — F.8). Эти формулы
относятся к чодйой грани дискретного элемента, имеющей нормалью
ось у (см. рис. 6.1—6.12). Для двух других граней, видимых на
рисунках, формулы можно получить циклической перестановкой
индексов. Такая циклическая перестановка равносильна повороту
осей координат. НаЪример, если в приведенных формулах заме-
нить х+-у+-г+-х; ii+-v+-w^u и i+-j+-k*-i, то получатся
формулы- для грани с нормалью z. Если же сделать такую циклическую
перестановку еще раз — то для грани х.
Таким образом, будут получены формулы для всех трех види^
мых на рисунках граней (их называют фасадными гранями).
Противоположные (задние) грани изображенного на-рисунках
элемента будут фасадными гранями соседних элементов, и
соответствующие напряжения, силы и моменты будут вычисляться
по тем же формулам, но для соседних элементов.
Ускорения вычисляются до разностной, формуле F.10), при
этом используются значения перемещений или углов поворота
дискретных элементов на трех временных слоях. Их нужно
вычислять в каждом ш^ге по времени после вычисления обобщенных
перемещений на следующем временном слое ш+\, когда в памяти
машины будут находиться все три значения каждого обобщенного
перемещения в моменты т—1; т; т+\.
Таким образом, параллельно с вычислением перемещений
производится вычисление и всех интересующих конструктора
величин: деформаций, напряжений, сил, моментов и ускорений.
Заметим, что все эти величины входят как составные части в
уравнения равновесия и при соответствующем построении алгоритма рас-.
чета их значения получаются как промежуточные при
вычислении обобщенных перемещений. ч *.*
Следующий этап анализа результатов вычислений —
обнаружение максимальных по модулю значений указанных величин. Для
этого каждое вычисленное новое значение производной, величины
сравнивается по модулю со значением, которое до этого было
максимальным. Если новое значение больше старого, то оно
записывается на место старого. Кроме того, для максимальных
значений нужно указывать место, в котором они возникли: координаты
узла (t, /, &), время (т), направление действий (ж, у или г) и
грань, для которой они вычислен^ (#, у или z). Таким рбразом,
если других требований конструктора нет, в результате
получается всего от одного до восьми значений указанных величин для
всей конструкции в целом или для каждого материала,
применяемого в конструкции.
Если. полученной информации о максимальных величинах
конструктору недостаточно, то можно продолжить анализ резуль-
149
татов. Например, можнб сравнить полученные максимальные
чения с максимально допустимым значением и получить информа|
цию о запасах прочности, виброустойчиво^сти, усталостной прочш
сти, допустимой степени деформирования.
В. любом случае выходная информация должна быть предст,
лена в компактной, удобной для койСтруктора форм.е. На
этой информации конструктор судит о качестве проектируемой^
конструкции, Если конструкция «выдержала» испытание и сойт-f
ветствует требованиям вибропрочности технического задания, то|
задача решена. Если же конструкция «не выдержала» испытаний;!
то в конструкцию нужно внести изменения, снова сформировать!
расчетную-модель, выполнить численное эксперименты и аналиЙ
результатов. Может оказаться, что конструкция «сломается» Щ
другом месте. Тогда весь цикл повторяется. Происходит то же < '
мое, что и при натурных экспериментах: делается новый опытн
образец,, проводятся новые испытания и анализируются резуль
таты.
В приложении 2 приведена, блок-схема пакета прикладных прей
грамм для анализа динамических характеристик слъжных
стинчато-стержневых конструкций/ ^
Численные эксперименты позволят выявить причины появлений
отказов и сбоев. Но путь улучшения конструкции конструктор
должен выбирать сам. Здесь не может быть общих рецептов,
как это — творческий процесс.-Однако можно сформулировать
этот счет некоторые общие правила и дать рекомендации, что
делается в следующей главе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие преимущества и недостатки имеет теоретическая (расчетная)
верка, вибропрочности проектируемых конструкций по сравнению с эксперимент¦
тальной проверкой? ':-°\
2. В чем состоят достоинства и недостатки натурных испытаний и числеаИ
ных экспериментов при анализе виброударопрочности аппаратуры?
3. Что положено в основу построения рассматриваемой имитационной
стемы? • •
4. Из каких основных этапов состоит построение расчетной модели конст-:
рукции в имитационной системе? - • с;^S
5. Какая исходная информация должна быть задана в систему для
строения расчетной модели конструкции?
6. В каком виде получается расчетная модель конструкции?
- 7. Каким образом при динамических расчетах задается начальное
яние конструкции (начальные условия задачи)?
8. Каким образом задаются внешние воздействия на конструкцию
ничные условия задачи)?
9. Каким образом обеспечивается при численных экспериментах заданя|
нулевых граничных условий на Свободных границах, т. е. отсутствие сил и мо|;
ментов? ^ i '
Ю. Каков порядок вычислений при расчетах нестационарных процессбв а
помощью явных схем? ^ J '>'
150 / , •"&
11. В каком виде представляют результаты вычислений в блоке численных
экспериментов?
12. Каковы источники погрешностей расчетов «в имитационной системе
анализа вибро- и ударопрбчности конструкций?
13. Каковы особенности - вычислений при решении стационарных и
нестационарных задач? -
14. Что следует предпринять, если процесс вычислений с помощью явной
разностной схемы получился неустойчивым?'
15. Каким образом можно включить в расчетную модель помимо упругих
сил также силы, определяемые потерями энергии при деформировании конст-~
рукций на внутреннее трение в материалах?
16. Что такое логарифмический декремент затухания колебаний?
17. Какую полезную для конструктора информацию и в каком виде
можно получить на выходе имитационной системы?
Глава 7. СПОСОБЫ ПОВЫШЕНИЯ ВИБРО- И
УДАРОПРОЧНОСТИ КОНСТРУКЦИЙ
РЭА
Радиоэлектроника и вычислительная техника применяются практически во всех
отраслях* народного хозяйства для выполнения однотипных задач — сбора,
обработки и выдачи информации. Но условия эксплуатации в разных областях
могут быть неодинаковыми. Поэтому при изготовлении аппаратуры
различными предприятиями, объединениями складываются определенные t приемы
конструирования и типовые конструкции. Типовые конструкции многократно
испытаны, проверены многолетней практикой, и нет сомнений в их высокой
надежности. Они вошли в соответствующие стандарты и отступление от них
рассматривается как нарушение закона.
Но постоянное расширение сферы применения аппаратуры, новые условия
• эксплуатации, новые требования заказчиков приводят к необходимости
пересмотра сложившихся приемов конструирования и к разработке принципиально
новых конструкций. Именно в этот ответственный период имитационные
системы и позволяют уменьшать объем экспериментальных работ, сокращать сроки
разработок и уменьшать их стоимость, получать конструкции высокого
качества. , ' •
Для этого каждая новая идея, каждое новре конструкторское решение
должно вначале проверяться теоретически — с помощью имитационной системы, и
только после этбго, если проверка дала положительный результат, можно
переходить к изготовлению макетов и опытных образцов и проводить натурные
испытания.
Если же теоретическая-проверка дала отрицательный результат, то нужно
вносить изменение в конструкцию.
151
' 7.1. ПОВЫШЕНИЕ ЖЕСТКОСТИ
КОНСТРУКЦИИ
Предположим, что с помощью численных экспериментов
веряется действие на конструкцию низкочастотной вибраций. Д
пазон частотчисточника вибрации fH.,./B охватывает частоты до^]
200... 300 Гц, и более высокочастотных воздействий на конструкЩ
цию нет. Предположим далее, что нижняя резонансная частотой
конструкции fi попадает в интервал ^;
/h</i</b. , GЛ||
Следовательно, неизбежно возникновение резонанса на частой
те fi, что и вызывает отказы или сбои. В этом случае можно по%)
пытаться повысить нижнюю резонансную частоту конструкции такЭ;
чтобы выполнялось условие f\>U. Тогда резонансов в диапазоне!!
fn... /в не будет. Повысить резонансные частоты конструкций мож^|
но двумя путями: или уменьшить массы деталей, или увеличить^
жесткость упругих звеньев несущих конструкций. л?
Выше была получена формула для резонансной частоты ^
на амортизаторах
j
где с — жесткость амортизаторов; т — масса блока. Щ
Формула G-2) показывает, что для повышения резонансной ча-^|
стоты вдвое необходимо уменьшить массу - или увеличить жест-SI
кость в 4 раза. Эта зависимость справедлива только для пружин^
кого маятника. Но ее можно использовать для качественных оде- )'t
нок й более сложных конструкций. ^:
Уменьшение массы деталей всесда целесообразно, и всякуюк~*
такую возможность, необходимо использовать. Но вряд ли удает- \?
ся уменьшить массу всех деталей в такой степени. ^
Другое дело — жесткость конструкции. Здесь возможности бо-*\
лее широкие. В гл. 5 получено аналитическое выражение E,29) ,4?*
из которого можно определить резонансные частоты прямоуголь- *;
нрй пластины, шарнирно закрепленной по контуру. Представим.^
это. выражение в виде Г
(О :
где кг — толйхина пластины. ' .
Следует обратить внимание на" то, ^то ив формуле G.3) отра-
жена зависимость G.2). Действительно, если считать, что жест-
кость пластины пропорциональна модулю Юнга Е, а масса про-
порциональна плотности материала р, то зависимость G.2) вы-
полняется с точностью до некоторого постоянного множителя. То»
•152 ' .
5ке самое можно сказать.про любую конструкцию; например,
увеличение модуля Юнгя всех деталей конструкции в 4 раза
приводит к увеличению любой резонансной частоты в 2 раза. Но
жесткость конструкции зависит не только от модуля Юнга материалов^
но и от размеров и конфигурации* деталей. Например,
формула G.3) показывает, что увеличение толщины пластины вдвое
увеличивает все резонансные частоты также вдвое. Наличие на
поверхности пластины (печатной платы) навесных, элементов
существенно не меняет этой закономерности. Можно считать в
первом приближении, что жесткость платы от жесткости навесных
элементов не зависит.
Таким образом, можно повысить нижнюю резонансную частоту7
за счет увеличения толщины пластины. Отрицательный эффект от
такого увеличения толщины пластины — увеличение расхода
материалов и массы изделия.
Еще больший эффект, дает уменьшение размеров платы й
увеличение жесткости крепления*. Например, уменьшение длины т
ширины платы вдвое уменьшает при резонансе длину волны в на^
правлении х и у также вдвое. Волновые числа kx п. ky при этож
возрастают, вдвое, а все резонансные частоты возрастают в 4 раза..
Однако, й здесь налицо отрицательный эффект от такого
увеличения нижней- резонансной частоты — уменьшение полезной площади:
для размещения навесных элементов. Поэтому у конструктора
чаще всего имеется один путь повышения нижней резонансной ча^
стрты — применение более жесткого крепления.
Труднее с помощью формулы G.3) определить эффект от
повышения жесткости крепления. Будет ли эта формула
справедлива для других способов крепления краев пластины? Будет,,если
форму колебаний можно представить в виде произведения двух.
Л/2
Рис. 7.L Изгиб пластины при
шарнирном (а) и жестком (б)
закреплениях
Рис. 7.2/- Дополнительное винтовое
крепление в центре пластины
синусоид E.28) или косинусоид и при этом выполняются
ные условия. ^ i;
Если, например, перейти от шарнирного закрепления всех кШЦ.
«ев к жесткому закреплению, то синусоиды остаются (рис. ~?§Щ
а длины волн уменьшаются вдвое. Поэтому волновые числа &* й&^
увеличиваются вдвое, а все частоты, в том числе и нижняя резо|
нансная частота, возрастают в 4 раза. ' ** ^
Случаи шарнирного закрепления по контуру и жесткого |$*
;крепления по контуру можно считать предельными случаяари|
шарнирное — самым мягким, а жесткое — самым жестким креЩ
.лением. Между ними лежат крепления с помощью различного
ла винтов или болтов, расположенных по контуру.,
Если увеличение жесткости крепления по контуру дает не/
статочный эффект, то используют различные виды дополнит
ного крепления по площади пластины. И здесь возможности
статочно широкие. В зависимости от формы несущих конструкций %
применяют дополнительное крепление винтами в различных
жах вблизи центра (рис. 7.2). . .. .
В приложении 2 приведены резонансные частоты для
яого числа винтов, расположенных по краям пластины и в центре^
-а также расчетные и экспериментальные значения первых двузе|
резонансных частот для плат. Расхождение между ними объ5йЦ|
няется в основном тем, что в расчете трудно^ учесть реальн} ~
жесткость винтового крепления. Сказываются и погрешности
кретизации. Для увеличения жесткости используют такж^ допол^|
нительную арматуру (рйс. 7;3). В пределе если считать арматур?
по сравнению с пластиной абсолютно жёсткой^ то фактичёс
шместо одной пластины нужно рассматривать четыре пластин!
меньших размеров. Эта мерд|
повышает резонансные частси|
ты в 4 раза. Фактически
ра .жесткости и арматура
ют конечную жесткость, и
фект от их применения
ется. Дальнейшее повышений
жесткости пластинчатых
струкций за счет дополнитёлк?|
ных ребер, арматуры и других^
дополнительных деталей «?*
всегда дает положительны^ {
результат. Методы повышени
жесткости других , конструк^
"Рис. • 7.3. Увеличение жесткости конст- ций, например ' стержневьШ
рукции с пбмощью доподнительной ар- или пластинчато-СТ€
матуры: ^ -
й — пластина; 2 - дополнительная арматура ООЛее МНОГОЧИСЛвННЫ И раЗНО*
154
2
образны. Можно привести очень много примеров и при этом не
исчерпать всего разнообразия удачных конструкций. Хорошие
примеры способов повышения жесткости можно наблюдать в
строительной механике сооружений, кораблей, летательных аппаратов,
различных механизмов и машин. Л*акие примеры постоянно
находятся перед нашими глазами.
, До кдкого же предела следует увеличивать жесткость
конструкции? Считается, что если нижняя резонансная частота
конструкции вдвое превышает верхнюю частоту внешних воздействий,
. ¦ ,. ¦ ' G.4)
то это является достаточной гарантией от возникновения в
конструкции резонансных явлений.
Следует заметить, что если опасность возникновения
резонансных явлений остается, то повышение жесткости конструкции
может привести к отрицательным результатам и нужно заботиться
не о повышений жесткости, а о повышении прочности конструк-
дии, о чем будет сказано ниже.
Мы рассмотрели случай ограниченного диапазона частот
внешних возмущений, когда этот диапазон — в области относительно
низких частот и можно вывести, резонансные частоты
конструкции за пределы этого диапазона, повышая резонансные частоты.
Если же диапазон частот внешних возмущений достаточно
широкий и резонансные частоты конструкции попадают в этот
диапазон, то можно ослабить резонансные колебания путем защиты
конструкции с помощью амортизаторов и демпферов.
7.2. ЗАЩИТА КОНСТРУКЦИИ
С ПОМОЩЬЮ АМОРТИЗАТОРОВ
И ДЕМПФЕРОВ
В гл. 1 бььли рассмотрены колебания блока на амортизаторах.
Было показано, что если рассматривать блок как жесткое неде-
формйруемое тело, то при установке его на амортизаторы
получается колебательная система, в общем случае имеющая шесть
степеней свободы. Обычно рассматривается только одна степень
свободы — в направлении, наиболее опасном с точки зрения
внешних воздействий. Тогда резонансная частота соо определяется
формулой G.2). Эта частота обычно является довольно низкой и не
превышает 100 Гц. В этом -случае весь диапазон частот внешних
возмущений оказывается выше соо. И только при условии
2к ,
сказывается защитное действие амортизатора. Амцлитуда
колебаний блока уменьшается по сравнению с амплитудой колебаний
155
'////////////////////////Л
Рис. 7.4. Амортизаторы с
дополнительными
пружинами
Рис. 7.5. Амортизаторы с
коническими пружинами
точек крепления амортизаторов к источнику вибрации в к раз
Если измеряется не амплитуда колебаний, а амплитуда ускорен
ний (перегрузок), то она уменьшается в р = соо/со2 раз. *К
То, что блок аппаратуры не является абсолютно жесткий #1
сам деформируется при колебаниях на амортизаторах, практичен
ски мало влияет на защитные свойства амортизаторов и, кроме^
того, это влияние положительно, поскольку установка более ият
кого блока на амортизаторы уменьшает резонансную частоту f^;
G другой стороны, установка конструкции.на амортизаторы измёя*
няет резонансные частоты самой конструкции. Все резонансны^
частоты становятся несколько ниже. '
Стремление повысить эффективность применения амортизато*
ров привело к изобретению множества различных конструкций^
амортизаторов. Помимо рассмотренных выше обычных конструк-^;
ций в виде пружин с вязким или сухим трением появились
личные оригинальные амортизаторы:
Рис. 7.6. Проволочно-пружинные
амортизаторы
Рис. 7.7. Пружинно-сеточные
амортизаторы
156
1. Амортизаторы с дополнительными пружинами (рис. 7.4).
Дополнительные пружины имеют длину, меньшую, чем у основной
пружины, и вступают в действие при увеличении амплитуды
колебаний. В результате получается нелинейная ступенчатая
характеристика жесткости. Дополнительные - пружины могут
устанавливаться как; рядом с основной, так и внутри ее.
2. Амортизаторы с коническими пружинами,. позволяющими
плавно,, изменять жесткость с ростом растяжения и сжатия .
(рис. 7.5). У таких пружин наружные витки, которые имеют
больший диаметр, имеют Меньшую жесткость. Поэтому при
небольшом сжатии работают тЬлько эти большие витки. При
увеличении сжатия большие витки касаются нижней жесткой
поверхности и начинают сжиматься верхние витки меньшего диаметра.и
большей жесткости. Прскольку амортизатор имеет начальное
сжатие под действие массы блока, то аналогичный процесс
получается и при растяжении амортизатора, когда начинают
растягиваться сначала витки* меньшего диаметра, а затем большего. В
результате при растяжении жесткость плавно уменьшается.
3. Проволочно-пружинные (сетчатые) амортизаторы (рис. 7.6),
получающиеся*прессованием упругого элемента из тонкой
спирали. В качестве материала спирали используется тонкая проволока ,
из легированной стали или бериллиевой бронзы. Трение проволо^
ки при деформации упругого элемента создает большие потери,
энергии в упругом элементе. При больших деформациях,
например при растяжении, отдельные спирали вытягиваются в одном
направлении. При этом получается картина такая же, как*и при
деформации материалов с длинными волокнами, например
резины. Поэтому материал упругого элемента сеточного амортизатора:
стали называть металлической резиной.
Основной недостаток металлической резины — непостоянство
во времени ее- упругих свойств. Поэтому промышленностью
выпускаются пружинно-сеточные амортизаторы (рис. 7.7), в которых
роль упругого элемента выполняет пружина ), а роль демпфера —
металлическая резина 2. -
4. Тросовые амортизаторы. Металлический трос, или канат,
свитый из множества тонких жил, при растяжении и особенно при
изгибе обладает свойствами упругого тела с большими, потерями
энергии-на трение между отдельными жилами. Эти свойства
изменяются в широких пределах в зависимости от материала жил, их
диаметра, способа изготовления троса и способа использования
его в качестве амортизатора. Поэтому возможно большое
разнообразие конструкций и характеристик ^тросовых амортизаторов
(рис. 7.8).
Заметим, что все амортизаторы, в которых используется
трение металлических частей, обладают тем недостатком, что
металлы истираются, образуя-металлическую пыль. Поэтому приходит-
157
Рис. 7.8. Троссовые амортизаторы * Кй*
ся принимать меры предосторожности, чтобы эта пыль не попад$|
ла на электрические цепи. ' v l<*
При создании различных амортизаторов конструкторы стремйр
лись обеспечить., во-первых, нелинейную характеристику ynpyrocilri
и, во-вторых, большие потери энергии на трени.е. V
'Нелинейность характеристики «сила — деформация» амортиза?
тора оказывается полезной по трем причинам. ';
Во-первых, она, позволяет уменьшать габариты амортизатору
Дело в том, что большой эффект защиты конструкции дают «мя^5
кие» амортизаторы, Но чем меньше жесткость, тем больше xogf
амортизатора при действии тех же сил. Приходится в конструкй*
ции выделять значительное место для устройств защиты. Для из?^
бежания ударов приходятся увеличивать габариты,амортизатора^
Установка дополнительных коротких пружин (см. рцс. 7.4) рлщ5/
конической пружины (см. рис. 7.5) позволяет с ростом амплитудш
колебаний включать дополнительные жесткйсти; и тем ограничив
вать амплитуды колебаний, не'допуская ударов об ограничители^
движения. "' ~:<
Во-вторых, движение блока на нелинейных амортизаторах бо^
лее сложно •*- несинусоидально по времени. Такое периодической
^сложное движение можно представить в виде суперпозиции ней
скольких гармонических составляющих. Таким образом, при за<
мене линейного амортизатора нелинейным помимо основной низ-*
шей гармонической составляющей колебаний, частота которой
равна частоте внешних воздействий, появляются более высокие^
гармоники. На возбуждение этих гармоник расходуется часть*>
энергии, передаваемой через амортизаторы от источника вибра^:
ции. Значит, меньшая часть энергии остается .на возбуждение ко*
лебаний низшей гармоники: Резонансные явления развиваются не?;
так интенсивно,*как при линейных амортизаторах. Возникающие^'
при этом высокочастотные гармоники быстро затухают вследствие
158 ' *;*
потерь энергии на трение в амортизаторах. Эта энергия потерь
тем больше, чем выше частота. .
Рассмотренный эффект отчетливо наблюдается Д1ри
длительных резонансных колебаниях. На практике часто встречаются
случаи кратковременйога возбуждения резонансных колебайий.
Например, при. запуске двигателей их обороты плавно меняются or
нуля до какой-то максимальной величины. При выключении
двигателя наблюдается обратный процесс — уменьшение частоты доО.
Наконец, при изменении скорости движения транспортного
средства обороты двигателя могут то возрастать, что убывать. При этом:
и аппаратура на транспортном средстве будет испытывать
колебания с возрастающей или убывающей частотой. %
В-третьих, если в этом диапазоне имеются резонансные
частоты конструкции, то начинают развиваться резонансные колебания.
В этом случае иногда говорят о переходе через резонанс. В
действительности, резонанс просто не успевает полностью развиться,-
поскольку для этого теоретически требуется бесконечное время.
Но и такой развивающийся резонанс может привести к отказам
и сбоям аппаратуры, например, если двигатель набирает илнп
сбавляет обороты медленно и на развитие резонанса приходцтся.
относительно большое время, измеряемое десятками периодов
резонансных колебаний. Здесь оказываются полезными нелинейные
амортизаторы, особенно если они обладают характеристикой
жесткости, показанной'на рис.~7<9,а или б< Такие симметричные
характеристики получаются «встречным» включением пар
амортизаторов (рис. 7.10) с возрастающей (и убывающей) жесткостью. Если:
амортизатор включает в себя несколько пружин различной
длины, то увеличение жесткости с ростом отклонения и происходит
дискретно и характеристика жесткости имеет вид ступенчатой
функции (рис. 7.9,в). При качественном рассмотрении работы
такого* амортизатора дискретность жесткости роли не играет.
Амортизаторы с возрастающей жёсткостью целесообразно
применять, когда опасным для конструкции является понижение ча-
Рис. 7.9. Нелинейные
характеристики амортизаторов
Рис. 7.10. Получение симметрических:
нелинейных характеристик
амортизаторов
Л4
стоты вибрации, и, наоборот, если более длительным и опасны^
яцляется процесс возрастания частоты* то следует применяй^
-амортизаторы с понижающейся жесткостью (см. рис. 7.9,в). ^
Физический смысл действия-нелинейных амортизаторов сост&§
ят в следующем. Предположим, что частота бибрации от источЦ
ника (двигателя)' постепенно возрастает. Резонанс развиваете*^
при частоте /, удовлетворяющей равенству ^.|
- ' 4
где со — жесткость амортизаторов при малой (нулевой) амплитуй
,де колебаний. * _зд
Амплитуда колебаний при резонансе возрастает, и некотораЩ
«средняя» жесткость, определяющая . частоту первой гармонику!
понижается. Таким образом, резонансная частота /о конструкций!
понижается, а частота внешнего возбуждения возрастает. РеззЦ
нанс развивается в течение меньшего времени. Щ
То же самое будет происходить и при убывании частоты щщ
-брации внешнего источника,, если средняя жесткость амортиза-|
тора будет возрастающей функцией амплитуды колебаний блокай|
В этом случае возрастание амплитуды при резонансе будет «уво*;|
дить» резонансную частоту вверх, а частота внешних возмущений^!
будет падать и резонанс также не будет развиваться. ' Щ
•Повышение энергии в амортизаторах за счет трения играё?|
очень большую роль в процессе гашения вибраций. Если бы не|
было таких потерь, то при длительном внешнем воздействии в,йй|
«брации на резонансной частоте амплитуда колебаний возрастала:^
бы теоретически до бесконечности. В реальных системах возраста?|
ние амплитуды при резонансах зависит в основном от величин^
этих потерь. Поэтому большие потери, энергии в амортизаторat?
являются фактором положительным.
Не нужно забывать, что вся энергия потерь переходит в тепло, в результ^*!
те чего амортизаторы нагреваются. Мощностть потерь (в ваттах) при вязко^"^|
трении определяется формулой *и* ^
где Р — коэффициент вязкости амортизатора, нс/м; ' tfm — амплитуда колеба* *
ний, м; со — круговая частота колебаний, 1/с. ' .
Например, если р = 100 нс/м, мт=0,01 м, й)=300 1/с, то №=1,5 Вт.
При сухом трении энергия потерь определяется формулой
>=4FTpwm/, G.9)?-
где F — сила трения, Н; f — частота вибрации, Гц. ч :Ь
Например, при FTP*=1 Н; «от=0,01 м ja f = 100 Гц получаем №Щ*
160
Повышение температуры амортизаторов изменяет их- упругие' свойства и
величину самих потерь энергии. При чрезмерном .нагревании амортизаторов
возможны их отказы. Поэтому приходится принимать меры па интенсивному
охлаждению амортизаторов с помощью теплоатводоя. Но^применение, в
амортизаторах различных пластмасс и резины усложняет задачу охлаждения,
поскольку они являются плохими проводниками тепла.
Рассмотренное выше конструкции амортизаторов обладают,
двумя недостатками: имеют довольно большие габариты и прл
интенсивной работе перегреваются.
% Чтобы улучшить условия охлаждения и уменьшить габариты
аппаратуры* переходят от рассмотренных выше амортизаторов;
которые можно.назвать амортизаторами с сосредоточенными
параметрами, к амортизаторам и демпферам с распределенными
параметрами. Другой причиной перехода к амортизаторам с
распределенными параметрами является микроминиатюризация
аппаратуры. • . ' * * ' - '
- Дело в том, что микроминиатюризация приводит к
уменьшению массы блоков РЭА. Жёсткости же стандартных
амортизаторов достаточно высоки и колеблются в пределах 10$...5(Ы05 Н/м.
Если, например, поставить блок массой в 10 кг на четыре самых
мягких амортизатора, то резонансная частота такой системы будет
Уг410'/1032 Гц,
Таким образом, защитные свойства амортизатора будут скз>
зываться на частотах внешних возмущений свыше'32 Гц. Если же
масса блока уменьшается до 1 кг, тЬ резонансная частота
возрастаете 3,16 раза и становится равной 100 Гц. Защитные свойства
амортизатора начинают проявляться на частотах свыше 100 Гц.
Применение стандартных амортизаторов становится
неэффективным. .
При малой массе блоков стали применять амортизаторы с
распределенными параметрами. Такими амортизаторами и демпферами можно считать
амортизационные прокладки, а также заливки $ засыпки-аппаратуры-рзличньши
синтетическими материалами. Амортизационные прокладки -применяют для защиты
от вибраций как целых блоков (рис. 7.11), так и отдельных частей внутри
блока (рис. 7.12).
К материалу амортизационных прокладок предъявляются высокие
требования. Во-первых, материал должен обладать хорошими упругими свойствами,
т. е. должен после снятия нагрузок полностью восстанавливать свою форму,
и должен быть достаточно мягким и эластичным. Во-вторых, он должен
обладать высокими потерями энергии, на внутреннее трение.. Эти потери зависят от'
внутреннего, строения вещества: чем сложнее макроскопическая структура, тем
больше потери.. В-третьих, материал должен обладать высокой
износостойкостью. Особенно он должен, хорошо противостоять истиранию. .
11-1215 161
Рис. 7.11. Защита блока с помощью
амортизационных прокладок:
/ — корпус; 2 — прокладки
Рис. 7.12. Защита плат с помощью^
амортизационных прокладок: Щ,
I — корпус; 2 — платы; 3 — прокладки;? :
4 — воздушные полости - \..jf
В различных конструкциях применяются сотни различных материалов,
по-видимому, самыми надежными материалами являются поролоны,
и резина. Поролоны являются хорошей защитой от 'акустических шумов. - Л ^
Для создания нелинейных характеристик упругости применяют прокладкц;
различной толщины (см. рис. 7.11) или прокладки, имеющие с одной сторонрг;$
воздушные полости (см. рис. 7.12). Для защиты от вибраций неремонтируемо)^
аппаратуры, а также .для повышения ее прочности применяют заливку anngj;f
ра*туры различными вязкопластическими материалами. Такая залитая annapaf^
тура представляет собой монолитную структуру, способную выдержать
большие механические нагрузки.' Однако заливка делает конструкцию ifepj
ной и очень ухудшает условия теплообмена. В какой-то мере лишена
недостатков ^асыпка внутренних полостей аппаратуры сыпучими материалами^
например шариками из пенопласта. * $$?
7.3. ПОВЫШЕНИЕ ПРОЧНОСТИ '***
конструкции g
Если принятые меры защиты аппаратуры от механически^
воздействий не дают результата и численные или натурные экспё51
рименты показывают, что «отдельные детали не выдерживают нф|
грузок и появляются отказы, например в результате поломок, т&!:
приходится принимать меры по повышению прочности констру^;
ций. Эти меры могут быть настолько разнообразны и неожиданна
* что указать какие-то определенные пути повышения прочность-
конструкций аппаратуры не удается. Все зависит от кон&ретнй|:'
условий. Часто работа конструктора выливается в изобретений
новой, неизвестной ранее конструкции. Г-
Однако анализ ошибок многих поколений конструкторов-
и не только в области радиоэлектроники-^-дает возможность bi
162
работать рекомендации, позволяющие избегать грубых ошибок.
Приведем некоторые из них:
1. Нужно стремиться к равнопрочным конструкциям. Конструкция, которая
должна выдерживать механические нагрузки, должна быть равнопрочной. Эго
значит, что все детали конструкции должны обладать одинаковым запасом
прочности, т. е. отношение предельно допустимых для материалов деталей
напряжений к реально возникающим во всех точках деталей должно быть одина*
ковым. -
В строительной механике сооружений, например, рассчитывают форму
равнопрочных колонн, у которых напряжения сжатия во всех точках одинаковы.
Поскольку колонны держат не только опирающуюся на них конструкцию, но
и собственную массу, нагрузка к низу колонны увеличивается. Поэтому
колонна имеет переменное по высоте сечение. Она расширяется книзу по
некоторому нелинейному* закону, который можно точно рассчитауь.
Большой опыт строительной механики позволяет производить
приближенные расчеты равнопрочных конструкций мостов, вышек, каркасов самолетов
и судов. . ' .' ' *
Конструкции радиоаппаратуры не предназначены для" выдерживания
больших механических нагрузок, как, например, мосты: У аппаратуры другое ос*
новное назначение, и поэтому часто с точки зрения механики деформации кон^
струкции аппаратуры представляются более сложными. Кроме того,
конструирование радиоаппаратуры такого опыта расчетов не имеет. Поэтому
разработать достаточно сложную равнопрочную конструкцию представляется нереальным.
Но если внимательно посмотреть на детали конструкции с точки зрения их
прочности, то почти всегда можно увидеть «слабые»* детали. Эти детали,
предположительно, и будут перегружаться и могут выйти из строя. Чаще всего-^
-это крепежные детали: болты, винты, шпильки, штифты, заклепки^и другие
мелкие детали. Например, тяжелые корпусные детали скрепляются винтами или
болтами недостаточно большого диаметра. Представим себе, что крышка
(рис. 7.13) массой в 1 кг крепится к корпусу четырьмя «болтами диаметром
5 мм. Если'эта "нормальная для обычных условий конструкция подвергается
действию вибрации; -то может возникнуть аварийная ситуация.
Допустимая сила из условия разрыва одного болта определяется простым
выражением * -
ТС**2 1 ; ^
,/%=-^°max-^> ; GЛ0)
где dBfl — внутренний диаметр резьбы; Ста*— допустимые напряжения
материала болта на разрыв; kK — коэффициент, зависящий от концентрации
напряжений. , •
Если принять ^вн*=3,5 мм, ата.ч-400 Н/мм2, ?к=3; то F*« 1282,8 Н,
Таким образом, каждый болт выдержит на разрыв силу в 1000 Н. Но это
только при действии силы в направлении осей болта. При сборке ^конструкции
болты получают предварительное натяжение, зависящее от момента затяжки
. болта. В результате предварительной затяжки- болт диаметром 5 мм уже будет
11* J 163
ж
.1. f
•ш
it
Рис.-?ЛЗ. Крепление крышки к блоку"
Рис. 7.14. Зазор в резьбовом
нении:
/ — зазор; 2 — крышка; 3 — корпус
испытывать-силу порядка 700 Н. Эта сила будет складываться с инерционно^;
силой крышки. Теперь уже отдельные болты могут нз. выдерживать приложей|у;
ную силу инерции, в результате чего "может возникнуть аварийная
Дальнейшие осложнения могут возникнуть в связи с недостаточной
ностью самой резьбы; Если.болт завертывается в гайку или в стальной
и если длина резьбы гайки достаточна, то прочность резьбового соедин
определяется разрывом болтаГ Если же высота гайки недостаточна (по
гайки размещается меньше 6—7Ч витков нормальной резьбы) или болт
вается не в стальную деталь, а в другой, менее прочный материал (силумин-
цинковый сплав, пластмасса), то возникает опасность «срыва» резьбы,
стимые нагрузки на болт будут меньше, чем в случае напряжений на
Опасность разрушения становится реальной. Такие динамические нагруз^
для данной конструкции недопустимы. Следует заметить, что болты и ви
диаметром меньше 5 мм применять в корпусных несущих конструкциях
рекомендуется. Еще более опасными для резьбовых соединений являются
брации в плоскости соединяемых деталей. Сила трения между соединяемыми
деталями равна силе* нормального давления, умноженной на коэффициент
'ния. А коэффициент трения между металлическими поверхностями невелик-^
". порядка 0,1. Поэтому, чтобы не было при вибрации относительного перемещер
ния в плоскости разъема, нужно повысить допустимые нагрузки еще в 10 ра^|
.Надо сказать, что сами резьбовые соединения всегда имеют зазоры между ци%
линдрическими поверхностями болта и крышки (рис* 7.14) и не препятствую^
небольшим перемещениям деталей в плоскости.разъема. Но и самые малые QTsg
носительные. перемещения деталей в плоскости разъема при вибрации недопуЙ
стимы. При таких перемещениях возникают сложные процессы, связанные -^-
трением, износом,'нагревом'и развинчиванием болта. Чтобы в принципе язбщ-'^
жать таких явлений, нужно- конструктивно, разгрузить резьбовые соединения^
исключая относительные перемещения соединяемых деталей. Для этого можн&
использовать различные буртики или цилиндрические и конические штифты. Ц
Применение клепаных соединений в нестационарной аппаратуре может при^г
вести к еще более сложным и неприятным явлениям, чем применение винтовыЦ
^
соединений. При ударах и вибрациях стоящие рядом заклепки могут оказаться
в совершенно разных условиях и нельзя избежать неприятностей путем
увеличения числа заклепок. Поэтому заклепки применяются редко. Гораздо более
эффективным является • применение ''сварных соединений, например точечной
сварки.
Помимо рассмотренных деталей крепежа в аппаратуре применяются
различнее гребенки, решетки и другие детали с пазами или вентиляционными
отверстиями. Часто,* например, для крепления плат применяют фрезерованные или
штампованные гребенки (рис. 7.15)^ Если пазы сквозные и близко расположены
друг к другу, перемычки являются слабыми звеньями несущих конструкций;
а если они еще нагружены дополнительными деталями, вставленными ~в пазы,
то под действием ударов и вибраций может произойти поломка.
.Неудачным нужно считать жонсольное крепление деталей, ^особенно если
эти детали длинные и тяжелые (рис. 7.16). При движейии подобной
конструкции с ускорением в направлении оси х возникает опрокидывающий момент
(рис. 7.17)
AfOnp = mlja, • . . ' G.11)
где т — масса блока; L\ — расстояние от плоскости крепления до центра
массы блока; а—ускорение.
Опрокидывающий момент уравновешивается моментом сил крепления
G.12)
где. ?г — плечо, откуда равнодействующая сил крепления
У консольно-закрепленных детаЛей отношение Li/L2 больше единицы.
Поэтому вследствие опрокидывания в точках крепления могут возникнуть ведопу-
Рис, 7.15, Приспособление для
крепления плат *
Рис. 7.16. Донсольное крепление
детали
165
/77
Hit
> *¦"• *
Рис. 7.17. К определению
опрокидывающего момента
Рис. 7.18. Брусок с отверстием
стимо большие напряжения. В результате может произойти разрыв болтов ил|$
могут отломиться лапки крепления. • . / |t
2. Нужно избегать концентраторов напряжения. Аналитические и числен^
ные решения задач "о сложном напряженном состоянии различных деталей .поС
казали, что далеко не всегда напряжения в материалах распределяются р-авнсЦ:
мерно по сечению, детали. Чаще всего происходит концентрация напряжений Ж
определенных местах. Эти места и называют концентраторами напряжений
Например, если бы в бруске (рис. 7.1*8) не было отверстия, то нормальны^-;
напряжения, возникающие при раетяжении, . определялись бы отношение^
о=Р/аЬ, где а, Ь — поперечные размеры бруска. И можно было бы считать^
что эти напряжения распределены равномерно по площади сечения S=ab. ЕслйГ;
же в бруске имеется малое ^отверстие, то картина резко меняется. Хотя отверг
стие мало изменяет площадь сечения 5 и среднее значение напряжений
тичёски остается прежним, происходит перераспределение напряжений. р^
жение концентрируется вблизи этого отверстия, в результате чего напряжения^;
могут возрасти в несколько раз. Поэтому такие места в конструкции называв-
ются концентраторами напряжений. . ' t);
Концентраторами напряжений являются отверстия, различные иазм;
(рис. 7.19, а), прямоугольные уступы (рис. 7.19,6)". Разумеется, полностью из*?
б) "
Рис. 7.19. Концентраторы напряжения
166
«бежать в конструкции подобных уступов и пазов нельзя. Но, как правило/ мож-
шо придать этим пазам и выступам сглаженные, закругленные формы •
(рис. 7.19,в). Чем больше радиус закругления, тем меньше эффект
концентрации напряжений.
Концентраторами напряжений являются также пузырьки, раковины И; ка~-
верны в; толщине и на поверхности металла или пластмассы. Могут
встречаться также неоднородные включения посторонних материалов и примесей.
Поэтому для вибропрочной аппаратуры используют высококачественные
материалы. ' * * ..
3, Следует избегать обработки . поверхности деталей со снятием стружки.
Заготовки деталей, полученные литьем или прессованием, имеют определенную
внутреннюю макроскопическую структуру. Это может быть
монокристаллическая или поликристаллическая структура у металлов или_ структура больших
(длинных) молекул у некоторых пластмасс. V поверхности деталей эта
структура повторяет форму поверхности и образует прочный запдитный слой, t
.Механическая обработка поверхности, например точение или фрезерование,
разрушает этот слой и, кроме того, оставляет на поверхности канавки риски,
царапдаы, что хахже снижает прочность.. Поэтому можно рекомендовать такие
прогрессивные -методы -• формообразования деталей несущих конструкций, как
-литье, прессование, штамповка без дальнейшей механической обработки
поверхности.
В процессе проектирования и изготовления таких деталей не нужно*
стремиться делать-их ..массивными, тяжелыми. Массивные детали не всегда прр^нее
^одее легких.-Но они всегда при ударах и вибрациях, оказывают сильное, воз-,
действие на соединенные с ними соседние детали. Поэтому в вибро- и
ударопрочных конструкциях можно и нужно применять тонкостенные детали. А для
исключения изгйбных колебаний большой амплитуды на таких тонких, стенках
делают ребра жесткости. . • %
4. Следует учитывать направление вибрации при установке аппаратуры на
транспортных средствах. Обычно нестационарная аппаратура проектируется для
установки на определенных транспортных средства^. Причем заранее известно*
хде и в каком месте она будет установлена и какие механические воздействия
Сбудет испытывать. В частности, конструктора должно интересовать направление
а)
Рис. 7.20. К определению ориентации плат
167
ударов и вибраций». При ударах и вибрациях точки конструкции церемеща^Й^
Зная направление вектора перемещения на транспортном средстве, можно
ентировать аппаратуру при ее установке так, чтобы она менее деформи
лась при ударах и вибрациях. ' ЩЛ
Например, аппаратура, устанавливаемая на автомобилях* при транспорт^
ровке по неровной дороге испытывает колебания в вертикальном направлен]
Кроме того, при разгоне и резком торможении появляются линейные ускорен
в направлении движения. Следовательно,. самым безопасным .является* гори
тальное направление, перпендикулярное движению (рис. 7.20,а).
В самолетах и кораблях вибрация от двигателя направлена вдоль оси
зеляжа или корпуса. Но так как. фюзеляж и корпус являются тонкими, ^
лочками, в них легко возбуждаются изгибные колебания, когда перемещений!
направлены по нормали к поверхности оболочки. Вследствие этого наиболее!
безопасным является направление,' перпендикулярное к направлению движени
и касательное к поверхности корпуса (рис. 7.20,6).
Плоские элементы конструкций, в частности печатные платы, наиболе
чувствительны к изгибным колебаниям, поэтому при их установке следует
миться к тому, чтобы нормаль к их поверхности совладала с безопасным на
правлением в транспортном средстве, (см. рис. 7.20)\ . • Щ4
' КОНТРОЛЬНЫЕ ВОПРОСЫ |
,ш
1. Какими способами рекомендуется выводить низшую резонансную частой!
ту конструкции за пределы рабочего диапазона частот? . * ч|
2. Как ослабить влияние резонанса? щ
3. Опишите наиболее распространённые типы амортизаторов. -,|
4. Что дает применение* амортизаторов с нелинейными характеристиками?^!
5. Объясните основные ^ способы' повышения прочности конструкций. Щ
¦-..•-• . .• 1
Г л а в а • 8. СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ!
: РАСЧЕТА УДАРОВ И ВИБРАЦИЙ 2
РАДИОАППАРАТУРЫ . * I
8.1. ВЫБОР МЕТОДА РАСЧЕТА УДАРОВ И *
ВИБРАЦИИ АППАРАТУРЫ - ' . 3
В предыдущих главах были ра1асмотрены расчеты ударов и вибра- J
ций в типовых конструкциях радиоаппаратуры. При этом исполь- »
зовались различные методы расчета — численные и аналитиче-.
ские, точные и приближенные. Возникает вопрос: каким методам и
в каких случаях отдавать предпочтение? 4
Расчеты процессов, деформирования конструкций относятся к. *
168 fc " •
краевым задачам' математической физики. При постановке такой
задачи необходимо определить область, в которой протекает
физический процесс деформирования^,внешние.воздействия, или
граничные условия, и начальное состояние конструкций (начальные
условия). Кроме того, нужно задать уравнения движения, или
уравнения взаимодействия соседних точек конструкции, в процесс
се деформирования. Для задания области, или конструкции,
необходимо определить,конфигурацию и материалы всех деталей
конструкции, их взаимное расположение и крепление друг к другу..
Граничные условия должны содержать сведения о воздействии на
конструкцию окружающей среды, например о внешних силах,
давлении, перемещении точек крепления-конструкции или ускорения,,
перегрузках в' точках крепления.. Начальные условия должны:
определять энергетическое состояние всех точек конструкции в
начальный момент (?=0). В начальных условиях задаются
перемещения и скорости всех точек при i=0. Упругое взаимодействие
точек конструкции между собой задается в виде системы
дифференциальных уравнений в частных производных. В общем случае
сложных трехмерных конструкций такими уравнениями являются
уравнения Ламе [12]. Решение краевой задачи в общем случае
сложйо] Поэтому всегда стремятся упростить задачу, используя
некоторые свойства конструкций или предварительные сведения-
о ее поведении в процессе деформирования. Наибольшие
упрощения задачи получаются, если "удается перейти от динамической
нестационарной задачи к статической или стационарной. . *
. В случае статической задачи внешние воздействия и состояние
конструкции во времени не меняются. Время как независимая
переменная исчезает. В стационарной задаче движение всех точек
конструкции происходит по • некоторому известному закону, чаще
всего по гармоническому. Тогда решение можно представить в
виде известной функции времени, и после подстановки этого
решения в дифференциальное уравнение* в частных производных
время, как независимая переменная исключается. В случае
статических и стационарных задач, естественно, начальные условия не
нужны.
Другой путь уменьшения количества независимых*
переменных— это использование различных 'особенностей формы
конструкций, .Например, учитывая малую толщину пластин по
сравнению с ее шириной и длийой и используя различные .гипотезы,о"
характере'деформирования пластин, приводят трехмерную задачу
к двухмерной (см. гл. 5). При этом остается только две
независимые переменные координаты, например х и у.' То же самое
делается при расчетах тонкостенных оболочек-в криволинейных
системах координат. При расчетах стержней исключаются две
координаты и остается одна независимая координата вдоль оси
стержня. Наконец, можно предположить, что конструкция абсолютна
169-
жесткая и не деформируется, тогда все три независимые,
. наты исключаются. К такому приему прибегают, при расчете
жения блоков на амортизаторах (см. гл. 2). Заметим, что
чение координат, как правило, сопровождается появлением. н
тролируемых погрешностей. Но в большинстве случаев этот
юправдан благодаря существенному упрощению картины фде
мирования и метода расчета. Полученные простые соотношение
позволят глубоко проанализировать механический процесс, п$р.*
исходящий в конструкции. ;^?
Таким образом, конструкторская задача должна быть сфррас^*:
лирована как краевая задача, в которой приводятся форма Jjj;
структура'рассматриваемой области, дифференциальные уравне*^
яия в частных производных, описывающие деформированное. с|§|
стояние в каждой точке конструкции, граничные»условия и.нЩ|
¦чальные условия (в случае нестационарных процессов). В завиЬ^Е
ности от вида задачи выбирают тот или иной метод расчета. Н§*|
удачный выбор метода приводит к неоправданным затратам и вШ
. дает положительных результатов.
Методы расчета разделяются на аналитические и численнь
При решении аналитическими методами получается формула
группа формул. В результате численного решения получаютсЦ
таблицы чисел. J|i
Аналитические решения бывают точными и приближенными^
При этом имеется в виду не точность решения исходной констру$|,
торской задачи, а точность решения сформулированной |сра^во|Л
задачи. Формулы, полученные при точном решении, удовлетвори^
юх условиям дифференциальной, краевой задачи. Точное решенй*||
можно получить только в простейших, случаях статического илщ
•стационарного процесса для области простой формы, например?
лдя движения блока-на амортизаторах, продольных и изгибны^!
колебаний стержцей в виде бегущих и стоячих волн, для пл^стий^
прямоугольной формы с простыми условиями закрепления по кра^|
ям (жесткое закрепление, шарнирное закрепление, свободны^
жрай). Несмотря на ограниченное применение точных аналитиче^|
*ских методов, ценность полученных решений чрезвычайно высока|,;
, поскольку решения в виде формул являются общими для целоШ
группы однотипных конструкций (например, прямые стержни раз?;|
личных размеров, материалов и различной формы, сечения) й|;
-определяют влияние параметров конструкции на процесс дефор|;
мирования. Если не удается получить точное аналитическое ре-^1
:шение; то пытаются получить приближенное аналитическое решё*;;
ние. Такое решение может точно удовлетворять уравнению и щ>лЩ
«ближенно — начальным или граничным условиямх или, наоборот,;;
точно удовлетворять начальным или граничным условиям и. прщ^
«ближенно — дифференциальному уравнению. Наконец^ возможецй
^случай, когда приближенно удовлетворяются все условия !^
170 ? '
Более подробно об аналитических методах решения будет
сказано в последующих разделах. * .
Численные методы решения краевых задач являются
приближенными. Наибольшее распространение получили дискретные
численные методы —метод конечных элементов (МКЭ), метод
конечных разностей (МКР), вариационно-разностные методы и их
различные модификации. Характерным для них является то, что
исходная дифференциальная задача заменяется алгебраической
(т. е. дифференциальные соотношения заменяются, «системой
алгебраических уравнений) и искомые функции, например
перемещения, вычисляются не в каждой тойке области, а только
в.отдельных точках, которые называют узлами сетки. Между, этими
точками предполагается, что искомая функция изменяется по
некоторому простому закону, который может быть.задан
аппроксимирующими полиномами. ,
Достоинство дискретных методов состоит 6 том, что нет
принципиальных препятствий для составления соответствующих систем
алгебраических уровней при любой конфигурации деталей
конструкций, и любых иачальных и граничных условиях. Поэтому с
помощью этих методов можно производить расчеты неоднородных
конструкций сложной формй. . .
Однако дискретные представления решения приводят и к
основным недостаткам методов:
необходимо решать системы алгебраических уравнений, в
которых количество уравнений равно произведению числа узлов на
число неизвестных в каждом узле и *на число шагов по времени,
Такие. большие объемы, вычислений можно выполнять только с
помощью ЭВМ;
дискретное представление решения вносит основную
погрешность— погрешность дискретизации. С уменьшением размеров
дискретных элементов погрешность дискретизации должна
'стремиться к нулю. Оценка погрешностей дискретизации представляет
собой задачу более сложную/ чем поиск основного -решения;
любое изменение конструкции, т. е. внесение изменений в
условие краевой задачи, приводит к неЪбходймостк повторного
решения на ЭВМ. * ' ,
' Для радиоконструктора наибольший интерес представляют
МКЭ и МКР. Рассмотрим достоинства и недостатки этих методов..
В МКЭ узлы сетки могут располагаться по области
произвольно. Например, фигуры между узлами в плоской задаче
могут представлять собой различные треугольники (рис. 8Л).
В объемной задаче такие фигуры — чаще всего тетраэдры
(рис. 8.2).
В МКР область разбивается на элементы плоскостями,
параллельными координатными плоскостями. Например, в
прямоугольной системе координат дискретные элементы будут иметь" прямо-
171
X
ш
а)
Рис. 8.1: Конечные эле- Рис. 8.2. Конечный эле- Рис. 8.3. Представление <Щ?
менты в форме треуголь- мент в форме тетраэд- ласти в методе конечш$&*
ника . ра разностей . >Щ
угольные формы. Узлы сетки помещаются или в вершинах пряшэШ
угольников {рис. 8.3, а), или в дентрах их (рис. 8.3, б).. Щ
Произвольное расположение узлов в МКЭ "определяет, преимЦ^
щества этого метода по сравнению с МКР. С помощью треугол^|
ников можно точнее аппроксимировать контур деталей сложно^
конфигурации. Кроме того, нерегулярное расположение узлов н§?^
ключает специфическое накопление погрешностей дискретизацн$||
свойственное регулярной структуре. ' ' ~Щ
В общем случае погрешности дискретизации в МКЭ получаю*^
ся меньшими, чем в МКР. Эти достоинства определили широко^
применение ^КЭ в строительной механике сооружений, кораблев^
самолетов. Разумеется, в МКЭ можно применять элементы той ж^
формы, что и в МКР. (например, в декартовой системе коорд)'"
нат — прямоугольники). Но тогда все преимущества МКЭ
ют, более того, расчетные соотношения получаются такими
как и в МКР. "•.'/'
В МКЭ дело осложняется при переходе к нестационарным заЩ
дачам! Если строго следовать- принципам МКЭ, то теперь нужн^
конечные элементы делать протяженными и во времени. Аппрок|1
симирующая функция в качестве независимой переменной такж|||
должна иметь вррмя. Такими элементами нужно «заполнить» иЩ
только рассматриваемую область, но и весь временной интервал^
в течение которого производится расчет." Такой подход являетс5зЩ
явно неприемлемым, так как приводит к очень громоздким систеС|
мам разрешающих алгебраических уравнений и соответственно к^
огромному объему вычислений. . ' Щ
- В МКР дело обстоит гораздо проще. Используя то свойств*)^!
что нестационарные уравнения отличаются от статических в co-Sj
ответствии с .принципом Даламбера только инерционным членомД|
включающим в себя произведение массы элемента на его ускорё-^
ние, вводят разностную аппроксимацию ускорения в виде второй|;
разности от перемещений по времени ' . |*
д2и
Это позволяет рассчитывать искомую функцию по временным:|5;
слоям, вычисляя ее значения на каждом следующем шаге по — *"
172 * .
мени (t+1). по известным значениям на двух предыдущих шагах
(см. § К2).
Более того, использование так называемых явных разностных
схем позволяет вообще избегать решения системы связанных
уравнений и решать в каждом узле в каждый момент одно
уравнение с одним неизвестным. Это достоинство МКР и определило
его монопольное применение в расчетах нестационарных про-
- цессов.
Заметим, что такая простота алгоритма расчета и малое время
вычислений не даются даром. Появляются свои трудности.
Основная из них — условная устойчивость явных разностных схем. Уо
. ловия устойчивости приводят к тому, что шаги по времени т при
расчете радиоконструкций приходится выбирать очень малыми —
обычно порядка нескольких микросекунд. Если производится
расчёт нестационарного процесса длительностью в 1 с, то необходимо
вычислять искомые функции в каждом узле в нескольких сотнях
тысяч моментах времени. Тем не менее использование явных
разностных схем представляется единственным способом,
позволяющим решать нестационарные задачи высокой, сложности — для
конструкций сложной конфигурации .при произвольных внешних
возмущениях." • . <
. В литературе по разностным методам расчета [10} при решении
нестационарных задач, описываемых уравнениями эллиптического
и параболического типа (например, тепловых задач), для
получения абсолютно устойчивого вычислительного процесса при любых
шагах по времени рекомендуется применять так называемые
неявные разностные схемы вместо явных.
Попытки использования неявных разностных схем для расчёта
нестационарных колебательных процессов не дают эффекта. Хотя
неявные, схемы устойчивы при любых шагах по времени, они тем
не менее приводят к искажению картины деформирования,
которая становится совершенно не похожей на реальный" процесс.
Подводя итоги, заметим, что точные аналитические решения
можно получить лишь в простейших случаях модельных задач, на-
лгример при свободных колебаниях систем с сосредоточенными па-,
раметрами, свободных колебаниях однородных стержней и пла-
'Стин прямоугольной формы с простым закреплением по краям.
Приближенные аналитические метрды несколько расширяют
круг решаемых задач. Об этих методах будет сказано в
последующих разделах.
' Особую группу конструкторских задач составляют нелинейные
задачи. В общем случае в природе все процессы нелинейны.. Но
цри формировании задач производится их линеаризация с целью
упрощения решения. Однако в конструкциях РЭА специально
применяют нелинейные элементы, например нелинейные
амортизаторы. Привести задачу к линейной.в этом случае не имеет смы-
"' ' . " "- / . 173
&•¦"
ела, так как теряется эффект влияния нелинейности на ход
цесса. Приходится решать нелинейную задачу. Наиболее
страненный способ решения нелинейных задач — разбиение
ния на отдельные участки и линеаризация задачи на каждом. щч
этих участков. Эта операция хорошо выполняется при использй|
вании явных разностных схем. Здесь линеаризация производит^
в пределах каждого шага по времени. Поскольку шаги по врем**^
ни очень малы, изменения нелинейных параметров конструкций
в пределах одного шага незначительны и можно считать эти -щ^
рамехры постоянными. Задача сводится к решению множества,
линейных задач. Объем вычислений ,в этом случае, пр^ктичеейй^
не возрастает по сравнению .с, расчетами'линейных процессов, "jj
. 8.2. АНАЛИТИЧЕСКИЕ МЕТОДЫ. РАСЧЕТА Hi
ДЕФОРМАЦИИ КОНСТРУКЦИИ - g
Выше были рассмотрены основные численные методы* расуеУ
та — дискретные методы, (метод конечных разностей и метод кдч?
нечного элемента). В процессе аналитического решения получает^
ся формула или группа формул. В предыдущих главах привода^;
лись аналитические решения нескольких задач. При этом основ^д
ное внимание уделялось результатам решения, т. е. поведении^
рассчитываемой конструкции при воздействии ударов и вибрациС^
Теперь обратим внимание на сам процесс решения и методы полу^;:
чения, аналитического решения в виде формул. Если эти формулй^
удовлетворяют всем условиям задачи, то порученное решение
дет точным. А таких условий достаточно много. Приведем
описание: .
1. Дифференциальные уравнения, описывающие деформиро?^
ванное состояние в каждой точке конструкции. Обычно —,это
нения равновесия в частных производных. Если конструкция
ставляет собой однородную область и состояние в каждой
определяется одной переменной, то уравнение будет одно,
мер, при расчетах изгибных деформаций пластин используют
но уравнение технической теории изгиба [12], в котором
искомая функция — прогиб w. Точное решение также может соЩ
держать одну,формулу. ^Щ
Если конструкция состоит из нескольких областей (деталей) &$
соединенных между собой, и рассматривается пространственное *
напряженное состояние, то для каждой области записывается тр#о|
дифференциальных уравнения равновесия для трех компонентов,
перемещений и, v, w в направлении, трех координатных осей [12]*Д^
В точном решении, если такое найдено, будет по три формулы?^
для иу v и w в каждой однородной части конструкции, т. е, в каж- ;\
дои детали. При подстановке формул точных решений в уравнения >у
равновесия последние обращаются в тождество. " . л .Ц
174 • :?
2. Граничные условия. Граничные условия в задачах теорий
упругости задаются по всему наружному контуру в виде переме-
щений (кинематическое возмущение) и напряжений или сил
(силовое возмущение). Если дифференциальные уравнения имеюг .
второй порядок производных, как это имеет место, например, в~
уравнениях продольных колебаний стержней, то достаточно
задать по одному какому-то условию на каждом краю (кинематиче- * •
скому или силовому). Если уравнения имеют четвертый
порядок производных, как в уравнениях изгибных колебаний, то на:
каждом краю должно быть задано по два условия. Причем
можно задавать прогиб, угол поворота сечения, изгибающий момент
и перерезывающую силу в любом наборе, например прогиб и угол
поворота, прогиб и изгибающий момент, или изгибающий моменг
и перерезывающую силу. Всего может быть шесть разных
сочетаний* - .
Заметим, что при заданий граничных условий необходимо
исключить движение всей конструкции как целого. Во-первы$, такое
движение не вызывает-возникновения напряженно-деформирован-^
ного состояния и в этом смысле интереса не представляем. Во-
вторых, при таком движений в расчете возникают большие
абсолютные перемещения, что приводит к потере точности расчета.
Поэтому при расчете кинематические граничные условия задаются
таким образом, чтобы исключить свободное движение
конструкции в любом направлении. Как правило, в расчетах вибраций
реальных конструкций такие условия задаются в местах их
крепления, в которых перемещения известны.
Граничные условия должны быть заданы во всех точках
границы области, т. е. на всех наружных* поверхностях всех деталей
конструкции. Если, например, при вибращш конструкции к
поверхностям не приложены внешние .силы, то нормальные и
касательные напряжерия во всех точках поверхностей должны „быть
равны нулю. Отсутствие напряжений на поверхности и
определяет нулевые силбвые граничные условия. * * ч
При Подстановке точного решения задачи в. виде формул *
граничные условия последние удовлетворяются тождественно.
3. Промежуточные граничные условия. Если конструкция
неоднородна, т. е. содержит соединения нескольких областей из
разных материалов, то на границе раздела.должны выполняться
промежуточные граничные условия.
В случае продольных колебаний неоднородного упругого
прямого стержня, состоящего из-двух областей* таких условий будет
два (расчет продольных колебаний приводился в гл. 4). Первое-
условие состоит в том, что стержни при прохождении продольных'
волн не разрушаются, поэтому перемещения в обоих материалах;
вблизи границы должны быть одинаковыми. Второе условие cocVo-
17S
Рис. 8.4. Неоднородный эле-
мент конструкции ч- „ "
т
шь
ит в том, что нормальные напряжешь
^вблизи границы в обоих материалах дй||;
жны ,быть одинаковыми, . пост
вблизи границы никакие внешние ра
гивающие силы не приложены. *
В других случаях на промежуточ
границах может потребоваться дру
"число промежуточных граничных ус
тзий. Например, при расчетах изгибных колебаний неоднородно
стержня необходимо на границе4 раздела сред задавать четы|
условия: равенство перемещений, равенство углов поворота сеч
ний, равенство изгибающих моментов и перерезывающих сил.
Таким образом, общее число граничных условий, которое
обходимо задавать в условиях'задачи, зависит от количества
ластей (материалов) в конструкции и порядка производных
уравнениях движения. Предположим, что производится >
деформаций некоторой неоднородной' конструкции сложной
(рис. 8.4). Если в ней провести произвольную линию JV, то
ние на этой линии в принципе может быть получено интегриров
ниевд уравнений движения на каждом из трех участков A, 2 и
Если уравнение движения имеет второй порядок производных
координатам, то при каждом интегрировании получится, по
постоянных на каждом участке. Для их определения, необходи
иметь шесть дополнительных условий. Это и будут условия
внешних поверхностях в точках 4 и 7 и по два условия на bhj
тренних поверхностях в точках 5 и '6.
4. Начальные условия. Трехмерную нестационарную задач
можно рассматривать как четырехмерную, т. е. считать время
волнительной координатой. Но'в отличие от пространственных
ординат, для которых все границы области идентичны и подверй
гаются известным внешним воздействиям, время — особая коор^|
дината. Начальное состояние конструкции задать можно, аконеч"
ное состояние, как правило, неизвестно. Часто неизвестно да>
конечное время в задаче, или оно нас не интересует. Таким обраЩ
лом, граничные условия'по времени задаются только в начальный
момент и называются начальными условиями.
В начальных условиях должно быть задано энергетическое ce^jt
стояние конструкции, т. е. кинетическая и потенциальная энергиЩ!
всех ее частей. Кинетическая энергия определяется скоростью дви|||
жения, а потенциальная энергия деформированного состояния-
относительным начальным положением всех точек конструкцией
Следовательно, в начальных условиях нужно задать перемещений
и скорюети во всех точках конструкции., . р
176 - ' '
Задание начальных условий в общем случае связано с
некоторыми трудностями. Если конструкция в начальный момент
находится в деформированном состоянии, то для определения
начальных перемещений необходимо вначале решить статическую, зада*
чу. Если же конструкция к тому же и движется, то нужно заранее
решить динамическую задачу о предыдущем движении, что
нерационально. Обычно в динамических задачах задается* такое
начальное состояние, в котором конструкция находится в состоянии
покоя, равномерного прямолинейного движения. За начальное
положение точек конструкции принимается то, которое они имеют в
начальный момент f=0. Тогда начальные перемещения всех точек
будут равны нулю, а начальные скорости во всех точках будут
одинаковыми.
При подстановке в точное решение значения f=0 должны
получаться заданные начальные перемещения, а после
дифференцирования по времени формул точного решения и подстановки f=
=0 — начальные скорости.
Таким образом, получить точное решение, удовлетворяющее
всем указанным условиям, чрезвычайно трудно, особенно если
конструкция имеет сложную форму и подвержена действию
произвольных нагрузок. Но даже в тех случаях, когда удается
получить такое решение, это еще не означает, что полученные
значения напряжений и деформаций точно соответствуют реальным
процессам, происходящим в рассматриваемой конструкции,
поскольку сама постановка краевой задачи содержит ряд
погрешностей. -Эти погрешности являются следствием неточного знания
условий работы конструкции и свойств применяемых в
конструкции материалов. Поэтому считают, что совпадение решения с
экспериментом с точностью 10...20% считается хорошим.
Возникает вопрос: может быть, вообще не стоит пытаться
искать точное аналитическое решение поставленной задачи,
поскольку все равно не избежать ошибок при постановке задачи?
Ценность полученных точных аналитических решений очень
велика, поскольку только они позволяют развивать теорию. Над
поиском точных решений работают многие специалисты в разных
отраслях, поэтому круг задач, имеющих точные решения,
постепенно расширяется.
8.3. ПРИМЕРЫ ТОЧНЫХ
АНАЛИТИЧЕСКИХ РЕШЕНИИ
Точное аналитическое решение краевой задачи можно
получить, если дифференциальные уравнения в частных производных
линейны, конструкция (область) имеет простую форму, начальные
12-1215 . . 177
120
250
У,мм
120
SO
О
150 250
г.. *№
Рис. 8.5. Примеры различной конфигу- Рис. 8.6. Область прямоугольно^
рации пластин . формы ~Э
и граничные условия выражаются простыми формулами и процесУ
в конструкции является установившимся, т. е. стационарным. ГкЁ|
ясним некоторые из этих ограничений. ^
Уравнения классической теории упругости для малых деформйЦ
цдй являются линейными. Большинство расчетов процессов дефор-|
мирования производится с помощью таких линейных уравнений^
Поэтому в современных условиях это ограничение можно считат^
несущественным. Только развитие теории может, привести к ширсиГ
кому использованию в расчетах нелинейных уравнений, например
уравнений пластичности. *
Простота формы конструкции (области) определяется <
ее наружных и промежуточных границ. Границы должны
ваться простыми аналитическими выражениями в выбранной
стеме координат, с тем чтобы искомые функции на границах и
ли простые выражения. На рис. 8.5 показана форма двух плайр
стин. Контур пластины на рис. 8.5, а определяется выражениям^
х=0у *=250, */=0, ?/= 120. ч Ц
Пластина; представленная на рис. 8.5,6, имеет ступенчатый^
вырез, и описать границы, без дополнительных условий не удает»;
ся. Поэтому выбрать простой вид искомых функций сложно. 5?
Основные вопросы, связанные с построением точных решений^
можно рассмотреть на нескольких примерах, ряд из которых pacf|
смотрен выше. Начнем с общего случая трехмерной нестационарЙ
ной задачи. - J2
. Рассмотрим упругие волны в твердом теле. Уравнения рав^ц
новесия теории упругости для общего случая трехмерного напря-7;
женного состояния однородной изотропной среды (уравнения Ла-?т:
ме) [12] имеет вид %
>/i
3
$!i
(8.1)
дгду) dt*
где X и \i — коэффициенты упругости среды (коэффициенты
Ламе); они могут быть выражены через модуль Юнга Е и
коэффициент Пуассона; иу vf w — компоненты перемещений; р —
плотность материала.
Решение в виде плоской бегущей волны имеет вид
u = Umsin(kx—C>t), у = 0; ш = 0, (8.2)
где Um — амплитуда; ?—волновое число; со — круговая частота.
Подставив решение (8.2) в первое уравнение (8.1), получим
— (л + 2|1)/г =—рог. (8.3)
Поскольку волновое число k определяет длину волны Д(& =
= 2л;/Л), то уравнение (8.3) показывает зависимость длины
волны Л от частоты .о. Таким образом, в области прямоугольной
формы (рис. 8.6) перемещения материала будут происходить только в
направлении оси х.
Чтобы решение (8.2) было точным решением задачи, на
границах области должны быть выполнены соответствующие условия.
Например, при # = 0 задняя стенка должна совершать
гармонические колебания по закону tt=?/msina>/, а перемещения иишпо
всем стенкам должны быть равны нулю.
Начальные условия должны быть следующими: при ? —0 и =
— Umsinkx, du/dt=—Umwcoskx.
Заметим, что создать в эксперименте такие условия на
границах очень сложно, поэтому задача представляет теоретический
интерес. Теоретически возможны также стоячие волны
и — Umsinkxsin'(dty. 0 = 0; w = 0 (8.4)
и суперпозиция стоячих или (и) бегущих волн, например:
v=Vmsm(kyy—G>yt), (8.5)
-W*=Wm Sin (kzZ—tizt).
Этими случаями практически и исчерпываются все возможные
виды точных аналитических решений трехмерных задач.
Уменьшение числа независимых координат в задаче расширяет круг задач,
12* 179
имеющих точное аналитическое решение. В предыдущих главах
были рассмотрены продольные и изгибные колебания пластин и'
стержней. При этом уравнения движения для пластин и стержней
были получены на основании общих физических представлений
теории упругости. Эти уравнения, естественно, должны быть част-:.
ным случаем уравнений Ламе (8.1). Действительно, уравнения
для стержней и пластин могут быть получены из уравнений (8.1)-,
формально, на основании некоторых гипотез, позволяющих
исключать одну или две координаты.
8.4. РАЗЛИЧНЫЕ ГИПОТЕЗЫ,
УПРОЩАЮЩИЕ ЗАДАЧУ 'л
РАСЧЕТА ДЕФОРМАЦИИ /
^Существует достаточно много различных гипотез, позволяю-1
щих исключать из расчетных уравнений независимые координаты,;,
т. е. приводить трехмерную задачу к двухмерной (плоской), а
двухмерную —к одномерной. Некоторые из этих гипотез очевидны,-
например гипотеза об однородном растяжении прямого стержня-
постоянного сечения. Другие гипотезы, наоборот, недостаточно ~
теоретически обоснованы и об их приемлемости судят лишь по?
совпадению с экспериментом. Это прежде всего гипотезы о дефор-;
мировании различных оболочек.
Для радиоконструктора представляют большой интерес гипоте-:
зы, позволяющие достаточно просто производить расчеты изгиб-.,
ных деформаций стержней и пластин. в * <
Исключение одной координаты из уравнений изгибных колеба^
ний пластин. Предположим, что пластины имеют прямоугольную^
форму и две поверхности находятся на близком расстоянии друг
от друга. Такое допущение позволяет строить различные гипотезы.
о характере распределения напряжений и деформаций по толщине <
пластины и тем самым исключать из уравнений движения одну
координату, перпендикулярную этим поверхностям. Заметим, что,,
все известные гипотезы упрощают картину деформирования и*:
вносят погрешности. Поэтому полученные таким образом
дифференциальные уравнения будут приближенными. Решения задач с
такими уравнениями будут несколько отличаться от решений
задач с уравнениями (8.1), т. е. будут содержать погрешности. Чем
пронщ гипотеза и соответственно проще картина деформирования,
тем больше погрешности. Рассмотрим наиболее известные
гипотезы.
1. Гипотеза прямых нормалей. Эта простая гипотеза уже
рассматривалась в гл. 4 и 5. В результате' ее применения получается ,.
уравнение изгибных колебаний тонких пластин. Это уравнение
приводилось в гл. 5.
Рассмотрим, какие упрощения вводятся в общую картину
деформирования в соответствии с гипотезой прямых нормалей:
а) перемещения и и v изменяются по толщине пластины по
линейному закону, a w от толщины не зависит:
u=uoz, v-=v0z9 w = Wb
где и0, vOi w0 — функции, не зависящие от z. Это предположение
позволяет интегрировать уравнения (8.1) по толщине пластины.
Причем при интегрировании нужно учитывать, к каким
напряжениям относятся члены уравнений. Если напряжения приложены к
граням элемента с нормалью г, то в результате интегрирования
по частям эти нормальные и касательные напряжения
«выводятся» на поверхности пластины;
б) в результате интегрирования по 2 в левых частях первых
Двух уравнений (8.1) получаются моменты упругих сил
относительно осей х и у, а в правых частях — моменты инерции
вращения относительно тех же осей. Второе упрощение состоит в том,
что пренебрегают инерцией вращения, т. е. приравнивают правые
части первых двух уравнений нулю;
в) выделяют из всех трех уравнений моменты от касательных
напряжений и моменты от нормальных напряжений. Из первых
двух уравнений моменты от касательных напряжений выражают
через моменты от нормальных и подставляют в третье уравнение.
При этом используют третье упрощение, которое состоит в том,
что сечения стержня, нормальные к серединной плоскости до
деформации, остаются нормальными к серединной поверхности в
процессе деформации:
du dw dv __ dw ш ~ fi.
dz dx * dz dy
г) последнее упрощение состоит в том, что срединная
поверхность не растягивается и не сжимается.
Полученное таким образом уравнение называют уравнением
технической теории изгиба тонких пластин. Оно широко,
применяется при расчетах прогибов пластин при их статическом нагруже-
нии, например в строительной механике сооружений. Результаты
расчетов хорошо согласуются с результатами экспериментов.
При расчетах динамических процессов распространения изгиб-
ных волн результаты не всегда согласуются с экспериментом.
Расхождение тем больше, чем короче длины волн. Считается [17], что
основная причина расхождения состоим в том, что принятые
выше упрощения предполагают отсутствие инерции вращения
элементов пластины. В результате с повышением частоты колебаний
скорости изгибных волн быстро растут. Полученные уравнения
E.26) не являются волновыми. В них порядок производных по
координатам и времени не одинаков. Инерция вращения элемен-
181
тов пластины учитывается другой гипотезой — гипотезой плоских-
сечений. *
2. Гипотеза плоских сечений. В отличие от гипотезы прямых
нормалей эта гипотеза предполагает, что при изгибных колебание
ях поперечные сечения пластины остаются плоскими, но не обяза-'
тельно нормальными к срединной поверхности. В результате вме^
сто условий (8.6) появляются новые условия
dU **--*. (8.7*
dz
dz
Первое условие соответствует рис. 8.7, а, второе — рис. &7, б[
Гипотеза плоских сечений приводит к появлению в расчет^
двух дополнительных переменных — углов поворота сечений. 7ъ$
перь в задачах об изгибных колебаниях пластин будет три неиз<-;
вестных функции: w, *рХу \<ру. Координата z будет по-прежнему Ер
уравнениях отсутствовать. Вместо одного уравнения для w nchr
явятся три уравнения: два уравнения моментов и одно уравнение!
сил. Эти уравнения будут соответствовать уравнениям (8.1). Вс&
три уравнения будут иметь второй порядок производных от неиз-(
вестиых w, (рХу <ру по координатам и времени, т. е. будут волно-|
выми, и скорость распространенияволн не будет зависеть от дли{
ны волны и частоты колебаний. Результаты расчета динамически^
процессов с помощью гипотезы плоских сечений получаются болёё?
точными, чем с помощью гипотезы прямых нормалей. В строи§
тельной механике сооружений гипотеза плоских сечений исполь4-
зуется при расчетах толстых пластин и стержней типа балок, бе^
тонных плит я т. п. Дальнейшего уточнения теории можно до*!
биться, если отказаться от предположения, что сечения пластинкЦ
при изгибных деформациях остаются прямыми или плоскими^
Наиболее общий прием исключения координаты z из уравнений!
(8.1) состоит в том, что искомые функции и, v\ w распределяют-А
ся по толщине пластины по закону степенного полинома. f:
3. Разложение ибкомых функций по полиномам Лежандра. Если"
сечения пластины при изгибных деформациях не остаются плоски-^
Рис. 8.7. К гипотезе плоских сечений
182
Рис. 8.8. Графики полиномов Лежаи-i
дра ?
ми, то естественно предположить, что форма сечений будет
достаточно простой и обладать некоторыми свойствами симметрии.
В [17] предложено для исключения координаты г представить
функции перемещения в виде разложения по полиномам Лежан-
дра (по толщине пластины z):
(8.8)
W ¦
где иПу vn, Wn — искомые составляющие перемещений, которые
являются функциями двух координатах х, у и времени; Pn(z) — сте*
пенные полиномы Лежаидра.
На рис. 8*8 показаны графики первых четырех полиномов Ле-
жандра (кривые 1—4). Эти графики нормированы, и на них
искомые функции моТут изменяться в пределах от —1 до 1.
Удобнее представить полиномы как функции от z[hz (А* —
полутолщина пластины):
(8.9)
После подстановки разложения (8.8) в уравнения (8.1),
умножения полученных уравнений последовательно на полиномы (8.9)
и интегрирования по толщине пластины от —h2 до Нг получают
Зп уравнений для определения составляющих ип, Vn и wn.
Координата z при интегрировании исключается. Эта процедура
подробно изложена в [11, 17].
При применении способа разложения функций перемещений по
полиномам Лежандра в направлении г исключается эта
координата, т. е. уменьшается мерность задачи, но при этом
увеличивается число неизвестных. Поэтому выигрыш в объеме вычислений
при численном решении задачи получается лишь в том случае,
если в разложении (8.8) сохраняется небольшое число членов.
При решении задачи, в которой сохраняются линейные члены щ
и v\ и нулевой член wOy получены результаты, аналогичные тем,
которые получаются с использованием гипотезы плоских сечений.
Разумеется, одновременно с лреобразованием самих уравнений
движения нужно соответственно преобразовывать и начальные и
граничные условия задачи с использованием принятых гипотез.
Исключение двух координат в уравнении изгибных колебаний
; ¦ 183
стержней» Стержни имеют два малых размера по сравнению с его-
длиной. У призматических стержней эти размеры постоянны по
длине. Это позволяет строить гипотезы о распределении
перемещений но двум координатам сечения стержня. Рассмотрим
исключение двух координат в уравнениях (8.1) при йзгибных
деформациях прямых стержней прямоугольного сечения.
1. Гипотеза прямых нормалей может быть использована дваж^
ды, по направлениям у и z, перпендикулярным оси стержня х.
При этом получаются два независимых уравнения йзгибных коле*"
баний: в плоскостях хОу и хОг. С помощью этих уравнений вычис-'
ляются два прогиба v и w в направлении у и z соответственно^
Если рассматривается один стержень, то задача распадается на
две независимые задачи о колебаниях и двух плоскостях. К этим:
задачам могут быть добавлены еще две независимые задачи а
продольных колебаниях и крутильных колебаниях стержня (см.
гл: 4). Каждый элемент стержня будет иметь четыре степени сво-:
боды. Если производится расчет сложной стержневой конструк-.
ции, то одни виды движения могут переходить в другие виды в пе-~
рекрестиях стержней.
2. Гипотеза плоских сечений, как и гипотеза прямых нормалей,
применяется для получения уравнения йзгибных колебаний
стержней в двух направлениях у и г. В соответствии с этой гипотезой
"сечения стержня могут не только смещаться в этих
направлениях, но и поворачиваться относительно этих осей, причем углы
поворота сечений <р* и ц>у не будут равны углам наклона середин-,
ной оси стержня. В то же время повороты сечений и прогибы
будут связаны между собой общей системой уравнений: прогиб w с
поворотом <pj/, а прогиб v с поворотом <p«. Каждый элемент стерж-:
ня будет иметь шесть степеней свободы. :
3. Разложение перемещений в ряд по полиномам Лежандра..
учитывает искривление сечений стержня при изгибах в двух
плоскостях. Для этого перемещения представляются в виде разложе-,
ния в двух направлениях: ч J
+ j) (»+ у)«.Лto)*.<*); л.
+ у
2 2
- 2 2 [т + 4") (л+ т)
Формальный переход от трехмерных уравнений (8.1) к
одномерным уравнениям для стержней приведен в [11]. В результате
в (8.10) ^получается система из Зтп уравнений для определения
составляющих итПу vmn и wmn. Для практических расчетов ис-
184
пользуется лишь небольшое число членов разложения, например
^оо, ЗД>оо, #оо, Моь им и Ми, которые соответствуют двум прогибам
(^оо, ^оо), растяжению «оо, углам поворота сечений при прогибах
(moi и Що) и кручению («п)'.
Заметим, что.указанные приемы исключения координат
широко применяются не только при расчетах стержней и пластин, но и
в ряде других задач, например при расчетах мембран,
цилиндрических и сферических оболочек.
Эффект от рассмотренного преобразования можно оценить по
сокращению объема вычислений. Этот эффект может оказаться
небольшим, особенно если учитывать появляющиеся погрешности.
Если же для сформулированной задачи оказывается возможным
цдйти аналитическое решение, то, наоборот, эффект может полу^
читься очень большим, например, если до такого* преобразования
задачу аналитически решать не удавалось.
8.5. ПОСТРОЕНИЕ ТОЧНЫХ И
ПРИБЛИЖЕННЫХ РЕШЕНИИ
С ПОМОЩЬЮ КООРДИНАТНЫХ ФУНКЦИИ
Выбор координатных функций ставит своей: целью
преобразование дифференциальной задачи к алгебраической, т. е. получение
системы разрешающих алгебраических уравнений. Иногда
удается исключить координаты последовательно, представив искомую
функцию, например, в виде произведения -трех координатных
функций: . '
u(x,y,z)~u(x)u(y)u(z). ' ' - . (8.11)
Если для и(х) райдено подходящее аналитическое выражение,
точно или приближенно удовлетворяющее уравнениям и
граничным услрвиям, то после соответствующих преобразований
уравнения координата х исключается* а координаты у п z остаются;
Подобным же образом иногда можно исключить и координаты у п z.
Тогда дифференциальные уравнения преобразуются в систему
алгебраических уравнений, в которых нет переменных х> у, г.
Неизвестными в этих уравнениях являются некоторые параметры,
которые эходят в координатные функции, например амплитуда
колебаний, максимальные перемещения при стационарном -йагру-
жении или другие величины. Нет общих рецептов построения
координатных функций. Имеются только отдельные удачные-случаи,
в которых такие функции удается построить. Рассмотрим один из
них —когда приближенное решение представляется в виде
суперпозиции частных решений* каждое из которых точно,
удовлетворяет дифференциальным уравнениям и граничным условиям. Этот
случай встречается, например, при рассмотрении свободных
колебаний конструкции после удара. Частное решение при этом удобг
но представить в виде собственной формы колебаний.
¦ * ¦ Ш
Пример.. Предположим, конструкция, включающая в себя упругий стержень'-
(рис. 8.9), движется вертикально вниз с постоянной скоростью v (см. рис. 8.9,ЩУ
и в момент /=0 встречает на своем пути жесткую преграду (см. рис. 8.9,6);^
Тогда крепления конструкции, в данном случае — концы упругого стержня,
останавливаются, а центральная часть между опорами продолжает двигаться. Если.,
точки опоры остаются неподвижными, стержень совершает сложные свободны^/;
изгибные колебания. Необходимо рассчитать эти колебания стержня после уДа*,<
ра. Поскольку все точки стержня двигались равномерно, а за начало отсчета I,
времени принят момент остановки- опор, то при f=0 премепдения всех точек |
были р^авны нулю, w(xt 0)=0, а скорости были постоянными:
dw(x,0) ^^ ¦ . -
di
Для свободных изгибных колебаний стержня, шарнирно закрепленного, по j
краям, частное решение уравнения D.47) получается в виде стоячей волна*/
где т0 — масса единицы длины стержня.. «. 4^
•Это частное решение точно удовлетворяет дифференциальному уравнению/
и определяет, собственную форму и частоту колебаний. Если длина волны > /§*.
выбрана такой, что точно удовлетворяются условия закрепления на концам"I
стержня, то волновре число ki принимает следующие значения: -;*¦ J
где L —длина стержня; пх —число полуволн, укладывающихся по длШге^
стержня. . . - . * -Щ
Поскольку уравнение D.^) является линейным, точным решением уравн||*|
.ния .будет и суперпозиция частных решений (8.12). *Ерли эти частные решейй^|
, представляют собой собственные формы, то получаем )^|
(8Л1
Амплитуды колебаний Wm, должны быть выбрдны такими, чтобы удовле#|
-ворялись начальные условия. Поскольку при /=0 sino)*?=0, то первое ^
рыполняется автоматически. Для удовлетворения второго условия необходим^;;
выражение (8.13) продифференцировать по времени и подобрать амплитуд^
' Ч,
xff) Рис. 8.9. К расчету изгиф|
^' . . ных колебаний стержня прй|
f ' ;- ударе-. .. . Т|
186 . '4
колебаний так, чтобы при любом значении х в начальный момент времени
удовлетворялось условие
dw/dt=v. _ \ ' (8.14)
' Если взять бесконечное число членов разложения (8.13), то условие (8.14)
можно удовлетворить точно* как я при разложении прямоугольных импульсов
в ряд Фурье. Если ограничиться небольшим числом ^членов, то начальные
условия будут удовлетворяться приближенно.
Укажем два случая определения амплитуд Wm;
Первый случай. Ограничимся в разложении п членами и возьмем
по длине стержня п произвольных тЬчек х\у Х2, ..., хп. Потребуем, чтобы в
каждой точке начальные условия удовлетворялись точно, например для точки х\\
гнх]=1>. " ;. ' (8.15)
В уравнении (8.15) <о**, kit xj определены. Неизвестными здесь
являются Wm . Поскольку таких уравнений будут п и-неизвестных также л, можно
решить систему уравнений и найти амплитуды составляющих собственных форм.
Второй случай. Можно при выбранном п поставить условие
наилучшего приближения начальных условий в приближенном решении к начальным
условиям задачи. В качестве критерия наилучшего приближения можно выбрать
интеграл - . *
i
"где А(х)-~ отклонение.начальной скорости в приближенном решении от точного
значения v для точки с координатой х;' * ' - . *
•л«пЬм0. - (8.17)
Задача теперь состоит в том, чтобы выбрать такие значения амплитуд Wm^
чтобы интегральная погрешность в была минимальной. Для этого в
соответствии с методом наименьших квадратов нужно продифференцировать критерий 0
по. каясдой искомой-амплитуде Ш^да и приравнять производные нулю. Техника
"вычисления в "данном случае; достаточно проста и. не представляет интереса.
Однако при вычислении .можно сужественно использовать свойство ортогоналъ-
¦ ности собственных форм колебаний. В данном случае свойство
ортогональности состоит а ТОМ,ЛТО /' , ' . .
}xdx =
\ «Свойство ортогональности позволяет вычислять "ампли1уды независимо
от друга, не решая систему- уравнений. В данном случае амплитуду ^щ мож-
, jfto формуле \; ./ ....
j
где i —номер гармоники» i=l, 3, 5, .... .
В силу симметрии задачи четные гармоники в разложение не вошли; С
растанием номера гармоники соответствующие амплитуды быстро уменьшаются¦}
Поэтому выбирать в разложении большое число членов не имеет смысла. V.,
Рассмотренный прием разложения свободных колебаний" по собственнйЦ^
формам целесообразно использовать только в тех случаях, когда собственны^
формы легко получить в виде простых функций. * ^;-
•- • - ¦. -:"•:.¦ - •- - ' а
8.6. ОСРЕДНЕНИЕ ХАРАКТЕРИСТИК Щ
НЕОДНОРОДНЫХ ОБЛАСТЕЙ КОНСТРУКЦИЙ
В РЭС часто используются конструкции, включающие в се^
множество деталей. Например, на поверхности плат располагавши
ся множество навесных элементов. Каждый элемент (найриме^
микросхема) крепится к плате с помощью выводов, занимающей
некоторую площадь. Если считать выводы недефармируемыми, тзЫ
эти. элементы Можно рассматривать как дополнительные массМ^
которые нужно учесть в расчете. Поскольку навесные элемен^!
могут располагаться на плате неравномерно и иметь разные май
су, при построении расчетноймодели можно представить, что пл jt**
та состоит из отдельных участков с различными распределении^
ми массами. Такой подход используется при численных расчеа^
вибравдй плат с навесными элементами; При поиске'
ского решения в такой постановке необходимо записать ффр^
циальное уравнение для каждого участка. В результате нуж|
найти отдельные решения каждого уравнения и «сшить» эти
шения по промежуточным граничным условиям. Такой подхс
практически невозможен. Поэтому используют прием осреднея
(«размазывания»), массы навесных элементов по поверхнос
платы. & результате приходят к одному уравнению изгибных
лебаний, которое решается * аналитическим методом. Если реш
ние.точно удовлетворяет граничным условиям и новому диф(
ренциальному уравнению, то оно будет решением новой задал
колебаний однородной: платы. Первоначальная же задача буд€Я
решена приближенно. Качество приближения оценить в данной|
случае трудно,, Можно получить некоторые представления о пЩ
грешностях только при сравнении численного решения первой^;;
чальной задачи и аналитического решения. \hx
Опыт показывает, что при таком осреднении получается хорб^
шее совпадение, с точным решением при сравнении интегральный
характеристик движения,, например резонансных частот колеб^|
ний. Осреднение по площади платы массы одинаковых элементов
занимающих всю поверхность платы, дает совпадение с эксперй?!
I
ментом с точностью в несколько процентов. Если элементы* разные
и занимают не всю поверхность платы, то погрешность по частоте
первой грамоники может составлять до десяти процентов, что так^
же, как правило, приемлемо. Однако отдельные характеристики
движения в различных точках могут отличаться значительно.
Например, осреднение может привести к отклонению амплитуды
перегрузок в разных точках в несколько раа.
Подобный прием осреднения может использоваться при
рассмотрении неоднородных структур с точки зрения их. упругих
свойств, например при. вычислении коэффициентов жесткости..
8.7. ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ
В ВИДЕ СТЕПЕННЫХ ПОЛИНОМОВ
Выше было рассмотрено представление решения в виде тригонометрических
функций. Эти функции удобны тем, что с их помощью можно легко
представить решения для прямоугольных пластин, если пластины закреплены жестко
или шарнирно. Если же края пластины закреплены в отдельных точках,
например в углах (рис. 8.10), то получить даже приближенное решение с помощью
тригонометрических функций трудно. В отдельных случаях более удобно
представление решения в виде степенных полиномов. .-
Пример. Плата, закрепленная по углам, является частью конструкции,
которая движется равноускоренно в направлении нормали к поверхности платы.
Уравнение изгиба при статическом нагружении платы силами инерции
имеет вид
дх* "*" дх*ду*
<? )
(8.19)
где р — плотность материала; h — толщина платы; аг — постоянное ускорение.
Представим искомое решение в виде двухмерного степенного полинома
W
Это решение должно удовлетворять
уравнению (8.19) и граничным условиям. В /точках
крепления платы (см. рис.. 8.10) возьмем
условия для шарнирного крепления, когда
перемещения о>*=-0 и оба изгибающих момента вокруг
осей, параллельных х, у, равны нулю. На
остальных краях платы нужно задать условия для
свободного края, т. е. считать равными нулю
изгибающие моменты и предыдущие силы.
Удовлетворить уравнению и граничным
условиям по всей области платы и ее контуру с
помощью, степенного полинома не удается.
Поэтому зададим несколько точек на поверхности и
(8.20)
15
0
X
w
Рис. 8.10. Пластина,
закрепленная в угловых
точках
189
краях и. потребуем, чтобы в этих точках выбранный полином точно удовлетно-у^
рял уравнениям и граничным условиям. : -:",
В ч:илу симметрии задачи относительно осей хну все члены полинома с -
нечетными степенями обращаются в нуль. Дли простоты будем считать, что
уравнение должно удовлетворяться только в одной точке —в начале
координат (х*=0, #=0). Подставив полином (8.20) в уравнение (8Л9), получим :*¦
/)[24Л4о+8Л2?+24Ло4]=рЛ#*- (8.21)
Для. удовлетворения граничных условий в точках шарнирного закрепления^
рассмотренный полином должен удовлетворять следующим условиям: . ?|
т
^^O при х=*а,у=*Ь. . ; ')
1=0 /«О , : "¦ i
« - -
Кроме того, чтобы изгибающие моменты в тех же точках были равны ну.г
лю, лбложим . . . -.:
т. е,
t - V
-22^V/</-l)^2«0, (8.23)
где t«0,2,4, ...; /-0, 2,4 ^ ^
. Условия симметрии приводят к тому, что уравнения (8.22), (8.23) гарант^
руют удовлетворение граничных условий ^ в остальных трех точках шарнирно^
закрепления. . ч I
Для удовлетворения граничных условий на свободных краях выберем !
точки (я=а, ^=0), (jt=O, у—Ь). Будем считать изгибающие моменты и
резывающие силы в этих точках-пропорциональными соответственно второй
третьей производной по координате, нормальной границе. Тогда в точке (х^
т. е.
izss0 ¦ . ' .,..'.... •¦V*-
190 " . ^
а в точке *=0, у*=Ь у ' .--"'- • ;
2 О,
где (,/-0,2,4,...". .
Таким образом, мы получили восемь уравнений для определения
неизвестных коэффициентов. Поэтому в разложении (8.20) нужно сохранить восемь
членов с четными локазателями степеней ухну. Требование симметрии при*
водит к единственному возможному варианту:
Х2уА. — - ; (8.24)
Решая, полученную систему относительно неизвестных коэффициентов,
получаем ~ < .
Лоо=— 3/7Sa2b29 А22 = В,
где В=*р_ка, а остальные коэффициенты равны нулю.
Приближенное решение задачи, буд^т иметь вид
— 2А2О- 2 2 2 2 4 2
lb2 ^
V). (8.25)
Полученное решение будет точно удовлетворять уравнению или граничным
.условиям только в указанных, выше точках. В. других- точках платы-Пол учен-
• ное решение не будет точно удовлетворять уравнению или граничным
условиям. Однако это решение будет точно удовлетворять решению некот:©рой другой
видоизмененной задачи, в которой правая часть уравнения и граничные уело-
вйя будут отличаться от исходной задачи. Пробные расчеты показывают, что
наибольшее отличие правых частей в исходной и видеоизмененной задачах по-
лучается в угловой точке платы (я=а, у=6). Если подставить полученное
решение (8.25) в левую часть уравнения. (8.19).. при *=а, у^Ь^. то левая часть
будет равна
т. е. в видоизмененной задаче правая часть будет*в A/7)[И+3(а4+&4)/а2&2] раз
больше, чем в исходной задаче. Если считать такое приближение грубым, то
можно повысить точность решения за счет Осложнения расчета. Введем в
рассмотрение еще один член в разложении (8.20), т. е. Представим решение
в виде - l . ~ - * -
W=Aoq + A20X2 + Aq
Потребуем, чтобы это решение точно удовлетворяло уравнению в угловой
точке (х=*а, у**Ь). Тогда появится дополнительное уравнение в системе разре-
* I 191
шающих уравнений. Решение системы для упрощенного случая -квадратной
платы (а=Ъ) будет иметь вид
±в1_
31 Ь4
31 »«. 31
Теперь максимальное расхождение левой и правой частей уравнения можно ,
ожидать в точке (а, 0) или @, а). Подставив решение в уравнение, получим.
в правой части -*• B3/31 )рНа. Таким образом, расхождение уменьшается. . |
' Если с целью дальнейшего уточнения решения потребовать точного удоз- ~\
летйорения уравнения в точках.(а, 0) и @, а), то в решение нужно ввести еще^
два члена, которые.не обращаются в нуль в этих координатах.. Такими членами ,
будут Лео*6 и Amtf* Решение новой системы уравнений имеет,вид 1
4
540 . а2 ' 540
Максимальное расхождение левой и правой частей ожидается в точке ^
х**у**а/2. Это расхождение составляет 0,031 Ард^ . ;;
Полученное решение в виде степенного полинома, содержащего 11. членов, <
может быть точным решением задачи, в которой масса платы распределена к
неравномерно (например, в точке (а/2, а/2) масса меньше, чем в центре на й
3,1%). Поскольку эта масса незначительна, можно считать исходную и видо-J
измененную задачи достаточно близкими друг к другу и утверждать* что по- Ц
лученное8 приближенное решение имеет достаточную точность. Картина функ- \
ции прогиба приведена на рис. 8.11. Цифры на рисунке обозначают значения
прогибов в относительных единицах. ;*
Таким образом, увеличивая число членов степенного полинома (8.20), мож"- |
но повышать точность решения до тех пор, пока исходная и видоизмененная *,
задачи не будут близкими друг к другу, :
Рис. 8.11* Прогиб пластины,
закрепленной в угловых точках
192
Заметим, что представление решения в виде степенного полинома дает
хорошие результаты в том случае, когда искомая функция не содержит резких
перепадов. Например, если в какой-либо точке платы приложена большая
сосредоточенная масса, то искать решение в виде степенного полинома
нерационально, поскольку даже при большом количестве членов полинома трудно
Судить о близости исходной и видоизменённой задач. ^
Мы рассмотрели только ограниченный класс задач и методов их решения
применительно к линейным задачам и простой форме конструкции. Для
приближенных аналитических расчетов конструкций более сложной формы
разработан деетод /^-функций [18], который можно рекомендовать для решения
стационарных задач. Применение /^-функций приводит к достаточно сложным
аналитическим выражениям. Однако затраты на решение задач оправданы тем>
что значительно расширяется круг задач, имеющих аналитическое решение.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Опишите сравнительные достоинства и недостатки аналитических и
численных методов расчета вибраций радиоаппаратуры.
2. Как задаются граничные и начальные условия?
3. Какие" основные гипотезы позволяют упростить задачи?
4. В каких случаях используется осреднение- характеристик неоднородных
конструкций?
б, В каких случаях и каким образом используется представление решения,
в виде степенных полиномов? ' '
13-1215
ПРИЛОЖЕНИЕ 1.
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
НЕКОТОРЫХ ВИБРОИЗОЛЯТОРОВ
Тип
виброизолятора
AHL-6
АН-10
АН-15
АН-30
АН-бО
АП-1-0,45
АП-1-1,80 * *
АП-2,2,70
АП-2-4,50
. АП-3-9
АП-3-11,35
Номинальная
нагрузка,' Н
-у
Прогиб, мм
Коэффициент
жесткости.
с\
Резинометаллические стержневые
60
100 .
150
300
500
1,6±0,4
* (для всех
видов)
40
65
95
' 185
310
Резинометаллические пластинчатые
.4,5
18
, -27 '
45
90
112,5
—
• -4
Резинометаллические судовые со
АКСС-10
АКСС-15
АКСС-25
АКСС-60
АКСС-85 ч
АКСС-120 - .
-.
АД-0,*
АД-1,5
АД-3
АД-5
АД-10 ""
АД-15
100
150
250
. 600
850
1200
0,8 •
0,8
0,9
1,1
1,4
1,3
2,5
11,5
17;2
28,6
57
•< 70
Н/мм*
С2
9,3
45
25
-46 *
80Г -
10
22,8
34,2
. 60
. 140 .
160
страховкой
120
170
280
430
610
920
110
150
250
380
540
830
Тружинные с воздушным демпфированием
3,06.., 6,12
10,2.,
15,3..
30,6..
71,4..
102..
. 15,3
.30,6 .
.51,0
.102 *
.153
2,5... 5,5
5,5... 7,5
4;0... 7,0
5,0... 7,5
5,5... 7^5
5,5... 8,0
1,2
2
4
7
12
19
'-
—
—
—
—
Пружинные с фрикционным демпфированием
АПН-1
AftH-2
АПН-3
АПН-4
АПН-5
АПН-6
5... 10
9,8... 24,5
19,6. ..49
39,2... 68,7
58,9... 98,1
88,3 ... 147,2
Цельнометаллические <
АЦП-30-0,6/10,
АЦП-33-2/10
АЦП-35-3/9
АЦП-38-7/9
АЦП-43-12/9
АЦП-48-20/10
5.,.15
• 10.
25,
40.
90.
1зо:
..30
..45
.. 100
..150
..360
—
—
—
—
.—
zo структурным
—
•—
— .
—
6,8
13,7
. 22,5
32,3
49,0
58,8
—
¦ —
. —
—
демпфированием
—1
—
*—
Масса» кг
* 0,012
0,012
0,038
0,038
0,046
0,007./.
0,008 ;
0,027...
0,028
0,068...
0,083
0,172
0,213
0,213
0,702
1,165
1,57
—
¦ —
—
—
—
0,041
0,074
0,079
0,126
0,135
0,225
—
—
194
АТ-6,5
АТ-8
АТ-Ю
АТ-13
АТ-17
6,5
80
100
130
170
Тросовые
0,15
0,15
0,22
0,23
0,27 .
• сх — жесткость в продольном направлении; с2 — жесткость в
поперечном-направлении. ' v
ПРИЛОЖЕНИЕ 2.
^ НАЗНАЧЕНИЕ И СТРУКТУРА ПАКЕТА
ПРИКЛАДНЫХ.ПРОГРАММ ПО РАСЧЕТУ
СЛОЖНЫХ ВИБРО- И УДАРОПРОЧНЫХ
КОНСТРУКЦИЙ РЭА .
Функциональное назначение пакета прикладных программ.
Специализированный пакет прикладных программ (ППП) предназначен для решения при,
кладных задач конструкторского проектирования — задач расчета динамических
характеристик объемных пластинчато-стрежневых конструкций нестационарной
РЭА при воздействии на них вибраций и ударов. Пакет обеспечивает
возможность проведения следующих видов расчетов:
расчет первой собственной формы и резонансной частоты колебаний
конструкции; . .. •
- расчет перемещений заданных точек (узлов) модели конструкции при
действии на нее вибраций и ударов; ,
расчет ускорений и перегрузок в заданных" точках (узлах модели);
>% расчёт напряжений и определение коэффициентов запаса прочности для
заданных,сечений конструкции.
Конструкция может быть закреплена произвольным способом. Блок-схема
ППП приведена на рис. П2.1. >
Состав пакета прикладных программ. Пакет состоит из расчетных и
обслуживающих программ. Основная программа осуществляет ввод исходной
информации. Данные о конструкции составляются пользователем, *
• Подпрограмма дискретизации производит разбиение конструкции на
дискретные элементы и формирует таблицу узлов (номера узлов и их координаты).
Подпрограмма формирования узлов закрепления выбирает из множества
узлов те, которые относятся к области закрепления. При расчете в эти узлы зд-
даютсл перемещения в соответствии с законом движения транспортного
средства или вибростенда.
Подпрограмма формирования узлов контроля выбирает из множества узлов
те, которые входят в выбранные конструктором области и в которых
необходимо определять напряжения, ускорения (перегрузки).
Подпрограмма вычисления характеристик дискретных элементов модели
13* ' - • ; 195
Начало
Подпрограмма дискретизации
Подпрограмма формирования
• у злоб " закреплений
Печать
Печать
Подпрограмма вычислений
характеристик элементов модели
Печать
Подпрограмма формирования
узлов контроля
Печать
Ь
Подпрограмма формирования
матрицы жесткости
Ь
Подпрограмма формирования
матрицы демпфирования
Подпрограмма формирования
инерционной матрицы
h
Подпрограмма моделирования
ударов и вибрации, определения на-
прятений перегрузок .
Подпрограмма
формирования контрольных
Подпрограмма расчета
резонансной частоты определения
напряжении, перегрузок
Подпрограмма контроля
результатов.
Печать результатов
Рис. П2.1: Блок-схема ППП для анализа виброударочных конструкций
определяет для каждого элемента моменты инерции сечений, массу и момент
инерции элемента.
Последующие подпрограммы формируют матрицы жесткости,
демпфирования, инерционную матрицу (матрицу обобщенных масс). Этим "заканчивается
построение расчетной модели конструкции.
Далее, в зависимости от задания, сформулированного' конструктором,
производится моделирование процессов ударов, вибрации или определение первой
196
резонансной частоты и формы колебаний конструкции. Ё обоих случаях
вычисляются напряжения, перегрузки в узлах модели.
Подпрограмма контроля. результатов производит сравнение расчетных и
предельно допустимых параметров (напряжений, перегрузок), определяет-запас
прочности конструкции..
Как правило, задачи расчета нестационарных процессов требуют большого
объема вычислений. С целью 'защиты от возможных сбоев введена
подпрограмма формирования контрольных точек, позволяющая в заданные контрольные
моменты времени фиксировать промежуточные результаты расчета и в случае
:боя возобновлять расчет с последнего фиксированного результата. Кроме того,
зто дзет возможность производить расчет в несколько этапов.
ПРИЛОЖЕНИЕ 3.
ЗНАЧЕНИЯ РЕЗОНАНСНЫХ ЧАСТОТ ПЛАТ
ПРИ РАЗЛИЧНЫХ СПОСОБАХ ЗАКРЕПЛЕНИЯ
В Приложении приведены некоторые результаты, сравнение расчетные и
экспериментальных данных определения первых двух- резонансных частот коле-,
баний плат. . - .
Таблица П3.1. Сравнение расчетных и экспериментальных данных
определения первых двух резонансных частот колебаний плат с
радиоэлементами
Схема закрепления
Размер, мм
Резонансная частота, Гц
расчет
эксперимент
Относительная
погрешность
i Af*
+
+
>
i
+
1
nr
120X80X1,5
229
362
240
290
0,046
0,260
120X80X1,5
140X87,5X1,5
300
334
341
402
310
330
480
445
0,032
0,012
0,280
0,188
197
В табл. П3.1 приведены результаты расчета первой и второй резонансных
частЬт для плат, закрепленных четырьмя и пятью винтами, а также для платы
с разъемом, закрепленной тремя винтами. Расчеты проведены на персональной
ЭВМ «Искр а-10.30 М» с помощью специализированного программного
комплекса REPLAT. Здесь же приведены экспериментальные данные и относительная
погрешность. '" ¦ .
ЗАКЛЮЧЕНИЕ
Рассмотрены вопросы разработки и совершенствования
конструкций, вибро- и ударопрочной РЭА и ЭВА. Успешное решение
этих вопросов зависит от развития: .
принципов конструирования аппаратуры, устойчивой к
механическим воздействиям;
методов расчета механических процессов в конструкциях;
методов экспериментального исследования механических про^
цессов. . . .
Трудно предвидеть пути развития, но некоторые перспективы
вырисовываются уже теперь.
В развитии принципов конструирования можно указать на
следующие тенденции: ' *
1. Дальнейшая интеграция аппаратуры на базе
микроэлектронной технологии. Получение монолитных сложных структур,
в частности монокристаллов.
2. Разработка равнопрочных конструкций. Хорошие модели
таких конструкций можно наблюдать в окружающей природе.
Деревья, например, являются „в определенном смысле
равнопрочными конструкциями.. Годичные кольца деревьев в виде
концентрических цилиндрических поверхностей, осевая симметрия плодоз
цитрусовых, переплетения волокон в корневой системе могут
натолкнуть конструктора на новые идеи создания несущих
конструкций.
3. Разработка средств защиты аппаратуры от механических
воздействий, и прежде всего средств активной защиты. И здесь
хорошие модели можно найти в живой природе. -
Развитие методов расчета связано с развитием
вычислительной техники и методов вычислительной математики, Разработка
и совершенствование систем автоматизированного проектирования
вибро- и ударопрочной аппаратуры (САПР) связаны с решением
следующих вопросов: — -
* совершенствованием расчетных моделей;
повышением надежности вычислений; . _
расширением эксплуатационных возможностей и обеспечением
простоты общения пользователя-конструктора с САПР.
Развитие экспериментальных методов направлено- на;
исследование комплексного воздействия различных дестабилизирующих
факторов (тепла, механики, климатики и др.). Важным вопросом
является автоматизация обработки результатов
198
; список литературы
1. Норенков И. П., Маничев 3. Б. Системы автоматизированного
проектирования электронной и вычислительной аппаратуры. — М.:* Высшая школа,
. 1983. —272 а .
2. Токарев ОД. Ф., Галицкий Е. Н., Фролов В. А. Механические воздействия и
защита РЭА,— М>.: Радио и связь^ 1984. —224 с " . *'
3. Ильинский В. С. Защита РЭА и прецизионного оборудования от динамиче-
. ских воздействий.—М.: Радио и связь, 1982.—295 с.
4. Проектирование датчиков механических величин/ Е. П. Осадчий, Av В.
Тихонов, В. Н. Карпов и др. —М.: Машиностроение, 1979.— 480 с.
5. Карпушин В. Б. Вибрации и удары в радиоаппаратуре.-т-М.: Сов. радио,
1971. —344 с.
6. Конструирование и расчет 'БГИС, микросборок и аппаратуры на. их
основе/ Г. В. Алексеев, В. Ф. Борисов, Т; Л. Воробьева и др. Под ред. Б. Ф. Вы-
соцкого.. — М.:' Радио и связь, 1981. — 214 с. г
7. Феодосьев В. И. Сопротивление материалов.-*-М.: Наука, 1986.-г-512 с.
8. Карпушин Ъ. Б. Виброшумы в радиоаппаратуре. — М.: Срв. радио, 1977. —
320 с.
9. Рощин Г И. Несущие конструкции и механизмы РЭА. — М.: Высшая школа,
1981. —375 с\ .
10. Самарский А. А. Теория разностных схем. — М.: Наука, 1983л—616 с.
11. Маквецов Е. Н. Цифровое моделирование вибраций в
радиоконструкциях.— М,: Сов. радио, 1976.— 120 с.
12. Тимошенко С. П., Гудьер Дж. Теория упругости. — М.: Наука, i979. — 560 с.
13. Андронов А. А:, Витт А. А., Хайкин С. Э. «Теория колебаний. — М.: Наука,
1981. —568 t. ' ' . . , .
14. Маквецов Е. Н., Тартаковский А. М. Дискретные модели приборов. —М.:
Машиностроение,. 1982.—136 с. ' >
15. Парлетт У. Симметричная проблема собственных, значений. — М.: Мир,
1983. —324 с.
16. Уилкинсон Р. Справочник алгоритмов на языке Алгол. Линейная алгебра:*
Пер. с англ./ Под ред. Ю. И. Топчеева. — М.: Машиностроение, 1976.-—
389 с. .
17. Слепян'Л. И. Нестационарные упругие волны.— Л.: Судостроение, 1971. —
386 с. . • . ч " .
' 18. Рвачев В. Л., Слесаренко А. П. Алгебра логики и интегральные
преобразования в краевых задачах. — Киев/ 1976. — 288 с.
ОГЛАВЛЕНИЕ
Предисловие . .*.,,•.«•,«••¦,» 3
Глава 1. МЕХАНИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА АППАРАТУРУ 6
1.1. Вибрации .«*••« , . . . 8
1.2. Удары ..•',...•..,... 10
1.3. Линейные ускорения ...«•..,¦#¦•«••• 18
1.4. Измерение характеристик вибрации # , , , .. , •••'«. 19
L5. Сложные механические воздействия .«,.,.•« • . 22
Глава 2. ОТКАЗЫ И СБОИ В РАБОТЕ АППАРАТУРЫ, ВОЗ-"
НИКАЮЩИЕ В РЕЗУЛЬТАТЕ УДАРОВ И
ВИБРАЦИЙ ...,.,.-. 23
2.1. Изменение характеристик электрорадиоэлементов при их деформации 26
2.2. Разрушение выводов электрорадиоэлементов , . ¦ . ¦ .« * 28
199
2.3. Разрушение деталей несущих конструкций * .'.."„.. 31
2:4. Вйброшумы и наводки • * 33
, Глава 3. КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ БЛОКОВ РЭА НА
АМОРТИЗАТОРАХ ...... 1 .... - 36
3.1. Собственные и вынужденные колебания, блока на амортизаторах . . 36
. 3.2. Удар блока на амортизаторах 43
3.3. Колебания блока на амортизаторах с демпфированием . . . . 47
'3.4. Колебания блока на амортизаторах с сухим трением 53
3.5. Колебания конструкций РЭА при двойной системе амортизации . » 56
3.6. Пространственные колебания блока РЭА на амортизаторах ... 58
Глава 4. - ВИБРАЦИИ СТЕРЖНЕВЫХ КОНСТРУКЦИИ . . 61
4.1. Продольные колебания прямых упругих стержней _ ...... 63"
4.2., Вибрации в виде стоячих волн ....... (« .... 66
4.3/Вибрации в виде бегущих" волн 68
4.4. Удар , ; . . 71
4.5. Аппроксимация, устойчивость и погрешности разностных решений . 75
4.6. Крутильные колебания . . ... . • . .. . ~ . . . . 78
4.7. Изгибные колебания стержня « . . 82
4.8. Изгиб консельно закрепленного стержня ...,..«. 85
4.9. Установившиеся изгибные колебания ....*..... 87
4.10. Распространение ударного импульса . . . . . .i f . . '. 90
4.11. Резонансные изгибные колебания , . . 93
4.12. Расчеты вибраций стержневых конструкций 97
Глава 5. ВИБРАЦИИ ПЛАСТИНЧАТЫХ КОНСТРУКЦИЙ . ' 103
> 5.1. Уравнения изгибных колебаний пластин . . . ... « . . 103
5.2. Свободные колебания пластины ' . ,. . ; 113
5.3. Удар пластины . . 117
5.4. Резонанс плат с навесными элементами 122
5.5. Расчеты вибраций несущих пластинчатых конструкций РЭА . . . 126
Глава 6, АВТОМАТИЗИРОВАННЫЙ РАСЧЕТ ВИБРАЦИЙ И
УДАРОВ СЛОЖНЫХ КОНСТРУКЦИЙ РЭА И ЭВА 129
6.1. Блок построения расчетной модели 130
6.2. Блок проведения численных экспериментов ,,.,.*« 140
6.3. Блок анализа результатов вычислений 148
Глава 7. СПОСОБЫ ПОВЫШЕНИЯ ВИБРО- И УДАРОПРОЧ-
НОСТИ КОНСТРУКЦИЙ РЭА 151
7.1.. Повышение жесткости конструкций -, 152*
7.?. Защита конструкций с помощью амортизаторов и демпферов ... 155
7.3. Повышение прочности конструкций i <\ '. ' . 162
Глава 8. СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ РАСЧЕТА
УДАРОВ И ВИБРАЦИЙ РАДИОАППАРАТУРЫ . . 1§8
8.1. Выбор метода расчета ударов и вибраций аппаратуры .... 168
8.2> Аналитические Методы расчета деформаций конструкций 174 '
8.3. Примеры точных аналитических решений . . . . . . . . 177
8.4. Различные гипотезы, упрощающие задачу расчета'деформаций . . • 180 *
8.5. Построение точных. и приближенных. решений с помощью
координатных функций .; * \ • 185
8.6. Осреднение характеристик неоднородных областей конструкций . . 188
8.7. Представление решения: в, виде степенных полиномов 189
* Приложение 1. Технические характеристики некоторых виброизоляторов . 194
Приложение 2. Назначение и структура пакета прикладных программ по
расчету сложных вибро- и ударопрочных конструкдий РЭА .... 195 f
Приложение 3. Значения резонансных частот плат при различных способах
закрепления » ...... в ..;...... 197
Заключение ....'...* 198
Список литературы •.«..,.¦ * 199
200 • *