А. А. ФРИДМАН
ОПЫТ ГИДРОМЕХАНИКИ
СЖИМАЕМОЙ ЖИДКОСТИ
ОНТИ ПТИ
1934

А. А. ФРИДМАН

А. А. ФРИДМАН
ОПЫТ ГИДРОМЕХАНИКИ
СЖИМАЕМОЙ ЖИДКОСТИ
Под редакцией, с примечаниями
Н. Е. КОЧИНА
с дополнительной статьей
Б. И. ИЗВЕКОВА, Я. А. КИБЕЛЯ,
И. Е. КОЧИНА
ОНТИ ГОСУДАРСТВЕННОЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО
ЛЕНИНГРАД 1934 МОСКВА

Огветсгв. ред. ?. В. Пулъкина Техн. ред. Р. В. Эмдинл
Печать с матриц Статформ. бумаги 62X94 Бум. дистов II1/2
Ленгорлит № 17286 Тираж 3000 экв. Зак. № 4253
2-я типография Издательства Леноблисполкома и Ленсовета
Ленинград, Улиці 3-го Июля, 55.

ОТ РЕДАКТОРА.
Предлагаемая вниманию читателя книга А. А. Фридмана „Опыт
гидромеханики сжимаемой жидкости" была издана в 1922 году
еще при жизни автора (скончавшегося в 1925 году) в
литографированном виде в весьма малом количестве экземпляров. В этой
книге Фридман подверг изучению некоторые фундаментальные
вопросы гидромеханики сжимаемой жидкости, чрезвычайно важные
как сами по себе, так и в виду тех приложений к динамической
метеорологии — науке, трактующей об атмосферных движениях,—
к которым рассмотрение этих вопросов может привести,
В основном текст литографированного издания был оставлен
мною без изменения. Я еще раз проверил все формулы, исправив
замеченные ошибки; в нескольких местах подверг изменению
текст с целью исправления вкравшихся в текст неточностей;
некоторые неупотребительные обозначения Фридмана заменил
более общепринятыми; выпустил несколько примеров, в которые
вкралась та или другая неточность.
В конце книги приложена статья „О некоторых работах,
связанных с «Опытом гидромеханики сжимаемой жидкости»,
написанная мною совместно с И. А. Кибелем и Б. И. Извековым. В этой
статье дается изложение некоторых работ, трактующих о тех же
вопросах, которые изучаются в книге Фридмана, с тем, чтобы
дать читателю ясное представление о том, что сделано в
направлении продолжения работы Фридмана. Мною написаны §§ 1, 2, 3
этой статьи, И. А. Кибелем —§§ 4 и 7, Б. И. Извековым —
§§ 5 и 6.
Н. Кочин.
25 декабря 1933 г.

ПРЕДИСЛОВИЕ.
I.
1. В классической гидродинамике изучаются обычно или
движения несжимаемой жидкости, плотность которой есть некоторая
физическая постоянная, характерная для данной жидкости, или же
такие движения сжимаемой жидкости, в которых давление является
функцией плотности, например движения при постоянной
температуре или частные виды адиабатических (без получения и отдачи
тепла) движений. Указанные нами движения являются
достаточными для тех технических и физических приложений, благодаря
которым развилась классическая гидродинамика.
Существует однако обширный класс физических явлений, до
сих пор еще очень плохо изученный как с экспериментальной,
так и с теоретической стороны, к которым указанные выше типы
движений имеют -сравнительно мало приложения. Мы имеем в виду
обширную область атмосферных движений, в изучении которых
трудности теоретические соперничают с трудностями
экспериментальными. Атмосферные движения являются движениями некоторой
сжимаемой жидкости — воздуха, — по свойствам своим весьма
близкой к идеальному газу. Эта сжимаемая жидкость движется однако
так, что, вообще говоря, давление не является функцией одной
только плотности; стремление применить к атмосферным
движениям представление об адиабатических движениях опровергается
фактом ежедневного притока тепла от солнца в атмосферу и
еженощной потерей тепла лучеиспусканием в мировое пространство.
Имея в виду, что развитие динамической метеорологии—науки,
трактующей об атмосферных движениях, — тесным образом
связано с теоретическим изучением общего случая движения
сжимаемой жидкости, мы поставили себе задачей в настоящей работе
осветить и разработать, насколько это оказалось в наших силах,
некоторые фундаментальные вопросы в области общей
гидродинамики сжимаемых жидкостей.
2. Главнейшее отличие движений, рассматриваемых в
классической гидродинамике, от движений общего типа сжимаемой
жидкости заключается безусловно в характере изменения вихревых
трубок. В классической гидродинамике, когда давление есть
функция плотности, имеют место две основные теоремы Гельм-
гольтца. Первая из этих теорем утверждает, что жидкая вихревая
трубка остается при движении жидкости вихревой трубкой,
5

состоящей из тех же самых жидких частиц; вихревая трубка
сохраняет, так сказать, свою индивидуальность. Вторая теорема
Гельмгольтца говорит, что напряжение вихревой трубки не
меняется при движении жидкости с течением времени. Для общего
движения сжимаемой жидкости обе эти теоремы Гельмгольтца
перестают быть справедливыми; вихревые трубки разрушаются, образуя
новые вихревые трубки, и напряжение трубок меняется с течением
времени при движении общего типа сжимаемой жидкости.
Это обстоятельство наиболее рельефно сказывается в том, что*
в противоположность теореме Лагранжа, в сжимаемой жидкости
могут иметь место движения, при которых возникают и
разрушаются вихревые трубки, хотя бы действующие при этом
внешние силы имели консервативный характер.
Вполне естественно, что первым вопросом, возникающим у
изучающего движения сжимаемой жидкости, является вопрос о
законах разрушения вихревых трубок и о законах изменения
напряжения этих трубок. Разработке этого вопроса, вопроса чисто
кинематического характера, посвящена первая часть нашей
работы, носящая название „Кинематика вихрей".
3. Если мы обратим внимание на метод получения теорем
Гельмгольтца, то без труда заметим, что в обеих этих теоремах
есть две части: первая, так сказать — кинематическая часть,
характеризующая те соотношения между слагающими скорости и их
производными по времени и координатам (подобные величины
будем называть кинематическими элементами движения), которые
должны быть выполненными, чтобы теоремы Гельмгольтца имели
место; и вторая, динамическая часть доказательства теорем
Гельмгольтца, заключающаяся в установлении справедливости
указанных выше условий, связывающих кинематические элементы,,
путем использования уравнений гидродинамики и исключения
из этих уравнений давления, плотности и их производных по
времени и координатам, величин, которые можно назвать
динамическими элементами движения.
С этой точки зрения три уравнения Гельмгольтца, из которых:
вытекают обе его теоремы, можно, по крайней мере для случая
несжимаемой жидкости, рассматривать как условия, налагаемые
на кинематические элементы движения для того, чтобы можно
было подыскать давление и плотность, удовлетворяющие всем
уравнениям гидродинамики. Иначе говоря, три уравнения
Гельмгольтца можно для случая несжимаемой жидкости рассматривать
как необходимые и достаточные условия динамической (а не только-
кинематической) возможности движения.
Рассматривая общий случай движения сжимаемой жидкости*
мы, следуя указанному кругу идей Гельмгольтца, должны
поставить себе два вопроса. Первый вопрос будет касаться условий
динамической возможности общего движения сжимаемой жидкости..
Вопрос этот заключается в установлении тех условий, коим
должны удовлетворять кинематические элементы движения для
того, чтобы можно было найти давление и плотность, удбвле-
6

творяющие всем уравнениям гидромеханики сжимаемой жидкости.
Исследуя этот вопрос, мы в самом процессе разработки его
приходим ко второму вопросу, а именно к вопросу установления
связи между величинами, характеризующими изменение вихревых
трубок, и динамическими элементами движения.
Этим двум вопросам: вопросу об условиях динамической
возможности движения сжимаемой жидкости и вопросу о связи
величин, характеризующих изменение вихревых трубок, с
динамическими элементами движения—посвящена вторая часть настоящей
работы, озаглавленная нами „Динамика сжимаемой жидкости".
4. Одно из крупнейших отличий задач, разбираемых в
классической гидродинамике, от задач, относящихся к общему случаю
движения сжимаемой жидкости, заключается в числе неизвестных
функций времени и координат, подлежащих определению. В
классической гидродинамике таких функций четыре: три слагающие
скорости по координатным осям и четвертая неизвестная
функция— давление; если мы имеем дело с несжимаемой жидкостью,
то плотность является величиной постоянной, а для движений
сжимаемой жидкости, изучаемых в классической гидродинамике,
плотность есть известная функция давления. Само собой
разумеется, что четыре уравнения классической гидродинамики (три
обычные уравнения динамики и уравнение неразрывности), вообще
говоря, достаточны для того, чтобы по начальным и граничным
условиям определить все четыре искомые функции. В случае
общего движения сжимаемой жидкости число неизвестных
функций возрастает до пяти, ибо к трем слагающим скорости по осям
координат и давлению прибавляется пятая неизвестная, а именно
плотность. Четырех условий классической гидродинамики
становится недостаточно для определения указанных пяти неизвестных,
и к этим четырем уравнениям приходится присоединять пятое,
чтобы задача общей гидродинамики сжимаемой жидкости стала
более или менее определенной. Это пятое уравнение, носящее
название уравнения притока энергии, получается с помощью
первого закона термодинамики, т. е. закона сохранения энергии, из
рассмотрения притекающей к жидкости извне энергии (тепла).
Величина притекающей энергии может зависеть самым
разнообразным способом от кинематических и динамических элементов
движения. Тепло может притекать к жидкости или помощью процесса
конвекционной передачи тепла (теплопроводности), или
посредством лучистого теплообмена частиц жидкости друг с другом
и с внешними телами, или благодаря каким-либо тепловым
процессам, происходящим в соприкасающихся с жидкостью (например
находящихся с ней в механической смеси) телах.
Изучая условия динамической возможности движения
сжимаемой жидкости, мы можем или принять во внимание уравнение
притока энергии, или попытаться, не рассматривая его,
использовать— в целях получения указанных условий динамической
возможности движения сжимаемой жидкости — четыре уравнения
классической гидромеханики. В первом случае мы должны будем огра-
7

ничиться каким-либо специальным предположением о характере
притока энергии в жидкости; при этом, по сложности вопроса,
особенно в случае лучистого теплообмена, результаты такого
исследования будут крайне сложны и громоздки. Во втором
случае мы будем иметь то преимущество, что наши условия
динамической возможности движения сжимаемой жидкости будут
необходимыми условиями динамической возможности движения при
любом способе получения тепла жидкостью. Подобная общность
результата в связи с относительной простотой его заставила нас
в настоящей работе воспользоваться именно вторым путем,
получения условий динамической возможности движения сжимаемой
жидкости. При этом оказалось, что процесс получения указанных
условий позволяет по заданным скоростям динамически
возможного движения определить, вообще говоря, плотность вплоть
до некоторого постоянного произвольного множителя, а
давление— до аддитивно входящей произвольной функции времени.
Первоначально мы имели в виду в настоящей работе коснуться
более подробно вопроса о решении различных задач
гидромеханики сжимаемой жидкости в том случае, когда задан
определенный процесс притока тепла в жидкости. Однако разросшийся
слишком размер первой и второй части нашей работы заставил
нас ограничить свою задачу и выделить указанное изучение
движений при заданном притоке энергии в особую работу *).
Этого вопроса о движении с заданным притоком энергии мы
лишь отчасти коснемся в конце третьей главы настоящей работы.
II.
1. Литература по вопросу о кинематике вихревых трубок
в случае, когда теоремы Гельмгольтца не имеют места, к
сожалению, почти отсутствует. Относительно условий, при которых
справедлива первая теорема Гельмгольтца, имеются некоторые
указания в книге Роіпсагё „Theorie des tourbillons", где говорится
об условиях выполнения первой теоремы Гельмгольтца для вязкой
несжимаемой жидкости. В статье Zorawski „Ueber die Erhaltung der
Wirbelbewegung" **) имеются необходимые и достаточные условия
для того, чтобы выполнялась первая или вторая теорема
Гельмгольтца. Однако до сего времени мы в литературе не встречали
никаких указаний на те величины, которые характеризуют
изменение вихревых линий; что же касается величин, характеризующих
изменение напряжения вихревых трубок, то введенное W. Thom-
воп'ом понятие циркуляции скорости и теорема его об
изменении циркуляции скорости по жидкому контуру при движении
Жидкости дают возможность установить подобную величину,
характерную для изменения напряжения вихревой трубки; эта теорема
*) Условия динамической возможности движения сжимаемой жидкости при
Заданном притоке энергии изучены И. А. Кибелем, который следовал методам
А. А- Фридмана. См. дополнение. Прим. ред,
¦**) Bulletin de Г Academic des sciences de Cracovie, 1900, p. 335.
8

послужила основой для указанной ниже теоремы Bjerknes'a.
Изложению исследования обстоятельств, сопровождающих изменения
вихревой трубки, и величин, характеризующих эти изменения,
посвящена первая часть нашей работы.
В первой главе этой части мы, после указания на основные
для кинематики сплошных средин понятия, излагаем необходимые
и достаточные условия того, чтобы векторные линии
удовлетворяли первой (соответственно, конечно, обобщенной) теореме Гельм-
гольтца.
Как было указано выше, для случая вихревых линий эти
условия были установлены в цитированной только-что работе Zorawski;
мы даем однако иное доказательство этому предложению, более
ясное, по нашему мнению, и более отвечающее тому кругу идей,
который главенствует в развитой нами кинематике вихревых
линий.
Первая глава первой части нашей работы разделена на три
параграфа. В § 1 мы указываем основные для кинематики
сплошных средин понятия; понятия эти хорошо известны в
классической гидродинамике, поэтому мы лишь кратко о них упоминаем.
§ 2 посвящен установлению условий, необходимых и достаточных
для того, чтобы первая теорема Гельмгольтца имела место, или,
как мы говорим, для того, чтобы векторные линии данного поля
векторов обладали свойством сохраняемости. В § 3 первой главы
мы перечисляем главнейшие понятия и формулы векторного
анализа, нужные нам в дальнейшем изложении; параграф этот является
вспомогательным в нашем исследовании, поэтому мы ведем в нем
особую, жирным шрифтом, нумерацию формул, причем в
большинстве случаев мы указываем формулы без доказательства их.
Необходимость ввести в наше изложение этот параграф
вытекает из двух соображений: прежде всего до сего времени
обозначения векторного анализа далеко еще нельзя считать
установившимися и общепринятыми; далее для последующего изложения
нам оказалось необходимым ввести некоторые новые векторные
символы и правила операций с ними, облегчающие исследование
движений сжимаемой жидкости.
По поводу применяемого нами в настоящей работе векторного
анализа уместно будет сделать следующее замечание. Первоначально
в работе своей мы им не пользовались; однако вскоре мы
убедились, что язык векторного анализа не только значительно
сокращает вычисления и формулировки теорем, но и дает
возможность вести исследование в симметричной форме, постоянно
имея в виду не случайные особенности выбранной координатной
системы, а существо дела — движение жидкости.
Само собой разумеется, что все вычисления нашей работы,
проведенные помощью векторных обозначений, можно было бы
выполнить и без помощи векторного анализа; однако усложнения,
которые при этом обнаруживаются, будут весьма значительны.
2. Вторая глава первой части нашей работы посвящена
изучению изменений вихревых линий и тех величин, которые эти изме-
9

нения характеризуют. Рассматривая два последовательных момента
времени, мы для данной жидкой частицы обращаем внимание
на три направления: направление вихревой линии к первому
моменту, направление жидкой линии, в которую ко второму
моменту времени перешла наша вихревая линия, и направление
вихревой линия ко второму моменту; условимся эти тр&
направления называть направлениями старого вихря, жидкой линии
и нового вихря. В общем движении эти три направления образуют
триэдр, который при наличии условий первой теоремы Гельм-
гольтца вырождается в плоский угол, ибо новый вихрь совпадает
с жидкой линией. Плоские и двухгранные углы этого триэдра
служат нам для установления тех величин, которые характеризуют
изменения вихревых линий; при этом, чтобы охарактеризовать
изменение вихревых линий к данному моменту, мы рассматриваем
предельный триэдр, когда второй из рассматриваемых моментов
стремится к первому, данному моменту времени. Двухгранные
углы триэдра стремятся в этом случае к некоторым конечным
пределам, тогда как плоские углы стремятся всегда к нулю»
Поэтому мы рассматриваем не пределы плоских углов, а пределы
их отношений к протекшему между первым и вторым моментами
промежутку* времени. Таким образом нами вводятся четыре
характерные для изменения вихревых линий величины: отклонение
вихря, образуемое пределом отношения угла между новым вихрем
и жидкой линией к протекшему промежутку времени; изгиб" вихря,.
образуемый пределом отношения угла между старым вихрем
и жидкой линией к протекшему промежутку времени; -уклон вихряг
образуемый пределом отношения угла между старым и новым-
вихрем к протекшему промежутку времени, и наконец кручение
вихря, являющееся пределом двухгранного угла нашего триэдра
при ребре жидкой линии.
Само собой разумеется, что движение, в котором имеет место
первая теорема Гельмгольтца, необходимо обладает отклонением
вихря, равным нулю; оказывается однако, что это условие является
условием не только необходимым, но и достаточным для
выполнения первой теоремы Гельмгольтца. Таким образом движение,,
в котором имеет место первая теорема Гельмгольтца, является
движением, в коем один из элементов нашего триэдра обращается
в нуль, а сам триэдр вырождается в плоскую фигуру; м» позволим
себе назвать это особое с общей точки зрения движение — гелъм-
голътцевым. Оно является первым в ряду тех специфических
движений, в которых указанный выше триэдр вырождается в
плоскую фигуру и которые рассмотрены нами с известной подробностью
в соответствующих местах второй главы.
Рассматривая вопрос об изменении напряжения вихревых
трубок, мы сталкиваемся с двумя точками зрения. Одна, классическая
точка зрения известного мемуара Гельмгольтца о вихрях,
предполагает наличность первой теоремы Гельмгольтца и изучает напряжение
вихревой трубки непосредственно. Другая, развитая W. Thomson'oM,
покоится на понятии о циркуляции скорости и дает представление
10

об изменении напряжения вихревой трубки независимо от
выполнения первой теоремы Гельмгольтца* Мы в соответствующем месте
второй главы развили обе указанные точки зрения, причем
оказалось, что вторая теорема Гельмгольтца может иметь место в
движении, в котором первая теорема Гельмгольтца отсутствует. Мы
позволили себе назвать движения, в которых напряжение вихревой
трубки не изменяется с течением времени — томсоновскимн движе-
ниями, а те движения, в которых имеют место обе теоремы
Гельмгольтца— главными гелъмголътцевыми движениями.
Вторая глава разделена нами на семь параграфов. В § 4 мы
излагаем основные понятия и указываем величины, относящиеся
к изменению вихревых линий при общем движении жидкости.
В § 5 мы изучаем отклонение вихря и условия, при которых
движение будет гельмгольтцевым. § 6 посвящен кручению и, как
оказалось, близко связанному с ним уклону вихря; здесь нами
разбирается особого рода движение, в котором новый вихрь всегда
заключен в плоскости старого вихря и жидкой линии. В § 7 мы
рассматриваем изгиб вихря и связанные с ним особенности
движения. В § 8 мы устанавливаем связь рассматриваемого нами
бесконечно малого триэдра с некоторым конечным тетраэдром,
образованным вектором вихря к данному моменту, и еще двумя векторами:
вектором Н и вектором D, играющими большую роль в кинематике
вихрей; в то же время мы указываем прием, как при помощи этого
тетраэдра можно, зная старый вихрь, построить новый вихрь,—
обстоятельство, имеющее известное практическое значение.
Полезно отметить, что вектор Н в случае движения, расхождение
скорости в котором равно нулю (несжимаемое движение), является
вихрем ускорения данной жидкой частицы, а геометрическая сумма
вектора Н и вектора D во всех случаях совпадает с индивидуальной
производной вихря по времени. Указанными пятью параграфами
исчерпывается наше исследование изменения вихревых линий.
§ 9 второй главы посвящен изучению изменения напряжений
вихревой трубки с тех двух точек зрения, о которых мы говорили
выше; в этом параграфе мы устанавливаем необходимые и
достаточные условия, при которых движение будет томсоновским или при
которых оно будет принадлежать к классу главных гельмгольтце-
вых движений.
Наконец, в § 10 второй главы мы вводим новое понятие о
характеристическом векторе и изучаем приемы его построения.
Характеристическим вектором для данного движения мы называем вектор,
образующий такое поле векторов, что векторные его линии
удовлетворяют в силу данного движения условиям первой теоремы
Гельмгольтца и обладают таким образом свойством сохраняемости.
Характеристический вектор, очевидно, обладает для данного
движения тем интересным обстоятельством, что его векторные
трубки во все время движения сохраняют свою индивидуальность*
В § 10 мы указываем методы отыскания, путем сходящихся для
некоторой области координат и промежутка времени рядов,
характеристических векторов для данного движения.
11

Отметим, что в целях иллюстрации различных положений
кинематики вихрей нами рассмотрен в первой части настоящей работы
целый ряд примеров.
3- Переходя к материалу, заключенному во второй части нашей
работы, отметим, что изучение условий динамической возможности
движения совершенно, поскольку нам известно, не затрагивалось
в литературе- Что же касается связи кинематических элементов
с динамическими, то здесь следует указать прежде всего на работы
Bjerknes'a, установившего связь между изменением циркуляции
скорости по контуру и числом трубок, пересекающих контур и
образованных изобарическими (поверхности равного давления) и
изостерическими (поверхности равного удельного объема)
поверхностями, проведенными через равные интервалы для давления
и соответственно для удельного объема. Это изящное предложение
было, в направлении приложения его к динамической метеорологии,
развито рядом учеников Bjerknes'a и сотрудников его по
Геофизическому институту в Лейпциге.
Далее следует упомянуть о работах Schiitz'a и Silberstein'a,
указавших простые геометрические законы, определяющие влияние
динамических элементов на возникновение вихревого- движения,
иначе говоря — на переход от безвихревого к вихревому движению.
Работами Bjerknes'a и Schiitz'a была между прочим выяснена
возможность образования вихрей под действием консервативных сил,
когда изобарические и изостерические поверхности пересекают
друг друга, т. е- когда давление не есть функция плотности.
Вторая часть нашей работы преследует две задачи. Первая
заключается в определении тех условий, которым должны
удовлетворять кинематические элементы движения, чтобы можно было
найти давление и плотность такие, при которых уравнения
гидродинамики удовлетворялись бы; по нахождении этих условий
надлежит установить метод, с помощью которого по заданным скоростям
можно определить давление и плотность, отвечающие данной
гидродинамической задаче.
Вторая задача состоит в определении кинематических элементов,
а особенно тех, которые характерны для изменения вихревых
трубок, при помощи элементов динамических. При изучении этого
вопроса оказалось, что из двух векторов, характерных для
изменения вихревых трубок,—вектора Н и вектора D,—лишь первый
(да и тот не во всех случаях) выражается через динамические
элементы; для выражения второго вектора, помимо динамических
элементов, т. е. давления, плотности и их производных по времени
и координатам, приходится прибегать к помощи величины притока
тепла в жидкости, величины расхождения скорости и наконец
величины, характеризующей изменение напряжения вихревой трубки.
Первая задача разбирается нами в третьей, а вторая — в
четвертой главе нашей работы.
Третья глава разделена нами на шесть параграфов. §11*
посвящен установлению основных уравнений динамики сжимаемой
жидкости, к числу которых мы- относим и уравнение притока
12

энергии в жидкости; в этом же параграфе мы изучаем теорему
живых сил, дающую при помощи уравнения притока энергии
возможность установить в общих чертах, куда поступает при*
текающая энергия и на что она тратится. Здесь следует
отметить неправильное применение теоремы живых сил, делаемое
в динамической метеорологии: рассматривая изменение энергии
некоторого жидкого объема, исследователи динамики* атмосферы
считают обращающимся в нуль тот член уравнения теоремы живых
сил, который зависит лишь от движения жидкости на границе
рассматриваемого объема; этот член действительно равен нулю
в случае, если выбранный нами объем граничит с твердыми
неподвижными стенками, но он отнюдь не равен нулю в случае, когда
мы имеем дело с объемом, не ограниченным такими стенками, как
это и наблюдается в свободной атмосфере.
§§ 12 и 13 третьей главы касаются установления условий
динамической возможности движения сжимаемой жидкости. Здесь мы
прежде всего рассматриваем (в § 12) общий случай движения,
в котором предполагаем отличными от нуля все величины, в ходящие
в знаменатели наших выражений. Исключение давления из
уравнений гидродинамики дает нам возможность установить вид
уравнении, которым должен удовлетворять удельный объем (или, что
по существу то же самое, плотность) жидкости; это же исключение
дает нам возможность ввести два вектора: динамический градиент,
являющийся разностью вектора действующей на единицу массы
силы и вектора ускорения данной жидкой частицы, и турбулизи-
рующий вектор, являющийся вихрем динамического градиента,
взятого с обратным знаком; этот турбулизирующий вектор играет
весьма большую роль в динамике сжимаемой жидкости. Именно
отличие его от нуля при наличии консервативных сил вызывает
вихреобразование.
Первым условием динамической возможности движения
сжимаемой жидкости является ортогональность динамического градиента
и турбулизирующего вектора; иначе говоря, динамический градиент
должен быть ортогонален своему вихрю, представляясь таким
образом незакручивающимся (по терминологии проф. Н. Е. Жуковского)
вектором. Это первое условие динамической возможности мы
назовем условием незакручиваемости.
Дальнейшее изучение указанных условий приводит нас ко второй
группе уравнений, характеризующих возможность движения;
оказывается, что некоторые векторы, определенным образом
составленные из скорости, динамического градиента и турбулизирующего
вектора, должны быть одинаково направленными; эти векторы
имеют близкую связь с величиной притока тепла в жидкости,—
мы назовем их поэтому тепловыми векторами^ а соответствующие
условия будем называть тепловыми условиями*
Наконец последняя группа условий, дающая уже возможность
определить удельный объем жидкости, была названа нами объемной
группой условий. Объемная группа условий распадается на две
половины: первая требует, чтобы некоторый вектор был потен-
П

циальным вектором, вторая налагает условия на производную этого
вектора по времени.
Определив объемные условия, мы устанавливаем, как с помощью
квадратур определяются удельный объем и затем давление по
заданным кинематическим элементам.
Указанные условия дают нам всего девять уравнений, связы*
вающих компоненты нашей скорости; однако не все эти уравнения
будут между собой независимы.
В § 13 мы изучаем случаи исключительного характера, спу«
щенные в предыдущем параграфе, и устанавливаем условия
динамической возможности движения сжимаемой жидкости во всех
случаях.
В § 14 мы упрощаем введенные в предыдущих параграфах уело*
вия и вместе с тем выражаем в раскрытом виде векторы,
установленные в §§ 12 и 13 через кинематические элементы. При этом
оказывается, что число условий динамической возможности
движения сжимаемой жидкости уменьшается в общем случае до пяти;
четыре из этих условий оказываются следствием остальных.
§ 15 посвящен нами выражению основных векторов, введенных
в предыдущих параграфах, через динамические элементы; в конце
этого параграфа мы прилагаем небольшую таблицу размерностей
введенных нами величин, весьма полезную как для поверки
выведенных формул, так и при численных вычислениях означенных
величин.
§ 16 третьей главы, наиболее обширный, рассматривает
применения условий динамической возможности движения сжимаемой
жидкости к некоторым. частным случаям. Путь, которым мы здесь
следуем, заключается в предварительном задании некоторой общей
кинематической формы рассматриваемого движения и в
последующем детальном определении компонентов скорости движения,
давления и удельного объема помощью методов, развитых в
первых пяти параграфах рассматриваемой главы. Так например, задав,
что частицы тяжелой жидкости движутся в направлении
перпендикулярном силе тяжести, причем движение является одинаковым
для двух любых горизонтальных плоскостей (мы назвали такое
движение плоским), мы определяем условия, которым должны
удовлетворять компоненты скоростей данного плоского движения, в
в ряде случаев доводим задачу об определении такого рода
движения до конца. Большинство рассмотренных нами случаев
относится к случаям движения тяжелой жидкости; однако лая того,
чтобы иллюстрировать применение наших методов в вопросах
движений, когда, кроме силы тяжести, действуют еще другие, не
консервативные силы, мы изучаем некоторое движение сжимаемой
жидкости относительно координатной системы, вращающейся вместе
с землей, имея в виду, что б такого рода движении действует
отклоняющая сила вращения земли, возникающая из ускорения
Кориолиса и не являющаяся, само собою разумеется, силой
консервативной.
Как мы уже говорили выше, в настоящей работе мы не касаемся
14

вопроса о движении жидкости, когда задан определенный способ
жритока энергии; однако, чтобы иллюстрировать применение наших
методов и в этом случае, мы рассматриваем в § 16
адиабатическое движение, т. е. движение без получения и отдачи тепла;
установив условия (налагаемые на кинематические элементы),
необходимые и достаточные для того, чтобы движение,
расхождение скорости которого равно нулю (несжимаемое движение),
было адиабатическим, мм показываем, что в адиабатическом
движении нет надобности предполагать связь между давлением и
плотностью, выражаемую графически адиабатой, иначе говоря — нет
надобности предполагать, что для адиабатического движения
энтропия постоянна; может иметь место такое адиабатическое движение,
при котором энтропия может меняться от точки к точке и в данной
точке может меняться с течением времени.
Попутно мы выясняем, что для адиабатического нзсжимаемого
движения векторные линии, отвечающие турбулизирующему вектору,
обладают свойством сохраняемости, т. е. удовлетворяют первой
теореме Гельмгольтца. Весьма интересный вопрос о том, возможны ли
адиабатические движения, в которых давление не есть функция
плотности, нами в настоящей работе оставлен открытым *). .
Четвертая глава предлагаемой работы изучает связь
кинематических элементов с динамическими. Она состоит из трех
параграфов: 17,18 и 19. В § 17 мы изучаем связь скорости с
динамическими элементами; для этого мы выбираем три вектора: градиент
давления, градиент удельного объема и турбулизирующий вектор,
перпендикулярный первым двум. Рассматривая движение, в котором
давление не есть функция плотности, мы пытаемся вектор скорости
представить в виде линейной комбинации указанных трех векторов.
Коэффициенты в этой комбинации определяются с помощью
динамических элементов, с помощью величины притока энергии,
расхождения скорости и некоторой величины, определяющей изменение
напряжения вихревых трубок. Выразив таким образом вектор
скорости, мы получаем возможность выразить через указанные
элементы вектор вихря, а также вектор Н и вектор D, введенные
нами в первой части настоящей работы.
§ 18 посвящен изучению зависимости изменения вихревых
трубок от динамических элементов. Здесь мы идем двумя путями:
с одной стороны определяем изменение вектора вихря в данной
частице или в данной точке при помощи динамических элементов;
мы рассматриваем этот вопрос с общей точки зрения, а для
случая возникновения вихрей излагаем две простые и изящные
геометрические теоремы" Silberstein а. С другой стороны мы изучаем
элементы, введенные во второй главе первой части, а именно
отклонение, кручение, изгиб и уклон вихря, и связываем их с
динамическими элементами.
*) Положительный отвег- иа этот вопрос заключается в работе Н. Е. К о ч и г а
„Ober einen Fall der adiabatischen Bewegunga,Zeitschrift fur Physik, Bd 17, S. 73,
• JL923. См. дополнение. _.
Прим. ред.
15

Наконец в § 19 мы кратко излагаем теорему Bjerknes'a и ее
видоизменение, сделанное AnsePeM и состоящее в установлении
связи между изменением циркуляции по контуру и числом трубок,
проходящих внутри контура и образуемых взаимным пересечением
изотермических (поверхности постоянной температуры) и изэнтро-
пических (поверхности постоянной энтропии) поверхностей,
проведенных через равные для температуры и соответственно
энтропии промежутки.
В заключение необходимо сказать несколько слов об отношении
наших исследований к изысканиям в области гидродинамики вязких
жидкостей. Большинство работ, относящихся к вязким жидкостям,
рассматривает случай несжимаемой вязкой жидкости. Сколько нам
известно, не существует в литературе исследований условий
динамической возможности движения вязких сжимаемых жидкостей,
каковые условия могут быть без труда получены методами,
аналогичными изложенным в третьей главе нашей работы *). Особняком
в области изучения движений вязкой жидкости стоят работы и
идеи Duhem'a, изложенные в его „Recherches sur PHydrodynamique".
Duhem, изучая движения вязкой сжимаемой жидк<3сти, обращает
главное внимание на термодинамическую сторону дела и связывает
вместе уравнение притока энергии и уравнение состояния; эти
работы стоят совершенно вне круга идей, развиваемого в
настоящем сочинении.
Равным образом в настоящей работе мы не касаемся
интересных исследований Rowland'a и Fabri, относящихся к так
называемым вихрям высших порядков; эти работы относятся или
к случаю несжимаемой вязкой жидкости, или к случаю хотя и
сжимаемой жидкости, но такой, в которой задана связь давления и
плотности, что коренным образом расходится с общей идеей
изучения движения сжимаемой жидкости, положенной нами в основу
при разработке настоящего сочинения.
А, Фридтлан.
20 февраля 1921 г.
г. Петроград.
Математическое бюро
Главной физической обсерватории.
*) Условия динамической возможности движения вязкой сжимаемой жидкости
получены по методам А. А. Фридмана Б. И. Извековым. См. дополнение.
Прим. ред.
15

I. КИНЕМАТИКА ВИХРЕЙ.
Глава L
СОХРАНЯЕМОСТЬ ВЕКТОРНЫХ ЛИНИЙ.
§ 1. Предварительные понятия.
1. Мы изучаем движение жидкости, рассматривая изменения
различных векторных величин, отнесенных к разным точкам
области, занимаемой движущейся жидкостью. Представляется поэтому
полезным перед изучением движения жидкости остановиться на
некоторых общих понятиях и представлениях, связанных с
изменением векторных полей и лежащих в основе дальнейшего
исследования кинематики жидкости.
Положим, что каждой точке М с координатами х, у, z,
отнесенными к некоторой неподвижной прямоугольной прямолинейной
системе координат, и каждому моменту времени t сопоставлен
некоторый вектор А, имеющий составляющими по указанным осям
координат величины Ах, Ау, As. Вектор А явится функцией х> у, z и /;
таким образом будем иметь равенства:
Ax = Az(t;x,y,z),
Aj^ ?*,(*; х, у, z),
Аг = Аш (t; х, yt z).
В дальнейшем мы будем обозначать векторы жирным шрифтом:
А, В, а, а и т. д. Соответственная буква, напечатанная обычным
шрифтом, будет означать тензор вектора: А, а, а. Составляющие
векторов по осям х, уу z будем обозначать соответственной буквой
со значком х, у или z.
Совокупность векторов А, отвечающих определенному моменту t
и отнесенных к разным точкам области, занимаемой жидкостью,
называется векторным полем. Условимся называть кривую,
касательная в каждой точке которой совпадает по направлению с
направлением вектора А в этой точке к моменту t> геометрической
векторной линией поля к моменту t.
Уравнение указанной векторной линии может быть найдено
2 Зак. 2-120. — А. А. Фридман, Опыт гидромеханики 17

в результате интегрирования следующих дифференциальных
уравнений:
dx dy dz
Ar Ay Лг
причем t играет роль некоторого параметра.
Каждому моменту t соответствует семейство векторных линий,
отвечающее моменту t; через заданную точку, вообще говоря,
проходит одна векторная линия данного семейства. Те точки, через
которые проходит более одной векторной линии данного
семейства, называются критическими точками данного векторного поля;
таких точек большей частью конечное число.
Совокупность всех семейств векторных линий, отвечающих
всевозможным t, условимся называть собранием векторных линий
данного векторного^ поля.
Не трудно видеть, что семейство векторных линий есть
многообразие сю2 объектов, а собрание векторных линий есть
многообразие ооз объектов.
Совокупность частиц жидкости, занимающих к моменту t
положения точек геометрической векторной линии поля, назовем жидкой
линией поля к моменту t.
2. Как уже было сказано, кинематика жидкости сводится к
изучению изменения с течением времени векторов векторных полей,
характеризующих движение жидкости. Изменения эти могут быть
двух сортов. С одной стороны можно изучать изменения вектора,
с другой стороны можно изучать изменения векторных линий.
Первая точка зрения дает нам возможность выяснить понятие
ускорения жидкой частицы, а также установить уравнения динамики
жидкости; вторая точка зрения дала возможность развить
классическую теорию вихрей в несжимаемой жидкости. В нашей работе
мы также будем следовать указанными двумя путями.
Обратимся к изучению изменения данного вектора с течением
времени. Мы можем изучать изменение вектора А, отнесенного
к определенной точке области, занимаемой жидкостью; изменение
это характеризуется тем обстоятельством, что координаты х, yt z
будут оставаться неизменными, а время t будет меняться. Следуя
Bjerknes'y *), мы будем называть эти изменения местными.
Легко видеть, что за меру указанных изменений рационально
взять следующий предел:
Нт А(* + Д*; x,g,z) — A(t; х,у,г)л
м+о At 9
этот предел будет при известных условиях относительно
характера функции A (t;x,y> z) вектором, являющимся частной произвол*
*) Bjerknes, Dynamische Meteorologie und Hydrographie, Bd II, Kinematik
der Atmosphare und der Hydrosphare, Braunschweig 1913.
13

дХ
ной А по L Обозначая этот новый вектор через -г-, найдем, что
его составляющие по осям координат будут:
(ЗАЛ =дАг
\ dt )я dt '
' (дк\ _дАу
\ dt /у~ dt '
(дА\ дА„
t
I dt /я dt *
Вектор -зт условимся называть местной производной вектора А
по времени*).
Мы можем, однако, изучать изменение вектора А, относя его
не к определенной точке пространства, занимаемого жидкостью, а
к определенной частице жидкости, и следить за изменениями, ка*
кие будут происходить с вектором А при движении той частицу
жидкости, к которой отнесен вектор А.
Пусть к моменту t частица наша была в точке Л/(л:, у, z)\ к
моменту t-\-bt частица перешла в точку М' (х\у\zf). За меру
изменения вектора А можно принять вектор, определяемый следующим
пределом:
А (< +Af; хг, д\ /) —А (і\ *,у, z),
нт т-, ;
этот вектор мы условимся обозначать через
dk
dt
и будем называть индивидуальной Производной вектора А по
времени г.
dk
¦ Легко видеть, что составляющие вектора —j- по осям координат
выразятся следующими формулами:
dA\
dt),
dA\
~dT)y~
dt).
dAx
dt
dAy
dt '
dA,
dt '
цричем обозначения -~г-~ и т. д^ясвы сами по себе.
*) См. В j е г к и е s, 1. с.
2* 19

Помня, что
,. х — л: ,. у —у .. z —z
lim г-— = Щ Ьт —т-~ = v, hm —— = zo,
где и, v, w суть составляющие по осям координат вектора V
скорости к моменту / жидкой частицы, занимающей к этому моменту
положение М (х9 у, z), без труда найдем:
dAx дАт . дАх . дАх . <?Л
Л Л ' (?д: ' ду ' dz
</Лу А4, f <ЭЛу <ЭЛу <?Л
іГ
у
Л dt ' с>лг
dA ' дА'< дА„ , А4. , 54
U
!-+^-^+^-гг-.
dt - dt l " дх ] " ду 1 ш dz
В одном из следующих параграфов мы введем соответственные
dX
векторные символы, позволяющие вектор —> - связать с векто-
дА
ром —.
3. Изучение изменения векторных линий имеет особое значение
тогда, когда эти линии мы рассматриваем как жидкие линии.
Собрания векторных геометрических линий данного поля,
рассматриваемых в связи с заданным движением жидкости, могут быть
разделены на два класса.
К первому классу мы отнесем векторные линии, обладающие
следующим свойством: если в некоторый момент t рассматривать
каждую из векторных линий семейства как жидкую линию, т. е. как
состоящую из частиц жидкости, то и в любой другой момент t'
частицы, жидкости, составляющие данную жидкую векторную
линию, будут образовывать жидкую линию семейства векторных
линий, отвечающего моменту ?.
Все остальные собрания векторных линий будем относить ко
второму классу.
Собрания векторных линий, принадлежащие к первому классу,
будем называть собраниями сохраняющихся векторных линий и,
соответственно, собрания векторных линий, принадлежащие ко
второму классу, будем называть собраниями разрушающихся
векторных линий. Для упрощения речи и в тех случаях, когда
недоразумения по- существу дела будут невозможны, будем просто
говорить о сохраняющихся и разрушающихся векторных линиях.
Свойство векторных линий быть сохраняющимися будем
называть в дальнейшем свойством сохраняемости.
Вся настоящая часть нашей работы будет посвящена вопросам
о сохранении или разрушении (и о законах, управляющих этими
явлениями) особых векторных линий, играющих чрезвычайно
важную роль в динамике- жидкости, а именно вихревых линий.
20

4. Кинематическими элементами, характеризующими движение
жидкости, являются скалярные и векторные величины,
образованные при помощи комбинации составляющих по координатным осям
скорости жидкости и, v, w (являющихся функциями ty х, у, z) и
различных их производных по t и координатам.
Совершенно ясно из соображений элементарной динамики, что
особую роль должен играть вектор ускорения данной жидкой
частицы. Обычный вывод основных уравнений гидродинамики в
форме Эйлера дает следующие выражения для составляющих по
осям координат вектора ускорения данной жидкой частицы:
<N \ du ди , ди , ди , ди
==z-dt==-dT+a-d^+v -fy+wm>
dv , dv
w
-5—i'W-ч—
di/ ' dz
dw , 'dw
w
dy ' dz'
Условимся вектор ускорения обозначать символом —т—.
at
Соответственно двум векторам, характеризующим движение
VaV
и ускорению —у-, можно построить
собрания векторных линий. Векторные линии, отвечающие скорости,
называются линиями тока и играют важную роль в классической
гидродинамике, особенно в безвихревом движении жидкости (с
потенциалом скорости) или в плоских движениях жидкости; характер
этих линий и их критические точки были рассмотрены проф. Н. Е.
Жуковским в его диссертации*). Следует отметить, что линии тока и
их критические точки имеют огромное значение для изучения
движений в атмосфере, для динамической метеорологии.
Меньшее значение должно приписать векторным линиям,
отвечающим ускорению; условимся называть эти линии линиями
ускорения] из динамических соображений будет далее ясно, что во
многих случаях линии ускорений суть ортогональные траектории
семейства изобарических поверхностей; в практических вопросах
(особенно в динамической метеорологии) линии ускорения удобно
изучать в плоском движении.
5. Третьей векторной величиной, имеющей огромное значение
в гидродинамике, является вектор вихря.
Напомним, что вихрем вектора А называется вектор С,
обозначаемый curl А и имеющий следующие составляющие:
dAz дАч
С — rnrl А= - -
*) Н. Е.Жуковский, „Кинематика жидкого тела". См. также известный мемуар
Роіпсагё, „Sur Iescourbesdefiniesparlesequations differentielles", Journ. de Liou-
ville 1881—1882 г., а также мемуар Bendixon'a, помещенный в Acta Mathema-
tica, Bd 24.
21

Г л к—дА* дА*
Су = curl, А --д- аг,
дАу дА,
С. = curl, А = -з
ду
да
dz
dv
dz '
dzu
дх'
du
дх ду
Понятие вихря играет огромную роль в изучении движений
вообще всякой непрерывной среды, например в электродинамике.
При изучении движения жидкости вихрем называется специально
вектор Q:
Q = curl V.
Мы условимся составляющие вихря по осям х, у, z обозначать ?, гі9 С:
dw dv
Ъ =
?
дх ду
Причина введения понятия вихря в гидродинамику выясняется
из рассмотрения относительного движения близких друг другу
частиц жидкости. Мы не останавливаемся на этих вопросах, подробно
разработанных в классической гидродинамике*).
Векторные линии, отвечающие вектору вихря скорости, называ
ются вихревыми линиями и играют особую роль в изучении
движения жидкости.
В классической гидродинамике вихревые линии суть линии не*
разрушающиеся, как это было впервые выяснено Гельмгольтцем**);
наоборот, при движении жидкости с притоком энергии вихревые
линии суть линии разрушающиеся; законы, управляющие их
разрушением, будут составлять содержание настоящей первой части
нашей работы.
Не трудно видеть, что дифференциальные уравнения,
определяющие вихревые линии, могут быть написаны следующим образом:
dx dy dz
~Т~~ч ~"
6. Из скалярных кинематических элементов, характеризующих
движение жидкости, особое значение имеет так называемое
расхождение (divergenz) скорости. Расхождением вектора А называется,
*) См. напр. Жуковский, „Кинематика жидкого тела", а также любой из
классических трактатов^ по гидродинамике, напр. Lamb, „Hydrodynamics".
**) Helmholtz, „Uber Integrate der hydro dynamischen Gleichungen, welche den
Wirbelbewegungen entsprechen", Creoles Journal, Bd 55.
22

как известно, скалярная величина, обозначаемая div А и опреде-
^яeмaя равенством:
а- д ^А дА, дАг
ниже, при установлении уравнений динамики жидкости, мы
встретимся с этой величиной в так называемом уравнении
неразрывности.
Помимо указанных выше векторных и скалярных
кинематических элементов, характеризующих движение жидкости, могут быть
вводимы в рассмотрение и более сложные скалярные и векторные
комбинации различных производных по времени и, по координатам
составляющих скорости частицы жидкости. Комбинации эти можно
назвать кинематическими элементами высшего порядка, тогда как
рассмотренные нами величины могли бы называться простейшими
кинематическими элементами.
Само собой разумеется, что кинематические величины высшего
порядка должны быть образованы таким образом, чтобы спбсоб их
составления не зависел от выбранной системы прямоугольных,
прямолинейных координат. Вышеприведенные простейшие
кинематические элементы обладают этим свойством.
Может возникнуть вопрос: существуют ли такие векторные
кинематические элементы высшего порядка, которые обладают
сохраняющимися векторными линиями для движений жидкости с
притоком энергии? Если бы такие элементы существовали, то они
играли бы в динамике указанных жидкостей ту же роль, какую
вихри играют в классической гидродинамике. Разыскание таких
элементов представляет поэтому весьма важную задачу для
гидродинамики указанных жидкостей; в настоящей работе мы, однако,
заниматься этой задачей не будем, предполагая посвятить ей одну
из следующих работ; некоторые соображения по поводу решения
этой задачи будут, изложены в §10 второй главы настоящей части.
Fabri и Rowland *) рассматривали особые кинематические
элементы высшего порядка типа curPV, причем сигГА определяется
следующей рекуррентной формулой:
curl А = curl (curPA).
Мы увидим в дальнейшем, что для жидкости, в которой имеется
приток энергии, более существенную роль играет не curl* V, а
особый вектор? равенство нулю которого составляет условие
сохраняемости вихревых линий.
В заключение настоящего параграфа сделаем следующее
замечание.
В кинематике деформируемой среды (особенно в вопросах те-
*) Работа Rowlands помещена в Amer. Journ. of Mathematics в 1880 г
С Fabri поместила ряд мемуаров в Nuovo Cimento 1892, 1894 и 1895 гг.; см.
также Encyclop. d. Math. Wissenschaften Bd IV, TeilbAid 3, S. 125.
21

ории упругости; важную роль играют так называемые сдвиги,
величины cjj, о>, а3, определяемые следующими формулами:
dw , dv
du . dzu
dv , d:i
dx l dy *
Легко видеть, что сдвиги являются такими кинематическими
элементами, форма которых зависит от выбора координатной системы*).
В этом отношении вихри обладают свойством, совершенно
противоположным сдвигам: изменения прямоугольных прямолинейных
координатных систем не отражаются на форме вихря. Переходя
к новым координатам х1У yv zx и полагая, что ?и у\і9 ?, и ии vl4wx
суть составляющие сооответственно вихря и скорости относительно
новой*координатной системы, будем иметь:
dwi dvx
61 =
•*1
дщ dwx
dzy дхх
dvx дщ
дхх дух
§ 2. Понятие сохраняемости векторных линий.
1. Так как при изучении законов сохранения или разрушения
вихревых линий нам придется постоянно сравнивать изменения
вихревых линий с изменениями соответственных жидких линий, то
настоящий параграф мы начнем с изучения изменения жидки*
линий.
Пусть (черт. 1) мы имеем жидкую линию ММ1 к моменту t; эта
линия вследствиэ движения жидкости перейдет к моменту ?-j-A?
в жидкую линию М/М[у причем частица жидкости, занимавшая
положение М, перейдет в положение М\ а занимавшая положение
М1 перейдет в положение М\.
При этом под величиной Л? мы подразумеваем некоторую
конечную величину.
В дальнейшем мы будем рассматривать жидкие линии в
соответствии с векторными геометрическими линиями; пусть поэтому
жидкая линия к моменту t являлась одной из линий векторного
поля вектора а.
*) Это обстоятельство представляется вполне естественным, если мы
вспомним физическое значение деформации сдвига параллельно некоторой плоскости.
24

Для нас впоследствии важно будет изучение направления
касательных к жидким линиям; поэтому в изучении жидких линий нам
достаточно будет ограничиться изучением бесконечно малых
элементов жидкой линии. Предположим, что Мг будет точкой,
бесконечно близкой точке М; тогда не трудно видеть, что координаты
*і> У\> zi точки Мг через координаты л:, у, z точки М выражаются
следующим образом:
Хь — х = л а.
ЛТ>
9і — !? = ь<*уу
Z\ — z = \az,
где X— бесконечно малая величина. Таким образом направляющие
косинусы касательной МТ в точке М к нашей жидкой линии
будут пропорциональны величинам ах, ауі а2.
2. Чтобы составить себе
представление об изменении жидкой линии к
моменту f-J-Д^ мы должны сделать
определенные предположения о зависимости
координат частицы жидкости от времени.
Будем предполагать, что эти координаты
вблизи момента t разлагаются в ряд Тэй-
лора по степеням Д?. При таких
предположениях не трудно видеть, что
координаты хг, у\ z\ которые будут отвечать
к моменту t-\-&t частице жидкости,
занимавшей к моменту t положение М (х> y,z),
могут быть выражены следующими формулами:
Черт. 1.
2 Л
J ы^ ' 2! dt п
^ ^2! dt Г
« —і
п\
1
п!
1
Л"-1
in — 1
П. V
л"-1
т71 — 1
a w
-Л^"+...,
п\
dt
и
\t
П і
•f
•f
где п! = 1, 2, З...п, ах, и,
da
, и т. д. относятся к моменту і и
к координатам л:, у, z частицы М.
Выражая таким же образом координаты х[9 yfv z[ к иомен і^
t-\-kt частицы, занимавшей к моменту t положение Мг (хь уи zL),
мы должны будем в предыдущем выражении, в коэффициентах при
различных степенях Af, каковые коэффициенты явятся функциями
t, Xj у, z, подставить вместо л:, у9 z заменившие их координаты
xv уи Zj. Так как лг1? уь zx бесконечно мало отличаются от x,y,z,
то указанную замену не трудно будет произвести.
Рассмотрим в общем виде только-что указанный вопрос. Пусть
25

/ (U х, у, z), будет некоторая функция времени и координат.
Относительно характера этой функции, как и всех тех, которые будут
встречаться у нас в дальнейшем, мы будем предполагать, что они
имеют столько непрерывных производных, сколько этого требуют
обстоятельства исследуемого вопроса; то рассуждение, к которому
мы перейдем, требует, чтобы функция / имела непрерывные
частные производные первого порядка по координатам.
Не трудно видеть, что
f(t\ xi,suzl)=f{t,x,y,z) + \y^ax + ^a^^aty
Выражение, стоящее в скобках при бесконечно малом множителе А,
будет играть в дальнейшем весьма важную роль. Для обозначения
этого выражения мы введем особый символ D&f:
а„.
Свойства этого символа будут изложены в конце настоящего
параграфа*). Фундаментальная роль его в теории изменения
векторных линий и в частности в теории разрушения вихрей выяснится
как в настоящем, так особенно и в следующих параграфах.
3. Пользуясь обозначениями предыдущего пункта, легко найдем.:
^'+x(a,+D.u^ + iB.fA(S + ... + -L0.pri(-+...),
W(^WiB.^+...+iz,1^..)l
при этом не трудно заметить, что
ag = Dmx, ау = Олу, • az = Daz,
каковые соотношения могут сделать предыдущие формулы более
симметричными.
Из предыдущих формул ясно, что направляющие косинусы
карательной М'Т' к.жидкой линии ММ{ в точке М' относительно
*) Очевидно, что при обычных обозначениях вектор Daf запишется так:
?./=(». grad/) = (a>V/).
Мы, однако, не решились изменять этого обозначения А. А. Фридмана.
Прим. ред*
ге

осей координат будут пропорциональны следующим выражениям,
обозначаемым нами через lu L, 4:
и
nl at
Д<" +
tn — 1
m
1
d»"1
«J
ь^Л==т*ч-...
(U
3 ."Г a T-21 . A T ¦ nI a^;
4. Для рассмотрения вопроса об условиях сохраняемости
векторных линий поля вектора а введем в рассмотрение векторную*
динию, отвечающую моменту t-\-At
и проходящую через точку М
(черт. 2).
Эта линия на черт. 2 будет
изображаться пунктирной линией М'АГ
с касательной М'Т". Направляющие
косинусы касательной М'Тп с
осями координат будут очевидно
пропорциональны составляющим
вектора а по этим осям, отнесенным к
моменту t -\- At и к координатам х\ Черт. 2.
у\ z точки Мг. Обозначая эти со-
г г t
ставляющие через ах,а , az, будем, очевидно, иметь:
д!' dt Л'
ая=ах
dt г^ 2! dP l ^
Д'+-^г
1 d*a.
2! -dP
Д*2
«;-«.+^+і-5ьа^
л
2! Ж-
1 «Га,
J -Atn~
^ л! Л" г '
4-1-^д*»
этим величинам, как мы уже сказали, пропорциональны
направляющие косинусы касательнрй М'Т".
Предыдущее исследование указало нам три важных для нас
направления: во-первых, направление
касательной к векторной линии,
соответствующей моменту t в точке М [направление
вектора a (t; х, у> z)]; во-вторых,
направление касательной к жидкой линии, в
которую наша жидкая векторная линия перейдет
к моменту t-\-At в той точке М' (x\yf, z')»
в которую переходит точка М (лг, у, z)
нашей жидкой векторной линии; в-третьих,
направление касательной к векторной ли-
Черт. 3. нии, отвечающей моменту t-\-At в точке
27

Mf [направление вектора а'= а (* ~f-Д*'; х\ f> z')\. Наиболее удобно
изучать эти три направления, построив сферу единичного радиуса
с центром в начале координат О и проведя через центр сферы
три радиуса, соответственно параллельные первому, второму и
третьему направлению (черт. 3). Пусть эти три радиуса
пересекут сферу в точках A, L, А\ мы получим тогда трехгранный
угол (триэдр) О ALA и сферический треугольник ALA,
расположенный на сфере единичного радиуса. Условимся в дальнейшем
этот триэдр и этот сферический треугольник называть, основным
триэдром и основным сферическим треугольником для поля век'-
тора а.
^Три точки A, L, А будем называть соответственно изобрази-
тельной точкой вектора а к моменту і, изобразительной
точкой жидкой линии к моменту t-{-kt и изобразительной точкой
вектора а? к моменту t-\-M.
5- Изучение основного триэдра или основного сферического
треугольника даст нам полное представление об изменении
векторных линий поля и о том, каким образом в общем случае эти Еек-
торные линии разрушаются, т. е., будучи в момент t жидкими,
перестают быть таковыми к моменту t-\-kt. Величины, которые будут
нами введены в связи с изучением основного триэдра, будут, как
это выяснится впоследствии, находиться в самой тесной связи с
динамическими элементами (давлением и плотностью),
характеризующими движение жидкости.
Рассмотрение основного триэдра дает нам возможность
установить необходимые и достаточные условия того, чтобы собрание
векторных линий поля вектора а обладало свойством
сохраняемости. Совершенно ясно, что необходимые и достаточные
условия, чтобы собрание векторных линий поля вектора а было
собранием сохраняющихся линий9 заключаются в совпадении
вершин L и Аг основного сферического треугольника, или, что
то же самое, в совпадении линий Ln А' основного триэдра для всех
значений t и для всех точек Af.
Не трудно аналитически выразить эти необходимые и
достаточные условия сохраняемости векторных линий поля вектора а
следующими формулами. Пусть аи а2, а3 будут величины,
соответственно равные ах, ау> az; a'v a'2, а'г будут соответственно
равны а'х, ау, a'z, и пусть наконец /х, /2, /3 будут
обозначать выражения формул (1). Очевидно, что направляющие
косинусы ребер А, А и L основного триэдра будут соответственно
пропорциональны (аи а2, а3), (а'17 а'2, а3) и (Zlt /2, /3)» Таким образом
наши условия могут быть выражены следующими равенствами:
' t t *
аі а2 а3
являющимися условиями совпадения линий L и А. Эти равенства
можно переписать так:
28

a\ l2 — a2 lx = 0.
Подставляя разложения по степеням&t для а! и lt в эти равенства»
найдем следующие соотношения:
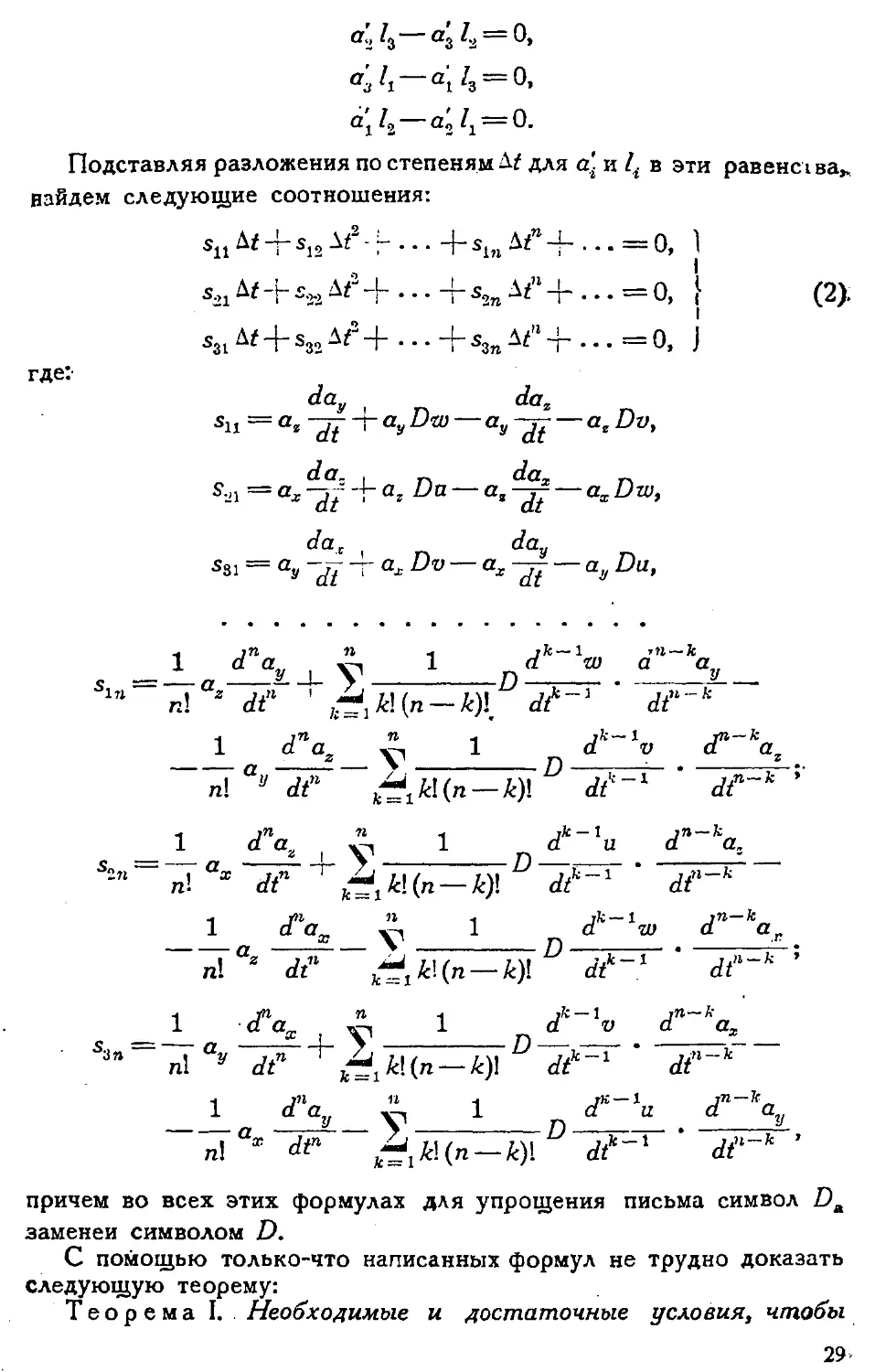
^Д' + ^Д^Н" •¦• 4-^Д^-Ь ••• =0, [ (2).
%Д^+з32дг+'--+^Д^-Ь.-.=о, J
где:
da* ' п Л» п
da. . -, Лг, _
S,J1 = а*~о7 * a*Da~~a'~j?~а*Dzv>
dae day
ssi^ay~di^a?Dv~~~ax~dt~ayDu'
а а„ v^ 1 а -и а а,
2 У ?>
<v—I 7,n-fc >
1 о а„ ж-^ I а и а а
2П п! х dtn ' ^А!(л —А)! Л""1 Л"""
Л** dtn ?xkl{n — k)\ dt-1 ' dtn~k ;
Iiti n ¦* jk — 1 in—А'
Sin~ n\ay df ^Щп-ку. dtk~x ' dtn-k
причем во всех этих формулах для упрощения письма символ Пл
заменен символом D.
С помощью только-что написанных формул не трудно доказать
следующую теорему:
Теорема I. Необходимые и достаточные условия, чтобы
29

собрание векторных линий поля вектора а было собранием сохра*
няющихся линий, заключаются в выполнении следующих равенств'.
dax da7J daz
— — ¦ . (о)
о, S а=
Прежде чем доказывать эту теорему, сделаем следующее
замечание, разъясняющее ее формулировку:
Если свойство сохраняемости выполняется для некоторого ин*
тервала t и внутри известной области значений х, у> z, то для
того же интервала и для той же области должны выполняться
соотношения (3); обратно, если для некоторого интервала t и
некоторой области значений Ос, у, z) выполняются соотношения (3), то
для этого же интервала и для этой же области выполняется
сохраняемость векторных линий.
При доказательстве нашей теоремы мы, конечно, будем
предполагать, что свойство сохраняемости векторных линий и
соотношения (3) имеют место для конечного интервала значений t и внутри
конечной области значений х, у, z9 хотя и интервал и область
могут быть как угодно малы.
Необходимость условий, указанных в теореме, вытекает из того,
что при наличии равенства (2) должны быть соблюдены равенства:
sn = 0, 521 = 0, sB1 = О,
которые и являются несколько преобразованными условиями нашей
теоремы.
Для того, чтобы доказать достаточность условий нашей теоремы,
необходимо установить, что из соотношений (3), справедливых для
конечного интервала t и внутри конечной области для х, у, z, как
следствия вытекают равенства:
при п = 2, 3..., причем равенства эти остаются выполненными для
того же самого интервала /ив той же самой области х, у, z.
Непосредственным вычислением легко обнаружить
справедливость следующего равенства:
df dDJ df(dax \ dfldav \ df/Ja, \
Условия, указанные в нашей теореме, дают следующие равенства:
D.« =
DKv^
?>,«> =
dt + а"
dt +Ха*'
. <fe. 11.
,t 1 Чр
где X есть некоторая функция t, xf y9 z*
30

df
Точно так же преобразование Da -4г при условиях нашей теоремы
может быть сформулировано следующим образом:
df dDJ
Обозначим через \і функцию от ty х9 у, z такую, что имеет место
соотношение:
1і ~ ;
если через /lfc> /2Л, /гк обозначим выражения:
fik=e D«"^T'
hk U* dtk '
hk e ^a nk »
ik
то из формулы (4), последовательно примененной к символу ?а—^
и т. д., без труда найдем:
f — jLbl
hk- dtk .
hk ^
d /2p
J /30
IT
Замечая далее, что
, ^ « ^ rfaz , , (a de aT
мы легко напишем следующие соотношения:
а е а«
/it
/» =
.'/
?-М '

Подставляя эти формулы в выражения для sln, s2n, s.sn>
предварительно умноженные на e*\ и применяя формулу Лейбница, мы после
несложных преобразований найдем следующее соотношение:
v, d еа at d е аяа
откуда sln = 0; точно так же докажем, что s2n = 0, s3n = 0, а вместе
с тем докажем и всю теорему.
6. Применим изложенные в п. 5 соображения к нескольким
примерам и прежде всего к условиям сохраняемости линий тока.
В этом случае вектор а есть v, поэтому условия нашей
теоремы перепишутся таким образом:
du n dv . n dw „
-a-d*u it~D^ -df-D-w
V
J
и v w
не трудно видеть, что:
_. ди . ди , ди
v дх х ду [ dz
поэтому предыдущие условия могут быть написаны в виде:
д]% и dig v d]gw ,-
Один из случаев, при котором линии тока обладают свойством
сохраняемости, имеет место при стационарном движении, когда
и, v, w не зависят от t явно и когда следовательно линии тока не
зависят от параметра і и семейство линий тока совершенно не
меняется с течением времени.
Самое общее решение уравнений, выражающихся условиями (5),
может быть представлено в таком виде:
u=f{t; х, у, z) и0 О, у, z\
v = f(t; х, у, z) vQ (х, у, z\
w=f{t; х, у, z) w0 (x,y} z).
Дифференциальные же уравнения линий тока могут быть
написаны в форме:
dx dy dz
"о v0 wQ'
и следовательно семейство линий тока и в этом случае не меняется
с течением времени. Совершенно очевидно, что линии* тока в
практических вопросах могут быть с пользой применяемы лишь тогда,
когда семейство линий тока не меняется с течением времени, т. е.
когда линии тока суть сохраняющиеся жидкие линии.
32

Вторым примером на приложение общих соображений п. 5
выберем линии ускорения. Условия нашей теоремы дают:
d2u ди du да dv ди dw d-v dv da dvdv dv dm
1F~~dx4t~~d^~df~ dz 1П~_7f*~dxllt~fy~dt~l)zlit _
da dv
It ~dt
drw dw da * dw dv dw dw
_~<№ dx4t~~d^~di~1z"lf
~ dw '
dt
мы не будем однако останавливаться на дальнейшем изучении этих
уравнений, в виду их сравнительно малого значения.
7. Исключительное значение в дальнейшем изложении будут
иметь собрания векторных линий вихря или так называемые
собрания вихревых линий. В целях упрощения письма мы освободим от
лишних значков многие из символов, введенных в предыдущих
пунктах, относя их не к какому-либо произвольному вектору, а
к вихрю.
Пусть 2 будет вектором вихря к моменту t частицы М,
имеющей к этому моменту координаты x,ytz. Составляющие Q по осям
координат пусть будут S, f\> С; той же буквой Q будем обозначать
тоЗку единичной сферы, в которой эту сферу пересекает радиус,
параллельный вихрю Q; направление этого радиуса будем
обозначать как направление 2.
Положим, что к моменту t-\-&t частица М (дг, у, z) пришла
в положение М (дг>\ у\ z')\ вихрь к моменту t-{-kt в новом
положении частицы обозначим через Q'; соответственную точку на
единичной сфере и соответственное направление радиуса единичной
сферы будем обозначать &.
В дальнейшем сферический треугольник QLQ' и
соответственный триэдр для сокращения речи будем называть основным
сферическим треугольником и основным триэдром.
Общий символ Z)a/ в применении к вихрю будем обозначать
просто D/f таким образом:
Если вектор А имеет составляющие Ах> Аи^ А2, то условимся
называть вектором DA вектор с составляющими DAX, DA^ DAS
Легко видеть, что вектор DV будет иметь такие составляющие-
*
/тліт\ п ди у , ди . ди г
(Dv)x=Du = -^<+^rl+~t:, .
/гчтг\ n dv t і dv . dv r
Зак. 2420. — А. А. Фридман, Опыт гидромеханики 33

/п\т\ п dzo , , dtv , dw
этот вектор DV будет часто встречаться нам в дальнейшем; мы
будем называть его вектором D.
Не трудно видеть, что необходимые и достаточные условия
сохраняемости вихревых линий, согласно теореме I, выразятся
следующими равенствами:
d\ n drt аХ п
__Z)U -д-Dv -д-Dw
В дальнейшем будем обозначать через Н и называть вектором
Н*) вектор, имеющий составляющими по осям х, у> z следующие
величины:
H, = ~ — Dzu.
dt
Вектор Н может быть определен следующим векторным
равенством:
dQ
at
Наиболее простая формулировка теоремы I может быть
выполнена помощью введения вектора Н.
Теорема I-bis. Необходимое и достаточное условие, чтобы
собрание вихревых линий было собранием сохраняющихся
линий, состоит в совпадении по направлению вектора Н с
вектором вихря-
Мы увидим в дальнейшем, что отклонение направления вектора
Н от направления вектора вихря дает естественную меру для
оценки разрушения вихревых линий, для оценки того, насколько
новая вихревая линия отходит от отвечающей ей жидкой линии.
Первая теорема Гельмгольтца **), к которой мы еще вернемся
впоследствии, утверждает, что для несжимаемой жидкости и для
некоторых движений сжимаемой жидкости условия теоремы I-bis
выполняются, а следовательно вихревые линии обладают
свойством сохраняемости. Как мы увидим далее, это не имеет места
в общем случае движения сжимаемой жидкости.
8. Для иллюстрации только-что развитых положений разберем
*) Причина, почему этот вектор заслуживает особого внимания, выяснится
в следующих параграфах.
**) См. Helmholtz, 1. с, особенно § 2 мемуара Гельмгольтца.
34

простейший пример движения жидкости, в котором скорости
являются линейными функциями координат с коэффициентами,
зависящими от L Пусть скорости ы, v, w определяются формулами:
и = а-\-агх-\-а<2у-га^,
v = Ь -J- Ьхх -j- b& -p b2z,
w = с 4- с^х -р c<&-\~cbz;
такое движение можно назвать коллинеарным движением. Вводя
вихрь с составляющими ?, % ^, а также (в целях большего
удобства вычислений) сдвиги з1э а2, с3, параллельные трем координат
ным плоскостям, и удлинения е19 г2, s3 *) по трем координатным осу
найдем следующие формулы:
Г-»3 - Зо -+- Т,
с,
откуда:
аі = 8і» аа="—2""' аз==
^1 = ? 02 = 22, . &з—- 2~-
2
т . і Со х-4-3,2: . **—$2:
v = b-\-%g + 2 Н 2 '
ш = с + s8 г + J Г —2
Простые вычисления дают:
L>u = e1?+—2 ,
Op ? -(- Оі С
D а; = г3 С + -1 2 —¦,
¦"«—6 — si; 2 '
Ну^Ъ — ?2гі- 2
»
* би dv dw ,r i і da» . dv
*) ?і = -^'^==^Г е3 = -й7, откуда dlv V = ?l + %-rs3; ^1 = -^ + ^;
du dw dv . du
3*

2
Слг-
2
ъ-
¦fe
TjAT
где буквы с точками обозначают производные по времени, причем
следует заметить, что ?, т„ С зависят только от * явно, так как
х, у, z в S, у\, С не входят.
Пример 7. Чтобы применить теорему I, рассмотрим движение
жидкости, аналогичное движению твердого тела.
Такое квази-твердое движение определяется тем, что все
удлинения и сдвиги равны 0; таким образом:
, rlZ — Oj
w = c+ 2 '
Нх = ?, Ну = т], Нг = С.
Отсюда видно, что условия теоремы I-bis могут быть
выражены равенствами:
J—Л—jL
откуда после интегрирования найдем:
ті = тю/ (0.
где /(*) — произвольная функция ? а ?0, ?і0, ?0 — произвольные
постоянные.
Интерпретируя геометрически квази-твердое движение, убедимся,
что линии вихрей во всяком квази-твердом движении должны быть
прямыми параллельными мгновенной оси, как это следует в
результате интегрирования дифференциальных уравнений вихревых линий:
dx dy dz
где 5, *ч> С не зависят от х, у, z.
Из предыдущих формул следует, что необходимое и
достаточное условие сохраняемости вихревых линий в квази-твердом
движении состоит в том, чтобы мгновенная ось, перемещаясь,
оставалась постоянно параллельной некоторому неизменному в
пространстве направлению.
Пример 2. Рассмотрим далее движение жидкости, в котором
сдвиги равны нулю; такое движение будем называть движением
36

без сдвигов. Скорости при движении без сдвигов определяются
формулами:
u = a-fei* +
г
Ъ* — -*9
Zx — \х
откуда
2
т \»
?
Пользуясь теоремой I-bis и интегрируя полученные из этой
теоремы условия, найдем, полагая, что /(*) — произвольная
функция /, а S0, iq0, С0 — произвольные постоянные:
t
J\<tt
t
je>dt
j t3dt
C = C0/We° ,
для случая сохраняемости вихревых линий.
Рассмотрим теперь пример, который даст нам иллюстрацию,
когда условия теоремы I-bis, являющиеся, вообще говоря, под видом
двух уравнений, вырождаются в одно уравнение.
Пример 3. Пусть движение жидкости таково, что и, v не зависят
от х, у> a w обращается в 0 *).
В этом случае:
откуда
dt di ' dt ~~ dt ' dt
= 0,
Яг==1Г' я»в~зЬ я«=0-
*) Подобный случай движения жидкости может представиться в атмосфере,
когда вертикальные течения слабы и ветер мало меняется с изменением координат
местности; такие условия соответствуют слабо искривленным изобарам. О
практическом вычислении вихрей см. мою статью „Об атмосферных вихрях",
Геофизический сборник, т. Ш, стр. 91,1916.
37

Условия теоремы I-bis будут:
dt ~ dt
откуда после интегрирования найдем:
где «р а2» ^о — произвольные функции своих аргументов. Изтолько-
что написанных выражений получаем следующие формулы для
составляющих скорости:
/»
ц= J ^(z)i0(t,z)dzJru0(t)9
с
Z
v = — J *1(z)Z0(l,z)dzJt-v0(t),
w = 0,
где с — произвольная постоянная, н0 и v0 — произвольные
функции t.
Не трудно видеть, что в разбираемом нами примере семейство
вихревых линий, отвечающее моменту t, будет семейством прямых
линий, расположенных в плоскостях, параллельных плоскости хут
Вообще говоря, с изменением t это семейство прямых будет
изменяться; условия сохраняемости требуют, чтобы семейство указанных
прямых вихревых линий оставалось неизменным при любом t\
в самом деле," при условии выполнения теоремы I-bis имеем для
вихревых линий следующие дифференциальные уравнения:
dx dy dz
откуда видно, что
z = c19
аЛсі)у — аз(сі)* = с2
(сі» с2 — произвольные постоянные) — уравнения вихревых линий,
одинаковых для любого момента U
Теорема сохранения вихревых линий может иметь место в слу>
чаях гораздо более общих, чем только-что разобранные; в этих
случаях щ v, го будут обладать большей произвольностью,, чем
это имело место в предыдущих примерах; для подтверждения
сказанного рассмотрим следующий пример.
Пример 4. Положим, что рассматриваемые нами вихри образуют
вихревые линии, состоящие из прямых, параллельных неизменному
направлению (случай прямолинейных вихревых трубок). Выбирая
38

ось z-ов параллельно этому неизменному направлению, мы Судей
иметь в нашем случае, что
5 = 0,
при всех /, дг, у, z.
Отсюда получаем:
dw dv dw ди
ду dz ' дх dz
т. е., по исключении wf
Я
= 0.
Таким образом Z. не зависит от z.
Имеем:
условия теоремы I-bis будут:
Нх __ Ну __ Нг
о о с
Если положим Zф0, т. е. рассмотрим случай действительной
наличности вихрей, то предыдущие равенства перепишутся так:
#.=о, ну=о,
откуда
dz v> dz U'
а следовательно (пользуясь тем, что & = y] = 0):
dw Hw ___
5л: (?!/
Таким образом теорема сохраняемости вихревых линий в нашем
случае требует, чтобы и, v не зависели от z, a w не зависело
от л: и у.
Полагая, что вертикальное направление совпадает с осью zt
мы можем выразить условие сохраняемости вихревых линий
следующим образом: горизонтальные составляющие скорости не
должны зависеть от высоты, а вертикальная составляющая
может зависеть только от времени и высоты *).
*) Разбираемый случай может иметь место в атмосфере, когда ветер мало
меняется с высотой, а вертикальные токи мало меняются с изменением
географических координат пункта.
39

Заканчивая настоящим случаем примеры на приложение теоремы
о сохраняемости вихревых линий, сделаем следующее общее
замечание. В дальнейшем мы будем иллюстрировать примерами лишь
наиболее характерные особенности кинематики нашей жидкости;
более подробному обследованию и приложениям наших результатов
к различным частным случаям мы предполагаем посвятить особую
работу. Подобное выделение рассмотрения частных случаев имеет
своим преимуществом возможность рассмотрения этих случаев не
только с неполной кинематической точки зрения, но и с
всесторонней динамической точки зрения, что в свою очередь даст
возможность избежать ненужных усложнений и, воспользовавшись
динамическими соображениями, рассмотреть лишь те частные
случаи движения жидкости^ которые могут иметь место в
действительности.
§ 3. Формулы векторного анализа.
1. В предыдущем параграфе мы выяснили, какую роль в
изучении изменения векторных линий и в частности вихревых линий
играют некоторые векторы и некоторые операции, векторного
анализа.
Дальнейшее наше изложение стало бы чересчур сложным,
если бы мы не воспользовались тем значительным сокращением
письма и упрощением вычислений, которое нам доставляет
символика векторного анализа. Однако в виду того, что с одной
стороны до сего времени многие символы и обозначения векторного
анализа не обладают общепризнанным однообразием, а с другой
стороны нам придется пользоваться рядом новых символов и
связанных с ними правил вычислений, мы решили выделить в особый
параграф первой главы те необходимые символы векторного
анализа и правила операций над ними, которые будут встречаться
в дальнейшем нашем изложении. Быть-может в целях более
систематического изложения было бы рационально поместить этот
параграф в начале настоящего сочинения; мы однако предпочли
говорить о новых векторных символах уже после того, как
предыдущие соображения, особенно касавшиеся введения вектора D
и.вектора Н, в известной мере оправдали введение ряда новых
векторных символов и операций с ними.
2. Мы уже условились обозначать векторы жирными буквами,
а составляющие вектора по осям координат — соответствующей
курсивной буквой со значками х, у, z; составляющие вектора А по
осям координат будут Ах> Ауі Ае.
Величину вектора А (тензор вектора) будем обозначать |А"
или А; таким образом:
А = ^=УК + Аі + Аі*). (1)
*) Квадратный корень берется у нас всегда со знаком плюс.
40

Скалярным тпроизведением *) вектора А на В называется
величина АХВХ~\- A?By-\-A%Bti обозначаемая символом (А, В):
(А,В) = АгВх~ A, B,+AzBt. (2)
Непосредственное вычисление дает:
(А,В) = (В,А),
Л
<A,B)i=,45cos(A,B),
(А,А) = Л*, Л = /(АГА),
Л
причем (А, В) есть угол меньший 180° между направлением
вектора А и направлением вектора В.
Необходимое и достаточное условие того, что два отличные от
нуля вектора А и В ортогональны друг другу, заключается в
равенстве:
(А, В) = 0.
Векторным произведением двух векторов А и В называется
вектор, обозначаемый символом [А, В], составляющие которого
определяются формулами:
[А,В1, = і4,Д,-і4,Я„
\А,ЩУ = А, Вг-АхВ„ (3)
[А,Щ,^АХВ,-АУВХ. .
Вектор [А, В] перпендикулярен к плоскости, проходящей через
Л
векторы А, В, по величине равен АВ sin (А, В) и расположен
так же относительно векторов А, В, как ось z-ов расположена
относительно осей jc-ob и #-ов. Таким образом:
(А, [А,В]) = 0, (В,[А,В]) = 0,
Л
| [А, В] | = АВ sin (А, В)..
Формулы (3) показывают далее, что
[А, В]--[В, А],
[А, А] = 0.
Необходимое и достаточное условие того, чтобы два отличные
от нуля вектора А и В были направлены по параллельным прямым,
заключается в равенстве:
[А,В] = 0.
До сих пор мы рассматривали алгебраические операции,
составленные из компонентов векторов; перейдем теперь к установлению
*) Мы не останавливаемся на операции сложения векторов, равно как и
правилах вычисления, связанных с этой операцией, считая их общественными, а
обозначения общепринятыми.

операции, составленной не только из комбинации алгебраических
действий, но также и процесса дифференцирования; для
гидродинамических исследований это одна из важнейших операций.
Градиентным произведением векторов А и В мы назовем
вектор, обозначаемый символом (В, V) А, составляющие которого
определяются формулами *):
((В, V)А), = Вх 4^- + Bs 4f- + В,
{(B,V)A},=A
clx
dx
dA.
\<fi,S7)A}. = Bx-fc
+ B
+b
dA
У
Ъ
+ B,
и
dAz , д
dAx
dz
dAy
dz
dA,
dz
W
Геометрическая интерпретация вектора (В, V) А может быть
формулирована следующим образом: это есть вектор, равный
вектору производной вектора А в
направлении вектора В, увеличенному
в [ В [ раз.
Пусть (черт. 4) ОА будет вектор
А, ОВ— вектор В; отложим по
направлению ОВ от точки О длину /ив
полученной точке (У построим
соответственный вектор А (следует
помнить, что А есть функция х> у, z); пусть
это будет вектор ОгА , который мы
обозначим знаком А'. Отношение
разности А7 — А,
Черт. 4.
вектора, равного
А' а
к длине / будет равно j . Таким образом:
(В, V)A=|B|lim
I
Градиентное произведение имеет самую близкую связь с
гидродинамикой, как это показывают следующие формулы:
^=4r + (V'V)A' (5)
DA = (2, V) А = (curl V, V) A. (6)
К сожалению градиентное произведение не обладает столь
простыми свойствами, как скалярное и векторное произведения;
*) А. А. Ф р и д м а н употреблял для этого вектора друтое обозначение {А, В}
Мы решили пользоваться более или иенее вошедшим в употребление символом
(В, V) А, где V — * -д hi ~д Ь Ь ~3— ~ символический оператор
Гамильтона, читаемый „набла". Этот оператор, будучи применен к скалярной величине <?»
дает вектор градиента V 9 = JP"*d 9-
Прим. ред.
42

ниже будут однако даны некоторые правила вычислений,
упрощающие иногда формулы, куда входит градиентное произведение.
3. Выше у нас уже встречались символы расхождения и вихря
вектора; повторим их здесь для полноты.
Расхождение вектора А есть скалярная величина, обозначаемая
символом div А и определяемая равенством:
дАх дАу дАх
Вихрь вектора А есть вектор, обозначаемый символом curl A
и определяемый равенствами:
&4.
UUIJT Л -ч
curLA— д х -
Л4 '
лиг! Д— . У
дАу
dz
дА,
дх
дАх
*\
дх dg h
Параллельно с этими двумя символами большую роль играет
символ градиента.
Градиентом скалярной величины <? называется вектор,
означаемый символом grad <p и определяемый следующими формулами:
і dv . tfo . до _л.
gradar? = — , gradycp = -^, grad2c?=:-^-. (9)
Геометрическая интерпретация вектора-градиента может быть
осуществлена введением в рассмотрение поверхности <р = const;
grad <? есть вектор, перпендикулярный в точке (л:, у, z) к
поверхности 9 — const, .проходящей через эту точку, и по величине
равный производной <р по нормали к этой поверхности.
Не трудно видеть, что:
div curl А = 0, (10)
curl grad ? = 0, (11)
~|- = -§- + (V,grad<?). (12)
Этот последний символ (V, grad о) мы будем в дальнейшем
обозначать через Е (<р); он сыграет большую роль в вопросе о связи
вектора D с динамическими элементами, определяющими движение
жидкости; из формулы (12) найдем:
?(<?) = (V, grad ср) = -§---g-. (13)
*) Гидродинамическое и геометрическое значения расхождения и вихря
общеизвестны; отчасти они выяснены были нами выше.
43-

Векторы по отношению к операциям div и curl делятся на два
класса; к первому классу относятся векторы, расхождение которых
равно нулю- Такие векторы называются соленоидальными.
Если А есть соленоидальный вектор, то всегда существует такой
вектор В, вихрь которого равен А:
curl В = А.
Вектор В называют вихревым или векторным потенциалом А.
Ко второму классу векторов относятся векторы, вихрь которых
равен 0; такие векторы называются потенциальными.
Если А—потенциальный вектор, то всегда существует скалярная
величина <?» такая, что градиент ее есть вектор А:
grad 9 = А;
?та величина называется скалярным потенциалом или просто
потенциалом вектора А.
В основных курсах векторного анализа доказывается, что любой
вектор А может быть представлен как сумма соленоидального и
потенциального. векторов. Таким образом для всякого вектора А
всегда можно найти такой вектор В и такую скалярную величину <pj
чтобы имело место равенство:
А = curl В ~\- grad <p;
в тех же основных курсах векторного анализа излагаются способы
нахождения векторного и скалярного потенциалов; мы не
останавливаемся на этом вопросе, так как в настоящем сочинении нам
не придется иметь дело -с указанными разложениями.
4. Вектор D привел нас к операции градиентного произведения,
известной уже давно в векторном анализе (под иным
наименованием); вектор Н и связанные с ним вопросы сохраняемости
вихревых линий приводят нас к двум новым операциям векторного
анализа. Эти две операции определяют все свойства кинематики
разрушающихся вихревых линий и настолько тесно связаны с
динамикой жидкости при наличии притока энергии, что нам
представляется полезным избрать для обозначения их особый символ
и особое наименование. Главную из этих операций мы позволили
себе связать с именем гениального Гельмгольтца, впервые
осветившего (в 1858 г.) гидродинамику идеальных жидкостей своими
двумя основными теоремами сохранения вихрей.
Вектор -~J2 (А» V) V мы назовем гелъмгольтцианом А
(сокращенно—гельм А) и будем обозначать знакоположением Helm A;
Helm А = ~~ — (А, V) V. (14)
Не трудно видеть, что вектор Н предыдущего параграфа есть
не что иное, как гельм вихря, иначе говоря:
Н = Helm ^ = Helm curl V.
44

Условие сохраняемости вихревых линий состоит в том, чтобы
гельм вихря совпадал по направлению с вихрем; иначе говоря,,
это условие заключается в выполнении равенства:
[Н, Q] = [Helm curl V, curl V] = 0.
Вектор, стоящий в левой части этого равенства и
обращающийся в нуль, когда вихревые линии обладают свойством
сохраняемости, определяет собой для вихревых линий, не обладающих
свойством сохраняемости, степень отклонения вихревой линии от
соответствующей жидкой линии; этот вектор пблезно отметить
особым названием и символом.
Вектор [Helm А, А] мы назовем деклинацией А (сокращенно
„декль А") и обозначим знакоположением decl А:
decl А = [Helm А, А]. (15)
Условие сохраняемости вихревых линий заключается в том,
чтобы деклинация вихря была нулем.
Помимо гельма А нам нужны будут следующие векторные
символы:
//А
Helm (п, А) = ~ (А, V) V + л А, (16)
helm А = -^- — fA,V)V + AdivV; (17>
первый будем называть гелъмголыпицаном А рода л, второй -
полным гехьмголыпцианом А.
Легко видеть, что:
helm А = Helm (divV,A),
decl A = [Helm (n, A), A] = [helm A, A].
В дальнейшем нам понадобятся еще некоторые редко
встречающиеся векторные и скалярные символы, которые мы
непосредственно выписываем.
Скаляр ( ц )•
(18)
Вектор *)
' *-,» - дА- , - <>А і і дА
*) Если ввести в рассмотрение тензор V А = і —s |-j —^ j- к
дх ^J ду ^~ dz
45

IH-
дА.
дВу дА,
f-4-
дх дх ду ду
дВу дА
4-
55.
¦&4„ <?Д
[
А
В
дх дх
I дА, дБ
+ дА*
дВ.
ду ду
, дА, дВ
+ <И,
dz dz
дВя
dz dz
дА, дВ,
дх дх ду ду
4-
дА. дВ
-г
дх дх
+
дА. дВ.
1Н-(-?
дА, дВ.
ду ду
дА.. дВ
4-
dz dz
дА, дВ, \
У
dz dz J
дА., дВ„
дх дх ' ду ду
4-
'V,
dz dz
дА.
dBv дА.
4-4-
дВ.
дА, дВ.
(19)
дх дх ' ду ду dz dz
Не трудно обнаружить справедливость следующих формул:
А
В
В
А
А
В
В
А
( В )==(sr*dA» 2radB,) + (gradi4,, grad В,) + (grad A., grad Вг),
А
А
= 0.
дА .
= grad Ах і -f- grad ^4у j + grad As к и сопряженный с ним тензор А V — ~у~ i ~h
Ч"""5~"і "^—л—к = і gradi4tf + J grad Л;/-}-к grad Л г, то скалярное
произведение двух тензоров AV и VB будет равно *
(AV. VB)= (*)
= (grad Ах, grad Вх) іі -f (grad Axt grad By) ij + (grad A& grad Вг) ik -f-
+tgrad Ay, grad 5,) ji + (grad Ay, grad ?,,) jj + (grad Ay, grad Яа) jk +
+ (grad Л 2, grad Bx) ki + (grad A2, grad?y) kj + (grad Az, grad Be) kk.
Беря в каждом члене (*) скалярное произведение обоих ортов, получим
первый инвариант тензора (А V- V В), который можно рассматривать как биска-
лярное произведение тензоров А V и VB:
((А V, V В)) = (grad Ах, grad Вх) +
-(А
+ {gradAy, gradВу) + (gradAet grad^s)~ . fi
беря же в каждом члене (*) векторное произведение обоих ортов, получим вектор:
((А V, У В)) = {(grad Ау, grad Bs) - (grad A„ grad By)} i +
+ {(grad4s, grad Bx)~ (grad Axt grad Вz)} j +
+ {(g™&Ax, grad By) — (grad Ay9 gradSx) k —
В
A
]¦
клк известно, тесно связанный с антисимметричной частью тензора (А V» V В)у
Прим. ред.
46

5. Правила вычислений, на которые опираются все
преобразования векторного анализа, могут быть распределены, в целях
удобства обозрения формул, на две категории. В первую входят
различные комбинации скобок (т. е. главным образом скалярного,
векторного и градиентного произведений), во вторую входят
операции curl, div, grad, Helm и т. п. в комбинации как между собой,
так и со скобками.
Все формулы настоящего пункта получаются с помощью
совершенно элементарных, хотя иногда и несколько длинных
вычислений; поэтому мы приводим эти формулы без подробного их
доказательства.
Формулы со скобками одного сорта:
(А, X В) = (X А, В) == X (А, В). (20)
[А, X В] == [X А, В] = X [А, В]. (21)
(ХВ, V)A = X(B,V)A. (22)
(В, V) X А = X (В, V) А + А (В, grad X). (23)
ХА
В
Х( В ) + (MsradX,V)B).
ХА
В
= х
А
В
+ [(grad X, V) В, А].
Формулы со скобками нескольких сортов:
(24)
(25)
(А, [В, С]) = (В, [С, А]) = (С, [А, В]) =
АхАу
вхвЙ
СшС,
Аг
вг
с,
(26)
[А, [В, С] = (А, С) В - (А, В) С. (27)
([А, В], [С, D]) = (А, С) (В, D) - (A, D) (В, С). (28)
[ [А, В], [С, D] ] = ([А, В], D) С - ([А, В], С) D. (29)
[A,(C,V)B]-[B,(C,V)A] = (C,V)[A,B]. (30)
(А, (С, V) В) + (В, (С, V) А) =.(С, grad (А, В)). (31а)
(А, (С, V) В) + (В, (А, V) С) = (A, grad (В, С)) + (A, [curl В, С]). (316)
Не трудно видеть, что условие компланарности векторов А, В, С
может быть выражено равенством:
(А,[В,С]) = 0.
Формулы^ содержащие одни основные дифференциальные
операции:
t grad ©ф = © grad 6 -f- Ф grad ©. (32)
div <?A ===== <? div A + (grad ?, A). (33)
curl <?A == <? curl A -f- [grad ©, A]. (34)
47

Helm?A = oHelmA+A-^ = ?Helmf^|p, a\. (35)
decl <?A = <?2 decl A. (36)
Формулы, содержащие дифференциальные операции и скобки:
div [А, В] = (В, curl А) — (A, curl В). (37)
curl [А, В] = A div В — В div А + (В, V) А — (А, V) В. (38)
grad (А, В) = [A, curl В] + [В, curl А] + (В, V) А + (А, V) В. (39)
1
(B,V)A
curl [А, В] +
2
f- -f grad (А, В) —j [A, curl В] - -±-[В, curl A] -f
+
BdivA — AdivB
(40)
div (В, V) A = (В, grad div A) — (curl A, curl B) + ( ? j . (41)
curl (B, V) A = (B, V) curl A — (curl B, V) A +
+ [curl A, curl B] -\- div A curl В -j-
A
В
(42)
С помощью формулы (38) можно получить следующие
выражения для операции гельма:
helm А = -§?• + curl [А, V] + V div A,
Helm А = -^- + curl [А, V] + V div A—A div V.
(43)
(44)
В частности:
6Q
helm 2 = ~^- + curl [О, V].
Все только-что написанные формулы получаются совершенно
простыми вычислениями, и лишь формула. (42) требует некоторых
преобразований, облегчающих вычисление; выведем эту формулу.
Введем еще один векторный символ, который позволит нам
вычислить вихрь вихря. Назовем символом ДА вектор с
составляющими:
мА) я *Ае . ^А+^ = дл
^А)х— д ¦+- dus -Г дял — *лх,
dy<
д*~Аи д*Ач , д*А.
дх-
(ДА) =^4
dy'
dy* ^ dz» *'
(45)
43

Нетрудно проверить справедливость следующей Формулы:
curl (curl A) = curl'2 A = grad div A — ДА. (46)
Пользуясь формулой (38), найдем:
curl2 [А, В] = curl (В, V) А — curl (А, V) В —
-fdivB curl A — div A curlB-f [grad div В, A] —[grad div A, B].
Замечая, что согласно (46):
curl* [А, В] = grad div [A, B] — A [A, B],
и применяя формулу (37), найдем:
curl (В, V) А — curl (А, V) В = (curl А, V) В +
-г (В; V) curl А — (curl В, V) А — (А, V) curl В +
+ 2 [curl A, curl В] + div A curl В — div В curl А + (*)
+ [А,ДВ]-[В,ДА]-Д[А,В].
Взяв curl от обеих частей равенства (39), помня, что
curl grad (А, В) = 0, и пользуясь формулой (38), найдем:
curl (В, V) А + curl (А, V) В = (А, V) curl В +
+ (В, V) curl А — (curl В, V) А — (curl А, V) В + (**)
-f- div A curl В -f- div В curl A;
складывая формулы (*) и (**) и замечая, что
[А, ДВ] - [В, ДА]-Д [А, В] = 2 Г *
докажем формулу (42).
6. В дальнейшем нам очень часто придется представлять
векторы в виде суммы трех векторов, направленных по трем заданным
векторам; подобное представление соответствует разложению
вектора на составляющие по трем неортогональньш (вообще говоря)
координатным осям. Разберем, какие формулы определяют
'подобное разложение.
Пусть нам заданы три вектора: А, В, С. Тогда, если эти векторы
не компланарны (не лежат в одной плоскости), то всякий вектор D
может быть представлен следующей формулой:
D = aA + AB-fcC, (47)
где
(D,[B,C])
а —
(А, [В, С])
(D,[C,A])
(В, [С, А])
(Р, [А, В])
(С,[А;В])
(48)
причем знаменатели в этих формулах (все одинаковые) отличны
от нуля в силу того, что векторы А, В, С не компланарны.
4 Зак. 2420. — А". А. Фридман, Опыт гидромеханики
49

В случае, если векторы А, В и С компланарны, тогда, очевидно,
лишь те векторы могут быть представлены формулой (47), которые
лежат в плоскости, проходящей через векторы А, В, С. Если два
какие-либо из векторов А, В, С, например А и В, не лежат на
параллельных прямых, то всякий вектор D, компланарный с А, В, С,
может быть представлен формулой:
D==aA+6B,
где
11 '[А, В]
61=4
[В, А]"
причем по условию [А, В] ф 0.
Разбор случая, когда все три вектора А, В, С лежат на
параллельных прямых, не представляет никаких затруднений.
Если векторы А и В не лежат на параллельных прямых, то три
вектора А, В и [А, В] не компланарны, как это ясно
непосредственно из геометрических соображений; разложение вектора D по
указанным трем векторам осуществляется такими формулами:
D = aA-b6B-bc[A,B],
(Р,А)(В,В)-(Р,В)(В,А)
(А,А)(В,В)-(А,В)(А,ВГ
а
А _ (D, В) (A, A)-(D, А) (А, В)
(А,А) (В,В)-(А, В) (А,В)'
\
с =
(D, [А, В])
(49^
(А, А) (В, В)-(А, В) (А, В)'
этими формулами мы часто будем пользоваться в дальнейшем,
особенно во второй части нашей работы.
7. В заключение разберем вопрос о правилах применения
операций дифференцирования к векторным символам. Не трудно
видеть, что получить правила дифференцирования частным образом
по t, х, у, z не представит больших затруднений; наоборот,
пользование символом —— повлечет за собой значительные усложнения
формул и вычислений. Установим сначала ряд формул, дающих
правила дифференцирования частным образом по t9 л:, у, z, причем
д * д д д
символом -т— будем обозначать одну из производных-^—, -<-, —
д У
или
дг '
д_
ds
д
(А, В)
1і <»' V) А
ds
дА
ds
. в) + (а,
В
4
А,
дВ
ds
дВ
ds
(B,V)-f-4
db_
ds
,V A,
(50)
(52)
50

^-grad^grad-^,
ds
a
~dT
div A = div
curl A = curl -
d_A_
ds '
dA
dA
dt
J_
ds
-г— Helm A = Helm ,
ds as
d_ I dA
dt [ ds
dA
ds '
d\
Ц-
ds
-|-curl
+
dV
A,
av
V) a,
dV
(531
(54)
(55)
(56)
ds
+
, div A — A div -j
ds ds
(57)
-r— Helm (n, A) = Helm ( n> -3—
-j- curl
A,
ds
+
ds
helm A = helm —5 j- curl
ds
A,
-div
dV •
ds
dV \
ds J'
(58)
(59)
Перейдем теперь к установлению некоторых правил, дающих
возможность вычислять *~77" различных векторных выражении. Не
трудно видеть, что формулы (50) и (51) остаются справедливыми,
б d
если в них —г— заменим на—у—; этого нельзя утверждать
относись at
тельно остальных формул.
Пользуясь формулами (41) и (42), установим следующие
равенства:
div4L = ^A _(curlAj curiV) + ( t \, (60)
dt
dt
(curl A, curlV) + ( * j,
curl -~ = d™fA - (curl V, V) A + [curl A, curl V] +
-j- div A curl V -j~
отсюда, заменяя А на V, получим:
A
V
(61)
,. dV ddivV , c c
du_
dx
. _ dw dv . » du
>zu
dg dz
curl
dx
+ 2
dv du
fzu
+
dx dg
dV
dt
= helm curl V.
4*
(62)
(63)
51

Последняя формула играет большую роль в гидродинамике?
с помощью ее вектор Н связывается с динамическими элементами
(давлением и плотностью или температурой) движения жидкости.
Выведем еще одну формулу, которая окажется нам весьма
полезной в дальнейшем:
-^- (grad/, А) = (grad -^-, А) + (grad /, Helm A). (64)
(
Так как непосредственный вывод этой формулы требует очень
длинных вычислений, то мы укажем следующий путь; имеем:
с/А \
= (^Г^. А) + ((V. V) grad/, А) + (grad /,
dt Г
откуда:
/grad -JL-, A J — -^- (grad/, А) =
= (grad (V, grad /), А) - )(V, V) grad/, A) - ( grad f,^~),
или
(grad-^, A)+forad/, Helm A)- ^ (grad/, A) = (grad(V, grad/), A) -
- (V, V) grad/, A) - (grad/, (A, V) V).
Пользуясь теперь формулой (31а) и непосредственно
проверяемым тождеством:
(V, (A, V)grad/) = (A, (V, V) grad/),
найдем, что правая часть предыдущей формулы обратится в нуль,
что и докажет формулу (64).
Формула (64) дает нам возможность установить ряд формул,
позволяющих переставлять операции -уг и D. Одною из таких
формул мы уже пользовались в § 2 для доказательства условий
сохраняемости вихревых линий. Символ Df может быть
представлен в следующем виде:
D/=(srad/,Q);
отсюда и из формулы (64) не трудно вывести следующее*
соотношение :
D& = ^-(gradf, HelmQ) = -^-(grad/, E). (65)
Обобщая формулу (65), мы можем найти простое и симметрич-
ное выражение для D-y~. Для вывода этого выражения нам
at
понадобится образовать особую последовательность векторов;
52

эта последовательность будет играть известную роль в
кинематических вопросах движения жидкости при наличности притока
энергии.
Условимся векторы этой последовательности обозначать
символами
Н, Hi» Н-2-.. Ид...,
образуемыми по следующему рекуррентному закону:
Ht = HolmHfc_1| (k = l, 2...)
Н0 = Н = Helm &
Легко видеть, что
Щ = Helmfc+1 Q = Helm* H *);
іоэтому Щ уместно будет назвать гельмго.лтцианом (к-{-1)-го
порядка („гельм (&-j~l)-ro порядка").
Условившись в указанных обозначениях, напишем формулу
для ¦Ь'т.й в следующем виде:
где
п]
р*' (f-bl)I(n — і— 1)! '
Формула (66) доказывается методом полной индукции, причем
никаких затруднений это доказательство не представляет.
Из формул (65) и (66) не трудно получить соответственные
формулы для символа D, приложенного к вектору А; вспоминая
обозначение градиентного произведения, найдем следующие две
формулы:
D^ = ^-(E,4)A, © (67)
п «ГА <Г?>А vi1 „ m 0. Л"-'"1 А
^ = ^-LP^H^^^-' (б8)
где рп і имеет то же значение, как и в предыдущих формулах.
8. Нам придется сравнительно редко пользоваться двумя
преобразованиями интегралов, известными под именем формул Гаусса
и Стокса. Для полноты мы приведем однако без доказательств
обе эти формулы. (
Пусть у нас имеется замкнутая поверхность S, ограничивающая
* Helmfc А есть операция гельм, повторенная последовательно к раз над
вектором А.
53

область ^; пусть л будет нормаль к поверхности S, направленная
вовне области ~; такая нормаль называется внешней.
Условимся проекцию вектора А на направление внешней
нормали обозначать через Ап; при этих обозначениях формула Гаусса
может быть написана следующим образом:
fdivAdz = fAndS, (69)
- s
где d'z и dS суть элементы объема области ^ и поверхности S;
первый интеграл распространен по всей области ?, а второй — по
замкнутой поверхности S.
Положим, что у нас имеется замкнутая линия К; через эту
линию проведем поверхность S и выберем определенное
направление нормали к этой поверхности за положительное; проекцию
вектора А на положительное направление нормали обозначим
через Ап. Условимся положительным обходом контура К считать
такой обход, который по отношению к положительной нормали
совершается в ту же сторону, как и кратчайший переход от оси
х-ов к оси 1/-ОВ по отношению к положительной оси z-ов.
При таких соглашениях теорема Стокса может быть
формулирована следующим равенством:
j\Axdx+Aydy + Azdz) = fcmlnAdS, (70)
К S
причем криволинейный интеграл / взят по положительному обходу
к
замкнутого контура Ку а интеграл по поверхности / распростра-
8
нен на кусок поверхности, растянутой контуром К.
Глава II.
ИЗМЕНЕНИЯ ВИХРЕЙ.
§ 4. Элементы, определяющие изменения вихревых линий.
1- В § 2 мы познакомились с понятиями основного триэдра и
основного сферического треугольника. Этот основной сферический
треугольник QL2', само собой разумеется, является бесконечно
малым сферическим треугольником, если промежуток времени Д?
стремится к 0; таким образом, если мы желаем определить элементы,
характеризующие изменения вихревой линии в момент t (т. е.
при &і -> 0), то мы должны рассматривать не сами элементы
основного сферического треугольника, а их предельные значения
при A*->0, или же, если эти предельные значения суть 0, — их
отношения к соответственно выбранной степени А*.
Элементами, определяющими основной сферический треугольник,
будут три его стороны и три его угла.
54

Пусть (черт. 5) QLQ' будет сферический основной треугольник.
Наиболее важен нам угол между линией L и линией Q'; в случае,
если имеет место сохраняемость вихревой линии, этот угол
обращается в 0.
Угол LQ', измеряемый дугой oLQ' основного сферического
треугольника, назовем отклоняющим углом и будем его
обозначать через а*).
Не трудно видеть, что lim а = 0. Таким образом для характе-
ристики того, насколько вихревая линия в момент t стремится
отделиться от соответствующей ей жидкой линии, необходимо ввести
предел отношения угла ее к некоторой степени Л?
Отклонением вихря будем называть предел отношения
отклоняющего угла а к промежутку времени Ц (в течение
которого образовался основной сферический треугольник) при Д? —>0
и будем обозначать его через 6. Отклонение вихря есть
положительная величина или нуль:
,. «
о = hm —г-..
Как мы докажем ниже, если 6 = 0, то имеет место
сохраняемость вихревых линий, так как отклоняющий угол а обращается
в 0 при всех Л? (во всем промежутке
времени, в течение которого
рассматривается движение). Уже одно это
обстоятельство позволяет считать
отклонение вихря весьма важной
величиной для кинематики вихревых линий;
впоследствии мы увидим тесную связь
отклонения вихря с динамическими
элементами, характеризующими движе- Черт. 5.
ние жидкости.
2. Менее важны два другие угла основного сферического
треугольника, однако и они дают некоторые интересные соотношения.
Угол Q'Q, измеряемый дугой uQ'S основного сферического
треугольника-) назовем уклоняющим углом и будем обозначать
через of; угол QL, измеряемый дугой о QL основного сферического
треугольника, *назовем изгибающим углом и будем обозначать
через а".
Не трудно видеть, что Hm а' = lim а" = 0.
Само собой разумеется, что движение, в котором а = 0, т. е.
в котором имеет место сохраняемость вихревых линий, совершенно
не влечет за собой равенства нулю величин а' и а"; для этого
движения будем иметь только: а' = о!\
*) Само собой разумеется, что за угол двух направлений мы будем принимать
угол меньший 180°.
55

Уклоняющий угол характеризует собой, насколько новая
вихревая линия к моменту t-\-Af уклонилась от старой (к моменту t);
изгибающий угол характеризует собой уклонение к моменту t -f- А*
жидкой линии от ее положения, совпадавшего с направлением
вихря к моменту L
Так как lim а' = lim а" = 0, то нам (аналогично предыдущему
пункту) необходимо для характеристики изменения вихря к
моменту t ввести отношения о! и а" к некоторым степеням At
Уклоном вихря назовем предел отношения уклоняющего угла
к At при Д?->0; изгибом вихря назовем предел отношения
изгибающего угла к At при Af->0.
Уклон вихря будем обозначать через 3', изгиб — через 3*.
Согласно определению имеем:
nr rtr/
о = ііт -т—, о = nm -г— .
л*-*о ^t м-уо &t
Ниже будет выяснено, что в обычных случаях движения
жидкости все три предела, определяющие отклонение, уклон и изгиб
вихря, существуют. Все эти три величины имеют размерность
угловой скорости, почему мы будем иногда называть их
скоростными элементами изменения вихревых линий.
3. Перейдем теперь к изучению двугранных углов бесконечно
малого основного сферического треугольника.
Из этих углов наиболее важен угол при вершине L
треугольника, характеризующий в известной мере, насколько повертывается
плоскость, проходящая через вихрь и жидкую линию в течение
промежутка времени А?.
Двугранный угол QLQr основного сферического треугольника
назовем крутящим углом и обозначим через А,
Если имеет место сохраняемость вихревых линий, то крутящий
угол становится неопределенным, но в этом случае он становится
совершенно излишним при описании изменения вихревых линий.
Во всех остальных случаях крутящий угол при любом А*, как это
будет выяснено в § 6, будет иметь вполне определенное значение
и будет стремиться к определенному пределу А9 коль скоро А/ -> 0.
Кручением вихря будем называть предел^ к которому
стремится крутящий угол А основного сферического треугольника,
когда At—>Q.
Кручение вихря будем обозначать через А\ согласно
определению, имеем:
lim A=Am
Кручение вихря даст возможность разобраться в тех изменениях
вихревых линий, которые они претерпевают когда отклонение
отлично от нуля, когда следовательно вместо сохранения вихревых
линий наступает их разрушение.
56

Остальные два двугранных угла основного сферического
треугольника имеют меньшее значение и в настоящей работе
рассматриваться нами не будут; давать им особых наименований мы
не будем, а условимся угол LQ'L* основного сферического
треугольника называть сопряженным уклоняющему углу и обозначим
через А' иуголй'Й/, основного сферического треугольника назовем
сопряженным изгибающему углу и обозначим через /і".
Предел угла, сопряженного уклоняющему углу при A* -> О,
назовем сопряженным уклоном вихря и обозначим через Ar \
предел угла, сопряженного изгибающему углу при Д*-*0, назовем
сопряженным изгибом и обозначим через А".
Согласно определению имеем:
lim А' = А', lim АШ = А". •
Кручение, сопряженный уклон и сопряженный изгиб суть
величины, не имеющие размерности (как углы); мы будем называть их
иногда угловыми элементами
изменения вихревых линий.
Изучение этих угловых
элементов значительно упрощается, если мы
построим триэдр, дополнительный
нашему основному триэдру.
Условимся символом [АВ\
обозначать направление, совпадающее с
направлением векторного произведения
векторов А и В; это будет очевидно
перпендикуляр к плоскости,
проходящий через направления А и В и
ориентированный относительно этих
направлений так же, как ориентировано
векторное произведение.
Для нашего основного триэдра
проведем (черт, б) через центр
единичной сферы направления [2L], [?-'],
[2', Щ. Мы получим новый триэдр, дополнительный основному,
в котором углы между направлениями [2L], J^^'] и [й'2] будут
последовательно 180°—Д 180°—-А', 180° — А". __
Таким образом А будет угол между [&L] и [2'L]; А'будет угол
между [&L] и [2'2], и А" будет углом между [Q'Q] и [LQ]. Это
замечание облегчит нам впоследствии вывод формул,
определяющих А, А', А".
4. Изучение угловых и скоростных элементов изменения вихря
значительно облегчается тем обстоятельством, что эти шесть
элементов образуют всегда три угла и три стороны некоторого
плоского треугольника.
- г,
[oil
Черт. о.
57

Докажем следующее предложение:
отклонение 3, уклон 8' и изгиб 8" суть стороны плоского
треугольника, углы которого, заключенные между о" к о, S и 8', У и
8", соответственно сцтъ кручение Л, сопряженный уклон А' и
сопряженный изгиб А* (черт. 7).
Согласно основным формулам сферической тригонометрии имеем
для основного сферического треугольника:
sin Л sin Л' sin Л"
sin of sin of sin a
Разделив знаменатели этих равенств на М и замечая, что при
* , т sin of a' ^
А* -*0 имеем lim —т-т- = hm — = & и т. д., найдем, переходя
к пределу при Д?-*•():
sin Л sin Л7 sin Л"
(*)
Обозначая через з сферический избыток основного
сферического треугольника, будем иметь:
г = Л + Л' + Л" —180°.
Из геометрии сферы известно, что сферический избыток для
треугольника на единичной сфере численно равен его площади;
так как площадь основного
сферического треугольника стремится к
нулю, когда Д*-?-0, то lim е —О,
поэтому
А~\-А' + А' = 180°; (**)
формулы (*) и (**) являются
доказательством нашей теоремы.
Только-что полученный плоский
треугольник мы назовем
сопряженным основному треугольником.
Из доказанного предложения вытекает, что мы будем знать
скоростные и угловые элементы изменения вихревой линии, коль
скоро будем знать все элементы сопряженного треугольника.
Элементы этого сопряженного треугольника будут известны, коль
скоро будут известны три основные величины, определяющие
сопряженный треугольник. За эти три основные величины мы
примем отклонение \ кручение А и уклон 8'. Причина, почему мы
выбираем отклонение и кручение за основные величины, в
известной мере выяснилась из предыдущих соображений; причина, почему
уклон о' взят нами за основную величину, выяснится в дальнейшем.
Отклонение, кручение и уклон будем называть главными
элементами изменения вихревых линищ остальные будут называться
второстепенными-, они без труда выражаются через главные
элементы изменения вихревых линий.
5S

Движение жидкости может быть распределено на классы
смотря по тому, в каком направлении и при каких условиях
проявляется вырождение сопряженного треугольника, т. е. обращение
в нуль одного из его элементов.
Хотя указанное разделение будет предметом дальнейшего
исследования, но мы считаем полезным уже в этом месте сделать
несколько замечаний по поводу означенной классификации.
Первый класс движений включает в себя те движения, в которых
отклонение о обращается в нуль. Ниже будет доказано, что в этом
случае имеет место сохраняемость вихревых линий, иначе говоря —
в этом случае -' постоянно совпадает сіи отклоняющий угол а
обращается в нуль при всех Д?; при этом движении наш плоский
треугольник вырождается в прямую линию. Движения, в которых
отклонение обращается в нуль, мы назовем гелъмголътцевыми
движениями жидкости, имея в виду, что главный фундамент при
изучении этого рода движений был заложен Гельмгольтцем в его
двух основных теоремах теории вихрей.
При рассмотрении негельмгольтцевых движений обращает на
себя внимание прежде всего второй класс движений, обладающий
тем свойством, что кручение А для этого класса движений
обращается в нуль или 180°. Отсюда, разумеется, нельзя еще заключать,
что А, т. е. крутящий угол вихря, при всех Л* обращается в 0°
(или в 180°), а можно только утверждать, что этот крутящий
угол А отличается от 0° или 180° величиной по меньшей мере
второго порядка малости относительно Д/. Тот случай движения,
когда не только А обращается^в 0° (или 180°), но и для всех М
А тоже равняется 0е (или 180°), мы назовем случаем незакручи-
вающегося движения.
Само собой разумеется, что для незакручивающегося движения
кручение обращается в 0° (или 180°), но этого конечно мало;
в незакручивающемся движении новое положение вихря (к
моменту 2-рЛ/) постоянно остается в плоскости, проходящей через
старое положение вихря (к моменту t) и через жидкую линию L
(соответственно к моменту ?-[-Д/). Из сопряженного плоского
треугольника следует, что в незакручивающемся движении или 5' =0
или sin А/ = 0.
Особого внимания заслуживает случай, когда 3' = 0, т. е. когда
уклон вихря равен нулю. В этом случае, так как мы
рассматриваем негельмгольтцевы движения, из сопряженного треугольника
найдем, что
8 sin і4 = 3'sim4" = 0, 3^:0,
и следовательно
sin А = 0,
т. е. А = 0 или 180°.
При изучении кручения вихря будет показано, что когда уклон
равен 0, то нетолько кручение А = 0° или 180°, но мы имеем
дело с незакручивающимся движением, т. е. А = 0° или 180° при
всех Д*.
59

Движение, в котором уклон вихря обращается в нуль, будем
называть главным незакручивающимся движением,
В параграфе, посвященном изучению кручения вихря, мы
укажем на ряд соображений, которые могли дать возможность
утверждать, что всякое незакручивающееся движение есть главное
незакручивающееся движение. j
Однако несколько примеров, которые своевременно будут нами
приведены, показывают, что это утверждение неправильно и что
возможны незакручивающиеся движения, не принадлежащие к классу
главных незакручивающихся движений. Вероятно однако, что
незакручивающиеся движения, не принадлежащие к классу главных
незакручивающихся движений, возможны лишь в исключительных
случаях. '
Равенство нулю уклона вихря влечет за собой, — как это будет
показано в дальнейшем, — обращение в нуль уклоняющего угла а'
при всех Д? Таким образом в главном незакручивающемся
движении новый вихрь постоянно будет по направлению совпадать со
старым вихрем.
К третьему классу движений относятся те движения, в которых
изгиб вихря Ь" обращается в нуль.
Здесь, как будет подробно выяснено в параграфе, посвященном
изучению изгиба вихря, можно подбором определенного частного
случая показать, что из равенства S" = 0 не вытекает еще, что
сс" = 0 при всех Д?; вследствие указанного, класс движений
жидкости, в которых изгиб вихря равен 0, характеризует движение
жидкости не в течение некоторого промежутка времени, а лишь в
данный момент t\ вид основного -сферического треугольника для этого
класса движений не будет представлять никаких особенностей.
Вследствие изложенного этот класс движений не представляет
особого интереса.
Мы назовем движения, в которых изгибающий угол а"
обращается в 0 при всех Af, прямыми движениями. Во всяком
прямом движении изгиб вихря ь" обращается в 0; однако этого
обстоятельства недостаточно для того, чтобы движение было
прямым. __ С
Движение, в котором сопряженный уклоняющий угол А/
обращается в 0 при всех Д?, сводится или к прямому или к незакручи-
вающемуся движению; точно так же движение, в котором
сопряженный изгибающий угол А' обращается в 0 при всех Д?, сводится
или к гельмгольтцеву движению, или к незакручивающемуся
движению.
Таким образом мы имеем три класса движений: гельмгольтцево
движение, незакручивающееся и прямое движения. При этом
в незакручивающемся движении особое значение имеет случай
главного незакручивающегося движения; следует еще раз
напомнить, что возможно незакручивающееся движение, не
принадлежащее к классу главных незакручивающихся движений.
Основной задачей следующих параграфов этой главы будет
изучение связи главных и второстепенных элементов изменения
60

вихревых линий с теми векторакл, которые характеризуют собой
движение вихрей. Мы увидим, что три вектора: вихрь Q, гельм Н
и вектор D будут достаточны для выражения через них всех элементов
изменения вихревых линий; выразив эти элементы через
указанные векторы, мы установим условия осуществления гельмгольтцева-
незакручивающегося (общего и главного) и прямого движения;
о гельмгольтцевом движении мы уже говорили в § 2 и будем
говорить еще в следующем параграфе настоящей главы.
§ 5. Отклонение вихря.
1. Займемся теперь наиболее важным кинематическим
элементом, а именно отклонением вихря.
Напомним, что косинусы направления Q с осями координат
были пропорциональны величинам аг, а2, а3; косинусы направления
L с осями координат были пропорциональны величинам /lf /2> /3> и
наконец косинусы направления Q' с осями координат были
пропорциональны а[, а'г, Од. При этом только-что указанные девять
величин могут быть определены следующими формулами:
ах = Ъ, а2 = tj, а3 = С, (6)
4_с+Л*+^>(-?>+ ... ->(?=)* + ....
Легко видеть, что справедливы следующие формулы:
cos (*СХ) = gl =- cos (jOO === Zl
К ax+ <*% + <*
"3
Co
cos (2, Y)= ' I2 cos (L, Г) =
J/ ax -f a2 + a а'
cos OO) = —p- % —r cos (C ^) =* - r , >
K4 + «2 + «2' К $ + ? + *;
V7
к
4
h
61

V <
V а;
а1
г '2
~а2
г
а..
">5
-t-a„
cos (Q', JQ
cos (Q', Г) =
cos(Q',2) = ._ .
К «i "Г <*2 Ta;1
Пользуясь этими формулами, найдем:
sm- a = sm- (L, 2 ) = ¦ ~т^ го™ ЧГ,7Г—#—~л\ 5
(«1 "Г С2 "Г «3 ) ('l і" 4 "Г U
отсюда, деля на Д?2 и переходя к пределу, получим основную
формулу:
8^ = ^
dt
dt
Dv
H-
(P + tf + C8)8
(S'+tf-K*)9
или
Отсюда, помня, что 8 не отрицательная величина, найдем:
[Н, Q] | | decl curl V |
Q2
(curl V, curl V) •
(9)
(10)
(11)
Вспоминая, что представляет собой векторное произведение, и
помня, что углы наши все содержатся в первой половине
окружности, найдем следующее выражение для отклонения:
о
Я sin (Q, Н)
Q
(12)
что и является основной формулой, выражающей отклонение 8.
2. Отклонение 8 обращается в нуль, если Н = 0 или если Н и
Q совпадают по направлению; таким образом условие 8 = 0
эквивалентно условию:
decl curl V = 0,
62

и это есть как раз условие сохраняемости вихревых линий; при
сохраняемости вихревых линий, вихревая линия остается постоянно
жидкой линией, т. е. 2' и I при всех Лг совпадают, а значит
а = 0 при всех &t. Отсюда получаем следующее предложение:
Теорема 2. Для того, чтобы движение жидкости было
гелъмгольтцевым, необходимо и достаточно, чтобы отклонение
вихря равнялось нулю.
В случае негельмгольтцева движения, т. е. когда сохранение
вихревых линий не имеет места, отклонение характеризует в
известном смысле степень разрушаемости вихревых линий. Чем
больше о, тем больше стремится отклониться новая вихревая линия
Qr от той жидкой линии, в которую к моменту *-}-Af перешла
жидкая линия, занимавшая к моменту t положение вихревой линии Q.
Имея отклонение вихря в виде функции координат и времени, мы
можем составить себе представление об отклоняющем угле и
о том,. как этот угол меняется в данный момент в зависимости от
координат частиц. При достаточно малом b.t можно написать
следующую приближенную формулу:
а =- o\t,
по которой и рассчитывать угол а; подобный способ расчета
может найти себе применение в динамической метеорологии, так
как величина S связана с одной стороны с распределением
вихрей к данному моменту, а с другой стороны с вектором Н,
который просто выражается через хорошо измеряемые динамические
элементы (см. ниже главу IV),
3. Чтобы иллюстрировать введенное нами понятие отклонения
вихря, приведем несколько примеров. При этом будем
рассматривать лишь негельмгольтцевы движения, так как ряд примеров на
гельмгольтцевы движения был нами рассмотрен в § 2 главы I.
Пример 5. Рассмотрим прежде всего квази-твердое движение
жидкости; тогда
[Н, SL = ^-6], [Н, Q], = « —К, [Н, QL-Jr,-^,
I ded Q |* = (p -f 1? -rr^2) (?+tf+Ф - (5+m -r ::)*;
P + f+C« \ dt J 9 v i ' ^ '
отклонение не зависит от координат и зависит только от
времени L
Рассмотрим такой частный вид квази-твердого движения,
в котором вихри пульсируют, затухая согласно формулам
? = е~ cos \*>t, Tj == е~ " sin pt, С = 0. О
Тогда после вычислений найдем, что отклонение будет величиной .
постоянной и равной р.
63

Пример б. Рассмотрим движение, в котором ц, v суть функции
t, z, a w = 0. В этом случае будем иметь:
*¦ _ _ d%L ., _ dlL * — n
; ~ "dz ' ' ~~ ~дг ' * ~~ '
И.
dt
, #; = 0;
~ 6-
д-ч
S^
1 dt - dt
Полагая:
% = 2 cos '¦?, ъ = 2 sin о,
т. е. вводя в рассмотрение отдельно величину и направление
вихря, после несложных вычислений найдем:
82
ch_\2
dt Г
до
Указанное движение, как мы уже говорили, может иметь место
в атмосфере, когда ветер мало меняется с изменением координат
места, а вертикальные течения слабы.
Пример 7. Положим и = v = 0, иначе говоря — положим, что
течения наши параллельны оси z-ов. В этом случае:
у dw d<w „
полагая:
будем иметь:
<?? . ді „ дщ , d-q
Oz
9. cos ?, '1
до ,
It
-w
w
dz9
2 sin o9
do
!z~
Я2 = 0;
§ 6. Кручение вихря.
1. Для изучения кручения вихря необходимо рассмотреть
крутящий угол, а значит необходимо принять во внимание триэдр,
дополнительный основному. Направления ребер этого триэдра
(черт. 6) были нами обозначены символами [2L], [?2'], (272]; угол
между [2?] и [L27) равен 180° — А, поэтому для определения
крутящего угла нам нужно рассматривать направления [2L] и
[2'L]; к этим двум направлениям присоединим еще направление
[22'], противоположное направлению [2'2], которое нам будет
нужно в дальнейшем. Обозначим величины, которым пропорцио-
64

кальны косинусы направлений [QL], [QrL\ и [?-'] с осями
координат, следующими буквами:
для [QL]: bv bo,t &3>,
для [Q'L]: b\9 b[2, b'z>
для [2Q'J: ml9 ma, /n3.
Из определения символа, характеризующего направление [АВ],
будут следовать такие формулы для Ьі9 Ъг и т. д.:
Ь3 = аги — ajv ^з == аі 4 — а2 А> ^з = аіа->
а'2а1 9
где а1? а.>, а3 и т. д. имеют то значение, какое им придано нами
в § 2 и в § 5.
Дальнейшее наше изучение величин Ьи &2 и т. д. будет
заключаться в разложении этих величин по степеням А/, для чего
чрезвычайно удобными являются формулы векторного анализа.
Обозначим символами a, at 1, Ь, Ьх, m векторы, имеющие следующие
составляющие по координатным осям:
ах = aV ах = а\> 1х = Ъ К = ЬХ> К = b'l у тх =
т
і>
ау = а2» ay==za^ ly = 4» Ьу = b2, by = bi9 ™y = ™2>
аг = а3> а'г = а'*> h = 73' K = hV bz = ?3> mz = m3*
Легко видеть, что при таких обозначениях будем иметь:
Ь = [а, 1], Ь' = [а', 1], т=[а, а'].
Соглссно формулам § 2 будем для разложений а, а' и 1 по
степеням А* иметь следующие формулы:
і
а , a"iJn' dt )ш
Для определения разложения векторов b, b', m по степеням
Af и в целях сокращения письма введем векторы Вп, Вп и Мп при
помощи следующих формул:
со со , со
2 ВПАЛ Ь'= 2 ВпМ\ т= 2
» = О « = О П—0
*) Будем, как это общепринято, считать 0! = 1.
5 Зак. 2420. — А. А. Фридман, Опыт гидромеханики 65

тогда, после элементарных вычислений, будем иметь:
іП — 1 хт
В0 = 0, В„ = -!р Q, D
А"
п
+ 2
в. = о, в,
Г |Н — ft
d*Q
Q
n! L A"
D
,2
n!
2,
s: —i
(и = 1,2 ...);
H-
(n = l, 2...);
(/1 = 1, 2,...).
> (13)
2. После этих предварительных замечаний перейдем к
установлению величин крутящего угла А и кручения А. Выше было уже
замечено, что для гельмгольтцева движения вектор Ь' обращается
в 0, и таким образом направление [Q'L] становится
неопределенным; равным обравом мы уже говорили, что для гельмгольтцева
движения крутящий угол становится неопределенным и является
излишним, ибо в этом движении направление Qr совпадает с
направлением L.
Все эти замечания могут быть высказаны и при рассмотрении
прямого движения. В прямом движении направление Q совпадает
с направлением L, значит вектор Ь обращается в нуль при всех
Д?, направление [QL] становится неопределенным, а вместе с ним
становится неопределенным крутящий угол и кручение вихря;
само собой разумеется, что и, для прямого движения понятие
кручения вихря является излишним.
При выводе дальнейших формул, касающихся кручения вихря,
мы будем предполагать, что наше движение не есть ни гельм-
гольтцево, ни прямое движение.
В этом случае по формулам аналитической геометрии найдем:
cos A = -
Ai*t +А3*2 + Мз
Vb\+b\ + %V^+b?+^
что может быть переписано с помощью векторных обозначений
следующим образом:
~л~ (Ь,Ь,) (14)
COS
А = ~
Ь|-|Ь'
Не трудно видеть, что для sin А может быть получена
следующая формула (sin А — величина положительная):
[Ь, Ъ']
sin
А =
(15)
,Ь|-|Ь'
каковая формула даст нам весьма удобные выражения для синуса
крутящего угла.
66

Из того обстоятельства, что Ь' не равен 0, следует, как мы
это показали в § 2, что коэффициент при М в первой степени
в разложении Ь' отличен от нуля. Ниже в § 7 будет показано,
что отличие от нуля вектора Ъ еще не означает отличия от нуля
коэффициента при А? в первой степени в разложении Ь по
степеням А*.
Обстоятельство это, как увидим в § 7 настоящей главы,
зависит от того, что отсутствие изгиба вихря (о" = 0) еще не означает
наличности прямого движения (изгибающий угол а" не равен 0 при
всех Д?); таким образом разложение Ь может начаться с Мп при
п > 1. Рассмотрим общий случай, когда это разложение начинается
с членов первой степени относительно Д? остальные случаи,
требуя выполнения определенных условий, налагаемых на скорости,
очевидно представятся лишь при особых частных обстоятельствах.
Переходя, при этих предположениях, в формулах (14) и (15)
к пределу при Д?->0 и принимая во внимание, что
lim ? = P,DV], lim-^ =
найдем следующие формулы:
^ Q
л*
-НО, ?>V]=[H, Q]=decl curl V,
.о, Л - i[Q' °П [H' Q]) (Ш
cos A~ |[fi, DV]\-\[H, Q]| ' (1 }
. л \№ ДУ], [H, Q]]' ,1<n
s |[0, ?>V]|-|[H, 0]| ' K }
Из этих формул последняя является особенно удобной для
преобразований; в самом деле, пользуясь формулой (29), будем иметь:
«:„ л- Q-1([Q> ДПН)!
Последняя формула приобретает простой геометрический смысл,
если мы введем кроме направлений основного триэдра еще
направления вектора Н и вектора D, причем направления эти будем
обозначать буквами Н и D; эти векторы вместе с вектором Q
образуют уже конечный тетраэдр, который мы будем называть
главным тетраэдром. Оказывается, что главный тетраэдр вполне
определяет предельное положение бесконечно малого
основного триэдра, иначе говоря — элементы сопряженного треугольника
(см. § 8).
С помощью направлений Н и D последняя формула примет
следующий вид:
. , | cos ([QD0Z) і , %
sin А = ~ -—^—^. (19)
* sin (Я, 2)
5*
67

Формула (lt>) для А показывает, что угол А есть не что иное,.
как угол между [QD] и [//2]:
А = ([QD]?[HO]). (20)
Не трудно для со*4 Л, применяя формулу (28), написать
следующее выражение:
(Q, И)(ДУ, Д)-(ДУ, H)(Q, Q)
cos л j [Q, Z)V] I - i [H, Щ i
откуда легко найдем:
A cos (Q^//) cos (LCQ) — cos (D^H) /0,4
cos Л = ^ — ; \21)
sin (Д Q) sin (О, Я)
последняя формула может быть полезна при рассмотрении свойств
главного тетраэдра.
Формула (19) для sin А показывает, что следует отличать два
случая: первый, когда угол между [-D] и Н меньше 90°, и второй,
когда он больше 90°. В первом случае будем иметь:
^A^cos([QDlH);
sin {Ну Я)
во втором случае найдем:
sin A
cos ([QDl H)
sin (#, 2)
Два эти случая (см. черт. 12 и 13 на стр. 119) отличаются друг
от друга тем, что в первом из них плоскость, проходящая через Q
и L, переходит в плоскость, проходящую через S' и'і, вращаясь
против часовой стрелки относительно направления L, а во
втором— вращаясь по часовой стрелке *). Положение это будет
установлено при изучении главного тетраэдра и его взаимоотношений
к основному триэдру; пока же указанное различие позволяет нам
назвать первый случай правым кручением, а второй — левым
кручением вихря.
Итак при правом кручении вихря вектор Н лежит по ту же
сторону от плоскости, проходящей через Q и D, как и направление
[22)]; при левом кручении вихря вектор Н и направление [2D]
лежат по разные стороны плоскости, проходящей через 2 и D.
На черт. 12 и 13 (стр. 119) показаны случаи правого и левого
кручений вихря и сообразно этому показано расположение
вектора Н относительно плоскости, проходящей через Q и D и
направление [ЙД|. Подробнее эти вопросы будут рассмотрены в § 8,
посвященном главному тетраэдру.
3. Чтобы разъяснить, каким образом в различных частных
случаях вычисляется кручение вихря, приведем простейший пример
*) При этом координатная система такова, что от оси л:-ов к оси у-оъ
переходим, вращаясь по часовой стрелке относительно оси z (французская координатная
система).
р8

из области движения жидкости, в котором скорости суть линейные
функции координат.
Предварительно, однако, укажем обозначения и приемы, с
помощью которых без труда вычисляется sin А по формуле (18).
Обозначая векторы [Н, Q] и [Q, Z>V] через d и <Г, а
определитель ([Q, DV\f Н) через А, будем иметь:
rf=|[H, QV> d'= \[Q,DV]\;
Hx, Hyi H,t
д =
'П
l2
Duy Dvf Dzv
H% (?Dv — фи).
При таких обозначениях формула (18) перепишется следующим
образом:
• a Q•1А[
sin Л = jJf
act
Не трудно видеть, что знак cos ([QD], Н) будет совпадать со
знаком А; таким образом мы будем иметь случай правого кручения
при А > 0 и левого при А < 0.
Пример 8. Разберем случай движения, в котором скорости суть
линейные функции координат; положим при этом, что все сдвиги
равны нулю. Вспоминая формулы § 2, мы после простых
преобразований найдем:
2 2 2
<*»=(г(с - б,)*+(« - К)»+(k - tf)9+W (4г+-й-+-ч- )+
+ 2" (vsr9-v,:»)+2tli (v1C2-v3^)-f2;t(v^-V1^);
/2 2 2
/V V >
С2
2і
д=^(^і+^+^і),
где V, = е3— е.2,
s = Sjl — е3, v3 = е2 — gj, причем очевидно vx -j-
4-v2fcbv3===0j из этих формул без труда получается выражение
для sin A. v
Рассмотрим еще более частный случай, когда % и *], равно как
и ^і, у2і суть постоянные величины; при этом конечно удлинения
еі» s2» вз могут и не быть постоянными. Для этого частного случая,
вводя постоянные
2 2 t 2ко >-2 2
69

и обозначая, для краткости, величину Vg^^^i-j-^)2^ через с,
будем иметь:
sin2 A = cft^Ofr
(і^2 -г с) (V? -1- 2ft.CC + К-2 -г с) *
в то же время А будет определяться соотношением:
Предполагая ?, ?], ^ положительными, найдем, что правым
кручением будет случай:
v3 > 0, s2 > г19
а левое кручение будет иметь место при:
v3 < 0, е3 < sle
Поставим себе задачей разыскание таких зависимостей ? от t,
чтобы кручение вихря было постоянной величиной. Обозначая
С2 через <?, постоянную величину sin2 А через т и вводя
постоянные т1 и то следующими равенствами:
ті = т>^г — с, т2 = (т — 1)\с$
найдем, что © должно удовлетворять дифференциальному
уравнению
?2 (™i? + ™*) + 4<р<?тц2 (th® + с) + 4т© (ад ¦+- с)2 = О,
интегрирование которого не представляет ни малейших затруднений.
Полагая А = 90°, иначе говоря т = 1, получаем, после
некоторых упрощений, следующее решение только-что написанного
уравнения: '
.а „о і .2
ввгй = *в V'-V _. K+v2W
2 3 і 2 t-
где ф0 — постоянная интегрирования (очевидно положительная).
Полученное только-что выражение для вихря С дает повод
сделать следующее замечание. Если v^r,2—^2?2<0, то должен
наступить такой момент t0 (больший 0), при котором о обращается
в 0 и после которого <р будет отрицательна. Таким образом
движение с углом кручения в 90°, у которого С вначале (при і = 0)
было отлично от 0, через некоторый промежуток времени будет
иметь С обращающимся в 0, и следовательно такое движение
возможно только до ограниченного момента времени. Этого
обстоятельства не случится, если varj2 — v2?2 > 0.
В следующем пункте будут подробно рассмотрены случаи как
незакручивающегося движения, так и такого, в котором Л = 0.
4. Известный интерес представляет тот случай, когда крутящий
угол А равняется 0° или 180° при всех Л/ в некотором интервале.
Таксе движение мы назвали выше незакручивающимся движением.
В незакручдівающемся движении всегда направление новой вихре-*
70

вой линии лежит в той же плоскости, как и направление старой
вихревой линии и направление жидкой линии L; в известном
смысле незакручивающееся движение есть переход от гельмгольт-
цева движения к такому, в котором происходит полное разрушение
вихревых4 линий.
Условие необходимое и достаточное для того, чтобы движение
было незакручивающимся, заключается в равенстве нулю sin A
или—согласно формуле (15) настоящего параграфа — в обращении
в 0 вектора [Ь, Ь7]. Из этого условия с помощью формулы (13)
мы могли бы, приравнивая нулю коэффициенты при различных
степенях Д?, получить бесчисленное множество условных равенств,
которые должны удовлетворяться, для того чтобы движение было
незакручивающимся; мы предпочтем однако, для вывода
следующей теоремы о необходимых и достаточных условиях незакручи-
вающегося движения, итти иным, более простым путем.
Теорема 3. Для того, чтобы .движение было
незакручивающимся, необходимо и достаточно выполнение следующей бес-
конечной последовательности условий относительно скорости V:
DV,
dQ_
dt
D
dV
dt '
dQ_
dt
, ^
, ^
Idv,
=o,
d? '
= 0,
m
k = l
(m — k-\-l)\ k\
D
di
m — Tc '
L dt'
= 0,
(22)
Согласно толіжо-что сказанному, необходимым и достаточным
условием незакручиваемости движения является обращение в 0
для всех Л* вектора [Ь, V]. Пользуясь равенствами:
Ь = [а, 1], Ъ' = [а', 1],
и применяя формулу (29) § 3, будем иметь:
[Ь, Ь'] = [[а, 1]. [а', 1]] = -[[а', 1],[а,Ц] = 1 (а [а', 1])
откуда по формуле (26) найдем, что равенство
[Ь, Ь'] = 0
а([вМ],1),
эквивалентно равенству:
(1, [а', а]) = 0.
Случай 1 = 0 исключается, так как он приводит к движению с
потенциалом скоростей, ибо условие 1 = 0 влечет за собо*й
равенство ?2 = 0, т. е. отсутствие вихря.

Легко получить следующие формулы:
со
[а', а] = У
СО
т
(1, [а', а]) = У \tm У
П—0
1
Мп Г rf"fi о
Л" '
«1 = 0
М-0 ^ — П)! П[
D
j))l — 1l~lfj
- in
di
т — n — l j
<TQ
<&
s-, 2
,_1
причем символу и ^—условимся придавать значение вектора У.
dt
Приравнивая нулю коэффициенты при различных степенях А/,
получим при т = 0 и т = 1 два равенства, выполняющиеся
тождественно, а начиная с тп = 2 получим условия теоремы 3.
Может показаться, что приведенная система бесчисленного
множества условных уравнений лишь в исключительных случаях
удовлетворяется; это однако не так, ибо не трудно заметить, что
уравнения (22) удовлетворяются, коль скоро обращается в 0
(это отвечает главному незакручивающемуся
вектор
dQ
dt '
L>
движению), т. е. коль скоро уклон вихря обращается в 0 (см.
выше, § 4).
Случаем главного незакручивающегося движения мы займемся
в следующем пункте. Главное незакручивающееся движение, как
это будет показано в п. 7 настоящего параграфа, есть однако не
единственное незакручивающееся движение. Бесчисленное
множество уравнений (22), содержащих, если написать их в развернутом
виде, три неизвестных функции и, v, w, всегда может быть
преобразовано таким образом, чтобы можно было решить вопрос
(в данном случае конечным числом действий) о совместности этих
уравнений. В настоящей работе мы однако не будем заниматься
этим вопросом, предполагая посвятить ему впоследствии отдельное
исследование.
5. Так как понятие о главном незакручивающемся движении
тесно связано с понятием уклона вихря, то мы разберем прежде
всего это понятие.
Не трудно для уклоняющего угла (угол между 2 и Q')
написать следующее выражение:
(а, а')
откуда
cos а =
. , 1 [а, а'] | |
а1'1а I ja
m
(23)
Движение, в котором уклоняющий угол будет равен нулю,
определится условием равенства нулю вектора m при всех Atf; эти
условия, в свою очередь, с помощью равенства (13) п. 1
настоящего параграфа при посредстве приравнивания нулю коэффици-
72

ентов при различных степенях А/ в векторе ш, выразятся
системой следующих уравнений:
1
п\
2,
dnQ
dt"
О,
(п = 1, 2,...). (24)
От уклоняющего угла перейдем к уклону вихря V, т. е
к lim -г-; с помощью формулы (23) без труда найдем:
о'
Q
dQ
dt
dQ
dt
sin
Q,
dQ
dt
Q*
о
(25)
связь уклона с отклонением и изгибом вихря будет изложена
далее в параграфе, посвященном главному тетраэдру.
Теорема 4. Необходимое и достаточное условие, чтобы
уклоняющий угол был постоянно равен нулю, состоит в
равенстве нулю уклона вихря, иначе говоря — в выполнении равенства:
dt
Q
= 0.
(26)
Это условие необходимо, так как, при я' = 0, имеем 8' = 0.
Покажем, что оно и достаточно. Для этого нам нужно показать, что
коль скоро выполнено условие (26), то все условия (24)
выполняются сами собой. Из условия (26) вытекает, что векторы Q и
dQ
—г- расположены по параллельным прямым, иначе говоря — выте-
dt
кает следующее равенство:
dQ_
dt
= И>,
<*)
где ^ — некоторая скалярная величина- Покажем, что при наличии
условия (*) имеет место выполнение равенств (24). Положим, что
эти равенства соблюдены для индексов до некоторого п
включительно, и покажем, что в таком случае справедливо и равенство
для индекса п-}-1. Из справедливости равенств (24) до
некоторого индекса следует, что
^| = XSQ, (k = l, 2,...n),
dt
причем X1 = ?v. В частности имеет место равенство:
dnQ . 0
dt
Прилагая к этому равенству операцию -т? j будем иметь согласно
13

правилам применения операций -j-, изложенным в § 3 предыдущей
главы:
т. е.
dtn + 1 n dt
^,
^=ы
dt
Q,
dn + 1Q
dt
П+ 1
= 0,
что. и доказывает нашу теорему.
Условие (26) теоремы 4 совпадает с условием, чтобы движение
было главным незакручивающимся движением; поэтому в
добавление к теореме 4 можно высказать еще такое предложение:
Теорема 5. Главное незакручивающееся движение
одинаково с движением, в котором уклоняющий угол равен нулю при
всех А/.
Таким образом в главном незакручивающемся движении
уклоняющий угол равен нулю и крутящий угол также обращается в 0°
или в 180°. Выясним прежде всего, когда имеет место случай
равенства 180° крутящего угла; очевидно, что для этого случая
крутящий угол можно заменить кручением вихря А и написать
следующую формулу для cos А:
([Q, DW], [HQ])
cos Л =
Так как в нашем случае
fli, DV\ | • j [HQ]
dQ
Q.
dt
= 0, то, помня, что DM-
= —j- H, без труда найдем:
at
cos A = 1.
Таким образом в главном незакручивающемся движении круче»
ние вихря и крутящий угол равны нулю.
Не трудно видеть, что в случае общего незакручивающегося
движения coSi4===tl, причем, так как в этом случае DV
компланарен с Н и 2, toDV = XH + ^j а тогда cosA = — signX*).
Для более детального выяснения характера условий для главных
незакручивающихся движений полезно ввести особую операцию
над векторами, дающую некоторое число.
Центробежной мерой Ц А сектора А назовем следующую
разность:
ЦА =
dA
dt
dA
dt
(27)
Чтобы пояснить, почему эту разность мы назвали
центробежной мерой, рассмотрим случай A = U, где U — скорость некоторой
*) sign /=-(-1, 0 или —1, смотря по тому />0, /" = 0 или /<0.
4

материальной точки; в этом случае -—у— будет ускорением этой
материальной точки, а —~гг будет абсолютной величиной
касательного ускорения, значит LJU будет разность квадратов величины
ускорения материальной точки и величины касательного ускорения
материальной точки, иначе говоря — Ц11 будет квадратом
нормального ускорения материальной точки. Центробежная сила вектора
характеризует до известной степени изменение направления вектора
с течением времени.
Пользуясь формулой (28), будем иметь:
а,
dQ
dt
= Q*
2,
dQ
dt
)=(a, ^)
dQ
dt
— 2*
откуда
^,
dQ \
dt J
dQ
Q2
dQ_ JQ_
'dt ' dt
dQ
dt
%
dQ
dt
)-
dQ
dt'
- *>
dt
Q2LJQ.
(28)
Таким образам необходимое и достаточное условие, чтобы
движение было главным незакручивающимся движением, состоит
в равенстве нулю центробежной меры вихря.
Формула (25) для уклона вихря дает нам непосредственно:
у«= * цо,
(29)
иначе говоря—квадрат уклона вихря равен центробежной мере
вихря, деленной на квадрат вихря, каковое выражение дает
возможность наиболее просто вычислять уклон вихря.
Приведем для пояснения предыдущей теории примеры
вычисления уклона вихря, а равным образом примеры главного незакру-
чивающегося движения; при этом следует помнить, что
рассматриваемое в наших примерах движение не должно быть прямым или
гельмгольтцевым.
Пример 9. Рассмотрим общий случай движения, в котором
скорости суть линейные функции координат. - Составляя
центробежную меру вихря, в этом, случае будем иметь: *
ЦО = Р
откуда нетрудно вычислить величину 8 . В более простом случае,
когда і и т, суть постоянные, найдем:
й'2
О
РСЧ-ч»)
(Р-Н8-К*)а'
Поставим себе задачей разыскание таких движений с постоянными
75

; и f{, при которых уклон является величиной постоянной.
Обозначая постоянный уклон буквой т и полагая л = V^S2 "KV»
будем иметь:
т =
л2-ь:2'
откуда, по интегрировании при пфО,
Z = ntg(mtJrm0),
где т0— постоянная интегрирования.
Если п = О, то и т = 0, т. е. мы будем иметь главное незакру-
чивающееся движение; в. этом случае движение, вообще говоря,
•будет не гельмгольтцевым и не прямым. Не трудно видеть, что
центробежная мера вихря, а значит и уклон вихря, обращается
в нуль во всяком движении, в котором \ = 0, т( = 0.
Пример 10. Рассмотрим случай, когда и —0, v = 0, т. е-
скорость направлена постоянно по оси z-ов. Обращаясь к случаю
стационарного движения, найдем по составлении центробежной
меры вихря, что
с
т.а I ' dz <te
причем
,. <?w dzv
Следует отметить, что в этом случае проще можно получить
уклон вихря, не прибегая к вычислению центробежной меры вихря,
а пользуясь формулой (25).
Рассмотрим задачу об определении движения с постоянным
уклоном вихря. Обозначая =о через —-*-, и полагая — =е >
после простых вычислений найдем:
W — у. ").
ой
"dz~
Легко видеть, что:
Ф . дх т _ 1 <?ф __ ду м.
/л ' zu ch Ф dz dz '
д —
ZU
Оу
где ? = arcsin th'r{\ Простые преобразования дают:
') sh *l, ch h, th ^ — гиперболические синус, косинус и тангенс.
76

Уравнение (*) может быть переписано таким образом:
s \ 4 ' 2 ) dydz ¦ dxdz и'
или, полагая -д-~г-я~=/, перепишем последнее уравнение в виде:
tg/-іЧ-Т--/-7-== 0, * = Intg/,
интегрирование какового уравнения представляет значительные
трудности.
6. Мы говорили уже выше, что главное незакручивающееся
движение не есть еще общий случай незакручивающегося
движения. В настоящем пункте мы выясним этот вопрос на
определенном примере; предварительно однако укажем, каким образом
в одном весьма значительном классе случаев могут быть
упрощены условные уравнения, характеризующие незакручивающееся
движение.
Рассматривая последовательность векторов:
' dt ' dp9"-' Л™' ¦"
мы можем встретиться с тремя случаями:
1) Вектор —тг параллелен вектору 2, иначе говоря—
' dt
о,
т. е. имеем случай главного незакручивающегося движения.
2) Вектор —у- не параллелен вектору U, но вектор , 0 ком-
о dQ
планарен с векторами U и —у-, иначе говоря — выполняется
равенство:
(?0_
\ df-' l~; dt j
Л
= 0:
в этом случае легко доказать, что любой вектор предыдущей
последовательности компланарен с векторами Q и "гг*
В самом деле, положим, что это свойство справедливо для
первых п векторов нашей последовательности, и докажем
справедливость его для (n-j-l)-ro вектора последовательности. По пред-
77

«Г-Чі п dQ
положению n _— компланарен с У и ; таким образом
существуют два числа ^п_г и pn_t таких, что
с/
прилагая к этому векторному равенству операцию -тт и замечая,
(PQ, , dQ
что -jT = X21JT!J2-тг> найдем:
Л2 * ' ™ Л
dtn \ Л
і 'н-1 2
'что и доказывает наше положение. Заметим, что Хл и (а„
определяются рекуррентными соотношениями:
^п = Х»-1 + ^-1^
3) Наконец третий случай обнимает собою движения, в которых
, векторы м, —т— и , 0 не компланарны; само собой разумеется,
что в этом случае любой из векторов нашей последовательности
может быть выражен в виде линейной комбинации векторов Q,
dQ d*Q
dt И d? '
Как мы уже отметили, первый случай даст при изучении неза-
* кручивающихся движений главные незакручивающиеся движения.
Оказывается, что и во втором случае вносятся в изучение неза-
кручивающихся движений значительные упрощения. ¦
Мы будем называть незакручивающиеся движения, в которых
d*Q ¦ п dQ
, 2 компланарен с Ьг и —тг, планоидными незакручивающимися
движениями *).
Упростим условные уравнения незакручивающегося движения для
случая планоидного движения. В этом случае имеем:
d*Q і'о_і_ dQ
г— = A.ft Ы -4- ы.,. ;
dtk " ^ * dt
*) Мы ввели термин „планоидные" (подобные плоскостным), основываясь на
¦ d"Q
том, что в этом случае все векторы —- лежат в каждый данный момент и для
каждой данной частицы в одной плоскости.

вставляя это выражение в т-ое равенство теоремы 3, будем иметь:
t»
а,
^ (т — k+1)1 Id
D
d'
м — Ьі
di
,т — 1; >
L dt
, Q
= 0.
Так как "^ = 1, то указанное равенство перепишем в таком виде.
J»J — 1
m!
D
«T^V
dt
m — 1 '
dQ
m
+s
!x*
, 2
?* (m— *+1)Ш
D
V
A'
ЛП—fc >
dQ
. dt
,Q
= 0;
применяя непосредственно эти равенства, без труда обнаружим
справедливость следующей теоремы:
Теорема 6. Для того, чтобы движение было планоидным
незакручивающимся движением, необходимо и достаточно
выполнение следующих условных равенств:
ld*Q Г dQ л"|\ „
dQ
D
DV,
dV
dt'
dt '
dQ
dt '
Q
Q
= 0,
= 0, }
D
dnV
df
dQ
——. Q
dt '
= 0,
(30)
Совершенно очевидно, что равенства эти выражают свойство
векторов ^-~пгг быть компланарными с векторами м и —гг.
Теорема 6 дает нам бесчисленное множество условных
уравнений, которым должно удовлетворять планоидное незакручиваю-
щееся движение; можно однако показать, что все эти равенства
сводятся к конечному числу уравнений.
Чтобы выполнить приведение системы (30) к конечному числу
уравнений, обратимся к случаю, когда наше планоидное незакру-
чивающееся движение не принадлежит к классу главных незакру-
- _ ^ dQ
чивающихся движении, т. е. когда
О,
di
ф0. В этом случае
каждый вектор может быть представлен в виде суммы трех векто-
dQ
ров, направленных соответственно по векторам 2, -j- и
*.§
79

очевидно не компланарным между собою. Обращая внимание на
вектор , т , мы напишем* его в таком виде:
rf"V_ о , 0 dQ
Л*
л
m
Q
JQ
' dt
*),
(31)
где ctm, pm> 7m суть три скалярные величины, определяемые по
формулам (49) § 3 предыдущей главы.
Производя над обеими частями предыдущего равенства опера-
d d*ft
иию -jT и помня, что —т.™ в планоидном незакручивающемся дви-
dt
dt
о
dQ
жении компланарен с ьг и —?т-> найдем следующую систему
рекуррентных соотношений:
do.
m I 'л
э = -^-4-^„+«„, (щ = о, і, 2,...)
Tm -f 1 ^ ' '^ш'
причем в этих формулах X и \± имеют значения, определяемые
равенством:
Л2 ~l dt '
о ^
которое является следствием компланарности векторов м, -~тт~
J2Q
и
Л- *
Не трудно видеть, что всегда можно выбрать такие две пары
а, Ь и а!, V решений уравнений:
da ,
был отличен от нуля; равным образом
чтобы определитель
dt
db
dt
а Ь
а'Ь'
й.
оь
*) В дальнейшем индекс 0 будем опускать, так что вместо а0, Р0, Yo будем
писать а, р, f.
**) Полезно отметить, что, переходя к лагранжевым переменным, мы
превратим нашу систему уравнений в систему линейных обыкновенных
дифференциальных уравнений.
80

всегда можно найти с, отличное от^нуля, являющееся решением
уравнения;
dc
С помощью пяти величин а, Ь, а, Ьг и с из а|Д> gWJ ym можно
образовать такие линейные комбинации с|Я, <!*т, <оЛ1:
?« = да» т- *?«.
^ = cYm,
чтобы имели место рекуррентные соотношения:
dv
с
m
m-f 1
л •
J6
Л '
со
О)
и»
ш + 1
л *
Из этих соотношений следует:
о
т
di
,У-
dmA
О
т j
Ywi —
А
m >
(О.
ffl
rf"
со
d(
Не трудно видеть, что ода, рто, тж выражаются в виде линейной
, а 6 ' '
комбинации <?т, 7т, <о„ в силу того, что с и
' L/
а'*
отличны от нуля.
Таким образом рекуррентные соотношения для аті $т, чт
оказываются решенными; на этом вопросе мы не останавливаемся, так
как для последующего эти рекуррентные соотношения нам не
понадобятся, тогда как величины отУ 6ОТ, <пт, значительно упрощая
дальнейшие формулы, позволят нам свести уравнения теоремы 6
к конечному числу уравнений.
d^V
Подставляя в уравнения (30) выражение (31) для -гж , получим,
что уравнение:
D
dmV
di
m t
dQ-
Г' dt л
о
0
эквивалентно уравнению:
(grad тт, Q) = аад ~х -f р„ ~2 + «уи ~3,
6 Зак. 2420. — А. А. Фридман, Опыт гидромеханики
(32)
81

где:
(<W)2,
(Я V)
о .
""»
'•'о
dQ
dt '
dQ
dt
Q
*-o
(2, V)
Q,
dQ
dt
dQ
dt
^,
dQ
dt
Q,
dQ
dt
Q,
dQ
dt
(33)
При выводе формулы (32) постоянно приходится пользоваться
соотношением (23) § 3 *).
Чті бы заменить в уравнении (32) «т, іл„, Т« на более удобные
для вычисления <?т9 4v> <*>И1, введем вместо *х, ъ& ^з величины
ъ[, ~1, ^з П°Д следующими условиями:
с^з= с^з — (grad с, Q).
Помощью элементарных соображений можно доказать, что
уравнение (32) эквивалентно уравнению:
(grad ©да, Q) = от к\ + фт Ц
Гю«*8«
(34)
В уравнение (34) входят <?т, &«> ®т при разных тп; можно однако
эти уравнения заменить такими, в которые будут входить лишь
величины <?, Ф» ш **)» но зато вместо вектора Q будут входить
векторы Н, Ии Но, •. -, введенные нами в п. 7 § 3; так как
указанное преобразование уравнений (34) нам в дальнейшем
понадобится, то мы его здесь рассмотрим в несколько более общем виде.
Покажем, что система уравнений:
(gradcom+j! й) = *т+і*1+Ъм+№ +**+}•% (/ = 0,1,2, .. .,*) (*)
эквивалентна системе
(grad%, H. .,) = ?.
d*<
1 L*
(/ = С, 1,2, ...,*),
-4-<о
\
т
df
3 1
I
(**)
где для сокращения письма положено Н_х = Q, Но = Н.
*) Щ отлично от нуля, ибо рассматриваемое движение не есть движение главное,
незакручивающееся.
**) <Ро = Ь Фо = '^ ш0 = ш*
82

Установим прежде всего, что из уравнений (*) следуют
уравнения (**). Применяя операцию -jr к обеим частям первого из
уравнений (*), найдем по формуле (44):
(grad
О)
ш 4-1'
2) + (grad «> , Н) =
т Jt
со
т
dt•
откуда второе из уравнений (*) даст прямо второе из уравнений (**).
Проделывая то же преобразование со вторым, третьим и т. д. из
уравнений (*), получим следующую систему уравнений:
(grad ш
WI+J
,Н)
cfej
fife»
чп + j Jt і >m+j fa
(/=0, 1, 2,..., * —1).
-j-O)
m
Применяя к этой системе тол^ко-что указанные преобразования,
найдем систему (к— 1) уравнений:
d% d% f «РЦ
(/ = 0, 1, 2,..., Л-2).
Продолжая производить указанным приемом преобразование
системы (*), найдем, что совокупность первых уравнений в
образуемых этим путем системах составит как раз все уравнения (**);
таким образом уравнения (**) являются следствием уравнений (*).
Покажем теперь, что из уравнений (**) будут следовать
уравнения (*). Для доказательства выпишем системы, полученные нами
из (*):
&га<1ст+я S) = ?m+j<4-^m+J^ + %l+j^ 0* = 0,1, 2,..., к), (*о)
Йъ г*х' гіт' \
0' = 0, 1, 2, .... к — 1),
(s-adcDm,_., HJ
о
а-т^
<Р-.>
:*> Г iiii+J JjQ Г w
**;
(; = 0, 1,2, ...,* —2),
С%)
(grada>TO+j,Hi_,) =
Л —2 »
JK — Z P jfC — 2 • J"
лл
(/=0, 1, 2),
<V.)
83

d
m+f "A — 2J
7fc —1
ife -1
A- 1
m+j
dt
1 i f 2 i
- 1 "T Vm 4- j j fc - 1 I
CO
dt
(/ = 0, 1),
m+j
df-
ic—i
> (**_i)
(grradcc„ ..„H*^)
<*»*:
со
«+J df
(/ = 0)..
" L_ jj)
I
В силу уравнений (**) каждое первое из уравнений (*0), (*і). • • (**)
удовлетворяется. Прилагая операцию -тт к первому из уравнений
(*&_і) и пользуясь формулой (44) и уравнением (*fc), найдем второе
из уравнений (*&_1). Прилагая операцию -,-- к первому из уравне-
нений (*л_«) и пользуясь уравнениями (*ft_x), найдем второеурав-
нение из (*я._2); прилагая операцию -у- ко второму из уравнении
С\._2)> найдем третье из уравнений (*А_2)« Идя таким образом
снизу вверх, покажем, что из уравнений (**) будет следовать вся
предыдущая таблица уравнений, а значит и уравнения (*0), т. е. наши
уравнения (*); указанный прием напоминает последовательное
вычисление разностей разных порядков.
Дальнейшие наши выводы будут основаны на делении движений
жидкостей на три класса. К первому будут относиться случаи,
когда ускорение направлено по скорости, т. е. когда имеет место
соотношение
v,
dt
0.
(35)
Ко второму классу отнесем те случаи, не входящие в первый
„ dV J2V
класс, когда векторы *>-уг И —~щ компланарны, т. е. когда имеет
место соотношение:
1?
» >
v,
dt
0.
(36)
Все остальные случаи отнесем к третьему классу *).
*) Так tax мы не будем в дальнейшем подробно заниматься общим случаем
иезвкручивающегося движения, то указанным классам мы не даем особых
наименований; вообще все рассуждения настоящего пункта мы, по указанной только-
что причине, стремимся изложить по возможности кратко, опуская многие детали.
84

Покажем, что для первого класса будем иметь формулы:
¦1т = 1тЧ> (/j = /, Лі = 1, 2, - . •)
где 1т — величины, удовлетворяющие рекуррентному соотношению:
Из условия (35) следует, что а1==/а, рй = /t3, 4l = lyt тогда по
формулам, определяющим о, &» <°> найдем:
?i = fo; ^1 = ^; «і = /«».
Производя кад этими равенствами несколько раз операцию -р,
at
докажем без труда наше утверждение.
Совершенно аналогично можно. показать, что для второго класса
движений будут справедливы формулы:
'?*¦ = *« ? + *„?!,
** = 1т '1» +¦ пт4р (4 = /, п2 = л, m = 2, 3...),
& = / CD —I— 77 О).
где /TO, nw удовлетворяют рекуррентным соотношениям:
А'
Т 7 _| •#_
йл.
Лт+1- Птп + lm "Г -^ ' (т = 2, 3. . .)•
Для случаев третьего класса точно так же установим формулы
Ф« = /«Ф + пя|^і + 9,»*а» *3 = n, (т = 3, 4...)
при рекуррентных соотношениях:
dnm
nm + i = ?iHn+/» + "S-» (т = 3,"4...)
Jo
л 1 f "w
После приведенных предварительных вычислений не трудно
будет доказать следующие три теоремы, сводящие бесчисленное
множество уравнений теоремы 6 к конечному числу их.
85

Теорема 7а. Для тою, чтобы движение, отнесенное к
первому классу, было планоидным незакручивающимся движением,
необходимо и достаточно выполнение следующих уравнений:
d*Q
\ dfi ' I
Q,
dt
= 0,
D
D
D
V,
(DV,
dt '
rff
dW
dp'
dV_
dt
Q.
Го
о,
L
Q.
Q.
dQ
dt
dj^
dt
dQ
dt
dQ
dt
= 0,
= 0,
= 0,
= 0.
(37)
Необходимость условий этой теоремы непосредственно следует
как из теоремы 6, так и из того, что наше движение — планоидное,
отнесенное к первому классу. Обратимся к доказательству
достаточности этих условий. Из последних трех уравнений (37) следуют
такие соотношения:
(grad a>lf Й) = ©хъг + Фх< + <°і*з *
(grad соа, Q) = ?2^ + %< + <»2*і,
(grad <о3, Q) = ?з< + Ф8*2 -f- а^.
Из этих соотношений, на основании доказанного выше, выте
кают равенства:
(grad©^ Щ^^К-г^^г^Л*
d<
u„1 cnLg d'-3
(grad «J, H) = ?! -^- + фі
+
CO,
dt [ ~x dt'
<Pk[ d% d%
(grad «p Hx) = ?a -^- -f ^ -^j- + oj —^.
Равным образом последние четыре из соотношений (37) дают
следующие равенства:
(grad со, О) = сртг; + <К + «*» >
(grado), Н)==?-^- + ф-^" + °
(grad ш, Н,) = ? -тз- + Ф -ЕГ +
А»
<tf
СО
dt '
~dF*
86

Из этих равенств, помня, что '~і = l'h 'W = ^» <°і = 1®9 получим
следующие три соотношения:
(grad Л Q) = (grad /, Н) = (grad /, Нх) - 0. (а)
Рассматривая последовательность векторов Q, Н, H1? Н2, . . .,
не трудно сделать следующие заключения об этой
последовательности. Так как мы имеем негельмгольтцево движение/ то векторы
Н к Q не обладают одинаковым направлением (decl ?2 =? 0); если
Q, Н, Нг компланарны, то Нл компланарен с Q и Н. Для
доказательства этого положения примем его справедливым при индексах
меньших или равных к и установим правильность его для индекса
к-{-1. Пусть имеет место равенство:
приложим к обеим частям этого равенства операцию Helm;
пользуясь формулой (35), найдем:
dhk dh'k
Так как Ht компланарен с 2 и Н, то и Нк+1 компланарен с этими
векторами; таким образом наше утверждение можно считать дока-'
занным.
Из предыдущего рассуждения следует, что всегда Н,. можно
представить формулой:
Н^Л^ + ^Н-Ь^Н,. (Ь;
В самом деле, если Нх, И, 2 не компланарны, то формула эта
следует из возможности представления любого вектора в виде
суммы трех векторов, параллельных трем данньім некомпланарным
векторам; если же Нх, Н, м компланарны, то Н? компланарен с Н, Q,
следовательно и в этом случае наша формула справедлива. Не
трудно видеть, что hk, h'Jc9 hk удовлетворяют следующим
рекуррентным соотношениям:
Йа + і = льа-1—5Г* А2 —Л,
dh'
*; + i = ^' + A» + "rfr' ^ = А" (* = 2,3,...)/ (с)
K+i = Kh" + h'b + -jf> til^h". j
Из формулы (Ь) и из уравнений (а) следует, что:
(grad/, НА) = 0
при всех к (к = —1, 0,1, 2,...) (см. выше, значение векторов И~х и Н0).
87

Покажем теперь, то если имеют место равенства (grad /, НА.) == О
при к = — 1, 0, 1, 2, ..., то будут справедливы и равенства:
(grad /,„, Н,,) = О, при к = - 1, 0, 1, 2, ... (d)
Положим, что эти равенства справедливы для индексов меньших
или равных т, и покажем их правильность для индекса 777-4-1.
Применяя к каждому равенству операцию -~т~, найдем [см.
формулы (44)]:
dl
grad---, Hj + (grad/m, Hfc+1) = a
Но:
откуда:
dl
т
dt
'?» 4-1 *-т *»
(grad lm + lt Щ) = lm (grad /,Hu)-f/ (grad lm, H,) - (grad/,„, Hfc + I) = 0,
в силу наших предположений; таким образом равенства (d) можно
считать доказанными.
Не трудно видеть, что условие (Z)V, Q,—y-
собой равенство:
(grad о), Q) = оъ[ + <К + <°~з 5
= 0 влечет
за
помножая это равенство на 1т и помня, что (grad lm> Q) = О по
только-что доказанному, найдем следующее соотношение:
(gradcv Й) = ?те*і + ?п*з + Шт<>
приняв при этом во внимание, что <рда = /жв, Ф,» = /«ф, о>т = /1По),
Это последнее равенство, как было выяснено выше,
эквивалентно уравнению:
(
D
(TV
dt
ти >
Q,
dQ
dt
= 0,
что и доказывает достаточность условий нашей теоремы.
Не трудно видеть, что условия теоремы 6 будут выполнены,
коль скоро будет выполнена следующая система условий:
ld*Q \Q dQ^
\ dP ' L dt
= 0,
v, k
d\_
dt
dQ
= 0,
(
DV, Q,
dt .
dQ
dt
-0
= 0.
(38)
88

Это предложение доказывается очень просто, если обратим
взимание, что второе и третье равенства из (38) дают следующие
соотношения:
V,
л*
==о,
<ГУ
dtm'
Q,
dQ
dt
= 0,
откуда следует:
V
ітя
С.
/ dmV
Условие I Z) -7TST»
-О,
С». Р« = 4?; т = 0, 1,2,-.
dQ
Q,
dt
= 0 эквивалентно равенству
которое будет выполнено, коль скоро выполняется равенство:
aiTj -j- р-2 = 0,
т. е. коль скоро справедлива последняя из формул (38), что и
доказывает правильность нашего утверждения.
В то время как теорема 7а требует выполнения семи скалярных
уравнений, тогда как неизвестных функций всего три (и, v, w —
составляющие скорости V), указанные условия дают лишь пять
скалярных уравнений.
Для случая планоидных движений, отнесенных ко второму и
третьему классам, можно высказать предложения, аналогичные
теореме 7а и доказываемые совершенно таким же образом. Мы
выскажем их, не приводя доказательств.
Теорема 7Ь. Для того, чтобы движение, отнесенное ко
второму классу9 было планоидным незакручивающимся движением,
необходимо и достаточно выполнение следующих уравнений:
&Q
dfr'
УсРУ
\ dP *
dQ
Й,
dQ
dt
V,
dt
= 0,
= 0,
НИ*it])-0 «-*1-***
(39)
Теорема 7c. Для того, чтобы движение, отнесенное к
третьему классу, было планоидным незакручивающимся движением,
необходимо и достаточно выполнение следующих уравнений:
{
( <Р Q
*7-1*
Q,
dQ
dt
= 0,
dt
= 0 (/ = 0,1,2,3,4,5).
(40)
89

Ьо всех указанных уравнениях мы имеем три неизвестных
функции и, v, w от переменных і, х, у, z, которые должны
удовлетворять, вообще говоря, семи дифференциальным уравнениям. Можно
думать, что для неглавного незакручивающегося движения найти
эти функции и, v, w невозможно и что, как мы говорили выше,
все незакручивающиеся движения суть главные незакручивающиеся
движения. Однако пример, разбираемый нами в следующем пункте,
показывает, что подобное заключение было бы ошибочным.
Чтобы решить задачу о разыскании планоидного
незакручивающегося движения, необходимо из наших семи уравнений исключить
функции ы, v, щ в результате мы или получим указание на
несовместность наших уравнений, или же определим u, v, w. В
настоящей работе мы однако не будем касаться этого вопроса.
7. Желая подыскать пример незакручивающегося движения, не
являющегося главным незакручивающимся движением, обратим
внимание на то обстоятельство, что уравнения (32), а значит и
условия теоремы 6 выполняются, коль скоро имеют место
следующие четыре равенства:
d2Q
dP
%
dQ_
dt
= 0,
Q,
(2. V) ^
dQ
dQ
dt
=o,
dQ
dt
= 0,
(CV)
dt
Q,
dQ
dt
= 0.
(41)
В самом деле, второе из указанных равенств вместе с первым
<TV n dQ
показывают, что - , т компланарно с У и —гг, значит Тм = 0; два
последние равенства показывают, что ^ и я2 обращаются в нули,
следовательно удовлетворяется уравнение (32), а вместе с тем
и условие теоремы 6.
Пример 11. Рассмотрим случай скоростей, линейно зависящих
от координат х, у, z. Пользуясь данными примера 1, найдем, что
составляющие векторов У и —у- будут зависеть только от г и не
будут зависеть от координат, следовательно в этом случае (Q, V) &
и (2, V) 7, обращаются в нули и два последние уравнения из (41)
удовлетворяются.
Первые два уравнения из (41) напишутся следующим образом
(см. пример 1):
ё (4 - о$+ч (« - к)+с & - 4)=о,
90

8i(f»'-*ri)i 2— ' — "> ^ "~2— ';T' ~~ ^ = *
¦'s
*~2~<V~^)+22(«-K) -f -^ (;r,-r,;) = 0,
Полагая в этих формулах ; = 0, ?і = 0, іфО, иначе говоря —
считая ?, ?] постоянными ? = со> ^ = 'По, найдем следующие
соотношения, в которые превращаются предыдущие уравнения;
аТо — ^'о= 0>
е.тп
і'іо
о» — С
'з
сл-4-х
to ,
ю
°8"К
2
^о — а
°і-
У
2*0 =
-$о>
= 0,
= 0,
Из этих уравнений могут быть определены четыре элемента
из двенадцати, характеризующих движение, в котором скорости
суть линейные функции координат.
Полагая ?]0 = 0 и считая ? и ?о отличными от нуля, найдем, что
7=0; с другой стороны предыдущие соотношения
удовлетворяются, если мы положим: Ь = 0, ог = ?0j s3 = — С, е3 = 0
Таким образом движение, скорости в котором определяются
формулами:
^ = с -г гз г ~г -о# — -|" Л
где ?0 — постоянная отличная от нуля, ч,— функция от ? такая, что
С ф 0, а, ер с, s3l а2 — произвольные функции і, является планоид-
ньш незакручивающимся движением, не принадлежащим к главным
незакручивающимся движениям.
Итак незакручивающееся движение может быть главным, пла-
ноидным и общим; мы оставляем без рассмотрения здесь весьма
интересный вопрос о том, в каких случаях движение может быть
планоидиым незакручивающимся движением и существуют ли не-
закручивающиеся движения отличные от главного и планоидного
*) Не трудно видеть, что выбором коэффициентов можно достигнуть того,
чтобы .разбираемое нами движение не было ни гельмгольтцевым, ни прямым.
91

8. В заключение скажем несколько слов о движениях, в
которых кручение обращается в нуль, тогда как движение не является
незакручивающимся, иначе говоря — крутящий угол не обращается
в нуль при всех Д? Такие движения очевидно своим условием
будут иметь равенство:
Q
\
DV,
dt
= 0.
(42)
Условимся движения, удовлетворяющие этому равенству,
называть квази-незакручивающимися; само собой разумеется, что из
числа квази-незакручивающихся движений не исключается гельм-
гольтцево и прямое движение, хотя для этого рода движений
понятие кручения отсутствует. Легко видеть, что равенство (42)
может быть заменено следующим условием:
dQ
Н, ' ~
о
dt
= 0,
(43)
эквивалентным условию (42).
Зто последнее условие может быть написано в форме равенства
нулю определителя:
<>
d-
at'
$2.
dt
Нх, #„, Нг
= 0.
(44)
Могут иметь место два вида квази-незакручивающегося
движения: общее квази-незакручивающееся движение, когда не все
миноры второго порядка определителя (44), соответствующие какой-
либо строке, обращаются в нуль, и специальное, ко гда все миноры
одной какой-либо строки обращаются в нули. Специальное
движение может быть трех типов:
1) Все миноры третьей строки обращаются в нуль, т. е. имеет
место равенство:
Q,d*
dt
о,
иначе говоря — имеет место главное не$акручивающееся движение.
2) Все миноры второй строки обращаются в нуль, т. е. имеет
место равенство:
[Q, Н]=0,
иначе говоря — имеет место гелъмгольтцево движение.
3) Все миноры первой строки обращаются в нуль, т. е- имеет
место равенство:
~, н]=0. (45)
Это будет новое движение; мы назовем его особым квази-
92

незакручивающимся движением. Очевидно, что условия для
особого квази-незакручиввющегося движения могут быть переписаны
следующим образом:
dt
=0. (46)
Для иллюстрации вышесказанного разберем пример особого
квази-незакручивающегося движения.
Пример 12* Положим, что u, vy w суть линейные функции
координат; принимая, что Duf Dv7 Did соответственно равны4 31э 82, о3,
найдем, как это будет указано ниже в § 8, посвященном
главному тетраэдру, что при ?, rt, С отличных от нуля:
где ^
Условия для особого квази-незакручивающегося движения могут
быть написаны таким образом:
. ¦ і -п і
о, о,, с.
откуда
и следовательно
'3
°2 = -^г(А'-2кщ-\-2Ч-П*),
«а = -?~ (А' — 2WC + 2ц С2),
А'=х (к + тт+Ш — ч *—ч -п2 - ч с*.
Легко видеть, что, полагая st — е2 = е3 = 0, С = ч0 — const, X = — ?,
Е= т), будем иметь: ?, =0, о9 = 0, о8 = &; откуда
ы = а+_-у + —у—,
, ,..S(g-*)
и, = с^--^_ .
93

Не трудно видеть, что указанное движение, вообще говоря, не есть
главное незакручивающееся или гельмгольтцево движение.
§ 7. Изгиб вихр».
1- Выше мы определили изгибающий угол как угол ап между
направлениями 2 и L; изгиб вихря 8" был нами определен
формулой:
8" = lim-^-. (47)
Пользуясь обозначениями § 3, мы без труда получим
следующие выражения для изгибающего угла:
ллс лп (а, 1) . „ _ ! [a, I] I
cos о. = -,—j—г— , sin а =
, , , *! іаі I1!
Разделив вторую из этих формул на &t и переходя к пределу
при Лг->0 (пользуясь формулами § 3), найдем
,7/ _ 1 [Q, ДУ] | __ D sin (^, D)
~" os 2 ;
6"= " \„ - = ~ -\ ' ' : (48)
при этом предполагается, что вектор Q отличен от нуля, а | DV \ = D.
Из рассмотрения сопряженного основному треугольника не
трудно установить связь между изгибом вихря, с одной стороны,
и отклонением, уклоном и кручением вихря, с другой стороны.
Эта связь получится, если мы выразим сторону сопряженного
основному треугольника, являющуюся уклоном вихря, через две
другие стороны (отклонение и изгиб) и угол между ними (кручение
вихря); вспоминая наши обозначения, будем иметь:
3'2 = 32 + 8*« — 2В8" cos А (49)
Для иллюстрации вычисления изгиба вихря приведем два
примера.
Пример 13. Положим, что наше движение обладает вихрями,
параллельными некоторой, не меняющей своего положения, прямой
линии. Не трудно соответствующим выбором координатных осей
свести этот случай к такому, при котором ?=0, ?] —О, а С отлично
от нуля. Скорости и, vy w должны удовлетворять условиям:
дно du dw dv_
дх ~ dz ' dy~dzf
откуда следует, что —— = 0, т. е. , зависит только от г, х, у.
OZ
Совершенно-ясно, что рассматриваемое нами движение относится
к случаю главного незакручивающегося движения. Составляя
компоненты вектора DV> найдем:
dz dz dz
94

Отсюда нетрудно определить геличину изгиба; согласно
формуле (48) найдем:
?„2= t ди
dz
нш-тнш-
Легко видеть, что по заданному изгибу можно определить
движение в разбираемом частном случае, т. е. найти и, v, w,
обладающие заданным изгибом вихря. Для этого мы должны
определить w из дифференциального уравнения:
после чего и и V определятся без труда из написанных выше
соотношений. Приведенное только-что уравнение, как известно,
встречается в теории конформного преобразования и достаточно
хорошо изучено. Не останавливаясь на общих случаях, разберем
частный вид задачи, когда Ь" — изгиб вихря — зависит только от t
u z. Вводя вспомогательную функцию Ф при помощи уравнений:
—- = о cos V; т~ = ° sin 7,
'дх ду
придем к выводу, что Ф должно удовлетворить следующему соог*
ношению:
т дх ' ' ду
Интегрирование этого уравнения даст, что Ф будет определяться
решением уравнения:
F(t, z, Ф, дгбіпФ—#cos'!>) = О,
где F—произвольная функция своих аргументов.
Зная функцию Ф, помощью квадратур определим і:, vt w.
Полагая Ф ™ arct? —j будем иметь:
и = -,-—— + Сі \t, .х, у),
го^у-^f^ ^§^ + С(t,z),
где 9> Сі> Со, С суть произвольные функции своих аргументов.
Переходя к цилиндрическим координатам г, 6, z, полярная ось
которых направлена по оси *-ов, а цилиндрическая ось — по оси
95

z-ов- и обозначая vr> vHf vz проекции скорости на нормали к трем
координатным поверхностям, будем иметь:
vr = *(z, ') + «,(', Ъ 0),
do(z, t) , пел
v*=r —— 1- С{U z);
9, аи а2і С суть произвольные функции своих аргументов.
Указанное движение может представлять известный интерес
в динамической метеорологии; в нем вертикальная скорость (vf)
зависит от высоты (z) и времени и кроме того изменяется в
зависимости от расстояния от центра (начала координат).
Пример 14, В только-что разобранном примере мы видели,
каким образом определяется изгиб вихря для одного из случаев
главного незакручивающегося движения. Посмотрим, как изгиб
вихря определится для такого движения, которое не подходит под
тип главного незакручивающегося движения.
Рассмотрим движение, в котором вихри остаются постоянно
параллельными некоторой неподвижной плоскости; соответственным
выбором координатных осей не трудно свести этот случай к такому,
в котором С = 0, а Е и т\ от нуля отличны или по крайней мере
не обращаются в нуль одновременно. Так как С = О, то существует
функция 9 от Ъ х* У> z такая, что
до до
и = -тЧ v =
дх' О у
Полагая
найдем:
до до до
дх ду ' dz "
* ду ' * дх> ^ и'
Dw=*
д<ь д*о д<ь д*2о
дх дх ду ду дх2'
д& д^о дь д2о
дх ду- ду дх ду '
д$ д^о дб д2о.
а отсюда
й
п2
дх dzdy ду dzdx*
(Р + rfi (Dw)* -f (Wv — фи)*
Последняя формула с помощью предыдущих соотношений может
быть переписана так:
11 <м "Mdjj J
2
8"2 —
96

•
тчт
дь
fc
д'Ь
дп-
'¦Э
дх dz ду ду dz ox
±\l(?t\*—(j!lY\ &2? <?6 д^ /д^
д*ъ
-\\ду } \бх J J дхду ~ дх ду \dx2 dy-J_
Это соотношение содержит три неизвестных функции: 8", »і и ?;
по о" и ? не трудно определить 6. Введем две новіях функции R и Ф
помощью соотношений:
-fo=R cos®, ^~=^l< вшФ;
(*)
тогда предыдущее условие по сокращении его на 7?4 даст
следующее трансцендентное уравнение для определения Ф*):
Г-ГГ.у
о"*= созФ
д^ь
dzdt/
sm Ф т—т- I +
+
_ cos 2Ф f-f- + 4
дхду* 2
;іп2Ф
dzdx
dr2
(
дуЧ\'
Определяя из этого уравнения Ф, будем иметь возможность
определить R из следующего условия интегрируемости уравнений (*):
интегрирование какового уравнения совершается обычными
приемами.
2. Изгиб вихря связан очень простыми соотношениями с
некоторыми элементами основного триэдра и основного сферического
треугольника. Рассмотрим три
точки единичной сферы,
изображающие направления Н, Q к L
(черт. 8); очевидно, что дуга
большого круга kjHQ и дуга kjHL
стремятся по величине совпасть
друг с другом, когда А*
стремится к нулю, ибо в этом случае L
стремится к совпадению с Q; с
помощью разности этих дуг можно
выразить изгиб вихря. Обозначая
дугу о HQ через &, дугу о HL
.и
через &', докажем следующую
формулу:
Черт. S.
lim
=Ь* cos A.
(50
*) Уравнение это сводится обычными приемами к решению алгебраическое
уравнения.
7 Зак. 2420. — А'. А. Фридман, Опыт гидромеханики 97

и
меем:
lim
At+Q
О'—ft
Hm
COS"
COS '»
C\f
sin
ho:
a_(H^)
cos *> = —
#9
, cos^'
ft + fl'
(H,I)
л*
откуда, замечая, что lim sin 0
lim
Ді->0
!>'—ft
(H, D)
+
tf.|i|'
sin (//, Q), найдем:
(H, Q) (Q, D) *
A' #Q sin (#f 9) #Q3 sin (Я, 9)
?> {— cos (#ГЬ) + cos (Д^) cos(QTb)}
) =
о
sin (#, Q)
Рассматривая сферический треугольник HQD (черт. 8) и
пользуясь тем замечанием, что угол при вершине Q этого
треугольника равен 180° — А, как это будет выяснено в следующем
параграфе, найдем:
cos (ЮЗ) = cos (fCQ) cos (Q^D) — sin (H^Q) sin (oTd) coc A,
каковая формула преобразует предыдущее
равенство в соотношение (50).
Из геометрических соображений ясно, что
дуга о HQ' стремится совпасть по величине
с дугой 'w> HQ, когда А/ стремится к нулю.
Простыми вычислениями обнаружим
справедливость формулы:
ЛУ/
Hm
>" —&
S4
S" cos A,
(51)
Черт. 9.
где $" есть о #Q'.
Простое соотношение между изгибом,
кручением и отклонением вихря получается, если
ввести направление Р> перпендикулярное
Q и [2ZJ], иначе говоря — лежащее в плоскости векторов 2 и D,
и перпендикулярное направлению 2. Условимся для сокращения
письма плоскость, проходящую через точки единичной сферы,
изображающие направления векторов А и В, обозначать' знакоположе-
нием
АВ ; направление Р будет лежать в плоскости
QD
и
будет перпендикулярно направлению Q. Обозначая через ? угол
*) Напомним, что через D мы, ради краткости, обозначаем вектор DY.
9S \

между направлениями —т-тлН, путем простых вычислений
установим следующее соотношение:
1_
о
dQ
dt
cost = o" —3 cos A (32)
Мы не останавливаемся на подробном выгоде этих
соотношений, так как в настоящей работе мы не будем касаться ни их
теоретических приложений, ни практического их значения для
вычисления кинематических элементов. Заметим только, что
последняя формула может быть полезна при изучении движения,
в котором вектор -г- занимает огределенное положение
относительно вектора Q. Так например! условие, чтобы вектор -у- лежал
з плоскости _L Р, сводится к условию cos т = 0, т. е. о cos А = о".
3. Перейдем к изучению случая, когда изгибающий угол равен
нулю при всех А*, т. е. когда жидкая линия, будучи к моменту t
вихревой линией, не меняет своего вида *). Такое движение мы
газвали прямым движением. Оно характеризуется условием:
ее" = 0, при всех Д?, где а" — изгибающий угол.
Совершенно ясно, что необходимым условием прямого движения
является равенство нулю изгиба вихря: S" = 0. Однако в то время,
как равенство нулю отклонения или уклона вихря является
условием достаточным для того, чтобы соответственно или
отклоняющий угол или уклоняющий угол обращались в нуль при всех
Д?, — указанное свойство не имеет места, как покажет приводимый
ниже пример, для изгиба вихря. Изгиб вихря может быть равен
нулю, в то время как изгибающий угол будет отличен от нуля.
Движение, в котором изгиб вихря равен нулю, назовем
квазипрямым движением*
Условие, чтобы Ь" обращалось в нуль, приводит нас к следую-
тцей теореме:
Теорема 8. Для тпою> чтобы движение было квази-прямым,
необходимо и достаточно, чтобы ректоры 2 и DV были
направлены по одной прямой **).
В самой деле, равенство о' = 0 сводится к равенству jDV='0
или [2, DV\ — 0, что и доказывает нашу теорему.
Для того, чтобы выяснить условия, когда движение становится
прямым, необходимо заметить, что прямое движение — это такое
движение, в котором направления 2 иі совпадают друг с другом,
т. е. мы имеем соотношение
[2,1] = 0,
которое должно быть справедливым при всех Дг.
*) Такая линия может перемещаться как твердая линия.
**) При этом, конечно, не исключается случай, когда DV = 0. Этот случай
разбирается далее.
7*
99

Приравнивая нулю коэффициенты при разных степенях А;
в этом соотношении, приходим к следующей теореме:
Теорема 9. Для того, чтобы движение было прямым,
необходимо и достаточно выполнение следующих условий:
[О, Z)V] = 0,
Q, D
A"
0, (n = 1, 2...).
(53
При изучении прямого и квази-прямого движения естественно
возникает ряд вопросов об отношении этого рода движения к ранее
уже разобранным нами гельмгольтцеву, незакручивающемуся и
главному незакручивающемуся движениям; кроме того возникает
вопрос о возможности существования квази-прямых движений,
отличных от прямых, а также о возможности существования
прямых движений. Дело в том, что прямое движение характеризуется
бесчисленным множеством условий, которые могут находиться
между собой в противоречии или же приводиться к ранее уже
изученным типам движений.
Прежде всего не трудно видеть, что всякое прямое движение
удовлетворяет всем условиям теоремы 3 и, следовательно, могло бы
быть отнесено к разряду незакручивающихся движений, если бы
для прямого движения имело смысл понятие кручения вихря; но,
в силу совпадения 2 и I, понятие кручения вихря для прямого
движения теряет всякий смысл; мы увидим ниже, что понятие
кручения вихря сохраняет свое значение для квази-прямого движения,
хотя в этом случае уже нельзя пользоваться выведенными нами
в § 6 формулами кручения вихря.
Дальнейшее изучение прямого движения будет основано на
одной формуле, позволяющей написать в несколько иной форме
условия теоремы 9.
Докажем, что для квази-прямого движения, если [Q, DA] = 0,
то имеет место соотношение
2 Я —
* dt
(2р —divA)
+
Q
dQ
dt
dQ
dt
Й,
dQ
dt
+
(54;
где р определяется из равенства DA = pQ.
Хотя только-что указанная формула и поверяется простым
вычислением, но мы считаем небесполезным указать вкратце путь,
которым эта формула выводится. По формуле (47), вспоминая
значение Н = -тг—DV, найдем:
dA _ dDA I dQ
D dt ~ dt \ dt
, v)a-kj3v, V)a;
100

так как движение квази-прямое, то D\f = lQ; с другой стороны
по условию DA = pQ, поэтому:
п с/А dQ
(^,V)A+(i+v)fi.
Образуем составляющую по оси z вектора
Q, D
dA
dt
; после
того как в этой составляющей соберем члены, имеющие
множите dr, d-. e
телями -у-, -J— и —г-, будем иметь равенство:
Q,D
rfA
dt
? I ,дАу
<?і4
<?*
¦ж i i
di\
It
+ 4\l&
6 dg +' dy
)+?(-'
&4.
i 'i
oz
d\
Прибавим и вычтем в множителе, стоящем при -г:, выражение
¦»1
дА, .дА
<Ь\
UZ
? -т^> а. в множителе, стоящем при -~тт, выражение
t дА, , гдАх
тогда предыдущее равенство преобразуется в такое:
Q, D
dX
dt
dX
= ^ (- P-I ~ ФА)„ + -Ч div А) +
dt
дА.
dQ
Q,
dt
+
x
^ dz
Q,
dt
^ dz
dQ
Q —
' dt
Js
и на основании формул
(Z>A), = /*, фА), = рті,
+ curly А, -г^=-зг- —curl^A,
dz ti*:
Cz
dg
легко обнаружим справедливость соотношения (54).
Г~ dQ
Из этой формулы получаем, что, при
Q, D
с/А
А
= 0, будем иметь
= 0, коль скоро справедливы равенства [Q, Z)V] = 0
в [Q, ЯА] = 0.
Отсюда нетрудно будет доказать такое предложение:
Теорема 10. Квази-прямое движение, принадлежащее кглав-
, ным незакручивающимся движениям^ является прямым
движением'
101

Так как в квази-прямом движении имеет место соотношение
2, DV] == 0, а для главного незакручивающегося движения имеем
= 0, то в силу формулы (54) и предыдущего замечания
Q
9 dt
получим:
S, D
c/V
= 0. Из этого равенства найдем, что
d*V 1
Q, В , = 0 и т. д.; таким образом все условия теоремы 9
будут соблюдены, что и докажет наше предложение. Следует
заметить, что квази-прямое движение, у которого уклон вихря равен
нулю, обладает одновременно и равным нулю отклонением вихря;
это ясно из рассмотрения треугольника, сопряженного основному,
равно как и из равенства:
[Н, Q] = [^-,a]-[2>V, Щ,
потому что оба слагаемых в правой части этого равенства
обращаются в нуль. Таким образом квази-прямое и одновременно
главное незакручивающееся движение есть в то же время и
гехъмголътцево движение*
Хотя случай прямого движения, установленный теоремой 10,
представляет собой обычный случай гельмгольтцева движения,
тем не менее мы укажем один пример такого движения.
Пример 15, Рассмотрим случай движения жидкости, в котором
? = і] —0 (см. пример 13). В этом случае имеем:
D
df
таким образом условие Q, D
dz \ dtn
^dz
df
d [dnV
df
0 сводится к двум условиям:
=о,
dz
(?)-*
Эти условия удовлетворяются, коль скоро u, v зависят только от
. т у л dw du dw dv _
г, х, у. 1 ак как к = г\ = 0, то -гг~ = -^— = 0, -^— =*~т- = 0; таким
образом V) зависит только от / и 2. В этом движении, которое
будет главным незакручивающиадся и гельмгольтцевым в одно
и то же время, мы будем иметь:
u = u(f, х, у), v = v(t, дг, у), w=w(t, z\
dz'
0, ij = 0, 'C = C(/, x,g),
#, = 0, //, = 0, #z= , -
dt
'W
dz '
4. Естественно возникает вопрос: всякое ли прямое движение
102

сводится к главному незакручивающемуся движению, или же имеют
место прямые движения, не принадлежащие к классу главных не-
закручивающихся движений? Оказывается, что подобно тому, как
класс главных незакручивающихся движений не исчерпывает всех
незакручивающихся движений, подобно этому существуют прямые
движения, не принадлежащие к классу главных незакручивающихся
движений. Мы найдем эти движения, поставив себе задачей
разыскание прямых движений для случая обобщенного плоского
движения, в котором скорости и вихри (могущие зависеть от всех трех
координат и времени) остаются параллельными некоторой
неподвижной плоскости.
При этих условиях мы будем (после соответствующего выбора
координатной системы) иметь w = Q, ? = 0; таким образом:
дъ до л
¦и==Тх> Vsss^'WSBS°>
где ? — функция времени и координат.
Применяя к нашему случаю формулу (54), где вместо А
подставлен вектор V, найдем:
Q, D
dv
dt
= (2p-divV) U^
?¦
4 Л
тогда как составляющие вектора
' U dt
по осям х и g
обратятся в нули. Отыскивая прямые движения, мы должны будем
рассматривать такие движения, которые во всяком случае удов-
летворяют условию
движения, не
% D
dt
0; так как нас интересуют
незакручи-
принадлежащие к классу главных
,. df[ <R , л
вающихся движении, то ? —гг —1\ -jr^FV', поэтому предыдущая фор-
dt
dt
мула дает нам равенство:
„_*,*_*+*.
о
Вспомнив, что значение величины р определяется из условия
будем иметь следующие равенства:
ди у . ди f.
dvу . dv
103

откуда, пользуясь выражением для р, данным формулой (*), будем
иметь:
Так как ? и ч\ не могут быть "равны нулю одновременно (каковой
случай не представляет для нас интереса), то определитель
предыдущей системы линейных однородных уравнений обращается
в нуль, т. е. мы имеем равенство:
[дх ду) "г4 ду дх~ '
откуда, подставляя найденные ранее значения для и и v9 найдем:
Поскольку мы рассматриваем только случаи вещественных
движений, то предыдущее разенство дает:
dx~tg~ ' Ш>~1)у*'
откуда видно, что:
с
? = ?о + а*+6» + уС*а +У3),
где <?о, а, 6, с — произвольные функции t, z.
Таким образом прямые обобщенные плоские движения, не
принадлежащие к классу главных незакручивающихся движений и не
являющиеся движениями с потенциалом скоростещ необходимо
должны иметь для скоростей следующие выражения9.
и = a -\- сх, і) = Ь-\-су) w == О,
>
где а, Ъ, с — произвольные функции t иг.
Установив необходимую формулу для скоростей, при которой
обобщенное плоское движение может быть прямым, покажем, что
обобщенные плоские движения, определяемые предыдущими
формулами, будут действительно прямыми, причем функции а, Ь, с
можно подобрать так, чтобы рассматриваемое движение не
принадлежало к классу главных незакручивающихся движений.
Только-что сказанное наложим в примере 16.
Пример 16. Движение, скорости которого выражаются
формулами
и = а-\-сх, v=b-\-cy, w = 0,
где а, 6, с суть функции t и z, есть движение прямое.
104

Легко видеть, что
. t ап , cnxt -н —дп t спуі . „¦ —U,
где ам Ьп7 сп—функции от t и z, определенным образом
составленные из функций а, Ь, с и их производных по времени.
Положим, что написанные формулы справедливы для некоторого
значения п, и покажем верность их для индекса п -f-1:
Л»*1 Л \ dtn 1 А \ Л" / + u ^ \ Jf I+ * дд \ df I ~
дап дсп
откуда
an+i =
с«+і =
= а* + сс*>
и точно так же:
дЬп
Эти рекуррентные соотношения и доказывают справедливость
нашего положения.
Легко получить из предыдущих формул следующие выражения
составляющих вектора и ¦ *п :
откуда непосредственно находим:
dnV
[
Q, D
df
= 0, (71 = 0,1,2,...)
т. е., согласно теореме 9, движение наше будет прямым.
Чтобы выяснить возможность выбрать наше движение не
входящим в класс главных незакручивающихся движений, составим
t d-n dk
выражение 6-^ -4-j:
. 56 дс da , дс
<#_ ** а^?. / дс 1 *te \
Л~ ЛА 6 <fe Г «?г + й»л)л
dt\ _ (Pa , _^с_і_/ _^? _і_ J^?_\
Л ~~ <ЬЙ +a <?z "'"Г dz "+~ dzdt)*'
105

А,
Л
d3* da
Л Гі dt dzdt dz dzdt dz
д2а дЬ ¦ дс
+ dz
+
<Jz& dz dz <?гЛ * dz
д-а дс да д*с , дс
"Г
dz Л dz dz dz dt ' dz
для случая a—b = k(t)c будем иметь:
a
дс
dz
, да
'-?-
дЬ\
да
db\i
31
K dt
dt
= *<0 (¦?)'(*-*).
что очевидно отлично от нуля при произвольном выборе k(t)
и с (f, z); движение будет в этом случае определяться формулами
u=c(t, z) [*(*)+*],
v = c(t, z) [k(t)+g],
zu = 0.
Значительно проще выяснить вопрос, указанный в начале
предыдущего пункта, а именно вопрос о том, что квази-прямое
движение не есть еще прямое движение.
Ответом на этот вопрос будут служить два следующих примера:
Пример 17. Рассмотрим снова обобщенное плоское движение.
Для этого движения будем иметь:
ц =
до
<Э2?
до
1 dxdz'
Полагая* что движение квази-прямое, найдем:
ди ч\ dv до j_
ду Т * ~ду ~р ох у\9
откуда
ди * dv _ ^ J__u J^L ^ — ^2? "2 4~ 'П9.
(*)
2/>
<Эх д# дх t\ dy % дхду Ь\
таким образом
Q, D
dV
dt
1 <R
д*
¦П dt Е dt)*^*' дхду
Отыщем движение, в котором т] = %е; тогда:
1 d-ц _ J_ &_
dt
tj dt
106

Уравнения (*) и условие т] = ;е дают:
Второе уравнение дает:
тогда первое уравнение может быть переписано таким образом:
= е
отсюда:
дб (х\ t)
С помощью этих обозначений найдем:
1 + е
где ф и Ф — произвольные функции своих аргументов; ясно, что
можно распорядиться этими функциями так, чтобы -у V не = 0;
Гл ~dV
тогда окажется, что [2, D4] = 0, а л ~
2 D —-
не = 0, т. е. мы
получим квази-прямое движение, не являющееся прямым. Делая
частное предположение относительно функций ф и Ф, установим
следующие формулы:
1 + е 1-}-е
что соответствует
После простых вычислений будем иметь:
\ = е'\ tj = 1, С = 0,
du e~t г,— — 2~'~е

в то же время:
1 ^_lii=1 ?2_Lr2=i4-e-2' _^=__У___
= е
7V
/1 dr,
б9+ча = і-Ь*
-т §) ('2+^2)
как и следовало ожидать.
Пример 18. Рассмотрим движение, в котором щ v суть
функции ?, х9 г/, a zu — функция всех четырех переменных. Поставим
условием, чтобы это движение было квази-прямым
В этом движении вихрь и вектор D определяются следующими
формулами:
у dw п jfa_ dw_ du^ dw
dzv ^ dv dw dv dw
^_^ Dw_
dx ay dz
для квази-прямого движения будем иметь следующие условия:
Du Dv Dw
_________
Обозначая через а выражение:
dw
дх
а =
д'ч
перепишем условия следующим образом:
ди du dv dv 1
dx б у dy dx a *
dw __ du du_
dz ~~dx dy
Отыщем частное решение этой системы уравнений, отвечающее
-лучаю, когда а обращается в 1. Предыдущая система уравнений
может быть переписана в этом случае следующим образом:
dw dw du du dv dv
Заменяя
дх
ду '
dw
dz
переменные х и
х+У =
дх
ди
~ дх
у на ;
*',
ду
ди
V
*'и/
х—у
ду'
по
= 3
дх9
формулам:
г
108

н помня, что и и v не зависят от z, получим следующее решение
нашей задачи: ~
и',
г; = у'Н',<Н-Л(^'),
«=-J§-H'.*')+/3(',*'),
т=*е\ (t, *')-J-^ (*,*'),
причем функции, входящие в эти формулы, суть произвольные
функции своих аргументов. С помощью указанных формул
найдем:
5. Среди квази-прямых движений особняком стоит движение,,
в котором DV обращается в нуль.
Рассмотрим пример такого движения, которое в дальнейшем
будем именовать особым движением.
Пример 19, Рассмотрим квази-прямое движение, в котором
вихрь совпадает по направлению со скоростью, т. е. имеют место
условия: [V, Q] = 0 и [&,?>V] = 0; равенства эти могут быть
переписаны таким образом:
dw dv dv. dw dv du
du
ndx
dy
+ v
dz
и
du ,
dy '
и
и
dz
du
WTz
dw ,
dx +
dx
V
dv .
dw ,
v d9+w
dx
w
dv
V
dw
dz
oy
•A-w
j
dv
dz
w
Полагая u=v и считая и независящим от z, найдем, что
предыдущие уравнения обратятся в следующие:
dw , dw n dw du , du
l)x^~~dy~~ ' dz ~'dx^"dg
dw I du , du \
dx \dx dg j9
(*>
109

интегрирование этих уравнений дает следующее частное решение*
u = y = 6(x—y,t),
w = Vc{t) — 2^{x — y,tfy
тде 4* и с являются произвольными функциями своих аргументов.
Не трудно видеть, что в этом случае
У7(0=24(х - #,')2 ' Ус(0-26(х-я,О8 ' ' '
где
V =—^,— при х ==*—#.
Из этих формул получим:
I 2'/ г, 2</ : 2-У
точно так же:
Du = О, ZX/ = 0, Z)o> = 0.
Таким образом получаем особое движение.
Систему уравнений (*) не трудно проинтегрировать сполна;
порученное общее решение или будет относиться к классу
безвихревых (с потенциалом скоростей) движений, или будет особым.
Для интегрирования уравнений (*) введем новые переменные:
*' = *—у, у' = х-\-д\
первое из этих уравнений даст нам условие:
w = zu (X, z,t); I -~- = 0 j;
вторые два уравнения перепишутся таким образрм:
дги -ди 0 ди . dw f
откуда
w
2+u' = f(g,z,t). (**)
Так гак и не зависит от z, то
д*у> _ „ д?и
dz* ~ дудг '
и следовательно
го '=Ых',{) z+<k(*V4
110

Соотношение (**) дает:
?* + 2-Vbz + % +1 ('?</3 + 44,'Ь»' -г 4ф = 2/ (у', z, /).
Отсюда ясно, что все коэффициенты при степенях гиг/'
должны зависеть только от t; значит, или ^ отлично от нуля и
тогда фі, 'Ьо, Фз зависят только от t9 или же '^ = 0, тогда между
^2 и Фз имеется зависимость
4-*+24* = с (fl;
с (?) — произвольная функция г*. Второй случай был нами только-что
рассмотрен и привел нас к особому движению, когда ?>V = 0.
Первый случай дает следующие формулы для и, v, w:
и = * = у Фх (0^+Ф. (*), в> = *і (<) * + ** С),
откуда легко найти:
$ = 0, ч = 0, С=*0.
Таким образом первый случай настоящего примера приводит
нас к классу безвихревых движений.
6. В заключение настоящего параграфа рассмотрим, как
видоизменяются формулы для определения кручения в случае
квазипрямого движения. В то время как для прямого движения понятие
крутящего угла и кручения не имеет смысла, для квази-пря-
мого движения (в случае если оно не есть прямое движение)
крутящий угол имеет вполне определенное значение, ибо направление
L в этом случае не совпадает с направлением вихря Q? хотя и
подходит к последнему теснее, чем в общем случае движения.
Формулы (16) и (17), данные нами в § 6 настоящей главы, были
выведены в предположении, что движение не было квази-пря-
мым, т. е. в предположении, что [Q, DV] не обращалось в 0; для
квази-прямого движения эти формулы уже не имеют места, и нам
необходимо вывести другие формулы, выражающие величину
кручения для случая квази-прямого движения. Формула для синуса
крутящего угла остается и в случае квази-прямого движения
без изменений; она может быть написана следующим образом:
мЛ- іы-іь'і
[см. § б настоящей главы, формулу (15)].
Как уже было выяснено, вектор V обладает (для негельмгольт-
цева движения) *) таким свойством, что коэффициент Bt при
первой степени А* в векторе V отличен от нуля. В случае
квазипрямого движения коэффициент при Af в разложении по степеням
А* вектора Ь будет равен нулю; так как мы имеем дело с
движением непрямым, то наверное б разложении вектора Ь по степеням
._>
*) Если движение гельмгольтцево, то понятие кручения вихря теряет смысл.
111

Af встретится такой коэффициент, который будет отличен от
нуля. Пусть этот коэффициент будет стоять при Д?п, таким
образом Вя не будет равно нулю; тогда легко получим:
[В„ [H,Q]]|
in A = -
sin
ВвН[іі,0]Г
Обозначим через Dn вектор D ———; тогда, помня, что
at
Цп = _ [Q, DJ, легко получим:
sin Л- QKH>[Q-Pn])l
«in Л- l^^^L, (55)
sin (Я, Q)
где [?, D„] есть направление вектора [Й, D„].
Чтобы иллюстрировать вычисление кручения для квази-пря-
мого движения, рассмотрим кручение для примера 17 § 7.
Пример 20.
При таких скоростях будем иметь, согласно вычислениям
примера 17, следующие выражения для составляющих вектора Dg
2* dt 14- е2і '
п. = /)Л=2 + в«
A, = Z>^- = 0;
точно так же:
**, = у Р>. D.J, = 0, Вгу = і [Q, DJ, = О,
** = ¦?¦ P. DJ. = -§-*-';
таким образом коэффициент при Д/3 разложения вектора Ь является
отличным от нуля.
Помня, что с = е~ , г\ = 1, ? = 0, найдем:
Нх=-2е~\ Ни=-1, #г = 0,
откуда
112

Отсюда легко получим
[В„[Н,О]] = 0,
а значит:
sin Л = 0.
Так как в данном случае
Л dK л п _ dtl~xw
то очевидно, что все условия (30) теоремы 6 выполняются,
следовательно рассмотренное движение принадлежит к числу планоид-
ных незакручивающихся движений,
§ 8. Главный тетраэдр.
1. Формулы (12), (19), (25) и (48) для отклонения, кручения,
уклона и изгиба вихря показывают, что все эти элементы связаны
с тремя векторами: вектором вихря 2, вектором Н и вектором
D; таким образом все элементы, характеризующие, по крайней мере
в первом приближении, изменения вихревых линий в жидкости,
вполне определяются, коль скоро заданы три вектора 2, Н, D.
Это обстоятельство указывает нам на то, что представляется
необходимым ввести в рассмотрение особый геометрический образ —
тетраэдр, образованный векторами 2, Н и D.
Хотя рассмотрение этого тетраэдра и связи его элементов
с элементами основного триэдра не даст нам теперь ничего
существенно важного, однако мы считаем необходимым остановиться
на изучении этого тетраэдра, так как подобное изучение может
быть весьма полезно для более детальной классификации
движений жидкости; само собой разумеется, что в настоящем параграфе,
имея в виду его сравнительно малое значение для дальнейшего
нашего изложения, мы ограничимся лишь кратким изложением
весьма немногих свойств, характеризующих связь тетраэдра с
элементами основного триэдра.
Тетраэдру образованный векторами 2, Н и D, мы будем
называть главным тетраэдром.
Формулы, указанные в начале настоящего параграфа,
позволяют выразить отклонение, кручение, уклон и изгиб через
элементы главного тетраэдра. Все остальные элементы плоского
сопряженного основному треугольника выражаются через npej^w-
дущие; поэтому главный тетраэдр вполне определяет собой
плоский сопряженный основному треугольник. Что же касается
основного триэдра (бесконечно малого триэдра, образованного
направлениями Q, L, 27), то можнс* высказать, — как это будет сделано
в п. 2 настоящего параграфа, — ряд предложений, указывающих на
связь предельного положения граней основного триэдра с гранями
главного тетраэдра, равно как и ряд предложений, указывающих
взаимное расположение основного триэдра и главного тетраэдра,
8 Здк. 2420. — А. А. Фридман, Опыт гидромеханики ИЗ

о чем мы уже упоминали в § 6, п. 2, говоря о правом и левом
кручении.
Здесь уместно будет отметить, что положение вихревой линии
к моменту г-рЛ* („новой" вихревой линии) будет определено по
положению вихревой линии к моменту /, коль скоро мы будем
знать: 1) положение плоскости QL | и 2) основной сферический
треугольник. В частности положение новой вихревой линии
определится по положению старой вихревой линии, по положению
плоскости
QL и по величинам изгибающего угла, крутящего
угла и отклоняющего угла. Как мы увидим далее, положение
, изги-
плоскости
QL \ будет близко к положению плоскости QD
бающий угол а." приближенно равен &"А/, где <* — изгиб вихря;
крутящий угол А приближенно равен кручению А, и отклоняющий
угол а приближенно равен ol{f где о — отклонение вихря. Таким
образом положение новой вихревой линии вполне определяется по
положению старой вихревой линии и по элементам главного тетраэдра.
Мы не останавливаемся здесь на вопросе о том, с помощью каких
графических процессов можно определить положение новой
вихревой линии.
Не трудно усмотреть, что в случае, когда движение
приобретает особый характер, главный тетраэдр также приобретает особый
вид, например сплющивается и, вырождаясь, превращается или
в плоскую фигуру, или даже в отрезок прямой.
Для гельмгольтцева движения главный тетраэдр обращается
в плоскую фигуру, указанную на черт. 9. Для главного незакручи-
вающегося движения главный тетраэдр обращается в плоскую
dQ
фигуру, изображенную на черт. 10, ибо в этом случае —jr и Q
dQ
совпадают по направлению, а потому И = , -—D лежит в
плоскости
QD I. Для прямого движения, где Q и D совпадают по
направлению, главный тетраэдр обращается в плоскую фигуру,
изображенную на черт. 11; а для незакручивающегося движения, в кото-
dQ „
ром —тгі и следовательно И, перпендикулярны к направлению
[2J5], т. е. лежат в плоскости QD , тетраэдр обращается в
плоскую фигуру (черт. 10). В случае прямого движения, которое
является одновременно и главным незакручивающимся движением,
а следовательно, как было показано в § 7, и гельмгольтцевым,
главный тетраэдр обращается в отрезок прямой.
Быть-мОжет небесполезно указать на кинематический смысл
тех особых движений, которые мы подробно исследовали в
предыдущих параграфах. Гельмгольтцево движение характеризуется тем,
что вихревые линии в нем сохраняются, т. е. жидкая линия, будучи
114

вихревой линией к некоторому моменту, продолжает оставаться
вихревой линией во все последующие моменты *).
В общем иезакручивающемся движении жидкая линия, будучи
вихревой к некоторому моменту, перестает быть таковой с
течением времени; однако движение таково, что новая вихревая линия,
рассматриваемая в бесконечной близости данной частицы,
удерживается в плоскости старой вихревой линии и той линии, в которую
превратился жидкий вихрь- Главное незакручивающееся движение
еще проще: в нем вихрь в данной частице меняет с течением
времени лишь свою величину, но оставляет неизменным свое
направление; таким образом элемент вихревой линии, проходящей через
данную частицу, перемещается параллельно самому себе, хотя
обычно (для негельмгольтцева движения) перестает быть жидким
элементом.
Для прямого движения мы имеем совпадение жидкой линии L
с направлением вихря Q. Таким образом элемент жидкой линии,
вихревой к некоторому моменту, перестает менять свое
направление с течением времени и может
только растягиваться или сжиматься;
конечно, для негельмгольтцева дзиже-
о о
Черт. 10. Черт. 11.
ния он перестает уже быть элементом вихревой линии.
Выделение особых движений, которое мы произвели в
предшествующем параграфе, основывалось в конце концов на изучении
случаев вырождения плоского сопряженного основному
треугольника в отрезок прямой. Не трудно усмотреть, что этот плоский
треугольник может вырождаться в прямую линию или тогда, когда
одна из сторон его обращается в нуль, или когда один из углов
его обращаетсял в 180°, а два других в 0°; следовательно или
обращается в нуль одна из величин 8, о', о", или же кручение А
обращается в 0° или 180°. Таким образом все случаи вырождения
плоского треугольника, сопряженного основному, учтены нами
в предыдущих параграфах. Без труда можно установить, что все
случаи вырождения главного тетраэдра в плоскую фигуру подхо-
*) Напомним, что жидкая линия во все время движения состоит из одних и
тех же жидких частиц.

дят под установленные нами особые классы движений. Главный
тетраэдр обращается в плоскую фигуру или когда Q, Н, D лежат
в одной плоскости, будучи отличны от нуля, или когда один из
этих векторов обращается в нуль. Первый случай очевидно
подходит под один из типов движений, рассмотренных нами выше;
конечно, в этом случае возможно движение не незакручивающееся,
а квази-незакручивающееся, и не прямое, а квази-прямое. Если
один из векторов, образующих главный тетраэдр, будет нулем, то
движение, такому случаю отвечающее, будет подходить к
установленным нами классам движений. Если Q обращается в нуль, мы
имеем безвихревое движение (с потенциалом скоростей); если Н
обращается в нуль, мы имеем гельмгольтцево движение
(обладающее некоторыми особенностями, о чем будет сказано в § 9); если
D обращается в нуль, мы имеем дело с особым движением
(см. конец § 7).
Таким образом все элементы, определяющие (по крайней мере
в первом приближении) изменение вихревых линий, выражаются
через элементы главного тетраэдра.
Выше мы видели, каким образом векторы Q, Н и D выражаются
через скорость V и производные ее по времени и по
координатам, иначе говоря — через кинематические элементы,
характеризующие движение жидкости.
Чтобы сзязать изменение вихревых линий с теми причинами,
которые вызывают движения, мы должны будем элементы главного
тетраэдра выразить при помощи динамических элементов
движения, т. е. при помощи давления, температуры (или, что то же самое,
при помощи давления и удельного объема), и действующих на
жидкость сил; это будет выполнено нами во второй части
настоящей работы, причем окажется, что вектор Н будет выражаться
только через давление и температуру (или, что то же самое, через
давление и удельный объем), тогда как для изучения вектора D
потребуется ввести притекающую энергию и изменение
температуры данной частицы жидкости.
Что же касается вектора вихря Q, то, являясь исходным
элементом, от которого мы считаем изменение вихревых линий,
вектор Q не подлежит выражению через динамические элементы;
этот вектор указывает, об изменении какой именно из вихревых
линий идет речь.
В заключение настоящего пункта установим формулы, которыми
мы отчасти уже пользовались для случая движения со скоростями,
линейно зависящими от координат и которые нам пригодятся
впоследствии. G
Поставим задачу о связи компонентов вектора DV с
компонентами вихря ?, t|, С, с тремя удлинениями ех, е2, е3 и с тремя
сдвигами ох, о2, о3; при этом указанные девять величин определяются
формулами:
h dw dv_ ? ди dzv dv ди
116

с1 =
отсюда
•
?і бх
dw , <fo
~!fy+~d7;
ди
0* 2
At ~~ 2
cs — ) >
ди , до;
°2_c?z + дх'
ди __ о3 —', _
Ой' 2 '
о г*
dw ox -j- 5
ду~ 2
dw
^3 <te'
??И 5., -j- Tj
<?Z 2 '
oz.» ^i —;
dz _ 2 '
Вспоминая формулы § 2 главы I, для составляющих DV будем
иметь:
Dw = е/, + ^
=,тп-г V
(56)
Отсюда не трудно получить обратно выражения з1я з2> а3 через
вихрь, составляющие вектора D и удлинения.
Определитель системы уравнений (56), в которые неизвестными
будем считать сдвиги оі9 оъ з3, будет равен -^ ;*?; таким образом
при условии, что ?, г\, С все отличны от нуля, мы можем
определить сдвиги ои о2, о3 через компоненты вектора Z)V. Рассматривая
только этот случай, будем иметь:
с1=А(Д-2*:?>и-г2«1Р),
^
Ч = -fir (А - 2т, Dv -f 2^),
^ = т^(А-2:^+2в/Л
*N
(57)
где
Д = I Du + т, Dv + С Dw — в,Р — з^з — =,го.
(58)
2. В настоящем пункте займемся вопросами, касающимися
предельного положения граней основного триэдра, а равно и
расположения этого триэдра по отношению к главному тетраэдру.
Из рассмотрения формул § 6 не трудно будет доказать следующее
предложение:
117

Теорема 10. Предельное положение плоскости QL , когда А;
стремится к нулю, есть плоскость QD L а предельное положение
плоскости
Q'L
есть плоскость
HQ
кости
При этом, конечно, рассматривается общий случай, когда плос-
имеют вполне определенное положение, т. е.
QD
и
НО.
когда мы имеем движение, не принадлежащее ни к классу гельм-
гольтцевых движений, ни к классу прямых (вернее — квази-пря-
мых) движений.
Легко усмотреть, что вектор Ь (см. § 6) есть перпендикуляр
к плоскости
QL у а вектор W — перпендикуляр к плоскости
Q'L
; так как с другой стороны:
urn .
?- = ыЦ?- = [в,іщ,
М->0
то очевидно, что предельное направление векторов b и I/
соответственно перпендикулярно плоскостям
QD
и
№
, что и
доказывает наше предложение.
Не трудно усмотреть из самого определения кручения А, что
угол между плоскостями QD и j QH *) в главном тетраэдре
равен 180° — А- В самом деле, на основании сказанного в § 6, Л
есть угол меньший 180° между направлением вектора [Q, JDV] и
вектора [Н, Q]; поэтому (согласно геометрическому значению
векторного произведения) угол главного тетраэдра между плоскостями
QD
и
QH равен 180° — А. Не трудно проверить означенное
замечание в случае совпадения этих плоскостей; когда Н и D
будут расположены по одну сторону от вектора &, мы будем иметь,
что угол между плоскостями
ЯП , ЯН
в главном тетраэдре
равен нулю, тогда как А = 180°. Сообразно сказанному в п. 2 § б
установим следующие определения:
Правым кручением назовем тот случай, когда дуга oLQ
основного сферического треугольника переходит в дугу о Lc2fr
вращаясь против часовой стрелки вокруг направления L; левым
кручением назовем тот случай, когда дуга О LQ переходит в дугу
о LQ\ вращаясь по часовой стрелке вокруг направления L.
*) Следует отметить, что эа угол между плоскостями АВ
и
А'В'
мы
будем считать угол меньший 180° между направлениями АВ
118
и
'D/
А'В

Как мы сейчас увидим, можно будет доказать предложение, свя"
эывающее вопрос об определении правого и левого кручения
с величиной угла между направлениями [QD] и //.
Предварительно, для упрощения дальнейших рассуждений,
условимся пользоваться так называемой французской системой
координат, т. е. такой, в которой переход от оси X к оси Y совершается
вращением по часовой стрелке вокруг оси Z. Приняв эти
замечания во внимание, докажем следующее предложение:
Теорема 11. Если угол между напрс злением \QD\ и Н острый,
то мы имеем правое кручение; если угол между направлениями
[QD] и Н тупой, то мы имеем левое кручение (черт. 1'г и 13).
Доказательство этой теоремы будем основывать на
нижеследующей лемме.
Условимся называть направлением обхода сферического
треугольника ABC направление контура ABC, составляющего этот
'¦?#
Черт. 12. Правое кручение.
Черт. 13. Левое кручение.
треугольник, по отношению к внешней нормали к сфере.
Как это видно из черт. 14 и 15, если направление обхода
треугольника ABC противоположно направлению вращения часовой
стрелки, то АС переходит в ВС, вращаясь вокруг С против
часовой стрелки; если же (см. черт. 15) направление обхода
треугольника ABC совпадает с направлением вращения часовой стрелки,
то АС переходит в ВС, вращаясь вокруг С по часовой стрелке.
Лемма. Если направления [АС] и В лежат по одну сторону
плоскости
АС , то направление обхода треугольника ABC
противоположно направлению вращения часовой стрелки; если
направления [АС] и В лежат по разные стороны плоскости
АС , то направление обход а треугольника ABC совпадает
с направлением часовой стрелки.
Заметим, что направлением А мы условились называть
направление вектора А из центра сферы к точке А на ее поверхности,
направление же [АС] совпадает с направлением вектора [А, С],
119

каковой вектор направлен так, чтобы вращение от- А к С на
кратчайший угол совершалось по часовой стрелке относительно
вектора [А, С]. После этого замечания справедливость леммы при
помощи черт, 16 и 17, исчерпывающих все случаи взаимного
расположения точек А, В, С, становится очевидной.
На основании определения понятия правого и левого кручения мы
можем сказать (черт. 12 и 13), что кручение будет правым, коль
Черт. 14.
Черт. 15.
скоро направление обхода треугольника 22'L будет против часовой
стрелки, и, наоборот, кручение будет левым, коль скоро
направление обхода этого треугольника буд§т по часовой стрелке. Только-
что доказанная лемма сводит изучение направления обхода тре-
Черт. 16.
Черт. 17.
-м
угольника QQ'L к изучению расположения направлений [QL] и Q'
относительно плоскости QL - Докажем прежде всего, что эти
направления лежат по одну или по разные стороны плоскости
J QL , коль скоро направления [2.D] и Н лежат соответственно по
одну или по разные стороны плоскости 2D . Обозначая через R
120

радиус-вектор точки с текущими координатами X, Y, Z, будем
иметь, что уравнение плоскости АВ в векторной форме
выразится следующим образом:
(R,[A,B]) = 0.
Легко видеть, что выражение ([а, 1], [а, 1]) имеет знак плюс,
поэтому направления [QL] и 2' лежат по одну или по разные
стороны плоскости QL |, смотря по тому, имеет ли выражение
(а', [а, 1]) знак 4~ или —. Точно так же не трудно показать, что
направления][2Щ и //лежат по одну или по разные стороны
плоскости
QZ? , смотря по тому, имеет ли выражение (Н, [2, D]) знак
-д- или —.
Вспоминая формулы, выражающие а'', а и 1, найдем, что знак
(а', [а, і]) одинаков со знаком (Н, [Q, D]), что и докажет наше
утверждение. Таким образом, если [QD] и Н лежат по одну
сторону от плоскости QD (т. е. если угол между [QD] и Н острый),
то [QL] и 2' лежат по одну сторону от плоскости QL
что
отвечает правому кручению.
Наоборот, если [QD] и Н лежат по разные стороны от
плоскости J 2Z? J (угол между [&D] и Н тупой), то [?L] и Q' лежат по
разные стороны от плоскости
QL
что отвечает левому
кручению.
Таким образом теорему 11 следует считать доказанной.
В настоящем пункте мы не приводим примеров, характеризующих
правое и левое кручение вихря, так как таковые примеры были
уже нами разобраны в п. 2 § 6.
3. Для более детальной характеристики изменения вихревых
линий, тех элементов (отклонение, кручение и т. д.), которые мы
ввели, само собой разумеется — недостаточно. Эти элементы, будучи
или конечными величинами, или бесконечно малыми первого
порядка относительно А*, могут быть названы элементами первого
порядка^ характеризующими изменения вихревых линий.
Рассматривая величины второго порядка малости относительно
А/, мы, конечно, получим более детальные сведения об изменении
вихревых линий; в настоящей работе мы не останавливаемся
подробно на изучении этих элементов второго порядка*
характеризующих изменение вихревых линий, но для иллюстрации того,
каким образом можно ввести в рассмотрение элементы второго
порядка, исследуем некоторые из них.
Как было показано в предыдущем пункте, плоскости 12Н
и
Q'L стремятся совпасть друг с другом, когда Af стремится
к нулю; линия пересечения их стремится занять некоторое пре*
121

дельное положение П, зависящее, как мы сейчас увидим, от
коэффициентов при второй степени А; в разложении введенных нами
в § 6 векторов а, а' и т. д. Это предельное положение, которое
мы для краткости назовем предельной прямой, представляет собой
геометрический образ, дающий возможность ввести ряд элементов
второго порядка. В настоящем пункте мы рассмотрим лишь
направление предельной прямой.
Обочначим через R радиус-вектор точки с текущими
координатами X, Y, Z\ не трудно видеть, что уравнение плоскости,
проходящей через векторы А и В, напишется в следующей форме:
(R,[A,B]) = 0;
таким образом уравнение плоскости Q// будет:
(н,[а,Щ) = о,
а уравнение плоскости QrL будет (см. § 6):
Ю = 0.
Вспоминая разложение Ь' по степеням А* и производя простые
преобразования, получим:
в;=-[о,н],
откуда найдем, что пересечение наших плоскостей будет опреде*
ляться из уравнений
(R, [2,Н]) = 0, .
(r, ~jt [Q,E\) —\ (R, [Q, HJ) = 0.
He трудно видеть, что пересечение двух плоскостей:
(R,A) = 0 и (R,B) = 0
совпадает с прямой, на которой лежит вектор С:
С = [А, В].
Таким образом предельная прямая является прямой, на которой
расположен вектор П, определяемый соотношением:
п=={^—^' [Q'H]) Q~{^' EQ>Hl)H- <59>
Этот вектор можно назвать предельным вектсром; не трудно
Усмотреть, что для случая общего незакручивающегося движения
или для случая квази-незакручивающегося движения предельный
вектор совпадает по направлению с вектором вихря.
Для иллюстрации образования предельного вектора рассмотрим
следующий пример:
122

Пример 21. Рассмотрим случай движения, в котором скорости
суть линейные функции координат с коэффициентами, зависящими
от времени. Пользуясь обозначениями предыдущих параграфов и
полагая сдвиги а19 з2, аг равными нулю, получим следующие
выражения для компонентов вектора
dtt Н,
dt
dH
X
я
\х
dt
dH
о.
2 ч,. , •»!'•. — '-*1 , _., е2
+ ^
У
Я
dt
dH
2
Я
2
& + #ч + -^Ч-^ + « **
10
-{[H+'iJt'
2
si - 4
+*
»»1
А 2 2 L' v"3 ' ~8/" ' 2 ' "' 2
Составляя выражения для компонентов вектора [2, Н], найдем:
Р, Щ,=к:-сч+чс (¦„-«,),
Полагая ? = 2, ? = 2, е1==еа = 1, е3 = 3, будем иметь:
П = (4-п — 16т, + 2-f -}- 4тл -f 4ті«+16) Q — 8-пН.
Вторым элементом высшего порядка, который мы рассмотрим»
будет величина, характеризующая степень близости плоскостей | &L
и
QD у совпадающих между собой при Д?—>0.
Обозначим наименьший угол между этими плоскостями через jJ;
a priori ясно, что J5 будет бесконечно малой величиной по
сравнению с Д?.
Отношение р к Д/2 назовем мерой второго порядка и
обозначим через М:
М= lim
р
д*^-о
Д/2 *
Очевидно, что, вычислив М, легко будет для каждого проме-
, коль
жутка Д? построить приближенное положение плоскости QL
скоро известно будет положение вихря и плоскости
QD
Принимая во внимание, что угол между плоскостями
QL
я
QD совпадает с углом между направлениями [Q?l и [QD],
найдем:
l[b,[Q,Dl]
smp— |b!-|[0-D]
Ш

откуда, помня, что:
B^IQ.D], Ba = y[Q,Dj, D8 = ?>-^-?
без труда получим формулу, выражающую меру М:
и 1 I (°2> 1М)±?. - ^» lcos(Z?„tQZ>])| ,_
М-2 iIfl,D]|- — 2Z>- sin(Cz)) * (60)
Из этой формулы, вспоминая выражение для изгиба вихря 8*,
найдем:
о'' • М = -^- | cos (D~[QD]) I. (61)
Пример 22. Рассмотрим движение, указанное в предыдущем
примере, когда скорости суть линейные функции координат, а
сдвиги olf а,, с3 отсутствуют.
Дая компонентов вектора D2 не трудно получить следующие
выражения:
Atf = (^ + ea)l-
А, = & + Ф'--
Вектор [Й, D] будет иметь следующие составляющие:
[Q,D], = «(ei-4),
[Q,D], = {4(^—в1);
•с помощью этих формул найдем, положив ? = $0> C = C0, V-—^ —-о»
.где $0, С0, s0, s3 — постоянные величины:
^ — -,г,
2
2
iTj— T(S
^ 2
гр.ез—еі,
2 '
* ?1—?о
— ?-п —± z- .
м-1
(^o+*nJ)(s3— «о) і
Полагая ?і = "4о СПо—постоянная величина), получим:
M=Q_yf+lo* + cS
4 4
124

§ 9. Напряжение вихревых трубок.
1. Вторая теорема Гельмгольтца в классической гидродинамике
устанавливает определенную закономерность изменения величины
зихря с течением времени. Две точки зрения могут быть приняты
во внимание при изучении этого изменения величины вихря с
течением времени* Первая точка зрения, которой придерживается
Гельмгольтц в своем классическом вышецитированном мемуаре,
предполагает наличность свойства сохраняемости вихревых линий,
иначе говоря, в нашей терминологии, предполагает движение гельм-
гольтцевым; с этой точки зрения вторая теорема Гельмгольтца
является лишь дополнением первой; метод доказательства второй
теоремы Гельмгольтца, принятый при ее изложении с только-что
развитой точки зрения, предполагает наличность свойства
сохраняемости вихревых линий, а потому первая точка зрения [лишает
вторую теорему Гельмгольтца самостоятельного значения.
Вторая точка зрения, развитая впервые в классической
гидромеханике W- Thomson'oM *) и примененная к самому общему случаю
движения жидкости V. Bjerknes'oM, рассматривает вторую теорему
Гельмгольтца как имеющую самостоятельное значение и
независимую от того обстоятельства, имеет ли место первая теорема
Гельмгольтца или нет.
В классической гидродинамике обе эти точки зрения
равноправны и различие между ними чисто методологическое, ибо все
движения в классической гидродинамике гельмгольтцевы и
следовательно первая теорема Гельмгольтца всегда имеет место.
Наоборот, в гидромеханике общей, в которой движения не
являются гельмгольтцевыми, в которой может иметь место приток
энергии, различие между двумя упомянутыми точками зрения
играет роль фундаментальную.
Первая точка зрения в общей* гидромеханике дает возможность
изучать лишь изменения величины вихря гельмгольтцевых
движений; в других движениях она не дает никаких критериев
относительно закона изменения величины вихря. Вторая точка зрения,
наоборот, в общей гидродинамике дает возможность изучать
изменение величины вихря во всяком движении жидкости. Вследствие
этого вторая точка зрения в общей гидромеханике является более
полезной, чем точка зрения первая. Это обстоятельство в истории
развития общей гидромеханики было учтено тем, что первые ее
основы были установлены путем обобщения метода доказательства
второй теоремы Гельмгольтца при помощи идеи Thoms^n'a о
циркуляции скорости, как это было сделано в работах Bjerknes'a и
других.
Признавая вполне преимущественное значение второй точки
зрения в доказательствах второй теоремы Гельмгольтца для общей
гидромеханики, не следует, однако, по нашему мнению совершенно
отбрасывать первую, классическую точку зрения на вторую теорему
*) W. Thomson, On Vortex Motion, Edinb. Transact, t. XXV, I860.
125

Гельмгольтца. Как мы увидим из дальнейшего, применение
классического метода доказательства второй теоремы Гельмгольтца
оказывается очень полезным при изучении гельмгольтцевых движений
и для их классификации.
Перед изложением идей, положенных в основу второй теоремы
Гельмгольтца, полезно будет сделать следующее замечание:
Наиболее детальное знание движения мы получаем, когда имеется
возможность судить об изменении кинематических элементов
движения или в данной точке пространства или для данной частицы
жидкости; изучая изменение величины вихря (или интенсивности,
связанной с величиной вихря), мы -должны установить, каким
образом для данной точки пространства или данной частицы жидкости
меняется величина вихря в зависимости или от кинематических
элементов или от динамических элементов (давления, плотности и
сил) данного движения. Bjerknes в своей вышеупомянутой работе,
устанавливая теорему об изменении циркуляции скорости по
жидкому контуру, приводит в связь это изменение с динамическими
элементами и указывает очень изящное
графическое решение этого вопроса; Bjerknes
однако не устанавливает связи изменения
величины вихря с кинематическими элементами;
мы считаем полезным * обратить внимание на
эту сторону дела, тем более, что в
выражение закона изменения величины вихря
входит тот же вектор Н, который был нами
введен при изучении законов изменения вихре-
( ( вых линий.
\ \ \ \ После этих предварительных замечаний
перейдем к установлению основных понятий
и предложений, необходимых для изучения
Черт, 18. законов изменения вихрей в общем движении
жидкости.
2. Рассмотрим некоторый жидкий контур К; пусть к моменту t
¦он будет обозначен нами символом Kt. Через каждую точку
контура -Kt'"') проведем вихревую линию, отвечающую моменту t;
образованная всеми этими вихревыми линиями трубка (черт. 18) будет
называться мгновенной вихревой трубкой, отвечающей моменту
і; иногда, для краткости, мы будем эту трубку называть просто
вихревой трубкой к моменту і.
Совокупность частиц жидкости, занимающих точки мгновенной
вихревой трубки (так сказать заполняющих мгновенную вихревую
трубку), назовем жидкой вихревой трубкой к моменту L
Когда жидкость движется, то жидкая вихревая трубка к
моменту U придя в движение, будет оставаться жидкой трубкой, но»
вообще говоря, к некоторому последующему моменту f перестанет
*) Будем в настоящем пункте предполагать, что черев все точки контура Kf
к моменту t проходят вполне определенные вихревые линии. Значит во всех
точках контура вихрь будет отличен от нуля.
\\
126

быть вихревой трубкой. Однако в гельмгольтцевом движении, где
вихревые линии обладают свойством сохраняемости, жидкая трубка,
будучи мгновенной вихревой трубкой к моменту і, перейдет к
моменту f также в мгновенную вихревую трубку, этому моменту
соответствующую.
Назовем сечением мгновенной вихревой трубки кусок некотороГ
поверхности 5, вырезываемый данной мгновенной вихревой трубкой;
это сечение для момента t можно обозначить через Sr Контур,
ограничивающий сечение, назовем контуром сечения.
Выберем некоторое направление обхода контура сечения за
положительное и назовем положительным направлением нормали
к сечению в данной точке то направление нормали к сечению
в данной точке, относительно которого положительный обход
контура сечения совершается по часовой стрелке *).
Напряжением I мгновенной вихревой трубки называется
следующее выражение;
1= f<±ndS> (62)
St
где 2П есть проекция вектора вихря на положительное
направление нормали в некоторой точке сечения мгновенной вихоевой
трубки, dS — элемент поверхности этого сечения,
отвечающий указанной точке, а интеграл
распространен на все сечение мгновенной вихревой трубки.
Не трудно видеть, что напряжение данной
мгновенной вихревой трубки не зависит совершенно от того,
какое сечение трубки мы взяли; таким образом
напряжение вихревой трубки есть величина, вполне для
данной мгновенной трубки определенная.
Теорема 12. Напряжение вихревой трубки не
зависит от того, какое сечение трубки мы
рассматриваем.
Чтобы доказать эту теорему, проведем в данной Черт. 19.
вихревой трубке два сечения: St и S't (черт. 19) и
образуем замкнутую поверхность из обоих этих сечений и из
поверхности трубки, заключенной между контурами наших сечений.
Обозначая через N направление внешней нормали к образованной
таким образом поверхности V, будем иметь на основании формулы
Гаусса:
.' *j
IS) (V
ибо div 12 = 0. На поверхности вихревой трубки 2д- = 0, а на
сечениях St и Sf- ?# = — ^п, причем, если для одного сечения будем
*) Напомним, что нами принята французская система координат.
127

иметь знак -j-, то для другого будет знак —¦ ; таким
образом из предыдущей формулы получим:
s't
что и доказывает нашу теорему.
Доказанную только-что теорему иногда относят к той же
категории, как и две основные теоремы Гельмгольтца; это однако
едва ли рационально, так как теорема 12 выражает свойство любого
вихря, а не только вихря скорости, тогда как остальные две
теоремы Гельмгольтца относятся лишь к вихрю скорости и имеют
глубокий динамический смысл. Мы привели здесь доказательство
теоремы 12, имеющее совершенно обычную форму, главным
образом в видах полноты изложения.
Таким образом на основании теоремы 12 мы можем выбирать
сечения мгновенной вихр'евой трубки произвольным образом*,
руководясь наибольшей простотой вычислений.
В дальнейшем нам важен будет определенный выбор так
называемых нормальных сечений. Вихревую линию, идущую внутри
мгновенной вихревой трубки, назовем осью этой трубки; ясное
дело, что выбор таких осей можно сделать бесчисленным
множеством способов. Сечение, ортогональное оси трубки, будем
называть нормальным сечением трубки; в связи с известной
произвольностью выбора оси трубки, и нормальное сечение обладает известной
степенью произвольности.
Перейдем теперь к установлению понятия напряжения вихря.
Пусть к моменту t через данную точку пространства проходит
некоторая вихревая линия; сделаем эту вихревую линию осью
мгновенной вихревой трубки бесконечно малого сечения; тогда
напряжение этой вихревой трубки и будет называться напряжением
вихря, проходящего через данную точку к моменту t.
Это напряжение будет бесконечно малой величиной; в оценке
его изменений придется сравнивать изменение напряжения с какой-
либо другой бесконечно какой величиной, большей частью с самим
напряжением.
Не трудно, вычисляя по формуле (62) напряжение бесконечно
малой вихревой трубки и пользуясь нормальными сечениями,
получить следующее равенство:
Q = lim • — *), (63)
сг->0 °
где /—напряжение бесконечно малой вихревой трубки с
нормальным сечением площади о. Из этой формулы получаем весьма
важную для практических применений приближенную формулу,
связывающую напряжение вихря с величиной вихря и площадью нормаль-
*) При этом положительный обход контура выбирается так, чтобы
положительная нормаль к g имела направление близкое к ".вправлению вектора Q.
128

ного сечения соответствующей бесконечно малой вихревой трубки:
/ = Qa. (64)
3. Вместо напряжения вихревой трубки, W- Thomson, как
известно, ввел понятие циркуляции скорости по контуру, дающее
возможность обобщить понятие напряжения мгновенных вихревых
трубок и на тот случай, когда на контуре имеются точки или
области точек, в которых отсутствует вихрь скорости.
Циркуляцией вектора А по контуру К мы назовем криволинейный
интеграл:
Ck{X)= f Axdx + Aydg-Azch= fA„ds,
к к
взятый по положительному направлению обхода контура К.
Здесь величина А8 есть проекция вектора А на направление
касательной в некоторой точке к контуру К, совпадающее с
положительным направлением обхода контура, a ds обозначает элемент
дуги контура К в этой же точке.
Иногда, ради краткости, мы будем при обозначении циркуляции
опускать индекс, указывающий контур, или аргумент, указывающий
вектор, циркуляция которого берется.
Непосредственно из теоремы Стокса [см. формулу (70)] следует,
что напряжение вихревой трубки равно циркуляции скорости по
замкнутому контуру, лежащему на боковой поверхности этой
трубки и охватывающему трубку:
/ = C4(V).
Не трудно также выяснить, что циркуляция скорости по любому
контуру есть сумма напряжений всех вихревых трубок, проходящих
внутри контура и обладающих свойством заключать в себе все
вихревые линии, проходящие внутри контура.
Напряжение вихря представляет собой очевидно циркуляцию
скорости по бесконечно малому контуру нормального сечения
соответственной бесконечно малой вихревой трубки.
С помощью понятия о циркуляции скорости легко установить
закон изменения величины вихря; для этого необходимо только
изучить, каким образом изменяется с течением времени циркуляция
по жидкому контуру; тогда не трудно будет усмотреть, как меняется
напряжение вихря.
Перед тем как перейти к установлению закона изменения
циркуляции по данному жидкому контуру, сделаем одно замечание.
Так как мгновенная вихревая трубка существует только для
момента t, то нет никакого смысла говорить об изменении
напряжения мгновенной вихревой трубки с течением времени; при
отсутствии свойства сохраняемости вихревых линий, мгновенные
вихревые трубки немедленно разрушаются, так что напряжение их
перестает существовать. Представляет однако большие упрощения
говорить об изменении напряжения вихря, понимая под этим
изменение циркуляции по бесконечно малому жидкому контуру, окру-
9 Зак. 2420. — А'. А. Фридман, Опыт гидромеханики

жгіющему вихрь в данной тбчке. В этом смысле мы и будем в
дальнейшем говорить об изменении с течением времени напряжения
вихря.
Изменение циркуляции скорости по жидкому контуру
определяется следующей теоремой, принадлежащей W. Thomson'y, которую
мы и будем называть в дальнейшем теоремой Thomson'a:
Теорема 13. Индивидуальная по времени производная цир*
куляции скорости по некоторому жидкому контуру есть цирку-
ляция* ускорения частиц этого контура по тому же самому
контуру.
^(V)=cj^v\
dt * \ dt .
Если К! есть контур, в который перешел жидкий контур К
через промежуток времени Д?, и V есть скорость, в которую
перешла скорость V данной жидкой частицы через промежуток
времени Д/, то по определению индивидуальной производной будем
иметь:
dCk(V) Ckr{V')-Ck{V)
—-J*— = nm г; •
at д«-»о At
В целях полноты изложения мы приведем доказательство
теоремы Thomson'a. Разобьем контур К на п частей, n-f-1 точками
Рі(і=0, 1, 2,-. .,л), причем Рп совпадет с Р0; пусть частица,
занимавшая положение Рі к моменту t, имела координаты лг^, уь zi
к этому моменту и координаты х\, у\, z\ к моменту і-{-&і; пусть
скорость частицы в точке Рі к моменту t имела компонентами по
осям координат величины иіУ vi9 wiy а к моменту t-{-&t скорость
той же частицы имела своими компонентами щ, vrif &)'4; тогда,
принимая во внимание общеизвестные ограничения относительно
расположения точек Рі на контуре, будем иметь:
п—г
Ск (V) г= ііш У {щ{хі+х — *.) -f v. (уі+1—^) + «>< (*<+1 — К),
CV{Y) = lim 2 {«;«hl-^)T- <(^+1-^) + ^«+1-^)!.
Полагая, что
dut
' ' 9
и принимая во внимание аналогичные формулы для других
координат и компонентов скорости, будем иметь:
130

Г dv-
^
"л1 (z<+i— ^+^(ю*+1—ет<)
A*f...t
д*+...,
причем ненаписанные члены будут порядка Af2 или высшего
относительно промежутка АЛ
Простое преобразование дает нам:
п—1
4=0
4=0
4=0
2 2
й« —"о
2 ^2
П—1
—у 2 (°<+і—u*)t;
і=0
так как (по свойству замкнутости контура) і:л = Щ, а
п-1
ііш ^ (и,+1 —а,)а = 0,
і'О
и*°° ;=о
Л—1
lim У а<(и<+1 — иг) = 0;
і=0
то же самое равенство будет иметь место, если вместо а подста"-
вить v или w.
Пользуясь всем вышесказанным, найдем следующее равенство:
п— 1
lim"] 2 {"iW+i — ^D-b^O/i+i—У0-Ью<(«і^а — *0>
{
I
n—l
A*
2 {u» (*i+1 — *і) Ч- wi (Уч-і —Л) "f «»< (zi+1 — 2i)} ^ =
I
<- )
Д*
' П—1
('"I
a^
*<) + "л" (Л+i — Sd-
dwj
-J™, 2 t AL<*<+i л*' > Л w+1_ *" l Л ч^+і
J
(Z4*4-l — Zi) И"7!»
4=0
где ij — величина такая, что lim v\ = 0. Переходя к пределу при
Д?>0
А/->0 и замечая, что первый член в только-что написанной
формуле от А/ не зависит, докажем теорему Thomson'a.
С помощью теоремы Thomson'a Bjerknes получил возможность
связать изменение циркуляции с динамическими элементами; об этом
будет сказано во второй части настоящей работы, сейчас же мы
9*
131

приведем, с помощью теоремы Thomson'a, в связь изменение
циркуляции с кинематическими элементами.
Обозначая, для краткости, циркуляцию скорости по контуру К
через С на основании теоремы Стокса в связи с теоремой
Thomson'а, получим следующее равенство:
dC ГI du j , dv r . dzv , \ Г , dV /e
~it = J (~dt dxt- w ¦& + ж dz) = J CUil>- л" ^
A' *
где iV—положительное направление нормалт; к поверхности *S,
опирающейся на контур К.
Формула (63) дает нам:
curl 4г" = helm curl V = Helm Q -!- 9 div V = H +- 2 div V,
at
откуда
-^= f(Hy-$-2„dW\)dS, (65)
где Лл- обозначает, как мы условились, проекцию вектора А на
положительное направление нормали N-
Во второй части нашей работы будет показано, что вектор
—у— при отсутствии действующих сил обладает свойством нсза-
dt
кручиваемости, иначе говоря — этот вектор ортогонален своему
вихрю; подобное свойство, как выяснил в своей магистерской
диссертации проф. Н. Е. Жуковский"*), обусловливает возможность
существования поверхности, ортогональной векторным линиям
вектора—г:-. г-сли бы было возможно эту поверхность взять за
/dV
curJiV —j—dS Обра-
тился бы в нуль, и следовательно имело бы место равенство —т—=0.
Это, как будет выяснено во второй части нашей работы,
чрезвычайно важное свойство движения идеальной жидкости **)
обусловливает невозможность возникновения вихря» перпендикулярного
указанным ортогональным поверхностям, каковые поверхности
являются изобарическими поверхностями. Этим свойством
объясняется невозможность (правильнее — малое напряжение)
вертикальных вихрей в атмосфере. Следует однако заметить, что наличие
указанной поверхности ни в коем случае не обусловливает
отсутствия изменений циркуляции, так как далеко не для всякого
контура можно подыскать опирающуюся на него поверхность, ортого-
d\f
нальную векторным линиям вектора
dt
••¦) Жуковский, Кинематика жидкого тела. Сочинения, т. I, стр. 76—79.
**) Для вязкой жидкости свойство это не имеет места.
132

4. Чтобы ссязать изменение циркуляции с изменением
напряжения ьихря, введеы особую величину, которую мы назовем
вихревой мерой. Пусть напряжение вихря к моменту t в некоторой
точке будет равно /; / будет циркуляцией скорости по бесконечно
малому жидкому контуру К, окружающему наш вихрь*). К моменту
/-{-А/ циркуляция по этому контуру изменится и получит
величину /'. Назовем двойной предел отношения
/' —/
когда &і стремится к кулю, а бесконечно малый контур К
стремится к изучаемой нами точке, вихревой мерой в данной точке
ц и данному моменту L
Обозначая вихревую меру через jt будем иметь:
/— Нт ііік —(г—, (бб)
где символ ііт употреблен в том смысле, что бесконечно малый
К + 0
контур К стремится совпасть с точкой, для которой
рассматривается зихревая мера.
Докажем следующую формулу, вполне определяющую вихревую
меру:
.^HcosIHM +d.vVj (67)
По определению индивидуальной производной имеем:
" Г — / dl
но по теоремй Thomson'a:
a 3
где интегралы распространены на поверхность, опирающуюся на
контур К. Применяя к предыдущему интегралу теорему о среднем,
найдем:
где HN, и 2ду, — значения нормальных составляющих векторов Н
и 2 в некоторой средней точке поверхности о, div V—значение
div V в этой точке, а о есть площадь нашей поверхности.
Из предыдущей формулы можно найти следующее соотношение
*) За К берем непременно контур нормального сечения вихревой трубки.
133

при условии, что поверхность о ортогональна вихрю Q в данной
точке:
1 dl HN, + <faVQN,
Qa dt ^ *
отсюда, переходя к пределу, когда контур К обращается в данную
точку, и замечая, что lim ~^~=1 [см. выше формулу (63)], а на-
правление N' в пределе совпадает с направлением ?, без труда
докажем формулу (67).
Из формулы (67), помня, что вектор Н + 2 div V обозначается
нами как helm 2, и вводя для helm Q сокращенное обозначение Ь:
h = helm Q,
без труда получим следующее соотношение:
._ Л cos (О) _(Ь, Q) /68у
' — g ~ а* • v '
Подобно тому, как мы, исходя из идеи сохраняемости вихревых
линий, установили особый род движений жидкости, так называемые
гелъмголътцевы движения, подобно этому, рассматривая вихревую
меру, мы должны выделить те движения, в которых вихревая мера
равна нулю и следовательно имеет место закон сохранения
напряжения вихря; такие движения мы будем называть тпомсонов-
скими движениями, имея в виду ту фундаментальную роль, которую
идея циркуляции, введенная W. Thomson'oM, играет при изучении
напряжения вихря.
Не трудно доказать следующую теорему:
Теорема 14. Для тою, чтобы движение было томсоновским,
необходимо и достаточно? чтобы helm вихря был перпендикулярен
вихрю:
(helm curl V, curl V) = 0 (69)
или
(h,fi) = 0.
Доказательство этой теоремы непосредственно вытекает из
предыдущей формулы (68). Ниже мы увидим, что когда движение
одновременно является томсоновским и гельмгольтцевым, то
helm curl V = 0; именно этот случай рассматривается в
классической гидромеханике и служит, в виде двух основных теорем
Гельмгольтца, базой для классической теории вихрей.
Само собой разумеется, что могут существовать гельмгольтцевы
движения, не принадлежащие к классу томсоновских; это
обстоятельство будет выяснено ниже. Точно так же могут иметь место
томсоновские движения, отличные от гельмгольтцевых, примеры
чему будут приведены в настоящем пункте.
Прежде чем, однако? перейти к примерам, долженствующим
разъяснить понятие о вихревой мере и о томсоновских движениях
134

сделаем одно замечание по поводу вычисления —у интенсивности?
характеризующей изменение величины вихря через посредство
вихревой меры. Замечая, что приближенно /=2з, будем иметь:
.__ 1 dQ 1 cfr-
J Q it + о dt '
откуда
JL-**-=• L Ji.
& dt J a dt *
Эта формула показывает, что на относительное изменение
величины вихря влияют два обстоятельства: величина вихревой меры и
относительное изменение бесконечно малой жидкой площадки,
расположенной около точки, где изучается изменение вихря.
Предполагая А* очень малым, получим следующую приближенную формулу:
' Q' _ Q с ¦ _ „
J
Q
=/д, (70)
где 2' и з' суть значения 2 и а через промежуток времени, равный А*;
по только-что приведенной формуле можно приближенно вычислять
изменение величины вихря. Формула (70) имеет большое
практическое значение в виду того, что / очень просто определяется по
динамическим элементам.
Пример 23. Рассмотрим сначала движение, в котором скорости
суть линейные функции координат. Простые вычисления дают
в этом случае:
Л =T]-f flf2Y)-
2
^ + ^
7, _r } - Г аіП + ^
К = ^ + а?-
2
где
а остальные обозначения прежние.
Не трудно видеть, что вихревая мера определяется формулой:
._ 66 + VI + СС + а^ + «2ті2 + «в?» — У* — °8« — qsbj
Для движения, аналогичного вращению твердого тела» будем
иметь:
Томсоновское движение характеризуется здесь постоянным по
135

вихрем; например движение, в которбм а = & = с = ?1 =
= е2 = е3 = а2 = ал = о8 = О, $ = a cos ®t, tj = а sin atf, ? = О, oj —
постоянная, будет движением томсоновским:
a sin to/ a cos ®t а , , . ,ч
ц_——Zj v = _—Zj w~~o G/cos°*—A'sina>0;
это есть движение с периодически меняющимися угловыми
скоростями по осям х is. у.
Для движения без сдвигов будем иметь:
Рассматривая частный случай, когда «х = х2 — а3 = а, получим
2 Л
. 1 dQ
= а.
откуда между прочим найдем
z dt
Не трудно получить движение без сдвигов с постоянными
удлинениями и постоянной вихревой мерой; мы ограничим^ случаем
томсоновского движения (/ = 0); тогда:
при постоянном я. Легко видеть, что движение, в котором:
? = ae~a cos<о/, т\ = ае~а sin <о/, С = 0 (<о постоянное),
зсть томсоновское движение; полагая
a
Sj = е2 = г3 = — ,
найдем, что скорости в этом движении будут:
a i a -at . a a -at ,
и = -^- х -р — ze sm< v=~ у — ze cos <or,
w = -y z-j-— e~a (ycosvf— Jtrsinotf).
Непосредственное вычисление показывает, что рассматриваемое
нами движение не есть гельмгольтцево; таким образом
устанавливается возможность существования томсоновского движения, не
принадлежащего к классу гельмгольтцевых движений.
Пример 24. Рассмотрим случай, когда щ v суть функции t, z,
а гу —0. В этом случае:
Е — — dv *• — 5и '—п
л*в-а-' А*в-5Г' А-=0'
136

откуда
*¦?-+
Y,
dt l ' dt 1 dQ
Полагая /=-y <p'(0> будем иметь
i-e"(f)
где v(z), f(?)— произвольные функции своих аргументов. Отсюда
0* = ф(*)е*№ ,
или, обозначая е*и через <?(*), найдем:
(?)'+(?Г-*«<*
откуда по заданным v(t} z), 'К2)» ?(') определим и; при этом не
трудно видеть, что
J 2 W
°ассмотрии; случай затухающего вихря:
Q2 = (a -f ?2)2 е~»¦' sin2 wtt
?(/) = e-2Usin2^, u(z) = (a-f fe)»,
у = — X -J- to ctg &t,
где X, <u, a, b—постоянные величины.
Легко видеть, чіО, вводя произвольную функцию Ф (t9 z)s имеем:
~z— = (a4-bz)e~"' sin ®i sin Ф (/, z), -т~-==(a+6z)e~ sino>/cosO(/,z)
O'z Cz
откуда без труда можно определить а и v.
Пример 25. Весьма простые соотношения получаются для
случая, когда две составляющие скорости равны нулю. Пусть
ц = 0, а —0; тогда
А. = 0.
137

откуда
*Tt^'fi dt dw
._ 1 dQ .dw 1 dQ__ . dw
J~lT~d7^~~te' ~Q dt ~~J ~Jz~m
Таким образом быстрое изменение скорости w с координатой z
уменьшает при данной вихревой мере величину относительного
изменения вихря.
Рассмотрим случай томсоновского движения. Вопрос об
определении w при условии, что движение будет томсоновским, сведется
к интегрированию следующих двух уравнений в частных произ*
водных с неизвестными функциями w и 2:
1 dQ w dQ . дго
Q dt "*" Q dz ^~ dz '
Положим, что w (а значит и 2) не зависит от t (движение
стационарное). Написанные выше уравнения тогда дают:
%™=^С(х,у),
где ty — vr, а С—произвольная функция х, у. Интегрирование
этого уравнения может быть выполнено, если положим
<5'1> -, > ч . d'l ~, v . _
~~ = C(x,g) cos Ф, -^ = С(х, у) sin Ф,
где Ф — неизвестная функция х, у, z, могущая быть определенной
из условия интегрируемости предыдущих равенств:
созФ^ + 3іпФ^ + зіпФ^-созФ^=0.
дх * dy ' dx dy
Полагая С независящим от х и у, будем иметь, что Ф
определится как решение уравнения:
Р(Ф, л: sin Ф — у cos Ф, z) = О,
где /'—произвольная функция своих аргументов.
Подбором этой функции можно найти следующее частное
решение нашей задачи:
* = с l/[*-«(z)p+Q/-pW2,
138

Ус
2f[jr-a(*)p+[y-p(z)]*
где с—произвольная постоянная, a(z), P(z)—произвольные функции г.
Пример 26. Рассмотрим еще случай, когда два компонента
вихрей обращаются в нуль: ? = 0, ?] = 0; тогда * не зависит от zy
и и v определяются формулами
dw ди dzo dv r dv ди
дх 6z 9 ду dz * " ~ дх ~ду '
простое вычисление дает нам:
ди
h=-
А„ = —С
дх9
dv
, dt , д? . Л . т ( ди . dv \
Отсюда для вихревой меры найдем следующее выражение:
задавая / и С, можно из выражения для С и из последней формулы,.
определяющей /, найти компоненты и и v скорости, а по этим
компонентам определить величину w. Рассмотрим случай томсонов-
ского движения с постоянным вихрем, ? = ?0:
ди . ду
Q°~ ду^дх'
и- дх^ ду'
Последнее равенство дает I отметим, чро рассматриваемый случай
J- \т ди , dv ,
не есть движение несжимаемой жидкости, ибо div V = -~^~ -+- -^— -+--
. dw дго \
+ ~dz~~~dz):
откуда г _ ^Ф і ^Ф
1Э*

Полагая ?=:—- (л:-- -j-;;-)-}- 'if найдем для ? уравнение Лапласа*
иначе говоря—сведем определение <р к известным процессам.
4- Как мы уже говорили выше, в случае, когда первая теорема
Гельмгольтца имеет место, т. е. когда вихревые линии обладают
свойством сохраняемости, является полная возможность
воспользоваться . для решения вопроса об изменении напряжения вихревой
трубки классическим приемом, изложенным впервые Гельмгольтцем
в его, много раз уже цитированной, работе. Это г классический
метод, названный нами выше первой точкой зрения, применим
лишь, как об этом было уже сказано, а движении гельмгольтцевом;
но зато в применении к этим движениям указанный метод даег
несравненно более детальное знание изменения напряжения
вихревых трубок и позволяет установить признак, пользуясь которым
можно классифицировать гельмгольтцевы движения.
Прежде чем перейти к изложению классического метода
изучения изменений напряжения вихревой трубки, сделаем одно
замечание. В предыдущих параграфах (до § 9) мы не пользовались
идеей циркуляции скорости; между тем в обычной гидродинамике
изучение циркуляции скорости по контуру, расположенному на
| боковой поверхности вихревой трубки, дает
) / чрезвычайно простое и изящное доказательство
первой основной теоремы Гельмгольтца. Этот
изящный прием доказательства свойства
сохраняемости вихревых линий становится, однако,
совершенно неприменимым в тех случаях,
когда вихревая трубка разрушается и когда
приходится изучать законы, по которым это
разрушение происходит; жидкая поверхность мгно-"
венной вихревой трубки ь следующий момент
времени перестает быть поверхностью вихревой
трубки, и 'изменение циркуляции скорости по
контуру, расположенному на поверхности
мгновенной вихревой трубки, показывает нам лишь то, что
в общем случае сохраняемость вихревых линий
не будет иметь места, но не отвечает нам на вопрос, каким
образом будет разрушаться вихревая трубка. По этим причинам
мы в предыдущих параграфах не пользовалась понятием
циркуляции скорости.
Метод Гельмгольтца изучения изменения напряхіЭвкия вихря
заключается в том, что из бесконечно тонкой нихревой трубки
вырезывается двумя сечениями, нормальными к ее оси, кусок и
рассматривается масса жидкости, заключенная в этом куске; через
промежуток времени А/ бесконечно тонкая вихревая трубка перейдет
в бесконечно тонкую также вихревую трубку, а тогда обычное
условие постоянства массы жидкости, заключенной в данном куске
трубки (в существе дела условие неразрывности), дает нам,
соотношение для определения изменения напряжения вихревой трубки,
Черт. 20.
140

что приведет нас к формуле, аналогичной выражению (67) для
вихревой меры.
Пусть (черт. 20) к моменту t через точку М (х, %j} z) жидкости
проходит вихревая линия Q; п? этой вихревой линии на бесконечно
малом расстоянии As наметим точку Мх (хи ух> гг):
*і = х 4- лс, у, = д -\- лт1( г, =» z -f ^
ГдеХ —-^. К моменту t-\-&t частица, занимавшая положение М
к моменту ty перейдет в точку № (х\ у', z), вихревая линия 2
перейдет в вихревую линию 2 , причем по свойству сохраняемости
вихревых линий, имеющему место для рассматриваемых нами
гельмгольтцевых движений, частица жидкости, занимавшая к
моменту t положение Мі9 перейдет к моменту t-\-&t в положение
Мх С*і> В\* zi)> расположенное по вихревой линии Q\ Согласно
сказанному в § 2 гл. 1? координаты точек М и М1 определятся
следующими формулами:
х = х J - и Д/ -и *' Л Л х[ = х +1 (; -f- Du М -f а" ДГ ),
и' = у + г; Л/ -f /ЛГ, */ = ,/ 4- л ( ч + Du -V + Э'ДГ),
г =r z 4- «,А/ -f V д'\ ^ = * "Г Х (- "h DwM --,- "" ДГ);
здесь а7, р', т', а", J3", у" — конечные величины, зависимость кото*
рых от & и ДЛ может быть без труда, определена; но она для нас
не существенна.
Найдем, во что обратится величина Д$, расстояние точек М и Мх
к моменту і\~Ы\ она к этому моменту будет расстоянием точек
М\ Мл обозначим это расстояние через Д 5. Рассматриваемое нами
движение есть движение гельмголътцево, поэтому имеют места
соотношения:
Ъ п *» п Л л
Tt~Da _7T-Dv _ ~3t'D7V
ё _ _ -_-__-
Обозначая через п общую величину этих равных между собой,
отношений, будем иметь:
lDu = ft+n\, Dv = ¦&¦ + ** Dvj^-^-Vnl:
определяя величину v под условием
rflnv
rfTen'
141

получим:
Пусть v' будет значение v для момента t -j- А/» тогда из предыдущих
формул легко найдем:
A's = ^-/Q'~i-aA**, (*)
где a — некоторая конечная величина.
Через точку М проведем нормальное сечение площади з
вихревой трубки, имеющей осью вихревую линию, проходящую через М;
через точку М1 проведем также нормальное сечение этой вихревой
трубки. Получим кусок (~) вихревой трубки, объем которого будет
равен ъ*.
х = As • a
с точностью до бесконечно малых высшего порядка.
Полученный кусок вихревой трубки к моменту ^ —J—А^ "перейдет
в кусок (*') новой вихревой трубки (напомним, что мы
рассматриваем гельмгольтцево движение); объем ^ этого куска выразится
(до бесконечно малых высших порядков) соотношением:
г! = A's . с',
где о' — площадь, в которую к моменту іА^Ы. перейдет нормальное
сечение в точке М нашей вихревой трубки.
Обозначим через р плотность частицы жидкости в точке М
к моменту t и через р' плотность той же частицы к моменту 2-f-A?;
масса куска (") вихревой трубки, долженствующая по закону
сохранения массы оставаться неизменной, будет равна массе куска
(т') вихревой трубки к моменту t~\-&t\ поэтому
откуда
р • As ¦ о — р' ¦ A's • a';
пользуясь определением As и формулой (*) для A's и отбрасывая
бесконечно малые высших порядков, получим:
рШо = р' — v'2'a' + рАг5,
где р есть величина того же порядка малости, как и величина
объема т куска бесконечно тонкой вихревой трубки. Замечая,
что ?з есть интенсивность / бесконечно тонкой вихревой трубки,
142

а 2'з' — интенсивность той же вихревой трубки к моменту і-\-1і,
іудем иметь:
откуда, составляя выражение для , и переходя к пределу при
Лі-*0 и при з-»0, найдем следующее выражение для вихревой
меры /:
dt '
У
ибо lim yt есть величина конечная по условию, сказанному
выше о порядке малости р.
Помня, что, согласно уравнению неразрывности, имеет место
равенство:
сЛп? ,. л«
_^ = — divV*),
и замечая, что, при decl 2 = 0,
„ _ (Н, Q)
найдем . (Н,2) , ,. х , хт
J = -^о2"^ "Г dw V = — п -[- div V.
Эта формула в ее первой половине была уже нами выведена
в предыдущем пункте при более общих предположениях о характере
движения [см. формулу (67)]. Как следствия из этого равенства
получаются условия теоремы 14, чтобы движение было том-
соновским. Такое движение, принадлежащее одновременно и к классу
гельмгольтцевых движений и к классу томсоновских движений,
условимся называть главным гельмгольтцевым движением.
Главное гельмгольтцево движение обладает как свойством
сохраняемости вихревых линий (первая теорема Гельмгольтца), так
и свойством постоянства напряжения вихревой трубки (вторая
теорема Гельмгольтца). Условие, необходимое и достаточное для
того, чтобы движение было главным гельмгольтцевым,
устанавливается следующей теоремой:
Теорема 15, Для того, чтобы движение было главным
гельмгольтцевым движением, необходимо и достаточно) чтобы
вектор helm curl V обратился в нуль:
h = helm curl V = 0.
Покажем сначала необходимость этих условий. Всякое главное
гельмгольтцево движение есть гельмгольтцево движение, поэтому
[Н, Q] = 0
согласно теореме 1 bis.
*) Это равенство будет указано в следующей части*
143

Так как b = II-j-QciivV, то из предыдущего равенства следует:
[Ь, 0]=0.
С другой сто„отты главное гельмгольтцево движение есть
движение томсоновское; поэтому согласно теореме 14 будем иметь:
(h, fi) = 0;
это равенство и предыдущее показывают, что Ъ = 0.
Установим теперь достаточность условий теоремы. Если Ь = 0, то
H = -QdivV,
откуда
[Н, Q] = О,
а значит наше движение — гельмгольтцево; с другой стороны, при
h = 0 очевидно будет (h, Q) = 0, следовательно наше движение есть
движение томсоновское. Соединяя все сказанное вместе, найдем,
что наше движение есть главное гельмгольтцево движение, что и
докажет достаточность условий нашей теоремы.
Замечая, что
dV
Ь = helm Q — helm curl V = curl —r—,
at
из теоремы 15 получим следующее предложение, служащее базисом
классической гидродинамики:
Теорема 16. Для того, чтобы движение было главный
гельмголътцевым, необходимо и достаточно, чтобы вектор уско-
рения ~jr был потенциальным вектором.
Примеры на главное гельмгольтцево движение будут нами
приведены в следующем пункте, где главное гельмгольтцево
движение будет выделено нами как один из классов гельмгольтцевых
движений.
В конце концов каждое вихревое движение обычной
гидродинамики может служить примером главного гельмгольтцева движения;
мы выберем лишь такие примеры, которые являлись бы
естественным продолжением примеров на гельмгольтцевы движения,
приведенных нами в главе I настоящей части.
5. Кроме напряжения вихря J=Qo9 которое мы назовем теперь
истинным напряжением вихря, введем еще понятие об обобщен*
ном напряжении вихря ]{, определяемом равенством
J,=fJ=fQ°,
где/—некоторая функция времени и координат точки, в которой
рассматривается напряжение вихря. Чтобы охарактеризовать, что
обобщенное напряжение вихря зависит от выбора функции /, мы
будем величину Jf называть обобщенным напряжением вихря,
соответствующим функции /.
¦ Оказывается, что для любого гельмгольтцева движения можно
подобрать такую функцию / и такое обобщенное напряжение вихря,.
144

чтобы это обобщенное напряжение вихря не менялось при
изменении данной вихревой трубки во время движения.
В соответствии с понятием обобщенного напряжения вихря
можно было бы установить и понятие об обобщенной вихревой
мере; вспоминая, что контуром К мы обозначали замкнутый контур,
расположенный на поверхности бесконечно тонкой вихревой трубки
и стягивающий трубку, мы можем определить обобщенную
вихревую меру jf следующим образом:
/r = Iim lim IlZIl.
Введя указанные определения и обозначения, мы без труда
докажем следующее предложение:
Теорема 17. Для всякого гелъмгольтцева движения
существует такая функция /, что обобщенная вихревая мера, ей
соответствующая, равна нулю, иначе говоря — что обобщенное
напряжение вихря не меняется при движении жидкости*
Выбрав функцию v, удовлетворяющую условию:
d In v
причем наши обозначения совпадают с обозначениями предыдущего
пункта, найдем, что искомая функция / определяется равенством:
где р — плотность жидкости к моменту t и в данной точке. В самом
деле, согласно рассуждениям предыдущего пункта мы до бесконечно
малых высшего порядка имеем равенство:
т. е.
fJ=f'J',
где /'—значение / к моменту *-}-Д/ для частицы, которая к
моменту / была в точке M(x,y,z). Предыдущее равенство дает:
Jf=Jf>
это и доказывает теорему в ее второй части; первая ее часть
может быть выведена или непосредственно, или же из второй части
нашей теоремы.
Каждому гельмгольтцеву движению отвечает определенное
значение п; но одному и тому же гельмгольтцеву движению может
отвечать бесчисленное множество функций /. Чтобы установить
связь всех этих функций друг с другом, введем понятие об
инвариантной для данного движения функции, понятие, которое
окажется нам весьма полезным в следующем параграфе настоящей
главы.
Инвариантной для данного движения функцией мы назовем
такую функцию <р от времени t и координат точки, значение
которой остается одним и тем же для данной частицы жид-
10 Зак. 2420. — А. А. Фридман, Опыт гидромеханики
145

кости во всяком положении этой частицы, двигающейся задан*
ным образом.
Вспоминая обозначения и определения § 1» без труда
установим, что необходимые и достаточные условия
инвариантности функции о для данного движения заключаются в
выполнении равенства:
dt U*
Это равенство в раскрытой форме дает для определения
функции 'f следующее уравнение с частными производными первого
порядка:
до , <?? , <Ь до
dt ' дх і ду ' dz
где и, и, а/— заданные функции t, х9 у, z*
Во второй части мы увидим, что несжимаемость жидкости не
означает еще постоянства ее плотности и указывает лишь на то,
что плотность для такого движения жидкости есть инвариантная
функция; равным образом адиабатическое движение жидкости
(движение без получения энергии извне) еще не означает, что
давление есть функция плотности, как это обычно принимают, а
означает лишь, что энтропия является для этого движения инвариантной
функцией.
Не трудно видеть, что если для данного гельмгольтцева
движения существуют два обобщенных напряжения вихря,
удовлетворяющих теореме 17 и соответствующих функциям /і и /2, то
где © — инвариантная для данного движения функция. ч
В самом деле, по определению имеем:
откуда: _
v2 = vi e? = ?vlf /2 = cp/j,
гдеср = е" является также инвариантной функцией. Легко убедиться,
что Jf = <?/^; а так как <р не меняется при движении данной частицы,
то изменения ]и будут пропорциональны изменениям Jfy
величина же обобщенной вихревой меры и вовсе не изменится:
* •
Jf*=Jfim
Таким образом, хотя можно разными способами выбирать
функцию / так, чтобы обобщенное напряжение, ей соответствующее,
сохранялось при движении вихревой трубки, однако все эти
функции будут составлять определенный класс, отвечающий
определенному сорту движений, и какая-либо функция / этого класса
является лишь представительницей класса.
146

Отсюда ясно, что гельмгольтцевы движения можно разделить
на роды; каждый род будет отвечать некоторому значению л,
определяемому из уравнения
Helm (n, Q) = Н -f n Q = 0.
Каждому роду будет отвечать класс функций / таких, что
обобщенное напряжение вихря, отвечающее любой из функций этого
класса, будет постоянным при движении данного жидкого вихря.
Этот класс функций будет таков, что отношение любых двух
функций этого класса будет инвариантной функцией для данного
движения. Величину п назовем для краткости индексом рода,
а одну из функций / указанного выше класса назовем
представительницей рода.
Подобное разделение гельмгольтцевых движений на классы
является естественным обобщением и развитием идеи о главном
гельмгольтцевом движении. В самом деле, главное гельмгольтцево
движение обладает тем свойством, что ті = divV — =—, значит
at
главное гельмгольтцево движение принадлежит к определенному
роду, представительницей которого является функция /,
тождественно равная 1:
1 * 1
v = _t /s5B5Vp = _pel.
Этот род можно было бы назвать главным родом.
Известный интерес может представить случай, когда п = 0;
этому случаю отвечает условие:
HelmQ = H = 0.
С другой стороны, так как за v можно взять 1, то
представительницей этого рода гельмгольтцева движения можно взять функцию,
равную плотности жидкости:
v = l, /=vp = p;
этот род гельмгольтцева движения можно назвать нулевым родом.
В примерах, далее приводимых, мы разберем прежде всето ряд
движений, относящихся к числу главных гельмгольтцевых
движений, покажем возможность неглавных гельмгольтцевых движений,
затем укажем, каким образом определять род данного
гельмгольтцева движения, и наконец разберем пример гельмгольтцева
движения нулевого рода.
Пример 27. Рассмотрим движение жидкости, в котором скорости
линейно зависят от координат. Для этого движения не трудно
будет показать возможность гельмгольтцева движения, не
относящегося к классу главных гельмгольтцевых движений, а также
выяснить, каким образом определяется род движения (его индекс)
и как выбирается представительница рода.
10*
147

Сохраняя прежние обозначения, будем иметь следующие
выражения для векторов Н и h:
причем a1 = s2-f-es; cc2 = e3-f si; а^ = гх-^-е2.
Рассмотрим сначала крази-твердое движение (sj =su — ?$ = v1 =
= с2 = с;3—-0); условия того, чтобы такое движение было главным
гельмгольті^евым, выразятся равенствами:
? = 0, 4=0, С = 0,
иначе говоря — I, *], \ будут постоянными величинами. Таким образом
мы имеем в этом случае дело с движением, аналогичным вращению
твердого тела с постоянной угловой скоростью вокруг оси,
постоянно параллельной некоему неизменному направлению.
Из сказанного в § 2 главы I настоящей части следует, что
в рассматриваемом нами случае движение будет гельмгольтцевым,
если вихри определяются равенствами:
где Cq, *)о» ^о суть постоянные величины. Нетрудно видеть, что
в рассматриваемом случае индекс рода п, определяемый из
уравнения Н -4-/г2 = 0, будет выражаться следующим равенством:
rflnv ^ 1
отсюда v, удовлетворяющее условию —гг~ = п> будет равно —,
а значит представительница рода / будет определяться формулой:
і
Таким образом на этом простом примере ясно, что могут иметь
место гельмгольтцевы движения, не принадлежащие к классу
главных.
Рассмотрим движение без сдвигов и с постоянными
удлинениями. Условие, чтобы такое движение было главным
гельмгольтцевым, выразится следующими равенствами, определяющими
величину вихрей:
где $0, tqq, С0—произвольные постоянные величины.
148

Чтобы иллюстрировать, каким образом для только-что
разобранного движения напряжение вихря остается постоянным, рассмотрим
частный вид этого движения, когда Е0 == тю = 0, а также е2 = е3 = 0.
В этом случае скорости выразятся таким образом:
г> =
~2
причем для простоты в этих формулах положено а = Ь = с = 0.
Рассмотрим вихревую трубку, имеющую к моменту t вид
кругового цилиндра с осью, параллельной оси z, и с радиусом равным г;
площадь, а сечения этой вихревой трубки какой-либо плоскостью,
•параллельной плоскости хоу (черт. 21), будет площадью круга
радиуса г: а = ісг2; напряжение вихря для указанной вихревой
трубки будет (предполагая г достаточно малым)
Через промежуток времени А; круговое сечение нашего вихря
перейдет в первом приближении в эллипс с осями, параллельными
осям х и у, и с полу-
осями равными гі и г
(полуось параллельная оси х
равна ги а другая равна г);
из указанных выше формул
для скорости, а равно и из
непосредственного
определения удлинения ех получим
следующее выражение для гхг
Черт. 21.
n-rCl + e^);
Черт. 21а.
таким образом площадь </, в которую превратится площадь з
к моменту t-\-&t, будет выражена следующим образом:
</ = гг2 (1 + ех Д*).
Цользуясь указанными выше формулами для выражения вихря,
получим і.еличину С вихря к моменту t-\- &t: C = ?e~Cl , ибо а3=е1
в нашем случае; таким образом напряжение ]' вихря к этому
моменту будет:
/ = 0'С'=7СГ2(1+е1Д'К<2
+Л—¦¦•
-еіА* _-.^Г
ъг*
(1 + г1М)(і-гіМ +
ъгЧ
*) Для простоты предполагаем К, > 0.
149

Таким образом величина напряжения вихря при движении не
меняется с точностью до величин второго порядка.
То обстоятельство, что величина напряжения вихря остается
постоянной лишь до величины второго порядка малости, является
следствием нашего утверждения о переходе круга в эллипс, каковое
утверждение справедливо также только до величины второго
порлдка.
Если мы движение без сдвигов и с постоянными удлинениями
подчиним условию быть гельмгольтцевым, то, как это было
выяснено в § 2 настоящей части нашей работы, выражения для
вихрей будут даны следующими формулами:
\ = %e-^o(t), 4 = V-'!t?(/), C = ^-^'?(0.
Определяя индекс рода этого движения п, найдем:
с сохранением предыдущих обозначений.
Рассмотрим далее движение с постоянными удлинениями и
сдвигами; условия, чтобы движение это было главным гельмгольтцевым,
сводятся к тому, чтобы вихри определялись формулами:
1~^е^ +S2e- +Ese ,
<.= ^е -- Це -f-Лзв ,
где ?„ т](., "j — постоянные, определенным образом между собой
связанные, а X, суть корни (предполагаемые различными) уравнения:
уравнение это имеет вещественные корни.
Случай, когда это уравнение имеет кратные корни, разбирается
методом обычным в теории систем дифференциальных линейных
уравнений с постоянными коэффициентами.
В заключение рассмотрим случай, когда составляющая по оси z
вихря постоянна, а составляющие по осям х и у скоростей не
зависят от z. Этот случай отвечает атмосферным течениям с
неменяющимися с высотой горизонтальными скоростями и с
постоянным вертикальным вихрем. В этом случае ах = ?, а2 = — т\9 С = 0;
150

поэтому условия, чтобы рассматриваемое движение было главным
гельмгольтцевым, напишутся в следующем виде:
ё+«іЕ
Зо
і1 = О,
Последнее равенство дает два случая: 1) С = 0, 2) аз — О-
Рассмотрим первый случай; в нем ? и Г[ определяются равенствами:
(*)
Л'
)../
7] = 7і1е1 +^2е* ,
где ?,, т)х-— между собой связанные постоянные, а X, суть корни
уравнения:
2
Ь"+("і + «й)* + <*Л—j = 0.
Так как дискриминант этого уравнения равен («2—аг)"'"4* °j и
больше нуля, то оба корня этого уравнения вещественны.
Во втором случае а8 = 0; очевидно, что ? и т{ выражаются
формулами (*), причем X,. суть корни уравнения
с-ь°з
2
Х-|-а2
= 0.
Корни этого уравнения будут:
К г = ЧГ1-"^ (аі_аг) + '3 ~ '
при достаточно большом |С|, а именно при |С| > ^ (cij — <*2)~ -J- a^
корни эти будут комплексные, так что при ct1-j-a2>0
составляющие вихря в плоскости хоу будут совершать затухающие
гармонические колебания.
Для случая, когда ссг -j— a2 = 0, мы имеем:
6 = 60 sin (Х0* + р),
ij = ilo sin (M + Tf);
So 5 *)о» P> 1 — постоянные, связанные между собой, а Iq =
-\V7-
о2 (a a г; в этом случае мы получаем вибрирующие
3 ^ 1 2'
составляющие вихря в плоскости ход.
Пример 28. Рассмотрим случай, когда две составляющие
скорости по осям л: и j/ не зависят от координат, х и #, иначе
151

говоря — случай, когда и и г; суть . функции і и z.
Разыскивая главное гельмгольтцево движение, выгоднее
воспользоваться не обычными условиями в форме h = 0, а вспомнить,
что а = curl —j~ и что значит для главного гельмгольтцева
движения curl —тг= 0» т. е. —тт потенциальный вектор, а следовательно
at at
существует функция ? такая, что —j- = grad <р; таким образом
условие, чтобы рассматриваемое нами движение было главным
гельмгольтцевым движением, выразится тремя равенствами:
ди . du до
ді ' w dz dx
dv , dv до
dw
и
dw
v
dw
dt l " dx l v dy
Два первых равенства дают:
w
dw
dz
до
ді
(*)
ди dw dv dw _
dz Ъу dz dx~~ y
du dv
откуда, предполагая, что ->-- и -г- одновременно не равны нулю,
каковой случай будет рассматриваться в конце настоящего
примера, получим:
<?Ф
«у^ф^оэ, Zy *) = ^f Ф = Ф(о>, z} t),
du . dv -
где<о = дг^+^-,?
произвольная пока функция своих
аргументов.
Отсюда, соответственно выбирая функцию Ф? будем иметь:
du t dv , - , л
сведем для краткости обозначения: Фц =-=—-. ф.0 = -——— ,
г lL aw2 l- a<o dz
Ф*3 — дтді
> Ф2 =
Л
*\.
); тогда последнее из равенств (*) даст
нам следующее соотношение:
*) При этих дифференцированиях все три переменные, входящие в Ф,
считаются независимыми.
152

я ГгтА *,>+*'»
(¦
дхді ' * dzut I "¦" ' ~1В ' \" dz ' " дх
*$^ Ф„ +
jn
+*
4- U
іак как по предположению ^— и -* обе одновременно не
нули, то одну из переменных х к у можно заменить на другую и
на неременную ш; полагая для определенности -у- :± 0
(случай ^— :? 0 разбирается совершенно так же 1, будем иметь;
1 о dz *
где а = -^—, р = — -г—; после такой замены предыдущее равен-
dz dz
ство (**) перепишется следующим образом:
(**')
*(Фц-1)
C/2W , d2W
Так как л: и ю— независимые переменные, то коэффициент при х
в этом выражении должен быть нулем; это даст нам два случая
смотря по тому, первый или второй из множителей, составляющих,
этот коэффициент, обращается в нуль.
Разберем первый случай:
Ф„ = 1;
тогда
Ф = -^-Ні(*, 0° + %<*, &
откуда после несложных вычислений, пользуясь предыдущими
равенствами и вводя произвольную функцию л от z и t9 получим:
Таким образом решение нашей задачи даст нам, что и и и—произ-
153

вольные функции z и і, а ги = -р, где Ф определена только-что
ди , <?v
написанным равенством, а ш — х -^—г У ^~ -
Во втором случае будем иметь:
Здесь следует отличать два вида решения, смотря по тому, равен
или не равен нулю коэффициент при Фг.
Для первого вида решения будем иметь:
^?j_3— -о J*L±B — = 0 (***)
(Ь* +* dzn-~U' dzOt +Р dzdt а * }
Разбирая эти уравнения, положим, что ^р^О и не зависит
от z; тогда оба эти уравнения удовлетворяются (ибо j3 = 0), а для
определения v и Ф мы будем иметь дифференциальное уравнение:
- ^«-^ [шг+ъ? ф<)+* Йф»+ф»+ф»Фі=ф-(а)
Это уравнение определит нам Ф, коль скоро будет задано v,
причем v является произвольной функцией z и L Таким образом
в рассматриваемом случае и не зависит от z, v— произвольная функ-
ция z и г, а гу=з—, где Ф определяется уравнением (а;; заметим,
dv
что в этом случае <ъ=у-г—.
Если для рассматриваемого нами первого вида решения -г—
будет отлично от 0 (р не = 0), то, интегрируя уравнения (***),
найдем:
и = cv +• u0 (*)>
где с — произвольная постоянная, а uQ (t) — произвольная функция с;
функция Ф будет в этом случае удовлетворять такому
дифференциальному уравнению:
+(и й-+w 1г )Фи+Фі3+Фі2Фі=Фа-
(Ь)
Таким образом в этом случае v есть произвольная функция z и f,
а = cv + ц0 (/), где с — постоянная, а и0 (*) — произвольная функция *
и w==3— j причем Ф удовлетворяет уравнению (Ь).
154

Положим теперь, что коэффициент при Фі в соотношении:
dz dt + ?dz dt + \ dz*^? dz>) Фі - °
отличен от нуля. Тогда, как нетрудно из предыдущего равенства
вывести,
и в этом случае уравнение (**') даст нам следующие два
соотношения, получаемые путем сравнения коэффициентов при
одинаковых степенях а) в правой и левой частях этого равенства:
Первое из этих соотношений дает:
по самому определению Р, будем иметь:
наконец, вспоминая, что Ф1 = 4'і> найдем;
л ' і1а
Z
Решение нашей задачи определяется в рассматриваемом случае
тремя только-что написанными уравнениями. Функцию &х мы
можем выбрать произвольно. Таким образом w выбираем
произвольной функцией zh/, ш = <1'1; уравнение (bt) после
интегрирования даст нам vy уравнение (Ь3) даст (3, и наконец, пользуясь
уравнением (Ь2), получаем и.
Нами был временно оставлен без рассмотрения случай з_ =
dv _
~ 7Г=== ' в этом слУчае и и v не зависят от г и суть функции
от t
u = u0(t), v = v0(t).
Первые два уравнения (*) дают для разбираемого случая:
9 = xu0($+gv'0(t)-\-y(z, t);
последнее из этих уравнений может служить для определения w
155

по заданной произвольной функции & Сг> 0; это уравнение
напишется в виде:
интегрирование его совершается обычными приемами.
Предыдущее решение задачи значительно упрощается, когда
движение является стационарным, т. е. когда и, v> ги не зависят
от t; не разбирая всех случаев, остановимся лишь на последнем
из разобранных выше случаев, когда Ф линейно зависит от а>:
• dv
v> = (гі (z), <W ^г = Т, (т = const)
Ф = Фі(г)<»-НоОг)»
dv
w = I 6 , v -+¦ ^о> (с и и0 = const)
е
и = — J -рт^- + "о> ("о = const)
с
ибо величина р в силу уравнения (Ь3) постоянна.
Определим вихри для разобранного нами движения:
<К W Фі (^)
Рассматривая случай, когда w = 0, а и и ^зависят только от
z и ?, мы могли бы применить результаты предыдущих выкладок;
здесь однако проще решить задачу о нахождении главных гельм-
гольтцевых движений непосредственно, замечая, что составляющие
вектора h в этом случае будут:
поэтому для главного гельмгольтцева движения будем иметь, что 5
и у\ не зависят от t, а тогда и~л v можно будет определить
формулами:
и = аі(*) + ио(0»
« = »1.(2) + ©о(0»
где ц0, v0, щ, v^—произвольные функции своих аргументов.
В заключение рассмотрим случай, когда не только и и v, но
также и w суть функции от z и t и не зависят от х и #; проще
в этом случае не пользоваться вышеизложенными общими
методами, а непосредственно написать выражение условия, чтобы дви-
156

жение было главным гельмгольтцевым, причем условия эти мы
напишем в форме curl -у- = О, -т— =-- grad 9:
du , ди до dv , dz> do fe r)w cfo
откуда
причем
<fe ~ a^ ~ ш dz '
где ^ и ^2 — произвольные функции L
Таким образом в этом случае движение таково, что
w—произвольная функция z и t, а и и v определяются из предыдущих
уравнений.
Случай, разобранный нами в примере 28, имеет большое
значение для динамической метеорологии, характеризуя собой частный
тип ветра, мало меняющегося по горизонтальному направлению
сравнительно с изменениями его по вертикали.
Пример 29. Рассмотрим движение, в котором и и v суть
функции і9 х, г/, a W есть функция от z и t; в виду того, что для такого
движения ? = т] = 0, ?=?0 (вообще говоря), движение это всегда
будет гельмгольтцевым.
Не трудно видеть, что составляющие вектора Н в этом случае
будут:
Определяя из уравнения Н -j- nQ === 0 индекс рода п, найдем:
dw d\ п С
п =
dz dt
Для случая го = 0 будем иметь:
rflnC 1
а значит представительница рода будет:
157

где р — плотность движущейся жидкости. В этом случае обобщенное
напряжение вихря приобретает очень простое значение:
Таким образом произведение из плотности жидкости в данной
частице на площадь бесконечно малой перпендикулярной оси z
площадки при движении жидкости в рассматриваемом случае не
меняется.
Пример 30. Рассмотрим движение жидкости, в котором две
составляющие скорости равны нулю, и = v = 0. В этом случае
условие, чтобы движение было главным гельмгольтцевым, на-
писанное в форме -т- = grad ср, выразится следующими соотноше-
шениями:
дх ' ду и'
w , дги д?
И^Ь^Ъ.
Первые два равенства дают, что ср не зависит от х ку. ОбОЗНа-
чая -V- через Ф (z, t), найдем, что w определяется
интегрированием уравнения:
где Ф(г, і) — произвольная функция.
Рассматривая случай стационарного движения и замечая, что
Ф (z, t)y не нарушая общности, можно заменить в этом случае
на -<—, где »— произвольная функция z, будем иметь:
где'Ь — произвольная функция своих аргументов. Вычисляя
компоненты вихрей, получим:
1 * 1 ^С-О»
не трудно видеть, что семейство линий вихрей определяется двумя
уравнениями:
z = cl9 &(х, #) = с2,
где с: и с2 — произвольные постоянные.
Полагая, что та не зависит от z, будем иметь:
Ф(г, *) = *'(*).
поэтому
где W и "/- суть произвольные функции своих аргументов.
158

В этом случае ; и *і не будут зависеть ни от z ни от і.
Пример 31. Рассмотрим движение, в котором отсутствует одна
из компонент вихря, ^==0- Тогда, как мы видели выше:
и
дез
дх~;
0\
v
Ф'
W
4/
дх';
CJz
; = о.
v;
Написав условия, чтобы это движение было главным гельигольт-
цевым, в форме —у- = grad Ф, и полагая
Ф = —
dt
lh{%b
dz)
ф,
найдем следующие уравнения:
. дЧ дФ
д2© дФ
' dxdz дх ' V dydz ду *
I
ъ
д^о д^ д^д^_ до дь
dz* ~ dt ~ дх дх ' ду ду : dz Oz Y dz dz ' j
dv д<Ъ
dty __дФ j
\ <*)
Исключая Ф из этих уравнений, получим:
где М—произвольная пока функция. Вместо Мвведем функцию М
под условием:
где М будет также функцией &, z, L
Продолжая далее исключение Ф из уравнений (*), получим
в результате этого следующие соотношения:
dz^~ д^ dz~^ dt^dx дх^ду ду V dz ~ '
6'М дсо
__ '
дФ dz
(**)
уравнения (**) служат нам для определения искомых функций
с? и ф.
Рассмотрим частный случай задачи, когда <р и & не зависят
от z и ?. В этом случае будем иметь, что Л/ не зависит от ^ и что
дМ , с^ ^_ , ду дф _
dz ^ дх дх ~г ду dy '
159

дМ
откуда -д- = — с, с — постоянная, а о и v удовлетворяют
уравнению:
дс? <?& dip <?ф
дх дх'*' ду ду ~
В случае с = 0, последнее уравнение показывает, что линии © = с4»
й = с2 (сх, с2 — постоянные) друг другу ортогональны и семейство
этих линий образует координатную сеть для некоторых
криволинейных ортогональных координат.
Пример 32. Рассматривая движение, в котором две компоненты
вихрей отсутствуют и в котором следовательно вихревые линии
параллельны некоторому неизменному направлению, будем иметь при
соответствующем выборе координат:
В этом случае С не зависит от z, т. е. С = С (і, х, у), a w
определяется по и и v соотношениями:
dw ди dw dv
дх dz* ду дг '
для этого случая
Отсюда ясно, что условие принадлежности разбираемого движения
к классу главных гельмгольтцевых движений заключается в том,
чтобы ии^не зависели от zy a w не зависело от х и у
(подобно движению, разобранному в примере 29). Совершенно ясно,
что в этом случае С можно задать в виде произвольной
функции х, у и t, а и и v определятся тогда из уравнений:
dv ди
дх~~ ty~^
Полагая ? = — © (*), будем иметь:
ди dv /л
ди , <^_ ©'(*)
полагая ы==ер(')# + цх> »= Т^У^ + ^і» будем иметь:
ду дх * дх* ду
160

— уравнения, хорошо известные из теории функций комплексного
переменного.
Определим, какие из рассматриваемых нами движений могут
быть гельмгольтцевыми движениями нулевого рода. Для этого
необходимо и достаточно, чтобы вектор Н обращался в нуль;
это даст нам, что и и v не зависят от z, a w не зависит от х и у,
ибо Нх =f —"-> -JZ~Q> Hv= —\ -г- = 0. Используя условие
Н2 = 0, найдем:
откуда?
ц - и -г ¦,— = (),
dt 1 с)х ' ду ' d«
где с и со — произвольные функции. Что же касается и и и, то
они определяются из соотношений:
dint , 5Ь; . <?1пС
<^лг бу
— г.
выбирая ч произвольной функцией /, х, у, мы из этих
соотношений без труда определим и и г/.
§ 10. Об инвариантных функциях и характеристических
векторах.
1. Первую часть нашей работы мы закончим изучением двух
новых понятий, являющихся прямым обобщением идеи вихрей
в жидкости и позволяющих, изучая условия динамической
возможности движения, т. е. условия возможности движения при данной
категории сил, находить те скалярные и векторные величины,
которые, в силу условий динамической возможности, обладают
свойством инвариантности по отношению к движениям жидкости.
Первое из вводимых нами понятий встречается прежде всего,
когда мы изучаем движение несжимаемой жидкости.
Несжимаемость жидкости налагает определенные условия на ее
плотность; как это подробно будет выяснено во второй части,
несжимаемость жидкости не влечет за собой обычного
представления о постоянстве плотности жидкости, однако условие
неразрывности, соединенное с условием несжимаемости (div V = 0),
dp л
дает нам, что -Т7=0, где р — плотность; следовательно плотность
at
данной частицы жидкости не меняется при движении этой частицы.
Точно так же,, рассматривая адиабатические движения, т. е. такие,
при которых не получается и не отдается тепла, мы не получим
обычно предполагаемого в этом случае изэнтропического
движения (в котором давление р есть функция плотности), а найдем
11 За л 2-120. — А'. А. Фридман, Опыт гидромеханики 161

лишь, что энтропия данной частицы жидкости не меняется при ее
движении в жидкости.
Из этих двух примеров видно, что во многих случаях большую
роль играют при движении жидкости особые скалярные функции,
не меняющиеся для данной частицы жидкости при движении этой
последней; такие функции понадобятся нам в дальнейшем как для
интерпретации условий динамической возможности движения, так
и для решения вопроса о нахождении векторов, векторные линии
которых обладают для данного движения жидкости свойством
сохраняемости. Повторим еще раз определение этих функций,
названных нами в предыдущем параграфе инвариантными
функциями:
Инвариантной функцией для данного движения жидкости мы
назовем такую функцию ъ времени и координат данной
движущейся частицы, которая для этой частицы остается
постоянной во все время движения этой последней.
Плотность несжимаемой жидкости, энтропия для
адиабатического движения — все это примеры инвариантных функций при
некоторых добавочных, относительно движения жидкости,
условиях.
Не трудно видеть, что необходимым и достаточным условием
инвариантности функции <? служит следующее равенство:
if-0' ™
или
Задача нахождения инвариантной функции для данного движения
сводится к интегрированию уравнения (72), общее решение
которого может быть получено по формуле:
где <?!, ?©, ?з — ТРИ частных независимых интеграла уравнения (72).
Совершенно ясно, что при задании движения в лагранжевой форме
инвариантная функция 9 не содержит времени t и является лишь
произвольной функцией трех параметров) определяющих данную
частицу жидкости.
Мы не останавливаемся здесь на совершенно ясной и
очевидной связи понятия инвариантной функции с идеями теории групп
непрерывных преобразований и в частности с идеями теории групп
бесконечно малых преобразований; по всей вероятности всю
кинематику непрерывной среды можно было бы изложить, применяя метод
теории групп *); возможно, что подобное изложение отличалось
бы большей простотой и чрезвычайным изяществом; мы
*) Идеи теории групп непрерывных преобразований поименены Zorawski
в его вышецитированной статье.
162

однако, имея целью установить основные представления
гидромеханики жидкостей при наличии притока энергии, ограничивались
всегда элементарными методами, почему и в дальнейшем, не вводя
идей, развитых в теории групп, будем держаться прежнего
элементарного изложения.
Плотность не является, как это следует из уравнения
неразрывности, инвариантной функцией для любого движения жидкости;
согласно уравнению неразрывности (см. вторую часть нашей работы)
логарифм плотности удовлетворяет соотношению:
rflnp .
и, только когда движение жидкости несжимаемое, логарифм
плотности, а значит и сама плотность является инвариантной
функцией. Это обстоятельство в связи с только-что написанным
равенством даст нам возможность ввести понятие об
условно-инвариантной функции.
Условно-инвариантной функцией <р мы назовем такую
функцию времени и координат данной частицы, которая определяется.
и/о
равенством', -іт — Ф» где ^ — заданная функция времени и координат.
В некоторых случаях будем условно-инвариантную функцию ?,
удовлетворяющую соотношению -тг— V? называть
условно-инвариантной функцией, отвечающей функции &•
Совершенно ясно, что коль скоро движение жидкости обладает
свойством обращать в нуль функцию й, то условно-инвариантная
функция <р для такого рода движения превращается в
инвариантную функцию.
Плотность есть инвариантная функция, коль скоро движение
подчинено условию несжимаемости
div V = -—H^r + T"— 0*
Ox l dy dz
Если & есть заданная величина, зависящая от времени,
координат, компонентов скорости и других кинематических элементов, то
условно-инвариантная функция <р> отвечающая функции 'Ь, получится
как решение уравнения:
іъ t
В следующем пункте мы покажем, каким образом можно отыски-
Еать как инвариантные, так и условно-инвариантные функции.
Условно-инвариантные функции представляют прекрасное
орудие для механической интерпретации разного сорта условий
динамической возможности движения; кроме того метод интегрирования
предыдущего уравнения помощью особых рядов даст .возможность
решать многие задачи гидромеханики, например из уравнения не-
11*
163

разрывности определять плотность по данному расхождению
скорости.
2. Как мы видели» интегрирование уравнения (72), служащего
условием для инвариантной функции, сводится к интегрированию
линейного уравнения в частных производных, или, что то же самое, к
интегрированию трех обыкновенных дифференциальных уравнений
первого порядка, применяемых для перехода от движения жидкости
в эйлеровых переменных к движению жидкости в лагранжевых
переменных. Во многих случаях однако представляется более выгодным
обойтись без интегрирования этих уравнений и выразить
инвариантные функции при помощи особого бесконечного ряда; прием
этот, в случае сходимости ряда, дает нам возможность найти
как общее решение задачи о разыскании инвариантной функции,
так и решение задачи Коши для данного случая; подробнее об
этом будет сказано ниже. Следует отметить, что построениями
указанных рядов пользуются и в теории групп для разыскания
инвариантов.
Положим, что уравнению:
• $-°
можно удовлетворить, подставляя вгесто о следующий ряд:
Подставляя указанное выражение в наше уравнение и предполагая
(чтб будет выяснено ниже) равномерную сходимость ряда,
составленного из производных членов предыдущего ряда для о, найдем,
что указанный ряд будет представлять инвариантную функцию,
если коэффициенты его будут удовлетворять соотношения:.!:
*Л~°' "ЗГ-Ио-О, ... _4-ап_х=0;
таким образом получим для частного решения уравнения -—=0
at
следующее выражение:
?-/-' -Ж^ТГ2і?+-- ¦+(-!) -^г SF+--- > <73)
причем функция / является функцией пока совершенно
произвольной. Мы назовем ее начальной функцией.
Чтобы для данной инвариантной функции только-что указанные
формальные операции были законны, необходимо доказать
сходимость ряда (73) для <? и равномерную сходимость ряда, состав-
\енного путем почленного дифференцирования по t ряда (73)
/ d
для о (вернее — путем почленного применения операции-j- к этому
ряду). Для того чтобы доказать сходимость ряда (73) для <р, огра-
164

ничим начальную функцию / условием быть голоморфной
относительно своих переменных, коль скоро модули этих последних не
превышают заданной величины г. Согласно основному свойству
голоморфной функции будем иметь:
^«оЧ-Ні + п^ + п,.
dtn> дхщ ду"* dzn*
<
720! Пх\п^\щ\М
tto-f ^4- п,"+ *Ь
где М—число, превосходящее или равное наибольшему значению
модуля /в указанной выше области значений переменных, \f\^M.
Относительно рассматриваемого нами движения сделаем
предположение, что компоненты скорости также суть голоморфные
функции для значений времени и координат, лежащих в указанной
нами области. Обозначим через т положительную величину,
которая больше каждого из четырех чисел 1, [u[, \v\, \w\ в нашей
области значений переменных,
Пусть Мп будет величина, удовлетворяющая неравенству
dtn
<МЯ
во всей выбранной нами области значений переменных; займемся
разысканием зависимости Мл от значка л.
Так как
гп+1
f
di
,n + l
<
ді
dnJ
Л"
+ |я»|"
д_
дх
dz
All
df
dj_
df
-\-\v
dy \dtn
+
dnf
и так как ~ф — голоморфная функция, то
.dn+if
т. е.
откуда
di
М
п+х
^4т „,
4т
ra-f 1
мп =
мп,
Am \п
М.
Из этой формулы вытекает абсолютная и равномерная сходимость
ряда для <р в указанной области значений переменных:
1 /4тпЛ2 ,
|<?1<М
1+^ +
12
Me
4mt
г
165

Совершенно аналогичным путем доказывается равномерная
сходимость ряда, составленного путем почленного дифференцирования
ряда (73) для 9-
С помощью указанного ряда, выражающего частный вид
инвариантной функции, не трудно построить общее решение задачи
о нахождении инвариантной функции. Выбирая начальные функции
/і > U> /з таким образом, чтобы функциональный определитель
Д(/і,Л,/а)
D(x, 9*> z)
был отличен от нуля при * = 0 (что сделать всегда возможно
бесчисленным рядом способов), можем утверждать, что
образованные при помощи этих начальных функций инвариантные функции
'-Pi» ?2> ?в будут между собой независимы. В самом деле, не трудно
видеть, что по самому способу образования рядов для функций *р4
будет иметь место равенство:
р-(?і, ?«,?»)) =/Р(Л>Л,/8)\
¦ \ D(x, у, z) ) t = o \ D(x, yt z) /f = o'
следовательно ~ТТ7—~—Т~ не Ргвен НУЛЮ ПРИ * = 0, откуда и
будет вытекать правильность нашего утверждения о
независимости функций <р1э 92» ?з Друг от друга. Имея три независимых
инвариантных функции «іі ?э> ?з> мы получим общее выражение
инвариантной функции в следующем виде:
9 = F(ol$ 92, %),
где г*—произвольная функция своих аргументов.
Задача Коши при разыскании инвариантной функции может
быть формулирована следующим образом:
Найти инвариантную функцию 9» обращающуюся при ? = 0
в заданную функцию 9о (х> У> z) от координат.
Решение очевидно получится, если за начальную функцию /
при составлении ряда, определяющего инвариантную функцию, мы
возьмем такую функцию, которая при t = 0 обращалась бы
в 9о (*> fff *)•
Ряд (73) для инвариантной функции 9 приобретает весьма
простую форму, если от эйлеровых переменных мы перейдем к ла-
гранжевым переменным. Тогда, как легко заметить, будем иметь:
/(/; х, у, г) = Ф (і; а, Ьу с),
где а, Ь, с суть параметры, определяющие данную частицу. С
другой стороны:
d*f_d*Q
dtu ~ dtn '
откуда
<ЭФ , Р д-Ф ,
?иф_,_4- _ + ...=ф(*_*, «9 Ъ, с) = Ф(0; а, Ь, с);
166

из этого равенства ясно видна инвариантность '•?, ибо в лагран-
жевых переменных ? оказывается независящей от L
С помощью введения переменных Лагранжа становится ясным,
что решение задачи Коши для инвариантной функции, как и
следовало ожидать, единственное.
Тот метод для решения задачи Коши, который мы указали, по
внешнему виду содержит известную неопределенность, ибо мы за
начальную функцию / могли бы взять любую функцию,
обращающуюся при t = 0 в <?о(*> У * z)- Оказывается однако, что конечный
результат, т. е. выражение инвариантной функции '•? не зависит от
того, какую из функций /, обращающихся при f = 0 в ?0(-*» У* %)>
мы берем за начальную функцию; выясним это обстоятельство.
Пусть мы имеем две функции fx и /2, обращающиеся в f0(x9 у, z)
при * = 0; выбирая за параметры а, Ь} с, определяющие частицу
координаты ее при /==0, будем иметь:
Л = Фі0; я, Ь, с),
/о = Ф2 (t; а, Ьу с),
причем Фі(0; а, Ьу с) = ср0(а, Ь, с) = Ф2(0; а, 6, с). Согласно тому,
что выше было сказано о применении переменных Лагранжа, будем
иметь:
9і = Ф і (0; а, Ь, с) для начальной функции flf
и
ср2==Ф2 (0; a, by с) для начальной функции /2,
2>
откуда следует, что ?х = ?$>> как впрочем и следовало ожидать.
Из только-что скаазанного следует, что за начальную функцию
можно всегда брать <?о (х> У' z)> т- е- значение инвариантной
функции при t = 0.
3. Перейдем теперь к решению вопроса об определении условно-
инвариантных функций. Как мы уже виде;и, вопрос этот сводится
к интегрированию уравнения:
d? ,
где ty — заданная функция времени и координат. Не останавливаясь
на обычных методах интегрирования этого уравнения в частных
производных, применим к решению вопроса о нахождении условно-
инвариантных функций метод составления рядов, аналогичных
рядам, указанным в предыдущем пункте.
Не трудно видеть, что частное решение нашего уравнения
выразится следующим рядом:
м in—1 ,
+(~1Г1~4^+-"' (74)
сходимость которого исследуется так же, как и сходимость рядов
предыдущего пункта.
167

Имея частное решение, удовлетворяющее уравнению
мы найдем общее выражение для условно-инвариантной функции,
прибавив к этому частному решению общее выражение для
инвариантной функции; таким образом решение нашего уравнения будет
иметь вид:
<? = ?о + 'г,
где о — инвариантная функция.
Мы не останавливаемся зд^сь на подробном разборе задачи
Коши, возникающей в связи с вопросом о нахождении условно-
инвариантной функции.
Нам встретится в дальнейшем необходимость определять
функции, удовлетворяющие уравнению:
S + .7-0
и более общему:
dt~ '
где і> и 6 — заданные функции времени и координат. Покажем, что
определение функций, удовлетворяющих одному из предыдущих
уравнений, сводится к отысканию инвариантных и
условно-инвариантных функций.
Первое из этих уравнений может быть написано в виде:
^ In 9 п
таким образом In © определяется как условно-инвариантная^
функция; прием определения In 9 известен, а значит известно и
определение <?> удовлетворяющей указанному выше уравнению.
Чтобы установить, каким образом находится решение второго
из написанных выше уравнений, положим, что 9 = ?о.4'> где 9о
удовлетворяет уравнению
т. е. определяется по методу отыскания условно-инвариантных
функций. Не трудно заметить, что если ^ удовлетворяет уравнению:
^ = JL
dt ©о *
то cp = 'f($ будет удовлетворять уравнению:
$ + •,-,
168

легко видеть, что ^ определяется как условно-инвариантная
функция, а отсюда следует, что интегрирование только-что
написанного уравнения сводится к отысканию инвариантных и условно-
инвариантных функций.
Так как настоящий параграф не претендует на полноту
изложения, то мы ограничимся лишь немногими примерами,
иллюстрирующими приемы нахождения инвариантных и
условно-инвариантных функций.
Пример 33. Для движения, скорости в котором заданы
условиями и = О, v = О, w = 2, найти инвариантную функцию.
Применим сначала обычный метод интегрирования ур-ния -г-—О*
ді ^ *д
]z
общее решение этого уравнения будет:
?=F(ze™*, х, у).
Применяя ряды, указанные в предыдущем пункте, и выбирая за
начальные функции х> у и z, будем иметь :t
?і = х, <эа = у9 сз = ze -'.
Найдем для указанного движения условно-инвариантную
функцию из уравнения:
_ = div V = -г- = 1
dt dz
Образуя согласно методам настоящего пункта частное решение
этого уравнения, найдем:
откуда
o = t-\-F{ze~\ х, у).
Не трудно видеть, что о = — In р, где р—плотность нашей
жидкости; для определения плотности надо знать распределение ее при
2 = 0; полагая, что в начальный момент плотность есть линейная
функция z, p = a-{-bz при t = 0, найдем:
(?)t-o = — h (а + te) = F(zf * У),
<p = t — \n(a-\-bze~'t), p = e (a 4" bze~ ),
что и дает решение нашей задачи.
Пример 34. В качестве второго примера рассмотрим
определение плотности, коль скоро скорости суть линейные функции
координат.
При этом условии div V = e1-[-s24-s3 = e(0j решая уравнение
2?—«>»
169

получим:
i0 = ts(J)
ткуда
t
о
Составляя теперь по методу п. 2 ряды для инвариантных
функций в нашем движении, не трудно заметить, что инвариантные
функции будут линейными относительно х, у> z; таким образом
9 = s0 -г 5, х -j- s2y ~г 5az,
где 5l(, 5lf 5;>, s3 суть функции времени; эти функции определяются
из системы линейных дифференциальных уравнений первого
порядка. Рассмотрим случай движения без сдвигов и вихрей:
и = a -j- е^, v = Ь -4- г2#, w = с + s3z;
тогда s,- будут удовлетворять уравнениям:
50 -f *іл +«зЬ+53с = О,
si + гі5г — 0» 52 "і" s-252= 0> 5з + аз5з = О-
Из последних трех уравнений определим su $2, sB; тогда первое
уравнение даст нам возможность определить $0.
4. Две теоремы Гельмгольтца показывают, что для классической
гидродинамики вектор вихря играет исключительную роль:
вихревые линии обладают свойством сохраняемости, а напряжение
вихревых трубок не меняется при движении жидкости. Вектор
вихря не обладает этими свойствами, как это было нами выяснено
в предыдущих параграфах, для случая общего движения жидкости;
оказывается, как это будет указано во второй части нашей работы,
что в случае движения жидкости при наличности действия сил и
притока энергии, вектор вихря точно так же не удовлетворяет
указанным двум теоремам Гельмгольтца. Естественно возникает вопрос:
нельзя ли найти такой вектор, который бы или для всякого
движения жидкости, или же по крайней мере для только-что
упомянутого движения обладал свойством сохраняемости, иначе говоря —
удовлетворял обеим теоремам Гельмгольтца зараз? Совершенно
очевидно, что такой вектор играл бы роль в изучении движения
жидкости, аналогичную той, какую играет вектор вихря в
классической гидродинамике. При этом, само собой разумеется,
представляется желательным указанного сорта вектор представить в виде
известной комбинации кинематических элементов, характеризующих
движение, т. е. компонентов скорости и их производных по
времени и координатам, аналогично тому, как вихрь выражается через
компоненты скорости данного движения.
Надлежащее обобщение идеи вихря приводит нас к понятию
о характеристическом векторе, метод же его разыскания будет
L &'(t)
1-2 К)
170

основан на применении особых рядов, члены которых представляют
собой итерированную юперацию Helm над некоторым вектором.
Характеристическим вектором мы назовем такой вектора
векторные линии которого образуют собрание сохраняющихся
векторных линий.
Вспоминая изложенное в § 2 настоящей части нашей работы
и пользуясь обозначениями, введенными в § 3, и в частности
символом Helm, мы без труда придадим теореме 1, помещенной в главе I
нашей работы, следующую формулировку:
Теорема 18. Для того, чтобы вектор а был
характеристическим вектором, необходимо и достаточно выполнение следую-
щего условия:
decl а = [Helm а, а] = 0.
Мы не останавливаемся на доказательстве этой теоремы, так
как с достаточной подробностью это доказательство было
проведено в § 2 настоящей части нашей работы.
На основании теоремы 18, характеристический вектор а
обладает тем свойством, что всегда можно будет найти такую
скалярную величину ft (функцию t, ху у, z), чтобы имело место равенство-
Helm a -f ft a = 0; (75)
отсюда следует, что характеристический вектор можно разделить
на ряд родов, отвечающих различным значениям ft; при этом
характеристический вектор рода, отвечающего ft = div V, мы будем
называть главным характеристическим вектором.
Для главного характеристического вектора Ь будем иметь:
Helm Ь + div V • Ь = helm Ь = 0.
Не трудно понять, каким образом идея вихревой трубки может
быть применена к характеристическому вектору и к векторным
линиям, ему отвечающим. Напряжением характеристического
вектора мы будем называть произведение из его величины на площадь
сечения векторной бесконечно тонкой трубки, перпендикулярного
оси этой трубки. Рассуждая совершенно так ж?, как в § 9, мы
найдем, что для главного характеристического вектора напряжение
его не будет меняться при движении жидкости. В дальнейшем мы
будем заниматься исключительно характеристическими векторами
общего типа, не останавливая своего внимания на роде этих
векторов и в частности на главном характеристическом векторе.
Разыскание характеристического для данного движения вектора
сводится к интегрированию векторного уравнения (75),
являющегося системой трех линейных уравнений с частными производными
первого порядка с тремя незвестными функциями а„ а//9 а„\ в виду
однако произвольности функции &, одно из этих уравнений отпадает,
и мы имеем дело с интегрированием двух уравнений с частными
производными первого порядка (уже не линейных), содержащих три
і71

неизвестных функции. Интегрирование этих уравнений может быть
выполнено двумя способами. Первый способ заключается в
разыскании таких трех векторов, через которые,: характеристический
вектор выражается в виде их линейной комбинации, тогда как
коэффициенты в этой линейной комбинации получаются
интегрированием так называемого обобщенного уравнения Ricatti и
нахождением инвариантных функций (или, что то же самое, переходом от
эйлеровых переменных к лагранжевым). Второй способ
основывается на построении особых бесконечных рядов и требует для
своего осуществления исключительно нахождения инвариантных и
условно-инвариантных функций. Второй способ непосредственно
отвечает на наше требование выразить характеристический вектор
в виде комбинации кинематических элементов; правда, комбинация
эта выражается бесконечным рядом и лишь в исключительных
случаях сводится к конечному числу операций.
Подобно тому как в предыдущих пунктах мы кроме
инвариантных функций ввели еще условно-инвариантные функции, подобно
этому представляется необходимым ввести понятие об условно-
характеристическом векторе.
Необходимо заметить, что для общего случая движения вихрь
не есть характеристический вектор, но он становится
характеристическим вектором, коль скоро движение является гельмгольтце-
вым, т. е. коль скоро на движение наложено определенное условие.
Вектор а мы назовем условно-характеристическим вектором,
коль скоро он удовлетворяет соотношению:
Helm а -\- в а = а Ь,
где &иа — скалярные функции времени и координат, аЬ— заданный
вектор.
Если движение таково, что вектор b обращается в нуль, тогда
вектор а, удовлетворяющий предыдущему соотношению, будет для
этого движения вектором характеристическим.
Как мы увидим во второй части, вихрь будет как раз условно-
характеристическим вектором» обладающим свойством
характеристичности для случая, когда давление есть функция плотности.
5. Для решения задачи о нахождении характеристического ,и
условно-характеристического вектора нам необходимо будет ввести
особое понятие об инвариантных векторах и с помощью
построения таковых векторов отыскивать характеристические векторы.
Назовем инвариантным вектором такой вектор F, который
определяется условием:
Helm F = 0. (76)
Для решения задачи о разыскании инвариантных векторов
введем в рассмотрение последовательность векторов, в которой
каждый последующий вектор есть Helm предыдущего вектора.
Первый вектор этой последовательности условимся называть
начальным вектором*
172

Пусть указанная последовательность векторов будет иметь вид:
причем S, Si, S2, .. • Sn,
S1 = Helm S, So = Helm S^... 3;j+1 = Helm Sn,...,
вектор S пусть будет начальным вектором.
Образуем из векторов предыдущей последовательности
векторный ряд:
F = sS + «i Si + ssS2+ ... tt^S.,-!-...,
причем под этим векторным рядом мы будем подразумевать
совокупность трех рядов, отвечающих трем компонентам векторов,
входящих в наш ряд; совершенно ясно, каким образом понятия
сходимости, абсолютной и равномерной сходимости, установленные
для обычных рядов, можно перенести на ряды секторные; так
например векторный ряд будет называться сходящимся, коль скоро
будут сходящимися все три обычные ряда, отвечающие трем
компонентам входящих в векторный ряд векторов.
Подберем коэффициенты предыдущего векторного ряда таким
образом, чтобы вектор F, им представленный, был вектором
инвариантным; вспоминая формулу (35) § 3, без труда обнаружим,
что F будет инвариантным вектором, коль скоро будут выполнены
соотношения:
Л '
dt ^5»-i и'
Только-что написанные уравнения имеют следующее частное t
решение:
L / * \ н *•
S — 1, Si — t, S-2 — 1 . О > ' * "> Snz~ ( 1)
П
таким образом вектор
F = S-*Sl + r^Sa-...+(-l)";?-Se+...
в случае, если мы докажем законность всех операций,
произведенных нами с векторными рядами, будет инвариантным вектором.
Однако, прежде чем перейти к этому доказательству, установим
более общее выражение для инвариантного вектора F.
Коэффициент 5 векторного ряда должен удовлетворять соотношению
ds
-г- = 0, иначе говоря—5 должно быть инвариантной функцией. Усло-
dt
вимся символом (?) обозначать функцию <? от t, х, у, z, в которой
эйлеровы переменные заменены лагранжевыми переменными;
в таком случае не трудно получить выражения всех коэффициентов
173

нашего ряда, представляющего инвариантный вектор. Если о
является некоторой инвариантной функцией, то:
t t t
s = ?> (Sl) = - f(,)dt, fe) = //(?)dtdt,...
f) I) U
t t
(s„) = (-l)nf... f(*)dt...dt-t
il
П
откуда без труда найдем:
.(0 = (-1)" f^tJ^Kr^d-., (n = l, 2,...).
Из этой формулы не трудно получить неравенство для (sn)f
нужное нам впоследствии для доказательства сходимости
векторных рядов. Пусть, в рассматриваемой нами области значений / и
координат, <? не будет по абсолютной величине превосходить
числа ;j.;
і ? I О;
тогда из предыдущих формул будем иметь:
\s\<*, UJ<^, (n = l, 2...).
Докажем теперь, что при некоторых предположениях
относительно начального вектора и скорости нашего движения все
операции, необходимые нам для образования инвариантного вектора,
являются операциями законными.
Условимся считать компоненты начального вектора и вектора
скорости нашего.движения голоморфными функциями своих
переменных, коль скоро модули этих последних не превысят заданной
величины г.
Положим, что абсолютные значения компонентов нашего
начального вектора не превосходят числа Му а величины 1, [u[, | v [, \w\
не превосходят числа тп.
Покажем прежде всего сходимость ряда для F. Ради краткости
условимся наибольшее значение абсолютных величин компонентов
вектора а обозначать через ||a|j; таким образом || a |'j будет наибольшим
из чисел \ах\, |ау|, \а=\.
Установим неравенство для ||Sn|; положим [|Sn||--^Af„ и выясним
зависимость Мп от индекса п.
Согласно определению символа Helm, будем иметь:
V =; г- W-
бі x дх да ' dz
dx ' n-i»* du n -l>y dz °n~ l'z' '
174

откуда, пользуясь методом, аналогичным методу п. 2 настоящего
параграфа, найдем:
или:
Так как для нашего ряда] sn | <v—j-, то из этого и из
предыдущего неравенств получим:
F|<^(1+^+TV(^)'+...+i('f)" + ...),
что и докажет сходимость нашего ряда.
я d
Докажем теперь, что, применяя к нашему ряду операцию —j—,
мы можем применить эту операцию к каждому члену ряда отдельно
и результаты сложить. Для этого достаточно доказать равномерную
сходимость ряда:
it > dt т ' *' "*" л *"і - • •
cfe(lS.
л
Легко заметить, что
Js.
dt
SJ| + |sB
Л.
л
из только-что выведенных неравенств найдем:
iisjk(^)V,
а так как
то
dS
п
dt dt
rfS.
dx
-- v —> [- o>
<fc
dz '
л
< *». M)i < (^lV!+1 ^
поэтому
G?S„S
n**rt
Л
<k-J-(t-) M+\*n\-(?f)
^(^)V>(1+7f),
Af=
ибо:
>«--<*
175

Из этого неравенства будет следовать равномерная сходимость
ряда для F, иначе говоря — будет следовать возможность почленного
г- d
применения к ряду для г операции , •
Из равномерной сходимости ряда для F вытекает равенство:
(F, V) V = (sS, V) V-f (*А, V) V+ ... -f (5.S.. V) V+ ...;
так как с другой стороны по только-что доказанному:
dF _ dsS , dsfii , j_d?_«S»jL.
dt~ dt ^ dt ^ '" ' dt ' ¦¦"'
TO
Helm F = Helm (sS)-f-Helm (s, Sx) + .. - -f Helm (4hSB)-f ...
Указанным выше методом мы можем построить ряд разных
инвариантных векторов соответственно различным начальным
векторам.
Не трудно видеть, что если мы выберем начальные векторы
таким образом, чтобы при ? = 0 эти векторы были не
компланарны, то полученные с помощью таких начальных векторов
инвариантные векторы будут также не компланарны для значений t,
близких к /==0; если бы полученные таким образом инвариантные
векторы были компланарны, то при t = 0 они оставались бы
компланарными, но при t = 0 инвариантный вектор совпадает с начальным
вектором при ? = 0, значит при t = 0 инвариантные векторы не
могут быть компланарны. Следовательно, выбирая соответственно
начальные векторы, всегда можно образовать указанным выше
методом три некомпланарных инвариантных вектора: F1? F2> F3.
С помощью инвариантных векторов F1? F2, F3, не компланарных
между собой, не трудно будет решить задачу об определении
характеристического и условно-характеристического векторов.
Всякий вектор может быть представлен в виде линейной
комбинации трех некомпланарных инвариантных векторов. Установим
условия, которым должны удовлетворять коэффициенты в этой
комбинации, чтобы она представляла собой характеристический
вектор.
Положим, что искомый характеристический вектор а выражается
формулой
а = niFx + 7i2F2 + n3F3;
так как HelmFi = 0, / = 1, 2,3, a Helm а-[-^а = 0, то
¦^+4 = 0; -^ + 4 = 0; ^+ »л, = 0, (77)
где 0- — произвольная функция; определение пи п2, п3 из этих
уравнений производится на основании правил, указанных в предыдущих
пунктах настоящего параграфа, и сводится к разысканию
инвариантных и некоторых условно-инвариантных функций.
Произвольность функции & значительно упрощает задачу, В виду
176

произвольности Ъ мы можем одну из функций пі считать
произвольной; полагая пх произвольной, найдем:
где '-ро и <?3— произвольные инвариантные функции. Таким образом
общее выражение характеристического вектора а может быть
написано в форме:
а = п (Fx -f ?,F2 -f ?3Wg), (78)
где n — произвольная функция времени и координат, а о2 и 'f3 суть
произвольные инвариантные функции. Отсюда между прочим
следует, что общее выражение для инвариантного вектора имеет вид:
F = <PlF1 + ?2F2-b%F3,
где ?і,?о, <р3-—инвариантные функции.
Перейдем теперь к решению вопроса о построении
условно-характеристического вектора. Для решения этого вопроса
необходимо определить зектор а, удовлетворяющий условию:
Helm а + ^а = «Ь,
где Ь — заданный вектор. Так как введенные нами инвариантные
векторы F не компланарны, то всегда можно представить вектор Ь
в виде линейной комбинации векторов Fl9 F2, F3, причем
коэффициенты в этой комбинации будут известными величинами:
b=/1F1+/2F2-f/3F3)
где/j,/о,/з — известные функции времени и координат. Полагая, что
условно-характеристический вектор а ищется в форме:
а = nj?i т~ Яз^Ч-Лз^з»
мы будем иметь для определения щ следующую систему уравнений:
dnx
IF
drio
~dt
dn3
dt
Ьп2 = af29
+ °*з = a/3;
(79)
такая система, как это было нами выше в настоящем параграфе
показано, требует для своего интегрирования лишь уменья находить
инвариантные и условно-инвариантные функции, а эту задачу мы
умеем решать с помощью рядов, указанных в предыдущих пунктах.
Произвольность функций & и а может в частных случаях
облегчить интегрирование системы (79).
Указанный выше метод нахождения условно-характеристических
векторов может быть значительно упрощен, если воспользоваться
произвольностью величин 0 и а в уравнении:
Helma+&a = ab,
12 Зак. 2420.— А'. А. Фрігд??ап, Опыт гидромеханики 177

служащем для определения условно-характеристического вектора а.
Составим для а ряд с начальным вектором S~b: ^
a === s& ~^~ s^Si ~т~ - -. -р* 5иЛл | • • • >
где Sn = HelmSn_1.
Подчиняя коэффициенты этого ряда условиям:
ds fl
J+44-vi = o. (n = i, 2...)
<
*
найдем, что вектор а будет условно-характеристическим вектором.
Само собой разумеется, что необходимо будет доказать законность
производимых нами операций. Для частного случая 9=0, а = 1,
(—1)я*л+1
будем иметь s = t, sn — j—ТГТП—» л=1, 2,... В этом случае
сходимость полученного ряда докажется приемом, изложенным выше;
сам ряд будет иметь такой вид:
a = *S j^y Sx+--• + (—!) ^ _|_ гу Sw-{-...,
причем S —Ь.
В общем случае сходимость ряда для а можег быть доказана
путем оценки его коэффициентов sn9 определяемых из уравнений (*).
Полагая , = ft, будем иметь из уравнений (*) следующее их
частное решение:
о
Если jjl будет число, превосходящее |ф| в рассматриваемой нами
области значений переменных, am — число, превосходящее \s\
(s можно выбрать произвольно вследствие произвольности ос), то из
предыдущего равенства получим
е
каковое неравенство достаточно для установления законности
производимых нами операций.
6. В предыдущем пункте мы показали процессы, которыми
можно образовать характеристический и условно-характеристический
векторы для данного движения жидкости. Вообще говоря, мы
получаем решение задачи в виде бесконечных рядов, составленных из
кинематических элементов, характеризующих наше движение.
В исключительных случаях ряды эти обрываются, и мы получаем
решение в виде комбинации конечного числа кинематических
элементов.
Совершенно очевидно, что указанные нами ряды превратятся
173

в суммы конечного числа слагаемых, коль скоро существует
значение/г, для которого Sn = 0 тождественно, иначе говоря — S^_1
есть инвариантный вектор.
Изложенные в настоящем и предыдущем пунктах приемы для
определения инвариантных, характеристических и
условно-характеристических векторов настолько просты в их общем виде, что не
нуждаются в пояснении примерами. Следует однако отметить, что
применение указанных -методов в частных случаях лишь весьма
редко ведет к упрощению формул; хотя из полученных (довольно
хорошо сходящихся) рядов всегда могут быть определены искомые
векторы, но получить их в законченном виде удается лишь в редких
случаях. Мы ограничимся приведением двух примеров,
показывающих, каким образом по приведенному выше способу определяются
инвариантные векторы.
Пример 35. Положим, что мы имеем движение, в котором
скорости суть линейные функции координат, причем сдвиги в этоаг
движении отсутствуют и компоненты вихрей $ и ч\ равны нулю.
За начальный вектор примем S = Й,
Полагая, что величина т (функция времени t) определяется из
условия:
т
— — з3,
тп
где е3 — удлинение по оси z-ов, будем иметь:
1 dmS „ _ 1 d2mS - _ 1 dnmS
Отсюда для инвариантного вектора F найдем:
или
= (m$)f = 0
zr—o р — о F =
т
т
где mQ и ?0 суть значения т и Z. при t = 0.
Пример 36. Рассмотрим квази-твердое движение. При этом за
начальный вектор примем вектор S, зависящий явно только от
dS dS dS . _ о
времени, так что 75"== "3"== "5™==s " К Как В нашем слУчае ц
также будет зависеть только от t, то
с _ ^Иіі L го S 1
12*
179

будет также зависеть лишь от і; вычислим последовательно Si и S2:
д& 1
dt 2
Si
[Q, s],
s.,
of*
2,
dS
dt
2
^ S
dt' Ъ
+±(q, s) а_1(а,С) s.
из образованных таким образом S„ образуем ряд для инвариантного
вектора F.
Полагая, что вектор S постоянен (не зависит от t), будем иметь ¦
So =
1_
2
и т. д.
7. Процессы, помощью которых мы образовывали
характеристические и условно-характеристические векторы, требуют
применения последовательных операций, вводящих всё более и более
высокого порядка производные; в некоторых случаях более
рационально решать нашу задачу, вводя процессы, требующие
последовательного интегрирования, а не дифференцирования.
Рассмотрим сначала случай стационарного движения. В этом
случае определение условно-характеристического вектора сведется
к известной в гидродинамике или — правильнее — в векторном
анализе операции определения вектора по его вихрю.
Полагая в уравнении, определяющем условно-характеристический
вектор, & = divV и считая, что diva —0, будем иметь:
причем
curl [а, V] — аЬ,
div а = 0.
Первое из этих уравнений с помощью известных методов
(пользуясь векторным потенциалом) даст нам величину [а, V].
Пусть *)
[a, V] = A;
тогда
а
[У, А] , у 4-cV
— (V V) — rsv»
где 5 — произвольная функция времени и координат.
Эту функцию мы выберем под условием:
div (a0 + sV) = 0,
*) Вектор А определяется только с точностью до потенциального вектора:
А = А0 -f- grad 9» и очевидно можно f определить так, чтобы вектор А был орто*
гонален вектору V; для этого достаточно удовлетворить уравнению (grad <р, V) =
= — (Aq, V)t что очевидно возможно сделать.
Прим. ред.
ISO

лаковое услогие даст нам уравнение:
¦J-f sdivV-f divao = 0M
Пользуясь условием неразрывности:
найдем, что-.
где й есть решение уравнения:
</ф div ар
<'.t ~ ~ ~"'
Не трудно видеть, что, найдя предыдущим способом соленои-
дальный вектор а, мы можем получить вектор а' с каким угодно
расхождением и обладающий точно так же свойством условной
характеристичности; для этого достаточно вектор а помножить на
соответственно подобранную скалярную функцию X,
В случае, когда движение не стационарно, мы можем
разыскивать условно-характеристический вектор, сводя эту задачу к
последовательности задач о нахождении вектора по его вихрю. В самом
деле, уравнение для условно ^характеристического вектора в нашем
нестационарном случае может быть написано так:
да.
— + curl [а, V] -(- V divа — a div V + Оа = ab;
представляя а в виде ряда
а = ах -f- *ц + • - • *г а* "Г • * * *
определим члены ряда условиями:
curl [aj, V] = ab,
curl [аа, V] + -^ + V div аі - а2 div V + Оа, = О,
о о о о о
curl 1а„, V]+^i + Vdiva<I_1-aw_1divV-i-4-i=0,
Очевидно, что в случае сходимости этого ряда и законности
всех операций, с ним производимых, мы получим решение задачи
о нахождении условно-характеристического вектора.
131

Ту же задачу можно решить, подчиняя члены ряда для а
условиям:
да.}
ді
да
2
ді
да.
ді
Л,
curl [аь V] + V div а: — a, div V -f Ч = О,
r- + curl[an_1,V]+Vdiva,_1-a,„1divVi-4-1=0,
Для иллюстрации только-что сказанного рассмотрим следующий
пример:
Пример 37. Найти векторные линии, обладающие свойством
сохраняемости для стационарного движения. Уравнение для
определения условно-характеристического вектора напишется в виде:
Helma-|-$a = a -^т,
ибо условие стационарности будет -зт- = U.
Полагая сс = 1, найдем:
да±_ д\_
ді ~ ді'
^+curl[a1, VJ + Vdiva, — ах div V + «Ц = Q,
Эта система равенств удовлетворяется, если положить
»i = V, а2 = 0, а3 = 0, ..., & = 0,
каковое решение указывает, что для стационарного движения линии
тока будут обладать свойством сохраняемости.
В некоторых случаях представляется более удобным отыскивать
инвариантные и характеристические векторы не в* виде бесконечных
рядов, а в виде линейных комбинаций трех особо выбранных
векторов.
Положим, что у нас имеется вектор S, обладающий тем
свойством, что S, Sj = Helm S и S2 = Helm St между собой не
компланарны; в таком случае любой вектор можно представить в виде
линейной комбинации векторов S, ?г и S2. Вектор S3 = Helm Sj
также представится в виде линейной комбинации S, Sj и Sg;
положим, что коэффициенты в этой линейной комбинации будут: q,
Я\7 ft*
S3:=?S-l-<7iS1-f ?2S2.
182

Будем искать инвариантный вектор F в следующей форме:
F = sS-}-s1S1 j-saSa;
тогда найдем следующие равенства:
— — ^52 = 0,
ds2
dt
+ «і-Ь?а«9 = 0»
каковые уравнения в случае перехода от эйлеровых к лагран-
жевым переменным сведутся к системе трех линейных
обыкновенных дифференциальных уравнений первого порядка.
Применяя тот же метод для разыскания характеристического
вектора а в форме:
а = sS -4- SjSi -J- $oS2,
найдем следующие уравнения для определения s, $х и s2:
ds1
dt
+ * + ft*i + 9i*a = 0,
Решая вопрос об определении условно-характеристического
вектора а из соотношения
Helm a -f- &а = аЪ
и полагая, что
найдем а в форме:
a==sS4-51S1 + s2S2,
где s, Sj, s2 определяются уравнениями:
ds
+ bs + qsz = a%
dt
d$i
¦bs + ®Si + 9A==a3lf
¦^ -r Si + $s2 + qraS8—«p2;
вследствие произвольности & и ее всегда можно s и st выбрать
произвольными; тогда 52, если мы перейдем от эйлеровых к лагран-
183

жевым переменным, определится тлз обобщенного уравнения Riccati.
Не останавливаясь подробно на вопросе определения
характеристических векторов только - что указанным способом, заметим,
что в некоторых случаях представляется более рациональным
искать характеристический вектор в виде линейной комбинации
не векторов, из которых последующий является Неіт'ом
предыдущего, а каких-либо иных векторов. Такой случай представляется
например при изучении условно-характеристического вектора для
уравнений Максвелла-Герца, где более рационально рассматривать
линейные комбинации вектора скорости, электрического смещения
и магнитного напряжения поля. Во второй части мы также иногда
будем пользоваться для разыскания характеристических векторов
частными прчемами5 отличными от изложенных в настоящем
параграфе,,

II. ДИНАМИКА СЖИМАЕМОЙ ЖИДКОСТИ.
Глава III.
УСЛОВИЯ ДИНАМИЧЕСКОЙ ВОЗМОЖНОСТИ ДВИЖЕНИЯ.
§ 11. Основные уравнения движения жидкости.
1. Дифференциальные уравнения, управляющие движением
жидкости, служат для определения по заданным силам движения, этими
силами вызываемого. Жидкость мы рассматриваем как совокупность
частиц, непрерывно заполняющих пространство; частицы эти
действуют друг на друга, отчего возникают внутренние силы,
выражающиеся при посредстве давления жидкости. Таким образом задача
изучения движения жидкости распадается на две части: 1) определение
движения жидкости, иначе говоря—определение координат каждой
данной частицы жидкости в зависимости от времени или, что то же
самое, определение вектора скорости V в зависимости от времени
и координат того места в жидкости, к которому скорость относится,
и 2) определение внутренних сил (т. е. давления), возникающих
в жидкости при данных обстоятельствах динамической задачи.
Первая часть задачи гидромеханики сводится к определению
вектора скорости V в зависимости от t, х, у9 z, иначе говоря—
сводится к определению трех составляющих вектора скорости V:
u, v, п) в зависимости от времени и координат. Вторая часть задачи
сводится к определению давления р жидкости в зависимости от
времени t и координат х, y> z.
Для решения нашей задачи механика дает нам три уравнения;
кроме того условие, что частицы жидкости непрерывно заполняют
некоторую часть пространства в связи с законом сохранения
материи, дает нам еще одно дифференциальное уравнение, известное
иод именем уравнения неразрывности. В эти уравнения входят
в качестве неизвестных величин три компоненты скорости V и
давление р, кроме того в эти же уравнения входит плотность
жидкости р. В классической гидромеханике плотность жидкости р
считается большей частью постоянной величиной, характерной
физической постоянной для данного сорта жидкости; поэтому четыре
указанных выше уравнения гидродинамики в связи с начальными
и граничными условиями являются, вообще говоря, достаточными
185

для определения четырех неизвестных: трех компонент вектора
скорости и давления.
Точно так же эти уравнения достаточны, если, как это делают
иногда в классической гидромеханике, рассматривая движение
сжимаемой жидкости, предположить определенную, наперед заданную,
зависимость давления от плотности, например рассматривать
изотермическое движение идеального газа или изэнтропическое его
движение. Но если мы обратимся к общему случаю, когда плотность р
будет неизвестной функцией времени и координат, то указанных
выше четырех уравнений будет недостаточно для определения пяти
неизвестных функций: и, и, го, /? и р; в этом обстоятельстве
и лежит вся трудность изучения движений сжимаемой жидкости
в общем случае. К четырем уравнениям классической
гидромеханики приходится присоединить еще пятое уравнение —
уравнение притока энергии, являющееся следствием первого закона
термодинамики;, в это уравнение притока энергии, помимо
величин и, v, wy р и р, входит еще новая переменная
величина—температура Т; это обстоятельство однако не усложняет вопроса, так
как величины р, р, Т связаны между собой конечным уравнением,
так называемым уравнением состояния.
Условимся в дальнейшем кинематическими элементами
движения называть компоненты скорости V, их производные по
времени и координатам, а равно и различные функции этих величин.
Динамическими элементами движения будем называть давление pf
плотность р, температуру Т, их производные по времени и
координатам, а равно и различные функции этих величин.
К числу таких функций относится например удельный объем ш:
1
со = .
9
В некоторых вопросах важную роль играет особая функция р
и р или р и со, так называемая энтропия жидкости S, которая
будет определена нами в дальнейшем.
Уравнения гидромеханики сжимаемой жидкости делятс* на две
группы. К первой, которую мы назовем динамической группой,
относятся три уравнения механики и уравнение неразрывности;
ко второй группе, которую мы назовем тепловой группой,
относятся уравнение притока энергии, уравнение состояния и те соот«
ношения между динамическими и кинематическими элементами,
которые могут встретиться при установлении притока энергии.
Для установления уравнений динамической группы нам
необходимо прежде всего определить, с какими внешними силами мы
имеем дело при движении жидкости. Эти внешние силы могут быть
разделены на два класса: 1) силы массовые, обладающие тем
свойством, что каждая такая сила, действующая на частицу, по величине
пропорциональна массе частицы; таким образом заданной нам
величиной является сила, действующая на единицу массы жидкости,
каковую силу обозначим через F, а компоненты ее по осям
координат условимся обозначать через X, Y, Z\ 2) силы объемные^
186

обладающие тем свойством, что каждая такая сила, действующая
на частицу, по величине пропорциональна объему этой частицы;
таким образом нам задается сила, действующая на единицу объема
жидкости, каковую силу обозначим через Ф, а ее составляющие
по осям координат обозначим через Х\ У, Z\
С помощью указанных выше обозначений динамическая группа
уравнений гидромеханики, на обычном выводе которой мы не
останавливаемся, может быть написана следующим образом:
dv
~dt~
dzu
W
rflne>
(80)
du , dv , dxo
dt "Зг"1"^"1""^5
с помощью обозначений векторного анализа уравнения (80) можно
переписать, в виде:
dV I
—.== — ш grad р -Ъ F -f <оф,
= div V.
(А)
Массовая сила, вообще говоря, может состоять из трех частей:
1) консервативной силы К, обладающей потенциалом, т. е.
удовлетворяющей равенству curl К = 0, 2) инерционной силы U,
возникающей вследствие кажущихся сил инерции, проявляющихся, когда
изучаем движение по отношению к подвижной системе координатг
и 3) каких-либо неконсервативных сил F':
F-K+U + F'.
Обычно в практически важных приложениях гидромеханики
сжимаемой жидкости мы имеем дело с консервативной силой тяжести.
Для задач динамической метеорологии инерционной силой является
отклоняющая сила вращения земли. НеконсерваЛвные массовые
силы встречаются сравнительно редко в практике, почему мы и не
будем в дальнейшем принимать их во внимание, хотя, конечно)
многие из наших выводов сохраняют свою силу при рассмотрении
движений жидкости под действием массовых сил общего типа.
Сила тяжести является силой постоянной по величину и по
направлению; в общем случае мы обозначим составляющие ее по
координатным осям через gu g2> ?? в случае же, когда ось z-ов
нашей координатной системы выбрана вертикальной и направлена
187

вверх, компоненты силы тяжести будут 0, 0,—g, где
g—ускорение силы тяжести.
Рассматривая движение на поверхности земли и предполагая,
что в левую часть наших уравнений входит относительное
ускорение (относительно вращающейся смеете с землей координатной
системы), мы должны считать, что инерционными силами в данном
случае являются силы, происходящие от ускорения переноса и
ускорения Кориолиса. Ускорение переноса, постоянное для данного
места на земной поверхности, сказывается лишь на изменении
величины ускорения силы тяжести; это ускорение переноса,
постоянное на* данной параллели земной поверхности и не зависящее от
совершаемого жидкой частицей движения, обычно включается в
величину ускорения силы тяжести. Таким образом в введенных нами
постоянных glf g2j g$ мы будем учитывать и переносное ускорение,
происходящее от вращения земли.
Что же касается ускорения Кориолиса, то его необходимо
принять отдельно во внимание, ибо оно существенным образом
зависит от скорости движущейся жидкой частицы. Обозначая
через L вектор, отложенный по полярной оси к южному полюсу
земли и по величине равный угловой скорости вращения земли,
будем иметь, что ускорение Кориолиса выразится следующим
образом:
2[L, V];
инерционная сила, действующая на единицу массы движущейся
жидкости, выразится поэтому соотношением:
и = — 2[L, V].
Перейдем теперь к рассмотрению объемных сил Ф,
действующих на частицы движущейся жидкости. К числу этих сил следует
отнести прежде всего силу внутреннего трения или вязкости
жидкости. Обозначая эту силу (на единицу объема) через R,
будем, согласно уравнениям, впервые указанным Poisson'oM и Navier,
иметь:
R^AV+^graddivV,
откуда, пользуясь формулой (46), найдем:
4
R = — т] grad div V — г\ curPV,
где iQ есть особая постоянная, характеризующая данную жидкость
и называемая коэффициентом внутреннего трения жидкости.
В некоторых вопросах (особенно в случае течения жидкости
узким слоем) полезно ввести еще особую силу — силу внешнего
трения. Эта сила Ra (рассчитанная на единицу объема) прямо
противоположна скорости и по величине пропорциональна скорости:
188

где т,'—коэффициент внешнего трения, также особая постоянная»
характеризующая жидкость.
Заканчивая настоящий пункт, полезно будет сделать одно
замечание о так называемой несжимаемой жидкости. Обычно под
именем несжимаемой жидкости разумеют жидкость, у которой
плотность р постоянна, т. е. не зависит ни от времени, ни от
координат, являясь физической постоянной, характерной для
данной жидкости; движения такой жидкости, как это следует из
уравнения неразрывности, должны быть таковы, что div V = 0
( д& дм д& дм . din to \
{ иб° И = ^==д^=='д^ = 0' а потому ~ЗГ^0!'' однако мо"
гут иметь место движения жидкости, в которых divV = 0, но для
которых плотность р отнюдь не является постоянной, т. е. не
зависящей от U х, у, z, величиной. В самом деле, условие div V — О
при помощи урасчения неразрывности дает: -77 = 0, т. е.
до* , да* да> . дм л
Ot l Ox dg ' де y
из какового равенства отнюдь не следует, что <о (а значит и
плотность р) не зависит от t, х, у, z.
Условимся в дальнейшем называть жидкость несжимаемой»
когда плотность ее р не зависит от t> х, у, z; те же случаи
движения жидкости, в которых div V = 0, условимся называть
несжимаемыми движениями; такого рода несжимаемыми движениями
могут обладать (ниже увидим примеры этого обстоятельства)
сжимаемые, вообще говоря, жидкости.
В дальнейшем, в целях упрощения рассуждений, мы будем
предполагать отсутствие внутреннего и внешнего трения и так
называемых объемных сил. .
* 2. Перейдем теперь к установлению тепловой группы уравнений
гидромеханики. Здесь прежде всего необходимо обратить
внимание на то, каким образом жидкость получает извне энергию
в виде энергии тепловой, или энергии лучистой, или в виде какой-
либо иной энергии. Выделим некоторый жидкий объем (т),
заключающий в себе определенные частицы жидкости; этот объем
жидкости за время от момента t0 до момента t получит некоторое
количество энергии е', выраженной в тепловых единицах
(например в больших, малых или геофизических калориях)*).
Пусть величина рассматриваемого объема будет т; тогда в
большинстве процессов, совершающихся в природе, будет иметь ме^-то
наличность следующего предела:
е= lim lim
е'
t0 + t т>0 (t Г0)Х
*) См. мою работу „О вертикальных "течениях в атмосфере", Журнал Фязиі
математического общества при Пермском госуд. университете, вып. 2, 1920 г.
ли*
185

причем знакоположение Iim означает, что жидкий объем ~
стретто
мится к нулю, сохраняя внутри себя определенную частицу
жидкости, занимающую к моменту t положение с координатами я:, у> z.
Только-что указанный предел, являющийся, вообще говоря,
функцией t, х, у, z (времени я координат), может быть назван
плотностью тепловой мощности потока энергии, падающего на
жидкость.
Не трудно видеть, что, определив в каждый момент времени
в каждом данном месте плотность тепловой мощности е, мы
будем иметь для величины притока энергии, падающего на данный
объем (х) жидкости за время от tQ до t7 следующее выражение:
t
г' = fdt f я «ft.
г-)
Чтобы установить, на что расходуется этот приток энергии, нам
необходимо обратиться к первому закону термодинамики. На
основании этого закона *) мы будем иметь, что приток энергии
расходуется отчасти на повышение абсолютной температуры Т каждой
частицы жидкости, заключенной в жидком объеме (~), отчасти на
совершение работы внутренних сил, действующих в жидкости, иначе
говоря—на работу, производимую давлением путем уменьшения или
увеличения объема сжимаемой жидкости. Обозначая через cv
теплоемкость при постоянном объеме (<о = const), будем иметь, что
іасть притекшей энергии Ц, пошедшая на увеличение температуры
при постоянстве объема), выразится следующим равенством:
Точно так же, обозначая через А термический эквивалент
работы I А = —р , где Е—механический эквивалент теплоты 1, будем
иметь, что часть s^ притекшей энергии, пошедшая на внутреннюю
работу, выразится следующим образом:
'¦л r-d^]
dt
Но уравнение неразрывности вместе с механическим смыслом
расхождения скорости дает нам:
d{dz) _.. сПпсо d® ,
*) См. напр. Kirchhoff, Vorlesungen uber mathematische Physik, Bd IV.
190

откуда
е; = Л jdt | P-jj?d-.
Помня, что е[-?-Ц = г' (на основании первого закона
термодинамики^ будем иметь:
* t
л
dT
откуда
+*>*)>*¦-
(Ь)
Это соотношение носит название уравнения притока энергии.
В этом уравнении у нас введен новый динамический элемент —
температура Т; связь этого элемента с давлением р и удельным
объемом <*> выразится особым конечным соотношением,
характерным для данной жидкости. Это соотношение называется
уравнением состояния. В общем виде оно может быть написано
следующим образом:
f(p, со, 70 = 0.
Хотя многие наши дальнейшие выводы будут иметь место для
уравнения состояния в общем виде, однако мы, в целях упрощения
выкладок, будем предполагать, что уравнение состояния дано нам
в форме уравнения Клапейрона, оправдывающегося в
значительном интервале для аргументов в применении к газам, близким
к идеальным; в частности это уравнение с большой точностью
имеет место при явлениях, изучаемых в динамической метеорологии.
Таким образом уравнение состояния мы будем писать в
следующей форме:
рш = #Г, (с)
где R—так называемая газовая постоянная.
Уравнение притока энергии вместе с уравнением состояния и
уравнениями гидродинамики составляют всего шесть уравнений,
достаточных для определения шести неизвестных: трех компонент
скоростей, давления, удельного объема и температуры; таким
образом, коль скоро нам известен приток энергии, характеризуемый
величиной е, стоящей в левой части уравнения (Ь), то, при
известных начальных и граничных условиях, движение сжимаемой
жидкости, вообще говоря, будет вполне определено.
Чтобы пояснить эту мысль, рассмотрим движение
неограниченной массы жидкости. Положим, что к начальному моменту t0 нам
заданы величины и, v, w9 р, <о 1а значит и Т = -?т\: при ? —^0>
и = и0 (*, у, z), v = vQ (х, у у z), w = w0 (х, у, г), р =
— РоС*» У у z)> <о = «>о (х, у, z). Не трудно видеть, что три уравне-
191

кия гидродинамики, уравнение неразрывности и уравнение притока
энергии вместе с уравнением состояния можно представить в виде
ди dv dw dp дм
пяти уравнении, разрешенных относительно —, -гт, —с—, -зт, -л-;
таким образом при * = ^0 эти величины будут вполне определены
по начальным условиям; отсюда не трудно заключить, что вели*
dnu dnv dnzo днр d"« л л л
чины^рг, -^рг, -^іг, -^г, ^п-будут определены при t=t0
путем последовательного дифференцирования по t уравнений нашей
задачи, написанных в указанной только-что форме. Пользуясь
приведенными сейчас величинами, можно построить ряды, выражающие
и, v, щ р, °>; так например ряд для и будет:
где символ (?)о означает значение ?(г, х, у, z) при *=*0.
Если щ, vo> wo> Ро> шо будут голоморфными функциями своих
аргументов, если силы, величина г и т. п. будут также
голоморфными функциями своих аргументов, то не трудно показать, что
построенные нами ряды будут сходящимися рядами и будут
удовлетворять дифференциальным уравнениям нашей задачи.
Доказательство это или может быть построено обычным методом
мажорантных функций, или же может основываться на общих
исследованиях ортономных систем*). Мы не останавливаемся более,
подробно на этом вопросе, так как для нас этот вопрос не
представляет интереса и мы упомянули о нем лишь для иллюстрации
того положения, что задача гидродинамики неограниченной
сжимаемой жидкости становится вполне определенной, коль скоро
известна величина плотности тепловой мощности притока энергии е **).
Однако лишь в весьма редких случаях величина притока
энергии является заданной нам функцией времени и координат;
большей частью эта величина зависит в свою очередь от подлежащих
определению кинематических и динамических элементов. Следует
тем не менее отметить, что величина е обычно-зависит лишь от
компонент скорости, давления, температуры, удельного объема и
их производных разных порядков по координатам; таким образом
приведенное выше рассуждение о существовании решения
уравнений гидромеханики при заданных начальных значениях компонент
скорости, давления и удельного объема и в этом случае не теряет
своей силы.
Рассмотрим ближе, под влиянием каких причин к жидкости
притекает энергия в обычных случаях- Вообще говоря, могут иметь
место три причины притока энергии.
*) См. Н. М. Гюнтер, К теории характеристик систем уравнений в частных
производных, 1913.
**) Ср. аналогичные соображения проф. Н. Е. Жуковского, примененные
им к обычным случаям гидродинамики в книге „Лекции по гидродинамике",
1887, стр. 79.
192

Первая причина заключается в процессе теплопроводности
(конвекционная передача тепла); впервые величина для е в случае
притока тепла путем теплопроводности была установлена Fourier *).
Подробный разбор величины для е в указанном случае имеется
в статье С. Neumann 'а **), где с совершенной ясностью установлена
роль конвекционной передачи тепла- Величина для е : s„
полученная путем процесса теплопроводности, может быть определена
следующим равенством:
где к—коэффициент внутренней теплопроводности.
Второй причиной притока тепла в жидкости является как
лучистый теплообмен частиц жидкости между собой, так и получение
лучистой энергии извне. Процесс этот весьма сложен; он имеет
огромное значение для явлений, протекающих в атмосфере, однако
до сих пор лишь в весьма частных случаях удавалось устанавливать
величину s = е2 для случая лучистого теплообмена.
Ряд статических задач (V = 0) для случая лучистого
теплообмена был разрешен в последнее время Schwarzschild'oM, Emden'oM
и другими; динамическая задача, а именно стационарные
вертикальные течения в атмосфере при наличности лучистого
теплообмена земли и солнца, была поставлена и разрешена также в
недавнее время ***),
Третьей причиной притока тепла могут служить разнообразные
внутренние процессы, совершающиеся в телах, находящихся в
непосредственном соприкосновении (например в механической смеси)
с нашей жидкостью. Таковы например процессы выделения или
поглощения тепла при переходе воды, находящейся в атмосфере,
из одного состояния в другое и т. п. Они дают особое значение
для величины е, е = е3, зависящее от целого ряда кинематических
и динамических элементов.
Совершенно особо стоят те случаи движения жидкости, при
которых нет ни отрицательного, ни положительного притока энергии,
т, е. е = 0; эти случаи называются адиабатическими движениями.
Они обладают в известном смысле большей простотой, чем случаи
движений при наличности притока энергии; поэтому во многих
*) Fourier, „Sur le mouvement de la chaleur dans les fluides", Oeuvres, t. II,
p. 595.
**) Neumann, „Cfber die Bewegung der Warme in compressiblen oder auch
incompressiblen Fliissigkeiten", Berichte iiber die Verhandlugen d. Kon. Sachsischen
Gesellschaft d. Wissenschaften zu Leipzig, 1894 S. 1.
***) См. например: Schwarzschild, „Uber das Gleichgewicht der Sonnen-
atmosphare*, Gottinger Nachrichten, Math.-Phys. Klasse, 1906.
Emden, „Ober Strahlungsgleichgewichtundatmosphansche Strahlung", Sitzber.
d. math.-phys. Klasse des К. В. Akad. d. Wissenschaften zu Miinchen, 1913.
См. также Emden, „Gaskugeln", 1911 r.
Cm. A. Friedmann, „Sur la distribution de la temperature aux diverses
hauteurs", Геофизический сборник, 1914 г., а также мою работу „О распределении
температуры с высотой при наличности лучистого теплообмена земли и солнца",
Известия Главной физической обсерватории, 1920 г.
13 Зак. 2420.— А'. А. Фрпдосан, Олыт гидромеханики 193

практически важных вопросах вместо движения с притоком энергии
обыкновенно рассматривают адиабатические движения, подтверждая
этот способ изучения движений тем соображением, что величина
притока энергии мала. Так поступали в прежнее время в
динамической метеорологии; при этом, отбрасывая величину в как малую
величину, сохраняли в уравнениях другие величины того же
порядка малости *).
Хотя во многих практических вопросах движение ни в каком
случае нельзя считать адиабатическим, тем не менее
адиабатическое движение по своей относительной простоте представляет
большой интерес.
Чтобы с наибольшей простотой исследовать адиабатическое
движение, полезно ввести в рассмотрение новый динамический
элемент, так называемую энтропию жидкости, являющуюся функцией
давления и температуры или, что то же самое, давления и
удельного объема. Энтропия S определяется следующим равенством:
S = ^\nT+R\n<» + ^]nR. (81)
Отсюда не трудно видеть, что из уравнения (Ь) можно получить
следующее равенство:
_Ар dS
*~~R~" dt ;
(82)
таким образом условие адиабатичностй движения будет:
• dS л dS . dS . dS . dS n
^ = 0, или ^-+U5-+„?+a,^-=0,
иначе говоря — для адиабатического движения энтропия есть
инвариантная фУнкЦил (см* § Ю)> отсюда однако отнюдь не следует,
что для адиабатического движения энтропия есть величина
постоянная, т. е. энтропия не зависит от времени и координат; таким
образом для адиабатического движения давление, в противность
обычному изложению этого предмета, не есть, вообще говоря,
функция плотности, а значит для адиабатического движения в
идеальной жидкости, находящейся под действием консервативных сил,
возможно возникновение вихрей. Условимся движение, в котором
энтропия есть постоянная величина, называть изэнтропическим
движением;, само собой разумеется, что всякое изэнтропическое
движение есть адиабатическое движение; однако, как мы только-
что выяснили, обратное заключение не верно и могут иметь место
адиабатические движения, в которых энтропия не есть постоянная
величина. Подробнее об этом будет сказано ниже, когда будет
приведен пример адиабатического не изэнтропического движения,
*) См. об этом мою статью „О вертикальных течениях в атмосфере", Журнал
Физ.-матем. общ-ва при Пермском госуд. университете, вып. II, а также мою
работу совместно с Hessel b erg'oM „Die Grossenordmmgen d. meteorologischen
Elementen", напечатанную в Трудах Геофизического института в Лейпциге во
время войны 1913 г.
194

В настоящей работе мы не будем касаться вопроса определения
движения при заданном притоке энергии, равно как и вопроса
о формах, в которых проявляется приток энергии.
Наши рассуждения будут построены таким образом, чтобы быть
справедливыми при любом притоке энергии. Крайне важный вопрос
определения движения жидкости при заданном притоке энергии
мы предполагаем разобрать в другой работе; само собой разумеется,
что этот вопрос выходит из рамок обычной механики, соприкасаясь
с термодинамикой и с теориями излучения. В настоящей работе
будет до известной степени разобран вопрос об адиабатическом
движении *)*
3. Из сказанного выше видно, что для огисания движения
жидкости, помимо кинематических элементов, имеются еще четыре
динамических элемента: давление р9 удельный объем со | или, что
то же самое, плотность р —-~і, температура Т и энтропия S; при
этом два из этих элементов могут быть выражены при помощи
конечных соотношений через два других элемента. Условимся
в дальнейшем называть давление р и удельный объем <о— силовыми
динамическими элементами, а температуру Тн энтропию
S—тепловыми динамическими элементами.
Обычно все уравнения гидромеханики сжимаемой жидкости
выражаются через силовые элементы; для некоторых вопросов
выгодно выражать все элементы в тепловых динамических элементах;
наконец в вопросах динамической метеорологии, по чисто
практическим соображениям, удобнее всего уравнения гидромеханики
выразить, взяв за основные динамические элементы давление р и
температуру Т. Эту пару динамических элементов будем
называть метеорологическими динамическими элементами.
Не трудно из уравнения состояния и из определения
энтропии получить выражение динамических элементов через каЦую-либо
пару из них; динамические элементы, через которые выражаются
все остальные, назовем основными.
1. За основные взяты силовые динамические элементы р9 о>:
т—Р?!
С83)
где ср—теплоемкость жидкости при постоянном давлении,
удовлетворяющая соотношению:
с, - AR. (34)
с
V
*) И. А. К и б е л ь, следуя методам А. А. Фридмана, разработал ряд вопросов
о движении сжимаемой жидкости с заданным притоком тепла. См. дополнение.
Прим ред.
13*
195

2. За основные взяты тепловые динамические элементы Г, S:
где х =
X X S \
P = R Т в ,
In/? ——^-Н х_1 1пГ + х — 1 In/?,
1 1 5
In о> = — — In T — InVi
/? X —1 X— 1
= CJL.
(85)
3. За основные взяты метеорологические динамические
элементы р, Т:
RT )
ш
(86)
S=^lnT-Rlnp + ^*R'
Во многих вопросах гидромеханики сжимаемой жидкости
приходится иметь дело не только с динамическими элементами, но и
с их индивидуальными производными по времени.
Представляется поэтому полезным установить, с какими
физическими величинами связаны индивидуальные производные по
времени динамических элементов. Оказывается, что они связаны
с самими динамическими элементами, а также с величиной в
плотности тепловой мощности притока энергии и с величиной
расхождения скорости divV; обозначим для краткости через ?
расхождение скорости:
e = divV.
Выражая индивидуальные производные динамических
элементов, которые мы будем называть в дальнейшем вторичными
динамическими элементами (соответственно силовыми или тепловыми),
через е, ? и динамические элементы, мы должны будем, как и
раньше, рассмотреть три случая:
1) Силовые динамические элементы:
dp_R
dt
*р%
dT
dt:
dS
dt
О)
•-*н
А»'
(87)
196

2) Тепловые динамические элементы:
х х 8
HRX~X Т
1 S
Ы
а
= bR
*— 1 ~- * — 1 fi
Г
Д^ _ _f_D *-l 7* x-1 Я
dS_R^
dt~
x —1
x /7
x— 1 R
e e.
e*—(x —1)74,
(88)
3) Метеорологические динамические элементы:
-v.p%
dp =R_
dt c.
d* RT л
dt= — b>
^:в|1._(х_1)7и.
at C„p
dS
dt
E±
Ар'
(89)
Приведенные только-что формулы играют большую роль в
приложениях гидромеханики сжимаемой жидкости, позволяя вторичные
динамические элементы выражать через более или менее известные
величины.
Не трудно установить, каким образом изменяются уравнения
гидродинамики (включая и уравнение притока энергии), коль скоро
мы за основные динамические элементы будем брать одну из
указанных выше пар.
1) Силовые динамические элементы:
- j7 = — <°grad/>4-F,
d In to
dt
= divV,
R dt^~ R o> dt
(90)
197

2) Тепловые динамические элементы:
dV
dt
= 7"grad S— -r grad 7\
A
1 V5 1 Jig 7 ,. „
/? Л * — 1 Л
5
е = Л/2 Т е -77 *
3) Метеорологические динамические элементы
Л р
din Т dlnp ,. .
-а 5r=dlvV>
(91)
gradp-j-F,
e = Rp
dlnT
dt
dt
(92)
Из этих уравнений обычно применяют уравнения (90) в
силовых элементах; уравнения (91) в тепловых элементах особенно
удобны при изучении адиабатических движении, тогда как
уравнения (92) в метеорологических элементах представляют
значительные удобства при численных подсчетах.
Из уравнений, выражающих вторичные динамические элементы,
можно сделать ряд заключений об изменении этих элементов для
данной частицы жидкости* Так например первое и третье из
уравнений (87) для случая несжимаемых движений показывают, что
'емпература и давление в данной частице жидкости будут воз-
>астать, коль скоро имеется положительный приток энергии, и
убывать при отрицательном притоке энергии (иначе говоря — при
охлаждении). Сжимаемость жидкости видоизменяет это заключение;
если например плотность данной частицы возрастает (? < 0), то
давление и температура частицы возрастают еще в большей мере,
чем для несжимаемого движения. Само собой разумеется, что все
здесь сказанное относится к частице жидкости, а не к данному
месту в жидкости.
4. Как и везде в механике, в гидродинамике сжимаемой
жидкости террема живых сил играет фундаментальную роль; связав
ее с уравнением притока энергии, мы будем в состоянии сделать
ряд общих заключений о том, на что тратится поступающая извне
энергия, когда жидкость движется пол влиянием заданных сил.
Назовем вектор
G = F-g (93)
динамическим градиентом) этот вектор будет играть в дальней-
198

шем весьма большую роль. Не трудно видеть, каким образом
динамический градиент выражается через динамические элементы:
6 = о> gradp,
А
grad Т— 7* grad .S,
G = grad p.
(94)
Для вывода теоремы живых сил нам необходимо будет
различать два случая: в первом случае мы будем рассматривать работу
силы, отнесенной к единице массы, и живую силу движения,
отнесенную также к единице массы; во втором случае будем те же
самые понятия рассматривать отнесенными не к единице массы,
а к массе некоторого жидкого объема.
Работу силы, отнесенной к единице массы частицы жидкости,
совершенную, когда частица эта двигалась так, как она и должна
была двигаться согласно уравнениям гидромеханики от момента tQ
до момента t, назовем через а; живую силу единицы массы
жидкости к моменту t обозначим через к, а к моменту t0 через Icq.
Те же самые величины, отнесенные к массе данного жидкого
объема, обозначим большими буквами. Не трудно видеть, что имеют
место следующие формулы:
t
a = J(F,V)A, k=-^-=i^f
5
А = у р dx f (F, V) dt = у pa A,
Й h (?)
к=у pk л.
(95)
Вторая и третья из этих формул могут быть получены, принимая
во внимание, что для данного жидкого объема его масса не
меняется с течением времени (pdx не зависит от времени f).
Теорема живых сил указывает на связь производимой силами
работы с изменением живой силы; чтобы выяснить эту связь,
введем еще особую скалярную величину, которая будет играть
большую роль в дальнейшем и которая характеризует, какая часть
работы не пошла на увеличение живой силы нашего движения.
Назовем величину
tt = (VfG) = nGe + ©Gf + roG.
(96)
мгновенной мерой диссипатпивностпи, отнесенной к единице массы,
или просто мерой диссипативности>
199

Величину:
t
pdi
назовем интегральной мерой диссипативности за время от t0 до
t (за промежуток времени от tQ до /).
Наконец величину:
М= fpd* f^dt
назовем интегральной мерой диссипативности за время от tQ
до t массы данного жидкого объема.
Иногда для упрощения речи величину М будем называть просто
интегральной мерой диссипативности массы жидкого объема.
Введя указанные определения, можем формулировать теорему
живых сил следующим образом:
Теорема 19. Работа А сил, приложенных к частицам жидкого
с Иъема за некоторый промежуток времени, равняется изменению
живой силы массы данного жидкого объема за этот промежуток
времени, сложенному с интегральной мерой диссипативности
массы жидкого объема за тот же промежуток времени:
А=К—Ко + М. (97)
По определению динамического градиента будем иметь:
и, следовательно,
1x=(V,G) = (F,V)-(v, ^),
откуда
Помножая обе части только-что полученного равенства на pd> и
интегрируя по всему объему (~), докажем теорему.
Если мы будем рассматривать работу и живую силу
отнесенными к единице массы данной жидкой частицы, то формулу (97)
можно будет переписать следующим образом:
і
a = k — k0 + J\dt (98)
to
Займемся теперь вычислением величин, входящих в формулы (97)
или (98) теоремы живых сил. Начнем с меры диссипативности у*.
2?0

Так как G = <*> grad /?, то
j* = (V,G) = «(V,8Tadp) = «(-* -^-) = ш?(Р);
символ Е(р) был нами определен в § 3 нашей работы.
Вспоминая значение символа с(р), без труда получим
выражение меры диссипативности в разного рода основных динамических
элементах:
*і = ш?"(р),
?=-??-E(T)-TE(S),
^=—Цр)-
(99)
Приступим теперь к вычислению величины а. Положим, что
наша сила F состоит из консервативных сил К, имеющих
потенциал тс, не зависящий явно от U и из инерционных сил U; легко
видеть, что:
* г
а = f(K,V)Jt+ /(U,V)A.
Для случая движения на вращающейся земной поверхности мы
имели:
U = -2[L,V],
откуда:
(U,V) = 0.
С другой стороны, если тс есть потенциал консервативных
сил, то
К == — grad тс,
откуда:
«.»>—-?-.
ибо тс не зависит явно от t, а значит:
а = — (тс — тс0),
где тс0 — значение тс в том положении, которое наша частица
занимала в начальный момент t~t0.
Для вычисления А назовем потенциальной энергией массы
объема (т) жидкости к моменту t величину:
П — / тр сгс;
отсюда ясно, что значение П для t = t0) которое мы обозначим
через П0, определится формулой:
П0 = У -оР^">

откуда:
А = 170-П = -(П-И0), (100)
т. е. работа сил равна изменению потенциальной энергии,
взятому со знаком минус.
Сумму потенциальной энергии и живой силы (кинетической
энергии) массы данного жидкого объема назовем полной энергией
данного жидкого объема и будем обозначать через В: В = П-|-К;
значение полной энергии в начальный момент t = t0 будет Е0;
формула (97) теоремы живых сил может быть выражена следующим
образом:
Е = Е0 — М, (101)
иначе говоря—полная энергия массы данного жидкого объема
уменьшается на величину интегральной меры диссипативности массы
данного жидкого объема.
Не трудно заметить, что если через е обозначим сумму *гс и к:
е = те -f- к,
то: »
Е= / epd'z;
w
таким образом е есть полная энергия данной жидкой частицы,
отнесенная к единице массы. Мы будем называть величину е
плотностью полной энергии частицы.
Как мы уже говорили, соединение уравнения притока энергии
и теоремы живых сил дает нам возможность разобраться, на что
вдет указанный приток энергии.
Чтобы ввести в рассмотрение притекающую энергию, нам
необходимо выразить меру диссипативности через энергию и дина-
мические элементы; не трудно видеть, что -у— выражается через в
Л « din® dT dp
и о, а Ь= , в свс.о очередь выражается через - , и , ;
dp
отсюда получается возможность выразить —j-~ через динамиче-
dT
ские элементы, через е и —гг •
at
jfy_ = е , ср Р dT
dt А + AR ' Т dt '
откуда: „
«е <v dT dp
Via предыдущих рассуждений легко вывести равенство,
справедливое для любого момента / и выражающее индивидуальную
производную по времени плотности полной энергии е:
-# = -*• (из)
202

из этого равенства без труда найдем:
de ср dT dp шз
-dr+-zsr- ш^г="л-; <104>
отсюда следует, что притекающая энергия тратится: 1) на
увеличение плотности полной энергии, 2) на повышение температуры,
3) на изменение давления в данном месте.
При этом оказывается, что, чем более при положительном
притоке энергии повышается давление в данном месте, тем большая
часть притока энергии идет на повышение температуры и на
изменение плотности полной энергии. Из уравнения (104) можно
сделать целый ряд аналогичных заключений, играющих весьма
большую роль в динамической метеорологии; мы не останавливаемся
на этом вопросе, имеющем более практическое, нежели
теоретическое значение.
Кинетическая теория газов указывает нам на особую величину,
являющуюся мерой кинетической энергии молекул, составляющих
газ (по нашей терминологии — сжимаемую жидкость); оказывается,
что эта энергия, называемая внутренней энергией Т, определяется
для массы данного жидкого объема следующим равенством:
Т = /^7рА; (105)
вспоминая, что ср = ср — cv -f- cv = AR -j- cv, перепишем
равенство (104) в виде:
de.CidT.fdRT dp \ <ог /-гил
По причинам, которые выяснятся несколько ниже, мы на3Овем
величину:
^ dRT dp
dt dt
предельной частью; предыдущее равенство напишем, вводя
величину Г, следующим образом:
de с, dT <os
dt ^ A dt 'Г1" А1
таким образом приток энергии тратится на повышение плотности
полной энергии, на повышение температуры и на изменение
предельной части. В том виде, в каком написано у нас равенство (106),
оно не представляет никаких преимуществ перед равенством (104),
являясь даже менее наглядным; однако, как мы сейчас увидим, при
рассмотрении изменения энергии больших масс жидкости
указанное равенство представляет известные преимущества, так как
в этом случае та порция притока тепла, которая идет на
изменение предельной части Г, оказывается малой по сравнению с
остальной порцией притока энергии. В этом обстоятельстве лежит при-
203

чина того, что преобразованное равенство (106) имеет большие
применения в практических вопросах, особенно в вопросах
динамической метеорологии.
Вычислим следующее выражение:
Й
Легко видеть, что:
Г = ое> (gradp, V)-f-p —jT" — ® div/>V — <op div V-f-p-j^- = aidivpV,
согласно формуле (33) § 3 и уравнению неразрывности.
Отсюда, применяя формулу Гаусса, будем иметь:
Г= f Гр<Ь =* fdbr(pV)<b=* fpVndS,
Й Й (5)
где 5 есть поверхность, ограничивающая объем (х), a Vn есть
составляющая скорости V по внешней нормали к поверхности S.
Называя через 5 площадь этой поверхности, полагая, что //,
Vn суть некоторые средние значения давления и Vn для точек
поверхности S, по теореме о среднем будем иметь Г = р Vns.
Эта величина в некоторых случаях обращается в нуль, а в
других случаях является величиной сравнительно малой; так например,
при больших объемах s величина поверхности вообще мала
сравнительно с величиной объема. Если р и Vn—величины того же
порядка, как давление и скорости внутри данного жидкого объема,
то величина Г и I Т di мала по сравнению с остальными членами
полученных равенств; точно так же, если Vn = 0 на границах
данного жидкого объема (т. е. если объем этот ограничен твердыми
неподвижными стенками), то Г = 0, а следовательно и / ГЛ = 0.
Следует однако отметить, что в общем случае величина Г не равна
нулю; в этом отношении ряд лиц, работавших в области
динамической метеорологии, допускали ошибку, полагая Г == 0 для объема,
не ограниченного твердыми неподвижными стенками. Помножая
равенство (106) на pdzdt и интегрируя по жидкому объему (г)
в пределах от *0 до t, найдем, вспоминая введенные нами
обозначения, следующее равенство:
* t
Е + Т+ ГгЛ=-і- J'dtJerfx + Eo + To, (107)
*о Ч (т)
где Т0 есть значение внутренней энергии жидкости к начальному
моменту t = tQ,
204

Из только-что написанного равенства следует, что притекающая
энергия расходуется на увеличение полной энергии, внутренней
энергии и на изменение - предельной части, которая во многих
случаях обращается в нуль и зависит во всяком случае лишь от
движения жидкости на границах нашего объема. Из последнего
равенства следует, что возможны случаи притока энергии
(притока тепла), сопровождаемые столь большим увеличением«полной
энергии данной массы жидкости, что происходит не нагревание,
а охлаждение (т. е. понижение средней температуры) этой массы
жидкости; мы не останавливаемся на ряде аналогичных
заключений, представляющих интерес исключительно практический.
Применяя простые преобразования к формуле (107), получим
следующее соотношение:
Е+хТ —
Jdtj^dx = ±-jdt |\</, + Е0+хТ0. (108)
Соотношение это весьма важно в практических приложениях,
так как все входящие в это соотношение элементы без труда
могут быть вычислены *).
Рассматривая случай стационарного движения, будем на
основании последней формулы иметь: '
*
E + *T = E0 + xT0+Jj- jdt Jedt;
tQ {-)
таким образом для этого случая приток энергии расходуется на
изменение полной энергии и внутренней энергии. Предполагая, что
для этого случая предельная часть обращается в нуль, будем
иметь, что Т = Т0, т. е. средняя температура массы данного
объема жидкости не будет меняться.
Отсюда следует, что, коль скоро при стационарном
распределении давления I ~?і7- = ®) средняя температура данной массы
жидкости меняется, то обязательно предельная часть должна быть
отличной от нуля.
Теорема живых сил в связи с уравнением притока энергии
позволяет нам, как мы уже указывали, сделать ряд заключений
о том, куда идет притекающая энергия. Заключения эти однако,
по необходимости, будут иметь суммарный характер и являются
более важными для практических применений гидромеханики
сжимаемых жидкостей, нежели для теоретического изучения движения
этих жидкостей. Вследствие изложенного мы не будем вдаваться
в дальнейшие подробности относительно того, какая часть полной
*) Для вычисления третьего члена левой части этой формулы применяется
динамической метеорологии так называемый метод изаллобар.
205

энергии идет на вихревое движение и т. п. *), ограничившись
сказанным выше.
§ 12. Общие условия динамической возможности движения
сжимаемой жидкости.
1. Фундаментальные теоремы Гельмгольтца о сохраняемости
вихревых линий и напряжения вихревой трубки для несжимаемой
жидкости могут быть, как известно, получены путем исключения
из уравнений гидродинамики единственного существенного
входящего туда динамического элемента, а именно давления. Эти
теоремы Гельмгольтца могут быть таким образом истолкованы как
условия динамической возможности движения несжимаемой
жидкости, иначе говоря — эти теоремы выражают необходимые и
достаточные условия, каким должны удовлетворять компоненты
скорости (кинематические элементы) движения жидкости, дабы
в этом движении было возможно определить давление в качестве
функции координат и времени. Оказывается, что не всякое поле
скоростей отвечает возможному движению, а лишь такое, в
котором имеют место соотношение, приводящие к двум основным
теоремам Гельмгольтца; если эти соотношения имеют место, то
можно всегда подобрать таким образом давление как функцию
времени и координат, чтобы уравнения гидродинамики были
удовлетворены; иначе говоря, если указанные соотношения при
данном поле скоростей удовлетворяются, то существует движение
несжимаемой жидкости с таким полем скоростей. Эти
соотношения можно назвать условиями динамической возможности
движения несжимаемой жидкости**).
Следует заметить, что условие несжимаемости жидкости дает
еще одно соотношение, а именно div V = 0, которое тоже
следует причислить к условиям динамической возможности движения;
эно получается исключением из уравнений гидродинамики плот-
юсти или удельного объема, величины постоянной для
несжимаемой жидкости.
Всего таким образом получаем в качестве условий
динамической возможности движения несжимаемой жидкости три
соотношения, известные под именем уравнений Гельмгольтца, и одно
соотношение (div V = 0), известное под именем уравнения
неразрывности.
Эти соотношения являются фундаментом для классической
гидродинамики. Значение их двоякое: с одной стороны они
устанавливают ряд основных свойств движений несжимаемой
жидкости, с другой стороны они служат мощным орудием для
выбора из данной кинематической формы движения жидкости тех
сортов движения, которые динамически возможны, а лишь такие
Движения могут представлять интерес для гидродинамики.
*) См. мою работу „Об атмосферных вихрях*, Геофизический сборник, 1915.
**) Кинематически возможно движение жидкости при любых скоростях.
206

Так например, рассматривая квази-твердое движение, мы
благодаря условиям динамической возможности можем из всех
квазитвердых движений выбрать лишь такие движения, которыми
могут обладать несжимаемые жидкости; равным образом, изучая
практически важный случай движения, когда дано наперед, что
одна из компонент скорости не зависит от координат, мы
можем с большой определенностью указать, какие движения
данной кинематической формы могут иметь место в несжимаемой
жидкости.
Все, что зде?ь сказано относительно жидкости несжимаемой,
от слова до слова может быть применено к случаю общего
движения сжимаемой жидкости. Для сжимаемой жидкости точно так же
не все кинематически мыслимые движения будут возможны;
иначе говоря, задав компоненты скорости в функции времени и
координат, 'мы не всегда можем определить давление и удельный
объем (функции времени и координат) так, чтобы уравнения
гидродинамики удовлетворялись.
Чтобы по заданным компонентам скорости можно было
определить давление и удельный объем (или, что то же самое,
плотность), необходимо выполнение известных соотношений между этими
компонентами.
Эти соотношения, представляющие необходимые и
достаточные условия того, чтобы движение с данным полем скоростей
было возможно, мы будем называть условиями динамическом
возможности сжимаемой в общем смысле жидкости, Коль скоро
эти условия будут удовлетворены, всегда по компонентам скорости
можно будет определить давление и удельный объем так, чтобы
движение было возможно, т. е. чтобы можно было найти
давление и удельный объем в функции времени и координат,
удовлетворяющие уравнениям гидродинамики сжимаемой жидкости.
При этом само собой разумеется, что мы должны рассматри-
' вать лишь динамическую группу уравнений гидродинамики, та
как тепловая группа заключает в себе величину е (плотност
тепловой мощности), которая от давления и удельного объема
' может зависеть самым разнообразным способом, смотря по
характеру притока энергии.
Настоящий и следующий параграфы будут посвящены
установлению условий динамической возможности движения сжимаемой
жидкости, каковые условия будут конечно значительно сложнее
соответственных условий классической гидродинамики. Само собой
разумеется, что равенства для случая несжимаемой жидкости
(равно как и случай несжимаемого движения) будут заключаться
как частный тип соотношений в наших общих условиях.
Переходя к установлению этих условий, сделаем следующее
замечание. Мы будем в дальнейшем рассматривать исключительно
случаи идеальной (без объемных сил) жидкости *); однако анало-
*) В соответствия с моими заметками, помещенными в Сообщениях
Харьковского математического общества, в XV т. 2 сер. „О вихрях в жидкости с
меняющейся температурой" и в Comptes Rendus, 1916 г.
207

гичные методы могут быть применены и в случае вязкой
жидкости, каковым вопросом мы предполагаем заняться в одной из
ближайших работ *).
2. Для получения условий динамической возможности
движения сжимаемой жидкости нам необходимо из уравнений
гидродинамики исключить динамические элементы, т. е. давление и
удельный объем. Исключение это можно вести или с помощью общих
методов теории дифференциальных уравнений, или пользуясь
приемами векторного анализа и частным видом уравнений
гидродинамики. С точки зрения гидродинамики предпочтительнее второй
метод, сохраняющий симметрию и позволяющий установить те
скалярные и векторные величины, которые играют большую роль
в общей гидродинамике сжимаемых жидкостей. Мы будем
придерживаться этого второго метода.
Прежде всего исключим давление р, иначе говоря — определим
условия (необходимые и достаточные), которым должны
удовлетворять компоненты скорости и удельный объем для того, чтобы
из уравнений гидродинамики можно было определить давление
и чтобы таким образом эти уравнения удовлетворялись.
Вспомним, что динамическим градиентом G мы назвали
вектор:
6 = F — -jt = <о grad р,
и обозначим 1п«> через ?:
<Р==1а©. (109)
Для возможности исключения давления р из уравнений
гидродинамики нам понадобится новый вектор, составляющие которого
образуют левую часть классических уравнений Гельмгольтца.
Этот вектор определяется следующим равенством:
?>=— curlG, (110)
откуда не трудно получить два соотношения [см. формулы (34)
и (63)]:
? = helmcurl V —curlF, (111)
& = [grad/>, grade»]; (112)
мы будем называть этот вектор тпурбдлизирующим Б2кторому
имея в виду, что равенство его нулю является как раз
уравнениями Гельмгольтца, написанными в векторной форме; при этом,
чем более отличен от нуля турбулизирующий вектор, тем сильнее
развиваются вихри при наличности консервативных сил. Далее
мы увидим, что для консервативных сил (каковые особенно важны
в практике) турбулизирующий вектор входит в выражения всех
введенных нами в части I величин, характеризующих разруше-
*) Перенесение методов А. А. Фридмана на случай вязкой жидкости было
выполнено Б. И. Извековым. См. дополнение.
Прим. ред.
208

ние вихревых линий и изменения их напряжений. Для
неконсервативных сил кроме турбулизирующего вектора приходится
рассматривать еще вихрь силы. Подробнее о выражении
турбулизирующего вектора при помощи динамических и кинематических
элементов будет сказано ниже в §§ 14 и 15.
С помощью понятия о турбулизирующем векторе не трудно
Судет доказать следующее предложение:
Теорема 20. Необходимое и достаточное условие того,
чтобы из уравнений гидродинамики можно было определить
давление как функцию времени и координат, состоит в
выполнении следующего равенства:
$ = [G,gradcp]. (ИЗ)
Здесь следует прежде всего отметить, что мы исключаем из
рассмотрения случай а> = 0, не отвечающий коне .ному значению
плотности.
Докажем необходимость условий теоремы. Из уравнений
гидродинамики имеем:
grad/> = —,
отдода:
- С 1 1
0 = curl gradp = curl — = — curl G ^- [grad ®, G]
[см. формулу (34)]; no умножении этого равенства на « получим
соотношение (113).
Достаточность доказывается еще проще. Из условий теоремы
вытекает, что curl — = 0, а тогда, как известно, можно найти такую
функцию р от времени и координат, чтобы удовлетворялось
уравнение:
grad/>= —,
что и доказывает достаточность условий нашей теоремы. Таким
•образом»необходимые и достаточные условия того, чтобы
уравнения гидродинамики имели место, будут очевидно состоять из
условий теоремы 20 (благодаря которым можно найти давление,
удовлетворяющее первым трем уравнениям динамической группы)
и из уравнения неразрывности (служащего дополнительным
уравнением для определения удельного объема). Отсюда следует, что
коль скоро уравнения гидродинамики имеют место, ,о Ь
удовлетворяет следующим соотношениям:
[G,srad<?l=& \
^ + (V, grad?) = 8, )
где ? = div V.
14 Зак. 2420. — А'. А. Фридман, Опыт гидромеханики 209

С другой стороны и обратно, коль скоро <? удовлетворяет
соотношениям (114), то путем соответственного подбора
давления р можно будет удовлетворить всем уравнениям динамической
группы уравнений гидродинамики.
Из условий теоремы 20, а равно и из уравнений (114)
вытекает первое условие динамической возможности уравнений
гидродинамики:
(&, G) = 0.
Теорема 21. Необходимое условие динамической
возможности уравнений гидродинамики сжимаемой жидкости
заключается в том, чтобы динамический градиент был ортогонален
сзоему вихрю:
(& G) = 0, (115)
(curl 6, G) = 0. (116)
Видоизменяя несколько терминологию проф. Н. Е.
Жуковского *), мы будем называть векторы, ортогональные своему вихрю,
незакручивающимися векторами; таким образом динамический
градиент по теореме 21 должен быть незакручивающимся вектором.
Будем в дальнейшем условие (115) теоремы 21 называть условием
незакручиваемости.
Дальнейшие наши рассуждения будут существенно зависеть от
того, обращается ли мера диссипативности (стр. 199) в нуль или
нет. Общий случай будет, конечно, тот, в котором мера
диссипативности отлична от нуля. Движения, в которых ji^tO и которые
соответствуют общему случаю, назовем нормальными движениями.
Наоборот движения, при которых [і = 0 и которые
представляют таким образом исключительные случаи, мы назовем полу-
консервативными движениями, имея в виду, что согласно теореме
живых сил (см. предыдущий параграф) эти движения отчасти
напоминают движения под влиянием консервативных сил. В
настоящем параграфе мы будем рассматривать только общие случаи,
поэтому в дальнейшем будем заниматься лишь нормальными
движениями, отнеся изучение полуконсервативных движений к
следующему параграфу.
Не трудно показать, что для нормального движения уравнения
(114) эквивалентны следующим:
e + P^ = »rad?» (117)
где векторы « и Р определяются равенствами:
t
при условии (?>, G) = 0.
*) Н. Е. Ж уковский, „Кинематика жидкого тела", гл. II, § 17.
210

Уравнение (117), написанное в векторной форме, представляет
собою, конечно, совокупность трех скалярных уравнений.
Покажем прежде всего, что из уравнений (117) вытекают
уравнения (114). Уравнение (117) может быть переписано следующим
образом:
I&V]-MG=:*grad?-fG^; (*)
умножив векторно обе части уравнения на G, найдем*
№, [?, V]] = a [G, grad?],
откуда, применяя формулу (27* и помня, 4to(|),G)~0, a (V, G) =
— Н-, найдем:
У-? = Н- [G,grad?];
так как н- Ф 0 (ибо мы имеем дело с нормальным движением), то:
•S> = [6, grad ?].
Таким образом получаем первое из уравнений (114). Второе
из этих уравнений получим, помножая скалярно обе части
уравнения (*) на V:
<V[$,V]) + e^ = *(V,8rrad?)+,i|?,
что и является вторым из уравнений (114).
С другой стороны не трудно видеть, что из уравнений (114)
вытекают уравнения (117). Для этого, помножив обе части
первого из уравнений (114) на V векторно, получим следующее
равенство:
[V [G, grade?]] = (V, grad <p) G -(V, G) grad ? = [V, ?];
но второе из уравнений (114) даст нам:
(V,grad?) = 0-g;
подставляя это выражение в предыдущее равенство и деля обе
части на ^, получим уравнение (117), что и требовалось доказать.
Как мы увидим в следующем пункте, уравнения (117) позволят
нам исключить функцию <р и таким образом к .условию незакру-
чиваемости добавить еще ряд условий динамической возможности
движения сжимаемой жидкости. Во всех этих условиях векторы а
и Р будут играть весьма большую роль; представляется
желательным дать втим векторам особое наименование; имея в виду, что
одно из слагаемых в числителе вектора % имеет некоторое
сходство с моментом вектора ф, мы назовем вектор « тдрбомомен-
том; вектор (3 условимся называть приведенным градиентом,
3. В предыдущем пункте мы выяснили, что удельный объем
или вернее <? = In <" удовлетворяет и определяется уравнениями
(117). Эти уравнения представляют собой три дифференциальных
уравнения с одной неизвестной функцией; очевидно, что векторы а
14*
211

и {5, входящие в уравнения (117), должны удовлетворять известны*
условиям для того, чтобы существовала функция о от времени и
координат, являющаяся решением этих уравнений. Чтобы
получить эти условия, нам необходимо ввести два новых вектора f
и 5, определенным образом выражающиеся через турбомомент и
приведенный градиент. Эти векторы определяются следующими
равенствами:
Y = curl а -|-
8 = curl ?
- 3
гдс
dt' *
<12G)
так как векторы эти, как мы увидим ниже, выражаются через
dp
и значит просто выражаются через плотность тепловой мощности
притока энергии е, то мы условимся называть их тепловыми
векторами и считать X первым тепловым вектором, а 8 — вторым
тепловым вектором.
Эти векторы должны удовлетворять условиям, изложенным
в следующей теореме:
Теорема 22. Необходимое условие динамической
возможности уравнений гидродинамики сжимаемой жидкости
заключается в том, чтобы оба тепловые вектора были параллельны
между собойі
[Y,S] = 0. (121)
Прилагая операцию curl к обеим частям уравнений (117),
найдем:
откуда:
curl ( л -f- р Y* I = curl grad «р = О,
do
curl <z-{--^ curl 8
ot
dt
(*)
но из уравнений (117) мы имеем:
dgrad?_d« , do d$ . d2o ,
Ал Ал \ Ал A~T \ Ал-А Р>
dt dt ' dt dt ' dt*
откуда:
fdgrad? I ?da '
IP
dt
Ал > Г
а отсюда и из равенства (*), вспоминая значения тепловых
векторов, без труда получим равенство:
і * do .
(122)
Vro и доказывает нашу теорему.
212

Будем в дальнейшем условия теоремы 22 называть тепловыми
условиями.
Не трудно видеть, что дальнейшее рассуждение будет зависеть
до
от того, можно ли из уравнения (122) определить —¦, или этого
сделать нельзя, иначе говоря—обращается ли в нуль второй
тепловой вектор 3 или нет. Условимся нормальное движение, при
котором второй тепловой вектор 3 отличен от нуля, называть общим
нормальным движением, те же нормальные движения, в которых
второй тепловой вектор 8 обращается в нуль, будем называть
специальными нормальными движениями. Специальные нормальные
движения относятся к исключительным случаям движений, поэтому
они будут рассмотрены в следующем параграфе. Теперь же мы
займемся общими нормальными движениями.
Функция о от четырех переменных будет определена, коль
скоро будут известны ее частные производные по времени и
координатам. Для определения этих четырех величин нам
необходимо ввести одну скалярную и одну векторную величину-
Так как оба тепловые вектора параллельны, согласно
тепловым условиям, и так как ЪфО, ибо мы изучаем общее нормальное
движение, то всегда можно определить одну и только одну
скалярную величину X, удовлетворяющую следующему векторному
равенству:
Т + Х5 = 0; (123)
эту величину л, через которую, как мы увидим, определится -тт,
мы назовем стереоскаляром. С помощью векторов турбомомента
и приведенного градиента, а также с помощью стереосг.аляра
образуем вектор от, определяемый равенством:
в = в-|->3; (124)
этот вектор, служащий для определения производных <? по
координатам, мы будем называть стерео вектором-
Вычитая из равенства (123) равенство (122) и помня, что 3 ф 0,
найдем:
§ = *; (125)
df-0
подставляя это значение для -^ в равенство (117), получим
соотношение :
grad? = ff. (126)
Два последних равенства дают возможность определить © и
установить третью группу условий, которым должны удовлетворять
кинематические элементы, характеризующие движение сжимаемой
жидкости.
213

Теорема 23. Необходимые условия динамической
возможности уравнений гидродинамики сжимаемой жидкости
заключаются в выполнении следующих равенств:
curl сг = 0, *
** л А (127)
— = grad К )
Условия этой те. ^емы непосредственно вытекают из равенств
(125) и (126).
Условия теоремы 23 можно назвать объемными условиями.
Таким образом мы пришли к трем группам условий,
необходимых для динамической возможности движения сжимаемой
жидкости: 1) условие незакручиваемости, 2) тепловые условия и
3) объемные условия.
Не трудно показать достаточность означенных условий и
установить следующую теорему:
Теорема 24. Необходимыми и достаточными условиями
для динамической возможности уравнений гидродинамики
сжимаемой жидкости в случае общего нормального движения служат
три группы условий: 7) условие незакручиваемости^ 2) тепловые
условия и 3) объемные условия; условия эти могут быть наті№
саны ? виде следующих равенств:
[Y, 8] = 0,
curl <з = О,
fa = grad К
(128)
Необходимость услозий теоремы 24 была уже нами
установлена; покажем теперь достаточность этих условий. Объемные
ус/ ">вия позволяют нам найти функцию », удовлетворяющую
следующим соотношениям:
gjT = *! grad? = a = «-fX?;
отсюда следует, что функция -f будет удовлетворять уравнению (117),
а также, в силу условий незакручиваемости, и уравнениям (114);
тогда согласно теореме 20 можно будет определить р под
условием:
A G
gradp = —,
где1псо = 9> а>== е?. Принимая за удельный объем со = е? и за
давление только-что определенную функцию р, мы найдем, что
три первых уравнения динамической группы уравнений
гидродинамики, а также уравнение неразрывности, четвертое уравнение
214

атой группы, будут указанными значениями давления и удельного
объема удовлетворены, что и докажет достаточность условий
нашей теоремы.
Не трудно по внешнему виду условий теоремы 24 подсчитать,
какое количество условных скалярных уравнений влекут за собой
равенства (128). Условие незакручиваемости дает одно уравнение;
тепловые условия дают два уравнения, а объемные условия дают
шесть уравнений; всего таким образом мы получаем девять
уравнений; однако, как это будет выяснено в дальнейшем, четыре из
этих уравнений суть следствия остальных-
Условия теоремы 24 в виду их важности мы позволим себе
привести также и в скалярной форме; эти уравнения выразятся
в таком случае следующими равенствами:
&G, + ©,G, + &G. = 0,
Хг т, т,
дз> ^s —о дз" да* о да" д°х
ду dz ' dz дх ' дх дп ~
дах ді да,, д\ dzz дк
~ді~Тх' "Ш-!^' ~ді^Тг'
\
1
= 0,
(129)
Для установления условий динамической возможности
уравнений гидродинамики сжимаемой жидкости мы ввели шесть новых
векторов (турбулизирующий вектор, турбомомент5 приведенный
градиент, д^а тепловые вектора и стереовектор) и один скаляр
(стереоскаляр); в дальнейшем мы покажем связь этих векторов и
стереоскаляра с динамическими элементами, а также с вторичными
динамическими элементами и следовательно с плотностью е
тепловой мощности притока энергии.
В заключение настоящего параграфа укажем, каким образом по
заданному полю скоростей можно определить динамические
элементы и .тем решить вопрос о динамической возможности
движения с заданным полем скоростей. Прежде всего необходимо по
кинематическим элементам и по действующей силе определить
динамический градиент и турбулизирующий вектор; после этого
должно проверить, удовлетворяются ли условия незакручиваемости.
Затем вычисляется мера диссипативности, которая в общем
случае отлична от нуля; с помощью меры диссипативности
строятся турбомомент и приведенный градиент, а равно оба тепловые
вектора, и проверяется выполнение тепловых условий.
Далее, принимая, что в общем случае второй тепловой вектор
отличен от нуля, строят стереоскаляр и стереовектор, после чего
проверяют выполнение объемных условий.
Коль скоро все три группы условий выполнены, тогда с
помощью стереоскаляра и стереовектора определяют <? и удельный
215

объем » = е?, после чего из трех первых уравнений динамической
группы уравнений гидродинамики определяют давление р. Отсюда
следует, что удельный объем будет иметь множителем
произвольную постоянную, а давление будет иметь множителем постоянную,
зависящую от произвольной постоянной, входящей в определение
удельного объема, и кроме того будет аддитивно содержать
произвольную функцию времени. Понимая в дальнейших формулсх под
знаком f одно из значений интеграла, будем иметь:
р=! jv/(i*" *+"у д"+'2 *+г d''(G* dx+G»dy+G'dz) ~l~p°(0, (130)
где Си ;>o {t) соответственно — произвольная постоянная и
произвольная функция времени.
Примеры определения удельного объема и давления по только-
что приведенным формулам будут указаны ниже (§ 16}.
§ 13. Исключительные случав условии динамической зозмож-
аости движения сжимаемой жндкоста.
1. Установив ъ предыдущем параграфе условия динамической
возможности общего нормального движения жидкости, мы в
настоящем параграфе займемся различными исключительными случаями
движения сжимаемой жидкости.
Изучим прежде всего специальное нормальное движение, т. е-
такое движение, в котором второй тепловой векто*-- обращается
в нуль.
В этом случае для динамической возможности такого
движения необходимо прежде всего выполнение условия незакручивае-
мости- Так как с другой стороны второй тепловой вектор
обращается в нуль, 5 = 0,"то уравнение (117) для специального
нормального движения весьма просто может быть приведено к нормальной
системе трех уравнений s частными производными первого
порядка.
В самом деле, уравнение (122), являющееся следствием уравне*
няй (117), показывает, что, при 5=0, у также обращается в вулъ;
следовательно для динамической возможности специального
нормального движения первый тепловой вектор должен быть нулем.
Приводя систему (117) к системе однородных уравнений
обычным приемом, т. -е. полагая, что <? определяется из уравнения:
наидек, что Ф будет удовлетворять следующей системе ураз-
• нений:
216

57 ~^ "л
L *> _..- —Г
1 ' С-?
Составляя по обычному методу скобки Пуассона из левых
частей уравнений этой системы, найдем, что в силу обращения
в нуль обоих тепловых векторов скобки эти будут тождественно
равны нулю, т. е. наша система будет нормальной системой трех
уравнений с частными производными первого порядка и с пятью
независимыми переменными. Такая система имеет два независимых
между собою решения: Фх и Ф$ не трудно видеть, что одно из этих
решений может быть выбрано так, чтобы оно не зависело от 9»
тогда как другое решение может быть представлено в форме
разности 9 и некоторой функции t, х> уу z:
Фі = ? —/. (г, x9y>z),
Отсюда легко усмотреть, что общее решение уравнений (131)
может быть написано в форме:
? = Л (*. *> у, z) -f Ч [Д {L ху уу z)\,
где Ф — произвольная функция своего аргумента, fx — частное
решение системы (117), а /2 — частное решение системы
дх~?х dtr 'dg~**dt' dz ~**~dt*
каковая система нормальна е силу обращения в нуль BTqporo
теплового вектора
Соединяя вместе все сказанное выше* приходим к следующей
теореме:
Теорема 25. Необходимыми и достаточными условиями
динамической возможности специального нормального движения
служат. 1) условие незакручиваемости и 2) обращение і: нуль
обоих тепловых векторов:
(f>.G) = 0, ) _ (132)
г = 0, 5 = 0. I
Пря атом удельный объем определится формулой:
аі = ш1/='(а)2)) (133)
где F—произвольная функция своего аргумента, «1 = е1, о>2 = /*2,
/і и /а СУТЬ функции времени и координат, определяемые как
частные решения двух нормальных систем уравнений с частными
производными первого порядка*
217

После определения удельного объема, давление может быть
опрзделено по формуле:
_ Г Grdx + G„ds + Gsdz
jCdx + G^ + Cd* +pM
где ро (t) — произвольная функция времени.
В рассматриваемом случае в определение удельного объема
входит уже не произвольная постоянная, как в случае общего
нормального движения, а произвольная функция, которая войдет
конечно и при определении давления р. Примеры специального
нормального давления будут нами приведены ниже (§ 16).
2. Перейдем теперь к изучению полуконсервативного
движения, иначе говоря — такого движения, при котором мера
диссипативности и обращается в нуль. Движение это дает
значительное упрощение теореме живых сил. В этом случае
теорема живых сил показывает, что вся работа массовых сил
идет исключительно на изменение живой силы движения;
рассматривая случай консервативных сил, мы то же самое положение
можем видоизменить, указав, что для полуконсервативного
движения полная энергия остается постоянной. В случае, ког/а
интегральная предельная часть в уравнении (107) обращается
в нуль, мы можем сказать, что для полуконсервативного движения
вся притекающая энергия идет на увеличение внутренней энергии
сжимаемой жидкости. Не останавливаясь более на развитии столь
просто получаемых положений, перейдем к изучению условий
динамической возможности полуконсервативного движения.
Изучение полуконсервативного движения заставляет нас
выделить в нем три разных случая: 1) общее полуконсервативное дви-
жение, характеризуемое тем, что вектор
G,
ді
"ф. 0; 2)
специальное полуконсервативное движение, характеризуемое тем, что вектор
G, -кг- обращается в нуль, тогда как динамический градиент
отличен от нуля, и 3) безградиентное движение, когда
динамический градиент обращается в нуль.
Начнем наше изучение со случая общего полуконсервативного
движения.
Как это следует из предыдущего параграфа, для общего
полуконсервативного движения должно иметь место условие незакру-
чиваемости, т. е. должно выполняться равенство:
(&G) = 0,
в то же врекя с? должно удовлетворять соотношению:
? = [G, grad ?];
найдем общую форму вектора X, удовлетворяющего соотношению:
[G,X]-& (*)
218

это уравнение имеет частное решение:
^~ (G,G)'
ори этом (G, G) $z О, ибо динамический градиент в общем
полуконсервативном движении не может обращаться в нуль, так как при
также обратился бы в нуль и наше движе-
6—0 вектор
G,
dt
ние не было бы общим иолуконсервативным движением. Очевидно»
что общее решение уравнения (*) найдем, положив:
[G, X — Хо] = 0;
значит X—Хо одинаково направлено, как и вектор 6, так что:
x-7G7Gj" + nG'
г."е п — неопределенная функция временя и координат.
Таким стразом grad ф может быть написан в форме:
ггаа* = -^|і + пС, (133)
где тг — неопределенная пока функция.
Так как
то
№ ?, V;] = о,
т. е. вектор [ф, V] одинаково направлен с вектором G, значит
существует величина v такая, что имеет место равенство:
f.f,.V] = vG. (134)
Подставляя в это равенство вместо ф равный ему вектор
[G, grad ?j и аомня, что ** = (), получим:
(V, grad ?) = - v,
откуда, пользуясь уравнением неразрывности, найдем:
|^-И- (135)
Уравнения (133) и (135) позволяют определить производную г?
по времени t и координатам через кинематические элементы и через
неизвестную пока * функцию п. Для определения величины п
продифференцируем равенство (133) по t; тогда, пользуясь
равенством (135), будем иметь:
grad(v^6) = _i^+n__ + _G;
219

умножив обе части этого равенства векторно на G:
[G, grad (v + Ь)]
G,
ді "(С, G) J
+ п
G,
dG_
ді
(136)
сможем определить п, ибо мы имеем дело с общим полуконсерва-
тивным движением, в котором
ді
фО. Определив п из
последнего равенства, мы можем из уравнений (133) и (135) определить ?
при помощи квадратур; для этого однако необходимо, чтобы
только-что определенное п и кинематические элементы
удовлетворяли соотношениям, получаемым как условия возможности
решения уравнений (133) и (135) относительно <?.
Теорема 26. Необходимыми и достаточными условиями
динамической возможности общего полуконсервативного движения
сжимаемой жидкости служат следующие равенства:
(V,G) = 0,
(& G) = О,
[§.6] , dG
grad(v-H) = ^-
r,,rl №' G]
n
+?-«
(G,G) ' dt
n © + [grad n, G] = 0,
(137)
где v определяется равенством:
[©,V] = vG,
a n определяется соотношением:
^ - G,
dG
'dt
grad (v + 0)—-
dt[$,G]
^(G,G:
,G
(G,G)
0G_
ot
67
r dG\*
(138)
Необходимость условий теоремы 26 вытекает из только-что
приведенных рассуждений; последнее равенство (138) теоремы 26
получаем, умножая равенство (136) скалярно на **
G,
dt
и
применяя формулу (28) § 3.
Покажем достаточность условий теоремы 26. Последние два
равенства (137) показывают, что возможно найти функцию <?>
удовлетворяющую уравнениям (133) и (135). Уравнение (133) в связи
с условием незакручиваемости [вторым из равенств (137)] дает:
?> = [G, grad ?]. (*)
Уравнение (135) в связи с только-что полученным равенством и
с первым из равенств (137) дает
dt
=4,
Г)
220

а выполнение уравнений (*) и (**) согласно рассужденияи
предыдущего параграфа есть условие достаточное, чтобы из
динамической группы уравнений гидромеханики определить удельный
объем и давление, что и доказывает достаточность условий
теоремы.
Заметим, что в практических применениях не всегда удобно
определять п из условий (138); иногда выгоднее пользоваться
векторным равенством (136), проектируя обе его части на какое-либо
соответственно выбранное направление.
Как видно из предыдущих рассуждений, величина о определяется
при помощи квадратур, следовательно удельный объем <в будет
определен также при их помощи и будет содержать множителем
произвольную постоянную; в таком случае давление р определится
из первых трех уравнений гидродинамики н будет содержать
аддитивно произвольную функцию времени L
Мы не выписываем относящиеся сюда формулы, так как в общем
виде они сложны, а в частных случаях их можно предварительно
упростить.
3. Перейдем теперь к рассмотрению специального
полуконсервативного движения. В этом движении, как мы увидим, удельный
объем будет определяться уже не квадратурами, а путем
интегрирования некоторой нормальной системы уравнений с частными
производными первого порядка; разбор случая специального
консервативного движения проще вести, перейдя от векторных
уравнений к скалярным.
Величина о должна, как известно, удовлетворять следующим
уравнениям:
до г до
до до
*9
G ^ = Я
^' дх "•'
до . до , до . до
at 1 ох оу ' дг
=^?
(139)
в виду того, что р = 0, т. е. uG:c-j-vGyJr-zuGs = О, эта система
Оо
„т до до
уравнений неразрешима относительно -г-, -jS ~^-; так как с
другой стороны G ф 0, то один из компонентов по осям
координат вектора 6 отличен от нуля. Положим для
определенности, что Gf отличен от нуля; тогда систему (139) можно будет
до ду до
разрешить относительно -т-, -jr- и -т^; произведя это разреше-
221

иие, мы приведем систему (139) к следующей системе трех
уравнений:
до Gx д-^ fry _
дх G. д:
С
As
дд " G. dz "*" G, *"
Вспомним, что:
и что следовательно:
G.
§*»— dj,H = vGt.
-9 = 0.
Преобразуя предыдущую систему в систему однородных
уравнений, иначе говоря — считая, что Ф определяется из соотношения:
Ф(?, t,x,y,z) = 0,
найдем следующую систему для определения Ф:
G, д?
дх G. dz
дФ G„ дФ
0,
Gf dz
G. д<?
= 0,
+ (v -f V
dt
d'f
= 0.
(140)
Для интегрирования этой системы необходимо составить скобки
Пуассона из левых частей только-что приведенной системы.
Не трудно видеть, что условие незакручиваемости в нашем
случае должно иметь место, иначе говоря — мы должны иметь
следующее равенство:
Составляя скобки Пуассона из левых частей первых двух
уравнений системы (140), получим следующее'выражение для коэффи-
дФ
циента при -=р-:
д
"57
G.
j_
G, д I G.
+ ±(.СЛ G»
Gt! ' Gt dz \ G% ) ' dy \ G, / G, dz
Gx curl,. G + Gy curlff G + G9 curi, G (f f G)
(?)-
Gt Gl '
в с тлу условия незакручиваемости коэффициент этот обращается
в нуль. Произведя аналогичное вычисление и помня, что
222

ri 1*1
ф ——curlG и что div§> = 0, найдем, что и коэффициент при .--
в выражений, образуемом помощью скобок Пуассона из левых
частей первых двух уравнений системы (140), также обратится
п нуль. Таким образом скобки Пуассона ьз левых частей первых
двух уравнений системы (140) тождественно обратятся в нуль.
Образуя скобки Пуассона из левых частей первого и третьего
уравнений системы (140), а также из левых частей второго и
третьего уразнений этой системы, получим следующие два
уравнения:
1дСх СхдСЛдФ ,
V ді~ G, ді ) dz ¦'
-ь
G. dt
dt
<?(v+6)
dz
(дС
GydG1
й, dG, дЬ,
LG.
G. ді
ді
Из условия 16,
1 dG
-(«
dG.
ді Gz ді
ду
У
ді
0
следует, что
дх
дФ
dz
l-dG*
~G~:~dY
дФ
la
= 0;
(*)
дФ
до
1 dG.
G. ді
= s; отсюда получим, что коэффициенты при
дФ
~ Gz ді ' — —V—, -г*-* -г- dz
в уравнениях (*) обращаются в нуль- Таким образом для возмож-
дФ
ности решения системы (140), причем -з— =? 0, необходимо, чтобы
д$Г
и коэффициенты при -д— ь уравнениях системы (*) обращались
в нуль, а раз это будет иметь место, то система (140) будет
нормальной. Из предыдущих соображений легко будет показать
справедливость следующей теоремы:
Теорема 27. Необходимыми и достаточными условиями
динамической возможности специального полу консервативного
движения служат следующие равенства:
(V,G) = 0,
dG
6,
= 0,
ді
(&G) = 0,
д§
С$>-1Н+ [G' grad (v + ?)] = С *>*
(141)
*) Эго равенство можно записать в более простом виде:
[G,gradCv + e-s)l = 0,
223

где v и 5 определяются равенствами:
K>,V] = vG,
i®-sG * (142>
Необходимость условий теоремы 27 может быть доказана
следующим образом. Первые два равенства из (141) вытекают
из определения специального полуконсервативного движения, третье
равенство должно иметь место согласно изложенному п начале
предыдущего параграфа. Обозначая левую часть четвертого из
равенств (141) через А, будем иметь, что обращение в нуль хоэф-
фициентов при ~^- в уравнениях системы (*) требует равенства
нулю составляющих вектора А по осям дг, у:
но по самому определению вектора А будем иметь:
ибо
(&G) = 0.
Дифференцируя равенство (§, G) = 0 по t и помня, что
найдем:
или, так как
следовательно
но
(&G) = 0,
(<.fH
(G, A) = 0;
Ах = А!/ = 0,СгфО,
значит Лг = 0, что и доказывает необходимость условий теоремы.
Достаточность этих условий выводится еще проще. Так как
система (140) является при выполнении условий теоремы
нормальной системой, то она имеет решение; следовательно существует
функция <р> удовлетворяющая системе (139), а тогда, согласно
рассуждениям начала предыдущего параграфа, можно будет определить
ибо
[grad я, G] = curl (sG) — s curl G = curl -r- s curl G = 4?- + 5Ф«
Прим. ред.
224

удельный объем и давление таким образом, чтобы
удовлетворялась динамическая группа уравнений гидродинамики.
Рассуждая так же, как и в первом пункте настоящего параграфа,
мы найдем, что система (140) будет иметь два независимых
решения:
где /j есть функция t, х, yt zy удовлетворяющая нашей системе
(такая функция существует в силу нормальности системы), а/а есть
решение следующей системы (которая является также нормальной
системой):
дх G,dz-U> ду G9~dz~-"> ~dt~%
/12 не зависит явно от t, а есть функция одних только координат.
С помощью указанных частных решений легко получить общее
выражение для функции ср: ' ' '
где W — произвольная функция своего аргумента.
Отсюда без всякого труда получим выражение для удельного
объема, а также и для давления. Удельный объем будет содержать
одну произвольную функцию, а давление — две произвольных
функции, из которых вторая будет функцией от времени t и войдет
Э выражение для р аддитивно.
Нам остается рассмотреть еще случай безградиентного
движения. В этом случае три первых уравнения динамической группы
уравнений гидродинамики дадут нам, что давление р не зависит
от X>U>Z и есть произвольная функция только от времени Ь9
величина © = In to определится из четвертого уравнения гидродинамики»
а именно из уравнения:
до , до , дф , до ,л ,лч
-ш+иъ+° -?+«>-?=*• <143>
которое может быть проинтегрировано или обычным способом, или
же сходящимися процессами, указанными в § 10.
4. В заключение настоящего параграфа скажем несколько слов
о некоторых замечательных движениях- Движения эти играют
большую роль в практических вопросах. Первым из таких движений
мы рассмотрим движение, в котором турбулизирующий вектор
обращается в нуль.
Классическая гидродинамика, рассматривающая случаи
движения несжимаемой жидкости или же такие движения, в которых
давление есть функция удельного объема, изучает частные случаи
движения с равным нулю турбулизирующий вектором. Отсюда
понятна важность отдельного изучения движений с турбулизи-
рующим вектором, обращающимся в нуль.
Эти движения распадаются на три класса: 1) движения
жидкости, в которых удельный объем не зависит от координат; частный
15 Зак. 2420. — А'. А. Фридман, Опыт гидромеханики
225

случай этих движений есть движение несжимаемой жидкости;
2) движения жидкости, в которых давление не зависит от
координат, каковые движения мы назвали безградиентными, и 3) движения
жидкости с равным нулю турбулизирующим вектором, не
относящиеся к первому или второму классу.
Условие того, чтобы турбулизирующий вектор обращался
в нуль, может быть интерпретировано как с помощью
кинематических, так и с помощью динамических элементов- Заметим, что
через силовые динамические элементы турбулизирующий вектор §
выражается равенством:
©=ferad-/>, gradco].
Равенство нулю этого вектора дает нам следующие три
соотношения:
др _д<о
ду dz
др д<&
dz дх
др <?ю
дх ду
Соотношения эти показывают, что между р и а> имеется функ
циональная зависимость. Зависимость эта может однако содержать
в качестве параметра время /, обстоятельство, на которое обычно
не обращали внимания. Таким образом в случае равенства нулю
турбулизирующего вектора $> будем иметь следующее
соотношение:
Если мы исключим указанные выше первые два класса, то
только-что' написанное равенство не трудно пояснить
геометрически; оно означает, что в каждый данный момент изобарическая
поверхность (р = const) совпадает с некоторой изостерической
поверхностью (о>== const). Это свойство движений, в которых
турбулизирующий вектор обращается в нуль, позволяет нам назвать
такие движения стеробарическими движениями.
Стеробарическое движение, в котором удельный объем не
зависит от координат (движение первого класса), будем называть
специальным стеробарическим движением. Специальное
стеробарическое движение, в котором удельный объем (а следовательно и
плотность) не зависит от времени, мы назовем движением
несжимаемой жидкости; это как раз и суть те движения, которые обычно
изучаются в классической гидродинамике.
Стеробарические движения, в которых, давление не зависит от
координат, суть разобранные выше безградиентные движения.
Наконец остальные стеробарические движения условимся называть
общими стеробарическими движениями.
Не трудно видеть, что в стеробарическом движении в каждый
данный момент времени совпадают не только изобарическая и изо-
др да>
dz ду
др да>
дх dz
др да>
ду дх
226

стерическая поверхность, но вместе с этими же поверхностями
совпадают поверхности изэнтропические (5 = const) и
изотермические (7*= const), ибо температура и энтропия суть функции
давления и удельного объема.
Обычно в классической гидродинамике, когда рассматривают
движения сжимаемых жидкостей, предполагают, что давление есть
функция удельного объема и в зависимость давления от удельного
объема не входит явно время L Геометрически это означает, что
если в известный момент времени изобарическая поверхность р = р$
совпадала с изостерической поверхностью о> = odq, то и во все
последующие моменты будет иметь место совпадение именно этих
двух поверхностей друг с другом. Такой случай стеробарического
движения условимся называть стационарно-стеробарическим
движением. Если наоборот в выражение зависимости между давлением и
удельным объемом входит явно время і, то изобарическая
поверхность р = Ро> совпадавшая к некоторому моменту t с изостерической
поверхностью <о = а>0> будет к другому моменту if совпадать уже не
с этой изостерической поверхностью оо = а»(ь а с какой-то другой » = о^';
таким образом в этом случае сливавшиеся раньше поверхности
разойдутся, — такое движение будем называть мгновенко-стероба-
рическим движением.
Стеробарическое движение при наличности консервативных сил
обладает замечательным свойством быть главным гельмгольтцевьщ
движением, ибо при наличности консервативных сил
кинематическое выражение для турбулизирующего вектора может быть
написано в виде:
helm curl V = §,
а значит для стеробарического движения будем иметь:
helm curl V = О,
т. е. будем иметь главное гельмгольтцево движение, в котором
вихревые линии обладают свойством сохраняемости и в котором
напряжение вихревой трубки не меняется с течением времени.
Из сказанного вытекает следующее предложение:
Теорема 28. Необходимым и достаточным условием, чтобы
движение жидкости при наличности консервативных сил было
главным гелъмгольтиевым движением, является стеробаричность
такого движения.
В стеробарическом движении под действием консервативныдх
сил и притока знергии не мсжет возникнуть вихрей. Если на жи-
кость действуют неконсервативные массовые силы, то само собой
разумеется, что в таком случае эти силы и в стеробарическом
движении могут вызвать образование вихрей, ибо, хотя турбулизи-
рующий вектор и будет в этом случае нулем, однако helm curl V не
обратится в нуль и будет определяться из равенства:
helm curl V = curl F;
подробнее о возникновении и изменении вихрей будет сказано
в следующей главе.
15*
227

Стеробарическое специальное движение обладает тем свойством»
что в любой момент плотность во всех точках жидкости одинакова>
движение происходит так, что жидкость в каждый данный момент
остается однородной по плотности. Для такого движения очевидно
турбулизирующий вектор ?> обращается в нуль, а расхождение
скорости ? не зависит от координат, являясь функцией одного только
времени L
Изучим, обратно, динамические условия возможности движения,
в котором § = 0 и 6 = divV есть функция только от t. Условие
незакручиваемости очевидно выполняется. Для изучения тепловых
условий построим турбомомент и приведенный градиент. Так как
в нашем случае турбулизирующий вектор обращается в нуль, то
будем иметь следующие формулы для нормального движения:
» 1 dm
причем о = -кг не зависит от х, у, z; поэтому
= - 03;
таким образом тепловые условия выполняются, и ^ — ?. Образуя
стереовектор ct, найдем:
отсюда будет следовать выполнение всех объемных условий. Таким
образом в рассматриваемом нами случае установлена динамическая
возможность движения.
Из предыдущего рассуждения видно, что в случае нормального
общего движения необходимыми и достаточными условиями того,
чтобы данное движение было специальным стеробарическим
движением, являются равенство нулю турбулизирующего вектора и
независимость от координат расхождения скорости (divV). Для движений,
ае относящихся к общему нормальному движению, этих признаков
яе достаточно.
Другим важным классом движений является несжимаемое
движение, определяемое условием:
divV = 0.
Как мы уже говорили выше, это движение отнюдь не следует
смешивать с движением несжимаемой жидкости. В несжимаемом
движении удельный объем и плотность являются лишь
инвариантными функциями, но отнюдь не являются постоянными величинами.
Не трудно видеть однако, что в случае общего нормального
движения несжимаемое стеробарическое движение есть движение
несжимаемой жидкости. В самом деле, образуя турбомомент для
несжимаемого стеробарического движения, найдем, что он
обращается в нуль; отсюда будет следовать, что первый тепловой
вектор, а зсачит (в случае общего нормального движения) и сто-
Gcurip — ?
3L а
dt'?
228

реоскаляр обращаются в нуль, следовательно и стереовектор
равняется нулю (ибо а=0), значит <р==1па> не зависит ни от /,
ни от координат, что и требовалось доказать.
Это свойство отнюдь не имеет места в случаях движения,
отличных от случая общего нормального движения. Ниже мы
увидим, что объемные условия для несжимаемого движения дают
возможность в некоторых случаях найти
условно-характеристический вектор, выражающийся через турбулизирующий вектор и через
скорость.
Сделаем еще одно замечание о движении с потенциалом
скоростей. Движение это должно быть в случае наличности
консервативных сил стеробарическим, однако оно должно удовлетворять
и ряду других условий динамической возможности движения. В виду
того, что условия эти очень мало упрощаются сравнительно
с общими случаями, мы приводить их не будем. Заметим, что
в дальнейшем движение с потенциалом скоростей мы будем
называть безвихревым движением,
§ 14. Основные векторы и кинематические элементы.
1. Задачей настоящего параграфа будет выражение векторов,
введенных в § 12 и § 13, через кинематические элементы,
характеризующие движение жидкости. Параллельно с этим мы выразим
условия динамической возможности движения непосредственно через
кинематические элементы, что даст нам возможность во-первых
упростить эти условия, а во-вторых установить, что некоторые
из этих условии суть не что иное, как следствие остальных
условий.
Турбулизирующий вектор, турбомомент и приведенный градиент
были нами уже выражены через кинематические элементы; мы
приведем однако здесь, в целях полноты, формулы, выражающие
указанные векторы в кинематических элементах:
& = helm curl V — curl F = - curl G, (144)
« = ИН-С, р = -^; (145)
заметим, что в настоящем параграфе мы будем рассматривать
исключительно нормальное движение, и большей частью даже
общее нормальное движение.
Из формул (145) ясно, что величины у-аи р$ выражаются проще,
нежели величины аир; представляется поэтому рациональным
выразить тепловые векторы через у-л и у$. Не трудно проверить
справедливость следующих формул:
u28 = у. curl .t*(J — [grad p, pfl -f
Г д^%
dt
P-P
¦ряГ=-!*сиг11** — [gradt*, H + l -j%-> V>P — -Jf№» НЙ-
1 д\ь
\
(146)
229

Подставляя в эти формулы выражения для |іл и р$, вытекающие
из равенства (145):
Р«=[& V] + 6G, jip = —G,
после несложных вычислений получим следующее выражение для
второго теилового вектора:
^S = ji|)-f-[grad!x, G]-f
dt
], (147)
каковое равенство и дает нам выражение второго теплового
вектора через кинематические элементы.
В целях получения формулы для первого теплового вектора
необходимо будет ввести новый вектор, который назовем тпурбу-
•шэырующим вектором второго порядка и обозначим через 4^;
этот вектор определяется из условия:
& = helm ф. (148)
Выше, в § 10 мы видели, что ©j есть первое звено в
последовательности векторов, играющих известную роль в вопросе
разыскания характеристических векторов.
После простых вычислений будем иметь:
^Y = ^i-^8divV-[(grad|i,V) + (^-,v)]©+:
+ [(grad jx, ф) + ( ^-, $) ] V + v [grad div V, G], (149)
каковая формула и выражает первый тепловой вектор через
кинематические элементы.
Лая выражения стереовектора и стереоскаляра надо прежде
*сего определить X из векторного уравнения:
т-;-лг=0;
это уравнение является возможным в силу тепловых условий.
Очевидно, что наиболее простой способ определения X будет
заключаться в умножении обеих частей предыдущего уравнения
скалярно на некоторый вектор Г и в выборе этого вектора так,
чтобы (S, Г) было отлично от нуля. При таком выборе
лектора Г, X определится следующей формулой:
(Y,r)_ Gt»Y,D
(5, Г) >»8, Г)'
проще всего за Г взять вектор 8: тогда (в случае общего нор*
мального движения» каковой случай мы только сейчас и
рассматриваем) (8*8) =?0 и значит X определяется из предыдущей
формулы. Подобного рода выражение будет однако очень сложным,
поэтому мы рассмотрим определение X при помощи иного
вектора Г; определение это будет возможно не всегда, так как
отличие от нуля выражения (8, Г) наложит известные условия на
наши скорости. Мы будем однако рассматривать лишь движения,
230

подчиняющиеся этим условиям, каковые движения и будут общим
случаем движения; тот же случай, когда эти условия не будут
выполнены, являющийся особым случаем движения, мы сейчас
рассматривать не будем. В тех частных примерах, когда этот особый
случай имеет место, приходится пользоваться непосредственно
векторным уравнениеи у -)- Х8 = 0, которое в этих случаях
обыкновенно значительно упрощается.
За вектор Г выберем следующий вектор:
г=[С©].
Произведя вычисление, без труда найдем следующее равенство:
(ц28, Г) = (^8,[С, $]) = (6, G)(&,G). (150)
Обозначим величину (?)lf G) через v и будем предполагать, что
она отлична от нуля:
v = (&, 6)^0;
случай, когда v,= 0, и будет тем особым движением, которое мы
условились не рассматривать.
Выбрав за вектор Г указанный выше вектор, найдем следующее
выражение для стереоскаляра:
\ = d\vV + vmf (i51)
ГА6 ni_(graddivV,g)) (УЛЙ,, С]) "
V * (IV • * '
Пользуясь предыдущими формулами, выражающими стереоска-
ляр через кинематические элементы, получим следующее
выражение для стереовектора также через кинематические элементы:
ff = JM_ma. (153)
В том случае, когда v — О, приходится прибегать к иным
приемам для выражения стереоскаляра через, кинематические элементы:
или выбирать другой вектор Г, или же из векторного уравнения,
определяющего ^> брать одно из скалярных уравнений,
содержащихся в этом векторном соотношении; правда, в этом последнем
случае мы рискуем потерять симметрию расчетов.
Рассмотрим определение основных векторов через
кинематические элементы для случая стеробарического движения. Помня, что
в стеробарическом движении |) = 0, а значит и ^ = 0, будем иметь;
GdivV , G
а = , ? = -
Р'
Р»8 =
grad н- + ~^г
jl^y = — у2Ъ div V + V- [grad div V, G].
231

Предыдущий метод для определения А не годится, так как
v = (§1? G) = 0. Полагая однако и в этом случае:
X = divV-f-^m,
найдем, что т определится из условия:
[grad div V, G] = — т grad ц -j- -^-, G J ;
стереовектор в этом случае будет равен:
а=— ml.
. 2. Выяснив, каким образом наши основные векторы выражаются
через кинематические элементы, перейдем к выражению через
кинематические элементы условий динамической возможности
движений сжимаемой жидкости.
Не останавливаясь на условиях незакручиваемости, в достаточной
мере просто выражающихся непосредственно через кинематические
элементы, перейдем к изучению тепловых условий; при этом
окажется, что благодаря условию незакручиваемости из двух тепловых
условий одно будет следствием другого *).
Помножая обе части равенства, выражающего тепловые условия,
на ja4, перепишем эти условия в таком виде:
или, что то же самое:
Вычисление левой части этого равенства распадается на три части
соответственно с числом слагаемых в формуле (147), выражающей
Р>*8. Обозначая эти слагаемые через Аі9 А2, А3, будем иметь:
Aa-t^r+^SdivV,^],
Ао =
'of G
^r + Ps8divV,
А8 = fr» Г -Ь ^ 8 div V, [grad ji, GJ].
Произведя вычисления, найдем:
Ах =^ [&, ©] + ^ (&, grad div V) G + i^grad ? + ~,^>)[V, $];
A2 = ,Q f-G f , ^§)+(grad,, §) (у, 4* ) _
-fcradft V) ^„Щ+г^, [grad div V, G])};'
A3 = (iQ grad (i - G { (i (4>, grad p.) — (grad h '$) (V, Д6- ) -f
+ (grad щ V) ($,-—) + P. (grad ft [grad div V, G]) ),
6t
*) На зависимость одних условий динамической возможности движения о?
других указал мне проф. Н. М. Гювтер в 1916 году.
232

где Q определяется следующим равенством:
Q = (&, G) + (grad^, €>)-(б,^). (154)
Покажем прежде всего, что из условий незакручиваемости
вытекает обращение величины Q в нуль.
Помня, что ?>! = helm §, найдем:
& = -gf-KV,V)S-<©,V)V-i-$divV,
откуда, пользуясь условием незакручиваемости, получим
следующее равенство:
(?>., G) = (-^-, с) + ((V, V) €>, G) - (($, V) V, G).
Вставляя это выражение в равенство, определяющее Q, и пользуясь
формулой (31а) § 3, выражающейся в нашем случае равенством:
(6, (& V) V) + (V, (& V) 6) = ©, grad (V, G)),
найдем следующее выражение для Q:
Q = ((V,V)§,G)-b(V,(§, V)G).'
Применяя к этому выражению формулу (316) § 3, получим
равенство:
Q = - (V, [?, curl G])+ [V, grad ф, G)],
откуда и будет следовать, что Q тождественно обращается в О,
ибо curlG = — &, (§, G)=0.
Из формул, выражающих Aj и А$, получим, полагая Q = 0:
А, + A3 = -^G (§+[grad-iiv V, G], -^ +.grad ц). (155)
Нам остается только преобразовать вектор Аі-
Покажем прежде всего, что всегда можно подобрать такие две
величины h и d, чтобы имело место равенство:
[&,й=лс+«*№&]. (156;
Если ?> = 0, то, полагая Л = 0, d=0t удовлетворим равенству
(156); рассмотрим случай § фО. В этом случае не трудно
установить, что направления векторов G и [V, §] не параллельны между
собой; в самом деле вектор:
[G,[V,?>]] = -!^
является величиной, отличной от нуля, ибо ^ ф О (рассматривается
нормальное движение) и $ф0> по предположению- Так как G
и [V, §] суть два вектора, ортогональные вектору § и
неодинаковые по направлению, то каждый вектор, ортогональный §, можно
представить в виде линейной комбинации этих двух векторов; так
как вектор [фи $] ортогонален §, то всегда можно найти hud,
удовлетворяющие равенству (156).
233

Применяя для определения h и d формулы (48) § 3, най/ем:
д= <V,[&,S1) j ^ (С ft)
откуда получим следующее выражение для Агг
Аі = G { »і (V, [&, ?]) + ^ (?, grad div V) }+^Q [V, ©].
Вспоминая, что Q = 0, и составляя сумму двух векторов А1 и
А2 + Аз, найдем, что каждый из этих векторов имеет направление G
и выражается через вектор G, помноженный на некоторый скаляр»
Для того, чтобы сумма этих векторов была нулем, необходимо
и достаточно, чтобы множитель-коэффициент при векторе 6
обратился в нуль, ибо вектор G отличен от нуля, так как мы имеем
дело с нормальным движением. Отсюда следует, что тепловые
условия, выражающиеся через два скалярных равенства,. будут
эквивалентны одному скалярному равенству, которое может быть
написано в виде
(V, [&,й)+
+1* ©, grad div V) — ($j + [grad div V, G], 4? -f grad ji j = 0; (157)
это равенство представляет тепловые условия, выраженные при
посредстве кинематических элементов.
Для случая стеробарического движения (© = 0, |)х = 0)
предыдущее равенство значительно упрощается и может быть написано
так:
([grad div V, Gl, -^- + grad v) = 0,
каковое равенство удовлетворяется в случае несжимаемого
движения, т. е. когда div V = 0.
Для несжимаемого движения тепловое условие может быть
написано в такой форме:
(V, [0:, ?])- (&, ^"4-grad ц) =0.
Чтобы иллюстрировать, насколько громоздкими становятся
вычисления в случае, если мы не будем пользоваться сокращенными
обозначениями векторного анализа, напишем тепловое условие,
раскрыв некоторую часть символов:
и v w
Ф* Ьу Ьг
<5? ' д* ¦ дй\ f dG dG
дСЛ f . д? Л. ди.\ (дЬ дЬ \
23*

/Л Л WdG. , <?u\
3. Нам обтается теперь исследовать объемные условия; выражая
их через кинематические элементы, мы покажем, что объемные
условия, состоящие из шести .скалярных уравнений, на самом деле
сводятся лишь к трем скалярным уравнениям, остальные же три
суть следствия первых трех, условия незакручиваемости и
тепловых условий.
Покажем прежде всего» что объемные условия, выражающиеся
равенством:
curl а = О,
суть следствия объемных условий, выражаемых равенством*.
и тепловых условий.
Легко видеть, что имеет место следующее равенство:
curl <з = curl (а + ХР) = curl * -f л curl р + Ь™* x> PL
d<? d(«4
откуда в силу равенства grad л. = — = —^—-^—&- найдем следую
шее соотношение:
дя '
Ж'*
л,р] = т+м-о.
curl а 4" X curl р 4"
откуда получим:
curl or = О»
что и требовалось доказать.
Исследуем теперь вопрос о возможности из условия curlff = 0
вывести остальные объемные условия, выразив их через
кинематические элементы; для этого заметим, что формулы, выражающие
стереоскаляр и стереовектор ч^рез кинематические элементы, а
именно равенства:
g= ^,V^--mG, X = divV4-^m.
справедливы для всякого нормального движения безразлично,
обращается ли v = (?)ь 6) в нуль или нет. Из этих равенств получим
сиг1а=-^-4^+-^(8гас1^ф)У +
+ [ т —^ (grad fc V) } § - [grad яг, G]> (1Г8)

да
6t
1_
dG dm
)-?^»i-5
m
G;
(159)
dt dt
grad X = grad div V -f- P grad m -j- /n grad y. (160)
С помощью этих равенств не трудно показать, что из условия
незакручиваемости следует равенство:
(curl a, G) = 0. (161)
Из равенства (158), помножая его скалярнс на й, найдем:
(curie, 6) = -^-;
следовательно равенство (161) выполняется, ибо Q = 0 в силу
условия незакручиваемости.
Таким образом условие curl а — 0 сводится к двум соотношениям:
(curl а, ф) = 0, 1
(curler, [?,G]) = 0;f (162)
в самом деле, если имеют место два равенства (162) и если (в силу
условия незакручиваемости) имеет место равенство (161), то
компоненты curl ff будут удовлетворять трем однородным линейным
уравнениям. Определитель этих уравнений может быть написан
в форме:
(G,[&№,G]])=-(G,G)(&S); ;
этот определитель отличен от нуля, если мы предположим, что
наше нормальное движение не есть стеробарическое движение.
Таким образом для не-стеробарического движения из двух
равенств (162) будет следовать одно из объемных условий:
curl с — 0.
Покажем теперь, что из условия незакручиваемости, из
тепловых условий и из условия curl op = U вытекает, как следствие,
равенство:
— -gracU, g]=0. (1,3)
Обозначим через Р следующий вектор:
Р = ^~gradX.
Определяя из равенства curl ff = 0 вектор [grad m, G], получим
соотношение
Lgrad m,. G] = -і" curl [& V]+-^ (grad ji, ©) V+
-f
m —
^
(grad y-, V)
&
236

пользуясь этим соотношением, найдем следующую формулу:
[P,G] = |[[S,
dt
,6
+т[
'д$ у"
,G
-± %№ Пб]-
[grad div V, G] — curl [?, V] — — (grad |i, ф) V + — (grad jx, V) §
—{*+[-?.•
[gradn-, G]L
Вспоминая формулы (147) и (149) для у?Ъ и «J.2y и произведя
несложные преобразования, найдем:
[Р, G] = - щ*Ъ - -I 0»»ч + ^8 div V),
Г
откуда без труда получим*,
[P,C] = -ji[Y + (divV+^in)8] = -|*(T + W) = 0,
что и требовалось доказать.
Таким образом, при условии curl а = 0, остальные объеыіные-
условия будут выполнены, коль скоро будет иметь место
соотношение:
' (w~gradX' G)==°* (164>
В самом деле, по только-что доказанному, вектор Р имеет
направление, одинаковое с вектором G, а так как (Р, G) = 0, то Р = О,
и значит будут иметь место все объемные условия.
Собирая вместе все сказанное выше об объемных условиях,,
можно установить, что объемные условия для не-стеробарического
движения эквивалентны следующим трем скалярным равенствам:
(curl сг, §) = О,
(curla,[&G]) = Q,
(-^-jrradX, C)=0.
(165)
Само собой разумеется, что эта эквивалентность имеет место
лишь при наличности выполнения условий незакручиваемости и,
тепловых, t
Мы имеем теперь возможность установить» что для нормального
движения условия его динамической возможности состоят из пяти
скалярных уравнений.
Теорема 29. Необходимые и достаточные условия динами*
ческой возможности нормального движения сжимаемой жидкости
состоят:
1) из одного скалярного уравнения условия незакручиваемостиг
(&G) = 0;
237

2) из одного скалярного уравнения теплового условия
(V. [&,$])-f
-' f. (& grad div V) - ($, 4- [grad div V, G], -^- + grad (*) = С
9 из трех скалярных уравнений объемных условий.
дог д\. до# д\ доя ді
1Г~ дх' ~ді~~~ді* ~дГ~!к'
Следовательно имеется всего пить условий, которым должны
удовлетворять три функции и, v, w — составляющие скорости V
по осям координат. Таким образом число уравнений превышает
здесь число неизвестных; нельзя однако думать, что эти уравнения
не будут иметь решения, ибо ряд частных примеров показывает,
что число уравнений теоремы 29 в частных случаях понижается,
так что является возможным отыскать три функции и, vt w,
удовлетворяющие этим условиям. Подробнее об этом
обстоятельстве будет сказано в § 16, посвященном примерам нахождения
скоростей по условиям динамической возможности движения жидкости.
В частности для случая нормального движения несжимаемой
жидкости не трудно видеть, что условия теоремы 29 понижаются
до трех, каковыми условиями и являются знаменитые уравнения
Гельмгольтца.
Теорему 29 можно видоизменить следующим образом, приняв
во внимание сказанное выше об объемных условиях:
Теорема 30. Необходимые и достаточные условия
динамической возможности общего нормального не-стеробарического
движения сжимаемой жидкости состоят;
1) из одного скалярного условия незакручиваемостщ
2) из одного скалярного теплового условия,
3) из трех скалярных объемных условий:
(curl ff, ф) = 0,
(curl а> [ф, G]) = 0,
Для случая стеробарического движения будем иметь
с = — mG, X = div V-\-pm,
curl or = — [grad m, 6],
-_ = — П2 — ^-6, grad X = grad div V + P- grad m-f m grad p,
откуда не трудно получить в раскрытом виде объемные условия.
§ 15. Основные векторы и динамические элементы.
1. В настоящем параграфе мы займемся выражением основных
векторов через разные сорта динамических элементов. Часть этих
векторов, а именно динамический градиент и отчасти турбулизи-
рующий вектор, была нами уже выражена через динамические эле-
138

менты. Равным образом мы уже выразили через динамические
элементы весьма важную скалярную величину — меру диссипатив-
ности. Не останавливаясь таким образом на формулах,
выражающих динамический градиент [см. формулы (94)] и меру диссипа-
тивности [см. формулу (99)], перейдем прямо к установлению
формул, выражающих турбулизирующий вектор. Помня, что ф =—curl G,
и пользуясь формулами (94), легко найти следующие выражения
турбулизирующего вектора § в силовых, тепловых и
метеорологических элементах:
§ = [gradp, grade],
"Ф — — b^ad р, grad Т].
Р
(166)
Не трудно найти геометрическое толкование указанных
выражений для турбулизирующего. вектора. Очевидно это есть вектор,
лежащий на линии пересечения касательных плоскостей к
изобарической и изостерической, или же к изотермической и изэнтрогга-
ческой поверхностям. Величина этого вектора определится, если
мы сможем построить градиент давления и удельного объема *).
Мы не останавливаемся подробно на геометрической
интерпретации турбулизирующего вектора, так как в настоящей работе мы
не касаемся вопросов графических методов подсчета величины
рассматриваемых нами векторов, для каковых вопросов и бывают
необходимы геометрические истолкования' полученных скалярных
и векторных величин. Для выражения турбомомента и
приведенного градиента через динамические элементы займемся предвари-*
тельно вектором [ф, V], входящим ¦ в выражение турбомомента.
Пользуясь формулой (27) и замечая, что
(V, grad*)==?(*) = -J-^-,
найдем для рассматриваемого вектора следующие выражения:
К?. У\=Е(р) grade» — ?(«>) gradp,
[?, V\ = E(T) gr&dS-EiS) grad T,
[& V\ = y{E(p) grad Т-Е(Г) gradp}.
(167)
В формулы для этого вектора входят вторичные динамические
элементы, каковые желательно выразить через плотность те-
*) О построении турбулизирующего вектора см. Sllberstein, „Ober die
Entstebung von WirbelbewegTrngen", Bullet. Intern, de Г Acad, des Sc. de Cracovle,
1896, p. 280, а также диссертацию АпэеГя, .Beltrage zur Dynamik und
Thermodynamic d. Atmosphere", 1913.
239

пловой мощности притока анергии е и через расхождение
скорости 6:
^
Л
Е (<ю) == со Ь
(7*
?(Г) =
0>
/г
>,,)_
іі
л
*«>-?
AS
168)
Подставляя эти выражения в формулы (167) для вектора [?), V],
получим выражение этого вектора через е, Ь и динамические
элементы.
Установим теперь выражение для турбомомента и приведенного
градиента:
grad » -1 д<л grad р
а =
а =
а> а>
-^-?(7)-Г?(5)
Мх —1 Л
grad 7" . 1
?=-
(/ х AT ' Т dS
x—ldt R dt
(169)
J grad 5+
x/?
gradp
E(p) '
1
(X—1)2 T -dt
It л
т Ji T
Л
) grad 7*1;
-^jgrradp-
?-E(T)—TE(S)
J Tgrad^S —-^-gradrl.
2- Переходя к определению тепловых векторов, заметим, что более
удобные формулы получаются не для самих тепловых векторов,
а для произведения их на р2. Мы ограничимся лишь выражением
тепловых векторов в силовых динамических элементах; выражения
их в других динамических элементах отличаются значительной
громоздкостью. Формулы для тепловых векторов можно написать
в следующем виде: .¦'
Zv= —
r*Y
О)
grad-^, grxd/>
1
.у2§ = о>2 grad -JL t gracj
(170)
240

В виду важности для дальнейшего этих выражений приведем их
гывод.
Пользуясь формулами для ^ и у28:
д\*.а
р,2у = jj. curl pa — [grad jx, \lo\ -f-
dt
• ^]-7^l>e'rfl
|Д = ,і curl rf— [grad h рЯ+[^-, rP
и подставляя в эти соотношения выражения для ра и р-р из
формул (169) и выражения для ^ из формул (99), будем иметь
следующие равенства:
^2у = <!>Е (р) [grad Е (р), grad <и] + <&Е (р)
д<о
grad Ж' gradp
*E(p)(gradE(p), grad<o]—а>-^-[gradЕ(р), gradp] —
E(p)-fi-\s™d<°> gradp]—<»E(p) grad -^-, gradp] —
Р [grad о), grad р] — « -^ I grad -^, grad p J -f
?^у df J <°E (p) [grad«, gradp] ==
grad -^-, gradp ;
Й
+ (- —
CO
*radlP grad/>
ps8 =— <u?(p)[grad<D, grad/>]-{-^(p)05[grad<o, gradp]-f-
+ «* [grad E (p), grad p] -f ©2
==ш2 grad -^-, gradp -
В выражение тепловых векторов входит вектор:
Л=| grad-^, gradp ;
этот вектор очень просто может быть выражен через плотность
тепловой мощности в притока энергии и через расхождение скорости 6:
ъ
Л =-7-[grade, gradp] — хр [grade, gradp]. (171)
Рассмотрим теперь стереоскаляр и стереовектор; по самому их
определению найдем:
1 1 дТ , 1 дТ 1 др
ш dt9 ~ К ді
grad <о 1 с
=^-»5=xgrad5
х—1 Т ді'
1
Т dt р dt'
х — 1 Г
16 Зак. 2420. — А'. А. Фридман, Опыт гидромеханики
grad Т grad Т grad р #
1
(172)
241

Из рассмотрения предыдущих формул следует, что наибольшей
простотой отличаются те формулы, в которых мы выражаем наши
векторы через силовые динамические элементы.
Кроме указанных выше основных векторов полезно будет
получить выражение через динамические элементы ряда скалярных
и векторных величин, введенных нами раньше. Ограничимся
большей частью силовыми элементами. Рассмотрим прежде всего
две скалярные величины т и v, введенные нами при изучении
объемных условий-
А — div V
откуда:
J*
т = ^V' (173)
Для вычисления величины v необходимо знать выражение через
динамические элементы вектора §t. Так как:
& = heb§ = ^- + curlK>, У],
ибо div § = 0, то для фх получаем следующие формулы
[пользуясь формулами (166)]:
©і = I grad -?¦, grado> I -f-1 grad/>, ^ad-^-J , 1
?>i = [grad -jr-, gradSJ + f grad 7, grad -^-I >
откуда не трудно получить еще такое выражение для фх:
ірі = —[grade, grad<*>]— [grad ?, v,p grad со-J-ш gradp]-
(174)
или:
(у. — 1) ? [grad р, grad со],
/?
§і = [grade, grad<o] — (х— 1) р [grad ?, grad со]
(175)
— Л [grad ?, grad» Т] — (х — 1) ? [grad /7, grad ев].
Только-что написанные формулы дают нам возможность вывести
следующее соотношение для ^:
v = (?i> 6) = © (grad/),
dp
дх'
Ж9
О)
дх\ dt
grad
V
dg\dtj
dt
, grad to
др_
dz '
Ж'
dz\dtj-
(176)
242

В формулах предыдущего параграфа весьма часто встречалось
выражение:
¦(V, [&„$]);.
не трудно найти формулу, представляющую эту величину через
динамические элементы. Ограничиваясь силовыми элементами, будем
иметь:
decl ф = [?>!, §] = (grad ш, grad р, grad -^ J gp*ad р —
— (grad<o, gradp, grad -j~ jgrad»; (177)
<V, [§i, ©b=(*r*U, [grad p, grad ~ )?(/>) —
— grad o),
grad p, grad -^
ад-
(178)
В заключение этого пункта приведем формулу для вектора
ИМ-
, 6
щ2
grad"^' gra<1/>
(179)
3. Только-что выведенные соотношения полезны в двух
направлениях: они позволяют с одной стороны производить более
простым способом вычисление тех векторов и скалярных величин,
которые входят в наше исследование; с другой же стороны эти
соотношения служат прекрасным средством проверки правильности
выводимых формул. Чтобы показать, как такого рода проверка
производится, рассмотрим тепловое условие, выражаемое
соотношением (157).
Первое слагаемое этой формулы определится равенством (178).
Второе слагаемое вычисляется по формулам:
*х (?>, grad div V) = Е (/>)( [grad p, grad ю], grad -^ J.
Для вычисления третьего слагаемого установим формулы:
1 Л>
& + [grad div V, G] =
9G
grad ^-, grad©
o> dt
grad o>, grad p
dt -b grad ^ = o> grad -Jr -f-^j 2rad p-\-E(p) grad a>,
16*
243

эткуда для третьего слагаемого левой части формулы (157) будем
«меть следующее выражение:
(©i + fcraddivV, G], ^-+grad^) =
== —?(©)/grad p,
grad -^j, grad<o
приняв во внимание это равенство, легко найдем, что левая часть
формулы (157) действительно обращается в нуль.
В заключение настоящего параграфа сделаем несколько заме»
чаний по поводу размерности введенных нами в предыдущих
параграфах векторов. За основные единицы выберем единицы длины,
времени, массы и температуры, причем условимся размерность
величины А обозначать символом [Л], размерность длины, времени,
массы и температуры будем соответственно обозначать буквами
/, t, т и $;-так например размерность силы А выразится
следующей формулой:
[А] = т/Г2.
После этих предварительных замечаний мы можем составить
Ta*'VK> табличку размерностей разных введенных нами величин:
Обозначение Размерность
Скорость
Ускорение
Вихрь
Удельный объем
Давление
Температура
Энтропия
Расхождение скорости
Плотность тепловой мощности
Динамический градиент
Мера диссипативности
Турбулизирующий вектор
Турбомомент
Приведенный градиент
Первый тепловой вектор
Сторой тепловой вектор
Стереоскаляр
Стереовектор
Вспомогательные величины 1
Турбулизирующий
рядка
V
dV
di
Q
ш
P
T
s
6
e
G
z>
a
P
T
ь
X
0
V
m
it-1
it-2
Г"1
PnT1
тГЧ~2
r1
тГ1 Г*
It-2
t-2
r1
tr1
r2
tr2
t-1
Г1
ir*
/-V
вектор второго по-
ft
«—8
Пользуясь этой табличкой, можно с большим удобством
производить проверку формул; кроме того табличка эта совершенно
необходима при вычислении величину встречающихся в нашей работе.
744

§ 16. Частные случаи движения сжимаемой жидкости.
1. В настоящем параграфе мы разберем для иллюстрации
положений, высказанных в предыдущих параграфах, несколько типйв
движения сжимаемой жидкости. Мы будем задавать известный
кинематический характер движения и, пользуясь методами,
развитыми в предыдущих параграфах, будем отыскивать динамически
возможные случаи движения данного кинематического типа. Так
как^ілавное практическое приложение развиваемая нами область
гидродинамики имеет в вопросах движения тяжелых жидкостей,
например атмосферы, то почти во всех примерах мы будем
предполагать, что объемная сила, действующая на 'частицы нашей
жидкости, будет постоянной по величине и направлению (подобно
силе тяжести на земной поверхности). Относительно величины
притока энергии мы во всех почти частных случаях, за
исключением одного, не будем делать никаких предположений и лишь
в этом одном случае .будем рассматривать адиабатическое
движение, т. е. полное отсутствие притока энергии.
Первые три частных случая движения будут посвящены разбору
динамически возможных движений определенного кинематического
типа. Первый случай будет посвящен разбору таких движений,
при которых скорости частиц все параллельны между собой, все
перпендикулярны направлению постоянной действующей силы и для
- частиц, лежащих в данный момент в некоторой плоскости,
перпендикулярной направлению сил, все скорости одинаковы. Мы назовем
такого рода движения ортогональными движениями.
Ортогональное движение может иметь место в земной атмосфере, когда ветер
почти горизонтален и на большой площади мало меняется по
величине и направлению на данной высоте *).
Второй случай будет содержать в себе изучение таких
движений, при которых скорости всех частиц параллельны направлению
действующей силы; мы назовем движения этого случая
вертикальными движениями; эти движения имеют место в атмосфере при
слабом ветре.
Третий случай будет содержать в себе изучение движений, при
которых скорости лежат в плоскостях, перпендикулярных
направлению силы, и одинаковы для всех частиц, лежащих на линии,
параллельной направлению силы. Этот случай можно назвать
плоским движением. Он может иметь место в атмосфере, когда мы
пренебрегаем величиной вертикальных течений и считаем ветер
мало меняющимся с высотой. В указанных трех случаях мы будем
иметь примеры, иллюстрирующие разные классы движений, как-то
нормальное общее, нормальное специальное, полуконсервативное
н т. п.
Для того, чтобы показать, каким образом с помощью идеи
/характеристических векторов могут быть получены общие свойства
определенных классов движений, мы рассмотрим несжимаемое дви-
*) Этот случай был Рассмотрен иною в упомянутой выше заметке в Comptes
Rendus.
245

жение и покажем, каким образом для стационарного несжимаемого
движения находится условно-характеристический вектор,
векторные линии которого обладают свойством сохраняемости в силу
несжимаемости движения жидкости.
Для иллюстрации указанного выше различия адиабатического
движения от изэнтропического движения мы рассмотрим пример
плоского адиабатического движения, не совпадающего с изэнтропи-
ческими движениями; для этих движений, вообще говоря, можс:
иметь место образование вихрей, несмотря на то, что приток
энергии будет отсутствовать; этого обстоятельства мы однако не будем
касаться в разбираемых нами примерах, в которых турбулизирую-
щий вектор для адиабатического движения будет нулем.
Наконец, чтобы показать, как строятся основные уравнения
динамики жидкости и турбулизирующий вектор при наличности
неконсервативных сил, мы остановимся на случае движения тяжелой
жидкости относительно земной поверхности.
2. Разберем случай ортогонального движения; примем за ось
z-ов направление, противоположное действующей силе
(постоянной, как было условлено выше, по величине и по направлению).
За ось #-ов примем направление скорости, для ортогонального
движения одинаковое во все времена для всех частиц жидкости
и перпендикулярное направлению силы. Принимая во внимание»
что в ортогональном движении скорости в данный момент
времени всех частиц, расположенных в плоскости, перпендикулярной
направлению действующей силы, одинаковы, будем иметь
следующие кинематические условия, характеризующие ортогональное
движение:
u = 0, v = v(t, z), ги = 0; (180)
зависимость г; от t nz определяется с помощью условий
динамической возможности ортогонального движения, к изучению каковых
мы и перейдем.
Обозначим величину действующей на единицу массы
постоянной силы через g; в случае силы тяжести g будет ускорение силы
тяжести. Составляя динамический градиент G, найдем:
G, = 0,G, = --^, G. = -.*; (181)
отсюда не трудно установить величину составляющих турбулизи-
рующего вектора ?): 4
$, = --^-.#,=.0, & = 0. (182)
Образуя вихри, отвечающие указанному движению, будем иметь:
* = -¦?, Ч«0,С~0;
отсюда ясно, что:
, [©, ^] = oJ
или
[helmQ, S] = 0.

Таким образом ортогональное движение будет движением гельм-
гольтцевым; очевидно это движение будет главным гельмгольт-
цевым движением (helm Q = §) = 0) лишь при условии v = vx (t) +
-h г/2 (z)y где vі и v.y суть произвольные функции своих аргументов.
Ниже будет разобран вопрос о динамической возможности
главного гельмгольтцева ортогонального движения.
Не трудно видеть, что согласно формулам (181) и (182)
условие незакручиваемости удовлетворяется. Для дальнейшего изучения
условий динамической возможности ортогонального движения
необходимо составить меру диссипативности ц:
р=-*4г (183)
Отсюда ясно, что полуконсервативное ортогональное движение
си. = 0) может иметь место лишь в случае, когда скорость не зави-
ит явно от времени, т< е. когда мы имеем стационарное движение.
Само собой разумеется, что нри наличности силы (g^O) случай
безградиентного движения не может иметь места. Рассмотрим
сначала случай нормального, иначе говоря—нестационарного
ортогонального движения I-тт Ф 0}.
Составляя турбомомент и приведенный градиент, будем иметь:
divV = 0, [& VL = 0, Г& V]y = 0, [& V\, = -v^-}
отсюда:
#
V
ax = 0,«9 = 0,as=^|, (184)
P- = 0,& = -4-» P.- fc-. (185)
v-dt
Перед тем, как перейти к составлению тепловых векторов,
проверим, выполняются ли тепловые условия [равенство (157)].
Составляя турбулизирующий вектор второго порядка !qv найдем:
откуда
и так как (фь -gr + grad (і J = 0, то тепловое условие выпол-
няется.
247

Составляя тепловые векторы, получим:
0 I dv d*v дЧ) d*v \ 9 п о л >
дЧ dv I dv Y а* «о л ! (18б)
Дальнейшее наше исследование естественно распадается на
две части: &х=?0 — общее нормальное движение, и 3^ = 0 —
специальное нормальное движение. Обратимся сначала к общему
нормальному движению.
Непосредственное применение общих приемов заставило бы
нас определить сначала стереоскаляр К затем построить стерео-
вектор з и после этого уже* установить объемные условия, которым
должна удовлетворять функция v. Дело значительно упрощается,
если мы сначала, не определяя стереоскаляр, вычислим стерео-
вектор и после, помощью объемных условий, определим
стереоскаляр и установим уравнения, которым должна удовлетворять
функция v.
Образуя стереовектор, без труд_: найдем:
\ dt dz 'kg
IT ¦ ¦ — *
°х = 0, =„ = — — ,
s
v ' ~ dv dv'
так как X = — ~ фх ф. 0, по предположению), то к есть функция
х
z и /; тогда одно из объемных условий дает нам следующее
равенство:
д\_ ок _п
dt ~ ду~ '
с другой стороны объемное условие curl <х = 0 дает нам между
прочим равенство:
dy . dz ' .
Так как ое не зависит от у, то -5х = 0; <зу не зависит от х
и у, и так как —ф = -^*- = 0, то ау есть величина постоянная;
2с л
называя эту постоянную через —, будем иметь:
?
Помня, что л== ^-, с помощью формулы (186) по иыпол-
248

яении некоторых упрощений получим следующее уравнение,
которому должна удовлетворять функция у:
d*v , g ( д*у d*v ду dsy \ dv !ду\* ;10,ч
8 д& ~г 2с [ dzdt * dfi dt Ш?) ~lz~ \W) • (187}
В то же время стереовектор и стереоскаляр определятся
формулами:
2c-^^L
л 2с zc l dzdt , 2с ,„ооч
а.-О, *у = —, а,= ^ .,Х = __„, (188)
где с есть произвольная постоянная* Не трудно проверить, что
стереовектор и стереоскаляр, определенные равенствами (188), будут
удовлетворять всем объемным условиям, коль скоро будет
выполнено соотношение (187).
Таким образом функция v двух переменных t к z должна для
динамической возможности ортогонального движения
удовлетворять одному уравнению (187) с частными производными третьего
порядка. Интегрирование этого уравнения в общем случае
представляет некоторые трудности; мы приведем лишь один частный
пример решения этого уравнения, пример, могущий иметь
приложения в вопросах динамической метеорологии.
Пример 38. Разберем случай ортогонального движения, в
котором v есть функция t-\-z *). Случай этот отвечает обычному
в теории волн распространению некоторого явления в известном
направлении с постоянной скоростью- Пусть к моменту tt на
высоте zx **) скорость жидкости была vx; к моменту &>*і эта
скорость будет уже не на высоте zu а на высоте z2 = %\ -f- tx — t2y
меньшей высоты zx; таким образом данная величина скорости
распространяется, спускаясь с известной быстротой в виде плоской
волны, перпендикулярной направлению силы. В динамической
метеорологии этот случай отвечает довольно часто встречающемуся на
практике типу погоды, когда ветер—довольно большой силы на
некоторой высоте и сравнительно слабый на поверхности
земли—постепенно, как говорят, „спускается" до земной
поверхности.
Если у зависит от t-\-z, то и ^ есть функция t-\~z\ обозначая
эту последнюю функцию через F(t-\-z)y будем иметь:
I = F(t+z), v = -J-F(t+z).
*) Не трудно указанный в примере 38 способом разобрать случай, когда v
есть функция at~\-z, где ее есть некоторая постоянная.
""*) Ради краткости будем координату z называть высотой.
**'
249

Не трудно видеть, что уравнение (187), определяющее v, может
«быть заменено равенством:
<Ч = дк ,
ді dz
одним из объемных условий; пользуясь этим равенством, получим:
откуда, интегрируя по t обе части найденного равенства и помня,
что of есть функция t-\-zf получим:
°. = F(i-rz) + a,
где а—произвольная постоянная. Из последнего равенства найдем,
что F удовлетворяет следующему дифференциальному уравнению
второго порядка:
F = FF + aF + ~. (*)
Вычисляя стереоскаляр и стереовектор и пользуясь формулами
(130), определим о и р:
Р- — ^ 5 -l-/w)>
где <о0 — постоянная, a po(t) — произвольная функция времени.
Интегрирование уравнения (*) может быть выполнено помощью
бесселевых функций дробного индекса и им сопряженных*
Обозначая аргумент у F через л: и полагая
получим для определения и следующее уравнение:
<Рп (2с* ' \
-^ + іт"*+СіГ=0,
2с2
где сх—произвольная постоянная. Полагая - — jc -j— сг = Е, найдем еле-
о
дующее уравнение:
каковое уравнение интегрируется помощью бесселевой функции
с индексом —г- *). Обозначая через Zn общее решение бесселева
*) См. напр. Jahnke ui»d Emde, Functionentafeln, S. J.67.
250

уравнения индекса п (линейная комбинация бесселевой функция
с индексом л и ей сопряженной функции, причем коэффициенты
в этой линейной комбинации суть произвольные постоянные), после
простых преобразований будем иметь:
8 „ . 2с^ V Сі ' g х _ г , / , 2с9 чх
2с2 1 ,/ ,2с2 т12&\Сг~*~ g
F{x)=—~z ^~1/ сі-г—*
"(А
'*[*(*+?¦)*]
•а»
Легко видеть, что, хотя в ZJ- имеются две произвольные постоя»-
ные, значит по внешнему виду в F(x) входят три произвольных
постоянных (ибо с — произвольная постоянная), появившихся при
интегрировании нашего уравнения (*), однако на самом деле в F(x}
Z±
войдут лишь две произвольных постоянных, ибо отношение -~*
7
зависит только от одной произвольной постоянной.
Обратимся теперь к специальному нормальному движению. В этом
случае оба тепловые вектора должны обратиться в нуль, иначе
говоря— должны иметь место следующие уравнения:
dt dfidz dfi дідх~ ' ]
второе из этих уравнений, по разделении обеих частей его на
-5т I , даст следующее равенство:
(
/ d*v \
д / dtdz
ді I dv_
= 0;
очевидно, общее решение этого последнего уравнения может быть
написано в следующей форме:
где <К фц <*— произвольные функции своих аргументов.
То обстоятельство, что мы разбираем не полуконсервативное
движение ( значит -Д Ф О J, указывает на отличие от нуля
функции ^(z) и производной a'(t) функции «(*) по времени. Для
определения функций Ф, <h и а может служить первое из уравнений
(189). Подставляя в ато уравнение v, определенное из выраже-
251

вия (*), деля обе части уравнения на а'(/)* и дифференцируя
полученное соотношение по і, будем иметь
где сх — произвольная постоянная.
Отсюда ясно, что Фі(г) может быть найдено по формуле:
где сх и Со—произвольные постоянные. Определяя аналогичным
образом из первого из уравнений (189) функцию <J> (z), найдем, что
t? при СіфО будет иметь вид:
v = VclZ + Csf(t)+c, (190)
где си с%, с суть пока произвольные постоянные, а/(/)—
подлежащая определению функция-
В дальнейшем будем различать два случая: 1) сх ф б и 2) сг = 0,
когда v не определяется формулой (190).
*В случае Cj ф 0 будем иметь, что /(*) определяется [помощью
первого из равенств (187)] из такого дифференциального уравнения:
интегрирование которого не представляет ни малейших
затруднений. Обозначая через $(х) функцию, определяемую формулой:
найдем, что f(t) есть решение уравнения:
*[]/Г&)ш~е*і+*> (191)
te с3 и Сі—произвольные постоянные.
Так как в разбираемом случае мы имеем дело с специальным
нормальным движением, то для определения удельного объема <*>
(или для определения <р —1по>)нам необходимо проинтегрировать
следующую нормальную систему дифференциальных уравнений
с частными производными первого порядка:
дх U'
дъ _ 1
Vy v
d*v
д<р dz at
dz Ov
dt
do
g
dv
© —
di
do
~dt;
352

эта система является непосредственным следствием уравнений (117).
Уравнения эти показывают» что <р не зависит от х; подставляя
vy определяемое согласно предыдущим соображениям, в эти
уравнения, найдем после замены <? на <?0 по формуле
o = yln(c1z + c2) + ?o»
что <р0 должно будет удовлетворять такой системе уравнений::
ду l^CjZ+CaZ+c dt '
д<?о =_ 8 _ 1 д?о,
частное решение этой системы будет:
<?о = к[у— Усгг-\-с2 J fdt—ct)+—Vclz + Cb,
\ «f ¦ f / С\
где &—постоянная, определяемая равенством:
k-tf. (192)
Соединяя все вышесказанное, получим выражение для удельного
объема ш:
(193)
ф=Ус1г-{~с2Ф \к(у — V^z+Cbjfdi—<*) + —Vcxzfcu ,
где Ф — произвольная функция своего аргумента; определив е>, мы
с помощью квадратур найдем н давление р.
Перейдем теперь к случаю сх = 0; в этом случае Фі(г) не
зависит от z, поэтому скорость г; определится формулой:
таким образом в этом случае мы будем иметь главное гельмгольт-
цево движение. Обратим сначала наше внимание на случай
безвихревого движения, когда -г- =^/(z) = 0, поэтому v=f(t); первое
из уравнений (189) дает в этом случае:
v — at-\-b,
где а и Ь — произвольные постоянные.
Уравнения для определения <р в этом случае будут:
ад: и'
до 1 до
'ду==~ аі+Ь Ж$

s
до
a(at-\- Ь) dt'
интегрирование этих уравнений дает нам следующее выражение для
<о (ш = е'):
в=ф gz^a</-f(at*+2bt) . (194)
По найденному <» определяется помощью квадратур давление р.
Определение р облегчается тем обстоятельством, что разбираемое
движение есть движение стеробарическое, т. е. p=f(<Si1t).
Разбирая случай вихревого главного гельмгольтцева движения,
будем иметь:
* = *(«) + «('),
причем Ъ'(г)фО, равно как и a'(t)zpQf ибо мы разбирае**
движение неполуконсервативное.
Первое из соотношений (189) дает в стой случае:
Cj—произвольная, отличная от нуля, постоянная. Определив ty(z),
без труда найдем <*(і), после чего получим следующее выражение
для v:
Сх Z
г'
1п(сй*.+ с3),
(195)
где сг, с%, с3—произвольные постоянные, причем с^фО.
Система уравнений для определения <? напишется таким образом:
д?_
dz
1
CXZ — In (Cot -f-Co)
8
ii.
dt
cxz — In (c21 -f- c3)
8
c2
dt'
. ct с2і-і-с6
интегрируя элементарными приемами эту систему, получим
следующее решение для удельного объема о>:
ш
Ф
(<Ъ* + <ъ)(с1г + -&-^ ^ln(c2^+c3)
с<і9
(196)
где Ф — произвольная функция своего аргумента. Определив <о,
получим помощью квадратур р.
Перейдем теперь к случаю полуконсервативного движения.
В этом случае -зт — О, v зависит только от z, ©=/(z); нетрудно
254

видеть, что динамический градиент и турбулизирующий вектор для
рассматриваемого движения выразятся формулами:
движение это будет относиться к случаю специальных
полуконсервативных движений ( 6,—- =01. Условия (141) в этом случае
удовлетворяются, поэтому <р определяется по нормальной системе
(139) уравнений с частными производными первого порядка»
6 нашем случае эта система напишется так:
до „ ?® л до
^-^^ = 0,^ = 0;
отсюда ясно, что
О) = Ф (Z),
где Ф — произвольная функпчя своего аргумента.
Определяя давление р, без труда найдем:
= -г/щг)лгрЛі)-
где ро{і) — произвольная функция времени, a zQ — произвольная
постоянная.
3. Перейдем к разбору вертикального движения. В этом
движении скорости всех частиц жидкости параллельны направлению
действующей постоянной силы.
Выберем ось z-ов противоположно направлению действующей
силы; тогда кинематическая форма вертикального движения
определится следующими соотношениями:
ц = 0, v = 0, w =± w (t, х, g, z).
Обозначая через g величину постоянной силы, действующей на
единицу массы, найдем следующие выражения для динамического
градиента и турбулизирующего вектора:
Gx = 0, G„ = 0, G. = -f-%-„%; (197)
~ д I dw , dw \ ~ д I dw . dw \ ~ л іл лоч
*--т^ (-*+»-*)' *!=—ь[-ді+10-5;)' ф°=0-(198)
Из этих формул следует, что условие незакручкваемости
выполняется само чсобой.
Заметим, что рассматриваемое нами движение (в противность
ортогональному) есть движение не несжимаемое, ибо div V = -^-— ф. 0,
вообще говоря; ниже будут рассмотрены как раз такие примеры,
dw
когда -д— действительно .не равно нулю.
155

Определяя компоненты вихря вертикального движения, найдем:
? = -— Ті = -, С — 0;
ду ' с*лг '
таким образом вертикальное движение будет безвихревым только
в том случае, когда w не зависит от х, у; мы увидим ниже, что
этот случай отвечает специальному нормальному движению. Во всех
прочих случаях вертикальное движение будет обладать вихрями.
Образуя меру диссипативности, получим следующее для нее
выражение:
/ . дго , dw \
полуконсервативным наше движение может быть в случае, если
w = 0, когда имеет место равновесие,—разбор какового случая (не
представляющий ни малейших затруднений) мы производить не
будем, — или же в случае равенства нулю второго множителя,
входящего в выражение у-, иначе говоря — в случае безградиентного
движения, которое будет нами ни re рассмотрено.
Обратимся к изучению нормального вертикального движения;
обозначая через ф выражение:
dw . dzu
перепишем предыдущие формулы для турбулизирующего вектора
и меры диссипативности следующим образом:
&=dp *»=—яг» ®>=°>
Пользуясь этими формулами, образуем турбомомент и
приведенный градиент:
a* ф дх' a» ф dff' a° w dz ' j
1
Ф = ?+—r + w
} (200)
Обозначая b <J* через / и In id через R^:
/=1пф, W=\nw,
найдем следующие формулы для первого и второго тепловых
векторов:
1х~~ dgdz dsdz e dgdt' T» dx dz^~ dxdz"+~
R -WdW wdW
(201)
256

Из этих формул вытекает, что специальное нормальное
движение возможно лишь в случае, когда w не зависит от х и у\ ниже
мы рассмотрим этот случай, теперь же обратимся к общему нор-
^ dw
мальному движению и будем следовательно предполагать, что —т—
дхи
и —т- одновременно не обращаются в нуль.
Нам следовало бы, руководствуясь общим методом, установить
'теперь тепловые условия, определить стереоскаляр и стереовектор
и перейти к изучению объемных условий; проще однако будет
поступить несколько иначе и воспользоваться сначала частью
объемных условий, оставляя пока стереоскаляр неопределенным.
Образуя стереовектор, будем иметь
°х~ дх> a'~~dff' °«~ dz е ;
применяя к* этим формулам часть объемных условий, а именно два
скалярных равенства:
Оу ~ Ох у дх ~ dz *
вытекающих из объемного условия curl с = 0, и пользуясь тем, что
стереоскаляр У< должен удовлетворять равенствам: 4
после несложных'упрощений найдем следующие два соотношения:
бх~ dxdt' бу~~ дудё
пользуясь этими соотношениями, можно написать такое равенство,
выражающее стереоскаляр:
\ = % + c(t,z), (*)
где с—пока произвольная функция. При помощи равенств 7Х+Ь8Х=0,
у -|- ХВ == 0 и предыдущего равенства, определяющего \ легко
вывести следующие два соотношения:
откуда по интегрировании будем иметь
іі*=Д _».-»_ ел .* о
где С—пока произвольная функция. Обе функции с и С связаны
между собой; чтобы получить соотношение между ними,
продифференцируем обе части предыдущего равенства по Ц тогда, вос-
17 Вак, 2420. — А'. А. Фридман, Опыт гидромеханики 257

пользовавшись одним из объемных условий, а именно равенством
д\ до
-р = -rj, получим следующее соотношение:
д! frf = дС
cz dzdt dt '
откуда следует связь между с и С в форме, такого равенства:
дс ^дС
dz~ ді '
это равенство показывает, что с и С суть частные производные
по t и z некоторой функции A (tt z):
_дА г_дА
С~ of ' С" dz '
Вводя в рассмотрение функцию А, легко видеть, что равенства
(*) и (**) дадут нам следующие соотношения:
,_<?(/+ А)
dt '
d{W—f) . -w дА
dz Oz
(202)
где A — неопределенная пока функция t и z.
Соотношения (202) суть следствия тепловых и объемных
условий вертикального движения; покажем обратно, что, коль скоро
соотношения (202) имеют место, то, какова бы ни была функция
А от t и z, всегда следствием соотношений (202) будет выполнение
тепловых и объемных условий.
Дифференцируя второе из соотношений (202) по дг и по у9
получи*-
dzdx дх ' dx '
dzoy dy ' dy *
/оло\ 'д1 d2f
вспоминая первое из равенств (202), которое дает ~з~"= -% ^ и
т-== л , найдем, что написанные уравнения приведутся к виду:
Ya- Н~ '^* = 0» Ту + ^== ^' иначе говоря — тепловые условия будут
удовлетворены.
Объемные условия точно также будут удовлетворены, коль скоро
имеют место соотношения (202). Дифференцируя первое из равенств
(202) по х и по у, мы убедимся, что будут выполнены соотноше-
д'к до„ ді д
а
у
ния -3— = —~ у -т- = -дг-; дифференцируя первое из равенств (202)
по zt а второе из этих равенств по tf найдем, по исключении функ-
258

ции А из полученных таким образом соотношений, что н третье
е д\ до,
объемное условие, а именно равенство: -г" = —f-* также будет
удовлетворено.
Таким образом w должно быть таково, чтобы удовлетворялись
соотношения (202). Подставляя /> из первого из равенств (202) во
второе и замечая, что /=lnf!>, найдем следующее уравнение,
которому должна удовлетворять функция w\
j^o __1_ d^ ( dA
dz ~~ 6 dt l di '
Отсюда между прочим следует, что для - сжимаемого
вертикального движения j4-f-ln^ будет инвариантной функцией.
Предыдущее уравнение по раскрытии всех символов может
быть написано в виде:
dw d2w , п &2w . 0 (Fw .
5 dz dp ' dtdz l tiz* n
, / , <?w , <3w\ (dA . (ЭЛ\ /пло.
^1*+-дГ+*-йгД-й-+в,"л)- (203)
Если я> определяется этим соотношением, то для стереовектора
и стереоскаляра будем иметь равенства:
я d(f+A) a_d(f+A) „ d(f+A) ,d(f+A)
откуда без труда найдем:
<о==<о0<1еЛ{^, (204)
где ш0 — произвольная постоянная. Отсюда не трудно написать
формулу, определяющую р; р не зависит от х и у и определяется
соотношением:
*0
2 -А<*,»)
Po(t) < (205)
где z0 и ро (0 суть произвольная постоянная и произвольная
функция времени.
Таким образом решение вопроса об отыскании динамически
возможного вертикального движения сводится к интегрированию
уравнения (203). Не изучая указанного уравнения в общем случае,
разберем два частных примера, когда w не зависит от z или не
зависит от t.
Пример 39. Положим, что скорость вертикального движения не
зависит от z. Уравнение (203) в этом случае напишется в форме:
так как мы имеем случай нормального движения, то динамический
граДиент должен быть отличен от нуля, поэтому предыдущее урав-
17 259

dm.
нение можно разделить на g — ~)f и по разделении на эту
величину продифференцировать по z; тогда, обозначая через Аг
производную А по z:
а>-ё?
UZ
придеы к выводу, что Аг должно удовлетворять уравнению:
дА' . дА' л
(dw dw
так как одновременно — - и -^— не обращаются
в нуль), что А' удовлетворяет соотношениям:
ибо, если бы —5— было отлично от нуля, то из предыдущих
равенств мы имели бы:>
дА'
w =
dt
дА
г »
dz
т. е. w ье зависело бы от л: и у.
Таким образом А' есть величина постоянная; что же касается
функции A (t,z), то она определится равенством:
A(t,z) = Cz + a(t);
тогда w должно будет удовлетворять следующему уравнению:
,/, А*
где a W = -jf' .
Разберем случай определения w, когда С обращается в нуль.
Предыдущее уравнение может в этом случае быть написано
в виде:
d^w , ,, ч dw , ,, ,
Интегрирование только-что написанного уравнения даст нам
следующее выражение для w.
w=— gt+b{x,y)c{$-\-bx{x9y)9
где с {і) = е~ , и значит с(t) — произвольная функция времени,
а А и Ьг — произвольные функции своих аргументов. Определяя
260

для разбираемого движения обычным приемом удельный объе?і и
давление, найдем:
ш=б(|?)і p=_?(/)z+^(f)i
где Ь2 — произвольная постоянная, a p0(t) — произвольная функция
времени.
Пример 40. Рассмотрим теперь случай, когда w не зависит от
dzv
времени, -~дГ = ®.
Уравнение для определения W в этом случае перепишется
следующим образом:
dw дЧ) , / . dw \ I дА , дА\
Отсюда тем же приемом, как и в примере 39, получим, что
A (t9 z) должно определяться равенством:
A{t,z) = Ct+a(z),
где С— произвольная постоянная, a a (z) — произвольная функция г.
Подставляя найденное значение для A (t, z) в уравнение дая
определения za, найдем следующее равенство:
Рассмотрим частный случай движения, когда ar(z) = 0, С=0;
тогда w определится из уравнения:
dz1 ? dz
откуда видно, что w есть решение уравнения:
cw-\-g\n{cw— ?) = c2z-|-6,
где с и Ь — произвольные функции х и #.
Определение ю и р в этом случае не представляет никаких
принципиальных затруднений; мы этим определением заниматься
не будем.
Перейдем к рассмотрению случая специального нормального
движения; это случай, при котором w не зависит от х и у;
никаких дальнейших ограничений условия динамической возможности
движения на функцию w не налагают, так что to есть
произвольная функция z и L
Турбомомент и приведенный градиент в рассматриваемом
случае будут определяться равенствами:
1 dzv
% w dz
*. = 0, а, = 0, а
261

Таким образом для определения ср = In со мы будем иметь еле*
дующую нормальную систему уравнений с частными
производными первого порядка:
dx ~~ у dy ~~ ' 0z~~ w Oz to dt '
интегрирование которой зависит от выбора функции щ в
разбираемом случае <п есть функция только от t и z. To обстоятельство,
что в разбираемом случае условия динамической возможности
движения не налагают никаких стеснений на зависимость скорости w
от t и z, позволяет решить ряд задач, относящихся к
вертикальным движениям, возникающим под влиянием определенного
притока энергии. Нами в двух напечатанных работах был разобран
случай вертикальных течений, возникающих в земной атмосфере
под влиянием лучистого теплообмена земли и солнца *).
Нам остается рассмотреть теперь случай безградиентного
движения. Скорость zu в этом движении определяется уравнением:
интегрирование которого дает, что w есть решение уравнения:
где Ф есть произвольная функция своих аргументов.
Давление р в безградиентном движении не зависит от xf yf z
и является произвольной функцией времени; что же касается
удельного объема, то он определяется условием:
eta , dw dw
dt ' dz dz '
интегрирование какового уравнения и определит нам а>. Следует
отметить, что случай безградиентного вертикального движения в
атмосфере невозможен, так как требует для своего осуществления
слишком больших вертикальных скоростей, какие в
действительности не встречаются.
4. До сих пор мы изучали движения, в которых определялись
или одна искомая функция нескольких переменных, или несколько
функций одной переменной, а именно времени. Рассмотрим теперь
случай, когда приходится определять две функции нескольких
переменных. Положим, что действующая у нас сила является силой
постоянной по величине и по направлению, и примем направление,
противоположное направлению этой силы, за ось z-ов. Движение
жидкости, в котором жидкие частицы движутся в плоскостях,
перпендикулярных направлению силы, причем движение частиц
в двух таких параллельных между собой плоскостях одинаково.
*) См. указанные в § И две мои работы.
262

условимся называть плоским движением. Подобного рода
движение часто и с большим успехом изучалось в классической
гидродинамике, равным образом пытались помощью этого рода
движения объяснить ряд явлений, замечаемых в атмосферных движениях;
ниже мы увидим, что динамически возможное плоское движение
должно быть обязательно главным гельмгольтцевым движением,
иначе говоря — при наличии плоского движения вихреобразование
невозможно, обстоятельство, стоящее в коренном противоречии
с фактами, наблюдаемыми в атмосфере.
В силу этой особенности плоского движения нам
представляется, что такое движение может иметь мало применений в
вопросах динамики атмосферы.
При сделанных нами предположениях для плоского движения
мы будем иметь, что компонента по оси г-ов скорости V будет
равна нулю, а компоненты по двум другим осям не будут зависеть
от z:
u = u(t, x, g), v = v (t, x, ff), zu = 0.
Составляя компоненты вихря, будем иметь:
с л n r dv du
расхождение скорости определится следующим равенством:
дх ду'
Переходя к составлению динамического градиента, условимся
величину постоянной силы, действующей на единицу массы,
обозначать через g; в таком случае составляющие динамического
градиента определятся формулами:
отсюда не трудно найти следующие равенства, определяющие
составляющие турбулизирующего вектора:
Условие незакручиваемости сразу дает нам:
©/=-§ +«С = 0; (206)
таким образом плоское движение будет движением стеробариче-
ским; кроме того, так как действующая сила есть сила
консервативная, то § —helmQ, а потому равенство (206) показывает, что
динамически возможное плоское движение есть движение,
принадлежащее к классу главных гельмгольтцевых движений;
следовательно в плоском движении не могут возникать и разрушаться
вихревые трубки, обстоятельство, стоящее в разительном
противоречии с атмосферными явлениями. Мы ограничимся в дальнейшем
263

разбором случая нормальных плоских движений, не затрагивая
вопроса >о плоских полуконсервативных движениях. Таким образом
мы будем предполагать, что мера диссипативности у- будет отлична
от нуля.
Не трудно видеть, что Gx и Gy суть функции tf х, у, причем,
так как *?>, = (), то всегда можно найти такую функцию і, X, у,
П (/, х9 у), чтобы имели место равенства:
°'— дх' "~~ dy;
условимся эту функцию П называть потенциалом ускорения.
Составляя турбомомент и приведенный градиент, найдем
следующие равенства:
Н-а =?
ft3,=
дх '
'дх
й д'іі
p*z= —Ър- I
я,
<Ш
'2,
P?. = g-
\
(101)
dy' r!-'-f j
Для получения тепловых векторов выгодно воспользоваться
формулами (147) и (149), выражающими эти векторы через
кинематические элементы; тогда не трудно будет вывести следующие
равенства:
дН
ду
?'А20
аг»
v-\
дЬ дИ дЪ дП
u.av = u. I 5г—
'* ' \ Ох ду ду дх
і2.
— fj.j.as
г»
'J.-0,
g
_д_ (<т
ду \dt
+ V-).
и?г
'у = 8
Ох
діі. \
д I . дП\
ду оу [* +
діі
dt J дх
<208)
Рассмотрим сначала случай общего нормального движения, т. е.
'-р зависит действительно по крайней мере
предположим, что
Ot
от одной из переменных х, у. .заметим тут же, что —т—
быть представлено в следующем виде:
<?ТТ
Оі
. дИ , dU . дТХ dU
-}- Н- можеі
(209)
264

Таким образом случай общего нормального движения
характеризуется тем, .что -7Г зависит по крайней мере от одной из
переменных х и у.
Напомним, что тепловое условие в нашем случае (?) = 0)
напишется следующим образом:
("d7 + Zradii, [grad'J,G])=0;
раскрывая это равенство, найдем:
* * Ш~* *(<?Uc. (210,
дд бх \ dt )¦ дх ду \ dt
Последняя формула может быть получена из равенства:
О С
Формула (210) показывает нам, что следует отличать два слу-
іч дЬ дь лч
чая: 1) одна из производных -т—, —т— отлична от нуля, или 2) обе
дЪ дЬ ^ У
производные -г-» —г- обращаются в нули.
Разберемся сначала в первом случае. Равенство (210) в этом
случае эквивалентно равенству:
^у = Ф(М), (211)
где Ф—~ пока неопределенная функция. При наличности равенства
(211) тепловые условия очевидно будут удовлетворены, и нам
предстоит перейти к изучению объемных условий. Легко видеть, что
стереоскаляр ^ определится из равенства:
отсюда, пользуясь формулой (211), найдем следующее выражение
для h
¦Х='в-^, (212)
Фі
<?Ф
где Фг=—; отсюда не трудно уже будет получить компонента
дЬ
для стереовектора, выразив их равенствами:
1 дП 1 <Ш g ( _
°*= ф; а7> °*в фГ ^ °з==" фГ' (213)
265

Так как X не зависит от z, то одно из объемных условий
-~гг = -г- дает, что зг не зависит от ?, иначе говоря — ч^ не
зависит от ?; Фі может зависеть от t при посредстве 6 и
непосредственно*), поэтому предыдущее заключение напишется в виде
такого равенства:
^l^j-^i—0 (214)
или
д>Ф дЬ д*Ф _
<??« dt + дЬ dt ~
В силу только-что написанных равенств, получим:
dt ~ Фі dx dt' dt' Фх dy dt'
точно так же будем иметь:
dx ~~ dx \ ^ ф*
dy dy \1^ Фі
¦• _ д*Ф
где Фи = -^Г.
Замечая, что —— = Ф — и-, и пользуясь объемными условиями,
дох дХ діу ді
написанными в виде равенств ~7й~=~)—> —н= ТТ"' получим
следующие соотношения:
dx ' ф* - U' dy фі U*
Так как }і.±0 и по крайней мере одна из производных -г—
дЬ
или —т— отлична от нуля, то предыдущие два равенства дадут:
1
Фі
1
¦>1
д\і
дх9
интегрируя пг4«ученное равенство, найдем:
ф = с(*)е + а(*), Ф1 = с(0;
*) Само собой разумеется, что в этчх f осуждениях х, yt z, t рассматриваются
как независимые переменные.
266

и так как Фг не зависит от ty то с(і) является постоянной вели»
чиной, равной с:
ф = сЬ + с$,
где a(f) — произвольная функция (/).
Таким образом в результате нашего исследования мы пришли
к двум уравнениям, которым должны удовлетворять функции ник
(215)
dt
-§ = cH+a(t),
где П есть потенциал ускорения» с — произвольная постоянная,
a a(t) — произвольная функция времени. Предыдущее рассуждение
показывает, что условия (215) не только необходимы, но и
достаточны для динамической возможности разбираемого движения.
Оба приведенные выше соотношения могут быть истолкованы
с помощью понятия об условно-инвариантных функциях.
U ft ^1ПС0 г~і_л
Ь самом деле, о = , ; поэтому при С 7= 0 первое из
соотношений (215) может быть написано следующим образом:
dt u'
иначе говоря — а>С есть инвариантная функция для динамически:
возможного плоского движения. Таким образом для данной частицы
жидкости вихрь пропорционален плотности ее: чем более плотность-
частицы, тем сильнее ее вихрь. Полученная инвариантная функция
обладает тем недостатком, что в ее образовании участвовали не
только кинематические, но и динамические элементы; однако чз
предыдущих уравнений (215) можно получить инвариантную
функцию, в построении которой не участвуют вовсе динамические
элементы. Пусть a(t) равняется — $'(*); тогда второе из равенств
(215) напишется следующим образом:
Jt ~cU- с dt '
отсюда
^[П + с1пЧ-*(0]==0,
иначе говоря: П + с In С + ф (t) есть инвариантная функция. Так как
за потенциал ускорения можно взять функцию П-Ц-^г), то отсюда
следует, что всегда можно найти такой потенциал ускорения Щ»
чтобы IT0-f-cln? не менялось при движении данной частицы.
Определяя «> помощью стереовектора и стереоскаляра, а
равным образом находя давление р, получим:
11—8* П— в?
о>= со0е
, р=—^е с -fp0(4 (216)
267

тде p0(t)~произвольная функция времени: если р0(*)=0, мы будем
иметь RT=<up= —с, иначе говоря — движение будет
изотермическое, т. е. температура будет постоянная по всей массе жидкости
и не будет меняться с течением времени; реально такое движение
возможно лишь при с < 0. .
Чтобы показать, каким образом могут быть применяемы
уравнения (215) для определения искомых функций и и v, разберем один
частный пример.
Поимер 41? Положим, что мы имеем плоское безвихревое
стационарное движение; тогда ? = 0, и и v не зависят от времени L
Обозначая через—у потенциал скоростей, будем иметь:
Ох ду
Первое из уравнений (215) удовлетворяется в силу того
обстоятельства, что d == 0; для образования второго уравнения необходимо
найти потенциал ускорения. Не трудно видеть, что за потенциал
ускорения можно взять следующее выражение:
так как наше движение стационарное, то, очевидно, й можно
предполагать независящим от времени, равно как и функцию a(t) можно
без нарушения общности считать равной нулю; в таком случае
второе из уравнений (257) напишется в следующем виде:
\5і) dx*+ дх ds dxdy + \dsl да*~ с\дх^д^)'
Попытаемся найти частное решение этого уравнения, считая,
что ф зависит только от г = j/*2-р-уг. Обозначая производные^
по г разных порядков через
уравнение для определения ^:
по г разных порядков через о, 6" и т. д., получим следующее
интегрируя это уравнение, получим выражения г п й через
параметр q:
где А и В — произвольные постоянные, а 1і (х) есть интегральный
логарифм, определяемый формулой:
168
очевидно, что <7 = 7 — і •

Выражая потенциал ускорения через 4s найдем:
п=—U'2=_?
2 ' 2 "
Легко видеть, что изобары в рассматриваемом движении, в
плоскости z = const, будут круги с неподвижным центром. Применяя
формулу (216), найдем:
2с с С zc "*~ С і /,\
(w0
/>о(0—произвольная функция L
Перейдем теперь к случаю, когда 0 не зависит от х и у
-т- = -^-==0; в этом случае тепловое условие оказывается
выполненным, стереоскаляр вычисляется весьма просто и оказывается
равным А, где Ь по условию есть функция одного tz
Отсюда ясно, что стереовектор о равен нулю; таким образом
объемные условия выполняются, ш есть функция одного і,
о> = а>0(г); что же касается давления /?, то оно определяется равен*
ством
где Po(t) — произвольная функция L
Таким образом из условий динамической возможности остается
лишь условие:
Скорости в рассматриваемом движении можно выразить через
одну неизвестную функцию. Примем во внимание, что ? зависит
только от времени:
поэтому:
<--(3+?)' <217>
условие динамической возможности движения может быть в
рассматриваемом случае написано следующим образом:
^+(tx+^J^+U^-^)?+ :==0" (218)
*) ф есть функция, аналогичная функции тока С т о к с а.
269

Для иллюстрации указанного движения разберем два примера.
Пример 42. Разберем с указанной точки зрения движение, ана- *
логичнее классическому примеру из гидродинамики, когда $ есть
функция одного только расстояния до начала координат:
Ф = Ф(г),
где г = У х- -*- у-; условимся считать это движение стационарным.
Условие (218) даст в рассматриваемом случае соотношение:
-ограничиваясь случаем действительно сжимаемого движения (0 ф 0),
найдем:
тде А — произвольная постоянная. С другой стороны имеем:
дх*+ ~др ~ *'
откуда получаем, принимая во внимание, что ф есть функция /*,
следующее уравнение:
лз которого «I* может быть определено равенством:
Л, Д С—произвольные постоянные. Пользуясь указанными в
равенствах (217) выражениями для и и v, найдем:
Аі Ч* ОЛ /5 —Л1пг\2
ляТх"^"1 ^—)*;
отсюда не трудно определить П:
П=— — Г-+— arctg — -fi>(r),
где
ч^Пё^у±=ц_^г),цАВ^у„г+
, Д(Л —g) Л2
2 4
Зная функцию И, легко получить выражение для давления.
Заметим, что рассуждения наши имели место для случая, когда ЪфО,
270

При 6 = 0, & может быть любой функцией г, так как
соотношение (218) в этом случае удовлетворяется, какова бы ни была Ф
функция г. Таким образом в несжимаемом стационарном плоском
движении условия динамической возможности в разбираемом
случае (когда функция тока Ъ зависит лишь от г=]/ х*-\-у'2) не
налагают никаких ограничений на движение.
Разберем еще пример, когда скорости в плоском движении
суть линейные функции координат.
Пример 43. Пользуясь обозначением примера 1, § 2, найдем,
что скорости плоского коллинеарного движения выразятся форму-
\ами:
u= a-j-Cjjt-f
аз
ибо в силу условия для движения быть плоским с, е3, з1( s.2, %9 rt
обратятся в нули- В разбираемом случае:
иначе говоря — 6 является лишь функцией времени и не зависит от
координат. Единственное условие (218) динамической возможности
разбираемого движения выразится равенством:
С-Н^+е,) ?==().
Не трудно путем элементарных вычислений найти выражение
потенциала ускорения П:
+ (.1+.,'+^)f+(|+f(., + «!)K +
/ 2 r2
+ (4-К2 -f 3 4"
зная П, определим давление р; удельный объем <о в
рассматриваемом случае будет функцией одного времени.
Нам остается в заключение рассмотреть случай специального
нормального движения. гЗ означенном случае ~т~ и о не должны,
как это легко получить из равенств (208), зависеть от х, z/. Коль
скоро это выполнено, решение задачи сведется к интегрированию
известной системы трех уравнений с частными производными
первого порядка. Мы не будем останавливаться на подробном
разборе этого случая специального нормального плоского движения.
5. Представляется небесполезным указать, каким образом можно
интерпретировать условия динамической возможности движения и
в довольно общих случаях определить вектор, векторные линии
271

которого обладают свойством сохраняемости, иначе говоря —
определить характеристический вектор для данного движения.
Рассмотрим несжимаемое стационарное движение, иначе
говоря—рассмотрим движение, в котором div V = 0 и кроме того
кинематические и динамические элементы не зависят явно от времени L
Образуя стереоскаляр для этого движения, будем иметь:
Л ST U,
со Ot
в силу стационарности движения. Отсюда будет следовать, что
стереовектор совпадает с турбомоментом и мы получим равенство
отсюда не трудно заключить, что будет иметь место следующее
соотношение:
curl« = -± curl (?, V] + -V (grad }і, ?>) V - -L (grad а, V) $.
Если мы найдем условно-характеристический вектср а из
равенства:
Helm а -р &а = a curl о, ^й)
где & и а— неопределенные пока скалярные величины, то очевидно^
что при динамической возможности рассматриваемого
стационарного несжимаемого движения векторные линии,
отвечающие.вектору а, будут обладать свойством сохраняемости. Согласно
формуле (44) § 3 будем иметь:
да.
Helm а = -у -j- curl [a, V] -f- V div a,
ибо div V — 0. Будем искать а, удовлетворяющее соотношению (*),
в следующем виде:
a = *© + sV,
гг.еЛи s — скалярные величины, могущие, вообще говоря, зависеть
и от времени і. Подставляя это выражение для а в равенство (*)9
найдем следующее соотношение:
^ § + § V + A curl [& V] + (grad A,V) ? + (grad s, V) V +
+ &(A§ + sV)==^curl[?)V]-b-^(grad[v§)V-
j Г Г ,
— 4-feradhV)©.
г
Выбирая в полученной формуле а так, чтобы имело место
равенство :
V-
772

и сравнивая коэффициенты при $ и V, стоящие в обеих частях
предыдущего равенства, будем иметь следующие два соотношения;
-|- + ferad А, V) -:- »А - 4 fe™d IS V) - О,
~ -т (grad s, V) — Ws — -- (grad а, ?>) = 0;
следует при этом отметить, что случай h = 0 даст нам известный
факт, что для стационарного движения линии тока обладают
свойством сохраняемости. Опуская решение h = 0, найдем, что
предыдущие уравнения будут удовлетворены, коль скоро мы
положим, что
а 5 определяется из условия
(grad s, V) = — (grad —, ф;
это уравнение всегда можно проинтегрировать; таким образом для
несжимаемого стационарного движения вектор, определяемый
равенством:
будет обладать свойством сохраняемости.
6. В настоящей работе мы не ставим себе целью изучать
движение сжимаемой жидкости, когда задан определенный закон
притока энергии, например путем теплопроводности или лучистого
обмена тепла. Однако, для иллюстрации приемов, которые могут
быть применены при изучении таких движений жидкости, мы
разберем ниже два примера, относящиеся к адиабатическому
движению, т. е. к такому движению, когда приток энергии отсутствует,
причем на примерах этих выяснится, что обычное представление
об адиабатическом движении как о таком, в котором энтропия
есть величина постоянная, является представлением неправильным.
Перед тем однако, как переходить к указанным примерам,
сделаем несколько замечаний общего характера, относящихся к
движению жидкости, когда притсж энергии является заданной
величиной. Исключая динамические элементы из уравнений
гидродинамики, мы не пользовались уравнением притока энергии по
следующей причине. Плотность тепловой мощности е является
функцией не только кинематических, но и динамических элементов,
причем, как например в случае передачи, тепла путем
теплопроводности, эта величина зависит от вторых производных
динамических элементов по координатам; еще более сложной является
зависимость е от динамических элементов в случае наличности
лучистого теплообмена. Поэтому, присоединяя уравнение притока
энергии в целях определения динамических элементов, мы, вообще
говоря, не можем считать s величиной заданной или зависящей
18 Зак. 2420. — А. А. Фридман, Опыт гидромеханики 273

от кинематических элементов, а следовательно исключение дина"
мических элементов становится или весьма трудным, или же, если
зависимость в от них неизвестна, то и вовсе невозможным.
В этом лежит причина того, что мы, стремясь к наибольшей
общности результата, не принимали во внимание уравнение
притока энергии, когда выводили условия динамической возможности
движения. В наших формулах это обстоятельство сказалось тем,
что для определения частной производной давления по времени
у нас отсутствовало соответствующее соотношение, поэтому
в наших формулах всегда входила аддитивно в выражение для
давления р произвольная функция времени.
Определив динамически возможное движение согласно правилам,
изложенным выше, мы не можем, конечно, думать, что такое
движение будет возможно при всяком притоке энергии; но раз приток
энергия задан, то всегда возможно из числа динамически
возможных движений данного типа выбрать такое, которое соответствует
данному притоку энергии, или же показать, что такого рода
движения, отвечающего данному притоку энергии, существовать не
будет.
Только*что сказанное относится и к частному виду притока
энергии, к случаю адиабатического движения; само собой
разумеется, что значительная простота притока энергии в случае
адиабатического движения дает возможность сделать ряд общих
заключений относительно этого движения.
Выведем сначала несколько соотношений, относящихся к общему
случаю притока энергии, причем будем считать плотность
тепловой мощности величиной заданной.
Равенство (87) дает нам:
dp R ft
Рассматривая случай общего нормального движения, будем иметь:
grad р = — , grad ? = <у, -^ = л,
где о = In <».
Уравнение притока энергии может быть с помощью первого из
только-что написанных равенств переписано следующим образом:
dp R
а
— е
-*И-~-; (219)
ді с. ш
о
прилагая к обеим частям этого равенства операцию grad и помня
предыдущие равенства, определяющие grad ?, а также -кг grad p,
найдем:
— a) grad s— v.RT grad G = у-6 G + ?rad у.-j--* XQ — <а<т;
Сг Ot
вспоминая дальше, что jj-ct == \ia -}- ^P» и пользуясь выражениями
274

для турбомомента к приведенного градиента, будем иметь
следующее равенство:
R
— о) grade — *RTgr&dn*=(x — l)0G-r
+ *radsi+ »?-[& V]. /220)
Очевидно, коль скоро это равенство удовлетворено, то всегда
возможно из уравнения притока энергии и из остальных уравнений
гидродинамики определить р, так как будут известны все
производные давления по времени и координатам. Уравнение (220) не
является, конечно, свободным от динамических элементов и поэтому
не может служить для определения выражений скоростей движения
данного типа, удовлетворяющих не только динамической группе
уравнений гидродинамики, но и уравнению притока энергии.
Следствием уравнения (220) может служить соотношение, определяющее
турбулизирующий вектор и могущее быть полученным путем
векторного умножения обеих частей равенства (220) на нектор G;
производя вычисление, получим формулу:
р, <q = — о) [grad s, 6] — v.RT [grad fi, 6] — grad p '
^„ , _, 1Й._ , ^ ^ ,
; (221)
при этом принято во внимание равенство (§, G) = 0. Предыдущее
соотношение можем написать, пользуясь равенством (147)3 в
следующей форме:
и28 = — со [grad в, G] — xRT [grad ft, G]. (222)
Выведенные только-что соотношения служат основой теории
движения жидкости, когда задан определенный приток энергии.
Мы применим эти соотношения для случая адиабатического
несжимаемого движения. В этом случае е = 0, ? = 0, а значит, согласие
последней формуле (222), вектор 8 обращается в нуль; мы имееы
следовательно не общее, но специальное нормальное движение
(предполагая рфО); поэтому все предыдущие равенства,
выведенные в предположении общего нормального движения, могут и не
иметь места в настоящем случае специального нормального
движения. Займемся выводом условий, необходимых и достаточных
для возможности несжимаемого адиабатического движения.
Теорема 31. Необходимыми и достаточными ^условиями
возможности несжимаемого адиабатического (не
полуконсервативного) движения служат следующие равенства:
divV = 0,
№,G) = 0,
^-fgrad^[?,V].
(223)
18* 275

Покажем прежде всего необходимость этих условий. Функция
'f = lna> удовлетворяет следующим соотношениям:
grad ? = а ~ ?? . (224)
Давление р должно удовлетворять равенств м:
причем второе из этих равенств получается из условия адиабатич-
кости несжимаемого движения. Дифференцируя по t первое из
равенств (225), прилагая операцию grad к обеим частям второго из
равенств (225) и вычитая полученные равенства одно из другого,
придем к следующему уравнению:
-df -Г Srad l1 = G — + v- grad «;
пользуясь равенством (224), найдем третье из соотношений (223)
нашей теоремы. Первое из этих соотношений есть условие
несжимаемости движения, второе — условие незакручиваемости. Таким
образом необходимость соотношений (223) доказана.
Достаточность соотношений нашей теоремы устанавливается
с помощью теоремы 25 об условиях специального нормального
движения. Последнее из соотношений (223) путем векторного
умножения на G дает нам равенство:
FM=p$ +
grad^-r —, G
= 0.
Прилагая операцию curl к обеим частям последнего из
равенств (223), будем иметь:
?>і = helm?) = 0.
Пользуясь формулой (149) для определения первого теплового
вектора и замечая, что 3 — 0, ?)j = 0, найдем следующее равенство;
2v —
ПГ
grad Н--^г, [&V]
иначе говоря [см. последнее из соотношений (223)] у = 0. Таким
образом из условий нашей теоремы следуют условия теоремы 25,
посвященной специальному нормальному движению.
Таким образом возможно найти <о и р такие, чтобы имели
место соотношения:
grad? = a-f p-^-,
gradp = —;
последнее же из равенств (223) показывает, что, если <р удовле-
276

творяет первому из только-что написанных равенств, то возможно
найти р из уравнений:
, Q др у-
s и <и ' ді а) '
что и доказывает достаточность условий нашей теоремы.
В процессе доказательства теоремы 31 мы нашли равенство:
©I=helm$ = 0;
это равенство, без труда проверяемое путем применения формулы
(174), ибо —>- = О, -J-- = 0 в силу адиабатичности и несжимаемости
движения, показывает, что вектор ?) есть характеристический
вектор, векторные линии которого обладают свойствам сохраняемости.
Теорема 32. Для несжимаемого адиабатического (не
полуконсервативного) движения векторные линии турбулизирующего
сектора обладают свойством сохраняемости-
В качестве примера на приложение предыдущих теорем
разберем адиабатическое несжимаемое вертикальное движение.
Пример 44. Для вертикального' движения имеем:
и=0, v = 0, w=zu (/, х, y*z).
Условие несжимаемости дает:
divV = ^=Qs
w есть функция і, xt у.
Составляя динамический градиент, турбулизирующий вектор и
меру диссипативности, будем иметь:
Gx = 0, G„ = 0, а=-*-
Юх — ~А± А.. » Vtf ~
щ
dtdy>
dtdx
dt >
dt '
откуда без труда найдем, что условие незакручиваемости
удовлетворяется. Составляя вектор [?>, V], найдем:
Wdx W'
vi d'w
[Ь,П = о,
откуда третье из условий теоремы 31 дает нам:
_д
дх
д
03
¦из
W
?
а
о
. dzo
1 dt
, dm
d2zv
d*w
dtdx
#
w9
w
dtoy
= 0.
277

Из этих равенств без труда получим:
дт От п <f~w п
7ы^°> -ц=0> ~діг^0;
так как мы имеем дело не с полуконсервативным движением
(а ф 0), указанные только-что равенства дают*
w = at -f- Ь,
где а, Ъ — произвольные постоянные. Движение это является
движением стеробарическим, ибо і>х = О, фу = 0, фг = 0.
Пример 45. Рассмотрим еще составление условий теоремы 31
для движения, определяемого следующим образом. Ось z-ов
выбираем противоположно направлению силы тяжести, скорости
движения задаем условиями:
и = и (t, х, z), v = 0, w = m (t, x, z);
условие несжимаемости показывает в этот* случае, что существует
такая функция ¦!» (t, х, z), что имеют место равенства:
д& дЬ
dz дх
Составляя компоненты вихрей, найдем:
Турбулизирующий вектор определяется равенством:
& = 0, $. = % & = 0;
динамический градиент будет дан нам следующими формулами:
-, du п А п dm
G'=- dt ' G*= 0j G*= ~8—jF'
поэтому условие незакручиваемости (§, G) = 0 будет выполнено само
собой. Составляя вектор §, найдем:
Из теоремы 32 будут вытекать необходимые (но не
достаточные) условия адиабатичности рассматриваемого несжимаемого
движения:
dt* '
Третье уравнение (223) в нашем случае может быть написано в виде.
d'2u f ди du , dm dm .
dfi ' дх dt ' дх dt
~_d_(dw\ д__ idu_
_дх \ dt) dz \ dt
~dr{ . дь
. dm
-\- a
dt дх9
278

d*w \du du , dw dw ,
rg
dw
dz
эти уравнения дают два соотношения, которым должна удовлетворять
одна функция <Ь; мы оставляем открытым вопрос о возможности
существования такого рода функции й*
Предыдущие примеры, равно как и те, которые будут
приведены ниже, а также примеры разобранные нами, ноне включенные
в настоящую работу, все приводят к стеробарическим
адиабатическим несжимаемым движениям; естественно поэтому возникает
вопрос о возможности несжимаемого адиабатического не-стероба-
рического движения, т. е. такого движения, во котором турбули-
зирующий вектор отличен от нуля и в котором, значит, не имеют
места теоремы Гельмгольтца. Нам не удалось найти примера
такого движения, равно как и показать, что оно невозможно;
в настоящей работе вопрос этот остается открытым? он
представляется нам чрезвычайно важным, так как указывает на
возможность или невозможность образования вихрей - без притока
энергии *).
Выше мы указали, что адиабатическое движение не есть еще
движение, в котором энтропия постоянна и в котором,
следовательно, давление и удельный объем связаны соотношениями:
р&' = с,
где с -~ постоянная, не зависящая от времени и координат, величина.
Приведем два примера адиабатического движения: в одном будет
выполняться указанное равенство, в другом оно иметь места не
будет.
Пример 46, Направим ось z противоположно силе тяжести
и рассмотрим вертикальное движение. Обратимся к специальному
нормальному вертикальному движению, иначе говоря—предположим,
что компоненты скорости заданы нам равенствами:
и = 0, v = 0, w = w (tt z).
Динамическая и тепловая гругпы уравнений гидродинамики
дают нам для рассматриваемого случая адиабатического
вертикального движения следующие три уравнения:
dw , dw dp
dt ~ dz ё dz9
d In ш . d In ш dw
w
dt { dz dz'
dlnp , d In p . dw л
(*)
*) Возможность несжимаемого адиабатического не-стеробарического движения
показана Н. ?- Кочиным, применившим метод А. А. Фридмана. См. дополнение.
Прим. ред.
2П

причем р и ю зависят только от /иг. Рассматривая случай
стационарного движения, будем иметь:
р = с1иГ*з
где сг и са суть произвольные постоянные; только-что
написанные формулы дают:
р<я* = Cj Co*;
таким образом в рассматриваемом движении энтропия является
величиной постоянной.
Для определения w первое из вышенаписанных уравнений по
интеграции дает следующее соотношение:
1 — 7
2cxc_w , 0
w iZl/. r*Sz = cS'
где с3 — произвольная постоянная, а х. отлично от 1.
Пример 47. Рассмотрим вертикальное движение, аналогичное
движению, разобранному в предыдущем примере, но предположим,
что w не зависит от z.
Полагая: 1//л
где &'(0 есть производная по t неопределенной пока функции
4* (і), для определения о и р будем иметь следующие
соотношения:
откуда
где /^ и F<z — произвольные функции.
Подставляя найденные значения р и <» в первое из
уравнений (*), найдем:
</' (0=-т*-/ч(*-Ф (*)) ^2 (* - Ф (*)),
откуда
где Л — произвольлая постоянная величина. Вводя вместо А
величину а под условием:
будем иметь:
p = F(z + aP — bt — c),
2a-rg
®~ f(z-f-<^ —^ —с)
w= —2at-\-b\
280

а* Ь. с — произвольные постоянные, a F— произвольная функция сво-
его аргумента; ее можно всегда выбрать так, чтобы /х»х не было
величиной постоянной; отсюда следует возможность
адиабатического неизэнтропичес]КОго движения.
7. В заключение настоящего параграфа разберем движение,
совершающееся на поверхности земли.
Уравнения гидродинамики для рассматриваемого движения,
согласно сказанному в § 11 настоящей главы, напишутся в
следующем виде:
4f = -»Sfradp-bK-2[L, V],
^-=chvV,
где К есть вектор консервативной силы, действующей на единицу
массы, a L есть вектор, направленный вдоль по земной оси
к южному полюсу земли и по величине равный угловой скорости
вращения земли вокруг оси. При этом, конечно, движение
рассматривается в координатных' осях, неизменно связанных с
вращающейся землей. Динамический градиент для рассматриваемого
движения будет:
G=K-2[L,V]—^[-;
переходя к составлению турбулизирующего вектора, заметим, что
curl К = 0» и
curl [L, V] = helm L,
ибо "7)7* =0; L — постоянный по величине и направлению вектор.
Приняв эти замечания во внимание, найдем следующее равенство:
? = helm(Q-f2L);
таким образом в рассматриваемом случае турбулизирующий вектор
не есть helm вихря, а является Ьеіт'ом другого вектора Ql =
= Q -{- 2L *); рассматривая случай стеробарического движения, мы
увидим, что не вихревые линии обладают свойством
сохраняемости, а векторные линии вектора Q -f- 2L.
Таким образом в движении около поверхности земли при
наличности консервативных сил и при условии, что давление есть
функция плотности (стеробарическое движение), может возникнуть
вихрь, так как напряжение будет постоянным не для вихревой
трубки, а для трубки вектора Q-J-2L; в этом лежит отчасти
причина образования циклонов на земной поверхности**).
*) В динамической метеорологии этот вектор многие называют приведенным
вихрем.
**) К этой причине присоединяется, как выяснил Prof. В jerknes, и образо-
і ание вихрей под влиянием того, что давление не есть функция плотности.
281

Чтобы показать применение наших методов к случаю
наличности неконсервативных сил, разберем следующий пример.
Пример 48. Выбрав ось z-ов противоположно силе тяжести,,
рассмотрим ортогональное движение по отношению к осям,
неизменно связанным с вращающейся землей. Называя через Lu L.iy
L% проекции вектора L на выбранные нами оси, образуем
выражения для проекции инерционной силы U= —2 [L, V]:
Ux = 2Z,3u, Uy = О, U9=— 2Lxv;
отсюда нетрудно определить динамический градиент:
G, = 2L3«, G,= —»-, Ge= —8 — 2Цт
g — ускорение силы тяжести*). Образуя меру диссипативности и
турбулизирующий вектор, получим:
dv
«.= —зга* ^=-2L><h- *>*=°-
Составляя условие незакручиваемости, найдем:
/ ^ dv dv\
если L3 = 0 (движение происходит на экваторе), указанное
равенство выполняется само собой; если Lj^O (движение
происходит не на экваторе), то, интегрируя полученное уравнение,
определим v следующей формулой-
где / и $ — произвольные функции. Составляя турбомомент I в
предположении, что движение не полуконсервативно, -?т ф О ], будем
«меть:
.,-0, „, = 0, *> = Щ',
дсс
отсюда ясно, что -^- = 0, curl а = 0, а значит первый тепловой
вектор у обращается в нуль. Предполагая, что мы имеем дело
с общим нормальным движением, т. е. предполагая, что вектор Ь
отличен от нуля, будем иметь для стереовектора и для стереоска-
ляра следующие равенства: *
as
f(*)'
*) Само собой разумеется, что в величину ?* введена уже nonpros* на
центробежную силу вращения земли; так как мы предполагаем g постоянным, то это
значит, что мы рассматриваем движение на небольших участках земли.
282

<o = w
при этом очевидно, что как тепловые, так и объемные условия
будут выполнены; таким образом на f(z) никаких дальнейших
ограничений не налагается.
Определяя удельный объем о и давление ру получим:
где <о0 — произвольная постоянная, p0(t)—произвольная функция от
времени, a zQ — постоянная величина. Очевидно, что в плоскости,
перпендикулярной оси z, мы будем иметь прямолинейные
изобары, определенным образом отклоненные от перпендикуляра к
направлению скорости течения (под влиянием отклоняющей силы
земли).
Разобранное нами движение не должно быть специальным
нормальным движением; вычисляя величину Зв, мы найдем, что она не
обратится в нуль, коль скоро выражение:
&у 1 (ду\2
dt* v { ді]
будет отлично от нуля. Таким образом разобранное движение
будет иметь место, коль скоро ty(t) будет таково, чтобы выражение
Ф"(') ', /а было отлично от нуля; разумеется, можно выбрать
бесчисленное множество функций U удовлетворяющих этому
условию.
Перейдем теперь к рассмотрению опущенного ранее случая
специального нормального движения. Составляя компоненты
приведенного градиента, получим следующие равенства:
й ~_2^з р — L ft _ 2 2^і
где / и ф суть функции: первая z, вторая времени t, такие, что
скорость v выражается через них равенством:
причем /', ? суть производные этих функций по аргументам; так
как движение мы рассматриваем не полуконсервативное, то tyf
отлично от нуля.
Составляя компоненты второго теплового вектора, найдем
следующие формулы:
іиГ , 2Lsg_
о*

отсюда (принимая во внимание, что L^ -? 0) найдем следующее
равенство:
6"
h~j=0' w=f(*)/(z)-
Второе равенство показывает, что &(t) не зависит от і; это
противоречит условию *У(і)Ф0; таким образом специальное нормальное
движение в рассматриваемом случае невозможно.
Обращаясь к случаю полуконсервативного движения, найдем,
что из условия ;і = 0 следует:
~=0, «=/(*),
где f(z)—неопределенная пока функция своего аргумента. Составляя
динамический градиент и турбулизирующий вектор, будем иметь
следующие равенства:
Gx = 2LJ(z), Clf = 0, Gs = -g- 2LJ(z),
*, = 0, i\ = - 2Lf (z), *Л = 0;
отсюда ясно, что условие незакручиваемости выполняется;
замечая, что в рассматриваемом случае величины 5, v, 0, указанные
в условиях теоремы 27, обращаются в нули, найдем, что условия
этой теоремы выполняются. Удельный объем <*> (или ? — 1п<*>) и
давление определяются из следующих уравнений:
\g+2LJ(z)]^ = Q. 2Laf(z)d^ = 0,
[g-r2LJ(z)]ddt + 2L3f(z)pz = 2L3f'(z),
гнтегрируя эту систему, после совершенно элементарных
вычислений получим такие равенства:
(* = nz)4>\x— тгг- I Т7^-— т12 ,
-*>*(*-? j
Жі U
*0
г
где z„—постоянная, Ф — произвольная функция своего аргумента,
р0 (і) — произвольная функция времени, a F(?) определяется
равенством:
-rv \ ¦ &
С'
^0
Ф(а)'
здесь о0—постоянная величина.
284

Таким образом в рассматриваемом случае мы имеем стационарное
движение; сечения плоскостями z = const изобарических
поверхностей будут прямолинейными изобарами, параллельными
направлению движения. Мы получили таким образом случай движения вдоль
изобар — случай, наблюдаемый в атмосфере на больших высотах, где
уменьшается влияние таких диссипативных сил, как внутреннее и
внешнее трение.
Не трудно заметить, что, при дфО, безградиентное движение
в рассматриваемом случае при L3=?0 невозможно.
Случай, когда L3 = 0 (движение под экватором), не представляет
никаких трудностей для своего рассмотрения; мы, однако,
останавливаться на нем не будем.
Глава IV.
СВЯЗЬ КИНЕМАТИЧЕСКИХ И ДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ.
§ 17. Выражение скорости через динамические элементы.
1. В первой части настоящей работы мы установили ряд
векторных величин, управляющих изменением вихревых линий при
движении общего типа сжимаемой жидкости. В предыдущей главе
мы разбирали вопрос о том, какие движения сжимаемой жидкости
являются динамически возможными; при этом нами было устано*
влено деление ¦ элементов, характеризующих движение, на две
группы—кинематические и динамические элементы. В первой части
нашей работы мы выразили закон изменения вихрей при
посредстве кинематических элементов; в предыдущей главе некоторые иа
векторов, управляющих изменением вихревых линий (например
:урбулизирующий вектор), были нами выражены через динамичен
ские элементы; настоящая глава будет посвящена выражению всех
кинематических элементов и векторов, управляющих изменениями
вихревых линий и напряжений вихрей через посредство динамических
элементов.
Принципиально задача наша был" бы разрешена, коль скоро
нам удалось бы по заданным динамическим элементам определить
компоненты вектора скорости. Наилучшим решением вопроса было
бы выражение компонентов скорости через посредство давления,
удельного объема и их производных по времени и координатам.
Подобного рода решение представляет весьма значительные
трудности; кроме того в него не вошла бы явно плотность
тепловой мощности притока энергии, иначе говоря — приток энергии не
был бы учтен непосредственно. Оказывается однако, что путем
привлечения к рассмотрению динамических элементов второго
порядка, иначе говоря— предполагая известными плотность тепловой
мощности притока энергии и расхождение скорости, представляется
возможным выразить компоненты скорости, а, значит, и все
кинематические элементы через посредство динамических элементов
первого и второго порядка, их производных по времени и коорди-
285

¦натам, а также при помощи особой величины, входящей в
выражение вихревой меры и представляющей скалярное произведение
из вихря и турбулизирующего вектора, обозначенное нами
через TV:
N=(§, a).
Таким образом, коль скоро нам будут известны давление, удель»
яый объем, расхождение скорости, плотность тепловой мощности
притока энергии и указанная величина N, то мы можем определить
компоненты скорости, а значит и все кинематические элементы и
все векторы, характеризующие изменение вихревых линий при
движении сжимаемой жидкости. При этом самый процесс определения
скорости будет требовать знания указанных величин, а также
первых частных производных давления и удельного объема по
времени лишь для определенного момента времени.
Указанным приемом легко будет решить поставленную в первой
части задачу о вычислении вихревой линии и направления вихря
к моменту t -|- Л*, коль скоро известен вихрь к моменту і> а равно
известны к атому же моменту динамические элементы первого и
второго порядка, плотность тепловой мощности притока энергии
и расхождение скорости.
Небесполезно будет сделать следующее замечание.
Практически чрезвычайно важно уметь вычислять компоненты скорости,
а равно и векторы, определяющие изменение вихря с помощью
указанных выше динамических элементов, так как эти элементы,
в частности давление и температура, гораздо легче наблюдаются,
чей скорости движения жидкости (особенно так называемые
вертикальные течения* т. е. вертикальные составляющие скорости ветра
в атмосфере). Представляется, согласно только-что сказанному,
чрезвычайно выгодным определить величину компонентов скорости,
а равно и векторов, характеризующих изменения вихрей через
посредство легко доступных для наблюдения элементов.
Обращаясь в частности к определению изменения вихря, мы
должны будем вычислить вектор —%—, или же, применяя
соображения, изложенные в первой части настоящей работы, определить
элементы главного тетраэдра, знание которых позволяет нам
определить основной сферический треугольник и таким образом по
вихрю к моменту t построить новый вихрь к моменту *-рД*. Как
первая, так и вторая задача сводятся к определению двух
векторов: вектора Н и вектора D. Знание вектора D оказывается
ненужным в случае, когда к исходному моменту t вихрь Q
отсутствует; этот случай, наиболее простой, был рассмотрен Schutz'eM и
Silberstein'oM *), давшими простые геометрические предложения для
.построения вихря в случае, когда к исходному моменту движение
совершается при отсутствии вихря.
*) Si Iber stein, „Ober die Entstehung von Wirbelbewegungen in einer rei-
bungrslosen Flr-**«tkeit", Bulletin de l'Academie de Cracovie, 1896, p. 28Q—290; см.
также статью S e л u t z'a в Annalen d. Physik, 1895, S. 144—147.
286

_ Согласно только'что сказанному мы в дальнейшем обратимся
прежде всего к задаче о выражении вектора скорости, а равно и
иных кинематических элементов через динамические элементы.
При этом будем выбирать всегда силовые динамические элементы,
равным образом будем рассматривать движения, не принадлежащие
к классу стеробарических движений.
Для стеробарических движений анализ наш не может быть
применен; для вихрей в стеробарическом движении имеют место обе
теоремы Гельмгольтца, поэтому дополнительное рассмотрение
изменения вихревых линий в этом случае не является столь
необходимым, как в общем случае движения.
Выразив кинематические элементы через динамические, мы
перейдем к изучению изменения вихрей; это изменение мы будем
рассматривать с двух точек зрения: во-первых, будем строить
вектор —7г , иначе говоря—распространим исследование Silberstein'a
на более трудный случай изменения вихрей, когда имеет место
в исходный момент вихревое движение; во-вторых, разберем
изменение сначала вихревых линяй, а потом и напряжения вихрей
согласно положениям, установленным нами в первой части нашей
работы. При этом мы укажем, каким образом через динамические
элементы определяются отклонение, кручение, изгиб и уклон вихря,
а равно и остановимся несколько на вопросе, какие условия на
динамические элементы налагает та или иная особенность
вихревого движения, указанная нами в части I нашей работы.
Настоящую главу - мы закончим кратким изложением теоремы
Bjerknes'a о связи изменения циркуляции скорости или, что то же
самое, напряжения вихря с динамическими элементами.
2- При изучении связи скорости V с динамическими элементами
мы будем предполагать, что рассматриваемое нами движение не
относится к разряду стеробарических движений, иначе говоря —
будем считать, что турбулизирующий вектор ф — [grad p> grad <в]
отличен от нуля; это означает, что векторы grad/7, grade) не лежат на
одной прямой и, следовательно, три вектора
gradp, grad<o3 [gradp, grade»] (226)
не компланарны между собой- Раз это обстоятельство имеет место,
то всегда будет возможно всякий вектор разложить (см. § 3) по
указанным трем векторам. Разлагая вектор скорости V по этим
трем векторам, получим для него следующее выражение:
V = a grad р -f Ь grad о> + с $. (227)
Если бы величины а, Ь, с мы могли определить через
динамические элементы, то задача наша была бы решена. Определив
скорости через динамические элементы, мы без труда получили бы и
остальные кинематические элементы; при этом само собой
разумеется, что все векторные кинематические элементы было бы
чрезвычайно удобно разложить по векторам последовательности (226).
Оказывается, что а и Ь определяются через динамические эле-
287

менты первого и второго порядка, что же касается величгяы с>
то в определение ее, кроме динамических элементов первого и
второго порядка, входит еще указанная нами выше величина N:
N= (Q, ?); ' (228)
величина эта может считаться известной, коль скоро задан л вихри
и динамические элементы; она может быть написана в виде
определителя:
', 5 V ;
Л7=
др
дх
д<о
'дх'
др
ду
д&
?
др_
Oz
бы
Oz
(229)
точно так же эта величина N в случае наличности консервативных
сил может быть выражена через вихревую меру по формуле (68) § 19:
tf=Q3V, (230)
ибо, как мы увидим ниже, в следующем параграфе, вектор h
совпадает с турбулизирующим вектором в случае, бели силы
консервативны; в свою очередь вихревая мера приближенно
выражается через индивидуальную производную циркуляции по контуру,
т. е. по теореме Bjerknes'a выражается через, динамические
элементы Соб этом см. ниже в § 19. Следует оговориться, что
предыдущий результат будет иметь место лишь в общем случае,
когда некоторое выражение Р:
/>=(& curl ©),
отлично от нуля. Движение, в котором имеет место случай Р = 0
мы назовем исключительным; для этого движения необходимо'
пользоваться иными приемами для определения коэффициентов а,
Ь, с в формуле (227).
Приступая к определению коэффициентов а, Ь9 с в формуле (227)>
введем следующие обозначения:
(©, $) = |?1а = л,
, л л\\ <*? &і д<? дъ до д'Ь ,. \ (231)
(grad Ъ grad 6) = --+^-+-- =J(9, 6), J
при этом для сокращения письма введем еще символы:
Др)=Др. р\ /(«)=/(»,«), J=J(p,»>)- u32)
Напомним, что символом .?(?) мы условились обозначать
выражение:
Е (?) ^ Tt ~ %={V' grad ?)- (233)
Согласно сказанному в предыдущей главе, Е(р) и Е{<&) не трудно
будет выразить через плотность тепловой мощности е и расхожде-
288

ние 0 помощью следующих формул, являющихся повторением
формул (87):
Помножая равенство (227) скалярно на grad р и grad », будем
иметь для определения а и b следующие формулы:
E(p) = aJ(p) + bJ,
E(») = aJ+bJ(«);
определитель этих уравнений относительно неизвестных а и Ь
равен Л:
h=J(p)J{*)-J*.
Так как' движение не стеробарическое, то этот определитель не
обращается в нуль; отсюда, определяя а и Ь, найдем следующие
равенства:
а = Е(Р)Ш-Еп1,
b=~-E(P)? + E(»)JM
<234)
Для определения с применим к обеим частям уравнения (227)
операцию div; тогда, пользуясь формулой (33) § 3 и помня, что
div § = 0, получим следующее соотношение:
(grad с, §) = ? - аЬр - Ъ^ -J(a, p) -J (V), (235)
где символ Лср означает выражение:
Только что написанное соотношение дает возможность опреде
лить с путем интегрирования уравнения с частными производным!
первого порядка, коль скоро нам будут известны динамические
элементы, первого и второго порядка.
Если желаем получить с в конечном виде, то мы должны
обратиться к другим приемам. Применяя к обеим частям равенства (227)
операцию curl и пользуясь формулой (34) § 3, а также равенством
curl grad<p = 0, найдем следующее соотношение:
Q = [grad a, grad р] -f- [grad b, grad со] -f [grad с, ф] -j- с curl §. (236)
Умножая это соотношение скалярно на § и пользуясь
формулой (28), § 3 получим:
* = (Q, © = [/(в,»-У№,«)]-У-У(в. *)J(P) +
+J(b,p)J(<») + cPf
где Р <стуед?ляется, как уже указано было выше, равенством:
/> = (?, curl ф) (237)
15 3, ч. ?4і0.—А. А.<Йді«Вкак, Опыт гидромеханики 289

Если Р отлично от нуля, что мы и будем предполагать в
дальнейшем, то с определится из вышенаписанного равенства с фор*
мулой:
,__ N+J(*> «)J(P)-J(b, p)j(*)+J*U(b,*)-J(atp)]
С~ Р
(238)
Таким образом все коэффициенты формулы (227) определены
с помощью динамических элементов первого и второго порядка, а
также с помощью величины N.
Ниже мы укажем несколько примеров вычисления помощью
только-что установленных формул коэффициентов в равенстве (227).
Вычисления эти, хотя и достаточно длинны, не представляют,
однако, ни малейших затруднений.
Руководствуясь идеей, указанной в начале настоящего пункта,
нам предстоит разложить все встречающиеся у нас векторы, в том
числе и вектор D, по векіюрам последовательности (226).
3. Пользуясь предыдущей формулой (227), дающей выражение
скорости с помощью трех составляющих, направленных по grad p,
grad оо и ?>, не трудно будет ряд кинематических векторных
элементов представить разложенными по направлению указанных
векторов. Займемся прежде всего выражением вектора вихря 2.
Обозначая коэффициенты в указанном разложении вихря по
векторам grad р> grad о>, Jq, через &1т 22> ^з> напишем следующее
равенство:
Q = Qx ^ad я + Q2 grad <о — ?3 ?>; (239)
задачей настоящего пункта будет определение величин Qlf 22, 23.
Для вычисления величины Qt мы воспользуемся формулой (236),
выражающей Q; применяя к каждому из слагаемых этой формулы
разложение по векторам grad pf grad «о и §, указанное в формулах
(49) § 3, решим поставленную задачу.
В дополнение к обозначениям предыдущих пунктов настоящего
тараграфа введем еще следующие символы:
до д'$ дг$
#(<?) = (grad <р, §) =
дх
др
дх
да>
д9
др
дм
dz
дР
dz
<?<0
dz
(240)
дх di/
Q (?) = (grad о, curl ©); (241)
символы ати обладают рядом свойств, указанных равенствами:
К(р) = К(») = 0, )
([[grad?, grad/>], grad a], ?) JK{<o), [ (242)
[[grad <p, $], grad 4»] =/ (<?, 4) & '" ('Ю grad <p;
I
290

эти равенства или очевидны, или непосредственно выводятся из
формулы (27) § 3.
Для получения Q4 определим коэффициенты а4, bif с, в
следующих равенствах:
(243)
} (244)
[grad a, grad р] = аг grad р-*-Ьх grad g> -J- Сі ?),
[grad 6, grad со] = а<> grad р -j- &> grad <о -f- с2 ф,
curl § = а3 grad р -j- 63 grad со -j- с3 §,
[grad с, §] = а^ grad р -|" *4 ST^ad ш + с4 $>;
пользуясь формулами (49) § 3, без труда найдем:
hai = — K (a) J hb, = K Ш(Р)
h^-K (b)J («>), А63 = К {b)J,
ha5 = Q (P)J(<*>) - Q (из)/, hbB = - Q fa)/ + Q (»)/Ы,
«4 =/(c, °>), 64 = —/(c, p),
Лс^УСа,?)/-/^,»)/^),
Ас,=У(*./»)У(«)-У(*>-)У,
Ac3 = P,
c4 = 0.
Приняв во внимание только*что написанные формулы и
подставляя значения коэффициентов а, и т. д. в равенство (239) для Q,
найдем следующие выражения коэффициентов Qt:
hQt = hj(с, ») - [К (а) -Ь cQ («)] /- (# (6)- cQ (P)J./(•), \
hQt = -V(c,py+[K(b)-cQ(p)]J+[K(a) + cQ(»)]J(p), j (245)
hQ» = U(fi,p)-J(b,*)]J+J(b,p)J(*)-J(a, *)J(p) + cP. ]
Легко видеть, что написанные здесь выражения для Q4 зависят
от динамически.! элементов первого и второго порядка, а равным
образом и от величины N.
4. Для выражения вектора D через динамические элементы нам
необходимо будет рассмотреть разложение по векторам grad р,
grad ш и © ряда вспомогательных векторов, которые будут играть
роль при определении векіора D. Введем следующие обозначения:
grad с? =* ат grad р -f Ьс grad о> -f <ч 4>, |
I
[grad <р, grad р] = а? grad р + *? grad <о -f с? Jg>, [
[grad <?, grad <*>] = а^ grad /э -(- *« ?rad <° + S Ф- J
(246)
19*
291

Применяя к определению коэффициентов в этих формулах
равенства (45-) § 3, найдем:
Ч =/(?, р)/П -](?, °>)У> л*, = -У(т. />) У+
+ ¦/(?,«) У О»),
hb=K(o)J(p\
hb':=K(<?)j,
Ц = -*(?) У («О,
Ц=У(?>р)У-У(?,<»)У(/>),
Лс" =У (<?, />) У (ев) —у (о, о>)У.
(247)
В дальнейшем нам необходимы будут коэффициенты в
разложении следующих векторов:
(grad <?, V) grad ср = А^ grad р -f В? grad ш +¦ Ср &
(grad ф, V) grad <р = Л^ ф grad р + 5?і ф grad <о + С?Гф ?, ^ (248)
(& V) © = Лх grad р + Ля grad « +*8 ©•
Для определения коэффициентов первой строки воспользуемся
формулой:
(grad <?, V) grad ? = у grad / ('?, <р),
вытекающей из равенства (40) § 3, каковым равенством мы
неоднократно будем пользоваться в настоящем пункте.
Обозначая выражение J (?,<?) через / (о):
мы с помощью первой из формул (246) найдем следующие
равенства:
АА=^У [У_(?)>/>! У»-|У [У (<?)> «ОУ.
hBf=-±JUto),p\J+jJU(?),»]J(pl
(250)
Коэффициенты А^ ^ и т. д. нужны нам будут только в двух
292

случаях: или когда о = р, $ = ®, или когда <р = », '} — р. Замечая,
что на основании формулы (40) § 3:
(grad °>, V) grad p = j curl & ~ ^ STa<*/+-у grad o> — -у grad /?,
(grad p, V) grad © = — у curl © + у grad/+ "y grad /> ^ grad »,
и пользуясь первой из формул (246) и третьей из формул (243),
найдем следующие выражения искомых коэффициентов:
Р- и>
^ju^)m-^j^pnp),
hB
_ V
іЛ,р
г ар) j
j_
+|л/.<В)У(Р)-^/(р)+^Л
Коэффициенты /ц получаются применением к формуле
(251)
(©, V) & = 2 grad А ~~ [& curl
вытекающей из формулы (40), во-первых, формулы (246) и, во-
вторых, очевидного равенства:
[$ curl $] = Q(P) g^d *> — Q W grad />; (252)
293

произведя указанные выкладки, найдем:
ЛА1 = уУ(А>А»)У(<о)-і/(А.«.)У + АО(.),
АЛ,
\j{h,P)J-r±J(h,«)J{P)-hQ{p),
hh3 = ±K(h).
(253)
)
(254)
Установим еще формулы, выражающие коэффициенты в
разложении векторов (grad <?, V) $ и (?), V) grrad <р. Пусть эти
коэффициенты определятся формулами:
(grad », V) & = A, grad р + Мщ grad • + ЛГв ф, ]
(& V) grad * = L? grad р -f М? grad <n + #f ?. j
Применяя формулу (40), найдем:
(grad <р, V) $ = - curl [ф, grad «] + 2" ^rad **(?) —
— j ferad <?, curl б] ~ ф,
<& V) grad Т = —J curl l^' §rad в] ~f -¦ grad К (?) —
— ^ [grad ?, curl ф] + у ©.
Пользуясь формулой:
[ф, ^rad <р] =/(?, р) grad »—/(«, <») grad />,
а равным образом применяя равенство (243), выражающее curl ф,
и вспоминая формулу (34) § 3, гл. I, ч. I, преобразуем первую и»
формул (255) следующим образом:
(grad ?,V)|)=. [gradУ (о, р), grad со] — — [grad/(с?, ©), grad p]
(255)
2 L5—' *•»"'*— j 2
-f і grad К (с?) - A {Q (р) у («) _ Q (ш) )} [grad <?, grad р] +
Д<р
+ 2А {Q (р) У- Q («)У (р)} [grad =р, grad «] — ^ [grad ?, ©] —^ ©.
Исходя из этой формулы и применяя формулы (246), после

несложных вычислений получим следующие выражения
коэффициентов Le и т. д.:
А/ _ K[J(?.»)]J-K[J(*,p)\J(»)
, J[K(<?),p]J(*) — J[K(<?),»y , Q(g.)g(?>_/>/(?,«)
^ 2 "i" 2 2
i,f _kU(?.p)V-k[J(q,»)U(p)
? 2
•ТО?),рУ-Л^(?). <°V(p)_Q(p)g(?) , P/(?.P). I (256)
2 2 2 *
an - ¦/^(?,/>),ri-/(«)-{./[/(9,rt,»]+yr-/fa«>),ri}y ,
? 2
"*" 2 ¦ 2 •
Рассуждая совершенно аналогичным образом, мы получим
следующие выражения для коэффициентов L и т, д.:
W,-. ; 2 " +
, J[K(ilP)]J(*)-JlK(9),»)J .
_, _ +
і QfrW?) РЛ*,*)_.
+ 2 2 •
Ш' = *[У(?,р)]У-*[./(9.«>)]У(р)
ЛЛГ(?),р]У--УГ*(?).«]-/(р) Q0W?) ¦
2 2 "г
^ 2
AiV'=
У[У(ф,р),р1У(«)
2
{^[У(<р,р),«]+У[У(?.«).р]}У і JU(9,*)**U(p\ ,
2 ^ 2 ^
, *№?)] y(y,g»)Q(p)-yfop)Q(a) . Mo
(257)
295

К предыдущим вспомогательным формулам следует еще
присоединить формулы, служащие для вычисления символа Z (о),
определяемого равенством:
Zb) = <P, Srado). (258)
Вспоминая формулу (239), для выражения 2 будем иметь:
Z(?) = Qt J(*,P) + 22У (?,») + ss К (о). (259)
Установим более простое выражение для Z(c).
Помножая векторно равенство (236) на §, будем иметь:
[«*,&]=*: (<*) grad р + К (6) grado) + $ (& grad с) — Л grad с +
+ c[curl§, ?>]; (260)
из этого равенства можно определить grad с, причем, на основании
формулы (235) для (§, grad с) и равенств
(% &) — Z (») grad p — Z(p) grad <о;
[curl & §] = Q (<o) grad p — Q(p) grad <o,
найдем следующее выражение для grade:
A grad c = {^T(e) + cQ («) — Z(«) }"gradp + { A-(6) — cQ(p).+
1-^-аДр-6Д«)-У(а, р)-У(А, •) U, (261)
-f ^(p)l grad<o-f
откуда после элементарных вычислений найдем следующее
соотношение для Z (с):
hZ(p) = K(a)Z(p) + K(b)ZW + c { Q (<o)Z(p)-Q (/,)*(•)} +
+ tff-i-^-oAp — &A«—/(«./»)-/<*.<¦>) |. (262)
После изложенных предварительных замечаний будет уже
нетрудно определить коэффициенты вектора DV в разложении его
по векторам grad р, grad <о и ?>. В самом деле, вектор DV по
определению- равен градиентному произведению (?, V) ^5 подставляя
в это произведение вместо V и Q их выражения по формулам
(227) и (239) и пользуясь формулами (22) и (23) § 3, получим
следующее равенство:
DV = <&г (grad р, V) grad р -J- а22 (grad o>, V) grad p -|-
+ aQ3(§,V)gradpH-621(grad/?,V)gradco + 6Q2(grad<o,Vgrado>+
+ ^з (& V) grado) -f cQa (grad p, V) § + cQ2 (grad «, V) § +
+ c28 (& V) § + Z (a) grad /> -f Z (b) grad <o-fZ (c)'?.
Из только-что написанных выражений мы можем при помощи
предыдущих формул определить коэффициенты Dly D2, Ds в
равенстве
DV = Dx grad p -f Z)2 grad ш -f Z)3 $. (263)
296

і (264)
Произведя необходимые вычисления, найдем следующие
выражения коэффициентов Z)*:
А - sx Мр + Мш§, + eL,) + Qs (о4л ш + ЬАШ + rfj +
+ 23(aL; + <) + cA1) + Z(a),
D% = Q1(aBp -f ^ , + dig + 22(овл № -f ЬВФ -f cMJ +
+ ^з (««; + ЬМі +¦ cAJ -f Z(4),
где Ap, Bp> CpJ Аф% #ш, Сф вычисляются по формулам (250) после
подстановки в них —вместо $— р или ш; Ар>о), 5р ^ Ср ^ Л^
Дв,р» Cu),jp вычисляются по формулам (251); hv 7^, As вычисляются
пз формулам (253); Lpt Мр> Np, Lp, М"р7 Л? вычисляются по
формулам (256) и (257), где вместо ? подставлено соответственно р
или о>; Z(a), Z{b\ Z(c) вычисляются по формулам (259) путем
подстановки вместо <р соответственно а, Ь, с; наконец Qlf Q& Q&
а, Ь, с вычисляются по формулам (245), (234) и (238).
Равенства (264) решают нашу задачу о выражении вектора D
через динамические элементы первого и второго порядков я через
величину TV.
5. Скажем несколько слов, перед тем как перейти к примерам,
о случае, когда Р обращается в нуль. Пользуясь формулой (260),
найдем:
grad с = А — -г К), curl ф],
(265)
где:
/=(& grade).
(266)
Согласно предыдущим пунктам, Ли/ могут быть выражены
через динамические элементы и через компоненты вихря Q. *
Применяя к равенству (265) операцию curl, будем иметь
следующее соотношение:
сР = h curl A + /'& 4"/curl §,
(267)
где:
Р' = curl {?>, curl ф] — (grad In A, curl ф) §> + (grad In A, §) curl ?),
-/'=y(curl ©, [ft Q]) + ^(a)QW+{^(fc)Q(«);
само собой разумеется, что Р'и f выражаются через динамические
элементы и через компоненты вихря. В том случае, если Р' отлично
297

от нуля, равенство (267) дает возможность определить величину ст
иначе говоря — решает нашу задачу и в том случае, когда Р
обращается в нуль. Этим замечанием мы ограничимся при рассмотрении
Р = 0 и перейдем к изложению примеров, поясняющих общие
соображения, изложенные выше.
Пример 49. Рассмотрим, во что превратятся наши формулы
в случае движения, имеющего место в атмосфере. Направляя ось-
z (вертикально вверх, мы будем иметь, согласно обычным
условиям атмосферных движений, что векторы grad р и grad <*> будут
направлены почти вертикально (ибо давление и удельный объем
сильнее всего будут изменяться по вертикали), тогда как вектор ?>
будет почти горизонтален; так как с другой стороны вектор
скорости V имеет направление, близкое к горизонтальному
(вертикальная скорость воздушных течений мала), то коэффициенты а и
Ь в формуле (227) для скорости V можно считать весьма малыми.
Полагая, что аиі, равно как и их производные по координатам,
суть величины весьма малые, будем иметь следующее
приближенное выражение для с:
(2> $)_*
с р р.
Определяя коэффициенты 2„ найдем такие приближенные для них
выражения:
hQt = hj(ct*)-c[JQ (*)-/ (<¦>) Q(р)],
А92= -hj{c9p)-c [JQ (p)-J(p) Q(*)],
Предполагая, что горизонтальные составляющие вихря
значительно больше вертикальных составляющих, придем к выводу,
что ?*і и &2 значительно меньше Q3. Пренебрегая величинами Qt и
§2, получим для коэффициентов Dt следующие приближенные
выражения:
Ul Ph '
U*~ Ph ?
Л =
Л**в
Ph
Хотя выводы формул настоящего примера лишены надлежащей
строгости, тем не менее для практических подсчетов эти формулы,
значительно упрощенные сравнительно с формулами, следующими
*з общих соображений, могут оказаться весьма полезными.
Рассмотрим для иллюстрации применения общих формул случай,
согда движение является адиабатическим несжимаемым движением,
причем давление представляется квадратичной функцией координат,
а удельный объем — линейной функцией координат. При этом мы
оставляем открытым вопрос о динамической возможности такого
рода движения.
298

Пример 50. Рассмотрим адиабатическое несжимаемое движение,
в котором давление р и удельный объем "> заданы следующими
формулами:
р = ахх* -f- щд3-{-а3г-,
где аіг j34 суть, вообще говоря, функции времени t. Производя
соответствующие вычисления, без труда найдем следующие
формулы:
Ф* = ^ ЫіУ — a3ftjZ), сигЦ> = — 2& (а. 4- я3),
!0у = 2 (asplZ — щ р3дг), curl^ = — 2?2 (от, -J- aj,
ф, = 2(в1р4г — вгРху), curls? = — 2?, (в1 -г а,),
Р = 4агр2р8 (а3 — а2) х -f 4аар8Рі (оі — ав)у -f 4asp,& (а2 — щ)z.
Др) = 4(а1х2+а&+4*\
У = 2 (аА* -f а2р2# + а3М,
Из этих формул нетрудно определить величины
коэффициентов а и 6 в случае адиабатического несжимаемого движения.
Пользуясь формулами (234), найдем:
ha =2 (р0 + fa + %и + М (*А* + «А* 'Ь ОвМ —
Л6 = -г- 4 (р0 + р2х -f j»2y + М (а*лг2 + а\д% + ajza) +
+ 2 (ахд:2 + ад* + a,z^) (a,fa + а^У + asfa);
с помощью этих выражений нетрудно будет вычислить
коэффициент с, а, значит, и величины 2Х и т. д. Однако, для
определения коэффициента с нам нужно будет знать величину N. Будем
вести наши дальнейшие расчеты в предположении, что величина N
' есть постоянная, и кроме того будем рассматривать стационарное
движение. В этом случае величины а и Ь обратятся в нуль, а
величина с определится соотношением:
_ N _^ N
~ Р PiX + ptyj-ps?'
где р13 ръ, р? будут даны нам равенствами:
Рг = 4*hhfo (аз — <**)і Р-2 = 4а J33^ (aL — а^
р» = 4a$ih («2 — аі)-
Для определения в рассматриваемом случае коэффициентов 2,>
необходимо вычислить несколько вспомогательных величин.
Производя соответствующие вычисления, получим:
Q (Р) = — 4 [а$г (а2 -f d3) * 4- а2^(а3 + ах) # + а3р3 («і + а*) z];
Q (•) = - 2 [tf (*2 + <0 Н- Й («з + а,) + Й К + ОЬ
299

J <•) Q(p) \JQ («) = 4e,Pt №l («, - «2) + К («i - «s)] *+
+ P22(«8-<0]*;
У (p) Q (•) —/Q 0») = - 8eJ Й (°s + «i) + Pi (a, + <4»S -
-8«: [Й («, + a,) + p; (a, + <**~^l D? («»+ <0 +
+ p* (as + «i)] z2 + 8a2asp2ps (a2 + 2ax + a3)^2: — &&$& (a3 +
+ 2a2 + ai) z* + вс^&Ра («і + 2<*з + «2) xSi
J(P,.) = 0 J (P, p) = 8a2 P2P3 (a, -«0*4- 8aJ p3Px (a, - a3) jr +
Пользуясь формулами (245) для определения 2„ будем в нашем
"Случае иметь:
А9Х = - ^-/(Р,«») 4- с [/(») Q 0») -JQ(*)),
hQt = ^J{P,p) + c\J(p)Q(»)-JQ(p)],
hQs = cP.
Подставляя в эти равенства результаты предыдущих вычислений,
получим следующие выражения для 2,:
4- Й (а, - at)] *+а,в, $ («з - «О + PJ («з -«2)] ^] ;
*°e = -pjr [<Р2Р3 (аг — аг)х + 4hh (ai —' <*3) ST +
+ <*&&(«,-«О z]—^- К [Й («,+«04-Рз (0, + а^х1-^
+ а\ [% (а, 4-а2)4-^ («,+«,)]/ + а\ ]?\ (а% + а3) + р| (а, 4"
+ <0] z2 — [а2азРаРа (<*2 + 2aj -f a3) #z — aja^^ (a3 4- 2a2 +
+ aO ** — а^гРіРз (at + 2a3 4~ c2) xy};
Полученные формулы можно с успехом применять для грубой
•оценки, с помощью приближенных формул, движений, возникающих
"300

в жидкости под влиянием тех или иных обстоятельств. Рассмотрим
случай ах = а.2 = a0t а? = Ь^ Рі = Р2 = р, ps = -у, причем положим,.
что Р -мало по сравнению с остальными величинами; обозначая
через ?4 главный член в 2<, т. е. содержащий множителем
наименьшую степень Р, будем иметь:
' Q'-NZ±*. I ,
2 р Ь0-а0 2rt(g-x)'
>« 2 2 / 2 г 2л »
4?а0(*+у)
отсюда видно, что, при достаточной малости р, наибольшей
величиной будет обладать коэффициент 22, таким образом вихрь будет
расположен близко к направлению градиента удельного объема..
Аналогичные заключения можно сделать и в более общем случае.
Само собой разумеется, что такого рода результаты не имеют
надлежащей математической строгости, поэтому мы не считаем
нужным останавливаться на них подробнее; однако в приложении
к динамической метеорологии указанные соображения могут быть*
весьма полезными.
§ 18. Выражение элементов главного тгтраэдра черев дннанн-
ческие элементы.
В настоящем параграфе мы займемся решением вопроса
о том, каким образом изменения вихря можно учесть, пользуясь
динамическими элементами. Основная задача наша может быть-
формулирована следующим образом: зная вихрь Q к моменту і„,
определить вихрь 2' к моменту t-\-&t (в той же частице). Задача
эта может быть решена двояким образом: с одной стороны можно
определить вектор ~~гг и, зная этот вектор, найти И , пользуясь-
приближенным равенством:
dQ
dt
о^а+^уг-Дй
с другой стороны можно определить элементы главного тетраэдра
и тем самым иметь возможность, согласно § 8, построить вихрь 2'.
Первый прием дает особенно простые результаты для случая, когда
в начальный момент вихрь отсутствовал. Этот случай был
разобран Silberstein'oM в его упомянутой выше работе, указавшим
простые геометрические законы образования вихрей в сжимаемой
жидкости. Но в случае наличности вихря в начальный момент
простота рассуждений первого приема исчезает, и в таком случае
предпочтителен второй прием, глубже, по нашему мнению,
проникающий в сущность вихревых движений сжимаемой жидкости.
301

Вспоминая обозначения первой части, будем иметь:
при этом Н = Helm Q = helm Q — Q div V. С другой стороны,
согласно формуле (110), определяющей турбулизирующий вектор
еайдем:
ф = — curl G = curl -у? — curl F = helm Si — curl ?t
•откуда:
helm ^ = & -b curl F.
Соединяя вместе все эти формулы, будем иметь:
^- = ?-fcurlF — QdivV + D. (268)
at
Формула (268) показывает, что изменения вектора вихря в дан-
вой частице происходят от следующих причин: 1) от турбулизи-
рующего вектора 4?» иначе говоря — оттого, что под влиянием
движения изобарические и изостерические поверхности начинают
пересекаться; 2) от неконсервативности сил (curlF^O); 3) от
сжимаемости жидкости (— JJdivV) и 4) от наличности вектора D. Мы
позволим себе назвать вектор D, выраженный в динамических
элементах, конвективным вектором^ имея в виду его аналогию с груп-
яе§ членов в уравнениях гидродинамики, называемых РгапсШ'ем
конвективными *).
Рассматривая изменения вихря не для данной частицы, а в дан-
гом месте, мы можем воспользоваться предыдущей формулой (268),
іспомнив следующие формулы:
dQ dQ
а равно и формулу (38) § 3. Производя указанные преобразования,
найдем следующее соотношение:
dQ
-jf = © + curl F — curl [Qt V]. (269)
Эта формула показывает, что изменения вихря в данном месте
зависят от трех причин: 1) от турбулизирующего вектора ф, 2) от
неконсервативности сил и 3) от влияния прежнего вихревого-поля,
проявляющегося вектором curl [Q, V].
Не трудно с помощью формул предыдущего параграфа выра-
dQ dQ
зять как —7г 7 так и -^- через динамические элементы.
2. Перейдем к случаю, когда в начальный момент вихрь
отсутствует; тогда обе предыдущие формулы дают один и тот же
*) Prandtl, Abriss d. Lehre von der Fliissigkeits- und Gasbewegungeu, 1913.
302

результат, который (принимая во внимание, что 2 = 0) мы можем
написать следующим образом:
dQ dQ
^r = ^7=-$ + cyrlF. (270)
Таким образом изменение вихря данной частицы или в данном
месте при переходе от безвихревого движения зависит от двух
причин: 1) от турбулизирующего вектора и 2) от
неконсервативности сил. В случае сил консервативных на возникновени вихрей
влияет исключительно турбулизирующий вектор.
Рассмотрим подробнее случай консервативных сил.
Вихревое движение возникает, будучи направлено вдоль по тур-
булизирующему вектору, и за время А* равняется величине этого
вектора, помноженного на протекший промежуток времени. Так как
турбулизирующий вектор зависит от того, насколько круто
пересекаются друг с другом изобарические и изостерические
поверхности, то совершенно естественно возникновение вихря поставить
в тесную связь с характером пересечения указанных поверхностей,
что и было сделано Silberstein'oM, установившим следующие две
теоремы, по очевидности своей не нуждающиеся после развитой
нами формулы (270) в подробных доказательствах. Первая теорема
может быть формулирована так:
Теорема 33. Начальное положение вихревой оси частицы,
переходящей от безвихревого движения к вихревому, совпадает
<: линией пересечения изобарической и изостерической
поверхностей, на которых частица эта находится.
В самом деле, эта ось направлена, согласно равенству
-— = ,9) = [grad р, grad со],
но касательной к линии пересечения поверхностей р = р0, о> = й>0,
на которых лежит наша частица, а это и доказывает высказанное
положение.
dQ
Вторая теорема относится к определению величины ~j? , или
вихревого ускорения^ как называет эту величину Silberstein.
Теорема 34. Вихревое ускорение данной частицы
пропорционально синусу угла пересечения изобарической и изостерине-
•ской поверхностей, содержащих данную частицу; это ускорение
пропорционально производной давления по нормали к этой
изобарической поверхности и производной удельного объема по
нормали к соответствующей изостерической поверхности.
Легко видеть, что из формулы (270) следует равенство (силы
консервативные, поэтому curl F = 0);
dQ
dt
ь=тт-р*
3*3

Обозначая через л направление нормали к изобарической
поверхности и через v направление нормали к изостерической
поверхности, будем иметь:
др др , ч др др / \ др др . ч
? = fnCOs (п,х), ? = Fncos (п,у), ?z = Тпcos (п, г),
^=^cosM> ф^с^05^' й^005^'
откуда
Др)=т, /w_(^, /-?$«.<**
-Ш'(
^) Sin2(n,v);
значит, искомая величина -гг определится (путем рационального
выбора направлений нормалей п и v) следующим равенством:
Л
др дв> . . .
что и докажет нашу теорему.
Теоремы эти имеют весьма элегантную форму; к сожалению,
они применимы лишь в простейшем случае, когда движение
переходит от безвихревого к вихревому. Учесть изменения вихря при
наличности вихревого движения в начальный момент теоремы
Silberstein'a не могут; причина этого — наличность конвективного
вектора, лишь с большим трудом (да и то ке в полной мере), как
мы видели выше, выражающегося через динамические элементы.
3. Перейдем к изложению второго метода изучения изменения
вихря. Как мы видели выше, мы сможем построить вихрь в данной
частице к моменту 2-|-Д/, коль скоро нам будут известны следую-
t щие обстоятельства: 1) положение вихря к моменту /, 2) положение
плоскости
QZ) [ (назовем ее плоскостью отклонения), 3)
отклонение вихря, 4) кручение вихря и 5) изгиб вихря (см. § 8).
Из сказанного в главе II ясно, что все изложенные пять обстоя-*
тельств будут определены, коль скоро будут известны векторы Q, Н,
[Н, Q] = decl 2 и [2, D]. Займемся выражением этих векторов через
динамические элементы и величину N.
Вектор вихря выражается при помощи формулы (239)
предыдущего параграфа. Вектор Н определяется через турбулизирующий,
вектор равенством:
Н = § — QdivV,
которое дает нам следующее выражение для Н:
Н= — 6Qlgrad/> — eQ2grad<*-f (1 — ?23)?, (271)
где 6 = divV.
304
і

Не трудно видеть, что decl Q = [$, Q]; это дает нам следующее
выражение для decl 2:
decl Q = [Н, Щ = - Z(«) grad/> -f Z(p) grad о», (272)
где Z(«>) и Z(/>) определяются по формуле (303) предыдущего
параграфа.
Вычисляя вектор [Q, D], будем иметь:
[Q, D] = A [Q, grrad р] + Z)2 [2, grad о>] + Z)s [Q, ?].
Подставляя вместо 2 его выражение по формуле (239), получим
следующее равенство:
+ [Z>, №+У Н ^9) - ^s (УА -К/ («) A)] grad , -
-[А(У(^і -К/2.)-а»(У(/0А +УА)] grad «>. (273)
С помощью только-что указанных формул мы определим по
вектору [2, D] положение плоскости отклонения QJD . Далее,
пользуясь формулой (11) §5, найдем следующее выражение для
отклонения о:
8._-_. zwj{p)+z(PTm-2Z{<»)z{p)j , (274)
пользуясь формулами для Z (р) и Z(o>), вытекающими из
формулы (259), найдем формулу:
. 1ЛГ Vл^lУ(p) + ^22УH+2^1^2У
по которой наиболее просто вычисляется отклонение 8.
Для вычисления кручения А выразим прежде всего через дина*
мические элементы величину (Н, [Q, D]); нетрудно видеть, что эта
величина равняется выражению ($) [Q, D]); вычисляя с помощью
формулы (273) это последнее выражение, получим
(Н, [Q, D]) = h (D2 Qx - Д Q9); (276)
отсюда, пользуясь формулой (18) § 6 и предыдущими выражениями
для векторов [Н, Щ и [Q, D], без труда вычислим sin Л.
** Наконец, изгиб вихря о" получаем при помощи формулы (48)
§ 7, пользуясь формулой (273) для вектора [Q, D]. Так как в
настоящей работе мы не имели в виду давать какие-либо приложения
развиваемых в настоящем параграфе формул, то мы и
ограничиваемся лишь указанием процесса вычисления элементов главного
тетраэдра, останавливаясь лишь на формулах, имеющих простой вид.
"* Само собой разумеется, что предыдущие формулы без труда
дают возможность вычислить уклон вихря. Как мы видели в § б,
20 Зак. 2420. — А. А. Фридман. Опыт гидромеханики 305

уклон вихря связан с центробежной мерой вихря, а эта послед-
Го <**'
няя — с вектором ь!, - , -
; замечая, что
dQ.
dt
= Н
найдем:
Q.
dQ
dt
[Q, D] - [II, Q],
откуда, пользуясь формулами (272) и (273), будем иметь
следующее равенство:
^,
dQ
~dt
= (Z>2 Q,-A^*) ? +
1
(277)
+ {(Дs-fl)[/^1+УW^2]-^з[/A^-/И^2]}gradp-
- {(A, -¦:-1) U(p) Q. -f /Q2] - Q3 [/(*») A+/A]} grad ». J
В заключение настоящего параграфа укажем, какие
динамические условия необходимы для того, чтобы движение обладало той
или иной особенностью.
Теорема 28 выяснила уже нам необходимые и достаточные
условия того, чтобы движение было главным гельмгольтцевым
движением. Точно так же можно выяснить, что необходимыми и
достаточными условиями принадлежности движения к классу гельм-
гольтцезых служат равенства:
при этом предполагается, что рассматриваемое движение не
принадлежит к классу главных гельмгольтцевых движений.
Рассматривая главные незакручивающиеся движения, найдем,
что необходимые и достаточные условия наличности их
заключаются в пропорции:
D, Ц> ?>з +1
*і Ц
Q.
Ъ
dQ
dt
= 0. Для общих
которая является эквивалентной равенству
незакручи^ающихся движений необходимым условием является
пропорция:
А=А, *
которая, однако, не будет достаточным условием наличности общего
геаакручивающегося движения.
Разбор всех предыдущих формул показывает нам, что все
элементы, характеризующие изменения вихрей, выражаются через
динамические элементы первого порядка, через приток энергии,
через расхождение скорости и через величину N.
Нам не удалось получить соотношения, которое бы определяло
указанную величину N через динамические элементы; является ли
306

это обстоятельство лежащим в существе дела, или же путем
соответственных преобразований возможно и величину N выразить
через динамические элементы, мы установить не михем.
§ 19. Теорема Bjerknes'a.
1. До сего времени в настоящей главе мы рассматривали
изменения вихрей с точки зрения, изложенной в классическом,
цитированном выше, мемуаре Гельмгольтца. В настоящем параграфе
выясним связь, существующую между динамическими элементами
и теми величинами, которые характеризуют изменения вихревых
полей с точки зрения W. Thomson'a (см. выше, § 9)..
Связь между изменением циркуляции скорости и динамическими
элементами, определяющими движение, была впервые выяснена
V. Bjerknes'oM; связь эта, дающая весьма удобный прием для
вычисления изменения циркуляции скорости по некоторой замкнутой
жидкой линии, не дает однако, к сожалению, указаний на
детальный характер движения и не позволяет решить вопрос об
изменении вихря в данной частице или в данном месте. Это
обстоятельство и заставило нас в главе II части I и в двух предыдущих
параграфах настоящей главы изучить изменения вихрей главным
образом с точки зрения, указанной Гельмгольтцем и отличающейся
от точки зрения W. Thomson'a и V. Bjerknes'a.
Метод Bjerknes'a, крайне удобный для использования
экспериментального материала, не дает однако никаких указаний
относительно возможности того или иного сорта движения, чему была
посвящена третья глава нашей работы.
Теорема Bjerknes'a, равно как и развитие ее, сделанное AnsePeM *)
в его диссертации, основываются на свойстве некоторых
криволинейных интегралов, к изложению каковых свойств мы и перейдем.
Положим, что нам заданы две функции времени и координат
? и <!>:
<? = ? (t, х, у, z), ф = Ь (і, х, у9 z).
Выберем некоторый замкнутый контур К и рассмотрим
криволинейный интеграл:
к к
распространенный на указанный контур К с определенным
направлением обхода.
Проведя через контур К поверхность S, разобьем эту
поверхность на ряд клеток, пересекая ее двумя семействами
поверхностей (Sj) и (So); поверхность, стягивающая контур К, разобьется
указанным приемом на ряд кусков, каждый из коих будет
ограничен контуром Кі9 направление обхода какового контура будет
*) См. Ansel, Beitrage zur Dynamik und Thermodynamik der Atmosphare,
Gottmgen 1913.
20* 307
tz

определяться обычным приемом по направлению обхода всего
контура К (черт. 22). Обозначая через Jt предыдущий криволинейный
интеграл, распространенный на контур К{\
путем обычных в теории криволинейных интегралов рассуждений
докажем равенство:
где 2 распространена на все контуры, на которые распадается
вышеуказанным приемом наш контур К.
Выберем семейство поверхностей (SJ и (52) таким образом,
чтобы семейство (Sj) было семейством поверхностей <р = const,
а семейство поверхностей
(*S2) было сецейством
поверхностей ^ = const.
Указанные выше контуры
/^распадутся на два класса: к
первому классу отнесем те
контуры Кі9 которые
образованы пересечением
поверхностей (52), (52) с
поверхностью S; ко второму классу
Черт. 22. отнесем контуры Кі9
прилегающие к нашему
контуру К9 часть границы которых является куском контура К.
Назовем через У сумму 7t, распространенную на контуры второго
класса; тогда будем иметь:
./=27,+/',
где 2' распространится на все контуры первого класса, лежащие
внутри контура AT.
Если поверхности <р = const и & — const мы проведем достаточно
тесно, то величина ]п может быть сделана сколько угодно малой;
мы не останавливаемся на доказательстве этого положения, так
как оно доказывается обычными в теории криволинейных
интегралов приемами- Таким образом, проводя поверхности © = const
и ф = const достаточно близко друг от друга, мы можем при
вычислении величины J пренебрегать малой величиной f\ что мы
и будем делать в дальнейшем. Пусть Кь будет контуром первого
класса, образованным сечением поверхности S с поверхностями:
при этом будем предполагать поверхности (*St) и (52)
расположенными в таком порядке, что, обходя контур Kt в правильно
избранном направлении, мы будем итти по сечению поверхности S сначала
поверхностью <р = с', затем поверхностью ф —« » после
поверхностью © = с" и, наконец, повеохностью ф = d"\ назовем куски
308

контора Ки образованные сечением поверхности S поверхностями
? = с', ty = d't ? = cff, Ф = <Г, соответственно через Kw Kzi, Kzi, Ки.
Интеграл /4 может быть написан следующим образом:
?Н і"2г ?"зі А'«
Легко видеть, что:
Xi #3»
приняв во внимание эти равенства, найдем:
у;-=(с'-с") («/'-л-
Системой поверхностей <?=const, u=const разобьем все
пространство на ряд трубок — соленоидов по терминологии V. Bjerknes*a *).
Соленоиды эти, пересекая
поверхность S, стягивающую контур К,
образуют систему контуров Кк
первого класса. Назовем единичным
соленоидом соленоид,
образованный пересечением поверхностей
и образуем систему
соприкасающихся друг с другом единичных
соленоидов; эти соленоиды будут
образованы пересечением двух по-
следовательностей поверхностей: ерт" 23"
Не трудно видеть, что для каждого контура Кі7 образованного
пересечением единичного соленоида с поверхностью S, будем
иметь:
Выбрав некоторый обход контуров за положительный, будем
называть положительными единичными соленоидами те, у которых
Ji = -J-1, отрицательными единичными соленоидами те, у которых
Ji = — 1. На черт. 23 показаны сечения плоскостью
положительных и отрицательных единичных соленоидов; отрицательные
соленоиды заштрихованы, обход контура цринят за положительный
обход.
С помощью только-что указанных рассуждений не трудно будет
доказать следующую теорему:
*) V. В j е г k n e s, Dynamische Meteorologle und Hydrographie, Bd I.
309

Теорема 35. Интеграл J, взятый по положительному обходу
контура К,
к
равен разности числа положительных единичных соленоидов, пере-
секаюгиих контур К, и числа отрицательных единичных соленои-
дов, пересекающих этот контур *).
Единичные соленоиды относятся к поверхностям <р = const,
•', = const.
Из предыдущего ясно, что У=і J и // — -Ь 1 ?ля
положительного единичного соленоида и /,. = — 1 для отрицательного
единичного соленоида, откуда непосредственно следует наша теорема.
Само собой разумеется, что, если бы интеграл был взят по
отрицательному направлению обхода контура К, то он был бы
равен разности числа отрицательных единичных соленоидов и числа
положительных единичных соленоидов, пересекающих контур.
Знак единичного соленоида зависит, конечно, от того, в какой
последовательности стоят поверхности ? = const, 'Ь = const; так,
например, положительный единичный соленоид для поверхностей
? == const и г) = const будет отрицательным единичным соленоидом
для поверхностей ГЬ = const и ? — const, в полном соответствии
с очевидным равенством
/ в^ = — / ¦{></?.
А' А'
2- В § 9 нами было высказано следующее предложение,
установленное впервые W. Thomson'oM:
Индивидуальная производная по времени циркуляции скорости
по некоторому замкнутому жидкому контуру равняется циркуляции
ускорения по этому же контуру.
Вспоминая, что, согласно уравнениям гидродинамики:
— = —(ograd/> — F,
получим следующую формулу для индивидуальной производной
по времени циркуляции С скорости по жидкому контуру К:
¦^ = / <FX dx+F, dy + Fz dz) - f ш dp. (278)
А' К
Рассматривая случай консервативных сил, найдем, что первый
из написанных интегралов обратится в нуль, а второй будет равен
— / pd&, отсюда для случая консерзативных сил получается
А'
следующее равенство:
' А*
:!:) Само собой разумеется, что d теореме говорится о приближенном равенстве*
310

Образуем изобарические и изостерические поверхности и с
помощью этих поверхностей образуем систему единичных изобаро-
изостерических соленоидов, отвечающих последовательности
поверхностей р = const, to = const. Единичные соленоиды,
соответствующие последовательности поверхностей о> = const, р — const,
будем называть изостеро-изобарическими единичными соленоидами.
Пользуясь теоремой 35 и равенством (279), докажем следующую
теорему, установленную впервые V. Bjerknes'oM и послужившую
основой для его замечательных исследований в области
динамической метеорологии:
Теорема 36. Индивидуальная производная циркуляции
скорости по положительному обходу жидкого контура для случая
консервативных сил равна разности числа положительных и
отрицательных единичных изобаро-изостерических соленоидов,
пересекающих контур.
Пользуясь равенством (278), мы можем только-что высказанную
теорему формулировать и для случая наличности
неконсервативных сил:
Теорема 37. Индивидуальная производная циркуляции
скорости по положительному обходу жидкого контура равна
циркуляции по этому контуру силы, действующей на единицу массы,
сложенной с разностью числа положительных и отрицательных
единичных изобаро - изостерических соленоидов, пересекающих
контур.
Теорема Bjerlcnes'a дает чрезвычайно удобное в практическом
dC
отношении средство определять —г-, а, следовательно, и
вычислять циркуляцию скорости С по жидкому контуру К\ в который
перешел контур К к моменту і-\-Ы; вычисление С" можно вести,
пользуясь следующей, приближенной формулой:
с=с+*?ь.
Как было выяснено в § 9, циркуляция по данному жидкому
контуру дает нам указание на величину напряжения вихревых трубок,
пересекающих этот контур. Посмотрим прежде всего, какие
указания может дать теорема Bjerlcnes'a относительно возникновения
вихрей в атмосфере. Уравнения гидродинамики и условие незакру-
чиваемости показывают, что динамический градиент есть незакру-
чивающийся вектор, ибо:
— (G,©) = (G, curlG) = 0;
отсюда не трудно заключить, что возможно подыскать поверхность,
ортогональную векторным линиям вектора G. Само собой
разумеется, что эта поверхность будет изобарической поверхностью;
для контура, лежащего на такой поверхности, при наличности кон-
311

сервативных сил, как это следует из рассуждений § 9, а равно и
из формулы (278), будем иметь:
А '
таким образом не может под влиянием консервативных сил и
притока тепла возникнуть вихря, пересекающего изобарическую
поверхность; следовательно, все вихревые трубки, возникающие под
действием консервативных сил и притока тепла, располагаются
вдоль изобарических поверхностей. Так как в атмосфере
изобарические поверхности, особенно на некоторой высоте над землей,
расположены почти горизонтально (с весьма малым уклоном), то
отсюда ясна невозможность возникновения в атмосфере вихрей
с вертикальной осью. Подробнее это обстоятельство выяснено
в нашей заметке, напечатанной в Известиях Главной физической
обсерватории *).
В заключение настоящего пункта свяжем теорему Bjerknes'a
с величиной вихревой меры /. Выбрав вихревую бесконечно
тонкую трубку и расположив контур к (охватывающий трубку) по
поверхности этой трубки, будем иметь следующее
предложение:
Теорема 38. Вихревая мера для случая консервативных
сил равна отношению разности числа положительных и
отрицательных изобаро-изостерических единичных соленоидов,
пересекающих контур к, охватывающий бесконечно тонкую вихревую
трубку, к напряжению этой вихревой трубки*
Вспоминая сказанное в § 9 и пользуясь формулой (67) для
вихревой меры /, будем иметь следующее приближенное
равенство:
1 dC .
Qo dt h
• где С—циркуляция скорости по контуру k> стягивающему вихревую
трубку сечения з; указанная только-что формула в связи с
равенством (324) и теоремой 36 докажет высказанное
предложение.
3. Ansel в упомянутой выше диссертации видоизменил теорему
Bjerknes'a, рассмотрев связь изменения циркуляции скорости не
с силовыми^ а с тепловыми динамическими элементами.
Вспоминая уравнения гидродинамики в тепловых динамических
элементах [формулы (91) § 11], будем иметь следующее
равенство:
dV cp
-?¦= TgradS— — grad Г-fi.;
*) А.Фридман, „Об атмосферных вихрях с вертикальной и горизонтальной
осью". Известия Главной физической обсерватории, 1921.
312

отсюда, применяя теорему Thorason'a и замечая, что при
интегрировании по замкнутому контуру К
К *
получим следующее равенство:
JC.= J* TdS+ f (Fxdx + F,dg + F.Jz), (280)
К К
откуда для консервативных сил найдем такое соотношение:
-^- = fTdS. (281)
к
Применяя к последнему равенству теорему 35, можно
формулировать следующее предложение:
Теорема 39, Индивидуальная производная по времени
циркуляции скорости, взятой по положительному обходу
замкнутого контура К для случая консервативных сил, равняется
разности числа положительных и отрицательных изотермо-изэн-
тропических единичных соленоидов, пересекающих этот контур.
Пользуясь известным преобразованием Clebsch'a, Ansel
вычисляет циркуляцию скорости, также вводя некоторые единичные
соленоиды. В самом деле, согласно преобразованию Clebsch'a,
всегда вектор скорости V можно представить в виде:
V = — grad тс -f- © grad <Ь,
причем вихревые линии будут, как известно, линиями пересечения
семейств поверхностей <р = const, ф = const. Образуя единичные
соленоиды, отвечающие этим семействам поверхностей, найдем, что
циркуляция скорости по некоторому замкнутому контуру будет •
равна разности числа положительных и отрицательных
вышеуказанных соленоидов, пересекающих этот контур. Следует однако
заметить, что отмеченное сейчас обстоятельство имеет малое
практическое значение, так как на практике чрезвычайно трудно
определить «риф? необходимые для выражения скорости в форме,
предложенной Clebsch'eM. г
Видоизменение теоремы Bjerknes'a, предложенное AnseFeM, имеет
то значение, что оно связывает законы образования вихрей с
энтропией.

ДОПОЛНЕНИЕ.
Б. //- Извеков$ И, А. КибехЬу
Н. Е. Кочин.
О НЕКОТОРЫХ РАБОТАХ, СВЯЗАННЫХ С „ОПЫТОМ
ГИДРОМЕХАНИКИ СЖИНАЕМОЙ ЖИДКОСТИ".
Настоящая статья преследует в основном цель дать в кратком
виде обзор главнейших из тех работ как самого Фридмана, так и
его учеников, в которых идеи Фридмана, заключенные в его
„Опыте гидромеханики сжимаемой жидкости", получили свое
дальнейшее развитие. Эти работы относятся главным образом к
условиям динамической возможности движения. Кроме этого, нам
представилось небесполезным остановиться еще на нескольких вопросах
из теории вихрей в сжимаемой жидкости, в виду фундаментального
значения этих вопросов для современной гидромеханики.
§ 1. О сохранении векторных линий.
В § 2 „Опыта гидромеханики" подробно выяснено понятие
сохраняемости векторных линий и доказана основная теорема о
необходимых и достаточных условиях того, чтобы собрание векторных
линий поля вектора А было собранием
сохраняющихся линий. В этой теореме,
как и всюду в своем „Опыте гидромеха-
2^>м- ники", Фридман пользуется разложениями
^ ' рассматриваемых функций в ряды Тэйло-
ра, иными словами — он предполагает, что
все рассматриваемые им функции
являются аналитическими функциями от своих
аргументов в некоторой области. В виду
фундаментальной важности упомянутой
выше теоремы интересно дать другое ее
доказательство, свободное от указанного
недостатки. Это можно проделать например следующим образом:
Допустим, что в некотором жидком объеме Т (состоящем все
время из одних и тех же частиц) и аля некоторого интервала
времени і0^і^іг заданы вектор скорости V и некоторый вектор А.
Пусть кроме того в рассматриваемом объеме Т для всех
рассматриваемых моментов времени как составляющие обоих векторов V
314

и А, так и их первые производные по координатам, а для вектора
А еще и первые производные по времени, суть непрерывные
функции своих аргументов, т. е. х, у, z и t Кроме того пусть вектор
А всюду отличен от нуля.
При этих условиях необходимое и достаточное условие того,
чтобы собрание векторных линий поля вектора А было
собранием сохраняющихся векторных линий, заключается в выполнении
равенства
4y-(A,V)V,A
= 0. (1)
Заметим прежде всего, что при сделанных предположениях
дифференциальные уравнения векторных линий вектора А
dx dy dz
А(х> У, z, t)~~Ay(x, yt z, i)~~Ae(x, y, z, t)
имеют одно и только одно решение, проходящее через какую-либо
заданную точку данной области, иными словами — через каждую
точку объема Г проходит одна и только одна векторная линия
вектора А.
Необходимость условия (1) можно доказать следующим
элементарным рассуждением:
Рассмотрим в момент / (черт. 24) векторную линию вектора А,
проходящую через точку М. Возьмем бесконечно малый элемент
этой линии ММлі л . /ГкЧ
* or = sA, (2)
где е — бесконечно мглая величина, такая, что аЛ есть длина
рассматриваемого элемента- Если мы будем рассматривать этот
элемент как жидкий элемент, т. е. элемент, состоящий из жидких
частиц, то к моменту t-rdt он займет новое положение М'МХ> причем
очевидно —-+ ....
ММХ = or -j- dor;
так как
8г = га — гг,
то
dor dr* drx Х7 лт .„ д\ * , dV. t dV
dt ~ dt di a l Ox l dg * ' dz (3)
= (or,V)V = a(A,V)V. ^ I
За время dt точка М перейдет в положение М\ а вектор
А {Му t) примет значение
А' = А(М', t + dt) = A(M, г)-МА.
Для того, чтобы имела место сохраняемость векторных линий,
необходимо, чтобы векторы Sr-J-cZor и A~j-c?A были коллинеарны,
T- е. ЧТОбы -ч і ъ е/л \ JA\
or -f- dor = s'(A -p dA),
где e' может быть и отлично от е. Условие коллинеарности можно
записать также в виде
[о> + <йг, А + ^А] = 0
или, в силу того, что
[8г, А] = 0,
315

и в силу того, что величина
есть бесконечно малая величина высшего порядка, в виде
[dor, А] + [Зг, </А] = 0.
На основании (2) и (3) получим:
[в (A, V)V, A]
или
*А,
JA
А
= 0
^А -(A,V)V, A
= 0,
А
что и требовалось доказать.
Интересно попутно отметить условие для того, чтобы сохра
нялись не только векторные линии вектора А, но и интенсивности
векторных трубок. Рассмотрим бесконечно тонкую векторную
трубку с осью ММ-і и обозначим поперечное сечение этой трубки
через о, а плотность жидкости в точке М в момент t — через р.
Тогда масса жидкости, заключенной в цилиндре, поперечное
сечение которого равно о, а высота |8г', будет poj^rj. К моменту t-\-di
эта же самая масса жидкости будет заполнять цилиндр с осью
ММХ, поперечное сечение которого будет теперь </, а плотность
жидкости в точке ЛГ в этот момент будет о'л Поэтому имеем
равенство:
ра | 8г | = pV |ог + J3r |.
Для того, чтобы сохранилась интенсивность векторных трубок'
необходимо выполнение равенства
Сравнение этого равенства с предыдущим показывает, что если
ввести вектор
В-А. (4)
то должно быть
[or]_ |or-^cfirl _v
В ~~ ВТ ' ( }
а так как векторы В и 8г при условии сохраняемости векторных
линий должны быть коллинеарны, то в этом случае должны
выполняться равенства
ог = г,В,
8r-M3r = -ri(B + <ffl),
уже с одним и тем же і\л Из последнего равенства выводим
dh = т{ dB
и, в силу (3), после сокращения на tq
™-(B,V)V = 0.
316

Таким образом условие сохраняемости как векторных линий
вектора А, так и интенсивности векторных трубок состоит в
выполнении равенства
d_/A
dA r>
-,V V = 0.
(6)
Замечая, что
dA p
1 dX 1 do 1 dA , 1
7A-^лА~Т ^TAdlvV'
предыдущее равенство можно еще переписать в виде
dA
dt
(A, V)V + AdivV = 0
или, в обозначениях Фридмана,
helm А = 0.
(7)
<8)
Отметим, что условие (1) сохраняемости векторных линий
вектора А можно очевидно записать в виде
[helm А, А] = 0.
(9}
Вернемся теперь вновь к условию (1). Докажем, что оно
является необходимым и достаточным условием сохраняемости
векторных линий вектора А. Для этого очень удобно воспользоваться
лагранжевыми переменными а, 6, с. Примем за такие лагранжевы
переменные а, Ь, с.декартовы координаты каждой частицы в
момент *0; тогда к моменту t декартовы координаты какой-либо
частицы будут функциями от а, Ь, с и t:
Х = х(ал Ь, с, і),
У=у(а, Ь, с, і),
z = z(a, b9 с, t),
х(а, Ь, с, to) —а,
причем у (а, 6, с, і0) = Ь,
z(a, b, с, tQ) = c.
Рассмотрим теперь к моменту ^о бесконечно малый вектор Sr<>
декартовы составляющие которого равны оа, lb, ос; жидкие
частицы, образующие этот элемент, расположатся к моменту t вдоль
вектора 5г с составляющими
дх ,s . дх „ . дх *
da ' дЬ Лл
о» = ^~ оа
* да
дс
ду ч і <fy а
(10)
<?z ^ . <3z ^, , dz л
0z = _ua+__o6 4-^oc,
317

так что мы ножей написать Зг в виде скалярного произведения
тензора на вектор *)г.
гг=д.гГо, (И)
где А есть тензор или матрица
л =
дх
да
да
dz
да
определитель которого мы будем
| дх
да
D =
*У
да
dz
! да
дх
дЬ
ду
дЬ
dz
дЬ
дх \
дс
Оу
дс
dz
дс
обозначать
дх
дЬ
ду
db
dz
db
дх
дс
ду
дс
dz
дс
(12)
(13)
Ив самого понятия о сохраняемости векторных линий вектора А
следует, что для того, чтобы последняя имела место, необходимо
и достаточно, чтобы из коллинеарности векторов A(r0, t0) и огс
следовала коллинеарность векторов А (г, і) и <*г. Иными словами,
если
Sr0 = eA(r0l fc), (14)
то должно быть
гг = з'А(г, t). 15)
В силу (11) имеем:
А (г, /) = — Л-А(г0, /0) = ?Л.А(г0, h).
Итак необходимое и достаточное условие сохраняемости
векторных линий вектора А состоит в том, чтобы для каждой частицы
имело место равенство
А = U • Ао, (16)
где А—значение вектора к моменту ty Aq — его значение к моменту
t0 и >* — некоторый скалярный множитель, величина которого не
имеет значения.
'*) См. Н- Ко чин, векторное исчисление, ГТТИ, 1934, или В. Смирнов,
Курс высшей математики, т. Ill, ГТТИ, 1934.
318

Заметим, что из (16) обратно следует
ХА0 = й_1 -А,
(17)
где А- означает матрицу, обратную к А.
Допустим теперь, что (16) имеет место. Тогда, дифференцируя
это равенство по t, получим
dk , б?А А d\. д
(18)
где, по самому определению производной от матрицы по
скалярному аргументу, имеем:
db.
dt
д*;
д\
д*х \
Г ди
dadt
d*y
dadt
№z
dbdt
d'2y
dbdt
d*z
dcdt
d!'y
dcdt
d*z
da dt db dt dc di
da
du_
db
dv dv
» da db
*го
dw
l)a db
dc
dv
~dc
dw
(19)
при понятных обозначениях для составляющих вектора скорости V:
dx dv dz
* dt* dt9 at
Замечая еще, что
efr . - d\n Ь . A . </InX
лл-Ао==-5гХА-А°=^гА'
и принимая во внимание (17), получим из (18):
. , JlnX
rfA _ d\ i
dt ~ dt
it
A.
(20)
— 1
Так как матрица A 9 обратная для матрицы А, имеет очевидно
значение
А"'--
' да
dx
дЬ_
dx
dc
{ dx
da
ду
db
ду
дс
^
da \
dz
d±
dz
dc
dz J
3»

то легко выяснять значение произведения матриц
(
dt
ди
да
dv
да
дги
ди
дЬ
dv
дЬ
дхо
ди
Ос
dv
дс
дги
да
дЬ
дс
да
дх
Я.
дх
дс_
дх
да_
ду
дЬ_
дс_
ду
да \
dz
EL
dz
дс_
dz
ди да .ди дЬ .ди дс^ ди да . ди дЬ , ди дс_
д~ад~х^д~Ьд~х~^дс дх да ду "¦" db ду'дс ду
dv да .dv db , dv дс
да" д~і +Ж ~дх~"^ дс дх
{ ди
дх
dv
дх
dw
дх
ди
ду
dv
ду
dw
ду
ди )
dz
dv
dz
dw
dz
Но тогда очевидно, что вектор -у- А-1 • А есть вектор с
составам
ляющими
ди
дх
dv
~дх~
dw
дх
Ах
лх
лх
+
+
1
ди
ду
dv
ду
dw
ду
А
А
А
+
+
+
ди
dz
dv
17
dw
dz
A
A
A
2>
Zf
z>
т. е. есть вектор (А, V) V. Итак мы имеем следующее равенство:
d± ,_і
dt
Д-А.А-(А, V)V.
(21)
В силу этого равенство (20) дает нам
dA
dt
JA==(A)V)V + ^A,
di
(22)
320

откуда и следует, что
^Г-(А, V)V, A
= 0.
Доказательство достаточности последнего условия для
сохраняемости векторных линий вектора А теперь не представит ни
малейшего труда. Из этого условия следует, что
dX
~-(A,V)V==?A, (23)
где у- — некоторая скалярная функция. Перейдем в этом равенстве
к лагранжевым переменным а, Ь, с. В силу (21) можно написать,
что
?-*Л-.А-* (24,
Отыщем теперь функцию \ обращающуюся при / = /0в 1 и
удовлетворяющую уравнению
«Ппл
dt
Для этого надо очевидно взять
= \к
/ц(а, Ь, с, t)dt
X= е° , (25)
после чего, умножив обе части равенства (24) на А~ слева,
получим
А
— і
*_д-.*4-..А
А • А.
dt
(26)
Заметим теперь, что имеет место равенство
— і
<Ц =-А-"*ДА-1.
dt dt
в самом деле, продифференцируем по t тождество *)
ДД-1 =1,
и полученное равенство
¦**?+?-'-о
умножим слева на А г; в результате очевидно получится (27).
В силу (27) равенство (26) принимает вид:
(27)
д
_і </А , rfA
—і
А =
dlnl
dt ' dt ~ Л
1 0 0 1
Д-1 -А
*) I есть единичный тензор
21 Зак. 242?. — А. А. Фридман, Олыт гидромеханики
0 1 0 .
0 0 1 )
321

или
</Д_1 • A dlnl ,_, .
—чг~=~іг^ А
или л
По интегрировании получим
-А"1 А = С,
где С — постоянный вектор; но в силу того, что при і =¦ t,
должно быть С = А0, и следовательно мы получаем
Л"1 -А = лАо
или
А == )Л • А0,
что, согласно (16), выражает сохраняемость векторных линий
вектора А. Теорема доказана полностью.
Если мы хотим потребовать не только сохраняемости
векторных линий, но и сохраняемости напряжения векторных трубок, то
в силу равенств (4) и (5) мы должны будем иметь вместо (14)
и (15) следующие равенства:
'Sro = — A(r0, /0),
Ро
8г = уА'(г, *).
и следовательно вместо (16) будем иметь
A = -f Л-Ао, (28)
Ро
так что теперь скалярный множитель \ должен иметь вполне
определенное значение:
Ро . '
Поэтому выведенное выше равенство (22) принимает вид:
§=(A,V)V + ^A, (30)
и так как по уравнению неразрывности
^-=-divV, (31)
322

то его можно записать еще так:
^=(A,V)V-AdivV. (32)
Обратно, если мы имеем равенство (32), то в силу (31)
получим уравнение (30), т. е. уравнение (24), где надо положить
сПпг>
а
dt
Отыскивая по формуле (25) величину л, найдем, что ?. = — .
Ро
Но в результате интегрирования уравнения (24) мы получили ра-
генство (16). Подставляя сюда найденное значение /.==—, мы по-
Ро
лучаем уравнение (28), выражающее сохраняемость векторных
линий и напряжений векторных трубок вектора А.
Следовательно условие
dX
-^=fA,V)V — AdivV (33)
является необходимым и достаточным для
сохраняемости,векторных линий и напряжений векторных трубок вектора А,
Q 2. Об изменении вихрей в движении сжимаемой жидкости
под действием неконсервативиых сил.
В § 18 главы IV (стр. 302) Фридманом дана формула (268)
dt
(Q, V) V — 2 div V -f curl F -f §, (1)
выражающая изменение вектора вихря 2 данной частицы с
течением времени. В этой формуле F есть вектор силы, действующей
на единицу массы, а § есть турбулизирующий вектор, равный
?> = [gradp, gradco], (2)
где р — давление, ш — удельный объем; так что формула (1)
принимает вид:
¦^- = (2, V)V— GdivV + curlF+feradp, gradj»]. (3)
dt
Эта формула является непосредственным обобщением формулы
Гельмгольца для изменения вихрей. В самом деле, если
предположить, что сила F консервативна, т. е. имеет потенциал, так что
curl F = 0, '
и что плотность р, а следовательно и удельный объем <о есть
функция одного только р, так что
l^rad р, grad со] = 0,
21* 323 '

то уравнение (3) перейдет в
¦^=(Q,V)V-OdivV, (4)
откуда, согласно § 1, сразу следует сохраняемость вихревых
линий и напряжений вихревых трубок, т, е. сразу следуют теоремы
Гельмгольтца о вихрях.
Формула (3) является фундаментальной для всей гидромеханики
слушаемой жидкости (а также и для случая жидкости
несжимаемой, но неоднородной).
Поставим себе целью выяснить, какой вид примет эта формула,
если ее написать не в эйлеровых, а в лагранжевых
переменных.
Примем, как в предыдущем параграфе, за лагранжевы
координаты а, Ь, с какой-либо частицы ее декартовы координаты х, z/, z
в момент /0. Заметим прежде всего, что, согласно уравнению
неразрывности,
d In p
divV =
dt
и так как в лагранжевых переменных уравнение неразрывности
имеет вид
р(а, Ь, с, t)D(a, bt с, *) = Ро(а> 6, с), (5)
то
,. v dlnD I dD
Пользуясь обозначениями предыдущего параграфа, мы имеем
далее
(Q.VJV^-^-A-1 Q.
Умноткая обе части уравнения (3) на D, можем переписать его
в виде
Е>^ = ЖХ~1 ¦ DQ-Q ^ + Dcm\F + D[Sradp, gracb]
или
Умножим обе части этого равенства слева на А"1 и примем во
внимание формулу (27) из § 1; в результате получим
JA"1 - DQ
di - А ¦ • О сі:г F + Д -1 • D [grad р, grad ф\ О)
Так как, если
324

то
то мы имеем
DcurIF =
curlF
•
і
д
дх
\х
1
I
1
|
t
Е
•
3
д
ду
Y
dv
да
д
да
А
і
д
дх
X
к
д
dz
Z
дт
db
d
db
В
•
J
к
д д
ду dz
Y Z
-
дх
да
ду
да
dz
da
дг
дс
д
дс
С
э
J
дх
db
ду
ab
dz
db
где
А
В
Л -da~+Y-da-Zda'
Л дЬ±Г db'Z db'
дс ' дс ' дс
короче
L4+jB + kC = F-A.
Вычислим наконец
да
1
_1 -DcmlV =
дх
1 дЬ
дх
дс
{ дх
да
«у
db
дс
ду
да
dz
db
dz
dc
dz
да
_д_
да
А

составляющая этого вектора по оси Ох равна очевидно
да
дх
дх
да
д
да
А
дх
дЬ
д
дЬ
В
дх
дс
д
дс
С
+
да_
ду
дЪ
'а
_д_ j)_
да дЬ
А В
дс
дс
С
Л-
+
да
дг_
да
дх_
дЬ
д_ _д_
да дЬ
dz_
дс
_д_
дс
ABC
и следовательно
— і
Д -DcurlF =
Точно так же в силу того, что
•
I
д
1
д
да
А
•
J
д
да дЪ
А
В
0
д
дЬ
В
к
д
дс
С
0
д
ее
С
•
\gmdp, grrada>] =
МЫ ПОЛУЧИМ
[gradp, grad<o]?> =
дх
д®
дх~
дг_
да
др
<)а
діх>
Ja
і к
др др_
dg dz
д&- д<^
ду dz
дг
дЬ
др
дг
дс
др
?. дс
да>
Ж
—і
А • D [grad р, grad«] =
др_
да
дш
да~
дм
дТ |
J к
др др
д&
дЬ
д&
326

Введем теперь обозначения:
Q* =
t
д
да
А
г
f
•
j
д
дЬ
В
I *
dp dp
да' дЬ
да> д<а
Оа дЬ
к
д
дс
С
к
дР
дс
д<&
дс
Л^і^+і^ + кИ*
(14)
Л = *•+*» +К.
Тогда, подставляя в уравнение (7) выражения (11) и (13),
интегрируя полученное уравнение по /в пределах от ^ до t и замечая
что при * = *0 мы имеем Z) = l, A = Ij U = Q0, получим
A-1.z)^ = ^0-h^*4-^*>
откуда
Z>2 = A.(Qo + Q»-^*) Щ
или, в силу формулы (5),
р
Ро
(16)
В проекциях последняя формула напишется следующим образок:
дх
Р Ро д<* Ро ^ Ро &
?<.+?*+*» ау , ^іо+^+^ <fr , S+^-fc» fr
Ро
Ро
<??
Ро
<?с
' р Ро <?а ¦" р0 дЬ "¦" р0 дс
(17)
Итак, наше исследование показало полную эквивалентность
формул (3) и (16). Обе они выражают, что в общем случае
сжимаемой (или неоднородной) жидкости, движущейся под действием
неконсервативных сил, сохранение вихревых линий не имеет уже-
: более места. Более того, обе эти формулы дают количественную!
характеристику вихреобразования, происходящего как от
неконсервативности силы [член curl F в формуле (3) и член 2* в (16)], так
и оттого, что изобарические и изостерические поверхности
пересекаются друг с другом {член [grad />, grad о>] * формуле (3)
и член Q* в (16)}.
327

Отметим, что формула (3) была дана Фридманом еще в 1915 годух)
и впервые опубликована в 1916 году2). Формулы же (16) даны
Аппелем в 1917 году 3). Эти формулы послужили для Лихтенштейна
фундаментом <» доказательства существования решений уравнений
гидродинамики идеальной несжимаемой неоднородной жидкости4).
Перейдем теперь к рассмотрению одного вопроса, связанного
с вюсреобразованием и поставленного Фридманом в его „Опыте
гидромеханики" (ч. II, § 16, п. 6, стр. 279). Вопрос этот
заключается в следующем: возможно ли такое движение жидкости,
происходящее без притока тепла под действием консервативных сил,
в котором плотность каждой частицы остается неизменной, так что
я следовательно
divV-0 (18)
(Фридман называет такие движения несжимаемыми), и в котором
турбулизирующий вектор ф отличен от нуля, так что плотность
не есть функция давления, и в котором, значит, не имеют места
• теоремы Гельмгольтца?
Н. Е- Кочин дал положительный ответ на этот вопрос, указав
пример адиабатического несжимаемого движения, происходящего
под действием силы тяжести и такого, что турбулизирующий вектор &
отличен от нуля» так что вихревые линии не обладают свойством
сохраняемости 5).
Направив ось Oz вертикально вверх, будем иметь
Х=0, Y = 0,Z = — g; (19)
примем теперь
u = — l{z)y, v = X (z) дг, w — О, (20*
где 'к (z) — произвольная функция своего аргумента. Условие (18)
очевидно выполнено. *
Применим теперь условия динамической возможности. Составим
для этого векторы: динамический градиент
c-v М
и турбулизирующий вектор
?) = —curlG.
*) „О вихрях в жидкости с меняющейся температурой", Сообщения
Харьковского математического общества, 2 серия, т. XV, 1917, стр. 173—176 (датировано
10 сентября 1915 г.).
2) eSur les tourblllons dans un llquide a temperature variable", Comotes Rendus,
t. 163, 1916, p. 219-222.
3) Comptes Rendua, t. 164, 1917, p. 71.
4) L. Lichtenstein, Grundlagen der Hydromechanik, 1929, X und XI Kapitel.
5) N. К о ts chin, „Uber einen Fall der adiabatischen Bewegung", Zeitschrlft fur
Physik, Ed 17, 1923, S. 73-78.
323

После простых вычислений получим:
Ga = V(z)x, G, = >.*(*) у. G:=-g,
?* = 2а {г) >/ (г) #, S, = - 2/. (г) J/ (z) лг, & = О,
так что
H = (G,V) = 0,
dt '
K>,v]=o.
Мы видим, что движенке может быть только полуконсервативным
специальным, условия которого даны в теореме 27 „Опыта
гидромеханики" (стр. 223). Легко видеть, что все эти условия в данном
случае выполняются.
Путем интегрирования системы (140) (стр. 222) легко определим
<? = 1п(о, и следовательно
• = Х«(*)Л#(э), (21)
где М есть произвольная функция своего аргумента
Затем обычным способом найдем давление р:
/» = / jfff + Po® = N(°) + Po(t),
(23)
где Ро(*) — произвольная функция от времени.
Принимая во внимание, что уравнение притока тепла может быть
яаписано согласно формуле (219) „Опыта гидромеханики" (стр. 274)
в виде
dp R t*
dt cs н ю'
видим, что в данном случае условие адиабатичности состоит в том,
что
at '
и следовательно надо взять
p = iV(a)-fp0) (24)
где pj — произвольная постоянная.
Если X (z) действительно зависит от z, так что >/ (z) ф 0, то
турбулизирующий вектор *р будет отличен от нуля. Так как
в нашем случае
curl F = 0,
то из формулы (1) следует:
^._(Q,V)V, Q
329

Но очевидно, что
следовательно
К», <->] ф О,
т. е,, согласно § 1, вихревые линии рассмотренного адиабатического
несжимаемого движения не обладают свойством сохраняемости.
§ 3. Примеры на условия динамической возможности.
В § 16 главы III „Опыта гидромеханики" Фридманом был
разобран целый ряд примеров на условия динамической возможности
движения. В настоящем параграфе мы укажем еще на один пример
применения условий динамической возможности, пример, важный
с точки зрения применения его в динамической метеорологии.
Как раз в то время, когда Фридман разрабатывал свой метод
условий динамической возможности движения сжимаемой жидкости,
в ряде работ английских метеорологов и гидродинамиков вновь
был поднят вопрос о построении гидродинамической модели циклона.
В то время как в старых работах .(например Oberbeck'a или Marchі)
рассматривались почти исключительно движения несжимаемой
жидкости и притом стационарные, в указанных работах задача
ставилась шире, а именно жидкость предполагалась сжимаемой, а самый
циклон перемещающимся, что представляет гораздо более интереса.
Основная идея этих работ заключалась в задании известной
кинематической формы атмосферного движения, в данном случае
вращения жидкости' („revolving fluid"), и в использовании уравнений
гидромеханики в целях получения той картины распределения
давления, которая отвечает заданному кинематическому движению.
Однако во всех этих работах вводились те или иные предположения,
лежащие не в существе рассматриваемого вопроса, а введенные
исключительно в целях упрощения вычислений. Так например,
Рэлей (Rayleigh)г) предполагает плотность жидкости постоянной
и кроме того пренебрегает вертикальной составляющей
отклоняющей силы вращения земли. Метеоролог Шоу2) (Shaw) ввел
добавочное предположение о том, что изобары совпадают с линиями
гока. Наконец Грин3) (Green) ограничивает свою задачу случаем
і зотермических изменений жидкости, т. е. предполагает плотность
пропорциональной давлению.
Фридман в своей работе „Идея вращающейся жидкости в
атмосферных движениях"4) поставил себе задачу изучить все движения
сжимаемой жидкости самого общего типа, в которой плотность
.есть функция давления и температуры, которые происходят под
• действием силы тяжести и отклоняющей силы вращения земли
і) Proceed, of the R. ь-^ London 1917, vol. 93, p. 148, и Phil. Ma*. 1919,
vol. 38, p. 420.
2) Proceed, of the R. Soc. London 1917, vol. 94, p. 33.
3) Phil. Mag. 1921, vol. 40, p. 665.
4) Метеорологический вестник, т. 31» 1921, стр. 69—88.
330

и которые имеют следующую кинематическую структуру.
Вертикальная составляющая скорости равна нулю, причем движение
жидкости в каждой горизонтальной плоскости является вращением
с постоянной угловой скоростью С вокруг перемещающегося центра
с координатами x=af y = b; перемещающийся центр вращения
предполагается при этом различным для горизонтальных плоскостей
на разных высотах, а угловая скорость "* для всех высот считается
одинаковой, другими словами — а и Ь считаются функциями от z и t,
а С считается постоянной.
Таким образом для составляющих скорости мы получаем
следующие выражения:
да (z, О
и =
V
ді
db (z, t)
dt
С \я-Ь (аг, f)l
_К lx-a(zt 01
<1)
Направим ось Ох к северу, ось Оу — к востоку, ось Oz— по
вертикали кверху; широту рассматриваемого места обозначим
через 9 и будем ее считать для всей изучаемой нами области
постоянной, чем вводится конечно известное ограничение. Если
обозначить вектор угловой скорости вращения земли через X, его
проекции на оси координат через
Хх = — Xcos?, ^2 = 0, Ъ$ = — ^sin?, (2/
то для проекций силы, действующей на единицу массы, получим
Х=2^ъю, Y= — 2X3u, Z=—g — 2\v. (3)
Применяя свой метод условий динамической возможности,
Фридман отыскивает все движения идеальной сжимаемой жидкости
типа (1), могущие иметь место при наличии сил (3).
Не производя вычислений, ограничимся тем, что приведем
окончательные результаты, причем будем предполагать, что ? отлично
от нуля и от — 2\ч.
Движение оказывается возможным в двух случаях. Во-первых
может иметь место общее нормальное движение, в каковом случае
за функции а и bt не нарушая общности, можно взять
2\
ч (z, t)
2к
z + ,4(z)cos(; + 2X3)*-f
(4)
+ Я (z) sin С+ 2Xe)* +a ft)..
Ъ (z, /) = В (z) cos (С + 2Х3) t —
— i4(z)sin(C+2Xe)* + p(/),
где A iz) и В (z) — произвольные функции z, а а (t) и $(t) —
произвольные функции L Далее, должно быть
• —«Of
(5)
331

т. е- удельный объем или — что то же самое — плотность является
величиной постоянной. Наконец для давления получается формула
«оР--^ 22Ц) (*а+У8) + [9і(0-2^]
+ **(0іГ-** —2Ь,
^а dz-':-<o0p0tt),
(6)
где р0 (*)— произвольная функция времени, a g^f) и g*(t)
функции, определенные равенствами
(7)
Во-вторых может иметь место специальное полуконсервативное
движение, в каковом случае функции а и Ь имеют вид
2^
Ь = д%,
(8)
где <7і и д% — произвольные постоянные. Удельный объем а> и
давление р определяются формулами
?¦¦/¦
F(c)
где
= Г9
{(-
9і
2Х,
С-1-2).,
¦Ро (t),
(y-</J*
2g',z
С + 2Х,
(9)
(Ю)
а F(o) и />о (0 суть произвольные функции своих аргументов.
В упомянутой работе Фридман производит детальный разбор
обоих этих движений с кинематической точки зрения и указывает
на то значение, которое они могут иметь в динамической
метеорологии. Мы можем рассматривать оба движения как
гидродинамические модели циклона или антициклона, однако оба они обладают
с этой точки зрения недостатками. Первое движение соответствует
случаю перемещающегося циклона в несжимаемой жидкости (в силу
постоянства плотности), так что его можно рассматривать только
как модель достаточно низкого циклона. Второе движение свободно
от недостатка, выражающегося в постоянстве плотности, но зато
мы его можем рассматривать только как модель стационарного
циклона (ибо семейстно изобар в этом движении остается
неизменным). О - '
Существенно дальше пошел Н. Е. Кочин. Он, следуя методам
332
)

Фридмана, при тех же предположениях относительно действующих
сил, т- е. считая, что
X=2lhv, Y = — 2Х8ц, Z = — s~2XlVf
(ID
разобрал возможность движений идеальной сжимаемой жидкости
с таким полем скоростей:
ді
я> = 0.
(12)
Иными словами, в то время как Фридман считал угловую
скорость вращения неизменной по высоте и во времени, Кочин принял
ее зависящей как от z, так и от L Оказалось однако, что условия
динамической возможности не выполняются, если С действительно
зависит от і, так что необходимо принять С зависящей только от
высоты z. Этот последний случай и был подробно разобран
Кочиным *).
Не приводя вычислений, укажем только результат. В
динамически возможном движении, имеющем форму (12), функции а и Ь
должны иметь следующий вид:
a(z, t) = a(z, t) + A (z)cos(; + 2Xs)/ +
\
J_ P. I
В (z) sin ? -f 2X3) t -f 2^
2X. '
(13)
b (z, t) = ? (z, t)-A (z) sin CH-2X,) t +
-r5(2)cos(;-f2X8)f,
где С есть любая функция от z, Л (z) и 5 (z)— тоже произвольные
функции от z, a a(z, г) и [3 (z, *) суть какие-либо частные решения
уравнений
да
ді
(14)
в которых .дг(і) и ?і(0 означают произвольные функции L
Если взять одновременно qx = const, 92 — const, A (z) = 5 (z) = О,
что соответствует случаю специального полуконсервативного
*) „Теоретическая модель перемещающегося циклона*, Журнал геофизики
и метеорологии, т. I» стр. 47—66, 1924.
333

движения, то удельный объем <& и давление р даются
формулами
« = :(:+2х,)Ла), I
Jm+м !
(15)
2 lL
9l-2)
г
dz
(z) -г- 21,
+ [y-92?-2
?«k
./ :(z)[;(z) -2У J'
(16)
tL F(z) и p0(/) — произвольные функции своих аргументов. Это
движение определяет стационарный циклон или антициклон
аналогично второму случаю Фридмана.
В общем же случае мы имеем общее нормальное движение,
в котором удельный объем <*> и давление р даются формулами
« = СоС(г)[:(*Н-2У,
1
Р =
2с,
¦* —9і (0 — 2*! / Т72<ггж
т-[?-?»(')]*-2
g dz
J С СИ-2).,,)
> (17)
— 4Х
:(і+2^
л
4^
+ 2*8 J
гРо(*)>
тде с0 — произвольная постоянная, a p0(t) — произвольная функция
времени. Это движение определяет перемещающийся циклон (или
антициклон), в котором плотность меняется с высотой и в котором
изобарические и изостерические поверхности пересекаются друг
с другом, чего не было в случае, рассмотренном Фридманом.
Заметим, что формулы Фридмана содержатся, как частный случай,
в формулах Кочина.
В заключение этого параграфа заметим, что, в целях более
гибкого применения условий динамической возможности движения
-334

к построению моделей атмосферных движений, Фридман выдвинул
идею построения приближенных условий динамической возможности
движения *).
§ 4. Новая классификация условии динамической возможности.
Каждая из пяти категорий, на которые Фридман разбивает все
возможные движения идеальной сжимаемой жидкости (см. стр. 206—229;,
характеризуется с кинематической точки зрения своей группой
неравенств и равенств, связывающих компоненты скоростей,
заданных сил и ях производные по координатам и по времени, а с точки
зрения динамической — своей системой дифференциальных
уравнений, служащих для определения плотности.
Отправным пунктом в этих исследованиях является система
уравнение
[grad?,G] = — ф,
(стр. 209): причем особенное значение (придается мере диссипа-
тивности ц *Так, первые две категории („нормальные") Фридман
характеризует тем, что в |них мера диссипативности отлична от
нуля, а остальные („полуконсервативные") определяются равенством
нулю величины у. Вспомним при этом, что в случае общего
нормального движения плотность определяется путем квадратур (стр. 216),
в специальном нормальном движении — из системы трех
дифференциальных уравнений в частных производных первого порядка
(стр. 217), в движении общем полуконсервативном — вновь путем
квадратур (стр. 221), в специальном полуконсервативном — вновь
из системы трех уравнений первого порядка (стр. 225), наконец
в случае „безградиентном* — из одного уравнения первого порядка
в частных производных.
При поверхностном рассмотрении можно было бы объединить
первую и третью из перечисленных здесь категорий по признаку
количества и характера уравнений, служащих для определения
плотности, хотя с точки зрения Фридмана они различны
существенно, ибо одна из них отвечает рфО, а другая р. = 0. То же
самое можно сказать про вторую и четвертую категории.
Обстоятельство это имеет повидимому глубокое основание.
Действительно Кибелю удалось показать, что все движения
идеальной жидкости с динамическим градиентом G, отличным от нуля,
можно разбить на две, а не на четыре, как это делается у
Фридмана, категории, минуя отдельное рассмотрение случаев ;а ^ 0
и а = 0. Таким образом по Кибелю имеется три различных сорта
движений (третий сорт совпадает с безградиентным движением
Фридмана), из которых, полагая, если угодно, рфО илиу. = 0,
можно вновь получить пять категорий Фридмана.
1 *) А. А. Фридман, .О приближенных условиях динамической возможности
движения сжимаемой жидкости", Геофизический сборник, т. V, вып. 2
стр. 24-32, 1927.
(1)
335

К изложению работы Кибеля мы и приступаем *).
Уравнения движения напишем в их обычной форме, вводя вместо
удельного объема его натуральный логарифм <? = 1п<о:
grad p = e~T G. (2)
Уравнение неразрывности представим в виде:
^--MV, grad?) = 0. (3)
Легко показать, что следствием (2) и (3) является уравнение^
аналогичное (2), но содержащее под знаком градиента не само
давление, а его индивидуальную производную во времени:
grad ^f^6"*6'» (4)
где
G' = ^+gradu + [V, ©]-вй
Действительно, предположим, что (2) и (3) имеют место, и возьмем
частную производную от обеих частей (2) по времени:
^gradp-grad — = е ¦ Tf-в • G ^.
С другой стороны в силу того же (2) очевидно
(V, grad/>) = e~V,
так что
grad (V, grad/>) = е~ ? grad ^ — е~" * a grad о. (5)
Но мы можем найти выражение ^ grad? непосредственно из (1),
являющегося следствием (2), умножая обе части (1) векторно на V:
!* grad 9 — (V, grad ?) G = — [V, ?].
Внося это выражение u grad? в (5), придем к соотношению
grad (V, grad p)==e~Y grad p — e~r (V, grad 9) G-j- e~* [V, ?>],
а вспоминая уравнение неразрывности, сможем написать:
grad -J = grad { -J- + (V, grad p) } =
= e_? { -W"+^ada + [V, ©]-0G }.
Формула эта очевидно совпадает с (4). Наше утверждение
доказано.
Уравнение (4) мы можем теперь использовать для получения
*) И- А. К и б е л ь, „О дифференциальных уравнениях, служащих для
определения плотности движущейся сжинаемой жидкости". Мат. сб. т. 39:4(1932),
стр. 141-152.
336

нового соотношения, аналогичного уравнению (1). Для этого
возьмем вихрь от обеих частей (4). Получим очевидно
ferad ?, G'] = — ?>', (6)
где
©' = — curl G',
аналогично тому как § = — curl G.
Уравнения (1) и (6) представляют прежде всего систему шести
алгебраических уравнений, служащих для определения компонентов
градиента grad у.
Для совместности этой системы должны быть выполнены
следующие три соотношения:
(6. ?>) = О, (7)
(С, §') = 0, (8)
(?',6) = -(&G'). (9)
Первое из этих равенств есть условие незакручиваемости
(стр. 210) [чтобы получить его, достаточно умножить обе части (2)
скалярно на G]* второе — аналогично условию незакручиваемости
и отвечает группе (6). Наконец третье соотношение получим,
например, умножая скалярно (6) на G и вставляя [grad ?, GJ из (1).
Нетрудно убедиться, что условие (9) выполняется само собой.
Действительно, имеем
($',G) = (-^r,- G)-'r(curl[&, V]. G) + ([gradO, G], 6)-?(?, G) =
= (^f, G)+(curl[©,V]fG);
no
(9,0 = 0, ($,.)_-(ft»).
div [[&, V], G] = (G, curl [$, V]) - ([©, V], curl G) =
¦= (G, curl [& Vj) + ([& V], ©) = (G, curl [& V]);
кроме того
№ V], G] = V (©, G) - § (V, G) = - ix§,
div \l!q = y. div § -j- (§), grad «•), div ?> = — div curl G = 0,
поэтому *
(&',G) = -(&-^)-(&gradiO;
HO
(«), G')=(§, ^ + gradp + [V5 §]-6б) = ($,-^-4-grad^,
и мы приходим к (9).
Относительно условия (8) заметим, что оно было получено
иным путем Фридманом для случая общего нормального движения
(стр. 234).
22 Зак. 2420. — А'. А. Фридіган, Опыт гидромеханики 337

Предположив, что (7) и (8) имеют место, легко получим для
grad? из (1) и (6) соотношение *):
<В, В) srad ? = [§>', [В, G]] -f (В,. ©) G\ (10)
где
В = [G, G'].
Прежде чем игти дальше, заметим, что вектор В, имеющий
смысл созершенно независимо от того, равно илг не равно ;-*• нулю,
совпадает в точности с введенным Фридманом вектором —\*>'ло **)
(хотя 8 имеет смысл лишь для общего нормального движения,
р28 не зависит от условий, накладываемых на ;*). Именно этот
вектор и следует, по мнению Кябеля, положить в основу
разделения движений на категории.
Разобьем же все движения на две группы* К первой отнесем
такие движения, в которых вектор
В^О,
ко второй движения с
В = 0.
Обратимся сперва к первой группе. Здесь (В,*В):?0 и имеют
смысл вектор
, [У, [В, С]] + (В, 3)6'
0 = (вГв'і (11)
и Скаляр
1 = (іГв) "¦ а2)
Из уравнений (10) следует однако, что
grrad ? = о', (13)
а из ураЕнения (3) — что
%-у. (и)
Таким образом нам необходимо положить
да'
curl а' = 0, grad >/ = -—. (15)
Итак *ы видим, что для возможности определения давления и
плотности из уравнений гидромеханики, при наличии неравенства
В:?0, необходимо должны выполняться соотношения (7), (8), (15).
*) Для получения (10) можем поступить, например, так: умножим обе части (1)
скалярно на G': ([grad <рf G], G') = (grad <р, В) = — (?>, G') или (grad ?, В) В =
= - №,G') В, но - (grad <р,В) В - [B,[grad ?,В] ] - (В, В) grad <р = (G,[grad ?.B])G'—
— (С, [grad у, В]) G - (В, В) grad ? = ([G, grad ?], B) G' - ([C, flr*d *L B) G —
— (B, B)gradf, а отсюда по (lj, (6) и (9) получим (10).
**> В самом деле
B[G)^+^adE" + tVj$3"6G]==[C'^+3?radji]-^^
М
[см. стр. 230, формула (147)].
338

Легко показать, что этих соотношений и- достаточно для опре*
деления давления и плотности. В самом деле, из условий (15)
можно определить скаляр 6 такой, что
Но тогда, в силу самого построения з', из (11) можно вывести:
что
farad Ф, G] = - ?;
уравнение же неразрывности также может быть удовлетворено
с помощью ф, ибо
^- + (V>grad<i) = r + (V)a') =
= -^щ{ (& 6') (V, В) - (V, GO (?>, В) + ? (В, В) + IX ($', В) +
+ (?>', 6) (V, В) - ($', В) и + (В, $) (V, С) } = ?,
в силу (9). Мы можем, таким образом, принять ф за <?, давление же
определить как обычно на основании (1). Мы приходим к теореме,
Если В ф- О, тпо необходимыми и достаточными условиями
возможности нахождения давления и плотности из уравнений
гидромеханики являются равенства:
(G, ф) = 0, (С, §0 = 0,
сиг1<т' = 0, grad^ = -~. <А)
В этом случае плотность определяется путем квадратур из
уравнений (13) и (14).
Обратимся теперь к -оставленному нами случаю, когда
В = 0. (16)
Его естественно разбить на два подслучая: когда (іфО и
6 = 0. Обратимся сперва к более общему случаю
ЬфО.
Из (16) следует существование скаляра п такого, что
G =72G
(п может быть нулем). Обращаясь вновь к (б), получим:
п [grad <р, G] = curl (72G) = п curl G -f- [grad л, G].
Таким образом, если имеет место (1), то должно быть
[grad л, G] = 0.
Отметив попутно выпо \нение соотношения [после того как (7)
выполнено]
(G', §') = - л (G, curl л С) = л» (G, §)—л (G, [grad л, G]) = 0,
сможем утверждать, что если
22* 339

[6, GT = B = 0,
то необходимо должна выполняться лишь условия
(6, $) = 0, [grad/i, G] = 0.
Нетрудно убедиться, что этих условий достаточно для
возможности определения плотности из уравнений механики. В самом
деле, система уравнений
ferad?, G] = -& % + (V, grad?) = 6, ft?)
из которых нам придется находить теперь плотность, является*
как нетрудно убедиться, полной якобиевой в силу условий
(G,$) = B=kradn,G] = 0.
Мы приходим к теореме:
Необходимым и достаточным условием для возможности
определения давления и плотности из уравнений гидродинамики
в случае^ когда вектор 3 = 0, но G ф О, является выполнение
соотношений
В-0, (G, $) = 0, | ,Б)
[gradn, G] = 0; J
при этом плотность находится из полной якобиевой системы трех
линейных уравненией (17) в частных производных первого порядка.
Давление определяется, как всегда, путем квадратур.
Остается рассмотреть оставленный нами последний случай,
когда
G = 0.
Обращаясь к уравнениям Euler'a, имеем
grad р = 0,
т. е. давление есть произвольная функция одного только времени.
Плотность определяется при этом из одного уравнения
неразрывности:
-g + (V, grad=?) = e.
Таким образом единственным условием, накладываемым в этом
последнем случае на скорость, является выполнение трех
уравнений
G = 0. (В)
Движение это в точности совпадает с „безградиентным"
движением Фридмана и особого интереса не представляет.
Покажем теперь, как, предполагая заранее у. ф 0 или ^ = 0, мы
придем вновь к пяти категориям Фридмана. Положим, что нам
известно, что \*>фО. В таком случае, если ВфО, мы находимся
в случае (А). Нетрудно убедиться, что X' совпадает с введенным
340

в этом случае Фридманом скаляром Ь (стереоскаляром), а з'—со
стереовектором а *). При этом условие
curl а' = О
выполнится само собой, и наши условия (А) совпадут с условиями
динамической возможности „общего нормального движения" (стр. 214).
Если В = 0 (но н- Ф О попрежнему), мы будем в случае (Б). Условие
[grad л, G] = О
влечет за собой условие
^2Y = О,
и так как В — — ;х-8, мы приходим к условиям „специального
нормального движения" (стр. 217). Если же известно, что ^ = 0, то
в случае (А)
B = [G, G'] = Г~ dG
(
G> *
to
так как здесь 6'=-зт — &G-|-[V, ?>] j, т. е. мы имеем дело с
общим полуконсервативным движением, в случае же (Б)
G' Л
= 0,
т. е. нам приходится рассматривать „специальное
полуконсервативное" движение. Случай (В), как уже было сказано, отвечает
„безградиентному" движению.
Для иллюстрации теории рассмотрим элементарный пример
частного случая движения сжимаемой жидкости. Остановимся на
так называемом квази-твердом движении. Для простоты будем
считать, что компоненты скоростей (по осям х, yf z)
представляются в виде
С С
где с — функция времени, а С — постоянная. Возьмем при этом
постоянное поле сил:
/;=о, f,=o,% Fz=g.
Разбирая это движение по Фридману, мы пойдем к следующим
значениям функции о> в первых четырех категориях:
В случае общего нормального движение
ш = ш0 = const,
при этом с (t) — произвольная функция времени.
В случае специального нормального движения
*) Это следует из того, что, как легко показать, вектор [[?>, V] -f- 6G, G'] +
¦ -|~ рь^ совпадает с вектором р-2? Фридмана, аналогично тому, как (что уже
отмечалось) вектор ? совпадает с — (х2о.
341

где <о — произвольная функция своего аргумента, с, — постоянная
такая, "то і
«ate—Ъ)Ф0 (V-ФО),
а
Общее полуконсервативное движение в данном случае
невозможно.
Наконец в специальном полуконсервативном движении будет
* = «(*»+ у>), c = gt9 (19)
где функция w произвольна. ч
Посмотрим, что даст нам классификация Кибеля. Согтавіш
сперва В. Легко видеть, что
flfc
*=«(*-?). e-a
поэтому
c;=c,=o, 0;=-$,
акнм образом
и для случая (А) необходимо считать -j-j- :?0. Так как далел
то
и, следовательно» ? (т. е. и to) есть величина постоянная:
<р = ?о = const.
Отметив, что условия (А) все выполняются тождественно и что
таким образом можно считать? что с есть совершенно произвольная
функция времени | -^ Ф О I, перейдем ко второй категории, когда
В = 0.
Здесь
л» '
и мы возьмем
с (0 = с А
при этом
G* = G„ = C,=0,
а так как G :? О (иначе будет С = 0), то п ~ 0. Условия (Б)
соблюдаются тождественно, и мы имеем для определения <р систему
уравнений
342

до I
до 12
dc
dt
до «
dz 4
ff = Or
(й 4
д?_ С*
^ do
Ол:
?
Л
<fy 4
' Со
Л.
дг = 0,
= 0,
Тъ'"'*^0,
ЗЛИ
3*
у дд ~ ' ~dz
4с [g
*[g
{
dc\
dc\
dtj
>
dt
до
0У
dt • cv
Интеграция этой системы производится совершенно
элементарно. Мы иолучаем
Р
;e2 + ^+8_tol/z_,i_
где 9—произвольная функция своего аргумента.
Мы видим, что в случае если у-фО (т. е. g— с1ф0), мы вновь
приходим к формуле (18) для специального нормального
движения, тогда как при р = 0 (g — Cj) мы получим удельный объем
в форме (19).
§ 5» Условия динамической возможности в неременных Ла-
гранжа.
1. Уравнения гидродинамики в форме Лагранжа могут быть
написаны следующим образом:
д^гд* , д*у_ дд_, _^^?___ $Р . - Ёі.
д** да + дР da^ df да~ * да +> х да
ду_
да
+
+ F,
dz_
da'
cfi db~^ д& дЬ^~ dp дЬ~~ ш дЬ "+" х дЪ + * оЬ ^
+ РШ
dz
\0)
д*х дх_ | д^ ду_ , d*z dz _
"ллГ ~аТ "Г лл л~ ~Г лл л^ "
дЧ dz dp
— л\ •
dfi дс ' д? дс ' Л2 (?с
»^ + f.
дх
дс
дс
F &.+
* дс ^
4-F —
343

Здесь ш и р означают удельный объем и давление в момент t;
Fjg, Fyt F% суть проекции силы F на координатные оси; <»0 — функция
от а, Ь, с, удельный объем в начальный момент, причем за а, Ь,
с приняты декартовы координаты частицы в начальный момент.
Величина *
D (а, Ь, с)
означает якобиан функций х, у, z относительно переменных а,
Ь, с. Система (1) эквивалентна другой системе уравнений
grad р — е~? Г 1
^ = 0 (2)
в которой grad р есть вектор с составляющими:
др др др_
!кі9 ~дЬ7 !te;
удельныЗ объем о> определяется уравнением
о = Df, (3)
и составляющие вектора Г имеют сыражения:
д*х\ дх . /¦ д*д \ ду
Задача, аналогичная рассмотренной в „Опыте гидромеханики*
задаче нахождения условий динамической возможности движения
а переменных Эйлера, здесь может быть формулирована таким
образом:
Найти условия, которым должны удовлетворять функции xf у, z
переменных а, 6, с, t для того, чтобы можно было найти функции
р и <р> удовлетворяющие уравнениям (2). Эта задача была решена
в совместной работе Фридмана и Извекова, содержание которой
мы сейчас изложим*).
2. Применяя к обеим частям уравнений (2) операцию curl,
находим, что функции р и 9 должны удовлетворять такой системе
уравнений:
[Г, grad?] = H, \
#-* j (5)
*) A. Friedmann et В. Izvekov, „Sur le mouvement cPun fluide parfai?
compressible". Известия Российской академии наук, 1925, стр. 351—362.
344

где Н означает —curl Г относительно переменных а, Ь, с, так что
"а~ дс db' "b-~fa
дТ.
, н.
db
дТ,
дс ' "'" дЬ да'
Система (5) выражает условия, которым должна удовлетворять
функция '•?. Если такая функция найдена, то давление определяется
до произвольной функции времени
р=--РоИ) + f e~" [Tada^Vbdb + Vedcl (6)
Из системы (5), как необходимое условие, получается
(Г, Н) = 0. (а)
Это последнее уравнение и представляет первое условие
динамической возможности движения.
Для разыскания других условий надо различать следующие
случаи:
V4
2)
О,
О, но Г^О,
ді
дТ
' dt
3) Г = 0.
Рассмотрим вначале первый случай.
Решим систему (5) относительно grad <?. Тогда, обозначая через
л некоторую пока неопределенную функцию от а, Ь, с, t, напишем
систему уравнений в таком виде:
grad о = )^,\ + лГ,
(Г, Г)
dt и'
(7)
Продифференцируем первое уравнение по t, принимая во
внимание, что
-^ grad о = grad \-? \ = 0.
Если потом помножим полученное соотношение векторно на Г,
то получим уравнение
ан . \и> ді
ді + (Г, Г)
г,
dt
(Г, Г)
Н + Л
дТ
' dt
0.
(8)
Это уравнение служит для определения функции п. Умножая
дТ
скалярно последнее уравнение на вектор -лт, получим второе
условие динамической возможности движения
"Г№=0. (Ь)
(
dt9 dt
us

Если удовлетворены оба условия.(а) и (о), то, как нетрудно
убедиться, можно определить скалярную функцию X так, чтобы
при п = X уравнение (8) было удовлетворено. Тогда, применяя one-
р?цию curl к обеим частям уравнения (7), получим еще
[Н,Г]
(Г, Г)
+ ХГ =0, (с)
Это последнее уравнение (с) представляет собой третье
условие динамической возможности движения. Наконец, дифференцируя
обе части первого из уравнений (7) по t и пользуясь вторым из
уравнений (7), получим последнее условие динамической
возможности движения:
!.1РУЗ-мг1=о (d)
ді ((Г, Г) Х ( Ue w
Условия (а), (Ь), (с) и (d) являются очевидно не только
необходимыми, но и достаточными условиями динамической
возможности движения. При их выполнении, обогначая через L вектор
L-IM + XT
L~(r,r)+U'
определим <р и т по уравнениям
• = к С+ f(Lada + L>db + Lc dc), 1
\ (9)
<u = cJ{L*da+L*db + l°dc) j
где С есть произвольная постоянная, после чего, как было
показано выше, давление р определится до аддитивно входящей
произвольной функции времени формулой (6).
3. Переходя ко второму случаю, когда
дГ
Г'Л
= 0,
что означлет, что
?-* »
заметим, что первое условие динамической возможности для этого
случая также сохраняет свою силу, а уравнение (8) упрощается и
принимает вид
?~л (о
Если, как предполагается ъ этом случае, Г отлично от нуля, то
хотя одна из составляющих вектора Г отлична &т нуля. Не
нарушая общности исследования, можем считать, что Ге отлично от нуля,
346

и тогда система (5), служащая для определения с, может быть
переписана в виде
da Г, <ЭС Г, ~U) Об Гс дс ~ TV— U> d/ — U'
Легко проверить, что б силу условий (а), (е) и (і) эта система
уравнений в частных производных будет нормальной системой.
Таким образом все условия динамической возможности в этом
втором случае будут содержаться в уравнениях (а), (е) и (f).
Наконец в последнем случае, когда
г=о, (г)
это последнее уравнение является, как легко »идеть, единственным
условием динамической возможности движения. Удельный объем и
давление в этом случае определятся по формулам
« = о)0 (а, Ь, с) Д |
где % и />о суть произвольные функции своих аргументов.
Таким образом при рассмотрении условий динамической
возможности в лагранжевых переменных получаются три категории
движений, совершенно аналогично тому, как это имело место в
приведенной в предыдущем параграфе классификации Кибеля. Это
связано с тем обстоятельством, что классификация, данная Кибелем»
является по сути дела той же самой классификацией, которая только-
что была приведена, но только выраженной не в лагранжевых, а
' в эйлеровых переменных. Мы не приводим примера на применение
условий динамической возможности в лагранжевых переменных,
отсылая интересующихся к цитированной выше работе Фридмана
и Извекова.
3 6. Условна динамической возможности двюхеяи.. вязкой ежи-
всаемой ж :дкости.
Обобщение результатов Фридмана, касающихся условий
динамической возможности, на случай вязкой сжимаемой жидкости, было
выполнено Б. И. Извековым*).
Для того, чтобы установить условия динамической возможности
движения жидкости, обладающей внутренним трением, нужно
исключить удельный объем и давление из дифференциальных
уравнений движения вязкой сжимаемой жидкости, т. е. из уравнений
Навье-Стокса, подобно тому, как это было сделано с уравнениями
Эйлера в случае идеальной жидкости. При этом предполагается,
что рассматривается самый общий тип сжимаемой жидкости» для
которой удельный объем -или плотность есть функция не только
давления, но и температуры: a> — f(p, 7*), например идеальный газ,
*) Б. Извеков, .Об условиях динамической возможности движения вязкой
сжимаемой жидкости". Математический сборник, т. 32:1, 1924, стр. 58—100.
347

длк которого уравнение состояния есть уравнение Клапейрона
pa> = RT, или даже всякий реальный газ с определенным
уравнением состояния. Коэффициент внутреннего трения ч\ предполагается
постоянным. На ряду с уравнениями движения, конечно, необходимо
рассматривать также уравнение неразрывности.
Уравнение притока энергии, так же как в «Опыте
гидромеханики", вовсе не принимается во внимание, и таким образом,
выведенные условия надо рассматривать как общие условия, которые
должны быть выполнены всегда, каков бы ни был приток энергии.
Величина притока энергии есть величина, крайне трудно
поддающаяся учету при практических определениях. Так например, в
динамике атмосферы, которая представляет самое важное
приложение гидродинамики сжимаемой жидкости, величина притока энергии
определяется весьма сложно на основании косвенных соображений.
Если условия динамический возможности движения оказываются
выполненными, то по заданным скоростям и силам удельный объем
или может быть найден как некоторая вполне определенная
функция от времени / и пространственных координат х, у, z, или же
может быть получен путем интегрирования некоторой системы
линейных дифференциальных уравнений первого порядка в частных
производных с одной неизвестной функцией ф = In со. В этом
последнем случае о будет представляться некоторой произвольной
функцией от частных интегралов этой системы. Что же касается
определения давления по данным скоростям и силам, то оно
становится возможным после того, как удовлетворены „условия
динамической возможности движения" и определен удельный объем,
причем давление определяется только до произвольной, аддитивно
входящей, функции времени.
2. Напишем систему уравнений вязкой сжимаемой жидкости
в виде
-? = F — о) grad р + ш S, |
* , J (і)
где
іпш, 6 = chvV=--—Ь-з—Н-т—•
бх і ду l dz
о
Первое векторное уравнение заменяет три уравнения движения
в форме Навье-Стокса. Здесь вектор
S = -^grade + rtA7f
где Д означает дифференциальный оператор Лапласа, взятый
соответственно относительно всех трех составляющих вектора V:
и, v, w. Второе скалярное уравнение системы есть уравнение
неразрывности.
348

• Вводя в рассмотрение попрежнему вектор G = F™-.-, называ-
at
емый по Фридману динамическим градиентом, и решая первое
уравнение системы относительно grad р, получим
1
grad/> = — G + S
ш
или
gradp = e-"G+ S. (2)
Отсюда видно, что если удельный объем найден как функция
от U ¦*> у, zf то давление может быть определено простыми
квадратурами, причем при этом определении войдет аддиативно произ-
вольная функция времени р0 (t):
+ (1с.+5.)л). (3>
В дальнейшем мы будем называть вектор S первым
фрикционным вектором, а вектор curl S = D вторым фрикционным вектором.
Далее вектор — curl G = ф назовем турбулизирующим вектором,
согласно терминологии А. А. Фридмана. Вектор этот, как показал
Фридман, играет большую роль при образовании и разрушении
вихрей.
Докажем такую теорему:
Условие необходимое и достаточное для того, чтобы из
уравнений гидродинамики можно было определить давление как
функцию времени и координат, состоит в выполнении следующего
равенства:
&-f krad?fG] = e?D. (4)
Необходимость этого условия обнаруживается ясно, если
применить к обеим частям уравнения (2) операцию curl.
Достаточность условия можно легко показать таким образом»
Левую часть уравнения (4) можно написать в форме:
curI(e~*G + S) = 0.
В этом легко убедиться, если развернуть написанное
выражение по известным правилам векторного анализа. Но соотношение
curl (е-9 G -j-S) = 0 показывает, что можно найти такую функцию р
от времени и координат, чтобы было удовлетворено уравнение
grad/> = е_? G -f~ S,
что и доказывает вторую часть теоремы.
349

Итак, коль скоро уравнения гидродинамики имеют решение, то
выполняются соотношения:
$+[grado, G] = e*D| I
И обратно, если ? удовлетворяет этим соотношениям, то можно
найти давление р в функции времени / и координат так, чтобы
удовлетворялись уравнения гидродинамики.
3. Умножив первое из уравнений (5) скалярно на G, получим
(G,$) = e'(G,-D). ' (6)
Отсюда, если (G, D) не равно нулю, то
Проф. Н. Е. Жуковский нагтвает векторы, ортогональные
своему вихрю, незакручивающимися векторами. Так как в
рассматриваемом случае (6, ф) = — (6, curl G) отлично от нуля, то
рассматриваемый класс движений можно назвать закручивающимися
движениями.
Условия динамической возможности класса закручивающихся
движений таким образом будут:
§==mD-j- —[G, gradm],
(8)
тдс
m_№.&)
Заметим, что условий динамической возможности в данном случае
яе четыре, а только три, так как одно из уравнений системы (8)
является следствием трех остальных. В самом деле, если GtфО и
выполнены два первые уравнения
ft-*.i4(*.?-<i.?).
; +
то третье будет выполняться также, в чем убедимся, если первое
уравнение умножим на G& второе на Gyi сложим и вычтем из
тождественного равенства
(G,$) = m(G,D).
4. Если (G, D) = 0, то условия динамической возможности
движения будут иметь другой вид, В самом деле, тогда из основного
350

•уравнения (6) ясно, что скалярное произведение (G,$>) также должно
равняться нулю, ибо в противном случае удельный объем
обратится в бесконечность. Таким образом в этом случае вектор G
оказывается незакручивающимся и движения этого класса естественно
назвать незакручивающимися движениями. -»
Обращаясь к системе (5), заметим, что решение ее относительно
grad 7 всегда возможно, но существенно зависит от того,
обращается ли в нуль или нет скалярное произведение (V, G), которое
по Фридману называется мерой диссяпативности и обозначается
через **. Если у* отлично от нуля, то движения такого рода будем
называть „нормальными"» а если ^ равно
нулю,—полуконсервативны ми-
В случае нормального движения разрешаем систему (5)
относительно grad <р-
В этом случае решение этой системы возможно и оно
получается в виде:
grad9 = A + -^B + e*C, (9)
где векторы А, В, С имеют такие значения:
Ав[иО±^,в=_Д,с=ИЭ. (іо)
Для этих трех векторов вводятся специальные названия: А—
турбомомент, В—приведенный градиент и С—третий фрикционный
вектор.
Применяя к обеим частям уравнения (9) огерацию curl, получим:
*>Pfe*Q + R = 0, . (И)
.at
где векторы Р, Q и R выражаются так:
дБ
dt
P=curIB +
дС
,В
В
Л'
R = curlA +
¦fcurlC+LA, С],
ЗА
dt
,В
В дальнейшем надо различать два случая: 1) когда вектор Р не
равен нулю—общее нормальное движение и 2) когда вектор Р = 0
— случай специального нормального движения.
В случае общего нормального движения, умножив векторно
уравнение (11) на Р, получим:
е* [Р, Q] + [R, Р] = 0- (12)
Отсюда следует условие динамической- воз^^ности
[[Р,9И*.РП = о.
351

что равносильно равенству нулю такого определителя третьего
порядка:
р. р„ р.
а а Q..
(IP-Q1.R)
Rx Ry Rt
0.
После этого удельный объем ш = е* определится из уравнения
(12) как некоторая скалярная функция переменных t, xyy7z> а
условия динамической возможности движения будут
(6,©) = О, (G,D) = 0, ([P,Q],R) = 0,
*™d<i»0=A-j-^-B + Jc, } {13>
где ; определяется из уравнения:
IX Р] = ;[Р, Q].
Последнее уравнение (13) получается, если подставить в
уравнение (9) вместо <? его значение.
Особый случай получится, если [Р, Q]=0. Тогда из уравнения
(12) следует, что и векторное произведение [R, Р]=0. Условия
динамической возможности в этом случае будут иметь другой вид,
и на выводе их мы не останавливаемся.
Специальное нормальное движение (Р — 0) в свою очередь
разделится на два класса» для которых условия динамической
возможности движения исследуются отдельно. Один класс получится
ирн Q отличном от нуля, а другой—при Q = 0.
¦s Подобным же образом исследуется полуконсервативное
движение [\>> = (V, 6) = 0], причем оно сразу делится на два класса:
градиентные движения (когда вектор G ф 0) и безградиентные
движения (6 = 0), Градиентные полуконсервативные движения в свою
очередь имеют подразделения, которые могут быть исследованы
особо.
Полностью исследование всех случаев проведено в
цитированной выше статье Извекова. Там же приведена подробная таблица,
содержащая классификацию всех возможных случаев движения и
перечень условий динамической возможности.
5. В заключение мы рассмотрим здесь один пример,
относящийся к классу закручивающихся движений [см. формулу (8)]*
Именно, рассмотрим стационарное движение воздуха у земной
поверхности, в котором отсутствует вертикальная составляющая
скорости, а горизонтальная скорость меняется только с высотой.
Составляющие скорости в этом случае напишутся так:
и == и (z), v — v (z), w = 0.
Действующие силы суть: сила тяжести с постоянным
ускорением g, направленным противоположно оси Ог, и отклоняющая
сила вращения земли, которая, как известно, будучи отнесена
к единице массы, выразится по теореме Кориолиса векторным
произведением—2 [к, V].
352

Векторы G, §, D имеют такие составляющие (штрих означает
дифференцирование по z):
Gs = 2 X3v, Gy = — 2 Х3ц, G, = —?—2 (>4t/ — X2u),
&= — 2Х3ц', ? =— 2X3t/, &s = 0,
D, = - V", ?>„ = V, Dz - 0.
Составляем скалярные произведения:
(G, $)=— 4Х32(иЧ,_ига
(G, D)= — 2ХзТі (ua'" + TO'")-
Если они отличны от нуля, то удельный объем
(G>,^)_2XS „'o-ao'
m-(G, D) ~ Т^Ч7^' * (14)
_ ^
Обращаясь к условиям (8), видим, что второе из этих условий
удовлетворяется само собой, а первое условие, как легко показать,
сведется к одному уравнению:
2{u'u'" + v'v'")= UX~1U? (hh"'+pO-(hh(IV) + ™'IV')- (15)
Это дифференциальное уравнение 4-го порядка представляет
единственное условие, которому должны удовлетворять функции и
и v. Понятно, что можно самым различным образом выбрать и
и v так, чтобы последнее уравнение было удовлетворено и, вместе
с тем, чтобы скалярные произведения (G, ф) и (G, D) были от-
L
личны от нуля. Так, например, если положить u=z и v — z~f то
все условия возможности закручивающегося движения будут
соблюдены.
о
В 1908 г* F. Ackerbloom дал теоретическую модель
изменения скорости ветра с высотой под влиянием силы внутреннего
трения. Решение Ackerbloom'a, хорошо известное в динамической
метеорологии, имеет вид:
и = С -j- е (A cos тх — В sin mz\
v = e~ {A sin mz -f- В cos mz)?
*t> = 0.
Здесь предполагается, что коэффициент трения есть величина
постоянная, и атмосфера предполагается вязкой несжимаемой
жидкостью. Можно поставить вопрос: возможно ли движение
Ackerbloom'a для вязкой сжимаемой жидкости? Согласно предыдущему
надо исследовать, будет ли удовлетворено уравнение (15).
Подстановкой убеждаемся, что условие это будет выполнено.
Однако, определяя удельный объем по формуле (14), легко
убедимся, что он оказывается постоянным, чего конечно и надо
было ожидать.
Для определения движений, являющихся обобщением движения
23 Зак. 2420. — А. А. Фридман, Опыт гидромеханики 353

Ackerbloom'a на случай сжимаемой жидкости, надо совместно
решать уравнения (14) и (15), предполагая в нервом из этих
уравнений ш заданной функцией от высоты, дающей то
распределение удельного объема с высотой, которое имеет место в
атмосфере.
В заключение настоящего параграфа заметим, что Е. Н.
Блинова и Е. П. Охлопкова *) дали иную классификацию условий
динамической возможности движения вязкой сжимаемой
жидкости, аналогичную той, которая для случая идеальной жидкости
была дана И. А- Кибелем и была изложена выше в § 4-
И. А. Кибель **) рассмотрел вопрос об условиях
динамической возможности, которым должны удовлетворять бесконечно
малые движения сжимаемой жидкости, наложенные на некоторое
основное движение, которое предполагается тоже
удовлетворяющим условиям динамической возможности.
§ 7. Условия динамической возможности движения при
заданном притоке энергии.
1- Вопросам притока энергии в сжимаемой жидкости Фридман
уделял большое внимание. В „Опыте гидромеханики" имеется ряд
страниц, посвященных выводу шестого уравнения гидромеханики,
так называемого уравнения притока энергии (стр. 191), а также
подробно исследуются несжимаемые движения, происходящие без
притока тепла. При получении условий динамической возможности
движения Фридман оставлял однако шестое уравнение
гидромеханики в стороне. Объяснение этому мы находим еще в преди- .
словии к „Опыту гидромеханики", где между прочим Фридман
упоминает о возникшей перед ним дилемме—привлечь к
рассмотрению шестое уравнение гидромеханики, выбрав какой-нибудь
частный вид для функции s, представляющей плотность тепловой
мощности притока энергии, или же не привлекать шестое
уравнение совсем, но зато получить условия, которые должны были бы
необходимо выполняться, каков бы приток тепла ® ни был.
Фридман остановился на второй постановке вопроса и только (в 6-м
отделе § 16) разобрал с точки зрения первой постановки задачи
частные случаи адиабатических движений (несжимаемые и неполу
консервативные).
В „Опыте гидромеханики" мы имеем вместе с тем указания
на то, что автор хотел вернуться к изучению возможности
движения при наличии различных предположений о форме г. Работа
*) Е. Н, Блинова и Е. П. Охлопкова, „Об условиях динамической
возможности вязкой сжимаемой я-идкостн", Прикладная математика и механика,
т. I, вып. % 1933.
**) И. Л. Кибель, „Об условиях динамической возможности малых
колебаний вязкой сжимаемой жидкости". Журнал Русского физико-химического
общества, часть физическая, т. LX, вып. 5, 1928, стр. 421—443.
354

эта выполнена была уже после смерти Фридмана его учеником
.*. А. Кибелем *).
Кибель ставит своей целью найти условия необходимые и
достаточные для возможности движения жидкости (идеальной или
вязкой), осуществляемого при наличии притока энергии е,
являющегося известной, но произвольной функцией от координат,
времени и компонентов скорости.
К изложению содержания этих работ мы и переходим.
Представим себе некое общее движение сжимаемой жидкости,
происходящее при наличии притока энергии s. Мы предположим,
что коэффициент вязкости нашей жидкости равен нулю, и
ограничимся таким образом исследованием движений жидкости
идеальной; мы укажем впоследствии, как наши построения могут быть
обобщены на случай жидкости вязкой.
Уравнения движения возьмем в той обычной форме, какую
дает им Фридман:
gradp = -?-G (1)
(как всегда, р — давление, ш—удельный объем, G — динамический
градиент). Уравнение неразрывности напишем в виде:
i* = divV = e. (2)
о) at '
(как прежде, обозначаем divV = 6). В качестве уравнения притока
энергии примем соотношение (90) (стр. 197 „ Опыта гидромеханики"):
Наша цель заключается в построении условий динамической
возможности движения, элементы которого удовлетворяют
уравнениям (1), (2) и (3). Это означает, что мы желаем найти условия,
каким надо подчинить поле скоростей и заданных (внешних) сил,
чтоб возможно было затем определить две функции р и <о из
перечисленных уравнений. Подчеркнем еще раз, что величину г мы
считаем известной функцией координат, времени и, может быть,
скоростей, так что условия динамической возможности, которые
мы ищем, должны связать не только скорости и внешние силы,
но также и плотность теплового притока энергии е.
Задача наша, как и аналогичная задача, решенная Фридманом
для уравнений (1) и (2) [без уравнения (3)], складывается,
очевидно, из двух частей: исключения давления р и плотности <» из
всех шести уравнений механики и установления метода, согласно
которому можно было бы по заданным скоростям, силам и при-
*) И. А. Киб ель, „Условия динамической возможности движения
сжимаемой жидкости с веданным притоком энергии", Геоф. сб., т. V, вып. 3, стр. 3—49,
1931. См. также I. Kiebel, „Conditions de possibillte dynamique du mouvement
d*un flulde compressible avec affluence d'energle donnee". C. R. de III-ieme Congres
Intern, de Mecanique Appliquee. Stockholm 1930.
23*
355

току энергии определить давление и плотность. Чтобы облегчил
себе задачу исключения давления и удельного объема из наших
уравнений, мы постараемся построить сперва некое соотношение,
являющееся следствием (1), (2) и (3), в которое р к <а входили
бы непосредственно, а не под знаком производных, как это имеет
место в наших уравнениях. Возьмем градиент от обеих частей
уравнения (3) и заменим появляющийся при этом grad p его
выражением из (1). Получим:
gradS = |grad^-H^VG + ^grad°- (4)
С другой стороны
grad -? = grad -J? -f grad (V, grad p),
т. е. в силу (1)
где <*•— попрежнему мера диссипативности. Чтобы получить, затем,
иное выражение для u grad <», умножим соотношение
[grad<*>, G]+o>§ = 0, (?> = —curlG)
являющееся следствием уравнения (1), векторном образом на V.
Очевидно, будем иметь
pgradto — (V, grad to) G-f-« [V, ?)] =0
и таким образом
-^6(^ + (V, gradco)j. (5)
Вставляя это grad -77 в уравнение 1,4), приведем последнее
после простых преобразований к виду:
— grad в + *р*> grad Ь -f -^
о> — grad е -J- */><*> gradfj +" ~зт + grad у- -)-
J-[V, $] + (*- l)eG = i-GJ~f(V, grades) -«б 1
(6)
При установлении этого соотношения мы не пользовались
совершенно уравнением неразрывности, так что уравнение (6) есть
следствие одних лишь уравнений (1) и (2). Одного взгляда на
правую часть уравнения (6) достаточно однако, чтобы сделать сле-
^56

дующее заключение: если уравнения (1), (2) и (3) выполнены, то
следующее соотношение необходимо должно иметь место:
-^-+grad;x+[/,§]-[-(y. —I) OG — xpegradft — «grad^^O. (7)
с.
Обратно, если (1) и (2) выполняются и (7) имеет место, причем
G^O, то и уравнение неразрывности выполняется. Это позволяет
в том случае, когда G ^0, заменить уравнение неразрывности
соотношением (7), в которое р и со входят непосредственно, а не
под знаком производных.
Введем два вектора:
Г = ^ + gradf.-HV, й+(х-1) 6G
И
Е = grad — е.
с.
Первый из них, обращающийся в нуль вместе с динамическим
градиентом, Кибель называет градиентным вектором, второй,
зависящий от притока энергии, — энергетическим вектором *).
Преобразуя уравнение притока энергии путем замены -j -
at
па.~-\-—> мы приходим к необходимости исследовать с точки
зрения динамической возможности следующую группу уравнений:
grad р = — G, (8)
!--?+!-*. w
Г + у-/*© gradfl — шЕ = 0. (10)
Заметим, что в случае, когда G = 0, будет ^ = Г = 0,т. е.
члены с ш автоматически выпадают из наших уравнений,
соотношение же (7) должно попрежнему выполняться в силу (6); таким
образом и в этом случае надлежит исследовать (8), (9) и (10У
г для определения <о воспользоваться отдельно единственным
уравнением неразрывности.
Уравнение (10), как уже было отмечено, не содержит р и ш под
знаком производных, и потому удобно именно его взять в
качестве отправного пункта исследований.
Обе части этого уравнения умножим векторно на Е:
[Г, Е]+*/>* [grad 6, Е]=0. (11)
Теперь нужно различить два случая: векторное произведение
градиента дивергенции скорости на энергетический вектор может
*} Кибель, Геоф. сб., стр. 7.
357

равняться или не равняться нулю- Обратимся сперва к
последнему случаю: пусть
[gracU, Е]=±0. (12)
Умножая обе части (11) векторно на [grad'J, Е], мы должны
получить
[[grad*, Е], [Г, Е)] = 0
или, что то же самое,
[{grade, Е], Г) = 0.
Если равенство это выполнено и неравенство (12) имеет место,
мы можем определить скаляр t из соотношения
[Г, Е] - х- [grad Ь, Е] = 0. U3)
Переписываг это последнее в виде
[r-;-xTgradOfE] = 0,
заключаем о существовании скаляра ш, удовлетворяющего
равенству _
Г-|-хтггаа» = «Е (14)
[Е=?0по (12)]. Вычитая из уравнения (13) уравнение (11), мы
можем найти физический смысл величины т, определенной при
помощи одних лишь кинематических элементов и притока энергии
(х — Н brad 6, Е] = 0,
а по (12)
т== рой.
Вычитая затем из (14) (10), получаем аналогичным путем ^
(0 = 0).
Мы получили таким образом возможность, в случае
выполнения неравенства (12), определить в конечном виде две скалярных
величины т и ш, которые должны давать физические температуру
и удельный объем.
Нам остается наложить на найденные т и to ограничения,
проистекающие оттого, что р и о> должны удовлетворять уравнениям
(8) и (9). Предварительно заметим однако, что неравенство (12)
недостаточно для возможности физического решения, ибо
определенное из (13) т и из (14) да могут обратиться в нуль или даже
стать отрицательными. Поэтому нам придется ограничить наши
величины еще и другими неравенствами, на которых, впрочем, мы
не будем останавливаться (не только в этом случае, но и далее).
Мы можем теперь написать условия динамической возможности
движения в случае, когда
fcrrad6,E]:?0,
358

в следующем виде:
grad 4т = ^г G,
со о>
— 1і.і4-«0 =— е
Vt со со со су
(1)
([grade, E], Г) = 0,
где ~ и ш находятся из равенств (13) и (14) соответственно. Эти
пять уравнений, связывающие кинематические элементы движения,
силы и приток энергии, являются необходимыми для
существования движения, когда fgrad ?, Е] ф 0.
Легко видеть, что они и достаточны *). В самом деле, мы
можем всегда положить а> равным <ч и р равным —; тогда обе
эти величины, в силу выполнения наших условий, будут
удовлетворять уравнениям (8) и (9), а следовательно, по доказанному,
также и уравнению (2) [G=?0, ибо иначе Г = 0, т. е. по (13)
х=0, чего по предположению нет], и таким образом представлять
действительно удельный объем и давление в некотором реальном
движении. Интересно отметить, что, определивши скорость,
удовлетворяющую (1), мы находим затем давление и удельный объем из
некоторых конечных соотношений, не прибегая даже к
квадратурам.
Обратимся теперь к следующему случаю, более частному,
характеризующемуся тем, что
[grad 6, Е] = 0. (15)
Из уравнения (11) прежде всего следует:
[Г,Е]=0. (16)
Предположим на первых порах, что энергетический вектор
отличен от нуля:
ЕфО. (17)
Условия (15) и (16) при наличии неравенства (17) позволят
определить два скаляра т и п из соотношений
gradfi=-^E, (18)
Г = лЕ. (19)
Предполагая сперва, что
пФО,
получим на основании (8) и (10), после простых преобразований,
соотношение
curl(D+pcurl(^)„„.
*) Нужно только еще проверить, будут ли ш и р всегда положительны и т. п
359

Мы должны необходимо положить
»Г,1
= 0,
[
, G і /TiG
curl — , curl
п п
а тогда, если, что мы сперва предположим,
, тпб , л
curl — =f 0,
п
можно определить скаляр р из соотношения
А+рВ = 0,
г,-е
А = curl — , В = curl •
п п
Не представит никакого труда убедиться теперь, что необхо
димыми и достаточными условиями для возможности движения,
характеризующегося равенством
[gradft, Е] = 0
и неравенствами
К^О, пфО, B = curl — ^0,
п
являются соотношения
[Г,Е]-0, [А, В]=0, |
8р R у- (у-т , Л- _- 6 , m-r \ (2Х)
dt cv п \ п ] г х г п ' л r J
При этом давление р и плотность <*> определятся из конечных
соотношений
— п
р=р, <*> = —
1+тр
Обратимся теперь к случаю, когда
B = curl^ = 0.
п
Рассуждения приходится вести здесь несколько иначе. Опуская
детали, отметим, что снова приходится рассмотреть два случая
отдельно:
at п п
и
at тіл ' п
ЗбЬ

В первом случае условия динамической возможности напишутся
в виде
[grad6, Е] = 0, EzfcO, пфО, -?™_(х_1: Ь -фО,
dt п
[Г,Е]==0, curl "^ О, curl-G
п
at
п
grad/> = — pQ
п
о,
П
п
(2-2)
где р находится из соотношения
а давление и плотность суть
dlnn
* ft
Р и
тр + 1
71
соответственно-
Во втором случае, когда
dm m , л. ft л
— • (х —1)9 = 0,
at n п
условия возможности должны быть написаны в виде
[grade, Е] = 0, Е^О, п^О,
[Г,Е] = 0,сиг1-"?=0, curfA-O, і ^-^-(v—1)6 = 0,
л п ас л л
dn ь R л
V(2.)
причем для определения р мы должны обратиться к системе
дифференциальных уравнений (полной якобиевой):
^2—.*.._.?._ (-^ + *й)р, .gradp^+^G,
<о же найдется из соотношения
Л
1-j-mp"
Исчерпав случаи, когда пфО, предположим теперь, что
п = 0.
Тогда d силу (19) будет
Г = 0
361

и, если
G=?0,
то должно быть *)
[G, grad т] = 0;
при выполнении последнего условия можно найти скаляр <» из
условия _
m-G = о> grad m.
Простые выкладки приведут нас тогда к следующей группе
условий:
ЕфО, [grad Ь,,Е] = 0, G^fcO, ]
Г = 0, [G, grad /n] = 0, ——= — 7^~e'l
at m <о т О, J
причем как р, так и о определятся вновь из конечных соотношений
1
р = , о> = (о.
т
Требующий отдельного рассмотрения случай
G = 0
даст просто
ЕфО, G = 0 ]
w п д 1 Л , хв | (26)
так что „ = -і- будет здесь зависеть лишь от времени, . же
ТП
найдется, как всегда, при G = 0 из уравнения (2).
До сих пор мы предполагали, что Е ф 0. Обращаясь к случаю,
когда
Е = 0,
получим прежде всего из уравнения (10) непосредственно:
Г-Ь'/рш grad 6 — 0, (20)
причем задача естественно разбивается на два подслучая:
grades 0 (21)
или grad6 = 0. Предположив сперва, что (21) имеет место, мы
можем, если
[r.gradq-o,
определить скаляр * из равенства
Г-f- хх grad 6 = 0!,
*) Мы считаем, что определенное из (18) тфО, иначе уравнение (10) не
смогло бы удовлетвориться при Е=?0.

Замечая, что должно быть
pm = z9
мы придем затем, в том случае, когда
^-Н*-і)'*=?о,
к следующей группе условий возможности движения:
Е = 0, grad^O, ^-|-(^-l)^^0,
С
curl -- = 0, [grad ?, Г] = О,
дт (ft-|-^)ic /г , 6
37 Н" — ~ = — е> 2rad **== ^ *,
где те определяется из уравнения
При этом достаточно положить
(?
(22>
p = w, ш
іь
Если же
А
+ (х —l)te = 0,
уравнение (22) нам даст е = 0, скаляр те не может быть найден,
давление /? должно быть получено непосредственно из системы
дифференциальных уравнений
а-і-хг?
= Pt
л & dp
в условия динамической возможности этого случая
gradO фО, 8 = 0, [grad О, Г]=0, 1
(23)
curl -=- = 0,
•с
Л
dt
(х —1)?т = 0,
(2,)
сделают систему (23) полной якобиевой.
Исчерпав случаи, когда, при Е = 0, grad в ф 0, предположим
теперь, что
grad6 = 0.
Уравнение (20) заставляет нас теперь считать, что
Г = 0,
363

ti так как равенство Е = 0 предполагается выполняющимся,
уравнение (10) выполнится само собой.
Если, что мы предположим,
то давление придется определять из системы дифференциальных
уравнений:
[grad/>, G] = 0,
^-f(V,gradp) = -~S-^
•Условия динамической возможности этого случая
G^=0, E = 0, gradf)=0, |
Г = 0, (С,ф) = 0, / Лв/
обеспечат полноту этой системы; <*> найдется из соотношения
grad р = — G.
Наконец в случае, когда не только Е = grad 6 = Г = 0, но и
G = 0,
условия возможности будут
Е = 0, srad 6=0, 6 = 0, (29)
причем давление окажется функцией одного только времени и
определятся из уравнения
dp . R R
удельный же объем найдется из уравнения неразрывности
-^¦ + (V>grad<*>) = coft.
Перечисленные здесь десять сортов движений являются
единственными возможными в идеальной сжимаемой жидкости.
Представляют оссібый интерес движения адиабатические. В идеальной
жидкости последние характеризуются условиями
Е = ? = 0.
-Поэтому в идеальной жидкости возможны лишь три сорта
адиабатических движений: (27), (28) и (29). Отметим, что частным
случаем движения (28) является рассмотренное Фридманом
несжимаемое (Ь = 0) адиабатическое движение (см. стр. 275).
Как мы уже отмечали, Кибель рассмотрел сразу движения
жидкости вязкой. Число категорий здесь увеличивается с десяти
до двенадцати, но никаких принципиальных осложнений не
возникает; последнее объясняется тем обстоятельством, что и здесь
отправным пунктом является уравнение, заменяющее уравнение
неразрывности и совпадающее по начертанию с соотношением (10)
364

(в этом уравнении вектор Г имеет прежний смысл, вектор же Е
усложнен присутствием членов, содержащих коэффициент
вязкости).
Читателя, желающего ознакомиться с деталями, отошлем
непосредственно к цитированной работе Кибеля. Там же можно найти
подробный разбор двух примеров, служащих для иллюстрации общей
теории. Первый из этих примеров посвящен исследованию плоских
(происходящих в вертикальной плоскости) движений идеальной
жидкости, в которых скорости зависят лишь от вертикальной
координаты, а приток энергии представляется как произведение двух
функций, зависящих — одна от горизонтальной, другая от
вертикальной координаты. Второй пример трактует движение вязкой
жидкости со скоростями
и притоком энергии
В обоих движениях привлекается к рассмотрению сила тяжести,
действующая вдоль вертикальной (z) оси.
Отметим в заключение этого параграфа, что И. А. Кибелем
был также рассмотрен вопрос об условиях динамической
возможности малых движений» наложенных на некоторое основное
движение, при заданном бесконечно малом притоке энергии в частном
случае, когда за основное движение принята так называемая „схема
Маргулеса" *). Им же рассмотрен и общий случай малых колебаний,
наложенных на любое основное движение идеальной сжимаемой
жидкости и происходящих при заданном бесконечно малом притоке
энергии.
*) И. А. К и б е л ъ, „О некоторых малых движениях сжимаемой жидкости*,
Известия Главной геофизической обсерватории, 1932, стр. 31—37.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.
Адиабатическое движение 193, 194, 275,
276, 277, 278, 279, 280, 281, 354,
364
Адиабатическое несжимаемое движение,
330
Атмосферное движение, 330
Безвихревое движение 229
Без градиентное движение. 218, 225, 262,
352
Вектор [А, В^ 41
— (В, V) А 42
— D 34
— Н 34
— вихоя 21 г 43
— второй фрикционный 349
— первый фрикционный 349
Векторное поле 17
Векторный анализ 40
— потенциал 44 .
— ряд 173
Вертикальное движение 245, 256
Вихревая мера 133
Вихревой потенциал 44
Вихревые линии 20, 22
Вихреобразование 327, 328
Вихрь вектора, 21, 43
Внешняя нормаль 54
Внутренняя энергия 203
Вращение жидкости 330
Вторичные динамические элементы 196
Второстепенные элементы изменения
вихревых линий 58
Газовая постоянная 191
Гельмгольтцско движение 59, 60, 63, 66,
VA 102, 125, 134, 140
Гельмгольтциан 44, 45
Геометрическая векторная линия 17
Гидродинамика сжимаемой жидкости 348
Гид оодинамическая модель антициклона
332
циклона 330, 332
Главное незакручивающееся движение
60, 92, 102
Главные гельмгольтцевы движения 11,
143, 144
Главные элементы изменения вихревых
линий 58
» лавныи род 147
— тетраэдр 67, 11 3
— характеристический вектор 171
Градиентное движение 352
— произведение 42
Градиентный вектор 357
о
Движение Ackerbloom'a 353
— без сдвигов 37
— вязкой сжимаемой жидкости 354
— идеальной жидкости 354, 355
несжимаемой жидкости 333, 335
— несжимаемой жидкости 226
Деклинация 45
Динамика атмосферы 348
Динамическая группа уравнений
гидромеханики 186
— метеорология 330, 332
Динамические элементы 186
Динамический градиент 13, 198, 349
357
Жидкая вихревая трубка 126
— линия поля 18
Жидкий контур 126, 129, 130
Жидкость несжимаемая 189, 324
— сжимаемая 324, 327
Закон сохранения напряжения вихря 134
— сохранения энергии 7
Закручивающиеся движения 350, 352
Идеальная несжимаемая неоднородная
жидкость 328
— сжимаемая жидкость 364
Изгиб вихря 10, 56, 94
Изгибающийся угол 55
Изобарические поверхности 334
Изобары 330
Изобразительная точка 28
Изостерические поверхности 334, 330
Изотермические изменения жидкости 330
Изэнтропическое движение 194
Инвариантная функция 145, 146,' 162.
166
Инвариантный вектор 172
Индекс рода 174
Индивидуальная производная 19
Инерционная сила 187
Интегральная - мера Диссипативности 200
366

Интенсивность векторных трубок 316
Истинное напряжение вихря 144
Квази-незакручивающиеся движения 92
Квази-прямое движение 99, 101, 102,
107, 108, 109, 111
Квази-твердое движение 36, 63
Кинематические элементы 23, 186
Классификация Кибеля 342, 347
Коллннеарное движение 35
Конвекционная передача тепла 193
Консервативная сила 187
Контур сечения 127
Координаты Декарта 317
Коэффициент внешнего трения жидкости
189
Коэффициент внутреннего трения
жидкости 188
Критическая точка 18
Крутящий угол 56
Кручение вихря 10, 56, 64
Левое кручение 68, 118
.Линии тока 21, 330
— ускорения 21
Мгновенная вихревая трубка 126
— мера диссипативности 199
Мгновенно-стеробарическое движение 227
Мера второго порядка 123
— диссипативности 199, 210, 218, 335,
351
Местная производная 19
Местное- изменение 18
Метеорологические динамические элемен-
ты 195, 196, 197, 198
Модель стационарного циклона 332
Направление обхода 119
— вихр-я 128
. Напряжение мгновенной вихревой
трубки 127
¦ч— характеристического вектора 171
Начальная функция 164
Начальный вектор 172
Незакручивающееся движение 59, 70, 71,
72, 74
Незакручивающиеся векторы 350
Некомпланарные инвариантные вй* горы
176
Неконсервативная сила 187, 327
Несжимаемое движение 328
— стеробарическое движение 228
Нормальное сечение трубки 128
Нормальные движения 210
Нулевой род 147
Обобщенная вихревая мера 145
Обобщенное напряжение вихря 144, 145,
Общее квази-незакручивающееся
движение 92
Обшее нормальное движение 213, 214,
223. 334, 335. 337, 341, 351
Общее полуконсервативное движение 218,
220, 341, 342
Общие стеробарическне движения 226
Объемная группа условий 14
Объемные условия 214, 235, 238, 257
Оператор Гамильтона «набла» 42
Ортогональные движения 245, 246
Основной сферический треугольник 28,
33
Основной триэдр 28, 33
Основные динамические элементы 195
Особое движение 109
— квази-незакручивающееся движение
92, 93
Ось вихревой трубки 128
Отклонение вихря 10, 55, 61
Отклоняющий угол 55
Переменные Лагранжа 164, 167, 173,
317, 343
— Эйлера 164, 172, 173, 343
Перемещающийся циклон 334
Планоидные незакручивающиеся
движения, 78, 86, 89
Плоский сопряженный основному
треугольник 58, 113
Плоское движение 14, 245, 263
Плотность тепловой мощности 190, 192
Полная энергия 202
Положительное направление нормали 127
Полуконсервативное движение 210, 218,
332, 352
— движение специальное 329, 333
Построение приближенных условий
динамической возможности 335
Потенциал 44
— ускорения 264
Потенциальный вектор 44
Правое кручение 68, 118
Предельная прямая 122
— часть 203
Предельный вектор 122
Представительница рода 147
Приведенный градиент 211, 351
Простейшие кинематические элементы 23
Прямые движения 60, 99, 101
— обобщенные плоские движения 104
Расхождение вектора 43
— скорости 22
Род 147
Свойство неаакручиваемости 132
— сохраняемости 20
Сдвиги 24
Семейство векторных линий 18
Сечение мгновенной вихревой трубки 127
Сила внешнего трения 188
— внутреннего трения 188
— вязкости жидкости 188

Силовые динамически* элементы 195,
196, 197
Силы массовые 186
— объемные 186
Скалярное произведение 41
Скалярный потенциал 44
Скоростные элементы измерения
вихревых линий 56
Собрание векторных линий 18, 314
— вихревых линий 33
•— разрушающихся векторных линий 20
— сохраняющихся векторных линий 20,
3Ч
Соленоидальные векторы 44
Сопряженный изгиб 57
— основному треугольник 58
— угол 57
¦— уклон вихря 57
Сохранение вихревых линий 327
Сохраняемость векторных линий 314—
318, 321, 323. 324
— напряжения векторных трубок 322—
324
Специальное квази-незакручивающееся
движение 92
Специальное нормальное движение 213,
217, 341, 351, 352
Специальное полуконсервативное
движение 219, 221, 223, 341, 342
Специальное стеробарическое движение
226
Стационарное движение воздуха 352
Стапионарно-стеробарическое движение
227
Стационарные движения несжимаемой
жидкости 330
Стационарный антициклон 334
— циклод 354
Стереовектор 213, 341
- Стереоскаляр 213, 341
Стеробарическое движение 226, 227, 231
Тепловая группа уравнзний
гидромеханики 186
Тепловые векторы 13, 212
— динамические элементы 195, 196, 197,
198
Тепловые условия 13, 213,214,234,238
Томсоновские движения 11, 134
Турбомомент 211, 351
Турбулизнрующий вектор 13, 208, 225»
226, 227, 323,349
Турбулизнрующий вектор второго
порядка 230
Угловая скорость вращения 333
Угловые элементы изменения вихревых
линий 57
Удельный объем 186
Уклон вихря 10, 56, 75
Уклоняющийся угол 55, 73
Уравнение неразрывности 185, 356
<— притока энергии 7, 186, 191, 354
¦— состояния 186, 191
Ускорение Кориолиса 188
— переноса 188
Условия адиабатичности 329
— динамической возможности 206, 208,
210, 214, 216, 237, 238, 328. 330,
333, 334, 346—348, 351, 352
— коллинеарности 315
— незакручиваемости 13, 210, 337
Условно инвариантная функция 163
— характеристический вектор 172, 177»
178, 180
Фрикционный вектор. 351
Характеристический вектор 171, 172, 176
Центробежная мера 74, 75
Йиклон перемещающийся 330
иркуляция вектора по контуру 129
Элементы второго порядкэ 121
— первого порядка 121
Энергетический вектор 357
Энтропия жидкости 186, 194
Якобиева система уравнений 340

ОГЛАВЛЕНИЕ.
От редактора . . • 3
Предисловие $
Часть I.
КИНЕМАТИКА ВИХРЕЙ.
Глава I. Сохраняемость векторных линий Y/
§ 1. Предварительные понятия —
§ 2. Понятие сохраняемости векторных линий 24
§ 3. Формулы векторного анализа 40
Глава'II. Изменение вихрей 54
§ 4. Элементы, определяющие изменение вихровых линий —
§ 5. Отклонение вихря 61
§ 6. Кручение вихря 64
§ 7. Изгиб внхря . . 94
§ 8. Главный тетраэдр ИЗ
§ 9. Напряжение вихревых трубок 125
§ 10 Об инвариантных функциях.и характеристических векторах . . 161
Часть II.
ДИНАМИКА СЖИМАЕМОЙ ЖИДКОСТИ
Глава Ш. Условия динамической возможности движения 185
§ 11. Основные уравнения движения жидкости —
§ 12. Общие условия динамической возможности движения
сжимаемой жидкости 206
§ 13. Исключительные случаи условий динамической возможности
движения сжимаемой жидкости 216
§ 14. Основные векторы и кинематические элементы 229
§ 15. Основные векторы и динамические элементы 238
§ 16. Частные случаи движения сжимаемой жидкости . . • . . . . 245

Г л а в а IV- Связь кинематических и динамических элементов 285
§ 17. Выражение скорости я других кинематических элементов черев
динамические элементы —
§ 18. Выражение элементов главного тетраэдра через динамические
элементы • . ...... 301
§ 19. Теорема Bjerknes'a • • 307
Дополнение.
Б, И. Извеков, //. А. Кибелъ Н. ?. Кочин. О некоторых работах,
связанных с „Опытом гидромеханики сжимаемой жидкости" 314
Предметный указатель 366