Линейная алгебра в примерах и задачах - Жукова Г.С., Рушайло М.Ф.

Автор: Жукова Г.С. Рушайло М.Ф.
Теги: математика алгебра задачи по алгебре
Год: 2000
Похожие
Аналитическая геометрия
Курс высшей математики. Том третий, часть первая
Аналитическая геометрия
Текст
                    В ПРИМЕРАХМ ЗАДАЧАХ
Москва 2000
3
ВВЕДЕНИЕ
В настоящее время решение большинства возникающих задач
выполняется на компьютерах с помощью различных вычислитель-
ных алгоритмов, использующих "серьезную”математику.
Поэтому современный специалист кроме хороших знаний по
своей специальности должен обладать определенной математи-
ческой культурой и четкими математическими знаниями: необхо-
димо знать и уметь использовать в своей практической деятель-
ности возможности вычислительной техники, современные ма-
тематические методы, уметь выбирать наиболее подходящие к
анализу его задачи комбинации различных известных методов,
знать их сравнительные характеристики и т.п.
Эти обстоятельства предъявляют повышенные требования к
качеству математической подготовки в вузах. Выпускник вуза
должен знать теорию и овладеть навыками решения задач по
основным разделам высшей математики, уметь изложить их
основы на четком алгоритмическом языке, знать преимущества и
недостатки того или иного метода решения.
Настоящее пособие написано на базе лекций и практических
занятий по линейной алгебре, читаемых в первом семестре сту-
дентам первого курса всех факультетов и колледжей Российского
химико-технологического университета им. Д.И. Менделеева.
При написании пособия авторы стремились изложить матери-
ал кратко, но четко, чтобы было доступно вчерашнему выпускни-
ку средней школы.
4
В книге предложены практические занятия и образцы кон-
трольных работ для овладения навыками решения примеров и за-
дач следующих разделов высшей математики:
•	аналитическая геометрия на плоскости}
•	векторная алгебра}
•	комплексные числа}
•	разложение многочлена на множители; разложение рацио-
нальной дроби на сумму простейших дробей}
•	линейная алгебр;
•	квадратичные формы
Схема изложения материала каждого занятия следующая:
1.	Справочный теоретический материал, необходимый для успеш-
ного усвоения темы;
2.	Разбор примеров (с подробным их решением и анализом);
3.	Перечень задач для самостоятельного решения;
4.	Ответы ко всем задачам.
Нумерация теорем, формул, рисунков и примеров с решениями в
каждом параграфе самостоятельная. Нумерация задач для само-
стоятельного решения и ответов к ним начинается с указания
номера параграфа.
Для контроля полученных знаний студентам предлагается вы-
полнить четыре контрольные работы. В книге даны образцы
контрольных работ с подробным анализом.
Предложен перечень контрольных вопросов по теории.
Преподавателям вузов, ведущим практические занятия по ли-
нейной алгебре, можно было бы посоветовать следующий порядок
изложения материала, включенного в книгу.
СЕМИНАРЫ:
1.	Определители второго и третьего порядков. Решение сис-
тем линейных алгебраических уравнений с двумя и тремя
неизвестными (§ 1).
5
2.	Уравнение прямой на плоскости (§ 2).
3.	Кривые второго порядка (§ 3).
4.	Векторы. Операции над векторами. Скалярное произведе-
ние двух векторов (§ 4).
5.	Векторное произведение двух векторов. Смешанное произ-
ведение трех векторов (§ 5).
6.	Контрольная работа на темы: уравнение прямой на плос-
кости; кривые второго порядка; операции над векторами
(приложение I).
7.	Комплексные числа. Операции над ними (§ б).
8.	Разложение многочлена на множители. Разложение ра-
циональной дроби на сумму простейших дробей (§ 7).
9.	Матрицы. Операции над матрицами (§8).
10.	Приведение матрицы к ступенчатому виду и виду Гаусса.
Ранг матрицы. Ранг системы векторов (§ 9).
11.	Определитель и его свойства. Обратная матрица. Реше-
ние матричных уравнений (§ 10).
12,	Методы решения систем линейных алгебраических уравне-
13. ний: правило Крамера, использование обратной матрицы,
метод Гаусса (§ 11).
14.	Системы линейных однородных алгебраических уравнений.
Фундаментальная система решений (§ 12).
15.	Контрольная работа на темы: комплексные числа; разло-
жение рациональной дроби на сумму простейших дробей;
ранг, определитель матрицы, обратная матрица; решение
матричных уравнений; решение систем линейных алгеб-
раических уравнений ( приложение 11).
6
16,	Собственные значения, собственные и присоединенные
17. векторы матрицы (§ 13).
18.	Линейные векторные пространства. Базис в пространст-
ве. Процесс ортогонализации базиса (§ 14).
19.	Контрольная работа на темы: собственные значения, соб-
ственные и присоединенные векторы матрицы; базис в
пространстве, ортогонализация базиса. Коллоквиум (при-
ложения III - IV).
20.	Квадратичные формы (§ 15).
21.	Итоговая контрольная работа (приложение V).
Настоящее пособие может быть использовано студентами
вузов как для работы под руководством преподавателя, так и для
самостоятельного изучения курса векторной и линейной алгебры,
так как все задачи имеют ответы, а некоторые и решения. Этому
же способствуют краткие пояснения теории.
Рекомендуется преподавателям и студентам вузов, изучающим
высшую математику
7
И
РЕШЕНИЕ
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ДВУМЯ И ТРЕМЯ НЕИЗВЕСТНЫМИ
1. ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
Определение 1. Квадратной матрицей второго порядка
называется таблица чисел:
А-
Л12
<^21	^22 J
содержащая две строки и два столбца.
Числа ai} (/, J - 1,2) называются элементами матрицы, где
z - номер строки, а у - номер столбца, на пересечении которых в
матрице расположен данный элемент.
Числа ап,ы22 образуют главную диагональ матрицы Л; числа
а21, ^17 - побочную (второстепенную) диагональ матрицы
8
Определение 2. Квадратной матрицей третьего поряд-
ка называется таблица чисел:
			^12	^13	
А	—-	^21	&22	^23	1 э
		<^31	^32	^33 >	
содержащая трн строки и три столбца.
Числа afj (/,7 = 1,2,3) называются элементами матрицы,
где i - номер строки, а у - номер столбца, на пересечении которых
в матрице расположен д анный элемент.
Числа cin , а22 , а33 образуют главную диагональ матрицы; вде-
ла &31, а22,6Г13 - побочную ( второстепенную) диагональ.
Определение 3. Определителем квадратной матрицы А
второго порядка (короче — определителем второго порядка) назы-
вается число, обозначаемое
^11	^12
.^21
(или |у4 , или det А)
и вычисляемое по формуле:
Л]2
^21
а22	&2\ ’ ^12
(О
9
Определение 4. Определителем квадратной матрицы А
третьего порядка (короче - определителем третьего порядка)
называется число, обозначаемое
(или \А , или det Л)
и вычисляемое по формуле:

^22
а32
(2)
Для определителя используют те же термины (элементы, строки,
столбцы, главная и побочная диагонали), что и для соответствую-
щей матрицы, чей определитель вычисляется.
Свойства определителя.
1.	Определитель не меняется при замене в нем всех строк со-
ответствующими по номеру столбцами;
10
2.	Определитель изменит знак на противоположный, если в
нем поменять местами любые две строки или два столбца;
3.	Определитель равен нулю, если содержит нулевую строку
или столбец;
4.	Определитель равен нулю, если содержит две одинаковые
строки или столбца;
5.	Если все элементы некоторой строки (столбца) содержат
общий множитель, то его можно вынести за знак опреде-
лителя;
6.	Определитель не изменится, если в нем заменить строку
суммой этой строки и некоторой другой, предварительно
умноженной на какое-либо числом
7.	Определитель треугольной матрицы
\ ®	а22
равен произведению элементов главной диагонали.
Замечание. Определитель третьего порядка может быть
вычислен не только по формуле (2), называемой разложением оп-
ределителя по элементам первой строки.
11
1) Для вычисления определителя третьего порядка можно вос-
пользоваться правилом разложения определителя по элементам
любой строки (столбца) матрицы А. При этом элементы
выбранной строки (столбца) берутся со знаками, указанными в сле-
дующей схеме:
—	4-
- + - ,
4- — 4-
то есть знак «+» стоит у тех элементов а-, для которых сумма ин-
дексов / + j есть число четное, «-» - сумма индексов i 4- j не-
четная.
Например, выбрав для разложения вторую строку определите-
ля, получим формулу разложения определителя третьего порядка
по элементам второй строки:
#11	а12	й13	
^21	а22	^23	—
а31	а32	#33	
Л21	^12	а1з	+ fif22 *		а13	^23 ’	
	^32	а33		#31	а33		а31
а\2
^32
12
2)	Для вычисления определителя третьего порядка можно вос-
пользоваться правилом треугольников. схема которого указана ни-
же:
где выделенные элементы нужно перемножить.
3)	Второй, часто используемый прием, заключается в следую-
щем: определитель третьего порядка равен сумме шести слагаемых,
получаемых перемножением элементов, попавших на параллельные
линии матрицы, полученной из исходной матрицы А приписывани-
ем к ней справа дополнительно первых двух столбцов матрицы А :
12 3 12
12 3 12
13
4)	Определитель третьего порядка равен сумме шести слагае-
мых, получаемых перемножением элементов, попавших на парал-
лельные линии матрицы, полученной из исходной матрицы А
приписыванием к ией снизу дополнительно первых двух строк
матрицы А:
2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Определение 5. Системой линейных уравнений, со-
стоящей из двух уравнений с двумя неизвестными х и у, называется
система вида
a11x + aI2j = 61
^21^ а11У — ^2»
(3)
где (/,J = 1,2)
некоторые постоянные числа.
14
Определение 6. Матрица А =
<^21
#12
а22 >
называется
матрицей системы (3);
вектор
называется столбцом сво-
водных членов системы (3).
Теорема 1 {правило Крамера). Если определитель матри-
цы системы (3) не равен нулю, то система (3) имеет единственное
решение, вычисляемое по формулам:
где А = |Л|, A; \J = 1,2J - определители, полученные из А за-
меной его /-го столбца столбцом свободных членов.
Теорема 2. Если определитель системы (3)
А = 0,
но хотя бы один из определителей Aj или А2 отличен от нуля, то
система (3) не имеет решения. Если для системы (3)
А = Aj = А2 = О,
то система (3) имеет бесконечное множество решений.
15
Определение 7. Системой линейных уравнений, со-
стоящей из трех уравнений с тремя неизвестными х, у и z, назы-
вается система вида
Ц1Х + а12^ + а,32=*1
< Д21Х + &21У + ^23Z ~ ^2
а31 х + азгу+a33z = b3,
(4)
где	, bi (z, j = 1,2,3) - некоторые постоянные числа.
Определение 8. Матрица
Л 21
^12
а22
<«31	«32
зывается матрицей системы (4); вектор
«2з на-
азз)
называется
столбцом свободных членов системы (4).
Теорема 3 {правило Крамера). Если определитель матри-
цы системы (4) не равен нулю, то система (4) имеет единственное
решение, вычисляемое по формулам:
Д,	А?	А,
х = —, у = —, z = —,
Д	Д	Л
16
где Д = 14 Ду(/ = 1,2,3) - определители, полученные нз Л
заменой его /-го столбца столбцом свободных членов.
Теорема 4. Если определитель системы (4)
А = 0,
но хотя бы один из определителей Aj, А2 или А3 отличен от ну-
ля, то система (4) не имеет решения. Если для системы (4)
А - А1 = А2 - А3 = 0,
то система (4) или имеет бесконечное множество решений, или не
имеет решений.
X ПРИМЕРЫ С РЕШЕНИЯМИ
Пр и м е р 1. Вычислить определитель:
Решение.
Ответ: 15
17
Пример 2. Вычислить определитель:
Решение.
1-й способ (разложение по элементам первой строки):
1	2	6
3-1	4-1	4 3
4 3 -1=1-	-2-	+ 6-
-25	25	2-2
2-2 5
= (3.5-(-2)(-1))-2 (4 5-2.(-1))+6.(4 (-2)-2 3)=
= (15 - 2)-2-(20 + 2) + 6- (- 8-б) = 13 - 44-84 = -115.
2-й способ (присоединение двух дополнительных строк):
1 2
4 3
2 -2
6
= 1-3-5 + 4-(-2)-6 + 22-(-1)-6-3-2-
1	2	6	-(-1)(-2)-1 - 5-2 • 4 = 15 - 48-4-
4 3 -1	-36-2-40 =-115
Ответ: -115.
18
Пример 3. Вычислить определитель:
Решение.
1-й способ (правило треугольников):
-2 3
7 4
3 -3
= 1- 7-(-3) + (-2)-4-5 + 0- 3- 3- 5- 7- 3-
-3-4-1-0-(-2)-(-3)=-21-40-105-12 =-178 .
1
О
5
2-Й способ (приведение к верхнетреуголъному виду).
Ответ: -178.
19
Пример 4. Решить систему:
2x-2j = l
- Зх + бу = 4.
Решение. В данном случае
матрица системы;
столбец свободных членов.
Найдем определитель системы.
Следовательно, по теореме 1 система имеет единственное реше-
ние.
Чтобы найти решение системы, вычислим определители:
Тогда по теореме 1 получим:
20
A	14 7	A, 11
X = —- = = —;	V = —- - — .
A	6	3	A	6
Ответ: X = —;
11
и м e p 5, Решить систему:
Решение. В данном случае
А =
— матрица системы;
столбец свободных членов.
Вычислим определитель системы:
= 6-6 = 0.
Вычислим определитель :
1
4
-2
6
= 14^0.
21
Так как А = 0, Aj Ф 0, то определитель А2 не следует вы-
числять: по теореме 2 система не имеет решений.
Ответ: 0.
Пример 6. Решить систему:
х - 2 у - 3
-Зх + 6.у = -9.
Решение. В данном случае
А =
1	-2^1
-3
— матрица системы;
-9J
— столбец свободных членов.
Вычислим определитель системы:
-3
Вычислим определитель
А, =
-9
-2
Л,:
-2
= 6-6 = 0.
= 18-18 = 0.
Д =
22
Вычислим определитель Д2 :
^2
= -9 + 9 = 0.
Следовательно, по теореме 2 система имеет бесконечное множе-
ство решений.
Эти решения можно найти, предполагая, что одно неизвестное,
х-3
например х- любое число. Тогда у = —-—, что следует из перво-
го (или второго) уравнения исходной системы.
Ответ:
где х- любое число.
Пример 7» Решить систему:
х + 2у - 3z - 0
2х-jy + 4z = 5
Зх + у - z = 2.
Решение. В данном случае
~ матрица системы;
столбец свободных членов.
23
Вычислим определитель системы:
2
2
Следовательно, по теореме 3 система имеет единственное решение.
Вычислим определители Aj, Д2, А3
О
2
= 16-15-6 + 10 = 5;
2
0
2
= -5-12 + 45-8 = 20;
о
2
2
з
= -2 + 30-5-8 = 15.
2
Поэтому, согласно правилу Крамера (теорема 3), получаем.
х =— = —,
10 2
20
10
15 3
z =— = —
10 2
24
Пример 8. Решить систему:
х — у + z = 2
< 2у - z = 5
x + j/ =4.
Решение. В данном случае
- матрица системы;
Вычислим определитель системы:
1 -1 1
Д-0 2	-1 - 0 + ] +0-2+1+0 - 0.
1	1	0
Следовательно, по теореме 4 система не имеет единственного
решения.
Вычислим определпшн Д1, Л2 , Л;:
25
2 -1	1
Д, = 5 2
-l=0+4+5-8+2-0=3^0.
0
Следовательно, не вычисляя Д2, А3, заключаем по теореме 4:
система не имеет решений.
Ответ: 0.
Пример 9. Решить систему:
х - у + z = 2
<	2 у - z = 5
x + j =7.
Решение. В данном случае
О
2
— 1 — матрица системы;
столбец свободных членов.
Вычислим определитель системы:
26
2 -1 = 0 + 1 + 0-2 + 1 + 0 = 0.
1	1	0
Следовательно, по теореме 4 система не имеет единственного
решения.
Вычислим определители Л], Д2, Д3:
2-1	1
1	0
2 -1=0 + 7 + 5-14 + 2 + 0 = 0;
1 2 1
Д2 = 0 5 -1 =0-2 + 0-5 + 7 + 0 = 0;
1 7 О
1 -1 2
Д3 = 0 2 5 =14-5 + 0-4-5 + 0 = 0.
1	1	7
В сложившейся ситуации для ответа на вопрос, имеет система
бесконечное множество решений или не имеет решений (см. теоре-
му 4), заметим: первое уравнение системы является результатом
вычитания второго уравнения системы из третьего.
Следовательно, решим систему
f2_y-z = 5
\х + у = 7,
27
составленную из второго и третьего уравнений исходной системы,
например, относительно неизвестных х н Z.
Воспользовавшись методом исключения, приходим к следую-
щему результату: исходная система имеет бесконечное множество
решений, описываемое формулой
у - любое число,,
<х = 7- у,
z = 2y- 5.
Ответ: (7 — у; у,2у — 5), где у - любое число.
Приме Решить систему:
х + 2у + 3z = О
<2х + 4у + 6z = О
x + 2_y + 3z = 3.
Решение. В данном случае
<1 2 3^1
А =
— матрица системы;
2 4 6
(О}
— столбец свободных членов.
Вычисления определителя системы и определителей Aj, Д2,
Д3 приводят к следующему результату:
28
1 ’2 3
Д= 2 4 6 =12 + 12 + 12-12-12-12 = 0,
1 2 3
1 0 3
О
6 =18-18 = 0,
В сложившейся ситуации для ответа на вопрос, имеет система
бесконечное множество решений или не имеет решений (см. теоре-
му 4), заметим: второе уравнение системы является результатом
умножения первого уравнения системы на число 2.
Следовательно, перейдем к анализу системы
х + 2у + 3z = 0
х + 2у + 3z = 3,
(5)
составленной из первого и третьего уравнений исходной системы.
Очевидно, что система (5) не имеет решений. Значит, исходная
система не имеет решений.
Ответ: 0.
29
4. ПРИМЕРЫ
Вычислить определители:
	1	-1	0
1.3.	2	4	-3
	0	1	-1
1	0	1
Решить системы:
5х + 9у = 20.
х + 2у + 3z -1
1.9. < 2х + 4у + 6z - 2
Зх + бу + 9z = 3.
1.10. Определить, при каких значениях параметров а и Ь
система
30
' [5x-qy = 10
x + 2y = b
1)	имеет единственное решение;
2)	не имеет решений;
3)	имеет бесконечное множество решений.
♦ ♦
♦
Вычислить определители:
sin3x
cos3x
cos5x
sin 5x
1.13.
sinx
cosx
cosx
-sinx
	3	-2	0		1	3	2
1.14.	0	1	-3	1.15.	2	1	3
	1	0	2		3	2	1
1.16. Найти x из уравнения:
2 -5
31
Решить системы:
1.17.
х + 2у = 2
3x-4j? = 7.
Зх-4у = 1
1.18.	<!
I — 6х+8_у = -2.
1.19.
1.21.
2х — Зу + z = 2
<x + 5y-4z + 5 = 0
4х + у -3z + 4 = 0.
2x + _y + 3z = 2
< 5x-y + z = 0
Зх - 2у - 2z = 1.
2x-3j^ + z = 13
1.20. <x-5z = 2
x+y + z = -1.
х- y + 2z = 7
1.22. <2y-3z = -10
x+y-z = -3.
1.23.
Определить, при каких значениях параметров а и b
система
Зх - 2у + z = b
< 5х - 8у + 9z = 3
2x+y + az--l
1)	имеет единственное решение;
2)	не имеет решений;
3)	имеет бесконечное множество решений.
32
5. ОТВЕТЫ
1.1.
1.5.
1.8.
1.10.
1.11.
1.14.
1.17.
1.20.
1.23.
10.
-2j; у).
1) а Ф -10 ; 2) а = -10, b Ф 2;
1.12.
-cos8x.
12.
1.15.
1.18.
18.
3) « = -10, b = 2.
1.13.
1.16.
1.19.
-2.
(5;6;10)
1.22.
----z .
2 ’ J
33
§2.
УРАВНЕНИЕ
ПРЯМОЙ НА ПЛОСКОСТИ
1. РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ
1)	Уравнение прямой с угловым коэффициентом:
y-kx + b7
где к —угловой коэффициент прямой (k — tga, (X — угол наклона
прямой к оси Ох, где 0 < а < я, но а & я/2); Ь-ордината
точки пересечения прямой с осью Оу (см. рис. 1).
Рис. 1
34
2)	Уравнение прямой, проходящей через заданную точку
М} (х}; _У]) с заданным угловым коэффициентом к
(то есть, когда а Ф я/2, см. рис. 2):
(1)
3)	Уравнение прямой, проходящей через заданную точку
(х1; у}), но не имеющей углового коэффициента
(то есть, когда а ~ л/2, см. рис. 3):
X = Хр
(2)
Рис. 3
35
4)	Уравнение прямой, проходящей через две заданные точки
и М2(х2,у2):
у — у х — X
---------	, если Xj ^х2 и у} Ф у2 (см.рис. 4);
У2~У1
(3)
X = Xj ,	если Xj = х2, но у} Ф у2 (см. рис. 5);
у =	, если Xj х2, но У] = у2 (см. рис. 6).
Рис. 4
Рис. 6
36
5)	Общее уравнение прямой на плоскости:
Ах + Ву + С = О,
где Л, Д С — числа, А2 + В2 ^0.
В частности,
•	если А - 0, В Ф 0, уравнение прямой принимает вид
у — уу; прямая параллельна оси Ох; угловой коэффициент
равен 0;
•	если А 0, В = 0, уравнение прямой принимает вид
х = Xj; прямая параллельна оси Оу\ углового коэффициен-
та не имеет;
•	если А Ф 0, В 0, то уравнение прямой принимает вид
у = кх + Ьу где к =
6)	Уравнение прямой в в отрезках»:
— + — = 1, а, Ь ф 0,
а b
где а и Ъ — соответственно, абсцисса и ордината точек пересе-
чения прямой с осью Ох и осью Оу (см. рис. 7).
Рис. 7
37
2.	ПРИЛОЖЕНИЯ
1)	Угловой коэффициент прямой, проходящей через две точки
и М2(х2,у2У.

если Xj х2.
2)	Острый угол ф между прямыми, заданными уравнениями
у = к}х + Ь} и у ~к2х + Ь2,
вычисляется по формуле:
А, -к,
tg<P =	—— 
1 + • к2
Смежный с ф угол (тупой) равен я — ф.
3)	Точка пересечения прямых, заданных общими уравнениями
А,х + В}у + С} =0 и А7х + В7у + С- =0,
находится как решение системы:
А,х + В}у + С, = 0
1 1 1
А.,х + В7 у + С, = 0.
Z	Z •<	Z
38
4)	Координаты х0, у0 середины отрезка М	2 у
t
где Мх ; у}) и М2 (х2; у2), вычисляются по формулам:
5) Расстояние М}М2
между двумя точками

равно
2
~Х1)2 +(?2 -Ji)'-
6)	Необходимое и достаточное условие параллельности
двух прямых, имеющих угловые коэффициенты к} и к2 :
к — к
Л1 Л2 •
7)	Необходимое и достаточное условие перпендикулярности
двух прямых, имеющих угловые коэффициенты к} и к2 : ‘
k2
3.	ПРИМЕРЫ С РЕШЕНИЯМИ
П ример 1. Дано общее уравнение прямой:
Зх- 5у -10 = 0.
39
Найти угловой коэффициент прямой.
Решение. Разрешив уравнение относительно^, получаем
уравнение прямой с угловым коэффициентом:
3
5j/~3x —10 или у = ~х-2,
1	3
Отсюда к — — — угловой коэффициент прямой.
3
Ответ: —.
5
Пример 2. Составить уравнение прямой, проходящей через
точку А(— 1;3) и составляющей с осью Ох угол 135°.
Решение. Так как в данном случае к ~ /gl35° = — 1 и
Xj =-1, у} =3, TO j-3 = -l-(x + l).
Отсюда
у — —X 4-2 - искомое уравнение прямой.
Ответ: у = —х + 2.
Пример 3, Составить уравнение прямой, проходящей через
точку пересечения прямых
х + ^~1 = 0 и 2x4-3j 4-4 = 0
параллельно прямой Зх - у 4- 7 = 0.
40
Решение, а) Найдем точку пересечения прямых
х 4- у - 1 = 0 и 2х + 3_у + 4 = 0.
Для этого, решая систему уравнений
X 4- у - 1 - 0
[2x + 3j + 4 = 0,
находим: х ~ 7, у — —6.
Итак, точка пересечения данных прямых М\(1,б).
б) Составим уравнение прямой, проходящей через данную точку
М} (7;~б) параллельно прямой Зх — у 4- 7 — 0.
Найдем угловой коэффициент прямой Зх - у 4- 7 = 0 :
у = Зх 4~ 7, откуда к} — 3.
Из условия параллельности двух прямых находим угловой ко-
эффициент искомой прямой: к2 —кх ~3.
Пользуясь формулой (1), находим уравнение прямой, проходя-
щей через точку (7;-б) с угловым коэффициентом к2 ~ 3 :
у + 6 — 3(х — 7) или после упрощения Зх — у — 27 — 0.
Итак, искомая прямая имеет уравнение: Зх — у - Т1 — 0.
Ответ: Зх — у — 27 = 0.
41
Пример 4. Даны вершины треугольника: Л(0;1); 5(6;5) и
С(12;—1). Составить уравнение высоты треугольника, проведен-
ной из вершины С.
Решение. Составим уравнение стороны АВ, используя
формулу (2):
У-1_х-0
5-1"6-0
Отсюда:
- 1 = — х или у - — X 4 1.
6	3
Таким образом, угловой коэффициент прямой, на которой лежит
проведенная „ ч»™	,™.., -|. Уравне-
ние этой высоты имеет вид
или Зх + 2ф- 34- 0.
Ответ: Зх+2у — 34 = 0.
4. ПРИМЕРЫ
XX	3.* - ф 2 ~ С, 4х 4- 2 у - 5 — 0,
2х 4 7у - 0 привести к ваду уравнений с угловым коэффициен-
том.
42
2.2.	Найти углы, образуемые прямыми х — у 4- 5 — О,
2у — 3 = 0, 4х 4- 7 = 0 с осью Ох.
2.3.	Под каким углом прямая у = х 4- 2 пересекает ось Ох ?
2.4.	Составить уравнение прямой, проходящей через начало коор-
динат под углом сс — 60° коси Ох.
2.5.	Составить уравнение прямой, проходящей через точку (3;~2)
под углом
а) 45°, б) 135°, в) 90°, г) 0°
к осн Ох.
2.6.	Составить уравнение прямой, проходящей через точки
Л/(-1;3) и 2V(2;5).
2.7.	Определить острый угол между прямыми у 4- Зх — 7 ~ 0
и у - 2х - 1 = 0.
2.8.	Даны вершины треугольника АВС: А(— 2;5), 7?(7;7),
С(3;~5). Написать:
а)	уравнения сторон треугольника АВС;
б)	уравнение медианы BE.
2.9.	Составить уравнение прямой, проходящей через точку
Л/(5;-1)
а)	перпендикулярно прямой Зх — 7у 4-14 ~ 0;
б)	параллельно прямой Зх — 7 у 4 14 — 0.
43
2.10.	Даны вершины треугольника АВС: /1(1,1), 2?(4;5),
С(13;—4). Составить уравнение высоты, опущенной из вершины
С. Вычислить площадь треугольника АВС.
2.11.	Найти вершины и построить треугольник, стороны которого
лежат на прямых: х 4- у — 4; Зх — у ~ 0; х — Зу = 8.
2.12.	Составить уравнения биссектрис углов между прямыми
x + j>-5 = 0 и 7х->у-19 = 0.
2.13.	Составить уравнение прямой, проходящей через точку /1(2;3)
и составляющей с осью Ох угол 45°.
2.14.	Составить уравнение прямой, проходящей через точку
м(- 2,3)
а)	параллельно прямой 2х 4- Зу — 7 = 0;
б)	перпендикулярно прямой 2х 4- Зу — 7 = 0.
2.15,	Определить угол между прямыми 2х 4-	— 15 - 0 и
Зх-7>> + 2 = 0.
2.16.	Даны вершины треугольника АВС: А(2;2), 7?(- 2;—8),
С(— 6;-2). Составить уравнение медианы АЕ.
44
2.17.	Даны вершины треугольника АВС \ Л(0;1), 2?(б;5),
С(12;— 1). Составить уравнение высоты CD,
2.18.	Даны точки Л(— 2,5), 73(1;3). Составить уравнение сере-
динного перпендикуляра к отрезку АВ.
2.19.	Найти прямую, проходящую через точку пересечения
прямых
х 4- 2у 4-3 = 0, 2х 4- 3у 4- 4 = 0
и параллельную прямой 5x4- 8 у - 0.
2.20.	Даны вершины треугольника АВС \ Л(1;1)э 2?(10;13),
С(13;б). Составить уравнение биссектрисы угла Л.
2.21.	Составить уравнения трех сторон квадрата, если известно,
что четвертой стороной является отрезок прямой
'\
4х 4- Зу — 12 = 0, концы которого лежат на осях координат.
2.22.	Найти углы, образуемые с осью абсцисс прямыми:
а) 2у/Зх - бу 4-11 = 0,	б) у/Зх 4- у - V? = 0,
в) 2х-7 = 0,	г) 5у + 14 = 0.
2.23.	Найти прямую, проходящую через середину стороны АВ
треугольника АВС и перпендикулярную стороне ВС, если из-
вестны координаты вершин треугольника:
Я(7;5), В(-1;-3), С(2;-3).
45
2.24.	Найти площадь треугольника АВС, если известны коорди-
наты его вершин: Л (—1,-1), 2?(4;6), С(-1;7).
5. ОТВЕТЫ
2.1 45°, 0°, 90°.
2.3.	а = 45°.
2.4.	у = у/Зх.
2.5.	у = х - 5, у = -х +1, х = 3, у = -2.
2.6.	2x-3j + 11 = 0.
п
2.7.	—.
4
2.8.	(АВ): 2х-9.у + 49 = 0, (ВС): Зх-^-14 = 0,
(AC): 2х+у = 1,	(BE)::14х-13>> + 7 = 0.
19.	a) 7x + 3j-32 = 0; б) Зх-1у-22 = 0.
46
2.10. Зх + 4у - 23 =0, S = 31,5.
2.11. Л(-1;-3), 2?(1;3), С(5;-1).
2.12. Зх + у -11 = 0,
х-Зу + З = 0.
2.13. Д' = х + 1.
2.14. 2х +3^-5 = О, Зх-2>> + 12 = 0.
2.15. —.
2.16. 6^-7х + 2 = 0.
2.18. 6х-4у + 19 = 0.
2.17. Зх + 2у - 34 = 0.
2.19. 5х +	+11 = 0.
2.20.	7х-9у + 2 = 0.
2.21.	Зх - 4у - 9 = 0;	Зх-4>' + 16 = 0;
4х + 3у — 37 = 0 или 4х + Зу +13 = 0..
2.22.	а) б) —; в)—; г) 0.	2.23. х = 3.
6	3	2
2.24. 20.
47
КРИВЫЕ ВТОРОГО ПОРЯДКА
1. ОКРУЖНОСТЬ
Определение 1. Окружность - геометрическое место
точек на плоскости, равноудаленных от некоторой точки,
называемой центром.
Каноническое уравнение.
х2 -к у2 - г2.	(1)
Свойства:
1.	Точка О(0;0) - центр окружности;
2.	Г - радиус;
3.	Ох, Оу - оси симметрии;
4.	График изображен на рнс.1.
Рис.2
Рис.1
48
Окружность, задаваемая уравнением:
(х-х0)2 + (у-_у0)2 =г2,
обладает свойствами:
1.	Точка О} (х0; Jo ) ” центр окружности;
2.	г - радиус;
3.	Прямые х = х0, у = j0 - оси симметрии;
4.	График окружности (2) изображен на рнс.2 и получается из
графика окружности с уравнением (1) параллельным
переносом на вектор ОО} .
2. ЭЛЛИПС
Определение 2. Эллипс - геометрическое место точек на
плоскости, для каждой из которых сумма расстояний до двух
данных точек, называемые фокусами, есть величина постоянная.
Кан они ческое уравнение:
(а Ф Ь).
(3)
Свойства
1.	Центр эллипса - точка 0(0,0);
2.	Вершины эллипса - точки
ЛДа.О), A2(-afi\ Д(О:Л), /?2(0;- Ь);
3.	А\А21 = 2п, Ij5] В21 - 2Ь - оси эллипса;
4.	b - полуоси эллипса;
5.	Оси симметрии ~ Ох, Оу;
49
6.	Фокусы эллипса - точки
F} (с;0), F2 (- с;0), где с = у/а2 - Ь2, если а>Ь\
F}(0;с)3 F2(0 — с), где с = yb2 — а2, если b > а\
7.	График эллипса (3) изображен на рнс. 3.
Эллипс, задаваемый уравнением:
/ V /	\2
---	 	А2--1
а--------------------b
обладает свойствами;
1. Центр эллипса - точка Ot (х0; у0 );
2. Вершины эллипса - точки
(а ф б).
(4)
50
4(*о + <г>Уо\ Л2(х0-а;у0\ В}(х0;у0 +b\ В2(х0,у0-b),
2
~2Ь - оси эллипса;
4.	а, Ь - полуоси эллипса;
5.	Оси симметрии - прямые X = х0, у — yQ ;
6.	Фокусы эллипса - точки
С^о + с>.Уо)» ^*2(^0	где с — у1& b , если а > by
^*] (*о э У о +	F2 (*о ’	где с — у/ b	& ? если b > dy
7.	График эллипса (4) получается из графика эллипса (3)
параллельным переносом на вектор ОО} , где О} (х0, .У0 ).
X ГИПЕРБОЛА
Определение 3. Гипербола - геометрическое место точек
на плоскости, для каждой из которых модуль разности расстояний
до двух данных точек, называемых фокусами, есть величина
постоянная.
Каноническое уравнение
(5)
или
Ь2 а
(6)
51
Свойства:
1.	Вершины: А}(а,О), А2(—а,0) - для гиперболы (5);
В}(0;Ь\ В2(р-Ь) - доя гиперболы (6);
2.	Полуоси: а - действительная
b - мнимая
—	- для гиперболы (5);
а -мнимая —
b - действительная.,
- для гиперболы (6);
3 . Фокусы гиперболы: точки
а2 +Ь2 ;0
4.	Осн симметрии - Ох, Оу.
b	ь
5.	Асимптоты: прямые у — — X н у —-----X;
а	а
6.	График изображен на рис. 4.
Рис.4
52
Гиперболы, задаваемые уравнениями:
или
(7)
(8)
обладают свойствами:
1.	Вершины:
4(*о +ед)> Л(хо -ед) - для гиперболы (7);
(^0 ’-Уо +	В2 (х0 , j^0 — £>) - для гиперболы (8);
2.	Полуоси: а - действительная
Ь - мнимая —
а - мнимая	—।
b - действительная
- для гиперболы (7);
- для гиперболы (8);
3.	Фокусы гиперболы: точки
Fx (х0 + у! а2 +Ь2- у0), F2 (х0 - у/а2 +b2- j/0) - для
гиперболы (7),
Fi (*о > У о	U j У о у[@ 4~ Ъ — для
гиперболы (8);
4.	Оси симметрии: прямые х = х0, у —	.
5.	Асимптоты: прямые у =	—(х“хо) и
а
Ь z
У = Уо—(х-х0)-
а
6.	График гиперболы, задаваемой уравнением (7)
53
(уравнением (8)), получается из графика гиперболы, задаваемой
уравнением (5) (уравнением (6)) параллельным переносом на
вектор ОС\ ,гдеО1(х0;.у0).
4, ПАРАБОЛА
Определение 4. Парабола - геометрическое место точек
на плоскости, равноудаленных от данной точки, называемой
фокусом, и данной прямой, называемой директрисой.
Канони ческое уравнение.
у2 = 2рх	(9)
или
х2=1ру,	(10)
где р — некоторое число, называемое параметром параболы.
Свойства:
1.	Вершина: О(0;0);
2.	Фокусы параболы: F —,0
-для параболы (9),
-для параболы (10);
3.	Директриса: прямая х =
~ для параболы (9),
прямая у =
- для параболы (10);
54
4.	Оси симметрии: Ох - для параболы (9),
Оу - для параболы (10);
5.	График параболы (9) изображен на рис. 5,
параболы (10) - на рис. 6.
Параболы, задаваемые уравнениями
или
б-Л.)2 = 2р(х-х0)
(х-х0)2 = 2р(у~Уо)>
(И)
(12)
где р — некоторое число, называемое параметром параболы,
55
обладают свойствами:
1. Вершина точка Оу (х0; у0 );
2. Фокусы параболы:
-для параболы (11),
-для параболы (12);
3.	Директриса: прямая х - х0-------для параболы (11),
прямая у = у0-------для параболы (12)^
4.	Оси симметрии: прямая У — Уо - для параболы (11),
прямая х = х0 - для параболы (12);
5.	График параболы, задаваемой уравнением (11)
(уравнением (12)), получается из графика параболы, задаваемой
уравнением (9) (уравнением (10)) параллельным переносом на
вектор ООХ , где О} (х0; уь).
Замечание. Уравнение второй степени
Ах2 + Су2 + 2Dx + 2Еу + F - 0,	(13)
где числа Л и С не равны одновременно нулю, преобразуется к
каноническому виду методом выделения полных квадратов и по-
следующим параллельным переносом.
Тип кривой (13) определяется числами Л и С :
1)	если Л=С,то(13)-окружность;
2)	если Л и Л • С>0, то (13)-эллипс;
3)	если Л-С<0, то (12)-гипербола;
4)	если одно из чисел Л или С равно нулю, то (12) - парабола.
56
5. ПРИМЕРЫ С РЕШЕНИЯМИ
П Р и м е р 1. Составить уравнение эллипса, фокусы которого
лежат на оси Ох симметрично относительно начала координат,
зная, что малая полуось 6, а расстояние между фокусами 2-\/13 .
Решение. По условию b ~ 6; с — у/13. Причем
а2=Ь2+с2 =>а2 =36 + 13 = 49=> а-7.
Подставляя найденные числа а ~ 7, b — 6 в каноническое
х2 у2
1внение (3), получаем уравнение эллипса:--1—— ~ 1.
49 36
Ответ:------Ь — — 1.
49 36
3
Пример 2. Асимптоты гиперболы у = ± ~ X, а расстояние
4
между фокусами 20. Написать каноническое уравнение гиперболы,
зная, что ее фокусы лежат на оси Ох.
Решение. По условию 2с = 20. Поэтому с = 10. Кроме
Ь 3	2
того, — — Но а +о —с .
а 4
Следолзтоличо. получас?»? ел ж му:
 Ь 3
 — = —	с/ = 8,
< а 4
I ?	?	b “ 6.
[Й2 + *" =100
57
Подставляя найденные числа ауЬ в каноническое уравнение
Ответ:  ------— 1.
64 36
Пример 3, Уравнения линий второго порядка привести к
каноническому виду; определить их вид и построить, используя
параллельный перенос координатных осей:
а)	х2 У у2 у 4х - бу - 3 - 0;
б)	9х2 + 16^2 - 90х + 32^ + 97 = 0.
Решение, а) Покажем, что данное уравнение есть уравнение
окружности.
Сгруппируем в рассматриваемом уравнении слагаемые, содер-
жащие только X, и слагаемые, содержащие только у:
(х2 + 4х)+ (у2 - бу)-3 = 0.
В левой части уравнения выделим полные квадраты. Тогда
уравнение запишется так:
(х + 2)2 -4 + (у-3)2 -9-3 = 0
I	- -	> I	z	J
х +4х
у2-бу
ИЛИ
(х + 2)2 + (у-3)2 =16.
Перейдем к новой системе координат:
x + 2 = X]i y-3 = yv
58
Получим новое начало координат: О} (- 2;3).
В новой системе координат данное уравнение имеет вид:
х,2 + у2 =16,
то есть является уравнением окружности радиуса г = 4 с центром
в точке Oj (- 2;3), см. рис. 7.
б) Поступая аналогично, приведем к каноническому виду урав-
нение
9х2 H6j2 - 90х + 32>-+ 97 = 0.
Сгруппируем слагаемые, содержащие только х, и слагаемые,
содержащие только у, вынося коэффициенты при х2 и у 2 за скоб-
ки:
9(х2 - 10х)+ 1б(у2 + 2у)+ 97 = 0.
Дополним выражения в скобках до полных квадратов:
59
9(х2 - 2 • 5х + 25 - 25)+ 1б(у2 + 2у +1 -1)+ 97 = О,
9((х-5)2 - 25)+1 б((у +1)2 -1)+ 97 = О,
9(х-5)2 - 225 + 1б(у +1)2 -16 + 97 = 0,
9(х - 5)2 + 1б(у +1)2 -144 = 0.
Таким образом, исходное уравнение равносильно следующему:
9(х-5)2 +1б(у + 1)2 =144.
Разделив обе части уравнения на 144, получим уравнение:
(14)
Уравнение (14) - уравнение эллипса с полуосями а ~ 4, b ~ 3.
Центр эллипса находится в точке О} (5;—1).
Для того чтобы построить график этого эллипса, перейдем к но-
вой системе координат:
х-5 = х1,	^ + 1 = ^.
Получим новое начало координат: Ot (5;—1).
В новой системе координат уравнение (14) имеет вид:
60
16	9
Фокальная ось эллипса: ось О} х,.
Расстояние фокусов от центра:
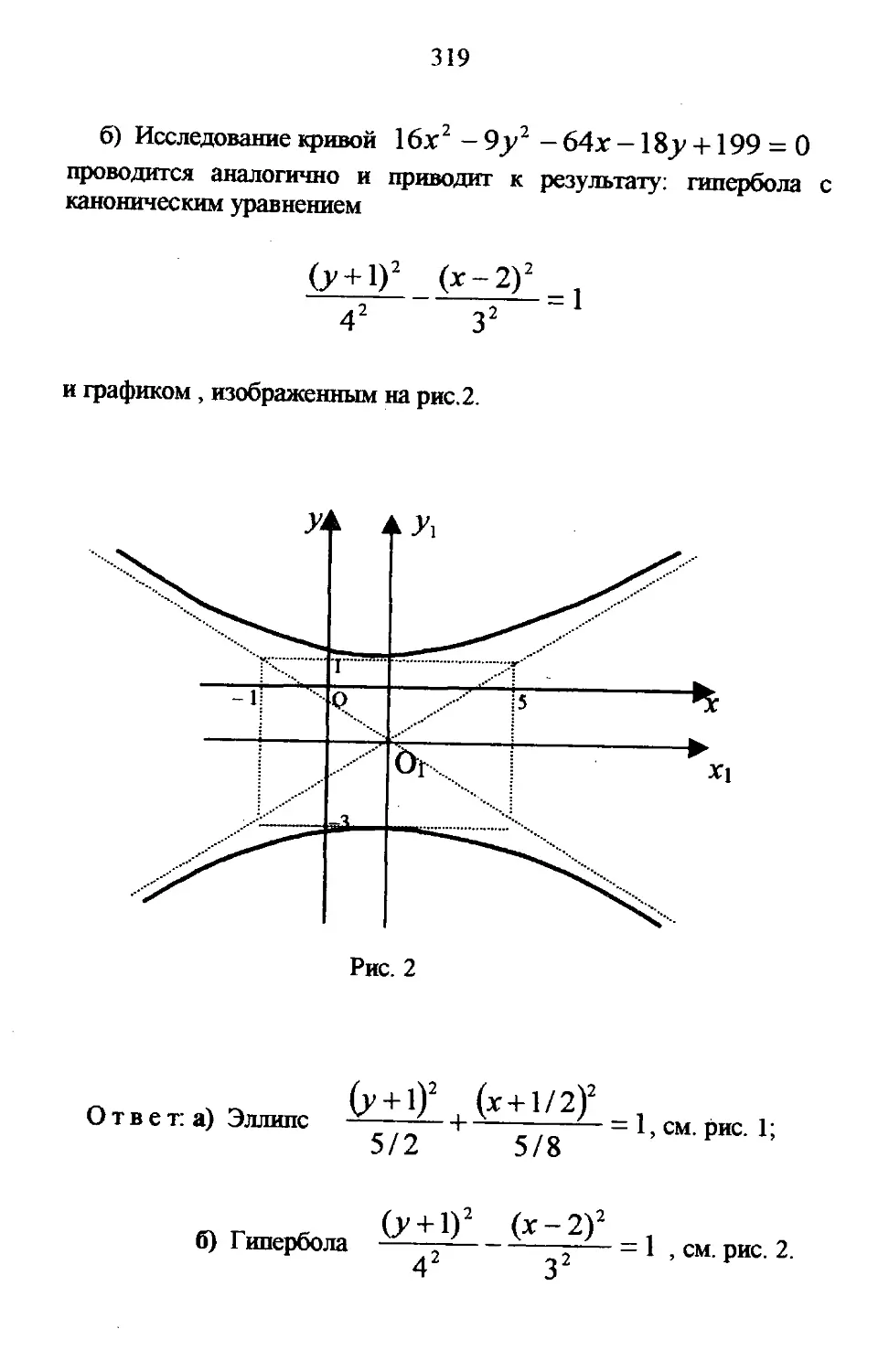
С = >/16-9 = 41 (« 2,б).
График эллипса (14) изображен на рис.8.
Ответ: а) окружность (х + 2)2 + (у-3)2=16 , см. рис. 7;
б) эллипс
= 1, см. рис. 8.
61
6.	ПРИМЕРЫ
3.1.	Составить канонические^, уравнение эллипса, фокусы кото-
рого лежат на оси Ох, если
а)	его полуоси л/7 и 2;
б)	его большая полуось 10, а расстояние между фокусами 12;
в)	расстояние между фокусами 2^5 , площадь четырехуголь-
ника с вершинами в вершинах эллипса равна 12.
3.2. Составить каноническое уравнение гиперболы, фокусы ко-
торой лежат на оси Ох, если
а) ее полуоси 5 и 3;
б) расстояние между фокусами 4^5 , мнимая полуось 2;
в) ее вершины находятся в фокусах, а фокусы - в верши-
2	2
х	У
нах эллипса------1--= 1.
9	5
3.3.	Написать уравнение параболы с вершиной в начале коор-
динат, проходящей через точку Л(2;4) и симметричной относи-
тельно оси Ох.
Определить тип кривой:
3.4.	Зх2 + 4у2 - 6х +16^ + 7 = 0.
3.5.	Зх2 + 3/ - 6х + 12j + 12 = 0.
3.6.	Зх2 - 12х - 2у +12 = 0.
3.7.	Зх2 - 4у2 - 6х +1= 25.
62
Уравнение линии второго порядка привести
к каноническому виду; определить тип кривой
и построить ее:
3.8.	х2 + у2 - 4 г +	+11 = 0.
3.9.	9х2 + 4j2 - 54х - 32_у +109 = 0.
3.10.	4г2 -9у2 -8х-36^-68 = 0.
3.11	у-х2 + 4х + 5.
3.12.	у-lx2 +8х + 12.
3.13.	у2 - 2х + 4у + 2 = 0.
3.14.	х2 -2х + у2 -4j + l = 0.
3.15.	9х2+4j2+30x-12j-2 = 0.
3.16.	Написать каноническое уравнение эллипса, фокусы кото-
рого лежат на оси Ох, малая полуось 2>/б , расстояние между фо-
кусами 8.
3.17.	Написать каноническое уравнение гиперболы, действи-
тельная ось которой 5 и у!а2 +Ь2 /а = 1,4.
3.18.	Парабола с вершиной в начале координат проходит че-
рез точку А(—2,—3) и симметрична относительно оси Ох, Напи-
сать ее уравнение; найти фокус и директрису.
Определить тип кривой:
3.19.	5х2 + 4j2 + 10х - 8j = 11.
3.20.	5х2 - 20г - 8у + 20 = 0.
63
3.21.	5х2 - 4у2 + 10х - 8j = 19.
3.22.	х2 + у2 + 2х - 2у +1 - 0.
Уравнение линии второго порядка привести
к каноническому виду; определить тип кривой
и построить ее:
3.23.	х2 + у2 - 2х + 4у - 4 = 0.
3.24.	х2 - 4у2 + 8х - 24у ~ 24.
3.25.	х2 + 4_у2 -6x + 8j/ = 3.
3.26.	у2 -8_у = 4х.
3.27.	Зх2 + 4_у2 - 6х + 16j + 7 = 0.
3.28.	у = х2 - Зх - 2.
3.29.	Зх2 - 4_у2 - 6х + 16j = 25.
3.30.	Зх2 + Зу2 - 6х + 12_у + 12 = 0.
7, ОТВЕТЫ
х у
3.1. а) — + —
7	4
б)
100
3.2. а)
3.3. у2 =8х.	3.4. Эллипс. 3.5. Окружность. 3.6. Парабола.
3.7. Гипербола.
64
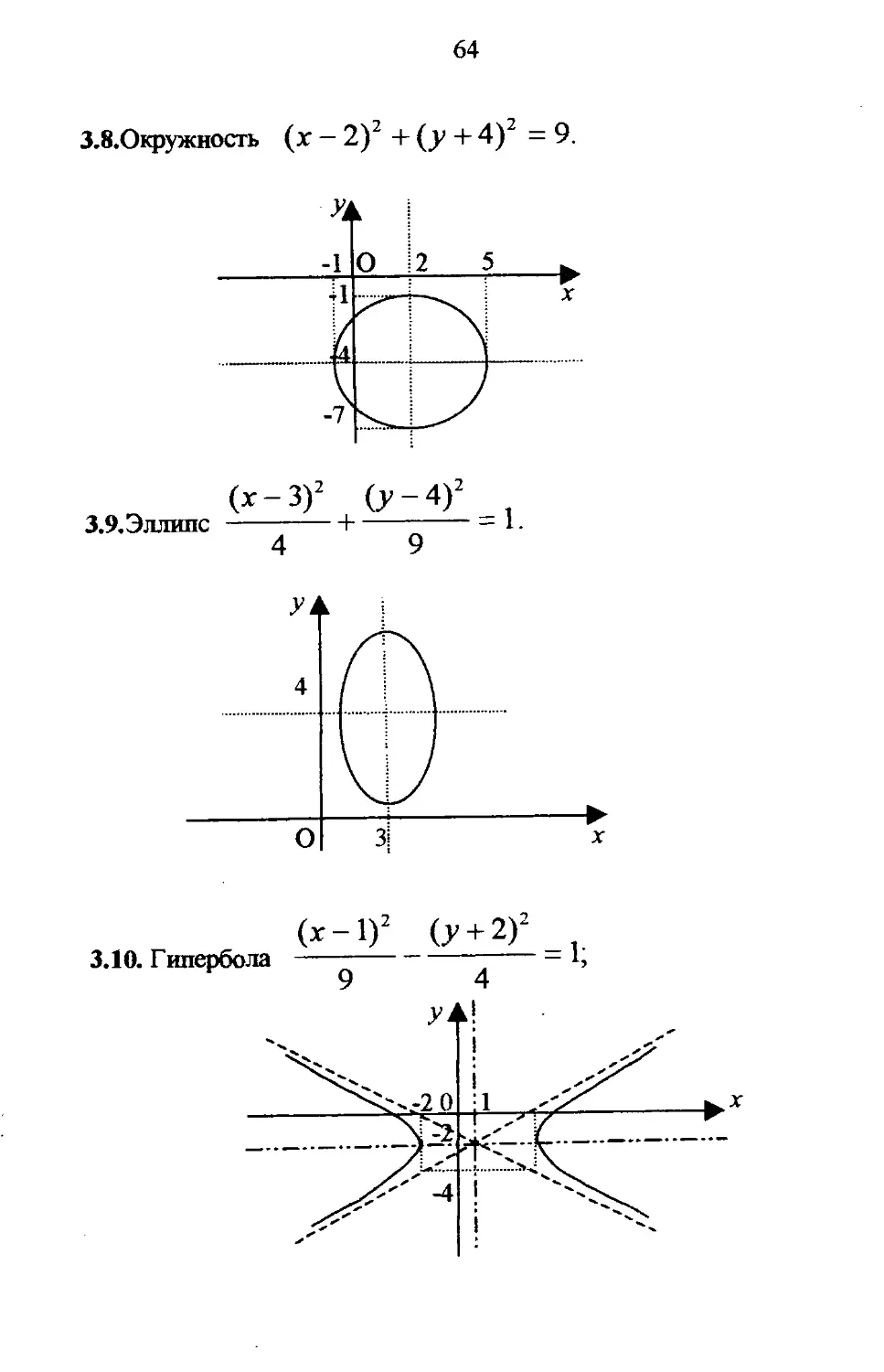
3.8.Окружность (г - 2)2 + (у + 4)2 = 9.
65
3.11, Парабола у — 1 = (х + 2)2.
3.12. Парабола у - 4 - 2(х 4- 2)2.
3.13. Парабола (>’ + 2)2 = 2(х 4 1).
66
3.14.	Окружность (х — I)2 + (j — 2)2 = 4.
<Х + 5/3>2 !
3.15.	Эллипс----------1-----------— 1.
4	9
X	у	X	у	2
3.16. ----+ — = 1.	3.17.-------- = 1.	3.18. у2
40	24	25	24
3.19. Эллипс. 3.20. Парабола.
9
=-----х.
2
3.21. Гипербола. 3.22. Окружность.
67
3.24. Гипербола
(г - З)2 (у +1)2
3.25. Эллипс--------1-------— 1.
16	4
68
3.26. Парабола (у — 4)2 = 4(х + 4) .
69
3.29. Гипербола
2	(J-2)2
3.30. Окружность (х — I)2 + (j + 2)2 = 1.
70

ВЕКТОРЫ.
ОПЕРАЦИИ НАД ВЕКТОРАМИ.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ
ВЕКТОРОВ
1. ОПРЕДЕЛЕНИЯ
Определение 1. Вектором АВ называется направлен-
ный отрезок с началом в точке А и концом в точке В.
Определение 2. Длиной вектора АВ (илимодулем)
называется длина отрезка АВ. Используется обозначение | А В | .
Определение 3. Два вектора а и Ь называются рав-
ными, если они имеют одинаковые длины, лежат на параллельных
прямых (коллинеарны) и направлены в одну сторону (сонаправле-
ны):
а ~ b
а = Ь
<а b
аШ.
71
Определение 4. Проекцией вектора а на ось Ои на-
зываются число, обозначаемое ПрОи а , вычисляемое по формуле:
ПрОи а = |а| • cos(a, Ои).
Определение 5. Направляющими углами вектора О на-
зываются углы между ним и координатными осями:
а = (а,Ох), 0 = (а,Оу} y = (a,Oz)
Определение 6. Косинусы направляющих углов назы-
ваются направляющими косинусами вектора.
О п р е д е л е н и е 7. Проекции вектора а на координатные
оси (9х, Оу. Oz называются координатами вектора а и обо-
значаются, соответственно, ах, ау, а2.
Замечание 1. Для любого вектора а верно равенство:
a = ax i + ay , j + a2 k,	(1)
где z, j, к — орты координатных осей Ох, Оу, Oz (то есть еди-
ничные векторы, сонаправленные с соответствующей осью).
Равенство (1) для сокращения записи заменяют следующим:
72
3 я м е ч а н и е 2. Для любого вектора а ~ \ах; а,; az) вер-
ны равенства:
COS6Z--~, COS/>“~~-
г
COS/ ,
1а
। ।
cosI 2 6Z4-COS2 /7 +cos2 / = 1.
Замечание 3. У равных векторов равны соответствующие
координаты:
а = Ь<^аж = Ьж,ау = Ьу,а2 =Ьг.
Замечание 4. У коллинеарных векторов координаты про-
порциональны:
Причем, если коэффициент пропорциональности к > 0, векторы
ci и b сонаправлены 1аТТЬ)\ если к<0^ векторы а и
Ь противоположно направлены
Замечание 5. Длина вектора а через координаты опре-
деляется по формуле:
I	М ,2 ,2
| d \ —	-
ул	_У	4-
73
Если известны координаты точек A(xA;yA;zA) и
В{%в > У в > Z s\ то
АВ ~ у1(Хв Ха ) ~Г’ (уВ Уа) *" (%В	) у
АВ = (хв-xA) i + (yB -yA) j + (zB-Za)-^
2. ОПЕРАЦИИ НАД ВЕКТОРАМИ
1)	Сложение
Рис. 1
2)	Вычитание
Рис. 2
74
3)	Умножение вектора на скаляр А :
а
3.	ОПЕРАЦИИ НАД ВЕКТОРАМИ, ЗАДАННЫМИ
КООРДИНАТАМИ
Пусть даны два вектора:
а = axi + ау ] + а2к
b = bxi + byj + b2k .
1)	Сложение:
a + b =(ax+bx)i + (ay+by)j + (a2 +b2)-k.
2)	Вычитание:
a-b =(ax-bx)i + (ay-by)-j + (a2-b2)-k.
3)	Умножение вектора на число Л
А-а = Аах • i4-Лау • j4-Aaz  к.
75
4.	СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Определение 8. Скалярным произведением друк векто-
ров а и b называется число, обозначаемое а- b или	и
вычисляемое по формуле	~
а-b =1 а| -I b I -cosla,Z>).
(2)
Физический смысл: скалярное произведение а  b есть раба
та силы а на пути вектора Ь .
Свойства скалярного произведения'.
1. а-Ъ-Ь-а,
(а • aj \p b)=aJ3 \a b), где а,/3 = const;
а • (Ь + с) = а • b + а • с;
\a+b)- с = ас+Ь -с,
4.	Если угол между векторами а и b острый, то а - Ь >0; если
угол тупой, то а  Ь <0;
5.	а1/юа-й = 0;
-2--------- 2
6.	а = а-а= а ;
7.	Если известны координаты векторов а = (ах,а аг) и
Ь = (Ьх,Ьу;Ьг), то их скалярное произведение вычисляется по
формуле:
76
a • b = ar • br + av • bv + a • b,.
у у it
(3)
8.	Проекция вектора а на вектор Ь вычисляется по формуле
пРьа =
а-Ь
(4)
b
9.
Если ф —угол между векторами
а и b, то
COS ^9 =
ab
(5)
5. ПРИМЕРЫ С РЕШЕНИЯМИ
П р и м е р 1. Даны точки
Л(1;0;2),5(3;-2;-1) и С(-1;-3;0)
Найти векторы а — АВ, b — АС, с — 2а~ ЗЬ.
Решение. Найдем векторы АВ, АС :
1) а = АВ = (xs-хА)i + (ув-уА) j + (zB -zA) k =
= (3-1)/ + (-2-0)у+(-1-2)1 = 2/-27-31
77
Следовательно, а — (2;—2;~3).
2) £ = ЛС = (хс -xj-z + (yc +	=
= (-1-1)/ + (-3-0)} + (0-2)1 = -2/-Зу-2Л.
Следовательно, b — (- 2;—3;—2).
Чтобы найти координаты вектора с— 2а — ЗЬ, найдем сначала
векторы 2а и — ЗЬ, а затем их сумму.
В данном случае
2а = 2 * (а -i' + av • j' + а • к}-2а* *i; + 2а • j + 2а • к -
\ *	У	i !	*	У **	А
= 2-2-/ + 2-(-2)-) + 2(-3)Л = 4/-4у-б1
Иначе это действие можно оформить так:
2а = (2аг ;2ау ;2аг) = (4;-4;-б)
Аналогично:
-зК = -з (^>, i+bv • j+b, k)=-3bx i-3bv • j-3b k =
= -3(-2)/-3(-3)-7-3(-2)Л = 6/+9}+6Л,
откуда — 3b = (б,9;б).
78
Теперь найдем вектор с :
ё = 2а-36 =
= ((2а)х + (- 3b)x )• i + ((2^ + (- 3b)y )• j + ((2а)г + (- ЗЬ)г )• к =
= (4 + б)/+(-4+9);+(-6 + б)Л = 10/ + 5/
Иначе это действие можно оформить так:
с = 2а - ЗЬ = (4;-4;-б) + (б;9;б) = (4 + 6;-4 + 9;-6 + б) = (10;5;0).
Ответ: а = (2,-2;-3); b = (-2;-3;-2^ с = (10;5;0)
ИЛИ
a -2i-2j-3k; b - ~2i-3j~2k\ c=10i + 5j.
Пример 2. Даны точки Л(3;1;1), В(5;2;0), С(2;—2;1) и
£)(— 2;4;3). Показать, что четырехугольник ABCD является тра-
пецией.
Решение. Известно, что у трапеции две противолежащие
стороны параллельны (основания трапеции), а две другие - нет.
Для решения данной задачи достаточно убедиться в коллинеар-
ности двух векторов, лежащих на противоположных сторонах че-
тырехугольника ABCD, то есть мы должны показать, что
~AB\\CD или ВС II ~AD.
79
Найдем эти векторы и рассмотрим отношения их соответствую-
щих координат, поскольку известно, что у коллинеарных векторов
координаты пропорциональны.
В данном случае
ЛВ = (хв - хА; ув - уА; zB - zA ) = (5 - 3;-2 -1;0 -1) = (2;—3;—1);
ВС = (хс — хв,ус - yB,zc ~^в ) = (^ — 5,-2 + 2,1 — о) - (— 3,0,1),
CD = (- 2 - 2; 4 + 2;3 -1) = (- 4;6;2>
AD = (- 2 - 3;4 -1;3 -1) = (- 5;3;2>
Нетрудно видеть, что АВ 11 CD, так как
2	-3 -1
-4" 6 ~ 2 ’
а векторы ВС и AD ие являются коллинеарными, поскольку их
соответствующие координаты не пропорциональны:
Следовательно, ABCD - трапеция, так как
ABWCD, ВС WAD.
Ответ: ABCD - трапеция.
80
Известны длины векторов: I а I =4; I b I =5. Найти длину вектора
с = 2а-~Ь.
Решение. Воспользуемся тем. что длина вектора равна
квадратному корню из скалярного квадрата этого вектора, то есть
।	/“2	// —	—\2	/ — 2	— —	—2
\с\ = ус = у1\2а~~Ь)	-4a-b + b
• Ъ • cos (р+ b
J4-42 -4.4.5.I4.52
V	2
764-40 + 25 = V49 = 7.
О т в е т: | с\ =7.
Пример 4. Даны векторы а - i 4- 5к и b ~ 31' - 4J 4- 2к.
Найти их скалярное произведение.
Решение. Воспользуемся формулой (3):
a b -a -bx +av b +а, -b. - 1 -3 + 0-(~ 4)+5-2 - 13.
Ответ: а • b — 13.
81
4.	ПРИМЕРЫ
4.1.	На плоскости даны векторы а и b .
Построить векторы 2 а; — b ; а + b ; а~Ь.
4.2.	ABCD - параллелограмм; АВ - р, AD = q.
Выразить через р и q векторы CD, ВС, BA, СА.
4.3.	Даны точки Л(1;4;—З), В(— 1;0;—2). Найти вектор АВ.
4.4.	Даны векторы
а = (1;3;0), Ъ = (0;~2;-4), ё = (-1;0;21 d = (0;5;0>
Каким координатным плоскостям параллельны эти векторы?
4.5.	a-2i- j + 5к; Ъ ~ -i 4- 3j: + 4к.
Найти векторы с — 2я3 d — а4-Л, е — b — a, f = 2а 4-ЗЬ.
4.6.	а = -6Z 4- 3J - 9к\ Ъ = 2/ - j 4- Зк.
Проверить коллинеарность этих векторов; выяснить, как они
направлены относительно друг друга; установить, какой из
них длиннее и во сколько раз.
4.7.	Даны точки Л(3;—1;2), В(1,2;~ 1), С(~ 1,1;—3) и£)(3;-5;3).
Доказать, ABCD - пгзвеция.
О, Наши разложение вектора с ~ (11;— 6;5) по векторам
p-3i~2j+k, q--i+j-2k и r = 2i+j~3k.
82
4.9.	Найти длину и направление (направляющие косинусы)
вектора АВ, если Л(1;2;3), 5(-1;3;5).
4.10.	Может ли некоторый вектор а образовать с координатными
осями Ох, Оу и Oz .соответственно, углы:
1)	а = 90°,р = 60”, г = 45”;
2)	а = 30”,/? = 45°,г = 135”;
3)	а = 30’,^ = 60°, / = 90° ?
4.11.	Найти угол между вектором а и осью Oz, если известно, что
а = ^z£bc)= 60”, р =	60”.
4.12.	a = U-3j-4k, b = i + 3k.
Найти a b.
4.13.	а = (- 1;1Хb = (1;31 с = 4а + Л,d = --а+-Ъ.
4	4
Найта угол (р между векторами end.
4.14.	Векторы р и q взаимно перпендикулярны, причем
I р 1=1, | #1=2; вектор а образует с векторами р и q уг-
л । ~i
лы, равные — , и I а I =3. Вычислить:
D (?+?) л;	з) y-p-qf,
83
2)	(а-р)-(2а + ?)	4) I 2р + ?|.
"Г"	I I	I "Z” 1
4.15.	Векторы ан о образуют угол <р — —; I a|=v3; I о 1=1.
6
Найти угол между векторами р и q, если
p-a + b,q = a-b.
4.16.	Л(- 2 -3,1), В(-C(4;l;l), D(- 5;5;3>
Доказать, что диагонали четырехугольника ABCD перпен-
дикулярны.
4.17.	а = / + Зу-2Л, b--i + mj + 4k.
При каких значениях числа тп векторы а и b перпен-
дикулярны ?
4.18.	Вектор а перпендикулярен векторам b = 3i + 2j + 2к и
с = 18/ — 22у — 5Л ; образует с осью Ох тупой угол; при этом
I <71=14. Найти координаты вектора а,
4.19.	а - 3/ - бу - к, b = i + 4j-5k, с- ~3i + 4j-\2к.
Найти проекцию вектора d — a + b на направление век-
тора с.
4.20.	Найти проекцию вектора а =(5; 1;-1) на ось, составляющую
с координатными осями равные острые углы.
84
4.21.	При каких значениях т и п векторы а = 2z — 3j + тк и
b~ni + 6j-4k коллинеарны ?
4.22.	Найти разложение вектора а — (5;—4) по векторам
р = (2;-3)и^ = (1;2).
4.23.	Даны точки Л(2;1;-1), В(5;4;—3) и С(3;—2;0). Найти ко-
ординаты вектора а = 2ЛВ-ЗСД его длину и направ-
ляющие косинусы.
4.24.	Может ли некоторый вектор а образовать с осями коорди-
нат углы:
1)	а = 0°,/?-90о,^ = 120°,
2)	а = 120°,/? = 150°, / = 90° ?
7	2
4.25.	Векторы а и b образуют угол (р = — п. Зная, что
I а I =3, | Ъ | =4, вычислить:
1)	а-Л; 2) ^z + Zj)2;	3) (за-2Л) (я + 2Л|
4)	I а + b |;	5) у/ = (а + Ь, а - />).
85
4.26.	Вектор Ь коллинеарен вектору а=(2;3;-6) и составляет с
осью Оу тупой угол. Найти координаты вектора b , если его
длина равна 21.
4.27.	Убедиться, что ЛАВС - равнобедренный, если Л(2;3;1),,
/?(4;0;7), С(8;5;—2). Найти углы треугольника.
4.28.	Даны точки у4(-4;-2;3) и В(5;-2;2). Найти проекцию
вектора АВ на ось, составляющую с осями Ох и Оу, со-
ответственно, углы (X = 60° и (3 — 120°, а с осью Oz ту-
пой угол у.
4.29.	Даны векторы а = 2i — J — 2к и b - -2i+ 3j — 6k Най-
ти:
1)	(a + i)2;	2)1 а + £I;
3)	р =	+	4) Пр-+Ь^-Ь).
4.30.	Даны точки Л(3;4;—5), 1?(2;0;— 1), С(7;3;2) и Z)(l;5;—3).
Найти:
86
5.	ОТВЕТЫ
4.2.	CD--/?, ВС = q, ВА = -р; CA = -p-q.
4.3.	АВ = (- 2;-4; 1)
4.4.	a 11 Оху, b 11 Оут, С11 Ох2\ d 11 Oxy и d 11 Oyz.
4.5.	c = (4;-2;10), rf = (l;2;9),
ё = (-3;4;-1), / = (1;7;22).
4.6.	aTJ^ Ial=3l5l. 4.7. ~AB\\CD, BC\№D
4.8.	c - 2p-3q + r.
—	2	12
4.9.1 AS 1=3; cosa =—; cos^ = —; cosx =—
4.10. 1)нег; 2) нет; 3)да.
4.11. у, =45°, у2 =135°.
87
4.12.	а-Л =-10.
4.13.	9> = 45°.
4.14.	1) 4-; 2) 18; 3)8; 4) 2 VI
^2/
4.15.	arccos
4.16. AC BD = Q. 4.17. m = 3. 4.18. a = -4i-6j+ 12k.
4.19. np-d = 4.
5>/з
4.20. -------.
3
4.21. m = 2; n = -4.
4.22.	a = 2p + q.
4.23.	a = -12j + 5£;	|a|=13;
12	5
cos a - 0; cosp =-------; cosy - —.
13	13
4.24.	1)нет; 2) да.
г—	ijwi
4.25.	1)-6; 2)13; 3)-61; 4) V13; 5) тг-arccos----
481
4.26.	b--&-9j + 13к.
12
= п -arccos—;
49
7 г	61
= Z.C = arccos —==.
7V122
4.28.
4.29.
о /77	5^51	20л/Г7
1)68; 2) 2V17; 3) © = л-arccos—-—; 4)---—
51	17
4.30.
5	8
i)-; 2)т-
88
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
ДВУХ ВЕКТОРОВ.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
ТРЕХ ВЕКТОРОВ
1. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Определение 1. Векторным произведением двух векто-
ров а и Ь называется вектор с, обозначаемый с - а х b, удов-
летворяющий трем условиям:
♦	clb (то есть вектор с перпендикулярен плоскости,
построенной на векторах а и Ь );
♦	векторы а ,Ь, с в указанном порядке образуют правую
тройку (то есть вектор с ~~ axb направлен таким образом,
что кратчай
пшт
поворот вектора а до совпадения с векто-
ром Ь виден из конца вектора с совершаемым против хода
часовой стрелян
I с 1Ч a I -I b I
89
Вектор c-axb изображен на рис. 1.
Рис. 1
Свойства векторного произведения:
1)	ах6 = -6ха;
2)	(аа)х (#/>) = {ap)axb,	а./З - const\
3)	(я + c = axc + Z>xc;
4)	ax(б + cj= axb + axc\
5)	Векторы а и b коллинеарны (то есть принадлежат па-
раллельным прямым) тогда и только тогда, когда их векторное
произведение равно нулю:
а II b <=> axb = 0;
6)	Площадь параллелограмма, построенного на векторах а
и b, численно равна длине векторного произведения этих векто-
ров:
90
7)	Площадь треугольника, построенного на векторах а и b ,
равна половине длины векторного произведения этих векторов:
5Д =-|а х b I;
8)	Если известны координаты векторов а =	и
Ь = (Лх, by, bz), то их векторное произведение вычисляется по
формуле:
axb =
(1)
9)	Физический смысл. Если вектор Ь рассматривать как силу,
приложенную к точке А , а вектор а - как вектор О А, то вектор
axb представляет собой момент М силы b относительно
точки О (см. рис. 2).
М
О а
Рис. 2
91
2, СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ
Определение 2, Смешанным произведением трех векто-
ров а ,b и с называется число, обозначаемое а • b • с, равное
скалярному произведению векторов а х b и с, то есть
а-b -с-^ахЬ^с'
Свойства смешанного произведения:
1)	(axb}c = а
2)	Абсолютная величина смешанного произведения трех век-
торов численно равна объему параллелепипеда^ построенного на
этих векторах (см. рис. 3):
^пар-педа ' О ' Ь ' с \ 7
Рис. 3
92
3)	Объем тетраэдра ( пирамиды, в основании которой лежит
треугольник, см. рис. 4), построенного на векторах а ,Ь и с,
численно равен:
И_.т_ = — I a b c\ ,
/лепр.	4 5 * 7
Рис. 4
4) Три вектора а , b и с компланарны (то есть параллель-
ны одной плоскости) тогда и только тогда, когда их смешанное
произведение равно нулю:
а ,Ь , с - компланарны <=> а  b • с =0 ;
5) Если известны координаты векторов а = (ах, ау, а2 j,
Ъ = (&x,Z>y,Z>z) и с - (сх,с?,сг), то их смешанное произведе-
ние вычисляется по формуле:
abc-
Ъх
Сх
ау а*
by Ъг
с с
у z
(2
93
3.	ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Д аны векторы
а - 2т3 j’ + к и b = -т’ + J - 2к.
Найти длину их векторного произведения.
Решение. Поскольку векторы заданы координатами, най-
дем их векторное произведение по формуле (1):
ах Ъ =
Найдем теперь длину полученного вектора:
Пример 2. Даныточки24(2;0;3)э 5(4;1;2) и С(1;—3;2).
Найти площадь треугольника АВС.
Решение. Известно,
ного на векторах а и
I ахб|.
что площадь треугольника, построен-
b, численно равна половине числа
Найдем векторы АВ и АС, на которых построен треугольник
АВС:
94
Следовательно, по формуле (1) находим:
2
Отсюда
Поэтому искомая площадь &АВС равна:
^=1|ЛВхЛС|=1-5Л = ^
_ 5^2
ДЛВС ~	2
п р и м е р 3. Показать, что точки Я(3;2;1), В(5;1;3),
С(4;4;—2) и D(6;—2; 8) лежат в одной плоскости.
Решение. Если точки А, В, С и D лежат в одной плос-
кости, то векторы АВ, АС и AD компланарны.
Эго можно выяснить, вычислив их смешанное произведение,
поскольку известно, что три вектора компланарны тогда и только
тогда, когда их смешанное произведение равно нулю.
95
Итак, найдем координаты векторов АВ, AC, AD и вычис-
лим по формуле (2) их смешанное произведение:
ЯВ = (5-3;1-2;3-1) = (2;-1;2);
АС = (4 - 3;4 - 2;-2 -1) = (1;2;-3);
AD = (6- 3;-2 - 2;8 -1) = (3;-4;7);
2
2
АВ-АС-А£>=1 2
-3 =28 + 9-8-12-24 + 7 = 0.
Следовательно, точки ,Л(3;2;1), 2?(5;1;3), С(4;4;~2) и
D (6;-2;8) лежат в одной плоскости.
Ответ: точки А, В, С и D лежат в одной плоскости.
4.	ПРИМЕРЫ
5.1.	Известны длины векторов I а 1=5, I b 1=6, а также угол
я
ними (р — —. Найти длину их векторного произве-
6
дения.
5.2.	Даны векторы а = 3z — j — 2k и b — i^2j — к.
Найти длину и направление (направляющие косинусы) их
векторного произведения.
96
5.3,	Найти длину векторного произведения векторов а и b ,
если известно, что I а I =10, | b I =2, а • Ь ~ 12.
5,5.	Даны точки Л(2;3;1), В(4,4;0) и С(3;1;-1). Найти:
1)	АВ х Л С;	3) площадь АЛВС;
2)	(вС — 2Сл)х (ЛВ + Лс); 4) высоту ВВ} в ДЛВС.
5.6.	Сила 1 — 5/ + 3j — к приложена к точке Л(2;~ 1;4).
Определить величину и направление (направляющие коси-
нусы) момента М этой силы относительно точки
<9(3;1;5)
5.7.	Найти смешанное произведение векторов а ,Ъ и с, если:
1)	а = /; b = у; с = к,
2)	а = i + j, Ъ = 2i -ЗА:; c-j-к.
5.8.	I а 1=6, \Ь 1=3, I с 1=3, \a,b}=—, cla, clb.
6
Найти а-Ь • с.
97
5.9.	Установить, компланарны ли векторы:
1)	а = (2;3;-1), Ъ = (1;-1;3} с =	1);
2)	а = (3;—2;1), й = (2;1;2), с = (3;-1;-2);
3)	а = (2,-1;2^ = (1;2;-3), с = (3;-4;7).
5.10.	Даны точки Л(1;3;5), В(2 —1;0), С(3; —2; —3) и
D(0;l; —1). Найти объем пирамиды DABC и длину ее
высоты DO.
5.11.	Доказать, что точки Л(1;1;5), 2?(2;3;6), С(4; —1;0) i
79(3; 0,2) лежат в одной плоскости. Найти площадь четы
рехугольника ABCD.
5.12..	Найти объем параллелепипеда ABCDAXBXCXDX, если
известны точки Л (2; —I;l), 2?(5;5;4), С(3;2; — 1),
4(4;1;3).
5.13.	Даны три вершины тетраэдра А(21;4), В(0;1;3),
С(~5;0; 1). Объем тетраэдра равен 7. Найти его четвер-
тую вершину 79, если известно, что она лежит на оси
абсцисс.
5.14.	I а I =3,1 b I =4, (р — (a, b I— 90°. Найти длины векторов
98
5.15.	Даны векторы a~i + 3j~kn b — —2i + к. Найти:
1)	ахЪ\	3) (2a + Z>)xZ>;
2)	(2a-Z>)x^i + Z>);	4) (2а + й)ха.
5*16. Даны точки: Л(2;3;1), 2?(4;4;0), С(3;1;~1). Найти
(4В + 2Вс)хЯС.
5.17.	Даны вершины треугольника АВС:
В(5;-6;2), С(1;3;-1).
Найти площадь треугольника АВС него высоту BD.
5.18.	Найти вектор с, перпендикулярный векторам
а = (2;—3;1) и b = (1;—2;3), удовлетворяющий условию
*
cf+ 2у-7^)=10.
5.19.	К точке ?4(1;0;1) приложены три силы:
^ = (2;-1;3> F>(5;4;-1) и F~3 = (-4;-2;-3).
Найти величину и направляющие косинусы момента М
равнодействующей этих сил относительно точки
5(3;-4;-5).
5.20.	Найти смешанное произведение векторов а ,Ь и с, если:
1)	а = 2к, b-3i, c--j,	2) a -i + к, b = i - к, с- j.
99
5.21,	Найти объем параллелепипеда, построенного на векторах
а = (1;-1;3); й = (-2;2;1) и с = (3;-2;5).
5.22.	Векторы а ,Ь и с, образующие правую тройку, взаимно
перпендикулярны. Зная, что I а 1-4, I b 1=2, I с 1=3, вы-
числить их смешанное произведение а-Ь-с.
5.23.	Объем тетраэдра равен 5, три его вершины известны:
Л(1;2;-1), В(-1;3;0) и С(2;-1;4).
Найти его четвертую вершину D, если она лежит на оси
Oz.
5.24.	Доказать, что точки Л(1;2;-1), 2?(0; 1;5), С(-1; 2; 1) и
29(2; 1; 3) являются вершинами параллелограмма. Найти
углы и площадь этого параллелограмма.
5. ОТВЕТЫ
5.1. 15.
73	73	7д/з
cos а =—;cosp = —; cosy =---
3	15	15
5.3. 16.	5.4. 1) 27; 2) 243.
5л/^	5л/2
5.5. 1) (-4;3;-5); 2) (l6;-12;20> 3)	4)
100
5.6.	VllO
cos a =
'110
——; cos/? = -
22
зУГТо
55
cosy =
7УГ10
ПО
5.7.	1) 1; 2) 5.
5.8.	+ 27.
5.9. 1)да; 2) нет; 3) да.
7	21Уб2
5.Ю.	VMBC=--DO = ^—.
2	02
7л/з
5.11.----.	5.12. 18.
2
5.13. яДо^ £>2(-15,8;О;О). 5.14.1) 168; 2) 36.
5.15. 1) (3;1;б), 2)(9;3;18), 3) (б;2;12), 4) (-3;-1;-б).
5.16. (4;-3;5).	5.17. 5Д =12,5; BD = 5.	5.18. (7;5;1).
л 2V10 а V10
cosa =-------; cosp =---; cosy =
15	6
5.20. 1) -6; 2) 2.
5.21. 7.	5.22. 24.
5.23. D,(0;0;-l), Z>2(0;0;ll).
5.24. zS4 — XB — ; ZC — zlD —	— 6^3.
101
КОМПЛЕКСНЫЕ ЧИСЛА
1. АЛГЕБРАИЧЕСКАЯ ФОРМА ЗАПИСИ
КОМПЛЕКСНОГО ЧИСЛА
Определение 1. Алгебраической формой записи ком-
плексного числа z называется его представление в виде
z = а + ib,
(1)
где а,Ъ — вещественные (действительные) числа, называемые, со-
ответственно, вещественной частью (Re z) и мнимой частью
(Im z) комплексного числа z; число Z, называемое мнимой еди-
•2	1
ницеи, определяется равенством I = — 1.
Множество всех комплексных чисел обозначается
Замечание 1. Любое вещественное число а является
комплексным, так как его можно представить в виде (1):
а - а + i • 0.
Следовательно, 7? С2 С. Причем для вещественного числа а
Re а = а,
1т а = 0.
102
Определение 2. Два комплексных числа
z} + ib, и ~а1 + ib^
Ill	X	X*	X*
называются равными* если равны, соответственно, их веществен-
ные и мнимые части:
а. Ь. -К.
Определение 3* Комплексное число, обозначаемое z и
вычисляемое по формуле
z = а - /А,	(2)
называется комплексно - сопряженным для числа z = a + ib .
Замечание 2. Для геометрического представления ком-
плексного числа вводят на плоскости прямоугольную систему ко-
ординат Оху. Тогда число z — a + ib можно рассматривать как
точку М (a; Z>) этой плоскости (см. рис.1) или же как радиус-
вектор ОМ (см. рис.2).
Рис. 1
Рис. 2
103
Операции над комплексными числами
z} + ib} и z2 = а2 + ib2 ;
1)	z, ±z2 ~{at ±a2) + i(b{ ±62);
2)	c • Zj = (cot]) + i(cb}), где с - вещественное число;
3)	z, -z, - (a, a, - b,b,)+ i(a.b0 + а2ЬЛ\
* Д A* X * 'i Af	1 4» j	\ 1 Лг	I f
z, a,a0 +b.b1	,aJ),-a.b2 ( , , 2	\
4)	_L = 11- ' A +	(	+ b2 ф oj
z2 a2 + b2 a2 + b2
l
Замечание 3. Для комплексно-сопряженных чисел спра-
ведливы равенства:
_ --------------------- --- -------------- --
z-z-a +b ; Z, +z2 =z, +z2; z, -z2 =z. -z2; \z)=z.
2.	ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ
КОМПЛЕКСНОГО ЧИСЛА
Определение 4. Тригонометрической формой записи
комплексного числа z называется его представление в виде
z = r(cos <р + i sin (р),
(3)
104
где Г — неотрицательное вещественное число, называемое модулем
комплексного числа z и обозначаемое z\ ;
угол (0 < (р < 2л"), называемый главным значением аргу-
мента комплексного числа z и обозначаемый argz (см. рис.З).
Для комплексного числа z — a + ib
справедливы соотношения:
a~r cos <р
b-r sin$9.
Следовательно.
г~\сГуЬ2 и (p~arctg — при а Ф 0; (р~—при а-0.
а	2
Замечание 4. Формула (3) верна при замене в ней (р на
<р + 2л£, где к — любое целое число.
3, ПОКАЗАТЕЛЬНАЯ ФОРМА ЗАПИСИ
КОМПЛЕКСНОГО ЧИСЛА
О пре деление 5, Показательной формой записи
комплексного числа z называется его представление в виде
z ~ ге1\
(4)
где Г — z
<р = arg z и обозначено е>(р - cos (р + i sin <р.
105
Операции над комплексными числами
Z] = r)e'<p’ и z2 = r2e'V2 :
то есть:
п
Геометра чески операции над комплексными числами выпол-
няются по следующим правилам (см. рис. 4-11):
Рис. 5
Рис. 4
106
Рис. 7
Рис. 8
107
Извлечение корня п-й степени из числа Z~rei(p
108
4, ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Выполнить указанные действия:
а) (3-2z) + (-7 + 4z), б) (2-z)-(l + 4z) в)
1 + /
Решение. Воспользовавшись правилами сложения, умноже-
ния, деления комплексных чисел, заданных в алгебраической фор-
ме, получаем:	*
а)	(3 - 2z) + (-7 + 4z) = (3 - 7)+(- 2 + 4)-г = -4 + 2z;
б)	(2 -/)• (1 + 4/)= (2 + 4)+ (8 -1)- i = 6 + 7z;
О т в е т: а) — 4 + 2z; б) 6 + 7z; в) 1 — 2/.
Пример 2. Решить уравнения:
а)х2+4х + 5 = 0,	б)х2+16 = 0.
Решение. Воспользовавшись формулой корней квадратного
уравнения, получаем:
а)
х2 + 4х + 5 = 0 =>
х12 =-2±7(-2)2 -5 =-2±л/4-5 = -2±V-T = -2±z
xt - -2 + i, х2 = -2 - ц
109
х2 + 16 = 0=>
х12 = лДТб = V16 • лЛч = ±4 • i
=> X] = 4z, х2 = -4i.
Ответ: а) х, = —2 + /, х2 — —2 — 7;
б)	х, - 4i, х. = -4i.
Пример 3. Представить в тригонометрической форме числа:
Z1 = -1; z2 =г, z3 =1-7.
Решение. Изобразим данные числа на комплексной плоско-
сти (см. рис. 12).
Для числа находим модуль и архумеит:

Следовательно, по формуле (3)
=COSfl' + /sin Л\
Аналогично находим:
4
по
Следовательно, справедливы представления:
я . . п
z~ ~ cos—Hsm —,
2	2	2
Ответ: z} = cosjt + isin я,
я .. я
Z, = COS----F 7 Sin — ,
2	2	2
При м e p 4. Вычислить:
a) (l-z)8, 6) V16.
Решение. . Воспользовавшись правилами возведения в сте-
пень и извлечения корня из комплексных чисел, заданных в показа-
тельной форме, получаем:
+ 7-0)=16;
Ill
2лк . . 2лк^
----+ l sin---
Следовательно,
Ответ: a) 16; б) 2, -2, 2/, -2/.
5. ПРИМЕРЫ
7.1. Выполнить указанные действия:
a) (-3 + 5/) +(4-8/);	б) (1 + 2/)-(3 + 2/) ;
в) (2 + 3/)-(3-2/);
7-4/
3 + 2/’
д)
2 + 5/
-3-4/’
ж) (1+/Г;
112
з) (л/з+z)3;
и)
(3 + 5/)-(2 + 3/)
1 + 2/
к)
л) V/.
7.2.	Представить в тригонометрической форме числа:
a) z = 1; 6) z = -3 + ЗУ; в) z = -1 - У;
г) Z-4^-l-
7.3.	Решить квадратное уравнение:
а) х2 + 6х +13 = 0, б) х2 + 2х +10 = 0, в) 9х2 +1 = 0.
7.4.	Представить в тригонометрической форме числа:
a) Zj = 3;	б) z2 = -2У;	в) z3 = 1 + л/ЗУ;
г) z4 = 2 - 2У; д) z5 = -3 + ЗУ.
7.5.	Выполнить действия:
а) 2 + ЗУ) + 2 ЗУ); б) (1 + 2У^•	2 +
д) (-1 +/)5;
е) ^2 +1' VI2 J
113
ж) VT;
з) V7/.
7.6.	Решить уравнения:
а)	х2 - 4х + 8 = 0;
б)	4х2 + 25 = 0.
6. ОТВЕТЫ
7.1. а) 1—3/; б) -1 + 8/; в) 12+ 5/; г) 1-2/,
д) -1,04 - 0,28/;
ж) 32/; з) 8/;
7.2 a) cosO + /sinO;
б) Зу/2 cos — + / sin
114
М 5л" . .
b)v2 cos— + zsm
_ f	. i
г) 2 cos —- + zsin -
7.4. a) Zj
7.3. a) - 3 ± 2i;
Z2
= 3(cos0 + i sin 0); 6)
f Зл . . Зл^
cos---1- z sin—
I 2	2 )
в) z3 - 2 cos— + z sin —
д) z5 = 3V2 cos—
I 4
2__2А .
25 25Z’
; r) z4 = 2>/2 cos— + z sin
+ z sin —
д) 4 - 4z;
e) 512(1-zVJ);
7.6. a) 2 ± 2z;
115

РАЗЛОЖЕНИЕ
РАЦИОНАЛЬНОЙ ДРОБИ
НА СУММУ
ПРОСТЕЙШИХ ДРОБЕЙ
1.	РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ
Определение 1. Многочленом от X степени П (или це-
лой рациональной функцией от х) называется функция вида
/(х) = />охп + />1хя“1 + ... + b„_}x + bn,
(1)
где Ьо О, Z>0? bu...,bn — некоторые комплексные числа, х-
независимая переменная, которая может принимать любые ком-
плексные значения.
Определение 2. Корнем многочлена (1) называется то
значение переменной х, при котором многочлен (1) обращается в
нуль.
Теорема L Всякий многочлен степени п имеет ровно п
комплексных корней СГ15 ...,6Zn и может быть представлен в виде
разложения на линейные множители:
116
/(х)= й0(х-«,)•.

(2)
Опред е л е н и е 3. Говорят, что корень имеет крат-
ность kj (k. g Дт), если множитель (х - а}) входит в разложе-
ние (2) к} раз.
С войс тв о 1. Если в формуле Ц) ьсе коэффициенты - ве-
щественные числа, но многочлен имеет комплексный корень
а + ib кратности к$ , где Ь Ф 0, то этот многочлен имеет также
сопряженный корень a — ib, кратность которого равна kQ .
Свойство 2, Если оставить в перечне корней многочлена
только различные и учесть их кратность, то многочлен (1) с веще-
ственными коэффициентами можно представить в виде произведе-
ния
/(х)=йо(х-°1)*'	(я2	+	•	(г2	+	,(3)
где
к} +... + кт + 2/j +... + 21 s — и,
числа ( 1 < j < т ), р-, qt (1 < z < 5) в разложении (3)
являются вещественными, причем
а,	(l<z’J<m);
р] <	j *);
117
2.	РАЗЛОЖЕНИЕ РАЦИОНАЛЬНОЙ ДРОБИ
Опр е деление 4. Рациональной дробью называется вы-
Р_(х) п t \ t \
ражение вида —т-т, где гт\х), (/„(xj —многочлены пох
степеней т и п соответственно.
Р(х)
Определение 5. Рациональная дробь —т-4- называет-
QA*)
ся правильной. если т < п. В противном случае, если ТП > и, то
она называется неправильной.
Опред е л е и и е 6. Простейшими рациональными дробями
называются дроби следующих четырех типов:
---- (А, а = const, A,a&R)-,
х-а
П. --------— (A,a,k = const,A,a&R,k&N,k>2)-,
(х - а)
III.
Mx + F
х2 + px + q
IV.
Mx+F
(x2 + px + q}k
'М, F, p,q- const, p2 < 4q,
l M,F,p,qeR j
'M, F, p,q,k = const,
M, F,p,q& R;
^k>2, keN; p2 <4q^
118
Теорема 2, Всякая неправильная рациональная дробь пред-
ставима в виде суммы многочлена (ее целой части) и правильной
рациональной дроби.
Замечание 1. Такого представления можно достичь, на-
пример, с помощью деления многочленов Рт(х) на Qn(x) «в
столбик», прекращая процедуру деления как только степень много-
члена, сформировавшегося в остатке, станет меньше степени мно-
гочлена Qn(x).
Теорема 3. Всякую правильную рациональную дробь мож-
но представить в виде суммы конечного числа простейших рацио-
нальных дробей.
Замечание 2. На практике осуществить разложение пра-
вильной рациональной дроби ---г-v на сумму простейших рацио-
нальных дробей можно по следующей схеме.
♦ Найти корни многочлена
<?и(х)=х” +Ьухп~х + ... + Ь }х + Ь
\ /	i	Л—1	Л
и представить его в виде разложения на множители:
2П(Х)=(Х-Й1Г • (х~аг)*г (x2 + Pix + ^J • --(х2 +px + qs^,
где
ai^aj (l<i,J<r);
P2i <	(1 < j < 5);
119
♦ Записать разложение с неопределенными коэффициентами:
(3)
содержащее к} + ... + kr +lx + ... + ls слагаемых.
♦ Определить коэффициенты Ли,	sl ,
F} j,..., Fsl > суммарное число которых равно П.
Замечание 3. Определить коэффициенты разложения (3)
можно многими способами. Например, приведя (3) к общему зна-
менателю, придем к задаче о равенстве двух многочленов. Прирав-
нивая в них коэффициенты при одинаковых степенях х, получим
систему и линейных уравнений с п интересующими нас неизвест-
ными, имеющую единственное решение. Такой метод называют
методом неопределенных коэффициентов.
Замечание 4. метод неопределенных коэффициентов при-
водит к цели всегда, но является довольно громоздким.
В ряде случаев удается определить коэффициенты, участвующие
в разложении дроби на сумму простейших рациональных дробей,
более простым способом, носящим название метода зачеркивания.
Изложим его суть.
120
Пусть знаменатель правильной рациональной дроби --
QAX)
имеет вещественное число а своим корнем кратности к .
В этом случае среди простейших дробей, на сумму которых рас-
Р (х)	А
кладывается дробь--, будет фигурировать дробь ------, а
QAX)	(x-af
многочлен Qn (х) представим в виде
£,(*)=(*-*)* •#(.*)>
где g(x)-~ многочлен по х степени п - к , причем g(p)^ 0.
Тогда коэффициент А равен:
_ л.(д)
Таким образом, для вычисления коэффициента А следует в
Рт(х)
знаменателе исходной дроби --«зачеркнуть» скобку
QAx)
/	\4
(X — а) ив оставшееся выражение подставить х = а .
3.	ПРИМЕРЫ С РЕШЕНИЯМИ
П рнмер 1. Определить, какие из указанных рациональных
дробей являются правильными:
121
Ax4 -lx+ 2
Решение, а) Дробь является неправильной, так как степени
многочленов, стоящих в числителе и знаменателе , совпадают
(равны четырем).
6)	- в) Дроби являются правильными, так как в числителе стоит
многочлен степени 4, а знаменателе - степени 5 в б) и 6 в в).
Ответ: б), в).
/(х)
Пример 2, Неправильную рациональную дробь за-
менять суммой многочлена и правильной рациональной дроби, если
а)	/(х) = Зх4 - 2V + 7х - 5, g(x) = х3 +2;
б)	/(х)-Зх4-2х2 +7х-5, g(x)=x2-x + 3.
Решение. Для решения примера разделим многочлен У(х)
на многочлен g(x)
а)
Зх4 -2х2 + 7х-5
Зх4 + 6х_____
- 2х2 + х - 5
Следовательно,
-2х2 +х-5
х3 +2
122
б)
Зх4 - Зх3 + 9х2
Зх2 +Зх-8
- 8х2 + 8х - 24
-Юх + 19 .
Следовательно,
-Юх + 19
Ответ:	а)
б)
”10x4-19
Та _ . э
Пример 3. Разложить на множители многочлен
/(х) - х4 + х3 4- 2х - 4.
Решение. Вещественный целый корень многочлена j (х)
следует искать среда целых делителей числа 4 ~ свободного члена
многочлена У(х). Ими являются числа 1; — 1; 2, — 2; 4, — 4.
Вычислим значения многочлена j(x) при указанных х:
123
/ОМ; /(-1) = -6<0; /(2) = 24>0;
/(- 2) = 0; /(4) = 324 > 0; /(- 4) = 188 > 0.
Следовательно, числа = 1, а2 — — 2 являются корнями
многочлена f (х ).
Отсюда вытекает справедливость представления:
(4)
где	— некоторый многочлен.
Найдем многочлен g(x), разделив /(х) на многочлен
(х — 1) • (х + 2), то есть на квадратный трехчлен х2 + х — 2 :
х4+х3+2х-4	х2+х-2
х4 + х3 - 2х2 х2 + 2
2х2+2х-4
2х2 + 2х - 4
0 .
Итак, вычисления показали, что в формуле (4)
g(x) = x2 +2,
причем g(X) не разлагается на линейные множители с веществен-
ными коэффициентами (так как дискриминант этого квадратного
трехчлена меньше нуля).
Следовательно, воспользовавшись равенством (4), получаем:
Ответ:
124
П_В. и м е р 4. Написать разложение дроби
4х4 + 5х3 ~ 1
х2(2х + 5)4(х2 -г б)3
на сумму простейших рациональных дробей, не находя коэффици-
ентов разложения.
Ответ:
П ример 5. Разложить дробь на сумму простейших рацио-
нальных дробей и найти коэффициенты разложения:
43х2 -5х-14
а) —:--;---—;
х3 + х~ - 2х
х + 4х + 3
в)
4х3 - Зх2 + 5х + 6
х4 -2х3 + 3х2
43х2 -5х-14
Решение, а) Дробь —;--------~------является правиль-
xJ + х - 2х
ной. Для ее знаменателя справедливо представление:
125
х3 + х2 - lx = X • (x -1)- (x + 2).
Запишем разложение дроби на сумму простейших рациональных
дробей с неопределенными коэффициентами:
43х2-5х-14 _А В С
х-(х-1)(х +2) х х-1 х + 2
(5)
Найдем коэффициенты разложения (5) методом неопределен-
ных коэффициентов.
Приведем равенство (5) к общему знаменателю и приравняем
числители получившихся при этом дробей:
43х2 - 5х -14 = Jx2 + Ах - 2А + 5х2 + 2Вх + Сх2 - Сх.
Отсюда, приравнивая коэффициенты при одинаковых степенях
х, приходим к системе:
X2:	А +В + С = 43
х1:	А + 2В — С
х°-	-2А=-\4
А = 7,
5 = 8,
С = 28.
Следовательно, подставляя найденные числа А, В, С в разло-
жение (5), приходим к равенству:
43х2-5х-14 7	8	28
--:-------= - +---+-----.
х + х -2х х х-1 х + 2
Покажем, как числа Л, В, С можно было найти из форму-
лы (5) методом зачеркивания:
126
-2
43 • 1 - 5 • 1 -14 _ 24
43-4-5-(-2)-14 _ 168
- 2 • (-3)	~ 6
= 28.
б) Дробь
х3 + 4х + 3
- правильная. Знаменатель этой
дроби представим в виде:
Поэтому
х3 + 4х + 3
С D
+ ~,—лГ + 7—7? (6)
(х +1) (х +1)
Коэффициенты А, В этого разложения найдем методом зачер-
кивания:
127
Для поиска коэффициентов С и D подставим в (6) вместо X
любые два числа (кроме тех, которые уже были использованы).
Например:
X = 0:
х = -2:
— —1 +1 + С + D\
Отсюда для поиска коэффициентов С и D получаем систему:
C-D = -3
с = -з
<
D = 0.
Подставив найденные числа
приходим к равенству:
С, D в разложение (6),
4х -Зх + 5х + 6
в)	Дробь --т----------z— - правильная. Ее знаменатель
х - 2х + Зх
имеет вид:
х4 - 2х3 + Зх2 = х2 (х2 - 2х + з),
128
причем у квадратного трехчлена X2—2х + 3 дискриминант
меньше нуля, и он не разлагается на линейные множители с веще-
ственными коэффициентами.
Поэтому
4х3 -Зх2 +5х + 6
х4 - 2х3 +3х2
4х3 -Зх2 + 5х + 6 _ А ±В Сх + Z)
х2 • (х2 - 2х + з) х2 х х2 - 2х + 3
Методом зачеркивания находим число А:
х = 0: А = 6/3 = 2.
Для поиска коэффициентов В, С, D приведем (7) к общему
знаменателю и приравняем числители:
4х3 - Зх2 + 5х + 6 = 2(х2 - 2х + з)+ Вх(х2 - 2х + з)+ (Сх + £>)х2.
Используем правило: многочлены равны, если равны коэффици-
енты при одинаковых степенях х. Это приводит к системе:
-3 = 2-25 + 1)
5 = -4 + ЗБ
6 = 6
129
Отсюда:
В = 3
2B-D = 5>
ЗВ = 9
Z) = l
Подставив найденные числа А, В, С, D в разложение (7),
приходим к равенству:
4х3-Зх2+5х + 6	2	3 х +1
------------- —----1~-1--------
х4-2х3+Зх2 х2 х х2-2х + 3
43х2-5х-14 7	8	28
а) — --------= —+----+----;
х3+х2-2х х х-1 х + 2
4х3-Зх2+5х + 6	2	3 х + 1
-------------- ----1--|~-------
х4-2х3+Зх2 х2 х х2-2х + 3
4. ПРИМЕРЫ
Разложить дроби на сумму простейших дробей:
(х-1)(х + 3)
8х +1
х2 - 4х + 4
х2 - х-6
130
8х + 8	Зх + х2+5х + 1
7.5. —--------.	7.6. ------------.
х + 10х2+9	х3 + х
х2 -Зх + 7	29х2 +169х + 599
(х-1)2х(х + 1)’	7'8* 1з(х2+9)(х + 2)2
♦ ♦
Разложить дроби на сумму простейших дробей,
не находя коэффициенты:
8х2 - 10х + 5
7.9.	т------г-
(Зх +1/ • (х2 + if
Разложить дроби на сумму простейших дробей:
7.15.
8х2-10х + 5
(2х -1)2 • (2х +1)
7.16.
131
7.18.
X4 - 16
5. ОТВЕТЫ
132
7.10.
7.14. х + 1-
2
л
...	3/2	1/2 ,	1/4
х + 1/2 х-1/2 (х-1/2)2
1	2
7.16. — +-----.
х	х + 1
2
2х-1
2 , ,
7.18. 1+
2
7.19. х + 2 -
1	1
7.20. - + — -
X	X
х + 3
х2 + 2х + 2
133
о.
МАТРИЦЫ.
ОПЕРАЦИИ НАД МАТРИЦАМИ
1. МАТРИЦЫ
О пр еделение 1. Матрицей размерности тхп называ-
ется прямоугольная таблица чисел вида:
А =
I а
J

содержащая т строк и п столбцов. Числа, составляющие матрицу,
называются ее элементами. Их обозначают , где i — иомер
строки матрицы, j — номер столбца матрицы, на которых располо-
жен данный элемент.
Матрицу обозначают:
А или (а..). —
7=1 Л
Определение 2. Две матрицы называются равными, ес-
ли они совпадают поэлементно.
140
Пример 5, Вычислить:
а)
б)
>
2
0
О
Решение, а) Первая из перемножаемых матриц имеет раз-
мерность 2 х 3 , а вторая матрица - размерность 2x1.
Так как число столбцов первой матрицы не равно числу строк
второй, то данные две матрицы перемножить нельзя.
б)	Пользуясь формулой (1), находим матрицу размерности
2x1:
в)	Пользуясь формулой (1), находим матрицу размерности 1x3:
0
141
г)	Пользуясь формулой (1), находим матрицу размерности 2x2:
Л О
к-1
' 0-1 + 1(-3)+2-2 j 01 + 10+2-(-1) Wi 1	-2^
J-ij-l + 7-(-3)+3-2! (-lj-l + 70 + 3-(-l)J”|Д 16 -4,
Ответ: а) не существует;
В)(3 -20 -7);
б)
г)
Пример 6. Найти и сравнить матрицы А-В и В- А, ес-
ЛИ
142
Решение. Перемножим данные в примере матрицы А, В ъ
порядке А- В и В • А :
=> А- В * В  А;
Ответ: а)
б)
в)
16;
143
Пример 7. Найти А2, если
в) А =
<1 О 0 0Л
1^0 О
2J
О
О
5
О
О О
О О
О
Решение. Так как А2 = А • А и все данные в примере мат-
рицы являются квадратными, то вычисляем:
О oY
О
в)
0 0	0 25
О 2) _Д0 О
О 0Л
О о
о о
0 4>
М О
О
5
О
^0 О
Ответ:
а)
г7 10\
ч15 22)
2>
fl О 0 0Л
25 О
О О
О
О
о
о
4;
144
4. ПРИМЕРЫ
8.1. Вычислить:
145
ж)
11
з) (3
л-1 2 -3 0\
к0 4 -2 3 J’
8.2. Вычислить:
а) АВ — В А, если
146
О
О
2
О

д)
(4
О -2
е)
О
ж)
О
-2
1 О
О
О
о
О ’
-2.
О 4)- О
147
5. ОТВЕТЫ
148
9 >
3
-6>
б) 3 10 О
в) (31);
<12 0 -6	9	3>
Д)
4
-4
20
О -10 15
0-2	3
0	2-3
8 0 -4	6	2)
л3 -9 0 -12^
2-2	1 О
-2 6	0	8
ч-3	1	-2	-4;
з) (14 -5);
И)
Г- 50Л
149
§9
РАНГ МАТРИЦЫ
1.	СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
Определение 1. Элементарными преобразованиями
строк матрицы называются преобразования следующих трех типов:
1)	перестановка местами двух строк матрицы (условное обо-
значение:^"
, где стрелки указывают на строки,
переставляемые местами);
2)	замена строки суммой этой строки и некоторой другой,
вспомогательной, предварительно умноженной на какое-либо
число а (условное обозначение: • (а), где стрелка указывает
на изменяемую строку; миожитель * (а) ставится рядом со
вспомогательной строкой);
3)	умножение строки на ненулевое число (X (условное обозна-
чение: • (а), ставится рядом с преобразуемой строкой).
Замечание 1. Аналогично вводятся элементарные преоб-
разования столбцов матрицы.
Определение 2. Опорным элементом строки матрицы
называется первый слева ненулевой элемент этой строки. (Услов-
150
ное обозначение: опорный элемент обводят кружочком или квадра-
том). Если строка нулевая, то опорного элемента у нее нет.
Определение 3. Матрица называется ступенчатой (или
имеющей ступенчатый вид), если выполнены следующие условия:
Д* если какая-то строка матрицы нулевая, то все последующие
строки - нулевые;
•	опорный элемент в каждой последующей строке расположен
правее, чем в предыдущей.
Определение 4. Говорят, что ступенчатая матрица имеет
вид Гаусса, если
•	все опорные элементы равны единице;
•	над опорными элементами стоят только нули.
Теорема!. Любая матрица А может быть приведена к сту-
пенчатой матрице А} даже только с помощью элементарных пре-
образований строк первого и второго типов.
Любая матрица А может быть приведена к ступенчатой матрице
А2 вида Гаусса с помощью элементарных преобразований строк
первого - третьего типов.
Определение 5. Ступенчатые матрицы А} и А2, постро-
енные по матрице А с помощью элементарных преобразований,
называются, соответственно, ступенчатым видом матрицы А и
видом Гаусса матрицы А.
Определение 6. Строки и столбцы матрицы А}, на пере-
сечении которых расположены ее опорные элементы, называются
базисными строками и базисными столбцами исходной матрицы.
Замечание 2. Ступенчатый вид у матрицы и ее вид Гаусса
не единственен. Набор базисных строк и базисных столбцов матри-
цы также не является инвариантом этой матрицы.
151
2. РАНГ МАТРИЦЫ,
РАНГ СИСТЕМЫ ВЕКТОРОВ
Определение 7. Рангом матрицы А называется число
ненулевых строк в ступенчатом виде этой матрицы. Используется
обозначение:
г(Л) или rang Л.
Замечание 3. Очевидно
О <r(A) <min (w, и).
Замечание 4. Ранг матрицы не меняется при применении
к матрице А элементарных преобразований, то есть ие зависит от
способа приведения матрицы к ступенчатому виду.
Определение 8. Рангом системы ги-мерных векторов
называется ранг матрицы размерности тхк , столб-
цами которой являются эти векторы.
3, ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Привести матрицу к ступенчатому виду
А-
О 1 2Л
2 1 О
2 2 2
2 0 ,3>
152
Решение. Выполним следующую цепочку элементарных
преобразований:
	<10 12^	(-2)(-3)	<10 1	2	
А =	2 2 10 3 2 2 2		02-1-4 0 2-1-4	i1}
^0 2 0 3J	^0 2 0	3 X
0 1
0 2-1
ООО
к0 0 1
Ч 0 1	2	>
02-1-4
О 0~| 1	7
^0 0 0	0	j
Ответ:
<10 1	2 >
02-1-4
0(Л 1	7
^0 0 0 О J
Пример 2, Указать два ступенчатых вида матрицы
(\	2	3	4	>
,	0	0	12
А —
12	4	6
^2	4	0	-4?
153
Назвать базисные строки и столбцы матрицы А .
Решение. Способ 1:
2 3
О 1
2 4
4 О
2
О
О
О
3
1
1
-6
2 3 4^
0 0 12
0 0 0 0
,0 0 0 0,
Отсюда заключаем: у матрицы А
базисные строки- Is, 2-;
базисные столбцы- Is,3й.
Способ 2:
2 3
О 1
2 4
4 *0
6V-1X-2)
2
154
rl 2 4
О О 1
OO-l
J) 0 -8
(0(8)
6
Г1 2 4 6Л
О р| 1 2
0 0 0 0
^0 О О О,
Отсюда следует, что у матрицы А
базисные строки - 2~ и 3-;
базисные столбцы - 1~ и 3- .
Ответ:
Г1 2 3 4А
0 0 12	базисные строки- 1, 2;
0 0 0 0	базисные столбцы- 1, 3.
к0 0 О О,
0 0 0 0
к0 0 0 0>
базисные строки- 2, 3;
базисные столбцы- 1, 3.
Пример 3. Привести матрицу к виду Гаусса
155
Решение:
''О 2 Зл	«-• Г1 2 3"(-2Х- 3)					f 1
О 2 1		О 2 1				0
1 2 3	<2	—->	0 2 3			—->	0
2 1 1		2 1 1				0
Ь 2 1J		<3 2 1J				<0
О
О
О
О
156
Л1 о оЛ
О 1 о
-> О oil
ООО
^0 О 0J
Ответ:
О 0л
~о| 1 о
О о[ 1
ООО
^о о о;
Пример 4. Найти ранг матрицы
4 0 6
2 3 0
Решение:
2 3 0V-2)
4 0 6
2 0 3
6 6 3 J<-
157
rl 2 3
0 4 0
0 2 0
J) 2 0
rl 2 3 0^
0~|4 0 6
0 0 0 0
J) 0 0 0;
=> r(A) = 2.
Ответ: r(A)=2.
4. ПРИМЕРЫ
9.L Привести матрицы к ступенчатому виду:
158
9.2. Привести матрицы к виду Гаусса:
Л2 7 3 1 6Л
в) 3 5
2 2 4
1 7 2;
9.3. Найти ранг матрицы:
(7	2	3	15л
5	3	2	9
10 -11 5 36
k2 -1 1 6;
159
9.4. Привести матрицы к ступенчатому виду:
<1 2 3 4 5 6 7>
а) 2	1	3	1	4	1	О
^0	3	О	4	О	5	О,
<3-13 2 5 А
2 3	4
-5 0 -7
1	4	1
9.5. Привести матрицы к виду Гаусса:
160
9.6.Найти ранг матрицы.*
r2 1 -1-1 Р
1-11	10
3 3 -3-32
ч4 5 -5-5 3;
'0 4 10
4	8 18 7
10 18 40 17 ’
Ч1 7 17 3;
I 3 0 V
4 5	6
7	8	9
J0 11 12;
5. ОТВЕТЫ
9.2.
Ч о -Р
О 1 2
ООО
ч0 0 0)
161
1 о
^0 о
1	9
Н	П
5	1
11	11
О	О
11
10
11
о ,
9.3. а) 2; б) 2; в) 3; г) 3.
9.5.
О
О
о
1
{0 0 0 0 О J
^0 0 О 0J
9.6. а) 2; б) 3; в) 2; г) 2.
162
S10.
ОПРЕДЕЛИТЕЛЬ
КВАДРАТНОЙ МАТРИЦЫ.
ОБРАТНАЯ МАТРИЦА
1. ОПРЕДЕЛИТЕ ЛЬ
Определение 1. Каждой квадратной матрице А порядка
п (где п >1) ставится в соответствие число, называемое опреде-
лителем матрицы А, обозначаемое \А I или det Л, вычисляе-
мое по правилу:
|^11 । — ^11 5
«12
— аи
«22	«21 ' «12 J
«11
«21
«22
«11 «21	«12 «22	«13 «23	= °и-	«22 «32	0 О UJ	к> Ш	UJ	«12 ’	«21 «31	«23 «33	+а13-	а21 «31	«22 «32
«31	«32	«33									
163
и так далее:
ап	а\2	• • •	а1п		^22	* .
а2\		« « •	а2„	= чг	• • •	• •
		- ’ ’	’ ’ ’		ап2	
а„1	ап2	• • •	апп			
а2„		а2] а23 ...	
•..	а\2 ’	• • • • • • • • • • • •	4-
аш,		Чй 4.3 ••• Чш	
0L 1
Z П~1
« « «
О и 1
П П—1
(1)
(Формула (1) иосит название разложения определителя по эле-
ментам первой строки. Определитель может быть вычислен раз-
ложением по элементам его любой строки или столбца.)
Замечание 1. Для определителя используют те же терми-
ны (элементы, строки, столбцы, главная и побочная диагонали), что
и для соответствующей матрицы, чей определитель вычисляется.
Свойства определителя.
1)
определитель не меняется при замене в нем всех строк соот-
ветствующими {по номеру) столбцами, то есть
2)	определитель равен нулю, если содержит нулевую строку или
нулевой столбец,
164
3)	определитель равен нулю, если содержит две одинаковые
строки или два одинаковых столбца,
4)	определитель треугольной матрицы равен произведению эле-
ментов главной диагонали',
5)	определитель изменит знак на противоположный, если в
нем поменять местами любые две строки или столбца (то
есть применено элементарное преобразование первого типа);
6)	определитель не изменится, если в нем заменить строку сум-
мой этой строки и некоторой другой, вспомогательной, пред-
варительно умноженной на какое-либо число (то есть приме-
нено элементарное преобразование второго типа);
7)	если строку (столбец) определителя умножить на некоторое
число (то есть применено элементарное преобразование
третьего типа), то определитель умножится на это число .
2> МЕТОДЫ ВЫЧИСЛЕНИЯ
ЭЕДЕЛИТЕЛЯ
Существуют различные способы вычисления определителя, на-
пример по формуле (1), путем понижения порядка вычисляемого
определителя. При этом разлагать определитель можно по любой
строке или столбцу.
Широко применяется способ, основанный на свойствах 5)-7), то
есть возможности преобразования определителя к треугольному
виду с помощью элементарных преобразований строк (или столб-
цов) и применению далее свойства 4).
165
3.	ОБРАТНАЯ МАТРИЦА
Определение 2. Квадратная матрица порядка п, обо-
значаемая А 1, называется обратной для квадратной матрицы А
порядка п, если выполняются равенства
АА'[ = А1 А = Е,
где Е - единичная матрица порядка п .
Теорема 1. Для того, чтобы квадратная матрица А имела
обратную, необходимо и достаточно, чтобы определитель матрицы
А был отличен от нуля.
Замечание 2. Одним из способов построения обратной
матрицы является следующий.
1)	Составить расширенную матрицу (Л|£), приписав после мат-
рицы А за вертикальной чертой единичную матрицу той же раз-
мерности, что и А.
2)	Матрицу (А Е) с помощью элементарных преобразований
строк привести к ступенчатому виду Гаусса.
Если при этом на месте матрицы А получилась матрица Е,
то за вертикальной чертой находится матрица А 1. В противном
случае IА | =0 и матрица А 4 не существует.
Определение 3. Минором элемента ai}. квадратной
матрицы А л-го порядка называется определитель матрицы
(л-1)-го порядка, получающиеся из матрицы А вычеркиванием
7-й строки и у-го столбца.
166
Определение 4, Алгебраическим дополнением эле-
мента матрицы А называется его минор, взятый со знаком
(—1)7+;. При этом используется обозначение:
4, =(-1Г-л/г
Замечание 3. Справедлива следующая формула, позво-
ляющая построить обратную матрицу для любой квадратной мат-
рицы А при условии А Ф 0 :
В частности, для квадратной матрицы второго порядка
для которой А Ф 0, из формулы (1) следует равенство:
167
4.	РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ
Теорема 2, Если IА I ^0 и А, В - матрицы порядка п,
то решение матричного уравнения
А* X — В (или X • А = В),
I
где X — квадратная матрица порядка W, находится по формуле:
Х = А~' В (или Х-В-А~}).
Теорема 3. Если IА | тЮ и I С | тЮ, где A, В, С - матри-
цы размерностью nxn,nxm9mxm9 то решение матричного
уравнения
где X — матрица размерности пхт, находится по формуле:
Х = А~' В С~\
4. ПРИМЕРЫ С РЕШЕНИЯМИ
При м е р 1. Вычислить определитель
2 3 10
0 2 0 0
4 12 1 5'
J 21 7 0|
168
Решение. Воспользуемся методом разложения определителя
по его второй строке, а затем по третьему столбцу:
2 3 1
о о
4 12 1
3 21 7
= -1011 = -110.
Ответ: -ПО.
Пример 2. Вычислить определитель
2-11 О
0 12-1
3-12 3
3 16 1
Решение. Воспользуемся методом приведения определителя
к верхнетреугольному виду:	*
169
2
О
О
о
-1
1
о
о
-1
1
о
о
Ответ: 0.
Пример 3. Найти обратную матрицу к матрице
Решение. Вычисляем определитель: А = 6 — 5 = 1.
Следовательно, обратная матрица существует. Найдем ее по
формуле из замечания 3:
Проверка'.
-1 2
170
Пример 4
Найти матрицу, обратную к матрице
Решение,
замечании 2:
Способ 7. Воспользуемся схемой, описанной в
о 0V1X-1)
2 3 10
3 5 11
12-10
0Л
О «
1
Г1 2 3
->012-
ч0 3 5
Г1 0 -1 3
-> О 1 2-1
к0 0 1-4
1 (-2Х-^)-> о
О
О
0-130 -2^
1 2-10	1
О
О
-1
-2'|<—
1
3j(-2Xl)
Г1 О О
О 1 о
,0 0 1
м
О
о
о
о
о
Следовательно,
171
Способ 11. Воспользуемся замечанием 3.
Вычислим определитель данной матрицы:
И
3
.5
2 =5 + 4-9-3-6 + 10 = 1.
Найдем алгебраические дополнения ко всем элементам матрицы А:
172
Следовательно, по формуле (1) получим:
Проверка:
2
1
3
О 0Л
1 О
0 Ъ
2
1
3
О 0Л
1 о
0 Ъ
И р и м е р 5, Решить матричное уравнение
А - X = В, где
173
Решение. Найдем матрицу, обратную к А:
А\ = 4 - 6 = -2 =>
Умножив обе части уравнения на А 1 слева, получим:
А~' АХ = А~1В или Х~А~‘В.
Следовательно, получаем:
5. ПРИМЕРЫ
10.1.	Вычислить определители:
3 2 0 0
4 5 0 0
6 7 2 3
8 9 3 7
2 14 3 5
3 4 0 5 0
4 6 0 7 0
174
6
9
7
-5 8
7 5
5 3
4
2
7
-4	8 -8 -3
10.2.	Найти обратные матрицы к матрицам:
10.3.	Решить матричные уравнения:
175
10.4. Вычислить определитель:
а)	2-341 4-232 1-110 3-143	;	б>	8	7	2	10 -8 2 7 10 4 4 4	5 0 4-32	5
	2	-1	1	0
	0	1	2	-1
в)				
	3	-1	2	3
	3	1	6	1
3 2 10
0 12 3
0 3 2 -1
3 16 1
10.5. Найти обратные матрицы к матрицам:
176
10.6. Решить матричные уравнения:
5. ОТВЕТЫ
10.1. а) 35; б) -4; в) 100.
10.2.
0,2>
177
' 1 -1 1 Л
-38 41	-34
ч 27 - 29 24 ;
г) -5 18 -7
1 -3
10.4. а) 5; б) -1800; в) 0; г) 162.
10.5. а)
(-3/5	2/5	1/5
б) -8/15 7/15
1^2/15 2/15
<2/31 -9/31 -3/62>
в) 9/31	6/31
^3/31
2/31
1/31
11/62,
(-7	5	12	-19>
3-2-5	8
41 -30 -69 111
к-59 43	99	-159,
10.6. а)
178
РЕШЕНИЕ
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
1. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕЬ
1515
О п р еделение L Системой линейных уравнений*
состоящей из т уравнений с п неизвестными
называется система вида
апх1 +-+а1пх„ =
<?21^1 + ’” + ®2»*и — ^2
(1)
^_]Х] + ••• + £/ X —
V ml 1	тп п т ’
где au,"-,amn,bi,--,bm -некоторыечисла.
Если в формуле (1) Ь} = 0, • • •, Ьт = О, то система называется
линейной однородной. В противном случае система (1) называется
линейной неоднородной системой.
179
где х —
Замечание 1. Система (1) может быть записана в
векторной форме
— вектор-столбец неизвестных,
столбец свободных членов,
матрица системы.
— вектор-
Определение 2. Расширенной матрицей системы (1)
называется матрица, полученная приписыванием к А справа после
вертикальной черты столбца Ъ , обозначаемая (А Ь).
Определение 3. Решением системы (2) называется
любой и —мерный вектор X, при подстановке которого в (2)
получаем тождество.
Определение 4* Система называется совместной^ если
она имеет хотя бы одно решение. В противном случае система
называется несовместной.
Теорема 1 ( Кронекера - Капелли ). Система (1) совместна
тогда и только тогда, когда ранг матрицы системы равен рангу
расширенной матрицы, то есть
180
г(а)=г(а b).
При этом, если г[А) = п, то система имеет единственное решение;
если г(А) < И, то система имеет бесконечное множество решений.
Теорема 2« Решение системы (2) имеет вид
х = Хо + Cj + • • • + ск 1к,
(3)
где число к , называемое числом свободных неизвестных системы
(2), вычисляется по формуле к ~п — г(а) ;
с1 ,..., ск — произвольные постоянные числа;
/],..., 1к — постоянные п — мерные векторы, являющиеся линейно
независимыми решениями соответствующей линейной однородной
системы А • х — 0;
Хо — частное решение линейной неоднородной системы (2).
2. МЕТОДЫ РЕШЕНИЯ
1.	С помощью обратной матрицы
Теорема 3. Если матрица А - квадратная и ее определитель
не равен нулю, то система (2) имеет единственное решение,
вычисляемое по формуле:
хо = А 1 -Ь,
где Л1 ~ матрица, обратная к матрицей.
(4)
181
2.	Правило Крамера
Теорема 4> Если матрица А ~ квадратная и ее определитель
не равен нулю, то система (2) имеет единственное решение Хо,
координаты которого могут быть вычислены по формуле:
(5)


где А — определитель матрицы Л, А; -определитель матрицы,
полученной из А заменой в ней j— го столбца на столбец b .
Замечание 2. Решения, построенные по формулам (4) и
(5), совпадают.
3.	Метод Гаусса
Для решения системы (1) нужно выполнить следующие
действия:
1)	Составить расширенную матрицу 1Л/> ) и привести ее к
ступенчатому виду с помощью элементарных преобразований
строк.
b L сделать выводы:
Если г(Л)-- / (А
-	система совместна;
-	базисными неизвестными объявить те, номера которых совпадут
с номерами базисных столбцов ступенчатого вида матрицы Л,
содержащих опорные элементы этой матрицы; остальные
неизвестные объявить свободными;
-	число свободных неизвестных равно к ~ п -~ г(Л);
-	перейти к выполнению следующего шага.
2)	Привести ступенчатую матрицу, полученную на шаге 1), к виду
Гаусса.
182
3)	Написать систему линейных уравнений, соответствующую
матрице, построенной на шаге 2), обозначив свободные
неизвестные числами с,,   •, ск.
4)	Выразить из полученной системы базисные неизвестные через
свободные.
5)	Записать ответ, воспользовавшись или векторной формой
записи (3), или покоординатной:

Замечание 3. Применение метода Гаусса не требует,
чтобы матрица системы А была квадратной и предварительного
вычисления ее определителя.
3.	ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Для системы
2x + 3y-z - 5
х - у + 5z = 3
4х + 7z = 7
указать матрицу системы А и столбец свободных членов b .
Записать систему в векторной форме.
Решение. Матрица А составляется из числовых
коэффициентов, стоящих в системе при неизвестных.
Поэтому в данном примере
183
Столбец Ъ составляется из свободных членов системы:
3
Если обозначить столбец неизвестных х —
то систему
можно переписать в векторной форме:
А • х - Ь .
Пр и м е р 2. Исследовать на совместность систему
х + 2z = 1
< Зх - у = 1
4х - у + 2z = 1.
184
Решение.
В данном случае А = 3 -1 0 ,
О 2>
Выполним шаг 1) метода Гаусса:
2
О
2
Г1 О
1V-3X-4) р
1 <J	—> О
1 <—о
о
-1
-1
о
о
-1
2
-6
О
о
Следовательно: г(л)=2, г(а Ь^—
Ответ: система несовместна.
Пример 3. Решить систему
х + 2z -1
Зх-у = 1
4х-j + 3z = l.
Решение. В данном примере
185
О
о
b =
1
и	А = det А — — 3 — 6 + 8 - — 1 ф 0.
Поэтому для решения системы можно воспользоваться (на
выбор) теоремой 3, теоремой 4 или методом Гаусса.
Способ I (с помощью
обратную матрицу:
А 1). Построим для матрицы А
(Л|Е)= 3
Оу-ЗХ-4)
О
О
2
О
о
о
О
1
О
О
2
О
О
О (Л
1 О
О
о
О
-1
О
2
-6
1
1
-3
-1
О
1
-1
О -1
1Дб)(-2) ^0 О
3
-9
-1
2
-5
-1
о
о
1
о
о
о
2
5
о
9
=(^4 1). Отсюда А 1
2
5
9
О
186
Следовательно, по формуле (4) вычисляем:
то есть х = 3, у = 8, z = -1.
Способ II {правилоКрамера). Вычислим:
О 2
1	0 1
Отсюда
187
Способ III (метод Гаусса).
<1 0 2 1V-3X-4) <10	2	1 >
0	2
->0—1—6
<0 0	1
<1
(б‘Х-2)
г(а)=г[а |Л )=3,
п = 3,
система совместна,
решение единственно
<1 0 0
->0—10
к0 0 1
U о
0 J
ч0 о
о
о
1
Ответ: х = 3; у = 8; z = -\.
Пример 4. Исследовать на совместность и решить систему

- X] + 7х2 +11х3 + Зх4 + 8х5 = 1
- 2Xj + 4х2 + 6х3 - 4х4 + х5 = 0.
188
Решение. Воспользуемся методом Гаусса. Для этого
составим матрицу системы, столбец ее свободных членов и
преобразуем расширенную матрицу (АЛ) к виду Гаусса:
3	5	7	0
5	8	5	4
10 16 10 8
10 16 10 1
(1	3	5	7
-1	2	3	-2
-1	7	11	3
<-2	4	6	-4
3 5 7
0 5 8 5
0 0 0 0
^0 0 0 0
0	р		f 1 3 5 7
4	1		0 5 8 5
0	0		0 0 0 0
-7		(-V7)	^0 0 0 0
г(А )= a*(v4| b )=3 =>
Л1.	3	5	7	0
0~|.5 8 5 4
0	0	0	0	[2
ко	о	о	о	о
система совместна;
П—5 имеет
бесконечно е
множество решений;
Л~Г=2 —число свободных
неизвестны х;
Xj, Х2, Х5 — базисные неизв.;
Х3, х4 - свободные неизв.
189
f 1 О
О 1
ко о
1/5 4 О 2/5^
8/5 1 О 1/5
0 0 1	0 }
Ответ:
-4с2
1 8
х4 — с2
х5 = О
с2 — произвольные постоянные.
Или в векторной форме:
где сА, с2
любые числа.
190
4.	ПРИМЕРЫ
Исследовать на совместность
и решить системы различными способами:
11.1.
2х - у + z = -2
< х + 2у + 3z = -l
x-3y + 2z = 3.
11.2.
11.3.
11.4.
11.5.
2Х] - Зх2 + х3 + 5х4 = -3
<
х, + 2х2 - 4х4 = -3
X] — х2 -4х3 +9х4 -22.
2х, + 7х, + Зх, + х. = 6
1	2	3	4
ЗХ] + 5х2 + 2х3 + 2х4 - 4
9х, + 4х2 + х3 + 7х4 = 2.
х, - Зх2 - 6х4 = 9
2х2 - х3 + 2х4 = -5
X] + 4х2 - 7х3 + 6х4 = 0.
ЗХ] - 5х2 + 2х3 + 4х4 = 2
< 7Х] - 4х2 + х3 + Зх4 = 5
5Х] + 7х2 - 4х3 - 6х4 = 3.
191
Исследовать на совместность
и решить системы при всех значениях параметра а\
(1 + а)х, + х2 + х3 = 1
5Х] - Зх2 + 2х3 + 4х4 = 3
11.7.
4Х] - 2х2 + Зх3 + 7х4 -1
8Х] - 6х2 - х3 - 5х4 = 9
7Х] -Зх2 +7х3 +17х4 =л
Исследовать на совместность
и решить системы различными способами:
х + 2у — 4z = 1
11.8. <2x + j>-5z = -l
х — у - z = -2.
X] + х2 - 6х3 - 4х4 = 6
11.9.
ЗХ] - х2 - 6х3 - 4х4 = 2
2Х] + Зх2 + 9х3 + 2х4 = 6
Зх, + 2х, + Зх, + 8х4 = -7.
V i	£	j	4
192
x + y-2z-6
11.10. < 2x + 3_y-7z = 16
5x + 2^ + z = 16.
X] + x2 + 3x3 - 2x4 + 3x5 = 1
2x, + 2x, + 4x, - x4 + 3x, = 2
11.11.
3X] + 3x2 + 5x3 - 2x4 + 3x5 = 1
2X] + 2x2 + 8x3 - 3x4 + 9x5 = 2.
3X] + 2x2 + 2x3 + 2x4 = 2
2X] + 2x2 + 2x3 + 5x4 = 3
11.1Z <9x, + x, + 4x, -5x4 =1
2X] + 2x2 + 3x3 + 4x4 = 5
7x, + x, + 6x, - x4 = 7.
X	J	"T
Исследовать на совместность
и решить системы при всех значениях параметра а:
193
2xj - х2 + Зх3 + 4х4 = 5
11.14. 4
4х] - 2х2 + 5х3 + 6х4 = 7
бХ] - Зх2 + 7х3 + 8х4 = 9
ах} - 4х2 + 9х3 +1 Ох4 =11.
5. ОТВЕТЫ
11.1.	11.2. (-1;3;-2;2)г.
9	10	5	1
11	11	11 1 и 2 1
11.4.	(3;-4;-1;1)г.	11.5. 0.
11.6.	0 при я = -3;
(1 - с} — с2; Cj; с2 )г при а = 0;
1
1
при а —3; а 0.
194
11.7. 0 при а 0;
11.13.	0 при а = -3;
О ^*2	^*3 ’ ^*1 ’ ^*2 ’ ^*3 ) 1ФИ 47 — 1,
Г 1	1	1	1 У
-----;-----;------;---- при а ф —3; а ф 1.
U + 3 а + 3 а + 3 a + 3J
11,14.	(с,; 4 + 2^ — 2с2; 3 — 2с2; при а = 8;
(0; 4 — 2^; 3 — 2с}; с} У при а Ф 8.
195
§12.
ФУНДАМЕНТАЛЬНАЯ СИСТЕМА
РЕШЕНИЙ
1. СПРАВОЧНЫЙ МАТЕРИАЛ
Определение 1. Линейная система, состоящая из т
уравнений с п неизвестными Х15"’3ХЛ5 называется линейной
однородной системой алгебраических уравнений^ если она имеет
вид:
ЪцХ1 +--- + a1„x„ =0
<......................
А • х = 0,
(1)
ci,x, +••• + ах„ = 0
ml 1	тп п
— матрица системы, х = : — вектор-
столбец из неизвестных.
Замечание!. Система (1) всегда совместна (то есть имеет
решения), так как всегда имеет решение X, = •   ~ хп — 0, назы-
ваемое тривиальным (или нулевым).
196
Т е о р е м а 1. Линейная однородная система (1) имеет нетри-
виальные решения тогда и только тогда, когда
г(Л)<п.	(2)
Напомним, что в случае (2) у системы (1) будет п — г(=к)
свободных неизвестных, которые обычно обозначают
Определение 2. Фундаментальными решениями систе-
мы (1) называются векторы-столбцы е\ ,•••,€ к, получаемые из
общего решения системы (1) подстановкой вместо вектора свобод-
ных неизвестных (с ],*•*, ск ) поочередно следующих векторов
(1;0;-;0), (0;1;0; • • •;()), - ,(0;-;0;1).
Замечание 2. С использованием фундаментальной систе-
мы решений общее решение системы (1) записывается в виде:
Х-С}в] + --- + сквк,
где	, • • •, ск - произвольные константы.
Замечание 3. Векторы	, • • •, вк линейно независимы и
образуют базис в пространстве решений системы (1).
Справедлива следующая связь между решениями линейной не-
однородной системы алгебраических уравнении
Ах = Ь	(3)
(если она совместна) и соответствующей ей линейной однородной
системы (1).
197
Теорема 2. Общее решение линейной неоднородной систе-
мы (3) вычисляется по формуле:
х = с}е\ +--- + скек +хо,
где 61, '",вк — фундаментальные решения соответствующей ли-
нейной однородной системы (1); х0 — некоторое решение линей-
ной неоднородной системы (3); с}, • • •, ск — произвольные кон-
станты.
2. ПРИМЕРЫ С РЕШЕНИЯМИ
Построить фундаментальные решения и решить
системы-.
Пример 1.
х + _у = 0
< 2х + у = О
х + 2у = 0.
Решение. Пусть А — матрица системы, Ь — столбец сво-
бодных членов системы. Для решения примера воспользуемся ме-
тодом Гаусса:
1
-1
0
198
1
1
О
(Г
о_
о,
Следовательно,
г(А) =2 = п,
свободных переменных нет;
общее решение : х — 0, у = 0;
фундаментальных решений нет.
Ответ: фундаментальных решении нет;
общее решение: х = 0, у — 0.
Пример 2»
х - у = 0
<х + у-z = 0
- 2х + z = 0.
Решение. Пусть А — матрица системы, b - столбец сво-
бодных членов системы. Для решения примера воспользуемся ме-
тодом Гаусса:
0
0
-1
0
О
199
1 0 -1/2
О] 1 -1/2
(Л
О
=> г(Л) = 2; свободная неизвестная z;
О
общее решение:
или
z - любое
Поэтому система имеет одно фундаментальное решение, полу-
чаемое из общего решения подстановкой в него с — 1:

Ответ: фундаментальное решение: е} =
общее решение:
= с-е1
Пример 3.
х + у + z-t = 0
х — у + 2z - О
2x + 3z-t -О
2j? - z -1 - 0.
200
Решение. Пусть А — матрица системы, Ъ — столбец сво-
бодных членов системы. Для решения примера воспользуемся ме-
тодом Гаусса:
о
О
0Х-1Х-2)
-1
2
0
-2
2
О
О
О
2
О
0
о
-2
•2
О
О
о
-2
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
-1/2
-1/2
(Г
о (-1X0
-1/2
Следовательно,
r(j) = 2;
1
о
0	0
О
О
О
0 О
О
и t, общее решение имеет вид:
з 2
2Z 2
i
2 2
2
или
-с.
2 1
2
Z,t — любые
= С,
2’
201
Фундаментальная система решений имеет вид:
О т в е т: фундаментальные решения: в\ —
общее решение:
-Суву +С2в2.
П ц и м е р 4. Определить, при каких значениях параметра а
система
г + 2 у - 0
ах - 3 у ~ 0
имеет нетривиальные решения. Найти их.
Решение:
(АЬ) =
а
202
г(Л) — 1, если — 3 — 2а = 0,
г(А) = 2, если — 3 — 2а 0.
Учитывая требование (2), гарантирующее существование нетри-
виальных решений, приходам к условию на параметр а:
-3-2б? = 0
При этом значении а имеем.
(P|	fx = -2j
0j	[ у - любое число
Ответ:
3
если а = —;
2
<у) W
при остальных значениях а.
Пример 5, Решить системы:
< 2у - z - 5 и
х - у + z = 0
< 2у - z = 0
r + j = 0.
Решение. Первая из данных систем - линейная неоднород-
ная, а вторая - соответствующая ей линейная однородная. Для этих
систем матрица системы имеет вид:
203
Решим методом Гаусса линейную однородную систему:
1
-1
о
~1
2
2
-1 1
2 -1
0 О
2
Z~C.
Следовательно, общее решение однородной системы имеет вид:
где с — любое число.
(5)
Решим данную в примере линейную неоднородную систему:
204
(1 -1 1
0 1 --
2
^0 0	0
<10 1/2
О 1 -1/2
1^0 О О
(6)
Общее решение неоднородной системы имеет вид:
с — любое число.
(7)
Замечание 4. Сравнивая цепочки преобразований (4) и
(6), заметим, что в них используются одни и те же преобразования
и результаты соответствующих шагов полностью совпадают в ле-
вой части расширенных матриц (до вертикальной черты). Ответы
(5) и (7) совпадают с точностью до последнего слагаемого (не со-
держащего произвольных постоянных).
Ответ: (7) - общее решение первой системы;
(5) - общее решение второй системы.
^ПРИМЕРЫ
Указать фундаментальные решения и решить системы:
12.1.
х 4- 2у - z - 0
2х + 9у - 3z - 0.
3xt + 2х2 + х3 = 0
12.2. 2xt + 5х2 + Зх3 - 0
3Xj + 4х2 + 2х3 = 0.
205
2х - 4у + 5z + 3t = 0
12.3.	< Зх - 6у + 4z + 2t = О
4х - 8j +1 lz +1V = 0.
Х| + 2х2 + 4х3 - Зх4 = О
4х, + 5х, - 2х, + Зх. = О
12.4. <
Зх, + 8х2 + 24х3 - 19х4 = О
Зх, + 5х2 + 6х3 - 4х4 = 0.
х, + х3 + х5 = О
х, -х2 +х5 -хб =0
12.5.	< х, - х. + х, = О
2	Ч	D
х2 + х3 + хб О
х, - х4 + х5 = 0.
12.6.	Определить, при каких значениях параметра а система
or2x + 3j + 2z = 0
lax - у + z = О
8х + у + 4z = О
имеет нетривиальные решения. Найти эти решения.
Указать фундаментальные решения и решить системы:
12.7.
х - 2у - 3z - О
<
- 2х + 4у + 6z = 0.
206
2х - Зу + z = 0
12.8. <x+j+z=0
Зх - 2_у + 3z = 0.
х + у + z — О
12.9. 2х - Зу + z = О
Зх - 2у + 3z = 0.
Зх, + 2х2 + х3 + Зх4 + 5х5 = О
12.10.
6х, +4х2	+ Зх3	+ 5х4	+ 7х5	= 0
9х, + 6х2	+ 5х3	+ 7х4	+ 9х5	-0
Зх, + 2х2	+ 4х4	+ 8х5	= 0.	
	5х,	+ 6х2	- 2х3 + 7х4 + 4х5 = 0
12.11. <	2х,	+ Зх2	- х3 + 4х4 + 2х5 = 0
	7х,	+ 9х2	- Зх3 + 5х4 + 6х5 = 0
	5х,	+ 9х2	- Зх3 + х4 + 6х5 - 0.
12.12. Определить значения параметра а, при которых система
2x + ^ + 3z = 0
< 4х-у + lz = О
х + ay + 2z = О
имеет нетривиальные решения. Найти эти решения.
ел
ОТВЕТЫ
208
S13
СОБСТВЕННЫЕ ЗНАЧЕНИЯ,
СОБСТВЕННЫЕ И ПРИСОЕДИНЕННЫЕ
ВЕКТОРЫ КВАДРАТНОЙ МАТРИЦЫ
1. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ВЕКТОРЫ
Пусть дана квадратная матрица порядка п с постоянными ве-
щественными элементами:
Л-
Определение 1. Число Л называется собственным зна-
чением (или собственным числом), а ненулевой вектор h называ-
ется соответствующим собственным вектором матрицы А, если
выполняется равенство
209
A-h = Ah.
Равенство (1) можно переписать в виде
(A-AE)-h = O
(1)
(2)
где Е — единичная матрица порядка п.
Тогда (2) есть линейная однородная система относительно век-
тора h. Так как по определению должно быть h Ф 0, то это воз-
можно только в случае вырожденности матрицы (А — Л  Е), то
есть при условии
det(J - Я • Е) = 0.
(3)
(Равенство (3) будем записывать далее в виде: | А — Л-Е\= 0.)
Теорема 1. Число Л является собственным значением
квадратной матрицы А тогда и только тогда, когда оно удовлет-
воряет уравнению (3).
Заметим, что уравнение (3) совпадает со следующим:
(«11 -Я)
«21
«12	«1»
(«22 —	«2 л
= 0.
(4)
«л2	•••, («лл"^)
Определение 2. Уравнение (4) называется характери-
стическим уравнением матрицы А.
210
Теорема 2> Для того чтобы число 2 было собственным
значением квадратной матрицы Л, необходимо и достаточно,
чтобы оно являлось корнем характеристического уравнения (4).
Замечание 1. Определитель в левой части равенства (4)
можно вычислить, например, разложив его по элементам первой
строки. После груг
шшн
вки подобных членов, характеристическое
уравнение (4) принимает вид
Лп +	+ Ь2Лп-2 +... + Ьп = О (5)
и является алгебраическим уравнением степени п относительно
2 , где Ь}, ЬгЪп — постоянные вещественные числа, в частно-
сти Ьп = (-l)n - det Л.
Следовательно, характеристическое уравнение (4) всегда имеет
ровно п корней (с учетом их кратности), которые в общем случае
являются комплексными числами.
Теорема 3> Любая постоянная квадратная матрица порядка
п имеет с учетом кратности ровно п собственных значений, сов-
падающих с корнями характеристического уравнения (5).
Обозначим: 21,...,2j; — различные корни алгебраического
уравнения (5) и ,..., кр — их кратности. Тогда
к}+... + кр=п и}<р<п.
Замечание 2. Задача нахождения собственных значений
матрицы А сводится к решению характеристического уравнения
(5). При этом полезно помнить следующее:
1) если уравнение (5) имеет целый корень 2^ и коэффициенты
уравнения - целые числа, то число 2^ является делителем
числа Ьп \
211
2) если какой-либо корень Л1 уравнения (5) найден, то многочлен
Лп + Ь}Лп} + Ь2Лп~2 +... + Ьп делится нацело на (Л — Л^),
например, «в столбик», в результате чего (5) принимает вид
(л-л,) -.(Z’1 + w2 + ... + £>;)=о
и задача сводится к поиску корней алгебраического уравнения
г-’ + ь;лп-2 +...+*;=о,
аналогичного уравнению (5), но степени на единицу меньшей.
Опред е л е н и е 3* Множество всех собственных значений
матрицы называется спектром матрицы.
Замечание 3. Если из характеристического уравнения (4)
найден корень Л^ кратности k} , 1 <	< и, то поиск соответст-
вующих числу Л] собственных векторов h & 0 матрицы А сво-
дится к решению линейной однородной системы
(А~Л} •£)•/? = О	(6)
с постоянной квадратной вырожденной матрицей (А — Л} Е)
порядка п.
Система (6) всегда имеет бесконечное множество решений, в
котором число базисных (то есть максимальное число линейно не-
зависимых) решений равно п —, где 1\ — rang(A — Л] • Е),
О < < п — 1 и 1\ — целое неотрицательное число.
212
Поэтому любому собственному значению квадратной матрицы
А соответствует хотя бы один линейно независимый собствен-
ный вектор.
Более того, число линейно независимых собственных векторов,
отвечающих собственному значению Л} кратности , не пре-
восходит числа к}.
2. СЛУЧАЙ ПРОСТОГО СОБСТВЕННОГО ЗНАЧЕНИЯ
Пусть Л1 — простое собственное значение матрицы А, то есть
его кратность к} — 1.
Тогда числу Л} отвечает ровно один линейно независимый
собственный вектор h\ Ф 0, который находим из системы (6),
например, с помощью метода Гаусса.
Замечание 4. Если все собственные значения матрицы А
являются простыми, то они различны и их ровно п:	,..., Лп.
У каждого из них существует только один линейно независимый
собственный вектор. Поэтому таких собственных векторов
. .,hn суммарно у матрицы А будет ровно п и между собой
они оказываются линейно независимыми.
3	СЛУЧАЙ КОМПЛЕКСНО-СОПРЯЖЕННЫХ
СОБСТВЕННЫХ ЗНАЧЕНИЙ
Пусть характеристическое уравнение (5) имеет комплексный
корень кратности кх > 1. Так как (5) - алгебраическое уровне-
213
ние с вещественными коэффициентами, то оно обязательно имеет
корень Л2, комплексно-сопряженный по отношению к . При-
чем кратность корня Я2 будет равна числу к}.
Тогда следует найти собственные векторы, соответствующие
собственному значению \ . Затем построить к ним комплексно-
сопряженные векторы, которые и будут являться собственными
векторами, соответствующими собственному значению Я2.
4.	СЛУЧАЙ КРАТНОГО СОБСТВЕННОГО ЗНАЧЕНИЯ
Пусть у матрицы А есть кратное собственное значение
кратности к} > 2.
Тогда, решая систему (6), будет найдено П — 1\ линейно не-
зависимых собственных векторов, отвечающих числу Л}. Причем
число п — г} удовлетворяет двойному неравенству:
1 < п - < кх, где = rang(A ~	• £’).
Замечание 5. Если оказывается, что п — 1\ =кх, то для
собственного значения будет найдено столько линейно незави-
симых собственных векторов, какова кратность рассматриваемого
собственного значения тЦ.
5.	ПРИСОЕДИНЕННЫЕ ВЕКТОРЫ
Пусть — кратное собственное значение матрицы А кратно-
сти к} > 2, для которого п — гх Ф к., где r\ ~ rang(A —	• Е).
214
Тогда числу отвечает только /Wj линейно независимых соб-
ственных векторов h\,... где обозначено:	~ п —
—1
Опред еление 4. Вектор hj называется первым присое-
диненным к собственному вектору hj , если выполнено равенство:
(7)
— 2
Вектор h j называется вторым присоединенным к собственно-
му вектору h j , если выполнено равенство:
— 2	—1
(A-^E}hj=h3.	(8)
Вектор hj называется l-м присоединенным к собственному
вектору h j , если выполнено равенство:
(A-At *E)hj - hj .	(9)
Теорема 4. У собственного значения Л} кратности к}
суммарно существует ровно к} линейно независимых собственных
и к ним присоединенных векторов.
Таким образом, у собственного значения \ существует п - г}
собственных линейно независимых векторов и к} — (п — г}) к ним
линейно независимых присоединенных.
Замечание 6. Нетрудно видеть, что (7), (8), (9) - линейные
неоднородные системы алгебраических уравнений, записанные в
215
векторной форме. Их анализируют и решают, как правило, с помо-
щью теоремы Кронекера - Капелли и метода Гаусса.
Замечание 7. Вопрос о том, сколько существует у собст-
венного вектора hj присоединенных векторов, решается, напри-
мер, по теореме Кронекера - Капелли при исследовании системы
(9) на совместность.
Теорема 5. Собственный вектор hj имеет первый при-
соединенный вектор h у тогда и только тогда, когда
rang(A -Я1 • Е | h}) - т\.
Теорема 6. Собственный вектор hj имеет максимально I
—1 —I
присоединенных векторов	тогда и только тогда, когда
rang(A -Я, • Е | h}) = rang(A - Ях E\tij)~... =
- rang(A -	• £|Л;1) = ^' и rang(A -Я^ -E\hlj)*rv
Зам е ч а н и е 8. При построении присоединенных векторов
нужно помнить следующее: если вектор h j имеет цепочку из при-
—1	— i
соединенных к нему векторов h} у, h3, то любой вектор вида
(с • hj ), линейно зависимый по отношению к вектору hj, также
—1	— i
имеет цепочку из присоединенных векторов (chj(chj ),
которые линейно зависимы с уже найденными.
216
Теорема 7. Пусть h — собственный вектор матрицы А,
—1	—т
h ,..., й — цепочка к нему присоединенных векторов. Тогда
— —1	— т
векторы й, h ,..., h — линейно независимы.
Замечание 9. Если для каждого из линейно независимых
собственных векторов h\,.. . ,й р построить его цепочку присое-
диненных векторов, то суммарно будет найдено кх + ... + к р век-
торов, что совпадает с числом п — порядком матрицы А. Все эти
векторы будут линейно независимыми.
6, ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Найти собственные значения и собственные век-
торы матрицы
Решение. 1) Найдем собственные значения матрицы А :
(1-2)	3
-1	(5-2)
= (1-2)*(5-2) + 3 = 22-62 + 8,
значит, 22 — 62 + 8 = 0 — характеристическое уравнение и
2j - 2, 22 — 4 — его корни.
217
2) Найдем линейно независимые собственные векторы, соот-
ветствующие собственному числу = 2 :
(Л-^Е 0) =
OV-l) f-1 з
oj^l 1^0 о
0J
'Ll
<0
-3
о
О?
о/
Поэтому координаты ах, а2 искомых собственных векторов h
связаны равенством: С1} = За2. Значит,
откуда
3) Найдем линейно независимые собственные векторы,
соответствующие числу Л2 = 4:
(А-л2е 0) =
р?
°>
218
Поэтому координаты а2, а2 искомых собственных векторов h
связаны равенством: ах — &2. Значит,
откуда
Ответ:	— 2,
Пример 2. Найти собственные значения и собственные век-
торы матрицы
Решение. 1) Найдем собственные значения матрицы А :
А-ЛЕ\ =
(4-Л)
1
= (4-2)(2-А) + 1 = А2-6А + 9 =
= (2-3)2 =0.
Поэтому
к. = 2.
— 3 — кратное собственное значение кратности
219
2) Найдем линейно независимые собственные векторы,
соответствующие числу = 3 :
(A-AtE 0) =
OV-1) 61 -1 | (Г
oJ^J (Jo о 0?
Поэтому координаты , а2 искомых собственных векторов h
связаны равенством:	— а2 Следовательно,
откуда А]
3) Найдем линейно независимые присоединенные векторы:

Поэтому координаты , а2 искомых присоединенных векто-
—]
ров h связаны равенством: = 1 + а2, откуда
Ответ:
220
Пример 3, Найти собственные значения и собственные век-
торы матрицы
Решение. 1) Найдем собственные значения матрицы А:
(4-2)
-1
(2-2)
= (4 - 2) • (2-2) + 5 =
= 22 -62 + 13 = 0.
Отсюда
2>2 = 3±V9-13 = 3±V^4=3±V4-VZT= 3±2/,
то есть - 3 + 2/, Л2 = 3 - 2/, кратность каждого из них
равна единице.
2) Найдем линейно независимые собственные векторы, отве-
чающие числу Л, = 3 + 2/:
221
Поэтому координаты а,, а2
искомых собственных векторов h
1 + 2/
связаны равенством: а, =--------а2. Следовательно,
Ответ: Я, 2 = 3±2/: А),2 =
Пример 4. Найти собственные значения н собственные век-
торы матрицы
Решение. 1) Найдем собственные значения матрицы А :
(4 -Л)
-1
(2-2)
-1
-1	=(4-Л)(2-А)2 +
(2-2)
+1 + 1 + (2-2)-(4-2) + (2-2) =
222
= (4 - A)  (2 - A)2 + 2 +2 - A - 4 + Л + 2 - Л =
= (4 -А)  (2 - А)2 + (2 - Л) = (2 - А) • ((4 - А)  (2 - А) +1) =
= (2 - А) • (А2 - 6А + 9) = (2 - А) • (А - З)2.
Поэтому характеристическое уравнение (2 — А) • (Л — 3)2 =0
имеет корни
Л, =2 кратности к} =1, Л2 =3 кратности к2 — 2,
являющиеся собственными значениями матрицы А.
2) Найдем линейно независимые собственные векторы, соот-
ветствующие числу \ = 2 :
о
(А-^Е 0)= 1
0>(-2)(-1)
0
0
0
0
О -1
о
0
о
о
о
о
о
о
о
о
ООО
223
Поэтому координаты а}, а2, а3 искомых собственных векто-
ров h удовлетворяют равенствам: а} = а3, а2= а3.
Следовательно,
откуда hi =
3) Найдем линейно независимые собственные векторы, соот-
ветствующие числу Л2 = 3 кратности 2:
(А-Л3Е 0)= 1
-1
-1
-1
-1
т
о
-1
"o’
о
0>|
о
Поэтому координаты а}, а2, искомых собственных векто-
ров h удовлетворяют равенству: а} —а2 + а3.
Следовательно,
224
откуда заключаем, что линейно независимыми являются векторы
Пример 5. Найти собственные числа и собственные векторы
матрицы
Решение. 1) Найдем собственные числа:
1-2 -2	3
-1 -Л 3
-1	-3	6-2
225
=> -2(1-2Хб-2)+6 + 9-32 + 9(1-2)-2(б-2) = 0,
-Л(б-7Л + Л2)+12-10Л = 0,
-Л3 + 7Л2 -162 + 12 = 0,
(Л - 2)(Л2 -5Л + б)= 0,
(2-2)2(2-3)=0.
Значит, собственными значениями матрицы А являются:
А} = 2 кратности 2, Л2 — 3 кратности 1.
2) Найдем собственные векторы для числа Л = 2 :
226
3) По собственному вектору h\ найдем присоединенный век-
тор h\, соответствующий собственному значению Л =2 ;
О
-1
О
1
1
О
-1
-1
о
о
0 >
а, = -1 +а.
Значит, <
1«2 = а3
4)
откуда
1
Найдем собственный вектор Лг, соответствующий собст-
венному значению Л — 3:
227
-1 -3	3 0	4-3	0^| (-1)		f\ 3	-3 0 1 -3/4	Ол 0	(-3)
	0	(1/4)-+			
ООО	0,		,00	0	°>	
Значит,
ах
а2
^0 о
откуда
-3/4
-3/4
О
228
7. ПРИМЕРЫ
Найти собственные значения,
собственные и присоединенные векторы матрицы:
13.4.
13.5.
13.6.
О
О
13.8.
-2
2
О
13.9.
13.10.
О
2
о
229
♦ Ф
❖
Найти собственные значения,
собственные и присоединенные векторы матрицы:
	л2	-1	1
13.И.	1	2	-1
		-1	2>
	л 2	1	(Р
13.13.	1	3	-1
	ч-1	2	3 ,
	' 2	-1	— 1
13.15.	2	-1	-2
	-1	1	2
8. ОТВЕТЫ
230
231
13.11.
13.12.
232
233
S 14.
ЛИНЕЙНЫЕ ВЕКТОРНЫЕ
ПРОСТРАНСТВА. БАЗИС
1. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА
Определение 1. Множество V называется линейным
векторным пространством, если для любых его элементов а и
Ь, называемых векторами этого пространства, и любого
действительного числа А так определены в V векторы а + Ь
и А  а, что верны следующие аксиомы:
1. В пространстве V есть нулевой вектор 0 такой, что
а + 0 = а УаеИ.
2. Для любого вектора a &V существует противоположный
ему вектор, обозначаемый — а, такой, что а + (— а) = 0.
X a + b = b + a \fa,b&V .
4.	(а + b) + с - а + {b + с) V a, b, с е V .
5.	1а = а УаеИ.
6.	А(а + Z>) = Аа + АЬ \fa,beV с R.
234
7,	(Л + fi)a = Ла + ца VaeV
8.	(Л//)а = Л(//а) WaeWA^eR.
Замечание 1. Пространство Rn - множество всех строк
из п действительных чисел (х,; х2;,..; хп ) - является линейным
векторным пространством, если суммой строк (xt;...; хп ) и
(Pii-iZ,) назватьстроку ((х, + j,);...;(x„ + _у„)), апроизве-
дением строки (х\^^хп} на число А назватьстроку
(Лх,Ахп ). При этом нулем пространства служит строка
О = (0;...;0); противоположной к строке	является
строка (—а17...;-ап) и верны все аксиомы 1-8.
bi; I:
2.J
:ЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ.
БАЗИС И РАЗМЕРНОСТЬ ПРОСТРАНСТВА
Опр еделение 2. Векторы а},а2^...^ап линейного век-
торного пространства V называются линейно зависимыми, если
можно указать числа ЛА,Л2,...Лп, не все равные нулю, такие, что
Да. + Да9 + ... +Да = 0.
11 L L	П И
(1)
Определение 3. Векторы а1эа2,...?ал линейного век-
торного пространства V называются линейно независимыми, если
выполнение равенства (1) возможно только при условии
235
Л = 2, = ... = 2=0..
1	2	П
Теорема 1, Система из к векторов a},a2,...,ak про-
странства Rn является линейно независимой тогда и только тогда,
когда матрица А , столбцы (строки) которой составлены из этих
векторов, имеет ранг к.
Следствие. Система, состоящая более чем из п векторов
пространства R”, линейно зависима.
Определение 4. Система векторов е} ,е2,...,еп линей-
ного векторного пространства V называется базисом этого про-
странства, а само пространство называется п - мерным, если для
любого вектора a G И найдется, притом единственный, набор
чисел Zj,Я2,...,Ял такой,что
<7.=	+ Я2в2 +... +	.	(2)
При этом говорят, что любой вектор пространства V од-
нозначно разлагается по базису.
Определение 5* Равенство (2) называется разложением
вектора а по базису ,е2,...,еп, а числа Л, ,22,...52л -
координатами вектора Ct в базисе в}1в2,..^еп. Число п на-
зывается размерностью пространства.
Теорема 2. Векторы е^е2,...,еп образуют базис линейно-
го векторного пространства V тогда и только тогда, когда этн век-
торы линейно независимы.
236
Следствие. Система из п векторов е15е2,...5еп образу-
ет базис пространства Rn, если ранг матрицы А , столбцы (строки)
которой составлены из этих векторов, равен п.
Замечание 2. Базисов в линейном векторном пространстве
бесконечно много, но все они имеют одно и то же число векторов,
совпадающее с размерностью рассматриваемого пространства.
3. ПРЕОБРАЗОВАНИЕ КООРДИНАТ.
МАТРВДА ПЕРЕХОДА
Пусть е15е2,...,ел и	-базисы линейного век-
торного пространства V, первый из которых назовем «старым», а
второй - «новым».
Векторы нового базиса, как и любые векторы пространства V ,
разлагаются по старому базису:
.	+ ai2e2 + ... + ainen,
где l<i<n, anyai2^..^am ~ координаты вектора j\ в старом
базисе.
Определение 6. Матрица А ~ (<г ).— называется
матрицей перехода от нового базиса к старому.
Замечание 3. Каждый вектор а пространства V имеет
координаты как в старом базисе, так и в новом. Справедливо ра-
венство
(У^У^-\Уп)-А =
237
связывающее координаты Xj, х2,..;,хл вектора а в старом ба-
зисе и координаты у}, ,..., у п вектора а в новом базисе, где
А - матрица перехода от нового базиса к старому.
4. ЕВКЛИДОВЫ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ
И ОРТОНОРМИРОВАННЫЕ БАЗИСЫ
Определение 7. Скалярным произведением векторов а и
Ъ линейного векторного пространства V называется число, обо-
значаемое (а, Ь) и удовлетворяющее следующим условиям:
1)	(a,b) = (b,a)
2)	((a + b),c) = (a,c) + (b,c) Xfa,b,ceV;
3)	(Ла,с) = Л(а,с) \fa,c eV VA е R;
4)	(а,а)>0 V а е И, причем (а, а) — 0 тогда и
только тогда, когда а — нулевой элемент пространства V .
Определение 8. Линейное векторное пространство V , в
котором определено скалярное произведение векторов, называется
евклидовым пространством.
Замечание 4. Пространство Rn является евклидовым, так
как оно линейное векторное и в нем определено скалярное произ-
ведение элементов:
(a,b)=xxy, + ... + хпу„,
238
гдеа=(х1;г2;...;хп) и Ъ =
Замечание 5. В любом евклидовом пространстве можно
определить
1)	длину вектора:
a| = 7(a,a),
2)	расстояние между двумя векторами:
р(а\ Ь) - \а - Ъ ,
3)	косинус угла (р между векторами а и Ъ\
cos(p -
(при а^О и b О ).
Определение 9. Базис е]5е2,...,ел евклидова про-
странства V называется ортогональным, если (еу, ej} = 0 при
любых 1 < i < j < п.
Определение 10. Ортогональный базис е13£2>--;еп
евклидова пространства V называется ортонормированным, если
(е.,е.)=1 при / = 1э2,...?и.
5. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ
Пусть /J, f2 ,.. ,fn - базис в евклидовом пространстве V .
239
Тогда п векторов, вычисляемых по формулам
е1 ~ f\>
k-\
ek = Л	(£ = 2,..л),
(г уе )
где С — У~~ V, к = 2, ..л, образуют ортогональный базис
в евклидовом пространстве V .
Процесс построения указанным способом ортогонального базиса
ех,е2,...,еп по некоторому данному базису Ур/г’-А называ-
ется процессом ортогонализации Шмидта.
Опред е л е н и е 11» Нормированием вектора а называется
а
замена его вектором ।—, имеющим длину, равную!.
6, ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Найти ранг и базис системы векторов
а = (1;0;1), Z» = (l;l;0), с = (1;1;1) и d =
Будут ли найденные векторы базисом в пространстве R3 ?
240
Решение. Составим матрицу, у которой, например, строка-
ми являются векторы a.b^d, и приведем ее к ступенчатому
виду:
0
1 1
1 1
к 0 1
f 1 0	1
~о! 1 -1
0 ° Ll
к О О О
Следовательно, ранг системы векторов ау с, d равен трем;
линейно независимыми являются векторы я, Ь, с; число найден-
ных векторов равно трем, что совпадает с размерностью простран-
ства R3. Значит, векторы а7 Ь, с~ базнс в пространстве R3.
Ответ: ранг системы векторов a, b, с, d равен трем;
базис этой системы векторов составляют а, Ь, с;
они же являются базисом пространства R3.
Пример 2, Показать, что векторы а ~ (1; 2; 3 ),
Ь~ ( 3; 2; 1) и с — (1; 0; 1) образуют базис в пространстве R3 и
найти координаты вектора т — ( — 1; 6; 13 ) в этом базисе.
Решение. Составим матрицу, столбцами которой являются
векторы а, Ъ, с, и приведем ее к ступенчатому виду"
241
Следовательно, ранг матрицы, составленной из векторов а, b,
с, равен трём; векторы а, Ь, с линейно независимы и образуют
базис в пространстве .
Тогда вектор т = ( — 1; 6; 13 ) должен разлагаться по этому ба-
зису:
т =	+ х2Ъ + х3с.	(3)
Значит, координаты разложения (3) удовлетворяют линейной
неоднородной системе алгебраических уравнений:
-1 = X] + Зх2 + х3
<j 6 = 2Х] + 2х2	(4)
13 = ЗХ] + х2 +х3.
Решим систему (4) методом Гаусса:,
3 1
2 2 0
<3 1 1
242
|^0 0	2 0 J(l/2)	^0 0	1 О J (2)(-1)
О 1 О
-2
Следовательно,
х, =5, х2 = -2, х3 = 0.
Итак, вектор т в базисе а,Ь, с имеет координаты:
(5;-2;0), откуда заключаем: т - 5а - 2Ь .
Ответ: а, b, с - базис пространства R3; т = 5а — 2Ь.
имев 3. Найти матрицу перехода от базиса =(1;1,0),
е2 = (2;0;1), ез =(0;1;1) к базису / = (1;1;1), /2 =(2;0;0),
Л=(о;о;2).
Решение. Найдем координаты	У1,У2’УЗ И
Zj, z2, z3 векторов , е2, е3 в базисе , f2, _/3 
243
Рассматривая каждое уравнение в отдельности, получим три
системы, соответственно, для координат х}, х2, х3,	, уг,
И з % 2 ’ ^3 
Xj + 2х2 = 1
Xj + 2х3 = О
У1 +	~
2) «У, = О
71 + 2 Л = 1
z} + 2z3 = 1.
Решая эти системы, находим:
Таким образом, вектор е1 имеет в базисе f}, f2, координа-
вектор е2 —
Значит, матрица перехода от базиса е1, е2, е3 к базису ,
/2, /3 имеет ввд:
244
Ч 0	-1/2>
О 1	1/2
J -1/2 О ,
Л1 О
л •*
1^1 -1/2
Пример 4. Применить процесс ортогонализации к базису
/, =(1;1;0), Л-(0;1;1), Л=(1;0;1)
пространства R3. Получить орто нормированный базис.
Решение. Вычисляем:
= Z = (1;1;0),
*1
= (0;1;1)-
0 + 1 + 0
1 + 1 + 0
 =
= (0,1,1) -1 (1;1,0) = (0;Ц) - Г+= (- 1+;?
J	4* 4 J
245
<11	11	1W2 2 2^
1 — +—;0~ ——;1— =
<26	2 6	3J <3 3 3)
Следовательно, векторы
образуют ортогональный базис в пространстве R3.
Чтобы получить ортоиормированный базис, найдем длины век-
торов е},е2,е3:
е,| = V12 +12 +02 =41,
£г'=ifFF'=)il •
[4 4 4 2-Л
е3 — J—I-1— —--
V9 9 9	3
Следовательно, векторы

е2
е2

= —-—О
I--- 7 I- 7V >
Va/2 V2 )
2 е3 _
^3
246
образуют ортонормированный базис в пространстве R3.
Ответ:
7, ПРИМЕРЫ
14.1.	Определить, являются ли линейно независимыми векторы
а = (1;0;1;0), b = (1;1;0;0), с = (1;0;0;1)
в пространстве R 4.
14.2.	Найти ранг и базис системы векторов пространства R4:
а = (1;0;0;-1), b = (2;1;1;0), с = (1;1;1;1), d = (1;2;3;4),
е = (0;1;2;3).
14.3.	Найти ранг и базис системы векторов пространства R4:
е, = (2;0;3;1), е2 = (1;2;0;2), е3 = (3;2;3;3),
е4 = (0;-4;3;-3).
14.4.	Доказать, что векторы ег, е2 , е3 образуют базис в про-
странстве R3 и найти координаты вектора а в этом базисе,
если: et = е2 = (1;1;2), е3 = (1;2;3), а = (б;9;14).
14.5.	Доказать, что векторы е}, е2, образуют базис в про-
странстве R2 и найти координаты вектора а в этом базисе,
247
если:
е1=(2;1Х е2=(-3;2), а = (5;б).
14.6.	Доказать, что векторы , е2, е3 , е4 образуют базис в про-
странстве R4 и найти координаты вектора а в этом базисе,
если:
е, = (1;2;-1;-2Х е2 = (2;3;0;-1), е3 = (1;2;1;4),
е4 = (1;3;-1;0Х а = (7;14;-1;2).
14.7.	Найти матрицу перехода от базиса 5 е2, е3 к базису
/пУз’Л пространства R3, если:
е. = (1;0;1Х е2 = (1;1;0), е3 = (0;1;1), /, = (1;-1;0),
/2=(1;0;-1), f3 = (0;1;-1).
14.8.	Применить процесс ортогонализации к базису пространст-
ва 7?3:
е,=(1;2;0Х е2 = (6;1;2), е3 = (1;0;2).
14.9.	Применить процесс ортогонализации к базису пространст-
ва 7?2:
ei = (l^),	=(2,1).
14.10.	Определить, являются ли линейно зависимыми векторы
248
л = (1;2;0;4), Ь = (-1;0;5;1), с = (1;6;10;14)
в пространстве R4 ?
14.11.	Найти ранг и базис системы векторов:
а = (1;0;2;3;0), b = (-с = (0;1;2;4;-1),
d = (0;1;0;0;0), е = (1;5;4;7;-1).
14.12.	Найти ранг и базис системы векторов:
а, = (0;1;0), а2 = (0;2,0), а3 = (0,3;0), а4 = (1;0;0).
14.13.	Доказать, что векторы
е, = (2;1;-3), е2 = (3;2;-5), е3=(1;-1;1)
образуют базис пространства R3 и найти координаты век-
тора а = (б;2;-7) в этом базисе.
14.14.	Найти матрицу перехода от базиса J\ = (1;3;2;1),
/2 =	, /3 = (1;0;-1;0), /4=(2;0;0;2)
к базису е} =(1;2;0;1), е2 =(1;0;-1;0), е3 =(0;1;2;0),
е4 = (1;0;0;1).
14.15.	Найти ортонормированный базис, применив процесс орто-
гонализации к базису:
л = (1;0;1Х * = (-1;1Д с = (-
пространства IV.
249
14.16.	Проверить, является ли базис	= (1;—2;1;3),
ортогональным и перейти к ортонормированному базису.
8. ОТВЕТЫ
14.1.	Линейно независимы.
14.2.	Ранг 3, базис а, Ъ, d.
14.3.	Ранг 2, базис е}, е2.
14.4.	(1;2;3).
14.6.	(0;2;1;2).
14.7.
( 1 0 - Р
О 1 -1
к-1 1 о,
14.5. (4;1).
14.8. (1;2;0); (-|;|;2j;
<8 4 2^1

14.9.
14.10. Являются.
250
14.13.
14.15.
Ранг 3, базис a, b, d.	14.12.
Ранг 2, базис ах,а4.
14.14.
1/2
О
О
1/2
О
;0;
14.11.
О
О
0
О
О
О
14.16.
2
715 ’ 715 ’ 715’715/
ГТз.Тз.Тз > ( Тз.Тз 7Г|
;о ,
251
S 15
КВАДРАТИЧНЫЕ ФОРМЫ
УЕДЕЛЕНИЯ
О пре деление 1. Квадратичной формой от переменных
х],..хп называется многочлен второй степени относительно этих
переменных, не содержащий свободного члена и членов первой
степени. Обозначение: f (X];...; хп ) .
Замечание 1. Если п = 2,то
f (Л]5 ^*2 ) —	1	+ 2^12	+ ^22 ^*2 •
Если П = 3 , ТО
/(*i; *2; х3) =
В общем случае квадратичную форму от переменных Xj,..., хп
можно записать следующим образом:
/(х1;...;х„) = ^а.х,2 +	а.х.Х].
(1)
Замечание 2. Если Л — действительное число, то спра-
ведливо свойство:

252
Определение 2. Матрицей квадратичной формы (1) на-
зывается матрица вида
	а\\	^12	- Л1я
А =		а22	-	а2„
		а1п 	• ат
(2)
Определение 3.
вается ранг матрицы (2).
Рангом квадратичной формы (1) назы-
Замечание 3. Матрица (2) является всегда квадратной по-
рядка п и симметричной, так как для ее элементов справедливо
равенство:
а = а
I]	£
(l<i<j<n).
Опред е л е н и е 4. Говорят, что квадратичная форма (1)
имеет диагональный вид (или канонический вид), если ее матрица
(2) является диагональной.
Замечание 4. Диагональная квадратичная форма содер-
жит только члены с квадратами переменных. В таком случае так же
говорят, что квадратичная форма имеет вид алгебраической сум-
мы квадратов.
Опред еление 5. Квадратичная форма (1) называется
положительно (отрицательно) определенной, если она положи-
тельна (отрицательна) для всех допустимых наборов переменных
Теорема 1 {критерий Сильвестра). Для того чтобы квад-
ратичная форма (1) была положительно определенной, необходимо
и достаточно, чтобы были положительны все главные диагональ-
ные миноры Дj,..Д „ ее матрицы (2):
253
Д, > 0, ... , Д > О.
Для того чтобы квадратичная форма (1) была отрицательно оп-
ределенной, необходимо и достаточно, чтобы знаки главных диаго-
нальных миноров А1,Ап ее матрицы (2) чередовались, начи-
ная со знака
Aj <0, А2 > О, А3 < 0,...
О пре деление 6- Знакоопределенн ыми называются квад-
ратичные формы, которые или положительно определены, или от-
рицательно определены.
2. ПРЕОБРАЗОВАНИЕ ПЕРЕМЕННЫХ
О пре деление 7. Преобразованием переменных х1...... х
называется переход к новым переменным	уп по формулам:
Ч =ьиу, +-+ь}пу„
<............................. (3)
А =ЬпМ +-+ЬтУ„
При этом квадратная матрица В = \Ь^ J р называется матри-
цей преобразования (или матрицей перехода) от старых перемен-
ных х]?...?хл1 к новым переменным У},...,УП-
Определение 8. Преобразование переменных называется
невырожденным, если определитель матрицы преобразования от-
личен от нуля.
254
Замечание 5. Если к квадратичной форме (1) от перемен-
ных Xj,..хп с матрицей (2) применить преобразование переме-
ных с матрицей перехода
) __ ? то получим квадратич-
ную форму от переменных ух,..., у п с матрицей
Л, -Вт А В.
3, ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ
К ДИАГОНАЛЬНОМУ ВИДУ
Теорема 2> Любая квадратичная форма (1) с помощью не-
которого невырожденного преобразования переменных может быть
приведена к диагональному виду:
^+...+Лгу2г,	(4)
где Лг — постоянные числа, г — ранг квадратичной фор-
мы (1).
Замечание 6. На практике привести квадратичную форму
(1) к сумме квадратов (4) можно с помощью метода собствен-
ных векторов:
•	Найти собственные значения Лп матрицы (2) квадра-
тичной формы (1) ;
•	Найти для каждого собственного значения соответствующие
ему линейно независимые собственные векторы;
•	Найти векторы ,..., ёп, ортонормировав набор собствен-
ных векторов Aj 5 ...9hn\
255
• Выполнить преобразование квадратичной формы (1) с помо-
щью матрицы В, столбцами которой являются векторы
ё ё
1? •** > п *
В результате выполненных действий квадратичная форма (1)
будет приведена к диагональному виду (4), где г ~п .
4.	КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Определение 9. Множество точек плоскости Оху, удов-
летворяющих уравнению
Ах2 + 2Вху + Су2 + Dx + Ey + F = 0,	(5)
называется кривой второго порядка.
Замечание 7. В уравнении (5) первые три слагаемые левой
части образуют квадратичную форму, которую методом собствен-
ных векторов можно привести к диагональному виду. Затем приме-
няют процедуру выделения полных квадратов, в результате чего (5)
сводится к одному из следующих канонических видов:
1)	AjX2 + Л2у2 +с = 0
2)	Л^х2+Ьу} =0
3)	A}x2+c = Q
(Л.2 * 0)>
(Л*о).
Определение 10. Множество точек в пространстве Oxyz,
удовлетворяющих уравнению
Ах2 + By2 + Cz2 + 2Dxy + 2Exz + 2Fyz +
+ Gx + Ny +Mz + L = Q,
(6)
называется поверхностью второго порядка.
256
Замечание 8. В уравнении (6) первые шесть слагаемых
левой части образуют квадратичную форму, которую методом соб-
ственных векторов можно привести к диагональному виду. Затем
применяют процедуру выделения полных квадратов, в результате
чего (6) сводится к одному из следующих канонических видов:
1)	Arf+Л2у?+с = 0	(4,2,3*°);
2)	4Х12 + +bz = 0	(4,2 * °)
3)	4Х]2 + А2у2 + с = О	(4 2 * 0) 
4)	4х2+бу]=о	(4* °);
5)	4Х12 +с - °	(4 * °) 
Поверхности видов 3)-5) являются цилиндрами; 2) - конусами;
1) - либо сферой, либо эллипсоидом, либо гиперболоидом.
5, ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Написать матрицу квадратичной формы
х2 +у2 +z2 +2ху
и найти ее ранг.
Решение. По формуле (2) находим:
<1
(Л
А= 1 1 0
1° ° V
Чтобы найти ранг матрицы, приведем ее к ступенчатому виду:
257
1 1 oV-i)
1 1 о
0 0 1.
(р
о <- ->
Q 10^
О 0 1
к0 О 0;
О О
о о
Следовательно, г(А) = 2.
Г1 1 о>
А = 1 1
Ответ:
г(Л) = 2.
^0 О
Пример 2. Выяснить, является квадратичная форма
знакоопределенной ?
Решение. В данном случае матрица квадратичной формы
имеет вид
Вычислим ее главные диагональные миноры:
258
Д3 = 1 3 3 = 15 + 6 + 6-12-9-5 = 1 > 0.
2 3 5
Следовательно, по критерию Сильвестра заключаем: квадратич-
ная форма является положительно определенной.
Ответ: положительно определена.
Пример 3. Как изменится квадратичная форма х2 + 2ху
при следующем преобразовании переменных:
х = Х1+^1, у = х1-у1 ?
(7)
Решение. Преобразуем квадратичную форму, воспользовав-
шись формулами (7):
х2+2ху = (х1 + у1)2+2(х1 +у1)(х1 -^) =
= х}2+ 2хАу} + у2 + 2х2 - 2у2 = Зх2 + 2xI j, - у2.
Ответ: 3Xj2 + 2xxyt — у2.
П ример 4. Как изменится квадратичная форма
Xj + 2x^2
-2х}х3
при следующем преобразовании переменных:
259
=x, + x2-x3,
У г = -X, + x2 + x3,
Л = X] - x2 + x3 ?
Решение. Матрица рассматриваемой квадратичной формы в
старых переменных х}, х2, х3 имеет вид:
О О
О 0 ;
Матрица перехода от новых переменных у}, у2, у3 к старым
переменным Xj, х2, х3 имеет вид:
Следовательно, находим матрицу перехода от старых перемен-
ных Xj, х2, х3 к новым переменным ух, у2 3 у3:
Тогда матрица квадратичной формы в новых переменных будет
следующей:
Д =вт-АВ =
260
Следовательно, в новых переменных у}, у2, у3 квадратичная
форма принимает вид:
Л 3	2	1 2 п
Ответ:—Jj ~~у;+2у}у3.
4	4
П ример 5, Привести квадратичную форму
4х}2 + 4х}х2 + х2
к каноническому (диагональному) виду.
Решение. Матрица рассматриваемой квадратичной формы
имеет вид:
2Л
Найдем собственные значения матрицы А , для чего составим и
решим характеристическое уравнение:
261
4-2
2
2
1-2
=> (4-2)(1-2)-4 = 0 =>
= 0
=> 4-52 + 22 -4 = 0 => 22 -52 = 0 => 2, = 0, 2^=5.
Найдем соответствующие этим числам собственные векторы
h}, h2 матрицы А .
Пусть = 0 . Тогда находим:
Следовательно,
Аналогично, пусть 22 = 5.
Тогда находим:
Следовательно, соответствующий числу = 5 собственный
вектор имеет вид:
262
Ортонормируем векторы hx, h2.
Нетрудно видеть, что векторы h} и h2 ортогональны. Дейст-
вительно, вычисляя их скалярное произведение, получаем:
= Ь2 + (-2)1 = 2-2 = 0.
Найдем длины векторов и й2 :
Таким образом, ортонормированиями по отношению к векторам
А] и Л2 будут следующие векторы:
Составим матрицу В , столбцами которой являются векторы
и е 2:
2/V^
1/^5 ;
263
Выполним с предложенной в примере квадратичной формой
преобразование переменных по формулам:
Матрицей этого преобразования является матрица В .
Тогда квадратичная форма 4Xj + 4х} х2 + х2 примет диаго-
нальный вид с матрицей
А} -Вт АВ =
ri/Vs -2/VT| Го io/VT|_Го о^
k2/V5 l/V? J 1^0 5/V5j~t° 5/
Следовательно, квадратичная форма 4х, + 4XjX2 + х2 имеет
следующий канонический вид; 5у?.
Ответ: 5у? •
Пример 6. Написать каноническое уравнение кривой вто-
рого порядка:
Зх2 + 3у2 ~2х-14у-13 ~ 0.	(8)
Определить ее тип.
264
Решение. Левая часть уравнения (8) представляет собой
многочлен второй степени относительно х и у .
Квадратичная часть этого многочлена имеет вид
Зх2 4- Юху 4-
и описывается матрицей:
Поступая по аналогии с решением примера 5, найдем
- собственные значения матрицы А :
ziq — 8, Л2 — -2;
- собственные векторы матрицы А :
- ортонормированные собственные векторы матрицы А :
rl/V2\
1/V2
-1/V2
Составим матрицу В , столбцами которой являются векторы
и ё2:
kl/V2
1/V2
-1/V2,
Выполним в уравнении (8) замену переменных по формулам:
265
11 11
Х=~Г^Х^~^У" У = 1^Х'--------КУ'-
V2 V2	V2 л/2
Матрицей этого преобразования является матрица В.
Тогда последовательно получаем:
Зх2 +10ху + 3/ -2x-14j-13 =
= 8Xj2-2у2 -8V2X, +6т/2^ -13 .
Следовательно, уравнение (8) принимает вид:
8Х]2 - 2у2 -8л/2Х] + 6л/2^ -13 = 0.	(9)
Выполним с уравнением (9) процедуру выделения полных квад-
ратов:
(8х12 - 8л/2х,) + (-2>’f + 6л/2у,) -13 = 0,
266
8(Xj2 - V2x,) - 2(>2 - зЛу,) = 13,
8(x,2-Лх, +|)-2O2-ЗЛу, + |) = 13+8-|-2-|,
8(x1-V2/2)2-2(j1 -ЗЛ/2)2 =8,
<Xj-у/2/2)2-~(У1 -ЗЛ/2)2 =1.	(10)
Таким образом, уравнение (10) - канонический вид кривой вто-
рого порядка (8).
Уравнение (10) описывает гиперболу в системе координат
с центром в точке
полуосями а = 1, b — 2.
Ответ:
1
гипербола (Xj -V2/2)2-— Зл/2/2)2=1
4
с центром в точке
полуосями
а — 1, Ь — 2, если выполнить преобразование
267
6.	ПРИМЕРЫ
Указать матрицы квадратичных форм:
15.1	. —2х2 + 16xy + 4j2 + 7z2 -4xz-20.yz.
15.2	. Зх/ +3х22 + Зх3 -2Х]Х2 .
15.3	. 5Х]2 + Зх22 + 4х3 + 4XjX3 + 4х2х3 .
15.4	. 27х/+3х22-10x,x2.
Найти ранги квадратичных форм:
15.5	. - 2х2 +1 бху + 4j2 + 7z2 - 4xz - 2()yz.
15.6	. 11х/ + 2x22 - 5x3 - 4X] x2 - 16x,x3 + 20x2x3 .
15.7	. 5x/ + 3x22 + 4x3 + 4X] x3 + 4x2x3 .
15.8	. 3(x2 + x2 + x3) - 2x,x2.
Привести квадратичные формы
к каноническому виду:
15.9	. -2х2 +16ху + 4}?2 +7z2 -4xz-20.yz.
268
15.10	. Зх,2 + 3х22 + 3xj -2XjX2 .
15.11	. 5Xj2 + Зх22 + 4х2 + 4X]X3 + 4x2x3.
15.12	. 27x.2 + 3x,2 - 10x,x,.
15.13	. x2 + 4x2 + x2 + 4x, x, - 2x, x. - 4x, x,.
15.14	. Их,2 +17x2 +11x3 -16X]X2 +8X]X3 -8x2x3.
15.15	. 11X]2 + 2x22 + 5x3 + 4x,x2 -16X]x3 + 20x2x3 .
15.16	. 2X] + 5x22 + 5x2 + 4x,x2 - 4x,x3 -8x2x3.
15.17	. x,2 + 5x2 + x2 + 2x,x2 + 6X]X3 + 2x2x3.
15.18	. x,2 + X-2 + x2 + 4x,x. + 4x,x, + 4x9x,.
15.19	. Зх/ + 4x22 + 5x3 - 4x,x2 - 4x2x3 .
Проверить квадратичные формы
на знакоопределенность:
15.20	. - 2х2 + 16ху + 4^2 + 7z2 - 4xz - 20yz.
15.21	. Зх,2 +3х22 +Зх3 -2Х]Х2 .
15.22	. 5х,2 +3х,2 +4х2 +4х,х, +4х,х..
X	J	J J
269
15.23	. 27Х]2 + Зх22 -1 Ох,х2 .
15.24	. - 2х2 +	- 4у2 - 3z2 + 2xz.
15.25	. - 4х2 + у2 - 5z2 + 2xz - 4yz .
15.26	. 4х2 + у2 - 5z2 + 2xz - 4yz - 20ху.
15.27	. - 4x2 - y2 - 5z2 + 2xz - 4yz.
15.28	. 4x2 - y2 - 5z2 + 2xz - 4yz.
Написать канонические уравнения
кривых второго порядка и определить их тип:
15.29	. 9х2 -4лу + 6>'2 +16х-8^-2 = 0.
15.30	. х2 -2ху + у2 -10х-6_у + 25 = 0.
15.31	. 5х2 +12ху-22х-12у-19 = 0.
15.32	. х2 — 4ху + 4_у2 — 4х — 3_у — 7 = 0.
7.	ОТВЕТЫ
( 3 -1 0>
15.1.	8	4-10
15.2. -1	3
-10
о
3;
< о О
270
л5 0
15.3. О 3
2
4?
15.5. 2.
15.7. 3.
15.9. 18х2-9у2.
15.11. yf + 4^2 + 7у23.
15.13. 6j2.
15.6. 3.
15.8. 3.
15.10. 2^2+4_у2+3_у2.
15.12. 2у2+28у2.
15.14. 9у2 + 9у2 + 27у3.
15.15.	9у2 +18у2 -9у3.	15.16. у2 + у2 +10.у2.
15.17.	-2у2 +6у2+Зу23.	15.18. -у?-у22+5у1-
15.19.	у2 + 4_у2 +7_у2.
15.20.	Не является.
15.21.	Положительно определена.
15.22.	Положительно определена.
15.23.	Положительно определена.
15.24.	Отрицательно определена.
15.25.	Не является.
271
15.26.	Положительно определена.
15.27.	Отрицательно определена.
15.28.	Не является.
15.29. Эллипс
с центром в точке
полуосями
а — \ 2, b ~ 1, если выполнить преобразование
15.30.	Парабола -1)2 = 4у[2  (х} - 2)
с вершиной в точке (2,1), если выполнить
преобразование
272
15.31. Гипербола
с центром в точке (1; 11, полуосями
а — 2, b = 3, если выполнить преобразование
х =
15.32. Парабола
с вершиной в точке
преобразование
если выполнить
2
273
ПРИЛОЖЕНИЯ
L КОНТРОЛЬНАЯ РАБОТА
на темы:
уравнение прямой на плоскости;
кривые второго порядка; операции над векторами
1. ПРИМЕРНЫЙ ВАРИАНТ
1. Даны вершины треугольника АВС : Л(5;-4), В(~1;3),
С(- 3;—2). Найти точку пересечения высоты BD с медианой
АЕ.
2. Определить тип кривой, заданной уравнением
х1 2 3 * + 2у2 + 4х — 4у = 10, и построить ее.
3. Даны три вектора:
а - -2z + j + к.> b-i + 5/, с - 4/ + 4j - 2k.
Вычислить проекцию вектора За — 2Ь на вектор с.
4.
Векторы а и b образуют угол (р = —. Зная, что а = 3
274
и
b = 2, вычислить
(зл - Z>)x (tz - 2Z>)
5. Даны вершины тетраэдра: Л(2;3;1), В(4;1;-2), С(б;3;7),
Z)(— 5;-4;8). Найти его объем и длину высоты, опущенной из
вершины D.
2. ОТВЕТЫ
<	109 19^
<	65 ’ 65/
2.
Эллипс
Рис. 1.
275
3.	-11.
4.	15.
tz 154	,	,,
5.	F,__ =---------; h - 11.
memp.	5
3. РЕШЕНИЯ
Пример 1. Зная координаты точек А и С, найдем угло-
вой коэффициент прямой АС:
к -Ус-У- -2~(~4L 2	1
АС хг - х. -3-5	-8	4
Тогда, так как BD1AC, то
к =
KBD
1
^АС
Поэтому уравнение прямой BD, проходящей через заданную
точку В(— 1;3) с известным угловым коэффициентом к ~ 4, име-
ет вид:
у - 3 = 4(х +1) или 4х - у + 7 “ 0.
Так как АЕ — медиана, то Е — середина отрезка ВС.
Поэтому, зная координаты точек /?(—1;3) и С(-3;~2),
находим координаты х0, yQ точки Е:
276
Зная координаты точек
-I-з „
хо “	-	— 2,
Л(5;-4) и £|-2;1
\. 2J
найдем
уравнение прямой АЕ:
или 9х + 14_у + 11 = 0.
Найдем точку	пересечения прямых BD и АЕ, ре-
шив систему:
(4х-у = -7
9х +14^ = -11.
Воспользуемся, например, правилом Крамера:
= 56 + 9 = 65;
-1
14
= -98-11 = -109;
4 -7
9 -11
= -44 + 63 = 19.
А
277
Отсюда
Ответ:
109 19л
65 ’ 65;
Пример 2. Чтобы определить тип кривой и построить ее,
приведем уравнение х2 + 2у2 + 4х — 4у = 10 к каноническо-
му виду с помощью процедуры выделения полного квадрата:
х2 + 2у2 + 4х - 4у -10,
(х2 +4х + 4)+2(у2 -2^ + 1)= 10 +4+ 2,
(х+2)2 +2(у-Д)2 =16,
16	8
Следовательно, данная кривая - эллипс, у которого
1. <7^-2;!) — центр;
2.	а = >/16^ — 4, b — V& ~ 2>/2 — полуоси;
3.	4(2;1), Л2(-6;1),	(-2;1+2>/2), В2(-2;1-2>/2) -
вершины;
278
4.	х = —2, у — 1 — оси симметрии;
5.	F} (- 2 + 2V2;1), F2 (- 2 - 2>/2;1) - фокусы;
6.
График кривой
= 1 изображен на рис. 1.
Ответ: эллипс
см. рис. 1.
Пример 3. Так как а(—2;1;1), Л>(1;5; О), с(4;4;—2),
то
За - 2Ь = 3 • (- 2;1;1) - 2 • (1;5;0) = (- 6;3;3) - (2;10;0)=(- 8;-7;
Поэтому
Ответ: —11.
Пример 4. Используя свойства векторного произведения,
найдем вектор с:
279
с = (За - brx\a - 2Ь]= За ха - b ха -6а xb + 2bxb =
= 3axa-5axb + 2bxb.
Однако справедливы равенства
аха = 0, bxb = O.
Поэтому
с = -5а хЪ.
Следовательно,
с =5- axb =5- а
Ответ: 15.
Пример 5. Найдем векторы АВ, AC, AD:
АВ = (2;-2;-3), АС = (4;0;б), AD = (- Т,-Т,1).
Так как
Vmmo =- AB AC AD
m€mp.
то, используя свойства смешанного произведения, получаем:
280
2 -2 -3
AB-AC-AD- 4	0	6 =0 + 84 + 84-0 + 84 + 56 = 308.
-7 -7	7
Следовательно,
V = 1-308 = —.
тетр 6 3
Но
тетр.
Поэтому длину высоты h тетраэдра можно вычислить по фор-
муле:
ЗИ
г тетр.
осн.
Причем SOCH
, где
к
АВхАС=
= -12/- 24/+8Л.
0
6
Отсюда
жн = - V144 + 576 + 64
, 154
h -----
14
TZ 154
Ответ:	= —;
А = 11.
281
II. КОНТРОЛЬНАЯ РАБОТА
на темы:
комплексные числа; разложение рациональной
дроби; ранг, определитель матрицы, обратная
матрица; решение систем матричных уравнений;
решение систем линейных уравнений
ПРИМЕРНЫЙ ВАРИАНТ
1.	Выполнить действия и изобразить ответ на комплексной
плоскости:
х2 + 2х + 3
2.	Представить дробь у---г-г ----г в виде суммы простейших
-1)
дробей
3.	Вычислить определитель:
282
-2-11 О
1	12-1
3 -12 3
3	16 1
4.	Исследовать систему на совместность и решить ее:
'2х} — х2 + Зх3 + 4х4 = 5
4х, - 2х2 + 5х3 + 6х4 - 7
6х} -Зх2 +7х3 +8х4 =9
8х, -4х2 +9х3 +10х4 =11.
5.	Решить матричное уравнение А • X = В, где
(Р
7
8>
6.	Разложить вектор b = (-4;5;5) по базису:
а,=(3;3;-9), а2 = (1;-8;4), а3 = (1;0;-2).
ОТВЕТЫ
ч 18	1 .	1 л/з.
1. а) — - — z, рис. 1; Ь) --——г, рис.2;
Л W Л W
283
Рис. 3
284
2.
3.	-20.
4.	Xj = -2 + 0,5c1 + c2, x2=c1? x3=3-2c2,
x4 = c2, где c}, c2 — произвольные постоянные.
Гб 4 5Л
5.	Х= 2 1 2
^3	3 3,
6.	b = -1-а, -1-а, + 0-а,.
РЕШЕНИЯ
Пример 1,
3 + 4/ _ (3 + 4/) (2-3z) _ 6-9/ + 8/-12/2
Я) 2 + 3/ “ (2 + 3/) (2-3/) "	4-9/2
6 + 12-/ _ 18 —г 18 1 .
4 + 9 - 13 "13 13*’
285
18	1 .
Комплексное число	изображено на рис. 1.
Z>) Найдем модуль г и аргумент (р комплексного числа
Z -------
2	2
5л
<р - 2л -
Поэтому
5л.
—i
z = е 3
Следовательно, получаем:
5я	100я"
20--i -------1
20	20 Л д	7
= z ~е 3 ~е 5
-), (^+-
3 = е 3
= е
Отсюда, воспользовавшись формулой Эйлера, находим:
2	2
20 = cos(X ч—) ч- i  sin(zr ч—) =
• - cos---I  sin — =
286
1 V3
Комплексное число----------i изображено на рис. 2.
2	2
с) Найдем модуль г и аргумент (р комплексного числа
z = — i :
г = д/(о)2+(-1)2 =71 = 1
Поэтому
Зя-.
—J
Следовательно, получаем:
у/— i = z3 = е3 2	- е2 * , где к = 0, 1? 2.
Поэтому, воспользовавшись формулой Эйлера, находим:
п 2я--0.	я-.
_ j	—f	ft	д
z.=e2 3 =е2 = cos— 4 i sin — -/;
л 2»1.
—Л----1
2	3 -еб
COS
п	. . л	л/3	1 .
= - cos----.’ sin — =---------1 ;
6	6	2	2
287
я. 2я-2, я 4я.	я
—1 + 1	—Z + 1	--1	JT	ТГ
z^=e2 3 =е2 3 -е 6 = cos(----------------------) + z-sin(------) =
Я	. . Я	у/З	1 .
= cos----zsin —=----------z .
6	6	2	2
Комплексные числа Z],z2,23 изображены на рис. 3.
Ответ: а)--------i, рис. 1; Ь)-------z, рис. 2;
13 13	2	2
ч .	л/3 1 . VI 1 .
С) 1,--------------1,----------1. рис. 3.
2	2	2	2
Рис. 2
288
Пример 2» Так как
то
(1)
Числа A^B.C.D найдем, приведя (1) к общему знаменатсщо
и приравняв в числителе коэффициенты при одинаковых степе-
нях х:
х2 + 2х + 3 =	+ х + 1)+В(х-1)-(х2 +x + l)+(Cx + D)-(x-l)2,
289
х + 2х + 3 —
= Ах2 + Ах + А + Вх3 - В + Сх3 + Dx2 - 2Сх2 - 2Dx + Cx + D,
х3 В + С = О
290
112-1
41-1-2-
-20.
Ответ: —20.
Пример 4. В данном примере
А =	4-256 6-378 .8 -4 9 10,	
Составим расширенную матрицу системы и, используя элементар-
ные преобразования строк, приведем ее к ступенчатому виду:
4
6
-2
-3
5
7
1^8 -4 9 10
291
Следовательно, ранг матрицы системы равен рангу расширен-
ной матрицы и равен 2; число неизвестных равно 4.
Поэтому с учетом теоремы Кронекера-Капелли делаем выводы:
•	система совместна;
•	имеет бесконечное множество решений;
•	х2, х4 — свободные неизвестные;
•	Xj, х3 — базисные неизвестные;
•	уравнения третье и четвертое исходной системы - зависи-
мые от первого и второго уравнений этой системы.
Чтобы найти решение системы, продолжим преобразование по-
следней полученной матрицы (2) к виду Гаусса:
292
<2-13	4	5 'I		<2-13	4		1
0 0-1-2	-3	(-0^	0 0 1	2	3	(-3) >
0 0	0	0	0		0 0 0	0	0	
/) 0	0	0	0 J		^0 0 0	0	°>	
(2 -1 0 -2 -4^(1/2) fl -1/2	0 -1	-2У 3
0 0 1	2	3	0	0	1 2	
0000	0	^0 0 00 .0 000	0	(о 000		0 0 .
Отсюда получаем решение исходной системы:
Xi — —2 Ч-Су +
2 1
J х2 — сх	где СХ^С2 — произвольные постоянные.
х3 = 3 - 2с2
^4 “	’
Или в векторной форме:
Ответ: Xj =-2 + 0,5с1+с2, х2=с1? х3=3~2с2,
х4 = С2, где Сх, С2 — произвольные постоянные.
293
Пл. и м с р 5. Если матрица А имеет обратную А 1, то данное
матричное уравнение А' X — В имеет решение, вычисляемое по
формуле:
X = А~} •В.
1) Проверим, существует ли матрица
(3)
А 1. Для этого выясним
выполнение условия I А 0:
= -24 + 25 = 1.
Следовательно, матрица А 1 существует.
2) Найдем матрицу А 1. Для этого составим расширенную
матрицу (#) и приведем ее к виду Гаусса с помощью элементар-
ных преобразовании строк:
(л|е) = 3
2 -3
2 -4
-1 О
1 О О+ЗХ-2)
О 1 о <-*
о о 1 -----
1 о оЛ
-3 1 О.<_]
-2 О 1J(-1)
294
A 2
-> 0 1
кО -5
Ч 2
-> О 1
кО О
-3
-1
6
-3
-1
1
1 о 0>
-1 1 -1 (?)-»
-2 0 1 7^
1 о о
"1 2
-> О 1
чо о
Л1 о
-> О 1
чо о
Следовательно,
А
-20 15 -12V-,
-8	6	-5 (-2)
-7	5	-4?
-4
-8
-7
г- 4 3 - 2>
-8 6 -5
к- 7 5 - 4;
295
Проверка:
3) Построим решение исходной системы.
Для этого по формуле (3) находим:
-3
2
7
296
П ример 6. Составим матрицу А, столбцами которой явля-
ются заданные базисные векторы
а}=(3,3;-9), а2=(1;-8;4), а3 = (1;0;-2):
Чтобы разложить вектор b = (—4;5;5) по данному базису,
са
(Е с ) с помощью элементарных преобразований строк. Тогда
вектор с и будет искомым.
Выполним преобразования:
297
Л3 1	0	-4>		Л3 1
0-9 0	9	(-1/9)->	0 1
к0 0 1	0 >		ко 0
0
О -1 (-!)->
1 0)
О О
->0-9 0
-3V1/3) р о
-1	-> 0 1
1^0 0 1
1^0 о
О -1'
О -1 = (е|с).
1 °>
0 )
Следовательно,
с=
и справедливо разложение:
b =-1-0] -1-а2 4-О
•а3.
Ответ: b = -1 • я, -1  а2 + 0-а3.
298
III. КОНТРОЛЬНАЯ РАБОТА
на темы:
собственные значения,
собственные и присоединенные векторы матрицы;
базис в пространстве; ортогонализация базиса
ПРИМЕРНЫЙ В А Р И А Н Т
1.	Найти собственные значения и собственные векторы матрицы:
—
13	16
-12 -15
2.	Найти собственные значения, собственные и присоединенные
векторы матрицы:
А =
14	16
{-9 -10J
3.	Среди векторов
ах = (3;3;-9), аг = (1;-8;4), а. = (-4;5;5), а4 = (1;0;-2)
указать линейно независимые. Выяснить будут ли они
базисом в пространстве R3.
299
4,	По базису
а2=(1;4;-1), а3 = (-1;7;0)
построить ортогональный базис А > 4 » 4 и ортонормированный
базис ё}, ё2, ё3.
ОТВЕТЫ
1. Матрица А имеет простые собственные значения
= 1, А2 = -3 ,
которым соответствуют собственные векторы
2. Матрица А имеет двукратное собственное значение
Л = 2, которому соответствует собственный вектор
и присоединенный вектор —
3. Векторы ах, а2, а4 — линейно независимые и являются ба-
зисом в пространстве/?2 3.
300
4. 7г=(1;-2;2), Z2 = (2;2;1), Z3 = (-2;1;2>.
РЕШЕНИЯ
Пример 1, 1) Найдем собственные значения матрицы
Для этого составим ее характеристический многочлен:
13-2
-12
16
-15-2
= (13-Л)-(-15-2) + 12-16 =
= 13-15+ 152-132+ 22 +12-16 = -195 + 22 + Л2 +192 =
= 22+22-3.
Характеристическое уравнение матрицы А имеет вид
22 +22-3 = 0
и имеет простые корни
2i2 =-l±VT+3 =-1±2.
301
Следовательно, собственными значениями матрицы А являют-
ся числа:
2, = 1, 22 - -3.
2) Найдем собственные векторы, соответствующие указан-
ным собственным значениям. Для этого решим однородные сис-
темы
(а-яе) • х = 0, где А — собственные значения.
Воспользуемся методом Гаусса.
a) — 1:
(л-ДЕо)^
( 12
С12
16
-16
*1
0\1)	(12 16
oj«-l До о
Х2
0Y1/12)
oj
о
Следовательно, координаты Xj
и х2 собственного вектора
связаны равенством х, = --х2 .
Значит, собственному значению — 1 отвечает семейство
собственных векторов вида
- любое число.
2
302
Следовательно, в этом семействе один линейно независимый
собственный вектор, например,
Л,=
16
-12
16 0>(3/4) Г16 16 (Г|(1/1б)
-12 ole-* "Ч о 0
I Л2
Следовательно, координаты Xj
связаны равенством Xj — — х2 .
Значит, собственному значению
и х2 собственного вектора
Л2 — -3 отвечает семейство
собственных векторов вида
, где х2 - любое число.
2
0
О О
2
О
\ 2 у
Следовательно, в этом семействе один линейно независимый
собственный вектор, например,
Л2 =
Ответ: Матрица А имеет простые собственные значения
которым соответствуют собственные векторы
А,=
Л2 =
303
Пример 2. 1) Найдем собственные значения матрицы
Для этого составим ее характеристический многочлен:
14-А
-9
16
-10-А
= (14-Я)-(-10-А) + 9-16 =
= -140-4Л + Л2 +144 = Я2 -4Л + 4 = (Л-2)2.
Следовательно, характеристическое уравнение матрицы А име-
ет вид
(2-2)2=0
и имеет двукратный корень
Л.2 “ .
Следовательно, у матрицы А двукратное собственное значе-
ние:
2 = 2.
2) Найдем собственные векторы, соответствующие указан-
ному собственному значению. Для этого решим однородную сис-
тему
(А - ЛЕ)-х = 0, где 2 = 2.
Воспользуемся методом Гаусса:
304
16 0V3/4)
2
0	0
о о
0
Следовательно, координаты X}
и х2 собственного вектора
связаны равенством: X, =-----Х2.
Значит, собственному значению

Л — 2 отвечает семейство
собственных векторов вида
, где х2 - любое число.
Следовательно, в этом семействе один линейно независимый
собственный вектор, например,
Л,=
3) Найдем для числа Л = 2 присоединенный вектор. Для
этого решим систему (А-2Е) х ~ hy ;
12
16
-4>(3/4)	<12 16 -4V1/12)
1
-9
0
0
305
Следовательно, координаты х1 и х2
собственного вектора
связаны равенством:
4	1
Значит, собственному значению 2 = 2 отвечает семейство при-
соединенных векторов вида
, где Х2 - любое число.
Следовательно, в этом семействе есть только один вектор ,
линейно независимый с собственным вектором .
Поэтому присоединенным к собственному вектору Aj будет,
например, вектор
Других присоединенных у вектора Aj нет, так как в сумме чис-
ло найденных линейно независимых собственных и присоединен-
ных векторов равно двум, то есть кратности собственного значения
2 = 2.
Ответ: Матрица А имеет двукратное собственное значение
2 = 2, которому соответствует собственный вектор
и присоединенный вектор
306
Пр и м е р 3. Составим матрицу А , столбцами которой явля-
ются данные векторы , а2, а3, а4 , и найдем ее ранг, а также
базисные столбцы.
Для этого приведем матрицу А к ступенчатому виду:
Следовательно, ранг матрицы А равен 3; базисными столбца-
ми являются первый, второй и четвертый.
Поэтому векторы , аг, а4 являются линейно независимыми
и базисом данной системы векторов.
Кроме того, так как базисных векторов оказалось найдено три,
то есть ровно столько, какова размерность пространства 7?3, то
они образуют базис в пространстве А3.
Ответ: Векторы ах, аг,	— линейно независимые,
являются базисом пространства R3.
307
Пример 4. Проверим, что векторы а1? а2,	— линейно
независимы (то есть действительно являются базисом).
Для этого составим матрицу, столбцами которой являются век-
торы ах, а2, а3 , и найдем ее ранг:
Так как ранг этой матрицы равен 3, то все три вектора, ее обра-
зующие, линейно независимы и являются базисом пространства
R3 — пространства трехмерных векторов.
Построим по векторам а}, а2 , а3 ортогональный базис
А, Л, /3, воспользовавшись процессом ортогонализации Шмидта:
А —	2,2);
К ”	’ А ’
где ах =
-9 ,
----= 1, то есть
308
/3 — Cl2) +	' /j + ^2 ’ 4 >
fc»A.)= ~15_5
то есть
4 - (- 2;1;2).
Построим по векторам alsa2ya3 ортонормированный ба-
ЗИС	, в2 ,	,
Зная координаты векторов	, /2 5 /3, вычислим их длины. В
данном случае
Следовательно, векторы ортонормированного базиса вычисля-
ются по формулам:
309
Ответ: Z, =(l;-2;2), Z2 = (2;2;1), Z3 = (-2;1;2>.
310
IV. ИТОГОВАЯ
КОНТРОЛЬНАЯ РАБОТА
ПРИМЕРНЫЙ ВАРИАНТ
1.	Определить тип кривой и построить ее:
а)	2_у2 + 8х2 + 4у + 8х -1 = 0,
б)	16г2-9/-64х-18^ + 199 = 0.
2.	Найти площадь треугольника АВС, если
Л(-1;2;-3), 2?(0;1;-2), С(-3;4;-7).
3.	Найти объем пирамиды A BCD, если
Я(3;10;-1), 5(-2;3;-5), С(-6;0;-3), £>(1; -1; 2).
311
4.	Вычислить определитель
2	2-6 3
-1 -1 2 -1
0	3	2	2
-5 2	0	6
	-3	3	-1	11	-3
	0	1	-2	6	-7
б)	3	-1	0	-2	-И
	0	3	-1	-11	-8
	3	0	-2	4	-18
5.	а) Вычислить 3zx  z2 ~4(zt -2z2)h--------,
z2 +zt
если Z] ; — 2—i, z2 = 3 — 2i.
6) На множестве комплексных чисел найти v64
6.	Разложить рациональную дробь на сумму простейших дробей:
2х4 - 6х3 + 4х2 - 8х + 2
х5 - х4 + 2Х3 - 2х2
2х3 -х2 -8х + 13
б)		2----------.
х +х-2
7.	Найти обратную матрицу:
312
8.	Найти ранг матрицы:
( 4	0	6	2	>
0-43-3
-3 -2 -3 -3
1	2	0	2	}
9.	Решить системы:
9. Решить матричное уравнение В • X = А,
где
313
11.	Доказать, что векторы
^i=(2;l;-2), а2 = (-2; - 4; - 4), а3 = (1; 5; -1)
образуют базис. Разложить вектор а4 = (5;10;—8) по этому
базису. Найти базисы ll7 l2J3 и е2,е3 , соответственно,
ортогональный и оргонормированный к базису а} , а2, а3.
12.	Найти собственные значения н собственные векторы матрицы
13.	Найти собственные значения, собственные и присоединенные
векторы матрицы
А= 0 2
(Р
4
I1 0 “V
ОТВЕТЫ
б) Гипербола
1. а) Эллипс
(J + 1)2	(х-2)2
42 З2
— 1 , см. рис. 2.
314
Рис. 2
315
2. л/2.
3. 45,5.	4. а) 22; б) 0.
5. а) 8,1 —9,7/;
6)2; 1-ь/л/З; -1 + л/З; -2; -1-/>/3; 1-/\/з .
2
а)
X X2
8.
б)
а)
-ОД
-0,4>
-0,2 ’
б)
-6
35
35
35
а)
X]
х2 = —
х3
35
2
2
2 ’
б) решений нет;
х2
3 ’
2
1
3’^3 С
х4 = 2 - Зс2,
^6 “ ^3’
^5 “ ^2 »
где с1, с2, с3 — произвольные числа.
316
11. а4 = 2й] + — а2 + 2а3;
/,=(2;1;-2), Т2 = (-2;-4;-4), ^ = (-2;2;-
= (2/3; 1/3; - 2/3), 72 = (-1/3; -2/3; - 2/3),
ё7 = (-2/3;2/3;-1/3).
12.
2з =10,
317
РЕШЕНИЯ
Пример 1. а) Преобразуем уравнение
2у2 + 8х2 + 4у 4- 8х -1 = О,
выделив в нем полные квадраты:
2
2	8
Следовательно, рассматриваемая кривая - эллипс с
каноническим уравнением (1).
Свойства эллипса (1):
1)
2)
Центр эллипса:
Полуоси эллипса: а =
318
3) Фокусы эллипса:
4) Вершины эллипса:
. ( 1 [Г J f 1 |5 /
2 Ъ’ /Д 2 v8’ J’
График эллипса (1) изображен на рис. 1.
Л ▲ кУ
Рис. 1
319
б) Исследование кривой 16х2 — 9j/2 — 64х —18^ +199 = О
проводится аналогично и приводит к результату: гипербола с
каноническим уравнением
(уч-I)2 (х-2)2
42 З2
и графиком , изображенным на рис.2.
(у +1)2 6 Ответа) Эллипс —	— + — 5/2 (.У + 1)2 б) Гипербола	?	с-4-1/2) = 1,см. рис. 1; 5/8 (х ~ 2)2 , = 1 , см. рис. 2.
320
Пример 2, Найдем векторы:
Тогда
АВхАС=
-2
-2
2
2
 k = 21 + 2j + 0k = (2;2,6)
Следовательно, площадь параллелограмма, построенного на
векторах АВ и АС, равна
S = АВ X АС = у/4 + 4 = 2V2 .
Поэтому
5^= 5/2= Л.
Ответ:
л/2.
Пример 3, Найдем векторы:
~АВ = (-5;-7;-4), АС = (-9;-10;-2), AD = (-2;-11;3) .
Вычислим их смешанное произведение:
321
ABACAD =
—5 -7 -4
-9 -10 -2
-2 -11 3
%
= 150 - 28 - 396 + 80+ 110-189 = -273.
Поэтому объем параллелепипеда, построенного на векторах
АВ, AC, AD, равен:
V = |- 273| = 273;
Следовательно, находим объем пирамиды ABCD:
ABCD g
273
~6~
= 45,5.
Ответ: 45,5.
Пример 4.
322
б) Вычисление определителя
-3	3 -1	И	-3
О	1-2	6	-7
3-10-2 -11
0	3-1	-И	-8
3	0 -2	4	-18
выполняется аналогично и приводит к результату: 0.
Ответ: а) 22; б) 0.
323
z.
Пример 5, a) 3zj • z2 — 4(Z] — 2z2) 4-!—
z2 +Zj
-2 - z) • (3 - 2z) - 4(-2 - i - 6 + 4/) +-:--
3 ~ 2z 2 ~” z
О
= 3(-6 - 3z + 4z - 2) - 4(-8 + 3z) +	=
1 -3z
= -24 + 3z + 32-12z + (- 2 ^1 + 3г) =8-9/ + ^—Л =
(1 - 3z)(l + 3z)	10
= 8-9z+ 0,1 - 0,7z = 8,1-9,7z.
б) Число 64 представим в тригонометрической форме:
64 = 64  (cosO + z sin 0).
Тогда
^64 =
0 + 2лк
cos-------
I 6
+ z sin
0 + 2лР
6 )
= 2- cos— + zsin— ,
где к = 0,1, 2, 3, 4, 5, 6.
Следовательно, находим шесть значений корня шестой степени
нз числа 64:
324
Z] = 2 • (cosO + i sin O) = 2;
z2 = 2- cos—+/sin —
_ ( 2n
z,=2- cos—
I 3
+ / sin
z4 = 2  (coszr + / sin ?r) = -2;
_ (	4/r . . 4тгл
z, = 2 • cos— +1 sin —
I 3	3 )
_ ( 5л .. 5л
z„-2- cos— + zsin —
Ответ a) 8,1-9,7/;
6
2x4 - 6x3 + 4x2 - 8x + 2
П p и м e p 6. a) ---j——3—~~2— =
x5 - x4 + 2x3 - 2x2
2x4 -6x3 +4x2 -8x + 2 _ 2x4 -6x3 +4x2 -8x + 2
x4 (x -1) + 2x2 (x -1)	(x4 + 2x2 )(x -1)
325
2х4 — 6х3 + 4х2 -8х + 2 _А_ В С Рх + Е
х2 (х2 + 2)(х — 1) х2 х (х-1) (х2 +2)
Следовательно, приводя к общему знаменателю, получаем:
2х4 -6х3 +4х2 -8х + 2 _
х2 (х2 + 2)(х -1)
А(х - IX*2 + 2) + Вх(х - IX*2 + 2) + Сх2 (х2 + 2) + Dx3 (х -1) + Ex2 (х -1)
х2(х2 +2Х*-1)
Приравнивая в числителях коэффициенты при одинаковых сте-
пенях х, получаем систему:
’ B+C+D=2
A-B-D + E = -6
< -А + 2В + 2С-Е = 4
2А-2В = -8
-2А = 2
Таким образом, получили разложение:
2х4 -6х3 +4х2 -8х + 2 __1_	_	2	,
х2(х2+2)(х-1) х2 х (х-1) (х2 +2)
326
2х3 - х2 - 8х +13
б) Дробь ------z------------ является неправильной.
х2 +х —2
Выделим ее целую часть:
2х3 -х2 -8х + 13
2х3 + 2х2 -4х
-Зх2 -4х + 13
-Зх2 -Зх + 6
-х + 7
х2 +х-2
2х-3
Поэтому можно записать
2х3-х2-8х + 13 _	-х + 7
---z-------= 2х - 3 + —-.
х+х-2	х+х-2
Разложим правильную рациональную дробь —------ на
х2 +х-2
сумму простейших дробей:
-х + 7 _ -х + 7	_ А В _ А(х-1) + В(х + 2)
х2 +х-2 (х + 2)(х-1) х + 2 х-1 (х + 2)(х-1)
Следовательно, получаем равенство:
А(х -1) + В(х + 2) = -х + 7
или
(А + В)х + (- А + 2В) = -х + 7.
327
Приравнивая здесь коэффициенты при х и свободные члены в
левой и правой частях равенства, получаем систему:
Следовательно, справедливо разложение:
2х3-х2-8х + 13	„	,	2	3
---- -------= 2х - 3 +----.
х+х-2	х-1 х+2
3	1	2	х-1
Ответ: а)-----------+ —г--;
х х2 х-1 х2 +2
б)
Пример 7. а) Вычислим определитель данной в примере
матрицы
= -6-4 = -10.
Так как это число не равно нулю, то матрица А имеет обрат-
ную:
328
-i
-10
°’3 -0’4>
2/^-0,! -0,2/
б) По данной матрице
-4 2 >
0 -3
-1	0 >
A
составим расширенную матрицу

где Е - единичная мат-
рица порядка 3, и приведем ее к виду Гаусса с помощью элемен-
тарных преобразований строк:
-4
0
-1
2
-3
0
1 0 о^«-
0 1 0 <-1 ->
О 0
1 О -3
о
1
о
1
о
о
О 1	0^1
329
Г1 0-3
—» 0 -1 -6
^0 0 35
О 1 (Р
О 2	1 (-4) ->
1 -з oj<-l
0	1	О л
О	2	1	(-1) ->
1 -11 -4j(l/35)
Следовательно, матрица А имеет обратную :
330
Пример 8. Приведем матрицу к ступенчатому виду:
4	0	6
0-4 3
-3 -2 -3
1	2 О
2 О
-4 3
-2 -3
О 6
2\3X-4)
331
rl 2	0	2	л
0 I 4 3 “3
0 0 0 -14
J) 0 0	0	,
Следовательно, ранг изучаемой матрицы равен 3.
Ответ: 3.
Пример 9, а) Составим расширенную матрицу данной сис-
темы и приведем ее к ступенчатому виду:
1 0
2 1 3
0 1 1
<3 1 4
1
0 -1
0 О
^0 о
1
О -1
о о
о
3
4
О
Следовательно:
1.	Система совместна;
2.	Четвертое уравнение системы - зависимое от остальных;
332
3.	Ранг системы равен 3;
4.	Базисные неизвестные: х1, х2, х3;
свободных неизвестных - нет;
5.	Система имеет единственное решение.
Продолжим преобразование расширенной матрицы к виду Гаус-
са:
1
-1
О
О
„ 111
Следовательно, х3 =-; х2 = —; х3 — —
Исследование систем б) ив) проводится аналогично.
Л 1 1
Ответ: а) х, =----; хэ = —
2	2 2
б) решений нет;
1
х3 = -
в) Xj = —с} - 2с2 + с3,
х3 — ,
х5 = с2,
где Су, с2 у с3
х2 = 1 + ^ +с2 -2с3,
х4 = 2 - Зс2,
произвольные числа.
333
Пример 10. Так как \В = -1 - 0 — 6 - 5 = -30 0, то у
матрицы В существует обратная матрица:
Поэтому матричное уравнение В • X — А имеет единственное
решение, которое найдем по формуле:
Пример 11. Проверим,что ах,,а3 — линейно
независимы (то есть образуют базис этой системы). Для этого со-
ставим матрицу, столбцами которой являются векторы
а15 а2, а3 , и найдем ее ранг:
334
О 6
О
6
О -12
О О
Так как ранг этой матрицы равен 3, то все три вектора, ее обра-
зующие, линейно независимы и являются базисом рассматривае-
мой системы векторов.
Найдем разложение вектора а4 по векторам ах, а2,
этого требуется решить систему
4 ~ •*!	' Л2 2 Л3 w3
(2)
Составим для системы (2) расширенную матрицу и приведем ее
к виду Гаусса
(«1 а2
а4
-12
1
О
о
6
335
О 6
О
-4 5
6 -9
О -9
-15
-4
1
О
0 0 Т"1
О 1/2 (4)
-> О
-18j(-l/9)
1 2 )
Г1 О О
О 1 о
кО oil
2 л
1/2
2 >
Следовательно, в формуле (2)
Значит, указанные числа являются координатами вектора а4
в базисе из векторов , а2, а3 .
336
Построим по векторам , а2, а3 ортогональный базис
, /2, /3, воспользовавшись процессом ортогонализации Шмидта:
А = = (2;1;-2);
^2	@2	’ А »
где О'] =
— = 0, то есть
9
/2=(-2;-4;-4);
/3 — Я3 + 6Z1 • A "t" (%2 ‘ ^2 >
где а, =
=_к^)==—
2 См 36 2>
9
то есть
/3=(-2;2;-1).
Построим по векторам , а2, а3 ортонормированный ба-
зис , е2, е3 .
Зная координаты векторов 1}, /2 5 /3, вычислим их длины. В
данном случае
337
A =V9 = 3,
/2 =д/36=6,
/3 =V9=3.
Следовательно, векторы ортонормированного базиса вычисля-
ются по формулам:
Ответ: А = (2;1;-2), /2 = (-2;-4;-4), /3 = (-2;2;-1).
Пример 12.	1) Найдем собственные значения матрицы
fl 4 5>
А= 3 2 5

338
Для этого решим характеристическое уравнение
det(/l-2E') = О:
(1-2)	4
3	(2-2)
3	1
5
(6-л)
= (1 - 2)- (2 - 2)- (б - 2)+ 60 + 5 -
-15(2-2)-5(1-2)-12(б-2) = 23 -922 -122 + 20 =
= (2-1Х2 + 2)(2-10)=0.
Отсюда: 2] =-2; 22 =1; 2j =10 - собственные значе-
ния матрицы А.
2) Найдем собственные векторы, соответствующие указанным
собственным значениям. Для этого решим однородные системы
(Л-2Е)-х = 0,
где 2 — собственные значения.
Воспользуемся методом Гаусса.
а) 2 =-2:
'3
3
к3
4 5
4 5
1 8
5
0
3
0	0-3 3
oj«e <о о о
(А <3 4 5
339
Отсюда для координат искомого собственного вектора получаем
зависимость:
х} = -Зх3; х2 ~ х3; х3 — любое число.
Следовательно, находим один линейно независимый собственный
вектор, например,
б)
<0
3
5
0
5
0
0
о
4
0
О
О
0
О
340
X] х2
х3
11 О 5/4
0~1 L V4
1^0 О О
ол
о
°>
Отсюда получаем следующие соотношения между координата-
ми искомого собственного вектора:
Xj =-----х3; х2 =------х3; х3 — любое число.
4	4
Следовательно, находим один линейно независимый собствен-
ный вектор, например,
в) 2 = 10:
1 -4
-9 9
7 -7
(Г
о (-1/9)
oj (1/7)
г3 1
0 1
<° 1
341
r3 1 -4
О 1 -1
J) О О
О -3
1 -1
О О
Отсюда получаем соотношения для координат искомого собст-
венного вектора:
xt = х3; х2 — х3; х3 — любое число.
Таким образом, находим один линейно независимый собствен-
ный вектор, например:
Ответ: матрица А имеет следующие собственные значения и
соответствующие им собственные векторы:
Пример 13. 1) Найдем собственные значения матрицы
342
Для этого составим и решим характеристическое уравнение:
О
(2-2)
О
1
1
(2-2)
О
4	=(2-2)2 (-1-2)+4 =
(-1-2)
= -(4 -42 + 22)(1 + 2)+ 4 = - 4 + 42 - 22 - 42 + 422 - 23 + 4 =
= -Л3 +ЗЛ2 = Л2 -(З-Л)= О .
Следовательно, Л^ 2 = 0; 23 = 3 — собственные значения
матрицы А.
2)	Наилем соответствующие собственные векторы.
а)	2 = 3:
^-1 1 О
0-14
ч 1	0-4
1
-1
1
1 Л2 3
о
1
-1
о
о
о
-1
о
-4
4
4
О
О
%
<0
О
Следовательно, координаты собственного вектора связаны ра-
венствами:
343
Xj = 4x3; x2 = 4x3; x3 - любое число.
Поэтому числу Л = 3 соответствует один линейно независимый
собственный вектор, например,
б)	2 = 0 (кратность Л=2 ):
1
2
0
0
4
-1
0 -1
2 4
1 0
<10-1
->024
<0 1 2
-1
2
4
2	3
(<
О
oj
Отсюда получаем соотношения для координат искомого собст-
венного вектора:
Xj = х3; х2 = — 2х3; х3 — любое число.
Поэтому числу 2 — 0 соответствует только один линейно неза-
висимый собственный вектор, например,
344
(Л-0Е)х = /12 :
3)	Найдем для числа 2 = 0 присоединенный вектор. Для этого
решим систему
Отсюда выясняем, что координаты присоединенного вектора
удовлетворяют условиям:
Xj = 1 + х3; х2 = -1 - 2х3; х3 - любое число.
Поэтому присоединенным к h2 будет, например, вектор
345
Других присоединенных векторов к вектору h2 нет, так как в
сумме число найденных линейно независимых собственных и при-
соединенных векторов равно кратности к собственного значения
Л = 0 , так как в данном примере Л=2.
Ответ: Матрица А имеет простое собственное значение
Я = 3 , которому соответствует собственный вектор
Л, = 4
двукратное собственное значение Я = 0,
которому соответствует собственный вектор
h2 = —2 и присоединенный вектор h2 = —1
к 1 J	1°>
346
V. ПЕРЕЧЕНЬ
КОНТРОЛЬНЫХ ВОПРОСОВ ПО ТЕОРИИ
1.	Уравнение прямой с угловым коэффициентом.
2.	Угол между двумя прямыми; условия параллельности и
перпендикулярности двух прямых.
3.	Эллипс, его свойства, каноническое уравнение.
4.	Гипербола, ее свойства, каноническое уравнение.
5.	Парабола, ее свойства, каноническое уравнение.
6.	Операции	над	комплексными	числами,	заданными	в
алгебраической форме записи.
7.	Операции	над	комплексными	числами,	заданными	в
показательной форме записи.
8.	Разложение многочлена на множители. Основная теорема
алгебры.
9.	Разложение рациональной дроби на сумму простейших дробей.
10.	Векторы, линейные операции над ними, свойства этих
операций.
11.	Скалярное произведение двух векторов и его свойства.
12.	Вычисление скалярного произведения двух векторов, заданных
координатами.
13.	Векторное произведение двух векторов и его свойства.
347
14.	Вычисление векторного произведения двух векторов, заданных
своими координатами.
15.	Смешанное произведение трех векторов и его свойства;
геометрический смысл.
16.	Вывод формулы для вычисления смешанного произведения
векторов, заданных своими координатами.
17.	Матрица, операции над матрицами.
18.	Элементарные преобразования строк матрицы.
19.	Ступенчатый вид матрицы; вид Гаусса.
20.	Обратная матрица. Алгоритм построения.
21.	Определитель, свойства определителя.
22.	Ранг матрицы.
23.	Линейная зависимость и независимость векторов. Ранг системы
векторов.
24.	Теорема Кронекера-Капелли.
25.	Правило Крамера.
26.	Метод Гаусса для решения системы линейных уравнений.
27.	Однородная линейная система. Фундаментальная система
решений.
28.	Собственные значения; собственные и присоединенные
векторы матрицы.
29.	Линейное пространство. Евклидово пространство. Базис в
пространстве. Матрица перехода к новому базису.
30.	Ортогональные и ортонормированные базисы. Процесс
ортогонализации Шмидта.
348
СПИСОК ЛИТЕРАТУРЫ
1.	Александров П.С. Курс аналитической геометрии и
линейной алгебры - М.: Наука, 1979.
2.	Головина ДИ. Линейная алгебра и векторные ее
приложения-М.: Наука, 1984.
3.	Дан ко П.Е., Попов А.Г., Кожевникова Т.Я.
Высшая математика в упражнениях и задачах: Т.1. - М.: Высш,
школа, 1996.
4.	Линейная алгебра (практические занятия): Учебн.
пособие / Под ред. Г.С. Жуковой; РХТУ им. Д.И. Менделеева.
М., 1999.
5.	Методические указания к решению задач по
линейной алгебре. Учебн. пособие / А.Х. Лившиц и др. / МХТИ
им. ДИ. Менделеева. М., 1987.
6.	Пискунов Н.С. Дифференциальное и интегральное
исчисления: Т. 1.-М.: Наука, 1985.
7.	Фаддеев ДК, Соминский ИС. Сборник задач по
высшей алгебре - М.: «Наука», 1968.
349
СОДЕРЖАНИЕ
Введение........................................ 3
§ 1.	Решение систем линейных уравнений с
двумя и тремя неизвестными.................. 7
§ 2.	Уравнение прямой на плоскости...... 33
§ 3.	Кривые второго порядка............. 47
§ 4.	Векторы. Операции над векторами.
Скалярное произведение двух векторов......	70
§ 5.	Векторное произведение двух векторов.
Смешанное произведение трех векторов....	88
§ 6.	Комплексные числа................. 101
§ 7.	Разложение рациональной дроби на сумму
простейших дробей......................... 115
§ 8.	Матрицы. Операции над матрицами...	133
§ 9.	Ранг матрицы...................... 149
§ 10.	Определитель квадратной матрицы.
Обратная матрица.................. 162
§ 11.	Решение систем линейных уравнений.	178
§ 12.	Фундаментальная система решений...	195
350
§ 13.	Собственные значения, собственные и
присоединенные векторы квадратной
матрицы....................................... 208
§ 14.	Линейные векторные пространства.
Базис................................ 233
§ 15.	Квадратичные формы.................... 251
Приложения......................................... 273
I.	Контрольная работа на темы:	уравнения
прямой на плоскости; кривые второго по-
рядка; операции над векторами........ 273
И. Контрольная работа на темы: комплекс-
ные числа; разложение рациональной дро-
би; ранг, определитель матрицы, обратная
матрица; решение матричных уравнений;
решение систем линейных
уравнений.................................... 281
III.	Контрольная работа на темы: собственные
значения, собственные и присоединенные
векторы матрицы; базис в пространстве;
ортогонализация базиса....................... 298
IV.	Итоговая контрольная работа........... 310
V.	Перечень контрольных вопросов по
теории.............................   346
Список	литературы............................... 348
Учебное издание
ЖУКОВА Галина Севастьяновна
РУШАЙЛО Маргарита Федоровна
ЛИНЕЙНАЯ АЛГЕБРА
В ПРИМЕРАХ И ЗАДАЧАХ
Редакторы: Р.Г. Чиркова
Г.П. Романова
Компьютерный набор и верстка: В.Ш. Дарсалия
Г.Г. Орлова
Лицензия ЛР №020714 от 02.02.98 г.
Подписано в печать 24.10.2000. Формат 60x84 1/16. Бумага газетная.
Отпечатано в типографии «Виктория - Принт». Лицензия АА №000012
от 12.11.95. Уч.-изд.л. 10,3. .Усл. печ. л. 20,4.. Тираж 2000 экз. Заказ 3847.
ТМО 7/1.
Российский химико - технологический университет им. Д.И. Менделеева.
Издательский центр РХТУ им. Д.И. Менделеева.
Адрес университета и Издательского центра: 125047 Москва, Миусская пл., 9.