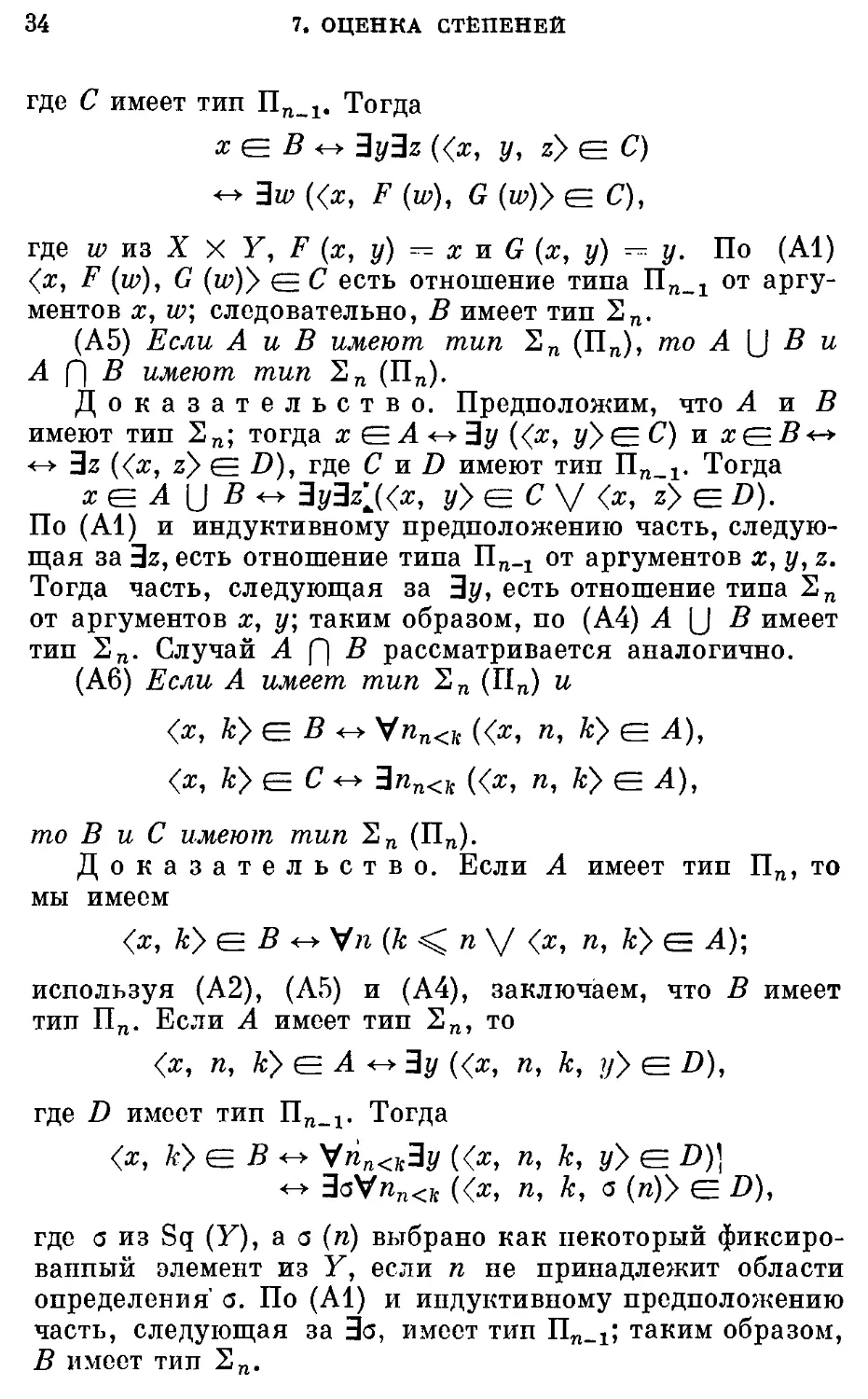Текст
Оглавление
МАТЕМАТИЧЕСКАЯ
ЛОГИКА
И ОСНОВАНИЯ
МАТЕМАТИКИ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1977
СТЕПЕНИ
НЕРАЗРЕШИМОСТИ
ДЖ. ШЕНФИЛД
Перевод о английского
И. А. ЛАВРОВА
Под редакцией Ю. Л. ЕРШОВА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1977
517
Ш 47
УДК 519.9
Joseph It. Shoenfield
DEGREES
OF UNSOLVABILITY
North-Holland Publishing Company
American Blsevier Publishing Company
1971
Джозеф Щепфилв
СТЕПЕНИ НЕРАЗРЕШИМОСТИ
Т. С. Вайсбер$
M., 1977 г., 192 стр. с илл.
Редактор В. В. Данченко
Техн. редактор Й. В. Кошелева
Корректоры Г. В. Подвольская,
Сдано в набор 17. 05. 1977 г. Подписано к печати 29.08.1977 г. Бумага 84Х108'/м
Физ. печ. я. 6. Условн. печ. я. 10,08. Уч.-изд. л. 9,57. Тираж 10 000 экз.
Цена книги 75 к. Заказ М 2444
Издательство «Наука»
Главная редакпия физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
2-я типография издательства «Наука», 121099, Москва, Шубинский пер., 10.
20203-137
Ш 053@2)-77 54'77
Перевод на русский язык,
Главная редакция
физико-математической литературы
издательства «Наука», 1977
СОДЕРЖАНИЕ
Предисловие редактора 6
Введение 9
0. Терминология и обозначения И
1. Рекурсивные функции 12
2. Изоморфизмы 15
3. Алгоритмы ; . ^ , . . . 18
4. Относительная рекурсивность 20
5. Рекурсивная перечислимость 24
6. Степени 29
7. Оценка степеней 32
8. Несравнимые степени 39
9. Верхние и нижние грани 42
10. Операция скачка 44
11. Минимальные степени 46
12. Простые множества 53
13. Метод приоритета 55
14. Теорема о разложении СО
15. Максимальные множества 04
16. Бесконечные нарушения 73
17. Индексные множества 80
18. Ветвящиеся степени . . . . 85
Дополнеиия . . . 95
К. Е. М. Ейтс. Три теоремы о степенях рекурсивно лерсчисли-
мых мпожеств 97
А. X. Лахлан. Решетка рекурсивно перечислимых множеств 109
Л. Фейнер. Иерархии булевых алгебр 163
Л. Фейнер. Гипотеза сильной однородности 180
Именной указатель 185
Предметный указатель 186
Указатель обозначений 191
ПРЕДИСЛОВИЕ РЕДАКТОРА
Предлагаемая вниманию читателей книга Дж. Шенфил-
да посвящена изложению основных результатов о степенях
неразрешимости (тьюринговых степенях). Эти результаты
традиционно считаются трудными, так как в их доказатель-
доказательствах используются различные формы так называемого
«метода приоритета». Автор книги поставил перед собой
цель изложить материал в максимально простой и ин-
интуитивно оправданной форме. И нужно сказать, что это
ему в основном удалось. Педагогическое мастерство авто-
автора, известного уже советскому читателю по переводу его
книги «Математическая логика» («Наука», М., 1975),
позволило ему создать небольшую книгу, которая содер-
содержит практически все принципиально важные результаты
о рекурсивно перечислимых степенях и которая тем не ме-
менее доступна для широких кругов читателей — математи-
математиков, интересующихся современными достижениями'теории
алгоритмов. Стоит, однако, предупредить, что чтение кни-
книги потребует от читателя напряженного внимания.
К переводу книги добавлены также переводы четырех
статей (К. Е. М. Ейтса, А. X. Лахлана и Л. Фейнера), ко-
которые расширяют круг проблем, обсуждаемых в книге, но
методы доказательств в которых близки используемым
в книге. Каждая из этих статей является весомым вкладом
в развитие теории алгоритмов.
Перевод книги и трех статей приложения выполнен
И. А. Лавровым, а перевод первой статьи Л. Фейнера —
С. С. Гончаровым.
Ю. Л. Ершов
Посвя1/{ается С. К. Клини,
который сделал теории:
рекурсивных функций теорией.
Дж. Шенфилд
СТЕПЕНИ
НЕРАЗРЕШИМОСТИ
ВВЕДЕНИЕ
Данные заметки возникли в семинаре, который я про-
проводил в Университете Калифорния — Лос-Анжелес в
1967 г. Несколько аспирантов семинара записали их. По-
После лекций, которые я читал в Католическом университете
в Сантьяго в 1969 г., я привел эти заметки в настоящий вид.
Подобная книга должна несколько отличаться от сбор-
сборника теорем, взятых из литературы. Моя главная цель —
показать, что доказательства в теории степеней не являют-
являются сложными и непонятными, как это могло бы показаться
из литературы (несколько статей Фридберга и Лахлана со-
составляют приятные исключения). Главное различие меж-
между доказательствами, которые я здесь привожу, и теми,
которые встречаются в литературе, состоит в том, что я
даю идею прямо перед доказательством, вместо того чтобы
переводить ее на неясный язык, с которого читатель должен
переводить обратпо. Я избегаю введения многих понятий,
а также специфических перечислений пар, конечных мно-
множеств, конечных последовательностей и т. д. Я уверен, что
если специалисты в теории степеней будут следовать этим
принципам при написании своих статей, то другие логики
будут читать эти статьи, вместо того чтобы заглядывать
в них со страхом (или отвращением). Меа culpa*).
Я также стараюсь показать, как мало нам нужно из тео-
теории рекурсии. Я даже не ввожу то, что обычно называется
«строгим» определением рекурсивной функции. Конечно,
такое определение нужно в различных приложениях тео-
теории рекурсивных функций, но не для теории степеней.
Я надеюсь, что, кроме упрощения всего изложения, это
поможет нам выделить те аксиомы, которые нам нужны
для построения аксиоматической теории рекурсивных
функций.
*) Моя вина (лат.).
10 ВВЕДЕНИЕ
У меня не было попыток охватить наиболее полно даже
сам предмет изучения. Главная задача — дать примеры
технических приемов, наиболее часто используемых.
Написание этой книги обязано многим обсуждениям
с различными людьми, в частности с Алистером Лахланом,
Хартли Роджерсом, Джеральдом Саксом и Майком Ейт-
сом. Национальный научный фонд обеспечил большую фи-
финансовую поддержку.
Дарем, Северная Каролина Дж. Р. Шенфилд
Август 10, 1971
0. Терминология и обозначения
Используем следующие логические обозначения:
| означает не; V означает или; & означает и; -*• означает
влечет; <-> означает тогда и только тогда. Символы |,
\/, &, —*¦ и <--> называем связками.
Если Р(х) — некоторое утверждение о х, то 3a:JP(a:)
означает, что Р (х) выполняется для некоторого х, а
VxP(x) означает, что Р(х) выполняется для всех х.
Эти обозначения будут использоваться только в случае,
когда областью изменения х является некоторое фикси-
фиксированное множество. Иногда это множество будет прямо
указываться в обозначениях. Так 3^же« Р{х) означает,
что Р(х) выполняется для некоторого х из у, а Ухх<у Р(х)
означает, что Р (х) выполняется для каждого х такого,
что х < у. Называем За; и V# кванторами, первый —
квантором существования, второй — квантором общности.
Термины отображение и класс используются в их обыч-
обычном понимании; терминам функция и множество будет
придан некоторый специальный смысл. Пустой класс бу-
будет обозначаться через 0. Мы не будем отождествлять
отображение с классом упорядоченных пар. Если F —
некоторое отображение из А на 5, то А называется об-
областью определения F, a В — областью значений F. Если
F является 1-1 отображением, то обращение F будет обо-
обозначаться через F~l.
Упорядоченную n-ку будем обозначать через <х1? . . .
. . ., хпу. Упорядоченная n-ка не отождествляется ни
с каким классом.
Натуральное число — это неотрицательное целое число.
Через N будем обозначать класс всех натуральных чи-
чисел; для обозначения натуральных чисел мы будем исполь-
использовать буквы г, /, k, m, n, r, s и t.
Бесконечная последовательность отождествляется с
отображением, областью определения которого является N.
12 i. рекурсивные функции
Как обычно, обозначаем через хп значение бесконечной
последовательности х при аргументе, равном п; бесконеч-
бесконечную последовательность будем обозначать через {а;п}.
Конечная последовательность длины п отождествля-
отождествляется с отображением, областью определения которого
является {0,1,. . ., п — 1} (но не отождествляется с упоря-
упорядоченной п-кой). Снова xt есть значение последовательно-
последовательности х при аргументе, равном г. Длину конечной последо-
последовательности х обозначаем через lh (x). Через 0 обозначаем
последовательность длины 0 (так же, как и пустой класс).
1. Рекурсивные функции
Теория рекурсии — это абстрактная теория вычисле-
вычислений. Все вычисления, которые мы будем рассматривать,
по крайней мере теоретически, могут быть проделаны в ко-
конечное время. Это означает, что объекты, которые мы вы-
вычисляем, должны быть конечными объектами, т. е. объек-
объектами, которые могут быть заданы с помощью конечного ко-
количества информации.
Несколько примеров сделают понятно конечного объ-
объекта более ясным. Всякое натуральное число — конечный
объект, так как оно может быть задано с помощью араб-
арабских цифр, входящих в обозначение этого числа. С дру-
другой стороны, действительное число, вообще говоря, не
является конечным объектом, так как для его задания мы
должны, например, задать каждый десятичный знак это-
этого числа, которых бесконечно много. Каждая п-ка конеч-
конечных объектов является конечным объектом, так как мы мо-
можем задать ее, задавая по порядку каждый из п объектов,
Всякий конечный класс конечных объектов является ко-
конечным объектом; бесконечный класс конечных объектов,
вообще говоря, не является конечным объектом. Каждая
конечная последовательность конечных объектов являет-
является конечным объектом; бесконечная последовательность,
в общем случае, не является конечным объектом.
Пространством называется бесконечный класс X
конечных объектов такой, что для любого конечного объ-
объекта а: мы можем решить, принадлежит х классу X или нет.
Дадим несколько примеров пространств.
1. Класс N натуральных чисел является простран-
пространством.
1. РЕКУРСИВНЫЕ ФУНКЦИИ [13
2. Если X и Y — пространства, то X X Y — прост-
пространство.
3. Если X — пространство, то класс Sub (X) конечных
подклассов X является пространством.
4. Если X — пространство или конечный непустой
класс конечных объектов, то класс Sq (X) конечных после-
последовательностей элементов X является пространством.
Для обозначения пространств будем использовать бук-
буквы X, Y и Z. Тогда, как правило, х, у иг будут обозначать
элементы пространств X,Y и Z соответственно.
Функцией из X eY называется всякое отображение из
X в Y; множеством в X называется всякий подкласс про-
пространства X. Под функцией мы всегда будем понимать не-
некоторую функцию из пространства в пространство, а под
множеством всегда будем понимать множество в некото-
некотором пространстве. Для обозначения функций будем ис-
использовать буквы F, G, II, L и М, а для обозначений мно-
множеств — буквы А, В, С, D и Е.
Функцию F из декартова произведения п пространств
будем называть функцией от п аргументов; вместо F (<х1,...
. . ., хпУ) мы пишем просто F {хх,. . ., хп). Всякое множе-
множество в декартовом произведении п пространств называется
отношением от п аргументов. Если мы рассматриваем
...х... у... как функцию от аргументов х и у, то мы имеем
в виду функцию F, определенную следующим образом:
F (х, у) — ...x...y..i Если мы рассматриваем ...х...у...
как отношение от аргументов х и у, то мы имеем в виду
отношение А, определенное следующим образом: <?, уУ%—
G^<-> ...x...y... Под отношением -•= мы понимаем отно-
отношение х = у от аргументов х и у; подобным обраэом пони-
понимаются отношения d, < и т. д.
Удобно отождествить каждое множество с некоторой
функцией, так что все определения, которые мы даем для
функций, будут применяться и к множествам. Мы отожде-
отождествляем множество А в X с функцией из X в N, которая
принимает значение 1 на аргументах, лежащих в А, и
значение 0 на аргументах, лежащих вне А. Для удобства
мы пишем «И» вместо 1 и «Л» вместо 0. Таким образом,
А(х) = И тогда и только тогда, когда ieA истинно,
и А(х) = Л тогда и только тогда, когда i6i ложно.
Функция F из X в Y называется рекурсивной, если су-
существует некоторый алгоритм, с помощью которого по дан-
14 1. РЕКУРСИВНЫЕ ФУНКЦИИ
ному элементу х из X мы можем вычислить F (х). Отсюда
следует, что множество А в X рекурсивно, тогда и только
тогда, когда существует некоторый алгоритм, с помощью
которого по данному элементу а; из X мы можем вычислить,
будет лих ^ А илих ф. А.
Дадим несколько примеров рекурсивных функций
и множеств. Функции сложения и умножения являются
рекурсивными функциями из N X N в N; алгоритмы для
этих функций изучаются в школьной элементарной ариф-
арифметике. Если F@) — 2, a F(n) для п ^ 0 равняется п-му
десятичному знаку действительного числа е, то F — ре-
рекурсивная функция из N в N: теория бесконечных рядов
дает нам алгоритм для вычисления F. Множество простых
чисел является рекурсивным множеством в N; требуемый
алгоритм — решето Эратосфена.
Тождественная функция из Хв X и проекции из X X Y
на X и У являются рекурсивными. Функция длины lh —
рекурсивная функция из Sq (X) в N. Отношение =¦ в
X х X и отношение d в Sub (X) X Sub (X) являются ре-
рекурсивными. Отношения <^,^>,<^и^> в N X N также ре-
рекурсивны.
Опишем теперь некоторые методы для получения
рекурсивных функций и рекурсивных множеств из других
рекурсивных функций и рекурсивных множеств. Ком-
Композиция двух рекурсивных функций является рекур-
рекурсивной функцией; действительно, мы можем вычислить
(F°G) (x), сначала вычислив G (х) = у, а затем вычислив
F (у). То же справедливо для любой композиции функ-
функций от нескольких переменных. Так, если F определена
следующим образом:
F (х, y) = G(H (у, х), L (х), у),
где G, Н и L рекурсивны, то F рекурсивна.
Если А определено так: х ?= А <-+ F (х) ?= В, где F
и В рекурсивны, то А рекурсивно. Опять это можно обоб-
обобщить на несколько аргументов. Так, если А определено
следующим образом:
<*, у> е А <-> <^п (х), G (у, х), у} е в,
где F, Gw. В рекурсивны, то А рекурсивно.
Объединение, пересечение и разность двух рекурсив-
рекурсивных множеств (в одном пространстве) являются рекурсив-
2. ИЗОМОРФИЗМЫ 15
ными множествами. Дополнение множества А в X, обоз-
обозначаемое через Ас, есть множество X \ А; Ас рекурсивно
тогда и только тогда, когда А рекурсивно.
Любая комбинация рекурсивных множеств, получае-
получаемая с помощью связок, является рекурсивным множест-
множеством. Так, если А определяется следующим образом:
где В, С и D рекурсивны, то А рекурсивно. Это утвержде-
утверждение перестает быть верным, если используются кванторы.
Предположим, что мы определили
х е А <-> ЗУ «х, у> е В),
где В рекурсивно. Проверяя, будет ли х ?Е А или х ф А,
мы должны будем проверить, будет ли (х, j)gB или
(х, уУ ф В для каждого у. Так как у существует бесконеч-
бесконечно много, то мы не сможем проделать1 это в конечное
время.
Такая проблема не возникнет, если областью измене-
изменения переменной под квантором является конечное множе-
множество. Так, если А определяется следующим образом:
(х, к) е А *-> Э«п<» ((х, п, ку е В),
где В рекурсивно, то А рекурсивно. Аналогичное замеча-
замечание применимо к кванторам Упп<ц, Зп»^ц, Vrea^/c и к
кванторам Эххеу и Ух^у, где У — Sub (X).
Пусть цге (...п...) означает наименьшее п такое, что
...п...; если не существует п такого, что ...п..., то
\т(... п...) считается неопределенным. Если множество А
рекурсивно и F (х) — цге ((х, ге> е= ^4) для всех х, то F —
рекурсивная функция; действительно, мы можем вычис-
вычислить F (х), испытывая пары (х, 0>, (х, 1> до тех пор,
пока не придем к первой, которая принадлежит А.
2. Изоморфизмы
Изоморфизмом между X и Y называется 1-1 функ-
функция F из X на Y такая, что F и F рекурсивны. Если та-
такой изоморфизм существует, то мы будем называть X и Y
изоморфными.
Мы будем рассматривать только такие свойства про-
пространств, которые являются инвариантными при изомор-
16 2. ИЗОМОРФИЗМЫ
физмах. Для примера покажем, что рекурсивность функ-
функций является инвариантным свойством при изоморфизмах.
Пусть F — рекурсивная функция из X в Y. Пусть G —
изоморфизм между X и X', а Н — изоморфизм между Y
и Y'. Функция F' из X' в У, соответствующая F, дается
следующей коммутативной диаграммой:
Jff
Таким образом, F' = H°FoG~l. Так как Я, F и G ре-
рекурсивны, то F' рекурсивна.
Теорема об изоморфизме. Любые два
пространства изоморфны.
В качестве первого шага к доказательству заметим, что
тождественное отображение из X в X является изоморфиз-
изоморфизмом, обращение изоморфизма является изоморфизмом,
композиция двух изоморфизмов является изоморфизмом.
Отсюда следует, что отношение «быть изоморфными»
является отношением эквивалентности. Поэтому нам нуж-
нужно лишь доказать, что N изоморфно X для каждого X.
Перечислением множества А в X называется 1-1
рекурсивная функция из N в X, областью значений кото-
которой является А. Другими словами, перечисление А есть
бесконечная последовательность {хп} элементов А, в ко-
которой каждый элемент из А встречается ровно один раз,
и такая, что для данного п мы можем вычислить хп.
Лемма 1. Если F — перечисление X, то F — изо-
изоморфизм между N и X.
Доказательство. Нужно показать только, что
F'1 рекурсивна. Для данного х мы вычисляем F @),
F A),. . . до тех пор, пока не найдем птакое, что F (п) = х.
Тогда F'1 (х) = п, что и требовалось доказать.
Лемма 2. Если А — бесконечное множество в X
и F — рекурсивная функция из N в X, область значений
которой есть А, то А имеет перечисление.
Доказательство. Определим индуктивно
функцию G из N в X следующим образом: G (п) = F (т),
где т — наименьшее число такое, что F (т) отличается
от G @), G A),. . ., G(n — 1). Такое т существует, по-
потому что А бесконечно. Ясно, что G — 1-1 функция из
2. ИЗОМОРФИЗМЫ 17
N в X, областью значения которой является А. Так как
F рекурсивна, то мы можем вычислить G (п), если G @),
G A),. . ., G (п — 1) известны. Поэтому G рекурсивна,
что и требовалось доказать.
Лемма 3. Если X имеет перечисление, то любое про-
пространство Y, входящее в X, имеет перечисление.
Доказательство. Пусть F — некоторое пере-
перечисление X. Выберем у0 ?Е У. Положим G (га) = F (га),
если F (п) ЕЕ Y, и G (п) — у0 в противном случае. Тогда
G — рекурсивная функция из N в X, областью значений
которой является Y; по лемме 2 Y имеет перечисление, что
и требовалось доказать.
Если х — конечный объект, то мы можем дать полное
описание х. Можно предполагать, что символы, использую-
использующиеся в таком описании, выбираются из конечного клас-
класса Г, не зависящего от ж. (Достаточно собрать в Г все
русские буквы, энаки препинания и все обычные математи-
математические символы.) Так как Г — конечный класс конечных
объектов, то Sq (Г) — пространство и все наши описания
принадлежат этому пространству.
Лемма 4. Пространство Sq (Г) имеет перечисление.
Доказательство. Пусть хх, х2, . . ., х, — сим-
символы из Г. Пусть F @) и F A) — пустые последователь-
последовательности. Если га^>1, то пусть дГ'Зг" ... qft — канониче-
каноническое разложение п на простые множители такое, что ql <
< <7г < • • • < Чп и все показатели степени положитель-
пы. Если все показатели степени <^ г, то пусть F (п) =
-¦- хП1х„, ... хПк; в противном случае пусть F (п) — пустая
последовательность. Тогда F — рекурсивная функция из
N на Sq (Г); таким образом, по лемме 2Sq (Г) имеет пе-
перечисление, что и требовалось доказать.
Пусть X — любое пространство. Из определения про-
пространства следует, что для данного элемента из Sq (Г) мы
можем решить, является ли этот элемент описанием не-
некоторого объекта из X, и если это так, то найти этот объект.
Пусть Y — множество описаний объектов из X, и для
у еЕ Y пусть F (у) есть объект, имеющий описание у.
Тогда Y — пространство, входящее в Sq (Г), и F — ре-
рекурсивная функция из Y на X.
По леммам 4 и 3 У имеет перечисление G. Тогда FoG —
рекурсивная функция иэ Л^на X. По лемме 2 X имеет пере-
18 з. алгоритмы
числение, и, следовательно, по лемме 1 N изоморфно X,
что и требовалось доказать.
Теорема об изоморфизме утверждает, что для наших
целей все пространства эквивалентны. Часто мы будем
молчаливо использовать этот факт. Так, мы можем утвер-
утверждать какой-нибудь результат для всех пространств,
а доказывать его только для N.
Допустим, что какое-то перечисление N X N раз и
навсегда зафиксировано. Если при этом перечислении па-
пара <i, ]У соответствует п, то скажем, что п находится в i-й
строке и /-м столбце. (Таким образом, можно представить
наше перечисление как расстановку натуральных чисел
в бесконечную матрицу.) Для данного п мы можем вычис-
вычислить его строку и столбец; по данным i и / мы можем вы-
вычислить число, находящееся в ?-й строке и /-м столбце.
3. Алгоритмы
Точная природа алгоритма зависит от метода вычисле-
вычислений. Если вычислитель использует карандаш и бумагу,
то алгоритмом может быть множество предписаний, напи-
написанных на русском языке; если вычислитель использует
какую-нибудь вычислительную машину, то алгоритмом мо-
может быть программа для этой машины. Выявим некоторые
свойства алгоритмов, не зависящие от таких рассмотрений.
Алгоритмом для функции F из X в Y называется пра-
правило, с помощью которого мы можем производить вычисле-
вычисления, приводящие от х к F (х). Назовем х входом, я у —
выходом вычисления. Считаем, что вычисление происходит
по шагам. Используя уже проделанные шаги и вход, алго-
алгоритм говорит нам, как проделать следующий шаг.
Алгоритмом из X eY называется правило, которое мо-
может быть применено к любому входу из X и конечной по-
последовательности шагов вычисления, для получения нового
шага вычисления или выхода из Y. Новый шаг или выход
получаются из входа и данной последовательности шагов
без каких-либо промежуточных выкладок, применения
каких-либо видов изобретательности и использования
любой дополнительной информации.
Всякий алгоритм есть правило и, следовательно, копеч-
ный объект; класс Alg (X, Y) алгоритмов из X в Y обра-
3. АЛГОРИТМЫ 19
зует пространство. Для обозначения алгоритмов исполь-
используем буквы /, / и К.
Пусть / ?Е Alg (X, Y). Для данного входа х ?еХ мы
можем, применяя /, получить какой-то шаг; применяя /
к этому шагу, получить другой шаг и так далее. В этом
случае говорим, что мы вычисляем согласно алгоритму I.
Процесс получения новых шагов может безгранично про-
продолжаться или он может оборваться на каком-нибудь
выходе из Y. Множество входов, для которых мы получаем
выход, обозначим через Wi. Если х е= Wi, то полученный
по входу х выход обозначим через [/] (х), а вычисление,
приводящее к этому выходу, назовем вычислением [/] (х).
Если х ф. Wi, to [/] (х) не определен.
Заметим, что [/] есть отображение из множества Wi,
лежащего в X, в У. Всякое отображение из множества, ле-
лежащего в X, в У называется частичной функцией из X
в У. Буквы, которые используются для обозначения
функций, будут также использоваться для обозначения
частичных функций, но только в тех случаях, когда это
явно оговорено. Частичная функция называется всюду
определенной, если она является функцией. Частичная
функция F из X в У называется рекурсивной, если сущест-
существует алгоритм / из X в У такой, что F = [/]. (Если F —
функция, то это согласуется с нашим прежним определе-
определением.) Любой такой алгоритм / называется в этом случае
алгоритмом для F.
Примем одно соглашение по поводу равенства между
выражениями (такими, как [/] {х)), которые могут быть не
определены. Пусть ?/=Увьшолняется, если как U, так и V
определены и имеют одинаковые значения, или если они
оба не определены. Во всех других случаях считаем
Используем данные выше определения для построения
нерекурсивной функции. Пусть \ln} — какое-нибудь пере-
перечисление Alg (TV, TV). Определим функцию F из TV в TV
следующим образом:
[JJ(w)+l, если neWrn,
О в противном случае.
Для каждого п имеем F (п) Ф [1п] (п); таким образом,
Fzf= [In] для всех п. Отсюда следует, что F нерекурсивна.
20 4. ОТНОСИТЕЛЬНАЯ РЕКУРСИВНОСТЬ
Можно также ноказать, что ie^i (где /е Alg (X, Y))
не является рекурсивным отношением от аргументов
х и /. Ввиду теоремы об изоморфизме достаточно доказать
это для X = Y = N. Если бы n e Wi было рекурсивным
отношением от аргументов х и /, то функция F, определен-
определенная в предыдущем абзаце, была бы рекурсивной.
Аналогичное доказательство показывает, что [/] (х) =
= у не является рекурсивным отношением от аргумен-
аргументов 1,хи у. Здесь функцию F нужно определить так:
, если \1п\ (п) = О,
в противном [случае.
Однако существуют некоторые аппроксимации этих от-
отношений и они являются рекурсивными. Пусть W/,n
будет множеством х ?Е Wj таких, что вычисление [/] (х)
имеет меньше, чем п шагов. Для ж?ЕИ0,п полагаем
[1]п (х) = [I] (х); для ж§Ё WI<n значение [1]п\х) не опре-
определено.
Мы утверждаем, что х 6Е Wi>n является рекурсивным
отношением от аргументов х, I и п, а [1]п (х) = у являет-
является рекурсивным отношением от аргументов /, п, х и у.
Действительно, пусть I, n, x ш у даны. Вычисляем соглас-
согласно алгоритму / с входом х, пока не получим выход или не
проделаем п шагов. Тогда х 6Е Wi>n тогда и только тогда,
когда мы получим выход, а [Л„ (х) = у тогда и только
тогда, когда мы получим выход у.
Заметим, что Wi>n и [7]п аппроксимируют Wj и [Л в
следующем смысле. Если х ф И^,то xQ=Witn для всех
п. Если х €Е Wi, то существует п0 такое, что х ф. WitTl
для в<В|,иге Wi>no, а [/]„ (х) = [1](х) для п > п0.
4. Относительная рекурсивность
В вычислениях, которые рассматривались до сих пор,
вся информация давалась алгоритмом и входом. Теперь
рассмотрим вычисления, в которых будет использоваться
некоторая дополнительная информация.
Пусть Н — некоторая функция из N в N, определим
F (п) = Н B-Я (п)). Если Я рекурсивна, то и F рекур-
рекурсивна. Независимо от того, будет Я рекурсивной или нет,
мы можем вычислять F (п) по п, если у пас будет какой-
4. ОТНОСИТЕЛЬНАЯ РЕКУРСИВНОСТЬ 21
нибудь объект, который по данному аргументу к будет
давать нам значение Н (к). Такой объект будет называться
оракулом для Н.
Мы обобщаем понятие алгоритма, позволяя пользо-
пользоваться оракулами. Обобщение будет состоять в разрешении
некоторой новой инструкции, появляющейся в алгоритме.
Эта новая инструкция говорит нам, что следующий шаг
вычисления состоит в получении значения с помощью ора-
оракула для аргумента, полученного ыа предыдущем шаге
вычислений. Такие инструкции ранее не допускались,
так как их выполнение требует получения дополнительной
информации.
Для вычисления согласно одному из наших обобщенных
алгоритмов мы нуждаемся и во входе, и в оракуле. При
этом мы можем встретиться со следующей проблемой: по
инструкции мы должны бы запросить оракул о значении,
соответствующем только что полученному аргументу z, a z
может не быть объектом из области определения функции,
для которой имеется оракул. Договоримся, что в этом
случае следующий шаг полностью повторяет предыдущий.
Это же соглашение позволяет нам использовать этот тип
алгоритмов для вычислений без оракула. Когда такой ал-
алгоритм будет отправлять нас к оракулу, мы будем полно-
полностью повторять предыдущий шаг. При таком соглашении
все наши предыдущие замечания об алгоритмах переносят-
переносятся на алгоритмы в данном обобщенном смысле. Все наши
результаты остаются правильными, но пам не нужно бу-
будет иметь дело с двумя видами алгоритмов.
Пусть / — какой-то алгоритм из X в Y, а Н — не-
некоторая функция. Тогда W? будет множеством таких х,
что мы получаем какой-нибудь выход, когда вычисляем
согласно /, начиная с входа х и используя оракул для II.
Полученный выход обозначим через [1]а (х), а вычисление,
к нему приводящее, называем вычислением [1]н (х). Если
х §ё W'i , то считаем [/]н (х) неопределенным.
Частичная функция /'' из X в Y называется рекурсив-
рекурсивной в II (или относительно II), если существует алгоритм
/ из X в Y такой, что F = [1]и. Любой такой / называет-
называется алгоритмом для F в И .
Пусть W"n — множество х ЕЕ W? таких, что вычис-
вычисление [1]н (х) заканчивается менее чем за п шагов. Для х е=
22 4. ОТНОСИТЕЛЬНАЯ РЕКУРСИВНОСТЬ
^ Wj1^ полагаем [1]%(х) ¦= И]Н(х); для х ф WjHn считаем
[/]„ (х) неопределенным. Тогда отношение х 6Е Wj,n яв-
является рекурсивным в Н отношением от аргументов х,
I, п, а отношение [1]п (х) — у — рекурсивным в // от-
отношением от аргументов /, п, х, у. Мы видим, что Wj,n
и \1\п аппроксимируют Wf и [7]я в ранее описанном
смысле.
Все, что мы сделали до сих пор,— заменили во всех пре-
предыдущих результатах вычисление на вычисление с ораку-
оракулом Н. Такой процесс называется релятивизацией к II.
Причина, по которой мы приходим к правильным резуль-
результатам, состоит в том, что мы пока не пользовались тем,
что вычисление не использует никаких внешних источни-
источников информации (и, в частности, оракулов). Так как мы
никогда и не будем использовать этого, то все наши ре-
результаты останутся верными при релятивизации к Н.
Часто мы молчаливо будем использовать этот факт.
Каждая рекурсивная функция рекурсивна в Н. Дей-
Действительно, если F рекурсивна, то существует алгоритм /
для F, не использующий оракула; следовательно, F =
= [/] - [/F.
Если F рекурсивна вЯиЯ рекурсивна в G, то F ре-
рекурсивна в G. Действительно, предположим, что мы имеем
оракул для G. Для данного х начинаем вычислять F (х),
как если бы мы имели оракул для Н. Когда мы будем
вынуждены спросить оракул о значении Н (z), мы вычис-
вычисляем /7 (z), используя наш оракул для G. Аналогичное
доказательство показывает, что если F рекурсивна в Н и
Н рекурсивна, то F рекурсивна.
Ясно, что Н рекурсивна в Н. Более общо, если F (х) =
= Н (х) для всех аргументов х, кроме конечного числа,
то F рекурсивна в Н. (Алгоритм будет снабжен конечным
списком этих аргументов и значениями F при каждом из
этих аргументов.)
Пусть Н — некоторая частичная функция из Z в не-
некоторое пространство. Оракул для Н — это объект, ко-
который по данному z из Z дает значение Н (z), если z при-
принадлежит области определения Н, и не будет давать ответа
в противном случае.
При вычислении согласно алгоритму / с оракулом для
частичной функции может возникнуть новая ситуация:
4. ОТНОСИТЕЛЬНАЯ РЕКУРСИВНОСТЬ 23
мы можем запросить у оракула некоторое значение и не
получить ответа. В этом случае вычисление останавливает-
останавливается без получения выхода. Тогда мы можем определить W^,
[Т]н, W[3 п и Ц]п для частичной функции Н, как раньше.
Пусть Н — некоторая частичная функция и х ЕЕ Wi •
Скажем, что z используется в вычислении [1]н (х), если в те-
течение этого вычисления мы будем запрашивать оракул о
значении Н (z). Следующий очевидный, но важный факт
называется принципом использования: если Н — частич-
частичная функция такая, что х ЕЕ Wj , a G — частичная функ-
функция такая, что G (z) = H (z) для каждого z, используемого
в вычислении [1]П (х), то i? Wf, [1]в (х) = [1]П (х) и
[/In (я) = [ITS (я) Для всех п.
Если GviH — частичные функции из X в Y, то G d H
означает, что Н является расширением G. Если G d H,
то ввиду принципа использования [I]G CZ [Лн.
Конечной функцией из X в Y называется частичная функ-
функция из X в Y, область определения которой конечна. Вся-
Всякая конечная функция является конечным объектом, а
класс всех конечных функций является пространством.
Конечные функции будем обозначать через аил.
Как следствие принципа использования имеем
x<=W?~3eecH(x^W4) A)
и
[7]Н (*) = »«- ЗО-асН ([/]" (X) = У). B)
Заметим также, что отношение х е= Wf, n является рекур-
рекурсивным отношением от аргументов х, а, /, п, а [/]? (х) =
= у — рекурсивным отношением от аргументов /, а, п, х, у.
Доказывается это так же, как и раньше; отметим при этом,
что знание сг позволяет определять, что отвечает нам оракул
для сг, если он дает ответ, и что он не дает ответа.
Элементы из Sq ({Л, И}) называются цепочками. Для
цепочек используем символы а, р, у и б. По принципу
использования для всякого подмножества А множества
N имеем
^E^iAo3aac4(xE^) C)
и
[/]А (.г) ---¦ у ¦-> Э<х,сл ([/]" W ^ У)- D)
24 5. РЕКУРСИВНАЯ ПЕРЕЧИСЛИМОСТЬ
Можно было бы обобщить рассматриваемые вычисле-
вычисления до вычислений, использующих несколько оракулов, но
легко заменить несколько оракулов одним. Пусть Я,- для
1 < i < п будет функцией из Х{ в Yt. Определим функ-
функцию #! х • . . X Нп из Хх х . . . X Хп в Yt X • • •
... X Yn следующим образом:
(#х х ... х Hjfa, ...,хп) = <ях (*!>,..., нп (*„)>.
Понятно, что можно получить ту же самую информа-
информацию от оракула для Я1 х . • . X Нп, что и от оракулов
для Ни. . ., Нп. По этой причине мы называем F рекур-
рекурсивной в Ни. . ., Нп, если F рекурсивна в Н1 х • • •
... X Нп. При конкретных описаниях вычислений F
мы предпочитаем использовать отдельные оракулы для
#!,. . ., Нп вместо одного оракула для Н1 х • • ¦ X Нп.
5. Рекурсивная перечислимость
Множество А в X называется рекурсивно перечислимым,
если существует пространство У и рекурсивное множество
В в X х Y такое, что
х е А +-> 3j/ «х, i/> e 5)
для всех ж. Ввиду теоремы об изоморфизме можно всегда
считать Y = N.
Например, эквивалентность
iGW,«3«(^ WUn) A)
вместе с фактом, что х ЕЕ Wj,n — рекурсивное отношение от
аргументов х, I, п, показывает, что х ?Е Wi является ре-
рекурсивно перечислимым отношением от аргументов х, I.
Аналогично,
[/] (х)=у~ Э/г ([/]„ (х) = у) B)
показывает, что [/] (х) = у является рекурсивно перечис-
перечислимым отношением от аргументов /, х, у.
Всякое рекурсивное множество является рекурсивно
перечислимым; действительно, х е А <-> Эу (х е= .4),
a iei — рекурсивное отношение от аргументов я, у.
Примеры, данные выше, показывают, что обратное ут-
утверждение ложно.
5. РЕКУРСИВНАЯ ПЕРЕЧИСЛИМОСТЬ 25
Селектором для отношения А в X х Y называется лю-
любая частичная функция F из X в Y такая, что для всех х
значение F (х) определено тогда и только тогда, когда суще-
существует такое у, что <х, i/> ?Е А, ив этом случае (х, F (х)> €=
ЕЕ ^4. Таким образом, F выбирает у — F (х) такое, что
<я, })е4, при условии, что такое у существует.
Теорема о селекторе. Если А — рекур-
рекурсивно перечислимое отношение в X xY, то существует
рекурсивный селектор для А.
Доказательство. Существует рекурсивное от-
отношение В такое, что
<х, у} е А <-» 3z «х, у, z> е В).
Пусть {(.Уп, zn» — перечисление Y x Z. Опишем алго-
алгоритм / из X в Y, указав процесс вычисления согласно /
на входе х. и-й шаг этого процесса состоит в вычислении
В (х, yn,zn). Если результатом будет И, то выходом будет
уп, в противном случае переходим к следующему шагу.
Ясно, что [Л будет селектором для А, что и требовалось
доказать.
Следствие 1. Множество А рекурсивно перечис-
перечислимо тогда и только тогда, когда оно есть область опреде-
определения некоторой частично рекурсивной функции.
Доказательство. Такая область определения
является рекурсивно перечислимой по A). Если А рекур-
рекурсивно перечислимо, то х €= А *-* Зу «х, у} €= В), где В
рекурсивно. Если F — рекурсивный селектор для В,
то А — область определения для F, что и требовалось
доказать.
Следствие 2. Если В рекурсивно перечислимо и А
определяется следующим образом:
х<=А*-+Зу «ж, г/> е В),
то А рекурсивно перечислимо.
Доказательство. Так как А является обла-
областью определения любого селектора для В, то результат
следует из теоремы и следствия 1, что и требовалось до-
доказать.
Например, область значений А произвольной частично
рекурсивной функции F является рекурсивно перечисли-
перечислимой. Действительно, если / — алгоритм для F, то
х е А <-* Эу ([/] (у) = х),
26 5. РЕКУРСИВНАЯ ПЕРЕЧИСЛИМОСТЬ
а [Л (у) = х является по B) рекурсивно перечислимым
отношением от аргументов х, у.
Ввиду следствия 1 и теоремы об изоморфизме, мно-
множество А в X является рекурсивно перечислимым
тогда и только тогда, когда А = W[ для некоторого
/ ЕЕ Alg (X, N). Любое такое / называется индексом А.
Теорема параметризации. Если А —
рекурсивно перечислимое отношение в X xY, то суще-
существует рекурсивная функция F из Y в Alg (X, N) такая,
что
х ЕЕ WF(V) ч-> <х, уУ ЕЕ А
для всех х и у.
Доказательство. Пусть / — индекс А, а
F (у) — алгоритм J такой, что процесс вычисления сог-
согласно / на входе х тот же самый, что и процесс вычисления
согласно / па входе <я, г/>. Тогда F рекурсивна и
х е WF(,,) *-> <х, y>^Wi *-> <ж, j)e4,
что и требовалось доказать.
Теорема о перечислении. Бесконечное
множество А рекурсивно перечислимо тогда и только тог-
тогда, когда оно имеет перечисление.
Доказательство. Если А имеет перечисление,
то оно есть область значений некоторой рекурсивной функ-
функции и, следовательно, рекурсивно перечислимо. Пред-
Предположим, что А рекурсивно перечислимо. Пусть х ?• А <-*¦
<-> Эу ((?, уУ ЕЕ В), где В рекурсивно, и выберем х0Е=А.
Положим F (х, у) = х, если (х, г/> е В, и F (х,у) =
= х0 в противном случае. Тогда F рекурсивна и ее об-
область значений есть А. По теореме об изоморфизме и лемме
2 из § 2 Л имеет перечисление, что и требовалось доказать.
Графиком частичной функции F из X в Y называется
отношение А в X xY, определенное следующим образом:
<х, уУ ЕЕ А <->• F (х) = у.
Теорема о графике. Частичная функция
рекурсивна тогда и только тогда, когда ее график рекур-
рекурсивно перечислим.
Доказательство. График для [/1 рекурсивно
перечислим по B). Так как селектором для графи-
графика F является сама функция F, то обратное утверждение
следует из теоремы о селекторе, что и требовалось до-
доказать.
5. РЕКУРСИВНАЯ ПЕРЕЧИСЛИМОСТЬ 27
Теорема о дополнении. Множество А
рекурсивно тогда и только тогда, когда множества А и Ас
рекурсивно перечислимы.
Доказательство. Если А рекурсивно, то Ас
рекурсивно; таким образом, А и Ас рекурсивно перечис-
перечислимы. Предположим, что А и Ас рекурсивно перечислимы
с индексами / и / соответственно. Для каждого х имеем
х ЕЕ Wi или х ЕЕ Wj\ поэтому мы можем определить ре-
рекурсивную функцию F следующим образом:
F (х) = цп (х (ЕЕ Wr.n V х ЕЕ Wj,n).
Тогда х ЕЕ А <-> х ЕЕ Wi,f(x) и, значит, А рекурсивно,
что и требовалось доказать.
Теперь отметим некоторые связи между рекурсивностью
и пределами. Если {хп} — бесконечная последовательность
в X, то говорим, что х есть предел {хп}, и записываем
lim хп = х, если хп = х для всех достаточно больших п.
Если {Fn} — бесконечная последовательность функций
из X в У, то говорим, что F есть предел) {Fn}, и запи-
записываем lim Fn = F, если lim Fn (x) = F (x) для всех х.
Если lim Fn = F, jo модулем для {Fn} называется вся-
всякая функция Я из X в TV такая, что
п > И (х) ^ Fn (х) = F (х)
для всех п и х.
Последовательность {Fn} называется рекурсивной,
если Fn (х) — рекурсивная функция от аргументов п, х.
Лемма о модуле. Если Л рекурсивно перечис-
перечислимо и функция F рекурсивна в А, то существует рекур-
рекурсивная последовательность {Fn} такая, что lim Fn — F,
модуль которой рекурсивен в А.
Доказательство. Предположим, что все рас-
рассматриваемые здесь пространства равны N. Пусть / —
индекс А и Ап = Wj,n. Тогда последовательность {Ап}
рекурсивна и lim Ап = А. Полагая G (к) = \т (к ЕЕ Ап),
если к ^ А, и G (к) = 0, если к ф. А, получаем, что G
является модулем для {-4П}; функция G рекурсивна в А.
Пусть / — алгоритм для F в А. Для любого г имеем
г ЕЕ Wf. Пусть Н (г) — наименьшее число т такое, что
г ЕЕ Wft т и т~^> G (к) для каждого к, используемого в вы-
вычислении [/]А (г). Если п !> Н (г), то ввиду принципа
28 5. РЕКУРСИВНАЯ ПЕРЕЧИСЛИМОСТЬ
использования
[/]> (г) = [/]? (г) = [/И (г) = F (г).
Следовательно, если мы положим Fn(г) = [/]„" (г), когда
г ЕЕ Wj%, и Fn (г) = 0 в остальных случаях, то lim Fn =
= F и Я — модуль для {Fn}. Наконец, Я рекур-
рекурсивна в А; действительно, оракул для А позволит нам
найти все z, используемые в вычислении [J]A (г), и вы-
вычислить G (z) для каждого такого z, что и требовалось
доказать.
Множество А в X называется рекурсивно перечислимым
в~Н, если существует пространство Y и множество В в
X х Y, рекурсивное в Н, такое, что для всех х
x^A^ly «х, у> е В).
Тогда мы можем релятивизовать к Н все вышеука-
вышеуказанные результаты. Индексом А в Н называется / ЕЕ
GE Alg(Z, ЛГ) такой, что А = Wf.
Если G рекурсивна в Я, то любое множество, рекурсив-
рекурсивно перечислимое в G, является рекурсивно перечислимым
в Я (вследствие соответствующего результата с заменой
рекурсивного на рекурсивно перечислимое).
Скачком функции Я называется отношение Я* в
, N) х N, определенное следующим образом:
Ясно, что Я* рекурсивно перечислимо в И. Каждое мно-
множество, рекурсивно перечислимое в Я, является рекур-
рекурсивным в Я*. Это достаточно доказать для множества А
в N. Пусть / — индекс А в Я. Тогда п Е= А +-> </, п> еэ
ЕЕ Я*, что и доказывает рекурсивность А в Я*.
Так как П рекурсивно в Я, а значит, и рекурсивно пе-
перечислимо в Я, то Я рекурсивно в Я*. Однако Я* не яв-
является рекурсивным в Я. Если бы это было так, то каждое
множество, рекурсивно перечислимое в Я, было бы ре-
курсивным^в Я, что противоречит /релятивизованному
к П ранее доказанному результату о том, что не каждое
рекурсивпо перечислимое множество является рекурсив-
рекурсивным.
6. СТЕПЕНИ 29
6. Степени
Будем писать F <[r G, если F рекурсивна в G. Как мы
видели в § 4,
F <r F, A)
F <R G & G <R Я -*- F <R Я. B)
Пусть F ~ G означает, что F <<r G и G <Jr F. Из A)
и B) мы видим, что ~ есть отношение эквивалентности
между функциями. Класс эквивалентности, содержащий F,
называется степенью F и обозначается через dg F. По ос-
основному свойству классов эквивалентности имеем
F ~ G <^ dg F = dg G. C)
Будеи обозначать степени через а, Ь, с и d.
Пусть a <J b означает, что для некоторых F и G имеем
а = dg F, Ь = dg G и F <R G. Тогда
dg F < dg G ~ F <R G. D)
Импликация справа налево очевидна. Если dg F < dg G,
то dg F = dg F', dg G = dgG' и F' <R G'. Используя C),
получаем F «^r F', F' <Jr С и С <[r G. Следовательно,
F <R G no B).
Из A) — D) следует, что отношение <! является час-
частичным порядком" на множестве степеней. Как обычно, пи-
пишем а < b вместо а < b & а Ф Ь. Используя D) и C),
получаем
dg F < dg G <r* F <R G & G <R F. E)
Можно считать, что F <!r G означает, что F легче для
вычисления, чем G. Тогда F —• G означает, что F и G оди-
одинаково легки для вычисления. Таким образом, степень F
есть некоторая мера трудности вычисления F; чем больше
эта степень (в частично упорядоченном множестве степе-
степеней), тем труднее вычислять F.
Если А — график F, то dg F = dg А; действительно,
отношение А рекурсивно в F по определению A, a F ре-
рекурсивна в А по теореме о графике, релятивизованной к А.
Таким образом, каждая степень есть степень некоторого
множества.-По теореме об изоморфизме мы видим, что для
любых ХиУ каждая степень является степенью некоторой
функции из X в У и некоторого мпожества в X.
30 6. СТЕПЕНИ
Если F рекурсивна, то F <^r G для всех С; таким об-
образом, dg F < а для всех а. Следовательно, существует
наименьшая степень 0 и 0 — степень каждой рекурсивной
функции. Обратно, если dg F — 0, то F рекурсивна. Дей-
Действительно, беря любую рекурсивную функцию G, будем
иметь F <^r G, и, значит, F рекурсивна.
Заметим, что в любом частично упорядоченном множе-
множестве имеет смысл говорить о наименьшей верхней грани
и о наибольшей нижней грани.
Пусть alt . . ., ап — степени, а ^ ,. . ., F,,. — функ-
функции такие, что dg Ft — аг. Применяя оракул, мы можем
вычислить Fx х . . . X Fn тогда и только тогда, когда мы
можем вычислять каждую из функций. На языке степеней
это означает, что dg (Ft X • • . X Fn) <, а тогда и только
тогда, когда а есть верхняя грань для {а^. . ., ап}. Сле-
Следовательно, dg (Fx x ... X Fn) является наименьшей
верхней гранью для {ах,. . ., ап}. Эта наименьшая верх-
верхняя грань обозначается через ах \J . . . \J an. Заметим,
что dg G <^ 8j U . . . U an тогда и только тогда, когда G
рекурсивна в F^. . ., Fn, a aj \J . . . [j an < dg G тогда
и только тогда, когда каждая Ft рекурсивна в G.
Так как пустое множество степеней имеет наименьшую
верхнюю грань, то каждое конечное множество степеней
имеет наименьшую верхнюю грань.
Если {Fn} — бесконечная последовательность функ-
функций из X в У, то ипогда будем отождествлять {/<*„} с функ-
функцией F из N х X в Y такой, что F (п, х) — Fn (x). Учи-
Учитывая это, мы понимаем, что означает {Fn} <Cr G или
{n}
Ясно, что Fn <r{/?\i}; следовательно, dg Fn ^ dg{Fn}.
Отсюда следует, что всякое счетное множество степе-
степеней имеет верхнюю грань.
Пишем A ^rb F для обозначения того, что А рекур-
рекурсивно перечислимо в F. Из результатов § 5 имеем
A <R F -> A <RB F, F)
A <rB F & F<R G -> A <rb G. G)
Говорим, что а рекурсивно перечислима в Ь, и записы-
записываем a ^rb Ь, если для некоторых А и F имеем а — dg.4,
b = dg F и A <rb F. Тогда по G) имеем A <RK G для
каждой G такой, что dg G = b. Однако для В с dg В = а
6. СТЕПЕНИ 31
не обязательно иметь В <^нв F. Например, dg A0 =
-¦ dg А — а, но по релятивизованной теореме о дополне-
дополнении, если не выполняется A <^R F, то мы пе будем иметь
АС <RE F.
По F) и G) получаем
a<b->a<REb, (8)
а < REb & b < с -> а < RBc. (9)
Если степень а рекурсивно перечислима в 0, то просто
говорим, что степень а рекурсивно перочислима. Таким
образом, степень а рекурсивно перечислима тогда и толь-
только тогда, когда она есть степень некоторого рекурсивно
неречислимого множества.
Для любой функции Н по основному свойству скачка
имеем, что dg II* есть наибольшая степень, которая яв-
является рекурсивно перечислимой в //. Следовательно, для
любой степени а существует наибольшая степень, рекур-
рекурсивно перечислимая в а. Эта степень называется скачком
степени а и обозначается через а'. Как мы только что ви-
видели, (dg#)' = dg#*. Так как Я<к II* и Я* <Rtf,
то в силу E) имеем
а<а'. A0)
Также
а<Ь_>а'<1>'. (И)
Действительно, a' <;RE а; если а <[ Ь, то а' <лш Ьиа'<
<Ь'.
Лемма о пределе. Функция F имеет степень
<[ а' тогда и только тогда, когда существует последова-
последовательность {Fn} такая, что dg {Fn} <; а и lim Fn = F.
Доказательство. Предположим, что такая
последовательность существует. Определим А следующим
образом:
<х, п} е А <-> Vmm>n(Fm (х) = Fn (x)).
Тогда
<в, п> е Ас <-> 1т (т > п & Fm (x) ф Fn (x)).
Значит, Ас рекурсивно перечислимо в {Fn} и dg A =
= dg Ае <; а'. Полагая Н(х) = цп «ж, п} 6Е А), ви-
видим, что Н — функция, рекурсивная в Л и поэтому
32 7. ОЦЕНКА СТЕПЕНЕЙ
имеющая степень < а'. Так как F (х) ¦-¦= Fh(x)(x),
то F рекурсивна в {Fn}, H и имеет степень < а'.
Теперь положим dg F <^ а'. Пусть А имеет степень а
и В = А*. Тогда по лемме о модуле, релятивизованной
к А, получаем требуемую последовательность, что и тре-
требовалось доказать.
Лемма о пределе также выполняется, если F и Fn
заменить на А и Ап. Нужно лишь показать, что если А =
= lim Fn, то А = lim An для некоторой последователь-
последовательности {Ап} такой, что {Ап} <^r {Fn}. Для этого достаточ-
достаточно положить Ап (х) = min (Fn (x), 1).
В заключение сделаем несколько замечаний о мощно-
мощностях. Так как Alg(N, N) имеет перечисление, то оно счет-
счетно. Таким образом, для любой фиксированной функции F
существует только счетное число [/]* таких, что Г ЕЕ
ЕЕ Alg(iV, N), и, следовательно, только счетное число функ-
функций из N в N, рекурсивных в F. Отсюда слодует, что каж-
каждая степень есть степень лишь счетного числа функций из
Nb N. Так как существует континуум функций из N в N,
то существует континуум степеней. Наш результат показыва-
показывает, что существует счетное число степеней, меньших любой
фиксированной степени; таким образом, всякое несчет-
несчетное множество степеней не имеет верхней грани.
Теория степеней — это теория частично упорядочен-
упорядоченного множества степеней с операцией скачка. Мы видели,
что это множество имеет некоторые довольно хорошие
свойства. Оно имеет наименьший элемент, каждое конеч-
конечное множество элементов имеет наименьшую верхнюю
грань. Операция скачка повышает степень и сохраняет
отношение ^. Оказывается, что подобных хороших
свойств не так много. Прежде чем перейти к таким резуль-
результатам, мы разработаем некоторые методы оценки степеней
специальных функций и множеств.
7. Оценка степеней
Множества типа 2„ и П„ определяем индукцией по п.
Множества типа 20 и По — это рекурсивпыо множества.
Множество А имеет тип 2п+1, если
х е А <- Зу «г, уУ ^ В),
где В имеет тип П„.
7. ОЦЕНКА СТЕПЕНЕЙ 33
Множесшо А имеет тип Пп+1, если
а: ЕЕ А «-> Vy «ж, у>е=_В),
где В имеет тип 2 п. (В литературе 2 п и Пп обычно обо-
обозначаются 2п и Пп, чтобы отличить их от других видов мно-
множеств, которые мы не рассматриваем.) Заметим, что мно-
множества типа 2^ — ото в точности рекурсивно перечисли-
перечислимые множества.
Теперь дадим песколько правил, с помощью которых
можно показывать, что некоторые множества имеют тип
2П или 11И. Во всех случаях доказательство ведется ин-
индукцией по п. Случай п — 0 в доказательствах опускается,
так как оп следует из предыдущих результатов.
(А1) Если А имеет тип Ъп (Пп) и
iGB <->• F (i)E4,
где F — рекурсивная функция, то В имеет тип 2П (П„).
Доказательство. Тривиально.
(А2) Если А имеет тип 2т или Пт для некоторого
т < п, то А имеет тип 2П и П„.
Доказательство. Предположим, что А имеет
тип 2т; случай Пт рассматривается аналогично. По ин-
индуктивному предположению А имеет тип 2п_х. Тогда
iEi« У у {х (= А), а по (Al) i?i- отношение
типа 2„_1 от аргументовх, у. Следовательно, А имеет тип
П„. Если п = 1, то А имеет тип Ii.n-i) подобное доказатель-
доказательство показывает, что А имеет тип 2П. Если п ^> 1, то х ЕЕ
ЕЕ А <-»• Зу «х, уУ е= В), где В имеет тип Пп_2. По ин-
индуктивному предположению В имеет тип nn_i; таким об-
образом, А имеет тип 2„.
(A3) Если А имеет тип 2„ (П„), то Ас имеет тип
П„ B„).
Доказательство. Пусть Л имеет тип 2П.
Тогда х GE ^ <-> Эг/ «а:, г/> ЕЕ 5), где В имеет тип Пп_!.
Следовательно, xeAcoVi/«я, г/>ЕЕ5е). По индуктив-
индуктивному предположению Вс имеет тип 2n_i-, таким обра-
образом, А" имеет тип Пп.
(А4) Если А имеет тип 2,nuxEzB<->3y «x, г/> Е:
ЕЕ А), то В имеет тип 2П. Если А имеет тип П„иа:Е
ЕЕ В +-»• Vi/ (<а;, i/> ЕЕ J5), wo Z? имеет тип П„.
Доказательство. Пусть Л имеет тип 2П; тогда
<х, уУ ЕЕ Л <-> Зг «х, у, z> ЕЕ С),
34 7. ОЦЕНКА СТЕПЕНЕЙ
где
С
имеет
тип
х е
Пп_!.
= в <-
3w «,
Тогда
* 3i/3z (
х, F (w)
(X,
, G
У,
(w
= 0
1С),
где w из X X У, F (х, у) — х и G (х, у) — у. По (А1)
(х, F (w), G (w)y ЕЕ С есть отношение типа Нп_1 от аргу-
аргументов х, w; следовательно, В имеет тип 2П.
(А5) Если А и В имеют тип 2„ (П„), то A (J В и
A f] В имеют тип Е„ (П„).
Доказательство. Предположим, что А и В
имеют тип 2„; тогда х ?Е А <-> Зу ({х, j)eC) и а; ее-#*->
<-> 3z (<a;, z> е ^), где С и D имеют тип П„_1. Тогда
x^A\JB^ 3y3z'S<x, уУ е С V <*, z> е D).
По (А1) и индуктивному предположению часть, следую-
следующая за 3z, есть отношение типа Hn-i от аргументов х, у, z.
Тогда часть, следующая за Зу, есть отношение типа 2П
от аргументов х, у; таким образом, по (А4) A [j В имеет
тип 2„. Случай A f] В рассматривается аналогично.
(А6) Если А имеет тип 2„ (Г1„) и
(х, &> е В <-> Vnn<ls ((х, п, к> е А),
<х, ^}ёСн Зпп<1с «ж, п, к} е 4),
то В и С имеют тип 2„ (П„).
Доказательство. Если А имеет тип П„, то
мы имеем
(х, i;)eB<-> V" (к ^ п \/ <ж, и, Л) е А);
используя (А2), (А5) и (А4), заключаем, что В имеет
тип Пп. Если А имеет тип 2П, то
<х, п, ку^А^Зу «х, п, к, ?/> е D),
где D имеет тип nn-1. Тогда
<ж, /с> е 5 <->• Уп'п<КЗу {(х, п, к, уУ е !>)]
3Vft (<ж, и, /с, а (ге)> е 1>),
где а из Sq (Y), a а (п) выбрано как некоторый фиксиро-
фиксированный элемент из Y, если п не принадлежит области
определения' а. По (А1) и индуктивному предположению
часть, следующая за За, имеет тип nn-1; таким образом,
В имеет тип 2П.
7. ОЦЕНКА СТЕПЕНЕЙ 35
Рассматривая С, заметим, что
<*, «:}ёСсн Vnn<k «я, п, к} ЕЕ Ав).
Если Л имеет тип 2П (Пп), то .4 е имеет тип Пп BП); та-
таким образом, Сс имеет тип Пп BП); следовательно, по (A3)
С имеет тип 2П (Пп).
Заметим, что (А6) можно также применить к кванто-
кванторам 3ran<fc и V^nOn действительно, можно переписать
их как Впп<1с+1 и Vran<k+i.
Скажем, что утверждение Р имеет тип 2П (Пп), если
оно есть отношение типа 2П (Пп) от всех (свободных) пе-
переменных Р. Тогда (A3) говорит нам, что если Р имеет
тип 2П (Пп), то ~Л Р имеет тип Пп BП). По (А5), если Р
и Q имеют тип 2П (Пп), то Р \/ Q и Р & Q имеют тип
2П (П„). Затем мы можем рассмотреть Р -> Q и Р <-* Q,
заметив, что Р -*¦ Q эквивалентно \ Р \J Q, а Р *-* Q
эквивалентно (Р ->- Q) & (Q -> Р). Ясно, что если Р име-
имеет тип 2П, то УхР имеет тип Пп+1, а если Р имеет тип П„,
то ^хР имеет тип 2п+1. По (А4), если Р имеет тип 2П,
то JxP имеет тип 2П, а если Р имеет тип П„, то УхР
имеет тип Пп. По (А6), если Р имеет тип 2П (Пп),
то V«n<» Р и Э"п<» Р имеют тип 2П (Пп). Часто мы
будем молчаливо использовать эти правила, чтобы пока-
показать, что определяемые множества имеют тип 2П илиПп.
Заметим, что мы также используем эти правила для того,
чтобы показать, что какое-либо множество рекурсивно
перечислимо, показывая, что оно имеет тип 2Д.
ТеоремаПоста. Множество Л имеет тип 2п+1
тогда и только тогда, когда оно рекурсивно перечислимо
в некотором множестве типа Пп.
Доказательство. Если А имеет тип 2п+1, то
х ЕЕ А *-* Jy (<?, уУ ЕЕ В), где В имеет тип Пп; таким
образом, А рекурсивно перечислимо в В. Теперь предпо-
предположим, что А рекурсивно перечислимо в множестве В в
N типа Пп. Пусть / — индекс А в В. В силу C) из § 4
имеем
х ЕЕ А <-+ х ЕЕ W?
<-* За (а С В & х ЕЕ \Уц).
Чтобы показать, что А имеет тии 2„+1, достаточно по пра-
правилам доказать, что а С В и х ЕЕ Wj являются отноше-
отношениями типа 2„+1. Последнее является рекурсивно пере-
36 7. ОЦЕНКА СТЕПЕНЕЙ
числимым; следовательно, имеет тип 2^ а значит, и 2„+1.
Рассматривая первое отношение, заметим, что
аС5о (Vran<lh(a))(a (п) = В (п));
тогда по правилам достаточно показать, что к = В (п)
имеет тип 2„+1. Но
* = В(«)н(ЬИ&пеВ) V (А - Л & (п е В));
таким образом, по правилам к = В (п) имеет тип 2„+1,
что и требовалось доказать.
Следствие. Множество А одновременно имеет тип
2„+1 и П„+1 тогда и только тогда, когда оно рекурсивно
в некотором отношении типа П„.
Доказательство. Используем релятивизо-
ванную теорему о дополнении, что и требовалось доказать.
Заметим, что по (A3) в обеих теоремах и следствии
Пп можно заменить на 2„.
Свяжем все это со степенями. Будем писать ап в слу-
случае, если к а применяются п скачков.
Лемма. Наивысшей степенью среди множеств типа
2„ (П„) является 0п.
Доказательство. Применяем индукцию по п.
Случай п = О тривиальный. Если теорема верна для
множеств типа П„, то по теореме Поста она верна и для
множеств типа 2„+1, а по (A3) и для множеств типа Пп+1,
что и требовалось доказать.
Данная лемма является основным орудием для оценки
степеней некоторых специальных множеств. Мы уже ви-
видели, как показывать, что некоторое данное множество
имеет тип 2„ или Пп; теперь объясним, как показывать, что
данное множество имеет наивысшую степень среди таких
множеств.
Скажем, что А т-сводится или просто сводится к В,
если существует рекурсивная функция F такая, что
х ее А *-* F (x) 6E В для всех х, т. с. такая, что F (A) CZ В
и F (Ас) С В". Ясно, что в этом случае имеем A <^R В.
Скажем, что А — полное множество типа 2„ (полное
множество типа П„), если А имеет тип 2„ (П„) и каждое
множество типа 2„ (П„) сводится к А. (Для полпых мно-
множеств типа St применяем термин полное рекурсивно пере-
перечислимое.) По ломме каждое полное множество типа 2„
или полное множество типа П„ имеет степень 0п.
7. ОЦЕНКА СТЕПЕНЕЙ 37
Легко видеть, что если А имеет тип 2„ (П„) и какое-
то полное множество типа 2 „ (Пп) сводится к А, то А —
полное множество типа 2n (tln). По этой причине полезно
иметь примеры полных множеств типа 2П и Ип. Найдем
песколько таких множеств.
Пусть Tot — множество всех таких / в Alg (N, N),
что Wj = N. (Таким образом, / ?Е Tot тогда и только
тогда, когда / всюду определен.) Покажем, что Tot —
полное множество типа П2. Имеем
/ <= Tot «-¦ Vn (п е Wi)\
так как п ?Е Wj рекурсивно перечислимо и, значит, имеет
тип 2lf то Tot имеет тип П2. Если А — любое множество
типа П2, то х €Е А <-* Vre «я, в) Е й), где В имеет тип
2Х и, зпачит, рекурсивно перечислимо. По теореме пара-
параметризации существует рекурсивная функция F такая,
что п GE Wp(X) <-* (х, пУ е В. Тогда
х е А <-> WF{X) = N
<^ F (x) e Tot;
таким образом, А сводится к Tot.
Скажем, что А сводится к В, С, если существует ре-
рекурсивная функция F такая, что F (A) CZ В и F (Ac) CI
d С. Отсюда следует, что А сводится к любому множеству
D такому, что В d D и С f~) D = 0.
Пусть Fin — множество всех таких / в Alg (N, N), что
Wi копечно. Покажем, что каждое множество типа 11а
сводится к Tot, Fin. Достаточно показать, что Tot
сводится к Tot, Fin. По правилам этого параграфа
V/cic<n (к ?Е Wi) — рекурсивно перечислимое отношение
от аргументов п, I; таким образом, по теореме параметри-
параметризации существует рекурсивная функция F такая, что
п ?Е WF{f) «-» Укъ<п (к ?Е Wi).
Отсюда без труда следует, что F (Tot) С Tot и F (Totc) CZ
С Fin.
Как следствие, получаем, что каждое множество типа
П2 сводится к Finc.
Имеем
/ е Finc ^ УпЗк (п < к & к е Wt);
38 7. ОЦЕНКА СТЕПЕНЕЙ
следовательно, Finc имеет тип П2. Итак, Finc — полное
множество типа П2, a Fin — полное множество типа 22.
Пусть Cof — множество всех таких / в Alg (N, N),
что Wj кокопечно *). Покажем, что каждое множество
типа П2 сводится к Tot, Cof \ Tot. Ввиду доказанного
выше достаточно найти рекурсивную функцию F такую,
что F (Tot) С Tot и F (Fin) С Cof \ Tot.
По теореме параметризации выберем F так, чтобы
п ЕЕ WFa) ~ Vrr<n (г ЕЕ Wj) V [ЗЛЙ<„ (к ф Wj, п) &
A Vfcft<n (к ЕЕ Wj,w-»kE Wj,„)].
Яспо, что F (Tot) CZ Tot. Теперь пусть Wj конечно, мы
должны показать, что Wptj) коконечно и отличается от
N. Если п достаточно большое, то 3&к<п (к ф Wf) и
Wi,n — WI<n+l = Wj. Все такие п лежат в Шрщ; таким
образом, Wf{I)коконечно. Пусть г — наименьшее число, не
лежащее в Wi. Тогда либо г ф Wp(i), либо существует
к < г такое, что к ф. Wj,r. В последнем случае к ЕЕ Wt\
таким образом, существует «такое, что и ^> г, к ф Wi%n
и к GE WIiTl+1. Так как к < л, мы имеем п ф Wpyy Та-
Таким образом, WV(j) ф N.
Теперь покажем, что Cof — полное множество типа 2 3.
Так как
/ е: Cof «-
то Cof имеет тип 23. Пусть А имеет тип 23. Тогда
хееА <-^ 3^ (<^, п}€ЕВ), где /? имеет тип П2. Тогда
3^п<»(<С-г> ге^ ? Щ есть отношение типа П2 от аргументов
х, к; по сказанному выше существует рекурсивная функ-
функция F такая, что
Зп71<К ((х, п> е /?) -> F (х, k) GE Tot,
HSnnOt «ж, п> е /?) -> F (ж, A') GE Cof \ Tol.
По теореме параметризации выберем G так, чтобы
<А\ m> GEE VFG(.v) <^ rn d- VFf(x,*).
Есл-и а; ЕЕ ^4, то для всех достаточно больших к имеем
F (х, к) Er Tot. Так как F (х, к) Е= Cof для всех к, то от-
отсюда следует, что Wc(X) коконечно. Если х фА, то F (х, к)ф
То есть имеет конечное дополнение.—Прим. ред.
8. НЕСРАВНИМЫЕ СТЕПЕНИ 39
^ Tot для всех к; отсюда следует, что VFg(*> кобеско-
нечно *). Теорема об изоморфизме теперь показывает, что
А сводится к Gof.
Результаты этого параграфа могут быть релятивизо-
ваыы ко всякому Я. При определении множеств типов
2П в Я и Пп в //, которые мы также пишем как 2П [Я] и
П„ [Я], вносим единственное изменение: множествами ти-
типов 20 в Я и По в Я теперь являются множества, рекур-
рекурсивные в II. Список правил и теорема Поста также реля-
тивизуются с помощью замены 2П и Пп на 2П[Я] и
ПП[Я]. Релятивизованная лемма утверждает, что наивыс-
наивысшей степенью среди множеств типов 2П [Я] и Пп [Я] яв-
является (dg Н)п.
8. Несравнимые степени
Результаты последнего параграфа могут навести
на мысль, что других степеней, кроме 0", нет. В противо-
противовес этому покажем, что существуют степени между 0 и О'.
Скажем, что степени а и b несравнимы, и записываем
а | Ь, если неверно а ^ b или b <; а.
Теорема (Клини-Пост). Существуют степени а и
b такие, что а | Ь, а ^ 0' и b <^ О'.
Следствие. Существует степень а такая, что
0<а<0'.
Доказательство. Возьмем а и b из теоремы;
имеем 0 < а < 0'. Так, как 0 < b < 0' и а | Ь, то а Ф О
и а Ф 0', что и требовалось доказать.
Так как доказательство теоремы будет служить мо-
моделью для нескольких других доказательств, то рассмот-
рассмотрим его в деталях.
Пусть F и G — частичные функции из X в У. Гово-
Говорим, что F и G совместны, и записываем Comp (F, G),
если F и G имеют общее расширение; в противном случае
называем F и G несовместными. Легко видеть, что F и G
несовместны тогда и только тогда, когда существует х
такое, что F (х) и G (х) определены и различны.
Сосредоточимся вначале на получении несравнимых
степеней а и Ь. Так как прямо строить степени трудно,
то будем строить функции F л G из N ъ N и возьмем
*) То есть имеет бесконечпое дополнение.—Прим. ред.
40 8.' НЕСРАВНИМЫЕ СТЕПЕНИ
а = dg F, Ъ — clg G. Мы хотим, чтобы F =^r G и G s^r F.
Эти условия можно разбить на бесконечное множество
условий (где / пробегает Alg (N, N)):
(lj) F ф [Л0,
Bi) G gt f/F.
Каждое условие есть конечный объект (а именно, некото-
некоторое выражение), класс всех условий составляет простран-
пространство. Пусть {Bs} — перечисление пространства условий.
Будем строить F ж Gno шагам. На каждом шаге будем
определять конечное число значений F и G. На шаге s
мы обеспечиваем условие Iis; другими словами, определяем
некоторые значения F и G так, чтобы независимо от того,
как будут определены оставшиеся значения, Rs выполня-
выполнялось. После всех шагов F, G будут определены полно-
полностью и будут удовлетворять всем условиям.
Пусть Fs и Gs — конечные части F и G, определенные
перед шагом s, т. е. Fe (к) — п тогда и только тогда,
когда F (к) = п получилось на некотором шаге до шага s.
Теперь опишем шаг s. Предположим, что Rs есть A/);
если Rs окажется Bj), то мы везде меняем местами F и G.
Пусть п — наименьшее число такое, что зпачение F' (п)
не определено. Имеются два случая.
Случай 1. Существует конечная фупкция а такая, что
Сотр (а, С)ип? W".
Выберем одну такую а. Положим G (т) = а (яг) для
каждого т из области определения функции а, для кото-
которого значение Gs (т) не определено, и положим F (п) =
= [Л"(л) + 1. Так как Comp (a, Gs), to этот выбор гаран-
гарантирует, что" а С G. Следовательно, мы будем иметь
[I]G (п) — [I]" (п) Ф F (п), а значит, условие (lj) выпол-
выполняется.
Случай 2. Случай 1 пе выполняется.
Положим F (п) — 0. Чтобы показать, что (lj) выпол-
выполняется, достаточно показать, что мы будем иметь п ф Wf*
Допустим, что п Е; Wf • По A) из § 4 существует веб
такая, что п Е:~ Wj. Так как о и С имеют общее расшире-
расширение G, то Comp (a, Gs). Это противоречит нашим допуще-
допущениям.
На бесконечно многих шагах определяем F (п), где
п — наименьшее число, для которого значение F (п) ра-
8. НЕСРАВНИМЫЕ СТЕПЕНИ 41
нее не было определено. Отсюда следует, что F (п) оп-
определено для всех п; аналогичное рассуждение справед-
справедливо для G. Итак, мы имеем несравнимые степени dg F
и dg G. Для завершения доказательства мы должны пока-
показать, что dg F < 0' и dg G < О'.
Можно отождествить нашу конструкцию с функцией,
значение которой в точке s является описанием тех зна-
значений F и G, которые были им приписаны на шаге s. Так
как каждое значение F и G определяется на некотором
шаге, то F и G являются рекурсивными относительно дан-
данной конструкции. Итак, нам нужно только показать, что
наша конструкция имеет степень ^ 0'. Другими словами,
мы должны показать, что по данному оракулу для подхо-
подходящей функции степени <^ 0' мы можем по данному s
вычислить, что произойдет па шаге у.
Можно предположить, что мы уже вычислили, что
произойдет на всех предыдущих шагах, так что мы знаем
Fs и Gs. Так как {Rs} — перечисление, то можно найти
Rs. Можно также вычислить п, о котором идет речь на
шаге s. Случай 1 выполняется тогда и только тогда, когда
Зз*(Сотр (с, G*)&n<= W°). A)
Так как Сотр (о, я) есть рекурсивное отношение от аргу-
аргументов с, я, то A) есть рекурсивно перечислимое отноше-
отношение от аргументов Gs, I, n (по правилам предыдущего па-
параграфа). Итак, это отношение имеет степень «^ 0'. Имея
оракул для этого отношения, мы можем решать, какой
же случай выполняется.
Если выполняется случай 2, то никаких проблем нет.
Если выполняется случай 1, то остается лишь проблема
нахождения о. Часть после Зз в A) является рекурсивно
перечислимым отношением от аргументов б, G*, I, п. Сле-
Следовательно, по теореме о селекторе существует частичная
рекурсивная функция L такая, что всякий раз, как толь-
только выполняется случай 1, L (Gs, /, п) есть подходящее б.
Тогда мы можем вычислить эту о, не используя оракула,
что и требовалось доказать.
Рассмотрим теперь релятивизацию данного выше до-
доказательства к функции Н. Это означает, что в любое
время можно использовать оракул для //. Следовательно,
когда мы обращаемся к G, мы имеем оракулы для G и Н
или, что эквивалентно, оракул для G X Н. Таким обра-
42 9. ВЕРХНИЕ И НИЖНИЕ ГРАНИ
зом, получающаяся F удовлетворяет условию F ^ rG X
X И. Апалогично G^RF X Н. Беря а = dg (F X Н) =
= dg F U dg Н и Ь = dg (G X Н) = dg G (J dg H, по-
получаем а | Ь. Так как A) является рекурсивно перечисли-
перечислимым в Н, то нам нужен оракул для функции степени
<^ (dg Н)'. Полагая с = dg II, получим а <1 с' иЬ^с'.
Так как ясно, что с ^ а и с ^ Ь, то устанавливаем, что
имеет место
Релятивизованная теорема. Для любой
степени с существуют степени а и Ъ такие, что а|Ь,
с <; а <; с' uc<b<c'.
Для всех результатов, которые мы доказываем о сте-
степенях, имеются подобные релятивизованпые варианты,
но мы не будем их упоминать, если они пе будут иметь
особого нптереса.
9. Верхние и нижние грани
Мы уже видели, что всякое конечное множество сте-
степеней имеет наименьшую верхнюю грань. Докажем, что
это утверждение ложпо для наибольшей нижпей грани, а
также что очень простые бесконечпые множества степеней
могут не иметь наименьшей верхней грани.
Возрастающей последовательностью степеней назы-
называется бесконечная последовательность {а„} такая, что
ап < а„+1 для всех п. Например, 0, 0', 0", ... — возрас-
возрастающая последовательность.
Теорема (Клини — Пост — Спектор). Пусть
{ап} — возрастающая последовательность степеней.
Тогда существуют верхние грани b и с для {а„} такие, что
никакая верхняя грань для {ап} не является нижпей гранью
для {Ь, с}.
Следствие 1. Никакая возрастающая последова-
последовательность не имеет наименьшей верхней грани.
Следствие 2. Существуют степени Ь и с такие,
что {Ъ, с} не имеет наибольшей нижней грани.
Доказательство. Возьмем любую возрастаю-
возрастающую последовательность {а„}, и пусть b и с таковы, как
в теореме. Тогда наибольшая нижняя грань для {Ь, с}
должпа быть верхпей гранью для {а„},что и требовалось
доказать,
9. ВЕРХНИЕ И НИЖНИЕ ГРАНИ 43
Теперь перейдем к доказательству теоремы. Пусть
Нп — функция из N в N степени ап. Построим функции
F и G из N X N в N и. возьмем b — dg F, с — dg G. Что-
Чтобы быть уверенными, что никакая верхняя грань для
{ап} не будет нижней гранью для {Ь, с}, мы должны удов-
удовлетворить условию:
(l/,j) Если [I]F = [J]G = L, то L <з Ип для некото-
некоторого п.
Пусть {Rs} — перечисление пространства условий.
Снова будем обеспечивать Rs на шаге s. На шаге s вначале
определяем конечное число значений F и G, затем поло-
положим
F (s, к) — Hs (к), если F (s, к) не определено, A)
G (s, к) = Hs (к), если G (s, к) не определено. B)
Во-первых, это обеспечивает нам то, что F и G по конст-
конструкции будут полностью определены. Далее, F(s, к) мо-
может быть определена перед последней частью шага s
только для конечного числа значений к; следовательно,
F (s, к) = Hs (к) для всех к, кроме конечного числа. Это
показывает, что Н, <^я F; таким образом, b — верх-
верхняя грань для {ап}. Аналогично,] с — верхняя грань
Для {ап}.
Теперь опишем шаг s. Пусть Rs будет (l/.j), a Fs и
Gs — уже определенные части F и G.
Случай 1. Существуют аия такие, что Comp (a,Fs),
Сотр (я, Gs), и [I]" и [/]* несовместны.
Выберем такие аия. Полагаем F (п, к) = а (п, к) для
всех (п, к) в области определения а таких, что Fs (n, к)
не определено; полагаем G(n, к) = я (п, к) для всех (п, к)
в области определения я таких, что Gs (n, к) не опреде-
определено. Затем приступаем к A) и B). Мы добились того, что
ad F vmdG. Следовательно, [/]" С Шр, и №с Ш°;
таким образом, [I]F и [/]G несовместны. Отсюда следует,
что A/,j) выполняется.
Случай 2. Случай 1 не выполняется.
Здесь мы сразу же приступаем к A) и B). Нам нужно
показать, что (l/,j) выполняется.
Во-первых, покажем, что множество а таких, что
Comp (a, Fs), рекурсивно в Hs. Выпишем конечное число
значений Fa, которые не определяются с помощью A) и
B). Чтобы определить, будет выполняться Comp (a, Fs)
44 Ю- ОПЕРАЦИЯ СКАЧКА
или нет, достаточно решить для каждого (ге, к) в области
определения 0, будет ли (ге, к) в области определения Fs
или пет, и если это так, то определить Fs (ге, к). Если
F* (re, к) попало в этот список, то данную операцию
можно проделать без оракула. В противном случае (ге, к)
лежит в области определения Fs тогда и только тогда,
когда ге < s; в этом случае Fs (re, к) — Нп (к). Для r< s
имеем ап < as и, следовательно, Нп <^ r77s. Таким об-
образом, оракула для Hs будет достаточно.
Теперь предположим, что [7]F = [J]G = L. Вначале
покажем, что
L @ = / <-» За (Сотр (а, F*) & [I]a (i) = j). C)
Если L (i) — /, то [7]F (i) = /; в силу B) из § 4 существует
а CZ F такая, что [7]° (i) = /. Так как а и Fs имеют об-
общее расширение F, то Сотр @, F*). Теперь предположим,
что Сотр (a, Fs) и [7]° (i) = / для некоторой о. Так как
[J]G (i) — L (i), то существует я d G такая, что [J]n (i) =
= L (i), и тогда Сотр (л, Gs). По предположению
Comp ([7]°, [/]"), следовательно, L (i) = /.
Comp (a, Fs) как отношение от аргументов a, i, j яв-
является рекурсивным в 77S и, следовательно, рекурсивно
перечислимым в Hs; [7]° (i) — j как отношение от аргу-
аргументов 0, i, j является рекурсивно перечислимым, следо-
следовательно, рекурсивно перечислимым в Hs. Тогда в силу
C) и релятивизации правил из § 7 график L рекурсивно
перечислим в 77S. Значит, по релятивизованиой теореме
о графике L <^ r77s и, следовательно, (lj,j) выполняется,
что и требовалось доказать.
10. Операция скачка
Перейдем теперь к определению области значений
операции скачка. По A2) из § 6 0' <[ а' выполняется для
всех а; таким образом, каждая степень в этой области
значений ^> 0'. Покажем обратное, что каждая степень
1> 0' есть скачок некоторой степени.
Теорема (Фридберг). Если 0' ^а, то существует
степень Ъ такая, что Ъ' = b (J 0' = а.
Хотя эта теорема и дает довольно хорошее свойство
операции скачка, она может быть использована для дока-
доказательства, что данная операция имеет и не очень хоро-
10. ОПЕРАЦИЯ СКАЧКА 45
шие свойства. Например, операция скачка не является
1-1 операцией. Действительно, используем теорему для
получения степени b такой, что Ь' — b (J 0' — 0". Тогда
Ь' = 0", но b ф О', иначе мы получили бы, что b (J О' =
= О' Ф О".
В действительности мы можем иметь а' = Ь' с любым
из альтернативных случаев а = b, a | b, a ¦< b, b < а.
Очевидно, что первый случай возможен. Для второго
случая возьмем а = 0', b — такая степень, как в преды-
предыдущем абзаце. Если бы 0' и b были сравнимы, то мы бы
имели b [J 0' = b или b (J 0' = 0', тогда как b (J 0' =
= 0", что отличается и от Ь, и от 0' (так как b Ф Ь'). Тре-
Третий случай выполняется, если взять а = 0. Затем надо
выбрать b так, чтобы b ф 0 и Ь' = 0'. В § 13 мы увидим,
что это возможно. Для подтверждения четвертого случая
мы меняем местами а и b в третьем случае. Третий случай
показывает также, что ^ нельзя заменить на <С в A1)
из § 6.
Перейдем к доказательству теоремы. Для каждой сте-
степени b имеем b ¦< Ь' и 0' <; b ; таким образом, b [j 0' ^
^ Ь'. Поэтому нам нужно только построить степень b
такую, что Ь' ^ а <; b (J 0'.
Пусть G — некоторая функция из N ъ N степепи а.
Будем строить некоторую функцию F из N в N и поло-
положим b == dg F. Будем добиваться того, чтобы F* и G
были рекурсивными относительно конструкции. Это даст
нам верхнюю грань Rnadg F* = b'ndgG =•- а; этих верх-
верхних граней будет достаточно, чтобы доказать Ь' ^ а ^
^ b (J 0'. Чтобы сделать F* рекурсивной относительно
конструкции, будем для каждых I и п добиваться на не-
некотором шаге конструкции, чтобы </, п) ?Е F* или
</, ri^E^F*, т. е. чтобы nEEWf или п ф. Wj . Когда мы сде-
сделаем это, то будем говорить, что вопрос one Wj решен.
Чтобы сделать G рекурсивной относительно конструкции,
мы сделаем каждое G (п) значением F при некотором
аргументе.
Все это приводит нас к следующим условиям:
A/, „) Решить вопрос опё Wf.
B„) Положить F (т) = G (п) для некоторого т.
Пусть {Bs} — перечисление пространства условий.
46 И. МИНИМАЛЬНЫЕ СТЕПЕНИ
Теперь опишем шаг s. Во-первых, предположим, что
Ra есть A/, „).
Случай 1. Существует о такая, что Comp (a, ^'s) и
гее Щ.
Выбираем такое о и, как в предыдущем доказательстве,
определяем значение F, которое будет гарантировать нам
а d F. А это гарантирует нам ге ?Е Wf.
Случай 2. Случай 1 не выполняется.
В этом случае новых значений не определяем. Тогда
мы утверждаем, что добились ге ф. Wi. Действительно,
предположим, что ге ?Е W*. Тогда существует о d F та-
такая, что re ?Е W"i. Так как а d F, то Comp (а, /"*), а это
противоречит нашим допущениям.
Теперь предположим, что Rs есть BП). Пусть /тг — наи-
наименьшее число такое, что F* (т) не определено, и полагаем
F(m)=G(n). В каждом из бесконечного числа шагов, посвя-
посвященных условиям BП), мы определяем F при наименьшем
значении аргумента, для которого F еще не была опреде-
определена. Таким образом, в конце конструкции F будет всюду
определена. Ясно также, что F* и G будут рекурсивными
относительно конструкции.
Посмотрим теперь, какие оракулы нам нужны, чтобы
знать, что случится на шаге s нашей конструкции. Пред-
Предположим, что мы уже знаем, что случается на предыдущих
шагах, т. е. мы знаем Fs. Можно найти Вг. Если Ва есть
(ii,n), то, как и при доказательстве в § 8, нам нужен лишь
оракул для некоторого отношения степени 0'. Если В,
есть BП), то найдем ге; здесь нам нужен оракул, выдаю-
выдающий нам общее значение F (т) и G (ге). Итак, здесь ораку-
оракулы для F и G вполне достаточны.
Мы уже показывали, что степень нашей конструкции
^ b U 0' и < a U 0' = а. Так как F* и G рекурсивны
относительно конструкции, то Ь' ^ а и а <^ b (J а', что
и требовалось доказать.
11. Минимальные степени
Степень а называется минимальной, если а ^> 0, но
не существует b такой, что а ^> b ^> 0. Следствие
из § 8 говорит нам, что степень 0' не является мини-
минимальной.
11. МИНИМАЛЬНЫЕ СТЕПЕНИ 47
Теорема 1. (Спектор). Существует минимальная
степень.
Множество А называется I-минималъным, если либо
[7]А не всюду определена, либо [1]А — рекурсивная функ-
функция, либо [/]А всюду определена и A <;R [/]А. Тогда сте-
степень dg А минимальна тогда и только тогда, когда мно-
множество А нерекурсивно и /-минимально для всех /. Ука-
Укажем теперь некоторые методы для получения /-минималь-
/-минимальных множеств.
Пусть St обозначает пространство цепочек. Если i — О
или i = 1, то а^ — цепочка, полученная добавлением в
конец цепочки а символа i. Скажем, что аир расщепляют
у, если yd a, у d P, а а и р несовместны.
Деревом называется рекурсивная функция Г из St в
St, удовлетворяющая условиям: если одно из Т (а^)
или Т (а^) определено, то и все Г (а), Т (а№) и Т (а^)
определены и Т (а^) и Т {a(V)) расщепляют Т (а). На-
Например, тождественное отображение из St в St является
деревом; его мы обозначаем через Id. Для деревьев ис-
используем обозначение Т.
Цепочка называется расположенной на дереве Т, если
она принадлежит области значений Т. Множество А в N
называется расположенным на дереве Т, если ad А для
бесконечно многих а, расположенных на Т.
Скажем, что Т' — поддерево дерева Т, если каждая
цепочка, расположенная на Т', также расположена на Т.
Отсюда следует, что каждое множество, расположенное
на Т', также расположено на Т.
Скажем, что аир I-расщепляют у, если у CZ а, у а
d P и [1]а и[/р несовместны. Отсюда следует, что аир
расщепляют у, действительно, если б — общее расширение
а и р, то [/]8 должно быть общим расширением [1]а и [/р.
Скажем, что у I-расщепляется на Т, если некоторые а и
Р, расположенные на Т, /-расщепляют у.
Лемма 1. Если А расположено на Т, а а А и а не
1-расщепляетпся на Т, то А является I-минимальным.
Доказательство. Предположим, что [/]А
всюду определена, и докажем, что она рекурсивна. По-
Покажем для этого, что [/]А (т) =&<->9P(adP&P рас-
расположена на Г & [/Р (т) = к).
Так как множество р, расположенное на Т, есть область
значений некоторой частичной рекурсивной функции и,
48 11. МИНИМАЛЬНЫЕ СТЕПЕНИ
следовательно, является рекурсивпо перечислимым, то
из этой эквивалентности следует, что график функции [1]А
рекурсивно перечислим; по теореме о графике [1]л явля-
является рекурсивной.
Пусть) [1]А (т) — к. Выберем 6с^ так, чтобы
[1]ь(т))= к. Для всех р d Л, кроме конечного числа, имеем
аСР и б d p. Поэтому существует р, расположенная
на Т, такая, что а С Р С А и б с Р- Тогда f Л*5 (m) = jfc.
Пусть a d Р, где р расположена на Т, и [/Р (in) — A.
По вышедоказанпому, существует у, расположенная на
Г, такая, что a CZ у и [/]Y (m) -~ [I]A (ш). Так как р и у
не /-расщепляют а, то [1]л (тп) = А, что и требовалось
доказать.
Дерево Т называется I-расщепленным, если как толь-
только Т (а@)) и Т (aW) определены, они/-расщепляют Т (а).
Лемма 2. .Если Т является I-расщепленным и А
расположено на Т, то А будет I-минимальным.
Доказательство. Предположим, что F = [1]А
всюду определена, и докажем, что A <^R F.
Пусть В — множество таких а, что Т (а) определено
и Т (а) С А. По определению дерева имеем
«ОЕВ-^аеВ&аМ^В. A)
Если А;п обозначает число цепочек из В длины п, то A)
показывает, что &n+i ^ кп. Но 5 бесконечно и к0 ^ 1;
таким образом, &п = 1 для всех п.
Пусть G (п) — цепочка из В длины п. Покажем, что
G <^r F. Предположим, что у нас есть оракул для F, и
вычислим G (п) индукцией по п. Понятно, что G @) =0.
Теперь предположим, что a = G (п) известна. Из A) ви-
видим, что G (п + 1) есть либо а@\ либо аA> мы хотим
узнать, какая именно. Так как Т (G (п + 1)) определе-
определено, то Т (а^) = р и Т (а^) = у определены и /-расщеп-
/-расщепляют Т (а); следовательно, для некоторых к и s значения
[/]s (к) и [/Ц (к) определены и различны. Мы можем вы-
вычислить р и у, затем можем найти такие к и s, перебирая
перечисление N X N. Если G (п + 1) = а@\ то р CZ A
и F (к) — [/]s (&). Аналогично, если G (га + 1) = а<1>, то
F (&) — \1\1 (к). Наш оракул- для F скажет нам, какой из
этих случаев выполняется.
11. МИНИМАЛЬНЫЕ СТЕПЕНИ 49
Чтобы закончить доказательство, покажем, что
Л ^rG. По определению дерева lh (T (G (п + 1))) >
> Hi {Т {G (и))); таким образом, lh {Т {G (п))) > п. Отсюда
следует, что А (п) = Т (G (п + 1))п, что и требовалось
доказать.
Теперь мы покажем, как строить /-расщепленные де-
деревья. Если / — алгоритм для Т, то а и р /-расщеп-
/-расщепляют у и расположены на Т тогда и только тогда, когда
уСа&уСр&Эб ([/] (б) = а) & Зб([/] (б) = р)
& 3n3i3; ([/]а (в) - » & [/Р (п) - / & i ф )).
Это есть рекурсивно перечислимое отношение от аргумен-
аргументов /, /, а, р, у. Следовательно, по теореме о селекторе
существуют частичные рекурсивные функции Lo и Lt
такие, что если у /-расщепляется на Т, то Lo (/, /, у) и
Lx (/, /, у) расположены на Г и /-расщепляют у; в про-
противном случае Lo (/, /, у) и Lx (/, /, у) не определены.
Теперь пусть б расположена на Т; определим Т' (у)
индукцией по lh (у) следующим образом:
Г @) = б,
Г (V(i>) = L, (/, /, Г
Легко заметить, что 7" имеет следующие свойства: а) Т' —
дерево; б) Т' — поддерево дерева Т; в) б расположена на
Т'; г) каждая цепочка, распложенная на Т'', есть расши-
расширение б; д) Т' является /-расщепленным; е) если Т' (у)
определено и /-расщепляется на Т, то Т' (у(-°'>) и Т' (уA^)
определены. Назовем Т' I-расщепленным поддеревом де-
дерева Т для б.
Чтобы доказать теорему 1, построим множество А в N
такое, что dg А минимальна. Пусть {/5} — перечисление
Alg (N, N). Тогда мы должны добиться, чтобы А Ф [ls]
и А было /5-минимал ьным для каждого s.
На шаге s определим всюду определенное дерево Ts
и цепочку б5, расположенную на Ts. Наша цель — пост-
построить А, расположенное па Ts так, чтобы 65(Ц^4. Мы до-
добиваемся того, чтобы А ф [Is] и А было /8-минимальным
на шаге s + 1. Другими словами, мы выбираем Ts+1 и
bSs.1 так, чтобы если А расположено на Tsyl и 6S+1 d А, то
Л Ф [Is] и А было /„-минимальным.
50 11. МИНИМАЛЬНЫЕ СТЕПЕНИ
Мы должны быть также уверены, что можно выбрать
такое А. Для этого выберем Г,+ 1 и б,+1 так, чтобы 6j,+ 1
была собственным расширением 6S и Тг+г было поддере-
поддеревом Т,. Первое гарантирует, что существует единствеппое
А такое, что?б, CZ А для всех s. Так как б, расположена
на Ts для всех s, то второе гарантирует, что все б,, 6j,+ 1, . . .
расположены на Т,\ таким образом, А расположено на Ts.
Теперь опишем шаг s. На шаге 0 полагаем То = Id
и б0 = 0. Теперь предположим, что шаг s закончен;
проделываем шаг s + 1. Так как б, расположена на Ts,
a Ts — всюду определенное дерево, то б, имеет два не-
несовместных расширения, расположенных на Tt. Следова-
Следовательно, существует собственное расширение б для 6S,
расположенное на Т$, такое, что б несовместно с [/,] *).
Выбираем 6,+i как расширение б; это гарантирует, что
6,+i — собственное расширение для б, и А Ф [/,!.
Имеются два случая. Сначала предположим, что неко-
некоторое расширение для б, расположенное па Т„ не^ /s-
расщепляется на Т,. Тогда пусть 6s+i — такое расширение
и Т,+1 = Т,. Тогда по лемме 1 А является /,-мини-
мальным.
Теперь предположим, что такого расширения не~суще-
ствует. Тогда положим as+1 = б, и пусть Г1+1 — /,-рас-
щепленное поддерево дерева Т, для б. Используя свойства
г) и е) расщепленных поддеревьев и то, что каждое рас-
расширение б, расположенное на Т„ /„-расщепляется на Т3,
легко доказываем индукцией по Ш (у), что ТгП (у) опре-
определено. Таким образом, Ts+1 — всюду определенное де-
дерево, а А является /8-мипимальным по лемме 2, что и
требовалось доказать.
Можно показать, что множество, которое только что
было построено, имеет степень ^ 0". Но вместо этого до-
докажем более сильный результат.
Теорема2 (Сакс). Существует минимальная сте-
степень а такая, что а <^ 0'.
Конструкция теоремы 2 является модификацией кон-
конструкции теоремы 1. Опять мы определяем б, на шаге s
так, чтобы 6s+i было собственным расширением для б„
*) Конечно, в том случае, когда [Is] всюду определена; в
противпом случае беспокоиться но о чем, за исключением того,
чтобы расширение было собственным. —Прим. ред.
11. Минимальные степени 51
и берем в качестве А единственное множество такое, что
б» CZ А для всех s. Однако деревья, с которыми мы будем
иметь дело, другие. На шаге s определяем дерево Т\ для
i <; к, (которое пе обязано быть всюду определенным).
Для i < ks дерево T\+i будет поддеревом дерева Т\, б,
будет расположенной на Т% и, следовательно, на всех Т\-
Всегда считаем Го = Id. В конце конструкции будет по-
показано, что Т\ сходится, в подходящем смысле, к некото-
некоторому дереву Tt.
Опишем шаг s. Для s = О положим б0 = 0, к0 = 0,
J% — Id. Теперь предположим, что шаг s закончен; про-
проделываем шаг s + 1. Пусть к — наибольшее число такое»
что к ^кв и 6S имеет собственное расширение, располо-
расположенное на Г*, которое несовместно с [Is] *). (Такое к долж-
должно существовать, так как Tl = Id.) Пусть 64+i — одно из
таких расширений; это обеспечивает нам А =?= [/,]. Пусть
ks+i = к -f- 1, и для г <1 к пусть Tl+1 = Т\. Остается вы-
выбрать поддерево rj+i дерева Т^1 — Т'н так, чтобы 6s+i была
расположена на Г1+\.
Случай 1. к = ка. Пусть Ткп — /^-расщепленное
поддерево дерева Г^1 для 6s+i.
С л у ч а й 2. к < ks. Пусть ТЦ\ = It1.
Докажем индукцией по г, что ks = i выполняется
только для конечного числа s. Так как к3 = 0 только для
s = 0, мы можем предположить i > 0. Выберем s0 с по-
помощью индуктивного предположения так, чтобы к3 > i
для s > s0. Можно предполагать, что к, = i для некото-
некоторого s ^> So, так как в противном случае наш результат
получается сразу. Поэтому мы можем выбрать s > s0
так, чтобы к3+1 — i. Тогда к на шаге s + 1 есть г — 1. Так
как kt ^ i > к, то на шаге s + 1 будет выполняться слу-
случай 2; таким образом, Т\+1'= Т?{.
Если наш результат ложен, то существует наименьшее
t ^> s такое, что kt+i = i. Так как все /cs+a, . . ., kt ^> i,
то Tl+1 =¦ Т\ и Т?\ = Tii, таким образом, Т\ = гЦ.
Отсюда следует, что к на шаге t + 1 не равно i — 1; сле-
следовательно, kt+1 ф Ц приходим к противоречию.
*) См. предыдущую сноску.—Прим. ред.
52 Н. МИНИМАЛЬНЫЕ СТЕПЕНИ
Если ks ^> i для всех s > s0, то Т\ определено и равно
Т\' для всех s ]> s0. Пусть 7,- равно 7?. Так как 8S распо-
расположена на Т\, как только Т\ определено, 6S расположена
на Tt; таким образом, А расположено на 7г.
Покажем, что если Z"|+1 определено, то либо оно
/^-расщепленное поддерево дерева Т\, либо 7f+i = 7? и
некоторая Ьп не /грасщепляется па 71. Допустив это, мы
видим, что тот же результат выполняется, когда все ин-
индексы s убираются; отсюда по леммам 1 и 2 следует, что
А является /^-минимальным.
Докажем этот результат индукцией но s. Если s = О,
то Tl+i не может быть определенным. Предположим, что
данный результат выполняется для некоторого s. Если
Л.+1 > i + 1, то Т1Х\ = Т-+1 и 7Т1 == У? и данный слу-
случай тривиален. Если /cs+i < i + 1, то r|JJ не определено.
Поэтому можно предположить, что &5+i = i ~\- 1; таким
образом, А; на шаге s + 1 есть г. Если на шаге s + 1 встре-
встречается случай 1, то результат очевиден; поэтому предпо-
предположим, что встречается случай 2. Конечно, TS?X = Т*+1.
Так как i = к < A;s, то Zi+i определено, по выбору /с ни-
никакое собственное расширение для 8S, расположенное
на Ti+i, не является несовместным с [/,]. По определению
дерева, 8S может не иметь собственного расширения, рас-
расположенного на 7"|+1. Из выбора к также следует, что 71 ^=
Ф Т{+1; таким образом, по индуктивному предположению
7|+1 — /,-расщеплепное поддерево дерева Т\. По свойству
е) расщепленных поддеревьев, 6S не /грасщенляется на
7? = ТТ.
Единственно, что осталось показать,— это dg A ^ О'.
Так как А (п) = (б,г+1)п> то достаточно доказать, что
dg {бп} <^ 0'. Сделаем это, показав, что конструкция имеет
степень <^ 0'. Однако сделанное высказывание имеет
смысл, если только объекты, строящиеся на каждом шаге,
являются конечными объектами. Поэтому мы заменяем
Т\ на алгоритм 1\ для Т\. Пусть 7° — алгоритм для Id,
а когда мы полагаем Т\ равным ранее определенному Т],
то считаем 7| - i]. Остается только случай, когда 7' есть
расщепленное ноддерево некоторого ранее определенного
12. ПРОСТЫЕ МНОЖЕСТВА 53
дерева. По определению расщепленных поддеревьев мы
видим, что можно в действительности вычислять алгоритм
для /-расщепленного поддерева дерева Т для б по /, б и
алгоритму для Т. Пусть этот алгоритм есть 1\.
Ясно, что оракулы пужны нам в конструкции только
для того, чтобы получить к и 6s+i на шаге s + 1. Тогда
«б имеет собственное расширение, расположенное на [J],
не совместное с [/] » — рекурсивно перечислимое отно-
отношение от аргументов б, /, /, так как оно может быть за-
записано как
За (б С а & б ф а & Зу ([J] (у) = а)
& ЗгЗге ([/] (г) = п& i < lh (а) & at ф п)).
Для получения к достаточно оракула для этого рекур-
рекурсивно перечислимого отношения. По теореме о селекторе
мы можем найти тогда 6s+i, что и требовалось доказать.
12. Простые множества
Единственными рекурсивно перечислимыми степеня-
степенями, с которыми мы пока встречались, были степени 0 и О'.
Это подсказывает следующую проблему Поста: существу-
существуют ли другие рекурсивно иеречислимые степени?
Пост надеялся положительно решить эту проблему,
построив «большое» нерекурсивное рекурсивно перечис-
перечислимое множество А и использовав его «величину» для до-
доказательства того, что А <С 0'. Хотя он не решил этой
проблемы, но доказал несколько интересных результатов
в этом направлении. Посмотрим на один из таких резуль-
результатов.
Наибольшими множествами являются коконечные мно-
множества, но они не подходят для наших целей, так как они
рекурсивны. По этой причине будем требовать от наших
больших множеств, чтобы они были кобесконечными.
Простым множеством в X называется рекурсивно пе-
перечислимое множество А в X такое, что Ас не имеет бес-
бесконечных рекурсивно перечислимых подмножеств. Такое
множество не может быть рекурсивным, иначе Ас было бы
бесконечным рекурсивно перечислимым подмножест-
подмножеством множества Ас
54 12. ПРОСТЫЕ МНОЖЕСТВА
Чтобы использовать простые множества для решения
проблемы Поста, мы должны доказать, что простое мно-
множество существует и что такое простое множество имеет
степень <^ 0'. Пост доказал, что простое множество су-
существует, но что не каждое простое множество имеет сте-
степень < 0'. Эти результаты входят в следующую теорему.
Теорема 1 (Деккер). Если а рекурсивно перечисли-
перечислима и &Ф 0, то существует простое множество степени а.
Доказательство. Пусть А — рекурсивно пе-
перечислимое множество в N, имеющее степень а. Так как А
нерекурсивно, то оно бесконечно, следовательно, по тео-
теореме о перечислении оно имеет некоторое перечисление F.
Определим рекурсивно перечислимое множество В сле-
следующим образом:
вё? <-» Зт(т> п& F (т) < F (п)).
Тогда п ЕЕ В тогда и только тогда, когда существует
k <C F (п) такое, что к ЕЕ А, и к отличается от F @),
F A), . . .,F (n — 1). Отсюда следует, что #^r А. Если
к дано и мы выберем п^>к так, чтобы F (п) было самым
маленьким, насколько это возможно, то п EJE В. Следова-
Следовательно, В кобескопечно.
Если и ЕЕ Вс, то элементы А, отличные от F @), F A),-..
. . ., F (п), все больше F (п); таким образом, если к <^F(n),
то к ЕЕ А тогда и только тогда, когда к есть одно из F @),
F A), . . .,F (п). Тогда по данному к и п ЕЕ Вс такому,
что к < F (п), мы можем решить, будет ли к ЕЕ А. Такое
п, конечно, существует, так как Вс бесконечно, a F — 1-1-
функция. По данному к с помощью оракула для В мы
можем найти такое и, испытывая 0, 1, . . .Следовательно,
А <^.е.В; таким образом, dg В = а.
Предположим, что Вс имеет бесконечное рекурсивно
перечислимое подмножество С. Тогда для каждого к су-
существует, как и выше, такое п ЕЕ С, что к < F (п), и мы
можем действительно вычислить такое п по к, если будем
использовать теорему о селекторе. Тогда, как и раньше,
А рекурсивно. Это противоречие показывает, что В —
простое множество, что и требовалось доказать.
Замечание. Множество В имеет следующее свой-
свойство: если Вс имеет бесконечное подмножество, рекурсивно
перечислимое в D, то В ^r D. Действительно, конец пре-
предыдущего доказательства показывает, что A ^r D и мы
13. МЕТОД ПРИОРИТЕТА 55
имеем В <^r.A. Простое множество с таким свойством на-
называется сильно простым.
Хотя мы не можем доказать, что каждое простое мно-
множество имеет степень < 0', мы докажем более слабый
результат.
Теорома2 (Пост). Простое множество не является
полным рекурсивно перечислимым множеством.
Доказательство. Пусть А — полное рекур-
рекурсивно перечислимое множество в N. Пусть {/„} — пере-
перечисление Alg (N, N). Так как п €Е Wi —рекурсивно
перечислимое отношение от аргумента п, то существует
рекурсивная функция F такая, что п €Е Wi +-* F (п) €Е А
для всех п. Пусть X = Sub (N), по теореме о параметри-
параметризации выберем рекурсивную функцию G такую, что
п €Е WG(X) <-»¦ F (п) Е= х для всех х и п. Пусть Н (х) =
= F (п), где п выбрано так, чтобы /n = G(x). Тогда по
лемме 1 из § 2 Н рекурсивна. Далее, имеем Н (х) €Е А <->
<-> Я (х) е х, откуда
хаАс-+Н{х)фА \J х. A)
Определим индуктивно L:
L(n) = H ({L @), L A) L (в - 1)}).
Используя A), легко видеть, что L (п) Е= Ас — 1-1
функция. Следовательно, область значений L — беско-
бесконечное рекурсивно перечислимое подмножество множества
Ае, и множество А не является простым, что и требовалось
доказать.
13. Метод приоритета
Проблема Поста была решена независимо Фридбер-
гом и Мучником, которые разработали для этого важный
метод, называемый методом приоритета. Мы используем
этот метод для доказательства другого результата, из
которого будет следовать решение проблемы Поста.
Теорема (Фридберг). Существует рекурсивно пе-
перечислимая степень а такая, что а ф- 0 и а' = 0'.
Следствие. Существует рекурсивно перечислимая
степень а такая, что а Ф 0 ма^О',
56 13. МЕТОД ПРИОРИТЕТА
Мы докажем эту теорему, построив рекурсивно пере-
перечислимое множество А в N и положив а = dg А. На шаге
s будем помещать конечное множество чисел в А. Тогда
А будет состоять из всех чисел, которые были помещены
в Л на каком-либо шаге. В отличие от предыдущих резуль-
результатов, наша конструкция должна быть рекурсивной, т. е.
по данному s мы должны уметь узнавать, что нужно де-
делать на шаге s.
Пусть А' — конечное множество чисел, помещенных
в А перед шагом s. Так как конструкция рекурсивна, то
вё4"—рекурсивное отпошеиие от аргументов п, s.
Так как п е= А <-> 3s (n ?E As), то А — рекурсивно
перечислимое множество.
Так как а' ^> 0' всегда выполняется, то мы должны
добиваться, чтобы было а ^Ои а'<; 0'или, эквивалентно,
чтобы А было нерекурсивным, a dg Л*^ 0'. Это приводит
нас к условиям:
A/) А ф [71.
Bji?c) Решить вопрос о к ЕЕ Wi .
(Как мы увидим, условие B/ifc) будет интерпретироваться
не так/как соответствующее условие из § 10.) Пусть"{Rn}—
перечисление пространства условий.
Наша идея достижения того, что А ф [I], состоит в
нахождении некоторого числа к такого, что А (к)Ф [I] (к).
Если [I] (к) = Л, то помещаем к в А и тогда имеем А (к) =
= И; если [/] (к) Ф Л, то с к мы ничего пе делаем и в
этом случае А (к) = Л.
Так как наша конструкция рекурсивна, то мы должны
действительно вычислить [I] (к). Если [/] (к) не определе-
определено, то это вычисление будет продолжаться все время.
В этом случае никаких беспокойств относительно к не
возникает, так как если [I] (к) не определено, то с ft мы
ничего не делаем. Трудность состоит в другом: мы никогда
не сможем обратиться к следующему условию.
Наше преодоление этой трудности будет состоять в
постоянном возвращении к каждому условию. Точнее,
если s лежит в строке п (в смысле терминологии § 2), то
мы посвящаем mar s условию RTI. В частпости, если Rn
есть А Ф- [Л, то на шаге s мы делаем s тагов в вычислении
[Л (к). Таким образом, если [Л (к) определено, то мы вы-
вычислим в конце концов это значение.
13. МЕТОД ПРИОРИТЕТА 57
Теперь предположим, что на mare s мы пытаемся решить
вопрос, будет к G= Wi или нет. Мы хотим вычислить
Wi (к), но это невозможно, так как А полностью еще не
определено. Правда, у нас есть конечная аппроксимация
А8 для А, по мы не можем даже вычислить Wf (к). Однако
мы можем сделать s шагов в вычислении [1]А* (к) и это,
возможно, приведет нас к заключению, что к €Е Wf .
Даже если мы убедимся на шаге s, что к ?Е Wi , то
уто не дает ничего хорошего, если мы не имеем к ?Е W% .
По принципу использования мы будем иметь к ?Е Wf, если
А (г) = А5 (г) для каждого г, использованного в вычис-
вычислении [7]А* (к). В зависимости от способа, которым А стро-
строится, мы можем это выразить различным образом. Скажем,
что г используется отрицательно в вычислении [7]AS (к),
если г используется в этом вычислении и г ф. А". Тогда
мы будем иметь к СЕ Wi i если никакое г, используемое
отрицательно в вычислении [1]Л* (к), не будет после шага
s помещено в А.
Если мы убедимся на шаге s, что к ?Е Wf\ то образуем
конечное множество х чисел таких, которые были исполь-
использованы отрицательно в вычислении [7]Л (к). Мы назы-
называем х п-требованием, где п — число такое, что Rn есть
B/ ft). Цель этого требования — напомнить нам, что мы
не хотим помещать элементы множества х в А.
Теперь предположим, что мы создали гс-требовапие х,
а позднее хотим поместить некоторое г ?Е х в А, с тем
чтобы удовлетворить условию Rm типа (ii). Решение этой
дилеммы — основная трудность метода приоритета: мы
даем приоритет условиям, имеющим меньшие номера.
Следовательно, если п <С т, то мы сохраняем г вне мно-
множества А; если же т ¦< п, то мы помещаем г в А.
Если мы нарушим процедуру удовлетворения Rn из-за
процедуры удовлетворения Rm, то мы скажем, что усло-
условие Rn повреждено условием Rm. Когда это случится, мы
можем начать снова выполнять процедуру удовлетворения
Rn. Причина, по которой Rn в конце концов удовлетворит-
удовлетворится, состоит в том, что оно может быть повреждено только
58 13. МЕТОД ПРИОРИТЕТА
конечным числом других условий, а именно условиями
Rm с т <С п.
Если на шаге s создается требование х, то х f] As= 0.
Если t ]> s и х f) А' = 0, то называем х активным па
шаге ?; в противном случае называем х неактивным на
шаге t. (Идея состоит в том, что пеактивное требование уже
не служит своим целям и поэтому может быть игнори-
игнорировано.)
Теперь объясним, как выбрать аргумент к, который ис-
используется, когда добиваются выполнения A/). Если Rn
есть (lj), то выбираем к в строке п; это обеспечит нам то,
что различные условия не будут мешать друг другу. Более
того, мы хотим избежать того, чтобы с помощью требова-
требований к сохранялось вне множества А; поэтому мы выбира-
выбираем к отличным от всех чисел в активных m-требованиях с
т <С п.
Теперь опишем шаг s. Пусть s лежит в строке п, и вна-
вначале предположим, что Rn есть (lj). Мы ничего не делаем
на этом шаге, если не выполняются условия: а) в строке
п нет чисел из А'; б) существует число к<С s такое, что к
лежит в строке п, к не находится в активном то-требова-
нии с m<n и [/]„ (к) = Л. Если же перечисленные ус-
условия выполняются, то мы выбираем наименьшее такое
к и помещаем к в А.
Теперь предположим, что Rn есть B/,^). Мы ничего
не делаем, за исключением случая, когда пе существует
.8
активного и-требования и i? Wi,s- В этом случае мы
создаем новое и-требовапие, состоящее из всех чисел, ис-
используемых отрицательно в[вычислении [I]A* (k)J
Описание конструкции закончено. Мы оставляем чи-
читателю проверку того, что она действительно рекурсивна.
Если х — требование и х f] A = 0 (таким образом,
х активно на каждом шаге, после которого оно создапо),
то мы говорим, что х постоянно; в противном случае на-
называем х временным.
Если мы поместим на шаге s число к из активного то-тре-
бования хъ Амк лежит в строке га, то п ^ т. Для каждо-
каждого п самое большее одно число из строки п помещается
в А. Из этих фактов следует, что существует только копеч-
ное число временных m-требований. Так как в одно и то
же время мы никогда по имеем двух активных то-требова-
13. МЕТОД ПРИОРИТЕТА 59
ний, то может существовать самое большее одно постояп-
ное гаг-требовапие. Следовательно, существует только ко-
нечпое число гаг-требований.
Теперь покажем, что Rn удовлетворится. Во-первых,
предположим, что Rn есть A/). Если число к из строки и
помещается в А, то это только потому, что мы узнали, что
\1](к) — Л. Так как А (к) = И, то (lj) выполняется.
Теперь предположим, что никакое число из строки и не
помещено в А. Выберем к в строке и так, чтобы к не при-
принадлежало никакому гаг-требованию с гаг < и. Так как
А(к) = Л, этого достаточно, чтобы показать, что [/] (к) =
= Л приводит к противоречию. Выберем s в строке га та-
таким большим, чтобы к ^ s и [7]s (к) = Л. Тогда некото-
некоторое число из строки и па шаге s помещается в А; получаем
противоречие.
Теперь предположим, что Rn есть Bхд). Смысл того,
что Rn удовлетворяется, состоит в следующем: мы имеем
к ее Wi тогда и только тогда, когда существует постоян-
постоянное «-требование. Действительно, предположим, что по-
постоянное «-требование х создается на шаге s. Тогда к ЕЕ
ЕЕ Wi . Так как х f] A = 0, то никакое число, исполь-
используемое отрицательно в вычислении [7]А8 (к), не будет
позднее помещено в Л; таким образом, А; ЕЕ Wi. Теперь
пусть к ЕЕ W*. Так как lim As = А, то по принципу ис-
пользования к ЕЕ Wi,s для всех достаточно больших s.
Поэтому мы можем выбрать s в строке п таким большим,
А8
чтобы было к ее Wi,< и каждое временное п-требование
являлось неактивным на шаге s. Либо существует актив-
активное тг-требовапие на mare s, либо некоторое и-требованне
создается на шаге s. В любом случае мы имеем постоянное
п-требование.
Теперь докажем, что dg А*^ 0'. Пусть </, k>EE#s, если
существует активное тг-требование па шаге s, где п есть
число такое, что Rn есть B/д). Так как {7?s} рекурсивна,
то по теореме о пределе достаточно показать, что lim Bs =
= А*. Если </, к} ЕЕ А*, то существует некоторое пос-
постоянное га-требование; таким образом, </, ку ЕЕ Bs для
всех достаточно больших s. Если </, кУфА*, то все
га-требования временные; так как их существует трлько
конечное число, то </, /с> е? Bs для всех больших s.
60 14. ТЕОРЕМА О РАЗЛОЖЕНИИ
14. Теорема о разложении
Используем метод приоритета для доказательства од-
одного результата, который дает некоторую дополнитель-
дополнительную информацию о рекурсивно перечислимых степенях.
Теорема о разложении (Сакс). Пусть С—
рекурсивно перечислимое множество, a D — простое мно-
множество. Тогда С является объединением непересекающихся
рекурсивно перечислимых множеств А и В таких, что D
не является рекурсивным ни в А, ни в В.
Чтобы перевести этот результат па язык степеней, до-
докажем следующую лемму.
Лемма. Если А и В — непересекающиеся рекурсивно
перечислимые множества, то dg (A (J В) = dg A |J dg В.
Доказательство. Мы должны доказать, что
Л {J В рекурсивно в А и В, а А и В рекурсивны в A (J В.
Первое очевидно. Чтобы показать, что А рекурсивно в
Л (J В, достаточно, ввиду релятивизованной теоремы
о дополнении, доказать, что А и Ас рекурсивно перечис-
перечислимы в A [J В. Так как А рекурсивно перечислимо,
то оно рекурсивно перечислимо в A (J В. Но Ас =
= (A U В)" U В; (A U В)° рекурсивно в A [j В; В
рекурсивно перечислимо. Отсюда следует, что Ас ре-
рекурсивно перечислимо в A (J В. Подобное доказатель-
доказательство показывает, что В рекурсивно в A (J В, что и тре-
требовалось доказать.
Теперь мы можем доказать некоторые следствия теоре-
теоремы о разложении.
Следствие 1. Пусть cud — рекурсивно пере-
перечислимые степени такие, что d Ф 0. Тогда существуют
рекурсивно перечислимые степени а и Ъ такие, что с =
= a (J Ь, d ^ a u d ^ Ь.
Д оказательство. Применяя теорему 1 из
§ 12, выберем простое множество D с dg D = d. Пусть С —
рекурсивно перечислимое множество с dg С = с, а А и
В такие, как в теореме. Взяв а = dg А и b = dg В, по
лемме получим с = a (J Ъ; ясно, что d ^ а и d ^ Ъ,
что и требовалось доказать.
Следствие 2. Если с — ненулевая рекурсивно пе-
перечислимая степень, то существуют рекурсивно перечис-
перечислимые степени aub такие, что с = a (J Ь, 0<а<;с,
0<b<cua|b.
14. ТЕОРЕМА О РАЗЛОЖЕНИИ 61
Доказательство. Берем d = с, и пусть а и Ь
таковы, как в следствии 1. Из a^a(Jb = cnc^a мы
заключаем, что а < с. Аналогично получаемЬ < с. Если
а = 0, то b = a U Ь = с; таким образом, а Ф 0. Анало-
Аналогично выводим, что b Ф 0. Если а и b сравнимы, то a \J
[_Jb=c должно быть равным а или Ь; таким образом, а|Ь,
что и требовалось доказать.
Следствие 3 (Фридберг — Мучник). Существу-
Существуют несравнимые рекурсивно перечислимые степени.
Следствие 4 (Мучник). Никакая рекурсивно пе-
перечислимая степень не является минимальной.
Следствие 5. Если d рекурсивно перечислима и
0 < d < 0', то существует рекурсивно перечислимая сте-
степень, не сравнимая с d.
Доказательство. Пусть с = 0', а а и b та-
таковы, как в следствии 1. Заметим, что по крайней мере
одпо из а и b несравнимо с d. Если это не так, то а < d
иЬ< d; таким образом, 0' = a (J b ^ d; получаем про-
противоречие, что и требовалось доказать.
Теперь перейдем к доказательству теоремы о разло-
разложении. Можно предполагать, что С и D являются множе-
множествами в N. Во-первых, покажем, как можно использо-
использовать эти рекурсивно перечислимые множества в некоторой
рекурсивной конструкции. Определим для / GE Alg (N, N)
Для фиксированного / множества Wj — это конечные
множества, возрастающие по s, a Wi — их объединение.
Далее, W\ может быть вычислено по sn I. Теперь зафикси-
зафиксируем индексы / множества С и К множества D и положим
Cs = Wj, Ds = Wr. На шаге s нашей конструкции мы
можем использовать Cs и Ds.
Мы добиваемся того, чтобы А и В были непересекаю-
непересекающимися, никогда не помещая одпо число и в А, и в В; мы
добиваемся того, чтобы А и В были подмножествами мно-
множества С, помещая в А и В па шаге s только числа из Cs.
Нам остается добиться выполпепия следующих условий:
A0 k^C-+k(EiAlJB;
Bi) D ф U\A;
(Зг) D Ф Шв.
62 14. ТЕОРЕМА О РАЗЛОЖЕНИИ
Пусть {7?„} — перечисление пространства условий. Ес-
Если 7?„ есть B/), то п назовем А-числом; если 7?„ есть Cj),
то п назовем В-числом.
Наша идея удовлетворить условию B/) состоит в том,
чтобы попытаться делать [7)А (к) = Л для различных к
до тех пор, пока мы пе доберемся до некоторого к из D.
Мы не можем сделать [1]А (к) = Л для бесконечно многих к,
чтобы при этом к не принадлежало D; действительно,
множество таких к будет рекурсивно перечислимым,
&D — простое множество. Если же мы добьемся [I]А (к) =
= Л только для конечного числа к, то пекоторое к, для
которого мы потерпим неудачу, будет находиться в бес-
бесконечном множестве Dc; таким образом, мы будем иметь
[1]А (к) ф Л = В (к).
В процессе построения мы пытаемся вычислить [7)AS (к).
Если мы находим, что [7]л* (к) = Л, то создаем некоторое
требование, пытаясь удовлетворить условию [7]А (к) = Л.
Мы называем такое требование п-требоеанием с аргумен-
аргументом к (здесь п — число такое, что 7?„ есть D Ф [1]А).
Все сказанное выше выполняется, если заменить B/)
на C/), а А на В.
Пусть х — и-требование, созданное на шаге s, и пусть
п — Л-число. Для t ^> s будем называть х активным на
шаге t, если х f] А' = 0; в противном случае называем х
неактивным на шаге t. Если х [Л А = 0, то х называется
постоянным; в противном случае х называется временным.
Аналогичные определения вводятся, когда А заменяется
па В.
Опишем теперь mar s. Пусть s находится в строке п,
и впачале предположим, что Rn есть (lfc). Ничего не дела-
делаем, если не выполняется к ее Cs и к ф As \J Bs. Пусть
к ее Cs п к ф. As \J Bs. Если к не находится пи в одном
активном требовании, то помещаем к в А. В противном
случае выбираем наименьшее т так, чтобы к находилось
в активном m-требовании. Если т — А -число, то помеща-
помещаем к в В; если т — 5-число, то помещаем к в А. (Таким
образом, условие Rm с меньшим номером т имеет прио-
приоритет над другими требованиями.)
Теперь предположим, что Rn есть B/). Ничего не де-
делаем, если не существует числа к <^ s такого, что: A) нет
аргумента активного и-требования, который был бы мень-
14. ТЕОРЕМА О РАЗЛОЖЕНИЙ 63
ше к и находился в D"; B) к не является аргументом
никакого активного тг-требования; C) [/]s (к) = Л. Если
же число к с данными свойствами существует, то мы выби-
выбираем наименьшее такое к и создаем тг-требование с аргу-
аргументом к, состоящим из всех чисел, которые отрицатель-
отрицательно используются в вычислении [1]А (к). Если Rn есть C/),
то мы продолжаем действовать так же, заменяя А на В.
Докажем индукцией по тг, что существует только ко-
конечное число тг-требований. Если тг — Л-число, а число
к из активного тг-требования помещается в А, то к должно
также принадлежать некоторому активному пг-требованию
с т ¦< тг. Это же выполняется, если А заменить на В. Ис-
Используя это и индуктивное предположение, видим, что
существует только конечное число временных тг-требо-
тг-требований.
Пусть Еп — множество аргументов постоянных тг-тре-
тг-требований. Пусть Е'п — множество аргументов тг-требова-
тг-требований, активных на шаге s. Тогда к ЕЕ Е*п — рекурсивное
отношение от аргументов к, s, п. В силу сказанного выше
можно выбрать s0 так, чтобы каждое временное тг-требова-
тг-требование было неактивным на шаге s0. Тогда
к е Еп ¦* 3s (s > s0 & к 6Е Esn).
Отсюда следует, что Еп рекурсивно перечислимо.
Предположим, что Еп бесконечно. Так как D — прос-
простое множество, то существует к ?Е D f] En. Если s доста-
достаточно большое, то на шаге s существует активное тг-требо-
тг-требование с аргументом к я к ?Е D*. Тогда никакое тг-требова-
тг-требование с аргументом, большим к, не может быть создано на
шаге s. Делаем вывод, что Еп конечно. Далее, не могут
существовать два активных тг-требования с одним и тем
же аргументом в одно и то же время. Таким образом, су-
существует только конечное число постоянных тг-требова-
тг-требований, а значит, только конечное число тг-требований.
Теперь можно доказать, что условие Rn удовлетворит-
удовлетворится. Допустим, что Rn есть (lk). Предположим, что к 6=
GE С, и выберем s в строке тг таким большим, чтобы к 6=
GE Cs. Тогда либо к е A' {J В\ либо к помещается в А
или В на шаге s. В любом случае имеем к Ei A \J В.
Пусть Rn есть B/). Предположим, что [I]A = D, и
придем к противоречию. Если какое-то тг-требовапие
04 15. МАКСИМАЛЬНЫМ МНОЖЕСТВА
с аргументом к создается па шаге s, то [1]л!!(к) = Л, а если
это требование постоянно, то [1]л (к) = Л, и, значит, кф.
?fc D. Таким образом, Еп с." D0. Так как Еп конечно, а
D просто, то можно выбрать к ф D \J En. Тогда [1]л (к) =
= D (к) = Л; таким образом, [1]^ (к) = Л для достаточ-
достаточно больших s. Выбором s в строке п таким большим, что-
чтобы все n-требовапия были созданы перед шагом s; все вре-
меппые n-требовапия являются неактивными на гааге s;
к ^ s и [7]f (к) — Л. Если 7г-тробование активно на ша-
шаге s, то оно долито быть постоянным. Тогда, если оно име-
имеет аргумент к', то к' €Е Еп; таким образом, к' €Е D0 и,
значит, к' ф. D"8. Далее, это требование не может иметь
аргументом к, так как к ф Еп. Отсюда следует, что какое-
то re-требование создается па шаге s, по это противоречит
выбору s.
Если Rn есть Cj), то проводим рассуждения таким
же путем, только Л заменяется на В, что и требовалось
доказать.
15. Максимальные множества
Покажем, что метод Поста не может быть использован
для решения его проблемы, если большое множество по-
понимать как множество, имеющее мало рекурсивно перечис-
перечислимых надмножеств. Чтобы доказать это, мы выбираем
наиболее сильное из возможных вариантов понятия боль-
большого множества и покажем, что все равно не сможем до-
доказать, что любое большое множество имеет степень <^0'.
Если А — кобескопечное рекурсивно перечислимое
множество, то среди его рекурсивно перечислимых над-
надмножеств есть множества, получаемые из А добавлением
конечного числа элементов, и кокопечные множества,
включающие А. Мы намерены исключить все другие воз-
возможности.
Максимальным множеством называется кобесконечное
рекурсивно перечислимое множество А такое, что для
каждого рекурсивно перечислимого множества В, вклю-
включающего Л, либо В \ А, либо Вс конечно.
Полезно немного переформулировать это определение.
В то время как В пробегает все рекурсивно перечисли-
перечислимые множества, A\JB пробегает все рекурсивно перечисли-
15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА 65
мые множества, включающие А. Далее, (A \J В) \ А =
= В П Ас и {A U В)с = Вс П Лс. Таким образом, ко-
бесконечное рекурсивно перечислимое множество Л мак-
максимально тогда и только тогда, когда для каждого рекур-
рекурсивно перечислимого множества В либо В f] Ac, либо
Вс П Ас конечно.
Максимальное множество просто и, следовательно, не-
нерекурсивно. Действительно, предположим, что Ас имеет
бесконечное рекурсивно перечислимое подмножество С.
Пусть F — перечисление С; положим G (и) = F Bи).
Тогда область значений В функции G является рекурсив-
рекурсивно перечиелммым множеством таким, что В (~| AcuBc f] Ac
бесконечны.
Существование максимального множества впервые бы-
было доказано Фридбергом. Результат, который нам нужен,
состоит в следующем: существует максимальное множест-
множество степени 0'. Это впервые было доказано Ейтсом. Мы до-
докажем еще более сильный результат.
Теорема (Мартин). Рекурсивно перечислимая сте-
степень а является степенью максимального множества тог-
тогда и только тогда, когда а' = О".
Если а рекурсивно перечислима, то а <; 0' и, следо-
следовательно, а' «^ 0"; таким образом, а' = 0* эквивалентно
а' > 0". Начнем с характеризации степеней а таких,
что а' > О".
Если F и G — функции из N в JV, то мы говорим, что
F доминирует G, если F (и) > G (и) для всех достаточно
больших п. Функция из N в N называется доминантой,
если она доминирует каждую рекурсивную функцию из
N в N.
Лемма 1. Для любой степени а имеем а' ;> О"
тогда и только тогда, когда существует функция-доми-
функция-доминанта степени ^ а.
Доказательство. Предположим, что F — до-
доминанта и dg F <^ а. Пусть А — полное множество типа
П2 в N. Тогда
п е А «* V/сЭг «и, k, r> e В),
где В рекурсивно. Положим
ке4,^ V&t<,3rr<F№««, к, г>еВ).
Тогда dg {As} <; dg F ^ а. Покажем, что А = lim As;
G6 I1»- МАКСИМАЛЬНЫЕ МНОЖЕСТВА
отсюда по лемме о пределе будет следовать, что 0" =
- dg Л < (dg {Л.})' < a'.
Если к t/E Л, то су1цостн\(-| /с такое, что <«, /с, г> ^? В
для всех г; таким обрлаом, n ^ /ls для s ]> /с. Если « Е Л,
то определяем рекурсивную функцию G следующим об-
образом:
G (я) — max \ir((n, ?, /-) g= В).
1К
Для больших s имеем С (s) < /<' (s) и. следовательно, /г ЕЕ
ЕЕ Л8, Таким образом, в любом случае lim As (п) — А (п).
Теперь пусть а' > 0". Тогда dg (Tot) = 0" < а'. Тог-
Тогда по лемме о пределе существует последовательность
{Ап} такая, что dg {Ап} ^ а и lim An = Tot. Для каж-
каждых па I существует s такое, что
[I](n) = s\/{s>n&I^At). A)
Действительно, если / ?f Tol, то берем s = [I] (n); если
/ ф. Tot, то / ф. As для всех больших s. Тогда A) рекур-
рекурсивно перечислимо в {Ап}; следовательно, по релятивизо-
ванной теореме о селекторе существует G степени <^ а
такая, что G (п, Г) для всех п и / есть s, для которого A)
выполняется.
Пусть {/„} — перечисление Alg (N, N); положим
F(w) = max С, (л, Ii)-\-i.
Тогда dg F <; а. Пусть // — рекурсивная функция из
N в N. Тогда II = [/,-], где /,- GZ Tot. Для большого п
имеем It ЕЕ Ак для каждого s ]> n; таким образом,
G (п, /;) = Ui](n) — II (п). Поэтому для больших п ]> i
имеем // (п) < F (и), что и требовалось доказать.
Если А — кобесконечное мно/кество в N. то La —
функция из N в N такая, что La @), La A), • • • — эле-
элементы Ас в порядке возрастания. Тогда dg La = dg A.
Действительно, с данным оракулом для А мы можем вы-
вычислять La@), La A)> ... по порядку. Обратно, с данным
оракулом для La мы можем решить, будет ли к ЕЕ А, вы-
вычисляя La @), La (i), ¦ ¦ -, пока не придем к к или к чис-
числу, большему к.
Лемма 2. Если А — максимальное множество в Л\
то La — доминанта.
15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА 67
Доказательство. Пусть F —рекурсивная
функция из N в N. Определим рекурсивную функцию Н
следующим образом:
Н (к) = рп (F Bп) + F Bп + 1) + п > к)
и рекурсивно перечислимое множество В следующим об-
образом:
* е Я <-> Vrr<k (Я (г) = Н(к) -> г е А).
Если Н (к) = п для некоторого к еЕ Ас, то в точности
одно такое к (а именно наименьшее) находится в В. Так
как либо В р А", либо 5е Г) ^4С конечно *), то отсюда
следует, что для больших п существует самое большее од-
одно к €Е Ас, для которого Н (к) = п. Из этого следует *),
что существует г такое, что для всех п существует самое
большее п + г чисел к Е= Ас таких, что Н (к) ^ п. Они
включают в себя все числа к ЕЕ Ас такие, что к ^ F Bп) +
+ F Bп + 1) + п. Следовательно,
F Bп) + F Bп + 1) + п < LA (n + г).
Если п > г, то LA (п + г) < LA Bn) < LABn + 1). От-
Отсюда следует, что LA доминирует F, что и требовалось до-
доказать.
Теперь мы можем доказать половину теоремы. Пред-
Предположим, что а — степень максимального множества А.
Также предположим, что А — множество в N. Тогда а' =
— (dg A)' = (dg ЬлУ > 0" по леммам 1 и 2. Так как а
рекурсивно перечислима, то а' = О".
Чтобы доказать обратное, будем строить рекурсивно
неречислимое множество специфической степени. Для это-
этого разработаем один метод.
Сдерживающей функцией назовем всякую рекурсивную
функцию F из N ъ N такую, что F (s) стремится к бесконеч-
бесконечности с ростом s. Для такой функции F определим
vF (п) - fts Vtt>l (F (t) > в).
Если vF (n) <; G (и) для всех п, то vP <^R G; действитель-
действительно,
Vj? (n) - H*V*i<G(n) (t>S^F (t) > П).
*) Для дальнейmcroнужно заметить, что на гамом доле Вср,.1с
конечно. Это следует из того, что функция И принимает одпо и то
же значение только на конечном множестве аргументов.—Прим. ред*
68 15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА
Конструкция рекурсивно перечислимого множества
А в N называется F-сдерживающейся, если как только п
помещается в А на шаге s, то п ^> F (s). Если F — сдер-
сдерживающая функция, а конструкция множества А являет-
является .F-сдерживающейся, то A <^R Vj?. Действительно, если
п помещается в А на шаге s, то п ]> F (s); таким образом,
s <Z Vf (п). Следовательно, п GF А +-*¦ п ЕЕ А*^п^.
Если мы строим рекурсивно перечислимое множество
А ъ N, то вместо ЬАя будем писать Ls. Конструкция мно-
множества А называется F'-поддерживающейся, если для каж-
каждого s некоторое число <J Ls (F (s)) помещается в А на
шаге s. T
Если F — сдерживающая функция, а конструкция
множества А является F-поддерживающейся, то v^^r
<^r А. Чтобы увидеть это, положим G (п) равным наимень-
наименьшему s такому, что каждое число ^ LA (n), которое нахо-
находится в А, находится и в А*. Тогда G ^я А; таким обра-
образом, достаточно показать, что vF ^r G. Для этого доста-
достаточно показать, что vF {п) <; G (п), т. е. что если s ]> G (п),
то F (s) ^> п. На шаге s мы помещаем в А число к <;
< Ls (F (s)). Так как s > G (п), то к ф AGW; таким об-
образом, к > LA (п). Так как А'С А, то Ls (F (s)) С
^ La (F (s)). Комбинируя эти три неравенства, получаем
La (F (s)) > La (n); таким образом, F (s) > п.
Пример. Пусть F — перечисление некоторого ре-
рекурсивно перечислимого множества А в N. Так как F —
1-1 функция, то она является сдерживающей. Мы мо-
можем строить А, помещая F (s) в А на mare s. Так как F (s) <
<^ Ls (F (s)), то эта конструкция /^-сдерживающаяся и
/^-поддерживающаяся; таким образом, dg А = dg vj?.
Лемма 3. Если а рекурсивно перечислима иа' = О",
то существует сдерживающая функция F такая, что Vp —
доминанта и dg vj? = a.
Доказательство. Пусть А — рекурсивно пе-
перечислимое множество в N степени а. Так как А нерекур-
нерекурсивно, то оно бесконечно; таким образом, по теореме о
перечислении оно имеет перечисление G. По лемме 1 су-
существует функция-доминанта Н, рекурсивная в А. По
лемме о модуле существует рекурсивная последователь-
последовательность {//„} с пределом // и модулем М для {Нп}, которые
рекурсивны в А.
15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА 69
Пусть F (s) — наименьшее число п <^ G (s) такое, что
Н& (п) ?= Яя+1 (ге), если такое ге существует; в противном
случае F (s) = G (s). Ясно, что F рекурсивна. Если s >.
> М (т) для всех m<nHs>vc (re), то F (s) > п. От-
Отсюда следует, что F — сдерживающая функция и
vf (re) ^ max M (т) -\- vr (re).
т^п
Следовательно, vF рекурсивна в М, vG, а значит, в А. Так
как F (s) ^.G (s), то vG (re) < Vp- (re); таким образом,
A <r vG < rVf- Следовательно, dg \F = a.
Осталось показать, что vP — доминанта. Если L ре-
рекурсивна, то #дП) (п) < Я (и) для всех достаточно боль-
тих п. Для любого такого п существует s ^> L (п) такое,
что Я8 (и) ф Я8+1 (ге) и, значит, F (s) ^ re. Отсюда следу-
следует, что L (п) < vjr (re), что и требовалось доказать.
Теперь переформулируем определение максимального
множества. Если А — множество в области определения
F и существует конечное подмножество Ао мгтожества А
такое, что ^есть констапта на А \ Ап, то будем говорить,
что F — почти константа на А. Тогда кобесконечпое ре-
рекурсивно перечислимое множество А является максималь-
максимальным в том и только в том случае, когда для каждого ре-
рекурсивно перечислимого В функция В является почти
константой на Ае.
и-цепочкой называем цепочку длины п. Зафиксируем
некоторое перечисление {/„} для Alg (N, N), и пусть
Sn W — re-цепочка
Тогда кобосконечное рекурсивно перечислимое мпожество
А в N является максимальным в том и только в том слу-
случае, когда каждая цепочка Sv (k) является по^ти констан-
константой на А°,
Упорядочим re-цепочки, положив а < р, если а,- <
< р,-, где i — наименьшее число такое, что а,- Ф рг. Лег-
Легко заметить, что это — линейный порядок на ге-цепочках.
Более 'того,
т < п & Sm @ < Sm (/) -+ Sn (i) < Sn (/), B)
так что
т < п & S,, (/) < Sn (i) -v Sm (/) < Sm (t). C)
70 15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА
Наша идея построения максимального мпожества А
состоит в следующем: поместить i в А, как только мы най-
найдем / ^> i такое, что Sn (/) ^> Sn (i). Если а — наиболь-
наибольшая n-цепочка такая, что Sn (;) = а для бесконечно мно-
многих ;, то каждое i с Sn (i) < а будет помещено в А. От-
Отсюда следует, что Sn — почти константа на Ас.
Необходимы два изменения. Чтобы быть уверенным,
что А кобесконечно, мы будем помещать i в А из-за Sn (/) ^>
]> Sn (i), только если существуют по крайпей мере п
чисел, меньших i, которые еще не помещены в А.
Второе изменение нужно пам, чтобы сделать конструк-
конструкцию рекурсивной. Пусть Sn (к) — n-цепочка
Тогда условия B) и C) будут выполпяться, если мы там
везде снабдим S верхпим ипдексом s. Кроме того, 5^ (^) —
рекурсивная функция от аргументов s, n, к. Так как Л <
< И, то
*<*-*$; (*)<$!, (*) D)
и, значит,
lim S'n (к) = Sn (к). E)
Изменяем нашу процедуру, заменяя Sn на Ssn на шаге s
конструкции.
Теперь закончим доказательство теоремы. Пусть а —
рекурсивно перечислимая степень такая, что а' = 0";
строим максимальное множество А ь N степени а. Пусть F
такова, как в лемме 3, и F' (х) = F (х) + 1. Наша конст-
конструкция будет F-сдерживающейся и ^'-поддерживающейся,
так что vF' <r A <r vf. Но vj? (n) = Vp- (тг -f 1); таким
образом, Vi? ^r Vp' и, значит, dg A = dg vp = а. Конеч-
по, чтобы сделать конструкцию /^-сдерживающейся и
F-поддерншвающейся, нам нужно будет внести еще неко-
некоторые изменения в пашу процедуру.
На шаге s будем говорить, что / п-держит i, если
Ls (п) < i < ;, Sn (i) < S'n (;) и i, j QE As. Отсюда сле-
следует, что ; < s; действительно, если / ^> s, то Ssn (/) =
= (Л, . . ., Л) — наименьшая тг-цепочка. Если некоторое
/ п-держит i, то будем называть i п-задержанным. Если
i является тг-задержаннымдля некоторого тг, то называем i
задержанным.
15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА 71
На шаге s мы помещаем в А все задержанные числа,
которые ^> F (s). Если пи одно из этих чисел не является
^ Ijs{F' ($))> то мы также помещаем LS(F' (*•)) в А. Так
как L3 (F' (s)) > F' (s) > F (s), то конструкция и F-сдер-
живающаяся, и F-поддерживающаяся.
Если / задержано на шаге s, то захватчиком числа /
называем наименьшее число / ^> i такое, что / ф. As и /
не является задержанпым. Тогда ото / мы не помещаем
в А на шаге s. Нам нужно лишь проверить это, если / =
— Ls (F' (s)). Тогда, по определению /, Ls (F (s)) является
задержанпым. Так как Ls (F (s)) > F (s), то Ls (F (s)) по-
помещается в Л, а значит, / нет.
Покажем, что если i является /г-задержанным на шаге
я и у— его захватчик, то / /г-задерживает i. Ясно,
что Ls (/г) ^ i < /. Пусть к — наибольшее число, ко-
которое /г-задерживает i. Если г ^> к и г ф. As, то Ssn (к) ^>
^> Ssn (г); таким образом, по B) и C) Ssm (к) > Ssm (r)
для всех т. Это показывает, что к не является задержан-
задержанпым н, значит, / <; к. По к не может /г-задерживать /,
таким образом, Sn (/') > Sn (к) ^> Ssn (i). Следовательно,
у «-задерживает i.
Теперь индукцией по п покажем, что lim La (/г) = L (/г)
существует. Используя индуктивное предположение, вы-
Перем s0 > Vf (и) так, чтобы для s > s0 иметь Ls (m) =
= L (т) для всех m < п. Во-первых, покажем, что
* > «„ & Ьш (и) Ф Lt (и) - ЯГ (L,+1 (/г)) > Ssn (L, («)).
F)
Так как Ls (то) — Ls+1 (т) для иг < /г и Ls (п) ф La+1 (/г),
то Ls (/г) — наименьшее число, помещенное в Л на шаге
s. Так как s > vp (n), то F' (s) > F (s) > га; таким образом,
Ls (/г) помещается в А, потому что оно задержанное и
;> F (s). Следовательно, все числа !> Ls (/г), которые за-
задержаны, помещаются в А. Зпачит, наименьшее число
!> Ls (/г), которое не помещается в Л8 и не помещается в
А па шаге s, является захватчиком для Ls (n). Таким об-
образом, Ls+1 (п) — захватчик для Ls (n). По B) Ls (n) яв-
является /г-задержанным и в силу сказанного выше Ls+1 (/г)
n-задерживает La (/г). Тогда по D) имеем
ST (ЬЙН (/г)) > S'n (Li+1 (/г)) > S°n (La (n)),
что доказывает F).
12 15. МАКСИМАЛЬНЫЕ МНОЖЕСТВА
Если L,+1 (и) = L, (и), то S*+l (Lm (и)) > Ssn (Ls (n))
по D). Из этого и F) мы видим, что Ssn {Ls (п)) для s > s0
возрастает по s. Так как существует только конечное чис-
число тг-цепочек, то Ssn (Ls (и)) в конце концов становится
константой. Из этого и F) мы видим, что Ls (n) со време-
временем становится константой; таким образом, lim Ls (n)
существует.
Для всех достаточно больших s имеем L (п) = Ls (и) ф
ф А8; таким образом, L (п) ф А. Если т Ф п, то Ls (m) ^=
Ф Ls (п) для всех s; таким образом, L (т) ф L (п). Все
это показывает, что А кобесконечно.
Остается показать, что Sn — почти константа на А".
Пусть а — наименьшая n-цепочка такая, что Sn (i) = a
для бесконечно многих i ЕЕ Ас. Достаточно предположить
$п @ ]> а Для бесконечно многих i ЕЕ Ас и получить про-
противоречие.
Пусть В — множество таких i ЕЕ Ас, что Sn (i) = a
и La (n) <^ i. Тогда В бесконечно. Пусть Cs — множество
таких i, что S'n (i) = а и i re-задерживается на шаге s.
Покажем, что
s<t->BnC'CC(. G)
с
Достаточно показать, что В f) Cs Cl Cs+1. Пусть i
?= В f| Cs и / — захватчик i на шаге s. Так как i ЕЕ А
и у — захватчик па шаге s, то i, j ф А41. Имеем Ls+1 (n) «^.
< LA {п) < i < у. Так как 5^ (i) = 5„ (?) = а, то по
D) и E) SnX @ = а. Теперь / /г-задерживает i на шаге s;
таким образом, S*1 (i) = 5^ (i) < 5^ (/) < S*1 (/) по
D). Итак, i ЕЕ Cs+1.
Пусть (i, $У ЕЕ D <-* i ф В \/ i ?E Cs. Мы утверждаем,
что Z) рекурсивно перечислимо. Так как i ЕЕ Cs — рекур-
рекурсивное отношение от аргументов i, s, то достаточно прове-
проверить, что Вс рекурсивно перечислимо. Но Ва есть объеди-
объединение четырех множеств: A, [i \Sn (i) ]> a], [i | i e= Ac &
& Sn (i) < а] и [i | i < ?A (и)]. Первые два рекурсивно
перечислимы, так как
по D) и E), а последние два конечны. Таким образом,
Ве рекурсивно перечислпмо.
16. БЕСКОНЕЧНЫЕ НАРУШЕНИЯ 73
Для каждого i существует s такое, что <?, s> ЕЕ D.
Это очевидно, если i §? В, потому предположим, что i EF
ЕЕ В. Так как существует бесконечно много / ЕЕ Ас таких,
что Sn (/) ^> а, то мы можем выбрать такое / с / ~^> i. Тог-
Тогда Sn (?) < Sn G), поэтому по E) S'n (?) < Ssn (?) для всех
достаточно больших s. Для всех s имеем г, / ф. AsnLs (n) <^
< La (п) < i < 7. Поэтому для больших s имеем i ^ С3
и, значит, <г, s> ЕЕ D.
По теореме о селекторе существует рекурсивная функ-
функция Я такая, что <г, // (г)> Ei D для всех i. Так как Vp- —
домипапта, то Н (г) < vF (i) для всех достаточно больших
г. Так как В бесконечно, то существует i ЕЕ В с // (г) <
< Vf @- Пусть s = Я (t). Так как ? ЕЕ 5 и <г, s> ЕЕ D,
то i ЕЕ Cs. Так как s < Vi? (г), то существует i !> s такое,
что F (t) ^ i. По G) имеем ? ЕЕ С. Таким образом, i за-
задерживается па шаге t и i ^> F (i) и, значит, ? помещается
в А на шаге ?. Это противоречит тому, что i ЕЕ Ас, что и
требовалось доказать.
16. Бесконечные нарушения
Мы могли бы попытаться улучшить результаты пос-
последнего параграфа, показав, что никакое понятие «боль-
«большого» для рекурсивно перечислимых множеств не может
привести к решению проблемы Поста.
Мы уже видели, что нам нужно, чтобы наши «большие»
множества были кобесконечными, и, конечно, хотим, что-
чтобы любое кобесконечное рекурсивно перечислимое мно-
множество, которое включает в себя «большое» множество,
было также «большим». Мы могли"бы, таким образом, дос-
достичь цели, если бы сумели доказать: каждое кобесконеч-
кобесконечное рекурсивно перечислимое множество включается в
кобескопечное рекурсивно перечислимое множество, имею-
имеющее степень О'.
Покажем, однако, что такой результат ложен. Если А —
максимальное множество, то каждое кобесконечное рекур-
рекурсивно перечислимое множество, включающее А, имеет
ту же степень, что и А. Тогда нам нужно доказать, что су-
существует максимальное множество, не имеющее степепи
О'. Это следует из результатов последнего параграфа и
следующей теоремы.
74 16. БЕСКО11КЧ11ЫЕ НАРУШКНИЯ
Теорема (Сакс). Существует рекурсивно перечис-
перечислимая степень такая, что а' =0" и & Ф 0'.
Если А — множество в X х Y, то через А(х) мы обоз-
обозначим множество таких у, что <#, уУ ?=Е А. Скажем, что
А кусочно рекурсивно, если каждое А(х> рекурсивно. Гус-
Густим подмножеством мпожества А назовем такое подмно-
подмножество В, что А(х> \ BW конечно для всех х.
Л е м м а (Шенфилд). Если С — кусочно рекурсив-
рекурсивное рекурсивно перечислимое множество в X xY, то су-
существует густое рекурсивно перечислимое подмножество
А множества С такое, что Ag А Ф 0'.
Вначале покажем, что из леммы следует теорема. Оп-
Определим рекурсивно перечислимое множество С: (J, к~) 6-1
ЕЕ С ++ Vrr<k (r e Wi). Тогда
/е Tot-^a11 --- -V, A)
/ ф. Tot-> C(l) конечно.
Таким образом, С кусочно рекурсивно. Пусть А таково,
как в лемме, и а = dg А. Тогда а Ф 0'. Положим Ак (/) ~
= А (I, к). Ввиду A) и густоты А имеем lim А^ = То1.
Тогда по лемме о пределе 0" = dg (Tot) <^ (dg A)' = а'.
Так как а рекурсивно перечислимо, то а' — 0", что и тре-
требовалось доказать.
Теперь перейдем к доказательству леммы. Берем X =
¦-- Y = N. Пусть D — простое множество в Лг. Мы до-
добьемся dg-4 Ф 0', если добьемся того, чтобы!) было нере-
нерекурсивным в А.
Для / ЕЕ Alg (TV x N, N) определим
<&, г} е W\ «-> (к, г>Е^ & к < в & г < s.
Выберем индексы J и К для С и D соответственно и поло-
положим С* — Wj и Ds — Wk- Чтобы добиться Л СИ С, мы
будем помещать в А на таге s только элементы из Cs. Еще
мы должны добиться того, чтобы С(т) \ А(т) было конеч-
конечным для каждого т и [1]А Ф D для всех /, Чтобы устроить
приоритет, фиксируем перечисление {/„} для Alg (N,N).
Тогда достижению того, что С(т*> \ Л'т) конечно, отда-
отдаем приоритет перед достижением [/„]А ф D, если т < п;
если п <, т, то делаем наоборот.
Если С(т^ бесконечно, то будем помещать бесконечно
много пар в А, чтобы сделать О-т) \ Л(т) конечным.
16. БЕСКОНЕЧНЫЕ НАРУШЕНИЯ 75
Делая это, мы можем бесконечно часто нарушать условие
1/п]а ф 1)ш По этой причине наша конструкция называет-
называется конструкцией бесконечных нарушений.
Наш метод, с помощью которого мы добиваемся [/„]А Ф
фВ, подобен методу доказательства теоремы о разложе-
разложении. Так, вычисляя, что [/,JaS (к) — Л для подходящего
к, мы создаем n-требование с аргументом к, чтобы добить-
добиться Un]A (к) = Л, если требование не окажется временным.
Так как при этом получается ситуация бесконечных нару-
нарушений, то мы не можем доказать, что существует только
конечное число n-требований. Однако, используя кусоч-
кусочную рекурсивность С, мы можем доказать, как и раньше,
что существует только конечное число постоянные п-тре-
бовани i.
Имеется еще одна трудность, состоящая в том, что пара
(тп, /•> из С может быть не помещена в А, потому что на
каждом шаге, после того как эта пара появилась в С, она
находится в активном, но временном требовании. Чтобы
предотвратить это, мы не разрешаем паре (тп, г> понадать
в требование на шаге s, если (т, г> Е: С", за исключением
случая, когда (m, r> помещена в А на шаге s. Вместо это-
этого мы помещаем в это требование некоторые пары, не на-
находящиеся в С3, по крайней мере ту, которую нужно бу-
будет поместить в А, перед тем как (тп, г) помещается в А.
Пусть Ps (тп, r) — множество пар (тп', г'У таких, что
тп' <т и <т', г'У принадлежит некоторому требованию,
которое активно на шаге s и содержит (тп, /•>. Если х — ко-
конечное множество в N х N, то пусть Qs (x) — наимень-
наименьшее множество такое, что х CZ Qs (x) и
<то, r> e= Qs (х) ПС!^ I\ (m, г) С Qs (x). B)
Ясно, что Qs (x) входит в объединение х и требований, ак-
активных на шаге s. Тогда Qs (x) конечно и может быть вы-
вычислено на шаге s; если х f ] А* —¦¦ 0, то Qs (x) f] A' -- 0.
Опишем теперь шаг s. Он состоит из двух частей.
В первой части мы помещаем в А все (тп, г) Е С \ 4',
которые не принадлежат активным n-требованиям с п <^
<^. тп.
Вторая часть: пусть s из строки п. Ничего не делаем,
если не существует к ^ s такое, что: а) нет аргумента в
активном я-требовании такого, что он < к и принадле-
принадлежит D'; б) к не является аргументом активного п-требова-
70 16. БЕСКОНЕЧНЫЕ НАРУШЕНИЙ
.8
ния; в) [/n]s (к) = Л. В противном случае находим ^наи-
меныпее такое к и пусть х — множество пар, используе-
используемых отрицательно в вычислении [1п\л$ (к). Пусть у —
множество (т, r> ЕЕ Q, (х) таких, что либо (т, г> ф. Cs,
либо (т, г> уже помещено в Л в первой части этого шага.
Тогда делаем у «-требованием с аргументом к.
Докажем ряд фактов, из которых будет следовать, что
все условия удовлетворятся.
(A) Если п-требование у создано на шаге s, то у постоян-
постоянно тогда и только тогда, когда у f) As+X = 0 и нет в
А такой (jn, r> е= у, что т < п.
Это следует из того, что если у (~) As+X = 0, то пер-
первый элемент у (если он есть), помещенный в А, должен
быть парой (т, г> с т < «.
(Б) Если (jn, r> ?Е С, то (jn, r> принадлежит только
конечному числу требований.
Действительно, если (jn, r> e С\ то (т, г> не поме-
помещается ни в какое требование после шага s, за исключе-
исключением, возможно, шага, па котором оно помещается в А.
(B) Если (jn, r> Е= С, то (jn, r> ЕЕ А тогда и только
тогда, когда (jn, r> не принадлежит никакому постоянно-
постоянному п-требоеанию с п ^ т.
Элементы А не могут принадлежать никакому постоян-
постоянному требованию. Предположим, что (т, г> §? А. По (Б)
мы можем выбрать s таким большим, чтобы (т, г) ЕЕ
ЕЕ С* и каждое временное требование, содержащее
(т, г>, пе было активным па шаге s. Так как (jn, r> ЕЕ
ЕЕ Cs \ А* и (т, г> не помещено в А на шаге s, существу-
существует n-требование с п^.т, которое активно на шаге s и со-
содержит (jn, r>. Это требование должно быть постоянным.
Пусть Еп — множество аргументов постоянных «-тре-
«-требований.
(Г) Еп и №> \ АЫ конечны.
Докажем это индукцией по п. Во-первых, покажем,
что Еп рекурсивно перечислимо. Пусть Е*п — множество
аргументов постоянных «-требований, созданных на ша-
шаге s. Так как к ЕЕ Еп <-> 3s (к ЕЕ i?n), то достаточно пока-
показать, что к €Е Еп является рекурсивным отношением от
аргументов к, s. По данным к и s мы можем решить, суще-
существует ли «-требование с аргументом к, созданное на шаге
s, и если это так, мы можем найти это требование у. Теперь
16. БЕСКОНЕЧНЫЕ НАРУШЕНИЙ 11
мы должны решить, будет ли требование у постоянным или
временным. По (А) достаточно будет решить для каждой
пары <яг, г)ё^ с т<.п, будет г Е? А^ или нет. По
индуктивному предположению О-™) \ AW конечно. Так
как С кусочно рекурсивно, то .4(т> рекурсивно. Таким
образом, мы можем решить, будет г ?? А("^ или нет.
Теперь предположим, что Еп бесконечно. Так как
D — простое множество, то существует к ?Е D f] Еп.
Для больших s имеем 1(ЕЙ'и существует га-требование
с аргументом к, активное па шаге s. Для такого s никакое
«-требование с аргументом ^> к не создается на шаге s.
Но тогда Еп конечно.
Из этого результата и индуктивного предположения
следует, что Ет конечно для т <^ п. Так как два иг-тре-
бования с одним аргументом не могут быть активными на
одном и том же шаге, то не могут существовать два по-
постоянных /^-требования с одним аргументом. Таким обра-
образом, существует только конечное число постоянных яг-тре-
бований си^п, По (В) получаем, что GW \ А(п конечно.
(Д) Если существует постоянное п-требование с аргу-
аргументом к, то [1п]А (к) = Л.
Предположим, что требование у создается на шаге s,
и пусть х такое же, как в описании шага s. Ясно, что дос-
достаточно показать, что х f] A =0. Предположим, что
х Р) А Ф 0 и, значит, Qs (x) f) А ^= 0. Выберем
<jn, r) ?E Qa (х) П А с минимальным т. Так как х f] A1" =
-- 0, to Q, (х) f) А* — 0; таким образом, <т, г> ф. As.
Так как у постоянно, то (т, r> ^ у; следовательно,
(jn, г)еС' и (тп, г) не помещается в А на шаге s. Отсюда
следует, что па шаге s пара (т, г)> принадлежит активному
«'-требованию г с л\ м. Так как (т, г) ? г f| ^> то z
временное. Так как z активно на некотором шаге, то по
(Л) существует <т', г'> ?Е z f) Л с m' < и' ^ m. Тогда
</?г', r'> e iJ, (m, г); таким образом, по B) <rn', r'> e
е ^, (ж). Это противоречит выбору (jn, r>.
Пусть Р (т, г) — объединение всех Рг (т, г) для s —
= 0, 1, ... Из (Г)) следует, что Р (т, г) конечно, если
(jn, r> е С. Мы называем множество у в N X N замкну-
замкнутым, если
<ш, г> е </ П С ^- Р (m, r) e г/.
Тогда если у замкнуто к х а у, то Qs (x) CZ у Для всех s.
78 16. БЕСКОНЕЧНЫЕ НАРУШЕНИЯ
(Е) Каждое конечное подмножество множества N х N
входит в некоторое замкнутое множество.
Так как объединение конечного числа замкнутых мно-
множеств замкнуто, то достаточно показать, что каждая (т, г>
принадлежит некоторому замкнутому множеству. Сделаем
это индукцией по т.
Если <m, r> fc? С, то {(т, г» замкнуто. Пусть
<jn, r> ЕЕ С. Для каждой <m', r'> ?E Р (т, г) выберем
по индуктивному предположению замкнутое множе-
множество, содержащее (т', г'). Объединение этих множеств
с «т, г)} замкнуто.
(Ж) Если [fn\A (к) определено, то существует только
конечное число п-требований с аргументом к.
Для больших s вычисление [1п]А& (к) то же, что и вы-
вычисление [1п]Л (к). Следовательно, существует конечное
множество х такое, что для каждого s, для которого
[/п]4" (к) определено, каждая пара, отрицательно исполь-
используемая в вычислении [1п]А<> (к), принадлежит х.
По (Е) существует замкнутое множество у, содержа-
содержащее х. Каждое и-требование с аргументом к входит в у.
Каждый раз, как такое требование становится неактив-
неактивным, некоторый элемент из у помещается в А. Следова-
Следовательно, существует только конечное число временных
w-требований с аргументом к; существует самое большее
одно постоянное и-требование с аргументом к.
C) Цп]А ф D.
Предположим, что [1п]л — D, и придем к противоре-
противоречию. Так как по (Г) Еп конечно, a D просто, то можно
выбрать к <= (D U Enf. Тогда Цп]А (к) = D (к) = Л. По
(Г) и (Ж) можно выбрать s в строке п таким большим, что:
(а) каждое постоянное гс-требование активно на шаге s;
(б) каждое временное гс-требование с аргументом <; к
неактивно на шаге s; (в) [1п]? (к) = Л; (г) к <^ s. Если
на шаге s существует активное «--требование с аргументом
т ^ к, то оно постоянно; таким образом, по (Д) D (т) =
= [1п1А (т) = Л и, значит, т ^Ds. Также т Ф к, так
как к ф. Еп. Все это показывает, что некоторое гс-требова-
ние с аргументом <; к создается на шаге s. Но по (а) и
(б) это невозможно.
Как следует из (Г) и C), все условия удовлетворены,
что и требовалось доказать.
16. БЕСКОНЕЧНЫЕ НАРУШЕНИЯ 79
В следующем параграфе нам нужны будут некоторые
дополнительные свойства только что сделанной конструк-
конструкции. Во-первых, покажем, что А рекурсивно в С. Предпо-
Предположим, что дан оракул для С, и покажем индукцией по
т, как вычислить, будет (т, г} ЕЕ А или пет. Если
(т, гУф.С, то (т,гУф.А; теперь предположим, что
(т, r> GE С. Найдем такое s, что (т, r> GE Cs. Требование,
созданное после шага s, может содержать (т, г>, только
если (т, г> ?Е А; таким образом, все постоянные требова-
требования, содержащие (т, г~), активны па mare s. По (В)
(т, г> с= А тогда и только тогда, когда никакое гс-требо-
вание х с п <^ т, которое активно па шаге s и содержит
<»i, г>, не является постоянным. Ввиду (А) и индуктивно-
индуктивного предположения мы можем узнать, будет выполняться
этот случай или пет.
Теперь рассмотрим, что мы могли бы доказать, если
бы не предполагали, что С кусочно рекурсивно. Мы могли
лишь, как и выше, доказать, что А рекурсивно в С. При
доказательстве (Г) кусочная рекурсивность была исполь-
использована только для доказательства, что С^^ рекурсивно
для т < п. Следовательно, если мы предположим, что
С(т) рекурсивно для т < п, то мы можем утверждать,
что С(п~> \ А^ конечно.
Теперь предположим, что С^т^ рекурсивно для всех
т ^> 0. Тогда мы можем доказать еще, что А — густое
подмножество множества С и D *^rA при условии, что
D — сильно простое множество и D ^r C^°\ Нужно лишь
одно изменение при доказательстве (Г). Так как С может
не быть рекурсивным, мы можем лишь утверждать, что
к GE Е'п рекурсивно в Cw и, значит, Еп рекурсивно пере-
перечислимо в С(о). Так как D — сильно простое множество
и D =4^к 6^°\ то этого достаточно, чтобы быть уверенным,
что Еп не является бесконечным подмножеством для Dc,
а ,по все, что нам нужно. Снова, если мы предположим,
чю С^ рекурсивно для 0 < т < п, то мы можем ут-
утверждать, что С(п) \ А(п) конечно.
Теперь рассмотрим, как А зависит от С. Чтобы сделать
конструкцию до конца, пам нужны индексы / для С и К
для D. Индекс / для А может быть тогда описан следую-
следующим образом: вычисление согласно / с входом <т, г)
состоит из проведения конструкции до тех пор, пока
80 17. ИНДЕКСНЫЕ МНОЖЕСТВА
<m, r> не будет помещено в А, и тогда даем выход 0. Если
предположить, что индекс К для D фиксирован, то ин-
индекс / для А есть рекурсивная функция от индекса / для С.
Суммируем эти результаты следующим образом.
Пусть D — простое множество в N. Тогда существует ре-
рекурсивная функция F из A\g (N х N, N) в Alg (N x N, N)
такая, что если С = Wj и А — Wp(j), то: (а) А рекурсивно
в С; (б) если С(т) рекурсивно для т < п, то C<n> \ 4(п)
конечно; (в) если С кусочно рекурсивно, то D ^.rA. Если
D — сильно простое множество и D =^r Cw, to: (б') если
&т) рекурсивно для 0<^т < п, то С<п) \4(п^ конечно;
(в') если С(т) рекурсивно для т ^> 0, то D =^r A.
17. Индексные множества
Теперь используем результаты предыдущего пара-
параграфа для оценки степеней некоторых множеств.
Индексным множеством для а, обозначаемым через
1х (а), называется множество /ЕЕ Alg (N, N) таких, что
dgWi — а. Если а не является рекурсивно перечислимой,
то 1х (а) = 0. Покажем, что если а рекурсивно пере-
перечислима, то dg (Ix (a)) = а3.
Если dg G = dg H, то одни и те же множества рекур-
рекурсивны в С и в //; таким образом, множества типа 2n [G]
(Пп [G]) являются в то же время и множествами типа
2n [H] (Пп [Я]). Это оправдывает следующее определе-
определение: множество называется множеством типа Бп [al
(Пп fa]), если оно является множеством типа Бп [Н]
(Пп [Н]), где Н — некоторая функция степени а. Следую-
Следующая теорема дает желаемый результат для степеней ин-
индексных множеств.
Теорема об индексном множестве
(Ейтс). Если а рекурсивно перечислима, то 1х (а) является
полным множеством типа 23[а].
В § 3 мы показывали, что если F рекурсивна в G, a G
рекурсивна в Н, то F рекурсивна в Н. В доказательстве
было указано, как получить алгоритм для F относительно
Н из алгоритмов для F относительно G и для G относитель-
относительно Н. Таким образом, существует рекурсивная функция
L такая, что если [J]H и [7]f;'w всюду определены, то
11]1ЛЯ = [L (I, J)f.
17. ИНДЕКСНЫЕ МНОЖЕСТВА 81
Теперь докажем, что если а рекурсивно перечислима,
то 1х (а) есть множество типа 28 [а]. Пусть А — рекурсив-
рекурсивно перечислимое множество в N степени а. Имея в виду
функцию L, описанную выше, получаем
/EElx (&)^AgWi = AgA
«¦+ 3J3K (Wi = [J]A&A = lK]Wl)
++ 3J3K (Wi = [J]A &A=[L(K, J)\A).
Поэтому нам нужно лишь показать, что Wi = [J]A и А =
= [L (К, J)]A являются множествами типа П2 [А].
Имеем
Wi = [J\A *-* Vn ((PTj (n) & ША (и) - И) V
V П W! (п) & [J\A (и) = Л)).
Так как Wi (n) рекурсивно перечислимо, a [J]A (n) = к
рекурсивно перечислимо относительно А, то они имеют
оба тип 2Х [А\. Отсюда следует, что Wi (n), [J]A (п) = И,
| Wj (n) и [/1А (п) =Л — множества типа П2 [А]', таким
образом, Wi = [J]A есть множество типа П2 [А]. Для
А = [L (К, J)]A рассуждаем подобным образом.
Лемма 1. Если А рекурсивно перечислимо и В —
множество типа Е^ [а], то х ЕЕ В <-> Vy «а;, уУ ее С),
г5е С рекурсивно в А и рекурсивно перечислимо.
Доказательство. Имеем ж ЕЕ 5 ¦*->• Vz«x, z>EE
ЕЕ Z)), где Z) рекурсивно в Л. По лемме о модуле D =
= limZ)n, где (Z),,} рекурсивна и имеет модуль Я, рекур-
рекурсивный в А. Тогда
х ЕЕ В <-+ Vz (lim Dn (ж, z) = Я)
<-+ VzVs3n (га > s & <х, z> ЕЕ Dn)
(так как UmDn (x, z) всегда существует). Пусть
<х, z, s> ЕЕ С «¦ Эп (и > s & О, z> ЕЕ Dn).
Таким образом, С рекурсивно перечислимо.В определении
С мы можем заменить Эй на 3ren<H(x,z>. Это показывает, что
С" рекурсивно в Н и, следовательно, в .4. Пусть У —
- Z х iV, F (z, /г) --= z, G(z,n) = n и
<х, г/> G С - <х, F (у), G (у)У ЕЕ С.
Тогда С имеет все требуемые свойства, что и треборалось
доказать.
82 17. ИНДЕКСНЫЕ МНОЖЕСТВА
Л е м м а 2. Пусть А рекурсивно перечислимо, а В —
множество типа 22Ы]. Тогда существует С, рекурсивное
в Л и рекурсивно перечислимое, такое, что С-х) рекурсивно,
если х ЕЕ В, и А рекурсивно в С-х), если х ф. В.
Доказательство. Предположим, что А —
множество в N. По лемме 1
х «= В <-> JtVs (<з , «, s> CE D),
где D рекурсивно в А и рекурсивно перечислимо. Пусть
(х, т, ii> Gt С <-> Зи<пУ^'С,1 (<>, t, s> ЕЕ D) \/ т 02 А.
Тогда С рекурсивно в А и рекурсивно перечислимо.
Пусть Е — С^ для фиксированного х. Если
</«, п) Е^. Е, то <пг, н'У С~ Е для всех п' <С п. Поэтому для
каждого т множество Е^п) конечно или равно N. Если
х ?Г- В, то существует t такое, что Vs «x, t, s) GE Z>).
Если т > f, то ?(m) = N. Следовательно, в этом случае Е
рекурсивно. Если х ф. В, то для каждого t существует s
такое, что <х, t, s> §? Z). Следовательпо, для данного тн
утверждение 3^<m Vss<,, «ж, f, s> GE Z?) ложно для боль-
больших п. Таким образом, I-Sm) --¦ N <-» т СЕ ^4; следователь-
следовательно, т?"#« Зг (<W) r> ^i Е). Это показывает, что Лс
рекурсивно перечислимо в Е. Но А рекурсивно перечис-
перечислимо и, значит, рекурсивно перечислимо в Е; таким обра-
образом, А рекурсивно в Е по теореме о дополнении,что и тре-
требовалось доказать.
Теперь мы можем закончить доказательство теоремы
об индексном множестве. Пусть а рекурсивно перечисли-
перечислима; мы должны доказать, что всякое множество типа
23 [а] сводится к 1х (а). Вначале пусть а = 0. (Этот слу-
случай рассмотрен Роджерсом.) Пусть А — рекурсивно пе-
перечислимое множество в N степени 0'. Если В имеет тип
2д, то В имеет тип 2,, [А'] для некоторого /Г, которое
есть множество типа 2j и, следовательно, реку решит в А;
таким образом, В имеет тин 2., [А]. Выберем С, как в лем-
лемме 2. Так как А нерекурсивно, то х ЕЕ В тогда и только
тогда, когда №> рекурсивно. По теореме о параметриза-
параметризации существует рекурсивная функция F такая, что
fu) = WFW. Тогда гЕ В <-> F (х) ?=_ 1х @), что доказы-
доказывает сводимость В к 1х @).
Теперь пусть а ^> 0. По теореме 1 из § 12 существует
простое множество D степени а. Пусть В имеет тип
17. ИНДЕКСНЫЕ МНОЖЕСТВА 83
2„ [Я]. Тогда
хевВс «-» V/c «ж, к><вС),
где С имеет тип 22 [D]. Но лемме 2 существует Е, рекур-
рекурсивное в D и рекурсивно перечислимое, такое, что
<х, к} <= С -> ?^- ^ рекурсивно, A)
<х, к) ф С ~+ D рекурсивно в №• *\ B)
Выберем по теореме о параметризации рекурсивную функ-
функцию G так, чтобы /?М — Wc^x)', пусть F такая же, как в
конце § 1G. Пусть Н (х) = F (G (х)). Мы завершим доказа-
доказательство, если покажем, что х (Е В <-> Н (х^ GE 1х (а).
Положив Ах = Wn(X), будем иметь: (а) Ах рекурсивно
в ЕЮ; (б) если Е^х' m> рекурсивно для т <^к, то
?(*, k) \ ,4^) конечно; (в) если ?W кусочно рекурсивно,
то D ^e, ij. Так как ?^rD, to из (а) следует, что
dg (Ax) < а.
Пусть х е- В. Выберем минимальное к такое, что
(х, ку i=? С. Для т -< к по A) ?^ т^ рекурсивно; такид!
образом, по (б) №•ft^ \ Ах конечно. Из этого и B) следу-
следует, что D рекурсивно в Ах)ш, таким образом, dgAx = a
и Н {х) е 1х (а). Теперь пусть х х? В. По A) EW кусочно
рекурсивно; тогда по (в) имеем D ^r Ax. Таким образом,
dgAx < а и II (х) ф 1х (а), что и требовалось доказать.
В действительности мы доказали немного больше.
Пусть 1х (Ь, а) — множество таких / GE Alg (N, N), что
b ^ dg Wi -< а. Мы доказали, что если а рекурсивно пере-
перечислима иа^-0, то каждое множество типа 28 [а] сво-
сводится к Ix (a), Ix @, а).
Усилим этот результат следующим образом: если а и Ь
рекурсивно перечислимы иЬ<а, то каждое множество
типа 28 [а] сводится к Ix (a), Ix (b, а). По замечанию из
§ 12 существует сильно простое множество D степени а.
Пусть В есть множество типа 28 [D\, и возьмем С и Е,
как раньше. Пусть D'— рекурсивно перечислимое мно-
множество в N степени Ь, и определим
<>, /с, »> ?Е Е' <^ (к --= 0 & п е D') V
V (к > 0 & <ж, к - 1, п> е Е).
Тогда Е' рекурсивно перечислимо и рекурсивное D', Е.
Так как Ь < а, то Е' рекурсивно в D. Выберем рекурсив-
84 ii- индексные множества
ную функцию G так, чтобы Wg(x) — Ег<-Х\ и положим
II {х) = F {G {х)). Покажем, что х ?Е В *-»- Н {х) GE 1х (а)
и х ф В *-»- Н (х) е Ix (b, а).
Имеем ?'(*,<>)= #' и ?'(*,/.-+» = ?(*,*). Так как Ь < а,
то D =^r Е'^х<°\ Следовательно, положив Лх = \УщХ), мы
будем иметь: (а) А^ рекурсивно в Е'Ю- (б) если Е(х'т)
рекурсивно для т <к, то Е^^ \ А(х+1) конечно;
(в) если ЕЮ кусочпо рекурсивно, тоD =^r Ax. Как и рань-
раньше, комбинируя эти результаты с A) и B), покажем, что
dg Ах — а, если х 6= В, и dg Ax < а, если хф.В. Кроме
того, ?'<*,о) \ а<?) конечно; поэтому D' = ?'(«.о) ^R
<r^3c0) <чк, Ах. Таким образом, Ь^ dg Ax. Наш результат
доказан.
Используем этот результат для доказательства одной
теоремы для рекурсивно перечислимых степеней. Во-пер-
Во-первых, докажем один важный результат, который показы-
показывает, что в определении рекурсивно перечислимого мно-
множества можно использовать индекс множества, которое
мы определяем.
Теорема о рекурсии (Клини). Если А —
рекурсивно перечислимое множество в Alg (N, N) х X,
то существует I такое, что х 6= Wi <-> </, Xs} 6Е А для
всех х.
Доказательство. По теореме об изоморфизме
можно отождествить Alg (N, N) с Alg (Alg (X, N) x X, N).
Тогда <•/, ху 6Е Wj является рекурсивно перечислимым
отношением от /, х; по теореме параметризации сущест-
существует рекурсивная функция F такая, что х ЕЕ Wf(J) <->
*-*¦ </, ху G Wj для всех J ъ. х. Выберем / так, чтобы
</, х) е Wj «-»¦ <F (/), ху еЕ А для всех / и х, и положим
/ = F (J). Тогда
что и требовалось доказать.
Следствие (теорема о неподвижной
точке). Если F — рекурсивная функция из Alg (X, N)
в Alg (X, N), то существует I такое, что Wi = Wpyy
Доказательство. Применим теорему о ре-
рекурсии к множеству А, определенному следующим
18. ВЕТВЯЩИЙСЯ СТЕПЕНИ 85
образом:
</, х} GEE A <-> х ЕЕ Wfo),
что и требовалось доказать.
Теорема плотности (Сакс). Если а и b —
рекурсивно перечислимые степени такие, что b <^ а, то
сугцествует рекурсивно перечислимая степень с такая,
что b <; с <; а.
Доказательство. Так как Ix (b) имеет тип
23 [Ь], а значит, и тип 23 [а], то существует рекурсивная
функция F такая, что / е= Ix (b) -»- F (I) ?E Ix (а) и
/ ф. Ix (b) —> F (I) c? Ix (b, а). Выберем /, как в теореме
о неподвижной точке. Если / еЕЕ Ix (b), то b = dg Wj =
= dg Wf(I) — а; получаем противоречие. Таким образом,
/ ф Ix (b) и, значит, dg Wj Ф b и b ^ dg Wjrt/) < a.
Тогда мы можем взять с = dg Wi = dg Wf(J), что и требо-
требовалось доказать.
18. Ветвящиеся степени
Современные работы в теории степеней больше всего
имеют дело с рекурсивно перечислммыми степенями. Рас-
Рассмотрим здесь только одну из проблем, которые изучались.
Рекурсивно иеречислимая степень а называется вет-
ветвящейся, если существуют рекурсивно перечислимые сте-
степени b и с, отличные от а, такие, что а есть наибольшая
нижняя грань для {Ь, с}. Ясно, что 0' не является ветвя-
ветвящейся. Существование ветвящихся степеней доказано
в первом из наших результатов.
Теорема 1 (Ейтс). Степень 0 ветвящаяся.
Доказательство. Построим два нерекурсив-
нерекурсивных рекурсивно перечислимых множества А и В так, что-
чтобы {dg^4,dgZ?} и.мело наибольшую пижнюю грань 0.
Будем удовлетворять следующим условиям:
Aг) А Ф [/];
B/) В Ф [/];
C;, j) если [1\Л — [J]B = F, то F рекурсивна.
Пусть {Rn} — перечисление пространства условий.
Наша идея удовлетворения условию C;, j) состоит
в достижении того, чтобы F (к) = г, если F — [1]л —
80 iS. ВЕТВЯЩИЕСЯ СТЕПЕНИ
= [J]ti и [1]aS (к) — [УРЧ (к) = i для некоторого s. Это,
очевидно, будет так, если для каждого I > s либо [1\А' (к) =
= i, либо [/]в (к) — г. Поэтому, когда мы увидим, что
[/]А (Л) = i, мы создаем требование, но мы не будем его
использовать для сохранения элементов вне А на шаге,
на котором существует активное требование, соответст-
соответствующее [J\ti (к) = i. Исключение будут составлять неко-
некоторые элементы требования, называемые ключевыми эле-
элементами, которые мы не можем номестить в А, пока требо-
требование остается активным. Цель этого — гарантировать,
что мы не создадим бесконечно много требований для
какого-нибудь единственного аргумента к.
Так как мы можем иметь бесконечно много «-требова-
«-требований, перед нами снова встает проблема — гарантировать,
что число не находится вне А (или В) из-за бесконечно
многих временных требований. Мы решим эту проблему
методом, отличным от того, который применялся в § 16.
На каждом шаге s некоторые числа помещаются в А (или
В), несмотря на существование w-требования, которое
в нормальной обстановке оставило бы их вне А. Позднее
мы опишем эти числа точно; грубо говоря, это числа, ко-
которые на многих предыдущих шагах оставались вне А
из-за то-требований с т <^ п.
Теперь дадим некоторые определения. Если Rn есть
C/,j), то мы можем создать n-требования. Каждое такое
требование является либо требованием для А, либо тре-
требованием для В. Далее мы часто будем рассматривать
лишь требования для А; понятно, что все будет выпол-
выполняться, если А и В поменять местами.
Каждое требование будет иметь аргумент и значение.
Если на шаге s мы создаем n-требование х для А с аргу-
аргументом к и значением i, то будем иметь х f] As — 0.
Для t ]> s требование х называется активным ыа шаге t, ес-
если х |~| А1 = 0; впротивпом случае х неактивно на шаге
t. Скажем, что х эффективно па шаге t, если оно на шаге
I активно и нет и-требования для В с аргументом к и зна-
значением г, активного на шаге t; в прошвном случае назы-
называем х неэффективным на шаге t. Элемент г из а: называет-
называется ключевым элементом, если г из строки т и т ^> к -+- п.
Теперь определим конечные множества РА (п, к) и
Q* (п) индукцией по s. Идея такова: РЛ (п, к) — множе-
18. ВЕТВЯЩИЕСЯ СТЕПЕНИ 87
ство чисел, которые мы не разрешаем ге-треоованию для
А с аргументом к оставлять вне А на шаге s; Qs (re) —
множество чисел, остающихся вне А на шаге s из-за
m-требований для А с аргументом к при т <^' п. Точнее,
г ge Pf (n, к), если г принадлежит re-требованию для А,
активному на шаге s, и г ЕЕ Qf (ге) для всех t таких, что
к <^ I <^ s и t находится в той же строке, что wr; r ЕЕ Qf (re),
если г принадлежит m-требованию для А с аргументом
к, эффективному на шаге s, m <J п и г ф. Ps4 (то, к).
Теперь опишем шаг s. Пусть s из строки п и вначале
предположим, что Rn есть (lj). Ищем число г^ s такое, что:
(а) нет чисел из As в строке ге; (б) г из строки ге; (в) [/]s(r) =
--= Л; (г) г — иеключевой элемент в некотором активном
требовании для А; (д) г д? ^ («). Если такое г существует,
то наименьшее помещаем в А.
Если Rn есть Bj), то везде в предыдущем абзаце ме-
меняем местами А и В. Теперь предположим, что /?,, есть
Cjv). Тогда шаг s имеет две части — Л-часть и 5-часть.
Опишем .4-часть; 5-часть получается так же, но А меняет-
меняется местами с В, а / с /.
Пусть к — наименьшее число, не являющееся аргу-
аргументом никакого активного re-требования для А. Ничего
не делаем, если не выполняется к ЕЕ Wj>g и нет эффектив-
эффективного ге-требоваиия, имеющего аргумент <С к. В противном
случае создаем re-требование для А с аргументом к и зна-
значением [ЛА<! (к), состоящее из всех чисел, используемых
отрицательно в вычислении [ЛА" (к).
Докажем несколько результатов, которые приводят
к тому, что все требования будут удовлетворены.
Постоянные и временные требования определяем как
обычно. Требование называется существенным, если оно
эффективно па шаге s для всех достаточно больших я; в
противном случае требование называется несущественным.
(А) Для каждых пик существует только конечное
число п-требований для А с аргументом к.
Если число г из некоторого активного «-требования
для А с аргументом к помещается в А, то г не является
ключевым п атом требовании; таким образом, г находится
в строке т, где т <J n + к. Для каждого т самое большее
одно число из строки т помещается в А. Из этого следует.
88 18. ВЕТВЯЩИЕСЯ СТЕПЕНИ
что существует конечное число временных п-требований
для А с аргументом к и существует самое большее одно
постоянное n-требовапие для А с аргументом к.
(Б) Если х — несущественное требование, то для всех
достаточно больших s требование х неэффективно на шаге s.
Пусть х — n-требовапие для А с аргументом к. Если
бы результат был ложен, то существовало бы бесконечно
много таких s, что х эффективно на шаге s и неэффективно,
но активно, на шаге s + 1.
Отсюда следует, что некоторое n-требование для В
с аргументом к создается на шаге s, а это по (А) не может
случаться бесконечно часто.
(В) Для каждого п существует самое большее конечное
число существенных п-требований для А.
Предположим, что существует существенное п-требо-
вание для А с аргументом к. Тогда после некоторого шага
никакое n-требование для А с аргументом ]> к не будет
создано. Тогда по (А) существует только конечное число
и-требований для А.
Пусть гё^а (п), если г ЕЕ QA (n) для всех достаточно
больших s в той же строке, что и г.
(Г) Если п — наименьшее число такое, что г ЕЕ QA (n),
то г принадлежит некоторому существенному п-требо-
ванию.
Предположим, что это не так. Выберем s0 так, чтобы
г ЕЕ Qf (п), если s > s0, hs было в той же строке, что и г.
По (А) г принадлежит только конечному числу п-требо-
п-требований для А с аргументами < s0. По предположению они
все несущественные. Тогда по (Б) существует s^ sa такое,
что для s > sx все эти требования становятся неэффектив-
неэффективными.
Так как г е QA (n) и г ф QA (n — 1), то существует
бесконечно много s в той же строке, что и г, таких, что
г ЕЕ: <?sA («) \ <?sA (п — 1). Выберем такое s с s ^ Sy. На
шаге s r принадлежит некоторому эффективному п-тре-
бованию х для А с аргументом к и г ф. Ps (n, к). Следова-
Следовательно, существует t в той же строке, что и г, такое, что
к <^ t < s и г ф. Qt (п). По выбору s0 имеем к ^ t < s0.
Но это противоречит выбору sx.
(Д) QA (n) конечно.
Это следует из (Г) и (В).
n.
18. ВЕТВЯЩИЕСЯ СТЕПЕНИ
Покажем, что A/) выполняется. Пусть AГ) будет Rn
Если число г из строки га помещается в А, то [/] (г) — Л;
таким образом, A/) выполняется. Теперь предположим,
что А не содержит чисел из строки га. Предположим, что
А = [/], и придем к противоречию. Выберем г из строки
га так, чтобы г не было ключевым элементом в требовании
для А и г ф. QA (га); uo (А) и (Д) это возможно. Так как
г^А, то Ц](г) = Л. Поэтому мы можем выбрать s из
строки га таким большим, чтобы s !> г, [I]s (г) = Л и
г ф()? (n). Тогда на шаге s некоторое число из строки п
помещается в А; получаем иротиворечие.
(Е) Для каждых пик имеем РЛ (п, к) CZ QA (га) для
всех достаточно больших s.
Так как Р^ (п, к) конечно и убывает с возрастанием
s, то достаточно показать, что если г ?Е .Р5А (п, к) для всех
s, то г ?Е QA (n). А это очевидно.
Перейдем к C/,/). Пусть Cj,/) будет Rn и предполо-
предположим, что [1]Л ¦— [J]B — F. Тогда каждое постоянное
га-требование с аргументом к имеет значение F (к). Пока-
Покажем, что для кажого к существуют постоянные несущест-
несущественные га-требования для А и для В с аргументом к. При-
Применяем индукцию по к. По индуктивному предположению,
(Б) и (А) имеем для всех достаточно больших s: (а) для
каждого / < к постоянное га-требование для А и В с аргу-
аргументом / неэффективно на шаге s; (б) каждое временное
га-требование для А или В с аргументом к неактивно на
шаге s; (в) к е Wft e f] Wf<s. Выберем такое s в строке га.
Тогда на шаге s либо существует активное га-требование
для А с аргументом к, либо такое требование создается.
В любом случае по (б) это требование постоянно. Анало-
Аналогично, существует постоянное га-требование для В с аргу-
аргументом к. Так как оба эти требования имеют значение
F (к), то они несущественны.
Выберем s0 так, чтобы QA (га) f] A CZ Л80, каждый эле-
элемент из А, который находится в строке т ^ га, уже нахо-
находился в А*° и чтобы соответствующие утверждения с заме-
заменой А на В также выполнялись. Используя ()А (га) и s0,
мы можем вычислить F (к) по к.
Пусть к дано. Выберем s± !> s0 так, чтобы Рл (га, к) С
С QA (n), и существует га-требование х для А с аргумен-
90 18. ВЕТВЯЩИЕСЯ СТЕПЕНИ
том к, которое активно, по неэффективно на шаге s1.
По (Е) такое sl существует и может быть найдено с по-
помощью проб.
Пусть i — значение х; покажем, что /' (к) --- L
Мы знаем, что для достаточно больших s должны су-
существовать активные n-требования для А м В, оба с аргу-
аргументом к и значением F (к). Поэтому достаточно показать,
что для каждого шага s > sl существует активное и-тре-
бовлнио для А или В с аргументом к и значением i. Это
выполняется для s — su поэтому достаточно показать, что
если это выполняется для s ]> s1, то выполняется и для
s + 1.
Предположим, что на шаге s существуют активные
п-требования для А и В с аргументом к и значением /.
Так как числа не могут одновременно на шаге к поме-
помещаться и в А и в В, то одно из ,>тих требований на шаге
.9+1 активно.
Теперь предположим, например, что па шаге s сущест-
существует активное n-требование для А с аргументом к и значе-
значением г, по для В такого требования пет. Это требование
;/ эффективно на шаге s; достаточно прийти к противо-
противоречию из предположения, что число г ЕЕ у помещается
в А на шаге s. Пусты из строки т. Тогда г ^ Q'^ (m) и по
выбору s0 имеет п <^т. Так как г лежит в эффективном
требовании у, то г ЕЕ Р* (п, к); таким образом, по выбору
Sj имеем г <= QA (и). Но это противоречит выбору я0, что
и требовалось доказать.
Теперь докажем, что существуют иеветвящиеся рекур-
рекурсивно перечислимые степени, отличные от 0'.
Теорема 2 (Лахлан). Если А — ненулевая рекур-
рекурсивно перечислимая степень, то существует неветвящаяся
рекурсивно перечислимая степень а такая, что а ^ d.
Лемма. Пусть Е — бесконечное множество в N,
рекурсивно перечислимое в А. Пусть G — функция из А
в N, рекурсивная в А. Пусть I 6E Alg (N, N) таков, что
dg A <^ dg Wi. Пусть Е' — множество таких г ЕЕ Е,
что некоторое число ^ г находится в Wj \ Wj lr\ Тогда
Е' рекурсивно перечислимо в А и бесконечно.
Доказательство. Так как
r (s S Wi & s <
18. ВКТПЯЩИКСЯ СТЕПЕПИ 91
то Е' рекурсивно перечислимо в А. Предположим, что Е'
конечно, так что Е \ Е' рекурсивно перочислимо в А
и бесконечно. По теореме о селекторе существует функция
F, рекурсивная в А, такая, что п <^ F (п) и F (n) GE
ЕЕ Е \ Е' для всех п. Тогда имеем
следовательно, Wi <rR A.' Это противоречит тому, что
dg А < dg Wi, что и требовалось доказать.
Теперь перейдем к теореме 2. Пусть D — рекурсивпо
перечислимое множество в N степени d. Так как D нере-
нерекурсивно, то оно бесконечно, поэтому оно имеет некоторое
перечисление F. Будем строить рекурсивпо перечислимое
множество A в TV и положим а = dg А. Будем делать Л ре-
рекурсивным в D, так что а ^ d.
Чтобы сделать А неветвящимся, мы должны добиться
того, чтобы всякий раз, когда
dg A < dg WT & Ag A < dg Wj, A)
dg А не будет наибольшей нижней грапью для
dgWj), т. е. существует Bitj такое, что В/, j ^
Вi, j <r Wj и В/, j ^El Основные усилия при построе-
построении будут направлены на то, чтобы сделать 5r,j ^r-4-
Таким образом, мы имеем условия:
Пусть {/?„} — перечисление пространства условий.
Скажем, что строка п является (/", J)-cmpoKoit, если
Rn есть Aг, j, к) для некоторого К. Если к находится
в строке п, то вместо п мы пишем rw (к). Пусть Bi, j — мно-
множество таких rw (к) для к Ег А, что rw (к) находится в
(/, /)-строке. Таким образом, если Rn есть (lr j. к), то мы
пытаемся добиться выполнения /?„, находя к такое, что
rw (к) находится в строке п и \К]А (rw (k)) — Л, и затем
помещая к в А и добиваясь [К]А (rw (k)) = Л. Для послед-
последнего мы можем ввести га-требование с индексом к.
Если n-требование х с индексом к 'создается на шаге s,
то мы имеемх (~) Ав — СЛ. Для t^> s x называется актив-
активным па шаго t, если ж f] А' — GS; в противном случае х
называется неактивным на шаге t. Скажем, что х эффектив-
эффективно на шаге t, если оно на шаге t активно и k S А .
92 18. ВЕТВЯЩИЕСЯ СТЕПЕНИ
Теперь опишем шаг s. Вначале предположим, что
s = 2t. Для каждого п мы помещаем в А наименьшее число
к, если оно существует, удовлетворяющее следующим ус-
условиям: (а) к — индекс некоторого активного я-требова-
ния; (б) не существует эффективного п-требования;
(в) к не находится в активном то-требовании с т < п;
(v)k>F(t).
Теперь предположим, что s = It + 1, и пусть t нахо-
находится в строке п. Если существует аффективное /г-требо-
вание, то ничего не делаем. В противном случае ищем чис-
число к < sтакое, что:
1) к не является индексом ранее созданного д-тре-
бования;
2) rw (к) находится в строке п;
3) [K]f (rw (k)) = Л;
4) к не используется в вычислении [К]л (rw (k));
5) некоторое число <^ rw (к) находится в W\ \ Wi",
6) некоторое число ^ rw (к) находится в Wj \ Wj-
Если такое к существует, то находим наименьшее и
создаем n-требование с индексом к, состоящее из всех чи-
чисел, используемых отрицательно в вычислении [К]л (rw (k)).
Во-первых, покажем, что A <^r D. Пусть нам даны
оракул для D и число к. Выберем t так, чтобы каждое чис-
число <Ы) было среди F @), F A) F (t — 1). Тогда
к не может быть помещено в А на шаге 2t или позднее;
таким образом, к 6= А <-> к ?Е А21.
Заметим, что по 1) и 2) никакое число не является ин-
индексом более чем одного требования. Если n-требование у
активно на шаге s, а число г из у помещается в А на шаге
s, то г является индексом некоторого активного то-требо-
вания хит ^ п по (в). Скажем, что х убивает у на шаге s.
По 4) х ф у.
Покажем, что если n-требование х убивает п-требова-
ние у на шаге s, то индекс к для у не помещается в А. По
(б) у неэффективно на шаге s; таким образом, к ф. А8. Так
как х является единственным «-требованием, чей индекс
помещается в А на шаге s, то к не помещается в А на шаге s.
После шага s единственное требование с индексом к не-
неактивно; таким образом, к никогда не будет помещено в А.
Как обычно, определяем постоянные и временные тре-
требования. Требование существенно, если оно постоянно и
18. ВЕТВЯЩИЕСЯ СТЕПЕНИ 93
его индекс принадлежит А; это означает, что оно эффектив-
эффективно на mare s для всех достаточно больших s.
Теперь покажем индукцией по га, что существует только
конечное число га-требований. Если существует какое-ни-
какое-нибудь существенное га-требование, то после некоторого
шага никакие га-требовапия пе будут созданы; поэтому
предположим, что нет существенных га-требований. По
индуктивному предположению только конечное число
га-требований будут убиты тга-требованиями с т <^п.
га-требование, которое убито га-требовапием, не может иметь
свой индекс в А, как мы видели выше. Отсюда следует, что
только конечное число га-требований имеют свои индексы
в А. Но если х убито у, то индекс для у находится в А.
Отсюда следует, что существует только копечное число
временных га-требований.
Предположим, что существует бесконечное число га-тре-
га-требований. Получим требуемое противоречие, доказав, что
D рекурсивно. Выберем s0 так, чтобы каждое временное
га-требование было неактивным на шаге s0 и каждое
га-требование, чей индекс находится в некотором тга-требо-
вании с т < га, создавалось до шага s0. Пусть г дано. Су-
Существует s > s0 такое, что некоторое re-требование х с ин-
индексом к~^ г создается на шаге s; можно найти такое s.
Если t > s, то никакое га-требование не является эффектив-
эффективным па mare 2t; x активно на mare 2t; к не находится в
тга-требовании с т <С га; никакой индекс re-требования не
помещается в Л на шаге 2t. Отсюда следует, что F (t) ]>
^> к > г для t ^> s; таким образом, г ЕЕ D тогда и только
тогда, когда г есть среди F @), F A), . . ., F (s — 1).
Предположим, что A) выполняется. Вначале покажем,
что 5/, j <^r Wf. Имеем г ЕЕ B\j тогда и только тогда,
когда г находится в некоторой (/, .7)-строке и некоторое к
из строки г находится в А. Так как A <^r W\, to достаточ-
достаточно показать, что мы можем ограничить это к при помощи
оракула для Wf. По 5) некоторое число ^ г должно быть
в Wj \ Wj. Следовательно, если выбрать s таким боль-
большим, чтобы каждое число <[ г из W[ было в Wi, то к <! s-
Аналогичное доказательство показывает, что 5/, j <з Wj-
Остается показать, что B\j ^r А. Предположим, что
5/, j = [К]л, и придем к противоречию. Выберем га так,
чтобы Rn было A/, j, к)- Предположим вначале, что сущест-
94 18. ВЕТВЯЩИЕСЯ СТЕПЕНИ
вует существенное и-требование. Если к — его индекс, то
[К]А (rw (к)) = Л и rw (к) ЕЕ Bit j. Это противоречит на-
нашему предположению.
Теперь предположим, что нет существенного «-требова-
«-требования. Пусть к0 больше, чем любой индекс и-требования;
пусть г0 больше, чем rw (к) для всех к < к0. Пусть Е —
множество чисел > г0 из строки и. Тогда Е рекурсивн0 и
бесконечно и Е f) Bx j = 0.' Таким образом, г ЕЕ Е ->•
-> тл (г) = л.
Для г ЕЕ Е пусть G (г) — наименьшее число к > к0 из
строки г, большее каждого числа, используемого в вычис-
вычислении [К]А (г); для г ф Е пусть G (г) = 0. Тогда G рекур-
рекурсивно в Л, а если г Fr Е, то G (г) — к удовлетворяет 1) —
4) для всех достаточно больших s. Используя два раза
лемму, получаем, что существует г ЕЕ Е такое, что и
Wi \ W['ir), и Wj \ Wjir) содержат число <[ г. Тогда
для всех достаточно больших s G (г) удовлетворяет 1) —
6). Так как нет существенного и-требовапия, то лет
эффективного n-требовагшя на шаге s для всех достаточно
больших s. Отсюда следует, что создается бесконечно
много требований, что приводит к противоречию, что и
требовалось доказать.
Лахлан показал также, что существует ветвящаяся
степень, отличная от 0; доказательство подобно доказа-
доказательству теоремы 1. Все это приводит нас к выводу, что
для ветвящихся степеней нет простой характеристики.
ДОПОЛНЕНИЯ
ТРИ ТЕОРЕМЫ О СТЕПЕНЯХ
РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ*)
К. Е. М. Ейтс
В связи с работой Поста [8] естественно возникает
вопрос о том, что можно сказать о степени неразрешимости
множества, если наложить на его дополнение некоторые
ограпичепия. Мы предлагаем три результата в этом направ-
направлении: во-первых, существуют полукреативные множест-
множества в каждой непулевой рекурсивно перечислимой степе-
степени; во-вторых, существуют негиперпростые множества
в каждой непулевой рекурсивно перечислимой степени;
в-третьих, существует максимальное множество степени О'.
Все необходимое можно найти в работах, перечислен-
перечисленных в конце статьи, в частности, в [5]. Как это принято,
но отличается от [5], рекурсивно перечислимым множест-
множеством мы называем множество вида
{х | Эг/Г (х, у)},
где Г — некоторый рекурсивный предикат; отсюда следу-
следует, что пустое множество рекурсивно перечислимо. Мы ис-
используем стандартное перечисление рекурсивно перечис-
перечислимых мпожеств /?0, i?!, . . ., где Re = {х | ЗуТ^ («i ?» у)}
для каждого е; положим
Ппе - {х | ЭУукпТг (е, х, у)}
для каждых ей п. По аналогии с определением рекурсивно
перечислимого множества мы будем говорить, что последо-
последовательность рекурсивно перечислимых множеств (Ео,
Еи . . .) рекурсивно перечислима, если существует рекур-
рекурсивный предикат Г такой, что Еп = {х \ ВуТ (п, х, у)} для
каждого п. В частности, последовательность конечных
множеств (Fo, /\, . . .) называется сильно рекурсивно пе-
перечислимой, если существует рекурсивная функция у
такая, что Fn — {х \ Зу [(у (га))у = х + 1]} для всех п,
*) С. Е. М. Y a t e s, Three theorems of the degrees of recursively
enumerable sets, Duke Math. J. 32, № 3 A965), 461—468.
98 К. Е. М, ЕЙТС
где (Z)i есть (i-{-i)-fi показатель степени в капопическом раз-
разложении Zna множители. Известно (см., например, [14]),что
существует рекурсивно перечислимая последовательность
конечных множеств, которая пе является сильно рекур-
рекурсивно перечислимой, и такая последовательность легко
строится. Читатель найдет в [14] определепие простых,
гиперпростых, гипергиперпростых и максимальных мно-
множеств. Далее, степень неразрешимости пазывается рекур-
рекурсивно перечислимой, если это степепь некоторого рекур-
рекурсивно перечислимого множества; степень рекурсивных
множеств обозначим через 0, наибольшая рекурсивно пе-
перечислимая степень обозначается через О'.
1. Полукреативные множества. Среди рекурсивно пе-
перечислимых множеств, которые не являются рекурсивны-
рекурсивными или простыми, имеются так называемые полукреатив-
полукреативные множества, неявно введенные Деккером в [2] при
рассмотрении полупродуктивных множеств: множество
полу креативно, если он® рекурсивно перечислимо, а его
дополнение полупродуктивно. Каждое креативное множе-
множество полукреативно, по как показал Шенфилд в [12], суще-
существуют полукреативпые, но не креативные множества.
Он определил промежуточный тин множеств, которые паз-
вал квазикреативными, доказав, что все такие множества
имеют степень 0', и построил квазикреативное, но не кре-
креативное множество. Здесь мы докажем теорему, из которой
вытекает существование полукреативных, но не квази-
квазикреативных множеств, ответив также отрицательно на
другой естественный вопрос: каждое ли полукреативпое
множество имеет степень 0'? Мы покажем, что каждая не-
ненулевая рекурсивно перечислимая степепь содержит полу-
полукреативное множество. Следующее определение эквива-
лентпо определению, приведенному в [2].
Определепие. Множество S полу креативно,
если оно рекурсивно перечислимо и существует рекурсив-
рекурсивно перечислимая последовательность Ао, Л1;. . . рекур-
рекурсивно перечислимых множеств такая, что для каждого е
ЛесЯ-^Аес5&Ае^ Re.
Нетрудно доказать, что класс множеств не изменится,
если в определении предполагать Ао, Alt ... конечными;
здесь этого не нужно, но доказательство можпо пайти
в [14], теорема 5. Если же мы сделаем дополнительное
ТРИ ТЕОРЕМЫ О СТЕПЕНЯХ 99
предположение, что последовательность Ао, А{, . . . силь-
сильно рекурсивно перечислимая, то получим квазикреатив-
квазикреативное множество, введенное Шенфилдом.
Теорема 1. Если А — произвольное нерекурсивное
множество, то существует полукреативное множество S,
имеющее ту же степень неразрешимости, что и А.
Доказательство. Пусть а — любая 1-1
рекурсивная функция, перечисляющая Л. Строим S как
объединение двух непересекающихся рекурсивно перечис-
перечислимых множеств Si и S%, где St состоит из всех чисел 5х
с х ge А, а 52 состоит из некоторых чисел вида 2е • 3й. За-
Заметим, что Sx той же степени, что и Л, и Л рекурсивно в S.
Это по зависит от степени S». Мы будем добиваться, чтобы
S2 было рекурсивным п А; отсюда будет следовать, что S
той же степени, что и Л, по легко доказываемой теореме,
что степень объединения двух непересекающихся рекур-
рекурсивно перечислимых мпожеечн есть наименьшая верхняя
грань их степеней; доказательство этого можно найти
в [10].
Определим функцию т следующим образом:
( max iz I u(z)<^ и}, если Jz[u(z)^Zu],
х(и)=-\ м
I 0 в противном случае.
Ясно, что т рекурсивна в А, так как а — 1-1 функция.
Положим
Имеем, что ?2 рекурсивно в Л и S имеет ту же степень,
что и А. Чтобы увидеть, что 5.2 рекурсивно перечислимо,
:saмстим, что
2е-3" Ci: 5, <-> 3y3z2>u \2e-3u EF. ПУе&ос (z) < и]
для всех е\\ и. Остается доказать, что S нолукреативпо.
Пусть Тч, — множество 2е-3" для различных и. Если
ЯССЦ S, то Н(, CZ S'., и Lr cz ^2. Элемент из Le может быть
положен в 52, только если он принадлежит Пе. St опреде-
определено так. что L,,CZS,, а значит, ил Л8 с ,? следует
Г'е ь^ >?• Пусть he ci /)'e. Тогда функция
рекурсивна. Если же L? [~] ?? = 0, то по определению
100 К. Е. М. ЕЙТС
5г для всех и имеем т (и) < tye (и) и
) (а (У) = м).
Но тогда бы А было рекурсивным. Значит, Le C? /?е. По-
Последовательность Lo, Llt ... рекурсивно перечислима и,
таким образом, S полукреативно. Теорема доказана.
Приводимое ниже следствие может быть прямо полу-
получено из теоремы 1 из [14] и метода, подобного процедуре
Шенфилда для построения квазикреативного множества,
которое некреативпо.
Следствие. Существует полукреативное мно-
множество, которое не является квазикреативным.
Доказательство. Как показано Шенфилдом,
каждое квазикреативное множество имеет степень 0', по
известпо (впервые это установили Фридберг в работе [3]
и Мучник в работе [7]), что существуют рекурсивно пере-
перечислимые степени, отличные от 0 и 0'.
Интересно отметить, что рекурсивно перечислимое
множество, построенное Фридбергом в работе [3] для ре-
решения проблемы Поста, полукреативпо. Ото обстоятельст-
обстоятельство натолкнуло нас на результат, полученный здесь.
2. Простые множества. Наш второй результат той же
природы и доказан подобным методом. (Ото является про-
простейшим методом, пригодным для доказательства того,что
для данного рекурсивно поречислимого множества А су-
существует нерекурсивное рекурсивно перечислимое мно-
множество В, степень которого меньше степени А. Это ре-
результат, впервые объявленный Мучником в [7], хотя эта
техника была предложена Деккером в [1].) Пост определил
гиперпростые множества и доказал, что простое множество
степени 0', построенное им, не является гипернростым.
Проблема Поста заключалась в нахождении рекурсивно
перечислимых множеств, не имеющих степени 0 или 0'.
Как было, однако, позднее доказано Деккером в [1], каж-
каждая ненулевая рекурсивно перечислимая степень содержит
гиперпростое множество, и, таким образом, в частности,
существуют гиперпростые множества степени 0'. Мы пока-
покажем сейчас, что каждая ненулевая рекурсивно перочис-
лимая степень также содержит простое множество, не яв-
являющееся гиперпростым.
Теорема 2. Если А — нерекурсивное рекурсивно
перечислимое множество, то существует множество S
ТРИ ТЕОРЕМЫ О СТЕПЕНЯХ 101
той же степени неразрешимости, что и Л, которое про-
просто, но не гиперпросто.
Доказательство. Мы знаем из работы Декке-
ра, что можно выбрать А гиперпростым. Пусть а — любая
1-1 рекурсивная функция, перечисляющая А. Строим
S как объединение двух непересекающихся рекурсивно
перечислимых множеств S-^ и 52 таких, что для каждого х
2х Е= 5Х <-> х ее А,
и В — некоторое простое множество, которое будет пост-
построено ниже. Сразу видим, что S — простое множество,
так как если S содержит бесконечное рекурсивно перечне^
лимое подмножество, то по крайней мере одно из Л или В
должно содержать бесконечное рекурсивно перечислимоо
подмножество, что невозможно. Мы будем также доби-
добиваться, чтобы В было рекурсивным в Л, а из этого будет,
как и в теореме 1, следовать, что S имеет ту же степень,
что и А.
Опишем теперь построение В. Пусть дано число е. Сре-
Среди чисел, превосходящих 2е, помещаем в В первое (если
оно есть) число х0, для которого число х ^ ха перечисля-
перечисляется в А, после того как хе перечислилось в Re.
Точнее, пусть
пе = \т (Зх [х ~^> 1с & х > а (п) & х ?Е Д™])>
хе — \ix [х > 2е & х > а (пс) & х <Е= Ree\.
Во-первых, покажем, что если Яе бесконечно, то пе п
х,, существуют. Предположим противное, что для некото-
некоторого е множество Не бесконечно, но такого п пе существу-
существует. Тогда число и принадлежит А в том и только в том
случае, когда оно перечисляется в А перед первым числом,
превосходящим и, которое перечисляется в Rc. Так как
Ле бесконечно, то ото дает нам эффективную процедуру для
решения для каждого числа и вопроса о том, будет это
число в А или нет. Это невозможно, так как А нерекур-
нерекурсивно. Таким образом, пе и, следовательно, хс существу-
существуют, когда Re бесконечно. Но тогда хе помещается в В и оно
уже принадлежит Rc. Итак, В пересекает каждое беско-
бесконечное рекурсивно перечислимое множество.
102 к. е. м. ейтс
Теперь заметим, что из каждого Ве самое большее одно
число помещается в В и, таким образом, из множества Rd
при d < е в В помещаем самое большее е чисел. Так как
из каждого Rd с d ^> e в В помещены лишь числа, превос-
превосходящие 2е, то из первых 2е + 1 чисел по крайней мере
е + 1 принадлежат В и, таким образом, если г0, гх, ... —
элементы В в порядке возрастания, то 2е + 1 > ге для
всех е. Мы заключаем, что В не гиперпросто либо сразу по
теореме 21 из [9], либо с помощью метода Поста из [8].
Отсюда следует, что существует бесконечная сильно ре-
рекурсивно перечислимая последовательность непересе-
непересекающихся конечных множеств Fo, Flf ... такая, что каж-
каждый со член пересекает В и, следовательно, существует
подобная последовательность Fo, Flt ... конечных мно-
множеств, где Fn состоит из чисел лида 2х + 1 с х Е? Fn,
такая, что каждое множество Fn пересекается с S. Итак,
мы доказали, что S — простое, но не гиперпростое мно-
множество.
Наконец, чтобы доказать, что В рекурсивно в А, заме-
заметим, что если число помещено в В, то оно помещается в В,
прежде чем все числа, не превосходящие его и прииадле-
;¦ ащие А, помещаются в А. Точнее: функция
{ max {z| a (z)<Ju}, если 3z[a(z)^u],
U в противном случае
екурсивна в А, так как а — 1-1 функция. Значит,
если и = хе для некоторого е такого, что 2е < ы, то и
помещается в В на шаге п и пе^ т (и). Теорема доказана.
3. Максимальные множества. В поисках рекурсивно
перечислимых множеств, степень которых заключена
строго между 0 и 0', Пост последовательно ввел понятия
простых, гиперпростых и гипергиперпростых множеств.
Как мы уже говорили выше, Пост доказал существование
простых множеств степени 0', а существование гиперпро-
гиперпростых множеств степени 0' следует из более поздней работы
Деккера. Оставшимися кандидатами иметь степень строго
между 0 и 0' были гипергиперпростые множества. Сущест-
Существование таких множеств было показано Фридбергом п [4],
который построил максимальное множество; каждое мак-
максимальное множество, очевидно, пшоргипорпросто. Ниже
мы даже докажем, что существуют максимальные множест-
ТРИ ТЕОРЕМЫ О СТЕПЕНЯХ ЮЗ
ва степени 0'. Заметим, что Сакс в [11] доказал существо-
существование максимальных множеств степени, меньшей О',
а Мартип в [(>], с другой стороны, показал, что гиперги-
перпростые множества содержатся пе в каждой непулевой
рекурсивно перечислимой степени. (В действительности
Мартип доказал, что рекурсивно перечислимая степень а
есть степень максимального множества тогда и только
тогда, когда а' = 0".) Эта очень привлекательная теоре-
теорема может быть использована при выводе всех настоящих
результатов о степенях максималышх множеств, так же
как и новый результат о том, что если а содержит макси-
максимальное множество, то это же справедливо для любой
рекурсивно персчпелимой степени > а.
Мы считаем, что наша конструкция максимального
множества очень естественна, если отвлечься от необхо-
необходимости делать это множество степени 0'; это легко заме-
заметить, если сравнить ее с другими известпыми конструкция-
конструкциями. Метод, который мы применяем, чтобы степень множест-
множества была 0', связан с одним замечанием Теппепбаума в [13].
Пусть Эе (х) — цу7\ (е, х, у) для каждого е и х е Яе.
Если Л/ рекурснвпо_перечнслимо и М бесконечно, а и0,
М], ... — элементы М в порядке возрастания и для каждо-
каждого е имеем их ^> ве (х) для всех х, для которых 0е (х)
определено, кроме конечного числа, то М имеет степень
О'. Тогда множество Se = {х | 3# [у < их & Тх (е, х, у)]}
рекурсивно в М и для каждого е отличается от /?ена конеч-
конечное множество.
О п р с д с л с п и е. Функция ср доминирует функ-
функцию^, если ср (х) определено и превосходит-ф (х) для всех
х, для которых гр (х) определено, кроме конечного числа.
Если ф перечисляет элементы множества Р в порядке
возрастания, то скажем, что Р доминирует \\>. С другой
стороны, если \\> перечисляет элементы множества Q в по-
порядке возрастания, то скажем, что ip доминирует Q. На-
Наконец, если выполняются оба случая, то скажем, что Р
доминирует Q.
Мы теперь докажем, что существует максимальное мно-
множество, дополнение которого доминирует каждую частич-
частично рекурсивную функцию. Таким образом, но замечанию
Тсппенбаума это множество имеет степень ()'. Теорема,
которую мы в действительности доказываем, носит даже
более общий характер.
104 U. E. м. ЕйтС
Теорема 3. Пусть S — любое множество, для кб-
торого существует рекурсивный предикат Г такой, что
S — {х \ Э^Уг/ Г (х, z, у)}. Тогда существует максималь-
максимальное множество М такое, что М доминирует S.
Доказательство. Удобнее строить дополне-
дополнение такого максимального множества. Это дополнение бу-
будет получено как предел убывающей цепи U° э U1 э • . .,
каждое множество в цепи будет рекурсивно. Точнее, мы
покажем, что если ы?, м™, . . . — элементы Un в порядке
возрастания, то ы™ — рекурсивная функция от е и п
и ие -- lim ы™ существует для каждого е.
п
Определим
т? = \it [t < п & Ууу<пТ ((Qo, (Oi, УI
т?+1 - ^ U < п & хпе < (Оо & Уг/„<„Г ((Оо, (Ol »)]•
Мы оставляем читателю доказать, что те = lim т" сущест-
п
вует для каждого е и что если s0, sy, ... — элемепты S в по-
порядке возрастания, то se << те для всех е. Пусть а™ (ж) =
= 22e~z, где суммирование ведется по всем z ^ e таким, что
х ЕЕ i??. Основное свойство а состоит в том, что если
с" (яд) > о? (я2), то а" (жд) > а" (ж2) для всех / > е.
Мы оставляем доказательство этого читателю. Другое,
более очевидное свойство а состоит в том, что ае (х) =
— lim а™ (х) существует для каждого е и х, если мы поло-
п
жим а" (ж) = 0, когда пе существует z <^ e такого, что
х е Яг. Заметим, что по терминологии Фридберга в [4]
а™ (х) есть е-высота числа х на шаге п.
Теперь определим последовательность U°, U1, ...
Положим и°е — е для каждого е, а и™1 определим по ы"
следующим образом.
Случай 1. п четное. Если существует число е та-
такое, что ы" ^ т™, то мы определим
еп = це (м" < т"),
zn = цг (unz > т^п)
и положим u"+1 = w"n+e-en Для всех е > еп, ы"+1 = ц"
ТРИ ТЕОРЕМЫ О СТЕПЕНЯХ Ю5
для всех е<еп. В противном случае положим ие =
= и™ для всех е.
Случай 2. п нечетное. Если существуют числа е
и z такие, что z ^> е и а™ (и™) ^> а" (и™), то определим
еп = [хе Cz[z > е & а? (и?) > а? (ы?)]),
zn - [xz [z > еп & а?п (и?) > а?п (и?пI
и положим ы™+1 — и™ .,?._,. для всех е ]> е„, щ+у = и"
для всех е < еп. В противном случае положим н™+1 -~ ы™
для всех е. Может быть, не очень ясно, почему щ — рекур-
рекурсивная функция от е и п, и следующее замечание поможет
понять это. В случае 1 мы можем определить, будет сущест-
существовать еп или пет, так как т™ ^ п, откуда щ ^ пи, таким
образом, еп<; п; в случае 2 мы можем определить, будет су-
существовать еп или нет, потому что отношение х ?Е /?" мо-
может быть истинным лишь при х < тг и е < и. Мы теперь
заметим, что если ?7°, L'1, ... определена, как выше, то это
убывающая цепь и ее предел будет дополнением мно-
множества М, определенного следующим образом:
хЕ М<-» 3^Vz [z ^ х ->¦ ы™ ^= х].
Так как ы™ —рекурсивная функция от z и и, то множество
М рекурсивно перечислимо.Остается доказать следующие
три леммы.
Лемма 1. М бесконечно.
Доказательство. Так как щ < щ < . . .
для каждого п, пам нужно лишь доказать, что для каждо-
каждого е существует число щ такое, что ие = lim u™. Во-пер-
п
вых, существует шаг п\ такой, что т™ =- тг для каждого
г^еи всех п ]> «е; таким образом, ы™ не меняется в слу-
случае 1 на любом шаге п ^ п\. Во-пторых, мы видим, что
если и* мепяется в случае 2, то должно существовать
г <^ е такое, что а™ (и"+1)~С> о™ («")• Так как существует
лишь конрчное число г ^ е и а™ (я) < 2е+1 независимо
106 К. Е. М. ЕЙТС
от п п от, мы заключаем, что сушсстлуст некоторый шаг п\
такой, что и]! не меняется в случае 2 на любом шаге
п > nl.
Таким образом, ие - lim и" существует.
_ п
Лемм а 2. М доминирует S.
Доказательство. Так как se < тс для всех е,
нам нужно лишь доказать, что те < и для всех с. Но если
м™ <1 т" и и четное, то н"+1 ^> и™, так что при и" = w-e
имеем т" < н"; таким образом, тР < we. Итак, se < ие
для всех е.
Л е м м.а 3. М — максимальное множество.
Д о к а з а т е л ь с т в о. Мы уже показали, что М
рекурсивно перечислимо и М бесконечно. Чтобы доказать,
что М — максимальное множество, мы заметим, что для
каждого е, если uz ЕЕ Яе, то о" (uz) нечетно, а если uz <= ffc,
то о" (и2) четно. Теперь лп.1 утверждаем, что если z ^> z ^> е,
то ое (ы2) <; ос (и-). Р1з лтого следует, что существует чис-
число ze такое, что ос (иг) — ае (uz ) для всех z ^& ze\ таким
образом, Re f] М и Яс С] М ие могут быть оба бесконеч-
бесконечными, и, значит, М — максимальное мпожество. Для до-
доказательства нашего утверждения предположим, что
2>!)>e)i о( (uz) ^> ае (иъ). Тогда существует нечетное
число п такое, что w" — uz, u" = и- и о" (unz) ^> а"(гД).
По ОСНОВНОМУ СВОЙСТВУ О МЫ ВИДИМ, ЧТО Oj («") ^> О^ (м^),
откуда Wj'1 ^> 7/j согласно случаю 2. По это певозможпо,
потому что и| -- i/j, и наше утверждение доказано.
Доказательство теоремы закончено.
Следствие 1. Если Е — любое рекурсивно пере-
перечислимое множество, то существует максимальное мно-
множество М такое, что М доминирует Е.
Следствие 2. Существует максимальное множе-
множество степени 0'.
Доказательство. Пусть sc = max 0r (е) для
всех е, и пусть S --¦- {s,,, .<;,, . ., }. Тогда
S = {у | Зе Зг[ (г < е & 7, (г, е, г/)) &
& Vz^vVr^eTj (г, с, z)]}
ТРИ ТЕОРЕМЫ О СТЕПЕНЯХ 107
и существует максимальное множество М такое, что Ms
доминирует S. Но если и0, щ, . . . — элемепты М в поряд-
порядке возрастания, то для каждого г имеем ие ^> Эг (ё) для
всех е ;> г. Следовательно, по замечаиию Тенненбаума
множество М имеет степень 0'.
Существует более короткий путь построения макси-
максимального множества степени 0', по метод, выбранный нами,
более интересный и позволяет нам получить немного более
общий результат, заключенный в теореме 3; на этот ре-
результат можно смотреть как на наиболее общий, так как
легко показать, что существует множество S такое, что
существует рекурсивный предикат Г, для которого
S = {х | VzlyT (х, z, у)},
и S доминирует каждое множество, которое выразимо в ду-
дуальной форме, в частности, каждое множество с рекурсив-
рекурсивно неречислимым дополнением. Следствие 2 показывает,
что существует максимальное множество, дополнение ко-
которого доминирует каждую частично рекурсивную функ-
функцию. Нетрудно доказать, что дополнение любого макси-
максимального множества доминирует каждую рекурсивную
функцию, а Мартин в [6] доказал, что дополнение любого
гипергиперпростого множества доминирует каждую ре-
рекурсивную функцию, хотя дополнение даже максималь-
максимального множества пе обязано доминировать каждую частич-
частично рекурсивпую функцию, как это следует из результата
Сакса в [11].
Мы заметим, что если дополнение рекурсивно пере-
перечислимого множества доминирует каждую рекурсив-
рекурсивпую функцию, то оно гиперпросто, а по теореме 21 из [9]
рекурсивно перечислимое множество гинернросто тогда
и только тогда, когда его дополнение не доминируется
никакой рекурсивной функцией; с другой стороны,
можно показать, что все результаты этого параграфа оста-
остаются истинными, если «максимальное множество» заменить
па «рекурсивно перечислимое множество с ретрассируемым
дополнением»: как известно из [14], такие множества пе
являются гипергиперпростыми. Также, классифицируя
множество всех номеров максимальных множеств, мы
доказали в [15], что если 0 ¦< а ¦< 0', то существует сте
пень b такая, что b | а и b содержит максимальное множе-
множество; ото обобщает результат Сакса.
108 К. Е. М. ЁЙТС
ЛИТЕРАТУРА
[1] D о к к е г J. С. Е., A theorem on hypersimple sets, Proc.
Amer. Math. Soc. 5 A954), 791—796.
[2] Dekker J. C. E., Productive sets, Trans. Amer. Math.
Soc. 78 A955), 129-149.
[3] F г i e d b e г g R. M., Two recursively enumerable sets of incom-
incomparable degrees of unsolvability. Proc. Nat. Acad. Sci. (U. S. A.)
43 A957), 236-238.
[4]Friedberg R. M., Three theorems on recursive enumeration,
I. Symbolic Logic 23 A958), 309—316.
[5] К 1 e e n e S. C., Introduction to metamathematics, N. Y., 1952.
[Русский перевод- К л и н и С. К., Введение в метаматематику,
ИЛ, М., 1957.]
[6] Martin D. A., A theorem on hyperhypersimple sets, J. Symbo-
Symbolic Logic 28 A9G3), 273-278.
[7] Мучник А. А., Отрицательное решение проблемы своди-
сводимости в теории алгоритмов, ДАН СССР 108 A956), 194—197.
[8] Post E. L., Recursively enumerable sets of positive integers
and their decision problems, Bull. Amer. Math. Soc. 50 A944),
284—316.
[9] R i с е Н. G., Recursive and recursively enumerable orders,
Trans. Amer. Math. Soc. 83 A956), 277—300.
[10] Sacks G. E., Degrees of Unsolvability, Ann. Math. Studies,
No. 55, 1963.
[11] Sacks G. E., A maximal set which is not complete, Michigan
Math. I. 11 A964), 193—205.
[12] Shoenfield J. R., Quasicreative sets, Proc. Amer. Math.
Soc. 8 A957), 964—967.
[13] Tennenbaum S., Degrees of unsolvability and tho rate of
growth of functions, Notices Amer. Math. Soc. E78—128), De-
December, 1961.
[14] Y a t e s С. Е. M., Recursively enumerable sets and retracing
functions, Z. math. Logik Grundl. Math. 8 A962), 331—345.
[15] Y a t e s С E. M., On the degrees of index sets II, Trans. Amer.
Math. Soc. 135 A969), 249—266.
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ
МНОЖЕСТВ*)
А. X. Лахлан
Даппяя статья содержит несколько новых теорем о ре-
рекурсивно перечислимых множествах. Цель этой статьи —
сделать некоторые продвижения в поисках разрешающей
процедуры для элементарной теории рекурсивпо перечис-
перечислимых множеств. Точнее, ищется эффективный метод для
решения того, будет ли произвольное предложение, сфор-
сформулированное в узком исчислении предикатов с единствен-
единственным пелогическим символом с:, истинным для рекурсивпо
перечислимых множеств или пет. Главным достижением
этой статьи является характеризация гилергиперпростых
множеств как тех рекурсивно перечислимых множеств,
имеющих бесконечное дополнение, у которых рекурсивно
перечислимые надмножества образуют булеву алгебру.
Читатель найдет в книге Девиса И] всю основную ин-
информацию о частичпо рекурсивных функциях и рекурсивпо
леречислнмых множествах **). Другие факты, которые
требуются для понимания дайной статьи, находятся в [8],
[3], теорема 2, [10], введение и § 4, и [5]. Мы используем
вариант узкого исчисления предикатов, даппый А. Робин-
Робинсоном в [9].
Натуральные числа будут обозначаться малыми латин-
латинскими буквами, множества натуральных чисел — малыми
греческими буквами. Пустое множество обозначим че-
через 0, а множество всех натуральных чисел — через v.
Дополнение множества а обозначим через ос'; а называется
коконечным или кобескоиечным в том случае, когда а' ко-
конечно или бесконечно соответственно. Для множеств ос, |3
мы пишем ос~Р, если множество (ос\|3) \J (Р\ос) конеч-
конечно; в противном случае пишем ос =?¦ |3. Под функцией мы
*) А. 1]. L а с h I a n, On the lattice of recursively enumerable
sets, Trans. Amor, Math. Soc. 130, № 1 A968), 1—37.
**) Советскому читателю можпо рекомендовать кпигу: Х.Род-
Х.Роджерс, Теория рекурсивных функций и эффективная вычис-
вычислимость, «Мир», М., 1972.— Прим. ред.
НО Л. X. ЛАХЛАН
понимаем отображение некоторого подмножества множе-
множества v X v X ... X v в v; функции и отношения па нату-
натуральных числах будем обозначать большими латинскими
буквами. Будем применять следующие логические сим-
символы: \/, &, —>-, ~~\, \fx, 3^i *->, которые будем соответ-
соответственно читать как «или», «и», «следует», «не», «для всех х»,
«существует хч>, «эквивалентны». Пусть Л — некоторый
конечный класс предложений; тогда &.Л, \/ А обозначают
их конъюнкцию и дизъюнкцию соответственно. Мы будем
применять обозначение {А (х) \ В (х)} для класса объектов
А (а), для которых В (а) выполняется. Если а — конечное
множество натуральных чисел, то через sup а будем
обозначать наибольший элемент множества а; в против-
противном случае sup а будет оо.
План статьи таков. В первом параграфе мы немного
поговорим об элементарной теории рекурсивно перечпе-
лимых множеств и докажем, что ее проблема разрешения
имеет ту же степень, что и элементарная теория решетки
классов эквивалентности рекурсивно перечислимых мно-
множеств относительно с?.. В § 2 мы докажем основную тео-
теорему: если а — рекурсивно перечислимос подмножество
рекурсивно перечислимого множества f>, -m либо существу-
существует рекурсивное подмножество 8 множества р* такое, что
a U б = Р, либо существует рекурсивная последователь-
последовательность {6;} попарно непересекающихся конечных подмно-
подмножеств Р такая, что 6г \ а Ф 0 для всех г. Эта теорема
навеяна рефератом Майхилла [7] на статью Ейтса [10].
Ейтс доказал в [10], что если ц.15 . . ., цп — максимальные
множества такие, что любые два таких множества отли-
отличаются друг от друга на бесконечное множество, то любой
класс попарпо непересекающихся рекурсивно перечис-
перечислимых множеств, каждый член которого имеет бесконеч-
бесконечное перечисление с (u.x f] . . . f] u.n)', имеет мощность <^ п.
Майхилл в своем реферате ввел понятие накрывающего
числа, где накрывающее число множества ос есть
sup {мощность 3( | 51 — класс попарно непересекающихся
рекурсивно перечислимых множеств, имеющих
бесконечное пересечение с а}.
Майхилл предположил, во-первых, что рекурсивно пере-
перечислимое множество максимально тогда и только тогда,
когда накрывающее число а' равно 1, и, во-вторых, что
РЕШЕТКА РЕКУРСИВНО ПЕГЕЧИСЛИМЫХ МНОЖЕСТВ
рекурсивно перечислимос множество гипергиперпросто
тогда и только тогда, когда накрывающее число а' конеч-
конечно. Ни одно из этих предположений не было подтвержде-
подтверждено. Результат Ейтса, приведенный выше, можно перефор-
переформулировать следующим образом; если \ix, . . ., цп — мак-
максимальные множества такие, что любые два таких множе-
множества отличаются друг от друга на бесконечное множество,
10 (Hi П ¦ • ¦ П Ил)' имеет накрывающее число п. Из ос-
пошюй теоремы мы доказываем обращение результата
Ейтса, что при n=d подтверждает первое предположение
Мамхилла. Другим следствием основной теоремы являет-
является следующая характеризация гипергиперпростых мно-
множеств: рекурсивно перечислимое множество гипергипер-
гипергиперпросто тогда и только тогда, когда a [J Р' — рекурсивно
иоречислимое множество для каждого рекурсивно пере-
чпелкмого множества р. Отсюда следует, что пересечение
двух гипергиперпростых множеств также гипергиперпро-
гипергиперпросто. Таким образом, с каждым гипергиперпростым мно-
множеством а мы можем связать булеву алгебру, образован-
образованную из решетки рекурсивно перечислимых надмножеств
множества ос; эту решетку обозначим через X (а), а решетку
классов эквивалентности рекурсивно перечислимых над-
надмножеств множества а относительно ~ — через X* (а).
В § 3 мы докажем ложность второго предположения
Маихилла с помощью построения гипергиперпростого
множества т), которое не имеет максимальных надмножеств.
В действительности множество т) обладает следующим
свойством: если |3 — любое рекурсивно перечислимое
надмножество множества т), то существуют рекурсивно
иерсчислимые надмножества (^ и C2 мпожества т| такие, что
Pi U Рг = P. Pi П Рг = Л* и такие, что
(Pi ~ т) V Рг ^ Л) -*¦ Р ^ Л-
Это свойство характеризует X (г\).
В § 4 метод построения множества т) из § 3, который сам
получен из проведенного Фридбергом в работе [3] построе-
построения максимального множества, приспосабливается для
следующей харлктеризацип булевых алгебр, связанных
с гиперпшерпростыми множествами. Пусть 7? — бинарное
3V9-oTiionieHHe, т. е. пусть существует рекурсивное
отношение S такое, что
R (х, у) <-> ^idv^wS (х, у, и, v, w).
112 A. X. ЛАХЛАН
Предположим также, что R рефлексивно и транзитивно.
Рассмотрим класс множеств А = {а0, а1} . . . }, где
at = {х | R (х, i)&R (i, x)},
и определим <; па А так:
а* < «j<-> Я (f. /)•
Класс Л частично упорядочивается отношением ^, так
как R рефлексивно и транзитивпо. При некоторых Я
класс А, частично упорядоченный отношением ^, обра-
образует булеву алгебру, т. е. А — дистрибутивная решетка,
имеющая наименьший элемент и наибольший элемент и
такая, что каждый элемент имеет дополнение. Всякая
такая булева алгебра называется 3\^гН>улевой алгеброй
при условии, что существуют рекурсивные функции U, V
такие, что для всех х и у
ЯЩх,у) — «я U al/> aV(x,y) = «ж П аУ
Мы покажем, что если а гипергиперпросто, то Ж* (а)
изоморфна ЭУЭ-булевой алгебре, и, обратно, если А
есть ЭУЭ-булева алгебра, то существует гипергиперпро-
стое множество а такое, что X* (а) изоморфна А.
В § 5 обсуждаются некоторые проблемы, связанные
с простыми и гипергиперпростыми рекурсивно перечис-
перечислимыми множествами. Здесь доказано, что если а — любое
нерекурсивное рекурсивно перечислимое множество, то
существует рекурсивно перечислимое подмножество р
множества а такое, что а \ р бесконечно, но для любого
рекурсивно перечислимого дополнения ш множества а
имеем р U и ~ v. Из этого факта и основной теоремы
получается результат, контрастирующий с результатом
Мартина в [5]; строится рекурсивно перечислимое множе-
множество, которое кобесконечно, но которое не имеет гипер-
гиперпростых надмножеств. Мы также построим г-макси-
мальное множество, не имеющее максимальных надмно-
надмножеств. Под г-максималъиым множеством мы понимаем
кобесконечпое рекурсивно перечислимое множество такое,
что для каждого рекурсивного множества р либо р f] a',
либо р' (~) а' конечно. Это является контрпримером
к предположению Р. Робинсона в [101 о том, что каждое
r-максималыюе множество имеет максимальное надмно-
надмножество.
[РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ ЦЗ
Наконец, в § 6 мы упомяпем пекоторые проблемы отпо-
сительпо элементарных свойств рекурсивно перечислимых
множеств, которые кажутся интересными и которые до-
доступны пастоящим методам.
1. Элементарная теория рекурсивно перечислимых мно-
множеств. Будет использоваться терминология и формальный
язык L книги А. Робинсона [9]. Однако этот язык L будет
применяться только для решеток X. Какие решетки будут
применяться, будет ясно из контекста. Индивидуальные
символы L будут поставлены в 1-1 соответствие С с эле-
элементами X, имеется также один 2-местный предикатный
символ Q (•, •)• Символы переменных L будут х1, х2, . . ¦
Кроме того, мы встретимся лишь с одной семантической
интерпретацией L, а имеппо, с той, в которой встречается
решетка X, индивидуальные символы интерпретируются
с помощью отображения С, a Q (•, •) означает отношение
включения на X. Далее, под предложением мы будем по-
понимать предложение, не содержащее индивидуальных
символов, а под предикатом — предикат без индивиду-
индивидуальных символов.
Пусть X—любой предикат и а„ . .., о„— ипдивидуаль-
пые символы, тогда X (%, . . ., ап) обозначает правильно
построенную формулу, полученную подстановкой аг, . . .
. . ., ап вместо хг, . . ., хп в X. Пусть R — некоторое
n-местноо отношение па X. Будем говорить, что предикат X
определяет R, если никакая переменная хп+1, ;г„+2, ... не
входит свободпо в X и для любых индивидуальных симво-
символов alt . . ., ап формула X (аг, . . ., ап) выполняется в X
тогда и только тогда, когда 7? (а*, . . ., а*), где ах, . . ., ап
соответствуют элементам а*, . . ., а* из X, Отношение
па X назовем элементарным, если существует предикат,
определяющий это отношепие.
Предположим, что задана некоторая гёделева нуме-
нумерация всех правильно построенных формул L.
Обозначая решетку рекурсивно перечислимых мно-
множеств через J?, определим некоторые отношения на Л:
In (х, у, z) <-> х Г) у = z,
Un (.г, у, z) <->¦ х U у = 2,
Emp (х) <-•> х = 0, АП (х) <-¦> х = v,
Rec (x) *-* х рекурсивно,
114 A. X. ЛАХЛАН
Fin (л) <-> x конечно,
Sim (х) <-> х просто,
Мах (х) <-* х максимально.
Каждое из этих отношений элементарно. Для первых
четырех соответствующие предикаты следующие:
Q (*з> *i) Л Q (хз> ъ) Л
Д V^4 [Q (*4, a,) /\ Q (хЛ, а,) -> Q (*4, xa)],
Q (*i. аг3) Л Q (*г. Хз) Л
/\ V^4 [Q (a-i, *a) A Q (^2, a,) — (? (x3, j4)],
V^2<? (a:lt a-2), V^2<? (^2. ^i)-
Мы можем построить соответствующие предикаты для ос-
оставшихся отношений, используя эквивалешпосш:
Rec (х) <-> 3y3z^w [In (а1, у, z) & Un (.г, г/, м;) &
& Emp (z) &Л11 (?r)],
Fin (ж) ^Vy[^(y,*)-^Poc(j/)],
Sim (.г) <-> VyVz [Emp (z) & In (jr, y, z) -*- Fin (//)],
Max (a) <-> Vf/3z3w [<? (a;, /y) -- [Fin B) & All (и>) &
& [Un (x, z, y) V Un (z, [/, »)]]].
Под проблемой разрешения для 2! мы будем понимать про-
проблему решения того, будет ли произвольное предложение
из L выполняться в X или нет. Точнее, мы определим про-
проблему разрешения рля X как степень неразрешимости
d (X) множества
D (X) = {х | х — гёделев номер предложения,
выполняющегося в X}.
Мы скажем, что проблема разрешения для X раз-
разрешима, если d (X) = 0, где 0 — степень рекурсивного
множества. Мы скажем, что проблема разрешения для X
сводима к проблеме разрешения для .//, если d (X) «^
< d (.#).
Как видно, из вышеприведенных элементарных отно-
отношений иг. Л, доказать разрешимость проблемы разрешения
для Я, по-видимому, непросто. Даже существование мак-
максимального множества не является тривиальным фактом.
С другой стороны, если Л имеет неразрешимую проблему
РЕШЕТКА РЕКУРСИВНО ПКРЕЧЙСЛИМЫХ МНОЖЕСТВ, Ц5
разрешения, то, чтобы доказать это, мы должны собрать
значительно больше информации про элементарные свой-
свойства рекурсивно перечислимых множеств, чем у нас
имеется сейчас.
Через Ж будем обозначать решетку всех подмножеств
множества натуральных чисел, и пусть X — произвольная
подрешетка решетки J/'. Предположим далее, что X замк-
замкнута относительно добавлений и вычитаний конечных
множеств, т. е. если ft, из X и \|) — конечное множество,
то ft, [J г|з и ft, \ г|з также принадлежат X. Обозначим через
X* решетку, элементами которой являются классы экви-
эквивалентности элементов X относительно отношения ~.
Будет доказано, что проблема разрешения для X может
быть сведена к проблеме разрешения для X*.
Теорема 1. Если X с JT и X* С Ж*, то проблема
разрешения для X сводима к проблеме разрешения для X*.
Доказательство. По условиям теоремы X
замкнута относительно добавлений и вычитаний конечных
множеств. Мы предположим в дальнейшем, что X содер-
содержит v и 0; в конце доказательства мы укажем, какие из-
изменения нужно сделать, когда v или 0 пет в X.
Пусть у обозначает и-ку ylt . . ., уп переменных,
область значений которых есть X. Пусть х = {1, 2, . . ., п)
и для каждого подмножества t множества х через у (i)
обозначим
Для каждого натурального числа т пусть Сп, С>т обо-
обозначают отношения па X, определенные следующим обра-
лом:
Ст (у) *-* У имеет мощность т,
С>т {у) <-* У имеет мощность > т.
Под п-местным А-отношением мы будем понимать п-мест-
поо отношение R па X такое, что R (у) эквивалентно
& {С, (у @) |icx}, A)
где каждое С\ имеет один из видов Ст, С>т или ложно.
Под п-местным В-отношением мы будем понимать п-мест-
ное отношение R на X такое, что R (у) эквивалентно
S {{у}), где 5 — n-местное отношение на X* и {г/} означает
п'кУ {г/Л. • • •. {г/n}; здесь {yi} — элемент X*, которому
116 A. X. ЛАХЛАЙ
принадлежит yt из X. Определим В-отношепие, соответ-
соответствующее А-отпошепию A), так:
& {Л({у}) hex}, B)
где /\ ложно, если Ct ложно, /'\ истинно, если Ct имеет
вид С>т, и /\ (z) есть
n{«il*ei}c=U{2/l'ex\i} C)
в остальных случаях. Левая часть этого последнего вклю-
включения будет {v}, если i —- 0; правая часть этого включе-
включения равна {0}, если i =- х. Заметим, что C) выполняется
для z — {у} тогда и только тогда, когда у (i) конечно.
Заметим также, что из A) следует B).
Под п-местпым ЛВ-отнсшением мы будем понимать
«-местное отношение R на X такое, что Я эквивалентно
\y{Al(y)&Bl(y)\i = O,i,...,p}, D)
где каждое А( есть Л-отношение и каждое Bi есть В-очио-
шение. Заметим, что любое n-местное Л-отношение есть
н-местисе Л/?-отноп1ение, то же самое справедливо для
n-местною ^-отношения.
Мы вводим гёделевы номера для Л-отношений так,
чтобы по ним можно было эффективно найти гёделевы
номера всех отношений 6\ в A), и наоборот. Число е
назовем гёделевым номером 5-отношения, если правильно
построенная формула языка L с гёделевым номером е
определяет соответствующее отношение на <?,*. Мы вводим
гёделевы номера для ЛБ-отношений так, чтобы но ним
можно было эффективно найти р и гёделевы номера
Ао, . ¦ ., Лр, Во, . . ., Вр в D), и наоборот. Теперь, когда
мы скажем, что «дано Л-отношение, #-отношение или
¦4#-отношенне», мы будем иметь в виду его гёделев но-
номер, а когда скажем, что можно эффективно найти А-от-
ношение, 5-отношение или Л^-отношение, то будем
иметь в виду, что можем эффективно найти его гёделев
номер.
Теперь мы изучим некоторые свойства класса АВ-от-
ношений. Ясно, что но двум данным Л5-отношениям мож-
можно эффективно найти их дизъюнкцию как Л^-отношение.
Докажем, что конъюнкция Л#-отношений может быть
эффективно найдена как Л^-отношение. Пусть R1 (у)
РЕШЁТКА РЕКУРСИВНО ЛЕРЕЧИСЛИМЫХ МНОЖЕСТВ Ц?
(при j -- 0, 1) эквивалентно
V Ш(у) & Щ (у) \i =-0,1,. . .,pJ},
где А\ — Л-отношения, В{ — /i-отношепия. Теперь
R0 (у) & R1 (у) эквивалентно дизъюнкции всех выражений
вида
Л% (у) & В% (у) & А\ (у) & И\ (у); 0 < g < р»,
Таким образом, ясно, что достаточно доказать, что по
двум Л-отношониям можно эффективно найти их конъюнк-
конъюнкцию как Л-отпошепие. Пусть для / — 0, 1 имеем
А'(у)<->& {С[ (у @) | i ? х},
где С?, С\ из A). Легко видеть, что Л° (г/) & Л1 (г/) экви-
эквивалентно A) при Си выбранных следующим образом.
Если СЧ, С\ представляют собой Ст, Ск соответственно,
то пусть d есть Ст, если т = Л, и тождественно ложно
н противном случае. Если С?, Ci представляют собой Ст,
С-л соответственно, то пусть Ct есть Ст, если т > Л;
то/кдественно ложно в противном случае. Если Ci, С\
представляют собой С^т, С^ соот)(етственно, то пусть
d есть С>тах(т,(Л Наконе}!;, если одно из СЧ, С\ тождест-
тождественно ложно, то пусть С тождественно ложно.
Отрицание D) может быть записано так:
& С\А< (У) V ~'\Bt (у) | i = 0, 1, . . ., р). E)
Для того чтобы эффективно найти E) как Л/i-OTHonie-
ние, достаточно показать, что по данному Л-отпошению
можно эффективно найти его отрицание как Л#-отношонио
и по данному .й-отпошепию эффективно найти его отри-
отрицание как ii-отношение. Последнее замечается сразу.
Теперь рассмотрим Л-отпошение A); его отрицание есть
дизъюнкция выражений вида ~| Ст (у (а)), " ] С>т {у (а)),
где т — натуральное число и a cz x. Мы можем опустить
случай, когда d. тождественно ложно, потому что истин-
истинное отношение мы можем заменить на С^о в A). Теперь
для т ^> 0
П Ст -> Wo V Сг V • • • V Ст-1 V
H8 A. X. ЛАХЛАН
и
k>m <-> It^о у ^1 V • • • V ^m-iJ'
Также 1 Со эквивалентно C>j и ~] С>0 тождественно лож-
ложно. Таким образом, достаточно показать, что для дан-
данного тиаСк можно эффективно найти Л-отношение R
такое, что R (у) эквивалентно Ст (у (а)), С^т {у (а)).
Для Ст (у (а)) надо взять конъюнкцию 6\, где С\ есть
С>0 для l Ф а и С а есть Ст; для С>т (г/ (а)) надо взять
конъюнкцию С, где Счесть С>0 для i ^= а и Сл есть С^^.
Итак, отрицание Л#-отношения есть Л5-отношение, ко-
которое можно найти эффективно.
Рассмотрим (п + 1)-местпое Л^-отношепие R. Можно
предположить, что И (у, z) *) есть
\/{Ai(y,z)&Bi(y, z)|* = 0, I, . ..р},
где Л г — Л-отношение, В; — /J-отнотение для 0 ^ i ^ р.
Докажем, что ^zR (у, z) можно выразить в виде D).
Так как квантор существования распределяется по дизъ-
дизъюнкции, то достаточно рассмотреть лишь случай р — 0.
Таким образом, предположим, что 7? (г/, z) есть Л (г/, z) &
& В (у, z), где Л — Л-отношепие, В — /i-отношение;
также предположим, что В (у, z) влечет /^-отношение,
соответствующее Л. Это не ограничивает общности, так
как А влечет Ti-отношение, ему соответствующее. Пусть
Л (у, z) имеет вид
& {с° (у (О п *). с\ (у (О п *') 11 e «)•
Мы определим и-местпое Л-отношение Л° следующим
образом. Если С?, С\ есть С^, Ск соответственно, то пусть
Ct есть Cmik. Если С?, С[ представляют собой С^.т, Cfc
или С-^тп, С^к в некотором порядке, то пусть С есть C>m+)j.
Если одно из С°, Cl тождественно ложно, то пусть CV тож-
тождественно ложно. Докажем, что
3z R (у, z) «-> [Л° (у) & 3z Д (у, z)]. F)
Слева панраво легко; нужно лишь заметить, что
(у (О П г) U (у @ П *') = »(О,
Здесь у — n-ка i/j, . . ., уп, а 2 — переменная. — Прим. ред.
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ Ц9
так что сумма мощностей у (i) f] z и у (i) f] z' равна
мощности у (i). Предположим теперь, что правая часть F)
выполняется для уг = щ, . . ., уп = юп в X и пусть
v — элемент X такой, что В (о>, и). Для каждого i мы опре-
определим конечные подмножества ср,,, i|it множества (о (i) та-
такие, что если о,, = (о \ <pt) U ifi, то С0 (ю (i) f] ut) и
С1 (со (i) П »i)- Есди С?, С[ есть Cm, Ск, то из A0 (со)
имеем Ст+к (to (i)). Пусть i|)t состоит из т наименьших
членов о) (i), a q\ состоит из к оставшихся членов. Если
С?, С\ представляют собой С^т, Ск, то из А0 ((о) имеем
C>m+s («* @)- Так как 5 влечет й-отношеиие, соответ-
соответствующее Л, vi С\ есть Ск, имеем по C), что 0) (i) (~) и'
конечно. Пусть ф^ состоит из к наименьших членов (о (i)
и ij)t = (о (i) f~| и' П ф,,. Если С°ь, С\ есть Ст, С>к, то мы
имеем C>m+(c (ft) @) и (о (i) f] u конечно. Пусть я|\ со-
состоит из m наименьших членов а> (i) и фь = (о (i) f] и.
Если C°lt C\ представляют собой C>m, C»f, to из Л° ((о)
имеем C^m^jc ((о @). Пусть ф! состоит из m -|- к наимень-
наименьших членов (о (i) и i^t состоит из т наименьших членов
со (i). Это полное определение ф1 и i|),, для всех i cz и.
Положим
«° = (о \ и(ф^ Il ^ «}) U U W>i Il s «}•
Так как все множества to (i) попарно непересекающиеся,
то (о @ f| u° = (о (i) f| ut. Таким образом, С? ((о (i) f") u°)
и С\ ((о (i) p| (о0)') для всех i с х, которые означают, что
Л ((о, о0). Так как »° только па конечное число элементов
отличается от и, мы имеем В ((о, и0). Таким образом, левая
часть F) выполняется для у = (о. Если (и + 1)-местное
отношение 5* на X* индуцирует отношение В на X, то
и-местное отношение на X*, выражаемое формулой
¦ЦгВ* (у, z), индуцирует n-местное отношение на X, выра-
выражаемое формулой 3z# (у, z). Таким образом, мы нашли
и-местное ЛБ-отношение S такое, что JzR (у, z) эквива-
эквивалентно S (у).
Итак, мы показали, что класс ?г-местпых Л/?-отнол10пий
эффективно замкнут относительно V» ^> i» a также что
применение квантора существования отображает класс
(п + 1)-местных Л5-отпошений в класс и-местных
Л?-отношений,
120 Л. X. ЛАХЛАН
Пусть X — любое предложение. Покажем, как найти
предложение X* такое, что X* выполняется в X* тогда
и только тогда, когда X выполняется в X. Можно считать,
что X записано в пренекспой нормальной форме и имеет
вид
где Y — предикат, не содержащий кванторов, и его пере-
переменными являются лишь х2, • . •, хк. Рассмотрим любой
подпродикат предиката Y: он построен из Q (xt, х}) с по-
помощью &, \/ и |. Q (xt, Xj) определяет fc-местное Л-от-
ношепие, полученное так: надо взять Со вместо С, если i
содержит г, но не содержит /, и С^о вместо Ct в остальных
случаях. Далее, если Yj,Y2 — подпредикаты предика-
предиката Y, определяющие Л#-отпотения Нг и R2, то [У, \/ Y2],
[Уг & У2], [~1 Y^] определяют Л5-отношения R1 V R^
Rt & R2, ~] Rt. Таким образом, применяя описанную
выгае процедуру, можно эффективно найти по X АВ-олю-
шепие, определенное Y. Назовем это отношение R. Далее
эффективно находим Л5-отношоние S такое, что
s (у) <-> Зг/2П Зг/зП • • • П ЗУ* R (у, уг, ¦ ¦ ¦, ук)-
По определению Л^-отношения существуют Л-отношения
Л,- и элементарные отношения 7?j па X* такие, что S (у)
эквивалентно
\/{Ai(y)&Bt({y})\i^O,l,...,p). G)
Мы зпаом, что S (у) не зависит от у, потому что Y не со-
содержит хх. Таким образом, X выполняется в X, только
если выполняется S @). Для каждого i можно эффективно
решить А-, @). Также для каждого i можно эффективно
найти предложение, которое выполняется в X*, только
если В* ({0}) выполняется в X*, потому что отношение
z = {0} элементарно на X,*. Таким образом, для данного
гёделева номера предложения X мы можем эффективно
найти гёдолев номер предложения X*, которое выполня-
выполняется в X*, только если X выполняется в X.
Доказательство теоремы закончено. Рассмотрим слу-
случай, когда 0 или v не принадлежит X. Если 0 не при-
принадлежит X, то мы ограничим Ск в A) либо С>0, либо
тождественно ложным отношением; если v не принадле-
принадлежит X, то мы ограничим С» в A) либо С>0> либо тождест-
Решетка рекурсивно перечислимых множеств 121
пенно ложным отношением; если и 0, и v не принадле-
принадлежат X, то мы сделаем оба ограничения. Сделаем соответ-
соответствующие изменения в определении А0 в F). В последнем
абзаце мы также сделаем следующие поправки, если
0 отсутствует в X. Если v есть в X, то вместо 0 подстав-
подставляем v. Если 0 и v отсутствуют в X, то вследствие нало-
наложенных ограничений каждое Аг в G) тождественно ис-
истинно или тождественно ложно. Мы все же можем найти X*
эффективно, так как X выполняется в X, только если
V {3z#f (z) | 1 < i < p & Ai истинно}
выполняется в X*.
Вышеприведенное доказательство представляет собой
непосредственную элиминацию кванторов. Используя ту
же технику в случае, когда X — булева алгебра, можно
доказать, что элементарные отношения на X являют-
являются дизъюнкциями Л-отпошений и, следовательно, X имеет
разрешимую проблему разрешения. Это объясняет, по-
почему не существует интересных элементарных свойств
решетки рекурсивных множеств.
Из нашей теоремы мы видим, что исследование элемен-
элементарной теории Я можно ограничить изучением элементар-
элементарной теории Я*.
Если X cz j\r и X* cz Ж*, можно доказать обращение
теоремы 1, т. е. что проблема разрешения для X* сводит-
сводится к проблеме разрешения для X, предположив, что отно-
отношение ух са у2 есть элементарное отношение на X. Для
данной формулы X*, определяющей элементарное п-мест-
ное отношение R* на X*, можно эффективно найти фор-
формулу X, определяющую отношение R на X, где R (у)
эквивалентно R* ({ух}, . . ., {уп})- Доказательство про-
проводится индукцией по длине X*. Вначале рассмотрим
случай, когда X* имеет вид Q (xu Xj); тогда в качестве X
возьмем формулу, определяющую n-местное отношение
R на X такое, что R (у) есть г/г f] yj ~ г/,. Мы можем
найти такую X, потому что отношение ~ элементарно
на X по предположению. Индуктивный шаг доказывается
сразу: в качестве соответствующих формул для X* & Y*,
X*\/Y*, X*Z)Y*, ~]X*, 3xtX*, Vxt X* возьмем
X&Y, X\/Y, XZJY, ~\X,qxi X, Vxt X, где форму-
формулам X*, Y* соответствуют формулы X, Y. Ясно, что для
любого предложения X* мы имеем, что X* выполняется
122 A. X. ЛАХЛАН
в X* тогда п только тогда, когда соответствующее пред-
предложение X выполняется в Ж.
2. Основная теорема, накрывающие числа, характе-
ризация гипергиперпростых множеств. Введем понятие
гипергиперпростого множества и максимального множе-
множества относительно данного рекурсивно перечислимого
множества следующим образом. Рекурсивно перечисли-
перечислимое множество а назовем гипергиперпростым в его ре-
рекурсивно перечислимом надмножестве р\ если р \ а
бесконечно и ire существует рекурсивной последователь-
последовательности попарно непересекающихся конечных подмножеств
множества C, каждое из которых пересекается с р \ о.
Подобным образом, а назовем максимальным в его рекур-
рекурсивно перечислимом надмножестве р, если р \ а беско-
бесконечно и если не существует рекурсивно перепислимого
множества у такого, что у \ а и р \ у бесконечны и
Теорема 2. Если а, р — любые рекурсивно пере-
перечислимые множества и a cz p\ то либо существует ре-
рекурсивное мноокестсо 6 такое, что a \J 6 = р, либо а не
гипергиперпросто в р.
Доказательство. Доказывать будем методом,
применяемым Фридбергом в [4] и позднее Ейтсом в [11].
Пусть R — трехместный рекурсивный предикат. Опре-
Определим функцию S:
S (х, у) = sup {г | 3«u<* Vi>»<2 Зи>«><у R (и, v,w)}.
Заметим, что для некоторых х и у мы можем иметь
S (х, у) = оо и что отношение х~^> S (у, z) рекурсивно.
По данному R мы строим рекурсивную последователь-
последовательность {б;} рекурсивно перечислимых множеств одновре-
одновременным перечислением но шагам 0, 1, ... Эффективно
перечисляем множества аир. Пусть а;, Pj б,-,; — конеч-
конечные мпожества, которые перечислены в а, р\ бг к концу
шага ;.
Шаг 0. Ничего не делаем.
Шаг у + 1. Пусть е — наимепыпее i из тех, для ко-
которых 6(,j \ а; пусто и Pj содержит число ^> S (г, /),
которое не лежит в a,- (J {8Xtj \ х > 0}. Если такое е
существует, то добавляем наименьший элемент из
(pj П {х | х > S (e, j)}) \ (a, U U (8*,; I * > 0})
в бе. В противном случае ничего не делаем.
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 123
Ясно, что данная конструкция по любому трехместному
предикату R порождает рекурсивную последовательность
{б,}попарно непересекающихся рекурсивно перечислимых
подмножеств множества р.
Лемма 1. Если JxVyJz R (х, у, z) выполняется,
то U {&х | х > 0} рекурсивно или существует рекурсив-
рекурсивное подмножество б множества ft такое, что a \J б = р.
Доказательство. Пусть е — наименьшее чи-
число такое, что Vyjz R (е, у, z). Тогда по определению S
имеем lim S (e, z) = оо. Также из определения S имеем,
2
что S (е, х) не убывает по х, и для любого у > е мы имеем
S (у, х) > S (е, х). Значит, множество а = \J {бж | х !> е}
рекурсивно, потому что по построению число может по-
попасть в а после шага /, только если оно ^>S (е, /)• Если
Р \ (а U а) бесконечно, то бесконечное число членов из
р \ а становятся и остаются пригодными для перечисле-
перечисления в б0, бц . . ., бс_а. Таким образом, каждое из б0, Ьи ...
. . ., 6P_j будет содержать член из р \ а и, значит, будет
конечным. Отсюда вытекает, что (J {бл. | х > 0} рекур-
рекурсивно. Однако, если р \ (a (J о) конечно, то, положив
^ = а U (Р \ (а U а))' видим, что б рекурсивно и
а U б = р. Доказательство леммы закончено.
Возвращаясь к доказательству теоремы, мы теперь
докажем, что для любой данной рекурсивной последова-
последовательности {е;} попарно непересекающихся множеств мож-
можно эффективно найти трехместное рекурсивное отноше-
отношение R такое, что
3*V?/3z R (х, у, г) « Р \ (a U е.„ U ?i U • • •) конечно.
(8)
По {ег} можно эффективно строить сильно рекурсивно
перечислимую двойную последовательность {е;,,} конеч-
конечных множеств такую, что {ег-,,} не убывает по / для фик-
фиксированного i, и такую, что lim ег,ж = ег- для каждого i,
X
Имеем
Р \ (a U е„ U Ej U . . . ) конечно <->
~ &Vy \у < х V у е (а и е„ U ei U • • ¦) V у ¦'? Р1 ^
^ \у < х V У С~ (а,„ U eolto U • • • U е"',№) V
V
124 A. X. ЛАХЛАН
Пусть Р и Q — одноместпые рекурсивные функции такие,
что (Р @), Q @)), (РA), <? A)),...— перечисление всех
упорядоченных пар патуральпых чисел. Тогда последнее
условие запишется так:
ЗхУуЗг [Р (у) < я V Р (У) е
е (аг U ев, г U elt г U • • •• ег, г) V Р (у) U РосУI-
Отношение внутри квадратных скобок рекурсивно и его
можно выбрать в качестве R (х, у, z).
Комбинируя эти две конструкции, мы получаем эф-
эффективную операцию, отображающую все рекурсивные
последовательности {е,} попарно непересекающихся мно-
множеств в рекурсивные последовательности {8;} попарно
непересекающихся подмпожеств р. Точнее, если Е — ча-
стичпо рекурсивная функция, определенная формулой
Е (х) = у ^ х СЕ ?,„
и D — соответствующая частично рекурсивпая функция,
определенная по {б;}, то номер D может быть найден эф-
эффективно по номеру Е. По теореме о рекурсии Г Я мы мо-
можем выбрать {е,} так, что {6,} — {е,}. Возвращаясь к до-
доказательству теоремы, предположим, что {g,} так выбрана.
Тогда имеются две возможности. Во-первых, мы можем
иметь 3^V.v3z R (х, у. z). тогда либо теорема следует не-
немедленно, либо IJ {8,. | х ;> 0} рекурсивно. Но из (8)
мы видим, что р \ (а {) б„ ¦ J 6-, [) . . .) конечно. Таким
образом, всегда, когда JxVyJz R (х, у, z), существует
рекурсивное подмножество б множества Р такое, что
а {) б = р. Во-вторых, может случиться, что
Vx^yVz['^,R(x,y.z)], ииз(8)следует,чтор\(а| )б„[)б, у...)
бесконечно. Вспоминая конструкцию {6,} по R, мы видим,
что в этом случае lim S (e, z) существует для всех е.
г
Отсюда следует, что каждое бг содержит число из Р \ а.
Предположим, что бе не пересекается с р \ а. Тогда мы
перечислим в бе некоторое число из Р \ а, которое
^> lim S (e, z) и которое не входит в другие 8j. Таким
г
образом, если б,, не пересекается с р \ а, то мы име-
имеем,что Р \ (a U 80 U ^1 U • • •) конечно, а это не-
невозможно. Этим полпостьто заканчивается доказательство
теоремы.
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 125
Как первое применение основпой теоремы, мы докажем
результат, подтверждающий первое из двух предположе-
предположений Майхилла, сформулированных во введении.
Следствие 1. Если дополнение рекурсивно пере-
перечислимого множества а имеет накрывающее число п ^> О,
то а есть пересечение максимальных множеств fx-,, . . ., fxn,
любые два из которых отличаются друг от друга на бес-
бесконечное множество.
Доказательство. Пусть а рекурсивно лере-
числимо и а' имеет накрывающее число п. По определению
накрывающего числа существуют попарно непересекаю-
непересекающиеся рекурсивно перечислимые множества х1; . . ., х„
такие, что пересечение каждого из них с а' бесконечно.
Кроме того, а должно быть гипергиперпростым, в против-
противном случае его накрывающее число равно оо. Взяв
E = a U Xj U х2 U . . . U х„ в теореме, видим, что суще-
существует рекурсивное множество б такое, что a (J б — E.
Таким образом, a (J Р' = а {J б' рекурсивно перечисли-
перечислимо. Перечисляем E и а (J Р' одновременно, и пусть
То ~ {х | х перечислилось в р раньше, чем в a [j P'},
Ух —¦ {х | х перечислилось в а U |У раньше, чем в |3}.
Так как |3 и a IJ Р' не пересекаются в а', то для
1 «С i <^ и мы имеем х; П Тп П а' = х; П а' и
Vi П а' ~ Р'- Таким образом, если бы Р' было бесконеч-
бесконечным, то мы имели бы п -| 1 попарно непересекающихся ре-
рекурсивно перечислимых множеств, а именно х, (П у0,
Х2 П Тп, • • .. У-п П У а и Ти каждое из которых имеет
бесконечное пересечение с а'. Значит, |3' конечно, и можно
предположить, что |3 — v. Для 1 ^ i ^ и положим
Hi — a U {хл | 1 <^ х <i n & х Ф /}.
Ясно, что любые два множества из Uj, . . ., \in отличаются
друг от друга на бесконечное число элементов. Теперь
покажем, что все ца, . . ., ц„ максимальны. Достаточно
рассмотреть лишь и,. Это множество кобесконечпо. Теиорь
пусть |3 (это не то |3, которое было выше) — рекурсивно
перечислимое мноичоство и (j, cz p ст. v. Строим б„ и бх
но аир так, как мы строили выше уп и уу; имеем, что
х-, П б0, . . ., х„ П 6„ и 6j — лолар}ю непересекающиеся
множества. Далее, так как р э Hi> то все множества
12fi Л. X. ЛАХЛАН
х, П fioi- • -А П б0 имеют бесконечное пересечение с а'.
Таким образом, либо б3 П а' копечно, либо х, (~) б0 Г) а'
конечно. Но р П Xi П «' = «1 П бо Г а' и Р' = б, П «'•
Поэтому в перлом случае Р' копочпо, а во втором Р \ Mi
конечно. Итак, |дх максимально. Подобт1ьтм образом дока-
доказывается максимальность \*2, . . ., |in. Доказательство
следствия закончено.
Это слрдствио является обращением результата Ейтса,
сформулированного но введении. Из теоремы Ейтса мы
видим, что если а' имеет пакрываюшее число п, то мак-
максимальные множества \xlt . . ., цп определяются по а с
точностью до конечных множеств.
Аргументы, применяемые при доказательстве след-
следствия, дают значительно больше информации. Опреде-
Определим разделяющее число множества % как
sup (мощность 3( | 31 — класс попарно непересекающихся
рекурсивных мпожеств, каждое из которых имеет
бесконечпое пересечение с у, и таких, что (J 3( = v}.
Предположим, что а гипергиперпросто, и заметим, что
И] П То. • • •> ип П То. Ti рекурсивны в первой части до-
доказательства следствия, так как они попарно непересе-
непересекающиеся множества, покрывающие v. Отсюда видим, что
разделяющее число а' ^> накрывающего числа а' и, таким
образом, для гипергиперпростых множеств накрывающее
и разделяющее числа для дополнения совпадают. Теперь
пусть р — произвольное рекурсивное множество такое,
что р (~| а' бесконечно, где а гипергиперпросто. Беря
р = хх во второй части доказательства следствия, видим,
что либо a (J р' максимально, либо можно разбить р
на два непересекающихся рекурсивных мпожества р Г) бп
и р Р) б,, каждое из которых имеет бескопечное нересечо-
пие с а'. Заметим также, что если разделяющее число
множества р [~| а' есть сю, то разделяющее число множе-
множества р П б0 П ос' или мпожества р f] 81 f] а' также рав-
ПО ОО.
Таким образом, если а гипергиперпросто и а'
имеет разделяющее число оо, то мы можем построить две
последовательности рекурсивных мпожеств {pj} и {ctJ
такие, что р0 \J an = v, pn (~| а„ ^ 0 и для всех i
множество рг \ а имеет накрывающее число оо, o"j \ oq
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 127
бесконечно,
Pin U °"m = Рг. Pin Л <7<м = 0-
Теперь определим
тг- = (at \ {0, 1, . . ., i - 1}) U ({0 \ («Jo U (Ti U
• • • U *<-i))
и мы видим, что {тг-} — последовательность попарно непе-
непересекающихся рекурсивных множеств, покрывающих v,
п такая, что каждый член имеет бесконечное пересече-
пересечение с а'.
Лторос применение основной теоремы связало с харак-
теризацией пшергиперпростых мпожеств.
Теорема 3. Рекурсивно перечислимое множество а
гипергиперпросто тогда и только тогда, когда оно ко-
бескоиечно и для любого рекурсивно перечислимого множе-
множества р множество a [J Р' рекурсивно перечислимо.
Доказательство. Для части «только тогда»
мы можем предположить, что р — рекурсивно перечисли-
перечислимое надмножество а, потому что а (J Р' = а (J (а (J р)'.
По если а гппергпперпросто, то оно пшергиперпросто
и любом надмножестве р. Поэтому по теореме 2 существует
рекурсивное подмножество 6 множества р такое, что
a U б — р. Следовательно, a (J б' = а (J р' рекурсивпо
перечислимо.
Для части «тогда» предположим, что а — рекурсивно
перечислимое кобескопечпое, но нз гипергиперпростое
множество, и построим рекурсивно перечислимое надмно-
надмножество р мпожества а такое, что a (J р' не является ре-
рекурсивпо перечислимым. Пусть {бг} — рекурсивная по-
последовательность конечных мпожеств, каждое из которых
пересекается с а', и пусть {ю;} — любое рекурсивное
перечисление всех рекурсивно перечислимых множеств.
Пусть р есть
а U U {б, Л <ох | х > 0}.
Если а [J P' рекурсивно перечислимо, то оно равно а>е
для некоторого с. Пусть / — элемент бе (~| а', тогда по
определению р
По из a (J P' = »f получаем противоречие. Поэтому
a (J P' не является рекурсивпо перечислимым.
128 A. X. ЛАХЛАН
Следствие 2. Если аг и а2 гипергиперпросты,
то а1 П «г гипергиперпросто.
Доказательство. По теореме достаточно дока-
доказать, что (ocj Г) а2) U Р' рекурсивно перечислимо для
любого рекурсивно перечислимого множества р. Но
ai U Р'» аг U Р' рекурсивно перечислимы, так как
ocj и а2 гипергиперпросты и
(«1 U Р') П («, U Р') = («1 П <Ч) U Р'.
Обобщим теперь метод теоремы 2. Р. Робинсон заметил,
что применение теоремы о рекурсии при доказательстве
теоремы 2 можно элиминировать. Мы используем его на-
наблюдение. Сперва дадим некоторые определения и леммы.
Множество а назовем гипергипериммунным, если оно
бесконечно и не существует рекурсивной последователь-
последовательности попарно непересекающихся конечных множеств,
каждый элемент которой пересекается с а.
Пусть со = (со], . . ., со„) — любая и-ка рекурсивно
перечислимых множеств. Порядком со назовем число под-
подмножеств i множества х =¦ {1, 2, . . ., п}, для которых
со (i) бесконечно, и обозначим его | ю |. Скажем, что упо-
упорядоченная пара (со0, со1) n-ок рекурсивно перечислимых
множеств есть разбиение я-ки множеств со, если сущест-
существуют непересекающиеся и взаимно дополняющие рекур-
рекурсивные множества б0, бх и 1-1 рекурсивные функции Do,
Dx такие, что Do (v) = 8„, Dx (v) = 8lt и такие, что
со? = Do1 (at), col = D? (сог) для 1 < i < k.
Лемма 2. Если w (i) — бесконечное и не гипергипер-
иммунное множество и если (о0, о1) разбивает п-ку ре-
рекурсивно перечислимых множеств ю, то одно из ю° (i),
«о1 (i) бесконечно и не гипергипериммунно.
Доказательство. Достаточно показать, что
одно из множеств w (i) f] б0, со (i) [~] бх бесконечно и не
гипергипериммунно, так как to0 (i) = D^1 (со (i) f] 60) и
со1 (i) = D^1 (со (i) П 6X). Если одно из множеств со (i) fN0,
со (i) П 8j копечпо, то доказывать нечего. Пусть оба эти
множества гипергипериммунны. По определению! to (i)
есть р \ а, где а — рекурсивно перечислимое подмно-
подмножество рекурсивно перечислимого множества р. Так как
со (i) р) Ьг гипергипериммунно, то б0 U а гипергипер-
гипергиперпросто в 8„ U р. Из теоремы 2 видим, что а (J б0 U Р'
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 129
рекурсивно перечислимо и поэтому a |J б0 (J Р' гипер-
гиперпросто, так как оно рекурсивно перечислимо и
имеет дополнение о (i) f] 6j. Аналогично доказывается,
что a (J 6X (J р' гипергиперпросто. Множество а (J р' --
= (а U б0 [J р') f| (а [j бх U р') гипергиперпросто по
следствию к теореме 3, и, таким образом, о (i) гиперги-
периммунно. Это доказывает лемму.
Лемма 3. Если о = (co^ . . ., <вп) — п-ка рекур-
рекурсивно перечислимых множеств и ни одно из множеств
соь . . ., (и'п не является конечным, но (Л @) конечно, то
существует разбиение (са°, о1) п-ки множеств (а такое,
что | в>° | < | а | и | «о1 | ¦< | «о |.
Доказательство. Пусть А, — подмножество
множества и такое, что (J {соя | ^ е Я,} коконечно и мини-
минимально относительно включения. Пусть р ?Е Я,. Пере-
Перечисляем сор и 5С = U {*** | * е Я, \ {р}) одновременно,
и пусть
6о = {у | У перечисляется раньше в <вр},
*>i = {У I У перечисляется раньше в %}.
Тогда б0, бх — непересекающиеся рекурсивно перечис-
перечислимые множества такие, что их объединение есть соР U X
и, следовательно, коконечно. Мы можем предположить,
что б0 U бх = v. Тогда существуют 1-1 рекурсивные
функции Do, Dx такие, что Do (v) = 80, D1(v) = 8г. Пусть
(са°, о1) — соответствующее разбиение о. Далее о0 (i)
или о1 (i) может быть бесконечным, только если со (i)
бесконечно. Также са° (i) не будет бесконечным, если i
не содержитр, хотя ю @ может быть бесконечным для не-
некоторых I, пе содержащих р, потому что сор бесконечно.
Также о1 (i) не будет бесконечным для любого i, не пере-
пересекающегося с % \ {р}, хотя (Л (i) будет бесконечным для
пекоторого такого i, потому что f) {w'x | х 6= % \ {р}}
бесконечно. Таким образом, | о0 | < | о | и | ю1 | < | о |.
Теорема 4. Пусть са = (<о1( . . ., соп) — п-ка ре-
рекурсивно перечислимых множеств и Ж Q {i С и & са (i)
ке является гипергипериммунным или конечным). Тогда
существует рекурсивная последовательность попарно не-
непересекающихся конечных множеств {Ь\ | i ЕЕ Ж & i ^ 0}
такая, что 8\ пересекается с о» (i) для всех i e= X и всех
-130 A. X. ЛАХЛАИ
Доказательство. Возьмем любое эффективное
1-1 отображение ЗС х v на v и обозначим через -^ линей-
линейный порядок на УС X v, индуцируемый естественным по-
порядком на v. Без ограничения общности можно предполо-
предположить, что все щ, . . ., con бесконечны, потому что если
©* получается из © отбрасыванием коконечного множе-
множества, то по модулю конечных множеств бесконечные
множества вида © (i) те же самые, что и вида ©* (i).
Если © @) конечно, то по лемме 3 получаем разбие-
разбиение (©°, ©J) n-ки множеств ©, |©°| < |©| и | ©х |<|©|.
Для г = 0, 1 определим
Жт = {i 11 е СК & сог (i) не является
гипергипериммунным или конечным}.
По лемме 2 имеем Х° (J Ж1 = X, а также что если тео-
теорема выполняется для ©° и ©*, то она выполняется и для ©.
Предположим теперь, что все а[, . . ., а>п бесконеч-
бесконечны и © @) бесконечно. Построим требуемую последо-
последовательность попарно непересекающихся конечных мно-
множеств одновременным перечислением по шагам 0, 1, 2, ...
Для i ?Е ЗС пусть Ь\г j — конечное множество, пере-
перечисленное в Ь\ к концу шага /. Для 1 <; i <! п пусть сог, j —
конечное множество, перечисленное в сог к концу шага /.
Если 0 €Е ЗС, то пусть а — рекурсивно перечислимое
надмножество множества © @)' такое, что © @)' (J а'
не является рекурсивно перечислимым; такое а суще-
существует по последней теореме. В противном случае положим
а = © @)'. Пусть ctj — конечное множество, перечис-
перечисленное в а к концу шага /. Для i =fc 0 пусть
©i (i) = п {«х,) | х е i} П П {v>'x,i |*ex\i};
положим
<М0) =¦¦<*} П П {<0х.Л*ек}-
Для каждого i e Jf определим бинарную рекурсивную
функцию S1:
S' (х, 0) - 0,
у (г 7 + 1) = l'^' ')' если ^. j пересекается с ©j(t).
161' (ж, /) + 1 в противном случае.
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 131
Шаг 0. Ничего не делаем.
III а г / + 1. Пусть (е, е) — наименьший член из Ж X
X v такой, что б*,,- П (Oj (е) = 0 и 0)j+1 (e) содержит
число / > max {5е (х, /) | (i, х) < (е, е)}, которое не со-
содержится в U {б*,,- I i е Ж & х > 0}. Если (е, е) су-
существует, то перечисляем наименьшее такое / в б*-
В противном случае ничего не делаем.
Легко видеть, что конструкция эффективна и также что
если Ь\ пересекает о) (i), то б,- конечно и lim Sl (i, у)
у
существует. Также легко видеть, что последовательность
{б,- | i Er Ж & i > 0} состоит из попарно непересекаю-
непересекающихся множеств, т. е. б; пересекается с бЦ, только если
t = т] и i -¦¦- h. Поэтому ничего пе надо доказывать, если
только не встречается случай, что 6J не пересекает о> (i)
для некоторой пары (i, j). Пусть (е, е) — наименьшая та-
такая пара; тогда S* (е, у) возрастает по у и имеет предел
оо. Следовательно, так как / ^> max {Sl (x, j) | (ц х) <
< (е, е)} на шаге j + 1, видим, что \J {8\ \ (i, i) ^>
> (е, е)} рекурсивно. Также по выбору (е, е) для (i, i) <
<^ (е, е) имеем, что б; конечно и lim Sl (i, у) существует.
v
Если е — 0, то IJ {б? | (i, i) > (е, е)} покрывает a f|
П ю @)> за исключением, может быть, конечного числа
элементов; в противном случае элемепт из a f] ы @)
должен перечислиться в б*. Но это влечет, что о> @)' (J
[J а' рекурсивно перечислимо, а это противоречит выбору
а; итак, е ф 0. Теперь (J {6;|(i, i) ^> (е, е)} покры-
покрывает о) (е), за исключением, может быть, конечного числа
элементов; в противном случае элемент из 0) (е) должен пе-
перечислиться в б'. Отсюда следует, что существует рекур-
рекурсивное множество б такое, что w (e) Q 8 с а, Берем
б0 — б и бх — б', и пусть (©°, оI) — соответствующее
разбиение о>. Определим
#"° = {i I i е # & i =7*= 0 & ю° @ не является
гипергипериммунным или конечным},
.Ж1 — {i | i (z- Ж & оI (i) пе является
гипергипериммунным или конечным}.
132 A. X. ЛАХЛАН
Если 0 ф. Ж, то ясно, что Ж° (J Ж1 = Ж по лемме 2.
Если 0 ЕЕ ^", то a' (J (бх f) ю @)') не является рекур-
рекурсивно перечислимым, потому что
а' U («1 П ю @)') U © @)' = а' U © @)''
и множество a'(J в> @)' не является рекурсивно перечис-
перечислимым по выбору а. Следовательно, в этом случае© @) П
П Ъх не является конечным или гипергипериммунным,
откуда заключаем, что ю* @) не является копечным или
гипергипериммунпым. Итак, во всех случаях Ж0 (J Ж1 =
= Ж. Теорема выполняется для {Ж, ю), если опа выпол-
выполняется для (Ж°, в>°) и (Ж1, (л1). Так как ю (е) сг б = б0,
имеем, что ю1 (е) = 0 и | ю11 < | ю |. Если 0 ^ Ж,
то из бСа имеем ю0 @) = 0 и | ю° | < | ю |. Если
0 ЕЕ •%", то, так как 0 QE •%"°, мощпость Ж° меньше, чем
мощность Ж. Теорема следует, если вести индукцию по
| ю | + мощность Ж.
Надо начать со случая, когда мощность Жесть 1; теоре-
теорема в этом случае очевидна.
3. Гипергиперпростое множество, не имеющее макси-
максимального надмножества. Данное построение связано со
вторым предположением Майхилла, сформулированным во
введении.
Пусть {%,} — рекурсивное перечисление всех рекур-
рекурсивно перечислимых множеств, т. е. такое перечисление,
что предикат х ЕЕ %у рекурсивно перечислим. На каждом
таге перечисляется одна пара(ж,г/), означающая, что яЕЕ%у
Для удобства положим, что каждая такая пара перечисля-
перечисляется бескопечпое число раз.
Пусть л, 6, ... обозначают конечные цепочки из О
и 1; возможна пустая цепочка. Множество всех таких
цепочек обозначим через S. Рассмотрим 1-1 функции
из S в v, которые будем называть числовыми деревь-
деревьями. Элементами числового дерева назовем элементы
его области значений. Обозначим через й * Ь цепочку,
полученпую приписыванием Ъ справа к л. Если Т — число-
числовое дерево и й GE S, то Т [й] будет обозначать число-
числовое дерево, определенное так: Т Ы (f) = Т (й * f).
Линейно упорядочим S следующим образом:
0, 0, 1, 00, 01, 10, 11, 000, . . .,
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 133
т. е. сперва по длине, а потом лексикографически. Когда
мы будем говорить о наименьшем элементе подмножества
D множества 8, будем иметь в виду элемент из D, кото-
который встречается раньше в этой последовательности; если
й расположена раньше, чем Ь, то будем писать а < Ь.
Элементы числового дерева Т линейно упорядочим отно-
отношением <^т (сокращенно <):
х < у *-» Э«Э& 1х = Т (й)&у = Т (Ь)&л< Ь].
Построение будет вестись по шагам 0,1,.. . На каждом
шаге s мы определяем числовое дерево Ts. Пусть тM состо-
состоит из тех чисел, которые не лежат в области значений Т„
тогда {т)я} — неубывающая сильно рекурсивпо перечис-
перечислимая последовательность, предел которой есть искомое
рекурсивно перечислимое множество.
Пусть со1;,а — конечное множество, определенное сле-
следующим путем. Во-первых, <о,л0 = 0 для всех у. Во-
вторых, если (х, у) — пара, перечисленная на шаге s, то
пусть
t«и, я U И. если z = у и х Ф «>!/,«.
az ,+1 = | со2, s \ {х}, если z > у и х ф го„, „
I coz, s в противном случае.
Л е м м а 4. Для всех у имеем Нт со„,2 = %у.
Z
Доказательство. Предположим, что лемма
выполняется для всех у < е. Имеем «>е, С %е. Пусть m —
любое число из %е, тогда по индуктивпому предположе-
предположению существует q такое, что для всех 1/<еи всех s ^> q
имеем, что тп ф. ю,;„,+1 \ со,,,. Для некоторого s^q
имеем m GE о),,,, потому что каждая пара, если она пере-
перечисляется, то бескоттечпое число раз. Также мы видим, что
тп Ег юе./ \ ыг,+] для некоторого t >= .9, только если су-
существует у <Z е такое, что m Е= гон,(+1 \ со,,,(. Но это пе-
возможпо по выбору q. Таким образом, тп- <= гаР,, для всех
достаточно больших s, и лемма доказана.
Определим вспомогательную фупкцию:
W (х, у, s) -¦= S {2v-* | ж еЕ со,„ & z < у}.
Ясно по лемме 4, что
Km W (х, у, t) - 2 I2""' I * е Х/& г < у}.
134 A. X. ЛАХЛАН
Ш а г 0. Определим То так:
То @) = 0,
то(г *о) = 2ro(s) + i,
То (*•!) = 2Т0 (?) + 2.
Шаг s + 1. Пусть (ж, у) — пара, перечисленная на
шаге s. Если ж ф. Ts или а; = Ts (?) и ? имеет длину
<^ у или х €Е «y.si то ничего не делаем. В противном случае
пусть ?0 — цепочка длины у, для которой ? есть расши-
расширение. Пусть уг — наименьшее расширение ?0 такое,
что ? j < ? и W (xu y,s)<W (х, у, s+ 1), где хх =
= Т (?х). Определим
(ж, если л = ?ь
Г8(й*0), если а — одно из у, f *0, f*00,...,
Гв(й) в противном случае.
Заметим, что область значений Ts+1 получается из обла-
области значений Ts выбрасыванием Ху. Если %х не существует
или ничего не делается, то полагаем Ts+1 = Ts.
Ясно, что данная конструкция эффективна. Для дан-
данного i можно эффективно перечислить т]{ и эффективно
найти его мощность. Мы видим также, что r\s cr r\sn. Сле-
Следовательно, {r\i} — сильно рекурсивно перечислимая не-
неубывающая последовательность, предел которой мы обоз-
обозначим через г\.
Лемма 5. lim Tx существует.
X
Доказательство. Пусть 6 —¦ наименьшая це-
цепочка такая, что lim Tx F) не существует; тогда суще-
X
ствует бесконечное число шагов s -f- 1, для которых
Ts F) Ф Ts+1 F). Для всех достаточно больших s таких,
что Ts F) Ф Т1+г F), имеем fx = 6; это потому, что на
любом шаге s -{- 1, для которого Ts Ф Ts+1, f, — наимень-
наименьшая цепочка, па которой Г8+1 отличается от Ts. На любом
шаге s + 1, где fx = 6, длина ?0 ^ длины 6. Также
если J, = 6 на шаге s + 1, то W(Ts(b), у, s) <
< W (Tsn (Ь), у, s -f 1). Пусть у0 — наименьшее число
такое, что существует бесконечно много шагов s -\- 1 с
fj = 6 и у = у0. Тогда для всех достаточно больших
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 135
s имеем W(T. (Ь), у0, *) < W (Т^ (Ь), у0, s + 1),- либо
потому что ух не определена, либо потому что уг ^> Ь, либо
потому что 5Х — Ь и у "^ у0. Для бесконечно многих s
неравенство строгое, потому что существует бесконечно
много s таких, что ух — Ь и у = г/0 на шаге s + 1- Это
противоречит неравенству И7 (Г, (Ь), г/0> s) < 2№>+1, которое
следует прямо из определения W. Лемма доказана.
Пусть Т = lim Тх и W (х, у) = lim W (х, у, г).
х z
Лемма 6. Пусть г — цепочка длины е. Пусть Ъ —
— Т (Ь), где Ь — расширение г. Пусть t — наибольшее
число такое, что на шаге t перечисляется пара (Ъ, е) и Ъ ej?
Оё (i>e t- Тогда Т~х (Ъ) — расширение г и W (Ъ, е, t + 1) =
= W(b, e).
Доказательство. Если t не существует, то
нечего доказывать. Во-первых, мы заметим, что для лю-
любого элемента Ъ ?Е Т длина Т^Х(Ь) не возрастает. Поэтому,
если Т'1 (Ъ) имеет длину ^ е, то это же будет справедли-
справедливо для 771 (Ь) при всех s. Существует цепочка е* длины е,
для которой TJl (b) является расширением. Пусть
я + 1 — наименьший шаг ^> t, если он существует, та-
такой, что 77+1 {Ь) не является расширением е*. Тогда мы
видим, что у0 на шаге s + 1 имеет длину у <С е и х = Ъ.
Таким образом, для пары (х, у), перечисляемой на шаге
s, будет и х = Ъ, и у <С е. Следовательно, Ъ ф. «вL+1,
что противоречит выбору t. Поэтому такого шага s + 1 не
существует и TJ1 (Ъ) — расширение (.
Если W (b, e, t + 1) Ф W (Ъ, е), то это может быть
лишь тогда, когда существует m <J e такое, что ЬЕхт\
\ ит, (+1- Ясно, что в действительности m <; е. Пусть
s — наименьшее число ^> t такое, что пара (Ь, т) перечис-
перечислена на шаге s. Тогда будем иметь то же противоречие, что
и ранее.
Лемма 7. Пусть г — цепочка длины е; тогда суще-
существует w такое, что для всех, кроме конечного числа, рас-
расширений у цепочки г имеем W (T (f), e) = и>.
Доказательство. Пусть С — цепочка длины
е — 1, расширение которой есть е. Можно предположить,
что существует w~ такое, что для всех, кроме конечного чис-
числа, расширений J цепочки е" имеем W (Т (у), е — 1) =
— w~. Из определения W мы видим, что для всех, кроме
136 A. X. ЛАХЛАН
конечного числа, расширений ? цепочки с имеем
2нг < W(T(s), е)< 2иГ + 1.
Предположим, что 1У (Т (у), е) - 2иГ -[- 1 для бесконечно
многих расширений ? цепочки с; в противном случае до-
доказывать нечего. Пусть а — произвольное расширение
С и s таково, что для всех х ^> s и всех ? ^ а имеем
Тх (?) -~ ?' (?). Существует бесконечное число элемен-
элементов b ЕЕ Т [с], для которых W (Ь, е) — 2w~ -f- 1. Каждое
такое 6 принадлежит %е, и поэтому существует такое на-
наибольшее число t, что b ф. o)Cif и пара (Ь, е) перечисляется
на шаге t. Так как существует бесконечное число таких Ь,
мы можем найти одно, чтобы TJ1 (Ь) —- ? ^> а и t ^ s.
По последней лемме f есть расширение си W F, е, ^ +
+ l) = W (b, e) = 2ыГ + 1. Так как Г(+1 (?) - Г4 (?)
для всех ? ^ а по выбору s, имеем W (Т (а), е, t) >
> PF F, е, t + 1). Следовательно, JF (Г (а), е) > 2w~ +
+ 1. Но а — произвольное расширение с и W (Т (?),
е) = 2и;~ + 1 для всех, кроме конечпого числа, расшире-
расширений ? цепочки е. Лемма доказана.
Лемма 8. Для любой цепочки е множество ц [j (об-
(область значений Т [t.]) рекурсивно перечислимо.
Доказательство. Пусть е имеет длину е. По
лемме 7 существуют w, Со такие, что с0— расширение с
и для всех расширений ? цепочки с, которые !> с0, имеем
W(T($),e) = w. Пусть .90 таково, что Ts (у) = Г (?)
для всех s !> s0 и для всех ? <^ с0.
Предположим, что для некоторых s > s0 и р мы имеем
VF (p, e, s) — w & р лежит в области значений
ts le] & т;1 (Р) > е0, (9)
тогда
[W (p, e, s + 1) •-- w & р лежит в области значений
Гт [с] & 77+\ (р) > с0] V Р е ть+1. A0)
Предположим противное; тогда мы видим, что р лежит
в области значений 7\,+1, так как р ф. iis+1. Если х в ут-
утверждении шага s -г 1 не есть р, то W (p, e, s -- 1) ¦-=
== W (p, e, s) и поэтому либо р не лежит в области значе-
значений Т$+1 [с], либо 77+х (р) 3> ^о- По выбору s0 имеем
?7+1 (р) ^> ^о и Р пс лежит в области значений Т$+1 (е),
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 137
что невозможно. Итак, х = р па шаге s + 1. Еели у в ут-
утверждении шага s + 1 больше е, то ТУ (р, е, s + 1) —
— W (р, е, s); далее, если ?0 и ?! определены, то они
являются собственными расширениями с. Это означает,
что р лежит в области значений Ts+1 [с], потому что Ts+1
может отличаться от Ts только на расширениях ?0- Теперь
^Т+i (р) ^> со> как выше, и у <^ е. Но имеем W (p, e, s) ^>
> W (Т (е), е, s) и W (Г (е0), у, s) <W(p, у, s + 1).
Значит, ?! определена и ^ с0. Так как Г8+1 (j^) ^
т^= 7S (fi) по выбору s0, приходим снова к противоречию.
Итак, (9) влечет A0), когда s^> s0.
Теперь заметим, что рекурсивно перечислимое множе-
множество
{и | 3z h > ,90 & W (u, e, z) — w & и лежит в области
значений Tz [е] & Т? (и) > е0]} (И)
есть подмножество множества i]U(область значений Г [с]).
Ясно, что все элементы из Т [с], кроме конечного числа,
принадлежат рекурсивно перечислимому множеству A1).
Лемма полностью доказана.
Теперь докажем, что т) — гипергиперпростое множе-
множество, не имеющее максимальных надмножеств. Пусть
С — цепочка длины е, по лемме 7 существует w такое, что
для всех элемептов ж из Г [с], кроме конечного числа,
имеем W (х, е) = w. Если w четно, то все элементы из
Т [с], кроме конечного числа, лежат в %е. Если w нечетно, то
все элементы из Т [с], кроме конечного числа, лежат в %е.
Пусть с1; . . ., cm — все цепочки длины е, для которых
соответствующие w четны, а ет+1, . . ., ет+п — все це-
цепочки длины е, для которых соответствующие w нечетны.
Тогда
Хе П U {область значений Т [г{\ | 1 <^ i <^ m)
и
U {область значений Т [ej | m < i ^ m + п) \ хе
конечны. Далее, множества
U {область значений Г [е;] | 1 =^ i ^ ?гг},
U {область зпачепий Т [tt] | m < i ^ те -f- ^}
це пересекаются и покрывают все т]'. Далее, т) (J Хе Ре*
138 A. X. ЛАХЛАН
курсивно перечислимо, так как оно на конечное число эле-
элементов отличается от множества
U {"Л U (область значений Т [вг]) | 1 ^ i <^ пг}.
Так как это верно для любого е, то т] гипергиперпросто
по теореме 3. Далее, если r\ [J %е не кокопечно, то m ^> О
и г) LJ (область значений Т [ex * 0]), r\ [j (область значе-
значений Т Ul * 1]) — рекурсивно перочислимые множества,
не пересекающиеся вне ц и имеющие бескопечное пересе-
пересечение с множеством (r\ [J %е)'. Итак, т] |J %e не является
максимальным надмножеством множества т], и поэтому tj
не имеет максимальных надмпожеств. Итак, доказана
Теорема 5. Существует гипергиперпростое мно-
множество, не имеющее максимальных надмножеств.
Заметим, что X* (г\) — счетная безатомная булева
алгебра; это определяет ее изоморфный тип как булевой
алгебры. Мы увидим далее, что X* (г\) определяет X (г\)
и тем самым существует только одна возможность для ре-
решетки рекурсивно перечислимых надмножеств множества г\.
4. Булевы алгебры надмножеств гипергиперпростых
множеств. Здесь мы покажем,'что X* (а) может иметь любой
возможный изоморфный тип, когда а гипергиперпросто.
Пусть {%t} — любое рекурсивное перечисление всех
рекурсивно перечислимых множеств, и пусть а — фикси-
фиксированное рекурсивно перечислимое множество. Рассмотрим
отношение В на натуральных числах, определенное сле-
следующим образом:
R (х, у) <-> (хх U «) \ (Xu U а) конечно.
Определим Л = (а0, аи ...}, где
аг = {х | R (х, i)&R (i, x)},
и отношение ^ на Л формулой
«г < «j *-»• В (U })•
Легко видеть, что отображение: а* переходит в %t [j а
есть изоморфизм из {А, «О на {X* (a), Q}. Определим
jy/J-решетку как решетку, имеющую вид {Л, ^}, где
Л и <| определены описанным способом по двуместному
ЭУЭ-отношению, и такую, что существуют двуместные ре-
рекурсивные функции U, V такие, что для всех х, у имеем
U а,, = ащх<чI ах С] a,j — оу(,
. у) -
РЕШЕТКА РЕКУРСИВНО ПЁРЕЧИСЛИМЫХ МНОЖЕСТВ 139
Так как на определенной выше решетке {А, ^.}-такие U и
V существуют, то имеем, что для любого рекурсивно пе-
перечислимого множества а решетка X* (а) изоморфна
3V3"Pe тетке.
Вообще говоря, неверно, что для данной 3V3-pemeTKH,
имеющей 0 (наименьший элемент) и 1 (наибольший эле-
элемент), можно найти рекурсивно перечислимое множество
а такое, то X* (а) изоморфна этой решетке. Например,
существует 3V3-peineTKa с 0 и 1 и еще одним элементом;
но известно, что если X* (а) конечна, то а ~ v или
X* (а) — булева алгебра, порядок которой есть степень 2.
Однако, если несколько изменить конструкцию послед-
последней теоремы, то можно доказать следующую теорему.
Теорема G. Пусть А — 3V'^-решетка, являющаяся
булевой алгеброй, тогда существует гипергиперпростое
множество а такое, что X* (а) изоморфна А.
Доказательство. Пусть f — цепочка длины
х\ далее мы будем отождествлять f с конечной функцией,
определенной так:
. _ | (п -{- 1)-му элементу цепочки f, если п<^х,
\ не определена в противном случае.
Пусть Л — счетная булева алгебра. Скажем, что после-
последовательность {а0, а1( . . .} элементов Л порождает Л,
если каждый элемент А может быть получен из элементов
этой последовательности с помощью операций объедине-
объединения, пересечения и дополнения. Отображение F множе-
множества S в @, 1} назовем союзником А, если существует по-
последовательность {а0, а±, . . .}, которая порождает А,
такая, что
= 0} Л П К |5 (У) = 1> = 0]-
Заметим, что каждый элемент А может быть выражен
в виде
где Ж — конечное множество цепочек. Назовем это множе-
множество а (Ж). Предположим, что каждая цепочка из Ж имеет
длину ^ви!0 — множество
{f 11 (~ 8 & 5 имеет длину и&Эп [и еЭЕ&ис fl}-
140 A. X. ЛАХЛАН
Легко видеть, что а(ЗЕ) = а ($0). Пусть §) —другое ко*
нечное множество цепочек, длина которых <[ п, и опре-
определим §H по §) так же, как Жо но Ж. Видим, что
Теперь заметим, что если ^°, Лх — две счетные булевы
алгебры с общим союзником, то Жй и Л1 изоморфны. Пусть
F — общий союзник и {а?}, {а*} — соответствующие по-
порождающие последовательности jl° и А1. Для каждого
конечного множества цепочек Ж мы отображаем а0 (Ж)
в а1^). Как следует из A2), ото отображение корректно
определено и является изоморфным.
Пусть Л —любая ЗУЗ-булева алгебра и a0, alt. . . —
ее естественная нумерация. Из рекурсивпости функций
U, V, дающих эффективно объединение и пересечение в
Л, ясно, что мы можем определить рекурсивные функ-
функции /, / такие, что
«Ду) = Г) {«« I 5 (У) = 0}, «Art = U К I 5 (У) = !}•
Теперь мы полагаем
/? E) = 1 *.» «1(у) f] a^0 = 0 <
Таким образом, для данной цепочки $ мы можем эф-
эффективно найти рекурсивное отношение Sf такое, что
( y )
Определим
¦фг,ж = {и | 3" [" < ^ & yyly^n-^-^zSf (и, у, z)]]}.
Назовем а сегментом v, если
VxVy [х < 1/&1/ е а -> х е а].
Ясно, что tyfiX рекурсивно перечислимо равномерно по $
и х. Кроме того, для фиксированной цепочки $ последова-
последовательность гру,,,, tyf.i, ... — неубывающая последова-
последовательность сегментов v. Далее легко видеть, что
F (f) = 1 <-> 3xVy \y>x-+ $fiV = v].
Цепочку и назовем сегментом цепочки f, записываем это
Й , если и=? или ? есть собственное расширение и. Пусть
)— длина ? и определим
= U {%,у I « — сегмент J& ^ = L (f) — L (u)}.
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ l4l
Ясно, что ору рекурсивно перечислимо равномерно по ?
и является сегментом v. Для последовательности {г|5у}
справедливы два свойства, которые нам будут нужны:
F (f) — 1 «-> [г|з^ = v для всех расширений it цепочки ?,
кроме конечного числа], A3)
¦фу конечно —>- [гр конечно для каждого сегмента
U цепочки $]. A4)
Для доказательства A3) заметим, что если F (f) = 1,
то для некоторого р множества т|5г,р, ipf.p+i,. • • все равны v.
Но если и — расширение ? такое, что L (f) + р ^ L (и),
то одно из 1|)г,р, i(V,p+i, . . . войдет в о]зц и поэтому г|зц = v.
Далее, если F (?) = 0, то %,„ г|5ГI, ... все конечны. По
определению союзника, из F (f) = 0 следует F (it) = О
для каждого сегмента и цепочки f; далее, из F (f) = О
следует, что каждое слагаемое в г|5у конечно и, следова-
следовательно, гру конечно. Поэтому A3) доказано, так как,
по определению союзника, из F (f) = 0 следует либо
F (? * 0) = 0, либо F (? * 1) =0, поэтому /" (и) = 0 для
бесконечного числа расширений it цепочки?. A4) истинно,
так как уже показано, что из F (f) — 0 следует, что г|5у
конечно и F (а) = 0 для каждого сегмента а цепочки ?.
Теперь проведем конструкцию, подобную той, которая
была в предыдущем параграфе; построим рекурсивно пе-
перечислимое множество т) такое, что X* (ц) имеет своим со-
союзником F. Этого будет достаточно для доказательства
теоремы. Пусть {%*} — рекурсивное перечисление всех
рекурсивно перечислимых множеств. На каждом шаге бу-
будет перечисляться либо пара из v x v, либо элемент из
S, но не оба вместе. Множество всех пар, которые будут
перечислены, есть {(#, у) | х ?Е %у}, и каждая такая пара
будет перечисляться бесконечное число раз. Каждый
элемент f из й будет перечисляться на Аг шагах, где к —
мощность ору.
Как и раньше, на каждом шаге s будет построено число-
числовое дерево Ts, и пусть r\s состоит из тех чисел, которые не
входят в область значений Ts. Мы определим coViS, как
раньше, аналогично определим вспомогательную функ-
функцию W. На шаге s будем определять функцию Са, отобра-
отображающую S X v в v. Роль функции Cs в конструкции
состоит в следующем. Скажем, что т занимает п-высоту
142 A. X. ЛАХЛАН
x на шаге s, если W (m, n, s) Ф х ¦-- W (т, n, s -(- 1). Для
любой цепочки S длины п функция Cs (s, x) подсчиты-
подсчитывает число тех т, тбЕю„, которые перед шагом s занимали
гс-высоту ж+1 из-за 7»6Есоп и которые «использовались» в кон-
конструкции. Считаем, что ? перечисляется без повторений
с помощью эффективной последовательности 20, Slt ...
Конструкция т] следующая.
Шаг 0. Определим То, как раньше. Пусть Со (п, п) —
- - 0 для каждой пары (п, п).
Шаг s+ 1. Существуют два случая в зависимости от
того, что перечислено па шаге s: либо элемент из v X v,
либо элемент из S.
Случай 1. Пусть (х, у) — пара, которая перечис-
перечислена на шаге s. Если х не является элементом Тв или если
S —- 771 (х) имеет длину <^ у, или если х (=Е coUiS, или
если ? ^ So * Sz, где So — сегмент s длины у и z —
— Cs ($o, W {х, у, s)), то положим Гт ^ Т, и Cs+1 — С,.
В противном случае положим
С (п п) = | ^ (П>") + lf если п = ?0 и п = ^ (ж' У's)'
\ Са (», «) в противном случае.
Также пусть Si — наименьшая цепочка, если она суще-
существует, такая, что So ^ ?i ^ ?о * Sz и W7 (а^, г/, s) <
<_W {х, у, s -\- 1), где жх = Ts (Si). Если такой Si не
существует, то положим Г8+1 = Ts. Но если Si определена,
то положим
х, если а = Sit
Т, (й * 0), если а — одпа [из S, $ * 0, s * 00,...,
Тв(а) в противном случае.
Заметим, что такое определение Та+1 дает, что т]8+1 =
~ Ti« U {^l}» а если ^«+1 — ^«>то 'Hs+i = ^s-
Случай 2. Пусть s — цепочка, которая перечис-
перечислена па шаге s. Положим
_ Та(а*О), если а —одна из S,S*°, S*00,..".,
:s+l \"'
\ Т,(й) в противном случае.
Если х = Ts (j), то имеем т]8+1 = т]8 U {х}.
Ясно, что данная конструкция эффективна. Для дан-
данного i мы можем эффективно перечислить г); и найти его
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 143
мощность. Далее, мы видим, что t)sQt)s+1. Итак, {t)J —
сильно рекурсивно перечислимая неубывающая после-
последовательность и поэтому она имеет рекурсивно перечис-
перечислимый предел т).
Докажем теперь леммы 9—12, соответствующие лем-
леммам 5—8 предыдущей конструкции.
Лемма 9. lim Tx (f) существует тогда и только
X
тогда, когда г|5у конечно.
Доказательство. Если т|>? бесконечно, то це-
цепочка f перечисляется на бесконечном числе шагов. Если
f перечисляется на шаге s, то Ts+1 (j) Ф Ts (f) по слу-
случаю 2. Итак, lim Г* E) не существует, если гр^ бесконечно.
х
Если г|)у конечно, то три конечно для каждого сегмента
« цепочки f. Это сразу следует из A4). Пусть % конечно,
тогда по индукции на й мы можем предположить, что
lim Tx (и) существует для каждого собственного сегмента
х
И цепочки Ь. Далее, только для конечного числа шагов
s мы имеем Ts+1 (Ь) ф Ts (Ь) по случаю 2 на шаге s + 1.
Предположим противное, что Ts+1 (Ь) Ф Ts (Ь) для беско-
бесконечно многих s. По индуктивному предположению, для
всех достаточно больших таких s мы имеем Ь = f или
Ь = ?х на шаге s + 1. Пусть Ъ — L (Ь) и е — наибольшее
число такое, что существует бесконечное множество а значе-
значений s, для которых Ts+l (Ь) ф Т, F) и W(TS (Ь), b, s + 1) = е.
Так как W (а, Ь, с) < 2Ь+1, то е определено. Для доста-
достаточно больших s в а мы не можем иметь Ь = fx на шаге
s + 1, потому что это может быть, только если W (Ta+1 (Ь),
Ь» s "\~ 1) ^> б, что противоречит определению е. Таким об-
образом, для достаточно больших s в а мы имеем Ь — f. Сле-
Следовательно, существует число г/ такое, что для всех доста-
достаточно больших s в а пара (Г, (Ь), г/) перечисляется па
mare s и Г8 (Ь) t^ (oy,s. Число *) у определяется как на-
наименьшее среди чисел z < Ъ таких, что 2b"z делит е. За-
Заметим, что тогда е0 — TF (Г8 (Ь), г/, s) = 2у"ье — 1. Сле-
Следовательно, для каждого достаточно большого s в а мы
имеем Сь+1 (f0, е0) -= G5 (f0, р0) + 1. Таким образом,
*) Начиная с этого места и до конца доказательства леммы,
текст п(! является переводом оригинала, содержащего неточности,
<i предложен редактором перевода.
144 A. X, ЛАХЛАН
С* (?<м ео) с ростом s принимает сколь угодно большие
значения. Так как существует лить конечное число це-
цепочек и таких, что ?0 * а <^ Ь, а последовательность 20,
8Х, . . . есть перечисление 8 без повторений, то существует
z0 такое, что Ь <^ ?0 * 8г для z > z0. Пусть достаточно
большое s из 0 таково, что Cs (?0, е0) ^> z0. Тогда на ша-
шаге s + 1 цепочка Ь не может совпадать с ?, так как Ь <^
<i Ео *Sc (?o,eo) по выбору.?. Полученное противоречие и до-
доказывает лемму.
Пусть Т (х) = Нт Гж (г), если этот предел определен,
X
и не определено в противном случае, и пусть W (х, у) =
= UmW(x,y,z).
Z
Лемма 10. Пусть t — цепочка длины е. Пусть Ъ =
= Т (Ь), где Ь — расширение г. Пусть t — наибольшее
число такое, что на шаге t перечисляется пара (Ь, е) и
Ъ ф. (Ле,. Тогда TJ1 (Ь) — расширение г и W (b, e, t -J- 1) =
- W (Ь, е).
Доказательство. Пригодно доказательство
леммы 6.
Лемма 11. Пусть г — цепочка длины е, тогда су-
существует w такое, что для всех, кроме конечного числа,
расширений ? цепочки t либо Т (?) не определено, либо
W (Т (?), е) = w и Нт Сх (е, и)] существует всегда, когда
X
U > W.
Доказательство. Пусть е~ — цепочка длины
е — 1, для которой е служит расширением, тогда мы можем
предположить, что существует w~ такое, что для всех, кроме
конечного числа, расширений ? цепочки е~ либо Т (?) не
определено, либо W (Т (?), е — 1) = w~. Из опреде-
определения И^мы видим, что для всех, кроме конечного числа,
расширений ? цепочки е либо Т (?) не определено, либо
2иГ <; W (Т (?), е) ^ 2w~ + 1 • Мы можем предположить,
что W (Т (?), е) = 2иГ + 1 для бесконечно многих
расширений ? цепочки е таких, что Т (?) определено;
в противном случае нечего доказывать. Пусть а — лю-
любое расширение е такое, что Т (а) определено, тогда по
лемме 9 Т (а) определено для каждого сегмента и цепочки а.
Поэтому существует а такое, что для всех х > а и всех
цел имеем Тх (и) = Т (п). Существует бесконечно много
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 145
чисел Ъ из Т [t], для которых W (Ь, е) = 2w~ + . Каждое
такое b лежит в %е, и поэтому с ним связано наибольшее
t такое, что Ьф. а>еЛ и пара (Ь, е) перечисляется па шаге t.
Так как существует бесконечно много таких Ъ, мы можем
найти одно, для которого T~l (b) больше любого данного
элемента из 8. Поскольку TJ1 (Ь) > Т~г (Ь) для всех t
и поскольку е с: TtX(b) по последней лемме и W (b, e, t + 1) =
= 2w~ + 1, то Cs (t, 2w~) принимает все значения, когда
s возрастает. Следовательно, существует бесконечно
много шагов s + 1 таких, что Cs+1 (e, 2w~) = Cs (t, 2w~) -\-
4- 1 = z 4- 1, где {С||С{*Йг, Выберем любое такое
s > а; тогда, так как ух на шаге s + 1 по является сег-
сегментом а, мы имеем И7 (Т (а), е, s)^W(x, e, s4-l)=2u;~4-l.
Следовательно, для любого расширения а цепочки t
такого, что Т (л) определено, мы имеем И7 (Г (л), е) !>
!> 2w~ -\- 1. Первая часть леммы доказана. Для окончания
доказательства леммы заметим, что если lim Cx (в, и) =
X
= оо, то W (Т (а), е) !> и 4- 1 для любого расширения
а цепочки в такого, что Т (а) определено. Итак, либо
существует только конечное число расширений л цепочки
t таких, что Т (л) определено (тогда w произвольно и
может быть, конечно, выбрано так, чтобы удовлетворялась
вторая часть леммы), либо w фиксировано в первой части
и lim Сх (е, и) существует для каждого и > w.
х
Лемма 12. Для любой цепочки t множество ц \J
(область значений Т [t]) рекурсивно перечислимо.
Д о к а з а"т е л ь с т в о. Пусть t имеет длину е.
По лемме 11 существуют w, t0 такие, что t0 — расшире-
расширение t и для всех расширений f цепочки в, которые
> в0, Т (f) не определено или W (T (f), e) = w. Пусть
«о таково, что для всех f <J е0 либо Т (?) не определено,
либо Ts (f) = Т (г) для всех s > s0. Пусть я состоит из
всех пар (р, s) с s > s0, которые удовлетворяют условию:
W (p, e, s) = w & р лежит в области значений Т, [t] &
& Т? (р) > в., A5)
но для которых
[W (p, e, s + 1) = w&p лежит в области значений
tiri A6)
146 A. X. ЛАХЛАН
ложно. Предположим (р, s) ЕЕ я. Если случай 2 выполняет-
выполняется на шаге s -f- 1, то Т71 (р) есть одна из f, f * 0, f *
* 00, . . ., где f — элемент ?, перечисленный на шаге s.
Поскольку A6) ложно, мы имеем р ф г\ и 771 (р) Ф ?.
Из A5) получаем Г^Ср) Э« и Т? (р) > е0 => е. Сле-
Следовательно, Г71 (р) — собственное расширение е, и, зна-
значит, р лежит в области значений Г8+1 [е]. Далее, W (р, е,
s + 1) = W (р, е, s), откуда, поскольку A6) ложно, имеем
Till (р) ^ *о- Но по выбору s0 мы знаем, что Т (Т7+1 (p))
не определено и можно доказать, что Т(T~t\(p)) не опре-
определено для t ^> s. Пришли к противоречию, и по-
поэтому случай 1 выполняется на шаге s + 1. Снова мы ви-
видим, что р ф г\ и таким образом, Ц1 (р) есть одна из f,
у * 0, у * 00, ... Теперь 77+i (р) > с0 по тем же при-
причинам, что и выше; отсюда следует, что Т11 (р) не может
быть ни одной из f * 0, ? * 00, . . ., потому что A6) лож-
ложно. Итак, Ц1 (р) --= I и либо W (p, e, s -f- 1) Ф w, либо
^s+i (?) = ? 1 ?j? ^s+i [в]. Мы получили, что на шаге s
перечислена пара (jp, у) с у ^ е.
Мы можем смотреть па я как на функцию от (е0, s0),
где эта пара должна удовлетворять всем условиям, накла-
накладываемым выше на (е0, s0). Если я содержит (р, s) такую,
что пара (р, у) перечислена на шаге s, то мы скажем, что
(е0, s0) соответствует у. Мы скажем, что е0 соответству-
соответствует у, если (е0, s0) соответствует у для бесконечно многих
значений s0. Так как у -^ е, то либо я = 0 для^ неко-
некоторой пары (е0, s0), либо существует у, которому соответ-
соответствует бесконечно много е0. Предположим последнее.
Пусть ех — сегмент е длины у, и пусть ц^ — значение
W (р, г/, s), соответствующее W(p, e, s)=w. Если С, (el7 ^j)
ограничено, когда s возрастает, то пусть lim Cx (^,^2) =
=z и предположим, что Cs (c1; u^i) = z для всех s ;> s^
Поскольку бесконечно много е0 соответствуют у, мы мо-
можем найти (е0, s0), соответствующее г/, такое, что е0 >
^ ех * 3?г, L (е0) >• г/ и s0 > s1. Теперь берем (р, s) в я
такое, что пара (р, у) перечислена на шаге s. Ясно, что
Cs+1 (ец ^ = С5 (Cj, h;j) + 1, а это противоречит s >
^ бро ^ sx. Итак, lim Cx (il, w^) — 00. Теперь из послед-
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 147
ней леммы сразу следует, что для всех расширений ?
цепочки et, кроме конечного числа, Т (?) не определено
или W {T (f), у) > Wl. Но из W {Т (?), у) > wx следу-
следует W (T (f), e) ^> w, значит, но последней лемме, Т (?) оп-
определено только для конечного числа расширений ? це-
цепочки е. В этом случае заключение леммы следует не-
немедленно. Остается лишь случай, когда я — 0 для неко-
некоторой пары (е0, s0). Фиксируем любую такую пару, тогда,
так как из A5) следует A6) для s !> s0, рекурсивно перечис-
лимоо множество
{и | 3z [z !> s0 & W (e, и, z) = w & и лежит в области
значений Tz [e] & Т;1 (и) > е„]} A7)
есть подмножество множества r\ (J (область значений
Пе]). Однако ясно, что все элементы Пе], кроме конечного
числа, принадлежат рекурсивно перечислимому мцоже-
ству A7). Доказательство леммы закончено.
Можно повторить рассуждения как после доказатель-
доказательства леммы 8 и доказать, что лЫХе—рекурсивно перечисли-
перечислимое множество и что существуют цепочки ет+1, . . ., em+n
длины е, где п может быть равно 0, такие, что
т] U Хе — Л U U {область значений Т [ег] | тп < i -^
Обозначим r\ U (область значений 7" [е]) через р (е).
Ясно, что классы эквивалентности {р (i)} порождают всю
X* (г\). Для i > 0 нусть
Pi = U {P (S ¦ 0) | L (?) = i}.
Пусть е — цепочка длины е и определим 0г«для i < e:
, если е (г) = 0,
1 ~~ \ р'., если e(i) = 1.
Ясно, что р (г) = П {0г- | i < е). Итак, последователь-
последовательность {ро}, {pi}, • • • порождает X* (г\). Пусть G — соот-
соответствующий союзник X* (г|), тогда имеем
G (е) = 1 <-[(") {Ы I«(У) •¦= 0} П П {{рЛ I е (у) = 1} =
{л)Ь
Условие справа эквивалентно р (е) с~ т], а это эквива-
эквивалентно тому, что Т (jc) определено только для конеч-
148 a. x. лахлай
ного числа расширений { цепочки е. По лемме 9 это
эквивалентно тому, что -фу конечно только для конечного
числа расширений ? цепочки е. По A3) это эквивален-
эквивалентно F (?) = 1. Итак, X* (т)) и Л изоморфны, поскольку
они имеют общего союзника. Доказательство теоремы пол-
полностью закончено.
Д. А. Мартин показал, что степени гипергиперпростых
множеств — те и только те степени а, для которых а' =
= 0", а также что каждая такая степень есть степень неко-
некоторого максимального множества. Его теорему можно ском-
скомбинировать с только что доказанной: для любой рекур-
рекурсивно перечислимой степени а такой, что а' = 0", и лю-
любой ЭУЭ-булевой алгебры Л мы можем найти гипергипер-
простое множество г\ степени а такое, что Л с^ X* (х\).
Далее, г) может быть выбрано так, что все кобесконечные
надмножества множества г\ имеют степень а. Недавно Р.
Робинсон доказал, что если а' = 0', то любое рекурсивно
перечислимое множество степени а имеет максимальное
надмножество. Вместо слов «максимальное надмноже-
надмножество» можно читать «гипергиперпростое множество т] с
X* (г\)~М.
Одно интересное следствие теоремы 6 состоит в том, что
существует множество натуральных чисел ? такое, что ре-
решетка множеств, рекурсивно перечислимых в ?, пеизо-
морфна решетке рекурсивно перечислимых множеств.
С каждым ординалом п мы свяжем булеву алгебру Хп сле-
следующим образом: Хп порождается всеми ординалами < п
и их включение определяется отношением щ Q п2 для
всех пар ординалов (щ, п2) таких, что и2 <^ п2. Ординал
р вложим в решетку X, если существует 1-1 строго мо-
монотонное отображение из множества ординалов <р в X.
Рассмотрим булеву алгебру Хп как решетку. Каждый
элемент этой решетки может быть выражеп единственным
образом в одном из пяти видов:
0.
U{«2i+2— n2i+1\ i = 0,1, . . ., / — 1},
п0 U U {п2Н2 — гегг+il i = 0, 1, . . ., /— 1},
U {па+2 — "гн-1 | i = 0, 1, ...,/ — 1} U (rcaj+i),
п0 U U {иаг+г — ra«+i | г = 0, 1, . . ., /—l}(J(j+i).
1,
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ .МНОЖЕСТВ 14У
где / — натуральное число, п0, щ, . . ., «2j+i — строго
возрастающая последовательность ординалов </г, 1 —
универсум. Скажем, что элемент а из 56п содержит ор-
ординал т < п, если а второго или третьего вида с т <^ n2j,
а также четвертого или пятого вида.
Лемма 13. Если т — ординал, еложимый в 56п, то
т <^ 2п*г.
Доказательство. Доказательство ведем ин-
индукцией по п. Для конечного п доказательство оставляет-
оставляется читателю. Пусть к — бесконечный ординал, тогда 56*
изоморфна 56к+г. Мы можем отобразить порождающую р
из 56*+1 в (р + 1)\ 0 из 56*, если р конечно, р из Х*п в
р \ О из ,32*, еслир бесконечно и р <^ к, и к в 0'. Таким об-
образом, если лемма выполняется для п = к, то она выпол-
выполняется для п = к + 1.
Теперь предположим, что к — предельный ординал и
лемма выполняется для всех п <Ск. Пусть а0, ccj, ... —
строго возрастающая последовательность в 56* порядко-
порядкового типа т. Пусть q — наименьший ординал, если оп
существует, такой, что aq дополняет порождающую
из 56*. Если q не определен, то любой собственный сег-
сегмент для а о, а1( . . . не имеет или имеет послед-
последний элемент а8 для некоторого s < т, который может
быть вложен в 561, где t — наибольший ординал, содер-
содержащийся в as. Таким образом, в этом случае по индук-
индуктивному предположению т ^ sup {2п+г | п < к} <^ 2к.
Если q определен, то либо а, = 1, либо а0 — элемент
56* второго или третьего вида. Если aq = 1, то q + 1 =
= т и вычеркивание aq из последовательности даст такую
последовательность, для которой q не определен. Поэтому
q ^ 2* и т ^ 2й+х. Предположим, наконец, что а, ^= 1
и а, дополняет порождающую г из 56**). Рассмотрим
последовательпости {ах | х < q) и {ах | ж > д} отдельно.
Первая имеет порядковый тип ^ 2* по тем же соображе-
соображениям, которые указаны выше, вторая может быть вложена
в ^г, и, следовательно, ее порядковый тип ^ 2* по индук-
индуктивному предположению. Итак, порядковый тип всей по-
последовательности снова <;2fe+1.
Лемма доказана.
*) То есть aq [j r= 1,— Прим. ред.
150 A. X. ЛАХЛАН
Хотя это не относится к предмету настоящей статьи,
любопытно знать: можно ли т <^ 2п+х заменить на т < 2л
в заключении этой леммы для бесконечного п.
Рассмотрим булеву алгебру X* (а), где а — гипер-
гиперпростое множество. Пусть Р — множество счетных
ординалов т таких, что существует гипергиперпростое
множество а, у которого X* (а) изоморфна Хт. Из по-
последней леммы следует, что, фиксируя гипергиперпростое
множество а, мы можем набрать самое большее счетное
число элементов Р. Следовательно, Р счетно, и существует
наименьший ординал р ф. Р. Нет гипергиперпростого
множества а такого, что X* (а) изоморфна Хр, но так как
р счетно, то существует полное упорядочение натуральных
чисел порядкового типа р. Отношение порядка для этого
упорядочения рекурсивно в некотором множестве ?, и Хр
есть ЭУЭ-алгебра относительно ?, т. е. при замене понятия
рекурсивности на рекурсивность в ?. Итак, для некото-
некоторого множества а, рекурсивно перечислимого в ?, мы име-
имеем X* (а) ~ Хр я. решетка множеств, рекурсивно пере-
перечислимых в ?, неизоморфна решетке рекурсивно пере-
перечислимых множеств.
Характеризуя решетку X* (а), когда а является ги-
пергиперпростым, мы тем самым характеризуем решетку
X (а); это вытекает из следующей леммы.
Лемма 14. Пусть Хх, Х2 — счетные подрешетки
решетки Ж такие, что X*, Xt — изоморфные подрешет-
подрешетки решетки Ж*. Если [0 е Хх <-» 0 е Хг\ & [v е Хх++ ve
еЖ|], то Ххс±.Х%.
Доказательство. Если а — элемент из Ж,
то пусть а* обозначает соответствующий элемент из
Ж*. Пусть Ф — изоморфизм из X* на X*. Выберем лю-
любые перечисления Хх и Х% и предположим прежде всего,
что ни 0, ни v нет в Хх и Хг. Мы строим последовательнос-
последовательности {pi}, {pi}, перечисляющие Хх и Хг соответственно.
Предположим, что р!, |3? уже определены для всех i < k и
что т шагов конструкции уже проделаны. Предположим
далее, что {|3{ | i < к}, {$\ \ i < к} — подрешетки 52Х и
Ха соответственно и что для всех i <Ck и / <Ск мы имеем
* Г
мощность (pi \ pj) = мощность (р? \ р|). A8)
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 151
Бели т четно, то пусть $\ — первый элемент %х, кото-
который не лежит в {Pi | i < к}. Так как Ф — изоморфизм,
имеем
конечно ~
Р* \ U (Pi Il < к) конечно <-» U {fit \i < к) э Ф
и для i, ]', меньших к,
Pifl(PJ\Pj) конечно
(Pl\Py)\Pl конечно
Рассмотрим v как объединение ({J {$ \i < A;})',
П {Pi I г<^} минимальных непустых множеств вида Р1\Р) с
i, j <i к. Мы видим, что существует представитель р^ из
Ф ф1*) такой, что A8) удовлетворяется для всех i, j <^k.
Пусть р|+1, . . ., Рр — оставшиеся элементы из ?и полу-
получающиеся из pj, . . ., pj с помощью объединений и пере-
пересечений, и пусть р|+1, . . ., Рр — соответствующие эле-
элементы из Хг. Шаг т завершен, индуктивные предположе-
предположения для шага т- + 1 будут выполняться. Если т нечетное,
то мы меняем местами верхние индексы 1 и 2 и ниж-
нижние индексы 1, 2, которые встречались выше. Из A8)
ясно, что отображение Cj в р? для всех i дает изоморфизм
из Хг на %г.
Если 0 е 5?! и 0 е 22, то положим PJ = Ро — 0;
если v E 2j и v Е ?3, то положим Ро = Ро = v, если 0
не присутствует, иначе положим pi = Р? = v. В осталь-
остальных случаях рассуждаем, как раньше. Лемма доказана.
Для того чтобы увидеть, что X* (а) определяет X (а)
для гипергиперпростого а, мы просто заметим, что суще-
существует изоморфизм решетки всех надмножеств а и JV.
5. Некоторые результаты, относящиеся к рекурсивно
перечислимым негипергиперпростым множествам. Здесь
мы приведем некоторые примеры, которые показывают,
что разработанный выше метод для построения гипер-
гиперпростых множеств, па который можно смотреть как
па обобщение конструкции максимального множества
Фридберга, можно применить в некоторых других си-
ситуациях.
152 A- X. ЛАХЛАН
Пусть а — рекурсивно перечислимое множество; ре-
рекурсивно перечислимое подмножество J3 множества а
назовем главным подмножеством а, если а\ р бесконеч-
бесконечно и для любого рекурсивно перечислимого множества
Y из a U 7 = v следует р |J 7 — v.
Теорема 7. Каждое нерекурсивное рекурсивно пе-
перечислимое множество имеет главное подмножество.
Доказательство. Пусть а — любое нерекур-
нерекурсивное рекурсивно перечислимое множество и {а,-} —
сильно рекурсивно перечислимая неубывающая последо-
последовательность конечных множеств, предел которой есть а.
Пусть также одновременно перечисляются все рекур-
рекурсивно перечислимые множества в последовательности
{%;•}, как в § 3, и пусть {%,,s} — множество чисел из %,-,
перечисленных к концу шага s. Определим F следующим
образом:
F (i, s) = min a', f] %[, „.
Заметим, что F (i, s) — неубывающая функция по s при
фиксированном i и lim F (i, х) = оо тогда и только тогда,
х
когда a U Х( = v.
Мы будем перечислять главное подмножество р мно-
множества а одновременно с перечислением всех %(; пусть
Ps — конечное множество, перечисленное в р к концу
raara s. Определим функцию W:
W (х, у, в) = 2 {2"-г | х ЕЕ %м &z^y&x<F(z, в)}.
A9)
Определим последовательность В @, s), В A, s), ...
для множества as \ ps:
В @, s) = min {x | х (В as \ ps & W (х, 0, s) =
= max {W (у, 0, s) | г/ е as \ p5}}
и для i ]> О
В (i, s) = min {х \ х ЕЕ ocs \ $s & х ^> В (i — 1, s) &
& W(x, i, s) = max {W (y, i, s) | у ЕЕ as \ ps &
&y>B(i-t,s)}}. B0)
Поскольку a ,\ ps конечно, то В (i, s) приданном s опре-
определено лишь для конечного множества чисел i. Копструк-
пия далее очень проста. На шаге 0 мы ничего не делаем, на
РЙ1ПЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 153
шаге s + 1 мы перечисляем в р все элементы as \ ps, ко-
которые не попали в последовательность Б @, s), В A, s), . . .
Лемма 45. Для любого фиксированного i В (г, s) оп-
определено для всех достаточно больших s и lim В (г, х)
X
существует.
Доказательство. Будем вести индукцию по
г. Предположим, что лемма верна для всех i < e; тогда
существует / и числа b0, bv . . ., be^1 такие, что для всех
s !> / и всех i < e В (i, s) определено и равно bt. Если
8]>/иаДР, содержит число ]> Ье^, то В (е, s) определено
согласно B0). (Случай, когда е = 0, оставляется чита-
читателю.) Такой шаг s существует, потому что а бесконечно
и ps Q as_! для всех s ]> 0. Далее, если В (е, s) определено
для некоторого s]>/, то as+1 \ ps+1 содержит число ]> 6е_1?
а именно В (е, s), и, значит, В (е, s + 1) определено. По-
Поэтому 5 (е, s) определено для всех достаточно больших s.
Если В (е, s + 1), Б (е, s) определены и отличаются
для некоторого s ]> /, то по B0)
НР(Д (е, s+1), е, s + 1)> W (В {е, s), e, s + 1)]\/
V [W E (е, s + 1), е, s + 1) =
= Ж (В (е, s), e,s+i)&B(e,s+l)<B (e, s)].
Поскольку W (х, г/, s) не убывает по s, мы можем замепить
W {В (е, s), e, s + 1) па W {В (е, s), e, s). Таким обра-
образом, W (В (е, s), e, s) не убывает по s, и так как W (х, у,
s) <^ 2y+1, то lim W (В (е, х), е, х) существует. Тогда, если
этот предел достигнут, В (е, s + 1) ф В (е, s) может быть,
только если В (е, s -\- 1) <^ В (е, s). Итак, lim В (е, х)
X
существует, и лемма доказана.
Лемма показывает, что a \ P бесконечно. Мы докажем
теорему, если покажем, что любое рекурсивно перечисли-
перечислимое дополнение а является почти дополнением р. Пред-
Предположим противное. Пусть %е — первое из %о, %i' ... такое,
что a U %е = v и р U хе кобескопечно. Пусть у =
= {х\ х<^е & aU Хх = v}. Обозначим lim W (х, у, z) через
Z
W (х, г/). Пусть Ьо, Ьх, ...— перечисление а \ р в порядке
возрастания. Устремляем s к оо в B0). Имеем
Vz Ix >i->W (Ья, i)^W (bt, OK
154 A. X. ЛАХЛАН
По A9) для любых чисел т, п, i имеем
Va: [*< *-* [W (т, 0 >W(n,i)->W (т, х) > W(n, x)]].
Отсюда следует, что
W (bt, i)>W (bi+1, i)>W (bM, i) > ...
и lim W (bx, i) существует для всех i. Если х ЕЕ f, то а \
X
\ (P U Хж) конечно и поэтому для всех, кроме конечного
числа, элементов Ъ из а \ р
6 е Хсс & а: < е & Ь < lim F (х, у). B1)
у
Если а: <^ е и х ф. у, то только конечное число значений Ъ
удовлетворяют B1), потому что lim F (х, у) существует.
у
Если а: = е, то a \ (P U %х) бесконечно и поэтому суще-
существует бесконечное число элементов Ъ из a \ P, которые не
удовлетворяют B1). Сравнивая A9) и B1), мы видим, что
W (Ь, е) = 2 {2е~х | * ?Е Y} B2)
для бесконечно многих b из a \ р. Поскольку для всех,
кроме конечного числа, значений Ъ из a \ P значения
W(b,e) одинаковы, мы видим, что B2) выполняется для всех,
кроме конечного числа, b из а \ р. Пусть Я — рекурсивно
перечислимое множество, состоящее из тех чисел, которые
перечисляются в р) {%х | а: ЕЕ V V а: = е) раньше, чем в
р, т. е.
[(z ЕЕ v V * = е) -¦ (* е %,• v & х ф ft,)]}.
Ясно, что Ь«'и, значит, Я f) a должно быть бесконеч-
бесконечным, так как а нерекурсивно. Пусть bf — наименьший
элемент иза\Рс/^>е такой, что Ъ = bf удовлетворяет
B2), и g таково, что В (х, s) = bx для всех х < / в s > g.
Так как X f| a бесконечно, то существуют т, s такие, что
т ^> bf, s~^> g, m <^ F {z, s), если z ^ у или z = е, и
m ЕЕ (а, \ рв) П П (Хг,. I z ЕЕ V V 2 = е>.
Отсюда следует, что
, е, *) - S {2е I ZEE V V я = е}>2 {2~ | z ЕЕ v}"=
= W (bf, e).
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 155
Следовательно, W (т, /, s) ]> W (bf, f) и, таким образом,
по определению В (/, s) мы имеем В (/, s) > bf, что проти-
противоречит определению 6/.
Теорема доказана.
Из этой теоремы легко получить кобесконечное рекур-
рекурсивно перечислимое множество р, не имеющее гипергипер-
гипергиперпростых надмножеств. (Мартин показал в [5], что можно
найти такое Р, включающее любое негиперпростое множе-
множество^ р можно сделать как гиперпростым, так и негипер-
простым. Эти более сильные результаты мы здесь пе полу-
получаем.) Пусть а — любое нерекурсивное множество и р —
главное подмножество множества а. Пусть F — 1-1 ре-
рекурсивная функция, отображающая v на а, тогда F~x (P)
не имеет гипергиперпростого надмножества. Для того что-
чтобы доказать это, достаточно показать, что ни р, ни любое
рекурсивно перечислимое множество между р и а не являют-
являются гипергиперпростыми в а. Из теоремы 2 следует, что либо
Р не является гипергиперпростым в а, либо существует ре-
рекурсивное множество б такое, что б (j p = а. В последнем
случае б' — рекурсивно перечислимое дополнение а такое,
что б' (J р кобесконечно и, значит, р не является гиперги-
гипергиперпростым в а. Если у — любое рекурсивно перечислимое
множество, удовлетворяющее условиям: рсуСа и
а \ у бесконечно, то у — главное подмножество множест-
множества а и, значит, не является гипергиперпростым в а.
Есть один небольшой вопрос, оставшийся открытым в
статье Мартина, который легко можно решить, используя
последнюю теорему. Для данного негипергиперпростого
множества р не всегда возможпо найти кобескопечное ре-
рекурсивно перечислимое надмножество а множества р, не
имеющее гипергиперпростых надмножеств. Пусть а —
максимальное рекурсивно перечислимое множество и р —
главное подмножество множества а, тогда р пе является
гипергиперпростым, потому что Р не гипергиперпросто в а.
Далее, если у — любое рекурсивно перечислимое надмно-
надмножество множества р, то либо у коконечно, либо v \ a ко-
конечно. Итак, не существует кобесконечного рекурсивно
перечислимого надмножества множества р, которое не
имеет гипергиперпростых надмножеств.
Для следующей теоремы нам необходим один результат
Мартина [5], который утверждает, что если существует
рекурсивная функция F и рекурсивно перечислимое
156 A, X. ЛАХЛАН
множество а такие, что
мощность (<т' П {х \ х < F (у)}) > у
выполняется для бесконечно многих у, то а не является
гипергиперпростым. Итак, а не является гипергиперпрос-
тым, если существует сильно рекурсивно перечислимая
последовательность {с^} непересекающихся конечных мно-
множеств такая, что
мощность (<т' П av) > у
выполняется для бесконечно многих у. Существует очень
простое доказательство этого результата с помощью теоре-
теоремы 3 настоящей статьи.
Множество называется r-максималъным, если оно рекур-
рекурсивно перечислимо и не существует рекурсивного множе-
множества, нетривиально разбивающего его дополнение. Легко
показать, что каждое r-максимальное множество гипер-
просто и что, с другой стороны, существует гиперпростое
множество, которое не является ни гипергиперпростым, ни
r-максимальным (например, каждое нерекурсивное рекур-
рекурсивно перечислимое множество с ретрассируемым дополне-
дополнением является таким множеством по одной из теорем в
[11]). Также, как следует из теоремы 3 настоящей статьи,
r-максимальное множество может иметь самое большее одно
гипергиперпростое надмножество (по модулю конечных
множеств) и это надмпожество должно быть максимальным.
Отсюда легко следует, что множество является немакси-
немаксимальным r-максимальным множеством с гипергиперпрос-
гипергиперпростым надмножеством тогда и только тогда, когда оно есть
главное подмножество максимального множества. Следу-
Следующая теорема, доказанная также независимо Р. Робинсо-
Робинсоном, показывает, что существуют r-максимальные множе-
множества, которые даже пе являются подмножествами макси-
максимальных множеств.
Теорема 8. Существует r-максималъное множест-
множество, которое не имеет гипергиперпростых надмножеств.
Д о к а з а т ел ь с т в о. Пусть %t и Xi,« такие же, как
при доказательстве последней теоремы. Пусть {аг} — ре-
рекурсивно перечислимая последовательность непересека-
непересекающихся конечных множеств такая, что мощность at равна
2*-? и U {a( \ i > 0} = v. На шаге s мы определим строго
возрастающую последовательность чисел /?0,4, plt „ ... и
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 157
сильно рекурсивно перечислимую последовательность р0, «>
pliS, ... непересекающихся конечных множеств. Мы опре-
определим также вспомогательную функцию
w (х, у, s) = SBV-Z I Р*.. е х*.. & z < у}.
Пусть я8 обозначает множество {pj,a \ i ^> 0}.
Мы скажем, что и требует внимания на шаге s + 1,
если гс е= па и существует т <Сп такое, что
2 (мощность pn,s П Xm,s) > мощность р„,3
и pn.s^Xm, s- Конструкция состоит в следующем.
Шаг 0. Определим р,-, 0 = «г и рг,о = i Для всех ?.
Шаг s+1. Этот шаг состоит из двух частей.
Часть 1. Пусть п — наименьшее число, если такое
существует, которое требует внимания па шаге s + 1, и
пусть соответствующее т выбирается наименьшим из воз-
возможных. Положим pn, s+1 = Pn, s П Xm, s и скажем, что п
уделяется внимание числом т на шаге s+1. Для i Ф п
или для всех'г, если п не определено, положим р,-, т = р,-, s.
Часть 2. Определим последовательность pOi s+1,
Pi, s+H". следующим образом:
Ро, s+i = min {х | а; е= я8 &
& TF (ж, 0, в) = max {TF (^, 0, s) ^ е я8}}
и для всех i ^> 0
Pi, s+1 = min {ж | a; G= я3 & а; > pMi s+1 & W (x, i, s) =
= max {W (y, i,s)\y^ns&y> рг_г, s+1}}.
Конструкция полностью описана. Легко видеть, что она
эффективна в том смысле, что р\_ s — рекурсивная функция
от i, я и {р,-, s} — сильно рекурсивно перечислимая двойная
последовательность конечных множеств. Нужно лишь
вспомнить, что (J {%i,s I i ^> 0} имеет мощность <^ s + 1,
и заметить, что {i \ р,-, s Ф at} имеет мощность ^ s. Поэто-
Поэтому для фиксированного s существует только конечное чис-
число пар (х, у) таких, что W (х, у, s) Ф 0, и мы можем най-
найти их.
Мы видим из части 1 шага s + 1, что p,-,s+i Q Рг,8 для
всех i; пусть lim рг-, х = р,-. Отсюда следует, что W (х, у, s)
X
для фиксированных х, у является неубывающей по s.
158 A. X. ЛАХЛАН
Далее, по определению W имеем, что W(x, у, s)<^2yn. Сле-
Следовательно, lim W (х, у, z) существует, и мы будем обозна-
2
чать его через W (х, у).
Легко доказать индукцией no i, что lim Pit x существует;
X
назовем его pt. Ясно, что lim ях существует; назовем его я.
X
Снова индукцией по i доказываем, что lim W (px, i) су-
X
ществует.
Рассмотрим последовательность множеств рг-,о,Р<,ъ •••
Если рг, 5 ф- р,-, 5+1, то существует т <^ i такое, что i
уделяется внимание числом т на шаге s -\- 1. Когда такое
случится, будет Р,-,5 (? Хт,*> .
2 (мощность f5,-,s П Хт,$) > мощность рг%5
и P(-,s+1 = Pi, в П lm, s- Заметим, что мощность |3;,8+1 не
меньше, чем половина мощности pi)S, и также что f>iti Q
S lm, t Для всех t~^> s. Отсюда следует, что i уделяется
внимание числом т самое большее на одном шаге. Следова-
Следовательно,
мощность Р; > i-2rj > s, B3)
где
j=мощность {х\х <^ i & i уделяется внимание числом х).
Покажем, что т] = ((J {$x \ x GE я})' удовлетворяет не-
необходимым условиям. Прежде всего, т] рекурсивно перечис-
перечислимо, потому что я' рекурсивно поречислимо и для каждого
i последовательность рг,о, Р,м, ••¦ невозрастающая. Пусть
?п фиксировано, тогда, так как lim W (рх, т) существует,
мы имеем, что W (р, т) постоянно для всех достаточно
больших р из я. Предположим, что W (р, т) нечетно для
всех достаточно больших р из я; тогда рр cz %m для всех
достаточно больших р из я. Таким образом, в этом случае
Ц U 1т коконечно. Предположим, что W (р, т) четно для
всех достаточно больших р из я; тогда для всех достаточно
больших р из я не существует шага, на котором р уделяется
внимание числом ти flp(j %m. В этом случае для любого
достаточно большого р из я и всех достаточно больших s
(зависящих от выбора р) мы имеем р ?Е яв, т <^ р, EР, s C|I
Я= У-т, s и Р все е1Де 1;е требует внимания числа т на шаге
s + 1. Следовательно, для достаточно больших р из я мы
РЕШЕТКА РЕКУРСИВНО ПЕРЕЧИСЛИМЫХ МНОЖЕСТВ 159
имеем 2 (мощность рр, а С] %т,«) <С мощность рР) s для всех
достаточно больших s. Тогда
2 (мощность рр \ Хт) > мощность рр. B4)
По B3) правая часть > 2р. Итак, для достаточно больших
р из я множество ар \ (ц (J Хт) имеет мощность ^> р.
Значит, Л U Xm не является гипергиперпростым.
Наконец, предположим, что %т и %п — непересекаю-
непересекающиеся рекурсивные множества, объединение которых есть
v и которые разбивают т)' нетривиально. Сразу видим, что
W (р, т) и W (р, п) четные для всех достаточно больших
р из я. В противном случае мы должны иметь, что т) (J %т
или т) (J Хп коконечпо. По B4) |3Р \ %т и рр \ %п имеют
мощность, превосходящую половину мощности рр для всех
достаточно больших р из я. Следовательно, (хт (J хп)'
непусто; получили противоречие. Теорема доказана.
Очевидной компонентой этой конструкции является
конструкция Фридберга максимального множества.
Если мы будем в копструкции применять лишь часть 2
па шаге s + 1 и переопределим W следующим образом:
W (х, у, s) = 2 {2«-г | * е Xz,* & z < у),
то л' — максимальное рекурсивно перечислимое множест-
множество. Для любого рекурсивно перечислимого множества г|
пусть Хг (т)) — решетка множеств вида т) (J р, где р рекур-
рекурсивно. Легко видеть, что ?г (л) есть ЗУЗ-булева алгебра.
Заменяя конструкцию максимального множества конст-
конструкцией предыдущего параграфа, можно получить следую-
следующее обобщение последней теоремы: пусть Л — любая ЭУЭ-
булева алгебра, тогда существует рекурсивно перечис-
перечислимое множество а, не имеющее гипергиперпростых
надмножеств, такое, что %* (а) си Л.
6. Заключение. Проблема, которая изучалась в этой
статье,— узнать, разрешима теория Я или нет,— еще да-
далека от решения. Теперь обсудим, как программа, начатая
в этой статье, может быть продолжена. Мы также укажем
некоторые новые теоремы относительно других элементар-
элементарных теорий, которые возникают в теории рекурсивных
функций.
Один из наиболее интересных вопросов, подсказанных
данной статьей, состоит в следующем: каким условиям
160 A. X. ЛАХЛАН
должна удовлетворять дистрибутивная ЭУЭ-решетка Л,
чтобы существовало рекурсивно перечислимоо множество
а такое, что X* (а) с~ Jll Часть ответа содержится в тео-
теореме 4, но это неполный ответ, как иллюстрируют две тео-
теоремы, доказанные автором, после того как данная статья
была написана:
Т1. Для данных рекурсивно перечислимых множеств а,
Р таких, что a cz р и a (J р" не является рекурсивно пере-
числимым,\ можно эффективно найти рекурсивно перечисли-
перечислимые множества pit р2 такие, что Pi U Рг = Р, Pi П Рг =
= a, Pj \ а бесконечно, р2 \ а бесконечно.
Т2. Для данных рекурсивно перечислимых множеств а,
Р таких, что a cz р и a (J P' не является рекурсивно пере-
перечислимым, можно эффективно найти рекурсивно перечисли-
перечислимое множество у такое, что у ^ а иу — главное множест-
множество р.
Более сильная теорема, чем Т1, была получена незави-
независимо Овингсом: в заключении этой теоремы еще добавлены
условия, что a (J Pi и a (J р2 не являются рекурсивно
перечислимыми. Его теорема может легко быть выведена из
Т1 и Т2. В настоящее время мы не имеем никаких гипотез,
как расширить известные условия на А, чтобы она была
изоморфна X*(а) для некоторого рекурсивно перечислимого
а. Как кажется автору, следующий шаг состоит в том, что-
чтобы попытаться строить рекурсивно перечислимое множест-
множество а, не имеющее гипергиперпростых надмножеств, такое,
что X* (а) заранее задана. По-видимому, это будет более
сложная конструкция, чем конструкция Фридберга для
построения максимального множества.
Более свежая работа самого автора посвящена построе-
построению частичной процедуры разрешения для Л*. А именно,
рассматривается теория, где вместо символа отношения Q,
применяемого в Я*, имеются функциональные символы
для объединения, пересечения и дополнения, а также два
одноместных предикатных символа В, Е. При интерпрета-
интерпретации кванторы релятивизованы по Л*; И (z) и Е (z)
понимаются как z 6E Я* и z = {0} соответственно. При-
Применяя методы настоящей статьи, можпо доказать разреши-
разрешимость множества УЭ-предложений этого нового языка в
Я*. Изучение теми же способами класса предложений
с тремя кванторами даст нам более глубокие результаты
о строении Я*, чем мы знаем сейчас.
РЕШЕТКА 1'ККУРСЙВНО ПЕРЕЧИСЛИМЬ1Х МНОЖЕСТВ 161
Проблема, оставшаяся в § 4, состоит в следующем:
для каких множеств ц решетка Ж^'' множеств, гипергипер-
нростых относительно ц, изоморфна Ж Я? В частности,
является ли Ж^ изоморфной Ж0 для каждого арифмети-
арифметического множества (х?
Другой и совершенно отличный путь, который может
оказаться очень плодотворным,— это исследование решет-
решетки рекурсивно перечислимых множеств по модулю простых
.множеств. Мы пишем а ~ C, если (а \ C) |J (C \ а) им-
.мунпо. Легко доказать, что ?=: — отношение конгруэнт-
конгруэнтности на М. Решетка, образованная классами конгруэнт-
конгруэнтности семейств Л относительно •х., называется решеткой
рекурсивно перечислимых множеств по модулю простых
множеств. Какие интересные результаты можно получить
для этой решетки?
Один специальный вопрос про максимальные множест-
множества: существуют ли элементарные классы максимальных
множеств, отличные от пустого класса и класса всех мак-
максимальных множеств?
Естественно задать подобные вопросы относительно
элементарных теорий других структур, которые изучают-
изучаются в теории рекурсивных функций. Немного известно в сле-
следующих трех случаях:
A) Как доказано автором, элементарная теория
иг-стененей неразрешима. А именно, доказано, что лю-
любая счетная дистрибутивная решетка с наименьшим и
наибольшим элементами изоморфна некоторому началь-
начальному сегменту m-степеней. Применяя подобный метод, мож-
можно доказать, что элементарная теория рекурсивно пере-
перечислимых те-степеней неразрешима.
B) Для 77-степепей Д. Ф. Хьюджил показал, что суще-
существует начальный сегмент, изоморфный любому счетному
линейно упорядоченному множеству с наименьшим эле-
элементом. Его метод обобщает конструкцию Спектора для
минимальных степепей и, вероятно, работает, когда слова
«линейно упорядоченное множество» заменяются на «дис-
«дистрибутивная решетка». Отсюда будет следовать, что эле-
элементарная теория Г-степеней неразрешима.
C) Пусть {i|)j}, {Xi} — две стандартные нумерации клас-
класса рекурсивно перечислимых множеств, a F и G — соот-
соответствующие бинарные отношения: F (х, у) <-> х ?Е tyy
и G (х, у) <-» х ?Е %v Можно показать, что существует
162 A. X. ЛАХЛАН
рекурсивная подстановка я такая, что F (ж, у) эквивалент-
эквивалентно G (я (х), л (у)). Отсюда следует, что элементарная тео-
теория /'' не зависит от выбора стандартной нумерации. Эта
элементарная теория, которую обозначим через SE, как
можно показать, неразрешима.
Добавление. Я благодарен К. Джокушу и А. Манасте-
ру за указание ошибки в моем доказательстве, что эле-
элементарная теория Ж* решетки коконечных и гипергипер-
простых множеств по модулю конечных множеств разре-
разрешима. Это доказательство изъято из статьи. Однако
Ю. Л. Ершов в [2] описал все полные расширения элемен-
элементарной теории RD дистрибутивных решеток с относитель-
относительными дополнениями и показал, что все они разрешимы.
Поэтому разрешимость Ж* есть следствие теоремы 3.
Из теоремы 6 можно видеть, какое полное расширение RD
есть элементарная теория Ж*; оказывается, оно имеет
паиболее богатую структуру.
ЛИТЕРАТУРА
[1] Davis M., Computability and unsolvability, McGraw-Hill
N. Y., 1958.
[2] Ершов Ю. Л., Разрешимость элементарной теории дистри-
дистрибутивных структур с относительными дополнениями и теории
фильтров, Алгебра и логика (семинар) 3, № 3 A964), 17—38.
[3] Friedberg R. M., Three theorems on recursive enumera-
enumeration, J. Symbolic Logic 23 A958), 309—316.
[4] Friedberg R. M., 4-quantifer completeness: a Banach —
Mazur functional not uniformly partial recursive, Bull. Acad.
Polon. Sci. Ser. Sci. Math. Astronom. Phys. 6 A958),^1—5.
[5] Martin D. A., A theorem on hyperhypersimple sets, J. Sym-
Symbolic Logic 28 A963), 273—277.
[6] Martin D. A., Classes of recursively enumerable sets and
degrees of unsolvability, Z. math. Logik Grundl. Math. 12 A966),
295—310.
[71 M у h i 11 J., Review of [10], Math. Rev. 26 A963), 691, # 3598.
[8] Post E. L., Recursively enumerable sets of positive integers
and their decision problems, Bull. Amer. Math. Soc. 50 A944),
284—316.
[9 Robinson A., Introduction to model theory and tbe meta-
mathematics of algebra, North-Holland, Amsterdam, 1963. [Рус-
[Русский перевод: А. Робинсон, Введение в теорию моделей и
^метаматематику алгебры, «Наука», М., 1967.]
[10] Yates СЕ. М., Recursively enumerable sets and retracing
functions, Z. math. Logik Grundl. Math. 8 A962), 331—345.
[11] Y a t e s G. E. M., On the degrees of index sets, Trans. Amer.
Math. Soc. 121 A966), 309—328.
ИЕРАРХИИ БУЛЕВЫХ АЛГЕБР •)
Л. Фейнер
1. Введение. Счетная структура называется рекур-
рекурсивной тогда и только тогда, когда ее основное множество
является рекурсивным подмножеством множества пату-
ральных чисел, а отношения и операции рекурсивны. На-
Например, стандартная модель теории чисел рекурсивна.
Структура пазывается рекурсивно представимой тогда
и только тогда, когда опа изоморфна рекурсивной струк-
структуре. Например, булева алгебра, порожденная счетным
числом свободных порождающих, как легко видеть, ре-
рекурсивно представима. (Основные факты, касающиеся бу-
булевых алгебр, читатель может найти в книге Сикорского [9]
и статье Тарского и Мостовского [10].)
Достаточно хорошо известны примеры структур, кото-
которые но являются рекурсивно представимыми, такие, как
(i) любая модель теории мпожеств (см. статью Рабина [7])
и (н) любая нестандартная модель теории чисел (см. статью
Тенпенбаума [11]). Оба эти результата следуют из сущест-
существования пары рекурсивно перечислимых рекурсивно не-
неотделимых множеств.
Тем не менее цель этой статьи — дать непосредствен-
непосредственное построение «рекурсивно перечислимой» булевой ал-
алгебры, которая не является рекурсивно представимой, и об-
обсудить некоторые интересные следствия этого построения.
Точнее, под булевой алгеброй мы будем понимать четверку
{A,\J,f),—}, где Л — основное множество алгебры, (J, П.—
будут отношениями объединения, пересечения и дополне-
дополнения, а отношение <^ определяется в терминах U'Cli—•
В дальнейшем f всегда будет обозначать некоторую фикси-
фиксированную рекурсивную бесконечную булеву алгебру, сво-
свободно порожденную рекурсивным множеством порожда-
порождающих.
*) L. F e i n е г, Hierarchies of Boolean algebras, J. Symbolic
Logic 35, № 3 A970), 365—374.
164 Л ФЕЙНЕР
Мы хотим построить рекурсивно перечислимый фильтр
V на ,f такой, что фактор-алгебра ,<f/V не является рекур-
рекурсивно представимой.
Это построение интересно по двум причинам. Во-пер-
Во-первых, оно позволяет, используя относительные формулиров-
формулировки структурных теорем Лахлана для решетки рекурсивно
перечислимых множеств, показать, как тип изоморфизма
решетки Х-рекурсивпо перечислимых множеств зависит
от X. В частности, если Xcf, то обозначим через Хх ре-
решетку Х-рекурсивно перечислимых множеств. Мы пока-
покажем, что если X' — теоретико-рекурсивный скачок мно-
множества X, то решетки Хх и Хх' неизоморфны.
Во-вторых, оно позволяет построить аксиоматизируе-
аксиоматизируемую теорию, у которой алгебра Линденбаума в стандарт-
стандартном понимании неизоморфпа алгебре Линденбаума ника-
никакой разрешимой теории. Это проливает некоторый свет на
гипотезу Ханфа об алгебрах Линденбаума теорий первого
порядка.
Для полноты мы заметим, что в [2] показано, что если
V является фильтром типа П\ алгебры $ и ,f7V имеет
счетное множество простых идеалов, то ,f /V — рекурсивно
представимая булева алгебра. Поэтому наша булева
алгебра ,f/V будет иметь несчетное множество простых
идеалов.
2. Предварительные сведения. ЛГ будет обозначать
множество натуральных чисел. Большими латинскими бук-
буквами будем обозначать множества. 0 — обозначение пу-
пустого множества. Маленькими латинскими буквами будем
обозначать числа или элементы структур. Структуры бу-
будем обозначать рукописными буквами, f), (J,— будут
обозначать булево объединение, пересечение и дополнение
или, в случае булевой алгебры мпожеств, объединение,
пересечение и дополнение. ^ будет обозначать алгебраи-
алгебраический изоморфизм, ,Л X Ш будет обозначать прямое
произведение структур Л и 53. .А2 — Л X Л. г\ — тип изо-
изоморфизма рациональных чисел.
Если X ~ {?,<} — линейный порядок с первым ипс
следним элементом, то D ? — булева алгебра всех подмно-
подмножеств из ,с?, которые являются конечным объединением ин-
интерпалов \а, Ь) из L (под [а, Ь) мы понимаем множество всех
а из L таких, что а ^ х < Ь) (см. [5], стр. 207). Как легко
ИЕ РАРХИИ БУЛЕВЫХ АЛГЕБР \ 63
заметить, изоморфизм X = ? влечет изоморфизм D е г^
^Z>2, и поэтому мы можем писать Z)a, где а — некоторый
порядковый тип. Если А — булева алгебра и а — один
из ее элементов, то через А [а] (А (а)) мы обозначим було-
ву алгебру, образованную главным фильтром (идеалом),
порожденным элементом а, т. е. булеву алгебру, образован-
образованную множеством всех элементов, которые содержатся в
элементе а (содержат элемент а), и имеющую те же опера-
операции, что и А, за исключением дополнения, которое бе-
берется относительно а.
Если Ж — решетка и а — некоторый ее элемент, то
Ж Ы {Ж (а)) определяется аналогично. Если А — булева
алгебра и S — подмножество из А такое, что (i) А по-
порождается S и (ii) S линейно упорядочено относительно
включения на А, то S называется упорядочешшм базисом
для А. Если А — булева алгебра и А имеет упорядочен-
упорядоченный базис порядкового типа а, то А = Da.
Замечание. <$/V будет иметь вид D е, где X есть
1 + Г S ((«2m + 1 + Л) X со»)] + 1
по модулю отождествления определенных нар соседних
изолированных точек *).
&, \/ и | будут обозначать соответственно конъюнк-
конъюнкцию, дизъюнкцию и отрицание, 3 и V соответственно
кванторы существования и всеобщности.
^Если XcJVh7cJV, то X @ Y = (X Г\У) [J (Y f)
П X), «3woz» означает «существует бесконечно много z
таких, что», «seq (s)» означает, что s — последовательност-
ное число. Если seq (s), to lh s равно длине последователь-
последовательности элементов, соответствующей s, и если i <; lh s, то
•i (i) есть i-ii член последовательности. Если а0,. . ., ап —
конечная последовательность натуральных чисел, то через
<ао, . . ., апУ будем обозначать последовательностное
число, которое соответствует а0, . . ., ап. Основное свой-
свойство последовательностных чисел состоит в том, что
<ао,\ . . ат> = <&„, . . ., ЬпУ тогда и только тогда,
когда т = п и Vti<n (a? = bt) (см. [8], стр. 482). Если
X Q N, то характеристическая функция сх множества X
*) Обозначения для порядковых типов сумм и произведений
порядковых типов те же, что и в [5].
166 Л. ФЕЙНЕР
определяется следующим образом:
сх (т) = 1 для теХ, сх (т) = 0 для т ф. X.
Через «3ziVz2 ... Rx (zu . . ., zn, m)» будем обозначать
предикат типа 2;f (см. [8], стр. 390) с Х-рекурсивной мат-
матрицей Rx (z,, . . ., zn, иг).
« < » есть лексикографический порядок па множестве
пг-ок. «[^» будем понимать как отношение истинности
между структурой и предложением в слабом языке второго
порядка.
В дальнейшем ссылки будут в основном на книгу Род-
Роджерса ([81, гл. 14). Тем не менее при доказательстве будет
удобно использовать также принадлежащую Девису ха-
рактеризацию относительной рекурсивности. Если XQiV,
то {е)х (п) будет обозначать одноместную Х-частично ре-
рекурсивную функцию, которой соответствует машина Тью-
Тьюринга с гёделевым номером е'АЫ обозначениях Девиса (см.
[11, стр. 22 и 56—64) {е}х (п) = Y^-x (п), где е — гёделев
номер машины Z]. Для наших целей удобно свойство фор-
формулировки Девиса: если у — вычисление {е}х (п), то у —
единственное вычисление {е}х (п).
Если X с: JV, то положим X' — {е\ {е}х (е) определе-
определено}. Пусть Х№ =Х иХ<"+« =(Х1»>)\ Обозначим Х^ =
= {<пг, | пУ\тЕЕХ^}.
Набросок конструкции. Мы будем ис-
использовать классификацию 0^-рекурсивных функций /,
основанную на ограничении «количества» информации об
оракуле 0(ш\ используемой при вычислении значения
функции / в точке п. Определим ее следующим образом.
Если (о, Ь) — пара натуральных чисел, е — натуральное
число, то пишем е ~ (о, Ь) тогда и только тогда, когда
(i) функция {е}0(ш) всюду определена;
(и) Уп Vmm>a+nbVq (вопрос «<д, т> е 0(ш)?» не зада-
задается оракулу 0(ш> при вычислении {е}0(ш) (и)).
В п. 4 мы определим последовательность {Ф„} предло-
предложений в слабом языке второго порядка теории булевых ал-
алгебр. Мы покажем, что {п \ Л[\= Фп} "f-B,2)*), если Л —
*) Под этим понимается, что существует такое eeJV, что
}0 — характеристическая функция множества, стоящего слева,
е + B, 2).— Прим. ред.
ИЕРАРХИЙ БУЛЕВЫХ. АЛГЕБР 167
рекурсивная булева алгебра. В п. 5 будет построен рекур-
рекурсивно перечислимый фильтр V на булевой алгебре $ такой,
что {п\& /V (z: Ф„) по ~ B, 2) *). Поэтому в слабой тео-
теории второго порядка булевых алгебр алгебра &IV не-
неэквивалентна никакой рекурсивной булевой алгебре.
3. Леммы из теории рекурсии. Пусть Ап = {(х, m> |
х <= 0<т) & т < п}. Если X cr N, то пусть Тх (в, п, у)
обозначает предикат «у — вычисление функции {е}х (п) с
оракулом X» (см. [1], стр. 57). Пусть U (у) — результат вы-
вычисления у (т. е. U (у) = {е}х (п)).
Теорема 3.1. Пусть <о, ЪУ — пара натуральных
чисел, X (о, Ъ) ={п\ пчетно и {n/2}Ao+nb (n) = 0}, тогда
(i) X (а, Ъ) ~ (а + 1, Ъ);
(ii) если X (а, Ь) 0 Y С {нечетные числа}, то Y не
~ (а, Ь).
Для доказательства теоремы 3.1 нам будут пужпы сле-
следующие леммы.
Лемма 3.1.1. (i) Предикат Тх (е, п, у) равномерно
рекурсивен в X.
(ii) Если е ~ (о, Ь), то для любых п, у
Лемма 3.1.2. Существует рекурсивная функция
р: N -*- N такая, что для любой пары <пг, п> имеем т ?Е
ЕЕ 0(п) тогда и только тогда, когда
3zi Vz2 . . . (р «Zn z2, . . ., zn, m» = 1).
Доказательство. Это переформулировка силь-
пой теоремы об иерархии ([8], гл. 14, теорема VIII,
часть с).
Лемма 3.1.2'. Лемма 3.1.2 сохраняет силу при заме-
замене «0<п)» на «Лп».
Л с м м а 3.1.3. Для любой пары <о, by существует ре-
рекурсивная функция P(a,bj: N->- N такая, что для любого п
имеем п ?= X (а, Ъ) тогда и только тогда, когда
. . . (р{а,Ь) «Zi, Z2, . . ., Za+1+nb» =1).
*) То есть (см. предыдущее примечание) не существует тако-
такого е, что [е\® — характеристическая функция этого множества в
о ~ B, 2).— Прим. ред.
168 Л. ФЕЙНЕР
Доказательство. X (а, Ь) = {п | * Зу (п чет-
четно и 2"Аа+пЬ (п/2, п, у) & U (у) — 0)}. Применяя алгоритм
Тарского — Куратовского ([8], стр. 394—400), 3.1.1 и
3.1.2 к выражению #, построим функцию р(а,ь;.
Лемма 3.1.4. Существует рекурсивная функция ср:
N2 ->¦ N такая, что для любой пары <jn, /г>, если функция
{т}0 всюду определена, то 3zxVz2... ({т}0 «zx, . . ., zn» =
= 1) тогда и только тогда, когда {ср(т, п)}0<~п\п) = 1.
Доказательство. Для иары <т, /г> такой, что
функция {т}0 всюду определена, положим
Вп = {z | z = z & 3zxVz2 . . . ({m}0«zi, . . . г„» = 1)}.
Применяя теоремы VIII и III из [8], гл. 14, найдем эффек-
эффективно по (т, пУ индекс i множества Вп как рекурсивно пе-
перечислимого в 0<-11~1). Теперь применяя [8], стр. 394, най-
найдем по i число ф (т, п) такое, что {ср (т, п)}0^— ха-
характеристическая функция множества Вп. Поэтому
{у(т, п)}0{-п) (п) = 1 тогда и только тогда, когда Вп не-
непусто.
Лемма 3.1.5. Если X ~ (а, Ь) и X ф Y конечно, то
Y ~ (а, Ь).
Лемма 3.1.6. Пусть /: N —> N — рекурсивная функ-
функция и X = {п | 3z!Vz2 . . . / «zx, . . ., za+nb» — 1}. Тог-
Тогда X ~ (а, Ь).
Доказательство. Пусть / = {е}0. По 3.1.4
X = {п | {ср (е, а + nb)}0^nb) (а + пЬ) =1}.
Из этого представления легко видеть, как построить маши-
машину Тьюринга q такую, что (i) q ~ (a, b); (ii) область значе-
значений функции {q}0^ С {0, 1}; (iii) {q}0W(n) = 1 тогда
и только тогда, когда вб!
Следствие 3.1.7. X {а, Ь) ~ (а + 1, Ь).
Доказательство 3.1. (ii) Мы покажем, что
X (а, Ь) не имеет характеристической функции вида {е}0^,
где е ~ (a, b).
Пусть е ~ (а, Ь). Если {е}0(а>) Bе) = 0, то в силу 3.1.1
{е}Аа+2гЬ Bе) = 0 и поэтому 2е е X (а, Ь).
В противном случае, если {e}0^w) Be) = q ф 0, то,
применяя 3.1.1, получаем, что {е}Аа+2еЬ Bе) =qфQ
и поэтому 2е ^ X (а, Ь). Следовательно, {е}0^ ф Сх(а,ъу
ИЕРАРХИИ БУЛЕВЫХ АЛГЕБР 169
4. Алгебраические леммы. Определим производную от
булевой алгебры, отождествляя в ней элементы, отличаю-
отличающиеся на конечное число атомов (см. [5], стр. 210). На-
Например, производная от булевой алгебры Дшг+1+1 равна
DJ+1- Если А — булева алгебра и«ё4, то определим
предикат Хп (а), который означает, что а содержит Хо
попарно различных атомных элементов, никакие два из
которых не отождествляются в (п — 1)-й производной от
алгебры А. Положим у„ (а), если Кп (а) & Vy ((а содержит
у & у — атомный элемент) -*¦ \Хп (у)).
Наконец, определим Фп, положив Ф„ — Зхуп {х). Фп
является предложением в слабой теории булевых алгебр
второго порядка (см. [2], стр. 54—58), хотя это нам не по-
потребуется.
Следующие леммы доказываются непосредственно.
Лемма 4.1. Если А = А, то для любого п имеем
,4 [г Ф» тогда и только тогда, когда А |и Фп,
Л е м м а 4.2. Если (п — 1)-я производная от „/ [а\
конечна, то ^„ (а) ложно.
Л е м м а 4.3. Если а = b U с, где b — атомный эле-
элемент, ас — безатомный элемент, то уп (а) ложно.
Следующие примеры несколько прояснят дальнейшие
построения.
11 р и м е p. -Dwn+ri+1 1= ф"-
Доказательство. Пусть х — интервал типа
со" +г\ (см. [5], стр. 209). со" + Л = (со" X со) + г\.со копий
(о" образуют бесконечное множество атомных элементов,
которые вырождаются в (п — 1)-й производпой в различные
атомы. С другой стороны, если х содержит у и у — атомный
элемент, то, поскольку у равен объединению конечного
числа интервалов, (п —1)-я производная Л [у] — ко-
конечная алгебра.
Пример. Пусть X cz N, тогда D i v, .. \ Ь cl),.
тогда и только тогда, когда п 6Е X.
Л е м м а 4.4. Пусть Л = {N, (J, П > —) — рекурсив-
рекурсивная булева алгебра и X = {п | A f= Фп}> тогда X ~ B, 2).
Доказательство. Мы покажем, что существует
множество Y, удовлетворяющее посылкам леммы 3.1.0
(где (а, Ъ) = B. 2)) и такое, что X © Y конечно. Мы распи-
распишем наще определение А \=. Ф„ и найдем место этого
170 Л. ФЕЙНЕР
отношения в иерархии предикатов (см. [8], стр. 389). Дадим
следующие определения:
Atom0 (х) ±? У у (у П х = у -> у = х \J у = 0J) & х Ф О*
(здесь Оей — нуль булевой алгебры,^). Предикат Atom0 (x)
имеет тип IlJ.
Atomistic (x) =*? Vy 3z (у f] % = У & У Ф 0^ ->
-»¦ (z П У = z & Atom0 (z))).
Предикат Atomistic (ж) имеет тип П*.
х =ly^3s3t (seq (s) & seq (f)& s @) = t @)&lhs = lhf&
& Vz2<ihs (Atom0 (s (г)) & Vz2<m/ (z > 0 -> * (z) = s (z) (J
U t B - 1)) & (a- r)y)U(ynx)=t (Ш *))•
Отношение «ж = гу» имеет тип 2°. Если мы заменим вхож-
вхождения «=» в определении Atom0 (x) на «=„», то получим
определение Atomn (x).
Если мы заменим вхождения Atom0 (x) в определении
«=х» на Atomn_x (x), то получим определение отношения
«=п». Отношение «х = пу» является равенством в n-й про-
производной. Поэтому
Кп {х) <-» Vm 3s (seq (s) & lh s > m &
& Vz (z < lh s -> Atomistic (s (z)) & ж П s (z) = s (z)) &
& Vz Vu> ((z < lh s & м> < lh s & z Ф w) -> ~]s (z) = n_!
Ф» «-> 3z (Я„ (ж) & Уг/ {(у П ^ = I/ & Atomistic (г/))
Легко пидеть,что существует процедура 9*, применяю-
применяющая эффективно по п к Ф„ алгоритм Тарского — Куратов-
ского, которая преобразует Ф„ к пренексной нормальной
форме, и если п> 3, то ^(Ф^) записывается в Егп+г-
Пусть i?n(zi,...,z2n+2) — рекурсивная матрица для {)
тогда определим рекурсивную функцию /, положив /«z,, ...
. . ., z2n+2» = 1 тогда и только тогда, когда выполнено
Л« (*i, • • ., гг„+г)- Пусть У={р|р>3* Л f= Ф„}.
ИЕРАРХИЙ БУЛЕВЬ1Х АЛГЁЁР 171
Множество Y удовлетворяет посылкам леммы 3.1.6 (где
(а, Ь) = B, 2)) и, следовательно, У ~ B, 2). Поэтому в силу
3.1.5 будет X ~ B, 2).
В п. 5 мы определим рекурсивно перечислимый фильтр
V булевой алгебры f такой, что {п | <f/V \= Фп} не ~ B, 2).
В силу 4.4 и 4.1 алгебра (f7V неизоморфпа никакой ре-
рекурсивной структуре.
Следующая лемма будет нужна нам при определении V.
Лемма 4.5. Пусть A: N3 -*• {порядковые типы).
Предположим, что для любой тройки <jn, i, К) имеем
оJ'" ^ Д (т, i, h) <^ со2, тогда для любого т
Л=В{% ^ Ц 1Д I'M. *>««>) + ! 1=Фда
т&& i&a hew
в том и только в том случае, когда
*3i ПЭ«0А (Л (т, i, h) = соат)).
Доказательство. Пусть хт CI Л\— макси-
максимальный интервал типа 2 2(^ (те> Ь ^) + 1 + л) (см-
ieu [Ье<л
[5], стр. 209). Из предыдущих лемм и примеров легко ви-
видеть, что Л (= Ф2т тогда и только тогда, когда Л \хт\ \z
\^ Ф2т- Предположим, что формула * верна для т. В этом
случае мы можем выбрать интервал у такой, что хт содер-
содержит у и у имеет тип (со27" + 1 + ц) X со *). Элемент у
содержит Хо непересекающихся интервалов типа со2.
Поэтому Х2т (у) выполнено. Пусть z — произвольный атом-
атомный элемент, содержащийся в у. Очевидно, что z объединя-
объединяет лишь конечное число интервалов типа со2™. Поэтому
алгебра (A [z]I-2™) конечна и Х2т (z) ложно. Следователь-
Следовательно, у2т (у) выполняется и А (= Ф2т-
Обратно, пусть * неверно для т. В этом случае можно
показать, что любой элемент у, содержащийся в хт, либо
(i) объединяет лишь конечное число интервалов типа со2
или 1 + г]' либо (а) содержит интервал типа со2. В этом
случае у2т (у) ложно.
*) Это не совсем точно, можно выбрать только интервал у типа
У (V/c + * + Л). гДе ш2т~1< у/с < ш2т; однако дальнейшие рассуж-
Iteo
дения справедливы и для такого у.— Прим. ред.
172 л. фёййёр
5. Построение V. В начале нашего построения зададим
представление для порядкового типа
2 ((со2 + 1 + т|) х со2).
теш
Определение. Пусть {N, а} — рекурсивный
линейный порядок тина 1 -\- ц.
Определение. Для удобства записи присоеди-
присоединим к N число V2. Положим
Lm -- {(m, i, h, Zi, . .. , zm, l,q)\l--Q -> (q -= -y
b.. . ,z2m) — f-g-,...,-^-
Пусть L = U Lm. Упорядочим L следующим обра-
обрате N
зом: (пг,; i, ^ h, z,, . . ., z2m, i, ?) -< (пг', i', h', zi, . . .
. • •, z^m, /', q') тогда и только тогда, когда (т, i, h, d) <iex
<lex (m1, i', h', V) или ((m, i, Л, /) = (m', i', A', V)
и ((/==1 и gcg') или (/ = 0 и (Zi, . . ., z2m) <
<(zi, . . ., z^m))). {L, -<} — рекурсивный линейный поря-
до1. типа 2 ((w2m + 1 + л) X со2).
теш
J1 е м м а 5.1.0. Существует рекурсивная функция г:
N -*- N такая, что для любой тройки <jn, i, /)
ЭгУг2 . . -Vz4m3 z4m+i (рBJ) «г, /, zlf . . ., z4m+1» = 1)
тогда и только тогда, когда
Э«^1— 3Xoz2m Уу (г «г, /, zi, . . ., z2m, у» = 1).
(Определение рB|2) см. в 3.1.3.)
Доказательство. Применим алгоритм Крайзе-
ла приведения к [/-форме ([8], стр. 422). Заметим, что ре-
рекурсивная матрица в записи с [/-кванторами эффективно
строится по рекурсивной матрице в предикатной форме.
Лемма 5.1.1. Пусть {N, \j , Г\ , —} — рекурсивная
булева алгебра и V cz JV — фильтр, порожденный рекур-
рекурсивно перечислимым подмножеством из N, тогда V — ре-
рекурсивно перечислимый фильтр.
Доказательство. Пусть V порождается рекур-
рекурсивно перечислимым множеством S. Тогда для любого х
ИЕРАРХИИ БУЛЕВЫХ АЛГЕБР 173
имеем х ?Е ^ тогда и только тогда, когда
//His x /Ihs u
Bs (seq (s) & Vti<lh (s) (s (i) ЕЕ Д1 & (( f] * (О) П * = (Ц * (Oj) •
Определение фильтра ?. Пусть ff — фик-
фиксированная рекурсивная бесконечная булева алгебра, опи-
описанная во введении; и {рп} — рекурсивное множество сво-
свободных порождающих алгебры tf.
Пусть к: N -> L —рекурсивное 1-1 соответствие, /:7V-*"
-.- Лг — рекурсивная функция такая, что V'reJXo«(/ (и) =
- т). Если к ЕЕ L, то пусть /> (/с) Pi-«(k)-
Пусть фильтр V порождается рекурсивно перечислимым
множеством элементов $
{Р (к) U Р (к) | к -< к или А - (m, i, h, zu . . . , z2m, 0, V2)
и к *- (m, i, A, zl5 . . . , z2m -h 1, 0, 72)
и 3»(r«*,/(A), zt, . . . , z2m, »»^1}*).
В силу 5.11 фильтр V рекурсивно перечислим.
Замечание. Алгебра J^/V имеет упорядоченный
базис типа
1 [1L №Ш + 1 + ^ Х
по модулю отождествления определенных пар соседних
изолированных точек.
Определение. Пусть 0 (т, i, h, z1, . . ., ггт-!) —
упорядоченный тип множества |j [p{m, i,h, zu . . .
z2me.v \
.. . , zim, 0, -s-H относительно отношения включения в
.f/V **).
Пусть
А (т, i, Л) ~ 2 ¦ • • S ° ("*' ^ Л» zl5..., z2m_!).
z«e<» Z2tn-iew
Паша конструкция удовлетворяет следующим свойствам.
*) Здесь мы поместили рп {J рт в фильтр V, чтобы было рп < рт
в упорядочении Ж/V. Тогда \рп) — упорядоченный базис алгеб-
алгебры .Г/9.
**) Здесь, конечно, два элемента тииа рп отождествляются, есди
они представляют один и тот же элемент Jf/
174 Л. ФЕЙНЕР
Лемма 5.1.2. (i) Д удовлетворяет посылкам лем-
леммы 4.5.
(ii) Если J (h) = / (h), то Д (т, i, h) = Д (т, i, h).
Лемма 5.1.3. Для любой тройки (т, i, 7г> имеем
Д (яг, i, h) < со2т тогда и только тогда, когда
~\ 3«0Z! ... Э«„22тУг/ (г «г, / (/г), г1} . . . , z2m, i/>) = 1).
Доказательство. Зафиксируем числа т, i и/г.
Пусть
Hi (zi, • • • , Zam-O = 0 (/re, i, h, zu . . . , z2m-i).
Пусть
(ir (Zi, . . . , Z2m-r) = S
Пусть
Ar (zlt . . . , z2m_r) ^
^ (r «i, / (/г), zb . . ., z2m, y}) = 1).
Мы хотим показать, что для 1 ^ г^ 2т:
(i) Vz, . . . Vz2m_r(Ar (zb . . . , z.2m_r)->
->• цг (zi, . . . , z2m_r) ---- cor);
(ii) Vzi ... Vz2m_r (П Лг (zi,..., z2m_r)->-
->- a'-^ цг (zb . . . , z2m-r) < cor).
Докажем это утверждение индукцией по г. Предполо-
Предположим, что (i) и (ii) верны для г ----- s — 1. Зафиксируем /те, г, h,
Zi, ¦ • •, z2m-,. Очевидно, что У /х,_! (. ..) = со" тогда и
только тогда, когда существует fc$0 z2m_s+1 таких, что
tVi(- • -.zam-e+i) = cos-i. В противном случае сй^^Ун^.-Х
<^ (о*. Таким образом, индукционный шаг доказан.
Пусть г — I. Зафиксируем т, i, h, zlt . . . , z2m_i.
Предположим, что n3«oz2mVj/ (r «i, / (h), zlt . . . , z2m,
уУ) = 1). Поэтому для достаточно больших z2m существует
ИЕРАРХИИ БУЛЕВЫХ АЛГЕБР 175
у такой, что г «i, / (h), zu . . ., z2m, z/>) ф 1. Следова-
Следовательно, для достаточно больших z2m все р (т, i, h,
Z], . . . , z2m, 0, */г) представляют один и тот же элемент в
ff/V и 1 <g: jlix (zb . . . , z2m_i) < со. Аналогично,
3«,z2mVj/(r «f, / (h), zb . . . , z2m, z/>) = 1)
влечет, что щ (z,, . . . , z2m) = со.
Положив r —- 2m, мы докажем лемму.
Лемма 5.1.4. Для любого т имеем f/V [= Ф2т тогда
и только тогда, когда
*3fVy П ЗиЛ ... 3Xoz2mV?/ (r «i, /, . . . , г/>) =- 1)).
Доказательство. Предположим, что утверж-
утверждение * выполнено. Тогда в силу 5.1.3, имеем Ji\/h(A(m,
i,/г)<0J7") и, следовательно, в силу 4.5 f /V f= Ф2т.
Предположим, что * неверно. Тогда в силу 5.1.3 имеем
VG/г (А (т, i, К) — со2т). А отсюда в силу 5.1.2 и опреде-
определения / получаем VG^»^ (^ (m> f> h) — со2). Следова-
Следовательно, f/V ф Ф2т.
Лемма 5.1.5. {п \ f /V |= Фп} не ~ B, 2).
Доказательство. Зафиксируем т. Обозначим
через А (т, i, j) выражение
, z2m) г/>) = 1),
•¦» = !)•
п =
а через В
Тогда
2т ge
где
A)
B)
C)
В (
35
X B,
... 3noz2
(т,
!lVz
,2)
следует
из 5.
из 5
силу
1.0,
.1.4.
3.1
2 ..
О)
из
imVz/ (г «i, .
f, Zi,
/) — выражение
. 3z4m+i (pB
3fVyS (m, i,
B)
<-> 3i
3.1.3,
получаем
,2) «'
B)
¦VjA
¦ •
, j,
(m,
C)
f/V \ Ф
2т,
{п | f/V fr Фп} не ~ B, 2).
Теорема 5.1. Булева алгебра $ /V неизоморфна ни-
никакой рекурсивной структуре.
Доказательство. Следует из 5.1.5 и 4.4.
176 Л. ФЕЙНЕР
Положение ,f/V в арифметической иерархии будет об-
обсуждаться в 6.1.3.
6. Приложения. Аналогично п. 1 мы можем определить
рекурсивно перечислимые (А\, 2}, Х-рекурсивные и т. д.)
структуры и рекурсивно перечислимо (А\, Б|, Х-рекурсив-
Х-рекурсивно и т. д.) представимые структуры.
Лемма 6.1.1. Любая рекурсивно перечислимая струк-
структура изоморфна рекурсивно перечислимой структуре с ос-
основным множеством N.
Доказательство. Изоморфизм получается
«переименованием» элементов основного множества рекур-
рекурсивно перечислимой структуры (см. [2], стр. 62).
Л е м м а 6.1.1'. Для любого X cz N любая Х-рекурсив-
Х-рекурсивно перечислимая структура изоморфна Х-рекурсивпо пере-
перечислимой структуре с основным множеством N.
Лемма 6.1.2. Любая рекурсивно перечислимая струк-
структура Л без предикатов изоморфна рекурсивной структуре.
Доказательство. Мы можем предположить
без ограничения общности, что основное множество модели
Л есть N. Пусть ц — гс-арная операция на Л. Отпошение
у =-• ц (хи . . . , хп) рекурсивно иеречислимо. Однако
у ф \х (хи . . . , хп) <-> Зг (г -- ц (хи . . . , хп) | & у ф г)
и поэтому отношение у ф (л (хх, . . ., хп) также рекур-
рекурсивно перечислимо. Следовательно, отпошение у =
-- fi (xu .... хп) рекурсивно.
Лемма 6.1.2'. Для любого X с. N любая Х-рекурсив-
Х-рекурсивно перечислимая структура без предикатов изоморфна X-
рекурсивиой структуре.
Лемма 6.1.3. Алгебра Линденбаума | Т | любой раз-
разрешимой теории Т рекурсивно представила.
Доказательство. Пусть G — множество
предложений языка теории Т. Используя разрешимость
теории Т, мы можем построить рекурсивную функцию
g: G ->- N такую, что если а, Р gG и \—т а <-> Р, то
g («) -~ g (P).
Определим операции f], (J,—следующим образом:
х U У ~= г ^ ЭаЗРЗа (g (а) -
¦=x&g (Р) - y&g(u) - г & [-т а V Р <-> f1).
х - у^ ЗаЗр {ц (а) - х & ц (Р) ^-у & \--т а -> П Р),
з- П у =* (НЛ).
ИЕРАРХИИ БУЛЕВЫХ АЛГЕБР 177
Алгебра | Т | з* {N, (J, f], — } рекурсивно перёчислима
и, следовательно, рекурсивна.
Лемма 6.1.3'. Если X Q N и V -- Х-рекурсивно
перечислимый фильтр на алгебре ^, то алгебра ^/V будет
X'-рекурсивно представимой.
Доказательство. V можно рассмотреть как X-
рекурсивно аксиоматизируемую теорию Т, сформулирован-
сформулированную в исчислении высказываний. Т будет Х'-разрепшмой.
Применяя релятивизацию утверждения 6.1.3, мы получа-
получаса, что | Т | является Х-рекурсивно представимой. Но
! Л ^f/v.
Теорема 6.1. Существует рекурсивно аксиомати-
аксиоматизируемая теория, формулируемая с одним бинарным пре-
предикатом, алгебра Линденбаума которой неизоморфна ал-
алгебре Линденбаума никакой разрешимой теории.
Доказательство. Пусть Н — теория следова-
следования, формулируемая с одним бинарным предикатом (см.
Г41, стр. 134). Пусть Р (т, п) — предложение, которое ут-
утверждает существование в точности т циклов следования
длины п. Применяя элиминацию кванторов, мы можем по-
показать, что | Н | свободно порождается множеством
{Р (т, n)}m^NtneN. Пусть J: N2 -+ N — стандартная спа-
спаривающая функция. Для любого п положим рп =р(/(и)).
Повторяя конструкцию п. 5, получим рекурсивно аксиома-
аксиоматизируемую теорию Т такую, что
(i) язык теории Т совпадает с языком теории //;
(ii) | Т | ^_ .f /V.
Так как ,f/V не является рекурсивно представимой, то
в силу 6.1.3 | Т | пеизоморфтта алгебре Линденбаума ни-
никакой разрешимой теории.
Замечание. В [4] Ханф предположил, что алгебра
Линденбаума любой рекурсивно аксиоматизируемой тео-
теории изоморфна алгебре Линдепбаума некоторой конечно
аксиоматизируемой теории. Применяя результаты из [3],
можно легко показать, что гипотеза Ханфа и теорема 6.1
влекут, что алгебра Липденбаума чистой теории первого
порядка, формулируемой с одним бинарным предикатом,
не является рекурсивно представимой. Мы опускаем детали
этого доказательства.
Теорема 6.2. Если X cz N, mo существует X-ре-
X-рекурсивно перечислимый фильтр V на $ такой, что tf7V не
является Х-рекурсивно представимой.
178 Л. ФЕЙНЕ1'
Доказательство. Следует из релятивиза-
релятивизации 5.1.
Аналогично п. 4, если X — решетка, то мы можем опре-
определить первую производную X* для X. Например, ато-
атомами решетки Хх (Х-рекурсивно перечислимых множеств)
будут одноэлементные множества, а Хх получается из Хх
отождествлением Х-рекурсивно перечислимых множеств,
отличающихся конечным числом элементов. Очевидно,
если Xt^?2, то X* &. Х\.
Лемма 6.2.1. Если X — Х-рекурсивно представимая
решетка и а ЕЕ X, то решетка X (а) является Х-рекур-
Х-рекурсивно представимой.
Теорема 6.3 (Лахлан). Если X с: Л', то решетка
Хх является Х^-рекурсивно представимой. Более того,
если V — ^-фильтр на f, то <f/V ^ Хх (я) для неко-
некоторого а ?Е Хх-
Доказательство. Определение Лахлана 3V3-
булевой алгебры ([6], стр. 138) соответствует <f no модулю
фильтра типа 2? *)• Поэтому 6.3 следует из 6.1.3 и роляти-
визовапной формулировки теоремы Лахлана ([61, теорема
6, стр. 139-148).
Следствие. Если X Q N, то Хх не является
Х^-рекурсивно представимой.
Доказательство. Пусть V — Х^-рекурсивно
перечислимый фильтр на § такой, что <$/V не является
.XW-рекурсивно представимой. Так как V — фильтр
типа 2*, то в силу 6.3 ,f /V ^ Хх {о) для некоторого
а ЕЕ 2$.
Следовательно, Х% (а) не является Х-рекурсивно пред-
представимой. Поэтому в силу 6.2.1 Хх тоже не будет Х<2>-ре-
курсивно представимой.
Следствие. Если X' сводится по Тьюрингу к У,
то %х неизоморфна Ху-
Доказательство. Х\ не является У^^-рекур-
сивпо представимой и, следовательно, так как X' ^г У>
%% не является (Х')B)-рекурсивно представимой. В силу
*) Лахлаповский союзник как раз отмсчарт все дополнппия из
векоторого фильтра типа S2 на У,
ИЕРАРХИИ БУЛЕВЫХ АЛГЕБР
6.3 Х\ неизоморфна Ж*. Следовательно, Хх неизоморф-
па %у.
В частности, решетка рекурсивно перечислимых мно-
множеств дает естественный пример структуры, которая пе
будет рекурсивно представимой.
7. Признания. Автор благодарен А. Нероуду за пред-
предложение основной проблемы этой статьи и В. Хапфу за
упрощение 4.5.
ЛИТЕРАТУРА
[1] Davis M., Computability and unsolvability, McGraw-Hill,
N. Y., 1958.
[2] F © i n e г L., Orderings and Boolean algebras not isomorphic
to recursive ones, Ph. D. Thesis, Massachusetts Institute of
Technology, Cambridge, Mass., 1967.
[3] 11 a n f W., Isomorphism in elementary logic, Notices Amer.
Math. Soc. 9 A962), 127—128.
[4] H a n f W., Model theoretic methods in the study of elementary
logic, The theory of models, North-Holland, Amsterdam, 1965,
133-146.
[5] H a n f W., On some fundamental problems concerning isomor-
isomorphism of Boolean algebras, Math. Scand. 5 A957), 205—217.
[6] L а с h 1 a n A., On the lattice of recursively enumerable sets,
Trans. Amer. Math. Soc. 130 A968), 1—37. [Русский перевод:
A.X. «Пахла н, Решетка рекурсивно перечислимых мно-
множеств, наст, кн., 109—162.]
[7] Rabin M., On recursively enumerable and arithmetic models
of set theory, i. Symbolic Logic 23 A958), 408—416.
[8] Rogers H., The theory of recursive functions and effective
computability, McGraw-Hill, N. Y., 1967. [Русский перевод:
X. Роджерс, Теория рекурсивных функций и эффективная
вычислимость, «Мир», М., 1972.]
[9] S i k о г s к i R., Boolean algebras Springer-Verlag, Berlin,
1964. [Русский перевод: Р. С и к о р с к и й, Булевы алгебры,
«Мир», М., 1969.]
[10] Т а г s k i A., and Mostowski A., Boolesche Ringe mit
geordneter Basis, Fundam. math. 32 A939).
[11] T e n n e n b a u m S., Non-Archimedean models for arithmetic,
Notices Amer. Math. Soc. 6 A959), 207.
ГИПОТЕЗА СИЛЬНОЙ ОДНОРОДНОСТИ*)
Л. Фей не р
1. Введение. Гипотеза сильной однородности утвер-
утверждает, что для любой Г-степени а существует изомор-
изоморфизм между верхней полурешеткой степеней и верхней
лолурешеткой степеней ^> а, сохраняющий операцию скач-
скачка. Роджерс (см. [2], стр. 335) сообщает, что эта проблема
открыта, и замечает, что ее истинность привела бы к упро-
упрощению многих доказательств в теории степеней. Но ги-
гипотеза в действительности ложна. Точнее, пусть 0 — наи-
наименьшая степень и (Кп> — ге-я итерация операции скач-
скачка, примененная к 0 (см. [2], стр. 329). Мы покажем, что
{A | СЬ6> ^С d <I 0W} не является изоморфным по упоря-
упорядоченности {d | 0 < d < 0<2>} **).
Предполагается, что читатель знаком с обозначениями
и терминологией из [2]. Если Р = {Р, <!} — частичный
порядок, то начальным сегментом Р называется множе-
множество вида {х | х ^L а} или вида {х \ х ^ а & х Ф а) для
некоторого а из Р. Если L = {L,< } — линейный по-
порядок, то сегментом L называется множество вида
{ос | a <gl х <С Ь} для а ?Е L, b ?E L. со* — порядковый
тип множества отрицательных целых чисел. Скажем, что
структура рекурсивна, если ее основное множество,
отношения и операции рекурсивны. Х-рекурсивные
(П?-, рекурсивно перечислимые и т. д.) структуры опреде-
определяются аналогично. Структура называется рекурсивно
представимой, если она изоморфна рекурсивной структу-
структуре. Например, любой полный порядок типа Sj является
рекурсивно нредставимым (см. [2], стр. 273 и упр. 16 —
*) L. V е i n е г. The strong homogeneity conjecture, J. Symbo-
Symbolic Logic 35 A970), 375—377.
**) К. Д ж о к у ш (письменное сообщение) независимо и дру-
другими методами опроверг гипотезу однородности. Он построил ана-
аналитическую степень а такую, что не существует изоморфизма, сохра-
сохраняющего операцию скачка, между {степени} и {степени ^ а).
Гипотеза сильной однородности 181
56 на стр. 576). Х-рекурсивно A1?-, рекурсивно перечис-
перечислимо и т. д.) представимые структуры определяются ана-
аналогично.
2. Построение контрпримера. Хьюджил в [1] показал,
что любой линейный порядок вкладывается в Г-степени
как начальный сегмент. Простое следствие конструкции
Хьюджила состоит в том, что если а — любая степень,
то любой линейный порядок степени а вкладывается в
{d | а <; d ^ а<2)} как начальный сегмент. Прямое при-
применение алгоритма Тарского — Куратовского показы-
показывает, что {d | 0 <; d ^ 0B)} является 0E)-рекурсивным
частичным порядком. Поэтому каждый начальный сег-
сегмент {d | 0 ^ d <; 0<2)} является 0E)-рекурсивным ча-
частичным порядком. Чтобы построить контрпример, ука-
укажем одну простую конструкцию 0F)-рекурсивного линей-
линейного порядка, не изоморфного никакому ^'^-рекурсивно-
^'^-рекурсивному линейному порядку, и вложим этот порядок в
{d | 0<в> <; d <; 0(8)} как начальный сегмент, используя
упоминавшееся следствие конструкции Хьюджила. Так
как {d | (К6> <; d ^ О^8)} имеет линейно упорядоченный
начальный сегмент, не являющийся 0E)-рекурсивно пред-
ставимым, то {d | 0 ^ d ^ (К2'} не может быть изоморфно
{d | 0<6) <; d <g; 0^'}. Следовательно, не существует
изоморфизма, сохраняющего операцию скачка, между
{степени} и {степени > 0<-в">}.
Осталось лишь построить требуемый 0^6)-рекурсив-
ный линейный порядок.
3. Линейные порядки. Здесь мы покажем, что для лю-
любого множества X Ci N существует Х'-рекурсивный
линейный порядок, не изоморфный никакому Х-рекурсив-
ному линейному порядку. Пусть L = {L, <;} — ли-
линейный порядок. Множество i'ci называется дискрет-
дискретным, если для любых a, b €E S множество {х \ а ^ х «^ Ь)
конечно.
Ясно, что любое дискретное подмножество может
быть расширено до максимального дискретного подмно-
подмножества. Также ясно, что для любого п существует пред-
предположение Р„ языка первого порядка теории линейного
порядка такое, что Р„ утверждает существование макси-
максимального дискретного подмножества длины п.
Теорема, (i) Если L — рекурсивный линейный
порядок, то {п | L ? р„} = т0C> (см. [2], стр. НО).
182 Я. ФЕЙНЕ*1
(ii) Существует рекурсивный линейный порядок L @)
такой, что {п \ L @) (= рп} = m0W\
Перед тем как доказывать этот результат, заметим, что
из него будет легко следовать следующий релятивизовап-
ный результат.
Следствие, (i) Если L — рекурсивный линейный
порядок, то
(ii) Для любого множества X с: N существует
Х-рекурсивный линейный порядок X (X) такой, что
{п | ? (X) (г pn} =m XW.
Следствие. L (X1) не является Х-рекурсивно пред-
ставимым для любого множества X.
Доказательство. Предположим, что L изо-
изоморфен L (X'), где L является X-рекурсивным. Тогда
XW = m{n\ L (X') (= pn} = {n | L (= pn} <
получаем противоречие (см. [2], стр. 327, теорема 1 (с)).
Итак, L @W) — требуемый линейный порядок. Ос-
Осталось лишь доказать теорему.
Доказательство теоремы, (i) Применим
алгоритм Тарского — Куратовского (см. [2], стр. 394) и
соотношения между кванторами и операцией скачка
(см. [21, стр. 403).
(ii) По [2] (стр. 419) имеем
0W> = m В — {п | Зт (т е Wn & Wn бесконечно)}.
(Этот результат, как и наше доказательство, может быть
релятивизован.)
Построим рекурсинный линейный порядок L @) та-
такой, что для каждого п > 2 имеем п ?Е В *-* L @) [= рп.
Вначале укажем рекурсивное представление порядкового
типа У ((п + со* ¦ со) • со) в терминах пятерок чисел, исполь-
используя следующий словарь:
21 ((п -\- со* • со) • со)
$ t I J I
п ж j i m
ГИПОТЕЗА СИЛЬНОЙ ОДНОРОДНОСТИ 183
Пусть L — следующее множество пятерок чисел:
{{(п, x,i,i,m)n>2&{x<n-> (j, i) = @,0)) &
&0< z< n).
Определим следующий линейный порядок на L:
(п, х, j, i, т) -< (ге\ х', у", V, пг) «-» (п, т) <]ех (п', т')\/
V ((», »») = (»', т')&х< х') V ((», т) = (»',»»') & ж =
= ж' = ге & i < г') V ((«. т) = (ге', ттг') & ж = ж' =
= ге & i = i' & ; > ;")•
Пусть S cz N — следующее рекурсивно перечислимое
множество:
(п, х, j, i, ra)eS<-» т (ЕЕ Wn & (j > 1 V
V 3t(«e Ж„,& t >;)).
{ } рекурсивно перечислим и, следовательно, изо-
изоморфен рекурсивному липейному порядку L @) (это
прямо можно доказать, используя связность линейных
порядков). Анализируя определение L @), приходим
к выводу, что справедливо следующее утверждение:
Если в > 2 в в Е 5, то? @) имеет начальный сег-
сегмент порядкового типа т + п + со*, где т не имеет мак-
максимального элемента (т может быть пустым) и, следователь-
следовательно, L @) |= рп. Обратно, если п !> 2 и п ф. В, то каждое
максимальное дискретное подмножество ?@) имеет длину,
не равную п, и, следовательно, L @) |^ |3П.
4. Замечания. Автором показано, что любой 0'-ре-
курсивный линейный порядок изоморфен некоторому под-
подмножеству рациональных чисел типа Пг Поэтому суще-
существует подмножество рациональных чисел типа П?, пе яв-
являющееся рекурсивно представимым.
Ейтс показал, что каждый 0'-рекурсивный линейный
порядок может быть вложен в множество степеней <; О'1
как начальный сегмент. Отсюда следует, что {d | d ^ 0")}
не является рекурсивно представимым частичным поряд-
порядком. Он высказал гипотезу, что любой 0<4>-рекурсивный
линейный порядок может быть вложен в множество
184 л. фейнер
{d | d <g; 0^} как начальный сегмент. Из релятивизации
этой гипотезы тогда следовало бы, что {d | d ^ 0^} не
является изоморфным по упорядоченности {d I 0W
< d 0<2>}
ЛИТЕРАТУРА
[1] II u g i I 1 D., Initial segments ol Turing degrees, Proc. London
Math. Soc. 19 A969), 1—15.
[2] Rogers H., The theory of recursive functions and effective
computability, McGraw-Hill, N. Y., 1967. [Русский перевод:
X. Роджерс. Теория рекурсивных функций и эффективная
вычислимость, «Мир», М., 1972.]
ИМЕННОЙ УКАЗАТЕЛЬ
Девис (Davis M.) 109, 162, 166, 179
Деккер (Dekker J. С. Е ) 54, 98, 100—
102, 108
Джокуш (Jockusch С.) 162, 180
Ейтс (Yates С Е. М.) 6, 10, 65, 80,
85, 97, 108, НО, 111, 122, 126,
162, 183
Ершов Ю Л. 6, 162
Клини (Kleene S. С.) 7, 39, 42, 84,
108
Крайзел (Kreisel G.) 172
Куратовский (Kuratowski К ) 168,
170, 181, 182
Лахлан (Lachlan A. H.) G, 9, 10, 90,
94, 109. 164, 178, 179
Линденбаум (Lindenbaum А ) 164,
176, 177
Майхилл (Myhill J) ПО, 111, 125,
132, 162
Манастер (Manaster А. В.) 162
Мартин (Martin D.) 65, 103, 107, 108,
112, 148, 155, 162
Мостовский (Mostowski A.) 163, 179
Мучник А. А. 55, 61, 100, 408
Нероуд (Nerode A.) 179
Рабин (Rabin M ) 163, 179
Райе (Rice H. G ) 108
Робинсон A. (Robinson A.) 109,
113, 162
Робинсон P. (Robinson R М ) 112,
128, 148, 156
Роджерс (Rogers H.) 10, 82, 109, 166,
179, 180, 184
Сакс (Sacks G.) 10, 50, 60, 74, 85, 103,
107, 108
Сикорский (Sikorski I! ) 163, 179
Спектор (Spector) С. 42, 47, 161
Тарский (Tarski A ) 163, 168, 170,
179, 181, 182
Тенненбаум (Tennenbaum S.) 103,
107, 108, 163, 179
Тьюринг (Turing A ) 166, 168, 178
Фейнер (Feiner L.) 6, 163, 179, 180,
183
Фридберг (Friedberg R М ) 9, 44, 55,
61, 100, 102,104, 108, 111, 122, 151,
160, 162
Ханф (Hanf W ) 164, 177, 179
Хьюджил (Hugill D. Г ) 161, 181,
184
Овингс (Owings J. С.) 160
Пост (Post E.) 35, 36, 39, 42, 53—55,
64, 73, 97, 100, 102, 108, 162,
Шенфилд (Shoenfield J R ) 7, 74,
98—100, 108
Эрастозфен 14
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра булева (Boolean algebra) 163
, образованная главным идеа-
идеалом (formed by the principal
ideal) 165
, фильтром (filter) 165
подмножеств (of subsets) 164
— Линденбаума (Lindenbaum algeb-
algebra) 164, 176, 177
Алгоритм (algorithm) 18
— для функции (for function) 19, 21
— из . в . . (from .. to.. ) 18
— Крайзсла (Kreisel) 172
— обобщенный (extended) 21
— Тарского — Куратовского (Таг-
ski—Kuratowski) 168, 170, 181,
182
Аппроксимация (appoximation) 20, 22
Аргумент требования (argument of
requirement) 86
Базис упорядоченный (ordered basis)
165
Влечет (implies) 11
Вход (input) 18
Выход (output) 18
Вычисление (computation) 19, 22,
166
— с оракулом (using an oracle) 21, 22,
167
— согласно алгоритму (according to
algorithm) 19
Гипотеза сильной однородности (the
strong homogeneity conjecture)
180
— Ханфа (Hanf conjecture) 164, 177
Грань наибольшая нижняя (greatest
lower bound) 30
— наименьшая верхняя (least upper
bound) 30
График (graph) 26
Дерево (tree) 47
— числовое (number) 132
— I-расщеплеиное (I-splitting) 48
Диаграмма коммутативная (com-
(commutative diaerani) 16
Дизъюнкция (disjunction) 110, 165
Доминанта (dominant) 65
Доминирование (dominantion) 65, 103
Дополнение (complement) 15, 109,
163, 164
Захватчик (holder) 71
Значение последовательности (value
of sequence) 12
— требования (requirement) 86
И (and) 11, 110
Идеал простой (prime ideal) 164
Иерархия предикатов (predicate hie-
hierarchy) 170
Изоморфизм (isomorphism) 15, 180
— алгебраический (algebraic) 164
Или (or) 11, 110
Интервал (interval) 164
Индекс (index) 26
— в... (in...) 28
Иптсрпретация семантическая (se-
(semantic interpretation) 113
Исчисление высказываний (ргоро-
sitional calculus) 177
— предикатов узкое (lower predicate
calculus) 109
Квантор (quantifier) 11, 110, 165
— общности (universal) 11, 110, 165
— существования (existential) 11,
110, 165
Класс (class) 11
— алгоритмов (of algorithms) 18
— конечных подклассов (of finite
subclasses) 13
последовательностей (of fini-
finite sequences) 13
— натуральных чисел (of natural
numbers) 11
— пустой (empty) 11
Композиция функций (composition
of functions) 14
Конструкция бесконечных нарушений
(infinite injury construction) 75
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
187
Конструкция F-поддерживающаяся
(F-supported) 68
— F-сдерживающаяся (F-restricted)
68
Конъюнкция (conjuction) НО, 165
Лемма о модуле (modulus lemma) 27
— — пределе (limit) 31
— Шенфилда (Shoenfield) 74
Матрица бесконечная (infinite square
array) 18
— рекурсивная (recursive matrix)
166, 170
Машина вычислительная (computing
machine) 18
— Тьюринга (Turing) 166. 168
Метод вычислений (method of com-
computation) 18
— приоритета (priority method) 55
Множество (set) 11, 13
— арифметическое (arithmetic) 161
— «большое» («large») 53, 64, 73
— в .. (in ..) 13
— гипергипериммунное (hyperhyper-
immune) 128
— гипергиперпростое (hyperhyper-
simple) 102, 107, 122
— гиперпростое (hypersimple) 100,
107
— дискретное (successor-chain) 181
— замкнутое (closed) 77
—, имеющее мало рекурсивно пере-
перечислимых надмножеств (having
few recursively enumerable super-
supersets) 64
— индексное (Index) 80
— квазикреативное (quasicrelative)
98. 99
— кобесконечное (coinfinlte) 39, 109
— коконечное (cofinite) 38, 109
— креативное (creative) 98
— кусочно рекурсивное (plecewise
recursive) 74
— максимальное (maximal) 64, 102,
122
— натуральных чисел (of natural
numbers) 109, 164
— одноэлементное (singleton) 178
— описаний (set of descriptions) 17
— основное булевой алгебры (uni-
(universe of Boolean algebra) 163
— полное рекурсивно перечислимое
(complete recursively enumerable
set) 36
типа 2П, П^ (complete 2n,
П„) 36
— полукреативное (semlcreative) 98
— полупродуктивное (semlproducti-
ve) 98
— простое (simple) 53, 100
— пустое (empty) 109, 164
—, расположенное на дереве (on
a tree) 47
— рекурсивно перечислимое (recur-
(recursively enumerable) 24, 97
Множество рекурсивно перечисли-
перечислимое в... (in .) 28, 30
¦ с ретрассируемым дополне-
дополнением (whose complement is
retraceable) 107
— рекурсивное (recursive) 14
— сильно простое (strongly simple) 55
V П„(Еп,гу 32
V „пу
, — В .. (in.. ) 39
2n [а], П„ [a] (Sn [а], Пп [а])
80
— I-минимальное (I-minimal) 47
— ^максимальное (r-maximal) 112,
156
— Х-рекурсивно перечислимое (Х-
recursively enumerable) 164
Модель нестандартная (nonstandard
model) 163
— теории множеств (model of set
theory) 163
Модуль (modulus) 27
He (not) 11, 110
Номер гёпелев (Godel number) 114,
116, 166
Нуль булевой алгебры (zero of Boo-
Boolean algebra) 170
Нумерация гёделева (G6del numbe-
numbering) 113
— стандартная (standard) 161
Обеспечение условия (insuring of
a condition) 40
Область значений (range) 11
— определения (domain) 11
Обращение отображения (inverse map-
mapping) 11
Объединение (union) 14, 163, 164
Объект конечный (finite object) 12
Описание конечного объекта (de-
(description of finite object) 17
Оракул (oracle) 21, 22
Ординал (ordinal) 148
—, вложимый в решетку (imbed-
dable In lattice) 148
Отношение истинности (satisfaction
relation) 166
— от л аргументов (of n arguments)
13
— элементарное (elementary) 113
Отображение (mapping) 11
— 1-1 (one-one mapping) 11
Отрицание (negation) 165
Пара рекурсивно перечислимых ре-
рекурсивно неотделимых множеств
(pair of recursively enumerable
recursively Inseparable sets) 163
Пересечение (intersection) 14, 163,
164
Перечисление (listing) 16
— рекурсивной всех рекурсивно пере-
перечислимых множеств (recursive
enumeration of all recursively
enumerable sets) 132, 138, 141
188
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Перечисление N X N (of N X \') 18
Повреждение (injure) 57
Поддерево (subtree) 47
— /-расщепленное (/-splitting) 49
Подкласс конечный (finite subclass)
13
Подмножество главное (major subset)
152
— густое (thick) 74
Подпредикат (subpredicate) 120
Полурешетка верхняя (upper semi-
lattice) 180
Порядок лексикографический (lexico-
(lexicographical order) 166
— линейный (linear ordering) 164,
180
— частичный (partial ordering) 180
— п-ки (order of л-tuple) 128
Последовательность (sequence) 11
— бесконечная (infinite) 11
— конечная (finite) 12
— рекурсивная (recursive) 27
— рекурсивно перечислимая (recur-
(recursively enumerable) 97
сильно (strongly) 97
— степеней возрастающая (ascen-
(ascending sequence of degrees) 42
Предел (limit) 27
Предикат (predicate) 113
—, определяющий отношение (de-
(defining a relation) 113
Предложение (sentence) 113
Принцип использования (the Use
Principle) 23
Проблема Поста (Post's problem) 53,
55, 73, 100
— разрешения (decision) 114
разрешимая (solvable) 114
сводимая (reducible) 114
Проекция (projection) 14
Произведение прямое (direct pro-
product) 164
Производная (derivative) 169, 178
Пространства изоморфные (isomor-
phic spaces) 15
Пространство (space) 12
— цепочек (of strings) 47
Процедура разрешающая (decision
procedure) 109
Равенство частичных выражений
(equality between partial expres-
expressions) 19
1'азбиение (splitting) 128
Разложение каноническое (factori-
(factorization) 17, 98
Разность (difference) 14
Расширение (extension) 23
Расщепление (splitting) 47
Результат иычислсиин (output of
computation) 167
1 екурсивность относительная (rela-
(relative recursiveness) 20, 16B
Гелнтивизация (relativization) 22, 41
I ешение вопроса (decision of a ques-
question) 45
Решетка замкнутая (closed lattice)
115
Решетка классов эквивалентности (of
equavalence classes) 111, 115
— подмножеств (of subsets) 115
— рекурсивно перечислимых мно-
множеств (of recursively enumerable
sets) 113
но модулю простых мно-
множеств (modulo simple sets) 161
— надмножеств (supersets) 111
— рекурсивных множеств (of re-
curvise sets) 121
— Х-рекурсивно перечислимых мно-
множеств (of Jr-rccursivcly enumerab-
enumerable sets) 164
Гешето Эратосфеяа (sieve of Erato-
sthanes) 14
Ряд бесконечный (infinite series) 14
Сводимость (reducibility) 36, 37
Связка (connective) 11
Сегмент (segment) 140, 180
— начальный (initial) 180
— — степеней (of degrees) 161
Селектор (selector) 25
Символ индивидуальный (ob)ect sym-
symbol) 113
Скачок степени (jump of degree) 31,
164, 180
— функции (of function) 28
Следует (Implies) 110
Сложение (addition function) 14
Соответствие (correspondence) 146
Союзник (associate) 139
Степени несравнимые (incomparable
degrees) 39
Степень (degree) 29, 180
— аналитическая (analytic) 180
— ветвящаяся (branching) 85
— гипергипсрпростого множества (of
hyperhypersimple set) 103, 148
— максимального множества (of
maximal set) 103
— минимальная (minimal) 46
— наименьшая (smallest) 30
— рекурсивно перечислимая (re-
(recursively enumerable) 31, 98
в . (in ) 30
Столбец (column) 18
Строка (row) 18
Структура (structure) 163, 164
—, представимая рекурсивно (re-
(recursively presentable) 163, 180
—, перечислимо (recursively
enumerable presentable) 176. 180
—, — JT-рекурсивно (JT-recursively
presentable) 176, 181
— рекурсивна» (recursive) 163, 180
— рекурсивно перечислимая (re-
(recursively enumerable) 176, 180
— Х-рекурсивная (X-recursive) 176
Теорема Деккера (Dekker theorem)
54
— Ейтса (Yates) 85, 110, 126
— Клинч — Поста (Kleene — l'ost)
39
ПРЕДМЕТНЫЙ. УКАЗАТЕЛЬ
189
Теорема Клини — Поста — Спектора
(Kleene — Post — Spector) 42
— Лахлана (Lachlan) 90, 139, 178
— Мартина (Martin) 65
— Мучника (Muchnlk) 61
— о графике (graph) 26
дополнении (complementation)
26
неподвижной точке (fixed
point) 84
перечислении (listing) 26
разложении (splitting) 66
рекурсии (recursion) 84, 124
селекторе (selection) 25
— об иерархии сильная (strong
hierarchy) 167
изоморфизме (isomorphism) 16
индексном множестве (Index
set) 80
— основная Лахлана (main of I ach-
lan) 122
— параметризации (parameter) 26
— плотности (density) 85
— Поста (Post) 35, 55
— релятивизованная (relativi7ed) 42
— Сакса (Sacks) 50, 74
— Спектора (Spector) 47
— Фридберга (Friedberg) 44, 55
— Фридбергч — Мучника (Fried-
berg — Muchnik) 61
Теория аксиоматизируемая (axioma-
ti7able theory) 164
— вычислений (of computations) 12
— линейного порядка (of linear order)
181
— первого порядка чистая (pure
quantification) 177
¦- рекурсия (recursion) 12
- слабая второго порядка (weak
second-order) 167
— следования (of successor) 177
- степеней (of degrees) 32
— олсментарнан (elementary) 159
дистрибутивных решеток с от-
относительными дополнениями (of
relatively complemented distri-
distributive lattices) 162
рекурсивно персчислимых мно-
множеств (of recursively enumerable
sets) 110, 113
решеток (of lattices) 161
F (of F) 162
m-степеней (of m-degrees) 161
Т-степеней (of T-degrees) 161
Тип изоморфизма рациональных чи-
чисел (type of isomorphism of ratio-
rational numbers) 164
Тогда и только тогда (if and only
if) 11
Требование активного (active requi-
requirement) 58, 62, 86, 91
— внимания (requirement of atten-
attention) 157
— временное (temporary) 58, 62, 87,
92
— для A (for A) 86
В (for B) 86
— неактивное (inactive) 58, 62, 86,
91
Требование несущественное (inesse-
(inessential)) 87
— неаффективное (ineffective) 86
— постоянное (permanent) 58, 62,
87, 92
— с индексом (with index) 91
— существенное (essential) 87, 92
— эффективное (effective) 86, 91
Убивать (kill) 92
Уделение внимания (receiving of at-
1елиоп) 157
Умножение (multiplication function)
14
Условия (conditions) 40, 43, 45, 56,
61, 85, 91
Фактор-алгебра (quotient algebra) 164
Фильтр (filter) 164
— типа П1, <nj) 164
Форма пренексная нормальная (pre-
nex normal form) 120, 170
Функции несовместные (incompa-
(incompatible functions) 39
— совместные (compatible functions)
39
Функция (function) 11, 13, 109
— длины (length) 14
— из . в (from. . to. .) 13
— конечная (finite) 23
— нерекурсивная (non-recursive) 19
— от л аргументов (of n arguments)
13
— почти константа (almost constant)
69
— рекурсивная (recursive) 13
— сдерживающая (restricting) 67
— спаривающая стандартная (stan-
(standard pairing) 177
— тождественная (identity) 14
— характеристическая (characteris-
(characteristic) 165
— частичная (partial) 19
всюду определенная (total) 19
рекурсивная (recursive) 19
в (in .) 21, 24
относительно . (relative
to...) 21
— Jl-чэстично рекурсивная (X-par-
tial recursive) 166
— 0(о))-рекурсивная @(m)-recursive)
166
Цепочка (string) 23, 47, 132
—, расположенная на дереве (on tree)
47
—, расщепляющаяся на дереве (split-
(splitting on tree) 47
Число действительное (real number)
12
• задержанное (held) 70
— «-задержанное (n-held) 70
—, используемое в вычислении
(used in the computation) 23
190
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Число, используемое в вычислении
отрицательно (used negative in
the computation) 57
— накрывающее (covering) 110, 122
— натуральное (natural) 11, 109
— последовательностпое (sequence
number) 165
— разделяющее (partition) 126
— рациональное (rational) 183
Эквивалентность (equivalence to) 110
Элемент ключевой (key element) 86
— наименьший (least) 133
—, содержащий ординал (containing
the ordinal) 49
— структуры (member of structure)
164
— числового дерева (member of a
number tree) 132
Элиминация кванторов (elimination
of quantifiers) 121, 177
Язык формальный (formal language)
113
— слабый второго порядка (weak
second-order language) 166
А-отношение (A-relatlon) 115
А-часть (A-part) 87
А-число (A-number) 62
АВ-отношение (AB-relation) 116
В-отношение (B-relation) 115
—, соответствующее А-отношению
(corresponding in the 4-relation)
116
В-часть (Л-part) 87
В-число (B-number) 62
е-высота (e-state) 104
Z-расщеплепие (Г-splitting) 47
— на дереве (on a tree) 47
(I, J)-CTpoKa((I, J)-ro\V)91
m-сводимость (many-one reducibiiity)
36
n-высота на шаге (n-state of step)
142
п-держит (n-hold) 70
n-ка упорпдоченпая (ordered n-tuple)
п-требование (n-requirement) 57
— о аргументом (with argument) 62
п-цепочка («-string) 69
Г-стенень (T-degree) 161, 180
U-квантор (U-quantifier)'172
[/-форма (ГУ-form) 172
ava-булева алгебра (ai'a-Boolean
alsrehra 112, 138, 178)
ЗУэ-отношение (ava' relation) 111
ЗУЭ-решетка (ava lattice) 138 t"
— дистрибутивная (distributive) 159
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
~1, V, &, ->, <-*, v, з 11, но,
165
0 11, 12, 109, 164
F~i 11
<«! ,. . ., Х„У 11, 165
Дг 11, 164
*„ 12
{*„} 12
Ш 12, 165
Sub, Sq 13
X х Y 13, 164
.:.х...у... 13
-= 13, 19
С, С, 13, 23, 109
<, < 13, 29, 163, 166
И, Л 13
F о G 14
Лс 15
цп 15
Г 17
Alg (X, У) 18
WIt [I] (х), {/„} 19
Wj, n, [/]„ (х) 20
Wf, [I]B (x), W^n 21
Wff (*) 22
#! х ¦ ¦ ¦ X Яп 24
lim 27
II* 28
<R, ~, dg 29
U, <RE 30
a' 31
2n, П„ 32
2», П» 33
a» 36, 180
Tot, Fin 37
Gof 38
2n [H], Un [H] 39
|, Comp 39
St, Id 47
2„ [а], П„ [a] 80
Re), Re 97
Ti («, x, y) 97
(Z)i 98
0, 0' 98, 180
a' 109
v 109
ea, & Ю9
{Л (x) | В (ж)} 110
sup, oo 110
2T (a), 25* (a) 111
L, (?, П 113
In, Un, Emp, All, Rec 113
Fin, Sim, Max 114
tf (,2T), D (ЙГ) И4
Ж 115
2T, ИГ* 115
y. 115
» (i) H5
M
%* 121
га, |ra| 1
{X} 132
28
127
, ||
{X{} 132,138,141,152,161
2 132
132
й*Ь 132
T [a] 132
<T 133
{X.J 152
ж 161
Ш 161
SE, RD 162
U, П, -163, 164
& 163
192 УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
V, Jf/V 164 К («), У„ (а), Ф„ 169
SCу 164 Atom,,, Atomistic, =„ 170
~" 164 Н< Р (т- ") 177
> 164 ? * 18°
n 1R4
л «в» (', /, А', т, п, г, s, I — мстанере-
¦? менные для чисел
\п, h) 164 х, У, Z — метапарсмсппмс для
^я 165 пространств
•Л [я], .// (л), ^ [я], ,i'? (я) 165 ж, 1/, 2 — мстанерсмонныс для
0 165 алемептов пространств
3Хо2 165 /•', G, Н, /., М — мстансремсн-
seq (s) 165 1ШС Для Фуикщ«1
,? («') 165 -^' ^' ^> ^' ^ — метаперемеи-
с к;5 ные для множеств и их ха-
х х рактеристических функции
3zx Vz2. . . Н lCli /i у^ др — метаперрмеиные для
1^ 166 алгоритмов
{<?}А (n), V^Xj (и) 166 а, я — мстансремсыныс для ко-
X' xW y'^ 1H(i иечных функций
• 'м- ' а, р, у, б — метанеременные для
(Ф i ш- цепочек
и ip- a> Ь, с, d — метапеременные для
" ' _ степенен
Т (е, я, у) 167 Т — метаперсменная для де-
U (у) 167 ревьев