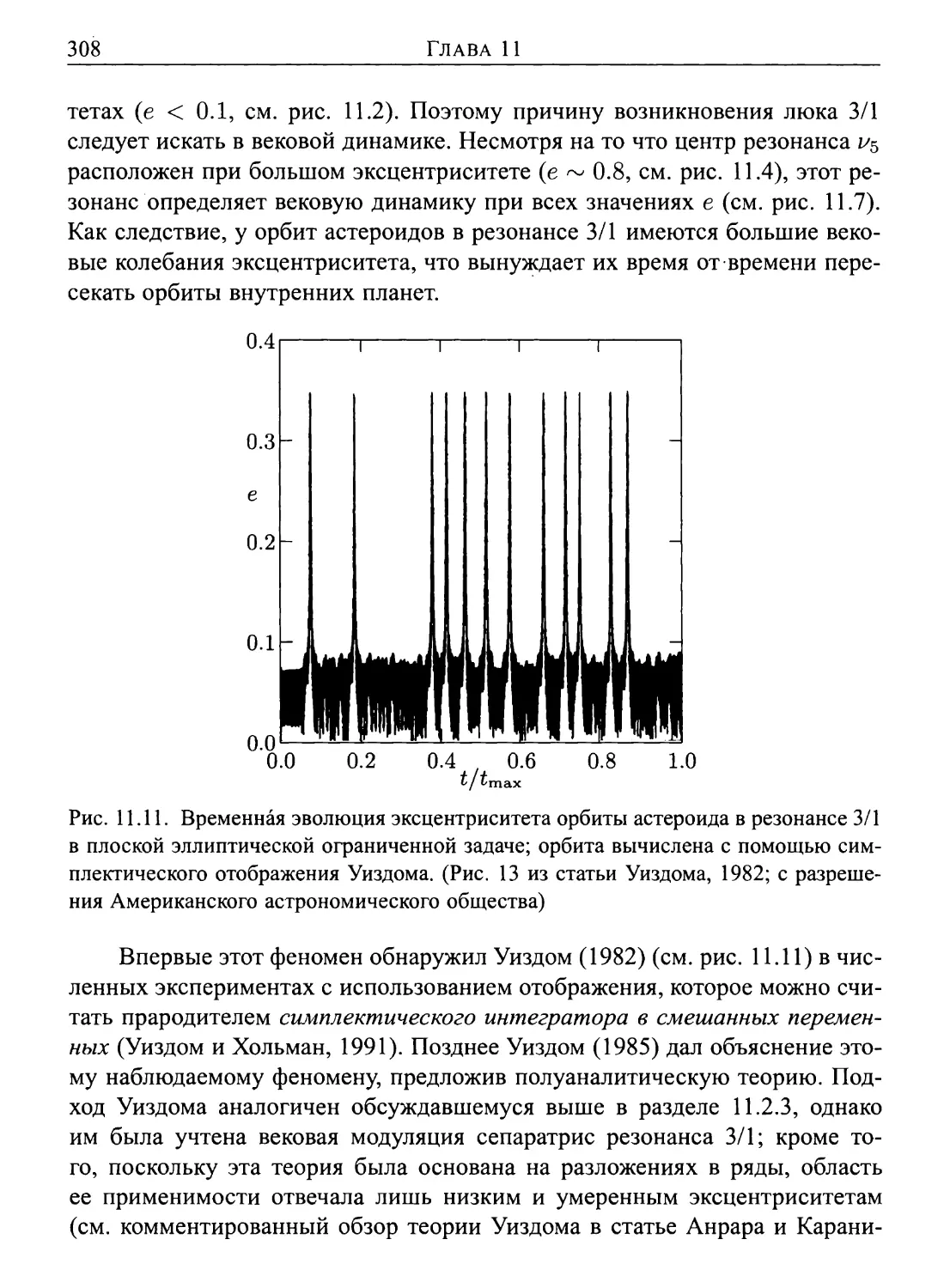
Автор: Морбиделли А.
Теги: prototheria (eplacentalia) яйцекладущие млекопитающие физика астрономия
ISBN: 978-5-4344-0209-5
Год: 2014
Текст
Алессандро Морбиделли
Современная
небесная механика
Аспекты динамики Солнечной системы
Modern Celestial Mechanics
Aspects of Solar System Dynamics
Alessandro Morbidelli
London and New York
Алессандро Морбиделли
СОВРЕМЕННАЯ
НЕБЕСНАЯ МЕХАНИКА
Аспекты динамики
Солнечной системы
Перевод с английского под редакцией
д. ф.-м. н. И. И. Шевченко
Москва ♦ Ижевск
2014
УДК 599.12-17
ББК 22.313.3
М79
Морбиделли А.
Современная небесная механика. Аспекты динамики Солнечной систе¬
мы. — М.-Ижевск: Институт компьютерных исследований, 2014. — 432 с.
Книга известного французского ученого, специалиста в области небесной ме¬
ханики и нелинейной динамики Алессандро Морбиделли «Современная небесная
механика. Аспекты динамики Солнечной системы» представляет собой введение
в современную небесную механику — резонансную и хаотическую динамику небес¬
ных тел, с приложениями к задачам орбитальной динамики тел Солнечной систе¬
мы. Фундаментальная тема книги — исследование проблем орбитальной динамики
в контексте современной теории гамильтоновых динамических систем. Как отме¬
чено автором в предисловии к русскому изданию, он надеется, что его книга «бу¬
дет побуждать молодых ученых к восприятию наследия великих русских учителей
и к продвижению этой области исследований». По полноте и современному уровню
изложения предмета книга не имеет аналогов на русском языке.
Монография предназначена научным работникам, специализирующимся в об¬
ласти небесной механики и динамики тел Солнечной системы, теоретической ме¬
ханики, нелинейной динамики и теории динамического хаоса, а также студентам
старших курсов и аспирантам университетов.
ISBN 978-5-4344-0209-5 ББК 22.313.3
© Taylor & Francis, 2002
© Перевод на русский язык:
Институт компьютерных исследований, 2014
Все права защищены. Никакая часть данной книги не может быть перепечатана, воспроизве¬
дена, передана или использована в какой бы то ни было форме электронными, механическими
или любыми иными средствами, которые известны в настоящее время или будут изобрете¬
ны впоследствии, включая фотокопирование, запись на магнитный носитель, микросъемку,
или при помощи любой другой системы хранения и обработки информации, если на то нет
письменного разрешения издательств.
http://shop.rcd.ru
http://ics.org.ru
Оглавление
Предисловие редактора перевода ix
Предисловие к русскому изданию xiii
Предисловие xv
Введение 1
Глава 1. Элементарная небесная и гамильтонова механика . . . 13
1.1. Уравнения движения 13
1.2. Элементы орбит 14
1.3. Возмущения задачи двух тел 18
1.4. Гамильтоновы системы и задача двух тел 20
1.5. Возмущения в гамильтоновом виде 23
1.6. Канонические преобразования 25
1.7. Свойства гамильтонова потока 28
1.8. Интегрируемые гамильтонианы 30
1.9. Переменные «действие-угол» 31
1.9.1. Переменные Делоне 33
1.9.2. Гамильтоновы уравнения в переменных Делоне для огра¬
ниченной и планетной задач 37
1.9.3. Правила Даламбера 39
1.10. Интегрируемая динамика 40
Глава 2. Квазиинтегрируемые гамильтоновы системы 43
2.1. Введение в теорию возмущений 43
2.2. Подход с применением рядов Ли 45
2.3. Проблема малых делителей 47
2.3.1. Нормальные формы 49
2.4. Порядки выше первого 51
2.4.1. Пример вычисления оптимального порядка нормаль¬
ной формы 53
vi
Оглавление
2.4.2. Генерирование старших гармоник в процессе норма¬
лизации 54
2.5. Усреднение по средним движениям 57
2.5.1. Вековая нормальная форма 59
2.5.2. Резонансная нормальная форма для резонансов сред¬
них движений 63
Глава 3. КАМ-торы 65
3.1. Теорема Колмогорова 65
3.1.1. Эскиз доказательства теоремы Колмогорова 66
3.2. Свойства КАМ-торов 69
3.3. Численные примеры 74
Глава 4. Динамика одиночного резонанса 79
4.1. Интегрируемое приближение 79
4.2. Резонансные переменные «действие-угол» 82
4.3. Возмущенная резонансная динамика 86
4.3.1. Величина остатка 86
4.3.2. Резонансные инвариантные торы 88
4.3.3. Расщепление сепаратрис 90
4.3.4. Размер хаотической области 94
Глава 5. Численные инструменты для выявления хаоса .... 99
5.1. Наблюдение временной эволюции в фазовом пространстве . . 99
5.2. Показатели Ляпунова 102
5.2.1. Вычисление МПЛ 105
5.3. Частотный анализ 109
5.3.1. Вычисление частот 113
5.4. Суррогаты 115
5.4.1. Быстрый индикатор Ляпунова 115
5.4.2. Углы спиральности и закручивания 116
5.4.3. Средний фактор экспоненциальной расходимости близ¬
ких орбит 116
5.4.4. Средние, максимальные и минимальные значения
действий 118
Глава 6. Взаимодействие резонансов 119
6.1. Две степени свободы 119
6.1.1. Гетероклинические пересечения 123
6.2. Более двух степеней свободы 126
Оглавление vii
6.2.1. Теорема Нехорошева 127
6.2.2. Нехорошевская структура 133
6.2.3. Суперэкспоненциальная устойчивость КАМ-торов . . 134
6.3. Исследование динамической структуры заданной системы . . 136
Глава 7. Вековая динамика планет 141
7.1. Решение Лагранжа-Лапласа 141
7.2. Решения более высокого порядка 146
7.3. Хаотическое вековое движение планет 149
7.4. Динамика осей вращения 155
Глава 8. Вековая динамика малых тел 165
8.1. Линейное интегрируемое приближение 165
8.2. Интегрируемое приближение Козаи 171
8.2.1. Динамика Козаи внутри орбиты главного возмущаю¬
щего тела 173
8.2.2. Динамика Козаи снаружи орбиты главного возмуща¬
ющего тела 178
8.2.3. Переменные «действие-угол» для гамильтониана
Козаи 183
8.3. Собственные элементы 185
8.3.1. Семейства астероидов 191
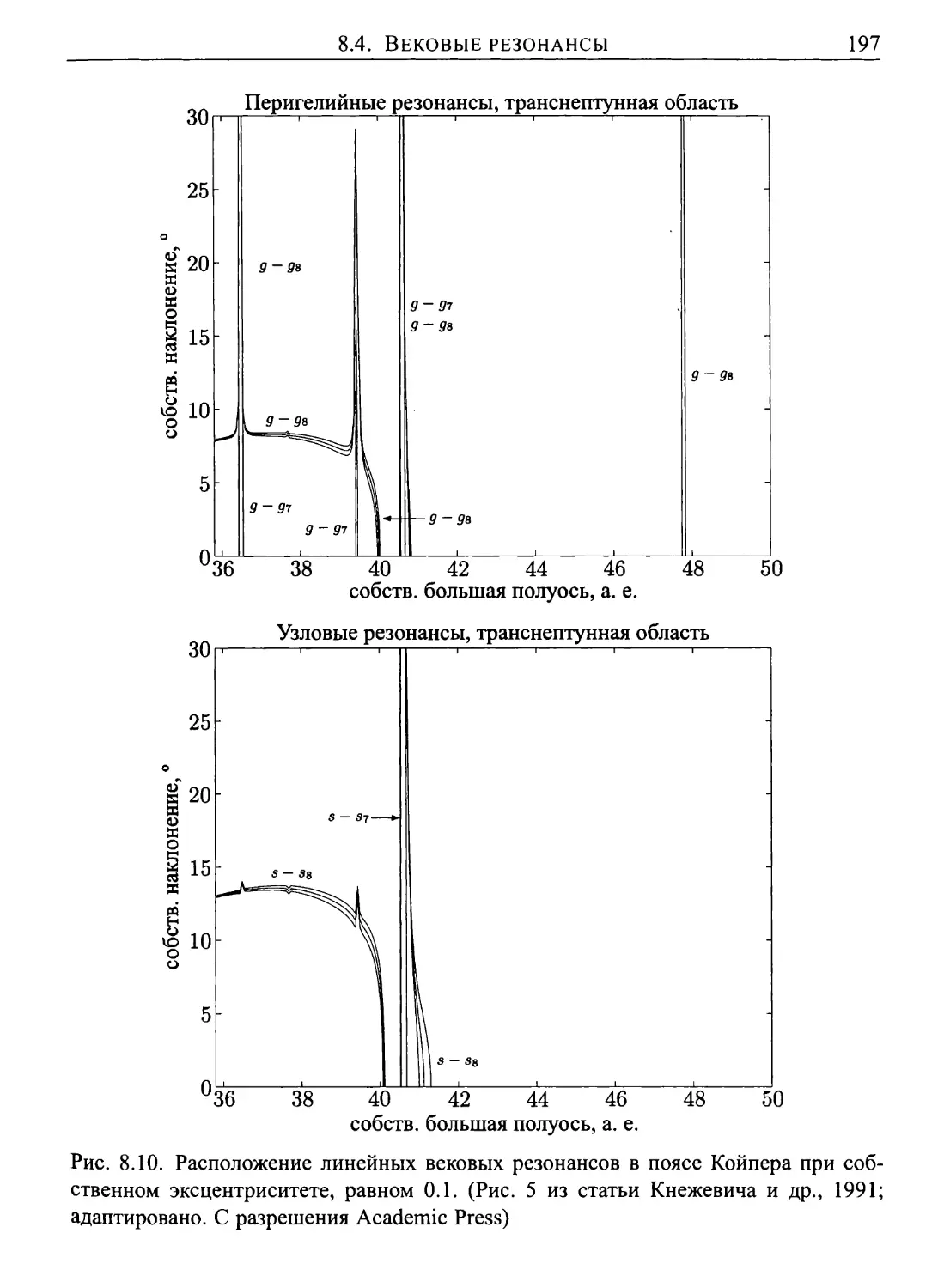
8.4. Вековые резонансы 193
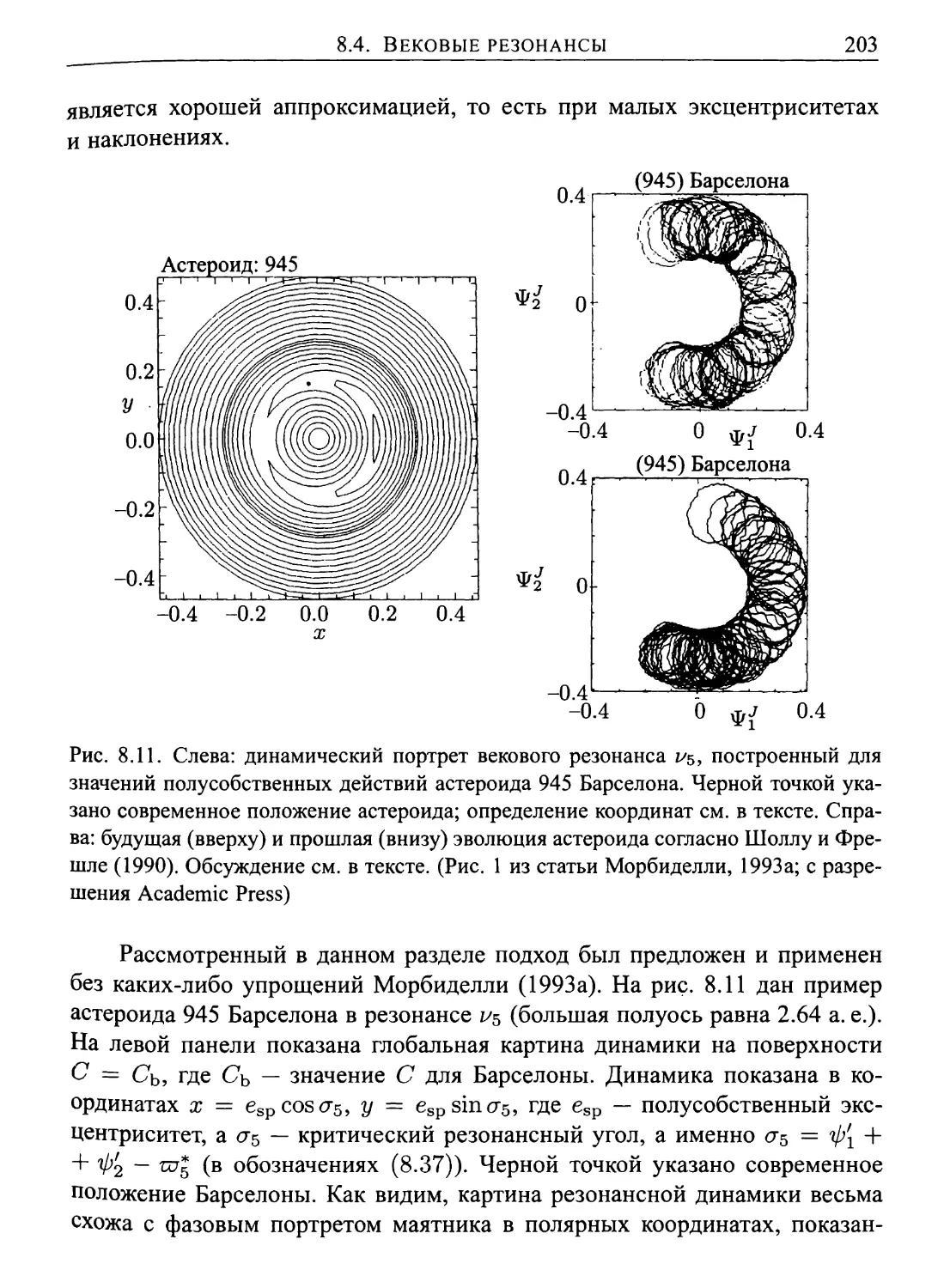
8.4.1. Динамика в вековых резонансах 199
8.4.2. Аномальный случай резонанса щ 207
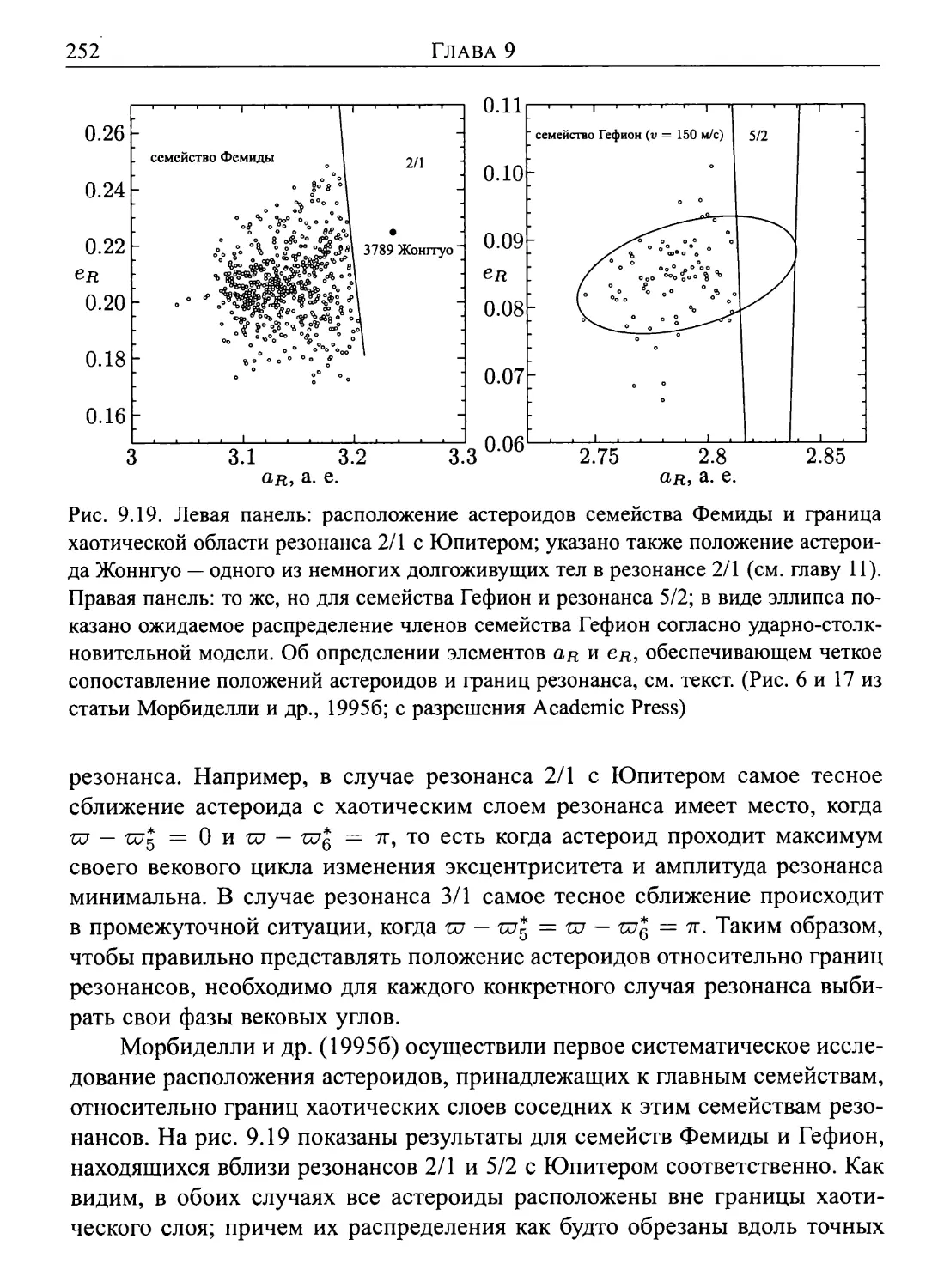
Глава 9. Резонансы средних движений 215
9.1. Простое интегрируемое приближение 215
9.1.1. «Фазовая защита» от столкновений с планетами .... 226
9.1.2. Случай резонанса 1/1 229
9.2. Перекрытие резонансов средних движений 232
9.2.1. Порог перекрытия вблизи планеты 238
9.2.2. Перекрытие планетных резонансов 239
9.3. Резонансные мультиплеты 243
9.4. Приближение модулированного маятника 247
Глава 10. Трехтельные резонансы 255
10.1. Происхождение резонансных членов в возмущении 255
10.1.1. Прямой эффект 256
10.1.2. Косвенный эффект 258
viii
Оглавление
10.1.3. Учет обоих (прямого и косвенного) эффектов в асте¬
роидной задаче 264
10.2. Трехтельные резонансные мультиплеты 265
10.3. Пояс астероидов и пояс Койпера 272
10.4. Хаотическая динамика планет-гигантов 280
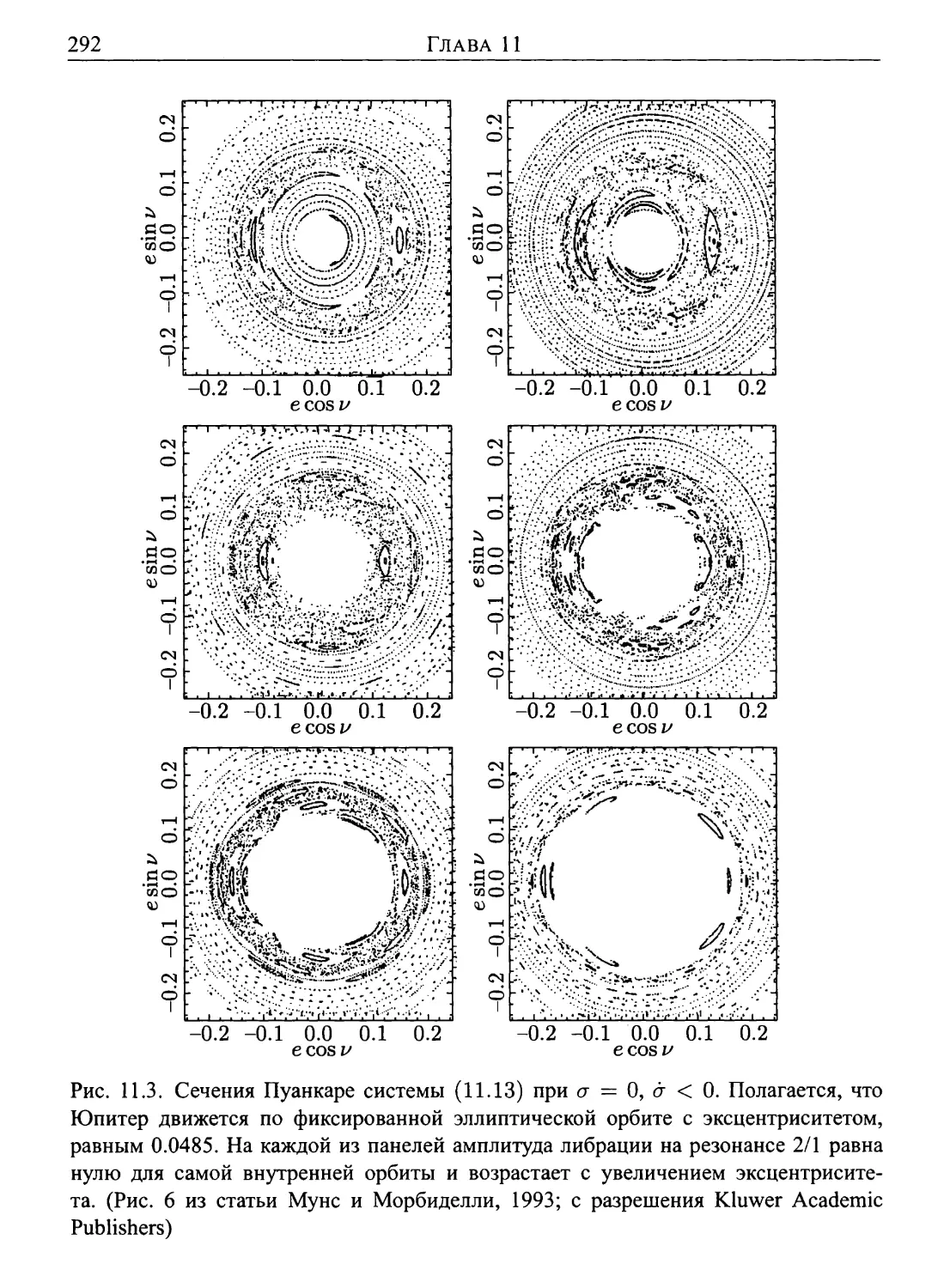
Глава 11. Вековая динамика внутри резонансов средних движе¬
ний 283
11.1. Последовательное исключение гармоник 283
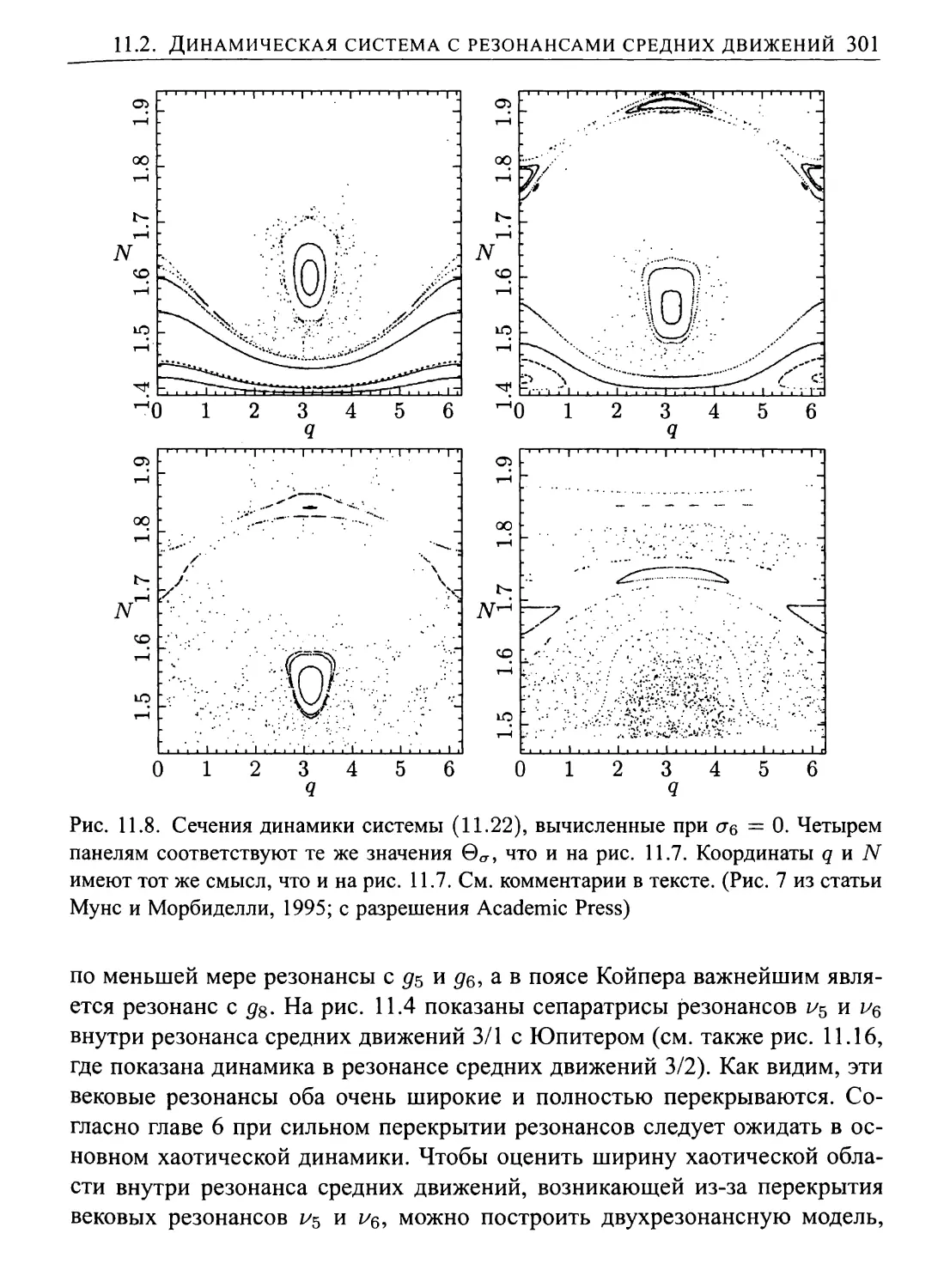
11.2. Динамическая система с резонансами средних движений . . . 286
11.2.1. Вторичные резонансы 289
11.2.2. Динамика Козаи 291
11.2.3. Перигелийные вековые резонансы 298
11.2.4. Узловые вековые резонансы 302
11.2.5. Трехтельные резонансы 304
11.3. Важнейшие резонансы в главном поясе астероидов 306
11.3.1. Резонанс 3/1 307
11.3.2. Резонанс 2/1 314.
11.3.3. Резонанс 3/2 320
11.4. Важнейшие резонансы в поясе Койпера 323
11.4.1. Резонанс 2/3 323
11.4.2. Резонанс 1/2 327
11.5. Резонансы 1/1 329
Глава 12. Глобальная динамическая структура поясов малых
тел 333
12.1. Обнаружение хаотических зон 333
12.2. Хаотическая диффузия и макроскопическая неустойчивость . 343
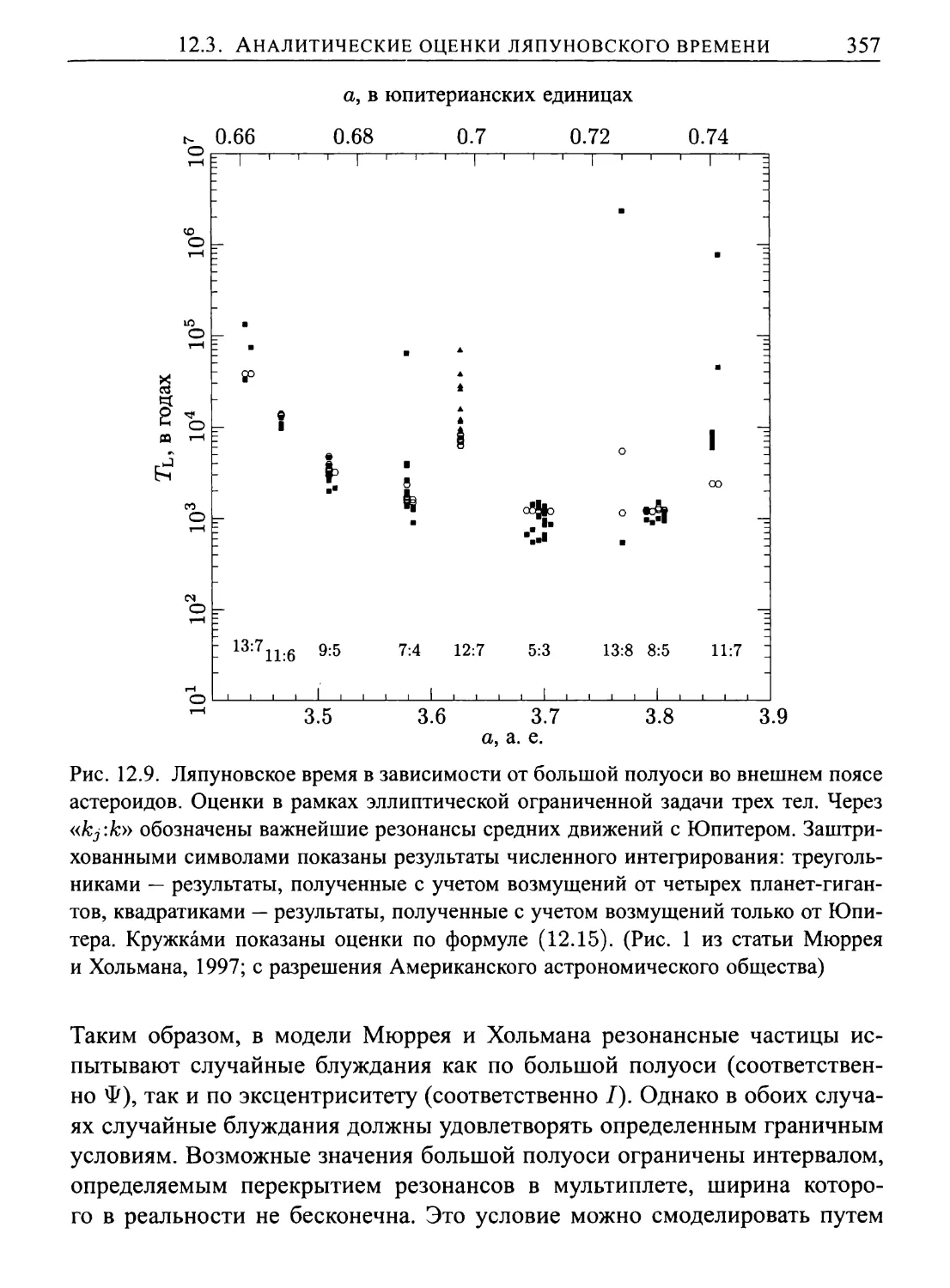
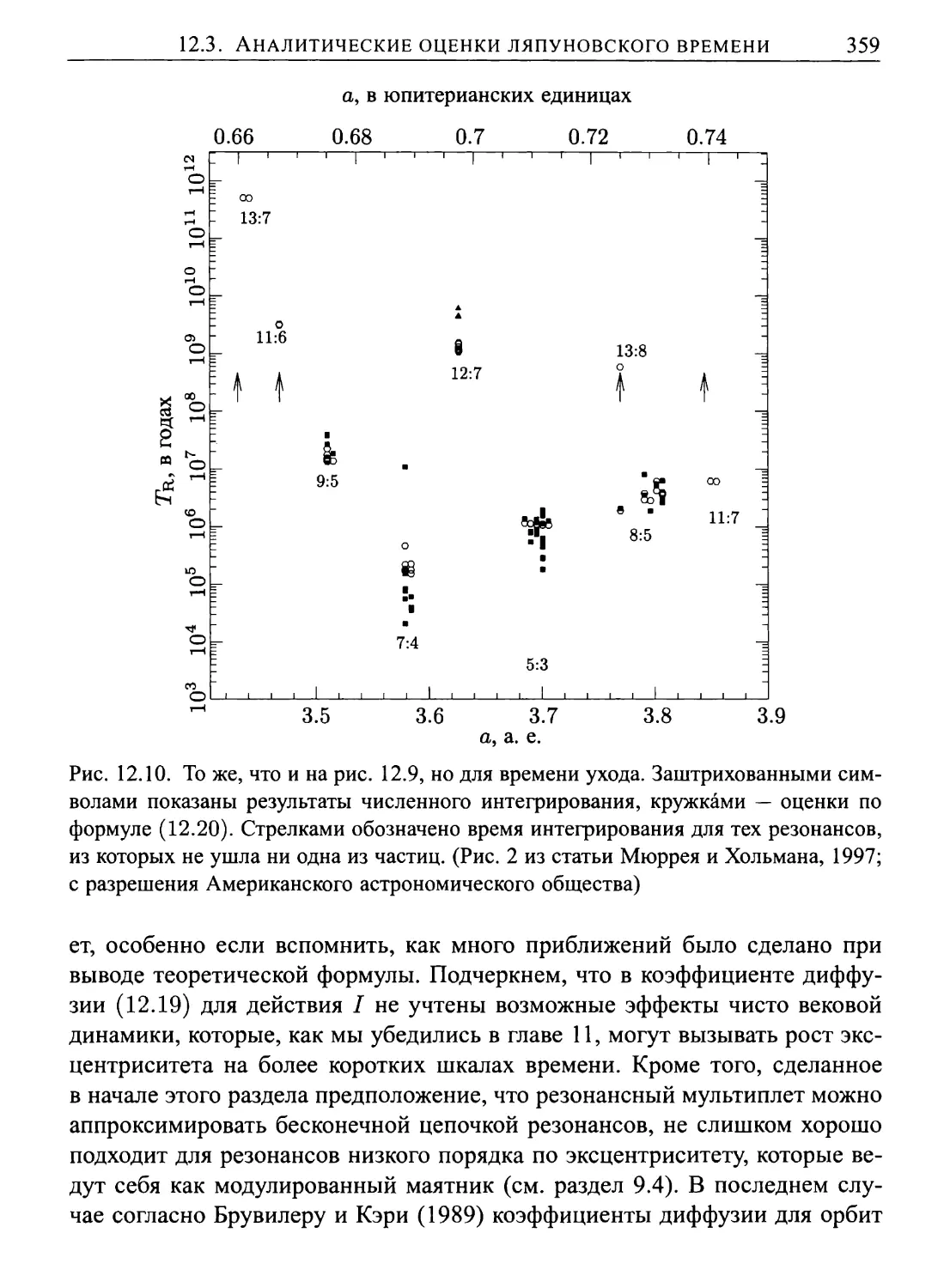
12.3. Аналитические оценки ляпуновского времени и времени
ухода 352
12.4. Применимы ли теоремы Колмогорова-Арнольда-Мозера
и Нехорошева к динамике малых тел? 360
А. Морбиделли, И. И. Шевченко. Douze ans apres. Заметки к русскому
изданию 365
Литература 387
Алфавитный указатель 407
Предисловие редактора перевода
Вниманию читателя предлагается русский перевод монографии из¬
вестного французского ученого, специалиста в области небесной механики
и нелинейной динамики Алессандро Морбиделли «Современная небесная
механика. Аспекты динамики Солнечной системы» (Morbidelli A. Modern
Celestial Mechanics. Aspects of Solar System Dynamics. London: Taylor and
Francis). Книга А. Морбиделли представляет собой введение в современ¬
ную небесную механику — резонансную и хаотическую динамику небесных
тел, с приложениями к задачам орбитальной динамики тел Солнечной си¬
стемы. Фундаментальная тема книги — исследование проблем орбитальной
динамики в контексте современной теории гамильтоновых динамических
систем.
Не так давно на русский язык была переведена и издана другая часто
цитируемая в современной небесномеханической литературе книга [1 ] —
монография К. Мюррея и С.Дермотта «Динамика Солнечной системы»
(Murray С., Dermott S. Solar System Dynamics. Cambridge: Cambridge Univ.
Press). Изложение в ней ориентировано на самую широкую аудиторию на¬
учных работников и студентов, интересующихся данной тематикой, и ве¬
дется без обращения к современной теории гамильтоновых систем. Поэто¬
му книга К.Мюррея и С.Дермотта может быть рекомендована для озна¬
комления с предметом на предварительном этапе, тогда как книга А. Мор¬
биделли — на более высоком и продвинутом. Без преувеличения можно
сказать, что книга А. Морбиделли уже успела стать настольной для аспи¬
рантов и исследователей в данной области науки.
Цели, задачи и содержание книги автор освещает в своем предисловии
и во введении, поэтому здесь нет необходимости о них говорить. Однако
подчеркнем, что эта книга пока единственная на русском языке, в кото¬
рой читатель может самым подробным образом и на современном уровне
узнать о разнообразных резонансных и хаотических эффектах в динамике
тел Солнечной системы и их математической теории.
Библиография в книге А. Морбиделли ориентирована на англоязычно¬
го читателя, поэтому уместно привести здесь краткий список книг и об¬
X
Предисловие редактора перевода
зоров по близкой тематике, изданных на русском языке. Тематика этого
списка следующая. Книга [1], как уже отмечено выше, может быть реко¬
мендована для предварительного ознакомления с предметом. В монографи¬
ях и обзорах [2-14] читатель может найти обширный материал для допол¬
нительного и углубленного чтения по общим вопросам небесной механики,
резонансной и хаотической динамики, теории гамильтоновых систем. В об¬
зорах [15-17] рассмотрены современные проблемы регулярной и хаотиче¬
ской динамики тел Солнечной системы.
Перевод книги осуществили: В. В. Куприянов (введение, гл. 1, разде¬
лы 11.3-11.5), В. Г. Соколов (гл. 2), В. В. Орлов (гл. 3, 6, разделы 8.1-8.2,
11.1-11.2), А. Т. Байкова (гл. 4), А. В. Мельников (гл. 5), В. В. Бобылев (гл. 7),
М. Ю. Ховричев (разделы 8.3-8.4), Е. Ю. Алешкина (гл. 9), Е. А. Смирнов
(гл. 10), А. В. Рубинов (гл. 12).
А. Морбиделли поддержал идею перевода книги на русский язык и лю¬
безно представил специально написанное им «Предисловие для русского
издания». Редактирование перевода осуществлено в творческом контакте
с автором. В частности, при переводе исправлен ряд обнаруженных в ори¬
гинале опечаток и неточностей — все эти исправления согласованы с ав¬
тором. Поскольку со времени публикации оригинала прошло более десяти
лет, автор книги и редактор перевода вместе подготовили краткий обзор
Douze arts apres о наиболее заметных результатах в данной области науки
за последние годы; он печатается как эпилог к переведенной книге. Редак¬
тор перевода глубоко благодарен автору книги за помощь и сотрудничество
при подготовке русского издания.
Редактор перевода искренне признателен В. К. Абалакину и К. В.Хол-
шевникову за ценные замечания. Участники проекта по переводу и изда¬
нию книги выражают благодарность Российскому фонду фундаментальных
исследований за частичную поддержку проекта.
И. И. Шевченко
Литература
[1] Мюррей К, Дермотт С. Динамика Солнечной системы / Пер. с англ.
под ред. И. И. Шевченко. - М.: ФИЗМАТЛИТ, 2009, 2010. - 588 с.
[2] Арнольд В. И. Математические методы классической механики. —
М.: Наука, 1989.-472 с.
[3] Арнольд В. И., Козлов В. В., Нейштадт А. И. Математические аспекты
классической и небесной механики. — М.: Эдиториал УРСС, 2002. —
416 с.
Предисловие редактора перевода
xi
[4] Белецкий В. В. Регулярные и хаотические движения твердых тел. —
М.-Ижевск: РХД, 2007. - 132 с.
[5] Белбруно Э. Динамика захвата и хаотические движения в небесной ме¬
ханике / Пер. с англ. под ред. В. Б. Титова. — М.-Ижевск: ИКИ, 2011. —
248 с.
[6] Лихтенберг А., Либерман М. Регулярная и стохастическая динамика /
Пер. с англ. под ред. Б. В. Чирикова. — М.: Мир, 1984. — 528 с.; Чере¬
повец: Меркурий-ПРЕСС, 2000. — 528 с.
[7] Маршал К. Задача трех тел / Пер. с англ. под ред. А. В. Борисова
и И. С. Мамаева. — М.-Ижевск: ИКИ, 2004. — 640 с.
[8] ТрещевД. В. Введение в теорию возмущений гамильтоновых систем. —
М.: ФАЗИС, 1998.- 184 с.
[9] Холшевников К. В. Асимптотические методы небесной механики. —
JL: Издательство ЛГУ, 1985. — 208 с.
[10] Холшевников К. В., Титов В. Б. Задача двух тел. — СПб: Издательство
СПбГУ, 2007. - 180 с.
[11] Чириков Б. В. Нелинейный резонанс. — Новосибирск: Издательство
НГУ, 1977. - 82 с.
[12] Чириков Б. В. Взаимодействие нелинейных резонансов. — Новоси¬
бирск: Издательство НГУ, 1978. — 80 с.
[13] Чириков Б, В. Нелинейные резонансы и динамическая стохастич-
ность // Природа. 1982. № 7. — С. 15-25.
[14] де ла Яве Р. Введение в КАМ-теорию / Пер. с англ. под ред. Д. В. Тре-
щева. — М.-Ижевск: ИКИ, 2003. — 176 с.
[15] Холшевников К. В., Кузнецов Э.Д Обзор работ по орбитальной эво¬
люции больших планет Солнечной системы // Астрон. вестник. 2007.
Т. 41 (4). - С. 291-329.
[16] Шевченко И. И. Резонансы и хаос в динамике тел Солнечной систе¬
мы // В книге: Орлов В. В. и др. Астрономия: традиции, настоящее,
будущее. Сборник обзоров. — СПб.: СПбГУ, 2007. — С. 284-314.
[17] Шевченко И. И. Непредсказуемые орбиты // Природа. 2010. № 4. —
С. 12-21.
Предисловие к русскому изданию
Когда я решил написать эту книгу, немногим более десяти лет на¬
зад, я руководствовался главным образом двумя соображениями. Прежде
всего, я чувствовал, что существует большой разрыв между классической
небесной механикой и теорией гамильтоновых динамических систем. То¬
гда как последняя самым захватывающим образом продвинулась в глубин¬
ном понимании механизмов, лежащих в основе порядка и хаоса, изложение
в учебниках по небесной механике было сосредоточено на разложении пер¬
турбационной функции в степенные ряды и ряды Фурье по орбитальным
элементам и на анализе простых задач, часто рассматриваемых в самом
низком порядке теории возмущений. Канонические переменные часто даже
не упоминались. Однако небесная механика становится глубоко взаимосвя¬
занной с теорией гамильтоновых систем, когда, в попытке описать дина¬
мику реальной Солнечной системы, она имеет дело с сильно нелинейными
задачами: при вычислении высокоточных интегралов движения (собствен¬
ные элементы), при исследовании взаимодействия нескольких резонансов,
при определении порога наступления глобального хаоса, если ограничить¬
ся упоминанием лишь немногих примеров. Таким образом, в своей книге
я ставил себе целью «навести мосты», ликвидирующие данный разрыв,
представляя динамику планет и малых тел как конкретные гамильтоновы
динамические системы. Во-вторых, я чувствовал, что динамическая астро¬
номия все более сдвигалась в сторону численных методов исследования,
чтобы справиться со сложностью реальной Солнечной системы. Числен¬
ные результаты можно получить относительно легко, но они нуждаются
в интерпретации, а для этого необходимо, чтобы современный специалист
по динамической астрономии знал теорию гамильтоновых динамических
систем и свойства, которыми такие системы могут обладать.
Поэтому с энтузиазмом и гордостью я приветствовал перевод моей
книги на русский язык. К русской школе, внесшей, возможно, наибольший
вклад в развитие теории динамических систем вообще и теории гамильто¬
новых систем в частности, принадлежат такие великие умы, как Колмого¬
ров, Арнольд, Нехорошее, Чириков, Нейштадт и многие другие. Интерес
xiv
Предисловие к русскому изданию
российского ученого сообщества к моей книге означал, что я сумел выпол¬
нить свою миссию, по крайней мере частично. Если у реалистичной и ана¬
литической небесной механики есть будущее, то оно, возможно, в России.
Я надеюсь, что моя книга будет побуждать молодых ученых к восприятию
наследия великих русских учителей и к продвижению этой области иссле¬
дований.
Алессандро Морбиделли
Предисловие
Последнее двадцатилетие XX века ознаменовалось захватывающими
достижениями небесной механики в познании структуры и эволюции Сол¬
нечной системы. Открытие хаоса в динамике планет, выявление главных
транспортных маршрутов, по которым астероиды покидают главный по¬
яс и выходят на угрожающие Земле орбиты, раскрытие динамических ме¬
ханизмов, вызывающих внутренний нагрев галилеевых спутников, — вот
лишь некоторые примеры достижений, сделавших небесную механику фун¬
даментальным разделом науки о Солнечной системе. Поэтому проводимые
во многих странах мира конгрессы по планетологии, такие как ежегодные
форумы Отделения планетных наук Американского астрономического об¬
щества и регулярные симпозиумы «Астероиды, кометы, метеоры», всегда
включают продолжительные и хорошо посещаемые сессии, посвященные
динамике.
Именно это я называю современной небесной механикой, хотя не сле¬
дует забывать, что у небесной механики есть и другие разделы, более скон¬
центрированные на строгих математических исследованиях простых «игру¬
шечных» моделей, а не на реалистическом описании эволюции Солнечной
системы, и недавно в этих исследованиях также были достигнуты иннова¬
ционные результаты.
В последние годы издан ряд книг по небесной механике, но ни одна
из них не описывает недавние результаты исследований динамики Солнеч¬
ной системы на основе фундаментальной теории. Изложение в них либо
сосредоточено на общей теории динамических систем, либо ограничено
базовыми элементами небесной механики. Настоящая книга призвана вос¬
полнить этот пробел. Надеюсь, она станет подспорьем для студентов стар¬
ших курсов и молодых ученых, вынужденных сегодня прокладывать себе
путь, изучая обширную научную литературу — статьи в первоисточниках —
без помощи «путеводителя», представляющего предмет в едином виде. Моя
цель состоит в том, чтобы подвести читателя к рубежу, где он смог бы при¬
ступить к самостоятельному исследованию.
Современная небесная механика глубоко взаимосвязана с теорией
гамильтоновых систем. Большинство аналитических исследований суще¬
ственным образом использует методы теории возмущений гамильтоновых
xvi
Предисловие
систем; зачастую также и для корректной интерпретации результатов чис¬
ленного моделирования требуется хорошее теоретическое знание гамиль¬
тоновой динамики. Поскольку гамильтонова теория не входит в обычный
багаж знаний изучающих небесную механику астрономов, в первой части
книги излагаются ее фундаментальные понятия. Без претензий на исчер¬
пывающую полноту первые шесть глав дают то, что нужно знать о га¬
мильтоновой теории, чтобы непринужденно работать над задачами небес¬
ной механики. Приводятся только основополагающие идеи — без деталей
и технических математических доказательств, но с необходимыми библио¬
графическими ссылками для тех, кто хотел бы освоить предмет более глу¬
боко. Вслед за первой главой, посвященной базовым понятиям небесной
и гамильтоновой механики, в главе 2 разъясняется основанная на рядах
Ли теория возмущений гамильтоновых систем. Главы 3 и 4 иллюстрируют
свойства инвариантных торов и резонансов соответственно. В отдельную
главу (главу 5) особо выделено обсуждение численных инструментов, по¬
лезных для обнаружения хаотического поведения. В главе 6 обсуждаются
динамические структуры гамильтоновых систем, обусловленные взаимо¬
действием резонансов, и детализируется, как эти структуры могут быть
отождествлены в численных исследованиях.
Вторая часть книги посвящена непосредственно предмету небесной
механики. Эта часть более техническая, тем не менее изложение здесь на¬
меренно сконцентрировано на процедурах и на идеях, а не на технических
деталях. Таким образом, книга должна представлять интерес также и для
специалистов по гамильтоновой теории, желающих быть в курсе происхо¬
дящего в современной небесной механике. В частности, в книге опущены
детали методов практических вычислений (методов разложения в ряд воз¬
мущающих функций или их вычисления по формулам в замкнутом виде,
вычисления интегралов действия и т. п.). Практические методы эволюцио¬
нируют очень быстро — параллельно с эволюцией мощности компьютеров,
тогда как идеи и концептуальные подходы сохраняют свое значение много
дольше. Главы 7 и 8 посвящены соответственно вековым движениям планет
и малых тел. В обсуждаемые здесь темы, среди прочих, входят: хаотиче¬
ская динамика планет земной группы; теории, созданные для вычисления
собственных элементов орбит астероидов; динамика вековых резонансов.
Последующие главы 9-12 посвящены сложной теме резонансов средних
движений. В частности, в главе 9 описана структура резонансов средних
движений, сначала в рамках относительно простой плоской ограниченной
задачи трех тел, а затем в более реалистичных моделях. Глава 10 посвящена
Предисловие
xvii
трехтельным резонансам, важность которых была совсем недавно осознана
как для динамики малых тел, так и для динамики планет. В главе 11 обсуж¬
дается вековая динамика внутри резонансов средних движений, которая,
по моему мнению, является одной из самых сложных тем в небесной меха¬
нике. Наконец, в главе 12 исследуется глобальная динамическая структура
областей Солнечной системы, плотно населенных малыми телами, и об¬
суждается модная тема медленной хаотической диффузии.
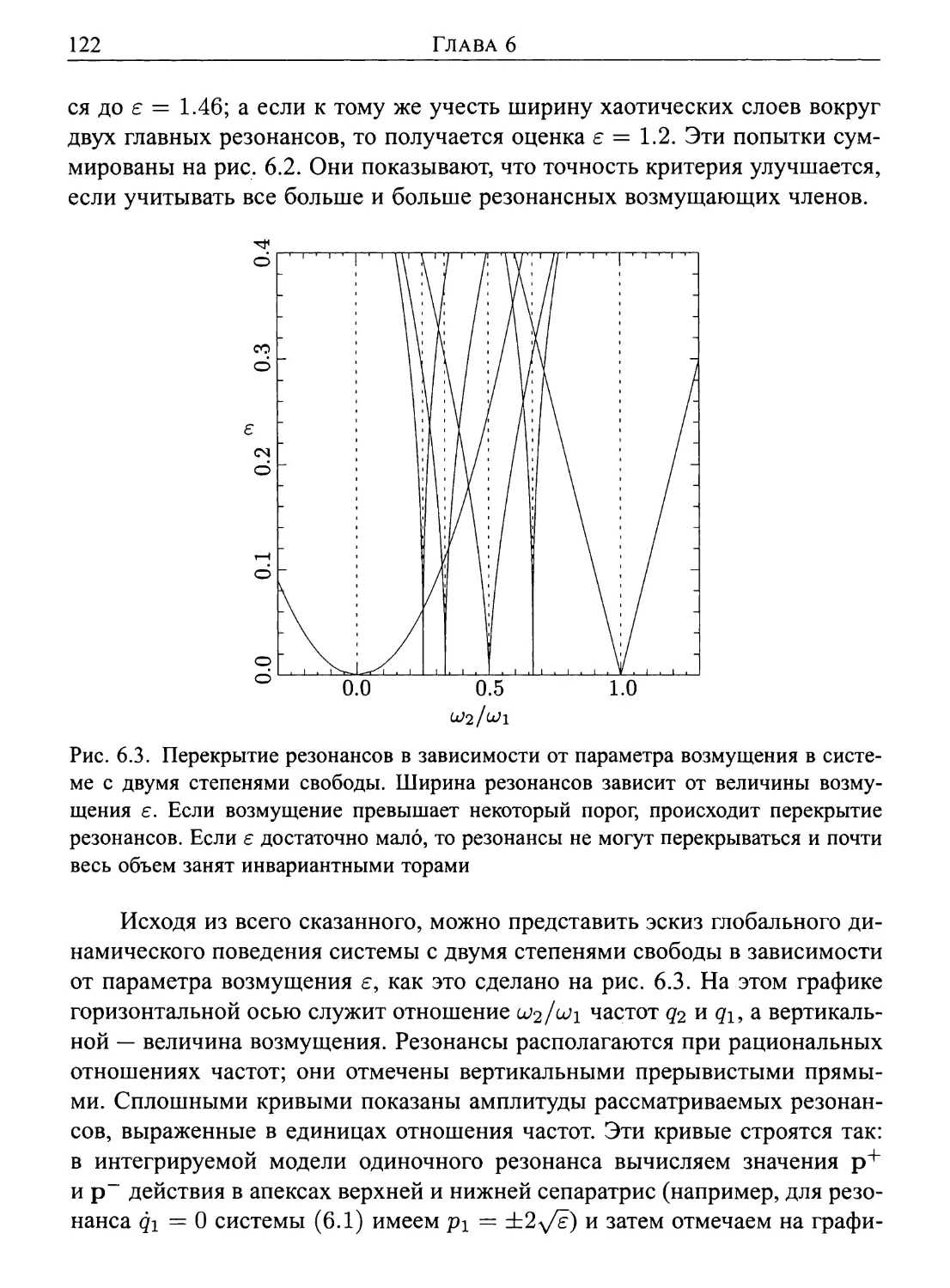
Можно видеть, что изложение в книге сосредоточено на динамике пла¬
нет и малых тел. Это объясняется главным образом пределами моих позна¬
ний. Важные проблемы динамики естественных спутников и планетных
колец (см. краткий обзор во введении) поэтому не обсуждаются. Однако
большинство развитых здесь концепций применимы также и к динамике
спутников и планетных колец, поэтому я надеюсь, что книга сможет послу¬
жить введением в предмет и для тех, кто интересуется данными темами.
Более того, я решил исключить из книги тему динамики тел, сближаю¬
щихся с планетами, поскольку она не входит в категорию квазиинтегриру-
емой динамики и ее связь с остальным изложением была бы очень слабой.
Действительно, динамика тел, сближающихся с планетами, изучается глав¬
ным образом численными методами, поскольку возможности аналитиче¬
ских и полуаналитических теорий в ее исследованиях весьма ограничены.
Завершение работы над этой книгой не стало бы возможным без под¬
держки некоторых моих коллег, прежде всего М. Фесту и К. Фрешле.
Я в долгу у главных «ревизоров» книги М. Гуццо, Д. Несворного и Ф. Тома¬
са за конструктивную критику и у рецензентов А. Джиорджилли, В. Гурза-
дяна, Ж. Анрара и Ж. Ласкара — за оценки и советы. По меньшей мере семь
читателей нашли в себе мужество прочесть каждую строку этой книги!
Также хочу поблагодарить А. Челлино, С. Ферраз-Мелло, Ж. Анрара,
М. Хольмана, 3. Кнежевича, Ж. Ласкара, Е. Лега, А. Леметра, К. Мюррея,
Н. Мюррея и Д. Несворного за предоставленные оригиналы рисунков из их
работ.
Я посвящаю эту книгу памяти моих друзей и коллег Паоло Фаринеллы,
Фабио Мильорини и Мишель Муне. Жизнь не дала им второго шанса, и мне
недостает их привязанности и их совета.
Ла Турби (Франция), 1 июня 2000 г.
Введение
Тела Солнечной системы и задачи небесной механики
В этом введении мы представляем общий обзор Солнечной системы
для неподготовленного читателя. Наша цель — показать, что практически
с любым телом Солнечной системы связаны какие-либо динамические за¬
дачи, что делает небесную механику важнейшей частью науки о Солнечной
системе. Некоторые из этих задач будут подробно рассмотрены в последу¬
ющих главах этой книги.
Первые попытки предсказать движение планет по небосводу восходят
к заре цивилизации. Однако то, что мы сейчас называем небесной механи¬
кой в точном значении этого слова, родилось с открытием закона всемир¬
ного тяготения Ньютоном в 1687 г. С этого момента вычисление точных
эфемерид стало сугубо математической проблемой. В ее исследовании осо¬
бенно велики достижения Лагранжа и Лапласа конца XVIII столетия. Решая
задачу повышения точности эфемерид, они сделали первый шаг в развитии
теории вековой эволюции планетных орбит, а второй из них осознал также
важность квазирезонанса между периодами обращения Юпитера и Сатур¬
на. В те времена любая видимая аномалия в движении планет, казалось,
могла быть объяснена с помощью достаточно точной теории в рамках нью¬
тонова закона тяготения. Этот успех выковал абсолютную веру Лапласа
в детерминизм, которая затем стала присущей и всей науке XIX столетия.
Поиск все более точных аналитических эфемерид продолжался, и продол¬
жается до наших дней. Однако два столетия спустя после работ Лапласа —
с открытием нового явления, названного хаосом, разработкой численных
методов для его обнаружения и созданием мощных компьютеров — бы¬
ло понято, что движение планет является в действительности хаотическим.
С этого момента важнейшей целью небесной механики стало познание при¬
чин такого хаотического поведения и его роли в долговременной эволюции
нашей планетной системы. Возможная связь между хаотическим измене¬
нием планетных орбит и климатической историей планет земной группы
продолжает занимать умы исследователей.
2 Введение
Рис. 1. Вверху: относительный масштаб орбит девяти планет1 (у орбит Меркурия,
Венеры и Земли названия планет не указаны). Внизу: приблизительный относитель¬
ный масштаб диаметров девяти планет. (Из фотогалереи NSSDC2)
Таким образом, планеты дают нам примеры интересного динамиче¬
ского поведения, но еще интереснее динамика астероидов. Так как их
очень много, для любого возможного динамического феномена, даже са¬
мого необычного, почти всегда найдется демонстрирующий его астероид.
Астероиды — это небольшие тела из скальных пород или льда; самый боль¬
шой из них, Церера, имеет диаметр 900 км. Орбиты большинства из них
расположены в главном поясе — области между Марсом и Юпитером — и не
пересекают орбиты планет.
Если мы построим распределения астероидов по большим полуосям,
эксцентриситетам и наклонениям их эллиптических орбит (см. главу 1, где
'По решению XXVI Генеральной ассамблеи Международного астрономического союза
(Прага, 2006 г.) Плутон более не считается планетой в строгом смысле этого термина. Он
отнесен к новому классу объектов — классу планет-карликов. — Прим. ред.
2National Space Science Data Center — Национальный центр космических научных данных
НАСА. — Прим. ред.
Введение
3
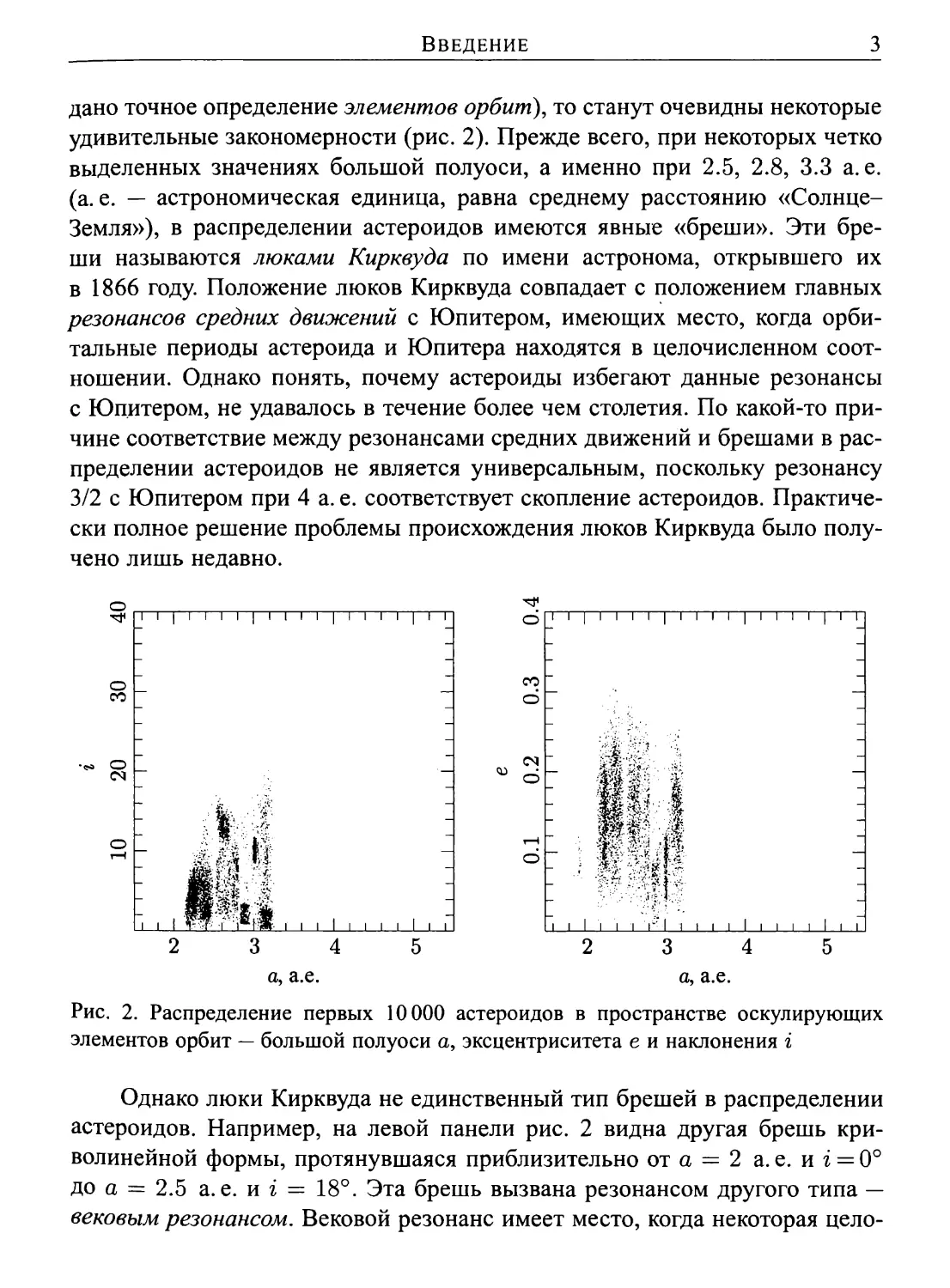
дано точное определение элементов орбит), то станут очевидны некоторые
удивительные закономерности (рис. 2). Прежде всего, при некоторых четко
выделенных значениях большой полуоси, а именно при 2.5, 2.8, 3.3 а. е.
(а. е. — астрономическая единица, равна среднему расстоянию «Солнце-
Земля»), в распределении астероидов имеются явные «бреши». Эти бре¬
ши называются люками Кирквуда по имени астронома, открывшего их
в 1866 году. Положение люков Кирквуда совпадает с положением главных
резонансов средних движений с Юпитером, имеющих место, когда орби¬
тальные периоды астероида и Юпитера находятся в целочисленном соот¬
ношении. Однако понять, почему астероиды избегают данные резонансы
с Юпитером, не удавалось в течение более чем столетия. По какой-то при¬
чине соответствие между резонансами средних движений и брешами в рас¬
пределении астероидов не является универсальным, поскольку резонансу
3/2 с Юпитером при 4 а. е. соответствует скопление астероидов. Практиче¬
ски полное решение проблемы происхождения люков Кирквуда было полу¬
чено лишь недавно.
a, a.e. а, а.е.
Рис. 2. Распределение первых 10000 астероидов в пространстве оскулирующих
элементов орбит — большой полуоси а, эксцентриситета е и наклонения г
Однако люки Кирквуда не единственный тип брешей в распределении
астероидов. Например, на левой панели рис. 2 видна другая брешь кри¬
волинейной формы, протянувшаяся приблизительно от а = 2 а. е. и г = 0°
до а = 2.5 а.е. и г = 18°. Эта брешь вызвана резонансом другого типа —
вековым резонансом. Вековой резонанс имеет место, когда некоторая цело¬
4
Введение
численная комбинация3 частот прецессии орбиты астероида равна некото¬
рой целочисленной комбинации частот прецессии орбит планет. Еще один
вековой резонанс, как было недавно обнаружено, отвечает за отсутствие
астероидов в промежутке между двумя четко очерченными группами, ви¬
димыми на рис. 2 при г ~ 20-28°, а ~ 1.9 а. е. и а ~ 2.3 а. е.
На рис. 2 очевидным образом проявляются также несколько скопле¬
ний астероидов. Напрашивается мысль, что тела в этих скоплениях свя¬
заны происхождением — например, образовались в результате разрушения
одного родительского тела. Однако простые небесномеханические расчеты
показывают, что большие полуоси, эксцентриситеты и наклонения осцил¬
лируют со временем из-за возмущений со стороны планет. Поэтому эти
очевидные скопления могут, в принципе, быть лишь видимостью. С другой
стороны, могут существовать и связанные происхождением группы асте¬
роидов, которые не видны на рис. 2 из-за тех же осцилляций. Поэтому
одной из задач современной небесной механики является нахождение ве¬
личин, квазиинвариантных во времени, — они называются собственными
элементами, — которые можно использовать для выявления статистически
значимых групп астероидов — так называемых семейств.
Астероиды с большими полуосями орбит вблизи 5.2 а. е. — это так
называемые астероиды-греки и астероиды-троянцы. Они имеют тот же
орбитальный период, что и Юпитер, и находятся приблизительно в 60°
впереди и позади планеты соответственно. Лагранж показал, что в первом
приближении их орбитальная конфигурация устойчива. Однако, если при¬
нять во внимание большие наклонения орбит этих астероидов, эксцентри¬
ситет орбиты Юпитера и влияние других планет, проблема устойчивости
греков и троянцев оказывается далеко не простой. Удивительно, что другие
планеты-гиганты не имеют своих греков и троянцев, что может быть след¬
ствием наличия орбитальных квазирезонансов между этими планетами. Из
планет земной группы лишь у Марса есть два астероида-троянца4.
У некоторых астероидов орбиты таковы, что они испытывают тесные
сближения с планетами земной группы. В зависимости от наблюдаемых
значений эксцентриситета и большой полуоси их называют аполлонцами,
амурцами, атонцами, Марс-кроссерами (астероидами, пересекающими ор¬
биту Марса); см. рис. 3. Первые три типа объектов входят в популяцию
астероидов, сближающихся с Землей (АСЗ).
3 Алгебраическая сумма величин с целочисленными коэффициентами. — Прим. ред.
4 К настоящему времени у Юпитера открыто более 2000 греков и троянцев. У Нептуна их
известно 6, у Марса — 4. — Прим. ред.
Введение
5
□ аполлонцы * атонцы
* амурцы • Марс-кроссеры
■ ■
большая полуось, а. е.
Рис. 3. Орбитальное распределение известных аполлонцев, амурцев, атонцев
и Марс-кроссеров. Сплошными и прерывистыми линиями нанесены границы этих
популяций, а пунктирными прямыми — местоположение некоторых из наиболее
важных резонансов. Как указывают стрелки, астероиды из внутренней и цен¬
тральной частей главного пояса могут мигрировать по эксцентриситету, становясь
Марс-кроссерами. АСЗ и Марс-кроссеры своим происхождением обязаны свой¬
ствам резонансной динамики в главном поясе
Численное интегрирование орбит показывает, что типичное время жиз¬
ни АСЗ составляет 10 млн лет. АСЗ «погибают» либо из-за падения на
Солнце, либо из-за ухода из Солнечной системы, либо из-за столкновения
с планетой. Динамические механизмы, приводящие к таким исходам, — еще
одна задача современной небесной механики, исследование которой вклю¬
чает моделирование расположения и силы резонансов, а также влияния тес¬
ных сближений с планетами. Короткое время жизни АСЗ означает, что все
они, безусловно, значительно моложе Солнечной системы, однако их попу¬
ляция должна поддерживаться в некотором стационарном состоянии бла¬
годаря притоку астероидов, покидающих главный пояс и начинающих пе¬
ресекать орбиты планет. Интуиция подсказывает, что происхождение АСЗ
связано с брешами в распределении астероидов главного пояса. Столкнове¬
ния и разрушение астероидов, вкупе со слабыми неконсервативными сила¬
6
Введение
ми, непрерывно поставляют новые астероиды в люки, однако воздействие
главных вековых резонансов и резонансов средних движений немедлен¬
но их «вычищает», заставляя тела покидать главный пояс и переходить на
орбиты, подобные орбитам АСЗ. Однако сосредоточение Марс-кроссеров
в области от 2.1 а. е. до 2.5 а. е. указывает на то, что зону главного пояса,
находящуюся в этом интервале больших полуосей, также покидают многие
тела, хотя в ней и нет ничего похожего на люк. Недавно было показано,
что причиной являются многочисленные слабые резонансы, дестабилизи¬
рующий эффект которых проявляется на временных масштабах, достаточно
больших для восстановления астероидной заселенности этой зоны.
За орбитой Нептуна располагается второй пояс малых тел, известный
как пояс Койпера. По данным на 9 июня 2000 года открыто 279 транснеп-
тунных объектов5. «Планета» Плутон также находится в поясе Койпера.
В 1999 г. бурно обсуждалось, следует ли продолжать считать Плутон пла¬
нетой, или же его следует понизить в статусе до малого тела Солнечной си¬
стемы. Международный астрономический союз принял решение сохранить
исторический статус Плутона6, хотя многие ученые едины во мнении, что
значительно большие, чем у других планет, эксцентриситет и наклонение
орбиты и малые размеры этого тела (диаметр 2340 км, то есть 2/3 диаметра
Луны) заставляют считать его просто самым крупным объектом, открытым
до сих пор в поясе Койпера.
Наше знание орбитального распределения тел в поясе Койпера все еще
весьма ограничено, поскольку, не считая открытия Плутона, первый объект
в нем был открыт только в 1992 году, а для уверенного определения па¬
раметров орбит требуется несколько лет наблюдений. Рис. 4, построенный
для объектов пояса Койпера, наблюдавшихся не менее чем в двух оппози¬
циях, является аналогом рис. 2.
Хотя полное число объектов (94) на графике невелико, очевидно, что
некоторые особенности их орбитального распределения напоминают свой¬
ства главного пояса астероидов. Скопление тел при 39.5 а. е. — в кото¬
ром находится и Плутон — соответствует резонансу 2/3 средних движений
с Нептуном. Кроме того, в области 40-42 а. е. виден «люк», обусловлен¬
ный вековыми резонансами. Где находится внешняя граница пояса Кой¬
пера, неизвестно. Наблюдательные трудности препятствуют открытию его
наиболее далеких от Солнца объектов, поэтому наши знания о поясе Кой¬
пера ограничены его внутренней частью. Одна из важных задач небесной
5Сейчас их открыто уже более тысячи. — Прим. ред.
6См. прим. ред. на с. 2. — Прим. ред.
Введение
7
а, а. е. а, а. е.
Рис. 4. Орбитальное распределение тел пояса Койпера, наблюдавшихся не менее
чем в двух оппозициях. Построено по данным Центра малых планет на 9 июня
2000 г.
механики состоит в прогнозировании обнаружения новых объектов пояса
Койпера и в предсказании их орбитального распределения на основе тео¬
рии.
Тогда как главный пояс астероидов ответственен за поддержание по¬
пуляции АСЗ, пояс Койпера считается ответственным за поддержание по¬
пуляции так называемых комет семейства Юпитера. Это короткопериоди¬
ческие кометы с малыми наклонениями орбит (рис. 5); их динамика опре¬
деляется сближениями с Юпитером. В последние годы был проведен ряд
исследований механизмов, заставляющих тела пояса Койпера сближаться
с Нептуном и в дальнейшем перемещаться во внутреннюю часть Солнеч¬
ной системы, находясь в которой они наблюдаются и классифицируются
как кометы семейства Юпитера.
Считается, что долгопериодические кометы и так называемые кометы
галлеева типа, поскольку их орбиты распределены по наклонениям изо¬
тропно (рис. 5), происходят не из дисковидного резервуара, подобного поя¬
су Койпера, а из квазисферического резервуара, называемого облаком Оор¬
та. Избыток комет с большими полуосями орбит порядка 10 ООО а. е. ука¬
зывает на то, что этот резервуар расположен на самых дальних рубежах
Солнечной системы. Полагают, что облако Оорта образовалось из плане-
тезималей, первоначально располагавшихся в области планет-гигантов, но
рассеянных при их сближениях с этими планетами с выходом на сильно
вытянутые орбиты с большими полуосями порядка 10000 а. е. На таких
8
Введение
долгопериодич.
кометы
кометы
. семейства
кометы юпитера
галлеева типа
Рис. 5. Орбитальное распределение и классификация комет. По определению,
долгопериодическими называют кометы, период обращения которых превышает
200 лет. Кометы с меньшими периодами подразделяют на кометы семейства Юпите¬
ра и кометы галлеева типа в соответствии с относительной скоростью пересечения
ими орбиты Юпитера
расстояниях от Солнца гравитационный потенциал нашей Галактики силь¬
но возмущает центральный потенциал Солнца. Изучение динамической ро¬
ли этого Галактического прилива совершенно необходимо для того, чтобы
понять, как образовалось облако Оорта и каким образом кометы споради¬
чески вбрасываются во внутреннюю Солнечную систему. Модели, прини¬
мающие во внимание Галактический прилив, а также близкие прохождения
звезд и гигантских молекулярных облаков, ставят своей целью определить,
сколько комет должно содержаться в облаке Оорта, чтобы получить наблю¬
даемое количество долгопериодических комет. Полученные данные, в свою
очередь, позволяют оценить полную массу исходного планетезимального
диска.
Системы колец Юпитера, Сатурна, Урана и Нептуна представляют со¬
бой удивительные естественные лаборатории для изучения действия как
Введение
9
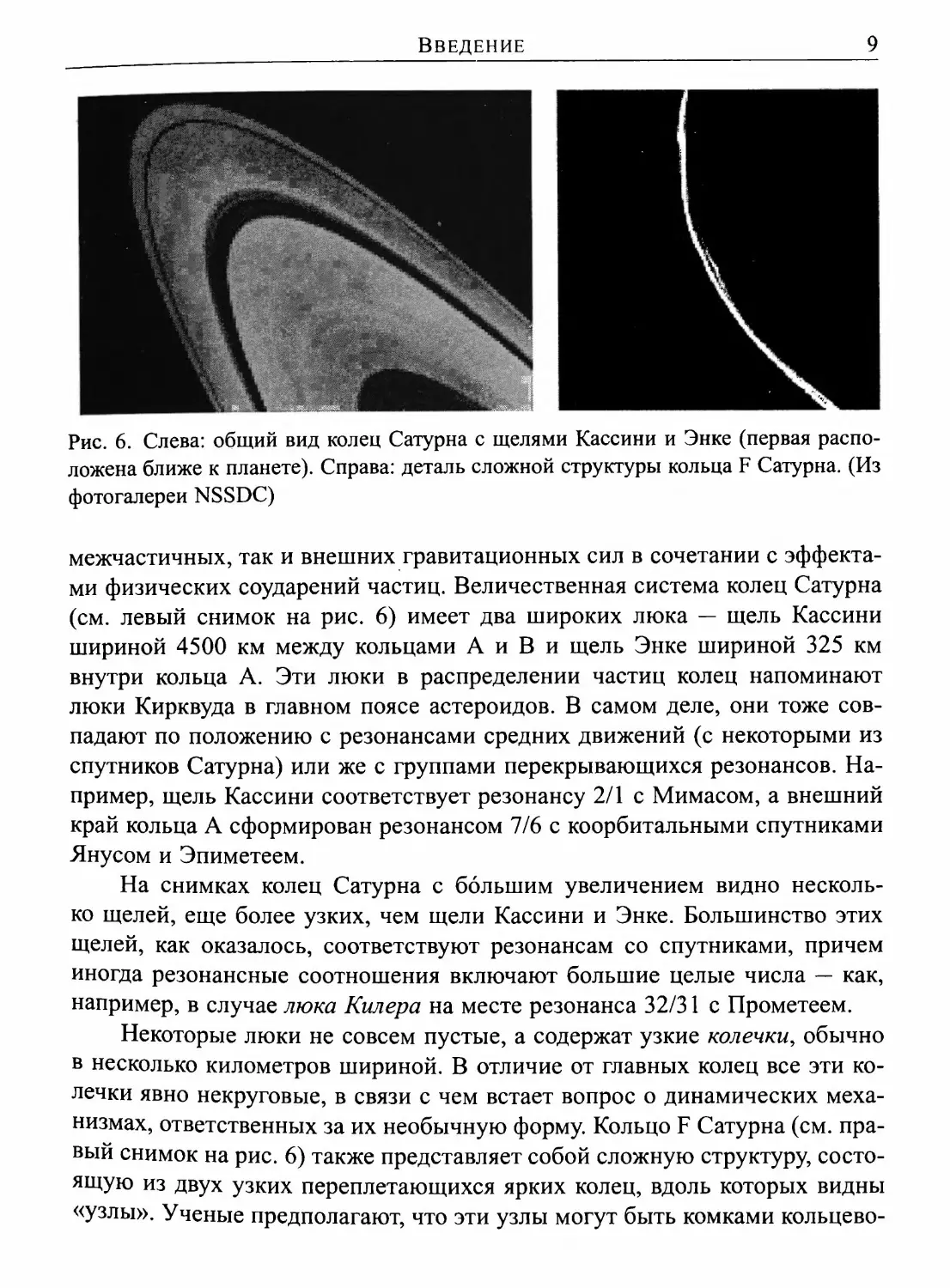
Рис. 6. Слева: общий вид колец Сатурна с щелями Кассини и Энке (первая распо¬
ложена ближе к планете). Справа: деталь сложной структуры кольца F Сатурна. (Из
фотогалереи NSSDC)
межчастичных, так и внешних гравитационных сил в сочетании с эффекта¬
ми физических соударений частиц. Величественная система колец Сатурна
(см. левый снимок на рис. 6) имеет два широких люка — щель Кассини
шириной 4500 км между кольцами А и В и щель Энке шириной 325 км
внутри кольца А. Эти люки в распределении частиц колец напоминают
люки Кирквуда в главном поясе астероидов. В самом деле, они тоже сов¬
падают по положению с резонансами средних движений (с некоторыми из
спутников Сатурна) или же с группами перекрывающихся резонансов. На¬
пример, щель Кассини соответствует резонансу 2/1 с Мимасом, а внешний
край кольца А сформирован резонансом 7/6 с коорбитальными спутниками
Янусом и Эпиметеем.
На снимках колец Сатурна с большим увеличением видно несколь¬
ко щелей, еще более узких, чем щели Кассини и Энке. Большинство этих
щелей, как оказалось, соответствуют резонансам со спутниками, причем
иногда резонансные соотношения включают большие целые числа — как,
например, в случае люка Килера на месте резонанса 32/31 с Прометеем.
Некоторые люки не совсем пустые, а содержат узкие колечки, обычно
в несколько километров шириной. В отличие от главных колец все эти ко¬
лечки явно некруговые, в связи с чем встает вопрос о динамических меха¬
низмах, ответственных за их необычную форму. Кольцо F Сатурна (см. пра¬
вый снимок на рис. 6) также представляет собой сложную структуру, состо¬
ящую из двух узких переплетающихся ярких колец, вдоль которых видны
«узлы». Ученые предполагают, что эти узлы могут быть комками кольцево¬
10
Введение
го вещества — миниспутниками. Форма этого кольца, по-видимому, опреде¬
ляется присутствием так называемых спутников-пастухов, обращающихся
по орбитам вдоль его обеих сторон.
Наконец, системы спутников планет-гигантов можно рассматривать
как миниатюрные солнечные системы, тоже богатые на увлекательные ди¬
намические явления. Резонансы средних движений здесь весьма распро¬
странены, потому что вызываемые планетой приливы приводят к медлен¬
ной миграции спутников во внешнем направлении. Поскольку относитель¬
ные периоды обращения изменяются при изменении больших полуосей,
при миграции спутники должны проходить через резонансные конфигура¬
ции. В некоторых случаях спутники захватываются в резонанс; при этом
большие полуоси их орбит далее увеличиваются таким образом, что отно¬
шение орбитальных периодов сохраняется постоянным. Особенно интере¬
сен так называемый резонанс Лапласа — тройной резонанс средних дви¬
жений галилеевых спутников Ио, Европы и Ганимеда: Ио совершает два
оборота вокруг Юпитера за один оборот Европы, а та, в свою очередь, —
два оборота за один оборот Ганимеда.
Взаимодействие приливных сил и орбитальной динамики объясняет
также, почему эксцентриситеты орбит многих близких к планетам спутни¬
ков отличны от нуля, несмотря на быстрое приливное затухание. Анало¬
гично и для наклонений: например, большое наклонение орбиты спутника
Урана Миранды (4°) объясняется временным захватом в резонанс 1/3 с Ум-
бриэлем, произошедшим в недалеком прошлом.
Приливы также приводят к замедлению скорости вращения спутни¬
ков — до тех пор, пока период вращения не станет равным орбитальному
периоду. В этом вращательном состоянии спутник всегда обращен к плане¬
те одной и той же стороной, как Луна к Земле. Однако в некоторых случаях
спутник может попасть в хаотическую область фазового пространства; при
этом вращение спутника становится неустойчивым относительно наклона
оси вращения и он начинает хаотически «кувыркаться». Так произошло, на¬
пример, со спутником Сатурна Гиперионом, вращение которого представля¬
ет собой один из первых примеров хаотического движения, обнаруженного
в Солнечной системе.
Внутренний нагрев некоторых спутников обязан сочетанию синхрон¬
ного вращения с движением по вытянутой орбите. Наиболее впечатляющим
является пример спутника Юпитера Ио — единственного, помимо Земли,
тела Солнечной системы, проявляющего активный вулканизм. У некото¬
рых спутников есть следы недавней тектонической активности, а у Европы
Введение
И
Рис. 7. Спутник Юпитера Ио — единственное, помимо Земли, тело Солнечной
системы, проявляющее вулканическую активность. Внутренний нагрев спутника
поддерживается приливными взаимодействиями между Ио, Европой, Ганимедом
и Юпитером. (Из фотогалереи NSSDC)
под твердой поверхностью до сих пор может существовать жидкий водный
океан.
Глава 1
Элементарная небесная и гамильтонова
механика
1.1. Уравнения движения
Согласно теории тяготения Ньютона, уравнения движения изолирован¬
ной системы, состоящей из двух сферически-симметричных тел с масса¬
ми 7720 и 7721, ИМеЮТ ВИД
d2u0 Qmx d2ui С?7720 , ч .
~Af2~ = й ЙЗ (U1 - Uo)> -Tj2~ = й ^(U0 - Ui), (1.1)
at Hui-Uoll at 11 u0 Ui ||
где uo и ui — векторы положений двух тел в инерциальной системе отсчета
(называемые также барицентрическими координатами, если начало коор¬
динат находится в барицентре системы), Q — гравитационная постоянная,
||х|| — евклидова норма вектора х.
Обозначая через г = ui — uo относительное положение тел (заме¬
тим, что г1?Г2,гз называют гелиоцентрическими координатами, если те¬
лом с координатами ио является Солнце), два векторных уравнения (1.1)
можно свести к двум следующим независимым векторным уравнениям:
уравнению
d2r <7(7720 + 772! )
„3
-г, (1.2)
dt2 ||г„
описывающему относительное движение двух тел, и уравнению
d2s
5^=0, (1.3)
которое показывает, что барицентр системы с координатами s = 7720U0 +
+ т 1Щ сохраняет инерциальное движение.
14
Глава 1
Уравнение (1.2) можно решить точно, причем решение зависит только
от начальных относительных векторов положения г(0) и скорости ^(0).
Подробное объяснение, как найти это решение, содержится в главе 6 книги
Дэнби (1962). Решение уравнения (1.2) стало первым выдающимся успехом
теории тяготения Ньютона благодаря его идеальному согласию — в случае
ограниченного движения — с тремя законами, эмпирически выведенными
Кеплером из наблюдений планеты Марс.
• I закон. Планеты движутся относительно Солнца по эллиптическим
орбитам; при этом Солнце находится в одном из двух фокусов эллипса.
• II закон. Скорость движения по эллиптической орбите такова, что век¬
тор положения планеты относительно Солнца заметает на плоскости
орбиты равные площади за равные промежутки времени.
• III закон. Квадрат орбитального периода Т прямо пропорционален ку¬
бу большой полуоси а эллиптической орбиты.
Таким образом, астрономам удобно характеризовать относительное
движение двух тел с помощью величин, описывающих геометрические
свойства орбитального эллипса и мгновенное положение на этом эллипсе.
Эти величины обычно называют элементами орбиты. Следует помнить,
что эллипс описывает движение одного тела относительно другого; обычно
эти тела называют соответственно вторым и центральным. Выбор цен¬
трального тела произволен: движение то вокруг mi описывается тем же
эллипсом, что и движение mi вокруг то. Если, используя решение урав¬
нения (1.3), вернуться к инерциальной системе координат, то легко видеть,
что тела описывают подобные друг другу эллиптические траектории во¬
круг их общего барицентра, причем отношение размеров этих двух эллип¬
сов обратно пропорционально отношению масс. Поэтому если отношение
масс близко к нулю (как в случае малого тела и звезды), то орбита звезды
стягивается к положению барицентра, а орбита малого тела относительно
звезды становится идентичной его орбите в инерциальной системе коорди¬
нат. По этой причине в качестве центрального разумно выбирать из двух
тел то, у которого больше масса; хотя с математической точки зрения этот
выбор и произволен.
1.2. Элементы орбит
Прежде всего определим величины, характеризующие эллиптическую
форму орбиты вокруг центрального тела и положение второго тела на этом
1.2. Элементы орбит
15
эллипсе. Затем введем величины, задающие ориентацию эллипса в про¬
странстве.
Форму эллипса можно полностью определить, задав две величины:
большую полуось а и малую полуось Ь, или же, что удобнее, большую
полуось а и эксцентриситет е (рис. 1.1). Название эксцентриситет проис¬
ходит из того, что е равно отношению расстояния «фокус-центр эллипса»
и большой полуоси эллипса. Таким образом, эксцентриситет служит мерой
отличия орбиты от круговой: е = 0 означает, что орбита круговая, а е =
= 1 — что орбитой является отрезок прямой длиной 2а, в одном из концов
которого находится центральное тело. Среди всех возможных «эллиптиче¬
ских» орбит только последняя является столкновительной, если пренебречь
физическими размерами тел. Большая полуось а = оо и эксцентриситет
е = 1 соответствуют параболическому движению, аа<0ие>1, по со¬
глашению, — гиперболическому. В нашей книге мы редко будем иметь дело
с этими типами неограниченного движения, поэтому сосредоточимся на эл¬
липтическом случае. Ближайшая к центральному телу точка эллиптической
орбиты называется перицентром (или перигелием, если центральное тело —
Солнце, или же перигеем, если центральное тело — Земля); расстояние q от
16
Глава 1
нее до центрального тела равно а(1 — е). Наиболее удаленная точка называ¬
ется апоцентром (соответственно афелием или апогеем)', расстояние Q от
нее до центрального тела равно а(1 + е).
Для определения положения тела на эллиптической орбите удобно ис¬
пользовать декартову систему координат qi, с началом в фокусе эллипса,
занятом центральным телом, и с осью q\, направленной к перицентру орби¬
ты. Можно использовать также и полярные координаты г, /. Угол / обычно
называют истинной аномалией тела. Элементарные геометрические соот¬
ношения (см. рис. 1.1) дают
где Е — угол (с вершиной в центре эллипса) между направлением на пе¬
рицентр и направлением на точку проекции положения тела на окружность
радиуса а, касательную к эллипсу в перицентре и апоцентре, как показано
на рис. 1.1. Этот угол называется эксцентрической аномалией. Положение
тела на орбите полностью задается значениями а, ей Е.
Из уравнений движения можно получить (Дэнби, 1962) закон измене¬
ния Е со временем, обычно именуемый уравнением Кеплера:
суть орбитальная частота или среднее движение тела (в согласии с третьим
законом Кеплера), t — время, to — время прохождения перицентра.
Астрономы обычно вводят еще один угол
называемый средней аномалией. Он изменяется со временем линейно и так¬
же определяет положение тела на орбите (посредством уравнений (1.6)
Чтобы задать ориентацию эллипса в пространстве в произвольной ор¬
тогональной системе координат (x,y,z) с началом в центральном теле,
qi = a(cosE — е), g2 = clV 1 — е2 sinE
(1.4)
И
г = а(1 — ecosE), cos / =
1 — е cos Е ’
cos Е — е
Е — esinE = n(t — t0),
(i.6)
где
п =
\/0{т0 + т{)а 3/2
(1.7)
М = n(t — to)
(1.8)
и (1.5)).
1.2. Элементы орбит
17
необходимо задать еще три угла (см. рис. 1.2). Первый из них суть на¬
клонение г плоскости орбиты (то есть плоскости, в которой лежит эллипс)
относительно координатной плоскости (ж, у). Если наклонение орбиты от¬
лично от нуля, она пересекает плоскость (х,у) в двух точках, называемых
узлами орбиты. Астрономы различают восходящий узел, где тело переходит
от отрицательных к положительным z, и нисходящий узел, где тело перехо¬
дит от положительных к отрицательным z. Ориентация плоскости орбиты
в пространстве в итоге полностью определена, если задано угловое поло¬
жение восходящего узла относительно оси х. Этот угол принято называть
долготой восходящего узла, а обозначают его П. Наконец, последний угол,
который необходимо задать, характеризует ориентацию эллипса в его плос¬
кости. Аргумент перицентра и (называемый также аргументом перигелия,
если центральное тело — Солнце) определяется в плоскости орбиты как уг¬
ловое положение перицентра, отсчитываемое от направления «центральное
тело-восходящий узел».
Орбитальные элементы а, е,г,а;,П и М полностью определяют по¬
ложение и скорость второго тела относительно центрального. Имеется
взаимно-однозначное соответствие между ж, у, z, dx/dt, dy/dt, dz/dt (ком¬
понентами г и dr/dt) и элементами орбиты. Оно дается соотношениями
dr dq
Г — Rxq^h (^•^)
где векторы q и dq/dt покомпонентно имеют вид
[gi,(?2,0] = [a(cosE — е),а\/1 — е2 sini£,0], (1-Ю)
18
Глава 1
dgi dq2
dt ’ dt ’
na sin E па\/1 — e2 cos E1
1 - e cos E’ 1 - e cos £?
,0
а матрица вращения Rxq суть
(cos П cos uj — sin Q cos i sin uj — cos П sin a; — sin П cos i coslj sin Q sin i \
sin Q cos ио + cos Q cos г sin a; — sin Q sin cj 4- cos П cos г cos uj — cos Q sin г .
sin г sin uj sin i cos uj cos г J
(1.12)
Заметим, что в случае, если наклонение равно нулю, при заданном на¬
ми определении орбитальных элементов элементы и и Q не определены,
поскольку тогда не определено положение восходящего узла. Более того,
элемент ио не определен и в случае нулевого эксцентриситета, поскольку
не определено положение перицентра. Поэтому удобно ввести долготу пе¬
ригелия w = ио + Q и среднюю долготу А = М + ио + П. Первый из этих
углов хорошо определен при г = 0, а второй — при г = 0 и/или е = 0. К то¬
му же очевидно, что набор элементов а, е, г, ш, О, А однозначно определяет
положение и скорость тела. Заметим, что если положить г = 0, то элемен¬
ты матрицы (1.12) естественным образом будут зависеть только от w, а не
от Q, и ио по отдельности; и аналогично, если положить е = 0, то соотно¬
шения (1.9) будут зависеть только от А — а не от ио и Е по отдельности.
Наконец, используя (1.9), можно убедиться в том, что уравнение (1.2)
сохраняет «энергию»
dr
dt
g(m0 + mi) _ g(m0 + mi)
Hrll “ 2a
(1.13)
и «угловой момент» г х dr/dt, модуль которого и проекция на ось z равны,
соответственно,
G = \/д{т0 4- mi)a( 1 - е2), (1-14)
H = Gcosi. (1-15)
Эти соотношения будут играть важную роль в разделе 1.9.1.
1.3. Возмущения задачи двух тел
Уравнения движения изолированной системы, состоящей из Солнца
массой то и N планет массами mi, m2,..., тдг, в барицентрической инер-
1.3. Возмущения задачи двух тел
19
циальной системе отсчета имеют вид
d2Uj Uj-ui
= -д^т з (1.16)
^ IIй* - Uj ||
где г и j принимают значения от 0 до N. Задав гелиоцентрические положе¬
ния планет г* = и* — ио, эти уравнения можно переписать как
N
d2I4 Gimo+rrii) r
~ш = ^r^ri+ Ъ Gm3
^ llr*ll Vll^ - rH|3 IMV (1.17)
i =
причем движение Солнца дается формулой u0 = - JZili miYi/ YliLo тг-
Уравнения (1.17) определяют задачу, называемую обычно задачей N 4-1
тел.
Аналогично, гелиоцентрическое уравнение движения тела пренебре¬
жимо малой массы в поле тяготения Солнца и N планет, движущихся по
заданным орбитам, имеет вид
d2r _ Gmo N
~dt? =
3 = 1
llrll3 I Mr, - rll llr.ll3 У
где г — вектор положения малого тела относительно Солнца, а — гелио¬
центрические векторы положения планет массами rrij. Уравнение (1.18)
определяет задачу, называемую обычно ограниченной задачей (либо огра¬
ниченной задачей трех тел, если планета только одна).
Если массы планет малы по сравнению с массой Солнца и ни одно
из их взаимных расстояний — г* не становится при движении малым,
то уравнения (1.17) и (1.18) очевидно близки к уравнению задачи двух
тел (1.2), причем член, зависящий от масс планет nrtj, играет роль малого
возмущения по отношению к двухтельному взаимодействию с Солнцем. По¬
этому движение, описываемое уравнениями (1.17) и (1.18), будет близким
к кеплеровому. Если выразить уравнения (1.17) и (1.18) через элементы
орбит при помощи соотношений (1.9), то уравнения для а, е,г,а;,П запи¬
шутся как da/dt = O(mj/mo), где а обозначает любой из этих элемен¬
тов, а O(rrij/mo) — функция того же порядка малости, что и масса планет
в единицах массы Солнца; уравнение для М примет вид dM/dt = п +
+ O(rrij/mo), где п — невозмущенное среднее движение в задаче двух тел.
20
Глава 1
Эти уравнения для орбитальных элементов обычно называют уравнения¬
ми Лагранжа; согласно им элементы а, е,г,о;,П изменяются со временем
медленно, a М медленно отклоняется от своего линейного невозмущенно¬
го хода. Поэтому движение планет и малых тел Солнечной системы удобно
характеризовать, как и в задаче двух тел, через элементы их орбит, имея
в виду, что эти элементы, как правило, очень мало изменяются за время
порядка времени человеческой жизни (именно в этом состоит причина то¬
го, что Кеплер открыл законы задачи двух тел, хотя он наблюдал движение
реальных планет)1. Тем не менее забывать о том, что элементы орбит в ре¬
альности изменяются со временем, не следует. Строго говоря, они задают
лишь мгновенную орбиту, по которой двигалось бы тело, если бы внезап¬
но исчезли все возмущения. Формулируя на языке математики, элементы
орбиты в момент t задают кеплерово движение, касательное к истинному
движению тела в момент t. По этой причине их называют также оскупиру¬
ющими элементами2.
С уравнениями Лагранжа трудно оперировать на практике, поэтому
нам потребуется переписать их в несколько ином — гамильтоновом — виде,
прежде чем мы сможем приступить к детальному изучению движения.
1.4. Гамильтоновы системы и задача двух тел
Система обыкновенных дифференциальных уравнений вида
имеет по определению гамильтонов вид, если г имеет размерность 2п и су¬
ществует функция 7i{vi,..., vn, xi,..., хп), такая, что уравнения (1.19)
можно записать в форме
где х\,..., хп и ^1,...,^ — 2 п компонент вектора г, г = 1,..., гг. Функ¬
ция Н называется гамильтонианом системы, а переменные х\,...,хп
1 Кеплер опирался на данные наблюдений Тихо Браге; сам он наблюдений не проводил и не
мог проводить (см., например, Берри А. Краткая история астрономии. — M.-JL: ОГИЗ ГИТТЛ,
1946). — IJpwit. ред.
2Это свойство нарушается в случае вводимых далее в разделе 1.9.2 формальных оскулиру-
ющих элементов, которые определяют эллипс, трансверсально пересекающий реальную тра¬
екторию. — Прим. авт.
(1.19)
dvi дН dxi дН
dt dxi ’ dt dvi ’
(1.20)
1.4. Гамильтоновы системы и задача двух тел
21
и v\,.. •, vn — координатами и импульсами соответственно. Для просто¬
ты изложения мы далее будем использовать векторный формализм, обозна¬
чая n-компонентные векторы х\,..., хп и v\,..., vn через х и v . Производ¬
ную по времени от произвольной переменной а будем обозначать через а.
Переменные v и х называются сопряженными переменными, а простран¬
ство (х, v) — фазовым пространством системы. Размерность п векторов х
и v называется числом степеней свободы.
Широкий класс обыкновенных дифференциальных уравнений — к нему
принадлежит и большинство уравнений небесной механики — может быть
записан в гамильтоновом виде. В самом деле, легко проверить, что уравне¬
ния второго порядка вида
= -gradrI/(r) (1.21)
можно переписать в виде (1.20), положив Xi = г*, г>* = п и Н = 1/2||v||2 +
+ Е7(х). В частности, уравнения задачи двух тел (1.2) записываются в га¬
мильтоновом виде с гамильтонианом
_ v\ + + v\ _ g(m0 + mi)
2 y/xl+xl + xl' ( ' ’
где xi,..., £з — обычные декартовы координаты с началом в центральном
теле, a Vi = Xi — скорости.
Вообще говоря, любая система, сохраняющая некоторую величину
(«энергию»), которую в переменных гиг можно записать как сумму «кине¬
тической энергии» Т(г, г) и «потенциальной энергии» U(г), допускает за¬
пись в гамильтоновом виде3. Представив Т как Т = Т2 + Т\ + Т0, где Г2, Т\
и Т0 — члены 2-го, 1-го и 0-го порядка по г соответственно, мы можем
записать уравнения движения в форме (1.20), причем
дТ
хг — Ti, Vi = И, = Т2 — Tq + U (1.23)
(вывод см. в книге Уиттекера, 1937, раздел 7).
Описанный рецепт очень полезен для нахождения гамильтониана си¬
стемы в таких координатах, в которых уравнения не записываются непо¬
средственно в виде (1.21), — например, при использовании сферических
координат или вращающейся системы отсчета.
3Сохраняющаяся величина не обязана быть равной реальной энергии системы. Например,
в рассматриваемых ниже первых двух случаях мы имеем дело с «энергией», равной реальной
энергии, деленной на массу тп\. — Прим. авт.
22
Глава 1
В качестве первого примера рассмотрим задачу двух тел (1.2), записав
уравнения в обычных сферических координатах д,$,(р. Используя форму¬
лы связи сферических координат с декартовыми г = (х, у, z), а именно
х = д sin $ cos (/?, у = д sin d sin (/?, z = д cos'd, мы можем записать «потен¬
циальную энергию» как U(g) = —Q{mо + mi)/д, а «кинетическую энер¬
гию» — как Т = 1/2[р2 + g2rd2 + g2 sin2 'дф2]. Отсюда находим гамильтониан
задачи двух тел в сферических координатах:
_«mi+mO
0
где r,d, (р — координаты, р6 = g, р$ = g2d, р^ = д2 sin2 &ф — импульсы.
В качестве второго примера рассмотрим задачу двух тел в декарто¬
вой системе координат, вращающейся с угловой скоростью и вокруг оси z.
Обозначая через X, У, Z декартовы координаты в инерциальной системе,
а через x,y,z — декартовы координаты во вращающейся системе и исполь¬
зуя соотношения X = х cos ut — у sin ut, У = х sin out + у cos cut, Z = z,
легко видеть, что «кинетическая энергия» Т = \/2\Х2 + У2 + Z2} записы¬
вается как Т = l/2[x2+ у2 + z2+и2(х2+ у2)— 2и(ху — ху)].3атем, следуя
приведенному выше рецепту и задавая импульсы рх = х — иу, ру = у + их,
pz = z, находим гамильтониан задачи двух тел во вращающейся системе
в виде
W = 1(р2х +Р2у + р2) + “(р*У - хРу) - (L25)
^ ^x2 + y2 + z2
Наконец, используя этот же рецепт, покажем, что задача двух тел в слу¬
чае т\ ф 0 допускает также гамильтониан
^ ||v||2 g(m0 + m i)/ii
н = 1ЦГ н <L26>
в декартовых координатах г и сопряженных им импульсах v = miг. Здесь
Mi = momi/(mo + mi) — приведенная масса второго тела. Действительно,
умножая правые и левые части уравнений (1.2) на мь находим выражения
для кинетической и потенциальной энергий системы в виде
'Г-1,,11;. II2 g(m0 + mi)/xi
2 ’ ||г|| ’ 1-27)
откуда, определяя импульсы v = <9Т/<9г и Н = Т + U, получаем (1.26).
1.5. Возмущения в гамильтоновом виде
23
Разумеется, гамильтонианы (1.22), (1.24), (1.25) и (1.26) полностью
эквивалентны в том смысле, что все они приводят к одним и тем же урав¬
нениям движения, хотя и в разных переменных. Наши примеры подчерки¬
вают, что у любой системы гамильтониан не уникален: его вид зависит от
выбора определения координат и импульсов. Выбор того или иного гамиль¬
тониана является лишь вопросом удобства.
1.5. Возмущения в гамильтоновом виде
Уравнения ограниченной задачи (1.18) тоже легко записываются в га¬
мильтоновом виде. Достаточно обратить внимание, что правая часть (1.18)
имеет вид —gradrf/(r), причем
ВДПТ ~ ППз )> (1-28)
где sj — гелиоцентрический вектор положения j-ой планеты, Aj = г —
— Sj, а г • sj обозначает скалярное произведение г и sj. Следовательно,
гамильтониан ограниченной задачи суть
||v|f дт0 ( 1 Г-sЛ
П~ 2 ||г|| gz2mi( ИД^-Ц ця..||з)’ (L29)
3 = 1
где г1? г2, гз — декартовы координаты, v\, г>2, — импульсы, причем v = г.
Заметим, что гамильтониан (1.29) имеет вид Но + Hi, где Но =
= ||v||2/2 — С/гао/||г|| идентичен гамильтониану (1.22) задачи двух тел при
mi = 0, а Н\ играет роль возмущения, величина которого относительно Но
пропорциональна отношению масс планет к массе Солнца. Далее, в (1.29)
предполагается, что планеты движутся по заданным орбитам, то есть век¬
торы sj — заданные функции времени. Гамильтониан (1.29), следовательно,
имеет вид H(v, г, t) и служит примером зависящего от времени, или неав¬
тономного, гамильтониана в отличие от гамильтониана задачи двух тел, не
зависящего от времени.
Неавтономные гамильтонианы всегда можно привести к автономному
виду, увеличив размерность фазового пространства. Это делается следую¬
щим образом. Введем новую координату т, сопряженный ей импульс Т
и новый гамильтониан
Н! = T + W(v,r,r).
(1.30)
.24
Глава 1
Легко проверить, что уравнение для т суть т = дН*/дТ = 1, что дает реше¬
ние r(t) = t; поэтому уравнения движения для v и г, порождаемые гамиль¬
тонианом Щ, идентичны уравнениям, порождаемым гамильтонианом Ti.
Посредством этого приема новый гамильтониан оказывается формально не
зависящим от времени, поэтому к нему применимы известные результаты,
справедливые для автономных гамильтоновых систем. На практике, когда
зависимость от времени имеет сложный вид и включает несколько незави¬
симых частот — как в случае, когда имеется несколько планет, каждая со
своей частотой обращения, — удобно еще более расширить фазовое про¬
странство, вводя координату Tj и сопряженный ей импульс 7} для каждой
независимой частоты Vj зависящего от времени возмущения. Гамильтониан
W(v, г, t) записывается тогда в виде
Опять же легко проверить, что уравнения движения для v и г остаются
неизменными; преимущество выражения (1.31), по сравнению с (1.30), со¬
стоит в том, что координаты Tj суть «углы»: гамильтониан периодичен по
всем Tj. Например, в ограниченной задаче углами tj будут средние ано¬
малии планет. Это обеспечивает возможность разложения гамильтониана
в ряд Фурье по Tj и применения пертурбационных алгоритмов, как будет
показано далее в главе 2.
Рассмотрим теперь гамильтониан планетной системы. Уравнения (1.17)
нельзя записать в виде (1.21), поэтому следует обратиться к уравнени¬
ям (1.16) в инерциальной системе отсчета. Если умножить обе части (1.16)
на rrii, то легко видеть, что правая часть может быть записана в виде
—gradr.Z7(i*o, • • • ^n), то есть «энергией» системы будет
Поэтому, как показано в предыдущем разделе, Н будет и гамильтонианом
системы, если ввести импульсы й* = дТ/дщ = га*и*. На первый взгляд
заманчиво преобразовать (1.32), задавая r* = u* — uq и v* = u* — uq,
чтобы перейти к гелиоцентрической системе координат. Однако не всякое
преобразование координат и импульсов сохраняет гамильтонов вид урав¬
нений движения (как оказывается и в данном случае). Это подводит нас
к понятию канонических преобразований.
(1.31)
3
1.6. Канонические преобразования
25
1.6. Канонические преобразования
Зависящее от времени преобразование координат и импульсов в фазо¬
вом пространстве называется каноническим, если оно сохраняет гамильто¬
нов вид уравнений движения для любого гамильтониана. В строгой форму¬
лировке преобразование (v,x) —> (v',x') является каноническим, если для
VW и заданного по определению
уравнениями движения для v' и х' будут
Класс канонических преобразований является весьма ограниченным среди
всех возможных преобразований в фазовом пространстве. Тем не менее мы
вынуждены ограничиться только каноническими преобразованиями, если
не хотим потерять гамильтонов вид уравнений, весьма удобный для ана¬
лиза движения. Поэтому важно иметь критерии каноничности заданного
преобразования. Не пытаясь привести исчерпывающий список, мы обсу¬
дим здесь три критерия, которые будут использованы далее в этой книге.
Наиболее полезным является критерий скобок Пуассона. Если заданы
сопряженные координаты и импульсы х и v и функции /(v,x) и g(v,x),
то скобка Пуассона / и д определяется как
где п — число степеней свободы. Можно доказать (см.: Уиттекер, 1937,
раздел 32, или Гантмахер, 2001, раздел 131), что преобразование (v,x) —►
—> (v',x') является каноническим тогда и только тогда, если, рассматривая
компоненты v[,..., v'n вектора v' и компоненты х[,..., х'п вектора х' как
функции от v и х, имеем
(1.33)
п
{/,9} = gradx/ • gradv<? — gradv/ • gradxg = ^
1=1
где Sij равно 1, если i = j, и 0 — в противном случае.
Этот критерий весьма практичен и полезен для проверки канонично¬
сти преобразований, и мы часто будем использовать его далее в этой книге.
26
Глава 1
В качестве первого примера вернемся к гамильтониану (1.32), чтобы пока¬
зать, как гелиоцентрические координаты можно задать канонически. Если
определить в качестве новых координат гелиоцентрические радиус-векторы
планет = uj — щ (j = 1,..., N), а также r0 = uo, то задача будет со¬
стоять в том, чтобы найти новые импульсы Vj такие, что преобразование
(й^,и^) —> (vj,Tj) было бы каноническим. Применяя критерий (1.36), на¬
ходим, что подходящим преобразованием будет Vo = йо + ui + • • • + u#
и Vj = iij (j = 1,..., N). Выбрав таким образом новые канонические коор¬
динаты и импульсы, легко проверить подстановкой их в (1.32), что новый
гамильтониан примет вид
П
1Ы1
2то
N
£
3 = 1
N 3-1
-«ЕЕ
j=l г=1
VQ ‘ Vj
т0
ТПоТПi
*г,3 |
+
|£|
j=i
N
-«Е
1
+
тп0
N j-1
+ ££V*'VJ
j=i i=l
m0
Tfl§TTlj
3 = 1
(1.37)
где = ri — Tj. Поскольку он не зависит от г0, уравнения движения
дают vq = 0, то есть барицентр системы движется равномерно и прямо¬
линейно. Без потери общности тогда можно положить Vo = 0 и опустить
в гамильтониане члены, содержащие vq. Тогда гелиоцентрический гамиль¬
тониан планетной системы запишется как
N ( " 112/ , _ \ _ _ "1 N j-1
« = Е
3 = 1
IIVj II (mo + mj)
2morrij
gmorrij 1 +
IV J~1 ,
EE ■
j=l1=1 ^
ппгт
m0
J)'
(1.38)
Заметим, что гамильтониан 7i можно представить в виде суммы гамильто¬
нианов
к
2/х,- IM (L39)
задач двух тел вида (1.26) с приведенными массами ^ = morrij/(гао+га^),
возмущаемой членами, величина которых по отношению к гамильтонианам
задач двух тел пропорциональна массам планет в единицах массы Солнца.
Путем перегруппировки кинетических членов гамильтониан (1.38)
можно привести к виду
2
N
* = Е
3 = 1
-G
morrij
+
1
2шо
N
Е-
3 = 1
N j-1
«ЕЕ
j=l г=1
mirrij
(1.40)
*1,3 I
1.6. Канонические преобразования
27
Такая запись гамильтониана (называемая иногда демократической гелио¬
центрической) представляет особый интерес для разработки алгоритмов
симплектического интегрирования (Коселефф, 1993, 1996; Тума и Уиздом,
19946; Дункан и др., 1998; Чамберс, 1999).
После этого небольшого отступления вернемся к обсуждению крите¬
риев, позволяющих отличить канонические преобразования от всех других
возможных преобразований фазового пространства.
Второй критерий, не слишком удобный в практических выкладках, но
используемый далее в теореме Арнольда -Лиувилля (см. раздел 1.9), фор¬
мулируется так: преобразование (v,x) —> (v',x') является каноническим,
если существует функция S(v', х) (называемая производящей функцией) та¬
кая, что
(см. Уиттекер, 1937, глава 4). Заметим, что не все канонические преобразо¬
вания можно записать в виде (1.41).
Третий критерий лежит в основе подхода Ли к теории возмущений
(что будет проиллюстрировано далее в главе 2). Он формулируется так:
преобразование (v,x) —> (v',x') является каноническим, если существуют
гамильтониан x(v',x') (называемый производящим гамильтонианом) и па¬
раметр е такие, что
где V и Xх даются гамильтоновыми уравнениями v' = —дх/д'х! и х.' =
= дх/длг1 (см. доказательство в книге Гантмахера, 2001, разделы 133-134).
Иными словами, преобразование фазового пространства является канони¬
ческим, если его можно интерпретировать как результат гамильтонова по¬
тока в некоторый момент «времени» е. Например, поворот на угол d по од¬
ной из степеней свободы в фазовом пространстве, конкретно х = xf cos d +
+ v' slu'd, v = — х' sin d + vf cos d, является каноническим, поскольку его
можно интерпретировать как поток в момент t = d, порожденный гамиль¬
тонианом xW,х') = 1/2(г/2 +х'2) гармонического осциллятора. Не всякое
каноническое преобразование можно записать как результат гамильтонова
потока; контрпримером служит каноническое преобразование декартовых
координат в полярные (х = y/2pcosq,y = ^/2psinq).
(1.42)
28
Глава 1
1.7. Свойства гамильтонова потока
Под гамильтоновым потоком мы подразумеваем эволюцию во време¬
ни координат и импульсов, описываемую гамильтоновыми уравнениями.
Гамильтонов поток имеет ряд важных свойств, полезных в дальнейшем.
А) Сохранение объема (теорема Лиувилля). Как известно, для системы
уравнений вида (1.19) объем SV бесконечно малого множества начальных
условий изменяется со временем согласно уравнению
1 dJF ^dFi _ , ._ч
= > . = dlvF> (!-43)
6V At ^ дг.
3 = 1
где т — число компонент векторов г и F. В случае гамильтоновой систе¬
мы (1.20), где т = 2п, г = (гц,..., vn, Х\,..., хп) и
дЛ дП дП дЛ\
дхп ды''"' dvn)' }
легко проверить, что divF = 0. Таким образом, гамильтонов поток сохра¬
няет объем. Это очень важное свойство, означающее, что мера эволюцио¬
нирующего облака начальных условий никогда не может уменьшаться или
увеличиваться. В частности, оно также означает, что гамильтоновы систе¬
мы не могут иметь аттракторов — многообразий размерности меньшей,
чем число степеней свободы системы, к которым может стягиваться поток.
Данное свойство будет играть важную роль в обсуждениях в главе 4.
Б) Сохранение Л. Скорость изменения Л со временем можно записать,
дифференцируя 7Y(v, х, £), как
61~С дЛ
— = gradxW • х + gradvW • v + —. (1.45)
Используя гамильтоновы уравнения (1.20) для v и х, получим
Другими словами, гамильтонианы, не зависящие явно от времени (то есть
автономные гамильтонианы), не изменяют своего значения на порождае¬
мом ими потоке, то есть они являются константами движения. Для си¬
стем (1.23) таких, что 7\ = То = 0, Л является полной энергией системы,
1.7. Свойства гамильтонова потока
29
поэтому сохранение значения гамильтониана есть не что иное, как сохране¬
ние энергии. Однако это неверно в общем случае, когда Т\ или То отлично
от нуля.
В) Временная эволюция функции на гамильтоновом потоке. Пусть /(v, х) —
функция, определенная на фазовом пространстве, a v и х изменяются со¬
гласно гамильтоновым уравнениям (1.20). Дифференцируя, имеем
^jj = gradx/ • х + gradv/ • v = {/, П}. (1.47)
Величина f(t) = /(v(t),x(t).) называется эволюцией f вдоль потока Н.
Выражение (1.47) позволяет записать f(t) как функцию от t, v(0) и х(0)
следующим образом. Если t достаточно мало, f(t) можно разложить в ряд
Тейлора:
/«>=/<°)+1:Ш«». о-4»)
i=1
где /(0) = /(v(0),x(0)) и dlf/dtl(0) = dl//d^(v(0),х(0)). Используя
соотношения
% = </.«>, § = {%»} = Ш,Ю,Ю, (1.49)
и обозначая
£nf = if, п}, су = суу/, (1.50)
в итоге имеем
00 fi
/W = /(o) + £tt£W (i.5i)
г=1 ‘
Это разложение обычно называют рядом Ли функции / вдоль потока Н.
В дальнейшем мы обозначаем его как S^f. Как и ожидалось, оно позво¬
ляет записать /(v(£),x(t)) в виде функции от v(0),x(0), причем время t
играет роль параметра. Это разложение будет представлять для нас особый
интерес в главе 2, где будет развит подход к анализу гамильтоновых систем
на основе теории возмущений.
Наконец, используя (1.51), мы можем переписать каноническое преоб¬
разование (1.42) в виде
v = 5®v', х = 5®х', (1.52)
где векторная запись а = S^o! означает ад = ..., ап = S^afn.
30
Глава 1
1.8. Интегрируемые гамильтонианы
Решение системы дифференциальных уравнений
Q.T'
-rr=-Fi(r), где i = 1,... ,п и г = (гь. ..,г„), (1.53)
можно записать в неявном виде как систему интегральных уравнений
Систему (1.53) называют поэтому интегрируемой, если интегралы в ле¬
вой части (1.54) могут быть вычислены явно и полученные соотношения
F}(r(t)) - F'(r(0)) = t, где F[ — первообразные от l/F*, могут быть обра¬
щены, давая в результате г(£) как явную функцию от t (см.: Арнольд и др.,
2002, глава 4).
Например, дифференциальное уравнение dx/dt = х является инте-
\nx(t) — 1пх(0) = t, откуда x(t) = х(0) exp(t).
Такое определение интегрируемости очень сложно использовать на
практике для выяснения, является ли данная система дифференциальных
уравнений интегрируемой или нет. Если интегралы не найдены, нельзя
сказать, вызвано ли это подлинной неинтегрируемостью системы или же
просто недостаточным мастерством при поиске первообразных F'.
В случае гамильтоновых систем отчасти помогает теорема Лиувил-
ля, утверждающая, что гамильтониан с п степенями свободы интегрируем,
если он допускает п независимых констант движения Фх,...,Фп таких,
что {Ф;,Ф^} = 0 при i ф j. Хотя константы движения найти легче, чем
непосредственно решить гамильтоновы уравнения, не существует общего
рецепта поиска всех констант движения. В частности, если найдено толь¬
ко т констант движения (га < п), то непросто выяснить, надо ли искать
остальные константы или их просто нет. Например, небесные механики
несколько лет искали третью константу движения для гамильтониана с тре¬
мя степенями свободы, описывающего движение звезды в кубическом по¬
тенциале галактики, пока Хенон и Хейлес (1964) не показали численно,
что третьей константы не существует. И наоборот, долгое время полагали,
что гамильтониан цепочки Тоды неинтегрируем, пока М. Хенон (1974) не
обнаружил последнюю недостающую константу!
(1.54)
грируемым, поскольку интегральное уравнение
nx(t)
/ dx/x =
dt дает'
Jx( 0) Jo
1.9. Переменные «действие-угол»
31
К счастью, сейчас ситуация не столь безнадежна, какой она была до
работы Пуанкаре (1892). Существует критерий неинтегрируемости — на¬
личие хаоса, обсуждаемое в главе 4, — который можно использовать как
аналитически, так и численно. В этой книге нам часто придется вводить
интегрируемые приближения для реальной динамики. Соответствующие
интегрируемые гамильтонианы будут всего трех типов.
1. Зависящие только от импульсов системы, то есть H(vi,..., г>п). В этом
случае решение тривиально: импульсы V{ являются константами дви¬
жения, поскольку dH/dxi = 0, а координаты я* изменяются линейно
со временем с постоянными скоростями = dH/dvi, 1 ^ г ^ гг.
2. Имеющие только одну степень свободы, то есть H(v,x). В этом слу¬
чае гамильтонова система интегрируема, поскольку она обладает од¬
ной константой движения, которой является сам гамильтониан. Дви¬
жение происходит вдоль линий уровня Н на двумерном фазовом про¬
странстве (v,x).
3. Зависящие только от одной координаты, то есть H(vi,..., vn, Хк).
В этом случае система интегрируема, поскольку она обладает п неза¬
висимыми константами движения v\,..., Vk-i, Vk+1,..., vn и H. При
движении сохраняются постоянными значения
Vfc+1, ..., vn, и оно происходит вдоль линий уровня Н на плоско¬
сти (Ук,Хк).
1.9. Переменные «действие-угол»
Важнейшее значение для интегрируемых гамильтоновых систем име¬
ет теорема Арнольда-Лиувилля — обобщение теоремы Лиувилля (см. раз¬
дел 1.8), полученное Арнольдом (1963а). Арнольд доказал, что при вы¬
полнении условий теоремы Лиувилля и в случае, если n-мерная поверх¬
ность, определенная неявно постоянными движения Ф1?...,ФП, являет¬
ся компактной, оказывается возможным ввести канонические импульсы р
и координаты q такие, что
1) координаты qi,..., qn являются углами, циклически определенными на
промежутке [0,27т], и каноническое преобразование исходных импуль¬
сов и координат v(p, q), х(р, q) 27г-периодично по углам q\, ..., qn\
2) гамильтониан в новых переменных есть функция только импульсов р,
то есть Н = Н(р).
32
Глава 1
Импульсы р обычно называют переменными действия системы. Набор ка¬
нонических переменных (р, q) (где координаты q являются углами) будем
в общем случае называть переменными «действие-угол». Хотя переменные
«действие-угол» и ранее использовались некоторыми авторами (Эпштейн,
1916; Зоммерфельд, 1922; Борн, 1927) при анализе частных задач, теорема
Арнольда-Лиувилля оказалась очень важной, так как она демонстрирует,
что в принципе любой интегрируемый гамильтониан можно записать, най¬
дя подходящие переменные «действие-угол», как функцию только перемен¬
ных действия. Поэтому, в свете теоремы Арнольда-Лиувилля, можно пред¬
ставить интегрируемые гамильтонианы в общем случае как функции Н(р)
и разработать общую теорию квазиинтегрируемой гамильтоновой динами¬
ки в переменных «действие-угол», что и будет выполнено в дальнейшем
в этой книге.
Более того, доказательство теоремы Арнольда-Лиувилля дает к тому
же конструктивный рецепт для введения переменных «действие-угол» на
практике. Существование п констант движения для гамильтоновой системы
с п степенями свободы гарантирует, что движение происходит на п-мерной
поверхности Мф, вложенной в 2п-мерное фазовое пространство. Посколь¬
ку {Ф*,Ф^} = 0 для г ф j, движение можно разложить на п независимых
потоков, порождаемых функциями Фх,..., Фп, каждую из которых можно
рассматривать как гамильтониан с одной степенью свободы. Это означа¬
ет, что состояние системы в момент t (то есть v(£),x(£)) можно получить,
следуя потоку Фх в течение времени t от начальных условий v(0),x(0)
до точки vx,xx, затем — следуя потоку Ф2 в течение времени t от vx,xi
до другой точки v2, Х2, и так далее. Последняя точка vn,xn будет совпа¬
дать с v(£),x(£). Требование компактности поверхности Мф означает, что
отдельные потоки Фх,..., Фп и, следовательно, движение в целом можно
разложить на независимые периодические циклы, которые мы обозначим
7i,...,7п- Тогда действия р задаются как
Записав v как функции от р и х, определим интегральную производящую
функцию
(1.55)
(1.56)
1.9. Переменные «действие-угол»
33
и введем новые координаты q:
лс
« = ^(Р,*). (1.57)
Преобразование (v,x) —> (p,q), определенное таким образом, имеет
вид (1.41) и, следовательно, является по построению каноническим. Мож¬
но доказать, что q\,..., qn — углы, а именно ^ возрастает на 2п за полный
цикл ть и что гамильтониан TL зависит только от переменных действия р
(см. Арнольд, 1963а).
1.9.1. Переменные Делоне
В качестве примера использования теоремы Арнольда-Лиувилля вве¬
дем переменные «действие-угол» для интегрируемого гамильтониана зада¬
чи двух тел. Мы используем эти переменные в дальнейшем для анализа
динамики в ограниченной и планетной задачах с помощью гамильтоновых
пертурбационных методов, следуя подходу Борна (1927), разработанному
для аналогичной задачи классического движения электрона вокруг ядра
атома водорода.
Удобно начать с гамильтониана задачи двух тел в сферических коорди¬
натах (1.24). Прежде всего, выписываем три независимые константы дви¬
жения
н-_„ г2 г,2 I И2 п 1 (г,2 I 2(mo + mi) ,, ,0>
Я-JV, G =Р<, + -^. + д (I'58)
и убеждаемся, что условия {Я, G2} = О, {Н,Н} = 0 и {G2,H} = 0 оче¬
видным образом выполняются (две последние скобки Пуассона показыва¬
ют также, что Н и G2 являются константами движения для Н). Используя
определение импульсов р$ и легко убедиться, что G есть модуль векто¬
ра углового момента системы, а Н есть проекция вектора углового момента
на ось г, причем обе величины нормированы на приведенную массу. Кон¬
станта 7i есть гамильтониан задачи двух тел.
Перейдем теперь к отождествлению циклов. Кеплеров случай про¬
ще общего, поскольку каждая константа движения (1.58) непосредственно
определяет цикл. Постоянная Н определяет цикл 7^ на плоскости (р^,<р),
задаваемый условиями р^ = Н и (р Е [0, 2тг] (напомним, что переменная (р
уже определена как угол). Постоянная G2 определяет не столь тривиальный
34
Глава 1
(а)
(6)
Рв
6
Рис. 1.3. (а) Цикл 70, определяемый константой движения G2; (б) цикл опреде¬
ляемый константой движения Н
цикл 70 на плоскости (р#, $); он показан на рис. 1.3а. Вдоль этого цикла пе¬
ременная d колеблется между двумя значениями ^min и $тах, причем ^min,
$тах и р0 ($) даются формулами
Наконец, константа Н определяет — если она отрицательна — цикл 7в на
плоскости (рв, д), как показано на рис. 1.36. Требование отрицательности Н
есть не что иное, как условие компактности поверхности Мф, играющее
решающую роль в теореме Арнольда-Лиувилля. Если бы Н не было отри¬
цательным, то движение было бы неограниченным и 7^ не было бы замк¬
нутым циклом. Вдоль этого цикла переменная д колеблется между двумя
положительными значениями дт[п и £тах, причем
втт - {-G(m0 + mi) + у/д2(т0+т1)2+ 2HG2}/2H,
Ртах = {-<?(т0 + mi) - у/д2(т0 + mi)2 + 2HG2}/2H, (1.60)
рв(в) = ±у/2 (Н + 0(то + mi)/в) - G2/q2.
(1.59)
Введем теперь переменные действия, используя (1.55). Поскольку
вдоль цикла 7^ изменяется только <р, то dd и dg равны нулю и сумма
в (1.55) сводится к единственному члену p^dip; аналогичная ситуация име¬
1.9. Переменные «действие-угол»
35
ет место для циклов 70 и 7е. Следовательно, с учетом (1.59) и (1.60) пере¬
менные действия записываются как
= i =i I Hdv = H’
Л Г 1 max
р2 = — ф p#di? = - / p#(i9)di9 = G - Н,
271" 7Г Ji?min
1 / J 1 /'emax / u , I G2(mo+mi)2
* = s t/‘de=; L р»<,г)а<?=~G+V 2Й—•
(1.61)
Обратив (1.61), легко видеть, что гамильтониан задачи двух тел равен
^ G2(m0 + m1)2
П = ~2Ы+Рг+Р3Г (1'62>
Наконец, чтобы ввести сопряженные углы q\,q2,qz, определим прежде
всего производящую функцию
S{pi,P2,P3,4>,‘&,e) = J Pe(Pi’P2iP3,e)de + p#{pi,P2,'&)d'&+pip(pi)d(p,
(1.63)
где выражения для ре (pi, р2, Рз, о), P-в (Рь Р2, $) и р,р (pi) получаются путем
обращения (1.58) и использования соотношений (1.61). Сопряженные углы
тогда запишутся как
OS dS dS
Qi = Я2 = , qs = . (1.64)
dp 1 др2 dps
Построение канонических переменных «действие-угол» для задачи двух
тел таким образом, завершено.
Коль скоро задан набор переменных «действие-угол», то любое линей¬
ное преобразование вида
J = Ар, ф = (^T)_1q (1.65)
(где А — матрица с целочисленными элементами и единичным определите¬
лем, а (Лг)-1 — матрица, обратная транспонированной А) определяет но¬
вые канонические переменные «действие-угол». Более того, если гамиль¬
тониан зависит только от переменных действия р, то он, очевидно, будет
36
Глава 1
зависеть только от переменных действия J. Иными словами, набор пере¬
менных «действие-угол» Арнольда не уникален. В случае задачи двух тел
форма (1.62) подсказывает, что в качестве канонических переменных «дей¬
ствие-угол» удобно использовать следующие:
L= Р1+Р2+Р3? I — Яз,
G = Р1+Р2, 9 = 42- <7з, (1-66)
H=pi, h = qx-q2.
При таким выборе переменных гамильтонианом задачи двух тел будет про¬
сто
Н = -gV. + ’n.)2 (167)
Канонические переменные «действие-угол» L, Z, G,g, Я, h обычно называ¬
ют переменными Делоне. Связь переменных действия G и Н с элемента¬
ми орбиты, определенными в разделе 1.2, нам уже известна по форму¬
лам (1.14) и (1.15) соответственно, а выражение для L легко получить из
(1.13). Чтобы установить связь с элементами орбиты для углов 1,д и /г,
необходимо выписать интегральные уравнения (1.64) и использовать (1.9).
В итоге получим
L = \/д{т0 + mi)a, I = М,
G = Ьу/ 1-е2, д = ш, С1-68)
Н = Geos г, h = Q.
Чтобы избежать проблемы с углами l,g,h9 плохо определенными, если на¬
клонение и/или эксцентриситет близки к нулю, часто используют модифи¬
цированные переменные Делоне:
k — L = у/д(то -Г mi)a, \ = l + g-\-h = M + m,
Р = L - G = L(l - л/l - e2), p = -g-h = -w, (1.69)
<5 = G-H = 2Gsin2|, q = —h = —O.
Эти переменные имеют то преимущество, что переменная Л всегда хоро¬
шо определена, тогда как переменные р и q не определены только тогда,
когда сопряженные им переменные действия Р и Q соответственно равны
нулю. Таким образом, (Р,р) и (Q,q) образуют полярные системы коорди¬
нат. Заметим, что при малых эксцентриситетах и наклонениях действие Р
пропорционально е2, а Q пропорционально г2.
1.9. Переменные «действие-угол»
37
1.9.2. Гамильтоновы уравнения в переменных Делоне
для ограниченной и планетной задач
Гамильтониан ограниченной задачи (1.29) можно переписать в пере¬
менных Делоне как
n = (1.70)
где Hi(L, G, iT, /, д, /г, t) получается посредством записи выражения
(1.71)
в оскулирующих элементах с помощью (1.9) и обращения (1.68). Время t
присутствует через радиус-векторы планет s^. Хотя итоговое выражение
довольно громоздкое, его можно выписать явно и использовать в практиче¬
ских вычислениях. Гамильтоновы уравнения имеют вид
+ т1
дПх
i =
Q2ml
Э1 ’
L3
дПх
&Hx
дд ’
9 =
8G ’
Шх
h =
dHx
dh ’
dH ‘
dL
6 = -^, 9=^г, (1-72)
L = -
Ввести переменные Делоне для гамильтониана планетной задачи (1.38)
несколько сложнее. Во-первых, заметим, что интегрируемое приближение
для (1.38) есть сумма гамильтонианов (1.39) — гамильтонианов задач двух
тел, записанных, однако, в виде (1.26), а не (1.22). Если бы мы начали
строить переменные «действие-угол» исходя из (1.26), то результирующие
переменные действия имели бы дополнительный множитель /xi по срав¬
нению с действиями, определяемыми посредством (1.68), а результирую¬
щий гамильтониан имел бы дополнительный множитель по сравнению
с (1.67)4. Во-вторых, напомним, что импульсы Vj в (1.39) не равны fijTj.
4Это легко видеть следующим образом. Умножим (1.26) на р\. Тогда гамильтониан (1.26)
будет формально равен (1.22), причем постоянная Q' = заменит Q. Переменные Делоне
и результирующий гамильтониан будут теми же, что и в (1.68) и (1.67), но с заменой Q на Q'.
Наконец, поделим результирующий гамильтониан на дх. — Прим. авт.
38
Глава 1
Это, однако, не изменяет соотношений между Vj, ft- и переменными Делоне
Lj, Gj, Hj, lj, ft, hj по сравнению с имеющими место в классической зада¬
че двух тел, где \j = PjYj\ действительно, гамильтонианы (1.39) и (1.26)
формально идентичны, независимо от того, что реально представляют со¬
бой импульсы. По этой причине можно определить формальные оскули-
рующие элементы ft, е^, Mj, ft, fij, используя формулу (1.9) с ft/ft
вместо dr/dt, и записать переменные Делоне для планетной задачи как
Lj = pj yjQ(m0 + rrij)aj, lj = M3,
Gj — Lj yl el-, ft
iTj = Gj cos ft, hj = Qj.
Тогда гамильтониан (1.38) принимает вид
и = £_в!(120+™iM+Kli (1.74)
J
J
dHi
7 .
Q2(m0
dlj ’
dHi
dHi
d9j ’
~ dGj ’
<9Wi
dhj ’
hj
9Hi
Щ
где 7ft можно выписать явно как функцию переменных Делоне (1.73) пу¬
тем прямой подстановки в (1.38), аналогично процедуре в случае ограни¬
ченной задачи. Тогда гамильтоновы уравнения запишутся как
, _ ^ v-u I дПх
3 ~ ™ ’ 3 ~ L) + дЬ, ’
= 9i = ^r, (!-75)
Lj
для каждого j. Уравнения (1.72) и (1.75) являются гамильтоновой версией
уравнений Лагранжа.
Как и в случае ограниченной задачи, чтобы избежать особенностей
в (1.75), возникающих, когда какие-либо из наклонений и/или эксцентри¬
ситетов принимают нулевые значения, обычно используют модифицирован¬
ные переменные Делоне:
= Lj » Aj = lj + ft + hj,
Pj = Z/j Gj?, ft — ft hj, (1.76)
Qj = Gj — Hj, ft = —hj.
1.9. Переменные «действие-угол»
39
1.9.3. Правила Даламбера
В классических работах о динамике в ограниченной и планетной зада¬
чах функцию Н\ в выражениях (1.70) и (1.74) обычно раскладывали в ряды
Фурье по углам Л, w и Q и в степенные ряды по е и г; или же, что экви¬
валентно, используя модифицированные переменные Делоне (1.69), в ряды
Фурье по \p,q и в степенные ряды по Р1/2, Q1/2. Хотя в этой книге мы
не будем работать с классическими явными разложениями, в последующих
главах нам будет крайне важно знать их общий вид.
Обозначим через A j,Pj, Qj,Xj,pj,qj (j = 1,..., N) модифицирован¬
ные переменные Делоне N тел (одного малого тела и А-1 планет, либо N
планет), а через Oij,fij, kj,rrij\ Sj — целые числа. Кроме того, традиционно
обозначим через Л, а, /3, k, m и s векторы, компоненты которых равны Aj,
Oij^^kj.rrij и Sj соответственно. Тогда наиболее общая форма разложения
в ряд Фурье по углам и в степенной ряд по yjPj, y/Qj записывается как
= X ca,/3,k,m,s(A) ^ Х (177}
a,/3,k,m,s у j J \ ' )
х exp
171 j Pj X j Sj Qj ) ] 5
где t обозначает л/~1> a 3,k,m,s — коэффициенты (об их вычислении
см. Брауэр и Клеменс, 1961; Дюрье, 1989; Ласкар и Робутель, 1995; Эллис
и Мюррей, 2000).
Из симметрий и аналитических свойств Hi легко вывести так называ¬
емые правила Даламбера:
1. Н\ должно быть инвариантно относительно одновременного изменения
знаков у всех углов Xj, pj, qj. Поэтому разложение в ряд Фурье должно со¬
держать только члены с косинусами, а именно: k,m,s = ca,/3,-K-m,-s?
причем все коэффициенты вещественны.
2. Н\ должно быть инвариантно относительно произвольного поворота си¬
стемы отсчета вокруг оси z. Поворот системы отсчета на угол д увеличи¬
вает долготы на величину $. Поскольку pj = —Wj и qj = —Qj,
инвариантность Н\ означает, что ]Г\ kj — JX mj ~ Yj sj = 0- Заметим,
что средняя аномалия lj = Xj — Wj и аргумент перигелия иjj = Wj — Qj
инвариантны относительно поворота системы отсчета.
3. Hi должно быть инвариантно относительно одновременного измене¬
ния знаков у всех наклонений, то есть относительно преобразования
40
Глава 1
QX-2 —> —Q1/2 Vj (напомним, что QlJ2 ~ ij). Это означает, что YjjPj/2
должна быть целым числом.
4. В исходных координатах и импульсах (см. (1.29) и (1.38)) все особен¬
ности Hi в действительном фазовом пространстве, очевидно, соответству¬
ют исключительно соударениям двух тел. Следовательно, особенности при
Pj = 0 и Qj = 0 у Н\, записанном в виде (1.77), присущи не самой
функции, а специальному выбору переменных «действие-угол». В самом
деле, углы pj и qj не определены, когда сопряженные им переменные дей¬
ствия Pj и Qj равны нулю, то есть при нулевых эксцентриситете и накло¬
нении. Эта особенность, типичная для канонических полярных координат,
должна устраняться при переходе к каноническим декартовым координа¬
там. Определим переменные Пуанкаре
Уз = '/ЩC0SPj. хз = у/ЩsinPj> „
, (l-'Oj
Zj = у/2Qj cos qj, Vj = у/2Qj sin qj.
Применяя критерий скобок Пуассона (1.36), легко проверить, что это пре¬
образование является каноническим и определяет Xj и Vj как новые коор¬
динаты, a yj и Zj — как сопряженные им импульсы. И (yj,Xj)9 и (zj,Vj)
хорошо определены при Pj = 0 и Qj =0. Поэтому в этих новых канониче¬
ских переменных свойства регулярности Hi должны восстановиться. Это
означает, что в (1.77) числа oij — \rrij | и Pj — | должны быть неотрицатель¬
ными четными целыми. Только в этом случае Hi аналитически выражается
через Xj,yj,Zj,Vj.
1.10. Интегрируемая динамика
В завершение главы изучим динамику интегрируемой системы, кото¬
рая, как мы убедились в разделе 1.9, в общем случае представима гамиль¬
тонианом Н(р), независимым от углов q системы.
Уравнения движения записываются просто:
Рз = = °» & = (L79)
Из них следует, что переменные действия являются константами движе¬
ния, а у угловых переменных qj производные по времени Uj постоянны.
Поскольку координаты qj представляют собой углы, их производные по
времени, ujj, фактически являются частотами.
1.10. Интегрируемая динамика
41
n-мерное многообразие, допускающее в качестве глобальной системы
координат п независимых углов, называется тором и обычно обозначает¬
ся Тп. Отметим для наглядности, что одномерный тор Т1 топологически
эквивалентен окружности, а двумерный тор Т2 — поверхности бублика.
Если движение задано интегрируемым гамильтонианом, то угловые пере¬
менные циркулируют с фиксированными частотами на торах, определяе¬
мых постоянными значениями действий р. Торы р = const, следовательно,
инвариантны для динамики в том смысле, что траектория, стартующая на
торе, никогда его не покинет, поскольку действия р являются константами
движения. Фазовое пространство расслаивается на инвариантные торы,
поскольку любые начальные условия р(0), q(0) порождают движение, ле¬
жащее на инвариантном торе.
Эволюция углов на торе определяется частотами ujj(p). Если частоты
таковы, что уравнение
допускает единственное целочисленное решение к = (0, то дви¬
жение всюду плотно покрывает тор. Это означает, что всякая область тора
посещается траекторией: для любой сколь угодно малой окрестности U(q°)
любой точки q° на торе траектория рано или поздно попадет внутрь U(q°).
В данном случае говорят, что частоты нерезонансны, а движение называет¬
ся квазипериодическим.
В противном случае, когда уравнение (1.80) в качестве решения допус¬
кает п — 1 независимых целочисленных ненулевых векторов к1,..., kn_1,
движение на торе является периодическим. Действительно, легко убедиться,
что в таком случае гг — 1 углов можно выразить как периодические функции
единственного угла. Частоты тогда называются полностью резонансными.
Наконец, существуют промежуточные случаи, когда уравнение (1.80)
в качестве решения допускает лишь т независимых целочисленных нену¬
левых векторов к1,..., кт, т < п — 1. Тогда движение на торе не явля¬
ется ни всюду плотным, ни периодическим. При этом т углов — скажем,
• • •, дш — можно представить как периодические функции от остальных
п — т углов gm+i,..., qn. Это означает, что проекция движения на (п — т)-
мерный тор, определяемый переменными gm+i,..., qn, всюду плотна, а ее
проекция на га-мерный тор, определяемый переменными <?i,..., gm, явля¬
ется периодической. В таком случае говорят, что частоты находятся в резо-
п
(1.80)
42
Глава 1
нансе кратности т. Величина
min1:£:KTO|kJ|, где |kJ| = \k{ \ Н + \к3п\
(1.81)
называется порядком резонанса.
Вообще говоря, частоты зависят от выбора тора, а именно от значений
действий р. Однако, если гамильтониан линеен по действиям, то часто¬
ты не зависят от р. Тогда говорят, что система изохронна. В более общем
случае гамильтонова система называется вырожденной, если определитель
матрицы ее вторых производных обращается в нуль:
Если система вырождена, существует по крайней мере одно направление
в пространстве действий, вдоль которого частоты не изменяются. Напро¬
тив, если система невырождена, то по крайней мере одна частота долж¬
на изменяться при любом сколь угодно малом смещении в пространстве
действий. В последнем случае резонансные торы всюду плотны в фазовом
пространстве — в том смысле, что сколь угодно близко к любой точке р*
существует точка р такая, что уравнению (1.80) удовлетворяет некоторый
ненулевой целочисленный вектор к.
Теоретическая гамильтонова динамика хорошо развита для невырож¬
денных систем с малыми возмущениями. Напротив, свойства динамики
вырожденных систем существенно зависят от специфики рассматриваемой
системы, в частности касающейся направлений, вдоль которых частоты по¬
стоянны, а также того, каким образом вырождение снимается при малом
возмущении системы.
К сожалению, задача двух тел является существенно вырожденной.
Как мы убедились в предыдущем разделе, гамильтониан этой задачи за¬
висит лишь от одной переменной действия (L) из трех. Это означает, что
частоты не зависят от переменных действия G и Н. Более того, две из трех
частот, а именно g и h, тождественно равны нулю, поэтому g и h являются
в задаче Кеплера дополнительными постоянными движения. Таким обра¬
зом, имеется вырождение вдоль двух направлений для I и вырождение во
всем пространстве действий для g и h. По этой причине даже малые воз¬
мущения задачи двух тел — такие, например, как ограниченная и планетная
задачи — могут порождать весьма сложную динамику.
(1.82)
Глава 2
Квазиинтегрируемые гамильтоновы
системы
2.1. Введение в теорию возмущений
Гамильтонову систему называют квазиинтегрируемой, если при зада¬
нии подходящего набора канонических переменных «действие-угол» ее га¬
мильтониан может быть записан в виде
W(p,q) = W0(p) +e«i(p,q), (2.1)
где е — малый параметр, a gradp7^o и Hi являются по предположению
величинами порядка единицы. Поэтому естественно рассматривать Но как
интегрируемое приближение, a Hi — как его возмущение. В самом деле,
поток, порождаемый Но (а именно, р = const и q = u>ot + q(0), где с^о =
= gradpWo), аппроксимирует реальную динамику, порождаемую Н, с точ¬
ностью порядка е в том смысле, что он отклоняется от реального решения
на величину порядка е на интервале времени порядка единицы и на величи¬
ну порядка единицы на интервале времени порядка 1/е. К сожалению, если
нас интересует очень точное описание динамики или же ее качественное
поведение на интервалах времени больше 1/е, то знания потока, порож¬
даемого Но, уже недостаточно и приходится искать существенно лучшие
приближения реального движения. Именно в этом состоит цель теории
возмущений. Как будет детально обсуждаться в разделе 2.5, гамильтониа¬
ны и ограниченной, и планетной задач ((1.70) и (1.74)) имеют вид (2.1),
где е — величина порядка массы Юпитера в единицах массы Солнца, то
есть ~ 10_3. Поэтому исследование квазиинтегрируемых гамильтоновых
систем не является лишь чисто математической проблемой, но и важно на
практике в небесной механике.
Мощь гамильтонова формализма состоит в том, что вместо поиска при¬
ближений для реальной динамики из анализа уравнений движения (обычно
44
Глава 2
связанного с громоздкими выкладками) он позволяет работать напрямую
с гамильтонианом. Говоря конкретно, общей стратегией для всех пертур¬
бационных подходов к гамильтоновым системам является поиск канониче¬
ского преобразования, близкого к тождественному, вида
р = р1 +efi(p1,q1), q = q1+£g1(p\q1), (2.2)
такого, что после подстановки (2.2) в (2.1) гамильтониан принимает вид
= WoCp1) +ffWi(p1) + e2W2(p1,q1), (2.3)
где Hi и H2 — некоторые новые функции порядка единицы (обычно Hi яв¬
ляется усредненной по углам q функцией Н\). Если этот поиск увенчался
успехом, то Но + еН\ является интегрируемым приближением порядка е2
для реальной динамики. В принципе, процедуру можно итерировать, ища
последовательность близких к тождественным канонических преобразова¬
ний
р-1 = р- +e’-fP(p’\q’-), qr_1 = qr + £rgr(pr, qr), (2.4)
таких, что гамильтониан как функция переменных «действие-угол» pr, qr
принимает вид
Wr(pW) = Wo(pr)+eWi(pr) + ---+^Wr(pr)+£r+1Wr+1(pr,qr). (2.5)
Тем самым получается последовательность все более точных приближе¬
ний реальной динамики. Казалось бы, можно надеяться, что повторение
данной процедуры бесконечное число раз преобразует исходный гамильто¬
ниан Н(р, q) в интегрируемый W00^00). Однако теперь мы знаем — бла¬
годаря работам Пуанкаре, — что такая надежда тщетна: в общем случае
процедура бесконечного порядка не может быть успешной (см. раздел 2.4).
Приходится останавливать итерирование при некотором оптимальном по¬
рядке г, зависящем от £ и свойств системы. Как следствие, наилучшим
интегрируемым приближением реальной динамики является pr = const,
qr = (jJrt + qr(0), где u>r = gradpr[Wo + • • • + erHr(pr)\. Образ этого
движения в исходных переменных р, q можно получить посредством ком¬
позиции всей последовательности канонических преобразований: p(£),q(t)
колеблются с амплитудой порядка е около значений pr,qr(£).
В последующих разделах мы детально рассмотрим эту процедуру
(а также трудности, с которыми приходится сталкиваться при ее примене¬
нии), следуя подходу, наиболее часто используемому в небесной механике,
а именно подходу с применением рядов Ли.
2.2. ПОДХОД С ПРИМЕНЕНИЕМ РЯДОВ ЛИ
45
2.2. Подход с применением рядов Ли
В процедуре, описанной в общих чертах в предыдущем разделе, боль¬
шой проблемой является нахождение среди всех возможных преобразова¬
ний (p,q) —* (p^q1), преобразующих (2.1) в (2.3), такого, которое было
бы каноническим. Разумно избежать этой проблемы (Гребнер, 1960; Хори,
1966; Депри, 1968), производя поиск «хорошего» преобразования внутри
класса преобразований, являющихся каноническими по построению. Это
достигается посредством определения преобразований как потока произво¬
дящих гамильтонианов х в ^-времени, как описано в разделе 1.6. Конкрет¬
но, преобразования определяются как в (1.42), или, в эквивалентной форме,
как
p = SJp\ q = S'£q1, (2.6)
где S£ — оператор ряда Ли, определенный в разделе 1.7, В (см. форму¬
лу (1.52)). Все преобразования этого типа являются в самом деле кано¬
ническими. Используя (1.42), путем подстановки получим выражение для
гамильтониана Н в новых переменных:
Щр, q) = ^(р1 (е), q1 (е)) = П1 (р\ q1). (2.7)
Таким образом, Н1 возникает как эволюция функции ^(р1^1) на момент
«времени» е (получаемая формальной заменой p,q на p^q1 в Н) вдоль
потока, порождаемого гамильтонианом х- Поэтому, как показано в разде¬
ле 1.7, В, Н1 можно записать, используя ряды Ли, в виде
П1 = S£XH. (2.8)
Теперь задача свелась к нахождению подходящего производящего га¬
мильтониана х такого, что если Н имеет вид (2.1), то Н1 имел бы вид (2.3).
С этой целью, используя (1.51) и (1.50), запишем (2.8) в явном виде до по¬
рядка е2:
Н1 = Но + sH\ + е{Но, х} + £2{Hi,x} + ~^{V~to, х}> х} + 0(£3)* (2.9)
В этом выражении Но, Н1 их следует все рассматривать как функции от
P1»q1. Из (2.9) сразу видно, что в Н1 членом нулевого порядка по е явля¬
ется Но(р1); поэтому Н1 будет иметь вид (2.3) тогда и только тогда, ко¬
гда член первого порядка по е будет функцией исключительно переменных
46
Глава 2
действия р1, то есть тогда и только тогда, когда уравнению
Wi + {Wo,x} = Wi, (2-10)
называемому гомологическим уравнением, удовлетворяют некоторые функ-
ции xCpW) и Witp1).
Чтобы решить уравнение (2.10), воспользуемся тем, что координа¬
ты q1 являются углами и гамильтониан Н периодичен по q1. Разложим Н\
в ряд Фурье:
Wi(p1,q1)= X c^p^exp^k-q1), (2.11)
kGZn
где k — целочисленный вектор, п — число степеней свободы, ь = у/^1.
Затем мы ищем решение х уравнения (2.10) в аналогичной форме
x(p1,q1)= rfk(pl)exp(tk'q1)’ (2Л2)
kGZn
так что можем записать
{W0,x} = -t X rfk(p1)k-OJ0(p1)exp(tk-q1), (2.13)
kezn
где u>o = gradpiWo- Тогда сразу очевидно, что решение уравнения (2.10)
дают производящий гамильтониан вида (2.12) с коэффициентами dк, зада¬
ваемыми как
do = 0, ^(р1) = vk ± °> (2-14)
и функция Hi, которая просто суть
^(р1) = Со(р1). (2.15)
Теперь, когда производящий гамильтониан х определен, определено
и каноническое преобразование, связывающее исходные переменные р, q
с новыми p^q1. Члены нового гамильтониана W1(p1,q1) второго или бо¬
лее высоких порядков по £ легко вычислить, используя полное выраже¬
ние (2.9).
Однако полученное нами решение уравнения (2.10) является всего
лишь формальным. Следует проверить, что производящий гамильтониан х
2.3. Проблема малых делителей
47
является аналитической функцией, то есть его ряд Фурье (2.12) с коэффи¬
циентами (2.14) сходится абсолютно. В принципе следует также проверить,
что степенной ряд по е, определяющий Н1 в (2.9), сходится абсолютно.
Однако последнее гарантируется при достаточно малых е, если х и ^ яв_
ляются аналитическими. В самом деле, в этом случае правая часть (2.9) по
определению представляет собой разложение в ряд Тейлора эволюции во
времени аналитической функции (Н) вдоль аналитического потока (порож¬
даемого гамильтонианом х), которое, как известно, сходится при условии,
что промежуток времени [0, е], на котором определено разложение, доста¬
точно мал.
Поэтому нам приходится заботиться только об аналитических свой¬
ствах функции х-
2.3. Проблема малых делителей
Из (2.12) и (2.14) сразу очевидно, что функция х не определена, если
существует целочисленный вектор к* такой, что знаменатель
к* • ^(р1) (2.16)
обращается в нуль для некоторого р1, причем соответствующий коэффи¬
циент Ск#(р1) отличен от нуля. В соответствии с определением (1.80) это
означает, что производящий гамильтониан х не определен ни на каком то¬
ре р1, несущем резонансное движение интегрируемого приближения Но-
Как было отмечено в конце главы 1, если гамильтониан Но невырожден,
то резонансы непременно являются всюду плотными; поэтому нельзя на¬
деяться, что функция х может в общем случае быть хорошо определена
в открытой области фазового пространства. Резонансы всюду плотны также
и в большинстве представляющих интерес вырожденных случаев, напри¬
мер, в ограниченной задаче трех тел. Другими словами, пертурбационный
подход, описанный в общих чертах в предыдущем разделе, в общем случае
не работает.
К счастью, имеется пара способов для выхода из этой неприятной си¬
туации. В основе первого — использование аналитических свойств функ¬
ции Н\. Всякая функция f(<p), 27г-периодичная по углам <р и аналитическая
на комплексном торе
Т" = {<£> € С" : Re<£j е [0,27г], | Im ipj \ < a, (2.17)
48
Глава 2
раскладывается в ряд Фурье
/(¥>) = Qk exp (tk • y>), причем |с*к| < Fexp (—|к|сг), (2.18)
kez
где |k| = |Ail| + ... + \kn\ — порядок гармоники Фурье с индексом к =
= (fci,..., kn), a F — точная верхняя грань |/(<р)| для (р е Т™ (Арнольд,
19636). Принимая во внимание экспоненциальное убывание коэффициен¬
тов, представляется естественным разделить разложение Н\ на две части:
Hi =Н<К +nfK, где
HfK= ^2 ck(p) exp (ik • q),
k€Zn,|k|<K'
(2.19)
nfK= ^2 ck(p) exp (tk • q),
k€Zn,|k|
причем К выбирается достаточно большим1 — таким, что Н{ является
величиной порядка е относительно HfK. Тогда в выражении (2.9) величи¬
ной порядка е будет только £HfK и уравнение (2.10) допускает решение
х= Е -kcj^)exp(tk-ql)- (2'20)
kEZn\0,|k|</C UV^ J
Теперь ряд, определяющий содержит лишь конечное число гармоник;
поэтому можно найти открытую область Ык в пространстве переменных
действия, такую, что знаменатели в (2.20) не обращаются в нуль для любых
Р1 £ Ык- Область Ык будем называть нерезонансной до порядка К.
Второй способ решения проблемы малых делителей состоит в выборе
точки р* в пространстве переменных действия, такой, что частоты и;о(р*)
удовлетворяют так называемому диофантову условию:
|k.«o(p,)|> VkeZMc^O, (2.21)
где 7 и т — некоторые подходящие положительные числа. Теория чисел
гарантирует существование таких частот (причем их множество в Rn имеет
положительную меру) при условии, что т > п — 1. Затем раскладываем Но
Некоторые авторы предпочитают выбирать К не зависящим от е, вводя, по сути, но¬
вый пертурбационный параметр ехр(—сгК). Преимущество такого приема состоит в том,
что нормализованный гамильтониан будет аналитическим по е, чего нет в случае, если К —
целочисленная (и потому разрывная) функция от е. — Прим. авт.
2.3. Проблема малых делителей
49
в степенной ряд относительно р = р - р*:
W0(P) = 5>о(р)> (2.22)
э>1
где Н30 — однородный полином степени j относительно р. Наконец, рас¬
сматриваем ^-окрестность точки р* в пространстве действий:
We(pJ = {р 6 R71 : ||р||<5}; (2.23)
так что члены Н30 при j ^ 2 имеют более высокий порядок по е чем Hq.
Поэтому в уравнении (2.9) Н\ будет играть роль Но, тогда как члены более
высокого порядка Н30 с j ^ 2 будут включены в Н\. В уравнении (2.10)
функция Но в скобке Пуассона с х будет полностью изохронна (так как она
линейна по переменным действия р) с фиксированными частотами и>о(р*),
поэтому формальным решением для х будет
£ “‘iri^exp(lk 4‘>' (224)
k€Z™\0
Теперь, принимая во внимание экспоненциальное убывание коэффициен¬
тов Ск (2.18) и используя определение (2.21) диофантовых частот о>о(р*),
легко видеть, что ряд (2.24) абсолютно сходится на комплексном торе Т™_6
при любых положительных 6 < <т.
В практических вычислениях, выполняемых обычно с помощью си¬
стем компьютерной алгебры, для решения проблемы малых делителей при¬
нято использовать оба изложенных выше способа в комбинированном виде.
Для обеспечения эффективности компьютерных выкладок функции долж¬
ны быть представлены в виде степенных рядов по переменным действия
и рядов Фурье по угловым переменным. Поэтому естественно расклады¬
вать Но в степенной ряд по р, что имеет также и то преимущество, что
в итоговом производящем гамильтониане х (2.24) знаменатели не будут за¬
висеть от переменных действия, поскольку точка р* фиксирована. С другой
стороны, так как компьютерная память всегда ограничена, все разложения
в ряды необходимо обрезать. Естественно сохранять в Н\ и х только гар¬
моники Фурье порядка |к| < К.
2.3.1. Нормальные формы
Из изложенного выше следует, что, хотя преобразовать исходный га¬
мильтониан Н в новый гамильтониан Н1 в виде (2.3) в общем случае нель¬
50
Глава 2
зя, все же достичь этой цели можно, если переменные действия ограни¬
чены локальной областью Ык, нерезонансной до порядка К (зависящего
от е\ или же окрестностью Ые тора р* с диофантовыми частотами. Если
гамильтониан преобразован к форме (2.3) в некоторой области переменных
действия, то говорят, что он представлен в нормальной форме Биркгофа до
первого порядка по е.
Однако в некоторых случаях представляет интерес область, пересека¬
емая резонансами порядка меньше К. В таких случаях соответствующие
члены в разложении Фурье еН\ не могут быть низведены в члены более
высокого порядка по е. С другой стороны, эти члены нельзя исключить
из-за проблемы малых делителей. Поэтому в таких случаях преобразовать
гамильтониан к нормальной форме Биркгофа невозможно и приходится со¬
хранять резонансные гармоники в новом гамильтониане Н1.
Конкретно, обозначим через U представляющую интерес область
в пространстве переменных действия и определим резонансное множество
/С = {k Е Zn , |к| < К : к • и>о(р) = 0 для некоторых р Е U} . (2.25)
Тогда Н\ удобно разбить на три части: Н\ = HR + HiR + 7i^K, где
Hi = ]Tck(p)exp(ik-q), HiR = ck(p) exp (tk • q),
k(E/C k£Zn,|k|<AT,k^/C
(2.26)
производящий гамильтониан x таким образом, что HiR + {Wo,x} =
полагая
Производящий гамильтониан х аналитичен по р1 еЫ, потому что ни один
из знаменателей к • а;о(р1) не обращается в нуль для р1 Е Ы и к ^ /С по
построению /С (заметим, что член с к = 0 также включен в HR), а так¬
же потому, что разложение Фурье в (2.27) содержит лишь конечное число
членов2. Поэтому каноническое преобразование (2.6) хорошо определено
2Поскольку ||р — р11| = О(е) (см. формулу (2.6)), то для того, чтобы гарантировать при¬
надлежность р1 Е U, следует выбирать р Е U — О(е), где последнее обозначает наибольшее
множество, содержащееся в U вместе с окрестностью радиуса О(е). Это означает, что раз¬
мер U должен быть по меньшей мере 0(e). — Прим. авт.
а 3-4^^ лппрттрп^ил ту а ъг г» (О 1 ТТгчтд (О ипритл плпатть-а с
keZn,\k\<KM#K
(2.27)
2.4. Порядки выше первого
51
и гамильтониан (2.1) преобразуется к виду
WV.q1) = WoCp1) + eHf (pW) + 0{e2). (2.28)
Данный гамильтониан Ttl находится, по определению, в резонансной нор¬
мальной форме до первого порядка по е.
Резонансные нормальные формы очень полезны при изучении резо¬
нансной динамики, поскольку в них удерживаются в низких порядках толь¬
ко существенные резонансные члены, а нерезонансные члены низводятся
в члены более высокого порядка. К сожалению, гамильтониан Но(р1) +
-h ^Wf(p1,q1) в общем случае неинтегрируем, если /С содержит более
одного резонанса3 или же единственный резонанс кратности больше 1
(см. определение кратности в разделе 1.10). Напротив, если /С содержит
только один резонанс кратности 1, то гамильтониан ^(р1) + sHi(р1, q1)
интегрируем, как будет показано в главе 4.
2.4. Порядки выше первого
Рассмотренная в предыдущем разделе процедура позволяет исключить
гармоники с коэффициентами порядка е, не принадлежащие резонансно¬
му множеству 1C. Естественно итерировать эту процедуру, чтобы исклю¬
чить также и нерезонансные гармоники с коэффициентами более высокого
порядка по е. Конкретно, будем искать последовательность производящих
гамильтонианов Хг и последовательность канонических преобразований
pr-x = 5^pr, qr_1 = qr, г > 1, (2.29)
таких, что гамильтониан в итоге преобразуется к виду
Wr(pr, qr) = Ho(pr)+eH?(pr, qr)+- • -+erW?(Pr, qr)+er+1Hr+i(pr, Цг),
(2.30)
где функции Hi',..., Н^ содержат только гармоники к • qr, к Е /Сг. Мно¬
жество /Сг представляет собой множество резонансов до порядка КТ, пере¬
секающих область U, то есть
K,r = {k Е Z71, |к| < Кг : к • о>о(р) = 0 для некоторых р Е U} , (2.31)
3То есть существуют по меньшей мере два значения р1 и р2 в U и два ненулевых цело¬
численных вектора ki и к2, таких, что ki • u>o(Pi) = k2 • ^(Рг) = 0 и ki • u>o(P2) Ф 0,
^2 * tJo(Pi) ф 0. — Прим. авт.
52
Глава 2
где Кг выбирается таким образом, что все гармоники порядка больше Кг
имеют коэффициенты меньше ет (см. ниже). Гамильтониан (2.30) будем
называть находящимся в резонансной нормальной форме до порядка ег по
отношению к /Сг. Заметим, что в случае /Сг = {0} (то есть когда резо¬
нансов до порядка Кг, пересекающих рассматриваемую область, нет) вы¬
ражение (2.30) приводится к виду (2.5), в таком случае.Ttr называется
находящимся в нормальной форме Биркгофа до порядка ег.
Чтобы определить производящую функцию Хг, возмущение Нг пред¬
ставляют в виде суммы НR + H^R + 'HfKr, где TCR и 7i^R определяются
как в (2.26), а Н^Кг — как в (2.19), но с JCr и Кг вместо /С и К. Обратите
внимание, что, тогда как HR и H^R содержат гармоники, коэффициенты
которых являются эффективно величинами порядка ет, 'HfKr содержит (по
определению Кг) только гармонические члены с меньшими коэффициента¬
ми. Далее, аналогично тому, как делается в случае резонансной нормальной
формы порядка 1 по е (см. раздел 2.3.1), \г выбирается таким образом, что¬
бы исключить нерезонансную часть возмущения порядка ег, а именно, как
решение уравнения
W?* + {Wo,Xr} = 0. (2.32)
Ключевым моментом этой процедуры является выбор Кг. Как указано вы¬
ше, Кг должно быть достаточно велико, чтобы все гармоники порядка
больше К г имели бы коэффициенты меньше ег. Обратите внимание, что
гармоники исходного возмущения еН\ порядка от 1 до К (где К опреде¬
ляется как в (2.19)) имеют коэффициенты порядка е\ поэтому вследствие
экспоненциального убывания (2.18) гармоники еН\ порядка от (г — 1)К
до г К имеют коэффициенты порядка ег. Как следствие, необходимо вы¬
бирать Кг ^ гК. Это означает, что резонансное множество Кг при уве¬
личении г должно содержать все больше и больше резонансных членов.
Поскольку в нормализованном гамильтониане 7ir удерживаются все резо¬
нансные члены, оказывается, что его вид не намного более удобен, чем вид
исходного гамильтониана TL. К примеру, нельзя надеяться в общем случае
построить гамильтонианы Ttr в нормальной форме Биркгофа до порядка ег
с произвольно большим г, то есть преобразовать исходный гамильтониан
в интегрируемый Н°°{р°°).
В практических приложениях обычно интересуются некоторой задан¬
ной областью U пространства переменных действия и стремятся преобразо¬
вать исходный гамильтониан по возможности к наипростейшей нормальной
форме в этой области. Поэтому обычно выбирают несколько независимых
целочисленных векторов к1,... ,кт, соответствующих главным резонан¬
2.4. Порядки выше первого
53
сам в этой области, и стремятся удержать в резонансной нормальной форме
только гармоники к • qr, где
кем = {kG Zn : к = nik1 Н Ь nmkm, где (щ,... ,nm) £ Zm} .
(2.33)
Легко видеть, что множество Л4, обычно называемое резонансным моду¬
лем, представляет собой целочисленное векторное пространство, порожда¬
емое базисом к1,..., кт (причем наиболее интересным случаем является
тот, когда базис сводится к одному-единственному вектору к1, поскольку
тогда получающаяся нормальная форма будет интегрируемой (см. главу 4)).
Далее, необходимо решать уравнения (2.32) при возрастающих значени¬
ях г, удерживая в Н^ только гармоники к • qr с к £ М. Очевидно, что этот
процесс должен быть прекращен при некотором порядке г, а именно ко¬
гда в HfKr обнаруживается первая гармоника, резонансная внутри U и не
принадлежащая резонансному модулю М. На этом шаге гамильтониан уже
преобразован к форме
7Г-1 = П0 + Ко™ + егПт + 0(er+1), (2.34)
где Ипогт = £Hi + • • • + er_1W^_1. Эту форму следует рассматривать как
оптимальную нормальную форму в том смысле, что при заданных U и Л4
она минимизирует величину ненормализованного остатка £rHr+0(£r+1).
Порядок г оптимальной нормальной формы и величина остатка полностью
определены, как только выбраны область U и резонансный модуль Л4. Фак¬
тически образ Ы в пространстве частот (то есть множестве частот с«;(р)
с р £ U) и М. определяют, какая гармоника низшего порядка является ре¬
зонансной в U и не принадлежит М. Обозначая ее порядок через ктш,
из (2.18) находим, что ее коэффициент не может превышать ехр(—кт[па)
с некоторым положительным а, определяемым аналитическими свойства¬
ми исходного гамильтониана. Как следствие, в общем случае эта гармоника
обнаруживается в процессе нормализации на шаге г = — кт-ша/ 1п£. (По¬
дробности см. в работе Морбиделли и Джиорджилли, 1997.)
2.4.1. Пример вычисления оптимального порядка нормальной формы
Рассмотрим гамильтониан (2.1) и точку р* в пространстве перемен¬
ных действия такую, что частоты и>о(р*) удовлетворяют диофантову свой¬
ству (2.21). Построим оптимальную нормальную форму Биркгофа в обла¬
сти £4(р*), определенной в (2.23). Обратите внимание, что, как объяснено
в подстрочном примечании в разделе 2.3.1, U£(p+) является областью ми¬
нимального размера, где можно попытаться построить нормальную форму.
54
Глава 2
Если гамильтониан Hq невырожден, то частоты сь>о(р) в области We(p*)
покрывают ^-окрестность и?о(р*)- Тогда, учитывая (2.21), в We(p*) имеем
|к • w0(p)| > ||k • w0(р.)| - e|k|| > ЩР ~ lkle> (2-35)
поэтому k*a;o(p) может обращаться в нуль, только если |к|
Таким образом, резонансы низшего порядка в Ы£(р*) имеют порядок
о ~ 1/е1^т+1\ а остаток оптимальной нормальной формы Биркгофа имеет
величину ~ ехр[—е_1^т+1^], то есть он экспоненциально мал по е (Морби-
делли и Джиорджилли, 1997). Можно заключить, что динамика в е-окрест-
ности невозмущенного диофантова тора аппроксимируется интегрируемой
динамикой на экспоненциально больших по 1/е интервалах времени.
Интересно отметить, что если в рассмотренном выше примере разло¬
жить Но в ряд Тейлора по р = р — р*, как в (2.22), и члены Н30 с j > 1
низвести в члены более высокого порядка по е (как сделано в разделе 2.3
при построении нормальной формы Биркгофа первого порядка по е), то
оказывается, что уже нет формальных препятствий для построения нор¬
мальной формы Биркгофа до любого произвольного порядка г. Фактиче¬
ски, поскольку ведущий член Н\ = и>о(р*) * Р является изохронным с дио-
фантовыми частотами и>о(р*), ни одна из гармоник возмущения, как пред¬
ставляется, не будет резонансной в Ы£{р#), в каждом порядке. Однако если
вычислить нетривиальные строгие оценки нормы возмущения (как сделали
Джиорджилли и Галгани, 1985), то оказывается, что в этом случае нор¬
ма Нг удивительно быстро растет с увеличением г — как r!s_rr^r+1\ то
есть егНг ведет себя как г\ег^т+1\ С увеличением г она сначала убыва¬
ет, а затем неограниченно возрастает при стремлении г к бесконечности.
Минимум достигается при г ~ 5~1/(т+1); он является величиной порядка
ехр[—е1^74-1)]. Таким образом, снова приходим к уже полученному выше
результату для размера остатка оптимальной нормальной формы.
Этот пример мы привели, чтобы показать, что никаким формальным
ухищрением нельзя построить нормальную форму до произвольно боль¬
шого порядка. Присутствие резонансов внутри заданной области является
существенным препятствием, которое нельзя обойти.
2.4.2. Генерирование старших гармоник в процессе нормализации
Во многих практически важных случаях исходный гамильтониан Н
имеет лишь несколько гармонических членов низкого порядка. Тогда мож¬
2.4. Порядки выше первого
55
но было бы ожидать, что резонансы высокого порядка, пересекающие за¬
данную область, не приводят к проблеме малых делителей, поскольку ко¬
эффициенты соответствующих гармоник тождественно равны нулю. Это
позволило бы строить нормальную форму до произвольно большого по¬
рядка.
Однако, вообще говоря, это не так. Даже если в исходном гамильтони¬
ане нет гармоник высокого порядка, такие гармоники обычно появляются
при построении нормальной формы, что легко видеть на следующем при¬
мере.
Рассмотрим гамильтониан (2.1) с двумя степенями свободы, где
Но = ujipi + ш2р2 + ^(Pi + pI)i ^ 36)
Hi = cos <71 + cos(<7i - q2) + cos(gi + q2) + cosq2,
причем ui и uj2 нерезонансны. Попытаемся построить нормальную форму
Биркгофа до первого порядка по е. Производящий гамильтониан х является
решением уравнения (2.10) и поэтому содержит те же гармоники, что и Н\.
Заметим, что функция Hi в (2.10) равна нулю, поскольку усреднение Hi
по qi,q2 дает нуль.
Представим спектр Фурье Hi и х в виде следующей схемы:
ki
fc2
Черными квадратиками на ней показаны гармоники (fci, к2) = ex.p[c(kiqi +
+ ^2^2)] с ненулевыми коэффициентами. Поскольку Hi и х являются веще¬
ственными функциями, то можно ограничиться рассмотрением полуплос¬
кости ki > 0. В самом деле, если коэффициент гармоники (ki,k2) нену¬
левой, то и коэффициент гармоники (—fci,— к2) должен быть ненулевым,
и наоборот.
Выясним теперь, у каких гармоник в преобразованном гамильтониане
Н1 = S^H коэффициенты ненулевые. Для этого достаточно заметить, как
гармоники компонуются в скобке Пуассона:
{o:(PbP2)exp[t(A:1g1 + k2q2)\,0(pi,p2)exp[L(m1q1 +m2<?2)]} = ^
= 7(Pi,P2)exp{tp1 +mi)qi + (k2+m2)q2]},
56
Глава 2
где а и /3 — функции общего вида от переменных действия р\ и р2, а 7 =
= ^(ак • gradp/? - /Зт • gradpa). Например, в {Н\, х} гармоника (1,1) в Hi
в сочетании с каждой гармоникой в х генерирует гармоники с ненулевыми
коэффициентами, показанные на следующей схеме белыми квадратиками:
кг
г
1 Г
1 Г
1
L
г
J L
1 I
J L
■ г
J
L
г
J 1
П Г
> L
т г
J
п
к2
В результате члены Н1 второго порядка по е, а именно СХН\ и 1/2£^Но,
имеют спектр Фурье в следующем представлении:
кг
г
п г
1 г
п г
п г
L
г
J L
п г
J L
1 г
J L
il П
J L
1 г
J
1
L
J 1!
1 С
1 1!
!) L|
J
к2
Аналогично, члены V} третьего порядка по е, а именно l/2£^TCi
и 1/6£хНо, имеют спектр Фурье в следующем представлении:
п
П Г1
п п
И Г
&1
1 Г1
tl ri
1 n
n.
L
г
J L
1 fr
J L
il IF
J L
il [г
J L
il 1г
J L
il fr
J L
il Г
J
“1
L
г
J it
1 (г
И It
il If
1 Е
1П 1й
JJ Е
iil fr
JJ tL
il lr
JJ L
il Г
J
"1
L
г
j IL
1 1г
JJ [1
il [г
11 Е
il 1г
HJ 11
ii т
JJ tt
il If
JJ L
il Г
J
-1 k2
Ц
щ 1L
РГ Е
JJ ty
J=U u
LI
Таким образом, все гармоники генерируются, вообще говоря, с ненуле¬
выми коэффициентами, хотя в исходном гамильтониане было всего лишь
несколько фурье-членов.
2.5. Усреднение по средним движениям
57
Легко видеть, что часть Н1 размера es имеет гармоники, вообще го¬
воря, до порядка |k| = 2s. Таким образом, коэффициенты гармоник поряд¬
ка |к| убывают как ехр(—|к|сг), где а = | Inб:|/2, так что закон Фурье (2.18)
выполняется. Фактически этот пример показывает, что после нескольких
шагов нормализации закон Фурье выполняет не только роль верхней гра¬
ницы для величины коэффициентов гармоник преобразованного гамильто¬
ниана: следует к тому же ожидать, что коэффициенты убывают не быстрее,
чем по формуле закона Фурье. Пример точного вычисления коэффициентов
гармоник приведен Морбиделли и Джиорджилли (1997).
2.5. Усреднение по средним движениям
Пертурбационный подход, рассмотренный в предыдущих разделах,
можно непосредственно применить к гамильтонианам ограниченной и пла¬
нетной задач с целью построения нормальной формы, не зависящей от
быстрых углов (средних аномалий, или, что эквивалентно, средних долгот).
Эту процедуру обычно (но неправомерно) на небесномеханическом жар¬
гоне называют усреднением — по той причине, что с точностью до первого
порядка относительно планетных масс она эквивалентна простому усред¬
нению по быстрым углам.
В ограниченной задаче мы начнем с гамильтониана (1.70), однако, что¬
бы избежать явных особенностей, перепишем его, используя модифициро¬
ванные переменные Делоне (1.69). Выберем единицы массы, длины и вре¬
мени так, чтобы QrriQ = 1, и обозначим через е массу самой массивной пла¬
неты в единицах массы Солнца. Векторы sj (t) можно записать как функции
элементов планетных орбит (предположим здесь, что планеты движутся по
кеплеровым орбитам)4. Таким образом, зависимость возмущения от време¬
ни проявляется только через средние долготы планет Xj. Предположим, что
последние изменяются линейно со временем, причем каждая со своей соб¬
ственной независимой частотой. Как объяснено в разделе 1.5, чтобы сде¬
лать гамильтониан автономным, удобно расширить фазовое пространство
путем введения пары сопряженных переменных «действие-угол» для каж¬
дой независимой пары «время-частота». Естественно выбрать в качестве
новых углов планетные долготы А^; если обозначить через A j сопряжен¬
ные им переменные действия, гамильтониан ограниченной задачи примет
4 На данном этапе отсутствует необходимость учета прецессии планетных орбит, так как
скорости прецессии малы, и тем меньше, чем меньше е. — Прим. авт.
58
Глава 2
вид (2.1), а именно:
1 N
Н = Но + еН\ — — ^д2 пз^з + £^i(A, Р, Q, А,р, g, Ai,..., Адг),
3 = 1
(2.38)
где rax,..., пдг — средние движения (то есть орбитальные частоты) АГ пла¬
нет. Возмущение Н\ является к тому же функцией планетных долгот пери¬
гелиев pj и долгот узлов qj, но они, будучи по предположению фиксиро¬
ванными, играют роль параметров. Эффекты, вызываемые их медленным
изменением, будут рассмотрены в главах 8 и 11. Согласно (1.29) возмуще¬
ние Н\ является суммой возмущений, вызываемых отдельно каждой пла¬
нетой, то есть Н\ = Ylj ^i^(A, Р, Q, А,р, q,\j,Pj, qj). Другими словами,
углы, относящиеся к разным планетам, не могут появляться в одной и той
же гармонике в Hi.
В планетной задаче мы начнем с гамильтониана (1.74), переписанного
в модифицированных переменных Делоне (1.76). Обозначим через е массу
самой массивной планеты в единицах массы Солнца, а через pj — массу
j-ой планеты в единицах массы самой массивной планеты; опять же еди¬
ницы выберем так, чтобы Q = то = 1. Тогда, используя принятые при за¬
писи (1.39) определения pj, имеем fij — ePj/(\ + ePj) и mo + mj = 1 + ePj.
Введем новые переменные действия Л' = Aj/e, Pj = Pj/e и Q' = Qj/e,
где Aj,Pj и Qj определяются формулами (1.76); при этом угловые пере¬
менные Aj,pj и qj оставляем прежними. Легко видеть, что гамильтонова
форма уравнений движения сохраняется, если определить новый гамильто¬
ниан Н' = Н/е.5 Он имеет вид (2.1), а именно:
N (1+е&)-\03
2(Л')2
+ £H'i(Ai, Р{, Q[, Ai,pi, qi,..., Л^, Р^, <5дг, Адг,рдг, #лг). (2.39)
W - Н'0 + еН[ --J2 —1 +
з=1
В дальнейшем для упрощения обозначений штрихи будем опускать. Со¬
гласно (1.38) Hi является суммой функций, описывающих парные взаимо¬
действия планет. Поэтому в его разложении в ряд Фурье ни одна из гармо¬
ник не может содержать комбинации углов более чем двух планет.
5Это преобразование относится к расширенному классу канонических преобразований,
при которых преобразуется и гамильтониан (в разделе 1.6 такой класс не рассматривался). —
Прим. авт.
2.5. Усреднение по средним движениям
59
Чтобы применить пертурбационный подход, возмущения eHi в (2.38)
и (2.39) раскладываем в ряды Фурье и сохраняем только гармоники с ко¬
эффициентами порядка е, а гармоники с коэффициентами порядка е2 или
выше низводим в возмущающую функцию более высокого порядка, е2Н<2\
таким образом, Н = Ho+eHi+£2H2- Функции Hi и еН2 играют роль Hfк
и HfК, определенных в (2.19). Аналитические свойства исходного гамиль¬
тониана совместно с правилами Даламбера гарантируют, что Н\ содержит
лишь конечное число гармонических членов, которые можно вычислить
в явном виде.
2.5.1. Вековая нормальная форма
Нормальная форма порядка е вычисляется как Hl = S^H, где х удо¬
влетворяет уравнению (2.10). Однако производящий гамильтониан х нель¬
зя выбрать так, чтобы усредненный гамильтониан Hi зависел бы только от
переменных действия. Фактически из-за вырожденности задачи двух тел,
в которой частоты перигелиев и узлов тождественно равны нулю, гармони¬
ки, не зависящие от средних долгот, но зависящие от перигелиев и узлов,
нельзя исключить.
Чтобы пояснить это, рассмотрим ограниченную задачу; анализ пла¬
нетной задачи отличен в основном только в обозначениях. В ограниченной
задаче, поскольку
W1=E Е Cbkm,mj,s,sM,P,Q)x
j k,kj ,m
m3’S'S3
X 6xp [^kX+kjXj+rnp+rrijPj+sq+Sjqj)], (2.40)
производящий гамильтониан x формально будет иметь вид
l—J 3: 3 х
^ (А1)3 к3п3
X exp [L(k\1+kj\1j+mp1+rnjpj+sq1+sjqj)\, (2.41)
где /с, kj, m,rrij, s, Sj — целые числа, а новые канонические переменные
л = s*x л1,...,л = sp1,.. . задаются посредством рядов Ли (см. форму-
ЛУ (2.6)). Тогда очевидно, что все гармоники с к = kj = 0 будут давать в х
* = £ £ -
j к,kj ,тп
60
Глава 2
знаменатели, тождественно равные нулю. Поэтому такие гармоники нельзя
исключить и они должны быть удержаны в Wi. Как следствие, наилучшая
нормальная форма, которую можно надеяться построить, имеет вид
п1 = fto(A\A)) + £H1(A\P\Q\p1,q1,pJ,qJ) + 0(е2). (2.42)
Гамильтониан Н1 представляет собой, по определению, вековую нормаль¬
ную форму до порядка г. В этой форме короткопериодические члены, от¬
носящиеся к орбитальным периодам, исключены в результате усреднения;
таким образом, итоговый гамильтониан описывает долговременную, или
«вековую», эволюцию орбиты, а именно эволюцию переменных Р1 и Q1,
обусловленную прецессионными движениями перигелия р1 и узла ql.
Новые переменные (A1, Р1, Q1, Л1,р1, д1), введенные при построении
вековой нормальной формы, называются средними модифицированными пе¬
ременными Делоне (порядка г). По построению они являются переменными
«действие-угол» для гамильтониана вековой нормальной формы. Форму¬
лы (1.69) позволяют по средним переменным Делоне определить средние
орбитальные элементы (а1, е1, г1, М1, а;1, ГР).
Вековую нормальную форму, однако, можно построить лишь в том
случае, если знаменатели к/(А1)3 + kjUj, появляющиеся в (2.41), отлич¬
ны от нуля при всех значениях к и kj, появляющихся в фурье-разложе-
нии Н\. Как обсуждалось в разделе 2.3, это накладывает ограничения на
область, где можно построить вековую нормальную форму. Конкретно, раз¬
ложение Н\ содержит лишь конечное число гармоник (k,kj), остальные
же низводятся в еН2\ поэтому уравнение к/А3 -У kjrij = 0 имеет конечное
число решений Ao(k,kj,rij). Вековую нормальную форму можно постро¬
ить лишь в области (назовем ее Ы) значений А1, где исключены подхо¬
дящие окрестности Aq(/c, kj, п/. Как будет пояснено в главе 4, область U
не должна содержать окрестности Ао размером у/е. Если А1 — Ао ~ у/е,
то производящий гамильтониан х тоже порядка у/е, как и получающаяся
разность |А — А11 между исходными и новыми переменными. Таким обра¬
зом, чтобы гарантировать принадлежность А1 е Ы, исходные действия А
должны выбираться в области, содержащейся в U вместе с окрестностью
радиуса |А — А1\. Эта ситуация эскизно показана на рис. 2.1. Резонансы
к/А3 + kjUj = 0 называют резонансами средних движений, поскольку они
включают средние движения рассматриваемого тела и jf-ой планеты. В пла¬
нетной задаче резонансы средних движений даются уравнением
и 1 + ePi)-1^/А? + kj( 1 + ер,)-10Цк) = 0, (2.43)
где индексы г и j обозначают две планеты.
2.5. Усреднение по средним движениям
61
yfi
Ло
у/ё у/е
///Л
У//,
////
/// А
Ло
Рис. 2.1. Эскиз геометрического построения вековой нормальной формы. Нормаль¬
ная форма может быть построена только в области \Аг — Ло | > у/е (заштрихованная
область на верхнем рисунке). Чтобы обеспечить попадание Л1 в такую область, ис¬
ходное действие Л следует выбирать в области |Л — Ло | > Ъу/ё (заштрихованная
область на нижнем рисунке). Фактически разность Л — Л1 зависит от углов и может
достигать величины ~ у/ё
Чтобы построить вековую нормальную форму более высокого поряд¬
ка по с, описанную процедуру следует итерировать, определяя последова¬
тельность производящих гамильтонианов Хт и последовательность кано¬
нических преобразований (Лг-1 = 5^ЛГ,..., Лг_1 = 5^АГ,...) таких,
что преобразованный гамильтониан 7ir = S^/Hr~l был бы в вековой нор¬
мальной форме до порядка ег. С этой целью Хг определяется как решение
уравнения {Но ,Хг} + Нт — Нг, где функция Нт зависит только от пе¬
ременных действия, а также от перигелиев и узлов. Однако, как обсужда¬
лось в разделе 2.4, в егНг должны содержаться все гармоники, коэффици¬
енты которых эффективно имеют порядок ег, поэтому количество членов
в его фурье-разложении растет вместе с г. Более того, следует отметить,
что в ограниченной задаче в порядке е2 член {Н\,х} также генерирует
гармоники, зависящие от средних долгот тела и двух планет, а в порядке
£ член {{Wi,xi},Xi} генерирует гармоники, зависящие от средних дол¬
гот тела и трех планет и т. д. Аналогично, в планетной задаче гармоники,
зависящие от комбинаций углов трех планет, появляются в порядке е2; гар¬
моники, зависящие от комбинаций углов четырех планет, — в порядке е3
и т.д. Это подводит нас к более общему определению резонанса средних
62
Глава 2
движений, задаваемому соотношениями
к/А3+ '%2kjnj = 0, fcj(l + £Pj)~1Pj/-h-3 = 0 (2.44)
3 3
в ограниченной и планетной задачах соответственно.
По причине роста числа гармоник область, в которой строится вековая
нормальная форма, необходимо уменьшать на каждом шаге г путем исклю¬
чения окрестностей резонансов средних движений (2.44), чьи соответству¬
ющие гармоники появляются в Нг. Размер этих исключенных окрестностей
составляет О (у/е) по Л, каков бы ни был порядок г шага нормализации, по¬
скольку |Л — Лг| ~ |л—л1! л/е (см. рис. 2.1). Разумеется, область опреде¬
ления исходного действия Л, где строится нормальная форма, должна быть
непустой. Этим накладывается ограничение на полное число окрестностей
резонансов, которые можно исключить. В свою очередь, это вынуждает
ограничить порядок г, до которого строится вековая нормальная форма.
К сожалению, из-за технических трудностей оперирования с рядами
при вычислениях на практике вековую нормальную форму строят лишь до
весьма ограниченных порядков по е. В нескольких приложениях в огра¬
ниченной задаче (см., например, Уильямс, 1969; Уильямс и Фолкнер, 1981;
Козаи, 1962; Накаи и Киношита, 1985; Иошикава, 1987) вековая нормальная
форма вычислена лишь до порядка е путем простого усреднения возмуще¬
ния по средним долготам. Более того, поскольку производящий гамильто¬
ниан в этих работах явно не вычислялся, средние элементы несколько непо¬
следовательно полагались просто равными начальным значениям оскулиру-
ющих элементов.
Более точное вычисление провели Милани и Кнежевич (1990), вычис¬
лившие вековую нормальную форму до порядка е2. Они учли в Hi возму¬
щения, вызываемые Юпитером и Сатурном, и разложили Hi в ряд Фурье,
удерживая в нем гармоники с |fc| и \kj\ не больше 14, а также разложили его
коэффициенты п0 степеням эксцентриситетов и наклонений,
удерживая члены до четвертой степени. Эти ограничения, в свою очередь,
ограничивают возможные значения га, raj, s и Sj согласно правилам Далам-
бера. Средние элементы были вычислены (при задании х в явном виде) до
порядка е, а не е2, поскольку второй производящий гамильтониан \2 не
вычислялся явно.
Леметр и Морбиделли (1994) осуществили схожее вычисление, не рас¬
кладывая, однако, возмущение в ряд по степеням эксцентриситета и накло¬
нения малого тела (но так же раскладывая по степеням эксцентриситетов
2.5. Усреднение по средним движениям
63
и наклонений планет). С этой целью в узлах регулярной решетки в про¬
странстве (а, е,г) они численно разложили возмущение и его производ¬
ные в ряды Фурье и построили вековую нормальную форму до порядка с2.
Затем в приложениях они вычисляли вековую нормальную форму в лю¬
бой произвольной точке пространства (а, е, г) путем интерполяции данных,
найденных для узлов решетки.
Что касается планетной задачи, построения вековой нормальной фор¬
мы в рамках гамильтонова подхода, описанного в этом разделе, по истори¬
ческим причинам не производилось. Тем не менее получены эквивалентные
результаты. Ласкар (1985, 1986, 1988) численно получил уравнения движе¬
ния, соответствующие вековой нормальной форме порядка е2. В них учте¬
ны все планеты от Меркурия до Нептуна, а возмущения разложены до ше¬
стого порядка по эксцентриситетам и наклонениям. Это потребовало удер¬
живать в рядах примерно 150000 членов. Бретаньон с сотрудниками в ряде
работ (см., например, Симон и Бретаньон, 1975; Бретаньон, 1974, 1982,
1990) строили аналитические эфемериды планет, представляющие все ор¬
битальные элементы в виде рядов Фурье по времени. Их последняя теория
для четырех планет-гигантов (все еще неопубликованная на момент напи¬
сания этой книги)6 эквивалентна вычислению вековой нормальной формы
и производящих гамильтонианов с удержанием всех членов, соответствую¬
щих колебаниям эксцентриситетов, наклонений и относительных больших
полуосей с амплитудами более 2 х 10“7.
2.5.2. Резонансная нормальная форма для резонансов средних
движений
В практических приложениях вековую нормальную форму обычно
строят лишь до весьма ограниченного порядка по е, но и здесь приходит¬
ся избегать окрестностей главных резонансов средних движений, а именно
резонансов, чьи гармоники проявляются в возмущении до порядка по е,
не превосходящего порядок нормальной формы. Чтобы изучать динамику
в окрестностях таких резонансов, прежде всего надо построить резонанс¬
ную нормальную форму, следуя подходу, обсуждавшемуся в разделе 2.3.1.
Например, в ограниченной задаче в окрестности резонанса к/А3 + kjUj = 0
необходимо удержать в нормальной форме гамильтониана не только веко¬
вые углы р и q, но и резонансную комбинацию средних долгот у? = кХ +
+ kj\j9 что порождает малые знаменатели в выражении (2.41) для произ-
6Эта теория остается неопубликованной и на момент выхода в свет перевода книги. —
Прим. ред.
64
Глава 2
водящего гамильтониана х- Поэтому последний определяется из решения
уравнения (2.10), при том что Н\ полагают функцией от р1,#1 и р1 (р =
— S^p\ q = р = S^p1). В общем случае говорят, что гамильтониан
находится в резонансной нормальной форме (для резонанса средних движе¬
ний) до порядка ег, если он преобразован к виду
пгммД = Но + еН*(Аг, Pr, Qr,pr,qr, рг) +
+ ... erH?(Ar, Pr, Qr,pr, qr, pr) + 0(er+1), (2.45)
где Ar, Pr, Qr,pr, gr, <pr — новые переменные (называемые полусредними
модифицированными переменными Делоне), связанные с A, Р, Q,p, <7, че¬
рез последовательность рядов Ли, а (р суть резонансная комбинация сред¬
них долгот, соответствующая заданному резонансу. Полусредние орбиталь¬
ные элементы определяются из полусредних модифицированных перемен¬
ных Делоне путем обращения формул (1.69).
В практических приложениях, когда рассматривают резонансы сред¬
них движений, связывающие средние долготы малого тела и единствен¬
ной планеты, резонансную нормальную форму обычно вычисляют лишь до
первого порядка по е (см., например, Анрар и Леметр, 1983, 1987; Сессии
и Ферраз-Мелло, 1984; Ферраз-Мелло, 1987; Иошикава, 1990, 1991; этот
список далеко не исчерпывающий). В случае же резонансов, связывающих
средние долготы малого тела и двух планет, нормальную форму вычисля¬
ют до порядка г2 (Несворный и Морбиделли, 1998), поскольку в данном
случае коэффициент резонансной гармоники имеет порядок е2.
Динамику, описываемую вековой нормальной формой, мы изучим
в главах 7 и 8 этой книги, а динамику, описываемую резонансными нор¬
мальными формами (для резонансов средних движений), — в главах 9, 10
и 11. Но прежде нам необходимо в общих чертах разобраться в свойствах
возмущенной гамильтоновой динамики (главы 3, 4 и 6) и овладеть некото¬
рыми полезными инструментами для численного исследования этих дина¬
мических свойств (глава 5).
Глава 3
КАМ-торы
3.1. Теорема Колмогорова
Из предыдущей главы следует, что для гамильтоновой системы в об¬
щем случае невозможно построить нормальную форму Биркгофа до про¬
извольного порядка по г на открытой области пространства действий из-за
плотного присутствия резонансов. Это препятствует глобальной интегриру¬
емости системы. Однако согласно главе 2 остается открытой возможность
интегрирования движения при частных значениях действий, соответствую¬
щих нерезонансным частотам.
Простым гамильтонианом, хотя вообще и неинтегрируемым, но допус¬
кающим одно точное решение, является
H(l,<p)=H0(I)+H1(l,v), где ||Wi|| =0(||1||2), (3.1)
а I и р — сопряженные переменные «действие-угол». Действительно, при
1 = 0 уравнения движения сводятся к
i = 0, Ср = gradjWoW, (З-2)
из которых очевидно, что I = 0 и р = gradjWoWt + р§ СУТЬ точное
решение, соответствующее начальным условиям (I, р) = (0,р0). Следова¬
тельно, тор I = 0, (р G Тп (где п — число степеней свободы) инвариантен
относительно потока (3.1), поскольку всякая орбита, стартующая на торе,
никогда его не покинет.
В 1954 году Колмогоров сформулировал теорему, гласящую, что
если заданы аналитическая квазиинтегрируемая гамильтонова система
^(p>q) = Wo(p) +eWi(p,q) и точка р0 в пространстве действий такие,
что
i) ujq = gradp7io(Po) удовлетворяет диофантову условию (2.21) с неко¬
торыми постоянными 7 и т,
66
Глава 3
ii) Но локально невырожден по р0, то есть матрица с элементами
(dHo/dpidpj(p0)) имеет ненулевой определитель,
то существует пороговое ё, зависящее от шо, такое, что для всякого е < ё
каноническое преобразование (р, q) —> (I, ф) позволяет записать гамильто¬
ниан в виде (3.1) с gradjWoCO) = ^о-
Теорема Колмогорова означает, что квазиинтегрируемые гамильтоновы
системы при достаточно малых возмущениях допускают инвариантные то¬
ры, несущие движение с диофантовыми частотами. Уравнения Гамильтона,
в общем случае неинтегрируемые, можно проинтегрировать на этих торах.
Теорема Колмогорова позднее была обобщена и улучшена Мозером (1962)
и Арнольдом (19636); поэтому сейчас она повсеместно известна как КАМ-
теорема. Инвариантные торы, несущие нерезонансное движение, обычно
называют КАМ-торами.
3.1.1. Эскиз доказательства теоремы Колмогорова
Доказательство теоремы Колмогорова интересно и поучительно, по¬
скольку его схема представляет собой замечательное приложение теории
возмущений и нормальных форм, проиллюстрированной в предыдущей
главе.
Прежде всего разложим гамильтониан в ряд Тейлора по переменным
действия в окрестности точки р0, вводя обозначение р = р — р0. Оче¬
видно, что р и q являются каноническими переменными «действие-угол».
В новых переменных гамильтониан записывается как
ЩР,Ч) = ^o-P+^P-C'p + 0(||p||3)+£[/o(q) + p-fi(q) + 0(||p||2)], (3.3)
где С — матрица значений вторых производных от Но в точке р0,
/о = Wi(p0,q), fi — вектор с компонентами dHi/dpj(p0, q), j = 1,... ,n.
Через 0(||p||J) обозначены члены, имеющие порядок по действиям не ни¬
же j.
Будем теперь искать каноническое преобразование, которое (3.3) пре¬
образует к форме (3.1) до порядка г2. Это делается путем композиции трех
канонических преобразований, каждое из которых задается посредством
подходящего производящего гамильтониана.
Первое из них имеет целью исключить в возмущении член /o(q). За¬
дадим производящий гамильтониан хо? не зависящий от действий, и ка¬
ноническое преобразование р = S£0Pi, q = *S'^0qi. В новых переменных
3.1. Теорема Колмогорова
67
гамильтониан (3.3) принимает вид
Sxon = ш° ' Pi + ^р1 ' Ср1 + °(llpil|3) + еК“о • Pi,Xo} + /o(qi) +
+ {Pi • CPdXo} + Pi • fi(qi) + 0(||Pl||2)] + 0{e2).
(3.4)
Легко видеть, что последние два члена в первой строке не зависят от дей¬
ствий, а первые два члена во второй строке линейны по рг. В дальнейшем
мы обозначаем выражение {рх • Ср1?хо} + Pi • fi(qi) через рх • flji(q1).
В качестве производящего гамильтониана хо выбираем решение уравнения
{^о,- PijХо} + /o(Qi) = /о, где через /0 обозначено среднее от /0 по уг¬
лам. Не зависящие от действий члены исчезают — от них остается лишь
константа, которую в итоговом гамильтониане можно опустить. Расклады¬
вая /о в ряд Фурье:
/оЫ = Y1 ckexp(tk-q1), (3.5)
k€Zn
имеем
Xo(qi) = —i7TrexP(tk-4i), (3.6)
k€^\0 k ’
где через k G Zn \ О обозначены все ненулевые целочисленные векторы.
Как мы уже убедились в предыдущей главе, поскольку /о является ана¬
литической функцией (что следует из аналитичности исходного гамильто¬
ниана), а о>о диофантово, ряд Фурье, определяющий хо в (3.6), сходится
абсолютно.
Второе преобразование служит для исключения нового члена
Pi * f 1,1 (Qi) в (3.4). Зададим производящий гамильтониан хь линейный
по действиям, и каноническое преобразование рх = S^p2, 4i =
В новых переменных гамильтониан (3.4) принимает вид
SxiSxon = шо ■ Ра + ^Р2 • Ср2 + 0(||р2||3) + ^
+ е[{^0 • Р2,Xi} + Р2 • fi,i(q2) + °(IIP2l|2)] + 0{е2).
Легко видеть, что первые два члена во второй строке линейны по действи¬
ям. Производящий гамильтониан xi определяется как решение уравнения
{^о • P2>Xi} + р2 * f 1,1 (Q2) — Р2 * f 1,1» гДе через обозначено среднее
68
Глава 3
от fi x по углам. Записывая xi — Р2 ’ ^(^2) и раскладывая f^i как
f 1,1(42) = XI dkexp(ik-q2), (3-8)
k£Zn
имеем
g(42) = -i ^2 77- ехР (tic - q2). (3.9)
k6^\o k'W°
Опять же, поскольку fi}i аналитична, a с^о диофантово, ряд, определяю¬
щий g, абсолютно сходится.
Однако это второе преобразование дает в итоге гамильтониан
SX1SX0н = • Р2 + ^Р2 • СР2 + 0(||р2II3) + ф2 ■ f 1,1 + 0(||р2II2)] + 0(е2),
(3.10)
где все еще присутствует линейный по действиям член (p2*f 1,1) в порядке е.
Из-за этого члена частоты тора р2 = 0 (вычисленные в пренебрежении чле¬
ном 0(е2)) теперь равны и?о + efi,i. Эти частоты отличаются от о; о лишь
на величину порядка е, но этого может оказаться достаточно для потери
ими их существенного диофантова свойства, что тем самым влечет запрет
итерирования описанной процедуры для исключения угловых членов, не
зависящих от действий и линейных по действиям при более высоких по¬
рядках по е. Однако невырожденность матрицы С в (3.3) (гарантированная
условием (ii) теоремы) обеспечивает, что вблизи тора р2 = 0 будет суще¬
ствовать тор р2 = б5р с ||<5р|| = 0(1), с частотами o>o + £fi,i +еС8р = о>о-
Фактически достаточно положить 5р = —C~liхд, где С~1 — матрица, об¬
ратная С (она существует, поскольку определитель матрицы С отличен от
нуля по условию невырожденности). Таким образом, мы задаем третье ка¬
ноническое преобразование: р3 = р2 — £<5р, q3 = q2. Его можно записать
как р2 = S^Spр3, q2 = S^,6pq3, где xsp = —<^Р • Чз- Как следствие, в новых
переменных «действие-угол» гамильтониан можно записать как
SxsPSxiSxоП = ^0-Рз + |рз*С'Рз+С>(||рз|Г)+£О(||рз|Г)+О(е2). (3.11)
Гамильтониан (3.11) имеет форму (3.1) — так называемую колмогоровскую
нормальную форму — до второго порядка по е.
Описанную процедуру можно итерировать, придавая гамильтониану
колмогоровскую нормальную форму до все более и более высокого поряд¬
ка по е. Используется последовательность трех преобразований вида р =
= 5^(r)p', q = S'^(r)q/, где через р, q, р', q', как обычно, обозначены старые
3.2. Свойства КАМ-торов
69
и новые переменные «действие-угол», а через х^ — подходящие произво¬
дящие гамильтонианы для исключения членов, не зависящих от действий
или линейных по ним в каждом порядке г по е. В данном случае не су¬
ществует принципиальных препятствий для итерирования нормализующей
процедуры до бесконечного порядка, поскольку колмогоровская нормаль¬
ная форма требует не полного исключения гармоник (что было бы невоз¬
можно из-за плотного присутствия резонансов), но лишь тех из них, чьи ко¬
эффициенты не зависят от действий или линейны по ним. Коэффициенты
гармоник могут иметь величину до 0(е||р||2). Строгие оценки показыва¬
ют, что ряд, получающийся при нормализации до порядка г, сходится при
г —> 6о, если е достаточно мало (см., например, Джиорджилли и Локателли,
1997). Это доказывает теорему Колмогорова.
Теорема Колмогорова также справедлива для гамильтонианов, зави¬
сящих от времени, вида Но(р) + sHi(p, q, v\t,..., vnt), если частоты
z/!,...,z/n диофантовы. Из главы 1 мы знаем, что гамильтониан можно
записать в автономной форме, как в (1.31). Очевидно, что теорему Кол¬
могорова нельзя применить к такому гамильтониану, поскольку 'Но(р) +
+ 'ZZjVjTj, очевидно, вырожден. Однако если обратиться вновь к схеме
доказательства, то станет очевидным, что, поскольку в возмущении Hi
нет действий Tj, частоты v\,..., vn в процессе построения колмогоров-
ской нормальной формы никогда не изменяются. Таким образом, никогда
не возникает необходимости применить третье преобразование (для кото¬
рого только и требуется выполнение условия невырожденности) к действи¬
ям Tj. Поэтому условие невырожденности Но(р) относительно действий р
является достаточным.
3.2. Свойства КАМ-торов
КАМ-теорема дает первичное представление о динамических свой¬
ствах квазиинтегрируемых гамильтоновых систем при достаточно малых
возмущениях. Как проиллюстрировано в главе 1, динамика интегрируемой
аппроксимации Но(р) дает слоение фазового пространства на инвариант¬
ные торы; при этом действия р постоянны, а углы q циркулируют линейно
со временем с частотами и>о(р) (левая панель рис. 3.1). Если добавить ма¬
лое возмущение eWi(p,q), то КАМ-теорема гарантирует, что некоторые
торы с диофантовыми частотами сохранят инвариантность относительно
потока полного гамильтониана Но + еН\. Для каждого инвариантного тора
можно задать новые локальные переменные «действие-угол» I, <р, такие,
70
Глава 3
что гамильтониан преобразуется к форме (3.1). В этих переменных движе¬
ние на торе является очень простым: действия I постоянны на инвариант¬
ном торе, а углы р циркулируют линейно со временем. В исходных пере¬
менных р, q движение на торе можно вычислить путем композиции всех
преобразований, потребовавшихся для приведения гамильтониана к фор¬
ме (3.1). Поскольку каждое из этих преобразований периодично по углам,
соотношение между p,q и I, р имеет вид р = P(I, р), q = Q(I, р), где
функции Р и Q периодичны по р, a Q-1 периодична по q. Следователь¬
но, на торе углы q уже более не являются линейными функциями време¬
ни, но их спектр Фурье имеет постоянные частоты, тогда как действия р
демонстрируют осцилляции, периодические по углам q (поскольку р =
= P(I, Q-1(q))) и квазипериодические по времени (поскольку углы имеют
нерезонансные частоты). Однако среднее от р по времени не равно зна¬
чению р0, при котором невозмущенные частоты Ыо(Ро) равны частотам
инвариантного тора. Другими словами, при заданном векторе частот воз¬
мущенный инвариантный тор испытывает сдвиг в фазовом пространстве
относительно невозмущенного тора. Эта ситуация проиллюстрирована на
рис. 3.1. Отметим, что о возмущенной динамике вне инвариантных торов
КАМ-теорема ничего не говорит. В этом случае, как будет показано в сле¬
дующей главе, требуется изучать резонансную динамику.
е = 0 £ Ф 0
Рис. 3.1. В случае интегрируемого гамильтониана фазовое пространство расслаива¬
ется на инвариантные торы. Согласно КАМ-теореме, торы с диофантовыми часто¬
тами сохраняются, если возмущение мало. Однако действия на возмущенных торах
являются уже не константами движения, а периодическими функциями углов. Более
того, средние значения действий на КАМ-торе в общем случае отличны от значений
действий, соответствующих невозмущенному тору с теми же частотами
3.2. Свойства КАМ-торов
71
Величина возмущения е определяет, какие торы сохраняют инвариант¬
ность среди всех невозмущенных торов с диофантовыми частотами. Теоре¬
ма Колмогорова утверждает, что величина е должна быть меньше порого¬
вой ё. Последняя зависит от вектора частот через константы 7 и т, харак¬
теризующие диофантово свойство (2.21). Согласно теореме Колмогорова
оказывается, что ё ~ 74. Следовательно, с увеличением возмущения число
сохраняющих инвариантность торов уменьшается; «выживают» лишь то¬
ры с достаточно большими 7. Если е достаточно велико, то инвариантных
торов не остается вообще. КАМ-теорема в версии Арнольда (19636) утвер¬
ждает, что мера Лебега множества инвариантных торов отлична от нуля,
если е достаточно мало. Более того, эта мера растет с уменьшением е,
и в пределе е —> 0 она стремится к 1. Более поздняя оценка Нейштадта
(1982) показывает, что эта мера стремится к 1 как 1 — у/е. Данный резуль¬
тат можно интерпретировать с вероятностной точки зрения. Представим
себе, что мы численно исследуем гамильтонову систему и, ничего не зная
заранее о ее динамике, задаем начальные условия для тестовых орбит слу¬
чайным образом. Если пренебречь ошибками округления, вероятность слу¬
чайного выбора начальных условий на КАМ-торе пропорциональна мере
Лебега множества КАМ-торов. Таким образом, в свете результата Арнольда
вероятность того, что орбита интегрируется на КАМ-торе, в пределе очень
малых возмущений близка к 1. Это свойство будет проиллюстрировано на
численных примерах в следующем разделе.
В гамильтоновых системах с двумя степенями свободы каждый КАМ-
тор разделяет фазовое пространство на две динамически несвязанные ча¬
сти. Фактически фазовое пространство четырехмерно, но сохранение га¬
мильтониана принуждает движение происходить в трехмерном простран¬
стве. Инвариантный тор представляет собой двумерное многообразие, по¬
груженное в это трехмерное пространство. Как следствие, траектории не
могут перейти из области с одной стороны инвариантного тора в область на
другой стороне, не пересекая тор; очевидно, это невозможно в силу опреде¬
ления инвариантности (инвариантность как раз и означает, что временная
эволюция при любых начальных условиях на торе никогда не приведет
к уходу с тора). В следующем разделе будет дана иллюстрация изолирую¬
щего свойства КАМ-торов в системах с двумя степеней свободы. Для га¬
мильтоновых систем с числом степеней свободы более двух изолирующее
свойство уже не имеет места из-за большей коразмерности КАМ-торов от¬
носительно размерности фазового пространства. В случае п степеней сво¬
боды размерность фазового пространства равна 2гг. Сохранение гамиль¬
тониана принуждает движение происходить в (2n — 1)-мерном простран-
72
Глава 3
стве. КАМ-тор имеет размерность п; следовательно, коразмерность равна
п — 1. Это означает, что фазовое пространство разделяется на несвязные
области, только если п ф 2. «Визуализировать» этот важный и строгий
геометрический вывод очень трудно, так как нельзя наглядно представить
себе пространство или поверхность, имеющие размерность соответственно
более трех или двух. Чтобы все же получить интуитивное .нестрогое пред¬
ставление, вместо рассмотрения динамики в фазовом пространстве удоб¬
но обратить внимание на пространство частот, которое, если учесть по¬
стоянство гамильтониана, в случае системы с п степенями свободы имеет
лишь (п — 1) измерений. В системе с двумя степенями свободы на поверх¬
ности постоянного гамильтониана пространство частот представляет со¬
бой прямую, параметризуемую отношениями На этой линии частот
КАМ-торы суть фиксированные точки, соответствующие диофантовым от¬
ношениям; здесь очевидно, что всякий КАМ-тор разделяет пространство
частот на две несвязанные части. Траектории, не лежащие на инвариант¬
ных торах, могут, в принципе, блуждать по линии частот, но не могут вы¬
ходить за точки, соответствующие диофантовым отношениям (см. рис. 3.2),
то есть движение ограничено КАМ-торами. В системе с тремя степенями
свободы на поверхности постоянного гамильтониана пространство частот
двумерно. В качестве координат можно выбрать отношения частот loi/uj3
и CJ2/W Опять же КАМ-торы на этой плоскости частот представлены точ¬
ками, а траектории, не лежащие на инвариантных торах, могут на ней блуж¬
дать. Из рис. 3.2 очевидно, что они могут демонстрировать «слалом» среди
КАМ-торов и «диффундировать», в принципе, повсюду.
Обрисованная картина, однако, несколько наивна, так как «слаломное»
продвижение среди КАМ-торов может быть экстремально долгим по вре¬
мени. В этом можно убедиться следующим образом. Если гамильтониан
записан в колмогоровской нормальной форме (3.1), то в окрестности ин¬
вариантного тора можно строить нормальную форму Биркгофа, то есть
исключать все члены порядка г по е, зависящие от углов, увеличивая г
до оптимального порядка. Эта процедура полностью аналогична проиллю¬
стрированной нами в разделе 2.4.1, так что оптимальная величина остатка
нормальной формы определяется минимальным порядком резонансов, пе¬
ресекающих область, где строится нормальная форма. В окрестности Ыв
(радиуса д) инвариантного тора 1 = 0 имеем
|к • u;(I)| = |к • и;(0) + к • (u;(I) - и>(0))| ^
^ ||к • о>(0)| - |k||u>(I) - w(0)|| > ~ 1к1<*0.
3.2. Свойства КАМ-торов
73
КАМ-торы
хаотическая орбита
\ t / -у
\
КАМ-торы
хаотическая орбита
х
X
(гг = 2)
(п = 3)
Рис. 3.2. Интуитивный эскиз инвариантных торов и «диффузии» в пространстве ча¬
стот. В случае двух степеней свободы пространство частот при заданном значении
гамильтониана является прямой (схема слева), а в случае трех степеней свободы —
плоскостью (схема справа). В пространстве частот инвариантные КАМ-торы яв¬
ляются инвариантными точками. Поэтому в системах с двумя степенями свободы
КАМ-торы ограничивают «диффузию» в пространстве частот, а в системах с тре¬
мя степенями свободы хаотические орбиты могут демонстрировать «слалом» среди
КАМ-торов и «диффундировать», в принципе, повсюду
где и>(1) — частоты тора I в интегрируемом приближении Но(1). Мы ис¬
пользовали диофантово свойство частот и?(0) и тот факт, что для всяко¬
го I G Ыв выполняется ||и>(1) — ы(0)|| ^ ад при некотором положитель¬
ном а. Как следствие, к • u;(I) может быть равно нулю только в случае
|к| > (7/ад)1^т+1\ Поэтому резонансы низшего порядка в UQ имеют по¬
рядок о а величина остатка оптимальной нормальной формы
Биркгофа составит ~ ехр[—Это означает, что «слалом» около
инвариантного тора на рис. 3.2 должен быть экспоненциально медленным
по величине, обратной расстоянию от него. В действительности, как будет
показано в главе 6, ситуация даже еще критичнее: существует пороговое д
такое, что внутри Uq дрейф в пространстве частот является суперэкспонен-
^тот результат можно сопоставить с результатом, полученным в разделе 2.4.1, если по¬
ложить q = е. Отличие состоит в том, что в разделе 2.4.1 минимальный размер области, где
можно строить нормальную форму, составляет ~ е, поскольку исходные действия р осцилли¬
руют с амплитудой порядка е. Здесь же, используя действия I, постоянные на инвариантном
торе, нормальную форму можно построить в любой окрестности произвольного малого раз¬
мера д. — Прим. авт.
74
Глава 3
циально медленным. Таким образом, в системах с более чем двумя степеня¬
ми свободы КАМ-торы, если они достаточно плотны, могут сохранять свою
роль эффективных барьеров для «диффузии» в фазовом пространстве. Эти
барьеры могут быть преодолены только по истечении экстремально долгих
интервалов времени.
3.3. Численные примеры
Наглядные примеры динамической структуры, описываемой КАМ-
теоремой, можно дать для гамильтоновых систем с двумя степенями сво¬
боды, так как в этом случае КАМ-торы легко визуализировать с помощью
так называемых сечений Пуанкаре.
Сечения Пуанкаре весьма полезны, поскольку они позволяют предста¬
вить динамику системы с двумя степенями свободы на двумерных изобра¬
жениях, соответствующих заданным значениям гамильтониана. Это дости¬
гается следующим образом. Рассмотрим гамильтонову систему
W(pi,gi,P2>tf2) (гДе Pi,qi и Р2><?2 — канонические переменные «дей¬
ствие-угол»), ограничившись траекториями, удовлетворяющими условию
W(pi, qi,P2, Q2) = С, где С — некоторая константа. Выберем двумерную
поверхность Е, трансверсальную большинству таких траекторий. Посколь¬
ку переменные действия системы в общем случае совершают лишь малые
осцилляции, а углы циркулируют (изменяясь от 0 до 2ж), в качестве ис¬
комой Е обычно выбирают поверхность, определяемую постоянным зна¬
чением одного из углов, например #2 = 0. При заданном значении С,
значения pi,qi на поверхности <72 = 0 однозначно определяют значение
оставшегося действия Р2, которое можно вычислить, решая неявное уравне¬
ние H(ph qi,P2,0) = С. Теперь, численно интегрируя уравнения движения
(см., например, Пресс и др., 1986), находим последовательные пересечения
каждой траекторией поверхности Е и учитываем только те из них, которые
происходят в заданном направлении, например для которых <72 > 0. По¬
следовательность точек p\,qi, отмечаемых таким образом на Е каждой из
траекторий, дает однозначное стробоскопическое изображение временной
эволюции траектории в фазовом пространстве.
Если траектория лежит на КАМ-торе, то последовательность точек
Pi, qi должна ложиться на одномерную кривую. В самом деле, на КАМ-
торе действия являются периодическими функциями углов; поэтому, обо¬
значая через pi = P{qi,q2) периодическую зависимость pi от обоих уг¬
лов и (72, находим, что на поверхности Е, определяемой условием <72 = 0,
3.3. Численные примеры
75
точки pi,qi должны лежать на кривой р\ = P(qi,0). Более того, посколь¬
ку углы имеют нерезонансные частоты (см. определение нерезонансности
в разделе 1.8), при каждом пересечении поверхности Е угол q\ должен
принимать на промежутке [0,27т] новое значение, и поэтому с течением
времени последовательность точек на Е должна плотно заполнять кривую
= P(qi,0). Следовательно, если вычислять сечение Пуанкаре достаточ¬
но долго, то КАМ-торы проявятся как сплошные кривые, охватывающие
весь промежуток [0,27т].
Чтобы привести пример, нам гораздо проще не выписывать гамиль¬
тонову систему с двумя степенями свободы и численно строить ее сече¬
ние Пуанкаре, а использовать так называемое стандартное отображение,
определяя последовательность точек p\,q\ явно путем итерирования соот¬
ношений
q[=Qi+Pi, p'i=Pi+esin(ql1). (3.13)
Стандартное отображение можно рассматривать как сечение Пуанкаре си¬
стемы с двумя степенями свободы (Анрар, 1970), хотя последнюю и нельзя
записать в явном виде2. Поэтому приведенные выше соображения о ви¬
де КАМ-торов на сечениях Пуанкаре применимы и в случае стандартного
отображения. Если в (3.13) положить е = 0, то стандартное отображение
сводится к сечению Пуанкаре при q2 = 0 для интегрируемой гамильтоно¬
вой системы Н(рг, q1.P2.q2) = Р?/2 + 2тгр2\ таким образом, е играет роль
параметра возмущения.
На рис. 3.3 приведены фазовые портреты стандартного отображения
для различных значений е. Обсудим эти портреты в свете КАМ-теории. Чи¬
татель может также сам легко запрограммировать уравнения стандартного
отображения на компьютере и познакомиться с динамическими структура¬
ми, характерными для различных значений параметра возмущения.
Для построения фазовых портретов на рис. 3.3 выбрано 20 начальных
точек на оси qi = 0, причем эти точки (начальные значения pi) распреде¬
лены на промежутке [—7г,7г] регулярно. При малом е (панель (а)) каждое
начальное условие порождает орбиту, лежащую на КАМ-торе. Это означа¬
ет, что занимаемый КАМ-торами объем велик. Отметим, однако, что торы
существенно искажены по сравнению со случаем е = 0, когда р\ было бы
постоянно на каждом торе. Благодаря искажению торов у прямой р\ = 0 со¬
здается «пустая область». Это не что иное, как резонансная область (соот¬
ветствующая резонансу qi = 0); траектории внутри нее не пересекают ось
2Можно, если использовать дельта-функции, см. Чириков (1979). — Прим. ред.
76
Глава 3
(б)£ = 0.6
0.0
Qi
(в) е = 0.9
0.0
qi
(г) е = 1.2
СМ
о
о
см
I
см
Й,
о
о
см
I
'■%де
Ж1
0.0 2 4 6 0.0 2 4 6
qi qi
Рис. 3.3. Фазовые портреты стандартного отображения при различных значениях £.
Обратите внимание, что с увеличением £ КАМ-торы все более искажаются и их
становится все меньше, тогда как хаотические области все более и более увеличи¬
ваются. См. комментарии в тексте
qi = 0, так что их нельзя построить при нашем выборе начальных условий.
Динамика внутри резонансной области будет детально исследована в сле¬
дующей главе. Наконец, отметим следующий факт: тогда как большинство
КАМ-торов проявляются на панели (а) как сплошные кривые, один из них,
проходящий через точку pi = —2.24 (а также, по симметрии, и через р\ =
= 2.24) на оси qi = 0, выглядит как пунктирная кривая. Объясняется это
3.3. Численные примеры
77
тем, что время, необходимое для видимого заполнения тора плотным (от¬
носительно разрешения графика) образом, зависит от частот на торе. Чем
ближе отношение частот к рациональному числу, тем больше это время.
При построении рис. 3.3 число итераций стандартного отображения для
каждого начального условия составило лишь 1000; если его удвоить, то
пунктирный тор также будет выглядеть сплошным.
В случае панели (б) значение е увеличено в три раза. Динамическая
структура существенно изменяется. Теперь лишь 14 начальных условий по¬
рождают траектории, лежащие на КАМ-торах. Начальные условия с pi =
= ±2.84 и р\ = ±1.36 порождают траектории, все еще лежащие на инва¬
риантных кривых, но эти кривые имеют топологическую структуру, отлич¬
ную от структуры КАМ-торов: они выглядят как цепочки кружков (остро¬
вов). Эти инвариантные кривые также соответствуют резонансной динами¬
ке; они будут обсуждаться в следующей главе. Наконец, траектории с на¬
чальными условиями pi = ±0.15, qi = 0 не лежат на инвариантных кри¬
вых, а выглядят как множество рассеянных точек. Область, покрытая таки¬
ми точками, называется хаотической областью. Мы увидим, что ее суще¬
ствование также связано с резонансной динамикой. В хаотической области
КАМ-торы отсутствуют и действия не являются периодическими функция¬
ми углов. Отметим, что искажения инвариантных торов и размеры «пустой
области» в центре портрета увеличились по сравнению с панелью (а).
В случае панели (в) лишь четыре начальных условия порождают тра¬
ектории, лежащие на КАМ-торах. Это наглядно демонстрирует, что объем,
занятый КАМ-торами, уменьшается с увеличением параметра е. Хаотиче¬
ские зоны проявляются теперь и вокруг некоторых цепочек островов, а не
только, как в случае панели (б), вокруг центральной «пустой области». Как
уже было отмечено в предыдущем разделе, «выживающие» КАМ-торы раз¬
деляют пространство (pi,(?i) на несвязанные области, ограничивая дина¬
мическую эволюцию траекторий в хаотических областях. Например, тра¬
ектория, стартующая с линии pi = —0.15, никогда не достигнет области
с pi < —2.5, поскольку для этого нужно пересечь КАМ-тор.
Наконец, на последней панели (г) КАМ-торов вообще нет. Хаотиче¬
ские области слились воедино и теперь доминируют на фазовом портрете
системы. В хаотической зоне невозможно различить траектории с разными
начальными условиями. Действие р\ может с течением времени принимать
на этих траекториях любые значения.
Из приведенных примеров ясно, что КАМ-теорема способна дать удо¬
влетворительное описание глобальной динамической структуры системы
78
Глава 3
лишь при малых значениях параметра возмущения. Если последний уве¬
личивать, то КАМ-торов становится все меньше и меньше и появляются
другие структуры. Поэтому, чтобы иметь полное представление о гамиль¬
тоновой динамике, необходимо исследовать также дополнение КАМ-торов,
а именно резонансную динамику и взаимодействие резонансов. Это будет
сделано в следующей главе и в главе 6.
Глава 4
Динамика одиночного резонанса
4.1. Интегрируемое приближение
Рассмотрим квазиинтегрируемый гамильтониан Н(р, q) = Wo(p) +
+ eWi(p, q) с n степенями свободы и сосредоточим внимание на обла¬
сти U с одним главным резонансом единичной кратности (см. раздел 1.10,
где дано определение кратности) в пространстве действий. Анализ резо¬
нансной динамики начнем с построения резонансной нормальной формы
с целью минимизации гармоник, не относящихся к главному резонансу.
Обозначим через к минимальный ненулевой целочисленный вектор, отно¬
сящийся к главному резонансу, а именно вектор минимальной нормы такой,
что к • о>о(р) — 0 Для некоторого р Е Ы\ и построим резонансную нор¬
мальную форму относительно резонансного модуля Л4, порождаемого к
(см. определение (2.33)).
Согласно главе 2 резонансная нормальная форма гамильтониана имеет
вид
Н = П0(р) + ^погт
(p,k-q)+ft(p,q), (4.1)
где для простоты для новых переменных «действие-угол», введенных для
построения нормальной формы, сохранено обозначение р, q. Нормализо¬
ванное возмущение 7Ynorm> величина которого не больше е, содержит толь¬
ко главную резонансную гармонику к • q и кратные ей; через 7Z обозначен
остаток оптимальной нормальной формы, величина которого будет обсуж¬
даться в разделе 4.3.
На данный момент мы пренебрежем остатком 7Z и рассмотрим толь¬
ко усеченный резонансный гамильтониан 7-{res = Но + Wnorm- С целью
анализа динамики 7ires удобно ввести новый угол ipi = к • q. Это можно
осуществить путем канонического преобразования. Согласно лемме 4 из
работы Морбиделли и Джиорджилли (1993), всегда можно определить мат¬
рицу U с целочисленными элементами, единичным определителем и пер¬
вой строкой, составленной из компонентов вектора k: /сх,..., /сп. Обозначим
80
Глава 4
через (UT)~l матрицу, обратную транспонированной матрице U. Преобра¬
зование р = Uq, I = (^Т)-1Р является каноническим, и по построению
оно дает р\ = к • q. Угол р\ обычно называют резонансным углом, или
критическим углом резонанса. В новых переменных HTes имеет вид
norm (4-2)
Так как система зависит только от одного угла (а именно, pi), гамиль¬
тониан Hres тривиально интегрируем1. Действия Д,... ,/п являются кон¬
стантами движения, поэтому интерес представляет динамика на плоскости
(Д, р\). На этой плоскости движение эволюционирует вдоль кривых посто¬
янного уровня HresihiPi), а остальные действия играют роль параметров.
В случае общего положения динамика HTes на плоскости (Ii,pi) имеет
локальную структуру динамики маятника. Это можно показать следующим
образом. Обозначим через р* значение вектора действий р, являющееся
точно резонансным, то есть удовлетворяющее уравнению к • и>о(р*) = 0.
Пусть I* = (UT)~1 р*. Положим теперь в (4.2) действия Д,..., /п равными
и разложим гамильтониан в ряд Тейлора по Д в окрестности
точки I*. Полагая Д = Д — I* и пренебрегая членами порядка Д в Но
и порядка Д в Нпотхп, находим, что (4.2) приобретает вид
nres = a(V)h + Ш/* + Пп огш(Г, Vi), (4.3)
где а и (3 — коэффициенты при членах первого и второго порядков разло¬
жения Но в ряд Тейлора. В этом выражении а должно быть равно нулю;
действительно, если ограничиться Но, то а равно ф\ в точке резонанса
Д = 0, a pi = к • q = к • с^о(р*) = 0. Наконец, в (4.3) разлагая НПОтш
в ряд Фурье по pi, оставим только главный член. Без ущерба для общ¬
ности предположим, что ведущей гармоникой является c(I*) cos</?i, тогда
гамильтониан HTes приобретает вид
Wres = 7^1 + CC0S¥>1, (4.4)
представляющий собой известный всем гамильтониан маятника.
]Если бы рассматриваемый резонанс имел кратность m > 1, то результирующая усечен¬
ная нормальная форма не была бы интегрируемой, так как в этом случае она зависела бы от
7п независимых углов. Случай резонансов более высокой кратности будет обсуждаться в гла¬
ве 6. — Прим. авт.
4.1. Интегрируемое приближение
81
Рис. 4.1. Интегрируемая резонансная динамика в локальных прямоугольных ко¬
ординатах (левая панель) и в глобальных полярных координатах (правая панель).
Жирной кривой показана сепаратриса; пунктирная прямая/окружность соответству¬
ет невозмущенному резонансному значению h = 7J*
На левой панели рис. 4.1 показана динамика маятника в случае, когда
коэффициенты (3 и с оба положительны; левая и правая границы панели
тождественны друг другу. Маятник имеет две точки равновесия, обе при
1\ = 0: одна из них при — 0 — неустойчивая, или гиперболическая,
другая при ipi = 7г — устойчивая, или эллиптическая. Жирная кривая, со¬
единяющая неустойчивую точку равновесия саму с собой (по модулю 27т),
называется сепаратрисой, так как она разделяет плоскость на три
области с различными динамическими свойствами. В области выше сепа¬
ратрисы угол pi циркулирует (изменяясь от 0 до 2тг) с положительной про¬
изводной; частота циркуляции монотонно растет с увеличением расстояния
от сепаратрисы. В области ниже сепаратрисы угол тоже циркулирует,
но с отрицательной производной. В области внутри сепаратрисы угол ipi
либрирует около значения 7г, и движение эволюционирует по замкнутой
кривой вокруг устойчивой точки равновесия. Частота либрации равна у/ф
для траектории, ближайшей к устойчивому равновесию, и уменьшается до
нуля с приближением к сепаратрисе. На сепаратрисе, требуется бесконеч¬
ное время для движения от точки неустойчивого равновесия к ней же, так
как при приближении к точке неустойчивого равновесия движение замед¬
ляется экспоненциально со временем. Области выше и ниже сепаратрисы
называются областями циркуляции, а область внутри сепаратрисы — обла¬
стью либрации. Резонансная область суть не что иное, строго говоря, как
область либрации, поскольку лишь для либрирующих орбит усредненная
производная от pi по времени равна нулю. Выше и ниже сепаратрисы
напротив, в среднем положительна или отрицательна. Полуширина резо¬
82
Глава 4
нансной области, измеряемая как значение Д в апексе сепаратрисы, равна
2 у/с/р. Поэтому минимальный размер области U для построения резонанс¬
ной нормальной формы должен составлять 4yjc/fi по Д. В разделе 4.3 мы
увидим, каким образом это определяет величину остатка оптимальной нор¬
мальной формы. Полуширина резонанса в пространстве невозмущенных
частот равна невозмущенной частоте резонансного угла в апексе сепа¬
ратрисы, а именно 2 у/]3с.
Разумеется, (4.4) является лишь локальной аппроксимацией динами¬
ки Hres около Д = Ц. Но в большинстве задач небесной механики Д и рi
образуют систему глобальных полярных координат. Глобальное представле¬
ние резонансной динамики в этих координатах показано на правой панели
рис. 4.1. Очевидно, около Д = Ц динамика топологически эквивалент¬
на показанной на левой панели; однако вблизи начала координат Д = О
имеется третья (устойчивая) точка равновесия. Фактически в канонических
прямоугольных координатах х = \/2Д sin</?i, у = yj2I\ cos<^i, коль скоро
гамильтониан Hres аналитичен в точке х = у = 0 (что для гамильтониа¬
нов небесной механики гарантируется правилами Даламбера), все кривые
должны быть гладкими; поэтому вблизи центра кривые должны быть топо¬
логически эквивалентны окружностям вокруг фиксированной точки. Свой¬
ство аналитичности в точке Д = 0 означает, что разложение (4.2) в ряд
Фурье имеет вид '£/т cm(h) exp[mwpi], где cm(Ii) ~ /,m/2+fe, k — неот-
рицательное целое число (см. обсуждение правила 4 в разделе 1.9.3). Если
сДД) = \/Д (то есть к = 0), то точка равновесия сдвинута относительно
Д = 0, а во всех других случаях она расположена в Д =0.
Портрет на рис. 4.1 можно считать парадигмой интегрируемой ре¬
зонансной динамики. Фактически учет гармоник более высокого порядка
по cpi и полный учет зависимости от Д для всех коэффициентов могут
деформировать динамический портрет HTes по сравнению с портретом на
правой панели рис. 4.1, но в общем случае это не изменяет его главных осо¬
бенностей: наличия устойчивой точки равновесия, окруженной сепаратри¬
сой, соединяющей неустойчивую точку равновесия саму с собой, и наличия
второй устойчивой точки равновесия вблизи начала полярных координат.
4.2. Резонансные переменные «действие-угол»
Так как усеченная резонансная нормальная форма (4.2) интегриру¬
ема, согласно теореме Арнольда -Лиувилля можно ввести новые пере¬
менные «действие-угол» J,^ и записать Wres в виде функции только
4.2. Резонансные переменные «действие-угол»
83
действий J. Назовем эти новые переменные резонансными переменны¬
ми «действие-угол». Введение резонансных переменных «действие-угол»
очень важно в небесной механике для возможности детального анализа воз¬
мущенной резонансной динамики. Поэтому в данном разделе мы подробно
рассмотрим, как эти переменные определяются и как в приложении к но¬
вому гамильтониану использовать численные методы.
Поскольку в (4.2) действия /2, являются константами движения,
новые действия J2,Jn просто равны исходным, то есть J2 = h, • ••, Лг =
= /п. Определить Ji сложнее. Коль скоро значения фиксирова¬
ны, гамильтониан (4.2) сводится к гамильтониану с одной степенью сво¬
боды. Таким образом, в переменных 1\,ц>\ каждая траектория представле¬
на замкнутой кривой. Эти кривые являются циклами, используемыми со¬
гласно рецепту Арнольда для определения нового действия. Как видно из
рис. 4.1, в резонансной задаче есть вращательные циклы (где принима¬
ет значения от 0 до 27т) и колебательные циклы (где ограничено между
^lmin и ^lmax)- На каждом цикле действие 1\ можно выразить как функ¬
цию от (/?ь решая неявное уравнение Wres^b^i) — гДе постоянная Е
суть значение гамильтониана на цикле. Согласно разделу 1.9 действие Ji
определяется как интеграл по циклу от действия 1\:
что является нормированной на 2тт площадью области между циклом
и осью Ii = 0 (см. рис. 4.2, панель (а)). В случае колебательного цикла
формула (4.5) приводится к виду
рис. 4.2, панель (б), разность этих двух интегралов представляет собой
площадь выделенной пунктиром области, то есть области, ограниченной
колебательным циклом.
(4.5)
В случае вращательного цикла имеем просто
2тг
h(E,<pi)d(pi
(4.6)
где If соответствует верхней части цикла, а 1г — нижней части. На
84
Глава 4
Рис. 4.2. В области вращений (панель (а)) действие J\ пропорционально площа¬
ди области между циклом и осью 1\ — 0, а в области либраций (панель (б)) оно
пропорционально площади области, ограниченной колебательным циклом
Что касается новых углов гр, то они могут быть заданы с помощью
производящей функции S= (см. формулу (1.56)). Одна-
** г=1
ко можно использовать тот факт, что новые углы являются ли¬
нейными функциями от времени (поскольку новый гамильтониан зависит
только от действий J) и что преобразование между старыми и новыми пере¬
менными является периодическим на цикле (что обеспечивается теоремой
Арнольда-Лиувилля). Поэтому имеем
1>х = Ц, ^ = щ1 ^№),<Рх(№ (1 = 2,(4.8)
где t — время, а Т — период (fi на цикле; причем Т положительно,
если ipi циркулирует с положительной производной или если движение
Ii,ifi происходит на циклах либрации в направлении по часовой стрелке;
в остальных случаях Т отрицательно. При этом соглашении преобразова¬
ние (I, ф) —> (J, гр) близко к тождественному в области вращений и близко
к преобразованию, определяющему переменные «действие-угол» гармони¬
ческого осциллятора в окрестности устойчивой точки равновесия. Из при¬
веденных формул следует, что производная ярх по времени равна частоте
движения на цикле (частоте либрации/циркуляции угла <рi), а производные
по времени от других углов яр1 (I ф 1) равны средним значениям производ¬
ных (pi по времени на цикле. Поэтому на каждом цикле зависимости
и Vii'ipi) можно легко получить из Д(£) и <pi(t) путем подстановки ярх =
4.2. Резонансные переменные «действие-угол»
85
= 27Гt/'T. К тому же, если записать y>i(t) как vfi + gi(t) (где функция Qi(t)
периодична с периодом Т), а щ в виде функции от фх и гр1 (I = 2,..., п),
то получим ф1=ф1 + д(Тфх/2п).
Рассмотрим теперь, как гамильтониан (4.1) выражается через резо¬
нансные переменные «действие-угол». В принципе, и Wres(J), и остаток
7£(J,ф) можно получить путем замены старых переменных на новые. Од¬
нако выписать соотношение между старыми и новыми переменными в яв¬
ной форме очень трудно. Требуется аналитически найти cp(t) и инте¬
грал (4.5). В случае точного гамильтониана маятника (4.4) это требует ис¬
пользования эллиптических функций; но для резонансных гамильтонианов
общего вида (4.2) такое аналитическое вычисление практически невыпол¬
нимо. Тем не менее гамильтониан и его производные в новых переменных,
как показал Анрар (1990), можно эффективно находить численно с помо¬
щью численных методов. Здесь мы приводим лишь некоторые примеры, как
это можно осуществить; более подробные сведения можно найти в статье
Анрара.
Движение на каждом цикле можно вычислить, используя численный
интегратор уравнений движения. Для каждого цикла значение действия J\
можно найти путем численного взятия интеграла (4.5). Это позволяет чис¬
ленно определить функцию J\{E, J2,..., Jn), которую можно численно об¬
ратить и таким образом найти 7iTes = E{J\, ^2, • • •» Jn)-
Легко вычислить и производные от 7ires(J) по J: численное интегри¬
рование дает частоту v\ либрации/циркуляции угла и частоты V2, • •., vn
циркуляции углов ip2,..., (/?п. Но эти частоты равны частотам новых углов
Ф2, • • •, фп- Поэтому имеем
91~Lres j 1 /л п\
= г = (4.9)
Наконец, на каждом цикле можно разложить остаток 1Z (или любую
другую функцию, первоначально записанную в переменных I, <р) в ряд Фу¬
рье по новым углам ф и численно определить коэффициенты этого ряда.
Это делается так. Численное интегрирование позволяет определить 1\ и (р
на каждом цикле как функции времени. Путем подстановки t = Тфх/(2тг)
находим функции /1(^1), (f 1(^1) и pz(V’i)- Затем запишем
к = In, Ф2 + в2{ф\), ■ ■ ■ ,Фп + en(ipi)) (4.10)
и численно найдем преобразование Фурье этого выражения. В результате
имеем коэффициенты фурье-разложения 7Z(J,'*/?) относительно ф\,... ,фп
86
Глава 4
для каждого значения J. Градиент этих коэффициентов по J можно далее
найти путем численного дифференцирования.
Как мы убедились в предыдущем разделе, резонансное фазовое про¬
странство разделяется сепаратрисой на три разные динамические области,
причем «период» на сепаратрисе бесконечен, а циклы в области либра¬
ции и в областях циркуляции имеют разную структуру. Поэтому наборы
переменных «действие-угол», заданных в области либрации и в областях
циркуляции, нельзя сшить гладким образом; особенность, соответствующая
сепаратрисе, неустранима. На практике введение резонансных переменных
«действие-угол» преобразует исходную интегрируемую резонансную дина¬
мическую систему WresC^^i) в три отдельные динамические системы ви¬
да Wres(J)) каждая из которых определена в своей динамической области.
Каждая из этих новых систем характеризуется постоянными значениями
действий J и линейной эволюцией углов ф, но действия и углы у этих трех
систем различны. Как следствие, также и возмущение 7Z в новых перемен¬
ных будет иметь в разных динамических областях разные представления.
Иными словами, всякая интегрируемая система 7iTes(J) будет иметь свое
собственное возмущение К(3,ф). Поэтому при использовании резонанс¬
ных переменных «действие-угол» исследование возмущенной резонансной
динамики разбивается на три параллельных исследования, каждое для сво¬
ей динамической области главного резонанса.
4.3. Возмущенная резонансная динамика
Рассмотрим теперь влияние остатка 7Z оптимальной резонансной нор¬
мальной формы (4.1) на динамику, определяемую интегрируемым прибли¬
жением Wres-
Чтобы зафиксировать терминологию, назовем главным резонансом ре¬
зонанс, для которого построена нормальная форма и чья динамика описы¬
вается 7^res- Вторичными резонансами назовем такие резонансы, которые
присутствуют в области построения нормальной формы, но чьи гармоники
не сохранились в 7ires. Ведущим вторичным резонансом назовем вторич¬
ный резонанс наинизшего порядка.
4.3.1. Величина остатка
Как показано в разделе 2.4, величина 7Z определяется величиной ко¬
эффициента гармоники ведущего вторичного резонанса, которая зависит от
4.3. Возмущенная резонансная динамика
87
рассматриваемой задачи, в частности от частот углов р2,... ,рп. Говоря об
«одиночном резонансе» мы неявно предполагаем, что все вторичные резо¬
нансы имеют существенно больший порядок, чем главный резонанс, так
что 1Z мало в сравнении с Нтеs. Если это не так, то модель «одиночного ре¬
зонанса» неприменима и следует рассматривать мультирезонансную задачу
(см. главу 6).
Отметим два случая, когда можно гарантировать, что 1Z много мень¬
ше Wres? по крайней мере в пределе малой величины коэффициента с гар¬
моники главного резонанса (см. формулу (4.4)).
i) Две степени свободы. Напомним, что согласно разделу 4.1 минималь¬
ный размер области построения резонансной нормальной формы, чтобы
охватить всю резонансную область, должен быть порядка ПО Д,
где с и /3 определяются как в формуле (4.4). Тогда как (3 обычно не за¬
висит от £, с является величиной порядка е или меньше. На этой области
ф\(= dHo/dli) принимает значения от 0 (при Д = 0) до ~ у/ф (напом¬
ним, что на границе области Д ~ ±у/с/(3). Вторичные резонансы соответ¬
ствуют соотношениям
к\ф\ + к2ф2 = 0 (4.11)
с целыми fci, к2 и к2 ф 0. Так как ф2{= дЛо/д12) является величиной
нулевого порядка по с, а ф\ не превышает ~ у/ф9 для выполнения (4.11)
нужно, чтобы ki ~ 1 /у/ф и к2 ~ 1. Поэтому ведущий вторичный резонанс
должен иметь порядок ~ 1/y/cj3. Как следствие, коэффициент соответству¬
ющей гармоники и величина остатка 7Z составляют ехр(-1 /у/ф).
ii) Фиксированные нерезонансные частоты с диофантовыми свойствами.
Предположим, что частоты углов р2,..., рп фиксированы (то есть не зави¬
сят от действий) и удовлетворяют диофантову условию
п
"52 k№ ^ Tv^iriw’ (k2,---,kn) е Zn_1, (4.12)
l=2 \2^i=2\ki\)
для некоторых положительных 7 и т. Тогда вторичные резонансы соответ¬
ствуют соотношениям
п
к\ф\ + = 0, (4-13)
1=2
где &2, ■.., кп не равны нулю все одновременно. Поскольку ф\ не превосхо¬
дит ~ фф
и выполняется (4.12), соотношения (4.13) могут выполняться,
88
Глава 4
только если Y^i=2 \ki\ ~ . Поэтому ведущий вторичный резонанс
должен иметь порядок l/y/cfi1^. Как следствие, коэффициент соответству¬
ющей гармоники и величина остатка 1Z сотавляют ~ ехр(—1 /у/ф1^т).
4.3.2. Резонансные инвариантные торы
Согласно предыдущему разделу, путем задания резонансных перемен¬
ных «действие-угол» в каждой из динамических областей гамильтони¬
ан (4.1) можно записать как Hres(J) + 7£(J,i/>). В предположении, что
Hres невырожден, применима КАМ-теорема. Согласно главе 3, если воз¬
мущение 1Z достаточно мало, должно существовать множество инвариант¬
ных торов большой меры. Эти торы должны быть «близки» к инвариант¬
ным торам интегрируемого приближения Hres» то есть к торам, определяе¬
мым условием J = const. Поэтому в переменных Ii,pi инвариантные то¬
ры возмущенного резонанса близки к инвариантным кривым маятника (см.
рис. 4.1). В частности, в областях циркуляции инвариантные торы имеют ту
же структуру, что и у обсуждавшихся в предыдущей главе: углы <pi,..., рп,
изменяются в пределах от 0 до 27т, а действия I являются периодическими
функциями углов. В либрационной же области движение на инвариантном
торе соответствует циркуляции углов р2,..., рп и либрации в ограни¬
ченном интервале; такой тор мы назовем либрационным, или резонансным,
инвариантным тором.
Согласно главе 3 инвариантные торы в задачах с двумя степенями сво¬
боды можно визуализировать, применяя сечения Пуанкаре. На рис. 4.3 дан
пример с использованием стандартного отображения (3.13). Здесь началь¬
ные условия выбраны на оси q\ = 7г, чтобы исследовать также и динамику
в области резонанса qi = 0, которая на рис. 3.3 получилась пустой.
На рис. 4.3 (построенном для того же значения £, что и рис. 3.35)
резонансная область получилась заполненной замкнутыми кривыми — так
на сечении Пуанкаре проявились либрационные инвариантные торы. Вне
резонансной области проявляются инвариантные торы, которые мы уже
видели на рис. 3.35. Цепочки островов, видимые выше и ниже области
главного резонанса, представляют собой сечения либрационных инвари¬
антных торов, соответствующих резонансам другого типа — типа kiq\ +
+ = 0. Отметим, что для этих резонансов сечение Пуанкаре по q2 дает
типичный фазовый портрет маятника к\ раз на промежутке [0, 27т] задания
переменной q\. Поскольку для стандартного отображения (3.13) q^ — 27г
и <?1 ~ pi, цепочка из трех островов при р\ ~ 27г/3 соответствует резо-
4.3. Возмущенная резонансная динамика
89
qi
Рис. 4.3. Фазовый портрет стандартного отображения при е = 0.6
нансу 3^1 — <72=0, а цепочка из двух островов при pi ~ тг соответствует
резонансу 2qi — <72 = 0. Если увеличить масштаб изображения окрестно¬
сти какого-либо из этих островов, то обнаружится структура, аналогич¬
ная структуре окрестности большого острова в центре рисунка. Разумеется,
острова могут также проявляться и между либрационными инвариантными
торами; они соответствуют вторичным резонансам между периодом либра¬
ции критического угла главного резонанса и периодом циркуляции q<i (это
резонансы между углами гр\ и^2, задаваемыми в области либрации для ин¬
тегрируемого приближения HTes главного резонанса). На рис. 4.3 эти ост¬
рова не видны, так как они слишком малы. Однако их можно различить на
рис. З.Зг, где область главного резонанса окружена цепочкой из 8 островов.
КАМ-теорема неприменима вблизи сепаратрис интегрируемого при¬
ближения Hres, поскольку это приближение, будучи записанным в резо¬
нансных переменных «действие-угол», на сепаратрисе теряет свои свой¬
ства регулярности. С другой стороны, как видно из рис. 4.3, инвариантные
кривые на границе между областями либрации и циркуляций отсутствуют.
Сепаратриса, присущая модели маятника, исчезла, а на ее месте появи¬
90
Глава 4
лась хаотическая область, имеющая на сечении Пуанкаре вид множества
рассеянных точек. Чтобы понять причину появления хаотической области,
необходимо тщательно проанализировать, что происходит с сепаратрисой
интегрируемого приближения Hres в присутствии произвольно малого воз¬
мущения 7Z.
Рис. 4.4. Слева: устойчивое и неустойчивое многообразия гиперболической точ¬
ки равновесия в локальном линейном приближении 7^res. Справа: устойчивые
и неустойчивые многообразия маятника
4.3.3. Расщепление сепаратрис
Неустойчивая точка равновесия маятника при Д = ipi =0 имеет ги¬
перболическую структуру. Разложение гамильтониана (4.4) в окрестности
этой точки в ряд Тейлора до второго порядка дает
Wres = ~ (4-14)
чьи траектории представляют собой гиперболы с асимптотами Е_ и Е+,
имеющими уравнения Д = y/c//3<pi и Д = — y/c/(3pi соответствен¬
но (рис. 4.4а). На линии Е_ движение описывается формулами =
= v?!(0)exp {y/cfit), Ii(t) = y/c/]i<pi(0) exp {y/cfit)\ при t —> — oo оно стре¬
мится к точке равновесия. Мы будем называть эту линию неустойчивым
многообразием. На линии Е+ движение описывается формулами p\(t) =
= Pi(0) exp (—y/cj3t), Ii(t) = —у/с/(Зрi(O) exp {—y/cfit)\ при t —> +oo оно
тоже стремится к точке равновесия. Мы будем называть эту линию устой¬
чивым многообразием. Если учесть в разложении Тейлора по Д и чле¬
ны более высокого порядка, то устойчивые и неустойчивые многообразия
4.3. Возмущенная резонансная динамика
91
в общем случае будут уже не прямыми, а некоторыми кривыми. В случае
маятника устойчивое многообразие точки равновесия при = 0 совпадает
с неустойчивым многообразием точки равновесия при = 2тт, и наоборот
(рис. 4.46). Устойчивое и неустойчивое многообразия вместе образуют то,
что в разделе 4.1 мы назвали сепаратрисой.
Рис. 4.5. Если бы неустойчивые (прерывистые кривые) и устойчивые (сплошные
кривые) многообразия не пересекались, два из них должны были бы закручиваться
по спирали к центру резонанса. Но это нарушило бы свойство сохранения объема
для гамильтонова потока. Поэтому устойчивое и неустойчивое многообразия долж¬
ны пересекаться
Введем теперь дополнительную несвязанную степень свободы и рас¬
смотрим динамику маятника в расширенном фазовом пространстве. Кон¬
кретно, пусть имеется интегрируемый гамильтониан
= h+'Hres(h,<Pl), (4-15)
где 7iTes — гамильтониан маятника с одной степенью свободы, подоб¬
ный (4.4), а переменные «действие-угол» /2,^2 представляют дополни¬
тельную несвязанную степень свободы. Динамика на плоскости /1,(^1, ра¬
зумеется, не изменяется, так что сечение Пуанкаре системы (4.15) по р2
дает портрет, идентичный портрету маятника (рис. 4.1). Зададим теперь
произвольно малую связь между двумя степенями свободы; а именно, рас¬
смотрим в общем случае неинтегрируемый гамильтониан
7i = /2 + Wres(A, <fi) + 7£(<Ръ ^2)? (4-16)
где 7iTes имеет форму (4.4). Можно доказать (Пуанкаре, 1892), что сечение
Пуанкаре новой системы сохраняет гиперболическую неподвижную точку
92
Глава 4
вблизи i\ = tpi = 0 (а также и устойчивую неподвижную точку вблизи
h = 0, (pi = 7г). Более того, устойчивое и неустойчивое многообразия
по-прежнему вынуждены пересекаться, так как иначе одно из них закручи¬
валось бы к центру резонанса по спирали (как показано на рис. 4.5), явно
нарушая присущее гамильтоновым системам свойство сохранения объема
(см. раздел 1.7). Однако здесь уже нет оснований ожидать, что устойчи¬
вое и неустойчивое многообразие совпадают, как в случае невозмущенного
маятника. В случае общего положения они будут трансверсально пересе¬
каться. Это явление известно как феномен гомоклинического пересечения,
или расщепления сепаратрисы (см. Пуанкаре, 1892; Арнольд и Авец, 1968).
о
Я1
Рис. 4.6. Трансверсальные пересечения устойчивого (жирная кривая) и неустойчи¬
вого (тонкая кривая) многообразий неустойчивой точки равновесия (0,0) стандарт¬
ного отображения. Для простоты показана только половина всей картины (та, что
образована верхними многообразиями); е — 2.5
На рис. 4.6 показаны верхние неустойчивое (тонкая кривая) и устой¬
чивое (жирная кривая) многообразия гиперболической точки (при qi — 0)
стандартного отображения (3.13) на промежутке [—27г,27г]. (Обсуждение
стандартного алгоритма компьютерного вычисления многообразий можно
4.3. Возмущенная резонансная динамика
93
найти в статье Симо, 1990.) Как видим, эти два многообразия пересекаются
трансверсально. Каждая из точек пересечения называется гомоклинической
точкой. Из рисунка следует, что число гомоклинических точек бесконечно.
Чтобы убедиться в этом, выберем одну из гомоклинических точек в каче¬
стве начального условия орбиты, скажем точку, обозначенную на рис. 4.6
цифрой 1. Поскольку начальное условие принадлежит как устойчивому, так
и неустойчивому многообразиям, вся орбита, по определению, принадле¬
жит обоим многообразиям. Более того, последовательные точки этой орби¬
ты на сечении Пуанкаре (обозначенные цифрами 2, 3, 4,...) не могут сов¬
падать, так как иначе орбита была бы периодической и не стремилась бы
к гиперболической неподвижной точке. Это доказывает, что орбита долж¬
на иметь на сечении Пуанкаре бесконечно много несовпадающих точек,
которые, по определению, все являются гомоклиническими.
Из рис. 4.6 также видно, что расстояние между двумя следующими
друг за другом гомоклиническими точками убывает, так как с приближени¬
ем к гиперболической неподвижной точке орбита экспоненциально «замед¬
ляется». Обратим теперь внимание на область, ограниченную устойчивым
и неустойчивым многообразиями; на рис. 4.6 она обозначена L\. Назовем
эту область петлей. По непрерывности можно доказать, что петля L\ отоб¬
ражается в петлю Z/2 и далее последовательно в петли L*, г — 3,..., -Ьоо,
являющиеся, таким образом, результатом итераций одной и той же петли.
Площадь каждой петли Li должна быть одной и той же, поскольку га¬
мильтонов поток сохраняет площадь. А так как длины оснований петель Li
убывают с г экспоненциально, то и их «высоты» должны экспоненциаль¬
но расти. Картина при этом все более усложняется: петли, как показано на
рисунке, должны пересекать друг друга, генерируя гомоклинические пере¬
сечения (второго порядка) устойчивых и неустойчивых многообразий. Ре¬
зультат обычно называют гомоклиническим клубком. Область, плотно пере¬
секаемую устойчивым и неустойчивым многообразиями, называют хаоти¬
ческой областью. Динамика в хаотической области эквивалентна динамике
так называемой «подковы» Смейла (Смейл, 1965, 1980; см. также Уиггинс,
1988). Произвольно близкие начальные условия принадлежат различным
частям гомоклинического клубка (то есть различным петлям), и поэтому их
Динамические эволюции совершенно различны; орбиты расходятся со вре¬
менем экспоненциально. Как показано на рис. 4.3, сечение Пуанкаре орби¬
ты в хаотической области дает множество рассеянных точек, чье распреде¬
ление очевидно нерегулярно; резонансный угол у хаотических траекторий
альтернирует между либрациями и циркуляциями случайным образом.
94
Глава 4
4.3.4. Размер хаотической области
Размер хаотической области зависит от «расстояния» между устойчи¬
вым и неустойчивым многообразиями. Как следует из рис. 4.6, это расстоя¬
ние на сечении Пуанкаре можно измерить как разность между значениями
действия на двух многообразиях при любом заданном значении угла. Если
устойчивое и неустойчивое многообразия совпадают, как в случае интегри¬
руемого резонанса, то расстояние равно нулю при всех значениях угла; если
же сепаратриса расщеплена, то расстояние равно нулю только в гомокли-
нических точках.
В принципе, расстояние между многообразиями можно измерить, ис¬
пользуя так называемый интеграл Пуанкаре - Мельникова (Пуанкаре, 1892;
Мельников, 1983; см. также Арнольд и др., 2002). Идея довольно проста.
Рассмотрим опять же гамильтониан (4.16). Если на сечении Пуанкаре зна¬
чение (fi фиксировано, то существует локальное взаимно-однозначное со¬
ответствие между 1\ и значением Нтеs. Поэтому расстояние между дву¬
мя точками на сечении Пуанкаре, имеющими одно и то же значение (pi,
можно измерить как разность между соответствующими значениями 7Yres- •
Обозначим теперь через HXsiVi) значение Hres на устойчивом многооб¬
разии в точке его первого пересечения с осью Аналогично, че¬
рез H~es((pi) обозначим соответствующее значение на неустойчивом мно¬
гообразии. Расстояние между многообразиями можно тогда измерить как
AHres = 'Hresi^i) ~ «res(^i)- Используя (1.47), имеем
Р~гОо
«г+ев(¥>?) = ««*(+00) - / {HTes,n}dt,
Jo
r°
««(¥>?) = Wres(-oo) + / {Hres,H}dt,
J — oo
(4.17)
где первый интеграл вычисляется на устойчивом многообразии, а второй —
на неустойчивом; значения Wres(H-oo) = Wres(—оо) суть значения 7i,Tes в ги¬
перболической неподвижной точке (достигаемой при t = +00 на устойчи¬
вом многообразии и при t = — 00 на неустойчивом многообразии). За на¬
чальный момент времени произвольно принят 0, так как функция {Hres,'H}
не зависит явно от времени; интегралы зависят только от значений коорди¬
нат в момент времени 0.
Интегралы в (4.17) нельзя вычислить, так как решение уравнений дви¬
жения на устойчивом и неустойчивом многообразиях в явном виде неиз¬
вестно. Заметим, однако, что многообразия Н отличаются от многообра-
4.3. Возмущенная резонансная динамика
95
зий Wres на величину, пропорциональную размеру 7Z; обозначим ее /х.
С другой стороны, скобка Пуассона {Wres>W} также является величиной
порядка 11. Поэтому вычисление интегралов в (4.17) на многообразиях Wres
дает точность приближения не хуже чем ~ fi2. Преимущество состо¬
ит в том, что уравнения движения на многообразиях Hres известны (так
как Hres интегрируем) и поэтому в принципе интегралы можно вычислить.
Используя это приближение, имеем
где интеграл вычисляется на сепаратрисе Hves. Интеграл в (4.18) обыч¬
но называют интегралом Пуанкаре - Мельникова. Он зависит только от вы¬
бранного значения при t = 0.
В качестве примера вычислим интеграл Пуанкаре - Мельникова для
модели (4.16) с R((pi,(p2) = fnpisin^ и Нтеs, как в (4.4). Имеем
£ = 0 определяются параметром sq- Кроме того, из уравнений, задаваемых
гамильтонианом (4.15), имеем
где (£2(0) — начальная фаза (для простоты принимаем ее равной нулю).
Таким образом, интеграл Мельникова равен
жительные значения в зависимости от «о- Это доказывает, что (i) существу¬
ют гомоклинические пересечения, которые имеют место при значениях
(4.18)
{Wres, = — sin V^2- Уравнения движения на сепаратрисе Hres в (4.4)
имеют решение
где т = \fcfi{t — sq). Таким образом, начальные значения (pi и Д при
т>2 (*) = t + У>2(0)
(4.20)
27Т/1
Как видим, M(sq) попеременно принимает нулевые, отрицательные и поло-
96
Глава 4
переменной ipi, определяемых so = ктг (к £ Z) в (4.19); (ii) пересечения
трансверсальны, так как расстояние между многообразиями равно нулю
только при дискретных значениях so (то есть (р\).
Вычисление интеграла Пуанкаре - Мельникова, хотя и осуществимое
в принципе, на практике осуществить непросто, за исключением случаев,
когда движение по сепаратрисе 7ires и скобка Пуассона {‘Tires? W} имеют
простые аналитические представления (см. обзор Делшамса и др., 1999).
Более того, в ряде случаев результат вычисления интеграла Пуанкаре-
Мельникова оказывается мал в сравнении с /х2, так что пренебрегаемый
член в (4.18), являющийся величиной порядка р'2, может доминировать.
В таких случаях необходимо выводить более сложные выражения для
A7ires с точностью до более высокого порядка по /х. Как следствие, в боль¬
шинстве случаев строгое аналитическое вычисление амплитуды расщепле¬
ния сепаратрисы остается открытой проблемой.
£ = 1(Г4, к — 50 е = /х = 1(Г4
Рис. 4.7. Слева: амплитуда расщепления в (4.22) в функции /х. Справа: то же
в функции к. (Рис. 4 и 5 из статьи Морбиделли и Джиорджилли, 1997; с разре¬
шения Elsevier Science)
Однако эвристические доводы и численные эксперименты (см. Морби¬
делли и Джиорджилли, 1997) указывают на то, что амплитуда расщепления
обычно определяется величиной коэффициента ведущего вторичного резо¬
нанса (см. определение в начале раздела 4.3), то есть величиной остатка 7Z
4.3. Возмущенная резонансная динамика
97
оптимальной нормальной формы. Рассмотрим в качестве примера гамиль¬
тониан н(р, q, t) = Wres(p, q) + Щр, я, *)> где
Wres(p,9) = - £COS<?,
2 (4.22)
n(p,q,t) = -^y{cos[(fc+ 1 )q - t] + cos[(fc - 1 )q - i]}.
Если выбрать целое к близком к 1/(2у/е), то гармоники в 7Z будут резонанс¬
ными на границе области |р| < 2у/е, охватываемой сепаратрисами гамиль¬
тониана маятника Нте8; таким образом, эти гармоники соответствуют вто¬
ричным резонансам. Поэтому в данном случае гамильтониан (4.22) мож¬
но рассматривать как парадигму оптимальной нормальной формы в задаче
о возмущенном маятнике. На рис. 4.1а показана амплитуда расщепления
сепаратрисы (измеряемая численно как расстояние Ар между устойчивым
и неустойчивым многообразиями при q — 7г) в функции /х; е и к фиксиро¬
ваны и положены равными 10-4 и 50 соответственно. Амплитуда расщеп¬
ления идеально масштабируется как у/р на интервале более 9 порядков по
/х. Степень р здесь зависит от значения q, для которого вычисляется ампли¬
туда расщепления: при q = 0 амплитуда пропорциональна /х. На рис. 4.76
показана амплитуда расщепления в функции к при фиксированных е = /х =
= 10-4. При к ^ \/(2у/ё) = 50 гармоники в 71 соответствуют вторичным
резонансам (поскольку они расположены при р ~ 1/к, то есть внутри об¬
ласти \р\ ^ 2у/ё, охватываемой сепаратрисами) и амплитуда расщепления
постоянна с точностью до порядка величины. При к < 50 гармоники в 7Z не
соответствуют вторичным резонансам, так что (4.22) нельзя рассматривать
как оптимальную нормальную форму. Используя алгоритм нормализации,
описанный во второй главе, можно исключить нерезонансные гармоники,
дойдя до порядка, при котором генерируются гармоники, соответствующие
вторичным резонансам. Это произойдет при достижении порядка |fc—501 по
ер, при этом коэффициенты гармоник будут иметь величину О((ерУк~Б01).
Из рис. 4.76 в самом деле видно, что амплитуда расщепления экспоненци¬
ально обрывается при к < 50.
Этот пример показывает, что «количественная характеристика» неин-
тегрируемости, то есть величина остатка оптимальной нормальной фор¬
мы, непосредственно связана с «количественной характеристикой» хаоса —
амплитудой расщепления сепаратрисы. Наличие хаоса является критерием
неинтегрируемости гамильтоновой системы (это строгий результат, извест¬
ный как теорема Зиглина; Зиглин, 1979; см. также Арнольд и др., 2002).
98
Глава 4
Строго доказать наличие хаоса обычно бывает очень трудно (поскольку
для этого надо аналитически взять интеграл Пуанкаре-Мельникова); одна¬
ко имеется ряд мощных численных методов, которые позволяют уверенно
обнаружить хаотическое поведение и широко используются для этого в со¬
временной небесной механике.
Глава 5
Численные инструменты
для выявления хаоса
5.1. Наблюдение временной эволюции
в фазовом пространстве
Как убедиться, что заданные начальные условия порождают хаотиче¬
скую эволюцию? Как убедиться, что орбита лежит на инвариантном торе?
Здесь мы рассмотрим эти важные вопросы.
В предыдущей главе мы выяснили, что построение сечения Пуанкаре
позволяет однозначно различить регулярные и хаотические орбиты. Однако
сечения Пуанкаре полезны только в случае систем с двумя степенями сво¬
боды. Если число степеней свободы больше, то размерность «поверхности»
сечения больше двух, и поэтому сечение Пуанкаре невозможно представить
графически.
Наглядно выявить динамический характер орбиты можно также из вре¬
менной эволюции канонических переменных р, q. На рис. 5.1 показана вре¬
менная эволюция действия р и угла q хаотической (панель (а)) и регуляр¬
ной (панель (б)) орбит простого гамильтониана Н(р, q, t) = р2 j2 + cos q +
+ l/4[cos(g -j- 51) + cos(q — 51)]. Различие между двумя типами движения
очевидно. В случае хаотической орбиты угол q попеременно демонстрирует
колебания большой амплитуды около 7г, циркуляции от 0 до 27т с положи¬
тельной производной и циркуляции от 27Г до 0 с отрицательной производ¬
ной. Соответственно, сопряженное действие р колеблется около р ~ 1, ес¬
ли q циркулирует с положительной производной, колеблется около р ~ — 1,
если q циркулирует с отрицательной производной, и колеблется около р ~ О
(с примерно удвоенной амплитудой), если q колеблется около 7г. Очевидно,
что эти три типа поведения соответствуют трем динамическим режимам,
близким к сепаратрисе интегрируемого резонансного приближения TCres =
= р2/2 + cos q. Для хаотической орбиты характерно именно чередование
100
Глава 5
различных режимов; чередование это происходит без каких-либо видимых
проявлений регулярности. В случае же регулярной орбиты (панель (б)) пе¬
реходов между динамическими режимами нет; колебания р и q регулярны
(квазипериодичны).
t t
Рис. 5.1. Временная эволюция хаотической (панель (а)) и регулярной (панель (б))
орбит возмущенного маятника. См. обсуждение в тексте
Однако ситуация оказывается не так проста, если рассматривать бо¬
лее сложные динамические системы с большим числом п степеней сво¬
боды. Из-за связи степеней свободы, здесь и в случае регулярных орбит
действия и углы демонстрируют сложную зависимость от времени, име¬
ющую п независимых частот. Поэтому хаотические орбиты могут не так
уж сильно отличаться от регулярных; визуально их различить становит¬
ся невозможно. Приведем пример: на рис. 5.2 сплошной линией показана
временная эволюция эксцентриситета орбиты Земли (являющаяся хаотиче¬
ской, см. главу 7), а пунктиром показана эволюция похожей, но регулярной
орбиты, полученной из интегрируемой аналитической аппроксимации.
Дело в том, что в случае квазиинтегрируемого гамильтониана Wo(p) +
+ £Wi(p, q) хаос может возникать из-за расщепления сепаратрис резонан-
5.1. Наблюдение временной эволюции в фазовом пространстве 101
Вековые изменения эксцентриситета Земли
00
о -
о
время, млн лет
Рис. 5.2. Временная эволюция эксцентриситета Земли, согласно результатам чис¬
ленного интегрирования (сплошная кривая), и в аналитической модели (пунктир¬
ная кривая). Какая эволюция является регулярной, а какая хаотической, определить
из рисунка сложно. (Рис. 1 из статьи Ласкара, 1988; с разрешения Astronomy and
Astrophysics)
са, гармоника которого имеет довольно малый коэффициент, скажем разме¬
ром s4. Тогда можно ввести новые переменные р1, q*,c тем чтобы преоб¬
разовать гамильтониан к резонансной нормальной форме HTes = ^(р1) +
+ £4^norm(р11Q1) + ^(р1? Q1)» где 7Z меньше е4. Затем, визуально просле¬
див временную эволюцию переменных р1, q1, легко определить, являет¬
ся орбита регулярной или хаотической, как в примере, представленном на
рис. 5.1. Амплитуда регулярных/хаотических осцилляций р1 является вели¬
чиной порядка ~ £2 (то есть порядка квадратного корня из коэффициента
главной резонансной гармоники), как показано в предыдущей главе. Одна¬
ко преобразование от исходных переменных р, q к новым переменным р1,
Ч — порядка е и периодично по углам q1 (см. главу 2). Таким образом,
временная эволюция р, q представляет собой квазипериодические колеба¬
ния с амплитудой е, на фоне которых совершенно теряются хаотические
колебания с амплитудами всего лишь е2.
102
Глава 5
Вывод состоит в том, что, вообще говоря, нельзя полагаться на визу¬
альный анализ временной эволюции переменных системы, когда требуется
выявить регулярный/хаотический характер орбит. Поэтому необходимо ис¬
кать более точные и математически обоснованные инструменты.
В этой главе мы подробно рассмотрим показатели Ляпунова, частот¬
ный анализ, а также их суррогаты. К декабрю 2013 года эти инструменты
используются наиболее часто в исследованиях динамики Солнечной систе¬
мы. Что касается методов, подобных основанным на КС-энтропии (Кры¬
лов, 1950; Колмогоров, 1959; Синай, 1959; см. также книгу Лихтенберга
и Либермана, 1983) и кривизне Риччи (Гурзадян и Кочарян, 1987; Эль-Зант
1997; Эль-Зант, Гурзадян, 1998), мы не будем вдаваться в их детали, по¬
скольку эти методы используются в основном для анализа глобально-ха¬
отических систем с эргодическими свойствами, таких как задачи TV-тел
с очень большими N, типичных для галактической динамики. Читатель,
интересующийся методами анализа хаотического поведения в таких систе¬
мах, может найти ряд интересных статей о них в сборнике под редакцией
Гурзадяна и Руффини (2000).
5.2. Показатели Ляпунова
Согласно предыдущей главе, сколь угодно близкие начальные условия
в хаотической области задают траектории, расходящиеся экспоненциаль¬
но быстро. Максимальный показатель Ляпунова (МПЛ) характеризует ско¬
рость такой экспоненциальной расходимости. Подробное изложение теории
показателей Ляпунова выходит за рамки данной главы; найти его читатель
может в статьях Ляпунова (1907), Оселедеца (1968) и Бенеттина и др. (1976,
1980), а также в книге Лихтенберга и Либермана (1983). Здесь мы обрисуем
лишь главные идеи и свойства, важные для приложений в небесной меха¬
нике.
Рассмотрим две орбиты с начальными условиями р^(0), q^(0)
и р(2)(0), q(2)(0). Измерить относительную расходимость этих орбит
(р(1)(f), q(1)M) и (p(2)(£), q(2)С0) нельзя, просто измеряя евклидово рас¬
стояние ||p^^(t) — р(2)(£)|| + ||q^^(t) — q(2)(£)|| между ними в функции
времени. В самом деле, когда движение ограничено, относительное рас¬
стояние не может неограниченно возрастать. Чтобы пояснить эту мысль,
рассмотрим две траектории на поверхности сферы: какова бы ни была на¬
чальная скорость их относительного расхождения, расстояние между ними,
очевидно, не может превысить диаметра сферы. Экспоненциальную рас¬
5.2. Показатели Ляпунова
103
ходимость можно измерить лишь локально. Удобно поэтому линеаризовать
уравнения относительного движения.
Обозначая 5р(£) = Р<2>(*)-Р(1)(*) и Sq(t) = q(2)(t)-q(1)W. выпишем
линеаризованные уравнения относительного движения:
Spi = -£k(pm(t)'4mmpi ~ ^Д;(р<1)(,)'ч<1|(,))^'
= £ж(р<"(,)'ч<“тъ+
(5.1)
где 7i(p, q) — гамильтониан системы, траекториями которой являются
p^(t),q^(t) и p(2)(t),q(2)(t); через 6pi,5qi,pi,qi обозначены компонен¬
ты йр, 5q, р, q; по индексу j подразумевается суммирование.
В принципе, уравнения (5.1) можно использовать лишь на относитель¬
но малых временах, таких, что Sp(t) и Sq(t) остаются достаточно малыми,
чтобы линеаризованные уравнения могли служить хорошей аппроксимаци¬
ей реального относительного движения. Однако на ограниченном интер¬
вале времени эволюция Sp(t), Sq(t) и ее скорость, конечно же, зависят от
начальных условий йр(0), <5q(0) и от величины заданного интервала време¬
ни, что неудобно для характеристики динамических свойств орбиты р^1) (£),
q^(t). Поэтому, «забывая» об исходном смысле йр, 5q, максимальный по¬
казатель Ляпунова (МПЛ) определяют как
С = lim llnEEffllMl, (5.2)
*->+оо t ||йр(0), <5q(0)||
где через ||йр(£), £q(£)|| обозначена евклидова норма вектора (Spi(t), ...,
Sqi(t)9 ..., 5qn(t)). Можно доказать, что С имеет одно и то же зна¬
чение для большинства начальных условий йр(0), <5q(0) (то есть мера мно¬
жества £p(0),5q(0), приводящих к иному значению £, равна нулю) и это
значение также не зависит от выбора канонических переменных р, q, ис¬
пользуемых для записи уравнений движения (5.1) (Оселедец, 1968). Бла¬
годаря этим свойствам можно заключить, что МПЛ характеризует орбиту
П^(^)- Вообще говоря, каждая из орбит динамической системы
имеет свой собственный МПЛ.
В том случае, когда траектория p^\t), q^(t) представляет собой
неподвижную точку, то есть р^(t) = р^(0) и q^(t) = q^(0), урав¬
нения (5.1) становятся линейными с постоянными коэффициентами, а сле¬
довательно — интегрируемыми. Обозначим через Аь ..., \2П собственные
104
Глава 5
значения (в общем случае комплексные) матрицы вторых производных Н
в точке р^(0), q^^(0). Гамильтоновы системы сохраняют объем, поэто¬
му если Л является собственным значением, то и 1/Л также является соб¬
ственным значением. Обозначим через Л собственное значение такое, что
|А| = тахг=1,...,2п |А*|; тогда либо |Л| > 1, либо |Л| = 1. В первом слу¬
чае линеаризованная динамика (5.1) имеет по меньшей мере одну гипер¬
болическую компоненту, то есть существует по меньшей мере одна пара
сопряженных переменных, поведение которых подобно изображенному на
рис. 4.4а. Поэтому для всех начальных условий 5р(0), <5q(0) (кроме тех, что
имеют нулевую проекцию на собственный вектор, соответствующий Л, —
они образуют множество нулевой меры) величина ||£p(t), <5q(t) || будет рас¬
ти при t —> +оо как ехрЛ£. Как следствие, из (5.2) имеем С = Л. В случае
же |А| = 1 линеаризованная динамика является эллиптической и эволюция
£p(t), 5q(£) ограничена, так что С = 0.
МПЛ орбит на КАМ-торах также равны нулю. В этом можно убедиться
следующим образом. В окрестности тора можно ввести новые переменные
«действие-угол» I, <£>, в которых гамильтониан записывается в нормальной
форме Колмогорова (3.1). В этих переменных уравнения (5.1) для орбиты
на торе принимают вид
61 = 0, б'ср = С61 + F((p(t))51, (5.3)
где ip(t) — вектор углов на торе, эволюционирующий линейно по t; матри¬
ца С — константа, а матрица F периодична по (р. Как следствие, для дви¬
жения относительно орбиты на торе имеем 61 = const и бср = at + (3(t),
где а — константа, (3(t) — периодическая функция. Поэтому в окрестно¬
сти торов экспоненциального расхождения орбит нет, что, в соответствии
с (5.2), дает С = 0.
Поскольку у хаотических орбит С > 0, а у орбит на КАМ-торах С = 0,
положительный МПЛ обычно считают индикатором хаоса. Однако положи¬
тельный МПЛ, вообще говоря, не означает, что рассматриваемая орбита яв¬
ляется хаотической, если подразумевать, что слово хаос служит синонимом
иррегулярного и непредсказуемого поведения. Строго говоря, положитель¬
ный показатель Ляпунова лишь указывает на наличие локальной гипербо¬
личности в окрестности орбиты. Например, гиперболическая неподвижная
точка маятника имеет положительный МПЛ, хотя динамика в данном слу¬
чае регулярна и предсказуема! Однако напомним, что в случае маятника ло¬
кальная гиперболичность означает существование устойчивого и неустой¬
чивого многообразий, которые при наличии возмущения в общем случае
5.2. Показатели Ляпунова
105
пересекаются трансверсально, порождая гомоклинический клубок, то есть
хаотическую область.
В дополнение к максимальному показателю Ляпунова можно эффек¬
тивно вычислять и остальные п — 1 положительных или нулевых пока¬
зателей Ляпунова (п — число степеней свободы), используя, однако, бо¬
лее сложный рецепт, описанный Бенеттином и др. (1980). Число поло¬
жительных показателей Ляпунова равно числу независимых направлений
в фазовом пространстве, вдоль которых орбита демонстрирует хаотическое
(или по крайней мере гиперболическое) поведение. Теорема Песина (1977)
утверждает, что КС-энтропию можно вычислить, если известны показатели
Ляпунова , по формуле
где суммирование производится для всех положительных показателей Ля¬
пунова, а интегрирование — по заданной области фазового пространства.
5.2.1. Вычисление МПЛ
Задача компьютерного вычисления МПЛ не имеет простого решения,
поскольку, чтобы вычислить предел в (5.2), формально необходимо инте¬
грировать систему (5.1) на бесконечном интервале времени. К тому же если
система является гиперболической, то 5р и <5q растут со временем неогра¬
ниченно, что при компьютерном вычислении их эволюции неминуемо ведет
к ошибке переполнения.
Эти трудности были блестяще преодолены Бенеттином и др. (1980).
Предложенный ими способ состоит в следующем. Начав с выбора про¬
извольных <Sp(0), <$q(0), вычисляем эволюцию 5p(£),5q(£) до некоторого
момента времени Т, достаточно малого, чтобы избежать ошибки перепол¬
нения на компьютере; затем, положив Si = ||<5р(Т), £q(T)||/||5p(0), <5q(0)||,
определяем 5рг = Sp(T)/si и 5qx = 6q(T)/su наконец, берем (Sp^*^
в качестве новых начальных условий 5p(0),5q(0) и итерируем описанную
процедуру. Таким путем мы получаем последовательность ренормирующих
факторов si, s2? ..., S/. Бенеттин и др. (1980) доказали, что
причем результат не зависит от выбора Т, если Т достаточно мало.
Ci> о
(5.4)
106
Глава 5
Рис. 5.3. Эволюция численной оценки С(1Т) показателя Ляпунова для хаотиче¬
ской (панель (а)) и регулярной (панель (б)) орбит стандартного отображения. Здесь
Т = 1, а I — число итераций стандартного отображения
Чтобы численно оценить этот предел, обычно строят график величи¬
ны £(1Т) = (2j=1 lnsj)//T в функции IT в логарифмическом масштабе
и пытаются определить ее асимптотическое поведение. На рис. 5.3 даны
примеры типичных результатов в случаях хаотической (панель (а)) и регу¬
лярной (панель (б)) орбит. Хотя величина С{1Т) сначала больше в случае
регулярной орбиты, она, как видим, в этом случае монотонно убывает с IT,
тогда как С(1Т) хаотической орбиты испытывает сильные осцилляции, но
в конце концов, по-видимому, стабилизируется (на рис. 5.3 при ~ 10-11).
Таким образом, есть основания полагать, что в случае (б) предел С(1Т) при
IT —+ + оо равен нулю, тогда как в случае (а) он равен ~ 10“1 л.
Чтобы выявить регулярные и хаотические орбиты, обычно бывает до¬
статочно построить графики, подобные рис. 5.3. Однако никогда нельзя
быть абсолютно уверенным, что для оценки предела выбран правильный
интервал времени. В некоторых случаях бывает, что С(1Т) сначала убывает,
как на рис. 5.36, но затем асимптотически сходится к некоторому малому,
но положительному значению. Таким образом, если эволюцию £(1Т) не от¬
слеживать достаточно долго, можно ошибочно прийти к выводу, что пока¬
затель Ляпунова нулевой. Вычисляя эволюцию С(1Т) на временах до неко¬
торого конечного IT, можно выявить лишь орбиты с МПЛ больше некото¬
рой величины, определяемой этим заданным максимальным значением IT.
Орбиты с меньшей величиной МПЛ можно выявить только путем увели¬
чения интервала времени, на котором проводится интегрирование. Чтобы
5.2. Показатели Ляпунова
107
выявить все хаотические орбиты, требуется точное вычисление показателя
Ляпунова, а значит, бесконечное время.
IT
Рис. 5.4. Эволюция численной оценки показателя Ляпунова С(1Т) для трех орбит
на разном (убывающем снизу вверх) расстоянии от главного резонанса стандартно¬
го отображения. Амплитуда осцилляций С(1Т) служит индикатором расстояния от
«наиболее эффективного» резонанса
Эволюция С(1Т) никогда не представляет собой строго монотонное
убывание: она всегда сопровождается малыми осцилляциями. Амплитуда
этих осцилляций определяется расстоянием от рассматриваемой орбиты до
«наиболее эффективного» резонанса1. В качестве примера на рис. 5.4 по¬
казана эволюция С(1Т) для трех орбит стандартного отображения. Ось IT
дана в линейном масштабе, чтобы лучше были различимы периоды ос¬
цилляций. Кроме того, чтобы избежать наложения кривых, к значениям
log £(1Т) каждой из орбит прибавлена подходящая константа. Показанные
три кривые соответствуют орбитам на разных (убывающих снизу вверх)
расстояниях от главного резонанса, расположенного при pi ~ 0. Осцилля-
1 Здесь и в подписи к рис. 5.4 под расстоянием до резонанса подразумевается расстояние
До сепаратрисы резонанса. — Прим. ред.
108
Глава 5
ции указывают на то, что вектор <Sp, <5q в (5.1) попеременно стягивается
и растягивается. Это происходит, когда орбита проходит вблизи гипербо¬
лической точки резонанса (в данном случае гиперболической точки р\ = 0,
qi = 0 главного резонанса стандартного отображения (3.13)). Амплиту¬
да сжатий и растяжений, очевидно, больше всего у орбиты, проходящей
на наименьшем расстоянии от гиперболической точки. Отметим также, что
период осцилляций возрастает с уменьшением расстояния от резонанса, по¬
скольку увеличивается период циркуляций резонансного угла. Таким обра¬
зом, из вида осцилляций зависимости С(1Т) можно оценить, не дожидаясь
окончания сходимости С(1Т) к асимптотическому значению, будет ли орби¬
та иметь в итоге положительный или нулевой МПЛ. Если эти осцилляции
почти неразличимы, значит, орбита не «чувствует» близкого присутствия
резонанса и она, скорее всего, находится вблизи инвариантного тора, то
есть ее МПЛ равен нулю. Напротив, если осцилляции сильные, то орби¬
та близка к резонансу и, скорее всего (но не наверняка!), орбита является
хаотической, то есть ее МПЛ положителен.
Кроме того, если у эволюции С(1Т) нет существенных осцилляций, то
орбиты с близкими начальными условиями будут иметь близкие друг другу
значения £(/Т) при любом фиксированном IT. Последнее не выполняется,
если осцилляции £(1Т) сильные, поскольку их период слегка изменяется
от одной орбиты к другой. Как следствие, С(1Т) является гладкой функ¬
цией начальных условий только в областях, где влияние резонансов пре¬
небрежимо мало, и, наоборот, является иррегулярной функцией в областях
хаотических или же, по крайней мере, подверженных сильному влиянию
резонансов. В качестве примера на рис. 5.5 показаны значения £(1000) ор¬
бит стандартного отображения в зависимости от начального действия р\
(при этом для всех орбит начальное значение q\ положено равным нулю).
Исходя из приведенного рассуждения, рис. 5.5 можно интерпретировать как
«карту» динамического характера системы: плато, где С почти постоянно
(£(1000) ~ 10—2 2), выявляют «регулярные» области, где относительная
мера КАМ-торов близка к единице, а пики и провалы (и вообще все разры¬
вы) — основные хаотические или резонансные области.
В заключение раздела необходимо предостеречь читателя. Некоторые
авторы при использовании основанного на формуле (5.5) рецепта Бенетти-
на и др. избегают вычисления линеаризованных уравнений движения (5.1),
вместо этого вычисляя 5p(t), 5q(£) как разность эволюций двух траекторий
системы. Это очень опасный путь, поскольку результат в таком случае зави¬
сит от интервала времени Т, на котором проводится ренормализация, и от
5.3. Частотный анализ
109
Pi
Рис. 5.5. Значение показателя Ляпунова стандартного отображения, вычисленное за
1000 итераций, в зависимости от начального значения действия. Параметр е равен
0.6, как и в случае рис. Ъ.Ъб
||<5p(0),<5q(0)|| , если только обе эти величины не являются чрезвычайно ма¬
лыми и все вычисления не проводятся с очень высокой точностью. Из-за
численных неустойчивостей получить неверные значения МПЛ очень лег¬
ко (см. обсуждение в статье Хольмана и Мюррея, 1996). Поэтому при вы¬
числениях эволюции 6p(t),5q(t) настоятельно рекомендуется использовать
линеаризованные уравнения движения во всех случаях, когда их можно вы¬
числить.
5.3. Частотный анализ
Частотный анализ, представляющий собой мощный инструмент для
выявления хаоса, был предложен Ласкаром (1990) с целью анализа вековой
эволюции планет (см. главу 7), а позднее с успехом применялся также для
изучения динамики малых тел (Несворный и Ферраз-Мелло, 19976; Робу-
110
Глава 5
тель и Ласкар, 2001) и галактической динамики (Папафилиппу и Ласкар,
1998). Его свойства и условия применимости подробно изложены в статьях
Ласкара и др. (19926) и Ласкара (1993).
Идея, положенная в основу частотного анализа, проста. Орбиты на
КАМ-торах имеют постоянные частоты (см. главу 3); у хаотических же
орбит, напротив, нет хорошо определенных частот: внутри хаотической об¬
ласти действия и углы эволюционируют случайным образом. Поскольку
значения частот можно численно найти на некотором интервале времени,
можно проверить, изменяются ли частоты или остаются постоянными от
одного интервала времени к другому.
Конкретно, найдя численным интегрированием орбиту р(t), q(£), чис¬
ленно определяем (следуя процедуре, описанной в разделе 5.3.1) фунда¬
ментальные частоты i/(£o) движения на временном интервале [to, to + Т\.
Продолжительность интервала Т должна быть выбрана больше величины,
обратной наименьшей фундаментальной частоте, с тем чтобы последнюю
можно было точно определить. Данное вычисление повторяем затем для
различных значений to, таким образом определяя частоты численно в функ¬
ции времени. Если они неизменны, тогда рассматриваемая орбита явля¬
ется «регулярной», то есть она либо лежит на КАМ-торе, либо является
периодической (Ласкар, 1999). Если же i/(£o) изменяется с to, есть силь¬
ное основание предположить, что она хаотическая. На рис. 5.6 дан пример
подобного анализа для группы орбит стандартного отображения, близких
к резонансу 1/6. На верхней панели показана временная эволюция часто¬
ты угла qi для орбит, расположенных на удалении от резонанса с обеих
его сторон (резонанс находится при v = 0.1666...). В случае наиболее
удаленных от резонанса орбит на графике получаются прямые линии, что
означает, что временные вариации частоты меньше разрешения графика.
Таким образом, данные орбиты предположительно лежат на КАМ-торах.
Напротив, у орбит, расположенных ближе к резонансу, частота v испытыва¬
ет временные вариации с амплитудой больше возможных численных оши¬
бок, с которыми частота вычисляется на каждом из интервалов (эти ошибки
показаны на графике вертикальными черточками). Следовательно, данные
орбиты должны не лежать на КАМ-торах, а, скорее всего, должны быть
слабо хаотическими. У орбит еще более близких к резонансу 1/6 (панель
(б)) амплитуда вариаций частоты увеличивается, что указывает на более
сильный хаос. Вторая орбита сверху находится как раз в резонансе 1/6,2
и поэтому ее частота испытывает сильные нерегулярные осцилляции около
2Точнее, в хаотическом слое резонанса 1/6. — Прим. ред.
5.3. Частотный анализ
111
t х 10"
t x 1(Г3
Рис. 5.6. Временная эволюция частоты у орбит стандартного отображения, близких
к резонансу 1/6. Орбиты, у которых частота приблизительно постоянна во време¬
ни, лежат на КАМ-торах, а остальные являются хаотическими. (Рис. 5 из статьи
Ласкара и др., 19926; с разрешения Elsevier Science)
112
Глава 5
точного резонансного значения; обратите внимание на ряд уходов частоты
в область значений меньше 0.166, что соответствует временным захватам
орбиты в область циркуляций ниже резонанса. Напротив, вторая орбита
снизу проводит большую часть времени ниже резонанса (у ~ 0.1654); два¬
жды она временно захватывается в резонанс (когда и ~ 0.1666).
0.170
0.169
0.168
v
0.167
0.166
0.165
0.164
-1.2230-1.2225-1.2220-1.2215-1.2210-1.2205-1.2200
У
Рис. 5.7. Зависимость частоты от начального значения у действия pi для орбит
стандартного отображения, близких к резонансу 1/6. Гладкие участки зависимости
соответствуют регулярным областям, а рассеянные точки выявляют области хаоса.
Горизонтальной линией показано точное резонансное значение частоты. (Рис. 6 из
статьи Ласкара и др., 19926; с разрешения Elsevier Science)
Второй путь, каким можно исследовать динамическую структуру си¬
стемы, состоит в вычислении частот в функции начальных условий. Кон¬
кретно, фиксируем начальные углы и задаем частую сетку начальных усло¬
вий р0 в пространстве действий; затем для каждого из начальных усло¬
вий на сетке вычисляем соответствующую ему частоту i/(p0) на интерва¬
ле [0, Т] с некоторым фиксированным большим Т. Теоретический резуль¬
тат Лазуткина (1973) гласит, что частоты на КАМ-торах можно описывать
гладкой (С°°) функцией действий. Поэтому в тех областях, где КАМ-торы
заполняют относительно большой объем, численно определяемая функ¬
ция 1/(р0) должна выглядеть гладкой. Напротив, эта гладкость должна утра¬
чиваться в хаотической области, где частоты плохо определены и на интер¬
вале [0, Т] вычисляются лишь грубые их приближения. Пример показан
5.3. Частотный анализ
ИЗ
на рис. 5.7 опять же для области в окрестности резонанса 1/6 стандарт¬
ного отображения. Частота v приведена в зависимости от начального зна¬
чения р\. Функция v(pi) выглядит гладкой при р\ < —1.222, причем v
медленно растет с р\\ затем она начинает испытывать скачки и выбросы
и наконец превращается в множество рассеянных точек. После пересече¬
ния точного резонансного значения зависимость v(p\) снова становится
гладкой.
Рис. 5.6 и 5.7 демонстрируют эффективность частотного анализа для
выявления хаотических орбит и хаотических областей. По сравнению с вы¬
числением показателей Ляпунова частотный анализ в принципе требует
меньше времени интегрирования. Нескольких периодов самого медленного
угла достаточно для точного определения частот и выявления их типа по¬
ведения во времени и/или относительно начальных условий, тогда как при
вычислении показателей Ляпунова приходится ждать, пока эволюция C(t)
достигнет своего асимптотического предела. Более того, из частотного ана¬
лиза можно непосредственно определить, какие резонансы ответственны
за выявленный хаос, тогда как вычисление показателей Ляпунова не дает
на этот счет никакой информации. С другой стороны, вычисление частот
требует весьма сложного программного обеспечения, в особенности в при¬
ложениях в небесной механике, где из-за вырожденности задачи Кеплера
есть как быстрые, так и медленные частоты. Из-за этой конкуренции пре¬
имуществ в настоящее время широко используются как расчеты показате¬
лей Ляпунова, так и частотный анализ.
5.3.1. Вычисление частот
В этом разделе мы дадим краткие рекомендации по практическому
применению частотного анализа. Подробности можно найти в оригиналь¬
ной статье Ласкара и др. (19926).
В системе с п степенями свободы регулярная орбита на КАМ-торе ква-
зипериодична с п независимыми частотами ..., vn. В принципе, из-за
связи степеней свободы эти п частот присутствуют во временной эволю¬
ции каждого из действий и углов системы. Однако каждая из частот i/j
является, вообще говоря, ведущей частотой своего угла qj\ поэтому, вместо
того, чтобы выявлять все независимые частоты во временной эволюции од¬
ной переменной, удобнее искать главную частоту каждого из углов qj(t).
Если искать частоту либраций на резонансе, разумно ввести критический
угол резонанса и сопряженное ему действие Ii (см. главу 4), а затем
задать угол, скажем определяющий в полярных координатах положение
114
Глава 5
точки 11, (fi относительно центра либраций. Частота либраций является
ведущей частотой di(t).
Во избежании сложностей, возникающих из-за взятия углов по моду¬
лю 2тг, для каждого из углов qj(t) вводят комплексную функцию fj(t) =
= exp[tqj(t)\. Ведущая частота qj(t) является, конечно же, и ведущей ча¬
стотой fj(t). Если использовать простое быстрое преобразование Фурье,
на произвольно взятом временном интервале [to,to + T] частоты fj нельзя
определить с хорошей точностью, поскольку fj (t) не является, вообще го¬
воря, на этом интервале периодической. Вместо этого вычисляют функцию
и ищут значение и*, при котором $j(u) максимальна. Значение и* ап¬
проксимирует ведущую частоту fj. Оно равно ей в точности, если функ¬
ция fj(t) является периодической: в самом деле, в случае fj = exp[wt\
формула (5.6) дает Фj(cj) = sin[(i/ — oj)T/2)/[(v — и)Т/2], — с абсолют¬
ным максимумом при и = и. Если fj имеет несколько независимых частот
i^i,..., ип, то и;* не будет в точности равно ведущей частоте, однако «ошиб¬
ка» будет невелика, если частоты хорошо разделены и амплитуда гармони¬
ки с ведущей частотой значительно больше амплитуд гармоник с другими
частотами.
В небесномеханических приложениях часто имеются сложности из-за
одновременного присутствия быстрых и медленных частот, связанных со¬
ответственно со средними долготами и с перицентрами и узлами небесных
тел. С точки зрения численной процедуры определения частот такая ситуа¬
ция эквивалентна случаю, когда частоты Vi,..., vn почти равны друг другу
и имеют сравнимые амплитуды в спектре Фурье. В первом исследовании
Ласкара (1990) этой проблемы не существовало, поскольку он рассматривал
исключительно вековую эволюцию Солнечной системы, начиная с вековой
нормальной формы (см. раздел 2.5), и поэтому быстрых углов не было.
Когда приходится иметь дело с орбитами, вычисленными в полных
задачах (то есть при наличии и короткопериодических членов), наилуч¬
шей стратегией является следующая: сначала, используя отдельную чис¬
ленную процедуру (Карпино и др., 1987), проводят фильтрацию орбиты,
чтобы осреднить все короткопериодические колебания, а затем применяют
частотный анализ к отфильтрованным углам. Полная процедура подробно
рассмотрена в статье Несворного и Ферраз-Мелло (1997а). Она позволяет
(5.6)
5.4. Суррогаты
115
эффективно вычислять частоты медленных углов, однако ее нельзя исполь¬
зовать в области высоких частот.
5.4. Суррогаты
Недавно были предложены новые численные инструменты для выяв¬
ления хаоса, представляющие собой вариации на темы показателей Ляпу¬
нова и частотного анализа. Здесь мы кратко рассмотрим только те из них,
которые были успешно применены в задачах небесной механики или же
являются перспективными для будущих приложений.
5.4.1. Быстрый индикатор Ляпунова
Этот метод предложили Фрешле и др. (1997). Для заданной орбиты
системы рассматриваем линеаризованные уравнения (5.1) и, задавая произ¬
вольные начальные <5р(0), <5q(0), вычисляем эволюцию 5p(t), 5q(£). Быст¬
рый индикатор Ляпунова FLI (fast Lyapunov indicator) определяется как вре¬
мя Т, на котором величина ||<Sp(£), 5q(£)|| впервые становится равной неко¬
торому большому произвольно заданному числу R. Интуитивно ясно, что
FLI имеет отношение к показателю Ляпунова: орбиты, для которых система
(5.1) сильно гиперболична, имеют малые FLI; если (5.1) слабо гиперболич¬
на, то FLI больше; если же изменения <$р, <5q ограничены, то FLI бесконеч¬
но. Однако FLI, очевидно, зависит от выбора начальных <5р(0), <5q(0), от
выбора значения R, а также от выбора канонических переменных р, q,
используемых для записи линеаризованных уравнений. Поэтому в отличие
от МПЛ FLI не характеризует рассматриваемую орбиту безусловно и его
нельзя использовать как абсолютную меру ее хаотичности.
Однако, коль скоро выбраны канонические переменные, заданы на¬
чальные <5р(0),<5q(0) и пороговое значение R, вычисление FLI позволяет
эффективно сравнивать динамическое поведение у различных орбит. В этом
смысле FLI можно рассматривать как индикатор хаотической природы од¬
ной орбиты относительно другой. Чтобы получить абсолютный индикатор,
необходима калибровка FLI с использованием реперных орбит, для которых
хаотическая природа уже определена, например из вычисления МПЛ.
Главным достоинством FLI является простота и скорость процедуры
его вычисления, что позволяет исследовать большие массивы орбит. Фреш¬
ле и др. (1997) успешно применили методику FLI в исследовании динами¬
ческой эволюции всех нумерованных астероидов; из его результатов стало
возможным выявить важность трехтельных резонансов для генерации хао¬
са в поясе астероидов (см. главу 11).
116
Глава 5
5.4.2. Углы спиральности и закручивания
Эту методику предложили Контопулос и Воглис (1996). Используя
линеаризованные уравнения (5.1), вычисляем ориентацию вектора 5p(t),
<5q(£) в зависимости от времени. В случае системы с п степенями свобо¬
ды ориентация определяется п — 1 углами — углами спиральности Фь ...,
Фп_1. Средние по времени значения углов спиральности (Ф\), ..(Фп-i)
зависят, в принципе, только от орбиты, относительно которой вычислены
линеаризованные уравнения движения (5.1), но они не зависят от началь¬
ного выбора вектора <$p(0),<Jq(0). Контопулос и Воглис показали, что для
орбит в однородной хаотической области средние значения углов спираль¬
ности инвариантны, а для регулярных орбит они плавно изменяются с на¬
чальными условиями. Это свойство позволяет легко разделить регулярные
и хаотические области, как только на регулярной сетке начальных условий
вычислены средние значения углов спиральности. Разумеется, для вычисле¬
ния средних углов спиральности требуется, в принципе, бесконечное время;
однако довольно точные оценки можно эффективно получить уже на отно¬
сительно малых временах, что с точки зрения практических вычислений,
делает данный метод привлекательным.
В дополнение к углам спиральности Контопулос и Воглис рассмотре¬
ли также их производные по времени — углы закручивания. Вычисление
средних значений углов закручивания также позволяет отделить регуляр¬
ные орбиты от хаотических. Они инвариантны для орбит в однородной
хаотической области, тождественно равны нулю для орбит на КАМ-торах
(в случае которых все углы циркулируют) и равны частотам либраций для
орбит на резонансных инвариантных торах (см. главу 4). Примеры поведе¬
ния среднего значения угла закручивания для орбит стандартного отобра¬
жения приведены в статье Фрешле и Лега (1998).
5.4.3. Средний фактор экспоненциальной расходимости близких орбит
Формулу (5.2) для вычисления максимального показателя Ляпунова
можно переписать в интегральной форме
(5.7)
где S = ||5р, <Sq||, а <5р(£), <Sq(£) являются решениями (5.1); S обозначает, как
обычно, производную от 6 по времени. Средний фактор экспоненциальной
расходимости близких орбит (MEGNO — mean exponential growth factor of
5.4. Суррогаты
117
nearby orbits), определяемый формулой
(5.8)
ввели Чинкотта и Симо (2000). Эволюция данной величины во времени
позволяет определить динамический характер рассматриваемой траектории
(траектории р(£),q(£), относительно которой вычисляются уравнения в ва¬
риациях (5.1)). Действительно, в случае квазипериодической траектории 8
линейно растет со временем, и поэтому Y(t) осциллирует с ограниченной
амплитудой около значения 2. В случае же хаотической траектории 8 рас¬
ходится со временем экспоненциально, и поэтому Y (t) осциллирует около
линейного решения у = at, где а — максимальный показатель Ляпунова.
Таким образом, если ввести текущее среднее MEGNO по времени
при t —» +оо в случае хаотической траектории.
На первый взгляд этот усредненный по времени показатель кажется со¬
вершенно эквивалентным максимальному показателю Ляпунова. Действи¬
тельно, у него такое же хорошее свойство, заключающееся в зависимо¬
сти исключительно от рассматриваемой траектории, но не от используе¬
мых при вычислениях координат и метрики. Однако Чинкотта и Симо по¬
казали, что Y(t) сходится к своему предельному значению быстрее, чем
оценка показателя Ляпунова. Причина состоит в том, что последний сохра¬
няет длительную память о начальной транзиентной эволюции касательного
вектора <5р, <5q; в интеграле же (5.8) предпочтительный вес имеет поздняя
эволюция 5р, 5q, что ведет к быстрой потере памяти о начальной транзи¬
ентной эволюции3.
3 Следует, однако, помнить, что при использовании малых времен счета получающаяся
оценка MEGNO не связана, вообще говоря, с истинным значением МПЛ, поскольку точную
численную оценку MEGNO, как и МПЛ, хаотической орбиты принципиально нельзя получить
иа временах меньше характерного времени диффузии по всей связной хаотической области,
которой принадлежит орбита. — Прим. ред.
(5.9)
имеем
i—►+оо
lim Y(t) = 2
(5.10)
в случае квазипериодической траектории и
(5.11)
118
Глава 5
Чинкотта и Джиордано (2001) привели многочисленные примеры при¬
менения MEGNO к системам с двумя и тремя степенями свободы. Во всех
случаях они нашли, что вычисление MEGNO выгоднее вычисления МПЛ:
при одних и тех же временах счета вычисление MEGNO позволяло выяв¬
лять более тонкие детали хаотических областей.
5.4.4. Средние, максимальные и минимальные значения действий
Идея данного подхода вдохновлена методом частотного анализа. Ес¬
ли орбита регулярная (то есть либо периодическая, либо лежит на КАМ-
торе), то не только частоты постоянны, но также и в поведении действий
есть периодические или квазипериодические повторения (см., например,
рис. 5.1а). Поэтому минимальное, максимальное и среднее значения дей¬
ствий на временном интервале [t0,to +Т] не зависят от начального време¬
ни to интервала, если Т достаточно велико.
Из этого соображения получается простой критерий для разделения
регулярных и хаотических орбит: регулярными орбитами являются такие,
для которых среднее, максимальное и минимальное значения действий не
изменяются при переходе от одного временного интервала к другому, а ха¬
отическими — такие, для которых эти значения изменяются с to. Впервые
этот критерий применил Ласкар (1994) при описании долговременной эво¬
люции планет; с тех пор его не раз применяли (см., например, Морбиделли,
1997; Морбиделли и Несворный, 1999) для выявления медленных измене¬
ний орбитальных элементов у астероидов и объектов пояса Койпера. Пре¬
имуществом данного подхода по сравнению с методом частотного анализа
является его намного более легкая реализация; к тому же он дает легче ин¬
терпретируемую информацию о долговременных изменениях средних ор¬
битальных элементов (большой полуоси, эксцентриситета и наклонения).
С другой стороны, частотный анализ позволяет легко отождествлять резо¬
нансы, ответственные за возникновение хаоса, чего нельзя достичь про¬
стым отслеживанием изменений действий.
Максимальное, минимальное и среднее значения, принимаемые дей¬
ствиями на временном интервале [0,Т], можно анализировать так же как
функции начальных условий, аналогично тому, как это делается в случае
частот. Это позволяет аналогичным образом разделять регулярные и хаоти¬
ческие области. Подробное обсуждение и примеры (для случая стандарт¬
ного отображения) можно найти в статье Контопулоса и др. (1997).
Глава 6
Взаимодействие резонансов
6.1. Две степени свободы
В главе 4 мы убедились, что резонанс, расположенный, скажем, при р0,
в действительности определяет динамику в окрестности р0, имеющей раз¬
меры ~ у/с, где с — коэффициент резонансной гармоники. Как следствие,
резонансы, расположенные в разных местах пространства действий, эф¬
фективно разделены только в том случае, если коэффициенты соответству¬
ющих резонансных гармоник достаточно малы; иначе их области влияния
перекрываются.
Чтобы пояснить эту мысль, рассмотрим квазиинтегрируемый гамиль¬
тониан
Р2
ft{Pi,P2,qi,q2) = у + 2тф2 +e[cos(gi) +cos(gi - q2)] (6.1)
и рассмотрим резонансы qi = 0 и qi — q<z — 0, расположенные соответ¬
ственно при pi = 0 и pi = 2тг для любого р2- Чтобы изучать динамику
этой системы, можно в первом приближении рассмотреть каждый из ре¬
зонансов отдельно, принимая во внимание только соответствующую ему
гармонику и пренебрегая другой гармоникой. Конкретно, мы используем
интегрируемые модели одиночного резонанса Н = р\/2 + 2тгр2 + £COs(<7i)
и Н = р\/2 4- 2ттр2 + £COs((?i — <72) Для построения сечений Пуанкаре
в окрестности pi = 0 и в окрестности pi — 2тт соответственно. Полученная
в итоге картина динамики показана на рис. 6.1. Если е мало, то сепаратри¬
сы этих двух резонансов находятся на удалении друг от друга; очерченные
прерывистыми прямыми области, где динамика сильно подвержена влия¬
нию резонансов, разделены большим расстоянием. Оказывается, что усло¬
вие разделения резонансов обеспечивает хорошую аппроксимацию дина¬
мики; согласно главе 4 сепаратрисы каждого из резонансов в действитель¬
ности расщеплены, образуя узкие хаотические области, но между двумя
120
Глава 6
резонансами, как ожидается, есть много КАМ-торов, так что хаотические
области локально ограничены. В частности, траектория не может перехо¬
дить из одного резонанса в другой.
Рис. 6.1. Сечения Пуанкаре для двух резонансов, вычисленные каждое в интегри¬
руемой модели одиночного резонанса. Когда ширина резонансов мала, резонансы
хорошо разделяются и для каждого из них применима аппроксимация в модели
одиночного резонанса (панель слева). Напротив, когда ширина резонансов велика,
они перекрываются (панель справа). В последнем случае можно ожидать наличия
крупномасштабного хаоса
Ситуация в корне отлична, когда е велико (рис. 6.1 б). Тогда области,
где динамика определяется отдельно каждым из резонансов, перекрывают¬
ся, а сепаратрисы резонансов, в том виде как они вычислены на сечении
Пуанкаре каждая в интегрируемой модели, оказываются пересекающими¬
ся. Таким образом, условие изоляции резонансов нарушается, и поэтому
глобальную динамику в данном случае нельзя исследовать, используя инте¬
грируемые модели одиночного резонанса. Естественно ожидать, что в дан¬
ном случае между двумя резонансами нет КАМ-торов, то есть хаотиче¬
ские области около сепаратрис обоих резонансов в действительности об¬
разуют единую связную область, охватывающую приблизительно все про¬
странство, занятое двумя резонансами. Образно говоря, начальное условие
в области перекрытия «не знает», какому резонансу оно принадлежит, и «не
уверено», вдоль какой ведущей траектории (кривые на рис. 6.1 б) оно долж¬
но эволюционировать. Как следствие, траектория с начальными условиями
внутри хаотической области может свободно переходить от одного резонан¬
са к другому, при этом действие р\ может изменяться от 0 до 27т и обратно,
а два резонансных угла qi и q\ — q<z — попеременно либрировать и цирку¬
лировать.
6.1. Две степени свободы
121
Р1
О
Qi
27Г
Рис. 6.2! Слева: простой критерий перекрытия для двух главных резонансов при
pi = 0 и pi — (е = 2.47). Посередине: критерий перекрытия с учетом также
резонанса при pi — 7г (е = 1.46). Справа: критерий перекрытия с учетом также
и ширины хаотических слоев (заштрихованные области) двух главных резонансов
(е = 1.2)
Чириков (1959, 1979) и Контопулос (1966) рассмотрели пересечение
сепаратрис разных резонансов, каждая из которых вычисляется в интегри¬
руемой модели одиночного резонанса, в качестве практического критерия
для количественной оценки порогового значения с, соответствующего ис¬
чезновению КАМ-торов и переходу к глобальному хаосу. Сейчас этот кри¬
терий обычно называют критерием Чирикова. Чириков (1979) исследовал
его точность на примере стандартного отображения (3.13). Учитывая толь¬
ко два главных резонанса, = 0 и q\ — q<2 = 0 при р\ = 0 и pi = 27т, он
получил критическое значение е ~ 2.47. Истинное же значение, при кото¬
ром происходит переход к глобальному хаосу из-за разрушения золотого
КАМ-тора (тора с отношением частот q±/q2 = (л/б — 1)/2), составляет
е « 0.9716, как численно установил Грин (1979). Таким образом, результат,
следующий из критерия Чирикова, выглядит лишь отчасти удовлетвори¬
тельным и весьма приблизительным с точки зрения возможности количе¬
ственных оценок. В общем случае критерий Чирикова дает завышенную
оценку порога перехода к глобальному хаосу в том смысле, что реальный
переход происходит при меньшем, чем предсказываемое критерием, значе¬
нии параметра возмущения. Это вызвано главным образом двумя причи¬
нами: во-первых, не учтены резонансы, чьи гармоники отсутствуют в ис¬
ходном гамильтониане, но генерируются при итерациях пертурбационного
алгоритма (см. главу 2) с коэффициентами более высоких порядков по е,
и, во-вторых, не учтены взаимодействие и деформации резонансов. Чири¬
ков попытался улучшить точность своего критерия, учитывая большее чис¬
ло возмущающих членов. Если учесть резонанс 2q\ — q2 = 0 при pi = п,
коэффициент гармоники которого порядка е2, то оценка порога уменьшает¬
122
Глава 6
ся до е = 1.46; а если к тому же учесть ширину хаотических слоев вокруг
двух главных резонансов, то получается оценка е = 1.2. Эти попытки сум¬
мированы на рис. 6.2. Они показывают, что точность критерия улучшается,
если учитывать все больше и больше резонансных возмущающих членов.
Рис. 6.3. Перекрытие резонансов в зависимости от параметра возмущения в систе¬
ме с двумя степенями свободы. Ширина резонансов зависит от величины возму¬
щения е. Если возмущение превышает некоторый порог, происходит перекрытие
резонансов. Если е достаточно мало, то резонансы не могут перекрываться и почти
весь объем занят инвариантными торами
Исходя из всего сказанного, можно представить эскиз глобального ди¬
намического поведения системы с двумя степенями свободы в зависимости
от параметра возмущения е, как это сделано на рис. 6.3. На этом графике
горизонтальной осью служит отношение частот и а вертикаль¬
ной — величина возмущения. Резонансы располагаются при рациональных
отношениях частот; они отмечены вертикальными прерывистыми прямы¬
ми. Сплошными кривыми показаны амплитуды рассматриваемых резонан¬
сов, выраженные в единицах отношения частот. Эти кривые строятся так:
в интегрируемой модели одиночного резонанса вычисляем значения р+
и р_ действия в апексах верхней и нижней сепаратрис (например, для резо¬
нанса qi = 0 системы (6.1) имеем р\ = ±2у/е) и затем отмечаем на графи¬
6.1. Две степени свободы
123
ке значения невозмущенного отношения частот, соответствующие р+ и р“.
Поскольку величина коэффициентов резонансных гармоник увеличивается
с ростом возмущения, а ширина резонансов пропорциональна корню квад¬
ратному из этих коэффициентов, амплитуды резонансов на рис. 6.3 име¬
ют характерный вид буквы V. Поэтому если величина возмущения меньше
пороговой (зависящей, вообще говоря, от отношения частот), то резонан¬
сы не перекрываются и между ними можно ожидать наличия КАМ-торов.
Траектории не могут переходить от одного резонанса к другому, и, таким
образом, движение ограничено в пространстве действий. Если же величина
возмущения больше пороговой, то резонансы перекрываются и КАМ-торы
исчезают. Тогда движение от резонанса к резонансу возможно; отношение
частот эволюционирует со временем как при случайных блужданиях. Ха¬
рактерная длина шага блужданий определяется амплитудами резонансов,
а характерное время одного шага равно по порядку величины типичному
периоду либраций резонансного критического угла. Далее мы называем это
явление диффузией Чирикова. Термин диффузия здесь не означает, что эво¬
люция отношения частот строго подчиняется диффузионному уравнению,
а означает лишь то, что эта эволюция испытывает макроскопические вари¬
ации — блуждания в пространстве действий.
Следует заметить, что на рис. 6.3 показаны только резонансы до неко¬
торого конечного порядка, тогда как необходимо, в принципе, рассматри¬
вать резонансы всех порядков. Однако из графика мы видим, что шири¬
на резонансов быстро убывает с порядком. Действительно, коэффициенты
резонансных гармоник экспоненциально убывают с порядком рассматри¬
ваемых резонансов, а расстояния между резонансами порядка К убыва¬
ют как 1/К. Как следствие, резонансы высоких порядков практически не
оказывают влияния на глобальное перекрытие резонансов. Резонансы, спо¬
собные перекрываться, имеют порядки меньше некоторого порогового зна¬
чения. Это справедливо и для систем с числом степеней свободы больше
двух; поэтому мы еще вернемся к данному важному факту в разделе 6.3.
6.1.1. Гетероклинические пересечения
Как мы видели, чириковский критерий перехода к глобальному хаосу
весьма привлекателен и интуитивно ясен; но, к сожалению, он является эв¬
ристическим и его полной строгой теории до сих пор не существует. Идею
перекрытия резонансов можно обосновать исходя из понятия гетероклини-
ческого пересечения. Это строгое математическое понятие: так называется
пересечение устойчивого и неустойчивого многообразий двух различных
124
Глава 6
(а)
(б)
0)
qi
Рис. 6.4. Гомоклинические и гетероклинические пересечения на примере двух глав¬
ных резонансов стандартного отображения для нескольких значений параметра е.
См. комментарии в тексте
6.1. Две степени свободы
125
резонансов (в отличие от обсуждавшегося в главе 4 гомоклинического пе¬
ресечения — пересечения устойчивого и неустойчивого многообразий од¬
ного и того же резонанса). К сожалению, гетероклинические пересечения
изучать гораздо труднее, чем гомоклинические. Последние можно изучать
в рамках задачи о возмущении интегрируемого случая, в котором устойчи¬
вое и неустойчивое многообразия совпадают. Гетероклинические же пере¬
сечения, напротив, нельзя изучать используя теорию возмущений, посколь¬
ку интегрируемого приближения с учетом обоих резонансов не существует,
по крайней мере в случае общего положения. Картина здесь в самом деле
очень сложная, и по сегодняшний день ясное представление о происходя¬
щем могут дать только численные эксперименты. Из главы 4 мы знаем,
что устойчивые и неустойчивые многообразия гиперболических периоди¬
ческих орбит можно находить численно. На рис. 6.4 показано, как происхо¬
дят гетероклинические пересечения многообразий двух главных резонан¬
сов стандартного отображения. Портрет на панели (а) построен для зна¬
чения е — 0.314, при котором динамика квазиинтегрируема: устойчивое
и неустойчивое многообразия каждого из двух резонансов, как видим, сов¬
падают с точностью до разрешения рисунка. На панели (б), где е = 0.942,
резонансы все еще хорошо разделены; однако вблизи гиперболических то¬
чек равновесия обоих резонансов стали заметны гомоклинические клубки.
На панели (в) (е = 1.632) петли устойчивого и неустойчивого многообра¬
зий двух резонансов уже очень близки друг к другу, но все еще не пере¬
секаются; по крайней мере, так следует из рисунка (многообразия имеют
бесконечную длину, но, разумеется, можно вычислить и изобразить только
конечные их фрагменты). На этой и последующих панелях показаны только
неустойчивое многообразие резонанса при р\ ~ 0 и устойчивое многообра¬
зие резонанса при pi ~ 27т, иначе изображение было бы слишком запутан¬
ным. На панели (г) (г = 1.696) петли наконец трансверсально пересекаются
в точках, называемых гетероклиническими точками. Следуя тому же рас¬
суждению, что и в главе 4 в случае гомоклинических точек, можно доказать
существование бесконечного числа гетероклинических точек и гетерокли-
нического клубка. У вычисленных фрагментов многообразий на панели (г)
кратные гетероклинические пересечения и гетероклинический клубок еще
не видны. Они все более и более проявляются на последующих панелях (д)
и (е), построенных для е = 2.198 и е = 3.14.
Интересно сравнить найденное здесь значение е, пороговое для по¬
явления гетероклинических пересечений, то есть £# ~ 1.66, с истинным
пороговым значением для перехода к глобальному хаосу (значением, при
126
Глава 6
котором разрушается золотой тор), то есть с eg = 0.9716, и с критиче¬
ским значением по критерию Чирикова, то есть с г с = 2.47. Отметим, что
£н £g> так как мы учитывали только два главных резонанса и прене¬
брегли всеми резонансами более высоких порядков, расположенными меж¬
ду ними; если бы мы искали гетероклинические пересечения в полной ре¬
зонансной цепочке, то получили бы критическое значение гораздо ближе
к истинному (см. Олвера и Симо, 1987). Альтернативой было бы вычис¬
ление устойчивого и неустойчивого многообразий двух главных резонан¬
сов на всем их бесконечном протяжении; но это, очевидно, невозможно.
С другой стороны, £н Ес, так как в критерии Чирикова учитывается
лишь амплитуда невозмущенных резонансов и пренебрегается взаимными
возмущениями и шириной гомоклинических петель. Результаты вычисле¬
ний, показанные на рис. 6.4, наглядно демонстрируют, насколько сложна
реальная картина динамики; и можно себе представить, насколько трудно
описать эти явления строгим математическим образом. Поэтому неудиви¬
тельно, что у критерия Чирикова и чириковской модели диффузии до сих
пор нет полного теоретического обоснования.
6.2. Более двух степеней свободы
Достичь понимания глобальной динамики систем с числом степеней
свободы более двух гораздо труднее, чем в случае двух степеней свободы.
География резонансов, а именно относительное расположение резонансов
в пространстве частот, здесь гораздо сложнее. В случае трех степеней сво¬
боды, например, положения резонансов можно представить на плоскости
в координатах uoi/uj2 и uji/us, где и>2, и)з — частоты системы. Все пря¬
мые на такой плоскости, имеющие рациональные наклоны, соответствуют
резонансам кратности 1 (см. определение кратности в разделе 1.10) и фор¬
мируют сеть, обычно называемую резонансной паутиной, или паутиной
Арнольда. Очевидно, что здесь, в отличие от случая двух степеней сво¬
боды, резонансные линии могут пересекаться, причем точки пересечения
соответствуют резонансам кратности 2. Из-за этих пересечений перекры¬
тие резонансов имеет место всегда (по крайней мере локально в окрест¬
ностях резонансов с кратностью больше 1), поэтому обобщение критерия
Чирикова неочевидно. Более того, как нам известно из главы 3, наличие
КАМ-торов теперь уже не препятствует «транспорту» в пространстве дей¬
ствий. Таким образом, тогда как в случае двух степеней свободы возможны
только две ситуации — глобально-устойчивая, когда резонансное движение
6.2. Более двух степеней свободы
127
ограничено КАМ-торами, и глобально-неустойчивая, вызываемая перекры¬
тием резонансов, в случае более чем двух степеней свободы динамическое
поведение является более сложным.
Тем не менее для достаточно малых возмущений Нехорошеву (1977,
1979) удалось достичь строгого результата о практической глобальной
устойчивости многомерных систем.
6.2.1. Теорема Нехорошева
Теорема Нехорошева касается квазиинтегрируемых систем с п сте¬
пенями свободы и гамильтонианами вида Н(p,q) = Wo(p) + £Hi(p,q),
где р, q — переменные «действие-угол», определенные в области V =
Q х Тп, пространство действий Q является областью в Rn, а пространство
углов Тп — n-мерный тор. В дальнейшем мы будем обозначать множество
точек р, содержащихся в Q вместе с окрестностью радиуса А, через Q — Д.
Тогда теорема Нехорошева может быть сформулирована следующим обра¬
зом.
Пусть W(p, q) = Wo(p) + £Wi(p,q) является аналитической функ¬
цией в V = Q х Тп, где Q С Rn — открытое ограниченное множество.
Рассмотрим матрицу С(р) с элементами Cij(р) = (р) и предполо¬
жим, что выполнено условие выпуклости:
C(p)v-v/0 Vp eg и Vv G Rn \ 0. (6.2)
Тогда существуют положительные постоянные £*, а, (3, а и Ь, такие что
для любого е < е* имеем
||p(i)-p(0)|| < Д = аеа
для всех р(0) G Q — А и всех |£| ^ Т{е), где
Г(£) = /З(^)%хр(^)6. (6.3)
Здесь уместно сделать несколько комментариев. Теорема Нехороше¬
ва не исключает возможности хаотических движений. В действительности
действия р могут изменяться хаотически: теорема утверждает лишь то, что
любые изменения р ограничены величиной А до времени Т. Медленный
дрейф может принудить действия измениться более чем на А относитель¬
но начальных условий только по прошествии времени больше чем Т, как
128
Глава 6
эскизно показано на рис. 6.5. Важно, что время устойчивости Т возраста¬
ет экспоненциально с величиной е*/е. Таким образом, если е оказывается
несколько меньше порогового значения £*, то время устойчивости стано¬
вится экстремально долгим и может превысить физическое время жизни
системы (например, время жизни Солнечной системы), что обеспечивает
практическую устойчивость системы. Подчеркнем, что столь важный вы¬
вод об устойчивости достигается равномерно по всем начальным услови¬
ям р, q при р, принадлежащих Q — А. Очевидно, что орбиты, проходящие
ближе чем на расстоянии А до границ области действий, исключаются, по¬
скольку они могут покинуть Q за малое время. Что касается условий тео¬
ремы, отметим, что условие иметь дело именно с аналитическими гамиль¬
тонианами является критичным. По причинам, которые будут объяснены
ниже, следует ожидать, что у дифференцируемых гамильтонианов время
устойчивости Т имеет степенную зависимость от £*/е, а не экспоненци¬
альную. Роль условия выпуклости (6.2) также будет объяснена ниже; здесь
же стоит отметить, что это условие можно ослабить, используя вместо него
более техническое условие, называемое крутизной (Нехорошее, 1979), об¬
суждение которого выходит за рамки данной книги.
Теорема Нехорошева — нечто много большее, чем сформулированный
выше знаменитый результат о долговременной устойчивости; а именно, она
доказывает существование специфичной структуры фазового пространства,
из чего выводится результат об устойчивости. Однако этот факт обычно
скрыт в доказательстве теоремы, и ему поэтому уделяется мало внимания.
Чтобы сделать эту структуру явной для читателя, приведем набросок дока¬
зательства теоремы Нехорошева.
Как мы убедились в главе 2, гармоники £Cfc(p) ехр(Пс • q) в возму¬
щении eH\ можно отнести к более высоким порядкам по е методом пре¬
образований Ли лишь вдали от соответствующих резонансов к • и — 0.
Вблизи резонанса гармонику нельзя исключить, то есть она должна быть
сохранена в резонансной нормальной форме. Поскольку резонансы плотны
в пространстве действий, на любом открытом подмножестве Q из возму¬
щения нельзя исключить бесконечное число гармоник. В общем случае это
препятствует интегрируемости системы (Пуанкаре, 1892). Идея Нехороше¬
ва состоит в том, чтобы рассматривать только резонансы порядка не выше
некоторого порогового К.
Выбор такого подхода очень важен. В самом деле, с одной стороны,
число резонансов порядка не выше заданного конечно, и поэтому всякое
открытое подмножество пространства действий содержит лишь конечное
6.2. Более двух степеней свободы
129
Р
2Д
I
t
t
Т ~ ехр(1/б:)
Рис. 6.5. Теорема Нехорошева: каковы бы ни были начальные условия, действия
могут эволюционировать хаотически, но время Т, требуемое для изменения более
чем на величину Д(е), экспоненциально велико по 1/е. Если параметр возмуще¬
ния е достаточно мал, то время Т превышает физическое время жизни рассматри¬
ваемой системы; то есть теорема Нехорошева обеспечивает вывод о «практической»
устойчивости. (Рис. 1 из статьи Морбиделли и Гуццо, 1996; с разрешения Kluwer
Academic Publishers)
число резонансных линий, как на рис. 6.6. С другой стороны, аналитич¬
ность гамильтониана означает, что пренебрегаемые члены, соответствую¬
щие резонансам порядка выше К, имеют величину не больше ехр(—Ка)
(где а — некоторое положительное число). Можно показать, что пороговое
значение К можно выбрать таким большим, как 1/еъ (с некоторым поло¬
жительным b < 1), поэтому пренебрегаемые члены оказываются экспонен¬
циально малыми по 1/еъ. Этот факт определяет время устойчивости Т(е),
экспоненциально зависящее от 1/еь, как в формуле (6.3). Заметим, что если
гамильтониан не аналитичен, а лишь г раз дифференцируем, то, как можно
ожидать, некоторые из пренебрегаемых членов имеют величину К~т, то
есть 1/егЬ. Как следствие, время устойчивости Т(е) получается не больше,
чем ~ 1/егЪ.
Ограничимся ради простоты случаем трех степеней свободы. К то¬
му же представим резонансную структуру системы при заданном значении
гамильтониана на плоскости частот в координатах и где и =
= Sradp7Yo. Такой выбор позволяет построить удобные поясняющие схемы
130
Глава 6
Рис. 6.6. Эскиз геометрической конструкции теоремы Нехорошева для системы
с тремя степенями свободы на плоскости частот с координатами оц/с^з и <^2/^3 •
Тремя жирными прямыми обозначены положения трех резонансов кратности 1;
они образуют ячейку паутины Арнольда. Точки пересечения этих резонансов друг
с другом соответствуют положениям резонансов кратности 2. См. обсуждение в тек¬
сте. (Рис. 2 из статьи Морбиделли и Гуццо, 1996; с разрешения Kluwer Academic
Publishers)
(рис. 6.6). Напомним, что на плоскости частот резонансы суть прямые с ра¬
циональными наклонами.
Прежде всего определим нерезонансную область как множество частот
достаточно далеких от всех резонансов порядка не выше К. На рис. 6.6а это
несвязная область, ограниченная пунктирными линиями. В точном опреде¬
лении она представляет собой множество частот таких, что |к • ш\ > \fe
для всех к, у которых |к| ^ К} В нерезонансной области можно построить
нормальную форму Биркгофа, исключив в возмущении eHi все гармони-
1 Напомним, что согласно главе 4 ширина резонанса пропорциональна корню квадратно¬
му из коэффициента (в данном случае е) резонансной гармоники; поэтому при определении
6.2. Более двух степеней свободы
131
ческие члены вида etk q с |к| ^ А". В самом деле, по построению все эти
члены нерезонансны в такой области. Полученный в результате гамильто¬
ниан зависит только от новых действий, если в гамильтониане не считать
остатка 7Zk, который (по своей сути) состоит из гармонических членов по¬
рядка больше К, являющихся экспоненциально малыми. Таким образом,
пренебрегая не более чем экспоненциально медленной диффузией, вызы¬
ваемой 1Zk, приходим к выводу, что частоты системы в нерезонансной об¬
ласти не изменяются со временем.
На втором шаге рассмотрим области одиночного резонанса, ограни¬
ченные на рис. 6.66 прерывистыми линиями. Каждая их этих областей ха¬
рактеризуется присутствием только одного резонанса порядка меньше К.
В этих областях можно построить нормальную форму одиночного резо¬
нанса, исключив все нерезонансные члены порядка меньше К. Затем при¬
водим гамильтониан к виду с лишь одним резонансным членом (порядка
|fc| ^ К) и с остатком 7Zk, состоящим из членов порядка больше К, —
опять же экспоненциально малым. Если им пренебречь, то гамильтониан
будет опять интегрируемым, но зависящим от одного резонансного угла,
так что действия (а следовательно, и частоты) уже не будут более фик¬
сированными. Из-за наличия резонансной гармоники они изменяются —
вдоль направления, обычно называемого направлением быстрого дрейфа.
На рис. 6.66 оно указано стрелкой. Условие выпуклости (6.2) гарантиру¬
ет, что резонансное движение ограничено, как в случае маятника. Фак¬
тически для выпуклого гамильтониана можно доказать, что направление
быстрого дрейфа трансверсально к резонансной линии. Таким образом, ес¬
ли следовать в направлении быстрого дрейфа неограниченно, то движение
попадет в нерезонансную область. Но это невозможно, поскольку в нерезо¬
нансной области частоты фиксированы, как объяснено выше. С другой сто¬
роны, движение, трансверсальное к направлению быстрого дрейфа, может
быть вызвано только неинтегрируемым остатком 7Zk, так что оно является
экспоненциально медленным. Это медленное движение обычно называют
диффузией Арнольда. Кроме того, остаток IZk вызывает расщепление се¬
паратрис, так что амплитуда расщепления не более чем экспоненциально
мала (Нейштадт, 1984).
На третьем шаге рассмотрим области двойного резонанса; их центры
приходятся на пересечения резонансных линий, соответствующие резонан¬
сам кратности 2. На рис. б.бв эти области ограничены сплошными тонкими
нерезонансной области необходимо исключать окрестности шириной у/е рассматриваемых
резонансных линий. — Прим. авт.
132
Глава 6
линиями. В таких областях резонансная нормальная форма содержит два
независимых резонансных члена порядка меньше К. Поэтому резонансная
нормальная форма, вообще говоря, неинтегрируема и можно ожидать, что
данные области характеризуются сильным хаосом, а частоты могут изме¬
няться на плоскости в окрестности пересечения резонансов в любом на¬
правлении. Однако это хаотическое движение вновь оказывается ограни¬
ченным. В самом деле, если бы частоты сместились достаточно далеко от
точки двойного резонанса, то они попали бы либо в нерезонансную об¬
ласть, либо в одну из областей одиночного резонанса. Но это невозмож¬
но, поскольку в нерезонансной области частоты фиксированы, а в обла¬
стях одиночного резонанса они могут изменяться только вдоль направления
быстрого дрейфа.
В итоге, если пренебречь экспоненциально малым остатком 7Zk, то
при любых начальных условиях движение удерживается в пределах од¬
ной из резонансных областей. Как следствие, частоты (и действия) мо¬
гут изменяться не более чем на величину радиуса областей двойного ре¬
зонанса (при числе степеней свободы п наихудшим является случай обла¬
стей, построенных около резонансов кратности п — 1). Можно доказать,
что этот радиус пропорционален еа9 где а — некоторое положительное
число меньше 1, которое уменьшается с увеличением числа степеней сво¬
боды.
Более того, чтобы получить самосогласованную картину, как на
рис. 6.6, резонансов порядка меньше К не должно быть слишком много,
так как иначе не осталось бы места для нерезонансной области и постро¬
ить рис. 6.6 было бы невозможно. Тот факт, что наибольшие резонансные
области имеют размер порядка еа, задает для выбора К верхнюю границу
вида 1/еь, как мы и предвидели.
Наконец, примем во внимание экспоненциально малый остаток 7£х-
Очевидно, что этот остаток может вызвать диффузию в любом направлении
пространства частот, но лишь с экспоненциально малой скоростью. Тогда
вывод об ограниченности движения, полученный в пренебрежении 7Zk,
будет справедлив, в принципе, лишь в пределах экспоненциально долгих
интервалов времени.
Рассмотренная здесь в общих чертах схема доказательства теоремы
Нехорошева описана со всеми математическими деталями в работе Пешеля
(1993). Читатель может обратиться также к статьям Нехорошева (1977),
Бенеттина и др. (1985) и Лошака (1992), где излагаются альтернативные
подходы.
6.2. Более двух степеней свободы
133
6.2.2. Нехорошевская структура
Конструкцию теоремы Нехорошева можно итерировать, чтобы иссле¬
довать динамическую структуру системы, обусловленную резонансами по¬
рядка выше нехорошевского порогового значения К 1/еъ (см. Морби¬
делли и Джиорджилли, 19956).
В самом деле, после исключения резонансов до порядка К в опреде¬
ленной выше нерезонансной области (обозначаемой далее как Qk) в новых
переменных «действие-угол» р', q' гамильтониан принимает вид
tf'(pW) = Wo(p') + e/Wi(P/-q'). гае e'Hi(p',q') = Пк{р',ч'). (6.4)
Как и прежде, это автономная выпуклая система, но здесь новое возмуще¬
ние экспоненциально мало относительно исходного возмущения, так как
е' ~ ехр(—1/£ь). Далее, применяя теорему Нехорошева к этому гамиль¬
тониану (то есть рассматривая резонансы до нового порядка обрезания
К' ~ 1/е'ъ ~ exp[Ь/еь]), мы доказываем глобальную устойчивость движе¬
ния в Qk на суперэкспоненциально долгих интервалах времени, а именно
до Т ~ ехр[ехр(1/еь)]6. Более того, мы находим новую нерезонансную об¬
ласть Qk', где нет резонансов до порядка К'. На Qk' можно ввести новые
переменные «действие-угол», чтобы преобразовать гамильтониан к виду
суммы интегрируемой части и остатка 7Zk' , где последний суперэкспонен¬
циально мал. Эту процедуру можно итерировать, причем доказано, что ите¬
рационный процесс сходится к множеству инвариантных КАМ-торов боль¬
шого объема (Джиорджилли и Морбиделли, 1997). Тот факт, что с каждым
шагом процесса нерезонансная область фрагментируется на все меньшие
и меньшие части, никогда не препятствует применению теоремы Нехоро¬
шева: в самом деле, наиболее существенный параметр, а именно отношение
величины возмущения и размера каждой из связных компонент области,
уменьшается на каждом шаге. Процедура итераций теоремы Нехорошева
резюмирована в таблице 6.1.
Итоговая глобальная картина, получаемая в свете теоремы Нехорошева
и ее последовательных итераций, эскизно дана на рис. 6.7. Если параметр
возмущения е достаточно мал, то теорема Нехорошева применима. Дина¬
мика структурирована (рис. 6.1а). Резонансы заданного порядка пересе¬
каются в резонансных узлах, соответствующих резонансам более высокой
кратности. В окрестностях последних присутствует выраженный хаос, но
резонансы не перекрываются полностью в том смысле, что внутри каждой
из ячеек резонансной паутины всегда есть нерезонансная область. Более то-
134
Глава 6
Таблица 6.1. Схема итераций теоремы Нехорошева. В первом столбце приведено
число итераций N; во втором — размер д связных компонент области определения
гамильтониана; в третьем — величина возмущения \\Hi\\; в четвертом — порядок
обрезания К для рассматриваемых резонансов; в пятом — нехорошевское время
устойчивости Ts\ в шестом — размер дк каждой из связных компонент нерезонанс¬
ной области; в последнем — величина остатка 7Zk построенной на нерезонансной
области нормальной формы. Итерация состоит в применении теоремы Нехорошева
последовательно на нерезонансной области, определенной на предыдущем шаге, то
есть в подстановке столбцов 6 и 7 в столбцы 2 и 3. Степени е не указаны
N
6
№11
К
TS
дк
№к\\
1
1
е
1/е
ехр(1/е)
£
exp-"T(l/e)
2
£
ехр-1(1/е)
ехр(1/е)
ехр*(1/е)
exp-i(i/£)
exp-'^l/e)
3
ехр-1(1/е)
exp-'J(l/e)
ехр^(1/е)
ехр3(1/е)
exp-^l/e)
exp“a(l/e)
п
ехр_п+‘!(1/е)
ехр_п+1(1/е)
ехрп-1(1/е)
ехрп(1/£)
exp-n+1(l/e)
exp~n(l/e)
го, этот сценарий справедлив на любом масштабе, если рассматривать резо¬
нансы последовательно увеличивающегося порядка. Ядром данной струк¬
туры служит множество инвариантных КАМ-торов, представляющее собой
в рамках данной схемы нерезонансную область в пределе, когда число ите¬
раций теоремы Нехорошева устремлено к бесконечности. В дальнейшем
динамическую систему с такой структурой мы будем называть нехорошев-
ской системой.
На рис. 6.76 показана обратная ситуация. При некотором порядке ре¬
зонансы перекрываются. Места для нерезонансной области нет, и инвари¬
антные торы более не существуют. Перекрытие резонансов позволяет ор¬
битам переходить от одного резонанса к другому посредством хаотической
«быстрой» (чириковской) диффузии. Фазовое пространство характеризует¬
ся крупномасштабным хаосом. Поскольку ширина областей одиночного ре¬
зонанса пропорциональна у/е, такая ситуация имеет место, если параметр е
не является достаточно малым.
6.2.3. Суперэкспоненциальная устойчивость КАМ-торов
Сравнение размера g нерезонансной области и времени устойчиво¬
сти Ts при каждом порядке N итераций теоремы Нехорошева (см. табли¬
цу 6.1) наводит на мысль, что время, требуемое для ухода из окрестности
КАМ-тора, суперэкспоненциально зависит от величины, обратной началь¬
ному расстоянию от тора.
6.2. Более двух степеней свободы 135
Рис. 6.7. Панель (я): эскиз нехорошевской структуры. Резонансы заданного порядка
пересекаются в резонансных узлах, но не перекрываются: внутри каждой из ячеек
резонансной паутины всегда существует нерезонансная область. При уменьшении
масштаба, если рассматривать резонансы последовательно увеличивающегося по¬
рядка, картина повторяется. Панель (б): при некотором порядке резонансы пере¬
крываются. Нерезонансную область нельзя определить. Инвариантные торы раз¬
рушены. Траектория может переходить от одного резонанса к другому. Как и на
рис. 6.6, резонансная структура эскизно представлена здесь на плоскости частот
для системы с тремя степенями свободы. (Рис. 3 из статьи Морбиделли и Гуццо,
1996; с разрешения Kluwer Academic Publishers)
Это можно доказать простым непосредственным образом (Морбидел¬
ли и Джиорджилли, 1995а). Как продемонстрировано в разделе 3.2, начав
с нормальной формы Колмогорова, в окрестности UQ радиусом д КАМ-тора
можно построить оптимальную нормальную форму Биркгофа, чей остаток
имеет величину е6 ~ ехр[£-1/(т+1)]. Тогда гамильтониан в Ыв запишется
как Н(I, <р) = Ho(I) + seTZ(I, ip). Если Hq(I) удовлетворяет условиям тео¬
ремы Нехорошева, то, применяя последнюю, мы доказываем, что время,
требуемое для ухода из UQ, если стартовать из Ы6 - ев, пропорционально
ехР[1/4] = ехр{ехр[6/£1/(т+1)]}.
Это улучшает уже обсуждавшийся в разделе 3.2 результат об устойчи¬
вости КАМ-торов и подчеркивает ту важную роль, которую играют КАМ-
торы в структурировании динамики гамильтоновых систем с любым конеч¬
ным числом степеней свободы.
136
Глава 6
6.3. Исследование динамической структуры
заданной системы
В свете раздела 6.2.2 приступать к исследованию заданной динамиче¬
ской системы разумно с поиска ответов на следующие вопросы. Обладает
ли система нехорошевской структурой? Если нет, то в каком порядке резо¬
нансы начинают перекрываться?
Рис. 6.8. Относительный объем Vk, заполненный всеми резонансами порядка К,
согласно формуле (6.5). На панели {а) е мало, поэтому при любом К объем Vk
всегда меньше объема фазового пространства (нормированного здесь на 1). Следо¬
вательно, резонансы не могут глобально перекрываться, существуют инвариантные
торы, и система имеет нехорошевскую структуру. На панелях (б) и (в) объем Vk
больше 1 при некоторых К. Поэтому резонансы должны перекрываться, а инвари¬
антные торы не могут существовать. Порядок, при котором резонансы начинают
глобально перекрываться, зависит от е. Если е очень велико (панель (б)), то этот
порядок мал; если нет (панель (в)), то он может быть очень велик и близок к поряд¬
ку, соответствующему максимуму Vk. (Рис. 4 из статьи Морбиделли и Гуццо, 1996;
с разрешения Kluwer Academic Publishers)
К сожалению, найти ответы на эти вопросы аналитическим путем
нелегко, что следует из следующего качественного анализа, вдохновлен¬
ного работой Арнольда (19636). Ширина резонансной области пропорцио¬
нальна корню квадратному из коэффициента соответствующей резонансной
гармоники, то есть она зависит от порядка К резонанса как л/ёехр(—Ка).
Количество резонансов порядка К растет с К как 2пКп~1, где п — чис¬
ло степеней свободы. Следовательно, относительный объем фазового про¬
странства, заполненный всеми резонансами порядка К, составляет
VK ~ 2плДКп~1 ехр(-Ка). (6.5)
Объем Vk максимален при К = (п — 1)/сг, а при больших К убывает экс-
поненциально. На рис. 6.8 показаны зависимости Vk от К при различных
6.3. Исследование динамической структуры заданной системы 137
значениях е. Если е мало, то при всех К объем, заполненный резонансами
порядка К, меньше объема всего фазового пространства (рис. 6.8а). Это
означает, что при всех порядках резонансы не могут перекрываться полно¬
стью: есть некоторый объем, свободный от резонансов, где могут существо¬
вать инвариантные торы; система имеет нехорошевскую структуру2. Если
взять е достаточно большим, то при некотором К относительный объем Vk
достигает единицы. Как следствие, резонансы порядка К должны пере¬
крываться полностью, инвариантные торы не могут существовать, и си¬
стема теряет свою нехорошевскую структуру. Минимальный порядок К,
при котором резонансы перекрываются, зависит от е. Если е очень велико,
то резонансы могут начать перекрываться уже при очень низком порядке
(рис. 6.8б); при меньших е перекрытие может происходить при К, близких
к Атах = (п — 1)/<г (рис. 6.8в). Последние могут быть очень большими,
если число п степеней свободы велико или параметр аналитичности а мал.
Например, динамическая система, описывающая движение астероида в ре¬
алистичной постановке задачи, имеет по меньшей мере 10 степеней свобо¬
ды, а а оценивается как ~ 0.1; поэтому глобального перекрытия резонансов
можно ожидать при порядке ~ 100(!).
На настоящий момент аналитические алгоритмы, реализуемые и ис¬
пользуемые на пределе возможностей современных технологий (системы
компьютерной алгебры, получисленные расчеты и т. п.), позволяют изучать
расположение и амплитуды резонансов лишь до весьма ограниченных по¬
рядков. Поэтому выяснить, имеет ли данная система нехорошевскую струк¬
туру, можно лишь в том случае, если Атах мало (число степеней свободы
мало, а велико). Фактически все успешные приложения чириковского кри¬
терия перекрытия резонансов (см. Контопулос, 1966; Чириков, 1979; Уиз-
дом, 1980) относятся к системам с двумя степенями свободы, где можно
получить хорошие результаты при низком или умеренном порядке.
Ситуация оказывается не столь безнадежной, если обратиться к чис¬
ленным методам исследования динамических систем. Инструменты, опи¬
санные в главе 5, позволяют эффективно выявлять резонансы и области ха¬
оса, так что можно надежно верифицировать, перекрываются ли резонансы
или же есть достаточно места для существования КАМ-торов. Прекрасные
2 Со строгой математической точки зрения для того, чтобы доказать существование инва¬
риантных торов, необходимо показать, что сумма Vk при К Е [1,оо) меньше 1; однако,
поскольку большинство областей резонансов высоких порядков в действительности покрыты
областями резонансов низких порядков, сумма Vk переоценивает полный резонансный объ¬
ем. Поэтому распределение Vk, показанное на рис. 6.8, существенней для нас, чем интеграл
от него. — Прим. авт.
138
Глава 6
0.32 0.34 0.36 0.38 0.4
3.5
см
о
0.32 0.34 0.36 0.38 0.4
3.5 4
Рис. 6.9. Динамическая структура системы (6.6) при двух значениях е, показанная
в двух разрешениях изображения. Координатами на всех панелях служат начальные
условия для действий р\ и р2 (при этом начальные значения углов выбраны равны¬
ми нулю). Десятичный логарифм быстрого показателя Ляпунова (FLI) представлен
в цветовой градации как функция начальных условий. Каждая из панелей построе¬
на для 250000 орбит; верхние панели — при е — 0.01, а нижние — при г — 0.04. На
правых панелях показаны в увеличенном масштабе особенно интересные области
на плоскости действий. Времена интегрирования для вычисления FLI взяты равны¬
ми 2000 (панели справа) и 1000 (панели слева). См. комментарии в тексте. (Рис. 2
из статьи Фрешле и др., 2000; с разрешения Американской ассоциации за научный
прогресс)
6.3. Исследование динамической структуры заданной системы 139
примеры такого подхода дали Ласкар (1993), Канеко и Кониши (1994) и, не
так давно, Фрешле и др. (2000). Фрешле и др. изучали гамильтониан с тре¬
мя степенями свободы
п=4+4+РЗ+е( !_—л. («.в»
2 2 \ cos q\ + cos q<2 + cos + 4 J
Необычная зависимость от углов искусно выбрана здесь таким образом,
чтобы в компактной записи получился гамильтониан, чье разложение в ряд
Фурье имеет бесконечное число гармоник3. Чтобы исследовать динамиче¬
скую структуру этой системы, авторы провели вычисления быстрых по¬
казателей Ляпунова (FLI; см. раздел 5.4.1) для 250000 орбит с начальны¬
ми pi и р2 на регулярной сетке и нулевыми начальными фазами углов. На
рис. 6.9 в цветовой градации показаны FLI как функция начальных (р\,р2)•
Обратим наше внимание сначала на верхнюю левую панель, относящуюся
к случаю е = 0.01. Через резкие изменения цвета относительно коричнево¬
го фона проявляются главные резонансы системы. Они проявляются в виде
прямых линий или прямых полос, так как частоты углов q\ и q2 линейны
по pi и р2, и поэтому резонансное соотношение k\q\ + А/2Ф2 + /адз = 0
сводится к линейному уравнению к\р\ + к2р2 + &з = 0 для pi и р2. Резо¬
нансы, проявляющиеся в виде полос, — это резонансы, у которых принятый
выбор начальных углов обеспечивает представительное разрешение обла¬
стей регулярных либраций. В противном случае резонансы проявляются
как одиночные желтые линии. Значения FLI у либрирующих орбит обыч¬
но меньше, чем у фоновых нерезонансных орбит, поэтому несколько полос
окрашены в синий цвет. Желтые линии (как границы резонансных полос,
так и одиночные линии) соответствуют сепаратрисам или же хаотическим
областям резонансов. Действительно, на сепаратрисах и в хаотических об¬
ластях движение в сильной степени гиперболично, поэтому значения FLI
велики.
Резонансная структура на верхней левой панели рис. 6.9 напоминает
рис. 6.7а, и это наводит на мысль, что при данном значении е система,
возможно, имеет нехорошевскую структуру. На нижней левой панели по¬
казана ситуация для учетверенного значения е\ здесь резонансные полосы
шире и проявляется больше резонансных желтых линий, так что наличие
нехорошевской структуры, по крайней мере в области, где |pi| и \р2\ мень¬
ше 0.5, вызывает больше сомнений. Истинная структура системы проявится
3Идея такого выбора восходит к работе Б. В.Чирикова «Нелинейный резонанс» (Новоси¬
бирск: Издательство НГУ, 1977), с. 51-55. - Прим. ред.
140
Глава 6
четче, если увеличить разрешение численного эксперимента. Это требует
задания более мелкой сетки начальных условий и интегрирования орбит
на более длительных временах, чтобы можно было выявить более слабый
хаос и более тонкие резонансы; так сделано при построении правых пане¬
лей рис. 6.9. Если система обладает нехорошевской структурой, то пере¬
крытия резонансов не должно быть при любом уровне разрешения. Тогда,
поскольку заполняемый КАМ-торами относительный объем велик, суще¬
ствование нерезонансной области при увеличении разрешения становится
более очевидным (верхняя правая панель). Напротив, если резонансы при
некотором порядке перекрываются, то при достаточно высоком разреше¬
нии выявляется глобальная хаотичность системы (нижняя правая панель).
Таким образом, из рис. 6.9 следует вывод, что в рассматриваемой области
пространства действий система (6.6) имеет нехорошевскую структуру при
е = 0.01, а при е = 0.04 она глобально хаотична.
Данный пример показывает, что численный анализ, применяемый в со¬
вокупности с теоретическими интерпретациями, представляет собой весь¬
ма эффективный способ исследования динамических свойств любой задан¬
ной системы. В современной небесной механике такой подход становится
все более распространенным (см., например, главы 11 и 12).
Глава 7
Вековая динамика планет
7.1. Решение Лагранжа-Лапласа
В предыдущих главах мы изложили основные концепции теоретиче¬
ской гамильтоновой динамики, что дает нам теперь возможность детально¬
го исследования динамики тел Солнечной системы. В этой и последующей
главах мы изучим вековую динамику. Это динамика, описываемая вековыми
нормальными формами (см. раздел 2.5.1), причем остаточные члены игно¬
рируются. Разумеется, вековая динамика правильно описывает реальную
динамику только в тех областях, где вековую нормальную форму можно
построить, то есть на удалении от резонансов средних движений, и ее точ¬
ность возрастает с увеличением порядка вековой нормальной формы.
Для упрощения записи формул далее мы не приводим в них верхние
индексы, употреблявшиеся в разделе 2.5.1 с целью подчеркнуть, что фи¬
гурирующие в вековой нормальной форме переменные — средние моди¬
фицированные переменные Делоне, а именно переменные, полученные из
исходных модифицированных переменных Делоне с использованием по¬
следовательности рядов Ли. Кроме того, говоря о средних орбитальных
элементах, определяемых из средних модифицированных переменных Де¬
лоне, мы будем опускать прилагательное средний.
Планетная вековая нормальная форма по определению не зависит от
средних долгот планет Аь ..., \N. Как следствие, действия Ль ..., An яв¬
ляются константами движения. Вековая система, таким образом, полностью
описывается каноническими переменными «действие-угол» Pj, Qj, pj, qj
(j = 1 , ...,7V). Тогда из нормализованного гамильтониана можно убрать
«главный» член Но(М,... ,Л#); в результате гамильтониан приобретает
следующую структуру:
^ • • •, An, Qi,..., Qn,pi,... ,pn, <ji,..., gn; Ai,..., Лп), (7.1)
142
Глава 7
где для упрощения записи в еН\ включены также и члены нормальной
формы более высоких порядков по е\ величины A j играют роль постоянных
параметров.
Малый параметр е (масса наибольшей планеты в солнечных едини¬
цах) служит множителем для всего гамильтониана (7.1). Таким образом, он
более не играет роли пертурбационного параметра, отделяющего интегри¬
руемую часть от возмущения, а лишь показывает, что движение, описы¬
ваемое гамильтонианом (7.1), является медленным: его естественная вре¬
менная шкала в 1/е раз дольше орбитального периода Юпитера. Поэтому,
чтобы обеспечить возможность исследования гамильтониана (7.1) с помо¬
щью инструментов, описанных в главе 2, необходимо прежде всего опреде¬
литься с интегрируемым приближением и новым пертурбационным пара¬
метром (последний назовем rf) такими, что в подходящих переменных «дей¬
ствие-угол» p,q можно было бы записать (7.1) в виде Но(р) + Wi(p, q),
где Н\ — величина порядка ij относительно Но.
Классическим является следующий путь. Учитывая малость эксцен¬
триситетов и наклонений планет, а также что
где W(n) — полиномиальная функция степени п от y/Pj, VQ~r в ря-
де (7.3) член Н(о) нулевой, так как из правил Даламбера (см. раз¬
дел 1.9.3) следует невозможность существования гармоник от Pj,qj с ко¬
эффициентами, не зависящими от Pj, Qj. Кроме того, нулевыми являются
все Н(п) с нечетными п, так как гармоники вековой задачи (общего ви-
да Y[j P^/2Qf12 ехр[^ J2j(mjPj + kjqj)]) должны удовлетворять условию
5+ kj) — это означает, что величина Ylj(\mj\ + IM) является
четной, а поэтому и Y^jiaj + Pj) будет четной. Как следствие, ведущим
членом в (7.3) является Н(2)- Опять же согласно правилам Даламбера об¬
щий вид Н{2) должен быть следующим:
(7.2)
раскладываем (7.1) в ряд Тейлора по y/Pj, y/Qj-
H(Pj, Qj, Pj, Qj) — H{n) (Pj, Qj, Pj, qj),
(7.3)
N N
n(v = 5353 -pk) +
(7.4)
j=1k=1
+ djtky/2Qjy/2Qk cos (qj - qk) ,
7.1. Решение Лагранжа-Лапласа
143
причем коэффициенты Cj^ и dj^k здесь зависят только от постоянных Aj,
то есть от больших полуосей планет. Отметим, что в случае к = j члены
суммы равны просто 2cjjPj -f 2djjQj. Если ввести канонические полино¬
миальные переменные (1.78), то (7.4) становится квадратичной полиноми¬
альной формой:
N N
w(2) = ^2^2lcjAxjxk +VjVk) +djtk(vjVk + ZjZk)}. (7.5)
j=i fc=i
Уравнения движения, задаваемые гамильтонианом (7.5), являются линей¬
ными, и, как и все линейные дифференциальные уравнения, они инте¬
грируемы. Поэтому в качестве интегрируемого приближения векового га¬
мильтониана (7.1) мы можем взять W(2)- Члены Н[п) с п > 4 будут иг¬
рать роль возмущения, причем их величина относительно Н{2) составляет
[ma,Xj(y/Pj, y/Qj)]^71^ ~ [maxj(ej>b')]^n-2^ Таким образом, тогда как
в исходной планетной задаче (2.39) естественным пертурбационным пара¬
метром е является масса наибольшей планеты в солнечных единицах, в ве¬
ковой задаче естественным пертурбационным параметром г] оказывается
квадрат наибольшего значения, принимаемого планетными эксцентрисите¬
тами или наклонениями в ходе вековой эволюции.
Найдем теперь решение уравнений движения, задаваемых гамильтони¬
аном 7i(2)> ~ так называемое решение Лагранжа-Лапласа — и введем под¬
ходящие переменные «действие-угол», позволяющие записать Н(2) в виде
функции от одних только действий. Имея ввиду эту цель, найдем прежде
всего новые канонические переменные х*-, у', г>'-, z'-, в которых (7.5) можно
записать как
w(2) = -
j
где qj и Sj — коэффициенты, зависящие только от средних значений боль¬
ших полуосей планетных орбит. Тогда, применяя преобразование, обрат¬
ное (1.78), легко ввести новые переменные «действие-угол» , Q',
в которых имеем
^(2 ) = -Е^+^1- <7-7)
j
Гамильтониан (7.5) можно записать в матричном виде как
9j
Ц)2 + (^)2 , (*4)2 + Ц)
+ Sj
(7.6)
Н{2) — х • + у • Ay + v • Влг + z • Въ,
(7.8)
144
Глава 7
где А и В — симметричные матрицы N х N. Таким образом, преобра¬
зование (7.5) к (7.6) сводится к простой диагонализации матриц А и В.
Поскольку последние симметричны, диагонализацию можно осуществить
поворотом векторов, то есть преобразование к новым переменным можно
записать как
где R1 и R11 — матрицы вращения N х N, а через х, y,v,z обозначе¬
ны векторы (£Ь...,жлг), (2/1,..., 2/n), Ол, • • •, vN), (zu...,zN) соответ¬
ственно. Наконец, докажем, что преобразование (7.9) — каноническое. Ли¬
нейное преобразование координат х = Сх.' является каноническим тогда
и только тогда, когда преобразование импульсов имеет вид у = (Ст)-1 у',
где {Ст)~1 — матрица, обратная транспонированной С. (Это легко прове¬
ряется непосредственной подстановкой в уравнения Гамильтона.) В форму¬
лах (7.9) координаты и сопряженные им импульсы преобразуются посред¬
ством одной и той же матрицы вращения, но матрицы вращения R как раз
обладают общим свойством R = (RT)~l.
Теперь, когда введены переменные «действие-угол» Р-, р', Q'-, q'-
и T~t{2) преобразован к виду (7.7), стало очевидным, что в пренебрежений
возмущением ^2п>2 В(2п) действия Pj и Q' представляют собой констан¬
ты движения, а углы р' и <?'• изменяются линейно со временем с фикси¬
рованными частотами — gj и — Sj соответственно. Посредством обратной
композиции предпринятых канонических преобразований легко вычислить
движение в исходных переменных «действие-угол» Pj,pj,Qj,qj в функ¬
ции времени. Тогда с помощью соотношений (7.2) находим, что планетные
эксцентриситеты, наклонения и долготы перигелиев и узлов выражаются
как функции времени следующим образом:
х = Д/х/, у = #У, v = Rnv', z = Ruz', (7.9)
N
k = 1
N
к=1
N
(7.10)
fc=l
N
к=1
7.1. Решение Лагранжа-Лапласа
145
Это и есть решение Лагранжа-Лапласа для векового движения планет.
Частоты Qk.Sk, коэффициенты и фазы на данном уровне
приближения (то есть при учете только члена 7Y(2) векового гамильтониа¬
на) зависят только от планетных больших полуосей; но, если учесть воз¬
мущающие члены Н(2п) сп ^ 2, они станут функциями также и от Р-, Q'
(см. следующий раздел). Численные значения будут приведены ниже, в таб¬
лицах 7.1, 7.2 и 7.3.
Одна из узловых частот с необходимостью равна нулю
вследствие сохранения полного углового момента. Фактически, если задать
произвольную ортогональную систему координат, х и у-компонентами век¬
тора полного углового момента будут
N
Сх = Q>j yjQ{mо + rrij)aj(l — е?) sinij cos Clj,
(7Л1)
Су = ^ pj yjG(mo + rrij)aj( 1 — Cj) sin ij sin Qj.
i=i
Поскольку Cx и Су — константы, одну из долгот узлов можно представить
как функцию от элементов орбит других планет, а именно:
Су — pjyjG{mo + mj)aj(1 — ej) sinЬ' sin^j
= — ===== . (7.12)
Cx — YsPjJejrno + mj)aj(l — e^) sinij cosQj
зФз
Поэтому система (7.7) может иметь лишь TV — 1 независимых ча¬
стот По соглашению, нулевую частоту обозначают s5. Поэтому из выра¬
жения (7.7) для 2) действие £% исчезает. Кроме того, каждый член Н^п)
в разложении (7.3) должен быть независим от (%; действительно, если
бы Q'5 появилось в одном из членов, скажем в Н{2п). тогда в порядке п
появилась бы и новая независимая частота qlb = дН\2п)/нарушая,
таким образом, сохранение углового момента.
Если система координат выбрана так, что плоскость х, у ортогональ¬
на вектору полного углового момента, то константы Nj^ равны нулю при
всех j. В этом случае плоскость х,у называют инвариантной плоскостью.
В противном случае все константы Nj^ равны некоторому значению, опре¬
деляемому наклоном плоскости х,у относительно инвариантной плоско¬
сти. Все остальные константы (при всех к) и Njtk (при к ф 5) не
146
Глава 7
зависят от выбора системы координат. Заметим, что согласно (7.10) при ну¬
левом Nj,5 все узлы Qj циркулируют. Напротив, если выбранная система
координат достаточно наклонена относительно инвариантной плоскости, то
узлы Qj либрируют. Именно так ведут себя узлы Юпитера и Сатурна, если
система координат — эклиптическая (в ней плоскость х, у совпадает с плос¬
костью орбиты Земли в настоящую эпоху).
На небесномеханическом жаргоне частоты дь, Sk обычно называют
собственными частотами к-ой планеты. На самом деле орбитальные эле¬
менты каждой из планет зависят от всех частот pi,... ,рдг, si,..., s^v,
как ясно видно из формулы (7.10). Данный жаргон мотивирован тем, что
в большинстве случаев частотам и Sk в динамике к-ой планеты соот¬
ветствуют наибольшие амплитуды, то есть \Мь,к\ = тах/ \Mk,i\ и |7Vfc,fc| =
= max/ |iVfc,z|. Однако это не всегда так: см. таблицу 7.2, где среди |М7Д
максимальна IM^I, то есть ведущей частотой перигелия Урана является р5.
7.2. Решения более высокого порядка
Выраженный в новых переменных «действие-угол» Ррр'3Q'j, pj, ве¬
ковой гамильтониан готов для изучения с помощью инструментов, опи¬
санных в главе 2. При этом гамильтониан 'H(2){PjiQj) и его возмущение
J2n>i'K(2n)(Pj,Qj,Pj,Qj) следует отождествить соответственно с Ло(р)
и еЛ\ (р, q) в (2.1). Пертурбационный параметр е здесь равен г), то есть
квадрату наибольшего значения, принимаемого планетными эксцентриси¬
тетами или наклонениями в ходе вековой эволюции. Здесь нет необходи¬
мости вводить обрезающее значение для порядка К гармоник (с целью
разбиения возмущений, как сделано в (2.19)), поскольку введение функ¬
ций Л(2п) с п > 1 уже обеспечило естественное разбиение 7^1 на члены
по возрастанию порядка относительно пертурбационного параметра. Каж¬
дая из функций Л(2п) содержит лишь конечное число гармоник благодаря
правилам Даламбера.
Для анализа вековой эволюции планет удобно построить нормальную
форму Биркгофа1. Как показано в главе 2, в порядке п нормальная форма
1 По сравнению с анализом в главе 2 здесь есть техническая трудность, состоящая в том, что
функции 7^(2п) неаналитичны, если одно из действий равно нулю, из-за присутствия членов
с квадратными корнями. Однако правила Даламбера гарантируют, что результаты применения
скобок Пуассона в рядах Ли всегда можно разложить в ряды по положительным степеням
квадратных корней из переменных действия. — Прим. авт.
7.2. Решения более высокого порядка
147
Биркгофа имеет вид
п+1
= £Wf2n)(PJ\Q]) + n{Pf,<?”), (7.13)
71— 1
где P™, Q™, р™, q™ — новые переменные «действие-угол», вводимые через
последовательность п преобразований Ли, а остаток 1Z содержит члены
порядка не ниже п + 2 по Pj1, Q7-.
Если пренебречь остатком, решением (7.13) будет просто
l(2n) I
р?(«) = Р”(0), рЩ = чтаарп yt+^(0),
(7.14)
Q?(i) = Q*(0), g»(t) = t + qf( 0).
Движение зависит от начальных значений Е^(0), Qj(0), р™(0), ^(0).
Их вычисляют (путем обращения рядов Ли) из начальных значений
Pj,Qfj,p'j,q'j, которые, в свою очередь, зависят от начальных Pj,Qj,pj,qj
через преобразования, описанные в предыдущем разделе. Как только на¬
чальные значения вычислены, движение Р™, Q™, р™, q™ полностью опре¬
делено, а его образ в исходных переменных можно легко найти путем
применения вновь (в обратном порядке) цепочки указанных канониче¬
ских преобразований. В итоге этой цепочки преобразований зависимость
ejcoszijj, ejSinwj, sin(ij/2) cosQj, sin (i j/2) sin Qj от времени оказыва¬
ется суммой двух слагаемых. Первое из них имеет такую же функцио¬
нальную форму, что и правая часть (7.10), но с модифицированными ко-
эффициентами дк, sk, (Зк, 6к, Mjtk, Njtk. Например, в, частотах дк и sk
появились соответственно члены —d(^™=2Hi£^/dPk(P!jl(0),Qn(0))
и ~d{^i^2Hi2n^/dQ^{Pf(0),Qn(Q))-, оба эти члена зависят от Р”(0),
Qj (0). Однако же заметим, что, поскольку ни один из членов Ti^n) не зави¬
сит от Q5,95, значения S5 и Nj$ остаются неизменными. Второе слагаемое
содержит новые гармоники, включающие целочисленные линейные комби¬
нации частот gk,Sk\ конкретно, в порядке п нормальной формы Биркгофа
имеются гармоники с комбинациями 2п + 1 частот.
148
Глава 7
Наиболее точной аналитической теорией векового движения восьми
планет Солнечной системы является теория Бретаньона (1974). Бретаньон
разработал свою теорию не используя уравнения Гамильтона, но его рас¬
четы эквивалентны вычислению вековой нормальной формы до второго
порядка (то есть е2) по планетным массам с последующим вычислением
нормальной формы Биркгофа (7.13) порядка п = 1; то есть в уравнениях
движения учитываются члены второго и четвертого порядков 0i(2) и 7^(4))
по планетным эксцентриситетам и наклонениям. Позднее Бретаньон (1984)
разработал более точную теорию исходя из модели, учитывающей также
релятивистские эффекты и возмущения движения внутренних планет со
стороны Луны.
Дюрье (1979) разработал аналитическую теорию векового движения
внешних планет (от Юпитера до Нептуна); его подход эквивалентен вы¬
числению нормальной формы Биркгофа до порядка п — 2.
Ласкар (1985) вычислил вековую нормальную форму до второго по¬
рядка по планетным массам и до шестого порядка по эксцентриситетам
и наклонениям для полной системы планет (от Меркурия до Нептуна), од¬
нако он не исследовал эту форму аналитически, а с целью определения ча¬
стот движения прибегнул к численному интегрированию на интервале вре¬
мени 10 млн лет (Ласкар, 1988). В принципе, частоты, вычисленные Лас-
каром, точнее вычисленных Бретаньоном, поскольку Ласкар использовал
вековую нормальную форму, содержащую больше возмущающих членов,
а численное интегрирование дало «точное» решение для системы, описы¬
ваемой этой формой.
Наиболее точные расчеты вековых частот внешних планет осуществи¬
ли Эпплгейт и др. (1986) и Нобили и др. (1989) путем численного ин¬
тегрирования полных уравнений движения (не прибегая, таким образом,
к вычислению вековой нормальной формы). Если сравнивать их результа¬
ты с результатами Ласкара, то наибольшее расхождение наблюдается для
частоты д6; полагают, что оно возникло из-за членов третьего порядка
по планетным массам, отсутствующих в вековой нормальной форме Лас¬
кара.
В таблицах 7.1, 7.2 и 7.3 приведены расчетные значения постоянных
в формулах Лагранжа-Лапласа (7.10), считающиеся сейчас наиболее точ¬
ными. Полные выражения для зависимости элементов планетных орбит от
времени, включая коэффициенты гармоник, соответствующих линейным
комбинациям планетных частот, можно найти в работах Бретаньона (1974),
Ласкара (1988, 1990) и Нобили и др. (1989).
7.3. Хаотическое вековое движение планет
149
Таблица 7.1. Планетные частоты и угловые фазы. Значения <71,...,#4 и si,..., S4
взяты из статьи Ласкара (1990); значения <75,..., д& и 56,..., 5s — из статьи Ноби¬
ли и др. (1989); частоты измеряются в "/год. Фазы /?i,..., /3s и 6\,..., 63 взяты из
статьи Ласкара (1990); они вычислены относительно эклиптической системы коор¬
динат 2000 года на эпоху JD 2451545.0
к
Як
РкП
Sk
М°)
1
5.5964
112.08
-5.6174
348.60
2
7.4559
200.51
-7.0795
273.25
3
17.3646
305.12
-18.8512
240.20
4
17.9156
335.38
-17.7482
303.75
5
4.2575
30.65
0.0000
107.58
6
28.2455
128.09
-26.3450
307.29
7
3.0868
121.36
-2.9927
320.62
8
0.6726
74.06
-0.6925
203.90
Таблица 7.2. Коэффициенты Mjtk решения Лагранжа - Лапласа (7.10). Значения
ci)5nfc)5 взяты из статьи Нобили и др. (1989); остальные — из статьи Ласкара
(1990), если они там приведены, в противном случае — из статьи Бретаньона (1974).
Все значения умножены на 106
лк
1
2
3
4
5
6
7
8
1
185444
-27700
1458
-1428
36353
113
623
7
2
6668
20733
-11671
13464
19636
-551
614
11
3
4248
16047
9406
-13159
18913
1506
650
12
4
650
2917
40133
49032
20300
7030
862
20
5
-7
-12
-1
0
44187
-15700
1814
58
6
-6
-12
-7
-7
32958
48209
1511
57
7
2
3
0
0
-37587
-1547
29033
1666
8
0
0
0
0
1881
-103
-3697
9118
7.3. Хаотическое вековое движение планет
Чтобы исследовать свойства вековой эволюции планет на очень боль¬
ших шкалах времени, Ласкар (1989) численно проинтегрировал уравне¬
ния движения, задаваемые его вековой нормальной формой, на интервале
200 млн лет. Он ввел эмпирические поправки к частотам д$, д? и 57 в W(2)?
приравнивающие эти частоты найденным при численном интегрировании
полных уравнений движения внешних планет; таким образом должно было
быть получено достаточно точное представление «истинного» движения.
Найденное Ласкаром численное решение вековых уравнений позднее было
150
Глава 7
Таблица 7.3. Коэффициенты Njtk- Источники те же, что и для Mjtk в таблице 7.2.
Для вычисления Nj^ использовалась эклиптическая система координат 2000 г. Все
значения умножены на 106
э\к
1
2
3
4
5
6
7
8
1
39957
30169
1678
72261
13772
-139
-1665
-724
2
6716
-4045
-9544
-5759
13772
-60
-959
-663
3
4960
-3431
8760
4024
13772
-1404
-866
-650
4
860
-566
-15421
34689
13772
-4579
-628
-615
5
-11
4
0
-1
13772
3153
-485
-584
6
-14
6
-2
-13
13772
-7858
-394
-564
7
11
-3
0
1
13772
353
8887
543
8
0
0
0
0
13772
38
-1062
5790
сопоставлено с результатами интегрирования полных уравнений движения
всех планет Солнечной системы на интервале времени 3 млн лет, осуществ¬
ленного Квинном и др. (1991), что подтвердило превосходную точность
решения Ласкара (Ласкар и др., 1992а).
Наряду с орбитальной эволюцией Ласкар (1989) вычислял и макси¬
мальный показатель Ляпунова, который составил ~ 1/5 (млн лет)-1. Это
свидетельствует, согласно главе 5, что орбитальная эволюция является ха¬
отической. Чтобы найти подтверждение хаотической природы вековой ди¬
намики Солнечной системы, Ласкар (1990) предпринял поиск резонансов,
ответственных за хаос. С этой целью он провел временной мониторинг раз¬
личных удовлетворяющих правилам Даламбера комбинаций углов p'j,q'j,
определенных в разделе 7.1, выявляя находящиеся в либрации, а также
те, у которых либрации и циркуляции чередуются. Согласно главе 4 та¬
кой подход соответствует поиску критических углов ipi (см. формулу (4.2))
существующих резонансов. Ласкар обнаружил две независимые резонанс¬
ные комбинации вековых углов и таким образом показал, что Солнечная
система пребывает в резонансе кратности 2 или выше (см. главы 1 и 6).
Резонансными углами являются р[ — pf5 — q[ + q'2 и 2{р,А — pf3) — q'4 + q^. От¬
вечающие им гармоники входят в Нщ и /Н(ъ) соответственно; то есть они
возникают в порядках 4 и 6 по эксцентриситетам и наклонениям планет.
На рис 7.1 показана эволюция этих двух резонансных углов во времени.
Первый из них либрирует в течение всего интервала времени, на котором
проводилось интегрирование2. Однако отметим, что амплитуда либраций
2Ласкар интегрировал назад во времени, от настоящей эпохи до —200 млн лет. Поскольку
гамильтонова динамика обратима, интегрирование назад и интегрирование вперед совершенно
эквивалентны. — Прим. авт.
7.3. Хаотическое вековое движение планет
151
27Г
О
— 27Г
— 47Г
—67Г
-8тг
ф
mjr
т
,11
I I
г
J/I
jr_
,.у
I 1
// If'
Л
f
"ПР^
2тт
О
—2тт
— 47Г
— 67Г
—87Г
млн лет -200
-150
-100
-50
0
Рис. 7.1. Эволюция углов р[ — р'5 — q[ + q'2 (вверху) и 2(^4 — р'3) — q'4 + q'3 (вни¬
зу) согласно результатам интегрирования вековой планетной системы, предприня¬
того Ласкаром. Как следует из поведения этих углов, Солнечная система пребывает
в вековом резонансе кратности 2, что объясняет хаотическую природу ее вековой
динамики. (Рис. 2 и 4 из статьи Ласкара, 1990; с разрешения Academic Press)
существенным и нерегулярным образом изменяется со временем, то есть
движение происходит не на инвариантной либрационной кривой, а в хаоти¬
ческой области; поэтому можно ожидать переходов к циркуляциям. При
интегрировании на более длительных интервалах времени такие перехо¬
ды действительно появляются (Ласкар, 1992). В поведении второго резо¬
нансного угла чередуются либрации и циркуляции, то есть оно явно ха¬
отическое. Кроме того, Ласкар показал, что линейные комбинации дей¬
ствий канонически сопряженные этим двум резонансным углам,
испытывают осцилляции в фазе с либрациями/циркуляциями последних,
обнаруживая динамику маятникового типа (в действительности весьма ис¬
каженную из-за наличия двойного резонанса). Хаотическую природу ди¬
152
Глава 7
намики Солнечной системы и описанный характер поведения резонансных
углов подтвердили Зюссман и Уиздом (1992) посредством прямого числен¬
ного интегрирования.
Ласкар подтвердил наличие хаоса, применяя свой метод частотного
анализа (см. раздел 5.3) к временной эволюции частот gk,Sk Солнечной
системы. Тогда как численно измеренные значения <75,... и
не испытывают за 200 млн лет относительных изменений более 10-4,
У <7ъ • • • > 04 и si,..., S4 они обычно составляют 10-2 (Ласкар, 1990). Та¬
ким образом, хаос проявляет себя в основном в подсистеме с 8-ю степенями
свободы, описывающей вековое движение внутренних планет (от Меркурия
до Марса), а подсистема, описывающая эволюцию внешних планет, будучи
слабо связанной динамически с первой подсистемой (возмущение, оказыва¬
емое внутренними планетами на движение внешних, по порядку величины
соответствует массе Земли в солнечных единицах), хаотична лишь в весь¬
ма ограниченной степени. Это привело Ласкара к предположению, что если
бы планет земной группы не существовало, то движение внешних планет
происходило бы на КАМ-торах. Очень похоже, что для вековой системы
так дело и обстоит; однако данное предположению неверно, если рассмат¬
ривать неусредненную систему, поскольку в последней присутствуют трех-
тельные резонансы средних движений высокого порядка (см. главу 10).
Работа Ласкара (1990), однако, оставила открытым вопрос о динамиче¬
ской структуре вековой планетной задачи. Действительно, в свете главы 6
естественно спросить, имеет ли вековая система нехорошевскую структу¬
ру, коль скоро хаотическое движение остается ограниченным на временах
больше возраста Солнечной системы. Ласкар (1994) дал частичный ответ
на этот вопрос, проинтегрировав уравнения движения, задаваемые его ве¬
ковой нормальной формой, на интервале времени 25 млрд лет (назад от
0 до —10 млрд лет и вперед от 0 до 15 млрд лет). Из-за хаоса движе¬
ние непредсказуемо на временах порядка величины, обратной показателю
Ляпунова, (в данном случае ~ 5 млн лет); поэтому результаты такого ин¬
тегрирования следует рассматривать лишь как представляющие возмож¬
ную эволюцию. Однако, согласно простым численным примерам в главе 4,
численное интегрирование может дать оценку протяженности хаотической
области, достижимой за время интегрирования. Кроме того, следует отме¬
тить, что время интегрирования здесь превышает физическое время жизни
Солнечной системы: она сформировалась, как полагают, ~ 4.5 млрд лет на¬
зад и просуществует еще, вероятно, лишь 5 млрд лет, прежде чем Солнце
в своей эволюции достигнет стадии красного гиганта и его радиус превы¬
7.3. Хаотическое вековое движение планет
153
сит радиус орбиты Земли. Долгая шкала времени была выбрана с умыслом,
чтобы лучше выявить динамический характер исследуемой гамильтоновой
вековой системы. Например, если эксцентриситет планеты через 10 млрд
лет испытал внезапный скачок, то вполне допустимо, что подобное явле¬
ние может произойти и за более короткое время, скажем, через 5 млрд лет.
Или, например, то, что согласно результатам интегрирования происходило
в прошлом, может произойти и в будущем.
Чтобы наглядно продемонстрировать хаотическую эволюцию планет¬
ных орбит и их «диффузию» внутри области хаоса, Ласкар применил «ме¬
тод максимального действия» (см. раздел 5.4.4), вычисляя максимальные
эксцентриситеты и наклонения, достигаемые каждой из планет на последо¬
вательных интервалах 10 млн лет. Как видим из рис. 7.2, у внешних планет
максимальные эксцентриситеты и наклонения постоянны во времени. Со¬
гласно разделу 5.4.4 это означает, что вековая динамика у внешних планет
очень близка к регулярной. У Земли и Венеры обнаруживаются связанные
нерегулярные вариации максимальных эксцентриситетов и наклонений, ко¬
торые, однако, ограничены пределами узкой горизонтальной полосы. Таким
образом, несмотря на хаотичность, орбиты Земли и Венеры едва ли могли
сильно измениться за время существования Солнечной системы. Этого не
скажешь о Марсе и в особенности о Меркурии. Проведя ряд расчетов, со¬
стоявших в численном интегрировании со слегка различными начальными
условиями, Ласкар показал, что в результате эволюции Меркурий может на¬
чать пересекать орбиту Венеры и это может привести к столкновению двух
планет либо к выбросу Меркурия из Солнечной системы после серии тес¬
ных сближений. Отсюда следует, что Солнечная система лишь маргинально
устойчива, то есть существует малая (но ненулевая) вероятность того, что
в Солнечной системе за ее физическое время жизни может произойти та¬
кое драматическое событие, как столкновение двух планет. Однако следует
заметить, что уравнения векового движения, полученные Ласкаром путем
обрезания рядов по степеням эксцентриситетов и наклонений, могут терять
точность, когда последние велики.
Вывод, что Солнечная система лишь маргинально устойчива, согла¬
суется с сегодняшними представлениями о ее формировании (см. обзор
Тейлора, 1999). Концентрация твердого вещества должна была привести
к формированию не только известных сейчас планет, но также и несколь¬
ких других планетных эмбрионов с массами, которые могли достигать (осо¬
бенно во внешней Солнечной системе) массы Земли. Такое представление
подтверждается данными современного численного моделирования форми-
154
Глава 7
<L>
к
cd
S
20
15
10
Венера
******
Земля
10
0
Урднч Сатурн^ Нептун^ “
10
.Юпитер/
Нептун^
10
15
0 5
время, млрд лет
Рис. 7.2. Долговременная вековая эволюция Солнечной системы. Максимальные
эксцентриситеты и наклонения, достигаемые каждой из планет на последователь¬
ных интервалах 10 млн лет, показаны в функции времени на интервале 25 млрд лет.
Сохранение этих величин постоянными (в случае планет-гигантов) свидетельствует,
что движение регулярно; а наличие вариаций — что движение хаотично. (Рис. 1 из
статьи Ласкара, 1994; с разрешения Astronomy and Astrophysics)
7.4. Динамика осей вращения
155
рования планет (Чамберс и Уэзерилл, 1998; Агнор и др., 1999), а также
и такими «вещественными доказательствами», как существование Луны
(предположительно возникшей в результате столкновения с Землей пла¬
нетного эмбриона размером с Марс; см. Хартман и Дэвис, 1975; Кэмерон,
1997) и наклон оси Урана (для возникновения такого наклона нужен удар
тела размером с Землю; Сафронов, 1965; Паризи и Брунини, 1996). Сол¬
нечная система, плотно населенная массивными планетными эмбрионами,
«бурно» неустойчива (Чамберс и др., 1996). Из-за их взаимных столкно¬
вений и выбросов на гиперболические орбиты система эволюционирует
к состоянию с меньшим числом планетных эмбрионов, соответственно ме¬
нее неустойчивому. Эволюция такого рода фактически «останавливается»,
когда система достигает маргинальной устойчивости. В данном сценарии
Меркурий — последний из планетных эмбрионов в Солнечной системе, ко¬
торому до сих пор не выпал шанс уйти из системы или столкнуться с дру¬
гой планетой.
7.4. Динамика осей вращения
Мы не будем описывать динамику осей вращения планет исчерпыва¬
ющим образом, так как это не входит в цели данной книги. Подробное
описание читатель может найти в работах Киношиты и Суше (1990) и Су¬
ше и др. (1999). Мы же рассмотрим упрощенное (но тем не менее весьма
интересное) описание динамики планетной оси вращения, получающееся
с использованием ряда приближений:
1) предполагается, что планета представляет собой однородное твердое
тело с главными моментами инерции Д, /2, /3, удовлетворяющими со¬
отношению Д = Д < /3, причем ось вращения совпадает с направле¬
нием Д;
2) пренебрегается всеми прямыми возмущениями, оказываемыми други¬
ми планетами на вращательное движение; учитываются лишь косвен¬
ные возмущения, то есть изменения орбиты планеты из-за влияния
других планет;
3) итоговые уравнения осреднены на орбитальных периодах, что эквива¬
лентно построению вековой нормальной формы первого порядка.
В неинерциальной прямоугольной системе координат x,y,z, плоскость х, у
которой совпадает с мгновенной плоскостью планетной орбиты, а ось х на¬
правлена на восходящий узел Г2 планетной орбиты, ориентацию оси враще¬
156
Глава 7
ния можно задать посредством углов еиА, определяемых соотношениями
sx=sin£sinA, sy = sinecosA, sz = cose, (7.15)
где sx, sy, sz — компоненты единичного вектора, направленного по оси
вращения, в системе координат x,y,z. Угол е обычно называют наклоном
планеты, а угол гр = А — Q, — долготой ее оси вращения. Коль скоро нами
введены три указанных упрощения, оказывается, что X = cos е и пред¬
ставляют собой канонические переменные «действие-угол», чья эволюция
описывается следующим зависящим от времени гамильтонианом с одной
степенью свободы:
H(X,ip,t) = ^(1 - e(t))~~3/2X2 + yjl - X2 (A(t) sin^ + B(t) cos яр)
(7.16)
(Ласкар и Робутель, 1993; Ласкар и др., 1993). Здесь e(t) — эксцентриситет
планетной орбиты, a A(t) и B(t) — зависящие от времени величины, опре¬
деляемые наклонением и узлом планетной орбиты относительно ее перво¬
начальной плоскости:
A(t) = 2(q + p(qp - pq))/\/l-p2 - q2,
B(t) = 2(p - q(qp - pq))/\/l-p2 - q2,
(7.17)
где p(t) = sin[z(t)/2] sinft(t), q(t) = sin[z(£)/2] cosfl(£), z(0) = 0. Пара¬
метр а дается формулой
3 <?M0 h~h ( .
“ = ■ -FT’ (7Л8)
где Mq — масса Солнца, Q — гравитационная постоянная, а — большая по¬
луось планетной орбиты (она считается фиксированной), v — частота вра¬
щения (обратная периоду вращения) планеты. В случае Земли влиянием Лу¬
ны нельзя пренебречь; если предположить, что Луна движется по круговой
орбите в экваториальной плоскости Земли, то к гамильтониану (7.16) необ¬
ходимо добавить член (ам/2)Х2, где ам дается формулой (7.18) с массой
Луны вместо массы Солнца и с радиусом лунной орбиты вместо а.
Гамильтониан (7.16) квазиинтегрируем: он представляет собой сум¬
му интегрируемой главной части (а/2)Х2 (или [(a -f ам)/2\Х2 в слу¬
чае Земли) и двух возмущающих членов, а именно (а/2)[(1 - е2)-3/2 -
— 1]Х2 и у/Т^ХР* (A(t) simp + B(t) cos^). Последние пропорциональны
соответственно квадрату эксцентриситета планетной орбиты и изменению
7.4. Динамика осей вращения
157
ее наклонения относительно исходного значения. Из вида интегрируемой
части следует, что в первом приближении наклон планеты постоянен. Ско¬
рость прецессии ф оси вращения планеты (так называемая прецессия рав¬
ноденствия) пропорциональна X; поэтому она максимальна, если наклон
нулевой (X = 1), равна нулю, если наклон равен 90° (X = 0; что при¬
близительно выполняется в случае Урана), и меняет знак, если наклон пре¬
вышает 90° (случай Венеры). Если элементы планетной орбиты, а значит
и возмущающие члены в (7.16), представляют собой квазипериодические
функции времени с диофантовыми частотами, то КАМ-теорема и теорема
Нехорошева — обе применимы к гамильтониану (7.16) при условии, что
возмущения достаточно малы (о КАМ-теореме см. раздел 3.1.1, а о теореме
Нехорошева — статью Гуццо и Морбиделли, 1997).
В частном случае, если эксцентриситет постоянен, a A(t) + tB(t) =
= /Зехр(tut), то (7.16) сводится к интегрируемому гамильтониану
Н = 7^(1 — е2)-3/2Х2 + (Зу/l — X2 sin (out + ф), (7-19)
описывающему волчок Коломбо, который назван так в честь работы Колом¬
бо (1966). Точки равновесия системы (7.19) называют состояниями Касси¬
ни; они особенно важны в динамике тел, испытывающих приливную эво¬
люцию, таких, например, как спутник Юпитера Ио (см., например, Глэдман
и др., 1996).
Согласно предыдущему разделу, в динамике планет Солнечной систе¬
мы зависимость орбитальных элементов от времени хорошо аппроксими¬
руется квазипериодическими функциями только в случае внешних планет.
В качестве иллюстрации на рис. 7.3 показан фурье-спектр A(t) + tB(t) для
Земли согласно решению Ласкара (1990) для векового орбитального движе¬
ния: видно, что спектр непрерывен, хотя имеются мощные пики на частотах
si>S2,53,54 и sq линейного решения Лагранжа-Лапласа (см. раздел 7.1).
Спектры A(t) + iB{t) для всех остальных планет приведены в работе Лас¬
кара и Робутеля (1993). Даже если ограничиться возмущающими членами
с коэффициентами больше некоторого порогового значения, все равно на¬
личие множества частот делает гамильтониан (7.16) весьма сложным для
анализа. Поэтому, исследуя динамическое поведение осей вращения планет
Солнечной системы, Ласкар и др. (1993) и Ласкар и Робутель (1993) при¬
бегли к численному интегрированию. В качестве сетки начальных условий
они взяли множество Х(0),^(0) с ^(0) = 0 и начальным наклоном е0 =
= arccosX(O) на интервале от 0 до 170° с шагом 0.1°. В каждом узле этой
158
Глава 7
A + iB
частота, "/год
Рис. 7.3. Фурье-спектр члена A(t) + tB(t) в гамильтониане (7.16) в случае Земли.
(Рис. 1 из статьи Ласкара и др., 1993; с разрешения Nature, Macmillan Magazines
Limited)
сетки они проинтегрировали на интервале времени 18 млн лет эволюцию,
описываемую уравнениями с гамильтонианом (7.16), где e(t),A(t),B(t)
были взяты из статьи Ласкара (1990). Для каждой вычисленной траекто¬
рии они нашли среднюю частоту ф, а также максимальное, минимальное
и среднее значения наклона. Согласно главе 5, по характеру зависимости
таких величин от начальных условий можно судить, является движение ре¬
гулярным или хаотическим.
На левой панели рис. 7.4 показаны результаты вычислений для Зем¬
ли, проведенных с учетом обоих вращающих моментов (с коэффициентами
а и ам) со стороны Солнца и Луны; для скорости вращения Земли было
взято современное значение v — 1/24 час-1. При исходных наклонах мень¬
ше 50° (напомним, что сейчас у Земли наклон равен 23.4°) эволюция оси
вращения выглядит весьма регулярной, причем частота и наклон являются
гладкими функциями от начального значения £q- Разность максимально¬
го и минимального значений наклона всегда очень мала, то есть наклон
7.4. Динамика осей вращения
159
О
50
100
0
100
50
€0, ° €0, °
Рис. 7.4. Частота прецессии (вверху) и максимальный, средний и минимальный на¬
клоны оси вращения Земли (внизу) в функции начального наклона ео. Панели слева
соответствуют модели с учетом вращающего момента со стороны Луны, а панели
справа — Земле без Луны. См. обсуждение в тексте. (Рис. 2 и 3 из статьи Ласкара
и др., 1993; с разрешения Nature, Macmillan Magazines Limited)
подвержен лишь малым осцилляциям. Заметим, что исследуемая система,
строго говоря, не имеет регулярных орбит, поскольку возмущение не яв¬
ляется квазипериодическим, и поэтому КАМ-торы не могут существовать.
Тем не менее не обнаруживается никаких следов хаоса. Причины этого сле¬
дующие: для рассматриваемых значений £q частота тр находится приблизи¬
тельно в пределах от 35 до 55"/год, а так как члены в возмущении (7.19)
относятся к типу sin('0 + ut), единственно возможными резонансами явля¬
ются резонансы с о; в интервале [—55, —35]"/год; но компоненты спектра
А + lB с частотой uj в таком диапазоне имеют, согласно рис. 7.3, коэффи-
160
Глава 7
циенты меньше 10-9. Как следствие, амплитуда хаотической компоненты
динамики X(t), 2p(t) на данной шкале времени так мала, что в разрешении
рис. 7.4 обнаружить ее нельзя.
Если исходный наклон находится в диапазоне 55-90°, то эволюция
оси вращения «бурно»-хаотична. Объясняется это тем, что данному диа¬
пазону наклонов соответствуют значения невозмущенной частоты ф от 0
до 30"/год, и поэтому она может быть в резонансах с главными компонен¬
тами спектра A(t) + tB(t). Тот факт, что независимо от начальных усло¬
вий наклон принимает за время 18 млн лет, принятое в вычислениях, все
значения примерно от 55 до 90°, свидетельствует, что главные резонансы
с критическими углами s^t 4- г/j, s^t + 'ф, «М + ф, S2t + ip и s\t + яр полно¬
стью перекрываются и образуют однородную зону хаоса, где идет быстрая
диффузия чириковского типа по действию X (см. главу 6). При наклонах £0
больше 90° движение оси вращения вновь становится практически регуляр¬
ным, так как ни один из компонентов с положительной частотой в спектре
A(t) + iB{t) не имеет достаточно большой амплитуды.
Ласкар и др. (1993) также выполнили аналогичные расчеты, чтобы .
ответить на вопрос о том, какова была бы динамика оси вращения Зем¬
ли, если бы Луны не существовало. Они обнулили в гамильтониане член
амХ2 и, кроме того, учли, что период вращения Земли увеличился в ходе
эволюции относительно его исходного значения из-за приливного трения,
вызываемого Луной, и поэтому рассчитали значение а по (7.18), полагая
частоту вращения v в 1.22 раз большей, чем наблюдается сейчас, что со¬
ответствует геологическим данным о частоте вращения Земли 2.5 млрд лет
назад. На правой панели рис. 7.4 показаны результаты, полученные в дан¬
ной модели. При всех начальных наклонах ео < 80° динамика, очевидно,
хаотична. Только при начальных наклонах £о > 90° динамика становится
явно регулярной. Таким образом, диапазон начальных наклонов, при кото¬
рых возникает хаос, больше, чем в модели с Луной. Причина этого про¬
ста: если в гамильтониане не учитывается вращающий момент со стороны
Луны (член ам^2), то при наклонах в диапазоне 0-90° частота прецес¬
сии составляет всего лишь 0-20"/год; если же его учитывать, то частота
прецессии принимает значения от 0 до 55"/год (сравните верхние графики
рис. 7.4); однако квазирегулярное движение возможно лишь при частотах
прецессии больше 30"/год, так как тогда нет резонансов с компонентами
спектра A(t) + tB(t), имеющих наибольшие амплитуды.
Отметим, что в отсутствие Луны область хаоса неоднородна. Фактиче¬
ски можно выделить три области: при начальных наклонах 0-45°, 45-60°
7.4. Динамика осей вращения
161
и 60-80°. При со в диапазоне 0-45° наклон за время интегрирования при¬
нимает все значения от 0 до 54° (минимальный и максимальный наклоны
не зависят от со). Ситуация аналогична при со в диапазоне 60-80°: на¬
клон меняется от 60 до 84°. Напротив, в области 45-60° вариации наклона
охватывают лишь малый участок в окрестности начального значения, так
что минимальный и максимальный наклоны зависят от со квазимонотонно.
Из всего этого следует, что скорость диффузии по действию X в обла¬
стях 0-45° и 60-80° велика, а в промежуточной области мала. Чтобы опре¬
делить, какие частоты угла яр соответствуют этим трем областям, взглянем
на верхний график панели справа. Области 0-45° отвечают значения яр,
меняющиеся от 16 до 20/;/год; эти вариации, по всей вероятности, имеют
место благодаря сильному перекрытию двух главных резонансов с крити¬
ческими углами sst + яр и s^t + яр. Аналогично, области 60-80° отвечают
значения яр от 5 до 10///год, и эти вариации, скорее всего, имеют место бла¬
годаря сильному перекрытию резонансов с критическими углами sit + яр
и szt + яр. Что касается области 45-60°, то ей отвечает такой диапазон яр,
в котором все резонансные компоненты спектра A(t) + uB(t) имеют малые
амплитуды. Таким образом, данная область образует «мост» между двумя
главными хаотическими областями. На этом «мосту» диффузия вызвана пе¬
рекрытием резонансов меньшей ширины, и поэтому она медленнее. Пере¬
сечь мост можно, но на шкалах времени больше чем принятое в описанных
расчетах время интегрирования (18 млн лет).
Интересен вопрос, почему подобного «моста» нет в модели с Луной,
в которой хаотическая область однородна во всем диапазоне частот 0-
30"/год. По-видимому, ответ состоит в следующем. Согласно разделу 4.1,
ширина резонанса в пространстве невозмущенных частот пропорциональ¬
на у//3с, где с — коэффициент резонансной гармоники, /3 — в данном случае
коэффициент вращающего момента. Если учитывать Луну, то коэффициент
вращающего момента равен а + ам', таким образом, он больше коэффици¬
ента а, соответствующего системе без Луны. Кроме того, в первом случае
резонансы расположены при больших значениях наклона, поэтому и коэф¬
фициенты с резонансных гармоник, пропорциональные у/1 — X2, больше.
Таким образом, в модели с Луной резонансы с критическими углами sst+яр
И stf+яр могут перекрываться с резонансами с критическими углами s\t+яр
и $2t + яр, тогда как в отсутствие Луны резонансы недостаточно широки.
Ранее Уард (1982) уже констатировал (в аналитическом исследовании
системы, эквивалентной (7.16), но включавшей лишь несколько членов
фурье-разложения A(t) + tB(t))9 что в отсутствие Луны наклон Земли ис¬
162
Глава 7
пытывал бы осцилляции ±10°. Согласно результатам Ласкара и др. (1993),
вариации наклона Земли были бы даже более драматичными (также и при
меньшем периоде вращения Земли). В отсутствие Луны климат Земли ме¬
нялся бы радикально на шкале времени в несколько миллионов лет, что
могло бы предотвратить развитие сложных форм жизни. Таким образом,
описанные результаты, по-видимому, означают, что наше собственное су¬
ществование обусловлено существованием Луны, которое, в свою очередь,
является, как полагают, следствием случайного события в ранней истории
Солнечной системы. Действительно, сходство составов Луны и земной ман¬
тии указывает на то, что Луна сформировалась путем аккреции вещества,
выброшенного с Земли после того, как произошла ее внутренняя диффе¬
ренциация на кору и мантию (Кануп и Эспозито, 1996; Ида и др., 1997).
Для выброса достаточной массы вещества требуется столкновение Земли
с планетным эмбрионом, сравнимым по массе с Марсом. Отметим также,
что ни у какой другой планеты (за исключением Плутона) нет столь массив¬
ного спутника, такого, что отношение масс спутника и планеты сравнимо
с отношением масс Луны и Земли. Небесная Механика здесь встречается
с Философией!
В реальности система «Земля-Луна» за время существования Солнеч¬
ной системы испытала сильную эволюцию под влиянием приливов: у Лу¬
ны медленно увеличивалась большая полуось орбиты, а скорости вращения
и прецессии Земли уменьшались. Динамику земной оси вращения в ходе
приливной эволюции системы «Земля-Луна» исследовали численными ме¬
тодами Тума и Уиздом (1994а) и Нерон де Сюржи и Ласкар (1997).
Ласкар и Робутель (1993) изучили также динамическую эволюцию
осей вращения других планет Солнечной системы, используя подход, ана¬
логичный описанному выше для случая Земли. Для планет-гигантов они
получили практически регулярные решения в широких диапазонах скоро¬
стей прецессии и начальных наклонов; в частности, согласно решению для
Урана большой наклон Урана (близкий к 90°) не может быть результатом
динамической эволюции. Скорее всего, он является следствием столкнове¬
ния Урана с планетным эмбрионом земной массы на ранней стадии эволю¬
ции Солнечной системы (Сафронов, 1965; Паризи и Брунини, 1996). Прак¬
тически регулярная динамика осей вращения планет-гигантов объясняется
простым видом спектра A(t) + tB(t) для этих планет: в нем присутствует
лишь ограниченное число хорошо разделенных линий.
Эволюция оси вращения Марса, напротив, является хаотической, при¬
чем наклон меняется в пределах от 0 до 60°. Причина состоит в том, что ча¬
7.4. Динамика осей вращения
163
стота прецессии Марса близка к некоторым главным вековым частотам его
орбиты; на это впервые обратил внимание Уард (1974). Хаотичность и раз¬
мах вариаций наклона оси вращения Марса были подтверждены в работе
Тумы и Уиздома (1993) путем интегрирования неосредненных уравнений
движения.
Наклон Венеры близок сейчас к 180°, и его эволюция является регу¬
лярной. Меркурий заперт в спин-орбитальном резонансе 2/3 (его орбиталь¬
ный период в полтора раза больше периода вращения), поэтому динамику
его оси вращения нельзя исследовать, используя осредненный гамильтони¬
ан (7.16). Обсуждение прошлой приливной эволюции осей вращения этих
двух планет также можно найти в работе Ласкара и Робутеля (1993).
Глава 8
Вековая динамика малых тел
8.1. Линейное интегрируемое приближение
Вековая нормальная форма в задаче динамики малого тела формаль¬
но эквивалентна вековой нормальной форме планетной задачи (см. раз¬
дел 2.5.1): она не зависит от средних долгот тела и планет, а зависит только
от средних эксцентриситетов, наклонений, долгот перигелиев и узлов. Как
и в предыдущей главе, верхние индексы у входящих в вековую нормальную
форму переменных, обозначающие, что те являются средними модифици¬
рованными переменными Делоне, далее при записи пропускаются. К тому
же, ссылаясь на средние орбитальные элементы, определяемые из средних
модифицированных переменных Делоне, мы будем опускать прилагатель¬
ное средний.
Если в вековой нормальной форме пренебречь постоянным членом
Wo(A, A j), она запишется как
Wsec = (8.1)
где еj, zuj, ij, flj — эксцентриситет, долгота перигелия, наклонение и долго¬
та узла j-ой планеты; в еН\ включены также и члены нормальной формы
более высокого порядка по е.
Пытаясь дать реалистичное описание векового движения малого тела,
нельзя не учитывать, что, как показано в предыдущей главе, ej, Wj, ij, Q,j
медленно изменяются со временем. В большинстве приложений предпо¬
лагается, что элементы орбит планет эволюционируют согласно реше¬
нию Лагранжа-Лапласа (7.10) с коэффициентами, чьи значения приведены
в таблицах 7.1, 7.2 и 7.3. Чтобы привести гамильтониан (8.1) к автономному
виду, вводятся новые углы тк — gkt + /3 к = Skt + 6к. Если обозначить
через А9к и ASk сопряженные им действия, то (8.1) запишется как
T^sec — ^ ^(fffcAgk + SfcASfc) + £l~L\(P,Q,p, q, ток, £\). (8*2)
к
166
Глава 8
Напомним, что согласно предыдущей главе S5 равно нулю и что при за¬
дании элементов орбиты относительно инвариантной плоскости планетной
системы гамильтониан Н\ не зависит от Щ.
В принципе, можно взять более реалистичные квазипериодические за¬
висимости элементов планет от времени, например зависимости, задавае¬
мые нормальными формами вековой планетной задачи более высокого по¬
рядка; это, однако, не привело бы к увеличению числа степеней свободы,
а следовательно, не изменило бы общей формы (8.2), но модифицировало
бы зависимость Н\ от углов и Щ. С другой стороны, чтобы сохранить
форму (8.2) вековой задачи, необходимо брать лишь квазипериодические
приближения векового планетного движения. Согласно предыдущей главе
вековое движение планет в действительности не является квазипериодиче-
ским; в особенности это явно проявляется в случае планет земной группы.
Если попытаться принять во внимание, что зависимости планетных эле¬
ментов орбит от времени имеют непрерывные фурье-спектры, то задачу ве¬
ковой динамики малого тела нельзя было бы записать в виде (8.2), так как
было бы невозможно ввести дополнительную степень свободы для каждой
независимой планетной частоты. К счастью, поскольку фурье-спектр ор¬
битальных элементов у наиболее массивных планет земной группы имеет
сильные пики на дискретном наборе значений частот, квазипериодическое
приближение для векового планетного движения является хорошим даже
в реалистичной постановке задачи исследования вековой динамики малых
тел. Фактически Гуццо и Морбиделли (1997) показали, что результат нехо-
рошевского типа об устойчивости векового движения малого тела, получае¬
мый в рамках квазипериодического приближения планетного движения, не
изменится, если принять во внимание непрерывность спектров планетных
элементов. Поэтому в данной главе изучение вековой динамики малых тел
мы начнем с вековой нормальной формы, имеющей вид (8.2).
Гамильтониан (8.2) не представлен в квазиинтегрируемой форме, по¬
скольку планетные частоты и Sk также являются величинами порядка е.
Таким образом, как и в вековой планетной задаче, необходимо найти ин¬
тегрируемое приближение и определить новый малый параметр, скажем 77,
задающий величину возмущения. Однако в данном случае выбор страте¬
гии не может быть единственным из-за того, что малые тела движутся
по весьма разнообразным орбитам, причем некоторые имеют большие экс¬
центриситеты и/или большие наклонения. В каждой из стратегий должны
использоваться свое интегрируемое приближение и свой малый параметр.
В данном разделе мы подробно рассмотрим «классическое» интегрируемое
8.1. Линейное интегрируемое приближение
167
приближение, справедливое для тех малых тел, чьи эксцентриситеты и на¬
клонения имеют тот же порядок величины, что и у планет. В следующем
разделе мы обсудим альтернативную стратегию, подходящую для других
малых тел.
Вспомним, что Р ~ фае2/2 и Q ~ 2фа sin2 (г/2) (где ей i — экс¬
центриситет и наклонение орбиты малого тела) и разложим функцию еН\
в (8.1) в степенной ряд по фР^у/Q и е^, sin(zj/2).. Мы рассматриваем
VP,VQ, 6j,sinzj/2 как величины одного и того же порядка, скажем фг\\
таким образом, можем записать еН\ = Н(п) с Н(п) порядка п по фд.
Рассуждая так же, как в разделе 7.1, легко показать, что благодаря прави¬
лам Даламбера (см. раздел 1.9.3) исчезают все члены Н(п) с нечетными п
или п = 0. Это означает, что rj является естественным «малым парамет¬
ром» в итоговом разложении. Также благодаря правилам Даламбера член
низшего порядка в разложении имеет вид
2) = — доР — $oQ + У^ [cj ej a/2P(cos р cos vjj — sin p sin voj) +
j
+ dj sin ^ \/2Q(cos q cos Qj — sin q sin Qj)], (8.3)
где — go, —so, Cj, dj — коэффициенты разложения, зависящие только от
больших полуосей орбит малого тела и планет. Для коэффициентов членов,
линейных по Р и Q, выбраны обозначения —до и — so с тем, чтобы запись
последующих формул была идентична обычно используемой в литературе.
Любопытный факт: если вековая нормальная форма построена только до
порядка £, то so оказывается равным —до при всех значениях большой по¬
луоси орбиты малого тела; если же в нормальную форму включены также
члены порядка е2 (как в работе Милани и Кнежевича, 1990), то, вообще
говоря, So ф -до-
Используя решение Лагранжа-Лапласа (7.10) для вековой эволюции
планетных элементов, находим, что (8.3) приводится к виду
Н{2) = —доР — SoQ + ^2 [сjЩ,к V2P(cosр cos w*k — sin p sin r?)*)-f
j к
+ djNj^\/2Q (cos qcosQl — sing sin fi£)]. (8.4)
Гамильтониан
T^int
'^2(9kh.gk + SkASk) + W(2) (8.5)
к
168
Глава 8
интегрируем. Если ввести обычные канонические полиномиальные пере¬
менные у = \/2Pcosp, х = \/2Psinp, z = y/2Q cosq,v = y/2Qsmq
(где x, v — новые координаты, a у, z — сопряженные им импульсы), то
уравнения движения для (8.5) запишутся как
Лдк = ^2 сз мз* [у sin W*k+x cos w*k\, Ib*k = gk,
3
ASk = ^ djNj^iz sinQl + vcosfijl], й*к = sk,
з
X = -9оУ + У У сзмз* cos V = 9ox + У У sin tujj;,
j к j к
V = —SqZ + EE djNj^k cos z — sqv -J- ^ ^ ^ ^ djNj^k sinS7£.
j к j к
(8.6)
С учетом тривиального решения = gkt + /Зк и &к = Sfct + послед¬
ние две строки (8.6) принимают вид хорошо известных уравнений для двух
несвязанных возмущаемых гармонических осцилляторов с общим решени¬
ем
х = Asin(-g0t + a) + '^2'22^3,ksinwk>
j к
у = A cos(-g0t + а) ~ 53 Ш ^>fc cos
Л Л (8-7)
v = Bsin(-s0t + (5) + >3/3 Уз,k sinOfc,
j к
z = Bcos(-s0t + /3) -
3 к
где А,а,В,{3 — постоянные интегрирования (зависящие от начальных
условий), а
_ cjMj,k _ djNjyk
£>j,k — ? Vj,k — (*•*)
9k~ 9o sk - s0
— амплитуды вынужденных колебаний. Отметим, что последние становят¬
ся бесконечными, когда частота до или so равна одной из планетных ча¬
стот дк или sk. В таком случае говорят, что имеет место резонанс. По¬
скольку соответствующие этим резонансам знаменатели дк — до и sk —
— so присутствуют в линейных уравнениях векового движения малого тела,
эти резонансы обычно называют линейными вековыми резонансами, или
8.1. Линейное интегрируемое приближение
169
вековыми резонансами первого порядка. Кроме того, резонанс до = 9 к
принято обозначать ик, а резонанс so = sk — через v1&. Поскольку ра¬
нее, в главе 4, были рассмотрены резонансы с динамикой маятникового
типа с ограниченными амплитудами колебаний, читателя может удивить
тот факт, что здесь амплитуды (8.8) в резонансах обращаются в беско¬
нечность. Расходимость амплитуд вынужденных колебаний (8.8) являет¬
ся в данном случае артефактом, возникающим из-за линейности уравне¬
ний движения (8.6) относительно переменных x, g, v, z. Напомним, что эти
уравнения получены из гамильтониана (8.5), в котором не учтены члены,
квадратичные по действиям Р и Q. Аналогично, если в гамильтониане (4.4)
пренебречь членом (/3/2), то движение Д станет неограниченным. Более
точный анализ динамики в вековых резонансах, учитывающий члены и бо¬
лее высокого порядка по переменным действия, будет предпринят в раз¬
деле 8.4.
Теперь, используя решение (8.7), гамильтониан (8.5) можно преобра¬
зовать к виду, зависящему только от переменных действия, при условии,
что линейные вековые резонансы отсутствуют. Прежде всего, найдем новые
канонические переменные у', аД z', vf, А'дк, vj*'k, A'Sk, такие, что (8.5)
запишется как
/2 ^2 ^2 /2
Пм = ^(9кЛ'дк+зкКк)-9оХ \У -s0^^+F(vu*'k,n*'k). (8.9)
Если сопоставить временную эволюцию х, g, v, 2, wk, С1к, даваемую фор¬
мулами (8.7), с эволюцией х', у', г/, 2Д zu*k, £1*к, описываемой гамильтони¬
аном (8.9), то естественно выбрать
х> =х~^2^2 €j,k sin wl, у' = y + J2J2 tj,k cos w*k,
j k j k (8.10)
v' = v Ъ,к sin Q.*k, z' = z + ^2^2 Vj,k cos n*k,
j к j к
а также w*fk = mk, Q*k = £lk. Далее требуется только определить А'дк
и Л' такие, что преобразование было бы каноническим. Для этой цели
мы используем критерий производящей функции (см. раздел 1.6 и, в част¬
ности, уравнение (1.41)): наше преобразование переменных можно пере¬
писать в виде неявных уравнений х' = dS/dyf,y = dS/dx,... ,П*к —
170
Глава 8
= dS/dA'Sk, если выбрать
к
-ED& к{у' sin ml + х cos wl) +
j к
+ Wj,k(z' sinOfc + vcosfi£)]. (8.11)
Это доказывает, что наше преобразование канонично, при условии, что пре¬
образование от Адк,А3к к A'gk,AfSk задается уравнениями Адк = dS/dw£
и ASk = dS/dQ,*k. По построению гамильтониан (8.5) преобразуется к ви¬
ду (8.9); функция F из гамильтониана исключается, так как она не зависит
от переменных движения малого тела ж', у', ?/, z'.
Теперь достаточно ввести новые канонические переменные «дей¬
ствие-угол» Pf,p',Qf,qf посредством формул
х' = л/2Р' sinp', у' = л/2Pf cos р\ v> = yj2Qf sin </, z' = л/2<2' cos
то есть к виду, зависящему только от переменных действия. Гамильтониан
готов для использования в качестве интегрируемого приближения при пер¬
турбационном анализе полной вековой нормальной формы. Введенные но¬
вые переменные «действие-угол» обычно называют линейными собствен¬
ными модифицированными переменными Делоне. Элементы, задаваемые
путем обращения (1.69) и (1.68), с Pf,pf,Q',q' вместо P,p,Q,q, а имен¬
но
называют соответственно линейными собственными эксцентриситетом,
долготой перигелия, наклонением и долготой узла. Из (8.13) очевидно,
что до и so являются частотами линейных собственных долгот перигелия
и узла соответственно; поэтому их называют линейными собственными ча¬
стотами.
Hint = + skA'Sk) - д0р' - s0Q', (8.13)
к
(8.14)
Г, Q' 1 <у
г = arc cos 1 — — , il = — q ,
Ij — 1
8.2. Интегрируемое приближение Козаи
171
8.2. Интегрируемое приближение Козаи
Найдем теперь интегрируемое приближение (8.2), подходящее для ма¬
лых тел, орбиты которых имеют эксцентриситеты и/или наклонения много
больше, чем у планет. В таком случае действия Р и/или Q, задаваемые фор¬
мулами (1.69), не являются малыми, поэтому раскладывать гамильтониан
в степенной ряд по у/2~Р и y/2Q, как в предыдущем разделе, нецелесообраз¬
но. Вместо этого, следуя схеме, впервые разработанной Уильямсом (1969),
мы разложим (8.2) в степенной ряд только по ej и sinZj/2, записывая
7~^sec — ^ /дкЛ-дк ~t~ Sfc ASfe) -f ^ ^ ^(n) Q't РчЧч ^кч ^к)4) (8.15)
к п^О
где /С(п) имеют порядок п по ej,sinzj/2. Ведущим членом этого разложе¬
ния является /С(0). В данном случае «малый параметр» г], характеризующий
величину возмущения относительно главной части гамильтониана, имеет
величину порядка планетных эксцентриситетов и наклонений (напомним,
что при подходе, основанном на линейном приближении, он имеет величи¬
ну порядка е|,ф.
Член нулевого порядка /С(0) не зависит от планетных эксцентрисите¬
тов и наклонений, поэтому благодаря правилам Даламбера он не зависит
и от планетных углов wk и С1*к. Из правила Даламбера об инвариантности
гамильтониана относительно вращений (правило 2 в разделе 1.9.3) следует,
что в фурье-разложении /С(0) ненулевые коэффициенты могут быть только
у гармоник exp t[mp + kq\ с т + к = 0; это означает, что /С(0) зависит толь¬
ко от аргумента перигелия д = q — р. Будучи зависимым только от одного
угла, /С(0) поэтому интегрируем (см. раздел 1.8). Вновь вводя переменные
Делоне G, Я, g,h (см. формулы (1.68)), примем гамильтониан
^int ~ ^(#fcAgfc + 5fcASfc) + /C(0)(G, Н,.д) (8.16)
к
в качестве интегрируемого приближения векового гамильтониана (8.2).
Чтобы записать (8.16) в виде функции одних только переменных действия,
что необходимо для изучения вековой нормальной формы методами гла¬
вы 2, требуется ввести новые переменные «действие-угол» согласно рецеп¬
ту Арнольда (см. раздел 1.9). Чтобы сделать этот шаг, который обсуждается
далее в разделе 8.2.3, прежде всего надо детально исследовать динами¬
172
Глава 8
ку, описываемую гамильтонианом /С(0). Впервые это сделал Козаи (1962,
1978)1, поэтому /С(о) сейчас обычно называют гамильтонианом Козаи.
Поскольку /С(о) не зависит от h, действие Н = у/а( 1 — е2) cos г являет¬
ся константой движения. Напомним, что Н есть z-составляющая углового
момента малого тела. Возвращаясь к средним элементам малого тела а, е
и г и принимая во внимание, что а постоянно, приходим к выводу, что
эволюции ей г (являющихся функциями аргумента перигелия д) связаны
соотношением Н = const. Естественными координатами на поверхности
уровня Н являются G и д, или же, что эквивалентно, е и д. На такой по¬
верхности эволюция е (или G) как функции от д следует кривой уровня
/С(о)(G, Я, д), где if играет роль параметра (см. раздел 1.8).
Если нормальная форма вычисляется только до порядка е, а члена¬
ми более высокого порядка по е пренебрегается, то практический способ
расчета кривых уровня /С(0) очень прост. Фактически в этом случае норма¬
лизованный гамильтониан есть просто возмущение в (1.29), усредненное
по средним аномалиям I и lj малого тела и планет, а именно
где векторы г и sj — гелиоцентрические положения малого тела и j-ой пла¬
неты соответственно; A j = г — s j; причем эти векторы должны быть пред¬
ставлены как функции орбитальных элементов. Таким образом, гамильто¬
ниан Козаи /С(0) дается выражением (8.17), где эксцентриситеты и наклоне¬
ния планет предварительно положены равными нулю. Если положить ej =
= ij = 0, то, как мы знаем уже из обсуждения выше, результат двойного
интегрирования в (8.17) не зависит от /г, а следовательно, зависит только от
a, e,i,g и а^. Значения а и aj фиксированы, потому что большие полуоси
являются постоянными для векового гамильтониана. Кроме того, из усло¬
вия пребывания на фиксированной поверхности Н = const следует соот¬
ношение г = arccos(#/y/a(l — е2)). Как следствие, значение /С(0) полно¬
стью определено, если заданы ей д. С технической точки зрения интеграл
по lj в (8.17) можно взять аналитически с использованием эллиптических
функций К первого рода. В самом деле, полагая эксцентриситет е7 и на¬
клонение ij планеты равными нулю, имеем (Уильямс, 1969; Бейли и др.,
'Еще раньше аналогичное исследование провел М.Л.Лидов (см. его статью в сб.: Искус¬
ственные спутники Земли. Вып. 8. М.: АН СССР, 1961. С. 5-45). — Прим. ред.
8.2. Интегрируемое приближение Козаи
173
1992)
Jo Ill'll J
где
тп = —— ,
г2 + a?j + 2аj у/х2 + у2
AajyJx2 + у2
(8.19)
г — вектор положения малого тела, х и у — координаты его проекций на
плоскость планетной орбиты, а г = ||г||. Интеграл по I в (8.17), напро¬
тив, взять аналитически нельзя, поэтому требуется численный алгоритм
(см., например, Пьессенс и др., 1983). Несложно написать компьютерную
программу для вычисления /С(0) в каждой точке е,д сетки на поверхно¬
сти Н = const, а затем построить кривые уровня /С(о) при помощи какого-
либо графического пакета.
Киношита и Накаи (1999) предложили для гамильтониана Козаи ана¬
литическую аппроксимацию:
где шс — масса центрального тела, rij — среднее движение j-го возмуща¬
ющего тела. Это выражение справедливо при любых значениях е и г, но
в нем пренебрегается членами порядка (а/а^)2, что жестко ограничивает
область его применения. Выражение (8.20) полезно лишь для спутниковых
задач, где отношение а/а7- очень мало.
Анализ динамики гамильтониана Козаи удобно проводить раздельно
для двух случаев: астероидного, когда большая полуось орбиты у малого
тела меньше, чем у главного возмущающего тела, и кометного — при об¬
ратной ситуации.
8.2.1. Динамика Козаи внутри орбиты главного возмущающего тела
На рис. 8.1 показана эволюция ей д, определяемая гамильтонианом
Козаи, на шести разных поверхностях Н = const. Динамика вычислена при
((2 + 3e2)(3cos2 г — 1) + 15е2 sin2 г cos 2д),
(8.20)
174
Глава 8
а = 3 а. е. и с учетом возмущений от четырех планет-гигантов, поэтому она
дает хорошее представление о типичном астероидном случае. Каждой по¬
верхности Н = const на рис. 8.1 отвечает (максимальное) значение накло¬
нения при е = 0, а именно гтах = arc cos(Н/у/а). Граничная окружность на
всех панелях соответствует максимально возможному на поверхности Н =
= const эксцентриситету, то есть етах = \А — Н2/а.
Отметим, что все графики симметричны относительно оси sin д = 0.
Причина заключается в том, что разложение /С(0) в степенной ряд по на¬
клонению малого тела включает благодаря правилам Даламбера только чле¬
ны in с четными гг; поэтому в фурье-разложение /С(0) должны входить толь¬
ко гармоники cos кд с четными к. Это означает, что функция /С(0) перио¬
дична по д с периодом тг.
При малом гтах (рис. 8.1 гг) кривые уровня /С0 по форме весьма близки
к окружностям. Это означает, что аргумент перигелия циркулирует, при¬
нимая значения на полном интервале 360°, эксцентриситет же (а следова¬
тельно, и наклонение) почти постоянен. Таким образом, линейное интегри¬
руемое приближение векового гамильтониана (см. раздел 8.1), в котором
пренебрегается всеми гармониками по аргументу перигелия, в данном слу¬
чае малого наклонения является хорошим приближением динамики Козаи.
При увеличении гтах (рис. 8.16) кривые уровня вытягиваются вдоль
оси esing. Аргумент перигелия по-прежнему циркулирует, но эксцентри¬
ситет либрирует, достигая максимума всякий раз при д = 90 или 270°;
наклонение при этом минимально. При гтах выше критического порога
структура динамики Козаи радикально меняется (рис. 8.1в). Точка е = 0
превращается в точку неустойчивого равновесия; сепаратриса соединяет
эту точку саму с собой и делит фазовое пространства на три части: две
области, где угол д либрирует около 90 или 270° (то есть он уже не пре-
цессирует), и область, где д циркулирует. Данная динамическая структура
типична для интегрируемого резонансного случая (глава 4), поэтому о ней
часто говорят как о резонансе Козаи. Резонанс Козаи можно рассматри¬
вать как резонанс 1:1 между частотами прецессии долготы перигелия w
и долготы узла Q малого тела. Таким образом, в терминах главы 4, аргу¬
мент перигелия д = w — £2 является критическим углом резонанса. Если
имеет место резонанс Козаи, то классическое интегрируемое приближение
(раздел 8.1) уже не может, очевидно, служить хорошим приближением для
реальной вековой динамики.
Рис. 8.1г, 8.16 и 8.1е соответствуют еще большим значениям гтах. Ре¬
зонанс Козаи становится сильнее в том смысле, что ширина области либра-
8.2. Интегрируемое приближение Козаи
175
а = 3.000 in
10.0 (а)
а = 3.000 гп
30.0 (б)
ecos(g)
а = 3.000 гтах = 33.0 (в)
ecos (д)
а = 3.000 гтах = 45.0 (г)
а = 3.000 гтах = 60.0 (д)
а = 3.000 гтах = 80.0 (е)
-0.5 0.0
е cos(^)
-0.5 0.0 0.5
ecos (д)
Рис. 8.1. Динамика Козаи в поясе астероидов, представленная в полярных коорди¬
натах е, д. Все панели построены при значении средней большой полуоси, равном
3 а. е. Наклонение гтах при е = 0 указано вверху каждой панели. Прерывистыми
кривыми обозначены е,д, соответствующие узловым пересечениям орбит планет.
(По данным Томаса, 1998; адаптировано)
176
Глава 8
ции увеличивается. При этом точка е = 0 всегда остается точкой неустойчи¬
вого равновесия. Как следствие, резонансная динамика вынуждает любую
орбиту с первоначально малым эксцентриситетом достигать больших е при
д = 90° или 270°. Большой эксцентриситет подразумевает малое гелиоцен¬
трическое узловое расстояние. Последнее определяется как расстояние от
Солнца при пересечении плоскости отсчета; оно дается формулой
о(1 - е2)
1 ± ecosg’ ( ^
где индексы «+» и «—» обозначают восходящий и нисходящий узлы соот¬
ветственно. Таким образом, астероид в некоторый момент его вековой эво¬
люции должен пересечь область орбит планет земной группы. На рис. 8.1 в
прерывистыми кривыми нанесено множество точек е, д, порождающих уз¬
ловые пересечения орбиты Марса (кривые построены просто путем под¬
становки г± = 1.5 а. е. в (8.21)); на рис. 8.1г дополнительно нанесены
аналогичные кривые для узловых пересечений орбиты Земли; кривые для
узловых пересечений орбит Венеры и Юпитера добавлены на рис. 8.Id,
а кривые для Меркурия различимы на рис. 8.1 е. Узловые пересечения с ор¬
битой планеты открывают возможность для тесных сближений астероида
с планетой; эти сближения дестабилизируют орбиту астероида. Таким об¬
разом, динамика Козаи объясняет, почему пояс астероидов малонаселен при
больших наклонениях. С математической точки зрения тесному сближению
соответствует истинная особенность (Aj = 0) гамильтониана (1.29). Ана¬
литическая конструкция вековой нормальной формы, следовательно, невоз¬
можна. Однако можно показать (Гронки и Милани, 1998, 1999), что двой¬
ные интегралы в выражении для гамильтониана Козаи (8.17) хорошо опре¬
делены даже в присутствии такой особенности. Поэтому, чтобы получить
первоначальное представление о вековой динамике с пересечениями орбит
планет, гамильтониан Козаи все же можно использовать (в чем мы убедимся
более конкретно в разделе 8.2.2).
Критический порог для гтах, при котором появляется резонанс Козаи,
зависит от а; его точное определение можно найти в работе Козаи (1962).
При любых значениях от 0 до 1 отношения а/а' (где а — большая полуось
орбиты малого тела, а' — большая полуось орбиты главного возмущающего
тела, то есть Юпитера в случае главного пояса астероидов) динамика Ко¬
заи оказывается весьма похожей на показанную на рис. 8.1. Таким образом,
описанная нами динамика не специфична для пояса астероидов, а характер¬
на для многих систем. Например, советский космический аппарат Лунник,
8.2. Интегрируемое приближение Козаи
177
запущенный первоначально на квазиполярную орбиту вокруг Земли, через
некоторое время упал на Землю, потому что резонанс Козаи, порожденный
совместно лунными и солнечными возмущениями, вынудил эксцентриситет
орбиты увеличиться настолько, что перигейное расстояние стало меньше
радиуса Земли2. В принципе, в любой динамической системе, описываемой
уравнениями ограниченной задачи трех тел, резонанс Козаи вызывает силь¬
ные вариации орбиты внутреннего тела, если ее наклонение относительно
орбиты внешнего возмущающего тела достаточно велико. Это справедливо
независимо от массы внешнего возмущающего тела или расстояния от него:
действительно, из-за вырожденности задачи двух тел величина возмущения
(е в формуле 8.1) сказывается лишь на временной шкале динамики Козаи,
но не на ее результатах. Однако если какие-либо иные возмущения вызы¬
вают прецессию аргумента перигелия д, то вековой гамильтониан в первом
приближении принимает вид
Wsec = aG + /C(0)(G,tf,s), (8.22)
где коэффициент а — частота вынужденной прецессии д, вызываемой до¬
полнительными возмущениями, а /С(0) — гамильтониан Козаи, определяе¬
мый присутствием удаленного возмущающего тела. Если /С(0) мало относи¬
тельно aG, то резонанс Козаи исчезает независимо от величины наклоне¬
ния. Пример этого дают спутники Урана. Их орбиты близки к экваториаль¬
ной плоскости планеты, то есть наклонены примерно на 90° относительно
плоскости видимого движения Солнца. Поэтому резонанс Козаи, вызывае¬
мый солнечным возмущением, должен вынуждать спутники упасть на пла¬
нету. Однако частоты прецессии их аргументов перицентра, вызываемой
сжатием планеты и их взаимными возмущениями, достаточно велики, что¬
бы подавить резонанс Козаи, что и обеспечивает долговременную устой¬
чивость орбит спутников. То же происходит и со всей нашей планетной
системой. Орбиты планет наклонены примерно на 60° относительно плос¬
кости Галактики. Если бы в Солнечной системе была лишь одна планета,
то возмущение со стороны концентрации вещества в плоскости Галакти¬
ки (так называемый Галактический прилив; см., например, Матесе и Уит¬
мен, 1992) периодически увеличивало бы эксцентриситет планетной орби¬
ты. Однако взаимные возмущения планет вызывают, согласно предыдущей
главе, прецессию аргументов перигелия с непренебрежимыми частотами,
2Речь идет о КА Луна-3, впервые в истории сделавшем фотоснимки обратной стороны Лу¬
ны. Его орбита была наклонена к плоскости эклиптики примерно на 90°. См. книгу В. В. Бе¬
лецкого «Очерки о движении космических тел» (М.: Наука, 1972), с. 113-119. — Прим. ред.
178
Глава 8
и поэтому воздействие Галактического прилива становится несуществен¬
ным. Напротив, в случае орбиты с большой полуосью в несколько тысяч
астрономических единиц частота прецессии, вызываемой планетами, очень
мала, и поэтому Галактический прилив становится доминирующим грави¬
тационным возмущением. Согласно наиболее популярной из теорий проис¬
хождения облака Оорта (резервуара долгопериодических комет), динамика
Козаи, порождаемая Галактическим приливом, ответственна за уменьше¬
ние эксцентриситетов тел, которые были рассеяны планетами на орбиты
с большими полуосями в несколько тысяч а. е. (см. Дункан и др., 1987).
8.2.2. Динамика Козаи снаружи орбиты главного возмущающего тела
Рис. 8.2 аналогичен рис. 8.1, за исключением того, что он построен
для малого тела с большой полуосью орбиты 45 а. е., то есть для малого
тела, внешнего по отношению к возмущающим телам (четырем планетам-
гигантам). Из этого рисунка сразу ясно, что во внешней Солнечной систе¬
ме динамика Козаи существенно отличается от таковой в главном поясе
астероидов. Если гтах мало, то аргумент перигелия всегда циркулирует
(рис. 8.2а), а эксцентриситет существенно не изменяется (кривые уровня
/С(0) по форме близки к окружностям), как и в астероидном случае. Однако
с увеличением гтах (в порядке следования панелей рис. 8.2) кривые уровня
при малых эксцентриситетах остаются квазикруговыми. На рис. 8.26 пре¬
рывистыми кривыми изображены семейства значений (е,д), соответствую¬
щих узловым пересечениям орбиты Нептуна. Орбиты с низкими эксцентри¬
ситетами всегда защищены от сближений с Нептуном; с другой стороны,
циркуляция д принуждает все орбиты с высокими эксцентриситетами пере¬
секать орбиту этой планеты. Заметим, что кривые уровня /С(о) имеют точки
излома на линиях узловых пересечений орбиты Нептуна, так как дважды
усредненная функция (8.17) при A j = 0 непрерывна, но не дифференци¬
руема (Гронки и Милани, 1998, 1999).
На поверхности Н = const, соответствующей гтах = 40° (см. рис. 8.2в)
фазовое пространство изменяется: появляется пара точек устойчивого рав¬
новесия при д = 0° и д = 180°. Эти точки равновесия служат центрами
островов, где аргумент перигелия либрирует. Среди всех орбит с высо¬
кими эксцентриситетами только орбиты на этих двух островах либраций
защищены от сближений с Нептуном. Для орбит с очень высокими эксцен¬
триситетами возможны также сближения с Ураном (узловые пересечения
орбиты Урана обозначены новыми прерывистыми кривыми). На рис. 8.2г
острова либраций гораздо больше, и орбиты с большой амплитудой либ-
8.2. Интегрируемое приближение Козаи
179
3
if
’ю
а = 45.000 гтах = 30.0 (б)
ecos (д)
а = 45.000 гтах = 41.0 (в)
ecos (д)
а = 45.000 гтах = 50.0 (г)
а = 45.000 гтах = 55.0 (б)
ecos (д)
а = 45.000 гтах = 60.0 (е)
ecos(^) ecos(p)
Рис. 8.2. То же, что и на рис. 8.1, но для значения большой полуоси, характерно¬
го для пояса Койпера. Прерывистыми кривыми обозначены е, д, соответствующие
узловым пересечениям орбит внешних планет. (По данным Морбиделли и Томаса,
1996; адаптировано)
180
Глава 8
рации вынуждены пересекать орбиту Урана. На рис. 8.2d кривые узловых
пересечений орбиты Урана разрезают каждый остров либраций на две ча¬
сти, создавая таким образом четыре малых либрационных острова, защи¬
щенных от сближений с планетой. При очень большом эксцентриситете
на графике появились прерывистые кривые, соответствующие сближениям
с Сатурном. Наконец, на рис. 8.2е выживают только два острова либраций
при д = 0°, 180° снаружи кривой пересечений орбиты Урана. Кроме того,
отметим появление еще двух островов либраций при д = 90°, 270°, огра¬
ниченных кривыми узловых пересечений орбит Нептуна и Урана.
Анализ панелей на рис. 8.2 позволяет сделать вывод, что в отличие от
случая главного пояса астероидов здесь резонанс Козаи не вынуждает ис¬
ходно малый или умеренный эксцентриситет увеличиваться, каким бы ни
было наклонение. Поэтому орбиты с малыми эксцентриситетами постоян¬
но защищены от сближений с планетами. И действительно, в поясе Кой-
пера, похоже, есть несколько тел с наклонениями гораздо большими, чем
в главном поясе астероидов. Однако динамика Козаи при больших эксцен¬
триситетах нетривиальна, что выражается в наличии островов устойчивого
движения, защищенного от сближений с планетами. Поэтому она представ¬
ляет интерес прежде всего при изучении вековой эволюции долгопериоди¬
ческих комет. Чтобы охватить диапазон эксцентриситетов, типичных для
кометных орбит, необходимо задать поверхности Н = const, соответству¬
ющие гтах > 60°. На рис. 8.3 показаны кривые уровня /С(0) на таких по¬
верхностях в декартовых координатах д и X = у/1 — е2. Благодаря такому
выбору координат видимая область высоких эксцентриситетов увеличена
относительно видимой области низких эксцентриситетов, поскольку функ¬
ция X сильно нелинейна по е.
Рис. 8.3а отвечает той же поверхности, что и рис. 8.2е, так что читатель
может установить прямое соответствие между двумя системами координат.
На рис. 8.36 нанесены также кривые узловых пересечений орбиты Юпите¬
ра. Каждый из больших островов либраций при д = 0°, 180° разделяется
на три острова кривыми узловых пересечений орбит Сатурна и Юпите¬
ра. Орбиты на каждом из этих островов защищены от сближений с пла¬
нетами. На рис. 8.3в два верхних острова при д = 0°(180°) разрушены,
и остается только третий остров, расположенный ниже кривых пересече¬
ний орбиты Юпитера. Однако кривые узловых пересечений орбит Нептуна
и Урана становятся ближе друг к другу, так что этот сохранившийся остров
теперь меньше, чем на панели (6). Однако появляется еще один остров —
также ниже кривых пересечений орбиты Юпитера, но при д = 90° (270°).
8.2. Интегрируемое приближение Козаи
181
а = 45.0 гтах = 60.0 (а) а = 45.0 гтах = 68.0 (б)
9 9
а = 45.0 гтах = 76.0 (в) а = 45.0 гтах = 86.0 (г)
Рис. 8.3. Динамика Козаи в поясе Койпера при очень больших эксцентриситетах
и наклонениях. Шкала вертикальной оси линейна по X = у/1 — е2, что увеличивает
изображение области больших эксцентриситетов фазового пространства. Панель (а)
построена для того же значения гтах, что и панель {ё) на рис. 8.2. (Рис. 5 из статьи
Томаса и Морбиделли, 1996; с разрешения Kluwer Academic Publishers)
Он увеличивается с гтах; на рис. 8.3г, соответствующем гтах = 86°, этот
остров при д = 90° (270°) доминирует в фазовом пространстве, тогда как
остров при д = 0° (180°) почти исчез.
Особенности динамики Козаи, проиллюстрированные на рис. 8.2 и 8.3,
типичны для внешней Солнечной системы, причем они качественно не
изменяются с изменением большой полуоси орбиты малого тела. Интуи¬
тивно это понятно. Появление и исчезновение островов определяются рас-
182
Глава 8
а = 91.60
= 89.41 At = 480000 лет
Рис. 8.4. Динамика Козаи, вычисленная для значений большой полуоси и гтах, та¬
ких, как у сангрейзера («царапающей» Солнце) кометы Икея-Секи. На график на¬
ложена кривая эволюции кометы, найденная численным интегрированием полных
уравнений движения на интервале времени 480000 лет. (Рис. 8 из статьи Томаса
и Морбиделли, 1996; с разрешения Kluwer Academic Publishers)
положением кривых узловых пересечений планетных орбит. Таким обра¬
зом, если увеличить большую полуось, то ситуация просто повторится при
большем эксцентриситете и том же наклонении, то есть при большем зна¬
чении гтах.
Как впервые отметили Бейли и др. (1992), острова либраций при д =
= 90°, 270° (видимые на рис. 8.3г) могут быть ответственны за происхожде¬
ние многих «царапающих» Солнце комет («сангрейзеров»), а также комет,
падающих на Солнце — наподобие тех, что часто открывают со спутника
SOHO. Последние являются долгопериодическими кометами с экстремаль¬
но большими эксцентриситетами, при этом их перигелийные расстояния
имеют величину порядка радиуса Солнца. По-видимому, они достигли сво¬
их нынешних эксцентриситетов, преодолев половину либрационного цикла
на одном из двух главных островов рис. 8.3г.
На рис. 8.4 приведен, в качестве примера, случай сангрейзера 1965VIII
Икея-Секи — одной из самых великолепных комет XX века. Показана ди¬
намика Козаи, соответствующая современным элементам орбиты кометы
(а = 91.6 а. е., е = 0.9999, г = 141.86°, д = 69.05°); положение коме¬
ты в координатах д, X указано стрелкой. На график наложены эволюци¬
онные треки кометы в прошлом и будущем, согласно точному численно¬
8.2. Интегрируемое приближение Козаи
183
му интегрированию полных уравнений движения на интервале времени
480000 лет. Как видим, эволюционные треки примерно следуют кривым
уровня гамильтониана Козаи; однако согласие неидеально, так как вековая
нормальная форма первого порядка дает лишь грубое приближение истин¬
ного движения, — ведь движение таких комет сильно возмущается при про¬
хождении через планетную систему; к тому же в гамильтониане Козаи не
учитываются вековые динамические эффекты, возникающие из-за наличия
у планетных орбит эксцентриситетов и наклонений. Подробное обсуждение
того, насколько уместно использование гамильтониана Козаи для описания
долговременной эволюции долгопериодических комет, можно найти в рабо¬
те Томаса и Морбиделли (1996). Однако уже из рис. 8.4 ясно, что простого
компьютерного расчета динамики Козаи достаточно для объяснения дина¬
мического происхождения комет-сангрейзеров.
Мишель и Томас (1996) показали, что динамика Козаи, подобная
представленной на рис. 8.2в, характеризует также движение астероидов
с умеренными наклонениями и с большими полуосями орбит, немного
большими, чем у Земли и Венеры. Острова либраций вокруг д = 0°, 180°
играют важную роль, защищая (временно) такие астероиды от тесных сбли¬
жений с планетами земной группы. Не следует удивляться, что в данном
случае динамика Козаи выглядит так же, как описано в этом разделе: в са¬
мом деле, при таких значениях больших полуосей и наклонений у орбиты
астероида Земля (или Венера) становится главным возмущающим телом,
доминируя относительно гравитационного поля Юпитера. Только при боль¬
шом наклонении гравитационные возмущения со стороны Юпитера стано¬
вятся преобладающими, и динамика Козаи опять выглядит так же, как на
рис. 8.1г.
Гамильтониан Козаи для «кентавров», орбиты которых имеют большие
полуоси 5-30 а. е., что соответствует внешней части Солнечной системы,
подробно изучен Гронки и Милани (1999); как и в случае долгопериодиче¬
ских комет, в их динамике присутствует несколько либрационных островов,
определяемых кривыми пересечений орбит планет.
8.2.3. Переменные «действие-угол» для гамильтониана Козаи
Поскольку гамильтониан Козаи интегрируем, можно ввести подхо¬
дящие переменные Арнольда «действие-угол», чтобы преобразовать /С(0)
в гамильтониан, зависящий только от новых действий. Как уже обсужда¬
лось в разделе 4.2, в областях, где д циркулирует, и в области, где д либри-
Рует, требуется задавать разные наборы переменных «действие-угол»; при¬
184
Глава 8
чем на сепаратрисе резонанса Козаи преобразование к новым переменным
будет сингулярным.
Поскольку действие Н является для гамильтониана Козаи константой
движения, одним из двух действий Арнольда, скажем J2, будет само Н.
При вычислении другого действия, J\, циклами, используемыми в теореме
Арнольда-Лиувилля, будут циклы, определяемые кривыми уровня /С(0).
Таким образом, имеем
для цикла либрации. В этих формулах через G(JC(0), Н,д) обозначена за¬
висимость G от д вдоль цикла, характеризуемого значениями констант Н
и /С(0); через G+ и G~ обозначены соответственно верхняя и нижняя ча¬
сти цикла в случае либрации, а через <7min, дшах — экстремумы д в ходе
либрации.
Что касается новых углов ярх и гр2, канонически сопряженных с J\
и J2, они, согласно теории Арнольда, линейны по времени, а их производ¬
ные по времени равны соответственно частоте циркуляции/либрации угла д
и частоте угла /г, усредненной по периоду изменения д. В полной вековой
нормальной форме новые переменные «действие-угол» вводятся, как опи¬
сано в разделе 4.2; тогда интегрируемое приближение (8.16) принимает вид
Для циклов, пересекающих кривую пересечений орбиты планеты,
в принципе, тоже можно ввести новые переменные «действие-угол». Фак¬
тически такой цикл хорошо определен (искусственно), так что интеграл,
определяющий Ji, можно вычислить; частоты углов д и h на кривых пе¬
ресечений орбит планет бесконечны, но их усредненные по циклу значе¬
ния по-прежнему конечны (Гронки и Милани, 1998, 1999). Однако гамиль¬
тониан, записанный в новых переменных, неаналитичен при всех значе¬
ниях Ji, J2, соответствующих циклам с пересечениями планетных орбит.
В действительности из-за тесных сближений с планетой динамика будет
сильно хаотической.
(8.23)
для цикла циркуляции и
Ji = — [ G+(IC^.H.a)da- I G~(IC{0),H,g)dg (8.24)
Wint — + 5fcASfc) + /C(0)(Jl, ^2)- (8.25)
к
8.3. Собственные элементы
185
8.3. Собственные элементы
Как уже упоминалось во Введении, из вида распределений астерои¬
дов по большим полуосям, эксцентриситетам и наклонениям оскулирую-
щих орбит (рис. 2) следует, что некоторые области главного пояса астеро¬
идов заселены менее плотно, чем остальные. Однако взаимные расстояния
астероидов в пространстве оскулирующих а, е, г изменяются на временной
шкале прецессии орбит, так как оскулирующие элементы непрерывно изме¬
няются из-за возмущений со стороны планет. Поэтому трудно делать какие-
либо выводы относительно того, насколько значимы эти области видимо
повышенной заселенности. Однако для астероидов на регулярных орби¬
тах, то есть на КАМ-торах, в принципе можно ввести переменные «дей¬
ствие-угол», такие, что действия являются константами движения. В про¬
странстве действий распределение астероидов было бы инвариантным во
времени, так что его анализ мог бы дать важную информацию о структуре
пояса астероидов (см. раздел 8.3.1).
Вычисление переменных действия, постоянных на КАМ-торе, нахо¬
дится за пределами любых практических возможностей. Однако, к счастью,
можно вычислить (путем построения нормальных форм Биркгофа низкого
порядка) действия, чьи амплитуды осцилляций во времени много меньше,
чем амплитуды осцилляций оскулирующих элементов. Для практических
астрономических целей эти действия можно рассматривать как квазикон¬
станты движения. Первый шаг при их вычислении состоит в построении
вековой нормальной формы (как уже объяснено в разделе 2.5.1), что позво¬
ляет в качестве первой приближенной константы движения отождествить
среднюю большую полуось. Второй шаг состоит в построении нормальной
формы Биркгофа первого порядка для векового гамильтониана (8.2). Этот
шаг подробно рассматривается в данном разделе.
Из предыдущих разделов мы знаем, что существуют два возможных
интегрируемых приближения векового гамильтониана. Процедура построе¬
ния нормальной формы Биркгофа зависит от выбора интегрируемого при¬
ближения, но формальная схема в обоих случаях одна и та же. Поэтому
в дальнейшем мы всегда будем через Но обозначать интегрируемое при¬
ближение, которым может быть либо (8.13), либо (8.25). Кроме того, че¬
рез /ь/2, <^2 мы будем обозначать задаваемые для интегрируемого при¬
ближения переменные «действие-угол», а именно P',Q',p',qf — в случае
линейного приближения, либо J\, J2, 'фх, Ф2 — в случае приближения Ко¬
зли. Наконец, через Н\ мы будем всегда обозначать член низшего порядка
186
Глава 8
в возмущении, то есть Нщ — при подходе, основанном на линейном при¬
ближении, либо /С(!) — при подходе, основанном на приближении Козаи.
В линейном приближении частоты долгот перигелия и узла у малого тела
зависят лишь от его большой полуоси. Чтобы иметь более реалистичное
приближение, мы включаем в Но члены Н\, не зависящие от углов. Та¬
ким образом Но становится нелинейным, тогда как среднее от Hi по всем
углам становится равным нулю. В приближении Козаи Но уже является
нелинейным, а среднее от Н\ по углам равно нулю, так что каких-либо мо¬
дификаций не требуется. В итоге нам предстоит работать с гамильтонианом
вида
Н = Ho{h,h, A5fc, ASk) + Hi(h,l2,<Pi,<P2, wl,Q,*k), (8.26)
где H\ — малая величина (скажем, порядка г/) относительно Но, имеющая
нулевое среднее по углам, а Но имеет вид
Ho(h,hAgk,Ask) =Yl(9kAgh +skASk) + W0(I1,I2). (8.27)
к
Функция Wo нелинейна по /ьД» поэтому частоты иi = dWo/dli, ll>2 =
= dWo/dl2 являются функциями от Д,Д. Напомним, что гамильтони¬
ан (8.26) параметрически зависит от А (квазипостоянного действия, ко¬
торое определяется при вычислении вековой нормальной формы; см. раз¬
дел 2.5), то есть от средней большой полуоси орбиты малого тела.
Чтобы вычислить нормальную форму Биркгофа, прежде всего раскла¬
дываем Н\ в ряд Фурье по углам:
Cj,i,m,n{h,h) exp +1(Р2 + m • 1Z7* + п • П*)], (8.28)
j,l, m,n
где zu* и ГГ — векторы, имеющие соответственно компоненты и Q*k;
индекс к изменяется в пределах рассматриваемого числа планетных ча¬
стот. В подходе, основанном на линейном приближении, разложение (8.28)
содержит только члены порядка 4 по эксцентриситетам и наклонениям, по¬
этому благодаря правилам Даламбера оно содержит лишь конечное число
гармоник. В подходе, основанном на приближении Козаи, ряд Фурье по р\
(то есть тД) бесконечен, поэтому приходится ограничивать |jf|, чтобы оста¬
вить в Hi конечное число членов. Если выбрать получисленную методику
(см. Леметр, Морбиделли, 1994), то можно работать без привлечения явного
8.3. Собственные элементы
187
фурье-разложения по углам, поэтому не требуется и ограничивать \j\. Для
простоты изложения мы будем использовать здесь явное фурье-разложение.
В главе 2 показано, как нормальную форму Биркгофа первого по¬
рядка можно вычислить с использованием рядов Ли: новые переменные
Г2, вводятся преобразованием вида (2.6) с производящим гамиль¬
тонианом х> который дается решением уравнения (2.10). Используя разло¬
жение (8.28), х можно записать как
где g и s — векторы планетных частот и Sk соответственно. Постро¬
ить нормальную форму не удастся, если один из знаменателей в (8.29)
близок к нулю; когда такое происходит, говорят, что есть вековой резо¬
нанс между планетными частотами и частотами малого тела. Поскольку
в подходе, основанном на линейном приближении, и в подходе, основанном
на приближении Козаи, определяются возмущения с разными фурье-
разложениями, в этих подходах различны и множества вековых резонан¬
сов, препятствующих построению нормальной формы первого порядка. Как
и при построении вековой нормальной формы (см. рис. 2.1), аналогично,
чтобы гарантировать, что знаменатели в (8.29) будут не меньше уту, значе¬
ния 7i и /2 малого тела должны отличаться по меньшей мере на 0(y/rj) от
решений уравнений
Как только х определено, значения I[, ^2» соответствующие
hyl2,<Pi,P2 астероида, можно вычислить до первого порядка по форму¬
лам
Cj,Z,m,n(-^ 1 ^ ^2)
X
X exp +п-П*)], (8.29)
mg+ns+ jcJi(/i,/2) + lw2(I1J2) = 0.
(8.30)
(8.31)
188
Глава 8
Однако эти уравнения являются неявными, так как производящая функ¬
ция х зависит от новых переменных. Поэтому решение (8.31) находят чис¬
ленно путем итераций, начиная с 1[ = Д, Г2 = Д, = <Pi, Ф2 — ^2-
Если производные от \ малы, то итерационный процесс сходится. Полу¬
ченные в качестве решения значения Д, Д» »^2 называют собственны¬
ми действиями и углами астероида. Частоты Д), и>2(Д i Д) являются
собственными частотами. Напротив, вблизи векового резонанса, где один
из знаменателей в (8.29) мал (меньше ~ y/fj), производные от х велики
и итерационный процесс обычно расходится.
Действия 1[ и Г2 (когда их можно вычислить) — это как раз и есть
те новые приблизительные константы движения астероида, которые в на¬
чале этого раздела мы намеревались искать. Вместо анализа распределения
астероидов в пространстве квазиинвариантных действий А, 1[, Г2 обычно
предпочитают предварительно задавать более легкотрактуемые величины,
называемые собственными элементами, то есть значения большой полу¬
оси, эксцентриситета и наклонения, определяемые квазиинвариантными
действиями. Делается это так. Собственную большую полуось отождеств¬
ляем со средней большой полуосью, то есть с ар = А2/(^М0), где Q —
гравитационная постоянная, М0 — масса Солнца. Затем, если использу¬
ется подход, основанный на линейной аппроксимации, полагаем, что ли¬
нейные собственные действия P',Qf равны собственным действиям I[,If2
(что в среднем выполняется), и, используя (8.14), вычисляем собственные
эксцентриситет и наклонение. При подходе, основанном на приближении
Козаи, полагаем, что действия J\ и Н гамильтониана Козаи равны соб¬
ственным действиям определяя таким образом специфический цикл
эксцентриситета и наклонения как функцию аргумента перигелия д\ затем
в качестве собственных эксцентриситета и наклонения выбираем некото¬
рые значения е и г, которые вместе с ар однозначно определяют этот цикл:
например, значения е и г на цикле при д = 0 или д = 90° или, как альтер¬
натива, усредненные е и г за цикл.
Хираяма (1918) был первым, кто применил подход, основанный на ли¬
нейной аппроксимации, для вычисления собственных элементов. Он ис¬
пользовал вековую нормальную форму первого порядка по массе Юпитера,
причем из нее он взял только линейную часть (избежав, таким образом,
вычисления нормальной формы Биркгофа). Позднее Юаса (1973) разрабо¬
тал более полную теорию векового движения астероидов, основанную на
вековой нормальной форме до второго порядка по массе Юпитера, при¬
8.3. Собственные элементы
189
чем он сохранил все члены до степени 4 по эксцентриситетам и наклоне¬
ниям. Однако Юаса никогда не использовал свою теорию для явного вы¬
числения собственных элементов астероидов. Это сделали Милани и Кне-
жевич (1990, 1992, 1994), которые развили теорию Юасы и предложили
метод, основанный на нормальной форме Биркгофа первого порядка (он
описан в данном разделе). В своем наиболее продвинутом алгоритме Ми¬
лани и Кнежевич (1994) учли возмущения со стороны Юпитера и Сатурна
и вычислили вековую нормальную форму до второго порядка по массам
планет, сохранив все члены до степени 4 по эксцентриситетам и наклоне¬
ниям; кроме того, они учли члены, отвечающие за поправки к собственным
частотам астероида из-за влияния планет земной группы; а для элементов
орбит Юпитера и Сатурна они использовали линейную теорию Лагранжа -
Лапласа, включающую все члены, относящиеся к вековой системе четырех
планет-гигантов, и дополненную главными членами нелинейной вековой
теории движения планет.
Метод, основанный на гамильтониане Козаи, впервые предложил Уи¬
льямс (1969). Уильямс не использовал гамильтонов формализм, однако его
алгоритм вычисления собственных элементов в основном эквивалентен
рассмотренному выше. В частности, его вековые уравнения эквивалент¬
ны уравнениям, определяемым вековой нормальной формой, вычисленной
до первого порядка по массе Юпитера. Леметр и Морбиделли (1994) пе¬
ресмотрели алгоритм Уильямса в рамках гамильтоновой теории, предло¬
жив процедуру, основанную на использовании переменных Арнольда «дей¬
ствие-угол» для гамильтониана Козаи (описанных в этом разделе). Кро¬
ме того, они исходили из вековой нормальной формы, вычисленной до
второго порядка по массам планет, и учли также возмущения движения
малого тела со стороны Сатурна. Для элементов орбит Юпитера и Са¬
турна они использовали линейную теорию Лагранжа-Лапласа с частота¬
ми 95,96,g7,S6,S7,S8, дополненную ведущим нелинейным членом с часто-
той 2д6 - д5.
Точность собственных элементов была проверена с помощью числен¬
ного интегрирования: орбиты астероидов интегрировались на интервале
времени в несколько миллионов лет и при каждом выводе результатов инте¬
грирования вычислялись собственные элементы. В принципе, собственные
элементы должны быть константами движения, то есть их значения должны
оставаться одними и теми же при каждом таком выводе; однако в реально¬
сти значения собственных элементов осциллируют (см. рис. 8.5) благодаря
членам, не учитываемым в использованных при их вычислении нормаль-
190
Глава 8
0.29
н °-28
ь
£ 0.27
О
| 0.26
Я
§ 0.25
п 0.24
CQ
| 0.23
О
u 0.22
0.21
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
х10®
время, в годах; интегратор Orbit8v
0.3
*0.295
£ 0.29
0 0.285
1 °-28
У 0.275
§ 0.27
а 0.265
ё 0.26
° 0.255
0.25
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
х10в
время, в годах; интегратор Orbit8v
Рис. 8.5. Эволюция во времени собственных элементов астероида 1021 Фламмарио.
Надписями ей I обозначены собственные эксцентриситет и наклонение, вычислен¬
ные с использованием алгоритма Милани и Кнежевича; надписями ех и 1х — соб¬
ственные эксцентриситет и наклонение, вычисленные с использованием алгоритма
Леметр и Морбиделли и определяемые как значения ей г при д — 0 на цикле Козаи,
задаваемом значениями собственных действий; еу, 1у — те же величины, что и ех,
/х, но определенные как значения е и г при д = 90° на цикле Козаи. Для этого
астероида (имеющего наклонение орбиты ~ 15.5°) точность различных наборов
собственных элементов (определяемая как отношение среднеквадратичного откло¬
нения к среднему значению) примерно одна и та же. (Рис. 2 из статьи Кнежевича
и др., 1995; с разрешения Astronomy and Astrophysics)
1021 Фламмарио
1021 Фламмарио
8.3. Собственные элементы
191
ных формах низкого порядка. Поэтому точность собственных элементов
измеряют как отношение среднеквадратичного отклонения к среднему зна¬
чению (на всем интервале времени интегрирования). Для астероидов с ма¬
лыми эксцентриситетами и наклонениями, не находящихся вблизи вековых
резонансов, точность собственных элементов Милани и Кнежевича пре¬
восходна: среднеквадратичные отклонения собственного эксцентриситета
и синуса собственного наклонения обычно много меньше 10-3 (Милани
и Кнежевич, 1994). Однако для астероидов с относительно большими экс¬
центриситетами и/или наклонениями точность падает, так как гамильтони¬
ан представляет собой усеченный степенной ряд по е и г, а линейная ап¬
проксимация подразумевает, что ей г постоянны в ходе прецессии аргумен¬
та перигелия; такое допущение для тел, не слишком далеких от резонанса
Козаи, является грубым (см. рис. 8.1). Для тел с i ~ 15° среднеквадратич¬
ные отклонения собственных элементов Милани и Кнежевича становятся
порядка 5 х 1СГ3 для эксцентриситета и 10-3 для наклонения, то есть они
становятся сравнимыми с типичной точностью собственных элементов Ле-
метр и Морбиделли (см. Кнежевич и др., 1995; а также рис. 8.5). Точность
последних в основном одна и та же для всех астероидов независимо от их
эксцентриситетов и наклонений, потому что не используется разложение по
степеням е и г и полностью учитывается динамика Козаи. В принципе, соб¬
ственные элементы Леметр и Морбиделли можно вычислить также и для
астероидов, либрирующих внутри резонанса Козаи, но этот факт не имеет
большого значения в практических приложениях, так как таких астероидов
известно немного. Однако, поскольку не учитываются члены порядков 2
и 3 по планетным эксцентриситетам и наклонениям (то есть /С(2) и /С(3)),
собственные элементы, вычисленные Леметр и Морбиделли, никогда не
достигают наилучшей точности элементов Милани и Кнежевича.
8.3.1. Семейства астероидов
На рис. 8.6 показано получающееся в итоге распределение астероидов
по собственным большим полуосям, наклонениям и эксцентриситетам, вы¬
численным Милани и Кнежевичем. Очевидно присутствие нескольких об¬
ластей явно повышенной плотности. Заппала и др. (1990) и Бенджоя и др.
(1991), используя два независимых метода классификации, осуществили
строгий анализ распределения астероидов по собственным элементам а, е
и г; в обоих случаях были получены схожие результаты (Заппала и др.,
1995). Оказалось, что в распределении астероидов (с собственными накло-
192
Глава 8
О.Зг
0.2-
0.1
‘f* щ
2.2 2.4 2.6 ‘ 2.8
а', а. е.
3.2
0.3
ft .ft#
§.§;т
-щтЩ
т
2.2 2.4 2.6 2.8
а', а. е.
Рис. 8.6. Распределение 12487 астероидов в пространстве собственных элемен¬
тов; а', е\ i' — значения собственных больших полуосей, эксцентриситетов и на¬
клонений, вычисленные Милани и Кнежевичем. (Рис. 1 из статьи Заппалы и др.,
1995; с разрешения Academic Press)
Рис. 8.7. То же, что и на рис. 8.6, но показаны только астероиды, входящие в 32
отождествленных семейства. (Рис. 12 из статьи Заппалы и др., 1995; с разрешения
Academic Press)
8.4. Вековые резонансы
193
нениями меньше 17.5°) есть 32 области со статистически значимой повы¬
шенной плотностью. По общепринятому мнению, эти области повышенной
плотности представляют собой результат распада родительского тела из-за
столкновения с другим (в общем случае меньшим) астероидом; поэтому та¬
кие скопления обычно называют семействами астероидов. Статистически
достоверно отождествленные семейства астероидов с собственными накло¬
нениями меньше 17° показаны на рис. 8.7. Форцони Акколти (1995), ис¬
пользуя собственные элементы Леметр и Морбиделли (1994), отождествил
еще шесть семейств при больших наклонениях: три в области Унгарии (это
область, населенная астероидами с а ~ 1.9 а. е., г ~ 22°), два в области Фо-
кеи (а ~ 2.35 а. е., г ~ 24°), а шестое ассоциировано с большим астероидом
2 Паллада (а = 2.77 а. е., е = 0.23, г = 34.8° на рис. 2).
Высокая точность собственных элементов Милани и Кнежевича поз¬
воляет астрономам изучать в деталях распределение астероидов внутри се¬
мейства, таким образом реконструируя поле скоростей, описывающее раз¬
лет фрагментов их родительского тела (Челлино и др., 1999). Это, в свою
очередь, позволяет выяснять свойства физики ударных столкновений асте¬
роидов в диапазонах размеров тел и скоростей столкновений на порядки
величины больших, чем достижимые в лабораторных экспериментах.
8.4. Вековые резонансы
Положения вековых резонансов вычисляются просто как наборы дей¬
ствий Л, 1\, /2 таких, что частоты интегрируемого гамильтониана (8.27)
удовлетворяют соотношениям вида (8.30) с коэффициентами m, n, j и I
такими, что соответствующие гармоники exp t(jpi + Ip2 + hi • vj* + n • Я*)
удовлетворяют правилам Даламбера и являются существенными в разло¬
жении возмущения в ряд Фурье. При подходе, основанном на линейной
аппроксимации, использование гамильтониана (8.27) для локализации ли¬
нейных вековых резонансов несколько некорректно. Фактически, если есть
линейный резонанс, одна из амплитуд (8.8) преобразования (8.7) беско¬
нечна, так что (8.27) нельзя построить, следуя пертурбационному подхо¬
ду, описанному в разделе 8.1. В этом случае интегрируемое «приближе¬
ние» (8.27) определяется просто путем отбрасывания всех гармонических
ЧЛеНОВ В Ц(2) и W(4).
Как только определены значения действий Л, /1, /2, отвечающие веко¬
вому резонансу, вычисляются соответствующие значения большой полуоси,
эксцентриситета и наклонения, как в случае собственных элементов.
194
Глава 8
собств. большая полуось, а. е.
Рис. 8.8. Расположение вековых резонансов и их оцениваемая ширина при соб¬
ственном эксцентриситете, равном 0.1. Показаны только те вековые резонансы, чьи
гармоники есть в Нр) или 7^(4) • (Рис. 5 из статьи Милани и Кнежевича, 1990;
с разрешения Kluwer Academic Publishers)
В поясе астероидов положения вековых резонансов вычисляли Мила¬
ни и Кнежевич (1990, 1992, 1994), используя подход, основанный на линей¬
ной аппроксимации, и Уильямс и Фолкнер (1981) и Морбиделли и Анрар
(1991а), используя подход, основанный на приближении Козаи. На рис. 8.8
показаны результаты Милани и Кнежевича: расположение вековых резо¬
нансов представлено на плоскости «собственная большая полуось - соб¬
ственное наклонение» при фиксированном собственном эксцентриситете,
равном 0.1. Показаны только линейный резонанс д — и те резонансы, чьи
гармоники есть в главном возмущающем члене Нщ. Данные о положени¬
ях резонансов при других значениях собственного эксцентриситета можно
найти в цитированных выше работах Милани и Кнежевича. В обозначе¬
ниях авторов д и s представляют собой соответственно частоту долготы
перигелия и частоту долготы узла, которые в уравнениях (8.30) следует
8.4. Вековые резонансы
195
отождествить с и — Для каждого резонанса центральная кривая
показывает точное положение, где соответствующее равенство (8.30) в точ¬
ности выполняется, а кривые по ее обеим сторонам показывают положения,
где та же комбинация частот равна ±1"/год (в случае резонанса д — д§) или
±0.5"/год (в случае других резонансов). Эти произвольные значения вы¬
браны, чтобы дать качественное представление о ширине резонансов. Об¬
ратите внимание, что некоторые резонансы кажутся сходящимися к одному
вертикальному положению, близкому к резонансу средних движений 3:1
(приблизительно при 2.5 а. е). Это артефакт метода вычислений: там, где
располагаются резонансы средних движений, вековая нормальная форма
сингулярна из-за малых знаменателей, которые присутствуют в (2.41) из-за
необходимости исключения соответствующих гармоник. Надлежащий спо¬
соб вычисления положений вековых резонансов внутри и вблизи резонан¬
сов средних движений будет описан в главе 11.
На рис. 8.9 показано расположение вековых резонансов, рассчитанное
Морбиделли и Анраром (1991а). Диапазон наклонений здесь шире благо¬
даря тому, что в подходе, основанном на приближении Козаи, вычисление
вековых частот астероида не теряет точности при больших г. Показаны все
резонансы, чьи гармоники есть в возмущающих членах /С^) и /С(2). Как и в
случае рис. 8.8, расчеты выполнены для собственного эксцентриситета, рав¬
ного 0.1. Здесь собственные эксцентриситет и наклонение определены как
значения, которые принимают е и г, когда аргумент перигелия равен нулю
на цикле, определяемом гамильтонианом Козаи. Положения вековых резо¬
нансов рассчитаны с использованием вековой нормальной формы порядка
2 по массе Юпитера; поэтому результат точнее, чем у Уильямса и Фолк¬
нера (1981), которые действовали аналогично, но исходили из вековой нор¬
мальной формы, вычисленной лишь до первого порядка по массе Юпитера.
Полосы из точек при 2.5, 2.8 и 3.3 а. е. обозначают «запрещенные зоны»,
где вековая нормальная форма сингулярна из-за присутствия резонансов
средних движений 3:1, 5:2 и 2:1 соответственно. Рис. 8.9 построен только
для орбит вне резонанса Козаи, у которых аргумент перигелия циркулиру¬
ет; однако подход, основанный на приближении Козаи, позволяет вычис¬
лять положения вековых резонансов и в областях, где аргумент перигелия
либрирует внутри резонанса Козаи. Там долгота перигелия астероида пре-
цессирует в направлении, противоположном прецессии долгот перигелиев
планет, поэтому вековые резонансы низких порядков, включающие периге-
3 Читателю не следует путать аргумент перигелия с частотой долготы перигелия, которые
в данной главе обозначаются оба через д (но всегда в разных контекстах). — Прим. авт.
196
Глава 8
а
Рис. 8.9. Расположение вековых резонансов при собственном эксцентриситете, рав¬
ном 0.1, вне резонанса Козаи. Показаны только те вековые резонансы, чьи гармо¬
ники есть в /C(i) или /С(2). Цифрами обозначены резонансы: 1 — д = д5 (i/5); 2 —
д = д6 Об); 3 s = sq Oi6); 4 - д + 5 = д5 + s6; 5 - д + s = д6 + 56; 9 —
= дъ + <7в; Ю — д — s = д*> — sq; 11 — д — s = дв — sq. Здесь д и s — собствен¬
ные частоты долгот перигелия и узла астероида, отождествляемые соответственно
с cji + CJ2 и Ы2, в обозначениях уравнений (8.30). Полосы из точек обозначают
области, близкие к главным резонансам средних движений, где вековая нормальная
форма сингулярна. (Рис. 9 из статьи Морбиделли и Анрара, 1991а; с разрешения
Kluwer Academic Publishers)
лии, не могут существовать. Как следствие, внутри резонанса Козаи найден
только резонанс s — sq (Морбиделли и Анрар, 1991а).
Мишель и Фрешле (1997) дополнили расчеты Морбиделли и Анрара
до малых эксцентриситетов орбит во внутренней Солнечной системе (об¬
ласть 0.5-2 а. е.), не пересекающихся с орбитами планет земной группы.
К тому же они приняли во внимание резонансы с вековыми частотами пла¬
нет земной группы, которые в расчетах динамики пояса астероидов обычно
игнорируют. Во внутренней Солнечной системе, как оказалось, много таких
резонансов, играющих заметную роль в динамической эволюции астерои¬
дов, сближающихся с Землей (АСЗ) (Мишель, 1997).
Из сравнения рис. 8.9 с левой панелью рис. 2 очевидно, что распре¬
деление астероидов сформировано главными вековыми резонансами. Резо¬
нанс д — де (называемый также резонансом щ) ограничивает распределение
8.4. Вековые резонансы
197
Рис. 8.10. Расположение линейных вековых резонансов в поясе Койпера при соб¬
ственном эксцентриситете, равном 0.1. (Рис. 5 из статьи Кнежевича и др., 1991;
адаптировано. С разрешения Academic Press)
198
Глава 8
основного населения главного пояса, тогда как группы Унгарии и Фокеи
(расположенные соответственно при а ~ 1.9 а. е., г ~ 22° и а ~ 2.35 а. е.,
г ~ 24°), по-видимому, ограничены также резонансами д — д$ (v$) и s — sq
(^1б). Как будет детально показано ниже, причиной этого являются боль¬
шие вариации эксцентриситета либо наклонения, которые эти резонансы
могут вызывать, дестабилизируя со временем движение астероида; таким
образом, резонансы i/5, щ и v\§ создали в распределении астероидов протя¬
женные «люки». С другой стороны, из сравнения рис. 8.8 и рис. 26 видно,
что главный пояс пересечен несколькими вековыми резонансами более вы¬
сокого порядка, которые на распределение астероидов заметно не влияют.
Фактически рис. 8.8 напоминает рис. 6.7а с наброском структуры Нехоро¬
шева, где резонансы пересекают друг друга в резонансных узлах, но пол¬
ностью не перекрываются. Наличие такой структуры указывает на то, что
астероиды в нелинейных вековых резонансах, несмотря на возможную ха¬
отичность движения, должны быть «устойчивыми» на весьма длительных
временах. Милани и Кнежевич (1990, 1992, 1994) численно проинтегриро¬
вали на интервале в несколько миллионов лет эволюцию астероидов в этих
вековых резонансах и не обнаружили проявлений макроскопического дрей¬
фа в значениях их собственных элементов. Например, астероид 221 Эос,
находящийся в резонансе д -f- s — дв — sq, является родительским телом
одного из самых населенных семейств, несколько членов которого, вклю¬
чая Эос, ведут себя хаотически благодаря резонансу; однако это семейство
остается весьма компактным и легковыявляемым из-за отсутствия макро¬
скопической диффузии. Понятие «практической» устойчивости, появивше¬
еся благодаря теории Нехорошева, находит в семействе Эос яркое реальное
воплощение.
Расположение вековых резонансов в поясе Койпера численно опреде¬
лили Кнежевич и др. (1991), используя тот же подход, что и Милани и Кне¬
жевич в случае главного пояса астероидов (но Кнежевич и др. учли так¬
же возмущения в движении малых тел, вызываемые Ураном и Нептуном).
В случае пояса Койпера можно ожидать, что результаты будут надежными
в большем диапазоне наклонений, чем в случае главного пояса, посколь¬
ку резонанса Козаи никогда не бывает при малых эксцентриситетах, как
можно убедиться из рис. 8.2. На рис. 8.10 показано получающееся располо¬
жение линейных вековых резонансов. Аккумуляция перегелийных резонан¬
сов приблизительно при 36.5, 39.5 и 47.5 а. е. является артефактом особен¬
ностей вековой нормальной формы из-за присутствия резонансов средних
движений 3/4, 2/3 и 1/2 с Нептуном. Помимо этих сингулярных ситуаций,
8.4. Вековые резонансы
199
в поясе Койпера под сильным влиянием вековых резонансов находятся три
области: область 40-42 а. е. находится под влиянием резонанса д—д$ (также
называемого z/g), резонансов s — sj (vw) и s — sg (z^is); область при ~36 а. е.
пересечена резонансами д — дч (у7) и Уп\ а в области между 36.5 и 39.5 а. е.
два резонанса щ и У\% присутствуют при наклонениях от 10 до 15°. Во
внешней части пояса Койпера (дальше 42 а. е.) линейные вековые резонан¬
сы не проявляются: там у орбит малых тел прецессия медленнее, чем у ор¬
биты любой из внешних планет, и поэтому можно надеяться найти только
резонансы высоких порядков.
Расположение вековых резонансов в областях между планетами-
гигантами численно определили Кнежевич и др. (1991); соответствующие
графики можно найти в их статье.
8.4.1. Динамика в вековых резонансах
Динамику тел в вековых резонансах можно исследовать аналитиче¬
ски путем построения резонансной нормальной формы, следуя подходу,
описанному в разделе 2.3.1. Для этой цели наиболее уместным является
подход, основанный на приближении Козаи. В данном разделе мы сосре¬
доточим внимание на случае вековых резонансов первого порядка, то есть
вековых резонансов, чьи гармоники проявляются в возмущающем члене
первого порядка /С(х).
В качестве отправного возьмем гамильтониан (8.26), который в подхо¬
де Козаи можно записать как
Н = ^(g^pfc+S/eASfc) + /C(0)(Jb ^2) + £(1)(Л, (8.32)
к
где Ji, J2, -02 — переменные «действие-угол» для гамильтониана Козаи,
вводимые, как описано в разделе 8.2.3. Подчеркнем следующее: угол *02
«близок» к долготе узла h малого тела; угол ф\ «близок» к аргументу
перигелия д в случае, когда последний циркулирует; если же последний
либрирует в резонансе Козаи, то ф\ характеризует угловое положение от¬
носительно либрационного центра. Частоты углов фх и ^2 равны и>х =
= <9/C(0)/<9Ji и и)2 = <9/C(o)/<9J2 соответственно. Благодаря правилам Да¬
ламбера возмущение JC(x) должно раскладываться в ряд Фурье вида
£(1) = ^2 Kfc(Ji, J2) cos(lipi + Ф2- Ъ>1) +
к,1
+ dt,k(Ji,J2) cos(^i + ^2 - О*)] • (8.33)
200
Глава 8
Если аргумент перигелия циркулирует, то в выражении (8.33) коэффициен¬
ты cijс с четными I и коэффициенты d^k с нечетными I равны нулю. В этих
переменных гармоника, относящаяся к резонансу д — дк, суть cos(/0i + ^2 —
— tu£), а гармоника, относящаяся к резонансу s — Sk, суть cos(^2 — Щ)-
Чтобы зафиксировать обозначения, рассмотрим тело, близкое к оди¬
ночному резонансу с гармоникой cos(Z*^i + Ф2 ~ Случай, когда тело
близко к одиночному резонансу с гармоникой cos(Z*^i + ^2 — триви¬
ально аналогичен. Как показано в разделе 2.3.1, резонансная нормальная
форма первого порядка строится с использованием рядов Ли: новые пе¬
ременные J[, , J2, Ф21А'дк, A'Sk (называемые полусобственными) вводятся
преобразованием вида (2.6) с производящим гамильтонианом который
дается решением уравнения
£( 1) + {^(0),х} = J2)cos(J*V>i +Ф'2 - ™1.)- (8-34)
где нет знаменателей, близких к нулю, в силу предположения, что тело
не находится вблизи какого-либо резонанса, отличного от рассматриваемо¬
го. Отметим, что, поскольку производящий гамильтониан х не зависит от
A'gk,A'Sk, это преобразование не изменяет планетные углы и
В первом порядке (то есть в пренебрежении членами более высоких
порядков, вводимыми посредством рядов Ли) гамильтониан в новых пере¬
менных сводится к
Поскольку этот гамильтониан не зависит от ъок (к ф /с*) и Щ, сопряженные
действия являются константами движения. Далее, если отбросить постоян¬
ные члены J2kytk* Л'9к и ^Гк SkAfSk и ввести новые канонические перемен¬
ные
у-
8т[1ф[ +Ф'2~ ъ>*к] +
(8.35)
sin[ZVi + Ф’2 ~
H — Уу2/{дк^'дк +sfcA:jb)+ /C(0)(Ji, J2)+ 0;,^, (J(, J2) C0S(Z»^1 +1p'2 — ^k,)-
к
(8.36)
a = 1,ф[ +ф'2- с?*,,
8.4. Вековые резонансы
201
то гамильтониан принимает вид
Н = /С(о) (S, С) -9kmS + cim ^ (5, С) cos а, (8.38)
где отброшен также и постоянный член дк*&дк#. Гамильтониан (8.38) три¬
виально интегрируем, так как он зависит только от одного угла. Отметим,
что (8.38) имеет тот же вид, что и (4.2), то есть стандартный вид интегри¬
руемой нормальной формы одиночного резонанса. Угол а суть критический
угол рассматриваемого векового резонанса.
На данном этапе рецепт расчета резонансной эволюции тела концеп¬
туально прост. Прежде всего, из исходных переменных «действие-угол»
J = (Ji, J2), ф = (^ъ^г) тела вычисляем полусобственные переменные
«действие-угол» J' = (Ji,*/^), 'Ф' = ('Фхт'Фъ), итеративно решая неявные
уравнения J = J' + {Л'.Х^'.^О}» Ф = ф' + {Ф',х(3',Ф')} (где X за-
дано формулой (8.35)), аналогично тому, как это делается в случае урав¬
нений (8.31) для вычисления собственных переменных «действие-угол»
нерезонансных астероидов. Затем, используя (8.37), вычисляем значения
Sb,(Tb, Сь переменных 5, а и С тела. Они используются в качестве началь¬
ных условий для вычисления эволюции в соответствии с интегрируемым
гамильтонианом (8.38). Чтобы получить глобальную картину резонансной
динамики на плоскости 5, а (где тело эволюционирует), можно просто на
поверхности С — Сь построить кривые уровня (8.38). На этой диаграм¬
ме эволюция тела описывается кривой уровня, проходящей через точку
Sb,(Tb• В приложениях на практике часто предпочитают представлять ди¬
намику в переменных более наглядных, чем действия S и С. С этой це¬
лью для всех значений 5 и С, обращая (8.37), вычисляют полусобственные
действия Затем путем, аналогичным применявшемуся для нахожде¬
ния собственных эксцентриситета и наклонения из собственных действий,
определяют полусобственные эксцентриситет и наклонение. А именно, по¬
лагают, что действия J\ и Н в гамильтониане Козаи равны значениям по-
лусобственных действий отождествляя, таким образом, конкретный
цикл эксцентриситета и наклонения в функции аргумента перигелия д\ за¬
тем полусобственные эксцентриситет и наклонение можно определить как
значения е и г на цикле при д = 0. Разумеется, эволюция полусобственных
эксцентриситета и наклонения представляет собой всего лишь «скелет» ре¬
альной эволюции тела: е и г орбиты тела осциллируют относительно полу¬
собственных эксцентриситета и наклонения из-за влияния динамики Козаи
и всех нерезонансных членов в /C(i), которые были усреднены при постро¬
ении резонансной нормальной формы.
202
Глава 8
Хотя описанная процедура в принципе проста, ее трудно реализовать
технически. Накаи и Киношита (1985) и Иошикава (1987), которые первы¬
ми исследовали динамику в вековых резонансах v\§ и щ, ввели поэтому
ряд упрощений. Во-первых, вместо введения переменных Арнольда «дей¬
ствие-угол» для гамильтониана Козаи (как описано в разделе 8.2.3) они
просто осреднили /C(0)(G, Я, д) по аргументу перигелия д. В терминах дан¬
ного раздела это эквивалентно сведению преобразования (8.23) к тожде¬
ству J\ = G, что является приемлемой аппроксимацией только при малых
эксцентриситетах и наклонениях, когда циклы гамильтониана Козаи в по¬
лярных координатах G,g близки к окружностям. Во-вторых, они вычис¬
лили среднее от К,^ по всем нерезонансным гармоникам, не определяя
производящий гамильтониан х, и отождествили полусобственные действия
J[, J2 с Ji, J2, то есть с действиями Делоне G, Я. Данное приближение бы¬
ло мотивировано тем, что цель авторов состояла не в вычислении вековой
эволюции конкретных астероидов, а в исследовании общих динамических
свойств резонансов i/ie и В-третьих, Иошикава (1987) разложил веко¬
вую нормальную форму в степенной ряд по эксцентриситету и наклонению
астероида до четвертого порядка. Мы не будем останавливаться здесь на
результатах, полученных Накаи и Киношитой (1985) и Иошикавой (1987);
с ними можно непосредственно ознакомиться в оригинальных статьях. От¬
метим, что эти результаты имеют приемлемую точность только при малых
и умеренных эксцентриситетах и наклонениях. В некоторых случаях мо¬
гут возникать и качественные отличия от реальной динамики: например,
в теории Иошикавы при большом наклонении либрационный центр резо¬
нанса щ оказывается сдвинутым на 180° относительно истинного положе¬
ния (см. осуждение в работе Морбиделли и Анрара, 19916).
Аппроксимации, предложенные Накаи и Киношитой (1985) и Иоши¬
кавой (1987), хороши тем, что они демонстрируют общее свойство веко¬
вых резонансов, которое иначе не проявляется явно в формализме перемен¬
ных «действие-угол», рассмотренном в этом разделе. Отождествляя J[, J2
с G,tf, для перигелийных вековых резонансов вида д — дь — 0 (что соот¬
ветствует Z* = 1) из (8.37) получаем S = #nC = G — Я, а для узловых
резонансов вида s — Sk = 0 (что соответствует Z* = 0, с заменой vd\ на Щ)
получаем S = Н, С = G. С учетом того, что G —Я ~ г2, а большая полуось
и С — константы, это означает, что перигелийные резонансы сохраняют на¬
клонение постоянным и вызывают изменения эксцентриситета, а узловые
резонансы сохраняют е постоянным и вызывают эволюцию наклонения.
Разумеется, это имеет место, только если отождествление J[ = G, J2 = Н
8.4. Вековые резонансы
203
является хорошей аппроксимацией, то есть при малых эксцентриситетах
и наклонениях.
Рис. 8.11. Слева: динамический портрет векового резонанса v5, построенный для
значений полусобственных действий астероида 945 Барселона. Черной точкой ука¬
зано современное положение астероида; определение координат см. в тексте. Спра¬
ва: будущая (вверху) и прошлая (внизу) эволюция астероида согласно Шоллу и Фре-
шле (1990). Обсуждение см. в тексте. (Рис. 1 из статьи Морбиделли, 1993а; с разре¬
шения Academic Press)
Рассмотренный в данном разделе подход был предложен и применен
без каких-либо упрощений Морбиделли (1993а). На рис. 8.11 дан пример
астероида 945 Барселона в резонансе v$ (большая полуось равна 2.64 а. е.).
На левой панели показана глобальная картина динамики на поверхности
С = Съ, где Съ — значение С для Барселоны. Динамика показана в ко¬
ординатах х = espcos<T5, у = eSpSin<75, где esp — полу собственный экс¬
центриситет, а (Т5 — критический резонансный угол, а именно <75 = +
~Ь ^2 ~ ^5 (в обозначениях (8.37)). Черной точкой указано современное
положение Барселоны. Как видим, картина резонансной динамики весьма
схожа с фазовым портретом маятника в полярных координатах, показан¬
(945) Барселона
-0.4
-0.4
0 0.4
204
Глава 8
ным на рис. 4.16. В частности, имеется точка устойчивого равновесия при
(75 = 0, окруженная бананоподобными кривыми, представляющими либра¬
ции в полярных координатах. Согласно диаграмме и современному поло¬
жению Барселоны на ней, можно ожидать, что астероид либрирует около
<75 = 0, причем его полусобственный эксцентриситет изменяется в прибли¬
зительных пределах от 0.15 до 0.2. Поучительно сравнить этот теоретиче¬
ский прогноз с результатами численного интегрирования, например полу¬
ченными Шоллом и Фрешле (1990); их результаты приведены на двух па¬
нелях справа на рис. 8.11. Верхняя и нижняя панели представляют резуль¬
таты интегрирования вперед и назад по времени соответственно; в обоих
случаях интервал времени равен одному миллиону лет. Координаты суть
Ф/ = [2(1 — х/Г^)]1/2со8(ш — wj) rsj ecos(w — zuj) и Ф2; = [2(1 -
— у/1 — е2)]1/2 sin(zi7 — wj)~ esin(c7 — wj), где e, w, wj — оскулирующие
эксцентриситет и долгота перигелия астероида и долгота перигелия Юпи¬
тера соответственно. Данные численного интегрирования вперед и назад
представляют собой бананоподобные «полосы», которые, по существу, об¬
разованы «эпициклическим» движением, наложенным на почти полукру-
говую дугу эволюции. Эти «эпициклы» обусловлены прецессией аргумен¬
та перигелия д, то есть динамикой Козаи. Полусобственный эксцентриси¬
тет esp, используемый для представления движения в вековом резонансе на
левой панели, соответствует значению е при д = 0, то есть минимально¬
му значению эксцентриситета на каждом «эпицикле». Поэтому ожидаемую
эволюцию Барселоны на плоскости esp, <75 следует сопоставлять с внутрен¬
ним краем «полос», полученных в результате численного интегрирования
на плоскости Ф/, Ф2. Тогда мы видим, что результат интегрирования впе¬
ред и результат интегрирования назад — каждый соответствует примерно
половине либрационного цикла в резонансе z/5 и что Барселона пересекает
ось Ф2 = 0 при esp « 0.15 и esp ^ 0.2 в ходе интегрирования вперед и на¬
зад соответственно. Это очень хорошо согласуется с результатом, получен¬
ным путем вычисления нормальной формы векового резонанса. Отметим,
что по данным численного моделирования полная вариация оскулирующе-
го эксцентриситета составляет от 0.15 до 0.4, и в основном она обязана
динамике Козаи, а не резонансной динамике z/5. В реальности амплиту¬
да вариации эксцентриситета, вызываемой вековым резонансом 1/5, обычно
довольно мала (~ 0.05 в данном случае), так как для больших полуосей
в диапазоне, соответствующем поясу астероидов, мал коэффициент гармо¬
ники cos(/0/i+V?2~wt): он обращается в нуль и меняет знак при наклонении
~ 30°, что близко к положению резонанса г/5 (см. Морбиделли и Анрар,
8.4. Вековые резонансы
205
19916). Общий дефицит астероидов в резонансе 1/5, следовательно, в боль¬
шей степени обусловлен динамикой Козаи (ответственной за общий эффект
истощения пояса астероидов при высоких наклонениях благодаря накачке
эксцентриситета до значений, соответствующих пересечениям орбит пла¬
нет), а не самим резонансом ^5.
Рис. 8.12. Динамический портрет векового резонанса v\q внутри резонанса Ко¬
заи, построенный для значений полусобственных действий астероида 2335 Джеймс.
Черной точкой указано современное положение астероида; определение координат
см. в тексте. (Рис. 5 из статьи Морбиделли, 1993а; с разрешения Academic Press)
Пертурбационный подход, рассмотренный в данном разделе, при-
менйм также и к изучению динамики вековых резонансов внутри резо¬
нанса Козаи, то есть к орбитам с либрирующим аргументом перигелия. На
рис. 8.12 дан пример астероида 2335 Джеймс (а ~ 2.12 а. е.), находящего¬
ся в резонансе v\§ внутри резонанса Козаи. Динамика векового резонанса
представлена здесь в полярных координатах: радиальной координатой слу¬
жит полу собственное наклонение гзр, которое здесь определяется как ми¬
нимальное значение, принимаемое наклонением за либрационный цикл Ко¬
заи; оно соответствует одному из двух пересечений цикла с осью д = 90°;
206
Глава 8
угловой координатой служит критический угол резонанса z/ie, сдвинутый
на 180°, а именно оде = т/4 ~ Цз+тг (Ф^а тг добавлена здесь, чтобы aie был
близок к разности ft — ft j оскулирующих долгот узлов астероида и Юпи¬
тера; см. формулу (7.10) и таблицу 7.3). Черной точкой на рис. 8.12 указа¬
но современное положение астероида в этих координатах. Кривые уровня
нормальной формы векового резонанса (8.38) построены только в обла¬
сти либраций аргумента перигелия; при пересечении сепаратрисы Козаи
они обрезаются. Как видно из графика, астероид Джеймс либрирует около
<Ti6 = 0, при этом его полусобственное наклонение изменяется приблизи¬
тельно в пределах от 37° до 42°. Его либрационная кривая пересекает сепа¬
ратрису Козаи при гзр ~ 37°, = 0; так что астероид может выходить из
резонанса Козаи, при этом его аргумент перигелия начинает циркулировать.
Как видно из рис. 8.9, резонанс присутствует в поясе астероидов
также и вне резонанса Козаи. Там его амплитуда много больше, чем внутри
резонанса Козаи: как впервые было показано Накаи и Киношитой (1985),
она может превышать 15°. Кроме того, устойчивый либрационный центр
резонанса uiq находится при ctiq = 180°, то есть он сдвинут на 180° в срав¬
нении со случаем резонанса Козаи на рис. 8.12. Отсутствие астероидов
в области между группами Унгарии и Фокеи (см. рис. 2) можно объяснить
наличием резонанса vi6. Фактически астероиды в этой области испыты¬
вали бы осцилляции наклонений, достаточно большие по амплитуде, что
приводило бы к воздействию на них либо резонанса щ (при низких на¬
клонениях), либо резонансов и Козаи (при высоких наклонениях), и это
воздействие увеличивало бы их эксцентриситеты до значений, достаточных
по меньшей мере для пересечений с орбитой Марса.
Согласно результатам численного интегрирования (Фрешле и др.,
1991), на длительных шкалах времени астероид 2335 Джеймс демонстриру¬
ет замечательное хаотическое поведение. Попеременно он то входит в ре¬
зонанс Козаи, то покидает его. Когда он вне резонанса Козаи, он одновре¬
менно находится в двух вековых резонансах v§ и z/ig, причем ctiq либри¬
рует около 180°; когда же он внутри резонанса Козаи, он вне резонанса v$
(напомним, что этот резонанс невозможен для орбит с либрирующим ар¬
гументом перигелия), но продолжает быть внутри резонанса причем
сг1б либрирует около 0°. Прохождения через сепаратрису Козаи спорадиче¬
ски вызываются сильными осцилляциями наклонения из-за резонанса v\§.
Любопытно, что астероид, солирующий в этом танце в вековых резонан¬
сах, назван в честь Джеймса Уильямса — пионера-исследователя вековой
динамики астероидов.
8.4. Вековые резонансы
207
Описанную в данном разделе пертурбационную схему использовал
также Мишель (1997) для изучения динамики в вековых резонансах с часто¬
тами планет земной группы во внутренней Солнечной системе (а < 2 а. е.).
Поскольку резонансы v3 и 1/4 (так же как и резонансы 1/13 и ^14) могут пе¬
рекрываться, нормальную форму вековых резонансов Мишель вычислил,
удержав в ней гармоники, относящиеся к обоим резонансам. Затем, чтобы
оценить протяженность хаотической зоны, он построил сечение Пуанкаре
результирующего неинтегрируемого гамильтониана. Он выяснил, что пери-
гелийные резонансы могут легко трансформировать орбиты тел из исход¬
но круговых в пересекающиеся с орбитами больших планет, и наоборот,
а узловые резонансы могут вызывать изменения до 10° в наклонении. Оба
эти явления важны для понимания эволюции и современного орбитального
распределения астероидов, сближающихся с Землей.
Что касается пояса Койпера, амплитуды вековых резонансов v7, v$, V17
и i/i8 были вычислены Морбиделли и др. (1995а) в упрощенных моделях,
аналогичных моделям Иошикавы и Накаи и Киношиты. Их результаты со¬
гласуются с результатами расчетов эволюции и показывают, что тела на
исходно плоских и круговых орбитах с большими полуосями 35-36 а. е.
и 40-42 а. е. вынуждаются пересекать орбиту Нептуна на временной шкале
~ 107 лет. Такое поведение впервые обнаружили Хольман и Уиздом (1993)
путем численного интегрирования.
8.4.2. Аномальный случай резонанса uq
Обсудим теперь отдельно резонанс vq, который благодаря своим ди¬
намическим свойствам является важнейшим вековым резонансом в поясе
астероидов.
Начиная с работы Фрешле и Шолла (1986) численное моделирование
движения реальных и модельных астероидов показало, что резонанс
в отличие от всех других перигелийных резонансов, способен «накачивать»
эксцентриситеты резонансных тел до значений, превышающих ~ 0.8. Фа-
ринелла и др. (1994) впервые показали, что у некоторых тел в резонансе uq
эксцентриситет увеличивается до единицы. В таких случаях перигелийное
расстояние уменьшается до нуля, так что астероиды падают на Солнце. На
рис. 8.13 показан пример такого феномена; интересно, что эксцентриситет
тела увеличивается от 0 до 1 очевидно регулярным образом на шкале време¬
ни порядка 1 млн лет. Благодаря большим эксцентриситетам, достигаемым
в резонансе щ, тела начинают пересекать орбиты планет либо становятся
208
Глава 8
сангрейзерами. Это объясняет, почему положение резонанса соответствует
области, почти полностью свободной от астероидов.
360°
270°
180°
90°
0°
0.8
0.6
0.4
0.2
0 в « '
-Ю6 0 106 2 х 106
время, в годах
Рис. 8.13. Эволюция астероида 1992 SZ в резонансе щ по результатам численного
интегрирования полных уравнений движения. (Рис. 1 из статьи Фаринеллы и др.,
1994; с разрешения Nature, Macmillan Magazines Limited)
Резонанс щ столь сильно влияет на эксцентриситет из-за своей
необычной динамической структуры, которая отличается от типичных ма¬
ятниковых моделей (4.4), справедливых для большинства других резо¬
нансов.
Причину этого различия можно понять на качественном уровне из вида
графика на верхней панели рис. 8.14, где показаны положения резонанса щ
на плоскости (а, е) при различных наклонениях; впервые эти положения
рассчитали Уильямс и Фолкнер (1981). Бросается в глаза, что по крайней
мере во внутренней части пояса астероидов (а < 2.5 а. е.) положение ре¬
зонанса щ описывается почти вертикальными линиями; при этом для за¬
данных значений наклонения и большой полуоси резонанс имеет место
при всех значениях эксцентриситета. Такая ситуация совершенно необыч¬
на; для сравнения на нижней панели рис. 8.14 показан аналогичный график
1992 SZ
и—1—■—■—■—
U) — LJS
■r;jf;if**w.:- •'
J.r • I
1 1 f\
эксцентриситет : i
8.4. Вековые резонансы
209
а, а. е.
а, а. е.
Рис. 8.14. Вверху: кривые положений резонанса vq по собственным большой по¬
луоси и эксцентриситету, маркированные соответствующими им значениями соб¬
ственного наклонения. Внизу: то же, но для резонанса г/5. Сплошными кривыми
показаны результаты первых расчетов Уильямса и Фолкнера (1981). Прерывистые
кривые построены с использованием более точных значений планетных собствен¬
ных частот дв и д$. (Рис. 5 и 6 из статьи Морбиделли и Анрара, 1991а; с разрешения
Kluwer Academic Publishers)
210
Глава 8
для резонанса z/5. Напомним, что перигелийные вековые резонансы нака¬
чивают эксцентриситет, сохраняя наклонение приблизительно постоянным;
поэтому тело, эволюционирующее в резонансе uq и чей эксцентриситет из-
за воздействия резонанса растет, никогда не покинет точного резонансного
положения, так что эксцентриситет может расти неограниченно.
С математической точки зрения эта ситуация является следствием по¬
тери свойства выпуклости резонансной нормальной формой гамильтониа¬
на (8.38). В главе 6 мы уже обсуждали в контексте теории Нехорошева роль
этого свойства для ограничения резонансных движений. Говоря конкретно,
невыпуклая резонансная нормальная форма — это гамильтониан вида (4.2)
такой, что коэффициент (3 в его локальном разложении (4.3) равен нулю.
Это означает, что частота резонансного угла равна нулю при любом значе¬
нии сопряженного ему действия (соответственно ipi и Д в (4.3)). Это как
раз и происходит в случае резонанса щ, где (при соответствующих значе¬
ниях большой полуоси и наклонения) частота резонансного угла +
+ -02 — Равна нулю при любом эксцентриситете, то есть при любом со¬
пряженном действии 5, о чем говорят вертикальные линии на верхней па¬
нели рис. 8.14. Поскольку (3 = 0, в аппроксимации, задаваемой локальным
разложением (4.3), действие Д может уйти на бесконечность для большин¬
ства начальных условий (что легко видеть из построения кривых уровня
гамильтониана (4.4)). Однако если Д увеличивается слишком сильно, то
локальное разложение (4.3) перестает быть хорошей аппроксимацией для
реального движения, что критически зависит от функционального вида Но
и коэффициента резонансной гармоники в полной нормальной форме (4.2)
при больших Д. Другими словами, у невыпуклых резонансных нормальных
форм нет единого общего динамического портрета в отличие от выпуклых
нормальных форм, которые все описывают маятникоподобное движение.
Поэтому первые требуют изучения в каждом отдельном случае.
На рис. 8.15 дан пример динамической структуры резонанса v§. На че¬
тырех панелях показаны кривые уровня нормальной формы векового резо¬
нанса (8.38) для различных значений константы движения С. Координаты
х = espcoscT6, у = espsincT6 аналогичны использованным на рис. 8.11 для
резонанса Графики ограничены областью esp ^ 0.65 из-за технических
трудностей точного расчета нормальной формы векового резонанса при
больших значениях полусобственного эксцентриситета. Панель (б) постро¬
ена для значения С, соответствующего фиктивному астероиду со средними
элементами орбиты а = 2.3488 а. е, е = 0.1802, г = 15.105°, и = 242.81°,
= 138.750°. Черной точкой указано его современное положение в коор-
8.4. Вековые резонансы
211
'-0.6-0.4-0.2 0.0 0.2 0.4 0.6 '-0.6-0.4-0.2 0.0 0.2 0.4 0.6
X X
Рис. 8.15. Динамические портреты резонанса щ при а ~ 2.35 а. е. и различных
наклонениях. См. объяснение в тексте. (Рис. 12 из статьи Морбиделли, 1993а; с раз¬
решения Academic Press)
динатах х,у. Из вида кривых уровня можно ожидать, что полусобствен-
ный эксцентриситет этого астероида будет осциллировать приблизительно
между 0 и 0.5, а его резонансный угол <Тб — около 180°. Этот прогноз
поведения подтверждается численным моделированием с использованием
полных уравнений движения (см. Морбиделли, 1993а). Из графика следует
присутствие точки неустойчивого равновесия (при х ~ —0.6, у = 0) и се¬
паратрисы, окружающей замкнутые циклы с центром в точке устойчивого
равновесия (при х ~ —0.27, у = 0). Снаружи сепаратрисы кривые уровня
разомкнуты: любое начальное условие в этой области приводит к полу-
собственному эксцентриситету, превышающему 0.65. Судя по виду кривых
212
Глава 8
уровня, логично ожидать, что эксцентриситет может увеличиваться и до
значений много больше 0.65, достигая, возможно, порога е — 1. Эволюция
эксцентриситета, показанная на рис. 8.13, соответствует диаграмме типа
рис. 8.156 для тела, которое вначале эволюционирует на замкнутом цикле
вблизи сепаратрисы (так что его эксцентриситет достигает первого мак¬
симального значения ~ 0.4), а затем пересекает сепаратрису, переходя на
разомкнутую кривую уровня, так что его эксцентриситет сначала уменьша¬
ется до нуля, а затем увеличивается до единицы. Поведение резонансного
угла (см. верхнюю панель рис. 8.13) подтверждает эту интерпретацию4. Не
следует удивляться тому, что тело переходит от одной кривой уровня к дру¬
гой, пересекая сепаратрису. Напомним (см. главу 4), что нормальная форма
одиночного резонанса, так как она интегрируема, имеет хорошо определен¬
ную сепаратрису; но остаток нормальной формы в общем случае разрушает
интегрируемость и расщепляет сепаратрису, создавая таким образом узкую
хаотическую зону. Орбита в этой хаотической зоне не следуют в точно¬
сти кривой уровня резонансной нормальной формы и может переходить из
области колебаний в область циркуляций и наоборот.
Рис. 8.15в построен для значения С, соответствующего тому же асте¬
роиду, что и на панели (6), но с наклонением, увеличенным до 15.6°. Точки
устойчивого и неустойчивого равновесий, характерные для динамики на
панели (б), здесь исчезли, и все кривые уровня разомкнуты. Это означает,
что, независимо от выбора начальных условий на этой панели, эксцентри¬
ситет накачивается резонансом до значений много больше 0.65. Наконец,
панели (а) и (г) демонстрируют резонансные портреты для значений С,
отвечающих наклонениям орбиты астероида г = 14.1° и г = 17.1°, при
которых астероид находится соответственно существенно ниже/выше точ¬
ного положения векового резонанса. Для динамики здесь характерно на¬
личие только одной точки устойчивого равновесия, смещенной от центра
диаграммы х = 0, у = 0. Все орбиты следуют циклам вокруг устойчивого
равновесия, при этом полусобственный эксцентриситет осциллирует, пери¬
одически принимая минимальное и максимальное значения. На большин¬
стве циклов резонансный угол циркулирует, принимая значения на всем
интервале [0°, 360°]; причем на панели (а) его производная по времени по¬
ложительна, а на панели (г) — отрицательна: для орбит ниже/выше резонан-
43аметим, что на рис. 8.13 показан угол ш — tus вместо ctq, где z&s — долгота перигелия
Сатурна. Угол vo — tus сильно осциллирует около сгб на временной шкале ~ 5 х 104 лет, так
как = vJq + где / — функция от всех планетных вековых перигелийных частот
(см. формулу 7.10). — Прим. авт.
8.4. Вековые резонансы
213
X X
Рис. 8.16. Слева: динамический портрет резонанса и6 для тела с теми же элемен¬
тами орбиты, что и у астероида 6 Гебы, кроме наклонения, увеличенного до 18.7°.
Координаты по осям: х = espcos<T6, у — espsincr6. Черной точкой указано со¬
временное положение тела. Справа: эволюция того же тела, полученная численным
интегрированием полных уравнений движения. Координаты по осям: х = ecos(t*7 —
— Тл7е), у — esin(zx7 — тд7в), гДе е и w — оскулирующие эксцентриситет и долгота
перигелия тела. (Рис. 11 из статьи Морбиделли, 1993а; с разрешения Academic Press)
са щ частота долготы перигелия астероида соответственно больше/меньше
планетной вековой частоты gQ. Если наклонение астероида уменьшать ни¬
же значения, отвечающего панели (а), или же увеличивать выше значения,
отвечающего панели (г), то есть в обоих случаях смещать дальше от резо¬
нанса, то динамические портреты существенно не изменятся по сравнению
с показанными на этих панелях. Всегда будет присутствовать точка устой¬
чивого равновесия, немного смещенная от е = 0. В этом легко убедиться,
если принять во внимание в линейных уравнениях движения (8.6) только
возмущающие члены с к = 6.
Диаграммы на рис. 8.15 нельзя считать типичными для резонанса vq
при любых значениях большой полуоси. Благодаря невыпукл ости нормаль¬
ной формы фазовый портрет резонанса может критически зависеть от боль¬
шой полуоси. В качестве примера на рис. 8.16 показаны кривые уровня
нормальной формы векового резонанса для астероида со средними элемен¬
тами а = 2.43, е = 0.20, i = 18.7°, и = 239°, Г2 = 139°. Как видим,
эта диаграмма сильно отличается от любой на рис. 8.15. Это не является
артефактом вычисления нормальной формы векового резонанса. Фактиче¬
ски на правой панели рис. 8.16 показана эволюция астероида, полученная
214
Глава 8
в осциллирующих координатах путем численного интегрирования полных
уравнений движения, и эта эволюция хорошо соответствует кривой уровня,
проходящей через современное положение тела в полусобственных коорди¬
натах. Как уже обсуждалось выше на примере астероида Барселона, кривая
уровня нормальной формы векового резонанса вычерчивает лишь «скелет»
реальной вековой динамики: эволюция в оскулирующих координатах ко¬
леблется около ведущей кривой уровня благодаря присутствию всех тех
нерезонансных гармоник, которые были усреднены при построении нор¬
мальной формы векового резонанса.
Глава 9
Резонансы средних движений
9.1. Простое интегрируемое приближение
Эта глава — первая из посвященных резонансам средних движений. Ре¬
зонансы средних движений составляют один из наиболее сложных аспектов
динамики Солнечной системы. Они отличаются от стандартных резонан¬
сов, описанных в главе 4, поскольку динамика Солнечной системы является
вырожденной, то есть она характеризуется наличием как быстрых угловых
переменных, связанных с орбитальными движениями тел, так и медленных,
обусловленных прецессионными движениями их орбит. В анализе вековой
динамики в главах 7 и 8 вырождение устранялось осреднением по всем
быстрым углам. В случае резонансов средних движений такое осреднение
согласно разделу 2.5 невозможно из-за наличия резонансной связи. Поэто¬
му нам придется в полной мере бороться с вырождением.
В этой главе мы изучаем структуру резонансов средних движений двух
тел. Мы сосредоточимся на случае резонанса астероида с планетой, потому
что двухтельных резонансов планеты с планетой в Солнечной системе не
выявлено. В следующей главе мы исследуем резонансы средних движений
нескольких тел, а в главе 11, в завершение темы, изучим вековую динамику
внутри резонансов средних движений низкого порядка.
Резонанс средних движений (часто называемый также соизмеримо¬
стью) между астероидом и J-ой планетой имеет место, если кп — ~ О,
где к и kj — положительные целые числа, щ — среднее движение J-ой
планеты, п = 1/А3 — среднее движение астероида. Отправным пунктом
для изучения резонанса средних движений служит нормальная форма, рас¬
смотренная в разделе 2.5.2. Нормальная форма гамильтониана резонанса
средних движений имеет вид
'Ншмк = W0(A, Aj) +eWi(A, P,Q,p,q, %Aj - kX(9.1)
216
Глава 9
В сравнении с (2.45) для упрощения записи здесь члены нормальной фор¬
мы высоких порядков по е включены в eHi, а также при записи пропуще¬
ны все верхние индексы, обозначающие, что появляющиеся в нормальной
форме переменные являются полусредними модифицированными перемен¬
ными Делоне. С другой стороны, мы подчеркнули, что нормальная форма
гамильтониана зависит от средних эксцентриситетов, перигелиев, наклоне¬
ний и узлов всех планет с j = 1,..., N). В сравнении с ве¬
ковой нормальной формой (8.1) Wmmr зависит также от средних долгот
астероида и J-ой планеты (A, Aj), так что А и Aj не являются постоянными
и главный член
Wo (Л, Aj) = —^д2 пз^з (9-2)
отбросить нельзя.
Чтобы исследовать динамику (9.1), разложим Hi в ряд по степеням
планетных эксцентриситетов и наклонений, как в разделе 8.2, и рассмот¬
рим пока только ведущий член НJ этого разложения, не зависящий от ej
и ij. Согласно правилам Даламбера (см. раздел 1.9.3), его фурье-разложение
имеет вид
Hi = ^2 cm,s,r (А, Р, Q) exp [t(m(kjXj - кХ) + sp + rq)], (9.3)
m,s,r
где га, г, s — целые числа, такие, что m(kj — к) — s — г = 0. Гамильтониан
Но + еН\ неинтегрируем, поскольку (9.3) содержит две независимые ком¬
бинации разных углов в противоположность тому, что имело место в ве¬
ковой задаче (где к = Щ = 0). Отметим, однако, что правила Даламбера
также подразумевают, что при малых наклонениях i астероида коэффици¬
енты cmjS?r пропорциональны Qr/2, где Q ~ г2/2. Поэтому если мы огра¬
ничимся плоским случаем г = 0, то гармоники с г ф 0 в (9.3) будут иметь
нулевые коэффициенты, так что гамильтониан Но + sH\ будет интегрируем
как зависящий только от угла kjXj — кХ + (kj — к)р и его кратных. Поэтому
рассмотрим гамильтониан
Wpc = Wo (A, Aj) + eW?(A, P, ЩXj — kX + (kj - k)p\ Q = 0) (9.4)
в качестве интегрируемой аппроксимации резонансной нормальной фор¬
мы (9.1). Заметим, что Wpc фактически суть гамильтониан резонанса сред¬
них движений в нормальной форме в рамках так называемой плоской круго¬
вой ограниченной задачи, в которой предполагается, что астероид и планеты
9.1. Простое интегрируемое приближение
217
движутся в одной плоскости и орбиты планет круговые. Плоская круговая
ограниченная задача, как мы убедимся в этой и последующих главах, — до¬
вольно грубое приближение реальной динамики, однако она является под¬
ходящим интегрируемым приближением для развития пертурбационного
анализа реальной динамики в резонансах средних движений.
Правила Даламбера также гарантируют, что при малом эксцентрисите¬
те е астероида коэффициент ведущей гармоники exp t[kjXj - кХ + (Щ - к)р]
пропорционален Рпричем Р ~ е2/2. Поэтому резонансы средних
движений вида кп — Щщ — 0 имеют ведущие гармоники, чьи коэффициен¬
ты экспоненциально убывают с \kj — к\. По этой причине астрономы назы¬
вают \Щ — к | порядком резонанса. Его не следует путать с порядком гармо¬
ники в определении, принятом в математике (он связан с общим убыванием
коэффициентов в рядах Фурье) и которого мы придерживаемся и в нашей
книге. Последний в данном случае был бы равен к + Щ. Чтобы устранить
двусмысленность, в дальнейшем мы будем называть величину \kj — к\ по¬
рядком резонанса по эксцентриситету. В действительности и астрономи¬
ческое и математическое определения оба правильны в своей мотивации,
поскольку коэффициенты ведущих гармоник резонансов средних движений
убывают пропорционально exp (—\kj — к|) ехр [—(к + kj)}.
Чтобы исследовать динамику гамильтониана (9.4), а затем и его воз¬
мущение (9.1), прежде всего введем следующий набор канонических пере¬
менных «действие-угол»:
Используя критерий «скобок Пуассона» (см. раздел 1.6), легко проверить,
что данное преобразование является каноническим. Угол <т называется кри¬
тическим углом резонанса средних движений. Глубокая причина, по кото¬
рой мы не определяем а просто как kj Xj — k\ + {kj — k)p, состоит в том,
что коэффициенты резонансных гармоник expim[kj\j-k\-\-{kj — k)p\ при
малых S пропорциональны 5,ТП1%-М/2 ~ еш\кэ-к\. Если а определяется как
5 = Р,
а =
kjXj — к\ + (kj — к)р
kj — к
N=klkA + p +
к
-к-\--и ь\
kjXj — кХ 4- (kj — k)q
kj — к
(9.5)
SZ = Q,
218
Глава 9
в (9.5), то резонансные гармоники суть exp t[m(kj—к)а]. Как следствие, га¬
мильтониан обладает свойством, аналогичным задаваемому четвертым пра¬
вилом Даламбера (см. раздел 1.9.3). Это свойство позволяет ввести канони¬
ческие декартовы переменные х = у/2~S sin <т, у = y/2S cos а, чтобы устра¬
нить особенность при S = е = 0. К тому же гамильтониан периодичен по
а с периодом 2n/\kj — к\.
3.0 3.2 3.4 3.6 47 48 49
а, а. е. а, а. е.
Рис. 9.1. Кривые уровня N согласно формулам (9.5) для резонанса 2/1 с Юпитером
(панель (а)) и для резонанса 1/2 с Нептуном (панель (б)). Значения N возрастают
слева направо на панели (а) и справа налево на панели (б). Вертикальными преры¬
вистыми линиями отмечены невозмущенные положения этих резонансов.
Отметим, что преобразование (9.5) сингулярно при Щ = к, то есть
в случае резонанса 1:1, имеющего место, когда астероиды находятся на од¬
ной орбите с планетой (подобно астероидам-троянцам). Поэтому для ана¬
лиза резонанса 1:1 требуется специальный формализм, который мы рас¬
смотрим в разделе 9.1.2.
В новых переменных гамильтониан (9.4) принимает вид
WpC = Wo(Aj, N, S, Sz) + eW?(S, (% - k)er, N, Sz), (9.6)
где согласно (9.2)
(kj-k)2 Га к-3
T-fn = - 1-77- A -
0 2 k2{N-S-Sz)2 J
(9.7)
Тогда очевидно, что Aj, N и Sz — константы движения для Нрс- Таким
образом, в (9.6) член щAj можно отбросить. Напомним, что Sz (то есть Q)
9.1. Простое интегрируемое приближение
219
был положен равным нулю, чтобы получить гамильтониан плоской зада¬
чи; так что интересующая нас часть динамики касается только перемен¬
ных S и <т и параметрически зависит от значения N. Поэтому динамиче¬
скую структуру резонанса можно представлять, строя кривые уровня га¬
мильтониана (9.6) на плоскости 5, сг для различных значений N.
Здесь полезно иметь в виду соотношение между действиями S, N и ор¬
битальными элементами а, е. Соотношение N = const определяет кривую
на плоскости «большая полуось - эксцентриситет». На рис. 9.1 такие кри¬
вые показаны для случая внутренних резонансов (kj > к; левая панель)
и для случая внешних резонансов (kj < к; правая панель). Поэтому движе¬
ние S на кривой N = const производит связанные колебания а и е. В невоз¬
мущенной задаче (е = 0) точный резонанс имеет место при значениях S
таких, что сг = дНо/dS = 0, а именно при
На рис. 9.1 невозмущенное положение резонанса отмечено вертикальной
прерывистой линией.
Динамический портрет резонанса средних движения первого порядка
по эксцентриситету (\kj — к\ = 1) давно известен из вычислений (Пуан¬
каре, 1902а, 19026; Мэсседж, 1966; Шубарт, 1964, 1968; Анрар и Леметр,
1983). На рис. 9.2 показано, как типичный динамический портрет резонан¬
са с Щ = к + 1 изменяется в зависимости от N. Если N достаточно мало, то
соответствующая ему кривая N = const на рис. 9.1 не пересекает линию,
которой отмечено невозмущенное положение резонанса. Результирующая
динамика на плоскости S, сг (рис. 9.2) имеет только одну точку устойчивого
равновесия при о — 0 вблизи начала координат S = 0 (расстояние от центра
уменьшается с А); никаких точек неустойчивого равновесия и сепаратрис
не наблюдается (верхние панели). Ситуация меняется, когда N становится
равным пороговому значению 7V* (средняя панель слева). Одна из кривых
уровня имеет угловую точку при сг = 7г; поскольку динамика регулярна
(в уравнениях движения нет особенностей), эта угловая точка должна быть
точкой неустойчивого равновесия, а кривая уровня, проходящая через эту
точку, суть сепаратриса, соединяющая точку неустойчивого равновесия са¬
му с собой (см. главу 4). При N > N* динамический портрет снова меня¬
ется (средняя панель справа). Появляется третья точка равновесия, также
при сг = 7г, но теперь она устойчивая, а сепаратриса, исходящая из этой
S = N —
то есть
(9.8)
220
Глава 9
Рис. 9.2. Фазовые портреты внутреннего резонанса первого порядка по эксцентри¬
ситету для различных значений N. Координаты по горизонтальной и вертикальной
осям суть у/2~S cos а ~ е cos <т и у/2~S sin а ~ е sin <т соответственно. Комментарии
см. в тексте. (Рис. 6 и 7 из статьи Анрара и Леметр, 1983; с разрешения Kluwer
Academic Publishers)
9.1. Простое интегрируемое приближение
221
Рис. 9.3. Отличие резонансных областей от областей либраций в случае резонансов
первого порядка по эксцентриситету для двух значений N. Заштрихованы чисто
резонансные области на верхних панелях, а также резонансные и нерезонансные
области либраций на нижних. Определения областей см. в тексте. (Рис. 2 и 3 из
статьи Анрара и Леметр, 1983; с разрешения Kluwer Academic Publishers)
неустойчивой точки, имеет две петли. Это типичный портрет резонанса
в случае, когда переменные «действие-угол» используются как полярные
координаты (см. рис. 4.1). С увеличением N выше порогового значения N.*
устойчивое равновесие при а = 0 и неустойчивое равновесие смещаются
к большим 5, а устойчивое равновесие при а = п приближается к центру
S = 0 (нижние панели). Как объяснено в разделе 4.1, причина, по кото¬
рой начало координат S = 0 никогда не бывает точкой равновесия, состоит
в том, что коэффициент ведущей резонансной гармоники exp ta пропорци¬
онален y/S. Благодаря этому специфическому свойству в случае резонансов
первого порядка по эксцентриситету необходимо проводить различие меж¬
ду резонансной областью и областями либраций. Как эскизно показано на
рис. 9.3, резонансной областью, по существу, является область, охватыва¬
емая сепаратрисами, окружающими устойчивое равновесие при а — 0 (на
верхних панелях она заштрихована). Когда сепаратрис нет (как на верхних
222
Глава 9
панелях рис. 9.2), не существует и резонансной области. Области либраций
суть множества орбит, на которых а либрирует либо около 0, либо около 7г
(заштрихованные области на нижних панелях). Как видим, в некоторых
случаях у резонансных орбит а может циркулировать, тогда как орбиты
с либрирующими а могут быть нерезонансными. В таких случаях геомет¬
рическое понятие либрации фактически не имеет реального динамического
СМЫСЛа. ИсТОрИЧеСКИ СЛОЖИЛОСЬ, ЧТО ОрбиТЫ С СГ, ЛИбрИруЮЩИМИ ОКОЛО 7Г,
называют апоцентрическими либраторами, поскольку устойчивое равно¬
весие при а = 7г соответствует периодической орбите, двигаясь по которой
астероид попадает в афелий всякий раз, когда он входит в соединение с ре¬
зонансной планетой (р = А + 7г, когда А = Aj). Несмотря на их либраци-
онный характер, эти орбиты динамически эквивалентны циркулирующим
орбитам маятника.
ecoscr
Рис. 9.4. Фазовый портрет резонанса 1:2 с Нептуном, демонстрирующий острова
асимметричной либрации. Жирными линиями показаны сепаратрисы, исходящие
из точек неустойчивого равновесия при а = 0 и а = 7Г. (По данным Томаса, 1998;
адаптировано)
9.1. Простое интегрируемое приближение
223
Динамический портрет внешних резонансов первого порядка по экс¬
центриситету (к = kj + 1) эквивалентен представленному на рис. 9.2, но
с сг, сдвинутым на 180°. Единственное исключение — резонанс 1/2 (/с = 2,
kj = 1). В его случае, при N больше некоторого порогового значения, внут¬
ри резонансной области точка равновесия при сг = 7г становится неустойчи¬
вой и появляются две новые точки устойчивого равновесия, расположенные
симметрично относительно горизонтальной оси (рис. 9.4). Сепаратриса, со¬
единяющая точку неустойчивого равновесия при сг = п саму с собой, окру¬
жает эти две точки устойчивого равновесия. Как следствие, в резонансной
области следует проводить различие между симметричными и асиммет¬
ричными либраторами: симметричные либраторы — это орбиты с а, либ-
рирующими около 7г в области, охватываемой сепаратрисой, исходящей из
точки неустойчивого равновесия при и = 0; а у асимметричных либрато-
ров сг либрирует около некоторого иного значения, и находятся они на двух
островах, охватываемых сепаратрисой, исходящей из точки неустойчивого
равновесия при а = п. Причина появления областей асимметричных либ¬
раций следующая. Из-за специфических значений коэффициентов с\ и С2
в месте расположения резонанса 1/2, гармоника C2Sexpt2a в возмуще¬
нии Hi начинает преобладать над «ведущей» гармоникой с\ yfS exp ш, ко¬
гда 5 достаточно велико. Согласно рис. 9.1, в месте расположения резонан¬
са значение 5 увеличивается с N\ как следствие, асимметричные либрации
должны возникать, когда N достаточно велико. Существование асиммет¬
ричных либраций впервые отметил Мэсседж (1958), затем их исследовали
Шубарт (1964) и Боже (1994); детали см. в их работах.
Динамические портреты резонансов, имеющих порядки по эксцентри¬
ситету выше первого, построены Леметр (1984). На рис. 9.5 дан портрет
внутренних резонансов второго порядка по эксцентриситету (Щ = к + 2).
При N меньше некоторого порогового значения начало координат 5 = 0
является точкой устойчивого равновесия, около которой циркулируют все
остальные орбиты (см. верхние панели). Если увеличивать N, то возника¬
ет первая бифуркация, при которой центр 5 = 0 становится неустойчивым
и появляются два устойчивых равновесия при 90° и 270° (см. средние пане¬
ли). Сепаратриса, соединяющая начало координат само с собой, окружает
эти устойчивые равновесия, охватывая две резонансные области, где а либ¬
рирует. При N больше второго порогового значения динамический портрет
меняется вновь. Центр 5 = 0 теперь устойчив, тогда как при а = 0,7г име¬
ются два неустойчивых равновесия. Сепаратриса теперь исходит из этих
точек равновесия, а резонансными областями по-прежнему являются обла-
224
Глава 9
Рис. 9.5. Фазовые портреты резонанса второго порядка по эксцентриситету для
различных значений N. Координаты по горизонтальной и вертикальной осям суть
л/25 cos а ~ ecos о и л/25 sin а ~ е sin а соответственно. Комментарии см. в тек¬
сте. (Рис. 1 из статьи Леметр, 1984; с разрешения Kluwer Academic Publishers)
9.1. Простое интегрируемое приближение
225
(
1 (С^л\
Г 1 \.ч5гг
г
i
I
1
}
Рис. 9.6. Фазовые портреты внешнего резонанса третьего порядка по эксцентриси¬
тету для различных значений N. Координаты по горизонтальной и вертикальной
осям суть л/25 cos а ~ ecoscr и л/25 sin а ~ esincr соответственно. Коммента¬
рии см. в тексте. (Рис. 4 из статьи Леметр, 1984; с разрешения Kluwer Academic
Publishers)
226
Глава 9
Рис. 9.7. Фазовые портреты резонанса четвертого порядка по эксцентриситету для
различных значений N. Координаты по горизонтальной и вертикальной осям суть
л/25 cos о ~ е cos сг и >/25 sin сг ~ е sin сг соответственно. Комментарии см. в тек¬
сте. (Рис. 7 из статьи Леметр, 1984; с разрешения Kluwer Academic Publishers)
сти, где орбиты либрируют около 90° или 270°. Внешние резонансы имеют
точно такой же динамический портрет, за исключением резонанса 1/3, для
которого равновесия при 90° и 270° становятся неустойчивыми, если N
превышает некоторое пороговое значение, причем появляются два новых
устойчивых равновесия, расположенных симметрично относительно вер¬
тикальной оси, внутри каждой резонансной области (см. Боже, 1994). Как
и в случае резонанса 1/2, асимметричными либраторами мы называем ор¬
биты, либрирующие около одного из этих устойчивых равновесий.
На рис. 9.6 дан портрет внешних резонансов третьего порядка по экс¬
центриситету (к = kj + 3), за исключением резонанса 1/4, у которого опять
же имеются асимметричные либрации. Динамический портрет внутренних
резонансов третьего порядка по эксцентриситету такой же, как на рис. 9.6,
но с сг, сдвинутым на 180°.
Наконец, на рис. 9.7 показан динамический портрет резонансов четвер¬
того порядка по эксцентриситету. Внутренние и внешние резонансы имеют
один и тот же портрет, за исключением резонанса 1/5, у которого имеются
асимметричные либраторы.
9.1.1. «Фазовая защита» от столкновений с планетами
В предыдущем разделе мы убедились, что во внутренних резонансах
неустойчивые равновесия расположены при сг = <тт = 7г[1 + 2mkj/(kj —
9.1. Простое интегрируемое приближение
227
— к)], где т — целое число в диапазоне [0,/cj — к). Заметим, что если
с7 = <тт, то р = А + тг всякий раз, когда Xj = А + 2гтт. Другими словами,
в неустойчивых равновесиях, если астероид находится в афелии, он при
этом находится и в одном из Щ — к различных соединений с резонансной
планетой. Напротив, во внешних резонансах неустойчивые равновесия рас¬
положены при о = ош — 2mkjTr/(kj — к) и соответствуют орбитам, на
которых астероид находится в перигелии, когда происходит одно из соеди¬
нений с резонансной планетой. Таким образом, неустойчивые равновесия
всегда соответствуют резонансным орбитам, обеспечивающим такое сбли¬
жение астероида и резонансной планеты, которое является наиболее тес¬
ным из возможных. Благодаря либрации устойчивые резонансные орбиты
избегают этой конфигурации наиболее тесного сближения.
Это свойство важно, когда велик эксцентриситет, потому что тогда наи¬
более тесное сближение может соответствовать физическому соударению
с планетой. Действительно, если значение N таково, что эксцентриситет
неустойчивых равновесий равен aj/a — 1 для внутренних резонансов или
1 — aj/a для внешних резонансов (здесь а и — большие полуоси ор¬
бит астероида и резонансной планеты соответственно), то неустойчивые
равновесия отвечают орбитам с соударениями в афелии (или перигелии)
с резонансной планетой. Когда N больше этого значения, типичный дина¬
мический портрет резонанса выглядит как представленный на рис. 9.8 (по¬
следний рассчитан для случая резонанса 5/6 с Нептуном). Жирной кривой
обозначено множество точек е, о, соответствующих соударению с плане¬
той. Эта кривая вычислена путем фиксации г = и / + w — Xj, где г
и / — гелиоцентрическое расстояние и истинная аномалия астероида, зада¬
ваемые формулами (1.5) и легко выражаемые как функции от /V, S и о. Все
орбиты, пересекающие эту кривую, имеют соударения или очень тесные
сближения с планетой. Заметим, что резонансные орбиты, благодаря либра¬
циям около о — 7г не пересекают эту кривую столкновений. Таким образом,
резонанс средних движений обеспечивает резонансным орбитам «фазовую
защиту» от столкновений. Плутон (крупнейший из известных объектов по¬
яса Койпера)1 дает самый известный пример этого свойства. Он находится
в резонансе 2/3 с Нептуном и проникает внутрь орбиты Нептуна. Одна¬
ко либрация о никогда не позволит ему пересечь кривую столкновений,
так что всякий раз, когда Плутон пересекает орбиту Нептуна, он находит¬
ся далеко от Нептуна. Этот своего рода «балет» в исполнении Плутона
1 Плутон уже не является крупнейшим из известных ТНО; см. прим. ред. на с. 325. — Прим.
ред.
228
Глава 9
и Нептуна, как полагают, устойчиво длится начиная с ранних фаз истории
Солнечной системы.
N = -0.920
ecoscr
Рис. 9.8. Фазовый портрет резонанса 5/6 с Нептуном; жирной кривой обозначе¬
но множество точек (е, сг), соответствующих возможному соударению с планетой.
Динамически устойчивыми могут быть только либрационные траектории, не пере¬
секающие эту кривую. (По данным Томаса, 1998; адаптировано)
Из рис. 9.8 также можно заметить, что точка равновесия при а = 0°,
обычно неустойчивая в случае внешних резонансов первого порядка по экс¬
центриситету, является теперь устойчивой. Эту точку окружает небольшая
область устойчивости, ограниченная с двух сторон кривой соударений. При
увеличении N (то есть при больших эксцентриситетах резонансных орбит)
область устойчивости вокруг точки равновесия при сг = 0 расширяется,
а вокруг точки равновесия при а = 7Г сжимается. Наконец, следует под¬
черкнуть, что резонанс средних движений обеспечивает защиту от тесных
сближений только с резонансной планетой; поэтому всякая орбита должна
в конечном счете стать неустойчивой, если ее эксцентриситет достаточно
9.1. Простое интегрируемое приближение
229
велик, чтобы стали возможными пересечения с нерезонансными орбитами
планет.
9.1.2. Случай резонанса 1/1
Чтобы исследовать резонанс 1/1 с планетой, нужен иной по сравнению
с (9.5) выбор резонансных переменных, поскольку (9.5) являются сингуляр¬
ными при Щ = к. Подходящими каноническими переменными для этого
резонанса будут
Введя эти переменные, исследовать динамику в резонансе 1/1 можно так
же, как объяснено выше для других резонансов.
На рис. 9.9 показан портрет резонанса 1/1 с Юпитером для N = 0 (то
есть е = 0); чтобы представить динамику нагляднее, в качестве радиальной
координаты мы используем а = S2 вместо S. Есть две точки, где гамиль¬
тониан имеет особенности типа «полюс»: начало координат а — 0 и точка
при а = 0, а = 5.2. Первая соответствует положению Солнца; квазикруго-
вые траектории вокруг нее отвечают квазикеплеровым гелиоцентрическим
орбитам, большие полуоси которых лишь слабо возмущены, в зависимости
от <т, резонансной планетой. Вторая точка соответствует положению Юпи¬
тера, которое в этих координатах фиксировано. Помимо этих двух точек, на
рисунке имеется пять точек равновесия — это знаменитые точки Лагранжа.
Две из них, обозначаемые через L4 и L5, устойчивы и образуют с Солн¬
цем и планетой два равносторонних треугольника. Либрации вокруг этих
точек обычно называют либрациями типа «головастик»; они аналогичны
асимметричным либрациям, существующим во внешних резонансах сред¬
них движений типа 1/га (то есть Щ = 1, k Е N; см., например, рис. 9.4).
Эти либрации ограничены сепаратрисой, соединяющей точку неустойчи¬
вого равновесия L3 саму с собой. Астероиды-греки и астероиды-троянцы
находятся на либрирующих орбитах типа «головастик». На рис. 9.9 так¬
же видна большая область либраций вокруг а = 7г, ограниченная сепара¬
трисами, исходящими из двух других точек неустойчивого равновесия, L\
и Ь2. Орбиты в этой области обычно называют либраторами типа «подко¬
ва»; они аналогичны симметричным либраторам, обсуждавшимся в связи
с рис. 9.4.
S = А,
N = Р,
SZ = Q,
v = р,
= q,
(9.9)
Aj — Aj + A,
230
Глава 9
е = 0
a cos сг
Рис. 9.9. Фазовый портрет резонанса 1/1 с Юпитером для значения N, соответству¬
ющего е = 0
Сепаратрисы, исходящие из Ь\9 не совпадают с исходящими из L2, но
из рис. 9.9 это трудно заметить, так как они очень близки друг к другу.
С другой стороны, эти сепаратрисы не могут взаимно пересекаться, по¬
скольку нормальная форма резонанса средних движений в плоской круго¬
вой задаче является интегрируемой.
Сепаратриса, соединяющая точку Li саму с собой, ограничивает ма¬
лую область либраций вокруг а = 5.2, а = 0. Здесь траектории окружают
планету подобно орбитам спутников. Так как <т должна быть положитель¬
ной при а <2j, траектории в центре рис. 9.9 должны циркулировать вокруг
начала координат против часовой стрелки. Тогда, по непрерывности, либра¬
ции типа «подкова» должны происходить по часовой стрелке, а траектории
спутникового типа вокруг Юпитера должны циркулировать против часо¬
вой стрелки. Вокруг своей оси Юпитер вращается также против часовой
стрелки, поэтому эти траектории спутникового типа называют проградны-
ми. Среднее значение, взятое от двух расстояний «Ь\ - планета» и «L2 -
планета», называется радиусом Хилла\ оно равно aj(£j/З)1/3, где £j — масса
планеты (в солнечных единицах).
9.1. Простое интегрируемое приближение
231
е = 0.2
acoscr
Рис. 9.10. Фазовый портрет резонанса 1/1 с Юпитером для значения N, соответ¬
ствующего е = 0.2 при а = 5.2 а. е.
На рис. 9.10 показан портрет резонанса 1/1 для значения N, соответ¬
ствующего орбитам с е = 0.2 при а = 5.2 а. е. Вновь мы видим два устой¬
чивых равновесия (теперь слегка смещенных относительно а = ±60°) —
центры либраций типа «головастик». Они ограничены сепаратрисой, ис¬
ходящей из точки неустойчивого равновесия при а ~ 5.2 а. е., а = 180°.
Новой деталью, по сравнению с рис. 9.9, является жирная кривая, окружа¬
ющая точку а = 5.2 а. е., а = 0°; она обозначает множество точек а, сг, для
которых может произойти соударение с планетой. Эта кривая вычислена,
как объяснено в разделе 9.1.1, и она аналогична кривой на рис. 9.8. По¬
скольку при этом значении N кривая столкновений ограничивает область
большего радиуса, чем радиус Хилла, неустойчивые равновесия, обозна¬
ченные на рис. 9.9 через Li и L2, исчезли, как и связанные с ними сепа¬
ратрисы2. Как следствие, максимальная амплитуда либраций типа «подко¬
2 При значении N, соответствующем более умеренному эксцентриситету, радиус области,
ограниченной кривой столкновений, будет меньше радиуса Хилла, а два неустойчивых рав¬
новесия при <т = 0° сохранятся; они соответствуют так называемым орбитам Ляпунова. —
Прим. авт.
232
Глава 9
ва» теперь диктуется расположением кривой столкновений. Глубоко внутри
кривой столкновений сохраняются траектории, либрирующие вокруг поло¬
жения Юпитера (а = 5.2, сг = 0) в устойчивом движении спутникового
типа. По непрерывности с направлением изменения сг на орбитах, пересе¬
кающих кривую столкновений (& > 0 на орбитах с а < 5.2 а. е. и & < 0 на
орбитах с а > 5.2 а. е.), либрации вокруг Юпитера теперь происходят по ча¬
совой стрелке, то есть они являются ретроградными по отношению к вра¬
щению Юпитера вокруг его оси. Поэтому орбиты ретроградных спутников
характеризуются большим гелиоцентрическим эксцентриситетом3, а орби¬
ты проградных спутников могут иметь лишь малый гелиоцентрический
эксцентриситет.
9.2. Перекрытие резонансов средних движений
В главе 6 мы убедились, насколько важно понятие перекрытия резо¬
нансов для понимания глобальной устойчивости или неустойчивости дина¬
мических систем.
Чтобы проверить, перекрываются или нет резонансы средних дви¬
жений, необходимо вычислить ширину каждого резонанса на плоскости
«большая полуось - эксцентриситет». Это делается следующим образом.
Как показано выше в разделе 9.1, на каждой поверхности N = const се¬
паратрисы (если они существуют) обычно пересекают ось сг = crstab два¬
жды (здесь crstab — значение а точки устойчивого равновесия в центре ре¬
зонансной области). Обозначим через Si(N) и S2(N) значения S в этих
двух точках пересечения (то есть минимальное и максимальное значения 5,
достигаемые на сепаратрисах). Затем вычислим образы (ai(iV),ei(N))
и (a2(i\0, е2(Л0) этих двух точек на плоскости (а, е), обратив (9.5) и (1.69),
а именно используя формулы
Наконец, соединим все точки (ai(7V), ei(7V)), полученные для возрастаю¬
щих значений N, и сделаем то же самое с точками (а2,е2). Полученные
таким образом две кривые представляют собой сечения сепаратрис резо¬
нанса при сг = crstab. Аналогично, обозначим через 5stab(N) значение S для
устойчивого равновесия и вычислим его образ (astab(N), estab(A0), найдя
3Его не следует путать с планетоцентрическим эксцентриситетом. — Прим. авт.
1/2
(9.10)
9.2. Перекрытие резонансов средних движений
233
таким образом кривую, представляющую собой семейство точек устойчи¬
вого равновесия, параметризованное через N. На рис. 9.11 показаны эти
кривые для резонансов 2/1 и 3/1 с Юпитером в поясе астероидов; также на¬
несено несколько кривых N = const. Как мы убедились в разделе 9.1, в ин¬
тегрируемой аппроксимации плоской круговой задачи каждая резонансная
орбита демонстрирует связанные осцилляции а и е на кривой N = const;
два экстремума этих осцилляций, достигаемых при а = crstab, лежат сим¬
метрично по обе стороны от семейства устойчивых равновесий, внутри
сепаратрис. Чем больше амплитуда либраций <т, тем ближе к сепаратри¬
сам лежат эти экстремумы. Заметим, что в обоих случаях ширина резонан¬
са возрастает с эксцентриситетом, потому что коэффициенты резонансных
гармоник пропорциональны некоторой положительной степени е.
со со
а, а. е. а, а. е.
Рис. 9.11. Сепаратрисы (жирные линии) и семейства устойчивых равновесий
(сплошные тонкие линии) резонанса 2/1 (панель (а)) и резонанса 3/1 (панель {б))
с Юпитером. Прерывистыми линиями показано несколько кривых уровня N
В случае резонанса 2/1 одна из двух сепаратрис не достигает е = О
(рис. 9.11а), так как в резонансах средних движений первого порядка по
эксцентриситету, когда сепаратриса появляется впервые (см. среднюю ле¬
вую панель рис. 9.2), она уже пересекает ось а = crstab при е > 0. Вторая
особенность этих резонансов состоит в том, что вдоль семейства устойчи¬
вых равновесий а —> 0, если е —> 0 (а для внешних резонансов а —► +оо,
если е —> 0); напротив, в случае резонансов большего порядка по эксцен¬
триситету семейство устойчивых равновесий достигает оси е = 0 при неко¬
тором определенном значении а (рис. 9.11 б).
234
Глава 9
Описанный рецепт определения ширины резонанса нельзя применять
к таким резонансам и при таких значениях N, для которых имеются асим¬
метричные либрации, а также в случае эксцентриситетов выше кривой пе¬
ресечений орбиты планеты. В первом случае ширина резонанса определяет¬
ся сепаратрисой, ограничивающей симметричные либрации (см. рис. 9.4).
Минимальное и максимальное значения 5 на этой сепаратрисе не дости¬
гаются, когда а = ас, где а с является центральным значением симмет¬
ричных либраций. Это делает вычисление Si(N) и 52(N) несколько более
сложным. Однако для многих практических целей 51 и S2 можно аппрокси¬
мировать значениями 5 на сепаратрисе при а = ас, поскольку отклонения
от реальных значений обычно невелики. Во втором случае, то есть для
значений N таких, что на портрете 5, а имеется кривая столкновений и от¬
сутствует хорошо определенная сепаратриса (рис. 9.8), ширина резонан¬
са определяется траекторией, имеющей наибольшую амплитуду либраций
среди траекторий, не пересекающих кривую столкновений. Si и S2 являют¬
ся минимальным и максимальным значениями 5 на этой траектории. По¬
скольку наибольшая амплитуда либраций бесстолкновительных резонанс¬
ных орбит уменьшается с увеличением N, выше кривой aj = а(1 ± е) пе¬
ресечений с орбитой планеты ширина резонансов средних движений с уве¬
личением эксцентриситета уменьшается.
Первые систематические расчеты ширины резонансов средних движе¬
ний в поясе астероидов выполнили Дермотт и Мюррей (1983). Они иссле¬
довали все резонансы средних движений с Юпитером вида n/rij = (2т +
4- 1 )/ш, (2т — 1 )/га, (3т + 1)/2т (где nj — среднее движение Юпите¬
ра, т — целое число), расположенные в диапазоне от 2.4 до 4 а. е., а также
резонанс 8/3 при 2.7 а. е. (рис. 9.12). В рассмотренном диапазоне большой
полуоси эти резонансы имеют наибольшую ширину. По сравнению с опи¬
санным выше рецептом авторы сделали несколько упрощений, чтобы об¬
легчить расчеты. Во-первых, в случае резонансов 2/1 и 3/2 (единственных
резонансов первого порядка по эксцентриситету среди рассмотренных) они
вычисляли ширину областей либраций, а не резонансных областей (в про¬
тивоположность рис. 9.11а). Это позволяет определить «границы резонан¬
са» и при малых эксцентриситетах, однако при е —> 0 граничные значения
большой полуоси стремятся к нулю и к бесконечности. Во-вторых, они
разложили гамильтониан в ряд по степеням эксцентриситета и сохранили
только ведущий член; тем самым теряется информация о влиянии кривой
столкновений с Юпитером на резонансную динамику и упускается из виду,
что резонансная область, защищенная от столкновений с планетой, сжима-
9.2. Перекрытие резонансов средних движений
235
Рис. 9.12. Распределение оскулирующих элементов астероидов (известных
в 1983 г.) в диапазоне 2.4 < а < 4.0 а. е. Сплошными линиями показаны грани¬
цы областей либраций основных резонансов средних движений с Юпитером. Внут¬
ри зоны перекрытия резонансов границы областей либраций резонансов 2/1 и 3/2
показаны прерывистыми линиями. (Рис. 5 из статьи Дермотта и Мюррея, 1983;
с разрешения Nature, Macmillan Magazines Limited)
ется с увеличением эксцентриситета, если эксцентриситет больше порога
пересечения с орбитой планеты. Однако для практических целей эти ап¬
проксимации обычно вполне допустимы, поэтому работа Дермотта и Мюр¬
рея остается ключевой ссылкой по данной теме. Как видно из рис. 9.12, ре¬
зонансы средних движений перекрываются при большом эксцентриситете,
приблизительно в области Q > 4.2 а. е., где Q = а( 1 + е) — афелийное рас¬
стояние астероида. Согласно главе 6, если имеется перекрытие резонансов,
лишь в центральных областях резонансов движение может быть регуляр¬
ным (на резонансных островах); остальное же фазовое пространство гло¬
бально-хаотично. В частности, нерезонансные регулярные орбиты не могут
существовать. Только ниже порога перекрытия резонансов движение асте¬
роида может быть глобально устойчивым (в рамках ограниченной плоской
круговой задачи). Хаотические орбиты могут существовать (вблизи сепа¬
ратрис резонансов), но отсутствие перекрытия резонансов гарантирует, что
движение локально ограничено (см. рис. 6.3). На рис. 9.12 также нанесены
236
Глава 9
положения астероидов, известных ко времени исследования; в качестве ко¬
ординат используются оскулирующие большая полуось и эксцентриситет.
Легко видеть, что подавляющее большинство астероидов находится в обла¬
стях между резонансами средних движений. Области резонансов средних
движений соответствуют выраженным «люкам» в распределении астеро¬
идов, если не считать резонансов 3/2 и 1/1 (последний расположен вне
диапазона больших полуосей, покрываемого графиком). Это заключение
подтверждает интуитивный вывод Кирквуда (1866), который первым обра¬
тил внимание на неоднородность распределения астероидов, построенного
им для выборки из 91 первых открытых астероидов. Области резонансов
средних движений, где нет астероидов, обычно называют люками Киркву¬
да. В рамках ограниченной плоской круговой задачи существование люков
объяснить нельзя, так как резонансные либрации устойчивы. Их происхож¬
дение будет объяснено в главе 11, где исследуется вековая динамика внутри
резонансов средних движений в рамках реалистичной модели планетной
системы. Обратите внимание, что несколько астероидов на рис. 9.12 все-
таки оказываются внутри резонансов, хотя и вблизи от границ. На самом
деле такие астероиды в большинстве своем нерезонансны, а внутри сепа¬
ратрис на графике оказываются потому, что их оскулирующие элементы
соответствуют значению сг, отличному от того, который использовался при
вычислении границ резонансов (сг = crstab). Если орбитальные элементы
этих астероидов интегрировать до выполнения условия сг = <Tstab> то в ре¬
зультате у них были бы значения а и е, соответствующие расположению вне
границ резонансов. Самосогласованный метод расчета расстояний астерои¬
дов от границ резонансов средних движений будет описан в разделе 9.4.
Аналитические расчеты ширины резонансов средних движений в по¬
ясе Койпера выполнили Морбиделли и др. (1995а). На рис. 9.13 показаны
сепаратрисы главных резонансов с Нептуном и Ураном, расположенных до
50 а. е. Как следует из графика, резонансы перекрываются вблизи линии
q = <2n = 30 а. е., где q = а(1 — е) — перигелийное расстояние малого тела,
ак — большая полуось Нептуна. Отметим, что при q < 30 а. е. резонансные
области сжимаются с увеличением эксцентриситета по причине, разъяснен¬
ной в этом разделе выше. Эти резонансные области являются единственны¬
ми областями с q < 30 а. е., где в рамках ограниченной плоской круговой
задачи могут быть регулярные орбиты. С другой стороны, все нерезонанс¬
ные орбиты должны быть хаотическими, поскольку они испытывают сбли¬
жения с Нептуном. Если же q несколько больше 30 а. е., то тела не пересе¬
кают орбиту Нептуна, а при q > 35 а. е. резонансы средних движений хо¬
9.2. Перекрытие резонансов средних движений
237
а, а. е.
Рис. 9.13. Расположение и ширина резонансов средних движений с Нептуном
(«Nn/nN») и Ураном («Un/пи») в поясе Койпера в интервале значений большой
полуоси от 32 до 50 а.е. Две жирные сплошные кривые соответствуют q = а( 1 —
— е) = 30 а. е. и q = 19.2 а; е.; они являются пороговыми кривыми пересечений
орбит Нептуна и Урана соответственно. Жирная пунктирная кривая соответствует
q = 35 а.е. См. комментарии в тексте. (Рис. 1 из статьи Морбиделли и др., 1995а;
с разрешения Academic Press)
рошо разделены, так что движение должно быть глобально-устойчивым —
опять же в рамках плоской круговой задачи. Расчеты ширины регулярных
областей внутри резонансов средних движений с Нептуном также прове¬
ла Мальхотра (1996) путем построения сечений Пуанкаре в ограниченной
плоской круговой задаче. Найденные ею значения ширины чуть меньше,
чем следует из рис. 9.13, поскольку при оценках она исключала хаотиче¬
ские области вблизи сепаратрис резонансных нормальных форм.
Существенная, но количественно не определенная часть объектов по¬
яса Койпера находится, подобно Плутону, в резонансе 2/3 с Нептуном. Та¬
кие объекты называется плутино. Кроме того, как полагают, один объект
находится в резонансе 3/4.4 Пока, однако, неясно, расположены ли объекты
4Согласно современным данным резонансное население пояса Койпера включает груп¬
пы во многих резонансах; в частности, исправленное за эффекты селекции население резо¬
нанса 2/5 не уступает населению резонанса 2/3 (Gladman В. et al. (2012) The resonant trans-
Neptunian populations. Astron. J., 144, 23). — Прим. ред.
238
Глава 9
с большими полуосями от 40 до 50 а. е. предпочтительно внутри резонан¬
сов средних движений или же вне их; наличие (гипотетическое) в поясе
Койпера эквивалентов люков Кирквуда пока не установлено.
9.2.1. Порог перекрытия вблизи планеты
Из рис. 9.13 видно, что резонансы первого порядка по эксцентриситету
(1/2, 2/3, 3/4, 5/6, ...) образуют последовательность, сгущающуюся с при¬
ближением к Нептуну; действительно, используя закон Кеплера, связываю¬
щий орбитальный период и большую полуось, легко видеть, что расстояние
между резонансами к — 1/ки к/(к+ 1) равно
где cij — большая полуось резонансной планеты. С другой стороны, с при¬
ближением к Нептуну ширина этих резонансов значительно не уменьшает¬
ся. Это означает, что резонансы первого порядка по эксцентриситету при
достаточно больших к могут полностью перекрываться, создавая хаотиче¬
скую область вблизи планеты, ширина которой существенна и при нулевом
эксцентриситете. Это явление впервые обнаружил Уиздом (1980). Он также
рассчитал, что пороговое значение к, при котором происходит перекрытие,
пропорционально е~2/7, где е — масса резонансной планеты. Этот резуль¬
тат справедлив как для внутренних, так и для внешних резонансов средних
движений первого порядка по эксцентриситету.
Чтобы воспроизвести результат Уиздома, требуется найти ширину ре¬
зонанса вида — к\ = 1 в функции от к. Эта ширина зависит от значе¬
ния N; как видно из рис. 9.2, если N достаточно мало, то точка устойчи¬
вого равновесия очень близка к е = 0, так что осцилляции большой полу¬
оси и эксцентриситета на либрационном цикле становятся пренебрежимо
малыми. Однако значения N, при которых это происходит, соответствуют
значениям а при е = 0, существенно отличным от невозмущенного поло¬
жения резонанса ares, определяемого законом Кеплера. Поэтому логично
выбрать значение N такое, что а = ares с ares, соответствующим е = 0.
Согласно (9.8) это имеет место для N = 1 /[к2(к + 1)п^]1//3 в случае внут¬
ренних резонансов и для N = —1/[к2(к — в случае внешних резо¬
нансов. Для простоты сосредоточимся на внутренних резонансах. Из (9.6)
и (9.7), проведя разложение в ряд Тейлора по y/S9 находим первые члены
2
2
9.2. Перекрытие резонансов средних движений
239
гамильтониана:
S 352
Нрс = ~кЧР ~ 2k*N* + + 1)nj5 + ecv/^cos<7’ (9Л2)
где все члены, не зависящие от S и сг, отброшены и сохранена только пер¬
вая гармоника; с — числовой коэффициент, приблизительно равный л/2 (& +
+ l)/7r[2if0(2/3) + jRTi(2/3)], где К0 и Ki — модифицированные функции
Бесселя (Мюррей и Хольман, 1997). При сделанном нами выборе N линей¬
ные по S члены взаимно сокращаются. Тогда (9.12) имеет единственную
точку равновесия (устойчивого) при crstab = 0, 5stab = (eck2N4/6)2/3; под¬
ставив зависимости с и N от к, имеем Ssta.ь ~ с2/3/с-2/3. Наличие точки
устойчивого равновесия, смещенной от 5 = 0, вынуждает действие S ос¬
циллировать с амплитудой SS ~ 2S'stab. Связанные осцилляции большой
полуоси имеют поэтому амплитуду 6а = 2 у/а6А = 2y/akSS (что следует
из определения N в формулах (9.5)). Таким образом, амплитуда резонанс¬
ных колебаний большой полуоси при рассматриваемом значении N про¬
порциональна е2!Ч1/\ Расстояние же по большой полуоси между двумя
соседними резонансами первого порядка по эксцентриситету дается фор¬
мулой (9.11). В итоге приходим к выводу, что перекрытие резонансов ста¬
новится возможным начиная с к ~ е~2!7.
Из третьего закона Кеплера следует, что резонанс первого порядка по
эксцентриситету с к ~ е~2!7 имеет место при значении большой полуоси а
таком, что |а — aj\/aj ~ е2!7. Это означает, что хаотическая область проле¬
гает по обе стороны от планеты на интервале большой полуоси (в единицах
большой полуоси планеты), пропорциональном г2!7.
9.2.2. Перекрытие планетных резонансов
Резонансы средних движений тела с двумя различными планетами так¬
же могут перекрываться друг с другом. На самом деле это довольно рас¬
пространенный случай, так как между планетами-гигантами есть квазире-
зонансные соотношения. Например, Юпитер и Сатурн близки к взаимному
резонансу средних движений 5/2. Как следствие, резонансы средних движе¬
ний п/m с Юпитером расположены вблизи резонансов средних движений
Ъп/2т с Сатурном. Ситуация аналогична для резонансов с Ураном и Неп¬
туном (эти две планеты близки к взаимному резонансу 2/1). Резонанс Ла¬
пласа — частный случай перекрытия резонансов средних движений; он име¬
ет место, когда два возмущающих тела находятся в точном резонансе друг
240
Глава 9
с другом. В динамике главного пояса астероидов и пояса Койпера резонан¬
сы Лапласа отсутствуют (так как между планетами нет точных взаимных
резонансов), но они довольно часто встречаются в спутниковых системах.
Наиболее известен резонанс Лапласа у галилеевых спутников, где Европа
одновременно находится в резонансах 1/2 с Ио и 2/1 с Ганимедом.
Когда два составляющих резонанса имеют сравнимую ширину, эффек¬
тивным способом изучения последствий их перекрытия является анализ
плоской бикруговой задачи. Гамильтониан этой задачи получается из (2.38)
при учете лишь двух резонансных планет в предположении, что они имеют
компланарные круговые орбиты. Наклонение малого тела также полагается
равным нулю. Благодаря правилам Даламбера гамильтониан зависит толь¬
ко от углов А, р, Aj1 и Xj2 (где последние два угла — средние долготы
резонансных планет) и, таким образом, фактически имеет четыре степени
свободы. В резонансной нормальной форме (см. раздел 2.5.2) в этом случае
от возмущений остаются только гармоники, зависящие исключительно от
резонансных углов, а именно от k'А — kj1Xj1 + (к' — kj^p для резонан¬
са kjx/к' с планетой j\ и от к"X — kj2 Xj2 + (к" — kj2 )р для резонанса kj2 /кп
с планетой fa- Все короткопериодические члены при построении нормаль¬
ной формы усредняются.
Первый шаг анализа осредненной бикруговой задачи состоит в поиске
набора канонических переменных, такого что среди новых углов два бы¬
ли бы критическими углами рассматриваемых двух резонансов. В случае
kjY ф к' и kh ф к" подходящими переменными будут
(9.13)
9.2. Перекрытие резонансов средних движений
241
Если один из двух резонансов — резонанс 1/1 (скажем, kjx = kf), то подхо¬
дящими переменными вместо (9.13) будут
si = Л + к - к" Р' a1=X-Xh,
J2 К
^ _ р _ _ khXj2-k"X
^2-А 2 , _ +Р,
*" - (9Л4)
Al = Aj! + Л + —у}Р, >
к
д . — Д 32 р \ . — \ .
1YJ2 — IVJ2 i Л32 — Л32-
32 Л
Читатель может проверить, что оба преобразования являются канониче¬
скими, используя критерий скобок Пуассона (см. раздел 1.6). В новых пе¬
ременных усредненный гамильтониан плоской бикруговой задачи зависит
только от углов <Ti и (Т2, то есть задача фактически имеет только две сте¬
пени свободы. Поэтому динамику можно относительно просто изучать пу¬
тем построения сечений Пуанкаре. Поскольку оба угла о\ и <Т2 могут по¬
переменно циркулировать и либрировать, логично взять сечение по углу
k"(kjl — k')ai — k'(kj2 — к")(Т2 (или k"ai — k'(kj2 — kf')<72> если kjx = к'),
который обычно циркулирует в фиксированном направлении5.
Возможно, наиболее интересным приложением такого подхода являет¬
ся анализ перекрытия резонанса 1/1 с Сатурном и резонанса 2/5 с Юпи¬
тером. Эти два резонанса имеют сравнимую ширину, если эксцентриситет
астероида равен примерно 0.1. Де ла Барр и др. (1996) высказали гипотезу,
что троянцы у Сатурна отсутствуют из-за этого перекрытия. На рис. 9.14
показана (штриховкой) область начальных условий (а, е) неустойчивого
движения, которая выявляется при интегрировании осредненной бикруго¬
вой задачи. Неустойчивым мы называем здесь движение с уходом из об¬
ласти определения гамильтониана, а именно движение, пересекающее кри¬
вую столкновений с какой-либо из планет. Как видим, орбиты в центрах
«головастиков» Сатурна (а ~ 9.5 а. е.) при е > 0.12 неустойчивы. При
учете одного лишь Сатурна эти орбиты были бы устойчивы; поэтому их
5Эта комбинация а\ и сг2 равна k//kj1Xj1 — k'kj2\j2 + [k',(kj1 — к') — к’(kj2 — к")]р.
Поскольку и Xj2 не находятся точно в резонансе, их линейная комбинация циркулирует
со временем. С другой стороны, изменение р обычно слишком медленно, чтобы изменить
направление этой циркуляции. Конечно, в случае резонанса Лапласа это не так. — Прим. авт.
242
Глава 9
неустойчивость должна вызываться перекрытием с резонансом 2/5 с Юпи¬
тером. Орбиты с таким же значением большой полуоси, но с начальным
эксцентриситетом меньше 0.12, в бикруговой задаче устойчивы. Однако
в разделе 11.5 мы убедимся, что вековая динамика «накачивает» их экс¬
центриситеты до значений выше 0.12, обеспечивая их попадание в область
неустойчивости.
ю
о ' ' ' ' 1 ' ' ' ' ■ 1 ' ' =
о
о
О ' ' ' 1 ' ' 1 ' 1 ' ' 1 ' '
8 9 10 11
большая полуось, а. е.
Рис. 9.14. Заштрихована область начальных условий (а, е) неустойчивого движения
в осредненной бикруговой задаче с гармониками резонансов 1/1 с Сатурном и 2/5
с Юпитером. Начальное значение критического угла резонанса 2/5 с Юпитером рав¬
но 7г, а начальное значение критического угла резонанса 1/1 с Сатурном зависит от е
и соответствует центру либраций типа «головастик» в интегрируемом приближении
без учета Юпитера. (Рисунок любезно предоставлен Д. Несворным)
Как отмечено выше, анализ в рамках осредненной бикруговой задачи
уместен в том случае, когда два резонанса имеют сравнимую ширину, так
что их перекрытие порождает сильный хаос. Но когда один резонанс гораз¬
до уже другого, как в случае узкого резонанса 5/1 с Сатурном и широкого
резонанса 2/1 с Юпитером, эффект перекрытия является весьма специфи¬
ческим, а бикруговая модель в качестве приближения реальной динамики
может быть слишком грубой. В подобных случаях для исследования дина¬
9.3. Резонансные мультиплеты
243
мики эффективнее использовать иерархический пертурбационный подход,
разъясняемый далее в разделе 11.2.5.
9.3. Резонансные мультиплеты
В этом разделе мы вновь обращаемся к динамике изолированного резо¬
нанса средних движений. Однако мы будем работать не с изученным нами
интегрируемым приближением (9.4), а восстановим в (9.1) отброшенные
ранее члены, а именно члены, содержащие наклонение астероида и эксцен¬
триситеты и наклонения планет. Для полноты картины мы также учтем ве¬
ковую прецессию планетных орбит; с этой целью, полагая, как и в главе 8,
что планетные элементы эволюционируют согласно решению Лагранжа-
Лапласа (7.10), введем новые углы w* = gjt + Pj иО* = sjt + Sj, а сопря¬
женные действия обозначим через Agj и ASj (j = 1,... ,п). Чтобы сделать
гамильтониан автономным, к интегрируемой части гамильтониана добавим
член ^2j(gjA9j + SjASj). (Напомним, что частоты прецессии орбит планет
малы, так что gj и Sj не превышают е.) В этой постановке нормальную
форму резонанса средних движений (9.1) можно записать как
где vj* и fi* — векторы с компонентами Wj и £2* соответственно;
где га, г, s — целые числа, a u = (iti,..., ип) и v = (^i,..., vn) — векторы
с целочисленными компонентами такими, что m(kj — к) — s — r + Yhj(uj +
+ Vj) = 0. Коэффициенты cm)U5V,s,r параметрически зависят от входящих
в (7.10) амплитуд Nj^ векового движения планет.
В разложении (9.17) гармоники с га = 0 качественно отличаются от
гармоник с га ф 0. Первые не зависят от быстрых углов А и А^; мы с ни¬
ми уже сталкивались в главе 8 в задаче о вековом движении астероидов.
7^0 — 2Д2 пз^з + + sj^Sj)i (9.16)
з
а возмущение sTL\ раскладывается в ряд Фурье:
X exp {t[m(fcjAj-fcA)+u-«7*+v-n*+sp+rg]}, (9.17)
244
Глава 9
Они определяют вековую эволюцию эксцентриситета и наклонения асте¬
роида. Гармоники с га ф 0, по существу, представляют собой гармоники
резонансов средних движений, поскольку все они содержат резонансные
комбинации kjXj — кХ.
Пренебрежем на время вековыми гармониками (га = 0) и проанализи¬
руем структуру динамической системы, обусловленную лишь гармониками
резонансов средних движений. Такая система, очевидно, неинтегрируема,
так как она зависит от нескольких независимых квазирезонансных комби¬
наций углов.
С целью изучения этой мультирезонансной динамики введем прежде
всего углы crm)U)V,s,r = m(kjXj — кХ) + и • zu* + v • fi* + sp + rq. Каждая из
гармоник резонансов средних движений имеет в качестве аргумента свой
угол 0-m,u,v,s,r- Затем рассмотрим гамильтонианы
'kim,u,v,s,r = Wo(A, Aj, Kg., Ks. ) + Со "Г CmjUjV,s,r COS CTm,u,v,s,r j (9.18)
где для упрощения записи через со обозначен коэффициент со,о,о,о,о> а так¬
же явно подчеркнут тот факт, что фурье-разложение (9.17) содержит только
косинусные члены. Эти гамильтонианы играют роль моделей одиночных
резонансов, использовавшихся в главе 6 для изучения взаимодействия резо¬
нансов. Для каждого из гамильтонианов Wm,u,v,s,r точный резонанс имеет
место при cJm,u,v,s,r = 0, то есть при
га
kjrij — к \ -+
1 дс0
А3 дА
+ sjp + + vi*i) = °- (9>19)
3
Решение этого уравнения дает значение А, зависящее от действий Р и Q,
а также от индексов га, u, v,s,r; однако, так как со, gj и Sj все являются
величинами порядка с, решение должно быть с-близко к А = (к^щ/к)1/3,
то есть к невозмущенному положению резонанса средних движений, опре¬
деляемому законом Кеплера. Отсюда мы заключаем, что резонанс средних
движений представляет собой мулътиплет субрезонансов6, чьи раздельные
положения по большой полуоси астероида s-близки друг к другу. Такая
мультиплетная структура является специфическим свойством резонансов
средних движений, а в общем случае — резонансов между быстрыми угла¬
ми в вырожденной системе (Гуццо и Морбиделли, 1997).
6В оригинале: мулътиплет резонансов. При переводе здесь и далее, чтобы четко проводить
различие между «родительскими» резонансами и резонансами - компонентами мультиплетов,
на которые первые расщепляются, для последних, как правило, используется термин «субре¬
зонансы». — Прим. ред.
9.3. Резонансные мультиплеты
245
(«)
(б)
0 <£
Рис. 9.15. Схема возможных динамических структур внутри мультиплета субре¬
зонансов резонанса средних движений, (а) Полное перекрытие, как в динамике
модулированного маятника; (б) частичное перекрытие; (в) разделение субрезонан¬
сов. Через сг^ единым образом обозначены углы crm,u,v,s,r различных субрезонан¬
сов. (Рис. 13 из статьи Морбиделли и Гуццо, 1996; с разрешения Kluwer Academic
Publishers)
Чтобы вычислить ширину каждого субрезонанса по большой полуоси,
обратимся вновь к интегрируемой модели (9.18); как и в главах 4 и 6,
ширина вычисляется как максимальное расстояние между сепаратрисами,
и она имеет величину порядка Напомним, что коэффициенты
Cm,u,v,s,r не могут по порядку величины быть больше г (так как они явля¬
ются коэффициентами фурье-разложения еН\), но могут быть много мень¬
ше. Обозначим величину наибольшего коэффициента (коэффициентов) че¬
рез е(3. Далее, возможные варианты показаны на рис. 9.15: если /3 ~ 1,
то главные субрезонансы имеют ширину много больше, чем расстояния
между ними (соответственно rsj
И ^ е), то есть перекрытие является
полным (панель (а)); если /3 ~ £, то главные субрезонансы имеют ширину
того же порядка, что и расстояния между ними (~ е), и перекрытие являет¬
ся частичным (панель (б)); наконец, если (3 <С е, то ширина субрезонансов
гораздо меньше расстояний между ними, и можно ожидать, что перекрытия
нет (панель (в)).
В резонансах средних движений с Юпитером значения \к — kj\, а также
эксцентриситета и наклонения астероида определяют, какая из трех описан¬
ных ситуаций имеет место. Фактически согласно правилам Даламбера каж¬
дый коэффициент cm?U5v,s,r равен величине ееИгИП^-МЙ'^Й1 с неко*
торым численным множителем (не обязательно порядка единицы). Здесь
Msj и Nsj — постоянные векового изменения элементов Юпитера, входя¬
щие в (7.10). Кроме того, s + г — Ylj(uj +vj) = т(к ~ Щ)- Как следствие,
246
Глава 9
у резонансов средних движений низкого порядка по эксцентриситету (име¬
ющих |к — Щ| порядка единицы) некоторые из коэффициентов cm)U5V,s,r
должны быть пропорциональны степеням е, г, или являющимся
величинами порядка единицы; поэтому такие коэффициенты не могут быть
существенно меньше £ (напомним, что согласно формулам (8.7) ей г осцил¬
лируют из-за планетных вековых возмущений, так что нельзя сделать до¬
пущение, что они существенно меньше, чем эксцентриситет и наклонение
Юпитера). Поэтому для резонансов средних движений с Юпитером низкого
порядка по эксцентриситету должна быть характерна ситуация, представ¬
ленная на рис. 9.15а. Эта динамическая структура, соответствующая моду¬
лированному маятнику, будет рассмотрена в следующем разделе. Ситуация
постепенно изменяется с увеличением |k — kj\: коэффициенты cmjUiV,s,r
становятся пропорциональными все большим степеням эксцентриситетов
и наклонений, так что возникают ситуации, представленные на рис. 9.156
и 9.15в, сначала для значений ей i того же порядка, что и эксцентриситет
и наклонение Юпитера, а затем и для больших значений.
Однако в случае резонансов средних движений с планетами, масса ко¬
торых много меньше массы Юпитера, частичное перекрытие субрезонан¬
сов в мультиплете может достигаться при меньших |к — Щ\. Фактически
из (9.19) следует, что расстояние между субрезонансами является величи¬
ной порядка £ (массы Юпитера в солнечных единицах) независимо от выбо¬
ра резонансной планеты; с другой стороны, коэффициенты cm)UjV,s,r субре-
зонансных гармоник пропорциональны массе резонансной планеты £j <С £.
У трехтельных резонансов (резонансов средних движений астероида
и двух планет) ситуация на рис. 9.156 является ожидаемой уже в случае
очень низких порядков по эксцентриситету. У таких резонансов коэффици¬
енты cm)ll5v,s,r являются величинами порядка е2, поскольку резонансные
гармоники появляются в нормальной форме только во втором порядке, как
объяснено в разделе 2.5.2. Трехтельные резонансы средних движений мы
подробно обсудим в главе 10.
Конечно, для детального понимания структуры мультиплета требует¬
ся количественный расчет сепаратрис каждого из гамильтонианов (9.18)
одиночных субрезонансов. Однако простую диагностику можно провести,
используя численное интегрирование на коротких интервалах времени. Так
как разделение субрезонансов в мультиплете пропорционально частотам ве¬
ковой прецессии (см. уравнение (9.19)), а амплитуда субрезонанса пропор¬
циональна частоте либраций его критического аргумента <7m>u v s r (см. гла¬
ву 4), динамическая ситуация, представленная на рис. 9.15а, характерна для
9.4. Приближение модулированного маятника
247
случая, когда частота либраций много больше частот вековой прецессии.
Для ситуации на рис. 9.156 требуется, чтобы эти частоты были величинами
одного порядка; а ситуация на рис. 9.15в имеет место только тогда, когда
частоты либраций всех углов crm)UjV5S?r много меньше вековых частот.
9.4. Приближение модулированного маятника
Рассмотрим зависящий от времени гамильтониан модулированного ма¬
ятника с одной степенью свободы:
Н = ^р2 + с(1 + a cos(et)) cos g, (9.20)
где p, q — общие переменные «действие-угол», t — время, е — малый пара¬
метр, а, (3 и с — числовые коэффициенты. Модулированный маятник пред¬
ставляет собой модель-парадигму системы полностью перекрывающихся
резонансов (рис. 9.15л). Действительно, путем тригонометрических преоб¬
разований легко показать, что (9.20) эквивалентен следующему гамильто¬
ниану с двумя степенями свободы:
Н = ^р2 + еТ + с ^cos q + ^(cos(q - т) + cos(q + т))^, (9.21)
где Т, т(= et) — сопряженные переменные «действие-угол». Гамильтони¬
ан (9.21) описывает мультиплет из трех резонансов с критическими угла¬
ми (/, q—т и q+т, ^-близких друг к другу: они расположены, соответственно
при р = 0 и при р = ±е. Полуширина каждого из них велика относитель¬
но е и составляет соответственно 2 у/с/(3 и 2 у/са/(3.
Гамильтониан (9.20) стал предметом ряда исследований, как аналити¬
ческих (см., например, Элскенс и Эсканде, 1991; Брувилер и Кэри, 1989),
так и численных (см., например, Анрар и Анрар, 1991). На рис. 9.16 пока¬
заны его сечения Пуанкаре. Они схожи с фазовым портретом маятника, но
вместо сепаратрис на них видны широкие хаотические слои, регулярные
островки внутри которых малы (размеры последних пропорциональны е).
Легко убедиться, что внешняя граница хаотического слоя на панели (а) по¬
чти совпадает7 с сепаратрисой маятника, имеющего гамильтониан /Зр2 /2 +
4- с(1 + a) cos q; аналогично, на панели (б) внутренняя граница хаотическо¬
го слоя почти совпадает с сепаратрисой маятника, имеющего гамильтониан
7Полное совпадение имеет место в пределе е —► 0. — Прим. авт.
248
Глава 9
Ч Я
Рис. 9.16. Сечения Пуанкаре гамильтониана (9.20) при et = 0 mod 27т (панель (а))
и et = 7г mod 27г (панель (б)). Сплошная кривая — сепаратриса маятника, вычис¬
ленная из (9.20) в предположении, что et — фиксированный параметр, равный 0 (а)
ИЛИ 7Г (б).
f3p2/2 + c(l — a) cosq. Таким образом, хаотический слой покрывает область,
заметаемую мгновенными сепаратрисами гамильтониана (9.20) за период
модуляции фактора с(1 + a cos (et)). (Мгновенными мы называем сепара¬
трисы, вычисленные из (9.20) при фиксации t.) Как следствие, регулярная
область, заполненная либрационными инвариантными торами, существует,
если и только если а < 1.
Разумеется, динамика в реальном мультиплете резонанса средних дви¬
жений, даже в случае полного перекрытия, является более сложной, чем
динамика (9.20). В действительности мультиплет резонанса средних дви¬
жений имеет в общем случае более трех компонент, к тому же у него нет
замечательного свойства симметрии мультиплета (9.21). Тем не менее ши¬
рину хаотического слоя все же можно вычислить с хорошей точностью,
используя рецепт, эквивалентный используемому для модулированного ма¬
ятника. В переменных (9.5) гамильтониан (9.15) записывается как
Wmmr = H0{N, S, Sz, Agj, ASj) + еНг(5, N, Sz,a, i/, w*, П*). (9.22)
Мы вычислим его мгновенные сепаратрисы в предположении, что вековые
углы г/, <jZ9 zn*, ft* и действия N, Sz — фиксированные параметры (так
что Нммк зависит только от S, а и поэтому интегрируем). Тогда хаоти¬
ческий слой должен покрывать область, заметаемую мгновенными сепара¬
9.4. Приближение модулированного маятника
249
трисами при изменении вековых углов, а границы слоя должны совпадать
с мгновенными сепаратрисами, соответствующими минимальному и мак¬
симальному значениям ширины резонанса. В качестве примера на рис. 9.17
показаны эти экстремальные мгновенные сепаратрисы в случае резонан¬
са средних движений 5/2 с Юпитером в упрощенной модели, где астероид
и планета находятся на компланарных орбитах, а орбита Юпитера — фик¬
сированный эллипс. Аналогичные рисунки для различных резонансов сред¬
них движений и различных значений вековых углов можно найти в статье
Иошикавы (1990, 1991). Как видно из рис. 9.17, ширина области либра¬
ций в случае минимума (левая панель) много меньше, чем в случае мак¬
симума (правая панель), но она никогда не бывает равной нулю; поэтому
можно ожидать существования регулярной области либраций, окруженной
хаотическим слоем, как у модулированного маятника при а < 1. В общем
случае можно ожидать наличия регулярной области либраций всегда, когда
наклонение орбиты астероида невелико, а ее эксцентриситет существенно
больше планетных эксцентриситетов, поскольку тогда, благодаря правилам
Даламбера, ширина субрезонанса, относящегося к плоской круговой огра¬
ниченной задаче (9.4), доминирует в сравнении с шириной всех других
субрезонансов в мультиплете. Определение области как «регулярная» здесь
не следует понимать буквально: она регулярна лишь в весьма упрощенной
модели, в которой предполагается, что действия N, Sz астероида — посто¬
янные. В реальности они эволюционируют вековым образом, причем эта
эволюция может быть неустойчивой и хаотической. Анализ вековой дина¬
мики в этих «регулярных» областях представляет собой одну из наиболее
сложных задач небесной механики; она будет обсуждаться далее в главе 11.
Чтобы выяснить, где находится конкретный астероид (вне резонанса,
или в хаотическом слое, или в «регулярной» области либраций), недоста¬
точно вычислить границы хаотического слоя резонанса средних движений,
так как прецессия вековых углов, вызывающая модуляцию ширины резо¬
нанса средних движений, вынуждает также осциллировать эксцентриситет
и наклонение орбиты астероида; это, в свою очередь, изменяет ширину ре¬
зонанса, поскольку последняя зависит от значений е и г. На рис. 9.18 дан
пример этих конкурирующих эффектов. Теперь модель учитывает члены
с частотами д5 и дв в уравнениях (7.10) для векового изменения эксцентри¬
ситета и долготы перигелия Юпитера. Двумя тонкими линиями показана
минимальная ширина резонанса 5/2 (на плоскости (а, е)), соответствующая
= 0 и го — zuq = 7г; а двумя жирными линиями показана его макси¬
мальная ширина, соответствующая w — w\ = 7г и tro-wj =0. Облако точек
250
Глава 9
О о
да, да,
Рис. 9.17. Динамика в резонансе средних движений 5/2 с Юпитером согласно ре¬
зультатам вычислений при ej = 0.05989, значении N, соответствующем е = 0.204
при а = 2.825 а.е., и двух разных значениях w — zuj: 0 (левая панель) и 7г (пра¬
вая панель). Горизонтальная ось имеет обозначение да = (kj — к)а, что в случае
резонанса 5/2 равно За. (Рис. 2 из статьи Морбиделли и др., 19956; с разрешения
Academic Press)
отслеживает эволюцию астероида, найденную численным интегрировани¬
ем уравнений движения для резонансной нормальной формы (9.15). В хо¬
де интегрирования астероид медленно перемещается по плоскости (а, е)
вверх-вниз, поскольку его эксцентриситет испытывает вековую эволюцию.
При этом астероид совершает быстрые почти горизонтальные осцилляции
из-за вариаций большой полуоси, вызываемых близостью к резонансу; они
коррелируют с циркуляцией ст. Максимальный эксцентриситет достигает¬
ся, когда vo — wl = 0 и vo — = 7г; в этот момент положение асте¬
роида следует сопоставлять с положением границ резонанса, нанесенных
тонкими линиями; минимальный эксцентриситет достигается, когда w —
— wl = 7г и w — zuq = 0, то есть когда ширина резонанса максимальна.
Конусообразная форма облака точек, отслеживающих эволюцию астероида,
говорит о том, что амплитуда осцилляций большой полуоси максимальна,
когда эксцентриситет проходит минимум своего векового цикла. Однако
согласно рис. 9.17 чем больше амплитуда осцилляций а, тем ближе астеро¬
ид к сепаратрисе резонанса. Поэтому мы можем заключить, что астероид
сильнее всего сближается с модулированным резонансом, когда w — = тг
и w — Wq = 0. Тот факт, что нижний левый угол конусообразного облака
лежит вне области, ограниченной жирными кривыми, означает, что астеро-
9.4. Приближение модулированного маятника
251
Рис. 9.18. Результаты численного интегрирования уравнений нормальной формы
резонанса средних движений 5/2 с Юпитером. Учтены вековые изменения орбиты
Юпитера с частотами д$ и дв. См. комментарии в тексте. (Рис. 3 из статьи Морби¬
делли и др., 19956; с разрешения Academic Press)
ид и при самом тесном сближении находится вне резонанса; в противном
случае следы осцилляций большой полуоси лежали бы внутри этой обла¬
сти и они были бы центрированы на ~ 2.825 а. е. Таким образом, следует
вывод, что данный астероид находится вне хаотического слоя резонанса
средних движений 5/2.
Если мы хотим однозначно представить положение этого астероида от¬
носительно резонанса 5/2, то естественно выбрать значения большой полу¬
оси и эксцентриситета его орбиты, соответствующие нижнему левому углу
конусообразного облака на рис. 9.18, (назовем их ад и ед), а в качестве
границ хаотического слоя взять жирные сепаратрисы. Таким образом, для
астероида и сепаратрис резонанса берутся одни и те же значения всех уг¬
лов (сг, т9 zu£, zuq), причем в момент времени, соответствующий их самому
тесному взаимному сближению.
Однако не у всех резонансов средних движений динамика аналогична
показанной на рис. 9.18, поскольку она зависит от локальной амплитуды ве¬
ковых осцилляций эксцентриситета астероида и от амплитуды модуляции
252
Глава 9
0.26
0.24
0.22
ея
0.20
0.18
0.16
Рис. 9.19. Левая панель: расположение астероидов семейства Фемиды и граница
хаотической области резонанса 2/1 с Юпитером; указано также положение астерои¬
да Жоннгуо — одного из немногих долгоживущих тел в резонансе 2/1 (см. главу И).
Правая панель: то же, но для семейства Гефион и резонанса 5/2; в виде эллипса по¬
казано ожидаемое распределение членов семейства Гефион согласно ударно-столк-
новительной модели. Об определении элементов ад и ея, обеспечивающем четкое
сопоставление положений астероидов и границ резонанса, см. текст. (Рис. 6 и 17 из
статьи Морбиделли и др., 19956; с разрешения Academic Press)
резонанса. Например, в случае резонанса 2/1 с Юпитером самое тесное
сближение астероида с хаотическим слоем резонанса имеет место, когда
vo — w% = 0 и w — zuq = 7г, то есть когда астероид проходит максимум
своего векового цикла изменения эксцентриситета и амплитуда резонанса
минимальна. В случае резонанса 3/1 самое тесное сближение происходит
в промежуточной ситуации, когда zu — = w — = 7г. Таким образом,
чтобы правильно представлять положение астероидов относительно границ
резонансов, необходимо для каждого конкретного случая резонанса выби¬
рать свои фазы вековых углов.
Морбиделли и др. (19956) осуществили первое систематическое иссле¬
дование расположения астероидов, принадлежащих к главным семействам,
относительно границ хаотических слоев соседних к этим семействам резо¬
нансов. На рис. 9.19 показаны результаты для семейств Фемиды и Гефион,
находящихся вблизи резонансов 2/1 и 5/2 с Юпитером соответственно. Как
видим, в обоих случаях все астероиды расположены вне границы хаоти¬
ческого слоя; причем их распределения как будто обрезаны вдоль точных
9.4. Приближение модулированного маятника
253
положений границ резонансов. Это наводит на мысль, что во время форми¬
рования этих семейств из-за катастрофического разрушения родительских
тел некоторые астероиды были вброшены в резонанс. Впоследствии они
были удалены в результате динамического воздействия этих резонансов.
Поскольку семейства астероидов должны быть много моложе Солнечной
системы (что следует из анализа столкновительных явлений; см. Марцари
и др., 1995, 1999), это означает, что формирование люков Кирквуда является
не феноменом ранней Солнечной системы, а результатом действия «неко¬
его» механизма динамической неустойчивости, активного и сейчас (см. гла-
ву И).
Глава 10
Трехтельные резонансы
10.1. Происхождение резонансных членов в возмущении
Трехтельные резонансы принадлежат к общему классу резонансов
средних движений, но в отличие от двухтельных резонансов средних дви¬
жений, обсуждавшихся в главе 9, в них вовлечены орбитальные частоты
трех тел. Конкретно, трехтельные резонансы соответствуют соотношению
kiXi + /С2А2 + &3А3 ~ 0, (10.1)
где Ai, А2, A3 — средние движения трех тел, а к\, /С2, к$ — ненулевые целые
числа. В данной главе мы потребуем, чтобы (10.1) не распадалось на два
соотношения
fciAi + (к2 - т)Х2 ~ 0, тА2 + /сзАз~0 (10.2)
для некоторого целого га. В противном случае трехтельный резонанс яв¬
ляется просто результатом наложения двух независимых двухтельных ре¬
зонансов средних движений (в случае точного наложения он называется
резонансом Лапласа) и может быть изучен, как описано в разделах 9.2.2
и 11.2.5.
Ввиду их важности в динамике планет, а также в динамике поясов
астероидов и Койпера, трехтельные резонансы заслуживают отдельной гла¬
вы. Если говорить о свойствах движения в резонансах, то в трехтельных
они в общем такие же, как и в двухтельных; однако, при том, что у трех¬
тельных резонансов коэффициенты гармоник квадратичны по массам пла¬
нет, у них сильнее проявляется мультиплетная структура, обсуждавшая¬
ся в предыдущей главе. Кроме того, не так просто понять происхождение
гармоник, относящихся к трехтельным резонансам, и вычислить их коэф¬
фициенты, так как в исходном гамильтониане ((1.29) в астероидной задаче
и (1.38) в планетной задаче), записанном в модифицированных перемен¬
ных Делоне (см. соответственно (2.38) и (2.39)), нет гармоник, зависящих
256
Глава 10
от комбинаций средних долгот трех тел. Поэтому можно было бы наивно
посчитать, что трехтельных резонансов не существует, поскольку коэффи¬
циенты соответствующих резонансных гармоник равны нулю. Конечно же,
это неверно. В этом разделе мы выясним, как возникают такие резонанс¬
ные гармоники. При этом мы будем различать прямой эффект, общий для
ограниченной и планетной задач, и косвенный эффект, присущий только
ограниченной задаче.
10.1.1. Прямой эффект
Гармоники, включающие комбинации средних долгот трех тел, скрыты
в исходном гамильтониане ((2.38) или (2.39)), но проявляются во втором
порядке по планетным массам, если осреднить гамильтониан по коротко¬
периодическим членам, используя пертурбационный алгоритм. Мы уже об¬
суждали это в разделе 2.5, а здесь детализируем процесс. Ограниченная
и планетная задачи формально эквивалентны; мы рассмотрим первую, где
запись выкладок проще.
Начнем с гамильтониана (2.38):
1 N
Н = Но + гН\ = — ^д2 + ^2njAj + еН\, (10.3)
з=1
где
N
eHi = ^riejH[j)(A,P,Q,\,p,q,\j,pj,qj), (10.4)
3 = 1
rtj — орбитальная частота j-ой планеты массы £j, N — число планет в си¬
стеме. Напомним, что все планеты, как предполагается, движутся по фикси¬
рованным кеплеровым эллипсам, поэтому pj, qj можно рассматривать как
параметры1, а действия A j, сопряженные Xj, введены для того, чтобы сде¬
лать гамильтониан независящим от времени.
В предположении, что среднее движение астероида не находится
в двухтельном резонансе со средним движением какой-либо планеты, все
гармоники в (10.4), зависящие от Л, Xj, можно удалить в порядке е пу¬
тем усреднения. Согласно разделу 2.5 в алгоритме Ли усреднение воз¬
мущения Tii по быстрым углам Л, Xj осуществляется путем введения
^чет медленной прецессии pj, qj ничего не изменил бы в дальнейшем анализе. — Прим.
авт.
10.1. Происхождение резонансных членов в возмущении
257
производящего гамильтониана х такого, что
1 N p2ir р2п
<«„, *> + *,= Я, I <<»
dAj, (10.5)
где {/, #} — скобка Пуассона функций fug. Решение уравнения (10.5)
имеет вид
N
ex = Y^£jX(j), (10-6)
3 = 1
где каждая ~ функция только от переменных, относящихся к астероиду
и j-ой планете.
В канонических переменных А1, Р1, Q1, Aj, А1, р1, q1, А] (полусред¬
них модифицированных переменных Делоне), вводимых с помощью ря¬
дов Ли 5£, а именно А = А1,..., А = 5JA1,..., новый гамильтониан
приобретает вид
Л1 = 7Yo + £ (Л\ + {Ло, х}) +
+ £2 ^ а}5 х} + {^i,x}j + 0(е3). (10.7)
По построению, {Ло,х} = Л\ — Л\, поэтому гамильтониан (10.7) можно
переписать как
Л1 = Но + еЛ\ + — ({Лг, х} + {Л\, х}) + 0(е3). (10.8)
Вспоминая выражения для Л\,Л\ и х в (10.4), (10.5) и (10.6), а также
определение скобки Пуассона, сразу находим, что £2{Л\,х) и £2{^ъх}
имеют вид
N N г dFjfT , дХ{к)
ЕЕ
j=1к=1
£з£к^{1^,^з) • -
дТ; dv(fc)
- e3£k~Qj~{Ii ф, <Pj) ■
, (Ю.9)
где через Tj обозначены Ti[3^ или Н^; переменные I и ip — канониче-
ские переменные «действие-угол» для астероида; переменные <pj и (fk —
258
Глава 10
углы j-ой и к-ой планет соответственно; через ^ обозначено скаляр¬
ное произведение двух градиентов. Таким образом, e2{Wi,x} и £2{^i,x}
содержат члены, связывающие переменные j-ой и к-ой планет. Гармо¬
ники, включающие комбинации средних долгот астероида и двух пла¬
нет (относящиеся, таким образом, к трехтельным резонансам), появляют¬
ся в e2{Hi,x}- Их коэффициенты прямо пропорциональны произведению
масс резонансных планет, то есть EjEk-
Чтобы построить нормальную форму трехтельного резонанса до вто¬
рого порядка по массам планет, усредним гамильтониан (10.8) по всем
нерезонансным комбинациям быстрых углов Л1, Aj (j = 1,..., N), остав¬
ляя только вековые и резонансные гармоники. В принципе это требует
введения нового производящего гамильтониана Х2 и новых переменных
(Л2, Р2, Q2, Л2, А2, р2, q2, А2) посредством канонического преобразования
Л1 = 5^ А2,..., А1 = 5£^ А2, — Как обычно (см. раздел 2.5.2), производя¬
щий гамильтониан выбирается так, чтобы
{Wo,X2}+W2=H2, (10-10)'
где Н2 = |({Wi,x} + {^ьХ})> аН2- функция, в которой сохранены
только гармоники Н2 вида
ехр
t(kiX2l 4- к2Х\ -Г кХ2 + TriiPj1 +
+ m2Pj2 + riqjl + r2qh + rap2 + rq2 (10.11)
с целыми k2, /с, либо равными нулю (что соответствует вековым чле¬
нам), либо удовлетворяющими резонансному соотношению + k2rij2 +
+ к/А3 ~ 0, где rij1 и rij2 — средние движения резонансных планет с ин¬
дексами j1 и j2.
10.1.2. Косвенный эффект
Косвенный эффект специфичен для ограниченной задачи, где полага¬
ется, что движение планет описывается известными функциями времени,
и только движение безмассового астероида вычисляется из гамильтоновых
уравнений. Напротив, в планетной задаче, где движение всех тел вычисля¬
ется самосогласованно, исходя из глобального гамильтониана (2.39)), о кос¬
венном эффекте беспокоиться незачем.
10.1. Происхождение резонансных членов в возмущении
259
В предыдущих разделах этой книги, изучая динамику астероидов, мы
всегда предполагали, что планеты движутся по фиксированным кеплеро-
вым орбитам или же по орбитам, медленно прецессирующим согласно ре¬
шению Лагранжа-Лапласа (7.10); в обоих случаях полагалось, что средние
долготы планет являются линейными функциями времени, а все остальные
элементы планетных орбит не испытывают короткопериодических колеба¬
ний. Для изучения трехтельных резонансов этот уровень аппроксимации
недостаточен.
В реальности орбитальные элементы всех планет испытывают корот¬
копериодические колебания из-за взаимных планетных возмущений. Явные
выражения для этих колебаний получаются при построении вековой нор¬
мальной формы планетной задачи, как описано в разделе 2.5.
Косвенный эффект состоит в возмущениях движения астероида, воз¬
никающих из-за короткопериодических колебаний орбитальных элементов
планет. Гамильтониан, учитывающий этот эффект, можно построить путем
подстановки в возмущающую функцию вместо оскулирующих планетных
элементов их выражений через средние элементы. Средние элементы по
определению свободны от короткопериодических колебаний; средние дол¬
готы являются линейными функциями времени. Поэтому получается выра¬
жение, формально эквивалентное (2.38), но с Ai,..., Адг в качестве средних
долгот планет; однако итоговое возмущение Н\ уже нельзя более запи¬
сать как сумму возмущений от отдельных планет. Фактически в результате
проделанной подстановки вводятся гармоники, связывающие средние эле¬
менты планет и имеющие коэффициенты, квадратичные по массам планет.
Среди этих гармоник присутствуют, среди прочих, и относящиеся к лю¬
бому заданному трехтельному резонансу. Для практических целей часто
бывает достаточно рассматривать только короткопериодические колебания
элементов орбиты главного возмущающего тела, то есть Юпитера для пояса
астероидов, а для пояса Койпера — Нептуна.
Далее мы детально рассмотрим процедуру подстановки вместо оску¬
лирующих планетных элементов их выражений через средние элементы,
следуя подходу Несворного и Морбиделли (1999). Чтобы обеспечить явный
и конструктивный алгоритм, этот подход использует разложения в ряды.
Без потери общности мы рассмотрим в возмущающей функции (10.4)
только член относящийся к J-ой планете. Ограничимся для просто¬
ты плоским случаем, то есть положим наклонения орбит астероида и пла¬
нет равными нулю (процедура замены планетных орбитальных элементов
в возмущающих членах, зависящих от наклонений, аналогична описывае¬
мой).
260
Глава 10
(i)
Классическое разложение Лежандра для е^Н\ записывается как
£]Н^ = — ^2 Ри(®)ерер cos (10.12)
Э и
где Фи = kjXj + к\ + IjWj + Ivo (мультииндекс и обозначает набор зна¬
чений целых kj, к, Ц, 1), а = a/aj. Через а3 е, Л, w обозначены большая
полуось, эксцентриситет, средняя долгота и долгота перигелия астероида
соответственно. Индекс j обозначает принадлежность к соответствующей
планете. Благодаря правилам Даламбера kj + к + lj + I = 0, Р = \1\ -Ь 2т
и Pj = \lj\ + 2га, где гга, п — положительные целые числа. Как вычислить
функции Pu(ol) в (10.12), описано в статье Шидлиховского (1990).
Разложение (10.12) содержит оскулирующие элементы рассматривае¬
мой планеты: aj, A j, ej и Wj. Зависимость этих переменных от средних
элементов планетной системы можно записать в следующем виде (см. Бре-
таньон, 1990):
аз — ЩР Х^ соэФ*, + 0(е2),
V
Aj = Aj + ^ Bv sin Фу + 0(г2),
V
e^exp (twj) = ё^ехр (lwj) + Х^ Cv exp (бФ-у) + 0(е2),
V
где Ф^ = rjXj + SjWj + TjXj -f SjWj (мультииндекс v обозначает на¬
бор значений целых rj, r^, Sj, Sj и индекса j ф j). Через cL,-, ej9 Xj
и wj обозначены средние большая полуось, эксцентриситет, средняя дол¬
гота и долгота перигелия j-ой планеты. Напомним, что средняя большая
полуось постоянна, средняя долгота является линейной функцией времени,
а средняя долгота перигелия испытывает лишь вековые изменения. Кон¬
станты Ay, Bv, Cv пропорциональны массе ej j-ой планеты. Символ 0(е2)
обозначает, что пренебрегаемые члены по меньшей мере квадратичны по
массам планет. Если бы мы рассматривали пространственную задачу, то за¬
висимость ijexp(iQj) от средних элементов планет имела бы ту же форму,
что и (10.15).
Выражения (10.13)—(10.15) можно подставить в уравнение (10.12), что
сделает н[^ функцией от средних элементов. Однако возмущающую функ¬
цию следует подвергнуть определенным упрощениям, чтобы записать ее
явно в виде рядов Фурье по косинусам. Подстановки выражений (10.13),
(10.13)
(10.14)
(10.15)
10.1. Происхождение резонансных членов в возмущении
261
(10.14) и (10.15) удобно осуществлять по отдельности, так как они требуют
разных технических процедур.
Подстановка aj
Чтобы подставить (10.13) в (10.12), прежде всего запишем Р(а) как мно¬
гочлен по а:
Р(а) = ^Рпап, (10.16)
П
а затем подставим (10.13) в каждый член:
-(п+1)
(10.17)
= z-an — (га + 1)-^ап Л^совФ^,
ау ау '
J J V
где а = a/aj, а — большая полуось орбиты астероида. Все члены в тейло¬
ровском разложении, по порядку величины равные или меньше, здесь
отброшены, так как они по меньшей мере квадратичны по планетным мас¬
сам.
Подставляя (10.17) в (10.16), имеем
-Р(а) = - У Рпап - Pn(n+l)anY Avcos$v. (10.18)
ау ау z' af zz—'
J J П J п V
При подстановке (10.18) в (10.12) первый член (10.18) дает исходное тей¬
лоровское разложение возмущающей функции, но теперь со средней боль¬
шой полуосью Щ вместо оскулирующей aj. Второй член генерирует новые
гармоники cos cos Ф^ = ^(cos(4/u + Ф^) + cos(4>u — Ф^)) с коэффициен¬
том
(X>(n+l)a^ ерер, (10.19)
квадратичным по массам планет.
Подстановка Xj
Подставляя (10.14) в (10.12), запишем
262
Глава 10
где Re обозначает вещественную часть, а Фи = kjXj + кХ + Ij'coj + Вя. Так
как
exp (ikjBv sin Фу) = Jn(kjBv) exp (тФД
п
где коэффициенты представляют собой функции Бесселя
(_l)r / z\ 2г
(•»»>«).
r^O V '
Jn(z) = (-1 )n J-nO) (если п < 0),
имеем
ехр |^Фи + ^ kjBv sin
= ехр(^Фи) П(Е Jn(kjBv) ехр (тФу) | . (10.20)
V \ п /
Так как коэффициенты Bv пропорциональны массам планет, для (10.20)
можно получить приблизительное выражение, сохранив в Bv только ли¬
нейные члены; тогда
Jo “ 1, Мк3Вь) “ (^), J-i(kjBv) “
и отсюда
ехр [г,(Ф„ + £ ЩВу sin Фу)} = ехр (^Фп) + ^ ехр [г(Фи + Ф„)] -
V V
2 ^ у kjBy ехр [^(Фп Ф^)].
(10.21)
Теперь в (10.12) вместо cos^u подставим вещественную часть (10.21):
первый член в правой части (10.21) дает гармонику cosT^, то есть исход¬
ную гармонику с формальной заменой оскулирующей Xj на среднюю дол¬
готу Л^; а два остальных члена дают гармоники соз(Фп+Фг;) и соз(Фп —Ф^)
с коэффициентами
±^-_kjBvP(a)epep, (10.22)
10.1. Происхождение резонансных членов в возмущении
263
квадратичными по массам планет; здесь знак «плюс» соответствует аргу¬
менту Фи + Фу, а «минус» — аргументу Фи — Фу.
Подстановка ej exp lwj
Прежде всего, используя представление через экспоненциальную функцию
и полагая, что Ij ^ 0, запишем
e?nej exp (djWj) =
ej exp (tvjj) + ^2 Cv exp (бФу)
V
ё^ехр (—LWj) 4- ^ Cv exp (—^Фу)
v
ej exp (twj) + exp (^Фу)
Выполним биномиальное разложение каждого из множителей и учтем толь¬
ко члены, линейные по Cv\ тогда имеем
e?nej exp (djWj) = е?пе^ exp (tljtuj) +
+ ej1 е/ exp (djWj) x
x (n + Ij)ej1 exp {—LWj) ^ Cv exp (^Ф„) + (10.23)
+ nej1 exp (tWj) ^2 Cv exp (—бФу)
Аналогично имеем
02n Ij ( , j r—r \ ^2n — ^j /
eJeJ exP (~Lhwj) = ejnej3 exP +
+ exp (—djWj) x
x (n + lj)ej 1 exp (6G7j) ^ Cv exp (-^Фу) + (10.24)
V
+ nej1 exp (—iWj) ^2 Cv exp (^Фу) .
26.4
Глава 10
Таким образом, сделав подстановки (10.23) и (10.24) в члене 6jJ cos^u
р- - —
из (10.12), мы получаем ё^э cos4/u, где = kjXj + кХ + Ijuij + Izu, (то
есть тот же самый член, но с формальной заменой ej и wj на ёj и Wj) плюс
новые гармоники по — Wj и + zuj. Коэффициенты этих
гармоник соответственно равны
(n + Ij) — СуР(а)ерёр~1 и п—СуР(а)ерёр~1. (10.25)
аз аз
Опять же эти коэффициенты квадратичны по массам планет.
10.1.3. Учет обоих (прямого и косвенного) эффектов
в астероидной задаче
Рассмотрим теперь, как можно учесть оба члена (и косвенный, и пря¬
мой) при построении нормальной резонансной формы для трехтельного
резонанса. Прежде всего, используя рецепт, описанный в разделе 10.1.2,
и вводя модифицированные переменные Делоне (A, Р, Q, А,р, q) для асте¬
роида, запишем возмущение в ограниченной задаче как
N
ёН\ = P,Q, +
3 =1
N
+ ЕЕ £j£k'kC2 (А, Р, А, р, q, Xj, zuj, Qj, Afc, 'CC7д., ^) —1- О(e ),
j=i k^j
(10.26)
где функции — те же, что и в (10.4), но с формальной заменой
Aj,vjj,Vtj на Xj,Wj,£lj, а каждая из функций зависит только от сред¬
них модифицированных переменных Делоне j-ой и к-ой планет. Средние
долготы планет Xj являются линейными функциями времени с частота¬
ми rij. Чтобы упростить обозначения, здесь и далее черточки сверху мы
отбрасываем и средние долготы обозначаем просто как Xj.
Теперь, как обычно, запишем гамильтониан астероидной задачи в ав¬
тономной форме, введя действия A j, сопряженные Xj, и добавив член
Y2j nj^j к интегрируемой части гамильтониана. Тогда гамильтониан асте¬
роидной задачи становится формально тождественным (10.3), за исключе¬
нием того, что здесь добавляется член Yhk^j £j£k'H<2,k^ квадратичный
по массам планет, а также члены более высоких порядков.
10.2. Трехтельные резонансные мультиплеты
265
Усреднение гамильтониана по быстрым углам A, A j в первом порядке
по е проводим так же, как в разделе 10.1.1; в результате до второго порядка
по массам планет имеем
ЕЕ £^£кП{2т, (10.27)
3 =1 кФз
где первые два члена в правой части те же, что и в (10.8). Таким обра¬
зом, возмущающие члены в усредненном гамильтониане во втором поряд¬
ке по массам планет представляют собой просто сумму членов, обуслов¬
ленных прямым эффектом, и членов, обусловленных косвенным эффектом.
Построение нормальной формы для трехтельного резонанса затем можно
выполнить так, как объяснено в конце раздела 10.1.1.
10.2. Трехтельные резонансные мультиплеты
Как только нормальная форма для трехтельного резонанса построена,
далее можно действовать так же, как описано в разделе 9.3 для случая двух-
тельных резонансов средних движений. Вековую прецессию планетных ор¬
бит учитываем, полагая, что средние планетные элементы эволюционируют
согласно решению Лагранжа-Лапласа (7.10), и вводим углы т* = gjt +
-f- (3j и (]• = Sjt + Sj. Чтобы сделать гамильтониан автономным, вводим
действия Agj и ASj9 сопряженные ш* и Щ (j = 1,..., iV), и добавляем
к гамильтониану член Ylj(9jA9j + SjASj).
Таким образом, нормальная форма для трехтельного резонанса k\Xj1 +
+ k,2Xj2 + кХ ~ 0 записывается как
'НЗВК = -^Д2 + П31 А?! + п32^32 +
N
+ + (PiQiT*7* i^l*) + (10.28)
з=i
+ £2H2(kiXjl + k2Xj2 -f kX9vj*9fl*9p9 q),
где rij1 = Xj19 rij2 = Xj2 и, как и в предыдущих главах, через vj* и Г2*
обозначены векторы с компонентами т* и П* соответственно. Функции
Hi и Н2 в (10.28) обе зависят от переменных действия А, Р, Q астероида,
266
Глава 10
а 0,2 можно разложить в ряд Фурье:
7^2 = ^ ^ Cm,u,v,s,r (А, Р, Q) exp (^CTm,u,V,s,r)? (10.29)
m,u,v,s,r
где <7m,u,v,s,r = m(fciA<7-1 +/c2Aj2 + кХ) + u • ш* + v • ft* + sp + rq; m, r, 5 —
целые числа; u = (щ,..., un) и v = (г>1,..., vn) — векторы с целочислен¬
ными компонентами такими, что т(к + ki + fc2) — s — г + Ylj(uj + vj) — 0*
Согласно разделу 9.3 каждый из углов crm)U?v,s,r является независимым
резонансным углом, поэтому трехтельный резонанс расщепляется на муль-
типлет резонансов. Так как коэффициенты резонансных гармоник являются
величинами порядка е2, ширина по большой полуоси у отдельного резонан¬
са в мультиплете составляет ~ е. Разделение резонансов в мультиплете по
большой полуоси пропорционально частотам прецессии вековых углов, по¬
этому оно также должно быть порядка е. Таким образом, можно ожидать,
что для типичного трехтельного резонанса характерно частичное перекры¬
тие субрезонансов в мультиплете. Несворный и Морбиделли (1999) путем
численных расчетов определили мультиплетную структуру некоторых важ¬
нейших трехтельных резонансов в поясе астероидов.
В таблице 10.1 дан список главных гармоник мультиплета резонанса
5Aj — 2As — 2А ~ 0 (далее мы называем его трехтельным резонансом 5-2-2),
где Aj и As — средние движения Юпитера и Сатурна, а А — среднее движе¬
ние астероида. Этот резонанс расположен в поясе астероидов на расстоянии
около 3.17 а. е. от Солнца. В первой колонке таблицы 10.1 дан порядко¬
вый номер гармоники, во второй — комбинация долгот перигелиев +
-1- uqzoq — su7, соответствующая резонансному углу <Ti,(o,...,o,tz5,u6,o...),o,s,o
(далее обозначаемому для простоты как сгП5 U6 _s). В третьей колонке дано
значение большой полуоси ares, при котором угол aU5^U6i-s является в точ¬
ности резонансным с учетом частот прецессии перигелиев. Наконец, в по¬
следней колонке дан коэффициент гармоники c1?(o,...,o,u5,u6,o...),o,s,o (далее
обозначаемый как cU5jU6)_s) в функции эксцентриситета астероида. Вычис¬
ления проведены в рамках плоской задачи, поэтому члены, включающие
наклонения и долготы узлов, не приводятся.
Как видно из таблицы 10.1, доминирующей гармоникой в мультиплете
является первая. Ее резонансный угол равен <7o,o,-i = 5Aj — 2As — 2А —
— w, а слагаемое в коэффициенте этой гармоники, линейное по эксцен¬
триситету, равно 45.59 х 10_8е. Эта гармоника в основном порождается
вкладом ej exp(cwj) косвенного эффекта; говоря более конкретно, большая
10.2. Трехтельные резонансные мультиплеты
267
величина ее коэффициента объясняется благоприятной комбинацией члена
Фу = Xj - 2As + в (10.15) и члена = 4Aj - 2А - wj - zu в (10.12).
Таблица 10.1. Коэффициенты гармоник трехтельного резонанса 5-2-2. (Табли¬
ца 3 из статьи Несворного и Морбиделли, 1999; с разрешения Kluwer Academic
Publishers)
№
Долготы перигелиев
&res 3.17
(10“3 a. e.)
C-U5 ,116, —s
(10 )
1
—ти
5.08
45.59e - 32.24e3
2
-ml
4.33
-2.76 + 0.93e2
3
— Wq
4.44
1.18 - 0.38e2
4
^5 ~ — &
5.19
—3.82e + 2.07e3
5
— 'СОъ + ^6 ~ ^7
4.97
—7.39e - 2.98e3
6
~2zd£ Н- т
3.57
0.15e + 0.73e3
7
—2т$ + т
3.79
О.ОЗе + 0.14e3
8
— ГО5 — Z&Q + ZD
3.68
-0.13e-0.60e3
9
—2zd% -Ь zdq
4.21
0.01 + 0.07e2
10
w% — 2zuq
4.55
0.01
11
ГО5 — 2m
5.83
—23.5e2
12
ZDq — 2 ZD
5.72
23.2e2
13
2 zd 5 — 3zd
6.58
0.64e3
14
2zDq — 3 ZD
6.36
1.42e3
15
ZD5 ZDq — 3ZD
6.47
3.41e3
Структура мультиплета трехтельного резонанса 5-2-2 довольно слож¬
на. Из таблицы 10.1 можно видеть, что мультиплет состоит из субмуль-
типлетов, образуемых почти полностью перекрывающимися резонансами.
Например, резонансы 4 и 5 перекрываются с резонансом 1 (у них почти
равные резонансные значения большой полуоси и к тому же их коэффи¬
циенты единообразно зависят от эксцентриситета астероида). Аналогично,
резонансы 3 и 9 перекрываются с резонансом 2; резонанс 12 перекрыва¬
ется с резонансом 11; резонансы 13 и 14 перекрываются с резонансом 15;
резонансы 7 и 8 перекрываются с резонансом 6. Как мы помним, согласно
разделу 9.4, когда у резонансов разделение гораздо меньше ширины, дина¬
мика подобна динамике модулированного маятника. Таким образом, каж¬
дый из этих субмультиплетов можно рассматривать как резонанс в модели
модулированного маятника.
К тому же эти резонансы, подобные модулированным маятникам, са¬
ми перекрываются; см. рис. 10.1, где изображены сепаратрисы резонансов
1, 2, 11, 15 и 6 (доминирующих компонент субмультиплетов) согласно таб¬
лице 10.1. Это перекрытие следует считать ответственным за общую гло¬
бальную хаотичность трехтельного резонанса 5-2-2. Только при больших
268
Глава 10
(а-3.17) х 10000
Рис. 10.1. Сепаратрисы пяти субрезонансов трехтельного резонанса 5-2-2. (Рис. 2
из статьи Несворного и Морбиделли, 1999; с разрешения Kluwer Academic
Publishers)
эксцентриситетах, где резонанс 1 много шире всех остальных резонансов,
следует ожидать наличия центрального острова устойчивого движения, как
у модулированного маятника типа (9.20) при относительной амплитуде мо¬
дуляции а < 1.
Приблизительное представление о динамике, порождаемой такой
мультиплетной структурой, можно получить путем расчета сечений Пуан¬
каре в упрощенной модели, включающей только две главные гармоники из
приведенных в таблице 10.1. Эта модель дается гамильтонианом
'Н — ~2д2 nj^j + nsAs + 9ъ^дъ +
+ /3е2 + с0,о,-1 cos (Т0,о,-1 + с—i)0)o cos<t_i,0,0. (10.30)
Фактически этот гамильтониан представляет собой упрощенную версию
модели (10.28), где теперь учтены только две гармоники из е2И,2, а вековая
часть еН\ сведена к единственному члену /?е2.
10.2. Трехтельные резонансные мультиплеты
269
4
О■ 0
-4
а 0
-4
-5Е-3 О 5Е-3 О 5Е-3
а - 3.1751 -5Е“3 а - 3.1751
Рис. 10.2. Сечения Пуанкаре модели (10.30) трехтельного резонанса 5-2-2. Боль¬
шая полуось и угол а = cro,o,-i отображаются при т — ml =0. (Рис. 3 из статьи
Несворного и Морбиделли, 1999; с разрешения Kluwer Academic Publishers)
Таблица 10.2. То же, что и в таблице 10.1, но для трехтельного резонанса 6 1-3.
(Таблица 6 из статьи Несворного и Морбиделли, 1999; с разрешения Kluwer
Academic Publishers)
№
Долготы перигелиев
Ures 3.13
(10“3 а. е.)
0^5 )и6, s
(10 )
1
—4т
8.88
—28.45е
2
—т$ — Зт
8.50
10.52е2
3
— Z&q — Зт
8.57
— 16.84е3
4
—2ml — 2т
8.13
—1.28е2
5
—2т q — 2т
8.27
—1.16е2
6
—т§ — т 5 — 2т
8.20
З.ЗЭе2
7
—3т1 — т
7.75
0.07е - 0.20е3
8
—Зт q — т
7.96
—O.Ole3
9
—2т ^ — mQ — т
7.82
—0.22е + 0.43е3
10
—ml — 2т% — т
7.89
0.17е — 0.42е3
На рис. 10.2 показаны сечения Пуанкаре на четырех энергетических
поверхностях; в правом верхнем углу каждой из панелей приведено зна¬
чение эксцентриситета, при котором соответствующая энергетическая по¬
270
Глава 10
4
2
о' 0
-2
-4
-5Е-3 О 5Е-3
а-3.1751
Рис. 10.3. Сглаженная траектория астероида 3460 Ашкова в наложении на сечение
Пуанкаре трехтельного резонанса 5-2-2 при е = 0.2. (Рис. 4 из статьи Несворного
и Морбиделли, 1999; с разрешения Kluwer Academic Publishers)
верхность Н = const (с Н как в (10.30), причем углы положены равны¬
ми нулю) проходит через резонансное значение большой полуоси ares =
= 3.1751 а. е. На таких энергетических поверхностях эксцентриситет при¬
мерно постоянен в принятом на графике интервале значений большой по¬
луоси.
На трех панелях, соответствующих е = 0.05, 0.1 и 0.15, хаос заполняет
почти все резонансное пространство. Только на панели с е = 0.2 относи¬
тельно большую долю фазового пространства занимает регулярная область
в центре, как и можно было ожидать, исходя из того, что при таком зна¬
чении эксцентриситета субрезонанс с углом oo,o,-i почти в два раза шире
субрезонанса с углом сг_10,о (см. рис. 10.1). Разумеется, реальная динами¬
ка гораздо сложнее представленной на рис. 10.2, так как модель (10.30)
является очень упрощенной. Однако интегрирование полных уравнений
движения астероида 3460 Ашкова подтверждает существование квазире-
гулярной области внутри этого трехтельного резонанса при е ~ 0.2. На
рис. 10.3 показана эволюция орбиты астероида Ашкова за 105 лет (причем
короткопериодические колебания эволюции сглажены путем фильтрации),
наложенная на соответствующее сечение Пуанкаре для модели (10.30). От¬
метим, что на данной шкале времени имеется довольно хорошее согласие.
10.2. Трехтельные резонансные мультиплеты
271
(а-3.13) х 10000
Рис. 10.4. Сепаратрисы четырех субрезонансов трехтельного резонанса 6 1-3.
(Рис. 8 из статьи Несворного и Морбиделли, 1999; с разрешения Kluwer Academic
Publishers)
Однако на больших временах орбита астероида Ашкова становится явно
нерегулярной; ее ляпуновское время составляет около 8300 лет.
Перекрытие резонансов в мультиплете ответственно за хаос также
и в большинстве случаев других трехтельных резонансов низкого поряд¬
ка. Несколько дополнительных примеров приведено в статье Несворного
и Морбиделли (1999). Только у резонансов относительно высоких порядков
по эксцентриситету компоненты мультиплета разделяются уже при малом
эксцентриситете.
В качестве примера можно привести трехтельный резонанс 6 1-3 (4-го
порядка по эксцентриситету). В таблице 10.2 даны коэффициенты гармо¬
ник, а на рис. 10.4 изображены сепаратрисы его субрезонансов. Согласно
рис. 10.4 область неперекрытия субрезонансов простирается до е ~ 0.07, то
есть до величины порядка амплитуды вековых колебаний эксцентриситета
астероида, вынуждаемых Юпитером.
272
Глава 10
Если рассматривать трехтельные резонансы все более высокого поряд¬
ка, то ширина у всех резонансных компонент должна убывать, тогда как
расстояние между ними должно оставаться по порядку величины одним
и тем же (так как оно определяется частотами вековой прецессии периге¬
лиев). Поэтому область неперекрытия субрезонансов должна простираться
до еще больших эксцентриситетов, чем наблюдается на рис. 10.4. Следо¬
вательно, динамика трехтельных резонансов очень высоких порядков по
эксцентриситету должна быть в основном регулярной.
10.3. Пояс астероидов и пояс Койпера
Трехтельные резонансы с Юпитером и Сатурном чрезвычайно важ¬
ны для понимания хаотической структуры пояса астероидов. Весьма яс¬
ный пример дает рис. 10.5 (из статьи Мюррея и др., 1998), где показано
ляпуновское время (величина, обратная максимальному показателю Ляпу¬
нова) в функции начального значения большой полуоси во внешней части
пояса астероидов. График на левой панели построен в модели, учитываю¬
щей только возмущения от Юпитера на прецессирующей вековым образом
кеплеровой орбите, а график на правой панели — в модели с учетом и Юпи¬
тера, и Сатурна (а также Урана и Нептуна), взаимодействующих друг с дру¬
гом.
Как уже обсуждалось в разделе 5.2 (см. рис. 5.5), минимумы зависимо¬
сти вычисленного ляпуновского времени от начальных условий выявляют
расположение хаотических областей, а горизонтальные плато, где ляпунов¬
ское время почти постоянно, соответствуют областям, где влияние резонан¬
сов несущественно и динамика поэтому регулярна. Тот факт, что вычислен¬
ное ляпуновское время в этих регулярных областях небесконечно, объясня¬
ется тем, что время интегрирования конечно. Имея в виду эти соображения,
на левой панели рис. 10.5 (то есть в модели с учетом возмущений только
от Юпитера) можно отождествить несколько изолированных хаотических
областей, разделенных интервалами, где движение регулярно. А на правой
панели, то есть в модели, включающей и Сатурн, динамика существенно
хаотична во всем рассматриваемом диапазоне значений большой полуоси.
С точки зрения резонансной структуры эти две модели отличаются друг
от друга тем, что во второй из них есть трехтельные резонансы «Юпитер-
Сатурн - астероид».
Причина столь сильного влияния трехтельных резонансов на хаотиче¬
скую структуру пояса астероидов состоит в том, что они гораздо многочис-
10.3. ПОЯС АСТЕРОИДОВ И ПОЯС КОЙПЕРА
273
Рис. 10.5. Ляпуновское время в зависимости от большой полуоси (во внешней ча¬
сти пояса астероидов). Панель слева: в модели учитываются только возмущения от
Юпитера, причем предполагается, что последний движется по эллиптической ор¬
бите, которая эволюционирует вековым образом согласно (7.10). Панель справа:
в модели учитываются возмущения от всех четырех планет-гигантов, взаимодей¬
ствующих друг с другом; вверху графика отождествлены резонансы средних дви¬
жений с Юпитером, все другие хаотические зоны предположительно соответствуют
трехтельным резонансам. (Рис. 1 и 4 из статьи Мюррея и др., 1998; с разрешения
Американского астрономического общества)
леннее имеющих сравнимую силу обычных резонансов средних движений
с Юпитером, так как включают три частоты средних долгот. Чтобы про¬
демонстрировать это свойство наглядно, на рис. 10.6 отмечены (вертикаль¬
ными линиями) положения как двухтельных, так и трехтельных резонансов
средних движений в диапазоне значений большой полуоси от 2 до 4 а. е.,
покрывающем весь пояс астероидов. Для двухтельных резонансов средних
движений с Юпитером (красные линии) высоты линий определяются фор¬
мулой 10—q, где q — порядок резонанса по эксцентриситету; таким образом,
показаны все резонансы до 9-го порядка включительно. Для трехтельных
резонансов средних движений (синие линии) высоты линий задаются ина¬
че, а именно, как 7 — q. Так сделано, чтобы учесть, что коэффициенты
гармоник трехтельных резонансов квадратичны по массам и что в случае
е = 0.066 масса Сатурна составляет « е3 (в солнечных единицах); други¬
ми словами, при эксцентриситете 0.05-0.10 трехтельный резонанс поряд¬
ка q должен иметь приблизительно ту же силу, что и двухтельный резонанс
с Юпитером порядка q + 3. Использование такого приема при задании вер-
274
Глава 10
большая полуось, а. е.
Рис. 10.6. Расположение резонансов средних движений ZcjAj — кХ ~ Ос kj +к < 20
(жирные красные линии) и трехтельных резонансов fcjAj + feAs + к\ гч> 0 С м +
+ \ks\ + \к\ ^ 20 (тонкие синие линии) в поясе астероидов. Вертикальная шкала
характеризует относительную силу резонансов. (По данным Несворного и Морби¬
делли, 1998; адаптировано)
тикальной шкалы рис. 10.6 позволяет качественно охарактеризовать отно¬
сительную силу резонансов; при этом высокая концентрация трехтельных
резонансов становится очевидной.
В отличие от резонансов средних движений с Юпитером низкого по¬
рядка, настолько мощных, что они выводят астероиды из мест расположе¬
ния резонансов (по причинам, которые будут объяснены в следующей гла¬
ве), трехтельные резонансы не вызывают каких-либо заметных минимумов
в распределении астероидов. Как следствие, большинство хаотичных реаль¬
ных астероидов находится в трехтельных резонансах. На рис. 10.7 показаны
значения большой полуоси, эксцентриситета и наклонения для каждого из
836 астероидов, хаотичность которых была выявлена Фрешле и др. (1997)
в модели с учетом возмущений от четырех планет-гигантов. При постро¬
ении графика использованы собственные элементы Милани и Кнежевича
(1994) либо оскулирующие элементы, если собственные не определены. На
нижней панели показано расположение некоторых важнейших резонансов
средних движений с Юпитером (жирные линии) и трехтельных резонансов
«Юпитер-Сатурн-астероид» (тонкие линии). Высоты этих линий масшта¬
бированы так же, как на рис. 10.6. Чтобы не загромождать график, показана
только часть резонансов, изображенных на рис. 10.6.
10.3. ПОЯС АСТЕРОИДОВ И ПОЯС КОЙПЕРА
275
2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5
а, а. е.
Рис. 10.7. Нумерованные астероиды, сильно хаотичные благодаря возмущениям со
стороны планет-гигантов (согласно Фрешле и др., 1997). Положения важнейших
двухтельных и трехтельных резонансов отмечены вертикальными линиями. Высоты
линий масштабированы как на рис. 10.6. Над каждой линией приведены целочис¬
ленные коэффициенты, характеризующие резонанс: через kj ks к обозначены трех¬
тельные резонансы kjXj + ksXs + кХ ~ 0, а через kj/k — двухтельные резонансы
kjXj — кХ ~ 0. (Рис. 5 из статьи Несворного и Морбиделли, 1998; с разрешения
Американского астрономического общества)
Из графика видно, что хаотичные астероиды в своем большинстве
скапливаются вдоль линий, легко отождествляемых с двухтельными и трех-
тельными резонансами умеренных порядков. Двухтельные резонансы сред¬
них движений 7/2, 10/3, 11/4, 8/3, 9/4, 13/6 (и т. д.) и трехтельные ре¬
зонансы средних движений 4-1-1, 3 1-1, 4-2-1, 5 3-2, 5 2-2, 2 2-1, 4-3-
1, 5 1-2, 3-1-1, 6 2-3, 5-2-2, 5 3-3 (и т. д.), по всей видимости, содер¬
жат большинство хаотичных астероидов главного пояса. Эти очевидные
корреляции были подтверждены Несворным и Морбиделли (1998) путем
анализа фильтрованных (сглаженных) зависимостей резонансных углов от
времени, полученных численным интегрированием на интервале времени
276
Глава 10
105 лет. К трехтельным резонансам были однозначно отнесены 255 асте¬
роидов, а к двухтельным резонансам средних движений с Юпитером — 63.
Так как исходный список из 836 хаотичных астероидов была составлен
Фрешле и др. (1997) на основе анализа динамики первых 5400 нумеро¬
ванных астероидов — числа, составлявшего менее 1/6 от числа всех ка¬
талогизированных астероидов, Несворный и Морбиделли заключили, что
из-за трехтельных резонансов должны быть хаотичными по меньшей мере
1500 реальных астероидов, а из-за резонансов средних движений с Юпи¬
тером — 380.2 Заметим, что эти оценки, должно быть, сильно занижены,
потому что эффективность отождествления (отнесения хаотичного астеро¬
ида к конкретному резонансу) у Несворного и Морбиделли (1998) не пре¬
вышала 50% (318 астероидов, отнесенных к резонансам, из 836), а также
потому, что в работе Фрешле и др. (1997), основанной на расчетах быстрых
индикаторов Ляпунова за время 50000 лет (см. раздел 5.4.1), скорее всего,
были выявлены лишь наиболее хаотичные астероиды. С другой стороны,
отношение 255/63 (числа тел в трехтельных резонансах к числу тел в двух-
тельных резонансах) не должно искажаться в расчетах и поэтому должно
отражать реальное положение дел в поясе астероидов.
Как видно из рис. 10.7, большинство хаотичных астероидов сконцен¬
трировано в области между 3.1 а. е. и 3.25 а. е. при е > 0.1; при этом в отли¬
чие от ситуации в других частях пояса в данной области они не скапливают¬
ся четко вдоль прямых а ~ const. Динамику в этой области детально изу¬
чили Несворный и Морбиделли (1998). Сплошная кривая на рис. 10.8 по¬
казывает зависимость максимального показателя Ляпунова (МПЛ) от боль¬
шой полуоси; эта зависимость построена по результатам интегрирования
орбит пробных частиц с учетом возмущений от четырех планет-гигантов
(время интегрирования 2 млн лет). Нижняя, средняя и верхняя панели от¬
носятся к астероидам с начальным эксцентриситетом, равным 0.05, 0.15
и 0.25 соответственно. Пунктирные кривые показывают относительное из¬
менение частоты долготы перигелия астероида за время 1 млн лет. Соглас¬
но главе 5 расчеты МПЛ и частотный анализ дают взаимодополняющую
информацию: МПЛ характеризует уровень хаотичности, а относительное
изменение частоты долготы перигелия — скорость хаотической диффузии
в пространстве частот. Напомним, что в обоих случаях наличие плато на
2Согласно современным данным, полученным на основе выборки, состоящей из ~ 250000
астероидов, в существенных трехтельных резонансах находится примерно 1 % всех астеро¬
идов (Smirnov Е. A., Shevchenko 1.1. (2013) Massive identification of asteroids in three-body
resonances. Icarus, 222, 220). — Прим. ред.
10.3. ПОЯС АСТЕРОИДОВ И ПОЯС КОЙПЕРА
277
а, а. е.
Рис. 10.8. Показатель Ляпунова (сплошная кривая) и относительное изменение ча¬
стоты долготы перигелия астероида (пунктирная кривая) в зависимости от большой
полуоси при трех значениях эксцентриситета. В данном диапазоне по большой по¬
луоси есть много хаотичных астероидов. (Рис. 6 из статьи Несворного и Морбидел¬
ли, 1998; с разрешения Американского астрономического общества)
278
Глава 10
Таблица 10.3. Численные характеристики трехтельных резонансов в поясе астерои¬
дов. Первая колонка: тройка чисел Zcj, /cs, к, обозначающая резонанс kjXj +ks As +
+ кХ — 0. Вторая колонка: каталожный номер резонансного астероида, для кото¬
рого приведена информация в последующих колонках (согласно результатам инте¬
грирования за время 2 х 105 лет): собственный эксцентриситет ер, среднее значе¬
ние ас и амплитуда осцилляций 8а большой полуоси, типичный период Т этих ос¬
цилляций. Последний обычно равен по порядку величины ляпуновскому времени.
Поскольку динамика большинства астероидов в трехтельных резонансах хаотична,
данные в последних двух колонках точны лишь по порядку величины. (Таблица 1
из статьи Несворного и Морбиделли, 1998; с разрешения Американского астроно¬
мического общества)
Резонанс
Астероид
Ср
Ас
(а. е.)
да
(1(Г3 а. е.)
Т
(103 лет)
4-1-1
2440
0.1113
2.2157
0.6
50
4-2-1
463
0.1795
2.3977
3.0
— 10
7-2-2
1966
0.1241
2.4476
0.6
-30
7-3-2
1430
0.1741
2.5599
0.5
-30
2+2-1
258
0.1687
2.6155
0.7
-20
6-1-2
53
0.2092
2.6190
-1.0
35
4-3-1
792
0.1604
2.6230
2.5
25
7-4-2
789
0.1471
2.6857
0.5
20
3-1-1
485
0.1958
2.7525
3.0
15
4-4-1
22
0.0881
2.9095
-1.0
-50
5-1-2
576
0.1758
2.9860
2.0
20
3-2-1
2395
0.0690
3.0790
4.0
10
6+1-3
936
0.1540
3.1385
0.4
10
8-4-3
10
0.1347
3.1418
0.5
-30
3+3-2
106
0.1466
3.1708
-2.0
—
5-2-2
490
0.0652
3.1738
4.0
10
7-2-3
530
0.1937
3.2080
<8.0
12
графиках говорит о гладкой зависимости индикатора от начальных усло¬
вий, присущей областям, где нет существенных резонансов, а пики вы¬
являют присутствие хаотических областей. Из рис. 10.8 видно, что рас¬
положение последних хорошо коррелирует с расположением резонансов
средних движений с Юпитером высоких порядков и трехтельных резонан¬
сов «Юпитер-Сатурн-астероид». С увеличением эксцентриситета хаоти¬
ческие области становятся шире (так как всем этим резонансам отвечают
гармоники, в коэффициенты которых входят е в положительных степенях),
к тому же появляются новые пики, относящиеся к резонансам высоких по¬
рядков, несущественным при малых е. Как следствие, начиная се~ 0.15,
хаотические области перекрываются, превращая эту часть пояса астерои¬
дов в глобально-хаотичную. Это объясняет, почему хаотичные астероиды
не скапливаются вдоль четко выраженных прямых. Отметим, что данное
10.3. Пояс астероидов и пояс Койпера
279
пороговое значение эксцентриситета, при котором происходит глобальное
перекрытие резонансов, гораздо ниже, чем порог, следующий из рис. 9.12,
так как в работе Дермотта и Мюррея (1983) не учитывались резонансы
с Юпитером высоких порядков, а также, что еще существеннее, и трех-
тельные резонансы с Юпитером и Сатурном. В таблице 10.3 представлена
компиляция свойств наиболее важных трехтельных резонансов в главном
поясе астероидов.
о
00
CD
<м
°35 40 45 50 55 60 65 70
большая полуось, а. е.
Рис. 10.9. То же, что и на рис. 10.6, но для резонансов средних движений с Непту¬
ном (красные линии) и трехтельных резонансов с Ураном и Нептуном (синие линии)
в поясе Койпера
В поясе Койпера самыми важными трехтельными резонансами являют¬
ся резонансы средних движений с Ураном и Нептуном. На рис. 10.9 (ана¬
логе рис. 10.6, построенном для пояса Койпера) представлены главные ре¬
зонансы средних движений с Нептуном и трехтельные резонансы с Ураном
и Нептуном в области от 35 до 70 а. е. Масса Урана меньше массы Сатур¬
на, поэтому теперь у синих линий высоты выбраны равными 6 — q (вместо
7 — q в случае рис. 10.6), где q — порядок по эксцентриситету у соответ¬
ствующего резонанса. Ситуация аналогична имеющей место в главном по¬
ясе астероидов: «плотность населения» по большой полуоси у трехтельных
резонансов гораздо выше, чем у обычных двухтельных резонансов сопоста¬
вимой силы, особенно вне 45 а. е. Поэтому, как будет подробно разъяснено
в главе 12, изучение трехтельных резонансов чрезвычайно важно для объяс¬
280
Глава 10
нения глобальной динамической структуры пояса Койпера и характеристик
его долговременной устойчивости. К сожалению, пока объектов пояса Кой¬
пера открыто немного и орбитальные элементы у открытых определены
неточно, поэтому сейчас нельзя оценить, какая доля реального населения
пояса Койпера хаотична из-за трехтельных резонансов.
10.4. Хаотическая динамика планет-гигантов
Согласно главе 7 вековая динамика планет земной группы сильно ха¬
отична, тогда как вековой динамике планет-гигантов свойственна лишь
очень слабая хаотичность, вызываемая взаимодействием с планетами зем¬
ной группы. Следовательно, если бы планет земной группы не было, то
система планет-гигантов сама по себе была бы регулярной (по крайней ме¬
ре с точки зрения вековой динамики).
Тем не менее Зюссман и Уиздом (1992) из проведенного ими чис¬
ленного интегрирования нашли, что показатель Ляпунова системы планет-
гигантов больше нуля. Однако этот результат никогда не подчеркивался,
поскольку вычисленный показатель Ляпунова странным образом зависел от
шага интегрирования и от начальных условий. Кроме того, Зюссман и Уиз¬
дом не смогли отождествить резонанс, ответственный за происхождение
хаоса. Фактически планеты-гиганты не находятся в каких-либо двухтель¬
ных резонансах средних движений, даже очень высоких порядков. Хорошо
известно, что Юпитер и Сатурн близки к резонансу 5/2, Уран и Нептун —
к резонансу 2/1, а Юпитер и Уран — к резонансу 7/1, но во всех этих слу¬
чаях резонансные углы циркулируют, то есть на самом деле эти планеты не
находятся в резонансах.
Недавно Мюррей и Хольман (1999) показали, что в системе планет-
гигантов имеется два трехтельных резонансных соотношения:
3Aj — 5As — 7Аи ~ 0 и 3As — 5Аи ~ 7An ~ 0, (10.31)
где Aj, As, Ац, An — средние движения Юпитера, Сатурна, Урана и Нептуна
соответственно. Эти резонансы не могли быть обнаружены Ласкаром (1985)
из расчетов вековой нормальной формы, так как соответствующие им резо¬
нансные члены появляются во втором порядке по планетным массам и в 9-
ом порядке по эксцентриситету, то есть за пределами имевшихся вычисли¬
тельных возможностей. Согласно оценке Мюррея и Хольмана, у первого из
резонансов (10.31) коэффициенты гармоник в уравнениях движения Урана
10.4. Хаотическая динамика планет-гигантов
281
являются величинами порядка 10 12 (в системе единиц с QMq = a\j = 1),
а у второго они меньше на фактор
~ (£n/£j) • [(5As — 2Aj)/(2An — Аи)] ~3x 10“3.
1
CQ
Dh
m
<u
§
au, a. e.
au, a. e.
Рис. 10.10. Ляпуновское время в зависимости от начального значения большой по¬
луоси Урана аи. См. комментарии в тексте. (Рис. 1 и 2 из статьи Мюррея и Холь-
мана, 1999; с разрешения Американской ассоциации за научный прогресс)
Чтобы понять в деталях сложную динамическую структуру системы
планет-гигантов, Мюррей и Хольман провели обзорный численный экспе¬
римент, в котором начальные значения элементов планетных орбит были
фиксированы, исключая начальное значение большой полуоси Урана аи,
которое варьировалось в диапазоне от 18.9789 до 19.3990 а. е. Для каждого
множества начальных условий было проведено интегрирование движения
на интервале времени 200 млн лет и вычислено ляпуновское время. На
левой панели рис. 10.10 показана полученная зависимость вычисленного
ляпуновского времени от начального значения аи- Область сильного хао¬
са, простирающаяся до 19.13 а. е., обусловлена резонансом 2/1 с Нептуном.
Она перекрывается с хаотической областью, порождаемой резонансом 1/7
с Юпитером на интервале 19.13-19.17 а. е. Трехтельными резонансами по¬
рождены хаотические области с центрами при аи = 19.219, 19.26, 19.29
и 19.34 а. е. Современное значение большой полуоси орбиты Урана (со¬
гласно эфемеридам DE200 JPL NASA) отмечено на рисунке вертикальной
прямой. На правой панели рис. 10.10 дан крупный план графика в окрест¬
ности этого значения. При аи < 19.218 а. е. можно различить узкие ха¬
282
Глава 10
отические области, порождаемые субрезонансами трехтельного резонанса
3Aj — 5As — 7Аи ~ 0; друг от друга их отделяют узкие регулярные об¬
ласти. Говоря конкретно, на интервале от 19.216 до 19.218 а. е. Мюррей
и Хольман отождествили субрезонансы с критическими углами 3A.j — 5As —
— 7Аи + qvo5 + 7wq + (2 — q)wj с различными целыми q. На отрезке
19.218 ^ a\j ^ 19.22 а. е. субрезонансы, напротив, частично перекрыва¬
ются, так что почти все орбиты хаотичны, то есть имеют конечное ляпу-
новское время. Критические углы этих субрезонансов равны 3Aj — 5Ag —
— 7Аи + + (3 — q)voj. Проявляют себя также некоторые субре¬
зонансы трехтельного резонанса 3Ag — 5Аи — 7An ~ 0, а именно субрезо¬
нансы с критическими углами ЗАу — 5Аи — 7An + 7+ (2 — q)w7 + Не¬
любопытно, что в настоящее время Уран находится в том единственном
месте внутри интервала 19.218-19.22 а. е., где субрезонансы полностью не
перекрываются. Это объясняет весьма сильную зависимость вычисленных
значений ляпуновского времени от начальных условий и от аппроксимаций
при интегрировании, обнаруженную Зюссманом и Уиздомом (1988).
Погрешность определения современного значения большой полуоси
орбиты Урана составляет 6 х 10-6 а. е., тогда как диаметр этой планеты
~ 1СГ4 а. е. Поэтому невозможно прийти к заключению, каково реальное
ляпуновское время Урана и какой именно субрезонанс в действительно¬
сти влияет на его движение. Тем не менее результаты Мюррея и Хольмана
не оставляют места для сомнений относительно важной роли трехтельных
резонансов в динамике планет-гигантов. Используя некоторую динамиче¬
скую модель (которую мы опишем далее в главе 12), Мюррей и Хольман
пришли к выводу, что благодаря хаотичности орбиты Урана ее эксцентри¬
ситет может возрастать до значения, при котором она начинает пересекать
орбиту Сатурна; однако для этого требуется время не менее 1018 лет, что
на 8 порядков превышает физическое время жизни Солнца. Таким образом,
система планет-гигантов является практически устойчивой.
Глава 11
Вековая динамика внутри резонансов
средних движений
11.1. Последовательное исключение гармоник
Как мы уже убедились в главе 9, резонансы средних движений низкого
порядка с планетой имеют в первом приближении динамическую структу¬
ру, типичную для модулированного маятника: имеется центральная область
«регулярного» движения, окруженная хаотическим слоем. Цель этой главы
состоит в изучении динамики внутри этой центральной области на масшта¬
бах времени много больше периода либраций внутри резонанса средних
движений. При этом необходимо также полностью учесть вековую часть
возмущения (9.17). Таким образом, мы приходим к изучению резонансов
внутри резонанса (или даже резонансов внутри резонанса внутри резонан¬
са, как в случае Плутона), то есть сильно нелинейной динамики.
Согласно главе 4 исключение зависимости от углов в резонансном
гамильтониане даже в интегрируемом случае не может быть достигнуто
посредством алгоритма Ли. Однако это можно сделать, введя переменные
«действие-угол» по Арнольду. В этих переменных интегрируемый резо¬
нансный гамильтониан записывается как функция исключительно перемен¬
ных действия и поэтому его можно использовать как стартовую основу
для дальнейшего изучения динамики. Таким образом, исследование зада¬
чи об иерархическом взаимодействии нескольких резонансов требует уже
введения последовательности преобразований к подходящим переменным
«действие-угол» по Арнольду. Использование переменных Арнольда в та¬
ких задачах позволяет нам вновь применить восходящий к Делоне (1867)
пертурбационный подход, основанный на последовательном исключении
гармоник возмущения вплоть до заданного порядка.
284
Глава И
Принцип алгоритма прост. Рассмотрим гамильтониан и разло¬
жим его в ряд Фурье
п = Но(Т) + ^2 ^m(I) exp (Ш1 • <р). (11-1)
ш
Затем выберем одну гармонику, например с индексом ш; и кратные ей
и рассмотрим неполный гамильтониан
Tim = Wo(I) + ^2 ^т(1) exp (i/cm • <р). (11.2)
fee z
Поскольку этот гамильтониан интегрируем, введем переменные «дей¬
ствие-угол» по Арнольду 3,ф, чтобы записать его как функцию новых
действий, то есть 7Yq(J); при этом вошедшие в (11.2) гармоники будут
полностью исключены. Запишем остаток
п= ^2 hm(T) exp(im • ip) (11.3)
m/fcm,/c£Z
в новых переменных J, ф и разложим его в ряд Фурье по новым углам ф:
^2 ^т(^) exp (im • ф). (11.4)
m/fcm,fc6Z
Новый гамильтониан Wq(J) + 7£(J, ф) формально эквивалентен (11.1); сле¬
довательно, чтобы исключить все главные гармоники, алгоритм можно ите¬
рировать (как показано на рис. 11.1).
Этот простой на первый взгляд алгоритм имеет ряд концептуаль¬
ных трудностей. Первая трудность касается последовательности, в которой
должны исключаться гармоники. Опыт подсказывает, что для эффективно¬
го и работоспособного приложения на практике необходимо на каждой ите¬
рации исключать ту гармонику, которая оказывает наиболее существенное
влияние на динамику переменных действия; в общем случае это гармоника,
имеющая среди резонансных гармоник наибольший коэффициент, обычно
ей также соответствует самая малая временная шкала либраций (так как
последняя обратно пропорциональна корню квадратному из коэффициента
гармоники; см. раздел 4.1). Если две гармоники резонансны в различных
частях пространства действий, то безразлично, какую из них исключать
первой. В следующем разделе мы увидим, что при применении данного
11.1. Последовательное исключение гармоник
285
Рис. 11.1. Эскиз алгоритма последовательного исключения гармоник путем введе¬
ния переменных «действие-угол» по Арнольду (см. текст)
алгоритма к динамике резонансов средних движений подходящая последо¬
вательность исключения гармоник возникает естественным образом.
Вторая концептуальная трудность состоит в том, что при исключении
резонансной гармоники переменные «действие-угол» по Арнольду вводят¬
ся не глобально по всему фазовому пространству (см. раздел 4.2). Фактиче¬
ски алгоритм задает фрагментацию фазового пространства на несвязанные
друг с другом области в соответствии с сепаратрисами рассматриваемого
резонанса. В областях либрации и циркуляций резонансного угла вводят¬
ся различные переменные «действие-угол», что приводит к определению
различных новых гамильтонианов Wq(J) -f 7£(J, г/>), своего для каждой об¬
ласти. Это отражает тот реальный факт, что динамика внутри резонанса
радикально отлична от динамики вне его. Таким образом, новые гамильто¬
нианы определяются на областях действий J внутри хорошо определенных
границ, задаваемых сепаратрисами предварительно исключенного резонан¬
са. Когда рассматривается новая гармоника, действия J уже не являют¬
ся более постоянными, поэтому некоторые траектории начинают пересе¬
кать границы своей области действий. Очевидно, что для этих траекторий
невозможно ввести новые переменные «действие-угол» по Арнольду, так
что алгоритм последовательного исключения гармоник нельзя итерировать.
Как следствие, наш алгоритм не позволяет исследовать области фазового
286
Глава 11
пространства вблизи сепаратрис резонансов. Однако это нельзя назвать его
дефектом, поскольку данные области фазового пространства должны со¬
ответствовать хаотическим областям (возникающим, как нам известно из
главы 4, в окрестности сепаратрис интегрируемого резонансного прибли¬
жения при введении возмущения).
Третья концептуальная трудность состоит в том, что уже исключен¬
ные гармоники появляются, вообще говоря, вновь в процессе выполнения
алгоритма, когда исключаются другие гармоники. Однако в предположе¬
нии, что исходный гамильтониан аналитичен и имеет квазиинтегрируемую
форму (2.1), легко показать, что исключенные гармоники могут появляться
вновь только с коэффициентами много меньшими, чем исходные. В этом
смысле метод последовательного исключения гармоник можно рассматри¬
вать как подлинно пертурбационный подход. Морбиделли и Джиорджилли
(1993) доказали, что если параметр возмущения достаточно мал, то алго¬
ритм сходится на множестве КАМ-торов.
Последняя трудность связана с технической реализацией алгоритма.
Как отмечено в разделе 4.2, весьма трудно, если вообще возможно, запи¬
сать гамильтониан Hq(J) в явном виде. С другой стороны, на каждом торе
J = const можно вычислить гамильтониан, его производные, а также оста¬
ток 7£(J, ф) и его разложение в ряд Фурье, используя получисленную про¬
цедуру. Таким образом, алгоритм последовательного исключения гармоник
можно реализовывать, вычисляя значения нового гамильтониана на сетке
в пространстве действий на каждой итерации. Гамильтонов поток затем
вычисляется в каждой требуемой точке фазового пространства с помощью
интерполяционного алгоритма. Данная техника практической реализации
алгоритма детально разъяснена в работе Морбиделли (19936) на нетриви¬
альном примере.
Опираясь на описанный алгоритм последовательного исключения гар¬
моник, мы можем теперь, используя структурный подход, исследовать
сложную динамику внутри резонансов средних движений низкого порядка.
11.2. Динамическая система с резонансами
средних движений
В качестве отправного пункта для изучения резонанса средних дви¬
жений kjXj — кХ ~ 0 между астероидом и J-ой планетой (при fcj ^ к)
мы возьмем гамильтониан (9.15). Напомним, что (9.15) представляет собой
неупрощенную нормальную форму резонанса средних движений, в которой
11.2. Динамическая система с резонансами средних движений 287
учтено также и вековое движение возмущающих планет. На первом шаге
процесса последовательного исключения гармоник требуется найти инте¬
грируемую аппроксимацию динамики. Согласно разделу 9.4, если у астеро¬
ида наклонение не слишком велико, а эксцентриситет существенно больше,
чем у планет, то резонансная гармоника с углом
доминирует в резонансном мультиплете, имея большую ширину, чем все
другие гармоники. Поэтому интегрируемую аппроксимацию На мы опре¬
делим, сохранив из возмущения Н\ в (9.15) только эту гармонику и крат¬
ные ей:
где ТСо дается формулой (9.7), а в сохранены все возмущающие члены,
не зависящие от углов, отличных от <т.
Здесь имеется трудность, вызванная тем, что фурье-разложение Н\
в (9.15) не сходится, если эксцентриситет астероида достаточно велик, так
что допускаются сближения с резонансной планетой при некоторых зна¬
чениях сг (см. раздел 9.1.1). В таком случае функцию Та все же можно
вычислить при всех значениях сг, не допускающих столкновений, запи¬
сав Н\ в виде функции переменных (9.5) без использования разложений
в ряд и усреднив ее по az, ъэ* и 17*. Локальное численное оценивание
Н\ и его производных без разложений в ряды можно осуществить, следуя
Ферраз-Мелло и Сато (1989) и Муне (1993, 1994).
Гамильтониан (11.5) формально эквивалентен гамильтониану плоской
круговой ограниченной задачи, однако в (9.4) полагалось Sz = 0, тогда как
теперь Та параметрически зависит от значения Sz (константы движения
для (11.5)). Напомним, что Sz сильно зависит от наклонения.
Коль скоро гамильтониан (11.5) интегрируем, введем переменные
«действие-угол» по Арнольду. Согласно разделу 4.2 преобразование имеет
вид
(kj — к)а = kjXj — кХ + (kj — к)р
На — Hq(Aj, N,S,SZ) + ^^(gjA9j + sjASj) +
з
+ £Fa(S, (kj - k)a, N, Sz), (11.5)
(11.6)
Фг — & z 9г(Фа, Ja,Jz,Jv), Jz — ^5
Фи = V Qvi^Pa, Ja , Jz, Jv), Jv ~ N,
288
Глава 11
где в первой строке в сокращенной записи приведено соотношение из раз¬
дела 4.2, связывающее исходные (5, сг) и новые (Ja^a) переменные «дей¬
ствие-угол», а функции gz и ди являются периодическими с нулевым сред¬
ним ПО фа.
Поскольку нас интересует динамика внутри резонанса средних движе¬
ний, вычислим расположение сепаратрис H.G в пространстве (<т, 5, SZ,N)
и введем переменные (11.6) только для траекторий внутри сепаратрис; то¬
гда \Та \ — период либрации, a Ja — нормированная площадь области, огра¬
ниченной либрирующей траекторией на плоскости (5, сг).1
Когда о либрирует около некоторого значения сг0, зависимость сг от фа
имеет вид сг = сг0 + я(Фа), где д — периодическая функция с нулевым
средним. Таким образом, из (9.5) вытекает, что az = сг0 + д(фсг) — V + Q —
= сг0 + д(фа)+ои и v = — сг0 — д(фа)-\-р = — <то — д{Фа) — Вспоминая, что
функции gz и д„ в (11.6) — также периодические с нулевым средним по фсг,
приходим к выводу, что фг и —фу можно отождествить соответственно
с аргументом перигелия и долготой перигелия астероида, усредненными за
период либрации на резонансе и смещенными на сг0.
Как функция от переменных (11.6), гамильтониан На зависит только'
от переменных действия, то есть
'На = '^2(9j^9j + sj^Sj) + СП Jzi Jv)' (H-7)
j
Переменные (11.6) войдут также в ту часть исходного возмущения, которая
не была включена в (11.5), а именно в
П\-Та= Т\(Фа,Ф^Ф1»ТЯ* М* ,Ja,JZ,Jv)- (П-8)
Поскольку (11.7) зависит только от переменных действия, частоты
• _дТо : _дТо J _дТ0 niQv
~ dja ’ ~ djz ’ ~ djv ( }
зависят только от (Jz, Ju) и поэтому постоянны. Следовательно, мы мо¬
жем теперь обратиться к другим возможным резонансам, чтобы решить,
1 Как эскизно показано на рис. 9.3, в резонансах первого порядка по эксцентриситету
угол сг может циркулировать на некоторых резонансных траекториях, однако переменные
«действие-угол» и в таком случае можно ввести по формулам (11.6), где под \Та\ теперь
понимается период цикла на плоскости (S', сг). Согласно соглашению, принятому в разде¬
ле 4.2, Та положителен у внешних резонансов (так как в них либрация на плоскости (сг, S)
происходит по часовой стрелке) и отрицателен у внутренних резонансов. — Прим. авт.
11.2. Динамическая система с резонансами средних движений 289
какую из гармоник Т\ следует рассмотреть на следующем шаге исследова¬
ния.
Отметим, что как только расположение резонансов определено в про¬
странстве (JCT, Л,Л), его можно легко определить и в пространстве
(а, е,г), используя сечение при а = сто- Процедура эквивалентна приме¬
нявшейся в главе 9 для построения сепаратрис резонанса средних движе¬
ний на плоскости (а, е). Фактически значения трех действий Ja,Sz,N
определяют на плоскости (5, сг) цикл, вдоль которого S принимает два
значения Si и S2, соответствующие сг = сг0. Используя (9.5) и опреде¬
ление (1.69) модифицированных переменных Делоне, преобразуем мно¬
жества значений (S\,SZ,N) и (S2,SZ,N) соответственно во множества
(ai, ei, zi) и (a2, б2,22) по обе стороны относительно центра резонанса.
11.2.1. Вторичные резонансы
Термин вторичный резонанс ввели Леметр и Анрар (1990) для обозна¬
чения резонанса между частотой угла фа и частотой комбинации вековых
углов, чья соответствующая гармоника проявляется в (11.8).
В задаче с учетом наклонения орбиты астероида имеется одно семей¬
ство вторичных резонансов, чьи гармоники удовлетворяют второму прави¬
лу Даламбера (см. раздел 1.9.3) и имеют коэффициенты, не зависящие от
планетных эксцентриситетов и наклонений. Это семейство отвечает соиз¬
меримостям
тфа + 2пфг = 0 (11.10)
с целыми тип. Поскольку фг — средняя частота аргумента перигелия со,
это семейство соответствует резонансам между периодом либрации угла о
и периодом циркуляции угла со.
Если учитывать также гармоники, чьи коэффициенты являются сте¬
пенями планетных эксцентриситетов и наклонений, то появляется много
других вторичных резонансов. Среди них выделим два семейства, соответ¬
ствующие соизмеримостям
тфа + пффу + gj) = 0 (11.11)
и
тфа + п(фг + фу + Sj) = 0. (11.12)
Поскольку фы равно средней частоте угла — w, первое семейство соответ¬
ствует соизмеримостям между периодом либрации на резонансе средних
290
Глава И
движений и периодом циркуляции угла w — w*, а второе — соизмеримо¬
стям между периодом либрации на резонансе средних движений и перио¬
дом циркуляции угла Q — Q*. В других семействах вторичные резонансы
включают комбинации перигелиев и узлов.
a/aj
Рис. 11.2. Расположение важнейших резонансов внутри соизмеримости 3/1. Двумя
очень жирными линиями по краям графика нанесены сепаратрисы резонанса 3/1
при сг = 90°. Внутри резонанса 3/1 жирными сплошными линиями показано распо¬
ложение вековых резонансов 1/5 и жирными прерывистыми линиями — вековых
резонансов и Козаи; тонкой сплошной линией — векового резонанса ди + дв +
+ 2,dz = 0; тонкой пунктирной линией — вторичного резонанса фа + 5(фи +дв) = 0
(она окаймляет область, затронутую вторичными резонансами вида (11.11) порядка
не выше пяти); тонкими прерывистыми линиями показано расположение трехтель¬
ных резонансов 2фа + 3(/?js + 9фи = 0 и Зфа + 3^js + 9— 0 (при большем
и меньшем эксцентриситетах соответственно). Напомним, что для внутренних ре¬
зонансов фа- < 0.
Согласно определению вторичного резонанса, вековые углы в них
должны циркулировать с периодом, по порядку величины равным периоду
либрации на резонансе средних движений; следовательно, вторичные резо¬
нансы как правило располагаются в областях, где нет вековых резонансов
низкого порядка, и поэтому доминируют в локальной динамике. Для этих
областей в общем характерны значения эксцентриситета от низких до уме¬
ренных. В качестве примера на рис. 11.2 показана (тонкой пунктирной ли¬
11.2. Динамическая система с резонансами средних движений 291
нией) верхняя граница области, затронутой резонансами семейства (11.11)
с m = 1 и п ^ 5, внутри резонанса 3/1 с Юпитером; все эти резонансы
расположены при е < 0.1. См. также рис. 11.10, 11.17 и 11.18, где показано
расположение вторичных резонансов внутри резонансов 2/1 и 3/2 с Юпи¬
тером и внутри резонанса 2/3 с Нептуном соответственно.
Как явствует из указанных рисунков, вторичные резонансы, как прави¬
ло, сконцентрированы в узкой области. Следовательно, довольно бессмыс¬
ленно пытаться последовательно исключать их соответствующие гармони¬
ки или развивать модели одиночного резонанса для описания их динами¬
ки. Эффективней будет выбрать семейство вторичных резонансов, скажем,
заданное соотношением (11.11) при фиксированном j, и вернуться к ис¬
ходному гамильтониану (9.15), записанному в переменных (9.5), сохранив
в нем все гармоники, зависящие от а и/или от v + ш*. Таким путем мы
получим систему с двумя степенями свободы вида
'Нам = Но{&э, N, S, Sz)+gjAgj+£j:r(T'l/(S, (kj-k)a, N, v+w*, Sz), (11.13)
которую можно исследовать с помощью сечений Пуанкаре. В качестве при¬
мера на рис. 11.3 показаны сечения Пуанкаре системы (11.13) (на шести
энергетических уровнях) для резонанса 2/1 с Юпитером в предположении,
что Юпитер движется по фиксированной эллиптической орбите (д7 = 0
в 'Нам)• Как видим, вторичные резонансы перекрываются, создавая хаоти¬
ческий слой, который простирается по эксцентриситету примерно от 0.10
до 0.15. При большем эксцентриситете движение, как видно из сечений,
регулярно, поскольку вторичные резонансы низкого порядка отсутствуют
(см. рис. 11.10). Аналогичный анализ можно провести для каждого из
семейств вторичных резонансов и таким путем получить представление
о протяженности хаотических областей, порождаемых этими резонансами.
11.2.2. Динамика Козаи
В областях, где нет вторичных резонансов низкого порядка, в динами¬
ке доминируют вековые гармоники, а именно гармоники не зависящие
от ipa. Если в (11.8) пренебречь членами, зависящими от то гамильто¬
ниан, описывающий вековую динамику внутри резонанса средних движе¬
ний, примет вид
T^sec — + SjASj) + Jz, Ju) +
j
+ Ja, Jz, Jv), (11.14)
292
Глава 11
-0.2 -0.1 0.0 “оа 0.2
ecos U
•I
-1Й- н
73%.,« «. .«-1 I,
-0.2 -0.1 0.0 0.1 0.2
ecos и
%
■| ' ?4 } ч.'гГг\.га_£Т^-Т,|.ТГ1 >|-т1
■ ^ С- 4%
• *-•л. А-Л/Д <, - . < Л г». У:,.. У
ь,\ л>^
жтжт.
<М
О '
/Ж
**Vj ’I
•ft1
А* :]\
cn ;
?■
-че
4
-0.2 -0.1 0.0 0.1 0.2
ecos и
-0.2 -0.1 0.0 0.1 0.2
ecos и
-0.2 -0.1 0.0 0.1 0.2
ecos и
Рис. 11.3. Сечения Пуанкаре системы (11.13) при сг = 0, <т < 0. Полагается, что
Юпитер движется по фиксированной эллиптической орбите с эксцентриситетом,
равным 0.0485. На каждой из панелей амплитуда либрации на резонансе 2/1 равна
нулю для самой внутренней орбиты и возрастает с увеличением эксцентрисите¬
та. (Рис. 6 из статьи Муне и Морбиделли, 1993; с разрешения Kluwer Academic
Publishers)
11.2. Динамическая система с резонансами средних движений 293
а
Рис. 11.4. Вековая динамика внутри резонанса 3/1 с Юпитером на плоскости (а, е)
при г = 0°. Тремя очень жирными линями обозначены сепаратрисы и центр резо¬
нанса. Пары пунктирных кривых, симметричные относительно центра резонанса,
обозначают множества (а, е), соответствующие Ja = const при а — 90°. Жирными
сплошными и прерывистыми линиями показано расположение резонансов v$ и vq,
соответственно. Пара тонких сплошных линий и пара тонких прерывистых линий
обозначают сепаратрисы этих двух вековых резонансов. Единицей измерения по
абсциссе служит величина большой полуоси орбиты Юпитера. (Рис. 6 из статьи
Муне и Морбиделли, 1995; с разрешения Academic Press)
где Т\ — среднее от Т\ по фа. Действие Ja является константой движе¬
ния системы (11.14). На рис. 11.4 для резонанса 3/1 с Юпитером показа¬
ны множества (а, е), соответствующие Ja = const при i = 0 и а = 90°
(значение для центра либраций). Пары пунктирных кривых, симметричные
относительно центра резонанса, соответствуют фиксированным значениям
Ja = const. От г вид этих кривых зависит слабо. Как видим, сохранение Ja
в ходе вековой эволюции эксцентриситета означает, что амплитуда колеба¬
ний большой полуоси (но не а\) остается почти постоянной. Парам пунк¬
тирных кривых, отстоящих на рис. 11.4 все дальше и дальше от центра ре¬
зонанса, отвечают возрастающие значения Ja. В противоположном пределе
Ja — 0 эти пары кривых стягиваются к кривой, отвечающей центру резо¬
нанса; действительно, Ja = 0 соответствует орбитам в точке устойчивого
294
Глава 11
равновесия резонанса средних движений. Если исследование вековой дина¬
мики ограничить случаем Ja = 0 (см., например, Иошикава, 1990, 1991), то
преобразование (11.6) для фг и фи становится тождественным, а гамильто¬
ниан (11.14) получается просто из исходного (9.15) подстановкой а = сг0
и А = А*(SZ,N), где A*(SZ,N) — значение Л в точке устойчивого равно¬
весия системы (11.5), которое слабо зависит от Sz и N.
Каким бы ни было значение Ja, гамильтониан (11.14) неинтегрируем,
поскольку он зависит от нескольких углов. Для исследования его динамики
требуется, как и выше, иерархическое рассмотрение его главных гармони¬
ческих членов. Благодаря правилам Даламбера все гармоники, зависящие
от ф„, vj* , Г2*, должны иметь коэффициенты, представляющие собой степе¬
ни планетных эксцентриситетов и наклонений; последние в общем случае
меньше, чем эксцентриситет и наклонение орбиты астероида. Таким обра¬
зом, как и в вековой задаче вне резонансов средних движений (см. главу 8),
ведущей гармонической частью гамильтониана будет та, которая зависит
только от аргумента перигелия, то есть от фг в координатах (11.6). Факти¬
чески эти гармоники — единственные, у которых коэффициенты ненулевые,
когда планетные эксцентриситеты и наклонения все равны нулю.
Поэтому следующим шагом процесса исключения гармоник будет ис¬
ключение членов, зависящих от фг. С этой целью, прежде всего, запишем
WsEC — + sj^Sj) + PFq + Tz + [T\ — PFZ), (11.15)
j
где Tz — среднее от T\ по ш*, Г2*;2 затем рассмотрим гамильтониан
7~tz — + sj^*j ) + Jzi Jv) + J<7', Jzi Jis), (11.16)
который интегрируем, поскольку зависит только от одного угла (ф2). Га¬
мильтониан (11.16) эквивалентен гамильтониану Козаи (8.16), но в данном
случае он описывает вековую динамику внутри резонанса средних движе¬
ний.
В динамике (11.16) сохраняется постоянным действие = N. На
поверхности в пространстве (а, е, г), определяемой равенствами Ja = const
и cr = ст0,3 условие Jy = const задает соотношение между эксцентриситетом
2Благодаря правилам Даламбера угол т/v исчезает при усреднении по vj* и ft*. В прене¬
брежении членами порядка (ej,ij)2 среднее по хи* и П* получается просто подстановкой
e-j = i j = 0 в Т\. — Прим. авт.
3 Первое из них во многих случаях можно аппроксимировать как а = const, чтобы облег¬
чить практические вычисления. — Прим. авт.
11.2. Динамическая система с резонансами средних движений 295
г cos из г cos из г cos из
Рис. 11.5. Типичные динамические портреты системы (11.16) для трех значений
постоянного действия Ju при Ja — 0. Координаты Jz, ipz конвертированы в на¬
клонение г и аргумент перигелия из. (Рис. 5 из статьи Морбиделли и Муне, 1993;
с разрешения Academic Press)
и наклонением; оно представлено на рис. 11.6 (для резонанса 2/1 средних
движений с Юпитером) пунктирными кривыми. Эксцентриситет и накло¬
нение благодаря этому соотношению испытывают связанные осцилляции,
коррелирующие с изменениями Jz^z- Эволюцию Jz, фг легко представить
наглядно путем построения кривых уровня гамильтониана (11.16) с Ja и Ju
в роли параметров. В качестве примера на рис. 11.5 построены кривые
уровня для резонанса 2/1 с Юпитером в случае Ja = 0 для трех значе¬
ний J„. Когда Ju достаточно велико, мы видим типичный резонансный
портрет; таким образом, внутри резонанса 2/1 средних движений с Юпи¬
тером присутствует эквивалент резонанса Козаи. Данное свойство присуще
и многим другим резонансам средних движений (см. Джеффрис и Стэн-
диш, 1972). Заметим, что движение 7г-периодично по фг, так как благодаря
правилам Даламбера гамильтониан (11.16) может иметь только гармони¬
ки ехр[ьтфг\ с четными т. Обозначим через ф® значение фг для одной
из точек устойчивого равновесия; сепаратриса резонанса Козаи пересека¬
ет ось фг = ф{] при двух значениях Jz (скажем, и ji2^), зависящих
от J,y. Вспоминая, что Jz = Sz и = TV, можно конвертировать значения
(Jzl\jy), Jv) и (j¥\Jv),Jv) в (ei(N),ii(N)) и (e2(N),i2(N)) на поверх¬
ности, соответствующей рассматриваемому значению Ja. Таким образом
получается изображение сепаратрис резонанса Козаи на плоскости «экс¬
центриситет-наклонение». Такую же процедуру можно осуществить и для
семейств устойчивых и неустойчивых точек равновесия системы (11.16).
На рис. 11.6 приведен пример такого графика, опять же для случая резо¬
нанса 2/1.
296
Глава И
о
ZO
о
0.2
0.4
0.6
0.8
е
Рис. 11.6. Вековая динамика в центре резонанса 2/1 (Ja = 0). Пунктирными кри¬
выми обозначены множества (е, г), соответствующие Jv = const. Тонкой сплошной
линией обозначено устойчивое семейство точек равновесия аргумента перигелия
(ф2 = 90°, 270°); прерывистой линией — неустойчивое семейство (фг = 0°, 180°).
Двумя жирными линями обозначены сепаратрисы резонанса Козаи, вычисленные
при фг = 90°. (Рис. 6 из статьи Морбиделли и Муне, 1993; с разрешения Academic
Press)
Далее, в каждой динамической области системы (11.16) (а именно,
в областях прямой циркуляции, обратной циркуляции, либрации фг) можно
ввести переменные «действие-угол»:
(здесь использованы те же условные обозначения, что и в (11.6)); тогда Ttz
будет зависеть только от переменных действия:
(11.17)
до = Vv - ^(^,©<7,02,0^), ©<7 = J<T,
= Фи ~ qU^z,&<t,Qz,&u), @v = J„
Hz = + SjASj) + /Co(@cr, ©2, ©i/). (11.18)
j
11.2. Динамическая система с резонансами средних движений 297
Если к новым переменным (11.17) перейти в члене /Ci = Т\ — Tz, которым
мы пренебрегли, то полный вековой гамильтониан (11.15) примет вид
Wsec = МЛ9., ASj, в*, ©Z, 0„) + tiv, «Л П*, Qa, &z, ©„).
(11.19)
«Невозмущенные» частоты гамильтониана (11.19) суть
^ =^о =^° ■д (1120)
dQa’ a©z’ ^ a©, -ZUj
наряду с планетными вековыми частотами gj и 5j. Знание этих частот поз¬
воляет локализовать резонансы, соответствующие гармоникам /Сь Среди
таких резонансов мы выделим два семейства.
(i) Перигелийные вековые резонансы отвечают соотношениям тду +
+ Yhj mj9j ~ 0» где т = Ylj mj согласно правилам Даламбера; факти¬
чески достаточно заметить, что преобразование от фу к^ в (11.17) близко
к тождественному, а также вспомнить, что —фу представляет собой среднее
значение долготы перигелия w астероида на периоде либрации о. Вековые
резонансы bv + gj ~ 0 будут детально рассмотрены (для случаев главных
частот д§ и до) в разделе 11.2.3.
(ii) Узловые вековые резонансы. Если фг циркулирует, то преобразование от
фг к dz в (11.17) близко к тождественному; поскольку фг представляет со¬
бой среднее значение аргумента перигелия на периоде либрации сг, узловые
вековые резонансы задаются соотношениями т(^2 + $„) + Yhj mjsj ~
где опять же т = J2j mj' ® разделе 11.2.4 мы рассмотрим резонанс dz +
+ + Sq ~ 0 внутри резонансов средних движений в поясе астероидов,
а также резонанс bz + + s% ~ 0 в поясе Койпера. В области либрации фг
узловые вековые резонансы задаются соотношениями mdu + rrijSj ~ 0.
Однако могут проявлять себя и многие другие вековые резонансы; на¬
пример, Плутон, находящийся в резонансе Козаи внутри резонанса средних
движений 2/3 с Нептуном, пребывает также и в резонансе между периодом
либрации фг и периодом циркуляции Щ (Милани и др., 1989).
Когда расположение резонансов в пространстве (0a50z?0i/) опреде¬
лено, его образ в пространстве (а, е, г) можно вычислить, применяя сле¬
дующую процедуру: вначале вычисляем значение Jz, соответствующее 0Z
при ф2 = ф®9 а затем преобразуем полученные значения (</г, Jv = 0^,
Ja = ©ст) в значения (а, е,г), как описано выше для случая сепаратрис
резонанса Козаи.
298
Глава 11
Заметим, что если ограничиться плоской задачей, то у всех гармоник
с ф2 в (11.16) коэффициенты будут равны нулю, поскольку они по мень¬
шей мере квадратичны по наклонению орбиты астероида. Таким образом,
преобразование (11.17) становится тождественным по всем переменным,
а гамильтониан (11.19) будет тождествен (11.14). Это позволяет упростить
вычислительную процедуру, но, с другой стороны, радикально ограничи¬
вает применимость результатов плоскостью г = 0. Для случая ненулевого
наклонения Иошикава (1990, 1991) упростил изложенную выше процедуру
путем усреднения (11.14) по фг и аппроксимации преобразования (11.17)
тождественным преобразованием; так он получил гамильтониан, формаль¬
но эквивалентный (11.19), но применимый лишь в области, где фг быстро
циркулирует и вызывает пренебрежимо малые осцилляции Sz. Поскольку
резонанс Козаи пересекает плоскость i = 0 при больших эксцентриситетах
(см. рис. 11.6, 11.9, 11.19), результаты Иошикавы справедливы только при
малых и умеренных значениях е.
11.2.3. Перигелийные вековые резонансы
На рис. 11.2, 11.10 и 11.17 показано расположение резонансов +
+ 05 = 0 и bv + 06 = 0 (также называемых г/5 и соответственно) при
i = 0 внутри резонансов средних движений 3/1, 2/1 и 3/2 в поясе астеро¬
идов. Согласно главе 8 вне резонансов средних движений данные вековые
резонансы проявляются только при больших наклонениях (за исключени¬
ем резонанса щ при а ~ 2.0-2.1 а.е.). Поэтому вековая динамика внутри
и вне резонансов средних движений совершенно разная. Эту особенность
вырожденной динамики можно хорошо уяснить, используя подход на ос¬
нове последовательного исключения гармоник: как обсуждалось в разде¬
ле 11.1, переменные «действие-угол» по Арнольду, вводимые в областях
циркуляций и либрации сг, совершенно разные, как и получающиеся веко¬
вые гамильтонианы.
Аналогично, на рис. 11.18 показано, как резонанс $„ + д$ = 0 (также
называемый щ) располагается внутри резонанса 2/3 с Нептуном в поясе
Койпера.
Чтобы исследовать резонанс вида + gj ~ 0, выделим в (11.19) гар¬
монику члена /Ci с аргументом сг? = <du + w* и рассмотрим интегрируемую
модель
nj = gj\gi+KQ{e<r,ez,eu) + K{{Qa,es,eu,aj), (11.21)
11.2. Динамическая система с резонансами средних движений 299
где функция К{ — среднее от К\ по всем углам, кроме ^ + zu*. В динами¬
ке (11.21) сохраняются постоянными Оа и 02; одно лишь 0^ = N эволю¬
ционирует, следуя циркуляции/либрации угла оу. Как обычно, динамику N
и aj можно описать с помощью кривых уровня гамильтониана (11.21), с 0а
и @z в роли параметров. В качестве примера на рис. 11.7 показана динамика
резонанса + #5 = 0 для четырех значений 0СТ и 02 = 0 внутри резонанса
средних движений 3/1 с Юпитером. Как видим, на фазовом портрете имеет¬
ся огромный остров либраций, охватывающий почти всю плоскость (А/, <75)
(кроме случая очень больших 0^, как на нижней правой панели). Это озна¬
чает, что вековая динамика резонанса 3/1 на плоскости г — 0 определяется
резонансом 1/5.
На панелях рис. 11.7, как обычно, верхняя граница N дается услови¬
ем е ~ 1. Поэтому те кривые, которые мы видим исходящими из верхних
границ панелей, отвечают траекториям, достигающим е ~ 1 в ходе своей
вековой эволюции; следовательно, астероиды на таких орбитах в итоге па¬
дают на поверхность Солнца. Нижней же границе по оси N соответствует
значение, которое совместно с заданным ©а = Ja определяет сепаратри¬
су (11.5). Как видно из рис. 11.4, кривые Ja = const внутри резонанса опре¬
делены только при достаточно больших эксцентриситетах, а именно при 7V,
больших некоторого нижнего порогового значения. Поэтому все те кривые,
которые мы видим исходящими из нижних границ панелей рис. 11.7, от¬
вечают траекториям, которые в ходе своей вековой эволюции пересекают
сепаратрису резонанса средних движений и поэтому должны быть хаоти¬
ческими. Однако заметим, что в нашем подходе к проблеме мы не учли
обсуждавшейся в разделе 9.4 модуляции амплитуды резонанса, вызывае¬
мой эволюцией вековых углов; фактически действие Ja было введено для
гамильтониана (11.5), в котором нет вековых углов, и при последующем
анализе это действие считалось константой.
Сепаратрисы, окружающие главный остров либраций (см. рис. 11.7),
можно представить в пространстве (а, е,г), используя процедуру, эквива¬
лентную обсуждавшейся выше для случая сепаратрис резонанса Козаи.
Вначале обозначим через а® значение aj для точки устойчивого равновесия
в центре острова; затем вычислим значения 0^ и ©[,2\ соответствующие
пересечениям сепаратрис с осью aj = а®. Разумеется, эти значения за¬
висят от ©сг и 02. Таким путем мы получаем представление сепаратрис
в пространстве (0а, 02,0^) и затем преобразуем его, как объяснено в раз¬
деле 11.2.2, в представление в пространстве (а, е,г).
300
Глава 11
q q
Рис. 11.7. Кривые уровня гамильтониана (11.21) для резонанса внутри соизме¬
римости 3/1. Значения Оа увеличиваются при переходе от панели к панели слева
направо и сверху вниз; эти значения соответствуют парам пунктирных кривых на
рис. 11.4. Через q обозначена величина w — а N = ©„ = у/а(3 — у/1 — е2).
В центре резонанса 3/1 значения N =1.4, 1.5, 1.6, 1.7, 1.8, 1.9 соответствуют значе¬
ниям эксцентриситета е =0.20, 0.55, 0.72, 0.84, 0.92, 0.97 соответственно. (Рис. 7 из
статьи Муне и Морбиделли, 1995; с разрешения Academic Press)
В каждой из относящихся к вековому резонансу областей циркуляций
и либрации можно ввести новые переменные «действие-угол» по Арнольду
Г£, Г^, Г£, 7^, 7^, 7^, чтобы исключить гармонику резонанса т?*, + д$ = 0.
Подобное исследование можно провести и для вековых резонансов,
включающих другие собственные частоты gj планетных перигелиев. В слу¬
чае резонансов средних движений в поясе астероидов следует рассмотреть
11.2. Динамическая система с резонансами средних движений 301
Рис. 11.8. Сечения динамики системы (11.22), вычисленные при <т6 = 0. Четырем
панелям соответствуют те же значения Оа, что и на рис. 11.7. Координаты q и N
имеют тот же смысл, что и на рис. 11.7. См. комментарии в тексте. (Рис. 7 из статьи
Муне и Морбиделли, 1995; с разрешения Academic Press)
по меньшей мере резонансы с д$ и д^, а в поясе Койпера важнейшим явля¬
ется резонанс с д%. На рис. 11.4 показаны сепаратрисы резонансов г/5 и щ
внутри резонанса средних движений 3/1 с Юпитером (см. также рис. 11.16,
где показана динамика в резонансе средних движений 3/2). Как видим, эти
вековые резонансы оба очень широкие и полностью перекрываются. Со¬
гласно главе 6 при сильном перекрытии резонансов следует ожидать в ос¬
новном хаотической динамики. Чтобы оценить ширину хаотической обла¬
сти внутри резонанса средних движений, возникающей из-за перекрытия
вековых резонансов и щ, можно построить двухрезонансную модель,
302
Глава 11
оставив в (11.19) гармоники с аргументами <75 = и <7б = +
+ w6' Практически мы рассматриваем гамильтониан
^5,6 = 9Ь^дь + 9б^д6 + /Со(©а? ©25 ©i/) +^i’6(0CT, ©2, 0„, <Т5, (Тб) (11.22)
в обозначениях (11.21). Этот гамильтониан неинтегрируем, поэтому опи¬
сываемую им динамику следует изучать численными методами. Ее мож¬
но представить на плоскости (05, 0^); например, посредством сечения при
сг6 = 0. Это не настоящее сечение Пуанкаре, так как угол сгб может либ-
рировать или циркулировать в обоих направлениях; но тем не менее оно
позволяет отделить регулярное поведение от хаотического. Чтобы постро¬
ить настоящее сечение Пуанкаре, надо задать = <75 -1- zu§ — Ше- и строить
сечение при некотором фиксированном — zn£. На рис. 11.8 показано се¬
чение по <7б динамики (11.22) для резонанса 3/1; используются те же зна¬
чения ©а, что и на рис. 11.7, и опять же Oz = 0. Отличие от рис. 11.7
впечатляет: большая часть фазового пространства является хаотической.
Как впервые показали Морбиделли и Муне (1993) и Муне и Морбиделли
(1995), такая ситуация типична для всех главных резонансов средних дви¬
жений с Юпитером в поясе астероидов; единственным различием является
протяженность областей хаоса.
В регулярной области, не затронутой хаотическим слоем, порождае¬
мым перекрытием резонансов и щ, можно ввести переменные «дей¬
ствие-угол», в которых гамильтониан становится в низком порядке неза¬
висимым от углов и Wq. Это делается за два шага: сначала вводим
переменные «действие-угол» Г®,Г^,Г^,7^,7^,7^, чтобы исключить гар¬
монику по + ^75, а затем вводим новые переменные «действие-угол»
Г®,Г®,Г®,7®,7®,7®, чтобы исключить гармонику по 7^ +
11.2.4. Узловые вековые резонансы
На рис. 11.2, 11.10 и 11.17 показано расположение резонанса dz + +
-f Sq = 0 (также называемого v\б) на плоскости г — 0 внутри резонан¬
сов средних движений 3/1, 2/1 и 3/2 в поясе астероидов. Аналогично, на
рис. 11.18 показано расположение резонанса bz + bv + sg = 0 (также назы¬
ваемого vi8) внутри резонанса 2/3 с Нептуном в поясе Койпера.
Чтобы исследовать резонанс вида dz + + sq ~ 0, мы выделим
в (11.19) гармонику члена JCi с аргументом qj = rdz+,dv + Q,* и рассмотрим
интегрируемую модель
~ Sj^Sj + ^о(©0-5 @25 ©I/) + fci (©0-5 ©25 ©1/5 Qj)-
(11.23)
11.2. Динамическая система с резонансами средних движений 303
е
Рис. 11.9. Вековая динамика в центре резонанса 3/2. Пунктирными кривыми обо¬
значены множества (е, г), соответствующие ©' = const. Жирной сплошной кривой
обозначена левая сепаратриса резонанса Козаи. Жирная прерывистая и тонкие пре¬
рывистые кривые обозначают соответственно центр и сепаратрисы векового резо¬
нанса 1/16. Точками показаны Тильды в координатах «оскулирующий эксцентриси¬
тет - оскулирующее наклонение». (Рис. 14 из статьи Морбиделли и Муне, 1993;
с разрешения Academic Press)
Функция JC{ представляет собой среднее от /Сi по всем углам, кроме +
+ + Щ. В динамике (11.23) сохраняются постоянными @а и ©' = @z —
— 0^, тогда как Qz (а поэтому и ©„) эволюционирует, следуя циркуля¬
ции/либрации угла qj.
Условие ©' = const можно преобразовать в соотношение между г и е
на поверхности, определяемой значением 0СТ и равенством а = сто, при¬
меняя следующую процедуру: для каждого значения ©z и ©„ = ©2 — ©'
вычисляем сначала значение Jz, соответствующее ©z при ipz = гр®, а. затем
преобразуем получающиеся значения (Jz, Ju = ©„) в (е, г), как объясне¬
но в разделе 11.2.2 для случая сепаратрис резонанса Козаи. На рис. 11.9
показано несколько кривых ©' = const на плоскости (е, г), определяемой
условием Qa = 0, для случая резонанса средних движений 3/2 с Юпи¬
тером. На этих кривых эксцентриситет почти постоянен, то есть узловой
вековой резонанс воздействует главным образом на наклонение астероида,
как и ожидалось.
304
Глава 11
Вековую эволюцию Qz и qj можно описать с помощью кривых уров¬
ня (11.23) с 0а и ©', играющими роль параметров (процедура аналогична
разъясненной в разделе 11.2.3 для случая перигелийных резонансов). Так¬
же можно вычислить экстремальные значения ©i1^ и ©12\ принимаемые
02 на сепаратрисах рассматриваемого векового резонанса. Множество зна¬
чений (©1Х\ ©*, = ©i1^ — ©') и (©12\ = ©i2^ — ©') можно преобразовать
в значения е и г на поверхности, определяемой значением ©а и равенством
а — сто, получая, таким образом, представление сепаратрис векового резо¬
нанса, подобное показанному на рис. 11.9.
Как обычно, в каждой из областей либрации и циркуляций векового
резонанса можно ввести новые переменные «действие-угол», чтобы исклю¬
чить рассматриваемую резонансную гармонику.
11.2.5. Трехтельные резонансы
То, что внутри двухтельных резонансов средних движений существу¬
ют и играют важную роль трехтельные резонансы, не так давно было вы¬
яснено Ферраз-Мелло с соавторами в серии работ (Ферраз-Мелло, 1996;
Ферраз-Мелло и др., 1997; Мищенко и Ферраз-Мелло, 1997; Несворный
и Ферраз-Мелло, 19976; Ферраз-Мелло и др., 1998а). Это соизмеримости
между частотой ipa и частотой квазирезонансной комбинации средних дол¬
гот двух планет, обычно 2Aj — 5As для пояса астероидов и Аи — 2An для
пояса Койпера, где Aj, As, Аи, An — средние движения Юпитера, Сатур¬
на, Урана и Нептуна соответственно. Эти резонансы можно рассматривать
как результат перекрытия резонансов средних движений с двумя разными
планетами в том случае, когда один резонанс гораздо сильнее другого. Ис¬
пользование термина «трехтельный резонанс» в данной ситуации не вполне
уместно; фактически далее будет показано, что коэффициенты соответству¬
ющих гармоник линейны по планетным массам, тогда как у «истинных»
трехтельных резонансов коэффициенты квадратичны (см. главу 10).
Для пояснения рассмотрим конкретный случай резонанса средних дви¬
жений 2/1 с Юпитером; так как разность 2Aj — 5As мала (соответствующий
период ~ 880 лет), астероид также близок и к резонансу средних движе¬
ний 5/1 с Сатурном. Поэтому при построении нормальной формы для резо¬
нанса 2/1 с Юпитером нельзя путем усреднения исключить в (2.38) гармо¬
ники с аргументами т(5As — АН ), где т — целое число, а через много¬
точие обозначены комбинации вековых углов, удовлетворяющие правилам
Даламбера. Коэффициенты этих гармоник пропорциональны £seae^si^i^s,
11.2. Динамическая система с резонансами средних движений 305
где £s — масса Сатурна в солнечных единицах; е, г, es, is — эксцентриси¬
теты и наклонения астероида и Сатурна; причем а + as + Р + Дз ^ 4га.
Так как эксцентриситет и наклонение Сатурна малы, гармониками с наи¬
большими коэффициентами будут такие, у которых as = /3s = 0. Если
наклонение астероида является умеренным, то для всякого га доминиру¬
ющей будет гармоника с аргументом m(5As — А — 4ш). Ее коэффициент
пропорционален £$е4гп. Разумеется, можно записать и так:
m(5As — А — 4w) —
= m(2Aj — А — w) + m(5As — 2Aj) — Зггш7 = та + mpjs — Smw,
(11.24)
где </?js — так называемый угол большого неравенства 5As — 2Aj.
Поскольку коэффициенты этих доминирующих гармоник гораздо
меньше коэффициента главной гармоники, относящейся к резонансу 2/1
с Юпитером, их влияние можно исследовать, используя характерный для
этой главы иерархически-пертурбационный подход. (Противоположный
случай, когда резонансы с двумя планетами имеют сравнимую силу, был
рассмотрен в разделе 9.2.2.) Сначала вводятся переменные (11.6) для ре¬
зонанса 2/1 с Юпитером. Тогда каждая гармоника с аргументом (11.24)
порождает ряд, состоящий из гармоник с аргументами
пфа- + тр JS + 3 тфи (11.25)
(где п С Z) и с коэффициентами, экспоненциально убывающими с |п|.
Для каждого резонанса вида пфа ~ трjg, таким образом, в возмущающей
функции существуют соответствующие ему гармоники с непренебрежимо
малыми коэффициентами.
Так как обычно эти члены тем не менее довольно малы, в процессе по¬
следовательного исключения гармоник анализ трехтельных резонансов ло¬
гично следует после рассмотрения главных вековых членов. При введении
переменных «действие-угол» Г£, Г^, Г£, 7^, 7^, 7^ для регулярных траекто¬
рий вне перигелийного векового резонанса с планетной частотой gj каждая
гармоника (11.25) порождает мультиплет гармоник с аргументами
+ трjs + (3m + k)jl + kw*, к е Z , (11.26)
где 7^ и 7^ — новые углы, «близкие» к фа и фу ~ — w соответственно.
Интуитивно это можно понять из следующих соображений: использова¬
ние данных новых переменных, по сути дела, эквивалентно тому, чтобы
306
Глава 11
положить, что эксцентриситет астероида имеет вековые осцилляции вида
е = во + 6 cos(w — w*); подставляя это выражение в член e4m cos(ni/v +
+ — 3тш), мы получаем гармоники с аргументами п^а + mcpjg —
— (3m + к) w + kzu* (где —4m ^ к ^ 4т), соответствующими аргументам
в (11.26). Фактически эти гармоники уже присутствуют в прямом возмуще¬
нии от Сатурна (с коэффициентами порядка вековые осцил¬
ляции эксцентриситета астероида порождают их вновь с коэффициентами
не меньше величин порядка ese^17 Так как амплитуда S в общем
случае много больше, чем эксцентриситет Сатурна es, косвенный эффект,
производимый вековыми осцилляциями эксцентриситета астероида, сильно
доминирует относительно прямого эффекта эксцентриситета Сатурна.
На рис. 11.10 показано расположение на плоскости г = 0 резонансов
с критическими углами фа + 2y?js - (6 — k)zu — kwl и фа + (/?JS — (3 —
— k)w — kwl для резонанса 2/1 с Юпитером. Оно рассчитано с исполь¬
зованием частот, задаваемых формулами (11.9). Как видим, эти резонансы
формируют очень плотную сеть, покрывающую почти всю резонансную
область соизмеримости 2/1. Хотя, взятые по отдельности, эти резонансы
слабы, их кумулятивное воздействие может быть достаточно существен¬
ным, чтобы хаотизировать области, не подверженные влиянию заметных
вторичных и вековых резонансов.
Роль трехтельных резонансов внутри двухтельных резонансов средних
движений не была до сих пор детально исследована с использованием ана¬
литических или полуаналитических моделей. Исключительно с помощью
численного интегрирования было показано (см., например, Ферраз-Мелло
и др., 1998а), что при внесении возмущений со стороны Сатурна дина¬
мика может хаотизироваться, причем сила хаоса зависит от частоты угла
большого неравенства (эту частоту можно варьировать, слегка изменяя ор¬
биту Сатурна). С другой стороны, как мы знаем из главы 6, очень трудно
выяснить аналитически, является ли данная система квазирегулярной или
полностью хаотической, когда в ней есть много узких резонансов высоко¬
го порядка. В таких случаях, чтобы достичь четкого понимания реальной
динамической структуры системы, следует прибегать к численным инстру¬
ментам, например к описанным в главе 5.
11.3. Важнейшие резонансы в главном поясе астероидов
В этом разделе мы обсудим современные представления о динамике
внутри наиболее важных резонансов средних движений с Юпитером в по-
11.3. Важнейшие резонансы в главном поясе астероидов
307
Рис. 11.10. Расположение важнейших резонансов внутри соизмеримости 2/1. Двумя
очень жирными линиями обозначены сепаратрисы резонанса 2/1 при сг = 0°. Жир¬
ными сплошными линиями показано расположение вековых резонансов v$ и uq,
жирными прерывистыми линиями — вековых резонансов v\q и Козаи (как и на
рис. 11.2). Тонкими пунктирными линиями показано расположение вторичных резо¬
нансов фа +п(фи+дь) = 0 (п = 2,..., 5), тонкими прерывистыми линиями — трех¬
тельных резонансов фа + 2<pjs — (6 — k)zu — kgs (к растет от 0 до 6 с уменьшением
эксцентриситета), тонкими штрихпунктирными линиями — трехтельных резонансов
Фа + Фзб — (3 — к)т — kgs (к убывает от 0 до —4 с увеличением эксцентриситета).
Напомним, что для внутренних резонансов фа < 0.
ясе астероидов. В качестве исторического обзора эволюции этих представ¬
лений рекомендуем статью Му не (1997).
11.3.1. Резонанс 3/1
Резонанс 3/1 средних движений с Юпитером при а ~ 2.5 а. е. соответ¬
ствует одному из наиболее явных люков Кирквуда в поясе астероидов.
Вторичные резонансы не играют заметной роли в динамике внутри
резонанса 3/1, поскольку они присутствуют лишь при малых эксцентриси¬
308
Глава 11
тетах (е < 0.1, см. рис. 11.2). Поэтому причину возникновения люка 3/1
следует искать в вековой динамике. Несмотря на то что центр резонанса
расположен при большом эксцентриситете (е ~ 0.8, см. рис. 11.4), этот ре¬
зонанс определяет вековую динамику при всех значениях е (см. рис. 11.7).
Как следствие, у орбит астероидов в резонансе 3/1 имеются большие веко¬
вые колебания эксцентриситета, что вынуждает их время от времени пере¬
секать орбиты внутренних планет.
0.4
0.3
е
0.2
0.1
0.0
0.0 0.2 0.4 0.6 0.8 1.0
t/tmax
Рис. 11.11. Временная эволюция эксцентриситета орбиты астероида в резонансе 3/1
в плоской эллиптической ограниченной задаче; орбита вычислена с помощью сим-
плектического отображения Уиздома. (Рис. 13 из статьи Уиздома, 1982; с разреше¬
ния Американского астрономического общества)
Впервые этот феномен обнаружил Уиздом (1982) (см. рис. 11.11) в чис¬
ленных экспериментах с использованием отображения, которое можно счи¬
тать прародителем симплектического интегратора в смешанных перемен¬
ных (Уиздом и Хольман, 1991). Позднее Уиздом (1985) дал объяснение это¬
му наблюдаемому феномену, предложив полуаналитическую теорию. Под¬
ход Уиздома аналогичен обсуждавшемуся выше в разделе 11.2.3, однако
им была учтена вековая модуляция сепаратрис резонанса 3/1; кроме то¬
го, поскольку эта теория была основана на разложениях в ряды, область
ее применимости отвечала лишь низким и умеренным эксцентриситетам
(см. комментированный обзор теории Уиздома в статье Анрара и Карани-
11.3. Важнейшие резонансы в главном поясе астероидов
309
х
Рис. 11.12. Вековое движение в резонансе 3/1 при одном из значений усреднен¬
ного гамильтониана плоской эллиптической задачи трех тел. Координаты по осям:
х = ecos(iu—Ш5), у = esin(w—ш?), где ewvj — эксцентриситет и долгота периге¬
лия, усредненные по сг. В виде заштрихованного кольца показана модулированная
сепаратриса резонанса 3/1. У траекторий внутри этого кольца угол а циркулиру¬
ет, у всех остальных — либрирует. (Рис. 5 из статьи Уиздома, 1985; с разрешения
Academic Press)
коласа, 1990). На рис. 11.12 (из статьи Уиздома, 1985) показана вековая
эволюция переменных х = ecos(w — w$), у = esm{vo — w£), полученная
путем усреднения по сг. Заштрихованное кольцо представляет собой моду¬
лированную сепаратрису резонанса 3/1; угол сг циркулирует внутри кольца
и либрирует вне его. Как видим, вековая динамика вынуждает почти все
орбиты, находящиеся в резонансе 3/1 (то есть вне кольца), достигать экс¬
центриситетов выше е = 0.3, что представляет собой пороговое значение
для тесных сближений с Марсом. Те траектории на рис. 11.12, которые
пересекают кольцо, все должны быть хаотическими; так что они могут со¬
вершать скачки к высоким эксцентриситетам нерегулярно во времени, как
и показывают представленные на рис. 11.11 результаты численного инте¬
грирования. Этот тип поведения присутствует также на графике на правой
верхней панели рис. 11.7 (построенном согласно рецепту раздела 11.2.3);
нижний край этой панели совпадает с сепаратрисой резонанса 3/1, и, таким
образом, он соответствует заштрихованному кольцу на рис. 11.12, тогда как
310
Глава 11
остров либраций вокруг q = w — vo^ =0 при малых N соответствует
бананоподобным кривым в правой части рис. 11.12.
Для орбит с меньшей амплитудой либраций внутри резонанса 3/1
(верхняя левая панель рис. 11.7) остров вековых либраций вокруг w —
— £7* = 0 исчезает, что впервые обнаружили Анрар и Караниколас (1990).
Однако те орбиты, что имеют наименьший возможный эксцентриситет при
w — т§ = 180°, все же достигают эксцентриситетов выше ~ 0.3 (то есть
N > 1.42), когда vo — w\ прецессирует до 0°. Хотя данная эволюция са¬
ма по себе и не является хаотической, достигнутый благодаря ей большой
эксцентриситет достаточен для тесных сближений с Марсом. Последние
вызывают случайные малые скачкообразные изменения большой полуоси
астероида, и поэтому рано или поздно они могут вывести его из резо¬
нанса 3/1. Благодаря такой «кооперации» вековой динамики и сближений
с Марсом, в течение ~ 100 млн лет на месте резонанса 3/1 в первоначально
однородном распределении частиц может образоваться люк (Уиздом, 1983;
Уэзерилл, 1975). Однако, как мы убедимся ниже, механизм, благодаря ко¬
торому резонанс теряет населяющие его объекты, на самом деле иной.
Большой остров либраций вокруг т — — 180° на рис. 11.7 соот-;
ветствует резонансу v$. Траектории, близкие к нижнему краю двух верхних
панелей, находятся вне этого острова и поэтому достигают лишь умерен¬
ных (хотя и достаточных для пересечения с орбитой Марса) значений экс¬
центриситета при циркуляциях угла w — или его либрациях вокруг 0°.
Траектории же, имеющие первоначально большой эксцентриситет (е ~ 0.45
при w — — 180°), следуют либрационному циклу вокруг vo — = 180°
и достигают эксцентриситетов, близких к единице. При большей амплитуде
либраций (нижняя левая панель рис. 11.7) большой остров либраций каса¬
ется сепаратрисы резонанса 3/1 (нижнего края панели), поэтому и орбиты
с самым низким исходным эксцентриситетом вынуждены приобретать экс¬
центриситет ~ 0.8-0.9, когда w — = 180°. Эту особенность впервые вы¬
явили Ферраз-Мелло и Клафке (1991) путем построения сечений Пуанкаре
в усредненной плоской эллиптической задаче трех тел (11.13) с Sz = 0. На
рис. 11.4 показано расположение сепаратрис большого острова либраций
на плоскости (а, ё) при а = 90°.
На этом же рисунке показано, как расположен резонанс щ и его сепа¬
ратрисы; данный резонанс сам по себе порождает вековую динамику, весь¬
ма похожую на представленную на рис. 11.7. Если же принять во внимание
оба резонанса v$ и то, как объяснено в разделе 11.2.3, вековая динами¬
ка полностью изменяется (рис. 11.8). Хаотическая область охватывает по-
11.3. Важнейшие резонансы в главном поясе астероидов
311
чти все фазовое пространство, вплоть до единичного эксцентриситета (до
верхнего края панелей). Помимо малых островков, погруженных в хаоти¬
ческую область, регулярными продолжают оставаться только траектории,
имеющие малые амплитуды либраций на резонансе 3/1 и малые эксцентри¬
ситеты (инвариантные торы внизу на двух верхних панелях рис. 11.8). На¬
помним, однако, что эти траектории периодически достигают эксцентриси¬
тетов, достаточных для тесных сближений с Марсом; последние вызывают
скачкообразные изменения большой полуоси и эксцентриситета астероида.
Эти изменения в общем случае очень малы, но при этом эффективно из¬
меняется амплитуда либраций астероида на резонансе 3/1. При больших
амплитудах либраций хаотическая область, порожденная перекрытием ре¬
зонансов i/5 и распространяется на все возможные значения эксцентри¬
ситета (нижние панели рис. 11.8), и поэтому орбита астероида может быст¬
ро и хаотически эволюционировать до очень высоких эксцентриситетов.
Данное сочетание крупномасштабного хаоса в вековой динамике со
сближениями с Марсом хорошо объясняет поведение астероидов в резо¬
нансе 3/1, наблюдаемое в экспериментах с численным интегрированием
полных уравнений движения. Как видно из рис. 11.13, если и эксцентри¬
ситет, и амплитуда либраций исходно малы, то астероид может проводить
~ 1 млн лет в состоянии с низким эксцентриситетом, осциллируя между
е ~ 0-0.1 ие~ 0.3-0.4 на шкале времени ~ 104 лет. При этом амплитуда
либраций большой полуоси изменяется благодаря сближениям астероида
с Марсом. В конце концов астероид попадает в протяженную хаотическую
область вековой динамики, и там его эксцентриситет очень быстро возрас¬
тает до значений, близких к единице. Тогда становятся возможными и ча¬
стыми тесные сближения с Землей и Венерой. Благодаря тому, что масса
любой из этих планет больше массы Марса, сближения с ними гораздо
эффективнее изменяют большую полуось орбиты астероида. Если проис¬
ходит тесное сближение, то астероид уходит из резонанса 3/1, а умеренные
сближения (как на рис. 11.13) приводят лишь к постепенному изменению
амплитуды либраций астероида, при этом его эксцентриситет продолжает
свою случайную эволюцию, вызываемую хаотической вековой динамикой;
в этом случае типичным итогом является падение на Солнце. Отметим, что
в ходе эволюции наклонение орбиты астероида также испытывает суще¬
ственные изменения благодаря наличию внутри резонанса 3/1 влияющих
на эволюцию наклонения вековых резонансов — резонанса Козаи, резонан¬
са z/i6 и резонанса + 2dz = 0. Их расположение на плоскости (а, е)
показано на рис. 11.2.
312
Глава И
1.0
0.8
0.6
0.4
0.2
0.0
30
20
10
0
2.6
2.5
2.4
Рис. 11.13. Типичная эволюция эксцентриситета, наклонения и большой полуоси
орбиты тела, находящегося исходно в резонансе 3/1 с Юпитером, согласно резуль¬
татам численного интегрирования полных уравнений движения в модели, включаю¬
щей все планеты Солнечной системы. Тело в конце концов падает на Солнце. (Рис. 9
из статьи Фаринеллы и др., 1993а; с разрешения Kluwer Academic Publishers)
, , , , I , , , , I , , , , I , J—i
0 5 x 105 10® 1.5 x 10® 2 x
время, в годах
11.3. Важнейшие резонансы в главном поясе астероидов
313
Представленная на рис. 11.13 динамическая эволюция вызывает быст¬
рое образование люка в распределении астероидов на месте резонанса 3/1.
В самом деле, результаты численного интегрирования, проведенного для
статистически значимой выборки частиц (Глэдман и др., 1997), показывают,
что среднее время жизни популяции, исходно помещенной в резонанс 3/1,
составляет ~ 2 млн лет, при этом менее 10 % популяции выживает дольше
10 млн лет, но все эти выжившие тела оказываются перенесенными в об¬
ласть а < 2 а. е. в результате повторяющихся тесных сближений с Землей
или Венерой, так что резонанс полностью освобождается от астероидов за
несколько миллионов лет. Эта шкала времени гораздо короче ~ 100 млн
лет, предсказываемых сценарием Уиздома.
То же самое происходит и во многих других важных резонансах
средних движений с Юпитером, соответствующих люкам Кирквуда. Муне
и Морбиделли (1995) показали, что хаотические области, порождаемые пе¬
рекрытием резонансов v§ и щ, доминируют также внутри резонансов 4/1,
5/2 и 7/3; поэтому астероиды, находящиеся в этих резонансах средних
движений, также могут приобретать весьма большие эксцентриситеты на
«короткой» шкале времени. Согласно результатам расчетов Глэдмана и др.
(1997) среднее время жизни частиц в резонансах 5/2 и 7/3 составляет 0.6
и 19 млн лет соответственно.
Благодаря своей эффективности в «накачке» эксцентриситета до значе¬
ний, при которых орбита астероида начинает пересекаться с орбитой Зем¬
ли, главные резонансы средних движений с Юпитером (в частности, ре¬
зонанс 3/1) считаются важнейшими «поставщиками» новых объектов для
популяции астероидов, сближающихся с Землей. Согласно общепринято¬
му сейчас сценарию население этих резонансов постоянно пополняется за
счет астероидов главного пояса с низкими эксцентриситетами благодаря
ударным столкновениям (Фаринелла и др., 19936, Меникелла и др., 1996)
и медленному воздействию слабой негравитационной силы (так называе¬
мому эффекту Ярковского4). Поскольку в хаотической области резонан¬
са 3/1 единичный эксцентриситет достигается на «короткой» шкале време¬
ни, в большинстве своем резонансные астероиды быстро погибают из-за
4Этот эффект порождается тепловым переизлучением с поверхности астероида. Благода¬
ря вращению тела и наклону его оси вращения наиболее горячий участок поверхности тела
испускает инфракрасные фотоны в направлении, смещенном по отношению к направлению
«тело-Солнце». Это приводит к слабому ускорению (положительному или отрицательному)
тела вдоль его орбиты, то есть к медленному дрейфу по большой полуоси. Этот эффект непо¬
средственно наблюдается у искусственных спутников Земли. См. статьи Фаринеллы и Вокро-
углицкого (1998), Боттке и др. (2000а). — Прим. авт.
314
Глава 11
столкновений с Солнцем (70 % выборки в расчетах Глэдмана и др.), и по¬
этому они не вносят заметного вклада (к счастью для нас!) в поддержание
популяции АСЗ.
Какой была бы динамика астероидов в резонансе 3/1, если бы Мар¬
са не существовало? Поведение траекторий, которые на верхних панелях
рис. 11.8 имеют регулярный вид, никогда не исследовалось детально с уче¬
том дополнительных гармоник и степеней свободы вековой динамики. Со¬
гласно рис. 11.2 эту область пересекает резонанс •&„ + д§ + 2bz = 0, и он
в принципе может дестабилизировать движение. Кроме того, эту область
пересекают два трехтельных резонанса, но их гармоники должны быть
очень высокого порядка по эксцентриситету, так как резонанс с Сатур¬
ном самого низкого порядка, который может взаимодействовать с резонан¬
сом 3/1 с Юпитером, — это резонанс 15/2 (порядка 13 по е). Численное
интегрирование, проведенное для той же выборки частиц, что и у Глэдмана
и др. (1997), но в отсутствие Марса показывает, что популяция резонан¬
са 3/1 убывает гораздо медленнее. По прошествии 10 млн лет в резонансе
выживает 15 % частиц, тогда как в численном эксперименте Глэдмана и др.
область резонанса 3/1 за это время полностью очищается.
11.3.2. Резонанс 2/1
Резонанс средних движений 2/1 с Юпитером соответствует люку Кирк¬
вуда, имеющему наибольшую ширину по большой полуоси. Поэтому он
стал первым резонансом, который исследовали детально начиная с работ
Пуанкаре. Любопытно, но это и резонанс, объяснить отсутствие астерои¬
дов в котором труднее всего. Найти удовлетворительное объяснение уда¬
лось лишь недавно.
Подробное исследование динамической структуры резонанса 2/1 вы¬
полнили Муне и др. (1998); впервые без упрощений они применили под¬
ход, описанный выше в разделе 11.2. Расположение различных резонансов
и их сепаратрис было численно определено для нескольких значений Ja,
а результаты были представлены в объединенном виде на плоскости (а, е)
для различных значений наклонения (рис. 11.14). На каждой из панелей
рис. 11.14 двумя очень жирными линиями слева и справа обозначены сепа¬
ратрисы резонанса средних движений 2/1, вычисленные при сг = 0. Отме¬
тим, что с увеличением наклонения область, ограниченная сепаратрисами
резонанса 2/1, несколько сужается. Расположение сепаратрис найдено чис¬
ленно из гамильтониана (11.5), параметрически зависящего от наклонения
через Sz. В пространстве между сепаратрисами точечной штриховкой вы-
11.3. Важнейшие резонансы в главном поясе астероидов 315
3.15 3.20
3.25 3.30
а
3.35 3.40 3.15 3.20 3.25
3.40
о
о
Г"-
Ь;
о
Козаи
О
CD
CD
Козаи
О
/ \
О
\
ю
/X у\
LO
V гХ ^ :
о
\ / /н
О
\ У ^\ 1 1
\ Л X
\ м Г
о
\ ^''' А ; \ /
о
\ А I
со
со
\ /
о
\ б /
о
\ X6 •' / "
см
' / /
см
\ / / :
о
-' /Б /
о
\Х,.. /.,/ /
т—Н
/
т—Н
\ '' / у
о
вторичные /
о
вторичные/ /
о
о
резонансы
о
о
резонансы '
3.30
а
3.35 3.40
Рис. 11.14. Сильно хаотические области (выделены точечной штриховкой) и ква-
зирегулярные острова (белые области А и Б) внутри резонанса 2/1 с Юпитером
при различных наклонениях. Двумя очень жирными линиями слева и справа нане¬
сены сепаратрисы резонанса средних движений 2/1; пунктиром показана верхняя
граница существования вторичных резонансов; прерывистыми, тонкими сплошны¬
ми и жирными сплошными линиями нанесены сепаратрисы резонансов Козаи
и z/5, соответственно. Комментарии см. в тексте. (Рис. 1 из статьи Муне и др., 1998;
с разрешения Academic Press)
316
Глава И
делены области, затронутые (индивидуально или совместно) вековыми или
вторичными резонансами, которые обсуждаются ниже. Это сделано с целью
обозначить области, где можно ожидать сильных (хаотических) изменений
орбитальных элементов.
Тонкими сплошными линиями на рис. 11.14 показаны сепаратрисы ре¬
зонанса Козаи. Ширина резонанса Козаи увеличивается с Наклонением, по¬
скольку коэффициент гармоники Козаи пропорционален е2г2. Как выглядит
этот резонанс на плоскости (е, г) в центральной части соизмеримости 2/1,
показано на рис. 11.6. При г ^ 20° верхняя сепаратриса резонанса Козаи
находится вне диапазона эксцентриситетов, покрываемого рис. 11.14 для
большинства значений большой полуоси, поэтому нанесена только нижняя
сепаратриса. Жирными сплошными линиями нанесены сепаратрисы резо¬
нанса vb. Угол w—vo% либрирует вокруг 0° (если большая полуось осцилли¬
рует в диапазоне 3.22-3.33 а. е.) либо вокруг 180° (в случае орбит с большей
амплитудой либраций на резонансе 2/1). Вековой резонанс щ также при¬
сутствует (Морбиделли и Муне, 1993): он расположен выше v$ и частично
перекрывается с последним, однако его сепаратрисы на рис. 11.14 не по¬
казаны, чтобы не перегружать график. Резонанс Козаи сильно взаимодей¬
ствует с резонансами 1/5 и i/6; частичное перекрытие имеет место при всех
наклонениях, и оно должно приводить (как в случае резонанса 3/1) к фор¬
мированию обширной хаотической области, где эксцентриситет астероида
может расти до единицы. Такой хаос покрывает область при больших зна¬
чениях эксцентриситета в центральной части резонанса 2/1, а при больших
амплитудах либраций он распространяется на все эксцентриситеты, следуя
расположению упомянутых выше вековых резонансов (см. рис. 11.10). Та¬
ким образом, если принимать во внимание только резонансы Козаи, г/5 и щ9
то область при малых и промежуточных значениях эксцентриситета в цен¬
тральной части резонанса 2/1 была бы регулярной. В отличие от случая
резонанса 3/1, чтобы добиться увеличения амплитуды либраций астерои¬
дов, исходно находящихся в этой области, здесь нельзя привлечь механизм
тесных сближений с Марсом, поскольку эксцентриситет не достигает значе¬
ний, достаточных для появления пересечений с орбитой Марса (напомним,
что в сравнении с резонансом 3/1 резонанс 2/1 находится гораздо дальше
от Марса).
Чтобы объяснить отсутствие астероидов в области малых и промежу¬
точных значений эксцентриситета, требуется дальнейшее изучение дина¬
мики в ней. Эту область пересекает резонанс чьи сепаратрисы обо¬
значены на рис. 11.14 прерывистыми линиями. Резонанс вызывает ко¬
11.3. Важнейшие резонансы в главном поясе астероидов 317
лебания наклонения с амплитудой ~ 15-20°. Кроме того, при более низ¬
ких эксцентриситетах имеется комплекс вторичных резонансов: пунктиром
обозначена верхняя граница по эксцентриситету для области, затронутой
вторичными резонансами порядка по эксцентриситету или наклонению не
выше 5. Следовательно, если принимать во внимание также резонанс v\§
и вторичные резонансы, то можно ожидать, что на рис. 11.14 регулярными
будут лишь белые области А и Б. Орбиты в зоне вторичных резонансов,
хотя и являются хаотическими, в плоской задаче покинуть эту зону не мо¬
гут, поскольку они должны были бы пересечь регулярные области А и Б
(см. рис. 11.3). В полной задаче, однако, вторичные резонансы вида (11.10)
и (11.12) вынуждают наклонение астероида расти. При больших наклонени¬
ях резонанс v\§ перекрывается со вторичными резонансами (нижние пане¬
ли рис. 11.14), поглощая область Б; при этом открывается выход к большим
эксцентриситетам через хаотическую область, порожденную резонансами
Козаи, i/5 и щ. Первым эту «извилистую тропу» обнаружил Уиздом (1987)
путем численного моделирования, а позднее Анрар и др. (1995) описали ее
детально, исходя из результатов массовых численных экспериментов.
Тем не менее ни вековые, ни вторичные резонансы не дают полно¬
го объяснения, почему области А и Б относительно свободны от астеро¬
идов. Эти области, однако, не являются в действительности регулярными,
как выяснили Франклин (1994) и Ферраз-Мелло (1994) путем вычисления
показателей Ляпунова для ограниченной выборки орбит. Несколькими го¬
дами позднее Несворный и Ферраз-Мелло (19976) впервые выполнили де¬
тальный численно-экспериментальный обзор динамической структуры ре¬
зонанса 2/1. На интервале времени в несколько сотен тысяч лет они про¬
интегрировали орбиты большой выборки пробных частиц с начальными
условиями на регулярной сетке, заданной на плоскости (а, е) при г = а =
= w — Wj = Q — = 0, где индекс J обозначает принадлежность к Юпи¬
теру. Для каждой частицы они измерили, как изменилась частота угла w
за время интегрирования. Согласно разделу 5.3, изменение частоты явля¬
ется индикатором хаотичности орбиты. Результаты показаны на рис. 11.15
в цветовой шкале: красным цветом окрашены наиболее хаотичные области,
а темно-синим — области начальных условий, где изменение частоты ниже
предела обнаружения. Впечатляет схожесть левой панели рис. 11.15 и верх¬
ней левой панели рис. 11.14 в том, что касается расположения наиболее
хаотичных областей. К тому же примененная мощная численная методика
позволяет увидеть, что для областей А и Б характерен протяженный сла¬
бый хаос (о чем говорит их почти однородный светло-голубой цвет), а не
318
Глава 11
г -Г т т i 1 . ! 1— I 1 1 1 1 1 1 1 1 I
0.5 0.4 0.3 0.2 0.1 0.0
Рис. 11.15. Динамическая структура резонансов 2/1 и 3/2 (панели внизу и вверху
соответственно). В цветовой шкале показан логарифм относительного изменения
частоты vj за 200000 лет; данная шкала служит для диагностики хаоса. (Рис. 2 из
статьи Ферраз-Мелло и др., 19986; с разрешения Тихоокеанского астрономического
общества)
11.3. Важнейшие резонансы в главном поясе астероидов
319
структура Нехорошева, обсуждавшаяся в главе 6. Поэтому астероиды, по¬
мещенные исходно в область А или Б, должны испытывать медленную хао¬
тическую диффузию на плоскости (а, е) и по прошествии большого време¬
ни в конце концов могут оказаться в областях сильного хаоса. Фактически
же результаты долговременного численного интегрирования, проведенно¬
го Несворным (частное сообщение), показывают, что у тел, помещенных
исходно в область А или Б, среднее время жизни превышает 1 млрд лет.
Мищенко и Ферраз-Мелло (1997) и Несворный и Ферраз-Мелло (19976)
высказали гипотезу, что протяженный слабый хаос в областях А и Б вы¬
зван резонансами между периодом либрации а и периодом вращения угла
большого неравенства (см. раздел 11.2.5). Чтобы найти этой гипотезе
косвенное подтверждение, они в своих вычислениях слегка изменили ор¬
биту Сатурна так, чтобы период угла большого неравенства уменьшился
в 2 раза. Оказалось, что хаотичность областей А и Б тогда сильно возраста¬
ет. Как видно из рис. 11.10, эти области пересекает комплекс «трехтельных
резонансов» с критическими углами, в обозначениях раздела 11.2.5 записы¬
ваемыми как фа + 2(/?js — (6 — k)w — kw$ и^-f 2(^js — (6 — k)vo — где
к = 0,.... 6. (Чтобы не перегружать график, на нем не приведены резонан¬
сы, включающие \ они располагаются вблизи соответствующих резонан¬
сов, включающих vj$.) Отсутствие различимой структуры Нехорошева на
рис. 11.15 указывает на то, что эти резонансы должны перекрываться друг
с другом. Если период угла большого неравенства (pjs уменьшить в 2 раза,
то этот комплекс резонансов замещается комплексом резонансов с крити¬
ческими углами 'фа- + (pjs — (3 — k)w — kw§ и фа — <^js — (3 — k)w — kw$.
У последних резонансов порядок по эксцентриситету ниже и коэффициен¬
ты гармоник, соответственно, больше, и поэтому порождаемый ими хаос
сильнее.
Общепризнанно, что в ранние эпохи существования Солнечной систе¬
мы Юпитер и Сатурн были несколько ближе друг к другу, чем сейчас (Фер¬
нандес и Ип, 1984). В таком случае, как отметили Несворный и Ферраз-
Мелло (19976), период угла большого неравенства должен был быть мень¬
ше. Поэтому логично предположить, что первичные астероиды, населяв¬
шие области А и Б, были удалены из этих областей, когда период угла <^js
составлял половину его нынешнего значения.
В действительности резонанс 2/1 не вполне свободен от астероидов.
В нем есть несколько объектов с сильно хаотическими орбитами (например,
1362 Гриква), которые, вероятно, были временно захвачены в резонанс из
числа астероидов, сближающихся с Землей, или комет семейства Юпитера.
320
Глава 11
К тому же в результате современных наблюдений обнаруживается все боль¬
ше мелких астероидов в области Б при малых наклонениях. Первым из них
был открыт 3789 Жонггуо. Из-за малых (не превышающих 10 км) размеров
этих тел их время жизни, обусловленное ударно-столкновительными про¬
цессами, меньше, чем возраст Солнечной системы, поэтому они не могут
быть первичными астероидами. Согласно рис. 9.19 (левая панель), в момент
ударно-столкновительного формирования семейства Фемиды некоторые из
его образовавшихся членов могли быть вброшены в резонанс 2/1; с другой
стороны, в корректно определенных координатах Жонггуо безукоризненно
выравнен с кластером Фемиды. Напрашивается вывод, что все астероиды
в области Б принадлежат семейству Фемиды и были вброшены в резонанс
относительно недавно, уже после того, как резонансное население первич¬
ных астероидов сошло на нет. Этот сценарий детально описан в работе
Муне и др. (1998). Хотя имеющаяся статистика все еще бедна, распределе¬
ние астероидов в области Б по размерам, по-видимому, является таким же,
как и в семействе Фемиды; при этом оно гораздо круче, чем у астероидов
главного пояса, не входящих в семейства (Ройг, частное сообщение). Если
это сходство подтвердится, оно станет сильным доводом в пользу сценария
родства этих астероидов с семейством Фемиды.
11.3.3. Резонанс 3/2
Среди резонансов средних движений низкого порядка в главном по¬
ясе резонанс 3/2 — единственный, который содержит много астероидов
(см. рис. 9.12). Исходя из названия первого открытого в нем объекта, насе¬
ление резонанса 3/2 принято называть Тильдами.
Из факта существования Гильд следует, что резонанс не синоним люка
в распределении астероидов. Действительно, в распределении астероидов
резонансу 3/2 соответствует пик на фоне нерезонансного населения. При¬
чина состоит в том, что нерезонансные астероиды с а ~ 4 а. е. и с не слиш¬
ком малыми эксцентриситетами испытывают тесные сближения с Юпи¬
тером и быстро дестабилизируются, тогда как резонансные тела согласно
разделу 9.1.1, «фазово защищены» от тесных сближений с планетами-ги¬
гантами.
Вековая динамика резонанса 3/2 весьма схожа с вековой динамикой ре¬
зонанса 2/1. На рис. 11.16 показано расположение резонансов и щ и их
сепаратрис. Угол w — w% либрирует вокруг 180°. Два вековых резонанса пе¬
рекрываются, порождая хаотическую область, простирающуюся примерно
от нижней сепаратрисы резонанса до верхней сепаратрисы резонанса щ.
11.3. Важнейшие резонансы в главном поясе астероидов
321
Таким образом, для регулярного движения остается область при умеренных
эксцентриситетах, где и находятся Гильды. Согласно рис. 11.16 несколько
Гильд оказались внутри резонанса на самом деле это артефакт, возник¬
ший из-за того, что сепаратрисы резонанса v$ нанесены для w — w£ = 180°,
тогда как положения астероидов приведены в текущих оскулирующих эле¬
ментах, независимо от значения w — vo%. Если бы орбиты астероидов были
проинтегрированы до момента, когда w — = 180°, то положения всех
астероидов на плоскости (а, е) оказались бы вне резонанса 1/5.
со
а
Рис. 11.16. То же, что и на рис. 11.4, но для резонанса 3/2 с Юпитером. Точками по¬
казаны положения известных Гильд в оскулирующих элементах. (Рис. 10 из статьи
Морбиделли и Муне, 1993; с разрешения Academic Press)
Согласно рис. 11.17, внутри соизмеримости 3/2 есть к тому же резо¬
нансы Козаи и v\q. На рис. 11.9 показано, как на плоскости (е,г) в центре
соизмеримости 3/2 пролегают левая сепаратриса резонанса Козаи, а также
резонанс v\§ и его границы. Как видим, Гильды избегают и этих резонан¬
сов. Вторичные резонансы низкого порядка оказываются перенесенными
в область с е < 0.15, причем они не порождают значимой хаотической
области, поскольку не перекрываются друг с другом (Мищенко и Ферраз-
Мелло, 1995).
322
Глава 11
Несворный и Ферраз-Мелло (19976) провели численный анализ дина¬
мики резонанса 3/2, аналогичный успешно проведенному ими для резонан¬
са 2/1. Результаты показаны на правой панели рис. 11.15. В данном случае
соответствие между сильно хаотической областью на рис. 11.15 и располо¬
жением сепаратрис векового резонанса на рис. 11.16 не слишком хорошее,
поскольку последние вычислены при — = 7г, а начальные условия для
пробных частиц взяты Несворным и Ферраз-Мелло при w — mj = 0. Как
следствие такого выбора начальных фаз, хаотическая область, порождае¬
мая перекрытием вековых резонансов, на рис. 11.15 сдвинута к большим
эксцентриситетам.
a/aj
Рис. 11.17. Расположение главных резонансов внутри соизмеримости 3/2. Жирные
сплошные, жирные прерывистые и тонкие пунктирные линии имеют тот же смысл,
что и на рис. 11.10, а тонкими прерывистыми линиями здесь показано расположение
трехтельных резонансов 4- 30js — 9w = 0 и 2-f 3<£>js — 9w.
Согласно рис. 11.15 область внутри соизмеримости 3/2, не затрону¬
тая вековыми резонансами, характеризуется гораздо более регулярной ди¬
намикой, чем области А и Б внутри соизмеримости 2/1. В интервале
0.2 < е < 0.35 (при w — zuj = 0) по центру резонанса 3/2 следов хаоса
не обнаруживается, то есть большая часть этой области заполнена инва¬
11.4. Важнейшие резонансы в поясе Койпера
323
риантными торами. Проинтегрировав орбиты всех астероидов до момента,
когда а = w — wj = 0, Несворный и Ферраз-Мелло установили, что в по¬
давляющем большинстве Гильды принадлежат этой устойчивой регулярной
области.
На рис. 11.17 показано расположение «трехтельных резонансов» с кри¬
тическими углами 'фа- + 3(£>js — 9w и 2фа + 3<^?js — 9w на плоскости i = 0.
Резонансы с аргументами ^+3(/?js —(9 —/с)^ —fctUg, Vv+3</?js“ (9 — к)т —
- kw% (к > 0) и 2фа + 3<pjs - (9 — k)w — kw%, 2фа + 3<рjs - (9-/с)ш-
(/с < 0) находятся в области между двумя резонансами, явно показанными
на рис. 11.17. Есть две причины, по которым трехтельные резонансы не
порождают хаоса в центральной области резонанса 3/2, тогда как внутри
резонанса 2/1 они его порождают: во-первых, резонанс с Сатурном самого
низкого порядка среди резонансов, способных взаимодействовать с резо¬
нансом 3/2 с Юпитером, — это резонанс 15/4 (порядка И по е); во-вторых,
период либрации на резонансе 3/2 меньше, чем на резонансе 2/1, вслед¬
ствие чего резонансы с периодом угла большого неравенства допустимы
лишь в более высоких порядках. По этим причинам коэффициенты гармо¬
ник трехтельных резонансов должны быть гораздо меньше, чем в случае
резонанса 2/1 с Юпитером, так что индивидуальные резонансы предполо¬
жительно не вполне перекрываются друг с другом.
11.4. Важнейшие резонансы в поясе Койпера
Исследования динамики внутри резонансов средних движений в поясе
Койпера начались совсем недавно, когда были открыты первые резонанс¬
ные объекты. Можно предположить, что они продолжатся и приведут к бо¬
лее детальному пониманию предмета изучения в ближайшем будущем —
параллельно с тем, как будут получены наблюдательные данные об ор¬
битальном распределении населяющих пояс Койпера объектов. Здесь мы
кратко обсудим современные знания о динамике внутри внешних резонан¬
сов средних движений 2/3 и 1/2 с Нептуном — резонансов, которые, судя по
всему, играют в поясе Койпера важнейшую роль.
11.4.1. Резонанс 2/3
Около 30 % тел, открытых на сегодняшний день в поясе Койпера, на¬
ходятся в резонансе 2/3 с Нептуном (а ~ 39.5 а. е.). Джуитт и др. (1998),
учтя эффект селекции, благоприятствующий открытию последних, оценили
заселенность резонанса 2/3 как 10-15% от всего населения пояса Койпера
324
Глава 11
макс. показатель Ляпунова
39.2 39.4 39.6
большая полуось, а. е.
-7.5
-7 -6.5 -6 -5.5 -5 -4.5
макс. показатель Ляпунова
Рис. 11.18. Показатели Ляпунова и расположение главных резонансов внутри соиз¬
меримости 2/3 с Нептуном. Жирные кривые слева и справа обозначают сепаратрисы
резонанса 2/3. Кривые «и8», «^18» и «Козаи» обозначают положения резонансов vs,
i/is и Козаи соответственно; прерывистые кривые «4:1» и «5:1» обозначают поло¬
жения трехтельных резонансов 4фа — <£>un ~ 0 и Ъфа — фип ~ 0 (напомним,
что для внешних резонансов фа > 0); кривая «sig5» обозначает верхнюю границу
области, затронутой вторичными резонансами не выше 5-го порядка по эксцентри¬
ситету. Черными кружками показано расположение известных плутино по большой
полуоси и эксцентриситету при а — 180° и о/ = 90°; причем кружком с крестиком
обозначен Плутон. В цветовой шкале показаны значения десятичного логарифма
максимального показателя Ляпунова, вычисленные для пробных частиц, исходно
размещенных на регулярной сетке на плоскости г = 0°. (Рис. 2 из статьи Несворно¬
го и Ройга, 2000; с разрешения Academic Press)
11.4. Важнейшие резонансы в поясе Койпера
325
в интервале 30-50 а. е. Плутон, самый крупный из известных объектов по¬
яса Койпера5 также пребывает в резонансе 2/3. Поэтому тела, находящиеся
в резонансе 2/3, принято называть плутино.
Детальное исследование динамики резонанса 2/3 выполнили Несвор¬
ный и Ройг (2000). На рис. 11.18 показано расположение главных вековых,
вторичных и трехтельных резонансов на плоскости (а, е) при г = 0° и а =
= 180° (устойчивый центр либраций на резонансе 2/3), рассчитанное по
рецепту из раздела 11.2. Кроме того, в цветовой шкале на графике показа¬
ны значения логарифма максимального показателя Ляпунова, вычисленные
для множества пробных частиц, исходно размещенных на регулярной сетке
на плоскости (а, е), опять же при % — 0° и а = 180°. Согласно разделу 5.2
значение показателя Ляпунова служит непосредственной мерой хаотично¬
сти. Как видно из рис. 11.18, значения показателя Ляпунова четко коррели¬
руют с расположением резонансов. Они очень велики вблизи границ резо¬
нанса 2/3 благодаря присутствию векового резонанса щ и его перекрытию
с резонансом При малых эксцентриситетах (е < 0.05) они меньше, но
все же явно больше нуля (благодаря присутствию резонанса ^8 и вторич¬
ных резонансов), как и вдоль трехтельного резонанса, соответствующего
отношению 4:1 между периодом либраций на резонансе 2/3 и периодом
угла большого неравенства </?un = 2An — Аи системы «Уран-Нептун». Те¬
ло в резонансе 2/3 с Нептуном находится вблизи резонанса 1/3 с Ураном,
так что прямые возмущения орбиты тела Ураном способны генерировать
гармоники трехтельных резонансов с довольно большими коэффициента¬
ми. Этот трехтельный резонанс «4:1» фактически является комплексом из
двух резонансов с критическими углами 4t/v — </?un + (1 ~ k)vo + kw% (к =
= 0,1). Оба резонанса пролегают весьма близко к кривой, приведенной на
рис. 11.18, поэтому область хаоса, порождаемого трехтельным резонансом
«4:1» на плоскости (а, е), сильно локализована в отличие от ситуации внут¬
ри резонанса средних движений 2/1 с Юпитером.
В центральной части резонанса 2/3 вычисленный показатель Ляпунова
по порядку величины равен 10-7 лет-1. Однако это значение, скорее всего,
не является истинным, а определяется интервалом времени интегрирова¬
ния (100 млн лет): если этот интервал увеличить, то вычисленный пока¬
затель Ляпунова, вероятнее всего, уменьшится. Таким образом, динамика
центральной части резонанса 2/3 оказывается практически регулярной, как
5 На 2013 год самым крупным объектом среди известных ТНО является Эрида (Eris, 2003
UB 313), чей диаметр, оцениваемый как 2400 км, хотя и ненамного, но превосходит диаметр
Плутона. — Прим. ред.
326
Глава 11
и в случае резонанса 3/2 с Юпитером (любопытное совпадение!). При по¬
мощи численного интегрирования полных уравнений движения Морбидел¬
ли (1997) показал, что движение тел в этой области регулярно и устойчиво
на временах порядка возраста Солнечной системы. Напротив, при больших
амплитудах либраций сильно хаотичные тела покидают резонанс и стал¬
киваются с Нептуном менее чем за 1 млрд лет. При умеренных амплиту¬
дах либраций тела, близкие к трехтельному резонансу «4:1», испытывают
медленную хаотическую диффузию, которая может вывести их в сильно
хаотическую область с большими амплитудами либраций за время, сравни¬
мое с возрастом Солнечной системы. Несворный и Ройг (2000) разработали
интересную получисленную модель этого диффузионного процесса.
На рис. 11.18 в проекции на плоскость (а, е) показаны положения плу-
тино на момент выполнения условия сг = 180°, полученные путем числен¬
ного интегрирования. Этот график недвусмысленно свидетельствует, что
плутино находятся в устойчивой центральной части резонанса 2/3. Однако
надо иметь в виду, что точность определения параметров орбит тел пояса
Койпера из наблюдений все еще невысока.
При ненулевых наклонениях (г > 0) важнейшим свойством вековой
динамики внутри соизмеримости 2/3 является наличие резонанса Козаи.
На рис. 11.19 показаны его сепаратрисы в плоскости (е, г), вычисленные
при со = ±90° в центре соизмеримости 2/3. Также показаны соответству¬
ющие положения Плутона (кружок с крестиком) и плутино. Плутон, как
впервые обнаружили Уильямс и Бенсон (1971), либрирует внутри резонан¬
са Козаи. Любопытно, что, помимо Плутона, в резонансе Козаи находят¬
ся лишь немногие плутино; это может быть вызвано дестабилизирующим
влиянием медленных сближений с Плутоном (Несворный и др., 2000). Как
впервые показали Зюссман и Уиздом (1988), движение Плутона хаотично.
Причиной служит резонанс между периодом либраций со и периодом цир¬
куляций П — fig, что путем численного интегрирования впервые установи¬
ли Милани и др. (1989). Этот резонанс, однако, вызывает лишь локальный
хаос, поэтому движение Плутона устойчиво (в том смысле, что он не по¬
кидает резонансов Козаи и 2/3) на временах порядка возраста Солнечной
системы (Киношита и Накаи, 1996). На рис. 11.19 графически представлены
также значения показателя Ляпунова пробных частиц с малой амплитудой
либраций на резонансе 2/3; начальные условия для движения этих частиц
взяты на регулярной сетке на плоскости (е, г). Единственной выдающей¬
ся особенностью графика является присутствие хаотической области при
низких эксцентриситетах для любых наклонений; причиной хаоса служат
резонанс vis и вторичные резонансы.
11.4. Важнейшие резонансы в поясе Койпера
327
-7.5
-7 -6.5 -6 -5.5 -5
макс. показатель Ляпунова
-4.5
Рис. 11.19. Резонанс Козаи внутри соизмеримости 2/3. Жирные и прерывистая кри¬
вые обозначают две сепаратрисы и центр резонанса Козаи соответственно. Черными
кружками показано расположение известных плутино по эксцентриситету и накло¬
нению при а = 180° и ш — 90°; причем кружком с крестиком обозначен Плу¬
тон. В цветовой шкале показаны значения десятичного логарифма максимально¬
го показателя Ляпунова, вычисленные для пробных частиц, исходно размещенных
на регулярной сетке на плоскости (е, г) в центре резонанса 2/3. (Рис. 8 из статьи
Несворного и Ройга, 2000; с разрешения Academic Press)
11.4.2. Резонанс 1/2
Резонанс 1/2 с Нептуном при 47.8 а.е. находится у внешнего края по¬
пуляции известных к настоящему времени объектов пояса Койпера6.
Этот резонанс необычен в том отношении, что, как отмечено в разде¬
ле 9.1, ему соответствуют два острова асимметричных либраций а внутри
большего острова симметричных либраций (см. рис. 9.4).
6К 2014 году обнаружено много объектов пояса Койпера, находящихся далеко за этим кра¬
ем, в том числе в различных резонансах (см., например, Gladman В. et al. (2012) The resonant
trans-Neptunian populations. Astron. J., 144, 23). — Прим. ред.
328
Глава И
Впервые динамику внутри резонанса 1/2 исследовали Несворный
и Ройг (2001). Чтобы представить области и симметричных, и асимметрич¬
ных либраций на одном и том же графике, они для каждого значения по¬
стоянного действия N вычислили значение crc(N) точки устойчивого рав¬
новесия системы (11.5) в центре одного из двух островов асимметричных
либраций; а затем численно определили соотношение между значениями
действий 5, N и значениями а, е для а — crc(N). Фактически из рис. 9.4
очевидно, что и симметричные, и асимметричные либрирующие орбиты
должны дважды пересекать ось о = crc(N) (или, что эквивалентно, ось
о — 2тг — crc(N)).
В таком представлении крайние жирные кривые слева и справа на
рис. 11.20 обозначают сепаратрисы острова симметричных либраций, а две
жирные кривые ближе к центру обозначают сепаратрисы островов асим¬
метричных либраций. Внутри последних Несворным и Ройгом были анали¬
тически определены положения резонанса Козаи и трехтельных резонансов,
соответствующих отношению 5:1 между периодом асимметричной либра¬
ции и периодом угла большого неравенства (/?un = 2 An — Ли - На рис. 11.20
графически представлены также значения показателя Ляпунова пробных
частиц, исходно расположенных на регулярной сетке на плоскости (а, е)
при i = 0 и а — crc(N). Можно видеть, что показатель Ляпунова велик у по¬
чти всех орбит в симметричных либрациях. Таким образом, здесь присут¬
ствует сильный хаос, чья природа пока еще детально не изучена. С другой
стороны, внутри острова асимметричных либраций показатель Ляпунова
в общем очень мал. По аналогии с резонансом 2/3 поэтому можно ожи¬
дать, что тела в центре островов асимметричных либраций выживают на
временах порядка возраста Солнечной системы. На сегодня7 единственным
кандидатом на нахождение в резонансе 1/2 является объект 1997SZi0, но,
как видно из рис. 11.20, он, скорее всего, пребывает в состоянии сильно
хаотичных симметричных либраций. Напомним, однако, что погрешности
наблюдательного определения орбит тел пояса Койпера пока еще остают¬
ся большими. Поэтому пока невозможно сделать вывод, является ли от¬
сутствие тел в островах устойчивых асимметричных либраций артефактом
из-за скудости наблюдательных данных о населении пояса Койпера или же
это реальный загадочный феномен8.
7 К 2002 году. — Прим. ред.
8К 2014 году открыто несколько объектов в состоянии асимметричных либраций в резонан¬
се 1/2 (Gladman В. et al. (2012) The resonant trans-Neptunian populations. Astron. J., 144, 23). —
Прим. ред.
11.5. Резонансы 1/1
329
макс. показатель Ляпунова
-8 -7.5 -7 -6.5 -6 -5.5 -5 -4.5 -4
макс. показатель Ляпунова
Рис. 11.20. То же, что и на рис. 11.18, но для резонанса 1/2 с Нептуном. Крайние
жирные кривые слева и справа обозначают сепаратрисы острова симметричных
либраций, а две жирные кривые ближе к центру обозначают сепаратрисы островов
асимметричных либраций. (Рис. 5 из статьи Несворного и Ройга, 2001; с разрешения
Academic Press)
11.5. Резонансы 1/1
Вековую динамику внутри резонанса 1/1 с планетой можно исследо¬
вать, используя тот же подход, что и применявшийся повсеместно в этой
главе. В самом деле, если ввести переменные (9.9), то интегрируемая ап¬
проксимация полного гамильтониана формально идентична (11.5), где Щ —
— к = 1. Поэтому в областях типа «головастик» и «подкова» можно ввести
переменные «действие-угол» вида (11.6) и тогда вековую динамику можно
исследовать, как описано в разделе 11.2.
В качестве примера применения данного подхода на рис. 11.21 пред¬
ставлена динамика резонанса щ в центре области типа «головастик» в резо¬
330
Глава 11
нансе 1/1 с Сатурном. «Истинный» резонанс (то есть резонанс, характери¬
зуемый точками устойчивого и неустойчивого равновесий и сепаратрисой,
окружающей область либраций) щ имеет место при большом эксцентриси¬
тете, вне границ этих диаграмм. Однако при малом эксцентриситете име¬
ется точка устойчивого равновесия при ш — Wq = 60°. Эксцентриситет,
отвечающий этой точке равновесия, близок к значению коэффициента Мб,б
в (7.10). Граница, разделяющая области либраций и циркуляций угла vo —
— vjq, не является сепаратрисой. В полярных координатах вековая динами¬
ка состоит просто из квазикруговых траекторий, смещенных относительно
центра е = 0.
долгота перигелия
Рис. 11.21. Динамика векового резонанса щ в центре области типа «головастик»
в резонансе 1/1 с Сатурном. На левой панели динамика представлена в декартовых
координатах, на правой — в полярных (х = ecosw, у = esintu). Здесь угол vj
отсчитывается относительно vjq . В расчетах учтены прямые возмущения со сторо¬
ны Юпитера, Урана и Нептуна (дважды усредненные по средним долготам планеты
и малого тела). (Рисунок любезно предоставлен Д. Несворным)
Вследствие существования этой точки равновесия все орбиты с началь¬
ным е ~ 0 достигают эксцентриситетов более 0.15 при ш — Wq = 60°. Со¬
гласно разделу 9.2.2 в центре области типа «головастик» динамика хаотич¬
на при эксцентриситетах больше 0.12 благодаря перекрытию с резонансом
средних движений 2/5 с Юпитером. Хаос проявляется на временной шкале
11.5. Резонансы 1/1
331
короче периода прецессии w — tuf*, так как он порожден резонансами сред¬
них движений. Поэтому благодаря ему тело может покинуть резонанс 1/1
прежде, чем вековая прецессия возвращает эксцентриситет обратно к мень¬
шим значениям.
При большей амплитуде либраций в областях типа «головастик» хао¬
тическая область, порождаемая перекрытием с резонансом 2/5 с Юпитером,
сдвинута к большим эксцентриситетам (см. рис. 9.14), и поэтому вековая
динамика уже не в состоянии вывести тела, исходно имеющие е ~ 0, в эту
хаотическую область.
Итак, сочетание вековой динамики с эффектами, возникающими бла¬
годаря перекрытию с резонансом 2/5 с Юпитером, действительно объясня¬
ет, почему у Сатурна нет троянцев с малыми амплитудами либраций, но
не может объяснить отсутствия у него троянцев с либрациями большей
амплитуды. Хольман и Уиздом (1993) путем долговременного численного
моделирования в полной задаче показали, что траектории типа «голова¬
стик» с большими амплитудами либраций и в самом деле устойчивы на
принятой ими шкале времени в 2 х 107 лет, а «головастики» с малыми
амплитудами либраций быстро прекращают существование. Поэтому при¬
чину отсутствия тел на орбитах типа «головастик» с большими амплиту¬
дами либраций следует искать в механизмах (до сих пор малоизученных)
формирования ранней Солнечной системы.
Детальные численные карты областей устойчивости в резонансах 1/1
с Сатурном, Ураном и Нептуном представлены в работе Несворного и До¬
унса (2002).
Глава 12
Глобальная динамическая структура
поясов малых тел
12.1. Обнаружение хаотических зон
В предыдущих главах мы проанализировали динамическую структуру
двухтельных и трехтельных резонансов средних движений различных по¬
рядков по эксцентриситету. В этой заключительной главе мы изучим, каким
образом все эти резонансы располагаются в поясе астероидов и поясе Кой-
пера, а также какова динамическая структура, возникающая при их взаимо¬
действии. В принципе, можно было бы аналитически рассчитать положения
сепаратрис каждого резонанса (или сепаратрис каждой компоненты каждо¬
го резонансного мультиплета) и построить график, аналогичный рис. 9.12,
но включающий двухтельные резонансы гораздо более высоких порядков
по эксцентриситету, а также и трехтельные резонансы. Однако на практи¬
ке это невозможно, так как пришлось бы вычислить и проанализировать
тысячи нормальных форм резонансов средних движений.
Наиболее простой и эффективный способ выявления резонансной
структуры поясов малых тел состоит в проведении численных исследова¬
ний с использованием инструментов, подробно описанных в главе 5. Знания
о резонансной динамике, приобретенные в предыдущих главах, позволят
нам интерпретировать результаты и получить представление об их возмож¬
ных приложениях.
Рис. 12.1 аналогичен рис. 10.8, но здесь анализ распространен на весь
пояс астероидов. Для 5700 пробных частиц начальные условия по большой
полуоси заданы на интервале от 2.1 до 3.24 а. е. с шагом 2 х 10-4 а. е.
Начальный эксцентриситет выбран равным 0.1, а начальное наклонение
и начальные фазовые углы — все положены равными нулю относитель¬
но плоскости эклиптики и точки весеннего равноденствия. Чтобы оценить
значения максимального показателя Ляпунова (МПЛ), уравнения движе¬
ния (с учетом возмущений от четырех планет-гигантов) интегрировались
334
Глава 12
-2
ьо -4 ~
-6
-2
ыэ -4
6
2.5 2.6 2.7 2.8
2
ьо 4
-6
Рис. 12.1. Максимальный показатель Ляпунова в зависимости от начального зна¬
чения большой полуоси орбиты астероида с начальным эксцентриситетом, рав¬
ным 0.1, и нулевым наклонением. В модели учтены возмущения только от четырех
планет-гигантов. Единицей измерения МПЛ служит год-1. Через «тп/п» обозна¬
чены двухтельные резонансы m/п с Юпитером, а через «га п к» — трехтельные
резонансы «Юпитер - Сатурн - астероид», соответствующие равенству гаЛл + nAs +
+ кХ = 0. Кроме того, через «S6/1» обозначен резонанс 6/1 с Сатурном, а через
«4J-2U-1» — трехтельный резонанс «Юпитер-Уран-астероид». (Рис. 1 из статьи
Морбиделли и Несворного, 1999; с разрешения Academic Press)
12.1. Обнаружение хаотических зон
335
совместно с уравнениями в вариациях на интервале времени 2.3 млн лет.
На рисунке 12.1 вычисленные значения показателя Ляпунова в логариф¬
мической шкале показаны в зависимости от начального значения большой
полуоси. Как всегда на подобных графиках, на рисунке имеется несколько
пиков, выделяющихся относительно уровня «фона»; а мы знаем из разде¬
ла 5.2, что пики, узкие минимумы и разрывы соответствуют хаотическим
или резонансным областям, тогда как уровень «фона» соответствует «ре¬
гулярной» области, причем «фоновое» значение МПЛ (на рис. 12.1 оно
составляет ~ 10-5,3 год-1) определяется временем интегрирования: при
увеличении последнего уровень фона в общем случае понижается.
Из рис. 12.1 видно, что с увеличением большой полуоси присутствие
хаотических областей становится все более заметным. Так происходит по
двум причинам. Во-первых, с приближением к Юпитеру резонансы сред¬
них движений фиксированного порядка встречаются чаще. Во-вторых, об¬
наруживаются резонансы все более высоких порядков по эксцентриситету
благодаря тому, что показатель Ляпунова коррелирует с величиной коэф¬
фициентов резонансных гармоник (см. раздел 12.3), а последние растут
с уменьшением расстояния до главного возмущающего тела.
Также отметим, что в расположении пиков есть особый порядок: они
образуют мультиплеты с ведущей компонентой в центре и вторичными ком¬
понентами слева и справа. Данную структуру не следует путать с муль-
типлетной структурой резонансов средних движений высоких порядков
(см. раздел 9.3), поэтому мы будем называть ее супермулътиплетной. Она
обусловлена тем, что Юпитер и Сатурн близки к резонансу средних движе¬
ний 5/2. Комбинация </?js = 5As — 2Aj является углом, который циркулиру¬
ет (причем производная по времени положительна) с периодом примерно
800 лет. Этот период много больше орбитального периода типичного асте¬
роида, поэтому при любых фиксированных целых m, mj и ms резонансы,
определяемые условиями тХ + (mj + 2/c)Aj + (ms — 5/с)As ~ 0 с раз¬
личными целыми /с, должны располагаться близко друг к другу (Мюррей
и др., 1998). Ведущая компонента супермультиплета чаще всего соответ¬
ствует резонансу наименьшего порядка по эксцентриситету или же резо¬
нансу с ms — 5/с = 0. На рис. 12.1 тройками целых чисел «т mj ms»
обозначены положения главных компонент наиболее важных супермуль-
типлетов. Считая от центральной компоненты, резонансы с к = 1,2,...
и с к = -1,-2,... расположены соответственно справа и слева от цен¬
тральной компоненты, если т < 0; или же соответственно слева и справа,
если т > 0.
336
Глава 12
Из рис. 12.1 следует, что большинство хаотических областей соответ¬
ствует либо обычным двухтельным резонансам средних движений с Юпи¬
тером (ms = 0), либо трехтельным резонансам «Юпитер-Сатурн-астеро¬
ид», хотя несколько малых пиков можно отнести к трехтельным резонансам
«Юпитер-Уран-астероид» низких порядков. Отметим, что нет пиков, явно
связанных с вековыми резонансами. Фактически вековые резонансы долж¬
ны давать значения показателя Ляпунова не больше ~ 10-6 год-1 благода¬
ря тому, что их критические углы изменяются медленно (типичный период
превышает ~ 1 млн лет). На рис. 12.1 виден только вековой резонанс щ,
расположенный у внутренней границы пояса астероидов. Орбиты тел
в этом резонансе могут со временем достигать очень больших эксцентриси¬
тетов (см. раздел 8.4.2), поэтому их интегрирование прекращалось раньше
2.3 млн лет; в итоге оценка показателя Ляпунова составила > 10-4 год-1.
Как отмечено в главах 9 и 10, у всех резонансов средних движений
(за исключением резонансов нулевого порядка по эксцентриситету) шири¬
на по большой полуоси тем больше, чем больше эксцентриситет орбиты
астероида. Как следствие, при больших эксцентриситетах в поясе астерои¬
дов хаоса больше, причем хаотические области, относящиеся к разным ре¬
зонансам, могут перекрываться, что делает пояс глобально-хаотичным. Для
части пояса за 3.1 а.е. этот эффект проиллюстрирован выше на рис. 10.8.
Что касается внутреннего пояса, Морбиделли и Несворный (1999) уста¬
новили, что при увеличении начального эксцентриситета астероида до 0.2
резонансы внутри супермультиплетов перекрываются, но сами супермуль-
типлеты продолжают оставаться хорошо отделенными друг от друга. По¬
этому в приближении, когда учитываются возмущения только со стороны
внешних планет, внутренний пояс имеет структуру, состоящую из хаотиче¬
ских полос, разделенных широкими регулярными областями.
Однако хаотическая структура внутреннего пояса радикально меняет¬
ся, если учитывать также и возмущения от внутренних планет. На рис. 12.2а
представлены результаты вычислений показателей Ляпунова во внутрен¬
нем поясе, полученные из численного интегрирования на интервале време¬
ни 2.3 млн лет с учетом возмущений от всех планет Солнечной системы
за исключением Меркурия. Этот график можно непосредственно сравнить
с верхней панелью рис. 12.1, так как начальные условия для пробных ча¬
стиц одни и те же. Такое сравнение впечатляет: оказывается, что внутрен¬
ние планеты «создают» очень много новых хаотических областей, причем
с уменьшением большой полуоси их присутствие нарастает. К тому же «фо¬
новый» уровень показателя Ляпунова между пиками оказывается весьма
12.1. Обнаружение хаотических зон
337
а, а. е.
Рис. 12.2. Панель вверху: то же, что и на верхней панели рис. 12.1, но также с уче¬
том возмущений со стороны планет земной группы. Панель внизу: минимальное
расстояние частиц от Марса в зависимости от начального значения большой полу¬
оси. Пики выявляют расположение внешних резонансов средних движений с Мар¬
сом. Через «Мп/Ь обозначены внешние резонансы п/к с Марсом. (Рис. 3 из статьи
Морбиделли и Несворного, 1999; с разрешения Academic Press)
нерегулярным по контрасту с плоским фоном, наблюдавшимся при учете
только внешних планет. Это еще раз указывает на плотную аккумуляцию
эффективных резонансов и на глобальную хаотичность в этой части пояса.
При больших полуосях меньше 2.16 а. е. уровня фона вообще не видно;
то есть при вычислении показателя Ляпунова положительный предел до¬
стигается для всех пробных частиц на временах меньше времени интегри¬
рования. Отметим, что на графике показатель Ляпунова в среднем растет
338
Глава 12
с уменьшением большой полуоси вплоть до 2.1 а. е., где расположен веко¬
вой резонанс щ. В сравнении с рис. 12.1 резонанс щ смещен влево (к мень¬
шему значению большой полуоси), потому что присутствие внутренних
планет несколько ускоряет прецессию перигелиев орбит астероидов.
То, что значения показателя Ляпунова в общем положительны, не явля¬
ется следствием тесных сближений частиц с Марсом. На рис: 12.26 показа¬
но минимальное расстояние, достигаемое при сближениях частицы с Мар¬
сом в течение всего времени интегрирования, в зависимости от большой
полуоси частицы. Оказывается, что оно больше радиуса сферы Хилла Мар¬
са (7.25 х 10 3 а. е.) для всех частиц при а ^ 2.103 а. е. и больше трех
радиусов сферы Хилла при а ^ 2.106 а. е. Таким образом, частиц, испы¬
тывающих тесные сближения с Марсом, почти нет, и, следовательно, по¬
казатель Ляпунова положителен благодаря резонансам с внутренними пла¬
нетами. Рис. 12.26 удобно использовать для отождествления некоторых из
них: пики на графике выдают присутствие внешних резонансов средних
движений с Марсом. Только находясь в этих резонансах, частица может
избегать тесных сближений с планетой благодаря обеспечиваемым резо¬
нансами защитным механизмам (см. раздел 9.1.1). На рис. 12.26 отмечены
главные внешние резонансы средних движений с Марсом. Обратите вни¬
мание, что пики на рис. 12.26 коррелируют с пиками показателя Ляпунова
на рис. 12.2д. Кроме того, при а < 2.15 а. е. на рис. 12.26 видно много мел¬
ких пиков, что говорит об аккумуляции в этой области внешних резонансов
средних движений с Марсом высоких порядков. Этим объясняется, почему
в данном диапазоне значений большой полуоси показатель Ляпунова всегда
положителен.
Однако одних только внешних резонансов средних движений с Мар¬
сом недостаточно для полного объяснения хаотической структуры внутрен¬
него пояса. Кривая показателя Ляпунова имеет гораздо больше пиков, чем
кривая минимального расстояния. Морбиделли и Несворный (1999) устано¬
вили, что многие из этих пиков на самом деле соответствуют трехтельным
резонансам средних движений «Марс-Юпитер-астероид». С другой стороны,
резонансы средних движений с Землей и Венерой и резонансы с участием
нескольких тел, включающие комбинации орбитальных частот планет зем¬
ной группы, по-видимому, не имеют отношения к хаосу в данной области.
Поскольку масса Марса мала (~ 3.3 х 10~7 массы Солнца), тот факт,
что на движение астероидов оказывают сильное влияние резонансы сред¬
них движений с Марсом высоких порядков или трехтельные резонансы
«Марс-Юпитер-астероид», может показаться на первый взгляд неожидан-
12.1. Обнаружение хаотических зон
339
большая полуось, а. е.
Рис. 12.3. То же, что и на рис. 12.1, но для пояса Койпера. Через «Nт:п» и «I)т\п»
обозначены двухтельные резонансы т/п с Нептуном и Ураном соответственно.
Через «mN+kU+j» обозначены трехтельные резонансы «Нептун - Уран - объект»,
соответствующие равенству гаАы + к\и + j А = 0. (Рис. 2 из статьи Несворного
и Ройга, 2001; с разрешения Academic Press)
340
Глава 12
ным. Однако не следует забывать, что астероиды внутреннего пояса нахо¬
дятся недалеко от Марса, так что его малая масса компенсируется малым
расстоянием до него. К тому же, поскольку расстояния до планеты при
сближениях меньше, область аналитичности возмущающей функции, от¬
носящейся к Марсу, много меньше области аналитичности возмущающей
функции, относящейся к Юпитеру; поэтому в первом случае коэффициенты
фурье-разложения возмущающей функции убывают с порядком гармоники
гораздо медленнее. Наконец, поскольку эксцентриситет Марса сравним по
величине с эксцентриситетами рассматриваемых астероидов, коэффициен¬
ты гармоник различных критических углов, пропорциональные произведе¬
ниям степеней эксцентриситета Марса ем и эксцентриситета астероида е,
являются величинами одного порядка, что вызывает сильную временную
модуляцию амплитуд резонансов (см. раздел 9.4). Например, коэффициент
гармоники cos(16Am — 27А + Зшм + 8ш) резонанса средних движений 16/27
с Марсом равен —5.6032 х 101 ем^ме%/где и ам — масса Марса
и большая полуось его орбиты. Таким образом, если е и ем оба равны
0.1, то ширина резонанса 16/27 составляет ~ 1.6 х 10-4 а. е. Для срав¬
нения: у резонанса средних движений 15/4 с Юпитером, расположенного
очень близко к резонансу 16/27 с Марсом, коэффициент ведущей гармо¬
ники cos(15Aj — 4А — 6wj — 5w) равен —6857ejeje5/aj, что при е = 0.1
и ej = 0.05 дает ширину резонанса всего лишь 6.5 х 10_6 а. е. Заметим,
что начальные условия по большой полуоси при вычислениях показателя
Ляпунова, результаты которых представлены на рис. 12.1 и 12.2, брались
с шагом 2 х 10~4 а. е., поэтому на этих графиках, вообще говоря, может
быть упущено много пиков, относящихся к более узким резонансам.
Несворный и Ройг (2001) провели аналогичное исследование динами¬
ки пояса Койпера. Распределив начальные положения 2800 пробных частиц
регулярно по большой полуоси в диапазоне от 38.8 до 50 а. е. (при началь¬
ном эксцентриситете, равном 0.1, и нулевых начальных наклонении и фа¬
зовых углах), путем численного интегрирования они рассчитали эволюцию
этих частиц с учетом возмущений от четырех планет-гигантов на интер¬
вале времени 100 млн лет. На рис. 12.3 показаны полученные значения
максимального показателя Ляпунова в зависимости от начального значения
большой полуоси. Из рис. 12.3 видно, что пояс Койпера, как и главный пояс
астероидов, имеет сложную хаотическую структуру.
Характерные особенности графиков на рис. 12.3, как и на рис. 12.1,
в большинстве своем обусловлены резонансами средних движений; что ка¬
сается вековых резонансов, у них показатели Ляпунова обычно меньше,
12.1. Обнаружение хаотических зон
341
поскольку их динамические шкалы времени длиннее. Единственным ис¬
ключением является интервал 40-42 а. е., где перекрываются вековые резо¬
нансы r'g, v 17 и vis (Кнежевич и др., 1991; см. рис. 8.10), что вынуждает
многие пробные частицы менее чем за 100 млн лет уходить на орбиты,
пересекающие орбиту Нептуна.
На рис. 12.3 для ряда резонансов средних движений приведены их
обозначения. Тогда как при а < 46.5 а. е. наиболее выдающиеся пики соот¬
ветствуют резонансам средних движений с Нептуном; при а > 46.5 а. е.
большинство пиков соответствуют трехтельным резонансам с Нептуном
и Ураном. Обратите внимание, что последние расположены по обе стороны
от резонанса 1/2 с Нептуном, образуя супермультиплетную структуру, ана¬
логичную обсуждавшимся выше структурам в главным поясе астероидов.
Она образуется потому, что Уран и Нептун близки к взаимному резонансу
1/2, так что угол <puN = 2An — Аи медленно циркулирует с положительной
производной и периодом « 4230 лет.
Отметим также, что на рис. 12.3 с уменьшением большой полуоси
присутствие хаотических областей нарастает. Этот феномен аналогичен ак¬
кумуляции резонансов средних движений с Марсом во внутреннем поясе
астероидов и резонансов средних движений с Юпитером во внешнем поясе
астероидов. Однако заметим, что важнейшие резонансы средних движений
с Нептуном во внутреннем поясе Койпера (2/3, 7/11, 5/8, 8/13, 3/5; а также
и резонанс 1/3 с Ураном) в общем вызывают понижения значения показа¬
теля Ляпунова относительно фонового уровня. Орбиты в этих резонансах
менее хаотичны, чем соседние нерезонансные орбиты, так как эти резонан¬
сы обеспечивают механизм фазовой защиты, а также из-за различий в ве¬
ковой динамике. Динамика внутри резонансов 2/3 и 1/2 довольно подробно
описана выше в разделе 11.4.
Робутель и Ласкар (2000), используя частотный анализ, провели иссле¬
дование динамики малых тел в масштабах всей Солнечной системы. Они
численно проинтегрировали эволюцию 192000 пробных частиц, исходно
расположенных на плоскости (а, е), с начальными наклонениями и всеми
начальными фазовыми углами, равными нулю. Регулярная сетка начальных
условий включала: 80 узлов по эксцентриситету в диапазоне от 0 до 1;
200 узлов на каждом из четырех интервалов [0.38, 0.9], [0.9, 2.0], [2, 5]
и [5, 10] а. е. по большой полуоси; 1800 узлов на интервале по большой
полуоси [10, 100] а. е. Интегрирование производилось на интервале вре¬
мени 0.5 млн лет для пробных частиц во внутренней Солнечной системе
(с учетом возмущений от всех планет) и 2 млн лет для пробных частиц
342
Глава 12
-8 -6 -4 -2 О
Рис. 12.4. Частотная карта динамики малых тел во всей Солнечной системе. На¬
чальные условия выбраны при наклонении и всех фазовых углах, равных нулю.
В цветовой шкале показаны значения log сг, где сг — относительное изменение ча¬
стоты средней долготы частицы, в единицах (млн лет)-1. Черным цветом обозначе¬
ны тела, отождествленные в двухтельных резонансах средних движений. Сплошные
кривые — кривые, соответствующие условиям пересечения орбит планет. (Рис. 2 из
статьи Робутеля и Ласкара, 2001; с разрешения Academic Press)
12.2. Хаотическая диффузия
343
во внешней Солнечной системе (с учетом возмущений только от планет-
гигантов). Интервал времени интегрирования [О, Т] был разделен на две
половины [О, Т/2] и [Т/2, Т], на каждой из которых вычислялись часто¬
ты средних долгот Л для всех малых тел. Изменение частоты находилось
согласно определению о = 1 — /п^1\ где и п^ — частоты, подсчи¬
танные последовательно на этих двух половинах. На рис. 12.4 в цветовой
шкале показаны значения log сг в зависимости от начальных условий; до¬
полнительно положено, что белым цветом, совпадающим с цветом фона,
обозначены начальные условия для тел, испытывающих тесные сближе¬
ния с планетой за время интегрирования, а черным цветом — начальные
условия для тел, отождествленных как находящиеся в резонансах средних
движений, независимо от их динамики (регулярной или хаотической).
Рис. 12.4 удачно описывает глобальную картину динамики малых тел
Солнечной системы. Разрешение здесь значительно ниже, чем на рис. 12.1,
12.2 и 12.3, поэтому тонкая структура, порождаемая резонансами средних
движений высоких порядков и трехтельными резонансами, неразличима;
однако рисунок дает полезное представление о наиболее вероятном распо¬
ложении областей регулярных и квазирегулярных орбит. Замечательно, что
в поясе астероидов такие орбиты (они обозначены темно-синим цветом)
можно найти в большом количестве только в области 2.15 < а < 3.2 а. е.
и е < 0.2. Что касается пояса Койпера, только у области а > 50 а. е. обна¬
руживается явно регулярная структура в широком диапазоне эксцентриси¬
тетов. К сожалению, в этой дальней части пояса Койпера пока не открыто
ни одного реального объекта.
Также замечательно, что в поясе астероидов и в поясе Койпера обла¬
сти умеренного хаоса (они обозначены на рис. 12.4 зеленым цветом) ре¬
ально населены, то есть хаос слишком слаб, чтобы вызвать уход большей
части тел за время, равное возрасту Солнечной системы (см. раздел 12.2);
с другой стороны, зеленые области, видимые на рис. 12.4 между планетами
земной группы, а также между планетами-гигантами, малыми телами не
заселены. Данное различие может дать важные подсказки об особенностях
процесса образования планет и/или ранней эволюции Солнечной системы.
12.2. Хаотическая диффузия и макроскопическая
неустойчивость
Тогда как для обнаружения хаотической структуры бывает достаточно
численного интегрирования на сравнительно малых временах, для изучения
344
Глава 12
влияния слабого хаоса на долговременную динамическую эволюцию тре¬
буется численное интегрирование на шкале времени настолько длинной,
насколько это возможно. Благодаря новому поколению высокопроизводи¬
тельных компьютеров и быстрых алгоритмов численного интегрирования
(Уиздом и Хольман, 1991; Левисон и Дункан, 1994; Дункан и др., 1998;
Чамберс, 1999) появилась возможность проводить численное интегрирова¬
ние на временах порядка 100 млн лет и даже 1 млрд лет. Таким образом,
начинает складываться грубая и лишь отчасти завершенная картина эво¬
люции пояса астероидов и пояса Койпера на шкалах времени, сравнимых
с возрастом Солнечной системы. В близком будущем она станет еще отчет¬
ливее.
Медленная хаотическая диффузия орбит во внутреннем поясе астерои¬
дов изучена в работах Мильорини и др. (1998) и Морбиделли и Несворного
(1999). Выборка из 412 реальных астероидов интегрировалась на интервале
времени 100 млн лет. Объекты были выбраны среди астероидов, у которых
оскулирующее перигелийное расстояние меньше 1.8 а. е., большая полуось
меньше 2.5 а. е., наклонение меньше 15°, и которые не пересекают орби¬
ту Марса в течение первых 300000 лет. Последнее условие позволяет ис¬
ключить из выборки популяцию «скрытых Марс-кроссеров», а именно тел,
пересекающих орбиту Марса на короткой временной шкале из-за вековых
колебаний их элементов орбит. Учитывались возмущения от всех планет, за
исключением Меркурия.
Чтобы явно представить малые изменения элементов орбит на длин¬
ных шкалах времени, численно находились собственные элементы асте¬
роидов и их изменения за время интегрирования. Это осуществлялось пу¬
тем усреднения элементов орбит (значения которых исходно выводились
с шагом 500 лет) методом скользящего окна, ширина которого была поло¬
жена равной 10 млн лет. Другими словами, если единым образом обозна¬
чить большую полуось или эксцентриситет через ж, то собственный эле¬
мент xp(t) находился по формуле
Г=£+5Му
xp(i) = х(12Л)
t'=t — 5Му
где N — количество выведенных значений х на рассматриваемом интервале
времени; время t увеличивалось на каждом шаге на 105 лет, начиная с t =
= 5 млн лет. Ширины окна в 10 млн лет достаточно, чтобы усреднить все
существенные квазипериодические осцилляции оскулирующих элементов.
12.2. Хаотическая диффузия
345
В результате, как объяснено в разделе 5.4.4, изменение собственных эле¬
ментов во времени дает представление о неквазипериодической эволюции,
то есть о хаотической диффузии. Напротив, у тел на регулярных орби¬
тах, чьи оскулирующие элементы испытывают лишь квазипериодические
осцилляции, собственные элементы во времени постоянны.
На верхней панели рис. 12.5 представлены начальные значения соб¬
ственных больших полуосей и эксцентриситетов тел из выборки Мильори-
ни и др., рассчитанные по формуле (12.1) за первые 10 млн лет интегри¬
рования. Красным цветом выделены тела, которые за время интегрирова¬
ния станут Марс-кроссерами. Только у трех тел динамическое время жизни
оказалось короче 10 млн лет, поэтому их начальные собственные элементы
вычислить нельзя. На нижней панели рис. 12.5 показана эволюция соб¬
ственных больших полуосей и эксцентриситетов тел выборки: у совсем
немногих из них орбиты регулярны (на графике они выглядят как точки),
тогда как подавляющее большинство испытывает макроскопическую диф¬
фузию по эксцентриситету, то есть существенное изменение собственного
эксцентриситета. Это согласуется с тем, что у большинства тел внутрен¬
него пояса орбиты хаотичны, как следует из рис. 12.2. На нижней панели
рис. 12.5 красным цветом выделена эволюция тел после того, как они стали
Марс-кроссерами, а именно когда в ходе интегрирования оскулирующее пе-
ригелийное расстояние стало меньше 1.665. Из-за сближений с Марсом эти
тела начинают случайные блуждания по большой полуоси, следуя пример¬
но вдоль кривой инвариантного параметра Тиссерана относительно Марса
(см. Эпик, 1976). Таким образом, их собственные большие полуоси изме¬
няются со временем. Эти изменения умеренны у тел, незначительно захо¬
дящих внутрь орбиты Марса, и гораздо сильнее у тел, заходящих глубоко
внутрь нее. При хаотической диффузии, напротив, у большинства тел соб¬
ственная большая полуось остается в общем постоянной, пока не достига¬
ется режим пересечений с орбитой Марса. Это означает, что при диффузии
по эксцентриситету тела всегда остаются в одном и том же резонансе сред¬
них движений или же попеременно находятся в близких друг к другу резо¬
нансах. Лишь немногие из астероидов, не пересекающих орбиту Марса, ис¬
пытывают макроскопическую диффузию по собственной большой полуоси;
это означает, что они мигрируют по цепочке перекрывающихся резонансов.
В разных частях внутреннего пояса скорость хаотической диффузии
различна. На рис. 12.5 видны участки, где изменения собственного эксцен¬
триситета велики, на общем фоне, характеризуемом малыми, но не пре¬
небрежимо малыми его изменениями. Такие участки мы будем называть
346
Глава 12
2.15 2.2 2.25 2.3 2.35 2.4 2.45
собств. большая полуось, а. е.
собств. большая полуось, а. е.
Рис. 12.5. Панель вверху: собственные большая полуось и эксцентриситет, вычис¬
ленные за первые 10 млн лет интегрирования орбит астероидов внутреннего пояса.
Красными точками обозначены объекты, которые станут Марс-кроссерами за вре¬
мя моделирования. Панель внизу: последующая эволюция интегрируемых орбит на
плоскости собственных элементов (а, е). Регулярные орбиты проявляют себя как
неподвижные точки, а хаотические мигрируют, оставляя на графике треки. Красным
цветом выделена эволюция тел после того, как они стали пересекать орбиту Марса.
Двумя сплошными линиями показаны кривые постоянных значений собственного
перигелийного расстояния, равных 1.92 и 1.84 а. е. (Рис. 8 из статьи Морбиделли
и Несворного, 1999; с разрешения Academic Press)
12.2. Хаотическая диффузия
347
главными диффузионными треками, а фон — диффузионным фоном. Глав¬
ными диффузионными треками являются: (i) трек при 2.256 а. е., связанный
с почти совпадающими по расположению резонансами средних движений
7/2 с Юпитером и 5/9 с Марсом (любопытно, что согласно расчетам по¬
следний более эффективен, чем первый); (ii) трек при 2.213 а. е., связанный
с резонансом средних движений 4/7 с Марсом; (iii) область при больших
полуосях меньше 2.17 а. е., где резонансы средних движений с Марсом пе¬
рекрываются друг с другом, что вызывает глобальный хаос (как видно из
рис. 12.2). Наиболее важным из последних резонансов является резонанс
средних движений 3/5 с Марсом при 2.142 а. е. Если перейти к внешней
части внутреннего пояса, то мы увидим два замечательных диффузионных
трека при 2.398 и 2.419 а. е., которые связаны с трехтельным резонансом
4-2-1 «Юпитер - Сатурн - астероид» и резонансом средних движений 1/2
с Марсом соответственно.
На рис. 12.6 сопоставлены зависимости максимального показателя Ля¬
пунова и амплитуды изменения собственного эксцентриситета от большой
полуоси. Последняя кривая получена путем вычисления максимального из¬
менения de собственного эксцентриситета каждой из представленных на
рис. 12.5 пробных частиц, имевшего место до перехода частицы в режим
пересечений орбиты Марса. Обе кривые на рис. 12.6 сглажены путем вы¬
числения средних по скользящему окну подходящей ширины. Сходство
рис. 12.6а и 12.66 впечатляет. С пиками кривой показателя Ляпунова сов¬
падают не только главные пики de, соответствующие рассмотренным выше
главным диффузионным трекам, но также и мелкие пики, определяющие
структуру диффузионного фона. В частности, на обеих панелях пиков осо¬
бенно много в области с большими полуосями меньше 2.25 а. е., а в более
регулярной области от 2.3 до 2.4 а. е. пики ниже и они лучше разделены.
Кроме того, в области а < 2.15 а. е. и МПЛ, и de имеют тенденцию к росту
с уменьшением большой полуоси.
Феномен медленной хаотической диффузии астероидов во внутреннем
главном поясе важен, так как он может дать объяснение, почему популя¬
ция Марс-кроссеров сохраняет стационарное состояние (Мильорини и др.,
1998; Морбиделли и Несворный, 1999). В свою очередь, популяция Марс-
кроссеров, в дополнение к резонансам 3/1 и г/б, считается сейчас одним
из главных транзиентных источников поддержания популяции астероидов,
пересекающих орбиту Земли (Боттке и др., 20006; Мишель и др., 2000).
Несворный и Ройг (2001) осуществили аналогичное исследование мед¬
ленной хаотической диффузии малых тел пояса Койпера. Они провели чис-
348
Глава 12
a, a. е.
Рис. 12.6. Зависимость максимального показателя Ляпунова от большой полуоси
(панель вверху) в сравнении с зависимостью амплитуды изменения собственного
эксцентриситета от большой полуоси (панель внизу). Через «Мп/т» и «Jт/п» обо¬
значены резонансы средних движений т/п с Марсом и Юпитером соответственно;
через «4J—2S—1» обозначен трехтельный резонанс «Юпитер - Сатурн - астероид»
4Aj — 2As — А ~ 0. (Рис. 9 из статьи Морбиделли и Несворного, 1999; с разрешения
Academic Press)
ленное интегрирование эволюции 101 пробной частицы на интервале вре¬
мени 4 млрд лет, причем начальные условия были выбраны следующим
образом: значения большой полуоси равномерно распределены в интерва-
12.2. Хаотическая диффузия
349
ле [37, 39] а. е., эксцентриситет и наклонение выбраны равными 0.01 и 2°
соответственно, а в качестве фазовых углов взяты случайные числа. На
рис. 12.7 показана эволюция собственных больших полуосей и эксцентри¬
ситетов этих частиц, вычисленная так, как описано выше для астероидов.
Черными точками эволюция обозначена до того момента, когда перигелий-
ное расстояние частицы впервые стало меньше 32 а. е.; затем она обозна¬
чается более крупными серыми символами. В общей сложности на орби¬
ты, пересекающие орбиту Нептуна, в течение всего времени интегрирова¬
ния перешло 16 частиц: две частицы (крайние слева) у границы резонанса
средних движений 3/4 с Нептуном (последний резонанс центрирован на
36.48 а. е.), одна частица (крайняя справа) у границы хаоса в резонансе 2/3,
а остальные 13 частиц стали Нептун-кроссерами в результате медленного
увеличения собственного эксцентриситета в резонансах средних движений
высокого порядка с Нептуном. Большинство (10 из 13) находилось в резо¬
нансе 5/7, причем среднее время перехода на орбиту, пересекающую орбиту
Нептуна, составило 666 млн лет. Остальные находились в резонансах сред¬
них движений 8/11 (время превращения в Нептун-кроссера 641 млн лет),
7/10 (620 млн лет) и 9/13 (1419 млн лет). Среди других частиц у некото¬
рых наблюдалась существенная диффузия по собственному эксцентриси¬
тету из-за трехтельных резонансов с Ураном и Нептуном, однако за время
интегрирования они не достигли режима пересечений с орбитой Нептуна.
Что касается собственной большой полуоси, она, как и в случае астерои¬
дов, почти не меняется со временем до тех пор, пока частица не начинает
испытывать тесные сближения с Нептуном, после чего происходят макро¬
скопические вариации.
Более общую картину динамики тел в поясе Койпера дали Дункан
и др. (1995). Они численно проинтегрировали эволюцию нескольких ты¬
сяч фиктивных частиц на интервале времени 4 млрд лет, задав начальные
условия на регулярной сетке на плоскости (а, е) при малом наклонении
и на регулярной сетке на плоскости (а, г) при малом эксцентриситете. При
этом начальные большие полуоси частиц были заданы в диапазоне от 32 до
50 а. е. На рис. 12.8 каждому начальному условию сопоставлено динамиче¬
ское время жизни частицы. Последнее определяется как время, прошедшее
до первого сближения с Нептуном на расстояние меньше трех радиусов
сферы Хилла. Желтым цветом обозначены частицы, которые за время ин¬
тегрирования никогда не сближаются с Нептуном, однако это не означает,
что их орбиты регулярны: они могут быть хаотичны и в отсутствие сближе¬
ний с Нептуном. Поэтому рис. 12.8 следует рассматривать в качестве карты
350
Глава 12
Рис. 12.7. То же, что и на нижней панели рис. 12.5, но для пробных частиц во
внутреннем поясе Койпера. Серыми точками показана эволюция тел после того,
как перигелийное расстояние впервые становится меньше 32 а. е. Указаны главные
резонансы с Нептуном и трехтельные резонансы с Ураном и Нептуном. (Рис. 3 из
статьи Несворного и Ройга, 2001; с разрешения Academic Press)
начальных условий, ведущих к макроскопической неустойчивости, а не как
карту хаотических областей.
Важнейшие из динамических свойств пояса Койпера, наглядно пред¬
ставленных на рис. 12.8, таковы. Кривая <7 = 35 а. е. разделяет плоскость
(а, е) на две части, в одной из которых динамическое время жизни до¬
стигает 4 млрд лет, а вторая неустойчива на гораздо более короткой шкале
времени. Выше кривой q = 35 а. е. большое время жизни имеют только ор¬
биты, относящиеся к резонансам средних движений первого порядка, по¬
скольку последние обеспечивают эффективную фазовую защиту от тесных
сближений с Нептуном (см. раздел 9.1.1). Ниже кривой q = 35 а. е. глав¬
ными областями неустойчивости (где даже частицы с исходно круговыми
орбитами имеют короткое динамическое время жизни) являются области
35-36 а. е. и 40-42 а. е., где расположены перигелийные вековые резонан-
12.2. Хаотическая диффузия
351
0.4
0.3 -
н
S
0
Я
е-
я
(U
1 0.2
1 1
-г — 1
I 1
1 1 1
1 1
I I
1 1 1 1
q = ЗДа.е.
—
Н
ИНН
-
q = 35 а. е.
-
4 х 109
35 40 45
начальная большая полуось, а. е.
Рис. 12.8. Динамическое время жизни пробных частиц в поясе Койпера в зави¬
симости от начальных значений большой полуоси и эксцентриситета. Начальное
наклонение положено равным 1°. Время жизни определяется как время до первого
сближения с Нептуном на расстояние меньше трех радиусов сферы Хилла. Через
«п : тп» обозначены главные резонансы средних движений с Нептуном. (Рис. 1 из
статьи Дункана и др., 1995; с разрешения Американского астрономического обще¬
ства)
сы и щ (см. рис. 8.10). Область неустойчивости 40^12 а. е. делит пояс
Койпера надвое. Во внутреннем поясе (а < 40 а. е.) устойчивые орбиты
относятся к резонансам средних движений первого порядка или же распо¬
ложены в области 36-39 а. е. при малых эксцентриситетах. Эту область, как
видно из рис. 12.7, могут покинуть совсем немного тел, — а именно, тела
в некоторых мелких резонансах. Во внешнем (а > 42 а. е.) поясе Койпера,
называемом также классическим поясом Койпера, большинство устойчи¬
вых орбит нерезонансны. В этом отношении динамическая структура пояса
Койпера похожа на зеркальное отражение динамической структуры главно¬
го пояса астероидов.
352
Глава 12
Из рис. 12.8 также следует существование орбит, начинающих испы¬
тывать тесные сближения с Нептуном лишь по истечении нескольких мил¬
лиардов лет эволюции. Некоторые из них, очевидно, принадлежат главным
резонансам средних движений и предположительно относятся к областям
медленной диффузии при умеренных амплитудах либрации, обсуждавшим¬
ся в разделе 11.4. Расположение остальных довольно хорошо коррелиру¬
ет с главными пиками кривой показателя Ляпунова на рис. 12.3. Поэтому
вполне вероятно, что эти орбиты медленно диффундируют по собствен¬
ному эксцентриситету в двухтельных и трехтельных резонансах высоких
порядков подобно тому, как проиллюстрировано выше на рис. 12.5 на при¬
мере главного пояса астероидов и на рис. 12.7 на примере внутреннего
пояса Койпера.
12.3. Аналитические оценки ляпуновского времени
и времени ухода
В предыдущих разделах мы убедились, что двухтельные резонансы да¬
же довольно высоких порядков по эксцентриситету и трехтельные резонан¬
сы играют важную роль в генерации хаоса и медленной диффузии орбит
малых тел по эксцентриситету и наклонению. Однако приведенные выше
результаты получены исключительно при помощи численного интегрирова¬
ния; поэтому феномен слабого хаоса в резонансах средних движений было
бы важно и полезно объяснить теоретически, а также получить аналитиче¬
ские оценки показателя Ляпунова и характерных времен диффузии.
Важную попытку в этом направлении предприняли Мюррей и Хольман
(1997). Поскольку очень трудно (если вообще возможно) решать эту задачу
строго и в общей постановке, они использовали ряд приближений; тем не
менее в большинстве случаев их подход дает оценки, верные по порядку
величины.
Согласно главам 9 и 10 в мультиплете субрезонансов резонанса сред¬
них движений хаос возникает благодаря частичному или полному перекры¬
тию субрезонансов. Чтобы описать подход Мюррея и Хольмана, используя
принятые в этой книге обозначения, начнем с гамильтониана (9.18) и огра¬
ничимся анализом плоской эллиптической задачи трех тел. А именно, из
всех гармоник cm)U)V)S,r cos<7m)U)V,s,r в (9.18) мы оставим только гармони¬
ки с v = 0, г = 0 и Uj = 0 для j ф j, где j — индекс резонансной планеты.
Кроме того, для простоты будем рассматривать только члены с т — 1, от¬
куда щ = —(kj — k — s). Используя укороченную запись cs = citlXj,o,s,o
12.3. Аналитические оценки ляпуновского времени
353
и со = со,о,о,0,0) в итоге записываем наш модельный гамильтониан в виде
Wr3B — Wo (A, Aj) -f со (A, Р) +
kj — k
+ ^ cs(A, Р) cos(kj\j — к\ + sp — (kj — к — s)wj), (12.2)
s=0
где Wj — долгота перигелия резонансной планеты. Ее. мы полагаем фикси¬
рованной, поэтому часть Но, зависящая от Agj, ASj (см. формулу (9.16)),
здесь опущена. Для простоты мы далее полагаем wj = 0 и исключаем Wj
из (12.2). Во всех коэффициентах cs сумма степеней эксцентриситетов ма¬
лого тела и резонансной планеты равна \Щ—к\. Введем новые канонические
переменные
Ф = (А — А о)/к, ф = кХ — kjXj,
I = P, <Р = Р, (12.3)
Aj = Aj -Ь kj(A — Aq)/к, Xj = Xj,
где Ao — невозмущенное положение резонанса средних движений, опре¬
деляемое из закона Кеплера. Раскладывая Но и со в (12.2) в ряд Тейлора
и сохраняя только члены низшего порядка по Ф, 7, имеем
к3-к
Hr3b = + 2еАГ + ce(/) cos(ip - s</?), (12.4)
s=0
где /3 = d2H0/d2A(A0,Aj), 2еА = дсо/д1(Ао,0) и cs(/) = cs(A0,I). Xo-
тя гамильтониан (12.4) получен в простых рамках ограниченной задачи
трех тел для двухтельного резонанса, его можно рассматривать и как бо¬
лее общую плоскую модель мультиплетной структуры резонанса средних
движений, справедливую также и для трехтельных резонансов. С этой точ¬
ки зрения коэффициент 2еА следует рассматривать как частоту прецессии
вековых углов, по порядку величины, очевидно, равную е (массе плане¬
ты, оказывающей доминирующее влияние на вековую динамику); коэффи¬
циенты cs тогда пропорциональны массе резонансной планеты в случае
двухтельных резонансов или же произведению масс резонансных планет
в случае трехтельных резонансов (в последнем случае эти коэффициенты
обычно меньше е); сумма гармоник должна быть распространена на все
комбинации вековых углов, дающие резонансные гармоники самого низко¬
го возможного порядка по эксцентриситету.
354
Глава 12
Чтобы получить общую модель, к которой можно было бы подсту¬
питься аналитически, Мюррей и Хольман положили все коэффициенты cs
равными ведущему коэффициенту сЧо, а также расширили пределы сумми¬
рования по s до — ос и +оо; отсюда
I +°°
Wr3b = + ЪеА1 + cS() (/) cos ф ^ cos s<p =
s=-oo (12.5)
= + 2eAf + cSn(I) cosф 6(ip),
где 5(у>) — периодическая дельта-функция Дирака, аргумента р. Интегрируя
уравнения движения, задаваемые (12.5) для переменных Ф и ф, на цикле
изменения получаем следующее симплектическое отображение (см. Чи¬
риков, 1979; Уиздом, 1983):
Ф' = Ф + 7rCs?^- sinф, ф, = ф+~\^'. (12.6)
С Л С Л
Коль скоро из (12.4) следует, что I ~ — 5оФ, для описания эволюции дей¬
ствия I имеем дополнительное к этому отображению уравнение
1' = J-ao--f-sin0. (12.7)
ел
Если ввести нормированную переменную Ф = Ф7Г/3/(еА), то (12.6) примет
в итоге вид стандартного отображения:
ф' = Ъ + КеяБШф, ^' = ф + ф', (12.8)
где
Ы»*-,г-(й)2- (12'9)
Хорошо известно (см. главу 4 книги Лихтенберга и Либермана, 1983;
а также раздел 6.1 нашей книги), что поведение стандартного отображе¬
ния (12.8) является глобально-хаотичным, если Ксн > ЛГснь где Kcrit ~ 1.
Заметим, что условие Ке^ > 1 аналогично условию перекрытия резонан¬
сов в резонансном мультиплете в модели (12.4); действительно, расстоя¬
ние между резонансами равно = 2еА/0, а ширина каждого составляет
ДФ ~ 2y/cSo/(3, так что Ке^ = (7гДФ/(!)Ф)2. Множитель 7г2 в этой формуле
12.3. Аналитические оценки ляпуновского времени
355
отражает тот факт, что согласно разделу 6.1 переход к глобальному хаосу
происходит прежде, чем в мультиплете начинают перекрываться резонан¬
сы низкого порядка, так как между ними есть перекрывающиеся резонансы
более высоких порядков.
Чтобы оценить величину показателя Ляпунова1, Мюррей и Хольман
выписали для (12.6) касательное отображение
£ф' = йф + 8ф
7Г/3
——cost/>, 5ф' = ёф Н
8 А 8 А
(12.10)
собственные числа которого даются уравнением
(1 — А)(1 + Keff cost/; — А) — Keff cosi/j = 0, (12.11)
где Keff дается формулой (12.9). Решение уравнения (12.11) имеет вид
Л = 1 + ~ Keff cos ф ± JКеff cos ф + ( ^ Keff cos ф
(12.12)
Логично ожидать, что в хаотическом слое переменная ф эргодически при¬
нимает все возможные значения от 0 до 2п, так что показатель Ляпунова
отображения можно оценить путем усреднения логарифма А по ф:
1 Г2п
7=— / 1пА<±0. (12.13)
27Г Jo
Согласно Мюррею и Хольману допустима аппроксимация2
i + ^s +
4
I Keff + (КМ\2
(12.14)
Поскольку период отображения (12.6) равен тг/(8А) (периоду угла р в га¬
мильтониане (12.4)), ляпуновское время рассматриваемого резонанса сред¬
них движений равно
(12.15)
’Способ, примененный Мюрреем и Хольманом, повторяет подход Б. В.Чирикова к ана¬
литическому оцениванию динамической энтропии стандартного отображения. Детали этого
подхода см. в работе Чирикова (1979). — Прим. ред.
2 В статье Мюррея и Хольмана (1997) в данной формуле допущена опечатка. — Прим. авт.
356
Глава 12
Чтобы проверить справедливость этой оценки, Мюррей и Хольман
провели ряд численных экспериментов. На рис. 12.9 представлены значе¬
ния ляпуновского времени для пробных частиц в различных резонансах
средних движений с Юпитером во внешнем поясе астероидов (при началь¬
ном эксцентриситете, положенном равным 0.05) в эллиптической плоской
ограниченной задаче трех тел. Значения ляпуновского времени, полученные
из численных экспериментов, показаны черными квадратиками, а оценки,
сделанные по формуле (12.15), — светлыми кружками. Как видим, по по¬
рядку величины в общем имеется хорошее согласие, хотя можно заметить
несколько исключений.
Чтобы оценить скорость диффузии орбит тел в резонансах средних
движений по эксцентриситету, Мюррей и Хольман в качестве отправной
точки взяли известный результат (см. главу 5 книги Лихтенберга и Либер-
мана, 1983), что при Кеfj > Kcrit в (12.8) транспорт действия Ф мож¬
но описать уравнением Фоккера-Планка. Это означает, что распределение
большого ансамбля частиц по Ф описывается функцией Р(Ф,/), эволюци¬
онирующей согласно уравнению
дР d(DdP\
dt дУ\ 2дФ)’ ( ^
где D = к/2 называется коэффициентом диффузии. Если применить уже
известную нам нормировку Ф = \1>7г/3/(еА), то коэффициент диффузии для
действия запишется как
°*=ктг=мш- <->
Учтя, что период отображения (12.6) равен тг/(еА), в итоге находим, что
коэффициент диффузии для Ф дается формулой
D* = \clWjA- (12Л8)
Поскольку инкременты Фи/в уравнениях (12.6) и (12.7) отличаются мно¬
жителем so, эволюция действия I будет описываться уравнением Фоккера-
Планка с коэффициентом диффузии
Di = si<WjA- (12-19)
12.3. Аналитические оценки ляпуновского времени
357
а, в юпитерианских единицах
а, а. е.
Рис. 12.9. Ляпуновское время в зависимости от большой полуоси во внешнем поясе
астероидов. Оценки в рамках эллиптической ограниченной задачи трех тел. Через
«kj'.k» обозначены важнейшие резонансы средних движений с Юпитером. Заштри¬
хованными символами показаны результаты численного интегрирования: треуголь¬
никами — результаты, полученные с учетом возмущений от четырех планет-гиган¬
тов, квадратиками — результаты, полученные с учетом возмущений только от Юпи¬
тера. Кружками показаны оценки по формуле (12.15). (Рис. 1 из статьи Мюррея
и Хольмана, 1997; с разрешения Американского астрономического общества)
Таким образом, в модели Мюррея и Хольмана резонансные частицы ис¬
пытывают случайные блуждания как по большой полуоси (соответствен¬
но Ф), так и по эксцентриситету (соответственно I). Однако в обоих случа¬
ях случайные блуждания должны удовлетворять определенным граничным
условиям. Возможные значения большой полуоси ограничены интервалом,
определяемым перекрытием резонансов в мультиплете, ширина которо¬
го в реальности не бесконечна. Это условие можно смоделировать путем
358
Глава 12
введения отражающих границ, расположенных при определенных значени¬
ях Ф. Что касается эксцентриситета, то он должен быть положительным,
что можно смоделировать путем введения отражающей границы при 1 = 0.
Благодаря этой отражающей границе пробные частицы на хаотических ор¬
битах с малыми начальными I диффундируют от малых эксцентриситетов
к большим. Когда орбиты частиц достигают эксцентриситета, достаточного
для пересечений с орбитой планеты, частицы выбывают в результате тес¬
ных сближений с планетой. Этот процесс можно смоделировать путем вве¬
дения поглощающей границы, расположенной при I = /тах. Решая урав¬
нение Фоккера-Планка, Мюррей и Хольман вычислили, что характерное
время ухода, то есть характерное время, за которое частицы, стартующие
от /о, достигают границы /шах, дается выражением
^ =. (12.20)
При помощи численного интегрирования Мюррей и Хольман провери¬
ли справедливость и этой оценочной формулы. Аналогично тому, как на
рис. 12.9 верифицированы оценки ляпуновского времени, на рис. 12.10 про¬
водится сравнение времен ухода, предсказываемых теоретически (обозна¬
ченных кружками), с наблюдаемыми в численных экспериментах (обозна¬
ченными заштрихованными квадратиками). Поскольку согласно (12.20) Xr
сильно зависит от эксцентриситета, дающего /о, Мюррей и Хольман в ка¬
честве эксцентриситета брали его среднее значение за первые несколько
тысяч орбитальных периодов, которое они находили из численного инте¬
грирования. Получаемый при этом разброс значений /0 ответственен за
разброс предсказываемых времен ухода частиц в каждом из резонансов,
показанных на рис. 12.10. При оценивании Х>/(7шах) также требуется опре¬
деленная осторожность. Действительно, если выбрать /тах исходя из значе¬
ния эксцентриситета, позволяющего частице пересекать орбиту Юпитера,
то коэффициент cSo(/max) обратится в бесконечность (поскольку гамильто¬
ниан неаналитичен и его нельзя разложить в ряд Фурье, как в (12.2)); тогда
и Х/(/шах) обращается в бесконечность, а Xr — в нуль. Поэтому прихо¬
дится выбирать несколько меньшее значение /гпах. Чтобы исключить при
этом произвол, лучше всего выбирать /тах так, чтобы значение Xr было
максимальным.
Из рис. 12.10 видно, что теоретически предсказываемые и численно¬
экспериментальные времена ухода в общем хорошо согласуются по поряд¬
ку величины, хотя можно заметить некоторые исключения. Это впечатля-
12.3. Аналитические оценки ляпуновского времени
359
а, в юпитерианских единицах
0.66 0.68 0.7 0.72 0.74
а, а. е.
Рис. 12.10. То же, что и на рис. 12.9, но для времени ухода. Заштрихованными сим¬
волами показаны результаты численного интегрирования, кружками — оценки по
формуле (12.20). Стрелками обозначено время интегрирования для тех резонансов,
из которых не ушла ни одна из частиц. (Рис. 2 из статьи Мюррея и Хольмана, 1997;
с разрешения Американского астрономического общества)
ет, особенно если вспомнить, как много приближений было сделано при
выводе теоретической формулы. Подчеркнем, что в коэффициенте диффу¬
зии (12.19) для действия I не учтены возможные эффекты чисто вековой
динамики, которые, как мы убедились в главе 11, могут вызывать рост экс¬
центриситета на более коротких шкалах времени. Кроме того, сделанное
в начале этого раздела предположение, что резонансный мультиплет можно
аппроксимировать бесконечной цепочкой резонансов, не слишком хорошо
подходит для резонансов низкого порядка по эксцентриситету, которые ве¬
дут себя как модулированный маятник (см. раздел 9.4). В последнем слу¬
чае согласно Брувилеру и Кэри (1989) коэффициенты диффузии для орбит
360
Глава 12
в хаотическом слое были бы просто пропорциональны кубу частоты моду¬
ляции, то есть (£А/7г)3 (опять же если пренебречь важными эффектами чи¬
сто вековой динамики), что меньше, чем дают формулы (12.18) и (12.19).
Этим могут объясняться некоторые из наиболее существенных расхожде¬
ний, видимых на рис. 12.10.
Несмотря на модельные ограничения, теоретические оценки времени
ухода, сделанные Мюрреем и Хольманом, представляют собой важную по¬
пытку продвинуться дальше классической теории возмущений и охаракте¬
ризовать статистические свойства хаотической эволюции.
12.4. Применимы ли теоремы Колмогорова-Арнольда -
Мозера и Нехорошева к динамике малых тел?
На данном этапе нашего изложения естественно возникает вопрос,
подходит ли теоретическая картина глобальной динамики, следующая из
теорем КАМ и Нехорошева (см. главы 3 и 6, соответственно), для описания
реальной динамики малых тел в Солнечной системе?
Разумеется, напрямую обе теоремы неприменимы, поскольку они до-;
казаны для невырожденных динамических систем. Прежде чем применять,
их необходимо адаптировать к случаю возмущенного кеплерова движения.
В этом направлении уже работали Арнольд (1963в) и Нехорошее (1977);
а не так давно Гуццо и Морбиделли (1997) переформулировали обе теоре¬
мы с учетом наиболее важных особенностей динамики малых тел.
Из предыдущих глав нашей книги с очевидностью следует, что, вне
зависимости от величины планетных масс и эксцентриситетов, было бы
безнадежно пытаться доказать результат об устойчивости нехорошевского
типа, который был бы справедлив во всем фазовом пространстве (исключая
множество орбит, пересекающих орбиты планет). Действительно, резонан¬
сы средних движений, чей порядок по эксцентриситету и фурье-порядок3
оба имеют значения от низкого до умеренного (пороговое значение порядка
зависит от эксцентриситета малого тела), обладают общим свойством рас¬
щепляться, порождая мультиплеты перекрывающихся субрезонансов (см.
раздел 9.3). При помощи адекватной модели (см. раздел 12.3) можно пока¬
зать, что макроскопические изменения эксцентриситета малого тела, дви¬
жущегося внутри мультиплета, могут происходить на короткой шкале вре¬
мени, а именно, в течение времени, пропорционального некоторой степе¬
ни возмущающих параметров (см. формулу (12.20)). Верно, что резонансы
3См. определения в разделе 9.1. — Прим. авт.
12.4. Применимы ли теоремы Колмогорова-Арнольда-Мозера 361
низших порядков ведут себя как модулированный маятник (см. раздел 9.4)
и поэтому могут иметь центральные острова, где движение устойчиво; но,
как мы убедились в главе 11, в этих случаях свойства устойчивости или
неустойчивости в конечном счете зависят от особых свойств вековой дина¬
мики, которые меняются от резонанса к резонансу. Таким образом, возмож¬
но и есть шанс доказать результат об устойчивости нехорошевского типа,
чья область применимости ограничена каким-либо одним определенным
резонансом (например, центральным ядром резонанса 3/2 с Юпитером), но
нельзя получить общий результат, справедливый для всех резонансов низ¬
кого порядка.
Как следствие, общий вывод нехорошевского типа об устойчивости
можно установить только на многосвязной области, из которой исключены
все резонансы средних движений порядков от низкого до умеренного. Эта
область существует только в том случае, если такие резонансы не перекры¬
ваются друг с другом, что накладывает условия на максимальное значение е
планетных масс, на минимальное расстояние от резонансной планеты и на
максимальное значение эксцентриситета малого тела. Мы будем называть
эту область областью Нехорошева.
Подробное описание, как можно получить результат нехорошевского
типа, выходит за рамки данного раздела, поэтому мы дадим лишь общий
эскиз. Заинтересованный читатель может обратиться к статье Гуццо и Мор¬
биделли (1997). В области Нехорошева сначала следует рассмотреть субоб¬
ласти, где нет резонансов средних движений фурье-порядка меньше 1/е. На
этих субобластях можно построить вековую нормальную форму с остатком,
экспоненциально малым по 1/е, и таким образом свести анализ устойчи¬
вости к вековой задаче. Так как последняя не вырождена, теорема Нехо¬
рошева применима в ее классическом виде (см. главу 6). Есть некоторая
техническая трудность, состоящая в том, что для векового гамильтониана
не выполняется условие (6.2), но в общем случае движение в вековых ре¬
зонансах можно ограничить, используя производные третьего порядка по
действиям. Таким путем по-прежнему можно получить время устойчиво¬
сти, экспоненциально долгое по 1/т/, где rj — некоторый малый параметр,
обычно выражающийся через планетные эксцентриситеты и наклонения.
Вековой резонанс z/6 является исключением; и действительно, как показано
в разделе 8.4.2, эксцентриситеты тел в резонансе могут расти от нуля до
единицы на «короткой» шкале времени.
В других частях области Нехорошева приходится иметь дело с резо¬
нансами средних движений непренебрежимого порядка (то есть порядка
362
Глава 12
меньше l/е). Однако согласно определению области Нехорошева у этих
резонансов компоненты резонансных мультиплетов не перекрываются. По¬
этому, используя процедуру, аналогичную кратко описанной в разделе 6.2.1,
по-прежнему можно получить вывод об устойчивости, также справедливый
на интервале времени, экспоненциально долгом по I/77.
Имея доказанный результат нехорошевского типа об устойчивости на
области Нехорошева, процедуру можно итерировать, как описано в разде¬
ле 6.2.2; тем самым доказывается также существование КАМ-торов. Таким
образом, как и в случае невырожденных систем, результат нехорошевско¬
го типа об устойчивости непосредственно соотносится с существованием
специфичной динамической структуры.
Данные результаты свидетельствуют, что теоремы КАМ и Нехорошева
при подходящей адаптации в принципе применимы для описания динамики
малых тел, по крайней мере в некоторых частях фазового пространства. Од¬
нако на сегодняшний день нет аналитических средств, чтобы решить, при¬
менимы ли эти теоремы к реальной Солнечной системе (с определенными
значениями планетных масс, больших полуосей, эксцентриситетов и на¬
клонений) и в каких областях. С другой стороны, как продемонстрировано
в разделе 6.2.2, для выяснения, описывается ли динамическая структура
заданной системы теоремами КАМ и Нехорошева, очень полезно числен¬
ное моделирование. Хотя подробный анализ (в рамках которого необходимо
было бы выяснить, как динамическая структура изменяется с повышени¬
ем точности выявления хаотических областей) никогда не проводился, из
рис. 12.1 следует, что при учете возмущений только от четырех планет-
гигантов внутренняя и центральная части пояса астероидов действительно
могут иметь динамическую структуру, описываемую теоремой Нехороше¬
ва, по крайней мере при умеренных эксцентриситетах. Внешняя же часть
пояса, напротив, испытывает гораздо более сильные возмущения со сторо¬
ны Юпитера; поэтому здесь хаотические области, соответствующие двух-
тельным и трехтельным резонансам средних движений, с увеличением экс¬
центриситета астероидов быстро сливаются друг с другом (см. рис. 10.8).
Если учитывать возмущения и от внутренних планет, то согласно рис. 12.2
уже вряд ли можно надеяться, что структура Нехорошева во внутреннем
поясе сохранится (по крайней мере до 2.15 а. е.), поскольку эта зона плотно
заполнена резонансами средних движений с Марсом. Таким образом, в рам¬
ках полной планетной задачи следует ожидать, что структура Нехорошева
существует лишь в центральной части пояса при малых эксцентриситетах.
На это указывают и карты частотного анализа, представленные на рис. 12.4.
12.4. Применимы ли теоремы Колмогорова-Арнольда-Мозера 363
Согласно этому же рисунку не следует ожидать, что теорема Нехорошева
применима к динамике малых тел где-либо еще во внутренней Солнечной
системе или в области планет-гигантов. Лишь в поясе Койпера, на достаточ¬
ном удалении от Нептуна, можно вновь обнаружить структуру нехорошев-
ского типа. Между 43 и 50 а. е. присутствие структуры Нехорошева огра¬
ничено зоной малых эксцентриситетов, тогда как за пределами 50 а. е. зона
преобладания регулярной динамики существенно расширяется, при этом
она сегментирована четко отделенными друг от друга резонансами. Вполне
возможно, что будущие высокоточные численные эксперименты покажут,
что во всей Солнечной системе реальная структура Нехорошева существу¬
ет только в глубине пояса Койпера.
Отметим, однако, что поиск структуры Нехорошева интересен ско¬
рее с точки зрения математики, а не астрономической необходимости.
По имеющимся оценкам, характерные времена устойчивости, относящи¬
еся к структуре Нехорошева, на много порядков превосходят физическое
время жизни Солнечной системы. Поэтому также и в резонансах средних
движений с перекрывающимися компонентами мультиплетов время жизни
малых тел может быть сопоставимо с возрастом Солнечной системы, если
время ухода (12.20) достаточно велико. Похоже, например, что именно так
обстоит дело с астероидом Хельга (находящимся в резонансе 12/7 с Юпите¬
ром), время ухода которого, согласно аналитическим оценкам и результатам
численного интегрирования, составляет ~ 5 млрд лет (Мюррей и Хольман,
1997).
Проблема справедливости результатов нехорошевского типа об устой¬
чивости осложняется еще и тем, что возмущающие планеты сами демон¬
стрируют хаотическое поведение (см. главу 7 и раздел 10.4). Это должно
разрушать структуру Нехорошева динамики малых тел на некотором ее
уровне и предотвращать существование инвариантных торов, в чем мож¬
но убедиться из следующих соображений. Неквазипериодические возму¬
щения имеют непрерывный спектр Фурье. В случае слабого хаоса, подоб¬
ного планетному, логично предположить, что непрерывный спектр Фурье
отличен от нуля лишь в некоторых окрестностях (шириной До;) дискрет¬
ных значений частот, соответствующих квазипериодической аппроксима¬
ции движения планет. Из-за непрерывности спектра возмущения каждый
резонанс расщепляется на непрерывный пакет резонансов. Ширина этого
пакета в пространстве частот равна Да; независимо от порядка резонан¬
са. Тогда ширина каждой резонансной области должна быть больше Да;,
вместо того чтобы, как обычно, экспоненциально убывать с порядком ре¬
364
Глава 12
зонанса. Модифицируя формулу (6.5), находим, что объем, заполняемый
резонансами порядка К, становится больше, чем
VK ~ 2пКп~1 [v^exp (-Ка) + До;] . (12.21)
Таким образом, он неограниченно возрастает с К. Поэтому в некотором
порядке К резонансы должны перекрываться, разрушая структуру Нехоро¬
шева и делая невозможным существование инвариантных торов. Следова¬
тельно, если точность численного анализа динамики астероидов повышать
в достаточной мере, то хаотический континуум будет проявляться рано или
поздно даже в тех областях, которые сейчас выглядят «самыми регулярны¬
ми». При этом, независимо от начальных условий, максимальный показа¬
тель Ляпунова будет положительным.
Однако в случае Солнечной системы размеры интервалов До;, опре¬
деляемые относительно некоторой пороговой величины, также довольно
невелики, так как частоты внутренних планет (орбиты которых наиболее
хаотичны) испытывают относительные вариации всего лишь в несколько
процентов (см. раздел 7.3). Поэтому хаотичность возмущений может и не
влиять на устойчивость движения малых тел на временах порядка возраста
Солнечной системы.
Douze ans apres
Заметки к русскому изданию
А. Морбиделли, И. И. Шевченко
Прошло двенадцать лет, как в этой книге были сделаны последние
штрихи. Очевидно, наука продолжает эволюционировать в быстром темпе,
и небесная механика здесь ни в коем случае не исключение. За прошедшие
годы было достигнуто немало новых результатов и, если бы книга писалась
сегодня, в нее потребовалось бы включить несколько новых тем.
В этих заметках мы даем краткий обзор тем, в которых, по нашему
мнению, достижения были наиболее существенными. Не вдаваясь в детали
(это потребовало бы существенного увеличения объема книги) и не пыта¬
ясь дать исчерпывающий список литературы, мы просто укажем предметы
исследований и приведем некоторые ссылки, чтобы заинтересованный чи¬
татель имел ориентиры в современной литературе.
Некоторые из недавних результатов представляют собой естественное
развитие уже рассмотренных в книге тем. Например, с использованием та¬
ких инструментов, как FLI (быстрые индикаторы Ляпунова, раздел 5.4.1)
и динамические карты (подобные представленным на рис. 6.9), исследова¬
лись тонкая структура фазового пространства гамильтоновых систем и роль
паутины Арнольда в обеспечении хаотической диффузии (Фрешле и др.,
2006; Лега и др., 2007). Что касается планетной динамики, сеть трехтель-
ных резонансов (см. главу 10) во внешней Солнечной системе была деталь¬
но исследована Гуццо (2006); в итоге было найдено наконец объяснение,
почему согласно некоторым модельным расчетам планеты-гиганты Солнеч¬
ной системы имеют хаотические орбиты, а согласно другим — регулярные
(см. также Хэйес, 2008). Аналогично, Робутель и Габерн (2006) отожде¬
ствили сеть резонансов и построили карты устойчивых и неустойчивых
областей фазового пространства для троянцев Юпитера.
Следует подчеркнуть, однако, что в прошедшем десятилетии эволюция
небесной механики стимулировалась главным образом новыми наблюдени¬
ями, открывшими новые области для исследований.
366
А. Морбиделли, И. И. Шевченко
Прежде всего, открытие внесолнечных планет: первые экзопланеты
были открыты раньше, чем была написана эта книга; однако на момент
написания были известны, за немногими исключениями, только однопла¬
нетные экзосистемы. К декабрю 2013 года открыто « 900 планет (и более
чем 3000 кандидатов в планеты по результатам миссии Кеплер), существен¬
ная часть которых входит в более чем 130 мультипланетных систем. (Всего,
включая и однопланетные системы, сейчас известно более 700 экзосистем.)
Они дают материал для многих интересных динамических задач.
В некоторых мультипланетных системах планеты находятся в резонан¬
сах средних движений друг с другом (Ферраз-Мелло и др., 2005; Райт и др.,
2011; Фабрицки и др., 2012). Известными системами с планетами в резо¬
нансе 2/1 являются Gliese 876 и HD 82943, в резонансе 3/1 — 55 Спс; тогда
как Gliese 876 — пример системы, где три планеты вовлечены в резонанс
Лапласа 4:2:1 (Марти и др., 2013) подобно трем внутренним галилеевым
спутникам Юпитера. (Более того, объявлено об открытии плотноупакован-
ной резонансной мультипланетной системы, KOI-730, с резонансом сред¬
них движений 8:6:4:3; Лиссауэр и др., 2011.) Как полагают, планетные ре¬
зонансы представляют собой естественное следствие примордиальной ми¬
грации планет, имеющей место благодаря их гравитационному взаимодей¬
ствию с протопланетным диском (см., например, Ванг и др., 2012). Факт
нахождения многих систем в резонансах средних движений стимулировал
исследования этих резонансов в рамках общей (неограниченной) задачи
трех тел.
Общая задача представляет собой весьма актуальный современный
раздел небесной механики. Фактически в нашей Солнечной системе пла¬
неты не вовлечены в резонансы средних движений друг с другом. В ре¬
зонансах наблюдаются только астероиды, объекты пояса Койпера, кометы,
спутники планет, пылевые комплексы. Поэтому резонансы ранее изучались
главным образом в рамках ограниченной задачи (см. главы 9 и 11). В об¬
щей задаче резонансы изучались в динамике спутников планет Солнечной
системы (см., например, Мальхотра, 1990, и ссылки там); однако в спут¬
никовом случае члены, возникающие из-за несферичности планеты, зна¬
чительно упрощают задачу, поскольку они вызывают быструю прецессию
орбит и расщепление резонансного мультиплета (см. главу 9)1.
Благодаря большему числу степеней свободы динамика резонанса
средних движений в общей задаче гораздо сложнее, чем в ограниченной
1В рамках общей задачи также изучались резонансы и периодические орбиты в динамике
тройных звезд, но главным образом в связи с «хореографиями», представляющими исключи¬
тельно математический интерес (см. Мартынова и др., 2005, и ссылки там).
Douze ans apres. Заметки к русскому изданию
367
задаче, особенно в отсутствие быстрой прецессии орбит. Поэтому иссле¬
дования проводились либо исключительно численными методами (см., на¬
пример, Марцари и др., 2006; Ли и др., 2006; Либер и Тсиганис, 2009,
2011), либо с использованием аналитических соображений, позволяющих
редуцировать систему к минимально возможному числу степеней свободы,
чтобы можно было численно строить сечения фазового пространства (см.,
например, Боже и др., 2005; Каллегари и др., 2004, 2006; Мищенко и др.,
2008а, 20086). Попытку построить аналитическую глобальную картину ре¬
зонансной динамики предприняли Батыгин и Морбиделли (2013 а), но за
счет принесения в жертву количественной точности в пользу качественно¬
го анализа. Фактически глобальную картину можно построить только пу¬
тем отождествления гармонических членов, используя разложения в ряды
по степеням эксцентриситетов, но эти разложения в действительности не
подходят для случая экзопланет, так как эксцентриситеты последних обыч¬
но велики. Присутствие резонансов средних движений и их взаимодей¬
ствие подразумевают возможность хаоса в динамике экзопланет, как, на¬
пример, в системе Кеплер-36 (Дек и др., 2012). Хаос может иметь место не
только благодаря взаимодействию резонансов средних движений, но также
и благодаря взаимодействию субрезонансов (в мультиплете, см. раздел 9.3)
с аргументами, содержащими различные комбинации вековых углов пла¬
нет (Батыгин и Морбиделли, 2013а). К тому же, как обсуждалось в разделе
10.4, хаос могут порождать трехтельные резонансы средних движений, на¬
пример, в динамике планет-гигантов в Солнечной системе. С увеличением
числа открытых экзопланетных систем исследования трехтельных резонан¬
сов были распространены на экзосистемы (Квиллен, 2011).
Вековая динамика планетных систем вне резонансов средних движе¬
ний также исследовалась (см., например, Ли и Пил, 2003; Мищенко и Маль-
хотра, 2004; Барнес и Гринберг, 2006; Ферраз-Мелло и др., 2005; Барнес,
2008; Барнес и др., 2011; Гринберг и ван Ларховен, 2012). (Фактически
эти исследования произросли из анализа вековой динамики тройных звезд¬
ных систем; см. Маршаль, 1990, и Форд и др., 2000.) By и Литвик (2011)
указали на возможность векового хаоса; это следует из обобщения динами¬
ческой картины, представленной в разделе 7.3 для планет земной группы
(также см., например, Ласкар, 1990, 1994, и Литвик и By, 2011, — об эво¬
люции Меркурия; Шидлиховский, 1990, — об эволюции астероидов), на
системы с много большим дефицитом углового момента, подверженные го¬
раздо более сильным неустойчивостям. В рамках общей задачи был также
переосмыслен эффект Лидова-Козаи (Либер и Анрар, 2007; Наоз и др.,
368
А. Морбиделли, И. И. Шевченко
2011). Этот эффект может быть широко распространен в планетных систе¬
мах двойных звезд или в мультипланетных системах, где планеты движут¬
ся по орбитам, сильно наклоненным относительно орбиты возмущающего
тела. Фактически эффект Лидова-Козаи мог бы объяснить наблюдаемые
сильно вытянутые планетные орбиты S-типа в некоторых двойных звезд¬
ных системах (Иннанен, 1997; By и Мюррей, 2003; Такеда и Расио, 2005):
при достаточно высоких наклонениях эксцентриситет планеты благодаря
этому эффекту может испытывать сильные колебания. В частности, пока¬
зано, что эффект возможен в системе 7 Cephei (Хагигипоур и др., 2010).
Кроме того, его привлекли для объяснения происхождения «горячих Юпи¬
теров» (Литвик и Наоз, 2011; Наоз и др., 2011). Наконец, отметим, что
подобно астероидам в Солнечной системе экзопланеты могут одновремен¬
но находиться в резонансах средних движений и в вековых резонансах;
пример такого рода динамики (хотя еще и не подтвержденный) — система
HD 12661 (см., например, Гоздзиевский, 2003).
Другим «неограниченным» следствием экзопланетного бума стал рас¬
тущий интерес к различного рода критериям устойчивости тройных гра¬
витационных систем (таких как две планеты на орбитах вокруг звезды
или же планета в двойной звездной системе). Зачастую ошибки опреде¬
ления орбитальных параметров непосредственно из наблюдений бывают
много больше, чем диапазон значений параметров, обеспечивающий дол¬
госрочную устойчивость системы. Поэтому анализ долгосрочной устой¬
чивости системы может накладывать более жесткие ограничения на воз¬
можные орбиты. Получили развитие как аналитические, так и численно¬
экспериментальные критерии устойчивости. В первом случае использова¬
лись подходы, основывающиеся на классическом критерии Хилла (Глэдман,
1993; Брассер, 2002; Верас и Армитидж, 2004; Доннисон, 2006) и крите¬
рии перекрытия резонансов Чирикова (Дункан и др., 1989; Мадрик и By,
2006). Во втором случае — вычисления FLI (быстрый индикатор Ляпу¬
нова, см. раздел 5.4.1; Пилат-Лохингер и Дворак, 2002), MEGNO (Mean
Exponential Growth Factor of Nearby Orbits — средний фактор экспонен¬
циальной расходимости близких орбит, см. раздел 5.4.3; Чинкотта и др.,
2003; Гоздзиевский, 2003; Гоздзиевский и др., 2013), расчеты подлинных
показателей Ляпунова (см. раздел 5.2.1; Попова и Шевченко, 2013), анализ
фундаментальных частот движения (частотный анализ, см. раздел 5.3.1;
Коррейа и др., 2009; Ласкар и Коррейа, 2009), а также простые условия
ухода/столкновений (Хольман и Вигерт; 1999; Пилат-Лохингер и др., 2003;
Холшевников и Кузнецов, 2011).
Douze ans apres. Заметки к русскому изданию
369
Обнаружение планет, обращающихся на орбитах, очень близких к ро¬
дительским звездам, дало старт исследованиям взаимосвязей динамики
и приливной диссипации в мультипланетных системах. Анализ вековой
эволюции читатель может найти, например, в статьях Мардлинг (2007), Ба¬
тыгина и др. (2009), Ловиса и др. (2011), ван Ларховен и Гринберга (2012),
Коррейа и др. (2013). Что касается резонансов средних движений, расхож¬
дение резонансных орбит исследовали Папалойцу и Теркем (2010), Лит-
вик и By (2012) и Батыгин и Морбиделли (20136); феномен расхождения
резонансных орбит ведет к резонансным системам с отношениями перио¬
дов большими, чем номинальные рациональные числа. Эффект обусловлен
свойством резонансов средних движений первого порядка, обсуждавшимся
в главе 9, а именно искривлением семейства устойчивых равновесий в коор¬
динатах «большая полуось — эксцентриситет» (см. рис. 9.11а). Тенденция
к несколько большим, чем резонансные, значениям отношений периодов
явно проявляется в системах, открытых в обзоре с КА Кеплер. В этой свя¬
зи особого упоминания заслуживает работа Делиля и др. (2012), в которой
продемонстрирована эквивалентность вековых и резонансных нормальных
форм для таких «квазирезонансных» планетных систем.
Более половины наблюдаемых звезд главной последовательности вхо¬
дят в кратные (главным образом двойные) звездные системы (Дюкеннуа
и Мейор, 1991; Матье и др., 2000). Особый вызов теоретикам — динамика
и формирование циркумбинарных планет, поскольку условия устойчивости
выполняются у наблюдаемых систем лишь на пределе. Недавно открытая
циркумбинарная планета Кеплер-16Ь обращается вокруг двух звезд глав¬
ной последовательности (Дойл и др., 2011). Хотя она и находится в опас¬
ной близости к хаотической области вокруг двойной, Кеплер-16Ь выживает,
будучи в безопасности в области, ограниченной неустойчивыми резонан¬
сами 5/1 и 6/1 с двойной (Попова и Шевченко, 2013). Вероятно, планета
Кеплер-16Ь (так же как и другие недавно открытые циркумбинарные плане¬
ты) испытала миграцию извне, так как формирование in situ проблематично
из-за условий, враждебных для аккреции планетезималей, в частности из-за
высоких столкновительных скоростей и низкой концентрации планетезима¬
лей (Мескиари, 2012; Пардекопер и др., 2012).
Особого упоминания заслуживает разработка метода TTV (Transit
Timing Variations) и исследования, проводимые с его помощью. Транзитная
планета, испытывающая возмущения от другой планеты, проходит по дис¬
ку родительской звезды нерегулярно во времени. Колебания ее орбиталь¬
ных элементов вызывают изменения времени прохождения относительно
370
А. Морбиделли, И. И. Шевченко
строгопериодического сигнала. Путем моделирования TTV можно полу¬
чить важную информацию о массах и орбитальных свойствах транзит¬
ных и возмущающих планет. Исторически вначале была разработана тео¬
рия TTV (см., например, Агол и др., 2005; Хольман и Мюррей, 2005;
Несворный, 2009; Несворный и Боже, 2010), а впоследствии, с ростом
числа открытий внесолнечных планет в транзитных обзорах (обзоре с КА
Кеплер в первую очередь), метод TTV стал реальностью. Первые TTV были
обнаружены в мультипланетных системах (Лиссауэр и др., 2011), и они поз¬
волили Лиссауэру и др. (1) подтвердить, что планетные «кандидаты» явля¬
ются реальными планетами, и (2) определить их массы. Недавно из анализа
TTV-сигнала транзитного компаньона этим методом впервые была открыта
и охарактеризована нетранзитная планета (Несворный и др., 2012). TTV-
анализ возрождает славные времена небесной механики, когда Леверрье
предсказал существование и положение Нептуна из анализа аномалий дви¬
жения Урана. «Чудо» Леверрье стало в наше время обыденным явлением.
Вернемся теперь к нашей старой доброй Солнечной системе. За время,
прошедшее с 2001 года, новые открытия глубоко преобразили наши знания
о ней и породили новые динамические исследования. Резко возросло число
известных астероидов. В 2000 году было известно приблизительно 100000
астероидов, теперь же — более чем полмиллиона. Это накопление наблю¬
дательных данных позволило астрономам отождествить много семейств
астероидов (групп астероидов, порожденных ударной дезинтеграцией ро¬
дительского тела) и охарактеризовать их орбитальную структуру. Теперь
семейства проявляют себя в пространстве собственных элементов не как
размытые «облака», а как четкие и интригующие особенности. Спектраль¬
ные обзоры (например, SDSS и WISE) позволили выяснить связи физиче¬
ских свойств со свойствами орбит, и это оказалось полезным для обосно¬
вания, что некоторые аномальные орбитальные структуры действительно
относятся к семействам, а не вызваны «чужаками». Анализ этих структур
позволил продемонстрировать, что давно уже предсказанный «эффект Яр-
ковского» (он упомянут в разделе 11.3.1) реален и играет существенную
роль. Данный эффект состоит в дрейфе вращающегося тела по большой
полуоси его орбиты, вызываемом анизотропным тепловым переизлучени-
ем поглощаемых телом фотонов. Первоначально он был предсказан в 19-ом
столетии Иваном Ярковским, а впоследствии возродился в работах Дэвида
Рубинкама и Паоло Фаринеллы (Рубинкам, 1995; Фаринелла и др., 1998).
Однако то, что эффект Ярковского определяет распределение астероидов,
было показано только в 2001 году в работе Боттке и др., которые проана¬
Douze ans apres. Заметки к русскому изданию
371
лизировали и воспроизвели орбитальную структуру семейства Корониды.
С тех пор эффект Ярковского изучается на основе данных о семействах.
Показано, что взаимодействие дрейфа по большой полуоси, вызываемого
эффектом Ярковского, и вековых резонансов может приводить как к про¬
хождению резонансов (см., например, Боттке и др., 2001), так и к захвату
в них (см., например, Вокроуглицкий и др., 2006а). В обоих случаях вли¬
яние на итоговые орбиты оказывается явным и индивидуальным. Кроме
того, с течением времени определяемая эффектом Ярковского эволюция на¬
кладывает характерный отпечаток на распределение астероидов семейства
по большой полуоси, зависящий от их физических размеров; этот эффект,
должным образом изученный, стал стандартным инструментом оценивания
возрастов семейств с хорошей точностью (см., например, Вокроуглицкий
и др., 20066; Боттке и др., 2007). Определить возраст более точно можно
только для очень молодых семейств, что достигается путем фиксирования
момента апсидального и узлового выравнивания орбит в ходе интегрирова¬
ния назад по времени (см. Несворный и др., 2002).
Параллельно с тем, как изучался эффект Ярковского, была установлена
важная роль YORP-эффекта. Этот эффект, названный по инициалам перво¬
открывателей (Yarkovsky- O’Keefe - Radzievskii - Paddack), заложивших ос¬
новы для его понимания, влияет на вращательную динамику несфериче¬
ских тел, изменяя скорость и наклон оси вращения. В этой книге враща¬
тельная динамика была затронута лишь вкратце (см. раздел 7.4), главным
образом в отношении эволюции осей вращения планет земной группы. Вра¬
щательная динамика астероидов, испытывающих YORP-эффект, оказалась
очень богатой. Вокроуглицкий и др. (2003) нашли, что астероиды могут
быть захвачены в вековой спин-орбитальный резонанс (резонанс между ча¬
стотой прецессии оси вращения и узловой частотой орбиты) и эволюцио¬
нировать ко второму состоянию Кассини (Коломбо, 1966). Этим объясняет¬
ся наблюдательный факт (Сливан, 2002), что многие астероиды семейства
Корониды имеют сходные направления осей вращения. Интересно, что по¬
добный же резонанс (между частотой прецессии оси вращения Сатурна
и частотой узловой прецессии Нептуна), по-видимому, ответственен за на¬
клон оси Сатурна (Гамильтон и Уард, 2004; Уард и Гамильтон, 2004; Буэ
и др., 2009). Конечно, в последнем случае действует не YORP-эффект, а,
скорее всего, медленное изменение узловой частоты Нептуна из-за мигра¬
ции планеты (см. ниже) или потери массы поясом Койпера.
Благодаря этим исследованиям возродилась теория адиабатического за¬
хвата в резонанс и прохождения резонанса. Данная теория не нова (см., на¬
372
А. Морбиделли, И. И. Шевченко
пример, Нейштадт, 1975), и о ней в книге не говорилось (кроме как вкратце
в разделе 9.4 о модулированном маятнике), — и только потому, что пол¬
ный обзор приложений адиабатических инвариантов в небесной механике
уже был опубликован ранее (Анрар, 1993). Однако до 2000 года исследо¬
вания адиабатического захвата в резонанс касались главным образом спин-
орбитальных резонансов и резонансов средних движений. Только когда по¬
явились указанные выше задачи, предметом изучения в небесной механике
стало и адиабатическое взаимодействие с вековыми резонансами.
Другая тема, которая почти не рассматривалась в книге, и тоже не но¬
вая, — движение комет и, в более широком контексте, возмущенное сильно¬
эксцентрическое движение. В реальных системах такое движение, как пра¬
вило, хаотично, даже когда отсутствуют близкие столкновения с возмуща¬
ющими телами; фундаментальной причиной для кометного хаоса является
аккумуляция резонансов тг: 1 между орбитальными частотами «планеты»
(внутреннего возмущающего тела) и «кометы» (пробной частицы) вблизи
параболической траектории, которая играет роль сепаратрисы, разделяю¬
щей ограниченные (эллиптические) и неограниченные (гиперболические)
движения. Впервые это показали Петроски (1986) и Чириков и Вечесла-
вов (1986); для описания хаотического движения комет на возмущенных
почти параболических орбитах они вывели специальное двумерное сохра¬
няющее площадь отображение. Главная цель состояла в том, чтобы каче¬
ственно охарактеризовать движение кометы Галлея в ожидании ее очеред¬
ного возвращения в 1987 году. Аналогично тому как вращение Гипериона
стало первым наблюдаемым примером хаотического вращательного дви¬
жения в Солнечной системе, движение кометы Галлея послужило первым
наблюдаемым примером хаотического орбитального движения, как следо¬
вало из анализа исторических хроник ее явлений, выполненного Чирико-
вым и Вечеславовым (1986, 1989). Выведенное отображение было впослед¬
ствии названо кеплеровым, поскольку его вторая строка выражает третий
закон Кеплера. Основное модельное предположение состояло в том, что
главный возмущающий эффект планеты сконцентрирован при нахождении
кометы вблизи перигелия ее орбиты. Использование современных версий
кеплерова отображения позволяет охарактеризовать эффекты хаотической
диффузии в динамике комет и метеорных потоков (Емельяненко, 1992; Лиу
и Сан, 1994; Емельяненко и Бейли, 1998; Малышкин и Тремейн, 1999; Жоу
и Сан, 2001; Жоу и др., 2000, 2002).
Кеплерово отображение принадлежит к классу обобщенных сепа-
ратрисных отображений (Шевченко, 2010). Классические сепаратрисные
Douze ans Aprils. Заметки к русскому изданию
373
отображения (Чириков, 1979) — эффективный инструмент для анализа дви¬
жения в хаотических слоях, образуемых расщепленными сепаратрисами
нелинейных резонансов (Пифтанкин и Трещев, 2007), и их теория может
использоваться для оценивания ляпуновских и диффузионных времен в ха¬
отических слоях (Шевченко, 2011) в тех случаях, когда стандартное отоб¬
ражение, описывающее бесконечный мультиплет равноотстоящих друг от
друга резонансов одинаковой ширины, как модель неприменимо. (Оценки
на основе теории стандартного отображения описаны в разделе 12.3 этой
книги.)
Еще одна классическая тема, не нашедшая отражения в книге, — ор¬
битальная и вращательная динамика спутников планет, демонстрирующая
разнообразие интересных типов динамического поведения, включая исто¬
рически первый случай предсказанного и непосредственно наблюдавше¬
гося хаотического движения, а именно хаотического вращения Гиперио¬
на — 7-го спутника Сатурна (Уиздом и др., 1984; Харбисон и др., 2011).
Гиперион остается единственным примером наблюдаемого хаотического
вращения в Солнечной системе; второй предполагаемый пример (Нере¬
ида) не был подтвержден (Доброволскис, 1995; Хессельброк и др., 2013;
Тераи и Ито, 2013). Путем массового анализа устойчивости возможных
вращательных состояний спутников планет (определяемой положением на
плоскости «инерционный параметр — эксцентриситет орбиты») Мельни¬
ков и Шевченко (2010) показали, что, хотя подавляющая часть спутников
с известными вращательными состояниями находится в синхронном спин-
орбитальном резонансе, более чем 60% всех спутников с неизвестными
состояниями находятся в иной (быстрой или, что менее вероятно, хаотиче¬
ской) моде вращения.
Что касается резонансной орбитальной динамики планетных спутни¬
ков, многие из них образуют резонансные или околорезонансные орбиталь¬
ные конфигурации. В спутниковой системе Юпитера галилеевы спутники
Ио и Европа, как и Европа и Ганимед, находятся в резонансе средних дви¬
жений 2/1; таким образом, система этих трех спутников вовлечена в трех-
тельный резонанс 4:2:1 (резонанс Лапласа). В системе Сатурна Мимас и Те-
фия, как и Энцелад и Диона, находятся в резонансе средних движений 2/1,
Диона и Рея близки к резонансу 5/3, Титан и Гиперион находятся в резонан¬
се 4/3. В системе Урана все резонансы приблизительные: Миранда и Ум-
бриэль близки к резонансу 3/1, Ариэль и Умбриэль — 5/3, Умбриэль и Ти-
тания — 2/1, Титания и Оберон — 3/2. Захваты спутниковых систем в ор¬
битальные резонансы представляют собой естественные стадии приливной
374
А. Морбиделли, И. И. Шевченко
эволюции этих небесномеханических систем. Особенно интересно, что дви¬
жение системы «Прометей - Пандора» (16-ого и 17-ого спутников Сатур¬
на — спутников-пастухов кольца F) является хаотическим, что следует как
из наблюдений, так и из теории. Ляпуновское время этой системы, находя¬
щейся в резонансе средних движений 121/118, было оценено как численно¬
экспериментально, так и аналитически; оказалось, что оно составляет все¬
го лишь « 3 года (Голдрайх и Раппапорт, 2003; Шевченко, 2008). Отметим,
что в отличие от других примеров наблюдаемого хаоса в Солнечной систе¬
ме здесь наличие хаоса было выявлено сперва из наблюдений и лишь затем
объяснено теоретически. Общие обзоры динамики планетных спутников
даны Пилом (1976, 1986, 1999); теоретическое введение и интересные фак¬
ты можно дополнительно найти в статье Мальхотры (1998).
Согласно главе 12, двухтельные и трехтельные резонансы средних дви¬
жений определяют динамическую структуру пояса астероидов; более того,
динамическое взаимодействие астероидных семейств с трехтельными резо¬
нансами и двухтельными резонансами высоких порядков является важным
фактором в транспортировке астероидов. Примером служат диффузионные
процессы в семействе (490) Веритас, протекающие благодаря резонансу (5,
-2, -2) (Качучо и др., 2010). Недавно Смирнов и Шевченко (2013) выпол¬
нили массовое отождествление астероидов главного пояса в двухтельных
и трехтельных резонансах с планетами: для астероидов из базы AstDyS2
(примерно четверть миллиона объектов) были проведены расчеты траекто¬
рий и поведения резонансных аргументов во времени; как оказалось, асте¬
роиды в чистых трехтельных резонансах до 6-ого порядка включительно со¬
ставляют приблизительно 1 % от всех объектов в хорошем согласии с более
ранней оценкой Несворного и Морбиделли (1998), сделанной на основе вы¬
борки из нескольких сотен астероидов. Современный атлас двухтельных ре¬
зонансов средних движений в поясе астероидов составлен Галлардо (2006).
Современные наблюдательные открытия не просто завершили карти¬
ну пояса астероидов: они буквально революционизировали наши позна¬
ния о Солнечной системе в целом благодаря открытию новых популяций
(троянцев Нептуна, нерегулярных спутников планет-гигантов) и описанию
пояса Койпера. Когда эта книга вышла из печати, было известно менее
трехсот объектов пояса Койпера, причем лишь у менее ста из них орби¬
ты были определены относительно точно (см. рис. 4). На сегодня известно
уже « 1000 транснептунных объектов с хорошо определенными орбитами.
В итоге компоненты и характеристики пояса Койпера предъявлены нам во
2Сайт AstDyS: http://hamilton.dm.unipi.it/cgi-bin/astdys/
Douze ans apres. Заметки к русскому изданию
375
всем их разнообразии: сосуществование нескольких населений (холодное,
горячее, резонансное, рассеянное, удаленное; объяснение терминологии см.
в статье Глэдмана и др., 2008), его внешняя граница (зависящая от рас¬
сматриваемого населения), дефицит массы, корреляции между физически¬
ми и орбитальными свойствами (см. обзор в статье Морбиделли и Брауна,
2004). Исправление наблюдаемой статистики за эффекты селекции показа¬
ло, что резонанс 5/2 с Нептуном населен даже больше, чем резонанс 3/2
(Глэдман и др., 2012).
Наблюдательный бум в исследованиях пояса Койпера имел еще од¬
но радикальное следствие: число планет Солнечной системы формально
уменьшилось до восьми, когда в 2006 году решением 26-й Генеральной
Ассамблеи MAC в Праге Плутон был отнесен к новому классу небесных
тел — классу карликовых планет (к которому были отнесены также круп¬
ные астероиды типа Цереры). Главной причиной для такого решения стало
открытие крупных тел в поясе Койпера, в частности объекта более крупно¬
го, чем Плутон, а именно Эриды (Eris), диаметр которой больше диаметра
Плутона на « 10 %.
Интересно, что поток новой информации о поясе Койпера не породил
многих новых динамических исследований в сравнении с уже обсуждав¬
шимися в этой книге. Причина состоит в том, что динамика пояса Койпера
относительно проста. Но зато эта новая информация дала старт числен¬
ным экспериментам по массовому моделированию формирования и ранней
эволюции Солнечной системы — с целью выяснения, какие процессы, уже
не работающие сейчас, придали поясу ту сложную структуру, которой он
в итоге обладает.
До 2001 года попытки моделирования примордиального формирова¬
ния пояса Койпера основывались на простой концепции радиальной ми¬
грации Нептуна, вызываемой его взаимодействием с примордиальным пла-
нетезимальным диском (Фернандес и Ип, 1984; Мальхотра, 1993, 1995).
В прошедшем десятилетии был развит намного более сложный сценарий.
Стало ясно, что для объяснения всех особенностей пояса Койпера и Сол¬
нечной системы в целом необходимо учитывать глобальную динамическую
неустойчивость системы планет-гигантов, описываемую, например, в так
называемой «Nice-модели» (Тсиганис и др., 2005; Гомес и др., 2005; Морби¬
делли и др., 2007; Левисон и др., 2011). Концепция неустойчивости планет-
гигантов также проявила себя как наилучшее объяснение для больших экс¬
центриситетов орбит внесолнечных планет-гигантов (см., например, Джу-
рич и Тремейн, 2008; Чаттерджи и др., 2008). Это дает единое представ¬
376
А. Морбиделли, И. И. Шевченко
ление об эволюции нашей Солнечной системы и эволюции внесолнечных
систем (см. обсуждение в работе Морбиделли, 2013).
Здесь, однако, мы покидаем почву «традиционной» небесной механи¬
ки, если под ней подразумевать исследования динамики в математически
строгих задачах, подобных всем рассмотренным в этой книге. Когда мы
исследуем происхождение планетной системы, главная трудность состоит
не в том, чтобы изучить ее динамику: это можно сделать путем примене¬
ния «грубой вычислительной силы». Реальный вызов состоит в том, чтобы
понять, какой система была изначально и каковы главные ингредиенты,
которые следует включать в упрощенную модель. Тогда эволюцию систе¬
мы можно рассчитывать численно (аналитические модели здесь редко при¬
менимы), чтобы проверить, эволюционирует ли постулируемая начальная
система естественным образом к финальной, имеющей желаемые характе¬
ристики, например воспроизводящие наблюдаемую структуру Солнечной
системы. Обычно исследуемые системы имеют очень много степеней сво¬
боды: например, включаются все планеты (или даже еще более многочис¬
ленный набор протопланет) и большая популяция массивных планетезима-
лей; иногда учитывается влияние газовой составляющей протопланетного
диска, при этом используются уравнения гидродинамики. Научный язык
смещается здесь от языка гамильтоновой динамики к языку статистической
механики. Мы вправе сказать, что это уже более не небесная механика, а ди¬
намическая планетная наука (где объект более важен, чем сама динамика):
актуальная тема для совершенно новой книги.
Литература
Агол и др. (2005) Agol, Е., Steffen, J., Sari, R., and Clarkson, W. (2005) On detecting
terrestrial planets with timing of giant planet transits. Month. Not. Roy. Astron. Soc.,
359, 567.
Анрар (1993) Henrard, J. (1993) The adiabatic invariant in classical mechanics. In:
Dynamics Reported. Jones, C.K.R.T., et al. (Eds.) Springer: Berlin. R 117.
Барнес (2008) Barnes, R. (2008) Dynamics of multiple planet systems. In: Exoplanets:
Detection, Formation, Properties, Habitability. Mason, J.W. (Ed.). Springer: Berlin.
P. 177.
Барнес и Гринберг (2006) Bames, R., and Greenberg, R. (2006) Extrasolar planetary
systems near a secular separatrix. Astrophys. J., 638, 478.
Барнес и др. (2011) Bames, R., Greenberg, R., Quinn, T.R., McArthur, B.E., and
Benedict, G.F. (2011) Origin and dynamics of the mutually inclined orbits of Upsilon
Andromedae с and d. Astrophys. J., 726, 71.
Douze ans apres. Заметки к русскому изданию
377
Батыгин и Морбиделли (20J3a) Batygin, К., and Morbidelli, А. (2013а) Analytical
treatment of planetary resonances. ArXiv: 1305.6513.
Батыгин и Морбиделли (20136) Batygin, К., and Morbidelli, A. (2013b) Dissipative
divergence of resonant orbits. Astron. J., 145, 1.
Батыгин и др. (2009) Batygin, К., Laughlin, G., Meschiari, S., Rivera, E., Vogt, S., and
Butler, R (2009) A quasi-stationary solution to Gliese 436b’s eccentricity. Astrophys.
J., 699, 23.
Боже и др. (2005) Beauge, С., Callegari, N., Ferraz-Mello, S., and Michtchenko, T.A.
(2005) Resonances and stability of extra-solar planetary systems. In: Dynamics of
Populations of Planetary Systems, Proceedings of IAU Colloquium 197. Knezevic,
Z., and Milani, A. (Eds.). Cambridge Univ. Press: Cambridge. P. 3.
Боттке и др. (2001) Bottke, W.F., Vokrouhlicky, D., Broz, М., Nesvomy, D., and
Morbidelli, A. (2001) Dynamical spreading of asteroid families by the Yarkovsky
effect. Science, 294, Issue 5547, p. 1693.
Боттке и др. (2007) Bottke, W.F., Vokrouhlicky, D., and Nesvomy, D. (2007) An
asteroid breakup 160 Myr ago as the probable source of the K/T impactor. Nature,
449, Issue 7158, p. 48.
Брассер (2002) Brasser, R. (2002) Hill stability of a triple system with an inner binary
of large mass ratio. Month. Not. Roy. Astron. Soc., 332, 723.
Буэ и др. (2009) Boue, G., Laskar, J., and Kuchynka, P. (2009) Speed limit on Neptune
migration imposed by Saturn tilting. Astrophys. J. Letters, 702, LI9.
ван Ларховен и Гринберг (2012) Van Laerhoven, С., and Greenberg, R. (2012)
Characterizing multi-planet systems with classical secular theory. Celest. Mech. Dyn.
Astron., 113, 215.
Ванг и др. (2012) Wang, S., Ji, J., and Zhou, J.-L. (2012) Predicting the configuration
of a planetary system: KOI-152 observed by Kepler. Astrophys. J., 753, 170.
Bepac и Армитидж (2004) Veras, D., and Armitage, PJ. (2004) The dynamics of two
massive planets on inclined orbits. Icarus, 172, 349.
Вокроуглицкий и др. (2006a) Vokrouhlicky, D., Broz, М., Bottke, W.F., Nesvomy, D.,
and Morbidelli, A. (2006a) The peculiar case of the Agnia asteroid family. Icarus,
183, 349.
Вокроуглицкий и др. (20066) Vokrouhlicky, D., Broz, М., Bottke, W.F., Nesvomy, D.,
and Morbidelli, A. (2006b) Yarkovsky/YORP chronology of asteroid families.
Icams, 182, 118.
Вокроуглицкий и др. (2003) Vokrouhlicky, D., Nesvomy, D., and Bottke, W.F. (2003)
The vector alignments of asteroid spins by thermal torques. Nature, 425, Issue 6954,
147.
By и Литвик (2011) Wu, Y., and Lithwick, Y. (2011) Secular chaos and the production
of hot Jupiters. Astrophys. J., 735, 109.
By и Мюррей (2003) Wu, Y., and Murray, N. (2003) Planet migration and binary
companions: The case of HD 80606b. Astrophys. J., 589, 605.
378
А. Морбиделли, И. И. Шевченко
Галлардо (2006) Gallardo, Т., 2006. Atlas of the mean motion resonances in the Solar
System. Icarus, 184, 29.
Гамильтон и Уард (2004) Hamilton, D.P., and Ward, W.R. (2004) Tilting Saturn. II.
Numerical model. Astron. J., 128, 2510.
Глэдман (1993) Gladman, B. (1993) Dynamics of systems of two close planets. Icarus,
106, 247.
Глэдман и др. (2012) Gladman, В., Lawler, S.M., Petit, J.-M., et al. (2012) The resonant
trans-Neptunian populations. Astron. J., 144, 23.
Глэдман и др. (2008) Gladman, В., Marsden, B.G., and Van Laerhoven, C. (2008)
Nomenclature in the outer Solar System. In: The Solar System Beyond Neptune.
Barucci, M.A., Boehnhardt, H., Cruikshank, D.P., and Morbidelli, A. (Eds.). Univ.
of Arizona Press: Tucson. P. 3.
Голдрайх и Раппапорт (2003) Goldreich, P., and Rappaport, N. (2003) Chaotic motions
of Prometheus and Pandora. Icarus, 162, 391.
Гомес и др. (2005) Gomes, R., Levison, H.F., Tsiganis, K., and Morbidelli, A. (2005)
Origin of the cataclysmic Late Heavy Bombardment period of the terrestrial planets.
Nature, 435, Issue 7041, 466.
Гоздзиевский (2003) Gozdziewski, K. (2003) Stability of the HD 12661 planetary
system. Astron. Astrophys., 398, 1151.
Гоздзиевский и др. (2013) Gozdziewski, К., Slonina, М., Migaszewski, С., and
Rozenkiewicz, A. (2013) Testing a hypothesis of the и Octantis planetary system.
Month. Not. Roy. Astron. Soc., 430, 533.
Гринберг и ван Ларховен (2012) Greenberg, R., and Van Laerhoven, C. (2012) Aligned
major axes in a planetary system without tidal evolution: the 61 Virginis example.
Month. Not. Roy. Astron. Soc., 419, 429.
Гуццо (2006) Guzzo, M. (2006) The web of three-planet resonances in the outer Solar
System. II. A source of orbital instability for Uranus and Neptune. Icarus, 181, 475.
Дек и др. (2012) Deck, K.M., Holman, M.J., Agol, E., et al. (2012) Rapid dynamical
chaos in an exoplanetary system. Astrophys. J., 755, L21.
Делиль и dp. (2012) Delisle, J.-B., Laskar, J., Correia, A.C.M., and Boue, G. (2012)
Dissipation in planar resonant planetary systems. Astron. Astrophys., 546, A71.
Джурич и Тремейн (2008) Juric, М., and Tremaine, S. (2008) Dynamical origin of
extrasolar planet eccentricity distribution. Astrophys. J., 686, 603.
Доброволскис (1995) Dobrovolskis, A. (1995) Chaotic rotation of Nereid? Icarus, 118,
181.
Доннисон (2006) Donnison, J.R. (2006) The Hill stability of a binary or planetary system
during encounters with a third inclined body. Month. Not. Roy. Astron. Soc., 369,
1267.
Дойл и dp. (2011) Doyle, L.R., Carter, J.A., Fabrycky, D.C., et al. (2011) Kepler-16:
A Transiting Circumbinary Planet. Science, 333, 1602.
Douze ans apres. Заметки к русскому изданию
379
Дункан и др. (1989) Duncan, М., Quinn, Т., and Tremaine, S. (1989) The long-term
evolution of orbits in the solar system — a mapping approach. Icarus, 82, 402.
Дюкеннуа и Мейор (1991) Duquennoy, A., and Mayor, M. (1991) Multiplicity among
solar-type stars in the solar neighbourhood. II — Distribution of the orbital elements
in an unbiased sample. Astron. Astrophys., 248, 485.
Емельяненко (1992) Emelyanenko, V.V. (1992) Dynamics of periodic comets and meteor
streams. Celest. Mech. Dyn. Astron. 54, 91.
Емельяненко и Бейли (1998) Emelyanenko, V.V., and Bailey, M.E. (1998) Capture of
Halley-type comets from the near-parabolic flux. Month. Not. Roy. Astron. Soc.,
298, 212.
Жоу и Сан (2001) Zhou, J.L., and Sun, Y.S. (2001) Levy flights in comet motion and
related chaotic systems. Phys. Lett. A, 287, 217.
Жоу и dp. (2000) Zhou, J.L., Sun, Y.S., Zheng, J.Q., and Valtonen, M.J. (2000) The
transfer of comets from near-parabolic to short-period orbits: map approach. Astron.
Astrophys., 364, 887.
Жоу и dp. (2002) Zhou, J., Sun, Y., and Zhou, L. (2002) Evidence for Levy random
walks in the evolution of comets from the Oort cloud. Celest. Mech. Dyn. Astron.,
84, 409.
Иннанен (1997) Innanen, K.A. (1997) The Kozai mechanism and the stability of
planetary orbits in binary star systems. Astron. J., 113, 1915.
Каллегари и dp. (2006) Callegari, N. Jr., Ferraz-Mello, S., and Michtchenko, T.A. (2006)
Dynamics of two planets in the 3/2 mean-motion resonance: Application to the
planetary system of the pulsar PSR В1257+12. Celest. Mech. Dyn. Astron., 94, 381.
Каллегари и dp. (2004) Callegari, N. Jr., Michtchenko, T.A., and Ferraz-Mello, S. (2004)
Dynamics of two planets in the 2/1 mean-motion resonance. Celest. Mech. Dyn.
Astron., 89, 201.
Качучо и dp. (2010) Cachucho, F., Cincotta, P.M., and Ferraz-Mello, S. (2010) Chirikov
diffusion in the asteroidal three-body resonance (5, -2, -2). Celest. Mech. Dyn.
Astron. 108, 35.
Квиллен (2011) Quillen, A.C. (2011) Three-body resonance overlap in closely spaced
multiple-planet systems. Month. Not. Roy. Astron. Soc., 418, 1043.
Коломбо (1966) Colombo, G. (1966) Cassini’s second and third laws. Astron. J., 71,
891.
Коррейа и dp. (2009) Correia, A.C.M., Udry, S., Mayor, М., et al. (2009) The HARPS
search for southern extra-solar planets. XVI. HD 45364, a pair of planets in a 3:2
mean motion resonance. Astron. Astrophys. 496, 521.
Коррейа и dp. (2013) Correia, A.C.M., Boue, G., Laskar, J., and Morais, M.H.M. (2013)
Tidal damping of the mutual inclination in hierarchical systems. Astron. Astrophys.,
553, A39.
Ласкар (1990) Laskar, J. (1990) The chaotic motion of the solar system. — A numerical
estimate of the size of the chaotic zones. Icarus, 88, 266.
380
А. Морбиделли, И. И. Шевченко
Ласкар (1994) Laskar, J. (1994) Large-scale chaos in the solar system. Astron.
Astrophys., 287, L9.
Ласкар и Коррейа (2009) Laskar, J., and Correia, A.C.M. (2009) HD 60532, a planetary
system in a 3:1 mean motion resonance. Astron. Astrophys., 496, L5.
Ли и Пил (2003) Lee, M.H., and Peale, S. (2003) Secular evolution of hierarchical
planetary systems. Astrophys. J., 592, 1201.
Ли и др. (2006) Lee, M.H., Butler, R.P., Fischer, D.A., Marcy, G.W., and Vogt, S.S.
(2006) On the 2:1 orbital resonance in the HD 82943 planetary system. Astrophys.
J., 641, 1178.
Лега и др. (2007) Lega, E., Froeschle, C., and Guzzo, M. (2007) Diffusion in
Hamiltonian quasi-integrable system. In: Topics in Gravitational Dynamics Solar,
Extra-Solar and Galactic Systems. Lecture Notes in Physics, v. 729. Benest, D.,
Froeschle, C., and Lega, E. (Eds.). Springer: Berlin. P. 29.
Левисон и др. (2011) Levison, H.F., Morbidelli, A., Tsiganis, K., Nesvomy, D., and
Gomes, R. (2011) Late orbital instabilities in the outer planets induced by interaction
with a self-gravitating planetesimal disk. Astron. J., 142, 152.
Либер и Арнар (2007) Libert, A.-S., and Henrard, J. (2007) Exoplanetary systems: The
role of an equilibrium at high mutual inclination in shaping the global behavior of
the 3-D secular planetary three-body problem. Icarus, 191, 469.
Либер и Тсиганис (2009) Libert, A.-S., and Tsiganis, K. (2009) Kozai resonance in
extrasolar systems. Astron. Astrophys., 493, 677.
Либер и Тсиганис (2011) Libert, A.-S., and Tsiganis, K. (2011) Formation of 3D
multi-planet systems by dynamical disruption of multiple-resonance configurations.
Month. Not. Roy. Astron. Soc., 412, 2353.
Лиссауэр и др. (2011) Lissauer, J.J., Ragozzine, D., Fabrycky, D.C., Steffen, J.H.,
Ford, E.B., Jenkins, J.M., Shporer, A., Holman, M.J., Rowe, J.F., Quintana, E.V.,
Batalha, N.M., Borucki, W.J., Bryson, S.T., Caldwell, D.A., Carter, J.A., Ciardi, D.,
Dunham, E.W., Fortney, J.J., Gautier, T.N. Ill, Howell, S.B., Koch, D.G.,
Latham, D.W., Marcy, G.W., Morehead, R.C., and Sasselov, D. (2011) Architecture
and dynamics of Kepler’s candidate multiple transiting planet systems. Astrophys.
J. Suppl., 197, 8.
Литвик и By (2011) Lithwick, Y., and Wu, Y. (2011) Theory of secular chaos and
Mercury’s orbit. Astrophys. J., 739, 31.
Литвик и By (2012) Lithwick, Y., and Wu, Y. (2012) Resonant repulsion of Kepler
planet pairs. Astrophys. J. Letters, 756, Lll.
Литвик и Наоз (2011) Lithwick, Y., and Naoz, S. (2011) The eccentric Kozai mechanism
for a test particle. Astrophys. J., 742, 94.
Лиу и Can (1994) Liu, J., and Sun, Y.S. (1994) Chaotic motions of comets in near¬
parabolic orbits: mapping approaches. Celest. Mech. Dyn. Astron., 60, 3.
Ловис и др. (2011) Lovis, С., Segransan, D., Mayor, М., Udry, S., Benz, W.,
Bertaux, J.-L., Bouchy, F., Correia, A.C.M., Laskar, J., Lo Curto, G., Mordasini, C.,
Douze ans api^s. Заметки к русскому изданию
381
Рере, F., Queloz, D., and Santos, N.C. (2011) The HARPS search for southern
extra-solar planets. XXVIII. Up to seven planets orbiting HD 10180: probing the
architecture of low-mass planetary systems. Astron. Astrophys., 528, 112.
Мадрик и By (2006) Mudryk, L.R., and Wu, Y. (2006) Resonance overlap is responsible
for ejecting planets in binary systems. Astrophys. J., 639, 423.
Малышкин и Тремейн (1999) Malyshkin, L., and Tremaine, S. (1999) The Keplerian
map for the restricted three-body problem as a model of comet evolution. Icarus,
142, 341.
Малъхотра (1990) Malhotra, R. (1990) Capture probabilities for secondary resonances.
Icarus, 87, 249.
Малъхотра (1993) Malhotra, R. (1993) The origin of Pluto’s peculiar orbit. Nature, 365,
Issue 6449, 819.
Малъхотра (1995) Malhotra, R. (1995) The origin of Pluto’s orbit: Implications for the
Solar System beyond Neptune. Astron. J., 110, 420.
Малъхотра (1998) Malhotra, R. (1998) Orbital resonances and chaos in the Solar
system. In: Solar System Formation and Evolution, ASP Conf. Ser. 149. Lazzaro, D.,
Vieira Martins, R., Ferraz-Mello, S., Fernandez, J., and Beauge, C. (Eds.). Astron.
Soc. of the Pacific: San Francisco. P. 57.
Мардлинг (2007) Mardling, R.A. (2007) Long-term tidal evolution of short-period
planets with companions. Month. Not. Roy. Astron. Soc., 382, 1768.
Марти и др. (2013) Marti* J.G., Giuppone, С.A., and Beauge, C. (2013) Dynamical
analysis of the Gliese-876 Laplace resonance. Month. Not. Roy. Astron. Soc., 433, 928,
Мартынова и др. (2005) Мартынова, А.И., Орлов, В.В., и Соколов, JI.JI. (2005) Ана¬
лиз окрестности резонанса 2:1 в задаче трех тел равных масс. Письма Астрон.
журн. 31 (3), 234.
Марцари и др. (2006) Marzari, F., Scholl, Н., and Tricarico, P. (2006) A numerical study
of the 2:1 planetary resonance. Astron. Astrophys., 453, 341.
Маршалъ (1990) Marchal, C. (1990) The Three-Body Problem. Elsevier: Amsterdam.
Матье и др. (2000) Mathieu, R.D., Ghez, A.M., Jensen, E.L., and Simon, M. (2000)
Young binary stars and associated disks. In: Protostars and Planets IV. Mannings, V.,
Boss, A.P., and Russell, S.S. (Eds.). Univ. Arizona Press: Tucson. P. 703.
Мельников и Шевченко (2010) Melnikov, A.V., and Shevchenko, I.I. (2010) The rotation
states predominant among the planetary satellites. Icarus, 209. 786.
Мескиари (2012) Meschiari, S. (2012) Circumbinary planet formation in the Kepler-16
system. I. N-body simulations. Astrophys. J., 752, 71.
Мищенко и др. (2008a) Michtchenko, T.A., Beauge, C., and Ferraz-Mello, S. (2008a)
Dynamic portrait of the planetary 2/1 mean-motion resonance — I. Systems with
a more massive outer planet. Month. Not. Roy. Astron. Soc., 387, 747.
Мищенко и др. (20086) Michtchenko, T.A., Beauge, С., and Ferraz-Mello, S. (2008b)
Dynamic portrait of the planetary 2/1 mean-motion resonance — II. Systems with
a more massive inner planet. Month. Not. Roy. Astron. Soc., 391, 215.
382
А. Морбиделли, И. И. Шевченко
Мищенко и Мальхотра (2004) Michtchenko, Т.А., and Malhotra, R. (2004) Secular
dynamics of the three-body problem: application to the upsilon Andromedae
planetary system. Icarus, 168, 237.
Морбиделли (2013) Morbidelli, A. (2013) Dynamical evolution of planetary systems. In:
Planets, Stars and Stellar Systems. Oswalt, T.D., French, L.M., and Kalas, P. (Eds.).
Springer: Dordrecht. P. 63.
Морбиделли и Браун (2004) Morbidelli, A., and Brown, M.E. (2004) The Kuiper belt
and the primordial evolution of the Solar System. In: Comets II. Festou, M.C., Keller,
H.U., and Weaver, H.A. (Eds.). Univ. Arizona Press: Tucson. P. 175.
Морбиделли и др. (2007) Morbidelli, A., Tsiganis, K., Crida, A., Levison, H.F., and
Gomes, R. (2007) Dynamics of the giant planets of the Solar System in the gaseous
protoplanetary disk and their relationship to the current orbital architecture. Astron.
J., 134, 1790.
Наоз и др. (2011) Naoz, S., Farr, W., Lithwick, Y., Rasio, F., and Teyssandier, J. (2011)
Hot Jupiters from secular planet-planet interactions. Nature, 473, Issue 7346, 187.
Нейштадт (1975) Нейштадт А.И. (1975) Прохождение через сепаратрису в резо¬
нансной задаче с медленно изменяющимся параметром. Прикл. мат. и мех., 39
(4), 621.
Несворный (2009) Nesvomy, D. (2009) Transit timing variations for eccentric and
inclined exoplanets. Astrophys. J., 701, 1116.
Несворный и Боже (2010) Nesvomy, D., and Beauge, C. (2010) Fast inversion method
for determination of planetary parameters from transit timing variations. Astrophys.
J. Letters, 709, L44.
Несворный и др. (2002) Nesvomy, D., Bottke, W.F. Jr., Dones, L., and Levison, H.F.
(2002) The recent breakup of an asteroid in the main-belt region. Nature, 417, Issue
6890, 720.
Несворный и др. (2012) Nesvomy, D., Kipping, D.M., Buchhave, L.A., Bakos, G.A.,
Hartman, J., and Schmitt, A.R. (2012) The detection and characterization of a
nontransiting planet by transit timing variations. Science, 336, Issue 6085, 1133.
Пардекопер и др. (2012) Paardekooper, S.-J., Leinhardt, Z.M., Thebault, Т., and
Bamteau, C. (2012) How not to build Tatooine: The difficulty of in situ formation of
circumbinary planets Kepler 16b, Kepler 34b, and Kepler 35b. Astrophys. J. Letters,
754, L16.
Папалойцу и Теркем (2010) Papaloizou, J.C.B., and Terquem, C. (2010) On the
dynamics of multiple systems of hot super-Earths and Neptunes: tidal circularization,
resonance and the HD 40307 system. Month. Not. Roy. Astron. Soc., 405, 573.
Пил (1976) Peale, SJ. (1976) Orbital resonances in the Solar system. Ann. Rev. Astron.
Astrophys., 14, 215.
Пил (1986) Peale, S.J. (1986) Orbital resonances, unusual configurations and exotic
rotation states among planetary satellites. In: Satellites. Bums, J.A., and Matthews,
M.S. (Eds.). Univ. of Arizona Press: Tucson. P. 159.
Douze ans apres. Заметки к русскому изданию
383
Пил (1999) Peale, S.J. (1999) Origin and evolution of the natural satellites. Ann. Rev.
Astron. Astrophys., 37, 533.
Петроски (1986) Petrosky, T.Y. (1986) Chaos and cometary clouds in the solar system.
Phys. Lett. A, 117, 328.
Пилат-Лохингер и Дворак (2002) Pilat-Lohinger, E., and Dvorak, R. (2002) Stability
of S-type orbits in binaries. Celest. Mech. Dyn. Astron., 82, 143.
Пилат-Лохингер и др. (2003) Pilat-Lohinger, E., Funk, B., and Dvorak, R. (2003)
Stability limits in double stars — a study of inclined planetary orbits. Astron.
Astrophys., 400, 1085.
Пифтанкин и Трещев (2007) Пифтанкин, Г.Н., и Трещев, Д.В. (2007) Сепаратрисное
отображение в гамильтоновых системах. УМН, 62 (2), 3.
Попова и Шевченко (2013) Popova, Е.А., and Shevchenko, 1.1. (2013) Kepler-16b: safe
in a resonance cell. Astrophys. J., 769, 152.
Райт и др. (2011) Wright, J.T., Veras, D., Ford, E.B., et al. (2011) The California planet
survey. III. A possible 2:1 resonance in the exoplanetary triple system HD 37124.
Astrophys. J., 730, 93.
Робутель и Габерн (2006) Robutel, P., and Gabem, F. (2006) The resonant structure of
Jupiter’s Trojan asteroids — I. Long-term stability and diffusion. Month. Not. Roy.
Astron. Soc., 372, 1463.
Рубинкам (1995) Rubincam, D.P. (1995) Asteroid orbit evolution due to thermal drag.
J. Geophys. Res., 100, 1585.
Сливан (2002) Slivan, S.M. (2002) Spin vector alignment of Koronis family asteroids.
Nature, 419, Issue 6902, 49.
Смирнов и Шевченко (2013) Smirnov, E.A., and Shevchenko, I.I. (2013) Massive
identification of asteroids in three-body resonances. Icarus, 222, 220.
Такеда и Pacuo (2005) Takeda, G., and Rasio, F.A. (2005) High orbital eccentricities of
extrasolar planets induced by the Kozai mechanism. Astrophys. J. 627, 1001.
Тераи и Ито (2013) Terai, Т., and Itoh, Y. (2013) High-precision measurements of the
brightness variation of Nereid. Publ. Astron. Soc. Japan, 65, no. 2, article no. 46.
Тсиганис и др. (2005) Tsiganis, К., Gomes, R., Morbidelli, A., and Levison, H.F. (2005)
Origin of the orbital architecture of the giant planets of the Solar System. Nature,
435, Issue 7041,459.
Уард и Гамильтон (2004) Ward, W.R., and Hamilton, D.P. (2004) Tilting Saturn. I.
Analytic model. Astron. J., 128, 2501.
Уиздом и др. (1984) Wisdom, J., Peale, S.J., and Mignard, F. (1984) The chaotic rotation
of Hyperion. Icarus, 58, 137.
Фабрицки и др. (2012) Fabrycky, D.C., Lissauer, J.J., Ragozzine, D., et al. (2012)
Architecture of Kepler’s multi-transiting systems: II. New investigations with twice
as many candidates. ArXiv: 1202.6328.
Фаринелла и др. (1998) Farinella, P., Vokrouhlicky, D., and Hartmann, W.K. (1998)
Meteorite delivery via Yarkovsky orbital drift. Icarus, 132, 378.
384
А. Морбиделли, И. И. Шевченко
Фернандес и Ип (1984) Fernandez, J.A., and Ip, W.-H. (1984) Some dynamical aspects
of the accretion of Uranus and Neptune: The exchange of orbital angular momentum
with planetesimals. Icarus, 58, 109.
Ферраз-Мелло u dp. (2005) Ferraz-Mello, S., Michtchenko, Т., Beauge, C., and
Callegari, N. Jr. (2005) Extrasolar planetary systems. In: Chaos and Stability in
Planetary Systems. Dvorak, R., Freistetter, F., and Kurths, J. (Eds.). Lect. Notes
Phys., 683. Springer: Heidelberg. P. 219.
Форд u dp. (2000) Ford, E.B., Kozinsky, B., and Rasio, F.A. (2000) Secular evolution
of hierarchical triple star systems. Astrophys. J., 535, 385.
Фрешле u dp. (2006) Froeschle, C., Lega, E., and Guzzo, M. (2006) Analysis of the
chaotic behaviour of orbits diffusing along the Arnold web. Celest. Mech. Dyn.
Astron., 95, 141.
Хагыгипоур и dp. (2010) Haghighipour, N., Dvorak, R., and Pilat-Lohinger, E. (2010)
Planetary dynamics and habitable planet formation in binary star systems. In: Planets
in Binary Star Systems. Haghighipour, N. (Ed.). Springer: Dordrecht. P. 285.
Харбисон и др. (2011) Harbison, R.A., Thomas, PC., and Nicholson, PC. (2011)
Rotational modeling of Hyperion, Celest. Mech. Dyn. Astron., 110, 1.
Хесселъброк и dp. (2013) Hesselbrock, A.J., Alexander, S.G., Harp, T.W., and Abel, N.P
(2013) An investigation of the relationship between shape and rotation to explain
the light curve of Nereid. Astron. J., 145, 144.
Хольман и Мюррей (2005) Holman, M.J., and Murray, N.W. (2005) The use of transit
timing to detect terrestrial-mass extrasolar planets. Science, 307, Issue 5713, 1288.
Хольман и Вигерт (1999) Holman, M.J., and Wiegert, PA. (1999) Long-term stability
of planets in binary systems. Astron. J., 117, 621.
Холшевников и Кузнецов (2011) Kholshevnikov, K.V., and Kuznetsov, E.D. (2011)
Stability of planetary systems with respect to masses. Celest. Mech. Dyn. Astron.,
109, 201.
Хэйес (2008) Hayes, W.B. (2008) Surfing on the edge: chaos versus near-integrability in
the system of Jovian planets. Month. Not. Roy. Astron. Soc., 386, 295.
Чаттерджи и dp. (2008) Chatterjee, S., Ford, E.B., Matsumura, S., and Rasio, F.A.
(2008) Dynamical outcomes of planet-planet scattering. Astrophys. J., 686, 580.
Чириков (1979) Chirikov, B.V. (1979) Universal instability of many-dimensional
oscillator systems. Phys. Rep., 52, 263.
Чириков и Вечеславов (1986) Chirikov, B.V., and Vecheslavov, V.V. (1986) Chaotic
dynamics of comet Hailey. INP Preprint 86-184. Institute of Nuclear Physics,
Novosibirsk.3
Чириков и Вечеславов (1989) Chirikov, B.V., and Vecheslavov, V.V. (1989) Chaotic
dynamics of comet Hailey. Astron. Astrophys. 221, 146.
3http://www.quantware.ups-tlse.fr/chirikov/publbinp.html
Douze ans apres. Заметки к русскому изданию
385
Чинкотта и др. (2003) Cincotta, P.M., Giordano, С.М., and Simo, С. (2003) Phase
space structure of multi-dimensional systems by means of the mean exponential
growth factor of nearby orbits. Physica D, 182, 151.
Шевченко (2008) Shevchenko, I.I. (2008) Adiabatic chaos in the Prometheus-Pandora
system. Month. Not. Roy. Astron. Soc., 384, 1211; 407, 704.
Шевченко (2010) Shevchenko, I.I. (2010) Hamiltonian intermittency and Levy flights in
the three-body problem. Phys. Rev. E, 81, 066216.
Шевченко (2011) Shevchenko, I.I. (2011) Lyapunov and diffusion timescales in the solar
neighborhood. Astrophys. J., 733, 39.
Шидлиховский (1990) Sidlichovsky, M. (1990) The existence of a chaotic region due to
the overlap of secular resonances nu5 and nu6. Celest. Mech. Dyn. Astron., 49, 177.
Литература
Агнор, Кануп, Левисон (1999) Agnor С.В., Canup R.M., and Levison H.F.
(1999) On the character and consequences of large impacts in the late stage
of terrestrial planet formation. Icarus, 142, 219.
Анрар (1970) Henrard J. (1970) On a perturbation theory using Lie transforms.
Celest. Mech., 3, 107.
Анрар (1990) Henrard J. (1990) A semi-numerical perturbation method for
separable Hamiltonian systems. Celest. Mech., 49, 43.
Анрар, Анрар (1991) Henrard J., and Henrard M. (1991) Slow crossing of a
stochastic layer. Physica D, 54, 135.
Анрар, Ватанабе, Муне (1995) Henrard J., Watanabe N., and Moons M. (1995)
A bridge between secondary and secular resonances inside the Hecuba gap.
Icarus, 115, 336.
Анрар, Караниколас (1990) Henrard J., and Caranicolas N.D. (1990) Motion
near the 3/1 resonance of the planar elliptic restricted three body problem.
Celest. Mech., 47, 99.
Анрар, Леметр (1983) Henrard J., and Lemaitre A. (1983) A second
fundamental model for resonance. Celest. Mech., 30, 197.
Анрар, Леметр (1987) Henrard J., and Lemaitre A. (1987) A perturbative
treatment of the 2/1 Jovian resonance. Icarus, 69, 266.
Арнольд (1963a) Арнольд В.И. (1963a) Об одной теореме Лиувилля, каса¬
ющейся интегрируемых проблем динамики. Сиб. мат. журнал, 4, № 2,
471.
Арнольд (19636) Арнольд В.И. (19636) Доказательство теоремы А. Н. Колмо¬
горова о сохранении условно-периодических движений при малом из¬
менении функции Гамильтона. УМН, 18, вып. 5 (113), 13.
Арнольд (1963в) Арнольд В.И. (1963в) Малые знаменатели и проблема
устойчивости движения в классической и небесной механике. УМН,
18, вып. 6 (114), 91.
388
Литература
Арнольд, Авец (1968) Arnold V.I., and Avez А. (1968) Ergodic Problems
of Classical Mechanics. Benjamin, New York. [Имеется перевод: Ар¬
нольд В.К, Авец А. Эргодические проблемы классической механики. —
Ижевск: РХД, 1999.]
Арнольд, Козлов, Нейштадт (2002) Арнольд В.И., Козлов В.В., Ней-
штадт А.И. Математические аспекты классической и небесной меха¬
ники. М.: Эдиториал УРСС, 2002.
Бейли, Чамберс, Хан (1992) Bailey М.Е., Chambers J.E., and Hahn G. (1992)
Origin of Sun-grazers: a frequent cometary end-state. Astron. Astrophys.,
257, 315.
Бенджоя, Слезак, Фрегиле (1991) Bendjoya Ph., Slezak E., and Froeschle C.
(1991) The wavelet transform: a new tool for asteroid family determination.
Astron. Astrophys., 251, 312.
Бенеттин, Галгани, Джиорджилли (1985) Benettin G., Galgani L., and
Giorgilli A. (1985) A proof of Nekhoroshev’s theorem for the stability
times in nearly integrable Hamiltonian systems. Celest. Mech., 37, 1.
Бенеттин, Галгани, Стрельцин (1976) Benettin G., Galgani L., and Strel-
cyn J.M. (1976) Kolmogorov entropy and numerical experiments. Phys.
Rev. A, 14, 2338.
Бенеттин, Галгани, Джиорджилли, Стрельцин (1980) Benettin G., Galga¬
ni L., Giorgilli A., and Strelcyn J.M. (1980) Lyapunov characteristic
exponents for smooth dynamical systems and for Hamiltonian systems;
a method for computing all of them. Part 1: Theory: Meccanica, March,
9-20; Part 2: Numerical application: Meccanica, March, 21-30.
Боже (1994) Beauge C. (1994) Asymmetric librations in exterior resonances.
Celest. Mech., 60, 225.
Борн (1927) Bom M. (1927) The Mechanics of the Atom. Bell, London. [Име¬
ется перевод: Борн М. Лекции по атомной механике. — Харьков-Киев:
ГНТИ Украины, 1934.]
Боттке, Рубинкам, Бернс (2000а) Bottke W.F., Rubincam D.P., and Bums J.A.
(2000a) Dynamical evolution of main belt meteoroids: numerical simula¬
tions incorporating planetary perturbations and Yarkovsky thermal forces.
Icarus, 145, 301.
Боттке, Едикке, Морбиделли, Пти, Глэдман (20006) Bottke W.F., Jedic-
ke R., Morbidelli A., Petit J.M., and Gladman B. (2000b) Understanding
the distribution of Near Earth Asteroids. Science, 288, 2190.
Литература
389
Брауэр, Клеменс (1961) Brouwer D., and Clemence G.M. (1961) Methods of
Celestial Mechanics. Academic Press, New York. [Имеется перевод: Брау¬
эр Д., Клеменс Дж. Методы небесной механики. — М.: Мир, 1964.]
Бретаньон (1974) Bretagnon Р. (1974) Termes a longues periodes dans le
systeme solaire. Astron. Astrophys., 30, 141.
Бретаньон (1982) Bretagnon P. (1982) Theory for the motion of all the planets:
the VSOP82 solution. Astron. Astrophys., 114, 278.
Бретаньон (1984) Bretagnon P. (1984) Improvement of analytic planetary
theories. Celest. Mech., 34, 193.
Бретаньон (1990) Bretagnon P. (1990) An iterative method for the construction
of a general planetary theory. Astron. Astrophys., 231, 561.
Брувилер, Кэри (1989) Bruhwiler D.L., and Cary J.R. (1989) Diffusion of
particles in a slowly modulated wave. Physica D, 40, 265.
Гантмахер (2001) Гантмахер Ф.Р. (2001) Лекции по аналитической меха¬
нике. М: Физматлит.
Глэдман, Квинн, Николсон, Рэнд (1996) Gladman В., Quinn D., Nicholson Ph.,
and Rand R. (1996) Synchronous locking of tidally evolving satellites.
Icarus, 122, 166.
Глэдман, Милъорини, Морбиделли, Заппала, Мишель, Челлино, Фрешле, Jle-
висон, Бейли, Дункан (1997) Gladman В., Migliorini F., Morbidelli А.,
Zappalla V., Michel P., Cellino A., Froeschle Ch., Levison H.F., Bailey М.,
and Duncan M.J. (1997) Dynamical lifetimes of objects injected into
asteroid main belt resonances. Science, 277, 197.
Гребнер (1960) Grobner W. (1960) Die Liereihen und ihre Anwendungen. D.
Verl. d. Wiss., Berlin. (2nd ed. 1967.)
Грин (1979) Green J.M. (1979) A method for determining stochastic transitions.
J. Math. Phys., 20, 1183.
Гронки, Милани (1998) Gronchi G.F., and Milani A. (1998) Averaging on
Earth-crossing orbits. Celest. Mech., 71, 109.
Гронки, Милани (1999) Gronchi G.F., and Milani A. (1999) The stable Kozai
state for asteroids and comets with arbitrary semimajor axis and inclination.
Astron. Astrophys., 341, 928.
Гурзадян, Кочарян (1987) Gurzadyan V.G., and Kocharyan A.A. (1987)
Relative chaos in stellar systems. Astr. Sp. Sci., 135, 307.
390
Литература
Гурзадян, Руффини (2000) Gurzadyan V.G., and Ruffini R., editors. (2000)
The Chaotic Universe. World Scientific, Singapore.
Гуццо, Морбиделли (1997) Guzzo М., and Morbidelli A. (1997) Construction
of a Nekhoroshev-like result for the asteroid belt dynamical system. Celest.
Mech., 66, 255.
Дела Барр, Каула, Варади (1996) De la Barre С.М., Kaula W.M., and Varadi F.
(1996) A study of orbits near Saturn’s triangular Lagrangian points. Icarus,
121, 88.
Делоне (1867) Delaunay C. (1867) Theorie du mouvement de la Lune. Mem.
Acad. Sci. 29, Paris.
Дельиамс, Рамирес-Рос, Ceapa (1999) Delshams A., Ramirez-Ros R., and
Seara T.M. (1999) Splitting of separatrices in Hamiltonian systems and
symplectic maps. In Hamiltonian Systems with Three or More Degrees of
Freedom. C. Simo, ed. Kluwer, Dordrecht, 39.
Депри (1968) Deprit A. (1968) Canonical transformations depending on a small
parameter. Celest. Mech., 1, 12.
Дермотт, Мюррей (1983) Dermott F.S., and Murray C.D. (1983) Nature of
the Kirkwood gaps in the asteroid belt. Nature, 301, 201.
Джеффрис, Стэндиш (1972) Jefferys W.H., and Standish E.M. (1972) Further
periodic solutions of the three dimensional restricted problem. Astron. J.,
77, 394.
Джиорджилли, Галгани (1985) Giorgilli A., and Galgani L. (1985) Rigorous
estimates for the series expansions of Hamiltonian perturbation theory.
Celest. Mech., 37, 95.
Джиорджилли, Локателли (1997) Giorgilli A., and Locatelli U. (1997)
Kolmogorov theorem and classical perturbation theory. Z. App. Math.
Phys., 48, 220.
Джиорджилли, Морбиделли (1997) Giorgilli A., and Morbidelli A. (1997)
Invariant KAM tori and global stability for Hamiltonian systems. Z. App.
Math. Phys., 48, 102.
Джуитт, Луу, Трухильо (1998) Jewitt D., Luu J., and Trujillo C. (1998) Large
Kuiper belt objects: the Mauna Kea 8K CCD survey. Astron. J., 115, 2125.
Дункан, Квинн, Тремейн (1987) Duncan M.J., Quinn Т., and Tremaine S. (1987)
The formation and extent of the solar system comet cloud. Astron. J., 94,
1330.
Литература
391
Дункан, Левисон, Бадд (1995) Duncan M.J., Levison H.F., and Budd S.M.
(1995) The long-term stability of orbits in the Kuiper belt. Astron. J., 110,
3073.
Дункан, Левисон, Ли (1998) Duncan M.J., Levison H.F., and Lee M.H. (1998)
A multiple time step symplectic algorithm for integrating close encounters.
Astron. J., 116, 2067.
Дэнби (1962) Danby J.M.A. (1962) Fundamentals of Celestial Mechanics.
Willmann-Bell Inc., Richmond, Virginia.
Дюрье (1979) Duriez L. (1979) Approche d’une theorie generate planetaire en
variables elliptiques heliocentriques. Ph. D. thesis, Univ. de Lille, France.
Дюрье (1989) Duriez L. (1989) Le developpement de la fonction perturbatrice.
In Les Methodes Modemes de la Mecanique Celeste. D. Benest and
C. Froeschle, eds. Ed. Frontieres, Gif sur Yvettes, France.
Заппала, Челлино, Фаринелла, Кнежевич (1990) Zappalla V., Cellino A.,
Farinella P., and Knezevic Z. (1990) Asteroid families. I. Identification
by hierarchical clustering and reliability assessment. Astron. J., 100, 2030.
Заппала, Бенджоя, Челлино, Фаринелла, Фреилле (1995) Zappalla V., Bendjo-
уа Ph., Cellino A., Farinella P., and Froeschle C. (1995) Asteroid
families: Search of a 12,487-asteroid sample using two different clustering
techniques. Icarus, 116, 291.
Зиглин (1979) Зиглин С.Л. Неинтегрируемость задачи о движении четырех
точечных вихрей. ДАН СССР, 250, № 6, 1296.
Зоммерфельд (1922) Sommerfeld А. (1922) Atombau und Spektrallinien.
Vieweg, Braunschweig, Germany. [Имеется перевод: Зоммерфельд A.
Строение атома и спектры. — М.: ГИТТЛ, 1956. (В 2-х томах.)]
Зюссман, Уиздом (1988) Sussman G.J., and Wisdom J. (1988) Numerical
evidence that the motion of Pluto is chaotic. Science, 241, 433.
Зюссман, Уиздом (1992) Sussman G.J., and Wisdom J. (1992) Chaotic
evolution of the solar system. Science, 257, 56.
Ида, Кануп, Стюарт (1997) Ida S., Canup R.M., and Stewart G.R. (1997)
Lunar accretion from an impact-generated disk. Nature, 389, 353.
Иошикава (1987) Yoshikawa M. (1987) A simple analytical model for the
resonance. Celest. Mech., 40, 233.
Иошикава (1990) Yoshikawa M. (1990) Motions of asteroids at the Kirkwood
gaps. I. On the 3:1 resonance with Jupiter. Icarus, 87, 78.
392
Литература
Иошикава (1991) Yoshikawa М. (1991) Motions of asteroids at the Kirkwood
gaps. II. On the 5:2, 7:3, and 2:1 resonances with Jupiter. Icarus, 92, 94.
Канеко, Кониши (1994) Kaneko К., and Konishi T. (1994) Peeling the onion
of order and chaos in a high dimensional Hamiltonian system. Physica D,
71, 146.
Кануп, Эспозито (1996) Canup R.M., and Esposito L.W. (1996) Accretion of
the Moon from an impact-generated disk. Icarus, 119, 427.
Карпино, Милани, Нобили (1987) Carpino М., Milani A., and Nobili A.M.
(1987) Long-term numerical integrations and synthetic theories for the
motion of the outer planets. Astron. Astrophys., 181, 182.
Квинн, Тремейн, Дункан (1991) Quinn T.R., Tremaine S., and Duncan M.J.
(1991) A three million year integration of the Earth’s orbit. Astron. J., 101,
2287.
Киношита, Наши (1996) Kinoshita H., and Nakai H. (1996) Long-term
behavior of the motion of Pluto over 5.5 billion years. Earth, Moon and
Planets, 72, 165.
Киношита, Накаи (1999) Kinoshita H., and Nakai H. (1999) Analytical
solution of the Kozai resonance and its application. Celest. Mech., 75, 125.
Киношита, Суше (1990) Kinoshita H., and Souchay J. (1990) The theory of
the nutation for the rigid Earth model at the second order. Celest. Mech.,
48, 187.
Кирквуд (1866) Kirkwood D. (1866). In Proceedings of the American
Association for the Advancement of Science for 1866.
Кнежевич, Милани, Фаринелла, Фрешле, Фрешле (1991) Knezevic Z., Mila¬
ni A., Farinella P., Froeschle Ch., and Froeschle C. (1991) Secular
resonances from 2 to 50 AU. Icarus, 93, 316.
Кнежевич, Фрешле, Леметр, Милани, Морбиделли (1995) Knezevic Z.,
Froeschle Ch., Lemaitre A., Milani A., and Morbidelli A. (1995)
Comparison between two theories of asteroid proper elements. Astron.
Astrophys., 293, 605.
Козаи (1962) Kozai Y. (1962) Secular perturbations of asteroids with high
inclination and eccentricities. Astron. J., 67, 591.
Козаи (1978) Kozai Y. (1978) Secular perturbations of asteroids and comets. In
Dynamics of the Solar System. Reidel, Dordrecht, 231.
Литература
393
Колмогоров {1954) Колмогоров А.Н. О сохранении условно-периодических
движений при малом изменении функции Гамильтона. ДАН СССР, 98,
№ 4, 527.
Колмогоров {1959) Колмогоров А.Н. Об энтропии на единицу времени как
метрическом инварианте автоморфизмов. ДАН СССР, 124, 754.
Коломбо {1966) Colombo G. (1966) Cassini’s second and third laws. Astron.
J., 71,891.
Контопулос {1966) Contopoulos G. (1966) Resonance phenomena and the
non-applicability of the «third» integral. In Les Nouvelles Methodes de
la Dynamique Stellaire. F. Nahon and M. Henon, eds. CNRS, Paris. Cm.
также: Bull. Astron., Ser. 3, 2, 233 (1967).
Контопулос, Воглис {1996) Contopoulos G., and Voglis N. (1996) Spectra of
stretching numbers and helicity angles in dynamical systems. Celest. Mech.,
64, 1.
Контопулос, Воглис, Эфиомопулос, Фрешле, Гонци, Лега, Дворак, Лохин-
гер {1997) Contopoulos G., Voglis N., Efthyomopoulos С., Froeschle С.,
Gonczi R., Lega E., Dvorak R., and Lohinger E. (1997) Transition spectra
of dynamical systems. Celest. Mech., 67, 293.
Коселефф {1993) Koseleff P.V. (1993) Relations among Lie formal series
and construction of symplectic integrators. In Applied Algebra, Algebraic
Algorithms and Error Correcting Codes. Lecture Notes in Comp. Sci., 673.
Springer-Verlag, Berlin, 213.
Коселефф {1996) Koseleff P.V. (1996) Exhaustive search of symplectic
integrators using computer algebra. In Integration Algorithms and Classical
Mechanics. Fields Inst. Commun., 10. Amer. Math. Soc., Providence, R. I.,
103.
Крылов {1950) Крылов H. (1950) Работы по обоснованию статистической
физики. М.-Л.: Изд-во АН СССР.
Кэмерон {1997) Cameron A.G. (1997) The origin of the Moon and the single
impact hypothesis. Icarus, 126, 126.
Лазуткин {1973) Лазуткин В.Ф. (1973) Существование каустик для билли¬
ардной задачи в выпуклой области. Изв. АН СССР. Сер. матем., 37,
вып. 1, 186.
Ласкар {1985) Laskar J. (1985) Accurate methods in general planetary theory.
Astron. Astrophys., 144, 133.
394
Литература
Ласкар (1986) Laskar J. (1986) Secular terms of classical planetary theories
using the results of general theory. Astron. Astrophys., 157, 59.
Ласкар (1988) Laskar J. (1988) Secular evolution of the solar system over 10
million years. Astron. Astrophys., 198, 341.
Ласкар (1989) Laskar J. (1989) A numerical experiment on the chaotic
behaviour of the solar system. Nature, 338, 237.
Ласкар (1990) Laskar J. (1990) The chaotic motion of the solar system: a
numerical estimate of the size of the chaotic zones. Icarus, 88, 266.
Ласкар (1992) Laskar J. (1992) A few points on the stability of the Solar
System. In Chaos, Resonance and Collective Dynamical Phenomena in the
Solar System. S. Ferraz-Mello, ed. Kluwer, Dordrecht, 1.
Ласкар (1993) Laskar J. (1993) Frequency analysis for multidimensional
systems. Physica D, 67, 257.
Ласкар (1994) Laskar J. (1994) Large-scale chaos in the solar system. Astron.
Astrophys., 287, 9.
Ласкар (1999) Laskar J. (1999) Introduction to frequency map analysis. In
Hamiltonian Systems with Three or More Degrees of Freedom. C. Simo,
ed. Kluwer, Dordrecht, 134.
Ласкар, Робутелъ (1993) Laskar J., and Robutel Ph. (1993) The chaotic
obliquity of the planets. Nature, 361, 608.
Ласкар, Робутелъ (1995) Laskar J., and Robutel Ph. (1995) Stability of the
planetary three-body problem. I. Expansion of the planetary Hamiltonian.
Celest. Mech. 62, 193.
Ласкар, Жутелъ, Робутелъ (1993) Laskar J., Joutel F., and Robutel Ph. (1993)
Stabilization of the Earth’s obliquity by the Moon. Nature, 361, 615.
Ласкар, Квинн, Тремейн (1992a) Laskar J., Quinn Т., and Tremaine S. (1992a)
Confirmation of resonant structure in the solar system. Icarus, 95, 148.
Ласкар, Фрегиле, Челетти (19926) Laskar J., Froeschle C., and Celletti A.
(1992b) The measure of chaos by the numerical analysis of the fundamental
frequencies. Physica D, 56, 253.
Левисон, Дункан (1994) Levison H.F., and Duncan M.J. (1994) The long-term
dynamical behavior of short-period comets. Icarus, 108, 18.
Леметр (1984) Lemaitre A. (1984) High-order resonances in the restricted
three-body problem. Celest. Mech., 32, 109.
Литература
395
Леметр, Анрар (1990) Lemaitre A., and Henrard J. (1990) On the origin of the
chaotic behavior in the 2/1 Kirkwood gap. Icarus, 83, 391.
Леметр, Морбиделли (1994) Lemaitre A., and Morbidelli A. (1994) Calculation
of proper elements for high inclined asteroidal orbits. Celest. Mech., 60, 29.
Лихтенберг, Либерман (1983) Lichtenberg A.J., and Lieberman M.A. (1983)
Regular and Stochastic Motion. Springer-Verlag, New York. [Имеется пе¬
ревод: Лихтенберг А., Либерман М. Регулярная и стохастическая дина¬
мика. — М.: Мир, 1984; Череповец: Меркурий-ПРЕСС, 2000.]
Лошак (1992) Лошак П. (1992) Каноническая теория возмущений: подход,
основанный на совместных приближениях. УМН, 47, вып. 6 (288), 59.
Ляпунов (1907) Lyapunov A.M. (1907) Probleme general de la stabilite du
mouvement. Ann. Fac. Sci. Univ. Toulouse, 9, 203. Reproduced in Ann.
Math. Study, 17, Princeton (1947). [Русские издания: Ляпунов A.M. Об¬
щая задача об устойчивости движения. — М.-Л.: Гостехиздат, 1950;
Ляпунов А.М. Общая проблема устойчивости движения. — В кн.: Ляпу¬
нов А.М. Собрание сочинений. Т. II. — М.-Л.: Изд-во АН СССР, 1954.
С. 7.]
Малъхотра (1996) Malhotra R. (1996) The phase space structure near Neptune
resonances in the Kuiper belt. Astron. J., Ill, 504.
Марцари, Дэвис, Ванцани (1995) Marzari F., Davis D., and Vanzani V. (1995)
Collisional evolution of asteroid families. Icarus, 113, 168.
Марцари, Фаринелла, Дэвис (1999) Marzari F., Farinella P., and Davis D.R.
(1999) Origin, aging, and death of asteroid families. Icarus, 142, 63.
Mamece, Уитмен (1992) Matese J.J., and Whitman P.G. (1992) A model of the
galactic tidal interaction with the Oort comet cloud. Celest. Mech., 54, 13.
Мельников (1963) Мельников В.К. Об устойчивости центра при периодиче¬
ских по времени возмущениях. Тр. Моск. мат. общества, 12, 3.
Меникелла, Паоликки, Фаринелла (1996) Menichella М., Paolicchi P., and
Farinella P. (1996) The main belt as a source of Near Earth Asteroids.
Earth, Moon and Planets, 72, 133.
Милани, Кнежевич (1990) Milani A., and Knezevic Z. (1990) Secular
perturbation theory and computation of asteroid proper elements. Celest.
Mech., 49, 247.
Милани, Кнежевич (1992) Milani A., and Knezevic Z. (1992) Asteroid proper
elements and secular resonances. Icarus, 98, 211.
396
Литература
Милани, Кнежевич (1994) Milani A., and Knezevic Z. (1994) Asteroid proper
elements and the dynamical structure of the asteroid main belt. Icarus, 107,
219.
Милани, Нобили, Карпино (1989) Milani A., Nobili A.M., and Carpino M.
(1989) Dynamics of Pluto. Icarus, 82, 200.
Милъорини, Мишель, Морбиделли, Несворный, Заппала (1998) Migliorini F.,
Michel P., Morbidelli A., Nesvomy D., and Zappalla V. (1998) Origin of
Earth-crossing asteroids: a quantitative simulation. Science, 281, 2022.
Мищенко, Ферраз-Мелло (1995) Michtchenko T.A., and Ferraz-Mello S.
(1995) Comparative study of the asteroidal motion in the 3:2 and 2:1
resonances with Jupiter. I. Planar model. Astron. Astrophys., 303, 945.
Мищенко, Ферраз-Мелло (1997) Michtchenko T.A., and Ferraz-Mello S.
(1997) Escape of asteroids from the Hecuba gap. Planet. Sp. Sci., 45, 1587.
Мишель (1997) Michel P. (1997) Effects of linear secular resonances in the
region of semimajor axes smaller than 2 AU. Icarus, 129, 348.
Мишель, Томас (1996) Michel P., and Thomas F. (1996) The Kozai resonance
for near-Earth asteroids with semimajor axes smaller than 2 AU. Astron.
Astrophys., 307, 310.
Мишель, Фрешле (1997) Michel P., and Froeschle Ch. (1997) The location of
linear secular resonances for semimajor axes smaller than 2 AU. Icarus,
128, 230.
Мишель, Мильорини, Морбиделли, Заппала (2000) Michel P., Migliorini F.,
Morbidelli A., and Zappalla V. (2000) The population of Mars-Crossers:
classification and dynamical evolution. Icarus, 145, 332.
Мозер (1962) Moser J.K. (1962) On invariant curves of area-preserving
mappings of an annulus. Nachr. Akad. Wiss. Gottingen, Math. Phys. KI.,
2, 1. [Имеется перевод: Мозер Ю. Об инвариантных кривых отображе¬
ний кольца, сохраняющих площадь. — В кн.: Мозер Ю. КАМ-теория
и проблемы устойчивости. — Ижевск: РХД, 2003. С. 28.]
Морбиделли (1993а) Morbidelli А. (1993а) Asteroid secular resonant proper
elements. Icarus, 105, 48.
Морбиделли (19936) Morbidelli A. (1993b) On the successive elimination of
perturbation harmonics. Celest. Mech., 55, 101.
Морбиделли (1997) Morbidelli A. (1997) Chaotic diffusion and the origin of
comets from the 2/3 resonance in the Kuiper belt. Icarus, 127, 1.
Литература
397
Морбиделли, Анрар (1991а) Morbidelli A., and Henrard J. (1991а) Secular
resonances in the asteroid belt: theoretical perturbation approach and the
problem of their location. Celest. Mech., 51, 131.
Морбиделли, Анрар (19916) Morbidelli A., and Henrard J. (1991b) The main
secular resonances щ, v$ and v\§ in the asteroid belt. Celest. Mech., 51,
169.
Морбиделли, Гуццо (1996) Morbidelli A., and Guzzo M. (1996) The Nekhoroshev
theorem and the asteroid belt dynamical system. Celest. Mech., 65, 107.
Морбиделли, Джиорджилли (1993) Morbidelli A., and Giorgilli A. (1993)
Quantitative perturbation theory by successive elimination of harmonics.
Celest. Mech., 55, 131.
Морбиделли, Джиорджилли (1995a) Morbidelli A., and Giorgilli A. (1995a)
Superexponental stability of KAM tori. J. Stat. Phys., 78, 1607.
Морбиделли, Джиорджилли (19956) Morbidelli A., and Giorgilli A. (1995b)
On a connection between KAM and Nekhoroshev theorems. Physica D, 86,
514.
Морбиделли, Джиорджилли (1997) Morbidelli A., and Giorgilli A. (1997) On
the role of high order resonances in normal forms and in separatrix splitting.
Physica D, 102, 195.
Морбиделли, Муне (1993) Morbidelli A., and Moons M. (1993) Secular
resonances inside mean motion commensurabilities: the 2/1 and 3/2 cases.
Icarus, 103, 99.
Морбиделли, Несворный (1999) Morbidelli A., and Nesvomy D. (1999)
Numerous weak resonances drive asteroids towards terrestrial planets
orbits. Icarus, 139, 295.
Морбиделли, Томас, Муне (1995a) Morbidelli A., Thomas F., and Moons M.
(1995a) The resonant structure of the Kuiper belt and the dynamics of the
first five trans-Neptunian objects. Icarus, 118, 322.
Морбиделли, Заппала, Муне, Челлино, Гонци (19956) Morbidelli A., Zappal-
la V., Moons М., Cellino A., and Gonczi R. (1995b) Asteroid families close
to mean motion resonances: dynamical effects and physical implications.
Icarus, 118, 132.
Муне (1993) Moons M. (1993) Averaging approaches. Dep. of Math. Rep., 19,
FUNDP, Namur, Belgium.
Муне (1994) Moons M. (1994) Extended Schubart averaging. Celest. Mech.,
60, 173.
398
Литература
Муне (1997) Moons М. (1997) Review of the dynamics in the Kirkwood gaps.
Celest. Mech., 65, 175.
Муне, Морбиделли (1993) Moons М., and Morbidelli A. (1993) The main
mean motion commensurabilities in the planar circular and elliptic problem.
Celest. Mech., 57, 99.
Муне, Морбиделли (1995) Moons М., and Morbidelli A. (1995) Secular
resonances inside mean-motion commensurabilities: the 4/1, 3/1, 5/2 and
7/3 cases. Icarus, 114, 33.
Муне, Морбиделли, Мильорини (1998) Moons М., Morbidelli A., and Migliori-
ni F. (1998) Dynamical structure of the 2/1 commensurability and the origin
of the resonant asteroids. Icarus, 135, 458.
Мэсседж (1958) Message J. (1958) The search for asymmetric periodic orbits
in the restricted problem of three bodies. Astron. J., 63, 443.
Мэсседж (1966) Message RJ. (1966) On nearly-commensurable periods in
the restricted problem of three bodies, with calculation of the long-period
variations in the interior 2/1 case. In The Theory of Orbits in the Solar
System and in Stellar Systems. G. Contopoulos, ed. Academic Press,
London, 197.
Мюррей, Хольман (1997) Murray N., and Holman M. (1997) Diffusive chaos
in the outer asteroid belt. Astron. J., 114, 1246.
Мюррей, Хольман (1999) Murray N., and Holman M. (1999) The origin of
chaos in the outer solar system. Science, 283, 1877.
Мюррей, Хольман, Поттер (1998) Murray N., Holman М., and Potter M.
(1998) On the origin of chaos in the asteroid belt. Astron. J., 116, 2583.
Накаи, Киношита (1985) Nakai H., and Kinoshita H. (1985) Secular
perturbations of asteroids in secular resonances. Celest. Mech., 36, 391.
Нейгитадт (1981) Нейштадт А.И. Оценки в теореме Колмогорова о сохра¬
нении условно-периодических движений. Прикл. мат. и мех., 45 (6),
1016.
Нейштадт (1984) Нейштадт А.И. О разделении движений в системах
с быстро вращающейся фазой. Прикл. мат. и мех., 48 (2), 197.
Нерон де Сюржи, Ласкар (1997) Neron de Surgy О., and Laskar, J. (1997) On
the long term evolution of the spin of the Earth. Astron. Astrophys, 318,
975.
Литература
399
Несворный, Доунс (2002) Nesvomy D., and Dones L. (2002) How long-lived
are the hypothetical Trojan populations of Saturn, Uranus and Neptune?
Icarus, 160, 271.
Несворный, Морбиделли (1998) Nesvomy D., and Morbidelli A. (1998) Three-
body mean motion resonances and the chaotic structure of the asteroid belt.
Astron. J., 116, 3029.
Несворный, Морбиделли (1999) Nesvomy D., and Morbidelli A. (1999) An
analytic model of three-body mean motion resonances! Celest. Mech., 71,
243.
Несворный, Ройг (2000) Nesvomy D., and Roig F. (2000) Mean motion
resonances in the transneptunian region: Part I. The 2:3 resonance with
Neptune. Icarus, 148, 282.
Несворный, Ройг (2001) Nesvomy D., and Roig F. (2001) Mean motion
resonances in the transneptunian region: Part II. The 1:2, 3:4, and weaker
resonances. Icarus, 150, 104.
Несворный, Ферраз-Мелло (1997a) Nesvomy D., and Ferraz-Mello S. (1997a)
Chaotic diffusion in the 2/1 asteroidal resonance: an application of the
frequency map analysis. Astron. Astrophys., 320, 672.
Несворный, Ферраз-Мелло (19976) Nesvomy D., and Ferraz-Mello S. (1997b)
On the asteroidal population of the first-order Jovian resonances. Icarus,
130, 247.
Несворный, Ройг, Ферраз-Мелло (2000) Nesvomy D., Roig F., and Ferraz-
Mello S. (2000) Close approaches of trans-Neptunian objects to Pluto have
left observable signatures on their orbital distribution. Astron. J., 119, 953.
Нехорошее (1977) Нехорошее H.H. Экспоненциальная оценка времени
устойчивости гамильтоновых систем, близких к интегрируемым. УМН,
32 (6), 5.
Нехорошее (1979) Нехорошее Н.Н. Экспоненциальная оценка времени
устойчивости гамильтоновых систем, близких к интегрируемым. II.
Труды семинара им. И.Г. Петровского, 5, 5.
Нобили, Милани, Карпино (1989) Nobili A.M., Milani A., and Carpino М.
(1989) Fundamental frequencies and small divisors in the orbits of the
outer planets. Astron. Astrophys., 210, 313.
Олвера, Симо (1987) Olvera A., and Simo C. (1987) An obstruction method
for the destmction of invariant curves. Physica D, 26, 181.
400
Литература
Оселедец {1968) Оселедец В.И. (1968) Мультипликативная эргодическая
теорема. Характеристические показатели Ляпунова. Труды Московско¬
го матем. обьц-ва, 19, 197.
Папафилиппу, Ласкар {1998) Papaphilippou Y., and Laskar J. (1998) Global
dynamics of triaxial galactic models through frequency map analysis.
Astron. Astropys., 329, 451.
Паризи, Брунини {1996) Parisi M.G., and Brunini A. (1996) Dynamical
consequencies of Uranus’ great collision. In Chaos in Gravitational N-
body Systems. J.C. Muzzio, S. Ferraz-Mello and J. Henrard, eds. Kluwer,
Dordrecht, 291.
Лесин {1977) Песин Я.Б. (1977) Характеристические показатели Ляпунова
и гладкая эргодическая теория. УМЫ, 32, вып. 4 (196), 55.
Петель {1993) Poschel J. (1993) Nekhoroshev’s estimates for quasi-convex
Hamiltonian systems. Math. Z., 213, 187.
Пресс, Тьюкольски, Веттерлинг, Фланнери {1986) Press W.H., Teukols-
ky S.A., Vetterling W.T., and Flannery B.P. (1986) Numerical Recipes.
Cambridge Univ. Press, Cambridge. (3rd ed.: Cambridge Univ. Press,
Cambridge, 2007.) [Имеется перевод: Пресс В., Фланнери Б., Тьюколь¬
ски С., Веттерлинг В. Численные рецепты. — М.: Мир, 1990.]
Пуанкаре {1892) Poincare Н. (1892) Les methodes nouvelles de la mecanique
celeste. Gauthier-Villar, Paris. [Имеется перевод в кн.: Пуанкаре А. Из¬
бранные труды. (В 3-х томах.) Т. 1-2. — М.: Наука, 1971.]
Пуанкаре {1902а) Poincare Н. (1902а) Les solutions periodiques et les planetes
du type d’Hecube. Bulletin Astronomique, 19, 177.
Пуанкаре {19026) Poincare H. (1902b) Sur les planetes du type d’Hecube.
Bulletin Astronomique, 19, 289.
Пьессенс, де Донкер-Капенга, Юберхубер, Каханер {1983) Piessens R.,
de Doncker-Kapenga E., Uberhuber C.W., and Kahaner D.K. (1983)
Quadpack: A Subroutine Package for Automatic Integration. Springer-
Verlag, Berlin.
Робутель, Ласкар {2001) Robutel P., and Laskar J. (2001) Frequency map and
global dynamics in the Solar System I. Short period dynamics of massless
particles. Icarus, 152, 4.
Сафронов {1965) Сафронов B.C. (1965) Размеры наибольших тел, падав¬
ших на планеты в процессе их образования. Астрон. журн., 42, 1270.
Литература
401
Сессии, Ферраз-Мелло (1984) Sessin W., and Ferraz-Mello S. (1984) Motion
of two planets with periods commensurable in the ratio 2:1. Solutions of
the Hori auxiliary system. Celest. Mech., 32, 307.
Cumo (1990) Simo C. (1990) On the analytical and numerical approximation of
invariant manifolds. In Modem Methods in Celestial Mechanics. D. Benest
and C. Froeschle, eds. Ed. Frontieres, Gif sur Yvettes, France.
Симон, Бретаньон (1975) Simon J.L., and Bretagnon P. (1975) First order
perturbations of the four big planets. Astron., and Astrophys., 42, 259.
Синай (1959) Синай Я.Г. (1959) О понятии энтропии динамической систе¬
мы. Докл. Акад. наук СССР, 124, вып. 4, 768.
Смейл (1965) Smale S. (1965) Diffeomorphisms with many periodic points.
In Differential and Combinatorial Topology: A Symposium in Honor of
Marston Morse. S.S. Caims, ed. Princeton Univ. Press, Princeton N.J., 63.
Смейл (1980) Smale S. (1980) The Mathematics of Time: Essays on Dynamical
Systems, Economic Processes and Related Topics. Springer-Verlag, New
York.
Суше, Луазель, Киношита, Фолгейра (1999) Souchay J., Loysel В., Kinoshi-
ta H., and Folgueira M. (1999) Corrections and new developments in rigid
Earth nutation theory. III. Final tables «REN-2000» including crossed-
nutation and spin-orbit coupling effects. Astron. Astrophys. Suppl. Ser.,
135, 111.
Тейлор (1999) Taylor S.R. (1999) On the difficulties of making Earth-like
planets. Meteoritics and Planetary Sci., 34, 317.
Томас (1998) Thomas F. (1998) La dynamique resonnante dans le systeme
solaire. Application au mouvement des objets transneptuniens. Ph.D. thesis,
Obs. de Paris.
Томас, Морбиделли (1996) Thomas F., and Morbidelli A. (1996) The Kozai
resonance in the outer Solar System and the dynamics of long-period
comets. Celest. Mech., 64, 209.
Тума, Уиздом (1993) Touma J., and Wisdom J. (1993) The chaotic obliquity of
Mars. Science, 259, 1294.
Тума, Уиздом (1994a) Touma J., and Wisdom J. (1994a) Evolution of the Earth-
Moon system. Astron. J., 108, 1943.
Тума, Уиздом (19946) Touma J., and Wisdom J. (1994b) Lie-Poisson
integrators for rigid body dynamics in the Solar System. Astron. J., 107,
1189.
402
Литература
Уард (1974) Ward W.R. (1974) Climatic variations on Mars. I. Astronomical
theory of insolation. J. Geophys. Res., 79, 3375.
Уард (1982) Ward W.R. (1982) Comments on the long-term stability of the
Earth’s obliquity. Icarus, 50, 444.
Уиггинс (1988) Wiggins S. (1988) Global Bifurcations and Chaos. Springer-
Verlag, New York.
Уиздом (1980) Wisdom J. (1980) The resonance overlap criterion and the onset
of stochastic behavior in the restricted three-body problem. Astron. J., 85,
1122.
Уиздом (1982) Wisdom J. (1982) The origin of the Kirkwood gaps: a mapping
for asteroidal motion near the 3/1 commensurability. Astron. J., 87, 577.
Уиздом (1983) Wisdom J. (1983) Chaotic behavior and the origin of the 3/1
Kirkwood gap. Icarus, 56, 51.
Уиздом (1985) Wisdom J. (1985) A perturbative treatment of motion near the
3/1 commensurability. Icarus, 63, 272.
Уиздом (1987) Wisdom J. (1987) Urey Prize Lecture: chaotic dynamics in the
solar system. Icarus, 72, 241.
Уиздом, Хольман (1991) Wisdom J., and Holman M. (1991) Symplectic maps
for the N-body problem. Astron. J., 102, 1528.
Уильямс (1969) Williams J.G. (1969) Secular perturbations in the solar system.
Ph.D. dissertation, University of California, Los Angeles.
Уильямс, Бенсон (1971) Williams J.G., and Benson G.S. (1971) Resonances in
the Neptune-Pluto system. Astron. J., 76, 167.
Уильямс, Фолкнер (1981) Williams J.G., and Faulkner J. (1981) The position
of secular resonance surfaces. Icarus, 46, 390.
Уиттекер (1937) Whittaker E.T. (1937) A Treatise on the Analytical Dynamics
of Particles and Rigid Bodies. Cambridge Univ. Press, Cambridge. [Имеет¬
ся перевод: Уиттекер Э.Т. Аналитическая динамика. — М.: Эдиториал
УРСС, 2010.]
Уэзерилл (1975) Wetherill G.W. (1975) Late heavy bombardment of the Moon
and terrestrial planets. Proc. Lunar Sci. Conf., 6, 1539.
Фаринелла, Вокроуглицкий (1998) Farinella, P., and Vokrouhlicky D. (1998)
Semimajor axis mobility of asteroidal fragments. Science, 283, 1507.
Фаринелла, Фрешле, Гонци (1993a) Farinella P., Froeschle Ch., and Gonczi R.
(1993a) Meteorites from the asteroid 6 Hebe. Celest. Mech., 56, 287.
Литература
403
Фаринелла, Гонци, Фрешле, Фрешле (19936) Farinella P., Gonczi R.,
Froeschle Ch., and Froeschle С. (1993b). The injection of asteroid
fragments into resonance. Icarus, 101, 174.
Фаринелла, Фрешле, Фрешле, Гонци, Хан, Морбиделли, Валъсекки (1994)
Farinella P., Froeschle Ch., Froeschle С., Gonczi R., Hahn G., Morbidel¬
li A., and Valsecchi G.B. (1994) Asteroids falling onto the Sun. Nature,
371, 315.
Фернандес, Ип (1984) Fernandez J.A., and Ip W.H. (1984) Some dynamical
aspects of the accretion of Uranus and Neptune: the exchange of orbital
angular momentum with planetesimals. Icarus, 58, 109.
Ферраз-Мелло (1987) Ferraz-Mello S. (1987) Averaging the elliptic asteroidal
problem near a first-order resonance. Astron. J., 94, 208.
Ферраз-Мелло (1994) Ferraz-Mello S. (1994) Dynamics in the asteroid 2/1
resonance. Astron. J., 108, 2330.
Ферраз-Мелло (1996) Ferraz-Mello S. (1996) A symplectic mapping approach
to the study of the stochasticity in asteroidal resonances. Celest Mech., 65,
421.
Ферраз-Мелло, Клафке (1991) Ferraz-Mello S., and Klafke J.C. (1991)
A model for the study of the very high eccentricity asteroidal motion: the
3:1 resonance. In Predictability, Stability and Chaos in N-body Dynamical
Systems. A.E. Roy, ed. Plenum Press, New York, 177.
Ферраз-Мелло, Camo (1989) Ferraz-Mello S., and Sato M. (1989) The very-
high-eccentricity asymmetric expansion of the disturbing function near
resonances of any order. Astron. Astrophys., 225, 541.
Ферраз-Мелло, Мищенко, Ройг (1998a) Ferraz-Mello S., Michtchenko T.A.,
and Roig F. (1998a) The determinant role of Jupiter’s great inequality in
the depletion of the Hecuba gap. Astron. J., 116, 1491.
Ферраз-Мелло, Несворный, Мищенко (1997) Ferraz-Mello S., Nesvomy D.,
and Michtchenko T.A. (1997) On the lack of asteroids in the Hecuba gap.
Celest. Mech., 69, 171.
Ферраз-Мелло, Несворный, Мищенко (19986) Ferraz-Mello S., Nesvomy D.,
and Michtchenko T.A. (1998b) Chaos, diffusion, escape and permanence
of resonant asteroids in gaps and groups. In Solar System Formation and
Evolution. D. Lazzaro, R. Vieira Martins, S. Ferraz-Mello, J. Fernandez,
and C. Beauge, eds. Astron. Soc. of the Pacific, Conf. Series 149, 65.
404
Литература
Форцони Акколти (1995) Forzoni Accolti Е. (1995) Identificazione statistica
delle famiglie di asteroidi ad alta inclinazione e/o ad alta eccentricita. Ph.D.
thesis, University of Turin, Italy.
Франклин (1994) Franklin F.A. (1994) An examination of the relationship
between chaotic orbits and the Kirkwood gap at the 2:1 resonance.
Astron. J., 107, 1890.
Фрешле, Лега (1998) Froeschle С., and Lega E. (1998) Twist angles: a method
for distinguishing islands, tori and weak chaotic orbits. Comparison with
other methods of analysis. Astron. Astrophys., 334, 355.
Фрешле, Шолл (1986) Froeschle Ch., and Scholl H. (1986) The secular
resonance щ in the asteroidal belt. Astron. Astrophys., 166, 326.
Фрешле, Гонци, Jleaa (1997) Froeschle С., Gonczi R., and Lega E. (1997) The
fast Lyapunov indicator: a simple tool to detect weak chaos. Application to
the structure of the main asteroidal belt. Planet. Space Sci., 45, 881.
Фрешле, Гуццо, Лега (2000) Froeschle С., Guzzo М., and Lega E. (2000)
Graphical evolution of the Arnold web: from order to chaos. Science, 289,
2108.
Фрешле, Морбиделли, Шолл (1991) Froeschle Ch., Morbidelli A., and
Scholl H. (1991) Complex dynamical behaviour of the asteroid 2335 James
associated with the secular resonances and numerical studies and
theoretical interpretation. Astron. Astrophys., 24, 553.
Хартман, Дэвис (1975) Hartmann W.K., and Davis D.R. (1975) Satellite-sized
planetesimals and lunar origin. Icarus, 24, 504.
Хенон (1974) Henon M. (1974) Integrals of the Toda lattice. Phys. Rev. B, 9,
1921.
Хенон, Хейлес (1964) Henon М., and Heiles C. (1964) The applicability of the
third integral of motion: some numerical experiments. Astron. J., 69, 73.
Хираяма (1918) Hirayama K. (1918) Groups of asteroids probably of common
origin. Astron. J., 31, 185.
Холъман, Мюррей (1996) Holman M.J., and Murray N.W. (1996) Chaos in
high order mean motion resonances in the outer asteroid belt. Astron. J.,
112, 1278.
Холъман, Уиздом (1993) Holman M.J., and Wisdom J. (1993) Dynamical
stability in the outer solar system and the delivery of short period comets.
Astron. J., 105, 1987.
Литература
405
Хори (1966) Hori G.I. (1966) General perturbations theory with unspecified
canonical variables. Publ. Astron. Soc. Japan, 18, 287.
Чамберс (1999) Chambers J.E. (1999) A hybrid symplectic integrator that
permits close encounters between massive bodies. Monthly Not. Roy.
Astron. Soc., 304, 793.
Чамберс, Уэзерилл (1998) Chambers J.E., and Wetherill G.W. (1998) Making
the terrestrial planets: N-body integrations of planetary embryos in three
dimensions. Icarus, 136, 304.
Чамберс, Уэзерилл, Босс (1996) Chambers J.E., Wetherill G.W., and Boss A.R
(1996) The stability of multi-planet systems. Icarus, 119, 261.
Челлино, Мишель, Танга, Заппала, Паоликки, дельЮро (1999) Cellino А.,
Michel R, Tanga R, Zappalla V., Paolicchi P., and dell’Oro A. (1999) The
velocity-size relationship for members of asteroid families and implications
for the physics of catastrophic collisions. Icarus, 141, 79.
Чинкотта, Джордано (2001) Cincotta P., and Giordano C.M. (2001) Global
dynamics through the Mean Exponential Growth factor of Nearby Orbits
(MEGNO). Preprint of Obs. of La Plata, Argentina.
Чинкотта, Симо (2000) Cincotta P., and Simo C. (2000) Simple tools to
study global dynamics in non-axisymmetric galactic potentials. Astron.
Astrophys. Suppl., 147, 205.
Чириков (1959) Чириков Б.В. (1959) Резонансные процессы в магнитных
ловушках. Атомн. энергия, 6, вып. 6, 630.
Чириков (1979) Chirikov B.V. (1979) A universal instability of many¬
dimensional oscillator systems. Phys. Rep., 52, 265.
Шидлиховский (1990) Sidlichovsky M. (1990) Tables of the Disturbing
Function for Resonant Asteroids. Czechoslovak Academy of Sciences,
Prague.
Шолл, Фрешле (1990) Scholl H., and Froeschle Ch. (1990) Orbital evolution of
known asteroids in the vb resonance region. Astron. Astrophys., 227, 255.
Шубарт (1964) Schubart J. (1964) Long period effects in nearly commensurable
cases of the restricted three-body problem. Smithsonian Astrophys. Obs.
Spec. Rep., 149.
Шубарт (1968) Schubart J. (1968) Long-period effects in the motion of Hilda-
type planets. Astron. J., 73, 99.
406
Литература
Эллис, Мюррей (2000) Ellis К.М., and Murray C.D. (2000) The disturbing
function in solar system dynamics. Icarus, 147, 129.
Элскенс, Эсканде (1991) Elskens Y., and Escande D.F. (1991) Slowly pulsating
separatrices sweep homoclinic tangles where islands must be small: an
extension of classical adiabatic theory. Nonlinearity, 4, 615.
Эль-Зант (1997) El-Zant A.A. (1997) On the stability of motion of N-body
systems: a geometric approach. Astron. Astrophys., 326, 113.
Эль-Зант, Гурзадян (1998) El-Zant A.A., and Gurzadyan V.G. (1998) Relative
chaos in gravitating systems with massive centre. Physica D, 122, 241.
Эпик (1976) Opik E.J. (1976) Interplanetary Encounters. Elsevier, New York.
Эпплгейт, Дуглас, Гурсел, Зюссман, Уиздом (1986) Applegate J.H., Doug¬
las M.R., Gursel Y., Sussman G.J., and Wisdom J. (1986) The outer solar
system for 200 million years. Astron. J., 92, 176.
Эпштейн (1916) Epstein P.S. (1916) Zur Quantentheorie. Ann. d. Physik,
51, 168.
Юаса (1973) Yuasa M. (1973) Theory of secular perturbations of asteroids
including terms of higher order and higher degree. Publ. Astron. Soc. Japan,
25, 399.
Алфавитный указатель
FLI, 115
MEGNO, 116-118
Аномалия
— истинная, см. истинная аномалия
— средняя, см. средняя аномалия
— эксцентрическая, см.
эксцентрическая аномалия
Апогей, 16
Апоцентр, 16
Апоцентрический либратор, 222
Аргумент перигелия, 17
Арнольд
— диффузия, 131
— паутина, 126
Арнольда-Лиувилля теорема, 31-33,
82, 184
Астероиды, сближающиеся с Землей,
196, 207,313,347
Астероиды-греки, 229
Астероиды-троянцы, 229, 241, 331
Аттрактор, 28
Афелий, 16
— расстояние, 16
Биркгофа нормальная форма, 50, 52
Большая полуось, 15
Большое неравенство, 305, 325
Вековая динамика
— малых тел, 165-214, 291-304
— планет, 141-163
Вековая нормальная форма, 59-63, 165,
361
Вековой резонанс, 168, 187, 193-214,
297-304, 340
- 1/5, 198, 203-205, 210, 298, 299, 301,
308-310, 313, 316, 320
- г/6, 196, 202, 207-214, 298, 301, 310,
313,316, 320, 329,336, 361
- i/ie, 198, 202, 205-206, 302, 311,
316-317, 321
- г/17, 207, 341
- г/is, 199, 207, 302, 325, 326, 341
- г/7, 199, 207,351
- г/8, 199, 207, 298, 325,341,351
— Козаи, см. Козаи, резонанс
— внутри резонансов средних
движений, 297-304
— критический угол, 201
— линейный, 168, 193
— нормальная форма, 200-201, 204, 206,
207, 210
— первого порядка, 169, 199
Венера, 153, 163
Возмущение, 18-20, 23-24, 43
Волчок Коломбо, 157
Вращающаяся система, 22
Выпуклость, 127, 128, 131, 210
Вырождение, 42, 59, 177, 215, 244
Галактический прилив, 177
Гамильтониан, 20
— зависящий от времени, см.
гамильтониан, неавтономный
408
Алфавитный указатель
— задачи N тел, см. гамильтониан,
планетной задачи
— интегрируемый, 29-33
— квазиинтегрируемый, 43
— неавтономный, 23-24
— ограниченной задачи, 23, 57-58
— планетной задачи, 24-27, 58
— потока свойства, 27-29
— производящий, 27, 45-50
Гармоника
— генерирование, 54-57, 256
— порядок, 48
— последовательное исключение,
283-286
— преобразование, 264
Гетероклиническая точка, 123-126
Гетероклиническое пересечение, см.
гетероклиническая точка
Гильды, 320-323
Гиперболическая точка, см. точка
равновесия, неустойчивая
Гиперболичность, 90, 104
Главный пояс астероидов, 173-178,
188-198, 203-214, 234-236, 272-279,
306-323, 333-340, 344-347, 356,
358-360, 362
«Головастик»
— либратор, 229
— траектории, 329-331
Гомоклиническая точка, 93
Гомоклинический клубок, 93, 105
Гомоклиническое пересечение, см.
гомоклиническая точка
Гомологическое уравнение, 46
Движение
— квазипериодическое, 41
— кеплерово, см. Кеплера задача
— константа, см. константа движения
— периодическое, 41
— хаотическое, см. хаос
Делоне
— переменные, см. переменные Делоне
Делоне переменные
— модифицированные, 38
Дельта-функция Дирака, 354
Диофантово условие, 48
Диффузия, 72, 123, 343-360
— Арнольда, см. Арнольд, диффузия
— Чирикова, см. Чириков, диффузия
— коэффициент, 356-360
Долгота восходящего узла, 17
Долгота перигелия, 18
Задача двух тел, см. Кеплера задача
Задача N тел, см. планетная задача
Закручивания угол, 115-116
Земля, 153, 157-162
Изохронная система, 42
Импульсы, 21
Инвариантная плоскость, 145
Интеграл Мельникова, см. интеграл
Пуанкаре - Мельникова
Интеграл Пуанкаре - Мельникова, 94-96
Интегрируемость, 30
Истинная аномалия, 16
КАМ
— теорема, 65-69, 360-362
— тор, см. тор, КАМ
КС-энтропия, 102, 105
Каноническое преобразование, 24-27
Кассини состояния, 157
Кеплер
— задача, 13-18, 33
— законы, 14
— уравнение, 16
Козаи
— гамильтониан, 172, 294
— динамика, см. Козаи, резонанс
— резонанс, 170-184, 191, 195, 198,
205-206
Алфавитный указатель
409
внутри резонанса средних
движений, 291-298, 311, 316, 321,
326, 328
Колмогоров
— нормальная форма, 68
— теорема, см. КАМ, теорема
Комета, 180-183
— долгопериодическая, 180-183
— сангрейзер, 181-183
Константа движения, 28, 30
Координаты, 21
— барицентрические, 13
— вращающиеся, см. вращающаяся
система
— гелиоцентрические, 13, 19, 24-27
— сферические, 21-22
Кратность, см. резонанс, кратность
Кривая столкновений, 227, 231
Кривая узловых пересечений, 176-182
Кривизна Риччи, 102
Критерий Чирикова, 121
Лагранжа уравнения, 38
Лежандра разложение, 260
Либратор
— апоцентрический, см.
апоцентрический либратор
— асимметричный, 223, 226, 229
— типа «головастик», см. «головастик»,
либратор
— типа «подкова», см. «подкова»,
либратор
Либрация
— асимметричная, 328
— область, 81, 221
— тор, см. тор, либрационный
Лиувилля теорема, 28, 30
Луна, 148, 155, 156, 159-162
Лунник, 176
Люк Кирквуда, 236, 253, 307, 313, 314
Ляпунов
— орбита, 231
— показатели, 102-109
Малые делители, 47^19
Марс, 153, 162
Маятник, 80-82, 91
— модулированный, 246-248, 359-360
Меркурий, 153, 155, 163
Многообразие
— неустойчивое, 90, 92-96
— устойчивое, 90, 92-96
Модуль резонанса, см. резонанс, модуль
Мультиплет, 243-247, 255, 265-272, 335,
352,354, 359
Наклон, 156
Наклонение, 17
Направление быстрого дрейфа, 131
Нептун, 280-282
Нехорошев
— область, 361
— система, 134
— структура, 132-134, 137, 139-140,
362-364
— теорема, 127-132, 360-364
Нормальная форма
— Биркгофа, см. Биркгофа нормальная
форма
— Колмогоров, см. Колмогоров,
нормальная форма
— вековая, см. вековая нормальная
форма
— векового резонанса, см. вековой
резонанс, нормальная форма
— оптимальная, 53-54
— остаток, 53, 54, 86-88
— резонансная, см. резонанс,
нормальная форма, см. резонанс,
нормальная форма
— трехтельный резонанс, см.
трехтельный резонанс, нормальная
форма
410
Алфавитный указатель
Облако Оорта, 178
Область
— Нехорошева, см. Нехорошее, область
— нерезонансная, 48, 130, 133, 134, 140
— резонансная, см. резонанс, область
Ограниченная задача, 19, 23
— плоская круговая, 216
динамика, 216-243
Орбитальные элементы
— полусобственные, см.
полусобственные элементы
— полусредние, см. полусредние
элементы
— средние, см. средние элементы
Оскулирующие элементы, 14-18, 20
— формальные, 20, 38
Остаток, см. нормальная форма, остаток
Остров, 77, 88, 178, 180, 181, 183, 235
Паутина, см. Арнольд, паутина
Переменные
— действие-угол, см. переменные
«действие-угол»
— полусобственные, см.
полусобственные переменные
— полусредние, см. переменные
Делоне, полусредние
— собственные, см. собственные
переменные
— сопряженные, 21
— средние, см. Делоне переменные,
средние
Переменные «действие-угол», 31-33
— резонансные, 82-86
Переменные Делоне, 33-38
— полусредние, 64
— средние, 60, 165
Переменные Пуанкаре, 40
Перигей, 15
Перигелий, 15
— аргумент, см. аргумент перигелия
— долгота, см. долгота перигелия
— расстояние, 16
Перицентр, 15
Планетная задача, 18-19, 24-27
Плоскость частот, 129
Плутино, 237, 325, 326 •
Плутон, 227, 297, 325, 326
«Подкова»
— Смейла, 93
— либратор, 229
— траектории, 329
Полусобственные переменные, 200, 201
Полусобственные элементы, 201
Полусредние переменные, см.
переменные Делоне, полусредние
Полусредние элементы, 64
Порядок
— гармоники, см. гармоника, порядок
— по эксцентриситету, см. резонанс
средних движений, порядок по
эксцентриситету
— резонанса, см. резонанс, порядок
Постоянная движения, 31
— задачи Кеплера, 33, 42
Пояс Койпера, 198-199, 207, 236-238,
279-280, 323-328, 340-341, 343,
347-352, 363
Правила Даламбера, 39-40
Преобразование
— близкое к тождественному, 44
— каноническое, см. каноническое
преобразование
— полярных координат в декартовы, 27,
40
Прецессия равноденствия, 157
Приведенная масса, 22, 26
Пространство частот, 72
Пуанкаре
— переменные, см. переменные
Пуанкаре
Алфавитный указатель
411
Разложение
— Лежандра, см. Лежандра разложение
Расщепление, см. сепаратриса,
расщепление
Резонанс
— Козаи, см. Козаи, резонанс
— Лапласа, 239, 255
— взаимодействие, 119-140
— вторичный, 86, 289-291
— задача трех тел, см. трехтельный
резонанс
— кратность, 42
— критический угол, 80
векового резонанса, см. вековой
резонанс, критический угол
резонанса средних движений, см.
резонанс средних движений,
критический угол
— модуль, 53
— мультиплет, см. мультиплет
— нормальная форма, 49-53, 63-64, 79
— область, 75, 81, 87, 131-132, 136, 221,
236
— одиночный резонанс, 79-98, 119, 131,
134
— определение, 41^12
— остров, см. остров
— паутина, см. Арнольд, паутина
— перекрытие, 120-123, 126, 134,
136-140, 160—161, см. также
резонанс средних движений,
перекрытие, см. также мультиплет,
см. также резонанс средних
движений, перекрытие
— переменные «действие-угол», см.
переменные «действие-угол»,
резонансные
— порядок, 42
— сепаратриса, см. сепаратриса
— тор, см. тор, резонансный
Резонанс средних движений, 60, 62,
215-253,283-331,333-364
— 1-го порядка по эксцентриситету,
219-223, 314-328
— 1/1,229-232,241-242,328-331
— 1/2 с Нептуном, 326-328
— 2-го порядка по эксцентриситету,
223-226, 307-314
— 2/1 с Юпитером, 314-320
— 2/3 с Нептуном, 323-326
— 3-го порядка по эксцентриситету, 226
— 3/1 с Юпитером, 307-314
— 3/2 с Юпитером, 320-323
— 4-го порядка по эксцентриситету, 226
— внешний, 219
— внутренний, 219
— критический угол, 217
— модуляция, 248-253, 299, 308, 340
— мультиплет, см. мультиплет
— нормальная форма, 215, 286
— перекрытие, 232-243
— порядок по эксцентриситету, 217
— с Марсом, 336-340, 345-347
Ряд Ли, 29, 44-47
Ряд Тейлора, 29
Ряд Фурье, 47
Сатурн, 280-282
Семейство астероидов, 191-193, 198,
252-253, 320
Сепаратриса, 81, 86, 121
— расщепление, 90-98, 131
Сечение Пуанкаре, 74-75, 88, 99, 241,
247, 268, 291,302
Скобка Пуассона, 25, 49, 55, 95, 96, 146,
257
Собственная частота, 146, 188
— линейная, 170
Собственные переменные, 188
— линейные, 170
412
Алфавитный указатель
Собственные элементы, 184-193, 274,
344-345
— линейные, 170
Сохранение объема, 28
Спин-орбитальная динамика, 155-163
Спиральности угол, 115-116
Спутники
— Урана, 177
— Юпитера, 240
— проградные, 230
— ретроградные, 232
Среднее движение, 16
Средние элементы, 60, см. элементы
Делоне, средние
Средняя аномалия, 16
Средняя долгота, 18
Стандартное отображение, 75-77,
88-90, 121, 125-126, 354
Степени свободы, 21
Теорема Колмогорова, 65
Теория возмущений, 43-54
Тесное сближение, 153, 176, 311, 313,
345, 349
— защита, 226-229, 320, 350
Тор, 41
— КАМ, 65-78, 104, 110, 113, 118-120,
123, 134-135
золотой, 121
изолирующее свойство, 71-72
мера, 71
сдвиг, 70
сохранение, 69
суперэкспоненциальная
устойчивость, 134-135
экспоненциальная устойчивость, 73
— инвариантный, 41, 65, 66, 69-74
— комплексный, 47
— либрационный, 88
— резонансный, 88-90
Точка равновесия
— гиперболическая, см. точка
равновесия, неустойчивая
— неустойчивая, 81, 90
— устойчивая, 81
— эллиптическая, см. точка равновесия,
устойчивая
Точки Лагранжа, 229
Траектории
— типа «головастик», см. «головастик»,
траектории
— типа «подкова», см. «подкова»,
траектории
Трехтельный резонанс, 255-282
— (5-2-2), 266-271
— (6 1-3), 271-272
— в движении планет, 280-282
— внутри резонансов средних
движений, 304-306, 319, 323, 325
— мультиплет, см. мультиплет
— нормальная форма, 258, 265
Угол
— большого неравенства, см. большое
неравенство
— закручивания, см. закручивания угол
— резонансный, см. резонанс,
критический угол
— спиральности, см. спиральности угол
Узел, 17
— долгота, см. долгота узла
Узловое расстояние, 176
Уравнение
— Кеплера, см. Кеплера уравнение
— Фоккера - Планка, см. уравнение
Фоккера - Планка
— гомологическое, см. гомологическое
уравнение
Уравнение Фоккера-Планка, 356
Уравнения Лагранжа, 20
Уран, 155, 162, 280-282
Алфавитный указатель
413
Усреднение, см. также Биркгофа
нормальная форма, 57-63
Устойчивость практическая, 127, 128,
198, 282
Фазовое пространство, 21
Функции Бесселя, 239, 262
Функция
— Бесселя, см. функции Бесселя
— Гамильтона, см. гамильтониан
— Дирака, см. дельта-функция Дирака
— возмущающая, см. возмущение
— производящая, 27
— эволюция во времени, 29
— эллиптическая, см. эллиптическая
функция
Хаос, 31, 90-126, 133-134
— в движении малых тел, 232-253,
265-280, 289-291, 300-302, 306-331,
333-364
— в движении планет, 149-163, 280-282
Хаотическая диффузия, см. диффузия
Хаотическая область, 77, 90, 93
Хилла радиус, 230
Циркуляция, 81
Частота, 40
— диофантова, 48, 66, 69
— нерезонансная, 41
— полностью резонансная, 41
— собственная, см. собственная частота
Частотный анализ, 109-115
Чириков
— диффузия, 123, 134
Эксцентриситет, 15
Эксцентрическая аномалия, 16
Элементы Делоне
— полусредние, 216, 257
Элементы орбиты
— оскулирующие, см. оскулирующие
элементы
Эллиптическая функция, 85, 172
Эффект Ярковского, 313
Юпитер, 280-282
Полный ассортимент литературы издательств
«Институт компьютерных исследований»
и «Регулярная и хаотическая динамика»
по самым доступным ценам представлен
в отделах прямых продаж:
R&C
Россия, Москва
Институт машиноведения им. А. А. Благонравова РАН
ул. Бардина, д. 4, корп. 3, к. 415 (м. Ленинский пр-т)
тел.: +7 (499) 135-54-37
e-mail: rhd-m@mail.ru
Россия, Ижевск
Удмуртский государственный университет
ул. Университетская, д. 1, корп. 4, оф. 201 а/207
тел./факс: +7 (3412) 50-02-95
e-mail: subscribe@rcd.ru
Интернет-магазин
http://shop.rcd.ru
• Отправка заказов осуществляется
почтой РФ из г. Ижевска
• Цены на сайте указаны
без учета стоимости доставки
Книги можно приобрести также:
Московский дом книги
Москва, ул. Новый Арбат, д. 8 (м. «Арбатская»)
Тел.: +7 (495) 789-35-91
Дом технической книги
Москва, Ленинский проспект, д. 40
(м. «Ленинский Проспект»)
Тел.: +7(499) 137-60-19
Книжные киоски ООО «Аргумент»
Москва, Ленинский проспект, д. 65
(м. «Ленинский Проспект») Главное здание
РГУ нефти и газа им. И. М. Губкина
ООО «Санкт-Петербургская книготорговая
компания»
Санкт-Петербург, ул. Капитана Воронина, д. 8
Тел.: +7 (812) 295-06-57
ООО «Киви»
Самара, ул. Ново-Садовая, д. 381,4-й этаж —
«ТЦ на Ново-Садовой»
Тольятти, ул. Дзержинского, 21, минус 1 -й этаж,
секция 803а — «ТЦ Капитал»
ООО «Пермкнига»
Пермь, ул. Лодыгина, д. 6
Тел.: +7 (342) 242-84-90,242-72-74
ООО «Издательство «Инфра-Инженерия»
Вологда, ул. Машиностроительная, д. 19, оф. 238
Тел.:+7 (911)512-48-48
ООО «ВЕЛЕС»
Омск
тел.: +7 (3812) 46-31-12,46-31 -41
Алессандро Морбиделли
Современная небесная механика
Аспекты динамики Солнечной системы
Дизайнер А. А. Гурьянова
Технический редактор А. В. Бакиев
Компьютерный набор и верстка А. В. Моторин
Корректор Е. В. Огородникова
Подписано в печать 28.09.2014. Формат 60 х 84 Vi6-
Печать офсетная. Уел. печ.л. 25,11. Уч. изд. л. 26,87.
Гарнитура Таймс. Бумага офсетная № 1. Заказ № 14-68.
АНО «Институт компьютерных исследований»
426034, г. Ижевск, ул. Кооперативная, д. 5.
http://shop.rcd.ru E-mail: mail@rcd.ru Тел./факс:+7(3412) 50-02-95
ISBN 978-5-4344-0209-5
9
785434
402095