Text
В.И.Баженов, М.И.Осин
Посадка космических
аппаратов на планеты
В. И. БАЖЕНОВ, М. И. ОСИН
ПОСАДКА КОСМИЧЕСКИХ
АППАРАТОВ НА ПЛАНЕТЫ
Москва
«МАШИНОСТРОЕНИЕ»
1978
ББК 39.61
Б16
УДК 629.785.001
Рецензент канд; техн, наук А. Ф. Евич
Баженов В. И., Осин М. И.
Б16 Посадка космических аппаратов на планеты. — М.:
Машиностроение, 1978.— 159 с., ил.
55 к.
В книге рассмотрены вопросы, с которыми встречаются разработчики
посадочных и спускаемых космических аппаратов при исследовании их струк¬
туры и режима движения. Изложены методы параметрических расчетов спу¬
скаемых аппаратов различных типов, сформулирована задача поиска их
оптимальных параметров и описаны методы физического моделирования.
Аналитические методы исследования динамики мягкой посадки, изложен¬
ные в книге, по точности результатов и трудоемкости вполне приемлемы для
практики инженерных расчетов. Книга может быть полезна конструкторам
космических аппаратов, научным работникам, занимающимся исследованием
вопросов спуска и посадки, а также аспирантам и студентам вузов соответст¬
вующих специальностей.
31901-170
038(01)-78
170-78
ББК 39.61
6Т6
© Издательство «Машиностроение», 1978 г.
«...Человечество ставит себе
всегда только такие задачи, кото¬
рые оно может разрешить, так
как при ближайшем рассмотрении
всегда оказывается, что сама за¬
дача возникает лишь тогда, ког¬
да материальные условия ее ре¬
шения уже имеются налицо, или,
по крайней мере, находятся в
процессе становления».
К. Маркс, Ф. Энгельс
ПРЕДИСЛОВИЕ
Предлагаемая вниманию читателя книга посвящена проблемам
спуска и посадки космических аппаратов (КА) на планеты. Успехи
космической техники в этом направлении очевидны: аппараты, соз¬
данные руками человека, совершают посадки на Луну, Венеру и
Марс, успешно возвращаются на Землю с орбит и межпланетных
траекторий.
К настоящему времени в отечественных и зарубежных публика¬
циях описаны методы расчета траекторий, газодинамики и тепло¬
обмена при движении КА в атмосфере. Как правило, в этих книгах
содержатся способы и алгоритмы, требующие трудоемких числен¬
ных расчетных процедур для определения всего лишь некоторых
параметров космических аппаратов. К сожалению, невозможно
строго формализовать все операции процесса проектирования кос¬
мических аппаратов, и на практике приходится искать аналогии и
общие черты в конструкции новых космических аппаратов; исполь¬
зовать методы приближенных параметрических проектных оценок
по упрощенным расчетным моделям; привлекать результаты экспе¬
риментов, применяя методы теории подобия и анализа размернос¬
тей для определения облика космических аппаратов, работающих в
новых и необычных условиях.
Очевидно, что охватить все многообразие проблем, связанных с
посадкой на планеты и возвращением на Землю, невозможно в пре¬
делах одной книги. Даже краткое перечисление этих проблем с
описанием и постановкой основных задач, решаемых при проек¬
тировании и наземной отработке посадочных аппаратов различных
типов, эквивалентно по объему монографии из нескольких томов.
Поэтому авторы данной книги ограничились рассмотрением основ¬
ных вопросов, связанных с проектированием перспективных спус¬
каемых и посадочных аппаратов, и освещением проблем, которыми
предстоит заниматься в ближайшем будущем.
В первой части книги, посвященной проблемам снижения в ат¬
мосферах различных планет, приведены результаты решения про¬
ектно-поисковых задач, связанных с определением конфигурации
и режима движения спускаемых аппаратов. В частности, для усло¬
вий спуска на Землю обоснован режим движения по перегрузоч¬
ным критериям пилотируемых космических аппаратов, входящих в
400
3
атмосферу Земли с гиперболической скоростью, и предложены
приближенные математические модели для расчета траектории
управляемого спуска. Применительно к условиям спуска на Марс
путем параметрических расчетов определяется оптимальная на¬
грузка на несущую поверхность; для Венеры определяются рацио¬
нальные траектории спуска из условий перехода к последующему
погружению в более плотные слои атмосферы; для Юпитера сфор¬
мулированы современные представления о способах проектного
расчета характеристик спускаемого аппарата планетного зонда.
Проблемы контактирования космических аппаратов с грунтом
планет и связанные с ними задачи проектирования посадочных уст¬
ройств могут быть в ’известной степени обособлены и рассмотрены
независимо от проблем движения в атмосфере и на участке пред¬
посадочного торможения. Вторая часть книги посвящена комплексу
вопросов, возникающих в процессе создания посадочных аппара¬
тов: от теоретических методов расчета динамики мягкой посадки,
методов моделирования и проектирования опорной кинематики,
средств поглощения энергии и повышения устойчивости посадоч¬
ных систем до экспериментального подтверждения теоретических
результатов на натурных макетах и динамически подобных мо¬
делях.
Во второй части книги обоснованы приемы физического модели¬
рования мягкой посадки в земных условиях, получены и проанали¬
зированы условия подобия, необходимые для воспроизведения про¬
цессов посадки на Луну и другие планеты при наземной отработке
посадочных космических аппаратов.
Книга может быть полезна специалистам по проектированию и
отработке посадочных отсеков лунных, венерианских, марсианских
и других спускаемых аппаратов, лицам, занимающимся исследо¬
ванием частных проблем механики посадки и термодинамики спус¬
ка, а также студентам соответствующих специальностей.
Авторы благодарны кандидатам технических наук А. Ф. Евичу
й Р. П. Белоногову за полезные советы и замечания, сделанные ими
при просмотре рукописи, а также инженерам А. И. Гончарову,
А. И. Бурцеву, Ю. В. Захарову и В. Ф. Малыхину за помощь при
подготовке материалов рукописи к публикации.
Авторы с признательностью примут все замечания читателей по
книге.
Часть 1
ВОПРОСЫ ПОСАДКИ КОСМИЧЕСКИХ АППАРАТОВ
НА ПЛАНЕТЫ С АТМОСФЕРОЙ
Предлагаемый вниманию читателя раздел посвящен проблемам
спуска космического аппарата в атмосферах Земли и планет. Ши¬
рокому кругу специалистов известны книги и учебные пособия, в
которых приведены методы расчета и обобщены задачи термодина¬
мики спуска (см., например, [1, 20, 40, 43]). В этих работах упор
сделан на получение приближенных зависимостей общего характе¬
ра, пригодных для качественных выводов на этапе проектно-бал¬
листического анализа. Методы и результаты аналитических оценок,
изложенные в этой литературе, несомненно, полезны для лиц, при¬
ступающих к изучению проблем движения в атмосфере спускаемых
аппаратов традиционного типа.
Однако космическая техника развивается, создаются новые ап¬
параты с применением современных технических средств и с уча¬
стием большого количества различных специалистов. Этим специа¬
листам недостаточно общих сведений по баллистике и термодина¬
мике спуска, их интересуют профессиональные аспекты проектиро¬
вания новых летательных аппаратов. Именно поэтому в данной
книге сделана попытка осветить проблемы проектирования перс¬
пективных спускаемых аппаратов. Рассматривая в пределах одной
части особенности спуска для каждой из планет, авторы намеренно
ограничились изложением общих закономерностей и основных, прин¬
ципиальных отличий техники спуска в условиях каждой планеты,
преследуя цель охватить проблему в целом, сопоставить возможные
технические решения по каждому типу спускаемых аппаратов и ус¬
тановить общие черты, присущие облику и режимам движения
перспективных спускаемых аппаратов.
В первой части книги рассмотрены вопросы выбора режима по¬
садки и расчета проектных характеристик будущих спускаемых
аппаратов (СА). Прежде всего обобщены особенности, свойствен¬
ные процессу проектирования спускаемых аппаратов в отличие от
других объектов, входящих в ракетно-космическую систему. Описа¬
на типовая проектно-поисковая задача, решаемая в системе машин¬
ного проектирования на верхнем уровне поиска и выбора проект¬
ных решений, т. е. при автоматизированном синтезе конфигурации
и структуры с учетом режима движения в атмосфере. Методы и
5
результаты анализа режима движения рассмотрены применитель¬
но к потребностям весового моделирования перспективных аппа¬
ратов. Такими аппаратами, по мнению авторов, являются много¬
кратно возвращаемые на Землю ракетно-космические системы, а
также аппараты, совершающие посадку на Марс или возвращаю¬
щиеся на Землю после межпланетных экспедиций. Определенный
интерес представляет собой проблема спуска тяжелых управляемых
автоматических планетных комплексов при исследовании Марса и
Венеры, а также вопросы автоматического зондирования атмосфе¬
ры Юпитера.
Все эти проблемы с той или иной степенью детализации после¬
довательно освещены в первой части книги.
Итак, начнем с особенностей спускаемых аппаратов, определяю¬
щих специфику их проектирования в сравнении с другими косми¬
ческими аппаратами.
Глава 1. ОСОБЕННОСТИ СПУСКА НА ПЛАНЕТЫ С АТМОСФЕРОЙ
Посадка на планеты с атмосферой или возвращение на Землю
из космоса •— один из наиболее сложных и важных этапов косми¬
ческого полета. Задачей спускаемого аппарата является высадка
на поверхность планеты или возвращение на Землю некоторого по¬
лезного груза. При посадке на планету таким грузом является на¬
учно-исследовательское оборудование, а при возвращении на Зем¬
лю — результаты исследований по программе полета. Для обитае¬
мых космических аппаратов, полезным грузом которых считается
также экипаж и пассажиры, возвращаемые из космоса или десан¬
тируемые на планету, период спуска в атмосфере представляется
одним из самых ответственных участков экспедиции. Происходит
это потому, что спускаемые аппараты испытывают экстремальное
воздействие факторов космического полета. Спускаемые аппараты,
так же как орбитальные, межпланетные или напланетные косми¬
ческие аппараты, работают в условиях вакуума, невесомости, сол¬
нечной радиации и метеорной эррозии. Однако все эти воздейст¬
вия, обычные для каждого космического объекта, отступают на
второй план перед факторами, определяющими действие атмосфе¬
ры. Подлет к планете и погружение в ее атмосферу происходит со
скоростью, в несколько раз превышающей скорость полета самого
скоростного самолета, и гашение этой скорости осуществляется за
счет аэродинамического торможения в атмосфере. При таком тор¬
можении на конструкцию и экипаж действуют инерционные силы,
превышающие вес; теплозащита аппарата предохраняет его гермо¬
кабину от мощных тепловых потоков, поступающих от ударного
слоя газа, нагретого в передней части аппарата до нескольких ты¬
сяч градусов. Помимо статических нагрузок, аппарат испыты¬
вает также вибрационные и ударные перегрузки. Процесс тормо¬
жения в атмосфере, как правило, скоротечен; и при этом с боль¬
шими градиентами меняются перегрузки, высота и скорость полета,
тепловые потоки и температуры в различных точках конструкции.
6
Итак, экстремальность нагрузок — есть первое отличие спускаемых
аппаратов от других космических объектов.
Изложенные особенности процесса спуска в атмосфере опреде¬
ляют второе отличие спускаемых аппаратов от других объектов
ракетно-космических систем. Оно заключается в высоких требова¬
ниях к надежности всех систем спускаемого аппарата. Действитель¬
но, если мы можем, спасая экипаж и полезный груз, прервать полет
и возвратиться на Землю, или эвакуировать экипаж с помощью
транспортного космического корабля, то спасти экипаж из гермо¬
кабины спускаемого аппарата во время аварии на участке тормо¬
жения в атмосфере почти невозможно. Заметим, что спасение с
орбиты или с трассы выведения на орбиту осуществляется с ис¬
пользованием того же спускаемого аппарата, и вероятность отказа
средств спуска и посадки определяет безопасность полета. Итак,
надежность средств спуска и посадки должна быть выше, чем на¬
дежность других блоков и кораблей ракетно-космического комп¬
лекса.
Третья особенность спускаемых аппаратов определяется жест¬
кими весовыми ограничениями со стороны всего ракетно-космичес¬
кого комплекса. Спускаемые аппараты работают, как правило, на
завершающей стадии космического полета и каждый лишний кило¬
грамм их веса эквивалентен нескольким килограммам веса разгон¬
ных блоков экспедиционного комплекса или десяткам килограммов
стартового веса носителя. Задачи оптимизации средств спуска и
посадки по весовому критерию являются важными в силу изложен¬
ного обстоятельства. Кроме того, эти задачи являются сложными
и интересными, поскольку при минимизации средств спуска и по¬
садки по весовому критерию приходится детальным образом учи¬
тывать связи между режимом движения и конфигурацией аппарата.
Эти связи определяют четвертое отличие спускаемых аппаратов от
орбитальных или межпланетных кораблей и отсеков, а именно
сложную зависимость весовых характеристик от геометрических
параметров, определяющих формы СА. Именно от этих параметров
зависит, с одной стороны, распределение тепловых потоков и массы
теплозащиты и, с другой стороны, несущие и тормозные характе¬
ристики аппарата, которые определяют протяженность, теплона-
пряженность и перегрузочный режим траектории спуска, т. е. в ко¬
нечном счете массу конструкции, теплозащиты и топлива двига¬
тельных систем, используемых для торможения и управления дви¬
жением.
Только комплексный подход к задаче оптимизации геометричес¬
ких, компоновочных и весоэнергетических параметров спускаемых
аппаратов может гарантировать получение достоверных результа¬
тов при выборе рациональных проектных решений. К сожалению,
часто можно наблюдать, как на базе детального анализа отдель¬
ных, не связанных друг с другом, проблем баллистики, управления
или аэродинамики делаются ошибочные выводы о преимуществах
той или иной конфигурации аппарата. Если проводится оптимиза¬
ция параметров СА по весовому критерию, то в расчетной модели
7
необходимо предусмотреть процедуры для описания конфигурации,
оценки аэродинамических и центровочных характеристик, модели¬
рования режима движения и теплообмена, а также процедуры для
оценки веса конструкции, теплозащиты и посадочных систем с уче¬
том нагрузок на аппарат, компоновочных особенностей и требова¬
ний к участку посадки. Для каждого типа летательного аппарата
расчетная модель строится по-разному и по-разному учитываются
проектные критерии и ограничения. Примеры учета ограничений
для аппаратов различного назначения рассмотрены в последующих
главах книги. Можно указать на некоторые общие принципы пост¬
роения расчетных моделей и попытаться объединить общей поста¬
новкой задачи оптимизации параметров спускаемых аппаратов раз¬
личных типов. Предполагается, что при оптимизации используются
численные поисковые методы, и выбор проектных параметров осу¬
ществляется в системе автоматизированного синтеза конфигурации
спускаемого аппарата.
Типовой алгоритм проектного или поверочного расчета, приме¬
няемый в системе автоматизированного поиска и выбора проект¬
ных решений по спускаемому аппарату в целом, должен обязатель¬
но включать в себя специализированные расчетные модули по сле¬
дующим проектным направлениям:
1. Модуль или группу модулей для описания конфигурации ап¬
парата, математического моделирования обводов, расчета габарит¬
ных, объемно-центровочных и компоновочных характеристик. Для
аппаратов простой формы, состоящих из нескольких геометричес¬
ких тел, должен быть предусмотрен специальный блок расчета раз¬
меров, площадей и объемов.
Как правило, группа модулей, описывающих конфигурацию, сты¬
куется со специальной процедурой, формирующей образ аппарата
для устройств графического отображения информации (графичес¬
ких дисплеев, графопостроителей или цифровых печатающих уст¬
ройств).
2. Группу модулей, предназначенных для расчета аэродинамиче¬
ских характеристик. Для различных классов форм и разных режи¬
мов обтекания создаются, как правило, различные модули.
3. Модули или блоки для расчета режима движения. Эти блоки
могут отличаться степенью детализации проектных оценок, исполь¬
зовать различные принципы и процедуры расчета, и входить в
состав модулей расчета аэродинамических или весоэнергетических
характеристик.
4. Модули для сводного расчета весоэнергетических характе¬
ристик. Эти модули перерабатывают и формируют итоговую ин¬
формацию, по которой можно судить об облике аппарата в целом.
В зависимости от постановки проектно-поисковой задачи в составе
этих модулей или отдельно от них могут быть предусмотрены про¬
цедуры расчетов на прочность, термодинамического расчета, расче¬
та динамических процессов, оценки стоимости, синтеза компоновоч¬
ной схемы и т. д.
8
Все параметры, определяющие облик типового спускаемого ап¬
парата, можно условно разделить на несколько групп. В первую
группу следует отнести геометрические характеристики, определяю¬
щие внешние обводы корпуса. Параметры этой группы непрерывны,
они являются исходными для расчета аэродинамических характе¬
ристик и, следовательно, определяют во многом проектно-баллисти¬
ческие параметры и теплонапряженность траектории движения, а
также режим обтекания и теплообмена в различных зонах поверх¬
ности аппарата. Во вторую группу можно отнести параметры, опи¬
сывающие управление движением. В их числе коэффициенты, фор¬
мирующие закон программного изменения угла атаки или крена,
или показатели, определяющие момент перехода на тот или иной
тип управления, например, движение по изовысотной, изоперегру-
зочной или изотемпературной траектории,
Третья группа проектных параметров включает в себя весоэнер¬
гетические и конструктивно-компоновочные характеристики СА. Это
прежде всего размеры элементов конструкции и теплозащиты, пара¬
метры двигательных установок, а также данные, определяющие
размещение отсеков и агрегатов на борту аппарата. В числе этих
параметров могут быть такие, которые меняются дискретно или
принимают целочисленные значения.
Еще сложнее обстоит дело, когда при автоматизированном по¬
иске конфигурации и структуры СА ведется просмотр различных
конструктивно-компоновочных схем и разнообразных вариантов
комплектации аппарата приборами и агрегатами, входящими в
состав бортовых систем.
Варьируемыми переменными в такой задаче оптимизации явля¬
ются формальные параметры, целочисленные значения которых со¬
ответствуют определенным вариантам компоновочных или схемных
решений. Задача автоматизированного синтеза структуры аппара¬
та формулируется в этом случае как задача дискретного програм¬
мирования и для решения ее используются специализированные
методы поиска, описанные в книге [23], где содержится т^кже и по¬
становка задачи синтеза структуры космического аппарата. В этой
же книге на примерах, взятых из практики проектирования косми¬
ческих аппаратов, рассмотрены особенности решения задач опти¬
мального проектирования в системе автоматизированного поиска и
выбора формы, траекторий спуска, конструктивных и весоэнергети¬
ческих параметров спускаемых аппаратов различных типов. Поэто¬
му здесь мы ограничимся описанием общих положений задачи
поиска проектных параметров СА и изложением некоторых наибо¬
лее интересных приемов проектного расчета и результатов поиска,
а также выбора режима движения и конфигурации перспективных
спускаемых аппаратов.
В наиболее типичной и широко распространенной задаче поиска
геометрических и траекторных параметров, решаемой обычно на
начальном этапе проектирования при определении облика спускае¬
мого аппарата, варьируются только непрерывные параметры, вхо¬
дящие в первую и вторую группы, и определяются те их значения,
9
которые соответствуют минимуму весового показателя. Таким пока¬
зателем может быть масса аппарата или масса средств спуска и
посадки. Вопрос о критериях, определяющих весовое совершенство
аппарата, будет поставлен ниже при рассмотрении понятия полез¬
ной нагрузки СА. Задача оптимизации формы совместно с режи¬
мом движения обычно формируется как задача нелинейного про¬
граммирования и решается с применением известных численных
методов поиска, основанных на шаговом продвижении в простран¬
стве параметров к оптимальному варианту. Значения проектных
параметров СА определяют вектор состояния оптимизируемой сис¬
темы: X(Xi, Х2, • • ..., Хп). Каждому значению этого вектора
Х^ соответствует значение целевой функции Ф (X) и значения
у(^). функциональных ограничений
У1(Х), Уг(Х), ..., УДХ), ..., Ут(Х). При этом вектор X определен
на множестве У?, которое ограничено из-за диапазона изменения
каждой переменной, определяемого неравенствами типа:
Bt < Аг (ограничения первого рода), (1.1)
а также из-за функциональных ограничений, т. е. из-за неравенств
типа
Yj (X) < у/о (ограничения второго рода). (1.2)
Целью оптимизации является нахождение наилучшего значения
критерия FOpt при X<=R. Цель поиска шире и она может заклю¬
чаться в нахождении целого семейства предоптимальных решений.
Именно среди этих решений, близких к оптимальному, но отли¬
чающихся от него рядом дополнительных качественных инеформа-
лизуемых признаков, разработчик будет искать рациональный ва¬
риант конструкции аппарата, приемлемый при принятых проектных
ограничениях. Выбирая такой вариант на современном уровне про¬
ектирования, конструктор должен знать, насколько он отступает от
строго оптимального решения по каждому критерию.
Общая цель проектных исследований еще шире, и она заклю¬
чается в получении зависимости оптимальных или предоптималь¬
ных решений от основных исходных данных и ограничений.
При выборе проектных параметров спускаемых аппаратов при¬
ходится иметь дело с несколькими критериями, зачастую противо¬
борствующими друг с другом. Как правило, один из них определяет
весовое совершенство, а другой целевую задачу, например, дости¬
жение максимальной боковой дальности, снижение перегрузочного
воздействия, снижение скорости полета в конце траектории спуска
перед посадкой. Задача поиска рациональных параметров СА раз¬
бивается при этом на ряд частных задач оптимизации, в каждой из
которых находится одно из лучших решений по одному критерию,
причем другие критерии рассматриваются, как ограничение.
Путем «дрейфа» оптимума по основным ограничениям определя¬
ются граничные множества оптимальных решений, т. е. предель¬
ные зависимости наилучших решений по каждому из критериев при
фиксированных значениях других критериев.
10
Критериями или ограничениями в задачах поиска рациональных
параметров спускаемых аппаратов могут быть весовые или массо¬
вые показатели всего аппарата, расходы рабочего тела двигателей
ориентации или торможения, величина характеристической скоро¬
сти этих двигателей, скорость полета на определенной высоте или
высота полета при определенной скорости, перегрузка, скоростной
напор, перегрузочное воздействие на экипаж, боковая дальность
или угол поворота траектории, продольная дальность полета, тем¬
пературы, удельные тепловые потоки или уносы покрытия в тепло¬
напряженных точках аппарата, толщины или плотности теплоза¬
щиты, время полета или время пролета через атмосферу. Выбор
критериев и ограничений определяется постановкой конкретной по¬
исковой задачи и зависит от целевого назначения аппарата. Назна¬
чение аппарата определяет способ управления движением, тип
конструкции и класс форм, рассматриваемых при поиске конфигу¬
рации.
Несмотря на короткий период развития космической техники, в
настоящее время приходится сталкиваться с многообразием спус¬
каемых аппаратов, и это многообразие вызывает необходимость
хотя бы какой-то их классификации. Авторы не претендуют на
всеобщую и окончательную систематизацию признаков СА и счи¬
тают, что возможны другие способы деления спускаемых аппара¬
тов на классы и группы и в будущем следует ожидать более обос¬
нованных приемов классификации СА.
Можно, например, условно делить спускаемые аппараты по ха¬
рактеру их полезной нагрузки и это будет первым признаком их
классификации. Наличие человека на борту аппарата, а вернее,
наличие систем, обеспечивающих его жизнедеятельность, работо¬
способность и участие в управлении, существенным образом влия¬
ет на состав полезной нагрузки и отражается на облике аппарата
и траекториях спуска и посадки. СА, создаваемые для полета в ав¬
томатическом режиме, могут быть рассчитаны на значительные
перегрузки, в силу чего исчезает потребность в управляемом спуске
и высоких несущих способностях аэродинамической формы.
Вторым признаком классификации следует, очевидно, считать
целевое назначение аппарата. Облик аппарата зависит от условий
входа в атмосферу, от параметров атмосферы и гравитационного
поля планеты, а также от перечня операций, которые необходимо
осуществить на участке спуска и посадки.
Возможно еще дополнительное деление аппаратов, предназна¬
ченных для околопланетных операций у одной планеты, по целево¬
му назначению и условиям полета. Спускаемые аппараты могут
входить в атмосферу с подлетных траекторий с гиперболической
скоростью или с околопланетных орбит. И в том и в другом случае
зачастую предъявляются различные требования к несущим способ¬
ностям аппарата. Кроме того, СА могут проникать в атмосферу,
доставляя туда полезную нагрузку, или пронизывать ее, выходя на
околопланетную или отлетную траекторию. В первом случае достав¬
ка осуществляется либо на поверхность, причем применяются спе¬
11
циальные посадочные средства, либо на определенную глубину в
атмосферу планеты.
Внешний облик аппарата, его конфигурация и режим движения
в атмосфере во многом зависят от того, как используются несущие
способности аэродинамической формы. При этом имеется в виду
максимально достижимое аэродинамическое качество, т. е. распо¬
лагаемое качество данной формы при принятых компоновочных и
центровочных характеристиках. В полете аппарат может быть сба¬
лансирован на угле атаки, дающем качество меньше располагае¬
мого. Соотношение между несущими и тормозными свойствами по¬
служит третьим признаком классификации, по которому СА можно
условно разделить на пять разновидностей: аппараты баллистичес¬
кого спуска (без аэродинамического качества), аппараты с малым
аэродинамическим качеством (7<<0,4); аппараты с умеренным аэ¬
родинамическим качеством (/( = 0,4—0,7); аппараты со значитель¬
ными несущими способностями (/(=0,7—1) и аппараты планирую¬
щего типа с высоким аэродинамическим качеством.
Аппараты баллистического спуска могут в свою очередь обла¬
дать разными тормозными способностями и иметь две крайние кон¬
фигурации: форма с развитым аэродинамическим тормозным уст¬
ройством (как правило, это затупленный лобовой щит) или
заостренная форма с большой нагрузкой на мидель.
Существует много способов классификации аэродинамических
форм, обеспечивающих получение умеренного или большого аэро¬
динамического качества. При этом классы форм образуются путем
трансформаций различных исходных конфигураций путем соедине¬
ния нескольких тел или рассечением конических и сферических
форм. Многообразие всех мыслимых форм вряд ли поддается опи¬
санию.
Сравнение различных классов аэродинамических форм целесо¬
образно только применительно к аппаратам определенного назна¬
чения при заданном уровне потребного аэродинамического каче¬
ства.
Один из распространенных приемов классификации СА по спо¬
собам полета в атмосфере использует различие в принципах управ¬
ления на основном участке траектории спуска. Спускаемые аппара¬
ты могут совершать неуправляемый баллистический спуск, как это
проектируется у автоматических аппаратов; могут плавно или скач¬
кообразно менять в процессе полета тормозные характеристики,
управляя тем самым траекторией спуска без аэродинамического
качества; могут, имея постоянную подъемную силу, соответствую¬
щую балансировочному углу атаки, менять ее проекцию на верти¬
каль, управляясь креном, т. е. вращаясь вокруг вектора скорости;
и, наконец, могут менять в процессе полета величину и направление
подъемной силы, управляясь креном и углом атаки. Управление
креном достаточно просто реализовать для аппаратов затупленных
форм с малым значением располагаемого качества, поскольку вра¬
щение вокруг вектора скорости можно организовать с помощью га¬
зоструйных органов, не меняя балансировочный режим аппарата,.
12
и такой спуск, получивший название «скользящего», был реализо¬
ван на кораблях «Союз» и «Аполлон».
И, наконец, все многообразие типов СА можно также разделить
по конструктивным признакам, определяющим принцип работы от¬
дельных средств спуска и посадки.
По принципам использования конструкции и теплозащиты спус¬
каемые аппараты могут быть одноразового и многоразового дейст¬
вия, а спускаемые аппараты многоразового действия могут отли¬
чаться способом тепловой защиты («горячая конструкция», испари¬
тельная теплозащита, теплозащита с аккумулирующим или радиа¬
ционным экраном и т. д.).
Посадочные системы СА также влияют на их облик и могут
служить признаком отличия аппаратов друг от друга. Различают
средства для предпосадочного торможения и средства амортизации
при мягкой посадке. В качестве последних могут применяться шас¬
си с различными поглотителями энергии в опорной кинематике,
надувные баллоны или двигатели мягкой посадки, обеспечивающие
вертикальный импульс в момент контакта с поверхностью. В каче¬
стве средств для предпосадочного маневра и торможения могут
применяться крылья, жидкостные ракетные двигатели, турбореак¬
тивные или турбовентиляторные двигатели, роторные системы с
различными способами привода лопастей, парашютные и параба-
лонные средства торможения, складные крылья с мягкой оболочкой
и надувным или жестким каркасом.
Существует еще много различных способов, позволяющих отли¬
чать СА по конструктивным особенностям отдельных систем. Попы¬
таемся теперь выделить общие критерии, которые можно использо¬
вать для сравнения СА одного назначения, т. е. перейдем от приз¬
наков, которые разъединяют СА различных типов, к признакам,
которые их объединяют.
Одним из основных безразмерных критериев, используемых при
сопоставлении характеристик СА, является критерий весового со¬
вершенства средств спуска и посадки. Представляется ошибочным
широко распространенный взгляд на критерий весового совершен¬
ства, так как отношение веса (массы) средств спуска и посадки
Gccn к суммарному весу (массе) аппарата, поскольку суммарный
вес аппарата сам включает в себя вес средств спуска и посадки.
Только отношение веса средств спуска и посадки к эталонному ве¬
су, неизменному для всех вариантов СА, может объективно свиде¬
тельствовать о весовом совершенстве аппарата. Таким эталонным
весом следует считать вес (или массу) полезной нагрузки Gn.n.
Действительно, если у двух аппаратов весовой КПД, т. е. от¬
ношение Gcen/Go составляет 50% и 70% и на первый взгляд отли¬
чие составляет всего 20% от суммарного веса, то на самом деле
при заданных единых ограничениях на вес СА со стороны всего
космического комплекса мы вынуждены уменьшить вес полезной
нагрузки у второго аппарата почти вдвое по сравнению с первым
аппаратом. Отношение
Gcen __ Gcen/Go ,
б?и.н“ 1-Gcen/Go’ j
13
в первом случае составляет 100%, а во втором — 2,33%. При неиз¬
менной полезной нагрузке действительное различие в весе состав¬
ляет 60%.
Полезной нагрузкой для типового спускаемого аппарата удобно
считать не только то научное оборудование, которое возвращается
Рис. 1.1. Общий вид спускаемого
аппарата с умеренным аэродина¬
мическим качеством:
/—лобовой щит; 2—передний объем; 3—
обтекатель полезной нагрузки; 4—зад¬
ний объем; 5—несущая поверхность
на Землю или доставляется на
планету, а также все бортовые
системы, сохраняемые постоянны¬
ми при изменении проектных па¬
раметров аппарата, т. е. при пере¬
ходе от одного варианта аппарата
к другому.
Таким образом, полезная наг¬
рузка есть все то, что не входит в
состав средств спуска и посадки.
Как правило, в состав средств
спуска и посадки входит конст¬
рукция гермокабины, планера или
аэродинамического тормозного
устройства, теплозащита и тепло¬
изоляция, двигательные установ¬
ки для ориентации и предпоса¬
дочного торможения и системы, обеспечивающие мягкую посадку.
Все остальные бортовые системы, а именно: набор систем жизне¬
обеспечения, системы терморегулирования, энергопитания, радио¬
связи и аппаратурная часть системы управления входят в состав
полезной нагрузки спускаемого аппарата.
Указанные системы размещаются в корпусе аппарата, и способ
размещения в отсеках принятой конфигурации определяет объем¬
ные и центровочные характеристики. Один из безразмерных крите¬
риев, косвенно отражающих увеличение веса аппарата с ростом его
несущих способностей, определяется по следующей известной фор¬
муле:
(1-4)
где Vp — располагаемый объем аппарата (по внешнему контуру);
S •— полная поверхность аппарата. Этот критерий представляет
собой отношение поверхности данного аппарата к минимально воз¬
можной поверхности при заданном объеме и может рассматривать¬
ся как своеобразный КПД использования полной поверхности ап¬
парата.
Для аппаратов с удлинением, близким к единице, и не имеющих
крыльев и других выступающих поверхностей, этот критерий при¬
ближается к единице. Типовая форма СА с малым или умеренным
качеством состоит из двух тел: переднего объема и заднего объ¬
ема (рис. 1.1). Передний объем может иметь форму сегмента или
затупленного конуса, кругового или эллиптического. Задний объем
имеет сферическую или коническую форму. Оба объема стыкуются
14
по общей поверхности, которую можно условно считать плоскостью
и относить к ней все аэродинамические характеристики. Эта плос¬
кость, называемая несущей плоскостью, перпендикулярна плоско¬
сти симметрии аппарата, в которой лежит, как правило, его центр
масс и равнодействующая аэродинамических сил.
Аэродинамические силы, используемые для торможения и управ¬
ления траекторией спуска, создаются в основном поверхностью пе-’
реднего тела. При гиперзвуковом режиме обтекания причиной соз¬
дания аэродинамических сил является давление в потоке, затормо¬
женном в передней части аппарата. Передняя несущая поверхность
покрывается слоем теплозащиты и является лобовым щитом или
экраном. Боковая поверхность заднего тела находится в донной,
области (области затенения), требует меньше теплозащиты и слу¬
жит обтекателем полезной нагрузки. Основную часть потребного
объема СА составляет объем заднего тела, и поверхность его боль¬
ше поверхности лобового щита, благодаря чему приобретается
выигрыш в весе, поскольку плотность единицы площади лобового
щита в два-три раза выше плотности единицы площади донного
обтекателя.
Центровочные характеристики аппаратов такого типа можно
сопоставлять с компоновочными параметрами с помощью безраз¬
мерного критерия Kv, определяемого для расчетного режима ба¬
лансировки и соответствующего ему положения равнодействующей
аэродинамических сил. Критерий представляет собой отношение
минимально возможного объема, отсекаемого от аппарата плосг
костью, проходящей через равнодействующую, к половине суммар¬
ного располагаемого ' объема. Минимально возможный объем
ограничен при этом поверхностью аппарата с наветренной стороны
и плоскостью, проходящей через равнодействующую перпендику¬
лярно плоскости симметрии аппарата.
Центр масс аппарата на расчетном режиме балансировки дол¬
жен находится на равнодействующей аэродинамических сил. Если
активными средствами стабилизации и управления обеспечивается
перед входом в атмосферу заданное положение аппарата по отно¬
шению к вектору скорости, то, как правило, не существует требо¬
ваний к положению центра масс на равнодействующей. Именно
так должно обстоять дело у спускаемых аппаратов, режим движе¬
ния которых подчинен определенным задачам.
В любом случае, будь то управление с целью снижения интег¬
рального перегрузочного воздействия до допустимого уровня (спуск
на Землю), или формирование пологой траектории с целью подлета
к поверхности с минимальной скоростью (спуск на Марс), или вы¬
вод аппарата в режим снижения на возможно большей высоте
(спуск в атмосфере Венеры), расчетный режим полета определяет¬
ся способом управления спуском. Какие-либо отклонения от управ¬
ляемой траектории, связанные с нерасчетным входом в атмосферу
аппарата, обтекаемого под произвольным углом атаки, недопусти¬
мы, ибо это приведет к невыполнению основной задачи полета.
Прямым следствием такого подхода к выбору режима движения
15
является главное требование к положению центра тяжести: его
место должно быть на равнодействующей аэродинамических сил
при расчетном угле атаки, и при незначительных отклонениях от
этого угла атаки аппарат должен быть статически устойчив. Усло¬
вимся поперечным направлением считать направление, параллель¬
ное несущей поверхности аппарата, а продольным — направление,
перпендикулярное несущей поверхности.
Итак, продольное смещение центра тяжести, как правило, ничем
не ограничено, если рассматриваются углы атаки, близкие к рас¬
четному. Иначе обстоит дело со смещением центра тяжести в по¬
перечном направлении, ибо здесь мы обязаны центровку аппарата
увязать с положением равнодействующей аэродинамических сил,
которая почти перпендикулярна несущей поверхности. Для аппара¬
тов с умеренным аэродинамическим качеством такое смещение
центра связано с определенными затруднениями. Если плоскость,
проходящая через равнодействующую, делит объем аппарата попо¬
лам, то обеспечение заданной центровки достигается без весовых
затрат. И напротив, по мере того, как потребное положение равно¬
действующей уходит в сторону от геометрического центра объема
аппарата, возрастают компоновочные затруднения и вес балансиро¬
ванного груза. Названный выше критерий косвенно отражает воз¬
можности для тех или иных форм аппаратов использовать внутрен¬
ний объем при создании аэродинамического качества. Особо важ¬
ным это свойство становится в тех случаях, когда потребная
величина качества приближается к значению 0,5—0,7. Получение
такого качества у традиционных сегментально-конических форм,
имеющих хорошее отношение поверхности и объема и малую отно¬
сительную поверхность лобового щита, является проблематичным
по ряду причин и в том числе из-за сдвига равнодействующей и
связанного с этим плохого использования объема при обеспечении
потребной поперечной центровки.
Двигаясь по пути улучшения таких форм для управляемых ап¬
паратов, входящих с гиперболическими скоростями в атмосферу
Земли, Венеры и Юпитера, вспомним о соотношении конвективных
и радиационных тепловых потоков, и о требованиях к заострению
лобовых щитов. В таких обстоятельствах нельзя не сказать о фор¬
мах с коническим лобовым щитом, обтекаемым под нулевым углом
атаки.
Если у традиционных сегментально-конических форм заменить
сегментальный щит на шит в форме косо-срезанного эллиптического
конуса, обтекаемого под нулевым углом атаки (рис. 1.2, 1.3), то
образованная таким образом форма будет иметь те же самые объ¬
емы и поверхности, что и сегментально-коническая, но приобретает
при этом ряд преимуществ. Основные из этих преимуществ следую¬
щие:
1. Большее аэродинамическое качество при равных углах атаки.
2. Меньшие углы атаки относительно несущей плоскости при
равном аэродинамическом качестве.
16
Рис. 1.2. Внешние обводы и положение равнодей¬
ствующей аэродинамических сил сегментально-ко¬
нической и биконической форм аппаратов с ма¬
лым аэродинамическим качеством:
/—положения центров масс; аппарат с сегмен¬
тальным лобовым щитом; аппарат с лобовым щи¬
том в форме косо-срезанного конуса
Рис. 1.3. Аэродинамические характери¬
стики сегментально-конической и бикони¬
ческой форм на различных углах атаки
для аппаратов с малым аэродинамиче¬
ским качеством:
аппарат с сегментальным лобовым щи¬
том; аппарат с лобовым щитом в форме
косо-срезанного конуса
17
3. Меньший вес конструкции несущей оболочки лобового щита
и меньший вес теплозащиты в тех случаях, когда радиационные
тепловые потоки от ударного слоя превосходят конвективные (для
аппаратов, входящих с гиперболической скоростью в атмосферы
Земли, Венеры и Юпитера).
4. Более благоприятное с точки зрения потребной поперечной
центровки положение равнодействующей аэродинамических сил.
Рис. 1.4. Внешние обводы и положение равнодействую¬
щей — аэродинамических сил сегментально-конической и
биконической форм аппаратов с умеренным аэродинами¬
ческим качеством:
/—положение центров масс; — аппарат с сегментальным
лобовым щитом; аппарат с лобовым щитом в форме
косо-срез энного конуса
Последнее обстоятельство становится особенно важным в тех
случаях, когда необходимо перейти к повышенному значению аэро¬
динамического качества (7<=0,7—0,8). Получение такого качества
у форм с сегментальным щитом (рис. 1.4) затруднено из-за жест¬
ких требований к положению центра тяжести, которой должен
вслед за равнодействующей смещаться к наветренной образующей
обтекателя полезной нагрузки.
Центровочные преимущества рассматриваемых форм видны на
рис. 1.2, где показаны исходная и трансформированная форма и по¬
ложения равнодействующей при углах атаки, соответствующих ве¬
личине качества 0,3 и 0,5.
Еще более наглядно эти преимущества просматриваются для
форм, предназначенных для получения повышенных значений аэро¬
динамического качества (К=0,7—0,8). На рис. 1.4 показана одна
из возможных несимметричных сегментально-конических форм и
биконическая форма, полученная путем замены сегментального ло¬
бового щита на щит в форме косо-срезанного эллиптического ко¬
нуса.
18
Графики на рис. 1.3 и 1.5 показывают аэродинамические харак¬
теристики при различных углах атаки исходных и новых форм, при¬
чем можно убедиться в первых двух преимуществах новых форм.
Нельзя не сказать еще об одном преимуществе биконических форм,
у которых ось переднего конуса, образующего поверхность лобово¬
го щита, параллельна вектору скорости набегающего потока. Лобо¬
вой щит обтекается под нулевым углом атаки и при таком сим-
метричном обтекании проще
рассчитать аэродинамиче¬
ские характеристики и пара¬
метры, определяющие тепло¬
обмен на поверхности лобо¬
вого щита. Последнее преи¬
мущество немаловажно для
аппаратов, которые должны
летать в ночных условиях, а
именно входить с гиперболи¬
ческими скоростями в атмо¬
сферу Земли и планет.
Условие обтекания под
нулевым углом атаки озна¬
чает, что передний конус
должен быть эллиптическим,
причем косой срез его может
быть как эллипсом, так и ок¬
ружностью, как например, у
формы, показанной на рис.
1.2. Обтекатели в донной ча-
К с<
1
IX
XX
XX
‘\
0,5 <
XX
XX
ч.
*
Хч
Х^
4 с,
25 50 Л 4Z7 50 c(°sc
Рис. 1.5. Аэродинамические характери¬
стики сегментально-конической и бикониче-
ской форм на различных углах атаки для
аппаратов с умеренным аэродинамическим
качеством:
. — аппарат с сегментальным лобовым щитом;
аппарат с лобовым щитом в форме косо-
срезанного конуса
сти аппаратов, как обычно, являются круговыми конусами. Таким
образом, определенные сложности в технологии изготовления кор¬
пуса и нанесения теплозащитного покрытия свойственны только ло¬
бовым щитам новых форм.
Нельзя обойти молчанием и такое свойство рассматриваемых
биконических форм, как способность к сохранению центровочных
характеристик с ростом потребного качества. Производные dKjda
или dK/e/Ут для этих форм значительно больше, чем у сегменталь¬
но-конических. Если говорить о влиянии разбросов центровки на
аэродинамические характеристики готового изделия, то названное
свойство классифицируется как недостаток. Если же ориентиро¬
ваться на систему регулирования центровки перед полетом в про¬
цессе полета или, если принимать во внимание такое свойство, важ¬
ное в процессе проектирования, как адаптацию формы и компоно¬
вочной схемы к изменению режима балансировки, например, к по¬
вышению располагаемого качества, то указанное свойство следует
рассматривать как преимущество.
Для того, чтобы при изменении массовых или габаритных раз¬
меров аппаратов одной и той же фермы не производить нового
расчета траекторий спуска, целесообразно разработать способ, поз¬
воляющий определять характеристики траектории без интегриро¬
19
вания уравнений движения, зная в общих чертах лишь вид управ¬
ления на спуске. Необходимость таких оценок ощущается также в
задачах оптимизации формы аппарата, когда известен тип траек¬
торий спуска, т. е. известна программа перегрузки по времени или
по скорости полета. В упомянутых задачах оптимизации для каж¬
дого рассматриваемого варианта спускаемого аппарата проводится
проектный расчет, заключающийся в оценке весовых характерис¬
тик средств спуска и посадки при различных ограничениях. Для
определения веса при проектном расчете используется итерацион¬
ная процедура, ибо для того, чтобы рассчитать вес, необходимо
знать траекторию спуска, а для этого нужно задаться нагрузкой на
несущую плоскость, т. е. тем же весом аппарата. Кроме того, рас¬
четные случаи для большинства систем, обеспечивающих спуск и
посадку,’ориентированы на предельные режимы полета. Определе¬
ние предельных режимов по перегрузке, тепловым потокам, темпе¬
ратуре, времени и дальности полета связано с серией итерации, в
каждой из которых рассчитывается своя траектория спуска.
Все вышеизложенное диктует несущую потребность в методах,
позволяющих экономить машинное время и приближенно оценивать
параметры траектории. Известные методы [6, 20, 40] для проектных
целей неудобны, поскольку величина перегрузки теплового потока
на траектории не задается, а получается в результате расчета. Тем
самым исчезает основное преимущество таких методов для целей
проектного поиска, а именно, пропадает возможность прямого вы¬
хода в расчетах на предельные по перегрузке и теплообмену режи¬
мы полета. В предлагаемом методе расчета движения тип траекто¬
рии задается сочетанием законов управления, в числе которых изо-
перегрузочные законы; программы, позволяющие путем
отслеживания заданной зависимости перегрузки от скорости полета
формировать изовысотную траекторию или обеспечивать попадание
в заданные ограничения по температуре и дальности‘полета.
Единая последовательность законов управления определяет
целое множество траекторий, и каждая траектория в этом множе¬
стве отличается одним проектно-баллистическим параметром-нагру¬
зкой на несущую площадь. Шкалой переменных является скорость
полета, ибо назначение моментов переключений в скоростной шка¬
ле позволяет все возможные траектории объединить в один класс
и установить общие пределы для управляющих воздействий.
Для оценки параметров движения, перегрузок, тепловых потоков
и температур, а, следовательно, уноса и прогрева теплозащитного
покрытия, достаточно получить зависимости скорости и высоты по¬
лета от времени.
Интегрируя четыре основных уравнения движения, мы получим
указанные зависимости с точностью, достаточной для проектных
расчетов. Эти уравнения, записанные в скоростной системе коорди¬
нат с учетом общепринятых допущений (см. [1, 6]) в унифицирован¬
ной форме, пригодной для любой планеты, имеют вид
dV
dt
(1-5)
20
clb
dt
dH
dt
V sin 6;
(1.6)
(1.7)
cosO, (1.8)
df k
где V — скорость полета; 9 — угол наклона траектории к местно¬
му горизонту; £з — ускорение свободного падения на поверхности
Земли; gn — ускорение свободного падения на высоте полета в
атмосфере планеты; 7?п — расстояние от центра планеты до той вы¬
соты, на которой движется аппарат; Н — высота полета; L — даль¬
ность полета; р — плотность атмосферы, определяемая на задан¬
ной высоте полета; Рх — нагрузка на несущую площадь.
При этом Px = Ql(CxS) или Px=tng3!(CxS\
где G — суммарный вес аппарата; Сх — лобовое сопротивление;
5 — несущая поверхность; т — масса аппарата.
Считается, что известен закон изменения плотности с высотой
полета и вычисление плотности означает оценку высоты.
Величина эффективного аэродинамического качества К в каж¬
дый момент времени определяет управление спуском. При постоян¬
ном угле атаки Рх аппарата практически не меняется по траекто¬
рии, а величина эффективного качества определяется углом крена у
и располагаемым качеством аппарата Кр, а именно
/C = ZCpcoisy. (1.9)
Как будет показано в последующих главах, предпочтительные
траектории движения перспективных спускаемых аппаратов, вхо¬
дящих в атмосферы Земли, Марса и Венеры, используют режимы
выравнивания с изовысотными или изоперегрузочными площадка¬
ми. Переход на режим выравнивания реализуется после участка
входа в атмосферу, т. е. после достижения максимальных перегру¬
зок или температур на поверхности теплозащиты. Управление на
участке входа в атмосферу, позволяющее гибко реагировать на из¬
менение условий входа и характеристик аппарата с тем, чтобы
ввести управляемый объект в заданные перегрузочные или темпе¬
ратурные ограничения, используют алгоритмы наведения или набор
программных зависимостей перегрузки от времени или от скорости
полета.
В самом простом случае участок входа в атмосферу может мо¬
делироваться линейными зависимостями перегрузки от времени.
Считая угол входа в атмосферу малым (управляемый спуск), пола¬
гаем в уравнениях движения 9~0; cos 0^1 и sin6 ~0 и получаем
следующие зависимости для участка полета с постоянным градиен¬
том нарастания перегрузки:
1 .
(1-10)
21
Q
L
ПетЗХ 2РХ г
(1.11)
дтвЦ1+/<2 У'2 ’
пе-Петах т;
Дтв
(1. 12)
— 1/вхт ■ с т3,
ВХ a 1 / л . /л2
(1.13)
p
где VBx — скорость входа в атмосферу; с= £ma—go —градиент из-
Дтв
менения ускорения при торможении; пе max — максимальная пере¬
грузка, характерная для данного коридора входа и располагаемо¬
го качества аппарата; Дтв — интервал времени от момента входа
в атмосферу (перегрузка 0,05—0,1 ед) до момента прохождения
максимума перегрузки. Если в период входа в атмосферу приме¬
няется гибкий алгоритм, позволяющий обеспечивать общую для всех
условий входа зависимость потребного ускорения от кажущейся
скорости, то тем самым совершается маневр, обеспечивающий за¬
хват аппарата (при движении Что верхней границе коридора входа)
и выведение его на допустимый уровень по перегрузке или темпе¬
ратуре. Предположим, что отслеживается линейная зависимость
продольного ускорения Vx от кажущейся скорости (Евх—V), т. е.
зависимость типа
Vx = a + b(Vm-V).
(1-14)
Зависимость продольного ускорения подставим.в уравнение (1.5).
Номинальная, или опорная траектория, общая для всех условий
входа, в таком случае определяется следующими, уравнениями, по¬
лученными интегрированием уравнений движения с учетом урав¬
нения (1.14) при тех же предположениях, что и в предыдущем
случае:
V=yB-4- (е6х—1);
U
(1-15)
(1-16)
(1- 17)
(1-18)
Сразу после прохождения максимума перегрузок, т. е. в тот мо'
мент, когда аппарат в состоянии дальше двигаться рикошетом с
максимальным эффективным качеством, угол наклона траектории
близок к нулю и затем меняет знак, приобретая положительное
значение.
22
Интервал времени от момента входа в атмосферу до момента
прохождения пика перегрузки будет Дтв, а скорость полета в этот
момент обозначим VB. Изовысотный режим выравнивания выгодно
начинать в этот момент, ибо программа управления формирует эф¬
фективное качество исходя из равенства нулю производной угла
наклона траектории. Принимая это во внимание, проинтегрируем
уравнение (1.5), считая плотность атмосферы постоянной. Получим
следующее выражение для скорости полета на изовысотном уча¬
стке:
V
1
1
0£з_
2РХ
(Т — ДТВ)
(1-19)
Плотность атмосферы на участке изовысотного полета равна:
(1.20)
° V2 /1 + К2 '
Перегрузка определяется из выражения
„ _ _ "етах^2
Пе~ ~V2 •
г в
Приращение дальности полета по траектории определяется по фор¬
муле
(1-21)
Д£=£-£.=^Г1п (
Ы3 L V
)-'"£](L22)
'3—^£з.ДТв_|_^£зт
ув 2РХ 2РХ
Движение по изотемпературной траектории начинается обычно
при достижении предельной температуры. Будем считать, что вре¬
мя полета в момент перехода на изотерму будет Дтв, а скорость Ув.
Условие постоянства равновесной температуры означает, что на
траектории сохраняется постоянный тепловой поток в теплонапря¬
женной зоне аппарата. Для оценки величины конвективного тепло¬
вого потока используются обычно формулы вида
q=CqQmVn. (1.23)
Будем предполагать, что поддерживается достигнутая величина теп¬
лового потока, равная qQ. Плотность атмосферы в том случае, если
система управления обеспечивает движение по изотерме, будет
зависеть от скорости полета следующим образом:
1
(1-24)
ут
Интегрируя уравнение движения (1.5) при условии (1.24) и в пред¬
положении, что угол наклона траектории равен нулю, получим сле¬
дующую зависимость скорости полета от времени:
1 "I т
п-т / М-
т [С9 ) 2РХ 1 B7J
Г п—т
(1.25)
23
Перегрузка на изотемпературнои траектории меняется по времени
полета следующим образом.
[п—т
vT
(1.26)
Дальность при полете по изотемпературному участку траектории
приближенно можно определять по следующей формуле:
(1-27)
Изоперегрузочный участок начинается после точки выравнива¬
ния или после полета в изовысотном режиме. Сход с изотермы так¬
же может быть организован по изоперегрузочной траектории. Пред¬
полагая угол наклона вектора скорости к местному горизонту ма¬
лым и принимая перегрузку, много большую чем величина gn sin 0,
получим приближенные выражения для параметров траекторий на
изоперегрузочных площадках:
г- ёз (г
И + Кр
С , / 2 ’
V 1 + K2pV2
(1-28)
(1-29)
AZ = L - Д 1/н (г - Дгн) - -т^= g3 (т - Дгн)2, (1.30)
V1 +к2
где LH, VH и Атн — начальные дальность, время и скорость полета,
соответствующие моменту перехода на изоперегрузку.
Все приведенные выше зависимости характерны для различных
участков управляемого спуска, когда система управления, исполь¬
зующая несущие характеристики аппарата, формирует пологую
траекторию, обеспечивая при этом тот или иной закон изменения
перегрузки от скорости полета.
Знание законов изменения скорости и высоты полета позволяет
оценить тепловые потоки, а затем массу уносимого теплозащитного
покрытия.
На этапе предварительного проектирования, когда применяется
набор приближенных моделей, вычисляются по корреляционным
формулам удельные тепловые потоки. В общем случае корреляци¬
онные зависимости для оценки тепловых потоков имеют вид
24
qr = kr&Vb„Rm\ (1.31)
qK = k^ViR\ (1.32)
где qr и qK — удельные радиационные и конвективные тепловые по¬
токи в критической точке аппарата; R — радиус затупления.
При входе в атмосферу Венеры и Земли с гиперболическими
скоростями радиационные тепловые потоки сопоставимы с конвек¬
тивными, а при входе в атмосферу Юпитера радиационные потоки
преобладают. В таких условиях оценка оптимального радиуса за¬
тупления представляет определенный интерес на этапе качествен¬
ного анализа вопросов торможения в атмосфере. Находить опти¬
мальный радиус затопления имеет смысл на классе траекторий,
оптимальных по критерию, определяющему целевую задачу, реше¬
ние которой подчинено управление режимом движения. При входе
в атмосферу Земли такой задачей является, как будет показано в
следующей главе, обеспечение минимального интегрального пере¬
грузочного воздействия; при входе в атмосферу Венеры — завер¬
шение торможения в высоких слоях атмосферы. И в этом и в дру¬
гом случае предпочтительны траектории с изовысотной площадкой
и дальнейшим пологим снижением по изоперегрузочной траекто¬
рии. Параметры траекторий такого типа могут быть определены без
интегрирования уравнений движения; поэтому для аппаратов с раз¬
личной нагрузкой на несущую поверхность можно оценить опти¬
мальный радиус затупления при различных условиях входа в ат¬
мосферу.
Выражение для оптимального радиуса затупления выводится из
условия
-^(Q,+QK)=o. (1.33)
aR
где Qr и QK — интегральные тепловые потоки в критической точке.
С учетом зависимостей (1.31) и (1.32) определяем оптималь¬
ный радиус затупления через единичные интегральные тепловые
потоки, т. е. через тепловые потоки в точке затупления с радиу¬
сом 1 м:
На рис. 1.6 читатель может видеть типовую зависимость оптималь¬
ного радиуса затупления от скорости входа в атмосферу Земли для
аппаратов с различной нагрузкой на несущую поверхность и рас¬
полагаемым качеством, равным 0,6. Данная зависимость построена
для траекторий, свойственных нижней границе коридора входа, и
при условии, что режим движения после прохождения максималь¬
ной перегрузки соответствует минимальному интегральному пере¬
грузочному воздействию (см. гл. 2).
Отметим, что величина оптимального радиуса затупления, опре¬
деляемая ПС- формуле (1.34), никоим образом не свидетельствует о
25
необходимости делать аппарат именно с таким радиусом затупле¬
ния, а лишь позволяет судить о соотношении интегральных тепло¬
вых потоков в критической точке для данного типа траекторий
спуска.
Проигрыш в суммарных тепловых потоках зависит от оптималь¬
ного радиуса затупления, что подтверждается графиком на рис. 1.7,
где показана в относительных единицах величина проигрыша в ве¬
личине суммарных интегральных тепловых потоков при отклонени-
Рис. 1.6. Зависимость оптималь¬
ного радиуса затупления от ско¬
рости входа в атмосферу Земли
Рис. 1.7. Зависимость проигрыша в
суммарных тепловых потоках ра¬
диуса затупления (Q — тепловой
поток в зоне затупления с радиу¬
сом R' R=R/Rom', AQ=(Q—
—Qoht) /фонт)
Истинная величина оптимального радиуса затупления должна
определяться по массе уносимого и прогреваемого теплозащитного
материала в самой критической точке и в ее окрестности на лобо¬
вом щите, причем необходимо учитывать также массу конструкции
несущей оболочки щита.
Величина радиуса затупления, как правило, мало влияет на
массу аппарата. Решающими факторами здесь являются размеры
поверхности лобового щита и общая кривизна его поверхности по
отношению к местным углам атаки, поскольку они определяют, с
одной стороны, сопротивление аппарата, его несущие характерис¬
тики, а следовательно, теплонапряженность траектории спуска и, с
другой стороны, массу всего экрана через массовую плотность
квадратного метра площади.
Глава 2. ПРОБЛЕМЫ ВОЗВРАЩЕНИЯ НА ЗЕМЛЮ, ХАРАКТЕРНЫЕ
ДЛЯ ОКОЛОЗЕМНЫХ И МЕЖПЛАНЕТНЫХ КОСМИЧЕСКИХ ПОЛЕТОВ
Большинство вопросов, связанных с созданием перспективных
спускаемых аппаратов, относится к проблемам спуска в атмосфере
Земли. Именно в атмосфере Земли и околоземном космическом про¬
26
странстве проверяется большинство новых технических решений.
Возвращение на Землю при межпланетных пилотируемых поле¬
тах связывают обычно с экспедицией, в ходе которой совершается
облет Марса и Венеры с автоматическим зондированием этих пла¬
нет или десантированием на поверхность Марса. Скорость входа в
атмосферу Земли превышает вторую космическую и достигает 16—
17 км. На рис. 2.1 можно проследить, как меняются с ростом ско¬
рости потребная величина аэродинамического качества при задан¬
ной предельной суммарной перегрузке, равной 10 ед, а также вели¬
чина предельной перегрузки для аппарата, имеющего опреде¬
ленное аэродинамическое качество в предположении; что несущими
Рис. 2. 1. Зависимость потребного
качества, перегрузки и коридора
входа скорости входа в атмосферу
Земли
Рис. 2. 2. Зависимость пере¬
грузки от предельного вре¬
мени действия:
/—тренированный организм; 2—
детренированный организм
способностями аппарата обеспечивается коридор входа в атмосферу
размером 20 км. Вывод из результатов расчетов предельных траек¬
торий спуска, которые обобщены на этом графике, следующий: если
мы ориентируемся на существующие представления о точности на¬
вигации на припланетном участке и, если мы хотим сохранить тра¬
диционные принципы спуска (аппарат с умеренным качеством, уп¬
равляемый по крену), то мы столкнемся с перегрузками на спуске,
максимальное значение которых будет таким же, как при первых
полетах в космос (8—12 ед), причем время торможения в атмосфе¬
ре возрастает примерно в 2 раза.
Если теперь обратиться к зависимости предельной перегрузки
от времени, приведенной, например, в работе [12] и показанной на
рис. 2.2, то можно путем несложных оценок установить, что пере¬
грузочное воздействие на экипаж при оптимальной позе пилотов
относительно вектора перегрузки (~78° к линии позвоночника в
направлении грудь — спина) будет близким к предельному. Поло¬
жение усугубляется тем, что экипаж детренирован из-за длитель¬
ного полета в невесомости. В таких условиях перегрузочное воздей¬
ствие на экипаж оказывает существенное влияние на выбор режима
торможения в атмосфере, и получение критериев, моделирующих
27
О,с
/ООО
zw
Woo
$00
\0пр
--
'км/с
км/с
•км/с\
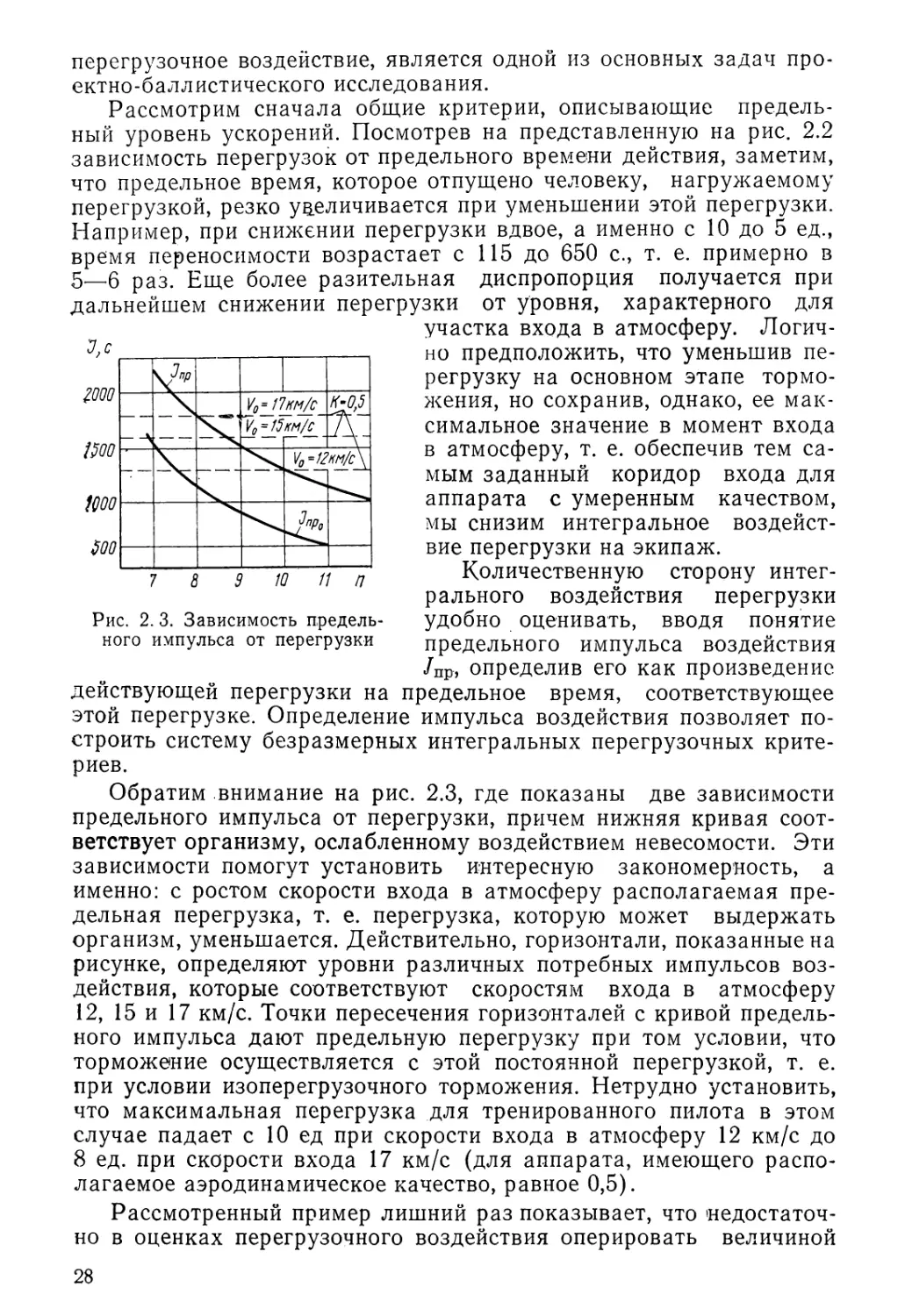
Рис. 2. 3. Зависимость предель¬
ного импульса от перегрузки
перегрузочное воздействие, является одной из основных задач про¬
ектно-баллистического исследования.
Рассмотрим сначала общие критерии, описывающие предель¬
ный уровень ускорений. Посмотрев на представленную на рис. 2.2
зависимость перегрузок от предельного времени действия, заметим,
что предельное время, которое отпущено человеку, нагружаемому
перегрузкой, резко увеличивается при уменьшении этой перегрузки.
Например, при снижении перегрузки вдвое, а именно с 10 до 5 ед.,
время переносимости возрастает с 115 до 650 с., т. е. примерно в
5—6 раз. Еще более разительная диспропорция получается при
дальнейшем снижении перегрузки от уровня, характерного для
участка входа в атмосферу. Логич¬
но предположить, что уменьшив пе¬
регрузку на основном этапе тормо¬
жения, но сохранив, однако, ее мак¬
симальное значение в момент входа
в атмосферу, т. е. обеспечив тем са¬
мым заданный коридор входа для
аппарата с умеренным качеством,
мы снизим интегральное воздейст¬
вие перегрузки на экипаж.
Количественную сторону интег¬
рального воздействия перегрузки
удобно оценивать, вводя понятие
предельного импульса воздействия
/Пр, определив его как произведение
предельное время, соответствующее
действующей перегрузки на
этой перегрузке. Определение импульса воздействия позволяет по¬
строить систему безразмерных интегральных перегрузочных крите¬
риев.
Обратим внимание на рис. 2.3, где показаны две зависимости
предельного импульса от перегрузки, причем нижняя кривая соот¬
ветствует организму, ослабленному воздействием невесомости. Эти
зависимости помогут установить интересную закономерность, а
именно: с ростом скорости входа в атмосферу располагаемая пре¬
дельная перегрузка, т. е. перегрузка, которую может выдержать
организм, уменьшается. Действительно, горизонтали, показанные на
рисунке, определяют уровни различных потребных импульсов воз¬
действия, которые соответствуют скоростям входа в атмосферу
12, 15 и 17 км/с. Точки пересечения горизонталей с кривой предель¬
ного импульса дают предельную перегрузку при том условии, что
торможение осуществляется с этой постоянной перегрузкой, т. е.
при условии изоперегрузочного торможения. Нетрудно установить,
что максимальная перегрузка для тренированного пилота в этом
случае падает с 10 ед при скорости входа в атмосферу 12 км/с до
8 ед. при скорости входа 17 км/с (для аппарата, имеющего распо¬
лагаемое аэродинамическое качество, равное 0,5).
Рассмотренный пример лишний раз показывает, что недостаточ¬
но в оценках перегрузочного воздействия оперировать величиной
28
перегрузки, а необходимо вводить критерий, определяющий по пре¬
дельному импульсу величину интегрального перегрузочного воз¬
действия.
Зависимость предельного импульса от величины перегрузки для
оптимальной позы пилотов может быть аппроксимирована следую-
щими
форм
улами:
а)
при
5<га<8,67
J -14
J пр
000 180 (га 8);
п
(2.1)
б)
при
8,67 < п <16
Лр
-.14 000 1 20;
п
(2.2)
в)
при
16 < п < 20
'/пр
_ 11500
/г — 0,8 ’
(2.3)
Уменьшение предельного импульса для организма, ослабленного
пребыванием в невесомости и в условиях гипокинезии, приближен¬
но можно учитывать по формуле /Про~ (/пр—450)0,85.
Соотношение между достигнутым значением импульса воздей¬
ствия 7 = пДт при постоянной перегрузке п и предельной его вели¬
чиной /пр = пДтПр послужит основой для формирования механисти¬
ческих безразмерных интегральных перегрузочных критериев, учи¬
тывающих накопление во времени перегрузочного воздействия.
Если на траектории спуска в течение малого отрезка времени Дг
действует перегрузка п, то доза т от предельного импульса воз¬
действия, соответствующего этой перегрузке, для указанного про¬
межутка времени будет
(2.4}
/пр (И) мДТпр
При J(n)>JUp(n), т. е. при т>1, действие перегрузки приведет к
необратимым изменениям в организме.
Суммируя дозы воздействия перегрузки на отдельных участках
траектории и в пределе интегрируя по времени отношение перегруз¬
ки к предельному ее импульсу, получим безразмерный критерий,
который называется мерой интегрального перегрузочного воздей¬
ствия:
М
о
п
/пр (^)
dx.
(2.5)
Если при данном способе торможения в атмосфере Л4<1, то ус¬
ловно считаем, что интегральное воздействие меньше предельного.
Указанный критерий описан в работе [11]. Тот же физический смысл
имеет критерий, предложенный в ряде работ и не использующий
понятия предельного импульса [18].
29
Понятие импульса воздействия методически оправдано, посколь¬
ку с ним связано построение более сложных критериев, учитываю¬
щих предысторию процесса нагружения. Дело в том, что мера ин¬
тегрального воздействия описывает механистически процесс накоп¬
ления физиологических изменений в организме человека, как бы
суммируя мощность воздействия нагрузок на органы тела, находя¬
щиеся под напряжением из-за противодействия силам инерции и
внешнего давления со стороны ложементов кресла. Кроме того, этот
критерий отражает явление накопления перегрузочного воздейст¬
вия односторонне, без учета предыстории процесса нагружения, без
учета действия других перегрузочных факторов на организм. Про¬
цесс воздействия ускорений растянут по времени, и небезразлично,
в какой период нагружения организм подвергается воздействию
максимальной перегрузки. Можно предположить, что форма эпюры
перегрузки по времени влияет на интегральное воздействие пере¬
грузки. Пиковые нагружения в конце траектории спуска или пов¬
торные пиковые нагружения будут восприниматься хуже, чем на¬
чальное воздействие перегрузки в момент входа в атмосферу. Преды¬
стория процесса нагружения может быть до некоторой степени
учтена с помощью безразмерного критерия, представляющего собой
максимальное отношение интеграла от перегрузки к предельному
импульсу воздействия, соответствующему этой перегрузке. Макси¬
мальное значение этого отношения выбирается из всех вычислен¬
ных в процессе нагружения. Этот критерий назовем степенью на¬
гружения импульсом перегрузки, он определяется по формуле
ndz
C(HJ) — max . (2.6)
Л.Р(и) k
ПриСн7)>1 следует предполагать, что организм перегружен, а при
ChJ)<C1 степень остаточной жизнеспособности ^oJ)b результате
действия импульса перегрузки логично оценивать как CoJ) = 1 — •
Нельзя не отметить, что рассматриваемый критерий учитывает
предысторию процесса нагружения односторонне, поскольку не
используется информация о достижении предельных значений пере¬
грузки и ее градиента. Поэтому при выборе траектории спуска по
критерию интегрального перегрузочного воздействия степень на¬
гружения оценивается одновременно с проверкой предельных уров¬
ней перегрузки, что дополняет основной критерий, в качестве кото¬
рого используется мера интегрального воздействия. Определение
траекторий, оптимальных по перегрузочному воздействию, произ¬
водится с использованием численных методов поиска, причем зада¬
ча оптимизации формулируется как задача нелинейного програм¬
мирования.
В качестве ограничений при поиске принимаются предельные
значения перегрузки и ее градиента, тепловые потоки, унос массы
теплозащитного покрытия, высота и скорость полета. Варьируемые
в ходе поиска параметры определяют (по шкале кажущейся скоро¬
30
сти полета) моменты переключений одного значения угла крена на
другое или моменты переключения на другую программу измене¬
ния перегрузки, отслеживаемую системой управления.
На рис. 2.4 в координатах высота — безразмерная скорость по¬
лета показаны две траектории входа в атмосферу с гиперболичес¬
кой скоростью. Одна из траекторий, которая была исходной при
поиске (показана пунктиром), имеет короткий изоперегрузочный
участок торможения с предельной перегрузкой, равной макси¬
мальной при входе в атмосферу. На рисунке показано, как накап¬
ливается в процессе полета мера интегрального воздействия. Исход¬
ная траектория является оптимальной по массе уносимой и прогре¬
ваемой теплозащиты. Завершением поисковых расчетов явилась
траектория, показанная сплошной линией, т. е. траектория с дли¬
тельным изовысотным режимом выравнивания, позволяющим без
рикошета и вылета из атмосферы, а значит без существенного уве¬
личения дальности и массы теплозащиты, снизить интегральное
воздействие перегрузок, сохранив их максимальное значение в мо¬
мент входа в атмосферу.
Рис. 2. 4. Зависимость меры
интегрального воздействия
для двух траекторий спуска
при входе в атмосферу с ги¬
перболической скоростью:
’ — исходная траектория;
оптимальная траектория
2
/
////////
'/////
//////
//////
/
t
Т
/
/*
J
.,1
с
Рис. 2.5. Предельные значения
меры интегрального воздействия
при различных углах входа в ат¬
мосферу;
/—граничное множество оптимальных
решений; 2—зона возможных траекто¬
рий движения: 3—граница допустимого
перегрузочного воздействия на экипаж
На рис. 2.5 показаны результаты дрейфа оптимума по одному
из ограничений, а именно по углу входа в атмосферу для траекто¬
рий спуска, реализуемых при возвращении с лунных трасс и с вы¬
соких околоземных орбит. Приведенная зависимость есть семейство
оптимальных решений, и можно определить предельный угол входа
для данного аппарата при оптимальном управлении — максималь¬
ный угол входа, соответствующий предельной мере интегрального
воздействия.
Рассмотренные нами критерии: мера интегрального воздействия
нагружения импульсом перегрузки применяются при выборе тра¬
ектории только при условии, что известны органичения на саму
31
перегрузку и ее градиент. Информация о приближении к предель¬
ным значениям перегрузки и ее производной по времени дополняет
интегральные критерии и позволяет построить систему комплекс¬
ных показателей, свидетельствующих о жизнеспособности организ¬
ма, подвергаемых воздействию переменных ускорений.
С физиологической точки зрения действие ускорений можно
условно разделить следующим образом:
действие на костно-мышечные ткани;
действие на органы, заполненные жидкостью (мозг, печень, же¬
лудок) ;
действие на сосуды кровеносной системы (изменение гидроста¬
тического давления в крови);
действие на колебательные процессы в организме (частотные
ритмы сердца, дыхание);
уменьшение рабочего объема легких из-за снижения мышечной
активности;
ухудшение идеомоторных реакций, ограничение двигательных
функций;
уменьшение телесного угла зрения.
Различные факторы перегрузки по-разному действуют на орга¬
низм. Массовые инерционные силы и внешние сосредоточенные ре¬
акции приводят к напряжениям в соединительных, костных и мы¬
шечных тканях, ограничивают двигательную активность. Градиент
изменения перегрузки оказывают действие на частотные процессы
в организме, меняя ритм сердца, частоту дыхания, а также воздей¬
ствия на вестибулярный аппарат. Импульс перегрузки определяет
работу противодействия притоку и оттоку крови, затрудняя крово¬
снабжение мозга, определяя застой крови, повышение давления и
местные кровоизлияния. Для того, чтобы судить о жизнеспособно¬
сти организма, подвергаемого экстремальному действию всех пере¬
грузочных факторов, необходимо рассмотреть степень остаточной
жизнедеятельности после действия каждого из факторов. По анало¬
гии с импульсом перегрузки, степень нагружения которым опреде¬
ляется по формуле (2.6), оценивается степень нагружения воздей¬
ствием самого ускорения С(НЛ) и степень нагружения градиентом
ускорения C(Hdn/dx):
СнП)=шах— ; CHJ/Z/Jt) = max
^пр
dn/dx
(d n/dT)n^
Степень остаточной жизнеспособности после действия названных
перегрузочных факторов определяется так же, как и для импульса
перегрузочного воздействия:
С&л)=1—с£л); (2.7)
Вычисляя поочередно степень остаточной жизнеспособности после
действия каждого фактора, следует учитывать достижение предель¬
ных значений импульса, перегрузки и градиента. Предельной вели¬
32
чиной перегрузки необходимо считать то ее значение, после кратко¬
временного действия которого в организме наступают необратимые
изменения. По ряду данных это величина перегрузки равна 30—
40 ед. Применяя эти критерии для оценки работоспособности пило¬
тов, мы обязаны снизить этот предел и считать пороговым значе¬
нием ускорения то, при котором происходит временное нарушение
отдельных функций организма при условии, что после снятия
перегрузки эти функции восстанавливаются.
Предельная величина градиента ускорения определяется еще
более расплывчато и, по-видимому, она находится в диапазоне
5—10 м/с3.
Нельзя не отметить, что большинство исследователей-медиков
считает интегральное действие перегрузки определяющим, причем
обеспечение нормального кровоснабжения организма — решающим
условием сохранения жизнедеятельности.
В работе [12], где обобщены результаты исследований переноси¬
мости перегрузок для тренированных и детренированных пилотов,
утверждается, что «одно из ведущих лимитирующих обстоятельств
переносимости человеком ускорений — нарушение кислородного
баланса организма».
Проблема переносимости перегрузок только исследуется и по¬
этому в ряде вопросов нет полной определенности. Это касается,
в первую очередь, определения степени важности тех или иных
факторов перегрузочного воздействия, уровня достоверности и во¬
просов точности оценки предельных величин перегрузки, градиента
и импульса воздействия.
Если не рассматривать вопросы работоспособности пилотов, то
в качестве единого критерия для оценки суммарного воздействия
перегрузки выступает вероятность благополучного исхода процесса
нагружения для всего экипажа. Каждому из факторов действия
перегрузки: градиенту ее изменения, величине инерционной силы, а
также интегральному воздействию ускорений свойствен разброс
значений вблизи пороговых величин. Этот разброс считается задан¬
ным, причем известны функции распределения предельных значе¬
ний перегрузочных факторов. В таком случае определение вероят¬
ности Pi превышения для одного члена экипажа предельного зна¬
чения при данном законе торможения для известной эпюры изме¬
нения перегрузки во времени не составляет большого труда, если
такая вероятность определяется только для одного фактора воздей¬
ствия перегрузки. Сделанный расчет ляжет в основу «оптимисти¬
ческой» модели перегрузочного воздействия, которая основана на
предположении о независимом действии перегрузки, ее градиента и
импульса воздействия.
Вероятность успешного исхода нагружения Р s определится в
такой модели следующим образом:
^ = [(1-Л)(1-Л)(1-^з)Ь (2.9)
где Рь Р2, — вероятности превышения предельных значений пе¬
регрузки, градиента импульса воздействия, определяемые по дан¬
2 400
33
ным, полученным для детренированного экипажа; п — число чле¬
нов экипажа.
Модели, в которых учитывается зависимость факторов нагру¬
жения друг от друга и от предыстории процесса нагружения, более
близки к действительности. В основе предельной модели такого ти¬
па лежит схема расчета вероятности успешного исхода по «песси¬
мистическим» оценкам. Такие оценки касаются корреляции перегру¬
зочных воздействий и делаются по каждому из предельных воздей¬
ствий при условии, что степень нагружения определяется с учетом
степени остаточной жизнеспособности организма, подвергаемого
ранее воздействию других перегрузочных факторов. Моделирование
суммарного перегрузочного воздействия производится методом
статистических испытаний.
Каждая серия испытаний проводится для одной конкретной
траектории спуска, и результаты сравниваются с целью выбора
наилучшего режима движения. В каждом из испытаний определя¬
ется на начальной фазе торможения степень нагружения градиен¬
том ускорения для данной случайной величины предельного гради¬
ента, полученной исходя из закона распределения порогового зна¬
чения этого градиента.
Мера остаточной жизнеспособности является новым уровнем,
в соответствии с которым уменьшается полученная путем очередной
случайной пробы величина предельной перегрузки. Определив вели¬
чину предельной перегрузки по закону распределения порогового
значения этой перегрузки и уменьшив ее в соответствии с мерой ос¬
таточной жизнеспособности, вычисляем степень нагружения вели¬
чиной перегрузки. Для этого сопоставляем максимальную величину
перегрузки на траектории с уменьшенным значением предельной
перегрузки. Новая вычисленная мера остаточной жизнеспособ¬
ности будет таким образом, учитывать два перегрузочных фактора.
При расчете каждой из рассматриваемых траекторий следует поза¬
ботиться о том, чтобы определить заранее максимум отношения
интеграла от перегрузки к предельному импульсу, соответствую¬
щему этой перегрузке. Запоминается величина перегрузки, соот¬
ветствующая этому максимуму, и производится случайная проба,
исходя из закона распределения предельного импульса, после чего
реализованное пороговое значение импульса корректируется и
уменьшается в соответствии с мерой остаточной жизнеспособности,
вычисленной ранее исходя из действия двух других перегрузочных
факторов.
Степень нагружения импульсом учитывает предысторию тормо¬
жения и в данном случае выглядит как отношение интеграла от
перегрузки, характерного для исходной вычисленной на траектории
степени нагружения, к новому скорректированному пороговому
значению импульса.
Производя многократно указанную операцию для данной траек¬
тории спуска и моделируя для этой траектории, каждый раз слу¬
чайным образом, появление пороговых значений градиента, пере¬
34
грузки и импульса, можно с заданной достоверностью оценить ве¬
роятность благополучного исхода процесса нагружения для одного
человека и всего экипажа в целом.
Если необходимо оценить уровень работоспособности пилотов,
который также влияет на благополучный исход процесса тормо¬
жения, то приходится учиты¬
вать следующие параметры,
описывающие пилотов, как
звено в системе управления
летательным аппаратом на
участке спуска:
время информационного
запаздывания в процессе пе¬
реработки сигналов от чув¬
ствительных элементов кон¬
тура управления';
время операционного за¬
паздывания в реакциях пи¬
лотов; время переходного
процесса управляющего
звена, включающего пилота
и орган управления.
Номинальные значения и
разброс этих параметров за¬
висит от перегрузочного воз¬
действия, и в общем случае
вероятность благополучного
исхода процесса торможе¬
ния определяется с учетом
надежности системы управ¬
ления.
Рассмотрим еще один из
аспектов проблемы возвра¬
щения на Землю при меж¬
планетных экспедициях, а
именно, попытаемся опреде¬
Рис. 2.6. Пути трансформации форм
при поиске рациональной конфигурации
спускаемого аппарата:
1—^посадочный отсек
лить возможный облик спу¬
скаемых аппаратов при условии, что принципы спуска в атмосфере
сохраняются неизменными.
Одним из условий при выборе формы аппарата пусть будет ус¬
ловие сохранения существующих способов торможения в атмосфере
и управление спуском. Рассмотрим аппараты затупленных и уме¬
ренно-заостренных форм с минимальным располагаемым качеством,
близким по величине к потребному (Лр = 0,65—0,78). Траектории
спуска выбираются по критерию минимального интегрального пере¬
грузочного воздействия. Максимальная перегрузка после погруже¬
ния в атмосферу составляет ~10 ед. при скорости входа 17 км/с.
Рис. 2.6 иллюстрирует один из возможных путей поиска рациональ¬
ной формы аппарата, предназначенного для входа в атмосферу со
2*
35
скоростью 17 км/с, с экипажем из шести человек. Последователь¬
ный переход к лучшим формам производится путем трансформа¬
ции отдельных частей рассмотренных форм; причем считались неиз¬
менными потребный объем, вес полезной нагрузки, величина пре¬
дельной перегрузки, располагаемого качества и тип траектории
спуска, т. е. совокупность изовысотного и изоперегрузочного участ¬
ков после прохождения пика перегрузок.
Исходная форма, близкая к формам существующих СА, с при¬
емлемыми объемными характеристиками не обеспечивает потреб¬
ного аэродинамического качества, поэтому на первом этапе транс-
формации формы изменим конфигурацию заднего объема, изменив
угол атаки несущей поверхности.
Два крайних пути трансформации заднего объема показаны на
рис. 2.6, и они приводят к формам 1 и 2. Один из таких путей свя¬
зан с косым срезом тела несущей плоскостью (форма 7); другой—
с увеличением угла раствора заднего конуса и, следовательно, с
увеличением несущей поверхности у симметричных форм (форма
2). Рядом с каждой из форм приведены значения коэффициентов
использования полезного объема (Ку), а также массы теплоза¬
щиты и средств спуска и посадки в целом. Массовые характеристи¬
ки приведены в относительных единицах и отнесены к массе полез¬
ной нагрузки спускаемых аппаратов, в которую включается экипаж,
результаты исследований, системы жизнеобеспечения, терморегули¬
рования, энергопитания, управления (аппаратурная часть), радио¬
системы и оборудование для проведения операций в период под¬
лета к атмосфере и после посадки.
Средства спуска и посадки включают в себя остальные системы
СА, масса которых непосредственно или косвенно зависит от его
размеров и формы, а именно: теплозащиту с теплоизоляцией, кон¬
струкцию гермокабины, донного обтекателя и переднего отсека с
лобовым щитом, парашютно-реактивную систему приземления, ис¬
полнительные органы системы ориентации и систему регулирования
центровки с запасами рабочего тела.
Путь, приводящий к формам со значительной несимметрией из-
за косого среза, приводит к конфигурациям типа формы 1 с малой
поверхностью лобового щита и относительно малой суммарной по¬
верхностью, но с крайне неудобными центровочными ограничения¬
ми, следствием чего являются неприемлемые массы систем регули¬
рования центровки и значительная суммарная масса СА при малой
массе теплозащиты и конструкции оболочки корпуса.
Компромиссное решение, представленное на рис. 2.6 формой 3,
обладает лучшими центровочными характеристиками.
Применение симметричных форм с малым удлинением (форма
2) дает удовлетворительные условия при обеспечении поперечной
центровки (Ку = 0,75), но из-за развитой поверхности лобового
щита, значительной суммарной поверхности и превышения распо¬
лагаемого объема над потребным массу средств спуска и посадки
и в том числе массу теплозащиты нельзя признать приемлемыми.
36
Характеристики аппаратов всех трех названных форм улучша¬
ются, если на следующем этапе трансформации видоизменить кон¬
фигурацию передней части, придав ей форму кососрезанного эллип¬
тического конуса, обтекаемого под нулевым углом атаки. Резуль¬
тат такой замены скажется на массе систем регулирования цент¬
ровки из-за улучшения объемно-центровочных характеристик (см.
гл. 1). На рис. 2.6 можно видеть, как изменяются при этом центро¬
вочные критерии, масса теплозащиты, а также средства спуска и
посадки в целом.
Компромиссное решение (форма За) привлекательно не только
удовлетворительными массовыми и центровочными характеристи¬
ками, но и тем обстоятельст-
рис. 2.6, может быть применен I i | п* ]
в составе других спускаемых 0 ~ lo SD
аппаратов, имеющих традици¬
онную симметричную сегмен- Рис. 2.7. Изменение по времени полета
тально-коническую форму и расхода массы уносимой теплозащиты:
предназначенных для входа в в2°вдхэдпопо нв“й r.plS коридора31
атмосферу с околоземной ор¬
биты и лунных трасс.
Одним из преимуществ умеренно-заостренных форм аппаратов,
входящих в атмосферу с гиперболическими скоростями [в дополне¬
ние к объемно-центровочным преимуществам (см. гл. 1)] является
меньшая масса теплозащиты и простая схема обтекания переднего
конуса, угол атаки которого близок к нулю. Оптимальный радиус
затупления в условиях преобладания в критической точке радиа¬
ционных тепловых потоков значительно меньше метра. Оценка ве¬
личины уноса покрытия должна производиться с учетом обратной
связи в механизме разрушения теплозащиты, т. е. с учетом блока¬
ды конвективных потоков и экранирования радиационных тепловых
потоков пристеночным слоем пиролизного газа, образованного про¬
дуктами разрушения теплозащиты.
На рис. 2.7 показано, как в трех характерных точках лобового
щита аппарата, имеющего форму За (см. рис. 2.6), меняется по вре¬
мени расход теплозащитного материала при входе в атмосферу по
нижней границе коридора входа. Одновременно можно проследить,
как меняется по времени масса уносимого покрытия с квадратного
метра площади в критической точке.
37
Рассмотрим вопросы управления при движении по траекториям,
для которых характерно ограничение по температуре, перегрузке
или тепловым потокам.
При движении по изотемпературным траекториям отслеживает¬
ся предельное или меньшее, чем предельное, значение тепловых по¬
токов; при этом постоянство тепловых потоков означает постоянст¬
во равновесной температуры в критической точке [20, 40]. Движение
по изотемпературной траектории (по изотерме) может быть органи¬
зовано путем поворотов по крену без изменения режима баланси¬
ровки. Номинальная величина потребного угла крена определяется
по значению эффективного качества.
В гл. 1 приведены уравнения движения в скоростных осях, из
которых, полагая на участке изотермы угол наклона траектории
близким к нулю, причем sin 0^0, a cos 0—1, получим для условий
движения в атмосфере Земли следующие соотношения:
dt=—^-dV-, (2.10)
dV 2PX g 2PX R '
(2.11)
Определим dtildV через q и V. Подставляя (2.10) в (1.7), получим
dH = 2РХ 0
dV QgV
Уравнение, связывающее плотность и высоту, продифференцируем
по V и получим выражение
— = — — — . (2.12)
dV dV ₽е v z
Приравняв правые части выражений для
g-У dQ
2РХ$ dV ‘
dH
dV'
получим
(2.13)
Продифференцируем 9 по V:
I dQ \
dV ~ 2РХ$ \dV^ ^dv)'
(2. 14)
Подставим (2.14) в (2.11) и найдем исходное выражение для оцен¬
ки эффективного качества, потребного для движения в режимах
выравнивания:
QV2 i ' vД _ QgV3 Л*22 у I \
2РХ "Г" 4Р^ ЧУ2 dV ) '
(2. 15)
Из выражения (2.15) выводится зависимость для изовысотного
(см. гл. 4), изоперегрузочного и изотемпературного режимов движе¬
ния. Для последнего выведем зависимости производных плотности
от скорости, использовав условие постоянства теплового потока,
определяемого по формуле
q=C^mVn.
(2. 16)
38
Взяв производную по V от q и приравняв ее нулю, найдем выраже¬
ние для первой производной плотности по скорости:
dQ п 1
dV ~ mQ~V ’
Продифференцируем (2.17) еще раз по V:
__ п О Л I » \
dV2 т 72 1 Т га / '
(2. 17)
(2. 18)
Подставив (2.17) и (2.18) в (2.15) и учитывая, что пхях ,
2Р х
получим результирующую формулу для эффективного качества:
1 / j 72 gn2x П2 j\
ПХ \' gP ₽ m2 72 )
(2.19)
Первые два члена за скобками в выражении для определения
потребной величины эффективного качества определяют условие
полета по изовысоте (с постоянным углом наклона траектории), а
третий член формирует приращение качества (отрицательное), не¬
обходимое для снижения в плотные слои атмосферы по мере умень¬
шения скорости полета. В частности, снижение по изоперегрузочной
траектории соответствует условию т = 0,5; п = 2, а снижение по
изотермам определяется условиями:
т = 0,5; /г = 3—3,75.
Анализ выражения (2.19) показывает, что при спуске с низких
околоземных орбит величина эффективного качества не может
быть меньше нуля при движении по изотерме. В начальный момент
при прохождении точки выравнивания угол крена близок к 60—•
70° и в дальнейшем по мере погружения в атмосферу он, как пра¬
вило, возрастает с тем, чтобы потом, снова уменьшаясь, обеспечить
увеличение эффективного качества при скоростях полета меньше
6 км/с. Перегрузка в период полета по изотерме растет, как это
можно видеть, например, из формулы (1.26).
Мы коснулись проектно-баллистических вопросов, связанных со
спуском, и не затронули вопросов предпосадочного маневра и по¬
садки, хотя проблемы автоматической посадки на аэродром не ме¬
нее сложны и интересны, нежели проблемы входа в атмосферу и
преодоления температурных и перегрузочных воздействий при дви¬
жении с гиперзвуковыми скоростями.
Анализ проблем посадки аппарата с высоким аэродинамичес¬
ким качеством, управляемого по тангажу, рысканию и крену, бли¬
же разработчикам самолетов, и в проблемах посадки на планеты
трудно найти в обозримом будущем аналогии задачам планирую¬
щей посадки на аэродром. Поэтому коснемся вопроса, знакомого
разработчикам спускаемых аппаратов традиционного типа, но
интересующего также исследователей многоразовых ракетно-кос¬
мических систем и перспективных тяжелых спускаемых аппаратов.
Речь пойдет о хорошо известных системах приземления, исполь¬
39
зующих парашютные средства и ракетные двигатели. Без сомнения*
системы такого типа будут еще долго применяться для решения
задач спуска и посадки, и было бы наивно предполагать, что в
ближайшем будущем все операции по возвращению из космоса бу¬
дут завершаться планирующей посадкой на аэродром. Посадка
спускаемых аппаратов, входящих в атмосферу с межпланетных
трасс, а также посадка ракетных ускорителей будет ориентиро¬
ваться на оптимальные по весу парашютно-ракетные системы, поз¬
воляющие полностью использовать двигатели с бортовой энергети¬
кой и совершать приземление в различные районы Земли.
Было бы заманчиво для СА межпланетных комплексов или для
многоразовых ракетных блоков сохранить традиционные приемы
предпоследнего торможения и, в частности, применить парашют¬
ные системы существующих размеров. Под этим углом зрения рас¬
смотрим оптимальные характеристики парашютно-реактивных сис¬
тем. Масса средств посадки Л4с.п в относительных единицах, т. е.
отнесенная к массе посадочного груза Л40, будет состоять из сле¬
дующих компонентов:
^с.п — ^с.пМ—А?авт, (2- 20)
где ЛТп.с — относительная масса парашютных средств;
Л/д.у — относительная масса двигательной установки предпосадоч¬
ного торможения с запасом топлива; Мавт — относительная масса
автоматической аппаратуры и оборудования для управления рабо¬
той посадочных средств. Оптимальная скорость парашютирования,
соответствующая минимуму массы средств посадки, весьма велика
и измеряется десятками метров в секунду. Убедимся в этом. Ско¬
рость снижения на парашюте Vc, соответствующая минимальной
массе, определяется из условия
^Н-=0. (2.21)
Л/авт составляет для больших Л4о величину порядка 0,01. Будем счи¬
тать, что Л7авт не зависит от Vc- Из условия установившегося сни¬
жения на парашюте получаем выражение для относительной массы
п.с
парашютных систем:
(1 4- Ал +'/С2)
п,с— C^ocose^ ’
(2. 22)
где 5 — удельный вес квадратного метра купола; Ki — отношение
массы строп со стренгами к массе куполов; К2 — отношение массы
элементов крепления и средств раскрытия парашютов к массе ку¬
полов; Сх —• коэффициент сопротивления парашюта; р0 — плот¬
ность атмосферы в районе посадки; 0 — угол отклонения оси пара¬
шютов от вектора скорости (для многокупольных систем). Значения
всех перечисленных коэффициентов и параметров будем считать не
зависящими от скорости парашютирования. Относительная масса
посадочного жидкостного реактивного двигателя определяется по
следующей формуле:
40
Л1д.у = (1 + «т.о)(1-e Jg) + Yx.y»o- (2.23)
Пояснения к формуле (2.23) см. в гл. 3. Относительную массу
твердотопливного двигателя можно определять, используя следую¬
щее выражение:
<у = Жкорп + (1-е-^), (2.24)
где AfKopn — относительная масса корпуса двигателя. Тяговоору-
женность при посадке будем считать намного больше единицы и
тогда VX^VC.
Для жидкостных двигателей, которые, как правило, предназна¬
чены для использования на других этапах полета, значения ат.о,
Уд.у и п0 не зависят от 7С, причем ат.0<С 1. Для твердотопливного
двигателя величина МкОрп зависит от Vx, но_составляет у больших
двигателей (0,1—0,2)Мд.у. Будем считать Л/Корп = const. Величина
Vc не превышает 100 м/с, поэтому с точностью до 2—4% считаем,
что
(2. 25)
Из условия (2.21), принимая во внимание (2.22), (2.24) и (2.25),
получим
(2. 26)
Нетрудно убедиться, что при любых сочетаниях значений вели¬
чин, входящих в выражение (2.26), оптимальная скорость парашю¬
тирования находится в пределах 20—30 м/с.
Оптимальная масса парашютно-реактивных систем при таких
скоростях снижения составляет 54-6% от массы посадочного груза,
т. е. примерно вдвое меньше, чем у большинства применяемых сис¬
тем, рассчитанных на скорость парашютирования 7—8 м/с. Изло¬
женные соображения по поводу оптимальной скорости парашютиро¬
вания не являются чем-то новым для лиц, занимающихся система¬
ми посадки. Реализация систем с неоптимальной скоростью пара¬
шютирования объясняется тем, что приходилось рассчитывать на
возможность аварийной посадки без двигателя, а также на труд¬
ности в обеспечении точности систем управления посадкой при
больших скоростях снижения. Ошибка чувствительных элементов
(как правило высотомеров) зависит в основном от скорости сни¬
жения, импульса и высоты включения двигателя.
Одним из возможных способов снижения разброса посадочной
скорости является ступенчатое включение двигателей с постепен¬
ным гашением скорости. Задачей первого этапа гашения скорости
является снижение скорости парашютирования до величины поряд¬
ка 10—15 м/с, причем двигатель первой ступени имеет тяговоору-
женность меньше единицы и работает под куполом парашюта, как
41
бы снижая посадочный вес. Ошибка включения двигателя (по вы¬
соте) компенсируется увеличением времени его работы в расчет¬
ном режиме, т. е. запасом топлива на предпосадочное подторма¬
живание.
Второй этап торможения происходит традиционным образом,
т. е. сообщением мощного импульса всей системе на малой высоте
у поверхности Земли.
Основные затруднения в реализации ступенчатого торможения
связаны с операцией подтормаживания на первом этапе гашения
скорости, причем приходится формировать программу работы дви¬
гателя с постепенным увеличением тяги, чтобы исключить динами¬
ческое воздействие на систему парашют — груз.
Рис. 2.8. Диаграмма изме¬
нения тяги посадочных дви¬
гателей и типовая форма
заряда двигателя первой
ступени
V,M/C
Рис. 2. 9. Параметры дви¬
жения парашютно-реак¬
тивной системы в случае
ступенчатого предпоса¬
дочного торможения
На рис. 2.8 одновременно с диаграммой изменения тяги твер¬
дотопливных двигателей для груза весом 5 тс приведена одна из
возможных форм заряда, обеспечивающая прогрессивное горение с
выходом на постоянную тягу для двигателя первой ступени.
Из диаграммы тяги двигателей первой и второй ступеней вид¬
но, что производится параллельно-последовательное включение
двигателей. На рис. 2.9 можно видеть, как меняются по времени
номинальные значения скорости снижения и высоты в случае тор¬
можения по программе, приведенной на рис. 2.8.
В приведенном примере рассмотрен только один из многих воз¬
можных путей предпосадочного торможения парашютно-реактивных
систем, обеспечивающих близкие к минимальным массовые харак¬
теристики посадочных средств.
42
Глава 3. ВЫБОР ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ ПАРАМЕТРОВ
ПОСАДОЧНЫХ АППАРАТОВ МАРСИАНСКИХ ПЛАНЕТНЫХ
КОМПЛЕКСОВ
Основной особенностью операций, связанных с высадкой на
Марс, является разреженность марсианской атмосферы. Поэтому
при анализе задачи спуска на планету приходится определять ра¬
циональный способ торможения, учитывая, с одной стороны, воз¬
можность применения развитых аэродинамических тормозных уст¬
ройств и, с другой стороны, способности аппарата к активному
предпосадочному торможению с помощью двигательных установок.
В будущем следует ожидать создания тяжелых спускаемых ап¬
паратов, совершающих управляемый спуск на поверхность Марса,
с целью доставки туда крупноразмерных планетных комплексов.
. Рассмотрим методы проектного расчета оптимальных проектно¬
баллистических параметров таких спускаемых аппаратов.
Выбор рациональных размеров и компоновочной схемы марси¬
анских СА определяется, как правило, компромиссом между несу¬
щей площадью аппарата и запасом топлива на торможение перед
посадкой.
При параметрических расчетах на этапе предварительных про¬
ектных оценок зачастую необходимо аналитически определить ра¬
циональные баллистические параметры и размеры аппарата при
условии, что движение в атмосфере осуществляется по энергети¬
чески оптимальным траекториям. Задача оптимизации решается
при этом раздельно, так как определяется класс оптимальных за¬
конов управления спуском и затем на множестве оптимальных
траекторий определяются проектно-баллистические параметры, а
именно, нагрузка на мидель и располагаемое аэродинамическое
качество. После таких расчетов можно для конкретных конфигура¬
ций аэродинамических тормозных устройств переходить к размерами
тормозного экрана.
Рассмотрим приемы аналитической оценки оптимальных проект¬
но-баллистических параметров, решая раздельно задачу выбора
оптимального закона управления спуском и задачу поиска проект¬
но-баллистических параметров и, в частности, нагрузки на мидель
аппарата. При этом будем предполагать, что в конструкции аппа¬
рата используются простые и апробированные решения, т. е. для
аэродинамического торможения на гиперзвуковых скоростях при¬
меняется лобовой теплозащитный экран. Лобовой экран обтекается
под углом атаки, достаточным для получения небольшого аэродина¬
мического качества, причем угол атаки и величина качества опреде¬
ляются весовой балансировкой или несимметричной формой экра¬
на и сохраняются неизменными в процессе спуска. Управление
движением осуществляется путем переворотов по крену вокруг век¬
тора скорости. Считается, что все предпосадочное торможение
осуществляется двигательной установкой, используемой в даль¬
нейшем для юстировочного маневра и мягкой посадки на поверх¬
ность.
43
Будем предполагать также, что схема обтекания аппарата и
способ получения аэродинамических сил, используемых для тор¬
можения и управления траекторией спуска, являются традицион¬
ными, т. е. используются аппараты простых аэродинамических
форм с малым располагаемым аэродинамическим качеством. Такой
аппарат имеет развитый аэродинамический тормозной экран, на
котором располагается полезная нагрузка, закрытая в зоне затене¬
ния легким обтекателем. Контуры экрана могут выступать за обво¬
ды полезной нагрузки, а сам экран имеет затупленную или умерен¬
но заостренную форму. Рассмотрим тип траекторий спуска, для
которых целесообразно определять оптимальные проектно-баллис¬
тические параметры аппарата.
Выбор оптимального закона управления спуском производится
для марсианских СА по критериям, описывающим конечную фазу
спуска в момент подлета аппарата к поверхности планеты. В об¬
щем- случае таким критерием является масса двигательной уста¬
новки при фиксированных размерах аэродинамического тормозного
экрана. Идя на некоторые упрощения, допустимые при параметри¬
ческих оценках, весовой или массовый критерий имеет смысл раз¬
делить и не рассматривать тяговооруженность и массу камер сго¬
рания, оперируя только запасом топлива на предпосадочное тормо¬
жение и посадку. Вопрос выбора оптимальной тяговооруженности
должен решаться комплексно с учетом изменения скорости полета
на разных высотах включения двигателя и с учетом программы
управления тягой при торможении. Некоторые результаты расчетов
оптимальной тяговооруженности будут обсуждаться в конце главы.
Скорость входа в атмосферу Марса значительно меньше скоростей
входа в атмосферу Земли и Венеры; она колеблется от 3,6 км/с
(спуск с низких околопланетных орбит) до 4,8—6 км/с (спуск с
высокоэллиптических ареоцентрических орбит или подлетных тра¬
екторий). На таких траекториях спуска максимальные конвектив¬
ные тепловые потоки (а именно они доминируют в теплообмене)
не превышают, как правило, 102 кВт/м2 и поэтому ограничения по
тепловому и перегрузочному воздействию не являются решающими
для спускаемых аппаратов марсианских планетных комплексов.
Если не рассматривать тяговооруженность и в качестве крите¬
рия при поиске режима управления на спуске принять характери¬
стическую скорость посадочного двигателя, то можно пойти на
дальнейшее упрощение задачи, сводя задачу оптимизации весо¬
энергетических характеристик к задаче минимизации характерис¬
тик траектории спуска.
Наиболее наглядно выглядят результаты решения такой задачи.,
когда определяется минимум всего одной, основной характеристики
траектории — скорости на заданной конечной высоте пассивного
полета в момент включения посадочного двигателя.
Строго говоря, мы не правомочны, оптимизируя режим движе¬
ния на спуске по критерию минимума характеристической скорости,
пренебрегать особенностями режима активного торможения и, в ча¬
стности, пологостью траектории, определяемой углом наклона век¬
44
тора скорости к горизонту в конце участка аэродинамического тор¬
можения. Характеристическая скорость Ух для посадочных опера¬
ций включает в себя следующие компоненты:
УГо — скорость полета на высоте Но в конце аэродинамическо¬
го торможения и перед включением двигателя предпосадочного тор¬
можения (величина Vh0 зависит от типа траектории спуска и бал¬
листических характеристик аппарата);
ДУг.п — гравитационные потери скорости на участке активного
торможения (определяются программой управления вектором тяги
и протяженностью участка торможения, т. е. тяговооруженностью
двигателя, которая, в свою очередь, зависит от высоты Яо и началь¬
ного угла наклона траектории 0 о). Величина ДУГ.П невелика и сос¬
тавляет 2—4% от VHo> поэтому в параметрических оценках опти¬
мальных проектно-баллистических параметров можно пренебречь
влиянием, характеристик конечного участка траектории спуска
на АУГ.П;
АУупр — затраты характеристической скорости на управление
на участке активного предпосадочного торможения. В целом по¬
тери на управление составляют 2—5% от VHo-
Три названных компоненты можно объединить, поскольку они
определяют запас топлива на предпосадочное торможение. При
ЭТОМ А Их.торм= Уно' + АУг.п+А Уупр и АУХ .торм — KvVIlQi где Kv =
= 1,04-4-1,10. Остальные составляющие характеристической скоро¬
сти определяют затраты топлива на участке посадки (АУх.ПОс) й
запасы неизрасходованного топлива в баках (ДУгар). АУх.1юС прак¬
тически не зависит от характеристик траектории спуска:
А^х.ПОС А1/ман-|-
где АУман — запас скорости на предпосадочный маневр. ДУман
зависит от времени, отпущенного на маневр. При времени маневра
60 с АУмаи = 270 м/с; ДУЮСТ — затраты скорости на юстировочное
торможение при мягкой посадке. Величина ДУЮСт, как правило,
невелика и составляет 20—60 м/с. ДУгар — компонента характе¬
ристической скорости, определяемая гарантийным запасом топлива
в баках. Величина ДУгар определяется обычно баковым коэффици¬
ентом и практически не зависит от параметров траектории спуска.
Проследим, как влияет режим движения на участке аэродина¬
мического торможения на конечную фазу этого торможения. Пара¬
метрами траектории, варьируемыми при оптимизации, являются
балансировочный угол атаки для аппарата принятой конфигурации
и набор управляющих воздействий, определяющих закон изменения
угла крена, т. е. величину эффективного качества. Эти управляю¬
щие воздействия могут формировать программу разворотов, опреде¬
ляя мо,менты включений двигателей ориентации или, что более
наглядно, определить моменты переключений с одного значения
эффективного качества на другое или с одного закона программ¬
ного отслеживания перегрузки на другой.
На рис. 3.1 приведены в координатах высота, •— скорость полета
четыре характерные траектории спуска аппарата, имеющего кони-
45
ческий лобовой щит с углом полураствора 70° и с удлинением 0,9.
Считается, что аппарат сбалансирован на угле атаки, соответст¬
вующем аэродинамическому качеству К = 0,4; имеет нагрузку на
мидель 5900 Н/м2 (600 кгс/м2). Расчеты проводились для модели
атмосферы, близкой к номинальной [24], при скорости входа в ат¬
мосферу 4,6 км/с и при условии, что в момент первого погружения
в атмосферу в режиме полета с максимальным эффективным каче¬
ством реализуется предельная перегрузка 5 ед.
Траектория 1, как видно из рисунка, является траекторией с от¬
ражением; это предельно рикошетируется траектория, поскольку на
ней поддерживается максималь¬
ное эффективное качество (угол
крена постоянен и равен нулю).
Траектория 2 есть предельно
глубокая траектория, поскольку
на ней в течение всего полета
поддерживается максимальная
перегрузка, в результате чего ап¬
парат не успевает затормозиться
и у поверхности имеет скорость
полета, соответствующую этой пе¬
регрузке (1,7—1,9 км/с).
В первом случае скорость
подлета к поверхности также ве¬
лика, поскольку повторный ны¬
рок в атмосферу происходит по крутой траектории.
Предпочтительными оказываются режимы полета с пологой тра¬
екторией после первого нырка, поскольку аппарат имеет значитель¬
ное время торможения в плотных слоях атмосферы и полого под¬
ходит к поверхности планеты. Две такие траектории показаны на
рис. 3.1. В обоих случаях аппарат подлетает к поверхности с мак¬
симальным эффективным качеством так, как это производится на
всей траектории 1. Однако после прохождения максимальной пере¬
грузки сразу после входа в атмосферу предусмотрено, в отличие от
траектории 1, снижение эффективного качества, т. е. проекции
подъемной силы на вертикаль. На траектории 3 организован поло¬
гий рикошет за счет того, что в период полета, начиная со скоро¬
сти 3,2 км/с и кончая скоростью 1,2 км/с, аппарат движется с уг¬
лом крена 10°, соответствующим значению эффективного качества
0,135. Траектория 4 имеет в тот же период полета участок изовы-
сотного выравнивания. Текущее значение угла крена определяется
на этом участке из условия равенства нулю производной угла
наклона вектора скорости к горизонту/
На траекториях 3 и 4 реализуются на высотах 2—4 км близкие
к минимуму значения скорости полета, причем на траектории с
пологим рикошетом величина этой скорости несколько ниже. Одна¬
ко предпочтительнее траектория с изовысотной площадкой, по¬
скольку из-за более пологого подлета к высотам 3—4 км затраты
46
топлива на предпосадочное торможение будут несколько ниже, чем
на рикошетирующей траектории.
Рассмотрим теперь, как меняется для таких настильных траек¬
торий скорость подлета к поверхности при изменении несущих и
тормозных характеристик аппарата. Зависимость конечной скоро¬
сти полета на различных высотах при спуске с изовысотным участ¬
ком от нагрузки на мидель аппарата при различных величинах
располагаемого качества для номинальной модели атмосферы пред¬
ставлена на рис. 3.2. Можно отметить резкое возрастание скорости
при малых нагрузках, увеличивающихся ог 200—500 Н/м2 (20—
50% кгс/м2) до 2000—3000 Н/м2 (200—300 кгс/м2) и дальнейший
пологий рост при Рх больше 4000 Н/м2—5000 Н/м2 (400—
500 кгс/м2).
Рис. 3. 2. Зависимость конечной ско¬
рости полета от нагрузки на модель
аппарата
Рис. 3. 3. Зависимость конечной
скорости полета на высоте
2 км от нагрузки на мидель
(при неизменном) и зависи¬
мость той же скорости от ка¬
чества при неизменной нагрузке
на мидель
р^р-о^гв)
KpfPt-SOOO)
0,
2 Z7,
6 о\
□
1
3 1,0 /тд
Как видно из рисунка (нижние кривые), чувствительность тра¬
екторий по критерию конечной скорости к располагаемому аэроди¬
намическому качеству нелинейна. Эта нелинейность более нагляд¬
но просматривается на графике рис. 3.3, где показано, как меняет¬
ся на высоте 2 км скорость полета для траекторий с режимом
выравнивания при возрастании располагаемого качества для неиз¬
менного Рх (Рх = 7850 Н/м2 (800 кгс/м2), а также при возрастании
нагрузки на мидель для постоянного качества (/<=0,526). Еще раз
проследим, как в области больших Рх конечная скорость растет с
ростом Рх довольно вяло. Градиент изменения скорости по вели¬
чине располагаемого качества явно не постоянен, и более всего
уменьшается скорость при возрастании качества от 0,2 до 0,6.
Вообще говоря, нельзя рассматривать раздельно зависимость
конечной скорости от Рх и К, поскольку обе эти характеристики
тесно связаны между собой через поляру аппарата. Для аппарата
47
одной и той же аэродинамической формы и размеров увеличение
его несущих способностей сопровождается ухудшением тормозных
характеристик, и правильнее было бы рассматривать влияние угла
атаки на величину конечной
формы аппарата зона
балансировочных уг-
на рис. 3.4 просматри-
зона для аппарата
форме симметричного
конуса с углом
70°. “
скорости полета
от угла атаки
траекторий,
конеч-
балан-
Рис. 3.4. Зависимость
ной скорости полета от
сировочного угла атаки
по-
Приведены две
на
для
скорости. Оказывается, существует
для каждой
наилучших
лов атаки, и
вается эта
со щитом в
затупленного
лураствора
зависимости
высоте 2 км
изовысотных траекторий, причем
одна зависимость характеризует ап¬
парат с развитым лобовым щитом,
а другая — свойственна аппарату с
относительно малым диаметром и
удлинением, близким к 'единице.
Значения конечной скорости полета, рассмотренные ранее, име¬
ет смысл аппроксимировать приближенными формулами, опреде¬
ляющими для оптимальных траекторий спуска эту скорость в зави¬
симости от высоты полета и нагрузки на мидель аппарата для диа¬
пазона рациональных режимов балансировки, т. е. при определен¬
ных значениях располагаемого качества (Кр), характерных для
затупленных и умеренно-заостренных форм.
Для большинства моделей атмосферы структура формул может
быть предложена из условия равновесного движения, благодаря
чему эти формулы имеют вид:
(3. 2)
где Ку — коэффициент, определяющий способ управления на уча¬
стке спуска и особенности применяемой модели атмосферы; gn —
ускорение свободного падения вблизи поверхности планеты; g3 —
ускорение свободного падения в атмосфере Земли; — плотность
атмосферы на конечной высоте полета; f(Kp) — функция, опреде¬
ляющая зависимость скорости от величины качества в области оп¬
тимальных значений Кр.
При изовысотном законе управления и для сегментальных или
конических затупленных форм для номинальной модели атмосферы
формула (3.2) имеет вид
1/'яо=0,49ея0'5Р^(1,26/<^0,77/<р + 0,45)0’5, (3.3)
и при этом описывает в диапазонах 980 Н/м2 (100 кгс/м2)
^6800 Н/'м2 (700 кгс/м2); 0,2Кр0,6, с точностью в пределах
десяти процентов величину скорости полета на высотах от нуля
до 4 км.
48
Предлагаемый метод определения оптимальных параметров
средств спуска и посадки опирается на параметрические расчеты,
в которых используются распространенные понятия: нагрузка на
мидель, удельная масса квадратного метра конструкции, удельная
масса камер двигательной установки, относительный вес системы,
тяговооруженность и т. д. Авторы не решились перейти к массо¬
вым показателям и сохранили общепринятые весовые критерии,
поскольку это допускается ГОСТом.
Вес средств спуска и посадки GCCn состоит из следующих ком¬
понентов:
^ссп ^к.т ^д.у ^оборуд’
где GICT — вес конструкции и теплозащиты аэродинамического
тормозного устройства; Од.у — вес двигательной установки с запа¬
сом топлива; ООборуД — вес оборудования.
Третья из названных составляющих практически не зависит от
проектно-баллистических параметров аппарата, поэтому будем оп¬
ределять оптимальную нагрузку на мидель исходя из минимума
веса конструкции с теплозащитой и двигательной установки.
Для марсианских тяжелых СА весовые характеристики конст¬
рукции корпуса входят в противоречие с аналогичными характе¬
ристиками посадочной двигательной установки и при этом основ¬
ным параметром, их связывающим, является скорость полета в мо¬
мент включения двигателя перед посадкой. Задачей оптимизации
является выявление оптимальной нагрузки на мидель. Будем опре¬
делять оптимальный вес средств спуска и посадки в относительных
единицах, не привязывая оптимальную нагрузку на мидель к кон¬
кретным размерам аппарата и соотнося компоненты веса средств
спуска и посадки с начальным весом Go, который характерен для
аппарата перед входом в атмосферу.
Вес конструкции и теплозащиты обычно в параметрических про¬
ектных расчетах оценивают через удельный вес несущих или сма¬
чиваемых поверхностей. Будем и мы оперировать удельным весом,
приняв в качестве такой величины приходящийся на каждый 1 м2
несущей плоскости вес конструкции и теплозащиты:
(3.4)
Из определения Рх
защиты
получим для веса конструкции и тепло-
О у л Qxpx • (3.5)
Предполагать, что 6-уд сохраняется неизменным для аппаратов раз¬
личной конфигурации и размерности не следует даже при парамет¬
рических проектных оценках. Рост размеров аппарата и его несу¬
щей поверхности при одном и том же суммарном весе должен
неизбежно приводить к уменьшению веса одного квадратного метра
несущей поверхности в силу нижеследующих обстоятельств. Во-
49
первых, с уменьшением нагрузки на мидель снижается теплона-
пряженность траекторий спуска, аппарат тормозится в более верх¬
них слоях атмосферы и вес покрытия, защищаемого от теплового
воздействия каждый квадратный метр поверхности лобового щита
и донного обтекателя, уменьшается. Этому уменьшению способст¬
вует также дополнительное снижение конвективных тепловых пото¬
ков из-за увеличения радиуса затупления с ростом размеров ап¬
парата.
Во-вторых, с ростом размеров несущей поверхности уменьшает¬
ся доля веса конструкции, приходящаяся на единицу площади этой
поверхности, которую составляют силовые элементы каркаса ап¬
парата, крепеж полезной нагрузки, узлы и агрегаты люков, меха¬
низмы разделения и т. д. Некоторое увеличение веса работающей
на устойчивость несущей оболочки лобового щита из-за возраста¬
ния радиуса затупления замедляет общую тенденцию к снижению
веса 1 м2 несущей поверхности с ростом ее площади.
В пределе при значительном увеличении размеров щита (Рх—>
—>0) вес конструкции каждого метра такого щита будет стремить¬
ся к очень малой величине.
Для аппаратов с. привычными соотношениями диаметра и дли¬
ны, с умеренными размерами и значениями нагрузки на мидель
(Рт = 4000—8000 Н/м2 (400-Н800 кгс/м2) удельный вес конструкции
и теплозащиты корпуса, приходящийся на каждый квадратный метр-
несущей площади, меняется незначительно с изменением диаметра
аппарата.
Из всего изложенного следует, что, во-первых, удельный вес
конструкции и теплозащиты, приходящийся на 1 м2 несущей пло¬
щади, не является постоянной величиной для аппаратов с различ¬
ными размерами несущих площадей, и, во-вторых, этот удельный
вес зависит от нагрузки на мидель нелинейно, возрастая с увели¬
чением этой нагрузки, причем наиболее интенсивное приращение
удельного веса следует ожидать при увеличении малых нагрузок
на мидель. _
В общем случае соотношение между удельным весом £уд и на¬
грузкой на мидель аппаратов затупленных форм имеет смысл опи¬
сать, используя закономерности вида:
(3.6)
где С2 — показатель степени, меняющийся в диапазоне между ну¬
лем и единицей.
На рис. 3.5 показаны типовые зависимости удельного веса от
нагрузки на мидель, полученные при аппроксимации результатов
проектно-компоновочных проработок аппаратов, имеющих различ¬
ные соотношения площади лобового щита и суммарной смачивае¬
мой поверхности. Эти зависимости имеют вид
Оуд = ^к.г^’5> (3.7)
где /<к.т — коэффициент, определяющий градиент роста 6УД, для
конструкции с теплозащитой. Подставляя (3.6) в (3.4) и переходя
50
к относительным единицам, получим
(3.8)
/7 IS 1
vrK.T к.т г .->0,5
Несомненно, приведенные зависимости отражают скорее качест¬
венную, нежели количественную сторону закономерностей, связы¬
вающих вес конструкции и размерность лобового щита спускаемого
аппарата. В каждом конкретном случае весовые характеристики
будут зависеть от силовой схемы аппарата, особенностей нагруже¬
ния, расчетных случаев, конструктивной схемы узлов и агрегатов
лобового щита и применяемых материалов для конструкции и теп¬
лозащиты. Однако при параметрических оценках, как правило, при¬
ходится пренебрегать особенностями конструкции с тем, чтобы,
определив область оптимальных значений проектных параметров,
уточнить их значения, использовав дополнительные более деталь¬
ные расчетные модели.
Рис. 3. 5. Зависимость удельного веса квадрат¬
ного метра несущей площади от нагрузки на
мидель
Рассмотрим весовую модель двигательной установки для пред¬
посадочного торможения и посадки. Вес двигателя состоит из сле¬
дующих компонентов:
^д.у = Окам + ^тонл + Обак» (3. 9)
где бКам — вес камер сгорания; GTOna — вес топлива на все опе¬
рации, связанные с посадкой; Ggan — вес баков с арматурой.
Переходя в формуле (3.9) к относительным единицам и относя
все компоненты к суммарному весу аппарата, получим
^д.у = Ткам^оН (1 +#т.о)’ (3- Ю)
G0
где уКам — удельный вес камер сгорания (кгс веса на кгс тяги):
л0 — начальная тяговооруженность посадочного двигателя; ат.о —
51
баковый коэффициент, являющийся отношением веса баковых сис¬
тем к весу топлива.
Поскольку
Go-G-гопл =е (3. Ц)
°о
то
^д.у = (1 +аг.о) (1 —eJg) +Ткам^О- (3.12)
В начале главы мы рассмотрели составляющие характеристической
скорости, причем разделили на следующие компоненты:
Ух = УН0~Г ^Уг.и + ДУу11р + &VмакДУюстДУгор =
= АКс.торм + ДУх.псс + ДУ гар-
Величина AVrap определяется баковым коэффициентом и учитыва¬
ется в ат о.
о 1бд год здо <м здо рк,кгс/нг
Рис. 3.6. Изменение составляющих массы
средств спуска и посадки при трансформации
несущей площади аппарата
Учитывая (3.1), получим зависимость от ИГо):
У^КуУнЛ^У^ (3-13)
где АУх.пос не зависит от УНо-
Величина Vx не превышает 1500—2000 м/с, поэтому без боль-
ших погрешностей формулу (3.12) можно преобразовать в следую¬
щее выражение:
a„=d+»,j(^-^)+v„A. (3.14)
52
Учитывая выражение (3.3) для 17Hoi, получим
Если тяговооруженность ДУ посадки при параметрических оценках
принять постоянной для разных вариантов спускаемых аппаратов,
Рис. 3.7. Зависимость массы средств
спуска и посадки от полезной нагрузки
для аппаратов с различной несущей пло¬
щадью
то высота включения двига¬
теля предпосадочного тор¬
можения также будет неиз¬
менной для аппаратов с лю¬
быми нагрузками на мидель.
Задавшись величиной Лр>
G Vh,m/q
Рис. 3. 8. Зависимость отно¬
сительной массы двигателя
и скорости полета в момент
его включения от начальной
тяговооруженности
близкой к оптимальной для рассматриваемого класса форм,
можем определить оптимальный Рх из условия
(^к.т + ^д.у) = 0- (3. 17)
Подставив (3.8) и (3.15) в выражение (3.17) и предполагая
AVx.noc малой величиной, получим результирующее уравнение для
определения оптимальной нагрузки на мидель:
(3.18)
где у=\/У Рх.
При реальных значениях Сх, J, HQ, ат.о оптимальная величина
Рх находится в диапазоне 1500 Н/м24-3500 Н/м2 (150 кгс/м2н-
350 кгс/м2).
На рис. 3.6 показана типовая картина изменения составляющих
веса средств спуска и посадки при трансформации несущей площа¬
53
ди аппарата для одного из возможных сочетаний названных выше
исходных данных.
Как уже говорилось в гл. 1, относительный вес средств спуска
и посадки не может быть объективным критерием для сравнения
и рис. 3.7 подтверждает это обстоятельство. На нем изображены
зависимости отношения веса средств спуска и посадки к весу по¬
лезной нагрузки СА от нагрузки на мидель, т. е. от размеров несу¬
щей площади при постоянном суммарном весе аппарата. Оптимум
в районе Рх= (1500 Н/м2-^3000 Н/м2) (150 кгс/м2н-300 кгс/м2), раз¬
мытый на графике рис. 3.6, на рис. 3.7 проступает более отчетливо.
Рассмотрим в заключение вопрос об оптимальной тяговоору-
женности посадочного двигателя. Для марсианского посадочного
аппарата определение оптимальной тяги на участке посадки следу¬
ет производить, учитывая как гравитационные потери при предпо¬
садочном торможении, так и прирост характеристической скорости
при изменении начальных условий в момент включения двигателя.
Поскольку аппарат при подлете к поверхности активно тормозится
за счет аэродинамического сопротивления, то выгоднее включать
посадочный двигатель как можно ниже, реализуя тяговооружен-
ность около 2 ед. На рис. 3.8 приведена типовая зависимость отно¬
сительной массы топливного отсека (GT.o) и двигательной установ¬
ки Од.у, а также скорости полета в момент включения двигателя
от начальной тяговооруженности посадочного аппарата.
Глава 4. АНАЛИЗ ХАРАКТЕРИСТИК ТРАЕКТОРИЙ
ПРИ УПРАВЛЯЕМОМ ВХОДЕ И СНИЖЕНИИ
В АТМОСФЕРЕ ВЕНЕРЫ
Высокая плотность атмосферы Венеры определяет облик спус¬
каемых аппаратов и перечень операций, проводимых во время
спуска и последующего снижения на поверхность. Противоречивые
требования, предъявляемые к аппарату на разных этапах движе¬
ния, заставляют менять конфигурацию аппарата по мере проникно¬
вения в атмосферу. Вход в атмосферу происходит со значительной
скоростью, которая достигает 12 км/с при спуске с подлетных тра¬
екторий, 10,2 км/с при спуске с высокоэллиптической орбиты и
7,5 км/с при сходе с околопланетных орбит. Аппарат интенсивно
тормозится в верхних слоях атмосферы, и при пологом входе его
режимы движения и теплообмена подобны аналогичным процессам,
протекающим в земной атмосфере. Облик спускаемого аппарата,
предназначенного для задач торможения в период входа в атмос¬
феру, не отличается от традиционного облика СА. Однако процесс
интенсивного торможения завершается, как правило, уже к высо¬
там 30—40 км, после чего аппарат начинает плавно снижаться,
погружаясь в плотную, разогретую до 700° С атмосферу.
Аппараты для снижения или дрейфа в атмосфере, давление в
которой достигает 100 кгс/м-, по конструкции и внешнему виду
54
ближе к глубоководным батискафам, нежели к летательным аппа¬
ратам.
Существуют две группы проблем, с которыми приходилось стал¬
киваться в прошлом при создании баллистических спускаемых ап¬
паратов и придется столкнуться в будущем при создании тяжелых
управляемых аппаратов для исследования Венеры.
Первая группа проблем связана с выбором рациональных спо¬
собов торможения в верхних слоях атмосферы, со снижением уров¬
ня перегрузок и теплонапряженности траекторий спуска.
Вторая группа проблем определяется режимом работы при
высоких наружных давлениях и температурах и задачами сниже¬
ния и посадки в таких условиях.
Рис. 4. 1. Область дости¬
жимых скоростей сниже¬
ния при посадке на по¬
верхность Венеры
Рис. 4. 2. Начальная высота
снижения при различных
характеристиках спускае¬
мых аппаратов
Одним из путей решения задач посадки на Венеру является
функциональное разделение планетного посадочного комплекса на
спускаемый и посадочный аппараты, причем второй является по
лезной нагрузкой для первого. Условия на планете, по-видимому,
непригодны для проведения десантных операций и создания в обо¬
зримом будущем планетных комплексов, оборудованных средствами
возвращения на Землю или околопланетную орбиту. Однако созда¬
ние тяжелых управляемых СА, способных эффективно тормозиться
в верхних слоях планеты, доставляя туда посадочные или дрейфую¬
щие аппараты, совершающие полет в более плотных слоях атмос¬
феры, является по-видимому, одной из задач космонавтики в бли¬
жайшем будущем. Рассмотрим применительно к таким аппаратам
проектно-баллистические вопросы, связанные, во-первых, со сни¬
жением перед посадкой, и, во-вторых, с управляемым полетом на
границе плотных слоев атмосферы.
В отличие от спуска в атмосфере Марса (см. гл. 3) задача га¬
шения энергии аппарата и получения приемлемых посадочных ско¬
ростей для Венеры осуществляется без специальных изменений в
конструкции и без проведения особых операций, связанных с уп¬
равлением на участке спуска. Аппарат баллистического спуска,
входящий в атмосферу в широком диапазоне углов входа (от—30
до —90°) затормозится до скоростей, необходимых для работы по¬
садочных систем. Скорость снижения на поверхность планеты
определяется удельной нагрузкой на мидель аппарата, зависит от
55
условий входа в атмосферу и практически не зависит от аэродина¬
мического качества. На рис. 4.1 приведена область достижимых
скоростей снижения, характерная для различных тормозных харак¬
теристик аппарата при отклонениях параметров атмосферы. Видно,
что достижение приемлемых посадочных скоростей обеспечивается
без применения специальных систем подтормаживания. Завершение
режима интенсивного торможения при входе в атмосферу и пере¬
ход к снижению с медленным погружением имеет смысл зафикси¬
ровать, так как именно в этот период меняется способ управления
траекторией, прекращают работу системы спускаемого аппарата,
Рис. 4. 3. Зависимость
максимальной пере¬
грузки от располагае¬
мого качества при
коридоре входа 40 км
и при спуске с под¬
летных траекторий
(для аппаратов с на¬
грузкой на мидель
2000—5000 н/м2) со
скоростью входа в
атмосферу:
7—12 км/с; 2—11 км/с
Рис. 4.4. Зависимость
максимальной перегрузки
от располагаемого каче¬
ства при спуске с около¬
планетных орбит (Рх =
= 20004-5000 Н/м2; V=
=94-10 км/с) с коридо¬
ром входа:
/—80 км; 2—40 км; 5—20 км
начинают функционировать средства для посадки или развертыва¬
ются парабалонные системы, предназначенные для аэростатическо¬
го торможения посадочного аппарата. По-видимому, именно пере¬
ход на дозвуковые скорости полета означает, что можно переходить
к развертыванию посадочных систем. На рис. 4.2 можно проследить,
когда наступает такой момент для определенных условий входя в
атмосферу (скорость входа 11 км/с, угол наклона траектории на
высоте 130 км составляет 30°). Переломным моментом в режиме
движения считалось достижение скорости полета, равной 200 м/с.
Зависимость конечной высоты полета в этот момент (//к) для но¬
минальной модели атмосферы для траектории спуска в режиме
максимального эффективного качества и для аппаратов, имеющих
различные несущие характеристики Кр и удельную нагрузку на
несущую поверхность Рх позволяет сделать вывод о том, что при
приемлемых размерах аппарата рост располагаемого качества поз¬
воляет переходить в режим снижения на больших высотах, увели¬
56
чивая тем самым время пребывания аппарата в верхних слоях ат¬
мосферы и эффективность операций по зондированию атмосферы
планеты. Характерно, что даже при баллистическом спуске началь¬
ная высота снижения равна 20—40 км. Однако баллистический
спуск в сочетании, с крутыми углами входа в атмосферу сопро¬
вождается высокими перегрузками и тепловыми потоками. Приме¬
нение малого или умеренного аэродинамического качества позволя¬
ет при пологом входе в атмосферу (углы входа меньше 30°) снизить
перегрузки и уменьшить теплонапряженность траекторий спуска.
График на рис. 4.3 иллюстрирует результаты расчетов предельных
траекторий входа, реализуемых при движении вблизи верхней гра¬
ницы коридора входа (условие захвата атмосферой) и вблизи ниж¬
ней границы коридора входа, определяемой максимальной пере¬
грузкой. Потребный размер коридора входа определялся по раз¬
нице высот фиктивных перигеев, и результаты соответствуют
коридору входа размером 40 км при условии, что аппараты имеют
тормозные характеристики, близкие к общепринятым [Рх = 2000—
5000 Н/м2 (2004-500 кгс/м2)]. На графике показана зависимость
максимальной перегрузки, реализуемой при входе по нижней
границе коридора (углы входа 5—7° на высоте 130 км) от распола¬
гаемого качества при условии, что захват при движении по верхней
границе коридора заданного размера обеспечивается рассматривае¬
мым'’значением качества (при отрицательной подъемной силе).
Область между двумя приведенными кривыми характерна для
большинства подлетных траекторий, скорость входа в атмосферу у
которых колеблется между 11 км/с (нижняя кривая) и 12 км/с
(верхняя кривая). По аналогии с возвращением на Землю с под¬
летных межпланетных траекторий увеличение аэродинамического
качества позволяет при пологом входе в атмосферу резко снизить
предельные перегрузки. Например, перегрузки уменьшаются в 2,5—■
3 раза при переходе от баллистического аппарата к аппарату с
умеренным аэродинамическим качеством величиной 0,6—0,8.
Еще большее снижение перегрузок ожидается при спуске с око¬
лопланетных орбит. Дополнительные высокоэнергетические затраты
при таком способе зондирования атмосферы окупаются возможно¬
стью обстоятельного выбора района исследования в атмосфере с
тем, чтобы направить туда планетный комплекс. На рис. 4.4 мож¬
но видеть, как для аппаратов с названными выше тормозными ха¬
рактеристиками меняется величина максимальной перегрузки с
ростом располагаемого аэродинамического качества в случае входа
с припланетных орбит.
Заштрихованные зоны характеризуют возможности спускаемых
аппаратов, входящих в атмосферу с высокоэллиптических орбит,
причем нижние границы каждой зоны соответствуют скорости входа
в атмосферу 9 км/с, а верхние скорости входа 10 км/с. Для различ¬
ных зон, показанных на рис. 4.4, характерны разные требования к
управлению при операциях схода с орбиты планетного зонда. Зона/,
границы которой показаны штрих-пунктиром, соответствует не¬
высоким требованиям при управлении сходом с орбиты, но опреде¬
57
ляет высокие перегрузки для аппаратов традиционных форм, при¬
чем снижение перегрузок связано с переходом на аппараты с
высоким аэродинамическим качеством. Размер потребного коридора
входа в этом случае равен 80 км. Зона 2, ограниченная штриховы¬
ми линиями, свойственна коридору входа размером 40 км и, нако¬
нец, зона 3, границы которой показаны сплошными линиями, соот¬
ветствует коридору входа 20 км. В последнем случае оказывается
возможным для аппаратов традиционных форм снизить перегрузки
до приемлемых величин.
Выбор соответствующего режима движения на участке спуска
дает для аппарата с умеренным располагаемым качеством дополни¬
тельную возможность завершить торможение на больших высотах,
чем при полете с постоянной подъемной силой (см. рис. 4.2).
Рис. 4.5. Параметры траектории спуска с ре¬
жимом выравнивания:
I—участок входа в атмосферу; П—изовысотный уча¬
сток; III—изоперегрузочный участок
Применение режимов выравнивания после прохождения макси¬
мума перегрузок позволяет простым способом избавиться, с одной
стороны, от рикошета и вылета из атмосферы и, с другой стороны,
избежать нырка с потерей высоты. Одним из способов выравни¬
вания является управление с применением изовысотного закона
изменения эффективного качества. Условию равенства нулю произ¬
водной угла наклона траектории к местному горизонту соответст¬
вует в уравнениях движения вполне определенный закон изменения
располагаемого качества и сопротивления аппарата. Реализовать
полет с постоянным углом наклона траектории при постоянной
нагрузке на мидель без изменения угла атаки, т. е. при управлении
креном вокруг вектора скорости, возможно при малых начальных
углах наклона траектории, т. е. практически сразу после момента
прохождения максимальной перегрузки и перед началом рикошета.
Если углы наклона траектории считать малыми, то программная
зависимость для угла крена аппарата имеет вид
у„=агссозЦЛ(1_£_)<у,
где
58
пологим снижением. На
Кр. н,™
Л .
200100
ЮО
120
50
■80
4Z7
I
1
1
J
L-
: А
I.
г ■.
1
1
. ..1
1
IQ
Рис. 4.6. Отображение в координатах
высота — скорость полета траектории
спуска с изовысотной площадкой:
I—участок входа в атмосферу; II—изовысог-
ный участок; III—изоперегрузочный участок
При этом пХу — программное текущее значение перегрузки, опре¬
деляемое величиной скорости полета; gn, — ускорение силы тя¬
жести и радиус планеты; g3 — ускорение силы тяжести на Зем¬
ле; Не max — величина максимальной перегрузки перед выходом на
режим выравнивания.
Результаты поиска оптимального режима торможения показы¬
вают, что на основной части траектории спуска целесообразным яв¬
ляется движение с выравниванием или
рис. 4.5 приведен пример оп¬
тимальной траектории при
входе по нижней границе кори¬
дора размером 40 км. Ско¬
рость входа в атмосферу
составляет 11 км/с, нагрузка
на мидель 5000 Н/м2, распола¬
гаемое качество — 0,5.
Изовысотный участок вы¬
равнивания обеспечивается из¬
менением эффективного ка¬
чества, потребная величина
которого показана пунктиром
на том же графике.
Изовысотный участок тра¬
ектории и следующий за ним
изоперегрузочный участок более наглядно отображаются на гра¬
фике (рис. 4.6), где в координатах высота — скорость полета изо¬
бражена та же траектория. Пунктиром показано потребное номи¬
нальное значение угла крена, определяемое из условия реализа¬
ции заданных законов управления. Завершение участка интенсив¬
ного торможения в атмосфере производится при максимальной
подъемной силе с нулевым углом крена аппарата.
Результатом описанной программы торможения является вывод
спускаемого аппарата за относительно короткое время и без зна¬
чительной потери высоты в конечную фазу торможения, на которой
начинает функционировать посадочный аппарат.
Глава 5. ОПРЕДЕЛЕНИЕ ПРОЕКТНЫХ ПАРАМЕТРОВ СПУСКАЕМОГО
АППАРАТА ЗОНДА В АТМОСФЕРУ ЮПИТЕРА
Специфика входа в атмосферу Юпитера определяется большой
скоростью подлета-к планете. Эта скорость зависит в основном от
значения параболической скорости освобождения, величина которой
определяется мощным гравитационным полем планеты и превыша¬
ет 60 км/с.
При анализе условий входа в атмосферу Юпитера необходимо
учитывать вращение планеты. Это обстоятельство позволяет сни¬
зить скорость входа в атмосферу до 49—50 км/с, организовав вход
по пологой траектории в восточном направлении в районе экватора
59
по направлению движения вращающейся атмосферы. Основная
часть кинетической энергии аппарата гасится в процессе интенсив¬
ного торможения в верхних слоях атмосферы до достижения об¬
лачного слоя. Расстояние от центра планеты до облачного слоя
принимается обычно за нулевой уровень отсчета, и так же, как и в
земных условиях, давление на этом уровне равно одной атмосфере.
В настоящее время большинство моделей атмосферы планеты
Юпитер строится из предположения о незначительном изменении
температуры по высоте в верхних слоях атмосферы, при этом пред¬
полагается, что в составе атмосферы имеется в основном водород
(70—85%%) и гелий (30—15%%).
Осуществление спуска, целью которого является доставка кон¬
тейнеров с приборами для измерения параметров атмосферы, ос¬
ложняется высокой скоростью входа в атмосферу, приводящей к
интенсивному тепловому и перегрузочному воздействию на аппарат.
В аэродинамическом нагреве доминируют радиационные тепло¬
вые потоки от ударного слоя, аппарат тормозится интенсивно с пе¬
регрузками, достигающими сотен единиц, тепловое воздействие на
покрытие носит характер теплового удара.
В отличие от СА, входящих в атмосферу Земли, Марса и Вене¬
ры, СА зонда, предназначенного для Юпитера и других планет-ги¬
гантов, подвергается более мощному тепловому воздействию, и
проблема тепловой защиты такого аппарата является одной из
основных в процессе его создания. Выбор формы СА предопреде¬
ляет задачу минимизации веса конструкции и теплозащиты.
Представим себе, каковы могут быть режим полета и облик та¬
кого аппарата и чем должен отличаться этот аппарат от традици¬
онных СА, совершивших посадку на ближние планеты. Логично
предположить, что для первых экспериментов по зондированию
атмосферы Юпитера предпочтение будет отдано простым апробиро¬
ванным схемам и надежным техническим решениям. Можно также
предположить, что аппараты, создаваемые впервые, будут совер¬
шать баллистический, неуправляемый спуск по аналогии с первыми
марсианскими, земными и венерианскими спускаемыми аппара¬
тами.
В числе систем, обеспечивающих спуск и влияющих на выбор
формы основными являются конструкция и теплозащита. В конст¬
рукцию входят оболочка, силовой набор корпуса, крепежные дета¬
ли полезной нагрузки, узлы для крепления аппарата, люки и сты¬
ковочные шпангоуты. Оболочка аппарата может быть негерметич¬
ной, но должна быть жесткой, чтобы выдерживать динамические
нагрузки при колебаниях аппарата в момент входа в атмосферу.
Приборы и оборудование при этом располагаются в гермоотсеках.
Несущая часть оболочки (лобовой щит) работает на устойчивость
от наружного давления, достигающего при максимальных скорост¬
ных напорах величины порядка десятка атмосфер. Теплозащита
включает в себя уносимое покрытие, прогреваемую теплозащиту и
теплоизоляцию. Мощные тепловые потоки требуют применения
теплозащитных покрытий с высокой энтальпией разрушения, зна¬
60
чительной рабочей температурой сублимации, хорошими отражаю¬
щими свойствами твердой фазы в наружном фронте разложения
покрытия и высокими поглощающими характеристиками продуктов
разрушения покрытия, поступающих в пограничный слой. Процесс
работы теплозащиты сопровождается значительным расходом мас¬
сы покрытия, в силу чего в пристеночном слое образуется подушка
пиролизного газа, состоящего, в основном, из продуктов разруше¬
ния теплозащиты.
Поступление этого газа, более холодного, нежели водородноге-
лиевая смесь в ударном слое, блокирует конвективные тепловые
потоки, а пелена из продуктов разрушения поглощает в соответст¬
вии с интегральным спектральным коэффициентом поглощения
часть энергии, поступающей от ударного слоя в виде излучения.
Линейная скорость разрушения теплозащитного материала в этот
момент настолько велика, что продвижение вглубь покрытия фрон¬
тов разрушения составляющих теплозащиты опережает движение
«волны прогрева», т. е. перемещение слоя с предельно возможной
для конструкции температурой.
Режим обтекания аппарата на всей основной части траектории
спуска — гиперзвуковой, и аэродинамическая тормозящая сила
определяется распределением давления по поверхности аппарата,
причем сила эта создается сферическим или коническим лобовым
щитом затупленной или умеренно заостренной формы. Задний об¬
текатель аппарата-, находящийся в зоне затенения, может иметь
щитки, обеспечивающие пассивную стабилизацию аппарата при
неориентированном входе в атмосферу донной частью вперед по
потоку.
При выборе проектных параметров следует предположить, что
аппарат в состоянии двигаться по любой траектории внутри расчет¬
ного коридора входа в атмосферу. В данном случае верхняя гра¬
ница коридора входа определяется захватом атмосферой, а нижняя
соответствует максимальной перегрузке. Для аппаратов различ¬
ных форм, имеющих разные баллистические характеристики, за¬
хват атмосферой можно определять минимальным значением пре¬
дельной перегрузки для данного набора моделей атмосферы.
При поиске проектных параметров СА приходится оценивать
массу конструкции и теплозащиты различных конфигураций аппа¬
рата. В соответствии с общей постановкой проектно-поисковой за¬
дачи для СА каждая такая проектная оценка должна проводиться
путем сопоставления всех возможных режимов движения с целью
выделить те из них, которые обеспечивают максимальные значения
массы для конструкции и теплозащиты. Можно предположить, и
результаты расчетов для отдельных форм аппаратов подтверждают
эти предположения, что максимальная масса уносимой теплозащи¬
ты будет реализована на траектории глубокого погружения, отли¬
чающейся от полета при входе по верхней границе коридора.
Наибольшая масса теплоизоляции будет на наиболее протяженной
траектории, реализуемой при движении вблизи верхней границы
коридора входа. Максимальное наружное давление на несущую
61
оболочку лобового щита, определяющее расчетный случай для кор¬
пуса, будет при наибольшем скоростном напоре, т. е. в момент про¬
хождения максимума перегрузок на предельно-глубокой траектории.
Сформулируем допущения при проектном расчете, производимом в
ходе поиска рациональных параметров, определяющих форму,
конструктивные элементы и режим движения СА. Основные из этих
допущений следующие:
1. В расчете объемных и центровочных характеристик достаточ¬
но оперировать размерами внешнего контура аппарата. Варьируе¬
мые при выборе формы геометрические параметры формируют об¬
воды по наружной поверхности теплозащиты перед входом в ат¬
мосферу.
2. При расчете аэродинамических характеристик контур аппара¬
та можно считать неизменным, т. е. величиной линейного уноса и
эррозией поверхности в расчетах сопротивления аппарата имеет
смысл пренебречь.
3. Баллистические характеристики и, в частности, нагрузка на
мидель, определяются по траектории спуска с учетом изменения
размеров несущего сечения из-за линейного уноса. Одновременно с
этим в нагрузке на мидель учитывается уменьшение веса аппарата
в процессе полета из-за массового расхода теплозащитного по¬
крытия.
4. При оценке тепловых потоков необходимо учесть увеличение
радиуса затупления вследствие различного уноса массы покрытия
в критической точке и на периферии лобового щита. Указанное
обстоятельство особенно важно для малых начальных радиусов
затупления у конических лобовых щитов. Оптимальный начальный
радиус затупления, определяемый по соотношению рациональных и
конвективных тепловых потоков составляет 0,104-0,20 м для аппа¬
ратов с нагрузкой на мидель 20004-5000 Н/м2 (2004-500 кгс/м2).
5. Поскольку основная часть траектории спуска, на которой ап¬
парат проходит максимум перегрузок, тепловых потоков и осуще¬
ствляется гашение 99,8% энергии полета, реализуется при гипер¬
звуковых скоростях полета (при числах М>44-6), то для опреде¬
ления аэродинамических характеристик достаточно использовать
гипотезу Ньютона. Отношение давления к скоростному напору в
отдельных точках поверхности принимается при этом неизменным
по траектории спуска.
6. Унос массы теплозащитного покрытия необходимо определять
с учетом экранирования радиационных и блокады конвективных
тепловых потоков слоем газа, образованного продуктами разруше¬
ния теплозащиты.
Изложенные допущения приемлемы на наш взгляд при оценоч¬
ных проектных расчетах режима движения, аэродинамических и
весовых характеристик аппарата. При поверочных расчетах на эта¬
пе рабочего проектирования используют более сложные модели
обтекания и теплообмена.
На рис. 5.1 показаны параметры траектории спуска аппарата
с коническим лобовым щитом, имеющего перед входом в атмосферу
62
Рис. 5. 1. Параметры траектории
спуска в атмосфере Юпитера
нагрузку на мидель 1720 Н/м2 (175 кгс/м2), радиус затупления в
критической точке 0,2 м и угол полураствора конуса 70°. Там же
показано, как меняется для такого аппарата нагрузка на мидель
в процессе полета из-за расхода теплозащитного покрытия.
Поиск оптимальных парамет¬
ров, определяющих форму аппа¬
рата, разбивается на серию про¬
ектных расчетов, в каждом из ко¬
торых определяются массовые
характеристики. Каждый такой
проектный расчет носит итера¬
ционный характер, поскольку в
алгоритме расчета веса или мас¬
сы необходимо задаться бал¬
листическим параметром, кото¬
рый, в свою очередь, определяет¬
ся весом или массой аппарата.
Кроме того, как указывалось ра¬
нее, определение массы систем
должно производиться с учетом
расчетного случая для каждой
системы, т. е. с учетом наихудшей
из возможных траекторий спуска.
Следует учесть также, что для каждого нового сочетания геомет¬
рических параметров аппарата необходимо производить поиск
предельно возможных траекторий, соответствующих верхней и
нижней границам коридора входа. Все вышеизложенное опреде¬
ляет необходимость многократного пересчета траекторий в одной
процедуре проектного расчета. Сократить трудоемкость такой опе¬
рации и уменьшить затраты времени можно, поступившись точно¬
стью оценки характеристик траекторий спуска и отказавшись от
интегрирования уравнений движения. Как правило для оценки мас¬
совых характеристик необходимо знать распределение во времени
нагрузок на аппарат (масса конструкции), скорости полета и плот¬
ности атмосферы на данной высоте (тепловые потоки и масса теп¬
лозащиты). Для проектных оценок желательно знать сразу пре¬
дельные траектории, т. е. траектории с наибольшим и наименьшим
значениями максимальной перегрузки. Для таких целей может
быть предложен метод оценки параметров траектории, использую¬
щий тепловые зависимости перегрузки от времени полета.
Перегрузки при баллистическом спуске сначала резко нараста¬
ют, затем, пройдя максимум, полого падают. Как правило, при пре¬
дельных перегрузках свыше 100 ед. реализуется один максимум
перегрузки, и типовую зависимость ее от времени полета удобно
описать формулой вида
п = ах2е~сх,
где п — перегрузка; т — время полета; а и с — коэффициенты,
определяющие форму перегрузочной кривой, в зависимости от при¬
нятой модели атмосферы и условий входа в атмосферу.
63
Принимая в уравнениях движения перегрузку намного больше
единицы, угол наклона траектории на основном участке торможе¬
ния в атмосфере, близким к нулю, получим после интегрирования
уравнений движения в скоростных осях следующие зависимости
скорости и плотности атмосферы от времени:
1Де
6Z 7\4/2-П1ах/тв,
(5.3)
1тах
Гд
&ун
100
0,15
ж
75
0,15
Ж
50
0,1 и
■\Г
птах
! >
Г7"
Рис. 5. 2. Зависимость максималь¬
ной перегрузки, времени полета
и относительной массы уносимой
теплозащиты от угла входа в ат¬
мосферу
Vbx — скорость входа в атмосферу; тв — время прохождения мак¬
симума перегрузки; /zmax — максимальная перегрузка. Эта пере¬
грузка меньше предельно допустимой для аппарата Пщахн (нижняя
граница коридора входа) и больше минимально допустимой из ус¬
ловий захвата аппарата атмосферой ятахв (верхняя граница ко¬
ридора входа); Рх ср — средняя величина нагрузки на мидель на
траектории. В качестве минимально допустимой перегрузки /гтахв
может быть принята величина 100—150 ед.
На рис. 5.2 показаны результаты точного расчета траектории, а
именно: максимальной перегрузки от угла входа в атмосферу для
аппарата с нагрузкой на мидель
1720 Н/м2 (175 кгс/м2) и для но¬
минальной модели атмосферы.
Моментом входа в атмосферу
считается подлет к высоте 400 км
от облачного слоя. Там же пока¬
зано время торможения до ско¬
рости, равной 1 км/с и относи¬
тельная масса уносимой тепло¬
защиты при различных условиях
входа в атмосферу для аппарата,
имеющего конический лобовой
щит с углом полураствора 70°
и радиусом затупления 0,2 м.
В общем случае уровни максимальных перегрузок связаны за¬
висимостью, которую для проектных расчетов имеет смысл считать
линейной и определять максимальную перегрузку внутри коридора
входа по формуле
^шах ^шах в ( 1 (5.4)
где Д0 — приращение угла входа в атмосферу, определяющее поло¬
жение данной траектории относительно верхней границы.
Коэффициент Кп зависит от принятой хмодели атмосферы и
практически не зависит от баллистических параметров аппарата.
Для проектных расчетов можно принимать ^ = 0,19+0,03. Время
прохождения максимума перегрузки определяется в долях суммар¬
ного времени торможения те, которое, в свою очередь, зависит от
64
импульса скорости и максимальной перегрузки, а именно:
тв=/<хте, Хе==_^К (5.5)
«щах 9,8
где Дер — коэффициент, определяющий среднюю перегрузку или
степень «полноты» эпюры перегрузки, Кер = 0,34-0,36. Коэффициент
Кг зависит от принятой модели атмосферы и колеблется в диапа¬
зоне 0,31—0,34.
Методы проектной оценки массы уносимого и прогреваемого
слоя теплозащиты базируются на рекомендациях отечественных и
зарубежных работ (см. [1, 61, 62, 63]).
Основная сложность при расчетах уноса теплозащиты заключа¬
ется в необходимости учитывать ослабление конвективных и ради¬
ационных потоков слоем пиролизного газа, образованного продук¬
тами разрушения покрытия. Оценка расхода массы теплозащиты в
условиях, когда конвективный тепловой поток блокируется самим
этим расходом, а лучистый частично поглощается в соответствии 6
интегральным спектром поглощения расходуемых продуктов разру¬
шения теплозащиты, производится с помощью рассчитанных для
различных типов покрытий функций ослабления тепловых потоков.
Эти функции учитывают обратную связь в механизме разрушения,
покрытия и представляют собой зависимость отношения тепловых
потоков, поступающих через завесу паров покрытия, потокам, излу¬
чаемым ударным слоем или переносимым газом в пограничном
слое, от соотношения расхода массы теплозащитного покрытия и
расхода массы в набегающем потоке.
Рис. 5.3. Изменение по времени тепловых потоков
и массы уносимой теплозащиты:
для критической точки; для точки на краю ко¬
нического лобового щита
На рис. 5.3 показано, как меняются по времени конвективные
(7К) и радиационные (qr) тепловые потоки и масса уносимой теп¬
лозащиты на траектории с максимальной перегрузкой 200 ед. для
аппарата умеренно-заостренной формы с углом полураствора ко¬
нуса 50° и нагрузкой на модель 2940 Н/м2 (300 кгс/м2).
3 400
65
Делать какие бы то ни было выводы о преимуществах аэроди¬
намической формы только по расчетам уносимой теплозащиты, как
это, к сожалению, имеет место в ряде работ, преждевременно,
поскольку на суммарную массу аппарата влияют потребные толщи¬
ны прогреваемого пакета теплоизоляции, толщина оболочки и раз¬
меры силовых элементов корпуса, а также размеры стабилизирую¬
щих щитков юбки или масса балансировочного груза. Только при
комплексном учете всех указанных факторов, с рассмотрением
объемно-центровочных характеристик и вопросов прочности лобо¬
вого щита возможно достоверно судить о преимуществах той или
иной аэродинамической формы.
Расчеты показывают, что при значительном заострении носово¬
го конуса ухудшаются объемные характеристики аппарата, возрас¬
тает располагаемый объем, следовательно, поверхность аппарата.
Одновременно уменьшается КПД использования поверхности, т. е.
увеличивается суммарная поверхность и поверхность лобового щи¬
та, что могло бы привести к резкому возрастанию массы конструк¬
ции и теплозащиты. Однако относительный вес или масса 1 м2
конструкции лобового щита при этом падает из-за возрастания кри¬
визны оболочки, которая работает на устойчивость от наружного
давления. Радиационные и конвективные тепловые потоки на боко¬
вой поверхности острого конуса значительно меньше, чем в районе
затупления, но при заострении формы тепловые потоки в районе
затупления резко увеличиваются из-за того, что аппарат, обладая
малым сопротивлением и площадью сечения, т. е. большой нагруз¬
кой на мидель, движется при равной предельной перегрузке по
более глубокой и теплонапряженной траектории. Кроме того, при¬
ходится учитывать массу балансировочного груза или средств пас¬
сивной стабилизации (щитков и юбок), которая возрастает при
заострении носового конуса.
По-видимому, если не учитывать другие обстоятельства (компо¬
новка СА на борту космического аппарата, наличие эксперимен¬
тального и технологического задела, степень достоверности проект¬
ных оценок и т. д.) и при выборе формы аппарата исходить из
весовых или массовых критериев, то оптимальной формой для аппа¬
рата массой 500—2000 кг является форма с умеренно-заостренным
коническим лобовым щитом, имеющим угол полураствора 45—55°
и радиус затупления 0,15—0,25 м. Выбор диаметра или удлинения
аппарата зависит от способа, которым обеспечивается статическая
устойчивость при неориентированном входе в атмосферу.
Следует ожидать, что для спускаемого аппарата-зонда, достав¬
ляющего измерительные приборы в атмосферу Юпитера с подлет¬
ной траектории масса конструкции и теплозащиты составляет НО—
140% от массы полезной нагрузки, причем расход уносимого тепло¬
защитного покрытия составляет 204-30% от суммарной массы ап¬
парата.
Вопросы достоверности и точности проектных оценок являются
весьма важными для аппаратов, создаваемых для новых во мно¬
гом неизвестных условий полета, а именно такими являются СА
66
1,5 G
проектных
юпитерианского зонда. Неопределенность условий работы, порож¬
денная незнанием многих параметров атмосферы и планеты, а
также необычными, экстремальными условиями входа в атмос¬
феру, заставляет осторожно относиться к результатам проектных
расчетов по любым, сколь угодно сложным методикам, поскольку
все методики оперируют исходными данными, подверженными
существенному разбросу их значений. В таких условиях обязатель¬
ным дополнением к традиционным и известным проектным крите¬
риям должны быть критерии риска, определяющие прямо или
косвенно возможные колебания значений проектных характеристик,
степень влияния разброса отдельных параметров на разброс значе¬
ний проектных критериев и уровень достоверности сравнительных
оценок, получаемых при сопоставлении возможных значений про¬
ектных критериев с предельными нормами, допустимыми для этих
значений.
В данном случае разброс массовых или весовых характеристик
будет определяться, в первую очередь, разбросом данных, опреде¬
ляющих модель атмосферы, а также параметров, формирующих
условия входа в атмосферу. Определенное влияние на разброс
массового критерия оказывают колебания значений характеристик
материалов для конструкции и теплозащиты (эффективная энталь¬
пия, температура разрушения, степень черноты поверхности и т. д.)
и разброс аэродинамических характеристик аппарата.
На рис. 5.4 приведена гисто¬
грамма распределения, полу¬
ченного при статистическом
моделировании разбросов мае- п
сы конструкции и теплозащиты
для одного из типов спускае¬
мых аппаратов. Приведены от¬
носительные массовые показа¬
тели, причем масса средств
спуска отнесена к массе полез¬
ной нагрузки.
Одним из критериев, позво¬
ляющих оценивать риск, свой¬
ственный процессу принятия
решения по информации, при¬
обретаемой при проектных
расчетах, является вероят¬
ность реализации таких про¬
ектных оценок, при которых создание аппарата становится не¬
целесообразным или попросту невозможным. Предположим, что
существует определенное ограничение на суммарную массу аппара¬
та со стороны межпланетного комплекса. С другой стороны, имеет¬
ся вполне определенная предельная масса приборов, предназначен¬
ных для научных исследований. На рис. 5.4 отмечено предельное
ограничение по массе конструкции с теплозащитой, и это ограни¬
чение определяется минимальной массой полезной нагрузки.
37
33
tx
-
29
к
<
г
<
х
X
-
19
к
к
10
X
-
5
Гистограмма распределения
оценок массы конструкции
с теплозащитой
3*
67
Может сложиться такая ситуация, что масса конструкции и теп¬
лозащиты аппарата превысит пределы, определяемые для него
полезным грузом. В нашем примере вероятность такого события
весьма велика (Р = 0,08).
Изменение параметров аппарата или назначение более обосно¬
ванных и приемлемых весовых резервов со стороны всего космичес¬
кого комплекса позволит уменьшить степень риска при принятии
решений на этапе предварительного проектирования. Критерии,
оценивающие степень риска в условиях неопределенности проект¬
ных оценок, и примеры, иллюстрирующие способы применения
таких критериев, описаны в работе, например, [23].
Часть 2
МЕТОДЫ ИССЛЕДОВАНИЯ МЯГКОЙ ПОСАДКИ
КОСМИЧЕСКИХ АППАРАТОВ НА ПЛАНЕТЫ
БЕЗ АТМОСФЕРЫ
Основные вопросы выбора, расчета и управления на траектори¬
ях подлета и спуска КА на планеты без атмосферы и на Луну ши¬
роко освещены как в специальной, так и в научно-популярной тех¬
нической литературе [3, 16, 17].
Что касается самого последнего, заключительного этапа полета
аппарата (начиная с высот 30—40 м над поверхностью планеты),
включающего момент контакта аппарата с грунтом, скольжение по
грунту и, наконец, полное успокоение аппарата на поверхности в
положении, которое явится исходным для последующего функцио¬
нирования аппарата на данном небесном теле, то, несмотря на всю
ответственность этого этапа, в литературе он, как ни странно, не
нашел должного отражения.
Еще меньше «повезло» в этом смысле вопросам наземной экс¬
периментальной отработки посадочного аппарата межпланетных
станций, которые в лучшем случае только упоминаются с указани¬
ем на их сложность и трудоемкость.
Учитывая сказанное, во второй части книги речь будет идти в
основном о теоретических, экспериментальных и конструкторских
аспектах обеспечения безаварийного мягкого контактирования поса¬
дочного аппарата с поверхностью исследуемой планеты или другого
небесного тела.
Кроме обеспечения «мягкости», посадка аппарата на грунт
должна удовлетворять следующим требованиям:
непременное сохранение устойчивого положения аппарата в те¬
чение всего процесса посадки;
исключение возможности «подпрыгивания» аппарата после пер¬
вого удара о грунт;
положение аппарата на поверхности планеты после посадки
должно обеспечить нормальную работу всех его систем (а если
предусмотрено программой, то и благоприятные условия для после¬
дующего старта);
сведение к минимуму опасности возникновения различных ава¬
рийных ситуаций при посадке путем повышения надежности функ¬
ционирования систем аппарата.
69
Анализ условий посадки на поверхность планет показывает, что
скорость встречи аппарата с грунтом может находиться в пределах
от нескольких единиц до десятка и более метров в секунду. Отсюда
следует, что КА необходимо снабдить надежным посадочным уст¬
ройством со специальным амортизирующим приспособлением. Изве¬
стны различные конструктивные схемы посадочного устройства ап¬
парата, например, лепесткового вида, в виде стержневых опор,
ферменных конструкций, тонкостенных оболочек и пр.
Очевидно, что создание надежно функционирующего посадоч¬
ного устройства межпланетного космического аппарата невозмож¬
но без проведения целого комплекса исследований, включающего в
себя теоретические, экспериментальные, проектные и конструктор¬
ские работы.
Глава 6. ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ДИНАМИКИ МЯГКОЙ
ПОСАДКИ И КОСМИЧЕСКИХ ПОСАДОЧНЫХ АППАРАТОВ
Математическая модель КПА
Космический посадочный аппарат (КПА) вследствие наличия
упругих связей между его отдельными конструктивными элемен¬
тами (полезной нагрузкой, научным оборудованием, двигательными
и приборными отсеками, а также опорами) представляет собой
весьма сложную упругую систему взаимодействующих тел.
Математическое описание динамики посадки на планету без
атмосферы, например, на Марс или Луну такой сложной системы
в общем случае пространственного движения на этапе непосредст¬
венного контактирования опор аппарата с грунтом приводит к чрез¬
вычайно громоздкой системе дифференциальных уравнений, вклю¬
чающей в себя неизвестные величины коэффициентов упругих свя¬
зей между отдельными элементами КПА, которые могут быть опре¬
делены только экспериментально на натурном объекте. Поэтому
проведение расчетов по динамике посадки на поверхность планеты
с помощью такой математической модели КПА из-за их большой
трудоемкости возможно только в виде проверочных на избранные
критические случаи посадки для уже созданного космического ап¬
парата.
Всесторонние исследования динамики мягкой посадки КПА на
этапе эскизного проектирования требуют применения более прос¬
тых и нетрудоемких методов инженерного исследования, позволяю¬
щих оценить различные конструктивные схемы посадочного устрой¬
ства (ПУ) аппарата и выбрать его оптимальные параметры.
Рассмотрим общий случай пространственного движения КПА,
имеющего жесткий корпус и деформируемые посадочные опоры,
состоящие из системы стержней, образующей обратную подвесную
треногу. Центральный стержень треноги снабжен энергопоглотите¬
лем и может деформироваться (рис. 6.1). Сложное движение КПА
70
при мягкой посадке на поверхность планеты можно представить как
два более простых движения:
пространственное движение корпуса КПА;
движение оснований посадочных опор (имеющих некоторую
приведенную массу по поверхности грунта в любом направле¬
нии, но с ограничением, накладываемым самой поверхностью по¬
садки.
Пространственное движение жесткого корпуса КПА происходит
под действием возмущающих сил и моментов, являющихся резуль¬
татом взаимодействия ПУ с грунтом. При этом угол наклона по¬
верхности посадки 9 и коэффициент трения f оснований опор по
поверхности могут варьироваться в широких пределах.
Чтобы описать такое пространственное движение КПА при мяг¬
кой посадке, необходимо составить и решить систему из 6+22V
динамических уравнений, каждое из которых является нелинейным
71
■<
Рис. 6. 2. Блок-схема этапов интегрирования
дифференциальным уравнением второго порядка (Л/ — количество
опор ПУ). Сложность решения таких уравнений требует примене¬
ния численных методов и использования ЭВМ.
Для приведения этих уравнений к форме обычных линейных
дифференциальных уравнений вводится следующее допущение:
все силы, воздействующие на систему, считаются постоянными в
течение достаточно малого шага интегрирования дифференциаль¬
ных уравнений. На блок-
схеме (рис. 6.2) показаны
последовательные этапы
интегрирования.
Динамика мягкой по-
садки КПА в основном
определяется следующи¬
ми факторами:
конструктивными осо¬
бенностями аппарата и
свойствами его энергопо¬
глотителей;
наклоном планетной
поверхности в месте по¬
садки аппарата;.
ориентацией КПА в момент касания одной из опор поверхности
посадки (момент касания опорой поверхности удобно принять за
начало отсчета времени);
вертикальной и горизонтальной составляющими вектора скоро¬
сти КПА в момент касания поверхности планеты;
составляющими вектора угловой скорости аппарата в момент
касания поверхности;
внешними силами, действующими на космический аппарат при
посадке.
Геометрическая форма расчетной модели КПА для любого мо¬
мента времени процесса посадки (от момента первого контакта
какой-либо опоры КПА с грунтом до полной остановки) в целом
может быть охарактеризована координатами нескольких контроль¬
ных точек для этих моментов времени.
К контрольным точкам относятся: центр масс КГ1А (т. 0) и че¬
тыре точки на каждой из его опор П4-4г- (см. рис. 6.1). В процес¬
се посадки координаты контрольных точек 2г-4-4г в подвижной сис¬
теме координат (U, V, W) остаются постоянными, а координаты
точек 1г- (/ — номер опоры) будут переменными вследствие изме¬
нения геометрии ПУ.
Координаты контрольных точек 2iH-4i находятся по формулам
U2l = г cos Az
У 21= — ^2
W2i=r sin Az
£/3Z = r cos (Д,-Z74z = r cos (Д,-— 0);
(6.1)
72
^31 — ^з> ^4Z:
W3i = r sin (Az + P); W4l=r sin (Az-₽),
где Az = (Z — 1)^Ц-Д; Д=-^-; Д = 0 (см. стр.83), Z=l,..., N.
Координаты точек Ц до момента касания грунта основаниями
посадочных опор определяются по формулам
Uu =R cots Az;
Vu=-H> (6.2)
WU = R sin Az.
Координаты точек Д после момента касания грунта основания¬
ми опор определяются из решения уравнений движения опор, что
будет рассмотрено ниже.
Когда координаты всех контрольных точек известны, можно
рассчитать длину деформируемых элементов конструкции по фор¬
муле
j.
Л,2/ = [(^-^)2+(^н-^2+(^и-^2/)2]2- (6.3)
Массово-инерционные характеристики КПА (m=IFn/gn, Jv, Jv,
Jw, rrii и др.) считаются заданными, так как они определяются в
результате анализа компоновки и проведения весовых и центро¬
вочных расчетов.
Для поглощения энергии при мягкой посадке КПА в конструк¬
ции элементов ПУ предусмотрены специальные энергопоглотители.
Эти устройства поглощают основную часть располагаемой кинети¬
ческой энергии КПА. Другая, гораздо меньшая часть энергии, по¬
глощается за счет трения в шарнирах и трения о грунт, а также
внутреннего трения в элементах конструкции. Энергопоглотители
математической модели КПА могут иметь расчетные характеристи¬
ки усилие — деформация любого вида, однако в дальнейшем с
целью упрощения выкладок мы будем рассматривать только энер¬
гопоглотители, имеющие характеристику усилие — деформация в
виде ступенчатой функции (рис. 6.3). При повторном нагружении
энергопоглотителей в процессе посадки необходимо учитывать вели¬
чину остаточной деформации от предшествующего нагружения.
Для исследования динамики пространственного движения КПА
используют три системы координат (см. рис. 6.1):
подвижную систему координат (£7, V, 1^), жестко связанную с
аппаратом (главные центральные оси инерции КПА);
неподвижную систему координат (X Y, Z), связанную с поверх¬
ностью планеты (оси X и Z лежат в плоскости поверхности посад¬
ки, причем ось X совпадает с направлением максимального на¬
клона поверхности, а ось Y — с направлением местной нормали);
неподвижную систему координат (Х'> Y', Z'), связанную с по¬
верхностью планеты (оси X' и Z' лежат в плоскости местного гори¬
зонта, причем ось Z' совпадает с осью Z, а ось Y' — с местной вер¬
тикалью) .
73
Преобразование из системы координат (X Y, Z) в систему
(Х'> Y', Zz) записывается в виде таблицы косинусов углов между
осями этих систем,
Г X Y Z
X' cos 6 sin 6 О
Y' — sin 0 cos 6 О
(6.4)
Z' О
О 1 .
Рис. 6. 3. Ступенчатая характеристика усилие — деформация
При мягкой посадке космического аппарата на поверхность пла¬
неты в конструкции его посадочного устройства возникают опреде¬
ленные силы. В общем случае величины этих сил зависят от харак¬
теристик деформирующихся элементов, используемых в посадочном
устройстве аппарата. Внешние силы прикладываются в момент со¬
прикосновения основания опоры с поверхностью планеты и имеют
направления, противоположные направлениям скоростей оснований
соответствующих опор. Внешние силы определяются для каждого
шага интегрирования Д/ в зависимости от условий, при которых
находится в этот момент динамическая система.
Допустим, что деформирующиеся элементы посадочного устрой¬
ства аппарата изготовлены из разрушающегося материала с не¬
большой упругой деформацией, т. е. имеют ступенчатую характе¬
ристику усилие — деформация.
Представим в общем виде зависимость усилие — деформация
для деформирующихся элементов ПУ со ступенчатой характерис¬
тикой:
74
(6.5)
Л (8)=2 {PP (8 - 8(У+ П) 11 ~ (8 - 8y)] +
7=1
+ \k} (8 - 8(У)) 4-Fy-J [6/ (8 - 8;) - U (8 - 8(y))] |,
где (7(d) — единичная ступенчатая функция;
l/®=°
1
В<0
8 >0.
При повторном нагружении изменения в зависимости усилие —
деформация определяются условиями:
а) если |в(7)|<|В|<|Ву-|, то F}=0 и k] = 0 при l<Zj\
б) если |В;|< |8|< |в(7_ь1)\, то Р}=0 и k} = 0 при l<^j
* (л* F i F i—1
И =^рттг 7 •
ki
Параметры с индексом «*» используются для определения силы
в случае повторного нагружения опоры.
На основание каждой опоры КПА (1г) при движении по грунту
планеты действуют:
сила воздействия корпуса КПА (через элементы ПУ);
реакция грунта;
сила трения основания опоры по грунту.
Силовое взаимодействие посадочного устройства с поверхно¬
стью планеты зависит от ее рельефа, структуры и механических
свойств грунта в месте посадки. Для проведения теоретических ис¬
следований динамики мягкой посадки КПА выбирают расчетную
модель поверхности, обладающую характеристиками, не противо¬
речащими современным данным о планетном грунте.
В первом приближении можно в качестве такой модели поверх¬
ности посадки принять абсолютно жесткую плоскость, имеющую
некоторый угол наклона и высокий приведенный коэффициент тре¬
ния, позволяющий учесть сопротивление перемещению опоры по
реальной планетной поверхности.
Для каждого интервала времени при интегрировании находим
составляющие внешней силы, действующей на основание опоры If.
По формулам преобразования можно получить составляющие внеш¬
ней силы в любой системе координат.
75
В процессе мягкой посадки на КПА действуют силы, которые
определяются из условий;
Fn/0 при Гп<0;
Flz=0 при Кп>0.
Силы и моменты, действующие относительно центра масс КПА, на¬
ходим по формулам
Z=1 Z=1 Z=1
= 2 Mi(J = 2 (Fuw Vu - FuvWuy,
/“1 n' (6.6)
A4lz = 2^/v==2^1/{/^lz_ uwUu)’
i — 1 Z = 1
Mw = ^Miw = ^ ^uv^u-^ииУиУ
Z = 1 Z=1
Затем выражения для сил и моментов подставляются в формулы
(6.7) и (6.8) для определения координат и скоростей центра масс
аппарата.
Общие уравнения пространственного движения КПА
при мягкой посадке
В общем случае движение корпуса космического посадочного
аппарата как твердого тела может быть описано уравнениями Эй¬
лера. Запишем эти уравнения в проекциях на оси подвижной сис¬
темы координат U, V, W (см. рис. 6.1). Получим следующую сис¬
тему дифференциальных уравнений:
dVu _ Fy
dt т
g„ sin —1/^сок;
dVv
dt
Fy
m
gncos уw^u Уи^ж,
(6. 7)
dV w F w
dt m
sin & sin cp-f-1/У
(6. 8)
76
(6.9)
dt
yy COS cp co и sin (p.
-i-=o>j,—sin ®ctg& —<0y cos<pctgd;
dt
— = o)r sin cp cosec ft +co^ cosec & cos <p.
dt
Уравнения (6.7) описывают движение центра масс КПА, уравне¬
ния (6.8) — движение вокруг центра масс, а выражения (6.9) яв¬
ляются кинематическими соотношениями Эйлера.
Так как относительно подвижной системы координат U, V, W
нельзя задать абсолютное положение и ориентацию аппарата, то
остальные уравнения запишем в неподвижной системе координат
X', Y', Z':
dXr г г dY' тг dZ' т г /г»
—=1/.г; — = V> и—= (6.10)
dt dt dt
В результате интегрирования уравнений (6.7) определяются
проекции скорости центра масс КПА на подвижные оси координат
U, V, W. Компоненты скорости центра масс в системе Xf, Y', 7Y на¬
ходятся по формулам
Vx, = Ауи + A2Vv + A3VW; VY> = В У и + B2Vv + Byw^
v^=cyuyc2vvycyw. (6. 11)
где Д = cos ф cos ft cos ср — sin ф sin ср;
А2= — cos<p sin ft;- A3 = sin ф cos cpcos ф cos ft sin cp;
2?! = cos cp sin ft; 52 = cos&; B3= sin ft sin cp; (6.12)
Сг = — cos ф sin cp — sin ф cos ft cos cp;
C2 = sin ф sin ft; C3 = cois cp coiS ф— sin cp cos ft sin ф.
Затем по формулам (6.10) можно вычислить координаты центра
масс аппарата в неподвижной системе X', Yf, Z'.
Таким образом, решив систему уравнений (6.7) — (6.12), мож¬
но найти все основные параметры движения корпуса КПА:
компоненты скорости центра масс в неподвижной системе
Vxf, Vyf и Vzf\
координаты центра масс в неподвижной системе — X', Yf и Z';
компоненты мгновенной угловой скорости вращения относи¬
тельно центра масс — со^, coy и сщу;
угловые координаты (углы Эйлера), характеризующие положе¬
ние тела относительно системы, движущейся так, что ее начало ко¬
ординат всегда совпадает с центром масс, а оси остаются парал¬
лельными соответствующим осям неподвижной системы координат
X', Y', Z — ft, Ф и ф.
Для решения системы уравнений (6.7) — (6.12) необходимо
задать в момент времени / = 0 значения следующих параметров:
77
X'=X'Q; VX' = VX'Q; & = &o5 ^u=
y' = Yo\ УYf = Уу'; <р=сро; <*v=(oro;
Z' = Z0; Vz/ = yz'^ Ф = Фо5 O)w7 = t0iro-
Если при Z = 0 -0’0 = ф0 = 'ф0=0, то из уравнений (6.11), (6.12) будем
иметь V\' = V7/0; Ууц = Уу0‘1 ^' = 1/^0,т. е. при вычислении правых
частей в (6.7) можно сразу воспользоваться исходными данными.
Если же при Z = 0 Фо¥=О, срот^О, фо^О (или один какой-либо
угол не равен нулю), то значения Vv, Vv и Vw находятся из урав¬
нений (6.11) с использованием исходных значений углов Эйлера
#о, Фо и ф0.
Силы, действующие на динамическую систему (корпус аппара¬
та) при посадке, зависят от характера поверхности планеты в ме¬
сте посадки (наклон грунта, физико-механические свойства грунта,
строение поверхностного слоя и т. д.), конструктивных особеннос¬
тей КПА (число опор, положение центра масс, характеристики
энергопоглотителей и пр.), особенностей движения посадочных
опор при мягкой посадке (кинематические параметры элементар¬
ных движений, составляющих сложное движение аппарата).
Так как почти все указанные факторы изменяются в процессе
посадки, то и силовое воздействие на аппарат не остается постоян¬
ным. Это весьма усложняет рассматриваемую задачу. Однако она
решается с помощью ЭВМ методом численного интегрирования при
допущении, что силовое воздействие на КПА остается постоянным
в течение достаточно малого шага интегрирования.
Для этого уравнения (6.7) — (6.10) необходимо представить в
конечно-разностной форме:
Ми __
n sin 9- co.s^-\-Vv(£,w^Vw^v;
Д/
m
4
LVy
FV
gu
tn
ди^
(
tn
^U
CO’
Ju
A4y
- (0,
Д/
J у
Mw
--I-
COS В1 -J- У— У
grl sin & sin ср^У и^у — Уу^и',
(6. 13)
w j /
\ Ju /
//ir —
M JV г
/ J и — J у
—-r
Ы J w \ J w
Д&
= со^ COiS cp — co^ Sin <p;
Д/
Дер
Д/
—= —sin cpctgB- -—0)^ COScpCtgft;
78
(6. 14)
= sin ср cosec ft~H°/7 CQ,S ? cosec ft.
Рис. 6. 4. Силы, действующие на основа¬
ния опор КПА (пи — приведенная масса
основания i-й опоры)
Уравнения движения оснований опор составляются несколько
иначе, чем уравнения движения центра масс КПА. В том случае,
если основания опор не ка¬
саются поверхности плане¬
ты, их движение полностью
описывается уравнениями
движения корпуса КПА, так
как в этом случае опоры
являются частью жесткого
тела. Когда основания опор
находятся на поверхности
планеты, их следует рас¬
сматривать как массы, дви¬
жущиеся под воздействием
сил трения и сил, обуслов¬
ленных деформируемыми
элементами посадочного
устройства аппарата (рис.
6.4).
При этом движение КПА
складывается из простран¬
ственного движения жестко¬
го корпуса и движений ос¬
нований посадочных опор
по поверхности планеты.
Возникающие при движении
оснований опор силы и моменты приводят КПА в состояние покоя.
Рассмотрим относительное движение посадочных опор по по¬
верхности грунта. Суммируя силы, параллельные осям X и Z, по¬
лучим
b f*MX — 0,
T7 lzz F\iZ —
Общая сила трения действует по линии вектора скорости, а ее
составляющие определяются следующими уравнениями:
-/FlzrXlz [(Xlz)2 + (Zlz)2pL;
Fuz= -fPUYZu [(X1(.)2 + (Zn)2]"h
(6. 15)
(6. 16)
79
Подставляя выражения (6.16) в уравнения движения оснований
опор (6.15), получаем
Хи г X
mt [(Х1;)2 +
7 f^liY 7 PUZ Л
Z,1£. — z.JZ -— — и.
fPliY
^liX
lz
mi
о,
(6. 17)
у
mi [(Xi,)2 + (±1;)2]2
Если ввести допущение, что при интегрировании для каждого
достаточно малого интервала времени силы и результирующие
скорости остаются постоянными, то можно привести уравнения дви¬
жения оснований опор (6.17) к системе линейных дифференциаль¬
ных уравнений второго порядка:
Xu — aXu — b = Q*,
Zu—aZu—c=0,
; b=Z112L- C=ZXZ.
nil mi
mi
(6. 18)
где
£
м(А'1г)2я4я
Система линейных дифференциальных уравнений имеет
ния вида
(6.19)
peuie-
a
n—1
Xu 1 +—) (1 - - — A/;
a \ a / a
\ a J a
Zu = Z?"1 - — f Z?F1 +—) (1 - ea49 — — A/;
ZXi = (znu
\ a ) a
Величины, имеющие индекс (л—1), относятся к предыдущему
шагу интегрирования. Отметим, что в момент первого касания грун¬
та основанием опоры КПА (Z=0) точка 1 коснувшейся опоры ус¬
танавливается так, что Хи = У1Д = 0. При скольжении оснований
опор вдоль поверхности грунта имеют место следующие тождества:
Г^О и (6.21)
так как FUy=Fuy.
Полученные выражения позволяют определить в системе X, Y,
Z координаты и скорости точек 1г- КПА в случае касания основа¬
нием i-ii опоры поверхности грунта. Пересчет значений указанных
параметров для системы координат U, V, W осуществляется по
формулам преобразования.
Если основание ьй опоры не соприкасается с поверхностью грун¬
та, то составляющие его скорости определяются по формулам
(6. 20)
80
Z7lz —U-j-co^UZlz -r0)u7 |Vrh-|;
11 = ^ + t0U7^ 1/ — 0)Gr^l/’
WU = W-^ \vri\-^vuu.
В том случае, если основание f-й опоры КПА, предварительно
коснувшись грунта, вышло из соприкосновения с поверхностью пла¬
неты, определение координат точек Ь аппарата ведется по фор¬
мулам
(6. 22)
(6. 23)
где i= 1, . . ., М причем значения с индексом «*» берутся в момент
отрыва от поверхности грунта f-й опоры КПА.
После проведения указанных вычислений для каждого шага ин¬
тегрирования можно получить полную зависимость параметров про¬
цесса от времени при посадке КПА на поверхность планеты без
атмосферы.
Завершив процесс посадки на планету, космический аппарат
занимает положение, соответствующее его устойчивому равнове¬
сию. Однако не всякое положение устойчивого равновесия КПА
после посадки обеспечивает нормальную работу всех его систем и
возможность, если запланировано, успешного обратного старта с
планеты. Действительно, опрокидывание КПА при посадке на бок
должно классифицироваться как неудачная посадка (а при нали¬
чии на корабле экипажа — как катастрофа).
Поэтому принято называть устойчивым только такое положение
КПА после посадки, при котором все его опоры (или большинство
спор при А 3^4) касаются грунта, а продольная ось отклонена от
вертикали на небольшой угол, определяемый условиями обратного
старта аппарата.
Для оценки устойчивости на опрокидывание космического аппа¬
рата при теоретическом исследовании процесса мягкой посадки вво¬
дят специальный критерий опрокидывания КПА, определяющий
положение центра масс аппарата относительно ломаной линии,
проходящей через основания его опор. Момент совпадения центра
масс аппарата с указанной ломаной линией является критическим
и рассматривается как предельное отклонение, при переходе через
которое аппарат не возвращается к положению устойчивого равно¬
весия. В этот момент угол Эйлера 14 превысит свое критическое
значение
|&KP| = arctg4^; Z=l. 2,..., N, (6.24)
Г1/1
определяемое текущей геометрией аппарата и углом Эйлера <р.
Величина | Окр | служит критерием опрокидывания космического
аппарата при посадке и вычисляется для каждого шага интегри¬
рования.
81
При I'O’I | 'О'кр| космический аппарат становится статически
неустойчивым, и процесс интегрирования прекращается. При
и <|'0’кр| — аппарат устойчив. Процесс интегрирования в этом
случае может быть прекращен, например, в тот момент, когда ки¬
нетическая энергия КПА станет меньше некоторой достаточно ма¬
лой положительной величины £<т]-
Необходимо отметить, что получение решения системы уравне¬
ний движения (6.7) — (6.12) в общем виде представляет чрезвычай¬
но сложную задачу. Однако в ряде практических случаев бывает
достаточным найти частные решения этой системы методом чис¬
ленного интегрирования с помощью электронной цифровой вычис¬
лительной машины.
Частный случай двухмерного движения КПА
при мягкой посадке
Н-четное
Как уже отмечалось ранее, решение динамических уравнений,
описывающих пространственное движение космического аппарата
при мягкой посадке, весь¬
ма громоздко и требует
больших затрат машинно¬
го времени на расчет об¬
ластей устойчивости
многоопорного (А^4)
КПА, особенно при ана¬
лизе влияния на динами¬
ку посадки разнообраз¬
ных конструктивных па¬
раметров аппарата и за¬
даваемых в широких пре¬
делах посадочных усло¬
вий (посадочные скорости
и ориентация КПА; харак¬
теристики рельефа и грун¬
та планеты).
Поэтому был разрабо¬
тан инженерный метод
расчета двухмерного по¬
садочного движения ап¬
парата, позволяющий провести исследование устойчивости КПА с
различным количеством посадочных опор (3—6) и сделать предва¬
рительный выбор его посадочного устройства по принципу наи¬
меньшей массы при равной устойчивости.
Поскольку в этом случае все условия посадки аппарата сим¬
метричны относительно оси U, то нет необходимости оценивать
особенности движения всех его опор. Если N — количество опор
КПА, а N — количество опор, движение которых следует проана¬
лизировать, то i будет принимать значение от 1 до N. Приведем
6. 5. К определению
величины N
82
соотношения, связывающие между собой величины N и N
(рис. 6.5):
если N — четное, то а) N = N/2 и A = n/7V;
б) 7V=W+1 и Д=0; (6>25)
если 7V —нечетное, то N=(2V-|“ 1)/2 и a) k = tt/N;
б) А = 0,
где А — угол между осью U и первой опорой аппарата.
Существенное упрощение математической модели КПА может
быть достигнуто, если мы обратим внимание на то, что в результа¬
те обжатия энергопоглотителей опорные пяты перемещаются в ос¬
новном в направлении продольной оси аппарата с незначительным
боковым смещением (см. рис. 6.1).
Рис. 6. 6. Схематизация КПА трехопорной моделью
Другими словами, можно схематизировать космический аппарат
моделью, состоящей из трех опор (;V = 3), которые под прямым уг¬
лом жестко крепятся к общему основанию (рис. 6.6). В каждой
из опор установлены неупругие сминаемые материалы для погло¬
щения кинетической энергии аппарата в процессе мягкой посадки,
имеющие ступенчатую характеристику усилие — деформация и не¬
ограниченную величину обжатия.
Возможность рассмотрения различных конфигураций ПУ (по¬
садочного устройства) в плоской задаче обеспечивается соответст¬
вующим выбором линейных размеров L\\ L%\ L3 и сил Fij /*72; F£3,
кратных усилию обжатия § энергопоглотителя. Эти параметры, вы¬
раженные через R (радиус ПУ) и приведены в табл. 6.1.
83
Таблица 6.1
N
Параметры
Li
Lz
L3
FLt
fl,
3
R
0,5/?
0
6
25
0
4
0,71/?
0,71/?
0
25
25
0
5
/?
0,81/?
0,31/?
5
25
25
6
0,87/?
0,87/?
0
25
25
26
Например, конфигурации ПУ с тремя опорами при движении
вниз по склону соответствует схема касания опорами грунта 1—2,
т. е. КПА касается грунта сначала одной опорой, расположенной
выше по склону, а затем одновременно двумя опорами, располо¬
женными ниже по склону. В плоской задаче две «нижние» опоры
можно рассматривать как одну опору, создающую при своей дефор¬
мации сопротивление в два раза большее, чем каждая из трех опор
аппарата в отдельности. Таким образом, конфигурации ПУ с 3, 4, 5
и 6-ю опорами могут быть исследованы в двухмерной задаче при
помощи математической модели ПУ с тремя опорами. Соответст¬
вующие схемы касания грунта опорами приведены в табл. 6.2.
Кроме того, при такой-
постановке задачи можно-
оценить влияние на поса¬
дочную устойчивость
КПА его стабилизирую¬
щих двигателей, так на¬
зываемых двигателей при¬
жатия. Стабилизирующие
двигатели, прижимая ап¬
парат к грунту, создают
момент, препятствующий
его опрокидыванию при
посадке и стремящийся
возвратить аппарат в устойчивое положение.
Рассмотрим упрощенную схему с расположением двигателей
прижатия на основании каждой опоры и с совпадением вектора тя¬
ги двигателя с продельной осью опоры. Все стабилизирующие дви¬
гатели включаются одновременно в момент касания грунта опора¬
ми, находящимися ниже по склону.
Проанализируем наиболее опасный случай с точки зрения устой¬
чивости при посадке. Будем считать, что поверхность планеты —
абсолютно жесткая плоскость, т. е. полностью отсутствует внедре¬
ние в грунт посадочных опор аппарата. При этом коэффициент
трения посадочных опор о грунт можно варьировать в широких
пределах. Получим следующие уравнения движения КПА:
84
Таблица 6. 2
Конфигурация ПУ
Схема касания
грунта
3- х опорное
4- х опорное
5- ти опорное
6- ти опорное
/—2 или 2—1
2—2 или /—2—1
1— 2—2 или 2—2—1
2— 2—2
(6. 26)
dX
dt
dY
dt
dy
~[2F7'i“UZ" sin6+27'‘' sin(Y — 0) 1;
L /=i /=i J
Д ^^.-1Гпсо30-^Лсоз(у-0)1;
L i^i J
1 <-1 1=1 1=1 J
так как у<0 и 0<0,
где i= 1, 2, 3;
X, = Ll cos (у — 9) — (H — 8;) sin (y — 9);
8z = /7-|-Z/tg(Y — 9) — У sec (y — 9);
8/= — sec2(Y — 9) {Г cos(y —9) + [^ sin (y —9) —Z;] y};
Y=(H — 8i)cos(y —9)4-Zi sin(y —6).
Сила, действующая вдоль стойки Ай опоры, определяется
ловий
(6. 27)
из ус-
FLi=0, если 8t<0;
Fl.=Q, если 8,>e2; 8,<8,-рт;
FLi=c^ если 8(>8,pm, B,->e2.
Тяги стабилизирующих двигателей принимают значения
Ti = Ki при /<7,д; 7\=0 при />Ад» если 82>0 (/=1, 2, 3),
где Ад — время отсечки z-ro двигателя.
Скорость скольжения i’-й опоры по поверхности определяется
выражением
X. = X + Гу _ Sin (Y - 8). (6. 28)
В зависимости от характера движения оснований посадочных
опор составляющие FN и FT. определяются для конкретных ча¬
стных случаев:
а) разрушение энергопоглотителя и скольжение Z-й опоры;
б) энергопоглотитель разрушается, скольжение отсутствует;
в) опора скользит, разрушение отсутствует.
Характерно: |8,-|<е2; Ft («-d>0.
В этом случае получаем системы дифференциальных уравнений
для каждой опоры, например, для опоры Г.
тХiY — sec pi cos p.t=FN, -фFN, — W„ cos 0 ф-
+ /пГ? - (7\ + r2 + Г3) cos (у - 0),
JirY + ^’£1sec₽1(Xricosp.i —Г sin^!)=
= (FTi + FTi} Y + FN,X2 - F„,X3 71A1 - T2L2 + T3L3.
(6. 29)
85
Решая соответствующую систему, определяем у и FL . Если
FL >0, то вычисленное значение FL. используется при интегри¬
ровании системы. Если FL.<0, то следует принять FL. =0. Угол p.i
X ’
вычисляется по формуле pz=• Используя найденные значе-
ния pi и FL., определяем pz = у — 6-pz; Fz=F£.sec^z; FN.=^F
FT[=F[ sin у.;',
г) опора не разрушается и не скользит.
Характерно: I^Ksj; |8г|<е2; FZ(„_d>0.
Для каждой опоры получаем системы уравнений, например, для
опоры 1:
FT1 + тГу =-FTi-Ft3 + Wn sin 0-tnXtf-
НП + Л + А)зш(у-6);
FNl — mXiY = — Fn2 — FN3 4- Wn cos 6 — mYy2 -f-
+ (Л + Л + Г3)со8(у-9);
Jwy +FN1X^FT1Y = (Fr. + FT3) Y +
“h-/7 — F n 3X i^i — TyL^-^-T 3Z,3.
(6.30)
Решая соответствующую систему, находим у, FT и FN.. Угол pz
определяется по формуле pi = arctgFrz/F;v.. При F>0 имеем:
если | pi | <ро, то вычисленные значения FN и FT используют¬
ся при интегрировании уравнений (6.26);
если | pi | >ро, то решение недействительно, так как опора
должна скользить (имеет место случай в), при FN[ <0 следует
принять Fj^l =0 и Fr. =0.
В этой главе мы уже рассматривали вопрос об определении ус¬
тойчивого положения космического аппарата после мягкой посад¬
ки на поверхность планеты. При решении плоской задачи критерии
опрокидывания КПА будут выглядеть несколько иначе, чем в слу¬
чае пространственного движения аппарата. Действительно, косми¬
ческий аппарат, движущийся в вертикальной плоскости, потеряет
устойчивость при мягкой посадке, если:
1) «1>0 или 2) а2<С0, (6.31)
где az=arctgy- 4-9 (при Z= 1, 2); (6.32)
(Xi (0С2) — угол между линией, проходящей через центр масс ап¬
парата и точку контакта опоры 1 (2) с поверхностью, и местной
вертикалью; — расстояние от центра масс аппарата до линии
действия силы FN. (Хг>0 — при совпадении направления отсчета
с направлением оси X).
Космический аппарат сохранит после посадки на поверхность
планеты устойчивое положение при одновременном выполнении сле¬
86
дующих условий:
«1<0; а2>0; E = ^-{mX2^mY2-YJw^<y\. (6.33)
Процесс интегрирования в этот момент можно прекратить, так
как кинетическая энергия КГ1А стала меньше некоторой достаточно
малой положительной величины т), а сам аппарат сохраняет устой¬
чивое положение.
Анализ устойчивости КПА при мягкой посадке даже в плоском
движении может быть проведен только с помощью ЭВМ (например,
методом численного интегрирования). Некоторые результаты ис¬
следований динамики мягкой посадки космического аппарата пред¬
ставлены в гл. 10.
Глава 7. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ МЯГКОЙ ПОСАДКИ
Экспериментальное подтверждение работоспособности и надеж¬
ности выбранной конструктивной схемы посадочного устройства
(ПУ) при полетах аппаратов (даже на Луну) из-за своей стоимо¬
сти может рассматриваться только как заключительная стадия
большого цикла экспериментальных исследований, проводимых в
наземных условиях на динамически подобных моделях и натурных
макетах космических посадочных аппаратов [8, 10].
Указанное обстоятельство является основной отличительной осо¬
бенностью экспериментального изучения большинства физических
явлений, связанных с проникновением техники в космическое про¬
странство (помимо мягкой посадки, к таким явлениям можно от¬
нести передвижение и строительные работы на поверхности Луны
и других небесных тел, стыковку на орбите и т. д.).
Если применение моделирования на основе теории подобия при
изучении таких явлений как флаттер самолета (ракеты), обтекание
тела потоком жидкости (газа), перенос тепла в движущейся среде,
механические колебания наземных сооружений, корпусов летатель¬
ных аппаратов с учетом подвижности топлива в баках и т. п. дает
исследователю определенные преимущества перед экспериментами
на натурных объектах (в выборе размеров системы, темпа разви¬
тия процесса, физических сред, значений режимных параметров
и пр.), то при изучении явления мягкой посадки на планеты в
наземных условиях метод научного моделирования оказывается
единственным средством, позволяющим качественно и количествен¬
но воспроизвести процесс и распространить полученные результаты
на натурное явление.
При экспериментальном исследовании мягкой посадки в зем¬
ных условиях должно быть соблюдено подобие с натурой по геомет¬
рическим и массово-инерционным параметрам аппарата, ускорению
силы тяжести, физико-механическим свойствам планетного грунта
и рельефу поверхности, а при испытаниях на натурных макетах
пилотируемых кораблей (или дистанционно управляемых автома¬
87
тов) еще и по специфической освещенности ландшафта, резкой
контрастности теней, отсутствию земных ориентиров.
Проведение таких исследований предполагает решение двух, в
сущности, самостоятельных задач: воспроизведение в наземных ус¬
ловиях явления, подобного натурному, и выполнение на нем всех
необходимых наблюдений и измерений.
Обращаясь к основным положениям теории подобия и размер¬
ностей, имеем следующее. Если между п размерными величинами
Уъ У2> • • Уп существует функциональная связь
^(г/i, г/л)=0, (7.1)
не зависящая от выбора системы единиц измерения, и при этом
среди величин z/b 1/2,, Уп р величин являются величинами неза¬
висимой размерности, то связь (7.1) всегда может быть записана
в виде
Ф(ПЬ П2,..., Пот)=0, (7.2)
уРп;
гДе H2=yse'y^... у%п-, (7.3)
ът=у^у^... ysnmn,
— безразмерные комбинации, составленные из размерных величин
Ух, У 2, • • -л У п, причем число этих безразмерных комбинаций т
равно
т = п — р. (7.4)
При этом предполагается, что безразмерные параметры П* ('/=1,
2, . . ., т) независимы, т. е. ни один из этих параметров не может
быть выражен через остальные.
Условие безразмерное™ параметров П—у^ур2... у^п,
(f=l, 2, .. ., т) накладывает определенные ограничения на выбор
элементов матрицы S показателей степеней размерных величин у^,
У2, . • Уп
5П
S12>..
^21
S22 • • •
$2п
$т1
$т2 • •
■ ^тп
Введенное понятие величин независимой размерности определя¬
ется следующим образом. Размерные величины у2) . . уР с раз¬
мерностями [i/i] = ai; [y2] = a2; .. [уР]=ар называются величинами
независимой размерности в том случае, если не существует таких
чисел q2, . . qP, удовлетворяющих равенству
аМ... арр=---\, (7.6)
из которых хотя бы одно было отлично от нуля. Все вышесказан¬
ное известно под названием П-теоремы.
88
Таким образом, П-теорема позволяет установить систему без¬
размерных параметров, определяющих данное явление. Можно по¬
казать, что для подобия явлений необходимо иметь значения этих
параметров одними и теми же. Иначе говоря, параметры Пг(/=
= 1, 2,..т) представляют собой критерии подобия.
Число определяющих безразмерных параметров зависит от сте¬
пени и характера идеализации физического явления при его изуче¬
нии. Поэтому говорить о совокупности этих параметров можно
только по отношению к принятой идеализированной схеме явле¬
ния.
Моделирование мягкой посадки
на абсолютно жесткие аналоги поверхности планет
Рассмотрим законы подобия при моделировании в наземных ус¬
ловиях динамики мягкой посадки КПА.
С физической точки зрения это явление определяется следую¬
щими параметрами: характерным линейным размером /, м; массо¬
вой плотностью конструкции q, кг/м3; модулем упругости материа¬
ла £, кг/м-с2; коэффициентом Пуассона материала ц, временем /, с;
ускорением силы тяжести / м/с2; коэффициентом трения Д т. е. у
нас п = 7; р = 3.
В соответствии с П-теоремой [31] можем составить четыре без¬
размерные комбинации (т=4):
П^; IL2=qIJ/E; IL3==t2j/h П4=/. (7.7)
Уравнение (7.2) принимает вид
ф^; т£;^)=0- (7-8)
Отсюда вытекает, что для того, чтобы моделируемое физиче¬
ское явление было подобно натурному, необходимо иметь равен¬
ство этих безразмерных комбинаций для натуры («н») и модели
(«м»).
Qf/нУн/^н Qm^m/m/^m’
^н/н/^н = ^м/м/^м’ fп= fм- (7*9)
Равенства (7.9) определяют условия подобия при моделирова¬
нии явления мягкой посадки космического аппарата на Луну и
планеты. Однако они имеют универсальный характер и справедли¬
вы для моделирования на Земле и других динамических процессов
(передвижение планетохода по поверхности, строительно-монтаж¬
ные работы и т. п.), совершаемых космическими объектами на лю¬
бых небесных телах, атмосфера которых не плотнее земной.
Рассмотрим следующие способы моделирования в наземных ус¬
ловиях процесса мягкой посадки на Луну и планеты Марс и Мер¬
курий: моделирование с помощью динамически подобных моделей
(ДПМ); моделирование с помощью натурных макетов КПА.
89
Совместное рассмотрение планет Марс и Меркурий объясняет¬
ся совпадением значений ускорений силы тяжести на их поверхно¬
сти (по современным данным расхождение в этих значениях менее
1,3% [41]). Конечно, вследствие различия на данных планетах дру¬
гих физических характеристик (температура и т. п.) и отличия па¬
раметров траекторий полета к ним аппараты мягкой посадки на их
поверхность не будут полностью идентичными. Что касается осо¬
бенностей температурного режима поверхности Меркурия из-за то¬
го, что «день» на этой планете равен ~88 земным суткам и плане¬
та близка к Солнцу, то посадка первых КПА, по-видимому, целесо¬
образна в теневой зоне его поверхности (т. е. после захода Солн¬
ца), имеющей примерно «земные» температуры.
Моделирование с помощью динамически подобных моделей. За
исходные масштабы моделирования принимаем масштабы величин
независимой размерности — длины, модуля упругости материала и
ускорения силы тяжести (так как р = 3) —Кь Ке и Kj.
Некоторые из производных масштабов, используемых при моде¬
лировании исследуемого явления, сведены в табл. 7.1. Производ¬
ные масштабы моделирования выражаются через исходные при по¬
мощи условий подобия (7.9). Например:
0к/н/н=0АЛ,; /<о=кЕ(к1К.у-1' (7.10)
£н
Условия подобия |1н=|Хм и /н=/м предполагают изготовление поса¬
дочных моделей из материалов с теми же коэффициентами Пуассо¬
на и коэффициентами трения, что и в натуре.
При моделировании явления посадки на поверхность Луны в
земных условиях однозначно получаем масштаб ускорения силы
тяжести К7 = 6.
Для упрощения как проектирования модели, так и технологии
ее изготовления наиболее целесообразно масштаб массовой плот¬
ности иметь равным единице, т. е. Ке = 1. Учитывая это, из форму¬
лы масштаба Kq (7.10) получаем простую зависимость:
Практический интерес представляют следующие случаи:
1) К/=1/6; Ке=1. В этом случае ДПМ следует изготавливать
из материалов натурных конструкций (титановые и алюминиевые
сплавы, сталь и пр., см. модели ДПМ-А; -Б; -В в табл. 8.1);
2) Ki= 1/3; Ке=2. В этом случае модель лунного аппарата дол¬
жна изготавливаться из материалов с модулем упругости £, в два
раза большим, чем у материалов натурной конструкции (например,
натурный материал — титановый сплав с £=11 • 1010 Па, а матери¬
ал модели —■ сталь с £ = 22 • 1010 Па);
3) Ki= 1/2; Ке = 3. В этом случае материал модели должен
иметь модуль упругости £ в 3 раза больше, чем у материалов на¬
турного КПА (например, натурный материал — алюминиевый
сплав с £ = 7* 1010 Па, а материал модели — сталь с £ = 21 X
Х1010 Па).
Более широкие возможности в выборе величины линейного мас¬
штаба ДПМ лунного аппарата можно получить, если отказаться
90
to to
04
of of
1O
II II
II
C4
Ю
CJ
CX
O, ||
c3
£
и i
IO
of
-
IQ
of
-
oq^
<^■*4
Ю
of
-
-
z^s ,
ю
of
z—
to
of
04
to
-
eq
to1
CM
/625
125
co
to1
to
04
CO
to
04
Ю
to
CM
to.
to
/625
to
CM
co
OQ
of
o'
ocf
CM
of
04
CO
- 12.
to
■ 04
to
CM
LO
О
to
CM
to
CM
04
ОС?
of
00
to^
04
to
04
to
04^
х—'ч
to
Ю
04
О
to
lof r-*
of
of
•x
91
от требования, что масштаб массовой плотности должен быть
равен единице (см. табл. 7.1).
Действительно, из формулы (7.10) при Kj = 6 имеем
К.
(7.11)
Рассмотрим следующий случай:
4) пусть 7(q = 1/6 и /Се=1. Получим Kz=l. Здесь мы встречаем¬
ся с противоречивым требованием, а именно — при натурных раз¬
мерах динамически подобной модели лунного аппарата необходи¬
мо получить общую массу модели в шесть раз меньше натурной
(см. табл. 7.1). Чтобы удовлетворить это требование, следует ос¬
новную часть модели лунного аппарата — его посадочное устройст¬
во и некоторые силовые элементы — изготовить в натуральную ве¬
личину из натурных материалов, а остальную часть модели (полез¬
ная нагрузка, макетные двигатели, приборный отсек, кабина кос¬
монавта и пр.) значительно уменьшить, но так, чтобы общая масса
полученной динамически подобной модели КПА соответствовала
масштабу /См= 1/6 и модель имела натурную центровку.
Особенностями натурной динамически подобной модели лунно¬
го аппарата являются:
увеличенное в 6 раз угловое ускорение;
увеличенные в Уб раз линейная и угловая скорости, и мощность;
натурные значения энергии (работы), напряжений, жесткостей
и сил, действующих_на модель;
уменьшенное в Уб раз по сравнению с натурным время проведе¬
ния испытаний;
уменьшенные в 6 раз масса, массовая плотность и моменты
инерции модели.
Натурная динамически подобная модель в отличие от натурных
макетов КПА (см. стр. 95) не нуждается в каком-либо механизме
«разгрузки» на 5/6 веса, что существенно упрощает испытательные
стенды и методику проведения самих экспериментов. Такая модель
позволяет провести экспериментальные исследования процесса мяг¬
кой посадки лунного аппарата и отработку его натурного посадоч¬
ного устройства путем простого сбрасывания модели со специаль¬
ного испытательного стенда или вертолета на площадку, имеющую
«натурный рельеф» местности. Эксперименты на натурной модели
очень интересны с точки зрения определения вероятности безава¬
рийной устойчивой посадки аппарата в обстановке, имитирующей
лунную.
принимает значение:7<y=/M//H=g3eMH/gMapc=|L^~-|-. Из (7.10)
Практический интерес могут представить следующие четыре
случая:
тогда Ас=2. Такую уменьшенную в пять раз
1)
92
динамически подобную модель, изготовленную из натурных матери¬
алов, но имеющую удвоенную по сравнению с натурным КПА мас¬
совую плотность конструкции (что достигается установкой допол¬
нительных грузов), очень удобно испытывать в специальном стенде
с площадками имитатора грунта планеты;
2) /<7 = 2/5; тогда Ке = 1. В этом случае уменьшенную в
2,5 раза динамически подобную модель КПА следует изготовлять
из материалов натурных конструкций, по-возможности пропорцио-
Рис. 7.1. Неустойчивая посадка ДПМ-Б в кратер, расположенный
на склоне 15°, со скоростями = 2,5 м/с, К = 2,0 м/с (схема по¬
садки «2—2», грунт жесткий, глубина кратера 0,1.5 м, шаг кино-
граммы ~0,06 с)
93
нально изменяя размеры всех элементов (см. модели ДПМ-А, -Б,
-В в табл. 8.1) ;
3) 7Сг = 2/5, Кв = 2/5; когда Ке=2/5. В отличие от предыдущего
случая такую уменьшенную в 2,5 раза динамически подобную мо¬
дель КПА изготовляют из материалов с модулем упругости Е в 2,5
раза меньшим, чем у материалов натурной конструкции, облегчая
при этом все основные элементы модели в 2,5 раза по сравнению
со случаем 2 (см. модели ДПМ-Г1 и ДПМ.-Г2 в табл. 8.1);
4) Kz=l; Ке=1, тогда К0 = 2/5. В этом случае посадочное уст¬
ройство и некоторые силовые элементы модели КПА необходимо
изготовить в натуральную величину из натурных материалов, а ос¬
тальную часть модели (полезную нагрузку, макетные двигатели,
приборный отсек и пр.) значительно уменьшить, но так, чтобы об¬
щая масса полученной модели КПА соответствовала масштабу
/<м = 2/5 = 0,4 и модель имела натурную центровку (см. модель
ДПМ-ГЗ в табл. 8.1). Этот случай аналогичен случаю 4 при мягкой
посадке на Луну.
Следует отметить, что при масштабе Ki—1/б (для Марса Ki =
= 2/5) масштаб линейной скорости принимает значение КУ=1, т. е.
динамически подобная модель будет иметь при посадке те же са¬
мые скорости, что и натурный КПА, совершающий мягкую посадку
на поверхность Луны (или Марса). Это упрощает эксперименталь¬
ные исследования и пересчет их результатов на натурное явление.
Допустим, что при эксперименте такая модель КПА сбрасывается
с 1/6 (2/5) высоты, имеющей место на Луне (на Марсе), а экспери¬
мент снимается на кинопленку с 1/6 (2/5) натурного расстояния и
в 6 раз (в 2,5 раза) быстрее нормального, тогда при просмотре
фильма с нормальной скоростью можно будет увидеть процесс мяг¬
кой посадки, эквивалентный действительному для лунного (марси¬
анского) КПА (рис. 7.1). Уменьшение же линейных размеров моде¬
ли в 6 раз (в 2,5 раза) по сравнению с натурой позволяет провести
некоторые экспериментальные исследования мягкой посадки в спе¬
циальной барокамере с имитацией лунного (марсианского) ваку¬
ума.
Моделирование с помощью натурных макетов КПА. При этом
методе моделирования для соблюдения подобия необходимо удов¬
летворить те же условия (7.9).
Поскольку мягкая посадка исследуется на макетах КПА, изго¬
товленных из натурных материалов и имеющих натурные массы и
габариты, то исходные масштабы моделирования определяются
сразу:
Ki= 1; KQ= 1 и 1 (как и ранее р = 3).
Из условий подобия (7.9) получаем следующие зависимости:
^=1; K^K^jKe1^ Z<z= 1,
откуда Kj=KE(KQI<l')~i; Kt=KtKfK~T. (7.12)
Подставляя в выражения (7.12) значения исходных масштабов,
находим Kj=l и /Q = l, т. е. сохранение подобия явлений при моде-
94
жировании мягкой посадки на натурных макетах КПА возможно
только в условиях искусственного создания на Земле планетного
ускорения силы тяжести (при этом натурное течение времени по¬
лучается как следствие). Достигнуть этого можно несколькими пу¬
тями. Единственный строгий путь получения планетного ускорения
силы тяжести — это помещение натурного макета в летающую ла¬
бораторию, подобную лабораториям для создания невесомости.
Однако для экспериментального исследования мягкой посадки ле¬
тающие лаборатории очень неудобны.
Более простыми с технической точки зрения, хотя и менее стро¬
гими, являются разнообразные способы «разгрузки», при которых
выполняется соответствие с натурой только по общему весу макета,
находящегося под действием земного притяжения (натурный ма¬
кет должен быть «разгружен» на [1—/С/1] часть своего веса).
В этом случае для получения более строгого подобия явлений сле¬
дует выбранный способ разгрузки применить к большому числу
элементов макета.
Способы разгрузки могут быть реализованы различными конст¬
руктивными средствами:
установкой на макете дополнительных реактивных двигателей;
применением противовесов (желательно иметь систему разгру¬
жающих противовесов для каждого элемента макета);
применением электродинамического тормоза;
с помощью гидропневматического механизма разгрузки;
использованием наклонной стенки и т. п.
Отметим, что в случае моделирования процесса посадки пило¬
тируемого корабля с помощью его натурных макетов для создания
космонавтам при тренировках условий, наиболее полно имитирую¬
щих планетные, необходимо дополнительно обеспечить следующее:
одинаковые с натурой характеристики ручного управления;
одинаковый обзор из кабин макета и пилотируемого корабля;
одинаковое положение космонавта в кабине натурного макета и
пилотируемого корабля.
Первый способ разгрузки предполагает, по существу, создание
летающего натурного макета КПА типа турболета [46]. Несмотря
на значительные трудности, связанные с его реализацией, этот спо¬
соб открывает богатые возможности исследования не только само¬
го процесса мягкой посадки, но и позволяет провести тренировки
космонавтов по отработке всего заключительного этапа полета пи¬
лотируемого корабля, включая маневры по выбору посадочной пло¬
щадки, проверку эффективности систем ручного и автоматическо¬
го управления, качества обзора из кабины и т. д.
Практический интерес могут представить отдельные варианты
разгрузки с помощью реактивных двигателей:
а) реактивный двигатель помещается в центре масс летающего
макета на двухстепенном кардане и удерживается системой корре¬
ляции в вертикальном положении в течение всего полета. Двига¬
тель создает тягу в 83,3% (Луна) или в 60% (Марс) земного веса
макета. В этом варианте необходима установка жестко укреплен-
95
ных на макете дополнительных двигателей, вызывающих линейные
перемещения макета при его вращении в плоскостях тангажа и
крена;
б) реактивный двигатель помещается в центре масс летающего
макета на двухстепенном карданном подвесе и связывается с ним
посредством гидроусилителей в продольной и поперечной плоскос¬
тях. Применяя комбинированную систему управления, включающую
в себя в качестве основных исполнительных элементов газовый
руль и бустер, обеспечиваем такое угловое положение макета и
двигателя в пространстве, при котором кинематические параметры
движения макета равны кинематическим параметрам движения
КПА.
Рис. 7. 2. Эстакадный испытательный стенд для отработки предпосадочного
маневра и посадки натурного макета КА «Аполлон»
в) реактивный двигатель жестко крепится к летающему макету
в его центре масс. Кабина же пилота устанавливается на макете
при помощи двухстепенного карданного подвеса. Система управле¬
ния посредством газовых рулей реактивного двигателя и гидроуси¬
лителей, связывающих поворотную кабину пилота с макетом, обес¬
печивает такое положение макета и кабины в пространстве, при ко¬
тором как линейные кинематические параметры движения макета,
так и углы поворота кабины равны соответствующим параметрам
движения пилотируемого корабля.
При всех остальных способах разгрузки натурный макет посто¬
янно связан поддерживающими тросами с разгрузочным механиз¬
мом, вследствие чего возможность маневрирования макета ограни¬
чена габаритами испытательного стенда. Однако отсутствие раз¬
96
гружающего реактивного двигателя существенно упрощает созда¬
ние натурного макета и технику проведения испытания (рис. 7.2).
Следует отметить отрицательную сторону второго способа раз¬
грузки, заключающуюся в том, что в момент контактирования ма¬
кета с поверхностью, т. е. в тот период, когда происходит встреча с
преградой, поглощение энергии и деформация посадочных уст¬
ройств и грунта, разгрузка оказывается не эффективной из-за инер¬
ционности противовеса.
В этом смысле более приемлемыми оказываются третий и, осо¬
бенно, четвертый способы разгрузки, отличающиеся малой инерци¬
онностью применяемых разгрузочных механизмов. С помощью не¬
сколько отклоненной от вертикали стенки можно получить имита¬
цию пониженной силы тяжести вследствие разложения веса маке¬
та КПА на составляющие. Однако при этом способе разгрузки
затруднена имитация рельефа посадочной площадки и свойств
рыхлого деформируемого грунта планеты.
Обеспечив при проведении экспериментов величину масштаба
тем самым добиваемся равенства единице и величин осталь¬
ных производных масштабов. Конечно, при таких испытаниях не
может быть выдержано подобие по температурному режиму и кос¬
мическому вакууму, так как проведение натурных экспериментов по
посадке в термобарокамерах практически исключено.
Экспериментальные исследования мягкой посадки на натурных
макетах являются одним из завершающих этапов эксперименталь¬
ной отработки ПУ в земных условиях. Такие исследования позво¬
ляют сделать окончательные выводы о пригодности как схемы ПУ,
так и его конструкции для успешной посадки на планеты, позволя¬
ют провести необходимые тренировки экипажа пилотируемого ко¬
рабля (или дистанционно управляемого автомата) по осуществле¬
нию мягкой посадки, обеспечивают требуемую надежность работы
ПУ и приводят к уменьшению числа дорогостоящих запусков КА в
рамках летных испытаний.
Моделирование мягкой посадки
на деформируемые грунты-аналоги поверхности планет
Рассмотрим теперь вопрос о моделировании в наземных услови¬
ях некоторых механических характеристик грунта планет, влияю¬
щих на процесс мягкой посадки КПА. Для этого случая существен¬
ными являются следующие величины: массовая плотность грунта
Qr (кг/м3), коэффициент сжимаемости грунта а (м-с2/кг), коэффи¬
циент внутреннего трения грунта ф [0], а также Z, t, f и /.
Известно, что при небольших изменениях давлений можно рас¬
сматривать грунты как линейно деформируемые тела и с достаточ¬
ной для практических целей точностью принимать зависимость
между напряжениями и деформациями линейной [39]. На рис. 7.3
изображена зависимость общей деформации грунта под штампом
от величины внешнего давления. Кривую деформации грунта мож-
4 400
97
Рис. 7.3. Зависимость деформация
грунта под штампом от внешнего
давления (0<р^р0)
но рассматривать состоящей из двух главных частей: I) от «О» до
некоторого давления р0, которая с достаточной для практических
целей точностью аппроксими¬
руется прямой линией (пунк¬
тирная линия на рисунке) и
2) при давлениях, больших
Pq,— криволинейная часть.
Практически все грунты имеют
«предел пропорциональности»
/?о между давлением и осадкой
6 при не очень больших внеш¬
них давлениях (до ~3 • 105Па)
[35]. Теория линейно деформи¬
руемого полупространства да¬
ет аналитическое выражение
для полной стабилизованной
осадки 6 однородного грунта
под действием внешнего дав¬
ления р:
§ = hbap, (7. 13)
где In — эквивалентная толщина слоя грунта, осадка которого при
сплошной нагрузке будет равновелика осадке слоя грунта при дей¬
ствии нагрузки на площадку заданных размеров.
Формула (7.13) справедлива для всех грунтов и учитывает огра¬
ниченность бокового расширения грунта, размеры, форму и жест¬
кость основания тела, воздействующего на грунт, влияние на осад¬
ку всех компонентов напряжения.
Тангенс угла а с учетом формулы (7.13) будет равен tga =
= /?6a=const при О<_р^ро. Так как для определенного грунта и
конкретного основания тела, воздействующего на грунт, величина
постоянна, то a=const при Формула (7.13) может
быть записана в виде
Р=~ = -, (7-14)
а
где Х==б/Лб — относительная деформация грунта при сжатии.
Коэффициент внутреннего трения грунта ф, равный tg <р, где
Ф — угол внутреннего трения грунта, характеризует сопротивление
грунта сдвигу.
Внутреннее трение грунта представляет собой сопротивление
взаимному сдвижению частиц и, в известных пределах, будет пря¬
мо пропорционально нормальному давлению, передаваемому на
твердый скелет грунта (закон Кулона):
*=ФЛ (7. 15)
где т — сопротивление сдвигу (сдвигающее напряжение в грунте).
Составляем в соответствии с П-теоремой безразмерные комп¬
лексы, дополняющие комплексы (7.7) и характеризующие процесс
98
взаимодействия грунта с опорной частью КПА:
П5 = Ф; Пб=арг/7, а также П3 = /2у’//; П4 = /. (7. 16)
Для того, чтобы поведение грунта при экспериментальном исследо¬
вании мягкой посадки в земных условиях было подобно натурному,
необходимо соблюсти равенство безразмерных комплексов для на¬
турного и модельного явлений:
4н = Фм’ ^н9гн/н^н~^м2гм/м^м’ Х = *2М/m/Zm’ f H = f M* (7. 17)
Особенности моделирования на динамически подобных моделях.
За исходные масштабы моделирования удобно принять масштабы
следующих величин независимой размерности: длины, массовой
плотности грунта и ускорения силы тяжести — Kqv и /Q. Произ¬
водные масштабы моделирования выражаются через исходные при
помощи условий подобия (7.17).
Условия подобия <фц='фм и = предполагают применение мо¬
дельных грунтов с коэффициентами внутреннего и внешнего трения,
идентичными грунту планеты. Масштаб ускорения силы тяжести
однозначно определяется из условий эксперимента (К;=6— Луна;
/Q = 2,5 — Марс и т.д.).
Учитывая необходимость соблюдения условия фн=фм, а также
то, что поверхностный слой рассматриваемых планет имеет малую
плотность, нецелесообразно при создании модельного грунта идти
по пути снижения его плотности. Поэтому принимаем KQr =1. Под¬
ставив в выражение для масштаба Ка значения Kj и К0г, получим
Ka = (KlKQKj)-h /<. = (6К/)-1(для Луны);
Марса). (7. 18)
Зависимость (7.18) показывает, что в случае применения дина¬
мически подобных моделей КПА в масштабе 1^1=1^^ масштаб
Ка=1. Другими словами, в этом случае при экспериментальном ис¬
следовании процессов мягкой посадки следует применять грунт-ана¬
лог, т. е. грунт, обладающий механическими характеристиками
грунта планеты. Для этой цели можно использовать некоторые спе¬
циальные материалы (естественные и искусственные) с характери¬
стиками, соответствующими новейшим данным о свойствах поверх¬
ностного слоя планет (см. табл. 7.2). В случае, если (на примере
Луны) К;>1/6, то Ка<1, т. е. модельный грунт должен быть менее
сжимаем (менее податлив), чем натурный. Он должен иметь мень¬
шую пористость (ноздреватость) и большую структурную проч¬
ность при значениях массовой плотности и коэффициентов внутрен¬
него и внешнего трения, соответствующих натурному грунту.
Окончательный выбор величины исходного масштаба Ki произ¬
водится с учетом габаритов испытательных стендов и полигонов и
возможностей создания и применения соответствующего имитатора
планетного грунта.
Особенности моделирования на натурных макетах КПА. При
исследовании мягкой посадки с помощью натурных макетов КПА
9J
4*
см
к
«з
3
к
Физические условия на поверхности планет, основные свойства их грунтов
и некоторых грунтов-аналогов
Несущая
способ¬
ность,
Па
ю
"ю
А?
О
X-
LO
О
7
*
LO
о
7
*
U0
О
см
Л
о
см
I
1
с_ Л со
о
1
1 *
1
5 н §
О о
1 о
о о
2 о
1
о ю
о о
о о
□ OU
1
о о
о ю
Г- О)
С х *
о
г—1 '
ОО —I
см см
СО
00
со
о
о
.1.
см
.1.
о
.1.
со
т
г
г
to
со
СО
о
см
г-
to
1 1
’ 1
см.
см
Tf
00
со
г-Г
со”
со
00
100
и
t-
С-.
t
О
о
о
о
о
о
ч
»=5
ч
ч
ч
t;
СО
со
СО
я
я
я
К
К
я
я
Я Ф
я
СО
СО
я
я
я .
я
г-
•Я
»я
»Я •
3
»я
3
»я
3 к
»я
я
3
я
3
® Он
3
к
я
я
я
я
я
Ф
н СО
я
Ф
И
F-
я
ф
ф -
gFT
я
ф
ф см
о ’—'
Г? со
Н и—1
О
ср со
СР
о
г?
н
о
си со
О со
о —
Г? Я
я
Е-
СР
Ф
я
I»
о Ё
щ >>
К Г''*
Е- н
о я
ш *
Я cj
ср ж
к £
Н
Щ
Е-
Я
сх
сх
сх
сх
сх
СХ
(X
X
X
X
t-H
X
ио
из
ио
СО
СО~
o'
о
о
1
о
1
1
1
ио
см~
1
см
о
о"
г-
1
1
1
1
1
СМ
1
1
1
1
1
Ю
1Л
LO
ю
ю
Ю
О
О
о
о
о
ю
’’7'
'У
’_7
’"7*
О
О)
гЗ
00
о
ио
А
СМ
см~
СМ
о
о
о*
о"
о*
о
1
о о
о
1
о о
о
о
[50
см
о см
о
•ф о
ио
со
СМ 1
"ф
см со
О 00
СО
1 см
ю
LQ
in
Ю
ш
LO
О
о
о
о
о
о
1—<
7
г
Примечание. Предположительная оценка по косвенным данным
н
я
ч
Я
я
я
я
ч
я
я
я
ф
ч
8
Я
я
я
я
\о
я
я
из
о
и
101
должны быть удовлетворены те же условия подобия (7.17),
В этом случае вопрос о моделировании планетного грунта требует
особого рассмотрения. Поскольку испытываемый натурный макет
вследствие разгрузки на (1— /CJ"1) х Ю0% своего веса имитирует
динамику посадки на планету, естественно проанализировать воз¬
можность применения при этом эксперименте грунта—аналога,,
свойства которого наиболее полно соответствуют характеристикам
планетного грунта. Поэтому исходные масштабы моделирования
принимают следующие значения: /Q=l; Крг =1 и Ка=1. Учитывая
это, из условий подобия получим K7-r = (Kz/<QrKfl)_1= 1.
Другими словами, полное подобие явлений при моделировании
с помощью натурных макетов и мягкого деформируемого грунта-
аналога может быть сохранено только в условиях искусственного
создания на Земле планетного ускорения силы тяжести. Так как
«разгрузить» на (1— /С/-1) часть своего веса каждую частицу грун¬
та в земных условиях невозможно, а создание искусственной гра¬
витации с помощью летающей лаборатории или воздействием элек¬
тромагнитного поля на частицы спецгрунта при экспериментах на
натурных макетах практически нереально, то остается только оце¬
нить величину погрешности, вносимой в эксперимент особенностя¬
ми динамики частиц грунта-аналога, находящихся в земном поле
тяготения.
В этом случае осадка грунта под действием макета КПА, опре¬
деляемая по формуле (7.13), будет отличаться от натурной вслед¬
ствие увеличенного в раз веса частиц грунта. Давление р, вхо¬
дящее в (7.13), состоит из двух частей [39]: внешнего давления на
грунт макета посадочного аппарата, равного натурному, — рап и
внутреннего давления в грунте от веса вышележащего слоя толщи¬
ной й, отличающегося от натурного — рг:
Р = Pan + Рг = Pan + Qpflg.
Отсюда находим погрешность в величине р при моделировании:
д (Рм — Рн) Um — £н) ( 7 I
Рп (Pan + Qrhgu)
ГДС gM— ёзем —бЙдун —2,5^Марса> fti~ёлун (Ян — ЙМарса) •
Формулу (7.19) для Марса можно записать так:
д_ 1>5^MapcaQr^ 1,5
Pan + QrhgМарс j Pan
Qr^^Mapcaa
или, для Луны:
Д = SgflynQMPan + бг^Лун) = 5 (1 Н Г’
к Qr^yJ
(7. 20)
(7.21)
Выражение (7.19) показывает, что погрешность в величине давле¬
ния р возрастает с ростом глубины слоя грунта. На поверхности и
в близлежащих слоях при й»0 имеем А^О. Оценим величину пог¬
102
решности давления в грунте на глубине h=i м. Приняв рап=
== 1 -105 Па, рг=1200 кг/м3 и £Лун =1,62 м/с2, £маРса = 3,74 м/с2, по¬
лучим А =0,095 или 9,5% (Луна); Д = 6,5% (Марс).
Поскольку и осадка 6 и сопротивление сдвигу т прямо пропор¬
циональны нормальному давлению р, действующему в грунте, то
погрешности в их величинах при экспериментах на мягком грунте
будут такого же порядка. Следовательно, с достаточной для прак¬
тики степенью точности можно применять «без разгрузки» грунты-
зналоги при экспериментальном исследовании процесса мягкой по¬
садки (а также и передвижения) на натурных макетах КПА.
Интересно отметить, что к аналогичному результату приводит
рассмотрение вопроса о моделировании планетного грунта в случае
исследования мягкой посадки с помощью динамически подобной
модели КПА в натуральную величину, но с уменьшенной в К7- раз
массой, так как и в этом случае внешнее давление модели на грунт
соответствует натурному.
Однако применение в качестве модельного грунта-аналога, со¬
ответствующего по своим свойствам натурному, при экспериментах
на динамически подобных моделях в масштабе приво¬
дит к существенному искажению картины взаимодействия опор
с грунтом планеты. Так, при масштабе модели (для Луны) К/=1/2
погрешность в величине давления на грунт (а, следовательно, и в
величине осадки грунта) составляет около 200%. Поэтому для та¬
ких испытаний необходимо создание специальных модельных грун¬
тов в соответствии с величиной масштаба Ка(Ка<1).
Экспериментальные исследования процесса мягкой посадки с
применением деформируемого грунта, свойства которого моделиру¬
ют характеристики поверхностного слоя планеты, позволяют полу¬
чить в наземных условиях полную аналогию посадки аппарата,
оценить величину погружения опор КПА при разных режимах дви¬
жения (особенно при необходимости его обратного старта), а так¬
же уточнить зоны устойчивой посадки, определенные ранее для
твердого грунта.
Имитация характеристик поверхностного слоя планет
в земных условиях
При рассмотрении вопроса о моделировании планетного грунта
была подчеркнута важность разработки для экспериментальных
исследований динамики мягкой посадки КПА полноценного имита¬
тора—аналога планетного грунта со свойствами, отвечающими сов¬
ременным представлениям о грунтах Луны и планет земной груп¬
пы *.
Несмотря на то, что наблюдения за небесными телами с помо¬
щью наземных установок ведутся очень давно, что космическая
эра уже вступила в свое третье десятилетие, а человечество осуще¬
* Хотя Луна является спутником, а не планетой, но, так как по своим физи¬
ческим характеристикам она близка к планетам земного типа, в дальнейшем
везде под термином «планета» будем подразумевать и Луну.
103
ствило более 25 мягких посадок автоматических и пилотируемых
аппаратов на Луну и планеты земной группы, наши знания о стро¬
ении и свойствах поверхностного слоя планет (см. табл. 7.2) явля¬
ются далеко не полными для правильного решения многих инже¬
нерных проблем, встающих при проектировании перспективных
средств посадки на планеты и передвижения по их поверхности.
Однако имеющиеся результаты исследования характеристик
поверхностного слоя планет свидетельствуют о том, что, несмотря
на существенные их различия (связанные со своеобразием геоло¬
гического развития планеты, атмосферными условиями, силой тя¬
жести, расстоянием от Солнца и т. д.), они имеют много общего,
особенно в отношении физико-механических свойств грунта. Поэто¬
му, обычно структуру и свойства грунта планеты дают в сравнении
либо с лунным грунтом, либо с различными земными горными по¬
родами.
Целесообразно, по-видимому, для имитации планетных грунтов
при наземных испытаниях КПА разработать несколько вариантов
грунта-аналога (см. табл. 7.3), охватывающих по своим физико-ме¬
ханическим характеристикам весь спектр значений этих свойств на
планетах земного типа (напомним, что такие свойства планетных
грунтов, как альбедо, цвет, угол поляризации, электрические и теп¬
ловые характеристики и т. д. не имеют принципиального значения
при исследовании динамических процессов). Комбинируя эти ва¬
рианты грунта-аналога, можно получать многослойные модели по¬
верхностей планет с необходимым изменением свойств по глубине и
заданным рельефом (уклоны, камни, кратеры и пр.).
Таблица 7. 3
Параметры
Варианты грунта-аналога
I
II
III
Плотность, кг/м3
(0,4-0,8)-103
(0,7-1,4)-103
(1,5-3,0).103
Несущая способность,
Па
(0,2—0,6)-105
(0,7—2,0). 105
(2,0-5,0).105
и более
Необходимо отметить, что варианты грунта-аналога, приведен¬
ные в табл. 7.3, представляют собой уточнение по современным
данным предварительной трехслойной модели строения лунной по¬
верхности, предложенной в середине 60-х годов членом-корреспон¬
дентом АН СССР В. С. Троицким на основании анализа результа¬
тов радиолокации Луны и определения вариаций радиояркостной
температуры в течение лунных суток [19, 70].
Для наземной отработки мягкой посадки КПА рационально вы¬
бирать наименее благоприятные варианты грунта-аналога. Так,
при исследовании работоспособности энергопоглотителей КПА, оп¬
ределении максимальных напряжений в элементах конструкции ПУ
и максимальных перегрузок в отсеках аппарата следует обратить¬
ся к наиболее прочному грунту-аналогу (вариант III), в качестве
104
Рис. 7.4. Газосиликальцит пониженной
прочности
которого можно использовать монолитные материалы — бетон, ас¬
фальт и т. п. Эти же материалы (как наименее благоприятные) це¬
лесообразно применять и в случае определения зон устойчивости
КПА на моделях и натурных макетах при посадке на площадки с
различными уклонами, выступами, коэффициентом трения.
При проведении экспериментов на ДПМ для изучения эффек¬
тивности той или иной схемы ПУ на рыхлых непрочных грунтах, а
также при испытаниях летающих макетов КПА для оценки специ¬
фики посадки и, особенно, обратного взлета с таких грунтов необ¬
ходимо использовать варианты I и II грунта-аналога. Материалы,
относящиеся к этим вариан¬
там, могут быть как естест¬
венного, так и искусственно¬
го происхождения.
К пористо-пенистым ма¬
териалам, вырабатываемым
промышленностью, относят¬
ся пенобетон и газосили-
кальцит, характеристики
которых приведены в табл.
7.2.
Пенобетон — монолит¬
ный материал, близкий по
механическим свойствам к
варианту II грунта-аналога, изготавливается с применением цемен¬
та по простой технологии.
Газосиликальцит изготавливается по специальной технологии,
разработанной по следующей методике [37]. При определенных со¬
отношениях CaO, SiO2 и А12О3 (без цемента) в зависимости от ре¬
жима термообработки получаются различные по механическим ха¬
рактеристикам материалы. Обычный газосиликальцит, используемый
для строительных целей, имеет прочность (5—8) -105 Па. Путем из¬
менения технологии и состава смеси удалось получить газосили¬
кальцит (рис. 7.4) прочностью ~105 Па (химический состав смеси:
СаО — 31,5%, SiO2 — 68,37%, А12О3 — 0,13%, Н2О — 42% от сухо¬
го веса смеси).
Искусственный грунт—аналог, приготовляемый на основе мел¬
козернистого песка, связность которого обеспечивается добавлени¬
ем некоторого количества минерального масла, обладает рыхлой
мелкодисперсной, зернисто-агрегированной связной структурой. По
своим физико-механическим свойствам его можно отнести к перво¬
му варианту грунта-аналога (табл. 7.2). Смесь песок-масло гото¬
вится порциями путем тщательного перемешивания и затем укла¬
дывается на твердом подслое в грунтовую площадку.
Сравнение полученного аналога и рыхлого планетного грунта
по гранулометрическому составу говорит о достаточной степени их
соответствия. Данные, приведенные в табл. 7.2, относятся к анало¬
гу, уложенному в грунтовую площадку методом свободной засыпки
без дополнительной обработки (средний коэффициент пористости
1Э5
аналога в этом случае 0,81). Путем уплотнения грунта-аналога или
рыхления различной интенсивности можно добиться изменения его
свойств за счет различной плотности упаковки [26]. Метод подго¬
товки грунтовой площадки к испытаниям влияет также на закон
изменения плотности и пористости аналога по глубине.
В работе [26] получена следующая зависимость давления в грун¬
те-аналоге под штампом от осадки: р = 8,5/г1’01646 • 105, Па (где Авм).
Доверительные оценки констант 8,5 и 1,01646, полученные по
критерию Стыодента, показывают, что с надежностью 95% их отно¬
сительные погрешности составляют соответственно 10% и 8,1%.
При создании искусственных аналогов грунта планеты необхо¬
димо постоянно иметь в виду то, что основными факторами, влия¬
ющими на его физико-механические свойства, являются специфиче¬
ские условия на поверхности данной планеты.
Глава 8. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ МЯГКОЙ ПОСАДКИ
С ПОМОЩЬЮ ДИНАМИЧЕСКИ ПОДОБНЫХ МОДЕЛЕЙ КПА
Экспериментальные исследования процесса мягкой посадки кос¬
мических аппаратов на динамически подобных моделях проводятся
со следующими основными целями:
а) изучить влияние на посадочную устойчивость аппарата: схе¬
мы ПУ аппарата (число опор ПУ, величина опорной базы и т. д.);
массово-инерционных характеристик КПА (величина моментов
инерции, положение ц. м., заполнение баков и т. д.);
конструкции энергопоглотительного устройства и его энергоем¬
кости;
различной начальной ориентации аппарата при посадке;
начальных угловых скоростей аппарата;
направления горизонтальной составляющей посадочной скоро¬
сти относительно КПА и поверхности;
величины наклона поверхности и ее неровностей («рельеф») ;
несущей способности поверхности грунта и коэффициента тре¬
ния.
Испытания необходимо проводить при разнообразных комбина¬
циях вертикальной и горизонтальной составляющих скорости встре¬
чи с поверхностью, обеспечиваемых испытательным стендом;
б) изучить влияние на массу аппарата различных схем и конст¬
рукций ПУ, а также кинематики его раскрытия;
в) проверить и уточнить математическую модель, принятую при
проведении теоретического исследования посадочной устойчивости
КПА на ЭВМ (сравнение и анализ теоретических и эксперимен¬
тальных результатов);
г) найти наиболее эффективные и быстрые пути эксперимен¬
тальной отработки натурного посадочного устройства аппарата;
д) выработать рекомендации по выбору схемы посадочного уст¬
ройства и его геометрических параметров, обеспечивающих как
устойчивость КПА на опрокидывание при посадке, так и прочность
элементов его конструкции и научного оборудования.
106
Весь объем экспериментальных исследований процесса мягкой
посадки на динамически подобных моделях целесообразно разде¬
лить на два этапа:
1 — исследование влияния условий посадки аппарата на поверх¬
ность планеты; 2 — исследование влияния на процесс посадки кон¬
структивных параметров КПА.
При проведении первого этапа исследований необходимо варьи¬
ровать:
величиной и направлением вектора посадочной скорости относи¬
тельно аппарата и поверхности;
величиной угла наклона поверхности и ее неровностей (имита¬
ция «рельефа» посадочной площадки);
величиной коэффициента трения опор о грунт, несущей способ¬
ностью и плотностью его верхнего слоя;
величиной углов начальной ориентации (тангажа, рыскания,
крена) и начальной угловой скорости вращения аппарата при сбра¬
сывании. При испытаниях значения вертикальной и горизонталь¬
ной составляющих посадочной скорости обычно берутся дискретно
(например, с шагом 0,5—1,0 м/с).
На этапе исследований влияния на устойчивость посадки конст¬
руктивных параметров КПА (второй этап) последние варьируются
в пределах, указанных проектировщиками. В этом случае с целью
сокращения количества экспериментов фиксируются значения или
же максимально сужаются пределы их изменения у группы пара¬
метров, характеризующих условия посадки КПА. Как правило, зна¬
чения параметров этой группы берутся близкими к критическим с
тем, чтобы наиболее отчетливо проявилось влияние конструктивных
параметров на устойчивость аппарата при посадке, на максималь¬
ные величины перегрузок, усилий, деформаций в элементах ПУ.
В случае обнаружения при испытаниях чрезмерных перегрузок,
деформаций или неустойчивости модели в диапазоне скоростей, воз¬
можных в натурных условиях, следует, изменяя отдельные конст¬
руктивные параметры ПУ модели (положение центра тяжести, ве¬
личину опорной базы, характеристики энергопоглотителей и т. п.),
попытаться получить приемлемые характеристики при устойчивой
посадке модели во всем требуемом диапазоне посадочных скоро¬
стей. Внесенные при этом конструктивные изменения явятся ценны¬
ми рекомендациями для доработки натурного посадочного устрой¬
ства.
Динамически подобные модели
Рассмотрим кратко особенности устройства и конструкции ди¬
намически подобных моделей (ДПМ), предназначенных для иссле¬
дования мягкой посадки на Луну и Марс (Меркурий). В табл. 8.1
приведены характеристики (осредненные по данным различных ис¬
точников) для трех моделей ДПМ-А, -Б и -В, соответствующих
трем лунным посадочным аппаратам (с уменьшением линейных
размеров в шесть раз — 7</= 1/6) с массами при посадке от 5,6 до
16 т [8, 47, 55].
107
Таблица 8.1
о
5Г
с
0—1,5
0-1,5
0-2,1
0-1,5
0-5
0-5
0-7
0-5
co co
1 1
о о
0-4,2
со
1
о
см см
o'o'
см см
о о
05
СО -ч
jj
см
*5г
СО со
F
со
Ю to
г-
to
co co
00
со
IF b-
f f
to^cM^
1 1
1
1
1 1
1
1
1 1
1
1
г г
г <!
r-?b>?
О о
о
о
о о
о
о
о о
о
о
8 8
о
о
со со
со
co
о о
о
о
00 оо
00 оо
б
б
Г-Н гЧ
1-Н
^Н у—ч
^н
o’4 o’4 1
1 1
1 1
о о
о о
1 1
1
1
1 1
1
1
•I* 1
•1-
•1-
1 I
1 1
1
1
tF
F F~
F
F
f" F*
FF
TF F 1
о о
о
о
о о
о
о
0*0
о"
О
о о
о о
о о |
СО
СО
F
i
см см
см см
со
со
СО
со со
см —<
О О [
г-н
со
со
' Ь-
со
CO
Г-н 00
со
СО
со
* СО
I
60
о о
о
о
о о
о
о
О С5
О*4
о”
о о
о о
О О }
1
СО
CM
05
F
со со !
00
оо о
f f
X
со
П’О
р (
to
1
05
Г'СО
т-ГСМ
to Ю !
Ю О
о
to
9 00
см
СО
о
ю
1 -1-
1
со со
1
1
1
-F
со
1
1
.1. .1.
•Ч
о о
■F
со
00 Д
СМ 2
1
tF
т-Н
F
ь-
г-н '
Г Г
05 05
и>
см
tF
,_7
F
s
o'
о
o' -н
оо оо !
л
Н
1
н
<D
S
В
F rt
F1
F1 tF
■F
F
F F
F
F
со СО
со со
i
СОСО
cd
Он
>Г
Л
1
с
1—Н г-Н
1-н
1-н
см см
CM
CM
F F
F
F
05 05
со со
со со
со со
со
со
о о
о
о
i"H i-H
см см
•f f
СМ СМ !
г-
1—1 у—Ч
1—H
—
см* см
^н ^н
СМ СМ !
1
ю см
F СО
!
s
to
CM CM
00 •
to СО
Ю Ю j
СО со
о
to
to о
ю
CM
tF co
со
оО
со см
СО со
F1 F
•»
**
•ч
to F
•S •»
о со
со
1—1
о со
см
i-H
О F
СО ■
т-Н
о »-<
г-н Г-н
о —"
j
S
СО tO
сО~
to
05 "F
to
to
CM
CO
to
to
IF
ОО О
F СМ
78
44
to to ;
Fb
"F 05
CM
CO oo
т_~
Ю
см со
СО 05
со СО '
о см
СМ*4
О** СМ
СМ*4
o'co’
со
о о
о" о"
О О
<м
* S
—• о
3
F1 О
о
tF
r-l О
05
CM
со
05
СО —1
ОО СМ
а 7
05 Ю
оо
О F .
to
05
05 О
о
оо
F СМ
о ю
-ОО
*-» о
-00
05
-со
CM
~F
со
-см
СМ г-н
►4
1—1 «F
СМ
СО СО
F
co о
со
О*4
СМ
co
о»
§?
05 О
53
ю
см о
F
b- о
ь-
оо
f
f f
СМ 05
b- со I
оо о
оо
см м<
CO
00 О
F
if
F т—1
О F
к*"> C-t
05
г—Ч
-о
о
CO
о
со
-см
со F1
►4
.-1 F1
см
со ю
to
co о
со
о
Ь- оо
I—1
см
CO
г-Н |
<М
СО О
см
F О
05
00
05 О
00
см
05 см
F 05
1
05 tF
со
05
юю
co
F
о о
см
о
05 F
F Ю
CM I
-см
о
-IF
05
CM
-о
00
со
-см
-СО
’-'05 |
1-< tO
со
СМ 05
co
со
F
о
СМ
1—1
<
. см
1
<э со
ю
СО
см о
о
о
^н о
о
00
со о
!
см о !
S2* с_*
см
о
-о
о
to
-о
СО
to
05 ОО '
£ а
со со
со
-F
ю со
CM
to
F О
со
см со
т-* F ;
см to
СО Ь~
CM
tF со
F
I—<
т—1 F
т-H Oi
F
’F
108
Тяжелый аппарат (вариант В) близок по своим характеристи¬
кам к лунному кораблю «Аполлон», с помощью которого были осу¬
ществлены первые полеты человека на Луну [55]. Аппарат вариан¬
та А (с массой около 5 т) следует отнести к классу автоматиче¬
ских, позволяющих доставить на поверхность Луны крупные беспи¬
лотные станции и подвижные лаборатории [47].
Методическая модель ДПМ-Б разрабатывалась для изучения
физической картины процесса мягкой посадки на планеты без атмо¬
сферы. Она позволяла широко менять основные конструктивные па¬
раметры посадочного устройства (например, число опор от 3 до 6
и т. п.) и испытывалась на различных посадочных режимах с при¬
менением жесткого и деформируемого аналогов планетного грунта.
В таблице 8.1 представлены данные четырехопорной модификации
модели. Натурный лунный аппарат варианта Б (полученный путем
пересчета параметров модели в соответствии с критериями подо¬
бия) с посадочной массой 7,6 т может быть отнесен к классу грузо¬
вых автоматических аппаратов, предназначенных для снабжения
перспективных стационарных лунных баз-станций.
Используя условия подобия (см. гл. 7, стр. 90), результаты экс¬
периментов (и расчетов) с моделью ДПМ-Б можно распростра¬
нить на случай мягкой посадки на поверхность Марса динамически
подобных марсианских аппаратов с посадочными массами 2200 кг и
550 кг. В таблице приведены также результаты аналогичного пере¬
счета характеристик моделей ДПМ-А и ДПМ-В на марсианские
(меркурианские) условия (для двух значений масштаба длин:
Kz=l/5 и 2<z=2/5 при Ке=1)-
Специально для изучения особенностей мягкой посадки на по¬
верхность Марса космического аппарата «Викинг» учеными США
были созданы и испытаны динамически подобные модели несколь¬
ких модификаций посадочного устройства этого аппарата. Три та¬
ких модели в масштабах Кг=2/5; КЕ=2/5 и 1; Км = 2/5 также
включены в табл. 8.1 (см. аппарат варианта Г [50, 69]).
Дадим краткое описание названных моделей.
Модель ДПМ-А состоит из несущего корпуса, опор с энергопог¬
лотителями, топливного бака, системы подвески и центровочного
груза. Каждая из четырех опор модели имеет по три стержня (стой¬
ка и подкосы) с амортизирующими устройствами и полусфериче¬
ский «башмак», на который наклеены сминаемые алюминиевые
соты.
Модель ДПМ-Б имеет жесткий цилиндрический корпус из алю¬
миниевого сплава, на котором можно смонтировать от трех до шес¬
ти одинаковых опор, узел подвески модели, несколько вариантов
топливного бака, центровочные и балансировочные грузы (рис.
8.1). Сменные опоры модели состоят из двух нижних боковых стер¬
жней (подкосов) и центрального стержня (стойки) с энергопогло¬
тителем (амортизатором). Энергопоглотитель представляет собой
точеный алюминиевый цилиндр, внутри которого свободно пере¬
мещается шток с поршнем. В цилиндр под поршень закладывается
патрон из алюминиевых сот, сминаемых при посадке модели на
109
грунт. Вместо применения амортизатора со сминаемыми алюмини¬
евыми сотами, в опорах моделей ДПМ-А и ДГ1М-Б предусмотрено
использование фрикционного энергопоглотительного устройства.
Модель ДПМ-В также имеет жесткий легкий корпус, выполнен¬
ный в виде крестовины с консолями Л-образного сечения. К кресто¬
вине крепятся четыре опоры, состоящие из основного стержня
(стойки) и двух боковых подкосов. Все стержни снабжены аморти¬
заторами для поглощения энергии удара с помощью сотовых алю¬
миниевых патронов. На каждой стойке модели вместо опорных пят
установлены небольшие иглы для моделирования повышенного ко¬
эффициента трения опоры при контакте с поверхностью. В центре
тяжести модели смонтирован вертикальный стержень с узлом под¬
вески модели на испытательном стенде. Стержень служит одновре¬
менно и для закрепления в заданном положении балансировочного
груза.
Рис. 8. 1. Испытательная установка:
а—стенд; б—динамически подобная модель ДПМ-Б
Модели ДПМ-Г являются аналогами основных модификаций
ПУ аппарата «Викинг». Две первые модели (Г-1 и Г-2) имеют
идентичный ферменный корпус, сваренный из алюминиевых трубок,
треугольный в плане, жесткий и легкий, удобный для крепления
центровочных и балансировочных грузов. Модели Г-1 и Г-2 отлича¬
ются друг от друга конструкцией посадочного устройства, а имен¬
но: первая модель имеет опоры в виде перевернутой треноги, к вер¬
шине которой шарнирно крепится пята; опоры второй модели вы¬
полнены по консольной схеме (два боковых подкоса подходят к ос¬
новной стойке опоры несколько ниже ее середины, образуя консоль¬
ную часть у основной стойки) и также имеют шарнирно закреплен¬
ную пяту.
Амортизатор основной стойки Г1У представляет собой цилиндр,
в который закладываются четыре алюминиевых сотовых патрона,
нанизанных на тонкий стержень. Каждый сотовый патрон деформи¬
руется под действием заданной силы. При деформации амортиза¬
110
тора зависимость силы обжатия от хода штока принимает вид сту¬
пенчатой функции (см. рис. 6.3).
Энергопоглотители бокоьых стержней (подкосов) опоры имеют
по два сотовых патрона, из которых один работает при сжатии под¬
коса, другой — при растяжении.
Последняя модель (ДПМ-ГЗ) в отличие от двух предыдущих
является натурной динамической моделью КПА «Викинг» с поса¬
дочным устройством в виде перевернутой треноги. Модель Г-3 име¬
ет габариты и центровку натурного КПА, однако ее масса в ~2,5
раза меньше, чем у натурного марсианского аппарата (см. табл.
7.1). Модель имеет жесткий и очень прочный корпус из алюминие¬
вых пластин и трубок, соединенных при помощи сварки. На корпу¬
се монтируются балансировочные грузы с целью придания модели
необходимых массово-инерционных характеристик. В энергопогло¬
титель стойки каждой опоры закладываются сотовые блоки (патро¬
ны) на четыре различных значения силы обжатия.
Особенности функционирования
модельных энергопоглотителей
Посадочное устройство КПА должно иметь специальные энерго¬
поглотители для обеспечения мягкой посадки на планету. К энер¬
гопоглотителям КПА предъявляют следующие требования:
малая масса и малый упаковочный объем;
запас по характеристикам на случай преждевременной отсечки
тормозного двигателя;
способность действовать в условиях глубокого вакуума и резко¬
го перепада температур;
прочность и живучесть при нерасчетных условиях посадки (удар
о камень, попадание в щель, посадка не на все опоры и т. д.).
Особое внимание при экспериментальных исследованиях про¬
цесса мягкой посадки на планеты в земных условиях (на моделях
или на натурных макетах КПА) необходимо уделять так называе¬
мым «модельным» энергопоглотителям, имитирующим натурные в
силовом и кинематическом отношениях. Снятие требования о функ¬
ционировании в глубоком вакууме открывает более широкие воз¬
можности (14] по выбору способов поглощения кинетической энер¬
гии при создании эффективных модельных энергопоглотителей. За¬
метим, однако, что отдельные результаты такого исследования
можно с успехом распространить и на натурные энергопоглотители
(например, на сотовые, на устройства типа «протяжки», на метал¬
лические торовые и шаровые оболочки, стальные стержни и т. д.).
Ниже приведены только основные результаты эксперименталь¬
ных исследований нескольких типов модельных энергопоглотите¬
лей, представляющих собой сотовую ячеистую конструкцию из алю¬
миниевой фольги различной толщины или спеченного алюминиево¬
го порошка (рис. 8.2), цанговых фрикционных энергопоглотителей,
а также устройств типа «протяжки» (см. рис. 8.6) и с пластически
деформируемым при растяжении стальным стержнем.
111
Сотовые энергопоглотители, полностью или частично разрушае¬
мые при посадке модели КПА, относятся к энергопоглотителям од¬
норазового действия. Низкая собственная масса, удобство в эксплу¬
атации и почти постоянная сила разрушения в процессе обжатия —
далеко не полный перечень их положительных качеств [22].
Экспериментальную зависимость силы разрушения сотового
энергопоглотителя от величины его деформации можно получить с
помощью статических (на прессе) и динамических (копровых) ис¬
пытаний. При таких испытаниях усилие обжатия должно прикла¬
дываться вдоль оси ячеек сотового блока.
Экспериментальное оборудование для статических испытаний —
гидравлический пресс и модельный цилиндр с поршнем (модель
опоры натурного ПУ), в свободное пространство которого заклады¬
ваются сотовые блоки.
Рис. 8. 2. Сотовый энергопоглотитель
Для проведения динамических испытаний используют копровую
установку, на которой груз тт свободно падает на цилиндр с сото¬
выми блоками.
Движение груза после момента удара о шток цилиндра описы¬
вается выражением
wrt/=Fp —mrg, (8.1)
где тг — масса груза; у — координата его центра тяжести; Fv —
сила разрушения сотового блока (или сила сопротивления фрикци¬
онного энергопоглотителя); g— ускорение свободного падения.
Из (8.1) получаем расчетную формулу для
FP = tnrg(y/g+V> (8.2)
где значения у определяются по осциллограммам, приче^м отсчет
следует вести от линии п= +1 (п— перегрузка).
Типовые результаты копровых испытаний сотовых энергопогло¬
тителей приведены на рис. 8.3. Отметим наличие характерной «по¬
лочки» ускорений в процессе пластической деформации сотового
блока и последующего «выброса» ускорений в том случае, если
энергия падающего груза больше энергоемкости поглотителя (при
112
60 /мм
м/с
этом возможен «жесткий» удар). Анализ результатов испытаний
позволяет отметить следующее:
достаточно хорошее совпадение данных динамических и стати¬
ческих испытаний сотовых энергопоглотителей;
сопротивление сотового блока смятию практически неизменно
на всем пути смятия (разброс по силе около 10%);
наличие в ряде случаев «пика» по силе в начальный период об¬
жатия сотового блока.
■Однако небольшим пред¬
варительным обжатием
сот такое явление можно
устранить;
имеющую место, иног¬
да, потерю устойчивости
сотовым блоком, сопро¬
вождаемую резким паде¬
нием величины силы соп¬
ротивления. Указанная
потеря устойчивости мо¬
жет вызываться несколь¬
кими причинами: искаже¬
нием формы ячеек сотово¬
го блока, предваритель¬
ной деформацией одной
из граней блока (что слу¬
чается при неаккуратной
закладке блока в ци¬
линдр), погрешностями
технологического процес¬
са изготовления сотовых
блоков (склейка фольги,
нарезка блоков и т. д.).
Приведем аналитиче¬
ское выражение для
оценки приближенного
значения среднего разру¬
шающего напряжения
<уСр гексагональной сотовой конструкции, подверженной статическо¬
му осевому нагружению и свободно опертой по торцам [22]:
оср=40,5-^ а0,2+1,155 4-ТоУз, (8.3)
d
где t — толщина стенки ячейки (толщина фольги); d — диаметр
вписанной в ячейку окружности; а0,2— предел текучести при растя¬
жении; то,з — предел текучести при сдвиге.
При выводе этого выражения материал конструкции полагался
жестко-пластическим с равными пределами текучести при растяже¬
нии и сжатии и не учитывалось влияние осевых напряжений на
характер процесса текучести.
сотовых энерго-поглотителей, сторона ше¬
стигранника 6 (2,5) мм; толщина фольги
0,05 (0,15) мм; материал Al-Т (САП);
mr=19,3 кг
ИЗ
Сравнение результатов расчета по формуле (8.3) с данными
вышеописанных испытаний показало, что формула (8.3) дает завы¬
шенную и весьма грубую оценку величины среднего разрушающего
напряжения сотовой конструкции (завышение достигает 50—70%).
Сравнение расчетов с экспериментом также свидетельствует о зна¬
чительном завышении расчетных величин [22].
кН
Fчач=
--200Н
Ущтока~200 5 м/с
—
— —
10 20 30 50 60 7Z7 80 90 (?мм
Направление хода штока при,,скатиа“—=►
Рис. 8.4. Типовые результаты статических испытаний фрикционного энео-
гопоглотителя:
сжатие; растяжение
5к
10
20
30
40
50
60
70
80
90
mF (5К)
0,127
0,135
0,164
0,209
0,245
0,295
0,322
0,376
0,476
D^(8K)-10‘
4,6
5,6
10,8
14,4
39,4
61,9
67,5
69,5
233
(8К)
0,021
| 0,024
0,033
| 0.038
■ 0,033
0,079
0,082
0,083
0,153
Фрикционные энергопоглотители. Наряду с сотовыми энергопог-
лотителями нашли применение модельные опоры КПА на сухом тре¬
нии. В этой конструкции опоры элементами, обеспечивающими пог¬
лощение кинетической энергии, являются клиновые вкладыши из
поликапролактама, поджимаемые к штоку специальной гайкой
[7, 13].
Испытания фрикционных энергопоглотителей можно проводить
на том же оборудовании и по той же методике, что и сотовых. На
рис. 8.4 и 8.5 приведены типовые результаты статических и дина¬
мических испытаний модельных опор КПА указанной конструкции.
Результаты испытаний фрикционных энергопоглотителей свиде¬
тельствуют о следующем:
рост силы сопротивления в процессе энергопоглощения имеет
место вследствие втягивания материала вкладышей внутрь цилинд¬
ра поглотителя по ходу движения штока (явление «самозатяжкл»
114
энергопоглотителя). По этой же причине величина силы сопротив¬
ления при «сжатии» поглотителя больше, чем величина силы соп¬
ротивления при его «растяжении» (т. е. при вытягивании штока из
цилиндра), причем это превышение в некоторых случаях достигает
30%. Отсутствие на осциллограммах «полочки» ускорений также
является следствием непрерывного роста силы сопротивления (ин¬
тересно сравнить с сотовыми поглотителями);
при ударах с большой начальной скоростью (~4,0 м/с) движе¬
ние штока поглотителя начинается при значениях силы сопротив¬
ления несколько меньших, чем статическая сила начальной за¬
тяжки;
Рис. 8. 5. Типовые результаты динамических испытаний фрикци¬
онного энергопоглотителя (датчик № 2 установлен на энерго¬
поглотителе, датчик № 5 — на падающем грузе, тг=19,3 кг):
а—испытание № 105 (^пачте400 Н; ^/нач.штока = 3’1 м/с); б—испытание
№ Ю4 (FHa4«400 Н; Упач,штока = 3.8 м/с)
в первый момент движения штока имеют место затухающие ко¬
лебания ускорения (и силы сопротивления), которые не могут быть
собственными колебаниями сейсмической массы датчика (так как
последний хорошо задемпфирован). Эти колебания, по-видимому
связаны с упругими свойствами вкладышей, трущихся о шток и втя¬
гиваемых внутрь цилиндра (разновидность автоколебаний);
на характер изменения силы сопротивления в процессе энерго¬
поглощения существенное влияние оказывают технологические отк¬
лонения при изготовлении штоков и поликапролактамовых вкла¬
дышей данной серии энергопоглотителей;
модельные энергопоглотители трения с вкладышами из поли¬
капролактама при нормальных условиях обеспечивают достаточно
высокую стабильность свойств поглощения энергии при повторных
испытаниях (тем самым открывается возможность создания мо¬
дельного энергопоглотителя многоразового действия).
115
Энергопоглотители среза представляют собой устройства, рабо¬
тающие по принципу «протяжки» [42]. Подвижный шток энергопог¬
лотителя—протяжка с режущими кромками (зубьями) —соединя¬
ется с опорой КПА. В момент посадки опоры КПА, воспринимая
нагрузку, обжимаются. Шток энергопоглотителя перемещается
внутри специальной втулки, и его режущие зубья поочередно сре¬
зают некоторый слой металла (рис. 8.6).
Рис. 8. 6. Энергопоглотитель среза (типа «протяжки»)
Величина силы сопротивления Fp, развиваемая таким энерго¬
поглотителем, зависит от материала втулки, числа одновременно
работающих зубьев, длины их режущих кромок и толщины среза¬
емого слоя металла, т. е.:
Fp = яр„Р 2 (8. 4)
1 = 1
где рПр — приведенное давление зуба протяжки на материал втул¬
ки при обжатии энергопоглотителя (из эксперимента) [42]; N — чис¬
ло одновременно работающих зубьев штока; di — диаметр режу¬
щей кромки f-ro зуба; Сг- — коэффициент длины режущей кромки
f-ro зуба (С^1; при = 1 — режущая кромка по всей окружно¬
сти зуба); ti — толщина слоя металла, срезаемого l-м зубом.
На рис. 8.7 представлены типовые результаты испытаний по оп¬
ределению зависимости силы сопротивления развиваемой энер¬
гопоглотителем среза, от величины перемещения его штока. При
испытаниях использовались сменные втулки из различных материа¬
лов (Д16Т, АМг-6 Д16М, АК-6 и др.). Полученные при копровых
испытаниях осциллограммы с ярко выраженной «полочкой» ускоре¬
ний очень напоминают осциллограммы испытаний сотовых энерго¬
поглотителей.
Экспериментальные исследования позволили установить следу¬
ющие основные особенности энергопоглотителей среза:
малая масса и малые габариты при большой энергоемкости;
простота получения необходимой величины силы сопротивления
и желаемого характера ее изменения (путем подбора материала и
ширины сменной втулки и профилирования зубьев протяжки);
116-
удовлетворительное совпадение величины силы сопротивления
при динамическом и статическом обжатии энергопоглотителя (рас¬
хождение может достигать ~15%);
отсутствие резких колебаний ускорения (и силы сопротивления)
в начальный момент энергопоглощения;
незначительное влияние
кость и пр.) на характе¬
ристики поглотителя;
высокая стабильность
характеристик поглотите¬
ля при повторных испы¬
таниях (при постоянстве
материала сменных вту¬
лок) ;
удобство в эксплуа¬
тации (перезарядка, «та¬
рировка» и т. д.).
Отмеченные особен¬
ности энергопоглотите¬
лей среза говорят о воз¬
можности успешного их
применения не только
при наземной отработке
процесса мягкой посад¬
ки, но и непосредственно
на натурном космическом
посадочном аппарате.
Энергопоглотители с
деформируемым
ным стержнем
иметь различную
рукцию,
ментами
ются две телескопически
соединенные
положенным
стержнем,
стержень
специальных
ков соединяется
ми трубами.
Ударная нагрузка при посадке модели КПА через внутреннюю
трубу (шток) энергопоглотителя передается на стержень. При
этом стержень растягивается, так как другой его конец жестко сое¬
динен с наружной трубой. Если усилие, растягивающее стержень,
превысит предел текучести его материала, то начнется пластиче¬
ская деформация стержня, в результате которой и происходит пог¬
лощение энергии удара.
сталь-
могут
конст-
основными эле-
которой явля-
трубы с рас-
внутри них
Стальной
посредством
переходни-
с обеи-
внешних условий (температура, влаж-
Рис. 8.7. Типовые результаты испытаний
энергопоглотителей среза (материал смен¬
ных втулок —Д16Т (а) и Д16М (б); мате¬
риал протяжки — Р18):
— статическое обжатие с
к штока
тие с
1,
/
v
f/
1
—V
\
1
/ z
у /
1 '
(!/
V
1
L
Д
60 £ мм
а)
б)
=2,5 • 10-4 м/с |
- • — динамическое обжа- ( ^=2 зуба
, ,.„=5,2 м/с J
с ч
^нач.штока=4>0 м/с 1д/-1 п
—динамическое обжатие Г7*-1 3У&
с ^нач.штока=^ м^с '
—. статическое обжатие с
^штока=2’5 • Ю—4 м/с
— динамическое обжатие Сч
Унач.штока = 3,3 м/с 1дГ=2 зуба
— • — — динамическое обжатие [ 1
с ^нач.штока = 3’0 м/с '
inc ь v нач.штока-м/с
I — — — динамическое обжатие с
117
Величина силы сопротивления обжатию Fp у такого энергопогло¬
тителя зависит от величины предела текучести на растяжение ма¬
териала стержня Go,2 и его диаметра на участке пластической де¬
формации <7Пласт, Т. е.
р = (8.5)
где у — эмпирический коэффициент, учитывающий влияние трения
между элементами амортизатора на величину силы его обжатия
(у>1).
Путем копровых и статических испытаний можно определить ха¬
рактеристики энергопоглощения такого амортизатора со стержня¬
ми из различных сталей (например, 1Х18Н9Т, Х17Г9АН4 и др.), об¬
ладающих хорошими пластическими свойствами. Как показывают
результаты испытаний, рассматриваемый энергопоглотитель отли¬
чается:
высокой энергоемкостью при малых габаритах и массе;
высоким коэффициентом полноты диаграммы обжатия;
хорошим согласованием результатов динамических и статиче¬
ских испытаний;
малыми упругими свойствами при снятии внешней нагрузки;
малым воздействием окружающих условий (положительных и
отрицательных температур, влажности и т. д.) на характеристики
энергопоглощения;
простотой конструкции с точки зрения технологии изготовления
и эксплуатации.
Следует отметить, что энергопоглотители с деформируемыми
стержнями (так же, как и сотовые амортизаторы) успешно были
применены на автоматических космических аппаратах «Луна-16»,
«Луна-17», «Луна-20», «Луна-21» и «Луна-24» [16], совершивших
мягкие посадки в различные районы лунной поверхности.
Модельные испытательные стенды
Испытательные стенды предназначены для экспериментального
изучения процесса мягкой посадки космических аппаратов на Лу¬
ну, Марс и другие планеты с помощью свободнопадающих дина¬
мически подобных моделей. Испытательные стенды позволяют про¬
вести в наземных условиях исследование устойчивости космическо¬
го аппарата при мягкой посадке, оценить действующие на него пе¬
регрузки, выбрать оптимальную по массе конструкцию посадочного
устройства и отработать его энергопоглотительные элементы. При¬
менение сменного грунта, имитирующего поверхностный слой Лу¬
ны, Марса и других планет, существенно расширяет возможности
стенда.
Испытательный стенд этого типа состоит из следующих состав¬
ных частей (рис. 8.8):
специального поворотного стола (платформы) с имитатором
грунта планеты;
118
маятниковой системы подвески и сброса модели КПА;
измерительной и регистрирующей аппаратуры.
Высота подъема модели КПА над столом h определяется требу¬
емой величиной вертикальной составляющей посадочной скорости
Ув и регулируется путем поворота консольной стрелы стенда в вер¬
тикальной плоскости. Величина горизонтальной составляющей по¬
садочной скорости 1/г зависит от угла р отклонений параллелограм¬
ма маятниковой системы подвески от вертикального положения.
Рис. 8. 8. Схема модельного испытательного стенда:
1—маятник; 2—трос к лебедке; 3—опоры; 4—модель
Величины h, р и Д вычисляются по следующим формулам:
p=arccos 1
g cos О
(8. 6)
где g=9,81 м/с2; I — длина боковой стороны параллелограмма
системы подвески; 0 — угол наклона имитатора грунта планеты.
Вследствие некоторого трения в подшипниках подвески и соп¬
ротивления воздуха при полете модели КПА составляющие ее поса¬
дочной скорости будут несколько ниже значений, принятых в (8.6).
При проведении наземных экспериментальных исследований
мягкой посадки обычно производятся измерения и регистрация (на
осциллограммах, магнитных лентах и т. п.) следующих параметров:
углов тангажа, крена, рыскания (ориентация модели);
вертикальных и горизонтальных перегрузок (в центре масс мо¬
дели и на всех опорах ПУ);
давления топлива на стенки модельных баков;
угловых ускорений и скоростей вращения модели;
деформаций опорных энергопоглотителей;
119
напряжений в элементах конструкции ПУ модели.
Для измерения вертикальных и горизонтальных перегрузок (ус¬
корений) применяются индуктивные датчики (ДУ-5) и малогаба¬
ритная аппаратура, например, ВИ6-5МА (датчики ДУ-5 можно ис¬
пользовать и в комплекте с тензоизмерительной аппаратурой).
Давления имитатора топлива на стенки баков модели КПА мо¬
гут измеряться датчиками давлений ДД-1-нДД-б (входящими в
комплект аппаратуры ВИ6-5МА). Датчики ДД также являются ин¬
дуктивными преобразователями измеряемых механических величин
в электрические сигналы.
Для измерения угловых ускорений и скоростей вращения моде¬
ли датчики, выполненные на основе гироскопов, весьма неудобны
из-за относительно больших габаритов, сильного воздействия на со¬
седние датчики и низкой ударной прочности. Датчик угловых уско¬
рений, свободный от указанных недостатков и нечувствительный к
действию линейных ускорений, предложен в работе [36]. Такой дат¬
чик состоит из статора и ротора, соединенных при помощи упругих
пружин. Ось пересечения пружин проходит через центр тяжести
ротора, являясь осью его вращения. Под действием измеряемого уг¬
лового ускорения происходит поворот ротора относительно статора.
Вследствие полной балансировки ротора датчик не чувствителен к
воздействию линейных ускорений.
Для измерения величины и характера деформаций опорных
энергопоглотителей по времени удара применяются специальные
датчики перемещений—потенциометры (см. рис. 8.2), состоящие из
константановой проволоки диаметром 0,5 мм, натянутой вдоль ано¬
дированного штока опоры, и скользящего контакта, охватывающе¬
го проволоку.
Напряжения, возникающие в стержнях опор при контакте моде¬
ли с грунтом, измеряются с помощью калиброванных проволочных
тензодатчиков.
Сигналы от всех датчиков модели передаются по легкому вися¬
чему кабелю в регистрирующую аппаратуру, в качестве которой
можно применять широко распространенные шлейфовые осцилло¬
графы, электронные осциллографы, ленточные магнитофоны с ви¬
деоприемниками, кинокамеры и т. п.
С помощью модельных испытательных стендов маятникового
типа в исследовательском центре Лэнгли (США) проводилась экс¬
периментальная отработка посадочного устройства марсианского
автоматического аппарата «Викинг» на нескольких его динамиче¬
ски подобных моделях (см. табл. 8.1, модели ДПМ-Г). Для испыта¬
ний малогабаритных моделей Г-1 и Г-2 (с уменьшением линейных
размеров в 2,5 раза по сравнению с натурой) и полноразмерной на¬
турной модели Г-3 (с уменьшенной в ~2,5 раза массой по сравне¬
нию с натурным аппаратом) применялись различные маятниковые
стенды.
В табл. 8.2 приведена краткая техническая характеристика
двух модельных испытательных стендов (исследовательский центр
Лэнгли [50, 69]).
120
Таблица 8. 2
Наименование параметра
Стенд для моделей
Г-1 и Г-2
Г-3
Номинальная высота подъема модели, м
~2,5
>7
Номинальный угол отклонения подвески, град
-40
>30
Номинальная вертикальная скорость посадки,
м/с
-7
-12
Номинальная горизонтальная скорость посадки,
м/с
-2
-3
Номинальный вес модели, Н
-130
-2000
Ширина посадочной площадки, м
1,8
-4
Длина посадочной площадки, м
3,7
-7
Номинальные углы наклона площадки, град
±20
±20
Номинальные углы тангажа модели, град
±15
04-10
Коэффициенты трения опор по площадке
0,4; 0,8
0,4-0,7
Посадочная площадка первого стенда изготовлялась из твердо¬
го дерева и покрывалась гладкой фанерой (толщиной в 1,9 см).
Один конец площадки мог регулироваться по высоте для получе¬
ния разных углов наклона. Алюминиевая пята модели при сколь¬
жении по гладкой фанере имела коэффициент трения 0,4. Коэффи¬
циент трения 0,8 получался при наклейке на опорную пяту модели
тонкого слоя резины.
Деревянная посадочная площадка второго стенда монтирова¬
лась на более массивной и жесткой платформе. Четырехстержне¬
вая маятниковая подвеска крепилась шарнирно к ферменной стре¬
ле специального крана на высоте около 14 м и отклонялась на за¬
данный угол с помощью троса и крановой лебедки.
Погрешности измерения основных параметров при эксперименте
Такими погрешностями, в основном, являются погрешности из¬
мерения физических величин, характеризующих динамику мягкой
посадки модели КГ1А, погрешности расшифровки (распечатки) ос¬
циллограмм (лент) и погрешности, вносимые реакцией массивного
стола стенда с имитатором грунта на удар.
Оценим погрешность приближенного определения составляю¬
щих посадочной скорости модели по формулам:
^в=[2ё-(Лзам + Дзам sin Vzr=gA3aMcos0aaMyr1. (8.7)
Имеем [30]:
1пУв=^-1п2^ + ^-1п(Л + Дзт9);
121
или
(8. 8)
d (In VB) =-^ = \dh-\- Д cos 0^0sin ©o' Д] [2 (й-J- Д sin 0)]-1,
AV7» _ Ай + Д COS 6Д8 + sin 0АД i qq 0/
VB~ 2 (Л + Д sin 0) ’ °
Так как максимальные абсолютные ошибки при измерении гео¬
метрических параметров Дзам, ^зам, 9зам не превосходят значений
ДЛ = ±0,02 м; ДД= ±0,02 м; Д0.= ±0,5°, то относительная ошибка
вычисления VB составит ~7%. Относительную ошибку вычисления
Vr можно найти по формуле
+ ЮОо/о. (8.9)
Находим, что погрешность вычисления Vr составляет ~10%.
Общую погрешность измерений при динамических испытаниях
моделей удобно определять через частные погрешности отдельных
элементов измерительной системы [28].
В нашем случае общая погрешность измерений слагается из сле¬
дующих частей:
погрешности чувствительного элемента (датчика) сгд;
погрешности усилительной аппаратуры оа;
погрешности гальванометра осциллографа огг;
погрешности записи и ее расшифровки су3.
Так, например, при измерении линейных ускорений комплектом
индуктивный датчик — тензометрическая аппаратура указанные
частные погрешности равны:
а) погрешность датчика ДУ-5 при нормальных условиях измере¬
ния в заданном амплитудном и частотном диапазоне — 3%; чувст¬
вительность к неизмеряемым компонентам ускорения — 0,5%;
температурная погрешность ~3%; погрешность от неточной уста¬
новки датчика — ~3%. Поэтому
ад = [32_ро,52-|-32-]-32]^ = 5,2%;
б) погрешность усилительной аппаратуры в комплекте с индук¬
тивным датчиком включает в себя чувствительность выходного то¬
ка к колебаниям питающего напряжения на ±10% —не более
1,5%; чувствительность выходного тока к взаимодействию между
каналами — не более 1%; погрешность частотной характеристики
усилителя в полосе 04-500 Гц— ~3%; нелинейность амплитудной
характеристики канала датчик — усилитель— ~4%. Поэтому
aa = [l,52+l2 + 32 + 42f=5,3%;
в) погрешность рамочного гальванометра с fo=4OO Гц в рабо¬
чем диапазоне частот (0—200 Гц) не превышает 1%, т. е. сгг= 1 %;
г) абсолютная погрешность записи и расшифровки включает в
себя неточность положения нулевой линии, отклонение ординаты
записи от нормали к нулевой линии, погрешности замеров по орди¬
нате и абсциссе при расшифровке, что составляет ~ ±0,4 мм. Та-
122
ким образом, относительная погрешность записи и расшифровки
при среднем отклонении светового луча в 20 мм равна 0*3=
= 0,4 : 20X100 = 2%.
Принимая закон распределения частных погрешностей нормаль¬
ным, находим общую погрешность измерения линейных ускорений:
°у = [°д сг +аз]2 =7,8%.
Определяя аналогичным образом погрешность измерения деформа¬
ций опор и напряжений (усилий) в элементах конструкции ПУ, на¬
ходим соответственно величины 5,6% и 5,3%.
Оценим влияние жесткости одного из вариантов специального
стола стенда (имитатора поверхности планеты) на динамику про¬
цесса мягкой посадки. С этой целью определим ту часть общей ки¬
нетической энергии модели, которая рассеивается конструкцией
стола стенда при колебаниях, возникающих в результате удара мо¬
дели при посадке.
Ферменную конструкцию специального стола, имеющего сред¬
нюю и боковые опоры, с аналогом грунта планеты схематизируем в
виде трехопорной балки с равными пролетами I и равномерно рас¬
пределенной погонной массой тпог. При основной форме колебаний
каждый пролет такой балки будет находиться в условиях стержня
с шарнирными концами [34]. С достаточной точностью можно при¬
нять, что изогнутая ось стержня в процессе колебаний имеет форму
статической кривой изгиба нагруженной посередине балки постоян¬
ного поперечного сечения, т. е.:
y(x, t) = A (/) (3/2х — 4%3)/~3,
где А (/) — перемещение в середине пролета колеблющейся двух¬
опорной балки.
Найдем выражение для кинетической энергии колебаний конст¬
рукции стола стенда:
'2Z . 114
Е„=-^пгаотуЦх, t)dx= 2А2^т™ =
о о
® т‘ют1'
Принимая A(t) =AQcospt, получим Лтах=^оЯ где Ло — амплитуда
колебаний в середине пролета при - р — угловая частота основ¬
ной формы колебаний стола стенда. Выражение для оценки вели¬
чины кинетической энергии, рассеиваемой конструкцией стола стен¬
да при колебаниях, принимает вид
E^^-Afam^l. (8.10)
Параметры Ло и р определяются экспериментально: р — резонанс¬
ным способом путем возбуждения основного тона колебаний стола;
123
До — при сбросах на стол динамически подобной модели КПА (см.
осциллограмму, рис. 8.9). Для нашего случая имеем
Доэксп = 3,33.1О-3м; тпог = 540 кг/м; / = 5 м;
рэкси=2л/эксп = 2л • 4,2 = 26,4 рад/с.
Подставляя эти значения в формулу (8.10), находим Ест= 10,1 Дж.
Общая энергия модели в начале испытания составляла Еобщ=
= /7/Mg7/ = 295 Дж, где тм = 35,2 кг — масса модели ДПМ-Б; й =
= 0,85 м — высота подъема центра тяжести модели при испытании.
Рис. 8. 9. к оценке влияния жесткости имитатора по¬
верхности планеты (/гСброса = 0,85 м; 0 — 0°, схе¬
ма 2—2):
I—ДП (точка 1 на середине стола), /Экс=4’2 Л0=3,3 мм;
//—ДУ (точка 2 на модели); n=4 g; III—ДУ (точка 3 на
краю стола); IV—ДУ (точка / на середине стола)
ДП—датчик перемещения; ДУ—датчик ускорения
Таким образом, в конструкции стола стенда рассеивается при
колебаниях £'ст = £’ст/£'обтц=0,0342 или 3,42% общей энергии мо¬
дели, что свидетельствует о пригодности специального стола стенда
для проведения экспериментов по моделированию мягкой посадки
на планеты.
Необходимо отметить, что схематизация стола, имеющего проги¬
бы в поперечном сечении, уменьшающиеся от середины к краям,
балкой с постоянными по сечению прогибами приводит к некоторо¬
му завышению оценки Ест. В рассматриваемом случае модель сбра¬
сывалась в центральную точку половины стола, возбуждая коле¬
бания с наибольшими амплитудами. Если же модель «садится» в
районе средней опоры стола (что имеет место в большинстве испы¬
таний,, особенно при посадке вниз по склону), то амплитуды коле¬
баний стола будут на порядок меньше. Отметим также, что в про-
веденном расчете не учитывалась ввиду малости доля энергии, рас¬
сеиваемая при колебаниях конструкции стола стенда по высшим
формам [32].
124
Глава 9. ОСОБЕННОСТИ НАЗЕМНОЙ ЭКСПЕРИМЕНТАЛЬНОЙ ОТРАБОТКИ
МЯГКОЙ ПОСАДКИ С ПОМОЩЬЮ НАТУРНЫХ МАКЕТОВ КПА
В гл. 7 указывалось, что сохранение подобия явлений при моде¬
лировании мягкой посадки на натурных макетах КПА возможно
только в условиях искусственного создания на Земле планетного
ускорения силы тяжести. Способы «разгрузки» натурного макета
КПА, применяемые для достижения этой цели, являются относи¬
тельно простыми с технической точки зрения и могут быть реализо¬
ваны различными конструктивными средствами, относящимися к
двум следующим группам:
разгрузка при помощи специальных реактивных двигателей, ус¬
танавливаемых на макете (создание бесстендовых летающих маке¬
тов КПА);
разгрузка при помощи стендовых механизмов, состоящих из сле¬
дящего подвижного устройства с разгружающим приспособлением
(создание стендовых натурных макетов КПА).
В связи с тем, что допустимое отклонение значений усилия раз¬
грузки от его номинальной величины, определяемой из условий по¬
добия явлений (7.9), составляет 1—3%, предельные отклонения
вектора разгружающего макет усилия от вертикали ограничивают¬
ся конусом с углом при вершине в 0,3—1,0°.
Основной особенностью экспериментальных исследований мяг¬
кой посадки на натурных макетах КПА является то, что они, поми¬
мо окончательной проверки работоспособности ПУ, оценки его эф¬
фективности и надежности, позволяют провести натурную отработ¬
ку заключительного этапа полета и посадки на поверхность плане¬
ты (что особенно ценно для пилотируемых или дистанционно управ¬
ляемых КПА).
Летающие макеты КПА
Летающие макеты можно создавать в соответствии с указанны¬
ми в гл. 7 вариантами «разгрузки» при помощи реактивных двига¬
телей (возможно также применение вертолетов, заменяющих эти
двигатели).
Первый вариант разгрузки позволяет получить наибольшую
точность имитации полета межпланетного корабля. Однако для то¬
го, чтобы в качестве летающего макета можно было использовать
натурный макет межпланетного корабля, необходимо установить
на него не один разгружающий двигатель, а несколько . с суммар¬
ным вектором тяги, проходящим через центр масс системы.
В качестве исполнительных органов системы управления можно
использовать струйные рули посадочного корабля, струйные рули
на сжатом воздухе, взятом от ТРД, или газовые рули, помещаемые
под обрезами сопел ТРД. Учитывая, что на пути создания такого
летающего макета стоят определенные трудности, целесообразно
рассмотреть возможность использования вертолетов, оборудован¬
ных специальным разгружающим летающий макет механизмом.
Горизонтальные перемещения натурного макета, вызываемые его
поворотом в карданном подвесе, могут отслеживаться вертолетом
125
так, что движение вертолета и макета происходит с равными кине¬
матическими параметрами. Обеспечение синхронности движения
вертолета и подвешенного под ним макета, исключение раскачки
макета на тросовой подвеске, оценка влияния возмущенного лопа¬
стями потока воздуха и вибраций вертолета, решение вопроса о
спасении летчика с помощью катапультной установки при аварии
вертолета или макета корабля — таковы основные трудности, кото¬
рые необходимо преодолеть при создании летающего макета по
этой схеме.
С точки зрения простоты конструкции летающего макета и его
эксплуатации более рациональными являются два других варианта
«разгрузки» с установкой на летающий макет только одного реак¬
тивного двигателя, несмотря на то, что в этом случае точность ими¬
тации полета межпланетного корабля ниже, чем при первом вари¬
анте.
Для проведения предварительных экспериментальных исследо¬
ваний динамики движения посадочного корабля, для отработки от¬
дельных его систем и начального этапа тренировок экипажа можно
взять в качестве летающего макета вертолет и установить в нем по¬
воротную кабину, имеющую две степени свободы по углам тангажа
и крена.
Имитация натурных линейных перемещений корабля с соответ¬
ствующими кинематическими параметрами обеспечивается систе¬
мой управления вертолетом и приведением его массово-инерцион¬
ных характеристик к натурным значениям.
Отметим, что в США в середине 60-х гг. работы по исследова¬
нию процесса мягкой посадки КПА получили особенно широкий
размах в связи с программой «Аполлон», предусматривавшей вы¬
садку американских космонавтов на Луну с последующим возвра¬
щением на Землю. Для осуществления мягкой посадки двух космо¬
навтов на поверхность Луны, обеспечения их пребывания на по¬
верхности и доставки затем на селеноцентрическую орбиту служит
специальный'лунный корабль.
Четыре телескопические опоры посадочного устройства корабля
имеют разрушающиеся вкладыши из алюминиевых сот, которые
амортизируют ударные нагрузки. Пяты опор, имеющие форму дис¬
ков, также изготавливаются из алюминиевых сот.
Для отработки методики заключительного этапа полета кораб¬
ля «Аполлон», тренировки космонавтов в условиях, имитирующих
посадку на Луну, исследования управляемости и устойчивости лун¬
ного корабля при посадке был создан летающий макет LLRV (рис.
9.1), [46]. LLRV представляет собой вертикально взлетающий аппа¬
рат, в центре масс которого подвешен на двухстепенном кардане
ТРД CF-700-2 с тягой, компенсирующей 5/6 веса аппарата для мо¬
делирования лунного притяжения. Этот двигатель поддерживается
во время полета в вертикальном положении (первый вариант «раз¬
грузки»). Для изменения вертикальной скорости аппарата исполь¬
зуются восемь ракетных двигателей с тягой ~2,25 кН, работаю¬
щих на продуктах разложения перекиси водорода.
126
Для обеспечения устойчивости и маневрирования применяются
16 струйных сопел с тягой по 80—410 Н. Размеры летающего маке¬
та: высота ~3,0 м, расстояние между опорами ~ 4,0 м.
Летные характеристики LLRV близки к характеристикам лун¬
ного корабля «Аполлон». Аппарат снабжен автопилотом. Для спа¬
сения пилота при аварии предусмотрены катапультируемое кресло
и 3—4 аварийных ЖРД. Кроме того, на аппарате установлен па¬
рашют с диаметром купола 9 м, обеспечивающий скорость сниже¬
ния 30 м/с. Запас топлива для ТРД рассчитан на 10—15 минут
работы. Максимальная величина вертикальной составляющей ско¬
рости полета 27 м/с, горизонтальной — 21 м/с. Аппарат может под¬
Рис. 9. 1. Летающий макет КПА (на земле и в полете)
127
няться на высоту 1,2 км и совершить посадку в пределах площад¬
ки радиусом 2,4 км.
Всего на этом аппарате было совершено 197 полетов на базе
ВВС им. Эдвардса и 50 полетов на базе им. Эллингтона. Фирмой
изготовителем — Бэлл Аэросистемз — было построено два аппарата
LLRV в 1964 г. В 1965 г. этой фирмой летающий макет был не¬
сколько модернизирован для изучения поведения человека в слож¬
ных условиях космического полета на конечной фазе управляемого
захода на посадку лунного корабля. Фирмой было изготовлено три
модернизированных аппарата LLTV (стоимость каждого— 1,9 млн.
долл.). В декабре 1968 г. при заходе на посадку с высоты ~150 м
аппарат потерял управление и разбился. Летчик-испытатель ката¬
пультировался и благополучно опустился на парашюте.
Стендовые макеты КПА
Стендовые макеты в отличие от летающих постоянно связаны
поддерживающими тросами с механизмами разгрузки, вследствие
чего их возможности маневрирования ограничены габаритами ис¬
пытательных стендов. В зависимости от сложности задач, решае¬
мых на стендовых макетах, последние можно (с известной степе¬
нью условности) отнести к одному из двух видов:
стендовые макеты, предназначенные для отработки непосредст¬
венно самой посадки (процесса контактирования КПА с грунтом);
стендовые макеты, предназначенные для отработки предпоса¬
дочного маневра КПА с последующей посадкой.
Стендовые макеты для отработки непосредственно самой посад¬
ки КПА являются дальнейшим развитием динамически подобных
моделей. Так же, как и модели они имитируют финальный этап по¬
садки на планету — свободное падение КПА после момента отсеч¬
ки двигателя. Для этих макетов характерно точное соответствие
с натурой только по конструкции посадочного устройства и по ос¬
новным массово-инерционным параметрам КПА. Поэтому прочие
элементы конструкции КПА (приборный отсек, двигатели, различ¬
ные системы, аппаратура и т. д.) моделируются лишь по своей
массе.
Все это существенно упрощает конструкцию макета, позволяя в
то же время провести экспериментальные исследования различ¬
ных схем натурных посадочных устройств, влияния на устойчивость
при посадке массово-инерционных характеристик КПА, конструк¬
тивных параметров ПУ и условий мягкой посадки, оценить опас¬
ность для полезного груза КПА (опрокидывание, перегрузки, раз¬
рушение конструкции), возникающую при аварийных ситуациях,—
словом полностью отработать мягкую посадку КПА, устранив вли¬
яние масштабного эффекта на результаты испытаний, имеющее ме¬
сто при использовании динамически подобных моделей. Однако
применение упрощенных стендовых макетов для тренировок экипа¬
жа пилотируемых КПА весьма затруднительно.
128
На рис. 9.2 схематически показан типовой испытательный стенд
для экспериментальной отработки процесса контактирования поса¬
дочного аппарата с грунтом и проверки эффективности выбранной
конструкции его посадочного устройства с помощью упрощенных
натурных макетов КПА. С этой целью стенд обеспечивает воспро¬
изведение в наземных условиях сил притяжения у поверхности раз¬
личных небесных тел, значительно меньших, чем силы притяжения
у поверхности Земли, варьирование по величине и направлению
вектором посадочной скорости космического аппарата, а также ими¬
тацию рельефа и свойств поверхностного слоя планет путем приме¬
нения сменного грунта.
Рис. 9. 2. Схема натурного испытательного стенда с ме¬
ханизмом разгрузки
Испытательный стенд обычно представляет собой мостовую фер¬
менную конструкцию. Основными его частями являются:
подвижная мостовая платформа с механизмом разгрузки и сис¬
темой подвески натурного макета;
специальная площадка с аналогом планетного грунта;
измерительная и регистрирующая аппаратура.
Подвижная мостовая платформа, установленная над площадкой
с аналогом грунта, служит для создания разгружающей макет си¬
лы в течение всего процесса посадки и для сообщения макету необ¬
ходимой скорости (горизонтальной и вертикальной составляющих).
Для реализации при испытаниях потребных значений верти¬
кальной составляющей посадочной скорости могут применяться
составные фермы. Изменяя длину ферм, можно получать различ¬
ную высоту подвески макета.
Разгрузка макета космического аппарата осуществляется меха¬
низмом, обеспечивающим любую силу разгрузки, а, следовательно,
и эффект уменьшения ускорения свободного падения макета кос¬
мического аппарата.
5 400
129
Рис. 9.3. Испытательный стенд для
отработки мягкой посадки натурного
макета КА «Викинг»
Специальная площадка с аналогом планетного грунта служит
для имитации как рельефа места посадки (камни, кратеры, укло¬
ны), так и физико-механических свойств поверхностного слоя пла¬
нет. Площадка для грунта может быть выполнена в виде бетонной
чаши или платформы, позволяющих воспроизвести местные укло¬
ны поверхности планеты до ±20° и имитировать изменение свойств
грунта по глубине.
Управление всеми этапами проведения эксперимента (разгон
платформы с макетом, сброс макета, торможение платформы пос¬
ле сброса, аварийный останов платформы и пр.) должно быть ав¬
томатизировано с сохранени¬
ем возможности у оператора
«вмешиваться вручную» с цен¬
трального пульта.
Испытательный стенд дол¬
жен быть укомплектован изме¬
рительной и регистрирующей
аппаратурой, необходимой для
записи следующих парамет¬
ров: вертикальных и горизон¬
тальных перегрузок при по¬
садке; угловых скоростей вра¬
щения макета; напряжений в
элементах конструкции ПУ;
давления топлива в баках;
деформаций энергопоглотите¬
лей ПУ (по времени); величин
погружения опор макета в
грунт и т. п. и т. д. Аппарату¬
ра и датчики, применяемые
для измерения этих парамет¬
ром, во многом аналогичны рас¬
смотренным ранее (см. гл. 8).
Рассмотрим в качестве иллюстрации применения упрощенных
стендовых макетов наземную отработку КПА станций «Викинг-1;
-2», совершивших в середине 1976 г. мягкие посадки на поверхность
Марса. В гл. 8 дано описание натурной динамически подобной мо¬
дели КПА «Викинг» (табл. 8.1, модель ДПМ-ГЗ), имеющей приб¬
лизительно в 2,5 раза меньшую массу, чем реальный космический
аппарат. В научно-исследовательском центре Лэнгли (СКА) эту
же модель путем установки на нее дополнительных грузов превра¬
тили в натурный стендовый макет, соответствующий по массово¬
инерционным характеристикам (масса 480 кг) одному из вариантов
КПА «Викинг» [50]. Полученный таким образом упрощенный на¬
турный макет испытывался на стенде с разгрузкой на 3/5 (или на
60%) своего веса для имитации марсианского ускорения силы тя¬
жести при отработке процесса мягкой посадки (рис. 9.3).
Разгрузка на 60% веса макета, сообщение ему необходимых
посадочных скоростей, «полет» макета до встречи с посадочной пло¬
130
щадкой обеспечивались на стенде системой тросов, блоков, катков
и грузов. В тросовую систему были включены динамометры для
контроля натяжения тросов при испытаниях. Система подвески ма¬
кета обеспечивала ему пять степеней свободы (шестая степень
свободы — боковые перемещения макета — подвеской не обеспечи¬
валась и была существенно ограничена). Натурный макет поддер¬
живался опорным тросом, перекинутым через верхний каток и сое¬
диненным с макетом при помощи разрывного болтового соедине¬
ния. Узлы крепления троса позволяли макету занимать перед сбро¬
сом различную ориентацию (например, угол тангажа макета уста¬
навливался в пределах 04-10°). Направляющие рельсы, по которым
перемещается каток, подняты над посадочной площадкой пример¬
но на 60 м.
Перед испытанием макет помещают на посадочную площадку,
силовые тросы натягивают с помощью лебедок и канатов до полу¬
чения разгружающего макет усилия ~60% от его веса. Затем ма¬
кет поднимают на расчетную высоту, обеспечивающую необходи¬
мую вертикальную скорость падения макета (номинальное значе¬
ние VB = 7 м/с), и закрепляют на опорном тросе. В этом положении
разгружающее макет усилие несколько снижается. Сброс макета
производится после срабатывания разрывного болта подвески. По
мере падения макета сила разгрузки увеличивается, достигая необ¬
ходимой величины в момент контакта опор макета с поверхностью.
Во время этого контакта возникают колебания в величине силы
разгрузки вследствие инерционности силовых тросов. Такие коле¬
бания имеют место в течение всего процесса посадки макета. При
этом точность получения разгружающего усилия составляет около
± 3 %.
Горизонтальный разгон макета и катка (массой 9,5 кг) произ¬
водится за счет энергии падающего груза с помощью двух натяну¬
тых буксирных тросов, связывающих макет через шкивы и каток с
грузом. При поднятии макета в исходное положение для сброса
производится и подъем груза на необходимую для получения задан¬
ной горизонтальной скорости высоту (номинальное значение Гг=
= 1,8 м/с). В исходном положении система макет — каток — груз
удерживается канатом. После отцепки каната под действием груза
каток и макет приобретают горизонтальную скорость. В заданный
момент груз замыкает контакты микровыключателя разрывного
болтового соединения. Освобожденный макет, имеющий определен¬
ную горизонтальную скорость, начинает свое падение на площадку
с имитатором грунта. Буксирный трос, соединенный с катком, не
отцепляется, но, будучи ненатянутым (так как груз опустился на
опору) и достаточно легким, не влияет на движение катка и ма¬
кета.
В качестве поверхности посадки использовалась жесткая мас¬
сивная деревянная платформа, которая покрывалась гладкой фане¬
рой или крупным гравием для получения коэффициента трения
0,4—0,7.
Сигналы, поступающие по кабелю во время испытаний, от аксе¬
5*
131
лерометров, потенциометров, тензометров и т. п., записывались на
магнитофоне методом частотной модуляции.
Испытания, проведенные в идентичных условиях на свободнопа¬
дающей динамически подобной модели и на натурном макете с раз¬
грузкой, при сопоставлении между собой показали хорошее согла¬
сование — большинство результатов (по измерениям ускорений в
центре масс, величин деформаций обжатия опор и усилий в их энер¬
гопоглотителях) попало внутрь ±10%-ного доверительного интер¬
вала.
Следует отметить существенное влияние ветра на величину го¬
ризонтальной посадочной скорости натурного макета. Так, при вет¬
ре, достигающем 4,5 м/с, отклонения в величине горизонтальной
скорости составляли около ±0,4 м/с.
Наземная отработка посадочного аппарата станций «Венера-9;
-10» производилась на натурном динамическом макете без раз¬
грузки, центровка и массово-инерционные характеристики которого
могли варьироваться в определенных пределах. Натурный макет —
упрощенная жесткая конструкция КПА со штатным посадочным
устройством. Номинальная масса посадочного аппарата — 660 кг.
ПУ макета — это тонкостенная оболочка тороидальной формы,
прикрепленная сварной фермой к прочному корпусу. В момент по¬
садки оболочка пластически деформируется, поглощая тем самым
энергию удара. Атмосферный газ, проникший во время снижения в
полость оболочки, выходит через специальные отверстия, уменьшая
подскок посадочного аппарата. Корпус натурного макета сварен из
согнутого в цилиндр стального листа и фланцев. Для получения не¬
обходимых массово-инерционных характеристик к корпусу макета
жестко крепятся передвижные балансировочные грузы. На стенке
корпуса вблизи центра масс макета смонтирована балка, обеспечи¬
вающая шарнирное крепление к подъемной системе стенда. Перед
каждым испытанием (сбросом) макет взвешивается, определяют¬
ся его центровка и массовые моменты инерции относительно трех
ортогональных осей.
С целью имитации теплового воздействия атмосферы Венеры на
КПА при стендовых испытаниях натурный макет нагревается до оп¬
ределенной температуры по интересующему конструкторов закону в
специальном термостате, смонтированном на стенде. На внутрен¬
ней поверхности термостата расположены нагревательные элемен¬
ты из нихромовой проволоки, намотанной на фарфоровые трубки.
Пространство между двойными стенками термостата заполнено
теплоизолирующей ватой. Испытания осуществляются путем сбро¬
са макета с заданной высоты при действии земной гравитации
(макет движется как свободнопадающее тело). Отличие ускоре¬
ния силы тяжести на Венере от земного притяжения учитывается
при расчете кинетической энергии удара макета о посадочную
площадку, а расхождение в величине аэродинамического сопро¬
тивления не принимается во внимание из-за его малости вследст¬
вие небольших значений посадочных скоростей (как известно,
132
при мягкой посадке КПА станций «Венера-9 и -10» имели скорость
встречи с грунтом планеты около 7 м/с).
Для имитации характеристик поверхностного слоя планеты
применяются бетон, пенобетон и аглопоритовый песок. Площад¬
ка с грунтом-аналогом может быть горизонтальной, иметь различ¬
ные углы склона, выступы и впадины. Требуемая пространствен¬
ная ориентация натурного макета при ударе о грунт обеспечива¬
ется путем соответствующего закрепления макета (имеющего
шесть степеней свободы) в исходном положении относительно
стендовой подвески.
Высотная часть испытательного стенда — стальная конструк¬
ция, состоящая из опорных колонн, поперечных прогонов и про¬
дольных балок. Натурный макет КПА подвергался нескольким
видам испытаний, в том числе:
связанным с оценкой посадочной устойчивости в момент кон¬
тактирования с грунтом при крайних значениях центровки, момен¬
тов инерции, углов ориентации макета и наклона грунта;
связанным с определением максимальных ударных перегрузок
при крайних значениях массы макета и нулевом относительном уг¬
ле между тороидальным ПУ и грунтом;
связанным с оценкой прочности элементов ПУ макета при его
максимальной массе и максимальном относительном угле между
посадочным устройством и грунтом.
Перегрузки при испытаниях натурного макета измеряются ин¬
дуктивными датчиками ДУ-7 с аппаратурой ВИ6-5МА и регистри¬
руются с помощью осциллографа (Н-115); измерение температуры
элементов макета производится хцомель-копелевыми термопара¬
ми ТКХ с записью электронными потенциометрами типа ЭПП-09
и КСП-4.
Процесс посадки макета и его результаты фиксируются с помо¬
щью кино- и фотосъемки [2, 10].
В заключение необходимо подчеркнуть, что нагрузки, дейст¬
вующие на КПА станции «Венера-9 и -10» при посадке на реаль¬
ную венерианскую поверхность, не превысили нагрузок, имевших
место при испытаниях их натурных динамических макетов [2].
Стендовые маневрирующие макеты служат для решения тех
же задач, что и летающие макеты КПА, конечно, в несколько ог¬
раниченных пределах, определяемых технической характеристикой
эстакадных испытательных стендов и габаритными размерами
пространства для маневрирования. Стендовый маневрирующий ма¬
кет по своей конструкции является натурной копией проектируемо¬
го КПА и оснащается натурными системами, необходимыми для
совершения предпосадочного маневра, в том числе, основными и
верньерными двигателями. Макет подвешивается с помощью двух¬
степенного кардана и системы тросов к специальной тележке, обо¬
рудованной механизмом разгрузки и отслеживающей перемещения
макета вдоль и поперек эстакадной ферменной конструкции стенда
(см. рис. 7.2). При этом вопрос о спасении испытателей (при отра¬
133
ботке пилотируемого КПА) полностью решается применением бе¬
зопасной и надежной тросовой подвески макета на стенде.
Основные части эстакадного стенда те же, что и у типового ис¬
пытательного стенда. Подвижная мостовая платформа стенда пере¬
мещается автоматически вслед за маневрирующим макетом, обес¬
печивая с помощью следящей системы постоянную вертикальность
тросов подвески (с точностью до 1/3 градуса) и разгрузку макета
КПА. Имитация угловых движений КПА осуществляется на маке¬
те с помощью расположенного в его центре масс кардана системы
подвески.
Такой испытательный стенд был сооружен в научно-исследова¬
тельском центре Лэнгли США. (установка LLRF) в 1965 г. Стои¬
мость установки 3,52 млн. долл. Установка представляет собой
мостовой кран высотой — 76 м, длиной — 120 м и шириной основа¬
ния — 90 м. Маневрирующий макет с двухместной кабиной имеет
шесть степеней свободы и благодаря кардану системы подвески
осуществляет имитацию угловых и поступательных движений лун¬
ного корабля «Аполлон». Изменение скорости «полета» произво¬
дится космонавтом путем управления тягой 10 ракетных двигате¬
лей, работающих на продуктах разложения перекиси водорода.
«Полеты» натурного макета могли продолжаться до 180 с со ско¬
ростями м/с; Кг^4 м/с [56].
Методика проведения испытаний
Целями экспериментальной отработки предпосадочного маневра
и процесса мягкой посадки КПА на его натурных макетах в зем¬
ных условиях являются:
1) окончательная проверка эффективности и надежности функ¬
ционирования посадочного приспособления в условиях, максималь¬
но приближенных к натурным; оценка возможности успешной по¬
садки в аварийных ситуациях (посадка на камень, в щель, с подло¬
манной опорой и т. д.);
2) определение характера и величины перегрузок, напряжений,
ходов энергопоглотителей при нормальных и аварийных условиях
посадки;
3) выяснение влияния масштабного фактора на характер изме¬
нения и величину параметров при мягкой посадке (сравнение с ре¬
зультатами испытаний моделей);
4) оценка эффективности применения натурных двигателей
«прижатия» с точки зрения аварийных посадочных условий;
5) проверка кинематики выдвижения посадочных опор и рабо¬
ты механизма выравнивания аппарата при необходимости обрат¬
ного старта с планеты;
6) отработка схемы заключительного этапа полета и посадки
автоматических, дистанционно управляемых и пилотируемых кос¬
мических аппаратов;
7) исследование устойчивости и управляемости межпланетного
корабля при полетах и посадке летающего макета;
134
8) отработка компоновки кабины межпланетного корабля;
9) оценка физиологических возможностей быстрого принятия
человеком правильных решений в сложной предпосадоч-ной обста¬
новке (особенно в случае возникновения отказов в системе автома¬
тики) ;
10) комплексная отработка системы управления КПА на этапе
посадки (включая имитацию аварийных ситуаций, отработку инди¬
кации положения аппарата в пространстве и пр.).
В соответствии с возможностями натурных испытательных стен¬
дов и особенностями используемых натурных макетов эксперимен¬
тальную отработку мягкой посадки КПА можно подразделить на
следующие этапы:
1 — отработка процесса контактирования КПА с грунтом;
2 — отработка предпосадочного маневра аппарата, завершаю¬
щегося его посадкой, на стендовых маневрирующих макетах;
3 — отработка предпосадочного маневра и мягкой посадки меж¬
планетного корабля на летающих макетах.
На первом этапе отрабатывается непосредственно процесс са¬
мой посадки на упрощенных стендовых макетах КПА. На этом эта¬
пе могут быть полностью решены первые пять из 10 указанных
выше задач. Особенностью первого этапа является использование
относительно простых натурных макетов и испытательных стендов.
На втором этапе осуществляется отработка не только непосред¬
ственно посадки КПА, но и его предпосадочного маневра. Приме¬
нение эстакадного испытательного стенда и маневрирующих маке¬
тов (автоматических и пилотируемых) позволяет решить все пере¬
численные задачи, т. е. полностью провести комплексную наземную
отработку мягкой посадки. Но для этого необходимы натурные ма¬
кеты, укомплектованные почти всеми системами космического ко¬
рабля, и грандиозный испытательный стенд.
Отработку предпосадочного маневра и мягкой посадки межпла¬
нетного корабля на летающих макетах (третий этап) следует про¬
водить в основном при отсутствии испытаний по предыдущему
этапу. Неограниченность пространства для маневрирования позво¬
ляет особенно хорошо проработать последние пять из названных
вопросов. Однако создание летающих макетов со специальными
двигателями разгрузки (по существу, создание летательных аппа¬
ратов нового типа) является задачей не менее сложной, чем соору¬
жение эстакадного испытательного стенда.
Отметим возможность параллельного проведения рассмотрен¬
ных этапов отработки мягкой посадки на натурных макетах КПА
вследствие использования разных испытательных стендов и маке¬
тов. На каждом этапе испытаний в соответствии с программой осу¬
ществляется варьирование в определенных пределах начальными
посадочными условиями и некоторыми конструктивными парамет¬
рами КПА.
На стендовых макетах КПА по аналогии с динамически подоб¬
ными моделями устанавливаются только датчики, а вся измери¬
тельная и регистрирующая аппаратура размещается дистанцион¬
135
но в наземном пункте. В отличие от стендовых на летающих маке¬
тах приходится устанавливать и аппаратуру, выдерживая при этом
подобие с межпланетным кораблем по массе.
Глава 10. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ТЕОРЕТИЧЕСКОГО
И ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ МЯГКОЙ ПОСАДКИ
При исследовании динамики мягкой посадки КПА основными
являются следующие случаи:
посадка аппарата с Квтах, Кг=0 на горизонтальную поверх¬
ность (0 = 0°) с ограничением перемещения оснований опор в плос¬
кости поверхности (возникновение максимальных вертикальных пе¬
регрузок) ;
посадка аппарата с КГтах и небольшой вертикальной скоростью
на горизонтальную поверхность (0 = 0°) с ограничением перемеще¬
ния оснований опор в плоскости поверхности (возникновение мак¬
симальных горизонтальных перегрузок);
движение аппарата вниз по склону (%=0; 0щах) с одной и двумя
опорами вперед с приведенным коэффициентом трения fmax и мак¬
симальными значениями составляющих посадочной скорости (воз¬
никновение критической ситуации из-за возможного опрокидыва¬
ния) ;
движение аппарата вверх по склону (Х=180°; Отах) с одной и
двумя опорами вперед с приведенным коэффициентом трения fmax
и скоростями Кв max; Кг max (возникновение критической ситуации
из-за максимального хода амортизатора вперед идущей опоры, или
опор, КПА) ;
движение аппарата поперек склона (Х = 90°; Отах) с приведен¬
ным коэффициентом Трения /max И скоростями Кв max, КгСКГШах
(для оценки особенностей энергопоглощения и устойчивости при
V'x
такой посадке), X = arctg—-p—угол, определяющий направление
V Z
горизонтальной составляющей вектора скорости центра масс КПА;
КВ=К/ — вертикальная составляющая вектора скорости центра
масс аппарата; K’r = (VrJ/4“^')2 ~~ горизонтальная составля¬
ющая вектора скорости центра масс аппарата.
В данной главе представлены только основные, являющиеся ха¬
рактерными, теоретические и экспериментальные результаты иссле¬
дования процесса мягкой посадки описанных в гл. 8 (см. табл. 8.1)
трех вариантов КПА — А, Б и В. Поскольку эти варианты КПА (в
отличие от варианта Г) рассматривались как прототипы соответст¬
вующих аппаратов для посадки на поверхность Луны, все резуль¬
таты— и теоретические (расчет на ЭВМ), и экспериментальные
(испытания моделей ДПМ-А, -Б, -В) даются в пересчете на натур¬
ный лунный КПА.
Однако при необходимости, пользуясь условиями подобия и со¬
ответствующими масштабами (табл. 7.1), можно от натурных лун¬
ных результатов вернуться к модельным, а модельные данные, в
136
свою очередь, пересчитать на натурные, но уже для другой планеты
(например, для случая посадки КПА на Марс) и, естественно, для
другого (с иными характеристиками) натурного посадочного аппа¬
рата.
На рис. 10.1 —10.3 представлены зоны устойчивости при мягкой
посадке КПА варианта Б на склоны 6 =—54—15°; Л, = 0°, постро¬
Рис. 10. 1. Зоны устойчивости при
посадке КПА. (вариант Б) вниз
по склону, %=0°; 9 = —5°; N = 4;
схема 2—2
Рис. 10.2. Зоны устойчивости при
посадке КПА (вариант Б) вниз
по склону, Х='0°; 0=—1<0°; А=4;
схема 2—2
✓
4
3
z
2
3 4-
Рис. 10.3. Зоны устойчивости при Рис. 10.4. Зоны посадочной
посадке КПА (вариант Б) вниз устойчивости КПА варианта Б,
по склону, %=0°; 0=—15°; А=4, построенные в осях Рг и 0 (циф-
схема 2—2 ры 1, 2, 3, 4, 5 у точек на гра¬
фике соответствуют скоростям
1, 2, 3, 4, 5 м/с), 5=1,5- 104 Н;
/=1,0; А=4, схема 2—2:
■ — теория; — эксперимент;
/эксп=0.6-1,2
1
Г7
енные в координатах VB и Кгс указанием значений параметров и ос¬
новных посадочных условий. На этих графиках областям, располо¬
женным слева от кривой устойчивости, соответствует устойчивая
посадка, а областям, расположенным справа от кривой, — опроки¬
дывание КПА при посадке. Для каждого значения угла наклона
грунта результаты теоретического исследования зон устойчивости
на ЭВМ. сравниваются с результатами эксперимента, проведенно¬
го на методической динамически подобной модели ДПМ-Б (см.
табл. 8.1).
При теоретических расчетах осуществлялось варьирование ве¬
личиной усилия обжатия энергопоглотителей — £. Как показывают
графики (рис. 10.1—10.3), экспериментальные результаты лежат
между кривыми с усилием обжатия энергопоглотителя от 10 кН до-
20 кН, что соответствует в пересчете на модель с /0=1/6 силе в
280—560Н (по сравнению с результатами испытаний сотовых энер¬
гопоглотителей; гл. 8).
На этих же рисунках результаты экспериментального исследо¬
вания мягкой посадки сравниваются с теоретическими расчетами,
выполненными для постоянной силы обжатия энергопоглотителя
£=15 кН при переменном коэффициенте трения опор по грунту
(f = 0,7-=-1,3). Поскольку опоры модели снабжались специальными
шипами, при посадке происходило постепенное внедрение их в
грунт (т. е. постепенное включение в работу). Поэтому сила трения
опор по грунту оказалась переменной — возрастающей с ростом ве-.
личины посадочной скорости. Этот вывод и подтверждается ре¬
зультатами эксперимента.
На рис. 10.4 приведены результаты теоретического и экспери¬
ментального исследований зон посадочной устойчивости лунного
аппарата, построенных в координатных осях Кг и 0 в зависимости
от величины Кв (при £=15 кН; /=1,0; схема посадки 2—2, Х = 0°).
На таком графике зоной устойчивой посадки корабля является об¬
ласть, расположенная слева от соответствующей кривой и включа¬
ющая начало координат. Области, расположенные за кривыми
(справа), определяют комбинации параметров прилунения, приво¬
дящие к опрокидыванию аппарата при посадке.
Графики, построенные в осях Кг и 0, позволяют более наглядно
показать зависимость величины площадей зон посадочной устойчи¬
вости КПА от угла наклона грунта, дополняя тем самым графики в
осях Уг и Ув. Кроме того, с помощью таких графиков удобнее срав¬
нивать результаты расчетов с экспериментом, так как при испыта¬
ниях действительные значения угла наклона грунта могут отли¬
чаться от значений,, заложенных в расчетную программ^.
Рис. 10.4 свидетельствует об удовлетворительном согласовании
результатов теоретического исследования с экспериментом. Расхож¬
дение составляет примерно 10%, что является следствием извест¬
ного ограничения объема испытаний, погрешностей замеров пара¬
метров, а также допущений, принятых при теоретическом исследо¬
вании. Отметим, что теоретический расчет дает границу устойчивой
138
посадки КПА с некоторым запасом, особенно при небольших значе¬
ниях составляющих посадочной скорости (до 2—3 м/с).
На рис. 7.1 и 10.5 показаны кинограммы процесса мягкой по¬
садки динамически подобной модели ДПМ-Б на наклонную (9 =
= —15°; Х = 0°) поверхность с жестким имитатором лунного грунта
(см. табл. 7.3; 3-й вариант; огр^ (2—5)-105 Па). Устойчивая по¬
садка (см. рис. 10.5) осуществлялась со скоростями 1/в = 2,7 м/с и
Vr = 3,7 м/с. Процесс посадки модели продолжался ~0,8 с с дости¬
жением максимальных перегрузок пв~5, пг^6. Кинограмма опро-
Рис. 10.5. Устойчивая посадка ДПМ.-Б вниз по склону (0 = 15°)
со скоростями VB = 2,7 м/с; Уг = 3,7 м/с (схема посадки Is—2—1,
грунт жесткий, шаг кинограммы ~0,05 с)
139
Рис. 10.6. Зоны устойчивости при по¬
гадке КПА (вариант A), g=3 104 Н;
f=0,8; JV = 4, схема 2—2:
теория; эксперимент;
— — схема 1—2—1
(теория)
^=~25°
0=-2О°
/(
А \
\\
SO q\
\ 1
(7=-Л7°
S'
\\
V '
Теория:
Т1=20кН
Т^ЮцН
Tz=0
Эксперимент:
q-Tt=20kH, 0=-25°\
&-Tz=27kH L=_j^<> устойчиво
^-Tz=56kH\ J
9-Tz=20kH-, 0=-М°неустойчиво
0- Уг,м/с
Рис. 10.7. Зоны устойчивости при посадке КПА
(вариант А) с двигателями «прижатия»,
£=3-104 Н; %=0°; W=4; f=0,8; схема 2—2
Рис. 10.8. Зоны посадочной устойчивости
КПА (вариант В), построенные в осях
Кг и 0 (обозначения точек см. на рис.
Ю.4), g=42,5-104 Н; W=4; схема 2—2
V8=5m/c
140
кидывания модели дПМ-Б при посадке в кратер глубиной 0,15 м
со скоростями 1/в = 2,5 м/с, Кг = 2,0 м/с представлена на рис. 7.1.
На рис. 10.6 и 10.7 приведены результаты теоретического и экс¬
периментального исследований посадочной устойчивости КПА ва¬
рианта А по схеме 2—2.
Теоретические исследования посадочной устойчивости проводи¬
лись в соответствии с гл. 6. Результаты экспериментальных иссле¬
дований, представленные на рис. 10.6, заимствованы из американ¬
ской работы [47] для модели ДПМ-А (см. табл. 8.1) при посадке на
склоны 0 =—5-4—15° с 7В= 14-4 м/с и Vr = 14-3 м/с.
На рис. 10.7 приведены экспериментальные точки, соответству¬
ющие испытаниям модели КПА с двигателями «прижатия» (в пе¬
ресчете на натурный лунный аппарат суммарная тяга двигателей
составляет 7\=20 кН4-36 кН) на склоны в —25°; —30°; —37° при
Кв = 34-4 м/с и Кг= 1,34-1,75 м/с. Как видим, результаты испыта¬
ний динамически подобной модели хорошо согласуются с расчетом
зон посадочной устойчивости на ЭВМ.
Расхождение между теоретическими зонами устойчивости КПА
варианта А и экспериментальными [47] не превышает 20%, и, в ос¬
новном, идет «в запас» (см. рис. 10.6).
На рис. 10.8 приведены для сравнения результаты теоретическо¬
го и экспериментального определений зон устойчивости при посад¬
ке тяжелого КПА (вариант В). Теоретические расчеты проведены
в соответствии с гл. 6 для пространственного движения КПА. Ре¬
зультаты экспериментального исследования взяты из американской
работы [55], посвященной анализу динамики посадки лунного ко¬
рабля по проекту «Аполлон», имеющего массу ~16000 кг (см.
табл. 8.1). Построение экспериментальных точек на графике в осях
Кг и 0 позволяет оценить величину расхождения результатов при¬
мерно в 10%.
Отметим, что графики, изображающие зоны посадочной устой¬
чивости КПА в координатных осях Кг и 9 (рис. 10.4 и 10.8) весьма
наглядно иллюстрируют опасность посадки аппарата вниз по скло¬
ну (0<0) с точки зрения возможного его опрокидывания.
Рассмотрим несколько подробнее влияние начальных условий
на динамику мягкой посадки КПА. Под начальными посадочными
условиями будем понимать комплекс внешних факторов, не связан¬
ных с конструкцией космического аппарата. К таковым можно от¬
нести:
характеристики поверхностного слоя планеты — угол наклона
поверхности в месте посадки 0; коэффициент трения f; выступы,
впадины или трещины; физико-механические свойства грунта и т. д.;
кинематические параметры движения космического посадочного
аппарата в момент контакта с поверхностью планеты — линейные и
угловые скорости, ускорения, ориентация КПА и пр.
Вертикальная VB и горизонтальная Vr составляющие посадоч¬
ной скорости КПА являются доминирующими факторами, опреде¬
ляющими динамику процесса посадки.
141
На рис. 10.14-10.3; 10,6; 10.8 показаны зоны посадочной устой¬
чивости КПА (варианты А, Б, В) при различных углах наклона
лунной поверхности для схемы посадки 2—2, Х = 0°; 180°.
При посадке аппарата на горизонтальную поверхность или по¬
верхность с уклоном до —5Р допустимая величина горизонтальной
скорости КПА возрастает с увеличением его вертикальной поса¬
дочной скорости (в диапазоне скоростей, представляющем практи¬
ческий интерес).
Очевидно, что случай движения вверх по склону (Z=180°, 2—2)
не является критическим для устойчивости аппарата при посадке,
так как область устойчивости расширяется с возрастанием угла 0
(см. рис. 10.6).
Рис. 10.9. Линии рав¬
ной посадочной устой¬
чивости КПА (ва¬
риант А), X—0; £ =
= 3-104 Н; 0 =—15°,
f = 0,8; N = 4; схема
1—2—1
Z7
1
\ВЯ^О,8В
к *4.
А
А
^4
1/7/7 /7/
n'A
Рис. 10. Ь0. Зависимость величины пло¬
щади зон устойчивости КПА (вариант А)
от числа посадочных опор, £=3104 II;
/=0,8; %=0°:
0 = 0°; 0 =—10°
Результаты исследования динамики посадки аппарата по схеме
1—2—1 (движение КПА одной опорой вперед) приведены на рис.
10.6; 10.9. Пунктирные линии на рис. 10.9 (движение аппарата
вниз по склону с 0= —15°) соответствуют линиям равной устойчи¬
вости КПА при посадке, т. е. таким линиям, каждая точка которых
определяет сочетание вертикальной и горизонтальной скоростей,
приводящих к достижению аппаратом в процессе посадки одного и
того же предельного угла О (см. гл. 6).
Сравнение зон устойчивости аппарата при посадке на склон с
0= —15° по схемам 1—2—1 и 2—2 (i=0°) (рис. 10.6) показывает,
что допустимые значения горизонтальной скорости посадки КПА по
схеме 1—2—1 более чем на 1 м/с превосходят соответствующие
значения Уг, имеющие место при посадке по схеме 2—2.
Влияние величины коэффициента трения оснований опор КПА
по лунному грунту на зоны устойчивости при посадке аппарата на
наклонную (0= —54 15°; 2i = 0°) поверхность показано на рис.
142
10.1 —10.3. Как легко заметить по этим графикам, области посадоч¬
ной устойчивости КПА имеют тенденцию к увеличению с умень¬
шением величины коэффициента трения. Это можно объяснить тем,
что с уменьшением величины коэффициента трения при постоянной
нормальной силе уменьшается составляющая общей силы (сила
трения), действующая на основание опоры вдоль поверхности, что
приводит к уменьшению опрокидывающего аппарат момента и про¬
скальзыванию опор по поверхности (с рассеиванием значительной
части энергии).
Наряду с рассмотренным выше влиянием начальных посадоч¬
ных условий, динамика мягкой посадки КПА во многом определя¬
ется конструктивными особенностями корабля, схемой и характе¬
ристиками его посадочного устройства, т. е. следующими парамет¬
рами: числом опор Г1У; относительной величиной радиуса_окруж-
ности, проходящей через основания опор до разрушения, R=R/H;
величиной тяги стабилизирующих двигателей (двигателей «при¬
жатия»); величиной силы сопротивления при обжатии опор (силы
деформации энергопоглотителей ПУ).
Зоны устойчивости КПА (вариант А), имеющего ПУ с различ¬
ным количеством опор (М=34-6), при посадке на горизонтальную
и наклонную поверхности представлены на рис. 10.10. Указанные
зоны получены при условии постоянства всех параметров, кроме
числа опор ПУ. Нетрудно заметить, что наименьшей устойчивостью
при посадке на горизонтальную поверхность обладает аппарат с
трехопорным ПУ. Зоны устойчивости аппарата с ПУ, имеющим 4—
6 опор, намного больше, но весьма незначительно отличаются меж¬
ду собой.
При оптимизации количества посадочных опор КПА необходи¬
ма комплексная оценка массы ПУ, его надежности и устойчивости
аппарата при посадке. Очевидно, что общая надежность успешной
посадки существенно возрастает с увеличением количества опор до
N=4, но при М>4 возрастание общей надежности не столь значи¬
тельно ввиду того, что отказ одной опоры не обязательно приводит
к аварийной ситуации. Более того, с ростом числа посадочных опор
возрастает вероятность отказа ПУ из-за большего количества дета¬
лей. В результате может быть потерян выигрыш в надежности, по¬
лученный за счет образования незначительной дополнительной об¬
ласти устойчивости в связи с лишней опорой.
Поэтому масса ПУ является основным критерием, определяю¬
щим выбор оптимального количества посадочных опор аппарата.
Массу ПУ можно сохранить неизменной при увеличении числа опор
только путем облегчения каждой опоры (путем уменьшения сече¬
ний ее силовых элементов), что, как правило, ведет к снижению
прочности отдельной опоры. Однако обычно считают, что снижение
прочности отдельной опоры, несмотря на увеличение их общего ко¬
личества, недопустимо, так как в случае отказа одной из опор на
оставшиеся опоры перераспределится вся нагрузка. К тому же кри¬
тические условия по поглощению энергии (посадка вверх по скло¬
ну одной опорой вперед) остаются одинаковыми независимо от чис¬
143
ла опор ПУ. Поэтому оптимизация количества опор по массе ПУ
при равной посадочной устойчивости производилась для случая
идентичных опор.
Для сравнения различных посадочных устройств условно мож¬
но взять параметр NQ/S, представляющий собой отношение массы
ПУ к площади области посадочной устойчивости. Здесь обозначено:
N — количество опор ПУ КПА; Q — масса одной посадочной
опоры, кг; S — площадь области устойчивости, ограниченная осью
ординат, кривой посадочной устойчивости и двумя прямыми, парал¬
лельными оси абсцисс и соответствующими условно выбранным ор¬
динатам, мм2.
Рис. 10. bl. Оптимизация
по массе посадочного
устройства КПА (ва¬
риант А), g=3-104 Н;
/=0,8; Л=0°
V6,m/c
п=1,27^
z
f/ /
/ / '
II
\
\\
°f 2 3 Vr,M/c
Рис. 10.12. Зависимость вели¬
чины площади зон устойчиво¬
сти КПА (вариант А) от отно¬
сительной величины радиуса
ПУ, Х=0; g=3-104 Н; W=4;
f=0,8, схема 2—2:
е=—10°; 6=0°
На рис. 10.11 представлены полученные зависимости параметра
NQ/S от количества опор ПУ при посадке КПА на горизонтальную
и наклонную поверхности. Из графиков видно, что ПУ с четырьмя
опорами является оптимальным по массе при равной устойчивости
среди рассмотренных посадочных устройств.
Результаты исследования влияния на динамику посадки КПА
относительной величины радиуса посадочного круга ПУ — r=R/H
указывают пути эффективного расширения зоны посадочной устой¬
чивости с целью обеспечения безаварийной посадки аппарата в тре¬
буемом диапазоне скоростей и возможных углов наклона планет¬
ной поверхности. Как видно из рис. 10.12 увеличение безразмерной
величины R (путем увеличения радиуса ПУ 7? или уменьшения вы¬
соты центра масс аппарата Я) ведет к существенному расширению
диапазона допустимых посадочных скоростей.
Другим средством повышения посадочной устойчивости КПА
(особенно при посадке на крутые склоны — до 30—35°), хотя и
приводящим к некоторой перекомпоновке аппарата, усложнению
144
его системы управления и возрастанию массы ПУ, может оказаться
применение двигателей «прижатия» КПА. Попутно заметим, что
вплоть до последнего времени необходимость в применении таких
двигателей на посадочных аппаратах для Луны и планет не воз¬
никала. Однако, учитывая, что космическая техника в целом, и,
особенно, космические аппараты мягкой посадки на поверхность
небесных тел находятся на ранней стадии своего «развития», а ко¬
личество мягких посадок составляет только 1—3 посадки за год (в
Рис. 10. 13. Изменение динамических парамет¬
ров при неустойчивой посадке КПА (ва¬
риант А) вниз по склону (0 = 20°):
I—смятие опоры № 1; II—вращение относительно
опоры № 1; III—смятие опоры № 2; IV—вращение
относительно опоры № 2; V—период работы стабили¬
зирующих двигателей; VI—смятие опоры № 2 с уче¬
том импульса стабилизирующих двигателей; VII—вра¬
щение относительно опоры № 2 с учетом импульса
стабилизирующих двигателей
145
Сводка осуществленных мягких посадок КА на Луну и планеты
Характеристика ПУ
Баллоны со сжатым
газом (сферическое)
4-х опорное стержне¬
вое, в виде треноги
3-х опорное с гидрав¬
лическими амортизатора¬
ми; в виде треноги
Район посадки
Н:
со
лЧ
и
Океан Бурь,
18,9° с. ш.; 62,0° з. д.
Море Изобилия,
0,7° ю. ш.; 56,3° в. д.
Море Дождей,
38,3° с. ш.; 35° з. д.
О
=s .
Я*
О и
Е- О
С1^
К СО
< ю
с1- 7Г
S 3
g.«
со
Море Ясности,
25,8° с. ш.; 30,5° в. д.
Море Кризисов,
12°45' с. ш.; 62°12' в. д.
со
-СМ
fQ --г
м 3
СО .
О О
W »
О °
ю
of
Океан Бурь,
3,0° ю. ш.; 23,3° з. д.
Море Спокойствия,
1,4° с. ш.; 23,2° в. д.
J
Уклон
поверхности,
град.
1
1
1
1
1
о
О
1
1
о
о
о
VQ
7
о
О
0
Ю
7
Посадочная
скорость, м/с
вертикальная
(горизонтальная)
оо
А
00
А
о
ю
сч
т
с?
т
1О
of
Z-^ч
х
о
СМ
о?
~3,0 (0,5)
О
СМ
4
о
о
оо
Масса
КПА,
кг
о
о
7
— 100
1880
о
8
7
о
ОО
ОО
о
о
СП
7
1880
О
СП
04
1
о
СП
см
1
о
СП
см
1
Дата
мягкой
посадки
3.02.66
24.12.66
20.9.70
17.11.70
21.02.72
16.01.73
18.08.76
2.06.66
20.04.67
11.09.67
Наименование
аппарата
«Лун а-9»
«Луна-13»
«Луна-16»
«Луна-17»
«Луна-20»
«Луна-21»
«Луна-24»
«Сервейер 1»
«Сервейер-3»
«Сервейер-5»
146
н
d
но
C и
O?1
co
CM
3,036° Ю. ш.;
23,416° з. д.
3
2 *
s. W
£м оо
о СМ
СО о
26,10° с. ш.; 3,60° в. д.
Н:
со
ю
со
но
а
2
о
о
СП
20,2° с. ш.; 30,7° в. д.
Электрис,
45° го. ш.; 158° з. Д.
Море Эритрейское,
24° ю. ш.; 19,5° з. д.
Хризе,
19,5° с. ш.; 34° з. д.
Утопия,
44,3° с. ш.; 1Ю° з. д.
о
/—ч
z-ч
z-s
Z—Ч
о
СО
о
о
о
о у
° tr
о ►>«
о
ОО
О
НО о
НО о
1
1
CH Q
СП о
*
)
)
еЗ
’—1 СЗ
1
1
' сЗ
1—1 сЗ
)
со
(
V/O;
V л
V/ ct
V/&
I
4Z
Z“4
/~ч
z—ч Я
z“ч
о
z-s
О
Z4
о
О
о О
z-ч
О
4«Z
см £
s«^ Qi
z~x
|
см 2
•ч
1,2
рас
О
г
со
о"
4Z
О
о"
1-3 1
(расч
1-3
(расч
к
НО
' tr
1 £
ч^
СМ
V/
V/^
Ч^
5
V/ —
хГ о
1 G5
00 Ct
см" S
~ сЗ
CM Ct
ч^
о
о
о
о
О'
О
О
о
О
о
о
О
о
о
о
О
О
о
о
НО
НО
й
НО
СО
со
со
СО
М4
'Ф
НО
s
но
но
J—4
)
)
)
(
(
(
(
о
сп
см
СМ
СО
ср
со
СО
О’
0^
С--
г-'
см
см
см
СО
(Р
СП
о
1
О
о
о
о
О
о
о
о
ю
о
см
см
о
см
СО
см
см
А
1—<
см
НО
СО
гС
т—1
1—<
’—<
’—<
’—<
А
А
л
л
д
д
л
к
А
’"Z
см
о
о
о
о
о
о
СО
CD
с.
ч
ч
ч
tj
О
л
д
ч
fc?
fcj
о
д
я
о
о
о
о
о
о
Ct
Q-(
я
я
с
к
к
я
к
к
я
сЪ
Ь-—(
к
я
<
<
<
<
<
<
CQ
PQ
у
у
147
Продолжение таблицы 10.1
сз
>3
CD
с
У
?
с
►
Ф
X
с
D
оЗ
X
\о
•
й
g
В
X
с
э
1
2
X
>>
X
03
S
CU
Ф
Н
X
X
1? си
2й н
S о
СП щ
X §
н
Q-.
t
с
t
с
Q
=5
3
<
Э
03
Рч
И
<
н
X
<р
о
н
X Р-
2 о
03 О
X
оЗ
° CU
«
СР
X
а
к 5J о
X § Н
щ X 03
«g
ч и
о
н
СЗ
ЕГ X
s*-*z
X
сЗ
О я
о
X
CJ
§
ХО
^2 я-
. о
S
CU
X
а? н
Z
СР
н
В
Райо
* 2
2 ср
*
СЧ С? Я
2^
°
о я
,—1 о
о
Р
СР
X
X
?§
СЧ
М< О
о Ю
d U
СЧ о
р *
} Я СР
3 си
СР
’—' о
СО о
< S &
о е-
1 о
Е-
&
00 О
03
03
си >>
О
сч
сч
S*
о
о
X
J
1О О
ю
2
г* ХГ
г-Ч
Е
2 и а
СР
1
1
СР
Я
° СР
О О
о
1 <*
ой
с
D
1
X
о
к й
х
03
03 X
X Я
1
I
✓■—ч
[
X ~
2 ч
1
1
1
£ Л
X 03
о н
оз £
К и
X X
03 X
х 2
Пос
СКОр(
н 2
И о
г
ю
со
г
1
оЗ
ю
ю
Ж ,
03
03
о
о
ЙЕ «
1
xf
1
со
со
со
со
о
СЧ
ю
ю
х
оз’§ X
Ь.
о-
X
<р
£ ?
-
сч
Г'.’
о
о
X
03 t
о
X
И X Ф
о
§ ё
1Q
сч
сч
ю’
X
к
сч
сч
сч
03
Е-1
-- /
СР
г>~»
ф
<Р
X
X
X
03
и
о
X
03
н
03
CU
А
t^-
03
00
03
А
03
03
А
О
03
ф
3
X
X
сЗ
<и
«2
cu
CU
CU
Рч
t=f
Ё
ф
СР
СР
СР
X
03
X
X
X
X
|
X
0)
СР
СР
СР
|
X
CQ
v
й
М
CQ
148
1972 г. были.осуществлены четыре мягкие посадки см. табл. 10.1),
можно не сомневаться, что в дальнейшем конструкция поса¬
дочных аппаратов станет более совершенной и более сложной, что
будут разработаны и применены самые разнообразные способы
обеспечения безаварийной мягкой посадки (например, посадка на
астероиды при отсутствии ощутимой силы тяжести без двигателей
«прижатия» представляется весьма затруднительной).
Приведем некоторые результаты оценки эффективности стаби¬
лизирующих двигателей при наиболее критических условиях посад¬
ки (движение вниз по крутому склону, Х = 0; 9тах = —30°). Двигате-
Рис. 10. 14. Изменение динамических параметров при
устойчивой посадке КПА (вариант А) вниз по склону
(0 = 20°):
I—смятие опоры № 1; II—вращение относительно опоры № 1,
III—смятие опоры № 2; IV—вращение относительно опоры № 2
149
ли прижатия располагаются на каждой опоре КПА (см. рис. 6.6).
Время работы двигателей ограничено. Легко заметить (см. рис.
10.7), что применение стабилизирующих двигателей с суммарной
4
тягой Tz = ^Ti= 100007/ увеличивает область устойчивости
Х=1
КПА в ~2 раза, применение двигателей с Те = 20000Н—в ~3 раза.
Расчеты показывают, что область устойчивости отсутствует при
посадке КПА на грунт с уклоном — 30° (см. рис. 10.7) без стабили¬
зирующих двигателей (заметим, что при этом статическая устойчи¬
вость аппарата сохраняется). Применяя стабилизирующие двигате¬
ли, можно добиться устойчивой посадки КПА па грунт с уклоном
—30° в требуемом диапазоне скоростей.
Изменение во времени ряда параметров, характеризующих ди¬
намику мягкой посадки аппарата с четырехопорным ПУ на склон
(О =—20°, схема посадки 2—2, Х = 0°), приведено на рис. 10.13
(посадочные скорости VB = yz = 3 м/с; Кг=Х/=1 м/с) и на рис. 10.14
(посадочные скорости VB = У/= 1 м/с; Vr=Xz=l м/с). На этих гра¬
фиках сплошными линиями показано изменение параметров в про¬
цессе посадки без использования стабилизирующих двигателей;
штрих-пунктирными — с использованием двигателей с суммарной
тягой 10000Н. В нижней части графиков обозначены характерные
моменты процесса мягкой посадки КПА.
Рис. 10.13 показывает изменение параметров в случае неус¬
тойчивой посадки аппарата при отсутствии стабилизирующих
двигателей (потеря устойчивости в момент /=1,65 с; ct2<0). Ис¬
пользование двигателей «прижатия» обеспечивает устойчивую по¬
садку (при /=1,35 с; «2 = 0,26 рад; Е = 58 Дж).
Рис. 10.14 иллюстрирует изменение параметров для случая
устойчивой посадки аппарата даже при отсутствии стабили¬
зирующих двигателей. Применение стабилизирующих двигателей
приводит к более быстрому окончанию процесса мягкой посадки.
Рассмотрим подробнее основные моменты этого процесса.
1. Опора 1 (сдвоенная опора) касается поверхности посадки и
деформируется (/ = 04-0,1 с). Вследствие деформации опоры 1 и на¬
личия трения о поверхность кинетическая энергия КПА уменьшает¬
ся (с 5800 до 4500 Дж). Деформация опоры 1 составляет 6im=
= 0,007 м.
2. КПА вращается относительно основания опоры 1 (/=
= 0,14-0,7 с). Центр масс аппарата продолжает опускаться до мо¬
мента прекращения деформации опоры 1. Поэтому кинетическая
энергия КПА возрастает (с 4500 до 9210 Дж).
3. Опора 2 (также сдвоенная) касается поверхности посадки и
деформируется (/ = 0,74-0,8 с). Вследствие деформации опоры 2 и
наличия трения о поверхность кинетическая энергия КПА умень¬
шается (с 9210 до 1400 Дж). Деформация опоры 2 составляет
б2т=0,17 м. При касании поверхности основанием опоры 2 основа¬
ние опоры 1 отрывается от поверхности посадки.
Согласно принятой схеме включения стабилизирующие двига¬
150
тели начинают работать в момент касания поверхности посадки ос¬
нованием опоры 2. На рис. 10.14 показано (штрих-пунктирной ли¬
нией) изменение параметров процесса в результате включения ста¬
билизирующих двигателей до момента удовлетворения критериям
устойчивости (6.33).
4. КПА вращается относительно основания опоры 2 (t=
= 0,84-1,0 с — при использовании стабилизирующих двигателей;
/ = 0,84-1,85 с — без стабилизирующих двигателей). При таком вра¬
щении центр масс аппарата поднимается и, следовательно, его ки¬
нетическая энергия убывает (с 1400 до 50 Дж).
В соответствии с критериями устойчивости (6.33) ai<0; ct2>0 и
£<ц = 50 Дж процесс посадки аппарата считается законченным в
моменты: /=1,85 с (без применения стабилизирующих двигателей)
или /= 1,0 с (с использованием двигателей).
На рис. 10.1 —10.3 представлено изменение области устойчиво¬
сти при посадке КПА (вариант Б) на наклонную поверхность в за¬
висимости от величины силы сопротивления при обжатии опор (g=
= 104-30 кН). Графики показывают, что при посадке на наклон¬
ную поверхность (0 =—54—15°; А,=0) зона устойчивости КПА
существенно сужается с ростом силы обжатия опор (особенно при
больших значениях посадочных скоростей). Причиной этого явля¬
ется возрастание опрокидывающего аппарат момента с увеличени¬
ем жесткости его опорных энергопоглотителей.
При изложении материала нами был рассмотрен весьма широ¬
кий диапазон посадочных скоростей (Ув=04-8 м/с; Кг = 04-5 м/с),
значительно больший того, который практически может быть обес¬
печен системой управления при нормальной посадке КПА на по¬
верхность планеты. Кроме того, как уже говорилось ранее (гл. 6)
деформации посадочных опор принимались (для упрощения рас¬
четов) неограниченными.
Отметим, что выбирать величину силы обжатия опорных энер¬
гопоглотителей целесообразно не только на основании определения
зон устойчивости КПА при посадке, но и с учетом допустимых для
полезного груза перегрузок и реальных величин деформаций поса¬
дочных опор.
Относительная простота изложенного в гл. 6 теоретического ме¬
тода исследования динамики мягкой посадки (и, следовательно, не¬
большие затраты при расчете машинного времени), возможность
учета влияния на динамику посадки конструктивных, параметров
аппарата и начальных посадочных условий, хорошее согласование
результатов с экспериментальными данными делают его вполне
приемлемым для практики инженерных расчетов в ОКБ с целью
уточнения компоновочной схемы КПА.
Обратимся теперь к особенностям деформации посадочных опор
космического аппарата при различных условиях посадки. Рассмат¬
ривая расчетные и экспериментальные данные по деформациям
опор КПА, можем отметить следующее:
деформации всех опор КПА возрастают с увеличением верти¬
кальной скорости посадки;
151
при посадке КПА вниз по склону (Х = 0°, схема 1—2—1) наи¬
большую деформацию имеет идущая вперед опора (5), а наимень¬
шую— задняя опора (/). Деформация опоры 3 в 24-2,5 раза боль¬
ше деформации опоры 1. Опоры 2 и 4 имеют примерно одинаковые
деформации, которые в 1,54-2 раза меньше деформации опоры 3.
С увеличением угла наклона поверхности посадки деформации
опор 3 и 1 увеличиваются;
при посадке КПА вверх по склону (Х= 180°, схема 1—2—/)
наибольшую деформацию имеет верхняя по склону опора (/), а
Вариант А Вариант В
Рис. 10. 15. Типовые деформации опор КПА
(варианты А и В) при посадке вверх по
склону, Х=180°; Рг=1 м/с; схема 1—2—1
наименьшую — нижняя опо¬
ра 3. Деформация опоры 1
в 24-2,5 раза больше дефор¬
мации опоры 3 и в 1,24-1,5
раза больше деформаций
опор 2 и 4. С увеличением
угла наклона грунта дефор¬
мация опоры 1 увеличивает¬
ся, а опоры 3 — уменьшает¬
ся. Этот случай движения
представляет наибольшую
опасность при посадке КПА
с точки зрения возможного
разрушения вперед идущей
опоры 1 из-за больших де¬
формаций ее энергопоглоти¬
теля (рис. 10.15);
при посадке КПА попе¬
рек склона (2i=9O°) реали¬
зуется схема касания опор
1—1—1—1, При этом наи¬
большую деформацию име¬
ет идущая вперед опора 4,
а наименьшую — задняя
опора 2. Это объясняется на¬
правлением вектора гори¬
зонтальной скорости в сто¬
рону опоры 4. Деформация опоры 4 в 2,5—3 раза больше деформа¬
ции опоры 2 и в 1,2—1,5 раза больше деформации опоры 1. С уве¬
личением угла наклона поверхности деформации опоры, идущей
вперед (4), и опоры, верхней по склону (/), увеличиваются; де¬
формации опор 2 и 3 уменьшаются;
при посадке КПА по схеме 2—2 вниз по склону для различных
значений составляющих посадочной скорости деформации опор,
идущих вперед (3, 4), в 2,5—3 раза больше деформаций задних
опор (/, 2);
характер деформаций опор различных КПА идентичен. Однако
абсолютная величина деформаций опор уменьшается с увеличени¬
ем жесткости их энергопоглотителей.
Сводка экспериментальных значений ускорений и деформаций
152
Таблица 10. 2
Испы¬
тание №
Схема и условия
испытания
Показания датчи¬
ков ускорений ДУ
и перемещений ДП
Примечание
30
А.
АГ
В ц. м.
Gr = 6g
GB=4,5g
На опорах
Gii = 7 g
Giii = 4 g
Giv=3,6 g
du = 85 мм
6ni=45 мм
div = 45 мм
В опоры заложены
соты энергоемкостью в
~2 раза большей, чем
при последующих испы¬
таниях. ДУШ и ДУ1У
показывают возникнове¬
ние колебаний вследст¬
вие сухого трения
Vr = 2,7 м/с
Ув = 2 м/с
Модель устойчива
31
че
Vr = 3,3 м/с
VB —2,0 м/с
0=—5°
Модель неустойчива
В ц. м.
Gr=llg
GB = 9g
На опорах
Cn=il,75g
Giii = 5,5 g
Giv=5,5 g
6ц=45 мм
din —77 мм
div =75 мм
ДПП показывает ха¬
рактерное поднятие пор¬
шня задней опоры
41
W I
ш п
Уг = 3,26 м/с
Ув=2,2 м/с
0 = —5°
Модель устойчива
В ц. m.
Gr=4,6g
Gs=4g
На опорах
Gi = 3,6g-
Gn=3,6 g
Gin=ll,6g
Giv = 1,6 g
di = 75 мм
du = 77 мм
din = 28 мм
6iv= —
Гальванометры не за¬
фиксировали момент ка¬
сания опорами грунта
вследствие нарушения
гальванической связи
между отдельными час¬
тями модели
42
Уг = 3,26 м/с
VB = 2,0 м/с
0 = —5°
Модель устойчива
В ц. м.
Gr = 5 g
G.^g
На опорах
Gi = 5£
Gn = 3,6 g
Gm = 1,7 g
Giv = 3,6 g
6i = 83 m.m
dn=!50 мм
dm =40 мм
div = —
ДУ II — «переворот»
сигнала характеристи¬
кой датчика
153
опор, зафиксированных при испытаниях модели ДПМ-Б с А=3; 4
при посадке на склон 0= —5° (Х = 0°), приведена в табл. 10.2.
Интересно заметить, что общее время процесса посадки модели
(включая подскоки после первого удара о грунт) существенно за¬
висит от величины и направления вектора посадочной скорости и
составляет 0,55—0,75 с, причем верхний предел относится к четы¬
рехопорному посадочному устройству. Своего максимального зна¬
чения ускорения в центре масс модели достигают примерно через
0,1 с (в пересчете на натурный лунный КПА — через 0,6 с) после
первого контакта с грунтом. Конечно, указанные временные отрез¬
ки имеют место при посадке модели ДПМ-Б на грунт с уклоном
—9°, но порядок величин этих временных отрезков сохраняется и
при изменении угла наклона грунта на i± 15°.
Результаты испытаний показали, что наибольшие перегрузки
возникают в опорах, идущих вперед и вниз по склону; они в 2—3
раза больше, чем в задних опорах. В случае посадки с одной опо¬
рой, идущей вперед (схемы 1—2—1 и 2—Г) это отличие становится
еще больше. Однако отметим, что при четырехопорном ПУ вслед¬
ствие большего числа опор этот эффект выражен слабее по сравне¬
нию с трехопорным ПУ. Другими словами, четырехопорный аппа¬
рат обладает известной степенью индифферентности к выбору схе¬
мы посадки. При трехопорном ПУ схема посадки аппарата 2—/,
Х=0 (одна опора вперед и вниз по склону), имеющая преимуще¬
ства с точки зрения устойчивости на опрокидывание по сравнению
со схемой 1—2, %=0о, является более опасной из-за больших пере¬
грузок в передней опоре.
Результаты испытаний при посадке вниз по склону свидетельст¬
вуют о большем обжатии энергопоглотителей опор, идущих вперед
и вниз по склону. При этом деформация опор достигает максималь¬
но возможной у модели величины 0,083—0,085 м (~0,5 м на на¬
турном лунном КПА), которая соответствует более чем 70%-ному
обжатию сотовых блоков.
В заключение, базируясь на изложенном материале, приведем
одну из возможных последовательностей разработки (ГОСТ
2.103—68) посадочного устройства перспективного космического
аппарата для мягкой посадки на планеты, их спутники, астероиды
или иные небесные тела.
А. На стадии разработки технического предложения (ГОСТ
2.118—73):
получение сведений о рельефе и свойствах грунта в месте пред¬
полагаемой посадки;
предварительный выбор схемы и габаритов посадочного устрой¬
ства в зависимости от назначения, компоновки и массы КПА и воз¬
можностей его системы управления;
проведение теоретического исследования динамики посадки ап¬
парата для выбранных схем его ПУ (при предельных значениях по¬
садочных условий).
Б. На стадии разработки эскизного проекта (ГОСТ 2.119—73):
получение уточненных сведений о поверхностном слое небесного
154
тела с помощью зондов жесткой посадки и пролетных, искусствен¬
ных спутников планет и пр.;
проведение детального теоретического анализа динамики посад¬
ки для наиболее вероятных схем посадочного устройства КПА;
проектирование, изготовление и испытания динамически подоб¬
ных моделей КПА с наиболее вероятными схемами посадочного
устройства.
В. На стадии разработки технического проекта (ГОСТ 2.120—
73):
проектирование, изготовление и динамические испытания стен¬
довых натурных макетов КПА (упрощенных и маневрирующих);
прочностные испытания натурного посадочного устройства на
расчетные случаи нагружения при посадке аппарата;
проектирование, изготовление и отработка летающего натурного
макета КПА; при отработке пилотируемого корабля—тренировки
космонавтов по совершению мягкой посадки на летающем макете и
по уточнению программы действий на планете (тренировки экипа¬
жа возможны и на стендовом макете с достаточным пространством
для маневрирования);
окончательная наземная отработка с целью оценки эффективно¬
сти посадочного устройства КПА при аварийных (нештатных) по¬
садочных ситуациях на стендовых натурных макетах.
Посадочное устройство, успешно прошедшее цикл наземной от¬
работки, передается на завершающую стадию испытаний — летные
испытания в составе КА.
СПИСОК ЛИТЕРАТУРЫ
1. Авдуевский В. С., Анфимов Н. А., Антонов Б. М. и др. Основы теории ^по¬
лета космических аппаратов. Под ред. Г. С. Нариманова и М. К. Тихонравова.—
М.: Машиностроение, 1972.—607 с.
2. Авдуевский В. С., Маров М. Я., Рождественский М. К. и др. Автоматиче¬
ские станции «Венера-9» и «Венера-10» — функционирование спускаемых аппа¬
ратов и измерение параметров атмосферы. — Космические исследования, 1976,
т. XIV, вып. 5, с. 655—666.
3. Автоматические планетные станции. Под ред. Ю. К. Ходарева.—М., Нау¬
ка, 1973.—279 с.
4. Алгоритмы и программы для решения технических задач оптимизации на
ЭЦВМ. Научно-технический отчет.—М.: Госфонд алгоритмов и программ, 1970.—
46 с.
5. Алексеев К. Б., Бебенин Г. Г., Ярошевский В. А. Маневрирование косми¬
ческих аппаратов.—М.: Машиностроение, 1970.—416 с.
6. Андреевский В. В. Динамика спуска космических аппаратов на Землю.—
М.: Машиностроение, 1970.—232 с.
7. Архангельский Б. А. Пластические массы. Справочное пособие.—Л.: Суд-
промгиз, 1961.—720 с.
8. Баженов В. И., Коваль А. Д., Страут Е. К. От модели к луноходу.—Ави¬
ация и космонавтика, № 8, 1966, с. 42—46.
9. Баженов В. Наземная школа лунохода,—Вестник АПН «По Советскому
Союзу», № 274, 23 ноября 1970, с.' 1—5.
10. Баженов В., Сахаров Ю. Земные репетиции «Венер». Газета «Ленинское
знамя», 26 ноября, № 277, 1975, 4 с.
11. Баженов В. И., Гончаров А. И., Осин М. И. Некоторые проблемы воз¬
вращения человека из космоса и их развитие от трудов К. Э. Циолковского до
наших дней. Труды десятых Циолковских чтений.—М.: ИИЕиТ АН СССР, 1977,
с. 28—40.
12. Барер А. С., Сорокина Е. И., Мураховский К. И. К вопросу о переноси¬
мости человеком ускорений после длительного пребывания в условиях, ими¬
тирующих невесомость. — Космическая биология и медицина, 1972, т. VI, № 3,
с. 49—53.
13. Билик Ш. М. Пары трения металл — пластмасса в машинах и механиз¬
мах. — М.: Машиностроение, 1966.— 311 с.
14. Бландов П. И. Амортизация и управление взлетно-посадочных устройств
самолетов.—изд. МАИ, 1962.—308 с.
15. Богданов В. А., Гурфинкель В. С., Панфилов В. Е. Стенд для моделиро¬
вания пониженной гравитации в наземных условиях. Авторское свидетельство
№ 215404.—Изобретатель и рационализатор, 1970, № 12, с. 12.
16. Борисов М. На космической верфи.—М.: Машиностроение, 1976.—136 с.
17. Кемурджиан А. Л., Громов В. В., Черкасов И. И. и др. Автоматические
станции для изучения поверхностного покрова Луны.—М.: Машиностроение,
1976.—200 с.
18. Климин А. В. Торможение в атмосфере аппарата с экипажем после меж¬
планетного перелета.—Космические исследования, 1973, т. 11, вып. 1, с. 31—37..
19. Кротиков В. Д., Троицкий В. С. Радиоизлучение и природа Луны.—
Успехи физических наук, 1963, т. 81, с. 51—56.
20. Лох У. X. Т. Динамика и термодинамика спуска в атмосферах планет.—
М.: Мир, 1966.—276 с.
156
21. Лунный грунт из Моря Изобилия. Под ред. А. П. Виноградова —М •
Наука, 1974.—624 с. F ’
22. Мак-Фарланд Р. К. Гексагональные сотовые конструкции под действие?л
закритической осевой нагрузки.—Ракетная техника и космонавтика 1963 № 6
с. 125—131. ’ ' ’
23. Мишин В. П., Осин М. И. Введение в машинное проектирование лета¬
тельных аппаратов. — М.: Машиностроение, 1978.—128 с.
24. Мороз В. И. Физика планет.—М.: Наука, 1967.—496 с.
25. Мороз В. И. О структуре марсианского грунта по оптическим и инфра¬
красным наблюдениям.—Космические исследования, 1976, т. XIV, вып 1
с. 85—96.
26. Наумов В. Н., Рождественский Ю. Л., Харитонова В. Е. Создание искус¬
ственного грунта. Труды МВТУ—№ 231, вып 1.—ХМ.: МВТУ, 1976, с. 32—37.
27. Нейланд В. Я-, Снигирев Ю. И. Тепловой режим летательного аппарата
при скоростях входа в атмосферу Земли, близких к 15 км/с.—Космические ис¬
следования, 1967, вып. 2, т. V, с. 205—211.
28. Пеллинец В. С. Об оценке погрешностей при измерении параметров виб¬
раций.—Л.: ЛДНТП, 1967.—23 с.
29. Пионеры ракетной техники. Избранные труды.—М.: Наука, 1964.—671 с.
30. Свешников А. А. Основы теории ошибок.—Л.: Изд. ЛГУ, 1972.—122 с
31. Седов Л. И. Методы подобия и размерности в механике.—М.: Наука,
1972.—440 с.
32. Стрелков С. П. Введение в теорию колебаний.—М.: Наука, 1964.—370 с.
33. Тейфель В. Г. Атмосфера планеты Юпитер.—М.: Наука, 1969.—183 с.
34. Тимошенко С. П. Колебания в инженерном деле.—М.: Наука, 1967.—444 с.
35. Трофименков Ю. Г., Воробков Л. Н. Полевые методы исследования стро¬
ительных свойств грунтов.—М.: Стройиздат, 1974.—175 с.
36. Угловой акселерометр, нечувствительный к действию линейных ускоре¬
ний. Патент США, № 316498, кл. 73—516.
37. Хинт И. А. Основы производства силикальцитных изделий. — М.: Строй¬
издат, 1962.—252 с.
38. Циолковский К. Э. За атмосферу.—Вокруг света, 1934, № 1, с. 10—14.
39. Цытович Н. А. Механика грунтов.—М.: Госстройиздат, 1963.—636 с.
40. Шкадов Л. М., Буханова Р. С., Илларионов В. Ф. и др. Механика оп¬
тимального пространственного движения летательных аппаратов в атмосфере.—
М.: Машиностроение, 1972.—240 с.
41. Штернфельд А. А. Введение в космонавтику.—М.: Наука, 1974.—240 с.
42. Щеголев А. В. Конструирование протяжек.—М.: Машгиз, 1960.—352 с.
43. Эльясберг П. Е. Введение в теорию полета искусственных спутников
Земли.—М.: Наука, 1965.—540 с.
44. Admire J., Mackey A. Dynamic Analysis of a Multilegged Lunar Landing
Vehicle to Determine Structural Loads During Touchdown. — NASA TN D-2582,
1965.
45. Bartolomew C. S. Risk Appraisal for Program Planning and Manage¬
ment. — Annals of Reliability and Maintainability, vol. 6, 1967.
46. Bellman D. R., Matranga G. J. Design and Operational Characteristics of
a Lunar Landing Research Vehicle (LLRV). — Flight Research Center, Edwards,
NASA TN D-3023, 1965.
47. Black R. J. Quadrupedal Landing Gear System for Spacecraft. — J. Space¬
craft and Roc., vol. 1, N 2, 1964.—p. 196.
48. Blanchard, Ulyssc J. Model Investigation of Technique for Conducting
Full-Scale Landing — Impact Tests at Simulated Lunar Gravity. — NASA TN
D-2586, 1965.
49. Blanchard, Ulyssc J. Evaluation of a Full-Scale Lunar-Gravity Simula¬
tor by Comparison of Landing — Impact Tests of a Full-Scale and a 1/6-Scale
Model. — NASA TN D-4474, 1968.
50. Blanchard, Ulysse J., Stubbs Sandy M. Martian Gravity Simulator for Full-
Scale Viking Landing Tests. — Space Simulation, NASA SP-298, 1972.—pp. 629—
646.
51. Congeion W. M. Investigation of Reflecting Heat Shield Materials for
Outer Planet Missions. — AIAA Paper, N 74-702.
157
52. Douglass D. R. and Austin C. R. Mission Risk Appraisal. — Annals of Re¬
liability and Maitainability, vol. 6, 1967.
53. Garden Huey D., Herr Robert W. and Brooks George W. Technique for the
Simulation of Lunar and Planetary Gravitational Fields Including Pilot Model
Studies. — NASA TN D-2415, 1964.
Touchdown Stability of Lunar-Landing Vehicles. — NASA TN D-4215, 1967.
54. Herr Robert W., Leonard H. Wayne. Dynamic Model Investigation of
55. Hylderman R., Mueller W., Mantus M. Landing Dynamics of the Lunar
Excursion Module. — J. of Spacecraft and Rockets, vol. 3, N 10, 1966.—pp. 1484—
1489.
56. Landley’s Lunar Landings. Lunar Landing Research Facility (LLRF).—Mis¬
siles and Rockets, vol. 17, N 2, 1965.—p. 8. Flight International, vol. 88, N 2940,
1965. —p. 111.
57. Leonard H. W., Walton W. C., Herr R. W. Studies of Touchdown Stabi¬
lity for Lunar Landing Vechicles. — J. Spacecraft and Roc., vol. 1, N 5, 1964.—
p. 552.
58. Mayo Etal E. E. Hypersonic Reentry Vehicle. — USA Patent N 3301507.
59. Me Gehee John R., Stubbs Sandy M. Experimental Validation of a Lan¬
ding Dynamics Computer Program for Legged Spacecraft Landers. — NASA TN
D-7301, 1973.
60. Miller R. E., Hansen S. D., Kawaguchi A. S., Redhed D. D., Southall J. W.
Cost Effectiveness of Integrated Analysis (Design Systems /IPAD/).—AIAA Paper,
N 74—960.
61. Moss I. N., Anderson E. C., Bold C. W. Viscous-Shock Layer Solutions
for Joyian Entry. — AIAA Paper, N 75-671.
62. Nicolet W. E., Morse H. L., Vojvodich N. S. Outer Planet Probe Entry
Thermal Protection. Part 1. Aerothermodynamic Environement. — AIAA Paper,
N 74-700.
63. Nicolet W. E., Mizines S. A. Outer Planet Probe Entry Thermal Protection.
Part 11. Heat Shielding Requirements. — AIAA Paper, N 74-701.
64. O’Bryan, Thomas C., Hewes Donald E. Operational Features of the Landley
Lunar Landing Research Facility. — NASA TN D-3828. 1967.
65. Rau T. R. and Decker J. P. Optimal Design Integration System for Syn-
tesis of Aerospace Vehicles. — AIAA Paper, N 74-72.
66. Schuring D. Scale Model Testing of Land Vehicles in a Simulated Low-
gravity Field. — SAE-660148, 1966.
67. Smith A. M. Risk Assesmeni in Complex Unattended Aerospace Systems.—
Annals of Reliability and .Maintainability, vol. 6, 1967.
68. Stubbs Sandy M. Investigation of Technique for Conducting Landing
Impact Tests at Simulated Planetary Gravity. — NASA TN D-6459, 1971.
69. Stubbs Sandy M. Experimental Investigation of the Landing Dynamics of
Three-Legged Spacecraft Models. — NASA TN D-7664. 1974.
70. Troitsky V. S. A 4-Meter Thick Porous Material Layer Covers the Moon.—
Space World,- vol. D-6 42, June, 1967. — pp. 44—45.
71. Warner R. W., Sorenson R. M., Kaskey A. J. An Investigation of a Defor¬
ming Energy-Absorption System for Space — Vehicle Landings.—NASA TN D-3061,
1966.
ОГЛАВЛЕНИЕ
Стр.
Предисловие 3
Часть 1. Вопросы посадки космических аппаратов на планеты с ат¬
мосферой 5
Г лава 1. Особенности спуска на планеты с атмосферой 6
Глава 2. Проблемы возвращения на Землю, характерные для околоземных
и межпланетных космических полетов 26
Глава 3. Выбор проектно-баллистических параметров посадочных аппара¬
тов марсианских планетных комплексов . 43
Глава 4. Анализ характеристик траектории при управляемом входе и сни¬
жении в атмосфере Венеры 54
Глава 5. Определение проектных параметров спускаемого аппарата зон¬
да в атмосферу Юпитера 59
Часть 2. Методы исследования мягкой посадки космических аппаратов
на планеты без атмосферы 69
Глава 6. Теоретический анализ динамики мягкой посадки космических по¬
садочных аппаратов . . 70
Г лава 7. Теоретическое обоснование физического моделирования мягкой
посадки 87
Глава 8. Экспериментальные исследования мягкой посадки с помощью ди¬
намически подобных моделей К.ПА 106
Г лава 9. Особенности наземной экспериментальной отработки мягкой по¬
садки с помощью натурных макетов КПА 125
Глава 10. Некоторые результаты теоретического и экспериментального ис¬
следования мягкой посадки 136
Список литературы . . 156
ИБ № 889
Владимир Иванович Баженов,
Михаил Иванович Осин
ПОСАДКА КОСМИЧЕСКИХ АППАРАТОВ НА ПЛАНЕТЫ
Редактор Е. В. Сербиновская Художественный редактор В. В. Лебедев
Технические редакторы Е. М. Коновалова, В. И. Орешкина Корректор А. И. Карамышкина
Обложка художника Л. С. Вендрова
Сдано в набор 29.03.78.
Формат 60X90V16
Печать высокая.
Тираж 2500 экз.
Подписано в печать 16.05.78. Т—09667
Бумага типографская № 2 Гарнитура литературная.
Усл. печ. л. 10,0 Уч.-изд. л. 11,05
Заказ 400. Цена 55 к.
Издательство «Машиностроение», 107885, Москва, Б-78, 1-й Басманный пер., д. 3.
Московская типография № 8 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
Хохловский пер., 7.
«МАШИНОСТРОЕНИЕ’