2. ОПРЕДЕЛЕНИЕ ДАВЛЕНИЯ НА ПОВЕРХНОСТИ ТЕЛА И
СОПРОТИВЛЕНИЯ, ОБУСЛОВЛЕННОГО ДАВЛЕНИЕМ
Арафайлов С.И.
Одной из наиболее важных аэродинамических характеристик тела
является сила лобового сопротивления. Она определяет во многом тра-
екторию летательного аппарата и его поведение в потоке. Наиболее про-
стой способ определить эту величину экспериментально - весовой - с
помощью специальных аэродинамических весов. Однако, в некоторых
случаях весовой способ измерения силы оказывается неприемлемым.
Например, если исследуемое тело находится на земле - это может быть
высотное сооружение типа трубы предприятия, плотины, башни и т.п.
Проблемы с весовым способом возникнут также и в случае, когда
нам понадобится знать детальное распределение сил, например, вдоль
несущей поверхности, которое необходимо для задания прочностных
характеристик материала, из которого изготовлена эта поверхность.
Лобовое сопротивление, обусловленное давлением
Для того чтобы справиться с подобными проблемами, в данной ра-
боте предлагается следующий способ измерения силового воздействия
потока на тело: сначала измеряется давление р на поверхности иссле-
дуемого тела, затем с помощью операции интегрирования по поверхно-
сти измеряется сила, создаваемая этим давлением:
Рд =-JpdS
S
Здесь индекс «д» означает, что сила соответствует только давле-
нию, минус перед интегралом стоит из-за того, что нормальный вектор п
имеет внешнее направление по отношению к телу, а, значит, направле-
ние элемента интегрирования dS противоположно давлению, оказывае-
мому обтекаемым потоком на тело (рис.1).
Очевидно, что полное силовое воздействие потока F не будет сов-
падать с силой, обусловленной только давлением - необходимо учиты-
вать касательные напряжения, обусловленные вязкостью:
F = Fa+JT„dS
5
17
Рис. 1
В общем случае оба интеграла в правой части этого равенства со-
поставимы. Однако, в некоторых случаях один из них может оказаться
несущественным. Скажем, если мы хотим определить вертикальную
составляющую этой силы К, называемую подъемной силой, - на боль-
шей части поверхности S тел типа фюзеляжа самолета, ракеты, крылово-
го профиля и т. п. проекция вектора тл на ось у будет невелика - т. е.
вязкий интеграл для определения подъемной силы можно не учитывать.
Тогда как для х - составляющей силы, которую в дальнейшем будем
называть лобовым сопротивлением X, ситуация совершенно противопо-
ложна - тЛ на большей части поверхности практически полностью про-
ецируется на осьх, поэтому, вклад вязкой составляющей силы сопротив-
ления обычно весьма существенен, несмотря на относительную малость
коэффициента вязкости.
Аналогично, расчитывая силу сопротивления при обтекании пло-
ской пластины, поставленной перпендикулярно вектору скорости набе-
гающего потока Уд,, получаем, что проекция вектора тл в равна нулю
и в данном частном случае плоской пластины:
Если форма обтекаемого тела похожа на такую плоскую пластину
(например, парашют) - очевидно, мы можем с большой точностью счи-
тать
X ~ ХД - - jp cos adS,
5
где а - угол между нормалью и поверхностью.
18
Более того - эту аппроксимацию можно применить и для плохооб-
текаемых тел, то есть тел, поперечные потоку размеры которых сопоста-
вимы с продольными - в частности для шара или для цилиндра.
Конечно, отбрасывать вязкий интеграл можно только когда вяз-
кость
невелика - то есть при больших числах Рейнольдса.
В данной работе рассматривается обтекание цилиндра и определя-
ется лобовое сопротивление только за счет давления. Если число Рей-
нольдса, соответствующее условиям эксперимента окажется достаточно
большим, то полученное значение будет достаточно хорошо аппрокси-
мировать полное лобовое сопротивление цилиндра.
Определение давления на поверхности тела
Для определения давления р проводится дренаж поверхности - на
поверхности высверливаются отверстия и в них устанавливается датчик
давления. Это может быть пьезоэлемент или конденсатор - устройства
преобразующие механическое напряжение в электрический сигнал. В
нашем эксперименте для наглядности используется «древний», но наи-
более наглядный способ измерения давления - с помощью жидкостно-
го манометра. Отверстие с помощью шланга подсоединяется к U-
образному сосуду с жидкостью известного удельного веса, второй конец
которого либо открыт в атмосферу, либо давление во втором колене р^
известно из каких либо других соображений. Тогда искомое давление
определяется по гидростатической формуле
р-р^
где к - коэффициент тарировки манометра, а - наклон манометра к по-
верхности горизонта.
Количество отверстий определяется необходимой точностью ап-
проксимации интеграла. Основная проблема при таком способе измере-
ния - техническая. Для измерения давления необходимо просверлить
отверстие строго по нормали к поверхности. Отклонение от нормально-
го направления приводит к искажению измеряемого давления (рис. 2) -
скос нормали навстречу потоку увеличивает снимаемое давление (за
счет динамического напора потока), скос по потоку уменьшает давление
(за счет срыва вихрей с острой кромки). Конечно нормаль невозможно
19
выбрать абсолютно точно, приемлемое отклонение определяется числом
Рейнольдса и скоростью потока на внешности пограничного слоя.

р
Рис. 2
Обезразмеривание параметров задачи
В аэромеханике в качестве обезразмеривающих величин обычно
берутся: р - плотность набегающего потока, - скорость набегаю-
щего потока и S - характерная площадь обтекаемого тела (обычно это
максимальное сечение плоскостью х = const). В качестве третьей обез-
размеривающей величины часто используется L - характерная длина -
вместо характерной площади. В случае обтекания цилиндра в силу дву-
мерности задачи обе эти величины можно считать одинаковыми и рав-
ными диаметру цилиндра 2R (под площадью сечения в плоском случае
подразумевается площадь, приходящаяся на единицу длины цилиндра).
С помощью этих трех величин можно обезразмерить любую раз-
мерную величину. Например, вместо размерной динамической вязкости
р можно рассматривать безразмерную —~— (равную, кстати, —).
pV^L	Re
Вместо размерного давления мы будем рассматривать безразмерный
коэффициент давления:
Силе лобового сопротивления соответствует безразмерный коэф-
фициент сопротивления
20
X
Аналогично, можно ввести коэффициент лобового сопротивления,
обусловленный давлением
cxa = ~\cpcosadS
S
Интеграл Бернулли для несжимаемой легкой жидкости
Р + \ру2 =Роо+|р(/»
1	7
после обезразмеривания (деления на динамический напор ~pV<x> ) пре-
вратится в более компактное выражение:
В соответствии с теорией размерности, обезразмеривание перемен-
ных и функций помогает моделированию задачи. В аэродинамике можно
привести наиболее характерный пример - для определения аэродинами-
ческих характеристик летательного аппарата необходимо изготовить его
«натурную» копию и, затем, прицепить его к другому летательному ап-
парату. Но такой эксперимент даст неточные результаты, поскольку за
несущей конструкцией образуется турбулентный след и, таким образом,
исследуемая конструкция будет обтекаться неравномерным потоком.
Лучше всего поместить эту конструкцию в аэродинамическую трубу.
Однако, размеры современных летательных аппаратов могут достигать
десятков метров - размеры рабочей части трубы должны хотя бы на по-
рядок превосходить размеры обдуваемой конструкции - то есть быть
порядка сотен метров. Труба, позволяющая проводить такие натурные
эксперименты имеет гигантские размеры и, кроме того, продувка в такой
трубе со скоростями, соответствующими скорости полета самолетов,
получается достаточно дорогостоящей.
Проще сделать уменьшенную копию - модель исследуемой конст-
рукции и в относительно небольшой аэродинамической трубе сделать
21
продувку и измерить сх. В результате, можно определить силу, дейст-
вующую на реальную, а не модельную, конструкцию по формуле
X = cx~pV^S
где р, и S - плотность, скорость набегающего потока и сечение для
обтекания реальной конструкции.
На вопрос почему сх можно считать одинаковым для маленькой мо-
дели и для реальной конструкции отвечает П - теорема, которая говорит,
что безразмерные величины (типа сх) не могут зависеть от размерных
величин - то есть неважно, каков размах крыльев обтекаемой конструк-
ции - десять метров или десять сантиметров - безразмерная величина
будет одинакова, если соблюдается геометрическое подобие. Конечно,
кроме геометрического еще должно быть соблюдено физическое подо-
бие, другими словами должны быть одинаковы все безразмерные харак-
pV L
теристики обтекания. В частности, число Рейнольдса Re =	----
безразмерная комбинация, значит величина сх от него зависит. Таких
безразмерных комбинаций в реальной задаче может быть достаточно
много. К наиболее важным, помимо Re можно отнести число Маха
.. к® .	_ kJ	l
-----, число Фруда Fr =----, число Струхала Sh ----- - харак-
^зв	&
терное время задачи). Однако, если мы будем рассматривать степень
влияния каждого из этих чисел на обтекание, то окажется, что, скажем,
для статических задач ( т —> ) число Струхаля становится несущест-
венным; при обтекании тела тяжелой жидкостью (например, водой) чис-
ло Фруда влияет на течение, в случае же аэромеханики - обтекания
«легким» газом, число Фруда учитывать не имеет смысла. То же самое
можно сказать о числе Маха при существенно дозвуковых течениях (кд-
гда скорость потока много меньше скорости звука язв . В итоге получа-
ется, что единственным важным параметром для сх является число Рей-
нольдса.
Зависимость сх от Re для плохообтекаемых тел весьма характерна.
На рисунке 3 приведена такая зависимость для шара (качественно гра-
22
фик сх = Re для цилиндра точно такой же, только цифры несколько
Рис. 3
Как видно из графика, при малых числах Рейнольдса коэффициент со-
противления падает (в соответствии с формулой Стокса). Затем падение
продолжается более медленно вплоть до Re»5-103, где достигается
локальный минимум сопротивления. В области чисел Рейнольдса
2-104-2-105 безразмерное сопротивление сх остается практически
постоянным. При Re «2 4-3 -105 наступает кризис сопротивления, вы-
званный турбулентностью - сопротивление падает примерно в 4 -5 раз.
Задача данного практикума - найти одну точку на аналогичной
кривой cx(Re) для цилиндра.
23
Плоские задачи аэрогвдромеханики
В аэромеханике очень важной проблемой является задача обтека-
ния несущих поверхностей (крыльев). В случае дозвукового течения
крылья большого удлинения обладают преимуществом, поскольку у них
мала индуктивная составляющая сопротивления. Для таких крыльев
пространственные эффекты обтекания проявляются только вблизи кро-
мок - в относительно небольшой области, поэтому большую часть пото-
ка, обтекающего крыло можно считать двумерным
Удобно рассмотреть предельный случай - крыло бесконечного раз-
маха, но здесь возникает следующая проблема: при вычислении коэф-
фициента сх для крыла бесконечного размаха придется интегрировать
по бесконечно большой поверхности. Чтобы обойти эту проблему вве-
дем профильное сопротивление крыла за счет давления и соответст-
вующий ему коэффициент профильного сопротивления.
В крыле (не обязательно бесконечного размаха) можно выделить
профиль - сечение плоскостью z = const, где z - координата, направ-
ленная вдоль образующей крыла. Профильным сопротивлением, обу-
словленным давлением, назовем следующий интеграл
А'д = jpcosc&fl
С
где I - элемент контура. Очевидно, что проинтегрировав профильные
сопротивления по размаху крыла, мы получим обычное сопротивление:
X = fxik
То есть X' можно считать производной по координате z от обычного
сопротивления X. Но, обычно, величину профильного сопротивления
интерпретируют следующим образом - если из крыла выделить элемент
длины равный единице на достаточном удалении от кромки крыла, то
сопротивление этого элемента будет
z0+l
Х= fX'dz = X'
в силу того, что профильное сопротивление, в данном случае не зависит
от z и интервал интегрирования равен единице.
24
Итак: профильное сопротивление - это есть сопротивление элемента
крыла единичной длины, который расположен достаточно далеко от
кромок крыла.
Для коэффициента профильного сопротивления, обусловленного
давлением можно написать формулу
схл
= fcp cosadr
где / - безразмерный элемент интегрирования по контуру.
Обтекание контура идеальной жидкостью
Итак, задача обтекания крыла воздухом, может быть существенно
упрощена в силу большой удлиненности крыла - можно считать течение
двумерным - и в силу большого числа Рейнольдса - можно считать что
все вязкие эффекты сосредоточены в тонком, по сравнению с размерами
крыла, пограничном слое, а вне пограничного слоя, который практиче-
ски не меняет форму крылового профиля, можно считать обтекаемый
воздух идеальной жидкостью. Кроме того, поскольку предполагается,
что скорости много меньше скорости звука, течение можно считать не-
сжимаемым.
Данная задача, несмотря на существенные упрощения осталась все
равно достаточно сложной в силу нелинейности уравнений, описываю-
щих это течение. Однако, она допускает аналитическое решение.
Уравнение неразрывности в декартовых координатах можно записать
так
ди dv
—+— = 0
дх ду
здесь и и v - компоненты скорости.
Поскольку на крыло набегает безвихревой поток и нет источников
тепла, то в идеальном газе можно считать, что вихрей не будет и в самом
течении. Поскольку течение плоское, то у завихренности со всего одна z-
компонента:
ди dv _
=------= 0
ду дх
JJpa последних уравнения составляют условия Коши-Римана -
то есть из функций и и v можно составить голоморфную функцию ком-
плексного переменного z = х+iy. Можно, так же понимать эти два со-
отношения как замкнутую систему уравнений с граничными условиями:
И.-’'.
Мс =0
25
то есть равномерный поток V на удалении от тела и условие непротека-
ния на поверхности обтекаемого тела.
Некоторое неудобство при решении такой задачи состоит в том, что
на поверхности в граничное условие входят обе переменные и и v. По-
этому, обычно, в таком виде задача обтекания не формулируется. Гораз-
до удобнее воспользовавшись условием отсутствия вихрей в потоке, ко-
торое означает, что для поля скоростей V можно найти потенциал <р:
др
дх
др
. Зи
Затем можно подставить эти соотношения в уравнение неразрывности -
получится уравнение Лапласа:
 ^-А
дх2 ду2
С граничным условием только для <р на поверхности контура С
££| .0
а» с
Такого рода задача называется задачей Неймана.
Можно пойти другим путем - в двумерном течении, в силу уравнения
неразрывности, всегда можно ввести функцию тока:
дм
и =----
др
v =----
дх
Подставив эту функцию р в уравнение отсутствия вихря, опять полу-
чим уравнение Лапласа
5 V ,	п
дх2 ду2
Граничные условия для ф:
Ис=0
Это задача Дирихле.
26
Можно решать задачу Неймана, или задачу Дирихле, но гораздо
удобнее воспользоваться теорией функций комплексного переменного -
ведь функции (р и так же как и и и v удовлетворяют условиям
Коши-Римана и	является голоморфной функцией; преобра-
зование, переводящее физическую плоскость z на плоскость w являет-
ся конформным (конформность обеспечивает условие непротекания).
Поскольку линии тока соответствуют линиям - const , на плоско-
сти w линии тока окажутся горизонтальными прямыми, а обтекаемый
контур - отрезком на координатной линии ср. То есть, если мы решили
задачу обтекания, значит мы нашли функцию w, конформно переводя-
щую наш контур на отрезок, лежащий на оси (р (рис 4).
Рис. 4
Верно и обратное - если мы нашли конформное отображение, пере-
водящее наш контур С в отрезок - значит мы можем определить все
параметры течения. Например, продифференцировав w, мы получим
комплексно-сопряженную скорость:
27
t да) .ду/
и> = —£- + /-= w-zv
дх дх
Взяв действительную часть w' мы получим х - компоненту скоро-
сти, взяв мнимую часть с обратным знаком - получим у - компоненту.
Для определения коэффициента давления ср необходимо восполь-
зоваться интегралом Бернулли:
V * Л'
cD = 1----= 1----v
р	и2
°о	У 00
Конечно, для определения течения около произвольного крылового
профиля довольно трудно найти такое конформное отображение w и
обычно такую задачу приходится решать численно (например, можно
заменить профиль ломаной и воспользоваться интегралом Шварца), од-
нако, для цилиндра данная задача решается достаточно просто.
Обтекание цилиндра идеальной жидкостью
Функция, отображающая внешность круга радиуса R на отрезок на
горизонтальной оси называется функцией Жуковского:
г *7
^=^00 Z +--------------------------------
I Z )
Конформность данного отображения обеспечивает условия непротека-
ния на поверхности тела. На бесконечном удалении от цилиндра должно
выполняться условие однородности поля течения. С помощью диффе-
ренцирования и можно убедиться в справедливости этого условия:
, VL я2)
=И00 1----у
Z J
При z -> оо сопряженная скорость стремится к . (Таким образом, со-
пряжение этого коэффициента в функции Жуковского - граничное усло-
вие на бесконечности).
Далее удобно использовать тригонометрический вид комплексного
числа z = ге® {г- радиус комплексного числа, 0- его аргумент). Нас
интересуют газодинамические параметры только на поверхности цилин-
дра, то есть г = R. Тогда, из безразмерного соотношения, соответст-
вующего интегралу Бернулли, получится и>7	= 1 - e~2l° и
28
cp =l-(l-e“2/0XI-e2'e)
Перейдя от мнимых экспонент к обычным тригонометрическим функци-
ям, получим теоретическое распределение давления на поверхности ци-
линдра в зависимости от угла 0 между осью х и радиусом точки на
поверхности:
ср =1-4 sin2 0	(♦)
Зная функцию распределения давления на поверхности ср(0)9
можно найти силу, действующую со стороны идеальной жидкости на
обтекаемое тело. В случае цилиндра удобно воспользоваться полярной
системой координат. Якобиан полярной системы координат равен R, то
есть dl = RdO. Следовательно, dl' - — = — d0. Поскольку для цилинд-
27? 2
pa cosa = cos0, получаем
1 п
сх* -— \cp(O)CQS0d0
~Л
В эксперименте угол удобно отсчитывать не от оси х, а от точки
растекания: 3 = п -0. Окончательно получаем формулу для коэффици-
ента лобового сопротивления
—л
где угол 0 отсчитывается от точки растекания в лобовой части цилинд-
ра.
Если в эту формулу подставить закон с р, полученный с помощью
метода конформных отображений, получим
1 к
с'Хд = - J(1—4 sin 2 &)cos(ff)d& = 0	(♦♦)
-л
Этот результат и должен был получиться в соответствии с парадок-
сом Даламбера. Забегая вперед можно сказать, что результаты экспери-
мента будут другими. Причиной несоответствия эксперимента и теории
в данном случае может быть только явление вязкости. При больших
числах Рейнольдса вязкость существенно проявляется только в тонкой
области, занимаемой пограничным слоем. Можно показать точно, из
уравнений Навье-Стокса, что при повышении давления вдоль движения
29
жидкости пограничный слой должен оторваться от поверхности тела. То
есть, рассмотренное здесь аналитическое решение задачи предполагает
безотрывное обтекание, а в реальной жидкости из-за явления отрыва
пограничного слоя это предположение оказывается неверным.
Тело, двигаясь поступательно и без ускорения, при безотрывном
обтекании не возмущает новые участки жидкости - поэтому на такое
движение на затрачивается энергия и нулевое сопротивление в данном
случае естественный результат. При отрывном обтекании тело при вне-
дрении в среду «тянет» за собой хвост жидкости, увлекая в движение все
новые и новые участки жидкости. При турбулентном движении точка
отрыва существенно смещается вниз по потоку - поэтому турбулентный
«хвост» занимает существенно меньший объем. Этим и объясняется тот
парадоксальный факт, что при турбулентном течении для многих плохо-
обтекаемых тел существенно - в несколько раз - падает сопротивление
(хотя из-за увеличения вязкого трения при наступлении турбулентности
это сопротивление должно было бы возрасти).
Эксперимент* >
В рабочей части трубы расположен цилиндр перпендикулярно набе-
гающему потоку. Торцы цилиндра выходят за пределы рабочей части
трубы. Площадь миделева сечения цилиндра много меньше площади
сечения рабочей части трубы, поэтому уменьшение площади живого
сечения трубы мало скажется на распределение скоростей около цилин-
дра. Цилиндр дренирован - 30 отверстий, направленных по радиусу ци-
линдра, отстоят на равных расстояниях друг от друга по углу. Тонкие
трубки изнутри цилиндра подсоединены к отверстиям и через его торец
выводятся наружу где с помощью резиновых шлангов соединяются со
стеклянными трубками жидкостного батарейного манометра (рис.5). Все
трубки батарейного манометр соединены снизу с бачком, в который на-
лита жидкость известного удельного веса /. Всю систему трубок бата-
рейного манометра можно считать соединяющимся сосудом и, в началь-
ный момент времени, когда течения в трубе отсутствует, можно пола-
гать, что все уровни одинаковы. Однако, закон сообщающихся сосудов
не учитывает капиллярных эффектов, вследствие которых начальные
При описании эксперимента используется методика, описанная в разделе:
Комаров А.М. «Определение местных давлений и их распределение на поверх-
ности тела в потоке» [5].
30
показания всех трубок батарейного манометра могут отличаться. До
включения трубы следует записать эти начальные показания hio. Ма-
нометр имеет наклон к горизонту на угол а- при малых углах а по-
вышается точность измерений, поскольку даже небольшие изменения
давления приводят к существенным отклонениям столбика жидкости в
трубке
манометра. При увеличении а точность уменьшается, но увеличивается
диапазон измеряемых давлений. Таким образом, а выбирается так, что-
бы соотношение диапазон-точность было оптимальным.
После включения трубы через определенное время течение выйдет
на установившийся режим, движение столбиков жидкости в батарейном
манометре прекратится. По уровням ht по гидростатической формуле
можно определить давление pt около соответствующего Z-ro отвер-
стия
Pi ~Ръ=	sin «
Здесь kj - тарировочный коэффициент Z - й трубки. Перепад уров-
ней Лй, можно считать равным й, - й/0 только тогда, когда суммарное
сечение всех отверстий много меньше сечения бачка, однако в данном
эксперименте это не так и необходимо учитывать изменение уровня в
бачке. Для измерения этого уровня в бачковом манометре предусмотре-
ны трубки с номерами 0 и 31 - они так же как и бачок открыты в атмо-
31
сферу (либо на них подается полное давление невозмущенного потока в
рабочей части трубы). Таким образом, падение уровня 8 в бачке можно
определить как среднее арифметическое: 8 = ~(ЛЛ0 + АЛ31). Тогда, в
соответствии с гидростатической формулой, разность давления рг -
будет определяться величиной АЛ, = Л, -Л,о -3.
Зная давление р, можно посчитать безразмерный коэффициент
давления cPj :
_ Pi Р<я
СР> ~ 1	,
2Р^
1 о
Для определения динамического напора в этом соотношении
предназначен манометр 1. Это бачковый манометр, верхний конец труб-
ки подсоединен к отверстию в рабочей части трубы - то есть измеряется
статическое давление на большом расстоянии от обтекаемого цилиндра.
Бачок открыт в атмосферу, либо подсоединен к трубке Пито, измеряю-
щей полное давление в потоке в рабочей части трубы. Для незамкнутой
трубы (прямого действия) можно с большой точностью считать, что
полное давление потока равно невозмущенному атмосферному давле-
нию. Следовательно, из интеграла Бернулли получаем:
+ Р ~ Ратм
2
гр	м.	00	W
То есть, динамический напор ., равный перепаду давления
Р “ Рэтм определяется по изменению уровня манометра АЛ = Л - Ло :
= АЛЛ/ sin а
Здесь к - коэффициент тарировки манометра, у - удельный вес жидко-
сти в манометре, а - угол наклона манометра. Отсюда, кстати, можно
получить и саму скорость потока, которая необходима для расчета числа
Рейнольдса:
_ 12АЛЛ/5та
32
В этой формуле плотность воздуха должна быть определена по уравне-
нию состояния совершенного газа р = pRT в которой R - газовая по-
стоянная воздуха. Поскольку известно, что при давлении р = 760 мм рт.
ст. и температуре 15°С (= 288 К) плотность воздуха равна
1 кГ-с2
Ро ------— 9 получаем
8 м4
р(мм) 288
Р ~Рй 760 Т(К)
Данные об условиях опыта и приборах заносятся в таблицы.
Таблица 1. Условия опыта
Барометрическое давление В = мм рт. ст
Температура t = °C
„ , л	см2
Коэффициент кинематической вязкости v= -----
с
Диаметр цилиндра	мм
Число Рейнольдса Re =---=
v
Таблица 2. Манометр 1.
sina =
у=	кГ/м3
к =
й0 =	мм
Л =	мм
= (рп-р*) =
= (h-h^yksina =	кГ/м2
[2
^’оо =. —(Рл-/’«)= м/с
VP
33
Таблица 3. Батарейный манометр
sina =
у= кГ/м3
ki =
- (Л-Л0)о+(Л-Л0)з1
П =------------------
Частично эти таблицы можно заполнять уже после включения тру-
бы во время ожидания выхода уровней жидкости в батарейном маномет-
ре на стационарный режим. До включения трубы следует заполнить
вторую строчку таблицы 4 - «нулевые» показания й0.
Таблица 4. Экспериментальные данные и вычисления
№тр.	0	1	2	3	4	5	...	28	29	30	31
мм											
hi0	мм											
й, - й/0 мм											
hi-h^-8											
Pi ~Р«> = = -(й; - й/0 - #)£;/ sin а											
_ Pi ~Рас СР> ~ 1	2											
%											
COS &i											
cD = (l-4sin2<9) г и ж											
34
Для заполнения строки «9, необходимо знать нахождение критиче-
ской точки - для этого во время эксперимента надо повернуть обтекае-
мый цилиндр так, чтобы критическая точка совпала с одним из отвер-
стий дренажа. Это состояние определяется по симметричному располо-
жению уровней жидкости батарейного манометра. В трубочке, соответ-
ствующей критической точке будет минимальный уровень, в соседних
трубочках - одинаковых уровень (с точностью до 1-2 мм). В ячейке таб-
лицы, соответствующей критической точке ставится 0, в ячейках слева и
справа 12 и -12 и так далее с шагом 12 градусов.
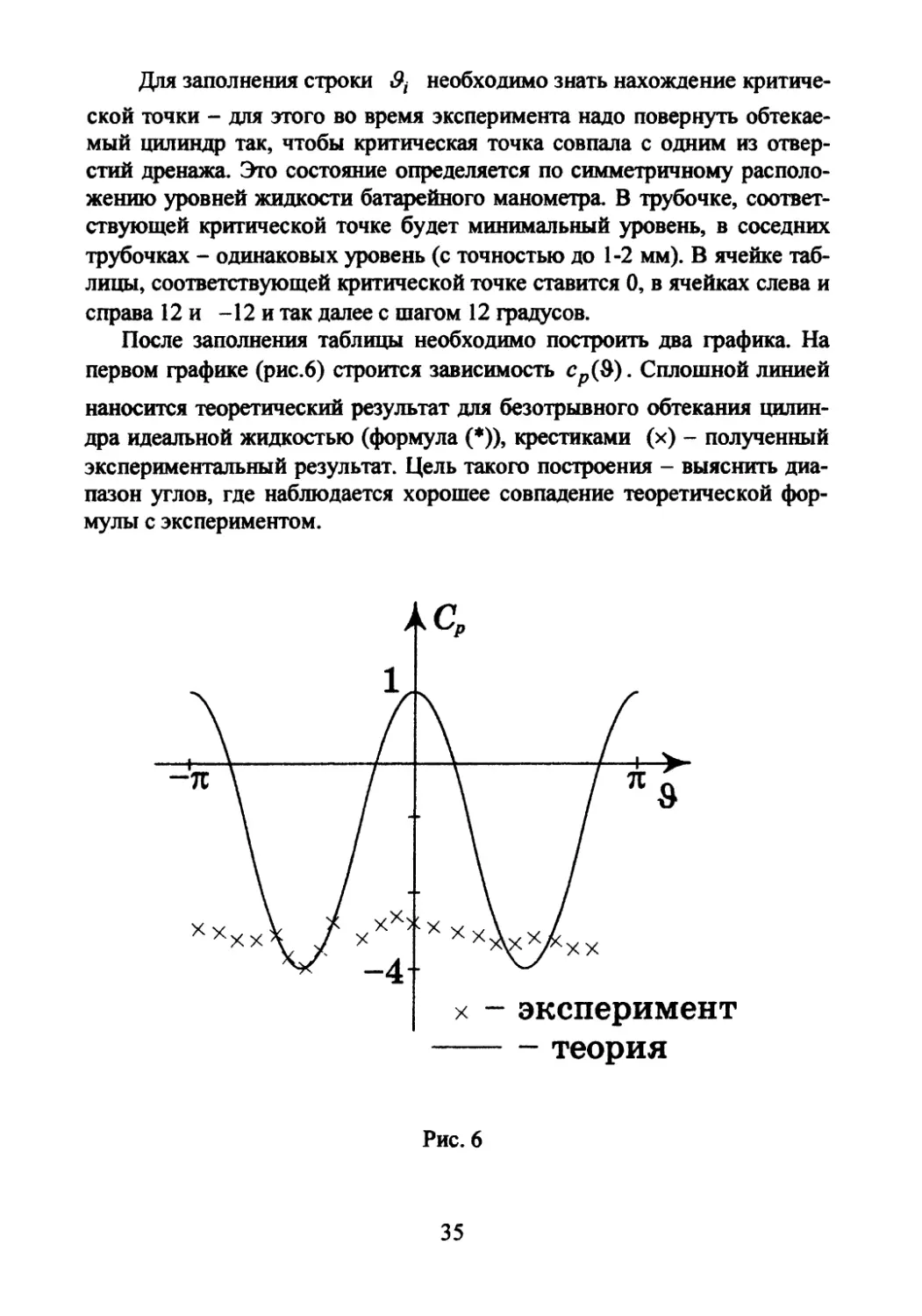
После заполнения таблицы необходимо построить два графика. На
первом графике (рис.6) строится зависимость ср(9). Сплошной линией
наносится теоретический результат для безотрывного обтекания цилин-
дра идеальной жидкостью (формула (*)), крестиками (х) - полученный
экспериментальный результат. Цель такого построения - выяснить диа-
пазон углов, где наблюдается хорошее совпадение теоретической фор-
мулы с экспериментом.
Рис. 6
35
На втором графике (рис.7) строится только экспериментальный график
ср (19) cos 19. Значения наносятся точками и соединяются плавной лини-
ей. Второй график необходим для определения интеграла (*♦) графиче-
ским способом. Полученное в результате значение с^д и является ос-
новным результатом данной работы.
ЛИТЕРАТУРА
1.	Попов С.Г. Некоторые задачи и методы экспериментальной аэ-
ромеханики. М., ГИТТЛ, 1952.
2.	Седов Л.И. Механика сплошной среды, ч. 1 и 2. М. «Наука»,
1976.
3.	Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромехани-
ка. М., Гостехиздат, 1955.
4.	Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидро-
динамика. М.: «Наука». 1986.
5.	Лабораторный практикум. Изд.Моск.ун-та, 1972.
36