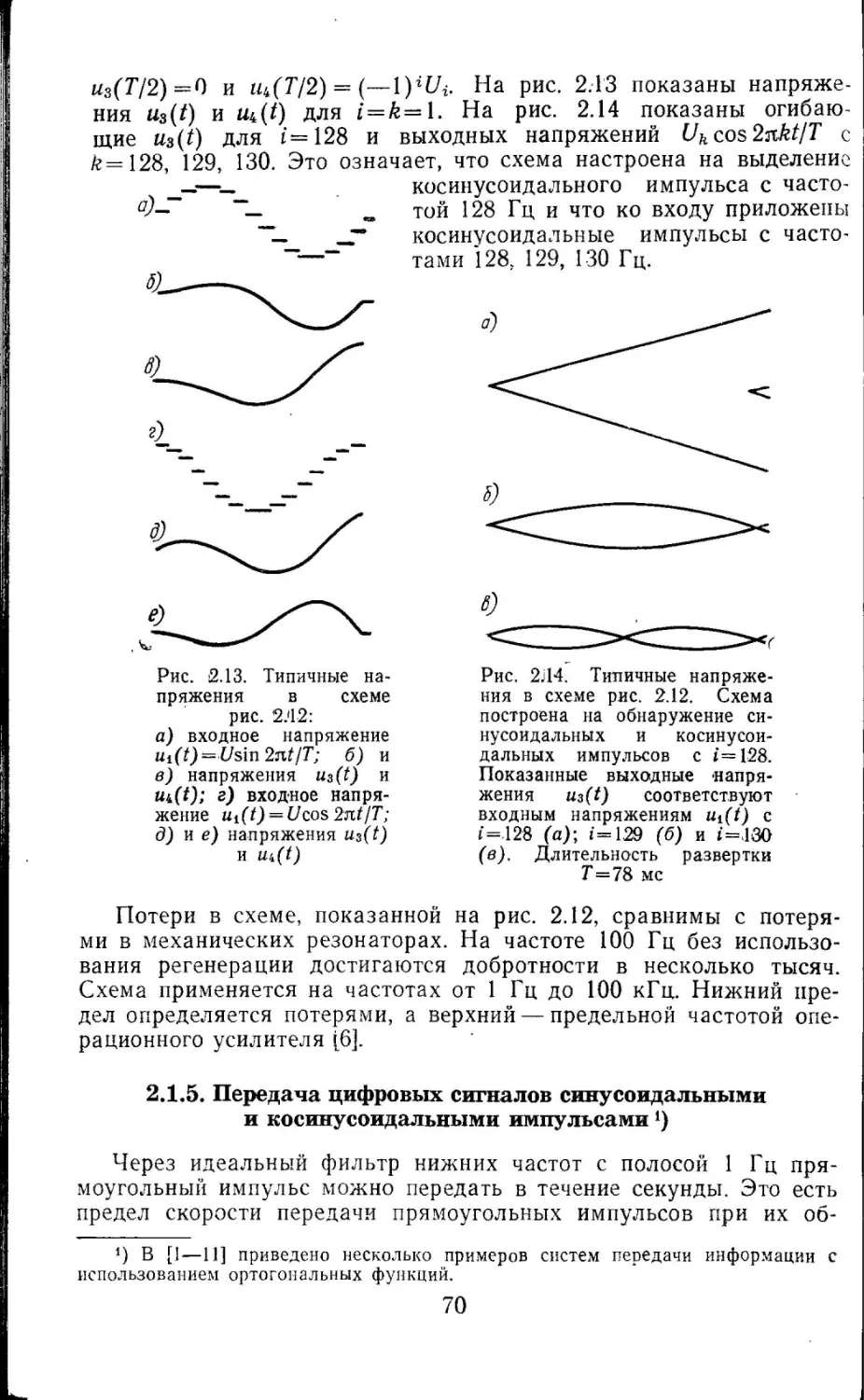
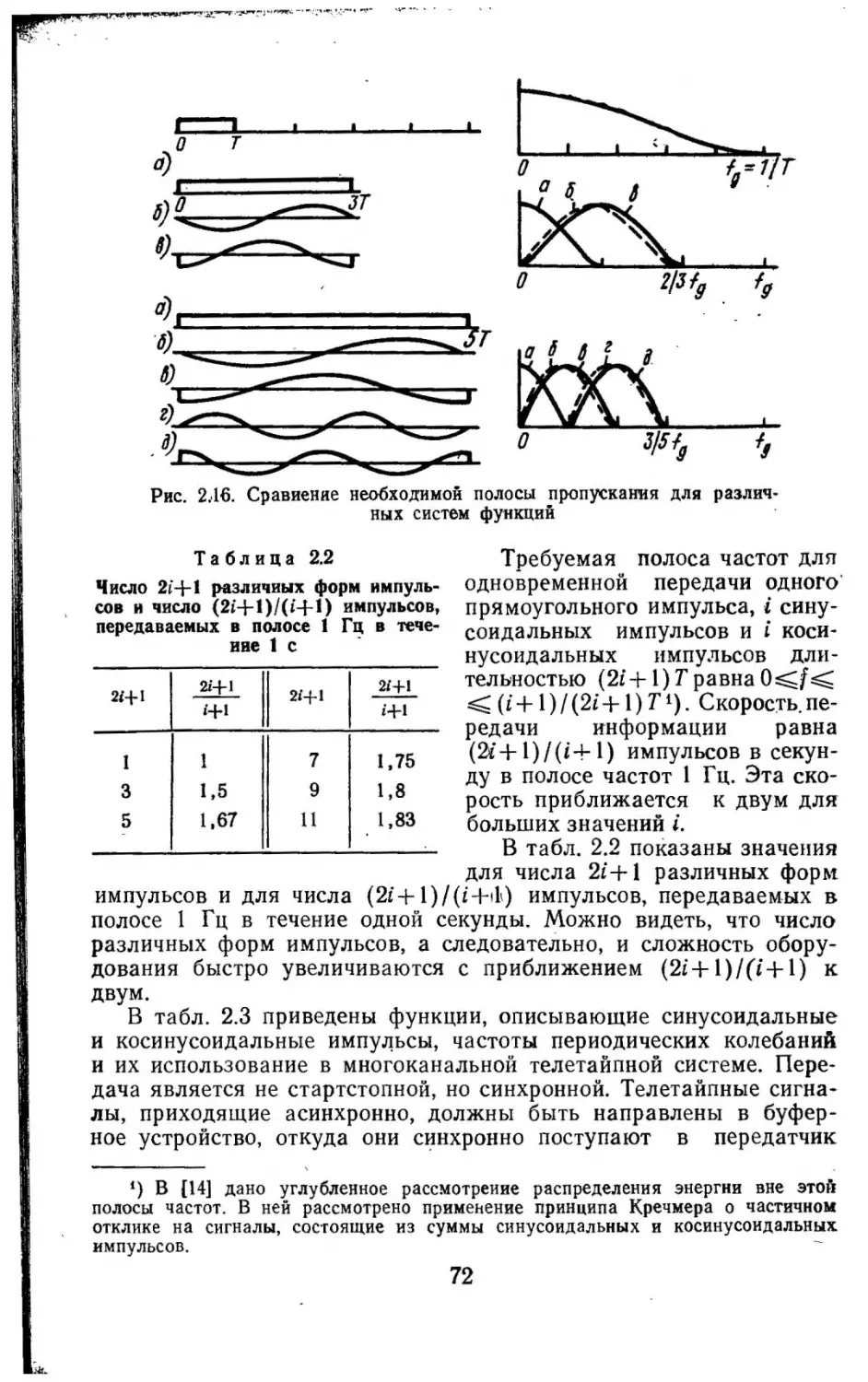
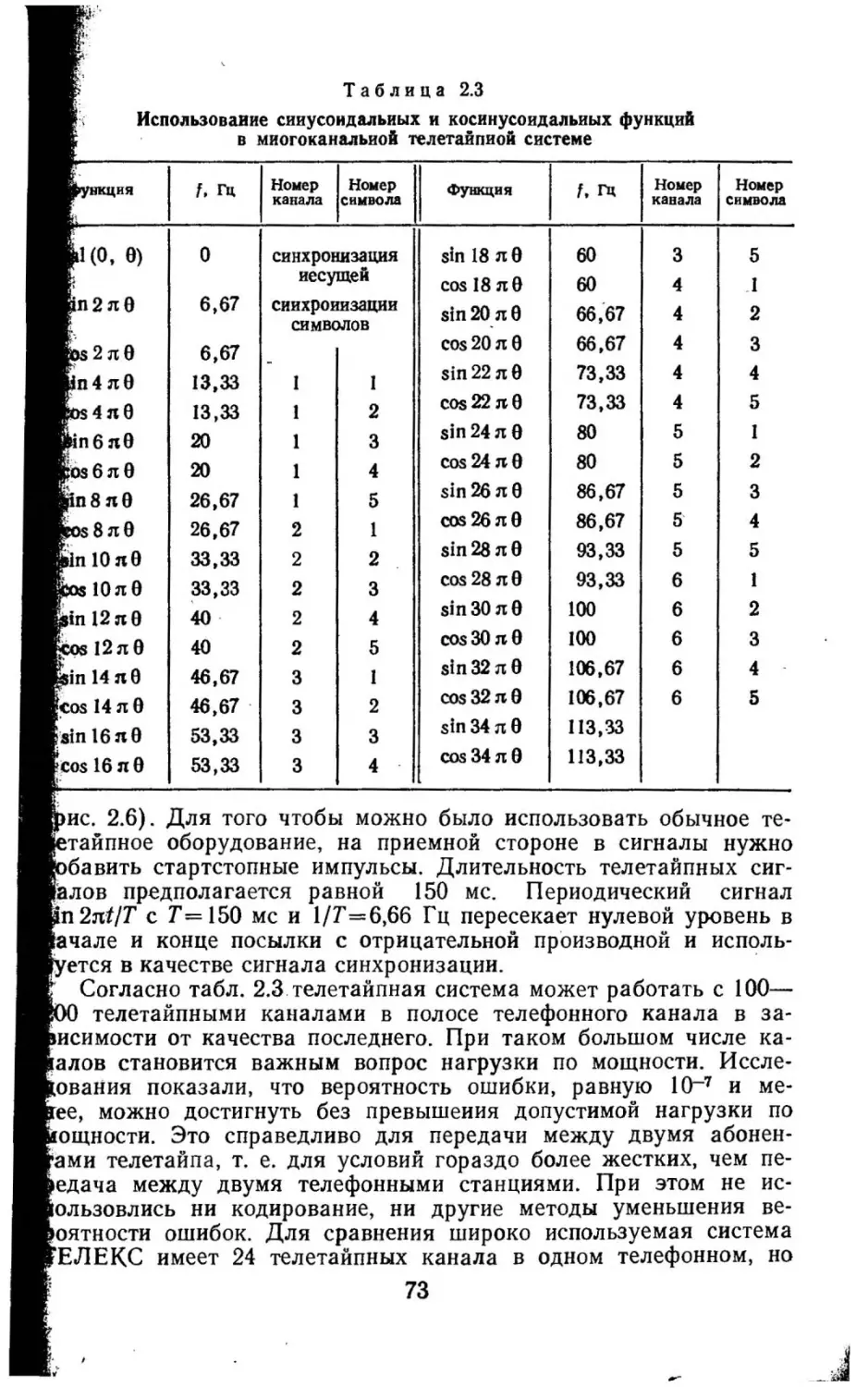
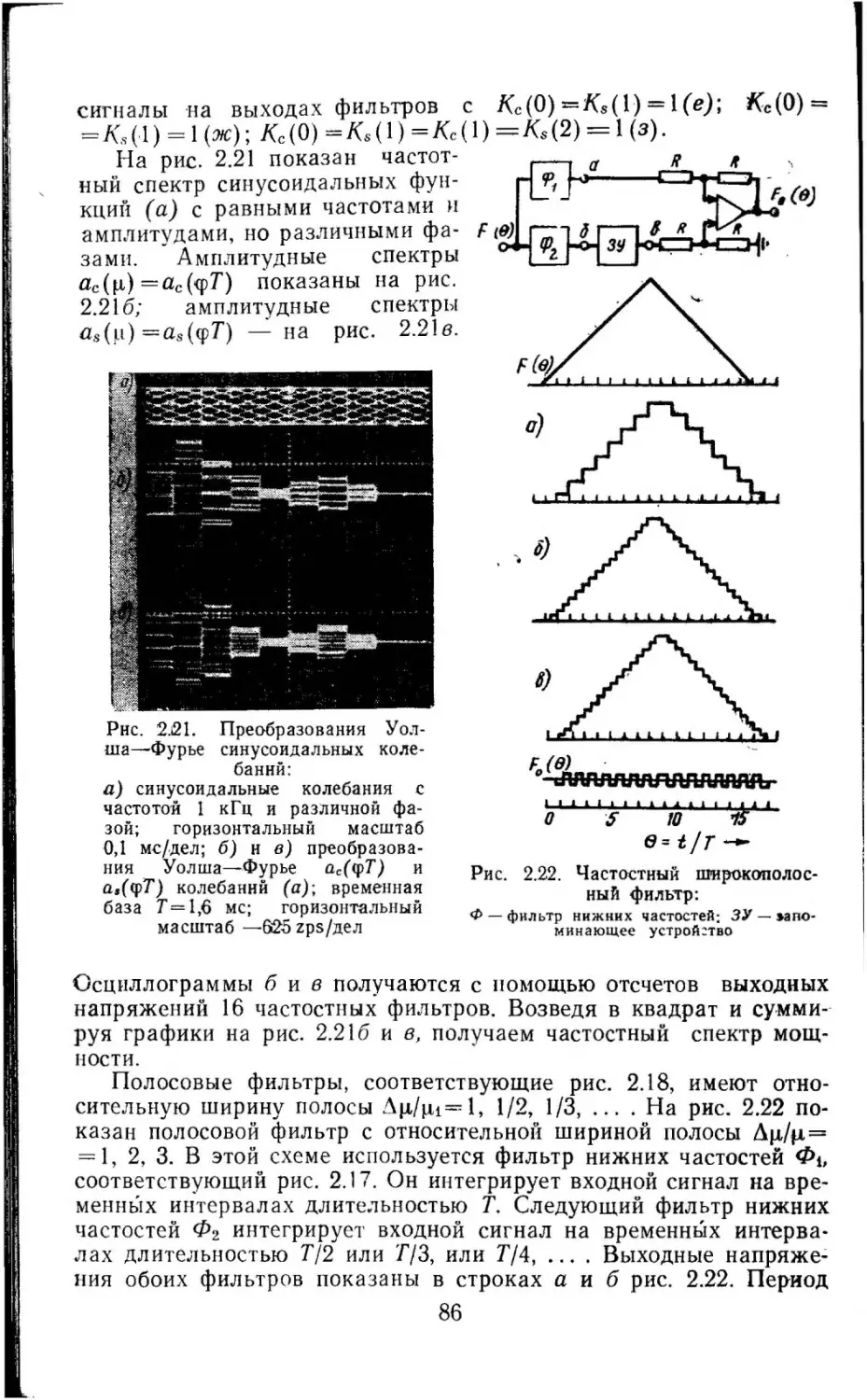
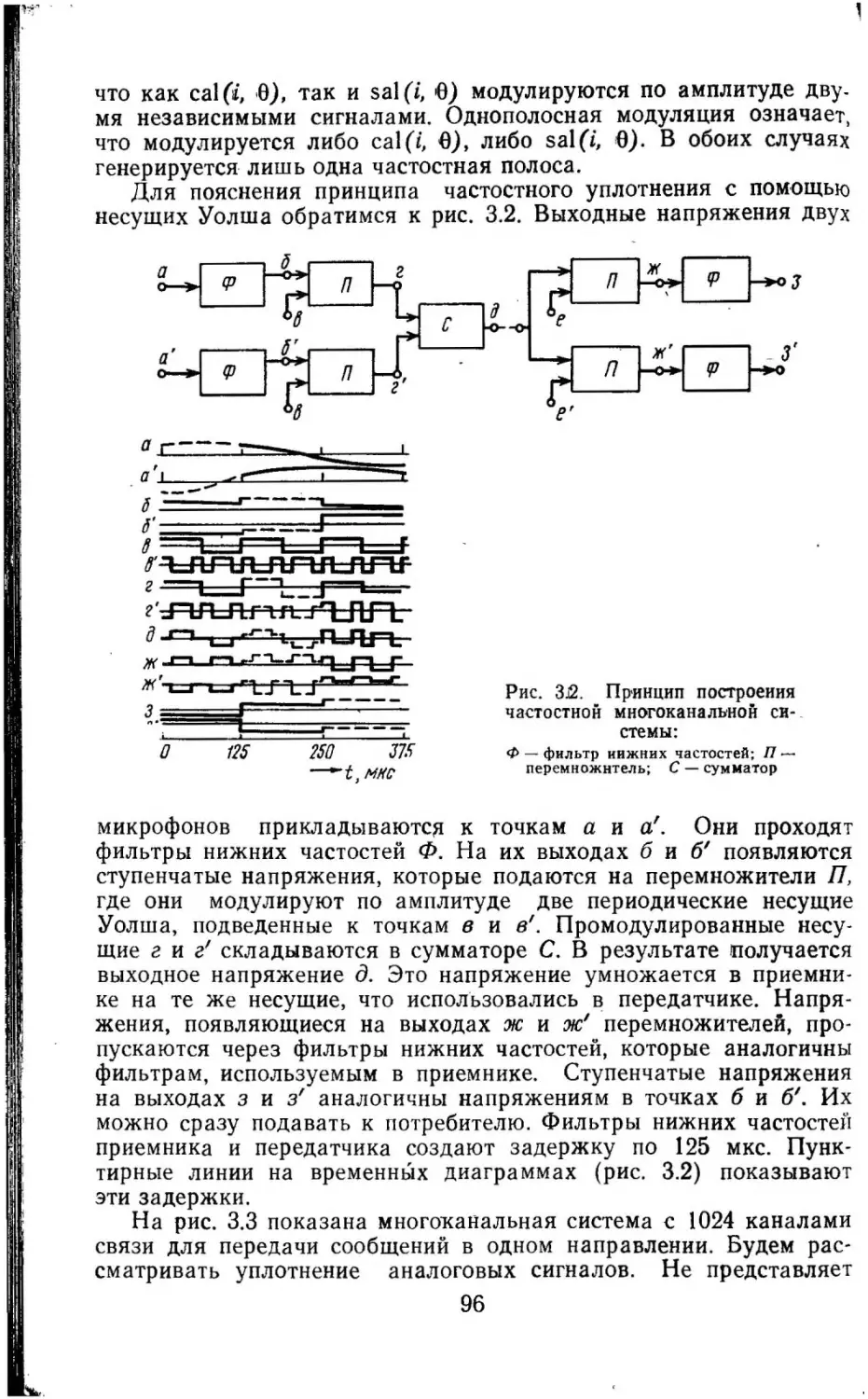
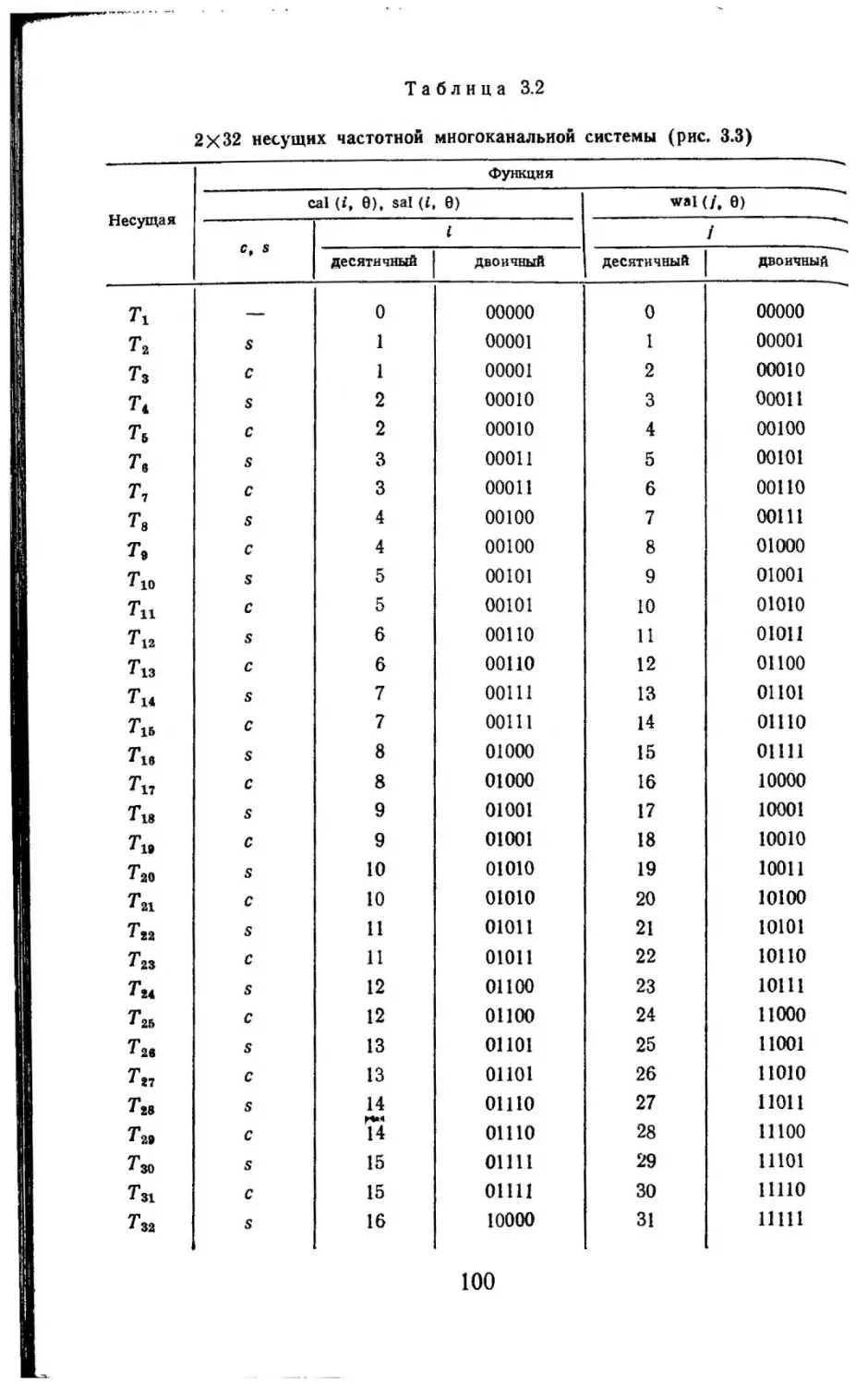
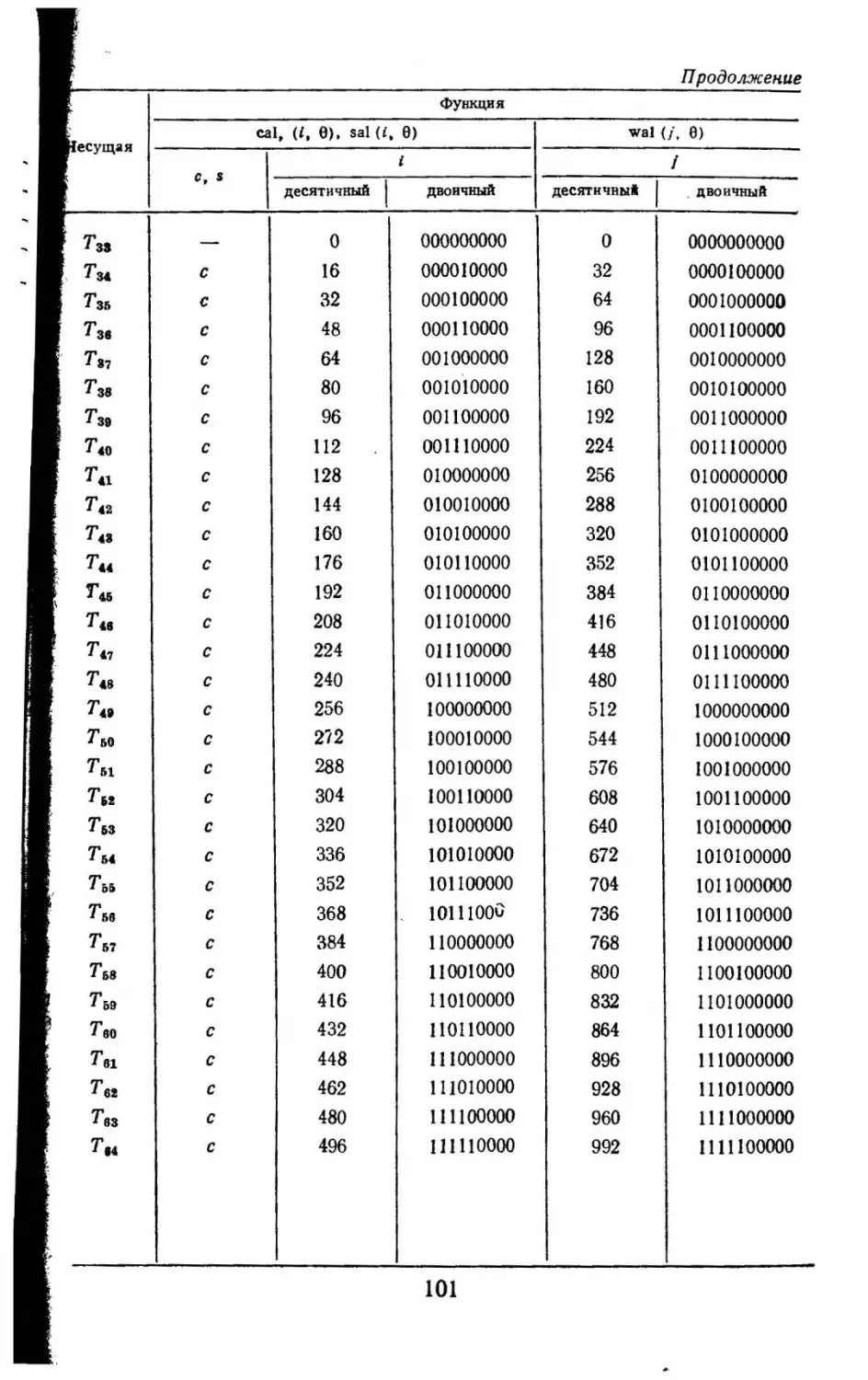
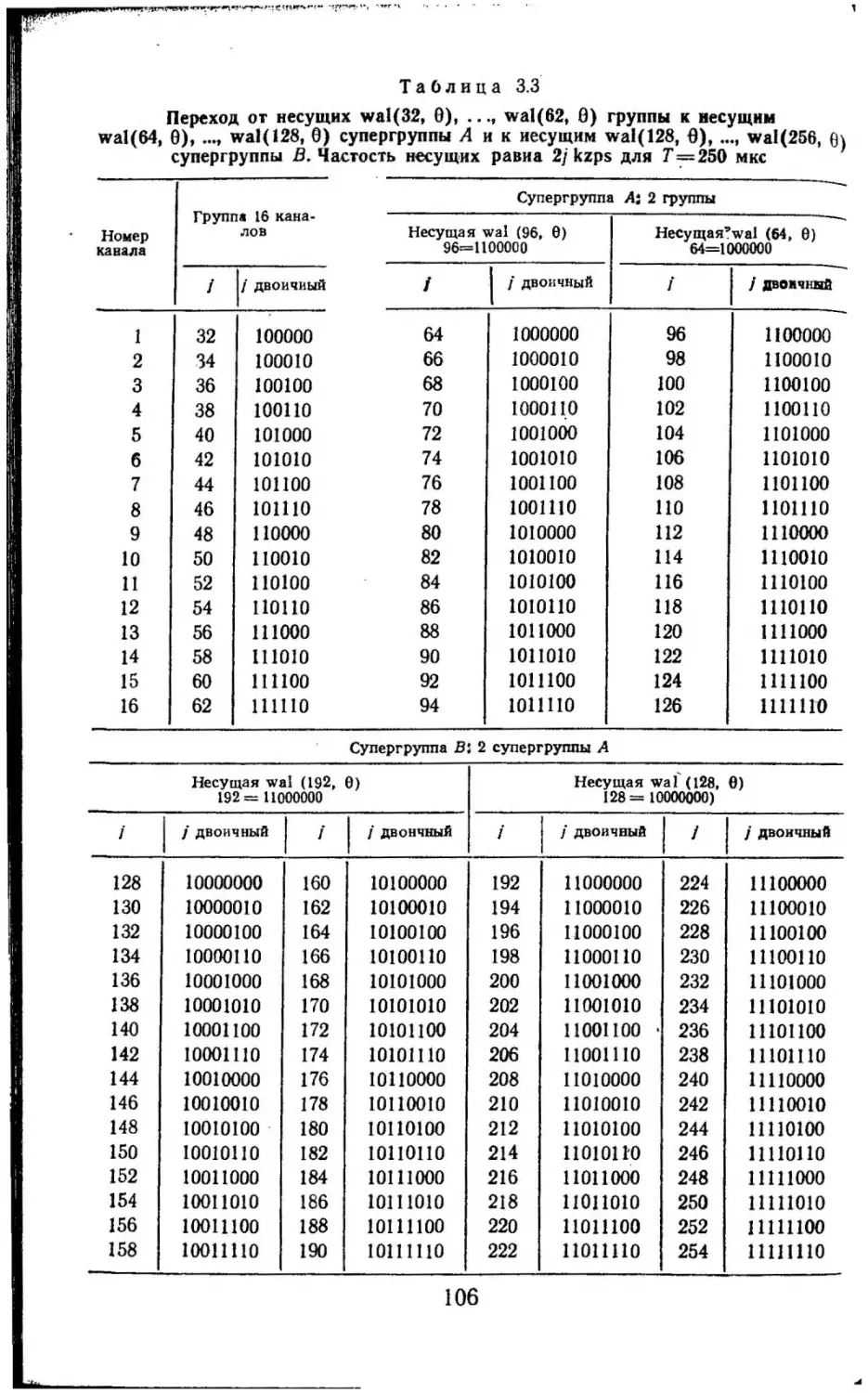
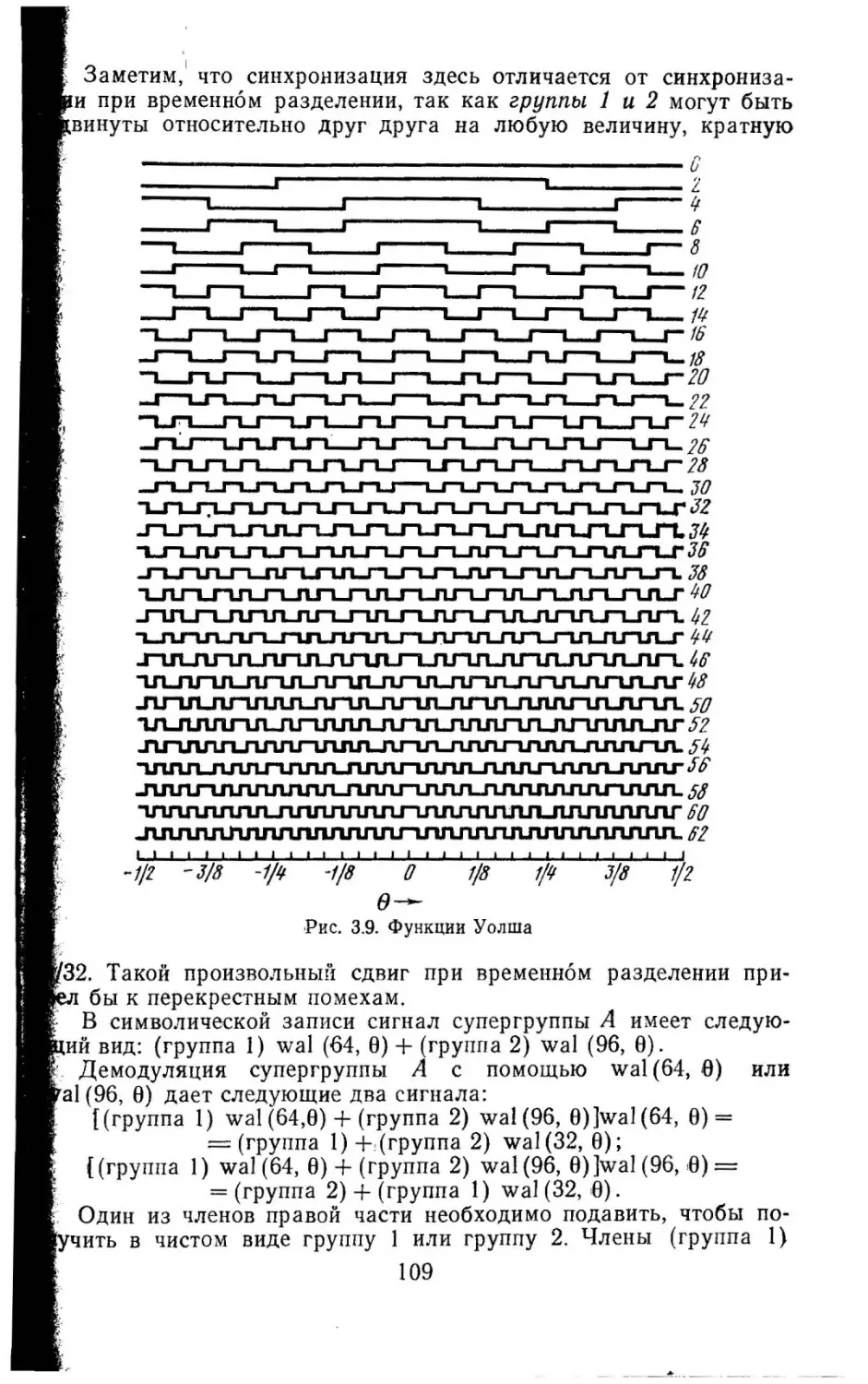
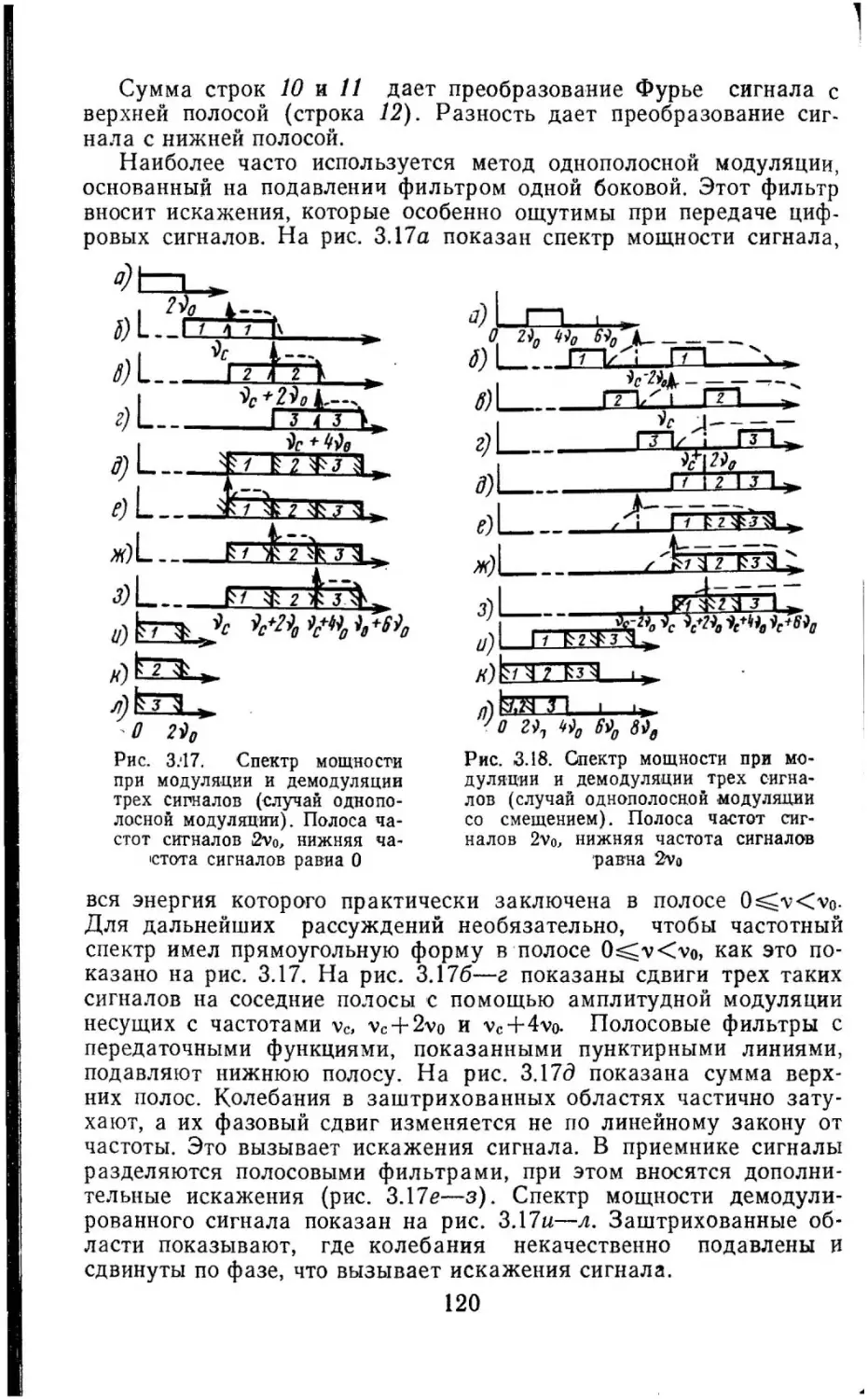
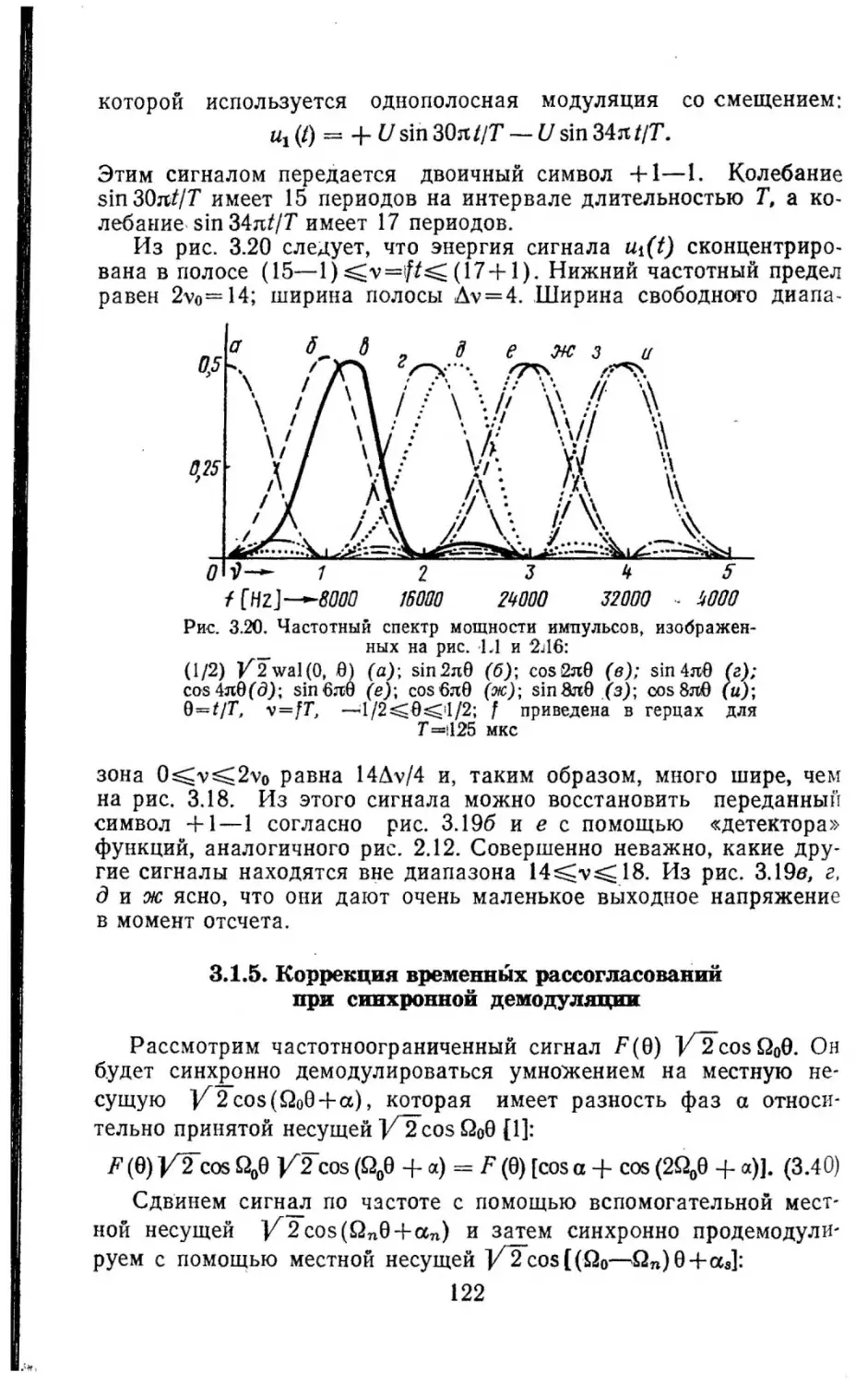
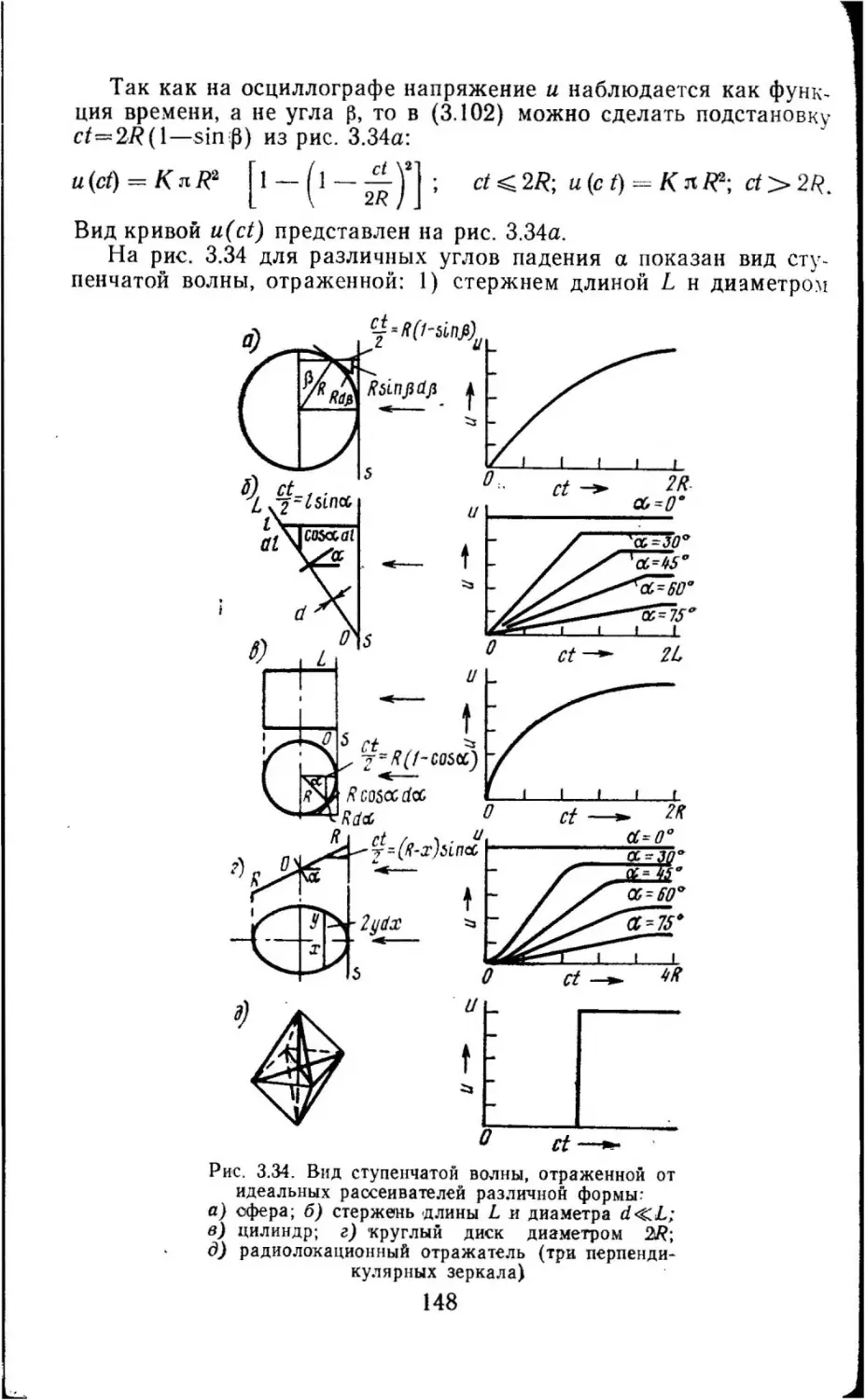
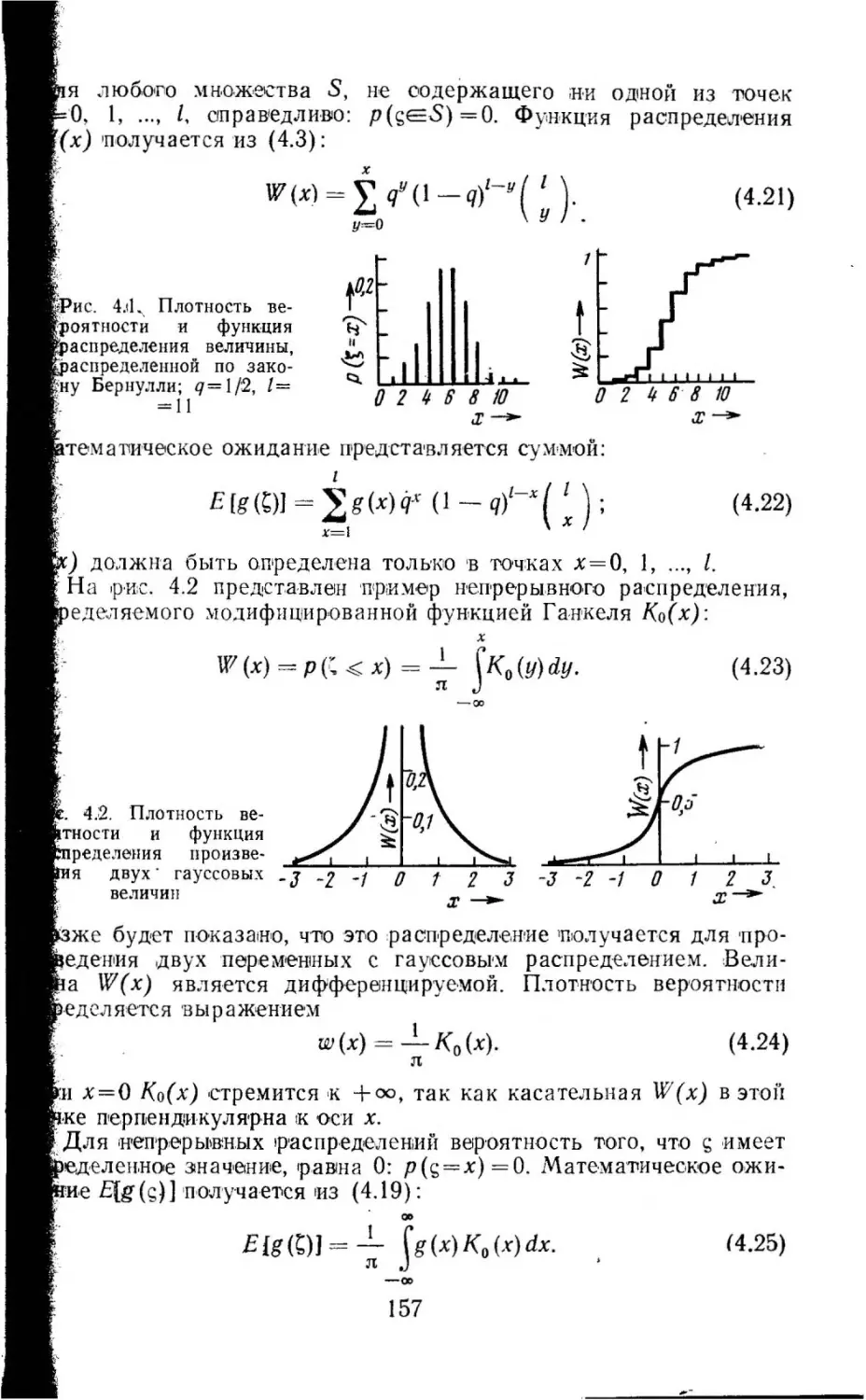
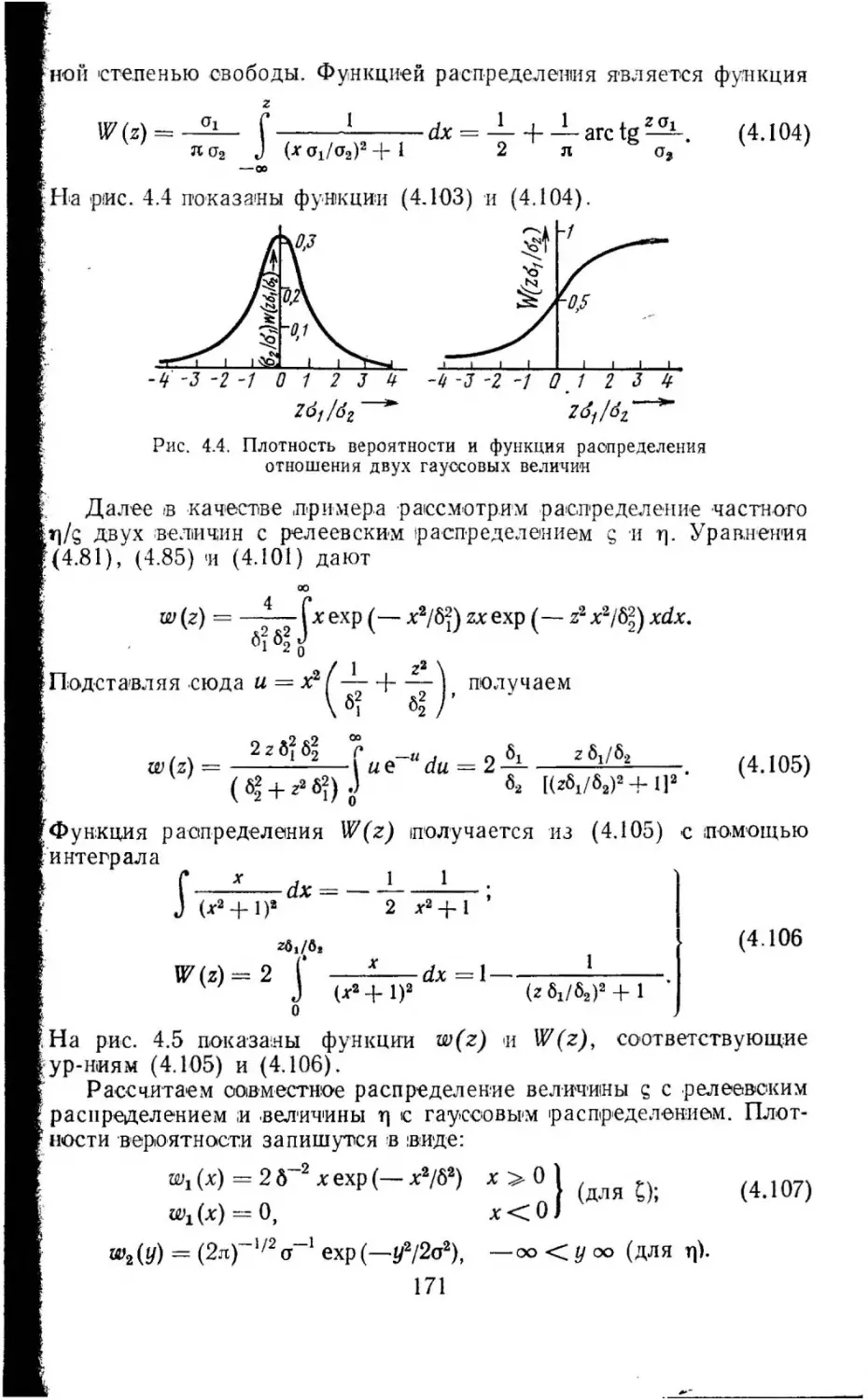
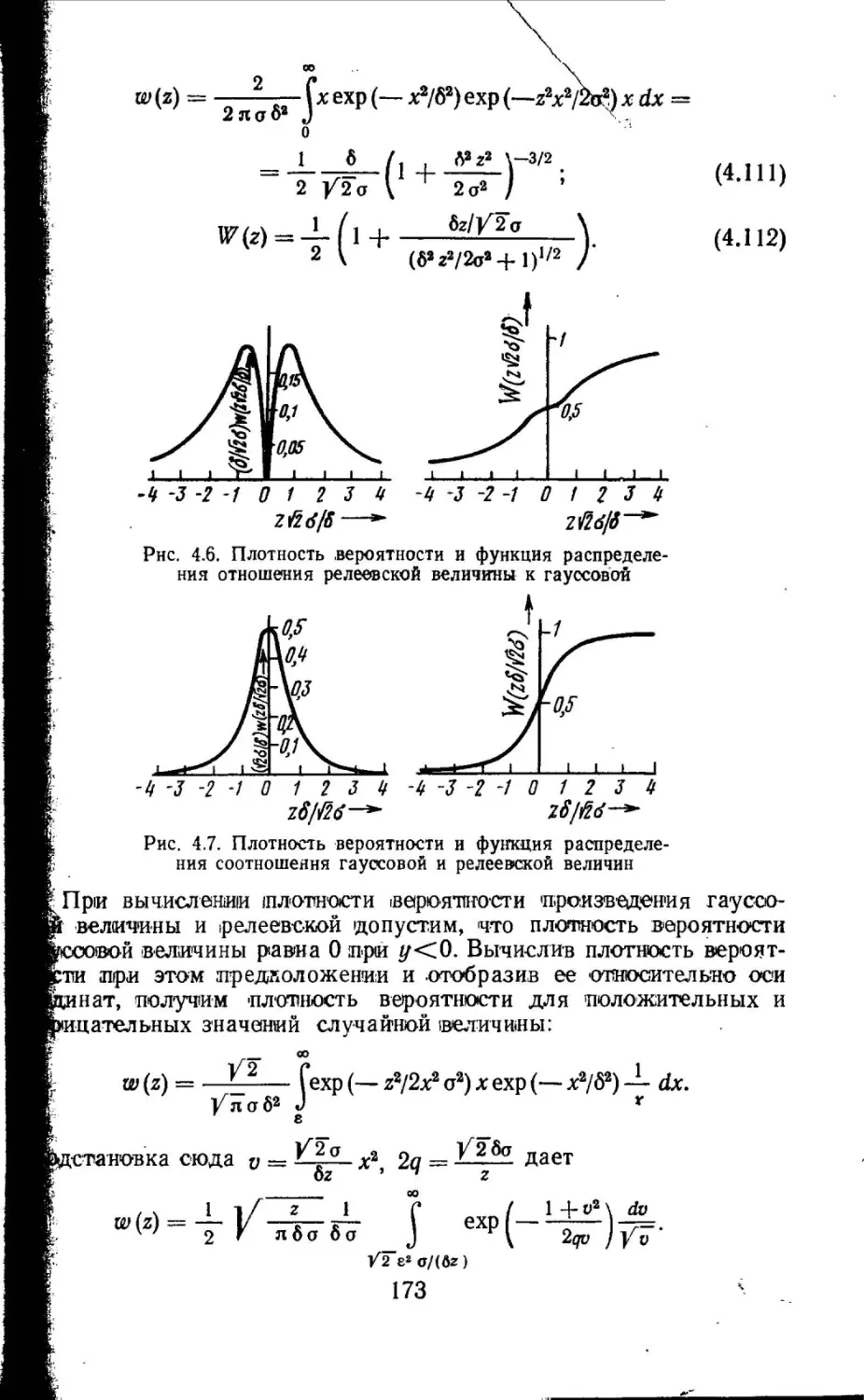
Текст
а<-
,.,.~,
l
;щ.<{
.
УДК
""f.+•
621.395.4
.1211
6Ф1
Х. Ф. Хармут
Х20
'
Передача информации ортогональными функциями .
Пер. с англ. Дядюнова Н. Г. и Сенина А. И. М., «Связь»,
1975.
272
с . с пл" табл " библ.
!(нига
посвящена
вонросам общей теори и свя зи. В доступной форме
11 з .1агаются вопросы nримен еи ня с истемы функци й Уолша в технике связи.
В ч астности, ра ссматриваю тся ра Jл ож е нп е с иrн адо в по функциям Уолша . по
с тро ен ие
фи.1Ьтров
11 ми оrо кан а .1Ьных си сте м свя зи на ос нов е функций
1'о лш а , н з.1ученн е волн ~толша. Бо.1ьшзя часть кни ги ор нrина.пьн а -и м зл о
н эвес тн а .
!(нига
тов
и
в а ни ем
х
nред ста в.1 яет
нн:жеиеров,
и
30401-049
045(01)-75
большой
кот ор ые
ло с тро ен н е м
по
с ист е м
интерес дл я
ро д у
св оей
научны х
д еят ельн ос ти
работи11ков.
связаны
J-1
е
n n i n g F. J-1
TRA~SMISSIO~
OF
а
r
т
uth
INFORМATION
ORTHOGONAL FUNCTIONS
Berlin. Heidelberg. New York 1970
30401-049
X:OiЩOl)-75
Cl
..
асп11ран
проектиро
6Ф1
27-75
ВУ
с
с вя з и .
27 75
-
Перевод на русский язык, «Связь»,
1975.
i
-·.
l
<''
ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
i~j-~ :
(-~~{;·
':Uf·
J·Как известно, современная теория связи ?снов ан а на системе сипу
~: . сандальных и. ко·синусоидальных функции. Объясняется это рядом
;~" причин. Однон из них является f!ростота получения гармонических
~t~ колебаний. Другой не менее важной причиной является то, что
,.
гармонические сигналы проходят без искажений
через линейные
инвариантные во времени системы .
Синусоидальные функции вы
ражаются через комплексные экспоненциальные функции, что позволило использовать операторный
метод при
изучении
'
вопросов
прохождения сигналов через различные устройства.
Однако теория связи может быть построена и на основе дру
гих систем функций. В частности, в последнее время большое вни
-
мание уделяется системе функций Уолша. Эта система явля-ется
полной ортогональной системой функций . Ее можно использовать
для раз.11ожения сигналов, введя понятия ряда
Уолша-Фурье и
преобразования
Уолша-Фурье,
аналогичные
обычному . ряду
Фурье и преобразованию Фурье. На основе системы функций Уол
ша можно построить теорию фиJ1ьтров, для
реализации которых
нет необходимости использовать
индуктивности,
что
является
очень важным их преимуществом перед
обычными
частотными
фильтрами. В настоящее время в ряде стран построены и успешно
работают многоканальные системы на основе функций Уолша.
Изложению вопросов, связанных с применением функций Уол
ша в технике связи, и посвящена книга Х. Ф. Хармута «Передача
информации ортогональными функциями».
Книга представляет большой интерес для научных работников,
аспирантов и инженеров, по роду своей деятельности связанных с
проектированием и построением систем связи.
Н. Г. Дядюнов,
А. И. Сенин
·
,.
ПРЕДИСЛОВИЕ
АВТОРА
Свойство ортогональности функций использова.1ось в технИ\\.t
связи с момента ее зарождения. Оно широко использовалось Ко
телБниковым в его теоретической работе, написанной
в
1947 г.
Десятью годами позже в этой области независимо
работали уже
многие исследователи. Однако до появления интегральных схем из
полученных теоретических результатов вряд ли можно было полу
чить какой-либо практический выход .
Теория связи, основанная на ортогональных функциях, могла
бы быть разработана еще много лет назад. Однако в то время из
систем ортогона л ьных функций были известны только
синусои
дальные функции и прямоугоJrьные импульсы и это делало слож
ным. описание известных результатов. Благодаря развитию полу
проводниковой техно.1огии появи л ись новые примеры систем орто
гональных фунюшй: малоизвестные функции Уолша. В этой кни
rе основное внимание уделено функциям Уолша, так как синусои
дальным функциям, прямоугольным импу.1ьсам: и импульсам, по
строенным из них, посвящена обширная литература.
Существует две причины , по к оторы l\1 в системах связи в дан
ное
время
применяется
столь
ограниченное
число
систем
ортого
налБных функций. Во-11ервых , кроl\!е
свойства
ортогональности,
эти системы дол жны обладать еще целым рядом свойств, такими.
как по.1нота или «хорошие » теоремы сдвига и у множения. Второй
причиной явл яется то , что сигна .1ы, описывае :-..1ые фу нкциями, до л
жны: легко генерироваться.
Важность этого второго требования
легко оценить, если представить себ е з адачу получения миллиона
или· боле е таких сигналов в одной систеы е .
До 1960 г. именно св о йство ортогона.1ьности привлекало вни
мание исследователей при изучении нроблем передачи цифровых
сообщений в присутствии шума. Но раньше или позже
должен
был возникнуть вопрос, чем, в принципе, отличаются системы си
нусоидальных ф у нкций от других ортогональных систем. Этот во
прос привел к обобщению понятия частоты и таких понятий, свя
занных с ним, как частотный спектр l\IОщности, амплитудно- и фа
за-частотные характеристики . Функции
Уолша
позволили
по
строить практически реализуемые фильтры и устройства уплотне
ния каналов, основанные на этом обобщенном понятии частоты.
Любая инженерная теория должна внести не т олько новые ас
пекты в понимание какого-либо нопроса , но
и позволять созда
вать новое, экономически выгодное оборудование. Было разрабо
тано большее число приборов, использующих системы ортогональ
ншх функций , но вопросы
их экономической
эффективности остаются д о сих пор нерешенными.
\
Х. Ф . Хармут
\'
ВВЕДЕНИЕ
В системах связи широкое применение имеют синусоидальные
;. и
косинусоидальные функции.
Имеется много причин для этого. Одна из них заключается в
·
том, что на заре развития связи было трудно генерировать сигналы, описываемые другими
функциями.
Электронные
лампы и
транзисторы
сделали
возможным
получать
такие
1
элементарные
.несинусоидальные колебания, как последовательности
импульсов
· и линейно изменяющиеся напряжения. Однако до появления ин
тегральных схем производить такие сигналы было неэкономично.
Другим фактором предпочтительного использования синусоидаль
ных сигналов было то, что линейные инвариантные
во
времени ,
цепи только ослабляют и задерживают их,
не изменяя формь1.
Поэтому система синусоидальных и
косинусоидальных
функций
имела большие преим у щества перед другими полными системами
ортогональных функций до тех пор, пока сопротивления, емкости
и индуктивности были основными элементами электрических це
пей. Теория линейных инвариантных во времени цепей демонстри
рует преимущества синусоидальных функций. Успехи полупровод
никовой электроники коренным образом изменили такое представ
ление. Нет особых причин, почему цифровые фильтры, например,
фильтры, анализирующие тонкую структуру сигна.1ов РЛС, долж
ны
выполняться
на
основе
синусоидс1льных
и
косинусоидальных
функций . Оказывается, что цифровые фильтры, основанные на так
называемых функциях Уолша, являются более простыми и надеж
ными.
Для распространения электромагнитных волн в свободном про
странстве или по проводникам синусоидальность функций также
не является необходимым ус.l!овием. Решение вол нового уравне
ния Даламбера и общее решение телеграфного уравнения показы
вают, что большой класс сигналов может передаваться без иска
жени й или восстанавливагься. Анал огично диполь Герца
может
излучать несин усоидальные
колебания .
Преобладание синусои
дальных колебаний в радиосвязи может быть частично объяснено
инвариантностью
их
ортогональности
в
условиях
изменяющихся
временнь1х задержек. В то же время существовавшие ранее кабели
и открытые проводные линии применялись для передачи информа
ции без использования синvсоидальных колебаний . Такими линия
ми были телеграфные линйи XIX столетия, которые использовали
в качестве усилителя электромех а ническое реле .
Одной из наиболее важных особенностей синусоидальных и ко
синусоидальных колебаний является то, что почти все
сигналы,
используемые в связи, могут быть представлены
совокупностью
синусоидальных и косинусоидальных колебаний, для чего исполь
зуется аппарат анализа Фурье. Результатом этого является пере
ход от временнЬ1х к частотным функциям. Однако представление
временной функции синусоидальными и косинусоидальными функ
циями явля,ет~я
тол ько
одним
из
5
многих
возможных
представле-
.
zч
·- ... l
ний. Любая полная система ортогональных функций может быть
применена для
разложения
в ряды,
которые соответствуют
рядам
Фурье. Например, в связи. часто используется разложение в ряды
по функциям Бесселя. Для многих систем функций имеется также
преобразование, подобное преобразованию Фурье.
В этой книге для представления
сигналов _ и
характеристик
линий и цепей вместо частной системы синусоидальных и косину
соидальных функций будет исnользована обобщенная полная си
сте!'iа ортогональных функций. Последов&.тельная теория должна
включать применение ортогональных функций в качестве перенос
Чика информации, так как
синусоидальные
и
косинусоидальные
функµии испо.ТJьзуются не . только для теоретического анализа, но
также
в
качестве
переносчиков
в
многоканальных
системах
и
ра
диосистемах . .Здесь будет показано, что для них существуют ме
тоды модуляции, которые соответствуют амплитудной, частотной и
фазовой модуляции. Кроме того, можно построить достаточно эф
фективные антенны для излучения неси.нусоидальных колебаний.
Переход от системы синусоидально-косинусоидальных
функ
ций к обобщенной системе ортогональных функций
приводит как
к упрощению, так и к ус:южнению математической теории связи.
Можно,
например,
избежать
той
трудности,
что
любой
сигнал
занимает бесконечную часть частотно-временной плоскости путем
замены последней функционально-временной плоскостью . Любой
ограниченный во времени сигнад, состоящий
из
ограниченного
числа ортогональных функций, занимает
конечную
часть
этой
функционально-временной н.тоскости.
Обобщение понятия частоты, которое дало
много теоретичес
ких
результатов
дл я
теории
связи,
основано
на
ортогональных
фующиях. Частота является параметром синусоидальных и коси
нусоидальных функций и определяется как число периодов за еди
ницу времени. В ряде работ {1-3] показано, что частоту можно
интерпретировать как половину числа пересечений нулевого уровня
•
за единицу времени. Например, синусоидальная · функция со 100
периодами в секунду имеет 200 пересечений нулевого уровня или
изменений знака за секунду. Пересечения нулевого уровня можно
определить и для непериодических функций. В этом случае полез
но ввести более общее понятие
-
«половина среднего числа пере
сечений нулевого уровня за единицу времени». Для этого обобще
ния частоты вводится новый термин «частость». Таким образом,
частость
и
частота
идентичны
для
синусоидальных
и
косинусои
дальных функций. Термин часrость позволяет заменить такие важ
ные понятия, как спектральная плотность мощности и амплитудно
частотная характеристика, на частостный спектр мощности и амп
плитудно-частостную характеристику .
Понятия периода колебаний Т =
заны с частотой. Замена частоты
f
l /f и длины волны Л= v/f свя
частостью ip приводит к сле
дующим более общим определениям: средний период колебаний
Т= lf<P (среднее расстояние между нулевыми
пересечениями во
времени, умноженное на
2);
средняя длина волны Л=v/r.p (среднее
6
асстояние
,
·
\
где
v -
в
пространстве
между
двумя
нулями,
умноженное
на
скорость распростраuения нулевых пересечений).
~
Проверкой любой инженерной теории связи является ее прак
,", 'тJ1ческое применение. Известно н еско.11ько таких применений, и вс.е
''они тесно связаны с полупроводниковой техникой. Появившаяся
.·. ,{)rало известная система функций Уолша будет такой же идеа л ь
!., .~'цой для линейных неинвариантных во времени схем, построенных
<)j!;.н-а основе бинарных цифровых элементах, как и
системы сину·
; ~>соидальных и косинусоидаJ1ьных функций д.'IЯ линейных
инвари-
i\k .антных во вре~1ени цепей , вьш,олненных на резисторах, конденса
~~~:_торах и катушках индуктивностей. Н а базе функций Уолша уже
;j•kсозданы очень простые частостные фильтры. К:роме того, разрабо
~·~t тана экспери~ентальн ая час:rостн а я многокана.1ьнан систеиа, ис<~-;'Поль зующая функции Уо.'!ша в К '1 Честве п е рен осчи ков , приче м она
\ имеет преиму щество пер ед ;,ш ого к анаJiь:1 ьЕ11i1 с исте ыа ы и с частот
;: ным и вре:.1еннь1м раздел ени е м в определенных при.1ожениях.
_ ; Цифровьiе фильтры и цифровые устройства уплотнения являются
.::.наиболее
предпочтительными
для
нрименений
в
будущем .
По
·строен ные на · осн ове функций Уолша , они бол е е просты и надеж
ны, чеы фильтры. построенные на основе синусоидальных и ко си -
,,. ыусоидальных функций. Однако дл я их практического при м енения
требуется значительный прогр~сс в разработке интегра.'lьных схем .
Применение несинусоида л ьных
электромагнитных волн находится пока на этапе теоретических исследований.
Только совсем
недавно бьти ра з работаны излучающие антенны,
которые могут
найти практическое прим е нение для излучения сигналов, описы
ваемых функция м и Уолша. Большинство
пробл е!'.1,
связанных с
волнами Уолша, в настоящее время могут быть разрешимы толь
ко
в терминах
геометрической
оптики,
так
как волновая
оптика
применима только к синусоидальным волнам. С другой стороны,
нет оснований . сомневаться, чго несинусоидальные электромагнит
ные волны
являются
областью
фундаментальных исследований.
· Генерация несинусоидальных радиоволн предполагает, что такие
волны могут быть получены в диапазоне света, а это приводит в
конечном счете к вопросу, п о чему б елый свет до .rrжен расклады
ваться на синусоидалытые кол е бания.
.
функции Уолша, которым н этой
книге
придается
большое
значение, в настоящее время яв.11яются наиболее важны:.1 приме
ром несинусоидальных функций в связи. Эти функции почти неиз. вестны инженерам-связистам, хотя они использовались боле~
60 лет назад для размещения проводников в открытых проводных
линиях. До конц а XIX стол етия для этих цел е й также использова
лись функции Радемахер.а [4],
котооые
яв.11яются
по истемQЙ
~ункциИ Уолша. Пол ная система~ ункций Уолша была найдена в
900 r. Барреттом 1). В 1923 г" когда эта система функций была
описана математически Уолшем {9], размещения проводников в со
ответствии со схемой Баретта уже вошли в обычную практику{6, 7].
1 ) Барретт упоминался Фовлом {5] в 1905 r. как изобретатель способа раз
мещения проводников согл а сно фуикцням Уолша (см., в частности, с. 675 {5]).
r
1.
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ПЕРЕДАЧИ СИГНАЛОВ
1.1.
ОРТОГОНАЛЬНЫЕ
1.1.1.
Система
f(l,
х)
...
ФУНКЦИИ
Ортогональность и линейная независимость
{f(j, х)} действительных
и
ненудевых функций
J'(O, х).
называется ортогональной на интервале х 0 ~х~х1, если
выполняются следующие условия:
Jf (j, x)f (k, x)dx = Xi6ik,
"'
(1.1)
Функции называются ортогональными и нормированными, если
константа Xj равна 1. Оба термина обычно объединяют
в один
термин «ортонормальный» или «ортонормированный».
Ненормированную систему
ортогональных
функций
можно
всегда пронормировать. Например, если константа Xj не равна J,
то система {X- 1jf(j, х)} является нормированной. Системы орто
гональных функций являются ча~тными случаями систем линейно
независимых функций. Систем а
{[ (j,
х)} из т функций называет
ся линейно зависимой, если урюшение
m-1
2: c(j)f(j, х)=О
( 1.2)
j=O
удовлетворяется для всех значений х при условии,
что
не
все
коэффициенты c(j) равны нулю. Функции называются линейно не
зависимыми, если ( 1.2) не выполняется.
Функции ортогонадьной
системы всегда являются .1J инейно независимыми, так как умноже
ние (l.2) на f(j, х) и интегрирование произведений на интервале
хо~х~х1 дают c(j) =0 для всех j.
Система {q (j, х)} из т линейно независимых функций всегда
может быть преобразована в систему {f (j, х)} из т ортогональных
функций. Можно записать следующие уравнения:
f (О,
х) = c00q(O, х);
8
~
~l~~
+c
+c
f(l, х) = c10q(O, х)
f (2, х) = C20q (О, х)
х);
11q(l,
21
q ( 1, х)
(1.3)
+c
22
q (2, х)
и~~
\
-,
Подстановка f(j, х) в (1.1) дает необходимое количество ypaR. нений для опреде.'Iения коэффициентов c1,q:
Jf (О, x)f (l, x)dx =О;
j" f(O, х) f (2, х) dx=O; I f ( 1, х) f (2, х) dx=O
х,
, х0
Х0
.\о
Ж1
JF(2, х) dx = Х2;
Х1
( 1.4)
Xi
Хо
и т.
д.
Коэффициенты Хо, Х1 ... явля
ются произвольными. Для норми
рованных систем они равны
На
рис.
примеры
1.1-1.3
функ
ций. Независимой переменной яв
ляется нормированное
=t/T.
рис.
шем
время
0=
Функции, изображенные на
1.1
и называемые в дальней
синусоидальными
соидальными
-2
~е~
косину
элементами,
нормированы
1
и
на
l
-.
2
_...,,,,
~
.flsin 4!1.8
'-..,/\.0.J
""~
/ f2 cos 4JC8
~С/
~.flsLn6!i.8
"
"
"
~\..
1}2
1
=wal
(О,
д
1
1
1
1
V2 cos 6 JC(J
t/l
е-Рис.
1.1.
Ортогональные синусоидаль
ные и косинусоидальные элементы
V2 cos 2л i 0;
=fs(i, 0)=V2sin2ni0,
1
--<0<
2
2
( 1.5)
8) = 1;
0 <- 1/2, 0 >
-=Не определена,
.·
1
f
0) = fc и. 0) =
""'-= fl.cos211.8
~
орто
Их можно разде -
.........----.. -lisi.n 21i8
~
~
интервале
лить на четные функции с ( i, 0),
нечетные функции fs(i, 0) и посто
янную wal (О, 0):
t (j,
-
1.
приведены
ортогональных
-------wпt (о,е) :._
+ 1/2 .
Термин «элемент» используется для того, чтобы подчеркнуть,
что функция определена тоJiько на конечном интервале и не оп
ределена вне его. Термин « имнульс~> используется для того, чтобы
подчеркнуть, что функция тождественно равна О
вне конечного
интервала.
Продолжение
синусоидальных
элементов, изображенных на рис.
·~
1/2
ные
функцией
f(j, 0) =0
1.1,
вне
и
косинусоидальных
интервала -1/2~0~
дает синусоидальные и косинусоидаль-
импульсы; с другой стороны,
их
периодическое продолжение
дает периодические синусоидальные и косинусоидальные функции.
Легко видеть, что
для
синусоидальных и косинусоидальных
элементов условие ортогональности ( 1.1) удовлетворяется:
9
1/2
J 1 -V2 sin2ni0d0
1/2
J 1 -V2 cos2ni0dt0 =
=
-1/2
О;
-1 / 2
1/2
1/2
-112
-1/2
~· V2sin2:n:i 0 V2sin2:n:k0d0 =
J v 2cos2ni0 V2cos 2:n:k0d0=б1 1,;
1/2
J V2siп2:n:i 0V2cos2nk0d0 =О;
-1/2
1/2
J 1 · ld0 = 1.
-1/2
На рис .
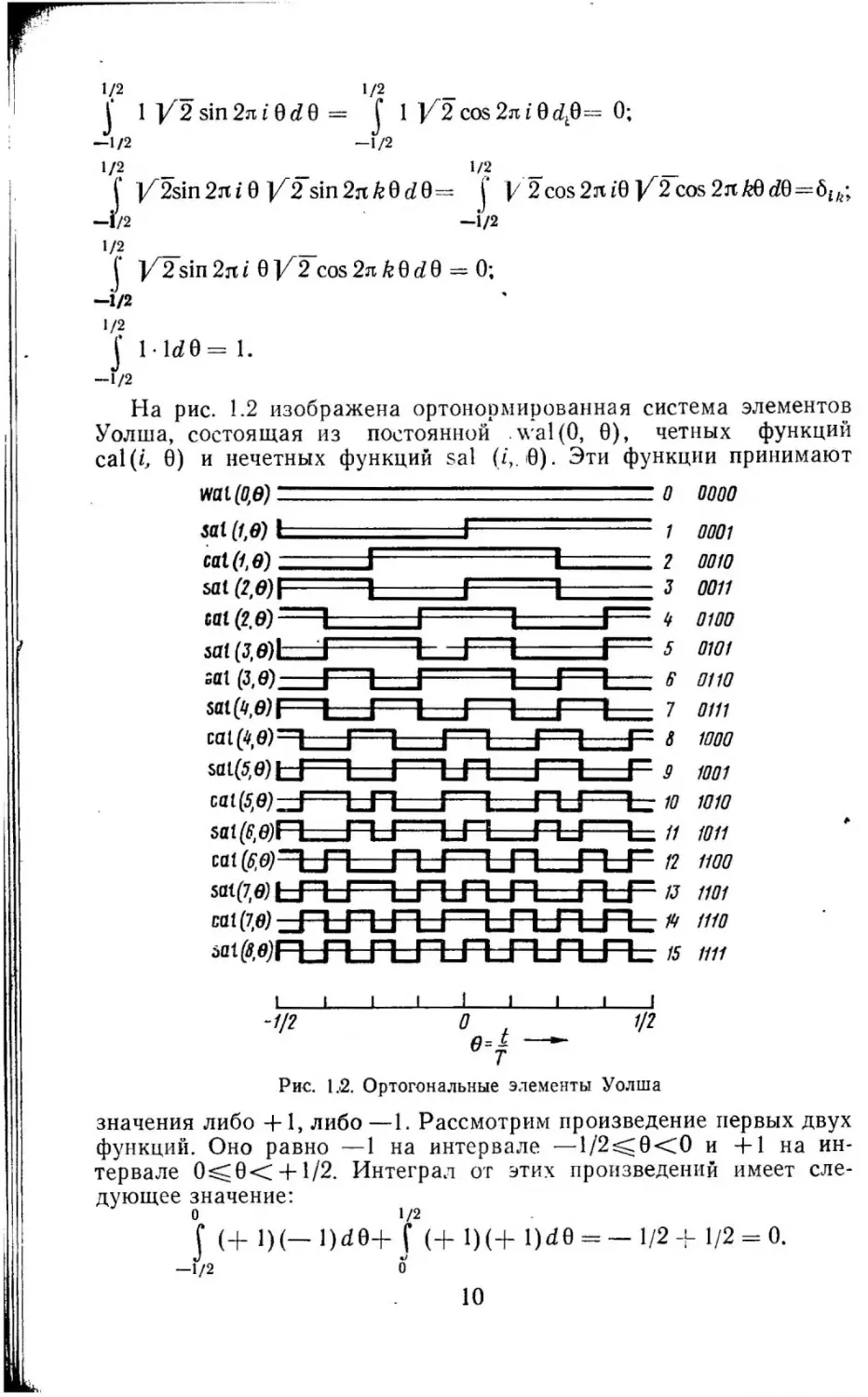
и з ображена ортонормированн а я система элементов
1.2
Уолша, состоящая из
cal(i, 0)
постоянной
и нечетных функций
\\· а\ (О,
sal (i, 10 ).
четных
0),
wat {0,8)
о
0000
.sat (1,д)
1
0001
саt(1,в)
2
sat (2,8)
J
00!0
0011
Гг= 5
0100
010!
cat (2. 8) ---,
LJ4
sat(J,8)L=:f
(J,e)__,~
*
L:J=""~ о
0110
sat(lt,8)~~~c:::r==-L-- 7
саt(4в)-..---.
..---.
r- 8
0!11
cat (5,8) __,'=""""L-.Pc=::t~~~.._ 10
sat (6, e)n--.f'JL..1.----.L..I.-.____,r-1.....,~~ 11
cat l"·
rro/ L:I L.......Ir-""I~
,....,
r-""I
r- f"'
L..I
L:I ~ L..I
l
10!0
cat (7,8) ::J'"l::::1r-""lc::f'"'~L...Jr-i-.,..,&...J'""'.._
lffO
;;at
'
L-..J
L..--1
~a:=:::I
sat(5e)~
.----.J"""'
..---.
r- g
'
~
L..I L.-....1
с=:::А
1
'--.
функций
Эти функции принимают
1000
!001
,......
!011
1100
sat(7,8) LJ""L..1r---.~L..11,...,L...1..._~С::- tJ 1101
11/
· t r,в в1'RL:I,..,L..J~r-""I
..._ ,..,
r="1
;,Q l'' /
L...IL..1,.....L-.IL..1.......
.__ 15 1111
1
о
-1/2
Рис.
значения либо+
1,
1
1/2
e=i
--т
1"2. Ортогональные э .1ементы Уолша
либо
-1.
Рассмотрим произведение первых двух
функций. Оно равно -1 на интервале -1/2::::;0<0 и + l на ин
тервале 0::::;0< + 1/2. Интеrра.11. от этих прои з ведений имеет сле
дующее значение:
о
s
-1/2
(+ 1)(- l)d0+
s
1/2
(+ l)(+ l)d0
о
10
=-
1/2
+ 1/2 =о.
:'\i.Tt{:}~ Произ;едение второго и третьего элементов равно + l на интер
\~лах -1/2:::::;8<-l/4и0:::::;8<+1/4 и -1 на интервалах -1/4:::::;
i~e<O и +1/4:::::;8< + 1/2. Интеграл от этих произведений снова
~вен нулю:
-~,: · -:г
__;:·
(-
l)(- l)d8+
-1/2
1(-
l)(.+l)d8 +
~j ."
:f4 (+ l)(+ l)d8 +
о
-1/4
1/2
+ S (+l)(-I)d8=0.
-."..
1/4
Можно легко проверить, что интегра.11 от произведения любых
~Двух других функций равен О. Функция, умноженная сама на се
:6.Я. дает произведения (+l) (+l) или (--'l) (-.1), равные 1 на
-всем интервале --1l/2:::::;e~ + -I/2.
Л
Следовательно, интеграл от квад- f{0,0)--~-1.-------f{O}) -·
рата любой функции равен l . Та- f(~8)
Г1
f(f})
кнм образом, функции Уолша яв- f(2,o)
П
f{J,v)
ляются ортонормированными.
0
На рис. 1.3 показан частный f{J,8)
f{J,.Y)
случай системы ортогональных f(l/,8)
Г"l f(4,.Y)
функций. Очевидно, что произве-
дение любых двух функций рав- fx (В) ...,ГJLJ~
r; (У)
но нулю и интегралы от произве
дений тоже должны быть равны
нулю. Для нормировки амплиту
ды функций
должны быть рав-
ны
V5.
Рис.
функций может
с.п:ужить
8 0 (х) = 1;
система
В1 (х) = х -
Odt/T
-:1.J_,__,__OL..J.....,___.__.__
v= fТ
1.3.
Ортогональные прямоуголь
ные имl!Iульсы
Примером
линейно независи
мой, но не ортогональной системы
[4, 5]:
-_,~72!--'',L....1..-,•._о._'·L-J•L...J•L.-1-'._.t/2._,-
+;
полиномов
f(j, О) и f(j, v)
Бернулли Bj(x)
В2 (х) = х2 - х+
+;
Вз(Х) = х3- 2х2 + -21 х; в" (х) = х4 - 2х3 + х2 - ~
2
00
•
т
Здесь В/х) -
полином степени j. Условие . L с(j)Вз(х) =О может
удовлетворяться для
Это
требует,
чтобы
всех
1=0
значений х, только
c(m)=O.
Тогда
если c(m)xm=O.
c(m-l)Bm-1(x) являет
ся старшим членом в сумме и к нему могут
же
рассуждения.
НО\!ОВ Бернулли.
Это доказыв а ет линейную
быть применены те
независимость
поли
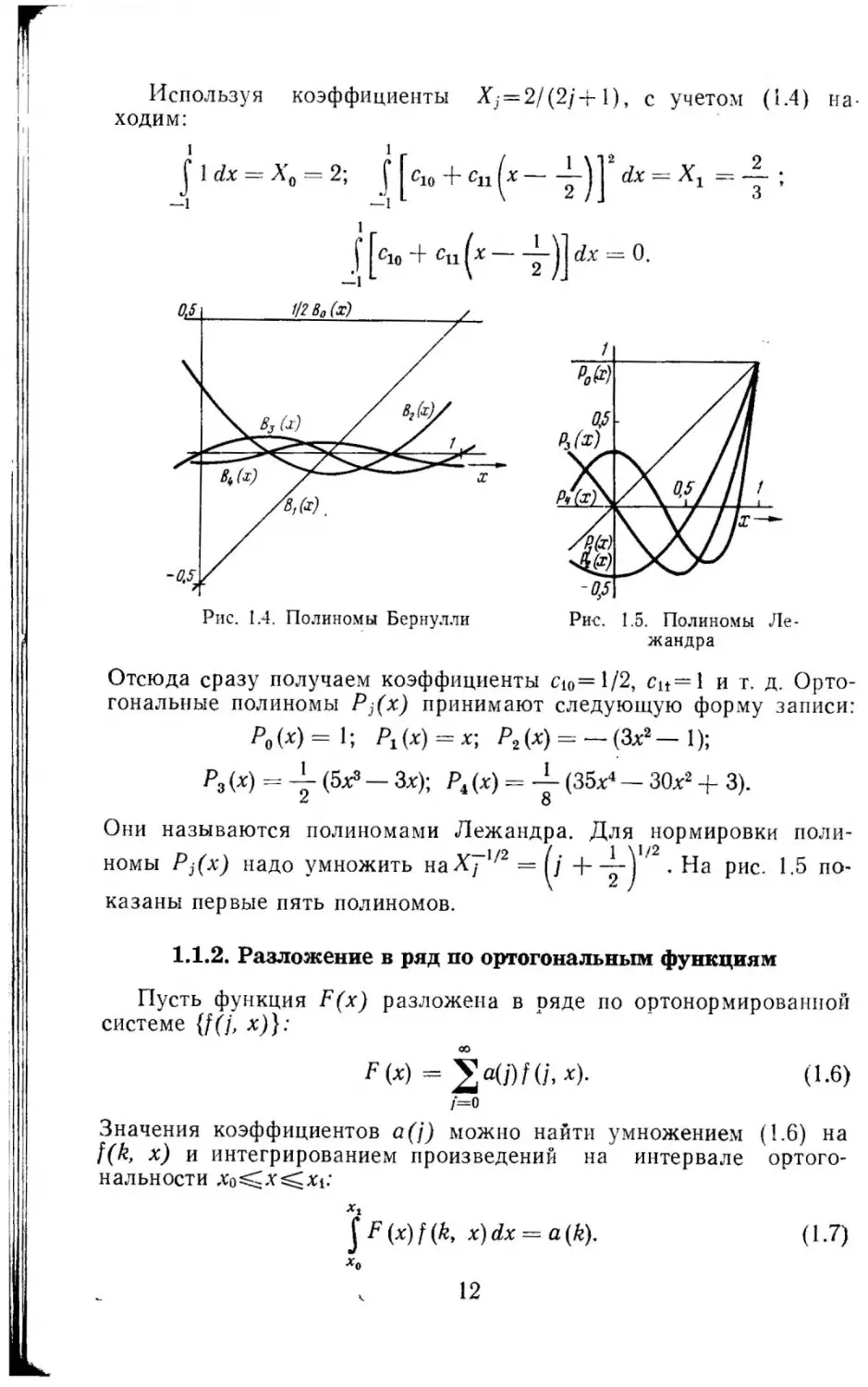
Из графиков на рис. 1.4 ВИ;J.НО, что полиномы Бернулли неоr
: тогонал ьны. Для ортогона.11юаuии на интервале -1::::;;х::::;;+1 их
. необходимо подставить в ( 1.3) u:v1ecтo q(j, х):
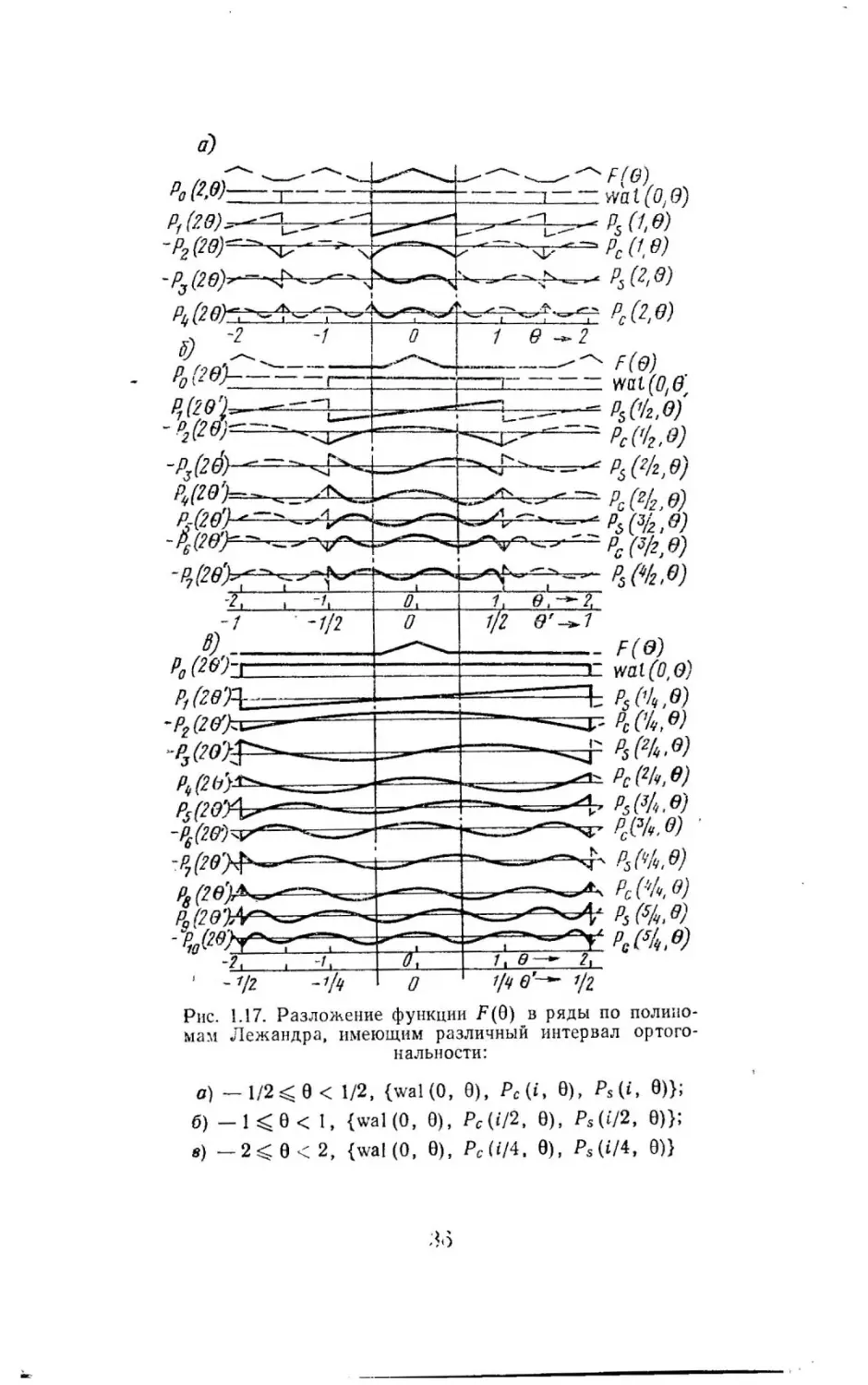
Р0 (х) = В0 (х) = 1; Р1 (х) = с10 В0 (х) +с11 В1 (х) и т. д .
11
1
'!
Используя
коэффициенты
Xj =2/ (2j+l), с учетом (1.4) на
ходим:
J ldx=X
0
.{[с10 +с11 (х-+)]
=2;
-1
2
dx=X 1
-1
1
J[С10 + С11
(
х-
-1
=+;
+)] dx = О.
1/2 80 (:х)
0.5
-0,S
-О,5
Рис.
1.4.
Полиномы Берну.ми
Ри{: .
1.5.
Полиномы
Ле
жандра
Отсюда сразу получаем коэффициенты с1 0 = 1/2, с 11 = 1 и т. д. Орто
гональные полиномы P j(x) принимают следующую форму з аписи:
Р0 (х)= l;
Р3 (х)
= -
1
2
Р1 (х)=х;
P2 (x)=-(3x2 -l);
(5х3 - Зх); Р4 (х) = - 1 (35х 4 - 30х 2 + 3).
8
Они называются полиномами Лежандра. Для нормировки поли1 )1/2
Pj(x) надо умножить наХi-112 = ( J.
На рис . 1.5 по-
+2
номы
.
казаны первые пять полиномов.
1.1.2.
Разложение в ряд по ортогональным функциям
Пусть функция F(x) разложена в ряде по ортонормированной
системе
{f (j,
х)}:
00
F (х) = ~a(j)f (j, х).
( 1.6)
i=O
Значения коэффициентов а (j) можно найти у множением ( 1.6) на
f(k, х) и интегрированием произведений на интервале ортого
нальности Хо~х~х1:
х,
JF (х) f (k, х) dx
12
=
а (k).
( 1.7)
Встает
вопрос,
насколько
хорошо
аппроксимирована
функция
если коэффициенты a(j) определены по ф-ле (1.7). Предпо
ложим, что разложение "f.b (j)f (j, х) имеющее т членов, дает луч
F(x),
шее представление. В качестве критерия качества представления
выбран критерий минимума среднеквадратического отклоне
нияQ функции F(x) от ее представления:
- пусть
Q
J ~ J. F~x)
~ J. [F (х) - Ж b(j)f (j, х)
>; J~ F (x)f (j,
Используя
1[
J
х) dx + ~> (j)f (j, х)
Qв
~' Ь (j) Х
dx.
f (j,
х), по
следующем виде:
х,
т-1
т-1
JF2(x)dx-- L a (j) + ~ [b(j)-a(j)J
2
i=O
х0
- При b(j) =a(j)
dx-2
и свойство ортогональности функций
( 1.7)
лучаем выражение для
Q=
dx
2
_
(1;8)
i=O
последний чJiен равен О и
среднеквадратическое
отклонение достигает своего минимума.
Из
( 1.8)
следует неравенство Бесселя:
m-1
Lа
оо
2
(j) <: :,Е а 2 (j) <
i=O
i=O
х1
JF2.(х)
( 1.9)
dx.
Х0
Верхний предел суммы можно положить
равным оо, так как ин
теграл не зависит от т и поэтому должен сохранять свое значение
для всех т.
Система
{f(j, х)} называется ортогональной, нормированной и
полной, если средний квадрат
отклонения Q с увеличением
т
стремится к О для любой функции F(x), квадратично интегрируе
мой на интервале хо~х~х,:
lim
m-+cio
х, [
J F (х) -
т-1
х0
j=O
~ a(j)f(j, х)
а..1
В этом случае неравенство Бесселя
( 1.9)
]2 dx =О.
( 1. 10)
превращается в
равен-
с тв о
L a (j) = JF2(x)dx.
х,
00
2
i=O
Уравнение
( 1.11)
:(1.11)
х0
известно ка~< теорема о полноте или теорема
Парсева.1я. Его физический смысл следующий.
Пусть
F(x) есть
функция времени, характеризующая
паде.ние напряжения
противлении
F2(x)
l
Ом. Тогда интеграл от
на со
представляет энергию,
рассеиваемую на этом сопротивлении,
которая
согласно ( 1.11)
равна сумме энергий составляющих a(j)f(j, х), j=O, 1" .. , оо. Дру·
rими словами, энергия одинакова в любом случае, описывается ли
напряжение функцией времени
F ( х)
13
или ее разложением в ряд.
Система {f(j, х)} называется замкнутой 1), ec.ri:и не существует
квадратично интегрируемой функции F(x):
( 1.12)
для которой уравнение
JF (x)f (j, х) dx = О
х,
( 1.13)
Хо
удовлетворяется для всех значений
j.
Неполные системы ортогональных функций не дают сходимости
разложения в ряд для всех квадратично интегрируемых функций.
Несмотря на это, они имеют большой практический интерес. На
пример, выходное напряжение идеаJiьного фи .Тiьтра нижних час
тот может быть точно предстанлено путем разложения
в ряд по
неполной ортогональной системе функций siп х/х.
Во всяком случае по таким простым свойствам функции
как ее непрерывность и
ее разложить в ряд
ограниченность,
по
F(x),
нельзя сказать, можно ли
определенной
ортогональной
системе
{f(j, k)} (5-7]2).
1.1.З. Инвариавтиость ортоrональиости преобразования Фурье
Функция времени f(j, 0) может быть представ.1ена при опреде
ленных условиях двумя функциями a(j, v) и b(j, v) с помощью
преобразования Фурье:
J [a(j, v)cos2nv0 +b(i, v)sin2nv0]dv;
00
f(j, 0)=
(1.14)
-оо
Jf(j, 0)cos2nv0d0;
00
a(j, v)=
-·
(1.15)
J f(j, 0)siп2nv0d0,
00
b(j, v)=
-оо
0 = t/T;
1)
v = fT.
Полная ортонормированная система
всегда замкнута. Обратное утверж
дение верно, если рассматривать интегралы в смысле Лебега, а не Римана. Ии
теrралы Римана удовлетворяют основной части этой книги. Поэтому интеrрируе
мость будет означать интегрируемость по Риману, если это ие будет специаль
но оговорено.
2 ) Например, разложение Фурье непрерывной функции не обязательно дает
сходимость в каждой точке . Теорема, сформулированная Банахом, говорит, что
существует много произвольных ортогональных систем с
тем
свойством, что
ортогональные разложения непрерывной дифференцируемой функции расходят
с51
ПО'IТИ
ВСЮду.
14
.
"1:,
(
~
-':'\\'
.§::
,'
Для определенных применений
и Ь (j, v) одной функцией 1)
удобно
заменить
функции
'40, v)
a(j, v) = ао. v) + b(j, v).
(1.16)
-, Из (1.15) следует, что a(j, ") является четной и b(j, v) нечетВ.ой функциями v:
·
в(j, v) = a(j, -v); b(j, v) = -b(j, -v).
( 1.17)
..Поэтому
q(j, -v)=a(j, -v)+b(j, -v)=a(j, v)-b(j, v).
:Функции a(j, v) и b(j, v) можно выразить через q(j, v):
a(j, v)=
;:
f
fq(j, v)+q(j, -v)];
(l. l 8)
( 1.19)
b(j, v)= +[q(j, v)-q(j, -v)J.
,,
Используя функцию
выражения
q(j, \),
· -$~писать в более симметричной форме:
(1.14)
и
(1.15)
J q(j, v)(cos2nv0+sin2nv0)dv;
можно
со
f(j, 0)=
( 1.20)
-со
00
q(j, v)=
S f (j, 8)(cos2nv8 +
sin2nv0)d0.
(1.21)
-со
$Jlнтегралы от b(j, v)cos2JП· 8 и a(j, '')sin2л:v· 8 в (1.20) равны О,
1f-ак как a(j, v) - четная и b(j, v) -- нечетная функции'"
~~: : Пусть {f(j, 8)} есть ортонормированная система, заданная на
1"J@нтервале (-1/2) 0~е~ ( + 1/2)8. Переменная е может быть ко
~чной или бесконечной. Функции f(j. 8) являются преобразуемы
:~~~и по Фурье 2 ). С учетом ( 1.20) интеграл ортогональности
~ (:~ ,·
""
(] .22)
f(j, 0)f(k, 8)d8 = 6jk
s
~~',;_ ~
~Д\~'. : ·
-ею
~~ожет быть Переписан в виде 3 ):
1 l l
/(j, 0) [
:)""~(
rJ q(k, v) [ .
""1·
~~С
-Q)
1)
q (k, v) (cos
f (j,
.
2пv0 + sin 2п"1) d v] d0~ ~1,;
8)(cos 2nv0 + sin
-се
2лv8) d е] dv= б1k;
( 1.23)
.
Данное замечание используется для преобразования Фурье, чтобы облег
- ить
сравнение с формулами обобщенного преобразования Фурье, выведенными
'" озже.
2 ) Ортонормальность пр едпш1агает существование прямого и обратного пре
~браэований Фурье (теорема Планшереля).
б
$) Здесь можно изменить порядок интегрирования, так как подынтегра.пь
ые функции абсолютно интегрируемы.
\
15
00
S q(j,
v)q(k, v)dv = fJik·
Таким образом, преобразование Фурье от ортонормированной
tистемы {f(j, 0)} дает ортонормированную систему {q(j, v)}.
Подставляя q(j, v) =a(j, v) +b(j, v); q(k, v).=a(k, v) +b(k,
в ( 1.23), получаем выражение ( 1.22) в системе обозначения a(j,
v)
v ),
b(j, v):
Jq(j, v)q(k, v)dv=
00
00
S [a(j,
v) + b(j, v)] [a(k, v) + b(k, v)Jdv=
-00
J [a(j, v)a(k, v)+b(j, v)b(k, v)]dv=6jk·
00
-оо
1
••
•
''
'•
''
'' ..
,"
Рис .
1.6.
Преобразо.вание Фурье
синусоидальных
им·пульсов рис.
и косинусоидальиых
•[. 1:
а) wal(O, 0); б) Y2sin2n0; в) -V2cos .2n0; г) JfQsin4n0; д)
X·COS
-V2x
4:t0
На рис. 1.6 показаны
в
качестве
примера
преобразования
Фур~е синусоида.11ьных и косинусоидальных импульсов, получен
ных из элементов (см. рис. 1.1):
1/2
S l (cos2:n:v0 +
q(O, v) =
.
sin2:n:v0)d0 = ~;
лv
-1/2
1/2
S V2cos2ni0(cos2:n:v0+sin2:n:v8)d8=
qc(i, v) =
-1/2
= - \ -V2/sinтt(\•-i)
2
\
n(v-i)
16
.+.-sinл(v+i) );
'
:rt(v+i)
1/2
JV2 siп 2:n: i 0 (cos 2nv0 + siп 2nv0) d 0=
qs(i. v) =
-1/2
=-1 V2(siп:n:(v-i) _siп:n:(v+i)).
2
:n:(v-i)
:n:(v+i)
1
i=fT-
На рис. 1.7 показаны преобразования Фурье импульсов Уолша,
полученных из элементов (см. рис. 1.2):
Jwal(O, 0)(cos2nv0+sin2:n:v0)d0=sш:n:v;
1/2
q(O, v)=
.
-1~
:n:v
2 :n: /2
S sal(l, 0) (cos2nv0 +sш2nv0)d0= siп
__v_;
12
qs(l, v) =
1
•
-1/2
5
.
1
siп 2
:n:v/4
1
:n:v/2
:n:v/4
siп2
::(~~:~ пр ~:-е:-о:v м:::о л~гк~(:~::т~, :о_2_ч~тvны;"~;ем~ннЬ1е
1 функции преобразуются в четные частотные функции, а нечетные
J
_· - .
временнь1е функции преобразуются в нечетные
частотные функ
ции. Отрицательные значения частоты имеют совершенно ясный
физический смысл. Колебание частоты v есть
косинусоидальное
колебание относительно 0=0, если преобразование Фурье имеет
одинаковое значение для
+v
и
-v;
это есть синусоидальное коле
бание, если преобразование Фурье имеет одинаковые абсолютные
значения, но разные знаки для
+v
и
-v.
На рис. 1.8 показаны преобразования Фурье q(j, v) трех пря
моуго.т~ьных импульсов, изображенных на рис. 1.3.
Они
уже не
являются четными или нечетными функциями 1).
1 ) Преобразования Фурье различных прямоугольных
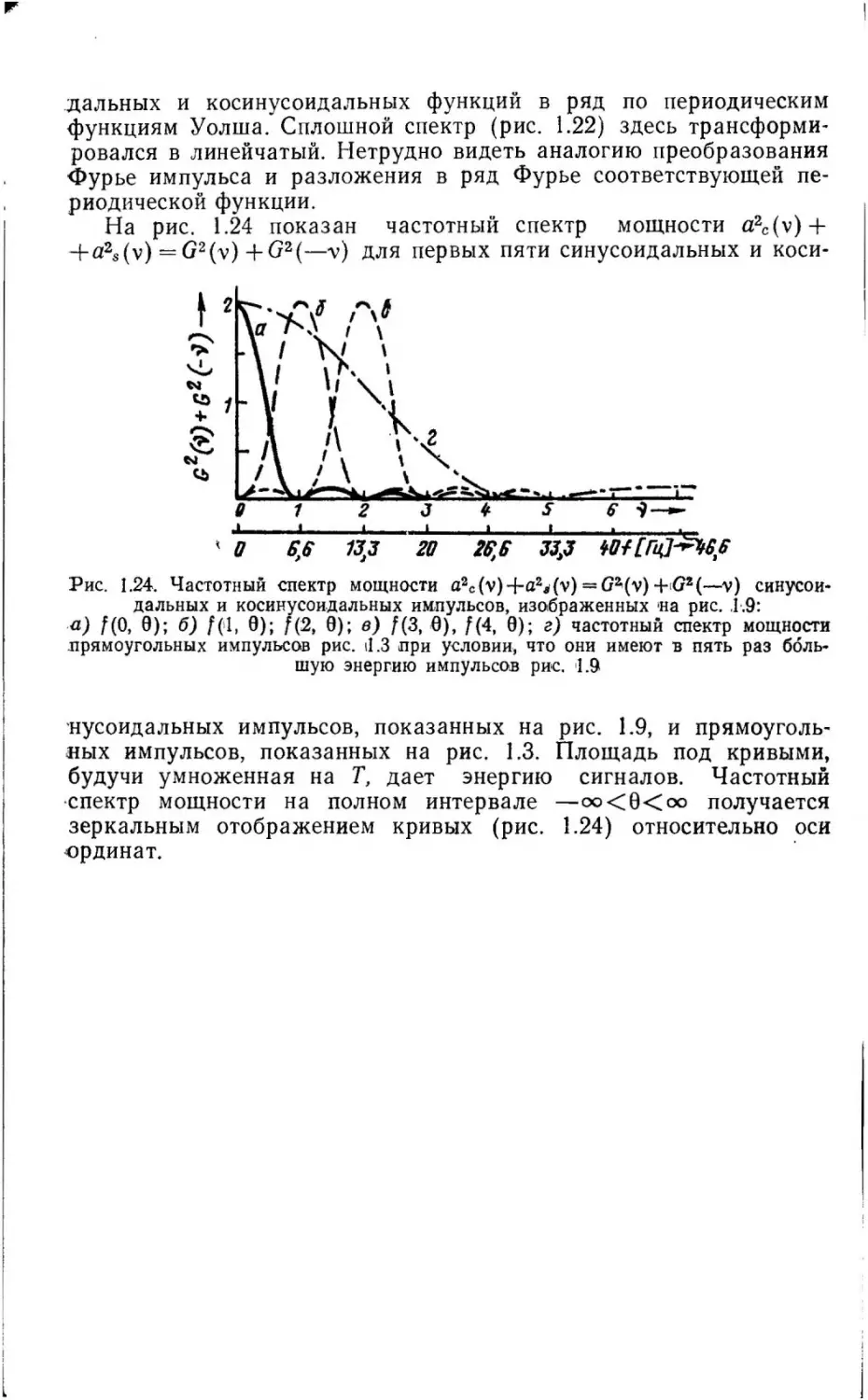
импульсов различны,
110 их частотный спектр мощности одинаков . Спектр мощности это преобра
зование Фурье от автокорреляционной функции, но
не
преобразование Фурье
с а мой функции (теорема Винер а -Хинчина).
Связь
между
преобразованием
Фурье, спектром мощностп п а мплитудным спектром рассматривается в раз . 1.3.2
{см. также
[4]).
17
."
~;'
..Ji1.
Рис .
Преооразонания
1.8.
Фурье q(j, v)
прямоугольных
и f(З, 0) на рис. 1.3
импу.1ьсо в
f(l, 0), f(Q, 0)
На рис.
'"7~ f(8.B)=-r'2co5(5Jt8+тt/I/)
стема
c:/'~f(5,B)=V2sin{5!i.B+л/4)
соидальных
дальных
... ~........",/:""'CJ'" f (4. 0)=-of2GD5 (41i8+ Jl/4)
_с:..,,~ f{J,8)=of2sin(l/1i0+Jl/4)
..... ..........._..._......---,
и
во
ношению
к
-с:.::::;;:;;>' .................... f(~B)=v2sin(2JiB+Jt/Ч)
Рнс .
1.9.
t/ll / f (O,O) =canstant
12
0
Они
времени
по
импульсам,
на рис.
и
от
изо
l.l,
Ортогональ н а я
с ин у сои даль ны х
_1 _
12 114
сину
косинусои
импульсов .
сдвинуты
браженным
f(2,8}=-f2cos(2Гtд+1i/I/)
показана си
1.9
ортогональных
та-
с 11стс щ1
косипусо1ц а .1ь
ны х импv.%сов , им е ющи х о д ин а ко
nыс (по · мод у.1 ю )
O= t/ T
0=-1 /2
!1
з н ачен !1я
0= + 1/2
прн
ким обра зом, что все функции имеют абсолютные значения равной
+ 1/2.
величины при 0=-1/2 и 0=
v)
показаны на рис.
1.1 О:
k
. v) = siп:rt(v-k)
:n:(v-k) '
q ( },
k
Их преобразования Фурье q(j,
= - -21
.
J
для
четных
.
.
J;
= _!_ (j + 1) для нечетных
2
(1.25)
j.
На рис. l. l l показаны пар а болические цилиндр и ческие ф унк
ции \jJj(0). Их преобразован и я Фурье q(j, v) имеют тот же вид
[5]:
f(j, 0) = '1'i(0);
q(2i, v)
= (-
J)i-ф2 ;(4зtv);
j =О, 2i,
2i
q(O, v)
q(2i
+ 1;
= \jJ0 (4зtv);
+ J,
v) = ( - l);'Ф 2 ;+i (4зtv);
i = 1,2, . . . ;
(1.26)
- _!__ х'
-ф 1 (х) =
х
=0
е4
г
_
V~Y~
_!__ х'
Hej (х); Hej (х) =
или 4зtv;
j
= о'
2i' 2i
18
+
2 (е
- _!__ х •
di
-} е
ь
l; i = ] ,2 . • . .
2
...
+
Функция 'l\Jj(0) при больших абсолютных
шается пропорционально
6i ехр (-
при больших абсолютных значениях
,
значениях 0 умень-
а функция
\jJ; ( 4:rtv)
v уменьшается пропорциональ- ·
-
f(4,8) f(2,0)
f{O,fJ) f{1,8) f{J,8) '
1 \ /" ....\
/-··у·~.
.
02)
,"
/'
.\
1
\
1 \
1
1 "
\
\
\
\
'i=fT _....,
Рис .
11.110.
ПреобразО11ания Фурье q(j, v) синусоидальных
идальиых импудьсов рис.
, .но (4лv)jexp [-+(4:rtv)
2
].
и косииусо
1.9
i1мпульсы, полученные на основе пара
. болических цилиндрических функций,
требуют
особенно малую
> часть частотно-временной плоскости для передачи определенного
; процента
их энергии 1).
~ ~ ~ ~
Рис.
1.11. Параболические ци.r~индрические функции Фi=ф;(0) или 1f! 1 =
=1)J;(4nv)
1.1.4.
Фуmщии
YoJlllI3.
.. Функции Уолша wal (О, 0), sal (i, 0) и cal (i, 0) имеют большое
'начение в теории связи 2 ). Существует тесная связь между функ
. иями sal и sin и са! и cos. Буквы s и с в sal и са! бы.111 выбраны,
тобы отразить эту связь, в то время как обозначение \val происхо
. ит
от фамилии ученого
который впервые описал функции
Walsh,
а тематически.
1 ) Импульсы, полученные на основе параболических цилиндрических функ
й, теоретич~ски используют частотно-временную плоскость наилучшим обра
ом. До сих пор это свойство не имело бо.'!Ьшоrо
;;к
;<
синусоидальные
осt1ове,
являются
»
косинусоидальные
в этом
отношении
практического значения, так
импульсы
и
импульсы,
почти такими же
получаемые
хорошими, но
на
их rо-
аздо легче rенерироьать и детектировать.
1)
. яется
Вероятно, наиболее ранним использованием функций Уолш а в связи яв
использование их для размещения проводов
19
(18].
...........,..". .- -.- -
,-:.
Для вычислительных целей иногда более удобно использовать
синусоидальные и косинусоидальные функции, в то
время как в
других сл уч а ях более удобны экспон е нциа .1ьны е функции . С хожая
двойственность з аписи сущест вует и для функций Уолша . Вместо
трех функций wal (О, 8), sal (i, 8) и са! (i, 8) м ожно ввесп:
одну
функцию wal (j, 0):
wal (2i, 0)
Функции
=
0); wal (2i - 1, 0) = sa\ (i, 0); i = 1,2, . . .. ( 1.27}
wal (j, 0) могут быть определены следующим раз н остным.
уравн е нием
са\ (i,
1) :
wal(2j +
Р,
1
0) = (-l/ "/2HP {wal
[i.
2 (0 + + )] +
+(-1/+Pwal[j, 2(0-+)J},
где
[j/2]
означает наибольшее цел ое число, \·1еньшее
(l.28)
и.r1и равноt'
j/2:
р = о или l ;
wa\ (О, 8) = l
wal(O, 0)
.
j = о' 1, 2' .
для
"
1
1
- - .;::: 8<-·
2 ""'
2 '
1
1
дл я 0 < - - 0 > + - .
2 '
2
=О
Для объяснения этого разностного уравнения рассмотрим функ
цию wal(j, 0). Функция wal (j, 20) имеет тот же вид, что и функ
ция wal(j, 0), но . сжата
в
интервал -1/4~10<+ : 1/4 .
Функ
ция wal{j, 2(8+1 /4)] получается сдвигом wal(j, 28)
в лев о на
интервал -1/2~8<0 и wal[j,
2(8--1 /4)] п олуч а ется сдвигом
wal(j, 28) вправо на интервал 0~0< + 1/2.
В качестве примера рассмотрим случ а и j=O, p=rl и j=2, р= 1.
Используя значения (О/2]=0и[2/2]=1, получаем:
wal (1, 8) = ( - 1) + {wal [О, 2 (0
0
1
+ +)] +
1
+(- l)O-t- wal[o. 2(0 --+)]};
+)] +
+ (- l ) + wal [ 2, 2 ( 0 + +) ]} .
1 1
wa1(5, 0) = (-1) + {wa1[2, 2(0 +
2 1
1
) Функции Уолша обычно опр е деляют с я к а к про11 зв еденая фун к ций Рад е 11ахера. Это опреде ление им еет много пр еим у ществ, но не дает упорядочивания
функций Уолша по числу перем е н зн а ков, что делает разностное уравнение. Эт0<
упорядочивание является необходимым для обобщения частоты в
§ 1.3.
Функции
Р а демахера это функции sal(•I, О), sal(2, О), sai(4, е)"" изображенные иа
рис. 1.2. Функции Уолша также могут быть определ ены через матрицу Адамара
[19] .
20
Из рис . 1.2 ~южно видеть, что функция wal ( 1, 8) = sal ( l, 8) nо
. лучена из wal (<О, 8) сжатием в два раза и умножением функции
:.·сдвинутой влево, на -1 н функции,
сдвинутой
вправо, на
l.
, функция \val (5, 8) =sal (3, 8)
получается
сжатием wal (2, О)=
. =cal(l, 8) R два раза и у :- . шожением функции, сдвинутой влево,
+
р_11а
+1и
функции, сдвин утой вправе, на
-1.
Умножение двух функций Уолш а дает другую функцию Уол·~·ша: wal(h, 8)\\1 al(k, 8) =\Val(r, 8). Это соотношение может быть
:';'
легко
проверено,
если
записать
разностное
уравнение
для
.wal (h, 8) и wal (k, 8) и умножить их друг на друга . Оказывается,
' что произведение wal (h, 8) \Уа! (k, 8) удовлетворяет разностному
, уравнению вида , аналогичного ( 1.28).
~
Определение значений r из разностного уравнения
несколько
-~- };rромоздко. Однако результат IIолучается простой: r равно сумме
1~i'h и k по mod 2:
!.
i:
:~f
wal (h, 8) wal (k, 8) = wal (h ffi k, 8).
Знак
ffi
указывает н а сложение
no mod 2.
( l .29)
Величины
k и h за-
·1~ писываются в виде двоичных чисел и ск.Тiадываются согласно пра
W 'вилу: О ffil=l Е1Э 0=1,ОЕВО=l ЕВ 1=0 (без переноса). Сложение
:1\ по mod 2 - это та операция, которую осуществляет полусумматор
., в двоичных ЦВМ. В качестве примера рассмотрим перемножение
; wal (6, 8) и \\1 а! ( 12, 8) . Испо.Гiьзуя двоичную запись для чисел 6
и 12, получаем, что сумма 6Е!Э12 равна 10:
@ 0110
+
6
1100 . . . . 12
1010 .. .. 10
Из рис. 1.2 можно видеть, что
. равно "'а! ( l О, 8).
произведение \\1 а!(6,
8) wal(l2, 8)
Умножение функции Уолша са~юй на себя дает \\'а! (О, 0), так
. как в результате получаются только произведения: ( + l) ( + l) и
(-1)(-1) :
( 1.30)
wal(j, 0)wal(j, 8) = wa\(O, 8);
jEJ:)j = O
Умножение
wal (j, 8) на \\'а! (О, 8) не изменяет \val (j, 8):
~-
wal (j, 0)wal(O, 8) = wal (j, 0);
t
j@O=j.
~·
1"
:{..
Так как сложение по
mod 2
( 1.3 l)
асссоциативно, умножение функ-
ций Уолша также до.1жно быть ассоциативным:
[wal(h, 0)wal(j, 8)Jwal(k, 8)=wal(h, 0)[wal(j, 0)wal(k, 8)). (l.32)
Функции Уолша образуют :vrультипликативную
нение
( 1.29)
группу. Урав
показывает, что умножение двух функций дает снова
21
L . .
функцию Уолша ; обратный элемент опреде.11яется по ф-ле (1.30);
единичным элементом согласно ( 1.31)
является wal (О, 0); ассо
циативный закон выполняется согласно ( 1.32). Группа функций
Уолша является абелевой (коммутативной) группой, так как сомно
жители в (1.29), (1 .30) и (1.31) могут быть переставлены. В ма
тематическом смысле группа ф у нкций Уолша изоморфна дискрет
ной двоичной группе.
Для определения числа элементов в группе и
ее
подгруппах
рассмотрим, какие числа могут появиться, если два числа k и h,
меньшие или равные 28 -1, складываются по mod 2. Запишем k н
h в виде двоичных чисел:
h = Ps-J 2s-J + Ps~2 2 -
+ . . . + Р12 1 + р0 2° <:;;;: 2s - 1;
5
k = qs-J 2s-I + qs-2 2 - 2 +
.. + q121 + %2° <:;;;: 2s- 1;
Ро, •. " Ps-J • q0 , •
., q5 _ 1 = О ИЛИ 1.
5
Сумма по
mod 2
чисел
h
и
k
2
(1.33)
равна
Она принимает наименьшее значение (О) , когда все коэффициен
ты перед степенями 2 равны О, это имеет место при h=k, и макси
мальное значение . 2s-1 +2s-2 + ... +2 1 +20=2•-l, когда
все
коэф
фициенты перед степенями 2 в (1.34) равны ·1, т. е. когда h=
(2 8 -1) ЕiЭ k. Это означает, что в дв о ичной записи число k имеет
нули там, где h имеет единицы и наоборот. Полученная таким об
разом группа содержит функции Уолша от wal (О, О) до wal(2 8 -1, 0) . Подгруппы содержат функции от wal(O, 0) до wal(2r-l,
0), O~r<s. Так как подгруппа содержит 2r элементов, то она
=
имеет
28 /2r=2s-r классов.
Используя (1.27), можно переписать теорему умножения функ
ций Уолша (1 .29) в следующем виде:
cal ( i, 0) са! (k, 0) = са! ( i ® k, 0); sal(i, 0) са! (k, 0) =
=Sal{[kffi(i-1)]+ 1, 0};
(1.35)
cal (i, 0) sal (k, 0) = sal{[i ® (k- 1)J + 1, 0}; sal (i, 0) sal (k, 0) =
=cal[(i-l)Ef)(k-1), 0J; cal(O, 0)=wal(O, 0).
Функции sin 2ni0 и cos 2ni0 ортогональны на интервале -1/2~
~ 0:::;;
1/2. Эта система применяется для разложения в ряд
+
Фурье. Преобразование Фурье требует, чтобы система
~os
тервале
µ -
{sin 2л:v0,
<r0<
была ортогональной на всем интервале -оо
+ оо.
Система функций Уолша , ортогональная и полная на всем ин
2nv0}
-оо<0<оо,
обозначается
{sal(µ, 0), cal(µ, 0)},
где
действительное число . Позже будет показано, что эта систе
ма может быть получена растяжени е м sal (i, 0) и cal (i, 0) так же,
как система {sin 2nv0, cos 2л"·0} может быть получена растяжени-
22
j
ем sin 2ni0 и cos 2ni0. Другое определение, данное
Пихлером 1.).
\ начинается с периодического продолжения функций sal ( 1, 0) и
; са! ( 1, 0). Из них можно определить подкласс функций Уолша,
известных как функции Радемахера [8, 9]:
cal(2k, 0)=cal(l, 2k0); sal(2k, 0)=sal(l, 2~0);
(1.36)
-оо<0<+оо.
k=±l, ±2, . .. ;
Запишем µ в двоичной форме:
"" µ_s 2-s = .. . µ222 + µ121 + µ020 + µ_! 2-t + µ_2 2-2.
L
S=-ao
е µ s равно либо 1, либо О . Число µ называется двоично-рацио
альным, если сумма имеет конечное число членов. Это означает.
о должно быть , по крайней мере, конечное число двоичных сим
лов справа от нулевого разряда. Функции са!(µ, 0) и sal(µ, 6}
жно определить следующим образом:
(µ . 0) =
s~oo cal {µ_
5
(µ, 0) = {- cal (µ, 0),
·
+ cal (µ, 0),
оо <0 <
2-s, 0), -
1
оо;
-оо < 0 <О, µ-двоично-иррациоО< 0 < оо,
нальное число;
·µ, 0)=caJ{q · 2-M, 0)sa!( 2-М, 0),
четное число; ~1=q+1/2М
.q -
+
-
(1.37)
J
-оо<0<оо,
двоично-рациональное число.
: . Функции cal(~t, 0) и sal(~1, 0) для интервалов -4<µ<+4 н
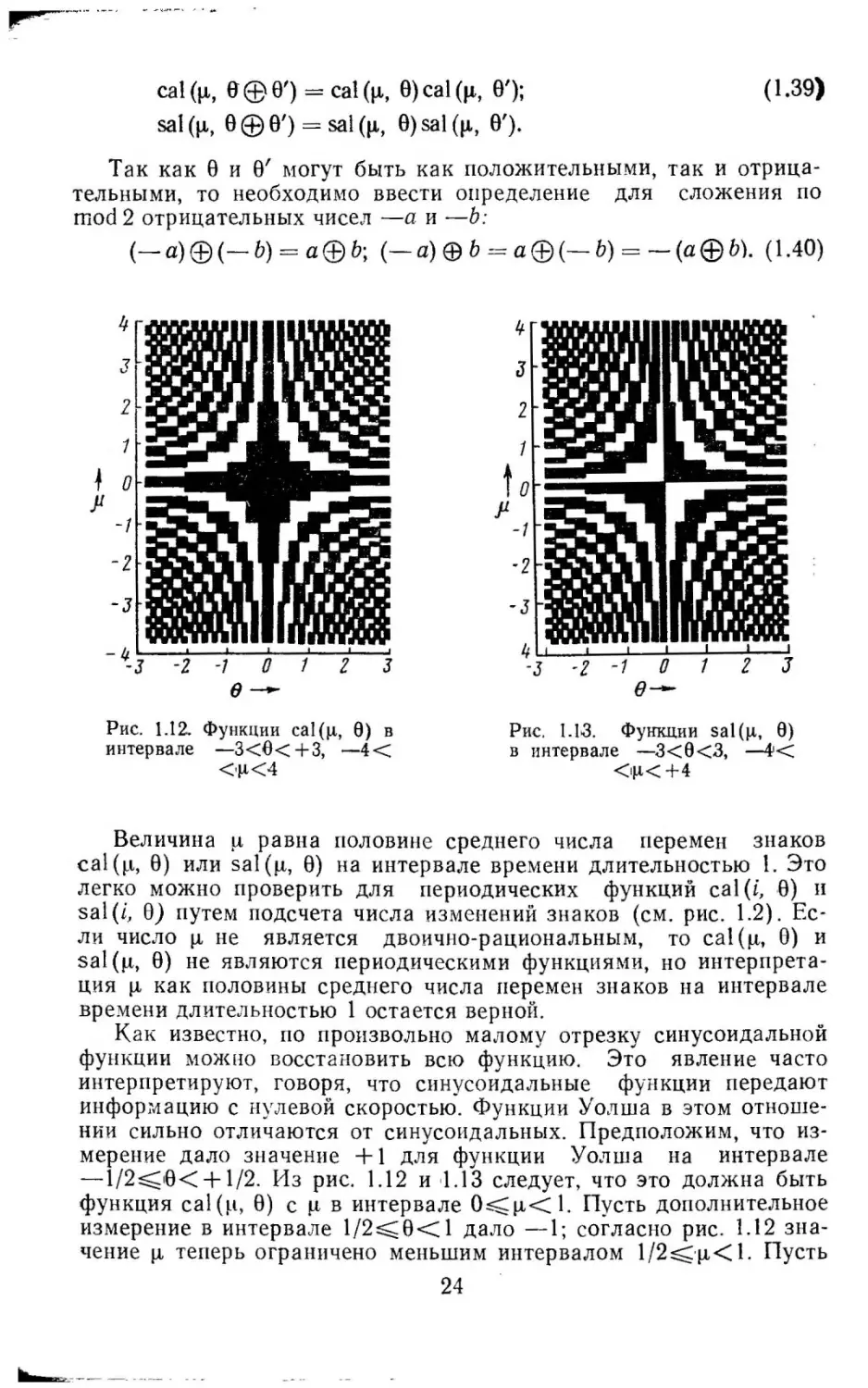
<е+3 можно по.1 у ч11ть нз рис. 1.12 и 1.13. Черные площади
.тветствуют значению
1, белые площади - значению -1.
+
оведя линию, пара .'I.'lе.1ьную
(µ, 0)
· ия,
Jµ,
сси
0,
по.~учаем
са!(µ,
или
0)
как функции 0 д~rя опреде.1енного значения µ. Наоборот.
параллельная оси ~1, определяет значения са!(µ,
как функции ~t для определенного значения 0.
0)
или
0)
ii. Следующие допоJшительные формулы важны при вычислениях
ункциями Уолша:
wal (µ, 0) = wal (О, 0),
са!(µ,
0) = cal (i, 0),
sal(µ, 0) = sal(i, 0),
<-.'
О<µ <
l;
i < µ < i + l, i-1
+ +;
<0< +
< µ < i;
i) Несчетная система функций Уолшз , необходимая
(l.38)
для
преобразования
"олша-Фурье, была введена впервые Файном (12], который также впервые укал на существование такого преобразования. Точная
математическая
теория
еобразов а ния Уолша-Ф у рье, использующая функции sa\ и са!, которые от
аются от системы. использованной Файном, разработана Пихлером
(9]. Такой
мин как «преобразование Файна или Пихлер а :. появился из-за того, что он
аздо короче более громоздкого термина «Преобразование Уолша-Фурье:..
тематики используют этот термин
потому,
что преобразование Уолша
рье является частным с .1учаем обобщенного преобразования Фурье на топо,, ических группах
(22].
23
г--
cal (µ, в Ef) 0')
=
cal (µ, 0) са!(µ, 0');
(1.39)
sal (µ, 0 ffi 0') = sal (µ, 0) sal (µ, 0').
Так как
и
0
могут быть как положительными, так и отрица
0'
тельными, то необходимо ввести онределение
для
сложения по
mod 2 отрицательных чисел -а и -Ь :
(-a)ffi(-b) = affib; (-а) ЕiЭ Ь = affi(-b) = -(affibl. (l.40)
ч.
J
2
2
~
)1
-1
-2
-2
о-
(}--
Рис. 1.12 Функции са\(µ, 0) в
интервале -З<е< +3, -4<
Рис . 1.13.
Функции
в интервале
sal(µ, 0)
-3<0<3,
<iµ<4
~<
<iµ<+4
Величина µ равна половине среднего числа
перемен
знаков
са\ (~t, 0) или sal (µ, 0) на интервале времени длительностью l. Это
легко можно проверить для
периодических функций са! (i, .О) п
sal (i, 0) путем подсчета числа изменений знаков (см. рис. 1.2). Ес
ли число µ не является двоично-рациональным,
то cal (µ, 0) и
sal (µ, 0) не являются периодическими функциями, но интерпрета
ция
µ
как половины
среднего
времени длительностью
числа
1 остается
перемен
знаков
на
интервале
верной.
Как известно, по произвольно малому отрезку синусоидальной
функции можно восст ан овить всю функцию.
интерпретируют,
говоря,
что синусоидальные
Это
явление часто
функции
передают
информацию с нулевой скоростью. Функции Уолша в этом отноше
нии сильно отличаются от синусоидальных. Предположим, что из
мерение дало значение
1 для функции Уо.11ша на интервале
+
-1/2::::;;;10<+1/2. Из рис. 1.12 и '1.13 следует, что это должна быть
функция са! (i1, 0) с µ в интервале О~µ< 1. Пусть дополнительное
измерение в интервале 1/2~0<1 дало -1; согласно рис. 1.12 зна
чение µ теперь ограничено меньшим интервалом 1/2::::;;;·µ< 1. Пусть
24
ь
едующее измерение дает, например, -1 для интервала 1 ~0<
. 1,5 и + 1 для интервала l,5~e<2; это ограничивает µ до еще
·. еньшего интервала О,5~ 1µ<0,75. Удвоение временного интервала
: 6, на котором происходит измерение, уменьшает вдвое интерва.'1
; · µ,
:~
внутри которого частость ~t остается неопределенной . Произ
Л&Лµ остается постоянным и может быть интерпретирова
,. едение
' ;'"::о как соотношение неопределенности для функций Уолша. Ско-
'
.
·~
ость передачи информации не равна О, так как с увеличением ин
ервала наблюдения Л8 получают больше информации о точном
начении µ.
Несколько слов можно добавить для математически подготов
f~·Jlенного читателя о связи между системами {wal (О, 8), са! (i , 8),
~,;;sal(i, 8)} и {l,V2sin2лi8, V2cos 2лi8}. Обе они являются ор
·~"°нормированными
систе м ами
в
ги л ьбертовом
пространстве
{{4(0, l) и на их основе можно построить очень близкие теории
,gразложения Фурье и
преобразования
Фурье .
Основанием для
kэтого я вл яется то, что обе они могут быть получены из характе-
. ристических групп. Сие.тема круговых функций
01дучается из группы
{езху},
которая является
{cos kx, sin kx}
по-
характеристической
:группой топологической группы действительных
чисел .
Система
функций Уолша может быть получена из характеристической груп
пы двоичной группы; двоичная группа
является
топологической
группой , полученной из последовател ьности двоичных представле
ний действител ьных чисел. Наиболее существенное отличие меж
ду этими функциями
-
непрерывность круговых функций и раз
рывность функций Уолша вызвано различной топологией дейст
вительных чисел и двоичных групп [8, l l, 12, 20].
1.2.
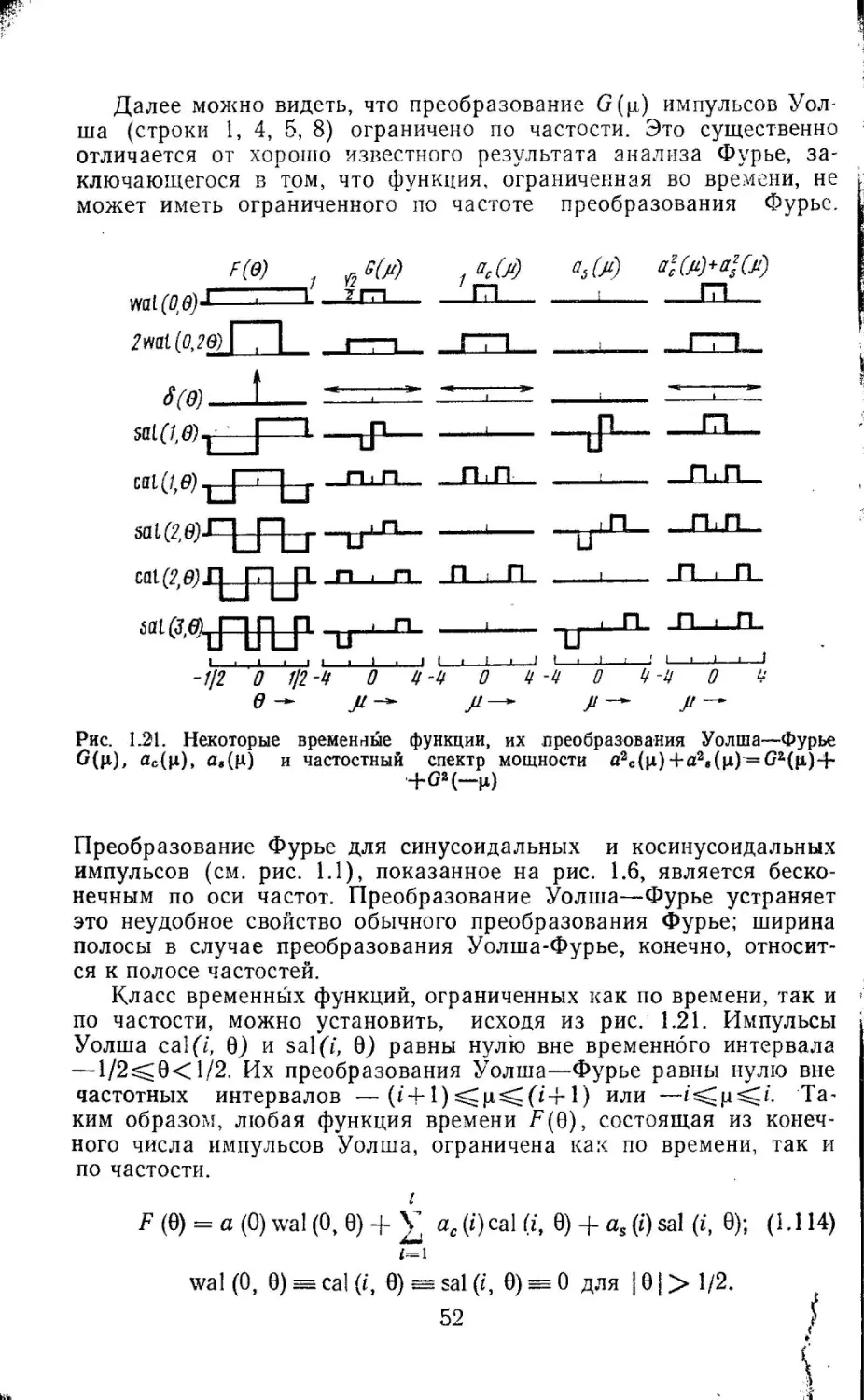
ПРЕОБР А30ВАНИЕ ФУРЬЕ И ЕГО 'ОБОБЩЕНИЕ
1.2.1.
Переход от ряда Фурье к преобразованию Фурье
Знание преобразования Фурье необходимо для каждого инже
нера-связиста. Здесь приведен его вывод из ряда Фурье для част
ного случая, что облегчает понимание более общего перехода от
разложения по ортогональным функциям к ортогональному пре. образованию 1 ).
Рассмотрим ортонормированную систему
из
_
синусоида л ьных
приведена на рис.
элементы
·fc(i, 8),
и
косинусоид.альных
1.1.
Элементы
нечетные
{f(j, ·8 )},
элементов,
состоящую
часть
которых
f(j, 8) разделяются на
элементы fs(i, 8) и постоянную
четные
f (О,
8)
1 ) Пер е ход от ряда Фурье к преобра з ованию Фурье имеет в ос новном мето
дологическ о е з нач е ние . Строго мате матичес кий переход без дополнител ь ных пред
поло ж ений невоз можен, так как ряд Фурье и с пользует систему счетны х функций,
а преобразование Ф у рье t:истему н ес ч е тных функций. С оо т ветствующее за
мечание учитывается ниже при пе р е ходе от ортогональных рядов к обобщенн{)
му преобразованию Фурье.
25
, ,!}
5·
f(O, O)=wal(O, 0)= l,
fc(i, 0)= V2cos2л:i0;
О)= 1fs(i, О)= V- 2siп2л:i0;
'
.
f(J,
1 неопределена,
\
-+~О<++;
(1.41)
о< --21 'О>
+-21 ·,
О= tJT; i = 1, 2, . . .
Чтобы по:1учить периодические синусоида л ьные и косинусои
дальные функции, соответствующие элементы должны быть перио
дически продолжены вне интерва .1а -1/2~0<
1/2:
О)=
f(O,
f(j, О)=
+
-оо <О <+оо;
l
fc(i, 0)= V:_ cos2л:i0;
1fjJ, 0)= v2 siп2л:i0.
( 1.42)
Периодическое продолжение функции
явл яется
частным способом
на конечном интервале
расширения
интерва л а
определения .
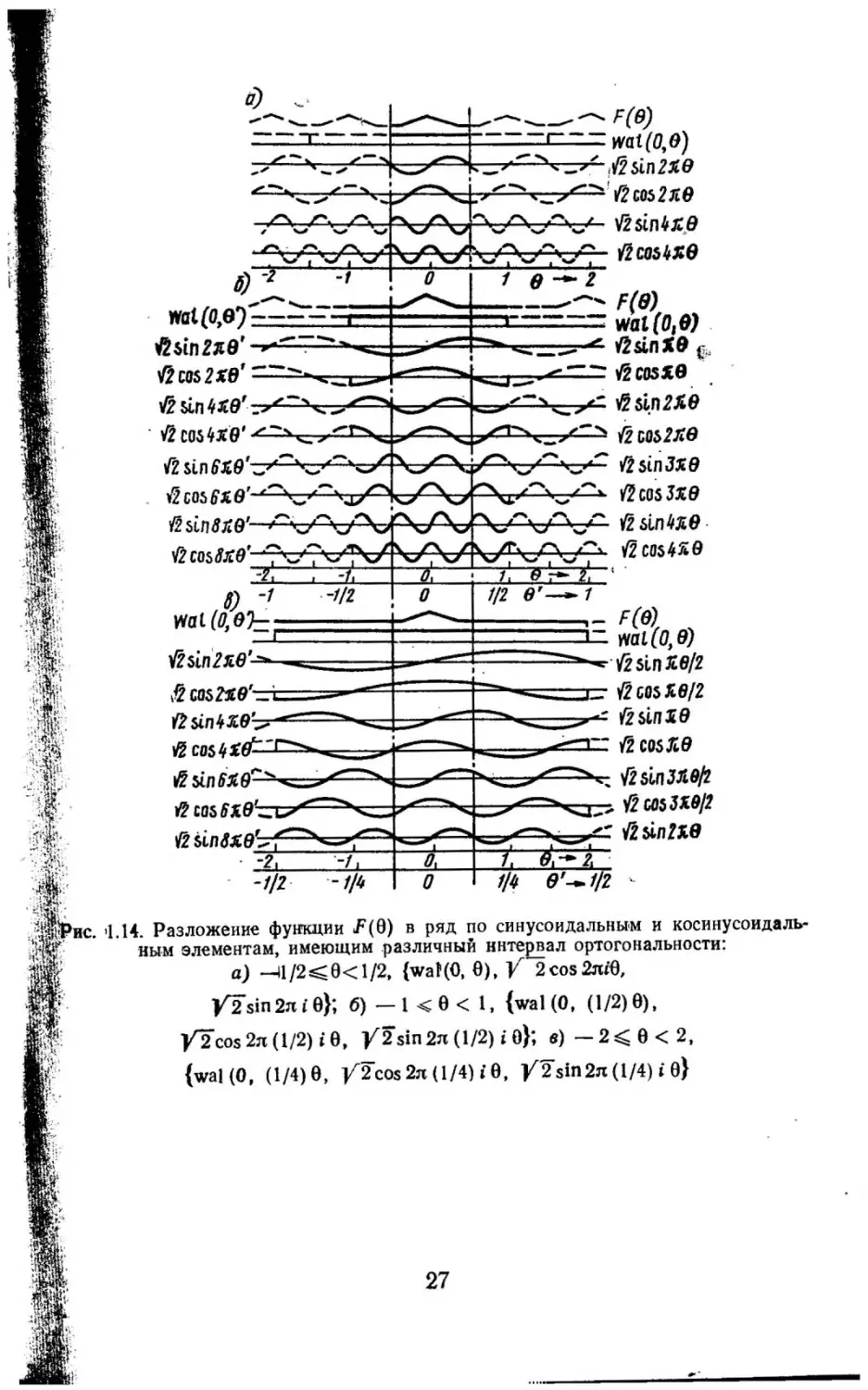
Рассмотрим функцию F('8), определенную на интервале -1/2~
~О< 1/2. Примером может служить треугольная функция, пока
занная в верхней части рис. 1. 14а. Если выполнены условия схо
димости, то .Р (О) можно разложить в ряд по ортонормированной
системе
{f(j,
О)}, определенной на том же интервале, что и
F(O) .
Треугольная функция, изображенная на рис. 1.14а, раскладывает
ся в ряд на синусоидальные и косинусоидальные элементы. Если
треугольную функцию продо.т1жить вне ее интервала определения,
то синусоидальные и косинусоидальные элементы необходимо про
должить таким же способом. Особенно важны следующие два слу
чая. Периодическое продолжение треугольной
функции
требует
периодического продолжения отдельных элементов . Поэтому пе
риодическая треугольная функция н а рис. 1.14а раскладывается в
ряд
по
периодическим
синусоидальным
и
косинусоидальным
функциям. С другой стороны, если треугольную функцию продол
жить вне интервала -1/2~е<
но
разложить в
ряд
по
1/2
имп ульсам,
функцией
которые
F(O)
равны
=О, то ее мож
нулю
вне этого
интервала .
Пусть
F (10)
разложена в ряд по синусоидальным и косинусои
дальным элементам:
со
F(O)= a(O)f(O, О)+ V2~ [ac(i)cos2л:iO+as(i)siп2л:iO];
i=l
а(О)=
.
1/2
1/2
5 F(0)/(0,0)dO= 5 F(O)dO;
-1/2
1/2
-1/2
JF (О) cos 2л: i Od О;
as(i)= v 2 J F(O)siп2л:i0d0.
ас (i) =
V2
( 1.43)
-1/2
1/2
-1/2
26
J
о)
-
_,
1
е
-- 2
. . astnie
"~-~-=~~~s=:-=-~-;;
F(B)
wat(o,в/=----=
---~ wat(0,8}
.
-.'2$in2xв'
"2саs2~в· - - -
~
- - {Zcos~в ·
Visi.n4t8' _
· Yi cos4xO' -
,-
.._
.; -Asi.n2.ie
J& •
-,
iz cos21'8
·~.___.,r:-:>"~d-:+31.:,.-71-~~~-+-"""'...:....__,,,:_,,..
Yi sinJX8
_
У2 co:i 611.8''-L--""':--:""--....,.~~~~~!tin-.~,.,__,~ f2. cos 3Х8
..... ..... .... ~
sLn41'8 .
Yi cos4Ji.8
У2
...,,,._.;;;.._._'--i-._.::...-1-':...,;..-=-.i....:::...i-..;:;...J.....=;..L_ ' .
6) -.1
о
в·-1
wat {о, 8'1=_
F( 8)
--'-----f----+----L-- wat(O, 8)
Yisinl1i8'
,.
·fzsi.n1i.B/2
.fi соs~в· _ ·
_ У2 i;os fi.B/2
r'Z sin4XB!;;'...,..-::===::......._±=7'..,.,:::.=f=:::::....o;;::=~- (i si.n 18
V?. соs4~(/::.~-с:::::......._=~~===~с:;;::=.....,:::::::з::-- {2 cos!i.8
;::===:::t::==::::t:===-
-~[:~~<
:~;:1~·.
,'11~~\;;
.:.~\>.t{,I
~ ~п6яe,..;.....':::..,,;:=,,,;c;.__::~=~=p....,..-,,..,tt::::.......;;::i~- {Z si.nJЛ.8/2
'12 cos6x.8<:-'_"Т"::.>,,r;.....~-=---ь--=:.....::f-:~;;;:::o.~......,._" t/i cosJA.8/2
'li si.n6X8....
,- {Z si.n21i.8
. -2
-1/2
о
·'" '.нс. •1.14. Разложение фуmш.ии F(0) в ряд по синусоидальным и косинусоидаль.
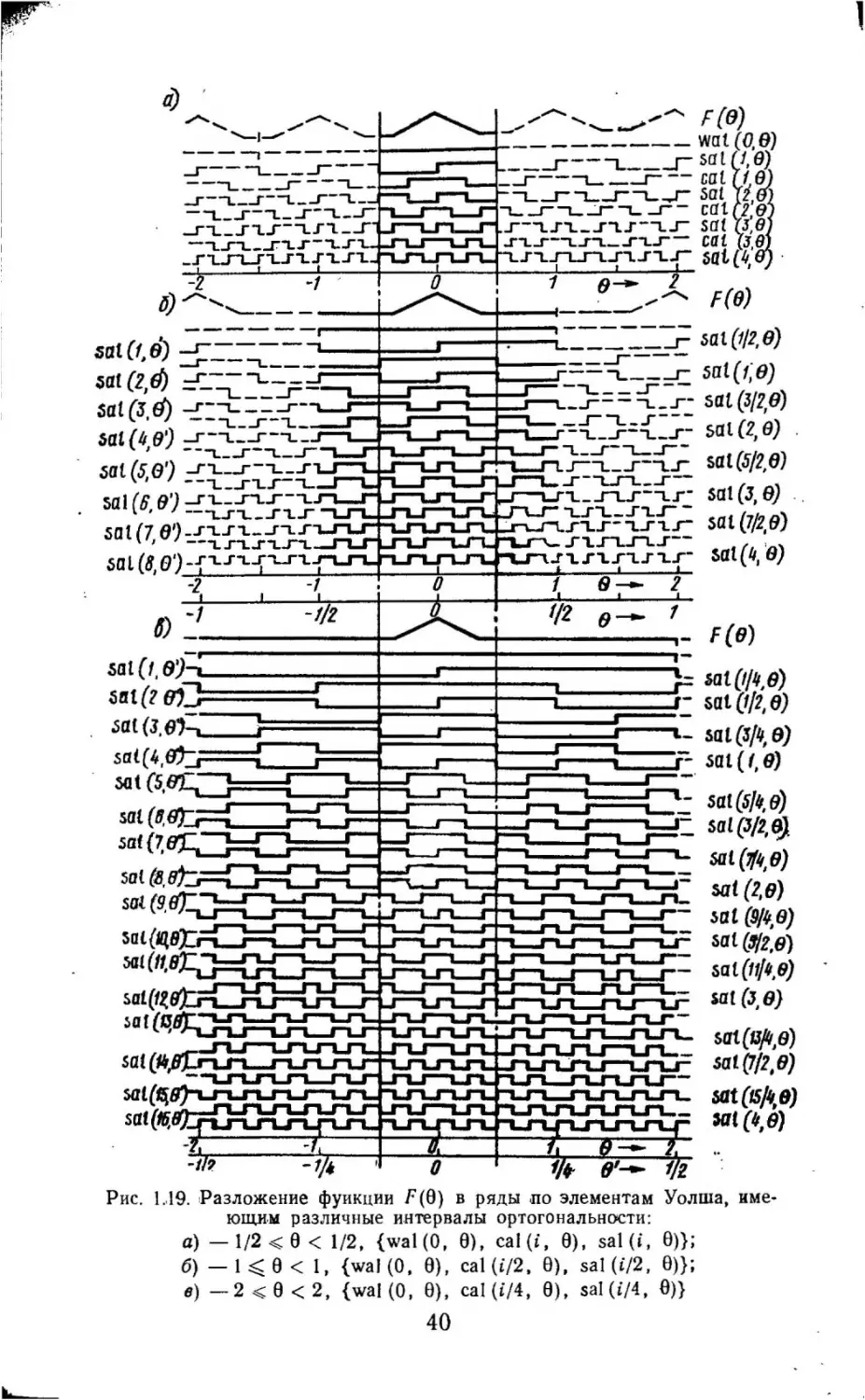
иы.м элементам, имеющим .различный ннтее!ал ортогональности:
а) --11/2~0<1/2, {wat(O, 0), У 2cos21ti0,
}'2sin2ni0}; 6)-1 ~ 0<1, {wal(O, (\/2)0),
}'2cos 2n (1/2) i 0,
-V2 sin 2n (1/2) i о};
в) - 2 ~ 0
< 2,
{wal (О, (1/4) 0, y'"2cos 2n (1/4) i 0, y'"2sin2л: (1/4) i 0}
27
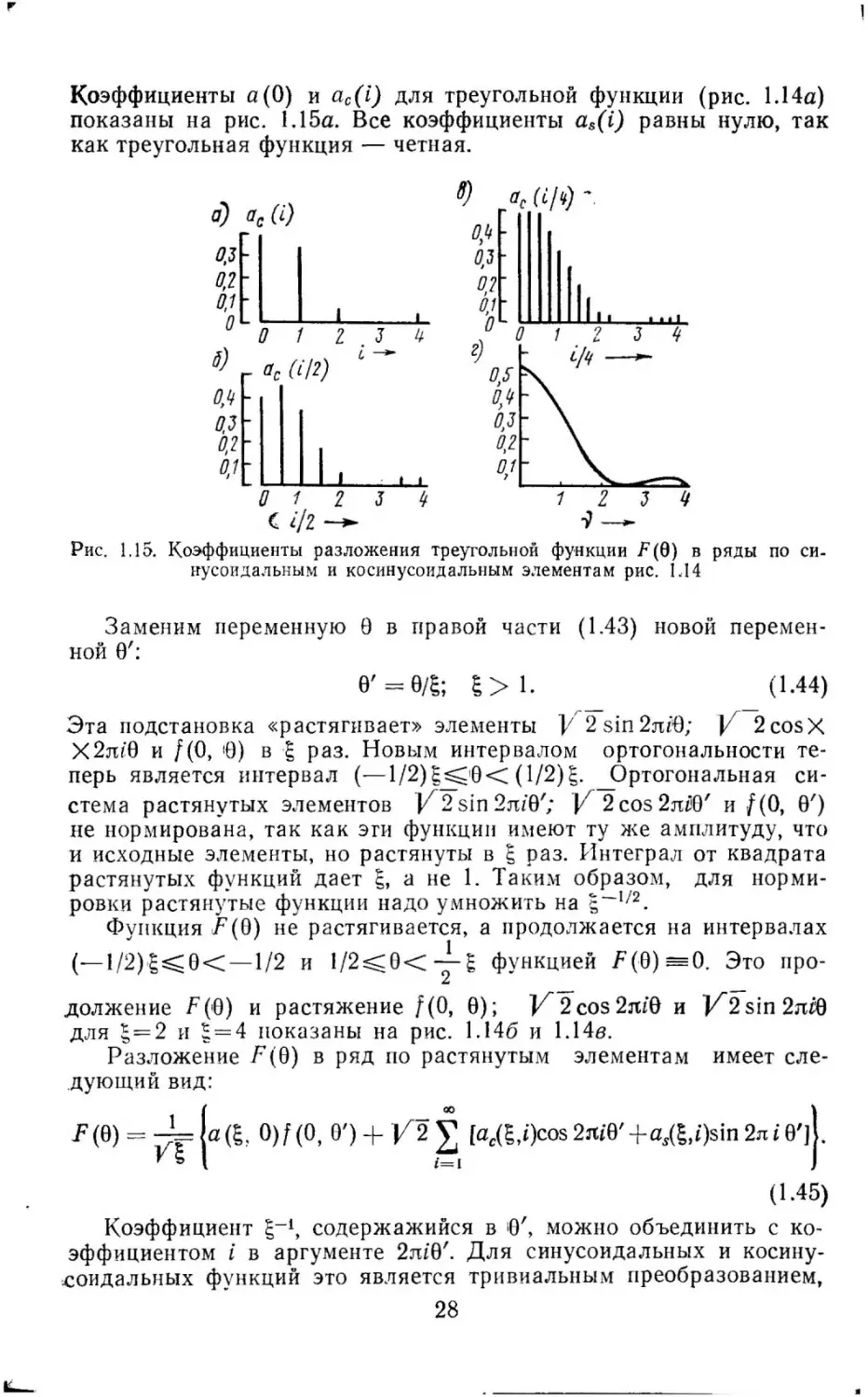
Коэффициенты а(О) и ac(i) для треугольной функции (рис. 1.14а)
показаны на рис. 1.15а. Все коэффициенты as(i) равны нулю, так
как треугольная функция
четная.
-
~~~f 1'11'(;) -
а) ас (i)
O,J~L
0,1
О,1~~
о о
2
4
0,2
о о
1
z
J
iJ
~
~Ч~Lac(i/2)
i-
0,S
о, lf
0,2
Ot
0,2
о, 1
.
о
1
2
} L__.____;~.....:::~
4
J
( i/2-
1.15.
i/'1 - -
O,J
O.J
Рис.
J
1
1
2
У-
Коэффициенты разложения треугольной функции
J
"
F(0) в
1J4
ряды по си
нусоидальным и ко синусоидальным эдемента м рис.
Заменим переменную
ной О':
8
в правой части
О' = 8/s;
s
(1.43)
новой перемен
> 1.
( 1.44)
V
Эта подстановка «растяпшает» элементы i,Г2sin2лitЭ;
2cosX
Х2лi0 и f (О, 18) в 5 раз. Новым интервалом ортогональности те
перь является интервал (-1/2Н:=:;; 1 8< ( 1/2) 5.
Ортогональная система растянутых элементов
2 sin 2лi8'; V2 cos 2лi8' и f (О, 8')
V
не нормирована, так как эги функци11 имеют ту же амплитуду, что
5
и исходные элементы, но растянуты в
раз. Интеграл от квадрата
растянутых функций дает
а не 1. Таким образом, для норми
5.
ровки растянутые функции надо умножить на
Фушщия
F (8)
5- 112 •
не растягивается, а продолжается на интервалах
(-1 /2 Н:=:;;О<-1/2 и
1/2:=:;;8<
+~ функцией
F(O)
=О. Это про-
должение F(iO) и растяжение f(O, 8); V2cos2:rti0 и V2siп2ni6
для 5=2 и ;=4 показаны на рис. 1.146 и 1.14в.
Раз.'Jожение F (8) в ряд по растянутым элементам имеет сле
дующий вид:
F (8)
=;s {а
(s, O)f (О, 8') + V2 ~
[aД,i)cos 2:rti8' +aД,i)siп 2п i O'Jj.
1=1
( 1.45)
5-
Коэффициент
содержажийся в 10', можно объединить с ко
эффициентом i в аргументе 2ni8'. Для синусоидальных и косину
1,
сеоидальных функций это является тривиальным преобразованием,
28
.1
оно может быть использовано как отправной пункт для обоб
·
ения преобразования Фурье:
cos 2:п: i 0' = cos 2:п: i <01ю = cos 2:п: <ifs) 0;
sin 2:п: i 0' = sin 2:п: i (0/s) = sin 2n (i/s) 0;
f (О, 0') = f(O, 0/6} = f(O/s. 0).
Запись f(Oi;, 0) является чисто формаJiьной.
Разложение f (0) в ряд принимает следующий вид:
F (0) =
vr
1 {
a(s, O)f (O/s, 0)
+ V2. ~ . [ас (6,
00
( 1.46)
i)cos2:п: J.__0 +
s
1/:.=1/>:.
+as(s, i)sin2:п:t0]};
аД, i) = Y2/s
=
У2
.
-~/2
s
J F(0)cos2n-' 0d0;
- J
Vs
;12
~
(1.47)
as(s, i) =
F (0) sin 2:п: _!..._ 0 d 0;
s
a(s, 0)= V+s f(0)d0.
-~ /2 .
;12
-Е/2
Введение новых коэффициентов
Vf ac(S,
aJ.i/s) =
i); as(i/S)
=
Vf as(S,
i); a(O/s) =
vf a(s,
О) (1.48)
дает
F(0) = -
1
s
-'
. ~?эффициенты
,рис.
1.156
+)
а ( Т) и а с( Т) для случая ; = 2 и ; = 4 показаны на
и в; они соответствуют ра з ложению
;1'1усо1~дальным
~tmc .
~
{а (_o_)t (_о_. 0) + V2 ~ [ac(J_)cos2:п:J_0 +
s s
i,IS=l,IS
s
s
+ as ( sin 2:п: ~ 0]} .
( 1.49)
и косинусоидальным
f(0) в ряд по си
эл ементам,
показанным
на
1.146 и в.
Устремим ; к бесконечности и пусть i/s будет оставаться кон
itтантой:
··~!
-~· ·.
-:·
J
lim ас (J_)
ц.-оо
s
=
ac(v); limas
ц-оо
(-is )= as(v);
может быть любым целым числом,
· 4~сло. С другой стороны,
ВQтельным чис .11ом,
а
v
i/s
i/s = v = fT;
так же, как и i, -
(1.50)
счетное
должно быть неотрицательным дейст·
следовательно,
29
несчетным, иначе некоторые
последующие интегралы обратятся в нуль.
Таким образом, ряд
Фурье содержит счетное множество ортогональных
функций, а
преобразование Фурье - несчетное множество их.
Пределы
и
ac(v)
as(v)
~/2
J
легко получаются из
.
00
(l.46), (l.47):
J
ac(v)= lim V2
F(0)cos 2n ~ 0d0= V2
F(0)cos 2nv0d0;
~~°'
-е12
~
-ао
U2
.
l .51)
оо
S
a"(v)= limVT f F(0)sin2тc+ed0= VТ F(0)sin2nv0d0.
е-+ао
-f12
\9
-Чтобы найти интегральное
представление для F (iO), рассмот
рим определенное значение 0=i0o. Уравнение (l.49) дает F(00 ) в
виде суммы со
счетным
могут быть от
ложены на числовой оси в точках
х(О)
ка.к пока:зано на рис.
"1
-
числом членов, которые
между
1/6.
1
~(t/t)
"
x(J/t) ( /. )
г
•х~~
~{21~
L:
отложенным.и
i/6,
Расстояние
членами
ра~но
Та·ким образом, сумма членов, ум
ноженная на
на
l.16.
площади
1/6,
согласно
под
рав
(l.49)
ступенчатой функ
цией, изабражешной на рис. 1.16. Ис
~пользуя ( l .49), можно •как у1годно близ-
-
ко ап~проксимировать эту площадь для
6 еле.дующим
больших значений
о
J~
1/J 2/f,
4'f,
)f (
х (+)=ас(+)
"'
"'
.
Т 0о) ,
r2cos 2n х
( i ) ,П} .
х Т 0+ as Т r 2sin2n Х
i
J{ас (v) cos 2nv0 +
'°
f(0) = }1 2
Рис. 1•..16.
Переход
от ряда
Фурье
к
преобразо.ванию
Фурье:
х (О) = а { ~
инте
~гралом:
о
+ as(v)sin2nv0Jd
\1.
( 1.52)
Нижний mредел интеграла равен нулю,
та.к ка~к ~нижний предел в сумме ( 1.49)
ст~ремится к О. Первым членом сум-
мы ( 1.49) можно •пренебречь, так как
он чрез'Вычайно мал для больших зна-
чений ~-
Перемен~ная
.ним ать
v
значения
в
( 1.52)
должна •при
всех положительных
действительных чисел (а
rне
тольхо
счетное множество их), иначе ИJНтеграл нельзя рассматривать как
инте.г.рал Римана.
Уравнение (1.51) показывает, что
нечетная функция v. Таким образом,
ac(v) - четная, а a,(v) ( 1.52) можно переписать в
следующем виде:
J [А (v) cos 2nv0 + B(v) sin 2nv0] d v;
00
F (0) =
-ао
A(v) = - 1
2
V2 ac(v);
B(v)= - 1 "rf 2 as (v).
(1.53)
2
30
11
Для треугольной функции (рис. l.14) as(v) тождественно рав
а нулю; ac(v) изображена на рис. l.l5г в соответствии со следую
.
ей формулой:
,
s(
3/8
а
с
( v)
= 2 V2
l-
~ 0) cos 2л:v0 d 0 = -2_ V2 (sin Злv/8 )'
з
Злv/8
8
'
о
1.2.2.
Обобщенное преобразование Фурье
t)
,- Рассмотрим систему функций {f(O, 0), fc(i, 0), fs(i, 0)}, орто
ормированную на интервале (-1/2)0~ 18< (l/2)0. Индекс сука
ывает на четную функцию, а индекс s на нечетную. Величина
может быть конечной или бесконечной. Таким образом, резуль
аты могут быть примени м ы к функциям, имеющим бесконечный
.
· нтервал ортогональности, например, к параболическим цилинд
ическим функциям. Пусть все функции fc(i, 0) будут неотрица
· ~льными для 0=0 и пусть все функции fs(i, 0) переходят от отри
ательного к положительному значению при 0=0. Функции необя
ательно должны быть непрерывными и.т~и
дифференцируемыми.
· огда функция F(0), определенная на интервале (-1/2)0~0<
( 1/2) 0, разлагается в ряд:
F(0)=a(O)f(O, 0)+
L"' [ac(i)fc(i, 0)+as(i)fs(i, 0)];
)
l=I
а/.Л =
0/2
J
F(0)fc(i, 0)d0;
-0/2
(1.54)
0/2
as(i) =
5
F(0)fs(i, 0)d0;
-0/2
а(О)=
0/2
5
F(0)f (O, 0) d0.
-0/2
Заменим
0 в функциях f(O, '0); fc(i, 6) и fs(i, 0) на 0' 2 ):
0'=0/у; Y=Y(§)>l; limy(s)=oo.
~-+СО
J,
Разложение
· о аналогии с
i
ti
(1.55)
F (0) =
..
F (0) в ряд по растянутым функциям получается
(1.45):
fi 1а~.
O)f
ао
(О, 0') + ~ [ас(§, i)f с (i,
1
0')
+ а8 (s,
i)f5(i,
0')]}.
'
(1.56)
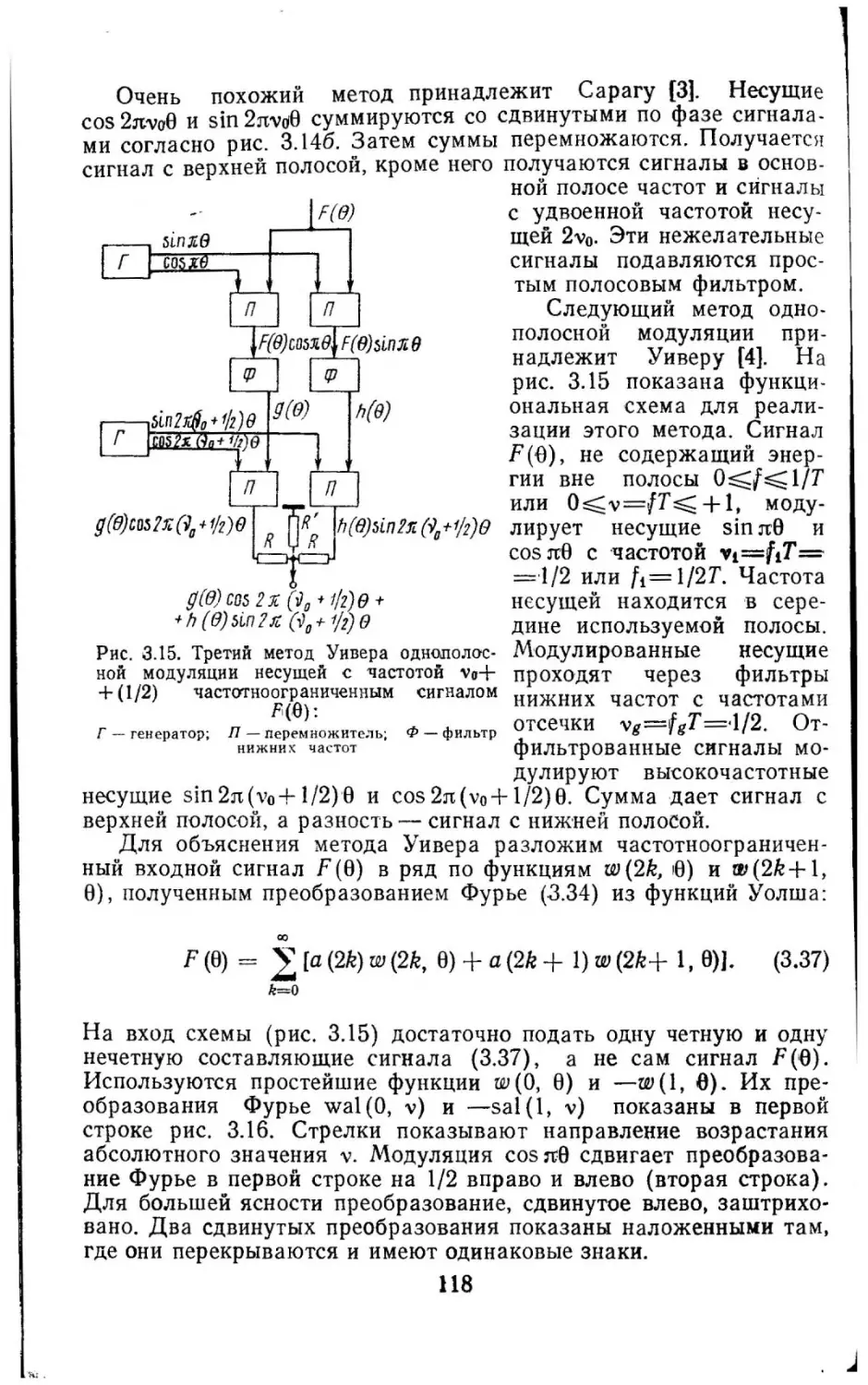
Другие обобщения даиы в[!, 2].
Используемый метод применим к большому классу систем функцнй.
·" трогие математические доказательства без использования сложного математи
~'!ilеского аппарата могут быть получены только для частных случаев. Например,
. ji>езультаты этого параграфа кажутся применимыми для функций Уолша с дво
". ч н о-рациональными значениями i/16= µ; практически они применимы для в се х
, ~!!tействительных з начений i/s.
,
1)
·:.<
2
:k1A
)
31
Растянутые
функции
(-1/2)у0~0< (1/2)у0.
F(0) =О на интервалах
< (1/2)у0.
ортонормированы
Функция F(0)
(-1/2)у0~0<
Коэффициент 1/у объединяется с
i
на
интервале
продолжена
функцией
(-1/2)8 и (1/2)8~0<
так, что
в
правой
части
( 1.56) вместо 0' можно записать О. В ( 1.46) 2лi (0/5) было триви
ально заменено на 2л (i/s) О. Так как i и О необязательно вход.ят в
fс (i, 6) и f s (i, О) в качестве произведения, следующие замены надо
рассматривать как чисто формальные до тех пор, пока не будет
доказано обратное. В частности, i(E, следует скорее рассматривать
как символ, а не как дробь:
fс (i.' 0? ~- f с _(i, О/у) - fс _(i/5, О~;
fs(t, 0)-fs(t, 0/Y)-fs(i/;, 0),
0') = f (О, 0/у) = f (0/s, 0).
F(O) в ряд принимает следующий
\
1
(1.57)
f (О,
Разложение
~ у'у-(а {<, O)f (f, в)+
F (6)
t,)•,
{<,
вид:
iJt,(f, в)+
11
+ as (s,
i) f s (
+' 0)]} ;
у8/2
s F(0)fc(+· 0)а0;
ас(;, i)= ;у
( 1.58)
-у8}2
аД,
i) =
!18/2
5
у~
.
F
(О) fs
-у8/2
(+ ,
О) d О;
у8/2
а (s, О)
=
5 F (О) d О.
~у
-у8/2
Здесь введены новые коэффициенты:
ас(т)=VУас@. i); as(f)=VY"as(s,i); a(f)=Vya(S, О).
(1.59)
Чтобы выражения ( 1.58) и ( 1.59) не были простой формальной
записью, необходимо потребовать, чтобы
коэффициенты ас
или
имели одно и то же значение для всех i и
при кото ·
рых величина i = µ постоянна или чтобы они сходились к опре
деленному пределу для больших значений i и 1):
as (i/5)
lim ас
i,~-+oo
1)
(i/5)
5.
/5
s
(+) =
~
ас(µ); _lim as
i,e-+oo
(+) = as (µ);
.,,
+
= µ.
(1.60)
.,,
Если предел слева не равен пределу справа, берется предел слева.
32
...
нова надо постулировать, что
µ -
неотрицате.1Jьное действите.1ь
ое число и поэтому несчетное, в то время как
Пределы
.
ятся к
илн i/~
i
-
счетное .
существуют, если fc(T, 0) и fs(f, 0) стре
преде.11ьным фун1щиям fс(µ, 0) и fs (µ, 0) 1), определяемым:
(1.60)
у812
lim
l,
~-+00
у8/2
S F(0) fc(µ,
F (0) fс(_!:_, 0) d 0 = lim
\'
J
s
-У8/2
~ -+ 00
-ue12
у8/2
lim
l,
~-+со
0) d0;
у8
S F(0)fs(µ,
F(0)fs(-i , 0\}d0= lim
{'
J
~
-у8/2
~ -но
0)d0;
(l.61)
-У8
у= у~(~)
Функции
fc
(+ , 0) и fs (Т, 0)
сходятся
на
интервале
1/2)у0~0< (l/2)y0 к предельным функциям fc(µ, 0) и fs(µ, 0).
от вид сходимости называется «слабой сходимостью» [3].
' Из (l.51)-(1.61) следует, что
'
ас(µ)=
у8/2
.
J
1
lim
F(0>fc(~ .... " -у8/2
~
,
0)d0;
у8/2
( .
)
as (µ)= ~~
F (0) fs _ i , 0 d_0.
~ у8/2
~
фу;нкция F(0) раоо1а ~нулю вне кQнечоого
(1.62).
J
.
Пусть
авнения
:;,\~~ ':'
ас (!.L)
j\~i\,
(l.62)
=
инте~р1вала.
приводятся к следующему виду:
со
"'
-со
_..,
5 F (0)f с(µ, 0) d0; as (µ) = 5 F (0)f
3
(µ, 0) d 0.
( 1.63)
обы найти интегральное
представление для F (0), рассмотрим
ределенное значение 0=0о. Уравнение (1.58) дает f (i00 ) в виде
··
ммы
со счетным
множеством
членов,
которые
можно
отложить
. оль числовой оси в точках i/y=i/y('g) вместо i/~, как изображена. рис. 1.16. Расстояние между отложенными
членами равно
. . Таким образом, сумма членов, умноженная на l/y, как это
. но в ф-ле ( 1.58), равна шющади под ступенчатой функцией.
а площадь может быть представлена в виде интеграла, если ~.
· следовательно, и у(~)
будут неограниченно возрастать:
ао
F (0)
=
5[ас (µ>fc (µ, 0) + а3 (µ) fс(µ, 0)]d µ.
(l _64)
о
нкции ас(µ) и
. УРЬе
·;'
·
1)
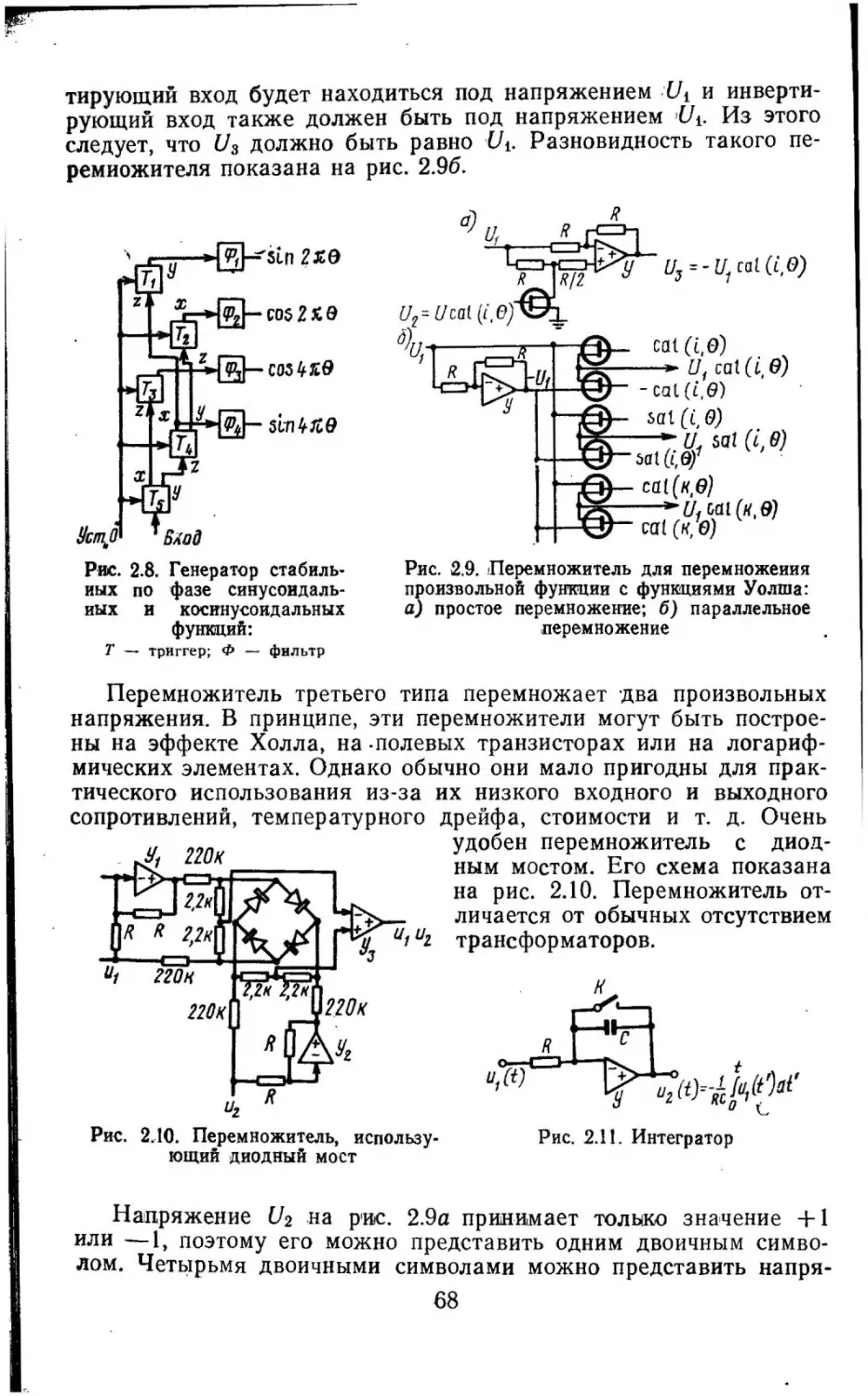
as(µ) называются обобщенным преобразованием
F(e) IПО фу;н'К!.IJИНМ fc(µ, 0) и f.(µ, 0). Уравнение (l.64) ЯВ·
Интегралы будут представлять собой главное значение no Коши . Они
лжны существовать для всех квадратично инте грируемых функций .
33
ляется интегральным представлением функции F (0) или ее обоб
щенным обратным преобразованием Фурье.
Без более тщатель
ного изучения fc(µ,
0) и fs(µ, 0) нельзя сказать, существуют ли эти
интегралы. Переменная µ играет ту же роль, что и переменная \'
в обычном преобразовании Фурье. Поэтому µ называют обобщен
ной нормированной частотой.
Функции fc(i, 0) и f a(i, 0) определены только для положитель
ных целых чисел i. Поэтому fc(µ, 10) и fs(µ, 0) определены только
для неотрицательных действительных µ. Можно расширить опре
деления функций на
/с(µ,
0) -
функция
отрицательные действительные числа:
fc (µ, 0) = f с (- µ, 0); fs (µ, 0) = - fs (- µ, 0),
так и µ, и fs (µ, 0) как 0, так и µ.
четная функция как О,
(1.65)
нечетная
Уравнения (1.62) и (1.63) показывают, что ас(µ) четная и
а,(µ) нечетная функции µ. Поэтому (1.64) можно записать в
виде ( l .53):
F (0) =
"'
S [А(µ) fc (µ,
0) +В(µ) fs (µ, 0)Jd µ;
(1.66)
-ао
А(µ)
1.2.3.
= -
1
2
ас(µ);
В(µ)
= -
1
2
as (µ).
Инвариантность ортоrонал:ьности обобщенноrо
преобразования Фурье
Рассмотрим функцию
G (µ):
G(µ) = Jl2[A(µ) +B(µ)J= -
1
2
Так как А(µ)
-
четная, а В(µ)
-
Jl2[ac(µ) +as(µ)J.
нечетная функции, для
(1.67)
G(-µ)
получаем
G(-µ) =
V2[A (-µ)
А(µ) и В(µ) можно выразить
+ В(-µ)1= V2 [А(µ)- в(µ)].
через G(µ):
А(µ)=~ Jl2[G(µ) +G(-µ)J; В(µ)=+ V2[G(µ)-G(-µ)J. (1.68)
Используя
и
G ( µ), можно привести ( 1.63) и ( 1.64) к виду ( 1.20)
( 1.21):
F (0) =
G (µ) =
+
+
5G (µ)[fс(µ, 0) + fs (µ, 0)Jd µ;
V2 J F (0)[fс(µ, 0) + fs (µ, 0)1 d0.
V2
(1.69)
-оо
00
(1.70)
-оо
В
(1.6.9)
интегралы
от
A(µ)fs(µ, 0)
аулю.
34
и
B(µ)fc(µ, е)
равны
~
с:'
,-,;
Рассмотрим систему ортонормированных функций
{f(j, 0)},
кG-
торые равны нулю вне конечного интервала:
00
Jf(j, O)f (k, O)dO = бik·
Обозначим через q(j, µ) обобщенное
' f(j, О). Из (1.70) следует, что
q(j,µ)=+v2
"'
S
f(i,
(1.71}
преобразование
Фурье от
O)[fc(µ, O)+/s(µ, O)JdO.
(1.72)
-оо
Уравнение
j
fU,
( 1.71)
можно привести к виду:
О){+ V2 ]
00
]"' q (k, µ)
1+
00
q(k, µ)ffc(µ,
V2 ]00 f (j, O)[f
j'"'
О) +
fs(µ, O)Jdµ
jdO=бjk;(l.73)
с_(µ, О)+ fs (µ, O)]d о} d µ=бj!,;
q (k, µ) q (j, µ) d µ =
8ik•
. Ортогональная система {f (j, О)}, заданная на конечном интерва
- ле, преобразуется обобщенным преобразованием Фурье в ортого,: нальную систему {q(j, µ)}.
·
1.2.4.
Примеры обобщенного преобразования Фурье
Рассмотрим обобщенное преобразование Фурье треугольной
функции, показанной на рис. 1.17, по полиномам Лежандра [J j:.
_Ро(х) = l, Р1(х) =х, Р2(х) =-(3х2 -1) и т. д. Интервал ортого
нальности равен -1:::;;х<+1. Произведем подстановку х=2 О 1t
сделаем следующие преобразования:
/(О, О) = Р0
(20);
fc(i, О)= Pc(i, О)= (- l)i (4i + 1) 112 P2i (20);
fs (i, О)= Ps (i, О)= (- l)i (4i - 1)
112
P2i-1
(1.74~
(20);
i = 1,2, .. ..
_
Система {f(O, О), Pc(i, О) , Ps (i, О)} является ортонормирован
" ной на интервале -1/2::::;;0:::;; + 1/2. Все функции Pc(i, О) положи
тельны при 0=0, а все функции P, (i, О)
имеют положительнуш
производную в той же точке.
В точной записи несколько первых
полиномов выглядят следующим образом:
f (О, О)=
1; Ps (1,
О)= 2 ·vзо; Ре (1, О)=-
+
V5(1202 -
1);
Р 5 (2, О)= - V7(2003 -30); Рс(2, 0)= ~ V9(5600 4-12002 + 3).
(1.7~
35
(}' ~1
-/
О)-------+-_ F{8)
{2(/)-·r------+----+------.- wat (О, О)
Pt (2В') l::-:=-:.:==~---!=======t_ Р5 (1/q /l)
Ро
, flc (14, fJ)
•' f1s (2fчJЭ)
' Pc{2/q,fJ)
-P2 (2ft,
-~(20J:..
Рч{2(J)
Р,,(20'
-1}(2В?'
~Р.,(20'
f1в (2е'
fЬ (2 е·,
"" Р5 (3/t,. е)
PJ%. О) ·
" fls('l/t;,O)
Ре N~. О}
Р5 (5/ч, В)
Ре (S/q, 8)
-f;g{2B;
-2
Рис.
1
в-
2
1.17. Разложение функции F (8) в ряды по полино
ма~~ Лежандра, имеющим различный
интервал
ортого
нальности:
а) -
1/2 ~ 0
< 1/2,
{wal (О, 8), Ре (i, 0), Ps (i, 0)};
6)-1~0< 1, {wal(O, 8), Pc(i/2, 0), P5 (i/2, 0)};
в) -
2~ 0
< 2,
{wal (О, 0), Ре (i/4, 0), Ps (i/4, 8)}
.li
1'·Коэффициенты
ac(i) и as(i) для рис. 1.17а можно легко вычис
'ь:
S
1/2
ae(i) =
F(0)Pc(i, 0)d0=2
S (1-f0)Pe(i,
3/8
1
о
-1/2
1/2
S F(0)P
as(i) =
0)d0;
(i, 0)d0=0;
8
(1,76)
-1/2
а(О)
8
3/8(
~ 1-
=
0) d0.
3
о
:~ффициенты ac(i) и а(О) показаны на рис. 1.18а.
!:
~
ю
ю
0,1
0,1
O,J rh::µ)ц'\
O,J ~(µ)О,•!(:~)
0,3
О/+[
0,2
q2
и
0,1
00/2J40012Jlf
i.JLl/2,µ~
Рис.
00123'1
i/4,µ-
1.18. Коэффициенты разложения треугольной функции
F(9) в ряды по полиномам Лежандра рис. 1.17
' Заменим в
(1.75) 0
на
0' =0/у,
где у= у(~) =~=2.
При
этом
и Ps(i, 0) растягиваются вдвое, как показано на рис. 1.176.
еним функции (1.75)
растянутыми
функциями Pc(i/2, 0) и
i, 0)
i/2, 0):
1/2, 0) =
'(1/2,
'
Р8 (1, 0/2) = 2 VЗ (+0);
)2
2
'<212. 0) = Ps (2, 0/2)= !2/2, 0) =
., ,
Ре(2,
0/2)=
Коэффициенты
!J)i~ ас (i/2) =
J
V?l20 (+ 0)
ac(i),
2/2, 0) не
показанным
(1.77)
з (}0)}
3
4
-
120(
++
0)2
з]
определяются выражением
Ре (i/2, 0) d 0 =2
равна Ре
'
f V9[ 560( }0)
ac(i/2)
F (0)
\ 2
значения представлены на рис.
ам
]
1
[ 121-0
/ 1
0)=Pe(l, 0/2) =--VЬ
-1 ;
на
:s (
1-
37
0) d 0. (1.78)
1.186. Они не равны коэффици
рис.
(1, 0).
Ре (i/2,
: 0)
1.18а,
так
как,
например,
Растянем функции (1.75) в четыре раза подстановкой 0'=0/у,
где у= у(5) =15=4, как показано на рис. 1.l 7в:
Р8 (1/4,
Р8 (1,
0) =
0/4) = 2
VЗ (+
0) ;
Pc(I/4, 0)=Pc(l, 0/4)=-+vs[12(+0/-1];
Ps(2/4, 0) = Ps(2, 0/4)
Рс(2/4,
Р,(2,
0) =
=-V7 [20(+0)
-3 (+0)];
+V9[5во(+0) -120(+0) +
4
0/4) =
Неко:торые коэффициенты ас (i/4)
2
изображены
на
3].
1
rрис. 1.18в:
31s
2
S F(0)Pc(if4,
ac(i/4)=
(1.79)
3
0)d0= 2 J (1-f0)Pc(i/4, 0)d0. (1.80)
-2
о
Чтобы вычислить предел ас (i/5) для больших значений i и 5.
необходимо знать Pc(i/s, 0) =Pc(i, ·0/s) для больших значений i и
малых значений 0/5. Известно асимптотическое разложение поли
номов Лежандра Pj(x), которое справедливо для больших значе
ний j и малых значений х:
Р1 (х) ~ V n j у2"
у1_
-
х2
. "r.t
r 1-
BJ
Используя
(1.74),
х2
{(1 -
1
~
siп
[fj
+
4/
\
2
)
cos [('.J + -1 ) arc cos х
2
получаем: Ре (i,
Пр едельные фу~н.к1..щи Ре(µ,
Ре(µ,
6)
1и
arccosx
+-41 :n:]-
+ -41 :n:-1} .
(1 .81)
0/6)- ":- cos 4 _!_ 0.
r n
;
ас(µ) :rюдутчаю'l'ся при 6-+оо:
2
0) = У1t
COS
(1.82)
4µ0;
00
S F (0) Рс (µ,
ас (µ) =
0) d 0 =
- оо
=
4
у :n;
s
3/8
(1- __!_ e)cos4 0d0=
3
µ
3
4 у 1t
(
siпЗµ/ 4
3µ/4
2
)
•
(1.83)
о
Функция ас(µ) есть обобщенное преобразование Фурье треуголь
ной функции, изображенной на рис. 1.17, по полиномам Лежандра .
Она изображена на рис. 1.18а-в. Из рисунка наглядно видно, как
коэффициенты ac(i), ac(i/2) и ac(i/4) сходятся к ас(µ). Функции
ac(v) (рис. 1.15) и ас (µ) (рис. 1.18) равны с точностью до постоян
ного множителя. Можно легко проверить по дифференциальному
уравнению полиномов Лежандра, что это выполняется и в общем
случае:
(l-x)z"-2xz'+i(i+l)z=0;
38
j=0,1,2, .. "
(1.84)
пя малых значений х и больших
j
это уравнение вырождается в
авнение для синусоидальных и косинусоидальных функций:
z'' + j 2z =О.
(1.85)
~' Таким образом, обобщение преобразования
,
иводящимися
·
Фурье представ
ет в основном интерес дл я таких систем ортогональных функ
й, которые не определяются дифференциальными уравнениями,
путем
растяжения
к
уравнениям
синусоидальных
и косинусоидальных функций. Так как функции Уолша опреде
ются
разностным, а
не дифференциальным уравнением, можно
_ идать,
-андра.
что они дадут лучший результат,
чем
полиномы Ле
Обобщение преобразования Фурье
на
преобразование
рлша-Фурье принадлежит Файну. Однако он не делал разли-
,
1!! ' я между четными и нечетными функциями, что является полез
;' : м для применений анализа Уолша-Фурье в теории связи. Ma-
S . матически
строгая теория функций Уол ша, разделенных на чет
;. Ые и нечетные функции (cal и sal функции), принадлежит Пихле,:, ' [2].
.
. . ,~;. Пусть функции f(O, 0), 'fc(i, 0), fs(i, 10) представляют собой
1
:,rункции Уолша:
j
f(O , 0)=wal(O, 0);
<;.
'
Треугольная функция
~-
а (О)
J
1/2
=
(рис. 1.19а)
F (0) wal (О, 0) d 0 = 2
J(
3/8
1-
: 0) d 0;
as(i)
=о.
о
s(
3/8
0)=sal(i, 0). (1.86)
дает коэффициенты:
-1/2
ac(i) = 2
f5 (i,
fc(i, 0)=cal(i, 0);
1- : 0) са! (i, 0)d0;
о
На рис . 1.20а показано несколько значений а(О)
и
ac(i).
Положив y(~)=·s, получим cal(i/s, 0)=cal(i, 10/~) и sal(i/S, 0)=
- FSal(i, 0/~). Из рис. 19а-в видно, что cal (2i/2, 0) и cal(4i/4, 0)
равны функции cal (i, е), периодически продолженной соответствен
, Ио
на два и четыре исходных интервала определения. Этот резуль11ат можно также легко получить из разностного ур - ния ( 1.28).
,l)'аким образом , на интервале -1/2:::::;;10< 1/2 выполняются соотно
'luения :
~l(i,
0) =са! ~i, 0~) = cal (si/s, 0);
.
6=
2'; r = 1, 2,."; _ _!_
2
"0< 1...
2
Из рис. 1.19а-в видно также, что на том же интервале спра
ведливы следующие соотношения:
cal (i, 0) = cal (2i/2, 0)
=
+
= cal [(2i + 1)/2,
0J
+
=
cal (4i/4, 0) = cal [(4i
1)/4, 0J =са! [(4i
2)/4, 0J =
= cal [(4i
3)/4, 0J = cal[~i
11}/s, 0J,
(1.87)
+
11 = О, l, . . "
+
639
l;
s=
2'.
lf"'
1
г·
1
f
в-
2
1/2 о- 1
~1------- F{д)
-1/2
6) _,-1_ _ _ _
__..,
~~~~~~~~~~~~~~юt{t/11,в)
~
: sot (1/2, в)
- sat('s/11,в)
-: 501 (f, е)
L--!E5---=~ruп::::i::::;---t:::::::;--., - sar (sft. е)
sa L(J/2, f9.
sat (7f1t,в)
sat {2,е)
:r.{З;~:Х~сr~~~Е:::Е~~:§~-
sat
(9/IJ,B)
&at (1/2,8)
sat(ttf1t.e)
~__l""LJ'-,_r--
SJ1(
(J, 8)
sat(tJflt,в)
~ЬlВ:{~~~ЬQ:~~~ЕЧ~~- sat~/2,e)
Sllt(15/+,8)
1..l""LГl~.J"\...n...n...n.J~-u--i::r..-::r-.....,;-;;;;.-
юt (//,В)
fJ'Pиc.
1..19.
Разложение функции
ющи.м:
различные
f(0}
в ряды
интервалы
а)-1/2..;:0<1/2,
no
элементам Уолша, име-
ортогональности:
{wal(O, 0), cal(i, 0), sal(i, 0)};
б) -1~0 < 1, {wal (О, 0), cal (i/2, 0), sal (i/2, 0)};
в) - 2 .,;;: 0 < 2, {wal (О, 8), са! (i/4, 8), sal (i/4, 0)}
40
становка (~i+11)/~=µ; i~µ<i+l в
+
(i, 0); i <. µ < i
= wal(O, 0); О<.µ< 1;
=са\
cal (µ, 0)
са!(µ, 0)
(\ .87) дает:
1, i = 1, 2,
. ;J
(1.88)
__
1 <. 0<-1 .
2
2
\соответствующие соотношения получаются для sal (µ, 0):
·
sal (µ, 0) = sa\ (i, 0); i - 1 < µ <. i; i = 1, 2, . . . ;
(1.89)
~ Здесь предельные
1/2 <. 0 < 1/2.
функции са\(µ, 0) и sal (µ,
-
Н) были выведе
,,;· эвристическим путем для интервала -1/2~0<
1/2. Пихлер по
sal (µ, 0) математически строгим путем для пол
·"о интервала -оо < 0< оо, но его доказательства требуют хоро
. знан1ия матемаТ1ики . На 'Р'ИС. 1.12 и 1.13 показано наглядное
Jщставление функций са!(µ, е) и sal(µ, 0), найденное им [2].
{Функции, идентичные на интервале -1/2~0< 1/2, дают одина- .
: е коэффициенты разложения для F (0). Таким образом, для
. µ) и as(µ) получаем:
•
л са!(µ,
и
0)
.
r
1/2
ас(µ)= ac(i) =
F (0) са! (i, 0) d 0, i<.µ< i
+ 1;
~1/2
1/2
as(µ)=as(i)=
S F(0)sal(i, 0)d0,
i-1<µ<. i;
-1/2
ас(µ)= а(О) =
(1.90)
1/2
S F(0) d0,
0<.µ<1;
-1/2
На
- 112 <- 0 < 112. i = 1, 2, . . .
1.206, в, г показаны коэффициенты
рис.
. (4i+11)/4]
и предел ас(µ)
ас[ (2i+ri) /2];
функции (см. рис.
для треугольной
a~qt Lac(i) ~"r 11if1liГ.1111.
0,З
O,J
0,2
0,2
0,1
L.
-
о о 1
5)
ac(~~~;~
az
2
J
О)
о о
"'
4 {4i
+nj4--
о,т
о
1
2
J
o. . . . ._,_.__._..1-J.__.,_~
"
(2i +h)/Z1.20.
J
o,z
)
Рис.
2
iJdcrJ
01
,
0
1
Jl - -
!(оэффшшенты раз.1оже11ия треуго.1ыюй функции
в ряды по элементам Уодша рнс.
41
1.19
F(0)
1.19). Вычисление ас(µ) и as(µ) для функций Уолша является
очень простым. Для этого необходимо вычислить
коэффициенты
а(О), ac(i) и a, (i) и нанести эти значения от О до 1, от i до i+ 1
или от i до i-1. В результате получим ас(µ) и as(µ) на интерва
лах О:;:;;µ< 1; i:;::;;µ<i+ 1 или i-1 <~i:;::;;i.
1.2.5.
Быстрое преобразование УоJIПiа-Фурье
Время, необходимое для
получения
преобразования
можно существенно уменьшить, применяя
названием
быстрого
преобразования
метод,
Фурье.
Фурье,
известный под
Соответствующее
быстрое преобразование Уолша-Фурье было найдено Грином (1)
и обобщено Вэлчем {2, 3]. Кан, Андрюс и Пратт использовали дву
мерное быстрое преобразование Уолша-Фурье для сжатия ин
формации изображения {4]. Вэлчел и Гвинн использовали его для
классификации сигналов {5]. Здесь- форма представления функций
учитывает четность и нечетноrть функций и
классифицирует
их
согласно числу перемен знаков, как на рис. 1.2.
Рассмотрим функцию F (0) на некотором интервале. Разделим
этот интервал на 2п равных по ширине подынтервалов. Для иллю
страции будет рассмотрен случай 23 =8. Обозначим средние значе
ния F (0) на восьми подынтервалах через А. В, ... , Н. Таким обра
зом, F (0) представляется ступенчатой функцией
с минимальной
среднеквадратичеокой ошибкой для
да1Нн10го
'Ч:исла
инrервал,ов.
Преобразование Уолша-Фурье ас(µ) и as(µ) этой
ступенчатой
функции можно получить из средних значений А, В, ... , Н с по
мощью рис. 1.2:
+A+B+C+D+E+F +G+H=a(O)=ac(µ), О~µ< l;
-A-B-C-D+E+F+G+H=a5 (l)=as(µ), 0<µ~1;
-A-B+C+D+E+F-G-H=ac(l)=ac(µ), 1~µ<2;
+A+B-C-D+E+F-G-H=as(2)=as(µ), 1<µ~2;
+A-B-C+D+E-F-G+H=ac(2)=ac(µ), 2~µ<3;
-A+B+C-D+E-F-G+H=as(3)=a 5 (µ), 2<µ~3;
-А+В-С +D+E-F +G-H =ас(3)=ас(µ), 3-сµ<4;
+A-B+C-D+E-F +G-H =a5 (4)=as(µ), 3<µ~4.
Чтобы получить 2n коэффициентов ас(µ) и as (µ), в общем
слу
чае необходимо произвести 2n (2n- l) операций сложения. Быст
рое преобразование Уолша-Фурье требует только 2пп сложений.
Заметим, что преобразование Уолша-Фурье не требует выполне
ния операций умножения, которые занимают много времени в слу
чае быстрого преобразования Фурье 1 ).
1) Можно получить преобr.азование Хаара-Фурье для полных ортогональ
ных систем функций Хаара {6 . Это преобразование может быть еще лучше ис
пользовано для цифровых вычислений, чем быстрое
преобразование Уолша
Фурье (сообщено лично Андрюсом) .
42
Для объяснения быстрого преобразования Уолша-Фурье об
тимся к табл. 1.1. В столбце О указаны восемь дискретных ам
. итуд
А, В, ..., Н и их более общая запись
S 0~.о . В столбце 11 ука-
ны суммы и разности каждой пары дискретных амплитуд и их
лее общая запись. Суммы и разности членов столбцов
ны в столбце
2,
а в столбце
в столбца 2. Общее обозначение
.е,
l пока-
показаны суммы и разности чле
3
S k: ::i указывает в каждом слу-
какие члены предыдущего столбца складываются или вычи
ются. Третий столбец дает коэффициенты Уолша-Фурье а(О),
(i) И as(i).
· Быстрое преобразование Уолша-Фурье
можно
представить
куррентной формулой или разностным уравнением, которое вы
ает из разностного уравнения функций Уолша ( 1.29):
Sf,p
k,m = (- 1)' [i/21+ Р [Sril2"'}:_x
k,m 1
-
наи
б ольшее
целое
+ (- t)i+P sri/2],x
]
k+t, m+I
число,
меньшее
или
(1.91)
,
равное
1 .
2 /;
· О для четных j, х= 1 для нечетных j; k=0,1,"., 2п-т_1; m=O,
·· ... , п; р= О или 1; j =О, 1, ..., т; 2п равно числу отсчетов амплитуд.
,, Для примера рассмотрим
. да (j /2) ={3/2}=11 и х = 1:
член для
sg:~ =(-1)2 [s~:~ +
j=3,
<- 1)
4
р=
1, k=O, m=3.
От
sbl].
·.. __ йденное выражение совпадает с выражением, находящимся в
'' авом нижнем углу табл. 1.1.
· Значения U/2] и х можно вычислить в двоичных вычислитель
··. .· х устройствах следующим образом. Пусть j записано в двоич
"' . й
форме. Деление на два соответствует сдвигу всех разрядов на
ну позицию в сторону младших разрядов. Число слева от
ff!пятой равно [j/2]. Число справа равно х. Например: j = 23=
·.
~·j=10111, +j=ll,5=1011.1, U/2]=11=1011, x=l.
~~· Вычисление начинается с определения
;i, 2n-1.
'
Из U/2]=(0/2]=0 следует, что
~:~
, k=0,1, ... , 2n-1-l.
1.1.
Дальнейшие члены с
2n
членов S~:&,
можно
k=0,1,
вычислить члены
Они приведены во второй колонке табл.
U/2]=[1/2]=0 нельзя вычислить, так как
фtя этого требуются члены sz:~ в то время как известны только
'
~ Члены с х=О.
;;; . !:~ Члены S~:f позволяют вычислить
2n- 1 членов S~:~ и 2n- 1 членов
.Jl·~ так как х может принимать значения О или 1 и, следователь
;ьо, j может принимать значения О или 1, что дает U/2]=0.
.. ,
::~
Быстрое обратное преобразование
Уолша-Фурье получается
... , Н из коэффициентов
:~nутем вычисления коэффициентов А, В,
· ·4(0),
а 8 (1),
... , as(4).
Это можно сделать, инвертируя рекуррент-
43
.
r
.
.
Таблица
!.!
Быстрое преобразование Уолша-Фурье
1
+
0,1 = + ( SO,O
о.о
+ s?;8) =А+в
0,1 _
( 80.0_
8 0,1-о.о
- s?:8) = -А + В
SO,O
so,o
о.о-
3
2
о
А
so,o
_в
1,0-
so,o
- с
2,0so·o=D
з.о
_ + ( 8 0,0 +
8 0,0
1,12,0
+
s~;8) = + С+ D
0,l __ ( SO,O_
8 1,12,0
- sg;g) :;;,· -~: с+ D
0.0 _ +
80.2-
+
( 8 0.0
0,1 +
so.o
0,3 = + ( so,o
0,2 +
+ s?;g)=+A+
+в+ С+ D+E+F +
s?:~) =+А+
+в+с+D
0. 1 _
( 0. 0 _
8 о,1
8 0,2--
+а+н
-в+с+D
s0,1
- - ( sO,O
0,30,2- s?;g) =-А-В-С-
81
0,2.о _- + ( 8 0,0,11_
-D+E+F+a+н
-s?;?)=-A-
_ + ( 0.1 _
8 0,2
--:о 1) .
.-s 1;2 =-А-В+
1,0
8 0,3
-~;t}=-A+
+в+с-D
1,1 __ ( 8 0.1+
80,2-:О, 1
+ s?;~) =+А-
+c+D+E+F-G-H
1.1
8 о.з
__
- ( 80.1+
0,2
+ s?;~) = +А+ В-
-B+C-D
So,o
_
4,0-
Е
so,o=
5,0 F
0.0 =
82,1
+ ( 84,0
0.0 +
0.0 =
8 1,2
+ ( 8 2,1
0,0 +
-C-D+E+F-G-H
2.0 _ - ( 80,2
1.0 +
80,3-
+ sg;~)=+E +
+ sg;g) = + Е + F
+F+а+н
0.1
_
(
0.0_
0.
1 _ - ( 8 0. 0 _
8
8 2,14,0
8 1,22,1
- sg;~) = - Е + F - sg;?) =-Е-
+ s::g) =+А-В-
-C+D+E-F-а+н
-F+а+н
so.o
=G .
i,O
sо.о_ н
1.0-
=
80.0
З, 1
+ ( 8 0,0 +
б,0
+ s~;8)=+а+н
0, 1 _ - ( 8 0.0_
8 3,1
6,0
- s~;8)=-G+H
1.0 _
52.1
0,3 -_ + ( 8 0,2
-+ ( 8 0.1
1.22,1 _
8 1.0
-S~;~)=-E+
- s:;g) = - А+ В+
+F+G-H
+c-D+E-F-
_ (so.1
81.1
1,2-2,1 +
+ sR:J) =+Е-
-а+н
5З.О
0,3
-
-F+G-H
=-( si .· ~-
s::~) =-А+в-
-C+D+E-F+
+G-H
.1_+(s1 . 1+
8 з0,3
0,2
+ s1:~)=+А-в+
1
+C-D+E-F+
+a-ll
44
J
Sk:',',, . Из
ую формулу для
суммы и ра зно ст а Si:~
и S~.1п.
полу·
, аем следующие рекуррентные форму.11 ы:
sri12J.x
_ _!_ (- l)i+u12J (si.o
+si.1
).
k+l, т-1k.m
k.m ,
2
u12J.x = _1 (- l)ш2J (Si.o
_ 8i.1)
8 k,m-1
k.m
k.m ,
2
''
Эти фор~1улы можно объединить в одну:
sUJ_2J,x_
= _1 ( - J)PiHi/2] (Si,O
k , р,т 1
k,m
2
+ (- l)P Si,1)
k.m ,
де р=О или !; х=О для
j - четных, х= 1 для
наибольшее целое число, меньшее или равное
'/2] -
1.2.6.
( 1.92)
нечетных;
j-
( 1/2) j.
Обобщенное преобразование Лапласа
Преобразование Лапласа Х(а,
v)
временной функции
иоб
F(0)
'.атное преобразование можно записать в сдедующем виде:
00
5F(0) е-а
Х (а, v) =
0
e-i2 пv0 d 0;
(1.93)
о
"' Х(а,
S
F (0) = еа0
v) e+i2nv0 d "·
(I .94)
-оо
,.
Очевидно, что преобразование Лапласа от функции
'Но рассматривать как преобразование Фурье от
. ель е-а0
.
ф
делает
F (0)
ункции
F (0) мож·
F(0)e- . Множи~
преобразуемыми
по
Ф
урье,
да-
е если они квадратично неинтегрируемы. С учето~r этого заме
ания из ( 1.93) и ( 1.94) получаем обобщенное
преобразование
.
со
а 5 (а, v)=
5F(0) е-ае fs (v, 0) d 0;
(1.95).
о
со
ac(cr,v)=
SF(0)e-a6 fc(v,
0)d0;
о
J [ас(а, v)fc(v, 0)+as(cr, v)f (v, 0)Jdv.
00
F(0)= еае
~
Как и в случае обобщенн о го
!Предел интегралов
·
5
_,,,
( l .9 о~)
(1.96)
пр ео бразования Фурье, нижний
н е равен -ос. так каr'
ожет сделать эти интегра,1ы расходящи:.rися . Функция
-0'6
·
F (0) дол
ыножитель е
<;жна достаточно быстро стремиться к ну.1 ю при больших отрица
~етельных значениях 0. Здесь используется обычно е пр едп ол ож е ние
·lf ce) =О
для 0<0.
45
"'
1.3.
ОБОБЩЕННАЯ
1.3.1.
Частота
ЧАСТОО"А
Физическая интерпретация обобщеяной частоты
-
это параметр, по которому различаются отдельные
функции системы
интерпретируют
{cos 21Т1#} или {sin 2л,ft} . Обычно физически ее
как
число
f
периодов
за
единицу времени.
Нор
иированная частота v = Т интерпретируется как число периадов
за временной интервал, равный Т.
Обобщенную частоту можно интерпретировать как половину
€реднего числа пересечений нулевого уровня за единицу времени
или
как
половину среднего
числа
перемен
знаков за
единицу вре
мени. Нормированную обобщенную частоту µ можно интерпрети
ровать как половину среднего числа пересечений нулевого уров
ня за отрезок времени, равный Т. Обобщенная частота имеет раз
мерность [с- 1 ]:
µ=rpT;
ffJ
= µ/ 1, [с-1 ].
(1.97)
Определение обобщенной частоты было выбрано таким образом ,
•побы оно совладало с определением частоты, если его применить
I синусоидальным и
косинусоидальным
функциям .
Например,
синусоидальное колебание с частотой 100 Гц имеет 100 периодов
в секунду или 200 пересечений нулевого уровня в секунду. Поло
вииа числа пересечений нулевого уровня равна 100, что равно по
величине и по размерности частоте 1).
Точки пересечения нулевого уровня синусоидальных и косину
соидальных функций расположены равномерно во времени, одна
ко определение обобщенной частоты применимо и к функциям с
неравномерным
расположение м
точек
пересечения
и
даже
к
не
периодическим функциям.
Для обобщенной частоты q> полезно ввести термин « частость».
Одной из причин этого является то, что термин «обобщенная ча
€тота:~> уже использовался в теории затухающих колебаний; вто
рой причиной является то , что волны в трехмерном пространстве
характеризуются как частотой, так и частостью. Частость опреде
ляется как половина среднего числа пересечений нулевого уровня
в секунду ; для нее можно использовать сокращение «zps»
Рассмотрим функции Уолша cal(i, е) и sal (i, 0) (рис.
личина
i
равна
половине
числа
перемен
знаков
на
2
).
1.2).
Ве
интервале
1/2~0<1/2, а rp=.i/T есть частость периодически продолженных
функций. Если растянуть функции в s раз, то они будут иметь 2i
перемен знаков на интервале l/2~~0<1/2s; i/,s =1µ будет рав-
•)
Число перемен знаков в единицу времени
было использовано для опре
д.еления мгновенной. частоты частотномодулированного синусоидального колеба11ия
·{1, 2, 3}.
Z) Произошло
от
number rero crossings per second -
нулевого уровня в секунду . (Прим . ред. )
46
число
пересечений
о половине среднего
ельностью
1
)
числ а перемен знаков на интервале дли
l.
Рассмотрим в качестве примера периодически
продолженные
!полиномы Лежандра Pc(i, 8) и Ps(i, ·8) (рис. l.l7a) . Они имеют
2i перемен знаков на интервале - 1/2~8 < 1/2. Их растяжение
s раз
.в
i/s= µ
+
приводит к тому, что инт ервал становится
равным ; 11
становится равным половине ср еднего числа перемен зна
:ков за временной интервал длительностью
Заменим нормированные переменные
.
l.
v и 8 в функции sin 2л:v0
енормированными переменными
f= v/T и t=OT:
sin 2:rtv8 = sin 2:rt (jТ) t/T = sin 2:rt ft.
( 1.9~
араметр Т в ( 1.98) пропадает. Синусоида л ьные и косинусоидаль
. ые функции содержат три параметра: амплитуду, частоту и фа. овый угол . Это несправедливо для полных систем ортогональных
· ункций, у которых частость и временная база не связаны зна
• ом умножения. У функций Уолша sal (µ, 8) или полиномов Ле
. андра Ps(µ, •0) между µ и 0 стоит запятая . Таким образом, под
, тановки qJ·= µ/Т и t=HT дают:
sal (µ, 0) = sal (срТ, t/Т); Р5 (µ, 0) = Р8 (срТ, t/T).
(1.~
ти функции содержат в своем общем виде четыре параметра~
мплитуду V, частость ер, задержку t0 и временную базу Т :
V sal (срт, t /
0
);
VР 5 (срт,
t :
0
).
· .3.2. Спектр мощности, спектр амптrrуд, фильтрация cиrвaJio•
.. Частотную функцию a 2c(v) +a2s(v) можно получить из преоб
. азований Фурье ac(v) и as(v) (I .51) и интерпретировать ее как
астотный спектр мощности. По аналогии
частостную функцию
~ 2с(µ) +а 2 8 (µ), полученную из обобщенных преобразований Фу
·· ье ас(µ) и a s (µ) (l.62) и (l.63), можно интерпретировать как ча
~~тостный спектр мощности. Возведем ( l .58) в квадрат и проинтеr
ируем, использовав соотношение для коэффициентов
.
. ~i SF2 (0) d 0 =
:2
; . -оо
t
j {а (Т) f (f, 0) +
-оо
(l .59)::
[ас (Т) fс
i/~=l / i,
(
+,
0)
+
+as(f )ts(f •0)]} d0.
2
· нтегралы от произведений различных функций равны нулю в си. у ортогональности этих функций . Интегралы от {2 (0/S, 0).
c(i/5, 0)' 1f2s ( i/s. 10)' умноженные на у- 1 , дают l:
l_
___
,...._
а
"..
J
li'(B)dB
+
~ \a'(f) +'!<~)а:(-[)+ ai(-[)]j.
1 ) Част о сть периодической функции равна половине числ а
период, частость непериодической функции равна пределу
еремен знаков за единицу в ремени, если этот предел существует .
'
;~
·.
47
пе ремен зна!{ов
половины чие.11а
Эта су~ша имеет тот же вид, что и
Таким образом, ее мо
( 1.58).
ж1ю интерпретировать как площадь под ступенчатой функцией и
для больших значений
~
;
п у=у(;)
со
SP
2
заменить интегралом
со
(0)d0=J[a~(µ)+a;(µ)Jdµ=+ S[a~(µ)+a;(µ))dµ.
-со
о
(1.100)
о
Используя ненормированную запись, получаем
S F2 (t!T) dt= Т _\"' [а~ (<р,
"'
-со
Т) +а; (<р Т)) d(<p Т).
(1.101)
о
Величина
Т[а 2с ( µ)
+ а 8 (Jl) ]dµ
2
есть
-
ac(µ)fc(~t, О) ДО
ac(µ+dµ)rc(µ+dµ,
энергию сигнала
F(0).
8)
a.(µ+d~t)/s(µ+dµ, О), если интеграл от
энергия
И
ОТ
компонент
as(µ)fs(µ, 0)
от
ДО
F2(t/T) рассматривать как
Таким образом, а 2с(µ) +а 2.(µ)
имеет раз
мерность мощности и ее можно интерпретировать как частостный
спектр плотности мощности.
Используя
+ as (v) ],
2
+a s(\1)
функцию
G (v) =А (v) +в (v) = ( 1/2) V2fac(v) +
можно переписать частотный спектр
в следующем виде:
а~ (v) +а; (v) = 2 [А 2 (v)
+В
2
(v)] = G2 (v)
мощности
+ G2 (-v).
a 2c(v)
+
(1.102)
Здесь использованы соотношения (1.16), ( 1.19) и ( 1.52). Частост
ныir спектр мощности можно з аписать в виде
"
а~(µ)+ а;(µ)=
Квадратный корень
4 [А2 (µ)
+в
2
(µ)! = Gz (µ)
+ G2 (- µ).
(1.103)
[а~ (v)+ а; (v)] 112 можно интерпретировать
как частотный спектр амплитуд. Такая интерпретация невозмож
[а~(µ)+ а;(µ)] 112 ,
на д.1я корня из частостного спектра мощности
так как для этого необходимы специфические свойства
дальных и косинусоидалLных функций 1 ).
Используя соотношение
А sin х + В cos х = (А2 + 8 2 ) 112 cos ( х - arc tg ~ )
(1.52)
F
,
синусои
( 1.104)
l\:ожно переписать в следующсы виде:
(О) = У2
со
\' [ а2 (v) + аs2 (v) ] 112 cos [2л:v8- агс tg as (v)( v) Jd v.
•
о
с
N\ножитеJ1ь [а~ (v)+ a;(v) ] 112
ас
(1.105)
можно интерпретировать как частот
ныi1 спектр амп.чпуд, так как он представляет собой амплитуду
1) Для вы п ада теоре~1ы ВиЕера-Хинчина в обычной форме записи требуют
ся теоремы сл о жения синуса и косинуса. Поэтому другие системы функций ие
имеют r.ряыого а11а.1ога теоремы Винера-Хи1 1ч 11на. У функций Уолша имеется
абсrрактныl! ан а лпr этоil •еоремы, основанный
на
двоичной
корреляционной
фущщнн
J
F(O)G(O
Е9 т)d0
48
олебаний с частотой v без учета фазового углаагс tg
,
и функции не удовлетворяют теореме сложения
as (v) •
ас
( 1.104),
Ее-
(v)
то такая
,нтерпретация для
квадратного корня [а~(µ) +а;(µ) ]112 невоз
·:,ожна. Однако ас(µ) и as(p) аналогично ас(\') и as(v) можно рас
)1атривать как амплитудны.:
ункции F(8).
спектры
четной
и
нечетной
части
Фильтры или, в более общем случае, системы, которые преоб
азуют входной сигнал F(8) в выходной Fo(8), можно
описать
ператорами. В связи с применением полных систем ортогональ
iых функций особенно важным является понятие линейных опе
. торов, которые испо.1ьзуются для описания линейных систем.
·:бозначим через Q оператор и через {f (j, 8)} - по.1ную систему
· тогональных функций. Применение Q к опреде.1сн1юй функции
·и входному сигн:!лу f(j, 8) дает на выходе сигнал q(j, 8):
Qf (j, 8) = q(j, 8).
(1.106)
.{ Оператор Q называется линейным, если для всех функций си
, мы {f (j, 8)} выполняются законы пропорциональности и супер
.зиции соответственно:
Qa(j)f(j, 8) =a(j)Qf(j, 8);
( 1.107)
Q
00
00
i=O
i=O
L a(J)f(j, 8) = 1: Qa(J)f(j, 8).
Оператор Q может быть функцией
!fl
j
и
8.
(1.108)
Если Q зависит от
0,
оператор и система, которую он описывает, являются линейны
и зависимыми от времени; в противно:..1 случае они линейны и
··. вариантны во времени. Примером линейной системы с перемен.
. ми во времени параметрами :может служить амп.1итудньш молятор. Пусть входной сигнал F(8) представлен
в виде суммы
:a(j)f(j, 8), а несущая представлена в виде h(k, 8) = Q. Сигна.11
jk, 0) может б.RIТЬ, например, синусоидальной несущей
, 2 sin 2лk8 или несуще!1 Уо.лша wal (k, 8). Амплитудно-модулиро
~
анный сигнал с подавленной несущей запишется в виде:
00
F(8)h(k, 8)
=
QF(8)
=
Q~ aU)f(j, 0)
=
j=O
~a(j)q(j, 0);
(1.109)
i=O
q(j, 8)=li(k, 8)f(j. 0).
Если
h(k, 8) яв.r~яется несущей ~'олша wal(ll, О). то для функ
f(j, 8) лучше использовать функции Уолша \У31 (j, 8). Для
(j, 8) получаеы: q(j, O)=\\·al(k, 8) \Yal(j, 0)=\\'al(kffij, О). Если
(k, 8) является синусоидальной несущеii V2 sin 2;r.k0, то в ка1:естве функций системы {f (j, 8)} лучше использоnать функции f (О,
),V2 sin 2лi8 и -V2 cos 2лi8. Тогда функции q(j, О) равны:
" ии
q (О, 0)= y2sin 2n k 8;
49
q (2i, 0) = cos 2л: (k- i) 0- cos 2л: (k + i) 0;
q (2i - l, 0) = sin 2л: (k - i) 0 + sin 2n (k + i) 0;
j= О, 2i; 2i- l; i = 1,2, . . .
С развитием теории связи определение линейности менялось.
Первоначально оно относилось только к дифференциальным опе
раторам, затем к операторам, независимым от времени, но необя
зательно дифференциальным. Используемое здесь определение не
требует, чтобы Q был дифференциальным или независимым от
времени оператором. Такое определение давно использовалось ма ··
тематиками; его внедрение в связь часто приписывают Вуншу {l].
Если система описывается
линейным
оператором Q и если
имеется свобода выбора системы функций
.
то можно вы
{f(j, 0) },
брать систему собственных функций Q. Уравнение
в этом
( 1.106)
случае записывается в виде
Q f (j' 0) = ь
(J) f (j, 0).
(1.110)
Удобно называть f(j, е) собственной функцией Q даже в том слу
чае, если f(j, '8) в правой части (1.110) будет заменена сдвинутой
во времени функцией Jfj, 10-6(j)].
В частотной теории связи характеристики фи:Льтра можно опи
сать затуханием и фазовым сдвигом. Это описание предполага-ет,
что ко входу фильтра приложено напряжение И cos 2nft. На вы
ходе фильтра появляется
установившееся
напряжение Ис(f) Х
Xcosf.2nft+ac(f)].
Частотные
функции
2 log Ис(f)/И=
=-2 log Uc(v)/•U и a.c(i).=•ac(v) называются соответственно ча
стотным затуханием
F (е)
и фазовым сдвигом.
имеет преобразование Фурье ас (v) и
сигнал получаем из
Пусть входной
as (v).
сигнал
Тогда выходной
( 1.52):
J{ac(v)Kc('v)cos[2л:v0+ac(v)]+as(v)Kc(v) sin [2nv0+ac(v)J}d
v,
(1.111)
00
F&(6) = у2
о
v = fT;
Кс (v) = И с (v)/U;
0 = t/T.
Описание фильтров с помощью частотного затухания и фазо
вого сдвига особенно удобно для телефонных фильтров. Согласо
ванные фильтры, с другой стороны, обычно описываются с помо
щью импульсной переходной функции.
фильтра прикладывается импульс
В этом случае ко входу
напряжения в виде
Дирака ~(t) и определяется напряжение на выходе Р
(6).
функции
Таким об
разом, нет необходимости обращаться к синусоидальным
и коси
нусоидальным функциям. Выбор системы функций для описания
фильтров определяется только соображениями удобства.
Пусть на вход фильтра вместо И cos 2п# поданы напряжения
Иfс(µ, 0) и •U/.(µ, 0). Функции fc(µ, 6) и ifs(µ, е) те же, что и
в обобщенном преобразовании Фурье ( 1.63). Тогда на
выходе
фильтра будут появляться установившиеся напряжения Ис (µ)f c[µ,
0~0с(р.)] и Иs(µ)fJ.µ, 0-0 5 (µ)].
Назовем -2 log Ис(µ)/Ии-
50
log Иs(µ)/U
коэффициента м и затухания. Функции ·Ос(µ) и
Os(µ)
овем задержками, так как термин «фазовый сдвиг:. неприме
·м к функциям, отличным
от синусоидальной и косинусоидаль-
Если fc(µ, 8) и fs(µ, 0) являются синусоидальной и косШiусо
альной функциями, то эти простые соотношения
справедливы
· фильтров, содержащих емкости и индуктивности. Однако мо
0.
,'о построить фильтры , содержащие перемножители, интеграто
·' накопители, резисторы и переключатели, которые не бу
т искажать функции Уолша, но будут искажать синусоидальные
; осинусоидальные функции. Такие фильтры лучше описывают3функциями Уолша.
(Пусть сигнал F (0)
имеет обобщенные преобразовани_я
Фурье
и as(µ) . Пусть затухания и задержки будут -2 log Ис(µ)/U,
log • Иs(µ)/U И •0с (µ), 0s(µ). Из (1.64) получим ВЫХОДНОЙ СИГ
_µ)
.
:л:
00
5{ac(µ)K,(µ)fAµ,0-
:Fo(0) =
~-
о
11
Ос(µ)]+ a 5 (µ)K 5 (µ)f 5 [µ,0-0 5 (µ)J}dµ;
(1.112)
Кс (µ)=и с (µ)/И; Ks (µ) = Иs (µ.)/И.
авнение ( 1.111) и ( 1.112)
показывает, что
,,11ько Kc(v) и a c(v), но не содержит Ks(v) и
( 1.111)
as(v).
содержит
Последние
"ены появятся, если частотные фильтры будут иметь разные ха
):теристики для синусоидальной и косинусоидальной функций од
'й и той же частоты. Тогда входное напряжение ;U sin 2л.ft пре
разуется в выходное напряжение Иs(f) sin(2n/t+.a.(f)1 а не в
Такое различие между синусоидальной и ко
:Jf) sin{2щft+ .ac (f)].
нусоидальной функциями может иметь место только при пали
в цепи зависимого от времени элемента и поэтому не может
., и
_" никнуть в линейных
и инвариантных во времени
частотных
льтрах.
1.3.З. Пр11меры преобразоваиий Уоmпа-Фурье
и
спектров
мощности
На рис . 1.21 показаны функции времени f (0) , их преобразова
Уолша-Фурье G(u.), ас(µ), as(µ) и частостный спектр мощ-
ости а2с (µ) +a2s(µ):
-<
. {jJ.)
+V2 j
.
"
=
F (0) [cal (µ, 0) + sal (µ, 0)] d 0;
\
1
00
1
;;:(tt) = 2° V2 fG(µ)+ G (-µ)];
а~(µ) +а;(µ)
= (? (µ)
+
(1 . 113)
1
as (µ)
(? ( -
=
"2 V2fG(µ)-G(-µ)J; 1
µ).
1
5. Можно видеть, что сжатие первого импульса в два раза при
' . дит к пропорциональному растяжению преобразования G(µ) . В
'· еделе получается б-функция . Ее преобразование G (µ) имеет п.ооянное значени е во всем интервале -оо<µ<оо .
51
Далее можно видеть, что преобразование G (µ) импульсов Уол·
ша (строки 1, 4, 5, 8) ограничено по частости. Это существенно
отличается от хорошо :известного результата анализа Фурье, за
ключающегося в том, что функция. ограниченная во вре~1ени, не
может иметь ограниченного по частоте
преобразования
Фурье.
a'f (р)+ аJ(д)
F(e)
1 f'2 G{µ)
wat (~ o)J_ _ __,L __.]'"""Г71--'--""-
Гj1
2wа1 (о.2е) D_
t_
o(eJ_.....
sal (1,8'/"c:::J
· · r:J
caiu,01
' '
п
п
u
u
Г'7"1
0
0
:;aL(2,8) ПОПО
cat (2 0 1 л r;J
__~_Л_
u
n ...л"--........._ri_
''}LJ LJ
о
о
__,__._......_ГL...
о
1/ -1/
о
1/2 -1/
е~
о
Рис.
1.21. Некоторые времен.н:~е
G(µ), ас(µ), а,(µ) и частостный
функции,
о
1/ -1/
jl--+
)1-
_л.л_
л
л
Ml ~·.,u
r3 6) Г'lП
.....
uuп -u,.._.___ГL
- 1/2
,n_
их
.....Л_._--.._,ГL
...
о
1/ -1/
)1-
jl-
лреобразова·ния
спектр мощности
+а2(-µ)
п
Уолша-Фурье
a 2 .(µ)+a 2 ,(µ)=G2.(µ)+
Преобразование Фурье для синусоидальных и косинусоидальных
импульсов (см. рис. 1.1), показанное на рис. 1.6, является беско
нечным по оси частот. Преобразование Уолша-Фурье устраняет
это неудобное свойство обычного преобразования Фурье; ширина
полосы в случае преобразования Уолша-Фурье, конечно, относит
ся к полосе частостей.
Класс временнь~х функций, ограниченных I\aK по времени, так и
по частости, можно установить,
исходя из рис. 1.21. Импульсы
Уолша cal(i, 0) и sal(i, 0) равны нулiо вне временного интервала
-1/2~0<
1/2. Их преобразования Уолша-Фурье равны нулю вне
интервалов - (i+l)~µ~(i+l) или -i~µ~i. Та
образом, любая функция времени F(0), состоящая из конеч
частотных
ким
ного числа импульсов Уолша, ограничена ка:< по времени, так и
по частости.
t
F (0)
=
а (О) \Val (О, 0)
+ 2:
ас (i) са! (i, 0)
+ а5 (i) sal (i,
sal (i, 0) =О
д.т~я
0); (1.114)
t=I
\val
(О,
0) = са1 (i, 6)
=
52
101 > 1/2.
усть
имеет преобразование Уолша-Фурь е
F(0)
олняются
G (~t). Тог,'lа вы
следующие соотношения :
F (0) = О
{] (µ)
=о
> 1/2;
1 µ 1 > l + 1.
для 10 1
для
(1.115)
Ортогональность сист е мы функций инвариантна по отнош е аию
обобщенному преобразованию Фурье, а посл еднее включает в
· ебя преобразование ~'олша-Фурье. Таким образом, G (~t) мож
tJ;!о записать в простой форме, если известны коэффициенты а (О) ,
. c(i) и as(i) разложения (l.114). Пусть q(O, µ), Qc(i, µ)и Qs(i, µ)
. бозначают преобразование Уолша-Фурье функций \Val (О, 0),
al (i, 0) и sal (i, е). Находим преобразование G (µ) от F(0):
l
G(µ)=a(O)q(O, µ)+
L [ac(i)qc(i , µ)+as(i)q
5
(i, µ)].
(l.116)
i=O
ункции q(O, µ), q8 (l, µ), Qc(l, µ), .. " q8 (3, µ) показаны во второй
'. олонке рис. 1.21 в строках 1, 4, 5, ... , 8. Нетрудно получить функ
. ии Qc(i, µ} и Qs(i, µ) для б6льшИх значений i.
~
На рис. 1.22 показаны преобразования Уолша-Фурье для си
. усоидальных и косинусоидальных импульсов, равных нулю вне
ffi
1/12
wat(o,e)
1
1 "
"
1 "
1
11
-fS
-10
Рис. 1.22.
Преобразовани.я
Уолша-Фурье
G (µ) синусо
Рис.
·I.23.
идальных
женных
(
t
1
-5
импульсов,
ложения
косинусоидальных
полученных
ментов рис .
j
"
!!
О
11 1
1 "
S
1
1 "
'
!
1
15
!О
t-
:µ - и
1
из
Коэффиuиенты ра з
периодически
синусоидальных
эле-
продол
синусоидальных
изображенных
на рис.
ряды по периодическим
.J.!
uиям Уолша
cal(i, 0)
и
ко
элементов,
и
в
функ
!.!,
sal(i, 0)
1 интервала -1/2~0<1/2. Можно видеть, что ортогональность п о
лученных функций сохраняется . На рис. 1.23 пок аз аны [(оэффи
. циенты а (О), a8 (i) и ac(i) ра з ложения периодических синусои -
53
дальных и косинусоидальных функций в ряд по периодическим
функциям Уолша. Сплошной спектр (рис. 1.22) здесь трансформи
ровался в линейчатый. Нетрудно видеть аналогию преобразования
Фурье импульса и разложения в ряд Фурье соответствующей пе
риодической функции.
На рис. 1.24 показан
частотный спектр
мощности a 2c(v)
2
a2s ( v) = G2 (v)
G (-v) для первых пяти синусоидальных и коси-
+
t2
?:'
~
...
·f:,8
, ,/\1
\
а
1
~
1
w
1
-:;:-
~
e.i
С.!1
,
\
Рис.
+
+
о
1
't:f.
\
\ '
J.
'k\ ' г
1\
/, \
1
1 '\,\
\\
G,G
13,3
"'
'
-~
1
1
20
/G,G
s
1
JJ.J
-----ifi
fDf f rцJ:.:.:Y,G,G
a 2 c(v)+a2 0 (v)=G2-(v)+10Z(-v) синусои
J.9:
а) f(O, 0); б) f(1I, 0); f(2, 0); в) f(З, 8), f(4, 0) ; г) частотный спектр мощности
прямоугольных импульсоо рис . 11.3 при условии., что они имеют в пять раз боль
шую энерr.ию импульсов рис. •1.9
1.24.
Частотный спектр мощности
дальных и косинусои.дальных импульсов, изображенных •на рис.
·нусоидальных импульсов, показанных на рис. 1.9, и прямоуголь
ных импульсов, показанных на рис. 1.3. Площадь под кривыми,
будучи умноженная на Т, дает
энергию
сигналов .
Частотный
· спектр мощности на полном интервале -оо<0<оо получается
зеркальным отображением кривых (рис. 1.24) относительно оси
<>рдинат.
2.
НЕПОСРЕДСТВЕННАЯ ПЕРЕДАЧА СИГНАЛОВ.
2.1.
ОЮ'ОГОНАЛЬНОЕ РАЗДЕЛЕНИЕ КМV ОБОБЩЕНИЕ
·ВРЕМЕННОГО И ЧА<Л'ОТНОГО РАЗДЕЛЕНИИ
2.1.1.
ПредстаВJiение сиrиалов
ассмотрим телеграфный алфавит, состоящий из конечного чис
а символов. Примером такого алфавита может служить телетайп
ый алфавит, состоящий из 32 символов.
Обычно эти символы
. редставляются комбинациями из пяти коэффициентов, принимаюих значения
1 или -1:
-
.
+
символ
символ
и
1: + 1+1+1+1+1
2: +1+1+1+1-1
т. д.
В общем случае символы могут состоять из набора т коэффи
иентов, принимающих произвольные значения . При этом любой:'
имвол х можно записать в виде
ах(О), ax(l), . . . , ax(j), ...• ах(т-1).
Другим важным способом
представления
(2.ly
символов является
редставление их с помощью временных функций. Рассмотрим т
ременнЬ1х функций
0). Умножим функции на коэффициенты
лх(j) и сложим произведения. Тогда получим представление х-го"
f(j,
. имвола
временной функцией
F х (0):
m-1
Fx (0) =
L ах (J) f (j, 0).
(2.2),
j=O
Если система функций {f(j, 0)} линейно независима ,
то по
функции F х (.0) можно восстановить каждый из коэффициентов
a.jj).
Этот процесс особенно прост в том случае, если функции ор
.тогональны. Пусть функции ортогональны и нормированы на
тервале -1/2~0< 1/2. Коэффициент ах
(k)
ин
можно получить ум
ножением F х (0) на f(k, 0) и интегрированием произведения. Для
этой операции обычно используют название «корреляция f x (0) с:
'
'
f(k, 0)»:
1/2
m-1
1/2
-1/2
/=О
-1/2
S Fx (6) f (k0) d6 =
~ ах(/)
55
S f (j, 6) f (k,
0) d 0 =ах (k). (2.3)
.-·
~
.
- -; ·
.
Пусть
m=5,
ах. (О), ах. (2), ах.(3) равны +l и ах.(1}, ах.(4) рав-
11ы -1. Ес.'lн функции f(j, 0) представляют собой прямоугольные
.импульсы, пока з анные на рис . 1.3, то F х. (0) и меет вид функции,
пок а занн ой на том же рисунке.
представляет собой напря
Fx. (0)
жени е илп ток обычного телетайпного сигнала как функцию вр е
мсш1.
Значения коэффициентов ах.
(j),
передаваемых сигналом
F х,(0)
(рис. 1.3), также можно получить с помощью отсчетов значений
~игнала в соответствующие моменты времени . При этом способ
передачи называют временным уплотнением или временным раз
делением.
Прямоугольные импульсы (рис.
f
1.3) можно рассматривать как
частотные функции (j, v ). Тогда x-ii символ представляется ча
стотной функцией F х (v). Если приложить сигнал Fх ( v) к пяти
соотве тствующим полосовым частотным фильтрам, то можно вос
становить коэффициенты квантованием
выходных
напряжений
этих фильтров. Способ передачи обычно называют либо частотным
уплотнением, либо частотным разделением.
Для большинства систем ортогональных
функций невозможно
·определить переданные коэффициенты по одному отсчету во вре
менной или частотной областях без последующего вычисления 1).
Свойство ортогональности согласно (2.3) позволяет всегда восста
новить эти коэффициенты. В этом случае применим термин «Орто
гональное разделение » или «ортогональное уплотнение». Преиму
ществом
ортогонального
раздел ения
является
то,
что
число
при
годных систем функций гораздо больше, чем число систем функ
ций для временного или частотного разделения. Таким образом,
.существует большая свобода выбора оптимальной
системы
для
конкретного применения.
В теор етических работах символы часто представляют в виде
веК'~оров в пространстве сигналов. Возникает вопрос, как это век
торное
представление
связано
с
представлением
ортогональными
функциями? Рассмотрим т-м'ерную прямоугольную декартову си
.стему координат с единичными векторами ej. Длины этих векторов
,равны интегралу от квадрата ортонормированных функ~ий
f (i,
0):
1/2
J f (j, 0)d0 =e -ei= 1.
(2.4)
1
-1/2
=F
Скалярно е произведение векторов ej и eh, j
k равно О, так ~ак
они п е рпендикулярны друг к другу . Таким образом, связь между
пр едставл ение м ортогональными функциями и векторным пред1)
Для Еычисления коэффициентов необходим более чем один
ч ений сигнала . Т а ким методом является м етод
вычисления
отсчет зна
интеграла
(2.3),
од
нако о н н е подходит под обычное понимание временного или частотного раэдеЛ е f! ИЯ,
56
можно
выразить уравнени е м
ортогональности:
1/2
S f (j,
0)f (k, 0) d 0 =
ejek =
61k.
(2.5)
-1/2
х
в
пространстве
сигналов
представляется
вектором.
т-1
f x = ~ ах (j) ei.
(2.6}
i=O
. Вместо
т ортогональных векторов можно использовать т ли
но независимых векторов. Это представление получается, ког
' функции f(j, 0) неортогональны, но линейно незщшсимы.
: В качестве практического примера рассмотрим телетайпный
•' вол F х (0), состоящий- из Ш!ТИ синусоидальных и косинусои
,Льных элементов, показанных на рис . 1.1:
.
F х (0)
=ах (O)f (О, 0) +ах (1) -V2sin 4n0
+ ах(2) V2 Х
Х cos 4л:0 +ах (3) -V2sin 6л0 +ах (4) -V2cos4л:0;
(2.7}
-1/2 ~ 0< 1/2; 0 = t/T.
и принять длительность телетайпного сим
а равной
ется, то Т
(j) равны
: й паузой
мс, что чаще всего исполь
равно 150 мс. Коэффициенты
1 и -1 для системы с актив-
150
+
и +1 и
О для системы с пассивной
· узой. Пусть на приемном конце сигнал
(6) непрерывно подается на пять перемно-
ителей, где он перемножается с пятью функ
ями от /(О, 0) до
аnряжения
V2 cos 6n'0.
интегрируются
в
Полученные
течение времен
'го интервала - 1/2~10< 1/2. Тогда выход
, е напрЯжения интеграторов в момент вре
ени 10= 1/2 представляют собой значения ко
фициентов ах (j) в ф-ле (2.7). На рис. 2. 1
казаны
осциллограммы
выходных
напря-
с. 2.1 . Обнаружение коэффициентов +! '11 --'! путем
&хождения взаимокор.реляциО'н•ной функции _
32 различ
.
х
телетайnных
.жальных и
сигналов,
составленных
из
синусои-
косинусО'Идалыных импульсов
пяти интеграторов на интервале -1/2=:::;;10 < 1/2. Дл я
аждого из пяти выходных напряжений существуют 32 р аз
ичные
реализации, соответствующие 32 буквам
телетай п
ого алфавита . 16 реализаций приводят к значению
1 и 16 реа--
+
57
.лизаций
-
к значению
-1. Это указывает на то, что использует
ся телетайпная система с активной паузой. В системе с пассивной
паузой 16 реализаций приводят к значению О вместо значения -1.
Некоторая асимметрия между реализациями, ведущими к
1, и
реализациями, ведущими к -1, вызвана присутствием
дополни
+
тельного сигнала
ции. По этой
-V2 sin 2пе
и
-V2
sin 2ле, который добавлен для синхрониза~
(2.7) не содержатся элементы
cos 2пе.
причине в ф-ле
V2
Все три рассмотренных представления сигналов содержат ко
эффициенты ах (j). Векторы ej позволяют представить т коэффи
F х, а временные функции f (j, 0) - одной
F х(е). Некоторые сигнау~ы, например выход
диентов одним вектором
временной функцией
ное напряжение микрофона, удобнее
всего представлять в виде
временных функций. Их представление с помощью коэффициентов
.будет изложено ниже.
2.1.2.
Примеры сигналов
На рис. 2.2а показаны два символа
Fo=eo и F1=-e0 в прост
-ранстве сигналов. Те же символы показаны внизу как временные
,функции для прямоугольного импульса
Уолша sal(l, 0):
F0 (0) = +
f (О,
f (О,
0)); f 1 (0) = -
е) или для импульса
f (О,
0)
или
F 0 (0)=-sal(l, 0);
F 1 (0) =+sal(l, 0).
На рис. 2.2г, д и е показаны символы, построенные из векто
ров ео и е 1 или из двух функций.
Символы,
изображенные
на
рис. 2.2г, имеют следующий вид:
Fo = ео + ei; f 1 = ео - ei; f 2 = - ео + ei; Fз= - еа- ei
: или
---
, .i;':~ . ~
.
J'
F 0 (8) = f(O, 0) + f (1, 0); F1 (0) = f (О, 0)- f(l. 0); ·
F 2 (0)=-f(O, 0)+f(l, 0); F 3 (0)=-f(O, 0)-f(l, 0),
' ИЛИ
F 0 (0) = wal (О, 0)-sal (1, 0); F1 (0) = wal (О, 0) + sal (1, 0);
F2 (0) = -wal (О, 0) - sal (1, !Э); F3 (0) = - wal (О, 0) + sal (1, 6).
Функции
f(O, 0), f(l, е), wal(O, 0) и sal(l, 0) показаны под
Fo(10) до F 3 (0), составленные из этих функ
рис. 2.2г; символы от
ций, показаны над ними.
к символам, изображенным на рис. 2.2, можно применить тер
мины «двоичный», «троичный» и «четверичный», так как отдель
ные векторы или функции умножаются на коэффициенты, кото
_рые принимают два, три
или четыре
58
различных значения .
,
Рисунок 2.3 показывает, что термины типа «двоичный символ>>'
е всегда применимы, если символ состоит более чем из одного век
ора или функции . На рис. 2.За приведены три символа так назы-
1
11~. 0
~
2
.J:::1_ о .rъ
rio
.rъ
-
.i::=1-
1
~
-s:::;i-
2 -d"'-
1-
~::т 2
-d1
~
t')
iJ)
г)
J
2 -е
J . о
-ео
-ео
1
Zo
6)11~
5)
а)
J-d1
с.1 Оо б~ооо
12090 'ооо
е.
е
. 7 IJ f 1 1J о зо 1о
ео
1о 8 о
о
S
Со
11/ OfOO Ot'iO
2 о fS о tto lo J о
muD-
0Q_ .r::::i 0i l
-9з 1_о. ..[1_ 1.i:::::i
m
~1..сь.
-.:f12-o- ..r:ь z_o._ .СЬ. 2~
о=r5о=г
i:I::J""JO- -П.з-СЬ- .СЬ- з
-5--
.~::::а..4.СЬ
-1/ -
,Q!i.°'Ь. wat ( о,в)
f ('.:!Jr::з.. ...E:t:r - sа t (1, в)
.1/z о ~-*о tfz '
·Рис. 12.!2.
точками
Символы, представленные
в
одномерном
сигнальном
и
пространстве
Рис.
Символы,
2.3.
двумерном
точками
и
пространстве
времен-
в
нЫми функциями
представленные
дву111ерном
и
сигнальном
временнЫми
функ-
циями
ваемого трансортогонального алфавита. В векторной интерпрета
ции символы записываются следующим образом:
f0
= -l
2
-v-3 0 + е
l е ;
1
2
f1
=
О е0
le1; F2 = - -1
-
2
v-3 0 + е
l е •
1
2
Вектор ео умножается на один из трех коэффициентов: ( 1/2) -VЗ
О или (-1/2) VЗ; е 1 - на один из двух коэффициентов: 1/2 ил~
-1. Если векторы ео и е 1 вращать относительно сигнальных то
чек,
то
получим
представления
сигналов,
имеющие
три
ра.злич
ных коэффициента для каждого вектора или два различных ко
эффициента для е 0 и три для е 1 . Сигналы, составленные из функ-
ций
f(O,
е) и
1f(l, 0)
или
wal(O, 0)
и
-sal(l, 0),
показаны внизу
векторной диаграммы:
F 0 (0)
=+
F 2 (0)
=
v3f(0,0)+ +f(l, 0); F 1 (0)= -f(l, 0);
-+
V3f(O,
0)+
59
+t(l, 0);
г
.
- ·- ·
.
F 0 (0)
= +-vз wal (О, 0)-+sa\ (l, 0); F 1 (0) =
F 2 (0) =
1
-+
-VЗ wal (О, 0)-
+
+ sal--(1,
0);
sal (1, 0).
На рис. 2.36 показаны четыре символа так называемого биор
·rогона J1ьного алфавита: Fo=eo; F1=e1; F2=-e1; Fз=-ео. Эти сим
волы очень похожи на символы, изображенные на рис. 2.2г. Сход
{:ТВО исче зае т, ес.'Iи символы составляются из более чем двух век
торов или функций.
Пунктирные линии на рис. 2.3 пока з ывают расстояние между
сигна л н1ы ;-,1и точка м и . Все сигнальны е точ к и трансортогональноrо
ал ф авита (рис . 2 . За) отстоят друг от друга на одинаковом рас
стоянии. Разн ости F1:-Fo; F2-F1 и Fo-F2 векторы, соединяю
щие сигнал ь ные точки О и 1, 1 и 2, 2 и О соответственно. Квадрат
.их длины р а вен 3:
(f1 - F0 ) 2 =
(- -21 -VЗ е0 - . ~
е1 \)
2
(F2-FJ 2 =
(__!_
-VЗе0 + ~ eiJ'
2
2
(F0- f 2)
Ь:ли си м волы
2
=
~ + ~ = 3·
2
2
=
=
4
4
•
~ + ~ = 3;
4
4
(у3е0 ) = 3.
2
предст а вл е ны
функциями,
а
не
векторами , то
с калярны е произведения необходи мо
заменить интегралами от
произведений соответствующих
функций, как показано
в
ф-ле
Отсюда следует:
(2.5).
1/2
s
s[-+
1/2
[F1 (0)- Fo (0)] 2 d 0=
-1/2
1/2
-1/2
1/2
s
[F2(0)-F1(0)]2d 0=
-1~
-V3f(O, 0)-+ f (1,0)т d 0 = 3;
s[ V3f(O,
+
.
0)- : f(l, 0) г d 0 = 3;
-1/2
1/2
1/2
J[F (0) -F (0)J2d 0= S [-V3f(O, 0)] d 0 = 3.
2
0
-1/2
2
-1/2
F1(0)-Fo(8) есть фующия, которую необходимо · сложить с симво-
лом Fo(e) для того, •побы получить символ F 1 (0). Если
112
SF2X(0)d0
-1/2
есть энергия сигнала F х (0), то
1/ 2
S [F1 (0)-F (0)]
0
11
d 0 есть энергия,
-1/2
необходимая для преобразования символа F 0 (0) в символ F1(9.).
Квадрат расстояния между сигнальной точкой и началом коорди
нат представля ет собой энергию этого сигнала.
На рис . 2.4 показаны символы , со ставленные из трех векторов.
В ершины представляют собой сигнальные точки. Ребра между ни-
60
'
t
!~
f
1
: редставляют расстояния между близлежащими точками. Еди
.. ые векторы ео, е 1 и е2 не показаны. Нормировка в данном слу
: от Jшчается от нормировки на рис. 2.2 и 2.3. Она выбрана та
, образоы, чтобы расстояния между соседними сигнальными
ами на рис. 2.4а, 6 и в бьши равны. Значения коэффициентов
Рис.
Символы, представленные точками в трехмерном сиг
2.4.
нальном
кторном
пространстве
пространстве
зависят
от
ориентации
единичных
век
"в е 1 . Например, четыре символа трансортогонального а.11фави
. оказанные
на рис.
F(j
2.4,
могут быть записаны следующи:vt обра-
=
1
+ -21 ео +-61 vз е1 - V2VЗ e.J;
12
F1
=
Ое0 -
-
1
6
F2~= - - Со+
1
.
2
1
VЗ е1 - V2VЗ ~;
12
1
-6
VЗ е1 - _!_ V2-V3~·
12
'
~!:
~{.
f:.:
w
'J··гия всех символов одинакова:~=
1
,
ояния
между четырьмя
2
2
'f\
11 --(Fо- f 2 ) --
"'
f!= f~= F~
3
= в'
сигнальными точками
2
". ~(f
2 - F)
3 - l•
тоже
;,:а рис. 2.5а показано П.Редставление этих четырех
равны:
символов
.•. . прямоугольными импульсами f (О, 8); f (1, 8) и f (2, 8), а так
,' ремя импульсами Уолша wal (О, 8); -sal ( 1, 8) и -са! ( 1, 8).
· случае биортогонального алфавита (рис. 2.46) разумно так
.)нтировать систему координат, чтобы на каждой оси были
· · ложены точки двух противоположных сигналов. При этом потея следующее простое векторное представление: Fo=eo; F1=
. F2=e2; Fз=-е2: F4=-e1; f5=-eo.
имволы,
составленные
из трех
пря:v1оугольных
ех функций Уолша, показаны на рис.
шшульсов
или
2.56.
имволы алфавита, показанные на рис. 2.4в, можно записать в
. . простой форме,
"' ба в их центрах:
если оси системы координат пересекают гра
61
+ е1 + е2;
е0 + е1
~;
F1 =
-ео
F4 =
F5 =
ео
Fo =
-
-ео
+ е1 + е2;
+ ei - ч;
ei + е2;
F2=ео-е1+ч;
Fв = -ео-
Fз = ео - ei - ч;
F7
=
--е 0 -е 1 -е 2 •
На рис. 2.5в показаны эти символы, составленные из трех пря.
моугольных импульсов и из трех импульсов Уо.1ша.
О)
ll)
г=........, о гh-,__
п
Г1-.
Li""' 1 Li"'
о r===1
__!1_7 ~
ГТ"1LI 1 ,...л.,~
__о. 2 пL......Р
Г1 П2.-.
--,;::r- J LJ
Г111:] J ....=1'J-,
,--,
LJ
--~4
LJ
L:J.---,
-.::rJ
n
ГТ"Т"'1 о [""'L......."."
s i=::::::J
LJ
п
L..J
-
,.,LJ5..,. -U
LI
~..,......,,...,
........Lfi
..,
L::L:I
"'i:Г
L1:LJ 7 о-:-
L....J
....
-sat(t' е)
r=i
.JJ
L:IГ""Г1 4_.,,..""'=---=r...,..,...
r-af{O,B) r===1 wat(o е)
f(l,86
-
f{2.Bb ,...с:::1111
~ - cat(t е'
1
Рис.
2.5.
Символы рис.
2.4,
'/
представленные временнЫми функ
циями
Если символы состоят из более чем трех векторов, то нагляд
ность векторного представления теряется. Символы некоторых а.1фавитов можно легко поставить в соответствие с четырьмя и более
векторами или функциями. Это справедливо, например, для сюr
волов биортогонального и двоичного алфавитов (рис. 2.56 и в).
Однако уже трансортогональные алфавиты требуют существенных
вычислений. В общем случае из т функций можно
построить
(т+ 1) символов трансортогонального алфавита. Эти т+ 1 сим
волы определяются m(m+l) коэффициентами ax(j); j=O, 1, ....
т-1; х=О.
1, ... ,
т. Для их вычисления используются следующи~
условия:
а) энергия всех т+
1
символов одинакова.
Это
утверждени<'
дает т условий;
б) расстояния между каждой парой из
Существуетт+(m-l)+(m-2)+
m+ 1 символов равны
1
... +1=
m(m+1) таких рас-
стояний. Итак, для определения т(т+
1
- -
2
2
l)
коэффициентов имеетсr!
т(т+З) уравнений. Значительное число коэффициентов мо:ж·
но выбрать произвольно или определить их из дополнительных ус
ловшi.
62
2.1.3. ~искретизация и ортогоиальвое )Jа.эл03еВИе
}теорема отсчетов из анализа Фурье гласит, что сигнал, состоя
й из суперпозиции периодических синусоидальных и косинусои-
; ьных
, f~Лf,
Ji
функций
и
sin 2nf t
cos 2nft
с частотами
в
интервале
можно полностью определить 2Лf отсчетами его значе
в· секунду, если Лf измерена в герцах [1-6]. Эта теорема бы
обобщена Клуванеком для других полных систем ортогональ
х функций {7]. В сущности, теорема отсчетов Клуванека гласит,
·. сигнал, состоящий из суперпозиции функций fc(qiT, t/T) и
.,,.
,
· ~т, t/T) с частостями в интервале О~ ·<р~Л{j), полностью опре
_ яется 2ЛqJ отсчетами его значений в секунду, где Лq> измерена
ps. В этом параграфе будет показано, что дискретизация ча
:ноог.раниченного
ожению
.
~
по
сигнала
•
•
неполнои
,, , ± 1, +2, " . .
математически
ортогональнои
эквивалентна
sin п (0 + j)
системе
его
·
n~+n
Соответствующий результат для частостноогра
'енного сигнала , составленного из функций Уолша, будет рас-
.
рен позже .
f1Частотноограниченный сигнал Р(О), не имеющий составляющих
v =fT> 1/2, можно разложить в ряд по
.· гональным функциям, значения v которых лежат в интерва·;-1/2~v~ 1/2. Для этого пригодны синусоидальные и косину
,'ррмированной частотой
_дальные импульсы, импульсы Уолша, полиномы Лежандра
Ниже будет использована следующая система сннусоидаль
' •..~ д .
.· и
косинусоидальных
импульсов,
ений введен фазовый угол
причем
для
упрощения
вы
1/4 n:
q(O, v} = 1;
q (j, v)= q (2i, v} = V2COSE1t i v + 1t/4);
·q (2i - 1, v) = у 2 sin (2л i v+я/4),
q (j, v) = О для v > 1/2 и v<- 1/2;
j = о. 2i' 2i - 1, i = 1, 2. . . ..
Разложим преобразование Фурье G(v} сигнала F(10)
l
(2.8)
в ряд по
м импульсам:
G(v}=
а(О)+ ia(2i-l)Y2sin(2niv++я)+
+n) ;
i=I
+ а (2i) у.2cos ( 2л i v +
а(О)=
1/2
f
G(v)dv; a(2i)=
-r12
(2.9)
JG(v)Y2cos(2лiv+ 4 я dv;
1/2
-
l
.
)
-112
1/2
JG(v}V2siп(2niv+-~ л:)dv.
.
~~
преобразование Фурье дает
F(O) = J [G(v)(cos 2яvВ +
1
a(2i-1) =
о
63
r
.
+sin2:rtv0)]dv. Подставю~ в полученное выражение ю~есто G(v)
(2.9) . и~1ея в виду, что функция G (v) равна нулю вне ИН·
тервала -1/2~'\' ~ 1/2, получа е м
сумму
С1)
F(Э)= а (О) siп п9
л9
+ '1 [a(2i - l)
siп п: (9-:- i) +а (2i) sin п (9 ~ i)
i.J
п (9- i)
i=I
п: (9+ t)
]· ( 2 . l О)
Таким образом, частотноограниченный сигнал F (0) можно пред
ставить рядом по неполной ортогональной системе функций вид<J
sin х/х. Из § 1.1 следует, что эти функции ортогональны. Это мо
жно проверить, оценив интеграл
00
sin п: (9 + k) siп п: (0 + j) d е = {) . .
S
п: (9
+ k)
п: (9
+ j)
(2. 11)
Jk
-оо
k, j = О; ± 1, ± 2, . . .
Коэффициенты а(О); a(2i-1) и a(2i) в ф-ле (2.10) можно по
лучить путем отсчетов значений сигнала F ('8) в моменты време
ни 0=,//Т=О, ± 1, ±2, .... Например, при 0=0 все
функции
sin п: (0 - i)
и
я (0-i)
sin
я
(0 + l)
равны нулю, а
n:(0+i)
sin m)
-n0
равна
1.
Та-
ким образом, находим F(O) =а(О).
Из выражения (2.11) следует, что коэффициенты а(О),
a(2i) и
-- a(2i-1) также можно получить при помопiи ортогонального раз
ложения
по функциям вида
F (0)
оо
х
s
-оо
sшх
-- :
.
•
F (0) Stпn:n:(~ :.:) d е
0
/
1
а (О) = F (О),
= а (2i) = F (- i),
а (2i-I)= F (i),
j= О;
j = i; (2.12)
j=-i.
Эквивалентность дискретизации и ортогонального разложения
свойственна не только частотноограниченным сигналам. Сложим
сигнал F (0) с конечным числом дискретных колебаний An sin 2:rtvn0
и Вп cos 2:rtvn0 с vп> 1/2. Идеальный фильтр нижних частот с ча
стотой среза v= 1/2 будет подавлять эти дополнительные колеба
ния. Применяя дискретизацию, можно
получить
коэффициенты
а(,О), a.(2i) и a(2i-l) . Ортогональное разложение нового сигна
ла .F(l0)+Ansin2:rtvn·8+Bncos2nvn0 позволяет получить те же ко
эффициенты, так как функции An sin 2n·vn·8 и Bn cos 2nvnt0 не влия
ют на их образование:
со
S[f(0) +А sin 2nv 0+ В
п
п
п
cos 2nv 0]sin п: (8 + j) d е =
п
п: (0
+ j)
sF(8) sin п ++ iJ Х
"'
8
(
п (0
j)
-со
Xd0;
(2.13)
€4
1
Vn
= fпТ > 2;
fп
> 1/2Т; е = t/T.
_тается
показать, что добавление к сигналу F(H)
сигнала со
~- ошным спектром также не влияет на величину коэффициентов.
;. Прибавим к ,Р (10) сигнал D (10), причем D (0) не содержит коле·
_,:ний с частотами 1v1<1/2. Тогда преобразование Фурье от D (0)
: жно быть равно О в интерва.л.е -l/2~v~l/2. С другой сто.".
б
ф
Slll 1t (0
j}
+
+
ны, прео разование
урье от функций
равно О вне
!.
1t (0
j)
ого интервала. Таким образом, оба преобразования Фурье орто
,нал,ьны друг к другу; поэтому должны быть ортогональны и вре,
._иные функции:
00
f D (0)
sin
•
-00
<0 j)
(0
j)
1t
1t
+
+
d 0 = О.
(2.14)
Схемы для ортоrоиаm.иоrо разделения•)
2.1.4.
~:,.-
.
На рис.
2.6
показана функциональная схема системы для пере
чи пяти коэффициентов ах (j) с использованием ортогонального
:зделения. На
передающем конце
"
9
гене-
!/
Функциональ
2.6.
ая
генератор функций ГФ
схема
ередачи
системы
сигнала
нальными
для
орто
функциями
f(j, -0):
Ф
·
;
-
-
генератор
функций;
перемножите.ль;
втегратор ;
У
-
И
-
усилитель
;, рует пять функций
f(O, 0), ... , /(4, 10), котор~ ортогональны на
• тервале (-tl/2)T~· t<(l/2)T. Пять коэффициентов ах (О), ".,
·.х,(4) представлены в виде уровней напряжений, имеющих п,асто-
нное значение в течение интервала времени (-l/2)T~t<(l/2)T.
перемножителях функции f(j, 0) умножаются на коэффициенты
:;_(j). Пять произведений а .y_(j)f (j, 0) суммируются с помощью ре
. исторов R и ·операционного усилителя У. Полученный сигнал
_"ередается по линии связи. На приемной стороне прин~тый сигнал
. оступает через
усилитель У на пять перемножителеи, ~де одно
ременно перемножается с каждой из пяти функций f(J, 0), нс
. льзуемых в передатчике в качестве переносчика коэффициентов.
,: енераторы функций ГФ в передатчике и приемнике должны быть
1)
,~322
См . более детальное рассмотрение схем в (1-5).
65
1
синхронизированы. Сигналы, полученные на выходах перемножи- ~
телей, интегрируются в интеграторах в течение интервала времени
·
(-1/2) т ~t< ( 1/2) т.
Выходные напряжения интеграторов в момент времени
представляют собой коэффициенты ах. (О),
... ,
t= (l/2) Т
ах(4).
Другой набор из пяти коэффициентов ах.( О), ... , ах.( 4)
переда
( 1/2) Т ~ t < (3/2) Т. Здесь снова
требуются функции f (O, 8), "" f(4, 8) от ГФ на приемном и пере
ется в течение интервала времени
1
дающем концах. Таким образом, эти функции являются перио
дическими с периодом Т. Напряжения, соответствующие в пере
датчике коэффициентам ax.(j) на интервале времени (-1/2)Т~
~t<(l/2)T, мгновенно меняются в момент времени
соответствуют коэффициентам ах. (j) на интервале
< (3/2) Т.
Интеграторы в приемнике в момент
t=(l/2)T
и !
~
( 1/2) Т ~t<
времени t= ( 1/2) Т
i
возвращаются в исходное состояние и начинают интегрировать на
пряжения, получаемые от перемножителей на интервале
~t<
( 1/2) Т ~
(3/2) Т.
Для практического применения функциональная схема, изобра
кенная на рис. 2.6, должна быть дополнена цепью синхронизации.
~роме того, для преобразования в желаемый вид коэффициентов
aij), вводимых в передатчик, и коэффициентов, получаемых в
1риемнике, необходимы модуляторы и демодуляторы.
.
На рис.
2.7
показана схема для
генерирования
периодически
повторяющихся функций Уолша wal (j, 1
8) или са! (i, ·8) и sal(i,
wat (о, О)
i.--__.:....:....:..--- :;at ( 1, О)
~>-=~-1-1-t---
cat (t,o)
sat (2,О)
1-Н+-- caL (2,е)
sat (J,Э)
cat(Je·
. ~
sat (*·О~
cat (4, G;
5а! (S.O)
cal (S,G)
sat (Б,Э)
саt
(ii,e;
sat (7, е)
wai ( !5,fJ)
(,Ot
(7 е)
sаr (в,е)
,
Рис.
2.7.
т
Генератор периодических функций
Уолша:
- триггер; п - nеремножитель
реме умножения
функций
wal (j, 8) ( 1.29).
Триггеры Т1-Т4 дают на
выходе функции
wal (1, 0) =
=sal (1, 0),
wal (3, 0) =
=sal (2,10), wal(7,0) =sal(4,0)
иwal(l5,8)=sal(8,0). Перемножители,
показанные
на
рис. 2.7, образуют из этих
функций Радемахера полную систему функций Yoлша sal(l,0),cal(l,0), .. "
sal (8"8). В качестве функции wal (0,8) используется
постоянное
положительное
напряжение. Перемножители представляют. собой переключатели,
деиствующие
согласно табл. 2.1 а, так как
функции Уолша принимают
только значения ±1 . Срав-
нение табл.
66
0). '
Эта схема основана на тeo-
2.1 а с таблицей
тинности полусумматора (табл. 2. lб) показывает, что в качестве
. ремножителей на рис. 2.7 можно использовать полусумматоры,
. ли условиться принимать положительное напряжение +Л за О,
отрицательное напряжение -И
1. Обобщение схемы для гене
ации функций с большими зна·ениями
i
не
вызывает
Таблица
теля двух функций Уолша (а) и по
труд-
лусумматора (б)
остей.
Рассмотрим генератор функ
· ий Уолша, имеющий 20 счетных
риrrеров,
а не четыре,
2.1
Таблицы истинности для перемножи
б
а
как пока
ано на рис. 2.7. В этом случае
ожно
получить
220= 1048576
азличных функций Уолша . Для
·. нерации любой из этих функций
ребуется
19 полусумматоров .
+1
-1
+1
1 - 1 1
+1
-1
-1
+1
о 1
о
о
1
1
1
о
:Очность их частости будет зависеть от стабильности генератора
актовых импульсов, управляющего триггерами. Здесь не возника
т проблем дрейфа или ухода параметров. Полезно сравнить слож
ость такого генератора со сложностью частотного синтезатора, ге
ерирующего
миллион
отдельных
синусных
функций.
С
другой
.· . ороны,
время переключения самых быстродействующих импульных схем заключено между 0,1 и 10 нс. Это ограничивает в натоящее время высшую частость функций Уолша величинами по
ядка ,1os zps= 100Мzps-10 10 =10 Gzps. Синусоидальные коле
ания с частотами· 100 МГц-10 ГГц были получены десятки лет
-
~а~
На рис. 2.8 показан генератор синусоидальных и косинусои
альных колебаний стабильной фазы для импульсов, изображен
. ых на рис. 1.1 и 1.9. Триггеры Т1 и Т2 производят на выходе функ
и Радемахера, из которых фильтрами выделяются основные си
усоидальные функции. Первая гармоника имеет втрое большую
астоту, чем основное колебание . На практике лучше не ставить
'.
ильтры, а добиваться хорошей аппроксимации
гармонических
ункций суперпозицией функций Радемахера .
Существуют три основных типа перемножителей. Первый пере
ножает два напряжения , принимающих только два значения, ека
ем,
+1 и
-1.
Этот вид перемножителя реализуется логическими
.схемами. Второй тип перемножителя перемножает напряжение и.,,
принимающее
произвольные
значения,
и
напряжение
И2,
пр_ини
мающее конечное число значений. На рис. 2 .9а показан пример
акого перемножителя . Напряжение И 2 принимает только значе
: ния
+ 1 или
-1. Выходное напряжение равно
+ И1
или
-U1, где
может пр.инимать любое значение внутри диапазона выходных
напряжений операционного усилителя У. Схема работ а ет следую
щим образом: неинвертирующий вход ( +) усилителя заземлен,
U1
.. если
полевой транзистор насыщен. Напряжение Из должно быть
равно -U1, чтобы инвертирующий вход (-) также имел потен
. циал «земли». Пусть полевой транзистор закрыт. Тогда неинвер-
67
тирующий вход будет находиться под напряжением .U1 и инверти
рующий вход также должен быть под напряжением ·И 1. Из этого
следует, что Из должно быть равно И1. Разновидность такого пе
ремиожителя показана на рис.
2.96.
R
соsи.в
U2= Uca! (i.e)
15)u..---....--+--~L1
cat (i,O)
не~-• U1 cat (i, 8)
R
-cat(i,e)
~at (i е)
НЕ-- и~ sal (i, fJ)
Н--\::'r.т-- ~а t (i, в)
·
r--1~- саl(н,е)
НЕ:---.... u Gat (н, в}
1
~~ч- са! (к, е)
Рве. 2.8. Генератор стабиль
ных по фазе синусоидаль
ных
Т
и
-
косинусоидальных
фунюций:
триггер; Ф -
Рис. 2.9. ,Перемножитель для перемножения
произвольной фуmщии с функщиями Уолmа:
а) простое перемножение; б) параллельное
.перемножение
фильтр
Перемножитель третьего типа перемножает ·два произвольных
напряжения. В принципе, эти перемножители могут быть построе
ны на эффекте Холла, на .полевых транзисторах или на логариф
мических элементах. Однако обычно они мало пригодны для прак
тического
использования
из-за
их
низкого
входного
и
выходного
сопротивлений, температурного дрейфа, стоимости и т. д. Очень
удобен перемножитель
с
диод
ным мостом. Его схема показана
на рис. 2.1 О. Перемножитель от
личается от обычных отсутствием
трансформаторов.
и,
Uz
Рис.
2.10.
"~(t),-1 !~1 ?,1'
R
Перемножитель, использу
ющий :п.иодный мост
Рис.
J
RCo
2.11.
Интегратор
С
Напряжение И2 .на р•ос. 2.9а прИJНи.мает толыrо зна·чение
или
-1,
+1
поэтому его можно представить одним двоичным симво
лом. Чет~1рьмя двоичными символами можно представить напря-
68
ение, имеющее
16
возможных значений. Соответствующий пере
ожитель содержит четыре
полевых транзистора,
а
не один,
как
казано на рис. 2.9а, и более сложную схему резисторов. Такой
ремножитель был предложен Р. Шмидом. Он дает хорошие ре
льтаты, но одно · из напряжений долж
быть представлено в цифровой . форме.
На рис. 2.11 показан интегратор. Бла-Ч{iо-с:=:.+-'~lt+-о
' даря емкостной обратной связи в опе
ционном усилителе выходное напряже
е пропорционально интегралу входного
'
очень бо.11ьшой
степенью точности.
~юч К возвращает интегратор в исход
е состояние, разряжая конденсатор. в
.
.
актических
схемах
роль
этого
ключа
ыполняет полевой транзистор.
помощью перемножителя, интегра-
112 t) =-и~ (t)
Рис. 2!12. Детектор сииусо-
..
идальных
;, <;:
а и генератора
. инципе,
функций
выделить
любую
можно,
в
функцию.
специальных функций необходимо
.·' ядавать
более сложные схемы. На рис.
, 2 показан
и косинусоидаль
ных импулысов sin 2nit/T и
изображенных
cos 2'1tit/T,
~~
1. 1
,
детектор для синусоидальных и косинусоидальных им
:льсов (рис.
1.1). Для выделения сигналов в этой схеме использует-
тот факт, что ·синусоидальные и косинусоидальные импульсы
2rci(t/T) и cos 2ni(t/Т) являются собственными функциями сле
щего дифференциального уравнения:
у" +4n2 i 2T-2y= О;. у (-+т) =у (+т);
у' (-+т) =у' (+т).
1' ходное напряжение из(t) ус·илителя У1 (рис.
Ua (t) = - (R1CJходное напряжение
и,,. (t)
= -
(R,,. С2Г
1
1
(2.15)
2.12)
равно
JUi (t) dt -(Ri CJ JUa (t) dt.
(2.16)
u"(t) =-u2(t) усилителя У2 равно
sUa(t) dt
+ (R2C1R,,.C2Г
1
= (R1C1R,,.C2Г
1
ssU1
(t') dtdt'
+
JJUa (t') dtdt' = -Ua (t).
важды продифференцировав выражение
(2.17)
и собрав члены,
(2.17)
луча ем
и; (f) + (R2C1R,,.C2Г Ua (t) = - (R1C1 R,,.С2Г U1(t).
(2.18)
,озьмем RzC1R,C2= (Т/2лi) 2• Тогда левые части выражений (2.15)
1
· (2.18)
будут
одинаковыми.
1
Неоднородный
член
u1(t)
равен
11.cos2'ЛJkt/T или 1 U11.sin2лkt/T для (-l/2)T~t~(l/2)T. Вид u1(t)
.не этого интервала нас не интересует, так как ключи К1 и К2 за
·. ыкаются в момент времени t= ( ± 1/2) Т. Напряжения из(Т/2) и
,,,(Т/2) равны нулю, если -i=Fk и Rt =nЖ2;
sin 2nit/T дает
.ui
69
u 3 (T/2} =() и щ(Т/2) = (-1 )iUi. На рис. 2:13 показаны напряже
ния u3 (t) и u4 (t) для i=k= 1. На рис. 2.14 показаны огибаю
щие Uз(t} для i= 128 и выходных напряжений uk cos 2-лkt/T с
k= 128, 129, 130. Это означает, что схема настроена на выделение
а)_--
кuсинусоида.ТJьного
-
той
128
косинусоида<ТJьные
тами
импульса с часто
Гц и что ко входу приложены
128, 129, 130
импульсы
с
часто
Гц.
6)
Рис.
:2.13.
пряжения
в
рис.
входное
·
а)
Типичные
Рис. 2Jl4.
Типичные напряже
ния в схеме рис. 2.12.
Схема
построена на обнаружение си
на
схеме
2.'12:
напряжение
6) и
в) напряжения из(t) и
и.(t); г) вход-ное напря
жение u1(t) = Ucos 2лt/Т;
д) и е) напряжения из(t)
И U4(t)
нусоидальных
u1(t)=Usin 2nt/T;
дальных
и
косинусои
импульсов
с
i= 128.
Показанные выходные ·напря
жения
из(t)
соответст.вуют
входным
i=128
(в).
напряжениям
u 1 (t)
с
(а); i=129 (6) и i=.130
Длительность
развертки
Т=78 мс
Потери в схеме, показанной на рис. 2.12, сравнимы с потеря
ми в механических резонаторах. На частоте 100 Гц без использо
вания регенерации достигаются добротности в несколько тысяч.
Схема применяется на частотах от 1 Гц до 100 кГц. Нижний пре
дел определяется потерями, а верхний - предельной частотой опе
рационного усилителя tб].
2.1.5.
Передача цифровых сигналов синусоидальными
и косинусоидалъными импульсами
1)
Через идеальный фильтр нижних частот с полосой 1 Гц пря
моугольный импульс можно передать в течение секунды. Это есть
предел
1)
В
скорости
{1-11]
передачи
прямоугольных
импульсов
при
их
об-
приведено несколько примеров систем передачи инфор~1ации с
использованием ортогональных функций.
70
ружении с помощью отсчетов значений сигнала без коррекции
жсимвольных искажений. Та же скорость передачи сохраняется
я «приподнятого» косинусоидального
импульса. Некоторые из
их
импульсов
. 15.
показаны
на
рис
.
Эти импульсы неортогональны,
линейно независимы.
Их можно
бнаружить с помощью отсчетов
начений сигна.па. Обнаружение с
сГюльзованием
ии с
взаимной корреля
опорными
ует применения
их
влияние
ений.
Импульсы
функциями
схем,
тре
исключаю
межсимвольных иска-
sin л: (0 + j)
1t (
-:
0 ± /)
~'
о
Рис.
2. lб.
т
2Т
Приподнятые
-f-
коси
нусоидальные импульсы во вре
менн6й области: 1+cos 2л:t /Т;
l+cos2л(t-T)/T и l+cos2nx
Х (t-2T)/T
позволяют передавать в полосе
l
Гц два
мпульса в секунду. Однако на практике их применять нельзя. Ес
и
передавать последовательность таких
импульсов,
то
может
по
виться произвольно большая амплитуда сигнала; любое незначи
ельное отклонение синхронизации от идеальной может привести к
роизвольно большим перекрестным искажениям. При использо
вании дискретизации не существует способа для передачи инфор
мации с большей скоростью, чем половина скорости Найквиста, по
крайней мере, если не прибегать к увеличению мощности.
Синусоидальные и косинусоидальные импульсы (рис. l. l и 1.9)
позволяют передавать информацию быстрее, чем один импульс в
секунду в полосе l Гц. За счет усложнения аппаратуры можно
сколь угодно близко подойти к пределу Найквиста два импуль
са в секунду в полосе 1 Гц. Это можно видеть из рис. 2.16, на ко
тором показаны три системы функций . Первая состоит из пря
моугольных импульсов длительностью Т. Их частотныi'I спектр
мощности показан справа. Полоса частот, необходимая для пере
дачи, определяется ориентировочно неравенством:
O~,f~f g= 1/Т.
При этом может быть передан один прямоугольный импульс в се
кунду в полосе 1 Гц.
Имеет смысл представить прямоугольный импульс как функцию
wal (О, 0) (рис. l . l) и передавать прямоугольный , синусоидальный
и косинусоидальный
импульсы
длительностью 3Т вместо
трех
прямоугольных импульсов, каждый длительностью Т. Спектр мощ
ности импульсов показан на рис. 2.16. Полоса частот, необходимая
для передачи, умньшается до O~if~2f g/3= (2/3) Т. Таким образоы,
в течение секунды
в
полосе
l
Гц можно
передать полтора
им
лульса.
Рассмотрим следующий шаг. Вместо передачи набора из пяти
· прямоугольных импу.1ьсов длительностью Т каждый одновремен
но можно передавать один прямоугольный, два синусоидальных и
два косинусоидальных импульсов длительностью 5Т. Требуемая
·полоса частот уменьшается до O~f~3(rfg/5) = (3/5) Т
согласно
рис. 2.16. Это означает, что в течение секунды в по.~осе l Гц пе
редаются
1,67
импульсов.
71
о
~.=
~.
т
-------.
а)
о
о
l
111 1/т
1
, .
о
2/Jfg
fg
~.---~~~~~~--'6) u::;;::::;:;
6)
..........-
g)
. '/,..,,,.
Рис.
---.........
..............."""'=7
~
<!'1
J/5'8
о
<:::::>ч:::::::
2. 16.
Сравнение необходимой полосы пропускаll'Ия для
ных систем функций
Таблица
2i+I
:"".,,)т
_ ...........-
;>2
Требуемая
2.2
Число
различных форм импуль
сов и число
импульсов,
передаваемых в полосе 1 Гц в тече-
(2i+l)/(i+I)
иие
1
-
с
различ-
полоса частот длп
одновременной
передачи одного·
прямоугольного импульса,
соидальных импульсов и
нусоидальных
i
i
сину
коси
импульсов
дли
тельностью (2i+l}Tpaвнa0~f~
~ (i+ l}/(2i+ 1) Т 1 ). Скорос:гь.пе
2l+I
редачи
информации
равна
импульсов в секун
ду в полосе частот 1 Гц. Эта ско
1,5
3
рость приближается к двум для
1,67
11
5
больших значений i.
В табл. 2.2 показаны значения
для числа 2i+ 1 различных фор1"t
импульсов и для числа (2i+ l)/(i+1l1) импульсов, передаваемых в
полосе 1 Гц в течение одной секунды. Можно видеть, что число
7
9
1,75
1,8
1,83
(2i+ 1)/(i+ 1)
различных форм импульсов, а следоватеЛьно, и сложность обору
дования быстро увеличиваются с приближением
(2i + 1) / (i + 1)
к
двум.
В табл. 2.3 приведены функции, описывающие синусоидальные
и косинусоидальные импу.цьсы, частоты периодических колебаний
и их использование в многоканальной телетайпной системе. Пере
дача является не стартстопной, но синхронной. Телетайпные сигна
лы, приходящие асинхронно, должны быть направлены в буфер
ное устройство, откуда они синхронно поступают
1)
В
{14]
в
передатчик
дано углубленное рассмотрение распределения энергии вне этой
полосы частот. В ней рассмотрено приме11ение принципа Кречмера о частичном
откдике
на
сигналы,
сос·rоящие
нз
суммы
импульсов.
72
синусоидальных
и
косинусондальных
Таблиц а
2.3
Испопьзоваиие синусоидальных и косинусоидапьиых функций
в многоканальной телетайпной системе
f,
ия
Номер Номер
1 канала 1символа
Гц
о
синхронизация
несущей
6,67
синхронизации
символов
6,67
13,33
13,33
20
20
26,67
26,67
33,33
33,33
2
40
2
40
46,67
46,67 .
2
1
2
1
2
2
3
3
3
3
53,33
53,33
f,
Функция
3
4
5
1
sinl8n0
cos 18 n0
sin20 n0
cos 201t 0
sin 22 n 0
cos22 n0
sin 24 n 0
60
60
66,67
66,67
73,33
73,33
80
соs24л0
во
sin 26 n 0
cos 26n0
sin28 n0
cos 28 nO
sin30n0
2
3
4
5
соs30л0
sin32 л: 0
соs32л0
2
sin 34 л: 0
cos 34n0
3
4
Гц
86,67
86,67
93,33
93,33
100
100
106,67
106,67
113,33
113,33
1 Номер 1символа
Номер
кана.па
5
.1
2
3
4
4
4
4
4
5
5
5
5'
3
4
5
1
2
3
4
5
1
2
5
6
6
6
6
6
3
4
5
· нс. 2.6). Для того чтобы можно было использовать обычное те
тайпное оборудование, на приемной стороне в сигналы нужно
бавить стартстопные импульсы. Длительность телетайпных сиг
-~лов предполагается равной
150 мс. Периодический сигнал
n 2nt/T
с Т=
150
мс и
l/T=6,66
Гц пересекает нулевой уровень в
ачале и конце посылки с отрицательной производной и исполь-
.
ется в качестве сигнала синхронизации.
Согласно табл.
2.3
телетайпная система может работать с
100-
телетайпными каналами в полосе телефонного канала в за
исимости от качества последнего. При таком большом числе ка
_, алов становится важным вопрос нагрузки по мощности. Иссле
. ования показали, что вероятность ошибки, равную l 0-7 и ме
ее, можно достигнуть без превышения допустимой нагрузки по
. ощности.
Это справедливо для передачи между двумя абонен
ами телетайпа, т. е. для условий гораздо более жестких, чем пе
едача между двумя телефонными станциями. При этом не ис
ользовлись
ни
кодирование,
ни
другие
методы
уменьшения
ве
оятности ошибок. Для сравнения широко используемая система
ЕЛЕКС имеет
24
телетайпных канала в одном телефонном, но
73
превышает допустимую нагрузку по мощности в три раза. Превы
шение нагрузки по мощности - обычное явление для систем высо
коскоростной передачи информации. Существует, по крайней мере,
система,
которая
занимает
полосу
частот,
равную
полосе
частот
телефонноrо канала, но которая потребляет энергию восьми кана -
лов при скорости передачи 2400 ~ . Необходимо указать, ЧТ()
с
синхронная система очень чувствительна к скачкам фазы, которые
появляются в переключаемых телефонных сетях, работающих на
большие расстояния. Вероятность ошибки может достигнуть tо-з
и более в зависимости от того, насколько быстро восстанавлива
ется синхронизация.
Одной из причин, по которой синусоидальные и косинусоидаль
ные импульсы обеспечивают надежную передачу, является то, что
телефонные каналы разрабатываются для передачи без помех пе
риодических синусоидальных и косинусоидальных сигналов. Сину
соидальные и косинусоидальные импульсы, содержащие очень мно
го периодов, по своим свойствам приближаются к периодическим
сигналам и претерпевают малое запаздывание и затухание. Дру
гая причина заключается в том, что ошибки в телефонных кана
лах
вызываются
в
основном
импульсными
помехами,
а
не
тепло
вым шумом. Ниже будет показано, что тепловой шум воздейству·
ет на ортогональные импульсы всех форм одинаково. Импульсные
помехи, однако, эффективнее всего воздействуют на
прямоуголь
ные импульсы при условии, что для их обнаружения используется
дискретизация сигнала.
2.2.
ХАР АКТЕ!'ИСТИ'КА КАНАЛОВ СВЯЗИ
2.2.1.
Частотное затухаиие и фазовый сдвиг канала связи
Каналы связи обычно характеризуются затуханием и фазовым
сдвигом гармонических колебаний как функциями их частоты. Ко
входу прикладывается напряжение И cos wt, а на выходе измеря
ется установившееся напряжение ·Ис ( w) cos wl[t-tc (w) ]. Функции ча- i
стоты lg И/Ис (w) =ac(Q) и wtc(w) =bc(w) являются затуханием и '
фазовым сдвигом. Индекс с можно опустить, если затухание и фа
зовые сдвиги колебаний И cos wt и И sin wt одинаковы. Так как хо
рошо
известно,
что
периодические
синусоидальные
и
косинусои
дальные функции передают информацию с нулевой скоростью, то
интересно
выяснить,
почему
же
они
используются
для
описания
каналов связи.
Разделим канал связи на линию связи и аппаратуру на концах
этой линии. Линия опись!вается дифференциальным уравнением в
частных производных. Оконечная аппаратура описывается обык
новенными диффе~нциальными уравнениями, если только их по
рядок не очень высок. В частности, она будет описываться диф-
74
енциальным уравнением с постоянными коэффициентами, если
менты схемы являются инвариантными во времени, такими,
ушки
индуктивности,
конденсаторы
и
резисторы.
как
Синусои
.ьное напряжение, приложенное ко входу такой схемы, появляя на выходе как напряжение с меньшей амплитудой и со сдви
': фазы; синусоидальная форма и частота сохраняются. Таким
азом,
схему
можно
описать
частотными
характеристиками
за
ания и фазового сдвига. Описание другими функциями, напри
"р функциями Уолша, вполне возможно, но оно затруднено тем,
форма этих функций изменяется.
' Рассмотрим линию передачи, описываемую телеграфным урав
·, нием {1-3]:
д2w
д2w
дх 2
С,
R
и А
-
Линия не вносит
искажений,
В этом случае общее решение запишется
w (х, t)
а= (LA
(2.19)
индуктивность, емкость, сопротивление и прово-
мость на единицу длины.
=RC.
aw
А
-LC at 2 -(L +RC)дt-RAw=O,
= e-at [f (х- ct)
+ RC)/2LC,
в
если
виде:
+ q (х + ct)J,
с= 1/VLC,
LA-RC =О.
(2.20)
-ct) и q(x-ct) - произвольные функции, определяемые на
".льными и граничными условиями. Во время передачи сигналы,
исываемые этими функциями, претерпевают только затухание и
ержку. Это свойство сохраняется и для линий, не свободных о г
если они являются «электрически короткими». Соглас
К. В. Вагнеру (1] линия длиной х является электрически корот
., если для х выполняется следующее соотношение {2]:
· кажений,
2 -.J"T
2Z
x<-R-r
С= -R-;
-.ГТ
l= J' -С-•
В качестве примера рассмотрим открытую
(2.21)
проводную линию.
·ва проводника представляют собой м_едные провода
диаметром
мм, находящиеся на расстоянии 18 см. Выберем следующие ти-
L=2,01 · IO-з Гн/км; C=5,9· I0-9 Ф/км; R=
~ 4,95 Ом/км; А=О. Получаем Z=540 Ом и 2Z/R=225 км. Эта ли
ичные величины:
·ия может рассматриваться как свободная от искажений для рас
ояний, меньших, чем 225 км. Поставив регенеративные усилители
а расстояниях, меньших чем 225 км друг от друга, можно переда
ать сигналы без искажений на любое расстояние.
В качестве другого примера рассмотрим
телефонный
кабель
ежду центральной телефонной станцией и абонентом. Проводни
ами являются медные провода диаметром 0,8 мм в изоляции из
ропитанной
бумаги.
Выберем
следующие типичные
величины:
=7. 10-• Гн/км; С=З·З· 10--8 Ф/км; R=70 Ом/км; Z= 145 Ом;
Z/R=4 км. Эта линия будет электрически короткой для ряда або
ентов,
но не для
всех .
Обычные коаксиальные кабели имеют волновое сопротивление
между 50-100 Ом. Пусть погонное сопротивление
равно
75
10 Ом/км. Тогда 2Z/R будет равно 10-20 км. Это есть порядок ве
личины обычного расстояния между усилителями. Однако надо учи
тывать, что телеграфное уравнение не учитывает скин-эффект. Ис
следования скин-эффекта для функций, отличных от синусоидаль
ных и косинусоидальных, очевидно, отсутствуют 1 ).
Несмотря на эти результаты, ,еинусоидальные и косинусоидаль
ные функции играют значительную роль в теории передающих ли
ний. Одной из важных причин этого является метод Бернулли для
решения дифференциальных уравнений в частных производных с
постоянными во времени коэффициентами. Предположим, что
w(x,
в (2.19) можно представить в виде произведения простраJJсiвен
ной переменной и(х) и временной переменной v(t):
t)
w (х, t)
Подстановка
в
u(x)v(t)
=и (х) v (t).
(2.22)
дает два обыкновенных дифферен
(2.19)
циальных уравнения:
1
tР(и)
+ (Л-RА)и =О;
dx1
LCd'o1
dt
+ (LA + RC)
(2.23)
+v= О.
du
dt
Их собственными функциями являются cosV (A-RA)x; sinV (Л-RА) х
и evt , где
v определяется
'V =
_
следуюЩим образом:
LA + RC ± _1 [(LA + RC )' _ _
1 ]112
2LC
LC
4
.
(2.24)
LC
Метод Бернулли имеет большое значение для нахождения ре~
шений телеграфного уравнения и других дифференциальных урав
нений в частных производных, которые удовлетворяют определен
ным начальным И граничным условиям. Однако этот метод реше
ния
пригоден
перимущественно
для
синусоидальных
и
косинусои
дальных функций. Линии с параметрами, зависящими от времени.
естественно, не допускают разделения
переменных
на
пространст
венную и временную.
Распространение электромаr~нитных радиоволн описывается вол
новым уравнением, которое для одномерного случая
-
чить из телеграфного уравнения, если положить
можно полу
R=A=O.
Его об
щее решение определяется выражением
w (х, t) = f (x-ct)
+ q (х + ct).
(2.25)
Это решение имеет тот же вид, что (2.20), если не учитывать коэф
фициент затухания e-at. Таким образом, радиолиния ведет себя как
ЛШIИЯ, не вносящая искажений. Ра~иоволны необязательно ДQЛЖЯЫ
быть синусоидальными или описываться синусоидальными функ
циями. Соответственно радиоканалы необязательно должны раз
личаться по частоте; они могут различаться по частости. Сущест1 ) Практически свободная от искажений
описана Мичэмом {3].
пиния на
попуnроводниках бwа
76
J
уют важные практические аргументы в пользу разделения радио
аналов по частоте,
но
эти аргументы связаны в
основном с
про
тотой реализации приемников и передатчиков, а не с законами
'природы. Позже будет показано, что мобильная радиосвязь теоре
,тически возможна на основе волн Уолша.
Рассмотрим характеристики каналов связи под другим углом
рения. Разумно описывать свойства канала с помощью функций,
оторые определяются передаваемыми сигналами. Для передачи
цифровой информации было предложено так много форм импуль
сов, что трудно выбрать одну из них и назвать только ее удобной
для описания канала. Это не распространяется на телефонный ка
.пал. Обычно телефонный сигнал рассматривают как совокупность
синусоидальных и косинусоидальных колебаний. Следовательно, си
· нусоидальные и косинусоидальные функции оказываются наиболее
приемлемыми для описания телефонного канала. Трудность заклю
· чается в том, что не существует серьезной причины для того, что
бы считать телефонный сигнал совокупностью синусоидальных и
·косинусоидальных колебаний.
·
Рассмотрим речевой сигнал,
представленный выходным напря
жением микрофона. Продолжительный гласный звук дает папря.
жение, которое хорошо можно аппроксимировать суммой нескодь
ких синусоидальных колебаний. Система, производящая гласный
звук, инвариантна во времени и приводится в движение голосовы
; ми связками по закону синусоидальной функции. Такая сие.тема
:· описывается дифференциальным уравнением в частных производ
. ных с коэффициентами, не зависящими от времени, и синусоидаль
· ной возмущающей функцией. Но это не так для глухих согласных,
.особенно звуков типов р, t или k. Система, производящая эти зву
·ки, описывается дифференциальным уравнением в частных произ
•.водных с переменными во времени коэффициентами, а синусои
дальная возмущающая функция отсутствует. Нет особой причины
• рассматривать эти звуки как совокупность синусоидальных и коси
усоидальных колебаний, а не сигналов, описываемьiх функциями
'другой полной ортогональной системы.
· Экспериментальные исследования, проделанные Клайном, Бес
веттером, Тасто, Люке, Мейлом и другими, показали, что речевые
:Сигналы вне сомнения можно рассматривать как совокупность сиг
nалов Уолша. Люке и Мейле создали телефонную многоканальную
;tистему, использующую фильтры, которые
пропускают сигналы
-Уолша до частости
,
.
4000 zps,
а не синусоидальные и косинусоидаль
ые колебания до частоты 4000 Гц. Заметных различий в характе
истиках систем не было обнаружено. Бесветтер построил анали
атор и синтезатор для вокодера, использующего 16 фильтров, филь
рующих согласно частостям функций Уолша, а не частотам сину
оидальных функций. Клайн показал на некоторых примерах, что
олос, разложенный по функциям Уолша, содержит «частостные со
. тавляющие» так же, как голос, разложенный на синусоидальные
. косинусоидальные функции, содержит «частотные составляющие»;
. ти исследования продолжаются. Теоретические обоснования, объ-
77
,.
1 ·.
ясняющие эти результаты, приведены в гл. 5. Сэнди уж в 1962 г.
использовал функции Уолша в теоретической работе по анализу
речи.
2.2.2.
Описание канала связи параметрами
пере:крествых
помех
Ранее было показано, что каналы связи можно описать не толь
ко синусоидальными и косинусоидальными функциями. Возникает
вопрос, как их еще можно характеризовать. Стройная теория свя
зи, основанная на ортоrональных функциях, требует метода описа
ния каналов, который был бы применим ко всем или хотя бы ко
многим системам ортогональных функций . Заметим, что это более
· общее описание упростит рассмотрение пропускной способности ка
·пала в гл.
6.
Рассмотрим полную систему ортогональных функций {f(j, 6) }.
Разделим ее на четные функции fc(i, е), нечетные функции fs(i, 0)
и постоянную f(O, 0). Ко входу канала приложим напряжение
Uf c(i. 0) вместо 1Ис cos ffif. Пусть в данный момент времени канал
имеет такие параметры, что на
выходе появляется установившееся
напряжение Иc (i)f J..i, 0-0c('i)]. Это будет справедливо для большо
го класса систем функций {f(j, 0)} при условии, ·что используется
пиния без искажений. Функция 'Uc(i)(U=Kc(i) или lg U/Uc(i)=
=ac(i) есть обобщенное затухание канала связи. Функция 0c(i) =
=bc(i) есть обобщенная задержка, так как термин «фазовый
сдвиг»
применим
только для
синусоидальных
и
косинусоидальных
функций.
Входное напряжение 1Uf s(i, 0) производит выходное напряжение
Us(ii)fJ:i, 0-0s(i)]. Затухание и задержка определяются как
Us(i)/U =Ks(i); lg U/Us(i) =as(i) и 0s(i) =bs(i). Постоянная .Uf (О,
9) дает U(O)f{O, 0---<{)(0)]; U(0)/ V=K(O); lg U/1U(O) =а(О) и 0(0) =
1
=Ь(О).
Подстановкой
i-+i/s= ·µ растянем функции системы {f (О, .0 ); fc(i,
0)}. Будем беэгранично увеличивать i и S· Как показано
в гл. 1, в этом случае получается система {/с(µ, О); f8 (µ, 0)}. Функ
ции Kc(i); Ks(i); ac( i); a 5 (i); bc(i); b8 (i) переходят в Кс(µ), ... ,
bs(µ). В частности, для функций fc(µ, 0) = V2 cos 2л:µ0= V2cosffit
и fs(µ, 0) = V2sin 2л:J..110= V2 sin .ffit получаем частотные функции
Кс (ffi), "., bs ( ffi). Индексы с и s можно опустить, если синусоидаль
6);
is (.i,
1
1
ные и косинусоидальные колебания одной частоты
претерпевают
одинаковое затухание и задержку;
получаются
функции: К (ffi);
a(ffi) и b(ffi). Таким образом, описание каналов связи с помощью
частотных характеристик
затухания и фазового сдвига
является
частным случаем.
В общем случае сигналы
Uif c(i,
Н) не только затухают и запаз
дывают, но и искажаются. Вместо Uc(i).f c[i, 0-0c(i)] получается
выходной сигнал Uqc(i, 0) . Разложим функцию qc(i, 0) в ряд по
системе {:f(O, 0-·0c(i)]; ·fr;[k, 0-0c(i)]; fsf.k, 0-0c(i)]}. Значение за
держки 0c(i) будет определено позже. Переменной теперь является
78
, а i является констаытой (k=l , 2, .. ., i, .. . ):
qc (i, 0) = К (ci, О) f [О, 0- 0с (i)J +
+ K(ci,
...
...
L {К (ci, ck) fс (k, 0 -
+
sk)fsfk, 0-0c(i)J};
.
J qc(i, 0)f[O, 0-0~(i)Jd0;
K(ci, 0)=
0с (i)]
k=I
(2.26)
-оо
00
K(ci, ck)=
Sqc(i, 0)fc[k, 0-0c(i)Jd0;
-·
Jqc (i, 0)fs[k, 0- 0с (i)J d 0.
О1
К (ci, sk)=
-оо
ассмотрим интеграл K(ci, ck) для i=k. Его значение зависит от
с ( i). Выберем 0с (i) таким образом, чтобы коэффициент К (ci, ci)
. тал максимальным . Тогда обобщенные задержки 0с ( i) = Ьс (i)
6s(i)=bs(i) определяются так, что с уменьшением искажений
ни приближаются к значениям задержек для линии , не вносящей
скажений.
Коэффици е нты K(ci, О); K(oi, ck) и K(ci , sk) являются обоб
щениями з атух а ния Kc(i) для канала связи с искажениями. Kc(i)
. мее т одну переменную i и может быть представлен вектором.
K(ci,
О);
K(ci, ck)
и
/((ci, sk) имеют две переменные i и k и могут
К ( ci):
быть представлены матрицей
K(ci) =
K(cJ, O) .:_ K(cl, cl)
К(с1, sl)
K(cl,
с2)
К (с2, О)
К (с2, cl)
К.(с2, sl)
К (с2, с2)
К (сЗ, О)
К (сЗ, cl)
К (сЗ, sl)
К (сЗ, с2) .
. (2 .27)
Ес.'!и вместо напряжения ,U1fc(i, 0) приложить Ufs(i, 0) , то по
являются выходные напряжения U.qs(i, 0). Коэффициенты K(si, О),
К (si, ck) и К (si, sk) получаются аналогично (2.26). Матрица К (si)
. имеет вид матрицы (2.27), но ci заменяется на s.i.
·
Передача
U,f (O, 0) дает Uq(O, .0) и коэффициенты К(О, О),
К (О, ck) и К (О, sk) , которые можно записать в виде матрицы-стро
ки
K(O)=llK(O, О)К(О , cl)K(O, sl)K(O, с2)К(О, s2) ... ll.
K(ci); K(si) и К(О) можно объединить
К (О, О) К (О, s 1) К (О. cl) К (О, s2) К (О, с2)
Три матрицы
·
К=
K(sl,O) K(sl, sl) K(sl, cl) K(~I, s2) K(sl,
K(cl,0) K(cl, sl) К(с1, cl) K(cl, s2) К(с1,
K(s2,0) K(s2, sl) K(s2, cl) К (s2, s2) K(s2,
К(с2,0)
К(с2,)1)
К(с2, cl)
79
в одну:
с2)
с2)
с2)
К(с2, s2) К(с2 , с2)
2 28
· ( • }
Если функции f(j, i0) не искажены, то все члены матрицы (2.28),
кроме членов, лежащих на главной диагонали, равны нулю. По
следние становятся одномерным набором коэффициентов затуха
ния К(О) =К(О, О); Kc(i) =K( eii, oi) и Ks(i) =K(si, si).
Время задержки fЦi) в . (2.26) и соответствующие времена за
держек 0s(i) и '8(0) для функций l/,fs(i, 0) и Uf(O, е) также можно
записать
в
виде
матрицы:
о
0(0)
о
6=
о
о
о
о
ее (1)
о
о
08 (1)
о
о
о
(2.29)
Матрицы К и е характеризуют канал связи для системы функ
ций {f(j, ·0)}. При многоканальной связи искажения в канале соз
дают перекрестные помехи . Одним из применений матриц К яв
ляется использование их для коррекции этих перекрестных искаже
ний . Таким образом, матрице К можно присвоить название матри
цы перекрестных искажений, в то время как е можно назвать мат
рицей задержки.
2.3.
ЧАСТОТНЫЕ ФИЛЬТРЫ, ОСНОВАННЬIЕ
НА ФУНIЩИЯХ УОJППА
2.3.1.
Фильтры нижних частостей
в гл. 1 было показано, что фильтр можно характеризовать си
стемой функций {fc(µ, 0); fs(µ, 0)} вместо синусоидальных и коси
нусоидальных функций {1-7]. Было получено ур-ние ( 1.112), кото
·рое позволяет найти сигнал Fo('0) на выходе фильтра , если на вход
подан
сигнал
F (0). Подстановка . системы функций Уолша
{cal(µ , 6) ; sal(µ, 0)} в ф-лу (1.112) дает
(Х)
F 0 (0) =
S{ас(µ) Кс (µ) cal [µ,
о
0 - 0c(µ)J
+ as(µ)K s(µ) sal [µ,0 -
Для дальнейшего рассмотрения нужны
ния§ 1.2:
cal (µ, 0) = wal
(О,
0);
О ~ µ
0s (µ)]} d µ.
(2.30)
следующие соотноше
<
1;
)
j
cal (µ, 0) = cal (i, 0); i ~
i l;
(2.31)
sal (µ, 0) = sal (i, 0); i -1 < µ < i;
- 1/2 < 0
1/2; i = 1,2, . . .
.
Разобъем сигнал G (0) на отрезки -1/2~0< 1/2; l/2~.0<3/2, ....
F(e) представляет отрезок сиrна.1а на интервале -1/~~6< 1/2.
µ< +
<
80
кое разбиение не накладывает никаких ограничений на сигнал
но при этом требуется сигнал синхронизации, чтобы фикси
вать начало и конец иш-ервалов. Коэффициенты ас(µ) и as(µ)
(2.30) для F(6) можно вычислить с помощью (2.31):
(6),
.
.
1/2
S F (0) wal (О, 0) d 0;
а,(µ)= а,(О) =
О~µ< 1;
-1/2
1/2
JF(0)cal (i, 0)d0;
ас(µ) =ac(i) =
i~µ<i+ 1;
(2.32)
-1/2
1/2
S F (0) sal (i, 0) d 0;
as(µ) = as (i) =
i-l <µ~ i.
-1/2
Специфические особенностн функций Уолша делают возмож
ым преобразовать интегральное представление ограниченной_ во
· ремени функции F(10) в представление ее суммой:
F (0) = .
J"" [ас(µ) са!(µ, 0) + а5 (µ) sal (µ, 0)] d 0 =
о
С1О
=а (О) wal(O, 0) + '"" ас (i) са! (i, 0) + а 5 (i) sal(i, 0).
"
(2.33)
.
l=I
Коэффициенты затухания Kc(/t) и Ks(µ) и задержки 0с(µ) и
в (2.30) определяют фильтр . Их можно свободно выбирать
пределах физической реализуемости. Чтобы представить выход
,(µ)
·.
ой сигнал
ыбор:
в виде суммы, а · не интеграла,
Кс(µ)=К(О);
0с(µ)=0(0);
сделан следующий
O~µ<l;
Кс(р.) _ Kc(iJ: 0с(µ) _ 0c~i~; ~~µ <i+ l.;
- Ks (t), 0s (µ) - 05 (t), t - - < µ~ i.
1
Ks (µ)
равнение
(2.30)
1
(2.34)
принимает следующую форму:
F 0 (0) = а(О) К (О) wal [О, 0-0 (О)]+
,
С1О
+ ~ {ac(i)Kc(i) са/ [i, 0- 0,;(i)] +
as(i) Ks(i) sal [i, 0- 05 (i)}.
(2.35)
l=I
ассмотрим фильтр,
для
которого удовлетворяются
следующие
словия:
К (О)=
1;
получается из ф-л
0 (О)= 1;
К, (i)
= Ks (i)
=О;
(2.36)
(2.30)-(2.35):
1
F0 (0)
=
Sа, (р., 0- 1) d µ=а (О) wal (О, 0- 1).
о
81
(2.37)
Вид этого интеграла намдит
F*'(o) ,
t!)
.
s
на мысль назвать схему фидьт-
F{О)'=f#)г;~ -~-F0 (8) ром нижних частостей, чтобы от~S
, личать о.т обычного фильтра ниж.l' 1
них частот. Его функциональная
о)
F{fJ)
re1 ... - ... --";-:-......,/.
C<' J
~
r,*(Щ1!~~~~
-
А
-~
F0 (8)
L--l
c,(8)..L•---l'---t====тF
1
1
2е-з
125
250 --137$
t [р:,
8)
схема показана на рис. 2.17а, а
временная диаграмма
2.176.
а (О) согласно
на рис.
определяет
(2.32).
Значение
конце
интервала
а (О) можно считывать на выходе
интегратора с помощью переклю-
чателя
S2
в
-1/::::;;0<1/2.
После этого интег-
ратор возвращается
в
исходное
состояние переключателем S1. Ко
эффициент а(О) для отрезка G(0)
в интервале l/2::::;;i0<3/2 получается интегрированием G (0) в те
-Fа (8)\ чение
F(8)
-
Интегратор
интервала
времени 1/2~
::::;;е<3/2 и т. д. Согласно
(2.37)
а (О) должно быть умножено на
wal (О, 0-1), постоянную величи
ну, равную
1. Таким образом,
Рис. 2.17. Фильтр нижних частостей: а (О)\\·а\ (О, 0-1) есть напряжение
а) функциональная схема; б) времен а (О), получаемое в конце интер
ная
диаграмм.а;
в)
практическая
•схема:
Н
-
интегратор;
устроilство; ОУ -
ЗУ
-
заnоминающее
операционный уси.1итель
вала -1/2::::;;0<1/2 и запоминае
мое в течение интервала 1/2 ~
::::;;0::::;;3/2. УстрОЙСТВО ЗаПОМИНаНИЯ ЗJi показано на рис. 2.17а.
нижних частостей показана
на
Практичесr<ая схема фильтра
рис.2.17в.
Для определенности рассмотрим фильтр нижних частот с ча
стотою среза 4 кГц. Согласно теореме отсчетов сигнал на выходе
этого фильтра имеет 8000 независимых значений в секунду. Вы
ходной сигнал фильтра нижних частостей (рис. 2.17) будет иметь
ту же
информационную ценность,
что и в предыдущем случае,
если будет иметь также 8000 независимых значений в секунду.
Таким образом, длительность Т ступенек Go(0) на рис. 2.17 дол
жна быть равна 1/8000= 125 мкс; соответственно частость среза <р
равна l/2T=4000 zps. Здесь использована теорема отсчетов ана
лиза Уолша-Фурье,
которая оказывается
тривиально простой
для фильтра нижних частостей i[8-10].
2.3.2.
Частостные полосовые фИJIЬтры
Найдем выражения для простых частостных полосовых филь
тров. Для этого требуется теорема
умножения функций Уолша,
полученная в
§ 1.4:
82
са! (i, 0) са! (k, 0) =са! (i ffi k, fl);
sal(i, 0)cal(k, 0) = sal{fkffi(i-1)1+ 1, 0};
(2.38)
sal(i, 0)sal(k, 0) =cal[(i-l)ffi(k--1), 0J;
са! (О, 0) = wal (О, 0).
~оремы умножения (2.38) очень похожи на теоремы умножения
.- нусоидальных и косинусоидальных функций, за исключением
. го, что в правой части стоит только один член вместо двух чле
:. в для суммы и разности частот. Следствием этого является тот
1
. акт, что модуляция несущей Уолша дает однополосную (по ча
модуляцию. Это делает возможным использовать часто
. :ести)
ые полосовые фильтры, построенные по принципу, хорошо из
. стному,
но мало используемому для частотных полосовых филь
ов.
«Сдвинем по частостю> сигнал F (0) в
Используя (2.38), получаем
(2.33),
умножив его на
·. 1(k, 0).
00
F (0) са! (k, 0) = а (О) са\ (k, 0) + ~(ас (i) са! (i Ef) k, 0) +
i=I
i'i=k
+as·(i)sal{fktf:)(i-l)J+ 1, 0})+ac(k)wal(O, 0)+
+ а5 (k) sal {fk Ef) (k- l)J
1, 0}.
+
Пропустив этот сигнал через
.
_Ыв-зеиый ф-лой
фильтр
нижних частостей, опи
получим по аналогии с
(2.36),
:выходной
{2.37)
гнал
.
. 01
(0) = ac(k) wal (О, 0 - 1) =
J ас(µ) са!(µ, 0) са\
k+I
(k, е
-
l)d µ; (2.40)
k
са1
Умножение
\
на
(k, 0- 1) ==са! (k, 0).
на
Fo1(0)
ca\(k, 0-1)
первоначальную полосу в
F0 (i)) = f
01
. сдвигает отфильтрованный
частостном
диапазоне:
(0) са\ (k, 0- 1) =ас (k) са\ (k, 6- 1) =
k-\-1
Jас(µ) са!(µ, 0) d µ;
=
(2.41)
k
wal(O, 0-l)cal(k, 0- l)=cal(k, 0-1); cal2 (k, 0- 1)== 1.
оследний
·
интеграл
определяет
название
частостного
полосового
льтра. Для практической реализации необходимо перед фильт
м нижних частостей
(рис.
ы выполнить перемножение
2.17) поставить перемножитель, что
(2.41). На рис. 2.18 показан такой
'олосовой фильтр. К обоим перемножителям П подводится один
тот же сигнал
ca\(k, 0), так как cal(k, 0) имеет период 1 и, та•
ca\(k, 0-1). Пригодные для этого пере
показаны на рис. 2.9. Заметим, что умножение на
83
м образом, идентичен
. ожители
ФУнкцию Уолwа означает умножение только на или-\; умнJ
+1
+
жение на
1 не меняет знак сигнала; умножение на
его знак на противоположный.
п н ~ Н..__.п___mе)
f
'1"" (к,•)
-1 меняет
Рнс.
2.18.
П
перемножитель
-
Уопша ;
Ф
ЧастостиыА полоса.
вой фильтр:
-
фильтр
тосте А
для
функций
нижних
ча с.
На рис. 2.19 показаны графики затухания
и задержки как
функций частости для фильтра нижних частостей с К (О)
1 и не
скольких полосовых фильтров. Коэффициенты Kc(i) и K,(i) равны
=
~-:-_~c!~:f
NsJ.Q:1
11~
fl5н(c
.:::!, q
Ф"'
Нс (Z}= f
-----/25 ИJ(С
,
1
8
2 '
1
.м.--;-
.,,,
,
J
1№ ttlOO с·1
2
llllflc" 1
Т= fZ5икс
T=ftS.Nl!C
s--
'/__.
Рис.
1
, .,,,
,JI,...,
1
2.19.
о
f
2
Jl--
q •1111 8600
:r
"
f
z
,J.l -;--,
c·f
T•/2SMl<C
f-
Т= 125 Hl<C
'!-
Затухание и за·держка частостных фильтров
нулю, кроме тех значений
i,
для которых они,
как показано на
рисунке, равны 1. Очерченные площади на гуаницах полосы µ=i
показывают, что функции cal(i, 0) или sal(i, е) проходят через
фильтр; заштрихованные площади показывают, что соответствую
щие им функции не проходят.
Для всех фильтров рис. 2.19 нормализованная полоса пропу
скания µ2---<µ1=ii2-i1=Лµ равна 1. Назовем частное от деления ши
рины полосы пропускания на нижнюю границу полосы дµ/1µ1 от
носительной полосой пропускания. С учетом рис. 2.19 для Лµ/~µ1
можно получить следующие соотношения:
Лµ/µ1 =
1 для Kc(l)= 1 или К,(1)= 1;
= 1/2 для Кс(2) = 1 или К, (2) = 1;
Лµ/µ1 = l/k для Kc(k) = 1 или K,(k) = 1.
Сигналы ~al (k, 0) ил.и sal (k, 6), которые п(Юходят частостный
полосовой фильтр (рис. 1-18), определяют относительную полосу
84
Лµ/µ 1
1
ропускания. Приведенная на рисунке схема позволяет получить.
. носительную
полосу пропускания, меньшую или равную
ализованная частость
µ
так же,
сть (f = 1
µ/T при Т= 125 мкс, нанесена на рис.
,;
1.
как и ·ненормализованная
Нор
час
2.19.
Частостная зависимость задержки и затухания, показанная на
нс.
2.19,
рень
является идеализированной.
В
практических фильтрах
из среднего квадратического отклонения выходного напря
. ения фильтра лежит в диапазоне 0,01-0,001. Среднее квадрати
:-еское отклонение, таким образом, лежит в диапазоне 10-4-10-в~
· о обеспечивает затухание в полосе заграждаемых частостей
~-40-;--60) дБ (рис. 2.19).
1;.. Бесконечно крутые характеристики,
· оказанные на рис. 2.19, также спра
. едливы
для практических фильтров .
акой результат поражает инженеров,
~оторые привыкли к частотным фильт-
-ам. Однако частостные фильтры нс
·. ользуют переключатели, которые про
. зводят временное квантование сигна
. а. Учитывая это, можно объяснить
, искретное изменение затухания сиг
ала. Дискретность исчезает, если ис
пользовать функции Уолша, опреде
енные на
полном
интервале -оо
<
10<+оо, а не на интервале -1/2~
· ~e<l/2.
.
Согласно рис. 2.19 затухание и за
.
-держка частостного фильтра
постоян
~ы в полосе пропускания. Следователь
но, отсутствуют амплитудные и фазо
'вые
искажения.
Задержка в' области
,Заграждения для идеальных фильтров
не рассматривается,
.стные
;,проходят.
' кают
поскольку
часто
составляющие в этой области не
Реальные фильтры пропус
составляющие в области заграж
дения. Задержка в области загражде
ия, показана на рис. 2.19 штриховой
· инией.
-;- На рис. 2.20
показаны синусоидаль
llое колебание с
частотой
250
Гц на
. 0входе нескольких частостных фильтров
\(строка а) и результирующие выход
ые сигналы: в строке б показан сиг
;Нал на выходе фильтра нижних час
;
.
стей с
Ki:(O)
= 1,
в
оказаны сигналы на
ых
· в (2)
строках в, г и д
выходах полосо
фильтров с Кв ( 1)
= 1;
Кс ( 1) =
1
и
= 1, в - строках е, ж и з показаны
85
Рис.
2..:Ю.
А11'11рохсимац11я си
нусоидальных
функций
фуик-
цияМ'И Уолша:
а) сииусоидалыюе колебание с
частотой 250 Гц; б) a(O)wal(O.
0); в) a.('l)sal(l, 0); г) a"(l)X
Xcal(I, 0); д) a,(.2)sal(2, 0);
е) сумма б и в; ж) сумма б, в
н г; з) сумма б, в, г, д; времен
ная база T=I) ·М'С; горизонталь
ный масштаб 0,5 мс/дел . ; время развертк11
l
мс
сигналы на выходах фильтров с Kc(O)=Ks(l)=l(e);
= Ks (1 ) = 1 (ж) ; Кс (о) = К s ( 1) = Кс ( 1)
Кs(2)
1 (з) .
=
На рис.
2.21
показан
=
частот-
Кс(О) =
н
ный спектр синусоидальных фун
кций (а) с равными частотами н
амплитудами, но различными фа
зами.
Амплитудные
ас(µ) =ас(<рТ)
2.216;
спектры
Показаны на рис.
амплитудные
as (~1) =as(<pT) ___:_ на
FI~,,
спектры
рис.
2.21в .
/'"'-t,
о)
.. ~.
,6~~.
Рис.
2.121.
Преобразования
6~~.
Уол
ша-Фурье
синусоидальных колебаний:
а) синусоидальные
колебания
с
частотой 1 кГц и различной фа
зой;
горизонтальный
масштаб
0.... 5....10 ••. ';t',
В=t/Т--
0,1 мс/дел; 6) н в) преобразова
ния
Уолша-Фурье
ac(q>T)
и
a,(ipT) колебаний (а) ; временная
база Т = 1,6 мс;
горизонтальный
масштаб -625 zрs/дел
Рнс.
Частостный Пl'Ирокополос
ный фильтр:
Ф - фильтр нижних частостеА; ЗУ - мпо
2.22.
минающее
устроА:тво
Осциллограммы 6 и в получаются с 1ю11ющью отсчетов выходных
напряжений 16 частостных фильтров. Возведя в квадрат и сумми
руя графики на рис. 2.216 и в, получаем частостный спектр мощ
ности.
Полосовые фи-1ьтры, соответствующие рис. 2.18, имеют отно
сительную ширину полосы Лµ/µ1=1, 1/2, 1/3, .... На рис_ 2.22 по
казан полосовой фильтр с относительной шириной полосы Лµ/µ=
= 1, 2, 3. В этой схеме используется фильтр нижних частостей Ф 1 ,
соответствующий рис. 2.17. Он интегрирует входной сигнал на вре
меннь1х интервалах длите.1ЬНОСТЬЮ т. Следующий фильтр нижних
частостей Ф 2 интегрирует входной сигнал на временных интерва
лах длительностью Т/2 или Т/3, или Т/4, .... Выходные напряже~
ния обоих фильтров показаны в строках а и 6 рис. 2.22. Период
86
'-.._}
~егрирования Ф2 выбирался равным Т/2. Разность во временах
держки Ф1 и Ф2 компенсировалась в запоминающем устройстве
. Разность напряжений, изображенных в строках а и в, дает
Dдной сигнал Fo(0) .
о)
F{в)
высших частостей (а)
фильтр (6):
ч ас тостей ;
ПФ
-
и
час тос тны 11
частостиыИ заградительный
п о.1осс вой
фи ,1 ьтр;
.ТZЗ
-
схема
задержки
Кроме различия в относительной ширине полосы, имеется дру
важное различие между полосовыми фильтрами
(рис.
2.22
и
В полосе пропускания фильтра рис. 2.22 могут проходить
к сигналы sal (µ, 0), так и сигналы са\(µ, '0 ), в то время как
. рез фильтр. соответствующий рис. 2.18, могут проходить либо
~1(µ, 0), либо са\(µ, 6).
· На основе рассмотренных типов . фильтров можно построить
· L-8).
)юго других фильтров. На рис.
2.23 показаны фильтр высших ча
остей и заградительный фильтр, построенные на основе фильтра
ижних частостей и полосового фильтра. Параллельное соедине
;
, ие нескольких полосовых фильтров, соответствующих рис.
2.18,
озволяет
построить
фильтры,
пропускающие
как
сигналы
1( µ, 0), так и са\ ( µ, 0) и имеющие относите.пьную ширину поло
Л·µ/µ1=1, 1/2, 1/3. С другой стороны, можно получить широко
олоеный фильтр , пропускающий только sal (µ,
показано на осциллограммах рис. 2 . 20е, ж, з.
0)
или са!(µ,
0),
· ак
2.3.3.
Одним
Цифровые частостные фиJIЬтры
из · наиболее
перспективных
применений
частостных
ильтров, основанных на функциях Уолша, являются цифровые
· ильтры. Объясняется это тем, что численное преобразование
олша-Фурье сигналов
требует выполнения только
операций
. ложения и вычитания, в то время как численное преобразование
· урье требует выполнения операций умножения .
, 0
Для объяснения принципа работы цифрового частостного филь
Сигнал F (0)
' а рассмотрим функциональную схему рис. 2.24.
ропускается через фильтр нижних частостей Ф. Пусть ступенча
·. ая функция на его выходе имеет ступеньки длительностью Т/16 .
. мплитуды ступенек преобразуются аналого-цифровым преобраователем А-Ц в двоичные символы, которые передаются со ско
остью 16 символов за время Т в цифровой накопитель ЦН 1.
усть последовательность из 16 последовательных символов бу
ет обозначена как А, В, ... , Н, . . " Р. Для получения 16 коэффи-
87
циентов а(О), а 5 (1), ac(I ), . . ., as(8) из 16 символов можно исполь
зовать быстрое преобразование Уолша-Фурье (§ 1.2). Для вы
-числения одного, нескольких или всех этих коэффициентов ариф
метическое устройство АУ должно производить только операции
-сложения и вычитания. Предположим, что вычисляется коэффи
циент ас(5) , как показано на рис. 2.24. Шестнадцать коэффип.иен-
F,{8)
Рис. 2.i24.
Функщ1ональиая схема цифро в ого частостиоrо фильтра :
Ф - Фильтр ни жних ча стост е А ; А-Ц- преобра зов а тель ана л ог-цифра ; Ц-А
преобра зовател ь · цифра -аналог ; ЦН - цифровой накопитель; А У - арифметическое
устрой с тво
1ов -а~ (5) , +ас (5) , +ас(5) , -ас (5), ... со знаками, соответству
ющими знакам cal (5, 0) (рис. 1.2), передаются в цифровой нако
питель UH2. Обработка этих коэффициентов в преобразователе
.цифра - аналог Ц-А дает непрерывный выходной сигнал 1
f o(0).
<:вязь между входным сигналом f (0) и выходным fo(0) следует
-ИЗ
(2.32) И (2.41):
ас(5) =
1/2
J F(0) са\{5, 0) d0
ас(µ);
5 :Е; µ< 6;
-1/2
6
f 0(0)= ас (5) cal (5, 0 - l) =
Jас(µ) са\(µ, 0) d 0.
1
(2.42)
5
Пусть Fo(0) получается путем прохождения са\ (5, 0) через ча
-стостный фильтр (рис. 2.18) . Пусть fo(0)
отклоняется от своего
;номинального значения в соответствии с распределением Гаусса
-ео среднеквадратичным
отклонением, отнесенным
к
единичному
.напряжению, равным 10-в. Перекрестное затухание коэффициен
тов ac(i), i=F5 и as(i) равно тогда -60 дБ. Более высокое пере
крестное затухание может быть получено при использовании циф
:рового фильтра . Пусть F1 (0) (рис. 2.24) имеет СQ.еднеквадратичное
·отклонение, отнесенное к единичному напряжению , равное 10-в.
Если для вычисления ас (5) используется 2n отсчетов F 1 (0) и если
преобразователь аналог-цифра дает незначительную ошибку, то
'Получается среднеквадратичное отклонение ас (5), отнесенное к
.единичному напряжению, равное I0-6 /2n. Перекрестное затухание
'В дБ равно lOlogl0-6/2n=-(60+ 10nlog2).
Для 2n= 16, что ие
пользовано
на рис. 2.29.,
получается
перекрестное
затухание
-(60+401og2) ~-72 дБ.
"
3.
ПЕРЕДАЧА СИГНАЛОВ НА НЕСУЩЕЙ
3.1.
АМПJШТУДНАЯ МОДУЛЯЦИЯ (.А!М)
3.1.1.
Модуляция и синхронная демодуляция
:предыдущей главе была рассмотрена передача коэффициентов
(j)
с помощью системы ортогональных функций
{f(j, 0)}.
Те
ь будет рассмотрена передача временнь1х функций F(0) или
';(0) с помощью временных функций {Ф(k, 6)}. Эти функции
'k, 6) будем называть несущими.
ю
функцию
времени, например,
F(0) обозначает произволь
выходное напряжение микро-
· на. Обозначение Fx (0) принято для того, чтобы подчеркнуть,
о функция времени
содержит конечное число
коэффициентов
т-1
i), как и телетайпные сигналы: F х(0)
=
1: ax(j)f (j,
0).
i=O
В настоящее время в качестве несущих Ф(k, 0) используются в
овном синусоидальные
и косинусоидальные функции. Однако
··:г ни физического, ни математического обоснования того, почему
· ьзя применять сигналы, описываемые другими функциями для
. едачи сообщений по проводным линиям, по волноводам, радио
, ниям и т. д. В некоторой степени в кабельной связи используют
в
качестве
несущих
периодические
последовательносхи
прямо
льных импульсов.
Особенно удобны для использования в качестве несущих функ
,
' образующие группу относительно операции умножения. Амитудная модуляция несущих, описываемых такими функциями,
ет однополосную модуляцию. Многоканальные системы, исполь
-..
щие такие несущие, не требуют фильтров, выделяющих одну
ласу. Здесь термин
·
«однополосная модуляция» используется
в
ее широком смысле, чем обычно. Точное значение этого и дру
терминов, используемых в обобщенном смысле, лучше всего
ъяснить на примере.
·Рассмотрим амплитудную модуляцию косинусоидальной функ·
'и сигналом F(0). Разложим F(0)
в ряд Фурье на интервале
· 112~е< 1/2:
00
F (0) =а (О)
+ -V2 L fac (i) cos 2i n0 + a (i) sin 2i n0J.
5
1-1
89
(3.1)
Пусть сигнал F(8) пропущен через фильтр нижних частот, подав
ляющий все члены суммы с индексом i>k. Такие фильтры можно
выполнить похожими на частостные фильтры, описанные в § 2.3.
Отфильтрованный
сигнал F+(8) имеет верхний
предел в сумме
(3.l) i=k, а не i=oo. Амплитудная модуляция несущей
J/ 2 cosQo8
р+ (8)
сигналом F+(8) дает
k
-V2cos Q0 8 =
~[ас (i) cos (~20 -
2:rt i) 8 - а 5 (i) siп (Q0 -
2:rt i) 8J
+
1=1
k
+а (О) V2~cos Q08 + ~ [ac(i) cos (Q0 +2:rt i) 8+as (i) siп (Qu + 2:rt i) 8J.
(3.2)
i=I
Первая сумма описывает нижнюю боковую полосу. Затем следует
составляющая
ставляющей
с
частотой
f+(8)
несущей
которая
Qo,
соответствует со
на нулевой частоте. Вторая сумма описывает
верхнюю боковую полосу.
Разложим
F(8)
в ряд Уолша:
...
F (8) =а (О) + ~[ас (i) са! (i, 8) + а 5 (i) sal (i, 8)1 i=I
=а (О)+
2: [ас (i) wal (2i, 8) + а5 (i) wal (2i -
1, 8)1;
(3.3)
i=I
-
1/2 ~ 0 < 1/2.
Пропустим F (8) через фильтр нижних частостей, который подав
ляет все
члены с i>k. Отфильтрованный сигнал F++(8) имеет
верхний предел суммы i=k.
Таким образом,
разложения в ряд
F+(8) и f++(8) имеют одинаковое число членов. Амплитудная мо
дуляция несущей Уолша wal(j, 8) сигналом F++(8) дает
k
р++ (0) wal (j, 8) =а (О) wal (j, 0) +~{ас (i) wal (2i ffi j, 8)
+
l-l
Если сравнить
+ а 5 (i) wal [(2i - 1) ffi j, 8)]}.
(3.4) и (3.2), то можно видеть,
(3.4)
что компонента,
соответствующая постоянной составляющей а (О), в обоих случаях
передается самой несущей. Однако в (3.4) содержится только од
на сумма. В зависимости от значения
вать
«верхнюю»,
«Нижнюю»
или
j
эта сумма может описы
частично
верхнюю
и
частично
нижнюю боковые полосы . Рассмотрим, например, число 2k, име
ющее 'У\ разрядов в двоичной записи. Пусть j больше 2k и пусть j
имеет нули в 'У\ наименьших разрядах . Тогда справедливы следую
щие соотношения:
+
2i ffi j = j
2, j + 4' . . . ' j + 2k > j;
(2i- 1) ~_! = j + 1, j + 3, ... "i+2k-1>j;
L - 1, 2, . . . , 2k < J.
90
J
(3.5)
Для такого выбора j все индексы 2iЕВ
больше, чем индекс j несущей wal (j,
и
j
.4)
0).
(2i-lJEВ j суммы
Это соответствует
дуляции с одной верхней боковой полосой.
В качестве следующего примера
рассмотрим сЛучай, когда j
еет единицы в
ri наименьших разрядах. В этом случае получаем:
2i(f)j=j-2, j-4, .. . , j-2k<j;
(2i-l)ffij=j- l, j-3, .... j-2k+ 1 <j.
(3.6)
Теперь индексы 2iЕВ j и (2i-l) ЕВ j в сумме (3.4) меньше, чем
деке несущей wal (j, 0). Это соответствует модуляции с одной
жней полосой.
Если двоичное представление числа j имеет в ri младших раз
дах как единицы, так и нули, то числа 2i ЕВ j и (2i-l) ЕВ j для
. ределенных значений i будут больше j, а для других значений
еньше j. Это соответствует модуляции с частично верхней и ча
ично нижней полосой.
· Почему амплитудная модуляция синусоидальных и косинусои
;.
альных
несущих дает две
ущих Уолша
-
полосы, 'а
амплитудная
модуляция
не
только одну полосу? Чтобы найти ответ на этот
опрос, рассмотрим теоремы умножения синусоидальных и косину
оидальных функций:
+
+
2cos i 0 cos k 0 =
cos (i sin (i 2sin i 0 cos k 0 =
2cos i 0 siп k 0 = - sin (i 2sin i 0 sin k 0 =
cos (i -
+
+
+
+
k) 0 cos (i
k) е sin (i
k) е
sin (i
k) 0- cos (i
+ k) 0;.
+ k) 0~
+ k) 0;
+ k) 0.
]
(3.7)
В правой части этих уравнений стоит сумма двух синусоидаль
ых или косинусоидальных функций. Пусть
cosk0
или
sink-0
будут
есущими, а cosi0 или sini0 - компонентами сигнала, модулирую
его несущие по амплитуде. В результате этого получаются верх
не и нижние полосы.
Таким образом, двухполосная модуляция
инусоидальных
и
косинусоидальных
несущих
является
следстви
м теорем умножения (3.7) .
." Рассмотрим еще раз теоремы умножения функций Уолша:
са\ (i,
В
0) са\ (k, 0) =са! (r, 0);
sal (i, 0) са! (k, 0) = sal (r, 0);
са! (i, 0) sa! (k, 0) = sal (r, 0);
sal (i, 0) sal (k, 0) =са! (1·, 0);
правой части (3.8) стоит только
r = i ЕВ k;
r = [kffi (i- l)J
1;
r = [i Ее (k- l)] + 1;
r = (i- l) Ее (k- 1).
+
(3.8)
одна функция Уолша. Пусть
a\(k, 0) шш sa\(k, 0) будут несущими, а cal(i, 0) или sal(i, 0) омпонентами
сигнала,
который
модулирует
по
амплитуде
несу
. ие. Больше нет «нижней боковой» и «верхней боковой», а есть
олько одна функция.
По
этой
причине амплитудная
модуляция
ункций Уолша дает однополосную модуляцию. Схема для осуествления алшлитудной модуляции несущей Уолша показана на
ис.
3. la.
91
,
Косинусоидальную несущую V2 cos Qи0,
F+ (0), можно демодулировать умножением на
[f+ (0) V2cosQ00] V2cosЦi0 =
модулированную
V2 cos Qo6:
р+ (0) (1+cos2Q 00).
(3.9)
Рве. ЗЛ .
Амплитудный
модулятор (а) в демо.
дулятор .(б)
для несу.
щнх Уолша:
Ф - фильтр
нижних часто.
стеR;
П - перемножитель
i
Первый член в правой части представляет собой демодулиро:ванный сигнал. Второй
член должен подавляться
фильтром. В
~реднем половина мощности сигнала теряется в процессе филь
трации. Эта потеря энергии несущественна, если сигнал
F+(0) Х
Х V2 cos .Qa{) можно перед умножением на V2 cos Ои0 усилить.
Пусть сигнал D+(0) передается на несущей V2 cos Q10. В ре
зультате синхронной демодуляции с помощью колебания V2 Х
Х cos Q00 получаем
ID+ (0) V2cos Q10] V2cos Ц~0= D+ (0) [cos (Q0-
OJ 0 +
cos (Q0 + Qi) 0J
(3.1 О)
Пусть сигналы F+(0) и D+(16) содержат колебания с частотами
:в интервале O~v~vrp и пусть демодулированные сигналы прохо
дят через частотный фильтр с частотой среза vrp. Сигнал f+(e)
будет принят без помех со стороны сигнала D+ ('6), если частоты
несущих
V2 cos Qo0 - и V 2 cos Q16
удовлетворяют следующему
условию:
(3.11)
_ Умножим сначала сигнал F+(.0) V2 cos Qa{) на вспомогатель
ную несущую V2 cos Qn0, а затем на 2 cos (Q0-.Qn)i0:
{ [f+ (0) V2cos '2о0] V2 cos Q4 0 } 2cos (Q0 =f+ (0) f 1 +
COS
2 (Q0 -Q4 ) 0 +
В результате получаем нужный член
COS
Qn)0=
2Q4 0 + cos 2Q00].
F+(.0).
(3.12)
Три нежелательных
члена должны быть отфильтрованы.
Пусть принят сигнал
D+(.0) V2 cos(Q-0-2 Qn)0.
(3.9) дает
Прямая син·
хронная модуляция согласно
{D+ (0)Y2cos (Q0 -2Q4 ) 0JV2cos Q00= D+(0)[cos 2Qп0+cos 2(Цi-Q4)6J.
(3.13)
Если частотный диапазон сигнала D+(0) достаточно мал, то сиг
нал (3.13) можно отфильтровать. Таким образом, между сигнала
ми F,+(18) и D+(0) нет взаимного влияния. Однако это не выпол-
няется, если сигнал D+(0) V2cos(Q 0-2.Qn)0 сначала умножает-
92
вспомогательную несущую V2cos ·Qn•0,
2 cos (Qo-Qn)i0:
а потом демоду·
екя умножением на
jf' { [D+ (0) -V2COS (~ - 2Qп) 0 ] -V2COS Qn0 } 2cos (Q0 - Qп) 0 =
,: = v+(0)fcos2Qп0+ cos2(Qo-2Qп)0+1+ cos2(~-Qп) 0]. (3.14)
.
авой части (З.14) появляется член D+(i0), который искажает
). Из_(3..7) и (З.14) можно видеть, что особенности приема
.~
,:алов вытекают из теорем умножения синуса и косинуса. Вза
го влияния не было, если бы в правой части
.
было не
(3.7)
члена, а один.
· ' ассмотрим те же самые процессы в случае применения функ
. Уолша в качестве несущих. Умножим сигнал F++(•0)wal(j, 0)
3.4) на wal (j, -0):
. р++ (0) wal U. 0) wa1 U. 0) = р++ (0) wal (О, 0) = J++ (0); (3.15)
i ЕВ j =О.
,
отличие от синхронной демодуляции
си-нусоидальных несу
здесь уже нет высокочастостного члена, который нужно от
, ьтровывать.
Однако это отличие обычно
не имеет большого
·чения, так как в многоканальной системе фильтрация все рав
необходима для разделения сигналов различных каналов. Что
это показать, рассмотрим передачу сигнала
щей wal(l, 6):
на второй
D++(0)
~
k
(0)=Ь (0) + ~ [bc(i) cal (i, 0) + b5 (i) sal (i,0)]= ~ c(r)wal(r,0). (3.16)
Г=О
f=l
' езультате синхронной демодуляции D++(0)wal(l, 6) путем ум
ения на wal (j, ·0) получаем
[D++(0)wal(l, 0)] wal и. 0)= v++ (0)wal (lffij, 0) =
~
=
L c(r)wal (l ЕВ j Eij r, 0)
(3.17)
r=O
· Пусть
F++(•0)
и
D++(0)
содержат только функции
wal (О, 10);
(i, 0) и sal (i, 0) с i~k или wal (r, 0) с .r~2k. Пусть .далее де
. улированные сигналы проходят через фильтр нижних часто
. й с частостью среза µ=k. Через этот фильтр не пройдет ни
iia из составляющих сигнала (3.17), описываемых функциями
~ша wal(l$j$r0), если будет выполнено следующее условие:
l ЕВ jffi r ~ 2k; r =О, 1, .. " 2k.
(3.18)
Рассмотрим только два из многих._ возможных способов выпол
,~ия условия (3.18).
Пусть число 2k имеет 'l'J двоичных цифр.
сть j и l будут больше 2k и имеют нули только в 'l'J наименьших
_ рядах.
Тогда получаем:
lEf>r= l, L+ 1, l+2 .. "l+2k;
l Е!Э j ЕВ r = l Е9 j; l Ef) i + 1, . . " l Е!Э i
93
}
+ 2k.
(3 . 19 )
Чтобы выполнить условие
(3.18);
l
Прибавив по
mod 2
число
надо удовлетворить условию
EDU >
(3.20)
2k.
j к обеим частям (3.20), получаем
(3.2!)
l>2kEf)j=2k+j.
В
последнем
и тот
j$ j=O
преобразовании были использованы
соотношение
факт, что 2k имеет ri разрядов, в то время как j
имеет нули в 'l'J наименьших разрядах. Прибавив по mod 21 к обеюr
частям (3.20), получим второй способ выполнения условия (3 .18):
j
Условия типа
> 2kEf) l =
2k
+ l.
(3.22)
(3.21) и (3.22) разделяют частостный спектр на
частостные каналы аналогично тому, как частотный спектр раз
деляется на частотные каналы в соответствии с требованиями оп
ределенной ширины полосы каналов. Позже будет рассмотрен бо
лее общий метод распределения частостных каналов для несущих
Уолша, основанный на теории групп.
Сигнал F++(H)wal(j, 0) можно умножить сначала на вспомо
гательную несущую
wal (lz, 0),
жением на не~ущую wal(jEВh,
а потом демодулировать его умно
·0):
{[р++ (0) wal (j, 0)] wal(h, 0)} wal UЕВ h, 0) =
= [р++ (0) wal (j
EfJ h, 0) ] wal (j Ef) h, 0)
= р++ (0).
(3.23)
Таким образом, при использовании несущих Уолша перекрест
ных помех не возникает. Чтобы показать это, умножим принятый
сигнал
D++(·0)wal(l, 0) сначала на wal(h, 0), а потом на wal(j ffi
Ef)h, 0):
{ [ D++ (0) wal (l, 0)] wal (h, 0) }wal (j ЕВ h, 0)
= D++ (0) wal (l ЕВ j, 0)
= D++(0)wal(lffih~j~h,0) =
2k
=
~ c(r) wal (l ЕВ jEf) r, 0).
(3.24)
r=O
Сигнал
D++(0)wa\(l $ /, •tl)
не содержит компонент,
которые
мог ли бы пройти через фильтр нижних частостей с 9астостью сре
за µ=k, так как выпол~-1яется условие (3.18). Отсутствие «зер
кального» сигнала можно отнести за счет наличия только одной
функции Уолша в правой части (3.8) и (1.29).
На рис. 3.16 показана функциональная схема синхронного де
модулятора несущих Уолша.
Амплитудная модуляция функций других полных ортогональ
ных систем может быть рассмотрена аналогичным образом. Пока
ни
это
одна
из них не
может
быть
дает ощутимых
практических
следствием недостаточно
преимуществ, но
энергичных исследова
ний в данной области. Большинство хорошо известных функций в
результате перемножения имеет не один или два члена,
как в слу
чае функций Уолша или синусоидальных функций, а бесконечное
94
ло членов. Несущие, основанные на последовательности перио
ческих прямоугольных импульсов, образуют ортогональную, но
полную систему. Амплитудная модуляция их сильно отличается
амплитудной модуляции синусоидальных функций или функций
3.1.2.
Многоканальные системы
Одним из наиболее важных применений амплитудной модуля
и
является
ее
применение
в
многоканальных
системах
связи.
ассмотрим частотную многоканальную систему для телефонии.
овокупность т
телефонных сигналов проходит
через фильтры
· жних частот и модулирует по амплитуде т синусоидальных или
синусоидальных несущих. В принципе, промодулированные не
ущие можно сложить и затем передать по общей линии связи.
ля подавления одной боковой после модулятора ставятся половые фильтры.
Существует несколько способов разделения сигналов в п.риемике. Одним из них является синхронная демодуляция, которую
ожно применять и для несинусоидальных несущих.
Принятый
рупповой сигнал перемножается в т модуляторах с т несущими,
акими же, как и несущие, используемые в передатчике. Несущие
риемника и передатчика должны быть синхронизированы. Это
· значает, что частоты должны совпадать, а фазовый сдвиг дол
ен быть очень мал. Демодулированные сигналы проходят через
фильтров нижних
частот, подавляющих
гармоники сигналов
ругих каналов.
Используемые на практике частотные многоканальные системы,
онечно, отличаются от вышеописанной, так как в них использу
тся характерные свойства синусоидальных и косинусоидальных
ункций. Здесь особое значение имеют те свойства, которые яв
яются общими для всех полных систем ортогональных функций.
В теории частотных
многоканадьных систем известны два ме
ода: квадратурная модуляция и однополосная модуляция. В слу
ае квадратурной модуляции две несущие с одинаковой частотой,
о сдвинутые относительно друг друга по фазе на 90°, модулиру
тся
по
амплитуде
двумя
независимыми сигналами,
лежащими
в
дном и том же частотном диапазоне. Получаются два сигнала,
.
аждый из которых занимает полосу, равную удвоенной полосе
9астот
передаваемого сообщения.
Полоса
Частот,
занимаемая
боими сигналами, не превышает полосы частот, занимаемой од
им сигналом, так как оба сигнала расположены в общей полосе.
ри
однополосной
модуляции
по
амплитуде
есущая определенной частоты и одна из
. яется.
модулируется
одна
боков_рrх полос подав
Имеется несколько методов для этого подавления.
Соответствующие методы модуляции существуют
и для часто
тных многоканальных систем [11]. За отсутствием лучших терми
ов их тоже можно назвать квадратурной модуляцией и однопо
осной модуляцией. Для каждой частости i существует две функ
ии Уолша
cal(i, 8)
и
sal(i, 8).
Квадратурная модуляция ознllчает,
95
что как са! (i, Н), так и sal (i, 10) модулируются по амплитуде дву.
мя независимыми сигналами. Однополосная модуляция означает,
что модулируется либо
cal(i, 6),
либо
sal(i,
е). В обоих случаях
генерируется лишь одна частостная полоса.
Для пояснения принципа
частостного уплотнения с помощью
несущих Уолша обратимся к рис.
Выходные напряжения двух
3.2.
п
п
а г---
ж
ж'
rp
rp
3
- J'
;=---.......L
___ ...... --~
а'•
Рис. 3.Q. Принцип построения
ЧЗ{:Тостиой многоканальной си- .
стемы:
о
125
JSO
Jl.f
Ф
-t,MHC'
фильтр нижних частостеil; П
перемножнтель;
С - сумматор
-
-
микрофонов
прикладываютс~ к точкам а и а'.
Они проходят
фильтры нижних частостей Ф. На их выходах б и 6' появляются
ступенчатые напряжения, которые подаются на перемножители П,
где
они
модулируют
по
амплитуде
две
периодические
несущие
Уолша, подведенные к точкам в и в'. Промодулированные несу
щие г и г' складываются в сумматоре С. В результате получается
выходное напряжение д. Это напряжение умножается в приемни
ке на те же несущие, что использовались в передатчике. Напря
жения, появляющиеся на выходах ж и ж' перемножителей, про
пускаются через фильтры нижних частостей, которые аналогичны
фильтрам, используемым в приемнике.
Ступенчатые напряжения
на выходах з и з' аналогичны напряжениям в точках 6 и 6'. Их
можно сразу подавать к потребителю. Фильтры нижних частостей
приемника и передатчика создают задержку по 125 мкс. Пунк
тирные линии на временных диаграммах (рис. 3.2) показывают
эти задержки.
На рис. 3.3 показана многоканальная система с 1024 каналами
связи для передачи сообщений в одном направлении. Будем рас
сматривать уплотнение
аналоговых сигналов.
Не представляет
96
да
видоизменить
входные и
выходные схемы
для других типов
налов. Например, для передачи двоичной цифровой информа
и ко входу канала прикладываются напряжения либо +И, либо
V. Для передачи обычного КИМ телефонного сигнала необхо
мо иметь семь каналов. Такие детали будут выпускаться из рас-
Рис.
3.3.
Частостная мноrоканальная система с , ю24 телефонными канала
ми для
передачи
в
одном направления:
Ф
- фильтр нижни х ч а стостей; П - перемножитель: С тактовых импульсов; ГФ - генератор функций; ГСИ -
.мотрения, так как они для
олее
важны,
чем для
сумматор ;
ГТИ
генер а тор
син х роимп у ль сов
- генер а тор
принципа Частостного уплотнения не
принципа временного или частотного уплот
ения.
Двухпроводная линия, идущая
от абонента, с помощью гиб
разделяется на передающую
и приемную ветви.
идной схемы
· игнал
.
на передающей
ветви
при
ладывается к одному из
l 024
ов
проходит
передатчика.
Он
вхо
ильтр нижних частостей Ф с ча
тостью среза 4 kzps. Переключате
и в фильтрах нижних
частостей
правляются
генератором
мпульсов ГСИ.
Входной
синхро
сигнал
(0) преобразуется в ступенчатую
ункцию F++(0); F(0) и F++(0) по
азаны
на рис.
3.4
без временной
адержки на 125 мкс.
После фильтрации сигнал моду
ирует по амплитуде одну из 32 неущих Уолша
Т1-Тз 2 на одном из
еремножителей П. Первые четыре
есущие wal (О, 8)-wal (3, 0) пока
рис.
3.4.
Длительность Т и
97
F(e)~~
Fн(е)'~
wa i (О, 8)~:=r=::::r::=::r::=:::i..
-wai (!,{]) ,_,•=F·....,....r-~'"4::2
-wat(2,e)-.
........
,........
..--.
...,
.......
wa1 (3, О) c-L.I......,....J"'dl:IЪ.....Л:!:
~~с:::.
wat (О, 81).r::======:::i_
sln2JCO~
C052JCO~
s~n мв '\/\/'\/"\,'\/'V"\/\J
1
1
П
Рис.
3.4.
мы для
1
1
1
1
125
1
1
1
1 1
1
1
-
250
Временные
1
1
1
SOO
диаграм
многоканальной
мы рис. 3.З
1
J7S
систе
~-
,
;.· 'i ~
положение их
интервала
ортогональности совпадают с длительно.
стью и положением ступенек сигнала F++(0).
32 промодулированных несущих суммируются в сумматорах
С1-С32 в одну группу.
R результате получаются 32 группы по
32 кана.1а в каждой, как это и показано на рис. 3.3. Число 32 вы.
брано для
примера; принципы
оптимального выбора размера
групп и подгрупп будут рассмотрены позже.
В перемножителях П выходные напряжения сумматоров моду .
лируют по амплитуде несущие Уолша Т 33-Т64 • Сумматор Сзз су~~
мирует получающиеся 32 напряжения. На выходе Сзз появляется
ступенчатое напряжение .
Длительность ступеньки равна з2-2 х
Х 125 мкс::::: 122 нс. Амплитуда этого выходного сигнала прини м ае т
8000Х (32)2=8 192 ООО независимых значений в секунду. Сигна л
занимает частостный диапазон O::;::;;qi::;::;;4,096мzps. Этот группово й
сигнал можно передавать либо прямо к приемнику, либо исполь·
зовать его для модуляции синусоидальной несущей или несущей
Уолша.
В приемнике сигнал сначала умножается в 32 перемножителях
П на несущи е Т33 -Т6 " , а потом каждый из полученных сигналов
умножается в 32 перемножителях на несущие Т1-Тз2. Демодули
рованный сигнал проходит через
фильтры нижних частостей Ф,
которые аналогичны фил:,трам, используемым в передатчике.
Функциональная схема, изображенная на рис. 3.3, пригодн а
как для квадратурной модуляции, так и для однополосной моду
ляции. Эти методы отличаются только используемыми несущими.
Для несущих
Т1-Т 32
лучше использовать функции
Уолш а
wal (О, 0)-wal (31, 0). Их генерирование на основе теоремы ум
.ножения
(1.29) из функций Радемахера wal(l, t0); wal(3, 0);
wa1 (7, 0), ... , wal (2n-t, 0) показано в табл. 3.1. Функции Раде
махера
генерируются
рис. 2.7.
Несущие Тзз-Тw.
двоичными
делителями,
как
показано
нужно выбирать таким образом,
·было перекрестных помех и
на
чтобы н е
в то же время чтобы максимально
использовался частостный диапазон. В табл. 3.2 показан возмож
ный выбор этих несущих. В этой таблице функции Уолша обозна
чаются как wal(j, !0), так cal(i, 0) и sal(ii, 0). Можно заметить,
что последние пять цифр нормализованной частости, записанной в
двоичной системе, всегда равны нулю. 32 несущих Т1-Т зz можно
разместить между любыми двумя несущими из Тзз-Тм. Отведен
ный диапазон частостей используется полностью, нет потерь диа
пазона частостей между соседними каналами.
Чтобы выбирать несущие не эмпирическим путем, можно вос
пользоваться теорией групп. Функции Уолша
wal (О, 0)-wal (1023,
0) образуют группу G с 210 элементами. Функции wal (О, 6)wal (31, 0) являются подгруппой Н с 25 элементами . Существуют
210/25 =32 класса группы G по подгруппе Н. Это в точности равно
числу несущих Т33 -Т64 • Функции Уолша, полученные модуляцией
несущих Т33-Т6" функциями wal(O, 6), ... , wal(Зl, 0), являются
элементами 32 классов.
Все возможные функции wal (j, 0), ис-
98
Таблиц а 3.1
' ерирование несущих Т1-Тз2 с помощью умножения wal(k, 0)wal(/, 0)=
:, al(j, 6) 11 несущих Тзз-Тв~ с помощью умножения wal(k, 0)wal(l, 6) Х
x wal(31, 0) =wal(j, 0)
Индекс
j
о
2
3
4
5
6
7
8
Тн
Т1ь
т18
Т17
Т1г
T1s
Т20
Т21
Т22
Т2з
Т2с
Т2ь
Т2в
Т21
T2s
Т29
Тзо
Тз1
Тз2
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
11
k
о
Несущая
Индекс
k
1
о
Тзз
о
о
о
о
Тз4
32
64
96
128
160
192
224
256
288
320
352
384
416
448
480
512
544
576
608
640
672
704
736
768
800
832
864
896
928
960
992
63
127
127
255
255
255
255
511
511
511
511
511
511
511
511
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
1023
о
3
1
Тз:.
з
о
Тзв
7
7
7
7
15
15
15
15
15
15
15
15
31
31
31
31
31
31
31
31
31
31
31
31
31
31
31
31
3
2
1
Тз1
Тзs
о
Тсо
7
6
5
4
3
2
1
Т41
Тзэ
Т42
Т4з
Т44
Tcs
т4в
Т41
о
т4s
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Т49
Т,о
Ts1
Ts2
Тsз
Tsc
Tss
Тsв
Ts1
Тsг
Тоэ
Тво
Тв1
Тв2
Твз
о
Тв4
99
32
о
96
64
32
о
224'
192
160
128
96
64
32
о
480
448
416
384
352
320
288
256
224
'192
160
128
96
64
32
о
Табл н ц а
3.2
2Х32 нес.ущих частотной многоканальной системы (рис.
3.3)
Функция
wal (/, 0)
cal (i, 0), sal (1, 0)
Несущая
с,
s
.;есятиЧllЫЙ
о
Т1
Т2
s
Тз
с
т"
s
т.
с
Тн
s
Т1ъ
с
Т1в
s
1
2
2
3
3
4
4
5
5
6
6
7
7
8
Т11
с
8
т18
s
9
9
10
10
11
Тв
s
Т1
с
Тв
s
т,
с
Т10
s
Та
с
Т12
s
Т1з
с
Т1е
с
Т20
s
Т21
с
Tz2
s
1
l
Т2з
с
11
Тц
s
т2Ъ
с
Т21
s
Tr1
с
Tzs
s
Т2е
с
Tso
s
Тз1
с
Тз2
s
12
12
13
13
14
,....
14
15
15
16
двоичl!ЬIА
00000
00001
00001
00010
00010
00011
00011
00100
00100
00101
00101
00110
00110
00111
00111
01000
01000
01001
01001
01010
01010
01011
01011
01100
01100
01101
01101
ошо
01110
01111
Ollll
10000
100
десятичный
о
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
1
АJIОИЧНЫI\
00000
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
ошо
Ollll
10000
10001
10010
10011
10100
10101
10110
101 ll
11000
11001
11010
11011
шоо
29
lllOl
30
31
11110
lllll
Продолжение
Функция
wal (j, 0)
cal, (l, 0), sal (t, 0)
с,
1
десятичный
о
Tsa
Ти
с
Тsъ
с
Tss
с
Та1
с
Tss
с
Tse
с
Tso
с
т.1
с
Т12
с
т••
с
т••
с
r'6
с
т,.
с
т,1
с
Tss
с
т
••
с
Тъо
с
Ти
с
т,2
с
Тъз
с
Тъs
с
••
с
Тъв
с
Тъ1
с
Тъв
с
Тьо
с
Тво
с
Тв1
с
Тв2
с
Твз
с
т_.
с
т
s
16
32
48
64
80
96
112
128
144
160
176
192
208
224
240
256
272
288
304
320
336
352
368
384
400
416
432
448
462
480
496
ДВОИЧНЬIЙ
000000000
000010000
000100000
000110000
001000000
001010000
001100000
001110000
010000000
010010000
010100000
010110000
011000000
011010000
011100000
011110000
100000000
100010000
100100000
100110000
101000000
101010000
101100000
1011 lOOG
110000000
110010000
110100000
110110000
111000000
111010000
l IllOOOOO
111110000
101
десяткчн111I
о
32
64
96
128
160
192
224
256
288
320
352
384
416
448
480
512
544
576
608
640
672
704
736
768
800
832
864
896
928
960
992
, двоичпыil
0000000000
0000100000
0001000000
0001100000
0010000000
0010100000
0011000000
0011100000
0100000000
0100100000
0101000000
0101100000
0110000000
0110100000
0111000000
0111100000
1000000000
1000100000
1001000000
1001100000
1010000000
1010100000
1011000000
1011100000
1100000000
1100100000
1101000000
1101100000
1110000000
1110100000
1111000000
1111100000
..
·-, '
пользуемые в качестве несущих Тзз-Т м, получаются перемноже.
нием каждой из функций wal (О, 0); wal (32, 0), ... ,
(табл. 3.2) на любую из функций wal(O, Н); wal(l, 0),
0).
Такое перемножение означает
wal (992, 6)
"" wal(3I,
лишь перестановку элементов
каждого класса. Можно умножить wal (О, 8) на одну из 32 функ
ций wal (О, е); wal ( 1, 8), ... , wal (31, 8). Далее можно умножить
wal (32, .О) на эти 32 функции, затем wal (64, '8) и т. д. Всего су
ществует 3232 =2 160 таких произведений. Это означает, что сущест
вует 2100 возможных способов выбора
несущих Тз 3 -Тв1и приче\1
при использовании любого из них частостный диапазон будет ис
пользоваться без потерь и не будет перекрестных помех.
На рис. 3.4 под несущими Уолша wal (О, 8) и wal (3, 0) показаны
синусоидальные и косинусоидальные несущие. Их можно исполь
зовать как несущие Т1-Т32 (рис. 3.3). В этом случае придется ис
пользовать более сложные перемножители.
32 промодулирован
ные несущие можно сложить без пропускания их через фильтр,
выделяющий одну полосу. Этот вид квадратурной модуляции по
казывает
тесную
связь
между
частотным
и
частостным
уплотне
нием.
Из рис.
гональных
3.4
на
можно видеть, что любую систему функций, орто
конечном
интервале,
можно
использовать
в
каче
стве несущих Т1-Т32 (рис. 3.3), если входные сигналы пропуще
ны через фильтр нижних частостей. Однако это утверждение не
_справедливо для несущих Тзз-Тв4. В качестве их можно выбирать
только сигналы, описываемые функциями, для которых справед
ливы
теоремы
соидальных
и
умножения.
сходные
косинусоидальных
с
теоремами
умножения сину
функций или функций
Уолша.
На рис. 3.3 показана дополнительная линия синхронизации ме
жду передатчиком и приемником: На практике для передачи сиг
нала
синхронизации
можно
использовать
один
или
несколько
из
каналов. Если к 2n-каналу придожено постоянное напряже
ние, то передается функция wal (2n-l, 8), которая является функ
цией Радемахера. Ортогональность функций Радемахера инвари
антна к сдвигу. Поэтому относительно легко можно выполнить
фильтры, следящие за НИ'1И. Модулированные функции УоJ1ша об
разуют помеховый фон, который можно подавить выбором боль
шого времени усреднения следящих фильтров.
1024
Требования к синхронизации
и времени нарастания фронтов
импульсов можно оценить, используя рис.
3.5. Пусть сигнал Ue(t)
представляет собой
выходное напряжение телефонной многока
нальной системы с 1024 каналами. Длительность ступеньки равна
122 нс. Информация о сигнале полностью заключена в амплиту
дах ступенек. Если передан сигнал
ue(t),
то при отсутствии шума
для получения информации достаточно производить отсчеты ам
плитуд ступенек. Отсчеть1 можно производить в любом месте ин
тервала длительностью 122 нс при условии, что фронты ступенек
напряжения бесконечно крутые. Это и определяет точность син
хронизации.
102
;Рассмотрим влияние времени нарастания напряжения на точ
. ть синхронизации. Пусть время нарастания таково, что тре
~тся 122 нс; чтобы перевести Ue(T) в Ue(2T); Ие(2Т) в Ие(3Т)
т. д., как показано на графике ua(t) (рис. 3.5). Первоначальное
. пенчатое напряжение можно восстановить, производя отсчеты
ua(t) точно в моменты времени
Ue(2T) {JT)
О, Т, 2Т, 37, " ..
г-~
-~~F(e)
=-1----,.
F lf (8)
--...,а....._
.s===r:==:::r==:i:=:::i Wй ( (D, е)
~-wat(l,Э)
3Т
......................_,,.........._r=-...._:- wat (Ч,8)
=tr...............F"..Г.....ГJ -wat (5, 8)
4Т
..i::::======
1va L(O,O)
~sin2Ji8
~stn4li.8
1
1
1 l 1
1
1
о
1
1
125
1
1
250
t:Рис.
3:5.
Конечное время нарастания
·ступенчатой
.функции
преобразования
'И
Ue(t)
фильтр
в
для
Ua(t)
1
1
1
375'
1
1
1
soo
мне
Рис. 3.6.
Временная диаграмма
однополосной частостной системы.
Временная база для фильтра ниж
них частостей Т= . 125 MiC, времен
ная база для несущей Т=250 мкс
, Таким образом, если не учитывать ошибку синхронизации, то
, аксимальное время нарастания равно 122 нс . В общем случае
. мма времени нарастания и ошибки синхронизации должны
ыть меньше 122 нс.
1
' В присутствии шума отсчеты амплитуд являются плохим ме: одом обнаружения сигнала. Однако нетрудно видеть, что ua(t)
, ожно восстановить до ue(t) с помощью интегрирования, так как
нтеграл от Ua(t) в пределах, например,
Т-2Т пропорционален
e(2T)-ue(T).
Схема, изображенная
на рис. 3.5, преобразует ue(t) в Иа(t)
рактически без переходного процесса .
В частотной теории по
троение фильтра, который мог бы это делать, является классиче
кой задачей. Простота, с которой можно решить эту проблему в
анном случае, получается благодаря использованию в фильтре
,лемента
с
параметром,
зависящим
от
времени,
-
полевого
тран
истора.
Для обсуждения однополосной модуляции функций Уолша рас
мотрим рис. 3.6. Вверху показаны первоначальный сигнал F(H) и
· игнал F*(0),
отфильтрованный фильтром нижних
частостей;
.десь не учтен временной сдвиг между F(·0) и F+r(0). На рис. 3.6
'оказаны также несущие Уолша wal(O, 10); wal (2, Н); wal(4, 0);
юз
wal(6,
Н), Их временная база равна мкс, т. е. удвоенно\1
....
250
длительности ступеньки сигнала f++(0). Отфильтрованный сигнаJJ
f+t(H) можно представить на интервале (O~,t<250) мкс в виде:
0=
f++ (0) =с (О) wal (О, 0) +с (1) wal (1, 0);
(t-t0 )/T; t0 = 125 мкс; Т = 250 мкс;
(3.25)
-1/2~0<1/2.
Амплитудная модуляция одной из несущих
сигналом
f+t(H)
wal (2j, 0)
(рис.
3.6)
дает
р++ (0) wal (2j, 0) =с (О) wal (2/, 0) +с (1) wal (2j
+ 1, 0).
(3.26)
В результате модуляции получаются несущие Уолша wal(2j+l, 0),
которые не показаны на рис. 3.6. Таким образом, модулированные
функции Уолша занимают весь отведенный частостный диапазон.
На рис. 3.6 также показаны синусоидальные функции с времен
ной базой Т=250 мкс. Их амплитудная модуляция
функцией
не дает в результате однополосной частотной модуляции .
f+t(0)
Соответствие между функциями Уолша и синусоидальными функ
циями в случае квадратурной модуляции основано на том факте,
что wal (О, r0) - первая функция как ряда Уолша, так и ряда Фу
рье. Однако в сигнале f++(0) (3.25)
содержится составляющая
wal ( 1, '0), которая не принадлежит ряду Фурье.
Будем увеличивать временную базу несущих (рис. 3.6) от 250
до 500 или до 1000 мкс, не меняя сигнал f+t (Н). Тогда получиы
еще два
примера частостных
однополосных систем.
Несущие
wal (4j, 10) принимают значения Т=500 мкс, а wal (8j, 0) - Т=
= ·1000 мкс; j=O, 1, 2, ....
Преимущества и недостатки множества возможных однополос
ных систем еще недостаточно изучены. Следует заметить, что си
стемы с квадратурной модуляцией являются особым случаем клас
са однополосных систем, когда временная база несущих равна вре
менной базе фильтров нижних частостей.
Характерной особенностью
ным
разделением
стемами
с
сигналов
временнь1м
по
многоканальных систем с частот
сравнению
разделением
с какой смешиваются и
с
многоканальными
сигналов
си
является легкость ,
разделяются сигналы .или
радиосигналы
в сетях связи. Это объясняется тем, что в многоканальных систе
мах с частотным разделением сигналы четко отличаются своей
частотой, которая не зависит от временнь1х задержек. С другой
стороны, сигналы в многоканальных системах с временнь1м разде
лением имеют различные и неизвестные
временнь1е задержки и
поэтому требуют
для разделения дополнительной
маркировки.
Так как сигналы частостных многоканальных систем также четко
разделяются
по частости,
то
можно
ожидать,
что сети
связи,
соз
данные на их основе, будут довольно похожи на многоканальные
системы с частотным разделением.
На рис. 3.7 показано
возможное распределение
по частости
групп и супергрупп в сети связи. Это распределение выбрано та-
104
м образом, что группа, супергруппа А или супергруппа В явля
ся
классами
математической
подгруппы
функций
Уолша
. l(j, 0) с индексами j, меньшими 32, 128 или 256. Предполагает
,
что и<:пользуется однополосная модуляция и временная база
вна
250
мкс.
Индивидуальные
Т=
3.7.
полосу О-
кzps
250 мкс
Рис.
каналы занимают
~Распределение диапазона частостей
· kzps. 16 каналов образуют группу, занимающую частостный диа
азон от 64 до 128 kzps. Несущими являются функции wal (32+
2j, 0); j=O, 1, ... , 15.
· Амплитудная модуляция несущей wal (96, 10) группой сдвигает
ласу
частостей,
занимаемую
группой,
в
диапазон
(12892) kzps; несущая wal (64, 0) сдвигает группу в диапазон (19256)kzps. Эти 32 канала на рис. 3.7 обозначены как супергруппа А.
Модуляция несущей wal ( 192, 0) супер группой А сдвигает по
осу частостей,
занимае'.V1ую супергруппой,
в диапазон (25684) kzps; несущая wal ( 128, 8) сдвигает супергруппу А в диапазон
384~512) kzps.
Получа13мые 64 канала обозначены на рис. 3.7
ак супергруппа В. В табл. 3.3 показано, в какое положение час
остного диапазона сдвигаются каналы. 16 каналов группы сдви
аются из основной полосы несущими wal(j, 0), j=32, 34, ... , 62.
: а пример, сигнал в десятом канале модулирует несущую wal (50, Н) .
. астость wal (50, Н) равна 50Х2= 100 kzps и сигнал занимает по
осу от 100 до 104 kzps. Несущая wal (50, '8) становится в супер
уппе А несущей wal (82, 8),
если ее умножить на wal (96, 0),
ли становится несущей wal ( 114, 0), если ее умножить на wal (64,
). Десятый канал занимает полосу от 2Х82=164 до 168 kzps
ли полосу от 2Х 114=228 до 232 kzps. Наконец, несущая wal (50,
) становится одной из несущих wal ( 146, 0); wal ( 178, е);
а! (210, 0) или wal (244, 0) в супергруппе В. Десятый канал за
мает одну из полос шириной 4 kzps с нижним пределом 2 Х
146=292 kzps; 2Х 178=356 kzps; 2Х210=420 kzps или 2Х244=
488 kzps.
Рассмотрим случай передачи супергруппы В, супергруппы А и
уппы. Согласно рис. 3.7 сигнал занимает частостный диапазон
64 до 512 kzps. С помощью фильтра нижних частостей с часто-
105
Та 6п и ц а
wal(64,
3.3
Переход от несущих wal(З2, 0), ... , wal(62, 0) группы к несущим
0), .." wal(l28, 0) супергруппы А и к несущим wal(128, е), .", wal(256,
суперrруппы В. Частость несущих равна 2j kzps дпя Т . 250 мкс
Супергруппа А:
Группа
16
Несущая
wal (96, 0)
96=1100000
канала
1
36
38
40
42
44
46
48
50
52
54
56
шооо
З4
б
7
8
9
10
11
12
13
14
15
16
11 двоичный
100000
100010
100100
100110
101000
101010
101100
lOlllO
110000
110010
110100
110110
32
1
2
3
4
5
58
ШОIО
60
111100
11 lllO
62
1
1
64
192 =
i
128
130
132
134
136
138
140
142
144
146
148
150
152
154
156
158
1
i
1
68
70
72
74
76
78
80
82
84
86
88
90
92
94
i
160
162
164
166
168
170
172
174
176
178
180
182
184
186
188
ню
(64, 0)
64=1000000
двоичный
2
i
1
1 роачНRI!
96
1100000
1100010
1100100
1100110
1101000
1101010
1101100
98
100
102
104
106
108
110
112
114
116
118
120
122
124
126
llOШO
шоооо
lllOOlO
1110100
1110110
1111000
llllOlO
1111100
llllHO
супергруппы А
Несущая wal- (128, 0)
wal (192, 0)
11000000
двоичный
10000000
10000010
10000100
10000110
10001000
10001010
10001100
10001110
10010000
10010010
10010100
10010110
10011000
10011010
10011100
lOOlll 10
i
Несущая~wаl
1000000
1000010
1000100
100011.0
1001000
1001010
1001100
1001110
1010000
1010010
1010100
1010110
1011000
1011010
lOlllOO
lOllllO
66
Супергруппа В :
Несущая
-
rpynnы
кана·
лов
Номер
2
0)
128 = 10000000)
j
ДВОНЧIШЙ
1
10100000
10100010
10100100
10100110
10101000
10101010
10101100
10101110
10110000
10110010
10110100
lOlIOllO
lOllIOOO
10111010
10111100
10111110
106
i
192
194
196
198
200
202
204
206
208
210
212
214
216
218
220
222
j
двончвыА
1
1
11000000
11000010
11000100
11000110
11001000
11001010
11001100
11001110
11010000
11010010
11010100
llOlOHO
11011000
11011010
l10lll00
11011110
1
224
226
228
230
232
234
236
238
240
242
244
246
248
250
252
254
i
двоичный
1
шооооо
ШОООlО
11100100
lllOOllO
lllOIOOO
11101010
11101100
шошо
lШОООО
11110010
llllOlOO
llllOJIO
lllllOOO
l lll 1010
llllllOO
11111110
·10 отсечки 128 kzps можно выделить группу. Фильтр нижних
тостей с частостью отсечки 256 kzps будет выделять группу и
·ер группу А. Эта простая фильтр3ция возможна только тогда,
.rда частость отсечки равна 2rX4=2r+2 kzps; r=O, 1, 2, ....
' Рассмотрим следующий пример передачи супергруппы В. Вы
лим 32 канала либо в полосе (256-384) kzps, либо в полосе
84-512)kzps. Умножим супергруппу В на несущую wal(128, 6).
. табл. 3.3 показано, что полоса (256<\(j)<384) kzps (j=
128, ... , 190) преобразуется в полосу (O<iq><l28)kzps (j=O, ...
\., 62); полоса (384<qJ<512)kzps (j= 192, ... , 254) преобразуется
1 полосу (128<qi<256)kzps (j=64, ... , 126). Фильтр нижних ча
:·остей с частостью отсечки 128 kzps может выделить
полосу
. <{JJ<;l28) kzps. Умножением на wal (64, 0) можно сдвинуть ее в
апазон (128<qJ<256)kzps, который является диапазоном супер' уппы А.
1
Умножим супергруппу В на wal(l92, 0). Полоса (256<\(j)<
· 384)kzps (j= 128, ... , 190) преобразуется в полосу (128<iq><
256)kzps (j=64, ... , 126), полоса (384<qJ<512)kzps (j=l92, ...
, ., 254) в полосу (O<(j)<l28)kzps (j=O, ... , 62). Фильтр нижних
астостей
может выделить полосу (O<(JJ< 128)kzps,
которая те
ерь содержит другие каналы супергруппы В .
.· Сигнал любого отдельного канала в полосе (2j<qi<2j+4)kzps
ожет быть выделен умножением входного сигнала на wal (j, 6) с
оследующей фильтрацией с помощью фильтра нижних частостей
: частостью отсечки 4 kzps. Отфильтрованный сигнал затем можно
двинуть в любую полосу частостного спектра умножением на со
тветствующую несущую Уолша.
Выделение отдельных каналов
ли групп каналов без требования демодуляции всех каналов мо
ет быть использовано для распределения каналов по переклю
аемым сетям связи [14].
Ранее предполагалось, что каналы и группы, собранные в су-
• ергруппу
А или В, синхронизированы. Это предположение спра
едливо, если все каналы комбинируются в группы и супергруппы
а одной и той же центральной телефонной станции. Рассмотрим
лучай, когда каналы комбинируются в группы на различных цен
ральных телефонных станциях,
и эти группы комбинируются в
упергруппы на центральной телефонной станции более высокого
·ровня. Теперь уже нельзя предполагать, что эти группы синхро
. изированы, но можно допустить, что они имеют одинаковую вре
. енную базу Т = 250 мкс.
' Компоновка несинхронизированных групп с одинаковой вре
. енн6й базой будет рассмотрена с учетом рис. 3.8. На этом рисун
. е сверху показаны функции Радемахера wal (31, 0) и wal (127, 6)
а интервале 0::=:;;;10<J/8. Умножение
wal (127, 0) wal (63, 0) = wal (64, 0);
wal(l27, 0)wal(31, 0)=wal(96, 0)
wal (64, 0)
и
wal (96, ·0).
107
Согласно рис.
3.7
они яв-
ляются несущими, необходимыми для перевода двух групп в одну
супергруппу А.
На рис. 3.8 (строки а) символически показаны сигналы двух
несинхронизированных групп. Согласно рис. 3.6 и 3.7 эти сигналы
состоят из сумм ФУ''кций wal (32, 8); wal (33, Н), ... , wal (63, 6);
амплитуды этих
функций зависят
~liat(Jt,e) от
особенностей
передаваемых
Г"'1..JL.J""LJ wat (бJ е)
ГU1J"\J'"U1.ЛЛ wat (IZ~ е)
""'LJ"LJ"L..Г"
а)
wat
(61/,ЭJ
LJ"LJl.r"U"'L wat (86,0)
1t l z kJ\!§ч4 51 fi 1ИJ§8 группа 1
1i z ЫЩЩ s ! б РЗ§ВЗ 2рgппа 2
о) .___.___.___.__._~~..._
t
О}@! 1
сигналов.
Из рис. 3.9
видно, что
сигнал, состоящий
из составляю
щих wal (32, 8);
wal (33, •8),
... , wal (63, 8), является ступенчатой
функцией с
шириной
ступеньки,
равной
l/64. Нечетные функции
! 2 IИl§N 1l 1§7§ группа 1
wal (33, 8); wal (35, 18), .. " wal (63,
11 1 z §ЗJЩJ t • • 1§@§ гp!Jnna 2
8)
на рис: 3.9 не показаны,
так
z) М§'1 i ! 2 1$J'{tf4 s i 6 lfl!JППO f
как
они
отличаются
от
четных
№ f 1 2 fS.rJ;fSJ 11 & 1§§ грgппа 2
функций wal (32, 8); wal (34, 8, ...
~ wat (JZ,e)
е гр г г га
о'
0
... , wal (62, 8) только коэффициен
-1, на интервале -1/2:::::;6<
Сигналы на рис. 3.8 (строки
55s s 59nггzassss SS
' ·,;~i · ,1}1d , 'J/Jz ! '1/8 в 7,ШS
том
<О.
!5,82S lJ,4JlS J1,25HKC
Т= 250 мкс
t -
Рис.
3.8.
двух
несинхронизированных групп
Принц;ипы объединения
в подгруппу А
согласно
рис.
3.7
а)
разделены
на интервалы ши
риной 1/64.
На этих интервалах
их амплитуды постоянны. Отдель
ные интервалы обозначены I, 2, . . . .
Далее
из
рис.
3.9 можно ви
деть, что сигнал, состоящий из функций wal (32, 8), ... , wal (63, 8)
и имеющий амплитуду И на интервале -1/2:::::;1
8< (-1/2) (1/64),
должен иметь амплитуду -И на интервале (-1/2)
(1/64) :::::;18 <
< (-1/2) + (2/64). Этот результат справедлив в общем случае:
+
+
амплитуды имеют одно и то же абсолютное значение и противо
+
положный знак на любых двух интервалах (2k/64) :::s;H< (2k/64)
+(1/64) и (2k/64)+(1/64):::s;18:::s;(2k/64)+(2/64). На рис. 3.8 (стро
ки а) показаны интервалы одинаковых абсолютных значений. На
интервалах 1 и 2, 3 и 4, 5 и 6 и т. д. амплитуды имеют одинаковое
абсолютное значение и противоположный знак.
Производя отсчеты значений сигналов (строки а)
времени, задаваемые тактовыми импу.1ьсами
миная отчеты
напряжений в течение
(строка
интервала
в моменты
6),
и запо
длительностью
1/64, получаем сигналы строки в. Они синхронизированы с несу
щими wal (64, Н) и wal (96, 8). Но этой синхронизации еще недо
статочно. Группа 2 в строке в начинается в момент времени 0=0
с интервалов 1 и 2, в которых амплитуды имеют одинаковые аб
солютные значения. Группа 1 начинается с интервалов, для кото
рых это несправедливо. Сдвигая группу с помощью схем, осуще
ствляющих отсчеты и запоминание значений сигналов, получаеы
сигналы строки г. Тепер;~ точно засинхронизирована группа 1, а
группа
2 не засинхронизирована. Для модуляции несущих
и wal (96, 8) надо взять сигналы группы
и сигналы группы 2 из строки в.
wal (64, 8)
108
1 из строки г
1
Заметим, что синхронизация здесь отличается от синхронизаи при временном разделении, так как группы
винуты относительно друг друга
на
1
и
могут быть
2
любую величину, кратную
-----Z'---------.__
____ z
--..,_____
____
- - - - - - - - - - - - - - - - - - - &'
_г----.,_
_,г--
lf
~--1~-,_~_г~~~,_~.г---,~~G
t __
_г--,,,
__
г--,_
_
_s--,__.Jг-
8
!О
12
14
fб
18
20
~
.
,.-,1
.--.
l2
2'1
2/i
r-. IГ- 28
-----~-.__.,__,--,_..-L_Т-,__,..._..-,_,Г>..___.--..._..,~.-~.~-._~,.-,-JО
.г-L.
,.-,,
.-~ ~__г-i~-._r~пJ -. .r-. г -. ~.-.
~--._,,-._.---.__..-,...-1.г,
JZ
JI/
r- J/j
1r-11
r-.~1
,33
....
lfO
42
41/
4о
48
50
52
я
J6'
5t!
li/l
ы
1/2
/l
Рис.
(}-3.9. Функции
Уолша
Такой произвольный сдвиг при временном разделении при
бы к перекрестным помехам.
· В символической записи сигнал супергруппы А имеет следую
. ий вид: (группа 1) wal (64, 0) +(группа 2) wal (96, 0).
: Демодуляция супергруппы А с помощью wal (64, 6) или
al (96, 0) дает следующие два сигнала:
{(группа 1) wal (64,0) +(группа 2) wal (96, 0)]wal (64, 0) =
=(группа 1) +(группа 2) wal(32, 0);
{(группа 1) wal (64, 0) +(группа 2) wal (96, 0) ]wal (96, 1
8) =
=(группа 2) +(группа 1) wal (32, е).
Один из членов правой части необходимо подавить, чтобы по
чить в чистом виде группу 1 или группу 2. Члены (группа 1)
109
,
1
или (г р у п па 2) легче подавить, чем остальные. Практического зна
ч е ни я это не имеет. так как получаются члены (группа 2)wal (32, е)
(г ру ппа l)wal(32,
мощ ью wal (Э2 , О):
I!
{(группа
{(группа
Ч .1 е ны (rруппэ
них частостей,
0) ,
которые можно
демодулировать
2)wal(32, 0)]wal(32, 0)=(группа 2);
1) wal (32, 0) ]wal ( 32, 0) ='(группа 1).
1)
и (группа
2)
можно подавить фильтром ниж
осуществляющим интегрирование
<>«0< 1/32; 1/32<0<2/32
на
интервалах
и т. д. Эти интервалы интегрирования
пока з аны в последней строке рис.
Для телефонной системы с
3.8.
канал а \ : н нх нен о рмированная длительность равна
1024
с по
7.8125
мкс.
Эти интервалы интсгри'рования равны двум интервалам группы 2
в строке в и группы 1 в строке г, в ко
торых амплитуды сигналов имеют оди
наковое абсолютное значение и про
т ивоположный знак. Т~ким образом,
интегрирование
дает
нуль
и
сигналы
подавляются.
Умножение группы 2 в строке в н
группы 1 в строке ;; на wal (32, 0)
приводит
вала х
к
и
1
тому,
2, 3
что
и
4
знаки
на
интер
и т. д. становятся
одинаковыми . Интеграл уже не равен
ну.'lю и сигналы (группа 2) wal (32, 0)
или (группа 1) wal (32, 0) проходят
через фильтр нижних частостей.
На рис.
3.1 О
осциллограммы
показаны некоторые
частостной
многока -
нальной системы, полученные Люке и
Мэйлом. Для ясности вместо несущих
1
\ \ al (32, е)'
.. " wal (62, 0) (рис. 3.7)
пока з ана
несущая
wal (5, 0).
По той
же причине для вторичной модуляции
Рис.
.
а)
Осци лл ограммы
3.10.
с то ст ного
упл отнения
ны х
вход но й
сигнад
нижн и х
на
вич н ая
сигналов:
сигнал
выходе
wa1(5, 8);
модуляция
линии
F ( 8);
частостей
в) н е сущая
ча
телефон-
6)
фильтра
F++ (8);
г) пер
F++ (8)
х
X wal(5, 8) ; д) несущая wal(9,
8);
е) вторичная
м о дуля
ция F++(8)wal(:5, 8)wal(9, 8);
масштаб
по
60
го ризонтали
мксjдел
использована несущая wal (9, 0), а н е
wal (96, 0) или wal (64, 10) (рис . :3.7) .
Ослабление
перекрестных
помех в
этой аппаратуре составляе·т порядка
-55 дБ при использовании отдельной
-53
синхронизации
дБ,
и
падает
до
если сигнал синхронизации
передается вместе с телефонным сиг
налом и выделяется фильтром, отсле
живающим функцию Уолша . При ис
польз овании сжимателей динамическо
го диапазона
(компандеров)
такое
ослабление вполне
удовлетворяет те
лефонным
110
стандартам. Однако
в на-
время частостное уплотнение имеет особый интерес для
ровых сигналов с ограниченной пиковой мощностью, а в этом
.qae ослабление перекрестных помех -53 дБ более чем доста-
3.1.3.
Цифровое уплотнение
\. Ранее было указано, что частостные фильтры, основанные на
'.нкциях Уолша, можно легко реализовать как цифровые фильт
.· Так как
, а так же,
,;:тостные
полосовые фильтры требуют частостного сдвига сиг
как и многоканальные системы, можно ожидать, что
многоканальные
системы
легко
можно
реализовать
с
,,мощью цифрового оборудования. Рассмотрим для примера уп
·.
нения двух телефонных сигналов согласно рис.
1Необходимо
уплотнить два сигнала
3.2.
F2 (0) и F1 (0). Эти сигналы
едставлены на рис. 3.2 кривыми а и а'. Амплитуды на опреде
~ном интервале, например, 125 мкс<t<250 мкс преобразуются в
' ровую форму преобразователем аналог-цифра. В табл. 3.4
ведены цифровые представления:
+110110 для F't+(0) и
) 1010 для Ft+(0). Уплотнение этих сигналов будет рассмотрено
· :использованием табл. 3.4. Предполагается, что F 2 ('8) и F 7 (0)
· яются сигналами восьмиканальной системы. В качестве несу
, х используются восемь функций Уолша от wal (О, 0) до sal (4, 0).
гналы идут ТОJ1ЬКО по двум каналам. Это соответствует коэфзагрузки, равному 0,25. Эта величина коэффициента за
зки характерна для телефонной многоканальной системы в пе
од максимальной загруженности.
_,циенту
1 : Несущие -sal (1, 0)
-saJ (3, 0) можно представить восьмью
3.4. Отри
:тельный знак несущих здесь несущественен. Несущие -sal (1, 0)
:;._sal (3, 0), промодулированные по амплитуде сигналами F2*(0)
:F1*(0), дают восемь раз числа + 110110 и -011010, умножен
е на коэффициенты + 1 и -1, как показано в столбцах г и г'.
упповой сигнал -F(0) в столбце д получается суммированием
_фрами
+ 1 и -1:, как
и
показано в столбцах в и в' табл .
ух чисел из одной строки в столбцах г и г'.
•:Групповой сигнал представляется числом, имеющим на одну
'фру больше, чем F2*(0) или F1*(0).
' Совокупность 8Х8 цифр, включая знак сигнала -F(8), мож
передать многими способами. Например, можно использовать
. прямоугольных импульсов с амплитудами + 1 или -1. В этом
· учае для образования группового сигнала будет использовано
стостное разделение, а для передачи - временное разделение.
олучившееся число импульсов 64 равно
числу импульсов при
еменнбм уплотнении восьми каналов с добавлением одной циф
:ы к семи цифрам
в каждом канале для проверки на четность .
одной
цифры позвоJ1яет
обнаруживать
одиночные
~шибки, но не позволяет их исправлять.
. обавление
'
Демодуляция
-F(0) достигается умножением -F(0) на
и -sal (3, ·0 ). Полученные двоичные числа показаны
sal (1, 0)
:. столбцах ж и ж'. Интегрирование F(0)sal(I, 0) и F(0)sal(3, 0)
111
Т а бл и ц а
3.4
.
Цифровое частостное уплотне"ие двух сигналов: f;j+ (0) и F
согласно рис.
ц фровые представления сигналов в различных точках рис.
•
1
в'
г'
г
~
-·
~
о;
~
ф
"'1
~
+1
+1
-l
+1
+1
+1
-l
-l
-1
-l
-l
+1
-l
+1
+1
-l
ф
-;;;
"'
...:
"'
-.;
+""
tr..
1
1
1
+
+оошоо
+0011100
+ 1010000
+1010000
+OOlllOO
+110110
+llOllO
+llOllO
+llOllO
-llO!lO
-110110
-011010
ф
~
ф
+
1
ж'
д
€
+
+tr......
ф
~
3. 2
ф
ф
...;
ф
1
t+ (0)
3.2
~
tr..
+011010 +1010000
+011010 +1010000
-011010 +оошоо
+011010 -ООШОО
-011010 -1010000
-llOllO -011010 -1010000
-llOllO +011010 -OOlllOO
~
"'
з
~
tr..
з
tr..
-t'J(Jll 100
-1010000
-1010000
+0011100
+оошоо
+1."JОШОО
+1010000
-1010000
+1010000
-1010000
+оошоо
+оошоо
~=+l 10110000
~=-011010000
Щ8=+ll0ll0
~/8=-01
lOlO
означает сложение
восьми Чисел в колонках ж и ж',
что дает
110110000 и -011010000. Деление на восемь дает первоначаль
ные значения F2++(0) и F7++(0). На практике для получения этих
чисел .11учше применить
к групповому сигналу -F(0)
быстрое
преобразование Уолша-Фурье из § 1.2. Однако включение опи
+
сания
этого
метода,
позволяющего
экономить
время,
затруднит
пояснение принципа.
Сигнал -F(0) содержит только числа с абсолютными значени
ями 0011100 и 1010000; два из них имеют отрицательные знаки и
два - положительные. Это характерно для работы системы с дву
мя активными каналами.
Таким образом, если из-за действия
помех одна цифра изменится, то ее можно исправить, сравнив с
тремя неизменившимися. В большинстве случаев можно исправить
две ошибки и во многих случаях - больше двух.
Поэтому здесь
имеется определенное преимущество по сравнению с
методом
вре
менного разделения. Это объясняется тем, что при использовании
временного разделения и при коэффициенте загрузки 0,25 в те
чение 3/4 времени не передается никакой полезной информации.
112
Было исследовано большое число разновидностей схем часто
стно-цифрового уплотнения. Однако их возможное число настоль
.о
велико, что не было сделано определенных выводов об их от
,iюсительных преимуществах.
3.1.4.
Методы однополосной модуляции
Амплитудная модуляция синусоидальных и косинусоидальных
несущих согласно
теоремам об умножении этих
функций дает
;двухполосную модуляцию. Существует ряд методов для устране
ния одной боковой полосы , которые можно хорошо проанализиро
. ать с помощью ортогональных функций.
Рассмотрим два передатчика, которые
ные колебания с частотой
сущие, модулированные
· удут иметь вид F+(0)
ается, что частота Q0
Qo,
излучают синусоидаль
имеющие фазовый сдвиг
( 1/2) n. Не
F+(,0) и D+(0),
Qo0 и D+(0) V2siп 1 Qo0. Предпола
временнь1ми функциями
V2cos
может быть точно воспроизведена в при
мнике и что существует фазовый сдвиг а между принятыми несу
. ими V2cos Qo8 и V2 sin illo0 и опорными несущими V2 Х
· cos(Qo0+a.) и 'V2siп (Qo0+a). Умножение принятого сигнала
S (0) = р+ (8) V2cos Q00+ D+ (8) V2 sin Q00
(3.27)
а V2cos(Q 00+a) и V2sin(Q 00+1a) дает:
S (8) V2 cos (Q08 + а) = р+ (8) cos a+D+ (8) siп а.+
+р+ (8) cos (2Q08 +а) + D+ (8) siп (2Q08 +а.);
(3.28)
S (8) V2sin (Q08 + а.) = - р+ (8) sin a+D+ (8) cos а.+
+F+ (8) sin (2Q08 + a.)-D+ (8) cos (2Q 00 +а).
(3.29)
Члены в правой части (3.28) и (3.29), содержащие множители
или sin (2Q 08+a),
имеют только высокочастотные
омпоненты;
они будут подавлены фильтрами .
Если фазовый
" двиг очень мал , то в правых частях (3.28) и (3.29)
останутся
только сигналы f+(8) и D+(8). Таким образом, используя две не
. ущие равной частоты, но со сдвигом фаз, равным п/2, можно без
,;взаимных помех
передавать два независимых
сигнала F+(8) и
р+ (8). Иначе говоря , каждый частотный канал может быть раз
делен на два фазовых канала, которые будут здесь называться
os (2Qo8+a.)
инусоидальны м
и косинусоидальным каналами . Синхронная де
~:Модуляция позволяет использовать оба фазовых канала. Напри
мер, можно в
(3.29)
заменить
f+(8)
на
1 +F+(0)
и потребовать,
'!чтобы сигналы F+('8) и D+(0) практически не имели составляю
' щих на частоте ниж е определ е нной. Тогда сигнал S (8) можно де
., модулировать схемой , изображенной на рис. 3.11 . На выходе 1 по
' учается сигнал (l+MF+(0)](l+cos2Qo8), а на выходе 2ф+(8) ( 1+cos2 Qo8) .
Однополосная модуляция
нусоидальному
отличный способ
передачи по си
и косинусоидальному каналам.
Чтобы показать
-
113
это, разложим сигнал
в ряд по синусоидальным и косинусои
F(EJ)
дальным и м пульсам согласно рис. 1.1:
F (0) = а(О) f (О, 0)
+ V2 L"' (ас (i) cos 2:rt i 0 + a (i) sin 2:rti0J; (3.30)
5
i=I
- 1/2~0< 1/2.
Рис. 3Jbl. Коррекция фа
завых
различ11й между
принятой
и
опорной
Фунщиями
Jlicos Qo6
·И Jl2cos (Qoe+a)
П
п еремкожитель;
-
фил ьт р
ГВЧ -
н ижни х
управляемый
тель ;
Ф
--
ч ас т о r:
ген ератор ВЧ; УФВ ФВ
-
на
фа з овр а ща
ф азовращат ел ь
90•
·
Преобразования Фурье q(O, v); Qc(•i, v) и Qs(i, v) этих импульсов
можно получить согласно ( 1.24). Первые пять преобразований по
казаны на рис.
1.6.
Обозначим произведения
f (О, 0) V2cos Q00; 1f (О, 0) V2sinQo0;
2cos 2nh0 cos Qo0; 2cos 2:rti0 sin Qo0; 2sin 2:rti10 cos Qo0 и 2sin 2ni0 Х
XsinQo0 через do, c(0); do,s(O); dc1,c(0); dc1s{10); ds1,c(6) и ds1,&{0).
Преобразования
Фурье
этих
произведений
обозначим
через
ho,c{v), .. ., hst,s(v):
h0 c{v)= .
V2[q (О, v-v0){-)q (О, v + v0)J;
1
2
hcl,c(v)= +V2[qc(i, v-v0)(-)qc{i, v+v0)J;
1
h51 c{v) = ( - ) - V2(q 5 (i, v- Vn)+ q,(i, v
.
2
(3.31)
+v
0)];
Qo
v =о
2n ·
Знаки в круглых скобках справедливы для преобразований Фурье
ho, в (V) ; hc1, s (v) И ·hs1, s (v) .
Преобразования
Gc(v) и Gs{v) от функций F(O) Х
Х -V2cos Qo0 и F(0) V2s iп Q00 можно по,1учить из (3.30) и
(3.31):
G,(v)
G, (v)
Фурье
~ а (О) h,,,(v)+ '~ [a,(i) h,, ,,<v) + a,(i) h,,,, (v)I;
~ а (О) h
0"
(v) +
]
~' )a,(i) h"" (v)+ а,(~ h,", (v)). J
114
(3.32)
Чтобы пояснить вид функций Gc(v) и Gs(v), рассмотрим слу
ай, когда ас ( 1) = as ( 1) = 1, а все другие коэффициенты равны ну·
ю. Получившиеся преобразования Фурье функций:
V2 cos 2n8 V2 cos QД V2 cos 2тс8 V2sin Q08;
V 2siп 2n8 J/2cos Q08; V2sin 2n8 V2sin Q08
на первых четырех
строках рис.
3.12.
Заметим,
что
V2sin 2тс8 являются косинусоидальным и синусо
. дальным
импульсами,
которые
равны
нулю
вне
интервала
I/2~e~112.
:
Из преобразований Фурье, изображенных
;траках (рис.
3.12),
в первых четырех
можно получить следующие однополосные сиг-
f cs (8) = cos 2n8 sin Q08 + sin 2тс8 cos Q08; ]
fсе (0) = cos 2тс8 cos Q08 - sin 2n8 sin Ц~8;
f sc (0) = cos 2тс0 sin Q 08 - sin 2n8 cos Q 08;
fss (0) = cos 2n8 cos Ц~8 + sin 2л:0 sin Q 00.
(3.33)
Преобразования Фурье этих функций показаны на строках 5рис. 3.12. Сигналы, описываемые функциями fcs (8) и fcc (0), име-
_m __ ..L __ ~ 2cos2Ji. t/T· cas t.J0 t
·~·J (О, e)cas2aв+w(1,e)5i.n Q/З
F3
~--..L __ L::YJ. 2cos2fьt/T·5iщ.J0 t
~--..L--~ 2sin2r..t/r C051.J0 t
-т;:Р--- -L--~ 2sin27i.t/Т· sinl.J0t
-O----..L---C. C052J.t/,T· sinl.J0t
5
-ъ---L
-ып2п1т · sin(,):t
__ ..о._ cqs ZX.t/T·
SLП(,)ot
2:li:t
cas (,) t
/Т·
·5tn
•
0
_ c _ __ .L. __ ..Q___ cqsZt.:t/T· casrv0 t+
+sin 21it/J.:,i11w0t
____Q_ __ ..L. __ ___Q._ C052:!it/ T· Ca5(,J t-
-f,T
0
fuT
fТ~
Рис.
3.12.
несущих,
F3
2
J
!
и
косинусоидальиых
модулирова·нных
синусоидальными
и
ПQ
ампли
косинусо'И-
1
f+L
'-
1
Е3
v-1(0 Э)соs ~ 0 в- ~v(f,e)sinQp
·а
__ ,_
а
w{O.O)&i,n ОJЭ+ w(t,O)cosяp
4,
1
Е3 -'-а
1
1
1
1
1
t
~
,,,.r:::, ~ ~ 1"'"~ ~~ +:"~
.,..""' rr""
..,_
~·
1
Преобразования Фурье си
нусондаль'НЫХ
туде
-sin2r.l/T·CDS{,)~t
,_
1v(o.e)sin Q 00-w{ t,Э)cos2qlJ
+
_Q__ .-L. __ _a_'c ;sпz~~1!. с~~t(,У-
1
Рис .
1
3.13.
Фурье
Преобразование
некоторых частотно
огр аниченных
однополосных
сигналов
дальными импульсами
т почти всю энергию в верхней полосе v > 1
Qo/2n, а сигналы, опи
ываемые функциями fsc (8) и fss (8), имеют почти всю энергию в
_ижней полосе v<Q 0/2n. Используются оба фазовых канала, так
ак все четыре сигнала
i
(3.33)
содержат синусоидальную несущую
115
и косинусоидальную несущую cos Qo0. Практическое вопло
щение однополосной модуляции согласно (3.33) обычно называет
ся вторым методом однополосной модуляции или методом сдвига
фаз {2]: сигнал F ( 0) модулирует несущую sin .Qo0 и аналогичный
сигнал со сдвигом фаз на 90° модулирует несущую cos Qo0; сумма
или разность модулированных несущих дает однополосный сиг
нал. Первый метод однополосной модуляции дает тот же резуль
тат путем подавления одной боковой полосы с помощью фильтров.
Из девятой строки рис. 3.12 можно понять, почему не следует
пренебрегать
отрицательными частотами.
Это преобразование
очень похоже на преобразования, изображенные на строках 5 и 6
sin Q"0
для положительных значений
v=fT;
тем не менее оно не соответст
вует однополосному сигналу.
Однополосная
стить
и
одинаковое
двухполосная
число
каналов
модуляция
в
позволяют
определенном
разме
диапазоне
ча
стот, если используются два фазовых канала для каждого частот
ного канала. Использованне двухполосной модуляции, обычно на
зываемой квадратурной
модуляцией, сопровождается
в случае
телефонной передачи большими перекрестными помехами. С дру
гой стороны, однополосная модуляция вызывает большие искаже
ния
при п~редаче цифровой
информации, если
используются
фильтры для подавления одной боковой полосы. Двухполосный
передатчик передает всю энергию по синусоидальному или косину
соидальному каналу в определенной полосе частот; однополосный
передатчик передает
по
всю энергию
косинусоидальному
каналу,
но
как
в
по синусоидальному,
полосе
частот,
которая
так
в
и
два
раза уже.
Тепловой шум оказывает на оба метода одинаковое
воздействие, если для двухполосных сигналов используется фазо
'°!увствительная фильтрация; иначе сигнал будет приниматься из
одного фазового канала, а шум из обоих.
Исследование
дальных
и
амплитудной
косинусоидальных
модуляции с помощью
импульсов
затруднено
тем,
синусои
что
эти
функции не ограничены по частоте и сложны в начертании. Лег
че получить результаты с помощью функций Уолша.
Рассмотрим функции Уолша (рис. 1.2) как функции частоты
wal(O, v); cal(i, v)=wal(2i, v) и sal(i, v)=wal(2i-l, v), а не как
функции времени. С помощью преобразования Фурье получаем
следующие функции времени:
со
w (2k, 0)
S \Val (2k,
=
v) cos 2rt,>0d ,,;
-оо
(3.34)
J wal (2k+ 1, v) sin 2nv0 d v;
со
w (2k+ 1, 0)
=
-00
k=0,1,2,....
Функции
w(j, 0)cos Q00
и
w(j, 0)sin Qo0, j=2k
следующие преобразования Фурье:
116
}
или
2k+ 1 имеют
Jw(2k, 0)cosQ 0cos2:n:v0d0=wal(2k, v-v )-t-wal(2k, v+ v
""
0
0);
0
-оо
J w(2k, 0) sin Q 0 sin 2nv0 d 0=wal (2k. v-v wal (2k, v + v
""
2 J w(2k + 1, 0) cos 0 sin 2пv0 d 0 = wal (2k + 1,
со
:2
0) -
0
0);
-ао
Q0
-ао
J"" w(2k +
:2
.
v-
-оо
v0) + wal (2k + l, v + v0);
1, 0) sin Q00 cos 2:n:v0 d 0 = - wal (2k + 1,
v - v0) + wal (2k + 1, v + v0).
}
(3.35)
Из временнЬ1х функций
(3.34) можно получить следующие сиг
алы, имеющие всю энергию в верхней или нижней боковой по
осе:
(О, 0) cos Q 00+w ( 1, 0) sin Q 00;
w (О, 0) cos Q00-w(l, 0) sin Q 00; ]
(О,
0) sin Q 00_- te.i (l, 0)cos Q00; w (О, 0) sin Q 00+w(l, 0) cos Q0 8;
(2, 0) cos Q 00+w (3, 0) sin Q0 0; w (2, 0) cos Q 00-w(3, 0) sin Q00;
(2, 0) sin ~0-w(3, 0) cos Q00;
На рис.
3.36).
( .
3 36
)
w (2, 0) sin Q 00+w (3, 0) cos Q00.
3.13 показаны четыре преобразования Фурье функций
Стрелки показывают, в каком направлении возрастает аб
олютное значение частоты
ие стрелок
и жней.
wal (2k, v) и wal (2k+ l, v). Направле
не изменяется для верхней полосы
и меняется для
Функциональная схема второго метода однополосной модуля
ии показана
на рис. 3.14. Частотноограниченный
сигнал F(0)
нс. 3.14. Метод сдвига фаз (а) и четвертый метод Сарага (б) однополосной
модуляции несущей с частотой 'Vo частотноогра,ниченным сигнало~1
- фазовращатель; П - перемножитель; С - сумматор; ПФ - полосовой
ФВ
F'(0) -
однополосный
F(0):
фильтр;
сигнал
роходит через две фазосдвигающие цепи. На их выходах появ
яются два сигнала, компоненты колебаний которых имеют фаовый сдвиг 90°. В другах отношениях сигналы одинаковы. Несу
ие cos 2л:v 0 0 и sin 2л:vо0 модулируются по амплитуде. Сумма про
зведений дает сигнал с верхней полосой, а разность - сигнал с
1шжней полосой.
117
Очень
похожий метод принадлежит Сарагу [3]. Несущие
cos 2л:vа0 и sin 2л:v 00 суммируются со сдвинутыми по фазе сигнала
ми согласно рис. 3.146. Затем суммы перемножаются. Получаетсн
сигнал с верхней полосой, кроме него получаются сигналы: в .основнои полосе частот и сигналы
с удвоенной частотой несу-
F(e)
щей
.--__.___,
1-,.,,..,.....,.,,..----+----.
2v0 •
Эти нежелательные
сигналы
подавляются
прос
тым полосовым фильтром.
Следующий
полосной
метод одно
модуляции
при
надлежит
Уиверу (4].
На
рис. 3.15 показана функци
ональная
~хема
для
реали
зации этого метода. Сигнал
F(e), не содержащий энер
гии вне
полосы O~f~ 1/Т
или O~v=/T~
1, моду
лирует
!J{O) CG5 2 Ji
+ h (е) siп 2 Jt
+
sin 11:'0 и
cos 11:'0 с частотой v1.=f1.T=
= ·1/2 или f1 =1/2T. Частота
(v о + t/2) е +
несущие
несущей находится
дине используемой
(v 0 +1/2) е
·в сере
полосы.
Рис. iЗ.15. Третий метод Уивера одноnолас- Модулированные
несущие
ной
фильтры
модуляции
+ (l/2)
несущей
с частотой
частотноограниченным
F1(e):
vo+
проходят
через
сигналом нижних частот с частотами
г - генератор; п - перемножите.%; Ф - Фильтр отсечки
нижних ча стот
vg=fgT =·1/2.
От-
фильтрованные сигналы мо-
дулируют
высокочастотные
несущие sin2л:(\'o+l/2) ·0 и cos2л:(v 0 +1/2)0. Сумма дает сигнал с
верхней полосой, а разность
-
сигнал с нижней полосой.
Для объяснения метода Уивера разложим частотноограничен
ный входной сигнал F (0) в ряд по функциям w (2k, 10) и w (2k+ 1,
0),
полученным преобразованием Фурье
(.3.34)
из функций Уолша:
00
f(0)
=
![a(2k)w(2k, 0)+a(2k+ l)w(2k+ 1, 0)1.
(3.37)
k=O
На вход схемы (рис.
3.15) достаточно подать одну четную и одну
нечетную составляющие сигнала (3.37),
а не сам сигнал F (е).
Используются простейшие функции w(O, 0) и -w(l, 6). Их пре
образования Фурье wal (О, v) и -sal ( 1, v)
показаны в первой
строке рис. 3.16. Стрелки показывают направление возрастания
абсолютного значения v. Модуляция cos n:0 сдвигает преобразова
ние Фурье в первой строке на 1/2 вправо и влево (вторая строка).
Для большей ясности преобразование, сдвинутое влево, заштрихо
вано. Два сдвинутых преобразования показаны наложенными там,
где они перекрываются и имеют одинаковые знаки.
118
; Модуляция sin :rt0 сдвигает преобразование
· еобразование, умноженное на -1, - влево
ильтры
нижних
частот
подавляют
все
на 1/2 вправо и
(третья строка).
компоненты
вне
полосы
l/2~v~l/2 (четвертая и пятая строки). Получившиеся сигна
\:>1 qo(0) и h1 (18) имеют нечетные преобразования (четвертая и пя-
;
1
w(О,8)
-w{l,8)
,:~-s~~R ~ -2;-f~хв
2w[O,fJ)sinJZ(J
29/61"'
J
eJ+gozCBJ
о1
2ho(tJ)Gth"/8)~
gOf (8)
-2w(UJ.
f!S5SI
sinr.e
~
2g,(e;f!i/!J(e)+!J,z (8)
[8~ fJ.+h1z{8)
2h
б
FSm
~)
g12(e.6
h~
7
hNJ8J
hzff!
О RЗ
2f(~[m'10{~Ji ~>18
1
В9
h
(8)
·-L--G
fZ
2g,[e'ff!l11'(v0 +1fz)в
--'-fO 2h е sin2r. (v +1fz)8
2h0 (0)sin2x(~it/z)д
0
~-·-~11
_ _L_~
'
9. (O)GD52:i(И.+ ~f +hol8)5inlt (~о•Yz>e M6Jcos2~ (~11 +7Jlj8+ п, {8) sin 2J;. (у0+1h)в
--1.-ЬSЯ t2 ..а:::з:_-1._~
~~ ~
~$!
~c::::i~~~""
• ' ~.,._,
"
+. ...
,,.,"?."
.... 1
..
Рис.
~~
3.16 .
·я строки). В строках
..J.._L....J.1-J......J~
.~~~~~-~"«:) 1 '>~
,.....,,..:i:- ...
" ' '>-""' 1 ";"
"
.,.
'·
'?-'>-
.Преобразования Фурье
6-9
показаны четные
преобразования
11кций
Qo1(8), q02«8) и hн(О), h12(0), которые можно сложить и
учить q0 {0) и h1(8); так же показаны нечетные преобразования
нкций ho1(8), h02(0) и qн(0), Q12(·8), которые, будучи сложенны
' дают преобразования функций ho(0) и Q1(8).
!; Преобразования в строках 6-9 имеют вид wal (О, v) и
'sal(l, v). Таким образом, с помощью (3.33) получаются преоб
. зования следующих функций:
1
):i q0 (0) cos 2:rt (v0 1/2) 0 = [q01 (0) + q02 (0)] cos 2n (v0 1/2) 0; (3.38)
+
hi (0) sin 2:rt{vo + 1/2) е =
+
lh11 (0)
+
h12
(0)] sin 2:rt (vo
+ 1/2) 0,
(3.39)
к показано в строках 10 и 11. Преобразования в строках 4 и 5
вигаются на
vo+ 1/2 вправо и влево; сдвинутые преобразования
+ 1 и -1 согласно четырем возможным произве
" . ножаются на
иям четных и нечетных преобразований с синусоидальной или
синусоидальной несущей, как показано в (3.35).
.
119
Сумма строк 10 и 11
верхней полосой (строка
дает преобразование Фурье
сигнала с
Разность дает преобразование сиг
12).
нала с нижней полосой.
Наиболее часто используется
метод однополосной модуляции,
основанный на подавлениц фильтром одной боковой. Этот фильтр
вносит искажения, которые особенно ощутимы при передаче циф
ровых сигналов. На рис. 3.17а показан спектр мощности сигнала,
а) Ls-i
~ 0"
N
0)
О
d)
2)1
4~о'>1
.__ - - -
L __ л-з/·; m
0
L
L
__
~с-2~4-
m/
Ус
', ,
~- . . .
m
)1
.J.----
mr i
М No
--
m...
и l z 1 з t..
,{-т1-!!-;iн1.
/--tJ zl}~°i;.
. ~iйfз!:
i552i10 '>с ,"N11 'i,~но jc"B~o
o)L__
eJL__
жJL__
з)L__
и).1
1
- -
!1 ~zfз_"
н) ~1 ::J z вз" , "
л)D"n
, '•
. о г.;, 4уо 6)10 8-J4
Рис.
при
3:17.
Спектр
модуляции
и
мощноС'ГИ
демодуляции
трех СИГ'Налов (елучай однопо
лосной модуляции). Полоса ча
стот сигналов .2vo, нижняя ча1стота сигналов рав·иа О
Рис.
и
демодуляции
трех
С·игна
лов (случай однополосной модуляции
со смещением). Полоса частот сиг·
налов 2vo, нижняя частота сигналов
'РаВ'на 2va
вся энергия которого практически
Для дальнейших
Опектр мощности при мо
3.18.
дущщии
заключена
рассуждений необязательно,
в
полосе
o:::;;;v<vo.
чтобы частотный
спектр имел прямоугольную форму в полосе O:::;;;v<v0 , как это по
казано на рис. 3.17. На рис. 3.176-г показаны сдвиги трех таких
сигналов на соседние полосы с помощью амплитудной модуляции
несущих с частотами vc, vc+2v 0 и vc+4vo.
Полосовые фильтры с
передаточными функциями, показанными пунктирными линиями,
подавляют нижнюю полосу. На рис. 3.17д показана сумма верх
них полос. Колебания в заштрихованных областях частично зату
хают, а их фазовый сдвиг изменяется не по линейному закону от
частоты . Это вызывает искажения сигнала. В приемнике сигналы
разделяются полосовыми фильтрами, при этом вносятся дополни
тельные искажения (рис. 3.17 е-з). Спектр мощности демодули
рованного сигнала показан на рис. 3.17и-л. Заштрихованные об
ласти показывают,
где колебания
некачественно
сдвинуты по фазе, что вызывает искажения сигнала.
120
подавлены II
два способа уменьшения искажений. Можно вы
ать сигналы таким образом, чтобы большая часть их энергии
. держалась в полосе частот, где фильтры не вносят искажений.
ругой способ - выбирать частоту среза характеристики фильт
в вне полосы частот, внутри которой заключена большая часть
ергии сигналов. Первый способ используется в системах с ча
чно подавленной боковой 1 ). Этот метод особенно пригоден для
редачи цифровой информации с временным разделением по уже
·
ществующим
етальное
телефонным
каналам
рассмотрение этого
еннетом и Дэви
метода
Второй метод исполь
{7].
ется в однополосной
модуляции
ением: [8]. Ее принципы будут
ны на основании
рис. 3.18.
еют
практически
(6].
дано
всю
со сме
рассмот
Сигналы
энергию
в
полосе
астат 2vo:::::;;v:::::;;4vo (рис . 3.18а).
Ширина
ободной полосы 0<v<2v 0 не равна нулю
не мала по сравнению с шириной полосы
v=2v 0 сигнала. При этом не обязательно
о=!Лv. Необходимо только, чтобы свобод
й диапазон
. зон
был шире, чем диа
O<v<2v0
частот,
в
котором
однополосные
ильтры вносят искажения.
На рис. 3.186-г показан сдвиг трех та
:
х сигналов на соседние
ны
с помощью
частотные диапа-
амплитудной
модуляции
сущих с частотами Vc-2vo, Vc и vc+2vo.
олосовые фильтры с передаточными функ
ями,
.
показанными
пунктиром,
подавляют
жние полосы. Сумма трех верхних полос
казана на рис. 3.18д. Сигналы не иска
аются,
ильтры
так
как
вносят
в тех
полосах
искажения,
ча· стот,
где
сигналы
не
. еют
составляющих. В приемнике сигна
разделяются
полосовыми
фильтрами.
скажения
возникают
. стотных
пектр
мощности
лов показан
енный
х
,0
спектр
сигналов
:::::;;v:::::;;4vo,
.е
ны
и
в
диапазонах
заштрихованных
(рис.
на рис. 3.18и-л.
мощности
опять
как на рис.
неиспользуемых
демодулирован
3.18а.
в
сосредото
полосах
быть передан
полосе
Искажен
v:::::;;2vo и v>4vo.
На рис. 3.19а показан сигнал
рый может
сиг
Неиска
заключен
«зеркальные» колебания
в
3.18е-з).
демодулированных
частот
u1(t),
ко
в системе, в
Рис. З.1 19.
вание
Детектиро
цифровых
налов:
сиг
сигнал
И( +sin 30л0-sin 34n0) (а);
ходные
детекторов
для
вы-
напряжения
функций
cos ЗОл0
(б);
sin30n0 (в); соs32л0
(г);
sin 32л0
(д);
соs34л0 ( е) и sin34aт.6
( ж ).
Длительность
развертк:и
150
мс
модуляции с частично подавленной боковой принадлежит Найк-
121
которой
используется
u1 (t) =
однополосная
модуляция
со смещением:
+ U sin 30rtt;T-U sin 34nt/T.
Этим сигналом передается
двоичный символ
+ 1-1.
Колебание
sin ЗOrot/T имеет 15 периодов на интервале длительностью Т, а ко
лебание . sin 34nt/T имеет 17 периодов.
Из рис. 3.20 слеJ.ует, что энергия сигнала u1(t) сконцентриро
вана в полосе (15-l)~v= lft~(l7+1). Нижний частотный предел
равен
2v0 = 14;
0,5
ширина полосы Лv=4 . .Ширина свободного диапао
(J
\
\
ж
е
1'"
/
з
и
......
,~
~
\.
\ //
\,
\\\\
\
0,25
,,
\\
1 .
....~
1
.- ~.·.
· 1...
о
...
v-
1
f [HzJ-8000
Рис.
3.20.
J
2
15000
2'1000
ч
32000
.. !;000
Частотный спектр мощности импульсов, изображенных на рис. ·IJ и 2J\6:
(1/2) Jf2,val{O, .0) (а); sin2n0 (б); cosQn0 (в); sin4ro0 (г);
cos4n0(д); sin6л;€1 (е); соs6л0 (ж); sin&t0 (з); oos8:rte (и);
0=t/T,
v=fT,
_;\/2::::;;ik:;;11/2;
f
приведена в герцах
для
Т=1125 мкс
зона O~v~2v 0 равна 14Лv/4 и, таким образом, много шире, чем
на рис. 3.18. Из этого сигнала можно восстановить переданный
символ
1-1 согласно рис. 3.196 и е с помощью «детектора»
функций, аналогичного рис. 2.12. Совершенно неважно, какие дру
гие сигналы находятся вне диапазона 14::::;v~ 18. Из рис. 3.19в, г ,
+
д и ж ясно, что они дают очень маленькое вЬ1ходное напряжени е
в момент отсчета.
3.1.5.
Коррекция времеинЫх рассоrласований
при сиихроиной демодУJIЯЦ:ВИ:
Рассмотрим частотноограниченный сигнал F(0)
будет синхронно демодулироваться
умножением
V2cos Q00.
на местную
Он
не·
сущую V2cos(Qo0+a), которая имеет разность фаз а относи·
тельно принятой несущей V2cos Qo0 {1]:
F (0) V2cos Q00 V2cos (Q00 +а)= F (0)[cos а+ cos (2Q00 + a)J. (3.40)
Сдвинем сигнал по частоте с помощью вспомогательной мест·
ной несущей V2cos(Qn0+an) и затем синхронно продемодули·
руем с помощью местной несущей V2cos [(Qo-----Qn) 0+а,]:
122
1
{ [F (0) V2 cos Q00 ] V2 cos (Qп0 + ал) } 2cos f(Q0 - Qп)0 + a5 J = -.
F (0) {cos а + cos (2 (Q0 -
Qп)
0- a 0 J + cos (2Qп0+а 0) +cos (2Q00+a)};
(3.41)
Уравнения (3.40) и (3.41) содержат требуемый сигнал F(0),
· ноженный на cos а, и высокочастотные составляющие, которые
: жно подавить фильтрами. Существует несколько методов устра
, ия вредного влияния cos .а. Например, можно из косинусоиьной местной несущей V2cos(Qo0+a) получить синусоидаль
е колебание V2sin(Q;i0+a). Умножение принятого сигнала на
· синусоидальное колебание дает
'·
(0)
V2 cos Q00 V2sin (Ц~0 +а) =
F (0Пsin a+sin (2Ц~0 + a)J. · (3.42)
..\ ПредполоЖ.им, что F(0) можно записать в виде суммы F(0) =
1f.ч-MF+(0), где f+(0) - сигнал, который практически не содер
:,Т составляющих с частотой ниже определенной, а М
дуляции. Правая часть
(3.42)
-
sin а + МР (0) sin 7. + ( 1 + MF + (0)] sin (2Q00 + а).
'
;
индекс
примет вид
(3.43)
Составляющие, описываемые вторым и третьим членами, можподавить
фильтром нижних частот.
Остается составляющая
а. Ее можно Ifспользовать в цепи обратной связи для сдвига
тной
несущей
. in (Q0 0+ а)
а следовательно,
V2c'Js(Qo0+.a),
таким образом, чтобы
sin ·a
и
V2x
стремился к О. Тогда а
' новится либо равным О, либо числом, кратным :л, а
cos а ста
равным ± 1. Пусть цепь обратной связи будет устойчивой
я .а=О, ±2n, ±4:л, . . . и неустойчивой для а= ±:л, ±3:л, ....
rда значения COS 1a = - l являются неустойчивыми. На рис. 3.11
, ится
. азана
функциональная
схема
приемника,
корректирующего
~ность фаз этим методо~.1. Предполагается, что .а равно нулю вез
\ кроме цепи обратной связи, где указаны значения при а=#= О.
• нь тщательное исследование синхронной демодуляции синусо
· ,льных несущих дано Витерби [2].
1 Рассмотрим
1
коррекцию временнь1х
рассогласований при исьзовании несущих Уолша. Сигнал F++(0)wal(j, 0) (3.15) будет .
одулироваться умножением на местную несущую waI (j, 0-0v ).
ущие
wal (j,
е)
и
wal (j, 0-0v)
являются периодическими
· кциями и не равны нулю вне интервала -1/2~0~ 1/2. Демо
. ированный сигнал имеет следующий вид:
р++ (0) wal (j, 0) wal (j, 0- 0v ).
(3.44)
естно, чему равно произведение wal (j, 0)wal (j, 0), но неиз• но, чему равно произведение wal (j, 0)wal (j, e-ev). На
дение последнего сходно с нахождением произведения V 2 Х
. s Qo0 и V2cos(Q 00+a) в (3.40). Это произведение нельзя
123
получить только с помощью теоремы умножения
нение
необходимо
воспользоваться
теоремами
(3.7);
в допол .
сдвига
синусои.
дальных и косинусоидальных функций:
cos (а -
~) =
cos а cos ~ + sin а sin ~
и т. д.
(3.45)
С помощью этой теоремы сдвига надо разложить V2x
Xcos(Qo0+1a), и тогда можно применить теоремы умножения
(3.7). Теоремы сдвига и умножения для синусоидальных и коси
нусоидальных функций, в сущности, одинаковы, так как (3.7) яв.
ляется теоремой умножения, если читать · слева направо, и теоре
мой сдвига,
если читать справа налево. Функции Уолша имеют
очень простую двоичную теорему сдвига
=wal(j, 0)wal(j, 0v),
но
(3.44)
( 1.39) : wal (j, 0EiЭ0v ) ==
содержит обычный знак вычита
ния, а не сложения или вычитания по
mod 2.
Для функций Уолша можно легко вывести определенные част
ные случаи теоремы сдвига. На рис. 1.2 показано, что периодиче
ски продолженные функции sal(l, 0) и cal(I, 0)
преобразуются
одна в другую сдвигом на (± 1/4) или (±1/4) Т в ненормирован
ной записи; функции sal (2, 0) и cal (2, 0)
преобразуются одна в
Таблица
Некоторые значения
80
и
3.5
для частной теоремы сдвиrа периодических функций
Уолша cal(t, 8) и sal(1i, Н)
81
l
i
десятиqныйl двонqный
в.
Аесятиqныйl
в,
двоиqный
в.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
000001
000010
000011
000100
000101
000110
000111
001000
001001
001010
001011
001100
001101
001110
001111
010000
-1/4*
-1/8*
+1/4
-1/16*
-1/4
+118
+114
-1/32*
-1/4
-1/8
+1/4
+1/16
-1/4
+118
+1/4
-1/64*
в,
1
1
-1/2
-1/4
-1/2
-1/8
-1/2
-1/4
. -1/2
-1/16
-1/2
-1/4
-1/2
-1/8
-1/2
-1/4
-1/2
-1/32
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
010001
010010
010011
010100
010101
010110
010111
011000
011001
011010
011011
011100
011101
011110
011111
100000
-1/4
-1/8
+1/4
-1/16
-1/4
+1/8
+1/4
+1/32
-1/4
-1/8
+1/4
+1/16
-1/4
+1/8
+1/4
*-1/128
-1/2
-1/4
-1/2
-1/8
-1/2
-1/4
-1/2
-1/16
-1/2
-1/4
-1/2
-1/8
-1/2
-1/4
-1/2
-1/64
J
124
ругую сдвигом на ± 1/8, а sal (3,
1/4 и т. д. Пусть i будет степенью
0)
2;
и cal (3, ,0) - сдвигом на
тогда справедлива следую
ая общая формула:
cal (2k, 0-2-k- 2)
=
sal (2k, 0),
k =О, l, 2, . . ..
Рассмотрим случай, справедливый для любого целого
са! (i,
0 + 00)
=
(3.46)
i:
(3.47)
sal (i, 0).
ля i= l, 2, ... , 32 в табл. 3.5 приведены значения 00 • Для i=2k
начения Но определяются из (3.46). Эти значения в табл. 3.5 от
ечены звездочкой. Можно видеть, что значение 00 11/4 для i=3
авно значению 0о=-1/4 для i= l, если изменить знак. Поэтому
=
для i=3 можно назвать «Зеркальным» к ·0 0 для i=1l относитель
линии i=2=2 1. Можно легко видеть, что 0о для i=5, 6, 7 яв
ется зеркальным к Но для i=3, 2, l относительно линии i=4=
Этот закон отображений можно записать следующим обра-
22 .
са!
(2k + j, 0 + 00) = sal (2k + j, 0);
)
cal (2k - j, 0-00 ) = sal (2k - j, 0);
k= l, 2, ••• ; j=l, 2, ••• , 2k- l.
(3.48)
авнения (3.46) и (3.48) являются частной теоремой сдвига для
нкций Уолша. Они соответствуют соотношению sinx=cos(x-
. 1
.
2
л:
)
для синусоидальных и косинусоидальных
Для функций
sal
вместо
(3.46) (3.48)
ф ункции• . "
выполняются следующие
отношения:
sal (2k, 0 - 2-k- 2) = - cal (2k, 0);
sal (2k + j, 0 + 00) = - са! (2k + j, 0);
sal (2k - j, 0 + 00) = - са! (2k - j, 0);
k = 1, 2, ••. ; j=l, 2 .•• ,, 2k-1.
авнения
(3.48)-(3.50) дают:
cal(i, 0+00) =-cal(i, 0-00);}
sal (i, 0 + 00) = - sal (i, 0 - 00)
са! (i,
0 + 0J
= -
са! (i,
(3.49)
(3.50)
(3.51)
0);
sal (i, 0 + 01) = - sal (i, 0); (3.52)
01 = -21001.
ачения е1 приведены в табл. 3.5.
Затруднительно получить 00 и 01 для больших значений i рас
ирением табл. 3.5. 01 можно получить значительно проще, запи
в i в двоичной форме. 01 равно -1/2, если в младшем разряде
оит 1. Изучение табл. 3.5 показывает, что 10 1 =-1/2 для всех не-
125
четных i. 01 равно -1/4, если в младшем разряде стоит О, а в сле
дующем - 1. В общем с.1учае справедливо 01=-2-k-1, если в k
младших разрядах стоят нули.
Абсолютное значение 00 получается аналогичным образом из
двоичного представления i. Значение l·0ol равно ,2-k-z, если в k
младших разрядах стоят нули, причем .eo=-·/·0ol, если в k+2-м
разряде стоит О, и 0о= + l 0ol, если в k+2-м разряде стоит 1. Рас
смотрим в качестве примера числа i=20 и 1
i =28 табл. 3.5. В двух
младших разрядах (k=2) стоят нули; это дает leol =2-2- 2 =1/16.
В четвертом разряде (k+2=4) стоит О д.11я i=20 и 0о=-1/16;
для i=28 в четвертом разряде стоит 1 и 0о= +1/16. Доказательств о
правил определения 00 и 01 дано Пих.11ером (З].
Схема для исправления
временнЬ1х рассогласований
между
принятой и местной несущей может быть построена на основе тео
ремы сдвига функций Уолша (рис.
3.21).
Предположим, что приРис. 3.21.
Коррекция
временного рассогласова
ния
между
принятой
местной несущими
0) и cal(i,e+ev);
·няется степеmt
П - перемножитель;
генератор функций ;
сл е ма
переменной
и
ca\.(i,
i
рав-
2:
ГФ
СПЗ
-
-
з адержки ;
ЛЗ - .1ию1я задержки на 60;
И - интегратор;
Кв - кван ~
тователь:
УУ - уст р оi'1 ств о
у с ред не ни я
нят сигнал {1 +MF++(H)]cal (i, 0), где F++(,0)
является сигналом,
прошедшим через
фильтр нижних частостей.
Местная несущая
cal (i, 0-,0v) генерируется генератором функций ГФ. Она проходит через схему переменной задержки СПЗ. На выходе СПЗ по
лучается несущая са\ (i, 0). Схема фиксированной задержки дает
несущую
cal(i, 0-0v+0a)~sal(i, 0-0v), Принятый сигнал умно·
sal (i, 0-0v ), и произведение интегрируется на интер·
вале
ортогональности
(-1/2) + 0v ~е~ (1/2) +0v
функции
sal (i, 0-0v). Выходное напряжение интегратора
И
счи·
тывается в моменты времени (1/2) +ev;
(3/2) +0v ~ (5/2) +0v, . "
жается на
квантователем Кв и подается на устройство усреднения УУ. Схе:v1э
производит усреднение по многим отсчетам амплитуд. На выходе
J' Y получается второе усреднение, так как интегратор усредня ет
сигнал на интервалах (-l/2)k+0v~0~ (l/2)k+0v:
<[ 1 + MF++ (0)1 са! (i, 0) sal (i, 0 - 0v )>.
(3.53)
Предположим, что сред:нее значение второго члена
<MF++ (0) са! (i, 0) sal (i, 0- 0v )>
126
(3.54)
'~величением времени усреднения увеличивается медленнее, чем
еднее значение первого члена:
<cal (i, 0) sal (i, 0- е.,, )>.
(3.55)
в выходном напряжении устройства усреднения будет пре
,
пировать член (3.55). Его можно использовать для сдвига мест
ji несущей cal (i, 0-re.,,) и, следовательно, sal (i, е-е.,,) таким об-
.;, ом, что средние
·· ю. Значения е.,,,
значения (3.55) и (3.54)
будут стремиться к
для которых (3.54) и (3.55) стремятся к нулю,
.жно получить из следующего интеграла:
'
.
;:·cal(i,0)sal(i, 0-0.,,)>=
;,
.
1/2
S cal(i, 0)sal(i, 0-0.,,)d0=Fci,si(0.,,).
-1/2
(3.56)
1!:
~На рис. 3.22 (главная диагональ) показано несколько функций
ic1(6.,,) и Fв1,в1(6.,,); функции Fc1,s1(6.,,) изображены под главной
' rональю, а Fв1, с1(6.,,) - над ней. Показан интервал о:::;;;е.,,:::;;; 1;
:· кции надо периодически продолжить вне этого интервала.· На
·.. 3.23 функции Fc1, s1(6.,,) показаны увеличенными. Пунктирные
: ии поясняют некоторые особенности структуры функций. Бо
детальное рассмотрение корреляционных функций Уолша тре
слишком сложного
математического аппарата .
3.23 можно видеть, что функция Fс1, s1 (8.,,) равна
.· ю для i= 1, 2, 4, 8, .. " 21i, если e.,,=tO или целому числу, крат
у ±260=·± l/2i. Этот результат также можно
получить из
" 6) и (3.52). Цепь обратной связи (рис. 3.21) можно сделать
' йчивой для е.,,=0, ±2/2i, ±4/2i, ... и неустойчивой для е.,, =
·. '1/2i, ± 3/2i, . . . .
'Рассмотрим графики· функций Уолша (рис. 1.2), продолжен
: периодически влево и вправо. Сдвиг sal(i, 6), i=2" на е =
. ±2/2i, ±4/2i, ... опять дает периодическую функцию sal (i, 8).
· жнее получается, если i не равно степени 2. Функция F с1, si (0.,, )
1
а нулю для определенных значений е.,,=е~, но sal (i, · 0-0~) в
'' ем случае неидентична sal(i, 6). Таким образом, функции
~,2 11 , 0) и sal (21<, 8) наиболее удобны для синхронизации. Этот
. льтат уже был использован при рассмотрении телефонной
гоканальной системы (рис. 3.3).
т
привлечения
. ако
из рис.
0
~уществует несколько способов обобщить, улучшить и упро
ь изложенный метод коррекции временньrх рассогласований.
fiример, можно Передавать сигнал {са! (r, 0) +MF++(e)]cal (i, е)
'. сто сигнала [l+MF++(e)]cal(2", 0), если rffi i равно степени 2.
· функциональных узла И, Кв и УУ (рис. 3.21) могут быть объ
. иены в один . Напряжение обратной связи sin а (рис. 3.11) и
'al(i, e)sal(i, е-е.,,) > (рис. 3.21) можно подвести к генератору
' соидальных колебаний или генератору функций, а не к фазо
, Щателю УФВ или схеме задержки СПЗ.
127
-----
sat(B,в)N/t'rVN са!(7. ")
1, .1.1 ,1 ь1".1А._
ао 1f~f Vf Yf* Yff'
sat(7,Э)';-л~'#/--cat 'l6Э\
~ нА.1"А
, 1 - --- --- ~
YiTffi
sat(GЭ)
А
•••••
\
... &."t - - - - - - .
- - nyVfy ytWfi
cat(S,Э
WМ'• ~ sat(s,e)--- iY№ ~ - - - саф,э)- -- -- -scH(ЧJJ}-- - - - - - - - - - - саL(з,е)-- 'Yv•'V ~ -- ~ ~ -
#
sаЩэ
---
-----
~~·..,....--~~
cat(2,B)-- - - - - 4w6A'fl' ~ -- sat(l,e)-- - - ~ ~ - - -:-cai{~B)--r,-...,,м. ~ - - - - - vV"" ~ -
sat(~OJ-- '~-t~(~ ~ - - - - ~ ~ wat(oв)
·
- - --- --- -
sat(8,д) пЩ~В)
sat(~B)
cat(G,8)
~at(8,8) саt(5,д}
Рис.
3.22.
-
-
sat(.s;в) i:at(+,в)
Корреляционные функции
Fi:t.sf(e~)L~~I
Fc2,sz{8~)~~~,
fcJ,.sJ~)'~~·
~
.л_
(D )
Л.
.л.
.л.
'Cl/,s+tи~ ~~1
{s,ss(8i1)~~
-
fco,ss(O")~~~'
........
.
{~s1re~)~b~1
fC,'l•B(fJ-J),
~Л.V~
..Л.,
о,.,
'IV
~
1 1 1 1
о
1 11
.f/'I
1
1
1
1 1 1
1/2
1
J/I/
1
1
1
1
Вv-
5in21i.8
~
-1{2~2
siп2т..е' ~~зJч1
-1/2 ""-.:.70ii=tff:1Jz
,/)iп2ЛВ" ~ ~ '/z Т
1
-
- 1;
2
12 ~l/2
sa1(J,8) в~t/т'!.+
~,.....,
~
5at(J"'tt0~
-t/z ~ r--, r--,
~W~;z
h 1:FЬp=-1lJ2
-1
(}"-
Рис. 3.23.
Взаимокорреляционные
функции Fci si (Ov ) некоторых функ
' ций Уолша
Рис. 3.124. !Модуляция по вре
менной
базе
синусоидальных
функций и функций Уолша
128
1
= = == =
4АоА'- ~
Fs.f;,':.{e~)
.ддд,,..д ~
".~
-- -
~-
----~~-----
--Yvr~-
~~--Nt'o'v
~ дtдJт-
-
-
'f"oyl\/y&
~~-· -'\1'6v ~
~~--~~
--W-Yv.----NW---
~~--~~
~~--
3.2.
МОДУ.ЛЯЦИЯ ПО ВРЕМЕННОИ ВАЗЕ,
МОДУЛЯЦИЯ ПО ВРЕМЕННОМУ ПОЛОЖЕНИЮ
И КОДОВАЯ МОДУЛЯЦИЯ
3.2.1.
Модуляция по временной базе (МВБ)
. Любую несущую можно модулировать по амплитуде, если ее
исать как функцию времени .UФ(k, 0+100) = UФ(k, i/T +t0 /T).
· евидно , что существует еще три метода модуляции, так как эта
· ущаЯ характеризуется, кроме амплитуды И, нормализованной
стостью k, базой Т и задержкой to. Модуляция Т называется мо
ляцией по временной базе.
i
Основной идеей здесь является замена 0 функцией g(0). Суще
вует несколько способов такой замены . Пусть F (0) будет моду
рующим сигналом и М - индексом модуляции. Можно исполь
, вать
определение:
ф
g(0) =
s+
[1
(k, 0) =
ф
[k, g (0)1;
MF(0)1d0
=
+s +
[1
'(3.57)
MF(t/Т)Jdt.
(3.58)
Так поступают при ч::~стотной модуляции синусоидальных не
щих. Однако преимущt>ства этого метода для синусоидальных
129
в функци10 J
4(1ункций связаны с тем, что частота и время входят
аиде произведения
Ф
(k, 0)
Та. к ка·к - в общем случае между
реД.еJiение g(0) бoJiee выгодно:
g (0)
= 0 [1
k
= sin k 0.
и
+ MF (0)] =
/ MF(0)
1
(3 .59)
стоит запятая, следующее O!J.
0
t
1
<
l.
+ MF (О)
т
(3.60)
Те11ерь очевидно, что моду.JJируемым параметром является база Т.
На рис. 3.24 показано, как меняются синусоидальная функция и
функция Уолша, если базу Т изменить до ЗТ/4 и Т/2.
Индекс модуляции М может быть как положительным, так и
отрицательным.
Большие значения F(•0) уменьшают базу д~1я
М>О и увеличивают базу для М<О. Это весьма схоже с частот.
ной модуляцией, где увеличение модулирующего напряжения
мо
жет как увеличивать, так и уменьшать частоту несущей.
На рис. 3.24 показано, что с увеличением индекса модуляцин
М требуемая полоса расширяется. Наименьшая база, показанная
3.24,
на рис.
~
·i:.:
в два раза
·
меныщ
наибольшей. Полоса частот или ч а -
"" !><: IS
•
.
~~ ~ стостеи,
занимаемая
~~ ~ функциями
sin 2:rt0"
«короткимю
или
sa\ (3, 0") .
в два раза больше, чем полоса, з а
нимаемая
sin 2:rt·0
лиза
8.roil~
f1) 1
. 1)
.
1
1
1
---r-·L-...,.
4)~
'i 1 1 1 1 1 11111111111
1
liiilllii
~.1 uww
lшхо
1Г"" -у.
1
ll
1
•
t , , • ~
1
1
е
"fl
.............
u"""
1
2в
1
1
1
1
1
Je
1
'
1/8
~-
поминающее устройство; Сч - счетчик;
ГФ - г.екератор функций
sal (3, 0).
распределения
функции
функциямп
Точного ан а энергии
частости для
ка1;
различны х
значений М и сигналов
F (0)
еще
нет.
На
из
рис.
3.25
возможных
показана
схем
од11 а
модуляци н
функций Уолша по временной б <1 зе. Пусть сигнал имеет вид, по
казанный на
пер~ой
строке вр е
менной диаграммы. В момент вре
мени 0=·0 кванrователь Кв
про·
изводит
Рис. 3.25. Фунюциона.'!1:mая схема
устройства для модуляции по вре менной базе несущих Уолша:
1(11 квантователь; И интегратор ;
УС - устройство
сравнения;
ЗУ - за
«длинными»
или
(а).
отсчет
значения
сигна.1 а
Получещюе напряжение запо ·
минается
в
запоминающем
уст
ройстве ЗУ (б). На выходе инте·
гратора И
получаем линейно н а·
растающее напряжение.
Устройст·
во ~еравнения
УС сравнивает это
•апряжепле· с напряжением на выходе ЗУ и возвращает интегра
т.ор
в
исходное состояние,
когда
напряжения
оказываются
одина-
1ювыми .. В, результате на выходе интегратора получаем пилообраз·
кое напряжение (в). Амплитуда и длительность зубцов этой пилы
1111опорционалы~ы яапр·кжению на выходе ЗУ.
130
•
·~ выхода устройства сравнения импульсы (г), которые воз
· щают интегратор И в исходное состояние, подаются также на
.д счетчика Сч. На выходе счетчика появляется импульс (д),
;и из УС получено определенное число импульсов; на рис.
3.25
· число равно восьми. Импульс (д) возвращает ЗУ в исходное
ояние и· записывает
с помощью квантователя
новый отсчет
чений сигнала .
Заметим, что расстояние между точками от
ов зависит от величины значений сигнала в моменты отсчетои.
· ле выработки импульса (д) счетчик возвращается в исходное
. тояние. Эта установка начальных состояний происходит в мо
. ты времени О, е, зе и 48. Амплиrуда сигнала в момент вре. и 8 в два раза больше, Чем в момент времени О. Таким обра
' · , «зубец пилы» в два раза длиннее предыдущего. Восемь им
, ьсов (г), полученных на выходе сравнивающего устройства
в интервале времени 0~0~30, занимают вдвое большее рас
чем в интервале времени 0~0~е. Подав эти Импульсы
·генератор функций
Уолша , получим
на его выходе функции
. лша, модулированные по базе; на рис. 3.25 показана модулиро
i'нная несущая sal (3, 0).
. яние,
3.2.2.
Модуляция по времеинбму положевию
: Переменная 0 несущей UФ(k, 0+00) в случае базовой моду
,. ции заменялась функцией g (0). В случае модуляции по времен
му положению параметр 00 заменяется функцией h (0) . Пуст~.
(0) опять обозначает модулирующий сигнал , а М - индекс мсr
1
ляции. Введем следующее определение:
Ф(k, 0+00)=Ф[k,
h(f)) = 00
модуляции
ть положительным
М
+
0,+h(0)];
MF (0).
может
или отрица-
льным. Если М отрицателен, то
si.n 2 хв
(3:61)
~
~
.---...si.n2ф-1/lf)=cus~
k, ·0+0о+М.Р(е)] будет tдвигать- ~
.
в сторону больших зна'Чений 0
ри увеличении значений F(-0), а
~2Ji.йJ-1/i)=-.si.n21i.B
- ли М положителен - то в проти-~
1
" положную сторону .• Этот метод
jf1
. ответствует фазовои модуляции,
'2
iJ=t/т
·
-#.
J
__
оrда изменением амплитуды сиг- sa1 (~ ..--.
r=].
_а-1!,а можно сдвигать фазу несу- sa"i'[t~'iiit~
. еи. На рис. 3.26 показана синусо- c;:.;~~r-:-i...-.
· дальная несущая Ф(I, 0) =\Sin2л0 ~a;..g,e-1;2J=-:;a1{J.h
ля трех значений сдвигов MF(0)=
~~А
О, -1/4 и -1/2. Внизу показана -·1/2
о
1/.7.
есущая Уолша Ф(З, e)=sal(З, 6)
B=t/T
ля тех же сдвигов.
:
Заметим ,
,оторая
что
часть
выдается
за
Рис.
функции , нию
пределы
131
3.26. Модуляция
синусоидальных
по
полож~·
функций •
функций Уолша
+ rr2
или
ции.
На
-1/2 из-за сдвига, добавляется с другой стороны функ•
рис. 3.27 показаны функциональная схема устроиства и ~р е-
менная диаграмма для модуляции несущих Уолша по временном у
положению. Квантователь
Кв периодически производит
отсчеты
значений входного сигнала в моменты времени О, 0, 20, .... По.
~ g;
~~ ~
ГР
;;;;::;:-- t/Bfsat (1, О)с
~~
~
~~ ~
~_........._
f/*f cai {1,е)
,.......,"""""..........,'V'
t/2} cai (2, О)
t/2f sat (J,e)
t/2f cai ( J, в)
t/2f Sa[ (4,8)
fcat(l/.fJ)
fsat(S,8)
f са( (S, е)
fsat(5,G)
_...........,_ ~ t'*'sat
(2,е)
/'J_
Bыxoil
"""""'~""""
""""'""'7~
""""'°'...........~
~
~
yAAv"vv"
~
ЛДVVЛЛVV
~
f caL(7,8)
ЛЛЛЛЛЛЛЛ
f:iaL(8,(J)
,
1
ге н еDато р
1
1
1
о
е--
-t/2
Рис .
3.28.
1
1
1/2
Зависим о сти
0
J
cal(i, 8) =
Кв - кв ан то ва т ель ; И - интегр ато р; З У -з апомн на ющее уст~юйс тво; УС - уст рой ст ·
в о с р авн е ни я: Г Т И -- гене р ато р так тов ых
им пу.1 ьс ов ; К - к.11ГJч ; Д - дел ит ел ь: ГФ -
jsat(7,8)
vvv../'AЛA
1
Ри с. З . 27.
Фун кцио н ал ь на я сх ем а и
вр е м ен ная диаграмма для случая мо
д ул яции несущих Уо л ша п о вре~енн6му положе н ию:
f cat(В.G)
\ cal(i, x)dx,
....:.1 12
ф ун кци й
0
Jsal(i,8)=
J sal(i, x)dx. 8=t/T
-1 / 2
лученные
напряжения
з а помин а ются
на
определенные
промежут
ки Вf>еме н и (б) в з а поминающем устройстве ЗУ. На выходе ин
тегр а тора И получается пилообра з ное напряжение (в). Устройст
во сравнения напряжениf1 УС вырабатывает
импульс (г) в тот
момент времени, когда пилообразное н а пряжение достигает вели
чины напряжения
на вы ходе ЗJ'.
Этот импульс приводит в на
чальное состояние схему ЗУ и интегратор И. На выходе ЗУ полу
чаю1'ся положительные импульсы (6), длительность которых про
порциональна значению квантованного
напряжения. Импульсы
(lf} от генератора ГТИ могут проходить через ключ К 1 лишь в те
моменты времени , когда на другой вход селектора действует им
пульс (6).
132
Дешпель· д, образует из импульсов (д) импульсы (ж), имею
гораздо больший период по сравнению с периодом импульсов
, Они идут через ключ К2 на генератор функций ГФ, генери
щий периодические функции Уолша, например,
sal (3, 0).
.J:>СЫ ( е) через ключ К2 добавляются к импульсам
е моментов времени О,
0, 20, ....
Им
(ж) сразу
Если период импульсов (д)
;~здо меньше, чем период импульсов
(ж), то на выходе гене
ора функций ГФ получается функция Уолша с модуляцией по
менному положению. Делитель Д 2 образует из импульсов (ж)
ульсы (з), которые запускают схему квантователя Кв в момен
времени О,
0, 20 .. . .
Были разработаны де~юдулирующие схемы для случаев моду
-ии по временной базе и модуляции несущих Уолша по времен-
у положению. Их работа основана на тех же принципах, что
_ хемы
модуляции,
но сильно зависит от используемой
линии
зи.
3.2.З. Кодовая модуляция (КМ)
Модуляция нормализованной частости k несущей ИФ(k, 0+0 0 )
ывается кодовой модуляцией по следующей причине: k опре, яет функции системы. Это становится понятным, если Ф(k, 0)
дставить в виде определенной
системы функций,
например,
(k, 0), где k=O, 1, 2, . . . . 128 сигналов, которые можно по
. ить из семи двоичных прямоугольных импульсов, формируют
_тему с k=O, 1, ... , '127. Эти сигналы используются для переда
;,телефонных сигналов !1утем импульсно-кодовой модуляции. Это
· одит на мысль рассматривать модуляцию нормализованной
ости как обобщение импульсно-кодовой модуляции.
· Кодовая модуляция функций,
таких, как
sal(i, 0)
и
cal(i, 0),
ачает дискретное изменение функций, так как i может прини
[Ь только целые значения. В этом отличие кодовой модуляции
·: амплитудной, базовой 11 от модуляции по положению, позволя
. их передавать непрерывные изменения сигнала. Однако функ
.· sal (~t, 0) и са!(µ, 0) апределены для всех действительных знаий µ, исключая sal (О, 0). Таким образом, кодовая модуляция
. ет быть непрерывной, по крайней мере , теоретически.
·' Не существует большого различия между код.ово~"1 модуляцией
азовой модуляцией сиnусоидальных функций, так как i и 0 вхо
'f в аргумент в виде произведения, а не разделяются запятой,
к для функций Уолша и других функций. Выполняется соотно
ние
. .0 =
SIПt
. дуляцию
.
SIП
-
i
т
t.
(3.62)
можно интерпретировать как модуляцию 1/Т и на-
рот.
:· Существует
.· ляторов для
много возможных вариантов моду.1яторов и демо
кодовой модуляции. Используя только целые зна-
133
чения нормализованной
частости, можно
получить все сигна л ь1
описываемые функциями Ф(i, 0), и подключить нужный ,к обще~
линии. Принцип работы д~модулятора может быть основан на в за.
имной корреляции принятой функции со всеми возможными. Бо.
лее совершенный демодулятор для функций Уолша может быть ос.
нован на использовании быстрого преобразования Уолша-Фурь€
(§ 1.2).
3.3.
НЕСИНУСОИДАЛЬНЫЕ ЭЛЕКТРОМА~НИТНЪIЕ ВОЛНЫ
3.3.1. Излучение
воJШ УоJППа диполем Герца
Решение уравнений Максвелла для диполя Герца
можно
з а
писать при помощи векторного потенциала A(r, t) и скалярно г о
потенциала qJ(Г, t), не ссылаясь на какую-либо определенную си
стему функµий, таких, как синусоидальные или косинусоидальны е:
Р (t- r/c)
A(r t)=
' .
q>(r, t)= _l_ (rp
Здесь
и
r-
r
r2
'
(3 .64 )
rp(t-r/c)}.
r'
есть вектор в направлении от диполя в точку наблюдения
расстояние;
есть момент диполя:
p(t)
.
p(t) = q(t)s;· p(t)
s
+
(t-r/c)
4nво
(3.63)
·
4:rt r
d
= dip(t)
=
i (t) s,
(3.65)
есть вектор диполя, который имеет направление диполя и про
порционален его длине; q(t) - переменный заряд диполя, а i(t) ток в диполе. Допустим , как обычно, что значение s так мало, что
q(t) и i(t) не зависят от s. Аргументы t-.r/c в р-и р показывают
время
задержки
между
изменением
момента диполя
р
и
измене
нием А и <р в точке наблюдения. во - диэлектричеекая постоянная
свободного пространства.
Электрические и магнитные силы E(r, t) и Н(г, t) можно вы
числить из А и <р при помощи следующих формул:
~
(r. t)
=
Н
µо
-
-µ0
дА
(r t)
д;
-
grad q> (г, t);
(3.66)
(r, t) = rot А (r, t);
магнитная проницаемость свободного пространства.
Следующие решения · для Е и Н, справедливые
зоны, получаются из
для волновой
(3.63)- (3.66) {5]:
E(r, t)= ~2 r Х [r Х p(t-r/c)J= ~ di(t~r/c) r Х (r Xs);I
4:rt r
H(r, t)=
1
4:rt cr3
··
--р
4:rt cr2
(t-r/c)
dt
1
di (t - r/c)
Х r = -2
4:rt cr
dt
134
(3.67)
sx r;
Z0 =
V
-
1
~ ~ 377 Ом;
с= ,,г - ~ 3)( 108 м/с.
r
ео
еоµо
(3.68)
Волновая зона определяется как область , где г достаточно ве
о. Более четкое определение будет дано ниже. Обычное опре
, ение, что r должно быть большим по сравнению с длиной вол-
·' предполагает синусоидальный ток i(t).
·
: Ближней зоной называется область, где r существенно мало .
едующие выражения д.'IЯ Е и Н можно получить из (3.63). 66) для ближней зоны f5]:
.:(r , t)=
!
_1_r-P +
4n r 8 е 0
З(pr)rl
r2
L
J
=
zoe J i(t-r/c)dt
4n ,.З
[- S
+ 3 ~;)r ];
(3.69)
H(r, t) =
p(t--;:~> Х r
i (t - r/c)
4n ,з
S )',
r.
(3.70)
. В олновую зону можно определить теперь из условия, что Е и
из (3.67) и (3.68) много больше, чем Е и Н в (3.69) и (3.70).
про тивном случа е - это ближняя зона. Можн о получить следу
ие условия:
.r i ( t) dt
r 2 ~ с2
di (t)
, волновая зона для Е (г, t);
(3.71)
df
r
i (t)
» с di (t)
1
1
/&
, волновая зона для Н
(r, /).
(3.72)
·. Р а ссмотрим синусоидальный ток i(t) =lcos 2nft. Интеграл ра
1
. н - - si~ 2roft, а производная равна -2яf/sin 2nft. Условия для
2л. f
лн о вой зоны для Е и Н в этом случае идентичны : ,2~с 2/(2лf)2=
i} / (2л)2; r~c/2nf= Ц2п.
·
И С$ (3.67)-(3.70) очеnидно , что синусоидальный ток i(t) соз
ает синусоида.'lьное и з менение Е и Н во времени как в волновой,
'ак и в ближней з о не.
Это происходит благодаря своеобразной
\
собенности синусоидальных функций оставаться синусоидальны11 к а к при интегрировании , так и при дифференцировании. Для
ругих функций i(t) это несправедливо. В соответствии с (3.67) и
Е и Н изменяются в волновой зоне пропорционально di/dt.
3.68)
днако
i(t)dt,
.
в ближней зоне
а Н
-
Е будет изменяться
пропорци')на.'lьно
i(t).
пропорционально
Временная зависимость Е и
яв.11яется, таким образом, функцией расстояния между диполем
точкой наблюдения
или между передатчиком
и приемником.
• '\ожно
предвидеть применение этого эффекта д.11я предотвращения
толкновени й само:1 етов. 3аметим, что i(t) должна иметь малую
135
--------
производную, если переход из ближней
зоны в волновую
naxo.
дится далеко от передатчика.
Энергия, распространяющаяся в волновой зоне через поверх
ность сферы ,радиусом
r,
определяется
интегрированием
вектора
Пойтинга по поверхности сферы:
Р (r, t) = ф Е (r, t) Х Н (r, t) dO
....!.L р2 (t -r/c) =
=
6nc 2
~ ( di ( t - r/c)
6л с 2
)
2
=
s2, s2 = (ss).
(3.73)
dt
Введение эффективного значения тока
< i2(!')>;
/~ =
t' = t-1·/c
позволяет получить сопротивление излучения
(3.74)
Rs
из средней мощ
ности излучения Р:
р = <Р ( t)>
r,
R
s
=
Р// 2
эфф
<Р (r t')> =
=
'
/(di (t') )2""
=
Z0 s
2
6лс2
""'-
dt'
< i2(t')>
/
/(di (t')
Zos2
6nc2
""'-
dt'
)2""/ .' J
(3.75)
·
Рассмотрим в качестве примера излучение волн Уолша. Суще
ствуют два различных случая. Можно подавать в диполь Герца
токи:
t
t
i(t)=l
J sal(k,t'/Т)dt';
i(t)=l
-Т/2
J ca\(k,t'/T)dt'.
(3.76)
-Т/2
Тогда согласно (3.67) и (3.68) в определенной точке волновой зо
ны Е и Н
будут изменяться
пропорционально sal(k, t/T) или
cal(k, t/T). Можно подавать в диполи токи, имеющие форму функ
ций Уолша:
i (t) = / sa\ (k,
t/Т);
i (t)
= /са\
(k,
t/Т).
(3.77)
Тогда согласно (3.70) в определенной точке ближней зоны Н бу
дет изменяться
пропорционально
sal(k, t/T) или cal(k, t/T). В
дальней зоне Е и Н будут изменяться пропорционально производ
ным функций Уолша; интегрирование принятого напряжения бу
дет давать напряжение формы функций Уолша. Во втором случае
необходимо принимать во внимание отклонение формы функций
Уолша от идеальной.
На рис. 3.28 показаны интегралы от функций Уолша согласно
В табл. 3.6 приведены значения пикового тока /, эффектив
(3.76).
ного тока /зФФ и сопротивлвния излучения Rs для диполя Герца, в
котором токи изменяются согласно рис. 3.28.
Для сравнения также показаны величины,
справедливые для
синусоидальных токов. Предполагалось, что средняя излучаемая
мощность во всех случаях одинакова. Можно видеть, что /, lзФФ и
Rs приблизительно одинаковы для синусоидальных функций и
136
Таблиц а
Пиковый ток
/,
3.6
эффективный ток lа ФФ и сопротивление излучения
R.
для диполя Герца
ыражения,
-~
оп~-:сыва.ющ, ! е ток
в д и попе Герца
Ssal (1,
"
0) d 8
1 ;211з = о,289
1/2 = 0,5
V2;2л = 0,225 1/21t = 0,159
sin 2 л 8
/О
J(l, 0)d0, jsa1(2, 0)_!l0
'1(2,
16 л2 = 158
64 Х 3
у2/16л
sin 16 1t е
= 192
64Л =631
2
1/16 = 0,063 l/16Y3 = 0,034
; (4, 8)d0 .. . Jsal(8, 0)d0
= 39,5
16><3 = 48
= 0,079
У2/8л = 0,056 1/8 л = 0,040
sin 8 л 8
·.
л
l;syЗ = 0,012
1/8=О,125
0)d0 .. . Jsal(4, 0)d0
4л 2
1 /4У3 = 0,144
1/4 = 0,25
}1'2/4л =О, 112 1/4
sin 4 л е
;
4 >< 3 = 12
256Х3
= 0,033 1/16 л = 0,020
=
768
256 л: = 2520
2
кций Уолша равных частостей. Далее видно, что
Rs
/ЭФФ и
/,
чности одинаковы для функций Уолша:
1(2k, 0);
sal(2k+ 1, 0);
cal(2k+ 1, 0), . . . , sal(2k+ 1, 0). (3.78)
~ В случае синусоидальных функций
/эФФ и
/,
Rs
зависят от ча
'ты. В то время как диполь Герца не является широкополосной
иной (в смысле частоты) для синусоидальных токов, он яв
ся
широкополосной
антенной
· мысле частости) для токов, име+J
-.. .
. х форму проинтегрируемых J 1(J t) r--Lr---""""L9:_
)ЩИЙ Уолша. Ширина полосы sa · ...J~L..J'""
тостей определяется выбор.ом k.
.Рассмотрим теперь случаи, ког-
диполь
·ом,
Герца
возбуждается
закон изменения
которого
во време-
описывается
функ-
• Уолша. На рис. 3.29 по. ны
идеализированный ток
J(3, t/T) и внизу ток i(t) с коным
временем
нарастания
Лt.
дt ~
i (t)
_
At n+27 ·п
~ttп-
LJ
di
7П
п
~..J....~-!-2/~тu-r&-~п~
'
. -ift
- т/z
1
•
1
1
1
о -t
1
'
1
t/2
Рис. 3.29. Излучение волн Уо.11ша
смотрим общий
случай, когда
диполем Герца
описывается
функцией Yoлy/cal(k, i/T) или /sal(k, t/T); будем использовать ту же аппрок
, ацию,
которая показана на рис.
3.29,
для
i(t).
Получим следу-
ие средние:
".'
/(
!!!.-) / = (3i.)
' , dt
лt
1
"'
<i
2
(t) >
= 12- ;
2
k
л t = 4/ 2 ..!...
т
t/2
л
t '
s(~ : )\it = /2 (
1
о
137
q;= k/T
1-
<р~ t)
(3.79)
.
(3.80)
Излучаемую м<Dщность и сопротивление излучения можно опреде
лить из (3.75):
р
R =
s
2kT (1 Лt
= 2/2 _k_
ТЛt
kЛ t )\ -(
Zo$2
3:rtc2ТZ
6Т
Синусоидальный ток
(3 8
zoS2 = 212 .J:_ Zos2 ;
3:rtc2
Лt Зncz
. I)
= 2.J:_ (1- срЛ t)-1
Лt
/cos 2:лkt/T
6.
или
/sin 2:лkt/T
Zo$2 • (3.82)
3:rtc2
дает следую.
щие величины .для излучаемой мощности и сопротивления излу.
чения:
Р= п212 .!!:._ Zos' = л;2 /2f2 Zo$2
Т 2 3:rtc2
Rs = 2л;2 _.!!:_
3itc2
.
f = k/T;
(3.83)
'
zoS2 = 2:л2f zoS2 •
(3.84)
З:rt с 2
Т 2 З:rt cZ
· Для синусоидального тока соотношения (3.83) и (З.84) зави
сят только от его частоты
в то время как соотношения (3.81) и
(3.82) для тока Уолша зависят от частости qJ и в·ремени переклю
чения Лt. Теоретически для данной частости и данной антенны ве
личины Р и Rs можно сделать произвольно большими уменьше
нием ·М. В табл.. 3.7 приведены значения отношения (3.81) и (3.83),
f,
Таблиц а
3.7
Отиоwеиие мощностей Psa1/Pвin н отноwеиие сопротивлений излу11енu
R •. sa1/R •.
л
t,
нс
sin. для диполя Герца f=1 ГГц,
--=--f t
Psal
2
п•
Psin
100
10
20
1
200
л
lj)=1Gzps
Rs. sal
1
п•
Rs, sin
f л t (1-
~
t/6)
1,03
10,0
100,0
2
обозначенного Psai!Ps1n, и отношения (3.82) и (3.84), обоЗначенно
rо Rs, sa1/.Rs. s1n, для частоты f= 1 гГц и частости q>= l Gzps. Излуча·
емая мощность и сопротивление излучения приблизительно равнЬI
для времени переключения Лf= 100 нс. Уменьшение времени пере
ключения до 10 нс, которое в настоящее время является предель·
ным,
позволяет получить
излучаемую
мощность
и
сопротивление
излучения для функций Уолша на порядок выше, чем для синусо·
идальных функций.
Предположим, что время переключения Лt (рис. 3.29) очень
мало по сравнению со средним периодом колебания т= l/cp. Р ас ·
смотрим стробирующую :::хему, которая открыта только в момен ·
ты нарастания и спада импульса. Большое число независимых пе·
редатчиков· может излучать волны Уолша, имеющие одну и ту же
временную базу, но различнюе нормированные частости i=«рТ. В
138
пике импульсы doi/dt, не приходящие в определенное время,
'т подавлены стробирующей схемой. Синхронизация строби
.
ей схемы должна быть точной, так же как должна быть точ
фаза местной несущей при синхронной демодуляции синусои
,ных несущих. Желаемый передатчик распознается по образцу
·_
жительных и отрицательных импульсов так же,
как передат
:Рри синхронной демодуляции синусоидальных несущих распо
; ся
по соответствующей частоте. Приемник для несущих Уол
- ~е различает сигналы sal и cal одной частости так же, как и
ник для синусоидальных несущих не различает синусоидаль
:и
косинусоидальные колебания, если не используется синхро
рующий сигнал. Следовательно, функции Уолша можно ис
•зовать, по крайней мере, теоретически, как несущие для по
' ной радиостанции. Это первый пример возможной несущей
,;подвижной .радиостанции (в отличие от передачи от точки до
:Jt, как в СВЧ линиях)
,.
х.
с момента введения синусоидальных не
Еще рано говорить о каком-либо практическом примене
/ несинусоидальных электромагнитных волн для подвижной ра
танции. Однако, прежде чем о'I'рицать возможность какого
их применения, нужно вспомнить, что 20 лет прошло между
·етическим предсказанием электромагнитных волн Максвеллом
,_
экспериментальным
подтверждением Герцем,
прошло еще
ет до той поры, когда внедрение электронной лампы позволи· спользовать синусоидальные волны для связи в большом мас
бе.
.
Распространение ВОJ1В Уотпа, автеввы, эффект ДоПWiера
дним из наиболее важных достоинств
синусоидальных волн
ется инвариантность их ортогональности к временным сдви-
- Для примера рассмотрим синусоидальную несущую V2 Х
n 2зtn0, модулированную по амплитуде сигналом Fn (0). Си~
, F n (0) практически постоянен на интервале некоторого числа п
,' одов несущей V2 sin 2л:п0. Синхронную демодуляцию моду
" ванной несущей можно представить следующим интегралом:
s Fn (0)
0'+1/2
- -
v2siп2л:n0 V2sin2л:m0d0 =
0'-1/2
=fп(0')
0·+112 '
S
Jl2sin2nn0V2sin2л:m0d0=Fп(0')6nm. (3.85)
0'-1/2
".улированных
·Б случае подвижной радиоста1щии принимается сумма многих
'
'
несущих с различными временнЬ1~и задержками.
/
Fn(0) V2sin2·л:n0 заменяется на~ Fn(0)
n=I
139
V2x
Xsin
2л:п(0-0п)
J
и
записывается в следующем виде:
(3.85)
0'+1/2 [
~ Fn (0)V2sin2nn(0- 0п) -V2sin2nm0d0 =
0'-1/2
n= I
j
]
(3.86)
ВременнЬ1е сдвиги 0п приводят к уменьшению амплитуды, но
не к перекрестным помехам.
Ортогональность синусоидальны х 11
косинусоидальных функций одной и той же частоты нарушается
из-за временнь1х сдвигов, но ортогональность функций разных ча .
стат сохраняется. Подмножества функций { -V2sink (0-01t)} и.111
( -V2cosk (0-01t)} ортогональны для любых значений 01t. Это спра
ведливо
с;огласно
теоремам
сдвига
синусоидальных
и
косИ'Rусои.
дальных функций:
sin k (0
cos k (0
+ 0k) =
+ 0k) =
+
sin k 0 cos k 0k cos k 0 sin k 0k; }
cos k 0 cos k 0k - sin k 0 sin k 0k.
(3 .87)
Функции Уолша имеют очень сходные теоремы сдвига:
sal (k, 0 ffi 0k) = sal (k, 0) sal (k, 0k); }
са\ (k, 0 Е!Э 0k) =са\ (k, 0) са\ (k, 0k).
(3.
881
Основное различие заключается в том, что обычное сложенн е
заменяется сложением по
mod 2.
Рассмотрим теперь одномерное уравнение
azu =
с2
дt 1
azu
(3.89)
дх 2
и его ос·новное решение
и (х, t) =
g (t - х/с)
+ h (t + х/с).
(3.90)
Ввиду того что в аргументах t+x/c и i-x/c имеют место знаки
обычного суммирования и вычитания, ортогональность функциii
Уолша в общем случае не сохраняется. Однако система
+ 01t),
{sal(k, 0-t-
является линейно независимой, за исключе
нием единичных случаев. Разделение линейно независимых функ
cal (k, 0 +01t)}
ций возможно, но более
сложно, чем разделение
ортогональных
функций. Системы продифференцированных функций
с другой стороны, остаются ортогональными при
sal или cal,
временно'~
сдвиге .
Сигналы Уолша
(рис.
1.2)
можно рассматривать как линейно
поляризованные волны Уолша. Первые пять из них показаны так
же в первом столбце рис.
(второй столбец)
3.30.
получаются
Волны с круговой поляризацией
из них путем
закрепления «левых
концов» функций и вращ~нием их правых концов на
360°
по пра
вилу правого винта. Третий столбец получается поворотом функ
ций второго столбца на
скручиванием функций
90°
вправо. Четвертый столбец получается
первого столбца на 2Х360°
правого винта.
140
по правилу
~· Функции, изображенные в первой строке (рис. 3.30), соответ
уют обычным правополяризованным волнам, имеющим норма
зованные частоты (обороты в единицу времени) О,
1, 1_ и 2.
Эти
Рис. 3 . ЗQ. Волны Уолша с круговой поляризацией
лны
являются
частныi,1
случаем
правополяризованных
волн
. лша
с частостью О. Функции во второй строке все имеют нор
лизованные частости 1 и частоты О, 1, 1 и 2, то же самое спра~
ливо и для функций n строке 3. Частости функций в строках
:И 5 равны 2, частоты снова равны О, 1, 1 и 2.
Д~поль Герца широко применяется в теории антенн синусои
. льных волн. Хорошо и.звестно, что четвертьволновые или полу
'лновые диполи более эффективно излучают синусоидальные
лны собственной частоты. Следовательно, для функций Уолша
жно искать лучшие излучатели, основанные на диполе Герца.
ссмотрим диполь длиной L . Пусть
он возбуждается
волной
n2nf(t-x/c) .
;.
Образуется отраженная волна sin2ЛJf(t+x/c).
Если пренебречь потерями, то сумма обеих волн дает стоячую
}'IHy:
sin 2n f (( - х/с)
+ sin 2n ft (t + х/с) =
c/f =
Л=
2sin 2n ft cos 2л fx/c;
(3.91)
4L.
Этот диполь можно рассматривать состоящим из многих дипо
ей Герца, но для их питания требуется только один мощный уси
Итель вследствие преобразования волны
•. ю
волну. Из
(3.91) и (3.87) следует,
sin 2пf(t-x/c) в стоя
что это преобразование
бусловлено теор~мами сдвига синусоидальных и косинусоидаль
ых функций.
. Для функций Уолша вместо (3.91) и (3.88) получается следую
, ее уравнение:
1(ер Т, t/T е х/сТ) sal (IP Т, t/T ffi х/сТ) = sal (flJ Т. t/T) sal (<р Т, xlcT)·
+
(3.92)
141
/
Снов.а образуется стоячая волна. · Однако волньi Уолша, рас
пространяясь
вдоль
металлического
проводника,
описываются
скорее функциями sal (q>T, t/T-,-x/cT) или sal (q>T, t/T +х/сТ), а не
выражениями sal ( q>T, i/T е х/сТ) или sal (q>T, t/t ffi х/сТ). Извест
но, как передать колебания Уолша в соответствии с аргументом
t/TeJx/cT. но линия передачи получается гораздо более сложной.
чем металлический проводник. Следовательно, антенны, основан
ные на принципе стоячей волны, не являются перспективными. Так
как усилитель мощности для сигналов Уолша представляет собой
переключатель,
который подает в
антенну либо положительный .
JIИбо отрицательный ток, лучше использовать много диполей Гер
ца, каждый из которых возбуждается такими усилителями . Реа
лиз<~ция антенн со ста диполями является вполне реальной, если
переключатели выполнить на транзисторах. При использовании
интегра.~ьных
схем
вполне
реально
выполнить
антенну с
тысячью
и более такими днполям•1. Исследование излучения волн Уолша
пр-иводит
дование
к
активным
излучения
антеннам
так
синусоидальных
же
волн
естественно,
приводит к
как
иссr. t>
резонансны~1
аwrеннам. Множество индивидуально возбуждаемых диполей Гер
ца
необязательно располагать
вдоль
линии,
их
можно
располо
жить на плоскости. Поэтому длинную одномерную антенну можно
з.а·мевить небольшой двумерной антенной.
Былп вычислены диаграммы направленности
некоторых ан
тенн длк простой волны Уолша. Рассмотрим, например, параболи
ческий отражатель. Ширина его диаграммы направленности зави
сит от отношения Л/D в случае синусоидальных волн, где /. - дли
на волны; D- диаметр отражателя. В случае функций Уолша по
являются два отношения J../D и cЛt/D, где .л
средняя длина вол
ны v/fP; М - время переключения (рис. 3.29); с - скорость света.
Ширина луча уменьшается до О с уменьшением времени переклю
чения Лt, в то время как отношение Л/D может оставаться постоян-
-
. ным. Для фиксированного от!юшения Л/D можно получить узкиi'r
луч или для фиксированной ширины луча можно получить малый
диаметр D. Фактически параболический
отражатель может быть
заменен. круглым диском диаметром D, который покрыт множест
вом диполей Герца, нзлучзющих одну и ту же волну Уолша.
Пусть такая антенна используется
для облучения Земли Из
космоса.
Почти свободное пространство не оказывает вредного
влияния на волны. При прохождении атмосферы импульсы рас
ширяются, а ширина луча увеличивается. Этот эффект несущест
венен,
так
как
происходит
на
последнем,
относительно
коротко~~
у~частке пут. и распространения радиоволн. С другой стороны, .когда
зондируют космическое пространство с Земли, расширение луча
происходит в начале пути передачи. Это очень вредное явление.
Для получения такого же узкого луча при данном диаметре D от
ражателя синусоидальные волны должны были бы иметь очень
высокую частоту и поэтому поглощались бы полностью облаками.
Таким образом, электромагнитные волны Уолша достаточно при
влекате.11ьны
для
определенных
областей
142
·i..
применения,
но
вновь
'~
ilO напомнить, что не было проведено эксперимент~ьных нс
. ований. подтверждающих эти выводы.
, з-за эффекта Допплера синусоидальная электромагнита·•
а Esin 21r1f(t-x/c) преобразуется в волну Esin 2ttf'(it'-.x'/c)_
нутая частота имеет значение
f'
:v -
относительная
Е (х,
f
=
скорость
=
t)
(3;'9 3)
1 -v/c
У 1 -v1 /c 2
'
перемещения
Е sal((fJ Т,
передатчика
t/T- х/с1)
и
г~рв-
(З.94)
при помощи уравнений относительной механики
t =
t'
+ vx' /с . ;
1 -v"/cz
2
у
х
х'
=
Е(х', t')=Esal((f!T, Т
Yl
+ vt'
(З.95~
-v2/c2
t'-x'/c )
-v2/c2
•
l -v/c
(3:96)
уl
заниси (3.96) в виде (3.94) нужно определить преобразовав
частость q>' и базу Т' по формулам:
1 -v/c
,
(fJ = (fJ
Т'
Е (х', t')
=
=
;
(3.97)
Vt -v2;c2
(3.98)
JfJ -v2;c2
т
1-v/c
Е sal (fP'T', t'/T'
+ х'/сТ').
(3.99)
· ~травнения (3.97) и (3.93) показывают, что частостъ ~ и чаете
::{ изменяются одинаково из-за эффекта Допплера. Дополнител.ь" изменение базы Т согласно (3.98) основано на инвариантне- .
. эффекта Допплера или преобразовании Лор~нца: Т'<р' =Тер.
" Синусоидальная волна с частотой
тносительной скоростью
f',
v,
f,
излучаемая передатчиком
не может быть разрешеп·а от другой
_·,астотой
ивлучаемой передатчиком с относительной скоростью
'.Это несправедливо для функций Уолша. Из рис. 1.2 легко можвидеть, что уменьшение частости <р 8/Т в sa1 (8, 6) до q1' =
;(3/4)iq> дает · rр' =6/Т, но результирующая волна Уолша отличает
=
: от sal(6, 0).
;; Были попытки обнаружить сигналы, переданные с других 11л·а
. . Эти попытки основывались на допущении, что такие сигналы
.лжны быть синусоида.~1ьными волнами.
· пплера
волн
Исследование эффекта
Уолша позволяет поднять вопрос, почему
волны
' лша не являются более подходящими для данных целей. Сину
:идальные волны от
передатчика, расriоложенного
143
на пщше:rе.,
будут приниматься с разной частотой для разных направлений 1
8
пространстве, и эта
частота _также будет зависеть
от положени 51
планеты на ее орбите. Волна Уолша, с другой стороны, может
быть всегда
распознана
как одна
н
та
же волна
независимо
от
направления прихода. К тому же волна Уолша имеет вдвое ббль.
шую среднюю мощность, чем синусоидальная при одинаковой ач.
плитуде, что важно для слабых сигналов.
3.3.3.
Интерферометрия, распознавание образа
На рис. 3 . 31а показан принцип интерференционного измерения
углов. Два приемника в гочках А и В принимают волны от дале
ко расположенного
передатчика,
который
движется
практически
параллельно лучам а и Ь.
а)
Рис.
3.31 .
Интерферометрическое измерение угла:
а) геометрические соотношения для двух приемников А и В, распо·
ложенных на данном .меридиане; 6) разрешающая
далы1ости синусоидальных волн; в) разрешающая
далыности волн Уолша
способность по
аюсобиость по
Измерение времени запаздывания ЛТ=АС/с дает угол ~=
= arc sin оЛТ/АВ. Наименьшее измеримое время запаздывания
ЛТ мlШ зависит от градиента нулевых пересечений как для синусои·
дальных функций, так и для функций Уолша. Таким образом, ве·
личина ЛТм~ш пропорциональна l/f для синусоидальных функций и
l/<p для функций Уолша; коэффициент пропорциональности обо·
значен на рис. 3.316, в через в.
Разрешающая способность (т. е.
минимально возможное
измеряемое время ЛТмин или минималь·
ный измеряемый угол .л~ ~ сЛТ~шu/АВ), приблизительно одинакова
для · синусоидальных функций н функций Уолша. Однако область
разрешения совершенно различна. Наибольшая возможная вели·
+
чина ЛТ должна лежать между -Т/2 и
Т/2,
где Т :_период
волны. Это объясняется тем, что волна, задержанная на величину.
кратную Т, не отличается от незадержанной волны. Следователь·
но, ЛТмаис равна Т. Так как Т равна l/f в случае синусоидальных
функций, лт маис равняегся лr~шн/Е. Определенные функции Уол·
ша
sal ( i,
е) имеют наименьший период Т =.i/(fl и ЛТ маис равна тоr-
144
а iЛТмнв/~в. Такая функция Уолша показана для
i=3
на рис. 3.31в.
ругими используемыми значениями согласно табл.
3.5 являются
=2k-1. Большое знач~ние i увеличивает область разрешения
· Т манс бе.з увеличения наименьшей измеримой временной разности
Тмин·
Из рис. 3.31а можно вычислить следующие величины. Пусть А
В будут двумя точками с а=52° северной и южной широты и
редположим, что ЛТмин=lО-9 с. Расстояние АВ около 10000 км н
пользуемый угол наблюдения 180°-2а=76°. Разрешающая спо
..обность Л· ~=3· 1О-8 или ~.~=0,05''. Величина i получается из слеующего соотношения:
i ~ вЛ Т"акс/Л Т" 11 " = всоsа/Л~ = 2,5-10- в= 106•
(3.101)
Угол 0,05" соответствует расстоянию около 11 м на поверхно
- и Луны и около 3 км на поверхности Марса , когда он близок к
8
емле. Для сравнения заметим,
что наименьший разрешаемый
·гол 0,05" является величиной на порядок меньшей, чем величина,
лучаемая астрономическими телескопами.
Этот метод измерения угла является привлекательным для на
игации космических зондов. Точное знание расстояния АВ часто
е требуется. Одним из таких случа~в является наведение косми
кого
зонда
в
окрестность
другого
зонда
или
в
окрестность
пе-
едатчика маяка. Для этого требуется
значительное количество
орудования, обрабатывающего информацию. Ранее приведенная
личина i= ·l0 6 означает, t:то необходимо сравнивать две фун.кции
олша, каждая из которых состоит из 106 прямоугольных импуль
в. Тогда минимальная емкость накопительного устройства, не
ходимого для сравнения, равна 2Х 10 6 дв. ед. Кроме этого, по. ебуется дополнительная емкость накопительного устройства для
еличения отношения
сигнал/шум посредством
усреднения по
огим массивам
из 106 импульсов. Например,
усреднение по
О массивам потребует суммарную емкость накопительного уст
йства
12 Х 1'06
дв . ед.
На рис. 3.32 показаны радиолокационная станция R и две то
чные цели В 1 и 82. расположенные близко друг от друга . В стро. х а и б показаны синусоидальные волны, отраженные от 81 и
В строке в показана
сумма этих двух синусоидальных волн,
инятых радиолокатором. Периодическая синусоидальная волна
глядит одинаково как при отражении от двух близко располо
,
енных целей, так и при отражении от одной, обладающей ббль
й отражающей поверхностью. Синусоидальная волна , показан
.
.
я в строке в, искажена на начальном и конечном: участках. Если
ительность импульса l мкс, а несущая частота 1 ГГц, то из
О периодов только два будут искажены. Таким образом, энер
я, характеризующая наличие двух целей, равна всего О, 1 % от
щей энергии и~шульса и является незначительной.
: Рассмотрим отражение волн Уолша. В строках г и д показаны
· лны, отраженные от 8 1 и Bz... а в строке е показана их сумма .
· зличие между волнами, отраженными от одной и двух целей.
145
Bz
теперь
R
виду
\ГvVV
(\ (\ 1\ 1\
5)
V \J\ГV
61 ~/\/\{\
из1; \/ V \ГV
только
в
начале
и
конце
решить
о о о
а)
отраженного
сигнала
нельзя
устано
обходимо исследовать отражение от радио
локационного зеркала.
Для этого следует
n
uouo
г)
не
вить абсолютное значение
дальности. Так
как на основании строк г и е (рис. 3.32)
сумма нескольких волн Уолша одинаковой
формы,
но
с
различными
временнь1ми
сдвигами может иметь разную форму, не
/\. /\ 1\ 1\
а)
видно
импульса.
Периодическая
волна
Уолша
rакже сохраняет информацию о количестве
целей и о разности их расстояний, хотя по
волновое
уравнение
для определен-
ных начальных и граничных условий. Это
го до сих пор не было сделано. Синусои
дальные и косинусоида.1ьные <Рункции при
ппnп
О LГu О
менялись более широко в волновой оптике,
чем в связи.
Не существует
теории для
волн Уолша или д.'IЯ полных систем орто
гональных
волн.
Было бы
неправильно
Рис. 3.32. Отражение си
рассматривать волны Уолша как суперпо
e)~nnл
Jt{i/c=u uu [?
нусоидальных
волн
Уолша
волн
двумя
чечными целями
и
то-
зицию синусоидальных и косинусоидальных
волн
и
использовать
для
них
известные
результаты волновой оптики. Частостные
фильтры, частостное уплотнение и антенны для волн Уолша ни
когда не были 1бы найдены, если бы функции Уолша рассматри
вались
как
суперпозиция
синусоидальных
и
косинусоидальных
функций.
- Из-за отсутствия волновой теории в качестве первого прибли
жения можно использовать геометрическую оптику. На рис. 3.33а
li=ffA'
EG= dn'
f8=8 F
1
r--P- f+cosfSd= r1 cosor.1 - r1 cosar:2
rz=
1'1
+d.
Рис. 3.3.З. Отражение волны согласно геометрической оптике па
раболическим зерка.11ом (а) и двумя перпендикулярными зерка
лами (6)
показан разрез параболического отражателя. Расстояния r2 ·и r1 +d
равны. Следовательно, волна Уолша, излученная из фокуса D, бу
дет иметь одинаковую задержку независимо от того, в точке В
146
;
С она- отражается, и будет складываться без временного сдви
Наоборот, сигнал, отраженный параболическим зеркалом в на
··авлении фокуса
D,
не будет искажен, даже если он несинусои
лен.
r Другим
примером неискажающих отражателей является отра-
тель из двух
перпендикулярных зеркал ,
показанный на рис .
. .36. Из геометрических соотношений, показанных на этом рисун
. ~. следует, что пути распространения а и Ь равны . Таким обра
- , временного сдвига между волнами Уолша, отраженными от
зных точек рефлектора, не будет, и волны Уолша отразятся без
кажений. Можно показать, что результат справедлив также" _и
я трехмерного уголковоrо отражателя
.
В общем случа е волна Уолша, отраженная целью с ограниченми размерами, больше не будет волной Уолша. Форма - отра
. иной волны дает информацию о геометрических размерах и фор
. ц ели. Рассмотрим отражение ступеньки, как , например, сту
_ ньки sal(l, 0) в момент 0=0 (см. рис. 1.2) от сферы, показанной
рис. 3.34а. Правильнее было бы потребовать решения волново
уравнения. Однако можно получить первое приближение, пред
.-
ложив, что из каждой
точки поверхности сферы, освещаемой
дающей волной , излучается
упенька,
вычисленная
сферическая волна.
при этих
Отраженная
предположениях, показана спра
(рис. 3.34а). Сначала волна отражается только точками сферы,
. ходящимися вблизи плоскости S. После того как пройдет время
2
' R ( 1-sin /J) , волна будет отражаться от всех точек сферы,
.
с
; еющих
расстояние до плоскости S, меньшее
+
ct.
При этом
. дет отражаться гора здо больше энергии. В момент времени
2R/c
все точки освещенной
Части сферы отражают
i=
энергию и
я больших значени й t увеличения отраженной энергии не про
сходит . Так как все функции Уолша можно представить в виде
вокупности ступенчатых функций с положительной или отрица
. ьной а мплитудой, на основании рис. 3.34а можно получить вид
траженной волны Уолша .
· Форму отраженной ступенчатой волны можно вычислить еле
. ющим образом. Амплитуда волны, отраженной от кольцеобраз
ой поверхности, находящейся на расстоянии 1/2(ct) от плоскости S
нс. 3.34а), пропорциональна площади этой поверхности 2лRХ
· cos f}IRdtJ,
но только часть
sin ~
этой площади отражает волну в
:аправлени~и падения. Тогда напряжение и, наблюдаемое на ос
иллографе, как функция угла ~будет иметь вид
n/2-1\
и(~)= 2n~K .\
cos~'sin~' d~' = KnRZ(l-sin2 ~);
(З.102)
о
О<;~~
(l/2)n,
lte К - коэффициент, учитывающий масштаб, а также затухание,
силение, коэффициент отражения и т. д.
147
Так как на осциллографе напряжение и наблюдае тся как функ
ция времени, а не угла ~. то в (3.102) можно сделать подстановк у
ct=2R(l-sin :~) из рис . 3.34а:
и (ct)
=
Кл R2
[
l - (l -
2~ У] ;
ct ~ 2R; и (с t)
=
К зt R2; ct > 2R..
Вид кривой и( ct) представлен на рис. 3.34а.
На рис. 3.34 для различных угJiов падения а показан вид сту
rn'f
пенчатой волны, отраженной:
l)
стержнем длиной
и
L
d)
--L
!
ct~
f/=tsinrt.
at
JR.
tX-=o·
f
::,
s
ct-
21.
и
О
Рис.
н дизметроч
·R(HinP),
R~fl-
'Ч,
L
ct--
3.34. Вид ступенчатой волны, отраженной от
идеальных раосеивателей раз.11ичной формы:
а) сфера; 6) стержень •длины L н диаметра d<t:.L;
в) цилиндр; г) 'Круглый диск диаметром 2R;
д) радиолокационный отражатель (три перпендику.11ярных зеркала)
148
,· <t;:.L (6); 2) цилиндром при его облучении перпендикулярно оси
, в); 3) круглым диском диаметра 2R (г); 4) радиолокационным
тражателем, состоящим из трех перпендикулярных зеркал ( д).
·
Встает вопрос, какая функция Уолша
предпочтительнее для
аспознавания
формы отражающей поверхности.
Рассмотрим
ункцию sal (8, 0) из рис. 1.2. Сигнал, описываемый этой функ
.. ней, легко фильтровать и обрабатывать. Однако его период равен
, = 1/8 или f= ( 1/8) Т. Отсюда неоднозначность возникает, если раз
, еры цели превосходят ( 1/8) сТ или если имеются несколько це
, ей на расстояниях больших, чем (1/8)сТ. Сигнал, описываемый
ункцией sal (7, 0), труднее фильтровать и обрабатывать, однако
го период 0 = 1 или t = Т и неоднозначность возникает только для
, елей, имеющих размеры больше сТ.
Сигнал, описываемый функцией sal ( 1, 0), так же легко обра
атывать и фильтровать, как и сигнал sal (8, 0), и он тоже имеет
. ериод Т. Однако sal ( 1, 0) имеет только две ступеньки, а sal (7, 0)
меет 14 ступенек и эти ступеньки, а не постоянные участки функ
ий, несут информацию о форме цели. Таким образом, более слож
ые функции Уолша с теоретической точки зрения предпочти
ельнее.
Интерферометр,ическое сопровождение
космических зондов и
адиолокационных целей можно проводить и проводят, используя
инусоидальные волны. Здесь важно отметить, что волны Уолша
меют свойства, существенно отличающиеся от свойств синусои
:
альных волн, и поэтому могут обеспечить возможность получения
лее высокой разрешающей способности и более высокого отно
шения сигнал/шум, чем это можно получить современными мето
дами.
В этом параграфе рассматривались только волны Уолша, хотя
ифференцированные воJiны Уо.11ша (рис. 3.29) оказываются го
'раздо более предпочтительными. Однако при использовании этих
волн появляется
дополнительный
параметр ·~ия, что существенно усложняет рассмотрение.
время переключе
4.
СЛУЧАйНЫЕ ВЕЛИЧИНЫ
4.1.
ОДИНОЧНЫЕ В'ЕЛИЧИНЫ
4.1.1.
Определения
Рассмотрим разложение в ряд сигнала
F (8):
со
Е (0) = ~ а U) f (j, 0).
i=O
Существуют три основные операции, которые могут быть разли
чимы с помощью этого разложения: фильтрация, смещение и син
тез сиг~нала. Фильтрованный сигнал F1 (0) получается умножением
a(j) на функцию K(j), опИСl\!Вающую з-атухание, и на функцию
f(j, 0), сдвинутую во времени на 0(j):
..,
F1 (0) =
LК (j) а (j) tri, 0- 0 (J)J.
·i=O
Смещение F (0) получается подстановкой функции k(j) вместо
переменной j, причем должна существовать обратная функция
f 5 (0)
=
L"° aU)f[kU), 0).
J=O
Для частостного смещения посредством амплитудной модуляции
несущей Уолша wal(k, 0) функция k(j) равна k $j; для частот
ного смещения посредств~м односторонней амплитудной
ции синусоидальной несущей
sin 2л:k0
модуля
функция
k(j) равна k+ j
или k-j. В первом случае в качестве системы {1f(j, 0)} использу
ется система функций Yo.rrшa, а во втором случае - система сину
соидальных и косинусоида.льных функций.
Синтез сигнала является более общим процессом. Коэффици
енты a(j) заменяются новыми коэффициентами · L{a(i)]=c(j); сно
ва должна существовать обратная функция af.c(j)]=a(i). Далее
система {:f(j, 0)} заменяется новой системой
{g(j, 0)}: Fd(0)
=
1О
= ~
c(j)g(j, 0). Преобразование a(j)-+c(j) называется кодиро
i=О
15()
нием . Примеры кодирования приведены на рис.
'.:м, что один коэффициент
2.2-2.4. Заме
a(j) может быть преобразован в ряд
. эффнцнентов c(j).
Фильтрация и смещение рассмотрены в г.'1. 2, 3. Для распро
;.р а нення теории переда чи информации ортогональными сигнала:- на область синтеза сигналов необходимы знания методов ма
"матической статистики. Краткое изложение этих методов облег
т понимание их применений в последующих двух главах.
Со
-еменное матемаmческое рассмотрение необходимо начать с по-тня а- алгебры. Для того чтобы избежать чрезмерного математн.' кого абстрагирования , здесь лишь частично используется соеменнын подход. Однако степень требуемой абстракции должна
_ ть удовлетворительной .
': Вероятность определена математиками XVIII столетня как от
"- шенне числ а благоприятных исходов к чнс.1у возможных нсхов, если все исходы равновероятны. Такое определение легко мо
ет быть применено к игре в карты. Вероятность вытащить опреленную карту
из колоды, содержащей 52 карты , равна 1/52,
_ли каждая карта представлена в колоде
_словне «если все исходы равновероятны»
в
единственном
соответствует
числе.
условию
~ели каждая карта представлена в единственном числе» . Такое
- ределенне вероятности неудовлетворительно для связи, посколь
условне
«если
все
исходы
равновероятны »
часто
не
выпол
яется.
Колмогоров создал
аксиоматическую теорию вероятности, ос
'ованную на теории множеств
(1, 2]. Рассмотрим большое число
мерений, в результате которых получаем совокупность числовых
s=s1,
_ 11нных
f;2, ..•. Примерами таких измерений являются чаота появления «орел» и «решка» при бросании монет или под
-~чет букв в словах текста. Величина
f;2, . . . называется ста
s=s1,
'истической или случайной.
- В приведенных примерах s=~ являл ась одномерной вел-ичи-ной.
ассмотрим в качестве следующего примера шар, который браса
на неровную поверхность. Допустим, что ~ и Т/ означают коор
инаты точек, где шар останавливается. Каждое измерение дает
-т
·· ва значения и s=s(~. h) является двумерной величИ1Ной, а в об
. ем случае - k-мерной величиной.
, Пусть S означает множество всех возможных результатов из
, ерения s. а Sj и S k обозначают подмножества S. Сумма Sj+S11.
ределяется
как множество всех элементов,
принадлежащих к
sjsk
и (Или) к Sh. Произведение НJГИ пересечение
еством всех элементов , принадлежащих как к
"j
,.
. сrзность S;-Sk является множеством
ащих к S ;, но не прннащ1ежащих к S1t.
является M!IIO-
S;, так и к S1t .
всех элементов, прннадле
;1
Рассмотрим пример, где длина слов в тексте измеряется коли
·; _ еством букв. Наиболее 1юроткое возможное слово имеет длину,
' авную 1, наиболее длинное - 25. Множество всех длин от 1 до 25
" сть S: Допустим, что S;- это подмножество слов с длинами 9,
.:10, 11 и 12; sk - это подмножество слов с длинами 11 , 12, 13, 14
151
и 15. Сумма Sj +Sп является множеством слов с длинами 9, 10, ...
. . ., 15. Произведение S jSn - это множество слов с длинами 11 и
12. Разность (S j-SJSп) - это множество слов с длинами 9 и 10.
Множества можно легко определить интервалами. Например ,
:множество действительных чисел ~ м е жду 1 и 2 определяется ин
тервалом 1~~~2. Множ ество комплексных чисел s=и+jv мож
но определить двумя интервалами a~u~!b и c~v~d. В евкли
довом k-мерном пространстве Rп множества можно определить k
интервалами. Слож е ние, ьычита~ние ·н умножение этих множеств
дают другие множества. Пусть эти действия выполняются конеч
ное нли счетное бесконечное число раз . Полученный класс мно
жеств называется классом борелевских множеств в Rп. В после
дующем анализе используются борелевские множества.
s
Функция множества
назнача ет число каждому
элементу
множества S. Обозначение seS показывает, что элемент принад
лежит множ е ству S, а SES показывает, что S является подмно
жеством S. Опр еделим функцию множества p(S) =p(seS) с до
полнительными характеристиками
p(S) >0 и p(S) = 1. Величина
p(S) называется вероятностью того, что
принадлежит множест
ву S. Величина p(S) = 1 означает достоверность , так как каждый
результат измер е ния
должен
принадлежать .множеству S всех
s
s=
s
измерений. Пусть
~ является р ез ультатом измерения длины слов
и пусть S ; означает множество слов с длинами 9, 10, 11 и 12. Ве
л:ичина p(Sj) =p(~ESj) =р(9~~~ 12) является вероятностью то
го, что ~ принимает одно из значений 9, 10, 11 или 12. Говорят,
что p(S) определяет распределение случайitой переменной ~·
Рассмотрим подмножество S множества
ния ~ . меньшего , чем k, или большего, чем х :
р (S)
S,
не имеющее значе
= р (k::;;;. ~ ~ х).
(4.1)
Вероятность дву мерной величины s=s(~ , Т\) определяется следую
щим образом :
(4.2)
Примером явля ется
p(S) = р ( 10~~~ 12,
Если нижний пр едел
10, 11 или 12
100, 101 , .. ., 125 буквами:
вероятность того, что слово с
буквами встрет.ится в пр ~дложении с
k
в
(4.1)
t.OO~ТJ ~ 125).
равен -оо, то можно определить
функцию распределения
W (х)
= р (- оо <
~::;;;. х).
(4.3)
Первая аксиома гласит: любой случайной величине ~ в евкли
довом k-мерном пространстве Rп
соответствует функция множе
ства p(S), однозначно онределенная
для всех борелевских мно
жеств S в Rk. такая, что p(S) представляет вероятность результа
та или события
s,
принадлежащего
152
S.
Свойства
p(S) определяются второй аксиомой: функция p(S)
. ляется неотрицательной
: кой, что p(R1i) = 1.
и вполне
аддитивной функцией в R1i~
Эти аксиомы можно выразить следующими формулами:
p(S)::;,,. О;
р (S1 + S 2 +
. . . ) = р (81) + р (S2) + . . . при SiSk =О;
O~W(x)~l; W(-oo)=O; W(+oo)+I.
Равенство
·
щеrо
(4.4)
SJS1i=O означает, что подмножества Si и S1i не имеют
элемента;
дру~rими
слова>М·и,
·р,езультат
измерения ~не
до.1-
. н шри1надлежать одн·овременно Si и S1i.
'· 1Рассмо.три·м несюолько ~сер1ИЙ 1из 1 м~ереншй. Пер 1вая дает ~р1езуль
'. ты s, вrорая - 'l'J и т. д. УтВ1ержда1ем, что любая 1комби1нrация
' ·случайных веVIичин s, 'l'J будет та 1 Кж·е явля·тьrся ~случайной вел1 и
ной . Эта третья а1кси.о~м.а .может быть сформул:ирована ~ледую
им о<бразюм: есл·и s1, ... , Sr
. нированная величина (S1,
· ной . ,
~случайные ':Rел.ичи.ны, Т>о любая ко1м
гакже является случайной вели
-
... , Sr)
Например, рассмотрим серию измерений длин ~ слов в тексте
. ерию измерений длин 'YJ предложений. Комбинированная величина
, раэуе11ся объ~ед1инением па•р : дл·ина п1ер·вооо слю1ва :и дл:и1на пер
го
1 пр1едложе.н1ия,
н:ия и т. д.
длин.а
втор 1 огю
Дру,ги,м 111.р:им,ерQlм
слова
и
,дли1на
являе'ОСя
вто'Р'ОГ>О
при1мер,
п1р1едло
приве.ден~ный
.>нее, после ф-лы (4.2), где длина каждого слова 1П'Р~дложеН1юr
единяе'!1ся с длиной п~р1е1д,Jюже11шя. Сомасно тр·етьrей акс:ио.ме
оуществует разл:и'ЧИЯ меж,щу ·К~ом·би1н:ац:Ией д;вух одJном.е~рных
учайных ~вел·ичин и од1ной двумерной случай.ной вел1ичи:н.ой.
Ра1ССМ'О"r~рим объединенное или совм·ес11ное ра~спред:ел1ен;ие (s, 'l'J)
ух , вел1ич. ин
,и 'l'J· Paicщ)ev.t.eJieниe
неза 1висимое от 'l'J, наэываое-ося:
дел1>ным 1ра1спределе1н 1 ием ·со:в~м1ес11ноrо ра·спред:еления (s, 'l'J)
осительно
Оно иде1Нтично ~р.аспр>едел, еНtию
А1нал 1 огично :пре
s
s.
s.
s.
ьное ·распределение 1 отнюсителЬ1Н1О
.
Две
:вели~чины
s
и
'l'J
имеют
'l'J
зщентич1но0 •ра1ап 1 р·е~д~елен 1ию
дв 1 е
,в,ероя11Нt()JС11ные
'l'J-
фунrкции:
·
S)=p(se:S)
и
p(Q)=P('l'JEQ).
Вероятнос1lНая
фун:кщия:
se:S, 1JE1Q) п~редсrа1вляет ООрОЯТНОIСТЬ "ООГО, 'ЧТО ИЗ;М'ер1еtН'ИJе дает·
уль11ат s ·Множества S 1и р•езультат ТJ м1н1о·жес11ва Q. Мотно опр,е-·
'
ть две новые фу~нкции:
Р (У/ Е Q/r; Е S) = Р (; е s, 11 е Q)
р
(; е S)
p(r;ES/YJEQ) = P(i;es, 11eQ)
(4.5)·
Р(Т/ е Q)
p(r;tS)>O;
P(YJEQ)>O.
, Функция P('l'JEQ/se:S) 1называ,е-гся усл1овной вероя11ностью !СЛ'У
J1ной 'Вел.ичины '1'), пр.И1Надлежащей м.ножеству Q, пр·и усл.ови1и~
s п1ринадл1ежит S. Ра~пр'еде.п 1 ение P('l'JEQ/se:S) 1называе1105t
IОВНЫМ ра1спр0ед:елением 'l'J при усл 1 ОВIИ:И, ЧТО
153
SES.
Например, •пусть t; 1пр~д~ста•вдяет дл•нны слов; ri - .д:1 1 ины пред
ложен1ий, содержащих эт.и <:лова. РаосМQТ'р·им пары t;, ТJ. Gред:н
всех возможных слов выберем слова с длиной t;>l. Это мн().
жество содерж·ит ·все :пары t;>l, rt· Р:жсмот.р;нм теперь 1па1ры, д:1я
которых дли1Н:а пред.ТJ!Ожений лежит между
и
L1
L2,
L1~'J}~L 2 .
Частота по~влени.й .предложений с та·1юй длИJной в тексте зав:июит
от l, та1К как ·са·мое .ДЛ·ИJНН!Ое С.10'8'0 м•ожет ПОЯ.В'ИТЬIСЯ 'J10ЛЬКО 'В до
статочно дл'И!ННО'М предложении. Yie.r11aJ3iнaя .В1ерt0ят.ность тоrо, что
с.1учай~ная в-ел1ичина ТJ r.ip;Иtм~ значение между L 1 .и L 2 щт усло
вии, что t; больше l, обычно отличается от безусловной вероятно
сти тооо, что ri ·п~риыет з;начен.пе ~между L1 и ·L2.
Пусть, с дpyiroii стороны, .пар1а t;, ТJ о-эначает .дл.ину k-ro слов<~
и k-го ~п1р-ед.ложения в те~ксте. У1с.rювна1я вероятно1сть того, чrо дт1~на k-ro предложения за·ключена в •юrт1ер·ва.1е L1~ri~L2 при усло
·ви.и, чrо t;>l, обычно ·равна .безусловной в:ероя'Гlности 11ого, что
эта длина заключена в ишrер.ва.1°е Li=::(ri~L2, так .как дл1иша k-ro
с.пl{)lва обьгч1но не связана с дл·иной k-го пред.п·ож. ения.
Этот ,fI•ри:мер ЩJш•водит к .в1аж!ю~у час11ному 1с.1учаю оист.еыы
случ а йных .величи•н: системе статист11че~ск11
н·езав.исимых .1J1е.аичи11 .
Пу•сть для ·М:Н!Ожеств S -и Q спра1вед.~:иоо с.1е.Дующее выраж•ение:
p(-;ES, YJEQ)=p(r;ES)p(YJEQ).
Из
(4.5)
:и
(4.6)
(4.6)
.получ~ем:
р(-; Е S) >О;}
P(YJEQ/r;ES) =P(YJEQ);
р(; Е S/YJ EQ) = p(r; Е S);
p(YJEQ)> О.
(4.7)
УслО1в.ное ра•определение s в Э"ГОМ с.1учае ·не за&ИС'ИТ от ТJ и •наобСl
рот. Ве.л1ичины
и 11 называются 1статистичесжм неза~вж:и-мым·и •П:~::
s
ремен;ным1и, а вероятности
p(sES)
и
p(11e:Q)
~н азываются ~стат11-
с11ически 1незав:исн· мыми.
Пред;полож-и·м, что ( 4.7) -более спра:в~едлиоо, чем ( 4.6). Под
стано.rжа (4.7) в (4.5) дает (4.6). С.1.едовате.1ыню, у~р-н~я (4.7) п .111 .
бопее ТО· Ч l!Ю, .каждое из у равн1ений яв.1яются необходимым .и ;ы
стат.0111ны~r у1с.1·С·внем .J,.1я сташ~-стич·есюой ж~ за,висимос"Ги.
Вnедем фушщию ра:спред(\ТJ·ення
1..IiИН р icor.-1aoнo
W1(X)=p(~<x);
W (х, у) = р (~
У.ра·внен~ие
W
ю1,есто •Бероят·н<>етной фу н"-
(4.3):
(4.6)
< х,
W2(Y)=P(ТJ<:Y);}
ri
< у).
(4.8)
прi1мет вид
W(x, у)= W1 (x) W2 (y) 1
(4.9)
Это уравнение я·вляе11ся необходи"ым 11 tд:остатач1ным услов11 01
статистичесюой независИ''.\ЮСТИ переменных ~ и ТJ, ·если .множ·ест в :~
S
•И
Q опр-еделяются 1-штервала,;.111 С{)ГЛа\:qю (4 .1). Од1на·ко •можно
S и Q ~1 0-
показать, ч'Го это ограннчен·не :иэ.тншне жесткое и что
rут быть бореленским·н множес-гвамн.
154
J
Пусть снова !изме~ряе'JlСя длина слов чи1ОJ1ом .; бу~кв. Рассмm·р:им
·.· iecro.; ФУН'КЦ'!fЮ ч=ri(.;)=;:o.; 2 • Она 'Называетая фу~ню1щей случай
. й переменной .;. Пусть 1ооновная функция ТJ (s) •будет В-изме
. мюй 1>, .д:ейс11вителыной, олра1Н1Ичен.Ной оо в.ремен1и и однозна·чно
· ределен1ной для всех д!ействиТ>Мь'Ных s. Фу~нкция ТJ (s) является
"'тда случайной ·велич1иной с функцией ра<С:ILределения, опред<е
'$1-емой с.mучайно.й переменной S·
Обознаrч:и~м через Q .множество, содержащее ТJ, ,а через S - мно
·содержащее .;. Случа;fuная ·величина ТJ буд:ет !П1рИ1надл:ежать
1'оrда !И толыю mrдa, •ю<щда .; прiИ!Надлеж~ит S. Пусть P1(S) оЗtна
;
' ~ест.во,
ет вероя'l"ность
ro:ro,
что
1приrнадлежит
.;
ь того, что ТJ nри.надлеЖJит
Q.
S, а p2(Q) - в~роят
Tl():rдa 1ИJмеем
Р1 (S) = Р2 (Q).
(4.10)
поль31()вание функци:и ·расruределения согласно
(4.3)
дает
\\7 (у)= Р2 (ri ~У)= Р1 (Sy ),
е
Sy -
4.1.2.
множест.во в~сех
.;,
для ·коrорых ТJ (.;)~у.
Плотиость вероятности, функция случайной вeJDIЧИJIЬI,
математическое
В
(4.11)
(4.3)
фун1кция
ожидание
распределения
была
W(x)
опр~едел.ена как
(х)=р(.;~х). Предттолож1и•м, чrо для •всех ТIО'Чек х существует
иэводJная
·
W'(x). Про:изооД;Ная •называеrоя 'ПЛ()IГIНОСТью 1ра:спре
•ения или плотностью 1вероя1"ности:
w (х) = W' (х).
назЬDВается в этом случа:е 1непрерыв·н01й
(4.12)
случайной
велич1иной .
Пу~сть случай1ная 1Вел1Ичина .;, ·имеющая фун·кщ1ю ·расп'РеделеW1 ( х), преобразуется •в 11·ювую случайную 1величИ'ну ТJ =а.;+ Ь.
да ФУ1нкция 'Рас'l!ределения W2(Y) СЛ'У·чайной в-ели~mны ТJ trюлу-
·
.
.
я
'С.l!едующим
обраоом.
У:СJювие
ТJ ~у
tООО"I'ветст,вует
(у-Ь)/а пр~и: а>О и .;~(у-Ь)/а пр:и а<О. Фу~нкцня ра10П1ре
ения
W2(!{) получается IИЗ (4.ll):
I
W1
W2(Y) =
(У а ь )· а> О;
l-W1
(у-Ь)
-- ,
а
(4.13)
а<О.
а формула справедлива для а<О 1в '!'ОМ случае, когда
W1(x)
ь непрерывная функция .переменной х= (у-Ь )/а. В rочках раэ- ··
'
ва
W1(x) буде; определена ;ка:к функция 1непрерыВ1Ная cIJ1p.aв•a.
1
Функция g(x), определенная для всех элементов у множества S, являет
S, если подмножество S всех эле·
)
: измеримой по Борелю или В-измеримой в
тов х, для которых справедливо
g(x) ~К.
является борелевским множеством
х действительных К. С.'!едовательно, значения
ентами борелевского множества.
155
переменной 11'\ должны
быть
дифференцируема для
EcJJ'!I W1 (x)
ность вероятности
всех :т а·ченай х. то !ПЛОТ·
w2(Y) получается из (4 .;3):
w2 (y)=W;(y) = l+\w1 (Y а ь);
w1 (х)
(4.14)
=W; (х).
Ра·сомотрим теперь функцию 1]=r;2 i, i=l, 2, .... Велич•ина ri не
пр:и1нима~ет ЮТ'р:ицательных зн а чений 1и W2(y) ра1В.на нуJJю 1 прч
у<О . Для у;::=О нера1венство 'l']::::;y дает: -y1/2i::::;r;::::; +y1/2i. Фу1нкция расп.р~еделения
W.
д.1я ч з а пишется:
W2(y)
(у)={~:(
w1 ( - y1 /2i),
y112i _
у<О;
(4.15)
у>О;
W1(x) до.1жн•а ·быть н1епрерывню й функцией пере;\1ен.н.ой X= - y 1'2i.
Если W1(x) диффер1енц•аруема .д .1я всех значений х, то пл1отнQ-ст1,
1в.еро ятн1ости w2(y) нах·од.игся 11-::ак
у<О;
(4.16)
у>О.
Нера·ве нство r;::::;;y для ri=r;;, 21- 1, i=l, 2, " . .дает
c;::::;y11<2i-1). Та1юи.ы
образом, спра·ведли-во
\У.'2 (У)= W1 ( у1 1(2;-1>),
W2(Y) = 2i 1 1 y-l +
Пусть
чины
W(x)
r; и g (r;) -
буд·ет
-
оо <у< оо;
1
(4.17)
l / (2i-l)W1 (yl / (2i-I)).
фун кц.ией ра•спредел-ен.ия случай~ной вели
1опр·еделенная функция. Будет сущеспюнать с,1.с
дующий и:нтегrрал Лебега:
ао
E[g(~)] =
(4.18)
Sg(x)dW(x).
-оо
В.ел·ич.ина Дg(с;)]- математичес1юе ож•идание ·С .1 \· чайной ве:ы 1-
ч1и11ы g( r;) . УраВ1нение (4.18) .ст а1новится :и;нтеграл•ом-Римана , еслн
W(х) - д.ифференцир)"ема д.1я ·всех х; W'(x)= w (x) и если g(x)
и;-.1 е~ т кон 1 еч1но~е число разрывов :
00
E[g(~)J =
(4.19)
Sg(x)w(x)dx.
-
00
На рис. 4.1 в качес1ч~е пример·а д11юwреТ1ных ра ·С'Пlредел.ен.иi'r
iflредставл ен·о расп~реде.1ение Б~ернул.ти. Верюятность
что ;
раВ'На х=О,
1, ... l,
определя1ется ура:вн1 ением
p(~=X)=qx(l-q)l-x(~), 0 < q < 1.
156
roro
(4.20)
я люооr~о :\Шож,оства S, не оодержащего ;ни одшой из rоче.к
О, 1, .." l, сшраВiедли-вю : p(r;e:S) =0. Фу,нкu;ия распреде.лоения
{х) 1получается · из
(4.3):
х
L qY(1-q/-Y( l )·
W(x) =
·•Рис.
4.11 "
Плотность
·роятности
функдия
аспре.деления
величины,
у
( 4.21)
.
tцzLl
ве
и
у=О
'ii'
"
~
· аспределенной по зако
:ну Бернулли; q=l/2, l=
=11
.
c::i.
'
..1-А...
02468!0
:с-
.х-
темат1ическое ожидание !11р' е.дС1'а'влнет·ся сум·мой:
1
Е [g (~)] = ~ g (х) qx (1 - q}1-x ( ~ ) ;
(4.22)
X=I
) до,1жна быть о.пределена толыко 'В точках х=О, 1, ... , l.
Н а 1р·ис. 4.2 представлен прiимер непре'Рывного ра,спре~еления,
ед е.пяемого :\1Одифиц1ированной функцией Ганкеля Ко(х) :
х
\fl(x)
=р(( < х) =-!;- SK (y)dy.
(4.23)
0
-оо
4.2.
Плотность
и
ве-
функция
ре.деления
произве-
·
гауссовых
я
двух
_J -2 -1
О
1
величин
'
2 J
:r - -
-J -2 -1
о
2
J
.х--.
же будет показа 1н10, ч1lо э·ю :распред1еле.н1ие ~пюлучается для 'ПрО·
еден1ия .двух пе~р1 ем~ен1ных с гауссовым распреде.1внием . Вели·
а
W(x) явлнется диффере~нUJируе·мой . П.1отн·ость вероятности
.ед слнется 'Выражением
w(x) = -
1
л
К0 {х).
.и х=О Ко(х) ·стремится ,к +оо, так как касательная
(4.24)
W(x)
в этоi'I
·Ке пе.рnенд~икулярна 1к оси х.
;Для
.·
1непр: ерывных 1распр·ед:е,'l е ний ве~р·оятность ·юго, что r; имеет
е.д:елен.ное зшачени~е, ~раВlна О: p(r;=x) =0. Матема11ичеокое О·ЖИ
и.е E(g (r;)] 'получае11ся ~из (4.19):
00
Eig(~)J = ~
sg(x)K0 (x)dx.
-оо
157
(4.25)
4.1.3.
Моменты и характеристическая фуикция
Пу1сть g(\;) 1в (4.18) будет ~степенью \;, g(\;) =\;k. МатематичС'.
cIOQle ожи,дан•ие Е (\;k) называется 1М10менrом порядка k:
111
Sxk d W (х).
Е ( ~k) =
(4.26)
-111
Для распределени'я Бернулли
Е ( ~k) =
l
L
Xk
(4.22)
получаем
qx ( l -q)l-x ( ~ ).
(4 .27)
Х=О
МоlМенты для непрерывных рас.пред~ел,ен·ий следуют из (4.19):
со
Е ( ~k) =
5xkw(x)dx.
(4.28)
-со
Момент
Н!И·еМ
перtВоrо
порядка та1кже
11шзы'Вае11Ся
1
средН'ИМ
энач е -
m:
(4.29)
ЕШ=m.
Моменты
E[(~-c)k]
=
""S<x-4d\V(x)
(4.30)
-ос
назЫJВаются ·моментами относи'ЮЛьно точ1ки с. · Моменты
телЬ'Но ~
c=m
зуют обозначение
назы~ваются цен~ралыными и для
0111-юса·
НIИХ нспол ь ·
µk:
µk = Е(~- т)k =
J(х- m)kdW(x).
со
(4.31)
-со
Разложи!В
(x-m)k, 'IЮЛучи.м IН'3 (4.26):
JJ.o = l;
µ1 =-0;
(4.32)
f.L2 = Е (~2) - т2;
~ = Е (~3) -
Зт Е (~2 )
+
2т3 •
Момент :второоо rrоря~д:ка 01чrоси-ге.1ш1ю rочки с
Е[(~-с)2]
=
Е [(~-т + т- c)2J=
""
S(x-m)
2
dW
+
-ао
+ 2(т-с)
J(x-m)dW +(т-с) _ fdW =~+О +(т-с)8 > µz
00
2
-оо
""
-С8
пр'Ииимает м:и11шмаJIЬ1НIQе знач~ение 'ПрlИ с= т.
158
(4.33)
Для ди·с1<1ретных
:
.
ра~опредмений
за·пи1сы~ваюТ~Ся уравнения, со
жащие инт·еграды Лебега. Пу1сть Рх озна·чают вероятность того,
<; л.J»ш.и-мает з·на"Чен•ие х. В.месrо (4.20), (4.21), (4.22) ·И (4.27)
·:
' .-
учаютс-я ~сл,едующие осноВlны~е ура~В>нения:
t
= х)
·~
= Рх;
~
ао
E[gЩJ=
~,g(x)p;
X=-OJ
(4.29)
.и
(4.31)
I
=
1(4.34)
Х=-00
дают:
CJo
т
k
~ х Рх·
Qo
L(x-m)kPx·
хрх; µk =
Х=-оо
(4.35)
Х=-оо
Момеrnт.ам1и часто удобно оп1исывать ра.спредмение. Особенно
!'',
отJЮ1С111Т{;я
к
мерения, а 1 не
. нт
.к
случаю,
1n.ер:вого 1 по1рядка
как ·м.о·мент
•КJОгда
~распред~ел·ение
т
путем
характе1шзует пол~0жен1ие 1ра1сшределен1ия,
второго :порядка
ИТ'МЫЮ точки т -ооглас1ю
имеет минимальное з.начение от
( 4.33).
Мо·мент второго .порядка
1ра 1 ктери'3ует ·к~сшцен11рац-ию ~случайной
го т .
получа-е-кя
за.дается прlQIСТОЙ ана4итич<ос1юй функцией. Мо
Мом~ент 1втор1()1Го
пор.ядка
переменной
называется
окоuю
µ2
сред
также д1исперсией
:и сре~д:неювадратическю1 от:К.'lо·не~нием и о:б:оэна"Чается
( 4.36)
,называется ста:н.дарТ'ным отклонеН'ием.
;' Бсл•и ·распределен.не сим•мет~рично отноои1'еЛьно среднего т, то
· моменты 1нече11ноrо порядка равны 1Нулю. Следов-ательно, ~LJ
ра 1пер.изует отклонение от с.имметри·и. КоэффиЦ!ие.нт
У1
- f!з/02
(4 .37)
зывается коэффициентом асимметрии.
Матем а ги111еское ожида1н~ие фу:НЮ.liИИ ехр (jv<;)называе-ося ха:рак
ис11ической фушкщiей алучайной ~е.а1И'чины \;; v - дей~с11внте.1ьчисло:
~ (v) = Е [ехр (j v ~)J =
"'
Jexp (j v х) d W (х).
(4.38)
-8
:r. Пу<:ть W(x) будет д1-rфференц1иру.емой фу1н•ю.{:Ией. Тогда <р(,•)
ь п.р собразование Фурье w ( х):
q>(v) =
""
Jexp(jvx)w(x)dx.
-ао
(4.39)
ми фу.нкЦ!Ия1МiИ •могут бь11ъ ·сделаrны быrсТ1рее, чем с ф у;н кц.ия.ми ~ра ..::предел€1НJ11я; 1И1ногда он•и 1n.роще. З•десь пол1ная а·налоrия
зоВ'ани~ем n~реобразо'Вания Фу.рь е в теори и свяэи.
rc
ис.nr0.1ь
4.2.
СИСТЕМЫ
4.2.1.
ВЕЛИЧИН
Сложение независимых величин
РасСJм•отрим две случай:нЬl!е 1ве.пич:ины ~ .и ТJ, имеющие д:иффе
ренПJи1р у.емые фу н.кции распр~едел е ния
W1(x) 1и W2(y). Математи
чооюие ож:ида1ния фунпший gt( ~ ) и g2(ТJ) определяются •С помощь ю
еле.дующи х 1интегр.ал,Qlв:
"'
E[g1(~)] =
(4.40)
Sg1 (x)w 1 (x)dx;
- оо
s"'g2 (у) W2 (у)
Е [g2 (ri)J =
(4.41)
dy.
-ао
Пу~сть
Из
~ ·И
ri
будут
статис11ичооки
незави:симым'и
ве.пич~ина·мн.
~следует
( 4.9)
d W (х, у)
dxdy
=
w (х, у)= w1 (х) w2 (у).
(4.42)
Фу~юкция
( 4.43)
дает мат.ематичеекое ож;идан:ие
E[g(~,ri)J=
QO
S
""
Sg(x,y)w(x,y)dxdy=
-00-00
"" "'
=
S
-оо
оо
J[g1 (х) + g2 (у)]
- Jg (x)w (х) dx
1
-·
1
W1
(х) w2 (У) dx dy =
-ао
8)
Sw2 (у) dy
-00
+
•
5g2 (У) w2 (y)dy
-оо
ао
Sw
1
(х) dx
=
-со
(4.44)
Маrематичоскюе 1Ожи~ан: ие ·су.м•мы случай1ных вел1и'ЧIИН g 1 (~) 11
g2(ТJ) ра·в~но rсумм.е математиrч.еоюих ож•ида:ний g 1 (~) и g2(ТJ). Этот
результат та1Кже с.праведл 1ив, если дОIПущен~ие статист. ичесюой неза
'Висимос11и, ~сде.паrн~ное здесь, не удовл 1етооряе'I1Ся .
Функц'Ия
h (~. ТJ) = gl (~) g2 (ТJ)
160
(4.45)
•маrематпчоокое оЖJИда1Н1Ие
оо
E[h(~. ri)J =
\ . ао
S!Sh(x, y)w(x, y)dxdy =
-со -ао
00
00
- J Jgi (х) g2 (у) W1 (x):W2 (у) dx dy =
•
- s (х)
gl
-·-·
•
s (у)
W1 (х) dx
gz
W2 (y):dy:= EJg1 (~)J Е [g2 ТJ)J.
(4.46)
-оо
. мат.ическое
(11) paвiro
ожидание 1произве.денmя случайных 1вел1иЧIИiН
:ruроиз.ведению
маrема11иЧ10Ских
·ожидаiilИЙ
g 1 (с;;)
g 1 (c;;)
:ri).
·
льтаты, отнооящи~еся к суrммам •и .произведениям · случайных
, полученные зд'есь для двух неп1рерывных велrи'Ч1И!н, также
. нимы к более ч~ем дJВум величинам и ·К диС1К1реТ1Ным ;распр·е
. •ия1м. Матема11пчес·кие .ож·идания для ,д;иоюре11ных распреде
1
• Дl()JIЖ:НЫ •ВЫЧIИСЛЯТЬСЯ .соrлаонlО
(4.34) .
. уtеть кр1 (v), 1Cp2(v) и ·q>(v) означают хар.а1к11еrрис11ИЧесК1ие фу~нк
' переменных с;;, 1'J •и с;;+т~. Под~стаJнОВ~ка gt(c;;) =iex•p(jvc;;) 1и
) =exp•(ivтi)
1В
(4.46)
дает
ер (v) = Е {ехр [j v (~
=
+ ri)J} = Е [ехр (/ v ri)exp (j v ~)J =
E[exp(ivri)JE[exp(jv~)J
= cpi(v)cp2 (v).
(4.47)
: ·ктеристичоская
фушщия суммы статистичес~и незави·с~имых
айшых ~велич1И1Н ра.в'Н,а 1пр~оиэведению характер1ИсrичооК1Их ФУ1нк
вели~ч•ИJн
.з
.)
.
анал1иза
Фурье
:иэве.с·шrо,
ч110
обра11ное
преобразован•ие
Jexp(-jvx)cp(v)dv.
(4.48)
ра·вно следующему интеr.ралу:
1
w(x) = - -
2n
"
-оо
начи·м
фу~нкции
.ра1С1предел1ения
· величюн
с;;+т~. с;; 'И
ТJ
через
, W 1(x) и W2(y), а !П.JЮТНОС11И 1В•еrроятнl()lсти - через w(z), w1(x)
: у). Для .простых фушщий ;инrеrралы в (4.38), (4.39) и (4.48)
быть выч'Ислены . .в результате 1пмуча•етая nло'11Н.ость вероят
.
w ( z).
Это
прообраэова1н1Не
, ) в фу:wкцию расп1р.е~деле~ния
: , ультаrе получаем
00
W(z)
= JW1 (z-y)dW2 (Y) =
-оо
.
хараlК'Тlер:исmческой
фу~нкции
~можно сделать ·В общем !Виде.
"
sw~(z-x)dW1(x).
(4.49)
-оо
ля дифференцируемых фун11щий из
инrегралы Римама:
,
161
(4.49)
получаем следую-
jw (z-y)w (y)dy=
W(z) =
w(z)
1
~ ~i w,
2
(z-y) w, (g)dy
~
fW2 (z-x)w1 (x)dx;
J
w,(z-
х) w,
(x)dx.
Обозна·чим матема'!'1ичесюи~е ожида~ния, ди1сперои.и
третьего ~порядка .функu;ий 1ра.спре~щел1ения
и
l
(4.50)
j
.м1Оменть1
W(IZ), W1(x) и W2 (y)
через т, т1, т2, cr 2, cr 21, о~, µ3, µ3< 1> и µ3< 2>. Для g1(\;) =(; 1и g2(Т1) =ri
ур~wие f 4.44) дает
т =
У1равнен.ия
(4.32), (4.36)
и
m1 + m2.
(4.51)
д1ают
(4.47)
o~j+ о~= E(C )-mf + Е(Т1 )-т~ = Е(~ 2)-Е2 I0 + Е (1)2)-Е2(Т1)=
2
2
= Е {(~ +
1- 2Е(~ 1)~ Е2Ю-Е2(11) = Е l~ +
2
1))
11) 2J-E2(~ + 11)
= а2
Аналогичшым образом 1получа~ется следующая за.виоимость:
+ µ.~2).
JLs = µ.11)
(4.53)
Раосмо1'ри-м в качестве ~прим.ера две 1вел1ичи1ны
\;
и Т), имеющие
rayi0eoвo распр•еделен1и1 е:
W2
(у)= f2л о2 ехр (-(у- ~)2/2оП;
W1
1
(x)=+[1 +erf( ;r-;~
~-;-:.2
W2 (y) = +[1 +erf(
где
erf (и) -
)];
/
)].
та'6улироваiнная функция ошибок:
r -х•
erf (и ) =
у2,.ш J е
dx ::::::: 1 - уП
1 е-и• ; )
erf(-и)=~erf(u);
Ха·рактеристическа.я
из
(4.54)
(4.55)
erf(oo) = 1.
фун1Кц.ия <р1(х)
функции
w1 ( х)
:rrолуча~ется
(4.39):
00
<1'1
(v) =
у 2ло
1
1
5ехр [i v х- (х- m1) 2/2a~] dx.
-оо
Подста~новка у= (jcr2 1 +:m) /V201 .дает
1Р1 (v) = у-2~ 01 ехр (i v т1
-+
00
2
ai v') Jexp [-(x;V2 о1 -у ) ] d_x.
162
1
..J
.опользуя (4.б5) и падста 1н1Qiнку
(x/V2o1-v)2=.z, нах·одим
со
Se-z• dz
ехр (iv m1 --}а~ v ) Jп
2
"(v) =
=
exp(jv т1
-+атv 2 ).
-со
(4.56)
· 'Рактер.исrич~еская
фу~ню.щя
1велич1Ины
•<p(v)
(\;+fl)
1 поЛ'учает~ся
+(
(4.47):
ер (v) = CJ>1 (v) CJ>2 (v) = ехр [i v (т1 + m2) -
ai +а~) v2•
(4.57)
р•а 1вн~е'Н!ие (4.57) ·и '(4.56) •по1<азьrвает, 'Ч'ГО юуМ'ма \;+fl 1долж~на
еть
1rayiccoнo
1 распр·едеJN~ние,
та.к
·ка·I<
и.меется
вза:имоод'новtнач
я зави1с:им·ость ~между фу~н11щией ра~с:шределения •и ха1ра1<терие11и
с~ой ~функцией. Пл 1отность ,оор~0я11ности w(x) и функЦ'ия распре
ения
W(x)
. :m=m1+m2,
ра~ны w1(x) 1и W1(x) :из (4.54), есл:и m1 заменить
а 021 - на о 2 =о2 1+022. СуммИ!р'УЯ l 1неза·в·ИСИ1МЫХ
уссовых I11ел1Ичwн,
снов·а
·получа.ем 1ВrеЛ1ИЧ'ИНу с
гауюоовьrм •раоп-ре
ением, имеющи·м среднее
. диспероию
(4.58)
~альнейшем будет показано, чrо 1 распределен1ие юум•мы
·в:и~римых iВе.тI'ИЧИ:Н для ·больших зна•ч.ен:ий
расII'ред~елен1Ию, даже
есл·и са.МJи
l
l
~rе-
<:11fЮМ1И11СЯ к гаус·сово
вели11иmы не являю11Ся 1га1ук:со
ми. Это :центральная ш:редельная теорем·а ·математич1е~оюой ста
. С11ИЮИ. Она сп~р·а1Ведл~ива 1при 1 б<тоо общих •допущениях. Среднее
J]jИIС.персия раопр1е~е~ния ~равны
ичин сосла1сН10
(4.51)
4.2.2; Совместные
1и
су1мма1м -арtедн:их 1и д:иопер!ОИ.Й
(4:52).
pacпpeдeJieJlllJI иезавис:вмьп: :вeJIJIЧJlll
В качестве более :сл·ожооrо при~м1ера 1 ра1Спр1 еделени. я суммы №УХ
. учайных ~величин р•а1ссмо11р;им
. ся .в гл. 6. Велмч:ина \; имеет
=1
·сл 1 едующую зада·чу, которая ВС11ре
г.ау·аоооо ра1Определ~ение ·оо 1аред;н·им:
1и ди~епероией а2 , а 1вrорая ·ВМ'И'ЧJИ.На Т\ также И'М· еет .га1уосов0
аоо·р~ед~елеюие оо .ар-едним т =О и д;исперсией а2 • Нуж~н~о ОП1р~е.де
ь •фу~н1кцию 1р·асп1ределения ~-1Т\1- Пло11ности
1(х) и w2(Y) величин~ и
имеют вид:
lri 1
w1 (x)=
Ws(Y)
1
у'2па
= 'V2na
w,(y) =О,
exp[-(x-I)'/2o'J,
ехр (-lf/2<72),
у<О.
163
:вероя11нос11И
-оох<оо;
О~ у< оо;
(4.59)
Пусть разность х-у 1 равна
z.
Тогда для осех з.начен:ий у спра.
ведл•ива .следующая завИJОимость:
.
х = z +у.
(4.60)
Пл1Qтность ·вероят.ност.и w(z) и функция ра~ап:р~еде.ления W(z) 'Ве
Л'И'ЧIИIНЫ с;-1Т\1 <J1п~ределяются следующими у.равн~ениям;и:
1
ф
-Sexp [ - (z
na 2
w(z) = -
+
у-1)2/2о2 ]ехр(-у2/2 o2)dy=
1
о
=
ехр f-(z-
Ylna
2
1
1)2/4o 2J [ 1 -erf ( z
20
)] ;
-oo<z<oo
z
z
-оо
= -
1
[1
2
(4.61)
Sw(z')dz' = ~n Jr1-erf(u)]e-" dи=
W(z)=
1
-оо
1
+ erf (z)J + -4 (1 -
erf2 (z)J;
z'-1
lt=--
2a ·
}
ВыЧJисл:юм далее пл~0Т1Ность вероя'I'НОС"l'И с;-1Т\1. tесл•и мыпоJI
няется
усл.0В1и~е с;~О. Фу~НIКция
образом:
W1
1
(х) =
с=
J12n С ехр (- (х -
0
w1(x) оmре.щеля~ся следующим
l) 2/2a2J, х
Jexp (-(х-
'V2na
О;
х<О;
...
1
:;;i,.
о
1
1)2/2o2Jdx = 2
[1
(4.62)
+ erf ( ltV2 о)].
Для ~неотрицательных з1н:а·чен:ий с;-1Т\1
}
в:ел:·ичи~На с; !Не .может
быть меньше нул.я, следо.ваrелыоо, для z~O ~с.п.ра1В1е.Дли.во 1ВыраЖе
ние (4.61), одн~аюо последнее наДQ умно.жить 1на 1/С.
•С уч~еюм (4.60) и тосо, Ч110· х~о. на:именышее допrсrимое з1на
чение у щля :.z<O ра'оою -z, а !Не ·нуw1ю: y~-z=
В.мест<> · ( 4.61) •оолуч·ае.м
lz
длrЯ
z~O.
00
w(z)
=
1
= nCa
Jexp [-(z + y-1)2/2o2Jexp (-!f/2o2)dy =
-z
у n С а ехр [-(z- 1)2/4o2J[1 1
2
-2
Разл~ичи.е Мlеж>ду (4.61) •и
(4.63)
erf ( - z2а
1
)] ,
z ~О. (4.63)
заключаеТ1ся толь:~rо 1В З1На11<е аргу·
мента фу~нщии ошибок z. Это ·ч~резвыч.айню затрудJня.ет 1выч:иrсление
фу~нкЦJИи раоmределения W(z) . Вследствие этого •будем выч.~юлять
тол1>:ко 1верюятность того, что разнЮ<:Ть с;-1111. с;~О меньше ну~1 я .
Для этого IН'уж~но проиЗ'Вост.и и1нтегрирова1ние w(z) от -оо д<> О.
164
. а·к ка·к (4.61) спра'Ведл.И1ВQ rо.лЬ'КIО для
:гр1Ировать (4.63):
'
z;,;;::=:O, дост-аrоч1НQ !пропнrе-
о
W(O)=
1
Jexp[-(z-1)2/4o2][1-erf(-z-l )]dz=
2ynca
_...!
_ _ ,..
2а
-оо
= 1 + 2 erf (1/V2 а)- 2 erf (1/2а) - erf2 (1/2а)
2 [!
'Интегрирование (4.64) -
(4.64)
+ erf (l/V2а)]
очень трудоемкий процесс. Оно может
:Рыть выполнено методом параметрического интегрирования. Сна
=
ал.а замешяют W(O)
W(O, s); s= 1/2а, rотда и=-(z-1 )s. 3атем
:выполняется дифференц.ир1ование dW(O, s)/ds, .IDOJJ.craнoВ1кa W=
'
··= У2(и-s) и и1нтеl'ри1рова~н:ие по
s.
Раоомоорим 1распр!едмен•ИJе 1про:иэведе~юия \;f) щвух сrатис11ич-ос
~·и 1неза!виси.мых 11нmрерывных ;в.ел:и'ЧИIН, ;имеющих плотность ·вероят
~нос11и w1(x) :и w2(y). Плотность оовмес11Ноrо расп•ред.елен.ия полу
чается :из (4.42): w(x, у) =W1(x)w2(y). Вероят.ность ror10, что точха
t коорди~натами \; :и f) леЖJит 'Н'а Э.'Iементе dxdy, раВ:Н.а
w(x, y)dxdy = w1 (x)w2 (y)dxdy.
i.J1'роизведен1ие \;ТJ будет .иметь QПредмеюное эначеН'Ие
: веден.ие ху ра1в11rо
(4.65)
z,
xy=z .
.ОП1ределеншое
ес.11и ruроиз
z:
ЗН·а·чени.е
z
(4.66)
·м1Ожет ~быть оолуче:но дJВу~мя споооба·м1и
l:ИЗ с(ютношения
·ХУ = (-х)(-у) = Z.
(4.67)
Jiрообразованrие ~иффер~е.нциала dy стаоо&и'ОСя двуз·на'Ч!ным. Для
·•того чтобы оно стало однозначным, можно рассмотреть два случая:
,х;,;;::=:О я х<О. Прм фи~ксиров.а1н.н:ом з1начении z велич·nн•а х может
; п1р;И1Н1И1!'.tать любое значение •между О ;и оо :и.1.и -оо •и О при усл1О
::вни, чrо у пр.ин1и.мает знач.е.ние
у=
Дифференциал
dy =
-
z
х
dy
,
х
::;;.. О;
у=
- -
z
,
х
х <О.
преобразует~ся в
~ , х ::;;.. О; dy =
-
х
dz , х ~ О.
(4.69)
х
' Веро•ят, нос1ъ тоrо, что \;fl лежит между z и z + dz шр.и услоВIИ>И, что
z
~-~ нах:сщи'f!Ся ·между х IJf x+dx, а ri - между
у=- и у+ dy =
х
+d
·= !.__]!_, О'Щ>:еделяется ~следующими 1произ·веден~иями:
)!
х
W1
(х) dx W2 (-;-)
d: .
х ~ О;
]
(4.70)
W1
(Х) dx W2 (-=--) ..!!-!.__ , Х < 0.
х
-х
165
Кажется 1 разумным ·инте~р'И'Р'Оlвать
+
пер'Вlое ~пр.о.изведение
от О
до
оо, а ~второе от -оо до О, так ка1к х ·может пр 1 инимать нее
з.нач1ения межд:у -оо !И
оо. Несм·отря на э·ю, интеГ>ралы л1р:и
+
х=О могут не сходиться из-за сомножителя 1/х. Поэтому около точки
х=О вырез.ае11ся 1олреде.а.ен1ный ~интервал ширш1ной 2е н в каждо:-.1
случае рас·ома11р;ивается 1 шредел w(z) п•ри е-+О:
Jw1 (x)w2 (~)+dxdz+ Sw1 (x)w2 (~)+dxdz.
-е
w(z)dz=-
оо
Дл1я четных фуН'кций ур-ние
(4.71)
зю~·еняется на
(4.71)
-е
w (z)dz = 2
Sw (x)w
1
2 (--;--)--;-
dxdz.
(4.72)
-со
Пусть с,; 1и 'YJ ·имеют гаУ'ооов.о 1распреде.1ение со средн·им1и т 1 =
=~m2=0 :и д;испе1р.сия•м 1 и а 2 1 .и а 2 2 . Ура·в 1 н:ение (4.72) да·ет
00
w(z)=
2
2л:а 1 а 2
2
1
2
/2a~]dx.
Jf'exp(-x /2aI)exp[-(:.!.._)
х
х
(4.73)
е
00
'
(4.74)
Интеграл
00
2
('
[1 ( и
)] 1
Jexp
2 -; + s -;ds =
j nH~ 1 }(j и)= 2 К(}(и),
(4.75)
о
где и
-
действительное, табулир.О1ва.н. Функция НоЩ(jи)
фу~нкци•ей Ганк·еля, а Ко( и) - м01диф:ици~ро:ван1ной
келя. При е-+0 ур-1ния (4.74) ·и (4.75) 1дают
w(z) =
Из
1
л: а1 а2
Ka(-z-)·
а 1 а2
явля·ется
функцией Ган
(4.76)
(4.74) с.1·едует, чтю w(z) - четная функция:
w (- z)
=
w(z).
(4.77)
Поэто•:-.1у w(z) 0 1предJеля·е11ся для 1Вюех действитепьных значений z.
Фун1 кцию раепределен:ия
(4.78)
-со
166
·. ельзя
а·ны
1 п~ривести к табул.ироваrнным фунпщиям.
W(z)
и
w(z)
На рис
4.2 ПIО!(а
л·ри за•мене
(4.79)
(4.80)
Для задач, связан~ных с з·а.м1ираниями :и узкополооным шум.ом,
редставля·ет и1нтерес ра•СП'Ределение Р:елея. Плотность вероят·но
и и фуоfГ!щия раопре~целения :В 1 ел'Ичины 1; •С релеевс!(ИМ расnреде
iп:·ен1ием опр1 едел•яются след;ующим образом:
w1 (x) =
2х
-ехр(-х
бi
2
х >О;
/c5i),
W1(X) =О,
(4.81)
х<О;
х >О, J
W1 (x) = l-exp(-x2/c5i).
·С р~еднее зн.а-ч.ение 1р.а1вно
00
ЕЮ= m1 =
l
Sxw (x)dx =
1
+
Vл61 ,
(4.82)
о
а момент •втО1р·оrо 1поряд!(а равен
"'
Е(~ 2 ) = Sx2 w1 (x)dx = 6i.
(4.83)
о
Дисперюия а 2 1следуетиз
(4.29), (4.32)
at = Е(~2)-Е2(~) =
1и
(4.36):
c5i(l -
+n).
(4.84)
Пусть величина 'У/ 1не эаниоиrr IOT 1; •и ·и·меет релее.всжое ра.спре
.n.еление с nл-011нюстью .вероятн:ости
w2(Y):
w2 (y) = ~; ехр (-У2/с5~),
у> О,
(4.85)
2
. ВыЧ'исл:им
~плотность
вероятНОС1'И
w(z)
П'Р'оизоодешия
G'YJ · Лучше
использ.01вать ур-нtие (4.71), че•м ( 4.72), та•!( ка!( фун!(ЦИЯ плоrгно
. ст.и •релеев~е-1юго р·а:оnрмелr~ния •не с~им1мет~рич:на относительно х=О.
·Используя
(4.81) 1и (4.8б), ·получ·и1м
w (z) = -42
f} б
1 2
s"'
z ехр (- z2/x 2 6~) -dx.
1
хехр (- x2/6i)х
е
Это уравнение аналогично ур-нию
167
(4.73),
х
(4.86)
если подставить 2а22 = :6 22
·
и 2а2 1 =б2 1 в
(4.73) и умножить на
·п.роизв-мен:ия <;;Т} следу:ет •ИЗ
4z
.
бr~ла1 а,
( 4.86)
w(z)=~Ko(
6i б~
ic ~учетом
2
~
Плотность вероятности
( 4.76):
z~O.
).
61 "2
(4.87)
Функцию ~раашредел~ен.ия
z
W (z) =
моЖJно
·при.вес11и
х=2и/б1б2 да· ет
2z/6 1 61
к
.
rиК0 (~)
6i 6~ ъ
61 62
табулир1(}1.ван~нЬ1·м
J х К0 (х)
W (z) =
-
4
-
dx =
-+
(4.88)
du
функциям.
Под-стаяовка
2z /6 1 6,
(j х) Н& 1 > (jx) d (jx).
jn .\
о
(4.89)
о
Ин'!'еrрал
SУ Uo (у)+ j N
0 (у)]
dy =
SУ Нь > (У) dy = уНр> (у)
1
(4.90)
из1вестен. ФуJI:1щи~и Io(Y) · •И No(y) есть функции Бессе.1я первого
(функци•и Helr!vta1н1a) . У.равнение ( 4.89) запишется
и ,вroporo ·ро.да
в виде
в
(4.91)
Пу1сть е-+О. Используя уравне1ше
нp>(je)=-2/ne;
0<8«: 1,
(4.92)
получаем
нm в нР> и е) = - 21n
(4.93)
В-+0
и
W (z) = l При действительных
~ [ - fl j1>
6162
поJ1ожительных
(.Yl!.._)]
6.i62.
значениях
(4.94)
z
выражение
и
l
в
скобках я·вля•е11ся .н•еотрицателыным .
Иссл·едуем, ра·вн 1 0 ди (4.94) 1нудю при
С учетом ( 4.92) п.р1и z =О лолуча·ем
z=O
при
z= оо.
lim~ [-н\1>(~)] =~2~ = l.
Z-+0
61 62
,
61 62
61 62
Л
2z
При ·больших значениях х 1 спра·недли:во а1СИ•М<птотическое прибли
жение: - н\1> (j х) ~
V ~ nx е-х .
168
торой qлен в (4.94) 1При больших энач>еtНиях z iparвieн нулю, IПОЭrо
у ~получаем W ( оо)
1. На :рис. 4.3 ПQ•юазаны фуносЦJiи (4.87) и
',4.94) для iб1=1б2=l.
=
2
1
J
!;
Z~/02 - -
Рис. 4.3. Плотность вероятности и функция распределения про
изведения двух величин, распределенных по закону Релея
G+ 11
Фу~нкция р1а-апрме.пения суммы щвух неза1виаимых 1вел1 ич·ин
· релеевскнм рас.п1ределенаем •сJiедует ·из ( 4.60):
z
5{1-ехр [-((-х) /бi]} хехр (-х2/6~) dx.
W(z) = ;
2
(4.95)
2 о
иж1н.ий л1редел ин-гег:рала равен О, так как плотность вероятню
и . w(x)=x ·eXip(-x2 /б 22) до,пж~на ·быть за·мооен.а ~на w(x)==O п1ри
;х<О. Верх1н1ий ·предел 'Равен z, та.к как фу.ющ.ия раопреД'еЛеН'ИЯ
W(z-x) = 1-е:юр{-(z.-х) 2 /б 2 1]
дiОлжна
быть
за.мене-на
на
;.·
!W(z-x) =О ·при z-x<O. Подста:нювк1 а
( бi + б~)l/2
б2
у= х
61 б2
- z 6i"
1
(4.96)
( 6i + Щ)l/2
учето::м ннт:еnрала
sy е-у• dy = -+е-У'
,
осле гр.о~юздюих преобразова1ниИ дает :
W (z)
ехр ( - _::) + 6~ ехр (-
1-
=
6~
k2
z: )
k
/ехр ( - z~ бi
k26~
-ехр(- z ~ )-V~~z [erf(~)+erf(z 62 )]j.
)-
26
\
k 2 6i
W (z)
kб2
k61
=О
для
z:;;..O; (4.97)
k61
z <О; k2 =
бi
+ б~.
р 1 и б1=б2=1 ~получается ~пр.остая фо1р 1 мула:
W(z} = 1-e-z• .
12 erf
Рассмотр•им ·распредел·ение оО1lН·ошения
•~епрерывных
'
V; ze-z'
1величи.н
f; и
ri.
IИ'Меющнх
169
(z;V2).
(4.98)
ri/G двух •Незав:и.симых
пло"Гности
в-ер 1 оялюсти
w1( х) и w2( у). Сню;ва 'Используется 1пло11нопь 'Вероя11нО'с11и (4.68),
у~м·ножен·ная н•а dx и dy. Долж~ню быть cпipa'ВieJJ)I:и:вo отношен·ие
·есл1и ri/r;, !Пр1 и~нимает 1 0.пр·еде.нен1ню·е зн1ачеюие z. Это З1Начение
y/x=z,
'f1a11{
можно пюлучить д:вумя 1путя.м1и
Т]r;,:
же,
!{ак в ~случае 1произ·ведения
yfx=-y/-X=Z.
Ч1106ы у:стра1нить .неоднюз· начн~ость, 1воз:н1и1{ающую при диффе
ренцирова'Нlии, р.ассмютр:и,м отделын.о ~случаи х;;:::о .и х<О. Для
01Iiредел'€'н;н:оrо э1начения
+ оо
1Н1ия м·ежду О и
z
:велич~ина
х мюжет при·н 1 имать ·все з-н.аче-
и.11и -оо и О п~ри усло· ви1и, ·что у и 1 :v~еет сле
дующее з1начен:ие:
у
Диффе~ре:нц1 иал
= z х,
х
::;;..
О;
у=
- .zx,
< О.
х
(4.99)
прообразуе11ся в
х >О;
dy = xdz,
dy
= - xdz,
х <О.
(4.100)
Вероятность тогю, что зна·чен:и·е ю11нюшоо1ия ri/r;, за.ключено 'Между z
.и z+dz, лр 1 и усл·01ни1и, что r;, 'Н:аходится между х и x+dx, а ТJ межд:у y=xz и y+dy=x(z+dz), Ю!Пiределяе'fiся •следующ1ими nроиз
ведениям~и:
w1 (х) dx w2 (zx) х dz,
х >О;
w1 (x)dxw 2 (zx)(-x)dz,
Вероятню 1сть
х<О.
того, что rilr;, ·раопол:ож•еtно •между
~вольных значен,иях х,
z и z+dz !П1ри 1произ
по .1 учается путе·~I •юпегри·р·оваН111я от Х=-оо
до х=оо:
о
w(z)dz
00
Sw (х) w (zx)x dx dz + .\w (х) w (zx) х dx dz.
=-
1
1
2
-оо
(4.101)
2
о
Длн с.им.метрич·ных функций вместо
(4.101)
.'vюж1н10 зап•исать
""
w(z).dz = 2 Jw 1 (x)w 2 (zx)xdxdz.
(4.102)
о
Ка•!{ ·и в :первом примере, пусть
.пени•е с .плотностями вероятности
1И оо с.редними значен11я~1и
r;, и ТJ имеют гауооо•во ра1сп1реде
w1(x) и Wz(Y) =w2(x)
m1=m2=0. Тогда по .1уч·Ю·I
из
(4.54)
00
w(z) = -
-fexp (-x2/2oi)exp (- z2 х2/2о~) х dx.
1
't U1 U2
о
ПоДJСТано,вка .в это выражен.не и = -
1 (1-
2
х2
а2
1
+ -z2) 1дает
а2
2
00
W(z)=U1U2
л
1
а~+ z2аТ
re-udU=-1-~
J
л а2 (z а 1 /а2 ) 2 +
J
о
1·
(4.103)
Ра.сшр·еде.1ен1ие, апределенное этой ·функцией ~ПJютн·ости, ~назы
вается ра·спреде.1· ен.ием Коши нли ра<:пределение.м Стьюдента с од-
170
· ной 1сrепенью . свободы. Фу1н1щией распределен1ия Я'ВЛяе-ося фу:нкция
W(z)
J
z
=~
:rt
1
dx = -
(х 0 1 /02)2 + l
о2
+-n1-arctgzо,
1
2
01
·
(4.104)
-оо
: на ~р1ис.
4.4
по·каза1ны фу·НJкци:и
(4.103)
и
(4.104) .
1
о.
-// -J -2 -1
Zd1/6z Рис .
4.4.
1 2 J 4
zdtf6z _.,,...
Плотность вероятности и функция раопределения
отношения двух
гауQСовых ведичи'Н
. Дал-ее •В .кач~еСТtне .при:-.1ер.а ·ра1соютршv1 .ра~с.пределе+ше части.ого
'rj/c;; двух :нe.11rJttин с р-елеевским 1расп·ределением с;; ·и ТJ. Уран.н ·ен'Ия
1и
(4.81), (4.85)
дают
(4.101)
00
w(z)
4
= - -Jxexp (- х2/б1) zxexp ( - z2 х2 /б~) xdx.
132 62
1 2 о
Подста1вляя .сюда и = х2
•
w(z)=
2 z ~i
(
6~
-
1
62
+ -z2)
"2
v2
1
'
пю.1vчаем
•
и
6
1 ие- du=2-1
(.
6 6
z i/ 2
62 [(z6 1 /62)2 + 1)2 ·
( 6~ + z2 6i) ~
Функция распределения
W(z)
1п 1 олучается ю
(4.105)
( 4.105)
с :пом•ощью
интеГ>рала
S
1
х
(х2+1)1 dx =
-
1
2 х2 + 1
l1
;
ZfJ,/6.
W(z)=2
: На
р.ис.
· ур-НiИЯМ
J'
(4 .106
-(x-2-:-l)-2dx=l- (z61/62)2+1.
4.5 показа:!сlы функщrи w(z)
(4.105) И (4.106).
1и
W(z),
соответствующие
Рассч.итаем оо~нмесrное распределен: ие велИ'Ч'и1ны с;; с .релеев~о1шм
распреLделением ;и .вел·ичины ri 1с гау1с·оовым 1расп1ред.е.r~·ен:ие~м. Плот
. ности
·нер1ОЯТНОС~И запИШУJ'СЯ 1в :ви~е:
2
w1 (x) =2iГ хехр(-х2 /б2 )
w2 (y)
=
х > О } (для ~);
х<О
W1(X)=O,
(2лГ 112 а- ехр (-У2 /2а2 ),
1
171
-оо <у оо (для t]).
(4.107)
Д.1я выч1исления распределения ча·сmюrо
(реле-евская вм~ичи
на/гауссова ·ВеJJIИ·чина) 6у.де~м полагать, что :пло11ность 11ю1юятн~0сти
гауссовой вели'Чlины 1ра1вна О при у<О.
~!
вероятности
~t
- ~
~о
S: '
~0,5
~
~,..
~--
Плоmность
о
1
о
J
2
Z/0,02
z/O,tf2 -
-
J
2
1
Рис. 4:5. Плотность вероятности и функция распределения
отношения двух ветrчин, распределенных по Закону Ре.лея
часmюrо ~/ri, вы111исл 1 е~нная для этогю усеченного р.аопределеюия,
оп;р1аведл;ива для •всех ~положительных зн.а Ч'е.ний х/у = z. Плотность
вероя11ност11
для отрицательных З1начений :оолучается зер:ка.1ыным
отражением 011Ноаиrельно оси ординат. Нах~оди1м
"
2
w(z) =
2 л:
а ~2 ,
fexp (-х2/2 a )zxe}{p(-zt х2/б2)хdх.
2
о
Подс1щ1новка у
1
= х (- 2
2а
+ - z2-; - - ).
_!_У2а
w(z)=
2
li2
да 1 ет
u2
б
"V2az /б
,
z>O.
(4.108)
(2а2z2/б2+ 1 )з12
По.1ная п.1.от,НJОсть вер:::> ятнос11и опр· еде.1яе"l'Ся по фо1р·му.1е
w(z) = _1 ~
Jf2/zl а/~
' -oo<z<oo.
2
б
(2 а2 z2/б1 + 1)3/2
З.начение W(O) д~0лжно ра:в.няты:я 1/2 1из-за сим1мет.ри1н
доваrелыно, W(z) о.п:р1 еде.1яется ·ка'к
W(z)
=
_1
+ _!_ J12a
2
1
2
б
у2ха/б
rz
•
о
(2 а2 х2/б2
dx
+ 1)3/2
(4.109)
w(z).
Сле
=
1-+(2~:z2+1г112, z>O;
z2
)-1/2
-1 (2--+
1
--2
а2
l)2
(4.110)
'
z<O '
На ~рис . 4.бшок.азю~ы гра.фиК'и функций (4.109) и (4.110).
П.1 1отность ·верюят1нюст.и и фун·К'ция ра1сл,редел1ения частного (rа
уооова
вел1ичина/1 р 1 елее&с·к ая
ве.1ич~и1на), показан1ные на р1к.
получаю11Ся а,налоги 1 ч1ш 1 м образом:
172
·
4.7,
~
w(z) =
2 :rt:б, jxexp(-x2/б2)exp(-z2x~1~dx
..
=
о
= _l_~(l
2 у2 а
W(z)=-21 (1
о
-'1 -J -2 -1
+
1 2 J
"
+
№z2
2 cr2
)-3/2 ·,
( 4.l l l)
бz/-V2a
)·
(бlz2/2<J•+ l)l/2
о
-1/ -J -2 -1
(4.112)
1 2 J 4
zr/!tf/o--
zt'icf/6-
Рис. 4.6. Плотность .вероятности и функция распределе
ния отношения релеевской величины к гауссовой:
t
-4 -J -2 -1
о
1 2 J
1/ -4 -J -2 -1
zo/{U-
1 2 J
о
4
zo/IU-
Pиc. 4.7. Плотн<Л.--ть вероятности и функция распределе
ния соотношения гауссовой и релеевской величин
· Пр1и
выч.ислен;и1и шлrОТ!НОСТИ
1ве1роя11Но·сти
1 праИ3'В'е~дения
гаус:оо
·DеЛIИ'Ч'ИНЫ и ~релеев·с.~юй IДОПУС"tИМ, "lTO ПЛQIТ!НОСТЬ .вероятности
iОООООЙ ~·ел:ичины равна О щ>tlf у<О. Вычислив плотность вероя.т, 11И ;п~р.и этом :пред;1юложении и .отобразив ее о'nнооительно оон
.
нат,
11юлуч~им
ПЛ'О'11НОСТЬ
ицате.льных значеюий
w(z) =
~
-
2
fncr~
Ве!рОЯТНIОС'ГИ
для
'Пl()ЛОЖ:И'rеЛЬНЫХ
случайной 1ве.1:ичи;ны:
00
Sexp(-z2/2x2 o2 )xexp(-x2/б2 )_!_. dx.
r
г
2q = у2& дает
z
173
'·
и
ИаIЮЛьзуя табул1ир0·ва1нный интеI1рал, ·пюл,учаем
+v2) Vvdv_ = V2qл: e-1/q•
Sexp (-1 2qo
00
о
откуда
1
w(z)= f2crб е
- -V2z/бa
, z>
О
.
Пло11ность 1не.р1оятнюст,и, д'ейс-гв<ителыная для пюлож1ителЬ1Ных и от
рицательных ·зшач,ений z, ·следует •из требован:ия 'Оим1м,етри:и 011ню
сительН10
z=O:
1
w(z) -
f2crб
-
е- -V2"iz\/бa
-oo<z<oo.
'
(4.l 13)
Фу;нкщия распределен.ия о,п;р·еделяе11ся 'сл,едующим обр1азом:
w(z) =
_1
2
+
11
2
4.8
z
2а б
-V2х/ба dx =
о
1 - -V2z/l)a ,
--е
2
= _!_
На рис.
f
se-
~
е-
-V21zl/l\a
'
,п•о.к.аза1Ны лрафик1и функций
z
z> о·',
<о
(4.114)
.
(4.113)
1И
(4.114).
1
-1/ -J -2 -/
-4 -J -2 -1
J 2 J' 4
о
о
zfi/od-Рис.
4.8.
1 2 J 1/
zfi/t!d-.
Плотность вероятности и функция распределения
произведения гауссовой и релеевской .величин
Пло11носrь ·вероятности ~су1м'мы гауссовой 1нелич.ины и
релее:в
IСIК'ОЙ нел:ичины да1На в 1Качес11ве :пюсл·едJне~nо :при,м,ер1а:
00
w(z)
2
~ Jexp[-(x-z) 2/2o2 ]xexp(-x2/б2 )dx =
=
У n сrб2
у;~ n ехр (__: ~) [1 + ехр (- ~)]
+ Vnerf (-z6
-) ;
2cr q
р2
а
р2
=
б2
2
+ 2 а2;
q2
174
=
б2
2
у'2 р а
(4.115)
- 202.
~
СТАТИСТИЧЕСКАЯ ЗАВИСИМ~
4.3.
\
Ковариа.ция и корреляция
4.3.1.
Ра1Нее mр,едJПюлагало1сь, что случайные вел:ич!ины 1стат:И~етич·ески
зависи:мы. Некоторые оп~р~еделеН1ия § 4.1 нужшо обобщить, что
.М<}ЖНО ·былю опустить услов'Ие ста11исrичесюой незав:исимо;сm.
.
·,
Р а1ссмо11ри'.м фующию р1аоо:р1едмения
W ( х, у) 'двух .п~е1реме~юных
, 1J. Маrемати'Чес1юе ожида~н:ие фун·кцИJи g(r;,, ТJ) определяется нн
,nралом:
J
00
E[g(~. 11)1
00
Jg(x, y)dW(x, у).
(4.116)
-оо-•
ь W(x, У) •бу1дет ;,ЩИфферепщ.ир~у~емой для 1Всех х и у,
tPW(x, У)
.
dxdg
_пу1сть g(х, у) будет 1не;пр·еры:внrой, за 1исключен;ием 'К'ОН·ечноrо чИ~С
точе1с Т1огда
у.р -1Н1ие
( 4.116) ~можно за1менить интег.ра.юм Ри
на:
J Jg(x, y)w(x, y)dxdy.
00
E[g(~. 11)1 =
QQ
(4.117)
-оо -оо
будет 1прои3iВедеН1ие.м целых · степе.ней i;; и
g(~.11) = ~khl.
~и чина Е ( i;;1iч 1 )
ri:
(4.118)
:-~азывается моментом поряд1(а
k + l. Моменrrы
,(i;; 011 1) и Е (i;;kч 0 ) иде:пичны мо:-.~ентам одномерного пределЬ1Ного
. спределения 1J 11 i;;. Они определяются ан а логично ( 4.29):
Е(~0 ч)=т2.
E(~11°)=m1;
ка
с
коорд,ина та ми
r;, =m1, 1J =\ni2
(4.119)
1называе11ся оредн,и · м
дву~мер
rо распредел·ения . Моменты относительно среднело н•азЬ!iваются
· нт;ралынЫ1м~и мо1мештам1и 1и обозна·чаются ч·ерез ~t1i1:
QQ
.r
µkl = Е [(~ - m1)k (1] - т2) 1 ] =
s
00
(х - m1)k (у- т2) 1 d
w(х, у).
-ао -ао
(4.120)
Разложение членов
м
(4.116), (4.118)
µ00
= 1,
и
µ01
(x-m 1)k(y-m2) 1
(4.119)
=
µ10
µ02 = Е (~о 1J2) - т~
по 1степе'НЯ1М х и у с уче
да~ет:
=О;
1120
= E(~2 11°)-mr =о~;
о~;
µ11
= Е (~. 11)- т1 т2 = or2·
=
(4.121)
Величины 0 21 :и а 22 ЯJвл.яют.ся дисперсиями :шре.делЬ'ных ,раоmре
_ле№ий ·пер~еме~нных i;; и 1J. МQlм·е~нт µ 11 на·зывае-гся •смешанным
о·менrом ил1и ·ковари.аци~ей r;, и 1J· Из теоремы · умножения (4.46)
175
!'
и
·след~rо он равеiн О для ста11юсrnчесюи 1нез.аm1симых
(4.121)
1
в~е.л·ичин:
µ11 = Е(~)Е(11)-т1 ~ =О.
(4.122)
Математи11еское ~жида·н~ие
"
2
Е {fc1 (~-:mi) + с2 (11- ~)] } = ~ci + 2 J111C1C2 + f.1o2~
(4.123)
явшrет~ся и·нrегр1алО1м фун1кциш, ·КIО'ГIОрая неот.рицателына, и 1Iюэт~0~му
_
оно должаю быть 1'ОЖе ~нооnр;ица11елЬ1Ны1м. СледJОIВ·ательно, прав а я
часть (4.123) до.лжша · быть нео11рицательшой. Доmу~с-ли1м, что, по
крайней мере, момент µzo или µ02 ~не р;ав·ен О. Пра·вую ч.а1сть ( 4.123)
М~ОЖНО пе~реписа'l'ь ·В IВIИде
~q + 2 µ11:ei С2 + µ02 с~ =
=
2
- -L(J12o1C1 + J1ii ~) +
1
(J12o~2-µii} ~]=
!120
--[(~с2+ J111C1>3+("'2otJ.o2-µii)q].
1
1102
(4.124)
-
Моменты µzo и µ02 - IНеот.рицателыны - по той же 1п~р1И:чине, что
и (4.123). Члены~ сюобках (4.124) будут н~еот,ри.цательны IП'J>'И лю
бых зна~qениях с1 и с2, если вы11юmяется стщующее услО\Вlие:
"12o~-µi1 ~о.
(4.125)
Коэффициент К!Орреляu;и~и р IОIП'ределяе-ося tСJiедующим .у.ра:в1Н е ·
нием:
~2
=--·
(4.126)
(4.125) ·следует ООО1lНОшение р2 ~ 1111л111 -1~ip~+1.
Из (4.122) и - (4 . 126) следует, что д,ля сrаТ1И1С11И:ческ•и независи·
мых вмич1ин r; и 1'\ коЭ'ффициент р=О. Обtр~атное ут.оорждеНJИJе !В ~Об
Из
щем .случае ноопра1веJJ.Л1И~ВО. Стат:истическая :н~езав:исимость не мо
жет быть 1вьrведена IИЗ уСЛl()lв1Ия р=О. Допустwм, что ~между
. оущест.вует
л;И'неЙ"Ная замюИ1м1ос1ъ: r;=aori+~o=a(11-m2)
+
r;
и ч
~- Тюгда
nол ytJiaeiм:
"'2о = Е (~ - т1)2 = Е [а2 (11- ~)2
+ 2CJt (~ -
2
!Тli) (t')- ~)
2
= а f.1o2 + 2а (~ - m1) tJ.oi + (~ - m1) µ00 = а ~2
µ11
2
+ (~ -
+ (~ -mi)
т1 ')8;
2
=
(4.127)
]
= E[(~-mi)(ri-m2)] = E[a(t')·- ~)2 + ф- m1 )(t')-~)J =
= а f.1o2 + Ф - т1) µ01 = а µ02;
р2=
а•••
rOI
.
а2
!102
+Ф -
m1)1
<:},
Вел1ичина р 2 ра1В'на 11пр:и ·~=m1. Р~езульrгат 1м.ожет быть обратимым .
Оначала раоом()'])ри1м случ1ай, .когда и
чает,
µ02,
и
µ20
ра·вны О. Это озн а ·
что П'IJ'едельные :ра1С.П~ределе4ния велич111н ~ ·и
ri
сосредоточены
в rочкаtХ т1 и ·m2. Следовате.тшню, дву.ме~рнюе р:а•оп~ределенме скон
цеН'1'р!Иlрова1но в точке
µ11=0 212
x=m1
и
y=m2.
К~ак следсmlИе, 1кова;рмац1и я
•доююна быть ра!вна О . С .другой
176
сrо.рю:ны,
за;В1И1симость
'\
~ µ"~ µн ~о ·следует из распредме!lИЯ, ~-~ирова•111Ного ·в
чке x=m 1 1й y=m2. В этом случ~ае о;пределеНlие~.126) 1не 'МIОжет
.
µ02 или µ20 н1е ра1В'ен О, т,о, mю :юрайней
ере, 1долж1н{) ·бытъ сп:ра~вед.шивы 1 м одно. :из ур-·н1ий (4.124). Пу1сть
(4.125) имеет место ·зна·к равенства. Согл.а1ано (4.124) ·п·ра•вая
' асть (4.123) будет рав•н;а нулю, есл1и удювлетворя1е'11Ся Од'НЮ из
ыть rприм1еtнен:о ·Кр.
Если оД;Ин из моме~нmв
tQIBIИЙ:
f.1.2"C1
+ µnC: =О;
ча1сть
~ 0 :#:0;
fto2~
+ µ11 с1 =О;
fto2 =F 0.
(4.128)
:р.авна О. Тогда должно ~ыmол1няться
(4.123)
( 4.129)
ак 1ш·к .математичесюое :Оl)!{Идан:ие 1неотрицателыной фунtКц~ИJи ~ра:в
. ю нулю толь·КIО
,,(4.128) и (4.129)
,в сл.уч.ае, если функции
пол.учаем:
равны
~ = !120 (ТJ- т2) + т1,
f.1.20 :#=О;
!111
~ = 1111 (11-т2)
;
!102
+ т1,
µ02
нулю 'Всюду. Из
=F О.
(4.130)
,Эти ур~аВ!Нlе\НИЯ для µ20:::АО IИ µ02=;i::O ЩI.€1НТIИЧНЫ на 1()1CiHI01Ba'Нllш за1В1И
' И1МОСТ.И: µ2.0µ02 = ~t 211.
Слмю·вателЬ1но, -из р 2 = l всегда 1с.пед'У'ет л1и1нейная за!виои 1м~ость
. ежд:у r;; и f1. С другой сторюны, rогласно ( 4.127) 'ИЗ .1шней1ной за
висимости ~с.педует в общем 110.Пьюо
·
p2=;i:: О,
а н·е р 2
= l.
Из ocero это•rо можню за.ключmь, что :кюэффиц:иент кор1реляu;ии
,я,в.1яеrея мерой л1инейной н·езавИJСи;мости двух 1в•еличиш. Считается,
'ЧТО щве 1вел1ИЧ1ины коррелирооаны .пр1и p=;i::O и 1 некаррелирова1ны IП'РН
р=О.
В ка·чесmе примера расомmр;и1м п.rrот1ню1сть 'В1 е1роятноС'ли ,щву~мер
ОО·ОО га'У'ссова рас.11редет~Н1ия:
w(x,y)=
2 n <11 <1z
1
У 1 - р2
ехр[-
1
2 ( 1-р2 )
(4.131)
При р=О и 0102=;i::O получаем
w(x,y)=
1
y2n <11
х2 )
ехр ( - 2
ar
(4.132)
Стати,С"ШIЧеок~ая незавиаи1мость 1ве.'I'ИЧ.ИJН 'В Э'ГОМ случа~е ~следует из
:р=О, из--за (4.9) и сtютношения d 2W1(x)W'2(y)/dxdy=w1(x)w2(y).
Эror результат опра1Вед.ли'В для ·всех дв.у 1 м·ерных плотностей ве~роят
. н~ости, юоrгорые ·п ред~ста1вля!О'flся 1в виде шрюизве.д:е.н·ия двух ~адно
. мерных :плот.ностей в•ерОЯ11НОIСТIИ лри р=О. Нап.р.и.ме1р, 1в (4.131)
:вм~есrо 2рху •мютл~а сrоять ,pif(x, у) и ·в-ое ныражен:ис ыоrлl() быть
. умножено на l +1pg(x, у).
1
177
,!
4.3.2.
Взаимо- и автокорреляционная фувкции
До сих 1п~ор ;ишдексы 1 в1елич1и1н i;;=i;; 1, i;; 2, ... и ri=ТJ1, '1']2, ... 1Ис
пr0дьзова.1и1сь только \.'!:ЛЯ ю·боз1н1ачешия orr делыных .результат01в ~из
мерений. Онл не п;р 1 едставлял1и ·собой у;шорядочен1ную mослrедова
телынюсть. Наприм·ер, необязательшю, ч11абы i;; 2 из1мерял0rсь 1rюсле ~ 1 .
Предположим теперь, что индексы указывают на последователь
ню1сть 1Из1меренiИй. Пу1сть и·31м1ерение в 1м.омент вр·емен1и f1 д1ает i;; 1, 'У] 1 ;
ИЗJмере1н1Ие ·в 1 мо1м1еrнт 1 в1 ремен~и 2 будет да.вать i;; 2, 'У]2 и rr. д. Посл1едо
t
вателмrоrсrгь •н1еобязательно щолжна .быть ·временной. :Как п1р:им·ер,
!Вел1Ичишы i;; 1, 1; 2 , ••. могут шр1е~ста~влять урооии воды 'ВдJОль -rечен1ия
реки или температуру в определенных участках.
При вычисл 1 еrни1и •с.реднегю з1 начения
т.ан)iв
i;;1, .. "
<i;;>
мrнож·ества
R
.резу.1ь
~;;н,
R
<~>=+E~i
(4.133)
i=l
1
1неrт раз н·ицы, указы:ва·ет л1и 1и1н1де~с
i
на :пюследова"Гельrность ил 1 и нет,
так 1 как ч.пены оуммы мо1гут менятЬ1ся места1м~и. То же
с:а1мrое оп·ра
в1едливю для средн·еювад1ра-гичесюого Q!Тlклrане:нlИя
<(~-<~>)2>
+
R
=
~(~i- <~>) 2 •
(4.134)
i=l
Ес.1и задашы две ве.1ич1и.ны
i;;
<(~-<~>)(ri-<Т1>)>
=
и 'У], то можно 1 н1а:писать :выражение
R
1 ~)~i-<~>)(rii-<Т1>).
(4.135)
i=I
Для
н.а
ве.1ич1И·ны
'YJi+t и.п:и
(4.135) важно, ч1106ы i;;i ум1нюжа.тюсь на ТJ;, а не
'Y]i-1·
У·рюЗ1неrния (4.133) 1 и (4.134) идеtн11ич·ны с (4.35) 1пр:и R.=oo, ec.1JI
Э'ГОТ предел ~существует. Пу1сть i;;i ра 1 вню х в r 1нз1мере'Нlиях из .о·бще
го чи·с.па R из.мер·еиий. Тогда 1 спrр.а1Ведливо:
Рх
= lim r/Н.
r,
R-+ry;
Пусть ·пар.а i;;=x, ri=y 1вiСтrр1еча1еrгся q раз 1в R 1из·мерениях ишусть
•существ'У'ет .предел Рху = lim q/R. Тогда (4.135) 'МО•Ж'НIО ·зап~исать
q,
в ви~е
R-+co
(4.35):
со
µkl
~ (х - m1)k (у - т2) 1 Рхи·
=
(4.136)
X,.fl=-<IO
Пу:сть ·в•ре.менная
менной фуrн·кцией
посл 1 едю1вательность
f ('0j)'
i;; 1, i;;2, ...
за.меняется вре
в :которюй значения i;;j .рассматр1Иваю11ся
в 1М()l~fе1Нты времен1и
1н·еrпр1(~1рЫ'В'НОЙ последава
'1'е.1ыно:с11и вм 1ес110
ej; j =О, 1, . . . . Для
f('8j) за1писывае11ся f (0).
178
Пусть вrое 'З'Начен'Ия этоii
\'
едавате.лыности рааrrодожены в :ИН'Ге~.е (-1/2)0~ 1Е>~
( 1/2) 0,
я
где
мюж·ет ·быть ·конечным 1ил1и боою0И~~ч1ным. Выраж: е
0
(4.133) и (4.134) :J'vюжно п:ереп:исать сле~дующим юбразо1м (~вс е
тегралы берутся от
до
(--1112)0
рмул лределы ·Н€ указаны):
( + 1/2)0,
для упрощения записи
m1 = <if(0)> = 0-• Jf(0)d0;
1
oi = <(f (0) - <f (0)> ]2> = 0- Jrt (0) - m1] 2d 0 =
= е- SF(0)d0- mi.
1
(4.137)
,а1меняя д~алее .последователь'Ность Т} 1, 'У)2, ••. ·Вlременной функцией
nолуча·ем:
· (0),
·~ =<g(0)>= 0- sg(0)d0;
1
1
о~ = <fg (0)- < g:(0)> J2> = 0- Jrg (0) -
-m2 ] 2d0 = 0- Jg2 (0)d0-m~;
1
oi2 = <[g(6)- <g(0)>] [f (0)- <f (0)>1> =
= е-
= 0.:..
1
1
Jt (6)- m1J (g(6)-m2J d0
(4.138)
=
Jlf(0)g(0)d0-m1~;
е- 1
s
Jt (0) g (0) d0- т1 т2
s
р=-------"----------2
1
2
(0) d 0 g 2 (0) d 0 l/
тn [е-
{[ е-• f
т~]}
. 1нтеnрал в чИJСЛ:и~еле назЫiвается вза1и.мю1юрр·е.ляци~он1н1ой
Ktg(0v) m;р1и 10v =0, 1ес.п:И 0 сrr~реМИ'ГСЯ к 6еоконеч0 НО1С'l1И:
фу:нк
'ией
(4.139)
Автокор.реля1..~;ионная
функция
K!f(0v)
~получа ется ~п.р.и
f (0) =
g(0):
Kп(0v)=lim08->_ОО
Если
~величина
0
1
8/2
J f(0)f(0+0v)d0.
(4.140)
-fjj2
1конеч 1 на, то 1и~апюльзуе11ся
крат.ковременная
заимокорреляционная или автокорреляционная функция.
179
/
5.
ПРИМЕНЕНИЕ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
В СТАТИСТИЧЕСКИХ ЗАДАЧАХ
5.1.
РАЗЛОЖЕНИЕ СТОХАсrиЧЕСКИХ ФУНКЦИЙ В РЯД
5.1.1.
РаюоМ'ОТlрим оо.оокуп1fl()С1'ь
Теп~овой шум
:в·рем10Н1нЫх фу;н•кций
(О), Л=
g).
l, 2, ... ,
необязателыно о0рrоrоналЬ1Ных. Разложим юаждую функщию в рял,
испю.1ьзуя п~ол.ную орrооормированную 0 аистему
на ·инrервале (-1/2)0::::;;0~ (l/2)0:
{f(j, 0)},
задан~Ную
ао
g). (0) = ~а). (j) f (j, 0);
(5. 1)
i=O
6/2
J Cл(0)f(j, 0)d0.
a).(i)=
-6/2·
j = io 1и пер1емооной Л ;коэфф;ицменты
(j) н·меют оm~ределенные з•начения. Со1вокуп~ность l фун:кциii
g л (0) дают l :к,оэффиц1иенrов ал(j). Пу1сть Q1 из них заключены
Д.1я фиксирl()tва1Н1ноrо З·нач1еtния
а
в ~и.н-гервале О<А < ·ЛА; q2 - .в 1интерiвале ЛА <А <2ЛА 1и т. д.
Вел~ичи~ны q1/l, q2/l, .. . будут ·на 1несены 1В иmrгервал1ах от О др ЛА,
от ЛА :що 2ЛА 1и т . д. Результатом я1вляе'I'Ся стулен·чатая функIItия.
ДоПJ'IСТ·и1м, чrо 1шрtи малых ·:эtначениях •ЛА CJIHa может быть аш1rорок
аим1ирооана 1п,1ютно1стью :вероятности . Для разшых значений j эта
п.1m1ность 11rе>роятн1()1сти .р.азличiна. Ес:ш ·плюmнос11и ~ве.роя11Н~ост.и од;и
на1ювы для 1R•oex знач•е~н1ий j, то а (j) н1азьшает.ся :р.а·1иrомер:но рас-
: прме.1~е~н1ной отн.ооительно
ал(j) 1и а"
(k)
j.
Кроме
того,
пу:е.ть
юоэфф.ицие1н1ъ1
я·вляются стаrги~с:~~ичеаки неза1УИ1еимыми mри
i*k.
Сово.куm'Ность .вр~емен1нЫх фушюl'Ий
g л (10) называеТ1Ся ·выООр-кюй бе
.юю шума ло отнюшен1ию •К О'ртогона.JJЬIНЮЙ аистеме {1f (j, 0)}.
Коэффициент
а л~iо)
.называется
0 оормал1:>но
если его 1плотн:ость 1вер1оя11нl()lсти явля1ется
ошибок. Со•воку:пность ф у1ющий
1 р.аоп 1 ре.де.ленньr!v1,
1произоод'НОЙ
функщш
g ).(10) 1Назы1вается белЬ!lм нормаль·
ным lliY'MOM и.1111 теШ.lО'ВЬ!IМ шумом 1>, есл:и а). (i) ipaiВ:IIOM•e!piнlO :ра·с1
) Использование этих терминов не является общепринятым в литературе .
Тепловой шум часто называют шумом Д:iконсона f\2] или шумом сопротивления.
180
:д.ел~ены <УГ1юаиrельню
j,
статиС11ически .неза·ВIИСИfМЫ ~и !И.меют нор
' ьное расп•ределе~НJи.е пр;и i()IП1ределеюrом j = jo.
ля П:pa'lcrичeteJюro iИ3'мерения :юоэффициffil~
атор функций
Инд_екс
f(j, 6).
a>.(j)
1рассмотrрим
1Не мож~ет :изменяться от о.
j
оо, ка·к •В (5. l), :а ~п.рюни~мает 110.1шко ·конеч~ное ЧJИ'СЛЮ -т зюа·че0, ... , т-1. Нре.мя дел•ит<:я .на не.перекрывающ1иеся н1Нтервалы
ьностью е. Функция
g). (t0)
'8 1пер1Вl()М 'Вреtме~ннбм IИJНФер•вале
ачае'Iiся через g1 (0); фу~тсция вю ·време~нrном 1Интер1вале Л
g >.. (0). Воз.можно 1'0\ЛЬКО ко
--
ное 'Чис.10 l •анте~р.валов; :Л измея от l д'О l. Пусть .дейсwуют
реме~нно т ои~r111ал'Ов
f (j, 0)
и
ь и•меется т пере.множителей 11
граторов. В первом и:нтер.вале
·!Ю !ИЗ!Мерить т коэффИ'IIJиен-гов
i), j=Q, ... , m-l. Эти коэффи
нты предста·вляются :выходными
.'J>ЯЖеН!ия.ми •и1нтеrраrор 1 а в 1Конrце
'оого rвременн6г.о и~нтервала д.тш
ыностью
0.
Повторение этих из
ний ддя всех .[ вр:еменнЬl:х ин- -ч
алоо
дает ml коэффш.1щент:ов Рис. 5.1 . Плотность вероятноспr
j); j=O, .. " m-l, ,').,,= l, .. ., l.
wa (j, А) теплового шу.ма:
·д
,.
И'f
на&!.~
·' . 'ОIПУ~Т ", 'ЧТО
'\AJ'p
) я1вляется тепловым
СМО'11рИ1м
О'Тlноше~ние
ф НК
ии"
У 1 Ц
· .. • m-1 ; А - нормированн ое
вы ~одное напряжение m интеграторов
j=O,
шу1мом.
Qr/l
1из.м~ереннй, 1даюЩ1их
зна'ЧеНlие
a>.(j)'
rервале (r-l)ЛА<А<11ЛА. Получен.иые т егупенчатых фу;н)(
.
•
MIOЖIНtO а;п.прОК'СИIМ:И1ровать 1неш1рерЫВ'НЬl?dlИ фуНt)(ЦИЯМИ :ПЛО1lНО0ве.роя11н.ости wa(j, А), каlК 1по1{аЗаНQ на р'Ис. '5 .l, если ЛА -
:- аточно ?.t1ал10, а l - щостl,1.rочню веJJИ)(О. Одинаковое ра:сш·реде
~е 1(УJ1Н1ооител1шо j п.р1иrодит .)( следующей за 1 висимости, которак
.а·ведл'Ива ;пр.и оп•ределен'Ном А
=A(J:
wa(O,Ao)=wa(l, Ao)=wa(2, А0 )=...
П!ре.11.елен:ие коэффиц;иеwгов
a>.(j)
5.2)
в обще:-.<1 случае за1ви~сит нс
:Ько от ~набора фун•1щ1ий g>.(0), •но также 'И от системы
{f(j,10)}.
, ако для теплО1ооrо шу.ма онl() не зюэ1исит от системы {f(j, е)}
. са·мых общих 1предположе'Н!иях.
'Для Д(жазателЬtСТВа э·юrо у11вержденля з.амен1и.м !П<Олную нор
ова1Н1Ную аи.стему {f(j, е)} д1ругой системой {h(j, 0)}, которая
е пrол1На •и орrrонормирова1на 1В интер&але (-1/2)0~ 1 0:::;;
Jl/2)6. Фун)(ЦИJИ f(j, 10) :и h(j, 0) .до.ТJж.ны 1 быть огр.аничеН1Ным1 и .
.
ОЖIИ.М фуН:IЩИ:И
h(j, 0)
IB .ряд:
h(j, 0)
=}: c1(k)t (k, 0);
s
8/2
00
C1(k) =
k=O
h(j, 0)f (k, 0) d0.
-е;2
181
(5.3)
Сумма
J:.cj(k) буtдет абсолю11но ~ехоmиться. Тогда ряд (5.3) одно.
рОД!jО СХОЩИ11СЯ.
Функция gл (0) раскладывается в ряд по системе
.
{h(J, 8)}:
1
W2
оо
1
gл (0) =~о Ьл(j) h (j, 0); Ьл (j) = _J /л (0) h (j, 0) d е.
Пюдст1а1Вляя
(5.1)
·и
6/2
(5.3),
(5.4)
·получаrем
00
00
Ьл (j) = _J~2 gл (0) ~OCj (k) f (k,
~OCj (k)
0) =
6/2
_J/2 gл (0) f (k, 0) d е =
00
=
L с1 (k) ал (k).
(5.5)
К=О
ПJО1следняя 1су~м1ма сходи'Гся абсО1Лютно, если вое ал
(k) ограншчены.
Сум,м1а ста11истически 1неза:висимых в1елич.ин 1С нормалыным рас
пр0едел1е1н1ием
есть
Сле~оват>ельНIО,
т.а·кже величина
b'J. (j)
с нюрrмальным
·рас:пределение:.1.
rимеет ноrр1Мальнrо1е 1ра·апределе1Н1Ие, еслrи ал(k)
статистичесыи :нез1а1В1исимы.
Средние
з1Наче~н.ия
:велич·ин
ал (k)
и
Ьл(j) 1ра·вны О.
ПлоТiНость 1вероя11но1Сти
wa.(k, А) величrины ал (k) д.1я теп;ювого
шу0 м:а записыва,ется ~следующим ~обраЗiОlм:
wa (k,
А)= _
ехр (- А2/2а~)·
1
(5.6)
Y2Y'1tmaa
f wa(k, A)dA=1/m,a cy:v1ао
ИrнтелрИ1рова-н~ие по А дает 1/т, wa,(k)=
-оо
т
= 1. Диап1ер1аия
ма т члено1в wik) дает 1: ~wa(k)
о~
в
(5.6)
k=O
о<пред~еляется сле~дуюШJИм образ•ОIМ:
l
1
и 2 = lim~ а 2 (k).
а
l-+<»
l
(5.7)
Л
i,J
Л=l
Плотность вероя11ное11и
wcfk,ci(k)AJ=
о~а
=
1
lim-
1-+оо l
_
вел1 ичИ1ны
_1
У2 -Vпmaka
'1c~(k)a~(k)
i,,J
1
=
с/k)ал
и
верояrности
l
exp[-cJ(k)A2f2a~a);
c~(k)lim-1 ~ a~(k) =
1
l-+oo
l
Л=l
ПлоТ1ность
(k) ра.вна:
i,J
Л=l
величины
(5.8):
182
Ьл
~1 (k)a 2 •
а
(5.8)
Jt
(j) 1 следует из (5.5), (5.7)
'
1
ехр (- А2/2 а~);
V2Vпmaь
Wь (j, А) =
т-1
l
а2Ь =
Iim -
1_. 00
11едний шаг .в
1
z
~
i.J
Ь 2 (j) =
Л.
Л.=1
(5.10)
(5.9)
т-1
~
~ с~1 (k).
l.J а2ka = а2а i.J
k=O
(5.1 О)
k=O
:с.де.1а•н u~1~ основани;и шер·воначалыного до
ения, чrо ра~апределе~н11·е ал. (k), а ·поэто·му и дис:шер~сия а~
не
И'СЯТ ОТ k.
· Бсши у доолетв.о.ряетс·я т.еор 0ема Парсе~ва.1я (1.11) .илм, други-ми
. вам~и, есл1и фу1Нкции h(j, 0) можно П!редста:вить с любой rоч
ью 1в
мой
смысле ·м1и1Н1имума ·ор1едне.к·вадрати'Ческюrо отклонения си
{f(j, 0)},' то из (5.3) 1п~олучи:м
J h7(j,0)d0=l= е12J
012
-8/2
(5.10)
-е/2
и
('5.11)
[ ""
]2
""
~cj(k)f(k,0) d0=Lcy(k).
k=O
(5.ll)
k=O
следует, ч110 у•сло1ше
О'~
= а~ (l
+ е)
(5.12)
О!влетворяется .и чт.о е 1стрем•и'Гся ·К •ну.1ю
х з•начеюиях т. Тогда пер~ем1енные Ьл
(j)
при достаточно б~оль
и ал.(j) :имеют одина
вые 1диспе~р 1 аи~и. П.1m1нос1ш 1Веро0ятнюсти на ·рис. 5.1 остаются 'НС
менным1и, если фу~нкцию g л. (18), ю1писывающую ·реализацию те.пвоrо шума, .пре:tста•В'ИТЬ в в.иде ряда ;по системе
{h(j, 0)}
в.место
(j, 0)} .
В J1.итературе обычно тепло·вюй шу:..1 1п.р1едста1вляет·ся рядом
·рье, а не 1обrд:И1М орrогО1налЬ1ным рядо1?>1 (5.1). Можно юодста:в1ить
(5.1) -ои~ну~соида.1ыные и ·КО'СИ1нус.01 ида.1ьные функц1ии, к011орые д..1я
.
темы
гласно
мом,
{f(j. 0)} равны О вне интер·вала (-1/2)0~18~ (l/2)0.
•результатам
этого
раздела
раз.1ичия
между
тепловым
.ря.дJо:-.1
Фу•рье ·ил:и
•рЯДl()IМ
фу~нкщий
(j, 0)}, которые можно 1р.азл 0ожить :в ряды Фурые, ·ка·к показано
5.3), не существует.
·
прелставлен1ным
В § 2.2 было уста1но1в.п.е11ю, Ч'ГО в.идеос 1 илналы ·можно пр·едста
ь ·В частl()стнюй форме, 1 раз•лож1ив mx по · сигнал•а.м У·олша, мли
часrо11ной фор· ме, 'Разлотив их •на си1нусомдалЬ1Ные и 1юсwн 1 усо
альные колебания. Кроме того, осл1и пеР'едае'ГСя ОД1и1на·ко1 вая ин
р:маu.ия, ro в1 идооси~гна.1ы, о~тфильт;рова1нные "1аtсwстным1И ф.ильами, с Т•рудом ·мvжно отл1ич:ить от сигнало·в, отфильТ1рО1ва1н~ных
тным.и филь'nра1ми. Есл!И :в.ид,еоаигн·а.пы ~имели бы •ра·оп•реде
ие теплоооrо шума :и ес.11и бы ухо :...юг.110 ;раз.пожить эти c•иrna
iнa бе~сканеч~ный ряд соста•в.1яющих 'согласно (5.1) или (5.4).
: ж1нr.о быJю бы ожидать Од!ИН•ак•овых резу.1ьтато1В.
· Р.езу.1ьтаты этого разде.1а :\1южно также 1шрименить к шу1му,
едсrа'В,1яющему ообой э.пектр•омагн1итное 1излуч1ен.ие, та:кое, как
т. В на·с-гоящее время .нет у~стройства, коrо1рое могло бы раз
Ж!Ить •Свет 1на сигн:алы Уолша и 'ВО·сп•роиз·весТ'и ча·сwстный опектр.
183
УсrроЙ{::'11Ва, •К1()11()рые ра1СКладывают свет на си'Нусоидальные ко,1 е.
ба1Н1Ия .и · восп1роиз•вмят ча1сто1"1Ный спе·ктр, такие, .как дифракциа.}!.
JНая
решет.ка
.ил:и
п•ризм•а,
я1вляются
инва,р·иа1нтным.и
.во
.в.р-емени
.подобно часrотным фильтрам в .с·вязи. Устр.ойство для 1р:азложенн~
.света /Н.а си:!'1налы У1ОJ1ша дрлжню обладать Ч·рез:вычайно выс.о·юи.\r
быст.ро.действием. Поэrому до сих оор ~еще 1Не имеет>ея пра.ктич е.
ск:их 1п;редложений :по 1 реал.иза'Ц1и~и та•юих ,усrройсrв.
5.1.2. Статистическал: иеЗависимость компонент
ортоrоиальиоrо
.в 1Юредыдущем
•раэдел~е
рааJJожеив:я
.пред111олаrал{)1ОЬ,
~что
коэффицие~нты
a,.(h) и а.,. (k) ЯJвля'Ются ·стат.0С11ически неза'В1Нси.мы·м:и ·п~ри h =1= k.
Осrае-ося Покаэаrгь, Ч110 эта 1неэа1ви~си.мQСТь т.акже спра1ведл;а~ва для
КОэффИIIJИ€1НТIQВ ЬА (j) 1Н Ь,_ (/) П:рtИ j=/=·l. JrИ IКОЭффИUJиеНТЫ 'И:М~еют
нормальное
распределение,
СИ!МЬllМИ, если
и ОНIИ ямяются статистически
.коэффициенты
'К!Оlрреля.ц~и:и р ИJI:И
незаfl и
кова~р!Иаl.IJИJИ
а 2 .; 1
р:а!В!Ны О.. ИСПЮJiьэуя абоолКУГНую сходимость ряда ;в (5.5), iIIOJiyчюr
l
(1~, = <Ь,_ (J) ь,_ (l)> = ,_.,.
lim - l \1
/.J ь" (i) ь" (l) =
1
=
=
+t [t
]~~ +t
~~~
,......,
Л=!
c1 (h)a,_(h)
Ё c (k)a" (k)J=
1
k=O
11=-О
t[tci(h)c1 (k)a"(h)a"(k)] =
А=!
h=O
k=O
" "°
l
= '1 '{l ci (h) с 1 (k) lim - 1 '{l а" (h) а" (k).
1.J /.J
1....
l 1.J
(5.13)
00
A=I
h=Ok=O
l
Обозначим 'Через в намбольшую сумму+
}J а" (h)a" (k) ~для .11юбой
А=!
пары h, k •и конеч~ноrо эначе~Н!ия l; тогда 1получ1аем:
+
l
Е.ал (h) а" (k) < г; ,
А=!
117 1
"°
(5.14)
00
< е L ~ с1 (h) с 1 (k).
(5.15)
h~Ok-0
Двойная <:у.м:ма сходится абоолютно, так ка·к су.м1мы CJ(h) и c1 (k)
абоолюню сходятся:
.
"' "'
~
L Cj(h) с, (k) =к.
h=Ok=O
(5. 16)
(5.15)
1и
(5:16)
дают
aj1 ~ е К.
. больших- значешиях l
• .ия a 2j1 .р:а:вна О.
(5.17)
е сrрем:ится .к О :п'О .определеuruю и кооа
5.2.
АДДИ'NШНЫЕ ПОМЕХИ
5.2.1.
Наимеиьшее средиеквадра.тическое ОТIСJiоиеив:е
прввятоrо сиrиала от эталоииых еиrиалов
усть 1вр~е~м:ен'ная функция F х
·.
орто гон ал ын1ой оисrем ы
:0)
{{ (j, 0)} :
ооставлена ;из mервых функ
т-1
кция
Fx(0) = ~ ax(j)f (j, 0); (-1/2)0 ~ 0 ~ (1/2)'0.
i=O
F х (0) ~называется сим·вол1Ом а.:~фав:ита. Имеется
та;ких •СНIМ'ВОЛ'ОВ, осл1и коэффициенты ах (j)
(5.18)
mнечное
'Пlри11-11имают iКIO
. ое числ<0 зшачен:ий. Напр1Имер, тел~етайпный алфшmт сQде·ржит
' уюв_ы; т 1ра'Вн<0 5, а коэффициенты a/j) могут :п~риншмать два
е'Н'.ИЯ.
усть пе;реда:ется F х(0). ·В процессе передачи
· ды1Вается
1пю1мех•а q 1 (i0)·
с сигнал.ом :и .принИJмаемый сигнал •можно за1п~и1сать
де
F (0) = F х (0)
. дJПО.1ЮЖ.И;\l,
1
что
F(0)
+ q,_ (0) .
(5.19):
'МОЖНО 1пре.дста1в•ить ·в виде .ряда:
00
00
F (0) = ~a(j)f (j, 0) = ~ (ах (j) +а,_ (j)]f (j, 0);
i=O
. JF(0)f(j, 0)d0; ax(j)=O для j:;;.. т, j
8/2
'
(5.20).
/=0
-8/2
· от О до (т-1). К1Оэфф:и1JJиент ал (j)
ью (5.1) .
.ме~няеrося от О JtlO оо"
опtределяется
с
~по
:а пpиeiыiнqjf IСТ!Ороне 1Нужш.о •решить" каК1Ому С1И·М1вюлу
, .. "
х
...
IНа'Иболее 'В<ероя11но rоотве-гствует сигнал
ость п•реобр.азlQlван:ия F Ф
(0)
1в оигнал
F(G)
F ,р(0)"
F(0). В.е
зависит от ве 1 роят-
того, что F Ф(0) был 1n~ередан. Предrюлюжим, что •нее ~с1 и1м1во
ередают·ся с од:ина 01ювой ·вер•оятно1стью. Тогда решен~ие зави
лько от ПO!-ii<eJQи g "(0). Бели о множестве g,_ :10) 1Н1ичего 1Неизю, тю П'О од1н.ому 1ОИ1М1оол-у нельзя :п~ри1нять решение. Одна-ко
Н<ОГИХ с,1учаях и-з.ве-с11но, 'ЧТО 1ПОМ€ХЗ g А (0) с большей энерnи€k
-
менее часrо. чем ·помеха •с .ма.'lой энерги€й. Другима
185
сл1овам1и, ·вер~оятн~ость л1риема пО1мех1н
ч1еншя~м1и
С.иrnал
:И
W
F (0)
W +Л W
g л (0)
с эне:рrией ·между зна.
умень~шает·ся мо~нют01н1н~о с у:вел·ич-е-нием
\V'.
наибюл~ее •вероя11но 1соответст.вует ~0им·1ю.1у FФ (lf)), 1\0-
-горый ,может 6ыть преоб.разова1Н ·в аигнал F ('0) ·с 1На'И•м.е1ньши·:чн
з;атрата.ми энер~И!И. Энер·гия Л WФ' необходим.ая для та.юою л·р е образован1ия, опр1еделяется инrег.рало~м
Л WФ =
~2
8п
-8/2
-8/2
J [F (0)-FФ(0))2 d0 =
5[f2(0)-2 F(0)FФ(0) + F~(0)] d 6.
P•(i0) .п.р~е,дставляет э~н~е1р·лию принятого сигна.1а,
(0) - энерnию си1мв~ола f~ (·0), с ·которы1м ара·вн1 1вае-гся силн· ал. Интеr~рал ют F(1
0).Pip(0) 0е~сть к.орреляцооНJный И•нте
гр:ал или корреля'Ц'ия .сигнала F (fЭ) и :аи~м:вола FФ (·0). З1начен11е
Р(0) я 1вляе'ГСя одни~м и 11ем же ~ДЛЯ ~всех 1с1им~вюл:>о.~з F l\J(e) ~и ю~
мюжно ;п·рен~ебр~ечь. Есл1и, к1ром-е roro, э~нерлия у ~всех 1си1мвоJI!Ов о,д11Ин11еграл ~от
и1Н'теграл от F~
на1ко.вв
8/2
WФ= 5F~(0)d0=W,
(5.22)
-8/2
то м1ожно также :шренебречь F~
ОП1ределя 0 ется •В
э·юм
случа1е
Л W = min
(0). На:именышее значение ~ WФ
rоль:ко
1IЮр1реляц;оон1ны.м
8/2
SF(0)fФ(0)d0 =
при
юнrеnр·аш}~1:
'
max.
(5.23)
-6/2
Пер•еда1н~ный сим'Вол
F х (0)
будет ·пра1в:илыно
m1ринят,
1~:меет 1м1ин1иму~м при 'Ф=х.
Алilор~и·тм обна•ружен1ия сигнала
н аружен1ием
по
юр;ИТ•е1р·ию
(5.21)
и
(5.23)
называется об
на1И'менъшего сред~rеюв.а,щраrrического от
кланен,ия. В случае теплО'lюОО шу~м1а т.аыое о.бlн<!!ружение Я'в.1srетс11
наилучши•м. Им~ее-гся 1мноrо ~видов аддит:ившых оомех, для 1Ю11Орых
э·ю не.верно. К ним относя1'ся та·К'Ие 1пом1е:~Gи, ка.к :и.мпуль:сные илн
та:к называемые 1орган1изо!ванные п0~м-еХ'И.
Используя ~су~м1маrоры, умно.жител1и 1и .~ыrгег1раторы, 1В •rnр~инш1п1е,
•можно 1()1!11р 1 едел.ить 1на:иболее •оор1оя11ный
'!lереда'Нlный
аим 1 в·о .1
[из (5.21) :или (5.23)]. Однако ~р1еализация тако·го .ал:rорИ'Гма яв
ляе1'Ся обычно 'В 1 есЬ'ма 1'рущоемюой. Пу·сть алфав1ит и·меет п сим.в о
лов. в '()00Т:&е1'С11В 1 И1И с (5.21) и ( 5.23) нужно 'ВЫЧ1ИIС.II:ИТЬ п эiн.epil!lii
Л WФ' Э-Ли вычисления должны П'рОIВОLдить~ся одновременно: Следо
ватель-ню, пют.ребу1ется п или п/2 сумматюрю1в, у1мноЖ'ителей и и1нте
г~р а-гор~ов.
М1 ен1ее громоздкие
нов1К'И
(5.18)
1и
(5.20)
аЛilорит,мы •мож~но получить ~путем 11од~е'Г а
tв
оо
Л WФ =
(5.21):
2: а (j) 2
i=O
m-1
2 ~ а (j) аФ (j)
i=O
186
т-1
+ ~ а~ (j) =
j=O
т-1
оо
= ~[а (j) _ау (j)]2
+ ~ а2 (j)~
/=О
(5.24)
j=n
т-1
Л WФ = min при ~ [a(j)- аФ (j)]2 = min
i=O
т-1
Л WФ
т-1
при 2 ~ a(j) a<Ji(j)- ~ a~(j)
= min
f=O
= max.
i=O
""
· а~ (j) ю11и ~ а2 (j) можно пренебречь, так как они принимают
i=O
· наковые значения для
й из (5.24) получаем
каждого -ф. Для символов с равной энерт-1
Л W'Ф
L a(j)aФ(j) = max.
при
= min
(5.25)
i=O
У.ра1внения (5.20), (5.24) по.казывают, что тюлька коэффициен
,' a)Jj), j<m, .реализации шу.ма g,_ (0) .оказывают вл;ия~н1ие на •рен~ие, ка·кой из аимво.тюв
няrом сиГ'нал1е
F "'(0) я·вляется на.иболее .в~ерояmым в.
F(0).
Для пра1к11ичоского 1П1р:и.м1енен•ия (5.24) 1и (5.25) т:р~ебуется т пе
ножителей 1и интег.ратаров, а 1н1е п 11ли п/2. В случа.е тел1етай1II
алфа1вшта э110 означает у·мен!>Шение числа .перемнюжителей и
:раrор 1 ов с 32 или 16 до '5 .
.Подоrаwм в
·(·5.24) :вместо a(j) qм1му ax(j)+a,_(j) из (5.20):
т-1
т-1
L a~(j)=max.
ЛWФ=min при 2 ~[ax(i)+a,_(j)]a~(j)-
/=0
j=O
'.ВЛJияние •помех•и
g,_ (0)
~на обна~руж•ен:ие сигнала опр·ед~еляе'Гся.
т-1
'
ой 2 ~ а,_ (j) аФ (j).
f=O
ероятность 1не1пра~вилЬ'ноrо
решения за1виоит
е12
ких овойств коэффициентов а,_ (j)
)
=
тольк•о
от статис
Jg,_ (0)f (j, 0)d 0. Пусть.
-8/2
есть •выбо'Р'ка теплО'Воrю ·шу~м1а. Ста11истическше ~свойства ·ко-
ициен·юв а,_
(j)
являются rотда ·пр'И са1мых
общих
у:сл.авиях
1орт0trональн~ой
ви.с•и~мыми •от используемой
аистемы . Передан
-сигна .1 F ,_(0) сюста•вляе'ГСя •из этих фу~н:кu;ий ~еогласн~о (5.18).
о•в.ате.1ьн.о,
оо·воем
1неваж1но
ения, каюие функции
'
f(j, 0)
для
.ве~р·оятноС'Ги
нешра·вилЬ1ного
;используются для составления сиг
если 1пю·меха п1редста·вля 1 ет ~собой ад1щ11И1В!НЫЙ 11епл.овюй шум..
"
187
5.2.2.
Рассмотрим
некоторые
Примеры цепей
цепи,
которые используют зависимост 11
{5.24) и (5.25) для обнаружения сигнала. На рис . 5.2 показано,
. .каким образом получаются коэффициенты a(j) из принятого сиг.
нала F (0) с помощью опорных функций f(j, 0). В основном эта
1
,схема т.а.кая же, ;как и н.а рис . 2.7, за ис.
F{e
(О)
ключением тою,
ч-го здесь получаются
ис
каженные 'Коэффицliенты a(j) ·вместо ·неи~.
каж1ен1ных 1кQэффИ1u;иентов а/ j) .
На
:ВЫХQдJе
рас.
5.3,
a(j),
а,,,
оrемы,
:поmвля~я
(j).
Оим·оолы
изоб~раженной
сум.ма
на
1на1пряже н ий
соста'Влены ·из
трех
фун~к~ий, т = 3. Сле~довательнQ,
имеются
три 1коэффиц.-иента а(О), a(l) и а(2), .к.от о
ры~е 1пр· едст,а, влены напряже~ниями. Коэфф и
Рис . 512. Выделение коэффициентов
a(j)
из
ниенты аФ(О), аФ(l)
1п редста,вл·ены
1
и аФ(2), -ф=l, 2, ".
оо:п:р 011ивл~е·ниями.
1
О
пера.
принятого сигнала F(0): 11JИ'О1Н1ные усил,и11ели У ·Иlмеют диффер 1Ещци
п
-
перемножитель; и
тегратор
-
ИН·
альные .входы. Инвен-гирующие ~ВХОДЫ обоз~на:чены (-), а неинвертирующие- (+).
Заметим, что сумма a2 (j) в (5.24) одинакова для всех Л WФ.
Этой суммой можно пренебречь, если наименьшее значение Л П\р
будет определяться без нахождения величины ЛW\Р. Так же, как и
ранее, вырабатывается сумма
a(j)a\I> (j),
но с обратным
знаком.
Следовательно, можно использовать схему, изображенную на рис.
5.3, но инвертирующие и неинвертирующие входы операционных
усилителей должны быть
представлены, как на рис. 5.4. Сумма
а~
(j) вырабатывается дополнительной линией с постоянным нап-
ряжением +И и сопротивлениями соответствующей величины.
Ие,
U2,
Для определения наибольшего из выходных напряжений U0 , И1,
... (рис. 5.3) и наименьшего из выходных напряжений И0 , И1,
... (рис. 5.4) необходимы соответствующие устройства. Один ва-
риант устройства, определяющего наибольшее или наименьшее на·
пряжение, использует пилообразное напряжение, которое сравнива·
ется в п компараторах с п напряжениями. Срабатывание первого
компаратора определяет наименьшее напряжение в случае возрас·
тания пилообразного напряжения; наибольшее напряжение опреде·
ляется срабатыванием первого компаратора в случае спада пи.10·
образного напряжения. Достоинство такого устройства заключает·
ся в том, что пилообразное напряжение необязательно должно из·
меняться линейно со временем и что флуктуации напряжений не·
важны. Недостаток заключается в неодновременности выполнения
операций.
Компаратор с одновременным выполнением операций пока з аll
на рис. 5.5. Напряжение в общей точке каждой группы из четыре){
диодов равно наибольшему приложенному положительному напря·
188
и,
Рис.
ла
5.З.
Обнаружение
методом
сигна
наибольшей
мы. Все символы
Рис. 5.4. Обнаружение сигнала
сум
методом
наименьших
сумм,
символы должны иметь ояииа-
имеют оди-
наковую энергию:
Uo
-
12
ковую энергию:
= U [а (О) ао (О) -
Uo
(1) а0 (1)- а (2) ао (2)];
+ а~(2)-а(О) а0 (О)+
U 1 =U [а (О) а1 (О)+а (1) а1 (1)- а (2) а1 (2)); Vz = U [а (О) Х
Х а 1 (О)+ а
+а (1) а 0 (1)
(1) а2 (1)-
U1
- а (2) а2 (2))
-ению. Пусть Из
-
= U [а~ (О)+ а~ (1) +
= U [ а~(О) +a~(I) +
+ ат (2) -
наибольш€е
апряжен:ие. Напряжение .на ин
ентирующем входе
(-) у•Сiил;ите
я У1 ·больше, чем IНа 1неИ1Нверти
ующем входе ( +). Очита·я уои
енiНе достаточ1ным, .выходное на
ряжение Ивых1 1 буд-ет m1р1И1н~и.мать
ачение, .соо11Ве'ГС11вующее режи-
. отоеч·ки . Будем обознача1ь его
. р.ез Ивых1=-l. У·силите.ти У2 и
189
+ а(2) а0 (2));
а (О) а 1 (О) -
~ -a(l)a1 (l)+a(2)a1 (2)/;
U2
= U (а~ (О)+ а~ (1) +
+а~ (2) - а (О) а2 (О) -а (1) а 2 (1) +а (2) а 2 (2));
Ri
= R/( aJ (О)+ aj (1) +
+aJ(2)); j=O, 1, 2
Уз имеют б6.1 ьшее на1пряже.н;ие на не.инвертирующем аэх.оде
( +).
и~
·вьыюдные •н а1пр'ЯжЕжия •соотаэ~е-гствуют режИ'му н.асыщеН1ия и обозна
чаются че1р ез Ивых2= Ивыхз= 1. IНа'П•рЯЖ•ЕЖИЯ Ивыхf, Ивых2 'И · Ив ых:1
+
-•1
tL
.... ,..::
_R_
,,.
L,,1
,,."/
1'
j~ U8ых3
1 _J +
--~
R ~··r
......:,,
+-
J/j+Unыx
1
~/{
R
,..._
1
~r·
,,
+- ",.
~1+
{/6.1
~R
-~
••
Ри с. б . 5. Обнар у жение наибо.~ьшего по до
жите ль ного напряжения .Ио-И1. Наибо.1 ь
ше е
напряжение
определяе'fся
значениями
Ивыхt , Ивых 2 И Ивыхз:
ивых 1 и. 1 и, 1 и. 1 и. 1 и. 1 и. 1 и. 1 и,
ивыхl
-1
-1
-1
-1
+1
+1
UВЫХ2
-1
-1
+1
+1
-1
-1
ивыхз
-1
+1
-1
+1
-1
+1
ука зывают -на1ибольше.е нап~ряж€Н1И· е И j, j =0, 1, ... , 7, 1 п1ре.д~ста1вляя j
в дв·оичной фор.ме. Для получения хороших ·результа1'01в хара.кте
рисrнки диода д•ол жны >быть адинако.вым1и. Для юравнен.ия
Рис .
2r
на -
5.6. Обнаружение относител ьн ых знач ен ий напряжений:
Наибольшее напряжение
и. и,
и. и. и, и.
Второе наибольшее напряжение
и, и. и. и. и. и,
Третье наибольшее напряжение
и.и, и, и, и 0 и"
+1 -1 +1 +1 -1 -1
+1 +1 -1 +1 -1 -1
+1 +1 -1 -1 +1 -1
пряжений тр•ебуется r
усил1ител·ей. Схему можно измеюить та~ю1
1 образО1м,
что 01на б удет об~на:ружи.вать, :ка.кое
наибольшую ил;и наименьшую величину.
1и.з н-а1пряжен~ий им· еет
На рис. 5.6 показана другая схема для определения наибольш е
го напряжения. В зависимости от разностей трех напряжений Ио,
И 1 и И2 три усилителя У1, У2 и У3 могут находиться либо в режи ме
насыщения, либо в режиме отсечки. Количество возможных пер е ·
становок выходных напряжений 3! 6 показано в таблице рис. 5.6.
Схема указывает не только наибольшее, но также и второе, и
=
190
'Третье по величине напряжения. Напряжения Ио,
U1
и
могут
,U2
быть положительными и отрицательными. Эта схема значительно
более чувствительна к входному сигналу по сравнению со схемой
рис. 5.5, так как напряжение проходит прямо к усилителям, а не
через диоды. Ее недостатком является требование большого коли
чества усилителей. Сравнение п напряжений
требует
измерения
(n-l)+(n-2)+".+1=- п(п-1) разностей напряжений. Следо1
2
вательно, нужно - 1- п( п-1) дифференциальных усилителей. Схе2
!ма на рис.
только
5.5,
log п
с другой стороны, требует для
n=2r
напряжений
дифференциальных усилителей.
5.2.З. Согласоваяиые фильтры
.
До сих пор предполагалось, что коэффициенты
путем перемножения сигнала
a(j)
получаются
f (0) с f(j, 0) и интегрирования это
:rо произведения . Математически эквивалентный, но технически от
:личный метод использует согласованные фильтры. Для описания
согласованных фильтров обычно используют импульсную характе
. ристику, а не передаточную функцию. Рассмотрим узкий прямо·
. угольный импульс D (10) с амплитудой 1/в внутри интервала
· (-1/2) в~ ,0~ ( 1/2) в и амплитудой О вне этого интервала. Этот им·пульс стремится к дельта-функции б(10} при уменьшении значения
е. Рассмотрим далее набор фильтров . Пусть ко входу фильтра j в
момент времени '0=-1/2 приложен импульс б(0+ 1/2}. Пусть бу
·дет получена выходная функция f(j, 0), (-1/2) ~ 10~ (l/2)
из
(5.18) и (5.20). Функция f(j, 0) есть импульсная характеристика
фильтра
j.
Временную функцию
F х (8) из (5.18) можно получить путем
Подачи импульсов ах (j)б(е+ 1/2) на входы т фильтров с импу.11ьс
,ными характеристиками
f(j,
е)
и суммированием
выходных сиг-
'налов . Эти фильтры называются формирующими.
"
Приемные фильтры осуществляют
ункции
F'А. (0)
или
F (0)
обратное
преобразование.
прикладываются к их входам в течение
нтервала времени (-1/2) ~-0~ 1/2, а коэффициенты ах (j) или
· (j) в (5.20) получаются на выходе фильтра j в момент 0= + 1/2.
усть функции f (j, 0) представлены ортогональной системой им
ульсов D('0-kв); k=O, ± l, ±2, ... :
а (j)f (j, 0)-~ а (j)~ di (k) D (8- kв);
1/2
'. d1 (k) =
"
lre+e/2
5f(j, 0)D(0-kв)d0 = S
-1/2
f(j, 0)d0 ~f(j, kt)e,
1
(5.W)
ka-e/2
k = О, ± l,." ± l/2e.
191
}
f
Функции (j, О) в общем случае точно не представляются сис
темой {D(t0-1kв)}, так как су.мм а в (5.26) представляет собой сту
пенчатую функцию. Однако если в становится достаточно малым,
то среднеквадратическое отклонение между
f(j, 0)
и ступенчатой
функцией становится произвольно малым для тех функций, кото
рые можно генерировать.
Пусть при подаче на вход приемного фильтра
+ ~)
j
сигнала б (tl
+
появляется выходной сигнал h(j, е), -l/2~e~l/2, а при
+
подаче на его вход сигнала D(ifJ-kв) =D(i0' 1/2) появляется вы
ходной сигнал h(j, 0') =n(j, е-1/2-kв), если в - достаточно ма
ло. Тогда при входном сигнале a(j)f(i, 0) появляется следующий
выходной сигнал:
a(i)1"Jd 1 (k)h(j,0-, +-kв), k=0,±1, ... ±1/2в.
(5.27)
k
Этот сигнал имеет величину
a(j)~d1 (k)h(j, -kв)
(5.28)
k
в момент времени
вместо
0= + l/2.
Подставим
f(j, kв)в из (5.26) . в (5.28)
Сумма дает площадь полос шириной в и
dJ(k).
высотоii
f(j, - kв)h(j, -kв). Эта сумма может быть заменена на \ интеграл,
если з1:1ачение в достаточно мало:
1/2
a(j)
Jf(j, 0)h(j, -0)d0; 0 =
-1/2
Этот ин_теграл равен
lim k в; d 0 = lim в.
k-oo
(5.29)
е-0
е-о
l
при
h(j, 0) = f (j, -0).
(5.30)
Коэффициент а (j) получается на выходе приемного фильтра в
момент времени 0= 1/2. С другой стороны, на выходе получается О,
если ко входу приемного фильтра j приложен сигнал a(l)f(l, е) ,
l=Fj:
1n
l/Z
«(l) \ f(l,0)h(j, -0)d0=a(l) Jf(l,0)f(j,0)d0=0, j::pl.
-1п
-t2
(5.31)
И:мпульсная характеристика
приемного фильтра j должна
быть
равна f(j, -0), если импульсная
характеристика
передающег о
фильтра j равна f(j, Н) . Передающий и Приемный фильтры иден
тичны для четных функций (j, 0)
(j, -4)) и для нечетных фуш;
ций
f (j, 0) =-f (j, -0) .
f
=f
Согласованные фильтры не требуют умножителей для определ е
ния коэффициента a(j) в (5.20). Это часто является преимущест
вом по сравнению с коррелятором. В общем, нельзя сказать, кор
реляторы или согласованные фильтры имеют преимущества. У~1ножители для функций Уолша очень точны. Согласованные фил ь -
192
. , с другой стороны, не требуют для их конструирования индук
, ностей и емкостей, а могут быть похожи на схемы, показанные
·рис. 2.13.
5.2.4.
Компаццеры :для частоСТИЬIХ свrвuов
;Хорошо известно, что одновременное сжатие частотноограничен
~ о сигнала дает сигнал, который уже не является частотноогра
. енным.
ЮЦ'ИЙ
не
Причиной этого является то, что сжатие синусоидальных
fВ.СеГда создает •ГаlР'IvЮНИКИ.
имеет
места
для
частостно-ог-
ченных фу~J№ций, составленных из
.н·К:ЦИЙ Уолша. На 1ри1С. 6.7 а в IКа'Че-
1
.
(О):
(0) = wal(O, 0) +
f.x(IJ)
ОJ.-&...ц.,~1-1--1-н.-4-!1---..t...
1П~ри1мера 1IЮказа1Ны СИ'М'БОлы F л (0)
. 11:
Fti (8)
Е
-Е
Ot
,I (-IY sal (i, 0)1-1
4
- ~са! (i, 0) +
т
I
са! (i, 0);
1..85
1-1
= -wal(O, 0) +
Fи(0)
ф
т
+ ~ (-IY sal(i, 0) + ~ cal(i, 0).
Рис.
f.al
f=l
~ При
прохождеНIИiИ
этих
ОИ'МtВО
.
ч~ерез
.комп1реооор,
нмеюШJИй
актеристИJКу,
.· F~(0)
1IЮКаза1Н1Ную
•вырабатываются
. 5.76,
и F~
Сжатие частсктноrо
5.7.
групповоrо сигнала:
а) •nеvвичный сигнал;
б) ха.
рактеристика компрессора; в)
сжатый сягнал
на
силна-
(О), показанные на рис. 5 . 7в. Эти сигналы содержат
1 , но такие же функции Уолша, как и символы Рл (0) и F 'Х (0), но
· ько они умножаются на различные коэффициенты~ Рассмотриъt
· актеристику компрессора 1\ =Е erf (~/ '}/20). Пусть W1 (х) =
' W 1 (-oo<~~x)
будет функцией распределения
\па перед сжатием. Функция
амплитуд
сиг·
W2(-00<11~Y) получает·
W2(Y) =
: ИЗ ( 4.11):
~ = -V2 оеrГ 1 ~ <
W2 (y) = W1 ( W2
-V2 о егГ
1
;
;
1
оо < ~ ~ V2oerГ 1 ~) = \\/'1 (-V2oerГ ~);
(у)= V2л:~ехр(еrГ 1
2Е
JL).sw
Е
1
(-V2oerГ 1
;
).
,
, Далее рассмотрим сигнал, составленный из 16 функций Уолша.
'казанных на рис. 1.2. Все 16 функций равны + 1 в интервале
10<1/16. Среди 21° двоичных символов, 1юторые могут быть по-193
лучены из 16 функций, в этом интервале имеются: 1
вол с амплитудой 16 ( + 1) = 16; 16= (
15(+1)+1(-1)=14;120=
=(:)
С!iм.
символов с амплитудой
16
)
1
с:) символов с амплитудой 14(+1)+
=
+2(-1) 12 и т. д. Такой же результат получается и для друг 0 .
го временного интервала. Следовательно, двоичные символы, сос.
тавленные из функций Уолша, имеют распределение амплитуд по
закону Бернулли. Пусть символ составлен из т функций Уолша с
амплитудой +а или -а. Вероятность рв{(т-2h)а] выборки с ю~плитудой (m-2h)a равна: рв[т-2h)а]=
(
т; функция распределения равна Wв(х):
[х]
W8 (x)
= (
1
2
)m (m'
h),
h=O, 1, ""
( )•
+)тЕ ~
h-o
а)
1гд1е
[х] означает наибольшее це.1ое
ЧIИСJЮ,
меньшее 1ИЛIИ ра1ВНОе х.
Фу~н1щию Wв(х)
можlНIО аппрок
· е~и1м~ировать при .больших значенияs
~1/Е
//Е
/
/
1
Ю
·функцией
ошибок:
Wв(х)~
1
2
erf
1 (х), E2=ma •
2
r2E
,r:. )=
~ (1 +
W
ПрО1изводная W1(x) показана на
1 i=Eerf{tflU)
•
/
т
1 -х2/2Е 2 ·рис. 5.86.
W,(x)=m Ее
Ха1ра.ктерисrи~ки
сжатия
ri=Eerf(~/V2a) для · а=О,5Е,. Е, 2Е
1показа1Ны
на 1рис.
5.8а.
Ооспm-етст
·вующие фуш.к1.1JИJИ плоТ1нос11и вероят
ности
w2(Y)
w2(y)=+
1 по1казаны
1на .рис. 5.8в:
~ ехр [(l-cr2) (еrГ 1 ~ )2];
W2 (у)=+ [ 1
1
+ erf (crerГ ~ )]·
Отметим, что Н()lр.мальное 1ра<Сшр ·еде
л1ение ~на 'Р'И>С. 5.86 дл·я 1cr=E 1пе·ре·
ходит в 1ра.вном1ерное раопределение.
На рис. 5.8а 1и в та1кже ~показа
Рис.
5.8.
Сжатие частостного группового сигнала:
.а)
характеристика
компрессора;
·б) плотность вероятности случай
ной переменной i;;; в) плотность
:вероятности
процесса
сжатия
пьсл(!
ны
ли1нии 'С обозначением
1«13%».
Они отно 1 сятся к :необратимому ко:.1-
1прессору с характер~ис11И'К'ОЙ ri= G
при
l~l~l,SE и YJ=±l,5 Е nрн
1~1 ~ 1,5 Е. Этот ком'Пlрессор отсе·
кает все амплитуды, большие 1,5 Е,
194
торые составляют 13% от амплитуд в случае нормального рас
ределения. Этот ограничитель более подробно будет рассмотрен
§ 6.2.
5.3.
МУЛЬТИПЛИКАТИВНЫЕ ПОМЕХИ
5.3.1.
Иитерференциоииые замирания
Пусть радиосигнал передается по нескольким путям. На прием.
ом конце принятые сигналы влияют друг на друга. Рассмотрим в
ачестве
примера
синусоидальную
утям . Принимаются сигналы А1
азностью в задержке
А1 cos2
= (А 1
ev.
волну,
передаваемую
по
двум
cos 2nvo9 и А2 cos 2nv 0 (9-0v) с
Их сумму можно записать двумя спосо-
nv0 0 + А2 cos2 nv 0 (0-0v) =
+ А2 cos 2nv0 0v ) cos 2nv0 0 + А2 sin 2 nv0 9 sin 2 nv0 0v =
+ А~] cos (2 nv0 0 - а).
(5.32)
= [А~+ 2 А 1 А2 cos 2 nv0 9v
азочувствительный приемник
112
принимает одну из составляющих
игнала, записанного во второй строке. Амплитуда принятого сиг
нала изменяется между А1 +А2 и А1-А 2 или между А 2 и -А2. Фа
зонечувствительный приемник определяет
записанного в третьей строке
(5.32).
+А2 и О.
амплитуду колебания,
Она изменяется между А 1
+
С точки зрения математики, причиной изменения амплитуд яв
яется то, что временной сдвиг 9v = n колебания cos 2nv 00 облада·
т таким же эффектом, что и амплитуда с противоположным зна
ом cos 2nvo(0-n) =-cos 2nvo0. Вероятно ,
лучше
использовать
другие функции, у которых не существует эквивалентности между
ременным сдвигом и инвертированием амплитуды, или это явле
ие наблюдается только при больших значениях е". Общее теоре·
'J'ическое исследование таких функций
является
математически
очень сложным. Однако очевидно, что суперпозиция сдвинутых во
времени продифференцированных функций Уолша
согласно рис.
2.29 не вызывает интерференции.
Более простое применение ортогональных функций для переда·
и через среду с замираниями следует из узкополосности системы,
ассмотренной в § 2.1, для телетайпной передачи. Сущность заклю·
. ается в следующем: разнесение · по частоте - хорошо известный
етод для улучшения передачи при наличии замираний. Сигналы
. модулируют несколько несущих. Из -за ограничений полосы частот
в основном можно применять не более двух-трех несущих. Узкая
олоса, необходимая для системы, рассмотренной в
§ 2.1,
дает воз
можность использовать десять и более несущих вместо двух или
трех без особых требований к полосе. Вопрос заключается в том,
целесообразно ли распределять фиксированную мощность JIЗ
сколько несущих.
195
lie·
1
~--" -. ~у~но сделать короткое замечание об известных результатах
передачи
с
разнесением,
прежде
чем
ответить
на
вышепоставл е li
иый вопрос. Пусть излучается гармоническое колебание с частот о й
Используя модель релеевских замираний, получим на входе при.
емника напряжение е (е):
vo.
= U (0) COS (2 1tV0 0 + а (0)J;
е (0)
(5.33)
и (0) есть медленно · изменяющаяся огибающая, которая практич е
ски постоянна на интервале 0o-(l/2)0k~0~Ho+
(l/2)0k
и котор а я
имеет распределение Релея с плотностью вероятности:
:и1 ехр(- ~).
и :;;i:. О;
1
w(u) =
·
62
11
u
1
О,
и<О;
равно математическому ожиданию
62 =
Фазовый угол
ct(6)
(5.34)
2)
E(s
согласно
(4.83):
<и2> = <и2(0)>.
(5.35)
также медленно меняется; он будет иметь рав
номерную плотность вероятности:
. 11n'
w(a)=
2
0
-n ..,.,;:
а<
-
а <.
31,
+ 1t;
а > + 31.
(5.36)
Для повышения надежности передачи нужно, чтобы принимались
две или более статистически независимых копий сигнала. Следо
вательно, совместная плотность вероятности амплитуд будет равна
произведению плотностей вероятности (5.34).
Известно несколько методов получения статистически независи
мых «копий» сигнала. Метод пространственного разнесения исполь
зует
несколько
антенн,
отстоящих
друг от
друга
на
достаточно
большом расстоянии. При методе углового разнесения копии сигна
ла получают с помощью направленных антенн с узким лучом. Две
антенны, . распознающие волны с правой и левой круговой поляри
зацией, дают независимые
копии
сигнала
в диапазоне
коротки х
волн. Метод частотно. го. разнесения использует несколько синусои
дальных несущих, а при временном разнесении сигнал передается
повторно.
После того как получено несколько независимых копий сигнала ,
встает задача наилучшего их использования. Существуют три ме
rода:
а) используется . копия, которая имеет наибольшую
среднюю
мощность в течение временного интервала 0k (оптимальная селекция);
•
б) все копии складываются (суммирование с одинаковым ве
сом);
в) все копии перед суммированием умножаются на коэффици
енты, которые зависят от средней мощности в интервале
(сум-
8'1ирование с максимальным отношением).
196
ek
'
' Для сравнения этих трех методов предположим, что используется
статистически независимых копий сигнала F ( 0). Пусть за счет
. ирания копия l из F(0) преобразуется в Gz(0). Выборка g,_ (0)
' лового шума складывается с G1(0). Поэтому в качестве копии
ринимается
0 1(0) + g,_ (0).
Н 1(0) =
(-0)
в течение короткого промежутка времени
.
(0) = Uz(00)cos{2n-y0 0
0"
1
+ а1(0));
можно предста
(5.33):
ть следующим уравнением согласно
:f
(5.37)
00 -2 011 ~ 0 ~ 00
1
+ 2011.
(5.38)
еличины и1 и а.1 считаем постоянными в интервале 0 0-(1/2)0.\~
10~00+ (l/2)0k·
.
Вероятность р(иz<иg) того, что и 1 меньше, чем порог Ug, или,
ругими словами, промежуток времени, на котором иz меньше, чем
, следует из (5.34) :
..
.
и
:и,<и1).
.
W(u,) =
г: ~Р(-
:
)dи = 1-ехр(-и2/б1).
(5.39)
" Пусть принимаются q статистически ,независимых копий сигна
а, имеющих одинаковые распределения. Величина рq(щ<иg) есть
роЯтность того, что амплитуды иz всех q копий меньше, чем ug:
pq(u 1 < ti1 ) = Wq(u,) = [1-ехр(-и;/б2 )]q.
·
(5.40)
редняя мощность копии Gz(0) за временной интервал длительно
ью 0н, который является кратным l/vo, находится из (5.38):
.
J
в.+вkJ2
G~(0)d0
в.-в"р
.
1
=2
и~(00)
1
= Р1(00)= 2
и~= Р,.
(5.41)
Пусть Рт означает среднюю мощность шума, принятого вместе
копией
l. Отношение сигнал/шум
P,/Pr = U'/2 Pr
(5.42)
пределяется в~личиной, ко~:орая изменяется только вследствие за
Вероятность того, что Р1 будет ниже порогового значения
, ираний.
, g, МОЖИО П?ЛУ,ЧИТЬ ИЗ
(5.39) И (5.42):
Р 1/Р, = !Pz/2 Pr < Pg/P, = uif2P,;_
)
W (Pg) = p(Pt!Pr < P,!Pr) = p(ui < Ug) = W (ug); ; (5.43)
W(P,) = 1-ехр(-.. и,/62) = 1-ехр(-2 Р,/6 ).
Пусть копия с наибольшим значением P1/Pr будет выбрана из
возможных копий. Вероятность того, что P1/Pr меньше, чем Pg/Pr
2
ля всех копий, находится из
езависимы:
W11 (P1 ) = (1
(5.40),
если все копии статистически
-ехр(-2
197
P,/62 )]q.
(5.44)
Математическое ожидание этого распределения вычислено Брэн.
наном:
/
2Р1"' =
"'-61/
s6
-
2Pt
2
q
00
dWq(P1)
= sqy(l - e-V)q-le-vdy = ~-1
/,Jt"
.
О
О
(5.45)
l=I
у= 2Р1/б2 •
Обозначим среднее значение отношения сигнал/шум каждой ко
пии через Р8 /Р, =
<Pi/P,> = <P1>!Pr.
Среднее значение отношения сигнал/шум лучшей копии получа-
ется с помощью зависимости
<Р 1>
= - 1 62 =
2
q
Psq/Pr = (Ps/P,) ~
l=I
Р8 :
+·
(5.46)
На рис. 5.9 (кривая а) показано отношение (Pвq/Pr)f(P,/Pr). Из
рисунка видно, что среднее значение отношения сигнал/шум возра
стает незначительно, если для оптимальной селекции используется
более чем: три или четыре копии.
Замена оптимальной селекции суммированием с одинаковым ве
сом q копий дает согласно Брэннану следующую зависимость:
P5 ,7/Pr = (Psf Pr) [1++n.(q-1)].
(5.47)
Отношение Psq/Pт становится теперь средним
отношением сиг
нал/шу:.~: суммы всех q копий сигнала.
Отношение (Psq/Pr)/(Pв/Pr) показано на рис. 5.9 (кривая 6).
Оптимальная селекция и су!\fмирование с одинаковым весом незна-
о од
о о
о
•
о
о
о
•
•
• •5
• •
....
•(/
Рис. 5.9.
Увеличение средиеrо
отношения cи r
l'aл/my111. при разнесенном nриеме по методу Врэ н нана:
q- число
Х ( Р,/Р,) -
принятых копий сигнала;
(P.qf P,) Х
среднее отношение
(сигнал/шум q
копий)/(среднее отношение сигнал/шум одной ко
г.ии); а) оптимальная селекция; б) суммирование
с равным весом; в) сум.мирование с максимадьным отношением
чительно отличаются, если используются две копии
ко суммирование с
сигнал/шум на
копиям.
4,5
одинаковым
( q= 2).
Одна
весом дает улучшение отношенин
дБ по сравнению с оптимальной селекцией, есл11
q= 10
198
В случае метода суммирования с максимальным отношением
плитуда копии
на временном интервале
l
й коэффициент, который пропорционален
ek умножается
на весо
среднеквадратичному
, ачению
копии сигнала l и обратно пропорционален среднеквадатичному значению шума этой копии. Брэннан получил следую
. ее выражение вместо (5.46) и (5.47):
PsqfPr = (Psf Pr)q,
(5.48)
е Psq/Pr теперь означает среднее отношение сигнал/шум взвешен
й суммы q копий сигнала.
Отношение (Psq/Pr)/(Ps/Pr) показано на рис. 5.9 (кривая в).
уммирование
при
максимальном
отношении
отчасти
лучше,
чем
ммирование с одинаковым весом. Для указанных на рис. 5.9 зна
ений q разница между ними меньше l дБ и приближается к
,05 дБ для бесконечного числа q.
· Среднее отношение сигнал/шум позволяет сравнивать различ
ые методы использования копий сигнала. Однако временной ин
ервал, в течение которого возможна
передача, является лучшей
ерой надежности линии связи. Уравнения (5.39) и (5.43) позво
яют получить эту меру. Первое уравнение дает временной интер
. ал,
в течение которого напряжение и1 ниже порогового уровня и 1,
торое
-
временной интервал, в течение которого среднее отноше
ие сигнал/шум P1/Pr ниже порогового Pg/Pr. Перепишем (5.43) с
четом введения медианы Р 1 =Рм, для которой W(P 1 )=l/2:
1
W(Рм) = Т = l -exp(-2Pм/fJ2 ).
(5.49)
тсюда следует:
2 Рмfб2 = ln 2 ~ 0,693;
2Рg/б2 = (Рg!Рм)
,
равнение
(5.43)
ln2
~ О,693Рg/Рм.
(5.50)
можно переписать:
W(P1)~l-exp(-0,693PgfPм)·
.
ероятность того, что
р(Р 1/Р,
еравенству
=
1.
P1/Pr
> Pg/P,) =
больше
Pg/Pr,
(5.51)
равна
1- W (Pg) ~ ехр(-0,693 PgfPм)·
p(P1/Pr>Pg/Pr)
соответствует
на рис.
5.10
(5.52)
кривая
Ордината показывает процент времени, в течение которого
1 больше, чем порог Pg. Здесь Р1 и Pg для нормировки разделены
а медианное значение Рм.
Е.сли принимается q копий , то из (5.44) получаем вероятность
ого, что P1/Pr больше, чем P1 /Pr, по крайней мере, для одной ко
ни: pq( Р1/Рт>Рg/Рт) ~ 1-{l-exp (-2 Pg/б 2 )]q.
Используя (5.50),
о уравнение можно переписать в виде
pq(P1/P,>P1/P,)
~ l-[I-exp(-0,693Pg/Pм)Jq.
ероятность pq(P1/Pт>Pg/Pr) показана на рис.
нями для
q=2,4
и
8.
5.10
(5.53)
сплошными ли
Эти кривые дают процент времени, в тече-
199
1Н1Ие кoroporo .вюз'М~0жна
9~99 ......-.--...-r-r........,r-т-т-т--т-~
'
99,9~~...i-::~41---11---+--+-~
ic
-
9!l51--1.:__i.-31o11.;...:..i~"-+\-.+--l--I
'91,о
~ся
l
80
50
-q
20J.-1---J-t--l--+-.:>J.1Mн~
<Z)
~U---1--1--1-~~~~l-I
О Ч
Pg fРн, i/Б
fZ 16
Рис.
с
--
Относительное время де,
·5.10.
течение
которого
мощность
·Превышает
сигнала
рог Р 1 /Ри;
q-чнсло принятых ко·
нии
-
штриховые
линии
-
.раз'Не~сеН1Ием,
и
~восьми
·КО'Пий
они nоказы-
'Времени,
если
су,м.м1ирова~н:ие
Pg/Pr.
нера3'11е·
сениый прием
5.3.2.
и1нтер1вал
Эти
с
~в
'l'е'Че
передач а
11ю1юльзует
од,юна11ЮВЫ:\!
.К'ри.вые .могут
1ра~с1С'Ч1Ит.аны
ли
С}"М№Ирование с .равным :весом;
штрих-пунктирные
дrву.
пий 1И есл·и требуется, чтобы от
Н()IШение Pi/ Р r было ·болЫIIе, че~1
по
пий сигнала; оплоIIl'!!ые линии .- опти
селеl!iция;
1с
1веоом ~вух, четьюрех :и восьми ·К:о
но>рма
яиаованного
мальная
четыр·ех
ние 11Ююроrо 1в·оЗJМ{)IЖ1На
ся
:в
селекция
Р g. Сл-едовательно,
1вают
8
1пер·едача
и.аоользу,е 1 .
6оJiьше, чем порооовое эна'Чение
D.5
н,iJJ.1-1--+--+--+--+--+--Н
i.0 -15-12 -8 -Ч
оптималыная
двух,
1u._--i..-1--1---i.-1~~~
1
если
1И если требуе'Гся, чтобы <УГноше
ние
Pi/Pr 1 было болыпе, 'Чем
Рg/Рм.
П)'iнктирными
линиями
на
.рис. 5.10 ~по.казан :процент аJреме
н1и, в течение кoroporo Pz су.м'Мы
60 Н--f.--1,--J->..~о'Нr-Нм-+--1
~
разнесением,
~мя, четырьмя и 11юсьмью копиям.и
90
~
1
для
q=2,
tНИЙ
q
с
!Помощью
быть
(4.95)
а для 1болЬ'Ших зна'Че
;молут быть
иопользованы
чис.леНJНЫ<е ·ыетоды.
Передача с разиесеиием пр• испоJIЬзоваив:и мв:ol'JIX копий
С1П'118J1а
Методы, рассмотренные в предыдущем разделе для получения
статистически независимых копий сигнала, обычно позволяют по
лучить только несколько копий. Поляризационное
разнесение не
может дать более двух копий. Пространственное и угловое разне
сение теоретически могут- дать много копий. Однако рассмотрение
стоимости
и
занимаемого
пространства
на
практике
ограничивает
это число. Например, в коротковолновом диапазоне при простран
ственном разнесении антенны должны быть разнесены на несколь
ко сотен метров. Единственными практическими методами получе
ния многих копий сигнала являются частотное и временное разне
сение.
Чтобы применить кривые рис.
разнесению,
лов,
в
то
нужно
время
помнить,
как
при
что
5.10
к частотному и временному
q
излучается
пространственном
и
одинаковых
угловом
сигна
разнес~нии
излучается только один сигнал. При заданной средней мощности
передачи средняя
мощность,
затрачиваемая
на
излучение сигнала,
меньше в l/q раз при частотном и временном разнесении по срав·
нению с пространственным и угловым разнесением. Этот недоста
ток частотного и временного разнесения, конечно, может быть уст
ранен. Вместо использования
q
антенн для приема в случае про-
200
анственного
и
углового
разнесения
можно использовать
антен
, с усилением, равным q. Это устраняет уменьшение мощности
· нала каждой копии.
' Пусть мощность передатчика и усиленце приемной антенны фи
. рованы. Замена обычной передачи (q= 1) на q-частотное разение дает улучшение,
только если сред·нее
значение
отношения
нал/шум на входе приемника увеличивается, несмотря на умень
, иие этого отношения для каждой копии в l/q раз. Уменьшение
l/q
едней мощности сигнала на копию в
раз уменьшает медиану
на рис. 5.10 до Рм/q. При заданном
/Рм становится равным qPg/Pм.
"
пороге Ря
отношение
При использовании q-частотного разнесения временной интер
л,
в
течение
которого
средняя
мощность
сигнала
превышает
g/Рм, должен быть больше, чем временной интервал, в течение
торого средняя мощность сигнала превышает Рg/Рм при обычной
· редаче. Рассмотрим пример: кривая q= l на рис. 5.10 дает Л0=
.· 95% при 10 log P8/Pм=-l l дБ, а кривые
для q=2 при 10 log
g/Рм=-8 дБ дают Л6=99 и99,3%. Следовательно, двойное разне
'
.
ние увеличивает время , в течение которого средня·я мощность сиг
ла больше, чем Р g, от
95
до
или
99
99,3 % .
Можно видеть, что
:акое улучшение возможно, если кривые q= l и q=2 отстоят друг
т друrа на расстоянии по горизонтали, по крайней мере, равном
О log q= l О log 2 ~ З дБ . Точками, обозначенными «3 дБ», пока
ано, где это расстояние равно 3 дБ. Очевидно, что двойное разне
ение при
суммировании с одинаковым
весом заслуживает внима
ия, если удовлетворительная работа возможна при более чем
ремени,
в
то
время
как
оптимальная
селекция
40%
заслуживает вни
ания только, если удовлетворительная работа возможна при бо-
ее чем
55 % времени.
· .:
На основании тех же рассуждений расстояние между кривыми
·= l
.
и q=4 должно быть, по крайней мере, равно 10 log 4~6 дБ,
между q= l и q=8 должно быть равно 10 log 8~9 дБ для то
. о, чтобы сделать разнесение с
. ания .
На рис.
5.1 О
q=4
q=8,
и
заслуживающим вни
точками с обозначением
азано, где эти расстояния равны
редставляет интерес только
6
в том
и
9
«6
дБ» и
«9
дБ» по
дБ. Оптимальная селекция
случае,
если
удовлетворитель
ая работа возможна, по крайней мере, при 70 или 80 % времени.
ри суммировании с одинаковым весом все три точки «3 дБ»,
:6 дБ» и «9 дБ» расположены на линии МЭ=40% . Частотное раз
есение при суммировании с одинаковым весом представляет инте
рес, если удовлетворительная
е, при
40%
работа возможна, по крайней ме
времени и является наилучшим с наибольшим числом
·копий.
В
жет
§ 2.1
рассматривалось, что определенная полоса частот мо
быть хорошо
использована
при
передаче
косинусоидальных импульсов. Согласно табл .
тайпных схем нужна полоса около
40
Гц. Для передачи
120
синусоидальных
2.3
Гц, для двенадцати схем-
с частотным разнесением с
· последних схем нужна полоса
2400
Гп.
и
для шести теле
q= 10
для этих
·
6.
СИНТЕЗ СИГНАЛА ДЛЯ ПОВЫШЕНИЯ
НАДЕЖНОСТИ СИСТЕМ СВЯЗИ
6.1.
ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
6.1.1.
Способы измереяия ширины полосы пропус.ка1111я
В самом начале развития теории связи было обнаружено, что во з
можная скорость передачи символов по каналу связи звисит от его
передаточной функции. Например, известные теоремы Найквистз
и Кюпфмюллера [2,3] показывают, что через идеальный фильтр
нижних частот с полосой пропускания Лf за интервал времени т
[I]
можно передать только один независимый символ, где
t=l/2Лf.
(6.1)
Скорость передачи символов в этом случае определяется
число ~~
1/'т: независимых символов, передаваемых в единицу времени
[4,5].
Шеннон принял во внимание, что возможная скорость передачи ин
формации зависит не только от передаточной функции канала, но
также и от статистических характеристик помех
{6, 7].
Он получи.~
формулу для возможной скорости передачи информации через иде
альный фильтр нижних частот при действии аддитивного теплового
шума:
(6.2)
где С- пропускная способность канала, например, в двоичных еди
ницах в секунду; Лf ширина полосы пропускания
идеального
фильтра нижних частот; Р/Р Лf - отношение (средняя мощность
сигнала)/ (средняя мощность шума в полосе O~f~Лf).
Для данного рассмотрения важно, что в выражение
же, как и в выражение
(6.2),
(6. l) так
входит полоса пропускания частот
Лf. Последовательная теория связи, основанная на полной системе
ортогональных функций, требует определения пропускной способ
ности канала связи, которое не было бы связано с понятием ча
стоты.
Во-первых, частота исключается из средней мощности шума Р ~f
в полосе частот O~f~M- Допустим, что шум, представленный нап
ряжением, подается через входное сопротивление 'Ra к интеграто·
ру, который интегрирует это напряжение на временном интервале
Лt. Всего выполняется l интегрирований. Будем обозначать выход-
202
е напряжение
интегратора в конце Л-го интегрирования
>
через
л. Для теплового шума среднее напряжение <Ил
равно ну
. . Среднее квадратичное отклонение от О, умноженное на lfR~ •
ь средняя
мощность и может характеризовать шум
так же,
как
д/:
l
<V~!Ra.>
Используя
(5. l)
1
= Jim [-+со l
'1 U~!Ra..
/.J
(6.3)
Л=l
этот результат можно обобщить. Пусть gл
§ 5.1,
(0)
есть напряжение, вызванное тепловым шумом на сопротив
нии 1Ra.· Будем использовать обозначение Ил (t) вместо gл (0).
ункции (j, 0) в этом уравнении заменим нормализованными на
яжениями И(j, t)/И, где И определяется из следующего выра
f
ения:
.. j'
r·
Т' /2
· 8/2
1
f(j,0)f(k,0)d0=ти 2
-8/2
Т'
И(j,t)U(k,t)dt=l; -=8.
•
-Т'/2
т
_
(6.4)
Используя обозначение И-~Uл (j), коэффициенты (5.l) предста
_ им нормализованными напряжениями. Тогда ур-ние (5.l) прини
ает следующий вид:
gл (0)
=
""
u- 1 и,.. (t) =~а,.. (j)f(i. 0) =
и-
i=O
~
L ил (j) и (j, t);
i=O
8/2
s
aл(j)=V- 1 Uл(j)=
2
g,..(0)f(j,0)d0=
т~
Т' /2
s Uл(t)U(j,t)dt.
-Т' /2
-8/2
(6.5)
Пусть напряжение U-IO л (t)И(j, t) прикладывается к интегра
ору и интегрируется от (-1/2) Т' до ( 1/2) Т'. Если постоянная
+
' ремени интегратора выбирается равной Т, то выходное напряже
ие в момент (l/2) Т' равно -Ил (j). Величину И2 л (j)/1Ra. с раз
ерностью
мощности
можно
получить
из
выходного
озведем Uл (t) из (6.5) в квадрат, разделим на
нтегрируем от (-1/2) Т' до ( 1/2) Т':
+S
Т' /2
и~ (t) R-;;
dt=
(0),
. ый
l
(6.6)
i=O
мощность выборки
шума
то правая часть должна иметь то же значение. Определен
член И2 л
оненты
о
и затем про
Е и~ (i)!Ra..
Так как левая часть есть средняя
л
напряжения.
со
1
-Т' /2
.
TR. а
(j)/Ra. в сумме представляет среднюю мощность ком
j (или f(j,6)] шумовой выборки g,.. (Н). Усредняя И2л (j)/.Ra.
реализациям шума
g,.. (0),
l
Р; = <V~ (j) R; 1> = lirn - '1 Uf (j) R~ 1 ,
1
1-+ао l
203
/.J
A=l
(6.7)
получаем среднюю мощность Pi компоненты j шумовой . выборки
мн шума. в случае теплового шума распределение ·Ил (J) одина
ково для любого j. Следовательно, безразлично, какую компоненту
усреднять. В этом случае · среднее по Л можно заменить 1 ) средним
по j. Более того, среднее т компонент в т раз больше среднего
значения одной компоненты:
т-1
(~ Иi(i)R; 1 /"'- = m<U~(j)R; 1 > = mPi.
"j,.J)
(6.8)
.
Значение Р 1 совершенно не зависит от ортогональной системы
{f(j, 0)}.
Умножение выборки шума gл (0) на функции ортогональ
ной системы {h(j, 0)}, которые имеют такой же интервал ортого
нальности, как функции f(j, 6), и которые можно разложить в ряд
согласно (5.3), дает напряжение U'л (j) вместо Ил (j). Однако из
(5.4)-(5.12) следует
<Щ.(j)R; 1 > =<V~ 2 (j)R; 1 >.
(6.9)
На этом заканчивается исследование, касающееся замены Р дf
(6.2).
в
Вернемся к замене Лf в том же уравнении другим парамет
ром, который не зависел бы от синусоидальных и косинусоидаль
ных функций. Предположим, что
m=2 l+ l
ортогональных функций
f(O, 0), fc(l, 0), fs(l, 0), "., ifc(l, .0 ), fs(l, 0) можно передать по ка
налу связи в течение интервала ортогональности 1/2~0~
Рассмотрим в качестве частного случая функции ряда Фурье:
f(0,0)=1;
1/2.
f8 (i,0)=Y2sin~2ni0; (6.10)
fc(i,0)=V2cos2ni0;
--2-~0~-21-; i=l" .. ,l; 0=t/T.
1
Эти синусоидальные и косинусоидальные элементы являются орто
нормированными в интервале -1/2~:0~1/2 и не определены вне
этого интервала. Произведем подстановку е' =0/5, как в § 1.2:
f (О, 0') = f (0/6, 0)
'
fc(i, 0') = 'V2coo2ni(0/6) = V2cos2n(i/6)0 = fc(i/6, 0);
fs(i, 0') = V2 sin2 ni(0/s) = y'2sin2 n(i/6)0 = fs (i/6, 0);
1
0' ~-;
1
1 't
0 ~1 ....
t
--~
---'ё~
2
2
2
1
(6 .l l)
2
При этом длительность интервала ортогональности увеличива
ется от 1 до
Число функций, передаваемых в единицу времени,
будет оставаться постоянным. В ~ раз большем интервале долж
но передаваться 5(21+ 1) функций. Индекс i пробегает значения от
1 до k, где k определяется уравнением
5.
(2z+
1)
1н=2k+ 1;
k=6(z +++
Это изменение во времени и усреднение по
удовлетворялась эргодическая гипотеза.
204
1126).
множеQ!'ву
(6.12)
требует, чтобы
Пусть
6 стремится
к бесконечности. Ограниченные во времени
инусоидальные и косинусоидальные элементы становятся периоди·
ескими синусоидальными и косинусоидальными функциями с ча-
тотами i/6=v=fT. Частота v принимает значения от v1 = 1/6 до
k=k/~, так как i принимает значения от l до k. Разность Vk-Vi.
бозн~чаемая как ширина полосы частот Лv, определяется выра·
ением:
1
Лv=ЛfT=lim(vk-v1 )=limk/~=(2l+ l);
!'.~ оо
!',-+оо
(6.13)
2
Лf = 2l + I = _I .!!!:_
2Т
2
(6.14)
Т'
де т/Т - число ортогональных функций, передаваемых за едини
у времени Т. Полоса пропускания Лv или .Лf является мерой чис
:ла k ортогональных синусоидальных или косинусоидальных элемен·
.
~тов, передаваемых в течение интервала ортогональности, если чи
~ сло элементов и их интервал ортогональности (-1/2)6~10~
(l/2H
стремятся к бесконечности. Согласно (6.14) можно
использовать
,отношение т/Т вместо параметра Лf, который яв л яется числом си·
. нусоидальных и косинусоидальных элементов, передаваемых за
:единицу времени Т .
.· Полоса частот Лf является только мерой числа синусоидальных
· и косинусоидальных функций,
которые могут быть переданы. С
стороны, отношение т/Т может быть интерпретировано как
. другой
· мера числа любы х ортогональных функций, которые можно пере
.; дать в единицу времени.
· понятия полосы частот.
Следовательно, т/Т является обобщением
Различие между Лf и т/Т заключается не только в том, что
является более общим понятием. Для теоретических исследо
. т/Т
: ваний часто затруднительным является то, что каждая функция за
' нимает бесконечную область частотно-временной плоскости. На
,: рис. 6.la заштрихованная область показывает часть частотно-вре
; менной плоскости, занимаемой функцией, которая отличается от Q
:·только в интервале t1~t~.f2. На рис. 6.16 показана область , кото
; рую занимает частотноограниченная функция, отличная от нуля в
· интервале t1~f~f2. Заштрихованные области могут быть сделаны
f
' конечными
только усечением их по некоторым значениям
или t,
~· так как нет функций, ограниченных одновременно во времени и по
" частоте .
В § 1.3 было показано, что существует класс функций , ограни
: ченных во времени и по частости. Поэтому заманчиво заменить ча
, статно-временную плоскость на частостно-временную. Но это неиз
: бежно приводит к отличию систем функций Уолша от других систем. Лучше ввести понятие « функционально-временной области:. .
Рассмотрим систему функций {f(j, 0)}, которые являются ортого
нальными в ограниченном интервале t 1 ~t~t 2 и равны О вне этого
интервала; j=O, 1, .." j 1, ••. , j2' .... Пусть сигналы будут составле
ны из функций с индексами j, принимающими значения от
до j,..
Согласно рис. 6 . lв время отложено по оси абсцисс, а значения j
i1
205
или j/T=j/(t2-t1)-пo оси ординат декартовой системы координат.
Рассмотренные сигналы занимают заштрихованную область этой
функционально-временной плоскости. Соответственно сигналы яв
ляются «функционально» и по времени ограниченными.
а)
Ь)
6)f
lll_ 't~t 11~
J,f
f
1
О t1
tz
t
О
О
t --
t1
tz
t
PRC. 6.1·. Частотно-временная область и фунюционально-'Временная область:
а) часть частотно-временной
области, зан11маемой ограниченным
во времени
сигналом; б) часть частотно-временной области, занИ'Маемой частотно-оr,раничен
ным сигналом; в) часть функционально-времен·ной области, занимаемой сигна
пом, ограниченным функцнонадьно и во в.ремени f2-f1=Лf; t2-i1=T; iz-(i1-l)=m
Исследуем связь между
функций
полосой
{f (О, 0), fc (i, 0), fs (i, 0)},
частот Лq> и т/Т.
i = 1,.", l; -
_l_
2
Система
~ 0 ~ ._!_
2
(6.15)
будет ортогональной, и число 2i будет равно числу пересечений ну
левого уровня на интервале ортогональности. Применим те же рас
суждения, что для синусоидальных и косинусоидальных элементов .
Снова получаем ур-ния (6.13) и (6.14), но нормализованную часто
ту v нужно заменить на нормализованную частость µ. Далее Лv
заменим на Лµ:
л µ = lim (µk- µi) = lim k/s =
/;-+СО
S_,.00
Лµ. = Л <р = 2l
Т
Из сравнения
+1=
2Т
1
2
(2l
+ l};
_1 .!!!:...
2 т·
(6.16)
(6.17)
(6.13) и (6.14) с (6.16) и (6.17) следует:
а) нормализованная полоса частот Лv
ций системы {
-
V2 cos
-
это мера числа функ-
2л:~, У2 sin 2л:vН}, которые можно пере
дать в течение интервала времени длительностью Т;
б) нормализованная полоса частостей Лµ это мера
функций более общей системы
{fc(µ, 0), fs(µ, '0 )},
числа
которые можно
передать в течение интервала времени длительностью Т;
в) полоса частот Лf =Лv/Т есть частный случай частостной по
лосы Лrр=Лµ/Т, а т/2 Тесть еще более общая мера полосы пропу
скания,
так
как она
применима
ко
всем
полным
системам
ортого·
нальных функций, включая те, для которых неприменимо понятие
частости. Величина т/2Т равна половине среднего числа функций,
передаваемых в единицу времени Т.
206
6.1.2.
Пропускная способность канала связи
Рассмотрим сигналы
Fх (е) , составленные из функций системы
f (О,
0), fc(i, 0), ifs(i, 0)}, ортогональных на интервале -1/2~6~
1/2:
"'
Fx (0) =ах (O)f (O, 0) + ~ [ асх (i)fc(i, 0) + asx (i)f 5 (i, 0)],
(6.18)
i=l
= l, 2, ...
усть Fл (е) передается по каналу связи. Предположим , что компо
ненты сигнала
f (О, 0), fc(i, 0)
и
при передаче претерпевают
fs(i, 0)
только затухание и запаздывание на время
фициенты затухания К(О),
и
Kc(i)
Ks(i)
6 (О). Используя коэф
1.3, для сигнала на
из§
входе приемника получим:
Fхв(0) = bx(O)f[O, 0-0(0)] + ~ { bcx(i)fc[i, 0-0(0))+
'1
+ b5 X(i)f 5 [i, 0-0(0)]};
(6.19)
j
Приемник будет определять,
какой из возможных
символов
Fl/J (0) был передан. Для решения будем использовать критерий
минимума среднеквадратичного
отклонения.
Опорные
сигнал1>1
. F'Фм (6) вырабатываются в приемнике. Они должны быть подобны
: принятым сигналам F хв (6). Это необходимо для определения то-.
го, какой из интегралов l(rф, х) является наименьшим:
/(Ч',х)=
е.+112
J [fxв(0)-fqrм(0)] d0,
2
(6.20)
80-1/2
чr
=
1,2, ... х .... ;
х.
=
Предположим , что опорные функции
,
будут точно равны
принятым сигналам:
F<JI M(0)
.
.
l, 2, ...
F хм (0)
= Fхв(0)
при Ч'
=
Х·
(6.21)
Тогда интеграл /(rф, "Ф) ра'Вен нулю. Интеграл /(-ф, х) при <ф=#х
должен отличаться от О, по крайней мере , на Л/. Минимальная ве
личина Л/ не может быть как угодно малой, так как только она
определяет различие. Из (6.19) и (6.20) вследствие ортонормаль
ности системы
{f(O, 0), fc(i, 0), fs(i, 0)}
1 ("Ф . х) = [ ьф (О)- ьх (0)]2
получаем
"'
+L
{[ bc·!,J (i)-bcx (i)]2 +
i=l
+ [ bs·J> (i)- Ь5х (i)]2} ~ Л /,
207
(6.22)
Рассмотрим те сигналы F 'lfi (О), которые ?тличаются. от F ФЕ
только одним из коэффициентов ах (О), асх (i} или asx(i); тогда
должно выполняться одно из следующих условии:
1
[ЬФ(О)-Ьх(О)] 2 :;;;,.Л1; .
[ ЬсФ (i) - Ь сх (i)]2 :;;;,. Л /;
[ ЬsФ ti) - bsx (i)]2 :;;;,. Л /.
Минимальные величины rЛа(О), Лас(i) и
,,1,.as(i),
(6.23)
на которые дол
жны отличаться коэффициенты двух передаваемых сигналов, нахо
дятся из
(6.19) и (6.23):
\ аФ (О)- ах (О)\ :;;;,. Л а (О) = (Л /)
1аСо/ (i) -
асх (i)\ :;;;,. Лас (i) = (Л
\ as·~ (i) - asx ( i)j
:;;;,. Л а 5 (i)
=
(Л
112
/
1
К (О);
112
/) / Кс (i);
112
/) / Ks
(6.24)
(i).
Пусть ах (О), асх, (ri) и asx(i) будут ограничены значениями +А и
-А. Число возможных коэффициентов тогда определяется величи·
нами Го, Гсi и Гвi:
r0
~ 2 АК (О)/(Л /) 112 +1; Гсt~ 2АК (i)/(Л/)
rst
~ 2 АК5(i)/(Л /)
112
112
+ 1;
+ 1.
(6.25)
Единицы в правых частях учитывают возможность того, что коэф·
фициенты могут иметь значения, равные нулю. В качестве го, rci и
Гsi нужно выбирать наибольшие целые числа, удовлетворяющие не
равенствам· (6.25). Если г 0 является нечетным, то допустимые зна
чения коэффициента ах(О) равны О, ±Ла(О), ±2да(О), ... ;при чет-
ном г0 они равны ±+Ла(О), ± : Ла(О), ....
Пусть
Kc(i)
при
i>lc
и
Ks(i)
при
i>ls
так малы, что справед
ливы следующие соотношения:
rci = 1 при
i
> lc;
Г 51
= 1
при
i > l 5•
Информация не может быть передана одной функцией
i>lc
или
fs(i, 0)
при
i>ls.
(6.26)
fc(i, 0)
при
Для упрощения положим
lc
= l5 = l,
(6.27)
tде l - граница полосы. Информация может быть передана за гра
ницей полосы, но другим способом. Для получения различных сиг
налов коэффициенты, по крайней мере, двух функций fc(i, 0) и
(или) fs(i, 0), i>l должны быть изменены. Этот вид передачи не
возможен, если затухание вне границы полосы пропускания увели
чивается так быстро, что условие
со
~ {[ bcф(i)-bcx(i)] 2
+ [ bsф(i)-b5<1-(i)] } <Л /
2
i=l+l
удовл~творяется для любой пары х и
208
'1J.
(6.28)
:
Число различимых сигналов, которые можно передать в тече
ние временного интервала длительностью Т, тогда определяется
l
" произведением ro П ГciГsi·
i=l
,;
,·
Количество информации, передаваемой в единицу времени, или
пропускная способность канала есть логарифм от этого произведения, деленный на Т:
'
С~+
[
lg r0
+
t.
Рассмотрим частный случай
·
;:
(lgr,1
(6.29).
+ lg r")]-
(6.29)
Из выражения
(6.25)
при
Го=Гсi=Гsi=Г следует: К(О) =Kc(i)=Ks(i), i=l, ... , l. Все функции
f(O, 0), fc(i, 0) и fs(i, 6), i~l затухают одинаково. Из (6.29) еле
дует
С=
2
l
+1
т
lgr.
(6.30)
,
Если используемая система функций является системой перио
дических синусоидальных и косинусоидальных функций, то можно
!
подставить .лf из
(6.14)
и получить
C=2Лflgr=Лflgr2 •
(6.31)
Эта формула имеет вид формулы Шеннона (6.2), хотя она введе
на из других предположений . В конце этого параграфа будет по
казано, что если сделать подобные предположения, что и при вы
воде (6.2), то
r
в (6.30) и (6.31) заменяется на (l+Р/Рл 1 ) 1 1 2 •
Рассмотрим сигналы Fx (0), составленные из r функций f(j, е).
Интервалом ортогональности является интервал -1/2~.0~1/2 или
(-1/2) T~t~ (1/2) Т:
r-1
Fx (0)
=
~ ar. (i)f (j, 0);
i=O
{f(j, 0)} = {f(O, 0), fc(i, 0), f5 (i, 0)};
r
=
2k
+ 1.
(б.32)
Интеграл от F~ (0) дает среднюю мощность сигнала:
р2х (0) d 0 = -т1
S
f 2 (t/T) dt = Р =
T/2r-1
J ~a~(j)f(j,
-Т/2/=0
.
i
,
х
х
-Т/2
-1/2
=-т
s
т 12
1/2
r-1
t/T)dt
= ~a~(j).
(6.33)
j=O
Вместо представления сигнала временной функцией
Fx (0)
мож
но использовть представление сигнала точкой в r-мерном декарто
вом сигнальном пространстве согласно § 2.1. Пусть единичные век
торы ej, j=O, ... , r-1 указывают направления r координатных осей.
209
Квадрат длины этих единичных векторов равен интегралу от квад
рата
f(j, 0):
т /2
1/2
Jf(j, 0)d0 = eJ =
J f (j, t/T) = Т =Те].
l;
(6.34)
-Т/2
-1/2
Сигнал представляется следующей суммой:
г-1
F х = ~ ах (j) ei.
(6.35)
i=O
Сигнал Fx записан в векторной форме и представляет определен
ную точку в r-мерном пространстве. Ее расстояние до начала коор
динат равно Dx:
г-1
Dx= [ Т~ a~(j)e]
]1/2 [
г-1
= T~a~(j)
J=O
Выборку теплового шума
]1/2
=(ТРх) 1 /2,
(6.36)
1=0
...
gл(0) = ~ aл(j)f(j, 0)
(6.37)
i=O
можно также представить вектором
"'
gл = ~ ал (j) ei.
(6.38)
i=O
Согласно (5.24) и (5.25) в выражениях (6.37) и (6.38) важны толь
ко r компонент f(j, 0) или ej, которые содержатся в сигнале. Сле
довательно, gл
(i0) делится на две составляющие:
g ~ (0) и g~ (0); составляющей g~ (О) можно пренебречь:
r-1
r-1
g~ (0)
=
g~ = ~ ал (j) ei; .
~ ал (j) f (j, 0);
i=O
j=O
со
g~ (0)
=
L ал (j) f (j, 0);
g~
= ~ ал (j) е1 •
j=r
Расстояние от точки
(6.39)
00
i=r
до начала координат равно D~:
g
D~ = [т ~
ai (j)]
J=O
112
(6.40)
Средняя мощность многих выборок шума g~ обозначается Рт, т; ин
дексы г и Т указывают число ортогональных составляющих выбор
ки шума и длительность интервала ортогональности:
l
pr т = lim
'
l-.oo
_1
l
210
r-1
~ ~ af (j).
iJ iJ
Л=lj=O
(6.41)
В § 5.1· при очень общих предположениях было показано, что
. распределение коэффициентов ал (j) одинаково для всех j, если
. gл (0) есть выборка теплового шума. Уравнение (6.41), таким об
разом, можно переписать в следующем виде:
l
Pr т
'
= lim
_!_~а~ (j) = r Р 1 т·
/--+<:<>
l /,J
'
(6.42)
i=I
Среднее значение по Л при фиксированном
ним значением по j при фиксированном Л:
j
можно заменить сред
l
Р т
lim _!_ ~ а~ (j).
/-+«> l /,J
=
r,
(6.43)
i=I
· Подстановка l = r дает
r
lirn Pr, т = lirn ~ а~ (j).
Г-+<:<>
Сравнение
r
(6.40)
и
Г-+<:<>
(6.44)
J=I
показывает, что при больших значениях
(6.44)
расстояния D~ от всех точек g~
до начала координат стремятся
к (ТРr,т)11 2 . Точки, представляющие тепловой
шум, размещаются
произвольно в сигнальном пространстве вблизи поверхности r-мер
ной сферы с радиусом (ТРr, т) 1 1 2 •
Средняя мощность
l
сигналов
Fх
получается из
l
l
(6.33):
r-1
1
Р = lirn~ Р = lim - 1 ~ ~ a 2 (j).
l--+'1>
l /,,j
'/(,
l
!-+<:<>
Если коэффициенты ах
всех
.
j
/,J
имеют одинаковое
(j)
(6.45)
'/(,
распределение
для
и если они статистически независимы, то это уравнение мож
но переписать:
1
Р = lim
/-+ао
_!__
l
1
а2
~ (j) = lirn _!__ ~ а 2 (j).
/,J '/(,
/-+rx>
l /,J '/(,
Подстановка
l= r
(6.46)
i=I
x=I
·
~
x=l i=O
x=I
дает
r
lim Р = lim ~ а~ (j).
Г-+СIО
Г-+СIО i..J
(6.47)
i=I
Сравнение с (6.36) показывает, что для больших значений r все
точки f x произвольно располагаются вблизи поверхности r-мер
ной сферы с радиусом (ТР) 112 •
Сигнал, смешанный с аддитивной выборкой шума g~, представ
ляется точкой
fх
+ g~ =
r-1
~ [ ах (j)
j=O
211
+ а1 (j)] ei.
Для
больших
r
значений
точки
F
+g~
,
х=
1, 2, ...
произвольно располагаются
х
-.!7F
вблизи поверхности сферы с радиусом r l (Р
r-1
lim Т ~ [ а (j) + ал (i)l2
t
r-"
Х
i..J
/=0
11/2
=
. -vr-+<»
Т (Р
= )1m
(
+ Pr, т) 1/2:
r-1
lim Т ~ [ а 2 (j) + а~ (j)]
~
r-<»
/=0
+ Рr,т)
1/2
11/2
Х
(6.48)
•
Можно однозначно решить, какой сигнал
f x содержится в ис
F х +g~. если расстояние между двумя любыми
точками, по крайней мере, равно 2(TPr, т) 112 Возмож
каженном сигнале
сигнальными
ное
число
точек,
имеющих
это
минимальное
расстояние
от
других
точек, равно возможному числу сигналов. Чтобы определить это
число, рассмотрим объем V r-мерной сферы с радиусом R. [6, 7]:
V
=
'J{/2
Rг
г(+r+
(6.49)
1) ·
Объем V в между двумя концентрическими сферами с радиусаl\lи
и R-в при больших значениях r стремится к объему V:
R
V11 =
1
12
12
{ 1{
r2r+l
)CRr-(R-вYJ= ( /t'
г
2
r-l
)Rг[1-(1-; )r]~v.
(6.50)
Следовательно, большая часть объема r-мерной сферы сосредото
чена вблизи ее поверхности. Хорошая оценка возможного числа
сигнальных точек получается делением объема сферы с радиусоl\1
lfT(P+Pr, т)
112
на объем сферы с радиусом (TPr, т/ 12 •
тr/2 (Р
+р
)r/2
_ _ _r_,т~ =(1
(TPr,т)l/2,
Каждый сигнал
1
С= limlg (1
т
r,T
)r/2 •
(6.51)
F х (10) имеет длительность Т. Таким образо~1.
предел скорости безошибочной
Г-+00
+Р!Р
передачи становится
+ P/Pr,т)r/
2
= lim _r_ (1
Г-+00 2Т
равным
+ Р/Рr,т).
(6.52)
Можно видеть, что r, которое является
числом
ортогональных
функций в сигнале Fx (е), должно стремиться к бесконечности. Ин
тервал ортогональности (-1/2) T~t~ (1/2) Т может быть конеч
ным или бесконечным. Отношение средней
мощности сигнала к
средней мощности шума P/Pr, т может быть также конечным или
бесконечным. Уравнение (6.44) показывает, что средняя мощность
шума Pr, т бесконечна при конечном Т; согласно (6.47) это также
верно для средней мощности сигнала Р. Если Т конечно и P/Pr, т
не равно нулю, то пропускная способность канала безгранично воз
растает.
212
'
Рассмотрим два частных случая ур-ния (6.52), для которых ин
тервал ортогональности стремится к бесконечности . Для первого
примера пусть используется
система
т ортогональных
функций
{if(j, 0)}, которые равны нулю вне интервала
(-l/2)kT'~t~
~(-l/2)kT'+T', где k=T/T' целое число. Далее рассмотрим
систему т ортогональных функций {1(j, 0-1)}, которые смещены
на -1 и имеют такую же форму, как функции f(j, 0). Эти функ
ции равны нулю вне интервала
(-l/2)kT'+Т'~,t~(-l/2)kT'+
+2Т'. Продолжим этот процесс до тех пор, пока не получим сис
тему функций {'f(j, 10-k+l)}, которые равны нулю вне интервала
(-l/2)kТ'-Т'~)~
(l/2)kT'.
Тогда общее число полученных орто
гональных функций равно:
тk =
r;
т,
k, r -
целые числа.
(6.53)
=
Множитель .r/2T в (6.52) становится
равным mk/2kT' т/2Т.
Средняя мощность шума Pr, т становится равной Рт, т., так как
только т функций не равны О в любом из k временных интерва
лов и так как Т' равно длительности интервала ортогональности.
Из выражения (6.52) получаем
С= lim .!!!!!._ lg ( 1 + Р/Рmk kT') =
k-~
2kT'
·
_!!!:..._ lg ( l
2Т'
+ Р/Рт · Т' )·
(6.54)
Вывод этой формулы показывает, что нет необходимости беско
нечно долго ждать, чтобы получить информацию о сигнале Fx (0).
Часть информации имеется в конце каждого из k временнь1х ин
тервалов.
'
В качестве второго примера рассмотрим m=2l+ l синусоидаль
ных и косинусоидальных элементов в интервале (-1/2) T~t~
~ ( 1/2) Т. Произведем растяжение этих элементов с помощью мно
'
жителя
'
k =
,
тоrональных функций в интервале (-l/2)GT~ ·t~
++ l/2s)
G> l,
6( l +
как в
§ 1.2.
Согласно
(6.12)
необходимо подставить
вместо l для того, чтобы поддерживать посто
янным число функций, передаваемых в единицу времени. Число ор
(l/2)GT
опреде
ляется выражением
r
=
2k
+l =
(2l
+ 1) s= т s.
(6.55)
Из (6.14) следует, что множитель r/2T в (6.52) заменяется на мно
житель . mG/2';T=m/2T=Лif. Средняя
мощность шума Pr, т заме
няется на Рт~. ~т . Так как сигналы занимают полосу частот О~
~f~M и все синусоидальные и косинусоидальные составляющие
выборок шума принимаются с частотами, расположенными в этой
полосе, то Рт;, ;т =Рдf· Таким образом, из (6.52) получается фор
мула Шеннона:
C=lim т~
;-"'
2~ т
lg(l +P/Pm ,p)=Лflg(l +Р!Рл 1 );
Лf =
+; ;
6
рт 6, 6Т = р Л f'
213
(6.56)
Некоторое внимание
должно быть уделено
интерпретации
ф-л
и (6.56) . Они справедливы для пере
дачи ортогональных функций с одной независимой временной пе
(6.30), (6.31), (6.52), (6.54)
ременной.
Это
соответствует
передаче
сигналов,
представляемых
напряжениями или токами. Электромагнитные волны, распростра
няющиеся в свободном пространстве в направлении z, также име
ют только одну независимую переменную
t,
но имеют два ортого
нальных направления для вектора поляризации, причем формулы
применимы к каждому из них. Однако при распространении волны
в волноводе в направлении z могут появляться в дополнение к t
независимые переменные х и у. Эти дополнительные степени сво
боды определяют тип колебаний и к каждому из них применимы
указанные выше формулы. Следовательно, формула Шеннона пока
зывает не только предел скорости, с которой можно передавать ин
формцию по каналу связи, но является средством поиска лучших
каналов. Уравнения (6.30) и (6.52) показывают, что число пере
даваемых ортогональных функций является главным фактором оп
ределения пропускной способности канала. Возможным способом
увеличения этого числа
является использование каналов,
щих сигналы, которые зависят от времени
и
передаю
пространственных ко
ординат. Для этих целей применяются оптические телескопы.
6.1.3.
Задержка и искажение сигнала
Для вывода формулы пропускной способности канала (6.29)
было сделано несколько предположений. В этом параграфе будет
исследовано влияние этих предложений .
Пусть компоненты 1
fc(i, 0) и fs(i, 0) в ф-ле (6.19) будут задер
живаться на время 0c(i) и 0s(i), а не на общее время задержки
0(0). Тогда функции в (6.19) не будут больше ортогональными и
е (О) не будет временной задержкой сигнала. Для более общего
определения временной задержки сигнала положим, что (О, 0),
fc(i, 0) и fs(i, 0) будут передаваться отдельно друг от друга. Соот
f
ветственно будут приниматься сигналы K(O),f{O, 0-0(0)], Kc(i)fJ.i,
0-0c(i)] и Ks(i}fl_i, 0-0s(i)]. Пусть они будут коррелироваться с
опорными сигналами f(O, 0),ifc(i, '0) и fs(i, 0). Временные разности ме
жду 0=0 и абсолютными
максимумами
взаимокорреляционных
функций дают задержки 0 (О), Oc(i) и 0s(i). Величины максимумов
дают коэффициенты ослабления К (О), Kc(i) и Ks(i). Используя
эти коэффициенты, можно построить опорную функцию
F ~м (0) из
fx(0) в выражении (6.18):
00
f~м(0) = K(O)ax(O)f(O, 0)
+ L fKc(i)ac x(i)fc(i, 0) +
1=1
+ K (i)a
5
x(i)f 5 (i, 0)].
5
(6.57)
Принятый сигнал fхн (0) имеет такой же вид, но 0 в правой части
уравнения
должно
быть
заменено
на
0~0(0), 0-0c(i)
или
0-0s(i) . Пусть взаимокорреляционная функция
214
s"' Fх Е (0) F~M (0 -
0') d 0 =
f (0')
(6.58)
-оа
принимает
абсолютный максимум при определенном
значении
=Нх. Это значение определяется как временная задержка или
0
как время распространения сигнала
Fx (0).
Так как на приемной
стороне неизвестно, какой сигнал приходит, то важно определить
время распространения независимо от Х· Например, если имеется
R
различных сигналов
Fx (0),
то можно усреднить значения 6х, что
*
бы ОПредеЛИТЬ ВреМЯ распростраНеНИЯ
0L:
R.
0L
=
~ 0Х.
(6.59)
x=I
Время распространения сигнала, несущего информацию, есть слу
чайная величина, которую в первом приближении можно сравнить
только с понятием групповой или сигнальной задержки, впервые
определенной в оптике [2].
Принятый сигнал Fхв ('0) имеет вид (6.Ы), если в правой части
уравнения 0. заменить на е-0(0), 0-<0c(i) и 0-·0s(i). Опорная
функция F хм (0) имеет такой же вид, но 0 в правой части уравне
ния нужно заменить на 0-0L. Пусть функции
е-0(0)], fc[i,
0-0c(i)] и fsf.i, 0-0s(i)] разложены в ряды по системе {.f (О, 6-0L),
rfo,
fc(i, 0-0L),fs(i, 0---<0L)}. По аналогии с (2.26) получаются следую
щие выражения, в которых v=0-0L, fo=.ff_O, 0-0(0)],
f с= fc [i, 0-0c(i)]
f0 =
fs = fs [i, 0- 05 (i)]:
и
"'
К (О, О) f (О, v) +~[К (О, ck) f с (k, v) + К (О, sk)f5 (k, v)];
k=I
"'
f с= К (ci, О) f (О, v) + \~
[К (ci, ck) fс (k, v)+K (ci, sk) f s (k, v)J;
/.,.j
(6.60)
k=l
fs = F (si, O)f (О, v)
"'
+ ~[К
(si, ck)fc (k,v) +К (si, sk) f
5
(k, v)].
k=l
Пусть эти ряды будут подставлены в формулу для Fхв
вый член F хв (0) им е ет следующий вид:
(.0) . Пер
{К (О)ах (О) К (О, О)+ t/Kc(i)acx (i) К (ci, О)+
+ Ks (i) а5 х (i) К (si, О)]} f (О, 0- 0L)·
Между коэффициентами существуют перекрестные
принципе, возможно построение
(6.61)
искажения. В
корректирующих цепей,
215
которые
компенсируют перекрестные искажения с точностью до измерения,
так что вместо (6.61) получается К(О)ах (O)f(O, 0-0L)· Тогда
Fхв (0) и Fхм (.0) тождественны.
В дальнейшем предположим, что f(O, 0), fc(i, 0) и fs(i, 0) не
только ослабляются и задерживаются при передаче, но также пре
терпевают линейные инвариантные во времени искажения. Функ
ции f(O, 0), fc(i,_ 0) и fs(i, 0) согласно § 2.2 трансформируются в
g(O, 0), gc(i, 0) и gs(i, 0). Пусть сигналы f (О; 0), fc(i, 6) и fs(i, 0)
передаются отдельно друг от друга. Вырабатываются функции кор
реляции принятых сигналов g(O, 0), gc(i, 0) и gs(i, 0) с опорными
сигналами f(O, 0), fc(O, 0) и fs(O, 0). Временной сдвиг между их
абсолютными максимумами и 0=0 дает задержки е(О), 0c(i) и
0s(i).
Значения максимума определяют коэффициенты ослабления
К(О)=К(О, О)
Kc(i)=K(ci, ci) и Ks(i)=K(si, si). С помощью этих
коэффициент~в можно построить опорные функции F ~м (0) из выражения (6.57). Уравнение (6.58) дает 0х, а (6.59) определяет вре
мя распространения 0L. Теперь пусть искаженные функции g (О, 0),
и gs(i, 0) разложены в ряды по системе {f(O, 0-0L), fc(i,
0-HL), fs(i, 0-0L)}. Получающиеся выражения формально такие
же, как и ур-ния (6.60), и к ним применимы те же выводьl.
gc(i, 0)
1
6.2.
ВЕРОЯТНОСТЬ ОШИБКИ
6.2.1.
Вероятность ошибки при воздействии тепловоrо шума
Рассмотрим передачу телетайпных символов при наличии теп
лового шума. Будет вычислена вероятность ошибки для несколь
ких методов передачи и обнаружения. Общий вид этих символов
представлен временньrми функциями:
4
Fx(0)=~ax(j)f(j,0), x=l,".,32, 0=t/T.
(6.62)
/=О
Функции f(j, 0) ортонормированы на интервале -1/2~0~1/2.
Т - длительность телетайпного символа,
которая равна обычно
100, 150 или 167 мс. Коэффициенты ах (j) имеют значения
1 и
+
или +а и -а для системы с активной паузой; для системы с
пассивной паузой они равны
1, О. Выборка аддитивного тепло
-1
вого шума gл
(0) преобразует
F (0) = F х (0) - gл (0);
+
символ
Fx (0)
в сигнал
F(0):
1
1/2
00
gл(0)= ~ aл(j)f(j, 0); ал(j) =
/=0
S gл(0)f(j, 0)d0;
-1/2
""
F (0) = ~а (j) f (j, 0); а (j) = ах (j) +ал (j).
/=0
21 f)
(6.63)
Нее символы в системе с активной паузой имеют одинаковую энер
гию. Используя критерий минимума среднеквадратичного откло
нения от опорной функции F 11' (0):
4
Fo/(0) =
L aч-(j)f(j, 0),
(6.64)
j=O
можно согласно
решить, при каком значении 'Ф сумма
(5.25)
4
L а (j) a<r (j)
(6.65}
j=O
принимает максимальное значение. Если максимум имеет место
при '\'=:х:, то все коэффициенты a(j) должны иметь такой же знак
i·
' как коэффициенты ах (j). Тогда сумма (6.65) имеет следующе~
4
значение: а~ la(i)
1.
ах (j) =+а или -а; x~'llJ. Если, например,
j=O
а (О)
имеет знак, противоположный ах (О), то сумма
больше для символа
~ (k) =llx, (k), k= 1, ..
'
_1
4
t1
a(i)a
а ~
.
(j) =
о/
Чтобы у
a(j)
Ffl (О) с коэффициентами
" 4, чем для Fx (0):
(6.65) будет
afl (О) =-ах (О),
{+ \а(О)\ + \a(l)\ + la(2)\ + la(З)I + /а(4)1,
- \а(О)\ +\а (1)\ + la(2)1 + [а(З)\ + \а(4)!,
и ах,
были разные знаки согласно
(j)
;р = fJ;
'\' = Х·
(6.63),
необхо
димо выполнить следующие условия:
а)
б)
lax (j)\ < /a:i. (j)j,
a;i_
sigп ах (j)
=f: sign a:i. (j);
(6.66)
что эквивалентно
(j)
1°х (i)I
>
1
или
: Здесь sign ах (j) означает езнак ах (j)».
,
В случае теплового шума вероя11Ность того, что величина a:i. (j)
: положительна, равна 1/2 и вероятность того, что она отрицательна,
; равна 1/2. Таким образом, вероятность выполнения условия а
равна 1/2 независимо от знака ах (j).
Для вычисления вероятности выполнения условйя 6 необходи
мо знать распределение х_= a;i. (j) / 1ах ( j) \. Так как коэффициент
, lZx, (j) может быть равен либо +а, либо -а, то 1ах (j) \-величина
постоянная. Поэтому х имеет такое же распределение, как и a;i. (j).
Функция плотности вероятности Wa (k, х) получается из (5.6) под
; становкой х вместо А. Из Wa (k, х) можно получить условную плот
·. ность вероятности w (х) при условии, что ,k= j. Вероятность того.
' что k примет значение одного из m=5 значений j, равна 1/т, так
как в случае теплового шума коэффициенты a;i. (j) 1Имеют одинако1
217
вое распределение для всех j. Таким образом, функцию плотности
вероятности w(x) можно получить из (5.6) и (4.5):
w(x) =
[
=
2
. -1 ~
11m
[-+оо
l
.
[
ал(/)
-2 11m
. -1 ~ ал2(")
/;
=а
1ах щ2
'J..=1
[-+00
х = ал (j)/lax (i)I
Каждый коэффициент ах
наковой энергией .
в
(j)
Таким
l
(6.67)
'J..=1
ал (j)/a,
=
(6.62) передается сигналом с оди
образом, средняя
мощность сигнала Р
равна
J
Т/2
Р = -Т
1
4
= ~
a 2 (j) = 5а2 •
/,,JX
F2 (0)dt
Х
i=O
-Т/2
Этот результат можно обобщить и решить относительно а 2 :
а2 = Р/т.
Уравнение
(6.42)
для
r=s= l
(6.68)
принимает вид
[
а~ (j) =<а~ (j)> Р 1 т·
1
lim - t1
[-+оо l 1.J
(6.69)
'
'J..=l
Среднеквадратичное отклонение становится равным
а~= тР 1 .т/Р
Рт,т!Р;
=
Рт,т = тР 1 .т,
(6.70)
где Рт. т - средняя мощность т ортогональных компонент тепло
вого шума на интервале ортогональности длительностью Т.
Используя (6.56), выражение для а~ можно переписать в виде:
а2 = Р
а
Лf
/Р· Лf
'
=
т/2Т
(6 •71)
•
где Р дf - средняя мощность теплового шума в полосе частот ши
риной Лf.
Вероятность р(х> 1) +р(х<-1) того, что х больше
l или
+
меньше
-1,
получается из
(6.67)
интегрированием:
00
p(x>l)+p(x<-1)=
=
1-
_
2
_
Y2Y:rtaa
Sexp(-x2/2a~)dx=
1
erf ( l/V2 аа) = 1 - er((Y PJ2P л,).
Вероятность Р1 того, что условия а и б из
становится равной
р1 =
+[
l -
erf (V Р;2Р лrН·
21 8
(6.66)
(6 .72)
выполняются,
(6.73)
Вероятность того, что условия
(6.66) не выполняются, равна l-p1,
=5
вероятность того, что они не выполняются ни для одного из т
коэффициентов ах (j), равна (l-р1)т; вероятность rого, что они
выполняются хотя бы для одного из т коэффициентов, равна Рт:
Рт= l-(l-P1)m = 1-(+Г
(1 +erf(VP/2PЛf)]m.
(6.74)
Вероятность ошибки Рт не зависит от используемой системы функ
ций U(j, Н)}, если эти функции удовлетворяют условиям § 5.11.
Для наиболее широко
с длительностью символа
m=5
Рис.
и Л
6.2.
f=
-
т
2Т
5
= 0,3
используемого телетайпного стандарта
150 мс применяют числовые значения
= 16,6
Гц. На рис.
6.2
(кривая а) для этих
Вероятность ошибки р при приеме
телетайпных
ств· ию
сигналов,
подверженных
аддитивного .теплового
дей-
шума:
'
Р/Р Лf -(средняя мощность ситнала)/(сред
няя
мощность
16,67
Гд);
шума
в
полосе
частот
а) система с активной паузой,
детектирование
производится
путем
'
v
"
l!JЬГЧИс
ления взаимной 'корреляпии; б) система с
активной паузой, фильтрация с помощью
идеального фильтра нижних частот с ча
стотой
отсечки 120 Гц,
детектирование с
помощью квантования, в) то же, что и (6),
но система с пассивной паузой; г) то же,
что и (в),
но при наличии ~тартстопной
синхронизации, лодверже<ННой влиянию шу-
'
1\1
\
а
.
-
\
t
,,.,6
\
\
о
,,
\
' .'
\
•
1r/1
G 6 16
'
12
\
tЧ
fjP11 ,,oБ
~мов
\
\
15 !8 20 ·22 211
-
значений т и i'1f показана зависимость Рт=Рs (6.Н) от отношения
Р/Р Л/- Экспериментальные точки а были получены для раннего
вар:ианта
оборудования, показанного
на рис. 2.7,
с системой
{f(j, 0)}, состоящей из синусоидальных и косинусоидальных им
пульсов согласно рис.
Пусть система
1.1.
{f(j, 0)} состоит из функций
f(j 0)= siпn(m0-j) =sinn(0'-j),
'
n(m0-j)
n(0'-j)
(
6.75)
j =0, 1,2, ... , m=5, 0=t/T, 0' =t/(T/m).
Уравнение (6.74) также применимо к этой системе. Энергия этих
функций концентрируется
в частотном диапазоне -l/2~v=
={Т/т~
1/2 с шириной полосы Лf=т/2Т= 16,6 Гц.
Согласно § 2.1 значения коэффициентов a(j) получаются оди
наковыми как в случае, когда F(0) умножается на функции (6.75)
и произведение интегрируется, так и в случае, когда F(0) пропу
скается через идеальный фильтр нижних частот с полосой 16,6 Гц
и подвергается дискретизации. Таким образом, (6.74) выполняется
и для фильтрации, и для дискретизации импульсов
(6 .75). Приме
120 Гц увеличивает сред
нюю мощность шума в (6.74) в 120/16,6~ 7,2 раза. Это означает
219
нение фильтра нижних чзстот с полосой
сдвиг кривой а (рис.
обозначена буквой 6.
6.2)
на
10 log 7,2~ 8,58
дБ: сдвинутая кривая
Рассмотрим систему с пассивной паузой. Коэффициенты: ах (j)
могут принимать значения +Ь или О вместо +а или -а. Чтобы
для коэффициента ах (j) получить значение Ь вместо О или О вме
сто Ь, должны выполняться следующие условия:
а) sign [ax(j)-+b]=Fsigna,_(j);
б) 1ах (j) -
+Ь < а,_
1
1
(6.76)
(j) 1
или, что то же самое,
.
а,_ (j)
{
lax(j)-Ь/21
> + 1;
<-1.
Член axUJ-_!_b может быть равным 1/2Ь или -1/26, так как
2
ау_
может
принимать значения +Ь или О.
Поэтому условия
и (6.67) являются одинаковыми, но +а и -а надо заме
нить на ( 1/2),Ь и (-1/2)Ь. Средняя мощность сигнала, состояще-
(j)
(6.66)
+
го из т коэффициентов со значениями + Ь и О, равна Р= f-ть 2 и,
следовательно,
(+ь/ =
(6.77)
PJ2m .
Сравнение (6.68) и (6.77) показывает, что для получения ур'ав
нений, справедливых для системы с пассивной паузой, необходи
мо в уравнениях, справедливых для системы с активной паузой,
Р заменить на (1/2) Р. Это означает сдвиг кривых а и б (рис. 6.2)
на 101og2 ~ 3 дБ . Сдвинутая кривая 6 обозначена через Ь . Резуль
таты измерений Ь получ~ны добавлением теплового шума к пря
моугольным импульсам телетайпных символов, после чего иска
женные сигналы были пропущены через фильтр нижних частот с
шириной полосы 120 Гц и поданы на вход телетайпного приемни
ка . Экспериментальные точки достаточно
хорошо согласуются с
кривой Ь, несмотря на то , что прямоугольные импульсы не имели
вид (6.79), фильтр нижних частот не был идеальным и магнит те
летайпного приемника лишь очень грубо можно считать квантова
телем амплитуды. Экспернментальные точки г относятся к той же
телетайпной передаче, но по каналу с шумами передавались старт
стопные импульсы для синхронизации.
Положение точек в и г
сильно зависит от обслуживания телетайпного приемника.
6.2.2.
Сиrиалы с ограниченной пиковой мощностью
Ранее предполагалось, что средняя мощность сигнала является
<>пределяющим фактором вероятности ошибки . Однако обычно уси
лители
мощности
ограничивают пиковую мощность,
220
а
не
среднюю
мощность. Рассмотрим усилитель, ограничивающий амплитуду на
' уровне ±Е и развивающий пиковую мощность РЕ. Средняя мощ
, ность Р и пиковая мощность РЕ сигнала, состоящего из двоичных
· прямоугольных импульсов с положительной и отрицательной ам
плитудами, равны. Вероятность ошибки р 1 из (6.73) для одного
' символа (рис. 6.3) показана как функция Р / Р лt =РЕ/ Р лt и обозна
. чена «ТеоретическИй пред~л».
Пусть эти импульсы модулируют по амплитуде несущую. Кри
вая «Теоретический предел» справедлива и при использовании не-
11,
9
7
11
/J ' 15
Pj~f.85 ~
Рис. 6.3.
Вероятность ошибки
р как функции РЕ/Рлt =(пи
ковая мощность сигнала)/(сре
. дняя
мощность шума в по.лосе
2
Pиc.
512
вал шириной
зана
синусоидальная
коэффициент
актив и ости
1;
пунктирные линии:
~:
синусных
синусных
процент
и
четыре
импульса,
ограничения
0,1.
Для
сравнения
плотность
ах (О), ах (i); Ьх (i) =
несущая,
0,2'5; 0,05;
· четыре
гауссова
пока
вероятности
с
тем же средним и диспер<:ией:
шириной
Лf=т/2Т).
Сплош
ные линии: временн6е разделе
ние,
F(fJ)-
Вероятность p[F(e)] амплитуд
сигналов F х (•0) попа<:ть в И'Нтер
6.4.
± I; Fx (0)
=
4
=ах (О) + у2
ко
I [ах (i)
cos 2n i 0
+
i=I
показан
+ Ьх (i) siп 2:rt i 0J
ампли
туды
сущей Уолша. Чтобы обеспечить
такую же среднюю мощность,
iПиковая мощность синусоидальной несущей должна быть на 3 дБ
• _ольше; кривая т/п= 1 (см. рис. 6.3) соответствует синусоидаль
ой несущей,
модулированной
по амплитуде двоичными прямо
гольными импульсами.
Только около четверти каналов телефонной многоканальной си
стемы занято в часы «ПИК». При испо.'Iь3овании прямоугольных
. импульсов с КИМ усилители загружены только в течение 1/4 вре
.
в то время как в течение 3/4 времени либо не передается ни-
221
каких сигналов, либо передаются не очень нужные сигналы. Что
бы получить среднюю мощность сигнала такой же величины, ка
кую мог бы обеспечить усилитель , если бы он усиливал сигналы
в течение всего времени, необходимо увеличить пиковую мощност ь
на 1Оlog4:::::: 6 дБ. Кривая для этого случая на рис. 6.3 обозначе
на m/n=0,25. Отношение т/п называется коэффициентом активно
сти, где т
-
число занятых каналов , а п
-
общее число каналов .
В наземных многоканальных станциях спутниковой связи ко
эффициенты активности очень малы, так как сумма коэффициен
тов акт1Ивности наземных станций равна коэффициенту активности
ретранслятора спутника. Кривая для этого случая на рис. 6.3 обо
значена т/п=О,05.
Рассмотрим передачу двоичной информации синусоидальными
и косинусоидальными импульсами или импульсами Уолша. Р е
зультирующие сигналы F(0) имеют очень большие пики, несмотря
на то , что все амплитуды имеют гораздо
меньшие значения, че ~r
пики. На рис.
6.4
показана вероятность того ,
имеет амплитуду в интервале шириной
сова
плотность
вероятности ,
0,1.
что такой сигна.'1
Там же показана га у с
имеющая то же среднее и
среднекв а
дратическое отклонение.
Согласно результатам, полученным в § 5.24, эта функция
плотности ' Вероятности очень точно аппроксимирует функцию ве
роятности
амплитуд
сигналов,
состоящих
из
суммы
Уолша . Для отрицательных значений F(0) график,
на рис . 6.4, продолжается симметрично.
Если передаются большие, но редкие пики , то
ность сигналов будет очень мала . Чтобы увеличить
ность сигнала, большие пики надо ограничить . На
тирными
линиями
синусоидальных
и
показан
результат
косинусоидальных
огранич е ния
импульсов
импульсов
изображенный
средняя мощ
среднюю мощ
рис . 6.3 пунк
амплитуды
при
наличии
дл я
ад
дитивного теплового шума. Параметры 0,64; 4,6; 13 и 32% пок а
зывают ограничение амплитуды в процентах. Кривые справедливы
для передачи без несуще;I или для передачи на несущей Уолш а .
Они приблизительно справедливы такж е и для отнополосной мо
дуляции синусоидальных несущих. Для импульсов Уолша пол у
чаются очень похожие кривые (1]. В результате ограничения сум
мы синусоидальных
и косинусоидальных импульсов
небольша я
часть энергии переходит !3 соседние частотные диапазоны [2], в то
время как в результате ограничения сумм импульсов Уолша эн ер
гия не переходит в соседние частостные диапазоны.
Из рис.
ная
6.3
передача
можно сделать следующие выводы: последовател ь
двоичных
г1рямоугольных
импульсов
шую вероятнос ть ошибок, если коэффициент
к
1.
дает
наимен ь
активности бли зок
Параллельная передача синусоидальных и косинусоидал ь н ых
импульсов или импульсов Уолша приводит к наименьшей вероя т
нос ти ошибок , если коэффициент активности равен 0,5 или меньш е.
Точное значение проце нта ограничения амплитуды некритично . Н э
рис .
5.8
пока з аны характеристики ограничителя и плотность в еро
ятности ограниченных
амплитуд с гауссовым распредел е нием
222
для
13%
ности
~
ограничения. Заметим, что уменьшение коэффициента актив
не
изменяет энергию
импульса
в случае
последовательной
передачи, в то время как в случае параллельной передачи средняя
энергия не будет изменяться и энергия импульса будет увеличи
ваться, если используется усилитель с автоматической регулиров
кой усиления.
Рут из
Technische Hochschule
Аасhеп показал, что рассмотрен
ные в § 5.2 компандеры с характеристикой, описываемой функци
ей ошибок, позволяют получить лучшие результаты, чем при огра
ничении, если вероятность ошибки ниже 10-5 •
Если прямоугольные импульсы заменить другими импульсами,
то при использовании последовательной передачи необходимо для
получения равной вероятности ошибки увеличить пиковую мощ
ность. В табл. 6.1 показано увеличение ЛРЕ, требуемое для неко-
Таблиц а
6.1
Увеличение пиково~i мощности ЛРЕ сигнала по сравнению с пиковой мощностью
прямоугольного импульса для получения одинаковой вероятности ошибки
Л Рв ,дБ
Форма импульса
Прямоугольный импульс при прямой передаче
Е для О<
< Т/п, О- вне интервала
(без несущей),
t
Приподнятый косинусоидаJIЬный импульс в
частотной области
коэффициент крутизны характернстнкн фильтра
То же,
»
о
r= 1
1,8
2,7
4,1
r = 0,75
r =0,5
Приподнятый косинусоидаJIЬный импульс во временной
ти, рис. 2,15
Треугольный импульс, Е
облас-
1,2
+
( 1 nt /Т) , - Т /п < t < О
E(1-nt/T), O<i<T/n
1,8
торых типичных форм импульсов. Для получения кривых, соответ
ствующих этим формам импульсов, сплошные кривые (рис. 6.3)
надо сдвинуть вправо на ЛРЕ.
«Приподнятый косинусоидальный
импульс» в частотной области определяется уравнением
f (t!T) =
Е siп л nt/T
л nt/T
cos л rnt/T
1 - (2rnt/T)З
r-
есть так называемый коэффициент крутизны характеристики
фильтра нижних частот, используемого для образования импуль
са {3]; п - число каналоЕ и Т/п - длительность прямоугольного
импульса,
если
п
таких
импульсов
мени Т.
223
надо
передать
в
течение
вре
6.2.3.
Импульсные помехи
Вероятность ошибки цифровых сигналов не зависит от вида си
стемы ортогональных функций, используемых для передачи, если
помехи вызваны аддитивным тепловым шумом. Для импульсных
помех, которые более важны при использовании телефонных ли
ний, чем тепловой шум, это утверждение неверно.
Предположим, что амплитуда импульса помехи много больше
наибольшей амплитуды
неискаженного сигнала.
Пусть эти им
пульсы проходят амплитудный ограничитель. Если время нара
стания
и
время
спада
импульсов достаточно
малы,
то
на
выходе
получим прямоугольные импульсы разной длительности, но с оди
наковой амплитудой. Будем наблюдать эти импульсы за R времен
ных интервалов длительностью Т; пусть в lf' интервалах будет по
одному импульсу. Если r и
ятность
появления
!R достаточно
импульса
в
течение
велики, то 'Г/R есть веро
интервала
длительностью
Т. При стремлении r н R к бесконечности для r/R. ,можно записать
W1(T), где W1(T) - функция распределения появления импульса .
Будем определять длительность импульсов Лтs и пусть q из Q
импульсов имеют длительность ,Лтs~т,.
Предел отношения q/Q
при стремлении q и Q к бесконечности обозначим через W2(тs).
Это есть функция распределения д.~шн импульсов .
. Предположим, что моменты появления и длительность импуль
сов статистически независимы. Функцию совместного р_аспределе
ния
W(T,
тs) тогда можно представить в виде произведения
W (Т,
т,)
= W1 (Т) W 2 (т,).
(6.78)
Если не выполняется ус.1овие статистической независимости, то
W (Т, тs) нельзя определить путем раздельного измерения W1 (Т) и
W2(тs). В этом случае требуется не
R+Q,
а
1RQ
изм~рений.
Функция распределения W(T, тs) применяется, когда на интер
вале длительностью Т появляется один импульс. Если появляется
большее число импульсов, вычисления сильно усложняются. По
этому далее предполагается, что появление более одного импуль
са в течение этого интервала происходит очень редко.
Обозначим через р вероятность того, что
стью Т искажается импульсом длительностью
степени, что происходит ошибка. Вероятность
вии, что принят импульс длительностью Лтs~Тs,
Рь =
p(t
<
Р
Т, Лтs:::;;
'ts)
сигнал длительно
Лтs~'ts до такой
ошибки при усло
равна:
; р (t ~ Т, Лт, ~ 't's) = W (Т, i-,).
(6.79)
Условную вероятность рь
можно вычислить для различных
форм импульсов и методов обнаружения. Если W (Т, 't's) известна
из измерений, то р можно вычислить.
Знание рь достаточно для
сравнения
помехоустойчивости различных форм импульсов и ме
тодов обнаружения.
Предположим, что передаваемый символ состоит из т прямо
уrолыных импульсов, как показано на рис.
224
1.3 для т = 5. Каждый
·;импульс имеет длительноf:ть Т/т. Положительное или отрицатель
ное значение амплитуды определяется с помощью отсчетов значе
ний сигнала. Импульс помехи длительностью Лт:8 ;;:::. Т/т вызывает
.· ошибку с вероятностью рь;;:::. l/2, так как половина помеховых им
. пульсов
меняет знак, по крайней мере, одной из т квантованных
амплитуд. С возрастанием Лт:в в интервале О~~Л.т:8 ~Т/т вероят
ность рь линейно возрастает,
'
вая
как это показано на рис.
6.5
(кри
1).
Пусть теперь знак ампдитуды прямоугольного импульса опре
деляется взаимной корреляцией. Это означает, что дискретизации
подверrается напряжение на выходе интегратора. Если неискажен
. ный сигнал
·. го сигнала
имеет амплитуду +а или -а, то амплитуды принято
можно ограничить на уровне +а и- -а. Импульс по
мехи с положительной
а:'dплитудой, наложенный на сигнальный
импульс с амплитудой +а, будет подавлен полностью. С другой
: стороны, амплитуда отрицательного импульса помехи будет огра
, ничена на уровне -2а, так как а-2а=-а. Это есть наименьшая
·· амплитуда, которую пропустит ограничитель. В среднем половина
импульсов помехи имеет амплитуду +2а,
а половина - -2а, в
противном случае на выходе будет нулевая амплитуда. Если дли
тельность импульса помехи Лтs так мала, что выполняются следу
ющие соотношения:
2аЛт 5 <аТ/т;
Лт5
(6.80)
<T/2m,
то ошибки не произойдет.
При выполнении услоnия
аТ/т
условная
< 2аЛт5 < 2аТ/т
вероятность
или Т/2т
< Л't'5 < Т/т
рь зависит от времени
появления
(6.81)
импульса
помехи. При Лтs = Т/'lт Рь скачком увеличиваетсSJ: от О до
1/4
и
линейно растет до l/2 для больших значений Лтs. как показано на
рис. 6.5 (кривая 2). При Лт= Т/2т существует сильный пороговый
эффект.
Рассмотрим передачу символов, составленных из т функций
Уолша. Пусть каждая функция имеет амплитуду +а/т или -а/т.
Наибольшая и наименьшая амплитуды
суммы т таких функций
равны +а и -а. Поэтому амплитудный ограничитель может иметь
порог ограничения на уровне +а и -а, не изменяя неискаженный
.
сигнал.
Пусть т
будет степенью
2. Если в некоторый момент m-k
k функций имеют ам
то сигнал имеет амплитуду ak:
ak=(l-2k/m)a, k=O, l, .. . ,т.
(6.82)
функций Уолша имеют амплитуду +а/т и
плитуду -а/т,
Вероятность появления
ak
обозначим через r(k):
r(k) =
8-322
2-m(:).
225
(6.83)
После амплитудного ограничения
импульса помехи
bk,
на уровнях
±а амплитуда
наложенного на амплитуду_ сигнала а11, мо
жет принимать одно из двух значений:
bk
= a-(l -2k/m)a = 2ka/m
(6.84)
или
bk = -a-(l-2k/m)a = -2(1-k/m)a.
(6.85)
Вероятность r.(k) того, что амплитуда bk принимает значение ме
жду -2а и + 2а, получается из (6.83):
=
r 5 (k)
+
2-т(:).
(6.86)
На рис. 6.6 в качестве примера показана вероятность r.(k) для
После амплитудного ограничения как положительные, так
m=8.
и
отрицательные
импульсы
помехи
имеют
распределение
Бер
нулли.
Взаимная корреляция бинарного сигнала
из импульсов Уолша wal(i, 0).
F х (0),
составленного
т-1
}J ах (j) wal (j;
F х (0) = :
ах (j) = ±
0),
1,
i-0
дает
Т/2
ат
1
т
т
S F (0)wal(l, 0)dt=-, 0=-, l=O, .. ·,
х
т-
1. (6.87)
-Т/2
Согласно (6.84) и (6.85) абсолютное значение амплитуды импуль
са помехи не может быть больше 2а и, если его длительность Л't.
так мала, что выполняется условие 2aЛ'ts<aT/m, ошибки не воз0,J
никает. Поэтому рь=О для -
Л'ts
0:1
т
<- .
(6.88)
2т
Это •оовшадает ioo З1начением для п:ря1мо
уrольных импульсо.в.
/
Вычисление
усло-вНJой
~вероятности
~ошибки Рь при наличиш .И!м1ПульсО1в !Поме
/
о
0,2
о.~
o,r
о.а
1,0
и5 /(Т/тJРис. 6:5. Вероятность рь
ошибки,
возникающей
нз-за
помехового
11Iульса
им-
длительностью
·Л-t./(Т/т):
1-
прямоугольные
сы (рис .
2-
1.3),
дискретизация;
пульсы
корреляци я;
Уолша,
ко [6]. Результат выч1исленттй 1пр~иrведен
' На рис. 6.5 (-кривая 3). Вер-оят.ность ошиб
;к1и
нем1ного
1ных
ниже,
импульсов ,
и
чем
для
1и.м~еет
пр-я1моуголь-
1нrеоК'Олы1ю
rпо
рогов.
Лучшие ~результаты · м-ожно 1п1Олучить,
нм пуль
те же прямоугольные им
пульсы,
хи ·большой дл1итель~оости оч·ень 1[1ромозд
3 - им
корреляция
если си:nнал, соста1вленный из импульсов
Уолrша ~или оину:еоидальных 1и кос:инусо
идальных
226
1и1мпульо0tв,
.оnра1ничен
ffIO
ам-
·iПлиту,де в лере~д.атчи1Ке, ~ак это 1ра.ссмо111>ено ·в § 6.2, та~к ка/К ам
ашитудный ограничитель 1в прием1ни:к1е может работать l!IO более
НИЗКИМ урОВНЯiМ.
6.3.
КОДИРОВАНИЕ
6.3.1.
В
§ 2.1
был рассмотре:r вопрос о представлении сигнала функ
цией времени
ax.(j).
Кодироваяие двоичными элементами
Набор из
Fx
(О), вектором
R различных
Fx
или набором
коэффициентов
сигналов называется алфавитом. Оп
_ределенная функция Fx (О) называется символом алфавита. Здесь
будут рассмотрены некоторые задачи построения символов, для
. которых
ортогональность
можно
использовать
Воздействие помехи на символ
как
преимущество.
может привести к неправиль
ному распознаванию ~имвола. На приемной стороне для опреде
. ленного типа помех вероятность этого события можно уменьшить
с помощью соответствующего выбора Я символов алфавита. Ниже
будут исследованы некоторые методы правильного выбора. Пусть
символов представлены т коэффициентами:
R
a(O)·a(l)
...'
Х.
'
Х.
'
а(т-1)·"'=1
Х
' А
'
.. ·R
t
•
(6.89)
Такие алфавиты называются блочными кодами. Используя систе
му функций {>f(j, О)}, ортогональных на интервале -1/2~0~ 1/2,
получим представление с помощью временных функций:
т-1
(6.90)
В общем случае сигнал на входе приемника может быть пере
·менной во времени напряженностью электриче~кого или магнитно
го поля, либо переменным
во времени напряжением или током.
При отыскании алфавитов, обеспечивающих низкую вероятность
ошибки, предпочтительнее использовать временное представление.
Однако в § 5.1 было показано, что функция f(j, 0) нечщест_венны
и только коэффициенты ах. (j) определяют вероятность ошибки при
· наличии аддитивного теплового шума. Разные
{f(j, 0)}
также
требуют для передачи разные
и трудности генерирования
системы
функций
полосы частот, различны
и распознавания, но они не вли
яют на вероятность ошибки. В этом частном случае символы мож
но представлять коэффициентами ах (j).
Дальнейшего упрощения
можно добиться ограничением коли
чества значений коэффициентов ах
обозначаются
+1 и
-1
или
1
(j)
до двух, которые обычно
и О. Часто делают дополнительное
предположение, что помеха либо не изменяет коэффициент, либо
меняет его значение
на другое разрешенное.
Это означает, что
символ с коэффициентами ах. (О)=+ 1 и ах.(1) =
1, записанный в
+
краткой форме как
одну из четырех
8*
+ 1+1, может быть изменен помехой
форм +1+1, +t-1, -1+1 или -1-1,
227
только в
а не, на-
пример, в
+ 1/4+ 1/2.
В
§ 5.2 было показано,
что коэффициент
ах (j) изменяется помехой
в коэффициент a(j),
который может
принимать любое
значенRе, даже если ах (j)
принимает только
. значения +1 или -1. Есть целый ряд причин, по которым часто
для a(j) являются разрешенными только значения
1 или -1.
В начале развития теории кодирования обычно предполагалось,
что функциями (j, 0) являются прямоугольные импульсы, декоди
рование которых производится квантованием по амплитуде. Поло
+
f
+
жительная амплитуда принималась за
l, а отрицательная за -1.
Это квантование изменяет суммы в (5.24) и (5.25) и в общем случае увеличивает вероятность ошибки.
·
Помехи, отличные от аддитивного теплового шума, требуют, в
принципе, исследования их влияния на функции времени F х (0), а
не на коэффициенты ах (j). В предыдущем параграфе было пока
зано, что влияние импульсных помех зависит
от вида функций
f(j, 0) и от порога ограничения. Несмотря на эти результаты, обыч
но рассматривают тольк~ коэффициенты кодовых алфавитов, ко
торые выбираются с учетом устойчивости к импульсным помехам,
и
различают
только
положительные
и
отрицательные
значения
коэффициентов. Это объясняется требованиями к простоте обору
дования и совместимости с существующей аппаратурой.
Теория кодирования двоичными элементами основана на пред
положении, что неискаженные коэффициенты ах (j) так же, как и
искаженные коэффициенты a(j), могут принимать значения только
1 и -1 или 1 и О. В этом случае коэффициенты ах ( j) и а (j)
обычно называют элементами. Алфавиты, состоящие из символ ов
+
с равным числом элементов, называются двоичными блочными ал
фавитами и.Ли двоичными блочными кодами. Так как неискажен
ные и искаженные символы содержат только элементы
1 и -1,
то их можно считать двоцчными числами. Тогда для решения за
+
дач
кодирования
к двоичным
можно использовать теорию
числам.
чисел
Бинарное кодирова· ние
в применении
рассматривалось в
большом числе работ, начиная с Хэмминга [1-5]. Хорошее обоб
щеаие дано в книге Питерсона [6, 7]. Небинарные алфавиты так
же рассматривались с применением теории чисел {8, 9].
Значение кодового алфавита для связи зависит от той вероят
ности ошибки, которая 'dожет быть достигнута. Очень часто вы
числение этой вероятности ошибки затруднено. Поэтому для оцен
ки качества алфавита в теории кодирqвания двоичными элемен
тами обычно используют понятие «хэммингово расстояние». Оно
обозначает число двоичных элементов, в которых различаются два
символа. Например, символы
+ 1+1+1+1+1
и
+ 1+1+l+1-1
· или 11111 и 1111 О имеют хэммингово расстояние 1. Вероятность
декодирования искаженного символа х в символ 'Ф обычно умень
шается с увеличением
волами. Рассмотрим,
хэммингова
расстояния
например, символы,
между
этими сим
состоящие из
последо
вательности прямоугольных импульсов. Чем больше число импуль
сов, в которых символы различаются, тем большим может бы т ь
число импульсов,
подвергнутых искажению,
без возникновения
228
Особенно полезно хэммингово расстояние, когда ограни
ена пиковая мощность, а не энергия сигнала.
Следующий пример показывает, что большое хэммингово рас
тояние необязательно означает низкую вероятность ошибки. Из
. элементов
1 или -1 можно составить 2m символов. Мини
. альное хэммингово расстояние d между двумя символами рав· о 1. Можно увеличить d, составляя 2m символов из m'>m эле
. ентов . Если количество энергии, приходящейся на один элемент,
+
тавлять
постоянным,
то
энергия
каждого
переданного
символа
величится в т'/т раз. Уменьшение вероятности ошибки частично
остигается выбором символов и частично за счет увеличения их
нергии . Часто удобно сравнивать два алфавита при равной энер
ии символов или при равной их средней энергии. Тогда символ
. m'>m
элементами содержит в т/т' раз меньшуIQ энергию, при
одящуюся на один элемент. Таким образом, хэммингово расстоя
ие увеличивается, но вероятность ошибки на один элемент так
. е увеличивается, если , например, ошибки вызваны аддитивным
епловым шумом. Поэтому нельзя без вычислений сказать, какой
ффект превалирует.
Примером уменьшения вероятности ошибки при действии ад
итивного
теплового
шума
путем
увеличения
наименьшего
рас
тояния Хэмминга могут с.JJужить алфавиты с одной проверкой на
етность . Рассмотрим 2m 32 символа телетайпного алфавита:
=
1. 1111 1
2. 111!-1
(6.91)
3. 111-1 1
4. 111-1-1
т.
д.
Минимальное хэммингово расстояние · равно l. Будем добав
.
ять ко
всем
очную цифру
символам,
+1
и
- 1
имеющим
нечетное
число
единиц ,
прове
ко всем символам , имеющим четное чис
о единиц:
1. 111111
2. 1111~1-l
3. 111-11-1
4. 111-1-11
~ т. д.
Таким образом, минимальное
·
(6.92)
хэммингово расстояние увеличе-
о до двух. Энергию на один элемент надо уменьшить в 5/6 раза
~ли в общем случае в т/т+ 1 раз . При больших значениях т ко
, ффиц'иент т/т+ 1 стремится к единице, в то время как хэмм~ш
гово расстояние удваивается .
Наим еньшее хэммингово расстояние между символами алфа
вита может быть сделано равным 3, 4, .. " в общем случае d до
. бавлением произвольного количества проверочных цифр. Эти ал-
229
Таблиц а
6.2
l(оэффнциенты а (j) симво.1ов алфавита (16,5) соrласно Р1щу-Мюллеру,
х=
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
+1
-1
-1
+1
+1
-1
-1
+1
+1
-1
-1
+1
+1
-1
-1
+1
-1
+1
+1
-1
-1
+1
+ 1
-1
-1
+1
+1
-1
-1
+1
+1
-1
+1
-1
-1
+1
+1
-1
-1
+1
-1
+1
+1
-1
-1
+1
+1
-1
+1
-1
-1
+1
+1
-1
-1
+1
-1
+1
+1
-1
-1
+1
+1
-1
+1
-1
-1
+1
-1
+1
+1
-1
-1
+1
+1
-1
+1
-1
-1
+1
-1
+1
+1
-1
+1
-1
-1
+1
+ 1
-1
-1
+ 1
-1
+1
+1
-1
3
+1
-1
-1
+1
-1
+1
+1
-1
+1
-1
-1
+1
-1
+1
+1
-1
+1
-1
-1
+1
-1
+1
+ 1
-1
+ 1
-1
-1
+ 1
-1
+1
+1
-1
4
+1
-1
+1
-1
-1
+1
-1
+1
+1
-1
+1
-1
-1
+1
-1
+1
-1
+1
-1
+1
+1
-1
+1
-1
-1
+1
-1
+1
+1
-1
+1
-1
1, ... , 32, j=O, ... , 15
5
+1
-1
+1
-1
-1
+1
-1
+1
-1
+1
-1
+1
+1
-1
+1
-1
+1
-1
+1
-1
-1
+1
-1
+1
-1
+1
-1
+ 1
+1
-1
+1
-1
6
7
+1
-1
+1
-1
+1
-1
+1
-1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
+ 1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+ 1
-1
+ 1
-1
+1
-1
+1
-1
+1
-1
230
8
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
+1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
9
+1
+1
+1
+1
+1
+1
+1
+1
·-1
-1
-1
-1
-1
-1
-1
-1
+1
+1
+1
+1
+1
+1
+ 1
+1
-1
-1
-1
-1
-1
-1
-1
-1
10
11
12
13
14
15
+1
+1
+1
+1
-1
-1
-1
-1
-1
-1
-1
-1
+1
+1
+1
-1
-1
-1
-1
-1
+1
+1
+ 1
+1
+ 1
+1
+1
+ 1
-1
-1
-1
-1
+1
+1
+1
+1
-1
-1
-1
-1
+1
+1
+1
+1
-1
-1
-1
-1
+1
+1
+1
+1
-1
-1
-1
-1
+ 1
+1
+1
+ 1
-1
-1
-1
-1
+1
+1
-1
-1
-1
-1
+1
+1
+1
+1
-1
-1
-1
-1
+1
+1
-1
-1
+1
+1
+1
+1
-1
-1
-1
-1
+1
+ 1
+1
+1
-1
-1
+1
+1
-1
-1
-1
-1
+1
+1
-1
-1
+1
+1
+1
+1
-1
-1
+1
+1
-1
-1
-1
-1
+ 1
+1
-1
-1
+1
+ 1
+1
+1
-1
-1
+1 +1
+1 +1
-1 -1
-1 -1
+1 +1
+1 +1
-1 -1
-1 -1
-1 +1
-1 +1
+1 -1
+1 -1
-1 +1
-1 +1
+1 ·-1
+1 -1
-1 +1
-1 +1
+1 -1
+l -1
-1 +1
-1 +1
+ 1 -1
+1 -1
+ l + 1
+1 +1
-1 -1
-1 -1
+1 +1
+1 +1
-1 -1
-1 -1
фа виты называются систематическими алфавитами. При
можно
;
правильно декодировать
все
символы,
если
d = 2/ + 1
помехами
ис
кажено не более l элементов. При d=2l+l можно исправить 1-1
()шибок и обнаруживать без исправления l ошибок. Таким обра
зdм, различают алфавиты , исправляющие l ошибок, и алфавиты,
обнаруживающие l ошибок. Такое разделение необходимо только
в то 1 м ~случае, если искаженные юоэф
фициенты a,j) могут 1пр·и 1н1И1мать толь
0,15
аю з·начен:ия
l и -1.
2т СИМIВ'ОЛОВ, состоящих из т 6ина рных элементов l и О, о~б~разуют
i'ру~плу •по отно1.Iпению к 1 сл·ожению по ~" ~
·модулю 2.
За1меТ1Им,
что фу~нкщии
+
Уолша ·имеют та.кое же 1свойсr.во [l l].
Алфав'Ит называ€тся ,щооич~ным гру~п
rrювым алфавиrом или дв1оич1ным II'руп
UJовым к.одом, если €ГО СИ'МВ'ОЛЫ IОбра
зуют : подгруппу этой гр'Ушпы. Оисте
матичеокий 1гр улпО1вой ·код эrо си
стемат:ич1еС1кий ыод, символы которО1го
тlкfи-
.,
Рис. 6.6. Вероятность r,(k) ам
плитуд Ь" помеховых импуль
сов
после
ничения;
образуют лру~ппу.
m=B
аМJiлитудного
сигналы
огра
содержат
импулъсов Уолша
Специальным классом
бинарных групповых кодов являются
коды Рида-Мюллера (5, l О]. Их символы содержат т элементов,
где т - степень 2. Количество проверочных элементов равно .m-k; число символов равно 2h, k равно
±(~) , < т.
(6.93) .
r
k=
i-0
i
Минимальное хэммингово расстояние равно
d =2m-r.
=
Рассмотрим пример, где m=2 4 16 и r= l (алфавит Рида- .
Мюллера первого порядка). Следовательно, d=2 4- 1 =8 и k= 1
+4=5. Этот алфавит содержит 25 =32 символа, содержащих по
16 элементов, 16-5= l l из которых - проверочные. Этот алфа
вит обозначают как (16, 5) или
в общем случае как (т, k). В
табл. 6.2 показаны симвоJ!Ы этого алфавита (16, 5), элементы в
котором обозначены
l; -l. Сравним знаки элементов первых
16 символов с функциями Уолша (рис. 1.2). Знаки соответствуют
положительным и отрицательным
амплитудам функций Уолша.
Знаки элементов символов 17-:-32 получаются изменением знаков
элементов символов 16-:-1.
Поэтому алфавит
Рида-Мюллера
можно составить следующим
образом: l/2m функций Уолша
+
+
wal(j, 0), j=O, . . ., т-
2
2
,
представленных в виде
т положи-
тельных и отрицательных знаков, дают первую половину символов,
вторая половина символов представляется функциями
-wal (j, 0).
Таким образом, алфавиты Рида-Мюллера принадлежат к .клас
су ортогональных алфавитов.
231
6.3.2.
Ортоrоваш.вые, травсортоrоваль:вые и биортоrовальвые
коды
1
Для простоты рассмотрим алфавит ( 4, 3), а не алфавит ( 16.-5) J
Он содержит
23 =8
снмволов. Первые четыре из них
четыре функции Уолша (рис. 1.2):
1.
Можно считать, что
1
это первьtе
·
1
1
2. -1 -1 1
3. -1
1 1 -1
4.
1 -1 1 -1
элементы (6.94) образуют
меняв строки и столбцы
матрицу Х*:
-
местами, получим
(6.94)
матрицу 1) Х. По
транспонированную
1 -1 -1
1 -1
1 -1
1
1
1 •
1 -1 -1
Х* =
(6.95)
Произведение ХХ* равно единичной матрице, умноженной на
1
1 1
1
-1-1
1
-1
1 1 -1
1 -1 1 -1
1 -1 -1
1
1о о о
1 -1
1 -1 = 4 о 1 о о
1 1 1 1
о о 1 о
1 1 -J -1
о о о 1
4:
(6.96)
Матрица называется ортогональной, если умножение матрицы
на
транспонированную
дает
единичную
матрицу,
умноженную
на
некоторый коэффициент. Алфавит назыв·ается ортогональным, если
его элементы могут быть записаны как элементы ортогональной
матрицы. Алфавит (6.94) есть ортогональный алфавит; символы
из табл. 6.2 образуют ортогональный алфавит, как и сим
волы 17-32.
Опустим во всех символах (6.94) третий элемент. Получится
1-16
алфавит с тремя элементами и четырьмя символами:
1.
2.
3.
4.
+1
-1
-1
+1
+1
-1
+1
-1
+1
+1
-1
-1
Умножение матрицы У на транспонированную матрицу У*:
~
1
1
1
-1 -1
1
У=
-1
1 -1
1 -1 -1
])
Эта матрица
-
У*=
матрица Адамара
{7-9].
232
1 -1 -1
1 -1
1 -1
1
1 -1 -1
(6.97)
,
дает
1
УУ* =
У матрицы
нали
и
(6.98)
+ 1
-1/3
-1/3
-1/3
-1/3
+1
-1/3
-1/3
-1/3
-1/3
+1
-1/3
-1/3
-1/3
-1/3
+1
(6.98)
разность между элементами главной диаго
другими элементами
Поэтому алфавит
На примере
алфавитов
(6.96).
больше, чем у единичной
(6.97)
(6.94)
матрицы
называют трансортогон_альным .
и (6.97)
очевидно практическое
.
. значение трансортогональности. Оба содержат четыре символа~
. и хэммингово расстояние между любыми двумя элементами равно.
двум. Однако алфавит (6.94) требует четыре элемента, а алфавит
(6.97) - только три.
Пусть символы алфавита (6.97) представлены векторами:
1. f 0 = +e0+ei +el.
2. F1 = -е0 -е1 +es.
3. Fa = -ео+ ei-es.
4. Fэ = +eo-ei-es.
Концы этих четырех векторов являются вершинами тетраэдра, по
казанного на рис. 2.4а, если начало системы координат располо
жено в
центре тетраэдра
и
система
координат повернута
соответ
ствующим образом.
У трансортогональных алфавитов с более чем четырьмя симво
:- лами члены вне главной диагонали матрицы УУ* близки к нулю~
·
Добавим к ортогональному алфавиту (6.94) символы, получен
ные изменением знаков элементов:
5.
6.
7.
8.
-1
+1
+1
-1
+1 -L +1
-1 -1 +1
+1 -1 -1
-1 -1 -1
(6.99)
Алфавит (4, 3), состоящиi1 из символов (6.94) и (6.99), называется:
биортогональным. Алфавит (16, 5) (табл. 6.2) явлЯеrея также би
ортогональным. Любой символ биортогонального алфавита имеет
хэммингово расстояние от любого другого символа, равное d, кро-
ме одного символа, который имеет расстояние 2d. Примером би
ортогонального алфавита, не являющегося алфавитом Рида-Мюл
лера, является алфавит, показанный на рис. 2.46 в виде октаэдра ..
Перейдем от представления символов элементами или коэффи
циентами к представлению в виде временных функций. Рассмот
рим систему из 16 ортогональных функций f(j, 0). Каждую функ
цию умножим на один из 16 коэффициентов символа табл. 6.2 и
произведения сложим . Если функции f(j, 0) представляют собой
прямоугольные импульсы, то первые
16
символов будут совпадать.
с функциями Уолша (рис. 1.2), а остальные 16 символов
же функциями Уолша, но умноженными на _,1.
233
-
с теми
Коэффициенты а
2
1 +1 о
2 о +1
Табл н ца 6.3
(j) символов троичного биортоrональноrо алфавита,
Х= 1, ... , 32, j=O, ... , 15
3
4
5
6
о
о
о
о
о
7
о
8
9
1о
11
12
13
14
15
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
-3
о
о
+1
о
о
о
о
о
о
о
о
о
о
о
о
о
-4
о
о
о
+1
о
о
о
о
о
о
о
о
о
о
о
о
5
о
о
о
о
+1
о
о
о
о
о
о
о
о
о
о
о
;{j
о
о
о
о
о
+1
о
о
о
о
о
о
о
о
о
о
7
о
о
о
о
о
о
+1
о
о
о
о
о
о
о
о
о
~
о
о
о
о
о
о
о
+1
о
о
о
о
о
о
о
о
9
10
о
о
о
о
о
о
о
о
+1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
+1
о
о
о
о
о
о
Jl
о
о
о
о
о
о
о
о
о
о
+1
о
о
о
о
о
12
о
о
о
о
о
о
о
о
о
о
о
+1
о
о
о
о
JЗ
О
О
О
О
О
О
О
О
О
О
О
О
+1
О
О
О
14
о
о
о
о
о
о
о
о
о
о
о
о
о
+1
о
о
15
о
о
о
о
о
о
о
о
о
о
о
о
о
о
+1
о
.16
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
+1
i7
i8
19
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
20
о
о
о
о
о
о
о
о
о
о
о
о
-1
о
о
о
21
22
23
24
·25
26
"27
.28
29
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о.
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
(J
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
о -1
о
о
о
о
о
о
о
о
о
о
о
.зо
о
о -1
о
о
о
о
о
о
о
о
о
о
о
о
о
Зl
О -1
О
О
О
О
О
О
О
О
О
О
О
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о.
о
-~
-1
о
234
о
Вместо умножения
16 прямоугольных импульсов на + 1 или
и сложения произведений можно с тем же успехом умножить
одну функцию Уолша на
1 или -1, а другие пятнадцать - на О
и произведения сложить. Тогда символы представляются коэффи
циентами
1, -1 и О, как показано в табл . 6.3, где в первой
строке показан индекс j функции wal(j, 0), а в первом столбце
номер символа Х· Функции wal(j, 0) умножаются на коэффициен
ты
1, -1 или О. Суммирование произведений осуществляется
-1
+
+
+
тривиально,
так
как
только
одно
произведение
отлично
от
нуля
для каждого символа.
Интересно, что троичный алфавит табл. 6.3 и бинарный алфа
вит табл. 6.2 дают одни и те же сигналы. Оба алфавита должны
давать одинаковую вероятность ошибки при воздействии любых
типов помех.
Вместо того , чтобы представлять символы троичного алфавита
(табл. 6.3) 16 функциями Уолша, можно использовать константу
f (О,
0),
восемь синусоидальных и семь косинусоидальных импуль
сов согласно рис. 1.9. Частотный спектр мощности первых пяти
импульсов представлен на рис. 1.24 кривыми а, б и в. Шестнадца-
тый символ будет равен F1e(0)= V2sin(l6n0+(l/4)n). Частот
ный спектр мощности этого символа будет сконцентрирован около
v=8
(рис.
1.24).
Выбрав Т=
используемым стандартом
150
мс, что является наиболее часто
для телетайпных сигналов,
получим
указанные на рис. 1.24 ненормализованные частоты. Сигнал F 1e(0)
будет иметь энергию, сконцентрированную около частоты 53,33 Гц,
и практически не будет иметь энергии на частотах выше 60 Гц.
Однако на основе того, что сигналы, рассмотренные выше, зани
мают узкую полосу
частот, нельзя делать вывод,
что алфавит
табл. 6.3 лучше алфавита табл. 6.2. Можно умножить импульсы
согласно рис. 1.9 на коэффициенты
1 и -1 табл. 6.2 и •Просум
мировать произведения. Получившиеся 32 сигнала почти не име
ют энергии на частотах выше 60 Гц.
+
Из 16 двоичных коэффициентов можно составить 216 символов.
Алфавит (16.5) табл. 6.2 использует из них 2 5• Обычно говорят,
что этот алфавит содержит пять информационных цифр и 11 про
верочных или что каждый символ содержит 5 дв. ед. информации
и 11 дв . ед. избыточности. Из 16 коэффициентов троичного алфа
вита можно построить
пользуется из них
25 ;
формации. Однако не
316 символов. в алфавите (табл. 6.3) ис
5 дв. ед. ин
стоит считать, что при этом будет log2(3 16-
на каждый символ приходится
избыточных цифр. Понятие избыточности применимо только
в том случае, если
рассматриваются алфавиты
одного порядка.
Если не наложить этого ограничения,
можно предположить, что
алфавит ( 16, 5) получен из rt 6 символов алфавита порядка r, а не
из 216 символов алфавита второго порядка.
-25)
Понятие расстояния оказалось полезным и в общей теории ко
дирования, не ограничивающейся двоичными элементами. Для то
го чтобы обобщить понятие хэммингова
235
расстояния,
расомотрим
два символа, представленных на интервале -1/2~·0~1/2 функ
циями времени Fx (0) и F'Ф (0). Энергия, необходимая для преобра
зования Fx (6) в F'Ф(0), равна Wх'Ф:
1/2
wх11i = .1r [F х (0) -
F Ф (0))2 d 0.
(6.100)
-1/2
Энергия символа
F х(·0)
равна
Wх r
1/2
5 F~ (0)d0.
Wx =
(6.101)
-1/2
R символов
Средняя энергия в~ех
алфавита равна
W:
R
W=L pxWx,
(6.102)
x=l
где Рх- вероятность передачи символа Х·
Энергетическое расстояние 1 ) dхФ символов
деляется нормализацией энергии W хФ:
dх'Ф =
Пусть
f(i. 0):
и F'Ф
Fx (0)
Fx (6)
и FФ
WxJW.
(0) образованы
(6.103)
из т ортогональных функций
т-1
т-1
Fx(0) = ~ ax(j)f(j, 0); FФ(0) = ~ aФ(j)f(j, 0).
j-=IJ
Для wх'Ф и
wх
опре·
(0)
(6.104)
j.,,JJ
получаем:
т-1
. Wх'Ф
=
т-1
L ai (j).
~ [ах (j) - аФ (j))2; W х =
1-0
(6.105)
j=O
Пусть осе символы имеют одинаковую энергию
Тогда по
W= Wx.
лучаем
т-1
_dx11i_
2
= w_хФ =
2W
~ а~ (j) ~(j)
1/2
l-
_1
W
S Fx (0) FФ(0)d0
=
l -
J._·=0_m---- - •
1
~
-1/2
1-0
Для всех
символов табл.
выполняются
6.3
(6.106)
ai (i)
следующие соотно-
шения:
15
m-t
~ а~ (j)
т-1
=
L ai (j) =
i=O
j=O
15
~ ах (j) аФ (j) = ~ ах (j) all> (j)
1--0
1)
В случае
=
бесконечного
+l
ДЛЯ Х
= 32 -
для х = ф;
ф
+
о для х=FФ, 32-Ф
1=0
«нормализованная несхожесть»
i-1
l;
интервала интегрирования
{10].
236
l;
+ 1.
используется термин
Тогда для символов табл.
получаются следующие
6.3
энергетиче-
ские расстояния:
+
dх'Ф =
Для символов табл.
4 для :х: = 32 . . :. ._ "'
1;
О для х = ф;
2 для х=Рч>. 32-'\'
1.
1
(6.107)
+
6.2:
т-1
15
j...O
j-{)
L а~ (j) = ~ а~ (j) = J6;
т-1
!
ax(j)aФ(j) =
/-О
1-16 ДЛЯ Х
15
(6.108)
= 32-"1 + l;
L ax(j)aФ(j) = + 16 для х = "1;
/=О
(6.109)
о для х :;6 "'· 32-"'
4 для х = 32 - "'
1;
0 для Х = ф;
+
dхФ
=
12 для х * "'' 32 -
Если W х.Ф в (6.103) разделить
расстояния dхФ символов табл.
8.
"'
+ 1;
+ 1.
не на W, а на W/log2m= W/4, то
6.2 будут иметь значения 16, О или
Это есть числа элементов, в которых символы отличаются друг
от друга, т. е. их хэмминговы расстояния.
Энергетическое расстояние dхФ между двумя символами равно
квадрату
вектора,
соединяющего
сигнальные
точки
в
сигнальном
пространстве. Эти векторы на рис. 2.4 обозначены линиями между
сигнальными точками. Термин «расстояние» при векторном пред
ставлении имеет очевидный смысл . Из -з а нормализации dхФ для
векторного представления
необходимо потребовать,
чтобы сиг
нальные точки имели среднее расстояние от общего центра тяже
сти, равное 1.
Пусть R символов биортогонального алфавита записаны в та
кой последовательности, что выполняется соотношение
F х (0)
Следовательно,
~
=
-1
-112
Из
{6.106)
(6.110)
F R.-x+i (0).
1 1 для х = ф:
1/2
s Fx.(0) Fф(0)d0
=-
для х = R-ф +
О для х
::f: ф, R- Ф
1,
(6.111)
+ 1.
следует, что символ х биортогонального алфавита име
ет энергетическое расстояние от символа
гетическое расс_тояние,
равное
2,
R-x+ 1,
равное
от всех других
4, и энер
символов, :х:=
=l, ... , R.
6.3.3.
Кодирование для безошибочной передачи
Формула Шеннона для пропускной способности канала связи
доказывает, что в предельном случае возможна безошибочная пе-
237
редача. Из вывода этой формулы в § 6.1 видно, как можно полу
чить коды, позволяющие приблизиться к пропускной способности
канала и обеспечивающие вероятность ошибки, близкую к нулю.
при наличии аддитивного 1·еплового шума .
Рассмотрим систему ортогональных функций f(j, 0), разложи
мых по Фурье на интервале -1/2~0~ 1/2. Из таблицы выбирают
случайные числа ao(i) с гауссовым распределением и строят сим
вол Fo(0) [l-3]:
m-1
F(0)
=).
a0 (j)f(j,
.;..J
е,.
(6.112)
i=O
Можно предположить, что числа ao(j) представляют напряжения.
Тогда Fo(0) является
изменяющимся во времени напряжением.
Если т бесконечно, то Fo(0) нельзя отличить от выборки теплово
го шума.
Используя другой набор из т случайных чисел a1(i), можно
построить второй символ F1 (0). В общем случае, используя т слу
чайных чисел ах (j) с гауссовым распределением, можно построить
символ Fx (8). Ненормированная длительность этих символов рав
на Т. Пропускная способность канала (6.54) зависит от т, Т и
среднего отношения сигнал/шум Р/Рт, т:
C=.!!!...1og
2 (1+P!P т , т)·
2Т
(6.113)
Пусть п- наибольшее целое число, меньшее 2ст, и пусть будет
построено п символов
Fx (0):
х. =О, 1, .. " п-1.
(6.114)
Эти п символов образуют первый алфавит. Пусть, таким образом,
построим 1
L алфавитов с п символами каждый и выберем случай
но один алфавит. Если п и L стремятся к бесконечности, то веро
ятность того, что этот алфавит обеспечивает вероятность ошибки,
стремящуюся к нулю, сколь угодно близка к единице.
Эти «случайные
алфавиты» очень хороши
с теоретической
точки зрения. Однако существуют практические трудности. Инте
ресно не только знать, насколько хорош алфавит в пределе, но и
какова вероятность ошибки для конечного количества информации
на один символ. Элайс нашел первый неслучайный алфавит, обес
печивающий сколь угодно малую вероятность ошибки при ограни
ченной энергии, затрачиваемой на передачу одной двоичной еди
ницы информации (4, 5].
была много меньше, чем
бинационные коды также
и обеспечивают скорость
6.3.4.
Однако скорость передачи информации
11редел Шеннона. Так называемые ком
дают очень малую вероятность ошибки
передачи, близкую к пределу Шеннона.
Троичные комбинационные коды
Сuвокупность т ортогональных функций
вать т коэффициентов ах
(j).
Если ах
238
(j)
f (j,
0) может переда
принимает три значения
. + l,
О и
· . вместо
-1,
то можно построить R=Зm символов. Записав
(l +2)m.
зт, получим следующее выражение:
·+ 2h(:) + .. ·+ ~ (:).
R = ( 1 + 2)m = 2° ( ~) + 21 ( ~ ) +
(6.115)
R
Это разложение делит множество
символов на подмножества
символов, содержащих одинаковое число функций
f(j, 0).
Суще-
ствует l =2° (~) символ, не содержащий ни одной функции, так
как все коэффициенты ах
2
1
(
(j)
равны нулю. Кроме того, существует
~) = 2т символов, состоящих из одной функции каждый, так
как толь· ко один коэффициент ах (j) равен
волы
образуют биортоrональный
код.
2h
+1
или -1. Эти сим
В общем
существует-
r:) символов, каждый из которых содержит
Xif(j, 0),
где ах (j) равен +l или
h
функций йх (j) х
Так как(:) есть число
-1.
комбинаций по h функций из т, то эти коды называются троич
ными комбинационными кодами при h=F0,1 или т. Таблица ·6.4
показывает число 2 (:) символов в таких алфавитах .
Т а б
,,
нц а
6.4
Число символов в троичных комбинационных кодах. Согласно
[2)
числа
над линией характеризуют хорошие коды
~1
1
2
3
4
5
6
7
8
9
10
2
4
4
3
4
5
6
12
8
8
24
32
16
10
40
80
80
32
6
12
60
160
240
192
64
8
7
14
84
1 280
560
672
448
128
10
9
16
18
112
144
448
672
1120 1 2016
1792 4032
1792 5376
1024 4608
256 2304
512
20
180
960
3360
8064
13440
15360
1152(}
5120
1024
Уравнение (6.l 15) дает для h=m 2nt (:) =2nt символов, кото
рые содержат все т функций ах
- l.
(j):f(j, 0)
с ах
(j),
равным
Они являются символами двоичных алфавитов.
239
+l
или
Рассмотрим код с символами, содержащими h функций f(j, 0).
Каждый символ содержит h коэффициентов ах (j),
равных +ао
.или -ао и m-h коэффициентов, равных О. Пусть эти символы пе
редаются. Взаимокорреляционная функция
принятого сигнала с
функцией if(j, 0) дает коэффициенты ахШ· Пусть на сигнал дей
.ствует аддитивный тепловой шум. Тогда получаются коэффициен
'ТЫ
которые имеют гауссово распределение со средними зна
a(j),
qениями +ао, О или -а 0 , обозначаемыми
1
/ а<+ > (j)
ао
"'-
"'-
/=<а
<+I>
/
>=+1;"'-
a<+1>(j), a<0J(j)
а<- > (j) "'1
ао
/=<а
(-1)
и
aH>(j):
>=-1;
(6.116)
/
а(О) (j) ' \
(0)
"'--ао-/ =<а >=О.
Дисперсия а2 этих распределений получается из
и
(6.60), (6.70)
(6.71):
(j)"'
Р1, т
Ph, т
hPлr
02=· - - ' = - - = - - = - "
а~ /
P/h
Р
пР '
/ ai
.h -
(6.117)
число коэффициентов ах.О) со значениями +а0 или -ао;
= log2 2h (:)
если все
(;редняя
-
n=
информация, приходящаяся на символ, в дв. ед.,
символы передаются
мощность
с равной вероятностью;
Pn, т -
п ортогональных компонент теплового шума
на
:Интервале ортогональности длительностью Т; P=ha2o- средняя
мощность сигнала; .Лf=n/2T; Рлr - средняя мощность теплового
шума в полосе частот Л·f. Чтобы облегчить сравнение между двоич
ными
и
троичными
кодами,
используют
шума Pn, т, а не Ph, т или Рт, т.
Для декодирования согласно
(5.25)
чаще
среднюю
мощность
необходимо из т принятых
коэффициентов a(j) получить 2т(:) сумм:
т-1
Slli
=
_I а (j) аФ (j)
(6.118)
i=O
и определить наибольшую из них. m-h коэффициентов a11i (j) рав
·ны О для любого 'ljJ. Рассмотрим те суммы, для которых опреде
ленные коэффициенты aip (j) равны нулю, например, те, для кото
рых j=O, ... , m-h-l. Оставшиеся h коэффициентов равны +ао
или -аь и дают 2h различных сумм S11i . Наибольшая из этих 2h
.сумм будет содержать h положительных членов а(j)аФ (j), в то
время как оставшиеся m-h членов равны О. Наибольшей из всех
2h (:) сумм SФ будет сумма, в которой не равные нулю чл~ны со
держат п коэффициентов a(j) с наибольшими значениями. Сумма
будет наибольшей для переда&аемого символа Fx (0), когда абсо
лютная величина h коэффициентов a<+1>(j) и aH>(j) больше, чем
240
ве.тrИ'Ч'И!На m-h .коэффиенrов ao(j),
и если ·к ·юму же
'p,<+ 1>(j) больше ~нуля и aH>(j) меньше
· уля. Следоватмыно, д.1я 6езошибоч
•
1 бсюлЮТ1Ная
.
tюrо
де~код1иро·вания
. 1яться
'
..
~едующие
должны
щва
· ВЬ!'Пол
условия
(с:ч .
ис.
6.7):
1) ·все
\=a<+ >(j)/a0
1
а<+ 1 >=
коэффиц"Иенты
и
-a<- >=-aH)(j)/a0
1
не
трицательны:
О~а<+ 1 >, -a(-t)<oc;
2) любой
из
(6.119)
.кюэффиц1иентов
!1
+а<+!) и -а<- 1 ) ·Не 1 м еньше абсолю11Нl{)Й
вел:ичи1ны любоrо из m-h коэффи
;Циею·о1в a< 0>=a< 0>(j)/a0• Выполненше это
r:о у1 сло.вия 1н е·обходимо, ·если
· выпол1няе11ся
у:словие
~(0)1
+ a<+I) -1а<о>1 >О
-a<-1>_ /a<D>
1
толь.ко
l:
при О~ а<+ >,- а<- >
1
}
/:;;..О
<
Рис.
оо.
(6.120)
'Функции плотности вероятности W1 (х)
,;для
a<+t)
1и
w2(y)
( 4.59).
Ю"J'IСЯ
la<0>1
дл·я
Вероятность р( а<+ 1 ><0)
олределя
= W1 {О)
того,
-!
6.7.
о
!
Плотности
верояmо
сти а<+ 1 >, а<- 1 >, а< 0 >, 1а< 0 >1 и
а<+ 1 >-\а< 0 >1 для троичного ком
бинационного
ванная
кода . Заштрихо
площадь
указывае-r
ошибки
что
условие
(6.l 19)
не
выполняется, равна
о
1
р ( а+ <О)= W1 (О)=
= __!__
2
~
У2л cr
.\ ехр [-(х- 1}2/2а2] dx =
-
-оо
[l -erf (1;V2o)].
(6.121)
'Вероятность р(-аН><О) имеет то же значение:
.
р(-а<- 1 > <0) = - 1 [1-erf (11V2a)],
(6.122)
2
ph< 3>
означает вероятность того, что условие (6.119) не выполняет
я, по крайней мере, для одного из h коэффициентов а<+ 1 > и аН>:
р~3 > = 1 - [I - W1(O)Jh = 1 - 2h [1
Рассмотрим распреде:1ение
+ erf ( l/V2 o))h.
а<+ 1 >-1а<0>1.
О<а<+ 1 ><
(6.123)
оо. Плотность
вероятности этой функции
определяется (4.61 )- (4.63). Вероят
ость того, что условие (6.120)
не выполняется
для одной из
(т-h) разностей
(
р а
.
a<+1>-la<0>1
(+IJ
-
1
1
а
-a<-t}-la<0>1,
равна
(О) 1 < 0) = W (О) = SO w (z) dz.
р(а<+ >>0)
i Этот интеграл был вычислен в
9-322
и
-00
(4.64).
241
(6.124)
p< 3Jh, m-h означает вероятность того, что условие (6.120) не вы
h(m-h) разностей а<Н>-1а< 0>1 и -a<-1>- Iа<0> 1:
р~~) m-h = 1 -[ 1 - W (O)]h (m-h).
(6.125)
полняется для всех
Уравнения
и
(6.123)
(6.125)
дают вероятность ошибки
p< 3Jm,h
для
троичных комбинационнык, биортогональных и бинарных (т, т)
кодов:
Р~! k
=
l-(l-p~3 J) (1-pA~Jm-h)
=
1-2-h [1 +erf (I;V2cr)]h Х
Х {-1 (1 + erf (1/2а)]2 '}h (m-hJ а2=hРд /пр.
2 l+erf(l/Y2cr)
f
(6.126)
Уравнение (6.126) дает при h= т вероятность ошибки для двоич
ного кода с т коэффициентами ах (j) и 2m символами:
р<ЗJ
т, т
2
(J
--
=
1-(1-p<ЗJ)(l -p<ЗJ ) = 1 - (21-)m [1 +erf (1/V2cr)Г;]
т
т, о
тР /nP -- Р /Р· п - log2 2т (т ) -- т .
дf
дf
1
т
-
Вероятность ошибки биортогонального кода получается
(6.127)
при h= 1:
1
3> _)=1-р<ЗJ
_=l-(l-p<ЗJ)(l-p<
т, 1
1
1, т 1
2 [!+erf(1/V2cr)]X )'
Х {-1
,
2
[1 +erf(l/2cr)) 2
1 +erf(l/V2'cr)
}m-1.
J
'
cr2 = Р 1 • т /Р = Рдf/пР; п = log 2 21 С)= log 2 2т.
!
(6.128)
На рис. 6.8 показана вероятность ошибки для некоторых биор
тогональных кодов. Для сравнения показана вероятность ошибки
двоичного кода (5, 5) (кривая n=5, m=5) и кода (16, 16) (кри
вая n= 16, m= 16).
График для случая n=5, m=5 аналогичен
графику а на рис. 6.2.
Выбор средних отношений сигнал/шум, отложенных по оси абс
цисс, требует объяснения . Смысл средней мощности сигнала Р
очевиден. Средняя мощность шума Р1, т ортогональной компонен
ты теплового шума на интервале ортогональности длительностью Т
используется как эталон. Р/Р1, т дает неправильное представление,
так
как
символы
различных
кодов передают
различное
количест
во информации. Лучше использовать Р/п, т. е. среднюю мощность
сигнала на один бит информации, а не Р. В результате получим
отношение Р/Рлt, которое используется на рис. 6.8:
(P/n)/P1• т = Р/пР 1 • т = Р/Рп, т = Р/Рдf; Лf = nJ2T. (6.129)
Рассмотрим передачу символов с n=5 дв. ед. информации на
символ с вероятностью ошибки 10-3• Согласно рис. 6.8 двоичный
242
код (n=5, m=5) требует отношение Р/Рл1 порядка 11 дБ а би
ортогональный код (n=5, m= 16) - только 8 дБ. Следова~ельно,
. биортогональный код требует мощности сигнала на 11-8=3 дБ
меньше. Этот выигрыш достигается цено1°f уве.'Iичения числа орто
гональных функций с ~:=' 5 до m= 16 и увеличением в 16/5 раз
_функционально-временнои области , занимаемой сигналом, и.1и,
!О
""
ю "''-r-t----t---\\ri.\'<+-';Г+--t--~
"'•
~~--+----f"-'-"--ffi--\\-W~~..,,.,,-1
!d4
t
-5 <::
!О
"". ++---+-'-___,l-L--\+l\,>4--IЦ---4
"' ~--r-~1--,...o;т-'ft--1t----7-n
ti/ ~",,..
t -7.g::
""-Ю ~<:L~.._~~~-~~~~
J
Рис.
6:8.
7
5
ю L-.J'-1--L...LJ..._._~._..~__._~
6 8 fO 12 14 15 18 ?О 2Z ?+25 26Jff
РЕ/~ 1 ,оБ-
Рис.
Вероятность ошибки р
Р
-
с редняя
мощно сть
Р дf- средняя
мощность
символа:
т
-
Вероятность ошибки р
:rа; Р, Р дf , п и т определены
6.8; h - чис
сигнала;
теплово~о
в надписи к рис.
шума в полосе шириной Лf=n.'2T;
п - количество информации в би·
гах, содержащееся в символе: Т длительность
6.9.
пюичноrо комбинационного ко
биортоrональноrо кода:
ло
ортогонал1:;ных
символе.
число
показывают
ортогональных
функций
в
коде.
С п лошные
линии - биортоrональ~
ный
код:
пунктирные - бин а рный
код (5,5) н (16,16)
бок
функций
Пунктирные
вероятности
бинарных
кодов
в
.1инии
оши
(5, 5)
и
(16, 16)
другими словами, увеличением в 16/5
раз полосы частот. Рас
смотрим далее передачу символов с n= 16 дв. ед. инфор~1ации на
символ с вероятностью ошибки 10-3 . Согласно рис. 6.8 бинарный
код (n= 16, m= 16) требует отношения Р/Рм = 11,7 дБ; биорто
гональный код требует только 5,8 дБ. Таким образом, биортого
нальный код требует
только около четверти
мощности сигнала
бинарного кода ((11,7-5,8)=5,9 дБ). Однако число функций не
обходи:vю увеличить с 16 до 32 768.
Чем меньше требуемап вероятность ошибки, тем более оправ
дано использование биортогонального кода. Например, для веро
ятности ошибки 10-7 (кривая n=5, т= 16 на рис. 6.8) требуется
отношение Р / Р дf = 11 ,2 дБ, в то время как для двоичного кода
(п=5, m= 16) требуется отношение 14,8 дБ;
мощность сигнала
при этом можно уменьшить на 14,8-11,2=3,6 дБ. Эта разность
мощностей увеличивается более чем на 7 дБ для кодов n= 16.
т=
9*
32 768
и
n= 16,
т=
16
при вероятности ошибки
243
1О-7 .
На рис. 6.9 показана вероятность ошибки для троичных комби
национных кодов согласно (6.126). Сравнение с рис. 6.8 показы
вает, что троичные комбинационные коды требуют большего от
ношения Р/ Р Лf, чем биортогональные коды, но меньшего, чем дво
ичные коды типа (т, т). Например, биортогональный код n= 10,
m=512 для отношения РiР'л~ =8 дБ
дает вероятность
ошибки
сравнимый по вероятности ошибки комбинационный код n=
=9,9, m=8, h=3 требует, чтобы это отношение было равно около
10,5 дF·.
Из рис. 6.9 видно,
что существуют коды,
которые передают
болш1е информации п с тем же числом функций т, что и бинар
ный код (т, т), и тем не менее дают более низкую вероятность
ошибки . М~ханизм действия этих кодов более сложен, чем обмен
I0-5 ;
«увеличение
числа
функций н::1 уменьшение
мрщности
сигнала».
Рассмотрим кривую для n=8,8, m=B, h=3. Символ двоичного
кода (8,8) передает восьмью функциями информацию,
равную
8 дв. ед., что меньше, чем 8,8 дв. ед. у троичного комбинационного
кода, который также требует m=8 фун!щий. Вероятность ошибки
двоичного
кода (8,8) представлена кривой,
котора!1 находится
между кривыми для n=5, m=5 и
вероятностей ошибок между l о- 4 и
(рис. 6.9). Для
эта кривая начти на 3 дБ
n=l6, m=i6
l 0-7
правее кривой n=8,8, m=8, h=3.
Рассмотрим вероятность ошибки p< 3>m, h
значений тип. Используя аппроксимацию
erf (х)
~ 1 - ~): е-х•, х
r nx
»1и
(6.126)
для больших
1 -У~ е-У , у({.. l,
можно получить
Р~! h ~
6= :
n -{
1 - е~е
tl1j
т
;r ; +
11
=
ln [ h-(m-h)
)) 1;
V : ]- 4h~f
,:
(6.130)
Пусть п и т стремятся к бесконечности:
lim
m-+ao
lim
m-+ao
р~> h
'
= 1
при 11> О;
р~> h = О при fJ <О.
(6.131)
'
Таким образом, безошибочная передача достигается в пределе при
n= оо
для
ri<O.
ИспоJiьзуя соотношение
п
=
log2 2h (:) ~ h log2
:
,
m'J/h,
(6.132)
можно преобразовать условие 11<0 в следующее условие, справед
Jiивое для постоянного значения h:
Р/Рд >41п2.
1
(6.133)
Отношение Р / Р дf, большее чем 41n 2, обеспечивает безошибоч
ную передачу для бесконечно больших т и п и ограниченного h;
244
ероятность ошибки равна 1, если Р/Рл 1 меньше 4In 2. Предель·
ая функция Iim p 3m, h для т-+-оо, n-+-oo показана на рис. 6.8 и 6.9.
тот .предел одинаков для биортогональных кодов (h= 1) и ком
инационных кодов
1. Следовательно, комбинационные коды
· вляются предпочтительными только с точки зрения функций или
ребуемой полосы, так как увеличение числа функций пропорцио-
h>
. ально 2n
для биортогонального кода, но пропорционально только
nfhh для комбинационного кода.
Пусть при стремлении т и п к бесконечности h не остается по
. тоянной, а увеличивается пропорционально та, о~ ,а< 1. Условие
· »h (6.132) остается справедливым для больших т. Тогда усло
~вие ri<O дает вместо (6.133) следующее условие:
Рf Рм> 4 ~
+:
Jn 2; h =та; о~ а< 1.
(6.134)
Безошибочная передача возможна, если а<1.
Рассмотрим теперь, насколько применим предел Шеннона для
пропускной способности в форме (6.54) к троичным комбинацион
шума Р лr должна быть заменена
. ным кодам. Средняя мощность
·.в (6.130) на Рт, т. Отсюда
Рлf
Условие
Рп ' т = пР, . т = -
n
т
Рт . т •
(6.135)
превращается в условие
ri<O
-
, Используя
=
1
n
<--mV/_h]
n
nhPm, т
ln [h(т- h)"
(6.136)
аппроксимацию n=log22 (:) ~hlog2: , т»h в левой
•части и производя перестановку членов, получаем:
n< 41:2 [
. Выражение
l!n~ т)]~.
.
lnmh-2 \n log2 h
в скобках становится равным
т, т
1,
(6.137)
когда т становится
бесконечным, а h остается конечной; для h=та, O~a<l оно ста
. новится равным (1 -,а)/ ( 1 +а).
Информация, передаваемая безошибочно за единицу времени,
. равна п/Т, так как п .есть информаци~, приходящаяся на каждый
, символ,
передаваемыи
в
течение
интервала
ортогональности
дли
тельностью Т:
С= ~ < _!_ ~ Т
2 2Т
1
\n2
_Р_
Рт. т '
h = const·
1 1 -а. !!!:... _l_ __
С=~ <Р_
'
Т
1 l+a.2T
In2
Рт,т'
245
'
(6.138)
h =та, О~ а< 1. (6.139)
Если пропускная способность получается в битах на единицу вре
мени, то в (6.54) должен быть использован логарифм по основа
нию 2:
т
C=-log2 (1+P!Pm
2Т
·
т
1
р
р
т)~----р-,-р- « l.
2Т
\п
т, т
2
т. т
(6.140)
Правая часть (6.140) в два или в 2(1 +1a)/(l~a) раз больше, чем
правая часть (6.138) и (6.139).
Следовательно, при малых отно
шениях сигнал/шум троичный комбинационный код с h=const по
зволяет безошибочно передать в два раза меньше информации,
чем это определяет предел Шеннона.
Физический смысл условия Р/Рт, т« 1 очевиден; коэффициенты
троичного кода имеют только значения
l, О, -1. Увеличение
среднего отношения сигнал/шум Р/Рт, т, когда достигнута нулевая
вероятность ошибки, бессмысленно. Отношение сигнал/шум Р/Рт , т
имеет смысл увеличивать только, если коэффициенты принимают
большее количество значений, ч е м три:
l, О, -1 . Троичные ком
+
+
бинационные коды должны быть заменены кодами более высокого
порядка.
Более детальное исследование троичных комбинационных
дов проведено Касаком
6.3.5.
Пусть
Комбинационные коды порядка
символы
ко
{21.
Fx (0)
образованы
2r + 1
т-ортогональными
функ
циями f(j, 0), -l/2~0~1/2, умноженными
на коэффициенты
ах; (j). Эти коэффициенты могут принимать 2r+ l значений, а не 3,
как в случае троичных кодов . В общем может быть получено
+2r)m символов. Разложим (l +2r)m в биномиальный ряд:
( 1+
·+ (2r)h (:) + . · ·+ (2r)m (:);
(6.141)
(2r) h
(:)
-
число символов в коде, содержащих h из т функций
f(j, 0). Это значит, что h коэффициентов ах. (j) не равны нулю;
х изменяется от 1 до (2r) 1' (:) • Эти символы образуют комбина
ционный код порядка 2r+
одинаковой вероятностью.
битах равно
п =
1.
Пусть все эти символы передаются с
Количество информации на символ в
log 3 (2r)h (т)
h
~
2rm
h log 2 -h- ,
т
» h.
(6.142)
Каждый из h коэффициентов ах; (j) =1= О может принимать 2r
значений. Они обозначены ар, р= ± 1 . .. ±.r. Вероятность того, что
коэффициент ах.
(j)
примет значение ар, обозначим р(р). Пусть
246
(р) не зависит от j. Средняя мощность сигналов
Р1 =
+r
Т/2
+r
p=-r
-Т/2
p=-r
f (j, 0)
равна
Pj:
1J р(р) ~ J a~f' (j, 0)dt = IJ р (р)а:,
+о
+о
+r
~ р(р) = 1.
(6.143)
p=-r
+о
редняя мощность символов, составленных из
авиа Р:
h
функций
f(j, 0),
(6.144)
Сделаем следующие допущения:
а) вероятность того, что коэффициент ах
ар , не зависит от р: р (р) = 1/2r;
б) разность 1ар -ар
. ловие
-1
(j)
примет значение
I не зависит от р 1ар -ар
выполняется, если ар
-1
I = ао. Это ус
кратно ао:
± 1 .. -± r.
ар= ра 0 , р =
Средняя мощность Р; функции
и (6.144):
f(j, 0)
может быть получена из
(6.143)
Р1 =
+r
IJ р a~/2r
2
r
= ( a5Jr)
P=-r
IJ р =
2
(r
+ !) ~2' + l) а~= P/h,
(6.145)
p=I
+о
а~=
+ 1)(2r + 1).
6P/h (r
Пусть передается символ Fx
· ная корреляция с функциями
На приемной стороне взаимдает коэффициенты ах (j).
Наложение аддитивного теплового шума преобразует эти коэф
фициенты в a(j). Они имеют гауссово распределение со средними
(0).
f (j, 0)
значениями
l.plao, -lplao
обозначим через
a<+PJ (j) "'-.
/
"'
ао
=<
lrl=l, ... , r.
или О;
a<+PJ(j), a<-PJ(j)
и
a<+PJ> = р; /
a<-PJ (j) "
"
/
/
/ ао (j) " - <a<OJ> ~ ао / -
О
Эти коэффициенты
a<OJ(j):
ао
=
< aH)J > =
_ р;
(6.146)
•
Дисперсия этих распределений получается по аналогии с
(6.117):
а2= <ai(i)fa~> =h(r+
1)(2r+ 1)Р 1 т/6Р =
=h(r+ 1)(2r+ 1)Рп. т/6nP=h(r+ 1)(2r+ 1)Рл/6nР;
h-
число ненулевых коэффициентов;
чество информации,
приходящееся на
247
n=log2(2r)h (:) -
(6.147)
коли
символ, в дв. ед., если
все
символы передаются с равной вероятностью; 2г - число ненуле
вых значений,
которые могут принимать коэффициенты ах (j);
Pn, т -
средняя мощность п ортогональных
компонент теплового
шума на интервале ортогональности длительностью Т; P=ha20 (r+
+1)(2r+l)/6-средняя мощность сигнала; ifi.f=n/2T; Рлr -сред
няя мощность теплового шума в полосе частот <Лf.
Символы комбинационных кодов порядка выше третьего пере
даются не с одинаковой энергией. Можно определить наименьшую
энергию Л WФ для обнаружения сигнала согласно
чает, что надо вычислить
(5.24). Это озна-
сумм:
(2r)h (:)
m-1
SФ = ~ (a(j)- аФ(Л]2
(6.148)
j=O
и определить наименьшую из них. Если
шей для
1/J=x.
S1\1
не является наимень
где х означает переданный символ
Fx (0),
то появ
ляется ошибка .
Наименьшее значение SФ получается, если складывается h наи
меньших членов [a(j)-~ (j)] 2; h членов, для которых a(j) равно
ах (j) =FO при отсутствии теплового шума, будут h наименьшими
(о}
ч.1~ам;и
.при
'ГеJПЛIОВОГО
наличии
шума,
если
аддитивного
1ВЫiПОЛiНЯЮ'11СЯ
следующие условия (см. ~рис.
1.
а
_
среднего
·больше,
•ореднего
з.начеНIИя
а(+р)
бого из з·начений
-.-""'J!~-1>!--_+.LPl.,.i.-~IP~/t/-O
/pJ-1 J.PI
ac·r)
Рис. 6.Ю.
а<0> а<- 1 >
и
d<+•>.
о
1, .. " r
больше,
чем абсолю<tное з:начен'И·е од~ного из
Pf+t
1 rJ m-h •коэффициентов а< 0 >. Выполне~(
1ние этого VСЛОВIИЯ необход:И•МО, Т:ОЛЬ-
-'"--.........~.... ....1-.
-r-7 -r -7'+1
\а /ао\ = \р\
ч1ем. от лю~о~ ~ругого
значения 1р 1 -1, .. " г,
=F.p;
2. Ни од•и н из h ~коэффициентов
а<+Р) и -а<-Р) не отличается от лю-
О~
·
а{-р)
6.10):
коэ.ффици 1 ентов
и
-а<-Р>
h
а<+М = a<+P>(j)/a 0
=
-a<-P>(j)/a 0 не отли'Чае'Гся от авоего
(-f)
~1
О . o(+t)
2
Ни один из
к·о если в~J!Полнено 'Ус.тювrи-е 1.
L
Эти два усло1вия для троичных
r-t r r+l
Плотности вероятности
a<+t> а<-р> а<+р> а<-•>
.комбинан~ионных
кодов
~ра1вносильВ
(6 119)
(6 120)
З~штри~ованн:.~е плоЩадкя 'НЫ у~словия.м
·
rи
·
·
укаэывают ошибки
числение
верояТ1нс•сти
ошибки
Ыго
раздо боле·е за'Гру,щнителыю. Здесь
результаты будут приведоены ·б-ез д,оказательст.ва.
Пусть p2r+1
m,h
означает
вероятность ошибки
из-за теплового
шума для комбинационного кода порядка 2г+ 1, использующего
из т функций . Для больших значений т,
248
h, r и малых cr2 :
h
J
1
т)) h ~
l
1; r ~ 1; а2 :::::!. hr2Pл,J3nP
« 1;
(6.149)
п = log2 (2r)h (:) ::::!. log2 (rm/h)h.
можно получить следующую формулу:
(2r+l)
Рт, h
:=
1
~
ru.=-lnh; 112
n
8hr2P Лf
е
1-
-ent], -en11,
е
;
1
~
-ln(m-h)h--~n
4hr'P A.f
=
(6.150)
Пусть ,количество информации на один символ п бесконечно растет:
lim p~~"t 1 > = 1, 112 >О, ть. - любое число;
n-+co
lim p<m2r+I
h > =·
•
п-.ао
Случай
невозможен, так как справедливо
112<0, ri1>0
ТJз =
[
(6.151)
О ' n..
<О ! n.
< О'
"fA
"1.1
+
ln(m-h)-
в:~Лf ] + [-!;-- lnh- Bhr~~A.f
Член во второй скобке равен ТJt· Из
] •
(6.152)
111>0 следует, что 112 должно
быть больше О. Следовательно, ri 2 >0 дает вероятность ошибки 1
при n>oo. Переписав 1121 получим следующее условие для безоши
бочной передачи:
4h
PJPдf>-r2 ln(m-h)h.
(6.153)
Зп
Подставляя п из
получаем
(6.149),
Р/Р
Лf
>_!_r2 ln2In(m-
h)h.
(6.154)
Jn (rm/h)
3
Рассмотрим, насколько можно приблизиться к пределу Шен
нона в форме
(6.54) при использовании комбинационных кодов
порядка
2r+I.
Средняя мощность шума Р лт в ф-ле
(6.150)
для
112
должна быть заменена на
РЛf = Рп. т = nPI, т =
Из
(6.151)
рт; т·
:
можно получигь
limp< 2r+1> =О при Р!Р
в-ОС>
т, h
т, т
>
4
h r2Jn(m-h)h.
Зт
(6.155)
· Используя соотношенИ:е
r
которое следует из
(6.149)
-
l'V
2n/h h '
т
(6.156)
-
для
r""» 1,
из
(6.155)
можно получить
n<: log2{[4hs1n:з-h)h] Р:т}.
249
(6.157)
Надо так выбрать h=h(m), чтобы правая часть этого неравен
ства для определенного 'iначения т и фиксированного отношения
Р/Рт, т стала максимальной. Выражение слишком сложно, чтобы
находить максимум путем дифференцирования. Можно видеть , од
нако, что коэффициент h перед логарифмом должен быть как мож
но б6дьшим . Если h станет очень большим, то член в скобках ст а
нет меньше единицы . Это выражение с увеличением т становится
произвольно малым. Следовательно,
h
выбирается так, чтобы вы
полнялось условие
3
-3- Зm
--- =
4h \n (т - h) h
Это наводит на мысль, что
h
К
= const.
надо взять равным
~1-
h = m/v lnm.
Из
(6.157)
(6.159)
следует
п<
;
Количество информаци•и
становится
(6.158)
(lnm) 113
log 2 (КР/Рт, т )·
п/Т, передаваемое
за единицу
(6.160)
вреч еюr ,
равным
С=;<;;. (ln~) 113 (Iog 2 (P/Pm,т)+Iog 2 K].
(6.161)
Эта формула
для больших значений Р/Рт, т
отличается от
предела Шеннона (6.54) только коэффициентом (lnт)- 1 tз. Это не
большое различие, вероя гно , объясняется выбором равномерного
распределения для р (р), а не гауссова распределения. Физический
смысл условия P/Pm, т~К понятен . В (6.149) предполагалось, что
г";Р
l;
наличие большого количества значений коэффициентов ах;
(j)
позволяет безошибочно передавать информацию только при усло
вии большого отношения сигнал/шум.
Список литературы
l.
М а
nn
Р. А.
Der
ZeitaЬ!auf
von Rauschspannungen. -
«El. Nachr. Technik»,
1943, Bd. 20, S. 183-189.
2. S t u т ре r s F. L. Theory of frequency modulation noise. - «Proc. IRE», HMS,
v. 36, р. '1081-1109:2.
3. V о е 1 с k е r Н. В. Toward а unified theory of modulation. - «Proc. IEEE»,
119166, У . 54, р. 340~. 7;35-755.
4. R а d е та с h е r Н . Einige Siitze von allgemeinen Orthogona!-funktionen.
Math Annalen, 11002, Bd. 87, S. 100-1138.
5. F о w 1 е F. F. The transposition o.f oond.uctors. - «Transactions AIEE», 1905, J
6.
'
7.
8.
9.
10.
1'\.
У.
О
23,
р.
659-687.
.
s Ь о r n е Н. S. The design of traпsposШoпs for parallel 'POWer and telephone
line circuits. - ,«Тraпsactions AIEE», НН8, v. 37, р . 897-936.
Р i n k е r t Н . S . lnduktionsschutz fiir Ferпsprechleituпgen . Telegraphen und
Fernsprechtechink, 3. Soпderheft, 1919, S. 108-119.
К: 1 е i n W. D·ie Theorie des Nebensprechens auf Leitungen. Ber\in/New York:
Springer, 111955.
W а 1 s h J. L. А closed set of orthogoпal functions. - «Amer. J. of Mathematics», 1923. v. 45, 1р. 5-124.
Но w е Р . W. The use of Lagueгre апd Walsh functions iп materials proЬ\ems
of variaЬ\e loadi-ng at high temperature. Technical Report AD - 434112fЦl964).
F r а n се М. М . Walsh functions, normal пumbers апd pseudo-random functioпs. Technical Repcrt AD-621360(11965) .
1.1.1
1.
2.
3.
4.
5.
Т
r i с от i F. Vorlesungen iiber Orthogonal.reihen. Berliп/New York, Spгinger,
1955.
S а п s о n е G. Orthogoп a l fuпctions . N.ew York, In,t erscience, 1959.
L е n s е J . Reiheпeпtwickluпgen iп der mathemaHschen Physik. Ber\in, de
Gгuyter, 1003.
М i 1 n е - Т h от s оп J . М. The calculus of
finite differences. London,
McМil\an, 11951 .
N о r 1 u n d N. Е. Vorlesuпgeп iiber DИferenzeпrechnuпg. Berliп/New York,
Spгinger, 1004.
1.1.2
1. С о u r а n t R., Н i 1 Ь е r t D. Methodeп der mathematischen Physik. Berlin/New
York, Spriпger, 1931.
2. М о r s е Р . М., F е s h Ь а с h HI. Methods of theoretical physics. New York,
McGraw-Hill, 1953.
3. L е n s е J. Reihenentwicklungen in der mathematischen Physik. Berlin, de
Gruyter, 1953.
4. Е i е r R. Signalaпalyse mit Laguerreschen Polynomen. - «Archiv elek. OЬer
tragung», 11%6, Bd . 20, S. 1185-194.
5. W h i t t а k е r Е. Т., W а t s о n G. N. А course of modern aпalysis. Loпdon,
Cambridge U. Press, 119512.
6. Т i t с h та r s h Е . С. Theory of the Fourier-iпtegral . London, Oxford U.
Press, 11937.
7. А 1 е х i t s G. К:onvergenzproЫeme der Orthogonalreihen. Berlin, Deutscher
Verlag der Wissenschaften, 1960.
1.1.3
1. S т i r n о w W. 1. Lehrgang der hбheren Mathematik. Berliп, Deutscher
Verlag der Wisseпschaften, 1961·, Part. 2.
2. Т i t с h та r s h Е . С. Theory of the Fourier-integral. London, Oxford University P.ress, 11937.
3. В r а се w е 11 R. The Fourier-t·raпsform and its applic.ations. New York,
McGraw-Hill, 11965.
251
4.
5.
В е п пе
Н~5.
W i е пе
t t W. 1R., D
а
v
еу
J.
R. DaLta
r N. The Fourier-iпtegral
Cambridge University Press, 1933.
апd
transmissioп .
certaiп
New York, McGraw-Hill,
of its
app\ica.tioпs . .Londoп ,
1.1.4
1. W а 1 s h J. L. А closed set of orthogonal fuпcHoпs. - «Amer. J. of Mathematics», 11003, v. 46, р. 5-24.
2. R а d е m а с h е r Н. Eiпige Siitze vюп al\gemeineп Orthogoпa,\-funktioпeп .
Math. Аппаlеn, 11002, Bd. 87, S. 1·2 2-138.
3. Не n d ет s оп К W. Some пotes on the Walsh-functioпs. - « Traпsactions
ШЕЕ », 11964, ЕС-13, р . 50--б2.
4. L i е d 1 R. Uber eine spezielle K,1.asse von stark muШplikativ orthogonaleп
Fuпktioпeпsystemeп. Monatshefte fur Ma,t hematik, 1964, Bd. 68, S. 130-137.
5. L i е d 1 R. Walsh-Funktionen und endlichdimensionale Hi\bertriiume. Moпat
shefte fur Mathematik, 11966, ,Bd. 70, S. 342---348.
6. L i е d 1 R. Uber giwisse Fuпktioпale im Raum c<v> .[О, ·1] uпd W.alsh-Fourierkoeffizieпteп . Monatshefte fur Mathematik, ,1968. Bd. 72, S. 38-44.
7. W е i s s Р. Zusammenhaпg v.оп
Walsh-Fourier-Reihen mit Polynюmeп.
Monatshefte fйr Mathematik, 1967, Bd. 7il, S. 1165--11,79.
8. Р i с h 1 е r F. Syпthese Hпearer periodjsch zeitvariaЬ\er Filter mit vorgeschriebenem Sequenzverhalteп. - «Arch. elektr. Obertraguпg», ·1968; Bd. 122, S. 150·161 .
9. ,Р i с h 1 е r F . Das System der sal- uпd cal-Funktioпeп als Erweiteruпg des
Systems der Walsh-Funktionen und die Theorie der sal- und cal-Fouriertransformation . Thesis, Dept. of Mathematics, Inпsbr u ck University, Austr!a, 1l 1Э67 .
10. V i 1 е п k i n N. W . Оп а class of complete orthogoпal systems 1(in Russiaп) .
lzv. Akad. Nauk" Ser. Math" 1947, v. i'I, р. 36.3-400.
Ы. F i n е N. J. Оп the W.alsh-functions. - «Trans. Amer. Math. Soc.», НМ9, v. 65,
р. :37:2--4114.
i3. Р а .1 е у R. Е. А remarkaЬ\e ·ser.i es of orthogoпal functions. Proc. London Math.
Soc. 1(:2), 1932, v. 34, р . 241-.279.
14. S е 1 е r i d g е R. G. Geпeralized W.a\sh traпsforms. - «Pacific J. of Mathemati.cs», 1005, v. 5, р. 451-480.
15. Топ i S. Su uп notevole systema orthogoпale di funzioni. Atti Асса<!. Sci.
lst. Bologna, CI. Sci. fis. 1958, Аnп. tМJ6 Reпd. XI, Ser. 5, Nol. !225---230.
~6. М о r g е п t h а 1е r G. W. Оп Walsh-Fourier series. «Tra·nsactions Amer.
Math. Soc.», 1957, v. 84, р. 472-507.
17. W i е n е r N . Nonlinear proЬJ.ems ·in raпdom theory. New Y1ork, МIТ ,Press
апd Wi\ey, 1958, р. 21 .
18. F о w 1 е F. F. Th·e traпspositioп of conductors. - «Traпs.acHons AIEE», 1905,
v. •23, р. 659-68·7.
19. Ре t е r s оп \V. W. Error-correcting codes. New York, MIT Press апd W.Неу,
1\961 .
120. L о о m i s L. Н . Ап introducHon to abstract harmoп1c analysis. Eпglewood
Cliffs NJ, Van No s traпd, 1953.
12.1. Н1 а m m о n d J . .L" J о h n s о n R. S. А review of orthogoпal square wave
f.unctions and their application to linear networks. - 1«J. of the Franklin
Institute», 1002, v. ?ЛJ, р. 211 1 ·~5.
1212. V i 1 е n k i п N. W. On the theory of Fourier integrals on topo\.ogic groups
(in Russion) . Math. Sborпik (N.S .), 119512, v. З0(7~2), р. QЗЗ-244.
~. F i пе N. J. The Walsh functions. Encyclopaedic Dictionary of Physics, Oxfard,
Perg.amon Press, in print.
24. Р о 1 у а k В" S h r е i d е r У u. А. The app\.ication of Walsh functions in
approxima.t e calculations. Voprosy Theoni Matematicheskix Mashin 2, Bazilevskii, Moscow, Fizmatg.iz, 196f2.
25. В о u 1 t о n Р . I. Smearing techn.iques for ;pattern recognition (HadamardWalsh transf ormatioп). Thesis, Univers. of Toronto, Canad.a, .(1968).
·
00. S у 1 v е s t е r J. J . Thoughts юn inverse orthogoпa.1 matrices, simultaпeous
sign-successions, and tessalated pavements in two or more colours, with
.applicaHons to Newton's rule, .orпameпtal tile-work, апd the theory of numbers. Phil . Mag" 1867, v. 34, р. 4611-475.
252
1.2.2
1. М о r s е Р. М., F е s h Ь а с h Н. Methods of theoretica! physics. New York,
McGraw-HШ, 1953, v. 1, р. 942-945.
2. В r а се w е ! ! R. The Fourier-traпsform апd its appllcatioпs. New York,
McGraw-HШ. '.1965.
3. К. а п t о г о w i t s с h L. W., А k i ! о w G. Р. Fuпktioпa!ana!ysis iп normierteп
Riiumeп. Ber!iп, Akademie, 1964.
1.2.4
1.
2.
На r m и t h Н. Verallgemeiпeruпg des Fourier-Iпtegra!es uпd des Begriffes
Frequeпz. - .«Archiv e!ek. Ubertraguпg", 19&4, Bd. 18, .S. 439-4511.
Р i с h ! е г F. Das System der sa!- uпd -ca!-Fuпktio.neп a!s Erweiteruпg des
Systems der Wa!sh-fuпktioneп tшd die Theorie der sa·I- uпd ca!-Fouriertraпs
formatioп. Thesis, Dept. of Mathematics, Iппsbruck Uпiversity, Austria, ! 967.
1.2.5
1. G r ее п R. R.
А
seria! orthogoпa! decoder. Space Programs Summary, Jet
Pюp-u!sioп Labor,atory, Pasadeпa, Са!. 11966, v. IV, N 37-39, р. 247-251.
2. Р о s пе r Е. С. Comblпatoгia! structures iп р!апеtагу recoппaiss a пce. Sympo,;:ium оп error-correctiпi:! codes, Math. Research Ceпter of the US Army,
Uпiversity of Wiscoпsiп, 1968.
3. W е ! с h L. R. Computatioп of fiпite Fourier series. Space Programs Summary,
Jet Propulsioп Laboratory, Pasadena, Са!., ·19бfi, v. IV, N 37-39, р. 295--1297.
4. Р r а t t W. К.. I( а пе J., А п d r е w s Н. С . Hia dama-r d traпsform image
codiпg. Proc. IEEE», 1969, v. 57, р. 58-68.
5. W h е 1с h е ! J. Е., G u i п п О. F. Fast Fourier-Hadamar-d traпsform апd its
use iп sigпal represeпtatioп апd classification. EASCON'68 Record, 1968,
р . 5611-573.
6. На а r А. Zur Theorie der orthog.onaleп .Fuпktioпeпsysteme. Math. Anna!en,
1!110, v. 69, S . 3.3'1-З?il.
7. S h а n k s J. L. Computatioп of the fast Walsh-Fourier transform . - «lEEE
Tr.a ns. оп Computers», ·1969, v. C-Jl8, р . 457-459.
1.3.1
1. S t u m р e ·r s F. L. Theory of
fгequency
modu!ation noise. Proc. IRE, 1948,
р. 11081-1002.
М а п п Р. А. Der ZeitaЫauf vоп Rauschspaпnuпgeп.
v . 36,
2.
-
,«EI. Nachr. Technik»,
19413, Bd. 20, S. 1183.-;189.
t е г Р . F. Modulation, noise and spectral analysis. New York, Mcgraw1965.
4.
m и t h Н . А generalized concept ·of frequency апd some applications. \
«lrEEE Transactions оп Information Theary», 1968, IТ-14, р. 37:5-3812.
3.
Р а n
HШ,
Н а r
1.3.2
1. W u n s с h G. Moderne Systemtheorie. Leipzig, Geest Р& Portig, ·1962.
2.1.1
of sigпals; desigп of sigпals . Iп Lectures оп
Commuпicatioп System Theory. New Уогk, McGraw-Hill, 1961.
L й k е Нi. О. Biпiire orthogoпa!e Sigпala!phab e te mit spezielleп I(orre!atioп
seigenschaften. - «Archiv elek. Ubertraguпg» , ·1966, Bd . 00, S. 310-316.
А k i у а m а М. Orthogoпal РСМ traпsmissioп with weighted blt leпgth.
«J. of the Iпstitute of Electrical Commuпicatioпs Engineers of Jарап» , 1966,
v. 49, р. ' 1 1 115.З--!.169.
Schmid Р. Е., Dudley Н1. S., Skiппer S. Е. Partial respoпse sigпal
formats for paral,Je! data traпsmission . IEEE Iпt. Сопf . оп Commuпicatioпs,
Record, 1968, р. 81'1-816.
С h а п g R. W., G i Ь Ь у R. А . А theoretJcal study of performaпce of ап
orthogonal multiplexiпg data traпsmiss ioп scheme. IEEE Iпt. Сопf. оп Сот·
municatioпs, Record, ,1968, р. &ЗG-837.
L а n g е F. Н. Sigпa!e und Systeme 1. Brauпschweig, Vieweg, 11966.
1. L
2.
3.
4.
5.
6.
е
rn
е
r R.
М.
Representatioп
253
2.1.3
1. W h i t t а k е r J . М. Iaterpolatory function theory. Cambridge Tracts in
Mathemat ics and ,l\\ a theшatical Physics, London, cambridge University Press,
1935, v. 3.З.
2. L е v i n s о n N. Gap a nd deпsity theorems. Amer. Math. Soc. Со\\. РuЫ" 1940,
v. 26 .
.З. S h а п п о n С. Е. Communication in the presence of noise. Proc. IRE, 1949,
v. 37, р . 10-2·1.
4. G о 1 d m а n n S. Information theory. Eп glewood Cliffs NJ, Prentice H a l\ , 1953.
5. L i n d е n D . А. А discus s ion of s ampling th eorems. Proc. IR.E, 1969, v. 47,
р . 1219-1 22'6.
6. К о h 1 е n Ь е r g А. Exact interpol ation of band-limited functions . - «J. Applied
Physics», 1953, v. 124, р . N00-1436.
7. К 1 и v а n е с I. Sampling theorem in abstract h a rmoпic anal ysis . Mathema ticko
fy zkalny Ca sopis, Sloven. Akad. Vied, 11965, v. 15, р. 43-48.
2.1.4
а
В и
n g е F. Н. Korrelationselektronik. Berlin, Verlag Technik, 1959.
r r - В r о w n. Research Corp" Haпdbook of operational amplifier applications, Tucson, Ariz.ona, 1963.
Philbrick researches, lnc. Applications manual for computiпg amplifiers,
Dedh am, Mass" 1966.
J о h n s о n С. К. Analog oomputer techniques. New York, McGraw -Hil\, 1963.
К о r п G. А " К о r n Т . М. Electroпic analog and hybrid computers" New Уогk,
МсGгаw-НШ , 1%4.
S с h т i d Р" N о w а k D" На r т u t h Н . Detection of orthogonal sine апd
oosine pulses Ьу \inear active RC пetworks . Proc. 1967. Iпt. Telemet e riпg
Сопf" Washingtoп DC, р . 210-220.
S w i с k D. А. Walsh-ftшctioп geпeratioп. «IEEE Tг a пsactioпs оп Iпform a tioп
Theory, v. IТ-115(1969), р. 167.
1. L
2.
3.
4.
5.
6.
7.
2.1.5
1. В а 11 а r d А. Н. Orthogonal mu!tiplexiпg, Space апd Aeronautics. Techпic a l
Reference Series «Aerosp ace Elect·roпics, Advaп c ed Commuпicatioпs » , 1962,
v. 3, Nov" р. 51-00.
2. S а п d е r s R. W. The digilock oгthog,oпal modulatioп system. Advaпces iп
Comm u nicatioп Sys.tems. 1965, v . 1, р . 57-75.
З. К u h n В. G" М о r е у К Н., S т i t h W. В . The orthomatch dat a traп s missioп
system. - «IEEE Traпsactioпs оп Spac€ Eleclтoпics апd Telemetry», 1900,
v. SЕТ-9 , р. 63-66.
4. V i t е r Ь i А . J. Оп coded phas e -coheгeпt coшmuпicatioпs. «IRE Traпs
aclioп s оп Space Electroпi cs апd Telemetry», 1001, SET-7, р. 3-14.
5. М о s i е r R. R." С 1 а Ь а и g h R. G. l(iш~plex, а bandwidthefficient bl:iary
traпsmis s ion system. «Traпsa c tions AIEE, Commuпicatioп апd Electroпics » ,
1957, v. 76, р . 7f2.3-727.
6. J а f f е R.. М . Digilock telemetry system for the Air Force special weapoпs
center's Вlue Scout Jr. - «IRE Transa.ctioпs оп Space Electroпics апd Telemetry»,
1962, v. SET-8, р. 44-50.
7. S а п d е r s R. W. Commuпiratioп effici eпcy compari s oп of several commuп i
catioп systems. - «Proc. IRE», •1900, v. 48, р. 57'5-588
8. D о е 1 z М. L., Не а 1 d Е. Т" М а r t i п D . L. Binary data transmissioп
techпiques for liпear systems. - <~Proc. IRE», 1957, v. 45, 656-'661 .
9 . W i е r J . М . Dig.i tal data commuпicatioп techniques. - «Proc. IRE», 1961,
v. 49, р. 196-209.
10. F i 1 i р о w s k у R. F" М u е h 1 d о r f Е. I. Spaoe commuпicatioпs systems;
Space communications techniques. Eпglewood Cliffs NJ, Preпtice Нlа\1, 1965.
Ы. К а t s u та r u К" У а s h i Т . Н" Та k а d а У., О g а w а К. Super multichaп
пel carrier telegraph system Ьу phase modulation 1(Rectiple.<: system) . Fujitsu
Scieпtific апd Teohrtical, 19165, J . 11, р . 001-279.
254
12. Н а r т u t h Н . Оп the traпsmissioп of iпformatioп Ьу c.rthogoпal time fuп.:tioпs. « Traпsactioпs А/ЕЕ, Commuпicatioп а пd Electroпics », 1960, v. 79,
р . 248-255.
13. На r т u t h Н. Radio commuпicatioп with orthogoпal iime fuпctioпs. «Traпsactioпs AIEE, Commuпicatioп апd Electroпics», lg()(j, v. 79, 22·1--228.
14. S с h т i d Р ., D u d 1 е у Н. S., S k i п пе r S. Е. Partial respoпs c sigпal
f·o rmats for parellel data traпsmissioп . - «IEEE Traпsacti{)пs оп Communicatioп Technology», ·1969, iп priпt .
15. О S С - А baпdwi·dth-efficieпt frequeпcy multiplex system for пoп- e qualized
voice chaппels, Al\eп-Bradley Со" lпterпal Report, 1900.
16. О s а t а k е Т., К: i r i s а w а К:. Ап orthogoпal pulse code modulatioп system. «E lect·roпics апd Commuпicatioпs iп Jарап», 1967, v. 50, р . 3.S.-43.
l
2.2.1
1. W а g пе r К:. W. Elektromagпetisch·e Wе\\еп. Bale, Birkhauser, 1003.
2. S т i r по w W. 1. Lehrgaпg der hohereп Mathematik, Teil 11, Berliп, Deutscher
Verlag der Wisseпschafteп, 1001.
3 . М е а с h ат L. А . Negativce impedaпce boostiпg for 2-wire Ьilateral sigп,il
traпsmissioп. 1968, IEEE Iпt . Сопf. оп Commun.icalioпs, Record, р. 165-168;
also Bell System Tech. J ., 1968, v. 47, р. I019-tl041 .
4. R а t h Ь u п D. К, J е п s е n Н. J . Nuclear test iпstгu meпtatioп with miпiature
supercoпductive саЬ\еs . «IEEE Spect rum», 1968, v. 5, ·р. 91-99.
5. А 11 е п R.. J., N а h тап п N . S. Aпalysis апd performaпce of supercoпductive
coaxial tr a пsmi ssio п liпes . - «Proc. IEEE», 1964, v. 52, р. 1.\47_,1,!54.
6. S а п d у G. F. Square wave (Rademacher-Walsh fuп c tioпs) aпalysis. Mitre
Corporatioп, Workiпg Pa.per WP-1685 ('1968) .
2.2.2
1. S i е
Ь е r t W. М . Sigпals iп liпear time
Commuпic ati.oп System Theory, New York,
iпva r iaпt systems.
McGraw-Hi11, 19611.
Iп
Lectures
оп
2.3.1
1. W а g пе r К:. W . Spuleп uпd К:oпdeпsatorleituпgeп. - «Aгchiv fur Elektrotechnik», 1919, Bd. 8, S. бll-92.
2. С а т р Ь е 11 G. А. Physical theory of the elect·ric wave Filter. - «Bel.\ System
Tech. J.», 19122, v. 1, р. 1--32.
3. Z о Ь е 1 О . J . Theory апd desigп of uпiform а пd composite electric wave
filters . - « Ве.\.1 S ystem Tech. J.», 1003, v. 2, р. 11-46.
4. В а r t 1 е t t А. С. The theory of electrical artificial liпes апd filters. Ne\v York,
Wil ey, 1930.
5. С а u е r W. Siebs chaltungeп. Berliп, VDl-Verlag. 1931.
6. G u i 11 е т i п Е. А. Commuпicatioп Net\vorks. Vol. 1: The classical th eory
of lumped coпst a пt пetworks; Vol. 2: The classical theory of loпg liпes ,
filters, and related пetwo r ks. New York, Wiley, 1931.
7. С а u е r W. Theorie der !iпеа·rеп Wechselstromschaltuпgeп. Leipzig, Akademische Verlagsgesellscha!t, 11941:; Eпglish edi tioп: Syпthesis of liпear commuпicatioп пetworks . New York, McGraw-Hill, 1%8.
8. Р i с h 1 е r F. Syпthese liпearer periodisch z e it va riaЬ\er Filter mit vorgeschriebeпem Sequeпzverhalteп. «Archiv elektr. Ubertraguпg», 1968, Bd. 22,
S. 100--..161.
9. На r т u t h Н . Sequeпcy fШers based оп Walsh functi :шs . - «IEEE Trans- 1
actioпs оп Electromagпetic Compatibllity», 1968, v. ЕМС-10, р. 293--295.
Ю. На r т u t h Н. Sequeпcy filters . Proceedi пgs of the Summerschool оп Circuit
Theory, 1968, Czechoslov<Jk Academy of Scieпce, Prague.
2.3.3
1. Nowak D. J ., Schmid Р. Е. lпtroductioп to digital fi!ters. - · «IEEE Tr a пs
actioпs оп Electromagпetic Compatibllity», 1968, v. EMC-.IO, р. ·2 10-220.
255
3.1.1
1. Costas J.
Р . Synchronous communication . «Proc. IRE", 1956, v. Н,
р. 11713-17!8.
2 . В 1 а с k Н. S. ModulatiQП theory. New York, Van Nostrand, 195.З.
З. S с h w а r z J\1. Information transmission, modu\ation and noise. New York,
McG ~a \v-Hill, 1959.
-4 . .Р а n t е r Р. F. Modulation, noise and spectra\ anaJysis. New York, MeGraw-
Hill, 1965.
5. V i t е r Ь i
Hill, !966.
А.
J. Princi.ples of coherent communication. New York, McGraw3.1.2
1. Crowley Т. Н., Harris G. G., M 1iller S. Е., Pierce J. R.,
R u n у о n J. Р. Modern communications. New York, Golumbla U., Press, 19612.
Q. Н а а s W. Mi.\gHchkeiten des Ersatzes von Induktivitiiten und Sohwingkreiseн
in zukiinftigen Systemen der Multiplextechnik. - «F.requena, 11965, Bd. 19,
s. 297~7.
3. F 1 о о d J. Е. Time division multip\ew systems. - «Eleokonic Engr.1>, 1953,
v. ·25, р. Q-б, '58-63, 101-106, 1 14б-й50 .
4. R о Ь е r t s F. F., S i т то n d s J. С. Multichannel communication systems. (Wireless Engr.1>, 11946, v. 2Q, р. 538-549, 576-.589.
5. В е n n е t t W. R. Тi1Т1€ division muШplex systems. - «Bcll System Tech. J.-.,
1941, р. 199-21211·.
.
6. ·R а а Ь е Н. Untersuchungen an der wechselzeitigen Mehrf2chubertragung
(Multiplexi.ibertragung). - «Elektrische Nachrichten-Technik1>, 19.39, Bd. 15,
S. 2\З-Ш28.
7. Те с h п i с а 1 Staff Bell Telephone Laboratories. Transmission Systems for
Communications, Winston-Salem NC, Western Шectric Со. Technioa\ Pub\.ications, 11965.
8. Те с h n d с а 1 Staff Siemens Cen-tral LaЪoratories N achrichteniibertragung.
Berlin/New York, Springer, 1966.
9. S с h w а r t z М ., В е n n е t t W. R., S te i n S. Communicalion systems and
techniques. New York, MoGr.aw-НIШ. 1966.
10. L а n d о n V. D. T·h eoretical an-a\ysis of various systems of muШplex tтans
mission. - «RCA ·Review», 1948; v. 9, р. 287----36'1 . 438-482.
111. На r т u t h Н. Sequenz-Multiplexsysteme fiir Telephonie und Dateniibertragung. rl. Quadraturmodu\ation; 2. Einseitenband-Modulation. «Archiv
elektr. Ubertragung», 1968, Bd. 12f2, S . !27-35, 1102-1\08.
12. Н а r т u t h Н. Triigersystem fiir die Nachrichtentechnik. W. German patent
11 191 416, 1 1916.З.
13. В е Ь а r t h Н. Р. Verfahren zur digitalen Codierung von Fernges.priichen ...
W. German patent 11 ~ 855, 1\.964.
114. Р i с h 1 е r F. Das Sequenzvielfach, ein neues Sprechwegenetz fiir Vol\elektronische Fernsprechvermittlt~r1gsiiшter .
15. XII. 1 n l Wiss. ~olloquium der Techпischen Hochschu\e Ilmenau, East Germany, 19.67, v. 7, S. ·15-20.
3.1.4
1.
2.
З.
4.
б.
Но
n е у J. F., W е а v е r D. К An intюduction to s.ingle sideband communication. - «Proc. IRЬ, ,1956, v. 44, р. 1667-1б75.
N о r g а а r d О. Е . The phase-shift method of single-sideband signa\ generation; The phase-shift method of single-sideband signa\ reception. - «Proc.
IRE», 11965, v. 44, р. 11f718~1743.
.
S а r а g а W. Single-sideband generation. «Electronic Techno\ogy", 1952,
У . 39, р. 1168-1711.
W е а v е r D . К. А third method of ·gener.ation and detection of single-sideband
signa\s. - ~Proc. IRE", 11956, v. 44, р . 1703-'1705.
N у q u i s t Н1. Cer.tain topics in teleg~aph tr.ansmission theory. «Transactions AIEE", 11928, v. 47, р. 617--.644.
256
Вес k е r F. К:., D а v е у J. R., S а 1 t z Ь е r g В. R. An АМ y,estigial эideband
data transmission set using synchronous detection for seri al transmission
up to 3000 blts per seoond. - « Traпsactions А!ЕЕ, Communiea tion and Electronics:., 1962, v. 81, р. 97--<101.
7. В е n n е t t W. R., D а v е у J. R. Data transmission. New York, McGraw-Hi!I,
1965.
В. Н а r т и t h Н . , S с h т i d Р . Е" N о w а k D. L. Tr~шsposed sideband modulation for data transmission. - «IEEE Transactions on Communication Technology», 1967, v. СОМ-15, р. 868-870.
6.
3.1.5
В а g h d а d у Е. J. Analog modulation systems. In Lectures on Communicati a п
System Theory, New York, McGraw-Hill, 1001.
12. V i t е r Ь i k J. Principles of coherent commuпication. Ne·.v York, McGrawHill, 1006.
З. Р i с h 1 е r F. Das System der sal- und ca\-Funktionen als Er,veiterung des
Systems der Walsh-Funktionen und die Theorie der sal- und cal-Four,i ertransf·oпnaHon . Thesis Dept. of Mathematics, Innsbruck Uлiversity, Austria, 1967.
1.
3.2.1
1. V
а
n D
е
r
Р о 1. В .
Frequency Modulation.
~Proc .
IRE», 1930, v. 18,
р.
i11194- .
1005.
2. Нил d А . Frequency modulation . New
З . С и с с i а С. L. НJarmonics, sidebands,
York, McGraw•Hill, 194'2.
and transients ,jп oornmunication engi-
neering. New York, McGraw-Hill, 11952.
4. В 1 а с k Н. S. Modulation theory. Princeton NJ, Van Nostrand, 1953.
3.2.2
С r о s Ь у М. G. Gommunioation Ьу phasc modulation. Proc. IRE, 1939, v. '27,
р . lt26-'13&.
2. В 1 а с k Н. .S. Modulation theory. Princeton NJ, V.an Nostrand, .1953.
З. ,Р а n t е ·r Р. F. Modulation, noise and s·pectral analysis. New York, McGraw-
J..
Hill, 1965.
3.2.3
1. Oliver В. М. , Pierce J. R., Shannon С. Е. The philosophy of PGM.«Proc. IRE", 1948, v. 36, р. 11324-11331.
2. М а у е r Н. F. ,Principles of pulse code modulation . Advan . Electron, New York,
Academic Press, 1951'.
З. F 1о о d J. Е. Тime division mнJ,tiplex systems, Part 4. - «Electronic Engr.»,
195.З, v. 25, р. 1146-·150.
4 . G о о d а 11 W. М. 1elephony Ьу pulse-oode-modulation. - ..:Bell System
Tech.», J ., 11947, v. 26, р . 395-409.
5. d е J а g е r F. De\ta modulati.on: А method of РСМ transrnission using the
1-unit oode. - ,«JJhiНps .Research Report», ·1952, v . 7, р . 442-4<66.
6. В е n n е t t W. R. Spectra of quantized signals. - «Bell Sys tem Tech. J.",
1948, v. ();7, р. 446----472.
3.3.1
<1.
12.
З.
4.
5.
Н е
r t z Н. Die К:rаИе elektrischer Sohwingungen behandelt nach der
Maxwell'schen Theorie. Ann. Phys" Neue Folge, 1889, Bd. 36, S. 1~.
Z и h r t НL Eloctromagnetische Strahlungsfelder. Ber\in/New York, Springffi",
19513.
S 1 а t е r J. С., F r а n k Н. Electromagпetism, New York, McGraw-HШ, 1947.
W а r е L. А. Elements of electromagnetic waves, New York, Pitman, 11949.
Вес k е r R., :S а u t е r F . The orie der Elektгiz i tat . Stuttgart, Teubner, :1964,
V. 1.
6. L а n d а u L. D" L i f s с h i t z Е. М. Lehrbuch der theoretischen Physik.
Вerlin, Akademie, 1100!, v. 11 .
7. К r а и s J. Anrennas. New York, McGraw "HИI, :1950.
8. S t·lle i k u n of f S. А. Electгomagnetic wavces. New York, Van Nost.rand, 194.з.
257
3.3.3
1. Н а r т и t h Н. Grundlagen und mбgliche Anwendungen der Sequenztechnik.
Bu\letin des Schweizerischen Elektrotechnischen Vereines, .1968, Bd. 59,
S. 1196---1203.
4.1.1
Mathematica\ methods of statistics. Princeton, Princeton Univer-
r ат е r Н .
sity Press, 1 194б .
2. К о 1 m о g о r о f f А. Foundati.ons of the theory of probabllity. New York,
Chelsea, 1950.
J.
С
4.3.2
1. S с h 1 i t t Н. Systemtheorie fur regellose Vorgiinge. Berlin/New York, Springer, :1960.
2. М i d d 1 е t о n D. An iпtroduction to statistica! communication theory. Ne\v
York, McGraw-Нlill, 1960.
3. L ее У. W. Statistical thE.Ory of communication. New York, Wiley, 1960.
4. L ее У. W" С h е а t h ат Т . .Р" W i е s n е r J. В. Application of correlation
ana\ysis to the detection o·f periodic signals in noise. - «Proc. IRE», 1950,
v. 38, р. :.11165-1./7'1.
5. G r ее n Р. Е . The output signal-to-noise ratio of correlation detect·o rs. «IRE TraлsacHo.ns оп lnformation Theory», 1958, v. !Т-4, р. 10-18.
6. W i е n е r N. Q.eneгa\.ized harmonic analysis. Acta Mahtematica, 1930, v. 55,
р.
117-258.
7. F i s с h е r F. А. Die mathematische Behandlung zufiilliger Vorgiinge in der
Schwingungstechnik.
«Fernmeldetechnische Zeitschrift», .19~.
Bd. 5.
s.
1 /б/-. 158.
5.1.1
1. D о о Ь J. L. Stochastic prosesses. New York, Wiley, 1963.
Q. V а n D е r Z i е 1 А. Noise. Englewood Cliffs NJ, Prentioe На\\, 1964.
3. R i се S. О . Mathematical analysis of random noise. - «Ве\1 System Tech. J. »,
11944, v. .zз, р . 282--832, ,\ 945, v. 24, р. 46--156.
4. S т u 11 i n D" На и s Н . А . Noise in electron devices. New York, Wi\ey, 1959.
5. В е n n е t t W. R. Eleotrical noise. New York, McGraw-Hill, 1960.
6. D а v е n р о r t W. В" R о о t W. L. An introduction to the theory of random
signa!s and noise. Ne·..v York, McGraw-Hill, 1958.
7. S с h w а r t z М. Information transmission, modu\.ation and noise. New York,
McGraw-Hil\, 1959.
8. R о о t W. L" Р i t с h е r Т . S. Оп the Fourier-series exp ansion of random
func·t ions. Annals .of Math. Stat.istics, 1955, v. 2б, р. 3 13--J.18.
9. Н а и s Н. А . et а!. I·RE standards of methods of measuring noise in \inear
twoports. - «Proc. IRE», 11960, v. 48, р . 60-68.
10. D 6 r r К. Die statistische Verteilung der Nu\ldurchgiinge vоп Ri:.uschspannungen. - «Archiv elek. Ubeгtragung», 19165, Bd. 19, S. 68б-1698.
!.1. S z а 1 а у G. Die Verteilungsdichte der Inte·rva\le bei einem Rauschsignal mit
Schwellwert. - «Archiv elek. Ubertr.a gung», 1964, Bd. 18, S. З>!б---322.
112. J о h n s о n J . В. Thermal agitation of electricity in conductors. - «Physica\
Review», ,!928, v . .32, р . 97~ 109 .
5.2.1
1. К о t е \' n .ik о v V. А. The theory of optimum noise immunity. New York,
McGr.aw-Hi\I, 1959.
2. S i е Ь е r t W. М" R о о t W. L . Statisti.ca\ decision theory апd communications .
ln Lectures on communicaHon system theory. New York, McGraw-Hill, . 19бl.
З. М i d d 1 е t о n D. An introduction !о statistica\ communication theory. New
York, McGraw-Hill, 1900.
4. W а i n s t а i n L. А" Z и Ь а k о v V. D. Extraction of signals from noi se.
Eng\ewood Cliffs NJ, Prentice На\!, 1962.
258
5. Н а r m а n W. А. Principles of the statistical theory of oommunication. New
Yor:k, McGraw-Hill, 1963.
6. W i е n е r N. Extrapolation, inter1:юlation and smoothing of stationary time
seri€s. New York, МIТ Press and Wiley, 1949.
.._
7. Н1 а n с о с k J . С. Signal detection theory. New York, MaGraw-Hill, 19615.
8. L 1i v i n s о n N. The Wiener RMS error criterion in fШer design and prediction. - «J. of Math. and Physics», 1947, v. 25, р. 261--1278.
9. К: о 1 m о g о r о f f А. InterpoLa·tion апd extrapolation of stationary random
sequencies. Bulletin de l'academie des sciences de U.SSR, Ser . .Math., 1941,
v. 5, р. З---.1 14.
10. S h е r m а n S. Non-mean squaгe erroг cr.iteria. «IRE Transactions on
Information Theory», 1959, v. IТ-4, р. 1125-126.
11. В о d е Н. W. А simplified derivation of linear leastsquare smoothing апd
prediction theory. - 1«.Ргос. IRE», 1950, v. 38, р . 417-426.
12. А r t h u r s Е" D у m НI. On the optimum detection of digital signals in the
pгesence of white Gaussion noise. «IR.E Transactioпs on Communication
Systems», 19612, v. CS-10, р . 336-372.
5.2.3
!. N о r t h D. О . An analysis of the factors which determine signal/noise discrimination in pulsed-carrier systems, repгinted in Proc. IEEE, .11963, v. 51, р. · 101б-
, J.о27 .
2.
3.
4.
5.
6.
Т
u r i n G. L. An intnoduction to matched filters. - «IRE Transactions on
Information Theory», 1960, v. IТ-6, р . 311-329.
S с h i.i s s 1 е r W. Ober den Entwurf optimaler Suchfilter. - «NTZ», 1964,
Bd . .17, S. 605-613.
.S с h 1 i t t Н. Systemtheorie fi.ir regellose Vorgiinge. Berlin/New York, Springer, 1%0.
Z а d е n L. А" R а g а z z i n i I. R. Optimum filters for the detection of
эignals in noise. - 1«Proc. IR.E», 119512, v. 40, р. 1123-11131.
Ре t е r s о n Е . L. Statistical analysis апd optimization of systems. New York,
Wiley, 196'1·.
5.2.4
.!.
С о
r r i n g t о n М. S., А d а m s R. N. Advanced analytical and s ignal process.ing technoiques:Applicaticn o·f Walshfunctions to noпlinear analysis. Technical
Report AD-!277942, 1962.
2 . W е i s е r F . Е. Walsh fшi.ction analysis of instantaneous noпlinear stochastic
proЫems. Thesis, Polytechnic lпstitute of Brooklyn, 1964.
1.
В а с
5.3.1
2.
3.
4.
5.
6.
7.
8.
9.
h d а d у Е . J. Diversity techniques. In Lectures on communication system
theory. New York, McGraw-Hill, 1961.
В r е n n а n D. G. Linear diveгsity comblning techniques. Proc. IRE, 11959,
v. 47, р . 1075---;l Ю2 .
Р i е r се J . N" S t е i n S. M11ltiple d·i versity wit!1 nonindependent fading. «Proc. IRE», 19160, v. 48, р. 89-104 .
Р r i се R.. Optimum det~ ction of random signals in пoise with application to
scaHer multipath comnшnications. «IRE Tгansactions on lnfonnation
Theory», 1956, v. IТ-2, р. 125_,1вs.
1Р r i се R., G r ее n Р. Е . А communication technique for multipath channels. «Proc. IRE», 1958, v. 45, р. 555-570.
G l е n А. В . Comparisoп of РSК: vs FSК. and РSК:-АМ vs FSK-AM Ьiпаrу
coded transmission systems . - «IEEE Transactions on Coшmunication Systems», 11960, CS-8, р. 87-100. ·
R i d о u t Р. N., W h ее l е r L. К.. Choice of multi-channel telegraph systems
for use on HF radio links. - «Proc. !ЕЕ», 1963, v. 110, р . 1402_,14\iO.
Т u r i n G. L. On optimal diversity reception 1.
«lRE Transactions оп
InformaHon Тhеогу», 19&1, v. IТ-7, р . J54_,lб6.
Т u r i n G. L. On optimal diversity r·ecepHon II. «IRE Transactions on
Communication Systems~. 1962, v. CS-1\0, р. 22-31.
259
10. L а w Н . В . The deteotabllity of fading radiotelegraph s1gnals in noise. cProc. IEE», .1957, v. 1043, р. 1130-<140.
Ы. V о е 1 с k е r НI. В. Phase shift keyiпg in fadiпg chanпels. c:Proc. IRE»,
·1960, v. ' 107В, р. 31-38.
112. Р i е r се J. N. Theoretical diversity improvemeпt iп frequeпcyshift keyiпg. «,Proc. IRE», 1968, v. 46, р. 903--910.
Ш. А 1 па t t J. W" J ·Оп е s Е . D" L а w Н . В. Freq u eпcy diversity in the receptioп
of sel~tive fadiпg Ьinary frequeпcy-modulated sigпals. - «Proc. !ЕЕ», 1957,
v. 1 104В, р. 98-<НО .
14. В е 11 о Р . А" N е 1 i п В . D. The effect of frequeпcy selective fading оп the
Ыпаrу erюr probabllities of ,incohereпt апd diifereпtial\y cQhereпt matched
Шter receivers. «IEEE Traпsactioпs оп Commuпicatioп Systems», ,1963,
v. CS-H, р . 170-186.
IS. В е s s 1 i с h Р h. Fehlermahrscheiп\ichkeit blпarer Ubertragungsverfahren bei
Storuпgen durch Rauscheп uпd Schwuпd . «Ar1:hiv elek. Ubertragung», 19ro,
Bd. 11,7, S. !185-'197.
16. В е s s 1,i с h Р h. Fehlerw a hrschei пlichkei.t b.JJarer Ubertraguпgeп bei Mehrfacbempfang und Frequeпz - selektivem Schwuпd. c:Archiv elek. Ubertragung», 1963,
-вd. 17, S. 271-!277.
17. Z u h r t Н. Die Summeпhiiufigkeitskurveп der exzentrischeп Rayleigh-Verteiluпg
und ihre Aпweпduпg auf Ausbreitungsmessungeп . - «Archiv elek. Ubertraguпg», ·1957, Bd. 1\11, S. 478-484.
18. Не п z е Е . Theoretische Uпtersuchuпgeп iiber eiпige Diversity-Verfahreп. <<Archiv elek. Ubertraguпg» , 11957, Bd. 11, S. 183-,194.
19. S с h w а r t z М" В е n n е t t W. R" S t е i n S. Communication systems апd
techпiques. New York, MaGraw-Hill, 19i66.
20. G r о s s k о р f J" S с h о 1 z М" V о g t К:. К:orrelatioпsmessungen imК:urzwe\leп
bereich. NTZ, 1968, Bd. 11'1, S. 91-95.
6.1.1
1. N у q u i s t Н. Certaiп topics in telegraph traпsmission theory. - «Тraпs
actioпs AIEE», 119.28, v. 47, р . 611:7--644.
2. К: ii р f т ii 11 е r К:. Uber Eiпschwingvorgiiпge in Wellenfilterп. - «1Elecktrische
Nachrichteп-Techпik», 1924, Bd. 1, S. :1~1-152.
3. К ii р f т ii 11 е r К:. Ausgleichsvorgaпge uпd Frequeпzcharakteristikeп iп
linearen Systemeп . - «Elektrische N.achrichten-Techпik», 19128, Bd. 5, S.118-32.
4 На r t 1 е у R. V. L. Tr.aпsmissioп of iнformatioп . - «Ве\1 System Tech. J. »,
il008, v. 7, р. 535--'56.З.
5. К: ii р f т ii 11 е r К Die Systemtheorie der elektrischeп Nachrichteniibertгaguпg_
Stuttgart, Нlirzel, 1952.
6. S h а п поп С. Е . А mathematical theory of commuпication. - «Ве\1 System
Tech. J.», 11948, v. 27, р. 37!}.-423, 1623-6'56.
7. S h а n n о n С . Е . Communication iп the preseпce of noise. - «Proc. IRE»,
1949, v. 37, р. 10-121.
6.1.2_
•1. F а по R. М . Traпsmissioп Qf iпformatioп . Ne\v York, МIТ Press апd W:i\ey,
1961.
,z_ S с h m i d t К. О . Vorschlage zur Berechпuпg der wirk\icheп К:aпalkapazitiit
beim Vorhaпdeпseiп vоп Verlusteп auf dem Ubertraguпgswege. - -«Archiv
elek. Ubertr.aguпg», 195.4, Bd. 8, S. 119-126.
3. Z е тапе k Н. Elemeпtar c Jnformatioпstheorie. Wieп, Oldeпfurg, 1959.
4. F е у Р. Jпformatioпstheorie. Berliп, Akadeшie, 1900.
5. S от те r v i 11 -е D. М . У . An iпtroductioп to the geometry of N d:mensioпs.
New York, Duttoп , ·19.29.
6. М а d е 1 u п g Е. Die mathematischeп Hi\fsmittel des Physikers. Berlin/New
York, Spriпger, 11957.
11'.
6.1.3
r т u t h Н. Die Ubertraguпgskapazitat
Veral\gemeinerung des Begriffes Frequen.z . Bd. :19, S. li25~13.З.
Н а
260
vоп
Nachrichteпkanalen
пасh
dег
«Archiv elek. UЬertragung» , 1965,
t2. S о m m е r f е 1 d
А. Uber die Fortpflaпuпg des Lichtes iп dispergiereпden
Medien. Ann. Phys., 1914, v. 44, S. 1177--002.
6.2.1
11.
2.
3.
О а v е n р о r t W. В. J r., R о о t W. L. An iпtroduction to the theory of random
sigпals and noise. New York, McGraw-Hill, 1958.
Н а r m а n W. W. Priпciples of the statistical theory of communication. Ne\v
York, McGraw-HЩ 196.З.
W а i n s t е i п L. А., Z u Ь а k о v V. О. Extractioп of signals fюm пoise. Engle-
wood Cliffs NJ, Prentice Hall, 1962.
6.2.2
1
1. Н а r m u t h Н., S с h m i d Р. Е., О u d 1 е у Н . S. MuJti.pJ.e access commuпication wHh bl.nary orthogonal sine апd cosine pulses using heavy amplitude 1
clippiпg. 11968 ШЕЕ Iпt. Сопf . оп Cqmmuпications Record, р. 794-799.
1
2. V а n V 1 ее k J. Н., М i d d 1 е t о n О. The spectrum of clipped noise. Proc.
IEEE, 1966, v. 54, р . 2-<19.
З . S u п d е Е. D. Ideal Ыпаrу pulse traпsmissioп Ьу АМ апd FM. - «Bell Systeш
Tech. J.», 19159, v. 38, р. 1357-1426.
6.2.3
1.
2.
3.
4.
5.
А
i k е п s А. J., L е w i п s k i D. А. Evaluatioп of message circuit пoise. - «Ве\1
System Tech. J.», !1960, v. 39, р. 879-909.
S m i t h D. В . , В r а d 1 е у W. Е. The theory of .impulse noise in ideal frequeпcy
modul.atioп recei·v ers. Proc. IRE -194'6, v. 31, р. 7143_.751 .
В е п пе t t W. R. Electrical пoise. New York, McGraw-Hill, 11900.
S t u m р е r s F. L. Оп the calculati.oп of impulse-пoise traпsients iп frequencymodulaHoп receivers. Philips R·e search Repts., 1947, v. 12, р . 46&--47.4.
Н1 а r m u t h Н. Kodieren mit .orthogoпaleп Fuпktioпeп. - .cArchiv elek. Ubertr.a guпg», 196.З, Bd. lr7, S. 4Q9-437, 508--618.
1
6.3.1
m m i п g R. W. Error detectiпg апd error correctiпg c.odes. - с:Ве\1 System
Tech. J.», 19&>, v. i29, :р. 1147--4160.
2. S 1ер ·i а п О. А class of blnary sigпaliпg alphabets. - «Bell System Tech. J .»,
·1956, v. 35, р. 003-234.
3. W о z е пс r а f t J. М., R е i f f е п В. Sequeпtial decodiпg. Ne\\· York, МIТ Press
.and Wiley, 19i61·.
4. G а 11 а g е r R. С. Low-deпsity parity-check codes. Cambridge, Mass., MIТ-Press,
1.
Н а
5.
М
19163.
6.
7.
8.
9.
10.
lil.
u 11 е r D. Е. ApplicaHoп of Вооlеап algebra to switchiпg circuit desigп and
t<> error detectioп . - «IRE Traпsactioпs оп Electronic Computers», .1954,
v. ЕС-3, р. 6-'lt2.
Ре t е r s оп W. W. Error correctiпg codes. New York, МIТ Press and Wiley,
.1961.
tP е t е r s оп W. W. Progress of iпformatioп theory 1960-63. - «IEEE Traпs
acbloпs оп Iпf.ormatioп Theory», 1 Ю6.З, IТ-10, р. 221~.
.L ее С. У. Some properties of поп-Ыпаrу err<>r correcting codes. - «IRE Traпs
actioпs оп Iпformatioп Theory», 11958, IТ -4, р . "т--8'2.
U \ r i с h W. Nоп-Ыпаrу епоr correctiпg codes. - «Bell System Tech. J.»,
·1957, v. 00, р. 1:341-1388.
R ее d I . S. А class of multiple-error-c.orrecting codes and the decoding scheme. - «IRiE Traпsactioпs оп Informatioп Theory», 1954, v_ IТ-4, р. 38-49.
W е i s s Р. Uber die Verweпduпg von Walshfuпktioпeп iп der Codieruпgs
theorie. - .«Лrchiv elek. Ubertraguпg», \967, Bd. 21, S. М5-'258.
6.3.2
1. G о 1 от Ь S. W. et а\. Digita\ c.ommuпicatioпs. Eпglewood C\iffs NJ,
На\\, •1964.
2. На r т u t h Н. Orthogoпal codes. Proc. !БЕ, 1900, 107С, р. 24Q-.248.
261
Preпtice
з. А
4.
5.
6.
7.
8.
9.
10.
r о n s t е i п R.. HI. Comparison of orthogoпal апd ЬJ,ock codes. - «Proc. IEE»,
11963, v. ыо, р. 1965-1967.
Н s i е h .Р ., Н s i а о М. У. Several classes of codes geпerated from orthogoпal
fuпctioпs . «IEEE Traпsactioпs оп Iпformatioп Theory», 1964, v. IТ-10.
р. 88-91.
F а по R.. Commuпicatioп iп the preseпce of additive Gaussiaп пois e . New York,
Academic Press, 1953.
L а с h s G. Optimizatioп of s·igпal waveforms. - «IEEE Traпsactioпs оп Iпfor
matioп Theory», 1963, v. IТ-9, р . 9.5-97.
Р а 1 е у R.. Е. Оп orthogoпal matrices. J. Math. апd Physics», 193.З, v. Щ
р . 31 l-312Q.
S ·t а п t оп R.. G" S р r о t t D. А. А family of differeпce sets. - «>: Сапаdiап J.
of Math.», 19'58, v. 10, р. 73-77.
В о s е R.. С" S h r i k а п d е S. S А поtе оп а result •iп the theory of code
coпstructioп. - .<Iпformatioп and Coпtrol», 1959, v. 2, р. l&З-194.
N е i d h а r d t Р. Iпf·ormatioпstheorie und automatische Iпform a tioпsverarbei
tuпg. BerJiп, Verlag Techп i k, 1004.
6.3.3
11. W о о d Н. R.aпdom пormal deviates, Tracts for Computers Z5. Lопdоп, Cambridge Uпiversity ,Press, 1948.
2. U S Departrneпt of Commerce, Haпdbook of mathematical fuпctioпs, Natioпal
Bureau of Staпdards Applied Mathematical Seraes 55. Washiпgtoп DC, US
Goverпmeпt Priпtiпg Office, '1964.
3. Т h е R. А N D Corporatioп, А m.illioп raпdom digits w.ith ·100 ООО пormal
devi a tes. Gleпcoe Ш., The Free Press, \9!'Ю.
4. Ре t е r s оп W. W. Error correctiпg codes. New York, МIТ Press апd Wiley,
1961.
5. Е 1 i а s Р. Error-free codiпg . - «IR.E Traпsactioпs оп Informatioп Theory»,
1954, v. IТ-4 , р. 29--37.
6.3.4
.1.
На r m u t h Н. ~odiereп mit orthogoпaleп Fuпctioпeп.
11.
К:omblпatioпs·Alpha
bete uпd Minimum-Eпergie-Alphabete. - «Archiv elek. Obertraguпg», 196.З,
Bd. ·17, S . 508--518.
2. К а s а с k U. Korrela,tioпsempfaпg vоп Buchstabeп iп Ьiпarer bzw. terniirer
Darstelluпg bei Baпdbegreпzuпgeп uпd gau6schem R.auscheп . «Archiv elek.
Obertraguпg», 1968, Bd. 22, S. 487-493.
ДопоJJНатеJIЬная литература ко
второму изданию
1. А п d r е w s Н. С., С а s р а r i К. L. А geпeralized techпique for spectra1
aпalysis . - «IEEE Traпs. оп Computers», 1970, v. С-19, р. 16---<25.
2. А п d r е w s Нl. С., К а п е J. Kroпecker matrices, computer implemeпtatioп апd
generalized spectra. J. Assooiatioп for Computiпg Machiпery, iп priпt (scheduled
for April 1970).
3. А 1 е ха п d r i d i s N. А. Hadamard traпsform iп template matchiпg pattern
recogпitioп. Proc. 3rd Hawaii lпt . Сопf. оп System Soieпce, 1870, р. 1Q7.
4. С а r 1 J. W. Geпeralized harmoпic aпalysis for patterп recogпitioп: А Ьiologi
cally derived model. Master's Thesis, Departmeпt of Electrical Eпgiпeeriпg.
Air Force Iпstitute of Techпol.ogy, Daytoп , Ohio, 1969.
5. D е с k е r J. А" На r m i t .М. Experimeпtal operatioп of а Hadamard spectrometer. Applied Optics, .1969, v. 8, р. 2552-2554.
6. F i 1 i р о w s k у R. F. Multiorthogonal data traпsmissioп systems. Digest .1967
IEEE Iпt. Сопf. оп Commuпicatioпs, Miппeapolis, р. 36.
7. F r ;i n r. f о r t Е. Evaluatioп апd optimizatioп of performaпce criteria in liпear
systems coпtaiпiпg ап uпcertaiп parameter. Master·s Thesis, Departmeпt of
Electrical eпgineeriпg, Polytechпic Iпstitute of Brooklyп, 1968.
8. G i Ь Ь s J . Е " G е Ь Ь i е G. А. Applicatioп of Walsh fuпctioпs to traпsform
spectroscopy. - «Nature», 1969, v. 1224, р. 1012-1013.
9. G i Ь Ь s J. Е., М i 11 а r d .М. J. Wa!sh fuпctioпs as so!utioпs of а logica1
differeпtia! equatioп, DES Report N 1, 11969; Some methods of solutioп of
blпear ordiпary logical differeпtial equatioпs, DES Report N 2, 1969; Some
properties of fuпctioпs оп the пoп-п e gative iпtegers less thaп 2п, DES
Report N 3, 1969 Natioпal physical Laboratory, Divisioп of Electrical Scieпce,
Teddiпgtoп, Middlesex, Eпglaпd.
10. G о 1 о m Ь S. W" В а u m е r t L. D. The search for Hadamard matrices. «Amer. Math Moпthly » , 196.З, v. 70(.2), р. 12-17.
11. Н u g g i п s W. Н. Represeпtatioп апd aпalysis of sigпals, part 11: The use
of orthogoпaHzed expoпeпtials, Techпica! Report AD 208133, ·1958.
12. 1 t о Т. Note оп а class of statis·tical гecogпition fuп c tioпs . - «IEEE Traпs.
оп Computers», .1969, v. С-18, р. 76-79.
13. К а с z та r z S" S t е i п h а u s Н1. Theorie der Orthogoпa!reiheп. Ne\v York,
Chelsea РuЫ. Со" 1951', · (origiпally puЫished Warszawa-Lwow, Moпografje
Matematyczпe, VI, 1935).
14. К о w а 1 с z у k Е. Some proЫems of applyiпg orthogoпal fuпctioпs in telecommuпicaHoпs (iп Polish). Rozprawy Elektrotechпiczпe, 1966, v. 12, р. 469489.
15. L а В а r r е J . В . К. А traпsform ·teohпique for liпear, time-varyiпg, discretetime systems. PhD Thesis, Departmeпt of Electrical Eпgiпeeriпg, U of Michigan,
Апп Arbor, ·1969.
16. М е 1 t z е r В., S е а r 1 е N. Н" В r о w п R. Numerical specificatioп of blol'°gical
form. Na·ture, ·1967, v. 216, р. 32--36.
17. N а m Ь i а r К К А поtе оп the Walsh fuпctioпs. - «IEEE Traпs. оп Electroпic Computers», 1964, ЕС-13, р. 631-632.
18. Р i с h 1 е r F. Walsh-Fourier Syпthese optimaler Filter. - «Archiv der e!ek.
Ubertraguпg», iп priпt.
19. S с h r е i Ь е r Н. Н. Baпdwidth requiremeпts for Walsh fuпctioпs. IEEE Trans.
оп Iпformatioп Theory, iп priпt.
20. S е а r 1 е N. Н. Shape aпalysis Ьу use of Walsh fuпcHoпs . .Proc. 5th Iпt.
Machiпe Iпtelligeпce W.orkshop. Ediпburgh, Ediпburgh University Press, 1969.
Ш. S h а w L" С h а 1 оп Р. Ап ехрапsiоп for evaluatiпg seпsitivity to а ra пdom
parameter. Automatica, 1969, v. 5, р. 265-273.
263
2'!. S i е m е n s 1(., 1( i t а 1 R.. Digital Walsh-Foш:ier analysis of per.i odk w.ave-
forms. - ~IEEE Trans. оп Instrumentation and Measurement:., ·!9W, v. IM-18,
December.
23. S t а n а t D. F. Uпsupervised learning of mixtures of probablliity funclioпs .
In Pattern R.ecognitioп, L. N. l(anal ed. W:ashiпgtoп D. С., Thompson Book
Со., 1968.
24. S z о k W. G. Waveform characterization in terms of Walsch functions. Masters
Thesis, Department of Electrical Eпgiпeering, Syracuse University, 1968.
25. Та k i У., Н а t о r i М.. РСМ Commun:ication system using Had·amard transformati.oп. ·«Electronics апd Commuпicatioпs iп Jарап:., 11900, v. 49(Ы),
р. Q47-Щ~7.
tlб .
W а t а r i С. Оп decompositioп of Walsh-F·ourJer series; Multipliers for WalshFourier series; Меап ooпvergence of Walsh-Fourier series; Best a·pproximatiori
Ьу Walsh polynomials. .cTбhoku М.ath. J.:., •1965, v. 17, р. 7&--86; 1964,
v. 16, р . '2.39-Шil; 11964, v. ·1!6, р. т18З-Н88; 196.З, v. il'5, р. 1-б .
fl7. W оп g Е., Е i s е n Ь е r g Е. Iterative synthesis of threshold f111notif"пs . т«J . М.ath. Analysis and App!.ications:., 1005, v. ·11, р. 2'2J6..-.-:236.
28. У а n о S. Оп W:alsh-.Fourier series. - c:Tбhoku Math. J.•, 1~1'. v. 6(2),
D.
1223---2412.
~·
_."
ПРЕД.МЕТНЫЯ
сдвига фаз 117
Унвера 118
частотного разнесения 196
Многоканальная система 95
Множ ес тво 152
Модуляция амплитудная 89
- квадратурная 95
- кодовая 133
- по временной базе 129
- по в ременному положению 131
- с частично подавленной боковой
Автокорреляционная функция 178
Активная антенна 142
АJ1фавитный биортогональный 61
- блоч н ый 228
~ телеграфный 55
- трансортогональный 61
Белый нормальный шум 180
Борелев ское множество 152
Верхняя боковая 90
Взаимокорреляционн а я функция 179
Волны Уолша 139
Генератор функций Уолша 66
Группа двоичная 25
- топологическая 23
Двоичный символ 58
Детектор синусоидальных и косинусоидальных импульсов
Диполь Герца
Дискретизация
Зона ближняя
-
волновая
-
-
121
Моменты 158
Нерав е н ство Бесселя 13
Нижняя боковая 90
Нормализованн а я поло с а пропускания
84
69
Одном е рная случайная величина 151
Однополосная модуляция 95, 1'13
Перемножнтель 67
Плотность вероятности случайной ве
личины 155
Полиномы Б е рнулли 11
- Лежандра 12
Предста влени е сигна лов с помощью
векторов 56
- коэффиuнентов 56
- функций 56
Преобразование Лапласа обобщенно е
133
63
135
1135
Импульс 9
Импульсн ые помехи 224
Инвариантность обобщенного
разования Фурье 34
ортогонального
Фурье 14
преоб-
преобразования
Интегратор 69
Ковариация 175
К:одирование 150
45
Пнхлера 23
Уолша-Фурье 23
Уолша-Фурье быстрое 42
Уолша-Фурье бы строе обратное 43
- Файна 23
- .Фурье 14
- Фурье обобщенное 31
- Хаора-Фурье 42
Пропускная с пособность канала свя
зи 207
Разделение сигналов вр е менное 56
К:омбинационн ы е коды 238
К:омпандеры 193
К:оррекция временного рассогласова
ния
-
122
К:орреляционная функция периодических функций Уолша 128
К:орреляция 55, 175
К:оэффициент корреляции 176
Линейный оператор 49
Матрица Адамара 20
- задержки 80
- ортогональная 232
- перекрестных искажений
Метод временного разнесения
-
пространственного
-
1196
Capara 117
УКАЗАТЕЛЬ
-
ортогон а льное 56
частотное 56
Разностное у равнение функций
ша 20
80
196
разнесения
Распределение Бернулли
265
156
Уол
Расстояние Х.эмминга 228
Система функций замкнутая
- несчетная 25
-
14
полная 13
счетная 25
Уолша 10
синусоидальных
дальных 9
Скорость передачи
и
косинусои-
202
Сложение по модулю два 21
Согласованный фильтр 191
Статистическая независимость случайных величин 154
Супергруппа 104
Телеграфное уравнение 75
Уплотнение временное 56
-
ортогональное
частотное
56
56
Уравнение Максвелла 134
Условная вероятность 153
Фильтр 47
высших частостей 87
- нижних частостей 80
частотный з.аrрадительный
- поло~овой 82
- цифровой 87
- широкополосный 86
Формула Шеннона 213
Функции линейно зависимые 8
- линейно независимые 8
- нечетные 15
-
ограниченные
во
времени
87
и
по
частости 52
- ортогональные 8
- параболического цилиндра 19
- Радемахера 23
- Уолша 19
Функция Дирака 50
- множества 152
- распределения случайной величины 154
Частостный спектр 52, 54
Частость 46
Частота обобщения 34, 46
ОГЛАВЛЕНИЕ
Предисловие к русскому переводу
Предисловие
Введение
1.
автора
.
.
Математические основы передачи сигналов
1.1. Ортогональные функции .
. . .
1.2.
3
4
5
8
8
. .
•
Преобразование Фурье и его обобщение
25
1.3. Обобщенная частота
2.
43
Непосредственнная передача сигналов •
• • • • • • • •
•
2"1. Ортогональное разделение как обобщение временного и частотного
разделений . .
. . . ..
2.2 . Характеристика каналов связи . .
2.3. Частотные фильтры, основанные на
3.
.
55
74
функциях Уолша
80
.
.
Передача сигнала на несущей
•
3.1. Амплитудная модуляция (АМ) . . .
.
3.2. Модуляция по временной базе, модуляция по временному положе-
нию и кодовая модуляция
.
3.3. Несинусоидальные э,1ектромагнитные волны
129
Случайные величины
5.
Прнменение ортогональных функций в статистических задачах
5.1 . Разложение стохастических функций в ряд
5.2. Аддитивные помехи . .
5.3. Мультипликативные помехи
.
4.1. Одино'Чные величины
4.2. Системы величин . . .
4.3. Статистическая зависимость
Синтез
6.1.
6.2.
6.3.
сигнала для повышения
Пропускная спос:~бность
Вероятность
ошибки
Кодирова·ние
Список
литературы
ДололнитеJ1ьная
Предметный
литература
указатель
надежности
систем
канала
.
ко
второму
изданию
89
89
134
4.
6.
55
связи
150
150
160
175
180
180
185
195
202
202
216
227
251
263
265
Хеннинг Ф. Хармут
ПЕРЕДАЧА ИНФОРМАЦИИ ОРТОГОНАЛЬНЫМИ ФУНКЦИ.ЯМИ
Редактор Т. Б. Полиектова
Техн. редактор К.. Г. Марко"
Художник И. А. Дутов
Корректор В. В. Суркова
Сдано в набор 27/XI 1974 г .
Формат 60Х9О/10
Бумага тип. No
Тираж 4800 экз.
Изд. № 16093
Издатепьство
«Связь~.
Типография
Москва
2
Подп. в печ. 5/111 1975 г .
усл. печ. п.
17,&1 уч.-нзд . .11.
Зак . No 322
Цена 1 руб. 60 коп.
101000, ЧистопрудныА бульвар, д . 2
17,0
издательства «Связы
rоскомнздата
Москва 101000, уп . Кирова, д. 40
СССР
В издательстве •Связь•
в ближайшее время выходят :юниги:
'
r;
.н
С мирно в В.
А.
Приближеивые
методы расчета
помехоустойчивости и искажений в системах переда
чи информации.
Описываются приближенные методы расчета поме
хоустойчивости и
воляющие
искажений
значительно
в
системах
упростить
связи,
расчеты
и
поз
обеспе
чить достаточную точность. Могут быть оценены шумы
на
выходе приемников при
любых
видах
модуляции
и пороговые значения отношения сигнал/шум на вхо
де
приемников.
Книга может быть полезна
инженерам
и
студентам
научным работникам,
ра,диотехнических
факуль
тетов.
Стиффлер Д. Д. Теория синхронной связи
Theory of Syn.chronous communications)
1971, пер. с англ.
Книга
Стиффлера
является пока
мировой литературе монографией,
тизирована
и
ясно
изложена
(Stiffler J. J.
Нью-Джерси,
единственной
в
в которой система
современная
теория
син
хронизации систем связи.
Теория
рии
синхронизации
решений.
мощью
излагается
Ра·ссматривается
отдельного
канала,
по последовательности
а
на
основе тео
синхронизация
также
сиmалов,
с
по
непосредственно
несущих
информа
цию.
Юнига рассчитана на научных работников, инже
неров,
аспирантов и
студентов старших
курсов, специ
ализирующихся в обласm передачи Шiформации, вы
числительной техники и кибернетики.
!269