OPTICAL WAVES
IN CRYSTALS
Propagation and Control of
Laser Radiation
AMNON YARIV
California Institute of Technology
POCHI YEH
Rockwell International Science Center
A Wiley-Interscience Publication
John Wiley & Sons
New York / Chichester / Brisbane / Toronto / Singapore
А. ЯРИВ, П.ЮХ
ОПТИЧЕСКИЕ
ВОЛНЫ
В КРИСТАЛЛАХ
Перевод с английского
канд. физ.-мат. наук С. Г. КРИВОШЛЫКОВА и
канд. физ.-мат. наук Н. И. ПЕТРОВА
под редакцией
д-ра физ.-мат. наук И. Н. СИСАКЯНА
Москва «Мир» 1987

ББК 22.34
Я73
УДК 535.5
Ярив А., Юх П.
Я73 Оптические волны в кристаллах: Пер. с англ. — М.: Мир, 1987.—
616 с. ил.
В книге известных американских специалистов рассматриваются вопросы распро-
распространения электромагнитных волн в периодических средах, теория волноводных мод в
диэлектрических волноводах и в волокнах, теория распространения поверхностных поля-
ритонов и т. п. Представлены также основы нелинейной оптики и явления оптического
фазового сопряжения. Большое внимание уделяется теории распространения электромаг-
электромагнитных волн в кристаллах, подверженных внешним воздействиям. Мо^ет использовать-
использоваться как учебное пособие.
Для физиков и инженеров, работающих в области квантовой электроники, инте-
интегральной оптики и волоконно-оптических линий связи, а также для студентов и аспиран-
аспирантов.
„ 1704050000—303 „
Я Т7-.—— 70—87, ч. 1
041A)—87
ББК 22.34
Редакция литературы по физике и астрономии
Научное издание
Амнон Ярив, Почи Юх
ОПТИЧЕСКИЕ ВОЛНЫ В КРИСТАЛЛАХ
Заведующий редакцией проф. А. Н. Матвеев
Зам. зав. редакцией С. М. Жебровский
Научный редактор А. Н. Куксенко
Мл. научные редакторы В. И. Аксенова, Р. X. Зацепина
Художник А. В. Дементьева
Художественный редактор К. В. Радченко
Технические редакторы Л. А. Тихомирова, Л. С. Тимофеева
Корректоры Н. А. Вавилова, Т. Б. Куликова
ИБ № 6023
Подписано к печати 06.08.87 г. Формат 60 х 9O'/i6. Бумага офсетная № 1.
Гарнитура тайме. Печать офсетная. Объем 19,25 бум.л.
Усл. печ.л. 38,50. Усл. кр.-отт. 38,50. Уч.-нзд.л. 35,30.
Изд. № 2/4756. Тираж 4200 экз. Зак. 63f . Цена 5 р. 60 коп.
Набрано в издательстве «Мир»
на фотонаборном комплексе «Компьюграфик»
129820, ГСП Москва, 1-й Рижский пер., 2.
Тульская типография Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли.
300600, Тула, проспект им. В. И. Ленина, 109
© 1984 by John Wiley & Sons, Inc.
All Rights Reserved. Authorized translation
from English language edition published by
John Wiley & Sons, Inc.
© перевод на русский язык, с исправлениями,
«Мир», 1987.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В настоящее время во всем мире происходит стремительное вне-
внедрение лазеров в науку и технику. Для многих применений необхо-
необходимы устройства, управляющие пространственными и временными
характеристиками лазерного излучения. Для создания таких уст-
устройств используются анизотропные среды, в частности кристаллы,
обладающие электрооптическими и акустическими нелинейными
свойствами. Монография известных американских исследователей
А. Ярива и П. Юха представляет собой современный курс кванто-
квантовой электроники, точнее той ее части, которая изучает распростра-
распространение лазерного излучения через анизотропные и нелинейные сре-
среды.
Проф. А. Ярив известен тем, кто работает в области квантовой
электроники. Ему принадлежит ряд монографий, пользующихся
большой популярностью среди специалистов. На русский язык пе-
переведены такие его книги, как «Квантовая электроника и нелиней-
нелинейная оптика» (М.: Сов. радио, 1973), «Квантовая электроника» (М.:
Сов. радио, 1980), «Введение в оптическую электронику» (М.: Вы-
Высшая школа, 1983), «Введение в теорию и приложения квантовой
механики» (М.: Мир, 1984).
В настоящей книге дается ясное изложение физических основ
распространения электромагнитного излучения в анизотропных
средах и рассматриваются физические принципы создания конкрет-
конкретных устройств электрооптики, акустооптики, интегральной оптики
и устройств, использующих нелинейные свойства среды.
Достоинством монографии является также помещенное в ней
большое число таблиц с материальными константами, которые
обычно приходится разыскивать по справочникам. Кроме того,
каждая глава завершается задачами, что весьма полезно и позволя-
позволяет рассматривать книгу как учебное пособие по квантовой электро-
электронике.
Мы надеемся, что данная книга вызовет большой интерес у ши-
широкого круга специалистов, работающих в области квантовой элек-
электроники, и у тех, кто занимается современной оптикой. Она будет

Предисловие редактора перевода
весьма полезной для студентов и аспирантов соответствующих
специальностей.
Перевод выполнили канд. физ.-мат. наук С. Г. Кривошлыков
(гл. 1—10) и канд. физ.-мат. наук Н. И. Петров (гл. 11—13).
Д-р физ.-мат. наук И. Н. Сисакян
ПРЕДИСЛОВИЕ
Предлагаемая читателю книга представляет собой учебное пособие
по курсу электрооптики для студентов, специализирующихся по
электротехнике и прикладной физике. Мы преследовали здесь две
главные цели: дать ясную физическую картину распространения ла-
лазерного излучения в различных оптических средах и научить чита-
читателя тому, как следует анализировать и конструировать электрооп-
электрооптические устройства.
Оценить характеристики оптических устройств и понять их
ограничения можно лишь, если хорошо изучить особенности рас-
распространения электромагнитного излучения. Это позволяет разра-
разрабатывать устройства для управления лазерным излучением. Поэто-
Поэтому основное внимание в книге уделяется изложению фундаменталь-
фундаментальных принципов. Мы постарались установить связь между теорией и
практикой путем рассмотрения конкретных примеров, основанных
на реальных ситуациях. Когерентное взаимодействие лазерного из-
излучения с различными оптическими средами мы рассматривали с
привлечением лишь классической электродинамики. Оптические
свойства этих сред описываются с помощью таких материальных
параметров, как диэлектрические тензоры, тензоры гирации, элек-
электрооптические коэффициенты, постоянные фотоупругости и нели-
нелинейная восприимчивость. Из оглавления нетрудно видеть, что здесь
рассмотрен очень широкий круг вопросов.
При написании этой книги мы предполагали, что читатель зна-
знаком с уравнениями Максвелла из курса электродинамики, а также с
интегралами Фурье, матричной алгеброй и дифференциальными
уравнениями.
Первоначальный вариант рукописи был положен в основу курса
для аспирантов по современной оптике, прочитанного летом
1982 г. П. Юхом в Тайваньском университете. Он хотел бы побла-
поблагодарить своих коллег и студентов этого университета за полезные
замечания и обсуждения. Особенно следует упомянуть проф.
К. П. Ванга [из Тайваньского университета], которому П. Юх обя-
обязан возможностью прочитать такой курс лекций. Он хотел бы по-
поблагодарить также д-ра Монте Кошневисана и д-ра Чан-Чинга Ши,

Предисловие
которые взяли на себя труд прочитать рукопись и сделали ценные
замечания, а также д-ра Хидехико Кувамото, д-ра Эмилио Соверо
и Марка Ивбанка за многочисленные полезные обсуждения.
Мы признательны Кармен Бирн и Руфь Стрэттон за их терпе-
терпение и аккуратность при напечатании рукописи. Мы также хотели
бы поблагодарить Филлис Форакер и Элен Куган за помощь при
получении разрешения на публикацию и при подготовке ссылок на
литературу. П. Юх признателен за поддержку научному центру
«Рокуэлл Интернешнл», а также за постоянную помощь д-ру Джозе-
Джозефу Т. Лонго и д-ру Джону М. Трэси.
Пасадена, Калифорния
Таузенд-Окс, Калифорния
Май 1983
Амнон Ярив
Почи Юх
Глава 1
ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ
Идеальный лазер генерирует когерентное электромагнитное излуче-
излучение, которое описывается с помощью векторов электрического и
магнитного полей. Поскольку распространение этого излучения
подчиняется уравнениям Максвелла, мы сначала познакомим чита-
читателя с основными свойствами электромагнитных полей.
В этой вводной главе дается обзор и вывод некоторых основных
соотношений для классических электромагнитных полей. Исходя из
уравнений Максвелла и материальных уравнений, мы получим вы-
выражения для плотности и потока энергии электромагнитного поля.
Будет доказана теорема Пойнтинга, а также выведены законы со-
сохранения и волновые уравнения. Мы подробно рассмотрим распро-
распространение монохроматических плоских волн и некоторые их важ-
важные свойства, а также обсудим понятия фазовой скорости и груп-
групповой скорости волнового пакета, распространяющегося в среде с
дисперсией.
1.1. УРАВНЕНИЯ МАКСВЕЛЛА И ГРАНИЧНЫЕ УСЛОВИЯ
1.1.1. УРАВНЕНИЯ МАКСВЕЛЛА
В классической электродинамике электромагнитное поле в свобод-
свободном пространстве описывается двумя векторами Е и Н, называе-
называемыми напряженностями соответственно электрического и магнит-
магнитного полей. Для учета влияния этих полей на вещество необходимо
ввести еще два вектора, а именно вектор электрического смещения
D и вектор магнитной индукции В. Эти векторы связаны между со-
собой уравнениями Максвелла, которые в системе единиц СИ записы-
записываются следующим образом:
V • D = p,
V -B = 0.
A.1.1)
A.1.2)
A.1.3)
A.1.4)

10
Глава 1
Здесь J — плотность электрического тока (ампер на квадратный
метр, А/м2), а /о — плотность электрического заряда (кулон на ку-
кубический метр, Кл/м3).
Эти четыре уравнения выражают основные законы электроди-
электродинамики в дифференциальном виде. Уравнение A.1.1) является диф-
дифференциальным выражением закона индукции Фарадея, описываю-
описывающего генерацию индуцированного электрического поля за счет из-
изменяющегося во времени магнитного потока. Уравнение A.1.2) —
это дифференциальная форма обобщенного закона Ампера, описы-
описывающего генерацию индуцированного магнитного поля потоком за-
зарядов. Уравнение A.1.3) является дифференциальной формой за-
закона Кулона, описывающего связь между распределением зарядов
и электрическим полем. Уравнение A.1.4) можно рассматривать
как условие отсутствия свободных магнитных зарядов (монополей).
Уравнения Максвелла A.1.1)—A.1.4) полностью описывают рас-
распространение электромагнитного излучения в любой среде.
Плотность заряда р и платность тока J можно рассматривать
как источники электромагнитного излучения. Во многих задачах
оптики приходится иметь дело с распространением электромагнит-
электромагнитного излучения в удаленных от источников областях, в которых как
/о, так и J равны нулю. К этой категории относятся и все задачи,
рассматриваемые в данной книге.
Уравнения Максвелла образуют систему дифференциальных
уравнений в частных производных, связывающую четыре основных
вектора электромагнитного поля: Е, Н, D и В. Для однозначного
определения векторов поля по заданному распределению токов и
зарядов эти уравнения следует дополнить соотношениями, учиты-
учитывающими взаимодействие электромагнитного поля с веществом.
Такими соотношениями являются материальные уравнения
D = еЕ = е0Е + Р,
В = МН = МоН + М.
A.1.5)
A.1.6)
В этих уравнениях параметры е и /х, характеризующие среду, пред-
представляют собой тензоры второго ранга, называемые соответствен-
соответственно тензором диэлектрической проницаемости (диэлектрическим
тензором) и тензором магнитной проницаемости; Р и М — векто-
векторы электрической и магнитной поляризации, а е0 и ц0 — диэлектри-
диэлектрическая и магнитная проницаемости вакуума соответственно. Для
изотропной среды указанные тензоры сводятся к скалярным вели-
величинам. Во многих случаях величины е и fx можно считать независи-
Электромагнитные поля
11
мыми от напряженности полей. Однако для достаточно сильных
полей, таких, например, как поля, возникающие при фокусировке
лазерного пучка или при облучении электрооптического кристалла
сильным электрическим полем, следует учитывать зависимость
этих величин от Е и Н. Такие нелинейные оптические эффекты мы
рассмотрим в гл. 7 и 12.
1.1.2. ГРАНИЧНЫЕ УСЛОВИЯ
Решения уравнений Максвелла можно получить в областях про-
пространства, в которых е и fx непрерывны. В оптике же нередко при-
приходится решать задачи, когда физические свойства среды (характе-
(характеризуемые величинами е и ц) резко изменяются при пересечении од-
одной или нескольких гладких поверхностей. Векторы Е, Н, D и В в
некоторой точке по одну сторону от гладкой поверхности, разделя-
разделяющей две среды, связаны с векторами Е, Н, D и В в соседней точ-
точке на противоположной стороне от границы раздела граничными
условиями, которые выводятся непосредственно из уравнений
Максвелла.
Рассмотрим очень короткий цилиндр, пересекающий поверх-
поверхность раздела, как показано на рис. 1.1, а. Верхнее и нижнее осно-
основания цилиндра расположены в областях 1 и 2 и параллельны по-
поверхности раздела. Высота цилиндра предполагается бесконечно
малой, поэтому его основания оказываются расположенными сколь
угодно близко от границы раздела. Применение известной теоремы
« *
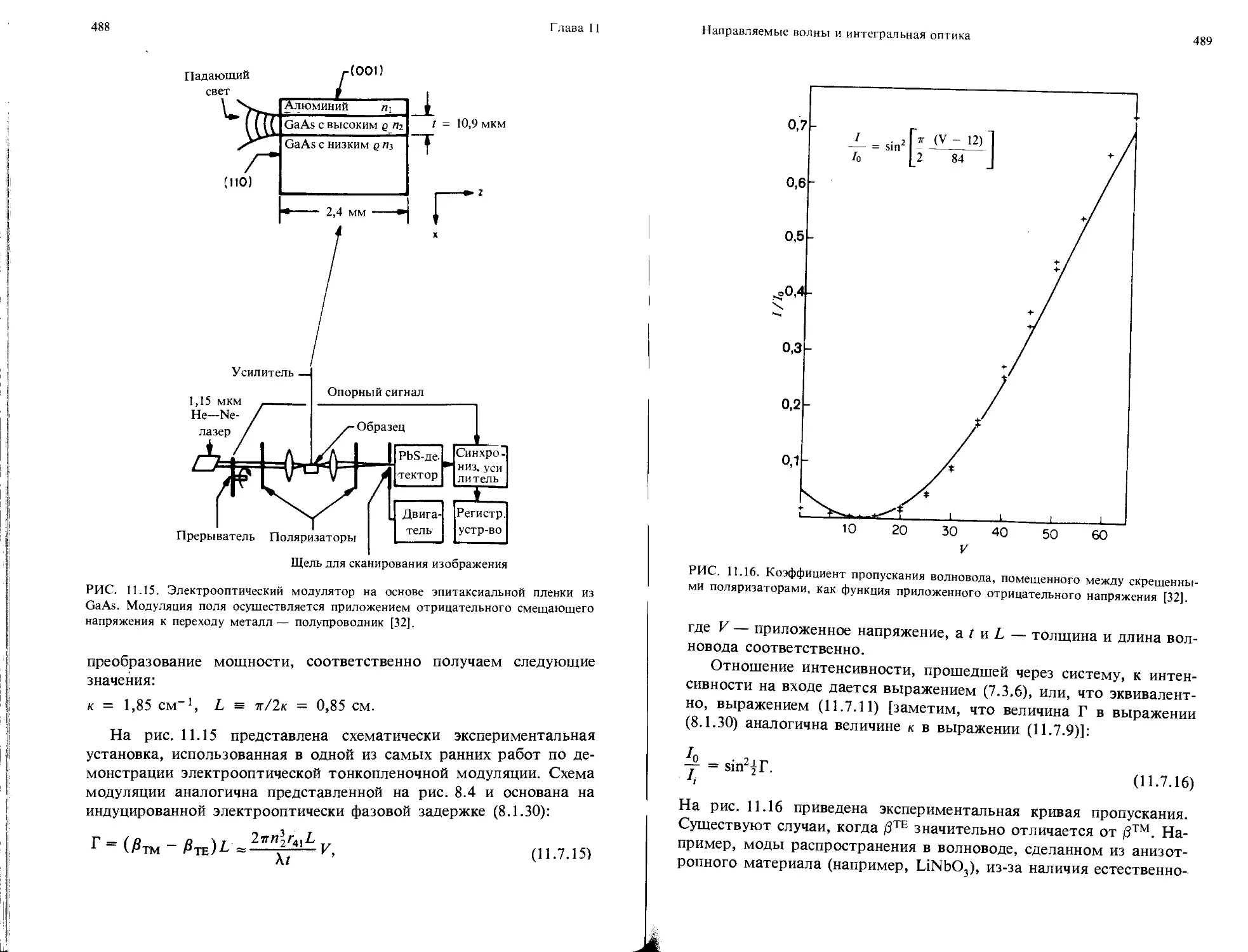
РИС. 1.1. а — короткий цилиндр, пересекающий границу раздела между двумя сре-
средами; 5 — поверхность цилиндра; б — узкий прямоугольный коитур, пересекающий
границу раздела между двумя средами; С — граница этого контура.

12
Глава 1
Гаусса — Остроградского
JV -FdV = JF-dS
к обеим частям уравнений A.1.3) и A.1.4) дает
n-te-Bj-O,
n-(D2-D,)-a,
A.1.7)
A.1.8а)
где п — единичный вектор, перпендикулярный поверхности раздела
и направленный из среды 1 в среду 2, о - поверхностная плотность
заряда (Кл/м ), а индексами отмечены величины на поверхности
относящиеся к какой-либо из двух сред. Граничные условия A.1.8а)
обычно записывают в виде
u = a,
A.1.86)
где В^ = В2 n, Bin = Bj-n, D^ - D2 n, а Dln = D,-n. Иными
словами, нормальная составляющая магнитной индукции В всегда
непрерывна, а нормальные составляющие электрического смещения
D претерпевают скачок, равный по величине поверхностной плот-
плотности заряда.
Рассмотрим малый, узкий прямоугольный замкнутый контур,
охватывающий часть границы раздела (рис. 1.1, б). Длинные сто-
стороны прямоугольного контура расположены в областях 1 и 2 и па-
параллельны границе раздела. Поскольку ширина контура предпола-
предполагается бесконечно малой, длинные его стороны оказываются распо-
расположенными сколь угодно близко к границе. Применяя теорему
Стокса
A.1.9)
A.1.10а)
к обеим частям уравнений A.1.1) и A.1.2), имеем
пх(Е2-Е,) = 0,
п X (Н2- Н,) = К,
где К — поверхностная плотность тока (ампер на метр, А/м). Гра-
Граничные условия для векторов электрического и магнитного поля
A.1.10а) часто записывают также в виде
Е2, = Е„, Н2, - Н„ = К,
Электромагнитные поля
13
где индексом t обозначены тангенциальные составляющие векторов
поля. (Примечание. Составляющие этих векторов, касательные к
поверхности раздела, являются также векторами, лежащими в пло-
плоскости, касательной к этой поверхности.) Иными словами, танген-
тангенциальная составляющая вектора электрического поля Е всегда не-
непрерывна на границе раздела, а разность между тангенциальными
составляющими вектора магнитного поля Н равна поверхностной
плотности тока К.
Во многих задачах оптики часто реализуется ситуация, когда по-
поверхностная плотность зарядов а и поверхностная плотность тока
К обращаются в нуль. В этих случаях тангенциальные составляю-
составляющие полей Е и Н, а также нормальные составляющие D и В непре-
непрерывны при пересечении границы, разделяющей среды 1 и 2. Эти
граничные условия играют важную роль при решении многих задач
оптики, связанных с распространением волн, например при изуче-
изучении оптических волноводов и распространения волн в слоистых
средах.
1.2. ТЕОРЕМА ПОЙНТИНГА И ЗАКОНЫ СОХРАНЕНИЯ
Сохранение энергии электромагнитного поля требует, чтобы сумма
скоростей изменения энергии электромагнитного поля во вре-
времени, содержащейся в некотором объеме, и изменения энергии
за счет вытекания через поверхность, ограничивающую этот объем,
были равны отрицательной полной работе, совершенной полями
над источниками внутри данного объема в единицу времени. Рабо-
Работа, совершаемая в единицу времени внешним электромагнитным
полем над точечным зарядом q, равна ^v-E, где v — скорость за-
заряда. Магнитное поле не совершает работы над точечным зарядом,
поскольку магнитная сила всегда перпендикулярна скорости заряда.
В случае распределенных зарядов и токов работа, совершаемая по-
полями в единицу времени в единичном объеме, равна J ¦ Е. Существу-
Существует уравнение непрерывности, описывающее этот баланс энергии.
Выведем это уравнение, исходя из уравнений Максвелла. Используя
A.1.2), работу электромагнитных полей в единичном объеме за
единицу времени можно записать следующим образом:
= E-(vxH)-E
дР
dt "
С помощью векторного тождества
V • (Е X Н) = Н • (v X Е) - Е • (V X Н)
A.2.1)
A.2.2)

14
Глава 1
и уравнения A.1.1) правую часть выражения A.2.1) можно предста-
представить в виде
dt '
A.2.3)
Если теперь предположить, что рассматриваемая среда обладает
линейными электромагнитными свойствами (т. е. е и /х не зависят
от напряженности поля), то A.2.3) принимает вид
•|j?+ V -S= -J-E,
где U и S определяются следующими выражениями:
S = Е X Н.
A.2.4)
A.2.5)
A.2.6)
Скалярная величина U представляет собой плотность энергии элек-
электромагнитного поля и имеет размерность джоуль на кубический
метр (Дж/м3). Вектор S является потоком энергии и называется
вектором Пойнтинга; он имеет размерность Дж/(м2-с). Величина
ISI -— это мощность, переносимая полем через единичную площад-
площадку в направлении вектора S и имеющая размерность ватт на ква-
квадратный метр (Вт/м2). Таким образом, величина V ¦ S представляет
собой результирующий поток электромагнитной мощности из еди-
единичного объема. Соотношение A.2.4) известно как уравнение непре-
непрерывности или сохранения энергии (теорема Пойнтинга). Аналогич-
Аналогичным образом можно получить законы сохранения импульса для,
электромагнитных полей. Мы предлагаем читателю вывести их са-
самостоятельно в качестве упражнения (задача 1.4).
1.3. ФОРМАЛИЗМ КОМПЛЕКСНЫХ ФУНКЦИЙ
В оптике обычно имеют дело со стационарными полями, изменяю-
изменяющимися во времени по синусоидальному закону. Такими свойства-
свойствами обладает, например, лазерное излучение. При этом векторное
поле удобно представлять в виде комплексной функции. Рассмот-
Рассмотрим некоторую составляющую векторного поля
a(t) = \A\cos(ut + а), A.3.1)
где ш — угловая частота, на — фаза. Определим комплексную ам-
амплитуду поля a it) следующим образом:
А=\А\е'а- A.3.2)
Электромагнитные поля
15
При этом выражение A.3.1) можно записать в виде
a(t) = Re[Aeiut].
A.3.3)
В дальнейшем вместо выражений A.3.1) или A.3.3) мы часто будем
пользоваться следующей записью для a (f):
a(t) = Aeiut A.3.4)
Такое представление не совсем корректно; всякий раз, используя
эту запись, мы будем подразумевать, что так же, как и в выраже-
выражении A.3.4), необходимо взять вещественную часть величины
Лехр(/а>0- В большинстве случаев представление полей в комплекс-
комплексном виде A.3.4) не вызывает затруднений при выполнении таких
линейных математических операций, как дифференцирование, инте-
интегрирование, суммирование и т. д. Исключение составляют случаи,
когда приходится вычислять произведения (или степени), например
при расчете плотности энергии и вектора Пойнтинга. В таких слу-
случаях необходимо пользоваться записью физических величин в ве-
вещественной форме.
В качестве примера вычислим произведение двух синусоидаль-
синусоидальных функций a (t) и b (t), где
a(t) =
а) =
A.3.5)
и
b(t) = |B|cos(«; + )8) = Re[Se'"'],- A.3.6)
причем A = 1^4 I e'" и В = \B\el13. При использовании веществен-
вещественных функций имеем
a(t)b(t) = {\AB\[cos{2wt + a + 0) + cos(a - /8)]. A.3.7)
Но если вычислять произведение a(t)b{t) в комплексном представ-
представлении этих функций, то мы получим
a{t)b{t) = ABei2ut = \АВ\е'Bш+а+Р\ A-3.8)
Сравнивая это выражение с A.3.7), видим, что в нем отсутствует
не зависящий от времени член A/2)\ АВ\ cos (а — /3). Таким обра-
образом, использование комплексной формы записи приводит к ошибке,
которая возникает из-за того, что в общем случае произведение ве-
вещественных частей двух комплексных чисел не равно вещественной
части произведения этих двух комплексных чисел. Иными словами,
если х и у — два произвольных комплексных числа, то в обшем

16
Глава 1
случае
A.3.9)
1.3.1. УСРЕДНЕНИЕ ПО ВРЕМЕНИ ПРОИЗВЕДЕНИЯ
СИНУСОИДАЛЬНЫХ ФУНКЦИЙ
Оптические поля являются быстроменяющимися функциями време-
времени. Например, период изменения поля во времени при длине волны
X = 1 мкм (один микрометр) равен Т = Х/с = 0,33-10~14 с. Во
многих случаях интерес представляют не мгновенные, а усреднен-
усредненные по времени значения физических величин, например, таких, как
вектор Пойнтинга и плотность энергии. Поэтому часто приходится
вычислять среднее по времени от произведения двух синусоидаль-
синусоидальных функций некоторой частоты:
(a(t)b(t)) = j jT\Afcos(a>t + a)\B\cos(a>t + р) dt;
A.3.10)
здесь a{t) и b(t) даются выражениями A.3.5) и A.3.6), Т = 2тг/а> —
период осцилляции, а скобки означают усреднение по времени. По-
Поскольку интеграл в A.3.10) является периодической функцией с пе-
периодом Т, усреднение можно производить по интервалу времени Т.
Используя A.3.7) и учитывая, что среднее по Т от члена, содержа-
содержащего cosBw/ + а + 0), равно нулю, получаем
= i\AB\cos(a-(i).
A.3.11)
Последнее выражение можно записать через комплексные амплиту-
амплитуды А к В, определенные из A.3.6):
, (L3.i2)
или непосредственно через аналитические функции a (t) и Ь (t):
<Де[в@]Де[б@]> = iRe[fl(/)H0]. A-3.13)
где звездочкой обозначено комплексное сопряжение. Правая часть
выражения A.3.13) не зависит от времени, поскольку a(t) и Ъ(t)
имеют одинаковую временную зависимость е'ш. Выражения A.3.12)
и A.3.13) имеют важное значение, и мы будем часто использовать
их на протяжении всей книги.
Если Е, Н, D и В записать в комплексной форме, то усреднен-
Электромагнитные поля
17
1Й по времени вектор Пойнтинга A.2.6) и средняя плотность
A 2.5) в случае синусоидально изменяющихся полей запи-
запишутся в виде
S = iRe[E X Н*]
и
(/ = jRe[E-D* + B-H*].
A.3.14)
A.3.15)
1.4. ВОЛНОВОЕ УРАВНЕНИЕ
И МОНОХРОМАТИЧЕСКИЕ ПЛОСКИЕ ВОЛНЫ
Уравнения Максвелла, рассмотренные в разд. 1.1, представляют со-
собой систему дифференциальных уравнений в частных производных.
Определенное преобразование этих уравнений позволяет получить
дифференциальное уравнение, которому удовлетворяет каждое из
векторных полей по отдельности. Ограничимся рассмотрением об-
областей, в которых как плотность заряда р, так и плотность тока J
равны нулю. Будем также предполагать в этом разделе, что среда
является изотропной, т. е. величины е и /х являются скалярами.
Подставив в уравнение A.1.1) материальное уравнение A.1.6)
для В, разделив обе части на /х и применив оператор ротора, полу-
получим
vx|-vxe)+|vxh =
A.4.1)
Дифференцируя A.1.2) по времени и используя A.4.1) совместно с
материальным уравнением A.1.5), имеем
= 0.
A.4.2)
Теперь воспользуемся векторными тождествами
vx(IvxE) = IVX(VXE)+(v^)x(VXE) d-4.3)
V X (V ХЕ)= V(V -Е) - V2E, A.4.4)
Тогда уравнение A.4.2) преобразуется к виду
V2E- це~+ (v In ju)x (V ХЕ)- v( V • Е) = 0. A.4.5)
Далее, подставляя выражение A.1.5) для D в A.1.3) и используя
2-631

Глава 1
векторное тождество
V-(eE) = eV.E + E.V?, AАб)
из A.4.5) получаем волновое уравнение для вектора поля Е:
•n/i)x (V XE) + V(E- у lne) = 0. A.4.7)
магнитного
V'H ~ ^"э^" + (V 1п ?) х (V X Н) + V(H . v In ft) = 0. A.4.8)
В однородной и изотропной среде градиенты логарифмов от а и м
обращаются в нуль и волновые уравнения A.4.7) и AА8) принима"
щ
= 0. A.4.9)
Эти уравнения являются стандартными волновыми уравнениями
для электромагнитного поля. Им удовлетворяет хорошо известное
решение в виде плоской волны"
ф = е«»,-к-т)^ A.4.10)
где угловая частота ш и величина волнового вектора к связаны со-
соотношением
|к| = «;/ме, A.4.11)
а под ф подразумевается любая декартова составляющая векторов
Е и Н.
Если наблюдатель перемешается таким образом, что он всегда
измеряет одно и то же значение поля, то траектория его движения
г (?) должна удовлетворять условию
wt - к • г = const, A.4.12)
где постоянная является произвольной и определяет значение поля,
«измеряемое» наблюдателем. Уравнение A.4.12) представляет со-
собой уравнение плоскости, перпендикулярной в любой момент вре-
'* Плоские волны не являются единственным решением этих волновых уравне-
уравнений. Другим решением являются так называемые «гауссовы пучки», которые мы
рассмотрим в гл. 2.
Электромагнитные поля
19
мени t волновому вектору к. Эта плоскость называется поверхнос-
поверхностью постоянной фазы. Нетрудно видеть, что она перемещается в
направлении к со скоростью
_w A.4.13)
v' к'
которая называется фазовой скоростью волны. Если мысленно за-
заморозить волну во времени, то расстояние между двумя соседними
максимальными значениями поля есть не что иное, как длина во-
волны, определяемая выражением
к «
Фазовая скорость волны является характеристикой среды и выра-
выражается через диэлектрическую е и магнитную /х проницаемости. Из
формул A.4.13) и A.4.11) получаем
1
v =
A.4.15)
Фазовая скорость электромагнитного излучения в вакууме равна
1
с =
= 2,997930- 108 м/с,
тогда как в веществе ее значение дается выражением
с
где п — V/xe/zzgEo — показатель преломления вещества (среды). В
табл. 1.1 приведены значения показателей преломления для некото-
некоторых наиболее часто используемых оптических материалов. Однако
следует иметь в виду, что для немагнитных материалов (р. = /х0) е,
а следовательно, и п зависят от частоты. Зависимость п от часто-
частоты приводит к хорошо известному явлению дисперсии в оптике. В
диспергирующей среде фазовая скорость световой волны зависит
от частоты.
Рассмотрим теперь решения уравнений Максвелла в виде пло-
плоских волн с учетом векторной природы электромагнитного поля.
Используя формализм комплексных функций, запишем плоские
электромагнитные волны в виде
Е = u1?oe'<""-k-r>, A.4.16)
Н = и2Яое'<ы'-к">, A.4.17)

20
Глава 1
ТАБЛИЦА 1.1. Показатели преломления некоторых оптических
материалов*
Материал
Показа-
Показатель пре-
преломления
Материал
Показатель
преломления
AgCl 2,05
As — S (стекло) 2,61
BaF2 1,47
Bi4Ge3O12 2,09
CaF2 1,43
CdF2 1,43
CdS 2,47
CdSe при X=l мкм 2,55
CdTe при X =
= 10,6 мкм 2,69
CsBr 1,69
Csl 1,78
CuBr 2,10
CuCl 1,96
Cul 2,32
Алмаз 2,41
Кварцевое стекло 1,46
GaAs при
X = 10,6 мкм 3,34
GaP при X =
= 10,6 мкм 2,90
GaSb при
X = 10,6 мкм 3,84
Ge при
X = 10,6 мкм 4,00
InAs при
X = 10,6 мкм
InP при
X = 10,6 мкм
InSb при
X = 10,6 мкм
КВг
КС1
KI
LiF
MgF2
MgO
NaCl
NaF
PbF2
Сапфир
Si при Х= 10,6 мкм
SiC
SrTiO3
TiO2
/3-ZnS
ZnSe при
X = 10,6 мкм
ZnTe
3,42
3,05
3,95
1,56
1,49
,66
,39
,37
,74
,54
,32
1,76
1,77
3,42
2,64
2,38
2,20
2,35
2,39
2,98
* Данные приведены для температуры 25 °С и X = 6328 А, кроме тех случаев, для
которых длина волны указана.
где и, и и2 — два постоянных единичных вектора, а Ео и Но — по-
постоянные в пространстве и во времени комплексные амплитуды. В
однородной среде, в которой отсутствуют заряды, вторая пара
уравнений Максвелла принимает вид V-E = 0 и VH = Оис уче-
учетом A.4.16) и A.4.17) дает
u,«k = u2«k = 0. A.4.18)
Электромагнитные поля
21
Это означает, что Е и Н перпендикулярны направлению распро-
распространения. Такие волны называются поперечными. Условие попе-
речности волны A.4.18) выполняется для всех четырех векторных
полей плоской волны, распространяющейся в однородной и изо-
изотропной среде. В общем случае анизотропной среды только векто-
векторы D и В плоской волны перпендикулярны направлению распро-
распространения.
Первая пара уравнений Максвелла накладывает дальнейшие
ограничения на векторные поля. Подставляя A.4.16) и A.4.17) в
уравнение A.1.1), имеем
к X и.
42 =
A.4.19)
A.4.20)
Это означает, что тройка векторов (и,, и2, к) образует взаимно ор-
ортогональный набор и что векторы Е и Н находятся в фазе и их
отношение в случае вещественных е и /л является постоян-
постоянным. В A.4.20) величина rj имеет размерность сопротивления и на-
называется характеристическим импедансом. Для вакуума rj0 =
= V/xo/eo = 377 Ом.
Рассмотренная выше плоская волна является поперечной и рас-
распространяется в направлении к. Ей отвечает усредненный по време-
времени поток энергии, описываемый, согласно теореме Пойнтинга, век-
вектором
|?Ql2u3
2т,
IF
A.4.21)
где u3 — единичный вектор в направлении к. Усредненная по вре-
времени плотность энергии имеет вид
t/ = 4е1?„|2_ A.4.22)
1.5. РАСПРОСТРАНЕНИЕ ЛАЗЕРНЫХ ИМПУЛЬСОВ;
ГРУППОВАЯ СКОРОСТЬ
В предыдущем разделе мы обсудили решения уравнений Максвелла
в виде плоских волн и изучили некоторые их основные свойства.
При этом мы рассматривали лишь монохроматические волны с
определенной частотой и волновым числом. Излучение от лазеров,

22
Глава 1
генерирующих в непрерывном режиме, можно считать монохрома-
монохроматическим и во многих случаях описывать плоской волной. Однако
во многих важных применениях требуются лазеры, работающие в
импульсном режиме генерации. В импульсе энергия может быть
сконцентрирована в чрезвычайно коротких временных интервалах,
что позволяет увеличить пиковую мощность. Это имеет большое
значение для многих промышленных применений, таких, как лазер-
лазерная обработка и сварка, а также для научных целей. В последнем
случае использование экстремально коротких импульсов позволяет,
например, исследовать переходные явления с очень коротким вре-
временем жизни (менее 10" п с).
Ограниченная длительность лазерного импульса приводит к су-
существованию некоторой конечной полосы частот или, что эквива-
эквивалентно, полосы длин волн. В силу линейности уравнений Максвел-
Максвелла распространение лазерного импульса в линейной среде можно
описывать с помощью соответствующей линейной комбинации
плоских волн с различными частотами. Однако при распростране-
распространении лазерного импульса в диспергирующей среде, в которой фазо-
фазовая скорость зависит от частоты, возникает ряд новых особенно-
особенностей. Так, различные частотные составляющие волны распростра-
распространяются с различными скоростями и стремятся изменить относи-
относительные фазы. Это приводит, как правило, к уширению лазерного
импульса при его распространении через диспергирующую среду.
Кроме того, скорость переноса энергии лазерным импульсом, рас-
распространяющимся в диспергирующей среде, может существенно
отличаться от фазовой скорости. Данный вопрос является непро-
непростым и требует более детального исследовайия.
Влияние дисперсии на распространение лазерного импульса
можно описать, если представить импульс в виде суммы многих
плоских волн, являющихся решениями уравнений Максвелла. В
предельном случае суммирование можно заменить интегрировани-
интегрированием. Для наглядности при введении основных понятий мы будем
рассматривать лишь случай одномерных скалярных волн. При
этом под скалярной амплитудой ф(г, t) будем подразумевать одну
из составляющих векторов электромагнитного поля. Если А (к) —
амплитуда плосковолновой составляющей с волновым числом к, то
импульс ^,0 можно представить в виде интеграла
*(*,/)= Г Л(*)е'<"<*>'-**>Л. A.5.1)
"'-00
Этот интеграл удовлетворяет уравнениям Максвелла, поскольку
интегрируются плоские волны, являющиеся решением тех же урав-
уравнений Следует заметить, что, если рассматривать Hz, t) ^Ц
Электромагнитные поля
23
РИС. 1.2. Лазерный нмпульс конечной длительности и его фурье-спектр в про-
пространстве волновых чисел к.
рый момент времени, скажем t = 0, то А (к) является фурье-обра-
зом функции \p(z, 0). При этом величину \А(к)\2 можно рассматри-
рассматривать как спектр Фурье поля ip(z, t). Дисперсионное уравнение, уста-
устанавливающее связь между со и А: для электромагнитного поля, запи-
записывается в виде A.4.11). В изотропной среде дисперсионные свойст-
свойства не могут зависеть от направления распространения; следователь-
следовательно, со должна быть четной функцией от к: со(-Аг) = со (А;). Далее в
этом разделе мы будем считать величины А: и со (А:) вещественными.
На рис. 1.2 показаны типичный импульс излучения и его спектр
Фурье.
Лазерный импульс обычно характеризуют его центральной ча-
частотой со0 (или соответствующим волновым числом Аг0) и шириной
полосы частот Дсо относительно соо (или соответствующей шириной
полосы в пространстве волновых чисел ДА:). Рассмотрим эволюцию
такого импульса во времени. Для этого разложим со(Аг) в ряд Тей-

24
Глава 1
лора в окрестности к0:
k-k0) + ---, A.5.2)
а затем подставим это разложение для со в интеграл A5 1) кото-
который, если пренебречь членами высшего порядка по к -'к прини-
принимает ВИД 0>
- *„)} dk. A.5.3)
, 0 =
Этот интеграл зависит только от комбинации переменных [z -
- (doj/dkHt] и называется огибающей E[z - (du>/dk)ot]. Таким
образом, амплитуду импульса можно записать в следующем виде:
A.5.4)
Отсюда следует, что с точностью до общего фазового множителя
лазерный импульс распространяется с сохранением своей формы
(рис. 1.3) и со скоростью
A.5.5)
которая называется групповой скоростью импульса. Это приближе-
приближение правомерно только в случае, когда распределение А (к) имеет
ярко выраженный пик при к0 и частота является медленноменяю-
щейся функцией величины к в окрестности к0. Если плотность эле
тромагнитнои энергии лазерного импульса связана с квадратом мо-
модуля амплитуды, то очевидно, что в этом приближении группова
скорость представляет собой скорость переноса энергии (см
1.7). Следует заметить, что в случае импульсного излучения *а ЧУ
вая и групповая скорости, вообще говоря, различны 3°
(dw/dk)Q * ыо/*о- Фазовая скорость, которая обычно прев'ыша "'
групповую, имеет тот же смысл, что и в случае плоской волны п"
совпадает со скоростью наблюдателя, находящегося на веп
или во впадине данной волны. вершине
В оптике дисперсионные свойства среды обычно описьт
помощью показателя преломления п(ш), зависящего от Ся с
(или длины волны). При этом соотношение мезвду и и h частотЬ1
WJ ш и л дается т,
ражением ьы-
к = «(w)-,
A.5.6)
Электромагнитные поля
25
РИС. 1.3. Схематическое изображение амплитуды поля, иллюстрирующее распро-
распространение волнового пакета в среде с дисперсией, определяемой выражением A.5.2),
в случае когда форма импульса остается неизменной.
где с — скорость света в вакууме. Фазовая скорость
оказывается больше или меньше с в зависимости от того, меньше
и (со) единицы или больше. Из A.5.5) и A.5.6) мы имеем следующее
выражение для групповой скорости:
v =
g n + u(dn/dw)
A.5.8)

26
Глава 1
При нормальной дисперсии (dn/dw > 0) групповая скорость мень-
меньше фазовой. Однако в областях аномальной дисперсии величина
dn/dw может быть большой и отрицательной. При этом групповая
скорость сильно отличается от фазовой и иногда превышает ско-
скорость света с. Последний случай имеет место, только когда dn/dw
является большой отрицательной величиной. Это эквивалентно ус-
условию быстрого изменения частоты w в зависимости от к что де-
делает наше приближение неприменимым. Следовательно, специаль-
специальная теория относительности здесь не нарушается.
Мы видели, что лазерный импульс, распространяющийся в дис-
диспергирующей среде, будет сохранять свою форму, если справедливо
приближение A.5.2). В случае когда следующим членом более высо-
высокого порядка (\/2)(d2w/dk\(k - kof нельзя пренебрегать, форма
импульса не будет больше оставаться неизменной и в общем случае
ширина импульса будет увеличиваться в процессе распространения.
Уширение импульса можно, понять, если заметить, что групповая
скорость vg может различаться для каждой частотной составляю-
составляющей лазерного импульса (дисперсия групповой скорости) Если
спектральная ширина импульса равна ДА:, то разброс в групповых
скоростях имеет величину порядка
d2w
dk1
Д*.
A.5.9)
При распространении импульса следует ожидать его уширения в
пространстве на величину порядка Avgt. Вопрос об уширении им-
импульса мы еще раз рассмотрим в разд. 2.5 и задаче 1.9.
ЗАДАЧИ
1.1. Для сохранения заряда необходимо, чтобы плотность заряда
в любой точке пространства была связана с плотностью то-
тока в окружающем пространстве уравнением непрерывности
др
Tt+ VJ-0.
Выведите это уравнение из уравнений Максвелла.
1.2.
Применяя теорему Гаусса к уравнениям Максвелла, найди
граничные условия для нормальных составляющих' полей ^
и D [выражения A.1.8)].
Электромагнитные поля
27
1.3. Применяя теорему Стокса к уравнениям Максвелла, получи-
получите граничные условия A.1.10) для тангенциальных составля-
составляющих Е и Н.
1.4. Плотность импульса электромагнитного поля и максвеллов-
ский тензор напряжений определяются выражениями соот-
соответственно
Р = Ме(Е X Н),
Ти =
Выведите гидродинамическое уравнение
f -VT-F,
где F — сила Лоренца, действующая со стороны электро-
электромагнитного поля на распределение зарядов и токов,
F = рЕ + J X В.
В области, свободной от источников, скорость изменения
плотности импульса поля равна силе, действующей на рас-
рассматриваемую область и определяемой максвелловским тен-
тензором напряжений.
1.5. Если магнитный монополь существует, то статическое маг-
магнитное поле, создаваемое магнитным зарядом, должно
удовлетворять следующему уравнению:
где рт — плотность магнитного заряда.
а) Покажите, что напряженность магнитного поля, созда-
создаваемая точечным зарядом т в вакууме, определяется
выражением
т
Н
гг>
где г — вектор, измеряемый от точки расположения
магнитного заряда.

28
Глава 1
б) Имеется электромагнитное поле, создаваемое точечным
электрическим зарядом е с координатами @, 0, d/2) и
точечным магнитным зарядом т с координатами (О, О,
— d/2). Плотность момента импульса поля дается выра-
выражением
L=rXP,
где Р — плотность импульса, приведенная в задаче 1.4.
Определите полный момент импульса поля, интегрируя
L по всему пространству. Ответ: — (ет/4жI. Заметьте,
что момент импульса не зависит от расстояния d.
в) Пусть начало системы координат выбрано в точке рас-
расположения магнитного точечного заряда. При этом
электрический заряд расположен в точке с координатами
(О, 0, d). Электрический заряд е перемещают из точки (О,
О, d) в точку @, 0, —d) по полуокружности. Определите
необходимый момент силы и проинтегрируйте его по
времени. Покажите, что момент импульса, необходи-
необходимый для перемещения электрического заряда, равен
-ет/2-к. Этот метод позволяет вычислить момент им-
импульса более простым способом, чем прямое вычисле-
вычисление, предлагаемое в п. б.
1.6. Выражения A.5.3) и A.5.4) дают приближенное описание ла-
лазерного импульса. В среде без дисперсии эти выражения ста-
становятся точными. Если распределение по волновым числам
А (к) известно, то вычисляя интеграл в A.5.3), можно полу-
получить огибающую ?Ч?). Найдите огибающую 2Г(?), изобрази-
изобразите графически зависимости \А(к)\2 и lff(?)|2, определите
стандартные отклонения Ак и Д? от средних и убедитесь в
выполнении соотношения неопределенностей Гейзенберга
ДАгД? ^ 1/2 для каждого из приведенных ниже распределе-
распределений А (к):
а) А(к) = А(ко)ехр[-(к - коJ/4д2). Это спектральное
распределение соответствует гауссову импульсу и пред-
представляет собой минимальный волновой пакет т
ДАгД? = 1/2. ' " -
б) А (к) = А(ко)ехр(- \к - ко\/2д). Это спектральное пас
пределение соответствует импульсу с лоренцевой фор-
формой.
в) A(k) = A(ko)sin[(k-ko)/g]/[(k-ko)/g]. Это
Электромагнитные поля
29
ральное распределение отвечает прямоугольному им-
импульсу.
1.7. Одномерный лазерный импульс имеет центральную частоту
ш0 и соответствующее волновое число к0. Огибающая E(z —
- vgt) для электрического поля определяется следующим об-
образом:
Ех = E(z - vgt)e*a<>'-k°z).
Найдите огибающую для магнитного поля Ну и вычислите
вектор Пойнтинга.
1.8. Дисперсия некоторого вещества описывается следующей за-
зависимостью показателя преломления от частоты:
= п0 -
Найдите групповую скорость vg импульса, распространяю-
распространяющегося в этой среде.
1.9. Если в разложении A.5.2) частоты ш(к) в окрестности к0
можно пренебречь членами второго и высшего порядков, то
огибающая лазерного импульса сохраняет свою форму. Рас-
Рассмотрите случай, когда член второго порядка не является
малым и его необходимо учитывать, в то время как членами
высшего порядка можно пренебречь:
ш{к) = ш0
dk V
-*о)+ 4
dk:
Найдите огибающую импульса со спектральным распределе-
распределением А (к), приведенным в задаче 1.6а, и определите зависи-
зависимость ширины огибающей от времени. При расчетах можно
использовать следующий интеграл:

30
Глава 1
В этом интеграле вещественная часть параметра а должна
быть положительной.
1.10. Пусть зависимость показателя преломления от длины волны
излучения известна. Покажите, что групповую скорость
A.5.8) можно вычислить по формуле
п -\{dn/d\) '
1.11. Покажите, что коэффициент разложения в ряд Тейлора
(\/2)(d2oi/dk2) пропорционален дисперсии групповой скоро-
скорости и что
s\c)dX2'
1.12. Пусть E = Е0(г)е'"* и Н = Н0(г)е'ш' являются решениями
уравнений Максвелла.
а) Покажите, что уравнениям Максвелла удовлетворяют
также комплексно-сопряженные величины Е* и Н*. За-
Заметим, что Е*, Н* и Е, Н отвечают одному и тому же
полю, поскольку физический смысл имеют лишь вещест-
вещественные части этих величин.
б) Покажите, что комплексно-сопряженные волновые поля
Ес = Е*0(г)е'ш, Нс = Щ(г)е'"'
также удовлетворяют волновому уравнению, при усло-
условии что среда не имеет потерь (т. е. ? и /х являются тен-
тензорами с вещественными элементами).
ЛИТЕРАТУРА
1. Born M., WolfE., Principles of Optics. — New York: Macmillan, 1964. [Имеется
перевод 2-го изд.: Борн М., Вольф Э. Основы оптики. — М.: Наука, 1970 1
2. Jackson J. D., Classical Electrodynamics. — New York: Wiley, 1962.
3. Ландау Л. Д., Лившиц Е. М. Электродинамика сплошных сред. _ м.: Физмат-
гиз, 1957.
Глава 2
РАСПРОСТРАНЕНИЕ ЛАЗЕРНЫХ ПУЧКОВ
Основная цель данной книги — показать, как происходит распро-
распространение лазерных пучков и каким образом можно управлять ими.
На рис. 2.1 схематически изображен типичный лазер с двумя зерка-
зеркалами и генерируемый им пучок излучения. В отличие от бесконеч-
бесконечных плоских волн, рассмотренных нами в гл. 1, генерируемый лазе-
лазером пучок ограничен в поперечном направлении и уширяется по ме-
мере распространения в направлении z. Понимание законов распро-
распространения таких пучков чрезвычайно важно для всех, кто имеет де-
дело с исследованием или применением лазеров. Несмотря на то что
этот вопрос рассматривался во многих учебниках, мы включили
его в нашу книгу для полноты изложения и как справочный мате-
материал для дальнейшего использования.
2.1. СКАЛЯРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ
Лазерный пучок представляет собой когерентное электромагнитное
излучение. Поэтому его распространение должно определяться
уравнениями Максвелла. Векторы поля Е и Н, которые описывают
распространение лазерного пучка, удовлетворяют векторным вол-
волновым уравнениям A.4.7) и A.4.8). Для пучков с малой угловой
расходимостью и сред, показатель преломления которых слабо из-
изменяется в поперечном направлении, векторное волновое уравнение
срядится к скалярному [1]. Действительно, из A.4.7) и A.4.8) мож-
можно получить скалярное волновое уравнение, если предположить,
что относительное изменение диэлектрической е и магнитной /х
проницаемостей мало в масштабе длины волны излучения. В этом
случае волновое уравнение A.4.7) или A.4.8) принимает вид
B.1.1)
с2 dt2
где 'Ф — любая декартова составляющая полей Е и Н, а п =
= cV/xe — показатель преломления. Лазерный пучок представляет
собой излучение с высокой степенью монохроматичности. Поэтому
естественно предположить, что временная зависимость поля имеет

32
Глава 2
Зеркало
Зеркало
~7
Активная среда
излучения СХеМаТИЧеСК°е изобРажение типичного лазера и
Выходной
пучок
генерируемого им пучка
вид f(x, у, z, 0 = Re[?(x,,у, z)eiat]. При этом скалярное волновое
уравнение B.1.1) запишется в виде
V2E + К2Е = О,
где величина
B.1.2)
B.1.3)
учитывает зависимость показателя преломления п от координаты
г. Уравнение B.1.2) называется волновым уравнением Гельмголь-
ца.
Большинство лазерных пучков, используемых в оптических ис-
исследованиях, имеют гауссово распределение интенсивности в пло-
плоскостях, перпендикулярных направлению распространения. Среда, в
которой распространяется лазерный пучок, во многих случаях име-
имеет цилиндрическую симметрию относительно оси пучка. В частно-
частности, мы будем рассматривать линзоподобную среду, показатель
преломления которой п = V,ue/>oeo изменяется по закону
B.1.4)
где к 2 — некоторая постоянная, характеризующая среду, и
казатель преломления на оси симметрии, г — расстояние от оси
к — волновое число (к = 2жпо/\). Поскольку фазовая задержка
волны, прошедшей отрезок dz среды с показателем преломления и
равна Bxdz/\)n, очевидно, что тонкий слой среды, описываемой
выражением B.1.4), будет действовать как тонкая линза и соз
вать фазовый сдвиг, пропорциональный г2.
В случае среды с показателем преломления и, определяемь
выражением B.1.4), член К2(г) в скалярном волновом уравне Ш
Гельмгольца B.1.2) принимает вид
К2(г) = к2 - кк2г2.
B.1.5)
Распространение лазерных пучков
33
Кроме того, поскольку нас интересует решение, зависящее только
от поперечной координаты г = V*2 + у1, в уравнении B.1.2) опера-
оператор V2 можно заменить на
, д2 д2
= 1 д { д2
dz2 дг2 г дг dz2
B.1.6)
Иными словами, будем искать цилиндрически-симметричные реше-
решения скалярного волнового уравнения Гельмгольца B.1.2).
Поскольку нас интересует распространение волн, которые незна-
незначительно отличаются от плоских и переносят энергию в основном
вдоль одного направления (например, в направлении z), использова-
использование скалярного приближения для волнового уравнения правомерно.
Подставляя в B.1.2) выражение B.1.5), выбирая Е в виде
у,
B.1.7)
и предполагая, что амплитуда поля меняется достаточно медленно,
т. е. величина d^/dz2 мала по сравнению с кф' или к2^, после не-
несложных преобразований получаем
- kkirV =
B.1.8)
где ф' = дф/dz.
Поскольку мы ищем амплитуду пучка с цилиндрической симмет-
симметрией, удобно ввести две комплексные функции P(z) nq(z) таким об-
образом, чтобы ф можно было записать в виде
B.1.9)
2q(zY
Подставляя это выражение для ф в B.1.8) и используя B.1.6), мож-
можно записать следующее волновое уравнение:
-2i\-\-k2r2
-\ - 2кР'- кк2г2 = 0,
B.1.10)
я) \ч.
где штрих указывает на дифференцирование по z- Если уравнение
B.1.10) справедливо для любого г, то коэффициенты при различ-
различных степенях величины г должны обращаться в нуль. В результате
имеем следующие соотношения:
B.1.11)
3-631

34
Глава 2
Таким образом, для пучка с цилиндрической симметрией в линзопо-
добной среде скалярное волновое уравнение B.1.2) сводится к соот-
соотношениям B.1.11).
2.2. ГАУССОВЫ ПУЧКИ В ОДНОРОДНОЙ СРЕДЕ
Если пучок распространяется в однородной среде, то в выражении
B.1.5) следует положить к2 = 0. При этом соотношения B.1.11)
принимают вид
-°- Г = -". B.2.1)
(штрихом обозначено дифференцирование по z). Вводя функцию
u(z) с помощью соотношения
и dz'
B.2.2)
из уравнения B.2.1) непосредственно имеем
^ = 0.
dz2
Следовательно,
du
-г- = а, и = az + b,
или в соответствии с B.2.2)
1 _ а
q(z) az + b'
B.2.3)
где а и Ъ — произвольные постоянные. Выражение B.2.3) можно
переписать в виде
Я = z + q0,
B.2.4)
где<70 — постоянное комплексное число [q0 - q@) = b/a]. Из урав-
уравнений B.2.1) и B.2.4) можно найти комплексную функцию Р(zy
i
a
Яо
B.2.5)
Распространение лазерных пучков
35
Интегрируя это выражение, получаем
B.2.6)
здесь произвольная постоянная интегрирования выбрана равной
нулю1'.
Подставляя B.2.4) и B.2.6) в B.1.9), решение скалярного волно-
волнового уравнения с цилиндрической симметрией можно записать в ви-
виде
= ехр{ -j| -
q0
2(qo
B-2.7)
Напомним, что q0 — произвольная комплексная постоянная. Из
выражения B.2.7) очевидно, что физически реализуемые решения ф,
которые обращаются в нуль при г -~ оо, определяются выбором
мнимой части постоянной q0. Перепишем q0 через новую постоян-
постоянную ш0:
Чо =
\ =
2ттп
B.2.8)
где п — п0 для однородной среды. Подставляя B.2.8) в выражение
B.2.7), рассмотрим по отдельности два входящих в него экспонен-
экспоненциальных множителя. Первый из них принимает вид
ехр
-In 1 -
\z
1
ехр
1 +
i arctg
\z
B.2.9)
где мы использовали соотношение \п(а + ib) = lnVa2 + b1 +
+ iarctg(b/a). Подставляя B.2.8) во вторую экспоненту выражения
B.2.7) и разделяя ее на вещественную и мнимую части, получаем
ехр
-ikr1
= ехр -
I
— г
ikr2
(\z/™2nJ] 2z[\ + (™2n/\zJ} I'
B.2.10)
'' Постоянная интегрирования будет влиять только на фазу решения B.1.7), что
эквивалентно только сдвигу начала отсчета времени.

36
Глава 2
Определяя параметры
A V
можно записать следующие соотношения:
1 _ 1 1_ ._ X
q(z) z + i(ircoi
и
/-
t\(z) = arctg
\z
= arctg | —
zo
B.2.11)
B.2.12)
B.2.13)
B.2.14)
где z0 = irwfyi/X. Тогда подставляя B.2.9) и B.2.10) в B.2.7), а так-
также учитывая то, что Е(х, у, z) = ФОс, У, z)e~'kz, получаем
B.2.15)
где, как обычно, к = 2тги/\. Это выражение представляет собой
наш основной результат. Будем называть это решение фундамен-
фундаментальным гауссовым пучком. Мы не рассматриваем более сложные
решения уравнения B.1.2) (например, решения с азимутальной зави-
зависимостью) и ограничиваемся зависимостью лишь от поперечной ко-
координаты г — (х2 + у2I12. Моды высшего порядка обсудим отдель-
отдельно.
Из выражения B.2.15) видно, что параметр w(z), изменяющийся
в соответствии с B.2.11), определяет расстояние г, на котором ам-
амплитуда поля убывает в е раз по сравнению со своим значением на
оси. Будем называть его радиусом пучка (размером пятна). Пара-
Параметр ш0 равен минимальному радиусу пучка в плоскости перетяжки
z = 0, a R представляет собой радиус кривизны практически сфери-
Распространение лазерных пучков
37
ческих волновых фронтов1' в сечении?. В справедливости этого ут-
утверждения можно убедиться, если вывести выражение для радиуса
кривизны поверхностей постоянной фазы (волновых фронтов) или
(более простым способом) путем анализа формы сферической во-
волны, испускаемой точечным излучателем, расположенным в пло-
плоскости z — 0. Такая волна описывается выражением
Е ос je~lkK= I exp(-ikjx2+y2
R
— ехр{ -ikz - ik
с2 + у2
2R
х2 + у2
B.2.16)
в котором квадратный корень в области?2 > х2 + у2 мы разложи-
разложили в степенной ряд и положили z равным радиусу кривизны сфери-
сферической волны R. Из сравнения выражений B.2.15) и B.2.16) видно,
что R можно интерпретировать как радиус кривизны гауссова пуч-
пучка. Знак величины R (z) обычно выбирается отрицательным, если
центр кривизны расположен при z' > z, и положительным, если он
расположен при z' < z-
Форма фундаментального гауссова пучка B.2.15) определена од-
однозначно, если заданы его минимальный радиус в перетяжке ш0 и
координата z относительно плоскости перетяжки. При этом радиус
пучка ш и его радиус кривизны R в любой плоскости z определяют-
определяются из выражений B.2.11) и B.2.12). На рис. 2.2 иллюстрируются не-
некоторые из этих характеристик пучка. Гиперболы, изображенные
на этом рисунке, отвечают траекториям лучей и являются линиями
пересечения плоскостей, проходящих через ось z, с поверхностями
гиперболоидов
х2 + у2 = const-w2(z).
B.2.17)
Эти гиперболы задают локальное направление распространения
энергии излучения. Радиусы кривизны изображенных на рисунке
сферических поверхностей определяются выражением B.2.12). На
больших расстояниях? гиперболоидых2 + у2 = ш2 асимптотически
11 В действительности из выражения B.2.15) следует, что всюду, кроме непо-
непосредственной окрестности плоскости г = 0, волновые фронты имеют параболиче-
параболическую форму, поскольку они удовлетворяют уравнению к [г + (r2/2R)] = const. Одна-
Однако при г1 < г2 различием между параболической и сферической поверхностями мож-
можно пренебречь.

38
Глава 2
Профиль
штенсивности
-Волновые фронты-
z ' О
Линии
распространения
РИС. 2.2. Распространение гауссова пучка.
стремятся к коническим поверхностям
B.2.18)
Половина вершинного угла такого конуса используется как мера
угловой расходимости пучка:
9пучок
Х/жи^ при 0пучок <§ ж. B.2.19)
Последний результат является строгим следствием волновой ди-
дифракции, согласно которой волна, ограниченная в поперечном на-
направлении апертурой радиусом ш0, будет расходиться (дифрагиро-
(дифрагировать) в дальнем поле (z > жш^г/Х) в соответствии с выражением
B.2.19).
2.3. ФУНДАМЕНТАЛЬНЫЙ ГАУССОВ ПУЧОК
В ЛИНЗОПОДОБНОЙ СРЕДЕ; ЗАКОН ABCD
Гауссов пучок B.2.15), рассмотренный в предыдущем разделе, яв-
является решением волнового уравнения B.1.2) для однородной сре-
среды (к2 = 0). Во многих случаях приходится сталкиваться со средой,
показатель преломления которой изменяется по квадратичному за-
закону B.1.4), причем к2 ^ 0. Например, показатель преломления
и (г) градиентных волокон (см. ниже рис. 2.5) приблизительно опи-
описывается распределением B.1.4). Другим важным примером явля-
является распространение гауссова пучка в среде с керровской нелиней-
нелинейностью [11]. В последнем случае к квадратичному распределению
показателя преломления приводит распределение интенсивности са-
самого лазерного пучка. Распространение волны в таких средах мож-
можно описывать двумя различными методами. При модовом описа-
Распространение лазерных пучков
39
нии произвольная волна представляется в виде линейной суперпози-
суперпозиции мод, каждая из которых характеризуется своей постоянной
распространения и поперечным электромагнитным полем (см.
разд. 2.5). При описании с помощью гауссовых пучков предполага-
предполагается, что распространение волны в каждой точке z подчиняется за-
закону B.1.9), причем параметры пучка Р и q изменяются в соот-
соответствии B.1.11). Последний подход представляется более нагляд-
наглядным и мы его рассмотрим в данном разделе.
Вернемся к рассмотрению общего случая линзоподобной среды,
когда к2 Ф 0. В выражении B.1.9) параметры Р и q в соответствии
с B.1.11) удовлетворяют следующим уравнениям:
- I + I - I + "Г =
q] \q) к
Р' = --.
q
B.3.1)
Вводя новую функцию и, определяемую следующим образом:
1 = HL B.3.2)
q и '
из B.3.1) имеем
B.3.3)
откуда
/ ч \кг \кг
u(z) = asiny — 2 + ocosy — z,
V /С V /С
B.3.4)
где а и Ъ — произвольные постоянные, а штрих обозначает произ-
производную по z.
Используя B.3.4) и B.3.2) и выражая параметры а и Ъ через
входное значение q @) = q0, можно написать следующее выражение
для комплексного радиуса пучка q (г):
-1
_ g0cosa2z + a2 sin a2
B.3.5)
-qoa2sma2z + cos a2z
где по определению a2 = (k2/k)w2. В геометрической теории по-
построения оптических изображений соотношение B.3.5) между пара-

40
Глава 2
метром q пучка на выходе и его значением q0 на входе известно как
условие коллинеарности [2].
Физический смысл q (г) в данном случае можно выяснить с по-
помощью B.1.9). Выделим часть амплитуды поля ф(г, г), которая со-
содержит г:
ос е~'кг2/2ч(-г'>.
B.3.6)
Если записать вещественную и мнимую части величины q (г) в виде
_J_ = _l \
q(z) R(z) ' B37)
то получим
ос ехр
-г2 . кг2
co2(z) l2R(z)
B.3.8)
Следовательно, как и в случае однородной среды, когда мы имеем
гауссов пучок, описываемый выражением B.2.15), величина со (г)
представляет собой радиус пучка, a R — радиус кривизны его вол-
волнового фронта. В частном случае однородной среды выражение
B.3.5) переходит в B.2.4).
2.3.1. ЛУЧИ В ЛИНЗОПОДОБНОЙ СРЕДЕ
Распространение оптических пучков можно адекватно описывать с
помощью уравнений Максвелла или (при определенных условиях) в
рамках скалярного волнового уравнения B.1.1). Показатель пре-
преломления п в волновом уравнении B.1.1) отражает свойства среды
и в общем случае зависит от положения в пространстве. Если п —
— const, то уравнение B.1.1) имеет решения в виде плоских волн
A.4.10). Если же п зависит от координат, то плоские волны уже не
являются решениями. Однако в случае, когда и медленно меняется
с расстоянием, решение можно искать в виде, близком к плоской
волне настолько, насколько это возможно. Иными словами, мы
ищем решение в виде
Ф = A(r)ei{ut-+(r>\.
B.3.9)
Здесь А (г) и ф(т) — искомые вещественные функции координат.
Следовательно, А (г) характеризует амплитуду волны. В случае ког-
когда п = const, функция ф(х) равна к-г, и поэтому ее называют фа-
Распространение лазерных пучков
41
зой волны; ее часто называют также эйконалом. Если подставить
выражение B.3.9) для Ф в волновое уравнение B.1.1) и предполо-
предположить, что относительное изменение п на расстояниях порядка дли-
длины волны пренебрежимо мало, то скалярное волновое уравнение
принимает вид
B.3.10)
В случае однородной среды интегрирование уравнения B.3.10) дает
ф(х) = кг, где ? = 27ги/Х. Вывод уравнения B.3.10) мы предлага-
предлагаем читателю провести самостоятельно в качестве упражнения (за-
(задача 2.5). Уравнение B.3.10) называется в геометрической оптике
уравнением эйконала. Поверхности постоянной величины ф, опре-
определяемые этим уравнением, представляют собой поверхности по-
постоянной оптической фазы, или волновые фронты. Световые лучи
определяются как траектории, ортогональные волновым фронтам
ф(х) = const, и, следовательно, описываются также уравнением
B.3.10). Если г — радиус-вектор некоторой точки на траектории
луча, а 5 — длина луча, измеряемая от некоторой фиксированной
точки на нем, то dx/ds представляет собой единичный вектор в на-
направлении V</>, перпендикулярный волновым фронтам. Таким об-
образом, извлекая квадратный корень из B.3.10), получаем уравнение
2чт dx
B.3.Н)
которое определяет траекторию луча посредством эйконала Ф(х). И
наоборот, эйконал ф(х) можно выразить через лучевой интеграл
Ф(г) = х/лЛ>
в котором интегрирование ведется вдоль траектории луча. Из
B.3.10) и B.3.11) можно получить дифференциальное уравнение, ко-
которое описывает распространение лучей непосредственно через по-
показатель преломления п (г):
d_
ds
dx
ds
= Vn.
B.3.12)
Для параксиальных лучей (т. е. для лучей, составляющих очень ма-
малые углы с осью z) можно заменить d/ds на d/dz. В случае линзо-
подобной среды, описываемой выражением B.1.4), уравнение для

42
Глава 2
лучей принимает вид
d2r
dz2
к2
-2.
к
B.3.13)
Следует заметить, что это уравнение аналогично B.3.3). Это озна-
означает, что в линзоподобной среде в параксиальном приближении
пространственная эволюция комплексного параметра пучка q и па-
параметра луча r(dr/dz)~l происходит одинаково. Иными словами,
для преобразования комплексного параметра пучка q можно приме-
применять тот же закон, что и при преобразовании параметра луча. Если
луч в любой плоскости z представить в виде вектора
(;¦)¦
dr_
dz'
то из уравнения B.3.13) для линзоподобной среды можно получить
лучевую матрицу, такую, что выполняется следующее преобразова-
преобразование:
B.3.14)
где /•' s dr/dz, а индексы 1 и 2 относятся к плоскостям zx и z2 со-
соответственно. В таблице 2.1 приведены лучевые матрицы для неко-
некоторых оптических элементов и сред. Заметим, что уравнение
B.3.14) можно также записать в виде
B.3.15)
2.3.2. ПРЕОБРАЗОВАНИЕ ГАУССОВЫХ ПУЧКОВ;
ЗАКОН ABCD
В предыдущем разделе мы получили законы преобразования гаус-
гауссова пучка B.3.5) и луча B.3.15) при их распространении в линзопо-
линзоподобной среде, характеризуемой постоянной к2. Было также показа-
показано, что параметр пучка q и параметр луча г/г' подчиняются одина-
одинаковым законам преобразования. Иными словами, преобразование
комплексного параметра пучка q можно записать в виде
Aqx + В
Cqx+ D'
B.3.16)
ТАБЛИЦА 2.1. Матрицы преобразования лучей для некоторых
часто встречающихся оптических элементов и сред
1. Участок одно-
однородной среды
длиной d
Выход
Вход
[1 d]
[О lJ
2. Тонкая линза с
фокусным рас-
расстоянием /
(при / > 0 со-
собирающая., при
/ < 0 рассеива-
рассеивающая)
3. Граница разде-
раздела диэлектри-
диэлектриков с показате-
показателями прелом-
преломления я, и «2
4. Сферическая
граница разде-
раздела диэлектри-
диэлектриков радиусом
R
5. Сферическое
зеркало радиу-
радиусом R
6. Среда с ква-
квадратичным
профилем по-
показателя пре-
преломления
Вход
Вход
Выход
Выход
Вход
Выход
Выход
1
-1
т
0
1
1 0
0 Hi-
n2R
О
"i
«2
1
-2
R
0
1
к . | / к2
— sin| i/ — i
k2
^sinU^I) <хя\\1-г,

44
Глава 2
где Л, В, С, D — элементы лучевой матрицы, связывающей луч в
плоскости z = z2 с лучом в плоскости z = zx [выражение B.3.14)].
Поскольку оптические элементы в табл. 2.1 можно рассматривать
как частные случаи линзоподобной среды, распространение излуче-
излучения через эти элементы или отражение излучения от них также
подчиняется закону B.3.16). Для дальнейшего рассмотрения полез-
полезно заметить, что для тонкой линзы с фокусным расстоянием / из
соотношения B.3.16) и табл. 2.1 (п. 2) получаем
Чг
J
/'
B.3.17)
откуда для пучка мы имеем
R,
R,
B.3.18)
f
где о), и со2 — радиусы пучка соответственно на входе и выходе лин-
линзы, а/?, и R2— соответствующие радиусы кривизны. Эти соотно-
соотношения применимы также для описания отражения от зеркал с ради-
радиусом кривизны R, если заменить в них/ на R/2.
Рассмотрим теперь распространение гауссова пучка через две
линзоподобные среды, примыкающие друг к другу. Пусть первая
среда описывается матрицей с элементами Ах, Вх, С,, ?>,, а вторая
среда — матрицей с элементами А2, В2, С2, D2. Обозначая входной
параметр пучка через дх, а выходной через др из B.3.16) получаем
следующее выражение для параметра пучка на выходе из среды 1
(плоскость 1):
х
а на выходе из среды 2 (плоскость 3) имеем
В2
Ъ C2q2 + D2 ¦
Сравнение последних двух выражений дает
ATq, + Вт
B-зл9>
где Ат, Вт, Ст, DT — элементы лучевой матрицы, связывающей
выходную плоскость 3 с входной плоскостью 1. Таким образом,
Распространение лазерных пучков
45
B.3.20)
AT Bt\ = [A2 B2\IAx Bx
CT DT] \C2 D2J\CX Dx
По индукции нетрудно показать, что выражение B.3.19) можно
применять для описания распространения гауссова пучка через про-
произвольное число линзоподобных сред и элементов. При этом мат-
матрица из элементов А т, Вт, Ст, DT является упорядоченным произ-
произведением матриц, характеризующих отдельные звенья такой цепоч-
цепочки.
Важное значение закона ABCD состоит в том, что он позволяет
рассчитать изменение параметра q(z) гауссова пучка при его рас-
распространении через сложную последовательность линзоподобных
элементов. Радиус пучка R (z) и его ширина ш (z) в любой плоскости
Z могут быть восстановлены с помощью соотношения B.3.7). Для
того чтобы понять, как можно использовать этот метод, рассмот-
рассмотрим следующий пример.
2.3.3. ПРИМЕР; ФОКУСИРОВКА ГАУССОВА ПУЧКА
В качестве иллюстрации применения закона ABCD рассмотрим слу-
случай гауссова пучка, который в плоскости его перетяжки падает на
тонкую линзу с фокусным расстоянием/ (рис. 2.3). Задача состоит
в том, чтобы найти положение плоскости перетяжки и радиус вы-
выходного пучка в этой плоскости.
На входе в линзу (плоскость 1) мы имеем ш = шх, Rx = оо, поэ-
поэтому
1 1 . А . X
Ч\ Л1 TWJ/J 7TWJ/J
Используя B.3.17), можно написать следующие соотношения:
J 1 i. J._ ._ЛГ_ 1 -а + jb
Яг <7, / / '™У qi
1 . А
Затем, учитывая B.2.4), в плоскости 3 имеем
. . -а Ц
12 + Ь2
+ 1 ,
R
1 X
- i—г
12 + Ь2
г2 + Ь2
' (а2
b2J

46
Глава 2
РИС. 2.3. Фокусирование гауссова пучка.
Поскольку по условию задачи выходная плоскость 3 отвечает пере-
перетяжке выходного пучка, R3 = оо. Учитывая это, из последнего вы-
выражения для координаты новой перетяжки получаем
/ = -г1-^ = ~ " = f~ V2 > B.3.21)
а отношение радиусов выходного и входного пучков в плоскостях
перетяжки дается выражением
"'
/А.
/
l +
+ (/А,J
B.3.22)
Параметр конфокальности пучка
z, s
пы.п
в соответствии с B.2.11) равен расстоянию от перетяжки, на кото-
котором ширина входного пучка возрастает в V2 раза, и является удоб-
удобной характеристикой сходимости входного пучка. Чем меньше z ,
тем сильнее сходимость пучка.
2.4. МОДЫ ГАУССОВА ПУЧКА ВЫСШЕГО ПОРЯДКА
В ОДНОРОДНОЙ СРЕДЕ
Мы рассматривали до сих пор гауссов пучок, в котором распреде-
распределение поля зависело лишь от продольного расстояния z и расстоя-
расстояния г от оси. Если мы не будем накладывать условия д/дф = о
[ф — азимутальный угол в цилиндрической системе координат
(г, ф, z)] и положим к2 - О, то волновое уравнение B.1.2) имеет ре-
решение вида [3]
Распространение лазерных пучков
47
X
X
Хехр
х2 + у2 ik(x2 + у2)
2*(z)
- ikz + /(/ + m + 1)tj
B.4.1)
где Н, — полиномы Эрмита порядка /, а величины u(z), R (z), g(z) и
rj определяются выражениями B.2.11)—B.2.14).
Для дальнейшего рассмотрения необходимо заметить, что сдвиг
фазы на оси дается выражением
Ч = kz - (/ + m + 1) arctg[-
B.4.2)
z —
Л •
Нетрудно видеть, что изменение электрического поля в поперечном
направлении вдоль координаты х (или у) имеет вид
//Д?)ехр( — ?2/2), где ? = V2x/u. Эта функция хорошо изучена, по-
поскольку она отвечает также квантовомеханической волновой функ-
функции и;(?) гармонического осциллятора [4]. На рис. 2.4 графически
представлены некоторые такие функции низшего порядка, норми-
нормированные на полную энергию пучка.
2.5. МОДЫ ГАУССОВА ПУЧКА В СРЕДЕ
С КВАДРАТИЧНЫМ РАСПРЕДЕЛЕНИЕМ
ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
В разд. 2.3 мы изучали распространение гауссова пучка с круговой
симметрией в линзоподобной среде, находя решение для комплекс-
комплексного параметра пучка q в зависимости от z. Здесь мы воспользуем-
воспользуемся модовым описанием и получим выражения для нормальных мод
пучка, распространяющегося в среде, показатель преломления ко-

«ю@
-5
РИС. 2.4. Функции Гаусса - Эрмита «/,(?) = (*и2П2'Г1/2Н{1-)е-&2, отвечающие
пучкам высшего порядка B.4.1). Кривые нормированы таким образом, чтобы пол
ная энергия во всех модах пучка была постоянной: ?auf (№ = 1. Сплошные кри
вые - функции и2(?) для / = 0, 1, 2, 3 и 10. Штриховые кривые - функции
Распространение лазерных пучков
49
|и„Ю|2
-0.5-1-
РИС. 2.4. (Продолжение.)
торой изменяется по закону
r2 = x2+y2, B.5.1a)
который совпадает с выражением B.1.4), если в нем положить
кг = 2жп2/Х.
В этом случае скалярное волновое уравнение B.1.2) принимает
4-631

50
Глава 2
ВИД
где
B.5.16)
Е(х, у, z) = }(х, y)exp(-ipz).
Записывая ф(рс, у) = f(x)g(y) и подставляя это выражение в волно-
волновое уравнение B.5.16), получаем
B.5.2)
Поскольку уравнение B.5.2) представляет собой сумму двух частей,
одна из которых зависит только от у, а другая — только от*, мы
можем написать следующие уравнения:
111
fdx2
8
B.5.3)
B.5.4)
где С — некоторая постоянная. Рассмотрим сначала уравнение
B.5.4). Вводя новую переменную ?, определяемую выражением
1/4
B.5.5)
уравнение B.5.4) нетрудно привести к виду
B.5.6)
Это хорошо известное дифференциальное уравнение, аналогичное
уравнению Шредингера для гармонического осциллятора [5]. Соб-
Распространение лазерных пучков
51
ственное значение С/а1 должно удовлетворять условию
4=B|я+1), т= 1,2,3,....
а
Решение, отвечающее данному целому числу т, имеет вид
B.5.7)
где Нт — полином Эрмита порядка т.
Проделаем теперь аналогичную процедуру с уравнением B.5.3).
Подставляя в него переменную
f = ах
получаем
d2f (
-П/=о.
Так же, как и в случае уравнения B.5.7), имеем
± а__к=B/+1), /=1,2,3,...
B.5.9)
Таким образом, полное решение для ф запишется в виде
„Ч.х2+у2)/а2
где радиус пучка ы в соответствии с B.5.5) определяется выражени-
выражением
B.5.11)
оп2
При этом полное (комплексное) поле имеет вид
р и [J-y _
B.5.12)

52
Глава 2
Выражение для постоянной распространения /3, ,„ моды (/, т)
находим из B.5.7) и B.5.9):
1/2
B.5.13)
Следует отметить две особенности модовых решений:
1. В отличие от решения для случая однородной среды (п2 = 0)
«радиус моды» со не зависит от z. Это можно объяснить фокуси-
фокусирующим действием распределения показателя преломления (п2 >
> 0), которое противодействует естественной тенденции ограни-
ограниченного пучка дифрагировать (уширяться). В случае когда пока-
показатель преломления возрастает с г (п2 < 0), из выражений
B.5.11) и B.5.12) следует, что со2 < 0 и решений, отвечающих не-
расходящемуся пучку, не. существует. Профиль показателя пре-
преломления в этом случае приводит к дефокусировке, усиливающей
дифракцию пучка.
2. Зависимость постоянной распространения C от модовых индек-
индексов /, т означает, что различные моды имеют разные как фазо-
вые (v/,m = °>/Pi,m)' так и групповые скорости [(уД т =
= ёы/d^! т], которые зависят от / и т.
Рассмотрим модовую дисперсию (т. е. зависимость от / и т)
групповой скорости моды /, т:
dco
B.5.14)
Если изменение показателя преломления мало, так что
-rJ— (/ + т + 1) <к 1,
к V По
то из B.5.13) приближенно получаем
т + IJ,
и в соответствии с B.5.14)
с/и„
()
B.5.15)
B.5.16)
B.5.17)
2к2
Распространение лазерных пучков
53
Влияние дисперсии групповой скорости на распространение импуль-
импульса мы рассмотрим в следующем разделе.
2.5.1. УШИРЕНИЕ ИМПУЛЬСА В СТЕКЛОВОЛОКНАХ
С КВАДРАТИЧНЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
Стекловолокна с квадратичным профилем показателя преломления
B.5.1а) являются превосходными каналами для систем оптической
связи [6, 7]. Поскольку информация кодируется последовательнос-
последовательностью оптических импульсов, информационная пропускная способ-
способность канала ограничивается в основном числом импульсов, кото-
которое может быть передано в единицу времени [8, 9].
Существуют две причины, по которым дисперсия групповой
скорости ограничивает частоту повторения импульсов в каналах с
квадратичным профилем показателя преломления.
Модовая дисперсия. Если оптические импульсы, падающие на вход-
входной конец волокна, возбуждают большое количество мод (как это
имеет место в случае, когда возбуждающий пучок сильно сфокуси-
сфокусирован и поэтому его «лучи» имеют большой угловой разброс), то
каждая мода будет распространяться со своей групповой скорос-
скоростью (у ), т в соответствии с выражением B.5.17). Если на вхо^е во-
волокна возбуждены все моды от @, 0) до (/max, wmax), to импульс на
выходе волокна при z = L будет уширяться на величину
1 1
TiT) 77T~ • С2-5-18)
Используя B.5.17) и условие (n2/no)(l + т + 1J/2к2 « 1, получаем
Дт= ^^-^(/max + wmax+ 1J. B.5.19)
Следовательно, максимальное число импульсов, которое может
быть передано за секунду без существенного перекрытия между со-
собой выходных импульсов, равно /max ~ 1/Дт. Поэтому для дости-
достижения высокой скорости передачи информации возбуждение дол-
должно быть одномодовым. Этого можно добиться, используя коге-
когерентное возбуждение одномодовым лазером [7—9].
Числовой пример. Рассмотрим волокно длиной 1 км с квадратич-
квадратичным профилем показателя преломления, у которого п0 = 1,5, пг =
= 5,1- 103 см. Пусть оптический импульс излучения с X = 1 мкм

54
Глава 2
возбуждает все моды вплоть до /тах = ттях = 30. Подстановка
этих значений в B.5.19) дает
Дт = 3,6Х Ю-9 с,
и для скорости передачи информации имеем /тах ~ (Дт) =
= 2,8-108 импульсов в секунду.
Дисперсия групповой скорости. Как уже отмечалось выше, ушире-
уширение импульса B.5.19), обусловленное многомодовым возбуждени-
возбуждением, можно устранить при распространении одной моды, например
моды /, т. Однако уширение импульса будет существовать и в
этом случае из-за зависимости (уД т от частоты. Это уширение
можно объяснить тем, что оптический импульс имеет спектраль-
спектральную ширину Дсо, которая приводит к его расплыванию на расстоя-
расстоянии L на величину (см. задачу 1.9)
аи
B.5.20)
Если импульс испускается непрерывным когерентным источником с
пренебрежимо малой шириной спектра, то спектральная ширина
импульса связана с его длительностью т соотношением Дсо ~ 2/т и
B.5.20) принимает вид
\ dus
B.5.21)
Если ширина линии излучения источника Дсо^ превышает т ', то в
выражении B.5.20) следует заменить Дсо на Дсо5. Таким образом,
уширение импульса обусловлено зависимостью групповой скорости
от со, т. е. дисперсией групповой скорости.
Для проверки нашего полуинтуитивного вывода соотношения
B.5.21), а также в качестве иллюстрации математического аппара-
аппарата, используемого при расчете дисперсии импульса, рассмотрим
распространение оптического импульса с гауссовой огибающей в
канале с дисперсией.
Пусть входной импульс имеет вид
E(z = 0, t) = *-«V"-' =
B.5.22)
Распространение лазерных пучков
где F(u) — фурье-образ огибающей е~а'2:
55
B.5.23)
Заметим, что частотный спектр гауссова распределения имеет мак-
максимум в точке соо. Поэтому поле на расстоянии z получается умно-
умножением каждой компоненты (со0 + 0) в B.5.22) на ехр[ —//3(соо +
]. Если разложить /3(соо + 0) в ряд в окрестности со0:
dB
Q+l\
fi2+ •••,
то можно записать следующее выражение
dQF(Q)expli
I
fiz
1 d I 1
где
B.5.24)
Огибающая поля дается интегралом в выражении B.5.24) и име-
имеет вид
B.5.25)
= f" dQF(Q)explia\(t- j-\-aQz\\,
где
1 d
a = 1
2 dec и
si 2v2gd<*'
Подставляя величину F(U) из B.5.23) в формулу для огибающей
B.5.25), получаем выражение
4тга ./_
которое после вычисления интеграла дает (см. задачу 1.9)
e(z,t)
1
/4aaz
exp
(< -
I/a + 16a2z2a
exp
Aaz{t-z/v?
1/а2 + 16аV
B.5.26)
Длительность импульса т на расстоянии z определяется как рассто-
расстояние между двумя моментами времени, когда квадрат амплитуды
огибающей импульса равен половине его максимальной величины:
B.5.27)
r(z) = i/21n2 J^ + 16a2z2a .

56
Глава 2
Исходная ширина импульса, определенная как ширина на полувы-
полувысоте интенсивности, дается выражением
/21п2\'/2
Таким образом, ширину импульса после распространения на рас-
расстояние L можно записать в виде
B.5.29)
B.5.30)
На больших расстояниях, для которых aL > т\, получаем
Если использовать определение коэффициента а [см. формулу, сто-
стоящую непосредственно после B.5.25)], то последнее выражение при-
принимает вид
du т0'
B.5.31)
что с точностью до множителя In 2 совпадает с B.5.21).
Дисперсию групповой скорости часто характеризуют величиной
D = L~ldT/d\, где Т — время распространения импульса через во-
волокно длиной L. Этот параметр связан со второй производной /3
по со:
B.5.32)
B.5.33)
а также с использованным выше параметром а:
4пс
D=-— a.
Выражение для ширины импульса B.5.29) можно записать через
новый параметр D следующим образом:
2 In 2 DLX2
ТС Т2
B.5.34)
Если величина DL измеряется в пикосекундах на нанометр, X — в
микрометрах, а т — в пикосекундах, то выражение B.5.34) прини-
Распространение лазерных пучков
57
мает вид
B.5.35)
Дисперсия групповой скорости (т. е. зависимость vg от со), при-
приводящая в соответствии с B.5.31) к уширению импульса, обуслов-
обусловлена двумя механизмами:
1. Групповая скорость vg зависит от со согласно B.5.17), поскольку
к = соя/с.
2. Групповая скорость vg неявно зависит от со вследствие зависимо-
зависимости показателя преломления вещества п от со. Подставляя
dvg/dw = dvg/dw + (dvg/dn)(dn/dw) в выражение B.5.20), получа-
получаем
Л 2L
Дт = —
с
ПоП2
dn
ск3
Аы,
B.5.36)
где во втором члене мы предположили, что (п2/2к2п()A + m +
+ IJ < 1. В большинстве волокон уширение импульса обуслов-
обусловлено в основном материальной дисперсией, характеризуемой ве1
личиной dn/dw.
На рис. 2.5 приведено реальное распределение показателя пре-
преломления в параболических волокнах на основе SiO2 — В2О3 при
п2 = 5-103 см. Рис. 2.6 иллюстрирует уширение оптического им-
импульса после прохождения им расстояния около 2,5 км. Входной
оптический импульс возбуждает большое число (/, ш) мод," и уши-
уширение описывается выражением B.5.19). Эти данные взяты из рабо-
работы [8], в которой исследовано также влияние важного явления меж-
модовой связи на уширение импульса.
Подставляя B.5.26) в B.5.24), нетрудно получить выражение
для полного поля на расстоянии z:
у/1 + iAaaz
exp (i
+
4az(t- z/vf
~2
16a2z2
I/a + 16a2z2a
B.5.37)

58
Глава 2
дпхКГ
10 10
Радиус, мкм
РИС. 2.5. Градиентный профиль показателя преломления по толщине волокна нз
SiO2 — В2О3. Штриховой линией изображен квадратичный профиль. (Согласно рабо-
работе [8].)
L'ZSWm
РИС. 2.6. а — форма импульса на входе в градиентное волокно из SiO2 — BjO3 с
квадратичным профилем показателя преломления, показанным на рнс. 2.5; б — фор-
форма импульса на выходе после прохождения волокна длиной 2516 м (обратите внима-
внимание на разные временные шкалы на рис. а и б). (Согласно работе [8].)
Таким образом, фазу электромагнитной волны можно записать в
виде
4az(t-z/vg)
а +
B.5.38)
Распространение лазерных пучков
59
При этом локальная «частота» ш(г, 0 дается выражением
u(zt)= — =u 8az(f ~ гЛт)
dt ° а-г + 16a2z2
B.5.39)
и представляет собой сумму из двух слагаемых, одно из которых
равно исходной частоте соо, а другое линейно меняется со временем
(chirp) и пропорционально параметру дисперсии групповой скоро-
скорости а. Это второе слагаемое можно качественно объяснить тем,
что из-за дисперсии групповой скорости разные частотные состав-
составляющие распространяются с различными скоростями. Из B.5.35)
следует, что относительное уширение t(L)/t0 для данного лазерно-
лазерного импульса, если произведение DL, характеризующее групповую
дисперсию, много меньше величины (tq/XJ, невелико (т. е. ~ 1).
Желательно, разумеется, создавать такие условия для распростра-
распространения импульса света, чтобы дисперсия групповой скорости от-
отсутствовала (D = 0). Это может иметь место в оптических волок-
волокнах, когда для некоторой длины волны излучения частотная и ма-
материальная дисперсии компенсируют друг друга. Недавно была
продемонстрирована возможность распространения практически
без искажений импульса длительностью 5 пс E-1О~|2с), ширина
которого ограничивалась лишь преобразованием Фурье, в двух
кремниевых одномодовых волокнах длиной 0,76 и 2,5 км соответст-
соответственно на длине волны X = 1,30 мкм, на которой дисперсия группо-
групповой скорости равна нулю (или почти равна нулю) [10]. На рис. 2.7
показано экспериментально измеренное уширение импульса.
РИС. 2.7. Уширение импульса в во-
волокне длиной 2,5 км, обусловленное
линейной дисперсией [10]. а — им-
импульс на входе в волокно; б — им-
импульс на выходе из волокна.
X = 1,30 мкм
-40 -20 0 20 40
Время задержки, пс

60
Глава 2
ЗАДАЧИ
2.1. Преобразование гауссова пучка линзой. Рассмотрим прохож-
прохождение гауссова пучка через тонкую линзу с фокусным рассто-
расстоянием /, предполагая, что пучок распространяется вправо.
Пусть перетяжка падающего пучка расположена на расстоя-
расстоянии dx от линзы и имеет ширину ыг Покажите, что в пере-
перетяжке ширина пучка, прошедшего через линзу, дается выра-
выражением
fl Г
и что перетяжка расположена на расстоянии d2 от линзы,
причем
Покажите также, что
<4 _d2-f
2.2. а) Пусть гауссов пучок падает перпендикулярно на призму
с показателем преломления п (рис. 2.8). Найдите угол
расходимости выходного пучка в дальнем поле,
б) Пусть призма перемещается влево, до тех пор пока ее
входная поверхность, на которую падает пучок, не сов-
совпадет с плоскостью z = — /г Чему теперь будет равен
радиус пучка в перетяжке и где перетяжка будет распо-
располагаться? (Предположите, что призма имеет достаточно
большую длину, так что перетяжка оказывается внутри
призмы.)
¦—1
:
z =
= 0
»
-/,
РИС. 2.8.
Распространение лазерных пучков
61
Линза
Образец
z = 0
г = /
РИС. 2.9.
2.3. Гауссов пучок с длиной волны излучения X падает на линзу,
расположенную в плоскости z = I (рис. 2.9). Вычислите фо-
фокусное расстояние линзы /, при котором перетяжка выход-
выходного пучка оказывается на передней поверхности кристалли-
кристаллического образца. Покажите, что при данных / и L существу-
существуют два решения. Дайте графическое изображение пучка на
входе и выходе в каждом из этих случаев.
2.4. Определите радиус пучка в перетяжке и максимальное число
импульсов в секунду, которое может переноситься оптиче-
оптическим пучком (X = 1 мкм), распространяющимся в стеклян-
стеклянном волокне с квадратичным профилем показателя прелом-
преломления при п — 1,5, п2 = 5-102см~2.
а) в случае одномодового возбуждения при / = т = 0 и
б) в случае, когда возбуждены все моды с /, т < 5. Ис-
Используя дисперсионные данные (зависимость от со) для
любого типичного промышленного стекла, сравните от-
относительные вклады межмодовой и материальной дис-
дисперсии в уширение импульса.
2.5. Подставьте выражение B.3.9) для ^ в волновое уравнение
B.1.1) и покажите, что
V2A -
?fn^A = 0
= 0.
Покажите, что если А (г) плавно изменяется в пространстве,
то величиной У2Л можно пренебречь и первое из приведен-
приведенных выше уравнений сводится к B.3.10).

62
Глава 2
ЛИТЕРАТУРА
1. Arnaud J. A., Hamiltonian theory of beam mode propagation. — In: Progress in
Optics XI (ed. E. Wolf)- — Amsterdam: North-Holland, 1973.
2. DrudeP., Theory of Optics. — New York: Longmans, Green and Co., 1933.
3. MarcuseD., Light Transmission Optics.— Princeton, N.Y.: Van Nostrand, 1972.
[Имеется перевод: Маркузе Д. Оптические волноводы. — М.: Мир, 1974.]
4. YarivA., Quantum Electronics, 2nd ed. — New York: Wiley, 1975, Sec. 2.2. [Име-
[Имеется перевод: Ярив А. Квантовая электродинамика. — М.: Сов. радио, 1980.]
5. Kogelnik H., Rigrod W., Visual display of isolated optical resonator modes. — Proc.
IEE, 50, 220 A962).
6. KawakamiS., Nishizawa J., An Optical waveguide with the optimum distribution of
the refractive index with reference to waveform distortion. — IEEE Trans.
Microwave Theory and Technique, MTT-16, No 10, 814 A968).
7. Miller S.E., Marcalili E. A. J., Li Т., Research toward optical fiber transmission
systems. — Proc. IEEE, 61, 1703 A973).
8. Cohen L. G., Presby H. M., Shuttle pulse measurement of pulse spreading in a low
loss graded index fiber. — Appl. Opt., 14, 1361 A975).
9. Cohen L. G., Personick S. D., Length dependence of pulse dispersion in a long
multimode optical fiber. — Appl. Opt., 14, 1250 A975).
Bloom D.M., Mollenauer L. F., Chin/on Lin, Taylor D. W., DelGaudio A. M.,
Direct demonstration of distortionless picosecond-pulse propagation in kilometer-
length optical fibers. — Opt. Lett., 4, 297 A979).
Yariv A., Yeh P., The application of Gaussian beam formalism to optical propaga-
propagation in nonlinear media. — Opt. Comm., 27, 295 A978).
10.
11.
Глава 3
ПОЛЯРИЗАЦИЯ СВЕТОВЫХ ВОЛН
Поля Е и Н, описывающие световые волны, являются векторными
величинами. В предыдущей главе распространение гауссовых пуч-
пучков мы рассматривали в приближении скалярных волн и нас не ин-
интересовало направление колебаний вектора электрического поля.
Мы лишь отметили, что вектор электрического поля лежит в пло-
плоскости, перпендикулярной направлению распространения. Во мно-
многих случаях характер распространения световых волн существенно
зависит от направления колебаний электрического поля. Действи-
Действительно, на протяжении практически всей книги мы будем изучать
главным образом распространение поляризованного света и вопро-
вопросы, связанные с его управлением. В данной главе мы рассмотрим
различные характеристики поляризованного света и ряд методов,
применяемых при изучении его распространения.
3.1. ЧТО ТАКОЕ ПОЛЯРИЗАЦИЯ?
Световые волны представляют собой электромагнитное поле, для
полного описания которого требуются четыре основных векторных
поля: Е, Н, D и В. Для определения состояния поляризации свето-
световых волн используется вектор электрического поля. Такой выбор
связан с тем, что в большинстве оптических сред физические взаи-
взаимодействия с волной осуществляются через электрическое поле. Ос-
Основной интерес к изучению поляризации световых волн обусловлен
тем, что во многих веществах (анизотропные среды) показатель
преломления зависит от направления колебаний вектора электриче-
электрического поля Е. Это явление можно объяснить движением электро-
электронов, которые раскачиваются электрическим полем световых волн.
Для иллюстрации этого предположим, что анизотропное вещество
состоит из несферических иглообразных молекул, причем все моле-
молекулы ориентированы таким образом, что их большие оси парал-
параллельны друг другу. Пусть в таком веществе распространяется элек-
электромагнитная волна. Вследствие анизотропной структуры молекул
электрическое поле, параллельное осям молекул, будет сильнее сме-
смещать электроны вещества относительно их равновесного положе-
положения, чем электрическое поле, перпендикулярное осям молекул. Поэ-

64
Глава 3
тому в первом случае следует ожидать более сильной вынужденной
поляризации электронов, чем во втором.
С поляризацией световых волн связано много других физических
явлений. Прежде чем перейти к изучению этих оптических явлений,
необходимо выяснить свойства поляризованных волн. Начнем рас-
рассмотрение с обзора состояний поляризации монохроматических
плоских волн.
3.2. ПОЛЯРИЗАЦИЯ МОНОХРОМАТИЧЕСКИХ
ПЛОСКИХ ВОЛН
Поляризация световых волн определяется вектором электрического
поля Е(г, /) в фиксированной точке пространства г в момент време-
времени /. Поскольку вектор электрического поля монохроматической
волны Е изменяется во времени по синусоидальному закону, коле-
колебания электрического поля должны происходить с определенной ча-
частотой. Если предположить, что свет распространяется в направле-
направлении оси z, то вектор электрического поля будет располагаться в
плоскости ху. Поскольку х- и/-составляющая вектора поля могут
колебаться независимо с определенной частотой, сначала следует
рассмотреть эффекты, связанные с векторным сложением этих двух
осциллирующих ортогональных составляющих. Задача о сложении
двух независимых ортогональных колебаний с некоторой частотой
хорошо известна и полностью аналогична задаче о классическом
движении двумерного гармонического осциллятора. В общем слу-
случае такой осциллятор движется по эллипсу, который отвечает не-
сфазированным колебаниям х- и /-составляющих. Существует, ко-
конечно, много частных случаев, имеющих большое значение в опти-
оптике. Мы начнем с рассмотрения общих свойств излучения с эллипти-
эллиптической поляризацией, а затем обсудим ряд частных случаев.
В представлении комплексных функций вектор электрического
поля монохроматической плоской волны, распространяющейся в
направлении оси z, дается выражением
*" -'J, C.2.1)
где А — комплексный вектор в плоскости ху. Выясним теперь, что
представляет собой кривая, которую описывает в некоторой точке
пространства конец вектора электрического поля Е. Эта кривая да-
дает эволюцию во времени положения точки с координатами (Ех, Ev):
Ех =
— kz
Еу = Aycos(ut - kz
Sx),
Sy),
C.2.2)
Поляризация световых волн
65
где комплексный вектор А определен следующим образом:
А = *.Aja- + №yeiS>', C.2.3)
здесь Ах иАу — положительные числа, а х и у — единичные векто-
векторы. Кривую, описываемую концом вектора электрического поля во
времени, можно получить, если из уравнения C.2.2) исключить
со/ — kz. После простых алгебраических преобразований получаем
( cos S
'ага„
где
= sy-sx.
C.2.4)
C.2.5)
Любой фазовый угол здесь удовлетворяет условию — тг < <5 ^ тг.
Уравнение C.2.4) описывает кривую второго порядка. Из выра-
выражений C.2.2) очевидно, что эта кривая ограничена прямоугольной
областью со сторонами, параллельными координатным осям и
имеющими размеры 2АХ и 2А . Следовательно, такая кривая дол-
должна быть эллипсом. В этом случае говорят, что волна, определяе-
определяемая выражением C.2.1), является эллиптически поляризованной.
Для полного описания эллиптической поляризации требуется знать
ориентацию эллипса относительно осей координат, его форму и на-
направление вращения вектора Е. В общем случае направление глав-
главных осей эллипса не совпадает с направлениями осей хну. Соот-
Соответствующее преобразование системы координат (вращение) позво-
позволяет диагонализовать уравнение C.2.4). Рассмотрим новую систему
координат с осямих' ну', направленными вдоль главных осей эл-
эллипса. В этой новой системе координат уравнение эллипса прини-
принимает вид
C.2.6)
где а и Ъ — главные оси эллипса, а Ех, и Еу, — составляющие век-
вектора электрического поля в этих координатах.
Пусть ф (О ^ ф < тг) — угол между направлением главной оси
эллипса х' и осью х (рис. 3.1). Тогда длины главных осей эллипса
определяются выражениями
„2 .
+
+ 2AxAycosScos<!>sm<l>,
- 2AxAycos8cos<$>sm<$>.
C.2.7)
5-631

66
Глава 3
РИС. 3.1. Эллипс поляризации.
Угол ф можно выразить через Ах, Ау и cos5 следующим образом:
-cos 8.
C.2.8)
Направление вращения эллиптической поляризации определяется
знаком sin 5. При sin 5 > 0 конец вектора электрического поля бу-
будет вращаться по часовой стрелке, а при sin 8 < О — против часо-
часовой стрелки. Рис. 3.2 иллюстрирует характер изменения эллипса
поляризации в зависимости от разности фаз д.
Прежде чем перейти к рассмотрению некоторых частных случа-
случаев поляризации, дадим ряд определений. Свет называется линейно
поляризованным, если конец вектора электрического поля Е пере-
перемещается вдоль прямой линии. В случае когда конец этого вектора
описывает эллипс, свет называется эллиптически поляризованным,
а в случае когда он описывает окружность, — циркулярно поляри-
поляризованным. Если конец электрического вектора перемещается про-
против часовой стрелки для наблюдателя, расположенного перед вол-
волной, то поле обладает правой поляризацией. На рис. 3.2 показано
также направление вращения эллипса поляризации. Наше определе-
определение правой и левой поляризации согласуется с терминологией сов-
современной физики, в которой фотон с правой круговой поляризацией
имеет положительный момент импульса в направлении распростра-
Поляризация световых волн
67
«=-Зтг/4
= -ir/2
-ir/4
6 = 0
6=ir/4
«= тг/2
6 = 3ir/4
6=-Зтг/4
= -ir/2
ir/4
6=0
6=тг/4
Ь="<2 «=,/4
б
' ?ллипсы П0ЛЯРизации при различных значениях фазы 6. а - Е
У = C0S(' k S) б

Поляризация световых волн
69
л
о
1
а»
V
о
л
о
V
О
g
¦а
§ ?
нения (см. табл. 3.1 и задачу 3.4). Однако в некоторых книгах по
оптике используется противоположное соглашение.
3.2.1. ЛИНЕЙНАЯ И КРУГОВАЯ ПОЛЯРИЗАЦИИ
Особенно важное значение имеют два частных случая, когда эллипс
поляризации вырождается либо в прямую линию, либо в окруж-
окружность. В соответствии с выражениями C.2.4) эллипс вырождается в
прямую линию, когда
8 = S-Sx = mv (w = 0,1).
C.2.9)
Напомним, что все фазы по определению изменяются в интервале
— тг < 5 < ж. В этом случае отношение составляющих вектора
электрического поля остается постоянным:
5:_(_l)»ii C.2.10)
Ex Ax
и свет является линейно-поляризованным.
Другой важный частный случай отвечает циркулярно-поляризо-
ванной волне, или волне с круговой поляризацией. В соответствии с
C.2.4) и C.2.7) эллипс вырождается в окружность, когда
S = 8у - 8Х = ±
C.2.11)
C.2.12)
Согласно нашему определению, свет является правоциркулярно-по-
ляризованным при 5 = — A/2)тг, что соответствует вращению век-
вектора электрического поля против часовой стрелки, и левоциркуляр-
но-поляризованным при 5 = A/2)тг, что отвечает вращению векто-
вектора электрического поля по часовой стрелке (см. табл. 3.1).
Эллиптичность эллипса поляризации характеризуется парамет-
параметром
е= +-, C.2.13)
где а и Ъ — длины главных осей. Эллиптичность считается поло-
положительной, если вращение вектора электрического поля является
правосторонним, и отрицательной в противоположном случае.

70
Глава 3
3.3. ПРЕДСТАВЛЕНИЕ КОМПЛЕКСНОГО ПАРАМЕТРА
В предыдущем разделе было показано, как состояние поляризации
световой волны можно описать с помощью амплитуд и фазовых
углов для х- и /-составляющих вектора электрического поля. Ока-
Оказывается, что вся информация о поляризации волны содержится в
комплексной амплитуде А плоской волны C.2.1). Следовательно,
для описания состояния поляризации достаточно использовать ком-
комплексный параметр х, определяемый выражением
Ay
~A~
C.3.1)
где угол ф по определению заключен в интервале от 0 до 7г/2. Па-
Параметры д и ф позволяют получить полное описание эллипса поля-
поляризации, для чего требуется задать его ориентацию, направление
вращения и эллиптичность [см. C.2.13)]. На рис. 3.3 изображены
различные состояния поляризации в комплексной плоскости. Мож-
Можно видеть, что все правые эллиптические состояния поляризации
расположены в нижней полуплоскости, а состояниям с левой эллип-
эллиптической поляризацией отвечает верхняя полуплоскость. Начало ко-
координат отвечает состоянию с линейной поляризацией, параллель-
о
о
о J0
\ Ч v n.
4 ч ч
1 Т
о О
О
о
о
РИС. 3.3. Каждой точке комплексной плоскости отвечает определенное состояние
поляризации.
Поляризация световых волн
71
ной осих. Таким образом, любая точка комплексной плоскости со-
соответствует одному состоянию поляризации. Каждая точка на оси
х отвечает состояниям с линейной поляризацией, но с различными
азимутальными углами колебаний. Круговой поляризации отвеча-
отвечают только две точки с координатами @, + 1) и @, — 1). Все осталь-
остальные точки комплексной плоскости соответствуют состояниям с
определенной эллиптической поляризацией.
Угол наклона ф и угол эллиптичности в (в = arctge), отвечаю-
отвечающие данному эллипсу поляризации, связаны с комплексным пара-
параметром х следующим образом:
tg 2ф
2Re[X]
i-lxl2
C.3.2)
C.3.3)
3.4. ВЕКТОР ДЖОНСА
Поляризацию плоской волны можно достаточно хорошо предста-
представить с помощью вектора Джонса, введенного в 1941 г. Р. Джонсом
[1]. В этом представлении плоская волна C.2.1) описывается век-
вектор-столбцом, составленным из ее комплексных амплитуд:
J =
C.4.1)
Заметим, что вектор Джонса является комплексным, т. е. его эле-
элементы задаются комплексными числами. Кроме того, J не являет-
является вектором в реальном физическом пространстве. Он представляет
собой вектор в абстрактном математическом пространстве. Напри-
Например, для получения вещественной величины х-составляющей элект-
электрического поля, необходимо выполнить операцию Re [У/""'] =
Ке[хе]
Вектор Джонса содержит полную информацию об амплитудах и
фазах составляющих вектора электрического поля. Если нас интере-
интересует только состояние поляризации волны, то удобно пользоваться
нормированным вектором Джонса, который удовлетворяет усло-
условию
J* - J = 1
C.4.2)

72
Глава 3
где звездочка (*) означает комплексное сопряжение. Таким обра-
образом, линейно поляризованная световая волна с данным направлени-
направлением вектора электрического поля может быть представлена векто-
вектором Джонса
cos ip
sin \p
C.4.3)
где ф — азимутальный угол между направлением поляризации и
осью х. Состояние поляризации, которое ортогонально состоянию
поляризации, описываемому вектором C.4.3), можно получить за-
заменой ф на ф + тг/2, что приводит к вектору Джонса
-sin
COS ip
C.4.4)
Частный случай ф = О соответствует линейно поляризованным
волнам, вектор электрического поля которых колеблется вдоль
осей координат. Векторы Джонса при этом имеют вид
-(!>)¦
$ =
C.4.5)
Световые волны с правой и левой круговой поляризацией описыва-
описываются векторами Джонса
C.4.6)
C.4.7)
Эти две круговые поляризации являются взаимно ортогональными
в том смысле, что
R*-L = 0. C.4.8)
Поскольку вектор Джонса представляет собой столбец из двух эле-
элементов, любую пару ортогональных векторов Джонса можно вы-
выбрать в качестве базиса в пространстве всех векторов Джонса. Лю-
Любая поляризация при этом может быть представлена как суперпози-
суперпозиция двух взаимно ортогональных поляризаций х и у, или Й и L. В
частности, базисные линейные поляризации х и у можно разло-
разложить на две круговые поляризации R и L и наоборот. Эти разло-
Поляризация световых волн
73
жения имеют вид
t--J=-(8 + /
i-ifl +
C.4.9)
C.4.10)
C.4.11)
C.4.12)
Мы видим, что круговая поляризация представляет собой суперпо-
суперпозицию двух линейных поляризаций вдоль осей х и у с равными ам-
амплитудами 1/\^2, но с разностью фаз A/2)тг. Аналогично, линейную
поляризацию можно рассматривать как суперпозицию двух проти-
противоположно направленных круговых поляризаций.
До сих пор мы рассматривали векторы Джонса для некоторых
простых частных случаев поляризации. Нетрудно показать, что в
общем случае эллиптическую поляризацию можно представить сле-
следующим вектором Джонса:
cos
C.4.13)
Этот вектор Джонса отвечает некоторому состоянию поляризации,
описываемому комплексным параметром х = e^&tgф. В табл. 3.2
приведены векторы Джонса для некоторых типичных состояний
поляризации.
Наиболее важное применение векторы Джонса находят при вы-
вычислениях состояния поляризации. Это мощный метод, используе-
используемый при исследовании распространения плоских волн с произволь-
произвольным состоянием поляризации через произвольную последователь-
последовательность двулучепреломляющих элементов и поляризаторов. В гл. 5
мы рассмотрим данный вопрос более подробно.
ЗАДАЧИ
3.1. Выведите уравнение C.2.4).
3.2. Получите соотношения C.2.7) и C.2.8).

74
Глава 3
Поляризация световых волн
75
ТАБЛИЦА 3.2. Векторы Джонса для некоторых типичных
состояний поляризации
Эллипс поляризации
Вектор Джонса
3.3. Покажите, что конец вектора электрического поля эллипти-
эллиптически поляризованного света при sin 5 > 0 будет вращаться
по часовой стрелке, а при sin 5 < 0 — против часовой стрел-
стрелки.
3.4. а) Волна с правой круговой поляризацией (sin5 < 0), рас-
распространяющаяся в направлении оси z, ограничена в на-
направлениях осей х и у. Предполагая, что модуляция ам-
амплитуды является плавной (ширина волны много боль-
больше длины волны), покажите, что электрическое и маг-
магнитное поля определяются приближенными выражения-
выражениями
3.5.
дх ду
б) Вычислите усредненную по времени составляющую мо-
момента импульса вдоль направления распространения
(+z). Покажите, что эта составляющая момента им-
импульса равна h, если энергия волны нормирована на hu.
Это означает, что фотон с правой круговой поляризаци-
поляризацией переносит положительный момент импульса h вдоль
направления его импульса (спиральность).
в) Покажите, что поперечные составляющие момента им-
импульса равны нулю.
Состояния с ортогональными поляризациями.
а) Найдите состояние поляризации, которое ортогонально
состоянию поляризации
cos \р
Ответ:
б) Покажите, что главные оси эллипсов двух состояний с
взаимно ортогональными поляризациями перпендику-

76
Глава 3
лярны друг другу, а направления вращения противопо-
противоположны.
3.6. а) Эллиптически поляризованный пучок, распространяю-
распространяющийся в направлении оси z, ограничен в х- и/-направле-
и/-направлениях:
Е(дс, у, z, г) = Е0(х, у)(ак
где а = соъф, /3 = sin\pe'&. Покажите, что электрическое
поле должно иметь составляющую в направлении оси z
(см. задачу 3.4а), и получите выражения для электриче-
электрического и магнитного полей.
б) Вычислите г-составляющую момента импульса, предпо-
предполагая, что полная энергия волны равна hoi. Ответ: Lz =
= — й sin 2^ sin 5.
в) Запишите волну с эллиптической поляризацией в виде
линейной суперпозиции правой и левой поляризаций R и
L; иными словами, если состояние поляризации в п. а
задачи описывается вектором Джонса J, найдите такие г
и /, чтобы выполнялось равенство
J =
it.
г) Пусть г и / — амплитуды вероятности того, что фотон
имеет соответственно правую и левую круговую поляри-
поляризацию. Покажите, что момент импульса можно вычи-
лить по формуле
д) Запишите момент импульса чгрез угол эллиптичности д.
3.7. Выведите соотношения C.3.2) и C.3.3).
3.8. Состояния с ортогональными поляризациями. Пусть име-
имеются две монохроматические плоские волны вида
Поляризации этих двух волн взаимно ортогональны, т. е.
А* В = 0.
Поляризация световых волн
77
а) Предполагая, что 8а и дь — фазовые углы, определяемые
выражениями C.2.2), покажите, что
б) Покажите, что, поскольку углы да и дь заключены в ин-
интервале — 7Г < 5 < 7Г,
«А < о.
в) Пусть ха и Хй — комплексные параметры, задающие со-
состояния поляризации этих двух волн. Покажите, что
ХаХь= -1-
г) Докажите, что главные оси эллипсов поляризации взат
имно ортогональны, а их эллиптичности имеют одина-
одинаковые значения, но противоположные знаки.
ЛИТЕРАТУРА
1. Shurdiff W- A., Polarized Light.— Cambridge: Harvard University Press, 1966.
[Имеется перевод: Шерклифф У. Поляризованный свет. — М.: Мир, 1965.]
2. Born M., WolfE., Principles of Optics. — New York: MacMillan, 1964. [Имеется
перевод 2-го изд.: Борн М., Вольф Э. Основы оптики. — М.: Наука, 1970.]
3. Azzam R. M. A., Bashara N. М., Ellipsometry and Polarized Light. — Amsterdam:
North-Holland, 1977. [Имеется перевод: Аззам Р., Башара Н. Эллипсометрия и
поляризованный свет. — М.: Мир, 1981.]
4. Wuhlstrom E. Е.„ Optical Crystallography. — New York: Wiley, 1969.

Глава 4
РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ
ВОЛН В АНИЗОТРОПНЫХ СРЕДАХ
Существует много веществ, оптические свойства которых зависят
как от направления распространения, так и от поляризации свето-
световых волн. К оптически анизотропным материалам относятся кри-
кристаллы, например кальцит, кварц и KDP, а также жидкие кристал-
кристаллы. Эти материалы характеризуются многими необычными опти-
оптическими свойствами, такими, как двойное лучепреломление, опти-
оптическое вращение плоскости поляризации, поляризационные эффек-
эффекты, коническая рефракция, электрооптические и акустооптические
эффекты. Анизотропные кристаллы используются во многих опти-
оптических устройствах, например в призменных поляризаторах, поля-
поляризационных пластинах и в двулучепреломляющих фильтрах. Ани-
Анизотропные нелинейные вещества используются также для достиже-
достижения фазового синхронизма при генерации второй гармоники. Таким
образом, очевидно, сколь важным для практического применения
этих свойств является четкое представление о процессе распростра-
распространения света в анизотропных средах. Данная глава целиком посвя-
посвящена изучению распространения электромагнитного излучения в
этих средах.
4.1. ДИЭЛЕКТРИЧЕСКИЙ ТЕНЗОР
АНИЗОТРОПНОЙ СРЕДЫ
В изотропной среде вектор индуцированной поляризации всегда па-
параллелен электрическому полю и связан с ним скалярным множите-
множителем (восприимчивостью), который не зависит от направления дей--
ствия внешнего поля. Для анизотропных сред это не справедливо,
за исключением лишь некоторых отдельных направлений распро-
распространения. Поскольку кристалл представляет собой регулярную пе-
периодическую систему атомов (или молекул) с определенной сим-
симметрией, следует ожидать, что индуцированная поляризация будет
зависеть как от величины, так и от направления приложенного по-
поля. При этом вместо простых скалярных соотношений, связываю-
Распространение электромагнитных волн в анизотропных средах
79
щих Р и Е, мы имеем
Ру = ?о(Х21?* + Х22Еу + Xl3Ez)>
D.1.1)
Здесь прописными буквами обозначены комплексные амплитуды
соответствующих величин, гармонически зависящих от времени.
Трехмерная матрица коэффициентов Ху называется тензором элект-
электрической восприимчивости. Величины х# зависят, конечно, от вы-
выбора направлений осей х, у и z относительно кристаллической
структуры. Направления этих осей всегда можно выбрать таким
образом, чтобы недиагональные элементы обратились в нуль:
Рх ~
Ру ~
D.1.2)
Эти направления называются главными диэлектрическими осями
кристалла.
Вместо D.1.1) диэлектрические свойства кристалла можно опи-
описать посредством тензора диэлектрической проницаемости е^, ко-
который определяется следующим образом:
D.1.3)
е22Еу + «23
Из D.1.1) и соотношения
D = е0Е + Р
получаем
ео = еоО + Х,7)-
D.1.4)
D.1.5)

80
Глава 4
Эти девять величин еп, е12, ... являются постоянными среды и со-
составляют диэлектрический тензор. Выражения D.1.3) часто записы-
записывают в виде тензора
D, =
D.1.6)
где подразумевается суммирование по повторяющимся индексам.
В большей части этой главы мы будем считать, что среда явля-
является однородной, непоглощающей и магнитно-изотропной. Плот-
Плотность энергии электрического поля, запасенной в анизотропной сре-
среде, равна
D
Дифференцируя D.1.7) по времени, получаем
D.1.7)
D.1.8)
При выводе теоремы Пойнтинга в разд. 1.2 мы видели, что поток
энергии в единичном объеме среды без поглощения дается выраже-
выражением
-V'(EXH) = E-D + H-B, D.1.9)
которое с помощью формулы D.1.6) для D можно записать в виде
- V (Е X Н) = ?,е/у?у + Н • В. D.1.10)
Поскольку вектор Пойнтинга равен потоку энергии в среду, первое
слагаемое в правой части выражения D.1.10) должно быть равно
Ue. Таким образом, мы имеем следующее уравнение:
Отсюда сразу следует, что
D.1.11)
D.1.12)
Это означает, что тензор диэлектрической проницаемости симмет-
симметричен и имеет, вообще говоря, лишь шесть независимых элемен-
элементов. Эта симметрия является прямым следствием определения
D.1.6) и предположения о том, что е представляет собой вещест-
вещественный тензор диэлектрической проницаемости. В случае когда сре-
среда без поглощения описывается комплексным тензором диэлектри-
диэлектрической проницаемости (например, оптически активная среда, см.
Распространение электромагнитных волн в анизотропных средах
81
разд. 4.9), аналогичный вывод приводит к условию
D.1.13)
Иными словами, для сохранения энергии электромагнитного поля
требуется, чтобы тензор диэлектрической проницаемости был эр-
эрмитов. В частном случае, когда диэлектрический тензор является
вещественным, свойство эрмитовости D.1.13) сводится к свойству
симметрии D.1.12).
4.2. РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН
В АНИЗОТРОПНЫХ СРЕДАХ
В анизотропной среде, такой, как кристалл, фазовая скорость све-
световой волны зависит как от состояния ее поляризации, так и от на-
направления ее распространения. Вследствие анизотропии состояние
поляризации плоской волны может изменяться в процессе ее рас-
распространения через кристалл. Однако в общем случае для данного
направления распространения в среде существуют две независимые
волны (моды) с хорошо определенными фазовыми скоростями и
направлениями поляризации. При распространении через анизот-
анизотропную среду состояние поляризации световой волны, поляризо-
поляризованной параллельно одному из этих направлений, будет сохранять-
сохраняться. Эти независимые поляризации, а также отвечающие им фазо-
фазовые скорости (или, что эквивалентно, показатели преломления)
можно определить из уравнений A.1.1) и A.1.2) с использованием
диэлектрического тензора.
С целью получения соответствующих выражений предположим,
что через анизотропную среду распространяется монохроматиче-
монохроматическая плоская волна с угловой частотой со, электрическое поле кото-
которой имеет вид
D.2.1)
Eexp[j'(«f - k-r)],
а магнитное поле записывается в виде
Hexp[j'(«f - к* г)],
D.2.2)
где k[=(co/c)«s] — волновой вектор (здесь s — единичный вектор
вдоль направления распространения) и п — показатель преломле-
преломления, который нужно определить. Подстановка выражений D.2.1) и
D.2.2) для Е и Н в уравнения Максвелла соответственно A.1.1) и
6-631

82
Глава 4
Распространение электромагнитных волн в анизотропных средах
83
A.1.2) дает
к X Е = соцН, D.2.3)
кхН= -соеЕ. D.2.4)
Исключая Н из уравнений D.2.3) и D.2.4), получаем
к X (к X Е) + и2цеЕ = 0. D.2.5)
В системе координат, которые совпадают с главными диэлектриче-
диэлектрическими осями, диэлектрический тензор имеет вид
е =
0
0 \
0
D.2.6)
О 0 ех
При этом уравнение D.2.5) можно записать следующим образом:
с ку kz
кукх
кгкх
кхку
*А
- к\ - к]
« V, - к\ - к)
= 0.
D.2.7)
Для того чтобы система уравнений имела нетривиальные решения,
детерминант матрицы в D.2.7) должен быть равным нулю. Это ус-
условие позволяет найти соотношение между шик:
det
_ 1.2 _ г. 2
с Ку Kz
kykx
Kkx
к к
k2 - k2
Kx Ky
= 0. D.2.8)
Данное уравнение можно рассматривать как уравнение трехмерной
поверхности в к-пространстве (пространстве импульсов). Эта по-
поверхность называется нормальной поверхностью (поверхностью
волновых нормалей) и состоит из двух оболочек, которые в общем'
случае имеют четыре общие точки (рис. 4.1). Две линии, проходя-
проходящие через начало координат и эти точки, называются оптическими
осями. На рис. 4.1 изображена одна из оптических осей. Для данно-
данного направления распространения существуют, вообще говоря, два
значения к, при которых направление распространения пересекается
с нормальной поверхностью. Эти два значения к соответствуют
Оптическая
ось
РИС. 4.1. Нормальная поверхность.
двум различным фазовым скоростям (ш/к) волн, распространяю-
распространяющихся вдоль выбранных направлений. Направления вектора элект-
электрического поля, связанные с распространением вдоль этих направ-
направлений, можно также вычислить из уравнений D.2.7), они определя-
определяются вектор-столбцом
D.2.9)
к2
к2
кх
- «V,
- а2реу
kz
A:2-co2
В разд. 4.3 мы покажем, что эти две фазовые скорости всегда отве-
отвечают двум взаимно ортогональным поляризациям (для вектора
электрического смещения D) (см. также задачу 4.1).
При распространении в направлении оптических осей существует
только одно значение к и, следовательно, только одна фазовая ско-
i _

84
Глава 4
рость. Однако имеются два независимых направления поляризации.
Выражения D.2.8) и D.2.9) нередко записывают через косинусы,
задающие направление волнового вектора. Используя соотношение
k = (ic/c)ns для плоской волны, описываемой выражением D.2.1),
уравнение D.2.8) и вектор-столбец D.2.9) можно записать соот-
соответственно в виде
1
n2 - ел/Ео
?v/?0
D.2.10)
~ ?х/?0
D.2.11)
1 - ?г/Е0 ,
Уравнение D.2.10) называется уравнением волновых нормалей
Френеля. Его решения дают главные значения показателей прелом-
преломления, а выражение D.2.11) определяет направления поляризации
независимых волн, которые могут распространяться в кристалле.
Уравнение D.2.10) является квадратичным относительно я2. Поэто-
Поэтому каждому направлению распространения (из набора sx, s , sz) со-
соответствуют два решения для п1 (задача 4.2). Для полного реше-
решения задачи мы должны подставить каждое из значений пг в выра-
выражение D.2.11), что позволяет определить поляризации соответству-
соответствующих независимых волн. Можно показать, что для непоглощаю-
щей среды эти независимые волны линейно поляризованы, по-
поскольку в D.2.11) все величины являются вещественными. Пусть Е,
и Е2 — векторы электрического поля, a D, и D2 — векторы элект-
электрического смещения линейно поляризованных независимых волн,
соответствующих п\ и п\. Из уравнения Максвелла V • D = 0 следу-
следует, что D, и D2 ортогональны s. Поскольку D,-D2 = 0, три векто-
вектора D,, D2 и s образуют взаимно ортогональную тройку векторов и
могут быть выбраны в качестве системы координат при описании
многих физических явлений, в том числе и оптической активности.
Согласно уравнениям Максвелла, векторы D, Е и Н связаны между
собой соотношениями
D= --s XH
с
D.2.12)
Распространение электромагнитных волн в анизотропных средах
85
= —sxE.
цс
D.2.13)
Отсюда следует,-что как D, так и Н перпендикулярны направлению
распространения s. Таким образом, направление потока энергии,
определяемое вектором Пойнтинга ЕхН, вообще говоря, не совпа-
совпадает с направлением распространения s. Подставляя выражение
D.2.13) для Н в D.2.12) и используя векторное тождество
Ах(ВхС) = В (А С) — С (А В), получаем следующее выражение:
D= ~
- " F
— I ^ попереч,
С2Ц
с р
D.2.14)
а поскольку s D = 0 и п2/с2ц = п2е0, имеем
?2 = -^E-D = n2e0E-D. D.2.15)
су
Иными словами, векторы D, Е и s лежат в одной плоскости. Мож-
Можно показать, что эти векторы связаны между собой следующими
соотношениями (см. задачу 4.1):
D, • D2 = 0, D, • Е2 = 0, D2 • Е, = 0,
S'D,=s«D7 = 0.
D.2.16)
Векторы Е, и Е2 в общем случае не ортогональны. Условие ортого-
ортогональности для независимых волн можно записать в виде
s«(E, X Н2) = 0.
D.2.17)
Последнее соотношение означает, что поток энергии в анизотроп-
анизотропной среде вдоль направления распространения равен сумме энергий,
переносимых каждой независимой волной.
4.2.1, СВОЙСТВА ОРТОГОНАЛЬНОСТИ НЕЗАВИСИМЫХ ВОЛН
Выведем теперь условие ортогональности D.2.17) для двух незави-
независимых волн, распространяющихся вдоль некоторого направления s.
Используя выражения D.2.1) и D.2.2) для электрического и магнит-
магнитного полей и теорему взаимности Лоренца, получаем
s-(E, XH2) = s-(E2X H,). D.2.18)

86
Глава 4
Подстановка выражения D.2.13) для Н, и Н2 в уравнение D.2.18)
приводит к уравнению
% • [Е, X (s X Е2)] = ^ls • [Е2 X (s X Е,)]. D.2.19)
Это уравнение можно упростить, используя векторное тождество
А-(Вх С) = С-(Ах В).
В результате получаем
— (s х E,)«(s x E2) = —(s x E.Ws x E2).
D.2.20)
Поскольку уравнение D.2.20) должно быть справедливо для любого
произвольного направления распространения s с и, Ф л2, оно мо-
может выполняться только в том случае, когда обе его части равны
нулю, т. е.
s-(E,
= s-(E2xH,) = 0.
D.2.21)
Таким образом, вдоль произвольного направления s могут рас-
распространяться две независимые линейно поляризованные плоские
волны. Эти независимые волны имеют фазовые скорости ±с/л, и
±с/л2, где п\ и п\ — два решения уравнения Френеля D.2.10).
На практике показатели преломления л,, л2 и направления век-
векторов D, Н и Е чаще всего определяют, используя не описанный
выше метод, а формально эквивалентный метод эллипсоида пока-
показателей преломления. Этот метод описан в следующем разделе.
4.3. ЭЛЛИПСОИД ПОКАЗАТЕЛЕЙ ПРЕЛОМЛЕНИЯ
Поверхность постоянной плотности энергии Ue в пространстве век-
векторов D определяется уравнением D.1.7) и имеет вид
D2 D1 D2
X | У . Z Луг
где ех, еу и ег
главные диэлектрические проницаемости. Заменяя
величину D/V2C/, на г и определяя главные показатели преломле-
преломления пх, пу и nz следующим образом: nf = е/е0 (/' = х, у, z), послед-
последнее уравнение можно переписать в виде
у2
п1
D-3.1)
Распространение электромагнитных волн в анизотропных средах
87
Это общее уравнение эллипсоида, главные оси которого параллель-
параллельны направлениям х, у иг, а их длины равны соответственно 2пх,
2л , 2лг. Такой эллипсоид называют эллипсоидом показателей пре-
преломления или оптической индикатрисой. Эллипсоид показателей
преломления используется в основном для определения двух пока-
показателей преломления и двух соответствующих направлений вектора
D, отвечающих двум независимым плоским волнам, которые мо-
могут распространяться вдоль произвольного направления s в кри-
кристалле. Этот метод состоит в том, что сначала находят эллипс пе-
пересечения плоскости, проходящей через начало координат и перпен-
перпендикулярной направлению распространения s, с эллипсоидом показа-
показателей преломления D.3.1). Две оси этого эллипса имеют длины 2л,
и 2л2, где л, и л2— два значения показателя преломления, пред-
представляющие собой решения уравнения D.2.10). Эти оси параллель-
параллельны соответственно векторам D, и D2, отвечающим двум допусти-
допустимым решениям (рис. 4.2).
Для того чтобы убедиться в том, что эта процедура формально
эквивалентна методу, описанному в предыдущем разделе, введем
тензор непроницаемости т^:
Чу = е0(е-%, D-3.2)
где ?"' — тензор, обратный диэлектрическому тензору ?. Исполь-
Используя это определение, можно записать следующее соотношение меж-
между векторами Е и D:
Е = — tjD. D.3.3)
Подстановка выражения D.3.3) для Е в волновое уравнение D.2.5)
приводит к уравнению
s X [s X tjD] +—D = 0,
л
D.3.4)
РИС. 4.2. Метод эллипсоида показателей преломления. Внутренний эллипс пред-
представляет собой сечение эллипсоида показателей преломления плоскостью, перпенди-
перпендикулярной вектору s.

Глава 4
где мы использовали определение к = п (w/c)s (s — единичный век-
вектор в направлении распространения). Поскольку вектор D всегда
перпендикулярен направлению распространения (s • D = 0), удобно
использовать новую систему координат, одна из осей которой вы-
выбрана вдоль направления распространения волны. Две другие оси
обозначим индексами 1 и 2. В такой системе координат единичный
вектор s дается выражением
D.3.5)
а волновое уравнение D.3.4) принимает вид
D.3.6)
Поскольку s • D = 0, третья составляющая вектора D всегда равна
нулю. Элементы тензора т/13, rj2i можно опустить и ввести тензор
поперечной непроницаемости rj, следующим образом:
'Ч|1 Ч|2
Ч' ~ I, 421 422
При этом волновое уравнение принимает вид
MD = 0,
D.3.7)
D.3.8)
где D — вектор электрического смещения.
Векторы поляризации нормальных мод являются собственными
векторами тензора поперечной непроницаемости с собственными
значениями \/п2. Поскольку т/, — симметричный тензор второго
ранга, он имеет два ортогональных собственных вектора. Эти два
собственных вектора D, и D2 отвечают двум нормальным модам
распространения с показателем преломления л, и п2 соответствен-
соответственно.
Пусть ?,, ?2, ?3 — координаты произвольной точки в новой си-
системе координат. Эллипсоид показателей преломления в этой си-
системе координат определяется выражением
4e/J?e?/?=l> D.3.9)
где мы предполагаем суммирование по повторяющимся индексам
а, /3 A, 2, 3). Подставляя в D.3.9) ?3 = 0, получаем эллипс сечения
Распространение электромагнитных волн в анизотропных средах
89
этого эллипсоида плоскостью (?3 — 0), проходящей через начало
координат и перпендикулярной направлению распространения. Та-
Таким образом, мы имеем следующее уравнение для эллипса в сече-
сечении:
D.3.10)
Коэффициенты в уравнении D.3.10) образуют тензор поперечной
непроницаемости т/г Следовательно, собственные векторы этого
тензора второго ранга направлены вдоль главных осей эллипса се-
сечения. В соответствии с D.3.8) значения п определяются длинами
главных осей. Это доказывает эквивалентность метода эллипсоида
показателей преломления и метода, описанного в предыдущем раз-
разделе.
4.4. ФАЗОВАЯ СКОРОСТЬ, ГРУППОВАЯ СКОРОСТЬ
И СКОРОСТЬ ПЕРЕНОСА ЭНЕРГИИ
Нормальная поверхность (поверхность постоянной ш в пространст-
пространстве к), описываемая уравнением D.2.8), содержит информацию как о
фазовой, так и о групповой скорости. Фазовая скорость плоской
волны по определению равна
со
D.4.1)
Групповая скорость волнового пакета дается выражением
vg=Vkw(k), D.4.2)
а скорость переноса энергии определяется следующим образом:
v = ? D.4.3)
е U'
где S — вектор Пойнтинга, at/ — плотность энергии. По опреде-
определению групповая скорость vg является вектором, перпендикуляр-
перпендикулярным нормальной поверхности. В разд. 1.5 мы показали, что груп-
групповая скорость представляет скорость переноса энергии при рас-
распространении лазерного импульса в диспергирующей среде. Ниже
мы увидим, что групповая скорость волнового пакета, распростра-
распространяющегося в анизотропной среде, также описывает перенос энер-
энергии, т. е. vg = ve.
Волновой пакет можно рассматривать как линейную суперпози-
суперпозицию многих монохроматических плоских волн, каждая из которых

90
Глава 4
имеет определенную частоту ш и волновой вектор к. Любая такая
составляющая в виде плоской волны удовлетворяет следующему
уравнению Максвелла в пространстве импульсов:
к X Е =
кх Н= -
D.4.4)
D.4.5)
Здесь величины е и /х рассматриваются как тензоры. Эти уравнения
можно получить из A.1.1) и A.1.2) в предположении, что J = 0, а
поля описываются функцией exp[/(w/ — к-г)].
Для доказательства равенства скоростей ve и v^ будем исходить
из уравнений D.4.4) и D.4.5). Предположим, что вектор к изменя-
изменяется на бесконечно малую величину <5к. Если 5ш, <5Е и <5Н — соот-
соответствующие изменения величин и, Е и Н, то
D.4.6)
D.4.7)
8к X Е + к X 8Е = SwjuH + ыц 8Н,
8к X Н + к X Ш = -SweE - weSE.
Умножая скалярно D.4.6) на Н, а D.4.7) на Е и используя вектор-
векторное тождество
А • (В X С) = В • (С X А) = С • (А X В),
получаем
8к • (Е X Н) + к • (8Е X Н) = 5со(Н • цН) + w(H ¦ ц8Н), D.4.8)
- 5к • (Е X Н) + к • (Ш X Е) = -8ы(Е • еЕ) - w(E • eSE). D.4.9)
Вычитание уравнения D.4.9) из D.4.8) дает
25к • (Е X Н) - Sw(E • еЕ + Н • цН) =
= Ш • (w^H - к X Е) + 8Е • (weE + к X Н). D.4.10)
Здесь мы использовали свойства симметрии тензоров е и /х:
Н • щШ = SH • цН,
Е • е8Е = 8Е • еЕ.
Правая часть уравнения D.4.10) в соответствии с D.4.4) и D.4.5) об-
обращается в нуль. Таким образом, D.4.10) принимает вид
5k«(EX H) = 5wHE-eE + Н-цН). D.4.11)
Распространение электромагнитных волн в анизотропных средах
91
ТАБЛИЦА 4.1
Оптическая
симметрия
Кристаллическая
система
Точечные груп-
группы симметрии
Диэлектрический
тензор
Изотропный
кристалл
Одноосный
кристалл
Двуосный
кристалл
Кубическая ДЗт
432
тЗ
23
тЗт
Тетрагональная 4
4
4/т
422
4тт
42т
4/ттт
Гексагональная 6
6
6/т
622
бтт
6т2
6/ттт
Тригональная 3
3
32
Зт
Зт
Триклинная 1
Т
Моноклинная 2
m
2/m
Орторомбическая 222
2mm
mmm
е = е0
п2
0
0
е = е0
и
0
0
е = е0
in1
11 X
0
0
0
п2
0
0
п\
0
0
п]
0
0
0
п2
<и
0
nlj
0
0

в
РИС. 4.3. Сечеиие нормальной поверхности плоскостью xz. a — двуосиые кристал-
кристаллы; б — положительные одноосные кристаллы; в — отрицательные одноосные кри-
кристаллы.
ТАБЛИЦА 4.2. Показатели преломления для некоторых
типичных кристаллов
Изотропный
кристалл
Одноосные
кристаллы:
положительные1
отрицательные
Двуосные
кристаллы:
CdTe
NaCl
Алмаз
Плавиковый шпат
GaAs
Лед
Кварц
ВеО
Циркон
Рутил
ZnS
(NH4)H2PO4(ADP)
Берил
KH2PO4(KDP)
NaNO3
Кальцит
Турмалин
LiNbO3
BaTiO3
Прустит
Гипс
Полевой шпат
Слюда
Топаз
NaNO2
SbSi
YAIO3
по
1,309
1,544
1,717
1,923
2,616
2,354
1,552
1,598
1,507
1,587
1,658
1,638
2,300
2,416
3,019
"х
1,520
1,522
1,552
1,619
1,344
2,7
1,923
2,69
1,544
2,417
1,392
3,40
"у
1,523
1,526
1,582
1,620
1,411
3,2
1,938
Пе
1,310
1,553
1,732
1,968
2,903
2,358
1,478
1,590
1,467
1,336
1,486
1,618
2,208
2,364
2,739
nz
1,530
1,530
1,588
1,627
1,651
3,8
1,947
Распространение электромагнитных волн в анизотропных средах
93
Согласно определению плотности энергии A.2.5) и вектора Пойн-
Пойнтинга A.2.6), уравнение D.4.11) можно переписать следующим об-
образом:
S
8ы = 8к-- = 8к-уе. D.4.12)
Из определения групповой скорости имеем
8ы = (vkw)-5k = 8к'\г.
D.4.13)
Поскольку <5к — произвольный вектор, из D.4.12) и D.4.13) следу-
следует, что
vg = ve. D.4.14)
Это равенство соответствует понятию групповой скорости, строгое
определение которой дается выражением D.4.2).
В приведенном выше доказательстве мы предполагали, что Е и
Н являются вещественными полями. Равенство D.4.14) можно так-
также доказать и для комплексного представления векторов поля (см.
задачу 4.3).
Если <5к — бесконечно малый вектор в плоскости, касательной к
нормальной поверхности, то бш обращается в нуль, поскольку нор-
нормальная поверхность есть поверхность постоянного ш. Из D.4.11)
при этом получаем
8к! • (Е X Н) = 0,
D.4.15)
где штрих означает, что <5к' лежит в плоскости, касательной к нор-
нормальной поверхности. Из этого уравнения следует, что как Е, так и
Н лежат в плоскости, касательной к нормальной поверхности, а
вектор Пойнтинга Е х Н всегда перпендикулярен этой поверхности.
4.5. КЛАССИФИКАЦИЯ АНИЗОТРОПНЫХ
СРЕД (КРИСТАЛЛОВ)
Выше было показано, что нормальная поверхность содержит важ-
важную информацию о распространении волн в анизотропных средах.
Эта поверхность однозначно определяется главными показателями
преломления пх, пу, nz. В общем случае, когда все три главных по-
показателя преломления пх, пу, пг различны, существует две оптиче-
оптические оси. Такой кристалл называют двуосным. Во многих оптиче-
оптических материалах два главных показателя преломления совпадают.

94
Глава 4
В этом случае уравнение нормальной поверхности D.2.8) фактори-
зуется:
к2
D.5.1)
здесь n20 = ?/?0 = ?/?0; л;г = ?г/?0.
Нормальная поверхность в этом случае состоит из двух оболо-
оболочек: сферы и эллипсоида вращения, которые касаются друг друга в
двух точках на оси z. Поэтому ось z представляет собой единствен-
единственную оптическую ось и такой кристалл называется одноосным. В
случае же, когда все три главных показателя преломления совпада-
совпадают, обе оболочки нормальной поверхности вырождаются в одну
сферу и кристалл является оптически изотропным.
Очевидно, что оптическая симметрия тесно связана с точечной
группой симметрии кристаллов. Например, в кубическом кристалле
три главные оси физически эквивалентны. Следовательно, можно
ожидать, что кубический кристалл является оптически изотроп-
изотропным. В табл. 4.1 перечислены оптические симметрии кристаллов
и отвечающие им тензоры диэлектрической проницаемости.
В двуосных кристаллах главные оси координат обозначают та-
таким образом, чтобы три главных показателя преломления образо-
образовывали следующую последовательность:
<ny<nz.
D.5.2)
При таком соглашении оптическая ось располагается в плоскости
xz. На рис. 4.3, а изображены сечения нормальных поверхностей
плоскостью xz. В одноосном кристалле показатель преломления,
соответствующий двум равным элементам (п2 = ех/б0 — е /е0), на-
называется обыкновенным показателем преломления п0. Другой по-
показатель преломления, соответствующий ez, называется необыкно-
необыкновенным показателем преломления пе. Если п0 < пе, то говорят, что
кристалл является положительным, а если п0 > пе, — отрицатель-
отрицательным. На рис. 4.3, бив показаны сечения нормальных поверхностей
плоскостью xz в этих случаях. Оптическая ось совпадает с главной
осью, которой отвечает один показатель преломления. Некоторые
примеры кристаллов и их показатели преломления приведены в
табл. 4.2.
Распространение электромагнитных волн в анизотропных средах
95
4.6. РАСПРОСТРАНЕНИЕ СВЕТА
В ОДНООСНЫХ КРИСТАЛЛАХ
Одноосные кристаллы используются во многих современных опти-
оптических устройствах. В качестве наиболее типичных примеров мож-
можно привести кварц, кальцит и ниобат лития. Для этих кристаллов
уравнение D.3.1) эллипсоида показателей преломления принимает
простой вид:
х2 У2 z2
* +2L + ?^i, D.6.l)
где в качестве оси симметрии, следуя нашему соглашению, выбрана
ось z.
На рис. 4.4 показан эллипсоид показателей преломления для по-
положительного одноосного кристалла. Направление распростране-
распространения совпадает с вектором s. Поскольку в этом случае эллипсоид ин-
инвариантен относительно вращения вокруг оси z, проекцию вектора
s на плоскость ху без потери общности можно выбрать совпадаю-
совпадающей с осью у.
, i (оптическая ось)
РИС. 4.4. Графический способ определения показателей преломления и поляризации
нормальных мод для данного направления распространения s. Рисунок соответству-
соответствует случаю одноосного кристалла с п = п = п , п = п .

96
Глава 4
Согласно процедуре, изложенной в разд. 4.3, найдем сначала се-
сечение эллипсоида показателей преломления плоскостью, проходя-
проходящей через начало координат и перпендикулярной вектору s. Это се-
сечение представляет собой эллипс, изображенный на рисунке. Длина
главной полуоси ОА равна показателю преломления пе(в) для не-
необыкновенного луча, вектор электрического смещения которого
De@) параллелен ОА. Обыкновенный луч поляризован вдоль ОВ,
т. е. его вектор D направлен вдоль ОВ, и показатель преломления
для него равен по.
Если обозначить через к волновой вектор, а через с единичный
вектор в направлении оси с (оси z), то поляризации для указанных
выше векторов электрического смещения можно записать соот-
соответственно в виде
к х с
D.6.2)
d =
|к X с]'
d =
е
D.6.3)
Из рис. 4.4 ясно, что при изменении угла в между оптической
осью и направлением распространения s направление поляризации
обыкновенного луча сохраняется неизменным (вдоль оси х на ри-
рисунке), а его показатель преломления всегда равен по. Напротив,
направление вектора De, как видно из рисунка, зависит от в. Значе-
Значение показателя преломления изменяется от пе(в) = по при в = 0°
до пе(в) = пе при в — 90°. Показатель преломления пе(в) необыкно-
необыкновенной волны равен длине отрезка ОА, и в соответствии с рис. 4.4
имеем
1
cos20 sin20
D.6.4)
В случае распространения света в одноосных кристаллах показате-
показатели преломления можно также определить непосредственно из урав-
уравнения D.5.1). Подставим в это уравнение А\, = n(u/c)cosd, kx = 0,
к}у = [(о)/с)п]2 — к\. Тогда, приравнивая первый множитель нулю,
получаем уравнение D.6.4), а приравнивая нулю второй множитель,
имеем обыкновенный показатель преломления по. Направление по-
поляризации для необыкновенной волны электрического поля опреде-
определяется из D;2.9):
Распространение электромагнитных волн в анизотропных средах
97
о
sin в
COS0
- п\
где пе(в) — показатель преломления необыкновенной волны, опре-
определяемый уравнением D.6.4). Следует заметить, что вектор элект-
электрического поля в общем случае не перпендикулярен направлению
распространения. На рис. 4.5 показано сечение нормальных поверх-
поверхностей плоскостью yz для положительного одноосного кристалла
(пе > по).
Таким образом, свет, распространяющийся в одноосном кри-
кристалле, в общем случае состоит из обыкновенной и необыкновен-
необыкновенной волн. Вектор электрического поля Е (и вектор электрического
смещения D) для обыкновенной волны всегда перпендикулярен как
оси с, так и направлению распространения. Фазовая скорость обык-
обыкновенной волны в любом случае равна с/по, независимо от направ-
направления распространения. Вектор смещения D необыкновенной волны
так же, как и вектор электрического поля обыкновенной волны,
перпендикулярен волновому вектору. Однако вектор электрического
поля необыкновенной волны в общем случае не перпендикулярен
волновому вектору. Он лежит в плоскости, образованной волно-
волновым вектором и вектором электрического смещения. Векторы
электрического поля для этих двух волн взаимно ортогональны.
РИС. 4.5. Сечеиие нормальных поверх-
поверхностей плоскостью sz в случае поло-
положительного одноосного кристалла
7-631

Глава 4
4.7. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
НА ГРАНИЦЕ РАЗДЕЛА
Рассмотрим плоскую волну, падающую на поверхность анизотроп-
анизотропного кристалла. В общем случае преломленная волна представляет
собой смесь двух независимых волн. В одноосном кристалле пре-
преломленная волна, вообще говоря, является смесью обыкновенной и
необыкновенной волн. При отражении и преломлении на плоской
границе раздела граничные условия требуют, чтобы все волновые
векторы лежали в плоскости падения и чтобы их тангенциальные
составляющие вдоль границы раздела была равны друг другу. Это
кинематическое условие остается справедливым и при преломлении
на границе анизотропного кристалла.
Пусть к — волновой вектор падающей волны, а к, и к2 — вол-
волновые векторы преломленных волн. Для данной проекции волно-
волнового вектора к0 на границу раздела две оболочки нормальной по-
поверхности в общем случае дают два волновых вектора, отвечающие
двум преломленным волнам, как показано на рис. 4.6. Кинематиче-
Кинематическое условие требует, чтобы для преломленных волн выполнялось
Пересечение поверхности
нормалей с плоскостью
падения
РИС. 4.6. Двулучепреломление на границе анизотропной среды и графический метод
определения углов в{ и в2-
Распространение электромагнитных волн в анизотропных средах
99
соотношение
k0sin60 = ?,sin0, = k2sin62. D-7Л)
Соотношение D.7.1) похоже на закон Снелля. Однако важно по-
помнить, что кх и к2 в общем случае не являются постоянными, эти
величины изменяются при изменении направлений векторов А:, и к2.
Положительный
одноосный кристалл
пе>п0
Отрицательный
одноосный кристалл
в
РИС. 4.7. Волновые векторы при двулучепреломлении в одноосных кристаллах, а —
оптическая ось параллельна границе раздела и плоскости падения; б — оптическая
ось перпендикулярна границе раздела, но параллельна плоскости падения; в — опти-
оптическая ось параллельна границе раздела, но перпендикулярна плоскости падения. Че-
Через 0 и Е обозначены соответственно обыкновенный и необыкновенный лучи.

100
Глава 4
Алгебраическая задача определения 0, и в2 состоит в решении ква-
квадратичного уравнения. Более простым оказывается графический
метод, соответствующий рис. 4.6.
В случае одноосных кристаллов одна из оболочек нормальной
поверхности представляет собой сферу. Следовательно, соответст-
соответствующее волновое число к оказывается постоянным для всех на-
направлений распространения. Эта волна является обыкновенной и
подчиняется закону Снелля
«,sin0o =
o
D.7.2)
где rij — показатель преломления внешней среды, а п0 — обыкно-
обыкновенный показатель преломления кристалла. Другой оболочкой нор-
нормальной поверхности является эллипсоид вращения. Следователь-
Следовательно, соответствующее волновое число к зависит от направления рас-
распространения. Эта волна является необыкновенной. На рис. 4.7 по-
показаны примеры некоторых случаев двойного лучепреломления.
4.8. РАСПРОСТРАНЕНИЕ СВЕТА
В ДВУОСНЫХ КРИСТАЛЛАХ
Исследуем теперь распространение электромагнитного излучения в
двуосных кристаллах. Нормальная поверхность [т. е. ш(к) = const]
для типичного двуосного кристалла изображена на рис. 4.1. Для
того чтобы лучше представить себе эту поверхность, рассмотрим
сначала ее сечения тремя координатными, плоскостями (рис. 4.8, а).
Подставляя в D.2.8) ку — О, получаем следующую систему двух
уравнений:
л? л? \с)'
D.8.1)
где пх, пу и nz — главные показатели преломления. Сечение нор-
нормальной поверхности плоскостью ку = 0 дает окружность радиу-
радиусом пуш/с и эллипс с полуосями пхш/с и nzw/c. Сечения двумя дру-
другими координатными плоскостями также дают окружность и эл-
эллипс. Вследствие нашего выбора осей координат (т. е. пх < п <
< nz) окружность и эллипс пересекаются только в плоскости
ку = 0. Эти четыре точки пересечения определяют две оптические
оси кристалла.
Распространение электромагнитных волн в анизотропных средах
101
РИС. 4.8. а — участки нормальной поверхности двуосного кристалла; б — кониче-
коническая рефракция. Пластинка двуосного кристалла вырезана таким образом, чтобы ее
поверхности были перпендикулярны одной из оптических осей.
Рассмотрим теперь распространение волны в координатной пло-
плоскости ку = 0. Обозначим направление распространения прямой ли-
линией OS. В общем случае существуют две точки пересечения. Рас-
Расстояния от начала координат О до этих точек пересечения равны
длинам волновых векторов. Волны, соответствующие окружности,
поляризованы перпендикулярно координатной плоскости к = 0, в
то время как волны, связанные с эллипсом, поляризованы в пло-
плоскости этого эллипса. Распространение волны в каждой из двух
других координатных плоскостей является аналогичным, за исклю-
исключением распространения вдоль оптических осей. Свет, распростра-

102
Глава 4
няющийся в направлении этих оптических осей, имеет однозначно
определенную фазовую скорость независимо от состояния поляри-
поляризации. Однако групповая скорость vg, определяемая выражением
D.4.2) как скорость потока электромагнитной энергии, в этом на-
направлении не имеет определенного значения, поскольку обе оболоч-
оболочки нормальной поверхности вырождаются в точку. Явления пре-
преломления при распространении в этом направлении тесно связаны с
природой сингулярности в этих точках.
Если мы нарисуем единичный вектор, перпендикулярный нор-
нормальной поверхности в бесконечно малой окрестности сингулярной
точки, то получим бесконечное число единичных векторов, соот-
соответствующих направлению потока энергии. Такие векторы образу-
образуют коническую поверхность. Поэтому следует ожидать, что поток
электромагнитной энергии будет иметь форму конуса. Данное явле-
.ние известно как коническая рефракция.
Для того чтобы изучить свойства конической рефракции, необ-
необходимо исследовать нормальную поверхность вблизи точки сингу-
сингулярности к0 (рис. 4.8, а). Волновой вектор света, распространяюще-
распространяющегося в направлении оптической оси, изображенной на рис. 4.8, а,
можно записать в виде
D.8.2)
где
куо = 0,
D.8.3)
а в — угол между оптической осью и осью z, определяемый выра-
выражением
пгу-п\
D.8.4)
Для исследования нормальной поверхности вблизи точки к0 требу-
требуется выполнить разложение в ряд Тейлора в окрестности этой точ-
Распространение электромагнитных волн в анизотропных средах
103
ки. Запишем следующие выражения:
D.8.5)
и подставим их в D.2.8). Тогда, отбросив члены высшего порядка
по ?, у] и f, получим
4(/сх0? + kzJ){n\kxOl + п]кг0$) + г)г{пгу - п2х)(п2у - п]) = 0. D.8.6)
Это уравнение второго порядка описывает конус, вершина которо-
которого лежит в точке к0 (т. е. ? = jj = f = 0). Вращение системы коор-
координат позволяет привести его к диагональному виду (см.
рис. 4.8, а):
1
D.8.7)
где х дается выражением
nlnl
D.8.8)
В соответствии с D.8.7) нормальная поверхность вблизи оптичес-
оптической оси представляет собой конус с вершиной в точке к0. Следова-
Следовательно, если волновой вектор совпадает с оптической осью, то су-
существует бесконечное число направлений потоков энергии (т. е. бе-
бесконечное число v ), которые лежат на конусе, описываемом урав-
уравнением
Г2 + A - tg2xh2 = r2tg2x- D-8.9)
Это уравнение описывает поверхность эллиптического конуса, ось
которого совпадает с осью ?', а вершина находится в точке к0.
Этот конус содержит оптическую ось ОА и при пересечении с лю-
любой плоскостью, перпендикулярной ОА, дает окружность (см. зада-
задачу 4.5). Угол расходимости этого конуса в плоскости xz равен 2х
(см. рис. 4.8, а). Любой единичный вектор, исходящий из вершины
конуса и лежащий на его поверхности, дает направление потока
энергии для волны, распространяющейся с волновым вектором к0.
Каждое такое направление отвечает состоянию с линейной поляри-
поляризацией. Например, направление КА соответствует потоку энергии
З'-поляризованной волны, а направление KB — потоку энергии
волн, поляризованных в плоскости xz (см. рис. 4.8, а).

104
Глава 4
Рассмотрим теперь пластинку из двуосного кристалла (напри-
(например, из слюды), обрезанную таким образом, чтобы две параллель-
параллельные ее поверхности были перпендикулярны одной из оптических
осей. Если эта пластинка освещается неполяризованным коллими-
рованным пучком монохроматического света, например лазерным
излучением, падающим перпендикулярно на одну из ее граней, то
энергия будет расходиться в пластинке, принимая форму полого
конуса, а после достижения ее другой поверхности примет форму
полого цилиндра, как показано на рис. 4.8. Таким образом, на
экране, параллельном грани кристалла, должно наблюдаться яркое
круглое кольцо.
4.9. ОПТИЧЕСКАЯ АКТИВНОСТЬ
Некоторые оптические среды вызывают вращение плоскости поля-
поляризации проходящего через них линейно поляризованного света.
Это явление называется оптической активностью и впервые было
обнаружено в кварце. Вращение плоскости поляризации оптически
активной средой иллюстрирует рис. 4.9. Величина поворота пропор-
пропорциональна длине пути света в среде. Принято вращательную спо-
способность среды условно выражать в градусах на сантиметр, т. е.
определять как величину угла поворота на единицу длины.
Знак вращения однозначно определяется направлением распро-
распространения световой волны. Так, если свет дважды проходит один и
тот же участок среды, но в противоположных направлениях, как
это имеет место в случае отражения от правой грани кристалла,
изображенного на рис. 4.9, то полное вращение оказывается рав-
равным нулю. Вещество называется правовращающим, если для наб-
Световой пучок
"А N
РИС. 4.9. Вращение плоскости поляризации в оптически активной среде.
Распространение электромагнитных волн в анизотропных средах
105
ТАБЛИЦА 4.3. Оптические вращательные способности
X, А р, град/мм
Кварц
AgGaSj
Se
Те
ТеО,
4000
4500
5000
5500
6000
6500
4850
4900
4950
5000
5050
7500
1000
6 мкм
10 мкм
3698
4382
5300
6328
10000
49
37
31
26
22
17
950
700
600
500
430
180
30
40
15
587
271
143
87
30
людателя, повернутого лицом к падаюшему световому пучку, пло-
плоскость поляризации вращается против часовой стрелки. Если вра-
вращение происходит по часовой стрелке, то вещество называется ле-
вовращающим. Кварц бывает как в правовращающем, так и в ле-
вовращающем кристаллическом состоянии. В настоящее время из-
известны многие другие вещества, обладающие оптической активнос-
активностью; к ним относятся киноварь, хлорид натрия, скипидар, сахар,
сульфат стрихнина, теллур, селен и тиогаллат серебра (AgGaS2).
Вращательные способности некоторых оптически активных сред
приведены в табл. 4.3.
В 1825 г. Френель впервые понял, что оптическая активность
возникает вследствие кругового двулучепреломления, при котором
распространяющиеся независимые волны (т. е. независимые реше-
решения уравнений Максвелла в виде плоских волн) представляют собой
волны с правой и левой круговой поляризациями.

106
Глава 4
Пусть пг и nt — показатели преломления, отвечающие этим
двум волнам. Предположим, что эти волны распространяются в
-(-^-направлении. Тогда амплитуды вектора электрического смеще-
смещения для этих двух волн можно записать в виде
Л А
где R и L — единичные векторы Джонса для круговых поляриза-
поляризаций C.4.9) и C.4.10) соответственно.
Пучок линейно поляризованного света с амплитудой Do, поляри-
поляризованный вдоль направления х и падающий на среду в плоскости
z = 0, можно представить в виде суммы двух^ таких волн с ампли-
амплитудами Do/\ 2. Тогда результирующее поле на расстоянии z в ореде
запишется в виде
v2
D.9.1)
Используя C.4.9) и C.4.10), это выражение можно переписать сле-
следующим образом:
где
-z\.
D.9.2)
D.9.3)
Выражение D.9.3) определяет поляризацию результирующей вол-
волны. Эта волна линейно поляризована, причем плоскость ее поля-
поляризации повернута против часовой стрелки относительно оси х на
угол b>z(n, - пг)/2с. Таким образом, вращательная способность в
данном случае дается выражением
Р = \(п1~ пг). D.9.4)
Если пг < и/( то оптическое вращение является правым (против ча-
часовой стрелки). Таким образом, плоскость поляризации вращается
в ту же сторону, что и волна с круговой поляризацией, распростра-
распространяющаяся с большей фазовой скоростью.
Вращательная способность кварца на длине волны А = 6328 А
составляет 188 град/см, что дает
\пг - п,\ = 6,6-Ю-5.
Распространение электромагнитных волн в анизотропных средах
107
Очевидно, что вращение плоскости поляризации дает чрезвычайно
чувствительный способ измерения очень небольших величин круго-
кругового двулучепреломления.
Диэлектрические свойства обыкновенных кристаллов, описывае-
описываемые материальным уравнением D.1.6), не допускают существова-
существования оптической активности. Дальнейшее развитие теории оптичес-
оптической активности требует обобщения материальных уравнений на
различные вещества. Электромагнитная теория оптической актив-
активности разработана главным образом Борном и его сотрудниками и
в окончательном виде была представлена Кондоном [3].
Согласно этой теории, оптическая активность определяется
свойствами молекулы, описываемыми параметром
р = аЕ- 0, D.9.5)
где р — индуцированный дипольный момент молекулы. Очевидно,
что для линейной молекулы C = 0. Отличные от нуля значения C
обусловлены спиральной структурой молекул. Когда такая спи-
спиральная молекула оказывается в переменном магнитном поле, из-
изменяющийся магнитный поток через молекулу приводит к возник-
возникновению индуцированного тока, текущего вокруг Н в направлении,
определяемом законом Ленца A.1.1). Этот индуцированный ток
будет приводить к образованию изменяющегося во времени разде-
разделения зарядов в направлении вектора Н и, следовательно, к возник-
возникновению электрического дипольного момента, который определяет-
определяется членом /3 в выражении D.5.9). Для плоской волны, распростра-
распространяющейся в однородной среде, материальное уравнение в случае
оптически активной среды можно записать в виде
D = еЕ + /e0G X Е,
D.9.6)
где е — тензор диэлектрической проницаемости в отсутствие опти-
оптической активности, a G — вектор, параллельный направлению рас-
распространения и называемый вектором гирации. Векторное произве-
произведение GxE всегда можно представить в виде произведения анти-
антисимметричного тензора [G] и Е. Матричные элементы тензора [G]
даются выражениями
[G]23 = - [G]32 = -Gx, [G]3l = - [G]n = -Gy,
D-9.8)
При этом выражение D.9.6) принимает вид
D = (е + ieo[G])E.

108
Глава 4
Часто оказывается удобным ввести новый диэлектрический тензор
e' = e + ieo[G]. D.9.9)
Этот тензор является эрмитовым, т. е. г'ц - е-*. Теперь мы можем
подставить е' в уравнение D.2.5) и, решая его, найти распространя-
распространяющиеся независимые волны. Пусть снова s — единичный вектор в
направлении распространения. Тогда вектор гирации можно пред-
представить в виде
G=Gs.
D.9.10)
Результирующее уравнение Френеля для показателей преломления
запишется в виде
.2 Г2 „2
+
+
п1 -я2. п1 - п2у п1 - п] п1
D.9.11)
= G2-
„V " »l){»2 ~ «,2)(«2 " п])
где пх, пу и пг — главные показатели преломления, a sx, s , s — со-
составляющие вектора s вдоль главных диэлектрических осей. Пусть
п\ и п\—¦ корни уравнения Френеля при G = 0. Тогда уравнение
D.9.11) можно записать через п\ и п\ следующим образом:
( ~ п\)( ~ п\) = G1. D.9.12)
Известно, что при распространении вдоль оптических осей выпол-
выполняется равенство и, = п2 = п. При этом уравнение D.9.12) прини-
принимает вид
п2 = п1 ± G,
а поскольку величина G мала, имеем
п = п ± ^-г.
2я
D,9.13)
Это выражение отвечает двум волнам с круговой поляризацией. Из
D.9.4) получаем следующее выражение для вращательной способ-
способности:
\п '
D.9.14)
Параметр G в D.9.12) зависит от направления волнового вектора и
Распространение электромагнитных волн в анизотропных средах
109
является квадратичной функцией направляющих косинусов sx, sy и
sz. Таким образом, мы имеем
q — о j2 + в 52 + в 52 + 2е 5 5+ 2? 55+ 2g s s D9 15)
или
= x,y,z,
D.9.16)
где gr — матричные элементы тензора гирации, описывающего оп-
оптическую активность кристалла.
Для исследования состояний поляризации независимых волн
(мод) удобно использовать вектор смещения D, поскольку D всегда
перпендикулярен направлению распространения (Ds = 0). Более
удобно также пользоваться обратным тензором е. При этом ма-
материальное уравнение можно записать в виде
D.9.17)
где е' дается выражением D.9.9). Обратный тензор 1/е' является
также эрмитовым. Распространяющиеся независимые волны мож-
можно получить из волнового уравнения D.2.5):
D.9.18)
Поскольку величина [G] мала по сравнению с е/е0, обратный тен-
тензор можно записать в виде
е' е ее
D.9.19)
Таким образом, уравнение D.9.18) можно записать через тензор не-
непроницаемости jj(= eo/e) следующим образом:
1
D.9.20)
где [s] — антисимметричное тензорное представление для s x,
определенное таким же образом, как и для [G] [см. D.9.7)]. Пусть
D, и D2 — нормированные распространяющиеся независимые вол-
волны в отсутствие оптической активности (G = 0):
1
'1,2
D.9.21)

по
Глава 4
Будем решать эту задачу на собственные значения в системе коор-
координат, образованной тройкой векторов (D,, D2, s). В данной систе-
системе координат уравнение D.9.20) принимает вид
1
iG
п\п\
п\п\
D.9.22)
Показатели преломления л для независимых волн удовлетворяют
следующему характеристическому уравнению:
М- ("-2з)
1
1
1
1
Корни уравнения D.9.23) записываются в виде
1 1
D.9.24)
Соответствующие состояния поляризации можно представить век-
векторами Джонса
1
/G
ЛГЛп
D.9.25)
Эти векторы Джонса отвечают двум эллиптически поляризован-
поляризованным волнам, которые ортогональны друг другу. Поскольку первая
компонента вектора является вещественной, а вторая — чисто мНи-
мой, главные оси эллипсов поляризации параллельны «невозмущен-
«невозмущенным» поляризациям D, и D2 (рис. 4.10). Направления их вращений
противоположны друг другу. Эллиптичность поляризационного эл-
эллипса (определяемая как отношение длин главных осей) дается вы-
выражением
-G
е = . D.9.26)
Распространение электромагнитных волн в анизотропных средах
111
А
РИС. 4.10. Эллипсы поляризации нормальных мод при наличии как двулучепрелом-
ления, так и оптической активности.
В случае изотропной среды (л, = я2 — п) показатели преломления,
отвечающие нормальным волнам D.9.24), даются выражением
_ = -^±3 = ^г11+-1. D-9.27)
п2 л2 л
что согласуется с D.9.13). Выражение D.9.25) для соответствующих
состояний поляризации принимает вид
D.9.28)
и описывает свет с правой и левой круговой поляризацией.
В случае анизотропных сред величина G обычно очень мала по
сравнению с п\ — и2 и эллиптичность эллипса поляризации оказы-
оказывается весьма небольшой (е <« 1), так что волны оказываются по-
почти линейно поляризованными (см. рис. 4.10). Например^ при рас-
распространении светового пучка с длиной волны X = 5100 А перпен-
перпендикулярно оптической оси кварца величина G по данным Шивесси и
Мунстера [4] составляет 6-10, а эллиптичность равна 2- 10~3.
Тензор гирации является симметричным и в общем случае имеет
шесть независимых компонент. Благодаря симметрии кристалла

112
Глава 4
ТАБЛИЦА 4.4. Структуры тензора гирации
Центросимметричная система
6/mmm, m3, тЗт):
Триклинная система:
Моноклинная система:
Орторомбическая
система:
Тетрагональная
система: 4,422
«.. о
0 «и
0 0
Тригональная и
2
«и
0
«13
m
0
«12
0
«11
0
0
0
0
«33
гексагональная системы
Кубическая система
:
/
\
A,2/т, ттт,
/0
0
U
«11
«12
«13
BИ*2)
0
«22
0
[т 1;
«12
0
«23
222
0
«22
0
«13
0
«33
с2)
0
«23
0
0
0
«33
«и
«12
0
3
«11
0
0
«11
0
0
0 (
0 (
0 (
J
«12
«22
«23
1
4
«12
-«1
0
)\
)
)/
«13 \
«23
«33 /
2
«11
«12
0
т
0
0
«13
0
«12
0
0
. о
0
, 32,622
0
«и
0
432,23
0
«и
0
0
0
«33
0
0
«11
4/т, 4/ттт, 3, Зт, 6/т,
BНх3)
«12 0
«22 0
0 «зз
(mlx3)
0 «13
0 «23
«23 0
2тт
«12 0
0 0
0 0,
42т B II х,)
0
«12 0
«12 0 0
0
0 0
Распространение электромагнитных волн в анизотропных средах
ИЗ
ТАБЛИЦА 4.4. (Продолжение)
Изотропная система (без центра
симметрии):
Другие системы Dmm, 43m, 3m,
6mm, 6, 6m2): /0 0 01
0 0 0
\0 0 0)
g
0
0
0
«
0
0
0
«,
некоторые его компоненты могут обращаться в нуль. Например,
кристалл, имеющий центр симметрии, не может быть оптически
активным (см. табл. 4.4). В табл. 4.4 приведены матрицы из необ-
необращающихся в нуль компонент тензора гирации для различных
классов симметрии кристаллов.
4.10. ФАРАДЕЕВСКОЕ ВРАЩЕНИЕ
Эффект Фарадея состоит в том, что прозрачные вещества, поме-
помещенные в магнитное поле, вызывают вращение плоскости поляри-
поляризации по мере проникновения в них света, распространяющегося
вдоль силовых линий магнитного поля. Точнее говоря, величина
вращения пропорциональна составляющей магнитного поля вдоль
направления распространения света. При этом вектор гирации,
определяемый выражением D.9.6), пропорционален внешнему маг-
магнитному полю:
где у — коэффициент магнитогирации среды. В оптически активной
среде направление вращения однозначно зависит от направления
распространения. Поэтому после отражения пучка света и распро-
распространения его в обратном направлении полный поворот плоскости
поляризации равен нулю. Однако в эффекте Фарадея направление
вращения однозначно определяется магнитным полем В, так что
отражение излучения назад приводит к удвоению вращения. Сте-
Степень вращения (т. е. вращение на единицу длины) часто определяет-
определяется следующим образом:
Р = VB;
D.10.2)
здесь V — постоянная Верде.
Эффект Фарадея обусловлен действием постоянного магнитного
поля на движение электронов. Электрическое поле оптического пуч-
8-631

114
Глава 4
ка приводит к смещению электронов относительно их положении
равновесия. Воздействие на это движение статического магнитного
поля описывается силой Лоренца vxB, которая вызывает движе-
движение электронов в поперечном направлении. В конечном итоге воз-
возникает индуцированный дипольный момент, пропорциональный
ВхЕ. При этом материальное уравнение принимает вид
D = еЕ + ieoyB X Е.
D.10.3)
Множитель / здесь учитывает задержку по фазе на 7г/2 между ско-
скоростью и магнитным полем. Фарадеевское вращение плоскости по-
поляризации наблюдается во многих твердых телах, жидкостях и да-
даже газах. В табл. 4.5 представлены значения постоянных Верде для
некоторых материалов.
4.11. АНАЛИЗ РАСПРОСТРАНЕНИЯ ВОЛН
В АНИЗОТРОПНЫХ СРЕДАХ МЕТОДОМ
СВЯЗАННЫХ МОД
В разд. 4.2 и 4.3 мы обсудили распространение электромагнитного
излучения в анизотропных средах, используя метод независимых
волн (нормальных мод). Эти нормальные моды характеризуются
четко определенными состояниями поляризации и фазовыми скоро-
скоростями; они получаются диагонализациеи тензора поперечной непро-
непроницаемости уI в D.3.8). Любая волна, распространяющаяся в ани-
анизотропной среде, может быть представлена в виде линейной супер-
суперпозиции этих нормальных мод с постоянными амплитудами. Пусть
ТАБЛИЦА 4.5. Значения постоянной Верде
при X = 5893 А
Вещество
Вода
Плавиковый шпат
Алмаз
Стекло (кронглас)
Стекло (флинт)
Дисульфид углерода
(CS2)
Фосфор
Хлорид натрия
Т, °С
20
18
20
33
V, (град/Гс-мм)
2,18-10-5
l,5-10
2,0-10-5
2,68-10-5
5,28-10-5
7,05-Ю-5
2,2-Ю-4
6,0-10-5
Распространение электромагнитных волн в анизотропных средах
115
е, и е2 — векторы, задающие направление поляризации вектора по-
поля Е нормальных мод, г. кх и к2 — соответствующие волновые чис-
числа. Произвольную волну, распространяющуюся в среде, можно за-
записать в виде
Е =
D.11.1)
где А, и Аг — постоянные, a f — расстояние вдоль направления
распространения s (т. е. f = s-r).
Следует заметить, что эти единичные векторы е, и е2 отличают-
отличаются от подобных векторов для электрического смещения и в общем
случае не ортогональны направлению распространения, т. е.
s-e, гФ 0. Однако для большинства кристаллов с незначительным
или малым двулучепреломлением векторы е, и е2 почти перпенди-
перпендикулярны s. Вдоль некоторого определенного направления векторы
е, и е2 перпендикулярны направлению распространения независимо
от анизотропии среды.
В случае когда существует внешнее или внутреннее возмущение,
такое, как механическое напряжение, магнитное и электрическое по-
поля или даже наличие оптической активности, е, и е2 не являются
более независимыми векторами распространяющихся мод. Тензор
диэлектрической проницаемости при наличии возмущений можно
записать в виде
е' = е + Ае,
D.11.2)
где е — невозмущенная часть, а Де — изменение тензора диэлект-
диэлектрической проницаемости, обусловленное возмущением. Если Де из-
известно, то распространяющиеся нормальные моды для вектора
электрического поля Е всегда можно определить с помощью мето-
метода, описанного в разд. 4.2.
Однако в некоторых случаях удобно и даже предпочтительнее
описывать распространение волн с помощью линейной суперпози-
суперпозиции невозмущенных нормальных мод, особенно в случае, когда воз-
возмущение мало (т. е. Де < е). При этом амплитуды мод А, и А2 те-
теперь не являются постоянными, поскольку е,е'(а' ' ' и е2е'"" 2)
при наличии возмущения Де в общем случае не являются нормаль-
нормальными модами. Тем не менее полное поле можно представить в
виде
) = Л.Ше,*'4"'-*^ + Л2(Ое2е'("'-*А D.11.3)
Поскольку е,, е2, кх и к2 известны как решения задачи в невозму-
невозмущенном случае (т. е. при Де = 0), поле Е однозначно определено,

116
Глава 4
если A ,(f) и А2(?) известны. Зависимость величин А , и ,42 от f обус-
обусловлена наличием возмущения Де диэлектрической проницаемости.
Выведем теперь дифференциальные уравнения для амплитуд мод.
Будем исходить из волнового уравнения
V X (V X Е) - ш2ц(е + Де)Е = 0.
D.11.4)
Поскольку волна распространяется вдоль направления s, дифферен-
дифференциальный оператор V можно заменить на sd/df. При этом волно-
волновое уравнение D.11.4) принимает вид
-^[Е - s(s • Е)]
0,
D.11.5)
где предполагается, что среда является однородной, а векторы по-
поля отвечают плоским волнам. В выражении D.11.5) величина в ква-
квадратных скобках представляет собой поперечную составляющую
вектора электрического поля. Пренебрежем теперь продольной со-
составляющей электрического поля и предположим, что s-E = О
(т. е. s-e, = se2 = 0) и е,-е2 = 0.
Подставляя выражение D.11.3) в уравнение D.11.5) и предпола-
гая, что е,е "и
возмущенной среды, получаем
d2A, ... dA,
являются независимыми модами не-
d2A2
2
dA2
l~df
D.11.6)
e,e
где было использовано условие А^ец — ш2^?ец = 0, а = 1,2. Пред-
Предположим теперь, что амплитуды А , 2 являются медленноменяющи-
мися функциями величины fu, т. е. что (d2Aa/d?2) « kJLAJdX, (a =
= 1, 2), и умножим скалярно уравнение D.11.6) на каждый из век-
векторов е, и е->. В результате получаем следующие уравнения:
D.11.7)
11 «Медленное» означает, что относительное изменение величины /1 в масштабе
длины волны излучения много меньше единицы.
Распространение электромагнитных волн в анизотропных средах
117
где мы использовали условие ортонормированности векторов е, и
е2. Величины Aeuli в D.11.7) являются матричными элементами тен-
тензора возмущения Де в системе координат, образованной векторами
е,, е2 и s. Уравнения связанных мод D.11.7) при заданных началь-
начальных условиях имеют единственное решение для состояния поляри-
поляризации волны.
В качестве примера, иллюстрирующего использование уравне-
уравнений D.11.7), рассмотрим распространение электромагнитного излу-
излучения в оптически активной среде с двулучепреломлением. Пусть
влияние оптической активности является малым возмущением Ае,
определяемым в соответствии с D.9.9) выражением
Де - ieo[G]. • D.11.8)
Матричные элементы этого возмущения запишутся в виде
Де12= -ieQG,
Де21 = ie0G.
D.11.9)
е21
Пусть А ,@) и А 2@) амплитуды мод при f = 0. Выражения для ам-
амплитуд мод А ,(?") и v42(f) в произвольной точке f получаются путем
решения уравнений D.11.7), в которых Асае даются выражениями
D.11.9). В результате получаем
D.11.10)
где л,, п2 — показатели преломления для мод (т. е. кх 2 = пх 2ы/с),
а
О)
Ак = к2- /с, = -(и2-и,),
2
D.11.11)
D.11.12)
Выражения D.11.10) показывают, как возмущенна Де12 приводит к
обмену энергией между модами 1 и 2. Следует заметить, что в слу-

118
Глава 4
чае, когда оптическая активность исчезает (G = 0), величина Д?12 в
соответствии с D.11.9) обращается в нуль и мы имеем А ^) =
= Д@) и А2(?) - Л2@). Следовательно, состояние поляризации вол-
волны зависит от координаты. Пусть х@) — комплексный параметр,
отвечающий начальной поляризации, а х (Г) — состояние поляриза-
поляризации в точке f. Тогда из выражений D.11.10) получаем
cos
/—sin зЦ -
D.11.13)
Из этого выражения видно, что состояние поляризации является
периодической функцией координаты f с периодом 7гА. В частном
случае, когда п2 = я, (т. е. Ак = 0), выражение D.11.13) для состо-
состояния поляризации принимает вид
D.11.14)
- x@)sin
где р — (u/c)G/2n — вращательная способность, определяемая вы-
выражением D.9.14). Если начальное состояние поляризации отвечает
линейно поляризованной волне с азимутальным углом ф0 [т. е.
х@) = tgi/-0], то в соответствии с D.11.14) состояние поляризации в
точке f равно х(Г) = tg(i/-0 + pf) и отвечает линейно поляризован-
поляризованному свету с азимутальным углом ф0 + pf. Иными словами, пло-
плоскость поляризации поворачивается на угол р$, что согласуется с
результатами, полученными в разд. 4.9.
Используя формализм связанных мод, можно также получить
распространяющиеся нормальные моды при наличии возмущения.
Для этого нам понадобится определить вектор Джонса для элект-
электрического паля, чтобы записать состояние поляризации волны сле-
следующим образом:
ад)
Из D.11.7) нетрудно видеть, что Е удовлетворяет уравнению
¦щЕ- ~iKeE.
D.11.15)
Распространение электромагнитных волн в анизотропных средах
119
Матрица Ке называется волновой матрицей и записывается в виде
е с
-Де,
и, + .
2я,
л Де21
2п2е0 21
2и,е0
Де1
1
2e0
D.11.16)
Для среды с оптической активностью Аеа13 дается выражением
D.11.9) и волновая матрица принимает вид
е с
2л,
JG_
2и,
D.11.17)
Согласно определению, распространяющаяся нормальная мода
имеет единственную постоянную распространения и единственное
состояние поляризации. Иными словами, нормальную моду можно
записать следующим образом:
Е = ее"'".
D.11.18)
Подставляя выражение D.11.18) для Е в уравнение D.11.15), это
дифференциальное уравнение можно свести к следующему компакт-
компактному алгебраическому уравнению:
Kjt = /се.
D.11.19)
Уравнение D.11.19) представляет собой характеристическое уравне-
уравнение. Отсюда следует, что поляризационные векторы нормальных
мод являются собственными векторами волновой матрицы Ке с
собственными значениями, отвечающими волновым числам распро-
распространяющихся мод. Пусть к = (ш/с)п, где п требуется определить.
Тогда из D.11.17) и D.11.19) получаем характеристическое уравне-
уравнение
п, — п —
Ю
2л,
JG
п-, — п
= 0,
или
(«1 -»)(»2~ П)= Ъ
\пхпг'
D.11.20)
D.11.21)

120
Глава 4
Корнями уравнения D.11.21) являются показатели преломления для
нормальных мод:
щ +п2
- п.
4И|И2
D.11.22)
Таким образом, волновые числа нормальных мод можно записать
в виде
к, + к-,
&ку /иу Gz
2 / \ с I 4п,п2
D.11.23)
где Ак определяется выражением D.11.11).
Соответствующие независимые векторы поляризации нормаль-
нормальных мод можно получить, если подставить D.11.23) в уравнение
D.11.19):
е —
iG
2п2
D.11.24)
Здесь п дается выражением D.11.22). При п2 « я, выражение
D.11.24) согласуется с D.9.25). Важно иметь в виду, что в анизот-
анизотропной среде состояния поляризации для вектора электрического
поля Е и вектора электрического смещения D, вообще говоря, раз-
различны. Выражения D.11.23) и D.11.24) для вектора электрического
поля получены в предположении, что продольная составляющая у
него отсутствует, а выражения D.9.24) и D.9.25) получены для век-
вектора смещения D. В следующем разделе мы выведем уравнение
движения, описывающее эволюцию вектора D.
4.12. УРАВНЕНИЕ ДВИЖЕНИЯ
ДЛЯ СОСТОЯНИЯ ПОЛЯРИЗАЦИИ
В предыдущем разделе мы получили матричное уравнение D.11.15),
описывающее эволюцию вектора электрического поля Е при усло-
условии, что его продольная составляющая пренебрежимо мала. Теперь
мы выведем уравнение движения для вектора электрического сме-
смещения D, который всегда перпендикулярен направлению распро-
распространения. Будем исходить из волнового уравнения A.4.2) и вос-
воспользуемся соотношением D.3.3), чтобы выразить Е через D. Тог-
Тогда можно записать следующее волновое уравнение:
D.12.1)
Распространение электромагнитных волн в анизотропных средах
121
Поскольку нас интересует состояние поляризации волны, распро-
распространяющейся вдоль направления s, дифференциальный оператор V
можно заменить на sd/df. При этом волновое уравнение D.12.1)
принимает вид
•х(.х
D.12.2)
Мы будем использовать здесь систему координат, введенную в
разд. 4.3, в которой вектор s определяет направление третьей оси.
В этой системе координат волновое уравнение записывается следу-
следующим образом:
D.12.3)
где t)t — поперечный тензор непроницаемости 2x2, определяемый
выражением D.3.7). Введем 2х 2-матрицу N следующим образом:
N\=\. С4-12-4)
Умножая D.12.3) слева на N2 и используя D.12.4), получаем
D.12.5)
Это дифференциальное уравнение эквивалентно следующей системе
двух линейных дифференциальных уравнений:
D.12.6)
D.12.7)
Матрица N называется матрицей показателей преломления и в слу-
случае изотропной среды сводится к показателю преломления п. По-
Поскольку мы используем зависимость от времени вида е'ш, уравнение
D.12.6) соответствует волне, распространяющейся в направлении
+ f> а уравнение D.12.7) отвечает распространению волны в направ-
направлении — f. Используем теперь уравнение D.12.6) для описания эво-
эволюции состояния поляризации в среде, характеризуемой матрицей
показателей преломления N.
Рассмотрим случай, когда существует внешнее (или внутреннее)
возмущение, такое, как механическое напряжение, магнитное поле,

122
Глава 4
электрическое поле или оптическая активность. Пусть индексы 1 и
2 отвечают нормальным модам, распространяющимся в отсутст-
отсутствие этих возмущений. Тогда тензор диэлектрической непроницаемо-
непроницаемости i)t можно записать в виде
Ч, =
D.12.8)
где Лгу представляет собой возмущение. Если величина Агу мала, то
для N можно получить явное выражение непосредственно из опре-
определения этой матрицы и выражения D.12.8):
N =
и, -
и, + п2
»2„2
И, + П.
Д?J1
п2 -
D.12.9)
Поскольку T)t — эрмитов тензор, эрмитовой является и матрица по-
показателей преломления N. Если матрица N известна, то уравнение
D.12.6), если заданы начальные условия для состояния поляриза-
поляризации, имеет однозначное решение. Распространяющиеся нормальные
моды можно найти путем диагонализации матрицы показателей
преломления при наличии возмущения.
Определим распространяющиеся нормальные моды в оптически
активной среде. Пусть величина Arj описывает влияние оптической
активности. В соответствии с D.9.20) эту величину можно записать
в виде
Дт)= -/t)[G]t). D.12.10)
Матричные элементы величины Ац даются выражениями
= 0,
ДЧ12
iG
п\п\ '
D.12.11)
л
ДЧ21 = ~
п\п\
Распространение электромагнитных волн в анизотропных средах
123
Таким образом, матрицу показателей преломления N можно запи-
записать следующим образом:
iG
и, + п2
-iG
и, + п2
«2
D.12.12)
Согласно определению, распространяющиеся нормальные моды
должны иметь четко определенные состояние поляризации и волно-
волновое число. Иными словами, нормальную моду можно представить
в виде
D = de '«. D.12.13)
Подставляя выражение D.12.13) для D в уравнение движения
D.12.14)
получаем
D.12.15)
здесь мы учли, что к = (со/с)и.
Таким образом, мы показали, что состояние поляризации d нор-
нормальной моды должно быть собственным вектором матрицы пока-
показателей преломления N. Собственное значение этой матрицы дает
показатель преломления, отвечающий распространению нормаль-
нормальных мод. Из D.12.15) и D.12.12) мы имеем следующее характери-
характеристическое уравнение для п:
(и- и,)(и - п2) =
(и, + n2f
Корни уравнения D.12.16) записываются в виде
и, + и.
(и, + n2f
D.12.16)
D.12.17)
Соответствующие векторы Джонса для состояния поляризации
нормальных мод даются выражением

124
Глава 4
п2- и,
D.12.18)
Этот результат совпадает с выражением D.9.25), полученным в
разд. 4.9.
ЗАДАЧИ
4.1. Состояния поляризации.
а) Получите выражение для состояния поляризации векто-
вектора электрического поля, определяемого выражениями
D.2.9) и D.2.11).
б) Используя соотношение D = еЕ, получите выражение
для соответствующих состояний поляризации вектора
электрического смещения D.
в) Пусть и, и п2— решения уравнения Френеля D.2.10), а
Е,, Е2, Dj и D2 — соответствующие собственные векто-
векторы поля. Вычислите скалярные произведения Е,-Е2 и
D,-D2 и покажите, что D, и D2 всегда взаимно ортого-
ортогональны, а Е, и Е2 взаимно ортогональны только в одно-
одноосном кристалле или изотропной среде.
г) Покажите, что E,-D2 = 0 и E2-D, = 0.
4.2. Уравнение Френеля.
а) Выведите уравнение Френеля D.2.10) непосредственно из
уравнения D.2.8).
б) Покажите, что уравнение Френеля представляет собой
следующее квадратичное уравнение относительно п2:
An4 + Вп2 + С = 0,
и получите выражения- для А, В и С.
в) Покажите, что в случае чистых диэлектриков с вещест-
вещественными ех, еу, ez выполняется соотношение В2 —
- ААС > 0.
г) Выведите D.5.1) из уравнения D.2.8) в случае одноосных
кристаллов.
д) Покажите, что в случае изотропной среды уравнение
D.2.8) сводится к
Распространение электромагнитных волн в анизотропных средах
125
4.3. Скорость переноса энергии и групповая скорость. При вы-
выводе равенства D.4.14) мы предполагали, что Е и Н являют-
являются вещественными. На самом деле уравнения Максвелла
D.4.4) и D.4.5) записаны для комплексных полей. Поэтому
вектор Пойнтинга S и плотность энергии U должны опреде-
определяться комплексными выражениями A.3.14) и A.3.15). Пока-
Покажите, что равенство D.4.14) справедливо также для ком-
комплексных амплитуд полей Е и Н.
4.4. Групповая и фазовая скорости.
а) Найдите выражение для групповой скорости необыкно-
необыкновенной волны в одноосном кристалле в зависимости от
полярного угла в волнового вектора.
б) Выведите выражение для угла а между фазовой и груп-
групповой скоростями. Этот угол является также углом
между векторами Е и D.
в) Покажите, что при в = 0 и тг/2 мы имеем а = 0. Опре-
Определите угол в, при котором угол а является максималь-
максимальным, и получите выражение для атах. Вычислите угол
атах для кварца при п0 = 1,544 и пе = 1,553.
г) Покажите, что при п0 = пе величина атах достигается
при в ~ 45° и что атах пропорциональна величине
\п0 - пе\.
4.5. Распространение света в двуосных кристаллах. Двуосные
кристаллы характеризуются тремя главными показателями
преломления и, < п2 < пу
а) Покажите, что сечение нормальной поверхности любой
координатной плоскостью состоит из эллипса и окруж-
окружности.
б) Покажите, что эти эллипс и окружность пересекаются
лишь в плоскости xz ¦ Эти точки пересечения определяют
оптические оси кристалла.
в) Найдите точки пересечения эллипса и окружности в пло-
плоскости xz и получите выражение D.8.4) для угла 9 между
одной из оптических осей и осью z. Покажите, что этот
угол обращается в нуль при и, = п2. Вычислите этот
угол для слюды при А?, = 1,552, п2 = 1,582 и «3 = 1,588.
г) Угол конической рефракции можно оценить по углу
между нормальными векторами эллипса и окружности в

126
4.6.
4.7.
Д)
е)
Глава 4
точке их пересечения. Получите выражение D.8.8).
Покажите, что этот конический угол обращается в нуль
при и, — п2 (или и2 = пг). Вычислите величину этого
конического угла для слюды.
Покажите, что поворот на угол ±х в плоскости ?'f
преобразует уравнение конуса D.8.9) к виду
(Г ± Н" tg 2ХJ + т,2 = Q?" tg 2ХJ.
Сечение этого конуса плоскостью ?" = const представ-
представляет собой окружность.
Призменные поляроиды. Двойное лучепреломление в ани-
анизотропных кристаллах можно использовать для поляризации
света. Рассмотрим пучок света, падающий на плоскую гра-
границу кальцита с внутренней стороны (п0 — 1,658, пе —
= 1,486), и предположим, что ось кристалла перпендикуляр-
перпендикулярна плоскости падения.
а) Определите диапазон внутренних углов падения, при ко-
которых обыкновенная волна полностью отражается. При
этом прошедшая волна оказывается полностью поляри-
поляризованной.
Призма Глана. Примените общие принципы, описанные
в п. а, для создания призмы Глана из кальцита, изобра-
изображенной на рисунке.
127
б)
с-ось
Определите диапазон вершинных углов а.
Четвертьволновая пластинка. Линейно поляризованная
электромагнитная волна с длиной волны X = 6328 А падает
нормально при х = 0 на yz-грань пластинки из кварца (х-
срез) таким образом, что она распространяется вдоль оси*.
Предположим, что волна была первоначально поляризована
так, что она имеет одинаковые составляющие вдоль осей у
и z.
а) Определите состояние поляризации волны в плоскостих,
Распространение электромагнитных волн в анизотропных средах
где
{kz-ky)x=\*.
Нарисуйте расположение вектора электрического поля в
этой плоскости в моменты времени t = О, тг/бсо, тг/Зсо,
tt/2w, 2тг/Зсо, 5тг/6ш.
б) Пластинка, удовлетворяющая условиям, описанным в
п. а, называется четвертьволновой, поскольку разница в
фазовых сдвигах для двух ортогональных состояний по-
поляризации равна четверти величины 2тг. Определите тол-
толщину четвертьволновой пластинки из кварца при длине
волны X = 6328 А.
в) Полуволновая пластинка. Определите состояние поляри-
поляризации в плоскости х, где
4.8. Дихроичные поляризаторы. Такие поляризаторы изготавли-
изготавливаются из веществ, у которых поглощающие и отражающие
свойства сильно зависят от направления колебаний электри-
электрического поля. Если коэффициенты поглощения для двух неза-
независимых поляризаций сильно различаются, то тонкого слоя
вещества будет достаточно для преобразования неполяризо-
ванного света в почти линейно-поляризованный.
а) Пусть а, и а2 — коэффициенты поглощения, отвечаю-
отвечающие двум независимым поляризациям. Получите выра-
выражение для отношения амплитуд этих двух прошедших
составляющих в зависимости от толщины среды.
б) Покажите, что при наличии поглощения распространяю-
распространяющиеся нормальные моды, строго говоря, не являются
линейно-поляризованными.
4.9. Эрмитов тензор диэлектрической проницаемости. Рас-
Рассмотрим добавку малого антисимметричного члена в тензор
диэлектрической проницаемости, т. е.
где 7у — антисимметричная (т. е. 7У = ~Т>,) часть, которая
не должна иметь омический, диссипативный характер, как в

128
Глава 4
случае комплексной диэлектрической проницаемости метал-
металлов. Кроме того, она должна быть консервативной, а это
означает, что у у не должна давать вклада в плотность элект-
электрической энергии Ue - A/2)(D-E), вычисленную из уравне-
уравнений Максвелла,
а) Вычислите DE и покажите, что
D-E = <
•j • j
при условии, что у^ антисимметричный тензор, т. е.
Уи= "ТО/-
б) Покажите, что выражение (А) можно записать в виде
D, = e,jEj + i(y X Е), ,
где у — вектор с компонентами
У\ = -Y23 = Гз2> Ъ = — Тз1 = Yi3. Y3=-Yi2 = Y2i-
в) Покажите, что тензор, обратный эрмитову, является
также эрмитовым и что
7)„Н (Б)
г) Покажите, что выражение (Б) можно переписать в виде
(В)
и что компоненты вектора А в главной системе коорди-
координат имеют вид
1
А, =
А3 =
?11е22еЗЗ
1
е11?22?33
1
е11?22?33
Тз?зз-
д) Покажите, что волновое уравнение D.9.18) можно запи-
записать в виде
X Is X (- - /А X )d| = - 4rD.
(Г)
Распространение электромагнитных волн в анизотропных средах
129
е) Пусть вектор А можно представить в виде
А = (А • s)s + А± ,
где А± — составляющая вектора А, перпендикулярная
направлению распространения. С помощью волнового
уравнения (В) покажите, что оптическая активность не
зависит от А±. Иными словами, только величина A-s
влияет на оптическое вращение плоскости поляризации.
ж) В анизотропных средах вектор А имеет вид
А = as,
где a — симметричная матрица. Покажите, что пара-
параметр оптической активности дается выражением
А = аиз,зг
з) Рассуждая, как и в предыдущем пункте, и предполагая,
что s-E = 0, покажите, что на оптическую активность
будет влиять лишь составляющая тензора G вдоль на-
направления распространения. В анизотропных средах
G = gs, где g — тензор гирации. Покажите, что пара-
параметр G в D.9.10) равен G-s, и получите выражение
D.9.15).
4.10. Векторы электрического смещения независимых волн (мод).
Волновое уравнение D.2.5) можно записать следующим об-
образом:
где s — единичный вектор в направлении распространения.
Пусть D, и D2 — нормированные собственные векторы с
собственными значениями \/п2 и \/п\ соответственно. Тен-
Тензор ео/е предполагается эрмитовым.
а) Покажите, что
9-631

130
Глава 4
б) Покажите, что
DT-D,
0.
4.11. Векторы электрического смещения независимых волн (мод)
в гиротропной среде. Воспользуйтесь уравнением D.9.20).
а) Получите уравнения D.9.22) и D.9.24).
б) Покажите, что векторы Джонса D.9.25) удовлетворяют
векторному уравнению D.9.22).
в) Покажите, что векторы Джонса D.9.25) ортогональны,
т. е. j;-j_ = о.
г) Пусть е± — эллиптичности двух собственных мод. По-
Покажите, что е+е_ = — 1.
4.12. Сохранение потока энергии.
а) Покажите, что поток энергии в направлении распростра-
распространения дается выражением
где D, и D2 — амплитуды вектора электрического сме-
смещения независимых волн, аи, и п2 — соответствующие
показатели преломления,
б) Используя соотношение D.2.14), покажите, что
S-s =
где А,, А2 — поперечные составляющие векторов элект-
электрического поля.
в) Покажите, что уравнения связанных мод D.11.7) совме-
совместимы с требованием сохранения потока энергии, т. е.
г) Покажите, что выражения D.11.10) согласуются с усло-
условием сохранения потока энергии, т. е. с выражением,
данным в п. в.
Распространение электромагнитных волн в анизотропных средах
131
ЛИТЕРАТУРА
1. Born M., WolfE., Principles of Optics.— New York: Pergamon Press, 1965.
[Имеется перевод 2-го изд.: Борн М., Вольф Э. Основы оптики. — М.: Наука,
1970.]
2. FowlesG. R., Introduction to Modern Optics.— New York: Holt, Rinehart and
Winston, 1968.
3. Condon E. ?/., Theories of Optical rotatory power.— Rev. Mod. Phys., 9, 432
A937); Handbook of Physics (eds. E. U. Condon and H. Odishaw). — New York:
McGraw-Hill, 1958, pp. 6—12.
4. SzivessyG., MunslerC, Lattice optics of active crystals. — Ann. Phys. (Leipzig),
20, 703-36 A934).

Глава 5
ИСЧИСЛЕНИЕ ДЖОНСА И ЕГО ПРИМЕНЕНИЕ
ДЛЯ РАСЧЕТА ДВУЛУЧЕПРЕЛОМЛЯЮЩИХ
ОПТИЧЕСКИХ СИСТЕМ
Многие сложные двулучепреломляющие оптические системы, та-
такие, как широкоугольные электрооптические модуляторы [1], све-
светофильтры Лио [2—5] и светофильтры Шольца [6, 7], используют
прохождение света через последовательность поляризаторов и фа-
фазовых пластинок. Действие каждого такого элемента (поляризато-
(поляризатора или фазовой пластинки) на состояние поляризации распростра-
распространяющегося света нетрудно рассчитать и без применения матричной
алгебры. Однако, в случае когда оптическая система состоит из
многих таких элементов, каждый из которых ориентирован под
разным азимутальным углом, расчет всей оптической системы ока-
оказывается весьма сложным. Существенно упростить его позволяет
лишь применение определенного систематического подхода. Исчис-
Исчисление Джонса, предложенное Р. Джонсом в 1940 г. [8], представля-
представляет собой мощный матричный метод, в котором состояние поляри-
поляризации задается двухкомпонентным вектором (см. разд. 3.4), а каж-
каждый оптический элемент описывается матрицей 2x2. Общая мат-
матрица полной системы получается перемножением всех таких мат-
матриц, а состояние поляризации распространяющегося света вычисля-
вычисляется как произведение вектора, определяющего поляризацию вход-
входного пучка, на общую матрицу. Сначала в данной главе мы изло-
изложим математический формализм матричного метода Джонса, а за-
затем используем его для расчета некоторых двулучепреломляющих
фильтров.
5.1. ФОРМАЛИЗМ МАТРИЦ ДЖОНСА
В предыдущей главе было показано, что свет, распространяющийся
в двулучепреломляющих кристаллах, представляет собой линейную
суперпозицию двух независимых волн. Эти независимые волны ха-
характеризуются вполне определенными фазовыми скоростями и со-
состояниями поляризации. Двулучепреломляющие кристаллы могут
быть как одноосными, так и двуосными. Однако большинство ши-
широко используемых кристаллов, например, таких, как кальцит и
кварц, являются одноосными. В одноосных кристаллах независи*
мые волны представляют собой обыкновенную и необыкновенную
Исчисление Джонса
133
волны. Направления поляризации этих волн взаимно ортогональны
и называются «медленной» и «быстрой» осями кристалла для дан-
данного направления распространения. Фазовые пластинки вырезают-
вырезаются обычно таким образом, чтобы с-ось располагалась в плоскости
пластинки. При этом падающий нормально на пластинку свет будет
распространяться в направлении, перпендикулярном с-оси.
Фазовые пластинки (называемые также волновыми пластинка-
пластинками) и фазосдвигающие устройства выполняют роль преобразовате-
преобразователей состояния поляризации. С помощью подходящей фазовой пла-
пластинки состояние поляризации светового пучка можно преобразо-
преобразовать в любое другое состояние поляризации. В формализме матриц
Джонса предполагается, что отражение света от любой поверхно-
поверхности пластинки отсутствует и что свет полностью проходит через
пластинку. Практически же любая пластинка всегда имеет конеч-
конечный коэффициент отражения, несмотря на то что большинство фа-
фазовых пластинок имеют специальное покрытие, чтобы уменьшить
потери на отражение от поверхностей. Френелевские отражения на
поверхностях пластинки не только уменьшают интенсивность про-
прошедшего излучения, но и влияют также на его тонкую спектраль-
спектральную структуру вследствие интерференции при многократном отра-
отражении (см. разд. 5.5). Опираясь на рис. 5.1, рассмотрим падающий
пучок света, состояние поляризации которого описывается векто-
вектором Джонса
V=l!*), E.1.1)
. 5.1. Задерживающая фазовая пластинка, имеющая азимутальный угол ф.

134
Глава 5
где
Vv и V — два комплексных числа. Оси х и у являются осями
х У _
фиксированной лабораторной системы координат. Для того чтобы
определить, как распространяется свет в фазовой пластинке, пред-
представим световую волну в виде линейной комбинации «быстрой» и
«медленной» независимых волн кристалла. Это можно сделать с
помощью следующего преобразования координат:
sin^\/K\ (Vs
E.1.2)
Здесь Vs — медленная составляющая вектора поляризации V, а
Vf — быстрая составляющая. «Медленная» и «быстрая» оси явля-
являются фиксированными в кристалле. Эти две составляющие пред-
представляют собой независимые (базисные) волны фазовой пластинки
и распространяются со своими собственными фазовыми скоростя-
скоростями и поляризациями. Из-за различия в фазовых скоростях одна со-
составляющая будет задержана относительно другой. Эта задержка
изменяет состояние поляризации выходящего пучка.
Пусть ns и rij — показатели преломления медленной и быстрой
составляющих соответственно. Тогда состояние поляризации выхо-
выходящего пучка в кристалле в .^/-системе координат дается выражени-
ем
VI
Vf
ехр -
о
ехр
Vf
E.1.3)
где / — толщина пластинки, а и — частота светового пучка. Фазо-
Фазовая задержка определяется как разность аргументов экспонент, вхо-
входящих в E.1.3), и равна
r = K~«/)f • EЛ.4)
Заметим, что фазовая задержка Г является мерой относительного
изменения фазы, а не абсолютным изменением фазы. Двулучепре-
ломление типичной кристаллической задерживающей пластинки ма-
мало, т. е. \ns - nf\ < ns, rij. Следовательно, абсолютное изменение
фазы, вызванное пластинкой, может быть в сотни раз больше, чем
фазовая задержка. Пусть ф — среднее абсолютное изменение фазы:
Ф
E.1.5)
Исчисление Джонса
135
При этом вектор-столбец E.1.3) можно записать через величины ф
и Г следующим образом:
= р-1*
е-|Т/2
О
О
E.1.6)
Вектор Джонса состояния поляризации выходящего пучка в систе-
системе координат ху получается с помощью обратного преобразования
из кристаллической системы координат sf:
cosxp - sin
sin \p cos
E.1.7)
Используя E.1.2), E.1.6) и E.1.7), преобразование, осуществляемое
задерживающей пластинкой, можно записать в виде
E.1.8)
где R (ф) — матрица поворота, a Wo — матрица Джонса для задер-
задерживающей пластинки, которые определяются соответственно вы-
выражениями
cos ф sin ф
- sin ф cos ф
E.1.9а)
Wo =
О
О
,'Т/2
E.1.96)
Если интерференционные эффекты не важны или не наблюдаются,
то фазовым множителем е'1ф можно пренебречь. Задерживающая
пластинка характеризуется величиной фазовой задержки Г и ее ази-
азимутальным углом ф и ее можно представить произведением трех
матриц, входящих в E.1.8):
IV = R(-4,IVORD,).
E.1.10)
Заметим, что матрица Джонса волновой пластинки представляет
собой унитарную матрицу, т. е.

136
Глава 5
где значком t обозначено эрмитово сопряжение. Прохождение по-
поляризованного света через волновую пластинку математически опи-
описывается унитарным преобразованием. Многие физические свойст-
свойства остаются неизменными при унитарных преобразованиях; к этим
свойствам относятся условие ортогональности между векторами
Джонса, а также инвариантность их длин. Таким образом, если со-
состояния поляризации двух пучков взаимно ортогональны, они оста-
останутся взаимно ортогональными при прохождении через произволь-
произвольную волновую пластинку.
Матрица Джонса для идеального однородного линейного пле-
пленочного поляризатора, ориентированного таким образом, что ось
распространения параллельна оси х лабораторной системы коорди-
координат, записывается в виде
^0 =
)¦
E.1.11)
где ф — абсолютная фаза, учитывающая конечную оптическую
толщину поляризатора. Матрица Джонса для поляризатора, повер-
повернутого на угол ф вокруг оси z, имеет вид
E.1.12)
Таким образом, если пренебречь абсолютной фазой ф, то представ-
представления в виде матриц Джонса для поляризаторов, через которые
распространяется свет с векторами электрического поля, парал-
параллельными осям х и у соответственно, имеют вид
lo о)
0 0
Чтобы определить, какое влияние оказывает последовательность
фазовых пластинок и поляризаторов на состояние поляризации све-
света, необходимо записать вектор Джонса входного пучка, а затем
матрицы Джонса различных элементов. Вектор Джонса выходного
пучка получается путем последовательного умножения матриц,
описывающих эти элементы.
5.1.1. ПРИМЕР: ПОЛУВОЛНОВАЯ ПЛАСТИНКА
Полуволновая пластинка имеет фазовую задержку Г = тт. В соот-
соответствии с E.1.4) х-срез1' (или у -срез) одноосного кристалла дейст-
' Кристаллическая пластинка называется л'-срезом, если ее грани перпендику-
перпендикулярны главной оси х.
Исчисление Джонса
137
вует как полуволновая пластинка, если его толщина равна / =
= Х/2 (пе — п0). Найдем, как изменится состояние поляризации
света, прошедшего через полуволновую пластинку. Пусть азиму-
азимутальный угол волновой пластинки равен 45°, а падающий пучок по-
поляризован вертикально. Тогда вектор Джонса падающего пучка
можно записать как
v =
E.1.13)
а матрица Джонса для полуволновой пластинки получается с ис-
использованием выражений E.1.9) и E.1.10):
1.14)
Вектор Джонса для выходящего пучка получается перемножением
матриц E.1.14) и E.1.13), что дает
E.1.15)
Этот вектор отвечает горизонтально поляризованному свету. Та-
Таким образом, полуволновая пластинка приводит к повороту векто-
вектора поляризации на 90°. Можно показать, что для произвольного
азимутального угла ф полуволновая пластинка поворачивает вектор
поляризации на угол 2ф (см. задачу 5.1). Иными словами, линейно
поляризованный свет остается линейно поляризованным, только
плоскость его поляризации поворачивается на угол 2ф.
Если падающий свет имеет круговую поляризацию, то полувол-
полуволновая пластинка будет преобразовывать свет с правой круговой по-
поляризацией в свет с левой круговой поляризацией и наоборот, неза-
независимо от азимутального угла. Доказательство этого утверждения
мы оставим в качестве упражнения (см. задачу 5.1). Действие полу-
полуволновой пластинки иллюстрируется рис. 5.2.
5.1.2. ПРИМЕР: ЧЕТВЕРТЬВОЛНОВАЯ ПЛАСТИНКА
Четвертьволновая пластинка создает фазовую задержку Г = тг/2.
Если пластинка представляет собой х-срез (или .у-срез) одноосного
анизотропного кристалла, то ее толщина должна быть равна / =
= Х/4 (пе - п0) (или кратна четному числу этой величины). Снова
предположим, что азимутальный угол пластинки равен 45° и что

138
Глава 5
Пластинка Х/2
Пластинка Х/2
РИС. 5.2. Действие полуволновой пластинки на отстояние поляризации пучка.
падающий пучок вертикально поляризован. Вектор Джонса падаю-
падающего пучка дается выражением E.1ЛЗ). В соответствии с E.1.10)
матрица Джонса для этой четвертьволновой пластинки запишется
в виде
о
!
1 I
1 -i
E.1.16)
Вектор Джонса выходного пучка получается умножением матоицы
E.1.16) на вектор-столбец E.1.13):
v' /
V5.1.17)
Исчисление Джонса
139
Пластинка
Х/4
Пластинка
Х/4
РИС. 5.3. Действие четвертьволновой пластинки на состояние поляризации линейно-
поляризованного пучка.
Он отвечает свету с левой круговой поляризацией. Таким образом,
воздействие четвертьволновой пластинки, ориентированной под
углом 45°, приводит к преобразованию вертикально поляризован-
поляризованного света в свет с левой круговой поляризацией. Если падающий
пучок горизонтально поляризован, то выходной пучок будет иметь
правую круговую поляризацию. Действие такой четвертьволновой
пластинки иллюстрирует рис. 5.3.
5.2. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ,
ПРОШЕДШЕГО ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
До сих пор мы использовали исчисление Джонса для расчета состо-
состояния поляризации светового пучка. Во многих случаях приходится

140
Глава 5
определять интенсивность излучения, прошедшего через оптиче-
оптическую систему. Например, узкополосный фильтр пропускает излуче-
излучение только в узком спектральном диапазоне и отклоняет (или по-
поглощает) излучение других длин волн. Для изменения интенсивно-
интенсивности распространяющегося пучка света обычно используют анализа-
анализатор. Анализаторами в основном служат поляризаторы, и называ-
называют их так просто из-за их расположения в оптической системе. В
большинстве двулучепреломляющих оптических систем поляриза-
поляризатор помещают перед системой, чтобы «приготовить» поляризован-
поляризованный свет. Второй поляризатор (анализатор) помещают на выходе
для анализа состояния поляризации выходящего пучка. Поскольку
фазовая задержка в каждой волновой пластинке зависит от длины
волны, состояние поляризации выходящего пучка также зависит от
длины волны света. Расположенный сзади поляризатор приводит к
тому, что полная интенсивность прошедшего излучения оказывает-
оказывается зависящей от длины волны. В представлении векторов Джонса
мы имеем информацию не только о состоянии поляризации свето-
светового пучка, но и о его интенсивности. Рассмотрим теперь световой
пучок, прошедший через поляризатор. Его вектор электрического
поля можно записать в виде вектора Джонса
Е =
E.2.1)
При этом интенсивность излучения рассчитывается следующим об-
образом:
/=Et.E = |?x|2 + |?/. ' E.2.2)
Здесь знак |, как и выше, означает эрмитово сопряжение. Если век-
вектор Джонса выходящего пучка после его прохождения через анали-
анализатор записать в виде
Е' =
E.2.3)
то коэффициент пропускания двулучепреломляющей оптической си-
системы вычисляется следующим образом:
т_ \е^ + \е;\>
\ЕХ\2 + \Ef
E.2.4)
Исчисление Джонса
141
Анализатор
Двулучепреломляющая
пластинка
Поляризатор
РИС. 5.4. Двулучепреломляющая пластинка, расположенная между двумя парал-
параллельными поляризаторами.
5.2.1. ПРИМЕР: ДВУЛУЧЕПРЕЛОМЛЯЮЩАЯ ПЛАСТИНКА
МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПОЛЯРИЗАТОРАМИ
Рассмотрим двулучепреломляющую пластинку, помещенную меж-
между парой параллельных поляризаторов, как показано на рис. 5.4.
Предположим, что пластинка ориентирована таким образом, что
«медленная» и «быстрая» оси составляют угол 45° с осью поляри-
поляризатора. Пусть двулучепреломление равно пе - п0 и толщина пла-
пластинки d. При этом фазовая задержка запишется в виде
Г = 2тт(пе- по
E.2.5)
а соответствующая матрица Джонса в соответствии с E.1.10) рав-
равна
-/sin| Г1
W =
-/sin| Г cos! Г
E.2.6)
Пусть падающий пучок является неполяризованным. Тогда вектор
электрического поля после прохождения пучка через первый поля-

142
Глава 5
ризатор можно записать в виде вектора Джонса
1°
E.2.7)
где мы предположили, что интенсивность падающего пучка равна
единице, а через поляризатор проходит только половина интенсив-
интенсивности. Вектор электрического поля прошедшего пучка можно запи-
записать с помощью вектора Джонса следующим образом:
Е'
E.2.8)
)
cos\T '
Прошедший пучок оказывается вертикально (вдоль оси у) поляри-
поляризованным, а его интенсивность дается выражением
E.2.9)
Из этого выражения видно, что интенсивность прошедшего пучка
является синусоидальной функцией волнового числа и максимальна
при X = (пе - no)d, (ne - no)d/2, (ne - no)d/3, ... , причем рассто-
расстояние между волновыми числами, отвечающими максимумам интен-
интенсивности, возрастает с уменьшением толщины пластинки.
5.2.2. ПРИМЕР: ДВУЛУЧЕПРЕЛОМЛЯЮЩИЕ ПЛАСТИНКИ
МЕЖДУ ПАРОЙ СКРЕЩЕННЫХ ПОЛЯРИЗАТОРОВ
Если повернуть анализатор, изображенный на рис. 5.4, на угол 90°,
то поляризаторы, помещенные на входе и выходе системы, ока-
окажутся скрещенными. В этом случае вектор Джонса для прошедше-
прошедшего пучка запишется в виде
E'
01/ cos±r
О/ -i
cosjr )yfl\\
E.2.10)
Исчисление Джонса
143
Этот пучок оказывается горизонтально (вдоль оси х) поляризован-
поляризованным, а его интенсивность дается выражением
v(ne- n.
E.2.11)
которое снова является синусоидальной функцией волнового числа.
Спектр пропускания состоит из ряда максимумов, соответствую-
соответствующих X = 2(пе — no)d, 2(ne — no)d/3, .... Эти длины волн отвечают
фазовым задержкам, равным ж, Зт, 5ж, ... , т. е. случаю, когда вол-
волновая пластинка становится полуволновой или кратна нечетному
числу полуволновых пластинок.
5.3. ПОЛЯРИЗАЦИОННЫЕ ИНТЕРФЕРЕНЦИОННЫЕ
ФИЛЬТРЫ
Спектральные фильтры могут быть основаны на использовании
интерференции поляризованного света. Такие фильтры играют
важную роль во многих оптических системах, от которых требует-
требуется выделение чрезвычайно узкой полосы частот с широкой угловой
расходимостью или способность настройки. Например, в задачах
физики Солнца распределение водорода может быть измерено пу-
путем фотографирования солнечной короны в свете линии излучения
На (X = 6563 А). Поскольку излучается большое количество энер-
энергии света на соседних длинах волн, для выделения этой линии необ-
необходимо иметь фильтр с чрезвычайно узкой (~ 1 А) полосой пропу-
пропускания. Такие фильтры состоят из двулучепреломляющих кристал-
кристаллических пластинок (волновых пластинок) и поляризаторов. Двумя
основными разновидностями таких двулучепреломляющих фильт-
фильтров являются фильтры Лио — Эмана [2—5, 12] и фильтры Шольца
[6, 7]. В них используется интерференция поляризованного света,
которая требует при прохождении излучения через кристалл опре-
определенной задержки между составляющими света, поляризованными
параллельно «быстрой» и «медленной» осям кристалла. Поскольку
фазовая задержка, создаваемая волновой пластинкой, пропорцио-
пропорциональна двулучепреломлению кристалла, при реализации такого
фильтра желательно иметь кристаллы с большим двулучепрелом-
лением пе — п0. В настоящее время для этой цели наиболее широко
применяются такие материалы, как кварц, кальцит и (NH4)H2PO4
(ADP).
Основной принцип работы фильтра Лио — Эмана очень прост;
его описание дается в задаче 5.5.

144
Глава 5
Исчисление Джонса
145
Исчисление Джонса, рассмотренное в предыдущих двух разде-
разделах, мы применим теперь для изучения характеристик фильтра
Шольца. Фильтр Шольца, названный по имени его изобретателя [6,
7], представляет собой стопку идентичных двулучепреломляющих
пластинок, каждая из которых ориентирована под определенным
азимутальным углом. Азимутальный угол каждой пластинки изме-
измеряется относительно оси пропускания переднего поляризатора. Весь
столбик двулучепреломляющих пластинок помещен между парой
поляризаторов.
5.3.1. СКРЕЩЕННЫЕ ФИЛЬТРЫ ШОЛЬЦА
Существует два основных типа фильтров Шольца: скрещенные и
веерные фильтры. Скрещенный фильтр Шольца работает между
скрещенными поляризаторами. В табл. 5.1 приведены азимуталь-
азимутальные углы отдельных пластинок. Геометрия фильтра Шольца из ше-
шести пластинок изображена на рис. 5.5. Согласно табл. 5.1, пропу-
пропускающая ось переднего поляризатора параллельна оси х, а ось за-
скающая ось переднего поляризатора параллельна оси х, а ось зад-
заднего поляризатора параллельна оси у. Полная матрица Джонса
Поляризатор -
M=[R(p)W0R(-p)R(-p)W0R(p)]m,
E.3.1)
где предполагается, что число пластинок четно, т. е. N = 2т. Под-
Подставляя E.1.9) в E.3.1) и выполняя матричное умножение, получа-
ТАБЛИЦА 5.1. Скрещенные
фильтры Шольца
Оптический
элемент
Передний поляризатор
Пластинка 1
Пластинка 2
Пластинка 3
Пластинка N
Задний поляризатор
Азимуталь-
Азимутальный угол
0°
Р
— р
Р
(-Dn-'p
90°
- Поляризатор
РИС. 5.5. Скрещенный фильтр Шольца из шести пластинок.
ем следующее выражение:
где
А =
= А В
С D
E.3.2)
- /cos2psinirJ + sin22psinHl\
В = sin4psin4r,
С= -В,
/cos2psinirJ
E.3.3)
10-631

146
Глава 5
а Г — фазовая задержка каждой пластинки. Следует заметить, что
эта матрица является унимодулярной (т. е. AD - ВС = 1), по-
поскольку в E.3.1) унимодулярны все матрицы. Используя тождество
Чебышева [9], выражение E.3.2) можно записать в виде
(А В\т_
\С D) '
A sin mKA - sin( т — 1) К А
sin КА
sin mKA
В
sin mKA
С-
sin К А
где
КА =
sin kA
Dsin mKA - sin(w - \)KA
sin К А
E.3.4)
E.3.5)
Мы используем обозначение К А для удобства сравнения с результа-
результатами, полученными с помощью теории связанных мод (см.
разд. 6.4).
Падающая и выходящая из системы волны связаны между со-
собой соотношением
E.3.6)
Выходящий пучок поляризован в направлении у, причем его ампли-
амплитуда дается выражением
Е; = М21ЕХ. E.3.7)
Если падающий пучок линейно поляризован в направлении оси х,
то коэффициент пропускания фильтра равен
Г=|М21|2.
Из выражений E.3.2) и E.3.3) получаем
Т =
где
sin mKA
cos AJ\. = 1 - 2cos22psin4r.
E.3.8)
E.3.9)
E.3.10)
Исчисление Джонса
147
Коэффициент пропускания Т часто выражают через новую перемен-
переменную х. определяемую следующим образом:
КА = -п - 2Х-
E.3.11)
Выраженный через эту новую переменную х коэффициент пропуска-
пропускания принимает вид
2
т =
sin JVv
tg 2pcosx—7 —
sinx
где
cosx = cos2psin2r.
E.3.12)
E.3.13)
Из E.3.12) и E.3.13) следует, что, когда фазовая задержка каждой
пластинки имеет значения Г = ?г, Зт, 5-я, ... , т. е. каждая пластин-
пластинка становится полуволновой, коэффициент пропускания равен Т =
= sin22/Vp. При азимутальном угле
Р =
4N
E.3.14)
коэффициент пропускания равен 100%. Такое пропускание при этих
условиях нетрудно объяснить, если рассмотреть состояние поляри-
поляризации после прохождения излучения через каждую пластинку внут-
внутри фильтра Шольца. Напомним, что при прохождении через полу-
полуволновую (Г = тг, Зт, ...) пластинку азимутальный угол между век-
вектором поляризации и быстрой (или медленной) осью кристалла ме-
меняет знак. После прохождения через передний поляризатор свет
оказывается линейно поляризованным в направлении оси х (азиму-
(азимутальный угол ф — 0). Поскольку первая пластинка имеет азиму-
азимутальный угол р, пучок после прохождения первой пластинки оказы-
оказывается линейно поляризованным с азимутальным углом ф = 1р.
Вторая пластинка ориентирована с азимутальным углом — р и со-
составляет угол Ър с вектором поляризации падающего на нее пучка.
Направление поляризации на выходной стороне этой пластинки
будет повернуто на угол 6р и ориентировано под азимутальным
углом — Ар (рис. 5.6). Пластинки ориентированы последовательно
под углами +р, —р, +р, —р, ... , в то время как направления по-
поляризации на выходе из пластинок имеют значения 2р, -Ар, 6р,
— 8р, ... . Таким образом, конечный азимутальный угол после N
пластин при этом равен 2Np. Если этот конечный азимутальный
угол равен 90° (т. е. 2Np = тс/2), то свет проходит через задний по-
поляризатор без какого-либо изменения интенсивности. Свет на дру-

з
s
к
S »
g X
D, 5
с «
I
1*
с
§
Исчисление Джонса
149
н
э
о
§
е §
I *
I1
L =0
3!
гих длинах волн, для которых пластинки не являются полуволно-
полуволновыми, не испытывает вращения поляризации на угол 90° и погло-
поглощается задним поляризатором.
С точки зрения распространения волн фильтр Шольца можно
также рассматривать как периодическую среду, в которой измене-
изменение азимутальных углов кристаллических осей создает периодиче-
периодическое возмущение по отношению к обеим независимым волнам и
приводит к связи между быстрой и медленной независимыми вол-
волнами. Поскольку эти волны распространяются с различными фа-
фазовыми скоростями, полный обмен электромагнитной энергией
возможен только в том случае, когда возмущение является перио-
периодическим, что позволяет поддерживать соотношения, необходимые
для непрерывного обмена энергией между быстрой и медленной вол-
волнами и наоборот. Это служит первой иллюстрацией принципа фа-
фазового синхронизма за счет периодического возмущения, к которо-
которому мы еще вернемся в следующих разделах. Основное физиче-
физическое объяснение этого явления состоит в следующем: если энергия
должна постепенно перекачиваться с расстоянием из моды А в мо-
моду В под действием статического возмущения, то необходимо, что-
чтобы обе волны распространялись с одинаковой фазовой скоростью.
Если фазовые скорости не равны друг другу, то падающая волна А
постепенно будет расфазироваться с волной В, с которой она связа-
связана. Это ограничивает полное количество энергии, которым можно
обмениваться. Такой ситуации можно избежать, если знак возму-
возмущения меняется на противоположный всякий раз, когда рассогласо-
рассогласование по фазе (между связанными полями) равно тс. Это меняет
знак перекачки энергии и таким образом поддерживает правильное
фазовое соотношение для непрерывной перекачки энергии. Теорию
связанных мод для скрещенных фильтров Шольца мы представим в
разд. 6.5.
Представляют интерес и заслуживают некоторого изучения ха-
характеристики пропускания фильтра Шольца в окрестности основно-
основного и побочных максимумов. Предположим, что каждая пластинка
толщиной d имеет показатели преломления пе и по.
Пусть \v — длина волны, при которой задержка по фазе равна
Bj- + 1)т. Фазовая задержка для произвольной длины волны равна
Если X мало отличается от Х(
приближенно записать в виде
Г= B*+ l)ff + ДГ,
E.3.15)
[т. е. (X - XJ <^ XJ, то Г можно

150
Глава 5
где
E.3.16)
Предположим теперь, что азимутальный угол пластинки удовлет-
удовлетворяет условию E.3.14), а N > 1. При этих условиях тригономет-
тригонометрическую функцию в выражении E.3.13) можно разложить в ряд,
что дает
X =
77 )
E.3.17)
Подставляя х в E.3.12), получаем
I ¦ 1\ I \^л N 2
Т =
E.3.18)
Это приближенное выражение для коэффициента пропускания спра-
справедливо при N > 1 и (X - Х„) < Х„. Из выражения E.3.18) следует,
что полная ширина полосы пропускания, измеренная на полувысоте
главного максимума пропускания, приблизительно равна ДГ1/2 =
= \,60ir/N, или в длинах волн
E.3.19)
Таким образом, для создания узкополосного фильтра Шольца с ши-
шириной полосы пропускания 1 А, необходимой для наблюдения ли-
линии Нц (Хо = 6563 А), требуется приблизительно 104 полуволновых
(v — 0) пластинок. Спектр пропускания состоит из главного макси-
максимума при Хо и ряда побочных пиков около него. В соответствии с
E.3.18) эти вторичные максимумы имеют место приблизительно
при условии
= Z/ + 1, / — 1, Z, J,. . . ,
причем коэффициент пропускания дается выражением
~ B/+1J'
E.3.20)
E.3.21)
Исчисление Джонса
151
1,0
0,8-
I
| 0,4
s
0,0
I I | Г I Т I |
_±>Kl/i \/ ¦ I | V/ iVxK^j^i i I i \^i^u>T\J\ Vl
0,0
0,5
1.0
1,5
Г/тг
2,0
2,5
3,0
РИС. 5.7. Расчетный спектр пропускания скрещенного фильтра Шольца.
На рис. 5.7 представлен расчетный спектр пропускания. Заметим,
что ширина полосы пропускания обратно пропорциональна полно-
полному числу пластинок.
5.3.2. ВЕЕРНЫЙ ФИЛЬТР ШОЛЬЦА
Веерный фильтр Шольца также представляет собой стопу одинако-
одинаковых двулучепреломляющих пластинок, каждая из которых ориенти-
ориентирована под определенным азимутальным углом. В табл. 5.2 приве-
приведена краткая характеристика типичного веерного фильтра Шольца,
а геометрическое расположение его элементов показано на рис. 5.8.
Согласно методу матриц Джонса, сформулированному в предыду-
предыдущем разделе, полная матрица для этих ./V пластинок дается выра-
выражением
М = R(-{т: + p)WqR{{tt - р) ¦ ¦ ¦ X
XR(-5p)W0REp)R(-3P)W0RCP)R(-p)W0R(p) =
= R{-fr + p)[W0RBp)]NR(-p), E.3.22)
где мы использовали следующее тождество для матриц поворота:
+ p2). E-3.23)

152
Глава 5
ТАБЛИЦА 5.2. Веерный фильтр Шольца
Элемент
Передний поляри-
поляризатор
Пластинка 1
Пластинка 2
Пластинка 3
Пластинка N
Задний поляризатор
Азимутальный угол
0°
Р
Ър
5р
BN - \)р =
= A/2)х - р
0°
Заметим, что в произведении E.3.22) последняя пластинка всегда
оказывается первой.
Используя тождество Чебышева E.3.4) и выполняя матричное
умножение в E.3.22), получаем
Л/,, = sin2pcosjr-^?—- ?
11 у 2 smx
а = -cosNX- isi
Мг, = cosNx - /si
21 л
sin
E.3.24)
M22 = MU ,
где
cosx = cos2pcos^r. E.3.25)
Эти выражения представляют собой элементы полной матрицы
Джонса, исключая поляризаторы.
Таким образом, падающая Е и выходящая Е' волны связаны
между собой соотношением
0\/Л/„ М12
0 0 М
'21
М
22
1 О
О О
E.3.26)

154
Глава 5
Выходящий пучок оказывается горизонтально поляризованным
(вдоль оси л:) с амплитудой, определяемой выражением
Е'х = МиЕх. E.3.27)
Если падающая волна линейно поляризована в направлении оси
х, то коэффициент пропускания равен
т=\мп\2- E.3.28)
Из выражения E.3.24) получаем следующее выражение для коэффи-
коэффициента пропускания:
, ~ sin Ny
tg2pcosx ¦
sinx
где
cosx = cos2pcos^r.
E.3.29)
E.3.30)
Следует заметить, что формула для коэффициента пропускания
E.3.29) формально совпадает с E.3.12). Максимальное пропускание
(Г = 1) имеет место при Г = 0, 2тг, 4тг, ... и р = тг/AN. Этот рав-
равный единице коэффициент пропускания объясняется тем, что для
рассматриваемых длин волн толщина пластинки соответствует це-
целой длине волны. Свет после прохождения через каждую пластинку
будет оставаться линейно поляризованным в направлении оси х и
не будет испытывать потерь в последнем поляризаторе. Свет с
другими длинами волн, для которого пластинки не являются полу-
полуволновыми, не будет линейно поляризованным в направлении оси х
и поглощается задним поляризатором. Пусть X,, — длина волны,
для которой фазовая задержка Г = 2ктг. Если X мало отличается от
А„ (т. е. X - Х„ < \), то Г дается приближенным выражением
Г =
+ ДГ =
2l»7T
E.3.31)
где v — 1, 2, 3, .... Случай v = 0 имеет место только для опреде-
определенных длин волн Хо, для которых двулучепреломление исчезает.
Этот частный случай находит ряд важных применений в широко-
широкоугольных узкополосных фильтрах и заслуживает особого внимания
(см. задачу 5.8). Если теперь предположить, что N s> 1 и использо-
использовать ту же процедуру, что и в E.3.17), то можно получить следую-
Исчисление Джонса
155
щее приближенное выражение для коэффициента пропускания:
Т =
in^w/l + (ЛГДГ/тгJ
/l
+
E.3.32)
которое совпадает с E.3.18). Ширина полосы пропускания АХ|/2, из-
измеренная на полувысоте максимального пропускания, дается снова
выражением
= 1,2,3,....
E.3.33)
Спектры пропускания веерного и скрещенного фильтров Шольца
совпадают с той лишь разницей, что в первом кривые сдвинуты по
фазе на Г = тт. Иными словами, коэффициент пропускания веерно-
веерного фильтра Шольца с фазовой задержкой Г такой же, как и у скре-
скрещенного фильтра Шольца с фазовой задержкой Г + тт. Это можно
также видеть из выражений E.3.12) и E.3.29) для коэффициента
пропускания. Расчетный спектр пропускания веерного фильтра
Шольца изображен на рис. 5.9.
Фильтры Шольца играют важную роль во многих современных
устройствах, например, таких, как электрооптические перестраивае-
перестраиваемые фильтры [10, 11] и узкополосные фильтры с широким полем
Т
А Ж
1,0 1,5 2,0 2,5
Г/тг
РИС. 5.9. Расчетный спектр пропускания веерного фильтра Шольца.
3,0

156
Глава 5
обзора. Более подробную информацию о фильтрах Шольца можно
найти в статье [12].
5.4. РАСПРОСТРАНЕНИЕ СВЕТА
В АНИЗОТРОПНОЙ СРЕДЕ С КРУЧЕНИЕМ
В данном разделе мы применим исчисление Джонса для исследова-
исследования распространения электромагнитных волн через анизотропную
среду со слабым кручением. Типичным примером такой задачи яв-
является распространение света в нематических жидких кристаллах с
кручением. Этот случай аналогичен веерному фильтру Шольца, чис-
число пластинок N которого стремится к бесконечности, а толщина
пластинок стремится к нулю как 1/7V. Действительно, анизотроп-
анизотропную среду с кручением можно разделить на N слоев, предполагая,
что каждый слой представляет собой волновую пластинку с неко-
некоторой фазовой задержкой и азимутальным углом. При этом пол-
полную матрицу Джонса можно получить перемножением всех мат-
матриц, отвечающих этим пластинкам.
Ограничимся рассмотрением случая, когда кручение является ли-
линейным и азимутальный угол равен
= az,
E.4.1)
где z — расстояние в направлении распространения, а а — постоян-
постоянная.
Пусть Г — фазовая задержка пластинки при отсутствии круче-
кручения. В частности, в случае нематического жидкого кристалла, ось с
которого параллельна поверхности пластинки, Г дается выражени-
выражением
Г -%(пе -поI, E.4.2)
где / — толщина пластинки. Полный угол кручения равен
а1. E.4.3)
Чтобы получить матрицу Джонса для такой структуры, необходи-
необходимо разделить эту пластинку на N пластинок равной толщины.
Каждая пластинка при этом будет иметь фазовую задержку T/N.
Пластинки ориентированы под азимутальными углами р, 2р, Ър,
... , (N — l)p, Np, где р — ф/N. Полная матрица Джонса для таких
N пластинок имеет вид
N
М= Y\R{mp)WQR{-m9).
E.4.4)
Исчисление Джонеа
157
Важно помнить, что в приведенном выше матричном произведении
член с т — 1 возникает с правой стороны. Используя тождество
E.3.23), эту матрицу можно записать в виде
м =
где
e-iT/2N q
О
,iT/2N
E.4.5)
E.4.6)
Используя E.1.9а) и E.4.6), получаем
N
\ N
E.4.7)
Выражение E.4.7) можно еще более упростить, если использовать
тождество Чебышева E.3.4). В пределе, когда TV стремится к беско-
бесконечности (Л/ — оо), имеем (см. задачу 5.10):
„ Г sin X
М=
где
ф-
2 X
sin X
sin X
. Г sin X
Т\2
2
E.4.8)
E.4.9)
Таким образом, мы получили точное выражение для матрицы
Джонса анизотропной пластинки с линейным кручением.
Пусть V — исходное состояние поляризации. Тогда состояние
поляризации V после прохождения пластинки можно записать в
виде
V = М\.
E.4.10)
5.4.1. АДИАБАТИЧЕСКОЕ ОТСЛЕЖИВАНИЕ
Нередко встречается ситуация, особенно в скрученных нематиче-
нематических жидких кристаллах, когда фазовая задержка Г значительно

158
Глава 5
больше угла кручения ф. Рассмотрим, например, слой жидкого кри-
кристалла толщиной 25 мкм с углом кручения -к/2. Двулучепреломле-
ние жидкого кристалла обычно имеет величину пе — по = 0,1. Для
длины волны X = 0,5 мкм мы имеем Т/ф = 20. Для более толсто-
толстого слоя это число может быть даже больше. В предположении
V > ф полная матрица Джонса E.4.8) принимает вид
,-'T/2
E.4.11)
Если падающий свет линейно поляризован вдоль медленной или
быстрой оси пластинки, то в соответствии с E.4.11) свет будет
оставаться линейно поляризованным вдоль «локальной» медленной
или быстрой оси. В этом смысле вектор поляризации отслеживает
вращение локальной оси, при условии что вектор поляризации на-
направлен вдоль одной из осей. Действие матрицы Джонса на любой
вектор поляризации можно разделить на два этапа. Сначала матри-
матрица фазовой задержки действует на вектор Джонса падающей вол-
волны, причем для света, линейно поляризованного вдоль одной из
главных осей, действие этой матрицы приводит только к фазовому
сдвигу светового пучка, а состояние его поляризации сохраняется
неизменным. Затем матрица R (ф) поворачивает вектор Джонса на
угол ф. В случае линейно поляризованного света такой поворот
приводит к тому, что вектор поляризации оказывается параллель-
параллельным главной оси на выходной грани пластинки. Таким образом, ес-
если падающий пучок света поляризован вдоль направления нормаль-
нормальных мод во входной плоскости (z = 0), то вектор поляризации све-
световой волны будет отслеживать вращение главных осей и оста-
оставаться параллельным локальной медленной (или быстрой) оси, при
условии что коэффициент кручения мал. Это явление называется
адиабатическим отслеживанием и имеет важные применения при
создании световых затворов на жидких кристаллах. Ниже мы рас-
рассмотрим принцип работы таких световых затворов.
Обсудим случай нематического жидкого кристалла с кручением
в четверть оборота (ф = -к/2). Если слой такого кристалла поме-
поместить между двумя параллельными поляризаторами, оси пропуска-
пропускания которых (х) параллельны оси с жидкого кристалла во входной
плоскости (z = 0), то для волны, прошедшей первый поляризатор,
можно записать следующий вектор Джонса:
E.4.12)
Исчисление Джонса
159
Матрица вращения Я(ф) в выражении E.4.8) запишется в виде
««-И! -J).
E.4.13)
В соответствии с E.4.8), E.4.12) и E.4.13) состояние поляризации
светового пучка после прохождения им жидкого кристалла дается
выражением
V' =
sin X
E.4.14)
Составляющая вдоль оси у не будет пропускаться вторым поляри-
поляризатором. Таким образом, коэффициент пропускания всей структу-
структуры запишется в виде
т =
+
(ГАJ)
E.4.15)
1 + (Г/77J
где мы использовали выражение E.4.9) для X с ф = ж/2.
Для кристаллических слоев с достаточно большой толщиной фа-
фазовая задержка много больше, чем ж (т. е. Г i> ж). При этом из
E.4.15) следует, что коэффициент пропускания фактически равен
нулю. Это есть следствие адиабатического отслеживания, посколь-
поскольку вектор поляризации отслеживает вращение осей и поворачивает-
поворачивается на угол ф = т/2, равный углу кручения. Поскольку это направ-
направление ортогонально оси пропускания анализатора, коэффициент
пропускания равен нулю.
Во многих жидких кристаллах с кручением, прикладывая элект-
электрическое поле (или создавая механические напряжения), можно воз-
воздействовать на ось с таким образом, чтобы она была направлена
вдоль заданного направления (см. разд. 7.7). Приложение электри-
электрического поля вдоль направления z будет разрушать такую скручен-
скрученную структуру (см. разд. 7.7). Это приводит к тому, что Г = 0 и,
согласно E.4.15), полному пропусканию света. После отключения
электрического поля жидкий кристалл восстанавливает свою струк-
структуру с кручением и свет блокируется. В этом состоит основной
принцип работы светового затвора на жидких кристаллах.

160
Глава 5
РИС. 5.10. Спектр пропускания фильтра Шольца; штриховая кривая — теория свя-
связанных мод; пунктирная кривая — исчисление Джонса; сплошная кривая — точный
расчет с помошью 4х4-матриц.
5.5. УЧЕТ ФРЕНЕЛЕВСКОГО ОТРАЖЕНИЯ
И ФАЗОВОГО СДВИГА
При формулировке исчисления Джонса пренебрегалось отражением
света от поверхностей волновой пластинки. Такие отражения обыч-
обычно уменьшают прохождение электромагнитной энергии. Однако ес-
если поверхности пластинки оптически гладкие, то интерференцион-
интерференционные эффекты могут приводить к уменьшению или увеличению ко-
коэффициента пропускания в зависимости от длины оптического пу-
пути.
Строгий подход, основанный на теории электромагнетизма, ис-
использует метод 4х4-матриц [13—15]. Световая волна пучка мате-
математически описывается вектором, состоящим из комплексных ам-
амплитуд падающей и отраженной волн. Каждая волна имеет медлен-
медленную и быструю составляющие. (Подробное изложение этого мето-
метода выходит за рамки данной книги, и читатель может найти его в
цитированных нами ссылках.)
Такой строгий подход позволяет получить точный спектр про-
пропускания двулучепреломляющего фильтра, поскольку он учитывает
Исчисление Джонса
161
интерференционные эффекты, обусловленные отражением волн.
При этом практические расчеты коэффициентов пропускания прихо-
приходится выполнять с помощью ЭВМ. Расчетный спектр пропускания
фильтра Шольца (рис. 5.10) имеет тонкую структуру, связанную с
интерференцией. Эта тонкая структура должна экспериментально
наблюдаться, если двулучепреломляющие пластинки являются тон-
тонкими и оптически гладкими. Такой анализ предсказывает также су-
существование сверхтонкой структуры, возникающей из интерферен-
интерференционных полос Фабри — Перо от всей стопки кристаллов, а не от
отдельных пластинок. Однако эта сверхтонкая структура выходит
за пределы разрешения масштаба графика, приведенного на
рис. 5.10. На этом рисунке для сравнения представлены также ре-
результаты расчета методом Джонса (в котором пренебрегается от-
отраженными волнами) и точным методом 4 X 4-матриц.
ЗАДАЧИ
5.1.
5.2.
Полуволновая пластинка. Полуволновая пластинка создает
фазовую задержку Г = ж. Предположим, что пластинка ори-
ориентирована таким образом, что азимутальный угол (т. е.
угол между осью х и медленной осью пластинки) равен ф.
а) Определите состояние поляризации прошедшего пучка в
предположении, что падающий пучок линейно полирязо-
ван в направлении оси у.
б) Покажите, что полуволновая пластинка будет преобра-
преобразовывать свет с правой круговой поляризацией в свет с
левой круговой поляризацией и наоборот, независимо от
азимутального угла пластинки.
в) Танталат лития (LiTaO3) представляет собой одноосный
кристалл с п0 = 2,1391 и пе = 2,1432 на длине волны
X = 1 мкм. Определите толщину полуволновой пластин-
пластинки на этой длине волны, предполагая, что пластинка об-
обрезана таким образом, что ее поверхности перпендику-
перпендикулярны оси х главной системы координат (т. е. х-срез).
Четвертьволновая пластинка. Четвертьволновая пластинка
создает фазовую задержку Г = т/2. Предположим, что пла-
пластинка ориентирована в направлении с азимутальным углом
Ф-
а) Определите состояние поляризации прошедшего пучка,
предполагая, что падающий пучок поляризован в на-
направлении оси у.
б) Покажите, что если состояние поляризации, найденное в
П-631

162
Глава 5
п. а, описывается комплексным числом в комплексной
плоскости, то при изменении ф от 0 до 7г/2 геометриче-
геометрическое место таких точек образует ветвь гиперболы. Полу-
Получите уравнение этой гиперболы.
в) Кварц (a-SiOj) представляет собой одноосный кристалл
с п0 = 1,53283 и пе = 1,54152 при длине волны А =
= 1,1592 мкм. Найдите толщину х-среза четвертьвол-
четвертьволновой пластинки из кварца на этой длине волны.
5.3. Преобразование поляризации волновой пластинкой. Волно-
Волновая пластинка характеризуется ее фазовой задержкой Г и
азимутальным углом ф.
а) Определите состояние поляризации выходящего пучка,
предполагая, что падающий пучок поляризован в на-
направлении оси х.
б) Запишите состояние поляризации, полученное в п. а, с
помощью комплексного числа.
в) Пусть состояние поляризации падающего пучка, поляри-
поляризованного вдоль оси х, задается точкой в начале ком-
комплексной плоскости. Покажите, что преобразованное со-
состояние поляризации может быть всюду на комплексной
плоскости, если Г может изменяться от 0 до 2ж, а ф —
от 0 до 7г/2. Физически это означает, что любое состоя-
состояние поляризации можно получить из линейно поляризо-
поляризованного света, если имеется соответствующая волновая
пластинка.
г) Покажите, что геометрическое место этих точек на ком-
комплексной плоскости, получаемое при вращении волновой
пластинки от ф = О до ф = ж/2, представляет собой ги-
гиперболу. Получите уравнение этой гиперболы.
д) Покажите, что матрица Джонса W волновой пластинки
унитарна, т. е.
где символом t обозначено эрмитово сопряжение,
е) Пусть VJ и \'2 — векторы Джонса, преобразованные из
V, и V2 соответственно. Покажите, что если V, и V2 ор-
ортогональны, то также ортогональны VJ и У2.
5.4. Поляризаторы и проекционные операторы. Идеальный по-
поляризатор можно рассматривать как проекционный опера-
оператор, действующий на начальное состояние поляризации па-
Рзспространение электромагнитных волн в периодических средах
163
дающего пучка и проецирующий вектор поляризации на ось
пропускания поляризатора.
а) Пренебрегая в E.1.11) абсолютным фазовым множите-
множителем, покажите, что
и
= р.
б)
в)
Операторы, удовлетворяющие этим условиям, называ-
называются в линейной алгебре операторами проекции.
Покажите, что если Е, — амплитуда электрического по-
поля, то амплитуда пучка после прохождения через поля-
поляризатор дается выражением
Р(Р'Е,),
где р — единичный вектор вдоль оси пропускания поля-
поляризатора.
Если падающий пучок вертикально поляризован (т. е.
Е, = уЕ0) и ось пропускания поляризатора направлена
вдоль оси х (т. е. р = х), то амплитуда прошедшего
пучка равна нулю, поскольку х • у = 0. Однако если пе-
перед первым поляризатором поместить второй и ориен-
ориентировать его под углом 45° относительно первого, то
амплитуда прошедшего поля не равна нулю. Найдите
эту амплитуду.
Имеется последовательность N поляризаторов, первый
из которых ориентирован под углом ф1 = ir/2N, вто-
второй — под углом ф2 = 2Gr/27V), третий — под углом
фъ = 3Gr/27V), ... , а п-й — под углом N-(w/2N). Пусть
падающий пучок поляризован горизонтально. Покажите,
что прошедший пучок поляризован вертикально и имеет
амплитуду
ИМ"-
Вычислите эту амплитуду для N = 1, 2, 3, ... , 10. Пока-
Покажите, что в пределе N — оо амплитуда стремится к еди-
единице. Иными словами, последовательность поляризато-
поляризаторов, ориентированная в виде веера, может вращать пло-
плоскость поляризации света без его поглощения.
5.5. Фильтр Лио — Эмана. В задачах физики Солнца распреде-
распределение водорода в солнечной короне измеряется путем фото-
г)

164
Глава 5
графирования линии Ни (X = 6563 А ). Для увеличения отно-
отношения сигнал/шум требуется фильтр с чрезвычайно узкой
полосой пропускания (~ 1 А). Поляризационный фильтр, со-
созданный Лио и Эманом, представляет собой последователь-
последовательность двулучепреломляющих пластинок, разделенных между
собой параллельными поляризаторами. Толщины пластинок
образуют геометрическую прогрессию (они равны d, Id, Ad,
8d, ...)• Все пластинки ориентированы под азимутальным
углом 45°.
а) Покажите, что если по и пе — показатели преломления
пластинок, то коэффициент пропускания полной стопы
из N пластинок дается выражением
Т = 5cos2xcos22xcos4x • • • cos2!** ,
где
ird(ne - по) trd{ne - no)v
б) Покажите, что коэффициент пропускания можно запи-
записать в виде
т I
2
в) Покажите, что полоса пропускания полной системы
определяется шириной полосы пропускания наиболее
толстой пластинки:
». " О
а свободный спектральный диапазон Av определяется
шириной полосы пропускания наиболее тонкой пластин-
пластинки:
d(ne-no)'
При этом добротность системы F, определяемая как от-
отношение Др/Др1/2, равна
F~2N.
Распространение электромагнитных волн в периодических средах
165
г) Рассчитайте фильтр с полосой пропускания 1 А для ли-
линии излучения На, используя в качестве двулучепрелом-
ляющего материала кварц. Предполагая, что по =
= 1,5416 и пе = 1,5506 при X = 6563 А, определите не-
необходимую толщину самой толстой пластинки.
д) Покажите, что, согласно п. б, ширина полосы пропуска-
пропускания на полувысоте максимума дается выражением
5.6. Внеосевые эффекты. Волновая пластинка, изготовленная из
одноосного кристалла, ось с которого параллельна поверх-
поверхностям пластинки, для нормально падающего пучка имеет
задержку 2тг(пе - no)d/\. Внеосевой пучок света будет пре-
претерпевать различное двулучепреломление, поскольку показа-
показатель преломления необыкновенной волны зависит от направ-
направления распространения пучка. Кроме того, длина пути в кри-
кристаллической пластинке не может превышать d (рис. 5.11).
а) Пусть во и ве — углы преломления для обыкновенной и
необыкновенной волн соответственно. Покажите, что
фазовая задержка равна
2тг
Г = -r-
e - nocosdo)d.
5.11. Внеосевые лучи.

166
Глава 5
Распространение электромагнитных волн в периодических средах
167
б) Пусть в — угол падения, а ф — угол между осью с и
тангенциальной составляющей волнового вектора. Пока-
Покажите, что фазовая задержка может быть выражена че-
через в и ф следующим образом:
sin
sin2#cos2</>
-п.
1 -
sin2»
в) Покажите, что в случае, когда sin2 в много меньше, чем
я2 и я2, фазовую задержку можно записать в виде
sin2</>
COS2</>
2и
г) В соответствии с формулой, приведенной в п. в, фильтр
Лио — Эмана с полосой пропускания при Хо для нор-
нормального падения будет иметь полосу пропускания при
Х() ± ДХ для внеосевого пучка света. Покажите, что при
'эфф
= «о ~ «2 величина ДХ дается выражением
Л sin2»
д) Покажите, что наиболее узкополосный фильтр Лио —
Эмана имеет предельную апертуру
= ±nt
где предполагается, что пе — по < по.
5.7. Фильтры Шольца. Коэффициент пропускания в области
максимума можно записать в виде
1 + х2
где
х =
а) Покажите, что Т — 0,5 при х = 0,8 и получите выраже-
выражение E.3.19) для ширины полосы пропускания на полувы-
полувысоте максимума.
б) Найдите длины волн, при которых коэффициент пропу-
пропускания обращается в нуль.
в) Определите коэффициенты пропускания для побочных
максимумов.
г) Оцените суммарный коэффициент пропускания, отвечаю-
отвечающий всем побочным максимумам, и сравните его с пло-
площадью под главным максимумом.
5.8. Изоиндексные фильтры Лио — Эмана. Рассмотрите фильтр
Лио — Эмана (задача 5.5), изготовленный из изоиндексных
кристаллов (т. е. кристаллов, у которых пе = по на опреде-
определенной длине волны Хс).
а) Получите выражение для ширины полосы пропускания в
зависимости от толщины пластинки и скорости измене-
изменения а двулучепреломления.
б) Выведите выражение для свободного спектрального диа-
диапазона в зависимости от а и толщины пластинки d.
в) Рассчитайте изоиндексный фильтр Лио — Эмана, ис-
используя CdS на длине волны 5245 А с полосой пропуска-
пропускания 0,1 А и свободным спектральным диапазоном по
крайней мере 10 А.
г) Объясните, почему полная толщина, необходимая для
получения данной полосы пропускания ДХ1/2, обычно
меньше, чем у обычных фильтров Лио — Эмана, изго-
изготовленных из кварца или кальцита. Покажите, что это
справедливо только в случае, когда а удовлетворяет ус-
условию
а >
где пе и яо — показатели преломления кальцита или
кварца.
5.9. Поле зрения изоиндексных фильтров. Используя результа-
результаты, полученные в задаче 5.6 (п. в), исследуйте поле зрения
изоиндексных фильтров Лио — Эмана.

168
Глава 5
а) Покажите, что полоса пропускания не зависит от угла
падения.
б) Выведите выражение для полосы пропускания в случае
внеосевых пучков в зависимости от 0 и ф.
в) Покажите, что для большинства экстремальных углов
падения полоса пропускания увеличивается или уменьша-
уменьшается в A ± 1/2л^) раз.
5.10. Нематические жидкие кристаллы с кручением.
а) Используя тождество Чебышева E.3.4), приведите выра-
выражение E.4.7) к более простому виду.
б) Получите выражение E.4.8).
ЛИТЕРАТУРА
1. West Е. A., Extending the field of view of KD*P electro-optic modulators. — Appl.
Opt., 17, 3010 A978).
2. Lyot В., Optical apparatus with wide field using interference of polarized light. —
Compt. Rend. (Paris), 197, 1593 A933).
3. Lyot В., Filter monochromatique polarisant et ses applications en physique
solaire. — Ann. Astrophys., 7, 31 A944).
4. Ohman Y., A new monochromator. — Nature, 41, 157, 291 A938).
5. Ohman Y., On some new birefringent filter for solar research. — Ark. Astron., 2,
165 A958).
6. Sold., Ceskoslov. Casopis pro Fysiku, 3, 366 A953); Csek. Cas. Fys., 4, 607, 699
A954); 5, 114 A955).
7. Sole !., Birefringent chain filters. — J. Opt. Soc. Amer., 55, 621 A965).
8. Jones R. C., New calculus for the treatment of optical systems. — J. Opt. Soc.
Amer., 31, 488 A941).
9. См., например: Yeh P., Yariv A., HongC.S., Electromagnetic propagation in
periodic stratified media. I. General Theory. — J. Opt. Soc. Amer., 67, 423 A977).
10. Pinnow D. A. et al.. An electro-optic tunable filter. — Appl. Phys. Lett., 34, 392
A979).
11. Tarry H. A., Electrically tunable narrowband optical filter. — Electronics Lett., 11,
471 A975).
12. Evans J. W., The birefringent filter. — J. Opt. Soc. Amer., 39, 229 A949); Sole
birefringent filter. — J. Opt. Soc. Amer., 48, 142 A958).
13. Yeh P., Electromagnetic propagation in birefringent layered media. — J. Opt. Soc.
Amer., 69, 742 A979).
14. Yeh P. Transmission spectrum of a Sole filter. — Opt. Comra., 29, A979).
15. Yeh P., Optics of anisotropic layered media: A new 4x4 matrix algebra. — Surface
Science, 96, 41—53 A980).
Глава 6
РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ
ВОЛН В ПЕРИОДИЧЕСКИХ СРЕДАХ
При распространении электромагнитного излучения в периодиче-
периодических средах возникает много интересных и потенциально полезных
явлений. К ним относятся: дифракция рентгеновского излучения в
кристаллах, дифракция света на периодических изменениях механи-
механических напряжений, возникающих при прохождении звуковой вол-
волны, и запрещенная зона для света в слоистых периодических сре-
средах. Эти явления используются во многих оптических устройствах,
таких, как дифракционные решетки, голограммы, лазеры на сво-
свободных электронах, лазеры с распределенной обратной связью, ла-
лазеры с распределенным брэгговским отражением, брэгговские отра-
отражатели с высокой отражательной способностью, акустооптические
фильтры, светофильтры Шольца и т. д. В данной главе мы рас-
рассмотрим некоторые общие свойства электромагнитного излучения
в периодических средах и общую теорию его распространения в
слоистой периодической среде. Эта теория имеет весьма близкую
формальную аналогию с квантовой теорией электронов в кристал-
кристаллах и поэтому позволяет использовать понятия блоховских волн,
запрещенных зон, затухающих и поверхностных волн. Наконец, мы
обсудим применение этой теории для решения ряда хорошо извест-
известных задач, таких, как расчет коэффициента отражения от брэггов-
ского зеркала, коэффициентов пропускания фильтра Шольца и оп-
оптических поверхностных волн. Кроме того, мы обсудим двойное
лучепреломление за счет формы и его применение в дихроичных по-
поляризаторах. Периодические структуры играют также важную роль
в интегральной оптике, рассмотрение которой мы отложим до
гл. 11.
6.1. ПЕРИОДИЧЕСКИЕ СРЕДЫ
Оптические свойства периодической среды описываются тензорами
диэлектрической проницаемости и восприимчивости, которые
вследствие трансляционной симметрии среды являются периодиче-
периодическими функциями координаты х:
е(х) = е(х + а), ц(\) = ц(\ + а),
F.1.1)

170
Глава 6
где а — любой произвольный вектор решетки. Эти формулы отра-
отражают лишь то, что наблюдатель, расположенный в точке х, «ви-
«видит» среду такой же, как и наблюдатель в точке х + а. В случае
трехмерной периодической среды, такой, как кристалл, периодич-
периодичность решетки определяется элементарными векторами а,, а2 и а3.
Среда остается инвариантной относительно перемещения на любой
вектор а, представляющего собой сумму целого числа этих векто-
векторов.
Распространение монохроматического (с частотой о>) лазерного
излучения в периодической среде описывается уравнениями Макс-
Максвелла
V X Н = шеЕ,
V X Е= -шцН.
F.1.2)
F.1.3)
Эти уравнения должны оставаться неизменными, если в оператор
V и е, ц вместо х подставить х + а. Трансляционная симметрия
среды позволяет выбрать нормальные моды в виде
F.1.4)
где Ек(х) и Нк(х) — периодические функции, т. е.
Ек(х) = Ек(х + а),
Нк(х) = Нк(х + а).
F.1.5)
Это свойство известно как теорема Флоке (или Блоха) и будет до-
доказано ниже. Нижний индекс К указывает на то, что функции Ек и
Нк зависят от вектора К, который называется блоховским волно-
волновым вектором. Величины ш и К связаны дисперсионным уравнени-
уравнением
¦ »(К).
F.1.6)
В случае когда периодичность исчезает, функции Ек(х) и Нк(х) ста-
становятся не зависящими от х, а нормальные моды — плоскими вол-
волнами с волновым вектором, равным блоховскому. Наша основная
цель состоит в определении Ек(х), Нк(х) и нахождении дисперсион-
дисперсионной зависимости w(K).
Paciipoci ранение элск ipoviai ни i иы\ ио.ш в периодических средах
171
6.1.1. ОДНОМЕРНЫЕ ПЕРИОДИЧЕСКИЕ СРЕДЫ
В современной оптике часто приходится иметь дело с одномерной
периодической средой, тензор диэлектрической проницаемости ко-
которой /; удовлетворяет условию
F.1.7)
где Л — период, а / — некоторое целое число. В данной главе мы
ограничимся рассмотрением распространения лазерного излучения
в одномерной периодической немагнитной среде. На рис. 6.1 пока-
показана типичная периодическая среда, представляющая собой череду-
чередующиеся слои двух прозрачных материалов. Предположим, что на
РИС. 6.1. Типичная периодическая слоистая среда, состоящая из чередующихся сло-
слоев GaAs и AlvGa|_vAs, выращенных на подложке из GaAs методом эпитаксии из
молекулярных пучков [7].

172
Глава 6
эту периодическую слоистую среду падает пучок лазерного излуче-
излучения. Свет будет претерпевать отражение и преломление на каждой
границе раздела. Пусть в — угол падения. Интерференционные
максимумы при отражении возникают при условии
2Acos0 =
F.1.8)
которое называется условием Брэгга. Его легко вывести, сравнивая
разность фаз между лучами, отраженными от последовательных
плоскостей решетки. Конструктивная интерференция возникает,
когда оптическая разность фаз между лучами, отраженными от по-
последовательных плоскостей решетки, составляет целое число длин
волн. Распространение электромагнитного излучения в таких сре-
средах подчиняется волновому уравнению
V X (V X Е) - <оVе = °-
F.1.9)
Поскольку среда является периодической, диэлектрический тензор е
можно разложить в ряд Фурье:
е(х) = I>Ge~'G'x, F.1.10)
где G пробегает все векторы обратной решетки, включая G = 0. В
нашем одномерном случае
= /^2, / = 0, ±1, ±2, ±3
F.1.11)
e(z) =
В физике твердого тела вектор G называется вектором обратной
решетки. В физике кристаллов этот вектор играет фундаменталь-
фундаментальную роль. В одномерной периодической среде вектор g параллелен
оси г. Вектор электрического поля в этой периодической среде в об-
общем случае можно выразить через интеграл Фурье:
Е
F.1.12)
Подставляя выражения F.1.12) и F.1.10) в F.1.9), получаем
:о2/х? fd3k eGA(k - G)e~'k'x = 0.
G
jd3kkX [k X A(k)]^"'k"]
Распространение электромагнитных волн в периодических средах
173
Это условие выполняется только тогда, когда все множители при
е-/к-х обращаются в нуль. Таким образом,
к X [к X А(к)] + <o2/x?eGA(k - G) = 0 для любого к,
G
F.1.13)
где суммирование производится по всем векторам обратной решет-
решетки. Это условие представляет собой бесконечную однородную си-
систему уравнений относительно неизвестных коэффициентов А(к).
Каждое уравнение в этой системе имеет свое, отличное от другого
значение к. В принципе для этой системы можно решить характе-
характеристическое уравнение, получаемое приравниванием детерминанта
системы уравнений F.1.13) нулю. Однако при более внимательном
рассмотрении системы F.1.13) можно заметить, что не все коэффи-
коэффициенты А(к) связаны между собой. Оказывается, что связаны
только коэффициенты вида A(k — G). Это позволяет разбить пол-
полную систему уравнений F.1.13) на много подсистем, каждая из ко-
которых относится к волновому вектору К и содержит уравнения от-
относительно А(К) и А(К - G) со всевозможными векторами G.
Каждая такая подсистема может быть решена по отдельности. Ис-
Используя это свойство для системы F.1.13), решение подсистемы,
характеризуемой вектором К, можно записать в виде
F.1.14)
В одномерном случае G = /g = I2irz/A. Поэтому
F.1.15)
является периодической функцией с периодом Л. Выражение F.1.14)
определяет нормальную моду распространения. Более общее реше-
решение F.1.12) теперь представляет собой линейную суперпозицию
этих нормальных мод. Тем самым мы доказали теорему F.1.5).
При условии что частота о> задана, из уравнений F.1.13) можно
получить волновой вектор К. Если среда однородна в х- и ^-направ-
^-направлениях, т. е. ? не зависит от х и у, то из F.1.14) и F.1.15) находим

174
Глава 6
следующее выражение для блоховской моды электрического поля:
Е - e-i(K*x+Krv)e->K<zEK(z), F.1.16)
где Ек(г) — периодическая функция от г. В этом случае, задавая ча-
частоту о) и набор величин (Кк, Ку), из уравнений F.1.13) можно опре-
определить К,. Существуют области значений ы, для которых Л', стано-
становится комплексным числом, и, следовательно, блоховская волна
F.1.16) оказывается затухающей. Падающее излучение от этих об-
областей будет полностью отражаться. В диапазоне рентгеновского
излучения это явление называется брэгговским отражением. По-
Поскольку наибольший интерес представляют явления и устройства,
использующие периодические среды в области их запрещенных зон,
мы будем искать приближенные решения для блоховских волн, ког-
когда условие Брэгга приблизительно выполняется. Чтобы проил-
проиллюстрировать основные идеи, для простоты в дальнейшем будем
предполагать, что волна распространяется в направлении z (т. е.
Кх = Ку — 0) и что вектор поля перпендикулярен волновому векто-
вектору (К-Е = 0). Кроме того, будем предполагать среду изотропной,
т. е. считать, что et является скалярной величиной. При этом систе-
система уравнений F.1.13) принимает вид
k2A(k) - w2n
- lg) = 0.
F.1.17)
Для нахождения блоховской волны с волновым числом К (здесь
для простоты опущен нижний индекс г) требуется решить систему
уравнений F.1.17) с А" = К, К ± g,K ± 2g, ... . Поскольку мы сно-
снова имеем бесконечное число уравнений относительно А (К), А (К ±
± g), А (К ± 2g), ... , для получения явного решения требуется сде-
сделать еще одно приближение. Чтобы это приближение было кор-
корректным, нужно исследовать все входящие в уравнения члены и
пренебречь малыми величинами. Записывая в F.1.17) несколько
первых членов для к - К, получаем уравнение
К2А(К) - ы2
g) - и2це_
g)
=.0,
F.1.18)
которое можно также переписать в виде
K2~
g)
F.1.19)
Распространение электромагнитных волн в периодических средах
175
Аналогично, уравнение F.1.17) для k = K-gnk =
записать соответственно в виде
можно
A{K-g) =
A(K+g)
1
u2fie-iA(K)+ ¦¦¦],
F.1.20)
[и2це1А(К) + u2ne_lA(K+2g)+ ¦¦¦]¦
F.1.21)
Из уравнений F.1.19) — F.1.21) следует, что если
\K-g\KK,
К2 =
F.1.22)
F.1.23)
то основными членами являются А (К) и А (К - g). Физически это
означает, что между составляющими плоских волн А (К) и А (К -
— g) имеется резонансная связь. Пренебрегая всеми другими коэф-
коэффициентами, систему уравнений F.1.17) для блоховских волн с вол-
волновым числом К можно переписать в виде
(К2 - w
[{К - gf -
- g) = 0,
-g) = 0.
F.1.24)
F.1.25)
Заметим, что е0 здесь представляет нулевую фурье-компоненту ди-
диэлектрического тензора, а ?,_, = ?*, если ?— вещественная диэ-
диэлектрическая функция.
Уравнения F.1.24) и F.1.25) представляют собой систему линей-
линейных уравнений для амплитуд поля А (К) и А (К - g). Она имеет не-
нетривиальное решение только в случае, когда детерминант системы
равен нулю:
К2 - и2р
или
(К2 ~ <ch
= 0,
= 0.
F.1.26)
F.1.27)
Последнее уравнение представляет собой явную запись дисперсион-
дисперсионного уравнения F.1.6), определяющего зависимость оз(К). Условие

176
Глава 6
Брэгга F.1.22) точно выполняется при К = (l/2)g — -к/К. При
этом значении К из уравнения F.1.27) получаем следующие два
корня со2:
к2
F.1.28)
Эти корни определяют границы спектральной полосы. При часто-
частотах со между со+ и со_ корни уравнения F.1.27) для К являются ком-
комплексными числами, вещественная часть которых равна 7г/Л. Вол-
Волны при этом являются затухающими, а их спектральный диапазон
называется «запрещенной зоной».
При частотах со, лежащих вне этой запрещенной зоны, корни
уравнения F.1.27) для К являются вещественными и решения отве-
отвечают распространяющимся волнам. Уравнение F.1.27), устанавли-
устанавливающее связь между и и К, называется дисперсионным. На рис. 6.2
представлено графическое изображение дисперсионного уравнения
F.1.27) для типичной периодической среды. Для трехмерной перио-
периодической среды дисперсионное уравнение F.1.6) соответствует по-
поверхностям постоянной частоты в К-пространстве. В случае трех-
трехмерных периодических сред могут также существовать запрещен-
запрещенные зоны частот со. Волны с частотами в запрещенных зонах не
могут распространяться, поскольку вследствие брэгговского отра-
отражения они затухают. Это нетрудно показать, если вычислить вол-
волновое число К в центре запрещенной зоны при со2 = (g/2J//i?0 [см.
F.1.22) и F.1.23)] и К = g/2 + х, где Ixl « g/2. При этом диспер-
дисперсионное уравнение F.1.27) принимает вид
F.1.29)
где мы пренебрегли числом, пропорциональным х4. Из уравнения
F.1.29) можно найти волновое число К в центре запрещенной зоны:
F.1.30)
Поскольку это волновое число является комплексным, оно отвечает
экспоненциально затухающей амплитуде. Следует отметить, что
это пространственное затухание существенно зависит от коэффици-
коэффициента ?, в фурье-разложении. Ширина запрещенной зоны определяет-
определяется величиной Acogap = 1со+ — со_ I и в соответствии с F.1.28) дается
выражением
F.1.31)
РИС. 6.2. а — дисперсионная кривая в области запрещенной зоны для периодичес-
периодической структуры, изображенной на рис. 6.3 при пх = 3,2, п2 = 3,4, а = Ь = 0,5Л; за-
заметим, что К становится комплексным, когда Ке(КК) = ж; б — общий вид диспер-
дисперсионных кривых и (AQ для основной запрещенной зоны (/ = 1) и запрещенных зон
высшего порядка (/ = 2, 3).
12-631

178
Глава 6
Таким образом, ширина запрещенной зоны Awgap пропорциональна
коэффициенту Фурье для диэлектрической проницаемости. Из вы-
выражений F.1.30) и F.1.31) можно заметить, что мнимая часть вол-
волнового числа в центре запрещенной зоны пропорциональна отно-
отнотй й (
р пропорциональна
сительной ширине этой зоны (Aa.igap/w) и дается выражением
со
F.1.32)
где, как мы помним, g — 2тг/Л.
Выше при получении формул мы предполагали, что распростра-
распространение волн происходит в направлении периодического изменения
диэлектрической проницаемости', т. е. вдоль оси z. Для произволь-
произвольного направления распространения (т. е. когда Кх или Kv Ф 0) дис-
дисперсионное уравнение оказывается более сложным и зависит от со-
состояния поляризации. Это будет показано в следующем разделе
при исследовании распространения волн в периодических слоистых
средах.
При выводе дисперсионного уравнения F.1.27) мы предполагали
\К - g\ « К [соотношение F.1.22)] и К2 ~ w2/xe0 [соотношение
F.1.23)], что следует из условия резонансной связи между коэффи-
коэффициентами А (К) и А (К - g). Запрещенная зона, связанная с брэггов-
ским условием F.1.22), определяется коэффициентом фурье-разло-
жения ?j диэлектрической функции e(z). В общем случае существует
запрещенная зона, связанная с каждым коэффициентом Фурье ?, ди-
диэлектрической функции e(z). Для иллюстрации этого рассмотрим
случай, когда
\K-lg\ "К, /= ±1,±2,...,
К2 « O32flEo.
F.1.33)
F.1.34)
Аналогично тому как были выведены уравнения F.1.24) и F.1.25),
можно получить
(К2 - u2tie0)A(K) - <с2ре,А(К - lg) = 0,
- i*2pt_,A(K) +[(K- lgJ - о2ре0]А(К - lg) = 0.
Это приводит к запрещенной зоне при
F.1.35)
F.1.36)
F.1.37)
Распространение электромагнитных волн в периодических срелах
179
Поскольку здесь предполагается, что е_/ = с*, ширина зоны дается
выражением
(Hap),=
F.1.38)
Если / Ф 1, то эти зоны называются запрещенными зонами высше-
высшего порядка, поскольку в соответствии с F.1.37) и F.1.34) они име-
имеют место при более высоких частотах. Во многих случаях коэффи-
коэффициент фурье-разложения с, с ростом / уменьшается (т. е. е, — 0 при
/ — оо). Как видно из F.1.38), соответствующие запрещенные зоны
имеют небольшую ширину. На рис. 6.2, б представлены дисперси-
дисперсионные кривые и (К) для общего случая.
6.2. ПЕРИОДИЧЕСКИЕ СЛОИСТЫЕ СРЕДЫ
Простейшая периодическая среда состоит из чередующихся слоев
прозрачных материалов с различными показателями преломления.
Современные достижения в технологии выращивания кристаллов,
особенно методом эпитаксии из молекулярных пучков, позволяют
выращивать периодические слоистые среды с хорошо контролируе-
контролируемыми периодичностью и толщинами слоев, соответствующими не-
нескольким атомным слоям. Распространение волн в периодических
слоистых средах изучали многие авторы [1, 2]. В этом случае мож-
можно получить точное решение волнового уравнения. Мы будем пред-
предполагать, что материалы являются немагнитными. Рассмотрим
простейшую периодическую слоистую среду, состоящую из двух
различных веществ со следующим профилем показателя преломле-
преломления:
'2'
причем
n{z) = n
О < z < ft,
b < z < Л,
А) .
F.2.1)
F.2.2)
Здесь ось z перпендикулярна границам раздела слоев, а Л — пери-
период. Геометрия этой структуры изображена на рис. 6.3. Для нахож-
нахождения блоховской волны, отвечающей векторам электрического по-
поля, будем использовать процедуру, описанную в [2]. Общее реше-
решение волнового уравнения для вектора электрического поля можно

180
Глава 6
Распространение электромагнитных волн в периодических средах
181
г= (и-2)Л
\
»= (и - 1)Л
/\
% - иЛ
_/
(п-\)-я элемент. элемент, ячейка
ячейка
РИС. 6.3. Схематическое представление периодической слоистой среды и амплитуд
плоской волны, отвечающих /7-й элементарной ячейке и соседним с ней слоям.
записать в виде
F.2.3)
где предполагается, что волна распространяется в плоскости yz, a
ку — составляющая волнового вектора, которая остается постоян-
постоянной при распространении через среду. Электрическое поле внутри
каждого однородного слоя можно представить в виде суммы пада-
падающей и отраженной плоских волн. Комплексные амплитуды этих
двух волн составляют компоненты вектора-столбца. Таким обра-
образом, электрическое поле в слое а {а - 1, 2) /7-й элементарной ячей-
ячейки можно записать в виде вектор-столбца
а= 1,2.
F.2.4)
При этом распределение электрического поля в рассматриваемом
слое можно записать следующим образом:
где
F.2.5)
F.2.6)
Вектор-столбцы не являются взаимно независимыми. Они связаны
между собой условиями непрерывности на границах раздела.
Вследствие этого только один вектор (или две составляющие раз-
различных векторов) могут быть выбраны произвольно. В случае ТЕ-
волн (вектор Е перпендикулярен плоскости yz) условие непрерывно-
непрерывности составляющих ?\ и Hv (H ~ dEx/dz) на границах раздела (см.
рис. 6.3) z = (п - 1)Л и z = {п — 1)Л + b приводит к следующим
уравнениям:
F.2.7)
п п п п *
iklz(eikl'acn - e~ik2'adn) = iklz(eik""an - e~ikl*"bn).
Эти четыре уравнения можно записать в виде системы двух мат-
матричных уравнений:
/ е'к*'А е'^г,А \[ cS
F.2.8)
I
1
1
-1
1
пп-
К-
\
1
1
е<к2:а _е-
d,
\ i
e~ik\,a
где
Исключая из этой системы вектор-столбец ( " ],
ричное уравнение \"„ /
A B\iar
С D]\b.
, F.2.9)
F.2.10)
получаем мат-
F.2.11)
В этом уравнении элементы матрицы записываются следующим
образом:
I

182
Глава 6
A = eik>-a cos k2zb + W-f*-
K2z
2z
C-e'*"e -i'hr^-T^
D
F.2.12)
cos k2zb " i'f-jp + xf
В выражении F.2.11) матрица представляет собой матрицу преоб-
преобразования для одной ячейки, связывающую амплитуды плоских
волн в слое 1 элементарной ячейки с аналогичными амплитудами
для эквивалентного слоя в следующей элементарной ячейке. По-
Поскольку эта матрица связывает амплитуды поля двух эквивалент-
эквивалентных слоев с одинаковыми показателями преломления, она является
унимодулярной, т. е.
AD- ВС= 1.
F.2.13)
Следует отметить, что матрица преобразования для элементарной
ячейки, связывающая амплитуды поля в слое 2, отличается от мат-
матрицы в уравнении F.2.12). Однако эти матрицы имеют одинаковые
следы. Ниже будет показано, что след матрицы преобразования
для элементарной ячейки непосредственно связан с зонной структу-
структурой периодической среды.
Матричные элементы А, В, С, D для ТМ-волн (вектор Н пер-
перпендикулярен плоскости yz) слегка отличаются от аналогичных
матричных элементов для ТЕ-волн. Для ТМ-волн имеем
л _ pikua
cos k2zb +
тм - e
«2^1.
sin /c,7ft
Распространение электромагнит!!
!ых волн в периодических средах
183
= eik"a
= e-'k>'a
«,^2,
sin^2zfe
F.2.14)
cos k2zb -
n\k\z
—
n2j.
VlW
Как уже отмечалось выше, только один вектор-столбец является
независимым. В качестве этого вектор-столбца можно выбрать, на-
например, вектор-столбец для слоя 1 в нулевой элементарной ячейке.
Оставшиеся вектор-столбцы эквивалентных слоев связаны с векто-
вектором для нулевой элементарной ячейки соотношением
i А В \п ia,
С D] \Ь
обращение которого дает
А В)
С D
y4 ?
С D)
F.2.15а)
F.2.156)
Используя тождество
А В
С D
D
-С
А )
справедливое для унимолулярных матриц, выражение F.2.15) мож-
можно упростить:
D
-С
F.2.16)
Вектор-столбец для слоя 2 той же элементарной ячейки можно
всегда получить с помощью F.2.9).
6.2.1. ЕЛОХОВСКИЕ ВОЛНЫ И ЗОННАЯ СТРУКТУРА
Периодическая слоистая среда эквивалентна одномерному кристал-
кристаллу, который инвариантен относительно трансляций на постоянную
решетки. Оператор трансляции решетки Т определяется выражени-
выражением Tz = z - /Л, где / — целое число. Отсюда следует, что
F.2.17)

184
Полученная выше матрица ABCD является представлением опера-
оператора трансляции на элементарную ячейку. Согласно теореме Блоха,
рассмотренной в разд. 6.1, вектор электрического поля нормальной
моды в периодической слоистой среде имеет вид
Е = EK(z)e~iKzei{"'-k>y\
где EK(z) — периодическая функция с периодом Л, т. е.
F.2.18)
F.2.19)
Нижний индекс К указывает на то, что функция ЕА(г) зависит от
К. Постоянная К называется блоховским волновым числом. Задача
теперь непосредственно состоит в определении величин К и B.K(z)
как функции от со и ку. (Заметим, что kv = Ку и нижний индекс у Kz
опущен для удобства обозначения.)
Используя представление с помощью вектор-столбцов и выра-
выражение F.2.5), условие периодичности F.2.19) для блоховской волны
можно записать в простом виде:
К-1
F.2.20)
Из выражений F.2.11) и F.2.20) вытекает, что вектор-столбец для
блоховской волны удовлетворяет следующему уравнению на соб-
собственные значения:
A B\ian
С D]\bm
F.2.21)
Таким образом, фазовый множитель е'кх является собственным
значением матрицы трансляции ABCD и удовлетворяет характери-
характеристическому уравнению
А - eiKK
С
В
D - е'КА
= 0.
Решение уравнения F.2.22) имеет вид
D) ±
D)]2 -
F.2.22)
Собственные векторы, отвечающие этим собственным значениям,
являются решениями уравнения F.2.21) и с точностью до произ-
Распространение электромагнитных волн в периодических средах
185
вольной постоянной записываются в виде
В
- А
F.2.23а)
Соответствующий собственный вектор-столбец для и-й элементар-
элементарной ячейки в соответствии с F.2.20) дается выражением
= е
-in К А
В
F.2.236)
Елоховские волны, получаемые из уравнений F.2.23), можно рас-
рассматривать как собственные векторы матрицы трансляции с соб-
собственными значениями е'кх, даваемыми выражением F.2.22). Два
собственных значения в F.2.22) являются взаимно обратными, по-
поскольку матрица трансляции унимодулярна. Уравнение F.2.22) дает
дисперсионную зависимость между со, к и К для блоховской волно-
волновой функции:
К{ку,о,) =
i-
F.2.24)
Режимы, при которых I (A + D)/2\ < 1, отвечают вещественному
К и, следовательно, распространяющимся блоховским волнам. Од-
Однако в случае I (A + D)/2\ > 1 мы имеем А" = тж/А + iKt, т. е. в
К присутствует мнимая часть А', и блоховская волна затухает. Эти
области отвечают так называемым запрещенным зонам периоди-
периодической среды. Частоты, отвечающие границам зоны, определяются
из условия I (A + D)/21 = 1.
С помощью F.2.5) и F.2.23) блоховскую волну в слое 1 и-й эле-
элементарной ячейки можно записать окончательно в виде
-iKz
F.2.25)
где а0 и Ьо даются выражением F.2.23а). Следует заметить, что
функция внутри квадратных скобок не зависит от и и, стало быть,
является периодической с периодом Л. На этом мы заверщаем по-
получение решения для блоховской волны.
Дисперсионное уравнение F.2.24) определяет блоховское волно-
волновое число К вдоль направления оси z для блоховской волны с ча-
частотой со и .у-составляющую к волнового вектора. Эту диспер-
дисперсионную зависимость можно представить в виде поверхности в
трехмерном пространстве (К, к , со). Сечения этой поверхности пло-

РИС. 6.4. Зонная структура в плоскости uAt лля ТЕ-волн (вектор Е перпендикулярен
периодически расположенным слоям). Темные области соответствуют разрешенным
зонам. Величина ш измеряется в елишшах < 'Л, а А — в единицах 1/Л.
РИС. 6.5. Зонная структура в плоскости o.Av для ТМ-волн (вектор Н перпендикуля-
перпендикулярен периодически расположенным слоям). Темные области соответствуют разрешен-
разрешенным зонам. Штриховая линия соответствует к, = (ш/с)«2 sin в„; и) — в единицах с/Л,
а к — в единицах 1/Л.
Распространение электромагнитных волн в периодических средах
187
скостями К = ттг/А представляют собой кривые, которые опреде-
определяют границы зоны. На рис. 6.4 и 6.5 изображены проекции этих
кривых на плоскость kvus для ТЕ- и ТМ-волн соответственно. За-
Заштрихованные области отвечают разрешенным зонам, для кото-
которых К является вещественным. Интересно отметить, что «запре-
«запрещенная» зона для ТМ-волн сокращается до нуля при ку =
= (o)/c)n2s\neH, где вв — угол Брюстера, поскольку при этом угле
френелевское отражение на границах раздела исчезает и падающая
и отраженная волны оказываются несвязанными. На рис. 6.6 пока-
показана эта дисперсионная зависимость ш(К) для частного случая
kv - 0 (т. е. случая нормального падения). Ее можно записать в ви-
виде
cosATA = cos A:,a cos A:2ft - - (— + — Isin *,esin*26, F.2.26)
I \ И] И2/
где А:, = (со/с)и, тл к2 = (со/с)и2.
В случае когда К находится в запрещенной зоне, уравнение
F.2.26) можно решить приближенно. В первой запрещенной зоне
Re А' = т/Л мы положим
КА = v ± ix. F.2.27)
Пусть ш0 — центр запрещенной зоны, для которой
kxa = k2b = iv. F.2.28)
Структура с такими условиями называется четвертьволновым эле-
элементом. Уравнение F.2.26) для частоты ш0 принимает вид
1 / Я,
cos
2\п
F.2.29)
Подставляя F.2.27) в F.2.29) и решая последнее относительно х,
получаем
F.2,30)
где приближенное равенство в правой части справедливо при 1и2 -
- п, I « я, 2- Это выражение дает мнимую часть величины К А в
центре запрещенной зоны. Внутри запрещенной зоны х изменяется
от нуля на границах зоны до ее максимального значения F.2.30) на
частоте соо.

188
Глава 6
РИС. 6.6. Дисперсионная кривая и(К) при ку = 0 (нормальное падение); ы в едини-
единицах с/А, а А" в единицах 1/Л. Пунктирные кривые дают мнимую часть величины К в
произвольных единицах.
Пусть у — нормированное отклонение частоты от центра запре-
запрещенной зоны ш0, т. е.
'о,
W — W(\ CO — id,
у = п,а =
J с ' с
Подставляя F.2.27) и F.2.31) в F.2.26), получаем
F.2.31)
chx
2\п, п2
cos2y — sin2у.
F.2.32)
Это есть выражение для мнимой части величины Л'Л в запрещенной
зоне в зависимости от частоты. Для получения границ зоны нужно
положить х - 0. При этом получаем
~ И,
./граница
и2 + и,
F.2.33)
Таким образом, ширина запрещенной зоны Awgap в частотном диа-
диапазоне дается выражением
Нар = «0-
|и, - и,
it п2 + и,
2 Ди
1Г И
F.2.34)
Распространение электромагнитных волн в периодических средах
189
в то время как мнимая часть величины Л'Л в центре запрещенной
зоны равна
Ди
F.2.35)
где Дя = 1и2 — л,1 и и = (я, + и2)/2. Эти выражения согласуются
с выражениями F.1.31) и F.1.32), полученными в разд. 6.1. В ка-
качестве упражнения читатель может самостоятельно найти коэффи-
коэффициенты фурье-разложения диэлектрической проницаемости для пе-
периодической слоистой среды. Ответ записывается следующим об-
образом:
4 \п2 - п.
F.2.36)
6.3. БРЭГГОВСКОЕ ОТРАЖЕНИЕ
Рассмотрим периодическую слоистую структуру, состоящую из N
элементарных ячеек. Геометрия такой структуры изображена на
рис. 6.7. Коэффициент отражения дается выражением
F.3.1)
'о/ ьК
и представляет собой отношение комплексной амплитуды Ьо отра-
отраженной волны на входе к амплитуде а0 падающей волны при гра-
граничном условии, отвечающем тому, что справа от оптического эле-
элемента отсутствует волна, падающая на него (т. е. bN = 0). Из
F.2.15а) мы имеем
A B\Nia
С D
Унимодулярную матрицу можно возвести в степень
следующего матричного тождества [см. E.3.4)]:
А В
С D
CUN_{
F.3.2)
с помощью
F.3.3)

190
Глава 6
РИС. 6.7. Геометрия типичного брэгговского отражателя, состоящего из N перио-
периодов.
где
sin(N + 1)КА
F.3.4)
а К дается выражением F.2.24).
Амплитудный коэффициент отражения rN получается из
F.3.1)—F.3.3):
CUN_X
F.3.5)
Коэффициент отражения (задача 6.10) вычисляется как квадрат мо-
модуля rN:
.- .2 - \С\2
11 \ sin NK А)
F.3.6)
Таким образом, мы получили аналитическое выражение для коэф-
коэффициента отражения от многослойного отражателя. Важно иметь в
виду, что эта формула для коэффициента отражения справедлива
Распространение элеюромагнитных волн в периодических средах
191
только для света, падающего из среды с показателем преломления
«j (задача 6.11). Величина \С\2 в F.3.6) непосредственно связана с
коэффициентом отражения от единичной элементарной ячейки со-
соотношением
\гА2 =
\С\2
или
|2 •
F.3.7)
F.3.8)
Коэффициент отражения 1л,12 для типичного брэгговского отража-
отражателя обычно много меньше единицы. Поэтому величина \С\2 при-
приблизительно равна If,]2. Второй член в знаменателе выражения
F.3.6) при больших Л^ представляет собой быстро меняющуюся
функцию величины К, или, что то же самое, величин kv и со. Следо-
Следовательно, структура спектра отражения определяется главным об-
образом этим членом. Между двумя запрещенными зонами имеется
ровно N — 1 узлов, в которых коэффициент отражения обращается
в нуль. Максимумы коэффициента отражения имеют место в цент-
центрах «запрещенных» зон. Существует также ровно N — 2 побочных
максимумов, каждый из которых лежит под огибающей
ICI2/[ICI2 + (sin К АJ]. На границах зоны Л'Л = тж и коэффициент
отражения
i2 -
F.3.9)
Внутри «запрещенной» зоны величина Л'Л является комплексным
числом:
ЛЛ = т-п -+¦ /Л,.Л, F.3.10)
а формула F.3.6) для коэффициента отражения принимает вид
\С\2
\С\2
а:, л
shNKA
F.3.11)
При больших N второй член в знаменателе выражения F.3.11) экс-
экспоненциально стремится к нулю как е~2<Л~1>А/Л_ Отсюда следует,

1,Or
1.0
о
1,0
о
1.0
1,0
ААЛЛА
в--85е
в =75°
9 = 65°
в = 55°
е=45°
1
1,0
1,0
о
1,0
о
1.0
о
1,0
Зтг
в - 4О° Г\
А
в = 20°
л
в=Ю°
л
л
л
л
л
тг/2
РИС. 6.8. Спектр отражения брэгговского отражателя, имеющего 15 периодов при
различных углах падения излучения, а — ТЕ-волны; б — ТМ-волны. Показатели
1,0 г
О
1,0
о
1,0
о
1,0
о
1,0
в = 85°
в =75°
в = 65°
в = 55»
I
в=45*
2тг
i 1
Зтг
0
1,0
0
1,0
0
ф
0
1,0
0
0 = 40*
в =30°
в = 20°
0=10°
в = 0°
А
л
л
л
/
л
Л
Л
б
преломления слоев: п] = 3, 4 и п2 = 3, 6, а толщины слоев выбраны таким обра-
образом, чтобы а = Ь = Л/2. Угол Брюстера 0S = 46,6°; ш в единицах с/Л.
13-631

194
Глава 6
что для брэгговского отражателя с большим числом периодов ко-
коэффициент отражения в запрещенной зоне оказывается порядка
единицы.
Структуры зон и коэффициенты отражения для ТЕ- и ТМ-волн
не одинаковы. Для ТМ-волны, падающей под углом Брюстера вв,
отраженная волна отсутствует независимо от числа пластинок N.
OaAs
а
100
Полоса
непрозрачности
0,90
1,00
1,30
1.40
1,50
Длина волны, мкм
РИС. 6.9. а — микрофотография под сканирующим электронным микроскопом (с
увеличением 11 000 х) тридцати пар слоев GaAs (темные полосы) и Al03Ga07As
(светлые полосы), выращенных на подложке из GaAs; б— микрофотография (с уве-
увеличением 55 ОООх), показывающая, что среда имеет период Л = 0,185 мкм; в — из-
измеренный спектр отражения света, падающего из воздушной среды [3].
Распространение электромагнитных волн в периодических средах
[95
Это связано с обращением в нуль динамического множителя ICI2
при значении угла Брюстера.
На рис. 6.8 и 6.9 приведены зависимости коэффициентов отра-
отражения для некоторых типичных брэгговских отражателей от часто-
частоты и угла падения.
В центре каждой запрещенной зоны период слоистой среды
приблизительно равен целому числу световых длин волн. Посколь-
Поскольку при последовательных отражениях от соседних границ раздела
свет оказывается сфазированным и, следовательно, интерферирует
конструктивно, световые волны будут сильно отражаться. Это яв-
явление аналогично брэгговскому отражению рентгеновских лучей от
кристаллических плоскостей. Такая высокая отражательная способ-
способность была продемонстрирована на брэгговском отражателе, изго-
изготовленном из чередующихся слоев GaAs и Al03Ga07As, выращен-
выращенных на подложке из GaAs методом эпитаксии из молекулярных
пучков (рис. 6.9, а). Измеренный коэффициент отражения представ-
представлен на рис. 6.9, в и хорошо согласуется с теорией [3].
6.4. ТЕОРИЯ СВЯЗАННЫХ МОД
В разд. 6.2 было получено точное решение задачи о распростране-
распространении электромагнитного излучения в периодической слоистой среде.
Существует, однако, много периодических сред, для которых мож-
можно получить лишь приближенные решения системы уравнений
Максвелла. Для решения этой задачи обычно используют два под-
подхода. Первый из них основан на формализме блоховских функций,
рассмотренном в разд. 6.1, а второй — на теории связанных мод. В
теории связанных мод периодическое изменение диэлектрического
тензора рассматривается как возмущение, которое приводит к свя-
связи между невозмущенными нормальными модами структуры.
Иными словами, диэлектрический тензор как функция пространст-
пространственных координат записывается в виде
е(х, у, z) = ео(х, у) + Де(х, у, z),
F.4.1)
где ео(х, у) — невозмущенная часть диэлектрического тензора, а
Ае(х, у, z) — периодический в направлении оси z тензор, являющий-
являющийся единственной периодически изменяющейся частью диэлектриче-
диэлектрического тензора. Сравнивая F.4.1) с фурье-разложением величины
е(х, у, z), приведенным в F.1.10), нетрудно видеть, что ео(х, у)
представляет собой нулевой член ряда, а остальные члены входят в
Ае(х, у, z).

196
Глава 6
Предположим, что распространяющиеся нормальные моды в
невозмущенной диэлектрической среде, описываемой диэлектриче-
диэлектрическим тензором ео(х, у), известны. Поскольку невозмущенная
диэлектрическая среда однородна в направлении оси z [т. е.
де (х, y)/dz = 0], нормальные моды можно записать в виде
Ет(х, у)е*"-Р-'\ <6-4-2)
где т — модовый индекс, который может принимать либо непре-
непрерывные значения для неограниченных мод, таких, как плоские вол-
волны, либо дискретные значения для локализованных мод, например
типа волноводных. Эти нормальные моды удовлетворяют уравне-
уравнению
дх ау1
Ет(х,у)
F.4.3)
где предполагается, что (V-E) = 0 и уравнение F.4.3) является
приближением волнового уравнения A.4.7) (см. разд. 2.1). Если
при z = 0 возбуждается произвольное поле с частотой со, то поле,
распространяющееся в невозмущенной среде, всегда можно пред-
представить в виде линейной комбинации нормальных мод:
Е = LAmEm(x, .y)e'(M'-*-*>, F-4.4)
где Ат — постоянные. Такое разложение возможно благодаря то-
тому, что эти нормальные моды образуют полный набор. Данные
моды обычно нормируют таким образом, чтобы поток энергии в
направлении оси z был равен 1 Вт. Следовательно, условие ортого-
ортогональности этих мод можно записать в виде (см. разд. 11.1)
F.4.5)
где
— магнитное поле, связанное с модой Ек. Если VE = 0 и
к
моды Ет удовлетворяют уравнению F.4.3), то это соотношение ор-
ортогональности принимает вид (см. разд. 11.1)
F.4.6)
где 8к/ — дельта-символ Кронекера для локализованных мод и
Распространение электромагнитных волн в периодических средах
197
дельта-функция для неограниченных мод. Если при 2 = 0 возбужде-
возбуждена только одна мода, например мода Е,(х, у)е >z\ то при рас-
распространении через невозмущенную среду электромагнитная энер-
энергия будет оставаться в этой моде.
Рассмотрим теперь распространение невозмущенной моды
Ej(.x:, y)e ' через возмущенную среду, описываемую диэлектри-
диэлектрическим тензором ео(х, у) + Ае(х, у, z). Наличие возмущения диэ-
диэлектрического тензора Ае(х, у, z) приводит к новому возмущению
поляризации:
ДР = Де(х, у, z)E,(x, у)е'1а'-**\
Если эта поляризационная волна, действующая как распределенный
источник, может перекачивать энергию в некоторую другую моду
Е2(х, у)е °" lZ) (или из нее), то можно говорить, что диэлектриче-
диэлектрическое возмущение Де(лг, у, z) приводит к связи (т. е. вызывает обмен
энергией) между модами Е, и Е2. Определим теперь, при каких ус-
условиях имеет место такая связь.
Обмен энергией между невозмущенными модами, обусловлен-
обусловленный возмущением диэлектрического тензора, аналогичен переходу
между состояниями атома под действием нестационарного возму-
возмущения. При этом метод расчета, который иногда называют мето-
методом вариации постоянных, является весьма простым. Он состоит в
том, что вектор электрического поля электромагнитной волны за-
записывают в виде суперпозиции нормальных мод, отвечающих не-
невозмущенному диэлектрическому тензору, причем коэффициенты
такого разложения, очевидно, зависят от z, поскольку при Де Ф 0
волны Ет(х, у)е "" '"z уже не являются независимыми модами:
Е = ?Am(z)Em(x, y)e-(»>-^\ F.4.7)
т
Подставляя выражение F.4.7) в волновое уравнение
(V2 + а2ц[е0(х, у) + Де(х, у, г)])Е = 0 F.4.8)
и используя F.4.3), получаем
, у, z)A,E,(x,
F.4.9)

198
Глава 6
Предположим далее, что возмущение диэлектрического тензора
«слабое», т. е. изменение модовых амплитуд является «медлен-
«медленным» и удовлетворяет условию
dz
гАь
F.4.10)
Это условие называется параболическим приближением и часто ис-
используется в случае малых возмущений. Таким образом, пренебре-
пренебрегая в уравнении F.4.9) второй производной, получаем
, у, z)A,E,(x,
F.4.11)
Умножим теперь скалярно уравнение F.4.11) на Щ{х, у) и проинте-
проинтегрируем его по х и у. Используя свойство ортогональности F.4.6)
нормальных мод, имеем
dz'
где
^ fE*k(x,y)'Ek(x,y)dxdy=
(k\Ae\l) = fE*k(x, y) • Ae(x, y, z)E,(x, y) dxdy.
F.4.12)
F.4.13)
F.4.14)
Поскольку возмущение диэлектрического тензора Ле(х, у, z) являет-
является периодическим по z, его можно разложить в ряд Фурье:
Де(>, y,z)= ? ет{х, j)exp -im-^-z
т*0 L iV J
F.4.15)
где в силу определения величины AeQc, у, z) в F.4.1) суммирование
ведется по всем т, кроме т - 0.
Подставляя выражения F.4.13)—F.4.15) в уравнение F.4.11), по-
получаем следующие уравнения:
d_
dzAk~
F.4.16)
Распространение электромагнитных волн в периодических средах
199
в которых коэффициенты связи С*™' определяются следующим об-
образом:
<#°s ^(k\Em\l) = ^JE*k{x,y)-Em{x,y)El{x,y)dxdy. F.4.17)
Эти коэффициенты С^"> отражают величину связи между к-й и 1-й
модами, обусловленную m-Vi фурье-компонентой тензора диэлект-
диэлектрического возмущения.
Уравнения F.4.16) представляют собой систему линейных диф-
дифференциальных уравнений, которые в принципе определяют беско-
бесконечное число модовых амплитуд. Однако на практике, особенно
вблизи условия резонансной связи, только две моды оказываются
сильно связанными и уравнение F.4.16) сводится к системе двух
уравнений относительно двух модовых амплитуд. Под условием ре-
резонансной связи мы подразумеваем следующее равенство:
Рк - ft,- т— = 0 , F.4.18)
где т — целое число. Это условие имеет фундаментальное значе-
значение, и мы будем называть его условием продольного фазового син-
синхронизма или просто фазового синхронизма. Условие F.4.18) явля-
является пространственным аналогом закона сохранения энергии в не-
нестационарной теории возмущений, и поэтому его можно называть
законом сохранения импульса. Резонансную связь можно объяснить
следующим образом. Из уравнения связанных мод F.4.16) видно,
что прирост амплитуды поля к-й моды dAk, обусловленный связью
с 1-й модой в области между z и z + dz, выражается через т-ю фу-
рье-компоненту возмущения диэлектрического тензора:
= ~'
\Ь
- ft - »*хJ]dz-
FА19)
Поскольку амплитуды представляют собой медленно меняющиеся
функции координат, выражение F.4.19) можно проинтегрировать
по расстоянию, которое много больше периода Л, но много мень-
меньше масштаба изменения амлитуд. Это приводит к следующему вы-
выражению для результирующего приращения амплитуды ЬАк, обус-
обусловленного связью с 1-й модой на расстоянии между z и z + L че-
через т-ю фурье-компоненту тензора диэлектрического возмущения:

200
Глава 6
Из этого выражения видно, что модовая связь между /с-й и 1-й мо-
модами является незначительной, когда условие F.4.18) при некото-
некотором целом т не выполняется. Действительно, в выражении F.4.20)
интеграл не обращается в нуль лишь в том случае, когда аргумент
экспоненты равен нулю. Это условие точно совпадает с условием
фазового синхронизма F.4.18).
Таким образом, для изучения распространения электромагнит-
электромагнитного излучения в диэлектрической среде с периодическим возмуще-
возмущением можно использовать метод вариации постоянных. Эти <*по-
стоянные» (модовые амплитуды) удовлетворяют уравнениям свя-
связанных мод F.4.16). Для того чтобы между модами /си/ имела ме-
место сильная связь, должны выполняться два условия. Первым из
них является F.4.18), называемое кинематическим условием. Вто-
Второе состоит в том, чтобы коэффициенты связи С^"> не обращались
в нуль. Последнее условие называется также динамическим, по-
поскольку оно зависит от таких характеристик волн, как поляризация
и конфигурация моды.
Описанные выше общие свойства модовой связи имеют важное
значение, поскольку они позволяют определить, какие процессы
могут иметь место и какой вид возмущений требуется для возник-
возникновения связи между данной парой нормальных мод. Этот вопрос
мы будем рассматривать на протяжении всей настоящей главы на
ряде конкретных примеров.
Соотношение F.4.18) называют также условием Брэгга, по-
поскольку оно совпадает с аналогичным условием для дифракции
рентгеновского излучения в кристаллах. В этом случае падающая
волна, описываемая плоской волной с пространственной зависимос-
зависимостью ехр( — ik у — iCz), сильно связана с отраженной волной, у кото-
которой зависимость от координат имеет вид ехр( — ikvy + ifSz). Посто-
Постоянная C является составляющей волнового вектора, перпендикуляр-
перпендикулярной соответствующим кристаллическим плоскостям. Из условия
F.4.18) следует, что расстояние Л между кристаллическими плоско-
плоскостями должно удовлетворять условию
/8 - (-/?) = 2/? = т~, F.4.21)
или условию
2Acos0 = тХ,
F.4.22)
поскольку /3 = kcosd, где в — угол падения, а т - 1, 2, 3, ... — не-
некоторое целое число. Выражение F.4.22) представляет собой хоро-
Распространение электромагнитных волн в периодических средах
201
шо известное условие Брэгга для дифракции рентгеновского излуче-
излучения. Как уже отмечалось выше, это условие является необходи-
необходимым, но не достаточным. Интенсивность дифракции зависит от ко-
коэффициентов фурье-разложения периодической диэлектрической по-
постоянной и от поляризации волн [выражение F.4.17)].
6.4.1. УРАВНЕНИЯ СВЯЗАННЫХ МОД
Уравнение F.4.16) описывает наиболее общий случай связи между
модами, обусловленной периодическим возмущением диэлектричес-
диэлектрической проницаемости. На практике во многих случаях имеет значение
связь лишь между двумя модами. Обозначим эти две связанные
моды индексами 1 и 2. Пренебрегая взаимодействием со всеми дру-
другими модами, уравнения связанных мод можно записать в виде
F.4.23)
±А --iK.Ae-*»
dz l
где
F.4.24)
а С^'1 и СB1'"> — коэффициенты связи, определяемые выражением
F.4.17). Из определения F.4.17) можно непосредственно показать,
что
сп) = \.сг\ т \* 1 F.4.25)
¦если Ае(х, у, z) — эрмитов диэлектрический тензор.
В случае когда диэлектрический тензор ? в F.4.1) является функ-
функцией только от z (т. е. не зависит от х и у), нормальные моды не-
невозмущенной среды представляют собой плоские волны и коэффи-
коэффициенты фурье-разложения ет возмущения диэлектрической проница-
проницаемости оказываются постоянными. В этом частном случае коэффи-
коэффициенты связи принимают вид
С{т) _
Р* • еир„
F.4.26)

202
Глава 6
где р^. и р, — единичные векторы поляризации плоских волн.
Заметим, что коэффициенты связи F.4.26) зависят как от состо-
состояний поляризации связанных мод, так и от тензорных свойств ко-
коэффициентов фурье-разложения ет.
Знаки множителей /3,/1/3,1 и j32/\j32\ в уравнениях F.4.23) ирра-
ют очень важную роль; они определяют характер поведения связи.
Эти знаки, разумеется, зависят от направления распространения
связанных мод. Поэтому можно рассматривать два типа связи, а
именно связь волн, распространяющихся в одном направлении, и
связь волн, распространяющихся в противоположных направле-
направлениях.
6.4.2. СВЯЗЬ МЕЖДУ МОДАМИ, РАСПРОСТРАНЯЮЩИМИСЯ
В ОДНОМ НАПРАВЛЕНИИ
Если связанные моды распространяются в одном и том же направ-
направлении, скажем в направлении +г, то оба множителя /3/1/3,1 и
/32/1/321 равны 1. При этом уравнения связанных мод принимают
вид
dz 2
где
к = С,BШ).
F.4.27)
F.4.28)
Напомним, что А , и А 2 являются комплексными амплитудами нор-
нормированных мод. Следовательно, величины \А ,12 и \А2\2 представ-
представляют собой потоки энергии мод 1 и 2 соответственно. Уравнения
связанных мод F.4.27) согласуются с условием сохранения энергии,
которое записывается в виде
^(|Л,Г + М2Г} = 0. F.4.29)
Общее решение уравнений F.4.27) получается путем интегрирова-
интегрирования от 0 до z. Таким образом, мы имеем
Ax(z) = ?>'
A2(z) = е
ism
F.4.30)
*{ -,-^sin5*4,@) + [cpssz + /|?
Распространенно электромагнитных волн в периодических срелах
203
где
52 =
F.4.31)
8/1,@) и Л2@) — модовые амплитуды при z = 0. С помощью вы-
выражений F.4.30) можно показать, что доля энергии, которая благо-
благодаря связи переходит из моды А 2 в А , на расстоянии z (или, наобо-
наоборот, из моды /1, в моду А2), равна
(Д/8/2J
-sin
к|2 +
Z.
F.4.32)
Максимальная энергия, которой могут обменяться моды, составля-
составляет Ы2/[Ы2 + (А/3/2J], причем при А/3 > \к\ она становится не-
небольшой. Передача всей энергии одной моды другой возможна,
только если А/3 = 0, т. е. если выполняется условие фазового син-
синхронизма. Типичным примером связи между модами, распростра-
распространяющимися в одном и том же направлении, является распростране-
распространение света через светофильтр Шольца. Такое распространение мы
рассмотрим в разд. 6.5 в рамках теории связанных мод.
6.4.3. СВЯЗЬ МЕЖДУ ПРОТИВОПОЛОЖНО
НАПРАВЛЕННЫМИ МОДАМИ
Если связанные моды распространяются в противоположных на-
направлениях, скажем при положительных /3, и отрицательных /32, то
множители /3,/1/3|1 и /32/1/321 становятся равными 1 и —1 соот-
соответственно. При этом уравнения связанных мод принимают вид
i*-
-iKA2e'Af*z,
F.4.33)
где к снова дается выражением F.4.28).
В этом случае полный поток энергии в направлении +z равен
1/1,12 - 1/4212. Уравнения связанных мод F.4.33) снова согласуют-
согласуются с условием сохранения энергии:
d
;х{И,|2 - |Л2|2} = 0. F.4.34)
Для противоположно направленных связанных мод граничные ус-

204
Глава 6
ловия записываются в виде А, = А @) при z = 0 я А2 = A 2(L) при
z = L. Общее решение для амплитуд этих мод имеет вид
sh s(L - z)
5 ch sL + /(Aft/2) sh
_jKei(№/2)L sh 5Z
A
s ch sL + /(Aft/2) sh sL
F.4.35)
A2(z) =
-iK* sh s(L - z)
s ch sL + /(Aft/2) sh
+
ch sz + i(Aft/2) sh sz
ch *L + /(Aft/2) sh 5L
2V ;
где
F.4.36)
Из общего решения F.4.35) видно, что энергия обмена между эти-
этими двумя модами в области между z = 0 и z = L дается выраже-
выражением
l*|2sh2sL . F.4.37)
s2ch2sL + (Aft/2) sh2sL
Можно снова заметить, что доля энергии, которой обмениваются
моды, уменьшается с увеличением А/3. Полный обмен энергией
между противоположно распространяющимися модами имеет ме-
место только при выполнении условия фазового синхронизма (А/3 =
= 0) и когда L — оо. Здесь ситуация отличается от случая связи
между одинаково направленными модами, когда две связанные мо-
моды обменивались энергией в том и другом направлениях и при ус-
условии А/3 = 0 происходил периодически в пространстве полный об-
обмен энергией. На рис. 6.11 показано, как обмениваются энергией
связанные моды, распространяющиеся в одном направлении, а на
рис. 6.14 иллюстрируется то же самое для противоположно направ-
направленных мод.
Брэгговское отражение представляет собой типичный пример
связи между противоположно направленными волнами. В разд. 6.6
мы применим теорию связанных мод для описания оптических
свойств брэгговского отражателя.
Распространение электромагнитных волн в периодических средах
205
6.5. ТЕОРИЯ СВЯЗАННЫХ МОД
ДЛЯ ФИЛЬТРОВ ШОЛЫДА
Фильтры Шольца мы рассмотрели в разд. 5.3, где для изучения их
характеристик пропускания использовался метод матриц Джонса.
Однако этот формализм не дает четкого представления о физиче-
физическом механизме действия такой структуры в роли фильтра. В дан-
данном разделе для изучения пропускания этих фильтров мы приме-
применим теорию связанных мод. Разумеется, эта теория применима
лишь к скрещенным фильтрам Шольца, которые представляют со-
собой периодическую структуру. Геометрия этих фильтров изображе-
изображена на рис. 5.5, а их характеристики были приведены в табл. 5.1.
Пусть л,, п2 и л3 — главные показатели преломления в каждой
кристаллической плоскости. Ось распространения z совпадает с
осью z (осью с) кристалла и перпендикулярна каждой плоскости.
Оси х и у параллельны направлениям пропускания соответственно
переднего и заднего поляризаторов. Диэлектрический тензор в
главных координатах кристаллических плоскостей имеет вид
? =
О
О
о
О п\
F.5.1)
где е0 — диэлектрическая проницаемость вакуума. Пусть ф — угол,
который составляют оси кристалла с координатными осями хну
(рис. 6.10). Тогда диэлектрический тензор в системе координат х, у,
z записывается в виде
О
О
О
F.5.2)
где
COS
sin i
О
-sin
COS
О
О
1/
F.5.3)
R — матрица вращения, для которой R~](\p) = Я(-ф).
Диэлектрический тензор F.5.2) можно представить в виде следу-
следующей суммы:
^ е0 + Де,
F.5.4)

206
Глава 6
Распространение электромагнитных волн в периодических средах
207
РИС. 6.10. Азимутальный угол
где е0 дается выражением
e0 = eo
«.
0
0
а Де имеет
Де = ео{п\
0
n\
0
вид
)
и
0
n\
sin2»p
sin \f/ cos ^
0
- sin >p cos >p
- sin2»p
0
0^
0
0
F.5.5)
F.5.6)
Поскольку разность п\ — п\ обычно мала по сравнению с п\ 2-> Ае
можно рассматривать как малое возмущение диэлектрического тен-
тензора. В структуре фильтра Шольца значение азимутального угла ф
колеблется в пределах от р до -р. Следовательно, возмущение Ае
диэлектрического тензора является периодической функцией от z.
Однако диагональные элементы тензора Де остаются постоянными
на протяжении фильтра и поэтому не входят в периодически изме-
изменяющуюся часть диэлектрического тензора. Если эти диагональные
члены входят в е() [выражение F.5.5)], то в силу их малости по
сравнению с п\ 2 ими можно пренебречь. Таким образом, будем
рассматривать F.5.5) как невозмущенный диэлектрический тензор и
предполагать, что периодическое возмущение дается выражением
Де = еп
0
0
~НИ2 ~ «2)sin2p О)
0 0
0 0
F.5.7)
где/(г) — периодическая прямоугольная функция величины г, опре-
определяемая выражением
'
-1,
F.5.8)
Период Л здесь равен удвоенной толщине кристаллической пла-
пластинки.
Нормальные моды невозмущенной диэлектрической среды пред-
представляют собой линейно-поляризованные плоские волны. Мы огра-
ограничимся рассмотрением волн, распространяющихся лишь в направ-
направлении z. Таким образом, нормальные моды — это х-поляризован-
ная плоская волна е
и ^-поляризованная плоская волна е
-ik-
волновыми числами соответственно кх и к2, причем
и
'1,2-
F.5.9)
Следует ожидать, что связь имеет место как между одинаково на-
направленными, так и между противоположно направленными мода-
модами, в зависимости от того, какой спектральный режим нас интере-
интересует. В обычных скрещенных фильтрах Шольца используется связь
одинаково направленных мод.
Разложим периодическую функцию /(г) в ряд Фурье:
cos т<п)
F.5.10)
Подставляя F.5.10) в F.5.7), получаем коэффициенты фурье-разло-
жения е1П для Де:
~?П/ ^ 'ч- !°1 О" I /A"COSW"). F.5.11)
0 0 0

208
Глава 6
Из F.4.26) и F.4.28) находим постоянную связи к между нормаль-
нормальными модами:
к =
? . „ /A — cosmir)
1 sin 2p -i i
/mr
F.5.12)
Заметим, что связь между четными модами {т — 2, 4, 6, ...) от-
отсутствует, поскольку ?,„ = 0.
Чтобы получить выражение для характеристик пропускания,
вспомним, что начальные условия при г = 0 записываются в виде
F.5.13)
Л2@) = 0,
где Л, — амплитуда х-поляризованной нормальной моды, а А2 —
амплитуда ^-поляризованной нормальной моды. Начальные усло-
условия определяются передним поляризатором, который пропускает
только х-поляризованный свет. Согласно F.4.30) и F.5.13), реше-
решение уравнений связанных мод F.4.27) записывается в виде
Ax{z) =
A2(z)
sz
F.5.14)
,-/(ДД/2)г/
Sin 5Z
где 5 определяется выражением s2 = к*к + (A/3/2J [см. F.4.31)], a
A/3 имеет вид
1,2,3,...
F.5.15)
На заднем поляризаторе (пропускающем ^-поляризованную волну)
при z = L амплитуда А, обращается в нуль. При этом коэффици-
коэффициент пропускания ^-поляризованного света дается выражением
sin25L F.5.16)
11 s2 '
Из этого выражения следует, что 100%-ный обмен энергией мод
имеет место при
Дув = о,
F.5.17)
Распространение электромагнитных волн в периодических средах
209
|k|L
F.5.18)
где L — длина фильтра. Заметим также, что полный обмен энерги-
энергией происходит периодически вдоль координаты z.
Мы предполагаем, что длина фильтра удовлетворяет условию
\к\Ь = тг/2 [(выражение F.5.18)], т. е. полный обмен энергией осу-
осуществляется лишь при А/3 = 0. При этом условии коэффициент
пропускания принимает вид
где
1 +
/A/3LV
I
211/2
F.5.19)
F.5.20)
Выражение F.5.19) аналогично E.3.18), выведенному с помощью
исчисления Джонса. Максимум пропускания имеет место при
А/3 = 0, что, согласно F.5.15), соответствует случаю, когда кри-
кристаллические пластинки являются полуволновыми (или составляют
нечетное число таких пластинок). Четный брэгговский порядок
(т = 0, 2, 4, ...) отвечает случаю, когда кристаллические пластинки
составляют полную волновую пластинку, которая не изменяет со-
состояние поляризации света. В этом случае связь между модами не
может существовать.
В соответствии с F.5.16) или F.5.14) при распространении волн
в периодической среде происходит обмен электромагнитной энерги-
энергией между связанными модами. На рис. 6.11 приведены зависимости
энергии мод в условиях фазового синхронизма (А/3 = 0) и при
А/3 Ф 0.
Периодическая среда фильтра Шольца может также приводить к
связи между противоположно направленными модами, что имеет
место, если выполняется следующее условие Брэгга:
/с, + к2 - 1и-д- =
F.5.21)
Это отражение света отличается от обычного брэгговского отраже-
отражения, описанного в разд. 6.3 и 6.6, и называется обменным брэггов-
ским отражением. Разница состоит в том, что при обменном брэг-
говском отражении изменение поляризации происходит одновре-
одновременно с отражением. При такой связи возникает обмен энергией
между двумя нормальными модами с различными состояниями по-
14-631

210
Глава 6
ДC>к
WWW
I/4, Ы12
л/wwv.
РИС. 6.11. Обмен энергией между двумя связанными модами в фильтре Шольца при
выполнении условия фазового синхронизма Л0 = 0 (а) и при Д/3 Ф 0 (б).
ляризации и различными фазовыми скоростями. Зонная структура
при таком виде связи отличается от обычной (прямой брэгговской
связи). При КЛ = ттг не обязательно должны быть запрещенные
зоны. Действительно, они могут находиться в любом месте в зоне
Бриллюэна [4].
6.6. ТЕОРИЯ СВЯЗАННЫХ МОД
ДЛЯ БРЭГГОВСКИХ ОТРАЖАТЕЛЕЙ
Применим теперь к брэгговским отражателям, описанным в
разд. 6.3, теорию связанных мод. Для простоты предположим, что
толщина всех слоев одинакова, а зависимость диэлектрической про-
проницаемости от z имеет вид
e(z)
I enn
;0я2>
епп
0я1>
< z < А,
F.6.1)
Распространение электромагнитных волн в периодических средах
2П
где
F.6.2)
В соответствии с F.4.1) эту диэлектрическую проницаемость мож-
можно разложить следующим образом:
e(z)
F.6.3)
здесь /(г) — периодическая функция прямоугольной формы F.5.8).
Нормальные моды невозмущенной среды представляют собой
плоские волны e~'kr с волновым числом, определяемым выражени-
выражением
F.6.4)
где п — (геометрически) усредненный показатель преломления сре-
среды. В соответствии с состоянием поляризации эти плоские волны
подразделяются на ТЕ- и ТМ-волны. Поскольку как возмущенная,
так и невозмущенная диэлектрические проницаемости являются
скалярными величинами, связи между ТЕ- и ТМ-волнами не су-
существует. Следовательно, связь между волнами может быть, толь-
только если они имеют одинаковые состояния поляризации. Это воз-
возможно лишь для случая противоположно направленных мод, по-
поскольку для одинаково направленных мод условие фазового син-
синхронизма вообще не выполняется [А/3 = /3, — /32 — тBтг/Л) =
= — апBтг/Л) Ф 0 для конечного Л].
Характер модовой связи как для ТЕ-, так и для ТМ-волн ана-
аналогичен. Единственное отличие состоит в том, что они имеют раз-
разные значения постоянной связи F.4.26). Пусть в — угол между вол-
волновым вектором к и осью z, а к' — волновой вектор отраженной
волны (рис. 6.12). В соответствии с F.4.26), F.5.10) и F.6.3) посто-
постоянные связи даются выражениями
/A -cosmv) U(n\-n2) (ТЕ-волна),
к = <
/A — cos/mr)
F.6.5)
-cos2в (ТМ-волна).

212
Глава 6
РИС. 6.12. Брэгговское отражение для внеосевых пучков света.
Следует заметить, что эти постоянные связи отличаются лишь на-
направляющим множителем cos 20, который равен косинусу угла
между векторами поляризации ТМ-волн. В соответствии с
F.6.5) для ТМ-волн при 0 = 45° постоянная связи обращается в
нуль. Это соответствует нулевому отражению ТМ-волн при угле
Брюстера (см. рис. 6.8, б). Действительно, при пг = «, вв =
= arctg(/i2//i,) «45°.
Величина фазового рассогласования Д/3 дается выражением
= 2kcos0 - m(-j^
F.6.6)
где Л — период слоистой структуры, а к — волновое число, опре-
определяемое выражением F.6.4). В соответствии с выражением F.6.5)
брэгговское отражение четных порядков отсутствует, поскольку
при т = 2, 4, 6, ... мы имеем к = 0. Это отвечает случаю, когда
толщина каждого слоя приблизительно составляет целое число
длин волн, что приводит к нулевому отражению.
Для того чтобы получить выражение для коэффициента отраже-
отражения, предположим, что для света, падающего при z — 0, выполня-
Распространение электромагнитных волн в периодических средах
213
ются следующие граничные условия:
A2(L)-0,
F.6.7)
где Л, — амплитуда падающей волны, &Аг — амплитуда отражен-
отраженной волны. Используя F.4.35) и F.6.7), получаем решение уравне-
уравнений связанных мод F.4.33):
A (z)
A2(z)
sL +
-iK*shs(L- z)
F.6.8)
schsL + i(bP/2)shsL
где s дается [так же, как и в F.4.36)] выражением s2 = к*к -
- (Д/3/2J, а А/3 — выражением F.6.6).
Коэффициент отражения брэгговского отражателя определяется
следующим образом:
R
Аг@)
МО)
В соответствии с F.6.8), его можно записать в виде
K*icsh2sL
s2ch2sL+ (&P/2Jsh2sL
Максимальное отражение имеет место при АC - 0:
К = th* \k\L.
F.6.9)
F.6.10)
F.6.11)
На рис. 6.13 построена зависимость вычисленных значений ко-
коэффициента отражения от A0L, откуда видно, что коэффициент от-
отражения является четной функцией величины А/3. Пусть ыт — ча-
частота, при которой удовлетворяется условие Брэгга F.6.6). Тогда
Д/3 можно записать в виде
Д/? = —(а) - wm)cos в.

РИС. 6.13. Коэффициент отражения от брэгговского зеркала, рассчитанный с по-
помощью теории связанных мод (\к\Ь = 2,0).
И, (ОН2
|Л2@>|2
\
\
\
\
\
\
\
\
Ч
р
Ч
ч
ч
ч
ч
ч.
ч
И, (ill2
Периодическая слоистая среда
РИС. 6.14. Интенсивности падающей н отраженной волн в периодической слоистой
среде при ДЗ = 0.
Распространение электромагнитных волн в периодических средах
215
Спектр состоит из основного пика с отчетливым максимумом и ря-
ряда побочных пиков. Ширина основного пика приблизительно равна
^ ' " F.6.12)
поскольку при А/3 = ± 21 к I параметр s обращается в нуль и коэф-
коэффициент отражения равен
R
к*кЬг
к*к
Ь2 '
F.6.13)
Коэффициент отражения F.6.13) обычно мал, поскольку в соот-
соответствии с F.6.11), чтобы получить большой коэффициент отраже-
отражения, должно выполняться условие \к\Ь > 1. Следовательно, выра-
выражение F.6.12) представляет собой хорошее приближение для шири-
ширины пика. Относительную ширину полосы Aw/w можно получить из
выражений F.6.5), F.6.6) и F.6.12):
А со
ы
\п% -л
n\
(ТЕ),
п\
{cos20 (TM),
т = 1,3,5,... .
F.6.14)
Эти выражения согласуются с F.2.34) для случая нормального па-
падения и т = 1, т. е. определенная в F.6.14) ширина полосы равна
размеру (в единицах а>) запрещенной зоны. Отсюда следует, что ча-
частоты, попадающие в запрещенную зону периодической среды, ко-
которые отвечают затухающим волнам, при падении на такую среду
испытывают значительное отражение.
В стороне от основного пика при А/3 = 0 спектр отражения так-
также состоит из ряда побочных максимумов по обе стороны от ос-
основного пика. Эти побочные пики имеют место приблизительно
при sL = Цр + 1/2)тг (р = 1, 2, 3, ...), что соответствует А/3 =
= ±2[к*к + (р + 1/2J(ж/ЬJ]1/2. В соответствии с F.6.10) макси-
максимальный коэффициент отражения для этих побочных пиков запи-
запишется в виде
R
F.6.15)
Эти побочные максимумы становятся существенными при \кЬ\ >
> тг/2. Действительно, при \kL\ — тг/2 максимальный коэффици-

216
Глава 6
ент отражения в первом побочном пике достигает 10%, в то время
как коэффициент отражения в основном пике в этой же точке со-
составляет лишь 84%. Коэффициент отражения обращается в нуль
при sL = iq-ir (q — I, 2, 3, ...), что соответствует А/3 = ±2(к*к +
+ (qir/LJy/2.
На рис. 6.14 построены графики для энергии мод l^4,(z)l2 и
\A2(z)\2 в этом случае. При достаточно больших аргументах гипер-
гиперболического косинуса и гиперболического синуса энергия падающей
моды экспоненциально затухает в области возмущения. Однако та-
такое поведение обусловлено не поглощением, а отражением энергии
в моду А2, распространяющуюся в обратном направлении, как по-
показано на рисунке.
Из выражений F.6.6) и F.6.8) нетрудно показать, что зависящая
от z часть волновых решений в периодической слоистой среде экс-
экспоненциально зависит от постоянной распространения
/
F.6.16)
Следует заметить, что в диапазоне частот, удовлетворяющих
условию \АC\ < 2\к\, величина А' имеет мнимую часть. Она отве-
отвечает так называемой запрещенной области, в которой волна зату-
затухает, как показано на рис. 6.14, и которая формально аналогична
энергетической щели в полупроводниках, где периодическое кри-
кристаллическое поле приводит к тому, что постоянные распростране-
распространения электронов становятся комплексными. Заметим, что для каж-
каждого значения т (т = 1, 2, 3, ...) существует запрещенная зона,
центральная частота w0 которой удовлетворяет условию kcos в =
= ттг/А. Исключение составляют значения т, для которых величи-
величина к равна нулю. Возвращаясь к выражению F.6.16) и используя
F.6.4) и F.6.6), имеем
F.6.17)
здесь центральная частота зоны и>0 равна значению частоты ш, при
котором ксоив = ттг/А (или АC = 0) и п = [{\/2)(п\ + и2)]172.
На рис. 6.15 изображены зависимости Re А" и ImA" от и> при
m = 1 и в = 0, вычисленные с помощью F.6.17). Заметим, что ши-
ширина запрещенной зоны частот равна
(A")gaP = у|*|, F,6.18)
Распространение электромагнитных волн в периодических средах
217
1,06
1,04
0,96
0,94
I I I Г
0,95
10 X К,
_L I I I I I I I I I I I I I I I I
1,00
1,05
К
1,10
1,15
1,20
РИС. 6.15. Дисперсионная кривая (зависимость ш от К) для периодической среды
при п{ = 3,4, п2 = 3,6 и а = Ь = 0,5Л. Эта зависимость получена расчетом по фор-
формуле F.6.17) из теории связанных мод или по точной формуле F.2.26). ш измеряется
в единицах ст/пЛ, а К — в единицах ж/Л.
где Ы в соответствии с F.6.5) является функцией порядка т. Из
выражения F.6.16) следует, что
|к| = коэффициент связи.
F.6.19)
Таким образом, при частотах вблизи брэгговского значения ш0 ко-
короткий отрезок периодической среды действует как зеркало с высо-
высоким коэффициентом отражения.
На рис. 6.15 представлена также дисперсионная зависимость
ы{К), вычисленная с помощью формализма блоховских волн. Сле-
Следует заметить, что теория связанных мод согласуется с формализ-
формализмом блоховских волн.
6.7. ФАЗОВАЯ СКОРОСТЬ, ГРУППОВАЯ СКОРОСТЬ
И СКОРОСТЬ ПЕРЕНОСА ЭНЕРГИИ
Выше мы получили некоторые важные характеристики электромаг-
электромагнитного излучения, распространяющегося в периодической слои-
слоистой среде. Мы нашли явное выражение для матрицы трансляции
на элементарную ячейку в периодической слоистой среде. При диа-

218
Глава 6
гонализации этой матрицы трансляции на элементарную ячейку
была получена зонная структура.
Понятия фазовой и групповой скоростей, а также скорости пере-
переноса энергии в периодической слоистой среде являются весьма тон-
тонкими и требуют внимательного анализа. Электромагнитные бло-
ховские волны определяются выражением F.2.25), а дисперсионное
уравнение, связывающее ку, К и со, можно получить из F.2.24).
Важно иметь в виду, что блоховское волновое число К определяет-
определяется выражением F.2.24) не однозначно, а с точностью до произволь-
произвольного целого числа, умноженного на 2тг/Л. Обычно используемая в
физике твердого тела схема приведения к зоне Бриллюэна неприме-
неприменима при рассмотрении фазовой скорости электромагнитной бло-
ховской волны. Если EK(z) разлагается в ряд Фурье
то блоховскую волну можно представить в виде линейной суперпо-
суперпозиции бесконечного числа элементарных плоских волн, называемых
пространственными гармониками. Из выражений F.2.25) и F.7.1)
имеем
Е =
F.7.2)
где ер — постоянные векторы. Таким образом, многозначная при-
природа блоховского волнового числа заключает в себе существование
полного набора пространственных гармоник. Если периодичность
отсутствует (т. е. и, = п2), то блоховская волна должна переходить
в регулярную плоскую волну, а К должен быть равен kz — z-coc-
тавляющей волнового вектора.
Главное значение К определяется таким образом, чтобы
|ef I > |e#>| F.7.3)
для любых / или, что эквивалентно, путем выбора такого К, чтобы
интеграл
F.7.4)
имел максимальную величину. Это гарантирует то, что при исчез-
исчезновении периодичности выживут лишь пространственные гармони-
гармоники е#> и К = kz.
Распространение злек грома! ни [ пых волн в периодических средах
219
Соответствующий выбор блоховского волнового числа К позво-
позволяет теперь определить фазовую скорость блоховской волны
V =
ур
\1/2
F.7.5)
В случае когда величина К комплексна, следует использовать лишь
вещественную ее часть.
Определенная выше фазовая скорость представляет собой, стро-
строго говоря, фазовую скорость основной пространственной гармони-
гармоники (/ = 0), которая имеет вид плоской волны
Е = (EK)e'(a'-k^~Kz\
F.7.6)
В длинноволновом режиме распространения, когда вся структура
ведет себя так, как будто она однородна, основная пространствен-
пространственная гармоника вносит преобладающий вклад в блоховскую волну и
может рассматриваться в качестве очень хорошего приближения
общей волны.
Групповая скорость блоховского волнового пакета, распростра-
распространяющегося в плоскости yz, дается выражением
V =
<?со
Ж
У I К
/к,.
F.7.7)
В однородной среде групповая скорость представляет собой ско-
скорость переноса энергии квазимонохроматической волны и, следова-
следовательно, параллельна вектору Пойнтинга, который в однородной
среде без потерь является постоянным. Вектор Пойнтинга блохов-
блоховской волны, определяемый выражением F.2.25), является периоди-
периодической функцией координаты z. Однако групповая скорость F.7.7)
той же самой волны является постоянным вектором. Противоречие
обусловлено тем, что в периодической среде поток энергии есть пе-
периодическая функция пространственных координат. Тем не менее
мы покажем, что средняя скорость переноса энергии, определяемая
выражением
1
Л J
(Вектор Пойнтинга) dz
V —
(Плотность энергии) dz
F.7.8)

220
Глава 6
в точности равна групповой скорости, определяемой выражением
F.7.7). Это весьма полезный результат, поскольку он позволяет
объяснить распространение локализованных пучков с конечной
апертурой в слоистой среде. Усредненные по пространственным ко-
координатам вектор Пойнтинга и плотность переноса энергии особен-
особенно полезны при рассмотрении длинноволнового режима распро-
распространения, когда среду можно рассматривать как квазиоднородную
и анизотропную.
Чтобы доказать, что скорость переноса энергии F.7.8) и группо-
групповая скорость F.7.7) в случае периодических слоистых сред равны
друг другу, мы можем воспользоваться результатами, полученны-
полученными в разд. 6.2, а также выполнить дифференцирование в F.7.7) и
интегрирование в F.7.8). Интересно показать, что это равенство
справедливо в произвольной периодической среде, в том числе и в
среде с периодическим двулучепреломлением при условии, что от-
отсутствуют потери. Тензоры электромагнитной восприимчивости
вследствие наличия у среды трансляционной симметрии являются
периодическими функциями координаты х:
е„(х) = в„(х + а), м,,(х) = м„(х + а), F.7.9)
где а — произвольный вектор решетки. Распространение электро-
электромагнитных волн описывается уравнениями Максвелла
V X Н = iueE,
V X Е =
F.7.10)
F.7.11)
где временная зависимость предполагается в виде е'"*.
Вследствие трансляционной симметрии среды [и(или) теоремы
Флоке; см. выражения F.1.4) и F.1.5)] будем предполагать, что
волна является блоховской:
Е-Ек(х)в-*'«, F7Л2)
Н = Нк(х)е <**, F.7ЛЗ)
где Ек(х) и Нк(х) — периодические функции:
Ек(х) = Ек(х + а), Нк(х) = Нк(х + а). F.7.14)
Нижний индекс К указывает на то, что функции Ек и Нк зависят
от блоховского волнового вектора К. Между К и ы существует дис-
Распространение электромагнитных волн в периодических средах
221
персионная зависимость
w = со(К).
F.7.15)
Усредненный по времени поток энергии электромагнитного поля
дается выражением
S=iRe[ExH*], F.7.16)
а усредненная по времени плотность электромагнитной энергии
равна
U= ЯЕ-еЕ* + H-(itH*]. F.7.17)
Тензоры электромагнитной восприимчивости предполагаются ве-
вещественными. В случае блоховских волн, распространяющихся в
периодической структуре, величины S и U являются функциями, пе-
периодическими в пространстве.
Определим скорость переноса энергии следующим образом:
V =
F.7.18)
где интегрирование ведется по элементарной ячейке, а V — объем
этой ячейки. Подставляя- выражения F.7.12) и F.7.13) в F.7.16) и
F.7.17), из F.7.18) получаем
V =
F.7.19)
где скобками < > обозначено усреднение по элементарной ячейке.
Групповая скорость V;,, определяемая как
F.7.20)
представляет собой вектор, перпендикулярный поверхности волно-
волновых нормалей. Подставляя блохокжие волны F.7.12) и F.7.13) в
уравнения Максвелла F.7.10) и F.7.11), имеем
V X Нк - /К X Нк = iweEK,
V X Ек - /К X Ек = -iwfiHK.
F.7.21)
F.7.22)

222
Глава 6
Чтобы показать, что Ye и Vg равны друг другу, будем исходить из
уравнений F.7.21) и F.7.22). Предположим, что К изменяется на
бесконечно малую величину 5К. Тогда если 5со, 5ЕК и 5НК являются
соответствующими изменениями величин со, Ек и Нк, то после ря-
ряда алгебраических преобразований (см. [4]) получаем
8и> = V, • 5К. F.7.23а)
Из определения групповой скорости мы также имеем
5ы = (VK«)*SK = Vg-5K. F.7.236)
Поскольку <5К — произвольный вектор, мы заключаем, что
V, = V,. F.7.24)
6.8. ДВУЛУЧЕПРЕЛОМЛЕНИЕ ЗА СЧЕТ ФОРМЫ
В предыдущих разделах мы рассмотрели некоторые наиболее важ-
важные характеристики блоховских волн, распространяющихся в пери-
периодической слоистой среде. Было получено точное выражение
F.2.24) для дисперсионной зависимости между величинами К, ку и
со. На рис. 6.16 эта дисперсионная зависимость представлена графи-
графически в виде контуров постоянной частоты в плоскости куК. Мож-
Можно показать, что эти контуры более или менее похожи на окружно-
окружности и имеют лишь небольшую эллиптичность. Начало координат
отвечает контуру с нулевой частотой. В длинноволновой области
(X > А) они аналогичны дисперсионным кривым для электромаг-
электромагнитных волн, распространяющихся в отрицательных одноосных
кристаллах. Рассмотрим теперь двулучепреломляющие свойства пе-
периодической слоистой среды. Для более коротких длин волн и око-
около границ зоны Бриллюэна (К А = тж), где длина волны сравнима
с размером элементарной ячейки, эти контуры начинают возму-
возмущаться и электромагнитные волны сильно взаимодействуют с пе-
периодической средой.
Рассмотрим теперь распространение электромагнитных волн в
бесконечной среде, состоящей из чередующихся слоев двух различ-
различных однородных и изотропных веществ. Хотя каждый отдельный
слой изотропный, структура в целом ведет себя как анизотропная
среда. Оказывается, что ТЕ- и ТМ-волны распространяются с раз-
разными эффективными фазовыми скоростями и периодическая среда
является двулучепреломляющей.
Если период Л достаточно мал по сравнению с длиной волны,
то структура в целом ведет себя так, как если бы она была одно-
Распросгранение электромагнитных волн в периодических среда>
22.1
РИС. 6.16. Контуры постоянной частоты в плоскости к К.
родной и одноосно анизотропной. При этом волна, определяемая
выражением F.2.25), ведет себя как плоская волна F.7.6).
Изображенные на рис. 6.16 контуры постоянной частоты со в
плоскости Кку представляют собой сечения нормальных поверхно-
поверхностей плоскостью Kkv при различных частотах. Из анализа этих кри-
кривых очевидно, что в длинноволновом пределе (X > Л) дисперсия
слоистой среды качественно аналогична дисперсии отрицательного
одноосного кристалла.
Чтобы продемонстрировать эту аналогию, рассмотрим предель-
предельный случай, когда киа < 1, kbb < \ и К А < 1, и разложим в ряд
все трансцендентные функции в F.2.24). После пренебрежения чле-
членами высшего порядка получаем
к
El
(ТЕ),
(TM),
F.8.1)
F.8.2)

224
Глава 6
причем
а
F.8.3)
Л „?
b_J_
Л „?
F.8.4)
Уравнения F.8.1) и F.8.2) описывают две оболочки нормальной по-
поверхности в плоскости Кку. Одна поверхность F.8.1) относится к
ТЕ-волне и представляет собой сферу, а другая нормальная поверх-
поверхность F.8.2) отвечает ТМ-волне и является эллипсоидом вращения.
Таким образом, ТЕ-волны формально аналогичны так называемым
обыкновенным волнам в одноосном кристалле, а ТМ-волны — не-
необыкновенным волнам. При более высоких частотах нормальная
поверхность имеет более сложную форму. Она состоит из двух
овальных поверхностей, соприкасающихся друг с другом при пере-
пересечении с осью К, когда частота попадает в область ниже первой
запрещенной зоны. Для частот, лежащих выше запрещенной зоны,
овальные поверхности разрываются на несколько участков. Точки,
в которых происходит разрыв, имеют место при условии
К = т-г, т — целое число.
F.8.5)
Это брэгговское условие для квазиплоской волны F.7.6).
Уравнения F.8.3) и F.8.4) играют очень важную роль в оптичес-
оптической теории дихроичных поляризаторов и при синтезе отрицатель-
отрицательных одноосных кристаллов с определенными свойствами. Чтобы
это проиллюстрировать, рассмотрим периодическую слоистую сре-
среду, которая состоит из чередующихся металлических и диэлектри-
диэлектрических слоев. Пусть и, — комплексный показатель преломления ме-
металлического слоя, а п2 — показатель преломления диэлектрическо-
диэлектрического слоя. Если металл является хорошим проводником, то 1/7,12 >
> п\. Таким образом, в соответствии с F.8.3) и F.8.4) обыкновен-
обыкновенный и необыкновенный показатели преломления для длинноволно-
длинноволнового света (X > А) принимают вид
1/2
-1/2
F.8.6)
Мы видим, что обыкновенный показатель преломления по аналоги-
Распространение электромагнитных волн в периодических средах
225
J,Ub
0,05
0,04
\
V
-
\
к
0,9
1,0
X, мкм
РИС. 6.17. Экспериментальная и теоретическая зависимости величины двулучепре-
ломления (яТЕ - ятм) в слоистой среде GaAs—AlAs. Точки отвечают измеренным
значениям двулучепреломления, а штриховая кривая получена расчетом по форму-
формулам F.8.3) и F.8.4). Сплошная кривая — зависимость, вычисленная по формуле
F.2.24) с учетом членов, пропорциональных к2, для GaAs и AlQ97Ga003As [5].
чен показателю преломления металла, а необыкновенный показа-
показатель преломления пе — показателю преломления диэлектрика. Сле-
Следовательно, обыкновенная волна (ТЕ) будет отражаться, как если
бы среда была металлической, в то время как необыкновенная вол-
волна (ТМ) будет проходить. С физической точки зрения векторы
электрического поля ТЕ-волн параллельны слоям и индуцируют то-
токи в металлических слоях, в то время как у ТМ-волн векторы
электрического поля перпендикулярны слоям. Поскольку металли-
металлические слои разделены диэлектрическими изолирующими слоями,
ток в этом случае не наводится.
Двулучепреломление за счет формы наблюдалось в периодичес-
периодической слоистой среде, состоящей из слоев AlAs толщиной 0,1235 мкм
и слоев GaAs толщиной 0,1062 мкм, выращенных методом эпитак-
сии из молекулярных пучков [5]. На рис. 6.17 показано измеренное
двулучепреломление пТЕ — птм в зависимости от длины волны.
6.9. ЭЛЕКТРОМАГНИТНЫЕ ПОВЕРХНОСТНЫЕ ВОЛНЫ
Цель данного раздела состоит в том, чтобы изучить затухающие
блоховские поверхностные волны, направляемые границей полубе-
15-631

226
Глава 6
сконечной периодической диэлектрической слоистой среды. Поверх-
Поверхностная волна по определению представляет собой распространяю-
распространяющуюся моду, которая локализована в непосредственной окрестно-
окрестности границы раздела между двумя полубесконечными системами.
Например, явление ряби на воде представляет собой поверхностные
волны, направляемые границей раздела между воздухом и водой.
Другая интересная разновидность поверхностных волн — это элек-
электронные поверхностные состояния, которые широко изучались в
физике твердого тела. В гл. 11 мы рассмотрим электромагнитные
поверхностные волны на границе раздела между диэлектриком и
металлом. Существование локализованных мод («поверхностных
состояний») около границы раздела между слоистой и однородной
средами было обнаружено Косселем [6]. В данном разделе зонная
теория периодических диэлектрических сред используется для изуче-
изучения поверхностных волн, волновые числа которых попадают в за-
запрещенную зону.
Сам факт существования таких поверхностных волн можно объ-
объяснить следующим образом. В разд. 6.2 мы показали, что для за-
заданной частоты существуют области ку, для которых величина К
комплексная, причем К — тж/А ± iKr Внутри бесконечной перио-
периодической среды волна с экспоненциальным изменением интенсивно-
интенсивности не может существовать, и мы называем эти области запрещен-
запрещенными зонами. Если периодическая среда является полубесконечной,
то экспоненциально затухающая волна может быть вполне закон-
законным решением в окрестности границы раздела, где его амплитуда
может иметь конечную величину. Огибающая поля внутри перио-
периодической среды убывает как е 'z, где z — расстояние от границы
раздела в глубь периодической среды. Она также экспоненциально
затухает по мере проникновения в полубесконечную однородную
среду при условии, что ску/ш > пи.
Для исследования свойств поверхностных мод рассмотрим полу-
полубесконечную периодическую многослойную диэлектрическую среду,
состоящую из чередующихся слоев с различными показателями
преломления. Пусть распределение показателя преломления имеет
вид
("a.
n(y,z) = ln2,
mA < z < тЛ + Ь,
пх, гаА + Ъ < z < (т + 1)Л
= 0,1,2,...).
F.9.1)
Распространение элек громагни гных волн в периодических средах
Воадт щк fkpuodut/есная слоистая
1 среда
РИС. 6.18. Полубесконечная периодическая слоистая среда.
Геометрия этой структуры изображена на рис. 6.18. Будем искать
локализованные волны, которые могут распространяться в поло-
положительном направлении оси у. Поскольку структура является полу-
полубесконечной, нас будут интересовать только направляемые поверх-
поверхностные волны. Ради определенности мы рассматриваем случай
поверхностных ТЕ-мод, электрическое поле которых направлено
вдоль оси х. Распределение электрического поля (ТЕ) подчиняется
волновому уравнению F.4.8). Будем искать его решение в следую-
следующем виде:
ае
<°ге-'к>>,
г < 0,
z>0,
где а — постоянная, величина qu дается выражением
1/2
|,2 I ш 1
-'74/ '
F.9.2)
F.9.3)
a EK(z)e~'Kz — блоховская волна, определяемая выражением
F.2.25).
Для существования направляемой волны постоянная К в выра-
выражении F.9.2) должна быть комплексной величиной, причем поле
должно обращаться в нуль при z — °°. Это возможно только в слу-

228
Глава 6
чае, когда постоянная распространения (ку) в периодической среде
соответствует запрещенной зоне. Другое условие состоит в том,
чтобы поле Е(х, у) и его производная dE/dz были непрерывны на
границе раздела z = 0 со средой а. Используя выражение F.9.25) и
явное выражение для блоховской волны F.2.25) при п = О, гранич-
граничные условия на границе раздела z = 0 можно записать в виде
а = а
о + Ьо,
F.9.4)
qaa = -ikl2(a0 - b0),
где а0 и Ьо определяются выражением F.2.23а). Исключая из F.9.4)
величину а и используя F.2.23а), получаем модовое условие для по-
поверхностных волн:
A + В - eiKA
Ча~1киА-В-е^
F.9.5)
где Л и В даются выражением F.2.12) для ТЕ-волн, а экспонента
е'КА определяется выражением F.2.22). Знак величины К выбран та-
таким образом, чтобы ее мнимая часть была отрицательной. При
этом в соответствии с F.9.2) амплитуда поля экспоненциально
убывает с увеличением z. Используя выражения F.2.12), F.2.24),
F.2.6) и F.9.3), можно показать, что для данной частоты со обе ча-
части выражения F.9.5) зависят от ку. Удовлетворяющие условию
F.9.5) значения ку, для которых К является комплексной величи-
величиной, отвечают поверхностным волнам.
На рис. 6.19 приведены расчетные поперечные распределения
поля ?¦((), z) для некоторых типичных поверхностных волн. Очевид-
Очевидно, что энергия более или менее сконцентрирована в первых не-
нескольких периодах полубесконечной периодической среды.Нетруд-
среды.Нетрудно показать, что
Энергия в первом периоде
Энергия во всей полубесконеч. периодич. структуре
—- = A -
F.9.6)
где Kj > 0 — мнимая часть величины К. Вообще говоря, фундамен-
фундаментальная поверхностная волна имеет наибольшие значения Kt и, сле-
следовательно, наивысшую степень локализации. Может оказаться
так, что фундаментальная поверхностная волна отвечает нулевой
или первой запрещенной зоне. Это зависит от величины показателя
преломления п Если па < п.
случаи, который представляет
РИС. 6.19. Поперечное распределение поля для типичных поверхностных мод, на-
направляемых поверхностью полубесконечной периодической стратифицированной сре-
среды [2]. а — основная мода; б — мода высшего порядка.

Периодическая слоистая среда
РИС. 6.20. Расчетное поперечное распределение интенсивности основной поверхно-
поверхностной моды в периодической слоистой среде. Пунктирная кривая — распределение
интенсивности, отвечающее свертке [7].
пни
Периодическая слоистая среда
РИС. 6.21. Фото участка слоистой среды, состоящей из чередующихся слоев GaAs и
AldjGapjjAs, полученное методом фазового контраста [7].
Распространение электромагнитных волн в периодических сред:
231
практический интерес {пи — показатель преломления воздуха), то у
фундаментальной поверхностной волны блоховский волновой век-
вектор находится в первой запрещенной зоне.
Распределение поля в каждом периоде для любой моды анало-
аналогично распределению поля в предыдущем периоде с той лишь раз-
разницей, что амплитуда умножается на величину (— \)'"е '' , где т —
целое число, соответствующее т-п запрещенной зоне.
Электромагнитные поверхностные волны наблюдались в перио-
периодической слоистой структуре, состоящей из 12 пар чередующихся
слоев Al02Ga08As толщиной 0,5 мкм на подложке из GaAs [7, 8].
При этих условиях для длины волны 1,15 мкм из модового условия
F.9.5) следует, что структура может направлять четыре поверх-
поверхностные волны. Вообще говоря, при пи < пх < пг максимальное
число поверхностных волн на данной частоте со равно пг, причем
пгж < Re[K(w, kv = паи>/с)\] < (т + 1Oг. На рис. 6.20 показано
поперечное распределение интенсивности фундаментальной моды.
Расчетное значение блоховского волнового числа равно
КА = it + /G.233 X КГ1)
при к = 3.357 Bтг/Х).
F.9.7)
РИС. 6.22. Измеренное поперечное распределение интенсивности поверхностной вол-
волны в слоистой среде длиной 15 мм. Горизонтальный масштаб соответствует
0,5 мкм на большое деление. Поверхность структуры отмечена стрелкой [7].

232
Глава 6
На рис.6.21 представлено фото поперечного сечения слоистой
структуры, полученное методом фазового контраста", а на
рис. 6.22 показано измеренное распределение интенсивности фунда-
фундаментальной поверхностной волны.
ЗАДАЧИ
6.1
Запрещенные зоны в одномерных периодических средах.
Пусть электромагнитное излучение распространяется в одно-
одномерной периодической среде с диэлектрической проницаемос-
проницаемостью
e(z) =
Л),
причем ось z совпадает с направлением распространения
электромагнитной волны.
а) Покажите, что конструктивная интерференция при отра-
отражении света имеет место, когда выполняется условие
Брэгга
которое можно также записать в виде \к - mg\ = к.
Физически это означает, что пространственные гармони-
гармоники к и к — mg резонансно связаны.
б) Предполагая, что свет падает теперь под углом в, пока-
покажите, что условие Брэгга Д/3 = 0 согласуется с выраже-
выражением F.1.8).
в) Пусть соо — центр запрещенной зоны; покажите, что
где g - 2тг/Л.
г) Пусть Kj — мнимая часть волнового числа в запрещен-
запрещенной зоне, так что
' Или теневым методом. — Прим. перев.
Распространение электромагнитных волн в периодических средах
233
Покажите, что связь между Л", и со дается выражением
2 En
Заметьте, что это выражение описывает эллипсоид с
центром со = со0 и К{¦ = 0.
д) С помощью выражений, приведенных в п. г, покажите,
что ширина запрещенной зоны дается выражением
Чар =
ио >
а максимальное значение Kt равно
(^i)max ~ 4
6.2. Полуволновая среда. Среда, в которой пространственный
период изменения диэлектрической проницаемости (показа-
(показателя преломления) равен половине полного периода, называ-
называется полуволновой средой. Иными словами, профиль показа-
показателя преломления такой среды дается выражением
п(г)
п2, 0<z<±A,
л„ jA < z < А,
причем
n(z + А) = n(z).
а) Пусть/(г) определена следующим образом:
причем/(г + Л) = /(г). Покажите, что
б) Покажите, что фурье-разложение функции/(г) имеет вид
tl \ V^ '0 ~ COS/w) Г ,27Г 1
]\z)— 2-, ', ехр—/7-7-2 .
, /w LAI

234
Глава 6
в) Покажите, что ширина первой запрещенной зоны (/ = 1)
для этой среды дается выражением
Да),
gap
6.3. Матричные элементы.
а) Получите выражения F.2.12) для матричных элементов
А, В, C,D.
б) Получите выражения F.2.14).
6.4. Елоховские волновые числа.
а) Выведите уравнение F.2.21).
б) Найдите решения F.2.22)—F.2.24).
в) Получите явные выражения для cosATA, используя мат-
матричные элементы F.2.12) и F.2.14) для ТЕ- и ТМ-волн и
дисперсионное уравнение F.2.24).
г) Покажите, что в случае нормального падения (kv = 0)
выражения, полученные в п. в, сводятся к F.2.26).
д) Покажите, что для волны, падающей под углом Брюсте-
ра \ку = (ш/с)п2 sinвв], блоховское волновое число всегда
вещественное. [Указание: В = С = 0, AD = 1.]
6.5. Четвертьволновый массив. Пусть имеется периодическая
слоистая структура, состоящая из двух чередующихся ди-
диэлектрических сред, профиль показателя преломления кото-
которой определяется выражением F.2.1).
а) Используя выражения, полученные в задаче 6.4 (п. в),
покажите, что максимум величины I cosATA I достигается
при
= j
i-ш 5„
Слоистая структура, удовлетворяющая этим условиям,
называется четвертьволновым массивом.
б) Получите выражения для максимальных значений cosATA
как для ТЕ-, так и для ТМ-волн.
в) Покажите, что при нормальном падении эти выражения
сводятся к F.2.29).
Распространенно j.ick громапш гны\ ноли в нсрно.шчсскнч срела\
235
г) Покажите, что амплитуда затухающей блоховской вол-
волны при нормальном падении на четвертьволновый мас-
массив уменьшается в п2/п} раз на каждом периоде (поло-
(положите я, < п2).
6.6. Сохранение энергии мод.
а) Покажите, что уравнения связи одинаково направленных
волн F.4.27) совпадают с условием сохранения энергии
F.4.29).
б) Покажите, что общее решение [выражения F.4.30)] это-
этого уравнения также подчиняется условию сохранения
энергии F.4.29).
в) Покажите, что уравнения связи противоположно направ-
направленных волн F.4.33) совпадают с условием сохранения
энергии F.4.34).
г) Покажите, что общее решение [выражения F.4.35)] так-
также согласуется с F.4.34).
6.7. Вращение кристаллической пластинки. Пусть ф — азиму-
азимутальный угол кристаллической волновой пластинки.
а) Покажите, что диэлектрический тензор определяется вы-
выражениями F.5.4) и F.5.6).
б) Докажите, что диэлектрический тензор является симмет-
симметричным.
в) Докажите, что след диэлектрического тензора остается
неизменным.
г) Покажите, что если угол у/ мал (т. е. ф <? 1), то возму-
возмущение диэлектрической проницаемости существенно
лишь для недиагональных членов.
6.8. Светофильтры Шольца.
а) Покажите, что F.5.19) эквивалентно E.3.18).
б) Покажите, что полоса пропускания фильтра Шольца об-
обратно пропорциональна длине периодической структуры.
6.9.
Брэгговские отражатели.
а) Выведите выражения для постоянных связи как для ТЕ-,
так и для ТМ-волн [выражения F.6.5)].
б) Покажите, что ширина полосы брэгговского отражателя
не зависит от длины структуры L.
Покажите, что коэффициент отражения при 5 = 0 коне-
в)
чен (т. е. Д/3 = 21 к I).
г) Покажите, что первый нуль коэффициента отражения

236
Глава 6
имеет место при sL = iir. Чему равна величина A(J в-
этой точке?
6.10. Коэффициент пропускания брэгговского отражателя опреде-
определяется следующим образом:
а) Покажите, что
1
*N
JN-2
б) Коэффициент пропускания энергии Т дается выражением
T=\tN\2-
Покажите, что
1
Т =
i+KT-
2 sin2NKA
Заметьте, что А * = D и \С\2 = \А\2 - 1.
в) Выведите F.3.6), используя соотношение R = 1 - Т.
6.11. Формулы для коэффициента отражения F.3.6) и для коэффи-
коэффициента пропускания, приведенные в задаче 6.10, справедли-
справедливы, только если свет падает из среды с показателем прелом-
преломления л,. Покажите, что если свет падает из среды с показа-
показателем преломления пи (для воздуха па = 1), то коэффициент
отражения записывается в виде
г А- г
где rs определяется выражением F.3.5), a rai — коэффициент
отражения света, падающего из среды с показателем пре-
преломления па на среду с показателем преломления пу Для
случая нормального падения
'а\
Распространение электромагнитных волн в периодических средах
237
[Указание: используйте формулу Эйри", предполагая, что
бесконечно тонкий слой с показателем преломления я, рас-
расположен между средой с показателем преломления па и брэг-
говским отражателем.]
ЛИТЕРАТУРА
1. См., например, Abeles F., Investigations on the propagation of sinusoidal elec-
electromagnetic waves in stratified media. Application to thin films. — Ann. Phys.
(Paris), 5, 596 A950); Investigations on the propagation of sinusoidal electromagnetic
waves in stratified media. Application to lhin films. II. Thin films. — Ann. Phys.
(Paris), 5, 706 A950).
2. Yeh P., YarivA., Hong C.S., Electromagnetic propagation in periodic stratified
media. I. General theory.— J. Opt. Soc. Amer., 67, 423—437 A977); YarivA.,
Yell P., II. Birefringence, phase matching, and X-ray lasers. — J. Opt. Soc. Amer.,
61, 438—448 A977).
3. Van der Ziel J. P., Illegems M., Multilayer GaAs—A1Q 3Ga0 7 dielectric quarter wave
stacks grown by molecular beam eptitaxy. — Appl. Opt., Й, 2627 A975).
4. Yeh P., Electromagnetic propagation in birefringem layered media. — J. Opt. Soc.
Amer., 69, 742 A979).
5. Van der Ziel J. P., /llegemsM., Mikulyak R. M., Optical birefringence of thin
GaAs—AlAs multilayer films. — Appl. Phys. Lett., 28, 735 A976).
6. Kossel D.,, Analogies between ihin-films optics and electron-band theory of
solids. — J. Opt. Soc. Amer., 56, 1434 A966).
7. Yeh P., YarivA., Clio A. Y., Optical surface waves in periodic layered media. —
Appl. Phys. Lett., 32, 104 A978).
8. Ng W., Yeh P., Chen P., YarivA., Optical surface waves in periodic layered
medium grown by liquid phase epitaxy. — Appl. Phys. Leu., 32, 370 A978).
9. Born M., WolfE., Principles of Optics.— New York: MacMillan, 1964, p. 62.
[Имеется перевод: Борн М., Вольф Э. Основы оптики. — М.: Наука, 1970.]
" Формулы Эйри для коэффициентов отражения и пропускания записываются в
виде [9]
I =
rl2r2ie
- 2|ф '
2 7гл ,f cos в7

Глава 7
ЭЛЕКТРООПТИКА
В гл. 4 мы исследовали распространение электромагнитного излу-
излучения в анизотропных кристаллических средах. Было показано, что
нормальные моды распространения можно определить из эллипсо-
эллипсоида показателей преломления. В данной главе мы рассмотрим рас-
распространение оптического излучения в кристаллах при наличии
внешнего электрического поля. Будет показано, что в некоторых
типах кристаллов внешнее электрическое поле приводит к измене-
изменению как размеров, так и ориентации осей эллипсоида показателей
преломления. Это явление называется электрооптическим эффек-
эффектом. Электрооптический эффект представляет собой удобный и ши-
широко используемый способ управления фазой и интенсивностью оп-
оптического излучения. Такая модуляция находит многочисленные
применения в различных устройствах, например для кодирования
информации в оптических лучах, дефлекторах оптических пучков и
спектральных перестраиваемых фильтрах. Некоторые из этих при-
применений мы обсудим в следующей главе.
7.1. ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ
Распространение оптического излучения в кристалле полностью
определяется тензором непроницаемости тц D.3.2). Напомним, что
г\ = СцЕ. Два направления поляризации и соответствующие пока-
показатели преломления (т. е. скорости распространения) нормальных
мод проще всего найти с помощью эллипсоида показателей пре-
преломления D.3.9). Эллипсоид показателей преломления наиболее
просто записывается в системе главных координат:
х2 у2 z2 _
l 2
G.1.1)
где х, у и z — главные оси, т. е. направления в кристалле, вдоль
которых векторы D и Е параллельны друг другу. Величины \/п\,
\/п\ и \/п2 представляют собой главные значения тензора непрони-
непроницаемости 1\ц.
Согласно квантовой теории твердых тел, оптический тензор ди-
Элсктрооп шка
239
электрической непроницаемости зависит от распределения зарядов
в кристалле. Наложение электрического поля будет приводить к пе-
перераспределению связанных зарядов и, возможно, к небольшой де-
деформации ионной решетки, что в свою очередь приведет к измене-
изменению оптического тензора непроницаемости. В этом и состоит суть
электрооптического эффекта. Электрооптические коэффициенты
традиционно определяются следующим образом:
Ч/у
= riJkEk + sijklEkE,=
= Jtjkrk + Sijkinfn G.1.2)
где Е — приложенное электрическое поле, а Р — вектор поляриза-
поляризации. Коэффициенты rjJk nfljk называются линейными электроопти-
электрооптическими постоянными (постоянными Поккельса), а коэффициенты
sijki и Sjjki — квадратичными электрооптическими постоянными (по-
(постоянными Керра). В приведенном выше выражении мы пренебре-
пренебрегли членами выше квадратичных, поскольку эти эффекты высшего
порядка для большинства применений оказываются слишком ма-
малыми. Квадратичный эффект впервые был открыт Керром в
1875 г. при исследовании таких оптически изотропных сред, как
жидкости и стекла. Электрооптический эффект Керра в жидкостях
обусловлен главным образом направленной ориентацией анизомет-
анизометрических молекул во внешнем электрическом поле. При этом веще-
вещество оптически ведет себя так, словно является одноосным кри-
кристаллом, в котором оптическая ось определяется электрическим по-
полем. Линейный электрооптический эффект был впервые изучен
Поккельсом в 1893 г.
На протяжении всей нашей книги мы будем использовать элек-
электрооптические коэффициенты г^к и stjkl. Некоторые авторы пользу-
пользуются также коэффициентами/^. ngikl. Величины rljk связаны cfljk,
a siJkl с g kl следующими соотношениями:
Jiik ~
Sijkl
~ ео)(е, - ?0) '
G.1.3)
G.1.4)
где Ек и ?/ — главные оптические диэлектрические проницаемости.
Таким образом, эллипсоид показателей преломления кристалла при

240
Глава 7
наличии внешнего электрического поля можно записать в виде
т},7(Е)х,х7= 1. G.1.5)
В случае когда электрическое поле обращается в нуль, эллипсоид
показателей преломления принимает вид G.1.1). В разд. 4.1 мы по-
показали, что в оптически неактивной среде без потерь диэлектриче-
диэлектрический тензор е/у является симметричным. Согласно определению
D.3.2) для rjjj, можно заключить, что в такой среде должен быть
симметричным также и тензор ^. Следовательно, нижние индексы
/ и у в G.1.2) можно поменять местами. В соответствии с G.1.2)
квадратичный электрооптический коэффициент определяется выра-
выражением
sijkl
д2,
1
2 дЕк дЕ,
G.1.6)
Поскольку порядок дифференцирования в частных производных не-
несуществен, индексы к и / можно тоже поменять местами. Свойства
такой перестановочной симметрии можно записать в виде
rijk
Sijkl
Sijkl sijlk-
G.1.7)
G.1.8)
G.1.9)
Вследствие этой симметрии удобно ввести условные индексы для
сокращения обозначений. Определим их следующим образом:
2 = B2),
3 = C3), G.1.10)
4 = B3) = C2),
5 = A3) = C1),
6 = A2) =B1).
Используя эти условные индексы, можно записать следующие ра-
равенства:
Электрооптика
24-1
г\к = г
11*'
Г2к ~ '22*'
Г3* ~ Г33*>
Г,ь = Г-
G.1.11)
'Ак
23* ~ '32*.
Г5* ~~ Г13* Г31*>
Г6* = Г12* = Г21*'
к= 1,2,3.
Необходимо помнить, что такие условные обозначения введены
лишь для удобства. Эти матричные элементы Fx3) не имеют
обычных тензорных свойств преобразования или умножения. Нали-
Наличие свойств перестановочной симметрии позволяет сократить число
независимых элементов rjJk от 27 до 18, а число элементов siJkl от 81
до 36.
7.2. ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ
В последнем разделе уже упоминалось, что возникновение электро-
электрооптического эффекта обусловлено перераспределением зарядов под
действием внешнего электрического поля. Поэтому можно ожи-
ожидать, что электрооптический эффект будет зависеть от отношения
величин внешнего и внутриатомного электрических полей, послед-
последнее из которых связывает такие заряженные частицы, как электро-
электроны и ионы. В большинстве практических применений электроопти-
электрооптического эффекта внешнее электрическое поле оказывается меньше
внутриатомного электрического поля, величина которого обычно
составляет 108 В/см. Поэтому следует ожидать, что квадратичный
эффект будет существенно меньше линейного, и при наличии линей-
линейного эффекта им, как правило, пренебрегают. Однако в кристаллах
с центросимметричной точечной группой линейный электрооптиче-
электрооптический эффект исчезает и преобладающим становится квадратичный
электрооптический эффект. Для доказательства последнего утверж-
утверждения рассмотрим пространственную инверсию кристалла.
Инверсия заключается в замене точки г кристалла на точку —г,
симметричную относительно центра инверсии. Среди 32 точечных
групп, перечисленных в табл. 7.1, имеются одиннадцать кристалли-
кристаллических систем, для которых операция инверсии / является симмет-
симметричной. Такие кристаллы называются центросимметричными. Рас-
Рассмотрим теперь преобразование линейного электрооптического тен-
16-631

ТАБЛИЦА 7.1. Точечные группы симметрии [1]
Кристаллическая Класс
система
международ-
международное обозна-
обозначение
Триклинная 1
Т
Моноклинная щ
2
2/т
Орторомбическая 2mm
222
mmm
Тетрагональная 4
4
4/m
4mm
42m
422
симметрии
в обозначе-
обозначениях Шен-
флиса
с,
с,
с,
с2
Сгн
c2v
D2
D2h
с4
S4
cZ
D4
Элементы симме'
E
El
Eah
EC2
EC2Ioh
EC2a'a"
EC2C&
E2C4C2
E2S4C2
E2C4C2I2S4ah
EC C'C"a'2S a
E2C4C22Ci2G'
Некоторые характерные кристаллы
KIO3
Слюда, Al2SiO5
3
KOH
AgAuTe4, PbSiO3
KNbO3,SbSI(r< Гс)*
KNa(C4H4O6) • 4H2O (сегнетова "соль)
SbSI (Г > Tc), СаС12, А12Ве04(александрит)
y-Fe2O3
4/mmm
4
AgIO4, NalO, KCuF4
BaTiO3 B5°C), KTN (Г < Tc)
AgGaS2, ADP, KDP
TeO2
TiO2,GeO2
Тригональная 3
3
3m
32
3m
Гексагональная 6
6
6/m
6m2
6mm
622
E2C3
Кубическая
6/mmm
23
m3
43m
432
m3m
C3p
Q
D6
о
E2C33o,
E2C33C2
E2C33C2I2S33av
E2C62C3C2
E2C3ah2S6
E2C62C3C2I2S32S6<j,
E2C33C2oh2S63o,
?2Q2C3C23<3a"
?2Q2C3C23Q3C^/2S32S6aA2a;3a,,"
?8C33C2
?8C33C2/8S33a
?8C33C26a6S4
?8C33C26C26C4
?8C33C26C26C4/8S33a6a6S4
S, Ge3N4, Asl3
Ag3AsS3, LiNbO3, LiTaO3
SiO2 (а-кварц) ,Те, Se, A1F3
A12O3, CaCO3 (кальцит) ,NaNO3
KLiSO4
Li2O2
PbSb2S4,/J-Si3N4
GaSe, GaS .
CdS, CdSe, ZnO, e-ZnS
CsCuCl3,BaAl204
BN,/8-Al2O3,NiAs
H2S, MnSe2, MgO2
CdTe, GaAs, InAs, ZnTe, MgO
LiFesO8
BaTiO3 {T > Tc), KTN (Г > Tc), SrTiO3, Ge, Si
• T — температура Кюри (или температура перехода)

244
Глава 7
зора гик при операции инверсии:
= -Г,
ijk •
G.2.1)
Но при инверсионной симметрии любое свойство тензора должно
оставаться инвариантным при операции инверсии; таким образом,
= r,t
G.2.2)
Уравнения G.2.1) и G.2.2) совместны, только если rljk = 0. Это до-
доказывает то, что линейный электрооптический эффект в центросим-
метричных кристаллах должен исчезать. Действительно, в один-
одиннадцати кристаллических системах, имеющих центр инверсии, все
тензоры третьего ранга должны быть равны нулю.
Используя условные индексы G.1.11), уравнение для эллипсоида
показателей преломления при наличии внешнего электрического по-
поля можно записать в виде
— + rXkEk \хг + | -^
и:
Z2 +
+ 2yzr4kEk + 2zxrikEk + 2xyr6kEk = 0,
G.2.3)
где Ек (к — 1,2,3) — составляющая приложенного электрического
поля, причем предполагается, что суммирование выполняется по
повторяющимся индексам к. Здесь нижние индексы 1, 2 и 3 соот-
соответствуют главным диэлектрическим осям х, у, z, а пх, пу и nz явля-
являются главными показателями преломления. При Ек = 0 этот но-
новый эллипсоид [G.2.3)] переходит в невозмущенный эллипсоид
[G.1.1)]. В общем случае главные оси эллипсоида G.2.3) не совпада-
совпадают с невозмущенными осями х, у, z.
С помощью поворота координат (это преобразование называет-
называется приведением квадратичной формы к главным осям) всегда мож-
можно найти новую систему главных осей. Размеры и ориентация эл-
эллипсоида G.2.3) зависят, разумеется, от направления приложенного
поля, а также от 18 матричных элементов г1к: Выше мы уже дока-
доказали, что в кристаллах, обладающих центром инверсии (центросим-
метричностью), г1к — 0. Вид тензора гш (но не его величина) может
быть получен из соображений симметрии, которые позволяют
установить, какие из 18 коэффициентов г1к равны нулю, и найти со-
соотношения между остальными коэффициентами. В табл. 7.2 пред-
представлены электрооптические тензоры для всех нецентросимметрич-
ных кристаллических классов, а в табл. 7.3 перечислены электрооп-
электрооптические коэффициенты для некоторых кристаллов.
ТАБЛИЦА 7.2. Электрооптические коэффициенты в условных обозначениях
для всех классов симметрии кристаллов*
Центросимметричная система
(I, 2/m, ттт, 4/т, 4/ттт, 3, Зт 6/т, 6/ттт, тЗ, тЗт):
0 0 0\
0 0 0
0 0 0
0 0 0
0 0
0
\0 0 0/
Триклинная система:
'31
'61
'32 '33
'42 Г43
'52 '53
'62
'63
Моноклинная система:
2
/ 0
0
0
'41
0
'61
m
('„
'21
'31
0
'51
0
Орторомбическая система:
/ о
0
0
'41
0
0
B 11
'12
C22
'32
0
'52
0
(m 1
0
0
0
'42
0
'62
222
0
0
0
0
'52
0
x2)
0
0
0
'43
0
'63
2
/ 0
0
0
'41
'51
0
x2) m
'13 \
'23
'33
0
'53
0
/'11
'21
'31
0
0
'61
0 \
0
0
0
0
'63 /
0
0
0
0
'51
0
B 11;
0
0
0
'42
'52
0
(m X
'12
'22
'32
0
0
'62
2mm
0
0
0
r
0
0
сз)
'13
'23
'33
0
0
'63
*з)
0
0
0
'43
'53
0 j
'13
'23
'зз
0
0
0

246
Глава 7
ТАБЛИЦА 7.2. (Продолжение)
Тетрагональная система:
0
0
0
'41
'51
0
4
0
0
0
'51
-'41
0
'13
'13
'33
0
0
о /
(°
0
0
0
'51
0
4mtr
0
0
0
'51
0
0
/ 0
0
0
'41
'51
0
1
'13
'13
'33
0
0
0 ,
4
0
0
0
-'51
'41
0
'13
— '13
0
0
0
'63 ,
42m
I 0
0
0
'41
0
0
B
0
0
0
0
Ui
0
/
IX,)
0
0
0
0
0
'63
0
0
0
'41
0
0
422
0
0
0
0
-'41
0
0
0
0
0
0
0
Тригональная система:
32
'И
-'11
О
'41
'51
~'22
Зт
О
О
О
О
'51
"'22
-'22
'22
О
'51
-'41
-'и
(mix,
-'22
'22
О
'51
О
О
'.3
'13
'33
О
О
О
'и
-'и
О
'41
О
О
) Зт
\
'13
'13
'33
О
О
О
'и
-'и
О
О
'51
О
О
О
О
О
-'41
-'и
(mix
О
О
О
'51
О
~'п
О
О
О
О
О
О
2)
'13
'13
'33
О
О
О
Электрооптика
247
ТАБЛИЦА 7.2. (Продолжение)
Гексагональная
/ 0
0
0
'41
'51
0
система:
6
0
0
0
'51
-'41
0
'13
'13
'33
0
0
0
'll
—'ll
0
0
0
-'22
'22
'22
0
0
0
-'ll
o\
0
0
0
0
0
/ 0
0
0
0
'51
0
6m2
0
0
0
0
0
-Г-,-,
6mm
0
0
0
'51
0
0
(m X
~'22
'22
0
0
0
0
'13 \
'13
'33
0
0
0 /
/ 0
0
0
'4
0
о
x,) 6m2
0
0
0
0
0
0
rll
-'1
0
0
0
0
622
0
0
0
0
-'4
0
(m X
0
0
0
0
0
-/•¦
0
0
0
0
0
o,
X;
)
0\
0
0
0
0
0
Кубическая система:
43m, 23
' 0
0
0
'41
0
0
0
0
0
0
'41
0
0
0
0
0
0
Га
432
/0 0 0^
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0/
* Символ над каждой матрицей отвечает условному обозначению соответствующей
группы симметрии.
7.2.1. ПРИМЕР: ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ В КН2РО4
Рассмотрим конкретный пример кристалла дигидрофосфата калия
(KHjPO^, называемого также KDP. Этот кристалл имеет инверс-
инверсную ось симметрии 4-го порядка, в качестве которой по строгому
соглашению выбирают ось z (оптическую ось) и две взаимно орто-
ортогональные оси симметрии второго порядка, расположенные в пло-
плоскости, перпендикулярной оси Z- Эти оси обозначаются через х и у.
Группой симметрии этого кристалла является 42т. Используя

ТАБЛИЦА 7.3. Линейные электрооптические постоянные
Вещество
Симметрия Длина волны Электрооптические коэффициенты*
X, мкм
r,t, 10
-12
м/В
Показатель
преломления
п, 10
-12
Диэлектрическая
проницаемость*
м/В
CdTe
GaAs
GaP
0-ZnS
(сфалерит)
ZnSe
ZnTe
43m
43m
43m
43m
43m
43m
1,0
3,39
10,6
23,35
27,95
0,9
1,15
3,39
10,6
0,55-1,3
0,633
1,15
3,39
0,4
0,5
0,6
0,633
3,39
0,548
0,633
10,6
0,589
0,616
0,633
0,690
3,41
10,6
G-)
G-)
G-)
G-)
G-)
G-)
G-)
G-)
(T)
(S)
(S)
(S)
(T)
G-)
G-)
(S)
(S)
G-)
(S)
(T)
(T)
(T)
(T)
(S)
G-)
(Г)
G-)
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
'41
= 4,5
= 6,8
= 6,8
= 5,47
= 5,04
= 1,1
= 1,43
= 1,24
= 1,51
= -1,0
= -0,97
= - 1,10
- -0,97
= 1,1
- 1,81
= 2,1
= -1,6
= -1,4
= 2,0
= 2,0
= 2,2
= 4,51
= 4,27
= 4,04
= 4,3
= 3,97
= 4,2
- 3,9
n = 2,84
n = 2,60
n = 2,58
n = 2,53
n = 3,60
n - 3,43
« = 3,3
« = 3,3
n = 3,66-3,08
n = 3,32
« = 3,10
n = 3,02
n = 2,52
n = 2,42
n = 2,36
n = 2,35
n = 2,66
n = 2,60
n = 2,39
« = 3,06
n = 3,01
n = 2,99
n = 2,93
n = 2,70
n = 2,70
103
120
94
82
51
58
45
54
35
33
27
18
35
108
83
77
(S) e-
(S) E =
(Г) e =
(S) e =
(Г) E =
(S) ? =
G-) e =
E) E =
G-) e =
(S) ? =
9,4
13,2
12,3
10
16
12,5
9,1
9,1
10,1
10,1
CdS
23
23
6mm
0,666
0,633
0,589
0,633
1,15
CdSe
ZnO
o-ZnS
(вюртцит)
(Ti,l6Zr114)O,
(PLZT)
6mm
6mm
6mm
3,39
10,6
3,39
0,633
3,39
0,633
0,546
G-)
(Г)
G-)
G-)
(Г)
G-)
G-)
G-)
G-)
(Г)
(Г)
E)
(Т)
(S)
(S)
to to
to to
'41 =
'41 =
'я =
'я ='
'31 -
'я =
'я =
'l.l =
'3.1 -
'51 -
'13 =
'11-
'п -
'1.3 =
'и =
'31 =
'и -
'11 =
3,22
5,0
3,7
'1,6
3,1
3,2
2,0
3,5
2,9
2,0
2,45
2,75
1,7
1,8
4,3
1,4
2,6
0,96
1,9
0,9
1,8
(T) r =4*
(Л r, - 4,8
(Г) r, =6,2**
(Г) r, -6,4**
(Г) г =5,2**
2320
п = 2,54
и = 2,54
я„ - 2,501
п, = 2,519
п„ = 2,460
п, = 2,477
п„~ 2,320
п, = 2,336
п., = 2,276
п.. = 2,292
п„= 2,226
и,. = 2,239
п„ = 2,452
п.. = 2,471
«„= 1,990
п,. = 2,006
п„= 1,902
пг = 1,916
п„ = 2,347
п,. = 2,360
п., = 2,55
53
82
(Л e, = 9,35
(Г) E, - 10,33
E) e, = 9,02
E) e3 = 9,53
(Г) ?, = 9,70
(Г) ?3 - 10,65
E) с, = 9,33
E) е, = 10,20
(Г) f,
E) e,
- е, - 8,15
- Ез
8,7

ТАБЛИЦА 7.3. Линейные электрооптические постоянные
Длина волны
Вещество Симметрия "¦ мкм
Электрооптические коэффициенты*
Показатель
преломления
n-V, 10"
м/В
Диэлектрическая
проницаемость*
LilO,
Ag,AsS,
LiNbO,
(Г, = 123О°С)
3m
3m
LiTaO,
3m
AgGaS2
42m
0,633
0,633
0,633
1,15
3,39
0,633
3,39
0,633
(S) r
3
(S) r4,
E) л
(S) n
G-) a
(Г) a
G-) a
3
I
П
(T) '51
(D A
G-) a
G-) a
G-) a
G-) f
G-) a
G-) a
G-) a
G-) ,
IS) A
E) a
(S) '
E) a
G-) r
G-) a
,2
,,
2,
33
13
5]
22
41
63
= 4,1
= 1,4
- = 70
r22 = 29
= 9,6
= 6,8
- 30,9
= 32,6
= 21,1
= 5,4
- 19
= 3,1
= 18
= 8,4
= 30,5
= -0,2
= 22
= 27
= 4,5
= 15
= 0,3
= 4,0
= 3,0
(S) «и
: 6,4
3,3
E) r,, = 8,6
E) л, = 3,4
IS) гл, = 30,8
E) г„ =28
(S) /•„ = 28
E) r22 = 3,1
E) /-,, = 6,5
E) r51 = 23
E) г,, = 7,5
(S) !•„ = 33
E) r5, = 20
no = 1,8830
no = 1,7367
"„ = 3,019
ai, = 2,739
ai,, = 2,286
Ai,. = 2,200
n,,= 2,229
n,. = 2,150
n,, = 2,136
n,. = 2,073
n,, = 2,176
л, = 2,180
л„ = 2,060
n,. = 2,065
л„ = 2,553
л,. = 2,507
G-) c,
(T) E3
(S) e.
(S) E,
€2
= 32
= E2 =
= 28
78
43
(Г) e, -e2 - 51
G-) e3 " 45
E) e, =e2 = 4l
(S) e3 = 43
C&H,AsO4
(CDA)
KH,TO4
(KDP)
KD,PO4
(KD*P)
42m
42m
42m
<NH4)H,PO4 42m
(ADP)
(NH4)D,PO4 42m
(AD'P)
BaTiO,
G; = 395 K)
KTa4Nb, 4O,
(KTN).x-'0.35
G; = 40-60°C)
4mm
0,55
0,546
0,633
3,39
0,546
G-)
G-)
G-)
G")
G-)
G-)
<n
(Г)
G")
(Г)
'41 ~
't.3 =
'41 =
'63 =
'41 =
'63 =
"«'63
'6i =
'41 =
14,8
18,2
8,77
10,3
8
II
= 33
26,8
8,8
0,633
0,546
0,633
0,633
0,546
0,633
Ba^SrD^NbO,, 4mm 0,633
G; = 395 K)
(П
24,1
(Л a4, = 23,76
(Г) a6, - 8,56
(Г) a41 = 23,41
(Г) n->6, = 27,6
(Л a4i = 40
G") 'M = 10
(Г) r5l = 1640
(Г) r, = 108
(Г) rsi - 8000G; - 28)
(Г) r, = 500G; - 28)
G") r5l = 3000G; - 16)
(T) r, = 700G; - 16)
(П rn = 67
(Г) r,_, = 1340
E) r5p = 820
E) r = 23
(Г) a5i = 42
E) r = 1090
n,. = 1,550
n,,= 1,5115
n,. = 1,4698
no= 1,5074
n,. = 1,4669
wA =
nt. =
n<>~
n <¦ =
n,, =
n г ~
nn =
n e =
"ll ==
nf =
ni>~
n(. =
n „ ==
"c =
W,, =
nf =
n „ =
л =
1^079
1,4683
1,502
1,462
1,5266
14808
1,5220
1,4773
1,516
1,475
2,437
2,365
2,318
2,277
2,318
2,281
2,3117
2,2987
G-) e, ¦
(S) ?, ¦
E) e3 '
= ?, = 42
¦21
¦ e, = 44
(S)
(T)
(T)
to to
«3
«1
«3
fl
«3
«1
f3
II II
= 48
= «2
= 15
= E2
= 14
¦ 58
56
58
(T) e, = e2 = 3600
G-) e3 = 135
e} = 3400
A5 МГц)

I
R
с
I
s
5 g
С е
О
О
141 1=
СЯ <N Ъ — <N
^ О i? С1 С
to to to ?T to
5
«1 q. q.
sD Г- NO
II II II
К К К К
3
8
о
X
d
2
Элекгрооп тка
табл. 7.2, запишем электрооптический тензор в виде
253
О
О
О
О
о
о
о
о
о
Г41
о
о
о
о
о
о
G.2.4)
где отличны от нуля только элементы г4] - г52 и г63. Используя
G.2.3) и G.2.4), для эллипсоида показателей преломления при нали-
наличии электрического поля Е(?\, Ev, E,) можно написать следующее
уравнение:
у2
2гаЕгху =
G.2.5)
где постоянные, входящие в первые три члена, не зависят от поля
и, поскольку кристалл является одноосным, выбраны в виде пк. =
— «,, = по, п. = пс. Таким образом, мы показали, что приложение
внешнего электрического поля приводит к возникновению пере-
перекрестных членов в уравнении для эллипсоида показателей прелом-
преломления. Эти члены содержат ху, xz, yz. Отсюда следует, что глав-
главные оси эллипсоида при приложении поля уже не остаются парал-
параллельными осям кристаллах, у nz. Поэтому для определения влия-
влияния внешнего электрического поля на распространение излучения
необходимо найти направления новых осей, а также соответствую-
соответствующие показатели преломления при наличии электрического поля Е.
Для конкретности выберем направление внешнего электрического
поля параллельным оси z. Тогда уравнение G.2.5) принимает вид
G.2.6)
Задача состоит в нахождении новой системы координат (л'', у', z'),
в которой уравнение эллипсоида G.2.6) не содержит перекрестных
членов, т. е. имеет вид
у'2
nl.
z'2
—
G.2.7)
При этом х', у' и z' представляют собой направления главных осей
эллипсоида во внешнем электрическом поле, приложенном парал-

254
Глава 7
РИС. 7.1. Оси х, у, z для кристалла с точечной группой симметрии 42т (такого, как
КН РО4) и оси х', у', z', где z — оптическая ось четвертого порядка, а х и у — оси
симметрии второго порядка.
лельно оси z. Длины главных осей эллипсоида [см. G.2.7)] равны
2пх., 2пу, и 2nz. и в общем случае зависят от приложенного поля.
Нетрудно показать, что для приведения уравнения G.2.6) к диа-
диагональному виду систему координат х', у', г' нужно выбрать та-
такой, чтобы ось z' была параллельна г. Поскольку уравнение G.2.6)
симметрично относительно х и у, координаты х' и у' получаются
из х и у поворотом на 45°, как это показано на рис. 7.1. Таким об-
образом, преобразование координат х, у в х', у' дается соотношения-
соотношениями
х = jc'cos45° -/sin45°,
у = jc'sin45° +/cos 45°,
которые при подстановке их в уравнение G.2.6) дают
1
у + —
"I
G.2.8)
Из этого уравнения видно, что х', у' иг действительно являются
главными осями эллипсоида в случае, когда внешнее электрическое
поле приложено в направлении оси z. Нетрудно также заметить,
что длина оси эллипсоида равна 2пх„, причем
Электрооптика
255
Отсюда в предположении, что r6iEz < no 2, и при использовании
дифференциального соотношения
получаем
и аналогично
"у »о + Wor63Ez,
"у =
п2 = пе.
G.2.9)
G.2.10)
G.2.11)
Рассмотрим теперь случай, когда приложенное постоянное
электрическое поле параллельно осих, т. е. уравнение G.2.5) прини-
принимает вид
х2 у2 z2
+ +
G.2.12)
Из уравнения G.2.12) видно, что в этом случае новая главная осьх'
будет совпадать с осью х, поскольку перекрестный член включает в
себя лишь у и z. Поэтому для приведения к диагональному виду не-
необходимо осуществить поворот осей в плоскости yz. Пусть в —
угол между новыми координатами /, z' и старыми координатами
yz. Преобразование от координату, z к /, z' записывается в виде
y = y'cosO - z'sinO,
z =/sin0 + z'costf.
G.2.13)
Подставляя теперь G.2.13) для у иг в уравнение G.2.12) и требуя,
чтобы коэффициент при/г' обращался в нуль, получаем
~ + (-2 + r4iEx tg в)у'2 + (\ - rMEx tg в)г'2 = 1, G.2.14)
где в дается выражением
tg20= 2гАХЕх{\/п\- 1/п2у
G.2.15)

256
Глава 7
Таким образом, в случае когда электрическое поле Ех приложено
вдоль оси*, главные оси нового эллипсоида показателей преломле-
преломления G.2.14) оказываются повернутыми на угол в вокруг оси* отно-
относительно главных осей невозмущенного эллипсоида. Этот угол
очень мал даже для умеренно сильных электрических полей. Так,
для кристалла KDP при Ех = 106 В/м этот угол составляет только
0,04°. Из G.2.15) следует, что этот угол существен лишь для ве-
веществ, у которых по ~ пе. В частности, при по = пе имеем в —
— 45°. В соответствии с G.2.14) новые главные показатели прелом-
преломления можно записать в виде
V = По - Wor4\Ex
9,
G.2.16)
G.2.17)
G.2.18)
Для кристалла KDP при умеренных значениях поля Ех угол в мал и
в соответствии с G.2.15) почти прямо пропорционален r^Ex. Поэ-
Поэтому изменение показателей преломления G.2.17) и G.2.18) имеет
второй порядок по Ех.
7.2.2. ПРИМЕР: ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ В LiNbO3
Кристалл LiNbO3 имеет точечную группу симметрии Зш. Согласно
табл. 7.3, электрооптические коэффициенты для него имеют вид
0
0
0
0
— г-
22
— Г-
22
'22
'51
0
о
гзз
0
0
0
G.2.19)
Рассмотрим теперь случай, когда электрическое поле приложено
вдоль оси с кристалла, так что в соответствии с G.2.3) уравнение
эллипсоида показателей преломления можно записать в виде
± + г„е\ = 1,
G.2.20)
где по и пе — обыкновенный и необыкновенный показатели прелом-
Электрооптика
257
ления соответственно. Поскольку в уравнении G.2.20) не возникает
перекрестных членов, главные оси нового эллипсоида показателей
преломления остаются неизменными. Длины этих новых полуосей
даются выражениями
G.2.21)
G.2.22)
G.2.23)
- \п\гггЕ.
Заметим, что, когда электрическое поле направлено вдоль оси с,
кристалл остается одноосно анизотропным (см. задачу 7.2). Для
светового пучка, распространяющегося вдоль оси х, двулучепре-
ломление равно
~ пу = (пе - по) -
- пъогп)Е.
G.2.24)
7.3. ЭЛЕКТРООПТИЧЕСКАЯ МОДУЛЯЦИЯ
В предыдущем разделе мы показали, что внешнее электрическое
поле может изменять эллипсоид показателей преломления опреде-
определенных кристаллов. Известно также, что характеристики электро-
электромагнитного излучения, распространяющегося в кристаллах,, опреде-
определяются эллипсоидом показателей преломления. Следовательно,
электрооптический эффект в этих кристаллах можно использовать
для управления распространением световой волны, в частности ее
состоянием поляризации. В качестве примера рассмотрим пластин-
пластинку, представляющую собой г-срез кристалла KDP, на которую дей-
действует внешнее электрическое поле Е, параллельное оси Z. Для све-
света, распространяющегося вдоль оси z, двулучепреломление в соот-
соответствии с G.2.9) и G.2.10) можно записать в виде
- п, = п\
, = п\гьъЕг.
G.3.1)
Пусть d — толщина пластинки. Тогда фазовая задержка этой пла-
пластинки дается выражением
^ = -{пу-nx,)d = ^-nlraV, G.3.2)
где V(— Ed) — приложенное напряжение. В гл. 5 мы показали,
17-631

258
Глава 7
\ пг = и.
РИС. 7.2. Участок эллипсоида показателей преломления для кристалла KDP и глав-
главные диэлектрические оси х', у' иг, возникающие при наложении внешнего электри-
электрического поля вдоль оси z. Направления осей х' и у' определены на рис. 7.1.
что такая задерживающая пластинка является преобразователем
состояния поляризации. В рассматриваемом случае фазовая задерж-
задержка пластинки пропорциональна приложенному напряжению. Следо-
Следовательно, с помощью внешнего электрического поля мы можем
преобразовывать состояние поляризации падающего пучка в состо-
состояние поляризации, которое нам хотелось бы иметь. Для иллюстра-
иллюстрации этого предположим, что падающий пучок света линейно-поля-
линейно-поляризован под углом 45° к оси х' (рис. 7.2). Тогда состояние поляри-
поляризации падающего пучка в плоскости z = О можно представить с по-
помощью вектора Джонса
m
G.3.3)
Состояние поляризации выходящего пучка в выходной плоскости
z = d записывается в виде
1
п
eiT/2
,-iT/I
G.3.4)
где Г дается выражением G.3.2).
На рис. 7.3 изображен эллипс поляризации выходящего пучка
при различных значениях фазовой задержки Г. Напряжение, кото-
которое соответствует фазовой задержке Г = тг, называется «полувол-
«полуволновым» напряжением и в данном случае определяется следующим
образом:
К
Г= 0°
Г = -я
РИС. 7.3. Линейно-поляризованная вдоль оси х оптическая волна падает в направле-
направлении оси z на электрооптический кристалл, в котором электрически индуцированны-
индуцированными главными осями являются х' и у'. (Этот случай отвечает кристаллу КН,РО4,
когда электрическое поле приложено вдоль оси г.) а — зависимость составляющей
Ех, в некоторый момент времени / от координаты z вдоль кристалла; б — зависи-
зависимость составляющей Е , от г в тот же момент времени t, что и в п. а; в — эллипсы
в плоскости х'у', описываемые концом вектора электрического поля оптической
волны в различных точках (от а до /) вдоль кристалла на протяжении одного перио-
периода оптической волны; стрелками обозначены направления мгновенного вектора поля
в момент времени t, а изогнутыми стрелками — направления, в которых перемеща-
перемещается эллипс; г — эллипс поляризации для двух ортогональных составляющих с фазо-
фазовой задержкой Г = тг/6 [т. е. Ег. = cosarf и Е , = cos(arf - тг/6)]; изображены так-
также векторы поля в различные моменты времени: wt = 0 A), ш = 60° B), oil = 120°
C), uit = 210° D) иш(= 270° E).

260
Глава 7
Электрооптика
261
здесь X — длина волны света. Для г-среза кристалла KDP это «по-
«полуволновое» напряжение на длине волны X = 6328 А составляет
9,3 кВ. Заметим, что полуволновое напряжение пропорционально
длине волны X и обратно пропорционально соответствующему
электрооптическому коэффициенту.
7.3.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
В конце предыдущего раздела мы показали, что двулучепреломле-
ние [выражение G.3.1)], индуцированное электрическим полем, при-
приводит к тому, что падающая в плоскости z = 0 волна, поляризо-
поляризованная вдоль оси*, приобретает поляризацию в направлении оси .у,
причем величина поляризации возрастает с напряжением за счет со-
составляющей х и при V = Уж поляризация становится параллельной
у. Если в выходной плоскости z = d поместить поляризатор под
прямым углом к поляризации падающего света, т. е. поляризатор,
пропускающий составляющую Еу, то при включенном внешнем
электрическом поле оптический пучок будет проходить без затуха-
затухания, а при выключенном поле (Г = 0) выходящий пучок будет пол-
полностью задерживаться скрещенным поляризатором, помещенным
на выходе. Такое управление потоком оптической энергии лежит в
основе приборов, осуществляющих электрооптическую амплитуд-
амплитудную модуляцию света.
На рис. 7.4 схематически показано устройство электрооптиче-
электрооптического амплитудного модулятора. Он состоит из электрооптическо-
электрооптического кристалла, помещенного между двумя скрещенными поляриза-
«Быстрая» «Медленная»
ось ось
Входной
пучок
Электрооптический
кристалл
Входной
поляризатор
Четверть-
Четвертьволновая
(F = тг/2)
фазовая пластинка
Выходной
поляризатор
РИС. 7.4. Типичный электрооптический амплитудный модулятор. Полная фазовая
задержка Г является суммой фиксированной задержки смещения (ГБ = тг/2), созда-
создаваемой четвертьволновой пластинкой, и задержки, возникающей в электрооптиче-
электрооптическом кристалле. Входной поляризатор параллелен оси х, а выходной — оси у;
«быстрая» ось направлена вдоль х', а «медленная» — вдоль у'.
торами, которые составляют угол 45° относительно новых глав-
главных осей*' и у'. Естественное двулучепреломление кристалла, со-
создающее постоянную задержку, также вносит вклад в длину опти-
оптического пути, так что полная задержка Г представляет собой сумму
задержки, создаваемой этим кристаллом, и электрически индуциро-
индуцированной задержки. В гл. 5 было показано, что коэффициент пропу-
пропускания такой системы для поляризованного света имеет вид
sin2l-
2 V.
G.3.6)
Последнее равенство в G.3.6) было получено с использованием
G.3.2) и G.3.5). На рис. 7.5 представлена зависимость коэффициен-
коэффициента пропускания Т от напряжения V.
Рис. 7.5 иллюстрирует также сам процесс амплитудной модуля-
модуляции оптического сигнала. На модулятор обычно накладывают сме-
смещающее напряжение таким образом, чтобы создать фиксирован-
фиксированную задержку Тв = х/2 и добиться коэффициента пропускания
50%. Этого смещения можно достичь, прикладывая напряжение
V = VJ2 или, что более удобно, используя кристалл с естествен-
естественным дзулучепреломлением (рис. 7.4) для создания разности фаз (за-
(задержки) между составляющими х' и у', равной я72. При этом ма-
2_ [ф ?]
Интенсивность
прошедшего света
Время
Приложенное
напряжение
Модулирующее _
напряжение |
РИС. 7.5. Зависимость коэффициента пропускания Т электрооптического модулято-
модулятора со скрещенными поляризаторами от приложенного напряжения. Модулятор сме-
смещен в точку Г = тг/2, что приводит к коэффициенту пропускания 50%. Малое сину-
синусоидальное приложенное напряжение обеспечивает модуляцию интенсивности на вы-
выходе относительно точки смешения.

262
Глава 7
лая синусоидальная модуляция напряжения будет приводить к по-
почти синусоидальной модуляции интенсивности выходящего пучка,
как показано на рис. 7.5.
Чтобы представить зависимость на рис. 7.5 с помощью формул,
запишем следующее выражение:
Г=
G.3.7)
где задержка, обусловленная смещением, выбрана равной х/2, а ве-
величина Гт связана с амплитудой. V
Vmsino3mt соотношением G.3.2),
G.3.6), получаем выражение
m модулирующего напряжения
т. е. Гш = vVm/VT. Используя
G.3.8)
G.3.9)
которое при Тт < 1 принимает вид
G.3.10)
Таким образом, модуляция интенсивности есть линейный отклик
на модулирующее напряжение Vтsinuimt. Из рис. 7.5 и выражения
G.3.9) следует, что если условие Гш <^ 1 не выполняется, то измене-
изменение интенсивности является возмущенным и содержит значитель-
значительное количество высших (нечетных) гармоник.
7.3.2. ФАЗОВАЯ МОДУЛЯЦИЯ СВЕТА
В предыдущем разделе мы показали, как с помощью поляризато-
поляризаторов можно преобразовать модуляцию состояния поляризации опти-
оптического пучка от линейного до эллиптического в модуляцию интен-
интенсивности. Рассмотрим теперь модулятор, схематически изображен-
изображенный на рис. 7.6, когда падающий пучок имеет неодинаковые со-
составляющие вдоль индуцированных осей двулучепреломления (осей
х' и у' на рис. 7.4), а поляризован параллельно одной из них, на-
например параллельно оси х'. В этом случае действие электрического
поля вдоль направления z не меняет состояния поляризации, а ме-
меняет лишь фазу выходного сигнала на величину
Электрооптика
263
Поляризатор
Электрооптический
кристалл Выходной пучок,
модулированный
по фазе ь
Несущая
волна
Волна, модулированная
по фазе
РИС. 7.6. Электрооптический фазовый модулятор. Ориентация кристалла и направ-
направления приложенного электрического поля отвечают кристаллу KDP. Направление
поляризации оптического излучения параллельно главной диэлектрической оси х',
индуцированной электрическим полем.
которая в соответствии с G.2.9) равна
G.3.11)
Если смещающее электрическое поле синусоидально, т. е.
E2 = EmsinUmt, G.3.12)
то падающее оптическое поле, которое на входной поверхности
(z = 0) кристалла изменялось по закону Ein = A cos at, на выходе
из него будет иметь вид
Еш1 = A cos L/ - -Чио- yr63
где d — длина кристалла. Опуская постоянную фазу, которая здесь
несущественна, перепишем последнее выражение в виде
?out = A cos[ Ш + 8 sin wmt ],
где величина
wnlr63Emd nn^r6iEmd
= Тс = А
G.3.13)
G.3.14)

264
Глава 7
называется индексом фазовой модуляции. Таким образом, оптиче-
оптическое поле оказывается промодулированным по фазе с индексом мо-
модуляции 5. Используя тождества для функций Бесселя
cos(fisinwm0 = JO(S) + 2J2(S)cos2umt + 2J4(8)cos4o>mt + ¦¦¦
+ 2/3(fi)sin3wmf + • • • ,
выражение G.3.13) можно переписать в виде
?om = A[J0(8)cosut + J{cos(u + um)t - /,(fi)cos(« - um)t
+J2(S)cos(u + 2wm)t + J2(S)cos(u - 2wm)t +
+/3(fi)cos(w + 3wm)t - /3(fi)cos(w - 3wm)t +
G.3.15)
Это выражение дает распределение энергии в побочных максиму-
максимумах в зависимости от индекса модуляции 5. Заметим, что J0@) = 1
и Jn (б) = 0 (п Ф 0) при 5 = 0. Другим интересным обстоятельством
является то, что индекс фазовой модуляции 5, определяемый выра-
выражением G.3.14), составляет половину задержки Г, определяемой
выражением G.3.2).
7.4. РАСПРОСТРАНЕНИЕ ВОЛН
В ЭЛЕКТРООПТИЧЕСКИХ КРИСТАЛЛАХ
До сих пор при рассмотрении электрооптической модуляции пред-
предполагалось, что фаза электромагнитной волны, выходящей из элек-
электрооптического кристалла, определяется мгновенными значениями
внешнего электрического поля. Понятно, что это предположение
теряет силу, когда поле, действующее на кристалл, является пере-
переменным с достаточно высокой частотой. В этом случае за время
прохождения света через кристалл внешнее электрическое поле
может существенно измениться (и даже несколько раз поменять
знак) и полная задержка (или изменение фазы) окажется очень ма-
малой. Высокочастотные модуляции особенно важны для систем оп-
оптической связи с большой скоростью передачи информации, в кото-
которых модулирующее поле может осциллировать на частотах микро-
микроволнового диапазона. Для учета этих высокочастотных эффектов
при электрооптической модуляции необходимо рассмотреть рас-
распространение света в кристаллах при наличии электрических полей,
изменяющихся как во времени, так и в пространстве.
Электрооптика
265
Будем исходить из уравнения для вектора электрического сме-
смещения D при наличии возмущения в анизотропной среде (см.
разд. 4.12):
G.4.1)
Напомним, что f — это расстояние в направлении распростране-
распространения, с — скорость света в вакууме, а N — матрица показателей
преломления, записываемая в виде
\п\
и, -
п\п
1
И, + И-,
„2„2
И, + И
Дч21
'/22
G.4.2)
где л, и л2 — показатели преломления среды, отвечающие распро-
распространению невозмущенных собственных мод. Величина ArjaC пред-
представляет собой изменение тензора диэлектрической непроницаемо-
непроницаемости, обусловленное возмущением. В случае электрооптической мо-
модуляции Д??а0, согласно определению G.1.2), дается выражением
ДЧа„ = г^уЕу, G.4.3)
где подразумевается суммирование по повторяющимся индексам у.
Мы использовали обозначение r'afiy для того, чтобы подчеркнуть,
что система координат, использованная в G.4.1) и G.4.2), вообще
говоря, отличается от главных диэлектрических осей. Пусть а^ —
матрица преобразования координат, поворачивающая систему ко-
координат от главных диэлектрических осей к осям, связанным с рас-
распространяющимся пучком (D,, D2, s). При этом электрооптические
коэффициенты в новой системе координат имеют вид
Г*РЧ ~ aaiafijaykrijk.
G.4.4)
где подразумевается суммирование по повторяющимся индексам /,
j и к. В выражении G.4.2) л, и п2 — показатели преломления рас-
распространяющихся нормальных мод при отсутствии возмущения
(т. е. Еу = 0).
Пусть Л, (f, t) иАг(?, t) — амплитуды мод. Тогда вектор элект-
электрического смещения можно записать в виде
D
G.4.5)
где d, и d2 — векторы поляризации нормальных мод, а к1 и к2 —
волновые числа распространяющихся волн, определяемые выраже-

266
нием
a= 1,2.
Подставляя выражение G.4.5) для D в G.4.1), получаем
7я-
Глава 7
G.4.6)
G.4.7)
где A7Vag — матричный элемент возмущения в матрице показателей
преломления:
(Дли)
«1
+
Зд
'2Ч"
и2 21
«1 +
1
«2
Ai
G.4.8)
Уравнения G.4.7) представляют собой систему линейных уравнений
в частных производных для амплитуд мод. Когда недиагональные
матричные элементы ANl2 обращаются в нуль, связь между мода-
модами исчезает. Это отвечает случаю чисто фазовой модуляции. Будем
решать уравнение G.4.7) для этого случая чисто фазовой модуля-
модуляции.
7.4.1. ФАЗОВАЯ МОДУЛЯЦИЯ
В данном случае внешнее электрическое поле не приводит к связи
между невозмущенными нормальными модами, поскольку Д?}12 =
= Д?721 = 0. Это имеет место, когда
Г'\2УЕУ
0.
G.4.9)
При этих условиях уравнения для модовых амплитуд А1 и А2 ста-
становятся несвязанными и могут быть решены по отдельности:
Пусть модулирующее поле имеет вид бегущей волны Emsin(wmt —
— kml). В соответствии с G.1.2) возмущение тензора непроницае-
непроницаемости имеет вид
ДЧаа = Су Ету sin( am t - kj), а = 1,2,
G.4.10)
где Е —7-составляющая поля Ет. Уравнение для модовых ам-
амплитуд можно записать в виде
L 1
% с'с
, t),
G.4.11)
Электрооптика
267
где
ыи3
1 or 2,
G.4.12)
в качестве п можно выбрать л, или п2, а в качестве А—/4, или А2.
Уравнение G.4.11) представляет собой линейное дифференциаль-
дифференциальное уравнение в частных производных и может быть проинтегриро
вано, если ввести новые переменные
— ? с
п '
С помощью замены
о ди о dv о
G.4.13)
dt dt ди dt dv n\ du dv
уравнение G.4.11) принимает вид
G.4.14)
Рассматривая и и v как независимые переменные, после интегриро-
интегрирования уравнения G.4.14) получаем
, 0 =
^ - kj)\,
G.4.15)
где С — произвольная функция, а пт = скт/шт. Граничное условие
на входной грани (f = 0) кристалла записывается в виде
где Ао — произвольная постоянная. Из этого условия следует, что
функция С имеет вид
G.4.17)
При этом, согласно G.4.15) и G.4.17), модовую амплитуду A (f, t)
можно записать в виде
х

268
Глава 7
С учетом тригонометрического тождества
cos a- cos /? = -2sin5(a + /?)sin^(a - /?)
для модовой амплитуды на выходной грани (f = L) кристалла по-
получаем
A(L, t) = Aoexp[iSsin(umt - ф)],
где
S = BL—-^— ,
G.4.19)
G.4.20)
Ф-?*(„ + „т)ь. . <7-4-21)
Если за плоскостью f = L возмущение отсутствует, то электриче-
электрическое смещение выходящего пучка можно записать в виде
, 0
- ф) -
G.4.22)
Выражение G.4.22) описывает модулированную по фазе волну с ин-
индексом модуляции 5. В этом случае величина д, определяемая выра-
выражением G.4.20), уже не пропорциональна длине кристалла L и ее
максимальное значение /3L меньше на множитель
sin AL
где
¦" /* »*'»« Л J sat I
G.4.23)
а и0 и vm — фазовые скорости света и модулирующей волны соот-
соответственно. С физической точки зрения возникновение этого огра-
ограничивающего множителя обусловлено рассогласованием фазовых
скоростей этих волн. В случае когда свет и модулирующая волна
распространяются с одинаковыми фазовыми скоростями, на свето-
световую волну при ее распространении через электрооптический кри-
кристалл будет действовать постоянное модулирующее поле. При
этом ограничивающий множитель оказывается равным единице,
т. е. уменьшение индекса модуляции д отсутствует. Таким образом,
Электрооптика
269
РИС. 7.7. Зависимость индекса модуляции S от длины кристалла L.
индекс модуляции оказывается прямо пропорциональным длине
кристалла. В случае когда фазовые скорости не равны друг другу,
величина 5 становится периодической функцией длины кристалла L.
Зависимость 5 от L приведена на рис. 7.7. Величина Ь достигает
своего максимального значения при
тг(и„-«)*• = ?. G-4.24)
а максимальное значение индекса модуляции 5тах дается выражени-
выражением
я а
fimax = 7Г
G.4.25)
Пример: фазовый модулятор на кристалле LiNbO3. Рассмотрим
кристалл LiNbO3 в виде прямоугольного стержня (рис. 7.8), вход-
входная и выходная грани которого параллельны плоскости главных
осей xz. На кристалл действует высокочастотное поле волны с век-
вектором Е, параллельным оси z. Пусть высокочастотная волна и оп-
оптический пучок распространяются в направлении у. Поляризатор,
расположенный перед входной гранью кристалла, обеспечивает по-
поляризацию света вдоль оси z кристалла. В соответствии с G.2.9),

270
Глава 7
G.4.12) и G.4.20) индекс модуляции 5 можно записать в виде
где ne — необыкновенный показатель преломления кристалла, L —
длина кристалла, а г33 — соответствующий электрооптический ко-
коэффициент. Пусть о)т/2х — 6 ГГц, пт — 0 и пе = 2,2. Тогда из
G.4.24) следует, что максимальная модуляция имеет место при
L = 6,8 см. Кристалл LiNbO3 имеет точечную группу симметрии
Зт. Из табл. 7.2 мы видим, что электрооптический коэффициент,
отвечающий структуре на рис. 7.8, равен г33.
7.4.2. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
Рассмотрим теперь случай, когда невозмущенные нормальные мо-
моды оказываются связанными благодаря наличию внешнего электри-
электрического поля. Это имеет место, когда в уравнениях G.4.7) недиаго-
недиагональные матричные элементы возмущения не равны нулю, т. е.
Дг?12 Ф 0. В этом случае при распространении волны в кристалле
происходит обмен электромагнитной энергией между связанными
модами. Поэтому величины модовых амплитуд являются функция-
функциями пространственных координат и времени. Модовые амплитуды
удовлетворяют уравнениям связанных мод G.4.7). Рассмотрим да-
Кристалл LiNbO3
Световой
пучок
Поляризатор
РИС. 7.8. Образец LiNbO3 в виде прямоугольного стержня, используемый в качестве
электрооптического кристалла для модуляции фазы. Модулирующее высокочастот-
высокочастотное поле поляризовано вдоль оси z и распространяется вдоль оси у.
Электрооптика
271
лее случай чисто амплитудной модуляции, т. е. случай, когда
Д?},, = Д?}22 = 0. Это соответствует условию
гиА = Г22А = °- G.4.26)
Снова предположим, что модулирующее поле имеет вид бегу-
бегущей волны E,,,sin(a)m/ - kmt). Тогда, согласно G.1.2), возмущение
тензора непроницаемости имеет вид
hi = r'l2yEmrsm(amt -
G.4.27)
где Ету — 7-составляющая электрического поля Е,„. Таким обра-
образом, уравнения связанных мод можно записать в виде
G.4.28)
[it + ^i
где
* = и +и 7Г'2 Ау G.4.29)
причем подразумевается суммирование по 7- В случае когда л. —
= л2 = л, уравнения связанных мод принимают вид
п д
G.4.30)
где
ыи3
G.4.31)
Решения уравнений связанных мод G.4.28) в общем случае («, ф
Ф п2) очень сложны, и мы не будем их здесь рассматривать. Запи-
Запишем общее решение уравнений связанных мод для случая, когда
л, = л = п:

272
Глава 7
Mi. О
Г. О = »
G.4.32)
здесь С, и С2 — произвольные функции. Пусть граничные условия
на входной (f = 0) грани кристалла имеют вид
^@, t) = A0, Л2@, f) = 0. G.4.33)
Эти условия отвечают случаю, когда поляризатор на входе парал-
параллелен вектору d, (одной из невозмущенных главных осей).
Пусть в G.4.32) f = 0. Тогда граничные условия G.4.33) прини-
принимают вид
^ / с \ Г кс 1
coswmn = Ао,
wm(n ~ пт)
С,( - -t)sm\ —т-^ г cos umt\-
Ч п I [Ыт{п-пт) \
-C2(--/)cos —т-^ rcoswmn = 0.
\ it ' I о)т [ it ~ w т) I
G.4.34)
Отсюда находим
(С
КС
ч„(л- пт)
КС
coswmr ,
G.4.35)
Электрооптика
273
Выражения G.4.35) определяют функции С, и С2 при f = 0. По-
Поскольку С, и С2 — произвольные функции разности f — (с/л)?, их
можно записать в виде
G.4.36)
Подставляя выражения G.4.36) в G.4.32), для модовых амплитуд
имеем
Л,(?, 0 = ^Ocos(^^-y [cos(«w/ - kj) - cos(«m/ - ~«f)]},
f, 0 = iA0sm
G.4.37)
•и соотношение km = (um/c)nm, модовые амплитуды на выходной
(f = L) грани кристалла можно записать в виде
Используя далее тригонометрическое тождество
cosa-cos?= -2sin^(a + 0)sin±(a - fi)
A{(L, t) = A0cos[Ssin(wmt - ф)],
A2(L,t) = i
где
G.4.38)
G.4.39)
fi = kL-
а ф определяется выражением G.4.21)
Заметим, что в G.4.39) величина 5 по своей зависимости от дли-
длины кристалла L аналогична- фазовой модуляции. Следовательно,
все результаты, полученные при рассмотрении согласования фазо-
фазовых скоростей в случае фазовой модуляции, применимы также для
амплитудной модуляции. В частности, максимальная модуляция
имеет место при выполнении условия G.4.24), а максимальная глу-
18-631

274
Глава 7
бина модуляции дается выражением
а "  г' f
тах ы In - и I Пу ту'
шт I" "ml
G.4.40)
Используя выражения, полученные в случае фазовой модуляции
при л, — п2, можно также прийти к выражениям G.4.38). Таким
образом, падающий световой пучок поляризован вдоль невозму-
невозмущенной главной оси d,. При наличии возмущения новые нормаль-
нормальные моды для случая и, = п2 поляризованы в направлениях, кото-
которые составляют угол 45° с невозмущенными осями (см. первый
пример в разд. 7.2). Падающую оптическую волну можно предста-
представить в виде линейной суперпозиции новых нормальных мод:
= -j=A0{#x + d'2),
G.4.41)
где dj и d2 — единичные векторы в направлениях поляризации но-
новых нормальных мод. Эти составляющие затем претерпевают чи-
чисто фазовую модуляцию, поскольку связь между новыми нормаль-
нормальными модами отсутствует. Оптическую волну в выходной (f = L)
плоскости можно записать в виде
^„{d',*""*"-'-*) + d^-"*-..'-*)}, G.4.42)
где 5 определяется выражением G.4.39). Эту амплитуду поля мож-
можно теперь представить в виде линейной комбинации невозмущен-
невозмущенных нормальных мод. Пусть А[ и А2 — амплитуды новых нормаль-
нормальных мод, а А, и А 2 — амплитуды невозмущенных мод. Тогда ам-
амплитуды А, и А 2 даются выражениями
А, = -^{А\ +А'2) = A0cos[8sin(o>mt - ф)],
v2
А2 = -}=г
G.4.43)
\- А'2) = iAosin[8sin(umt ~ «)]•
Выражения G.4.43) аналогичны выражениям G.4.38), полученным
непосредственно из уравнений связанных мод.
Пример- амплитудный модулятор на основе GaSe. Рассмотрим пря-
прямоугольный стержень из GaSe, показанный на рис. 7.9, входная и
выходная грани которого параллельны плоскости ху главной систе-
Электрооптика
275
Анализатор
Кристалл GaSe
Поляризатор
Входной
световой пучок
РИС. 7.9. Образец кристалла GaSe в виде прямоугольного стержня, используемый
для амплитудной модуляции.
мы координат. Поле высокочастотной волны и оптический пучок
распространяются вдоль оси z (с-оси) кристалла. Пусть этот кри-
кристалл помещен между двумя скрещенными поляризаторами. Кри-
Кристалл GaSe имеет группу симметрии 6т2. Используя табл. 7.2, на-
находим, что электрооптический коэффициент, ответственный за
связь х- и у -составляющих оптической волны, равен г61 = г121 = г22-
Таким образом, в соответствии с G.4.29) и G.4.39) индекс ампли-
амплитудной модуляции можно записать в виде
Тс'
sin %(n-nm)L
2c
(n-nm)L
где no — обыкновенный показатель преломления кристалла (г61 =
= г22)- Пусть шш/27г = 6 ГГц, пт = 0 и по = 2,46; таким
= г
образом, в соответствии с G.4.40) максимальная модуляция имеет
место при L = 6,1 см.
7.5. КВАДРАТИЧНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ
Квадратичный электрооптический эффект является эффектом вы-
высшего порядка, и при наличии линейного электрооптического эф-
эффекта им обычно пренебрегают. В отличие от линейного электро-
электрооптического эффекта он существует в среде с любой симметрией.
Используя условные индексы G.1.1), уравнение эллипсоида показа-

276
Глава 7
телей преломления при наличии электрического поля можно запи-
записать в виде
2sl4EyEz + 2sl5EzEx + 2sl6ExEy
+y\ —
ni
s22E2y
+ 2yz{sME2x + в,2Е
+ 2zx{sMExl + s52E
+ 2xy(s6lEx2 + sb2E
2suEyEz + 2s25EzEx + 2s26ExEy
2sMEyE, + 2s35EzEx + 2S36ExEy
2sMEyEz + 2s4iE,Ex + 2SA6ExEy)
2sMEyE, + 2s55EzEx + 2si6ExEy)
2sMEyEz + 2s65EzEx
G.5.1)
Коэффициенты s^ обычно задаются в главных координатных осях.
В случае когда электрическое поле отсутствует, уравнение G.5.1)
переходит в уравнение G.11) для невозмущенного эллипсоида. В об-
общем случае электрическое поле изменяет размеры и ориентацию эл-
эллипсоида показателей преломления. Это изменение зависит как от
направления внешнего электрического поля, так и от элементов s^
матрицы 6x6. Вид электрооптических коэффициентов s^ (но не их
величину) можно получить из соображений симметрии, из которых
следует, что 36 коэффициентов равны нулю, а между остальными
коэффициентами должны существовать определенные соотноше-
соотношения. В табл. 7.4 приведены электрооптические коэффициенты для
всех кристаллических классов. Квадратичные электрооптические ко-
коэффициенты для некоторых кристаллов приведены в табл. 7.5.
7.5.1. ПРИМЕР: ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ КЕРРА
В ИЗОТРОПНОЙ СРЕДЕ
Если оптически изотропную среду поместить в статическое элект-
электрическое поле, то она становится двулучепреломляющей. Это явле-
явление обусловлено главным образом направленной ориентацией мо-
ТАБЛИЦА 7.4. Квадратичные электрооптические коэффициенты
в условных обозначениях для всех классов
симметрии кристаллов
Триклинная система:
1,1
•$11
Моноклинная система:
Орторомбическая
система:
Тетрагональная
система:
/
c
(
1
11
Sj\
*3I
0
s5l
0
iSj j
^31
0
0
0
I
2
1
)
)
51
s
*3
0
0
0
sn
*32
0
sS2
0
2,m,
iS|3
*33
0
si3
0
2/m
0
0
0
¦*44
0
*64
sls
*25
*35
0
*55
0
2mm,222,mmm
*12
s22
Si2
0
0
0
¦S.2
su
0
0
-*6i
422,
¦S.2
SU
S3l
0
0
0
sn
i$23
^33
0
0
0
4,4,
*13
s,3
S13
0
0
0
4mm,
¦*13
sn
*33
0
0
0
0
0
0
544
0
0
4/m
0
0
0
¦S44
0
0
0
0
0
¦*55
0
0
0
0
¦S45
*44
0
42m,4/mm
0
0
0
*44
0
0
0
0
0
0
.S44
0
0 \
0
0
*46
0
*66
0 \
0
0
0
0
¦*66
— i
0
0
с
6 \
16
*« j
0
0
0
0
0
s№

ТАБЛИЦА 7.4. (Продолжение)
Тригональная система:
3,3
512
о
О
О
-S,
45
5l5
514
sn
— 5
О
14
41
0
0
— 54i
0
0
0
0
0
Гексагональная система:
32,3m, 3m
514 0
0
0
544 0
0 544
0 514
6,6,6/m
О
О
о
о
s
и
*.2
531
0
0
/
J
исте
'12
'31
0
0
0
via
^12
*ll
53,
0
0
-*6i
%
¦*13
533
0
0
0
0
0
0
¦**
-5
0
1
45
622,6mm,6m2,(
*12
0
0
0
f
513
¦S.2
0
0
0
5,3
S\3
533
0
0
0
5,2
5,,
*13
0
0
0
0
0
0
¦S44
0
0
23,
513
512
0
0
0
0
0
0
0
54,
0
m3
0
0
0
544
0
0
0
0
0
545
544
0
— s
61
1
¦*6i
0
0
0
H*n -^12)
5/mmm
»
0
0
0
0
iM
0
0
0
0
0
0 ,
,*11 -J12);
0 \
0
0
0
0
544
Электрооптика
ТАБЛИЦА 7.4. (Продолжение)
279
432,m3m,43m
12 *12 0
II *12 0
2 i|, 0
0
0
0
0
0
0
0
0
0
J44
0
0
0
0
0
0
0
Изотропная система:
12
0
0
0
sl2
0
0
0
sl
0
0
0
0
0
0
i(*n -
0
0
0
0
0
0
K*n -¦
0
0
0
0
0
0
лекул во внешнем электрическом поле. При этом среда оптически
ведет себя так, как будто она является одноосной кристаллической
структурой, в которой электрическое поле определяет направление
оптической оси. Поскольку среда изотропна, ось z можно выбрать
в направлении электрического поля. Из табл. 7.4 и уравнения G.5.1)
следует, что эллипсоид показателей преломления дается выражени-
выражением
ЛЬ+s"
G-5-2)
где Е — величина приложенного электрического поля, s13 = s2i =
= j|2hs33 = sl2. Эллипсоид показателей преломления можно запи-
записать в виде
х2 +у2 | z2 _
где
ие = и - \n3snE2.
G.5.3)
G.5.4)

Электрооптика
-О
Ж
<и
S
Я
•е
I
о
а
ID
с?
3"
s
с U
«Г.
г- S-
5 к
я х
el
•а
н
a
Я
¦&
И
8 =
о
s 2
a
о.
281
Л II
К Е-,
О VO
I
II II
«по
5
оо о
I I
сп О
о4©*
СП СП
СП СП
vo *о
©"о"
S
S
U
о
О
сч
S S
СП СП
S S
«2
00 1/4
сн^ ТГ^
CN~ CN*"
U
о
СП
и -
° I
vo 1 <
G
•"¦' © ЧО
СП "Л IN
II Л II
г} г
г
СП
г
*о оо
ю о
cs оо
~- сп" °V °«
СП ~- 00 СП
II II II II
ч ч ч г
I I I
(Л — Csl
(Л **1 —
ч ч ч
I I
С С й
s
8
'ОО О U
*л °
о Cs] с^ сп
j? ^-" w Ь.
0-1
г
г
я
с.
Pi
& s
С s?>
" о"
а S
I ч
Н я
ей Я
11ри этом величина двулучепреломления пе - п0 дается выражени-
выражением
И- - И- =
G.5.5)
где л0 — показатель преломления для света, поляризованного под
прямым углом к вектору электрического поля Е, а пе — показатель
преломления света, поляризованного в направлении вектора Е. Вы-
Выражение G.5.5) можно также переписать в виде
ие-и0= -n's^E2 G56)
если использовать соотношение su = (sn - sl2)/2, справедливое
для изотропной среды (см. табл. 7.4). Выражения G.5.5) и G.5.6)
нередко записывают в виде
пе - п0 = КХЕ2, G.5.6а)
где К — постоянная Керра, а X — длина волны в вакууме. Посто-
Постоянные Керра для некоторых веществ приведены в табл.7.6. Посто-
Постоянная Керра связана с квадратичными электрооптическими коэффи-
коэффициентами для изотропной среды соотношением
su = -К\/п\
ТАБЛИЦА 7.6. Постоянные Керра для некоторых
веществ
Вещество
Бензин
cs2
СС14
Вода
Нитротолуол
Нитробензол
X, мкм
0,546
0,633
0,546
0,633
0,694
1,000
1,600
0,633
0,546
0,589
0,589
0,589
п
1,503
1,496
1,633
1,619
1,612
1,596
1,582
1,456
1,460
К, м/В2
4,9 X 10-15
4,14 X 105
3,88 X 104
3,18 X Ю-'4
2,83 X Ю-'4
1,84 X 104
1,11 X 10~14
7,4 X 106
8,6 X 10"|6
5,1 X 104
1,37 X 102
2,44 X 102

282
Глава 7
7.5.2. ПРИМЕР: ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ В ВаТЮ3
Рассмотрим конкретный пример кристалла титаната бария
(BaTiO3). Он представляет собой сегнетоэлектрический кристалл с
температурой фазового перехода Тс = 120 °С. Ниже температуры
перехода (Т < Тс) кристалл является ацентрическим с точечной
группой 4mm и преобладает линейный электрооптический эффект.
Выше температуры перехода (Г > Тс) кристалл обладает симмет-
симметрией m3m (кубической) и линейный электрооптический эффект исче-
исчезает. Пусть поле действует вдоль направления <110> в кристалле:
G.5.7)
Из табл. 7.4 и выражения G.5.1) следует, что эллипсоид показате-
показателей преломления можно записать в виде
± + \suE2
+ z'
sl2E2\ + 2xys44E2
G.5.8)
Вследствие симметрии уравнения G.5.8) по х и у его можно приве-
привести к диагональному виду поворотом в плоскости ху на 45°:
и*, п;, п;,
здесь
G.5.9)
G.5.10)
Предполагая, что sE2 «и 2 и используя дифференциальное соотно-
соотношение dn - -(l/2)n3rf(l/«2), получаем
Электрооп гика
283
sn)E2,
In3(su + sn)E2,
G.5.11)
nz. = n —
7.6. ФИЗИЧЕСКИЕ СВОЙСТВА
ЭЛЕКТРООПТИЧЕСКИХ КОЭФФИЦИЕНТОВ
Электрооптические коэффициенты rijk usijkl, определяемые выраже-
выражением G.1.2), в общем случае зависят от длины волны света, часто-
частоты модуляции и температуры кристалла. Эти коэффициенты непо-
непосредственно связаны с нелинейными тензорами восприимчивости
х(}.\ х^ш и могут быть рассчитаны с помощью квантовой теории
(см. гл. 12 и приведенные там ссылки). Квантовомеханический рас-
расчет этих электрооптических коэффициентов выходит за рамки дан-
данной книги. Вместо него мы изложим лишь элементарную теорию.
Эта теория качественно объясняет как зависимость от длины вол-
волны, так и зависимость от частоты модуляции.
Пусть q и Q — динамические переменные (например, перемеще-
перемещения), которые описывают распределения электронных и ионных за-
зарядов соответственно. Оптическая диэлектрическая непроницае-
непроницаемость 77 непосредственно зависит от q и является неявной функцией
переменной Q, которая в свою очередь зависит от температуры Т.
Известно, что непосредственный ионный вклад в поляризуемость
молекул очень мал (в 2000 раз меньше электронного вклада). Одна-
Однако в твердых телах электрический потенциал в основном определя-
определяется распределением ионного заряда. Поэтому изменение в рас-
распределении ионного заряда будет приводить к соответствующему
изменению электронного потенциала, который в свою очередь из-
изменяет поляризуемость твердого тела.
Модулирующее поле Е («ш) индуцирует два независимых измене-
изменения в оптической непроницаемости:
=
L
dE
G.6.1)
Первое слагаемое здесь обусловлено только электронами, а именно
их перераспределением за счет модулирующего поля. Если электро-
электроны представить как затухающие гармонические осцилляторы с ре-
резонансной частотой «0, то величины (dr]/dQ)q и (d7]/dq)g имеют ре-
резонанс на частоте ш0 (обычно 1014—1015 Гц). Второй член учитыва-

284
Глава 7
ет изменение оптической непроницаемости, обусловленное перерас-
перераспределением ионного заряда (или деформацией решетки) под дейст-
действием модулирующего поля Е(ая). Если решетку представить как
затухающий гармонический осциллятор, то величина
3Q
е/М
G.6.2)
имеет резонанс на частоте собственных колебаний решетки шт с
шириной линии 2Г. Поскольку резонансная частота ат обычно мно-
много меньше оптической резонансной частоты а>0 (т. е. шт < <о„), то
дисперсионные свойства величины г можно рассматривать по от-
отдельности. Дисперсия на высоких частотах [зависимость г («J] име-
имеет место строго в окрестности резонансной частоты решетки («m ~
« ит), а дисперсия в области оптических частот [зависимость
г(а))] _ строго в окрестности частоты электронных переходов (а ~
• «-). Решеточные резонансы проявляются, как правило, вблизи
частоты 1013 Гц, а электронные резонансы — вблизи 10 Гц
C000 А). Частота модуляции «т в электрооптических устройствах
обычно много меньше резонансной частоты шт решетки (т. е. шт «
« шТ). Поэтому дисперсия для высокочастотных волн очень мала.
Исключение составляют лишь некоторые материалы в окрестности
их точек фазового перехода, где решетка «размягчается» (ат стано-
становится малой).
Прежде чем приступить к анализу экспериментальных электро-
электрооптических коэффициентов, следует в какой-то степени познако-
познакомиться с тем, как эти данные получают. Большинство общеприня-
общепринятых методов определения электрооптических коэффициентов за-
заключается в измерении изменений фазы света и интенсивностей по-
побочных максимумов. Все изменения фазы G.3.11) и интенсивностей
в побочных максимумах G.3.15) непосредственно связаны с соот-
соответствующими электрооптическими коэффициентами. Оба метода
измерений обычно реализуются при квазиэлектростатических усло-
условиях, т. е. при частотах модуляции, которые много ниже фунда-
фундаментальных частот акустических резонансов образца. При этих ус-
условиях кристалл может свободно деформироваться в соответствии
с законами пьезоэлектричества и изменение напряжения в нем от-
отслеживает модуляцию поля. Измеренный таким образом электро-
электрооптический коэффициент обозначают через rjjk (низкочастотный ко-
коэффициент). Если частота действующего электрического поля мно-
много выше фундаментальных частот акустических резонансов, то кри-
кристалл не деформируется и является фактически сжатым (т. е. нахо-
находится при постоянном сжатии). В этом случае измеренный электро-
электроэлектрооптика
285
. К
РИС. 7.10. Зависимость электрооп- . ?
тического коэффициента г63 от часто-
частоты для кристаллов KDP (/) и ADP
B), иллюстрирующая влияние упру-
упругого резонанса и различие между гТ,
и ? [3].
\(
1
1
;
<
Л
¦г-Н
I Т I
111
ю:
ю6
f, Гц
оптический коэффициент обозначают через rfJk (высокочастотный
) Кфф j f й
фф
коэффициент). Коэффициенты rjjk и rfJk
fJk
j J имеют одинаковые свойства
симметрии и отличаются друг от друга на величину, определяемую
непрямым электрооптическим эффектом:
1у* = г-
,jk
Pijlm dl,
mk >
G.6.3)
где pt lm и dlmk — электрооптический и пьезоэлектрический коэффи-
коэффициенты соответственно. Рис. 7.10 иллюстрирует эффект акустиче-
акустического резонанса и различие между г\ъ и г\ъ в кристаллах KDP и
ADP. На рис. 7.11 приведены зависимости г\г от длины волны для
кристаллов KDP, KD*P, ADP, AD*P и RDP.
Широко изучалась также температурная зависимость электрооп-
электрооптических коэффициентов. Известно, что в сегнетоэлектриках и дру-
других материалах, которые проявляют фазовый переход, электрооп-
электрооптические коэффициенты могут сильно зависеть от температуры
и при достижении температуры перехода Тс изменяются, как пра-
правило, приблизительно пропорционально величине (Г — Тс)~{
26
22
s
РИС. 7.11. Зависимость г^3 от длины волны для
кристаллов KDP, KD'P, ADP и RDP [4].
АО*Р
КОР
АОР
400 500 600 700
X, HM

286
Глава 7
х 10
-«О
РИС. 7.12. Температурные зави-
зависимости величин г6ъ и 1/г63 для
кристаллов KDP, KD*P и RDP
[5].
(рис. 7.12). Это явление можно объяснить «размягчением» попереч-
поперечной моды оптических фононов [т. е. уменьшением шт в выражении
G.6.2)], которое приводит к большим возмущениям ионной решет-
решетки, обусловленным слабым внешним электрическим полем.
7.7. ЭЛЕКТРООПТИЧЕСКИЕ ЭФФЕКТЫ
В ЖИДКИХ КРИСТАЛЛАХ
Жидкие кристаллы по определению представляют собой жидкости,
которые имеют упорядоченное расположение молекул. Они образу-
образуются при некоторых условиях в органических веществах, у которых
молекулы являются резко анизометрическими, т. е. имеют удли-
удлиненную (сигарообразную) или плоскую (дископодобную) форму.
Вследствие упорядоченности анизометрических молекул их механи-
механические, магнитные и оптические свойства становятся анизотропны-
анизотропными. Хорошим примером жидких кристаллов является р-метокси-
бензилиден-р'-л-бутиланилин (МББА), который проявляет жидко-
жидкокристаллическую фазу простейшего типа (нематического) в темпе-
температурном диапазоне 21—47 °С. Существуют три фазы жидких кри-
кристаллов, структуры которых изображены на рис. 7.13. Рис. 7.13, а
иллюстрирует нематическую фазу, в которой существует дальний
порядок ориентации осей молекул, а центры молекул распределены
хаотически. На рис. 7.13, б показана смектическая фаза, в которой
существуют как одномерный трансляционный порядок, так и ори-
ентационный порядок, а рис. 7.13, в иллюстрирует холестерическую
фазу, в которой также имеется ориентационный порядок, но моле-
Электрооптика
287
о
cf5\
РИС. 7.13. Фазы жидких кристаллов:
а — нематическая; б — смектическая;
в — холестерическая.
кулы ориентированы рядами, причем в каждом ряду молекулы за-
закручены на определенный угол. Смектические жидкие кристаллы по
структуре наиболее близки к твердым кристаллам. Интересно заме-
заметить, что в веществах, находящихся как в нематической, так и в
смектической фазах, изменение фаз с ростом температуры происхо-
происходит в следующей последовательности: твердый кристалл — смекти-

288
Глава 7
ческий жидкий кристалл — нематический жидкий кристалл — изо-
изотропная жидкость. Несмотря на то что высшая степень упорядоче-
упорядочения свойственна смектикам, в электрооптических приложениях наи-
наибольшее число применений находят нематики и холестерики.
Благодаря ориентационной упорядоченности анизометрических
молекул смектики и нематики являются одноосно симметричными
жидкими кристаллами, причем их оптическая ось параллельна осям
молекул. Оптическая ось холестерических жидких кристаллов опре-
определяется лишь локально. Анизотропия показателя преломления ха-
характеризуется величиной Ди = пе — п0. Во всех известных немати-
ках и смектиках An > 0. Анизотропия диэлектрической проницае-
проницаемости Де = ?ц — ех жидких кристаллов может быть либо положи-
положительной (вплоть до ~ + 15?q), либо отрицательной (до — 2е0). Че-
Через Сц и ех мы обозначили диэлектрические проницаемости для
электрического поля, соответственно параллельного и перпендику-
перпендикулярного оптической оси (называемой также директором). Положи-
Положительной величиной Де характеризуются молекулы с продольным
дипольным моментом. Именно параметр Де (его знак и величина)
является наиболее важным при определении того, как жидкий кри-
кристалл будет реагировать на приложенное электрическое поле.
В жидких кристаллах наблюдается много электрооптических эф-
эффектов. Большинство из них состоит в том, что оптические свойст-
свойства жидких кристаллов изменяются в присутствии внешнего элект-
электрического поля. У молекул жидких кристаллов была обнаружена
тенденция поворачиваться таким образом, чтобы максимум ди-
диэлектрической проницаемости имел место в направлении внешнего
электрического поля. Поскольку сам жидкий кристалл весьма ани-
анизотропен, любое изменение в его структуре легко обнаружить оп-
оптическими средствами. В жидком кристалле постоянная времени
переориентации молекул имеет величину порядка 10 с и зависит
от вязкости.
Ниже мы обсудим кратко и в основном качественно различные
электрооптические эффекты в жидких кристаллах.
7.7.1, ЭФФЕКТ ОРИЕНТАЦИИ
В нематических жидких кристаллах при наложении электрического
поля оптическая ось может переориентироваться. Рассмотрим сна-
сначала случай, когда ев > е ± (Де > 0). Пусть вначале оптическая ось
была ориентирована вдоль оси z. Если приложить внешнее элект-
электрическое поле перпендикулярно оси z, то оптическая ось стремится
установиться вдоль направления поля. Пусть 9 — угол между опти-
Электрооптика
289
ческой осью и осью z. В соответствии с D.6.4) необыкновенный по-
показатель преломления для света, распространяющегося параллель-
параллельно электрическому полю, дается выражением
1
cos2fl sin2fl
G.7.1)
где пе и по — необыкновенный и обыкновенный показатели прелом-
преломления соответственно. Угол 9 зависит от напряженности электриче-
электрического поля. В сильных электрических полях 9 обращается в нуль и
двулучепреломление [пе(9) — п0] исчезает. При снятии электриче-
электрического поля угол 9 становится равным 90° и снова возникает двулу-
двулучепреломление.
В случае когда е, < е ± (Де < 0) и оптическая ось первоначально
ориентирована вдоль оси z, внешнее электрическое поле должно
быть приложено также вдоль оси z. Оптическая ось стремится из-
изменить свое направление таким образом, чтобы быть перпендику-
перпендикулярной приложенному электрическому полю и иметь определенное
направление (вдоль оси х или у) в зависимости от направления дей-
действия дополнительного возмущения (например, магнитного поля
или физико-химической обработки электродов).
Такая переориентация оптической оси под воздействием внешне-
внешнего электрического поля позволяет переключать фазовую задержку в
тонком слое соответствующим образом ориентированного жидкого
кристалла от нуля до 2тг(ие - поI/\ и обратно. В некоторых случа-
случаях эта фазовая задержка может изменяться непрерывным образом.
7.7.2. ЭФФЕКТ КРУЧЕНИЯ
Тонкий слой нематического жидкого кристалла, у которого оптиче-
оптическая ось параллельна плоскости слоев, может быть закручен таким
образом, что локальная оптическая ось будет изменяться в зависи-
зависимости от z. При этом возникает анизотропная среда с кручением. В
линейно закрученном нематическом кристалле азимутальный угол
оптической оси является линейной функцией координаты z:
az.
G.7.2)
Распространение света в анизотропных средах с линейным кручени-
кручением мы рассмотрели в разд. 5.4. Было показано, что линейно поля-
поляризованный свет, плоскость поляризации которого параллельна од-
одной из локальных диэлектрических осей, будет оставаться связан-
связанным с локальной диэлектрической осью при распространении в сре-
19-631

290
Глава 7
де, если коэффициент кручения а мал [т. е. а < 2ж(пе — по)/\].
Иными словами, плоскость поляризации такого линейно поляризо-
поляризованного света будет вращаться таким же образом, как и оптическая
ось. Это часто ошибочно интерпретируется как оптическая враща-
вращательная способность.
Рассмотрим тонкий слой положительного (Де > 0) нематическо-
го жидкого кристалла, закрученного на одну четвертую оборота
(90°). Этот слой расположен между парой параллельных поляриза-
поляризаторов, оси пропускания которых параллельны оптической оси во
входной плоскости. Такая система не пропускает свет, до тех пор
пока к ней не приложено электрическое поле. Наложение электриче-
электрического поля приводит к тому, что локальная ось ориентируется
вдоль направления поля (оси г), вследствие чего возникает пропу-
пропускание света, обусловленное исчезновением двулучепреломления.
Существуют и другие электрооптические эффекты, такие, как
динамическое рассеяние света, фазовый переход холестерик — не-
матик и эффект «гость — хозяин». Рассмотрение этих эффектов
выходит за рамки данной книги. Соответствующие подробности
читатель может найти в работе Блинова [6].
ЗАДАЧИ
7.1. Линейные электрооптические коэффициенты и симметрия
кристалла. Если atj — матричное представление операции
инвариантной симметрии кристалла, то преобразованный
электрооптический тензор имеет вид
rljk = auajmaknrlmn-
Этот тензор вследствие симметричности совпадает с исход-
исходным тензором, т. е. r[jk — Гцк. Данное свойство можно ис-
использовать для приведения электрооптических коэффициен-
коэффициентов, представленных в табл. 7.1.
а) Моноклинная группа 2. Пусть z — ось двумерного вра-
вращения С2. Матричное представление С2 записывается в
виде
Электрооптика
291
Покажите, что
б)
в)
Таким образом, электрооптический коэффициент rljk ра-
равен нулю, если индексы 1 и 2 возникают один или три
раза, — иными словами, если индекс 3 возникает нуль
или два раза. Проверьте этот результат по табл. 7.2.
Моноклинная группа т. Пусть ху — плоскость зеркаль-
зеркальной симметрии а. Матричное представление для а имеет
вид
/1 0 0\
1 0 .
0 -1/
atj = 0
,0
Покажите, что, как в п. а,
rtjk = auajjakkrijk = (±)rijk.
Таким образом, электрооптический коэффициент r^k ра-
равен нулю, если индекс 3 возникает один или три раза.
Проверьте этот результат по табл. 7.2. Покажите так-
также, что обращающиеся в нуль элементы электрооптиче-
электрооптического тензора для точечной группы m являются допол-
дополнительными к элементам для точечной группы 2, если
двумерная ось в случае группы 2 перпендикулярна пло-
плоскости зеркальной симметрии в случае группы т.
Орторомбическая группа 222. Точечная группа 222 име-
имеет три взаимно перпендикулярные двумерные оси Л", у и
z. Покажите с помощью результата, полученного в п. а
задачи, что единственные отличные от нуля компоненты
электрооптического тензора равны г123, г231 и г312.
Тетрагональная группа 42 т {кристаллы типа
KDP — ADP). Точечная группа 42т имеет симметрию
группы 222, а также двумерную вращательно-инверсион-
ную симметрию 2S4 и две зеркальные симметрии. Вра-
щательно-инверсионная симметрия представляет собой
поворот на 7г/2 вокруг оси z с последующей инверсией
относительно начала координат. Покажите, что матрич-
матричное представление оператора этой симметрии имеет вид
/О -1 0\
аи= 1 0 о.
\0 0 -1/

292
Глава 7
Покажите, что г231_= г132. Из этого следует, что для
кристаллов группы 42т мы имеем г52 = г41.
д) Кубическая группа 43т. Точечная группа 43т имеет все
симметрии группы 42т, а также трехмерные вращения и
другие симметрии. Простейшей операцией трехмерного
вращения является л" — У, У — z иг — А", что можно за-
записать в виде матрицы
Покажите, что г123 = г231 = г312, откуда следует г63 =
7.2. Электрооптический эффект в одноосных кристаллах. Рас-
Рассмотрим случай, когда электрическое поле приложено вдоль
с-оси электрооптического одноосного кристалла.
а) Покажите, что все гексагональные и тригональные кри-
кристаллы остаются одноосно симметричными, т. е. пх. —
= "у
б) В тетрагональном кристаллическом классе только кри-
кристаллы с точечной группой 4, 422, 4mm или любые цент-
росимметричные кристаллы остаются одноосно симмет-
симметричными.
в) Покажите, что при наличии электрического поля, прило-
приложенного вдоль с-оси, кристаллы с точечной группой 4
или 42т становятся оптически двуосными. (Для группы
42т см. пример в тексте.)
г) Покажите, что в кристаллах группы 4 новый эллипсоид
показателей преломления имеет вид
А + г13Е\+у
+ — + 2xyr63E = 1
Д)
е)
Покажите, что новые главные оси получаются вращени-
вращением прежних главных осей на угол в вокруг оси z (с-оси).
Этот угол не зависит от напряженности электрического
поля Е и дается выражением
tg20 = ra/rn.
Покажите, что главные значения показателя преломле-
Электрооптика
293
ния записываются в виде
»Х' = "о ~ г»1гпЕ ~ Wo tg 9r63E,
"у = »о+ Wor\3E + 2»l tg вг63Е,
ж) Покажите, что для светового пучка, распространяюще-
распространяющегося вдоль оси z, двулучепреломление равно
"у ~ "х
з)
Придумайте физическую модель, объясняющую разру-
разрушение одноосной симметрии, даже если электрическое
поле действует вдоль оси симметрии.
7.3. Электрооптическая перестраиваемая фазовая пластинка (про-
(продольная). Пусть имеется волновая пластинка, изготовленная
из электрооптического кристалла толщиной d. Если поперек
пластинки приложено напряжение V, то фазовая задержка Г
оказывается пропорциональной приложенному напряжению,
т. е. ее можно перестраивать с помощью электрического по-
поля. Покажите, что фазовые задержки для разных пластинок
определяются представленными ниже выражениями,
а) Для х-среза (или у- и z -срезов) кристаллической пластин-
пластинки группы 43т, 23 или кубической группы (например,
кристаллов CdTe, GaAs):
Г = *п\У.
б) Для х-среза пластинки группы 6m2 (m Lx2; например,
GaSe):
T=~[(ne-no)d-inlrnv].
в) Для z-среза пластинки группы 42mm:
Г = ~nlr6iV.

294
Глава 7
г) Для г-среза пластинки группы 4:
2тг
\
г = 4%№W3.
д) Для г-среза пластинки группы 2mm:
Г ^ ) d *A
7.4. Осм распространения в кристалле кубической группы 43т.
Пусть в кристалле группы 43т распространяется световая
волна с волновым вектором К, направленным по радиус -
вектору полярной системы координат (в, </>). В системе коор-
координат, показанной на рис. 7.14, ось z' совпадает с волновым
вектором К, а ось х' выбрана таким образом, чтобы с-ось
кристалла (ось z) располагалась в плоскости x'z'¦ Ось у'
перпендикулярна осям z' их'.
а) Покажите, что это преобразование можно осуществить
поворотом на угол ф вокруг оси z с последующим пово-
поворотом на угол в вокруг оси у'. Покажите также, что
матрица преобразования записывается в виде
sm$\
О
— sin в cos ф — sin в sin ф cos в l
atJ
РИС. 7.14. Система координат для задачи 7.4.
Электрооптика
295
б) Используя формулу преобразования G.4.4) для электро-
электрооптических коэффициентов, покажите, что
ri23 = cos 2 0 cos 2 ф г, и (примечание: г123 = r4i),
s2e - 2sin20)r123,
в) Получите выражения для г'т, г'пъ и г'пу
7.5. Квадратичные электрооптические коэффициенты в изо-
изотропных средах. Покажите, что для изотропных сред
а) Рассмотрите прямое преобразование координат при по-
повороте вокруг оси z на 45°. Матрица этого вращения
имеет вид
1 -L о'
"и =
-± ± О
U v/2
о о
Заметьте, что su = s!2!2, и используйте соотношение
б) Приведите к диагональному виду эллипсоид показателей
преломления при наложении электрического поля Е =
= (l/V2)E(% + у). Покажите, что главные значения по-
показателя преломления определяются выражениями
п;. п<
nt пА

296
Глава 7
где х> _ направление электрического поля. При получе-
получении выражения для sM примените условие симметрии
п.,. = п,..
ЛИТЕРАТУРА
1. Bhagavantam S., Crystal Symmetry and Physical Properties.— New York:
Academic Press, 1966.
2. CookW.R., Jr., JaffeH., Electro-optic Coefficients, Landolt-Bornstein, New
Series, vol. 11 (ed. K.-H. Hellwege), Springer-Verlag, 1979, pp. 552-651.
3. ПисаревсшпЮ. В., Трегубое Г. А., Шалдин Ю. В. Электрооптический эффект
в кристаллах NH4K,PO4, КН2РО4 и N4(CH2N в полях СВЧ. — ФТТ, 1965, т. 7,
№2, с. 661.
4. Adhav R. S., Linear electro-optic effects in tetragonal phosphates and arsenates. —
J. Opt. Soc. Amer., 59, 414—418 A969).
5. Василевская А. С., Сонин А. С. Связь диэлектрических и электрооптических
свойств сегнетоэлектрических кристаллов группы KDP в параэлектрической фа-
фазе. — ФТТ, 1971, т. 13, №6, с. 1550.
6. Блинов Л. М. Электрооптические эффекты в жидких кристаллах. — УФН,
1974, т. 114, вып. 1, с. 67.
ГЛАВА 8
ЭЛЕКТРООПТИЧЕСКИЕ УСТРОЙСТВА
В гл. 7 мы рассмотрели электрооптические эффекты в кристаллах,
т. е. вопрос о том, как внешнее электрическое поле влияет на рас-
распространение электромагнитного излучения. Эти эффекты можно
использовать для создания модуляторов света, перестраиваемых
спектральных фильтров, электрооптических фильтров, сканирую-
сканирующих устройств и т. п. Электрооптическая модуляция позволяет
управлять лазерным пучком или контролировать сигнал излучения
с высокой скоростью (вплоть до частоты в несколько гигагерц), по-
поскольку при этом не используется механическое перемещение эле-
элементов. В данной главе мы рассмотрим различные такие устройст-
устройства, их характеристики и принципы действия. Рассмотрим также не-
некоторые важные особенности их конструирования. В гл. 11 мы об-
обсудим электрооптические приборы на основе направляемых волн,
такие, как модуляторы и согласующие устройства.
8.1. ЭЛЕКТРООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
В разд. 7.3 мы кратко рассмотрели электрооптическую модуляцию
света в г-срезе пластинки из KDP (поверхность пластинки перпенди-
перпендикулярна с-оси кристалла). Принцип действия здесь основан на изме-
изменении эллипсоида показателей преломления под действием внешне-
внешнего электрического поля. При распространении линейно-поляризо-
линейно-поляризованных нормальных мод через такую пластинку показатель пре-
преломления будет зависеть от напряженности поля. Очевидно, что
фазовый сдвиг этих нормальных мод при прохождении через кри-
кристалл зависит от показателя преломления. После прохождения в
кристалле расстояния L волна претерпевает следующий фазовый
сдвиг благодаря наложенному электрическому полю:
= f»VEL,
(8.1.1)
где X — длина волны света, п — показатель преломления, г — со-
соответствующий электрооптический коэффициент, а Е — напряжен-
напряженность приложенного электрического поля. Если Е изменяется во
времени синусоидально, то фазовая задержка волны следует за из-

298
Глава 8
менением приложенного электрического поля и также изменяется
синусоидально, если только частота модуляции не слишком высо-
высока. Таким образом, электрооптический эффект непосредственно
приводит к фазовой модуляции этих нормальных мод. Амплитуд-
Амплитудную модуляцию можно получить, комбинируя две распространяю-
распространяющиеся нормальные моды и два различных индуцированных элек-
трооптически фазовых сдвига. Обычно для создания фазовой за-
задержки линейно-поляризованного света необходимо иметь всего
один поляризатор. Для амплитудной же модуляции требуется до-
дополнительный поляризатор (анализатор), ориентированный под
определенным углом для получения соответствующей интерферен-
интерференции.
Электрооптическая модуляция световых волн также подразделя-
подразделяется на два основных типа в зависимости от направления прило-
приложенного электрического поля. Если электрическое поле параллель-
параллельно направлению распространения, то модуляция называется про-
продольной. Если же электрическое поле перпендикулярно направле-
направлению распространения, то модуляцию называют поперечной. Рас-
Рассмотрим ниже оба этих случая по отдельности.
8.1.1. ПРОДОЛЬНАЯ ЭЛЕКТРООПТИЧЕСКАЯ МОДУЛЯЦИЯ
На рис. 8.1 изображена геометрия продольного электрооптического
модулятора. Этот модулятор представляет собой тонкую электро-
Световой пучок
Электро-
оптический
кристалл
Прозрачные
электроды
РИС. 8.1. Геометрия типичного продольного электрооптического модулятора.
Электрооптические устройства
299
оптическую кристаллическую пластинку большой площади. Вектор
модулирующего электрического поля параллелен направлению рас-
распространения света всюду, кроме области электродов. В случае ли-
линейного электрооптического эффекта изменение показателя прелом-
преломления, вызванное электрическим полем, пропорционально напря-
напряженности электрического поля Е. Вызванное электрическим полем
изменение фазы (фазовая задержка) для света, проходящего через
кристаллическую пластинку, пропорционально величине EL, кото-
которая равна приложенному напряжению V и не зависит от толщины
кристаллической пластинки L. В следующих примерах приводятся
расчеты некоторых изменений фазы, обусловленных действием
внешнего электрического поля.
г-стЕЗ пластинки H3LiNbO3. Рассмотрим случай, когда электроопти-
электрооптический кристалл представляет собой z-срез пластинки из LiNbO3.
Кристалл LiNbO3 имеет точечную группу Зт. Из табл. 7.2 и выра-
выражения G.2.3) следует, что эллипсоид показателей преломления при
наличии внешнего электрического поля, направленного вдоль оси z
(т. е. Е = Еъ), описывается уравнением
1
= 1,
(8.1.2)
где по ипе — обыкновенный и необыкновенный показатели прелом-
преломления кристалла, а г13 н г33 — соответствующие электрооптические
коэффициенты. Поскольку уравнение (8.1.2) не содержит перекрест-
перекрестных членов, главные значения показателя преломления, согласно
(8.1.2), даются выражениями
"х = "
- l"l
l"lrl3E>
Пу = »о~ 1ПоГ13Е>
(8.1.3)
n=n.-
2»е'33
r33E,
где предполагается, что пъгЕ < п. В соответствии с (8.1.3) пх = пу,
так что кристалл является оптически одноосным и с-ось остается
неизменной. Свет, распространяющийся вдоль оси г, будет претер-
претерпевать один и тот же сдвиг фазы независимо от его поляризации.
Следовательно, такой модулятор может модулировать фазу непо-
ляризованного лазерного пучка. Световой пучок, прошедший через

300
Глава 8
модулятор, приобретает фазовый множитель е lkL, который содер-
содержит фазу, отвечающую нулевому полю (Е = 0), и электрически ин-
индуцированное изменение фазы
2iT
(8.1.4)
где V — приложенное напряжение. Напряжение, требуемое для из-
изменения фазы на тг, называется полуволновым напряжением фазо-
фазовой модуляции и дается выражением
v.=
(ФМ).
(8.1.5)
Если приложенное напряжение синусоидально изменяется во време-
времени по закону
V=Vmsmumt, (8.1.6)
то прошедший пучок будет модулированным по фазе и его можно
записать в виде
E(z.t) = Aexv\i(wt- kz - ^ + 5sinwm0], (8.1.7)
где а — постоянная амплитуда,
(8.1.8)
Поскольку в устройстве с такой геометрией электрическое поле не
индуцирует двулучепреломление, фазовая задержка между любыми
двумя ортогонально поляризованными волнами отсутствует. Без
введения обратной связи (см. разд. 8.2) такое устройство не позво-
позволяет осуществить амплитудную модуляцию.
Аналогичным образом ведут себя и z-срезы других одноосных
электрооптических кристаллов; исключение составляют кристаллы
с группой симметрии 42т или 4, которые под действием электриче-
электрического поля становятся двуосными (см. задачу 7.2).
г-сРЕз кубического кристалла. Рассмотрим теперь случай, когда
пластинка представляет собой г-срез кубического кристалла. При-
Примерами таких кристаллов являются GaAs, CdTe, InAs и ZnS. Эл-
Эллипсоид показателей преломления при действии электрического по-
Электрооптические устройства
301
ля вдоль оси z (т. е. Е = Ег) согласно табл. 7.2 и G.2.3) имеет вид
хг v2 z2
п2 п1 п1
Приложенное электрическое поле приводит к связи х- и j-поляризо-
ванных волн. Главные диэлектрические оси х и у поворачиваются
вокруг z на угол 45°, так как электрическое поле действует в на-
направлении оси z. Эллипсоид показателей в новой главной системе
координат (а"', у', z') принимает вид
(8.1.9)
Главные значения показателя преломления, согласно (8.1.9),
ся выражениями
пх, = п- \пъгЛ1Е,
дают-
дают(8.1.10)
п,,
п.
Если пластинку нужно использовать в качестве фазового моду-
модулятора, то свет должен быть поляризован в направлении либо оси
х', либо у'. При этом фазовый сдвиг, индуцированный приложен-
приложенным напряжением, дается выражением
Дф = ^и3г41К, (8.1.П)
где V — модулирующее напряжение (V = EL). Полуволновое на-
напряжение для фазовой модуляции равно
п'г
(ФМ).
Г41
(8.1.12)
Если модулирующее поле синусоидально изменяется во времени по
закону (8.1.6), то индекс модуляции можно записать в виде
8 = X"V41Fm = ^~ (ФМ).
(8.1.13)

302
Глава 8
Если пластинка применяется в качестве амплитудного модуля-
модулятора, то передний поляризатор нужно выставить вдоль оси х та-
таким образом, чтобы х'- и .у'-моды возбуждались с одинаковыми
амплитудами. При прохождении через кристалл в этом случае на-
накапливается фазовая задержка Г = Ък(пч. - wv.)L/X, определяемая
выражением
r = yVr41K. (8.1.14)
Полуволновое напряжение в случае амплитудной модуляции опре-
определяется как напряжение, необходимое для получения фазового
сдвига на -к, и дается выражением
2и3г
(AM).
(8.1.15)
14
Если модулирующее напряжение синусоидально изменяется во вре-
времени по закону (8.1.6) и последовательно с электрооптическим кри-
кристаллом располагается соответствующим образом ориентирован-
ориентированная четвертьволновая пластинка, то фазовая задержка принимает
вид
2тг
(8.1.16)
если поляризатор на выходе ориентирован перпендикулярно поля-
поляризатору на входе, то он преобразует фазовую модуляцию в ам-
амплитудную. Коэффициент пропускания полной структуры при этом
равен Т = sin2(IY2), где Г определяется выражением (8.1.16). Если
жУш <^ Vж, то коэффициент пропускания Т приближенно записыва-
записывается в виде
= ГоA
где То = 1/2, а Д дается выражением
¦ у •
(8.1.17а)
(8.1.176)
Величина Д называется глубиной модуляции. Благодаря симметрии
пластинки из х- или z-срезов кубического кристалла будут вести се-
себя точно таким же образом, как и пластинка из .у-среза.
Электрооптические устройства
303
Приведенные выше два примера показывают, что величина ин-
индекса (или глубины) модуляции пропорциональна приложенному
напряжению. Полуволновые напряжения прямо пропорциональны
длине волны света и обратно пропорциональны электрооптическо-
электрооптическому коэффициенту. Для света в видимом диапазоне длин волн эти
напряжения имеют величину порядка нескольких киловатт. Увели-
Увеличение толщины пластинки приводит к увеличению длины взаимо-
взаимодействия, но и к уменьшению напряженности электрического поля.
Следовательно, полное увеличение модуляции за счет увеличения
толщины пластинки при продольной модуляции отсутствует. Для
излучения ИК-диапазона из-за большой длины волны света (ска-
(скажем, 10,6 мкм) возникает необходимость в приложении высоких
напряжений. Продольные модуляторы используются только тогда,
когда требуются большие площади устройства и большое поле зре-
зрения. Можно показать, что угол поля зрения продольного модуля-
модулятора из z-среза кристалла с группой симметрии 43т составляет по-
почти 2тг (см. задачу 8.1).
8.1.2. ПОПЕРЕЧНАЯ ЭЛЕКТРООПТИЧЕСКАЯ МОДУЛЯЦИЯ
Геометрия поперечного электрооптического модулятора приведена
на рис. 8.2. При данной напряженности электрического поля такая
структура позволяет обеспечить большую длину взаимодействия.
Модулирующее поле является поперечным относительно направле-
направления распространения оптического пучка. Ограничиваясь рассмотре-
рассмотрением только линейных электрооптических эффектов, можно пока-
показать, что изменение показателя преломления, индуцированное
электрическим полем, пропорционально напряженности поля Е.
Электрически индуцированное изменение фазы (или фазовая за-
Электроды
Свет
Электрооптический
кристалл
т
РИС. 8.2. Геометрия типичного поперечного электрооптического модулятора.

304
Глава 8
держка) для света, проходящего через кристаллическую пластинку,
пропорционально при этом величине EL, или VL/d, где d — рас-
расстояние между электродами. Таким образом, изменение фазы про-
пропорционально длине кристалла L. Это преимущество было исполь-
использовано при создании электрооптических модуляторов лазерных пуч-
пучков с низкими управляющими напряжениями. Поперечную электро-
электрооптическую модуляцию можно проиллюстрировать следующими
примерами.
Электрооптический модулятор на кристалле LiTaO3. Рассмотрим
прямоугольный образец кристалла LiTaO3, изображенный на
рис. 8.3, входная и выходная грани которого перпендикулярны оси
у, а боковые грани — осям х и z соответственно. Кристалл LiTaO3
имеет точечную группу симметрии Зт (так же, как и кристалл
LiNbO3). Пусть модулирующее электрическое поле действует вдоль
направления оси г; при этом главные значения показателя прелом-
преломления определяются выражениями (8.1.3). Поскольку световой пу-
пучок распространяется вдоль направления оси у, двулучепреломле-
ние для него можно записать в виде
/ и\ J./3 3 \ г< /о 1 1 о\
Величина этого двулучепреломления равна сумме естественного
двулучепреломления (пе - п0) и электрически индуцированного дву-
двулучепреломления A/2)(«^зз — n*ru)E. При этом фазовая задержка
для света, проходящего через кристалл, дается выражением
р _ 21Г/И „ \г „3, „3, \L ,, (Q 1 1Q\
Свет
РИС. 8.3. Образец электрооптического кристалла LiTaO3.
Электрооптические устройства
305
где V — приложенное напряжение, ad — расстояние между элек-
электродами.
Если свет линейно-поляризован вдоль оси z, то изменение фазы,
индуцированное внешним электрическим полем, равно
чт ¦, L
Дф= д-"ггзз7К- (8.1.20)
В амплитудном модуляторе на кристалле LiTaO3 из-за наличия
естественного двулучепреломления приходится применять фазовый
компенсатор, который сдвигает фазу до тех пор, пока полная фазо-
фазовая задержка при отсутствии внешнего напряжения не будет со-
составлять нечетное число ж/2. Кроме того, входная и выходная гра-
грани кристалла должны быть параллельными друг другу, чтобы пу-
пучок претерпевал одинаковую фазовую задержку по всему попереч-
поперечному сечению модулятора. В этом случае полуволновое напряжение
запишется в виде
- п„г
(8.1.21)
о'13
Если приложенное напряжение синусоидально изменяется во време-
времени по закону (8.1.6), то фазовая задержка равна
7***"«' = г°
(8.1.22)
где Гц — полная фазовая задержка в отсутствие внешнего напряже-
напряжения. Если Гц составляет нечетное число ж/2, то глубина модуляции
дается выражением
Д = Гт = ^. (8.1.23)
Из (8.1.21) видно, что полуволновое напряжение можно умень-
уменьшить, выбирая более длинные кристаллические образцы, что по-
позволяет увеличить область взаимодействия. Были созданы модуля-
модуляторы интенсивности света на основе кристаллов LiTaO3 и LiNbO3
рассмотренной нами геометрии, обеспечивающие частоту модуля-
модуляции вплоть до 4 ГГц [1].
Электрооптические модуляторы на кубических кристаллах. Кубиче-
Кубические кристаллы оптически изотропны (не обладают двулучепрелом-
20-631

306
Глава 8
лением) и поэтому использование их во многих оптических систе-
системах позволяет получать широкое поле зрения. Здесь мы рассмот-
рассмотрим кристаллы с группой симметрии 43т (цинковая обманка). К
ним относятся кристаллы InAs, CuCl, GaAs и CdTe. Последние два
кристалла используются для модуляции ИК-излучения, поскольку
их прозрачность сохраняется на длинах волн более 10 мкм. Эти
кристаллы являются кубическими и имеют четырехкратные оси
симметрии вдоль кубических граней (т. е. <100>, <010>, <001>) и
трехкратные оси симметрии вдоль диагоналей куба (т.е. <111>,
В соответствии с табл. 7.2 и выражением G.2.3) эллипсоид по-
показателей преломления при наличии внешнего электрического поля
можно записать в виде
2rAl(yz?x + zxEy + хуЕ,) = 1,
(8.1.24)
где Ех, Еу и Ez — составляющие электрического поля вдоль кри-
кристаллических осей, а г41 — электрооптический коэффициент. В этом
случае все три переменные х, у и z оказываются связанными. Для
приведений уравнения (8.1.24) к диагональному виду необходимо
решить задачу на собственные значения:
"Г гм Ех
г
'41
(8.1.25)
Собственные векторы V представляют собой новые главные оси, а
собственные значения п' — новые главные значения показателя
преломления. Для конкретности рассмотрим случай, когда электри-
электрическое поле действует в направлении <110>. Если напряженность
поля равна Е, то
Е* = Еу=-^Е, Е: = 0. (8.1.26)
Подставляя выражение (8.1.26) для Ех, Еу и Ez в (8.1.25), получаем
Электрооптические устройства
307
следующее
' 1
п2
0
1
1
и'2
Е
характеристическое
0
1
п2
Ж*
1
и'2
1Е
1
'п2 ~
уравнение:
V2
= 0.
(8.1.27)
Корнями этого уравнения являются главные значения показателя
преломления:
пх, = п + in\E, ny, = n- ±n3rAlE, я,.-д.
Новые главные оси определяются выражениями
(8.1.28)
~X~±y.
(8.1.29)
На рис. 8.4 показан схематически работающий на этом принципе
амплитудный модулятор. Фазовая задержка в нем дается выраже-
выражением
2тг
(8.1.30)
Е II <110>
Входной
пучок
*
Входной
поляризатор
Выходной
пучок
Выходной поляризатор,
скрещенный со входным
РИС. 8.4. Поперечный электрооптический модулятор на основе кристалла типа цин-
цинковой обманки D3т), в котором внешнее электрическое поле Е параллельно диаго-
диагонали куба (направлению < 110>).

ТАБЛИЦА 8.1. Электрооптические свойства и фазовые задержки в кристаллах с симметрией класса 43т (структура
цинковой обманки) для трех направлений приложенного поля [2]
Эллипсоид пока-
показателей прелом-
преломления
п'х
п'у
<
Е ± плоскости
х2 + у
= 0,?г
2 + *2 ,
+ 2гмЕху = 1
по~ ir
"о
1г*\Е
«>4.?
@01)
= ?
X'
»о
"о
"о
Е
?х
-+>
п
+ f2
+ i
-i
i. плоскости (ПО)
=? = ?/V2, ? =0
У Z
2 + z2,
2 '
rME(yz + zx) = 1
x;
?
?,=
«2
.. 1
' 2^3
1
+ 2^
ГЙ
i. плоскости
ЕУ = Ег =
*2 +
E(yz + zx -+
">41^
>4.?
(HI)
?Af3
xy) =
1
Система коор-
координат x'y'z'
Направления оп-
оптического пучка
и осей скрещен-
скрещенных поляризато-
поляризаторов
Фазовая задержка
Г(К = Ed)
45
Г = 0
(ПО)
45° / 45° х
@01)
— к з
Г = 0

310
Глава 8
В табл. 8.1 приведены фазовые задержки и электрооптические
свойства кристаллов группы 43т в случае, когда электрическое по-
поле приложено вдоль направлений <001>, <110> и < 111>. Очевидно,
что максимальная достижимая фазовая задержка определяется вы-
выражением (8.1.30). Полуволновое напряжение при этом равно
V - —
2и3г
(8.1.31)
41
8.2. ЭЛЕКТРООПТИЧЕСКИЕ МОДУЛЯТОРЫ ФАБРИ — ПЕРО
Выше при рассмотрении электрооптических модуляторов, в частно-
частности с поперечной геометрией (рис. 8.2), было показано, что модуля-
модуляция пропорциональна длине взаимодействия L. Если Vm — ампли-
амплитуда модулирующего напряжения и на модулятор подано соот-
соответствующее смещающее напряжение, то глубину фазовой модуля-
модуляции (8.1.8) можно записать в виде
8 = тг —
* яг
(8.2.1)
а глубина амплитудной модуляции (8.1.23) принимает простой вид:
А К™
Д = 7Г—.
(8.2.2)
Согласно (8.2.1) и (8.2.2), для осуществления большой глубины мо-
модуляции полуволновые напряжения VT должны быть малы при дан-
данном напряжении модуляции, а для этого в случае поперечной схемы
модулятора требуются кристаллы большой длины.
В данном разделе мы исследуем вопрос о том, к чему приводит
включение электрооптического кристалла в резонатор Фабри — Пе-
Перо. Поскольку в оптическом резонаторе свет отражается много-
многократно, эффективная длина взаимодействия светового пучка в элек-
электрооптическом кристалле сильно возрастает. Это существенно уве-
увеличивает глубину модуляции как в фазовых, так и в амплитудных
модуляторах. Рассмотрим теперь эти устройства более подробно.
8.2.1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
Рассмотрим тонкую пластинку, представляющую собой z-срез кри-
кристалла LiNbO3 (или LiTaO3), помещенную между диэлектрическими
зеркалами с большой эффективностью отражения (рис. 8.5). На
Электрооптические устройства
311
Высокоотраж ающее
диэлектрическое покрытие
Прозрачные электроды
РИС. 8.5. Электрооптический модулятор Фабри — Перо.
внешнюю поверхность общей структуры наложены прозрачные
электроды. Коэффициент пропускания резонатора Фабри — Перо
дается выражением [1J]
Т =
О-*J
(8.2.3)
где R — коэффициент отражения зеркал, а ф — фазовый сдвиг све-
света при прохождении через среду, определяемый следующим обра-
образом:
-nL;
(8.2.4)
здесь L — толщина пластинки. В соответствии с (8.1.3) показатель
преломления п при наличии внешнего электрического поля записы-
записывается в виде
я - я, - \п\гпЕ. (8 2.5)
Подставляя выражение (8.2.5) для п в (8.2.4), получаем
Ф = -ynoL ~ ^nlri2V, (8.2.6)

312
Глава 8
Приложенное
напряжение
Модулирующее
напряжение
РИС. 8.6. Зависимость коэффициента пропускания электрооптического модулятора
Фабри — Перо от приложенного напряжения. Модулятор смещен в рабочую точку,
расположенную на полувысоте максимума пропускания. Небольшое приложенное
синусоидальное напряжение приводит к модуляции интенсивности на выходе относи-
относительно точки смещения.
где V — приложенное напряжение.
Если падающий световой пучок является монохроматическим,
то интенсивность прошедшего пучка зависит от величины ф, кото-
которая, как следует из (8.2.6), является электрически перестраиваемой.
Кроме того, если резонатор Фабри — Перо смещен таким образом,
что коэффициент его пропускания в отсутствие модулирующего
напряжения равен 50%, то интенсивность прошедшего излучения
будет сильно модулироваться относительно малыми модулирую-
модулирующими напряжениями. Это иллюстрируется на рис. 8.6. Большая
глубина модуляции обусловлена резким пиком пропускания, разу-
разумеется, при условии, что резанатор имеет высокую добротность.
Действительно, в соответствии с выражением (8.2.3) наклон кривой
пропускания в точке, расположенной на ее полувысоте, запишется в
виде
dT\ _ F
иф J 1/2 Я
(8.2.7)
Электрооптические устройства
313
где F — добротность резонатора. Нетрудно изготовить резонато-
резонаторы Фабри — Перо с добротностью F = 30. Таким образом, наклон
кривой пропускания, определяемый выражением (8.2.7), может
быть порядка 10. В обычных амплитудных модуляторах (см., на-
например, рис. 7.5) этот наклон равен 1. Пусть приложенное напря-
напряжение имеет вид V = Vmsinujmt. Тогда глубину модуляции прошед-
прошедшего пучка с помощью выражений (8.2.7), (8.1.4) и (8.1.5) можно
записать в виде
V
Ъ = Р—. (8.2.8)
Заметим, что по сравнению с выражением (8.2.2) здесь при. том же
глубина модуляции увеличивается в F/ж раз.
напряжении VJV.
8.2.2. ФАЗОВАЯ МОДУЛЯЦИЯ
Хотя амплитудно-модулированный свет после прохождения через
электрооптический модулятор Фабри — Перо оказывается промо-
Диэлектрическое
покрытие
(R < 1,0)
Полиостью
отражающее зеркало
(R • 100%)
»¦ Л
Электроопт.
кристалл
РИС. 8.7. Работа асимметричного реюнатора Фабри - Перо (эталона Жира-
»Урнуа) в качестве фазового модулятора.

314
Глава 8
дулированным также и по фазе, имеется необходимость в получе-
получении светового пучка с чисто фазовой модуляцией. Идеализирован-
Идеализированная структура чисто фазового модулятора изображена на рис. 8.7.
Он представляет собой асимметричный резонатор Фабри — Перо,
заднее зеркало которого имеет коэффициент отражения 100%. Пе-
Переднее зеркало имеет частично отражающее диэлектрическое по-
покрытие с R < 1,0. Это так называемый эталон Жира — Турнуа [9].
Коэффициент отражения полной структуры, очевидно, равен 100%,
поскольку свет не может проходить через второе зеркало и полная
структура не имеет потерь. Если в спектральном диапазоне, пред-
представляющем интерес, коэффициент отражения зеркала сохраняется
равным 100%, то будет отражаться вся электромагнитная энергия.
Действительно, коэффициент отражения можно записать в виде
J*
(8.2.9)
где мы положили гп = — V7?, г2Ъ = 1, аф дается выражением
ф=—пЬ. (8-2-10)
Фазовый сдвиг Ф после отражения определяется выражением (8.2.9)
и может быть выражен через ф следующим образом:
Ф = -2arctg
(8.2.11)
В предельном случае, когда коэффициент отражения переднего зер-
зеркала равен нулю (R = 0), мы имеем Ф = — 2ф, т. е. фазовый сдвиг
совпадает с полным оптическим фазовым сдвигом светового пучка,
прошедшего через резонатор в прямом и обратном направлениях.
Если коэффициент отражения больше нуля (R > 0), то в асиммет-
асимметричном резонаторе Фабри — Перо фазовый сдвиг Ф существенно
возрастает из-за многократных отражений (см. рис. 8.7).
Для пластинки, представляющей собой г-срез кристалла LiNbO3,
фазовый сдвиг ф при наличии электрического поля дается выраже-
выражением (8.2.6):
Ф = ^T-n0L - -n\rXiV. (8-2.6)
Кроме того, если к электрооптическому кристаллу приложено со-
соответствующее смещающее напряжение, то в отсутствие модулиру-
Электрооптические устройства
315
юшего напряжения мы имеем ф = тж. Таким образом, фазовый
сдвиг Ф отраженного пучка можно записать в виде
V/?
К)}
(8.2.12)
Предположим теперь, что модулирующее напряжение мало, так
что глубина фазовой модуляции
ДФ =
(8.2.13)
Заметим, что наличие переднего зеркала увеличивает глубину мо-
модуляции в A + VR)/(l - л/R) раз. Например, при R - 0,9 глубина
фазовой модуляции увеличивается в 38 раз. На рис. 8.8 представле-
представлена зависимость Ф от V/Vm. Выражение (8.2.13) является линейной
аппроксимацией зависимости (8.2.12).
Приведенные два примера продемонстрировали, что оптическая
обратная связь, создаваемая резонатором Фабри — Перо, значи-
значительно увеличивает длину взаимодействия и, следовательно, глуби-
глубину модуляции при данной величине напряжения. Однако это увели-
увеличение возможно лишь для тех оптических частот, которые удовлет-
удовлетворяют условиям резонанса Фабри — Перо. Иными словами, к
ф 2 -
0,00
0,1
рИС. 8.8. Зависимость Фот И при R = 0,95.

316
Глава 8
Электрооптические устройства
317
электрооптическому кристаллу необходимо приложить соответст-
соответствующее смещающее напряжение. Поскольку фазовое смещение за-
зависит от длины волны, на других длинах волн резонатор нельзя
сместить в нужную рабочую точку. Следовательно, присутствие
оптического резонатора уменьшает полосу пропускания модулято-
модулятора на оптических частотах.
В разд. 8.6 мы рассмотрим применение пассивного асимметрич-
асимметричного резонатора Фабри — Перо для сжатия импульса.
8.3. НЕКОТОРЫЕ КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
МОДУЛИРУЮЩИХ УСТРОЙСТВ
8.3.1. ВЫСОКОЧАСТОТНАЯ МОДУЛЯЦИЯ
В рассмотренных в двух предыдущих разделах примерах мы по-
получили выражения для фазовой задержки, индуцированной низкоча-
низкочастотными электрическими полями. Во многих практически важных
случаях приходится иметь дело с высокочастотными модулирую-
модулирующими сигналами с широкой полосой частот. В данном разделе мы
рассмотрим ряд основных факторов, ограничивающих максималь-
максимальные допустимые частоты модуляции в ряде типичных эксперимен-
экспериментальных ситуаций.
Рассмотрим сначала схему, показанную на рис. 8.9. В этом слу-
случае электрооптический кристалл помещен между двумя электрода-
электродами, к которым,приложено модулирующее поле с частотой ~шо/2х.
Пусть Rs — внутреннее сопротивление модулирующего источника,
а величина С — емкость конденсатора, образуемого плоскопарал-
плоскопараллельной пластинкой электрооптического кристалла. Если Rs >
> (ш0С)~', то основное падение модулирующего напряжения про-
происходит на /?л и, следовательноГтеряется, поскольку оно не вносит
вклада в задержку. Такого падения напряжения можно избежать,
/
Электро-
оптический
кристалл
если настроиться в резонанс с контуром, образованным емкостью
С и индуктивностью L кристалла [где ш„ = (LC)~]], как показано
на рис. 8.9. Кроме того, из-за наличия шунтирующего сопротивле-
сопротивления RL при ш = ш0 импеданс параллельной RLC-цепи оказывается
равным RL. Поскольку RL выбирается больше, чем Rs, модулирую-
модулирующее напряжение падает главным образом на кристалле. Резонанс-
Резонансный контур имеет конечную ширину полосы, т. е. его импеданс вы-
высок только в частотном интервале Дш/2х « \/BwRLC) (с центром в
точке ы0). Таким образом, максимальная полоса модуляции (т. е.
частотный спектр модулирующего сигнала) должна быть меньше,
чем
Ды I
; ' (8.3.I)
если модулирующее поле должно полностью повторять модулиру-
модулирующий сигнал.
На практике размер полосы модуляции Дш/2х определяется кон-
конкретными применениями. Кроме того, необходимо иметь опреде-
определенный максимум задержки Г/и. Используя G.3.2) для того, чтобы
связать F/H с максимальным модулирующим напряжением Vт —
= (?",)„,/>, с помощью (8.3.1) можно показать, что мощность
Vj;/2RL, необходимая для получения максимальной задержки Гш в
кристаллах типа KDP, связана с полосой модуляции Av — Дш/2х
следующим образом:
РИС. 8.9. Эквивалентная электрическая схема модулятора на электрооптическом
кристалле плоскопараллельной конфигурации.
где L — длина оптического пути в кристалле, А — площадь попе-
поперечного сечения кристалла, перпендикулярного L, а е — диэлектри-
диэлектрическая проницаемость на частоте модуляции ш0.
8.3.2. ОГРАНИЧЕНИЯ ЗА СЧЕТ ВРЕМЕНИ РАСПРОСТРАНЕНИЯ
СВЕТА ЧЕРЕЗ МОДУЛИРУЮЩИЙ КРИСТАЛЛ
Другой важной характеристикой В Ч -модуляции является ограни-
ограничение за счет времени распространения света через модулирующий
кристалл. В случае когда модулирующее поле является быстроме-
быстроменяющейся функцией времени, оптическая фаза не может отслежи-
отслеживать адиабатически изменение во времени показателя преломления,
особенно когда время распространения т = nL/c сравнимо с перио-
периодом 2ж/ыП1 модулирующего поля. Этот вопрос мы рассматривали в
Разд. 7.4. Согласно общему результату G.4.23), уменьшение глуби-
глубины модуляции для приведенного модулятора (п>п = 0) за счет ко-

318
Глава 8
Г I \
РИС. 8.10. Зависимость коэффициента р от ш t.
конечного времени распространения равно
(8.3.3)
где шш — частота модуляции.
Для р = 1 (уменьшение глубины модуляции отсутствует) необ-
необходимо, чтобы удовлетворялось условие штт <^ 1, т. е. время рас-
распространения должно быть мало по сравнению с самым коротким
периодом модуляции. Коэффициент р представлен на рис. 8.10.
Если мы условно выберем наивысшую частоту модуляции как
частоту, при которой шшт = -к (в этой точке, согласно рис. 8.10,
р = 0,64), и используем соотношение т = Ln/c, то получим выра-
выражение
с
2Ln'
которое для кристалла KDP (п ~ 1,5) и длины L =
(8.3.4)
2 см дает
8.J.3. МОДУЛЯТОРЫ БЕГУЩЕЙ ВОЛНЫ
В Методе, который в принципе позволяет избежать ограничений,
связанных с временем распространения, используется модулирую-
модулирующий сигнал В виде бегущей ВОЛНЫ (рис. 8.11). В разд. 7.4 МЫ ПОКа-
Электрооптические устройства
319
Оптическая
поляризация
I
«Быстрая» i
ось
Входной
«Четвертьволновая»
пластинка
Источник
модулирующего
сигнала
Выходной
поляризатор
РИС. 8.11. Электрооптический модулятор бегущей волны.
зали, что если фазовые скорости оптического и модулирующего по-
полей совпадают, то часть оптического волнового фронта при рас-
распространении через кристалл будет испытывать то же самое мгно-
мгновенное модулирующее электрическое поле, что и поле, с которым
оптическая волна встречается на входной грани, и рассмотренная
выше проблема времени распространения не возникает. Такой вид
модуляции в основном используется в случае поперечной схемы,
рассмотренной в предыдущем разделе, поскольку в большинстве
структур высокочастотные поля в основном поперечные.
В общем случае, если фазовые скорости модулирующей и свето-
световой волн различны, уменьшение глубины модуляции определяется
выражением G.4.23). Максимальная частота модуляции выбирается
такой же, как и при выводе выражения (8.3.4), и дается выраже-
выражением
('J™,- 2L(n-nmy (8-3.5)
из которого при сравнении с (8.3.4) следует возможность увеличе-
увеличения предельной частоты или длины кристалла в A - nm/n)~l раз.
Напомним, что п — показатель преломления среды на частоте све-
светового пучка, а п1П — показатель преломления на частоте модули-
модулирующего напряжения.
8.3.4. ГЕОМЕТРИЧЕСКИЕ ЭФФЕКТЫ
При рассмотрении поперечного электрооптического модулятора

320
Глава 8
2V2C1
РИС. 8.12. Пучок с гауссовым поперечным сечением, проходящий через образец диа-
диаметром d и длиной L.
было показано, что для уменьшения модулирующего напряжения
желательно использовать длинные кристаллы с малым поперечным
размером (с большими L/d). Однако поперечный размер d должен
быть достаточно большим, чтобы световой пучок мог быть промо-
дулирован. Световой пучок с конечным поперечным размером, во-
вообще говоря, будет расходиться в процессе распространения. Поэ-
Поэтому кристалл с данным поперечным размером d имеет некоторую
максимальную длину электрооптической модуляции.
Рассмотрим гауссов лазерный пучок, отвечающий поперечной
моде низшего порядка и распространяющийся в электрооптическом
кристалле цилиндрической формы длиной L и диаметром d. Можно,
показать (см. задачу 8.4), что для данного кристалла с фиксирован-
фиксированной длиной L диаметр цилиндра будет минимальным, когда гаус-
гауссов пучок сфокусирован таким образом, что параметр конфокаль-
ности z0 равен половине длины L, а перетяжка пучка располагается
в центре кристалла, как показано на рис. 8.12. При этих условиях
диаметр пучка в перетяжке равен 2а>0, а на входном и выходном ос-
основаниях цилиндра он равен \^8ш0, причем
XL
2irn'
(8.3.6)
величина ш0 названа в разд. 2.2 шириной перетяжки пучка. На прак-
практике с целью более простого согласования диаметр d выбирается
больше, чем Vlcoo. В гл. 11 мы рассмотрим электрооптические мо-
модуляторы направляемых волн, в которых свет локализован в очень
малой (~А) поперечной области. Поскольку свет представляет со-
собой направляемую волну, дифракция для него отсутствует (ском-
(скомпенсирована) и длина взаимодействия может быть очень большой.
Электрооптические устройства
321
8.4. БИСТАБИЛЬНЫЕ ЭЛЕКТРООПТИЧЕСКИЕ УСТРОЙСТВА
До сих пор мы рассматривали только оптические устройства, ин-
интенсивность пучка на выходе которых была прямо пропорциональ-
пропорциональна интенсивности на входе. Такие устройства называются линейны-
линейными оптическими устройствами и характеризуются величиной
>Х)> (8.4.1)
где 1О и /, — интенсивности входного и выходного пучков соот-
соответственно, а Т(п, X) — коэффициент пропускания, который явля-
является функцией распределения показателя преломления п и длины
волны излучения X. Коэффициент пропускания Т линейного уст-
устройства не зависит от интенсивностей входного и выходного пуч-
пучков. Эта линейная зависимость исчезает, когда п зависит либо от
интенсивности на входе /,, либо от интенсивности на выходе, либо
от обеих интенсивностей. Это, естественно, может иметь место в
случае, когда оптическая среда обладает нелинейностью, т. е. когда
= no(z)+n2I(z),
(8.4.2)
где I(z) — локальная интенсивность пучка в точке z, а п2 — посто-
постоянная величина. Нелинейность может возникать также искусствен-
искусственно, если в электрооптическом кристалле существует некоторая об-
обратная связь.
Нелинейные оптические устройства обладают многими интерес-
интересными свойствами. К ним относятся дифференциальное усиление и
бистабильность (гистерезис), которые можно наблюдать, напри-
например, исследуя пропускание интерферометра Фабри — Перо, содер-
содержащего пары Na, облучаемые светом непрерывного лазера на кра-"
сителях [3]. Бистабильные устройства обычно работают в режиме
больших мощностей, когда среда ведет себя нелинейно. Если нели-
нелинейность среды увеличивается за счет резонансных электронных пе-
переходов, то полоса оказывается очень узкой. В дальнейшем мы об-
обсудим ряд электрооптических устройств с искусственно созданной
нелинейностью, характеристики которых аналогичны оптическим
устройствам с естественной нелинейностью. Обладая теми же нели-
нелинейными свойствами, они позволяют избежать ряд трудностей при
решении задач, связанных с нелинейной природой.
8-4.1. БИСТАБИЛЬНЫЙ РЕЗОНАТОР ФАБРИ — ПЕРО
Рассмотрим изображенный на рис. 8.13 резонатор Фабри — Перо,
21-631

322
Глава 8
Усилитель
Электрооптический
кристалл
Детектор
Резонатор
Фабри—Перо
Расщепитель пучка
РИС. 8.13. Схематическое представление бистабильного устройства Фабри — Перо.
(Согласно [4, 5].)
внутри которого помещен электрооптический фазовый модулятор.
Небольшая часть выходного пучка подается на детектор, сигнал на
выходе которого пропорционален интенсивности прошедшего излу-
излучения и после усиления используется для управления модулятором
в резонаторе. Это устройство представляет собой модель нелиней-
нелинейной среды, поскольку в нем управляемый электрооптически показа-
показатель преломления зависит от интенсивности излучения. Коэффици-
Коэффициент пропускания такого резонатора можно записать в виде
гр __ ^_О_
где
Ф
О-*J
A -К) +
(8.4.3)
(8.4.4)
здесь ф0 — половина фазового сдвига света после его прохождения
через резонатор в прямом и обратном направлениях без вспомога-
вспомогательной обратной связи, а а — постоянная. Величина а/0 — это из-
изменение фазы, создаваемое электрооптическим кристаллом, когда к
нему приложено электрическое напряжение, пропорциональное ин-
излучения /0. Выражение (8.4.3) можно
тенсивности прошедшего
также переписать в виде
A-
(8.4.5)
I О .1
A-ЛJ
С помощью выражения (8.4.5) можно построить зависимости /0 (/,)
Электрооптические устройства
323
т—г
= 0,4?г
1 2 3
Входная мощность
б
а —
R.
стики оистабильного резонатора Фабри — Перо.
"" " V б ~ ПРИ Фо = О,5тг, а = 1 и различных

324
Глава 8
0 12 3 4
Входная мощность
РИС. 8.15. Выходная характеристика устройства, показанного схематически на
рис. 8.13.
для различных значений ф0 и R (рис. 8.14). Мы видим, что при со-
соответствующих условиях такое устройство будет обладать биста-
бильностью, дифференциальным усилением и оптическим ограничи-
ограничивающим действием.
Заметим, что для некоторых областей входной энергии энергия
на выходе является многозначной величиной и не может быть
определена однозначно. Действительное значение интенсивности на
выходе зависит от того, каким путем изменялась энергия на входе.
Иными словами, выходная интенсивность пучка при данной интен-
интенсивности на входе зависит от предыстории работы устройства. Это
явление называется гистерезисом. В качестве примера рассмотрим
зависимость 1О (/,), изображенную на рис. 8.15, когда энергия вход-
входного пучка постепенно увеличивается от нуля. Между началом ко-
координат и точкой А энергия на выходе определяется однозначно.
После того как энергия на входе достигает точки А, энергия на вы-
выходе становится неоднозначной. Если энергия на входе возрастает
адиабатически при достижении точки А, то на выходе энергия бу-
будет описываться кривой АВ до тех пор, пока энергия на входе не
достигнет точки В. В точке В бесконечно малое увеличение энергии
на входе приведет к резкому переходу энергии на выходе в точку С.
За точкой С любое увеличение входной энергии будет приводить к
Электрооптические устройства
325
однозначно определенной энергии на выходе. Рассмотрим теперь,
что происходит при постепенном уменьшении энергии на входе!
Энергия на выходе при этом будет следовать кривой CD вплоть до
точки D. В этой точке снова бесконечно малое уменьшение энергии
на входе приведет к резкому переключению энергии на выходе в
точку А. Экспериментально этот гистерезис наблюдался в резона-
резонаторе Фабри — Перо, содержащем электрооптический модулятор на
кристалле KDP; при этом использовалось излучение гелий-неоново-
гелий-неонового лазера с длиной волны 6328 А [4].
Переключение между состояниями с высоким и низким коэффи-
коэффициентами пропускания можно осуществлять либо кратковремен-
кратковременным увеличением энергии пучка на входе, либо изменением напря-
напряжения смещения модулятора (замечание: ф0 зависит от напряжения
смещения). Можно показать, что кривая BD отвечает неустойчиво-
неустойчивому состоянию и физически не реализуется. Доказательство этого и
рассмотрение динамики переключения выходит за рамки данной
книги. Особый интерес-представляет кривая рис. 8.14, а, отвечаю-
отвечающая ф0 = 0,6тг, поскольку она обладает свойствами, характерными
для большого дифференциального усиления. Если входная энергия
оказывается вблизи скачка кривой, то небольшая модуляция вход-
входной энергии будет приводить к большой модуляции энергии на вы-
выходе. Существует много других интересных возможностей исполь-
использования таких устройств, например для формирования импульсов и
ограничения мощности (см. задачу 8.6).
Были продемонстрированы также бистабильные оптические ре-
резонаторы Фабри — Перо с обратной связью за счет отражения све-
света [5] (см. задачу 8.7).
8.4.2. БИСТАБИЛЬНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ
АМПЛИТУДНЫЙ МОДУЛЯТОР
Оптическая бистабильность может быть получена также в электро-
электрооптическом амплитудном модуляторе, на кристалл которого пода-
подается сигнал обратной связи, пропорциональный интенсивности про-
прошедшего света. На рис. 8.16 схематически показано, как действует
такое устройство. Если поляризатор на входе ориентирован под
углом 45° относительно главных осей кристалла, к которому при-
приложено модулирующее напряжение, а анализатор на выходе скре-
скрещен с ним, то коэффициент пропускания этого амплитудного моду-
модулятора дается выражением E.2.11):
I, =
(8.4.6)

326
Глава 8
Усилитель Детектор
Электроопт.
кристалл
/9
Поляризатор
1
Анализатор
РИС. 8.16. Схематическое представление бистабильного электрооптического ампли-
амплитудного модулятора.
где /¦ и / — интенсивности на входе и выходе соответственно, а
Г — фазовая задержка кристалла. Из-за наличия сигнала обратной
связи модулирующее напряжение пропорционально интенсивности
прошедшего излучения. Следовательно, фазовую задержку можно
Входная мощность
РИС. 8.17. Выходные характеристики бистабильного электрооптического амплитуд-
амплитудного модулятора при различных значениях ф0.
Электрооптические устройства
327
записать в виде
ф0 +
(8.4.7)
где а — постоянная, а величину ф0 можно регулировать, подавая на
кристалл постоянное поле смещения или помещая последовательно
с кристаллом компенсатор Солея — Бабине. На рис. 8.17 приведе-
приведены зависимости /0 (/,), описываемые выражением (8.4.6), при раз-
различных значениях параметра ф0 и при а = 1. Эти кривые проявля-
проявляют все нелинейности, свойственные бистабильному резонатору
Фабри — Перо. Оптическая бистабильность была продемонстриро-
продемонстрирована экспериментально на электрооптическом модуляторе с кри-
кристаллом LiNbO3 [6, 7].
Рассмотренные выше бистабильные оптические устройства име-
имеют много потенциально важных применений, в том числе в оптиче-
оптических системах связи и в системах обработки сигналов. Они могут
использоваться в качестве дифференциальных усилителей, переклю-
переключателей, ограничителей, вентилей и т. п.
8.5. ЭЛЕКТРООПТИЧЕСКИЙ СДВИГ ЧАСТОТЫ
И СЖАТИЕ ИМПУЛЬСА
В нашем обсуждении фазовой модуляции мы почти всегда предпо-
предполагали, что модулирующее напряжение является синусоидально из-
изменяющимся во времени, так что показатель преломления кристал-
кристалла также изменяется по синусоидальному закону. Рассмотрим те-
теперь частный, но представляющий интерес случай, когда модулиру-
модулирующее напряжение изменяется во времени линейно. Вследствие элек-
электрооптического эффекта показатель преломления кристалла изме-
изменяется также линейно во времени. Таким образом, фазовый сдвиг
прошедшего светового пучка можно записать в виде
1=фо + в/, (8.5.1)
где 8 — постоянная. При этом прошедший световой пучок запи-
запишется следующим образом:
E(z, t) = е'(ыо'+в'+*о)-'** (8.5.2)
Это плоская волна с частотой ш0 + 8. Иными словами, благодаря
такой модуляции частота прошедшего пучка сдвигается вверх
(8 > 0). Действительно, если в (8.5.2) аргумент экспоненты обозна-
обозначить через ф((), то обобщенную частоту можно определить следую-

328
Глава 8
щим образом:
(8.5.3)
Согласно определению (8.5.3), обобщенная частота плоской волны
равна скорости изменения фазы во времени.
Рассмотрим теперь другой частный случай, представляющий
интерес, а именно случай, когда модулирующее наложение изме-
изменяется во времени по квадратичному закону. Вследствие электрооп-
электрооптического эффекта показатель преломления кристалла снова следу-
следует за напряжением и изменяется во времени также по квадратично-
квадратичному закону. При этом фазовый сдвиг прошедшего пучка дается вы-
выражением
МО = Фо - «Л
(8.5.4)
где а — коэффициент пропорциональности. В этом случае прошед-
прошедший пучок можно записать как
E(z) =
(8-5.5)
Если рассматривать дф/dt как локальную (или мгновенную) частоту
в момент времени t, то эту частоту можно записать в виде
= ы0 — 2at.
(8.5.6)
Данное явление называется «чирпингом». При прохождении лазер-
лазерного импульса через такой модулятор возникает линейное частот-
частотное уширение на протяжении импульса. Действительно, если в
центре импульса а > О и / = 0, то фронт импульса (передний край)
будет сдвинут по частоте вверх, а конец импульса (хвост) — вниз.
Это иллюстрируется на рис. 8.18.
8.5.1. СЖАТИЕ ИМПУЛЬСА
Рассмотрим теперь распространение модулированного по частоте
лазерного импульса через среду с дисперсией. Пусть длительность
исходного лазерного импульса равна т. В результате линейного
чирпинга передний фронт импульса сдвинут по частоте вверх, а за-
задний фронт по частоте вниз (см. рис. 8.18). Если такой импульс
распространяется в среде с дисперсией групповой скорости и если
дисперсия такова, что групповая скорость меняется с частотой ли-
Электрооптические устройства
329
A{t)
Передний
фронт
Задний
фронт
РИС. 8.18. Чирпинг лазерного импульса.
нейно, то задняя (низкочастотная) часть импульса может догонять
его переднюю (высокочастотную) часть и импульс может быть
сжат до минимальной ширины Bат)~1, где 2ат — величина разбро-
разброса частоты.
Пусть а — параметр, характеризующий дисперсию групповой
скорости в среде:
(8.5.7)
Этот же параметр был использован при описании уширения им-
импульса в разд. 2.5. Условие сжатия импульса состоит в том, чтобы
разность времен распространения передней и задней частей импуль-
импульса была равна первоначальной длительности импульса т. Пусть Г,
и Тг — времена распространения передней и задней частей импуль-

330
Глава 8
са соответственно. Тогда это условие имеет вид
L L
т
— Т.—
v (ы + ат) v (ы - ат)
-L-f -\-2ar,
или, что эквивалентно,
4aLa = 1,
(8.5.9)
где мы использовали (8.5.7), a L — длина среды. Для максимально-
максимального сжатия импульса условие (8.5.9) должно удовлетворяться для ко-
коэффициента линейного чирпинга а и параметра а, характеризующе-
характеризующего дисперсию групповой скорости.
Рассмотрим теперь задачу о сжатии импульса аналитически.
Пусть начальный импульс имеет вид
Ex(t) = A(t)eiu°', (8.5.10)
где А (/) — огибающая импульса. После линейного чирпинга лазер-
лазерный импульс принимает вид
E2{t) =
(8.5.11)
Этот импульс с чирпингом проходит затем через диспергирующую
среду. Чтобы найти, какое влияние оказывает эта среда на им-
импульс, разложим его в интеграл Фурье
(8.5.12)
где F(w) — частотный спектр импульса с чирпингом, определяемый
выражением
(8.5.13)
После прохождения через среду с дисперсией каждая частотная со-
составляющая импульса приобретает фазовый множитель e'~lkL, где
к — волновое число, зависящее от частоты ш. Разложим к в ряд
Электрооп гические устройства
331
Тейлора в окрестности
(8.5.14)
где к() — волновое число, отвечающее центральной частоте со0, а
(dk/du>H — обратная групповая скорость v,~] на частоте too. Исполь-
Используя определение (8.5.7) и определение групповой скорости, выраже-
выражение (8.5.14) можно переписать в виде
к(ы) - к0 + I — (ы - ы0) + а(и ~ "о)
\ s 'о
Прошедший импульс можно представить как
(8.5.15)
(U)elu'-'k<^Ldu. (8.5.16)
Подставляя выражение (8.5.15) для к (и) в (8.5.16), получаем
?з@ = fF(u)e'u'~'k<>L-i^~ao)T-ia(U-UoJL ju ¦ (8.5.17)
здесь Т — L/v4 — время распространения компоненты, отвечаю-
отвечающей центральной частоте. Подставим теперь выражение (8.5.13)
для F(u) в (8.5.17), используем (8.5.11) и выполним интегрирование
по to. В результате приходим к выражению
(8.5.18)
(8.5.19)
Определим огибающую Аъ(/) прошедшего импульса следующим об-
образом:
?з@ = A3(t)e'"°'~'koL. (8.5.20)
Тогда с помощью (8.5.18) эту огибающую можно записать в виде
1
fyimaL * 1 '
(8.5.21)
в котором мы использовали известную формулу

332
Глава 8
Предположим, что первоначальный импульс имел гауссову форму:
A(t') = е"''2/2т2. (8-5.22)
Подставляя выражение (8.5.22) для А {С) в (8.5.21) и используя
(8.5.19), получаем
(8.5.23)
здесь
В =
2т2
4aL
- а
(8.5.24)
Из (8.5.23) и (8.5.24) следует, что длительность прошедшего лазер-
лазерного импульса равна
211/4
(8.5.25)
Из этого выражения очевидно, что длительность импульса мини-
минимальна при а = \/AaL; это условие совпадает с выражением
(8.5.9), полученным полуинтуитивным методом. Подставляя aL =
= 1/4а в (8.5.25), находим следующее выражение для минималь-
минимальной длительности импульса:
(8.5.26)
Описанный выше метод был использован для сжатия импульсов от
500 до 270 пс [8]. С помощью выражений (8.5.9) и (8.5.26) можно
показать, что для получения максимального сжатия длина диспер-
диспергирующей среды должна быть равна
Hi
2а'
(8.5.27)
Эта длина прямо пропорциональна произведению начальной и ко-
конечной длительностей импульса и обратно пропорциональна дис-
дисперсионному параметру а. Для импульсов длительностью порядка
100 пс длина L большинства диспергирующих сред оказывается
слишком большой, чтобы ее можно было реализовать на практике.
В работе [8] в качестве диспергирующего элемента использовался
Электрооптические устройства
333
асимметричный резонатор Фабри — Перо, который впервые пред-
предложили Жир и Турнуа [9]. Можно показать, что фазовый сдвиг для
света, отраженного от асимметричного интерферометра Фабри —
Перо, обладает необходимыми дисперсионными свойствами, если
длина резонатора подобрана соответствующим образом и переднее
зеркало имеет высокий коэффициент отражения (см. задачу 8.8).
В соответствии с изложенным выше сжатие импульса проводит-
проводится обычно в два этапа. На первом этапе производится уширение
спектра. Второй этап заключается в том, что спектрально уширен-
уширенный импульс пропускают через диспергирующую среду. В качестве
диспергирующей среды можно использовать пару решеток. Таким
методом недавно были получены оптические импульсы длительнос-
длительностью 30 фс [12]. Для этого оптический импульс длительностью 70 фс
спектрально уширялся при распространении через оптическое во-
волокно, а затем сжимался до 30 фс с помощью пары решеток.
Спектральное уширение при прохождении импульса через волокно
обусловливается фазовой самомодуляцией за счет эффекта Керра и
изменения во времени оптической интенсивности.
8.6. ЭЛЕКТРООПТИЧЕСКОЕ ОТКЛОНЕНИЕ
СВЕТОВОГО ПУЧКА
Электрооптический эффект используется также для отклонения све-
световых пучков [10]. На рис. 8.19 иллюстрируется принцип действия
такого отклоняющего устройства. Представим себе оптический вол-
волновой фронт, падающий на кристалл, в котором длина оптическо-
оптического пути зависит от поперечной координаты х. Этого можно до-
достичь, если сделать так, чтобы скорость распространения (т. е. по-
показатель преломления п) зависела отх, как на рис. 8.19. Если пока-
\
D
\
/ *»
н(х)-п + — х
Iх
т шу
А \
Направление
распространения
пучка
РИС. 8.19. Схематическое представление принципа действия дефлектора пучка. По-
Показатель преломления изменяется линейно в направлении х по закону п(х) = по +
+ ах. Прн прохождении через кристалл фаза луча В возрастает быстрее фазы луча
Л, что приводит к повороту волнового фронта на угол в.

334
Глава i
затель преломления линейно зависит от х, то верхнему лучу А от-
отвечает показатель преломления п + An и, следовательно, время его
распространения в кристалле равно
Нижнему положению волнового фронта отвечает луч В, которому
соответствует показатель преломления п и время распространения
т - Ь„
в ~ 7
Разность времен распространения лучей А и В равна
и соответствует отклонению оси распространения пучка внутри
кристалла на выходной грани на величину
_ Ay _ LAn
L dn
(8.6.1)
где мы заменили An/D на dn/dx. Угол отклонения в оси вне кри-
кристалла относительно горизонтальной оси связан с углом в' зако-
законом Снелля
sin0
sin0' "'
откуда, используя (8.6.1) и предполагая, что sin 6* = в
ем
1, получа-
получаО
ах
(8.6.2)
На рис. 8.20 показана простая реализация такого отклоняющего
устройства на основе кристалла КН2РО4 (KDP). Устройство состо-
состоит из двух призм из кристаллов KDP, грани которых параллельны
осям х', у' и z. В случае когда электрическое поле приложено
вдоль оси z, эти оси совпадают с главными осями эллипсоида пока-
показателей преломления, как это описано в примере, приведенном в
разд. 7.2. Оси z обеих призм имеют противоположные направле-
направления, но ориентированы под одним и тем же углом. Электрическое
поле приложено вдоль оси z, а свет распространяется вдоль оси у'
Электрооптические устройства
335
Входной
лучок
Выходной
пучок
РИС. 8.20. Дефлектор пучка на основе двух призм из кристалла KDP. Оси z верхней
и нижней призм имеют противоположные направления. Отклоняющее поле прило-
приложено параллельно оси г.
и поляризован параллельно х'. В этом случае показатель преломле-
преломления для луча А, который распространяется целиком через верхнюю
призму, дается выражением G.2.9):
Поскольку в нижней призме электрическое поле имеет противопо-
противоположный знак относительно оси z,
Полагая в (8.6.2) An = пА — пв, получаем следующее выражение
для угла отклонения:
0=±n\raEz. (8.6.3)
Согласно B.2.19), любой оптический пучок имеет конечный угол
расходимости в дальнем поле; обозначим этот угол через 0пучок. Яс-
Ясно, что главное достоинство дефлектора состоит не в получении
угла отклонения в, который можно изменять просто с помощью
линзы, а в увеличении угла в по сравнению с #пучок в ./V раз. Напри-
Например, если бы нам потребовалось сфокусировать выходной пучок,
то N соответствовало бы числу разрешимых элементов, которые

336
Глава
можно было бы разместить в фокальной плоскости, используя
электрические поля величиной вплоть до Е..
Чтобы получить выражение для N, предположим, что кристалл
помещен в перетяжку гауссова (фундаментального) пучка, имею-
имеющую радиус ы0. Согласно B.2.19), угол дифракции в дальнем поле в
воздухе равен
й - Х
" пучок — .
1TU0
Такой пучок может проходить через кристалл толщиной D — 2соо,
поэтому, используя (8.6.3), для числа разрешимых элементов полу-
получаем
в
ттЬпъ
2\
'-?..
(8.6.4)
Из (8.6.4) непосредственно следует, что электрическое поле, ко-
которое обусловливает фазовую задержку за счет двулучепреломле-
ния (на расстоянии /) ДГ = тг, дает N = 1. Доказательство этого
предлагается провести самостоятельно в качестве упражнения. Сле-
Следовательно, электрооптическое запирание пучка, которое в соот-
соответствии с (8.6.4) требует, чтобы Г = тг, эквивалентно отклонению
на один диаметр перетяжки.
В гл. 10 мы рассмотрим отклонение оптического пучка вследст-
вследствие дифракции на звуковой волне.
ЗАДАЧИ
8.1
Поле зрения электрооптического модулятора на основе
кристалла группы 43т. Рассмотрим в кристалле с группой
точечной симметрии 43т электрооптический эффект, такой,
что при наличии электрического поля, направленного вдоль
кубической оси, главные значения показателя преломления
даются выражениями
пх, = и + \пъг*\Е,
пу, = п - \пггЛХЕ,
пг, = п.
а) Предполагая, что пластинка представляет собой г'-срез
толщиной /, покажите, что фазовая задержка для нор-
Электрооптические устройства
337
мально падающего света дается выражением
г0 = ^п\хт.
б) Пусть падающий световой пучок распространяется
вдоль направления (в, </>), где в — угол падения, а </>- —
азимутальный угол падения. Покажите, что волновой
вектор падающего света можно записать в виде
к = -у (sin в cos ф*' + sin в sin ф$' + cos 02')-
в) Покажите, что волновой вектор волны в кристалле име-
имеет вид
к' = *,,*' + ky,f + kz.t,
где
кх, = -г- sin в cos ф,
к , = -г- sin в sin ф.
' К
г) Подставьте кх,, ку, и кг, в D.2.8) и покажите, что при
этом получается квадратичное уравнение относительно
к\.. Найдите решения этого уравнения и вычислите фа-
фазовую задержку
д) Покажите, что в предельном случае (в = тг/2, ф = 0 или
тг/2)
Г0|1
1
1
1/2
4n2(n2-l)j "
22-631

338
Глава 8
В кристалле GaAs, в котором п = 3,4, фазовая задержка
при предельном угле падения отличается от задержки
при нормальном падении на множитель 1,0- 10.
8.2. Покажите, что наклон кривой пропускания резонатора Фаб-
Фабри — Перо в точке, расположенной на полувысоте этой кри-
кривой, записывается в виде
d<j>Jl/2
/R
1 - R'
Вычислите этот наклон в случае, когда коэффициент отраже-
отражения зеркала равен 90% (т. е. R = 0,9).
8.3. Ограничения, связанные с конечным временем распростра-
распространения. Уменьшение глубины модуляции для модулирующего
кристалла (8.3.3) можно получить из следующих полуинтуи-
полуинтуитивных соображений.
а) Покажите, что если поле Е существенно изменяется за
время распространения г = nl/c света через кристалл, то
фазовую задержку можно записать в виде
Г= ±
где Го — максимальное значение фазовой задержки при
постоянном поле (со,„ = 0) и поле, изменяющемся по си-
синусоидальному закону (т. е. Е ~ sincom?)-
б) Вычислите интеграл, приведенный в п. а, и покажите,
что
=
8.4. Модуляция гауссовых пучков. Рассмотрим распространение
гауссова пучка в кристаллическом образце, имеющем вид
стержня длиной /.
а) Покажите, что с точки зрения симметрии минимальный
диаметр образца имеет место, когда перетяжка пучка
расположена в центре кристалла.
б) Покажите, что когда перетяжка пучка расположена в
центре кристалла, минимальный диаметр образца отве-
Электрооптические устройства
339
В)
чает случаю, когда параметр конфокальности пучка z0
равен половине длины образца (т. е. z0 — 1/2).
Определите этот минимальный диаметр.
8.5. Дифференциальное усиление. Бистабильные оптические уст-
устройства нередко проявляют дифференциальное усиление. Ко-
Коэффициент усиления g определяется как
g = dlo/dlk.
а) Получите выражение для коэффициента дифференциаль-
дифференциального усиления g бистабильного резонатора Фабри — Пе-
Перо. Покажите, что g может быть положительным, отри-
отрицательным и даже обращаться в бесконечность.
б) Выведите выражение для коэффициента дифференциаль-
дифференциального усиления g устройства, показанного на рис. 8.16.
Покажите, что коэффициент усиления g обращается в бе-
бесконечность при
в) Объясните, как это дифференциальное усиление можно
использовать при создании оптического транзистора.
8.6. Формирование импульса. Пусть через бистабильное оптиче-
оптическое устройство распространяется световой импульс
(рис. 8.21).
з
б
РИС. 8.21.

340
Глава 8
а) Покажите, что форма прошедшего импульса будет отли-
отличаться от формы импульса на входе, даже если отсутст-
отсутствует дисперсия.
б) Формирование импульса при прохождении через биста-
бильные оптические элементы легко проиллюстрировать
с помощью графического метода. Пусть входной им-
импульс Ij(t) имеет вид, приведенный на рис. 8.21, а, а за-
зависимость /0(/;) показана на кривой рис. 8.21, б. Нари-
Нарисуйте форму импульса на выходе.
8.7. Бистабильный резонатор Фабри — Перо с обратной
связью за счет отражения.
а) Получите соотношение между мощностями входного и
выходного пучков, предполагая, что
ф = ф'0 + а'1г,
где 1Г — интенсивность отраженного пучка, а а' и ф'о —
постоянные величины.
б) Если резонатор Фабри — Перо не имеет потерь, то /0
можно заменить на /, — 1Г. Получите соотношение меж-
между 1Г и /;. Покажите, что бистабильность может сущест-
существовать и в этом случае.
в) Попытайтесь построить кривую зависимости /„(/,-) по
кривой зависимости /г (/,-).
8.8. Дисперсия групповой скорости в асимметричном резонато-
резонаторе Фабри — Перо.
а) Пусть / — длина диспергирующей среды. Плоская волна
e'(w'~ta), распространяющаяся в этой среде, приобретает
дополнительный фазовый множитель е~м. Пусть
Ф(со) = —к(со)/. Покажите, что дисперсия групповой ско-
скорости а связана с дисперсией Ф(со) соотношением
2/
б) Покажите, что условие максимального сжатия импульса
можно записать в виде
2а-
do,2
= -1.
Электрооптические устройства
341
в) Пусть 7, и 73 — начальная и конечная длительности им-
импульса соответственно. Покажите, что условие макси-
максимального сжатия импульса имеет вид
г) Покажите, что фазовый сдвиг Ф в пустом резонаторе да-
дается выражением
= arctg
С2')]-
tg -
где / — длина резонатора, a R — коэффициент отраже-
отражения переднего зеркала.
д) Предполагая, что R является постоянной величиной
(т. е. не зависит от со), покажите, что
2/ 1 + /R
1-JK A _ ^f + 4^sin2(w//c)
du
Кривая зависимости с1Ф/с1ш от со состоит из серии пиков,
аналогичных гребенчатой структуре резонатора Фаб-
Фабри — Перо с добротностью F, определяемой выраже-
выражением
i-/r'
е) Покажите, что в точке, расположенной на полувысоте
максимума величины б/Ф/б/со, справедливо выражение
/
1/2
2R1/4 1 + {К
1 - {К 1 - {К
где знак зависит от того, на какой стороне пика произ-
производится расчет. Таким образом, условие максимального
сжатия импульса принимает вид
2Rl/A 1 + {К
1 - /R 1 - /R
A\2
- = тт3.
ж) Пусть т — 100 пс, 73 = 10 пс. Определите длину резона-
резонатора для R = 0,5 и 0,9. Ответ: 0,16 см и 0,0250 см.

342
Глава 8
ЛИТЕРАТУРА
1. Kaminov I. P., Sharpless W. M., Performance of LiTaO3 and LiNbO3 light
modulators at 4 GHz. — Appl. Opt., 6, 351 A967).
2. Namba С S., Electro-optical effect of zincblende. — J. Opt. Soc. Amer., 51, 76
A961).
3. Gibbs H. M., Differential gain and bistability using a sodium-filled Fabry — Perot
interferometer. — Phys. Rev. Lett., 36, 1135 A976).
4. Smith P. W., Turner E. H., A bistable Fabry— Perot resonator.— Appl. Phys.
Lett., 30, 280 A977).
5. Smith P. W., Turner E. H., Mumford В. В., Nonlinear electro-optical Fabry —
Perot devices using reflected light feedback. — Opt. Lett., 2, 55 A978).
6. Garmire E., Marburger J. H., Allen S. D., Incoherent mirrorless bistable optical
devices. — Appl. Phys. Lett., 32, 320 A978).
7. Feldman A., Bistable optical systems based on a Pockels cells. — Opt. Lett., 4, 115
A979).
8. Duguay M. A., Hansen J. W., Compression of pulses from a mode-locked He — Ne
laser. — Appl. Phys. Lett., 14, 14 A969).
9. Gires F., Tournois P., An interferometer useful for pulse compression of a frequency
modulated light pulse. — Compt. Rend. (Paris), 258, 6112 (June 1964).
10. Fowler V. J., SchlaferJ., A survey of laser beam deflection techniques. — Proc.
IEEE, 54, 1437 A966).
11. См. например, Yariv A., Introduction to optical electronics. — New York: Holt,
Rinehart and Winston, 1976.
12. Shank С V., Fork R. L., Yen R., Tomlinson W.J., Compression of femtosecond
optical pulses, Confer, on lasers and electro-optics, Phoenix, Arizons, April 14—16,
1982.
ГЛАВА 9
АКУСТ00ПТИКА
Акустооптика изучает взаимодействие оптических волн с акустиче-
акустическими в различных веществах. Возможность такого взаимодейст-
взаимодействия впервые предсказал Бриллюэн в 1922 г., а затем ее эксперимен-
экспериментально проверили в 1932 г. Дебай и Сиарс в США и Люка и Бигар
во Франции. При взаимодействии света со звуковыми волнами наи-
наиболее интересное явление представляет собой дифракция света на
акустических возмущениях среды. При распространении звука в
среде возникает соответствующее поле напряжений. Эти напряже-
напряжения приводят к изменению показателя преломления. Такое явление
называется фотоупругим эффектом. Поле напряжений для плоской
акустической волны является периодической функцией координат.
Поскольку показатель преломления среды претерпевает периодиче-
периодическое возмущение, возникает явление брэгговской связи, как показа-
показано в гл. 6. Акустооптическое взаимодействие является удобным
способом анализа звуковых полей в твердых телах и управления ла-
лазерным излучением. Модуляция света при акустооптическом взаи-
взаимодействии находит многочисленные применения, в том числе в
модуляторах света, дефлекторах, устройствах обработки сигналов,
перестраиваемых фильтрах и анализаторах спектра. Некоторые из
этих устройств мы рассмотрим в следующей главе.
9.1. ФОТОУПРУГИЙ ЭФФЕКТ
Фотоупругий эффект состоит в том, что в веществе механическое
напряжение и оптический показатель преломления связаны друг с
другом. Этот эффект имеет место для всех состояний вещества и
традиционно записывается в виде
(9.1.1)
где Дт;^ [или ДA/«2),-/] — изменение тензора оптической непроницае-
непроницаемости, a Skl — тензор напряжений. Коэффициенты pijkl образуют
тензор фотоупругости. В выражении (9.1.1) пренебрегается членами
высшего порядка по Skl, поскольку эти члены обычно малы по
сравнению с линейным членом (типичное значение Skl ~ 10"). При

344
Глава 9
наличии поля напряжений эллипсоид показателей преломления кри-
кристалла дается выражением
UJ + PijkiSkl)xlxJ=l. (9.1.2)
В случае когда поле напряжений отсутствует (Skl = 0), эллипсоид
показателей преломления в главной системе координат определяет-
определяется выражением G.1.1). Поскольку r\tj и Skl — симметричные тензо-
тензоры, в выражении (9.1.1) нижние индексы / и у, а также к и / можно
поменять местами. Перестановочная симметрия тензора фотоупру-
фотоупругости piiki аналогична симметрии квадратичного электрооптическо-
электрооптического тензора s{-kl [выражения G.1.8) и G.1.9)]. Поэтому для краткости
обозначений удобно использовать условные индексы. При этом вы-
выражение (9.1.1) принимает вид
ь\-Л -
= l,2,....6,
(9.1.3)
где Sj — компоненты тензора напряжений. Теперь уравнение эллип-
эллипсоида показателей преломления при наличии поля напряжений
можно записать в виде
x\^2+PuS
Pl6S6)
p2iS5 + p26S6)
(— + PuSx + p32S2
+ 2yz(pMSl + pA2S2
/>45S5
Pi6S6)
+ 2zx(p5lSl + pS2S2
p55S5 + p56S6)
+ 2xy(p6lSt + p62S2
p65Ss + />66S6) =
= 1, (9.1.4)
Акустооптика
345
ТАБЛИЦА 9.1. Тензоры фотоупругости в условных обозначениях для всех
классов симметрии кристаллов
Моноклинная
' Ри
Рг\
Рп
0
Ps\
0
Рп
Рп
Ръг
0
Pb2
0
Рп
Ргъ
Ръъ
0
Psъ
0
Триклинная
1 Ри Рп
Рг\ Ргг
Рп Ръг
Ра\ РАг
Ps\ Рьг
Рв\ Рьг
система B0):
0 Ри 0
0 ргь 0
0 р„ 0
Раа 0 Ра6
0 Pii 0
РбА 0 РЫ,
Тетрагональная система A0)
классы '
1 Ри
Рп
Рп
0
0
Рб\
Рп
Ри
Рп
0
0
~Ры
», 4, 4/т
Рп
Рп
Ръъ
0
0
0
/ Рп
Рп
Рп
Рак
Ps\
~P\t
0 0
0 0
0 0
Раа Pas
~Раь Раа
0 0
Рч
Ргъ
Ръъ
Раъ
Psъ
Рвъ
'
i
Р\6
~Р\6
0
0
0
Ры, ;
система C6I:
Р\А PlS
РгА РгЬ
Ръа Ръь
Раа Раь
Рьа Рьь
РбА РбЬ
Р\6
Ргь
Ръь
Раь
Рьв
Ры,
\
1
Орторомбическая
Рп
Рг\
Рп
0
0
0
Рп
Ргг
Ръг
0
0
0
Рп
Ргъ
Ръъ
0
0
0
0
0
0
Раа
0
0
система A2)
0
0
0
0
Рьь
0
Тетрагональная система
классы 4mm,
[Рп
Рп
Рп
0
0
0
Тригональная система
классы
Рп Рп
Р\\ Рп
Рп Ръъ
-Pai 0
-Рп 0
Pit 0
з, з
PlA
-Р\
0
Раа
~Ра.
~Р\
Р\ь
» ~P\s
0
Раь
Раа
>
Ри
Рп
Ри
Рп
0
0
0
A2):
Нр
Рп
Рп
Ръъ
0
0
0
Р\б
~Р\ь
0
~Рь\
Ра\
i
422,-
0
0
0
Рм
0
0
~Рп)
t/mmm
0
0
0
» о
Раа
0
0 \
0
0
0
0
Рбб !
G):
0
0
0
0
0
Ры,

346
Глава 9
ТАБЛИЦА 9.1. (Продолжение)
Тригональная система (8):
классы Зт, 32, 1т
Ри
Рп
Рп
р*1
0
0
Рп
Рп
Ръ\
0
0
~Р\6
Рп
Ри
Рп
-P*i
0
0
Рп
Рп
Рп
0
0
0
Pi*
-Pi*
0
^44
0
0
0
0
0
0
^44
Pl*
0
0
0
0
P*i
K/'ii ~ Pn)
Гексагональная система (8):
классы
Рп
Ри
Ръ\
0
0
Ри
Рп
Рп
Рп
0
0
0
6, 6, 6/m
0
0
0
^44
-P*s
0
0
0
0
P*s
Paa
0
P\6
~Pi6
0
0
0
K/'ii ~ Pn)
Гексагональная система F):
классы 6m2, 6mm, 622, 6/mmm
Ри
Рп
Рг\
0
0
0
Рп
Ри
Ръ\
0
0
0
Рп
Рп
Рп
0
0
0
0
0
0
^44
0
0
0
0
0
0
^44
0 +1
0
0
0
0
0
( Ри -
Кубическая система D):
классы 23, тЗ
Ри
Рг\
Рп Рг\
О О
О О
О О
Рп Рг\
Ри Рп
Ри
О
О
О
^44
О
О
о
о
о
о
^44
о
о
о
о
о
о
РаА
Кубическая система C):
классы 43т, 432, тЗт
Р\\
Рп
Рп
О
О
О
Рп
Ри
Рп
О
О
О
Рп
Рп
Ри
О
О
О
О
О
О
Рал
О
О
О
О
О
О
^44
О
О
О
О
О
О
^44
Акустооптика
347
ТАБЛИЦА 9.1. (Продолжение)
IPu
Рп
Рп
О
О
О
Рп
Ри
Рп
О
О
О
Рп
Рп
Ри
О
О
О
Изотропная
О
О
О
K/'ii ~ Рп)
О
О
система B):
О
О
О
О
K/'ii -Pn)
О
О
О
О
О
О
K/'ii ~ Рп)
' Цифры в круглых скобках указывают число независимых коэффициентов.
где пх, пу и nz — главные значения показателя преломления. Коэф-
Коэффициенты фотоупругости р~ обычно определяются в главной систе-
системе координат. Новый эллипсоид показателей преломления при на-
наличии поля напряжений в общем случае отличается от эллипсоида
показателей преломления при отсутствии поля. Поле напряжений
изменяет как размерность, так и ориентацию эллипсоида показате-
показателей преломления G.1.1). В соответствии с (9.1.4) это изменение за-
зависит от поля напряжений и коэффициентов фотоупругости рг.
Свойства симметрии кристалла позволяют определить вид тензора
фотоупругости (но не величину коэффициентов/?^). Точечная группа
симметрии дает информацию о том, какие из 36 коэффициентов
равны нулю, а также соотношения, существующие между отличны-
отличными от нуля коэффициентами. В табл. 9.1 представлены тензоры фо-
фотоупругости (а именно вид этих тензоров) для всех классов симмет-
симметрии кристаллов. Заметим, что они записываются аналогично ква-
квадратичным электрооптическим тензорам (см. табл. 7.4). Экспери-
Экспериментально измеренные коэффициенты фотоупругости для некото-
некоторых кристаллов приведены в табл. 9.2.
9.1.1. ПРИМЕР: АКУСТООПТИЧЕСКИЙ ЭФФЕКТ В ВОДЕ
Рассмотрим распространение звуковой волны в воде. Пусть звуко-
звуковая волна представляет собой продольную волну, распространяю-
распространяющуюся вдоль направления г, смещение частиц в которой описыва-
описывается выражением
- Kz),

ТАБЛИЦА 9.2. Коэффициенты фотоупругости [1]
Вещество
Кварцевое стекло
(SiO2)
As2S3 стекло
Вода
(стекло)
Люсит
Полистирол
а)
Длина
волны
0,63
1,15
0,63
1,06
0,63
0,63
Изотропная система
Рп
X, мкм
0,121
0,308
±0,31
±0,21
±0,30
±0,30
Р\г
0,270
0,299
±0,31
±0,21
±0,28
±0,31
Вещество
б) Кубическая система: классы 43т, 432 и тЗт
Длина р р р Рц-Pu
ВОЛНЫ'X, МКМ
CdTe
GaAs
GaP
10,60 -0,152 -0,017 -0,057 -0,135
1,15 -0,165 -0,140 -0,072 -0,025
0,633 -0,151 -0,082 -0,074 -0,069
Ge
NaCl
NaF
Si
Y3A15O12
KRS5
KRS6
0-ZnS
2,0-2,2
10,60
,55-0,65
0,633
0,589
1,15
3,39
1,15
0,633
0,633
0,633
0,546
0,589
0,633
-0,063
0,27
0,115
0,08
-0,101
-0,094
±0,025
-0,029
±0,18
±0,28
0,091
-0,0535
0,235
0,159
0,20
0,0094
0,017
±0,073
0,0091
±0,27
±0,25
-0,01
-0,074
0,125
-0,011
-0,03
-0,021
-0,051
±0,041
-0,0615
±0,15
±0,14
-0,044
-0,137
0,075
-0,009:
-0,042
-0,12
-0,10
-0,110
-0,111
-0,038
010

ТАБЛИЦА 9.2. (Продолжение)
в) Гексагональная система: классы 6m2, 6mm, 622 и 6/mm
Длина волны
Вещество
CdS
SnO
a-ZnS
(вюртцит)
Вещество
А12О3
LiNbO3
LiTaO3
SiO2 (кварц)
Ag3AsS3
(прустит)
\, мкм
0,633
10,60
0,633
0,633
Ри
-0,142
0,104
±0,222
-0,115
г) Тригональная система:
Длина волны
\, мкм
0,644
0,633
0,633
0,589
0,633
1,15
Ри
-0,23
-0,026
-0,081
0,16
±0,10
±0,056
Рп
-0,066
±0,099
0,017
классы Зт,
Рп
-0,03
0,090
0,081
0,27
±0,19
±0,082
Pl3
-0,057
-0,111
0,025
32 и Зт
Рп
0,02
0,133
0,093
0,27
±0,22
±0,068
Ръ\
-0,041
0,011
±0,088
0,0271
Ри
0,00
-0,075
-0,026
-0,030
-0,20
-0,235
-0,13
Ръ\
-0,04
0,179
0,089
0,29
±0,24
±0,103
/>44
±0,054
-0,0585
-0,0627
Ръъ
-0,20
0,071
-0,044
0,10
±0,20
±0,100
/>41
0,01
-0,151
-0,085
-0,047
±0,01
/>44
-0,10
0,146
0,028
-0,079
Вещество
д) Тетрагональная система: классы 4mm, 42m, 422 и 4/mmm
Длина
волны|Л, мкм р.. р.. пп р,. р,.
Рбв
(NH4)H2PO4
(ADP)
MgF2
0,589
0,633
0,319 0,277 0,169 0,197
0,296 0,243 0,208 0,188
0,167 -0,058 -0,091
0,228
0,546 ри -рп = 0,892,/»,, -р31 = 0,0695,/>зз - Рп = ОД 128 0,0776 0,0448
КН2РО4
(KDP)
х - 0,75
ТеО2
TiO2 (рутил)
0,589
0,633
0,63
0,633
0,633
0,514
0,633
0,287
0,254
0,16
0,06
0,0074
-0,001
-0,011
0,282
0,230
0,10
0,08
0,187
0,113
0,172
0,174
0,233
0,08
0,17
0,340
-0,167
-0,168
0,241
0,221
0,11
0,09
0,0905
-0,106
-0,0965
0,122
0,212
0,47
0,23
0,240
-0,064
-0,058
-0,019
-0,17
0,0095
-0,064
-0,0552
-0,0463
-0,066
±0,072
е) Тетрагональная система: классы 4, 4 и 4/т
Вещество Длина
волны ^. мкм
РЬМоО4
CdMoO4
0,633
0,633
/,,,=0,24 рп= 0,24
Рз, =0,175 Рзз = 0,300
рм - 0,067 р45 0,01
р61 - 0,013 Рб6 - 0,05
рп = 0,0255
0,017
рп = 0,12 ^12 = 0,10 рп - 0,13
/>3, - 0,11 />зз = О»18

352
Глава 9
где А — амплитуда колебаний, П — частота звука, а К — волновое
число. Поле напряжений, связанное с этой звуковой волной, имеет
вид
S3 = KA si
- Kz) =
- Kz),
где S = KA. Вода представляет собой изотропную среду. Следова-
Следовательно, согласно табл. 9.1 и соотношению (9.1.3), изменения эле-
элементов тензора диэлектрической непроницаемости можно записать
следующим образом:
-\) =pi2Ssxn{Ut-Kz),
= д(-7| = рi2Ssin(Qt - Kz),
\ П /2
-т| = puSsin{Qt-Kz),
п /з
Atji7 = 0 for i =* j.
Новый эллипсоид показателей преломления определяется выраже-
выражением (9.1.4) и может быть записан в виде
pl2
- Kz)\ +У2\\ + />I2Ssin(B/ - Kz)\ +
\ + />,,Ssin(a/ - Kz)I = 0.
Поскольку это выражение не содержит перекрестных членов, на-
направления главных осей остаются неизменными.
Таким образом, новые главные значения показателя преломле-
преломления можно записать в виде
- Kz),
- Kz),
nz = n - |/j3/?uSsin(B/ - Kz),
Акустооптика
353
где/?и, рп — коэффициенты фотоупругости, an — показатель пре-
преломления воды. Заметим, что при наличии звуковой волны вода
становится периодической средой, которая эквивалентна объемной
решетке с постоянной решетки 2тг/К = Л.
9.1.2. ПРИМЕР: АКУСТООПТИЧЕСКИЙ ЭФФЕКТ В ГЕРМАНИИ
Рассмотрим распространение звуковой волны вдоль направления
оси <001> (оси z). Пусть волна представляет собой сдвиговую вол-
волну, поляризованную в направлении <010> (вдоль оси у), смещение
частиц в которой дается выражением
u(z, t) = $Acos(Qt-kz),
где у — единичный вектор вдоль направления <010>. Поле напря-
напряжений, связанное со сдвиговой волной, можно записать следующим
образом:
S4 = KA sin(B/ - Kz) = Ssin(B/ - Kz),
где S = KA. Кристалл германия является кубическим и имеет то-
точечную группу симметрии m3m. Из табл. 9.1 следует, что тензор
фотоупругости для него имеет' вид
Рп
Рп
Рп
0
0
0
Рп
Рп
Рп
0
0
0
Рп
Рп
Рп
0
0
0
0
0
0
Рал
0
0
0
0
0
0
Рал
0
0
0
0
0
0
Рал)
(А,)-
Таким образом, в соответствии с (9.1.3) изменение тензора диэ-
диэлектрической непроницаемости равно
а все остальные элементы тензора равны нулю. При этом эллипсо-
эллипсоид показателей преломления (9.1.4) описывается уравнением
пг\х
23-631
z2) + 2yzp4ASsin(Qt- Kz)

354
Глава У
Это уравнение аналогично G.2.12) при пи = пе = п. Новые главные
оси получаются поворотом старых осей на 45° вокруг оси*. Таким
образом, главные значения показателя преломления можно запи-
записать в виде
пу. = п - jn^p^Ssin(fi/ - Kz),
В этом случае мы снова имеем оптическую объемную решетку, воз-
возникающую под действием сдвиговой звуковой волны за счет фото-
фотоупругого эффекта. Эта оптическая решетка перемещется со ско-
скоростью v = п/К.
9.2. ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ ОБ
АКУСТООПТИЧЕСКОМ ВЗАИМОДЕЙСТВИИ
Рассмотрим теперь распространение плоской монохроматической
световой волны в среде, в которой возбуждена звуковая волна и по-
показатель преломления является периодически промодулированным.
Как было показано в разд. 9.1 на конкретных примерах, звуковая
волна вызывает изменение показателя преломления среды. При
этом среда становится периодической с периодом, равным длине
звуковой волны. Это периодическое возмущение изменяется как в
пространстве, так и во времени. Если звук представляет собой бе-
бегущую волну, то периодическое возмущение перемещается со ско-
скоростью звука (ее типичное значение порядка нескольких тысяч мет-
метров в секунду). Поскольку скорость звука на пять порядков меньше
скорости света (с = 3- 108 м/с), периодическое возмущение, вызван-
вызванное звуковой волной, можно считать стационарным. Задача при
этом сводится к задаче о распространении электромагнитного излу-
излучения в периодической среде, рассмотренной нами в гл. 6. Для ил-
иллюстрации акустооптического взаимодействия рассмотрим в ка-
качестве примера распространение светового пучка в воде. Благодаря
фотоупругому эффекту звуковая волна приводит к изменению пока-
показателя преломления. Пусть ось z совпадает с направлением распро-
распространения звуковой волны, а плоскость уг параллельна плоскости
падения. Если световой пучок линейно поляризован в направлении х
(ТЕ-мода), то, как мы показали в разд. 9.1.1 на конкретном приме-
примере, показатель преломления для этой моды записывается в виде
n-
- Kz),
(9.2.1)
Акустооптика
355
Средний
показатель Расстоя-
преломления ние
Z
f
Показатель преломления
РИС. 9.1. Звуковая волна, «замороженная» в некоторый момент времени. Она со-
состоит из чередующихся областей сжатия (темные области) и разряжения (светлые
области), которые распространяются со скоростью звука v. Показано также мгно-
мгновенное изменение показателя преломления в пространстве под действием звуковой
волны.
где п/К = v. Это синусоидальное изменение показателя преломле-
преломления иллюстрируется рис. 9.1.
Если в поперечном направлении звуковая волна имеет неограни-
неограниченные размеры, то, согласно кинематическим граничным услови-
условиям, отраженный пучок должен располагаться в плоскости падения
(плоскости yz), причем угол отражения должен быть равен углу па-
падения 9 (рис. 9.2). Согласно теории связанных мод, рассмотренной
в разд. 6.4, значительное отражение света имеет место в случае,
когда
27Г
2ksmd = тК = т ¦ -г-,
(9.2.2)

356
Глава 9
где k _ волновое число для светового пучка (к = п2ж/\), а т —
целое число. Число т отвечает /и-й компоненте Фурье возмущения
диэлектрической проницаемости. В случае чисто синусоидальной
акустической волны все компоненты Фурье с т > 2 равны нулю.
Следовательно, резонансное отражение света от звуковой волны
происходит при условии
2ksmd = K. (9.2.3)
С учетом того что К = 2тг/Л и к = п2ж/\, это выражение можно
представить в виде
Дифракция света, удовлетворяющая условию (9.2.4), называется
брэгговской дифракцией по аналогии с дифракцией рентгеновского
излучения в кристаллах. Для того чтобы оценить порядок величи-
величины угла в, рассмотрим случай дифракции света с длиной волны
X = 0,5 мкм на звуковой волне частотой 500 МГц. Выбирая из
табл. 9.3 скорость звука равной v= 1,5-103м/с, имеем Л =
= 3-10~6 м и из (9.2.4) получаем 0=6- Ю рад * 3,6°. Условие
брэгговской дифракции (9.2.4) найдено в предположении, что пери-
периодическое возмущение неподвижно относительно светового пучка.
Влияние движения можно учесть, если рассмотреть доплеровский
сдвиг для оптического пучка, падающего на зеркало, перемещаю-
перемещающееся со скоростью v под углом, удовлетворяющим условию Брэг-
Брэгга (9.2.4). Формула для доплеровского сдвига частоты волны, отра-
отражающейся от движущегося объекта, имеет вид
= 2ы
с/и'
где cv — оптическая частота, а у, — проекция скорости объекта на
направление распространения волны. Из рис. 9.2 видно, что у, =
= vsinB и, следовательно,
(9.2.5)
с/п
Используя для sin0 формулу (9.2.4), получаем
Ды = —г— = Й,
(9.2.6)
Акустооптика
357
1 Движущийся фронт
звуковой волны (fi)
РИС. 9.2. Отражение от двух эквивалентных плоскостей в звуковом пучке (т. е. пло-
плоскостей, расстояние между которыми равно длине волны звука Л), при котором про-
происходит сложение фаз вдоль направления в, если оптическая разность хода
АО + ОБ равна одной длине световой волны.
откуда следует, что частота отраженной световой волны возраста-
возрастает на величину П.
Если направление распространения звуковой волны изменить на
обратное тому, которое указано на рис. 9.2, то звук догоняет опти-
оптическую волну, так что знак доплеровского сдвига меняется на про-
противоположный и частота дифрагированного на звуке светового пуч-
пучка становится равной со — П.
9.3. КОРПУСКУЛЯРНАЯ КАРТИНА
АКУСТООПТИЧЕСКИХ ВЗАИМОДЕЙСТВИЙ
Многие характерные особенности дифракции света на звуковой вол-
волне можно получить из рассмотрения корпускулярно-волновой при-
природы света и звука. Согласно этому представлению, световой пу-
пучок с волновым вектором к и частотой со можно рассматривать как
поток частиц (фотонов) с импульсом йк и энергией Йсо. Аналогич-
Аналогичным образом звуковую волну можно считать состоящей из частиц
(фононов) с импульсом ЙК и энергией Ml. Дифракцию света на зву-
звуке, иллюстрируемую рис. 9.2, можно рассматривать как сумму от-
отдельных столкновений, каждое из которых заключается в аннигиля-
аннигиляции одного падающего фотона частотой со и одного фонона при од-
одновременном рождении нового (дифрагированного) фотона часто-
частотой со' = со + п, который распространяется в направлении рассеян-
рассеянного пучка. Закон сохранения импульса требует, чтобы импульс
й(к + К) сталкивающихся частиц был равен импульсу йк' рассеян-

358
Глава 9
ного фотона, т. е.
к' - к + К.
Закон сохранения энергии имеет вид
и' = ш + Й.
(9.3.1)
(9.3.2)
Таким образом, пучок при дифракции сдвигается по частоте на ве-
величину, равную частоте звука. Поскольку при таком взаимодейст-
взаимодействии происходит аннигиляция фонона, закон сохранения энергии оз-
означает, что сдвиг частоты оказывается таким, что со' > со и энер-
энергия фонона суммируется с энергией аннигилирующего фотона, а
это приводит к образованию нового фотона. Из такого рассмотре-
рассмотрения следует, что если направление звуковой волны на рис. 9.2 изме-
изменить на противоположное так, чтобы падающая световая волна
догоняла звук, то процесс рассеяния можно рассматривать как ге-
генерацию нового фотона (дифрагированного фотона) и нового фото-
фотона, в то время как падающий фотон аннигилирует. В этом случае
закон сохранения энергии дает
ы' = ы — Й.
Эта связь между знаком изменения частоты и направлением рас-
распространения звука согласуется с выводами, полученными при рас-
рассмотрении доплеровского сдвига в конце предыдущего раздела.
Условие сохранения импульса (9.3.1) эквивалентно брэгговскому
условию (9.2.3). Для доказательства этого обратимся к рис. 9.3.
Поскольку интересующие нас частоты звука ниже 10ю Гц, а часто-
частота оптического пучка обычно выше 1013 Гц, мы имеем со' = со, т. е.
Ik' I ~ Ikl, так что величину двух оптических волновых векторов
можно считать равной к. При этом величина звукового волнового
вектора запишется в виде
К= 2/csin0 , (9.3.3)
что аналогично выражению (9.2.3).
9.4. БРЭГГОВСКАЯ ДИФРАКЦИЯ
В АНИЗОТРОПНОЙ СРЕДЕ
В предыдущем разделе мы видели, что дифракцию света на звуко-
звуковых волнах можно рассматривать как процесс взаимодействия трех
частиц: падающего фотона, акустического фонона и дифрагирован-
дифрагированного фотона. Закон сохранения импульса требует, чтобы три векто-
Акустооптика
359
РИС. 9.3. Диаграмма, иллюстрирующая
условие сохранения импульса (9.3.1), ис-
использованное при выводе условия Брэг-
Брэгга 2Asin0 = \/n для оптического пучка,
который дифрагирует на приближаю-
приближающейся к нему звуковой волне. 0 — угол
между падающим (или дифрагирован-
дифрагированным пучком) и акустическим волновым
фронтом.
ра импульса, связанные с этими тремя частицами, образовывали
треугольник. В изотропной среде показатель преломления для све-
светового пучка не зависит от направления распространения волны и
поэтому Ik'l почти всегда совпадает с Ikl. Таким образом, треу-
треугольник является равнобедренным и из него следует условие брэг-
говской дифракции (9.2.3) или (9.3.3).
В анизотропной же среде показатель преломления для данного
светового пучка в общем случае зависит от направления его распро-
распространения. Поскольку направление распространения дифрагирован-
дифрагированного пучка, вообще говоря, отличается от направления исходного
пучка, величины волновых векторов теперь не остаются почти не-
неизменными. В некоторых случаях может даже происходить измене-
изменение состояния поляризации между падающим и дифрагированным
пучками. Пусть п' и п — показатели преломления, отвечающие ди-
дифрагированному и падающему пучкам соответственно. Стороны
треугольника, образованного векторами k', k и К, равны п'ш'/с,
пш/с и К соответственно. Поскольку в общем случае п' и п не рав-
равны друг другу, треугольник не является равнобедренным, даже ес-
если пренебречь небольшим различием между со и со'. Пусть в и в' —
углы между световыми пучками и волновым фронтом звуковой
волны (рис. 9.4). Условие брэгговской дифракции получается из
треугольника на рис. 9.4 и записывается в виде
2A;sin0 = К -
' = К +
к12 - к2
К
к'2 - к2
К
(9.4.1)
(9.4.2)
Это условие можно представить также в следующем эквивалент-
эквивалентном виде:
(9.4.3)

360
Глава 9
Падающий
пучок
Анизотропная_
среда ~
Дифрагированный
пучок
Преобразователь
а
к'-
РИС. 9.4. Брэгговская дифракция в анизотропной среде, а — дифракция светового
пучка на звуковой волне; б — сохранение импульса.
(9.4.4)
При п' — п мы снова получаем брэгговское условие дифракции
(9.2.3), если в' = в. Для иллюстрации эффекта анизотропии рас-
рассмотрим случай брэгговской дифракции в одноосном кристалле (на-
(например, в кристалле LiNbO3). Предположим, что как световой пу-
пучок, так и акустическая волна распространяются в плоскости, пер-
перпендикулярной оптической оси кристалла (оси с). Падающий свето-
световой пучок линейно поляризован в направлении, параллельном оси с,
так что он отвечает необыкновенной моде кристалла с показателем
преломления пе. Дифрагированный световой пучок предполагается
Акустооптика
361
-srlx-xW -г)].
РИС. 9.5. Брэгговская дифракция в отрицательном
одноосном кристалле (например, в кристалле
LiNbO3). Все три вектора импульса к, к' и К ле-
лежат в плоскости, перпендикулярной оси с. Падаю-
Падающий пучок отвечает необыкновенной волне, а ди-
дифрагированный — обыкновенной волне.
"оТ
линейно поляризованным в направлении, перпендикулярном оси с,
и, следовательно, отвечает обыкновенной моде кристалла с показа-
показателем преломления по (рис. 9.5). Из (9.4.3) и (9.4.4) следует, что
углы падения и дифракции пучков определяются соответственно
выражениями
(9.4.5)
(9.4.6)
Таким образом, как угол падения в, так и угол дифракции в' при
постоянных по и пе зависят от величины Х/Л для данного кристал-
кристалла. При Х/Л = \по ± пе\ и 10'I = 1(91 = 90° векторы к, к' и К
коллинеарны. Брэгговская дифракция возможна лишь тогда, когда
'ло ~ ле' ^ ^/Л ^ 'ло + ле' и Углы в' и в вещественны. В обла-
области Х/Л < \по — пе\ или Х/Л > \по + пе\ величины sin0' и sin0
становятся больше единицы и дифракция невозможна. На рис. 9.6
показана зависимость в и 9' от Х/Л для типичных одноосных кри-
кристаллов. Точка Х/Л = \по — пе\ соответствует коллинеарной брэг-
брэгговской связи для одинаково направленных волн, что имеет ме'сто,
например, в фильтре Шольца (см. разд. 6.5).

362
Глава 9
90°
50°
-50'
-90°
 1 I ' Г
i L
10
Х/Л
РИС. 9.6. Зависимость угла падения в и угла дифракции в' от отношения длин волн
света и звука в кристалле LiNbOj при п = 2,2 и п' = 2,3-
9.5. БРЭГГОВСКАЯ ДИФРАКЦИЯ
И ТЕОРИЯ СВЯЗАННЫХ МОД
В предыдущем разделе мы рассмотрели кинематические свойства
брэгговской дифракции, т. е. сохранение энергии и импульса. Эти
законы сохранения приводят к условию брэгговской дифракции, ко-
которое дает соотношение между углами падения и дифракции свето-
светового пучка. Чтобы ответить на вопрос, а каковы же интенсивность
и состояние поляризации дифрагированного пучка, необходимо рас-
рассмотреть электромагнитные свойства излучения. Для изучения
брэгговской дифракции света на звуковой волне мы используем
здесь формализм связанных мод, развитый в гл. 6. Для этого пред-
предполагаем, что акустическая волна является плоской и неограничен-
неограниченной, т. е. высшие дифракционные порядки отсутствуют (см. следу-
следующий раздел), и что под действием звука связанными оказываются
лишь две волны — падающая волна с частотой со и дифрагирован-
дифрагированная волна с частотой со + U или со - п, в зависимости от направле-
направления распространения звука относительно падающего оптического
пучка.
Как отмечалось в разд. 9.1, звуковая волна вызывает бегущую
модуляцию оптической диэлектрической непроницаемости, которая
Акустооптика
363
имеет вид
- Kz),
(9.5.1)
где Sk/ — амплитуда поля напряжений, вызываемых звуком, a z —
направление распространения, pijkl — коэффициенты фотоупруго-
фотоупругости. Здесь предполагается, что суммирование ведется по повторяю-
повторяющимся индексам к, I. Такая модуляция тензора непроницаемости
Дт7у отвечает бегущей модуляции диэлектрического тензора, опреде-
определяемого выражением
Ae(z, t) = 2e,cos(flf - Kz) =
- Kz),
где ?j — тензор, записываемый следующим образом:
_ e(pS)e
е, = -¦
2еп
(9.5.2)
(9.5.3)
a (pS) — матрица, состоящая из элементов p.k,Skr В (9.5.2) множи-
множитель 2 введен для удобства, так что е1 является первым (и единст-
единственным) коэффициентом фурье-разложения возмущения Де диэлект-
диэлектрической проницаемости [см. F.4.15)]. Согласно полученным в
гл. 6 результатам, при соответствующих условиях это периодиче-
периодическое возмущение диэлектрической проницаемости будет приводить
к связи двух распространяющихся мод падающей и дифрагирован-
дифрагированной волн.
Предположим, что полное электрическое поле выбрано в виде
E =
(9.5.4)
где kj и Ц — волновые векторы падающей и дифрагированной
волн соответственно, a cot и со2 — соответствующие частоты свето-
световых волн. Здесь Ej и Е2 — моды распространения, которые в одно-
однородной среде постоянны, а Ах и А2 — амплитуды этих мод. В при-
присутствии возмущения Де (9.5.2) диэлектрической проницаемости эти
две моды оказываются связанными и модовые амплитуды Ах и А2
зависят от пространственных координат. Зависимостью от времени
мы пренебрегаем, поскольку 0 значительно меньше, чем coj и со2, и
возмущение Де (9.5.2) является практически стационарным. Пусть
плоскость падения (т. е. плоскость, образованная векторами kj и
К) совпадает с плоскостью xz. Закон сохранения импульса требует,
чтобы вектор к2 также лежал в этой плоскости. Таким образом,
вектор электрического поля можно записать в виде
Е =
(9.5.5)

364
Глава 9
где j3j и j32 — z-составляющие волновых векторов kj и к2 соответст-
соответственно, а а, и а2 — составляющие этих волновых векторов, парал-
параллельные волновому фронту акустической волны. Модовые ампли-
амплитуды Ах и А2 зависят, вообще говоря, как от х, так и от z. Однако
имеется ряд случаев, когда конфигурация взаимодействия такова,
что модовые амплитуды Ах иА2 зависят только либо от х, либо от
z. Таким образом, акустооптическое взаимодействие можно под-
подразделить на две конфигурации, которые иллюстрируются рис. 9.7.
Для низких звуковых частот наиболее типична конфигурация, изо-
изображенная на рис. 9.7, а, а в случае очень высоких частот мы име-
имеем, как правило, плоскую волну конечной длины, показанную на
рис. 9.7, б. Для конфигурации, отвечающей малым углам брэгговс-
кой дифракции (рис. 9.7, а), модовые амплитуды Ах и А2 зависят
от х, как того требуют граничные условия. Для конфигурации, от-
отвечающей большим углам брэгговской дифракции (рис. 9.7, б), ам-
амплитуды Ах и А2 зависят только от z. В любом случае электриче-
Дифрагированный
свет
Звук
Дифрагированный
свет
РИС. 9.7. Две конфигурации взаимодействия, а — дифракция при малых брэггов-
ских углах; б — дифракция при больших брэгговских углах.
Акустооптика
365
ское поле Е, записываемое в виде (9.5.5), должно удовлетворять
следующему волновому уравнению:
О,
(9.5.6)
где е — диэлектрический тензор среды в отсутствие звуковой во-
волны, а Де — создаваемое звуком возмущение диэлектрической про-
проницаемости, определяемое выражением (9.5.2). Как Exexp[i(o)xt -
- ахх - 0xz)], так и Ejexp^co.,/ - а^ - 02z)] являются решениями
уравнения (9.5.6) при Де = 0. Подставляя выражение (9.5.5) для Е в
(9.5.6), получаем
/п-1,2
д_
'mdz
/-1,2
(9.5.7)
Вторыми производными d2A/dz2 и сР-А/дх2 часто можно прене-
пренебречь, поскольку акустооптическое возмущение обычно мало
(Де/е0 ~ 10~5) и основную роль в дифференциальном уравнении
(9.5.7) играет первая производная. Однако в двумерном случае
(т. е. для координат х и z) трудно решить даже дифференциальное
уравнение первого порядка. Поэтому мы ограничимся рассмотрени-
рассмотрением только двух типичных случаев, изображенных на рис. 9.7, когда
это дифференциальное уравнение становится одномерным.
9.5.1. БРЭГГОВСКАЯ ДИФРАКЦИЯ НА МАЛЫЕ УГЛЫ
Если угол между направлением распространения светового пучка и
волновым фронтом акустической волны мал, то длина взаимо-
взаимодействия L совпадает с шириной акустического пучка. Следователь-
Следовательно, амплитуды мод Ах и А2 зависят только от х, поскольку в дан-
данной конфигурации взаимодействия (см. рис. 9.7, а) координата х
определяет глубину проникновения. Нормируем поля Е, и Е2 таким
образом, чтобы
е,.
а.
/=1,2;
(9 5.8)
здесь р. — единичные векторы, определяющие состояния поляриза-
поляризации мод, а а( — х-составляющие волновых векторов. Такая норми-
нормировка согласуется с F.4.6), так что каждая мода представляет
поток мощности, равный 1 Вт/м2, в направлении х для случая изо-

366
Глава 9
тройной среды [см. выражение A.4.2)]. Уравнение связанных мод
(9.5.7) в этом случае принимает вид
X (АхЕхе'<-ы*'-а'х-р'г) +А2Е2еКы^-а^х-^2))' (9.5.9)
где мы подставили выражение (9.5.2) для Де в (9.5.7).
Умножая скалярно (9.5.9) на Е*ехр[-/(со,? - а,х - @,z)], / = 1,
2, и интегрируя по z и t, получаем следующую систему уравнений:
(9.5.10)
где к12 — коэффициент связи, определяемый выражением
при условии, что выполняются следующие соотношения:
& = /3. ± К ,
«2 = WI ± й.
(9.5.11)
(9.5.12)
(9.5.13)
Если какое-либо из этих двух условий не выполняется, то уравне-
уравнения связанных мод теряют силу. Величина Да представляет собой
рассогласование импульса в направлении х:
Да = а, - а2.
(9.5.14)
Эти две составляющие ах и а2 предполагаются положительными. В
случае анизотропной среды условие Брэгга (9.5.12) не может выпо-
выполняться при C, = —/32 = — к$твв = — К/2, когда фонон поглоща-
поглощается, или при C, = — C2 = &sin0B = А"/2, когда имеет место испу-
испускание фонона. При брэгговском угле падения
0„ = тс%ЩК/2к) = arcsin(X/2A)
(9.5.15)
Акустооптика
367
рассогласование импульса Да исчезает (Да = 0), ось х делит угол
между kj и к2 пополам и уравнения связанных мод принимают вид
АЛ dA-,
=? - -fcl2^2. -? = "«?2^1- (9-5-16)
В соответствии с F.4.30) решения уравнений (9.5.16) можно запи-
записать в виде
Ах(х) = yl1@)cosKX - i——yl2@)sinicx,
К
А2{х)
где
- i—Ax(Q))sva.KX,
К
к = |к.21- (9.5.17)
В частном случае, когда при х — 0 падает только одна волна [т. е.
Л2@) = 0], решения принимают вид
Ах(х)
(9.5.18)
Следует заметить, что
(9.5.19)
т. е. полная мощность, переносимая обеими световыми волнами,
сохраняется.
Если длина взаимодействия L двух пучков удовлетворяет усло-
условию кЬ = х/2, то вся мощность падающего пучка передается ди-
дифрагированному пучку. Поскольку это явление имеет многочислен-
многочисленные применения в науке и технике, стоит остановиться на оценке
эффективности такой дифракционной передачи энергии для извест-
известных акустических сред и практически достижимых уровней мощно-
мощности звука.
Используя (9.5.18), нетрудно получить долю мощности падаю-
падающего пучка, которая на расстоянии L передается дифрагированному
на звуке оптическому пучку:
7л-Фр/7пад = I>42(LIV 1^,@I2 = sin2*!, (9.5.20)

368
Глава 9
где к в соответствии с (9.5.2), (9.5.11) и (9.5.17) дается выражением
(9.5.21)
При выполнении условия Брэгга (9.5.12) мы имеем 1/3,1 = 1/321 =
= ksine = К/2 и а = kcosdB = (со/с)пcosвв. Следовательно, по-
постоянную связи к можно записать в виде
(9.5.22)
напомним, что здесь Де — изменение диэлектрической проницаемо-
проницаемости под действием акустической волны, ар, ир2 — единичные век-
векторы, описывающие состояния поляризации падающей и дифраги-
дифрагированной волн соответственно. Используя (9.5.2) и (9.5.3), постоян-
постоянную связи к можно выразить также через составляющие напряже-
напряжений и коэффициенты фотоупругости:
(О
к =
где
4nccos6B
|pf •
(9.5.23)
(9.5.24)
a (pS) — матрица с элементами Pijk,Skr Для изотропной среды
е' = и2 и выражение (9.5.23) принимает вид
к =
4ccos0B'
(9.5.25)
Поскольку составляющая напряжений S непосредственно связана с
вектором Пойнтинга или интенсивностью звука /зв, то эффектив-
эффективность дифракции (9.5.20) удобно выразить через эту величину. Для
этого запишем постоянную связи в виде
К = ^-pS, (9.5.26)
4с
где р — эффективный коэффициент фотоупругости, a S — эффек-
эффективная составляющая напряжений. Интенсивность звука можно за-
записать следующим образом:
Г2, (9.5.27)
Акустооптика
369
где v — фазовая скорость, ар — массовая плотность вещества. По-
Поскольку в выражении (9.5.26) амплитуда напряжений S прямо про-
пропорциональна квадратному корню из интенсивности звука /зв [см.
(9.5.27)], эффективность дифракции материала удобно характеризо-
характеризовать величиной
п6р2
При этом выражение (9.5.20) принимает вид
дифр пад
= sin2 (ж
¦)•
(9.5.28)
(9.5.29)
Величина М, определяемая выражением (9.5.28), представляет со-
собой эффективность дифракции акустооптических материалов при
данном уровне акустической мощности. Для конкретного вещества
величина М определяется неоднозначно, поскольку она зависит так-
также от конфигурации взаимодействия, направления распространения
и состояния поляризации волн.
Рассмотрим в качестве примера воду и предположим, что пада-
падающая и дифрагированная световые волны поляризованы парал-
параллельно плоскости падения (плоскости xz). Согласно рассмотренно-
рассмотренному в разд. 9.1 примеру, в этом случае соответствующим коэффи-
коэффициентом фотоупругости является pi2. Задаваясь длиной волны оп-
оптического излучения X = 0,6328 мкм и беря из табл. 9.3 остальные
постоянные, а именно и = 1,33, р = 0,31, v = 1,5-103 м/с и р =
= 1000 кг/м3, из выражения (9.5.29) получаем для этого случая
(9.5.30)
Для других веществ и других длин волн из последних двух выраже-
выражений можно получить удобную рабочую формулу
где Mw = М/Мн 0 — относительная эффективность дифракции дан-
данного материала М и воды Мн 0. Значения величин М и Mw для ряда
типичных веществ приведены в табл. 9.3 и 9.4.
Из (9.5.29) следует, что при низкой эффективности дифракции
интенсивность дифрагированного света пропорциональна интенсив-
интенсивности звука. Это используется в акустических модуляторах оптиче-
оптического излучения. Для модуляции интенсивности звука используется
сигнал, содержащий передаваемую информацию. Эта модуляция
затем в соответствии с (9.5.29) преобразуется в модуляцию интен-
интенсивности дифрагированного оптического пучка.
24-631

370
Глава 9
ТАБЛИЦА 9.3. Свойства некоторых материалов,
используемых обычно для получения дифракции
света на звуке*
Материал
Р-1СГ3,
кг/м3
км/с
м..
Вода
Сверхплотный флинт
Плавленный кварц (SiO2)
Полистирол
KRS-5
Ниобат лития (LiNbO3)
Флюорид лития (LiF)
Рутил (ТЮ2)
Сапфир (А!2О3)
Молибдат свинца (РЬМо4)
Йодноватая кислота
(НЮ3)
Двуокись теллура (ТеО2)
(медленная сдвиговая
волна)
1,0
6,3
2,2
1,06
7,4
4,7
2,6
4,26
4,0
6,95
4,63
5,99
1,5
3,1
5,97
2,35
2,11
7,40
6,00
10,30
11,00
3,75
2,44
0,617
1,33
1,92
1,46
1,59
2,60
2,25
1,39
2,60
1,76
2,30
1,90
2,35
0,31
0,25
0,20
0,31
0,21
0,15
0,13
0,05
0,17
0,28
0,41
0,09
1,0
0,12
0,006
0,8
1,6
0,012
0,001
0,001
0,001
0,22
0,5
5,0
*р — плотность, v — скорость звука, л — показатель преломления, р — эффективный коэффици-
коэффициент фотоупругости, определяемый выражением (9.5.26), и Мщ — относительная эффективность
дифракции, определяемая выражением (9.5.31). (Из работы [2].)
Числовой пример: рассеяние в молибдате свинца. Вычислим долю
мощности света с длиной волны 0,633 мкм, которая дифрагирует
при выполнении условия Брэгга на звуковой волне в РЬМо04 со
следующими характеристиками:
акустическая мощность
поперечное сечение акустического пучка
оптическая длина пути L в акустическом пучке
Mw (из табл. 9.3)
Подставляя эти значения в (9.5.31), получаем
= 1Вт,
= 1 ММ X 1 ММ,
— 1 мм,
= 0,22.
Рассмотрим теперь случай, когда угол падения слегка отличается
от брэгговского угла
0в = arcsin(/<:/2*:) = arcsin(X/2A).
(9.5.32)
3
t
о
I
а о
С я
I
III
СП Ш U
3 в
? ^.й Я -
5
н = =
= -t-t=-t=-l = ;
^ Q5 <
0<Г «Г Г
« 1
1=1=1111. = §
ссссссссссссссс
заз
о" о" о"
Э 2
ssss.s s s s, s. s. cs s. s « s.
o" «* о" о -^ о о о" о" о" о" о* о о" о" о' о*
i О О I
6 S
: §
о ч
X О
§ i.
i*S
О О.
о з
II!
s s
1Г1

Глава 9
372
Пусть угол падения равен
0, = вв + Ав,
(9.5.33)
где Ав — малый угол. Условие Брэгга (9.5.12) требует, чтобы
в2 = вв- Ав. (9.5.34)
Следовательно, величина рассогласования Да, определяемая выра-
выражением (9.5.14), принимает вид
Аа = 2кАвйпвв = КАв. (9.5.35)
Поскольку величина Да не равна нулю, из F.4.30) следует, что ре-
решения уравнений (9.5.10) при граничном условии А2@) = 0 имеют
вид
Ах(х) = e'^M^Ojfcoss* - /|~ sinsxl,
(9.5.36)
где
52 = К2
= к2
(9.5.37)
Из (9.5.36) видно, что передача мощности (или эффективность ди-
дифракции) никогда не может быть полной; таким образом, мы име-
имеем
дифр
к2 +
+
(КАв\2
(9.5.38)
Максимальная эффективность дифракции равна к2/ [к2 + (КАд/IkI]
и при КАв > к становится малой. Это угловое отклонение Ав мо-
может быть связано либо с рассогласованием лазерного пучка, либо с
возмущением акустического волнового фронта из-за конечного раз-
размера преобразователя. Последнее соотношение можно использо-
использовать для описания углового спектра плоских волн преобразователя
шириной L. Таким образом, измеряя мощность дифрагированного
светового пучка в зависимости от Ав, можно получить распределе-
распределение излучения преобразователя.
Акустооптика
373
9.5.2. БРЭГГОВСКАЯ ДИФРАКЦИЯ ПРИ БОЛЬШИХ УГЛАХ
Рассмотрим теперь акустооптическое взаимодействие, конфигура-
конфигурация которого изображена на рис. 9.7, б. Анализ распространения
волны в этом случае относительно прост, поскольку среда одно-
однородна как в х-, так и в ^-направлении. Граничное условие требует,
чтобы в (9.5.5) а2 = а,, а модовые амплитуды Ах и А2 зависели
только от z. Таким образом, электрическое поле можно записать в
виде
Е =
(9.5.39)
где
/3,
и
02 — z-составляющие волновых векторов, а
а — составляющая волновых векторов, параллельная волновым
фронтам звука. В представлении частиц составляющая волновых
векторов, перпендикулярная направлению распространения звуко-
звуковой волны, вследствие закона сохранения импульса будет оставать-
оставаться неизменной.
Нормируем векторы Ej и Е2 следующим образом:
'
(ж
р"
(9-5'40)
где р( — единичные векторы, описывающие состояния поляризации
соответствующих мод. Такая нормировка согласуется с F.4.6), так
что каждая мода в случае изотропной среды переносит мощность
1 Вт/м2 в направлении z [см. A.4.21)]. Используя процедуру, опи-
описанную в разд. 6.4, можно получить следующую систему уравнений
связанных мод:
d
TzA
где
(9.5.41)
(9.5.42)
(9.5.43)

374
Глава 9
Акустооптика
375
В выражении (9.5.42) знак перед К определяется тем, поглощается
ли фонон (знак «плюс», со2 = coj + п) или испускается (знак «ми-
«минус», ш2 = coj — Q). Поскольку со2 * сор величина со в (9.5.43) пред-
представляет собой частоту света. Из (9.5.41) видно, что необходимое
условие непрерывного кумулятивного взаимодействия между пада-
падающим и дифрагированным полем записывается в виде
02 — Pi ±
(9.5.44)
В противном случае из (9.5.41) следует, что вклад, например, в А2
от различных элементов пути не суммируется в фазе и непрерывное
пространственное возрастание амплитуды А2 невозможно.
Выражение (9.5.44) представляет собой общее условие Брэгга
для многих случаев брэгговской дифракции. Условие (9.2.3) являет-
является частным случаем этого общего условия, когда /32 = — 01 =
= ктпв при поглощении фонона (приближающаяся звуковая вол-
волна; .К и /3, имеют противоположные знаки), или когда /3, = —/32 =
= кs\n9 при испускании фонона (удаляющаяся звуковая волна; К и
/3, имеют одинаковые знаки). Условие Брэгга (9.5.44) отвечает так-
также сохранению импульса при взаимодействии одинаково направлен-
направленных световых волн в акустооптическом перестраиваемом фильтре
(см. следующую главу), которое не может быть описано с по-
помощью (9.2.3). Характер связи между двумя модами зависит от на-
направления распространения относительно оси z. Решения системы
уравнений (9.5.41) мы рассмотрим отдельно для двух случаев: связи
одинаково направленных световых волн и связи противоположно
направленных световых волн.
Взаимодействие одинаково направленных световых волн 08,/32 > 0).
При взаимодействии одинаково направленных волн дифрагирован-
дифрагированная (А2) и падающая (Ах) волны распространяются в одинаковом
направлении (либо в направлении +z, либо в направлении — z; см.
рис. 9.8, а). Характеристики распространения этих двух связанных
волн описываются уравнениями (9.5.41), которые теперь принима-
принимают вид
±A>--i
(9.5.45)
A
где Д/3 дается выражением (9.5.42), а к12 — выражением (9.5.43).
Пусть 0j и в2 — углы между волновыми векторами кх, к2 и акусти-
акустическим волновым фронтом. Тогда, используя (9.5.2) и (9.5.3), полу-
получаем
(9.5.46)
4c|H,H2sm0Isin02|I/2'
где «j и п2 — показатели преломления, отвечающие этим волнам,
р, и р2 — их состояния поляризации, a S — тензор напряжений.
Обшие решения уравнений (9.5.45) определяются выражениями
F.4.30). В случае когда при z ~ 0 падает одна волна, граничные ус-
Звуковая волна
-Звуковая волна-
РИС. 9.8. а
связь при распространении волн в одном направлении (/3,/32 > 0); б -
ространении в противоположных напрал C3 0
р распространении волн в одном направлении (/3,/3
связь при распространении в противоположных направлениях (/3j/32 < 0).

376
Глава 9
ловия имеют вид Ах@) = const и А2@) - 0. При этих условиях ре-
решения запишутся в виде
A,(z) = Л,(ОИ
- i|? Sin 5Zj
A2(z)= -iAi(O)e-f'^-sinsz (9.5.47)
s
где
s2 = |Kl2|2 + (iAjSJ. (9.5.48)
Из этих решений видно, что передача мощности от одной моды к
другой является наибольшей, когда Д/3 = 0. Доля мощности, пере-
передаваемая при взаимодействии на расстоянии L, дается выражением
(9.5.49)
Это выражение совпадает в точности с коэффициентом пропуска-
пропускания фильтра Шольца, рассмотренного нами в разд. 6.5. Зависи-
Зависимость передаваемой мощности от рассогласования Д/3 можно ис-
использовать для создания фильтра, который перестраивается при
изменении акустической частоты. Для иллюстрации этого рассмот-
рассмотрим следующий пример.
Пример: коллинеарное акустооптическое взаимодействие в кристалле
LiNbOj. Рассмотрим случай, когда акустическая сдвиговая волна и
падающий световой пучок распространяются параллельно оси у
кристалла LiNbO3, вдоль которой имеет место акустооптическое
взаимодействие. Пусть падающий световой пучок представляет со-
собой необыкновенную волну, поляризованную вдоль оси z (оси с)
кристалла, а дифрагированный пучок — обыкновенную волну, по-
поляризованную вдоль оси х кристалла. Звуковая волна, необходимая
для реализации такого брэгговского рассеяния, является сдвиговой
волной, поляризованной вдоль оси х кристалла. Таким образом,
амплитуду поля напряжений можно записать в виде
S =
(9.5.50)
Акустооптика
377
В соответствии с видом тензора фотоупругости, представленным в
табл. 9.1, изменение тензора оптической непроницаемости запишет-
запишется следующим образом:
At, = (pS)
0
А» А
0
0
о
о
(9.5.51)
/
Состояния поляризации падающего и дифрагированного пучков
описываются вектор-столбцами соответственно
(9.5.52)
Тензор диэлектрической проницаемости е' имеет вид
0
0 „;
о о
о
о
е,
(9.5.53)
где. п0 и пе — показатели преломления кристалла. Подставим те-
теперь в (9.5.46) п] = пе, п2 = п0 и 0, = 92 = х/2. Тогда, используя
(9.5.51)—(9.5.53), постоянную связи кр можно записать в виде
42
Ас
(9.5.54)
Из (9.5.49) очевидно, что максимальная передача мощности (sin2sL)
достигается при Д/3 = 0, или
2чт
(9.5.55)
Для ЮО'Уо-ного преобразования мощности требуется выполнение
условия
(9.5.56)
где L — длина взаимодействия. Амплитуда напряжений S6 непо-
непосредственно связана с интенсивностью звуковой волны (см. задачу
9.1):

378
Глава 9
Ч\ ¦ (9.5.57)
Для кристалла LiNbO3 длиной 10 см на центральной длине волны
излучения X = 6328 А из табл. 9.2 (п. г) имеем р41 = -0,151.
Пусть по = 2,29, пе = 2,20, р = 4640 кг/м3 и v = 4,0-103 м/с. Тог-
Тогда из (9.5.54), (9.5.56) и (9.5.57) следует, что для 100%-ного преоб-
преобразования плотность акустической, мощности должна быть равна
0,2 Вт/см. В соответствии с (9.5.55) частота звука должна быть
равна d,57 ГГц.
Связь противоположно направленных световых волн (/3,/32 < 0). В
этом случае z-составляющие двух волн отличаются знаком (см.
рис. 9.8, б). Следовательно, система уравнений (9.5.41) принимает
вид
Л2 1Кп
(9.5.58)
где Д/3 дается выражением (9.5.42), а кп — выражением (9.5.43) или
(9.5.46). При получении уравнений (9.5.58) из (9.5.41) предполага-
предполагалось, что /3j < 0 и /32 > 0; это соответствует конфигурации взаимо-
взаимодействия, изображенной на рис. 9.8, б. Общие решения уравнений
(9.5.58) записываются в виде F.4.35), причем к = — к12. В случае
когда при z = 0 падает только одна волна, граничное условие име-
имеет вид A2(L) = 0. При этом решения запишутся следующим обра-
образом:
A2(z)
5ch
~ z)
schsZ, + i
/icf2 sh s(L — z)
sL
schsL +
где
(9.5.59)
(9.5.60)
Из выражений (9.5.59) снова следует, что максимальная перекачка
мощности обратно в моду Е2 происходит при Д/3 = 0. Доля мощ-
мощности, передаваемая на длине взаимодействия L, дается выражени-
выражением
R =
А2@)
,4,@)
(9.5.61)
Акустооптика
379
Это выражение в точности совпадает с коэффициентом отражения
брэгговского отражателя [см. F.6.10)]. Характеристики акустиче-
акустического взаимодействия с противоположно направленными волнами
аналогичны характеристикам брэгговского отражателя, за исключе-
исключением того, что модуляция показателя преломления, создаваемая
звуковой волной, перемещается в пространстве. Поскольку ско-
скорость звука пренебрежимо мала по сравнению со скоростью света,
периодическое возмущение, вызванное звуковой волной, является,
по существу, стационарным. Следовательно, все результаты, полу-
полученные в разд. 6.6 для брэгговских отражателей, можно использо-
использовать для описания акустооптического взаимодействия противопо-
противоположно направленных волн.
Пример: коллинеарное акустооптическое взаимодействие противопо-
противоположно направленных волн в кристалле LiNbOj. Рассмотрим брэггов-
ское отражение света в кристалле LiNbO3. Геометрия задачи, со-
состояния поляризации и направления распространения в точности
такие же, как и в предыдущем примере, за исключением лишь того,
что дифрагированная волна распространяется в обратном направ-
направлении. Для выполнения условия фазового синхронизма (условие
Брэгга) А/3 = 0 необходимо, чтобы
2тг
(9.5.62)
где Л — длина звуковой волны. При X = 6328 А и скорости звука
v= 4,0-103 м/с частота звуковой волны должна быть равна
28 ГГц, а в большинстве твердых тел звук такой частоты сильно
затухает. В связи с этим акустооптические взаимодействия проти-
противоположно направленных волн при больших углах не находят прак-
практических применений.
Помимо необходимости в высоких частотах, в этом случае и ко-
коэффициент отражения энергии при условии k12L = ж/2 составляет
всего лишь R = th2(x/2) - 0,84.
Однако при малых углах вх и 92 между волновыми векторами кр
к2 и акустическим волновым фронтом связь между противополож-
противоположно направленными волнами сильно возрастает. Постоянная связи
к12 (9.5.46) при малых углах вх и 92 становится большой. Уменьше-
Уменьшение частоты звука также определяется аналогичным множителем
sin0, поскольку условие Брэгга (9.5.62) принимает вид
. 2w й
w2sin02) = -г- = —.
(9.5.63)

380
Глава 9
Акустооптика
3X1
Действительно, это и есть брэгговское взаимодействие, которое мы
уже рассматривали в связи с малоугловым взаимодействием
(разд. 9.5.1). Из выражения (9.5.63) следует, что с уменьшением
углов 0] и в2 частота звука п также понижается.
9.6. ДИФРАКЦИЯ РАМАНА — НАТА
До сих пор мы рассматривали дифракцию света на неограниченной
плоской звуковой волне. В представлении частиц неограниченной
плоской волне соответствует частица (фонон) с определенным им-
импульсом и определенной энергией. Брэгговская дифракция рассмат-
рассматривается как сумма отдельных столкновений, в каждом из которых
происходит поглощение или испускание фонона фотоном. Эти фун-
фундаментальные процессы могут иметь место, только когда сохраня-
сохраняются и энергия, и импульс. Поскольку частота звука существенно
меньше оптических частот, для сохранения энергии и импульса тре-
требуется, чтобы волновые векторы фотона и фонона образовывали
равнобедренный треугольник (см. рис. 9.3). Такая брэгговская ди-
дифракция означает, что волна, падающая под углом Брэгга вв —
= arcsin (Х/2/?Л), дифрагирует с поглощением фонона. Может ли
дифрагированная волна поглотить другой фонон и претерпеть рас-
рассеяние на больший угол? Для случая неограниченной акустической
волны ответ на этот вопрос отрицательный, поскольку в этом слу-
случае законы сохранения энергии и импульса не могут выполняться
одновременно. Это иллюстрирует рис. 9.9, б. Волновой вектор 0
соответствует волне, падающей под углом Брэгга вв. Волновой век-
вектор 1 представляет волну, дифрагированную с поглощением фоно-
фонона. При поглощении другого фонона с тем же волновым вектором
К закон сохранения импульса не будет выполняться (рис. 9.9, б).
На рис. 9.9, а показаны также многократный или последователь-
последовательный процесс трехчастичного взаимодействия, который включает в
себя поглощение фононов со слегка различающимися волновыми
векторами. В последнем случае выполняются как закон сохранения
энергии, так и закон сохранения импульса. Таким образом, можно
заключить, что многократные процессы рассеяния не могут проис-
происходить, когда волновой вектор звуковой волны однозначно опреде-
определен, как это имеет место в случае неограниченной плоской волны.
Многократные процессы рассеяния возможны лишь в том случае,
когда акустические волновые векторы К имеют некоторое угловое
распределение. Последнее отвечает случаю, когда акустическая вол-
волна представляет собой пучок конечного размера.
Исследуем теперь качественно критерий многократного рассея-
-2
-2
РИС. 9.9. Диаграммы волновых векторов при многократном рассеянии, а — много-
многократное рассеяние разрешено, когда волновой вектор звуковой волны имеет некото-
некоторое угловое распределение; б — многократное рассеяние запрещено, когда волновой
вектор звуковой волны имеет строго определенное направление.
ния. Из рис. 9.9, а следует, что многократное рассеяние имеет ме-
место лишь тогда, когда угловое распределение акустических волно-
волновых векторов К достаточно широко по сравнению с углом Брэгга
вв. Пусть L — ширина звукового пучка. Тогда угловая расходи-
расходимость пучка в дальнем поле дается выражением
Ф = A/L, (9.6.1)
где Л — длина волны звука. Из (9.2.4) следует, что угол Брэгга
приблизительно равен
вв = \/2пА. (9.6.2)
Для того чтобы различать два режима дифракции, обычно вводит-
вводится безразмерный параметр Q:
2irXL
пЛ2
Режим Q > 1 называют брэгговской
этом режиме многократное рассеяние
только один порядок дифракции света,
ляют как режим оптической дифракции
жиме угловой разброс акустического
чем угол Брэгга вв, и поэтому можно
дифракции. Начальный световой пучок
взаимодействия с акустической волной
(9.6.3)
оптической дифракцией. В
запрещено и имеет место
Область же Q < 1 опреде-
Рамана — Ната. В этом ре-
пучка существенно больше,
наблюдать много порядков
с угловой частотой ш после
расщепляется на несколько

382
Глава 9
пучков, отвечающих различным порядкам дифракции. Эти порядки
обозначаются числами 0, ±1, ±2, ±3, ..., ±т, которые соответст-
соответствуют частотам со, со ± П, со ± 2П, ..., со ± тп и волновым векто-
векторам к, к ± К, к + 2К, .... к ± тК. Пучок 0 — это падающий пу-
пучок, пучок + т отвечает поглощению т фононов, а пучок — т —
испусканию т фононов.
Для расчета эффективностей дифракции, отвечающих каждому
дифракционному порядку, рассмотрим в среде тонкий слой, в кото-
котором акустическая волна создает модуляцию показателя преломле-
преломления в виде бегущей волны:
bn(x,y,z,t) =
0
Кт), 0 < z < L,
в остальных случаях.
(9.6.4)
Для простоты иллюстрации основных идей предположим, что сре-
среда является изотропной и что An — скалярная величина. Запишем
падающую оптическую волну в виде
Е = Eoexp[i(wf - к-г)].
(9.6.5)
Пусть эта волна при z = 0 падает на тонкий слой среды, в которой
распространяется звуковая волна. В режиме дифракции Рамана —
Ната (Q < 1) длина взаимодействия L достаточно мала, так что
такой периодически возмущенный слой @ < z < L) действует как
фазовая решетка. Иными словами, при прохождении света через
возмущенную область 0 < z < L происходит лишь модуляция фа-
фазы плоской волны. Таким образом, прошедшую волну можно запи-
записать в виде
Е, = Еоехр[-/ф + i(m - к • г)],
(9.6.6)
где ф — фазовый сдвиг, возникающий при прохождении световой
волны через возмущенную область, который можно представить в
виде
¦¦ I — Дя ds.
J с
(9.6.7)
Интегрирование здесь ведется по траектории луча в области
0 < z < L. Пусть в — угол падения (т. е. угол между вектором к и
звуковой волной, которая параллельна оси z). Длина пути в возму-
возмущенной области равна L/cosd. Если величина L достаточно мала,
Акустооптика
383
то интеграл (9.6.7) можно записать в простом виде
Подстановка выражения (9.6.8) для ф в (9.6.6) дает
Е, = Еоехр[/(<о; - к • г) - iSsin(fo - К • г)],
где величина
ccosd Acostf
(9.6.8)
(9.6.9)
(9.6.10)
называется индексом модуляции. Следует отметить, что прошед-
прошедшее поле (9.6.9) оказывается промодулированным по фазе. Исполь-
Используя тождество для функций Бесселя
00
e-,«sin*= ? JmF)e-'mx, (9.6.11)
т= —оо
прошедшее поле (9.6.9) можно записать в виде
00
Е, = Е0 X /n(«)exp[i(<o-mfi)/-i(k-mK)-r]. (9.6.12)
/И- -00
В соответствии с этим выражением прошедшее поле представляет
собой линейную суперпозицию плоских волн с частотами со — mfi и
волновыми векторами к — тК, которые в точности совпадают с
рассмотренными выше дифрагированными пучками т-го порядка.
Амплитуда дифрагированного пучка т-го порядка равна / (б). Та-
Таким образом, эффективность дифракции при дифракции Рамана —
Ната т-го порядка можно записать в виде
(9.6.13)
ЛСО80
При отсутствии модуляции (Д«о = 0) вся энергия светового излуче-
излучения сосредоточена в порядке т = 0, т. е. г\о = 1 и r/m = 0 для
т Ф 0. Эффективность дифракции для порядков т = ±1 макси-
максимальна при индексе модуляции 8 - 1,85. Нулевой порядок полнос-
полностью гасится при 8 - 2,4, когда JQ B,4) = 0. Используя тождество
00
X У^(в)=Уо(О)= 1, (9.6.14)

384
Глава 9
мы видим, что
00
Е vm=i.
т= — оо
(9.6.15)
Иными словами, чтобы выполнялся закон сохранения энергии, сум-
сумма интенсивностей всех дифракционных порядков должна быть
равна интенсивности падающего пучка.
9.7. ПОВЕРХНОСТНАЯ АКУСТООПТИКА
До сих пор мы ограничивались рассмотрением взаимодействия
светв с объемной звуковой волной в материальных средах. В фото-
фотоупругой среде объемная звуковая волна приводит к образованию
объемной фазовой решетки. Вследствие периодической модуляции
показателя преломления свет испытывает в такой среде дифрак-
дифракцию. Поверхностные акустические волны (волны Рэлея) распро-
распространяются в свободном пространстве вблизи полубесконечной сре-
среды, причем их акустическая энергия концентрируется в приповерх-
приповерхностном слое толщиной порядка длины звуковой волны. Под дей-
действием поверхностной акустической волны оптические свойства ве-
вещества также изменяются. В 1967 г. появилось первое сообщение
Иппена [6] об экспериментальном наблюдении дифракции света на
рэлеевских волнах в кварце. Такая дифракция света может возни-
возникать вследствие двух различных причин:
1. Свободная поверхность, вдоль которой распространяется по-
поверхностная волна, претерпевает периодическое волнообразное
возмущение; эта бегущая периодическая волнистость действует
как поверхностная решетка, на которой дифрагирует свет.
2. Если вещество представляет собой фотоупругую среду, то поле
напряжений, индуцированное поверхностной акустической вол-
волной, приводит к периодическому изменению показателя пре-
преломления. Это периодическое изменение диэлектрической про-
проницаемости действует как поверхностная решетка и также при-
приводит к дифракции света. Однако в этом случае эффективная
длина взаимодействия оказывается порядка длины звуковой
волны Л и наблюдаемые эффекты малы [5, 6] по сравнению с
эффектами, возникающими при волнообразном возмущении по-
поверхности.
Рассмотрим теперь дифракцию света на волнообразном возму-
возмущении поверхности, обусловленном поверхностной акустической
волной. Предположим снова, что волнообразное возмущение по-
Акустооптика
385
верхности является стационарным, поскольку частота звука много
меньше оптических частот. Пусть К — волновое число акустичес-
акустической волны (К = 2ir/A). Профиль волнообразного возмущения по-
поверхности можно записать следующим образом:
х' =f(z') = asinKz',
(9.7.1)
где а — амплитуда поверхностного волнообразного возмущения,
которая обычно имеет порядок 10~3 Л. Эта поверхностная волни-
волнистость приводит лишь к очень слабому возмущению исходной по-
поверхности х' = 0. Дифракция света при этом может быть описана
с помощью элементарного принципа Гюйгенса. Так, каждую точку
поверхности можно рассматривать как вторичный источник излуче-
излучения, создаваемый падающим на поверхность светом. Поскольку ве-
величина а мала (а ~ 10~3 Л), большая часть света, падающего на
такую поверхность, преломляется или отражается согласно закону
Френеля.
Отраженный
пучок
Воздух и = 1
Преломленный пучок
РИС. 9.10. Система координат при дифракции света на поверхностной акустической
волне.
25-631

386
Глава 9
Пусть система координат выбрана таким образом, чтобы ось х
была перпендикулярна свободной поверхности вещества, а акусти-
акустическая поверхностная волна распространялась в направлении оси z
(рис. 9.10). Пусть в, вг и 0t — углы, которые падающий, отражен-
отраженный и преломленный световые пучки составляют соответственно с
осью х. Тогда волновые векторы отраженного и преломленного
световых пучков даются соответственно выражениями
kr = k(cos6rk + sin 0,2),
k, = пк(-со$в,$. + sin0,2),
(9.7.2)
где к — волновое число падающего света (к = 2тг/Х), аи — показа-
показатель преломления среды. Пусть Ео — амплитуда падающей плос-
плоской волны. Тогда на поверхности среды поле, создаваемое распре-
распределенным источником при рассеянии от поверхности, запишется в
виде
Е - ?оехр[-ik( — cos вх' 4 sinOz')].
(9.7.3)
Каждая точка х', z' поверхности будет рассеивать некоторую
часть излучения падающего пучка. Вклад элемента поверхности dz'
в точке Р в амплитуду отраженной волны в дальней зоне имеет до-
дополнительный фазовый множитель ехр(/клт') относительно соот-
соответствующего вклада от точки, отвечающей началу координат О
(см. рис. 9.10)._Здесь kf — волновой вектор отраженной волны, а
г' — вектор ОР. Предположим теперь, что амплитуда а волно-
волнообразного возмущения поверхности много меньше длины волны
света (т. е. ка < 1), так что каждая точка такой поверхности дает
одинаковый вклад. Тогда амплитуда отраженной волны в дальнем
поле пропорциональна интегралу
(9.7.4)
где г — радиус-вектор точки наблюдения, а C - /с sin Оr — z-состав-
ляющая волнового вектора кг. Интегрирование по г' в (9.7.4) ве-
ведется по поверхности х' = asmKz' от — оо до +°°. Интегрирова-
Интегрирование по /3 также ведется от — оо до +оо. Используя (9.7.2) и (9.7.3),
отраженную волну можно записать в виде
?, = CE0je'kx'(QOse+cose')-'iksm!>-^z'~'k'-Idz'dp,
(9.7.5)
Акустооп гика
387
где мы ввели обозначение /3 = ksindr, С — постоянная, ах' —
определяется выражением (9.7.1). Подставим теперь выражение
(9.7.1) для х' в (9.7.5) и используем следующее тождество для
функций Бесселя:
00
„iasinib V™1 г/ \ у/л
е = L ^(«)е''*. (9.7.6)
/=-оо
При этом выражение (9.7.5) принимает вид
1= -оо
где
а = ка(cosO + cos в».).
(9.7.7)
(9.7.8)
Выполняя в выражении (9.7.7) интегрирование по z', амплитуду от-
отраженной волны можно переписать в виде
V —
00
Е fj,(aJirt(p + IK- ksine)e-ik'-rdl3,
(9.7.9)
/= -оо
где б — дельта-функция Дирака. Интегрируя (9.7.9) по /3 с учетом
выражений (9.7.2), получаем
I 00
здесь вг определяется выражением
k(sin6r - sintf) = -IK.
(9.7.10)
(9.7.11)
Условие (9.7.11) представляет собой закон сохранения импульса,
который также определяет углы дифракции вг для различных по-
порядков 1-0, ±1, ±2, .... Это условие можно записать также в
виде
Л
(9.7.12)
На практике звуковая длина волны Л обычно много больше опти-
оптической длины волны X. Поэтому для угла вг можно получить следу-

Глава 9
388
ющее приближенное выражение:
IX
(9.7.13)
при условии что / не очень велико. Здесь Ав = вг — в — угол между
направлениями дифрагированного и отраженного пучков. Посколь-
Поскольку вг » в, величину а в (9.7.8) можно записать как а ~ 2касо%в.
Таким образом, амплитуда отраженной волны (9.7.10) принимает
вид
= 2тгСЕ0
(9.7.14)
/=-00
Постоянную С здесь можно определить из рассмотрения предель-
предельного случая, когда волнообразное возмущение поверхности исчеза-
исчезает (а = 0). В этом случае амплитуда отраженной волны равна про-
просто гЕ0 (здесь г — френелевский коэффициент отражения). Полагая
в выражении (9.7.10) а = 0, амплитуду Ег можно записать в виде
(9.7.15)
Следовательно, мы получаем С = г/2ж и амплитуда Ег отраженной
волны запишется в виде
/=-00
(9.7.16)
/= -оо
где г — френелевский коэффициент отражения, а / — порядок ди-
дифракции. Таким образом, мы получили выражение для отраженной
волны, которая представляет собой линейную суперпозицию со-
составляющих в виде плоских волн с волновыми векторами к — /Кг.
Каждое значение / отвечает определенному дифрагированному пуч-
пучку. Дифрагированный пучок, распространяющийся в направлении
вг, описывается выражением (9.7.11) или (9.7.12) с амплитудой
rE0JtBkacos0). Таким образом, эффективность дифракции, опреде-
определяемая как доля мощности падающего света, которая преобразует-
преобразуется в мощность дифрагированной волны, дается выражением
= \г\Ц2Bкасоьв).
(9.7.17)
Акустооптика
389
Используя аналогичные рассуждения, можно найти выражение
для преломленной волны:
? _ Qi? feikx'(cose-ncose,)-i(ksine-p-)z"-ik,-T fei jo
(9.7.18)
где /3 = nksmdr. Окончательный результат здесь можно получить
путем тех же преобразований, что и выше:
(9.7.19)
/--00
nk sin в, — k sin в = - 1К.
(9.7.20)
Из выражения (9.7.19) следует, что преломленная волна также со-
состоит из многих дифрагированных пучков. Каждый из них распро-
распространяется в направлении Bt и определяется выражением (9.7.20).
При этом эффективность дифракции преломленной волны запишет-
запишется в виде
(9.7.21)
COS0
где t — френелевский коэффициент преломления, а множитель
(«cos0,)/cos0 компенсирует различие скоростей распространения
света в двух средах.
Приведенный выше вывод выражения для интенсивности дифра-
дифрагированных пучков основан на скалярной теории дифракции и спра-
справедлив только в случае, когда ка < 1. Для типичных поверхност-
поверхностных акустических волн амплитуда волнистости имеет величину по-
порядка 10~3 мкм или меньше, так что для дифракции света имеем
ка ~ 10~3. Таким образом, скалярная теория, примененная нами
для получения выражений для амплитуд дифрагированных волн,
является очень хорошим приближением. Действительно, выраже-
выражения (9.7.17) и (9.7.21) согласуются с законом сохранения энергии,
что можно показать, если вспомнить равенство \г\2 +
+ (п cos0( \t\2)/cos9 = 1 и использовать (9.6.14).
ЗАДАЧИ
9.1. Акустооптическип эффект в кристалле LiNbO3. Пусть
правлении оси у кристалла LiNbO3 распространяется х-
в на-
¦поля-

390
Глава 9
ризованная волна. Смещение частиц среды описывается
функцией
и(у, 0 = хмоехр[/(Ш - А»].
а) Получите выражение для поля напряжений, созданного
этой сдвиговой волной.
б) Кристалл LiNbO3 имеет точечную группу симметрии Зш.
Используя табл. 9.1, получите выражение для созданно-
созданного полем напряжений изменения оптического диэлектри-
диэлектрического тензора непроницаемости Дт/...
9.2. Брэгговская дифракция рентгеновских лучей в кристаллах
имеет вид [7]
2dsin6 = т—,
и
т
1,2,3,...,
где d — расстояние между эквивалентными атомными пло-
плоскостями, в — угол падения, а Х/п — длина волны дифраги-
дифрагированного излучения. Брэгговская дифракция света на звуке
[см. (9.2.4)] имеет место при выполнении условия
9.3.
2Asin0 = -.
и
Таким образом, если сравнить это условие с условием брэг-
говской дифракции рентгеновских лучей при Л — d, то раз-
разрешенным оказывается лишь случай т — 1.
Объясните причину этого различия. Почему мы не можем
получить дифракцию света в направлениях в, отвечающих
т = 2, 3, ...? [Указание: предположите, что дифракция
рентгеновского излучения происходит на дискретных атом-
атомных плоскостях, которые можно представить как бесконечно
тонкие слои, а звуковую волну считайте непрерывной вдоль
оси z; см. рис. 9.2.]
Что происходит при брэгговской дифракции света на стоя-
стоячей звуковой волне? Определите смещения частоты и на-
направления дифракции.
9.4. Поверхностная акустооптика. Рассмотрите распростране-
распространение поверхностной волны вдоль свободной поверхности фо-
Акустооптика
391
тоупругой среды. Пусть поверхностная волнистость имеет
вид
х = a sin Кг.
а) Пренебрегая фотоупругим эффектом и предполагая, что
поверхностная волнистость действует как фазовая ре-
решетка, покажите, что для нормально падающего света
индекс модуляции равен
ф, - к(п - \Jа
б) Покажите, что амплитуда поля напряжений, обусловлен-
обусловленного поверхностной волной,
S = Ка.
в) Пренебрегая волнообразным возмущением поверхности,
рассмотрите только фазовую решетку, образуемую по-
полем напряжений. Предполагая, что иоле напряжений ло-
локализовано в области, находящейся на расстоянии \/К
от поверхности, покажите, что индекс модуляции равен
ф2 = kpS/K.
г) Используя выражение S ~ Ка из п. б задачи, покажите,
что
ф2 = кра и
д) Вычислите отношение фг/фх для кварца, германия и
LiNbO3. Покажите, что для поверхностных акустических
волн дифракция на поверхностной волнистости обычно
сильнее, чем на модуляции показателя преломления.
ЛИТЕРАТУРА
1. Landolt-Bornstein, New'Series, vol. 11 (ed. K.-H. Hcllwege), Springer-Verlag, 1979.
2. См., например, Adler R., Interaction between light and sound. — 1ЕЕ-П Spectrum.
4, 42 A967).
3. Dixon R. W., Photoelastie properties of selected materials and their relevance for ap-
applications to acoustic light modulators and scanners. — J. Appl. Phys., 38, 5149
A967).

392
Глава 9
4. Gordon E. I., A review of acousto-optical deflection and modulation devices.—
Proc. IEEE, 54, 1391 A967). [Имеется перевод: Гордон. Обзор по акустическим
отклоняющим и модулирующим устройствам. — ТИИЭР, 1967, т. 54, № 10,
с. 181.]
5. Salzmann Е., Weismann D., Optical detection of Rayleigh waves. — J. Appl. Phys.,
40, 3408 A969).
6. Ippen E. P., Diffraction of light by surface acoustic waves. — Proc. IEEE, 55, 248
A967).
7. KittelC, Introduction to Solid State Physics, 3 ed. — New York: Wiley, 1967,
p. 38. [Имеется перевод: Киттепь Ч. Введение в физику твердого тела. — М.:
Наука, 1963.]
8. Damon R. W., Maloney W. Т., McMachon D. H., Interaction of light with ultra-
ultrasound: Phenomena and applications. — In: Physical Acoustics, vol. VII (eds.
W. Mason, R. Thurston). — New York: Academic Press, 1970. [Имеется перевод:
В кн.: Физическая акустика. Принципы и методы. Т. 7/Под ред. У. Мэзона и
Р. Терстона. — М.: Мир, 1974.]
9. KorpelA., Acousto-optics. — In: Applied Solid State Science, vol. 3 (ed
R. Wolfe). — New York: Academic Press, 1972.
10. Lean E. G., Interaction of light and acoustic surface waves. — In: Progress in Op-
Optics, vol. XI (ed. E. Wolf). — Amsterdam: North-Holland, 1973.
11. Sapriel J., Acousto-optics. — New York: Wiley, 1979.
ГЛАВА 10
АКУСТООПТИЧЕСКИЕ УСТРОЙСТВА
В гл. 9 было показано, что при взаимодействии световых пучков со
звуковой волной в фотоупругой среде возникает много интересных
явлений. Эти явления (например, брэгговская дифракция) могут
быть использованы при создании модуляторов света, дефлекторов
пучков, перестраиваемых фильтров, анализаторов спектра и уст-
устройств обработки сигналов. Использование акустооптического вза-
взаимодействия позволяет модулировать лазерное излучение или обра-
обрабатывать с высокой скоростью информацию, переносимую излуче-
излучением, поскольку при этом отпадает необходимость в использова-
использовании каких-либо механических перемещающихся элементов. Это
свойство аналогично электрооптической модуляции с той лишь раз-
разницей, что при акустооптическом взаимодействии вместо постоян-
постоянных полей применяются ВЧ-поля. Последние достижения в приме-
применениях акустооптических устройств обусловлены главным образом
наличием лазеров, которые генерируют интенсивные когерентные
световые пучки, развитием эффективных широкополосных преобра-
преобразователей, генерирующих упругие волны с частотами вплоть до
микроволновых, а также открытием веществ, обладающих замеча-
замечательными упругими и оптическими свойствами. В данной главе мы
изучим различные устройства, основанные на брэгговской дифрак-
дифракции. Будут рассмотрены их характеристики пропускания, эффектив-
эффективность дифракции, рабочая полоса частот и другие параметры.
10.1. АКУСТООПТИЧЕСКИЕ МОДУЛЯТОРЫ
Акустооптическое взаимодействие можно использовать для созда-
создания различных модуляторов света. При этом можно реализовать
как амплитудные модуляторы, так и преобразователи частоты. Та-
Такие модуляторы могут работать либо в режиме дифракции Рама-
на — Ната, либо в режиме брэгговской дифракции. Первый акусто-
оптический модулятор [1, 2] работал в режиме Рамана — Ната на
частотах ниже 10 МГц. Принцип действия такого модулятора ил-
иллюстрирует рис. 10.1. В соответствии с полученными в гл. 9 ре-
результатами амплитуда дифрагированной волны в первом порядке
пропорциональна J{ (kAnL), где kAnL — индекс модуляции, кото-

394
Глава 10
Акустооитические устройства
395
Падающий
свет
I . I
| Модулированный
ВЧ сигнал
Дифрагированный
свет
| Модулированный
, ВЧ' сигнал
о
РИС. 10.1. Акустооптические модуляторы света, а — режим дифракции Рамана —
Ната; б — режим брэгговской дифракции.
рый пропорционален амплитуде звукового поля. Если высокоча-
высокочастотная звуковая волна промодулирована несущим информацию
сигналом, то дифрагированный свет будет также промодулирован
тем же сигналом. В таком режиме работы свет в нулевом порядке
должен быть экранирован с помощью соответствующим образом
расположенной диафрагмы. Если индекс модуляции kh.nL < 2,4
(см. разд. 9.6), то модуляция оказывается линейной. Недостаток
работы в режиме Рамана — Ната состоит в малой длине взаимо-
взаимодействия, определяемой критерием 2жХЬ/пА2 < 1. Для высоких ча-
частот (малых Л) максимальная достижимая длина L оказывается
слишком малой для практических применений (см. задачу 10.1)
вследствие того, что при этом требуется чрезвычайно большая
мощность звука. Поэтому модуляторы света Рамана — Ната мо-
могут работать лишь при низких частотах и, следовательно, иметь
ограниченные полосы.
В данном разделе мы рассмотрим главным образом модулято-
модуляторы, работающие в брэгговском режиме (когда выполняется условие
2тг\Ь/пА2 > 1), поскольку лишь высокочастотные модуляторы мо-
могут обеспечивать очень широкие полосы, представляющие практи-
практический интерес. Из выражения (9.5.29) видно, что относительную
величину дифрагированного света можно записать в виде
1
дифр . .
= sin''
над
тгЬ
Л/2 cos 0,
A0.1.1)
где L — длина взаимодействия, X — длина волны света, вв — угол
Брэгга, /в — интенсивность звука, а М — параметр, характеризую-
характеризующий фотоупругий материал. Для малых уровней звуковой мощно-
мощности эффективность дифракции г/ монотонно возрастает с увеличени-
увеличением интенсивности звука:
1) =
2A2cos20,
¦ML.
A0.1.2)
Следовательно, если интенсивность звука модулирована, то моду-
модулированной оказывается и интенсивность дифрагированного свето-
светового пучка. Таким образом, акустооптическая брэгговская дифрак-
дифракция позволяет закодировать информацию в оптическом пучке. Для
того чтобы эффективность брэгговской дифракции была достаточ-
достаточной, направления падающего и дифрагированного оптических пуч-
пучков должны быть приблизительно симметричны по отношению к
акустическим волновым фронтам. При этом как угол падения, так
и угол дифракции известны как угол Брэгга вв, который определя-
определяется выражением
вв = arcsin(X/2«A) = arc sin(\//2w), A0.1.3a)
где п — показатель преломления среды, v — фазовая скорость и
/— частота звука. На практике угол Брэгга вв является неболь-
небольшим, так что выражение A0.1.3а) можно записать в виде
2лЛ 2nv'
(Ю.1.36)
При малых углах вв угол отклонения 29В прямо пропорционален
частоте звука. В этом состоит основной принцип работы акустооп-
тических дефлекторов пучка (см. разд. 10.2). Ниже мы рассмотрим
некоторые важные параметры модуляторов, такие, как полоса и
эффективность модуляции.

396
Глава 10
10.1.1. ПОЛОСА МОДУЛЯЦИИ
Модулированная звуковая волна обычно характеризуется централь-
центральной частотой/0 и полосой Д/(т. е. полосой модуляции). Полоса Д/,
достижимая в акустооптических модуляторах, определяется глав-
главным образом, как мы увидим ниже, угловой расходимостью свето-
светового пучка. Для бесконечно широких звуковых и световых пучков
волновые векторы имеют хорошо определенные направления. Поэ-
Поэтому для данного угла падения и соответствующего ему угла ди-
дифракции условие брэгговской дифракции A0.1.3) может быть выпол-
выполнено на одной акустической частоте (нулевая полоса модуляции,
Д/ = 0). На практике приходится иметь дело с ограниченными зву-
звуковыми и световыми пучками, что приводит к конечной угловой
расходимости пучка. Конечное угловое распределение волновых
векторов позволяет получать брэгговскую дифракцию в некотором
диапазоне акустических частот (конечная полоса модуляции). Диф-
Дифференцируя выражение A0.1.3а), полосу модуляции можно записать
в виде
лд A0.1.4)
где Ав — изменение углов падения и дифракции, обусловленное
угловой расходимостью звукового и светового пучков. Величина Ав
представляет собой такое изменение угла Брэгга, которое необхо-
необходимо, чтобы выполнялись условия брэгговской дифракции в случае,
когда частота звука изменяется на величину Д/. Пусть 8в — угловая
расходимость оптических волновых векторов, а Ьф — то же самое
для звуковых волновых векторов. Эти углы расходимости пучков
связаны с длиной волны и шириной пучка и для пучков с дифракци-
дифракционной расходимостью определяются следующими приближенными
соотношениями:
2\
1ГПШ,
о
Л
L'
A0.1.5)
где w0 — размер лазерного пучка в его перетяжке, аи — показатель
преломления среды. Очевидно, что угол падения (т. е. угол между
волновым вектором света к и звуковым волновым вектором К) за-
занимает теперь диапазон
8ф.
A0.1.6)
Акустооптические устройства
397
В'
-Ьф
— Преобразователь
РИС. 10.2. Брэгговская дифракция светового пучка конечной ширины на модулиро-
модулированном акустическом пучке конечной ширины. Угловая расходимость светового пуч-
пучка равна &в, а звукового — Ьф.
Исследуем брэгговскую дифракцию светового пучка конечной ши-
ширины на модулированном акустическом пучке, имеющем конечную
ширину L. Расходящийся пучок можно представить в виде суперпо-
суперпозиции плоских волн, волновые векторы которых лежат в некото-
некотором диапазоне углов. Для каждой угловой составляющей светового
пучка условие Брэгга может выполняться в диапазоне звуковых ча-
частот, соответствующих разрешенным значениям волнового вектора
К в пределах Ьф. Дифракцию обеспечивает на каждой звуковой ча-
частоте своя плосковолновая составляющая, имеющая отличное от
других направление волнового вектора К. Дифрагированный свето-
световой пучок, отвечающий этому фиксированному углу падения света,
имеет угловую расходимость 2Ьф. Каждому направлению соот-
соответствует свой сдвиг частоты. Рис. 10.2 иллюстрирует угловую
расходимость световых пучков для двух крайних угловых составля-
составляющих. Чтобы осуществить модуляцию интенсивности дифрагиро-
дифрагированного светового пучка, спектрально сдвинутые составляющие ди-
дифрагированного света должны быть суммированы на квадратич-
квадратичном детекторе. Поэтому желательно, чтобы два крайних дифраги-
дифрагированных световых пучка (ОА' и ОВ' на рис. 10.2) имели некото-
некоторое угловое перекрытие. Для этого необходимо иметь 8ф ~ Ьв.
Подставляя 56 — 5ф = \/жпи>{), получаем полосу модуляции

398
Глава 10
A0.1.7)
которая приблизительно равна величине, обратной времени распро-
распространения звука через оптический пучок. Согласно этому выраже-
выражению, полоса акустооптического модулятора обратно пропор-
пропорциональна диаметру светового пучка. Для получения большой по-
полосы модуляции Д/ нужно использовать пучки малой ширины. Од-
Однако когда угловая расходимость 8в становится слишком большой,
дифрагированный световой пучок будет перекрываться с недифра-
гированным, что может нарушать работу модулятора. Следова-
Следовательно, максимальная относительная полоса акустооптического мо-
модулятора обычно определяется из условия отсутствия перекрытия
дифрагированного и недифрагированного световых пучков, для чего
требуется, чтобы 8в < вв. Таким образом, из выражений A0.1.3) и
A0.1.4) при условии Ав - вв получаем
/
2/<2-
A0.1.8)
Отсюда следует, что максимальная полоса модуляции составляет
приблизительно половину звуковой частоты. Таким образом, ши-
широкая полоса модуляции возможна лишь при высокочастотной
брэгговской дифракции.
10.1.2. ЭФФЕКТИВНОСТЬ МОДУЛЯЦИИ
Другим важным параметром акустооптического модулятора явля-
является эффективность дифракции, т. е. доля интенсивности падающе-
падающего света, которая подверглась дифракции. Из выражения A0.1.1)
следует, что интенсивность звука 1а, необходимая для того, чтобы
иметь 100%-ную модуляцию (т. е. полное преобразование падаю-
падающего света в дифрагированный), записывается в виде
_ X2cos20fi
A0.1.9)
где М — параметр, характеризующий фотоупругий материал и
определяемый выражением (9.5.28), а X — длина волны света. За-
Заметим, что требуемая интенсивность звука пропорциональна X2.
Пусть h — высота преобразователя. Тогда необходимая мощность
Акустооптические устройс гва
399
звука Ра равна
X2cos20b / h
2М
A0.1.10)
Отсюда следует, что для эффективной работы модулятора жела-
желательно иметь малое отношение h/L. В случае низкой эффективно-
эффективности дифракции (г/ < 1) выражение A0.1.1) можно приблизительно
записать в виде
дифр
A0.1.11)
или, используя соотношение Ia ~ Pa/hL, в виде
1} =
•л
2X2cos20,
(IK
A0.1.12)
В этом выражении параметр М часто обозначают через М2, для то-
того чтобы иметь возможность ввести другие полезные параметры.
Величину М2, определяемую выражением (9.5.28), во многих случа-
случаях формально записывают как
и.6.,2
pv
з •
A0.1.13)
Наиболее важной величиной следует считать ширину полосы моду-
модулятора, которая во многих случаях является важным конструктив-
конструктивным параметром. В соответствии с A0.1.12) эффективность ди-
дифракции г/ возрастает прямо пропорционально ширине акустическо-
акустического пучка L. Однако из A0.1.5) мы видим, что угловая расходимость
акустического пучка 8ф обратно пропорциональна L [а в соответст-
соответствии с A0.1.4) малые 8ф означают узкую полосу модуляции] и что
8ф ~ 8в - Д0/2. Подставляя 8ф = A/2L и используя выражения
A0.1.4)— A0.1.6), полосу модуляции можно записать в виде
2nvA
A0.1.14)
где Л — длина звуковой волны, а вв — угол Брэгга. Гордон [3] ввел
величину, которая не зависит от ширины модулятора L, а именно
h
A0.1.15)

400
Глава 10
где /0 — центральная звуковая частота (f0 = v/A). Фактор
pv
A0.1.16)
является полезным параметром, характеризующим фотоупругий
материал модуляторов (и дефлекторов).
Другая величина, введенная Диксоном [4], которая не зависит от
размеров акустического и оптического пучков, определяется выра-
выражением
— Р A0.1.17)
где мы положили A/L = 2А/тгяш0 (т. е. 8ф = 8в) и использовали ве-
величину h = iroH/2. Третий полезный параметр М3 записывается в
виде
" - 1?~ A0.1.18)
г- -
Каждый из введенных выше параметров Mv M2 и М3 играет опре-
определенную роль в работе модулирующего устройства. В случае низ-
низкой эффективности модуляции г/ величина М2 пропорциональна г/.
Для учета полосы модуляции Д/ следует использовать параметр
Mj, который пропорционален величине 2г)/0Д/. Значения параметров
Мр М2 и М3 для некоторых материалов приведены в табл. 10.1.
Эти параметры, хотя формально и выражаются через п, р, р и v,
определяются конфигурацией взаимодействия и состояниями поля-
поляризации волн. Как будет показано в разд. 10.2, эти параметры
можно использовать также для характеристики акустооптических
дефлекторов пучка.
10.1.3. ДВУЛУЧЕПРЕЛОМЛЯЮЩИЕ АКУСТООПТИЧЕСКИЕ
МОДУЛЯТОРЫ
Выше при выводе выражения для полосы модуляции предполага-
предполагалось, что волновые векторы падающей и дифрагированной свето-
световых волн равны друг другу. Для двулучепреломляющих материа-
материалов выполнение этого условия не обязательно. Как было показано
в гл. 9, условие Брэгга для акустооптического взаимодействия в
анизотропных средах изменяется, если падающий и дифрагирован-
дифрагированный световые пучки имеют разные фазовые скорости. Полоса мо-
о
о
s
а
S
х
В"
S
н
о
о
и.
л
л
е
о
s
<
Я Я)
в- "
С 1
я о »
' Ё §
S О в
S
Ъ
See
s я о
a g. в
к S о
г- Я м
X >,
о
С s
О
X
о
X
ч
о
а
С
о
С
ё §
о —
С в
§2"
о о
о
о
II
о —¦
С а
15 15
О О
II
о _
а —
С а
О
Н
I
а
С
26-631

ТАБЛИЦА 10.1. (Продолжение)
Материал
X, мкм п р, г/см3 Поляризация v, 103 м/с Поляризация Параметры качества фогоупругого
и направление и направление материала (в ед. СГС)
звуковой оптической
волны волны*
мг =
YAG
YIG
LiTaO3
As2S3
SF-4
/3-ZnS
0,63
1,15
0,63
0,63
0,63
0,63
1,83
2,22
2,18
2,61
1,15
1,616
2,35
4,2
5,17
7.45
3,20
2,46
3,59
4,10
Продольная
в [100]
Продольная
в [ПО]
Продольная
в[100]
Продольная
в [001]
Продольная
Продольная
Продольная
Продольная
в [110]
Поперечная
в [110]
Продольная
8,53
8,60
7,21
6.19
2,6
3,63
5,51
2,16
в [001]
nJp2/pv n6p2/pv3
0,16
0,98
3,94
11,4
762
619
1,83
24,3
a-AUO,
0,63 1,76 4,0 в [001]
2,165 Пили X в [001] 10,6
11,15 II в [1120] 7,32
0,012
0,073
0,33
1,37
433
347
1,51
3,41
0,57
0,34
n1p2/pv1
0,019
0,114
0,53
1,84
293
236
3,97
4,41
4,9
0,66
CdS
ADP
0,63 2,44 4,82
Продольная
в Г1120]
KDP
H,O
Те
ТеО,
ПА1 , со Продольная
°'63 1.58 1,803 в [100]
0,63 1,51 2,34
Поперечная
в [100]
Продольная
в [100]
Поперечная
в [100]
°'63 '.33 1.0 Продольная
'0,6 4,8 6;24
0,63 s 99
Продольная
в [1120]
Продольная
в [100]
Продольная
в [100]
Продольная
в [001]
Продольная
в [001]
4,17
6,15
1,83
5,50
1,5
2,98
4,26
51,8
II в [010] ,60
II или X в [001] 3.34
« в [010] 872
» или х в [001] ]57
4,36
11 в [0001] 10.200
[100] в [010] 0H97
[001] в [010] 22,9
[100] в [010] |42
[001] в [010] цз
12.1
2.78
6,43
1,91
3,83
160
4400
0,048
10,6
34,5
25,6
12,4
2,62
1,83
1,45
0,95
29,1
4640

ТАБЛИЦА 10.1. (Продолжение)
Материал X, мкм /; р, г/см3 Поляризация v, 103 м/с Поляризация Параметры качества фо гоупругого
и направление и направление материала (в ед. СГС)
звуковой оптической м — М — М
волны волны* _
РЬМоО4
0,63
[010] в [100] 3,04 Произв. в [001] 3,70
4,21 [НО] в [ГЮ] 323
[001] в [ТЮ] 16,2
3,64 [010] в [Т01] 101
Продольная
в [110]
Продольная
в [ПО]
Продольная
в [101]
Продольная
в [010]
[110] в [110]
[Ш1] в [101]
Продольная
6,95 в [100]
Продольная
в [100]
Продольная
в [100]
3,98 [001] в [010]
3,98 [100] в [010]
3,98 [010] в [001]
.n1p2/pv п 6
1,76
0,802
3,77
33,4
2,98
0,617
2,08
[101] в [101]
Произв. в 001
[100] в [010]
42,6
68,6
76,4
20,4
793
77
7,5
24
24
п 1p2/pv2
0,52
0,49
Bi,,GeO20(BGO) 0,63 2,55 9,2
Bi,,SiO20(BSO) 0,63
Sr075BaA2,Nb,O6 0,63 2,30
(SBN) 2,31
[100] в [010]
[100] в [001]
Продольная
в [001]
Продольная
в [001]
Продольная
в [001]
Продольная
в [001]
Продольная
в [110]
Продольная
в [100]
Продольная
в [001]
Продольная
в [100]
2,20 [100] в [001]
1,99
3,75 [100] в [010]
3,75 [001] в [010]
3,75 [100] в [010]
12,8
3,75
3,42
3,83
[100] в [010]
Произвольная
поляризация**
Произвольная
поляризация**
[001] поляри-
поляризация
[100] поляри-
поляризация
29,5
33,8
26,8
26,9
43,4
56,1
9,91
9,02
38,6
2,66
35,6
35,6
8,64
8,83
48,8
4,08

я
к , к
= н = н = н
л
EJ
О ^Г
IS
С a
EJ
О ZT
IS
I
4
о
a
С
4
с с
Е!
о
§
a
С
§
3
a
С
х х
л л
§ §
a a
С С
— (N
X X X X X X
л л л л л л
с; с; с; с; с; с;
о о о о о о
о о о о о о
а а а а а а
С С С С С С
О
E!
О
4
О
a
С
uo
и о
го
о
о.
S
I
I
S
с;
О
О
I
Акустооптические устройства
407
a
-е
о
оэ
! °
i g
I s
а т о
с с; О
л о ^
X со в
3 в н
>> о
со \л
Н
IS h
S О
= S9
| '-> 3
2-е;
со l_ cd
РИС. 10.3. Акустооптическое взаимодействие в одноосном кристалле, а — неколли-
неарное взаимодействие; б — коллинеарное взаимодействие.
дуляции двулучепреломляющего акустооптического модулятора
может отличаться от полосы модулятора в изотропном случае.
Для иллюстрации этого рассмотрим два следующих примера.
Пример- неколлинеарная акустооптическая модуляция в одноосных
кристаллах. Рассмотрим акустооптическое взаимодействие в одно-
одноосном кристалле (например, в LiNbO3), в котором плоскость рассе-
рассеяния перпендикулярна с-оси. Конфигурация взаимодействия изобра-
изображена на рис. 10.3, а. Предположим, что одноосный кристалл явля-
является отрицательным (пе <.по). Поскольку падающий свет линейно
поляризован^ вдоль с-оси, он распространяется в необыкновенной
моде кристалла с фазовой скоростью с/пе. Дифрагированный свет
предполагается линейно поляризованным в плоскости рассеяния
(плоскости ху) и представляет собой обыкновенную моду кристалла
с фазовой скоростью с/по. Углы падения и дифракции определяют-
определяются выражениями (9.4.5) и (9.4.6), и их зависимость от Х/Л =
= \f/v представлена на рис. 9.5. Из рис. 9.6 можно видеть, что
угол дифракции в' в широком диапазоне звуковых частот остается
почти постоянным, в то время как угол падения изменяется вблизи
в = 0. Действительно, из выражений (9.4.5) и (9.4.6) следует, что
Скорость изменения дифракционного угла в' с Х/Л при в = 0 обра-

408
Глава 10
щается в нуль (т. е. дв'/df = 0 при в — 0). Это соответствует кон-
конфигурации взаимодействия, изображенной на рис. 10.3, а. В соот-
соответствии с (9.4.5) частоту звука, отвечающую этой конфигурации
рассеяния с в = 0, можно записать в виде
A0.1.19)
где последнее приближенное равенство справедливо в случае, когда
An = по — пе < по. Предположим теперь, что падающий пучок
имеет угловую расходимость Ав. При этом звуковое волновое чис-
число может изменяться в диапазоне
АК=кеАв,
который соответствует звуковой полосе частот
A0.1.20)
A0.1.21)
Максимальная полоса модуляции определяется из условия того,
что дифрагированный пучок не перекрывается с недифрагирован-
ным, т. е. из условия Ав < в'. Таким образом, из выражений
«2I/2 и (ю.1.21) имеем
(9.4.6) при Х/Л = (п2о
A0.1.22)
Сравнивая этот результат с A0.1.8), получаем, что двулучепрелом-
ляющие акустооптические модуляторы в случае неколлинеарной
конфигурации взаимодействия не дают увеличения полосы модуля-
модуляции. Однако требование, накладываемое на угловую расходимость
акустического пучка (8ф « 89), в этом случае выполнить легче, что
позволяет увеличить длину взаимодействия без уменьшения полосы
модуляции и приводит к более высокой эффективности дифракции
г]. Приведенная на рис. 10.3, а конфигурация взаимодействия часто
используется при создании акустооптических дефлекторов пучка, в
которых звуковой волновой вектор тангенциален поверхности нор-
нормалей дифрагированной моды (см. разд. 10.2).
Пример- коллинеарная акустооптическая модуляция. Рассмотрим
акустооптическое взаимодействие, диаграмма которого изображена
на рис. 10.3, б, когда падающий и дифрагированный пучки распро-
распространяются коллинеарно вдоль оси у. Падающий световой пучок
представляет собой необыкновенную волну, поляризованную вдоль
Акустооптические устройства
409
с-оси кристалла. Дифрагированный свет является обыкновенной
волной, поляризованной вдоль оси х. Для сохранения импульса не-
необходимо, чтобы звуковая волна распространялась также вдоль
оси у и имела частоту
/о
A0.1.23)
При таком коллинеарном акустооптическом взаимодействии ди-
дифрагированный свет можно отделить от недифрагированного с по-
помощью поляризатора. Предположим теперь, что падающий пучок
имеет угловую расходимость Ав. Для сохранения направления ди-
дифракции вдоль оси у звуковое волновое число должно изменяться в
диапазоне АА', таком, чтобы выполнялось следующее равенство:
A0.1.24)
где ке = 2жпе/\ — волновой вектор падающего света. Этот диапа-
диапазон АК соответствует полосе модуляции
2/оА2
(А*J-
A0.1.25)
Используя выражение A0.1.23) и равенство /Л = v, относительную
полосу модуляции можно записать в виде
A0.1.26)
Из этого выражения может показаться, что для получения боль-
большой полосы модуляции необходимо, чтобы двулучепреломление
по — пе было мало и Д0 « по
пе. Однако при малом двулучепре-
ломлении значительно возрастает угловая расходимость акустиче-
акустического пучка. В действительности угловая расходимость акустиче-
акустического пучка должна быть равна Ьф - 2АК/К и в соответствии с
A0.1.23) и A0.1.24) должна определяться выражением
\2
A0.1.27)
Таким образом, из A0.1.26) и A0.1.27) имеем
A0.1.28)

410
Глава 10
Акус гооптнчсскис ус гройс гва
4] 1
Относительная полоса модуляции обратно пропорциональна длине
взаимодействия L. Следовательно, в случае коллинеарной акусто-
оптической модуляции трудно получить одновременно высокую эф-
эффективность и большую полосу модуляции.
10.2. АКУСТООПТИЧЕСКИЕ ДЕФЛЕКТОРЫ
Одним из наиболее важных применений акустооптического взаимо-
взаимодействия являются дефлекторы оптических пучков. Принцип рабо-
работы акустооптических дефлекторов в основном такой же, как и у
модуляторов, основанных на брэгговской дифракции. Единственное
различие состоит в том, что теперь изменяется не амплитуда, а ча-
частота звуковой волны. Использование акустооптического взаимо-
взаимодействия позволяет создавать дефлекторы пучков с высоким разре-
разрешением. При этом могут быть созданы сканирующие дефлекторы
как с произвольной выборкой, так и непрерывно действующие. Ос-
Основной принцип действия таких устройств иллюстрирует рис. 10.4,
а соответствующее объяснение можно дать с помощью рис. 10.5.
Для многих приложений важными параметрами таких устройств
являются число разрешимых элементов пучка, быстродействие и
эффективность.
Рассмотрим теперь брэгговскую дифракцию (рис. 10.4). Угол от-
отклонения при условии Брэгга равен 2вв = 2 arc sin(X/0/2w). На
рис. 10.5 приведена соответствующая этой дифракции векторная
диаграмма импульсов. Предположим, что частота звука изменяет-
изменяется от /0 до /0 + Д/. Поскольку К = 2irf/v, это приводит к измене-
изменению звукового волнового вектора на величину АК = 2-wkf/v, как
показано на рисунке. Поскольку угол падения остается неизменным
FВ) и фактически неизменной сохраняется длина вектора дифраги-
дифрагированной волны к, концы этих векторов к оказываются располо-
расположенными на окружности, изображенной на рис. 10.5. Таким обра-
образом, мы не можем замкнуть диаграмму импульсов и, следователь-
следовательно, закон сохранения импульсов не выполняется. Пучок будет ди-
дифрагировать в направлении, которое соответствует наименьшему
нарушению закона сохранения импульса". Дифракция происходит
Падающий
световой пучок
Пучок,
дифрагированный
на звуке частотой
/ + Д/
Пучок,
дифрагированный
в на звуке частотой
/о
Звуковая волна
переменной частоты
РИС. 10.4. Изменение частоты звуковой волны от /0 до /0 + Д/ приводит в соот-
соответствии с A0.2.1) к изменению направления дифрагированного пучка на угол Лв.
Окружность радиуса к
с центром в точке О X
РИС. 10.5. Диаграмма импульсов, иллюстрирующая отклонение дифрагированного
светового пучка от в до в + Ав, обусловленное изменением частоты звука от /„ до
/о + А/.
вдоль направления ОВ и приводит к отклонению пучка на величину
А6. Вспоминая, что углы в иДв малы и что Л: sin ^ = К, получаем
'* Это означает, что в направлении, которое отвечает максимальному значению
|ехр(/Дкт)с/3г, где Дк = к' — к — К, происходит рассогласование импульса и ин-
интегрирование ведется по области взаимодействия.
да:
k cos в,
в
nv cos в,
•А/,
A0.2.1)

412
Глава 10
где вв — угол брэгговской дифракции на частоте /0. Таким обра-
образом, угол отклонения пропорционален изменению частоты звука.
Как и в случае электрооптических дефлекторов, нас не интересует
абсолютное значение отклонения Ав. Гораздо больший интерес
представляет число разрешимых элементов пучка, т. е. число, опре-
определяющее, во сколько раз величина Ав превышает угловую расхо-
расходимость пучка. Если угловую расходимость пучка рассматривать
как 89 = 2Х/7г«ш0 [см. A0.1.5)], где ш0 — размер гауссова пучка в
перетяжке, то число разрешимых элементов запишется в виде
N = — = —
дв 2t>cos0B
Д/ = тД/,
A0.2.2)
где величина т = 7гшо/2г; cos вв приблизительно равна времени про-
прохождения звука через перетяжку гауссова оптического пучка и назы-
называется постоянной времени дефлектора.
Обычно качество дефлектора характеризуется параметром, рав-
равным отношению полного числа разрешимых элементов и постоян-
постоянной времени. Этот параметр, определяющий быстродействие де-
дефлектора, в соответствии с A0.2.2) записывается в виде
N
т
A0.2.3)
Таким образом, высокое быстродействие дефлектора возможно,
лишь когда полоса модуляции Д/ велика. Поэтому для дефлекторов
пучка желательно использовать высокочастотные звуковые волны,
поскольку, согласно A0.1.8), большая полоса модуляции Д/ воз-
возможна только в случае, когда частота модуляции/0 является доста-
достаточно высокой.
На практике полоса модуляции Д/ ограничивается широкополос-
широкополосным преобразователем и допустимыми отклонениями угла Брэгга.
Последнее связано с тем, что соответствующий угол падения света
при резонансной брэгговской дифракции зависит от частоты звука
FВ = \f/2nv). Для того чтобы дефлектор имел полосу Д/, угол па-
падения (угол между волновым вектором падающего светового пучка
к и звуковым волновым фронтом) должен перекрывать диапазон
порядка
A0.2.4)
Акустооптические устройства
413
что позволит получить высокую разрешающую способность. Пада-
Падающий световой пучок обычно хорошо коллимирован (т. е. угол
расходимости пучка Ьд мал). Следовательно, звуковая волна дол-
должна иметь конечную угловую расходимость 8ф, сравнимую с Авв
или даже больше (т. е. Авв < 8ф). Используя соотношение /0Л0 =
= v, из выражений A0.1.5) и A0.2.4) получаем
Д/" 2иЛ:
, < ¦
/о ~
о.
A0.2.5)
здесь Лц — длина волны звука с частотой /0. Таким образом, чтобы
иметь большую полосу модуляции, длина L преобразователя дол-
должна быть малой. Однако в соответствии с A0.1.12) небольшая
длина взаимодействия L приводит к низкой эффективности дифрак-
дифракции. Для преодоления этой трудности был предложен метод управ-
управления пучком, в котором звуковой пучок при изменении частоты
отслеживает угол Брэгга [6]. Этого можно добиться, если создать
систему акустических преобразователей, управляемых электриче-
электрическими сигналами с постепенно возрастающим сдвигом фаз между
последовательными элементами преобразователя (рис. 10.6). Такое
устройство позволяет избежать ограничивающего условия A0.2.5) и
существенно увеличить рабочую полосу Д/, а также эффективность
дифракции у] за счет концентрации мощности звука в соответствую-
соответствующем направлении, отвечающем брэгговской дифракции для всех ча-
частот в пределах Д/.
Для иллюстрации характеристик акустооптического дефлектора
пучка рассмотрим отклоняющую систему, в которой в качестве
среды используется флинт, а частота звука может изменяться от 80
до 120 МГц, т. е. Д/ = 40 МГц. Пусть диаметр оптического пучка
равен 1 см. Тогда из табл. 9.3 находим v = 3,1-105 см/с. Следова-
Следовательно, постоянная времени т равна 3,2 1О~6с, а число разреши-
разрешимых элементов равно ./V = тД/ = 130.
Увеличение полосы акустооптического дефлектора пучка было
продемонстрировано с помощью сфазированной решетки, схемати-
схематически показанной на рис. 10.6, в кристалле РЬМоО4 длиной 3 см [8].
Лазерный пучок (X = 5145 А) отклонялся в такой системе на 2000
разрешимых элементов с постоянной времени 8,5 мкс. При этом
была получена ширина полосы 200 МГц. При мощности 0,1 Вт де-
дефлектор отклонял 8% падающей мощности света.
Была также продемонстрирована работа двумерного акустоопти-
акустооптического дефлектора на основе кристалла РЬМоО4 [9], в котором ис-
используются два одинаковых отклоняющих устройства, расположен-
расположенных ортогонально друг к другу.

414
Глава 10
Падающий свет
Направление
вперед
Дифрагированный
свет
Результирующий
i/__ акустический
волновой фронт
Недифрагированный
РИС. 10.6. Акустооптическая брэгговская дифракция света на фазированной решетке
акустических волн [7].
10.2.1. ДВУЛУЧЕПРЕЛОМЛЯЮЩИЙ БРЭГГОВСКИЙ ДЕФЛЕКТОР
Выше при определении параметров акустооптических дефлекторов
мы предполагали, что среда является изотропной. Используя дву-
лучепреломляющие среды, можно существенно увеличить полосу, а
значит, и число разрешимых элементов дефлектора. Рассмотрим
изображенную на рис. 10.7 диаграмму акустооптического взаимо-
взаимодействия, в которой плоскость рассеяния (т. е. плоскость векторов
кик') перпендикулярна с-оси одноосного кристалла. Акустический
пучок падает таким образом, что для центральной рабочей часто-
частоты /0 волновой вектор к' дифрагированной волны перпендикулярен
звуковому волновому вектору Kq. Как мы показали в гл. 9 и в
предыдущем разделе, условие Брэгга может выполняться в широ-
широком диапазоне частот без использования сильно расходящихся (или
управляемых) акустических пучков. Из рис. 9.6 видно, что для ши-
широкого диапазона акустических частот угол падения остается почти
постоянным, в то время как угол дифракции сильно изменяется.
Поскольку в широком диапазоне частот звуковой волновой вектор
приблизительно перпендикулярен дифрагированному пучку, падаю-
падающий световой пучок должен отвечать моде с более высоким значе-
значением показателя преломления. В отрицательных одноосных кри-
Акуетооптические устройства
415
РИС. 10.7. Конфигурация взаимодействия в двулучепреломляющем акустооптиче-
ском дефлекторе пучка. Падающий световой пучок отвечает обыкновенной волне с
волновым вектором к = ОА, а дифрагированный световой пучок — необыкновен-
необыкновенной волне с волновым вектором к', направления которого изменяются в диапазоне
углов^У?. Звуковой волновой вектор К должен изменяться от А С до AD. Угловая
расходимость акустического пучка 6ф = BE/А В. Заметим, что звуковой волновой
вектор К перпендикулярен к '.
сталлах при пе < пд (например, в кристалле LiNbO3) падающий
свет должен соответствовать обыкновенной волне, а дифрагирован-
дифрагированный — необыкновенной волне. Отвечающие им волновые векторы
даются выражениями соответственно
k =
к' —
A0.2.6)
Из условия Брэгга (условия сохранения импульса) следует, что ча-
частота звука /0 записывается в виде
/о-J(«5-«2)
1/2
A0.2.7)

416
Глава 10
где п = {пе + по)/2 — среднее значение показателя преломления, а
An = \по — пе\ — двулучепреломление материала.
Пусть 8ф — угловая расходимость акустического пучка, необхо-
необходимая для того, чтобы отклонить световой пучок в угловом диапа-
диапазоне Ав (см. рис. 10.7). Величина 8ф связана с Ав соотношением
дф =
_ к' - k'cos^AO __ _^
К
8а:
A0.2.8)
Подставляя в это соотношение выражение A0.1.5) для 8ф, исполь-
используя A0.2.6) и учитывая, что К = 27г/Л, имеем
Ав
8Л
1/2
A0.2.9)
Из рис. 10.7 видно, что для отклонения оптического пучка в диапа-
диапазоне углов Ав звуковое волновое число должно лежать в диапазоне
АЛ', определяемом выражением
АК = к'АО.
A0.2.10)
Учитывая, что К = 2irf/v и используя выражения A0.2.6) и A0.2.9),
полосу частот Д/ можно записать следующим образом:
A0.2.11)
Если вспомнить, что г; = fo\, то относительная ширина полосы
запишется в виде
Д/
/о
8л \1/2
A0.2.12)
где мы вместо пе подставили п, поскольку в большинстве случаев
по~ пе « п. Сравнение выражения A0.2.12) с шириной полосы
изотропного дефлектора A0.2.5) дает следующее отношение полос
в этих случаях:
Д/двулу
^изотр
п J
A0.2.13)
Последнее равенство было получено благодаря использованию вы-
выражения A0.2.7). Из A0.2.13) следует, что полоса двулучепреломля-
Акуетооптические устройства
417
ющего дефлектора в 2{LAn/X)m раз больше полосы изотропного
дефлектора. В дефлекторе с длиной взаимодействия L = 1 см на
основе типичного двулучепреломляющего материала с An = 0,01
для светового пучка с длиной волны X - 1 мкм этот коэффициент
равен 20.
Относительная полоса двулучепреломляющего дефлектора
A0.2.12) всегда больше, чем для изотропного A0.2.5). Действитель-
Действительно, между этими двумя относительными полосами существует сле-
следующее соотношение:
т
J0
двулуч
A0.2.14)
Поскольку относительная ширина полосы обычно меньше едини-
единицы, это означает, что относительная ширина полосы двулучепре-
двулучепреломляющего дефлектора больше относительной ширины полосы
соответствующего изотропного дефлектора.
Такое увеличение полосы в двулучепреломляющем кристалле с
диаграммой взаимодействия, показанной на рис. 10.7, было проде-
продемонстрировано экспериментально [10]. Изменение частоты звуко-
звуковой волны в кристалле сапфира от 1,28 до 1,83 ГГц позволило осу-
осуществлять непрерывное отклонение оптического лазерного пучка
1200
1300
1400
«00
1600
1700 1800 1900
РИС. 10.8. Характеристики дефлектора на основе х-среза кристалла сапфира, в —
угол отклонения дифрагированного светового пучка относительно направления пада-
падающего пучка; ///тах — относительная интенсивность дифрагированного пучка (см.
текст);/0 — частота звука, вычисленная по формуле A0.2.7). (Из работы [10].)
27-631

418
Глава 10
(X = 6328 А) в пределах угла 4°. При этом была получена полоса
Д/ = 550 МГц. При типичной постоянной времени 2 мс число раз-
разрешимых элементов приблизительно равно 1000. Соответствующие
экспериментальные результаты приведены на рис. 10.8.
10.2.2. ПОВЕРХНОСТНЫЕ АКУСТООПТИЧЕСКИЕ
ДЕФЛЕКТОРЫ ПУЧКА
Недавно была продемонстрирована [11] возможность брэгговского
взаимодействия между поверхностными акустическими волнами и
оптическими направляемыми волнами (см. гл. 11) в тонкопленоч-
тонкопленочных диэлектрических волноводах. Поскольку эффективность дифрак-
дифракции г) [см A0.1.11)] зависит от интенсивности звука /а, локализация
акустической энергии вблизи поверхности (на глубине ~Л) приво-
приводит к низкой мощности модуляции или переключения. На рис. 10.9
схематически изображена экспериментальная установка, в которой
как поверхностная звуковая волна, так и оптическая волна направ-
направляются в одном кристалле LiNbOr Диэлектрический волновод об-
образуется вследствие диффузии Li из поверхностного слоя порядка
10 мкм, что приводит к увеличению показателя преломления в этой
области. На рис. 10.10 представлена фотография пятен отклонен-
отклоненных световых пучков, когда частота звука в дефлекторе изменялась
j Ось z(c)
Призмеииое
устройство
ввода
Недифрагиров.
световой пучок
Призменное
устройство
вывода
у срез пластинки
кристалла LiNbO3
Преобразователь 1 ^— Преобразователь 2
РИС. 10.9. Акустооптическая брэгговская дифракция направляемых волн на двух на-
наклонных поверхностных акустических волнах [12].
Акустооптические устройс г ва
419
РИС. 10.10. Неотклоненный и отклоненный световые пучки в дальнем поле, а — не-
отклоненный световой пучок; 6 — положения отклоненных световых пучков (пятен)
при изменении частоты звуковой волны от 155 до 410 МГц с интервалом 15 МГц.
(Из работы [13], copyright 1976 ШЕЕ.)
с помощью трех преобразователей, создающих наклонные поверх-
поверхностные акустические волны [13]. Были получены случайная посто-
постоянная времени т = 1,24 мкс и ширина полосы 358 МГц, что соот-
соответствует 400 разрешимым пятнам пучка.
Поверхностный акустооптический дефлектор пучка является
главным элементом в анализаторе спектра ВЧ-сигналов (см.
разд. 10.4).
10.3. АКУСТООПТИЧЕСКИЕ ПЕРЕСТРАИВАЕМЫЕ ФИЛЬТРЫ
Создание перестраиваемых спектральных фильтров — это еще одна
важная область применения акустооптического взаимодействия.
Акустооптические перестраиваемые фильтры используют, как пра-
правило, широкоугольное акустооптическое взаимодействие одинаково
направленных волн. Сильное акустооптическое взаимодействие
происходит только при выполнении условия Брэгга (условия сохра-
сохранения импульса). Если падающий пучок состоит из многих спект-
спектральных составляющих, то при данной акустической частоте толь-
только для одной из них будет выполняться условие Брэгга. Иными
словами, лишь одна спектральная составляющая будет дифрагиро-
дифрагировать при данной акустической частоте. Следовательно, изменяя ча-
частоту звука, можно изменять также частоту (или длину волны) ди-
дифрагированного оптического пучка. Относительная величина мощ-
мощности падающего пучка, преобразуемая в дифрагированный пучок
на длине взаимодействия L, в соответствии с выражением (9.5.49)
имеет вид
т =
A0.3.1)

420
Глава 10
где к12 — значение постоянной связи, определяемой выражением
(9.5.46), а Д/8 — рассогласование импульса:
д>в = д - & ± а:. (ю-з.2)
Здесь /Sj и /32 — составляющие волновых векторов падающего и ди-
дифрагированного пучков соответственно вдоль направления распро-
распространения акустической волны. Пусть в1 и в2 — углы, которые оп-
оптические волновые векторы составляют с волновым фронтом зву-
звуковой волны, так что
AО-3-3)
р2 — — n2smff2 = -r-
с л
где И[ и п2 — показатели преломления, отвечающие падающей и
дифрагированной волнам соответственно. Условие сохранения им-
импульса (условие Брэгга) Д/8 = 0 принимает вид
2тг / . а
— (и2яп02-
= ±
2тг'
A0.3.4)
где /— частота звука, a v — его скорость в среде.
Из выражения A0.3.4) видно, что волновое число Bя7Х) дифра-
дифрагированного света пропорционально частоте звука /. Идеальный
акустооптический перестраиваемый фильтр обычно работает в ус-
условиях, когда
к12Ь=\тг, A0.3.5)
т. е. при выполнении условия фазового синхронизма Д/3 = 0
A0.3.4) мощность падающей световой волны целиком переходит в
дифрагированную. Подставляя выражение A0.3.5) для к12 в A0.3.1),
эффективность преобразования мощности A0.3.1) можно перепи-
переписать в виде
A0.3.6)
1 +
Акустооптические устройства
421
Таким образом, эффективность преобразования падает до 50°7о,
когда
= +0,80тг;
A0.3.7)
здесь L — длина взаимодействия оптического и акустического по-
полей. С учетом A0.3.4) и A0.3.7) это соответствует ширине полосы
(ширине на полувысоте максимума)
ДЛ
0,80Л2
' |«2sin02 - п
A0.3.8)
которая в случае коллинеарного взаимодействия @, — в2 — тс/2)
принимает вид
ДА
0,80Л2
1/2
(коллинеарное взаимодействие).
A0.3.9)
Из A0.3.8) и A0.3.9) мы видим, что ширина полосы пропускания
обычно пропорциональна длине взаимодействия L. На рис. 10.11
построены зависимости пропускания фильтра Т (или эффективно-
эффективно0,8
I
§0,6
Q.
a
§0,4
о
0,2
0,0
Т
10
РИС. 10.11. Расчетный коэффициент пропускания акустооптического перестраивае-
перестраиваемого фильтра в зависимости от нормированного отклонения частоты Д0?/7г. Кри-
Кривая 1 — максимум пропускания равен 100% (а = 1); кривая 2 — максимум пропуска-
пропускания равен 50% (а = 1/2). Параметр а входит в выражение A0.3.13).

422
Глава 10
Прошедший
( i свет
Входной >v
световой пучок Поляризатор
¦!• 'В
LiNbOj \
Тонкопленочный
преобразователь
изСсШ
7000
6500 —
Ё
Л
6000 —
5500
750
Ю5О
РИС. 10.12. а — схематическое представление акустооптического перестраиваемого
фильтра на основе коллинеарного взаимодействия в кристалле LiNbO3; 6 — экспери-
экспериментальная кривая перестройки фильтра.
Акустооптические устройства
423
сти преобразования) для данной частоты звука от нормированного
отклонения оптической частоты A@L.
Харрис с сотр. [14, 15] предложили спектральный фильтр с элек-
электронной настройкой на основе коллинеарного акустооптического
взаимодействия в оптически анизотропных средах и продемонстри-
продемонстрировали его работу. В разд. 9.5.2 мы кратко рассмотрели одну из
конфигураций взаимодействия с участием сдвиговой волны. В дру-
другом эксперименте, выполненном этими авторами, оптические вол-
волны и продольная акустическая волна распространялись вдоль оси
х кристалла LiNbO3. На рис. 10.12, а показано схематически уст-
устройство этого фильтра. Падающий пучок может быть поляризован
либо вдоль оси у, либо вдоль оси z. Благодаря фотоупругому эф-
эффекту с постоянной ри (= p4i) (см. задачу 10.4) возникает брэггов-
ская дифракция в ортогональную поляризацию. Перестройка по
спектру от длины волны 7000 до 5500 А была получена изменением
акустической частоты от 750 до 1050 МГц (см. рис. 10.12, б). Для
кристалла LiNbO3 длиной 1,8 см с указанной на рис. 10.12, а ориен-
ориентацией двулучепреломление равно An = 0,09. Из A0.3.9) следует,
что ширина полосы пропускания ДХ1/2 на длине волны X = 6250 А
составляет около 2 А. Необходимо заметить, что в спектре пропу-
пропускания не присутствуют вторичные полосы или полосы высших по-
порядков, поскольку акустическая волна является синусоидальной.
Интенсивность звука 1а, необходимая для 100%-ного преобразова-
преобразования мощности (т. е. для того, чтобы к12Ь = тг/2), так же, как и в
A0.1.9), определяется выражением (см. задачу 10.4)
/ =
Л2
2M7L2
A0.3.10)
где
A0.3.11)
Если интенсивность звука 1а меньше величины, определяемой выра-
выражением A0.3.10), то из A0.3.1) следует, что максимальный коэффи-
коэффициент пропускания (см. задачу 10.4) дается выражением
— Sin —=r -г-
A0.3.12)
Интенсивность звука 1а пропорциональна приложенной к преобра-
преобразователю электрической мощности. Существуют, разумеется, опре-

424
Глава 10
деленные потери на границе раздела между кристаллом и преобра-
преобразователем, приводящие к конечным потерям при преобразовании
электрической мощности в акустическую.
Из-за нагревания кристалла вследствие диссипации мощности
звука в большинстве перестраиваемых фильтров трудно достичь
100%-ного преобразования мощности. Эти обстоятельства приво-
приводят к уширению полосы пропускания акустооптического перестраи-
перестраиваемого фильтра. Проиллюстрируем это на следующем примере.
Пусть условия работы таковы, что кпЬ = тга/2, где а может изме-
изменяться от 0 до 1. Максимальное пропускание в этом случае равно
Т - sin2Gra/2), и, поскольку 0 < а < 1, оно меньше 100%. В соот-
соответствии с A0.3.1) коэффициент пропускания дается выражением
sin2
+
A0.3.13)
1 +
Отсюда следует, что первый нуль (Г = 0) имеет место при
- 1 . A0.3.14)
При а = 1 максимальный коэффициент пропускания равен 100%.
Первый нуль возникает при Д/3 = V3ir/L. При a = 1/2 максималь-
максимальное пропускание равно 50%. При этом первый нуль соответствует
д/3 = \f\5ir/L, что означает уширение более чем в 2 раза. Однако
отношение главного и побочных максимумов пропускания умень-
уменьшается в [sin2Gra/2)/a2] раз. При a — 1/2, что соответствует коэф-
коэффициенту пропускания 50%, это отношение составляет лишь поло-
половину отношения в случае, когда пропускание равно 100% (а = 1).
Разумеется, все это за счет уширения полосы пропускания ДХ1/2.
Уширение полосы пропускания и уменьшение отношения главного
и побочных максимумов иллюстрирует рис. 10.11, б.
10.3.1. УГЛОВАЯ АПЕРТУРА
На рис. 10.13 представлена диаграмма волновых векторов, описы-
описывающая коллинеарное акустооптическое взаимодействие, рассмот-
рассмотренное выше. Геометрические места концов оптических волновых
векторов представляют собой концентрические окружности (в пло-
плоскости ху), причем в случае коллинеарного взаимодействия каса-
касательные к этим окружностям, отвечающие волновым векторам па-
падающей и дифрагированной световых волн, параллельны друг дру-
Акустооптические устройства
425
РИС. 10.13. Диаграмма волновых векторов для внеосевого оптического пучка в кол-
линеарном акустооптическом перестраиваемом фильтре. Взаимодействие в этом слу-
случае происходит в плоскости ху одноосного кристалла.
гу. Таким образом, при изменении угла падения условие согласова-
согласования импульсов A0.3.4) в первом порядке еще сохраняется. Это при-
приводит к большим угловым апертурам коллинеарных акустооптиче-
ских перестраиваемых фильтров, в которых волновые векторы на-
направлены вдоль главных осей при сохранении высокой разрешаю-
разрешающей способности (узкой полосы).
Пусть ф — угол между падающим световым пучком и звуковым
волновым вектором, т. е. ф = тг/2 - 0,. Поскольку п2 « «р дифра-
дифрагированный световой пучок составляет со звуковым волновым век-
вектором угол, приблизительно равный ф. При этом условие фазового
синхронизма A0.3.2) можно записать в виде
2тг,
К.
A0.3.15)
Пусть нормально падающий световой пучок (ф - 0 или 0, = тг/2)
на данной длине волны строго удовлетворяет условию фазового
синхронизма (Д/3 = 0). При отклонении угла падения от ф - 0 ус-

426
Глава 10
Акустооптические устройства
427
ловие фазового синхронизма выполняется для другой длины волны
(X + ДХ). Этот спектральный сдвиг связан с внутренним углом па-
падения ф следующим соотношением:
1 « t
A0.3.16)
X X + ?lX'
Если ф мал и спектральный сдвиг ДХ много меньше X (т. е. ДХ/Х <
< 1), то cos ф можно разложить в степенной ряд и мы имеем
4^ = -W. A0.3.17)
шетки. Обычная дифракционная решетка имеет угловую апертуру
порядка 1/N.
При создании перестраиваемых спектральных фильтров можно
также использовать неколлинеарное акустооптическое взаимодейст-
взаимодействие в анизотропных средах. Эти фильтры обладают некоторой уни-
универсальностью конструкции и имеют ряд важных практических пре-
преимуществ, а именно они позволяют в различных применениях сво-
свободно выбирать направления распространения и рабочую частоту
звука для данного кристалла. Большую угловую апертуру по-преж-
по-прежнему можно получить в случае, когда касательные к геометриче-
геометрическим местам концов волновых векторов падающего и дифрагиро-
Угловая апертура фильтра определяется как угол падения, при
котором спектральный сдвиг ДХ составляет половину полосы про-
пропускания ДХ1/2. Таким образом, в соответствии с A0.3.9) и A0.3.17)
угловую апертуру ф1/2 можно записать в виде
1/2
A0.3.18)
Угол ф1/2 является внутренним; реальный угол падения в воздухе
вследствие френелевского преломления на границе оказывается
больше. При ф1/2 « 1 внешний угол приблизительно равен пф1/2.
Интересно заметить, что как полоса ДХ1/2, так и угловая аперту-
апертура связаны с числом акустических длин волн, укладывающихся на
длине взаимодействия L (т. е. N — L/A). Если вспомнить, что ус-
условие фазового синхронизма A0.3.4) эквивалентно Л = Х/1Д«1, то
выражение A0.3.9) для полосы пропускания можно записать в виде
М/2
0,80
а угловую апертуру — в виде
0,80 \1/2
N ) ¦
A0.3.19)
A0.3.20)
Согласно A0.3.19), акустооптический фильтр по существу действу-
действует как решетка с разрешающей способностью (Х/ДХ1/2), пропорцио-
пропорциональной полному числу периодов (акустических длин волн). Угло-
Угловая апертура ф1/2 коллинеарного акустооптического фильтра, опи-
описанного выше, намного превосходит апертуру дифракционной ре-
реz (оптическая ось)
РИС. 10.14. Неколлинеарный акустооптический перестраиваемый фильтр, а — диа-
диаграмма волновых векторов в случае неколлинеарного акустооптического взаимо-
взаимодействия; 6 — схематическое представление акустооптического перестраиваемого
фильтра на основе кристалла ТеО2.

428
Глава 10
Акустооптические устройства
429
Кристалл FeO2
Акустическая
нагрузка
Падающий
свет
Отфильтрованный
свет
Преобразователь
Анализатор
РИС. 10.14. (Продолжение)
ванного световых пучков параллельны друг другу. Это иллюстри-
иллюстрирует рис. 10.14, а. Неколлинеарный акустооптический перестраивае-
перестраиваемый фильтр с полосой 40 А и апертурой//4 (±7°) был создан на
кристалле ТеО2 [16, 17]. При изменении частоты звука от 100 до
180 МГц была достигнута перестройка от 7000 до 4500 А. Недав-
Недавно появилось сообщение [18] о создании на основе неколлинеарного
взаимодействия в кристалле ТеО2 акустооптического перестраивае-
перестраиваемого спектрального фильтра для инфракрасного диапазона с отно-
относительной шириной полосы 1%. Была получена перестройка от 2
до 5,2 мкм при изменении частоты звука от 20 до 52 МГц.
10.4. АКУСТООПТИЧЕСКИЙ СПЕКТР-АНАЛИЗАТОР
Акустооптическая брэгговская дифракция может быть использова-
использована также для анализа энергетического спектра ВЧ-сигнала. В
разд. 10.2 мы рассмотрели обусловленное брэгговской дифракцией
отклонение светового пучка путем изменения частоты звука. В
этом случае эффективность дифракции пропорциональна мощности
звука. Каждому углу отклонения 2вв соответствует частота звука,
удовлетворяющая условию Брэгга:
2вв « —)
A0.4.1)
Рассмотрим схему акустооптического спектр-анализатора
(рис. 10.15) в случае, когда акустическая волна состоит из многих
частотных составляющих. Согласно A0.4.1), каждая частотная со-
составляющая звуковой волны будет приводить к отклонению свето-
светового пучка в определенном направлении. Поэтому дифрагирован-
дифрагированный свет представляет собой некоторое угловое распределение. Ес-
Если использовать линзу, то в ее фокальной плоскости каждому на-
направлению дифракции светового пучка будет соответствовать опре-
определенное пятно. Поскольку эффективность дифракции на каждой
частотной составляющей звука пропорциональна ее мощности, рас-
распределение оптической энергии в фокальной плоскости пропорцио-
пропорционально энергетическому спектру звукового ВЧ-сигнала. Интенсив-
Интенсивность оптического излучения в фокальной плоскости обычно изме-
измеряется с помощью линейки фотодетекторов. Поскольку работа аку-
акустооптического спектр-анализатора основана на одновременном от-
отклонении лазерного пучка во многих направлениях, такие его харак-
характеристики, как ширина полосы ВЧ-сигнала и число разрешимых
элементов, аналогичны характеристикам дефлекторов пучка.
Недавно Мергериан с сотр. [19] продемонстрировали работу ин-
интегрально-оптического высокочастотного спектр-анализатора, ис-
использующего поверхностную акустооптическую брэгговскую ди-
Частотная
плоскость
Коллимирующая
линза
Ячейка
Брэгга
Линза для
фурье-преобразования
РИС. 10.15. Основная схема акустооптического спектр-анализатора.
Линейка
фотодиодов

430
Глава 10
Акустооптические устройства
431
Лазер
ВЧ сигнал |—•
Детектор пучка
в нулевом
порядке
Линейка из
140 элементов
в фокальной
плоскости
2,0
1,5
§1,0
5
5
0,5
О Низкочастотный преобразователь
X Высокочастотный преобразователь
2,2мкмШГц
300 400 500 600
Частота, МГц
б
700
800
РИС. 10.16. а — схематическое представление интегрально-оптического спектр-ана-
спектр-анализатора ВЧ сигнала; 6 — зависимость отклонения направляемой оптической волны
от частоты поверхностной звуковой волны [19].
фракцию. На рис. 10.16, а схематически показано устройство этого
спектр-анализатора, а на рис. 10.16, б приведена зависимость от-
отклонения светового пучка от частоты ВЧ-сигнала. Спектр-анализа-
Спектр-анализатор был изготовлен из х-среза кристалла LiNbO3, с-ось которого
параллельна направлению звуковой волны. Оптическое излучение
было локализовано в тонкой пленке толщиной 280 А, полученной
путем диффузии титана. Геодезические линзы представляли собой
асферические углубления с круговой симметрией на поверхности
тонкопленочного волновода. Наклонные поверхностные акустиче-
акустические волны создавались двумя преобразователями (см. рис. 10.9) и
имели полосу 400 МГц с центральной частотой, равной 600 МГц.
Эффективность дифракции составляла около 5% при мощности
ВЧ-сигнала 60 мВт.
В традиционном спектральном анализе используется гетеродин-
гетеродинное сканирование сигнала от узкополосного частотно-
избирательного фильтра; при этом информация о различных спект-
спектральных составляющих поступает последовательно и слишком мед-
медленно для многих практических применений. Использование для
спектрального анализа акустооптического взаимодействия позволя-
позволяет обрабатывать сигналы параллельно и получать все спектраль-
спектральные составляющие одновременно в оптическом виде. Эти методы
играют важную роль для обработки сигналов в радарах.
10.5. АКУСТООПТИЧЕСКИЕ КОРРЕЛЯТОРЫ СИГНАЛА
Корреляция между двумя сигналами является одной из наиболее
важных характеристик при обработке сигналов радара. Для осу-
осуществления корреляции сигналов можно использовать акустоопти-
ческое взаимодействие. Рассмотрим акустооптический коррелятор,
изображенный на рис. 10.17, в котором входной электрический сиг-
сигнал (во многих случаях это принимаемый радаром эхо-сигнал) с по-
помощью электроакустического преобразователя кодируется в звуко-
звуковой волне. Результирующее поле напряжений в брэгговской ячейке
дается выражением
S(x, t) ~
A0.5.1)
где п — частота звука, v — скорость звука, а К = Q/v — волновое
число. Если на брэгговскую ячейку падает коллимированный свето-
световой пучок под углом Брэгга, то дифрагированный свет в случае
слабого взаимодействия можно записать в виде
Еа(х) ~ S,(* - or)exp[i(«
A0.5.2)
где ы — частота света. Первые две линзы (а, Ь) в совокупности с
диафрагмой действуют как фильтры, которые блокируют недифра-

432
Глава 10
Акустооптические устройства
433
Брэгговская ячейка Апертура
Транспарант
S2(x)i
(опорный сигнал)
Отверстие
Фотодетектор
] « Ь У
"колли ми poi
ванный
световой Входной сигнал
пучок Sl(t)
(принимаемый сигнал)
РИС. 10.17. Схематическое представление акустооптического коррелятора сигналов.
тированный свет. Дифрагированный свет A0.5.2) содержит инфор-
информацию, закодированную во входном сигнале S, (/). Действительно, с
помощью акустооптического взаимодействия входной сигнал S,(/)
оказывается «записанным» на световом пучке. В каждый момент
времени через апертуру проходит часть сигнала, закодированного в
дифрагированном пучке. Этот дифрагированный световой пучок за-
затем проходит через транспарант, содержащий информацию об
опорном сигнале S2(x). Распределение амплитуды светового пучка
сразу за транспарантом дается выражением
Ес ~
- vt)S2(x)exp[i(c>
A0.5.3)
Пучок затем фокусируется третьей линзой, расположенной таким
образом, чтобы транспарант находился в ее фокальной плоскости.
В задней фокальной плоскости линзы находится диафрагма с не-
небольшим отверстием на оптической оси. Поскольку третья линза
выполняет преобразование Фурье [20], поле на диафрагме d можно
записать в виде
Еd~
- vt)S2(x) dx,
A0.5.4)
где D — диаметр диафрагмы. Непосредственно за диафрагмой d
имеется квадратичный детектор, ток на выходе которого
~\j"D S,{x-vt)S2{x)dx
A0.5.5)
Следует заметить, что величина тока пропорциональна конечной
перекрестной корреляции между S, и Sr
Ток корреляции на выходе, определяемый выражением A0.5.5),
содержит существенное количество информации о сигнале S,(/), ко-
который может быть либо сигналом, принимаемым радаром, либо
сигналом в системе связи. В общем случае опорный сигнал S2(/)
обеспечивается приемным устройством и обычно представляет со-
собой сигнал, комплексно-сопряженный S,(/). В этом случае положе-
положение корреляционного пика дает время задержки между сигналами
и, следовательно, расстояние до цели. Ширина корреляционного
пика обратно пропорциональна ширине полосы Д/1/2 коррелирован-
коррелированных сигналов и дается выражением (см. задачу 10.5)
1
'1/2
A0.5.6)
Отношение сигнал/шум (ОСШ) для корреляционного пика можно
выразить через отношение сигнал/шум (ОСШ,) для сигнала на вхо-
входе S,(/) + «(/), где n(t) — дополнительный шум. Это соотношение
ТАБЛИЦА Ю.2. Параметры коррелятора
Акустическая мода
Материал
Постоянная времени Т
Диаметр апертуры D
Ширина полосы Д/1/2
Произведение &/1/2Т
Эффективность дифракции
(индекс модуляции)
Отношение сигнал/шум
Мощность звука
Необходимая мощность сигнала
Продольная
LiNbOj
10 мкс
5,5 см
300 МГц
3000
5%
43 дБ
1,2 Вт
5 Вт

434
Глава 10
Акустооп гические устройства
435
имеет вид [21]
ОСШ = (Д/1/2)ГОСШ,,
A0.5.7)
где Т — время корреляции сигналов (Г = D/v), а Д/|/2Г — произве-
произведение ширины полосы на время корреляции. Согласно A0.5.7), от-
отношение сигнал/шум для исходного принимаемого сигнала возрас-
возрастает в Д/|/2Г раз, что является основной целью преобразования
корреляции. В табл. 10.2 приведены параметры типичного брэггов-
ского акустооптического коррелятора [22], которые дают возмож-
возможность студентам познакомиться с основными характеристиками та-
такого коррелятора.
ЗАДАЧИ
10.1. Акустооппгические модуляторы Романа — Ната. Длина
взаимодействия L модулятора света, работающего в режиме
дифракции Рамана — Ната, должна удовлетворять условию
2-rrXL
пА2
а) Покажите, что максимальная возможная длина взаимо-
взаимодействия обратно пропорциональна частоте звука и да-
дается выражением
nv2
< 1.
тах 2тг\/2
б) Продольная акустическая волна в кварце имеет скорость
v = 5,95-105 см/с; показатель преломления кварца п =
= 1,46. Пусть свет отвечает линии гелий-неонового ла-
лазера с длиной волны 6328 А. Покажите, что максималь-
максимальная достижимая длина взаимодействия на частоте звука
10 МГц составляет 13 см.
в) Покажите, что на частоте 100 МГц максимальная длина
взаимодействия составляет 1,3 мм. Используя значение
М2 = 1,51 -10-15 из табл. 10.1 и выражение A0.1.11),
определите интенсивность звука, необходимую для полу-
получения эффективности дифракции 5%.
10.2. Расходимость акустического пучка. Имеется акустическая
система с полосой частот Д/ = 100 МГц. Если угол расходи-
расходимости акустического пучка достаточно большой для получе-
получения дифракции во всей этой полосе, то быстродействие ре-
рефлектора равно/Vr = 10s.
а) Покажите, что для типичных скоростей звука порядка
4- 103 м/с и для оптического пучка диаметром 1 см мож-
можно получить постоянную времени 2,5 мс и разрешение
250 элементов.
б) Покажите, что оптическому пучку диаметром 0,1 см от-
отвечает постоянная времени 0,25 мс и разрешение 25 эле-
элементов.
в) Пусть длина волны света равна 6328 А, а показатель
преломления среды п = 1,5. Покажите, что угол расхо-
расходимости акустического пучка Ьф должен быть порядка
или больше 5-1О~3 рад.
г) Для центральной акустической частоты 200 МГц найди-
найдите длину волны Л и длину взаимодействия, которым от-
отвечает расходимость пучка 5-10"~3 рад.
10.3. Брэгговский дефлектор на сапфире. Имеется двулучепрелом-
ляющий брэгговский дефлектор пучка, изготовленный на ос-
основе кристалла сапфира, диаграмма взаимодействия в кото-
котором изображена на рис. 10.7. Пусть свет испускается гелий-
неоновым лазером с длиной волны 6328 А. Предположите,
что по = 1,765 и пе — 1,757 и что звуковая волна распро-
распространяется вдоль оси х кристалла со скоростью 5,85-103 м/с.
а) Определите центральную частоту акустической волны,
необходимую для дифракции с изменением поляризации.
Ответ: /0 = 1,55 ГГц.
б) Покажите, что для длины взаимодействия L = 2,5 мм
ширина полосы составляет 350 МГц, а диапазон угловой
перестройки 2°.
в) Пусть диаметр оптического пучка равен 0,75 см. Опреде-
Определите постоянную времени г и число разрешимых элемен-
элементов.
10.4.
Фильтр Харриса. Пусть продольная звуковая волна взаимо-
взаимодействует с оптической волной, причем обе волны распро-
распространяются вдоль оси х кристалла LiNbO3 (см. рис. 10.12, а).
а) Покажите, что поле напряжений можно записать в виде
I S,
0
0
о
о
о/
- Кх)],

436
Глава 10
б)
где S, — единственная, отличная от нуля составляющая
напряжений.
Кристалл LiNbOj имеет точечную группу симметрии Зт.
С помощью табл. 9.1 и выражения (9.1.3) покажите, что
изменение оптической непроницаемости, обусловленное
полем напряжений, записывается в виде
в)
Дт,
0
о
о
о
Pusi
- Kx)].
Следовательно, брэгговская связь между у- и г-поляризо-
ванными волнами осуществляется благодаря коэффици-
коэффициенту фотоупругости pl4(= р41).
Покажите, что необходимая частота звука дается выра-
выражением
г)
Д)
где An = пе — гго — величина двулучепреломления кри-
кристалла. Для кристалла LiNbO3 с указанной ориентацией
скорость звука v = 6,57-103 м/с и An — 0,09. Определи-
Определите частоту звука, необходимую для работы на длине
волны 6328 А. Ответ: 934 МГц.
Определите полосу пропускания на длине волны 6328 А
для кристалла длиной 1,8 см. Ответ: 2 А.
Найдите угол захвата ф1/2, отвечающий ширине полосы
пропускания 2 А при X = 6328 А. Ответ: 1°.
10.5. Функция автокорреляции и теорема Винера — Хинчина.
а) Покажите, что энергетический спектр (спектральная
плотность) сигнала и автокорреляционная функция свя-
связаны преобразованием Фурье. Иными словами, пусть
S(w) — фурье-образ сигнала S(t). Покажите, что
Г S(t' + t)S*(t') dt'
du.
Это соотношение известно как теорема Винера — Хин-
Хинчина.
б) Покажите, что, согласно п. а задачи, ширина корреляци-
корреляционного пика обратно пропорциональна полосе сигнала и
определяется выражением A0.5.6).
Акустооптическне устройства
437
в) Пусть сигнал представляет собой гауссов импульс
5@ = е-'2/2т2е>"°'.
Покажите, что автокорреляционная функция дается вы-
выражением
Г@ = т^е-'2/4Л
а энергетический спектр имеет вид
Покажите также, что ширина корреляционного пика и
энергетический спектр даются следующими выражения-
выражениями:
At ~ у/2т, Аш ~ 1/г.
ЛИТЕРАТУРА
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
AdlerR. — IEEE Spectrum, 4E), 42 A967).
Bergmann L., Der Ultraschall. — Stuttgart: Hirzel, 1954, Ch. 5.
Gordon E. I. — Appl. Opt., 5, 1629 A966).
Dixon R. W. — J. Appl. Phys., 38, 3634 A967).
KorpelA., Acousto-Optics, Applied Solid State Science, vol. 3 (ed. R. Wolfe). —
New York: Academic Press, 1972.
Korpel A. et al. — Proc. IEEE, 54, 1429 A966). [Имеется перевод: Корпел и
др. — ТИИЭР, 1966, т. 54, № 10, с. 225,]
TsaiC. S., SPIE, 90, 69 A976).
Yao S. К., Young E. Я., SPIE, 90, 23 A976).
Pinnow D. A., Van Uitert L. G., Warner A. W., Bonner W. A. — Appl. Phys.
Lett., 15, 83 A969).
Lean E. G. #., Quote С F., Shaw H. J. — Appl. Phys. Lett., 10, 48 A967).
Kuhn L., DakssM. L., Heidrich P. F., Scott B. A. — Appl. Phys. Lett., 17, 265
A970).
Tsai С S., Nguyen Le Т., Yao S. K., AlhaiderM. H. — Appl. Phys. Lett., 26, 140
A975).
Tsai С S., AlhaiderM. A., Nguyen Le Т., Kim B. — Proc. IEEE, 64, 318 A976).
[Имеется перевод: Изай, Альхайзер, Ле Тронт Нгуен, Ким. — ТИИЭР, 1976,
т. 64, № 5, с. 295.]
Harris S. E., Wallace R. W. — J. Opt. Soc. Amer., 59, 744 A969).
Harris S. E., Nieh S. T. K., Winslow D. K. — Appl. Phys. Lett., 15, 325 A969).
Chang I. C. —Appl. Phys. Lett., 25, 370 A974).
Chang I. C. — SPIE, 90, 12 A976).
Khoshnevisan M., SoveroE., Newman P. R., Tracy J. — SPIE, 245, 63 A980).
Mergerian D. et al. — Appl. Opt., 19, 3033 A980).
Cutrona L. J. et al. — IRE Trans. Inform. Theory, IT-6, 386 A960).
Sprague R. A. — SPIE, 90, 136 A976).
Maloney W. T — IEEE Spectrum, 6, 40 (Oct. 1969).

Глава 11
НАПРАВЛЯЕМЫЕ ВОЛНЫ
И ИНТЕГРАЛЬНАЯ ОПТИКА
В данной главе мы рассмотрим вопросы, связанные с распростра-
распространением оптических волн в диэлектрических структурах (т. е. в тон-
тонких пленках и волокнах), размеры которых соизмеримы с длиной
волны. Известно, что лазерный пучок с ограниченным поперечным
размером расходится при распространении в однородной среде (см.
гл. 2). В волноводных диэлектрических структурах при определен-
определенных условиях это расхождение отсутствует. Оптические моды в
этих диэлектрических волноводах соответствуют локализованному
в пространстве распространению электромагнитного излучения с
поперечными размерами, определяемыми волноводом.
В начале нашего рассмотрения мы изучим основные свойства
направляемых волн в диэлектрических структурах общего вида. Оп-
Оптические моды представляются как решение характеристического
уравнения, к которому сводятся уравнения Максвелла, удовлетво-
удовлетворяющие граничным условиям, определяемым геометрией волново-
волновода. Этот подход мы применим затем к планарному диэлектриче-
диэлектрическому волноводу и получим выражения как для ТЕ-, так и для ТМ-
мод. Физика локализованного распространения объясняется при
этом с помощью явления полного внутреннего отражения плоских
волн от диэлектрических границ раздела.
Затем мы сформулируем теорию связанных мод и применим ее
для описания распространения излучения в волноводах, когда на
распределение мощностей мод оказывают влияние различные воз-
возмущения. Этот формализм применяется также при исследовании
большого числа имеющих важное практические значение устройств,
таких, как 1) периодические (гофрированные) оптические волноводы
и фильтры, 2) лазеры с распределенной обратной связью и 3) элек-
электрооптические смесители и направленные ответвители. В заключе-
заключение мы подробно рассмотрим характеристики распространения
волн в волноводах с металлическим покрытием, в волноводах на
брэгговском отражении и в волноводах с вытекающими модами.
11.1. ОБЩИЕ СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ ВОЛНОВОДОВ
Общее требование, которому должны удовлетворять волноводы в
случае электромагнитного излучения, состоит в том, что поток
Направляемые волны и интегральная оптика
439
РИС. 11.1. Общий вид цилиндрического
волновода.
энергии должен распространяться только вдоль направляющей
структуры и должен отсутствовать в перпендикулярном к ней на-
направлении. Это означает, что поля будут существенны лишь в не-
непосредственной близости от направляющей структуры. Таким вол-
волноводом может служить диэлектрический цилиндр с произвольным
поперечным сечением, изображенный на рис. 11.1, при условии что
его диэлектрическая проницаемость достаточно велика. Следова-
Следовательно, для оптических волн сердцевина волновода должна иметь
более высокий показатель преломления, чем его периферия. Вооб-
Вообще говоря, в соответствии с лучевым уравнением B.3.12) траекто-
траектория пучка, распространяющегося в неоднородной в поперечном на-
направлении среде, изгибается по направлению к области с высоким
показателем преломления. Таким образом, высокий показатель
преломления в волноводной области (сердцевине) производит тот
же эффект, что и собирающая линза. При соответствующих усло-
условиях такая фокусировка благодаря высокому показателю преломле-
преломления сердцевины точно компенсирует расхождение пучка, обуслов-
обусловленное дифракцией. При этом волноводная мода направляется ди-
диэлектрической структурой.
Рассмотрим волновод с произвольным поперечным сечением
(рис. 11.1). Ось волновода выбрана в направлении координаты z, a
временная зависимость предполагается в виде ёш. Тогда уравнения
Максвелла можно записать в виде
V X Н = ше0п2Е,
A1.1.1)
A1.1.2)

440
Глава 11
где п — распределение показателя преломления диэлектрической
структуры, зависящее только от х и у (т. е. dn/dz = 0). Поскольку
диэлектрическая структура однородна вдоль оси z, решения волно-
волновых уравнений A1.1.1) и A1.1.2) будем искать в виде
Ш-fiz)], A1.1.3а)
Н = %(х, y)exp[i(vt - pz)], A1.1.36)
где /3 — постоянная распространения, определяемая из уравнений
Максвелла. Мы ограничимся рассмотрением диэлектрических
структур, которые состоят из кусков однородных и изотропных
материалов, или материалов с небольшим градиентом показателя
преломления. Тогда волновые уравнения сводятся к A.4.9). Под-
Подставляя выражение A1.1.3а) для Е в уравнение A.4.9), получаем
A1.1.4)
где V2 = V2 - d2/dz2 — оператор поперечного лапласиана. Уравне-
Уравнение A1.1.4) определяет поведение поля в поперечном направлении.
В случае кусочно-однородной диэлектрической структуры уравнение
A1.1.4) справедливо отдельно в каждой из однородных областей.
Следовательно, поле должно быть найдено отдельно в каждой об-
области, а затем тангенциальные составляющие полей необходимо
сшить на каждой из границ раздела. Другим важным граничным
условием для волноводных мод является равенство нулю амплиту-
амплитуды полей на бесконечности. Для выполнения граничных условий во
всех точках границ раздела однородных сред параксиальная посто-
постоянная распространения /3 должна быть одинаковой во всей волно-
водной структуре.
Основной задачей при этом является нахождение решения харак-
характеристического уравнения A1.1.4), удовлетворяющего условиям не-
непрерывности тангенциальных составляющих полей на диэлектриче-
диэлектрических поверхностях раздела и граничным условиям на бесконечно-
бесконечности. Для данного профиля показателя преломления п2(х, у) сущест-
существует, вообще говоря, бесконечное число собственных значений /З2,
соответствующих бесконечному числу мод. Однако лишь конечное
число этих мод обычно удерживается вблизи сердцевины и беспре-
беспрепятственно распространяется вдоль волновода. Одним из необходи-
необходимых условий существования волноводной моды является отсутст-
отсутствие потока энергии в поперечном направлении, что эквивалентно
Направляемые волны и интегральная оптика
441
экспоненциальному уменьшению полей вне волноводной структу-
структуры. Следовательно, величина (ш2/с2)п2 — /З2 должна быть отрица-
отрицательной вдали от волноводной области (сердцевины). Иными сло-
словами, постоянная распространения /3 направляемой моды должна
удовлетворять условию
р->—п-{сс), A1.1.5)
где я2(оо) — показатель преломления на бесконечности (Vx2 + у2 —
— оо). Однако, если поля обращаются в нуль на бесконечности
(т. е. 1/Г(оо)|2 = 0), из условия непрерывности полей следует, что
амплитуда поля \Е(х, у)\ должна иметь максимальное значение в
некоторой точке плоскости ху. Обычно Е(х, у) является гладкой
функцией пространственных координат. Существование максимума
требует, чтобы лапласиан поля был отрицательной величиной.
Иными словами, постоянная распространения /3 направляемой мо-
моды в некоторой области ху (обычно в сердцевине) должна удовлет-
удовлетворять неравенству
-ги (*> У)-
с
A1.1.6)
В частности, если пс — максимальное значение показателя прелом-
преломления п(х, у), то постоянная распространения направляемой моды
в любом случае должна удовлетворять следующему условию:
/г-<—л;. A1.1.7)
В области, в которой выполняется условие A1.1.6), решения волно-
волнового уравнения A1.1.4) являются осциллирующими. Эти осцилли-
осциллирующие решения должны быть согласованы с экспоненциальными
решениями на поверхностях раздела диэлектрической структуры.
Следовательно, не все значения /3, удовлетворяющие условиям
A1.1.7) и A1.1.5), представляют собой допустимые собственные
значения направляемых мод. Это будет проиллюстрировано ниже
при исследовании мод планарного волновода. В следующем разделе
мы рассмотрим некоторые основные свойства волноводных мод.

442
Глава 11
11.1.1. ОРТОГОНАЛЬНОСТЬ МОД
Волноводные моды произвольной диэлектрической структуры об-
обладают важным и полезным свойством ортогональности. Пусть
поля Е,, Н, и Е2, Н2 представляют собой два линейно независимых
решения уравнений Максвелла A1.1.1) и A1.1.2). Так как в диэлект-
диэлектрической волноводной структуре источники отсутствуют, имеет ме-
место следующее уравнение:
V '(Ei X Н2 - Е2 X Н,)
0.
A1.1.8)
Уравнение A1.1.8) известно как теорема Лоренца и справедливо
при условии, что е и ц являются симметричными тензорами.
Если заменить оператор 7 на 7( + azd/dz и предположить, что
поля Ер Нр Е2 и Н2 записываются в виде A1.1.3а) и A1.1.36) с по-
постоянными распространения /3, и /32 соответственно, то уравнение
A1.1.8) принимает вид
V, '(Е, X Н2 - Е2 X Н.) - /(/8, + у82)аг-(Е, X Н2 - Е2 X Н,) = 0,
A1.1.9)
где V, — поперечный градиентный оператор, и аг — единичный
вектор вдоль оси z. Используя двумерную форму теоремы дивер-
дивергенции, получаем
х Н2 - Е2 х
A1.1.10)
где S — произвольная поверхность в плоскости ху, С — граница
поверхности S, а п — единичный вектор, перпендикулярный кривой
С и вектору а . Если в качестве S выбрать всю плоскость ху, то в
уравнении A1.1.10) контурный интеграл исчезает, поскольку поля
на бесконечности обращаются в нуль. Таким образом, получаем
@. +
х Н2 - Е2 х Н.)
= 0.
A1.1.11)
Направляемые волны и интегральная оптика
443
Подстановка выражений A1.1.3а) и A1.1.36) для Е и Н в A1.1.11)
дает
хЗС2-б2х %])-a2da = 0.
A1.1.12)
Здесь общие экспоненциальные члены можно опустить. Чтобы по-
показать, что в выражении A1.1.12) каждый член обращается в нуль
по отдельности, рассмотрим два решения Ц, Н, и Е2, Н2, где ре-
решение Е2, Н2 является зеркальным преобразованием решения Е2,
Н2 относительно плоскости z = 0. Благодаря симметрии структу-
структуры преобразования мода также является решением уравнений
Максвелла A1.1.1) и A1.1.2). Это зеркальное преобразование соот-
соответствует обращению направления распространения. Поэтому на-
направления продольного электрического и поперечного магнитного-
полей также обращаются, т. е.
Е'2, -
-S2iexp[i(«f
Н'2,=
Щ, =
fi2z)],
A1.1.13)
где индекс t означает поперечную компоненту. Так как лишь попе-
поперечные компоненты поля дают вклад в интегралы A1.1.11) и
A1.1.12), уравнение, соответствующее A1.1.12), в этом случае при-
принимает вид
б, x3C2-S2x3C,)-a,rfa = 0. A1.1.14)
Сложение и вычитание выражений A1.1.12) и A1.1.14) дает
//(б, x%2)-azda= ff{S2x%l)-azda = 0. A1.1.15)
При отсутствии потерь (т. е. е и /* являются вещественными тензо-
тензорами) аналогичный вывод приводит к уравнению
//(б, X %*) .uzda = ff{$* X %,) .zzda = 0.

444
Глава 11
Включив зависимости от времени и от z, условие ортогонально-
ортогональности можно записать в виде
J /е, X H*2-a2da = О,
A1.1.16)
где Н2* — вектор, комплексно-сопряженный с Н2. Из этого условия
следует, что поток мощности в диэлектрическом волноводе без по-
потерь равен сумме мощностей, переносимых каждой модой по от-
отдельности. Если мощность каждой моды нормирована на величину
1 Вт, то условие ортогональности мод можно записать следующим
образом:
A1.1.17)
где /, т — модовые индексы, а 5/ш — символ Кронекера. Для попе-
поперечных электрических (ТЕ) или поперечных магнитных (ТМ) мод
условие ортогональности A1.1.17) принимает вид (см. задачи 11.3 и
11.4)
A1.1.18)
2ы
(TM).
I I.I.2. ПЕРЕНОС ЭНЕРГИИ
В диэлектрических волноводах без потерь каждая мода переносит
энергию и распространяется вдоль волновода независимо от нали-
наличия других мод. Это видно из условия ортогональности мод
A1.1.17). Переносимая мощность определяется вещественной час-
частью интеграла от комплексного вектора Пойнтинга по всей плоско-
плоскости ху. Вследствие ортогональности мы можем рассматривать рас-
распространение мощности одной моды. Для данной моды мощность,
усредненная по времени, дается выражением
Р = ?Ref JExH*-azda. A1.1.19а)
Энергия поля моды на единицу длины волновода запишется в виде
H-ixH*)da,
A1.1.196)
Направляемые волны и интегральная оптика
445
где мы предполагаем, что е и д — вещественные величины, так что
подынтегральное выражение также является вещественным. По-
Поскольку уравнения Максвелла линейны, поток мощности Р и плот-
плотность энергии U пропорциональны друг другу. Постоянная пропор-
пропорциональности имеет размерность скорости и называется скорос-
скоростью распространения энергии:
ve = P/U. A1.1.20)
Можно показать, что эта скорость равна групповой скорости, ко-
которая определяется как
vg = dco/d/3. A1.1.21)
В диэлектрических волноводах постоянная распространения /3 для
каждой моды является функцией частоты со. При распространении
в волноводе импульса света с конечной шириной полосы частот 5со
возможен случай, когда мощность каждой спектральной компонен-
компоненты переносится только одной модой. Если 5/3 есть соответствую-
соответствующий разброс постоянных распространения моды, то скорость рас-
распространения импульса дается выражением A1.1.21).
Для доказательства того, что скорость ve равна групповой ско-
скорости vg, рассмотрим уравнения Максвелла A1.1.1) и A1.1.2) [или в
более общей записи уравнения F.7.10) и F.7.11)], в которые вместо
оператора V подставим V( + azd/dz. Таким образом, мы имеем
следующие уравнения:
V, X Н + а, X -^-Н = /ыеЕ,
V, X Е + az X д-Е = -шцН,
A1.1.22)
где, как и прежде, az — единичный вектор вдоль оси волновода.
Так как зависимость мод от z имеет вид, определяемый выражени-
выражениями A1.1.3а) и A1.1.36), уравнения A1.1.22) можно записать в виде
V, X Н - *0az X Н = /ыеЕ,
V, X Е - фл2 X Е = -шцИ.
A1.1.23)
Предположим теперь, что /3 изменяется на бесконечно малую вели-
величину 5/3. Если 5со, 5Е и 5Н являются изменениями величин со, Е и Н
соответственно, то, следуя рассуждениям, приведенным в разд. 6.7,

446
Глава 11
мы получим следующее уравнение:
V,-F- 4/80Re[(E X Н*) • aj = -2*8<о[Е«еЕ* + Н-/Ш*],
где F дается выражением
F = 8Е X Н* + 8U* X Е + Н X 8Е* + Е* X 8Н.
A1.1.24)
A1.1.25)
Выполняя в уравнении A1.1.24) интегрирование по всей плоскости
ху и используя двумерную теорему для дивергенции
ЛГУ, • Fda = (f)F 'ndl,
s Jc
получаем
- 8i8/3P = -
A1.1.26)
A1.1.27)
где с — контур на бесконечности, а Р и V определяются выраже-
выражениями A1.1.19а) и A1.1.196) соответственно. Контурный интеграл
в A1.1.27) обращается в нуль, поскольку на бесконечности амплиту-
амплитуды полей локализованных мод равны нулю. Это приводит к выра-
выражению
8{}P = 8wU. A1.1.28)
Используя определение групповой скорости и скорости распростра-
распространения энергии, выражение A1.1.28) можно записать в виде
A1.1.29)
Так как 5/3 — произвольное бесконечно малое число, мы заключа-
заключаем, что для волноводной моды в диэлектрической структуре
ve = v ¦ A1.1.30)
Чтобы проиллюстрировать некоторые особенности диэлектри-
диэлектрических волноводов, рассмотрим пленарный волновод толщиной t
из непроницаемого диэлектрика с показателем преломления п2, уло-
уложенного между непроницаемыми средами с показателем преломле-
преломления и, с одной стороны и пъ — с другой. Эта несложная структура
выбирается вследствие того, что решение задачи в этом случае за-
Направляемые волны и интегральная оптика
447
х- -t
РИС. 11.2. Пленарный диэлектрический волновод с дп/ду = 0. Ось у направлена
перпендикулярно рисунку на читателя. Ломаная ABCD соответствует полному зиг-
зигзагу луча.
писывается в простом виде. На рис. 11.2 схематически нарисована
такая волноводная структура. Пусть координаты выбраны таким
образом, что волна распространяется в плоскости xz, а показатель
преломления определяется следующим образом:
A1.1.31)
Поскольку в направлении оси у показатель преломления не изменя-
изменяется, в уравнении A1.1.4) можно положить д/ду — 0 и написать
уравнения отдельно для областей I, II и III:
Область I:
Е(х, у) + {kin] - /S2)E(x, у) = 0, (П.1.32а)
ОбластьП: — Е(х, у) + (Цп2 - Р2)Е(х, у) = 0, (Ц.1.326)
д2
ОбластьШ: —-Е(х, у) + (kin2 - /32)Е(х, у) = 0; A1.1.32в)
дх2
здесь к0 = со/с и Е[х, у) — компонента модовой функции <f(x, у)
A1.1.3а).
Прежде чем искать решения уравнений A1.1.32), с помощью
простых рассуждений исследуем физическую природу решений. Рас-

448
Глава 11
Направляемые волны и интегральная оптика
449
(e) (d) (с) (b) (a)
РИС. 11.3. Вверху: различные режимы (а), F), (г), (d), (e) постоянной распростране-
распространения /3 для волновода, изображенного на рис. 11.2. В середине: распределения полей
при различных значениях /3. Внизу: диаграммы волновых векторов, соответствую-
соответствующие различным режимам распространения.
смотрим решения как функцию постоянной распространения /3 при
фиксированной частоте со. Предположим, что л2 > л3 > л,. При
/3 > коп2 [т. е. режим (а) на рис. 11.3] из A1.1.32) непосредственно
следует, что (\/Е)(д2Е/дх2) > О всюду, а Е(х) является экспоненци-
экспоненциальной функцией во всех трех слоях (I, II, III). Из-за необходимо-
необходимости согласования как функции Е(х), так и ее производных на двух
границах раздела распределение результирующего поля должно со-
соответствовать случаю (а) на рис. 11.3. Поле увеличивается вне гра-
границ волновода по крайней мере в одну сторону, так что такое ре-
решение физически не реализуется и не соответствует реальной волне.
При коп3 < /3 < коп2 [режимы ф) и (с) на рис. 11.3] из уравне-
уравнения A1.1.32) следует, что решение является синусоидальным в об-
области II, так как (\/Е)(д2Е/дх2) < 0, и экспоненциальным в областях
I и III. Это позволяет получить решение Е(х), которое удовлетво-
удовлетворяет граничным условиям и в то же время экспоненциально спада-
спадает в областях I и III. Два таких решения показаны на рис. 11.3
[случаи ф) и (с)]. Энергия, переносимая этими модами, локализует-
локализуется в окрестности волноводного слоя II, и мы будем называть их
локализованными, или направляемыми, модами. Из обсуждения,
приведенного выше, следует, что необходимым условием их су-
существования является выполнение неравенств konv копг < /3 <
< коп2, так что локализованные моды существуют, только если
п2 > пх, п3, т. е. внутренний слой имеет более высокий показатель
преломления.
Модовые решения при коп1 < /3 < коп3 [режим (d)] соответству-
соответствуют, согласно A1.1.32), экспоненциальному поведению в области I и
синусоидальному — в областях II и III, как показано на рис. 11.3
[случай (сГ)]. Мы будем называть такие моды излучательными мо-
модами подложки. В случае 0 < /3 < коп} [режим (е)] решение Е(х)
становится синусоидальным во всех трех областях. Это так назы-
называемые излучательные моды волноводов.
Решения уравнений A1.1.32), удовлетворяющие граничным усло-
условиям на границах раздела (мы их запишем в следующем разделе),
показывают, что, в то время как в режимах (d) и (с) величина /3 яв-
является непрерывной, в режиме, когда коп3 < /3 < коп2, значения /3
являются дискретными. Число локализованных мод зависит от
ширины t, частоты со и показателей преломления и,, п2, nv При
данной длине волны число локализованных мод увеличивается от О
с увеличением t. При некотором значении t мода ТЕ0 становится
локализованной. Дальнейшее увеличение t приводит к моде ТЕ, и
т. д.
Для изучения распространения волн во внутреннем слое 2 полез-
полезно рассмотреть распространение плоских волн под некоторыми
углами в к вертикальной оси х, испытывающих серию полных
внутренних отражений на границах раздела II—I и II—III. Для это-
этого выберем уравнение A1.1.326). Предполагая решение в виде Е ~
~ sin(hx + a)e~ifSz, мы получаем
+ Л2 = к2п\.
A1.1.33)
А
29-631

450
Глава 11
Результирующие прямоугольные треугольники со сторонами /3, h и
к0п2 показаны на рис. 11.3. Заметим, что, поскольку частота посто-
постоянна, для случаев ф), (с), (rf) и (е) справедливо тождество к0п2 =
= (ы/с)п2. Таким образом, распространение излучения можно рас-
рассматривать как распространение плоской волны, направленной
вдоль гипотенузы с неизменяющейся постоянной распространения
к0п2. При уменьшении /3 угол в уменьшается до тех пор, пока при
/3 = коп3 не нарушится условие полного внутреннего отражения на
границе III—П. Это следует из того факта, что условие волновод-
ного распространения волн/3 = ?o/i2sin0 > к0п3 эквивалентно нера-
неравенству в > arcsin(/23/i2) - <?с» где "с ~ Угол полного внутреннего
отражения на границе раздела между слоями II и III. Поскольку
п3 > пх, полное отражение на границе раздела II—III гарантирует
полное внутреннее отражение на границе областей I—II. Использо-
Использование полного внутреннего отражения для получения волноводных
мод мы обсудим в конце следующего раздела.
11.2. ТЕ- И ТМ-МОДЫ В АСИММЕТРИЧНОМ ВОЛНОВОДЕ
Решим волновое уравнение A1.1.4) для диэлектрического волно-
волновода, показанного на рис. 11.2. Ограничимся при этом волноводны-
ми модами, которые, согласно рис. 11.3, имеют постоянную рас-
распространения /3, такую, что
копг
к0п2,
где и, < пг При условии д/ду = 0 уравнение A1.1.4) для модовой
функции принимает вид
A1.2.1)
~ + (konj - fi2)\& ^ 0, /= 1,2,3,
где значения / = 1, 2, 3 отвечают соответственно областям I, II,
III. В общем случае этот волновод содержит конечное число лока-
локализованных ТЕ- и ТМ-мод, первые из которых имеют компоненты
Е , Н и Н , а вторые — компоненты Н , Е и Е'
11.2.1. ТЕ-МОДЫ
Компоненту поля Е ТЕ-моды можно записать в виде
A1.2.2)
Направляемые волны и интегральная оптиьм
451
где модовая функция ^ (х) определяется следующим образом:
Се~"\ 0<х<оо,
С cos hx — — sin /
L h
C^
cos ht + % sin
A1.2.3)
Подставляя A1.2.3) в уравнение A1.2.1), получаем
А = {n\kl - р)Х/\ q={P~
ы
с
A1.2.4)
Решения
у и Jfz = (i/un)(d(f/dx) должны быть непрерывны
при х — 0 и х = —t. Выбор коэффициентов в A1.2.3) осуществля-
осуществляется таким образом, чтобы функция <§" была непрерывной на обеих
границах раздела, а ее производная д(?у/дх была непрерывной при
х = 0. Налагая требование непрерывности на д(?/дх при х — —t,
из A1.2.3) имеем
hsmht - qcosht = plcosht + -f sin An,
L n \
или
tght = (p + q)/h{\ - pq/h1).
A1.2.5)
Выражение A1.2.5) нередко называют модовым условием, подразу-
подразумевая при этом, что ему удовлетворяет постоянная распростране-
распространения /3 ТЕ-моды. При данных значениях показателей преломления
«,, «2 и п3 планарного волновода выражение A1.2.5), вообще гово-
говоря, дает конечное число решений для /3, при условии что толщина t
достаточно большая. Эти моды удовлетворяют условию ортого-
ортогональности в соответствии с общим рассмотрением, проведенным в
разд. 11.1.
Постоянная С в выражении A1.2.3) является произвольной; од-
однако для многих приложений, особенно для таких, в которых в рас-
распространении и обмене энергией участвует более чем одна мода,
удобно определить величину С таким образом, чтобы она пред-
представляла собой суммарную мощность моды. Этот вопрос мы рас-
рассмотрим подробнее в разд. 11.3. Выберем С таким образом, чтобы
поле <?у (х) в A1.2.3) соответствовало потоку мощности 1 Вт (на
единицу ширины в направлении у) в моде. При этом моде Еу =

452
Глава 11
= А<?(х) будет соответствовать поток мощности \А\2 Вт/м. Ус-
Условие нормировки при этом принимает вид
где индекс т относится к т-й локализованной ТЕ-моде [соответст-
[соответствующей m-му собственному значению выражения A1.2.5)] и Нх -
= -i(uix)-l5Ev/dz.
Подставляя выражение A1.2.3) в A1.2.6), после громоздких, но
прямых вычислений получаем
WLI
1/2
Условие ортогональности мод A1.1.17) принимает вид
A1.2.7)
A1.2.8)
11.2.2. ТМ-МОДЫ
Решение для локализованных ТМ-мод в принципе получается таким
же образом, как и для ТЕ-мод. Компоненты поля записываются в
виде
<1L2'9)
Модовая функция Jf(x) определяется следующим образом:
[А 1
- cos ht + sin ht ep(x+l), x < -1,
q J
, -/ < x < 0,
0 <x.
A1.2.10)
Направляемые волны и интегральная оптика
453
Используя условие непрерывности функций Н и Ez на границах
раздела, получаем характеристическое уравнение тем же способом,
что и уравнение A1.2.5):
tght = h(p + q)/(h2 - м), A1.2.11)
где
Постоянная нормировки С выбирается таким образом, чтобы по-
поток мощности поля, определяемого выражениями A1.2.9) и
A1.2.10), был равен 1 Вт на единицу ширины в направлении у:
2w J_,
e(x)
или, используя п2(х) = е(х)/е0,
п\х)
-dx
А» '
A1.2.12)
Выполняя интегрирование с учетом выражений A1.2.10), находим
С„ = 2
q2 + h< i t
A1.2.13)
|
| |
\ q1 + Л2 n\q р2 + Л2 п\р
ТМ-моды являются также ортогональными. В действительно-
действительности все ТЕ- и ТМ-моды являются взаимно ортогональными. Общее
условие ортонормированности записывается в виде A1.1.17).
Общие свойства решений для ТЕ- и ТМ-мод иллюстрируются
рис. 11.4. Мода оказывается локализованной, когда значение f/X
становится выше некоторого порогового. При пороговом значении
мы имеем р = 0 и /3 = п3к0, причем мода простирается до х —
= -оо. Согласно модовым условиям A1.2.5), A1.2.11) и A1.2.4),
пороговые значения f/X для ТЕ- и ТМ-мод даются соответственно

454
Глава
0,00 0,25 0,50 0,75 1,00 1,25 1,50 1,75 2,00
«3 = 3,20
РИС. 11.4. Дисперсионные кривые для локализованных мод пленки из GaAs на под-
подложке из AIGaAs; n = 1,0.
выражениями
тчт + arctg
п% - п;
п% - п\
\/2
A1.2.14)
тчт + arctg -—
и?
п\-п\
где w — целое число (т = 0, 1, 2, 3, ...,), которое соответствует
т-й локализованной ТЕ- (или ТМ-) моде. Заметим, что пороговое
значение для ТМ/);-моды всегда больше, чем для ТЕт-моды, по-
поскольку пх < п2. Если же значения t/Х ненамного больше порогово-
порогового, то р ? 0 и мода плохо локализована, при дальнейшем увеличе-
увеличении t/\ величина р также возрастает и мода больше локализуется в
слое 2. Это находит отражение в изменении эффективного показа-
показателя преломления моды j3\/2ir, который при пороговом значении
t/\ равен пъ, а при больших t/\ приближается к пг. В симметрич-
симметричном волноводе («, = пъ) низшие моды ТЕ0 и TMq не имеют порога
и локализуются при всех значениях t/Х. В работе [1] рассматрива-
рассматриваются вопросы селективного возбуждения мод волновода с по-
помощью призменных устройств ввода и определение их постоянных
распространения j3m.
Направляемые волны и интегральная оптика
455
Общее число локализованных мод, которые могут распростра-
распространяться в волноводе, зависит от величины t/\. Посмотрим теперь,
что произойдет с ТЕ-модой в данном волноводе (т. е. при фиксиро-
фиксированных значениях «,, п2, пъ и t), когда длина волны света постепен-
постепенно уменьшается, при условии что среда остается прозрачной и по-
показатели преломления и,, п2 и пъ не меняются значительно. По-
Поскольку к0 = 27г/Х, уменьшение длины волны приводит к увеличе-
увеличению к0. При больших длинах волн (низких частотах), таких, что
0 <
< arctg ¦
- п\
1/2
A1.2.15)
t/\ меньше пороговой величины и локализованные моды в волно-
волноводе отсутствуют. При уменьшении длины волны, так что
arctg -j—
\nl -
njkot
\п\- Щ) '
arctg ( —f \
A1.2.16)
существует одно решение, удовлетворяющее модовому условию
A1.2.5). Поперечный параметр Л моды ТЕ0 удовлетворяет условию
0 < h,t < чт,
A1.2.17)
поэтому мода ТЕ0 не имеет узлов пересечения внутри волноводного
слоя ( — t < х < 0). При дальнейшем уменьшении длины волны,
когда параметр 4п\ - n\kot попадает в область
7Г +
_ „2
A1.2.18)
модовое условие A1.2.5) имеет два решения. Одно из них соот-
соответствует величинам Ы < ж, т. е. моде ТЕ0 нулевого порядка. Для
следующей моды выполняется условие
h2t
2тг,
A1.2.19)
и, таким образом, она имеет один узел пересечения (т. е. точку, где
Е = 0) в волноводной области ( — t<x<0). Это так называемая
ТЕ,-мода. Обе эти моды соответствуют одной и той же частоте и
могут, следовательно, возбуждаться одновременно одним и тем же

456
Глава 11
падающим полем. Заметим, однако, что мода ТЕ0 имеет большую
величину р (т. е. р0 > р,) и, следовательно, более сильно локализо-
локализована в волноводном слое. Из выражений A1.2.4) вытекает, что
|80 > |8Г Поэтому фазовая скорость v0 = ш/0о моды ТЕ0 меньше,
чем моды ТЕГ Обобщая вышесказанное, мы заключаем, что т-я
мода (ТЕ или ТМ) удовлетворяет следующему условию:
тчт < hmt < (m
A1.2.20)
Отсюда следует, что m-я мода имеет т узлов пересечения в волно-
волноводном слое ( — t < х < 0). Общие свойства как ТМ-, так и ТЕ-мод
совпадают, за исключением того, что величина р для ТМ-мод не-
несколько меньше, что указывает на меньшую степень ее локализа-
локализации. Таким образом, по сравнению с ТЕ-модой такого же порядка
большая часть общей мощности ТМ-моды распространяется вне
направляющей среды. Этот вопрос рассматривается в задаче 11.5.
11.2.3. ГЕОМЕТРООПТИЧЕСКОЕ ПРИБЛИЖЕНИЕ
Моды ТЕ и ТМ волноводного слоя, рассмотренные выше, могут
быть получены также в рамках геометрической оптики. Это воз-
возможно вследствие того, что такой волновод состоит из участков
однородной среды с планарной геометрией. Волновое распростра-
распространение в каждой однородной области можно представить в виде су-
суперпозиции двух плоских волн. Как было показано в разд. 11.1, ло-
локализованные моды существуют только в области пък0 < /3 < п2к0,
где плоские волны испытывают полное внутреннее отражение как
на нижней (II—III), так и на верхней (II—I) границе.
На первый взгляд кажется, что условие полного отражения на
обеих границах является достаточным для существования волно-
водных мод. Однако полное внутреннее отражение — это лишь не-
необходимое условие. Иными словами, не все лучи, которые удовлет-
удовлетворяют условию полного отражения, образуют моду. Мода по
определению должна иметь одну постоянную распространения и
определенную амплитуду поля в каждой точке пространства и вре-
времени. Рассмотрим представление моды <?(x)exp[i(wt — j3z)] с по-
помощью зигзагообразной волны, определяемой выражением
Е(х, z, t) = Еоехр[/(ы/ - fiz - hx)],
A1.2.21)
где Ео — постоянная величина, а И — поперечное волновое число.
Пусть плоская волна за время At проходит расстояние Az по одно-
одному зигзагу ABCD (рис. 11.2). Если следовать по траектории луча
Направляемые волны и интегральная оптика
457
ABCD и учитывать при этом изменение фазы, обусловленное рас-
распространением и полными отражениями в точках В и С, то общее
изменение фазы запишется в виде
и At - /3Az - 2ht + 2ф21 + 2ф23,
где 2ф21 и 2ф23 — изменения фазы при полном отражении в точках
В и С соответственно. Мода S(x)exp[i(ut — /Зг)], распространяю-
распространяющаяся от точки А к точке D, приобретает изменение фазы uAt —
- PAz- Следовательно, испытывающий полное отражение зигзаго-
зигзагообразный луч отвечает моде лишь при условии, что дополнитель-
дополнительное изменение фазы является кратным 27г, т. е.
-2ht + 2ф21 + 2ф23 = ~2тчт,
A1.2.22)
где m — целое число. Знак минус перед 2тж ставится для того,
чтобы число т соответствовало модам ТЕт и ТМт волновода. Для
удобства изменения фазы 2ф2х и 2ф23 мод ТЕ или ТМ можно выра-
выразить через величины h, p и q следующим образом:
2Ф2Х =
2arctg-
h
2 arc tg
n\q
n\h
(ТЕ),
(ТМ),
A1.2.23)
(ТЕ),
(ТМ).
A1.2.24)
Эти фазовые изменения заключены между 0 и 7г. Следовательно,
основная мода соответствует условию, когда 2Ы — 2ф21 + 2ф2ъ,
т. е. т — 0. Чем выше номер моды, тем больше величина ht. Поэ-
Поэтому целое число т в уравнении A1.2.22) принимает только неот-
неотрицательные значения: т = 0, 1, 2, 3, ... . Условие A1.2.22) эквива-
эквивалентно модовым условиям A1.2.5) и A1.2.11), полученным в задаче
на собственные значения.
Рассмотрим конкретный пример. Пусть имеется волновод на ос-
основе пленки GaAs толщиной 1,0 мкм, выращенной на подложке из
AlGaAs. Показатели преломления при X = 1 мкм имеют следую-
следующие значения: я, = 1, 0, п2 - 3,50 и пъ = 3,20. Согласно рис. 11.4,

458
Глава 11
Направляемые волны и интегральная оптика
459
РИС. 11,5. Три низшие ТЕ-моды планарного волновода и соответствующие им зиг-
зигзагообразные лучи. ф} > ф2 > 0, (ф = я72 - в2).
в этой пленке существуют три локализованные ТЕ-моды. Эффек-
Эффективные показатели преломления 0/ко равны 3,473, 3,394 и 3,264 для
мод с т = О, 1 и 2 соответственно. Эти эффективные показатели
преломления соответствуют углам падения луча в2 (определяемым
из условия /3 = n2k0sin62), равным 82,9°; 75,9° и 68,8° соответст-
соответственно. Заметим, что все эти углы больше, чем критический угол
вс — 66,1°. Основная мода (т = 0) всегда имеет больший эффек-
эффективный показатель преломления и угол падения: ее эффективный
показатель преломления приближается к п2. У моды высшего по-
порядка эффективный показатель преломления наименьший и прибли-
приближается к и3; они имеют наименьший угол падения, почти равный
критическому углу. На рис. 11.5 показаны зигзагообразные лучи,
соответствующие волноводным модам, рассмотренным выше.
Лучевая оптика представляет собой удобный метод получения
модового условия для волноводного слоя. Однако в более сложных
волноводных структурах, состоящих из многих однородных слоев
или из неоднородных слоев, этот метод оказывается трудным для
использования. Кроме того, геометрооптический подход позволяет
получить лишь модовое условие и не дает распределения поля или
соотношения ортогональности для мод.
11.3. ВОЗМУЩЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ
ПРОНИЦАЕМОСТИ И ВЗАИМОДЕЙСТВИЕ МОД
В предыдущем разделе мы рассматривали некоторые общие
свойства мод диэлектрического волновода и, в частности, получили
решения для локализованных мод, распространяющихся в волно-
водном слое. Волноводные моды могут быть возбуждены и рас-
распространяться вдоль оси (z) диэлектрического волновода независи-
независимо друг от друга при условии, что диэлектрическая проницаемость
?(х> У) - е0п2(х, у) сохраняется постоянной вдоль оси z- В случае
когда имеется возмущение диэлектрической проницаемости Ае(х,у, z),
обусловленное несовершенствами волновода, искривлением оси,
наличием гофра на поверхности и т. п., собственные моды оказы-
оказываются связанными между собой. Иными словами, если на входе
волновода возбуждается чистая мода, то некоторая часть ее мощ-
мощности может перейти в другие моды. Существует большое число
экспериментов и устройств, в которых намеренно создают взаимо-
взаимодействие между такими модами [2—5, 7]. Два типичных примера
относятся к преобразованию мод ТЕ — ТМ электрооптическими
методами [4, 5], с помощью акустооптического эффекта [2] или вза-
взаимодействия прямой и обратной мод из-за наличия гофра на одной
из границ волновода. В данном разделе для описания такого взаи-
взаимодействия мод мы используем теорию связанных мод, развитую в
гл. 6. Некоторые из важных результатов можно кратко описать
следующим образом. Возмущение диэлектрической постоянной
представляется небольшим возмущающим членом Ае(х, у, z)- Тогда
тензор диэлектрической проницаемости как функция пространствен-
пространственных координат запишется в виде'
е(х, у, z) = ео(х, у) + Де(х, у, z),
A1.3.1)
где ео(х, у) — невозмущенная часть диэлектрической проницаемо-
проницаемости, определяющая структуру волновода. Волновое распростране-
распространение в таком возмущенном волноводе можно всегда представить в
виде линейной комбинации невозмущенных собственных мод:
Е
x, y)exp[i(ut -
A1.3.2)
где Am(z) — амплитуды мод, зависящие от продольной координа-
координаты z. Эти собственные моды <5т (х, y)exp[i(ut — I3mz)] удовлетворя-
удовлетворяют следующему волновому уравнению:
A1.3.3)
?^+ uipe0(x, у) - /ф„,(х, у) = 0,

460
Глава 11
Направляемые волны и интегральная оптика
461
где мы пренебрегли членом V(VE), что оправданно, если измене-
изменение величины ео(х, у) на длине волны мало. В случае пленарных
волноводов ео(х, у) является скачкообразной функцией на диэлект-
диэлектрических границах и для ТЕ-мод VE = 0, поскольку E-Ve = 0.
Следовательно, в этом случае уравнение A1.3.3) справедливо. В
случае же ТМ-мод планарного волновода уравнение A1.3.3) на гра-
границах не справедливо.
Эти моды являются взаимно ортогональными и удовлетворяют
следующему условию ортогональности:
Ж
°кт-
A1.3.4)
Условие A1.3.4) выполняется всегда, когда справедливо уравнение
A1.3.3).
Подставляя выражение A1.3.2) в волновое уравнение F.4.7) и
используя A1.3.4), получаем следующие уравнения:
A1.3.5)
A1.3.6)
где <?1Де1ю> определяется в виде
ю> = f&*k • Ae$mdxdy.
Уравнения A1.3.5) описывают эволюцию модовых амплитуд Ак(z)
в процессе распространения волн вдоль волновода и представляют
собой систему дифференциальных уравнений, решения которых
можно получить для целого ряда модовых взаимодействий [2]. В
следующем разделе мы рассмотрим некоторые важные примеры.
Частным случаем, заслуживающим внимания, является возмущение
диэлектрической проницаемости Де = Ае(х, у), зависящее только
от координат х и у (т. е. случай de/dz — 0). Этот вопрос мы обсу-
обсудим ниже.
11.3.1. ОДНОРОДНОЕ ВОЗМУЩЕНИЕ
ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ
Метод связанных мод, рассмотренный выше, позволяет исследо-
исследовать взаимодействие невозмущенных мод, обусловленное возмуще-
возмущением диэлектрической проницаемости, в частности когда возмуще-
возмущение не зависит от г. Во многих практических ситуациях задача со-
состоит в том, чтобы найти моды всей волноводной структуры, име-
имеющей возмущение диэлектрической проницаемости Ае(х, у). В слу-
случае когда волновое уравнение решить трудно (или его нельзя ре-
решить непосредственно), для решения таких задач применяется тео-
теория возмущений. Возмущение Де (х, у) нередко выбирают таким об-
образом, чтобы невозмущенная волноводная структура имела извест-
известное решение или решение для нее можно было легко найти.
Пусть невозмущенные моды имеют вид
m = 0,1,2,...,
поперечные модовые функции которых <?т удовлетворяют невозму-
невозмущенному волновому уравнению
[V,2 + ыгче{х, у)]&т(х, у) = ?&т(х, у).
A1.3.7)
Эти моды образуют полную ортогональную систему функций, как
было показано в разд. 11.1, и удовлетворяют условию ортогональ-
ортогональности
„/¦ A1-3-8)
i- m
Рассмотрим теперь влияние возмущения диэлектрической проницае-
проницаемости Ае(х, у), которое мало по сравнению с е(х, у). Предполо-
Предположим, что столь малое возмущение будет вызывать лишь неболь-
небольшие изменения модовых функций и постоянных распространения.
Пусть модовые функции изменяются на величину &<?т, а постоян-
постоянные распространения — на Ь02т. Правильное волновое уравнение те-
теперь принимает вид
[V,2 + «V + <о2ц Де](бт + 8&т) =
8бт). A1.3.9)
Если пренебречь здесь членами второго порядка малости Aeb<fm и
5/Зт5^ и воспользоваться соотношением A1.3.7), уравнение A1.3.9)
можно записать в более простом виде:
[V,2 + wV] 8Sm + «V
= /8m«Sm + 8р*&т. A1.3.10)
Чтобы решить это уравнение, разложим 5 <fm в ряд по невозмущен-
ньщ модовым функциям:
,(х,у)=
, у),
A1.3.11)

462
Глава 11
Направляемые волны и интегральная
оптика
463
где ат1 — постоянные коэффициенты. Подставляя в уравнение
A1.3.10) выражение A1.3.11) для 5(?т и используя A1.3.7), получаем
A1.3.12)
Умножим теперь это уравнение на <§"^ и проинтегрируем по всей
плоскости ху. При этом благодаря условию ортогональности
A1.3.8) выражение слева окажется равным нулю. Таким образом,
мы имеем следующее уравнение:
A1.3.13)
Поскольку 5/3^ — постоянная величина, из A1.3.13) следует
A1.3.14)
К dx dy
Это выражение дает поправку первого порядка к постоянной рас-
распространения E2т. Используя условие A1.3.8) и равенство 5/3^ —
= 2/3m5/3m, выражение A1.3.14) можно также записать в виде
A1.3.15)
Для получения поправки 5 ?т к модовой функции умножим левую и
правую части уравнения A1.3.12) на <f*(l Ф т) и проинтегрируем
по переменным х и у. Это дает
A1.3.16)
здесь мы использовали условие ортогональности A1.3.8) для не-
невозмущенных мод. Таким образом, коэффициенты разложения
A1.3.11) для 8<?т в ряд по функциям &! можно записать в виде
«?
т.
A1.3.17)
Величину атт нельзя получить из этой формулы. Она может быть
выбрана из условия нормировки возмущенной модовой функции со-
согласно A1.3.8) и имеет вид (см. задачу 11.7)
а =_1
4
Используя выражение A1.3.15) для Ь$т, коэффициенты ат
записать следующим образом:
dX dy.
A1.3.18)
можно
A1.3.19)
Удобно использовать выражение для «коэффициентов связи» [ана-
[аналогичное выражению F.4.17)]:
A1.3.20)
Тогда выражение для поправки первого порядка к модовой функ-
функции с учетом A1.3.17) и A1.3.11) принимает вид
— V
L 2 TJK/mfe/
1*т Рт ~ Pi
A1.3.21)
Таким образом, поправку 5/?m к постоянной распространения
A1.3.15) можно записать следующим образом:
S&, = /cmm. (П.3.22)
Результаты A1.3.21) и A1.3.15) будут использованы при вычисле-
вычислении коэффициентов затухания мод в волноводах с металлическим
покрытием (см. разд. 11.10).
11.4. ПЕРИОДИЧЕСКИЙ ВОЛНОВОД;
БРЭГГОВСКОЕ ОТРАЖЕНИЕ
Рассмотрим периодический диэлектрический волновод, в котором
периодичность создается за счет гофрирования одной из поверхно-
поверхностей раздела, как показано на рис. 11.6. Такие периодические волно-
волноводы используются в качестве оптических фильтров [8], а также в
лазерах с распределенной обратной связью [9—11]. Ниже мы обсу-
обсудим оба этих применения.

464
Глава 11
Направляемые волны и интегральная оптика
465
Гофрированная поверхность описывается функцией Де (х, у, z) =
= е0Дл2(х, у, z). Поскольку Дл2(х, у, z) является скалярной функци-
функцией, из A1.3.6) следует, что благодаря гофрированности поверхно-
поверхности моды ТЕ или ТМ взаимодействуют лишь между собой, а не
ТЕ с ТМ. Согласно гл. 6, правую часть уравнения A1.3.5) можно
рассматривать как источник, возбуждающий к-ю моду. Для того
чтобы амплитуда моды Ак непрерывно увеличивалась, правая
часть должна содержать член, который не изменяется существенно
на расстоянии z ^> Л, так чтобы интегрирование в среднем не при-
приводило к нулевому значению. Для этого необходимо, чтобы выпол-
выполнялось следующее условие:
(П.4.1)
где @т — постоянная распространения т-тл моды, а / — целое чис-
число. Если условие A1.4.1) выполнено, то к-я и т-я моды оказыва-
оказываются резонансно связанными между собой через 1-ю фурье-компо-
ненту периодического возмущения Де(х, у, z).
Для конкретности предположим, что период Л возмущения
Дл2(х, у, z) такой, что /(тг/Л) » /^ для некоторого целого числа /.
Условие фазового синхронизма A1.4.1) может быть выполнено по-
посредством связи моды fls с отраженной модой, имеющей постоян-
постоянную распространения -@s, так как /3$ - (-/35) = 2/35 * /Bтг/Л).
Для вычисления модовых амплитуд с помощью уравнений связан-
связанных мод F.4.33) возмущение Де(х, z) необходимо разложить в ряд
1
Волноводь
| 1 |
ый слой

я2
= 0
= — а
Подложка
РИС. 11.6. Гофрированный периодический волновод.
Фурье. Рассмотрим конкретный пример, когда гофрированная по-
поверхность имеет вид прямоугольных импульсов, как показано на
рис. 11.6. В этом случае возмущение диэлектрической постоянной
Де(х, z) можно записать в виде
где
0,
в остальных случаях,
A1.4.2)
A1.4.3)
а/(г) — прямоугольная функция, определяемая выражением F.5.8).
Используя для функции/(г) разложение Фурье F.5.10), выражение
A1.4.2) для возмущения диэлектрической проницаемости Де(х, z)
можно записать следующим образом:
g
exp[-//(f )zj} . (П.4.4)
Де(х, z) = ?e,(x)exp -/7(-^)z
A1.4.5)
Выражение A1.4.5) представляет собой более общую форму разло-
разложения. В случае гофрированной поверхности, имеющий вид прямо-
прямоугольных импульсов, 1-я фурье-компонента еДх) дается выражением
е,(х)
' /= +1,+3,±5,...,
/тг
^Де(х), 1 = 0,
0, /= ±2, ±4
A1.4.6)
Связь между прямой (/35) и отраженной ( — 0S) модами описывается
уравнениями связанных мод F.4.33), которые в данном случае при-
принимают вид
A1.4.7)
EL = iK*A
dz s
30-631

466
Глава 11
Направляемые волны и интегральная оптика
467
где Bs — амплитуда отраженной моды ( —/35), а Д/3 и к даются соот-
соответственно выражениями
A1.4.8)
A1.4.9)
Заметим, что полная мощность, переносимая обеими модами, со-
сохраняется, поскольку
i[\Af-\Bs\2)=0. (ПАЮ)
Используя выражения A1.4,3) и A1.4.6), постоянную связи к для не-
нечетных / можно записать в виде
к =
/= 1,3,5,....
A1.4.11)
На практике период Л выбирается таким образом, чтобы А/3 ~ 0
при некотором значении /. Заметим, что при А/3 ~ 0 справедливо
равенство
Л = 1Щ>/2,
где А^> = 27г//35 — длина волны 5-й моды в волноводе.
Теперь можно использовать явные выражения A1.2.3) для поля
<^ (х) в случае ТЕ-мод. Постоянная связи к принимает вид
A1.4.12)
~ °\1 2) I_С} [cos h5x - f- sin hsx j dx.
Хотя с учетом выражений A1.2.3) и A1.2.5) интеграл здесь может
быть вычислен точно, особенно просто его вычислить в области,
находящейся намного выше частоты отсечки [1(п2 - «,)/s\ > 1].
Тогда из выражений A1.2.4) и A1.2.5) получаем
А*«2*0.
, its
{ > s — 1.2, ... = поперечное модовое
число,
A1.4.13)
Эти результаты могут быть проверены с помощью соотноше-
соотношений A1.2.4) и A1.2.5). Кроме того, поскольку qs > hs, из A1.2.7)
мы имеем
A1.4.14)
В случае hsa < 1 интеграл в A1.4.11) равен
0 IV / \12 j 47rV«/i/a\3/. , 3 3 \
I S.(x)J dx = -т—г-Ч - 1 + + ——-
L jV n 3n2k0 \t { qsa qy
а постоянная связи принимает вид
.2тгУ п\- п\(а>
3/Л
- х
(\/аJ
A1.4.15)
Таким образом, задача сводится к решению системы двух диф-
дифференциальных уравнений A1.4.7), в которых постоянная связи
определяется выражением A1.4.15). Следует заметить, что выраже-
выражение A1.4.15) справедливо лишь для ТЕ-мод.
Общее решение уравнений связанных мод, имеющих противопо-
противоположные направления, дается выражением F.4.35). Рассмотрим вол-
волновод с гофрированным участком поверхности длиной L, как пока-
показано на рис. 11.6. Пусть слева на гофрированный участок падает
волна с амплитудой А @). В этом случае граничные условия запи-
записываются в виде A (z) = /1@) при z ~ 0 и B(z) = 0 при z — L.
Подставляя Ax(z) = А@) и A2(L) = 0 в общее решение F.4.35), по-
получаем следующие выражения для модовых амплитуд:
A (z) = A
- z) + /(l/2)A/3shj(Z, - г)
5ch^L + /(l/2)A/3sh5L

468
Глава II
A1.4.16)
B(Z) = A(V)e-*f*'2
— iK*shs(L — z) Л
TT7l/2)A3 h L J '
|_5ch5ZTT7(l/2)A/3 sh sL J
где 5 и Д/3 даются выражениями
-А-(-А)-'Х-
A1.4.17)
A1.4.18)
За исключением постоянной связи, эти выражения совпадают с со-
соответствующими выражениями для случая отражения от периоди-
периодически слоистой среды. Доля мощности, связанная с модой (- /35),
распространяющейся назад, называется коэффициентом отражения
моды и определяется следующим образом:
*=»
Л@)
Используя выражения A1.4.16), получаем
K*nsh2sL
^ch2$L +~(Ap/2Jsh2$L '
Это выражение также совпадает с коэффициентом отражения для
периодически слоистой среды F.6.10). В соответствии с A1.4.20)
при выполнении условия фазового синхронизма Д/3 = 0 коэффици-
коэффициент отражения R достигает своего максимального значения:
A1.4.21)
R -
Амплитуды мод при этом (Д/3 = 0) задаются, согласно выражени-
выражениям A1.4.16), следующим образом:
A(z) = А@)
- z)
chl/cLl
A1.4.22)
- z)
ch I k
На рис. 11.7 представлены зависимости мощностей 1Л(гI2 и
\B(z)\2 от z в этом случае. Следует заметить, что в возмущенной
области мощность падающей моды уменьшается по экспоненциаль-
Направляемые волны и интегральная оптика
I Возмущенная часть
( волновода
469
}—- Волноводный t
слой
1-1IWI1
Возмущение
~ вызывает—
модовую
связь здесь
Возмущенная
область
РИС. 11.7. Вверху: гофрированная часть диэлектрического волновода. Внизу: интен-
интенсивности падающей и отраженной волн внутри гофрированной области.
ному закону. Это полностью совпадает с тем, что происходит при
отражении света от периодически слоистой среды (см. разд. 6.6 и
рис. 6.14). Экспоненциальное затухание падающей волны, показан-
показанное на рис. 11.7, обусловлено ее взаимодействием с волной, распро-
распространяющейся назад. Такое уменьшение амплитуды моды можно
также объяснить, используя комплексные блоховские волновые чис-
числа, когда падающая волна удовлетворяет условию Брэгга (Д/3 = 0).
Из выражений A1.3.2), A1.4.16) и A1.4.18) следует, что в периоди-
периодическом волноводе зависящие от z части волновых решений являют-
являются экспонентами с постоянными распространения
Ij- ± 1]/к*к -
A1.4.23)
Эти постоянные распространения совпадают с блоховскими волно-
волновыми числами, если поле A1.3.2) записать в виде блоховской пол-
полны.
Пусть ш0 — частота, при которой выполнено условие фазового
синхронизма Д/3 = 0. Тогда Д/3 можно записать в виде
A1.4.24)

Глава 11
470
Направляемые волны и интегральная оптика
471
где „ _ эффективный показатель преломления направляемой вол-
волны (т. е. ?;= «со/с). Таким образом, блоховское волновое число
/3' можно записать следующим образом:
ij± «у к*к - G) (w ~ w°J ¦
A1.4.25)
Гофрированная область.
Длина волны, А
РИС 11 8 К иллюстрации действия фильтра на основе гофрированного тонкопле-
„очного волновода. Сплошная кривая - отражательная способность фильтра в за-
зависимости от отклонения длины волны от брэгговского условия; штриховая кри-
кривая - вычисленная по формуле A1.4.20) отражательная способность фильтра
15@O.4 @I2. (Из работы [8].)
Заметим, что в частотной области, для которой — 21 к I < ДЗ <
< 2Ы, величина /3' имеет мнимую часть. Эта область называется
«запрещенной зоной» периодического волновода, изображенного на
рис. 11.6; формально она совпадает с аналогичной зоной периоди-
периодической слоистой среды (см. разд. 6.6). Падающие волны, частоты
которых соответствуют этой области, являются затухающими на
гофрированном участке и испытывают сильное отражение при ус-
условии, что длина взаимодействия L достаточно большая. Таким
образом, гофрированная часть волновода действует как заграждаю-
заграждающий фильтр, ширина полосы которого в соответствии с A1.4.23)
определяется выражением Д/3 = 41 к I, или [см. A1.4.24)]
Ды = —Ы.
п '
A1.4.26)
Действие фильтра, основанного на брэгговском отражении волно-
водной моды в гофрированном волноводе, демонстрировалось экс-
экспериментально. Результаты измерений характеристик этого фильт-
фильтра показаны на рис. 1 L8.
11.5. ВСТРЕЧНАЯ СВЯЗЬ В ПЕРИОДИЧЕСКОМ ВОЛНОВОДЕ
В предыдущем разделе мы предполагали, что период Л выбирается
таким образом, что @s ~ 1ж/А для некоторой моды f$s и целого чис-
числа /. При этом условии мода 0S оказывается сильно связанной с мо-
модой, распространяющейся в обратном направлении. Обычно период
представляет собой величину порядка 1\/2, где X = 27Г/Д, — длина
волны 5-й моды в волноводе. Для эффективной связи целое число /
выбирают по возможности минимальным, поскольку, согласно вы-
выражению A1.4.11), постоянная связи к пропорциональна 1/7. Одна-
Однако получение минимального периода Л ограничено возможностями
технологии изготовления. Например, период, необходимый для
брэгговского отражения излучения с длиной волны 1 мкм в волно-
волноводе из GaAs (п = 3,3) (см. рис. 11.4), равен / х 1500 А. Из техно-
технологических соображений можно выбрать 1=3.
Если период гофра на поверхности многомодового волновода
достаточно большой, так что для некоторой пары мод /3, и /32 и це-
целого числа / мы имеем /3j — 02 = 1Bж/А), то эти моды оказывают-
оказываются сильно связанными при постоянной связи, не равной нулю.
Пусть Л, (г) и A2(z) — амплитуды связанных мод. В соответствии с
A1.3.5) или F.4.27) для них можно написать следующую систему

472
уравнений:
±Ах=-щ
где
«12 " Т /"
4 '-оо
, ±
Глава 11
e-'W\ A1.5.1)
i Л, (П-5.2)
A1.5.3)
Здесь е, (х) — 1-я фурье-компонента возмущения диэлектрической
проницаемости A1.4.5), определяемого выражениями A1.4.3) и
A1.4.6) в случае, когда гофрированная поверхность имеет вид пря-
прямоугольных импульсов. Заметим, что полная мощность, переноси-
переносимая обеими модами, сохраняется, поскольку
— {K|2 + l^2|2} = °- (П-5-4)
Пусть АЛО) и А2@) — амплитуды мод в плоскости z = 0. Тогда
решение системы уравнений A1.5.1) можно записать в виде
Ax{z)
A1.5.5)
A2(z) =
i
*i-i^f sinsz,4,@) +
+ \cossz + i-^- sin sz \A2@I,
L ?s J /
где
A1.5.6)
Из A1.5.5) следует, что доля мощности, которая из моды 2 перехо-
переходит в моду 1 (или наоборот) на расстоянии z, дается выражением
21
+ ид/о
A1.5.7)
Направляемые волны и интегральная оптика
473
т. е. представляет собой периодическую функцию координаты z.
Мы видим, что при достаточно большой длине взаимодействия
происходит обмен энергией между модами в прямом и обратном
направлениях. Максимальная доля мощности, которая может пе-
перейти из одной моды в другую, равна 1к,212/[1к]212 + (Д/3/2J] и в
случае 1Д/31 > \кХ2\ эта доля мала. Полный обмен энергией проис-
происходит лишь в случае А/3 — 0, т. е. когда имеет место синхрониза-
синхронизация фаз. Если это условие выполняется, мы можем написать следу-
следующие выражения:
Ax(z) = Ax@)coskz - /—/*2@)sin kz,
A2(z) = A2@)coskz - «—/4,@)sin jcz,
A1.5.8)
где
к = \кх2\.
A1.5.9)
Обмен энергиями при встречной модовой связи происходит так
же, как в случае связанных мод в фильтре Шольца. Поэтому
встречную модовую связь можно описать теми же кривыми для
\Ax(z)\2 и \A2(z)\2, которые были представлены на рис. 6.11 для
фильтров Шольца.
Встречная модовая связь зависит также от частоты излучения.
Пусть np п2— эффективные показатели преломления (т.е. 0а -
= па(ш/с), а = 1,2], отвечающие связанным модам, а соо — часто-
частота, при которой ДЗ = 0. Тогда выражение для Д/3 можно перепи-
переписать в виде
(л, - л2)(ы-ы0)
A1.5.10)
Сильная связь имеет место лишь в частотной области, в которой
1Д/31 < 2к. В переводе на частотную ширину полосы получаем вы-
выражение
Ды =
4кс
I". -«21'
A1.5.11)
где к — постоянная связи, с — скорость света, а л, — л2 — раз-
разность эффективных показателей преломления. Сравнивая A1.5.11) с
выражением A1.4.26) для брэгговского отражателя, находим, что

474
Глава 11
ширина полосы встречной связи много больше, так как \пх — п2\
обычно меньше по сравнению с п.
11.6. ЛАЗЕРЫ С РАСПРЕДЕЛЕННОЙ ОБРАТНОЙ СВЯЗЬЮ
В предыдущих разделах и в гл. 6 мы предполагали, что возмуще-
возмущение Де(х, у, z) диэлектрической проницаемости является веществен-
вещественной величиной, которая описывает пассивные неоднородности. На-
Наличие в среде небольшого усиления можно также рассматривать
как возмущение, и в этом случае Де(х, у, z) следует считать ком-
комплексной величиной. Рассмотрим распространение электромагнит-
электромагнитных волн в периодической среде с вещественной диэлектрической
проницаемостью е(х, у, z) и комплексным периодическим возмуще-
возмущением Де(х, у, z)- Ниже мы покажем, что генерация излучения мо-
может происходить и без наличия торцевых зеркал. При этом обрат-
обратная связь осуществляется за счет непрерывного когерентного рассе-
рассеяния от периодического возмущения. Общее рассмотрение, которое
мы проведем ниже, применимо как к объемной периодической сре-
среде (например, слоистой среде), так и к периодическому волноводу.
Усиление в объемной среде описывается комплексной диэлект-
диэлектрической проницаемостью ег + /е(. с положительной мнимой частью
е( > 0. При этом постоянная распространения к' плоской волны
запишется в виде
к'2 =
A1.6.1)
где к — постоянная распространения волны в отсутствие усиления,
определяемая выражением
= ,.,2,
к2 = и цег .
A1.6.2)
В случае е/ег < 1 выражение A1.6.1) можно записать следующим
образом:
A1.6.3)
Если подставить теперь это выражение для к' в A.4.10), то пло-
плоская волна, распространяющаяся в направлении оси z, принимает
вид
'2e,)ze,(o,,-*z) A1.6.4)
Направляемые волны и интегральная оптика
475
Отсюда следует, что интенсивность волны возрастает в соответст-
соответствии с выражением
где коэффициент усиления
ке,
8=
A1.6.5)
A1.6.6)
При наличии усиления в периодической среде тензор диэлектри-
диэлектрической проницаемости A1.3.1) можно переписать в виде
е(х, у, z) = ео(х, у, z) + Де(х, у, z) + iy(x, у, z),
A1.6.7)
где е(х, у, z) — невозмущенная часть тензора диэлектрической про-
проницаемости, Де(х, у, z) — возмущение диэлектрической проницае-
проницаемости (вещественная величина) и у(х, у, z) — часть возмущения,
обусловленная усилением. Заменяя в A1.3.5) величину Де на Де +
+ iy, получаем следующие уравнения связанных мод:
d_
dz'
A1.6.8)
где величина (к\Ае\т) определяется выражением A1.3.6), а
< к 171 /) — выражением
A1.6.9)
Для того чтобы показать, как влияет усиление на характеристики
связи встречных волн, рассмотрим усиление, которое является од-
однородным в направлении z, т. е. >(х, у, z) - т(х, у). Используя вы-
выражения A1.4.5) или F.4.15), уравнения связанных мод A1.6.8)
можно записать в виде
(П.6.10)
где gk — коэффициент усиления k-Vi моды, определяемый выраже-

476
Глава 11
нием
, у)
Мы пренебрегли членами, отвечающими за усиление, которые име-
имеют зависимость вида el<J3k~^l)z, поскольку они являются быстроме-
быстроменяющимися функциями координаты z и не дают вклада в модовую
амплитуду Ak(z).
Рассмотрим теперь частный случай, когда 0S = 1(ж/А), т. е. 5-я
мода сильно связана с распространяющейся назад модой ( — /35).
Оставляя в A1.6.10) лишь медленноменяющиеся члены, уравнения
связанных мод сводятся к следующей системе двух уравнений:
dz
dB
dz
A1.6.12)
где А и В — амплитуды мод As и A_s соответственно, величина к
определяется выражением A1.4.9), Д/3 — выражением A1.4.8), a g
равна gs [см. A1.6.11)]. В случае когда постоянная связи к обраща-
обращается в нуль, амплитуды мод принимают вид
B(z) =
A1.6.13)
что находится в полном согласии с выражением A1.6.5). При ко-
конечном значении к уравнения A1.6.12) нетрудно решить, если вве-
ввести функции A' (z) и В' (z), определяемые следующим образом:
B(z) = B'(z)e~'gz.
При этом система уравнений A1.6.12) принимает вид
Ц- =
dz
~ =
dz
A1.6.14)
A1.6.15)
Направляемые волны и интегральная оптика
477
Таким образом, мы получили уравнения, вид которых совпадает с
уравнениями A1.4.7), если сделать замену
Д0 -» ДK + ig.
A1.6.16)
Использование этой замены и выражений A1.4.16) позволяет нам
непосредственно написать решения для амплитуд падающей A (z) —
— A' (z)^2 и отраженной В(z) = В' (z)egz/1 мод в области длиной
L в случае, когда на гофрированный участок при z — 0 падает одна
волна с амплитудой А @):
A(z) =
s ch sL + ij(Afi + ig) sh sL
-/K*sh s(L - z)
B(z) = ..
s ch sL + ij(Ap + ig) sh sL
где s и Д/3 даются выражениями
.2тг
A1.6.17)
A1.6.18)
A1.6.19)
То, что 5 является теперь комплексной величиной, свидетельствует
о качественном различии между решениями в случае пассивного пе-
периодического волновода [см. выражения A1.4.16)] и в случае перио-
периодического волновода с усилением [см. выражения A1.6.17)]. Для ил-
иллюстрации этого различия рассмотрим случай, когда выполнено ус-
условие
sL
ig)
A1.6.20)
Из выражений A1.6.17) следует, что как коэффициент отражения
В@)/А @), так и коэффициент прохождения A (L)/A @) при этом об-
обращаются в бесконечность. Устройство действует как генератор,
поскольку оно обеспечивает ненулевые значения полей В@) и A (L)
на выходе при нулевом поле на входе И@) = 0]. Следовательно,
условие A1.6.20) представляет собой условие генерации для лазера
с распределенной обратной связью [9]. В случае g = 0 из выраже-
выражений A1.4.16) или A1.4.20) следует, что \A(L)/A@)\ < 1 и
1В@)/Л@I < 1, т. е. мы имеем пассивное устройство без общего
усиления.

478
Глава 11
Направляемые волны и интегральная оптика
479
1В@)Л4@)|
Я@|
ЛЮ)
Усиление Волноводныи
СЛОЙ
"з Подложка
» - о
РИС. 11.9. Амплитуды падающей и отраженной волн в усиливающем периодиче-
периодическом волноводе.
При соответствующих условиях и достаточно высоком коэффи-
коэффициенте усиления g, когда условие A1.6.20) приблизительно выпол-
выполнено, волновод действует как усилитель с большим усилением. При
эхом коэффициенты отражения и прохождения с усилением имеют
вид соответственно
в(о)
А@) s ch sL
A(L)
-/к* sh sL
+ ig) shsL
se
s chsL
ig) shsL
A1.6.21)
A1.6.22)
На рис. 11.9 приведены зависимости амплитуд падающей и отра-
отраженной мод для случая с большим усилением от координаты z. От-
Отметим качественное различие между этим случаем с усилением и
случаем пассивного волновода, представленным на рис. 11.7.
На рис. 11.10 представлены зависимости величины \В@)/А @I2,
а на рис. 11.11 — величины \A(L)/A@)\2 от Д/3 и g. На каждом из
рисунков мы видим четыре сингулярности, соответствующие беско-
бесконечному усилению, в которых выполняется условие генерации
A1.6.20). Этими сингулярностями являются четыре продольные
KL = 0,4
8 9 10 11 12 13 14
РИС. 11.10. Контуры коэффициентов отражения в плоскости A0L — gL. Величина
Д/3 определяется выражением A1.4.18) и пропорциональна отклонению частоты ы от
брэгговской частоты шп = жс/Ап.
\A(L)/A{0)\'
600
1000
9 10 11 12 13 14
РИС. 11.11. Контуры коэффициентов прохождения в плоскости A/3L — gL.
моды лазера. Моды высшего порядка, сушествующие при больших
значениях A/3L, на рисунках,не показаны.

480
Глава 11
11.6.1. УСЛОВИЕ ГЕНЕРАЦИИ
Условие генерации A1.6.20) можно записать в виде
5 - (l/2)fe - /Д8)Й1$? = 0. A1.6.23)
Это — трансцендентное уравнение для комплексной переменной
Д/3 + ig. Обычно для получения пороговых значений Д/3 + ig, при
которых выполняется условие генерации, прибегают к численному
решению уравнения A1.6.23). Однако в некоторых предельных слу-
случаях можно получить приближенные решения. В случае большого
усиления g ^> к из определения 52 = кк* — A/4)(Д/3 + igf- имеем
A1.6-.24)
Используя это приближенное выражение, уравнение A1.6.23) мож-
можно переписать в виде
1 - th sL
2к*к
2 '
A1.6.25)
Поскольку g > к, функция th sL примерно равна единице, и, следо-
следовательно, мы можем написать следующее приближенное равенство:
thsL = 1 - 2e~sL. A1.6.26)
Таким образом, условие генерации A1.6.23) принимает вид
к*к
A1.6.27)
Приравнивая фазы в обеих частях уравнения A1.6.27), получаем
, ±1,±2, .... (П.6.28)
В случае генерации вблизи брэгговской частоты соо (т. е. вблизи ча-
частоты, при которой Д/3 = 0) и в пределе Д/3 « g частоты генериру-
генерируемых мод определяются выражением
(Afi)mL = Bт +
A1.6.29)
Направляемые волны и интегральная оптика
481
а поскольку Д/3 = 2(со — шо)п/с [см. A1.4.24)], мы имеем
"ПС
A1.6.30)
Следует заметить, что генерация точно на брэгговской частоте
соо невозможна. Согласно рис. 11.10, она может иметь место на
различных частотах, не совпадающих с брэгговской. При этом мы
имеем g -4 Д/3 и условие для модовых частот записывается в виде
(&,fi)mL = 2т'чт, т' = большие целые числа.
A1.6.31)
В любом случае расстояние между модовыми частотами дается вы-
выражением
"ПС
A1.6.32)
причем оно приблизительно такое же, как и в случае лазерного ре-
резонатора с двумя зеркалами длиной L. Пороговое значение усиле-
усиления можно получить из амплитудного равенства A1.6.27):
= 1,
A1.6.33)
откуда видно, что пороговое усиление увеличивается с ростом мо-
дового числа [т. е. с увеличением (Д/3)^. Это также подтверждают
численные расчеты (рис. 11.10 и 11.11).
На рис. 11.12 показан схематически лазер с распределенной об-
обратной связью на основе структуры GaAs—GaAlAs. Волноводный
слой, который обеспечивает также усиление (активный слой), выпол-
неных из кристалла CaAs р-гипа. Обратная связь обеспечивается на-
наличием гофрированной границы между слоями p-GaQ 93Alo 07As и
/>-Gao,7A1o,3As-
Увеличение порогового усиления с возрастанием модового ин-
индекса т, предсказываемое выражением A1.6.33) и кривыми на
рис. 11.10 и 11.11, проявляется в лазере с распределенной обратной
связью как высокая степень дискриминации мод. Этот факт ил-
иллюстрируется также спектром генерации, приведенным на
рис. 11.13, на котором отчетливо видна отдельная (т = 0) мода.
31-631

482
Глава 11
Направляемые
483
Область
возбуждения
p-GaAs
Контакт Сг—Аи
Пленка из SiO2
,. Подложка из n-GaAs
Контакт Аи—Ge—Ni
РИС. 11.12. Непрерывный инжекционный лазер на основе GaAs — GaAlAs с гофри-
гофрированной поверхностью волноводного слоя. Во вставке помещена микрофотография
слоистой структуры, полученная с помощью сканирующего электронного микроско-
микроскопа. Обратная связь с / = 3 (третий порядок) обеспечивается гофром с периодом
Л = 3\g/2 = 0,345 мкм. Тонкий (/ = 0,2 мкм) слой из p-GaQ 83Al017As образует по-
потенциальный барьер, который локализует инжектированные'электроны в активном
слое (p-GaAs) и способствует таким образом росту усиления. (Из работы [11].)
т = 0
Г=30ОК
/ = 5,0 А
т= 1
Г=260К
/ = 4,8 А
8700
8800
Длина волны, А
8900
РИС. 11.13. Спектр генерации лазера с распределенной обратной связью на основе
двойного гетероструктурного диода GaAs — GaAlAs. Здесь т — модовый индекс.
(Из работы [11).]
11.7. ЭЛЕКТРООИГЧ.
И МОДОВАЯ С
МОДУЛЯЦИЯ
Одним из очень важных применений тонкопленочных волноводов
является использование их для оптической модуляции и переключе-
переключения вследствие следующих двух их преимуществ:
1. Благодаря локализации оптического излучения в области, срав-
сравнимой с длиной волны А, можно достичь величины электриче-
электрического поля, которая требуется для модуляции (см. разд. 8.1),
при относительно малых приложенных напряжениях. Это приво-
приводит к уменьшению мощности модуляции.
2. Отсутствие дифракции у направляемого оптического пучка дела-
делает возможным использование более длинных областей модуля-
модуляции (см. разд. 8.3).
Основной принцип электрооптической модуляции в диэлектриче-
диэлектрических волноводах заключается в отводе всей или части мощности из
моды ТЕ (или ТМ) на входе в моду ТМ (или ТЕ) на выходе с по-
помощью внешнего постоянного (или низкочастотного) электрическо-
электрического поля. Для определенности рассмотрим следующий случай преоб-
преобразования мод ТМ — ТЕ. Такое преобразование происходит из-за
возмущения функции диэлектрической проницаемости е(х), произво-
производимого внешним электрическим полем через электрооптический эф-
эффект. Пусть Де есть изменение тензора диэлектрической проницае-
проницаемости s(x), обусловленное наличием постоянного электрического
поля. В соответствии с результатами, полученными в разд. 6.4 и
11.3, в случае когда чистая ТМ-мода Ej возбуждается при z — О,
возмущение диэлектрической проницаемости приводит к возмуще-
возмущению вектора поляризации Р = ДеЕг Эта поляризация, действуя
как источник, может возбудить ТЕ-моду Е2 при условии, что про-
произведение Е2-ДеЕ, Ф 0 и /3™ а.- /31Ь.
Из определения тензора непроницаемости -ц = ?Q?~l [см. выра-
выражение D.3.2)] следует, что изменение тензора непроницаемости свя-
связано с соответствующим изменением тензора диэлектрической про-
проницаемости следующим соотношением:
Д?= -
A1.7.1)

484
Глава 11
Направляемые волны и интегральная оптика
485
Используя выражение G.1.2), находим следующее соотношение
между Де и приложенным электрическим полем:
Де= -
е(гЕ°)е
A1.7.2)
где (rE°) — 3 х 3-матрица, состоящая из элементов riJkE°k (rjjk —
электрооптический тензор, ЕРк — компонента приложенного посто-
постоянного электрического поля), и предполагается суммирование по
повторяющимся индексам (к). В случае планарных волноводов, вы-
выполненных из изотропных материалов, тензор ? становится скаляр-
скалярной величиной е0п2(х) и возмущение диэлектрической проницаемо-
проницаемости Де можно записать в виде
Де= -е0п4(х)(гЕ°), A1.7.3)
где ЕР — приложенное постоянное электрическое поле.
Рассмотрим теперь связь между модами ТЕт и ТМП, где т и
п— целочисленные модовые индексы (см. рис. 11.4). Предполо-
Предположим, что связь с другими модами отсутствует и возбуждены толь-
только эти две моды. Таким образом, электрическое поле волны можно
записать в виде
где S^- и d?™ — собственные моды планарного волновода с по-
постоянными распространения /З^е и /jtm соответственно, а Ат и
Вп — модовые амплитуды, которые при наличии связи между мо-
модами являются функциями от z. Согласно результатам, получен-
полученным в разд. 6.4, 11.3 и 11.5, эти модовые амплитуды подчиняются
следующим уравнениям:
= -in
1К
A1.7.5)
— й = -/к* А е~'*Р*
где
7Г
^ " — Г
A1.7.6)
WWW
АААААЛ
.,27Г
РИС. 11.14. Обмен мощностью между
связанными модами, а — условие фазо-
фазового синхронизма (|3™ = /3™) выпол-
выполняется [выражения A1.7.11)]; б— усло-
условие фазового синхронизма не выполня-
выполняется [выражения A1.7.12)] /3™ * 0™).
еДх) — /-й коэффициент фурье-разложения возмущения диэлектри-
диэлектрической проницаемости:
A1.7.7)
Выражение A1.7.3) является достаточно общим и может быть при-
применено во многих случаях. Зависимость ?° и г от х учитывает
связь, обусловленную электрооптическим материалом в волновод-
ном или пограничном слоях. Зависимость от z соответствует случа-
случаям, когда ?° или г зависит от продольной координаты. Для кон-
конкретности рассмотрим случай, когда волноводный слой — t < х <
< 0 электрооптически однороден и поле ЕР является однородным в
этом слое. Интегрирование в A1.7.6) выполняется от — t до 0. При
этом интеграл перекрытия в A1.7.6) имеет максимум, когда моды
ТЕт и ТМЛ являются хорошо локализованными и имеют один и
тот же порядок, т. е. т = п. Кроме того, согласно рис. 11.4,
/3™ « /3™ только при т = п. Если моды локализованы, то р,
q > И и эффективный показатель преломления C/Bж/\) приближен-
приближенно равен п2 (т. е. /3^Е = /3™ — /3 « п22ж/\). При этих условиях мо-
моды ТЕ и ТМ имеют приблизительно одинаковое распределение по-
поля и отличаются лишь направлением векторов их электрического
поля. Выражения A1.2.3), A1.2.9) и A1.2.10) для <?(х) в волновод-
ном слое принимают вид

486
Глава 11
ном слое принимают вид
- S
t
A1.7.8)
где мы пренебрегли ^-компонентой ТМ-волны, поскольку она мала
по сравнению с ^-компонентой (потому что к < C). В этом случае
константа связи A1.7.6) принимает вид
к= -\
A1.7.9)
где мы использовали условие /3™ = /3™ = п2к0 = п22ж/Х. Таким
образом, уравнения связанных мод A1.7.5) запишутся в виде
dz
dz
A1.7.10)
Следует заметить, что приведенные выше уравнения удовлетворя-
удовлетворяют условию сохранения полной мощности, т. е.
Уравнения A1.7.10) описывают связь между двумя встречными
модами. Общее решение этих уравнений записывается в виде
F.4.30). При выполнении условия фазового синхронизма (/3™ =
= C™) решения уравнений A1,7.10) в случае, когда на входе имеет-
имеется одна волна Ит@) = Ао, Вт@) ~ 0 при z = 0], запишутся следу-
следующим образом [см. F.4.30)]:
Ат = y40cosKz,
Вт = —iA о sin кг.
A1.7.11)
Используя выражение A1.7.9), можно показать, что значение
произведения напряженности электрического поля на длину E°L,
для которого kL — -к/2, необходимое для полного преобразования
Направляемые волны и интегральная оптика
487
мощности ТМ <- ТЕ на расстоянии L, такое же, как для перехода
от «включено» к «выключено» в объемном модуляторе, показан-
показанном на рис. 7.4. Этот результат применим только при жестких
ограничениях. Обычно коэффициент связи к меньше величины,
определяемой выражением A1.7.9), и значение произведения E°L,
необходимое для достижения полного преобразования мощности,
соответственно больше.
В случае когда /3™ Ф /3™, решения уравнений A1.7.10), удовлет-
удовлетворяющие граничным условиям Ат @) = Ао, Вт @) = 0, записыва-
записываются в виде
A1.7.12)
— I-
-sin к
Bm(z)= -iAoe-*z-
i
где
28 S /8™ - /В™.
in[(
sin[(K2 + 82I/2z],
A1.7.13)
чальной моды Ат на входе в моду В^, равна
Максимальная доля мощности, которая может перейти из на-
A1.7.14)
и становится пренебрежимо малой, если Ь > к.
Мощности мод для случаев 5 = 0 и 5^0 показаны на
рис. 11.14.
11.7.1. ПРИМЕР: ТОНКОПЛЕНОЧНЫЙ МОДУЛЯТОР
НА ОСНОВЕ GaAs ПРИ ДЛИНЕ ВОЛНЫ X = 1 мкм
Для оценки порядка величины связи рассмотрим случай, когда вол-
новодный слой образован из GaAs и X = 1 мкм. В этом случае (см.
табл. 7.3)
п2 « 3,5; п\г = 59-Ю2 м/В.
Если приложить внешнее поле Е° = 106 В/м, то из выражения
A1.7.9) для постоянной связи и расстояния, на котором происходит

488
Глава 11
Направляемые волны и интегральная оптика
489
Падающий
свет
@01)
п
(но)
^Алюминий щ
GaAs с высоким q г\г
GaAs с низким q п}
2,4 мм
t = 10,9 мкм
Г'
Усилитель —
1,1 ^ мкм .
Не—Ne- /
лазер /
Опорный сигнал
/- Образец
М-
1 V^
Прерыватель Поляризаторы
PbS-де.
тектор
Двига-
Двигатель
Синхро.
низ. уси
литель
¦
Регистр,
устр-во
Щель для сканирования изображения
РИС. 11.15. Электрооптический модулятор на основе эпитаксиальной пленки из
GaAs. Модуляция поля осуществляется приложением отрицательного смещающего
напряжения к переходу металл — полупроводник [32].
преобразование мощности, соответственно получаем следующие
значения:
к = 1,85 см, L = ж/2к - 0,85 см.
На рис. 11.15 представлена схематически экспериментальная
установка, использованная в одной из самых ранних работ по де-
демонстрации электрооптической тонкопленочной модуляции. Схема
модуляции аналогична представленной на рис. 8.4 и основана на
индуцированной электрооптически фазовой задержке (8.1.30):
гл,Ь
\t
A1.7.15)
0,7\-
РИС. 11.16. Коэффициент пропускания волновода, помешенного между скрещенны-
скрещенными поляризаторами, как функция приложенного отрицательного напряжения [32].
где V — приложенное напряжение, a t и L — толщина и длина вол-
волновода соответственно.
Отношение интенсивности, прошедшей через систему, к интен-
интенсивности на входе дается выражением G.3.6), или, что эквивалент-
эквивалентно, выражением A1.7.11) [заметим, что величина Г в выражении
(8.1.30) аналогична величине к в выражении A1.7.9)]:
Y =sin2il\ A1.7.16)
На рис. 11.16 приведена экспериментальная кривая пропускания.
Существуют случаи, когда /3ТЕ значительно отличается от /3™. На-
Например, моды распространения в волноводе, сделанном из анизот-
анизотропного материала (например, LiNbO3), из-за наличия естественно-

490
Глава 11
Направляемые волны и интегральная оптика
491
го двулучепреломления в волноводном слое и в подложке имеют
различные постоянные распространения, зависящие от их состоя-
состояния поляризации. В этих случаях для компенсации рассогласования
ехр[ЦР™ - fi™)z] в A1.7.5) можно использовать в соответствии с
выражениями A1.7.5) и A1.7.6) целенаправленное периодическое из-
изменение функции E°(z) или r(z) с периодом 2тг(]3^Е — /3™), что сно-
снова приводит к согласованию фазы. Недавно в работах [4, 5] было
сообщено о полном электрооптическом преобразовании мод
ТЕ «-» ТМ в волноводе из LiNbO3 с Ti-диффузией при использовании
периодического изменения приложенного электрического поля. При
данном периоде расположения электродов Л полное преобразование
мощности мод достигается только для длины волны Xq, удовлетво-
удовлетворяющей условию синхронизации фаз:
[100]
„ТЕ
„TMI _
2тг
2тг,
^l""--""¦'" л
где пГЕ и и™ — эффективные показатели преломления мод ТЕ и
ТМ. Таким образом, этот преобразователь мод действует анало-
аналогично фильтру. Преобразование поляризации в волноводе описыва-
описывается уравнениями связанных мод A1.7.5). Характеристики преоб-
преобразования при этом очень похожи на характеристики фильтра
Шольца (см. разд. 5.3 и 6.5) или акустооптического перестраивае-
перестраиваемого фильтра (см. разд. 10.3). Относительная ширина полосы про-
пропускания при отсутствии модовой дисперсии (см. задачу 11.8) рав-
равна ДХ/Х0 = A./L = 1/7V, где N — число периодов, a L — длина вза-
взаимодействия. Несколько более подробно такой электрооптический
преобразователь мод ТЕ <- ТМ мы рассмотрим в следующем раз-
разделе.
11.7.2. ПРИМЕР. ВОЛНОВОДНЫЙ ПРЕОБРАЗОВАТЕЛЬ —
ФИЛЬТР НА КРИСТАЛЛЕ LiNbO3
Рассмотрим волновод на кристалле LiNbO3 с Ti-диффузией, на по-
поверхности которого периодически располагаются электроды
(рис. 11.17). Предположим, что толщина волноводного слоя t на-
намного меньше, чем период Л. В практических случаях толщина t
обычно равна нескольким сотням ангстрем, а период Л — порядка
нескольких микрометров. При этих условиях электрическое поле в
волноводном слое, обусловленное приложенными к электродам на-
напряжениями с чередующимися знаками плюс и минус, дается приб-
приближенно выражением
Е° = *?
A1.7.17)
¦у [ою]
Падающий свет
Волновод
с Ti-диффузией
РИС. 11.17. Схематическое представление электрооптического волноводного преоб-
преобразователя мод ТМ " ТЕ на основе кристалла LiNbO3 с периодическими гребенча-
гребенчатыми электродами.
где V — величина напряжения, d — промежуток между электрода-
электродами, /0>) — периодическая функция в виде прямоугольных импуль-
импульсов, определяемая выражением F.5.8). Мы предполагаем, что ось
х перпендикулярна поверхности кристалла и волна распространяет-
распространяется вдоль оси у кристалла. Вследствие электрооптического эффекта
периодическое электрическое поле A1.7.7) вызывает периодическое
изменение тензора диэлектрической проницаемости. Кристалл
LiNbO3 обладает точечной группой симметрии Зт. Согласно
табл. 7.1 и выражениям G.1.2) и A1.7.1), xz-компонента диэлектри-
диэлектрического возмущения (Ае^), обусловливающая связь между модами
ТЕ (поляризованными вдоль оси z) и ТМ (поляризованными при-
примерно вдоль оси х), дается выражением
Aexz= ~е0пУог51^/(у), A1.7.18)
где пе, по — необыкновенный и обыкновенный показатели прелом-
преломления волноводного слоя. В хорошо локализованном случае модо-
вые функции определяются выражением A1.7.8), где у теперь нуж-
нужно заменить на z, поскольку здесь используется новая система ко-
координат. Постоянные распространения записываются приближенно
в виде
/8та»я«Х' /*™ ="„!?• (П.7.19)

492
Глава 11
Постоянная связи ктп между модами ТЕт и ТМЯ
обусловленная
1 l^V I I/Sljn.ГАМ» w»«»—- — "fjjfl """"¦ ' '" '*
компонентой / = 1 фурье-разложения функции Aexz, в соответствии
с выражениями F.5.10), A1.4.5), A1.7.6) и A1.7.8) записывается
следующим образом:
Kmn
\V2,
Г51
8'»"'
A1.7.20)
где g — дельта-символ Кронекера.
Полагая п™ = пе = 2,21 и л™ = я0 = 2,30 при X = 6328 А, из
выражения A1.7.6) получаем следующее значение периода Л, необ-
необходимое для согласованной связи:
Л = 7,03 мкм.
Используя г51 = 28- 102 м/В из табл. 7.2, d = Л/2 = 3,51 мкм и
V = 20 В, находим, что постоянная связи к - I ктп I будет равна
к = 28,8 м.
Таким образом, для полного преобразования необходима длина
взаимодействия
L - ж/2к = 550 мкм.
Следует отметить, что, поскольку к прямо пропорциональна напря-
напряжению V, для полного преобразования приложенное напряжение
должно быть тем меньше, чем больше длина взаимодействия L. На
рис. 11.18, а показана измеренная эффективность преобразования
ТЕ « ТМ как функция от приложенного напряжения V при согласо-
согласованной связи в волноводном канале с Ti-диффузией длиной L =
= 6 мм, а на рис. 11.18, б представлена зависимость преобразова-
преобразования мод от длины волны [4, 5].
Другим видом электрооптической тонкопленочной модуляции
является использование двумерной брэгговской дифракции волно-
водной моды на пространственной периодической модуляции пока-
показателя преломления. Периодическое изменение показателя прелом-
преломления можно получить с помощью периодического электрического
поля, создаваемого гребенчатой электродной структурой, показан-
показанной на рис. 11.19. Этот случай формально аналогичен случаю брэг-
говского рассеяния на звуковой волне (см. гл. 9), когда модуляция
показателя преломления была обусловлена акустической деформа-
деформацией.
Необходимое условие дифракции, когда мода с волновым векто-
вектором /?,. переходит в моду с волновым вектором /3d, по аналогии с
Направляемые волны и интегральная оптика
# 100
493
г з
Напряжение, В
100
РИС. 11.18. а — измеренная эффективность преобразования мод ТЕ « ТМ при усло-
условии фазовой синхронизации (X = XQ = 0,6 мкм) в зависимости от приложенного на-
напряжения; б — измеренная эффективность преобразования мод при фиксированном
значении напряжения (V = 2,5 В) для электрода длиной 6 мм [4,5].
выражением F.4.18) записывается в виде
2тг
= Э,
-т,
т= 1,2,3,...,
A1.7.21)

494
Глава 11
Направляемые волны и интегральная оптика
495
РИС. 11.19. Схематическое представление электрооптического модулятора из решет-
решетки в волноводе на LiNb^Taj ^.Oj — LiTaO3. Мода, возбуждаемая в волноводе с по-
помощью призмы, отклоняется на угол 2$д, когда к гребенчатой системе электродов
прикладывается напряжение; Л = 7,6 мкм и / = 0,3 см. Кривые показывают про-
процентное отношение дифрагированного света в зависимости от приложенного напря-
напряжения. О — 4976 А (Не — Se-лазер); + — 5598 А (Не — Se-лазер); • — 6328 А
(Не — Ne-лазер). Сплошные кривые соответствуют функции sin2(SKQ), нормирован-
нормированной к данным при 75%. [Из работы: Hammer J., Phillips W., Appl. Phys. Lett., 24,
545 A974).]
где Л — период пространственной модуляции и aG — единичный
вектор, перпендикулярный линиям с равными значениями показате-
показателя преломления (т. е. нормаль к электродам на рис. 11.19). Векто-
Векторы Зг и j8rf располагаются в плоскости волновода.
На рис. 11.20 представлена диаграмма «импульсов», соответст-
соответствующая условию A1.7.21) для случая т = 1.
Используя формальную эквивалентность этого случая брэгговс-
кой дифракции на звуковой волне, эффективность дифракции [см.
выражение (9.5.20)] можно записать в виде
A1.7.22)
РИС. 11.20. а — диаграмма «импульсов» при дифракции падающей моды OS) в моду
ffd в случае электрооптического изменения показателя преломления с периодом Л;
б — вид плоскости волновода сверху, показывающий направления падающего OS,) и
дифрагированного 0Srf) пучков, а также плоскость образующейся «решетки» показа-
показателей преломления.
где An — амплитуда модуляции показателя преломления, связанная
с соответствующей фурье-компонентой Е{ (т = 1 для брэгговской
дифракции первого порядка) низкочастотного электрического поля
соотношением G.2.9); таким образом,
?п3гЕ.,
A1.7.23)
где г — элемент электрооптического тензора, который зависит от
ориентации кристалла. Подставляя выражение A1.7.23) в A1.7.22),
имеем
't - -I 2Л
A1.7.24)
Поскольку поле ?, пропорционально приложенному напряжению
Vo, эффективность дифракции A1.7.24) можно записать в виде
A1.7.25)
где величина В обратно пропорциональна оптической длине вол-
волны X.
Экспериментальные кривые на рис. 11.19 находятся в согласии с
теоретическим выражением A1.7.25).
11.8. НАПРАВЛЕННАЯ СВЯЗЬ
Рассмотрим теперь связь между модами двух параллельных волно-
волноводов, разделенных конечным расстоянием. Обмен энергией между
направляемыми модами примыкающих волноводов известен как

496
Глава 11
Направляемые волны и интегральная оптика
497
-2t-s
-t-s -t
РИС. 11.21. а — общая волноводная структура, состоящая из двух параллельных
цилиндрических волноводов; б — два идентичных планарных волновода, разделен-
разделенных расстоянием (. Дя^(х) = (пгг - /ф при -t < х < 0; Ап^(х) = (пг2 — п2{) при
-2t - s < х < -t-s.
направленная связь. Это явление аналогично движению электрона в
двухатомной молекуле. Волноводные направленные ответвители
выполняют множество полезных функций в интегрально-оптичес-
интегрально-оптических устройствах, включая деление мощности, модуляцию, переклю-
переключение, частотную и поляризационную селекции.
Волноводная связь может быть исследована с помощью теории
связанных мод. Рассмотрим случай двух цилиндрических вол-
волноводов, изображенных на рис. 11.21. Пусть &а{х, у)е^1~&аг) и
4,(*' y)e((^~0bZ) — моды, каждая из которых распространяется в
своем волноводе, когда волноводы удалены друг от друга. Элект-
Электрическое поле в структуре двух связанных волноводов при условии,
что волноводы расположены не слишком близко друг к другу,
приближенно можно записать в виде
Е(х, у, z, 0 = A(z)Sa(x,
B{z)&b{x,
A1.8.1)
В отсутствие связи, т. е. если расстояние между волноводами а и Ъ
является бесконечным, A(z) и B(z) не зависят от г и друг от друга.
Поэтому каждый из двух членов в правой части выражения A1.8.1)
удовлетворяет волновому уравнению A1.1.4) по отдельности.
Пусть п2(х, у) — распределение показателя преломления комби-
комбинированной волноводной структуры. Для изучения модовой связи
запишем показатель преломления в виде суммы трех частей:
(х, у) = п]{х, у) + АпЦх, у) + АпЦх, у),
A1.8.2)
где n2s(x, у) — распределение показателя преломления окружающей
среды (покрытия), Дл^(х, у) и Дл^(х, у) — показатели преломления
волноводов а и Ъ соответственно. Таким образом, очевидно, что
отдельные волноводные моды <^(х, у) удовлетворяют уравнению
, у)
. у).
а = а,Ь. A1.8.3)
Присутствие волновода Ъ вызывает возмущение диэлектрической
проницаемости е0Лп1(х, у) при распространении моды #а{х,у)х
Xei(o>t-Paz) и наоборот. Полное электрическое поле A1.8.1) должно
удовлетворять волновому уравнению
JL + JL + JL
Эх2 ду2 dz2
, у) + АпЦх, у) +
Е = 0.
A1.8.4)
J
Для получения системы уравнений для модовых амплитуд A(z) и
B(z) подставим выражение A1.8.1) в уравнение A1.8.4) и воспользу-
32-631

498
Глава 11
Направляемые волны и интегральная оптика
499
емся уравнением A1.8.3) и предположением о слабом изменении
амплитуды моды F.4.10) с расстоянием z. Это приводит к уравне-
уравнению
A1.8.5)
Умножим теперь уравнение A1.8.5) скалярно на <f*(x, у) и <#?(*, у)
соответственно и проинтегрируем по х и у. Используя условие нор-
нормировки F.4.6), получаем следующую систему уравнений:
= -не
ab
где
Kab
кьа
)z - Ы А
b>* - 1КььВ,
A1.8.6)
A1.8.7)
кьь =
, y)&adxdy
, y)&adxdy,
, y)&bdxdy.
A1.8.8)
При получении A1.8.6) мы использовали предположение, что вол-
волноводы расположены не слишком близко друг к другу, так что ин-
интеграл перекрытия модовых функций мал, т. е.
f
s; • &а
A1.8.9)
Величины, входящие в выражения для киа и кьь, связаны с возмуще-
возмущениями диэлектрической проницаемости в одном из волноводов,
обусловленными наличием другого волновода. Эти величины пред-
представляют собой лишь малую поправку к постоянным распростране-
распространения )За и /Зй соответственно [см. выражения A1.3.15) и A1.3.22)].
Члены в каЬ и кЬа описывают обменную связь между двумя волно-
волноводами. Так, если вместо выражения A1.8.1) полное поле записать
в виде
Е
то уравнения A1.8.6) принимают вид
dz
где
28 = (Ра + Ка
~ (В„ + кьь).
A1.8.10)
A1.8.11)
A1.8.12)
Решение уравнений A1.8.11), когда на входе волновода а имеется
одна волна [т.е. А@) = Ао, В@) = 0], дается выражением
A1.7.12). Для мощностей Ра = А*А и^ = В*В в этих волново-
волноводах решения в случае каЬ = кЬа = к принимают вид
A1.8.13)
где Ро = \А @I2 — мощность волны на входе в волновод а. Пол-
Полная передача мощности происходит на расстоянии" L = ж/2к, при
условии что 5 = 0, т. е. при равенстве фазовых скоростей двух
мод. Из A1.8.13) следует, что при 5^0 максимальная доля мощ-
мощности, которая может быть перенесена, равна
A1.8.14)
Постоянная связи к = каЬ = кЬа дается выражением A1.8.7). Для
случая двух параллельных планарных диэлектрических волноводов
ее можно вычислить непосредственно из выражений A1.2.3) и
A1.2.10). В частном случае двух одинаковых планарных волноводов

500
Глава 11
Направляемые волны и интегральная оптика
501
постоянная связи к для ТЕ-мод записывается в виде
2/p)(h2+p2)'
A1.8.15)
где t — толщина волновода, s — расстояние между волноводами, а
величины р — q и А определяются выражением A1.2.4). В случае
хорошо локализованных мод (t > 2/р) выражение A1.8.15) прини-
принимает более простой вид [13]:
к =
2h2pe~ps
~ Pt(h2+p2)
A1.8.16)
При X « 1 мкм, / = s » 3 мкм и An » 5-10 3 мы получаем типич-
типичное значение к » 5 см~', откуда следует, что длины взаимодейст-
взаимодействия будут порядка к « 2 мм.
Основанный на направленной связи [12] электрооптический пере-
переключатель имеет следующие конструктивные параметры. Длина L
ответвителя выбирается таким образом, чтобы при 5 = 0 (случай
фазовой синхронизации) кЬ = -к/2. Из выражения A1.8.13) следует,
что при z — L вся мощность из волновода а переходит в волновод
Ъ. Переключение достигается приложением электрического поля к
волноводу а (или Ь). При этом изменение постоянной распростра-
распространения должно равняться
8L = Н& - Pb)L = 1/Зтг,
A1.8.17)
т. е. Ь = VJk. Из A1.8.13) следует, что при этом значении 5
Ра =
о,
т. е. мощность снова переходит в волновод а. Таким образом,
управляя величиной 8, можно получить любое разделение мощно-
мощности на выходе волноводов а и Ъ.
Действие переключаемого направленного ответвителя, основан-
основанного на таком принципе и использующего полосковые волноводы
на кристалле LiNbO, с Ti-диффузией и полосковые волноводы
на GaAs [15] с металлическим зазором, было продемонстрировано
в работе [17]. В этих устройствах важным моментом является то,
что длина взаимодействия L равна нечетному числу яУ2к. Это обес-
обеспечивает полную передачу оптической мощности из волновода а в
волновод Ъ, когда моды в волноводах удовлетворяют условию син-
синхронизации фаз (Д/3 = 0). Если длина взаимодействия не удовлетво-
удовлетворяет этому идеальному случаю, то в таких устройствах имеет ме-
место лишь частичный переход мощности (рис. 11.22, 6). Полный пе-
переход мощности из одного волновода в другой не может быть до-
достигнут с помощью электрической настройки. Таким образом, тре-
требование максимального условия перекачки мощности налагает
жесткие ограничения на допустимые отклонения размеров уст-
устройства.
Чтобы избежать этой проблемы, связанной с технологией, приво-
приводящей к разбросу длины взаимодействия L, в работе [16] были
предложены ответвители со знакопеременными значениями Д/3. Та-
Такая схема ответвителя (рис. 11.22, в) позволяет с помощью элект-
электрического напряжения регулировать мощность как в первом волно-
волноводе Ра, так и во втором волноводе Рь при любой длине взаимо-
взаимодействия, которая больше чем ж/2к. Для этого используются разде-
разделенные электроды, к которым прикладываются напряжения разной
полярности вдоль волноводов, чтобы создать знакопеременные Д/3.
Рассмотрим теперь принцип действия простейшего ответвителя со
знакопеременными Д/3, показанного на рис. 11.22, в.
Для получения выходных мощностей Ра и Рь необходимо ре-
решить уравнения связанных мод A1.8.11) в области 0 ^ z < L/2 и
найти модовые амплитуды A(L/2) и B(L/2). Эти две амплитуды
затем используются в качестве (граничных) входных условий при
решении уравнений связанных мод A1.8.11) в области L/2 ^ z < L
с противоположным знаком величины Д/3 (или 5). Из-за изменения
знака у Д/3 постоянные распространения /За + каа и fib + кьь двух
волноводов не являются постоянными, так как они теперь имеют
различные величины в двух смежных секциях. Амплитуды мод А (г)
и В (г), определяемые выражением A1.8.10), должны быть перео-
переопределены в области второй секции L/2 < z < L. Это очень не-
неудобно в случае, когда устройство имеет больше чем две секции.
Определим теперь две новые модовые амплитуды, которые не за-
зависят от изменения знака Д/З:
A'(z) = A(z)e-iS', B'(z) = B(z)ei8', A1.8.18)
где 8 дается выражением A1.8.12). Используя выражения A1.8.18),
полное электрическое поле можно написать в виде
Е = [A'(z)$a
A1.8.19)

100
-/>« f.so
L
a
Направляемые волны и интегральная оптика
Перекрестная
ветвь
+Д/3
-д/з
У- L/2—I— L/2—I
100
л 50
8
о „
10 20 30
Напряжение, В
6
Перекрестная J
ветвь
10 20 30
Напряжение, В
г
40
12
А
503
РИС. 11.22. а — переключаемый направленный ответвитель, состоящий из двух оп-
оптических полосковых волноводов с длиной взаимодействия L (из работы [16];
copyright 1976 IEEE); б — оптическая мощность, переходящая из переключателя в
прямую и перекрестную ветви волноводов, как функция напряжения для случая о;
в — схема с расщепленными электродами для переключаемого ответвителя с изме-
изменением знака Д/3 (знакопеременные Д/3 с двумя секциями электродов) (из работы
[16]); г — оптические мощности Ра и Рь как функции напряжения для случая в; д —
диаграмма переключений ответвителя с двумя секциями электродов, имеющих зна-
знакопеременные Д/3. Знак ® означает перекрестное состояние, а знак ® соответствует
прямому состоянию (из работы [16]).
где
= НРа + «аа + Рь + О-
A1.8.20)
Заметим, используя A1.8.19), что эти новые модовые амплитуды
А' и В' действительно не зависят от изменения знака величины Д/3.
Используя выражения F.4.30) и A1.8.18), амплитуды Л' A/2) и
В' (L/2) можно выразить через А' @) и В' @):
где
Х =
A1.8.21)
A1.8.22)
A1.8.23)
Коэффициенты S и X представляют прямую и перекрестную связи
соответственно. Аналогично А' (L) и В' (L) могут быть выражены
через A' (L/2) и В' A/2)
A1.8.24)
где мы учли изменение знака величины 6F = Д/3/2) в области
L/2 ^ z ^ L. Подставляя выражение A1.8.21) в A1.8.24), получаем
A'(L)\_(S*S-X*X -2iS*X \[A'@)\
()j-[ -2iX*S S*S-X*x}[b'{0))- A1-8-25)

504
Глава 11
Направляемые волны и интегральная оптика
505
Если предположить, что входная мощность Ро = \А' @)\2 отдель-
отдельной моды вводится в первый волновод, то В' @) = 0. С помощью
выражений A1.8.22), A1.8.23) и A1.8.25) оптические мощности мод
в волноводах при z = L можно записать в виде
Pa(L)
Pb{L) = P0- Pa(L).
A1.8.26)
Согласно формуле A1.8.26), полная передача мощности из вол-
волновода а в волновод b имеет место, когда
A1.8.27)
Определяя длину переключения 1С = х/2/с (/с — длина, на которой
происходит полный переход мощности из а в b при 8 = 0), мы мо-
можем переписать выражение A1.8.27) в виде
(L/leJ + B8LA
На рис. 11.22, д представлены кривые переключения, построенные
в соответствии с формулой A1.8.27а) в плоскости 8L — L/lc. Этим
кривым на рисунке соответствуют кривые, связывающие точки (х)
на оси ординат. Каждая точка на такой кривой соответствует паре
8L, L/lc, для которой имеет место полная передача мощности. По-
Показаны также кривые, соединяющие точки (=), которым соответст-
соответствует «сквозное» прохождение мощности.
Таким образом, возможно (например, при 1 ^ L/lc ^ 3) пере-
переключение из режима полного «сквозного» прохождения (=)к «пере-
«перекрестному» режиму (х) изменением величины 6Х/х от значения,
указанного на рис. 11.22, д точкой В, до значения, соответствующе-
соответствующего точке А.
В случае когда 5 = 0, условие перекрестной трансформации
A1.8.27) приводит к соотношению кЬ — х/2 + п-к {п = 1, 2, ...).
Если 8 выбрана правильно, то условие A1.8.27) может быть удов-
удовлетворено для большой области значений величины L. Действи-
Действительно, для kL в области х/2 ^ kL ^ Зтг/2 этому условию всегда
можно удовлетворить с помощью надлежащего выбора величины
5. Это можно показать, если построить кривую, отвечающую ле-
левой части уравнения A1.8.27), как функцию величины 8. При 6 = 0
левая часть равна величине sin2(/cL/2), которая больше чем 1/2 в об-
области х/2 ^ kL ^ ir/2. При больших значениях 8 левая часть урав-
уравнения A1.8.27) стремится к нулю как 8~2. Поскольку эта левая
часть является непрерывной функцией величины 8, в области ж/2 <
^ kL ^ Зж/2 всегда должно существовать решение.
Таким образом, если величиной 8 можно управлять с помошью
приложенного напряжения, то схема переключателя со знакопере-
знакопеременной Д/3 позволяет осуществить полную передачу света из одно-
одного волновода в другой. Электрооптически переключаемый направ-
направленный ответвитель, основанный на таком принципе, демонстриро-
демонстрировался в работе [17]. Получаемые при этом выходные мощности Ра
Сфокусированный свет
г-
'¦-.
}
\»
Г
X
|
Г
z=0
Г"
0,9 мм
1,5 мм
L
2,5 мм
t 6,4
I—HI-
4 2,4
мкм мкм мкм
GaAs
« б
РИС. 11.23. а —многоканальный оптический направленный ответвитель; показаны
потоки оптической мощности в смежные каналы; б — измеренные профили интен-
интенсивности направляемого света на различных расстояниях г; интенсивности представ-
представлены в относительных единицах; волноводы были изготовлены с помощью имплан-
имплантации протонов в кристалл р+ -GaAs. (Из работы [14].)

506
Глава 11
Направляемые волны и интегральная оптика
507
и Рь в зависимости от приложенного напряжения приведены на
рис. 11.22, г.
На рис. 11.23,0 показан схематически принцип действия много-
многослойного направленного ответвителя, описываемого системой урав-
уравнений
dA
= -1кА„_х -
A1.8.28)
которая представляет собой очевидное обобщение системы уравне-
уравнений A1.8.11) на многомодовый синхронный случай (<5 = 0), когда
только смежные моды связаны друг с другом. Решение уравнений
A1.8.28) в случае возбуждения лишь одного волновода [т. е.
Ап@) = 1, п = б; Ап@) = О, п Ф 0] имеет вид [14]
An(z) = (-i)n JnBKz),
A1.8.29)
где J — функция Бесселя порядка п.
Направленный ответвитель, основанный на этом принципе, по-
показан на рис. 11.23,йг, а предсказываемые распределения интенсив-
интенсивности в виде функций Бесселя представлены на рис. 11.23, б на раз-
различных расстояниях от основного волновода.
Из выражений A1.8.13) и A1.8.14) следует, что если 6 > к, то
доля преобразуемой мощности мала. Это имеет место, когда два
волновода имеют сильно отличающиеся диэлектрические проницае-
проницаемости, а значит, и постоянные распространения. Однако и в этом
случае возможна полная передача мощности при условии, что меж-
между двумя волноводами имеется периодическое возмущение диэлект-
диэлектрической проницаемости. Период такого возмущения должен быть
равен 2х/(|За + каа — /Зй - кьь), чтобы компенсировать рассогласо-
рассогласование фаз при однонаправленной связи, и должен быть равен
2ж/фа + каа + /Зй + кьь) при встречной связи. Вследствие периодич-
периодичности возмущения такие направленные связи являются частотно-из-
частотно-избирательными. Для данного периода Л максимальный обмен мощ-
мощностями между модами достигается лишь для длины волны Xq, для
которой выполнено условие синхронизации фаз
—I
^0
2т
A1.8.30)
где па, пь — эффективные показатели преломления для мод в вол-
волноводах а и Ь соответственно. Здесь знак плюс соответствует
встречной связи, а знак минус — попутной связи. Частотная изби-
избирательность этих направленных связей может быть использована
для частотного мультиплексирования и демультиплексирования
(см. разд. 11.9). Относительная ширина полосы пропускания при
этом будет порядка 1/7V (т. е. ДХ/Х « 1/7V), где N — число перио-
периодов, при условии что модовой дисперсией можно пренебречь.
Если волноводы сделаны из электрооптического материала, то
периодическое возмущение показателя преломления может быть
получено приложением вдоль волноводов знакопеременного напря-
напряжения. Использование электрооптического возмущения диэлектри-
диэлектрической проницаемости дает также способ электрического переклю-
переключения направленного ответвителя.
11.9. ЧАСТОТНЫЕ МУЛЬТИПЛЕКСОРЫ
Частотное мультиплексирование (иногда оно называется цветным
мультиплексированием или мультиплексированием по длинам
волн) позволяет значительно повысить информационную емкость
оптических волноводов. В системах с частотной мультипликацией
каждый информационный канал занимает соответствующий Диапа-
Диапазон частот (частотную полосу) для передачи. Важным элементом
таких систем является частотно-избирательный ответвитель для
сложения и разделения каналов. В этом разделе мы кратко опишем
некоторые различные типы частотных мультиплексоров, исполь-
используемых в волоконно-оптических линиях связи. Следует заметить,
что ответвители такого типа являются взаимными устройствами и
по существу могут как складывать, так и разделять частотные ка-
каналы.
11.9.1. ДИФРАКЦИОННЫЕ РЕШЕТКИ С ПЕРЕМЕННЫМ ПЕРИОДОМ
Рассмотрим диэлектрический волновод с гофрированным участком,
период гофрированности в котором равен Л. Пусть оптический пу-
пучок с длиной волны X падает на гофрированный участок под углом
а (рис. 11.24,йг). Согласно рассмотрению, проведенному в гл.6,
световой пучок отклонится на угол 2а, если выполнено условие
Брэгга
Л = 2/iAcosa, A1.9.1)
где п — эффективный показатель преломления направляемой вол-
волны.
Если гофрированный участок представляет собой решетку с пе-
переменным периодом Л(г), то, как показано на рис. 11.24, различ-

508
Глава 11
X
/j
W/
2
"У
X
j
A
3
б
РИС. 11.24. a — разделение пучка в диэлектрическом волноводе с постоянным пери-
периодом решетки Л; б — разделение пучка и демультиплексирование в диэлектрическом
волноводе с дифракционной решеткой с переменным периодом Л (г).
ные области гофрированного волновода отражают различные дли-
длины волн. Волна с определенной длиной волны X, будет отражаться
от того участка гофра, период которого Л, удовлетворяет условию
Л, = X, /Bл cos а), в то время как волна с другой длиной волны Xj
отразится от участка, период которого Л2 удовлетворяет условию
Л2 = Xj/^ cosa). Таким образом, эти две длины волны, которые
первоначально входили в один и тот же пучок, разделяются про-
пространственно. Доля светового излучения с длиной волны X,, кото-
которая отражается, зависит от длины участка волновода, для которой
длина волны X, попадает внутрь «запрещенной» зоны распростра-
распространения. Она является, таким образом, функцией плотности штрихов
и постоянной связи, которые в данном волноводе определяются
высотой и профилем гофра.
Основанный на этой идее демультиплексор по длине волны был
Направляемые волны и интегральная оптика
509
= 6О7ОД X, = 627ОД
i
б
РИС. 11.25. a — фото, полученное при двукратном экспонировании, показывает от-
отражение на двух различных длинах волн от двух различных областей дифракционной
решетки разделителя пучка; б — схематическое представление эксперимента, резуль-
результаты которого приведены на рис. а; штриховые линии обозначают границы гофри-
гофрированной области, а сплошные — контуры лазерных пучков.
продемонстрирован на одномодовом волноводе толщиной 0,95 мкм
[18, 19]. Период решетки изменялся от 2930 до 3210 А на расстоя-
расстоянии 6,5 мм, а высота ее неоднородностей в стекле приблизительно
равнялась 500 А. При угле падения 48° отраженные лучи на двух
длинах волн 6070 и 6270 А пространственно разделялись расстоя-
расстоянием 4 мм. Экспериментальное наблюдение такого разделения ил-
иллюстрируется на рис. 11.25.

510
Глава 11
Оптические волноводы
Область
взаимодействия
РИС. 11.26. Частотно-избирательиые ответвители для использования в волоконно-
оптической связи.
11.9.2. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ НА РЕШЕТКАХ
Направленная связь между двумя различными волноводами может
быть сделана частотно-избирательной и весьма эффективной при
условии, что достигнута синхронизация фаз с помощью периодичег
ского пространственного возмущения показателя преломления. При
этом в зависимости от периода решетки могут быть реализованы
как попутная, так и встречная связи. Согласно условию A1.8.30),
для попутной связи на длине волны \ требуется решетка с перио-
периодом Л = \/(па — пь), в то время как для встречной связи на такой
же длине волны период решетки должен быть равен Л = \/{па +
+ пь), где пи, пь — эффективные показатели преломления для мод
волноводов а и b соответственно. Поскольку относительная шири-
ширина полосы сильной связи порядка 1/7V (т. е. ДХ/Л ~ 1/7V), rneN —
число периодов, очевидно, что ответвитель на встречной связи об-
обладает большей частотной избирательностью (т. е. узкой шириной
полосы) на меньшей длине взаимодействия. Однако такой ответви-
ответвитель труднее изготовить, так как для этого нужно иметь решетки с
очень небольшим периодом. На рис. 11.26 показан схематически
ответвитель на встречной связи для применения в волоконно-опти-
волоконно-оптических линиях связи. Для подробного ознакомления со спектраль-
спектральными характеристиками и конструкциями направленных ответвите-
лей на решетках мы отсылаем интересующегося читателя к рабо-
работам [20, 21].
11.10. ДРУГИЕ ПЛАНАРНЫЕ ВОЛНОВОДЫ
При рассмотрении характеристик ТЕ- и ТМ-мод в разд. 11.2 мы
предполагали, что волноводы сделаны из диэлектрических материа-
Направляемые волны и интегральная оптика
511
лов с показателем преломления волноводного слоя п2, большим,
чем показатели преломления двух граничащих сред (т. е. пг > я, 3).
Это условие является необходимым для существования полного
внутреннего отражения на границах, которое ответственно за ло-
локализованное распространение излучения. В данном разделе мы
рассмотрим два других типа планарных волноводов, в которых это
ограничение снимается.
11.10.1. ВОЛНОВОДЫ С МЕТАЛЛИЧЕСКИМ ПОКРЫТИЕМ
Рассмотрим слоистую волноводную структуру (рис. 11.2) с метал-
металлической подложкой (среда III). Показатель преломления пг метал-
металлической подложки является комплексной величиной. Например,
комплексные показатели преломления меди, золота и серебра при
X = 6328 А равны соответственно пъ = 0,16 - /3,37; 0,16 - /3,21
и 0,067 — /4,05. Коэффициенты отражения этих металлических по-
поверхностей крайне высоки (почти 100%), особенно при скользящем
падении (в « 90°), вследствие большой мнимой части (большого
коэффициента экстинкции) и малой вещественной части показателя
преломления пг. Действительно, если п3 — чисто мнимое число, то
волна в среде III всегда затухает. Коэффициент отражения света от
такой идеальной металлической поверхности всегда равен 100% не-
независимо от угла падения и состояния поляризации. Таким обра-
образом, идеальный металл, подобный этому, может обеспечивать пол-
полное отражение, необходимое для локализованного распростране-
распространения. Среда с чисто мнимым показателем преломления имеет отри-
отрицательную диэлектрическую проницаемость и нулевую оптическую
проводимость. Для меди, золота и серебра мы имеем соответст-
соответственно п\ = -11,33 - /1,08; -10,28 - /1,03 и -16,40 - /0,54. За-
Заметим, что мнимая часть величины п\, которая пропорциональна
оптической проводимости а, мала для всех трех металлов.
Характеристики распространения волн в волноводах с металли-
металлическим покрытием, в которых подложка выполнена из меди, золо-
золота или серебра, можно получить приближенно, пренебрегая вещест-
вещественной частью показателя преломления п3 (или мнимой частью ве-
величины nf). Иными словами, мы можем предположить, что метал-
металлическая подложка является чисто «диэлектрической» с отрица-
отрицательной диэлектрической постоянной. В этом приближении при
рассмотрении волноводов с металлическим покрытием мы можем
применить все модовые функции A1.2.3), A1.2.10) и условия рас-
распространения A1.2.5), A112.11) для ТЕ- и ТМ-мод соответственно.
Поскольку п\ отрицательная величина, металлическая подложка

512
Глава 11
имеет большую постоянную затухания/? [см. A1.2.4)]. Это означа-
означает, что доля мощности моды внутри металла очень невелика. Та-
Таким образом, моды оказываются хорошо локализованными, а оми-
омические потери — малыми.
Так как металлическая подложка имеет отрицательную диэлект-
диэлектрическую постоянную (т. е. п\ < 0), на границе между волновод-
ным слоем и металлической подложкой всегда имеет место полное
отражение, независимо от величины п2. Следовательно, до тех пор
пока п2 > Яр показатель преломления волноводного слоя может
быть сколь-угодно малым. Постоянная распространения моды
может принимать любое значение между п}к0 и п2к0, т. е. пхк0 <
< /3 < п 2к0. Этот интервал значительно шире по сравнению с
обычным диэлектрическим волноводом. Таким образом, волново-
волноводы с металлическим покрытием обычно содержат большое число
локализованных мод.
Распределение поля и постоянная распространения /3 локализо-
локализованных мод в волноводе с металлическим покрытием могут быть
получены из решения уравнений A1.2.5) для ТЕ-мод и A1.2.11) для
ТМ-мод. Поскольку п\ комплексная величина, постоянная распро-
распространения является, вообще говоря, также комплексной. Волновод-
ная мода с комплексной постоянной распространения будет зату-
затухать при распространении вдоль волновода. Получение комплекс-
комплексных корней /Зт путем решения трансцендентных уравнений A1.2.5)
и A1.2.11) с комплексным п\ представляет собой непростую задачу.
В металлах с небольшой мнимой частью величины п2 комплексная
постоянная распространения может быть получена по теории воз-
возмущений. Небольшая мнимая часть величины п2 соответствует не-
небольшой оптической проводимости а и, следовательно, малому за-
затуханию вследствие омических потерь. По теории возмущений мы
сначала получаем решение для мод с вещественной величиной п2 и
затем вводим в л3 небольшую мнимую часть в качестве возмуще-
возмущения для вычисления малой поправки к постоянной распространения
/3. Пусть постоянная распространения записывается в виде
&, = y8j,0)-/iam, A1.10.1)
где /3<?> — постоянная распространения моды т с вещественной ве-
величиной п2, а iam/2 — поправка, обусловленная мнимой частью ве-
величины п2. Поток мощности моды т вдоль волновода с постоян-
постоянной распространения A1.10.1) дается выражением
Pjz) = Pm@)e~
A1.10.2)
Направляемые волны и интегральная оптика
513
где Р$ — мощность моды т при z = 0. Пусть An2 — небольшое
диэлектрическое возмущение, обусловленное мнимой частью вели-
величины /if. Малую поправку 5/3m = -iam/2 к постоянной распростра-
распространения в соответствии с A1.3.15) можно записать в виде
= iuej '&*-An2&mdx,
A1.10.3)
где </т — электрическое поле моды т, определяемое выражениями
A1.2.3) и A1.2.10) с постоянной распространения /3^'. Используя
выражение A1.3.14), поправка к ^запишется в виде
A1.10.4)
где Г3 — доля мощности моды, распространяющаяся в металличес-
металлической подложке (среда III) и определяемая как
A1.10.5)
Согласно этому определению и выражению A1.2.3) для поля, вели-
величину Г, для ТЕ-мод можно записать в виде (см. задачу 11.5)
рТЕ _
1з ~
h2+p2
t+
A1.10.6)
Пусть ni = n — iK, где n — вещественная часть величины п3, а к —
коэффициент экстинкции металла; при этом An2 = -2тк. Тогда
поправочный член <5/Зт можно записать в виде
Коэффициент затухания ат дается выражением
2пк/ оз \2
ат = -тг~ — Г,.
A1.10.7)
Заметим, что Г3 зависит от номера моды /», а также от состояния
поляризации. Вообще говоря, ТМ-волны имеют меньшие значения
/3 и такие же большие Г3. Поэтому, согласно A1.10.7), ТМ-моды
обладают большим затуханием, чем ТЕ-моды (т. е. а™ > а^Е).
33-631

514
Глава 11
ТАБЛИЦА ll.l. Эффективные показатели преломления
и потери в волноводах из полистирола с серебряным
покрытием (использовалась полистироловая пленка
толщиной 1,81 мкм) [23]
Мода
ТЕ„
и
ТЕ,
ТЕ2
ТЕ3
ТЕ4
ТЕ5
ТЕ
™0
ТМ,
тм2
тм3
тм4
тм5
тм6
Толщина полисти-
полистироловой пленки,
мкм
1
2
2,5
3
Эффективный показатель преломления
Измеренный
,582
,547
,503
,438
,349
,238
,092
,577
,543
,484
,407
1,304
1,169
1,004
ГЕо
13,609
1,85
1,03
0,63
Потери,
ТЕ,
51,77
'7,60
4,03
2,32
Вычисленный
1,574
1,547
1,502
1,438
1,351
1,238
1,095
1,571
1,538
1,484
1,406
1,302
1,168
1,014
дБ/см
™0
136,46
19,03
9,92
5,91
ТМ,
313,92
62,94
33,58
20,21
Моды высшего порядка (большие т) имеют меньшие /Зот и большие
Г3 (т. е. они менее локализованы). Следовательно, моды высшего
порядка обладают большим затуханием, чем моды низшего поряд-
порядка. В табл. 11.1 приведены результаты вычислений для волноводов
из полистирола с серебряным покрытием [22]. Локализованное рас-
распространение света в волноводах из полистирола с серебряным и
алюминиевым покрытиями исследовалось в работе [23] и иллюст-
иллюстрируется рис. 11.27.
Направляемые волны и интегральная оптика
515
РИС. 11.27. Распространение света в полистироловых волноводах с серебряным (о)
и алюминиевым (б) покрытием. Короткая длина пути распространения света на
этих фото объясняется большими потерями в волноводе [23].
Коэффициент затухания ат можно также вычислить непосредст-
непосредственно из скорости затухания энергии вследствие омических потерь.
Согласно выражению A1.10.2), коэффициент затухания может
быть определен как
Рт dz
A1.10.8)
где Рт — поток мощности моды т на единицу длины в направле-
направлении оси у, a -dPm/dz — мощность, диссипируемая за счет омиче-
омических потерь на единицу длины вдоль оси^ и на единицу длины вол-
волновода (вдоль оси z). Согласно закону Ома, плотность тока в ме-
металле дается выражением J = аЕ. Усредненная по времени ско-
скорость диссипации энергии за счет омических потерь на единицу объ-
объема равна A/2)J-E* = (l/2)alEI2. Таким образом, величину
~dPm/dz можно записать в виде
(П. 10.9)

516
Глава 11
Направляемые волны и интегральная оптика
517
где &т — модовая функция волновода. Если функция &т нормиро-
нормирована на мощность моды Рт = 1 Вт/м, то из A1.10.8) и A1.10.9)
следует, что коэффициент затухания ат может быть записан как
n2 n, n2
= ^/ 'a\&J2dx.
A1.10.10)
Этот результат совпадает с выражением A1.10.3), если сделать за-
замену &п\ - —1о/е0ш.
То, что ТМ-моды и моды высшего порядка обладают большим
затуханием, позволяет использовать волноводы с металлическим
покрытием в качестве фильтров или поляризаторов, которые про-
пропускают только ТЕ-моды низшего порядка.
11.10.2. ВОЛНОВОДЫ НА БРЭГГОВСКОМ ОТРАЖЕНИИ
Обращаясь к рис. 11.28, рассмотрим слоистый диэлектрический вол-
волновод с подложкой, состоящей из периодической слоистой среды с
показателями преломления пх и пг Волноводный слой имеет пока-
показатель преломления п такой, что па < ng < пх 2, где па — показа-
показатель преломления другой граничной среды (для воздуха па ~ 1).
Локализованное распространение формально можно рассматривать
как зигзагообразное распространение плоской волны в сердцевине
(ng), которая испытывает полное внутреннее отражение на границе
раздела х = — t со средой с низким показателем преломления (па) и
брэгговское отражение на границе х — 0 с периодически слоистой
средой. Для высокого брэгговского отражения необходимо, чтобы
угол падения удовлетворял условию Брэгга или, более точно, что-
чтобы условие распространения внутри слоистой среды выполнялось в
пределах «запрещенных» зон (см. разд. 6.6).
Для получения характеристик распространения мод предполо-
предположим, что периодическая слоистая среда является полубесконечной,
простирающейся от * = 0 до * = +оо.В случае ТЕ-мод существу-
существуют лишь компоненты Е' , Нх и Hz. Выберем поле Еу(х, z, t) в виде
A1.2.2). Поперечная функция (? (х) запишется следующим образом:
с1Ек(х)е-к\
c2|cos[/cg(* +
, -/<*<(),
A1.10.11)
РИС. 11.28. Диэлектрический волновод на брэгговском отражении (д/ду = 0).
где с, 2 — постоянные коэффициенты, Ek(x)e~iKz — блоховская вол-
волновая функция электрического поля в слоистой среде (см.
разд. 6.2) и
A1.10.12)
Поперечная функция <?у (х) в области между ^ = 0их= -1 анало-
аналогична поперечной функции планарного волновода [см. A1.2.3)]. Но-
Новой особенностью здесь является блоховская волна в полубесконеч-
полубесконечной периодической среде (х ^ 0). Явный вид блоховской волны в
областях с показателем преломления nt дается выражением F.2.25)
(замечание: вместо z здесь нужно брать х).

518
Глава 11
Возможные решения для ?у и Жг = (//со^)(д ?у/Ъх) являются не-
непрерывными при х = 0 и х = —t. Коэффициенты в A1.10.11) нахо-
находятся из условия непрерывности для ? и д <?у/дх при х = -t. Нала-
Налагая условие непрерывности на ? и д g/Ьх при х = 0, из выражений
F.2.25) и A1.10.11) мы имеем
6o) = c2\coskgt+ у-sin kgt\,
A1.10.13)
~ '*i*ci(°o ~ h) = c2[-kgsin kgt + qacoskgt];
здесь aQ и b0 определяются выражениями F.2.23), a
A1.10.14)
Исключая с, и с2 из выражений A1.10.13) и используя F.2.23), мо-
довое условие для ТЕ-волны можно записать в виде
qacos kgt - kgsin kgt
s\qasitikgt + kgcoskgt
= ik
\x
oiK\
- А- В
- A + В
A1.10.15)
где Л и В даются выражениями F.2.12), Л — период слоистой сре-
среды, а. К— блоховское волновое число. Постоянные с, и с2 опреде-
определяются выражениями A1.10.13) и условием нормировки A1.1.17)
или A1.1.18).
Локализованное распространение мод имеет место, если выпол-
выполнено условие A1.10.15) при вещественных параметрах /3, qa и кч и
если постоянная распространения /3 такая, что свет попадает в одну
из запрещенных зон. Последнее условие соответствует тому, что
блоховское волновое число является комплексным:
К= -д- - iKi A1.10.16)
и приводит к затуханию осцилляции амплитуды поля в слоистой
среде (х ^ 0). На рис. 11.29,6 показано распределение поля такой
локализованной моды, полученной из расчетов [24]. Локализован-
Локализованное распространение света в такой волноводной структуре наблю-
наблюдалось экспериментально в работе [25]. На рис. 11.30 показано из-
измеренное распределение интенсивности локализованной моды в по-
поперечном направлении.
Ъолноводнып
Ърэгговскшх
отрпж п '
РИС. 11.29. а — микрофотография (полученная с помощью сканирующего электрон-
электронного микроскопа) слоистого брэгговского волновода, образованного из чередующих-
чередующихся слоев GaAs и A^Ga^As [25]; б— профиль показателя преломления брэггов-
брэгговского волновода (вверху) и вычисленное поперечное распределение поля (внизу); по-
по43 GA)
казатели преломления: па = 1 (воздух), ng = 3,24
2As), n2 = 3,43 (GaAs) и
а g ^,, 62
= 3,35 (Al0 20Ga() 80As) при длине волны X = 1,15 мкм [i5].

520
Глава 11
РИС. 11.30. Измеренное поперечное распределение интенсивности локализованной
моды в брэгговском волноводе длиной 2 мм. Одно большое деление горизонтальной
шкалы соответствует 10 мкм [25].
Рассмотрение, проведенное выше, предполагает, что периодиче-
периодическая слоистая среда является полу бесконечной. Для локализованно-
локализованного распространения без потерь необходимо, чтобы коэффициент
отражения на границе между волноводным слоем и периодической
средой был равен единице, что возможно только в бесконечной
структуре. На практике число периодов всегда конечное. Поэтому
коэффициент отражения меньше единицы. Таким образом, в волно-
волноводе имеет место небольшая утечка энергии. Коэффициент затуха-
затухания а можно грубо оценить следующим образом. Пусть R — коэф-
коэффициент отражения света, обусловленный брэгговским отражением
на границе х = 0 (R ^ 1). Если dg — угол падения луча в волновод-
ном слое, то луч перемещается на расстояние 2/tg#g при каждом
возвращении назад к той же границе. Таким образом, на участке
длиной L число обратных возвращений равно N' — L/Bttg в ). При
этом коэффициент затухания дается выражением
RN' = e-"L.
Используя выражения /V = Z./B/tg {?,.,),
затухания а можно записать в виде
а = -(\nR)/Bttgde) = -(*?/20Oln/?.
A1.10.17)
kg tg вщ, коэффициент
A1.10.18)
Направляемые волны и интегральная оптика
521
Следует отметить, что а — 0, когда коэффициент отражения R -~
— 100%. Коэффициент отражения/? брэгговского отражателя с конеч-
конечным числом слоев дается выражением F.6.10). Если излучение па-
падает под таким углом, что коэффициент отражения достигает свое-
своего максимального значения th2 \k\NA [см. выражение F.6.11)], то,
используя соотношение ln(tgx) ~ —le'2* при больших х, коэффи-
коэффициент затухания а A1.10.18) можно записать приближенно в виде
-^ехр(-2|к|#Л),
A1.10.19)
где к — постоянная связи, определяемая выражением F.6.5). Заме-
Заметим, что коэффициент затухания а уменьшается экспоненциально с
увеличением числа периодов N.
11.11. ДИЭЛЕКТРИЧЕСКИЕ ВОЛНОВОДЫ
С ВЫТЕКАЮЩИМИ МОДАМИ
В разд. 11.2 мы изучили свойства ТЕ- и ТМ-мод, распространяю-
распространяющихся в тонких диэлектрических волноводах. Было показано, что
тонкие диэлектрические пленки могут поддерживать локализован-
локализованное распространение излучения без потерь при условии, что показа-
показатель преломления внутреннего слоя (сердцевины) превышает пока-
показатели преломления двух граничных сред, т. е.
пг> и,,3.
A1.11.1)
Это условие является необходимым для получения мнимой попе-
поперечной постоянной распространения, что соответствует бесконечно
малому значению поля моды в граничной среде. Существует много
практических приложений, когда бывает желательно или необходи-
необходимо направлять мощность в слое, у которого показатель преломле-
преломления меньше, чем в двух окружающих средах. Примером этого явля-
является волноводный лазер, в котором внутренний слой состоит из
молекулярного газа с п2 = 1. В таком случае полное отражение на
границах отсутствует. Волна, попадающая в такой волновод, теря-
теряет мощность из-за утечки в граничащие среды и затухает с расстоя-
расстоянием z (направление распространения).
Ряд исследователей [26] показали, что описанные выше потери
при определенных обстоятельствах ничтожно малы и такие волно-
волноводы могут быть использованы в лазерных системах [27]. Заметим,
что френелевский коэффициент отражения на границах раздела
приближается к единице, когда угол падения достигает 90°. Таким

522
Глава 11
Направляемые волны и интегральная
оптика
523
РИС. 11.31. Волновод с вытекающими модами, в котором я2 < п\ у ";> ^ и 9j —
углы, под которыми распространяются лучи в средах 1, 2 и 3 соответственно.
образом, потери из-за неполного отражения от диэлектрических
границ будут малы при скользящем падении лучей. Недавно в ра-
работах [28—30] были продемонстрированы так называемые «волно-
водные лазеры» на основе волноводов с вытекающими модами в
качестве передающей среды.
Ниже мы получим характеристики ТЕ-мод и коэффициенты за-
затухания для них. При получении выражений для постоянной рас-
распространения и коэффициентов затухания как для ТЕ-, так и для
ТМ-мод мы будем использовать также геометрооптическое приб-
приближение.
Обращаясь к рис. 11.31, рассмотрим распространение ТЕ-волн
вдоль оси z. Выберем Е (х, z, t) в виде
Е(х, z, t) = & (x)exp[i(ut - pz)].
A1.11.2)
Поперечная функция &у{х) определяется следующим образом:
Сехр(-/Л,х),
cosh2x - /— sinh2x , -t ¦
h2 J
cosh2t + ij-sinh2t ехр[/Л3(л: + tj\,
, A1.11.3)
где
°~7 = x
/-1,2,3,
A1.11.4)
Коэффициенты в A1.11.3) выбираются таким образом, чтобы
функция б? была непрерывной при х = 0их= -/, а//г была не-
непрерывной при х = 0. Налагая условие непрерывности на Нг при
х - —t, из выражения A1.11.3) получаем
tg
h2t
А2(Л, + h3)
(П.11.5)
Заметим, что модовое условие A1.11.5) может быть получено непо-
непосредственно из выражения A1.2.5) с помощью подстановок д — ihv
h -~ h2, p -~ ih3. Это соответствие между двумя группами постоян-
постоянных следует из сравнения формы решений для локализованной мо-
моды A1.2.3) с решением A1.11.3). Знаки перед hx и h3 в экспонентах
решения A1.11.3) выбираются таким образом, чтобы решение опи-
описывало распространение волн в граничащих средах. Это соответст-
соответствует утечке электромагнитной энергии из сердцевины в окружаю-
окружающую среду. Так как вся диэлектрическая структура является пассив-
пассивной (т. е. отсутствуют усиление или источники излучения), утечка
энергии должна соответствовать уменьшению энергии мод в серд-
сердцевине при распространении их вдоль оси z. Таким образом, посто-
постоянная распространения мод утечки должна представлять собой
комплексное число
^/а, A1.11.6)
где а > 0 — коэффициент ослабления мощности моды, а @@) — ве-
вещественная величина. Действительно, модовое условие A1.11.5),
полученное из электродинамического рассмотрения, не выполняется
для вещественных значений /3 в области 0 ^ ft2 ^ п\к\. Из выраже-
выражений A1.11.2)—A1.11.4) следует, что комплексная постоянная рас-
распространения C A1.11.6) приводит к экспоненциальному уменьше-
уменьшению мощности мод вдоль оси z и одновременно к экспоненциально-
экспоненциальному увеличению интенсивности волны с Ы в граничной среде. По-
Поскольку при 1x1 - оо амплитуды полей становятся бесконечными,
модовая функция A1.11.3) с комплексным 0 не является решением

524
Глава 11
уравнений Максвелла, если волноводная структура бесконечна в по-
поперечном направлении. Однако выражение A1.11.3) описывает
приближенно правильно поле вблизи сердцевины и внутри сердце-
сердцевины в волноводной структуре конечной протяженности. Уравне-
Уравнение A1.11.5) можно решить, если учесть выражения A1.11.4) для
величин А,, А2 и А3, определяющих комплексную постоянную рас-
распространения C. Приближенное решение можно получить методом
последовательных приближений (итераций), если волновод «широ-
«широкий» и угол падения в2 близок к углу скольжения @2 = тг/2), так что
О =» А2 < А, з- В этом случае модовое условие можно приближенно
записать в виде
tg
A1.11.7)
Поскольку А2 < А, 3, правая часть выражения A1.11.7) очень мала
и в первом приближении ею можно пренебречь. Тогда в первом
приближении для А2 имеем
SIT
-+, 5=1,2,3....
A1.11.8)
Для широких волноводов (т. е. больших /) величина А2 действитель-
действительно является небольшой при условии, что модовый индекс s мал.
Так как А2 = 0, из A1.11.4) получаем следующие выражения для C,
А, и /г3 в приближении первого порядка:
n2k0,
A1.11.9)
Во втором приближении мы подставляем Ар А2 и А3 из A1.11.8) и
A1.11.9) в правую часть A1.11.7). Это приводит к выражению
sir
tg A2r = i—
1
1
\'/2
A1.11.10)
которое можно рассматривать как приближенное выражение для
h2t, поскольку правая часть мала:
sir .sir
T + '7r
1
1
x'/2
A1.11.11)
Направляемые волны и интегральная оптика
525
Подстановка этого выражения в A1.11.4) дает второе приближение
для /3:
п2кЛ\ - - ——- -
°[ 2\n2kot \
— I
sir
knt
tn2{n\-n\)'/2 tn2{n]-n\)
1/2
A1.11.12)
Таким образом, коэффициент затухания для ТЕ^-мод можно запи-
записать в виде
sir
или, используя кп = 27г/Х, в виде
1
1
A1.11.13)
5=123
2и2Л(//Л)
A1.11.14)
Этот результат был получен в работе [31]. Мы видим, что коэффи-
коэффициент затухания уменьшается как г3. Поскольку такое затухание
обусловливается неполным отражением на диэлектрических грани-
границах (т. е. R < 1), коэффициент затухания как для ТЕ-, так и для
ТМ-волн можно вычислить с помощью модели зигзагообразного
распространения лучей..
П.11.1. ГЕОМЕТРООПТИЧЕСКОЕ ПРИБЛИЖЕНИЕ
Найдем теперь коэффициенты затухания и постоянную распростра-
распространения /3, используя геометрооптическое приближение (см.
разд. 11.2). Поскольку в случае, когда п2 < п 1}, фазовые сдвиги ф2|
и ф23 при отражении от диэлектрических границ равны 0 или ж, мо-
модовое условие A1.2.22) принимает вид
h2t = n2k0cose2t = sir, 5=1,2,3,...,
A1.11.15)
где в2 — угол падения (см. рис. 11.31). Пусть R2l и R23 — коэффици-
коэффициенты отражения на диэлектрических границах х - 0 и х = -t соот-
соответственно. Из выражений A1.10.17) и A1.10.18) следует, что коэф-

526
Глава 11
фициент затухания а можно записать в виде
A1.11.16)
При скользящем падении (cos02 «0) коэффициенты отражения R2X
и R23 можно приближенно записать следующим образом:
1 -4-
i
1 - 4-
R
23
(ТЕ),
(TM),
¦"«^ (ТЕ),
A1.11.17)
1 - 4
. w3cos02
w2cos03
A1.11.18)
(TM),
где 0, и 6»з — углы падения лучей (см. рис. 11.31) в средах 1 и 3 со-
соответственно. Используя закон Снелля, для этих углов можно на-
написать следующие приближенные выражения:
сое*,* 1- Р*
211/2
A1.11.19)
Подставим теперь выражения A1.11.17) и A1.11.18) для R2l и
R23 в A1.11.16) и используем соотношение 1пA + х) = х при малых
х. Тогда коэффициенты затухания для ТЕ- и ТМ-мод можно запи-
записать в виде
ХЕ _
2Л2
fit \ /J,COS0. ^ /J,COS&
_.тм
2Л21 /j,cos#2
fit I w2cos в.
A1.11.20)
Используя A1.11.15), A1.11.19) и выражение /8 = n2k0 (k0 = 2ir/X),
из A1.11.20) получаем следующие выражения для коэффициентов
Направляемые волны и интегральная оптика
527
затухания:
„ТЕ
2n2X(t/XK
A1.11.21)
2n2X(t/XK
A1.11.22)
Заметим, что это выражение, полученное в геометрооптическом
приближении, совпадает с выражением A1.11.14), которое было по-
получено методами волновой оптики. Из A1.11.21) и A1.11.22) следу-
следует, что ТМ-волны затухают сильнее, чем ТЕ-волны, поскольку
п2 < и, з- Это прямо связано с тем фактом, что коэффициент отра-
отражения для волн ТМ всегда меньше (или равен), чем для волн ТЕ
(т. е. R™ ^ RTE). Из выражений A1.11.21) и A1.11.22) следует, что
моды высшего порядка (большие s) обладают большими потерями,
чем моды низшего порядка. В случае когда и, < п2 < п3, выраже-
выражения A1.11.21) и A1.11.22) также справедливы, если мы исключим
чисто мнимый член (и2 - и2)"|/2 в квадратных скобках, который
является малой поправкой к постоянной распространения. В случае
симметричного волновода с п2 — 1 и пх = п3 = п0 выражения
A1.11.21) и A1.11.22) принимают вид
«Iе =
\1/2
s2X2nl
\1/2
1,2,3,
A1.11.23)
Некоторые типичные коэффициенты затухания для симметричного
волновода с s = 1, п0 = 2, 0 и X = 1 мкм приведены ниже:
мкм
1
10
50
аТЕ,
„тм
СМ
см
5774
23094
46,2
184,8
5
23
,8
,1
4,6 •
1,85-
10
10
-2
-1
Таким образом, в случае / > 10Х мы находим аТЕ X < 6-10 4. Та-
Такие потери легко могут быть перекрыты усилением в большинстве
лазерных сред [28, 30].

528
Глава 11
Окна Брюстера
из CdTe
Трубка из ВеО
Коваровые
электроды
Зеркала
\.
Фланец
металл—вакуум
4 Спай металла
с керамикой
РИС. 11.32. Конструктивные особенности лазера на капиллярной трубке из ВеО. (Из
работы [30]; copyright 1973 IEEE.)
На рис. 11.32 схематически показано устройство волноводного
СО2-лазера на длине 10,6 мкм, использующего описанные выше мо-
моды утечки. Волноводный режим достигается в капиллярной трубке
из ВеО.
11.12. ПОВЕРХНОСТНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
(ПОВЕРХНОСТНЫЕ ПЛАЗМОНЫ)
В разд. 6.9 мы показали, что на границе между однородной ди-
диэлектрической и периодической слоистой диэлектрической средами
могут существовать поверхностные электромагнитные волны. Эти
моды являются в действительности затухающими блоховскими вол-
волнами периодической среды. При данной частоте ш в такой струк-
структуре может распространяться большое число как ТЕ-, так и ТМ-
мод. Покажем теперь, что поверхностные электромагнитные вол-
волны могут также существовать на границе между двумя средами,
если диэлектрические проницаемости сред имеют противополож-
противоположные знаки (например, воздух и серебро). При данной частоте су-
существует лишь одна ТМ-мода. Амплитуда волны экспоненциально
уменьшается в обеих средах в направлении, перпендикулярном по-
поверхности. Эти моды называются также поверхностными плазмо-
нами вследствие вклада электронной плазмы в отрицательную диэ-
диэлектрическую проницаемость металлов, когда оптическая частота
меньше плазменной частоты (т. е. ш < ы ). Ниже мы получим ха-
характеристики распространения поверхностных электромагнитных
волн.
Обращаясь к рис. 11.33, рассмотрим распространение волны
вдоль границы раздела между средой с положительной диэлектри-
диэлектрической проницаемостью (п\ > 0) и средой с отрицательной диэлект-
Направляемые волны и интегральная оптика
529
¦>¦ z
РИС. 11.33. Электромагнитная поверхностная волна на границе между двумя среда-
средами. Показана зависимость амплитуды поля Н (или ?_) от х (расстояния вдоль нор-
нормали к границе раздела). Два эллипса указывают состояния поляризации вектора Е
в двух средах.
рической постоянной (п\ < 0). Типичным примером является грани-
граница между воздухом и серебром, когда п\ = 1 и п\ — — 16,40 -
— /0,54 при А = 6328 А. Если пренебречь малой мнимой частью
(—/0,54), то серебро можно рассматривать как материал с отрица-
отрицательной диэлектрической постоянной. Наличие мнимой части будет
приводить к затуханию волны при распространении, вдоль грани-
границы. Будем сначала искать решение для поверхностных мод, прене-
пренебрегая мнимой частью диэлектрической проницаемости. При этом
коэффициент затухания может быть получен с .помощью теории
возмущений или непосредственно из комплексного решения уравне-
уравнения, представляющего собой модовое условие.
Структуру, показанную на рис. 11.33, можно рассматривать как
частный случай волноводной структуры, изображенной на рис. 11.2
с / = 0. Следовательно, к волноводу на рис. 11.33 можно приме-
применить выражения для полей A1.2.3), A1.2.10) и модовые условия
A1.2.5) и A1.2.11) для ТЕ- и ТМ-волн. Полагая в выражении
A1.2.5) t — 0, получаем условие существования мод для поверх-
поверхностных ТЕ-волн:
p + q = 0, A1.12.1)
где р и q — постоянные экспоненциального затухания в средах 3 и
1 соответственно. Поскольку для локализованной моды требуется,
34-631

530
Глава 11
чтобы/? > 0 и q > О, условие A1.12.1) не может быть выполнено.
Это соответствует тому, что поверхностная ТЕ-мода не может су-
существовать на границе раздела двух однородных сред. Для ТМ-
волн модовая функция Жу (х) может быть записана в виде
Се'4*,
Серх,
х>0,
х < 0,
A1.12.2)
где С — постоянная нормировки. Условие существования мод мож-
можно получить из непрерывности функции Ег на границе х = 0 или не-
непосредственно из выражения A1.2.11), полагая / = 0:
4 + 4=0. A1.12.3)
Так как п2п2 < 0, условие A1.12.3) существования поверхностных
ТМ-волн может быть удовлетворено для локализованного распро-
распространения cp>0uq>0. Используя выражения A1.2.4) для/? и q
и модовое условие A1.12.3), постоянную распространения /3 можно
записать в виде
/8 =
и? + п\
1/2
(О
с
A1.12.4)
Распространяющаяся локализованная мода должна иметь вещест-
вещественную постоянную распространения. Для этого из A1.12.4) и усло-
условия п\п\ < 0 получаем
+ п\ < 0,
A1.12.5)
т. е. сумма диэлектрических проницаемостей сред должна быть от-
отрицательной. В соответствии с A1.2.4) и A1.12.4) постоянные зату-
затухания р и q можно записать следующим образом:
-иг
о>
03
A1.12.6)
Согласно условию A1.12.5), эти величины являются положитель-
положительными. Из A1.2.9) и A1.12.2) мы имеем следующие выражения для
Направляемые волны и интегральная оптика
531
составляющих электрического поля:
«е0 п2
A1.12.7)
— ег"е'
Е =
A1.12.8)
Мы видим, что вектор электрического поля Е является эллиптиче-
эллиптически поляризованным в плоскости xz, причем главные оси эллипса
параллельны осям координат. При распространении в направлении
+Z (/3 > 0) вектор Е имеет правую эллиптическую поляризацию в
верхней половине пространства х > 0 и левую эллиптическую поля-
поляризацию в нижней половине пространства х < 0. Эллиптичности
равны fi/q и — /3//? для верхней и нижней половин пространства со-
соответственно (см. рис. 11.33).
Нормировочная постоянная С выбирается таким образом, что-
чтобы мощность поверхностной моды, определяемой выражениями
A1.12.2), A1.12.7) и A1.12.8), была равна 1 Вт на единицу ширины
в направлении оси у. Используя выражения A1.2.12) и A1.12.2), по-
получаем
С2 =
-1
(П.12.9)
11.12.1. КОЭФФИЦИЕНТ ЗАТУХАНИЯ
Выше мы предполагали, что как п\, так и п\ являются веществен-
вещественными. Например, в случае когда рассматривается граница раздела
воздух — серебро, мы имеем для воздуха п\ = 1, а для серебра п\ с
небольшой мнимой частью. Действительно, диэлектрические про-
проницаемости еоп2 большинства металлов представляют собой ком-
комплексные числа в оптической частотной области. Поверхностная
волна, распространяющаяся на границе раздела металл — диэлект-
диэлектрик, испытывает омические потери. Поэтому она затухает в на-

532
Глава 11
правлении оси z. Это соответствует комплексной постоянной рас-
распространения
p-p«*-i\a, A1.12.10)
где а — коэффициент затухания мощности A1.10.2), а /3@)— ве-
вещественная часть постоянной распространения. Выражение для по-
постоянной распространения /3, полученное выше [выражение
A1.12.4)], в действительности справедливо также для комплексных
л2 и п\. В случае границы раздела диэлектрик — металл и2 является
вещественным положительным числом, а л] — комплексным чис-
числом (л — //сJ. Таким образом, используя выражение A1.12.4), по-
постоянную распространения поверхностной волны можно записать в
виде
/3 =
п2(п - пс)
п\ + (п - пс)
1/2
(О
с '
A1.12.11)
где к — коэффициент экстинкции металла. В представляющей инте-
интерес спектральной области п < к. Это соответствует малой мнимой
части величины п\, так как п\ = (л2 — к2) — 2/и/с. В этом случае по-
постоянная распространения /3 приближенно записывается как
1
гпкп\
(л2 - к2){п\ + л2 - к2)
п2+(п2-к2)
(О
с
A1.12.12)
A1.12.13)
Таким образом, согласно выражениям A1.12.10), A1.12.12) и
A1.12.13), коэффициент затухания а можно записать следующим
образом:
2пкп\
[{Я2 _
A1.12.14)
В выражениях A1.12.12)—A1.12.14) мы сохраняем член п2 — к2, так
как он пропорционален вещественной части диэлектрической прони-
Направляемые волны и интегральная оптика
533
цаемости металла. Используя диэлектрические проницаемости
A1.12.15)
е, = е0п2,
eR - ie, = (п2 - к2) - Ипк,
постоянную распространения и коэффициент затухания можно за-
записать соответственно в виде
а =
е.е
1/2<0
CR/ С
3/2
A1.12.16)
A1.12.17)
где е, — проницаемость диэлектрика, a sR - is, — комплексная ди-
диэлектрическая проницаемость металла. Отметим, что е, > 0,
eR < 0 и е, + eR < 0, причем е, всегда больше нуля.
Коэффициент затухания может быть найден также из вычисле-
вычисления омических потерь. При этом мы получаем следующее выраже-
выражение [аналогичное A1.10.11)]:
2/ °\Ц2<1х,
A1.12.18)
где а — проводимость, связанная с комплексной диэлектрической
проницаемостью соотношением
: 2ыеопк
- «еое,.
A1.12.19)
Используя выражения A1.12.7) и A1.12.8) для поля Е, а также вы-
выражения A1.12.4) и A1.12.6), после простого интегрирования в
A1.12.18) мы приходим к выражению для коэффициента затухания
а, аналогичному A1.12.14).
11.12.2. ПРИМЕР. ПОВЕРХНОСТНЫЕ ВОЛНЫ
НА ГРАНИЦЕ РАЗДЕЛА ВОЗДУХ — СЕРЕБРО
При длине волны X = 6328 А комплексный показатель преломле-
преломления серебра равен п — /к = 0,067 - /4,05. В соответствии с
A1.12.13) постоянная распространения поверхностной моды на гра-

534
Глава 11
Направляемые волны и интегральная оптика
535
нице раздела между воздухом и серебром равна
/3 = 1,032(ш/с) = 10,25 мкм-',
а коэффициент затухания [см. A1.12.14)] равен
а = 0,0022(«/с) = 220 см-'.
Постоянные затухания поля р и q вычисляются следующим обра-
образом:
р = 4,18(ш/с) = 26,26/Х, . q = 0,25(w/c) = 1,60/X.
Заметим, что амплитуда поля в серебре уменьшается до величины
е~26,26 _ 4- Ю"|2 на глубине, равной длине волны X = 6328 А. Та-
Таким образом, волна в основном распространяется в воздухе, хотя
направляется поверхностью серебра. Это находит также отражение
в фазовой скорости поверхностной волны, которая равна с/1,032 и
очень близка к скорости света в воздухе.
Коэффициент затухания а для серебра (и — /к = 10,8 - /60,7)
при длине волны X = 10 мкм равен
а = 0,6 см.
Если положить п2 = 1 и пренебречь величиной п2 в знаменателе
выражения A1.12.14) (поскольку п2 < к2), то коэффициент затуха-
затухания а можно записать в виде
а =
А-пп
A1.12.20)
Мы видим, что а уменьшается как к 3. Значения коэффициента экс-
тинкции к металлов, подобных серебру, золоту, алюминию и меди,
очень большие. Таким образом, из A1.12.20) следует, что в инфра-
инфракрасной области спектра коэффициент затухания а поверхностных
волн для этих металлов мал.
ЗАДАЧИ
11.1. Теорема взаимности Лоренца. Пусть (Е,, Н,) и (Е-,, Н2) два
независимых решения уравнений Максвелла A1.1.1) и
A1.1.2). Покажите, что
V «(Е, X Н2 - Е2 X Н,) = 0,
если е и in — эрмитовые тензоры (т. е. среда без потерь).
11.2. Зеркальное преобразование локализованной моды. Диэлект-
Диэлектрическая волноводная структура с профилем показателя пре-
преломления п2(х, у) является зеркально-симметричной относи-
относительно плоскости z = 0.
а) Пусть Е2 и Н2 — векторы электрического и магнитного
полей волны. Покажите, что зеркальные преобразования
полей Е2 и Н2 определяются выражением A1.1.13).
б) Покажите, что
\Re[E'2 X Н'*] • а, = -\Re[E2 XH*]-a:.
11.3. Соотношение ортогональности для ТЕ-мод. Пусть (Е,, Н,)
и (Em, Hm)— две произвольные моды вида A1.1.3а) и
A1.1.46) и задан интеграл
а) Покажите, используя уравнения Максвелла A1.1.1) и
A1.1.2) и операторУ = V, + a^d/dz, что
2<oju
Отсюда следует, что соотношение ортогональности
A1.1.17) для ТЕ-волн с Ег = 0 сводится к выражению
A1.1.18).
б) Покажите, используя интеграл из п. а задачи и интегри-
интегрируя его по частям, что
"lm
в)
Таким образом, достаточным условием для перехода от
соотношения ортогональности A1.1.17) и A1.1.18) явля-
является выполнение условия либо V • Е = 0, либо аг • Е = 0.
Волновое уравнение A1.1.4) справедливо при условии,
что V-E = 0. Получите соотношение ортогональности
A1.1.18) непосредственно из уравнения A1.1.4).

536
Глава 11
11.4. Соотношение ортогональности для ТМ-мод. Используйте
формулировку задачи 11.3 и такое же определение для //т.
а) Покажите, что
Таким образом, для ТМ-волн (Hz = 0) соотношение ор-
ортогональности A1.1.17) сводится к выражению A1.1.18).
б) Получите соотношение, аналогичное соотношению, за-
записанному в п. б задачи 11.3. Покажите, что условие
Н ¦ Ve = 0 или лг ¦ Н = 0 является достаточным для вы-
выполнения соотношения ортогональности A1.1.19).
11.5. Коэффициент локализованности моды. Пусть Г, — доля
мощности, распространяющаяся в среде / (/ = 1, 2, 3). В
частности, долю Г2 мощности моды в врлноводном слое п2
обычно называют коэффициентом локализованности моды.
Если мощность моды нормирована на величину 1 Вт, то Г,-
определяют в виде
XH*)-azdx, i-1,2,3,
где интегрирование производится по области, занимаемой
/-й средой.
а) Покажите, что для ТЕ-мод имеют место следующие вы-
выражения:
г Vq h2
1 t + l/q + Up h2 + q2'
г * i Vp pl -i
2 t + l/q + \/p t + l/q + l/ph2 + p2
Uq
t + l/q + l/ph2 + q
2 '
3 / + l/q + l/ph2 + p2
[Заметим, что Г, + Г2 + Г3 = 1. Это доказывает соот-
соотношение A1.2.7).]
Направляемые волны и интегральная оптика 537
б) Покажите, что для ТМ-мод справедливы выражения
Уд'^
г
1
г
2
^_
' + \/q' + \/р' h2 + q2'
'' I l/q>
2 /'
I
/' + l/q' + \/p' f + l/q' + \/p' h2 + q2
i
Up'
P'
f + l/q' + \/p' h2 + p2'
Up'
h2
t' + Uq' + Up' h2 + p2'
где
J_
n\q
n\p '
в) Покажите, что Г2 возрастает с увеличением /J и
lim Г2 = 1.
Таким образом, поскольку низшие моды имеют большие
постоянные распространения, они более локализованы
по сравнению с высшими модами. [Указание: используй-
используйте соотношения h2 + р2 = {п\ — п2)к2 и h2 + q2 =
= (п2 - п\)к2.)
г) Сравните коэффициенты локализованности Г2 для мод
д) Покажите, что в пределе, когда имеет место наилучшая
локализация (т. е. h — 0),
тм
4 +
п\ Я n
где р - ко(п2 - п\Г\ q = ко(п2 - п\
У2

538
Глава 11
е) Покажите, что для волноводов с металлическим покры-
покрытием (и2 < 0)
ТМ
рТЕ
1ъ •
Иными словами, моды ТМ проникают глубже внутрь
металла, чем моды ТЕ, и, следовательно, больше зату-
затухают.
11.6. Возмущенный диэлектрический планарный волновод. Пусть
возмущение диэлектрической проницаемости планарного
волновода записывается в виде
Ди2(л:) = { Ди2, -
где An2, An2, и Ап\ -— постоянные величины (могут быть
комплексными при наличии усиления или поглощения),
а) Покажите, что поправка к постоянной распространения
дается выражением
где
,- - 1 2 3
причем интегрирование |, осуществляется по /-й среде.
Величины Г определяют долю мощности, которая про-
протекает в соответствующей среде.
б) Для планарного волновода с фиксированной толщиной /
постоянные распространения $2т можно рассматривать
как функции величин п2, п\ и и2. Таким образом, для Ь$2т
можно записать
дп]
дп2
Направляемые волны и интегральная оптика
539
Функция /3^ = /3^(/2р п\, п\) входит неявно в выражения
A1.2.5) и A1.2.11). Покажите непосредственно из выра-
выражения A1.2.5), что
/=1,2,3.
11.7. Пусть некоторая мода имеет вид
где атт г?т — член в разложении функции 8 <?т, так что
Ь<?т ортогональна к (?т. Покажите, что если &'„ норми-
нормирована следующим образом:
где $'2 = /3?„ + 6/3,2„, то атт дается выражением
4
2 рт
11.8. Преобразование мод ТЕ «-> ТМ вследствие периодического
электрооптического взаимодействия описывается выражени-
выражениями F.5.19) и F.5.20).
а) Покажите, что преобразованная мощность равна поло-
половине максимального значения, когда
APL = 0,8тг,-
здесь Д8 определяется выражением A1.7.6).
б) Покажите, что полная ширина полосы пропускания
(определяемая на половине максимума) в длинах волн
при отсутствии модовой дисперсии дается выражением
N ¦
в) Покажите, что при учете модовой дисперсии относи-

540
Глава 11
тельная ширина полосы равна
ДЛ
1/2
0,80
N
Ди дХ
где
Д» = „ТЕ _ „ТМ_
11.9. Поверхностные плазмоны.
а) Покажите, что если металл рассматривать как газ сво-
свободных электронов с диэлектрической проницаемостью
где о — плазменная частота, то поверхностные плаз-
монные моды существуют только при условии
Здесь предполагается, что п\ = 1.
б) Покажите, что для постоянной распространения /3, опре-
определяемой выражением A1.12.4), справедливо неравен-
неравенство
если п\ > 0 и п\ + п\ < 0. Здесь kQ = о/с.
в) Покажите, что
и что состояния поляризации вектора Е в двух средах яв-
являются взаимно ортогональными.
г) Получите выражение для г-компоненты вектора Пойн-
тинга. Покажите, что в средах с положительной и отри-
отрицательной диэлектрическими проницаемостями потоки
мощности имеют противоположные направления. Таким
образом, поверхностная плазмонная волна, распростра-
распространяющаяся вдоль поверхности серебра в направлении +z,
имеет отрицательный поток мощности в серебре и поло-
положительный поток мощности в воздухе.
д) Комплексный показатель преломления золота при длине
волны А — 10 мкм равен п - in = 7,4 — /53,4. Найдите
Направляемые волны и интегральная оптика
541
постоянную распространения /3<0) и коэффициент затуха-
затухания а поверхностной плазмонной волны.
ЛИТЕРАТУРА
1. Tien Р. К., Ulrich R,, Martin R. J., Modes of propagating light in thin deposited
semiconductor films. — Appl. Phys. Lett., 14, 291 A969).
2. YarivA., Coupled mode theory for guided wave optics.— IEEE J. Quant.
Electron., 9, 919 A973).
3. KuhnL., DakssM.L., Heidrich P. F., Scott B. A., Deflection of optical guided
waves by a surface acoustic wave. — Appl. Phys. Lett., 17, 165 A970).
4. Alferness R. C., Electro-optic waveguide ТЕ « TM mode converter with low drive
voltage. — Opt. Lett., 5, 473 A980).
5. Alferness R. C, Efficient waveguide electro-optic ТЕ <-• TM mode con-
converter/waveguide filter. — Appl. Phys. Lett., 36, 513 A980).
6. Dixon R. W., The photoelastic properties of selected materials and their relevance to
acoustic light modulators and scanners. — J. Appl. Phys., 38, 5149 A967).
7. Stoll H., Yariv A., Coupled mode analysis of periodic dielectric waveguides. — Opt.
Commun., 8, 5 A973).
8. Flanders D. C, Kogelnik #., Schmidt R. V., Shank С. V., Grating filters for thin
film optical waveguides. — Appl. Phys. Lett., 24, 194 A974).
9. Kogelnik H., Shank C. V., Coupled wave theory of distributed feedback lasers. — J.
Appl. Phys., 43, 2328 A972).
10. Nakamura M., YarivA., Yen H. W., SomekhS., Garvin H. L., Optically pumped
GaAs surfase laser with corrugation feedback. — Appl. Phys. Lett., 22, 515 A973).
11. Aiki K., Nakamura M., Umeda J., Yariv A., KatzirA., Yen H. W., GaAs—GaAlAs
distributed feedback laser with separate optical and carrier confinement. — Appl.
Phys. Lett., 27, 145 A975).
12. SomekhS., докторская диссертация, Calif, lnst. Technol., 1973.
13. MarcatiliE. A. J., Dielectric rectangular waveguides and directional couplers for in-
integrated optics. — Bell Syst. Techn. J., 48, 2071 A969).
14. Somekh S., Garmire E., Yariv A., Garvin H. L., Hunsperger R. G., Channel optical
waveguide directional couplers. — Appl. Phys. Lett., 22, 46 A973).
15. CampbellJ. C, Blum F. A., Shaw D. W., Lawley K. L., GaAs directional coupler
switch. — Appl. Phys. Lett., 27, 202 A975).
16. Kogelnik H., Schmidt R. K, Switched directional couplers with alternating Д/3. —
IEEE J. Quant. Electron., QE-12, 396 A976).
17. Schmidt R. V., Kogelnik H., Electro-optically switched coupler with stepped A0
reversal coupler using Ti-diffused LiNbO3 waveguide. — Appl. Phys. Lett., 28, 503
A976).
18. Livanos A. C, KatzirA., YarivA., Hong C. S., Chirped-grating demultiplexers in
dielectric waveguides. — Appl. Phys. Lett., 30, 519 A977).
19. KatzirA., Livanos A. C., Shellan J. В., Yariv A., Chirped gratings in integrated op-
optics. — IEEE Quant. Electron., QE-13, 296 A977).
20. Miller S. E., Some theory and applications of periodically coupled waves. — Bell
Syst. Techn. J., 48, 2189 A969).
21. Yeh P., Taylor H. F., Contradirectional frequency-selective couplers for guided-wave
optics. — Appl. Opt., 19, 2848 A980).
22. Tien P. K., Integrated optics and new wave phenomena. — Rev. Mod. Phys., 49,
361 A977).

542
Глава 11
23. Tien Р. К., Martin R. J., Riva-Sanseverino S., Novel metal-clad optical components
and method of forming high-index sudstrate for forming integrated optical
circuits. — Appl. Phys. Lett., 27, 251 A975).
24. Yen P., Yariv A., Bragg reflection waveguides. — Opt. Commun., 19, 427 A976).
25. Cho A. Y., Yariv A., Yen H., Observation of confined propagation in Bragg
waveguides. — Appl. Phys. Lett., 30, 471 A977).
26. Marcatili E. A. J., Schmeltzer R. A., Hollow metallic and dielectric waveguides for
long distance optical transmission and lasers. — Bell. Syst. Tech. J., 43, 1783 A974).
27. Steffen H., Kneubuhl F. K., Dielectric tube resonators for infrared and submilli-
meter-wave lasers. — Phys. Lett., 27A, 612 A968).
28. Smith P. W., A waveguide gas laser. — Appl. Phys. Lett., 19, 132 A971).
29. Bridges T. J., Burkhardt E. C, Smith P. W., CO2 waveguide lasers. — Appl. Phys.
Lett., 20, 403 A972).
30. Abrams R. L., Bridges W. В., Characteristics of sealed-off CO2 waveguide lasers. —
IEEE J. Quant. Electron., 9, 940 A973).
31. Hall D. В., Yeh C, Leaky waves in heteroepitaxial films.— J. Appl. Phys., 44,
2271 A973).
32. Hall D., Yariv A., Garmire E., Optical guiding and electro-optic modulation in
GaAs epitaxial layers. — Opt. Commun., 1, 403 A970).
Дополнительная литература
1. Integrated Optics (ed. D. Marcuse). — New York: IEEE Press, 1972 (препринты по
интегральной оптике до 1972 г.).
2. Tien P. K., Light waves in thin films and integrated optics. — Appl. Opt., 10, 2395
A971).
3. Integrated Optics (ed. T. Tamir). — Berlin: Springer-Verlag, 1975. [Имеется пере-
перевод: Интегральная оптика/Под ред. Т. Тамира. — М.: Мир, 1978.]
4. Tien Р. К., Integrated optics and new wave phenomena in optical waveguides. —
Rev. Mod. Phys., 49, 361 A977).
Глава 12
НЕЛИНЕЙНАЯ ОПТИКА
12.1. ВВЕДЕНИЕ
В настоящей и следующей (заключительной) главах мы рассмотрим
некоторые явления и применения, которые относятся к нелинейной
оптике. Это ветвь оптики, которая использует преимущества нели-
нелинейного отклика атомов и молекул применительно к оптическим
полям излучения.
В любой реальной атомной системе поляризация, наведенная в
среде, не пропорциональна оптическому электрическому полю, а
может быть выражена в виде разложения в ряд Тейлора:
p. =
2diJkEjEk
A2.1.1)
где Р( — /-я компонента мгновенной поляризации, а Е( — /-я компо-
компонента мгновенного поля. Здесь предполагается суммирование по
повторяющимся индексам; Ху — линейная восприимчивость, тогда
как д-к и Хщ — нелинейные оптические восприимчивости второго и
третьего порядка соответственно. В выражении A2.1.1) предпола-
предполагается, что система не имеет потерь и, следовательно, отклик явля-
является мгновенным. В этом случае можно показать, что коэффициен-
коэффициенты Ху> diJk, Xjjirf инвариантны при любых перестановках их индек-
индексов; например, xi23i = Хгпз-
Нелинейный оптический отклик, характеризуемый параметрами
dyk и %*/» приводит к многочисленным интересным явлениям и
применениям. Нелинейность второго порядка Р(. = 2dijkEjEk от-
ответственна за генерацию второй гармоники [1] (удвоение частоты),
за генерацию суммарной и разностной частот и за параметрическое
усиление и генерацию. Член третьего порядка Pt = Ахнк,Е,ЕкЕ, фи-
фигурирует в разнообразных, явлениях, таких, как генерация третьей
гармоники [2], комбинационное рассеяние и рассеяние Бриллюэна
[3], самофокусировка и оптическое фазовое сопряжение (см. гл. 13).
В данной главе мы дадим описание основ генерации второй гармо-
гармоники, а также параметрического усиления и резонанса (два нелиней-
нелинейных явления второго порядка).
Мы не будем касаться в этой главе физического происхождения
нелинейных коэффициентов djk и Хукп а примем их в качестве мате-

544
Глава 12
риальных параметров и изучим электромагнитные явления и при-
применения, последние из которых стали возможными благодаря нели-
нейностям. Читатель, интересующийся физическими основами,
может обратиться к работам [4—7].
12.2. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ ВТОРОГО ПОРЯДКА;
ОБЩАЯ МЕТОДОЛОГИЯ
Рассмотрим нелинейную связь двух оптических полей. Первое из
них, выражаемое через компоненты электрического поля, дается
выражением
?и'@ = RelEpe"') = UEpe'' + компл.) (j = х, у, z), A2.2.1)
J V7 ' v ' сопр. '
в то время как поле при частоте ш2 записывается в виде
?,"*(/) = R^Epe1"*1) {к = х, у, z). A2.2.2)
Если среда нелинейная, то присутствие этих полей вызывает по-
поляризации на частотах пшх + mw2, где пит — любые целые чис-
числа. Представляя поляризационные компоненты на частоте о>3 =
= Wj + ш2 вдоль /-го направления как
Р»1-»>+»2(/) = Re(p,e'') A2.2.3)
и ограничиваясь рассмотрением в A2.2.1) членов второго порядка,
т. е.
P^ld^EjE,, A2.2.4)
мы получаем
РДО = id^Epe'' + \ЕреШг' + компл. сопр. ) X
X (^Е^'е'' + \Ере'Ш2' + компл. сопр. V A2.2.5)
Рассмотрим только член, соответствующий суммарной частоте:
p-. + »2(f) = Jrf ?-.?-2e'(«.+-2)« + rf ??-.е/<-2 + -,)» + КОМПЛ. 1,
сопр. J
A2.2.6)
где мы используем соглашение о суммировании по повторяющимся
индексам. В системах без потерь (с мгновенным откликом) dik =
Нелинейная оптика
= djjk [8], мы имеем
545
К0МПЛ сопр
+ компл. сопр.
или
гГ—^тг = 2diJkEpEp. A2.2.7)
В системах с потерями djjk обычно зависит от w, и us2 и рассмат-
рассматривается сумма или разность этих частот. Таким образом, нелиней-
нелинейность можнс- определить, вообще говоря, не через мгновенные оп-
оптические поля, как это было сделано/в A2.1.1), а через их комплекс-
комплексные амплитуды
p.,—1+«2 = 2diJk(-u3, «„
и
где коэффициент diJk (—с^,
плексной амплитуды />р~ш
что в общем случае
A2.2.8a)
)?7.(?-2)*, A2.2.86)
ш2) связывает /-ю компоненту ком-
комс произведением EjlE^2. Заметим,
поскольку два этих коэффициента относятся к случаям, когда поля
с частотами ш1 и ш2 имеют различные направления, так что резуль-
результирующая />р=ш1+ш2 для них не обязательно одна и та же. Однако
имеет место следующее равенство:
-"з. «1,
A2.2.9)
Мы будем рассматривать главным образом случай прозрачных
кристаллов без потерь, когда коэффициенты djk не зависят от ча-
частоты или от того, на суммарной или разностной частоте происхо-
происходит генерация. Ниже мы будем опускать любые их обозначения,
связанные с частотой.
Только кристаллы без центра симметрии обладают ненулевым
тензором djJk. Это следует из требования того, чтобы в центросим-
метричных кристаллах изменение знаков у ?"' и Е%2 приводило к
изменению знака поляризации р^^=ш1+ш2> но не влияло на значения
35-631

546
Глава 12
амплитуд. Используя выражение A2.2.8), мы получаем
так что с/ук = 0. Отсутствие симметрии относительно инверсии яв-
является также необходимым условием для линейного электрооптиче-
электрооптического эффекта и пьезоэлектричества, т. е. все электрические и пье-
пьезоэлектрические кристаллы проявляют нелинейные оптические
свойства второго порядка (Р ~ Е2). Этот же аргумент можно ис-
использовать для доказательства того, что все кристаллы, а также
жидкости и газы проявляют оптические нелинейности третьего по-
порядка.
Коэффициенты dljk измеряют чаше всего в экспериментах по ге-
генерации второй гармоники, когда о>, = ш2=-ш. В этом случае мы
имеем
~ "ijk^j
A2.2.10)
Заметим, что выражения A2.2.10) и A2.2.8) различаются множите-
множителем 2. Это следует непосредственно из A2.2.5). Поскольку в выра-
выражении A2.2.10) перестановка индексов./ и к местами не имеет ника-
никакого физического смысла, в соответствии с G.1.10) можем заме-
заменить нижние индексы kj и jk условными индексами:
XX
yz = zy = 4, xz = zx = 5, xy = yx = 6.
Получаемые коэффициенты </у образуют Зхб-матрицу, которая,
действуя на вектор-столбец Е1, дает вектор поляризации Р:
d22
'23
'эз
«14
'24
•34
'15
'25
«35
16
"У
Ej
2EzEy
2EZEX
A2.2.11)
Тензор dtj в условных обозначениях удовлетворяет тем же тре-
требованиям симметрии, что и пьезоэлектрический и электрооптиче-
ТАБЛИЦА 12.1. Нелинейные оптические тензоры в условных обозначениях
для всех кристаллических классов
Классы
Центросимметричные классы
1,2/m, ттт, 4/т, 4ттт, 3, Зт, 6/т, бттт, тЗ, тЗт:
Класс 1—С,:
0 0 0 0 0 0'
0 0 0 0 0 0
0 0 0 0 0 0j
Триклинная система
Моноклинная система
Класс т— С/.
Класс т—Cs:
т J. х2'
Класс 2—С,:
1 «22
о о
'23
0
0
0
0
^35
'26
A0)
о
о
0
«2
о
о
о
о
'24
d24
0
«",5
25
«26
о
о
о
"6
(Ю)
(8)
Класс
2-С2:
2
и V
0
dlx
0
0
«2
0
0
d23
0
rf14
0
d34
0
rf25
0
^16
0
rf36
(8)
Класс тт2— С
Орторомбическая система
2v
0
0
0
0
^33
'24
0
о
E)
1

ТАБЛИЦА 12.1. (Продолжение)
Класс 222—D2:
0
0
0
0
0
0
0
0
0
du
0
0
0
«5
0
0
0
«"зб
C)
Тетрагональная система
Класс 4—С4:
Класс 4—S4:
Класс 4mm—С4„
Класс 42m—D2d:
Класс 422—D4:
О* О
О О
36 / D)
О
о
О
О
«"зз
т II х,
О О О di4
ОООО
0 0 0 0
dxs 0
0 0
0 0
0
0
C)
О ^
О
B)
о
о
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
Тригональная система
КлассЗ—С*:
Класс 3m—C3v:
m
~d22
d3X
0
~d22
0
0
«"зз
0
d22
0
0
«".5
-dxA
0
0
dxs
0
-d
22
F)
0
0
0
0
/D)
ТАБЛИЦА 12.1. (Продолжение)
Класс 3m— C3v:
m ± x2
Класс 32— D3:
(dn
О
d3l
dl5
О О
D)
dn
0
0
-dn
0
0
0
0
0
d»
0
0
0
"<M4
0
0
-dn
0
B)
Класс 6—C3h:
Класс 6—Q:**
Гексагональная система
— f/,, 0 0 0 -d-,
Класс 6m2—?»
ЗА-
m _L x,
Класс 6m2—D3h:
m J.
Класс 6mm—C6v:
Класс 622—
—
d22
0
0
0
dix
' 0
0
d3l
0
0
0
d22
0
0
0
d3\ (¦
0
-^22
0
du
0
0
0
0
d3x
0 0
0 0
0 0
0
0
0
0
'зз
0
d2-.
0
-dn
0
0
0
0
d33
du
0
0
0
0
du
'.5
0
0
о
0
0
0
0
0
dl5
0
0
-a
0
0
0
dxs
-dx
0
0
0
0
0
0
0
dxs
0
0
'u
— <
in
0
0
4 0
0
0
0
0
0
0 -
0
0
0
0
0
0
0
(i)
/<2)
B)
-d22
0
0
0
-dxx
0
C)
A)
(I)

550
ТАБЛИЦД 12.1. (Продолжение)
Глава 12
Класс 23—Г:
Кубическая система
Класс 43m—Г„:
Класс 432—0:
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
«14
0
0
du
0
0
0
du
0
0
du
0
0
0
du
0
0
dt
A)
A)
'0 0 0 0 0 0\
0 0 0 0 0 0
^0 0 0 0 0 0/d)
* Общепринятая ориентация.
** Такая же, как и у класса 4—С,.
ский тензоры, и в кристаллах с данной симметрией точечной груп-
группы он имеет такую же форму. Соответствующие тензоры для лю-
любого класса кристаллов приведены в табл. 12.1. Например, в кри-
кристалле KHjPO^KDP), который обладает симметрией точечной
группы 42т, тензор dy записывается в виде
A2.2.12)
а компоненты нелинейной поляризации даются выражениями
Px = 2duEzEy, Py = 2duEzEx, P2 = 2d36ExEy. A2.2.13)
В табл. 12.2 приведен перечень нелинейных коэффициентов некото-
некоторых кристаллов, играющих важную роль.
Нелинейные коэффициенты dijk, определяемые выражением
A2.1.1), приводят к линейным электрооптическим коэффициентам
rijk согласно следующему соотношению1':
10
0
0
0
0
0
0
0
0
d\4
0
0
0
du
0
0
0
11 Линейный электрооптический эффект может быть, вообще говоря, обусловлен
движением ионов, которое не учитывается в выражении A2.2.14).
Нелинейная оптика
ТАБЛИЦА 12.2. Нелинейные оптические коэффициенты
некоторых кристаллов [9]
551
Кристалл
Точечная
группа
X, мкм
f
10
-22
ед. МКС
109 ед. МКС
GaAs
GaP
43m
43m
GaSb
InAs
InSb
P-ZnS
ZnSe
ZnTe
CdTe
CuBr
CuCl
43m
43m
43m
43m
43m
43m
43m
43m
43m
Cul
Bi4Ge3012
CdSe
43m
43m
6mm
CdS
a-ZnS
6mm
6mm
2,12
10,6
1,064
1,318
2,12
3,39
10,6
10,6
10,6
28
10,6
10,6
10,6
28
1,064
10,6
1,064
10,6
1,064
1,064
2,12
10,6
10,6
1,06
10,6
10,6
1,06
du
du
du-
du-
du'
du-
du-
du-
du-
du =
du =
«\4 =
du-
Wu\ =
d33 =
d3l =
Ksl =
d33 =
d3l =
Ksl =
d33 =
d3l =
«\, =
= 138
107
= 80 ± 14
65
62
53
46
= 311
= 207
= 462
= 24
= 64
= 72
= 48
= -8,29
-6,2
= -7,7
= -5,3
¦ -5,0
¦ 1,6
= 52
44
: -23
25
35
80
-21
23
29
-15
35
«u
«14
Su
«и -
«u =
«14 =
«14 =
«14 =
«U =
«U =
«14 =
«U =
l«ul =
«33 =
«3. =
l«isl =
«33 =
«3. =
«33 =
«31 =
= 1,9
= 1,6
= 2,0
= 2,3
= 3,0
= 6,8
= 9
= 9
= 3,6
= -2,5
¦ -3,7
¦ -0,7
= 0,7
= 5,7
; -2,9
3,2
8,0
-5,1
5,5
6,7
-3

552
ТАБЛИЦА 12.2. (Продолжеиие)
Глава 12
Кристалл
ZnO
ВеО
SiC
Agl
GaSe
LiIO3
LiKSO4
LiNbO3
LiTaO,
Ag3SbS3
(пирарги-
рит)
Ag3AsS3
(прустит)
Турмалин
а-Кварц
(SiO2)
Те
Точечная группа X, мкм 1/9-10 22 ед. МКС
Ю9 ед. МКС
6mm
6mm
6mm
6mm
6m2
6
6
3m
3m
3m
3m
3m
3 m
3m
1,06
1,064
1,064
1,318
10,6
1,064
0,6943
1,06
1,058
10,6
10,6
10,6
1,06
1,064
10,6
28
^зз =-7,2
«*3i - 2,2
\dl5\ " 2,4
dn 0,26
dix - -0,18
^33 = -18
dn = U
da ' 10
^зз " -21
d3l - 10
«/и- 64
d3X = -5,7
dJ3= -5,6
\dH\ = 0,25
\d33\ = 0,8
\dn\ = 0,5
d3i = ,7
d33 = -27
d22 = 3,2
«/„--1,4
^зз =-21
dn ' 2,2
Irfj.l = 10,0
\dn\ = 10,7
|«/,,|-14
Irfal = 22
Irfjjl = 0;62
Irfj.l = 0,18
\dn\ - 0,09
l^isl = 0,29
dn = 0,4
</,4- -0,0036
\du\ = 733
W..I-454
«зз " -4,5
«з. = 1.4
I«15I = 1,6
«зз = -0,52
«з. = -0,41
«зз = -1,2
531 = 0,85
a,5 = 0,78
«зз = -7,1
«з. = 3,7
«22 = 2,5
«з, = -7,3
«33= "LI
l«ul = 0,26
«з.= -1,1
«зз= -8,2
«22 = 0,72
«3. = -0,44
«зз- -6,7
522 - 0,73
1«з.1 - 0,66
l«22l - 0,62
1«з.1 = 1,0
l«22l = 1,4
1«зз1 - 2,44
|«з.1 = 0,66
l«22l = 0,35
I«15I = 1,08
«u - 2,5
514 = -0,02
l«ul=l-l
Нелинейная оптика
ТАБЛИЦА 12.2. (Продолжение)
553
HgS
Se
AgGaSe2
AgInSe2
CdGeAs2
CdGeP2
CuGaSe2
ZnSiAs2
ZnGeP2
KH2PO4
(KDP)
BaTiO,
3m
3m
42m
42m
42m
42m
42m
42m
42m
42m
42m
42m
42m
NH4H2PO4
(ADP)
KD2PO4
ND4D2PO4
RbH2PO4
42m
42m
42m
42m
4mm
10,6
1,32
10,6
2,12
10,6
10,6
1,064
10,6
10,6
10,6
10,6
10,6
10,6
10,6
10,6
1,318
0,6328
0,6943
1,06
1,15
1,064
0,6328
0,6943
1,318
0,6943
0,6943
1,0642
0,6943
1,058
l^il-
\du\ -
Wil-
1«*эв1 -
1«*зв1 -
^36-
^36 =
\d3t\ =
\dM\ -
\di6\ =
1«*зв1 =
\dM\ -
\dM\ -
\d*\ -
du~
d36 =
\dit\ =
\dM\ "
\dx\ =
1^361 =
\du\ =
1«*эв1 -
\d\A -
^33 =
d,x =
40
56
77
54
46
14
23
50
280
129
8,8
11 ±4
35
87
88
0,48
0,57
0,56
0,50
0,49
0,61
0,69
0,68
0,57
0,42
0.61
0,4
0,6
0,5
0,9
-7,03
-18
-18
l«ul =
l«ul =
l«36l -
«36-
1«3б1 -
1«3б| =
1«3б| -
1«3б1 -
1«3б| -
1«3б1 =
1«3б| =
«.4 =
«36 =
1«3б| -
1«3б1 =
1«3б1 =
1«3б| =
1*м1 =
«33 =
3,3
6
4,0
3,0
3,8
2,9
2,8
0,87
1,5
2,3
1,8
2,3
4,5
5,1
3,8
5,0 ± 0,8
3,4
4,5
-1,5
-3,4
-3.2

554
ТАБЛИЦА 12.2. (Продолжение)
Глава 12
РЬТЮ,
4mm
Sr05Ba0|5Nb2O6
(SBN)
ТеО2
CdGa2S4
InPS4
Ba,NaNb<0,<
4mm
422
4
4
4
Ksl
KNbO3
Li(COOH)H2O 4
1,064 \dl5\
1,064
1,064
1,064
1,064
1,064
1,064
¦ 41,7 ± 0,6 |515|
¦ 47,1 ± 0,3 |531|
9,3 ±0,2 l^l
5,3 ± 0,5 |031|
14,1 |533|
; 7,5 |515|
0,50 |514|
32 ± 0,2
22 ± 0,3
28 ± 0,6
-16
-16
-22
-16
-15
«u
1«3б1
32
«33
«.5
«
24
а-ШО,
222
1,064
1,064
Из.1
¦¦ 12
¦¦ 14
22
¦¦ 13
14
0,12
-1,4
2,1
6,6
l«32l
1«зз1
l«24l
«32
«33
¦¦ 3,78
0,76
' 1,1
3,43
¦ 1,67
0,10
5,2 ± 0,6
3,8
5,0
-3,7
-3,7
-6,3
-3,7
-3,5
3,4
3,5
7,1
3,5
3,3
2,0
-12
16
5,2
ds,
4е0
A2.2.14)
где ijk являются главными координатными индексами. Доказатель-
Доказательство этого соотношения оставляем читателю в качестве упражне-
упражнения (см. задачу 12.1).
Нелинейная восприимчивость третьего порядка Хде связана с
квадратичными электрооптическими коэффициентами sijkl G.1.2) со-
соотношением
12e0'
A2.2.15)
Нелинейная оптика
555
в котором компоненты тензора опять определяются в главной ко-
координатной системе (см. задачу 12.2).
12.3. ЭЛЕКТРОМАГНИТНАЯ ФОРМУЛИРОВКА
НЕЛИНЕЙНОГО ВЗАИМОДЕЙСТВИЯ
Запишем уравнения Максвелла, в которые вектор поляризации Р
входит в явном виде:
VXE=-^(MoH). A2.3.1)
Поляризацию. Р представим в виде суммы линейного и нелинейного
^PNL, A2.3.2)
членов:
где
A2.3.3)
и тензорным характером величины xL мы пренебрегли.
Первое из уравнений A2.3.1) можно записать как
at
at
A2.3.4)
Штрих в d!jk означает, что направления в декартовой системе ко-
координат /, j и к не обязательно совпадают с осями х, у, z кристалла
(в последнем случае мы снова имеем djJk). Символом а обозначена
проводимость (потери), а е = еоA +xL)- Взяв ротор от обеих ча-
частей второго уравнения в A2.3.1), подставив VxH из A2.3.4) и вос-
воспользовавшись тождеством V х V х Е = VV-E - V2E, получа-
ем
дЕ
где V • Е = 0.
С этого момента будем рассматривать одномерную задачу, по-
полагая д/ду = д/дх = 0 и считая, что волна распространяется вдоль

556
Глава 12
оси z. Мы ограничимся также рассмотрением трех частот ш,,^»
а>3, а соответствующие поля будем представлять в виде бегущих
плоских волн:
z, t) =
z, t) =
z, t)
л. сопр.],
+компл. сопр.],
сопр.],
A2.3.6)
компл
где индексы /, j, к означают декартовы координаты и каждый из
них может принимать значения х или у. Заметим, что при PNL = О
решение уравнения A2.3.5) записывается в виде выражений A2.3.6),
причем входящие в них величины Eu(z), E2k(z) и ?^(z) не зависят от
z.
Например, при частоте ш1 = ш3 — ш21-я компонента нелинейной
поляризации в соответствии с A2.3.3) и A2.3.6) запишется следую-
следующим образом:
™ A2.3.7)
Возвращаясь к волновому уравнению A2.3.5) и рассматривая /'-ю
компоненту (при д/дх = д/ду = 0), получаем
dz
z, 0 = I ^1
A2.3.8)
Производя указанное дифференцирование и предполагая, что изме-
изменение комплексной амплитуды поля с расстоянием z достаточно
мало, так что
dz
dz
2 '
из A2.3.8) мы имеем
+ сопр.
A2.3.9)
Аналогичные выражения имеются для V2?JW3>(z, t) и V2?^2)(z, /).
Используя уравнение A2.3.5), для поля &"l\z, t) можно написать
следующее волновое уравнение:
Нелинейная оптика
557
следующее волновое уравнение:
компл- С0ПР- =
+ компл. сопр.] -
д2
A2.3.10)
где мы приняли d/dt = /ы,. Мы также предположили, что если чис-
число взаимодействующих частот ограничено, то уравнение A2.3.5)
должно удовлетворяться отдельно для каждой частотной
компоненты.
Заменяя в последнем уравнении величину [P^^z, 01, выражением
A2.3.7) и вспоминая, что со^е = к], получаем
' E
или после деления на ikle~'kiZ (и принимая во внимание частотную
зависимость величины а) имеем
dE
dEu о, П^ г . ГЕ
ЕЕ и' f F
1Д j
* -
и аналогично
°2
~ 1 ]l i;Elk 2v
3
A2.3.11)
Эти уравнения составляют главный результат данного раздела. В
следующих разделах мы применим их к некоторым частным случа-
случаям.
12.4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ
В ОПТИЧЕСКОМ ДИАПАЗОНЕ
Эксперимент по генерации второй гармоники в нелинейной оптике
выполнили в 1961 г. Франкен, Хилл, Петере и Вейнрейх [1]. На
рис. 12.1 дано схематическое представление первоначального экспе-

558
Рубиновый
лазер Фокусирующая
линза Призма и собирающие
Кристалл кварца линзы
Глава 12
3471,5 А
6943 А
Фотопластинка
РИС. 12.1. Установка, использованная в первом эксперименте, в котором была по-
поручена генерация второй гармоники [1]. Пучок рубинового лазера (X = 0,694 мкм)
фокусируется на кристалле кварца, что приводит к генерации (слабого) пучка при
Х/2 = 0,347 мкм. Затем два пучка разделяются призмой и регистрируются на фо-
фотопленке.
римента. Пучок рубинового лазера на длине волны 6943 А фокуси-
фокусировался на передней поверхности кварцевой пластинки. Выходяшее
излучение исследовалось на спектрометре, и было обнаружено, что
оно содержит излучение на удвоенной частоте входного пучка (т. е.
в длинах волн мы имеем X = 3471,5 А). В этом первом экспери-
эксперименте эффективность преобразования была порядка 10~8. Примене-
Применение более эффективных материалов, лазеров большой мощности и
методов фазовой синхронизации позволило получить за последние
несколько лет эффективности преобразования, приближающиеся к
единице. Все эти возможности мы и обсудим ниже в данном раз-
разделе.
Рассмотрим уравнение A2.3.11) в случае генерации второй гар-
гармоники. Это предельный случай трехчастотного взаимодействия,
когда две частоты шх и w2 равны друг другу, а ш3 = 2ы,. Следова-
Следовательно, нам потребуются лишь два уравнения из A2.3.11), а именно
первое (или второе) и последнее. Чтобы еще более упростить ана-
анализ и тем не менее сделать так, чтобы он правильно отражал боль-
большинство экспериментальных ситуаций, мы предполагаем, что при
преобразовании во вторую гармонику потери мощности входного
(о>,) пучка ничтожно малы, так что dEu/dz « 0. При этом мы мо-
можем рассматривать лишь последнее из уравнений A2.3.11). Если
среда прозрачна при о>3, то а3 = 0 и мы имеем
dE
v
dz
= -iu>Jfd'JikEuElke
iAkz
A2.4.1a)
Нелинейная оптика
где
559
ДА: =
- к\к);
A2.4.16)
здесь kfp — постоянная распространения пучка с частотой ш1, поля-
поляризованного вдоль направления /'.
Предположим теперь, что /, j и к могут принимать значения х и
у, которые выбираются вдоль направлений поляризации собствен-
собственных мод в кристалле. Волна с частотой «р вообще говоря, являет-
является линейной суперпозицией этих двух собственных мод и, таким об-
образом, имеет как х-, так и ^-компоненту. Верхний индекс у к озна-
означает, что величина постоянной распространения зависит от состоя-
состояния поляризации пучка. Заметим, что в правую часть уравнения
A2.4.1а) входит коэффициент 1/2, обусловленный вырождением
и2 = Oj [см. выражения A2.2.8) и A2.2.10)].
Решение уравнения A2.4.1) при Е3ф) = 0 (т. е. при отсутствии
второй гармоники в начальной плоскости) для кристалла длиной L
имеет вид
- 1
/Д*
A2.4.2)
где мы напоминаем, что суммирование предполагается по повторя-
повторяющимся индексам (/, к = х, у). В правой части выражения A2.4.2)
имеется, вообще говоря, четыре члена. Рассмотрим случай, когда в
правой части преобладают два перекрестных члена dL и djki
(/ ф к), обусловленные синхронизацией фаз или большими нелиней-
нелинейными коэффициентами. Таким образом, используя симметрию от-
относительно перестановок индексов тензора d.jk, из A2.4.2) получаем
A2.4.3)
где i — х, к = у (или / = у, к = х) и отсутствует суммирование
по повторяющимся индексам. Множитель 4 является результатом
возведения в квадрат множителя 2 (два перекрестных члена). Что-
Чтобы получить выражение для выходной мощности второй гармони-
гармоники Р*2"), воспользуемся соотношением A.4.21):
Г

560
Глава 12
Подставляя в это выражение соотношение A2.4.3), получаем
площадь
или, записывая последнее выражение через мощность первой гар-
гармоники, имеем
Р}2а) _ /Мо\3
A2.4.4)
здесь /"И и 7^ш) — мощности мод на частоте ш (i Ф к). В случае
/*¦>) - P*jf> = A/2)Р<ш> выражение A2.4.4) принимает вид
A2.4.5)
(")
площадь
где мы приняли е, « е3 = еол2. Если бы мы использовали диаго-
диагональные члены (хх или уу), когда волна с частотой w поляризована
вдоль х или j>, то получили бы те же самые выражения A2.4.3) и
A2.4.5).
12.4.1. ФАЗОВЫЙ СИНХРОНИЗМ
ПРИ ГЕНЕРАЦИИ ВТОРОЙ ГАРМОНИКИ
Из выражения A2.4.5) следует, что для эффективной генерации вто-
второй гармоники необходимо выполнение предварительного условия
ДА: = 0, или, если учесть, что w3 = 2w, ы{ — ш2 = ш,
кB*у _ 2к<а\ A2.4.6)
где мы предполагаем, что Щ> = kf> = k^K
Если Ак Ф 0, то волна второй гармоники, генерированная в не-
некоторой плоскости (например, z{), дойдя до некоторой другой пло-
плоскости (z2), не будет находиться в фазе с волной второй гармоники,
генерированной в плоскости z2. Это приводит к интерференции,
определяемой в выражении A2.4.5) множителем
Нелинейная оптика
561
Два соседних пика этой пространственной интерференционной кар-
картины разделены так называемой «длиной когерентности»
_ 2тг _
с ~ Ак ~
2тг
(ПАЛ)
Таким образом, длина когерентности 1С является мерой максималь-
максимальной длины кристалла, используемого для получения второй гармо-
гармоники. В обычных условиях эта длина не больше чем 10~2 см. По-
Поскольку показатель преломления п, как правило, возрастает с и, то
Ак можно записать следующим образом:
ДА: =
= — (л2ш - л"),
с v '
где мы использовали соотношение
рентности равна
/, =
¦ПС
A2.4.8)
ип^/с. Тогда длина коге-
A2.4.9)
где X — длина волны основного пучка в вакууме. Если выбрать ти-
типичное значение волны X = 1 мкм и пBш) — п(а>) « 10~2, то мы
получим /с « 100 мкм. Если, скажем, увеличить /с от 100 мкм до
2 см, то из выражения A2.4.4) следует, что мощность второй гар-
гармоники возрастает в 4-104 раза.
Для того чтобы удовлетворить требованию фазового синхро-
синхронизма (Ак = 0), широко применяется метод [10, 11], использующий
явление естественного двулучепреломления анизотропных кристал-
кристаллов, которое мы рассматривали в гл. 4. Используя соотношение
&() V^fl", выражение A2.4.6) можно переписать в виде
п1ы = и*
A2.4.10)
т. е. показатели преломления на основной частоте и частоте вто-
второй гармоники должны быть равны друг другу. В обычных мате-
материалах с дисперсией показатель преломления для обыкновенной и
необыкновенной волн вдоль данного направления увеличивается с
возрастанием w, как видно из табл. 12.3. Отсюда следует, что не-
невозможно удовлетворить условию A2.4.10), когда оба пучка с ча-
частотами w и 2ш одинакового типа, т. е. когда оба являются необы-
необыкновенными или обыкновенными. Однако при некоторых условиях
36-631

562
Глава 12
ТАБЛИЦА 12.3. Дисперсионные характеристики
показателя преломления в кристалле КН2РО4
Длина волны, мкм
0,2000
0,3000
0,4000
0,5000
0,6000
0,7000
0,8000
0,9000
1,0000
1,1000
1,2000
1,3000
1,4000
1,5000
1,6000
1,7000
1,8000
1,9000
2,0000
Показатель преломления
по (обыкновенный
луч)
1,622630
1,545570
1,524481
1,514928
1,509274
1,505235
1,501924
1,498930
1,496044
1,493147
1,490169
1,487064
1,483803
1,480363
1,476729
1,472890
1,468834
1,464555.
1,460044
пе (необыкновенный
луч)
1,563913
1,498153
1,480244
1,472486
1,468267
1,465601
1,463708
1,462234
1,460993
1,459884
1,458845
1,457838
1,456838
1,455829
1,454797
1,453735
1,452636
1,451495
1,450308
можно получить равенство A2.4.10), если использовать две волны
различного типа, одна из которых является необыкновенной, а дру-
другая — обыкновенной. Чтобы показать это, рассмотрим зависи-
зависимость показателя преломления необыкновенной волны в одноосном
кристалле от угла в между направлением распространения и опти-
оптической осью кристалла (z). Эта зависимость дается выражением
D.6.4):
1
cos20 sin20
при котором п2еш (вт) —
Если л2ш < л?, то существует угол вт
таким образом, если основной пучок (с частотой со) распространя-
распространяется вдоль направления вт как обыкновенный луч, то пучок второй
гармоники будет образовываться вдоль этого же направления как
необыкновенный луч. Это поясняется с помощью рис. 12.2. Угол вт
определяется точкой пересечения сферы (показана на рисунке в виде
окружности), соответствующей поверхности показателей преломле-
преломления обыкновенного луча на частоте со, с эллипсоидом показателей
преломления A2.4.11) необыкновенного луча, который дает nf*(9).
Нелинейная оптика
563
Ось z (оптическая)
1Ш (О =
РИС. 12.2. Поверхности показателей преломления для-обыкновенного и необыкно-
необыкновенного лучей в отрицательном (пе < по) одноосном кристалле. Если nf" < ri*o, то
условие п^"(в) = л^ выполняется при в = вт. Эксцентриситеты показаны в увели-
увеличенном масштабе.
Для отрицательных одноосных кристаллов, т. е. для кристаллов, у
которых л™ < я™, угол вт есть угол, который удовлетворяет усло-
условию ri^ (вт) — п™ или, если использовать A2.4.11), — условию
A2.4.12)
Решая это уравнение относительно вт, получаем
**_ - Midori
i-2*
A2.4.13)
12.4.2. ПРИМЕР. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ
В КРИСТАЛЛЕ КН2РО4 (KDP)
Рассмотрим основной пучок, полученный от рубинового лазера
(X = 6943 А), и кристалл KDP. Экстраполируя данные из

564
Глава 12
табл. 12.3, получаем следующие значения показателей преломле-
преломления:
пе = 1,466, и2ш = 1,487, по = 1,506, п2ои = 1,534.
Подставляя эти значения в A2.4.13), находим вт = 50,4°.
Возможен и другой способ согласования показателей преломле-
преломления в кристалле KDP, если как /-я, так и к-я составляющие падаю-
падающего пучка на частоте со не являются обыкновенными лучами, а од-
одна из них (например, к) ведет себя как необыкновенный луч. Пучок
на частоте 2z остается необыкновенным. В этом случае условие со-
согласования показателей преломления (Ак = 0) можно записать в
виде
A2.4.14)
где индексы i, j, к представляют собой оси системы координат, ко-
которая выбирается в качестве системы отсчета. При этом угол со-
согласования показателей преломления вт дается выражением
-1/2\
sin0m
-1/2
1
__
2
I
+
/~г\с2Л
cos от
. (О2
1 A2.4.15)
Это выражение получено из выражения A2.4.14), в котором вели-
величины и?" (в) и и?е@) заменены их явными выражениями с помощью
A2.4.11).
В экспериментах по генерации второй гармоники необходимо
удовлетворить не только условию согласования показателей пре-
преломления A2.4.15), но и требованиям, налагаемым формой нели-
нелинейного оптического тензора, которая ограничивает свободу выбо-
выбора направлений поляризации. Например, в кристалле KDP в соот-
соответствии с выражениями A2.2.13) составляющие вектора нелиней-
нелинейной поляризации можно записать в виде
A2.4.16)
В схеме согласования показателей преломления, которая приво-
приводит к условию A2.4.13), основной пучок является обыкновенным лу-
Нелииейная оптика
565
чом и, следовательно, Щ = О1*. Это означает, что поляризация
второй гармоники определяется последним уравнением в A2.4.16) и
имеет лишь ^-компоненту. Компонента поляризации Pz, перпенди-
перпендикулярная направлению распространения, равна 2d36E%Eysinem и,
следовательно, достигает максимума при ?™ = Щ = ?"/V2, кото-
который имеет место, когда азимутальный угол для Еш равен тг/4, как
показано на рис. 12.3.,
Из выражения A2.4.4) следует, что при отклонении от условия
согласования показателей преломления при фиксированной длине L
мощность второй гармоники уменьшается в соответствии с выра-
выражением
рBы)
рBы)
* max
A2.4.17)
Это выражение нетрудно проверить путем изменения угла а =
= в — вт между направлением, соответствующим согласованию
показателей преломления, и направлением распространения. Для
небольших значений а величину Ак(в) = kf*(d) — 2к% можно ап-
РИС. 12.3. Генерация второй гармоники в кристалле KDP. Вектор Би направлен под
углом 45° к осям х и у. Вектор кш направлен под углом вт к оптической оси г. (Все
векторы, отмеченные точками, стянутыми дугами, лежат в плоскости ху.)
'* Здесь мы пренебрегаем тем обстоятельством, что равно нулю электрическое
смещение Dz, а не Ez. В случае пе « по векторы D.
иыми.
и Е являются почти параллель-

566
Глава 12
проксимировать следующим образом:
где /3 — постоянная распространения, которая зависит от л?, п2? и
л^". Таким образом, величина AkL/2 в выражении A2.4.17) равна
/3ctL; обозначим эту величину через ф. На рис. 12.4 построена зави-
зависимость мощности второй гармоники от а, полученная из экспери-
эксперимента. На рисунке представлена также теоретическая кривая, опи-
описываемая функцией (sin2 ф)/ф2.
12.5. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ
ПРИ НАЛИЧИИ ОБРАТНОГО ВОЗДЕЙСТВИЯ
При рассмотрении генерации второй гармоники, приводящей к вы-
выражению A2.4.4), мы предполагали, что интенсивность входного
излучения на частоте со не подвергается какому-либо воздействию.
Такое приближение справедливо лишь для случаев, когда мощность
получаемого излучения при частоте 2со по отношению к входной
мощности излучения при частоте со мала. В этом разделе мы сни-
снимем это ограничение.
Вернемся к уравнениям A2.3.11) и введем новые полевые пере-
переменные А(, определяемые следующим образом:
1= 1,2,3.
A2.5.1)
1,0
0,8
М 0,6
% 0,4
0,2
0
х 8,1 х 10-'4
о Эксперимент
ТЕМ00
Р, = 1,48-10~3 Вт
/ = 1,23 см
KDP
чх>-о°-а-
-О,
+0,1°
+0,2°
РИС. 12.4. Изменение мощности второй гармоники в зависимости от угла а между
направлением распространения основного пучка и направлением фазового синхро-
синхронизма. (Из работы [13].)
Нелинейная оптика
567
Тогда интенсивность на частоте со, можно записать в виде
A2.5.2)
Поскольку энергия фотона равна /гсо,, величина \At\2 пропорцио-
пропорциональна потоку фотонов на частоте со,, причем коэффициент
пропорциональности не зависит от частоты.
Уравнения A2.3.11) можно теперь записать следующим обра-
образом:
dAx
dA\
~dz~
1, - ЫА\Аъе~н
1кАхА*е'
A2.5.3)
где 1, 2, 3 — направления поляризации полей Ер Е2, Е3, а
= 23
Mo
е0 nxn2n3
A2.5.4)
Преимущество использования величины А! вместо Et теперь очевид-
очевидно, так как в отличие от уравнений A2.3.11) уравнения A2.5.3)
включают лишь один параметр связи к.
В случае генерации второй гармоники поле А2 отсутствует и си-
система уравнений принимает вид
-! Д/tz
A2.5.5)
Следует заметить, что наличие множителя 1/2 обусловлено вырож-
вырождением со2 = со, [см. выражения A2.2.8) и A2.2.10)]. Если величину
^j(O) выбрать вещественной,' то Ax(z) будет также действительной

568
Глава 12
величиной. Тогда в случае синхронизации фаз (ДА: = 0) уравнения
A2.5.5) принимают вид
KA3AU
az <*z
где Аъ = — 1А'Ъ. Отсюда следует, что
Поэтому, предполагая, что на входе отсутствует излучение на ча-
частоте со3, мы имеем
или из уравнений A2.5.6)
^ = \к[А\{0) - 2Af]
A2.5.7)
При этом эффективность преобразования дается выражением
i><2") 2H3(z)|2
th2
-KZ\.
A2.5.8)
Отметим, что когда кЛ,@)г — °°, величина Л3'(г) — AЛ/2)Л,@);
следовательно, не более половины всех фотонов на входе может
быть превращено в выходные фотоны (на двойной частоте).
На рис. 12.5 представлены эффективности преобразования, по-
полученные как в отсутствие обратного воздействия на падающую
волну A2.4.5), так и с учетом воздействия A2.5.8).
12.6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ
ГАУССОВЫМИ ПУЧКАМИ
При рассмотрении генерации второй гармоники в разд. 12.4 и 12.5
мы использовали приближение плоской волны. На практике имеют
дело с гауссовыми пучками. Поэтому возникает необходимость в
Нелинейная оптика
569
100
111 I 11 11 ' I I I I 111 I I 11 I I 11 11 11 [ 111 I 11 II111 111 11 111 111 I I 111 111 1111 [ I I
0 12 3 4 5 6
Интенсивность на входе, ГВт/см2
РИС. 12.5. Эффективность преобразования энергии во вторую гармонику (от X =
= 1,054 к X = 0,527 мкм) в кристалле KDP толщиной 12 мм. Штриховая кривая по-
получена расчетом по формуле A2.4.5) без учета воздействия обратной волны; сплош-
сплошная кривая представляет «точное» решение A2.5.8). Кружками отмечены экспери-
экспериментальные данные из работы [15].
Гауссов
пучок
РИС. 12.6. Гауссов пучок, сфокусированный внутри нелинейного оптического кри-
кристалла.

570
Глава 12
исследовании того, какое влияние оказывает дифракция таких пуч-
пучков на нелинейные процессы, скажем на генерацию второй гармо-
гармоники.
Вследствие того что эффективность преобразования обратно
пропорциональна площади поперечного сечения пучка [см. выраже-
выражение A2.4.5)], необходимо, чтобы пучок фокусировался внутри нели-
нелинейного кристалла. Типичная ситуация представлена на рис. 12.6.
На этом рисунке величина z0 = тгисо^/Х [см. выражение B.2.11)]
равна расстоянию, на котором площадь поперечного сечения пучка
удваивается по сравнению с его площадью в области перетяжки.
Если длина кристалла L много меньше, чем z0, то внутри кристал-
кристалла сечение пучка остается по существу постоянным и мы можем ис-
использовать результаты, полученные в приближении плоской волны
A2.4.3):
A2.6.1)
A2.6.2)
где
Используя выражение
Попер.
сечение
а. также A2.6.2), после интегрирования A2.6.1) получаем
A2.6.3)
где мы положили пы » п2" и d'ljk = d. Выражение A2.6.3) аналогич-
аналогично A2.4.5), за исключением того что площадь равна A/4)ttc0q и что
это выражение справедливо теперь и для гауссова пучка. Из-за ква-
квадратичной зависимости эффективности преобразования от длины L
на первый взгляд кажется, что выгоднее использовать длинные
кристаллы. Однако, согласно рис. 12.6, когда L > 2z0, увеличение
поперечного сечения пучка приводит к уменьшению эффективности
преобразования. Таким образом, максимальную эффективность
преобразования можно получить, когда L — 2zq = 2(тго^«/Х). Мы
будем называть это условие конфокальной фокусировкой. В этом
Нелинейная оптика
571
случае мы имеем следующее выражение:
рBы)
р(ы)
= _8_
конфок. nc \ e0 )
фоку сир.
A2.6.4)
Точный анализ [14] показывает, что оптимальное преобразование
имеет место, когда L = 5,68z0 и результирующая мощность приб-
приблизительно в 1,2 раза больше, чем та, которая определяется выра-
выражением A2.6.4I'.
Сравнивая выражение A2.6.4) с решением в приближении плос-
плоской волны A2.4.5), мы находим, что при оптимальных условиях
фокусировки эффективность преобразования увеличивается пропор-
пропорционально длине кристалла L, а не L2.
12.6.1. ПРИМЕР. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
Рассмотрим преобразование второй гармоники при условиях кон-
конфокальной фокусировки в кристалле КН2РО4, когда излучение на
длине волны X = 1 мкм преобразуется в излучение с X = 0,5 мкм.
Полагая L = 1 см, d = tf36sin0 = 3,6- Ю4 ед. МКС, п = 1,5, из
выражения A2.6.4) получаем
рBш)
рп = 1.75-
10-" ЯК
12.7. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ
Оптическая нелинейность второго порядка, которая отвечает за ге-
генерацию второй гармоники, может быть также использована для
усиления слабых оптических сигналов. Основная схема включает
в себя входной «сигнал» на частоте w,, который падает на нелиней-
нелинейный оптический кристалл вместе с интенсивной волной накачки на
частоте ш3, причем ш3 > w, [16—18]. Усиление волны с частотой со,
сопровождается при этом генерацией «холостой» волны на частоте
и-, — аь — со,.
' В недавних экспериментах [15] по генерации второй гармоники импульсными
пучками большой мощности достигнуты эффективности преобразования больше
80% на длине волны X = 1,06 мкм.

572 Глава 12
12.7.1. ОСНОВНЫЕ УРАВНЕНИЯ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
В приближении отсутствия взаимодействия с основной волной мы
полагаем A3(z) = А3@) и записываем первые два уравнения из
A2.5.3):
A2.7.1)
dz
где
Ak = k.
7, 7,
— /Ci /C2,
A2.7.2)
Рассмотрим общий случай, когда во входной плоскости имеют-
имеются как «сигнальная», так и «холостая» волны с комплексными ам-
амплитудами /4,@) и А2@) соответственно. Решения уравнений
A2.7.1) с а, = 0 (потери отсутствуют) записываются в виде
x@)\
chbz + i|?
t-%A*2@) sh bz
A2.7.3)
A* I
A2[
chbz - i^rr shbz | +
ib
ij^Ax@) sh bz
где
- kx - k2.
A2.7.4)
A2.7.5)
A2.7.6)
Нелинейная оптика
573
В простейшем случае параметрического усиления во входной
плоскости мы имеем одну волну, например А1@). Полагая А2@) =
= 0 и рассматривая для простоты случай фазового синхронизма,
из выражений A2.7.3)—A2.7.5) получаем
АЛг) = ^@) ch \gz,
sh
{gz.
A2.7.7)
Увеличение мощности «сигнальной» (ы,) и «холостой» (ы2) волн
происходит за счет волны накачки (ы3). На самом деле, используя
уравнения A2.5.3) с а( = 0, можно показать, что
dz
dz
dz
A2.7.8)
Поскольку величина AtA* пропорциональна потоку фотонов с
частотой ы;, можно считать, что, согласно выражению A2.7.8), на
каждый фотон, прибавляемый к «сигнальной» волне (ы,), добавля-
добавляется один фотон к «холостой» волне (ы2) и один фотон отбирается
у волны накачки (ы3). Поскольку ы3 = ых + ы2, энергия сохраняет-
сохраняется. Интегрирование соотношения A2.7.8) по всему объему взаимо-
взаимодействия позволяет нам получить следующее соотношение между
изменениями полной мощности во входной и выходной плоскостях:
A2.7.9)
здесь Р — мощность пучка. Выражение A2.7.9) известно как соот-
соотношение Мэнли —. Роу [19].
Числовой пример. Параметрическое усиление. Чтобы оценить
величину параметрического усиления, рассмотрим кристалл
LiNbO3. Подставляя в выражение A2.7.2), определяющееg, следую-
следующие значения:
v = v2 = 3 • 1014 Гц
v = 6-1014Гц,
rf3, = 0,5-Ю-22
л, = п2 « 2,2,
(X = X, = 1 мкм),
(см. табл. 12.2),
площадь
= 51О6 Вт/см2
(?• = 4,13-106 В/м),
v з • "

574
Глава 12
получаем g = 1,34см. Отсюда следует, что даже при больших
плотностях мощности накачки величина параметрического усиления
невелика. Это объясняется тем, что данный эффект используется
главным образом для получения генерации, а не для усиления.
12.8. ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ
В предыдущем разделе мы показали, что волна накачки с частотой
ы3 через взаимодействие в нелинейном кристалле может привести к
одновременному усилению оптических волн с частотами шх и со2,
причем w3 = coj + co2. Если нелинейный кристалл поместить внутри
оптического резонатора, который настроен в резонанс на частоте
сигнальной или холостой волн (или на обеих частотах), то при не-
некоторой пороговой интенсивности накачки параметрическое усиле-
усиление будет вызывать одновременную генерацию на частотах как сиг-
сигнальной, так и холостой волн. Пороговая интенсивность для этой
генерации соответствует значению, при котором параметрическое
усиление в точности компенсирует потери сигнальной и холостой
волн [16—18]. Это является физической основой оптического пара-
параметрического генератора. Практическое значение такого генератора
состоит в том, что он может преобразовывать выходную мощ-
мощность лазера накачки в когерентное излучение на «сигнальной» и
холостой частотах.
На рис. 12.7 представлен схематически оптический параметриче-
параметрический генератор на двойном резонансе, который резонирует как на
сигнальной, так и на холостой моде (и обладает высоким Q). Пре-
Прежде чем начать строгий анализ параметрической генерации, рас-
рассмотрим очень простую точку зрения, которая будет полезной для
иллюстрации основной природы взаимодействия. Прежде всего
Лазер
Фокусирующая
лииза
Оптическая ось
Я, г 100%
Я2 а 100%
Я, = 0%
кристалл
Я, (высокий, НО < 1)
Я2 (высокий, но < 1)
я,
0%
РИС. 12.7. Схематическое представление оптического параметрического генератора,
в котором для накачки используется излучение лазера с частотой а>3. Результирую-
Результирующее усиление вызывает в оптическом резонаторе, содержащем нелинейный кристалл
и настроенном на частоты о), и и2, генерацию на частотах о), и а>2 (а>, = а>. + «,).
Нелинейная оптика
575
рассмотрим уравнения A2.7.1), в которых величины Ax(z) и A2(z)
будем считать амплитудами волн параметрического генератора,
показанного на рис. 12.7. Коэффициенты распределенных потерь «j
и а2 можно отнести к потерям на зеркалах, при условии что потери
за каждый проход в резонаторе малы. При этом мы имеем
а,/=1-Я, (г =1,2),
A2.8.1)
где / — длина резонатора. В установившемся режиме dAx/dz =
= dA2/dz = 0 и уравнения A2.7.1) принимают вид
= 0.
A2.8.2)
Нетривиальные решения для А1иА2 существуют, если детерми-
детерминант, составленный из коэффициентов системы A2.8.2), обращает-
обращается в нуль, т. е. если
g? = «i«2- A2.8.3)
Рассмотрим теперь эту же проблему в более строгой форме.
12.8.1. САМОСОГЛАСОВАННЫЙ АНАЛИЗ
ПАРАМЕТРИЧЕСКОЙ ГЕНЕРАЦИИ
В данном разделе, используя самосогласованный подход, мы полу-
получим уравнения, описывающие установившиеся колебания в пара-
параметрических генераторах.
Основная схема, для которой мы будем проводить рассмотре-
рассмотрение, показана на рис. 12.8. Предположим ради простоты, что нели-
нелинейный кристалл имеет форму оптического резонатора, искривлен-
искривленные торцы которого отражают сигнальную и холостую волны с
Нелинейный
кристалл
РИС. 12.8. Кристаллический параметрический генератор.

576
Глава 12
коэффициентами отражения соответственно1' гх и г2 и прозрачны
для накачки. Общее поле, состоящее из сигнальной и холостой
волн, в произвольной плоскости z будет описываться вектор-
столбцом
A*2(z)eik*z
A2.8.4)
где kt = (ш/с)пг Величина A(z) на выходе нелинейного кристалла
длиной / в соответствии с A2.7.3) и A2.7.4) дается выражением
2b
ib
2b
4r
2b
А@).
A2.8.5)
Потребуем теперь, чтобы вектор A (z) воспроизводил себя после
полного цикла прохождения излучения внутри резонатора. Исполь-
Используя рисунок 12.9, это условие можно записать в виде
А~.-Ая.
A2.8.6)
Поле Ае получается из Аа умножением последнего на четыре мат-
матрицы, первая из которых учитывает отражение на левом зеркале,
вторая описывает распространение от правого до левого зеркала
(параметрическое усиление при этом отсутствует), третья учитыва-
учитывает отражение на правом зеркале и, наконец, последняя — прохож-
прохождение излучения от левого зеркала к правому в соответствии с
A2.8.5). Таким образом, предполагая выполнение условия фазового
синхронизма Ак — 0, полный цикл прохождения излучения можно
записать в виде
Л =
О
х
О г2*
e-'*''ch
ieik*' sh
,-ik.l
О
а,к21
О
-ie-" sh hi
eik>' ch hi
A2.8.7)
'' г. и r2 — коэффициенты отражения для комплексных полей. Они связаны с ко-
коэффициентами отражения от зеркал соотношением l/v I = /?..
Нелинейная оптика
577
Опорная
плоскость
Накачка
РИС. 12.9. Полное прохождение (в прямом и обратном направлении) в резонаторе
вектора Л, представляющего паразитную и сигнальную волны и используемого при
выводе условия генерации A2.8.12).
или
где
М =
A2.8.8)
Пе~
-" I (\2 8 9^
{i(r*Je'2^ sh |g/ (r*Je«M ch у)'
Условие самосогласования A2.8.6) можно написать теперь в виде
A2.8.10)
так что при нетривиальном Ла имеем
det|iU - /| = О,
или, используя выражение A2.8.9),
sh2 у.
A2.8.11)
A2.8.12)
Это выражение и есть условие параметрической генерации.
Из выражения A2.8.12) следует, что минимальное пороговое
усиление gl будет иметь место, когда каждый из двух сомножите-
37-631

578
Глава 12
лей в левой части является вещественным положительным чис-
числом. Для этого должны выполняться следующие соотношения:
A2.8.13)
A2.8.14)
-ф, + 2ft:,/=
- ф2 + 2k2l =
где т и s — целые числа и
Условия A2.8.13) означают, что сигнальная (со,) и холостая (со2) ко-
колебательные частоты должны соответствовать двум продольным
модам оптического резонатора.
Ниже мы используем выражение A2.8.12) с целью получения по-
пороговых условий для двух важных классов параметрических генера-
генераторов.
12.8.2. ДВУХРЕЗОНАНСНЫЙ ПАРАМЕТРИЧЕСКИЙ ГЕНЕРАТОР
В этом случае конфигурация обеспечивает резонансы с высокой до-
добротностью Q как для частоты со,, так и для со2. Используя выра-
выражения A2.8.12) в A2.8.13), получаем
(/?, + R2)ch(gl/2) - R{R2 = 1. A2.8.15)
Для зеркал с высокой отражательной способностью (Л,, R2 = 1)
мы имеем ch(g//2) « 1 + g2/2/8, и уравнение A2.8.15) принимает
вид
g,/ = 2^(l-JRl)(l^R2T. A2.8.16)
Используя выражение A2.7.2) и выражая поле накачки Еъ через ин-
интенсивность
из A2.8.16) получаем
3'
o
A2.8.17)
Нелинейная оптика
579
12.8.3. ПРИМЕР. ПОРОГОВОЕ ЗНАЧЕНИЕ НАКАЧКИ
ДЛЯ ПАРАМЕТРИЧЕСКОЙ ГЕНЕРАЦИИ
Оценим порог накачки для параметрического генератора, представ-
представленного схематически на рис. 12.8 и использующего кристалл
LiNbO3. Для расчета выберем следующие параметры:
1 - /?j = 1 - R2 = 2-10-2
(т. е. полные потери за проход на частотах СО] и со2 равны 2°7о),
X] = Х2 = 1 мкм,
/ = 1 см (длина кристалла),
«[ = п2 = л3 = 2,2,
tf3,(LiNbO3 = 5-1О-23ед. МКС.
Подстановка этих параметров в выражение A2.8.17) дает
/3, = 4,5-103 Вт/см2.
Такое значение интенсивности нетрудно получить даже в непрерыв-
непрерывном режиме. Таким образом, этот пример иллюстрирует привлека-
привлекательность оптического параметрического возбуждения колебаний
как способа генерации когерентного оптического излучения на но-
новых частотах.
12.9. НАСТРОЙКА ЧАСТОТЫ
В ПАРАМЕТРИЧЕСКИХ ГЕНЕРАТОРАХ
В отличие от лазера работа параметрического генератора не зави-
зависит от резонансных переходов и, следовательно, он может быть
настроен в широком частотном диапазоне. Частоты сигнальной
(со,) и холостой (со2) волн при этом одновременно удовлетворяют
условию фазового синхронизма
и закону сохранения энергии
и>ъ = и> \ + и>2.
A2.9.1)
A2.9.2)
Очевидно, что соотношение A2.9.1) является просто другой фор-
формой условия к} = кх + к2 для коллинеарного взаимодействия.
В кристаллах показатели преломления л,, л2 и л3 обычно зави-
зависят от ориентации кристалла (для необыкновенных лучей), темпе-
температуры, электрического поля и давления. Из выражения A2.9.1)
следует, что, изменяя любой из этих параметров, мы можем управ-

580
Глава 12
лять настройкой выходных частот со, и со2 параметрического генера-
генератора.
В качестве примера рассмотрим проблему угловой настройки.
Пусть параметрический генератор накачивается необыкновенной
волной с частотой со3. Частоты со, и со2 соответствуют обыкновен-
обыкновенным волнам. При некоторой ориентации кристалла в0 @О — угол
между осью с кристалла и осью резонатора) генерация происходит
на частотах со1О и со2о, для которых мы имеем показатели преломле-
преломления соответственно я10 и и20. При в = в0 выражение A2.9.1) можно
записать в виде
Повернем кристалл на угол Д0. Это вызовет изменение показателя
преломления пъ, а из-за необходимости удовлетворить условию фа-
фазового синхронизма A2.9.1) изменятся и частоты со, и со2. Новая ге-
генерация будет иметь место при следующих изменениях параметров
относительно генерации при 0О:
со, — со3 (частота накачки не изменяется),
и
!20
«30 + Д"з. «10 -» «10 + Д'
ы20 + Ды2, Ды2 = -Ды,.
п20
го
"ю
и
ю
Поскольку условие A2.9.1) должно удовлетворяться для нового на-
набора параметров, мы имеем
«i)("m + Дл,) + (со» - Д",)(и20 + Дл2).
= ("
ю
Пренебрегая членами второго порядка малости ДиДсо и используя
соотношение A2.9.2), получаем
A2.9.3)
~ И20
Поскольку волна накачки является необыкновенной, показатель
преломления и3 зависит от угла в. Показатели преломления пх и п2
для обыкновенных лучей зависят от частоты, но не зависят от угла
в. Таким образом, можно написать
дп2
Ды,,
A2.9.4)
Нелинейная оптика
581
Ди3 =
~дв
Ав.
A2.9.5)
Подставляя эти соотношения и равенство Дсо2 = — Дсо, в выраже-
выражение A2.9.3), получаем скорость изменения частоты колебаний в за-
зависимости от ориентации кристалла:
дп-.
дв
~дв
дп-
Используя выражение D.6.4) и соотношение d(l/x2) =
имеем
A2.9.6)
^dx,
Подставив затем это выражение в A2.9.6), получаем
и
sin 2в
дв
(«10 - «го) + wio^- - W2o^7Г
A2.9.7)
На рис. 12.10 приведена экспериментальная кривая, показывающая
зависимость частот сигнальной и холостой волн от в в кристалле
NH4H2PO4 (ADP). На этом же рисунке представлена и теоретиче-
теоретическая кривая, построенная по формуле A2.9.7) в квадратичном при-
приближении с использованием данных по дисперсии (т. е. зависимости
п от со) для кристалла ADP. На рис. 12.11 представлена кривая
угловой настройки генератора на кристалле CdSe [21].
Рассуждения, аналогичные тем, которые мы использовали выше
при получении выражения угловой настройки A2.9.7), можно при-
применить также для определения зависимости частот генерации и от
любых других физических величин.
12.10. ПОВЫШЕНИЕ ЧАСТОТЫ
Параметрические взаимодействия в кристалле можно использовать
для преобразования «низкой» частоты со, в «высокую» со3 путем

4500 5000
Длина волны, А
6000 7000 10,000 15,000
I
I Г
. Теория (квадратичное
приближение)
2,5
2,0 1,5
Энергия фотона, эВ
1,0
0,6 0,4 0,2 0 -0,2 -0,4
Относительное смещение частоты Д
-0,6
РИС. 12.10. Зависимость сигнальной частоты ш, от угла между направлением волны
накачки и оптической осью кристалла ADP. Угол в измеряется относительно на-
направления, для которого со, = со3/2; Д = (к, - 2ыъ)/ыу (Из работы [20].)
X, мкм
14
10
1 2
CdSe
О = с + О
= 2,36 мкм
о
70
80
90
РИС. !2.П. Кривые угловой настройки для кристалла CdSe при \} = 2,36 мкм; кри-
кривые 1 — коллинеарное взаимодействие, ф = 0; кривые 2 и 3 — неколлинеарное взаи-
взаимодействие соответственно для ф = 0,5 и 1°; кр к2, к3 — волновые векторы соот-
соответственно сигнальной, паразитной волн и волны накачки; в — угол между сигналь-
сигнальным волновым вектором и оптической осью кристалла CdSe; ф — угол между вол-
волновыми векторами волн накачки и сигнальной. (Из работы [21].)
Нелинейная оптика
583
смешения ее с частотой ш2 мощного лазерного пучка, причем
«, + «-, = (О,.
A2.10.1)
Основной процесс, имеющий место при частотной перестройке,
можно рассматривать, используя квантовомеханический подход [3,
22—25]. Этот процесс состоит в том, что «сигнальный» (ш,) фотон
и фотон накачки (w2) аннигилируют и одновременно рождается фо-
фотон с частотой шу Поскольку энергия фотона равна hu>, из закона
сохранения энергии получаем w3 = ш, + ш2, а из закона сохранения
импульсов имеем следующее соотношение для волновых векторов:
2,
A2.10.2)
Такой подход предполагает также, что число выходных фотонов
при w3 не может превышать число входных фотонов с частотой со,.
На рис. 12.12 приведена схема эксперимента по параметрическо-
параметрическому повышению частоты. Пучки с частотами ш, и и>2 складываются
после прохождения через частично пропускающее зеркало (или при-
призму), так что они вместе (почти параллельно)'распространяются в
кристалле длиной / с нелинейными оптическими характеристиками.
Рассмотрение параметрического повышения частоты можно на-
начать с уравнений A2.5.3). Предположим, что амплитуда волны на-
накачки (А2) пренебрежимо мала и потери на частотах ш, и и>2 от-
отсутствуют (а = 0). Тогда первое и третье из уравнений A2.5.3)
можно записать в виде
(?4з
Ж"
A2.10.3)
Отсюда, используя выражения A2.5.1) и A2.5.4) и выбирая без по-
потери общности фазу волны накачки равной нулю, так что А2@) =
= А2@), получаем
V И1«з «о
dE
'2>
A2.10.4)
где Е2 — амплитуда электрического поля лазерного излучения на-
накачки. Общие решения уравнений A2.10.3) имеют вид
A3(z)
A2.10.5)

584
Глава 12
Частично
отражающее
зеркало
Входной
сигнал
Ц)
Нелинейный кристалл
Фильтр
ft
Лазерная
накачка (а>2)
РИС. 12.12. Параметрическое повышение частоты, когда взаимодействие сигналь-
сигнальной волны на частоте cot н мощного лазерного пучка на частоте w2 приводит к гене-
генерации на суммарной частоте ш3 = а>, + ш2.
где А ,@) и Л3@) — комплексные амплитуды волн во входной пло-
плоскости.
В случае когда на входе имеется одна (низкочастотная) волна с
частотой шх, мы имеем Л3@) = 0. При этом
A2.10.6)
\Аъ{г)\2 ^
откуда следует, что
Выше мы отмечали [см. рассуждение после выражения A2.5.2)],
что величина 1ЛДгI2 пропорциональна потоку фотонов (числу фо-
фотонов на квадратный метр за единицу времени) с частотами шг Пе-
Переписывая выражения A2.10.6) через мощности, мы имеем
P,(z) =
*э(*)-?
и,
A2.10.7)
Таким образом, эффективность преобразования кристалла длиной /
дается выражением
A2.10.8)
Нелинейная оптика
585
Мы видим, что максимальное значение эффективности преобразо-
преобразования равно ojj/wj и соответствует случаю, когда все входные фото-
фотоны с частотой шх превращаются в фотоны с частотой w3.
В большинстве практических случаев эффективность преобразо-
преобразования мала (см. следующий числовой пример): так, используя
sinx = х при х < 1, мы получаем выражение
которое после подстановки в него выражений A2.10.4) и A2.5.2)
можно переписать в виде
P3(l) =
A2.10.9)
Л(°) И1И2«з\?о/ А '
где А — площадь поперечного сечения области взаимодействия.
Числовой пример. Главный интерес к параметрическому повы-
повышению частоты связан с практической возможностью регистриро-
регистрировать инфракрасное излучение (область спектра, где детекторы либо
неэффективны, либо требуют большого времени измерения, либо
их необходимо охлаждать до криогенных температур) с помощью
преобразования частоты в видимую или близкую к видимой обла-
области спектра. Это позволяет регистрировать излучение с помощью
эффективных и быстродействующих детекторов, таких, как фото-
фотоумножители или фотодиоды [23—26].
В качестве примера такого применения рассмотрим параметри-
параметрическое повышение частоты, когда сигнал с длиной волны 10,6 мкм,
излучаемый СО2-лазером, преобразуется в сигнал с длиной волны
0,96 мкм с помощью смешения исходного сигнала с излучением на
частоте 1,06 мкм Nd3+ — ИАГ-лазера. Нелинейный кристалл, вы-
выбранный для этой цели, должен иметь низкие потери на используе-
используемых длинах волн 1,06, 10,6 мкм и 0,96 мкм. Кроме того, двулуче-
преломление кристалла должно быть таким, чтобы выполнялось
условие фазового синхронизма. Этим требованиям удовлетворяет
кристалл прустит (Ag3AsS3) [26] (см. табл. 12.2). Используем следу-
следующие данные:
= 104 Вт/см2 = 108 Вт/м2,
1 y\J\j МКМ
/ = 1 см,
и3 = 2,6,
LI Ю-22
38-631

586
Глава !2
(величина d^ чуть меньше половины значения d22, приведенного в
табл. 12.2). Подставляя эти значения в выражение A2.10.9), получа-
получаем эффективность преобразования
Р /Р'
ГА = 0,96 мкм/7Л = 10,6 мкм
~3
В настоящее время эксперименты на кристалле LiIO3 [27] с исполь-
использованием для накачки излучения рубинового лазера с длиной волны
0,6943 мкм' дают почти 100%-ную эффективность преобразования
при X = 3,39 мкм.
Один из важных аспектов генерации на суммарной частоте со-
состоит в совместном смешении частот излучений от различных лазе-
лазеров для получения излучения с длиной волны около 16 мкм, необ-
необходимого в экспериментах по разделению изотопов урана из UF6.
ЗАДАЧИ
12.1. Связь между величинами d{jk и гГк. Пусть полное электриче-
электрическое поле задано выражением
Efc
Ц"Г + компл. сопр.).
а) Покажите, что из A2.1.1) следует
С = *оХ,Аш + 4JkE?E; .
б) Покажите, что приведенное выше соотношение можно
получить также из соотношения
Um
Ш| —»Ш
в котором pf3~a\±a2 дается выражением A2.2.8).
в) Если записать поляризацию Pf — (е^ + Ае^Еу, где из-
изменение диэлектрической проницаемости Де.. равно
4djJ-kEklc, и использовать соотношение
то можно показать, что
1_
«о
'"* = " 4гп
Нелинейная оптика
587
где суммирование предполагается по повторяющимся
индексам а, C.
г) В главной системе координат последнее соотношение в
п. в принимает вид
12.2. Связь между величинами xtjkl и Sykr
а) Покажите, что
б) Покажите, что
1_
Xijkl~ л-,. еи
в) Покажите, что в главной системе координат
ЕиеЛ
г) Докажите, что в изотропной среде
= = °
хуху ~ Хухху 12
где п — показатель преломления, К — постоянная Керра
и X — длина волны в вакууме. Оцените восприимчивость
третьего порядка хухху У CS2 при X = 1 мкм, используя
значение постоянной Керра, приведенное в табл. 7.6.
12.3. Свойства симметрии нелинейных восприимчивостеи. Нели-
Нелинейные восприимчивости, определяемые выражением
A2.1.1), можно записать следующим образом:
2!
d2Pt
>Е<дЕ>
3! I dEj дЕк BE,

588
Глава 12
а) Покажите, что индексы jkl допускают перестановку,
т. е.
Xujk-
б) Покажите, что если определить D(. = ?,-,?,-, то
в) Покажите, что если еу = е,-,-, то величины dijk и хт сим-
симметричны относительно любой перестановки их индек-
индексов.
ЛИТЕРАТУРА
Phys. Rev. Lett., 7, 118
1. Franken P. A., Hill A. E., Peters С W., Weinreich G.
A961).
2. Maker P. D., Terhune R. N., Savage С. М. — In: Proc. Third Confer, on Quantum
Electronics, Paris, 1963 (eds. P. Grivet, N. Bloembergen). — New York: Columbia
University Press, 1964, p. 1559.
3. Yariv A., Quantum Electronics, 2d ed. — New York: Wiley, 1975, Ch. 18. [Имеется
перевод: Ярив А. Квантовая электроника. — М.: Сов. радио, 1980.]
4. Bloembergen N., Nonlinear Optics. — New York: Benjamin, 1965. [Имеется пере-
перевод: Бломберген Н. Нелинейная оптика. — М.: Мир, 1966.]
5. Armstrong J. A., Bloembergen N., DucuingJ., Pershan P. S., Interactions between
light waves in a nonlinear dielectric. — Phys. Rev., 127, 1918—1939 A962).
6. Bloembergen N., Pershan P. S., Light waves at the boundary of nonlinear media. —
Phys. Rev., 128, 606—622 A962).
7. Bloembergen N., Shen Y. /?., Quantum-theoretical comparison of nonlinear suscep-
susceptibilities in parametic media, laser, and Raman lasers. — Phys. Rev., 133, A37—A49
A964).
8. Kleinman D. A., Nonlinear dielectric polarization in optical media. — Phys. Rev.,
126, 1977 A962).
9. Kurtz S. K., Jerphagnon J., Choy M. M., Nonlinear Dielectric Susceptibilities
(Landolt-Bornstein), New Series, vol. 11, (ed. K.-H. Hellwege). — Berlin: Springer-
Verlag, 1979.
10. Maker P. D., Terhune R. W., Nisenoff M., Savage С. М., Effects of dispersion and
focusing on the production of optical harmonics. — Phys. Rev. Lett., 8, 21 A962).
11. Giordmaine J. A., Mixing of light beams in crystals.— Phys. Rev. Lett., 8, 19
A962).
12. ZernikeF., Jr., Refractive indices of ammonium dihydrogen phosphate and
potassium dihydrogen phosphate between 2000 A and l,5/*m. — J. Opt. Soc.
Amer., 54, 1215 A964).
13. Ashkin A., Boyd G. D., Dziedzic J. M., Observation of continuous second harmonic
generation with gas laser. — Phys. Rev. Lett., 11, 14 A963).
Нелинейная оптика
589
14. BoydG.D., Kleinman D. A., Parametric interaction of focused Gaussian light
beams. — J. Appl. Phys., 39, 3597 A968).
15. Seka W., Jacobs S. D., Rizzo J. E., Boni /?., Craxton R. S., Demonstration of high
efficiency harmonic conversion of high power Nd-Glass laser radiation. — Opt.
Comm., 34, 469 A980).
16. Wang C. C, Racette G. W. Measurement of parametric gain accompanying optical
difference frequency generation. — Appl. Phys. Lett., 6, 169 A965).
17. Giordmaine J. A., Miller R. С, Tunable optical parametric oscillation in LiNbO3 at
optical frequencies. — Phys. Rev. Lett., 14, 973 A965).
18. Kingston R. H., Parametric amplification and oscillation at optical frequencies. —
Proc. IRE, 50, 472 A962).
Kroll N. M., Parametric amplification in spatially extended media and applications
to the design of tunable oscillators at optical grequencies. — Phys. Rev., 127, 1207
A962).
19. Mantey J. M., Rowe H. E., General energy relations in nonlinear reactances.—
Proc. IRE, 47, 2115 A959).
20. MagdeD., MahrM., Study in ammonium dihydrogen phosphate of spontaneous
parametric interaction tunable from 4400 A to 16 000 A. — Phys. Rev. Lett., 18,
905 A967).
21. Davydov A. A., Kulevskii L. A., Prokhorov A. M., Savel'ev A. D., Smirnov V. V.,
Shirkov A. V., A tunable infrared parametric oscillator in a CdSe crystal. — Opt.
Comm., 9, 234 A973); см. также: Herbst R. L., Byer R. L., Efficient parametric
mixing in CdSe. — Appl. Phys. Lett., 19, 527 A971); Herbst R. L., Byer R. L.,
Single resonant CdSe infrared parametric oscillator. — Appl. Phys. Lett., 21, 189
A972).
22. Louise/I W. H., Yariv A., Siegman A. E., Quantum fluctuations and noise in
parametric processes. — Phys. Rev., 124, 1646 A961).
23. Johnson F. M., DuradoJ.A., Frequency up-conversion.— Laser Focus, 3, 31
A967).
24. Midwinter J. E., Warner J., Up-conversion of near infrared to visible radiation in
lithium-meta-niobate. — J. Appl. Phys., 38, 519 A967).
25. Warner J., Photomultiplier Detection of 10.6^m Radiation using optical up-
conversion in proustite. — Appl. Phys. Lett., 12, 222 A968).
26. Hulme K. F., Jones O., Davies P. H., Hobden M. V., Synthetic proustite (Ag3AsS3):
A new material for optical mixing. — Appl. Phys. Lett., 10, 133 A967).
27. Gurski T. R., High quantum efficiency infrared up-conversion. — Appl. Phys. Lett.,
23, 273 A973).

Глава 13
ОПТИКА ФАЗОВОГО СОПРЯЖЕНИЯ
13.1. ВВЕДЕНИЕ
Оптика фазового сопряжения — новая область когерентной оптики
[1, 2]. Она включает в себя использование нелинейных оптических
методов для обработки электромагнитных полей в реальном мас-
масштабе времени. Такое название обусловлено тем, что все примене-
применения этой области, которые были осуществлены или предложены к
настоящему времени, основаны на обращении фазы падающей
электромагнитной волны.
Существуют многочисленные приложения оптики фазового со-
сопряжения для практических целей и научных исследований. К ним
относятся передача изображения, сжатие импульса, обработка изо-
изображения (включая свертку и корреляцию) и голография в реаль-
реальном масштабе времени. Прежде чем рассмотреть подробно тео-
теорию, опишем два таких приложения: распространение через неод-
неоднородную среду и передачу изображений в многомодовом волокне.
13.2. РАСПРОСТРАНЕНИЕ ЧЕРЕЗ НЕОДНОРОДНУЮ СРЕДУ
Рассмотрим в качестве примера задачу о распространении оптиче-
оптического пучка
= Re[^,(r)e""] A3.2.1)
через линейную искажающую среду без потерь в направлении оси z
(слева направо). Зависимость функции ф от г отражает пространст-
пространственную модуляцию информации, эффекты искажений и дифракцию.
Если в некоторой области пространства вблизи z0 мы каким-то об-
образом создали поле Е2(т, t), которое локально описывается выраже-
выражением
Е2(т, t) = ] [)
ТО / \ /
А2(т) = А\(г) для всех z < z0.
\ ' щ '
Оптика фазового сопряжения
591
Искажающая
среда
Устройство фазового
сопряжения
Ф, (г) г
РИС. 13.1. Комплексное сопряжение падаюшей волны
Нелинейная
среда
)е lkz
Поле Е2(т, t) будем называть комплексно-сопряженным по отноше-
отношению к Ех (г, ?)• Следует заметить, что для получения поля Е2 из Ех
мы проводим комплексное сопряжение части поля, зависящей толь-
только от пространственной координаты, оставляя множитель е'°" без
изменений. (Это эквивалентно обращению знака времени t при не-
неизменной пространственной части. Иными словами, поле Е2 связа-
связано с Ех операцией «обращения времени».)
Чтобы понять практические следствия фазового сопряжения,
рассмотрим поле Ех, распространяющееся слева направо через не-
неоднородную среду, как показано на рис. 13.1. Диэлектрическая про-
проницаемость среды задается функцией е(г), которая является вещест-
вещественной величиной. Скалярное поле распространяющегося в направ-
направлении (+z) пучка записывается в виде
?,(r, t) = Re[^,(r)e+'("'-*z)J. A3.2.3)
Скалярное волновое уравнение, которому удовлетворяет эта волна,
имеет вид
0.
A3.2.4)
Это уравнение справедливо, если относительное изменение диэлект-
диэлектрической проницаемости е(г) на оптической длине волны мало по
сравнению с единицей.

592
Глава 13
Запишем теперь уравнение, комплексно-сопряженное A3.2.4):
= о.
A3.2.5)
Этому волновому уравнению удовлетворяет волна, распространяю-
распространяющаяся в направлении —z, а именно
?2(г, t) = Ке[ф2(т)е+«ш1+кг)], A3.2.6)
если мы положим
f (г),
A3.2.7)
где а — произвольная постоянная. Таким образом, мы показали,
что волна Е2, комплексная амплитуда которой является комплек-
комплексно-сопряженной по отношению к амплитуде ?,, удовлетворяет то-
тому же волновому уравнению, что и ?,. (Это верно для произволь-
произвольной волны в любой среде без потерь с вещественной диэлектричес-
диэлектрической проницаемостью е; см. задачу 13.7.)
Практический вывод из формального доказательства, приведен-
приведенного выше, состоит в следующем. Пусть комплексная монохрома-
монохроматическая волна ?, распространяется от некоторой плоскости А к
другой плоскости В через среду с диэлектрической проницаемостью
е(г). Если в окрестности плоскости В мы генерируем каким-то об-
образом волну Е2, комплексная амплитуда которой в пределах площа-
площади, занимаемой падающим пучком, комплексно-сопряжена с ампли-
амплитудой волны ?, (с точностью до постоянного множителя), то вол-
волна ?2 будет распространяться назад и оставаться всюду комплек-
комплексно-сопряженной волне ?,. Таким образом, ее волновые фронты
всюду совпадают с волновыми фронтами поля ?,.
Этот аспект фазового сопряжения был продемонстрирован в не-
некоторых ранних экспериментах [3, 4].
13.3. ПЕРЕДАЧА ИЗОБРАЖЕНИЯ В ВОЛОКНАХ
Следующей потенциальной областью применения фазового сопря-
сопряжения является передача изображения на большие расстояния по
оптическим волноводам [5, 6]. Задачу фазового сопряжения в опти-
оптическом волноводе иллюстрирует рис. 13.2. Пусть падающее поле во
входной плоскости волновода записывается в виде
/,(*,>.*-0,0 «? 1.Ат„Етп(х,У)е<»; A3.3.1)
т-0 л-0
Оптика фазового сопряжения
593
РИС. 13.2. Компенсация и восстановление изображения за счет модовой дисперсии в
диэлектрическом волноводе с применением фазового сопряжения.
где Етп — пространственная модовая функция определенного вол-
волновода. Хуммирование осуществляется по дискретному спектру
волноводных мод, общее число которых равно N1. Выходное поле
на конце волновода длиной L при отсутствии потерь дается выра-
выражением
/2(х, у, L, t) =
п(х, y)txp[i(at - РтяЬ)],
A3.3.2)
где /Зтл — постоянная распространения моды щ, п. В общем случае
распределение поля A3.3.2) отличается от распределения поля
A3.3.1) на входе фазовыми множителями /3mnL. На практике это
соответствует пространственному искажению информации. Однако
если мы создадим поле, комплексно-сопряженное выходному полю
A3.3.2):
/3(х, у, L, г) = LLA*mnE*n(x, y)exp[i(Ut + fimHL)]
A3.3.3)
и подадим его в другой волоконный волновод длиной L, характери-
характеристики которого полностью идентичны первому волноводу, то на
выходе получим
/4(х, у, 1L,
, y)cxp[i(cct + pmnL - PmnL)] =
За исключением комплексного сопряжения, поле /4 при z — 2L со-
совпадает с входным полем/р и информация, переносимая волной,
при этом восстанавливается.
Для практической реализации этой схемы необходимо иметь два
отрезка идентичных волокон, которые имеют незначительные
внутримодовое рассеяние и потери для всех мод. Похожая схема с
использованием одного отрезка волокна была продемонстрирована
экспериментально в работе [13]. В этой схеме фазово-сопряженный

594
Глава !3
сигнал генерировался посредством вырожденного четырехволново-
четырехволнового смешения (см. следующий раздел) в кристалле ВаТЮ,, а затем
снова подавался в тот же самый волновод. Это приводило к вос-
восстановлению исходного изображения.
13.4. ТЕОРИЯ ФАЗОВОГО СОПРЯЖЕНИЯ
ПРИ ЧЕТЫРЕХВОЛНОВОМ СМЕШЕНИИ [7]
В этом разделе представлены основы теории фазового сопряжения
посредством четырехволнового смешения. Здесь рассматривается
нелинейность третьего порядка, которую в соответствии с A2.1.1)
можно записать в виде
Р, = 4Х,,*,?,ВД. <13-4Л)
Используя методы, аналогичные тем, которые приводят к вы-
выражению A2.2.7) (детали оставляем в качестве задачи), мы нахо-
находим, что комплексная амплитуда наведенной поляризации на часто-
частоте ы] — ы, + ш3 — ш4 связана с амплитудами электрического поля
следующим образом:
2)?*(«з)?,*(«4). A3А2)
В случае материальной среды с мгновенным откликом поляри-
поляризации величина х<д/ в выражении A3.4.2) численно равна Хщ в
A3.4.1). Множитель 6 в A3.4.2) обусловлен числом различных воз-
возможных способов, с помощью которых можно получить комбина-
комбинацию Ej(w2)Ek(wi)E*(wA) в A3.4.1). В отличие от коэффициента вто-
второго порядка drk, который не равен нулю лишь в нецентросиммет-
ричных кристаллах, коэффициент Хш не равен нулю в любой среде,
включая изотропные материалы (газы, жидкости, стекла), а также
кубические кристаллы. Однако форма тензора Хпк/ определяется
симметрией точечной группы среды. Эти тензоры для различных
случаев симметрии табулированы в книге Хеллворта [8]. В этой
книге рассматриваются подробно различные физические явления,
которые связаны с оптическими нелинейностями третьего порядка.
В табл. 13.1 мы поместили небольшой перечень величин хухху Для
некоторых материалов.
На рис. 13.3 иллюстрируется основная экспериментальная схема
четырехволнового смешения. Нелинейная среда накачивается двумя
интенсивными противоположно направленными пучками плоских
Оптика фазового сопряжения
ТАБЛИЦА 13.1. Значения ххуух (—со, со, со, —со) некоторых
материалов при \ = 694 нм [8]
595
Материал
cs2
cci4
Плавленый кварц
ИАГ
Бензол
Стекло LSO
Стекло ED-4
Стекло SF-7
Стекло ВК-7
Стекло LaSF-7
п
1,612
1,454
1,455
1,829
1,493
1,505
1,557
1,631
1,513
1,91
Ххуух (-<«>. W. ". -").
104 ед. МКС
441
6,2
1,5
7,41
68,9
2,26
2,8
9,8
2,26
12,4
и Е2 с частотой ш. В дальнейшем мы будем использовать
волн Ех 2
нижние индексы для обозначения волны, а не ее поляризации. По-
Поляризации предполагаются фиксированными. Волны Ех и Ег
сываются в виде
Еу,2 = АК2(т)е^'-к^'1 A3.4.3)
В среде вдоль некоторого произвольного направления z распростра-
распространяются также две другие волны в противоположные стороны. Их
комплексные амплитуды равны Л,(г) и Аг(т). Волны Еъ и ЕА, вооб-
вообще говоря, не являются плоскими волнами, и мы рассматриваем Е4
как волну на входе, а?3 — как волну на выходе. Если частота w4
г = L
РИС. 13.3. Схема экспериментального устройства для фазового сопряжения по-
посредством четырехволнового смешения.

596
Глава 13
волны 4 равна ш (т. е. частоте волн накачки 1 и 2), то волна 3 бу-
будет генерироваться на частоте ш3 = и, а ее комплексная амплитуда
будет всюду комплексно-сопряженной амплитуде поля Е4. Направ-
Направление распространения волны 4 произвольное. Волны предполага-
предполагаются поляризованными вдоль определенных направлений, и мы бу-
будем рассматривать взаимодействие, используя скалярные величи-
величины.
Четыре волны A, 2, 3 и 4) связаны между собой посредством
нелинейной поляризации A3.4.2). Рассмотрим в качестве примера
нелинейную поляризацию, обусловленную смешением волн 1, 2 и 4:
О =
A3.4.4)
Последнее выражение в A3.4.4) обусловлено тем, что kj + к2 = 0.
Сравнивая это выражение с A3.4.2), мы видим, что х<3) = 6Хукг
Выражение A3.4.4) соответствует волне поляризации с частотой ш
и волновым вектором k = — ezk. Таким образом, будет возбуж-
возбуждаться волна Е3 вида
E3 = A3(z)e'iul+kz\
Новая волна Е3, смешиваясь с волнами А х и А 2, генерирует вол-
волну поляризации
, 0 =
A3.4.5)
у которой частота и волновой вектор такие же, как и у волны Е4,
т. е. волна поляризации A3.4.5) должна взаимодействовать с вол-
волной Е4. Это показывает, каким образом происходит взаимодейст-
взаимодействие и обмен мощностью волн 3 и 4 с волнами накачки 1 и 2. При
математическом описании этого взаимодействия мы будем предпо-
предполагать, что волны накачки Ех и Ег очень интенсивны и, следова-
следовательно, не участвуют в обмене мощностью, так что амплитуды Ах
и А2 можно считать постоянными. Предположим также, что
\АХ\ = \А2\. Тогда замедление (оптический эффект Керра) каждой
волны накачки другой волной одно и то же, и, следовательно, им
можно пренебречь. Таким образом, нужно рассматривать распро-
распространение только волн Е3 и Е4.
Начнем рассмотрение с основного волнового уравнения A2.3.10)
в случае нелинейной поляризации. В случае обратной волны Е3 в
Оптика фазового сопряжения
597
A2.3.10) величину кх мы заменяем на -к. Предполагая, что потери
отсутствуют (со = 0), и вспоминая, что к2 = со2^0?, получаем
Подстановка в уравнение A3.4.6) выражения A3.4.4) для PNL дает
A3.4.7)
и аналогично
dA*
л
dz
2
В этих выражениях мы использовали соотношение к = о)у//л0е. По-
Последние два уравнения можно переписать следующим образом:
dz1 = iK*A*'
A3.4.8)
dA
dz
dA*
dz
где
В большинстве научных публикаций по оптике фазового сопря-
сопряжения используется система единиц СГС. Ниже рассмотрение осно-
основано на системе единиц МКС. Уравнения A3.4.8), которые приме-
применяются в качестве основных во многих практических приложениях,
остаются неизменными в системе единиц СГС (СГСЭ), за исключе-
исключением того что постоянная связи в ней определяется следующим об-
образом:
СГСЭ СП Л ' 2
A3.4.9)
где любая из физических величин х<3), Ах,А2пс должна быть выра-
выражена в единицах СГСЭ. Для удобства перехода из одной системы
единиц в другую напомним, что
1 статвольт/см = 2,99793 • 104 В/м

598
Ю
-18
Глава 13
A3.4.10)
Если задать комплексные амплитуды /13(L) и Л4@) двух слабых
волн в соответствующих им входных плоскостях (z — L, Z — 0), то
решения уравнений A3.4.8) можно записать в виде
cos|k|z , M K*sin|K|(z
- L)
—-Лд
sin
cos|k|(z - L)
cos|k|L
A3.4.11)
В большинстве практических случаев присутствует лишь одна вол-
волна А4@) при z = 0. В этом случае отраженная волна на входе (в
плоскости z = 0) дается выражением
A3.4.12)
в то время как на выходе (в плоскости z — L) мы имеем
cos|k|L '
A3.4.13)
Заметим, что амплитуда отраженной волны А 3@) пропорцио-
пропорциональна амплитуде А *@), т. е. амплитуде, комплексно-сопряженной
Л4@). Из линейности уравнений A3.4.8) непосредственно следует,
что если входное поле Е4 не является плоской волной, а имеет
сложную форму волнового фронта (но по-прежнему представляет
собой монохроматическую волну), так что
[здесь 1^(г) — некоторая комплексная функция], то отраженная вол-
волна Е3 принимает вид
?3(r)z<0=Re
-/ ?- tg \k\L
A3.4.14)
Следовательно, уравнения A3.4.8) применимы для анализа не толь-
только плоских волн, но и волн с произвольной формой волнового
фронта.
Оптика фазового сопряжения
599
Таким образом, мы установили, что геометрия четырехволново-
го смешения, представленная на рис. 13.3, выполняет функцию фа-
фазового сопряжения и что отраженная волна Еъ повторяет при ее об-
обратном распространении любое искажение, испытываемое падаю-
падающей волной Е4. Такой способ компенсации искажений продемонст-
продемонстрировали экспериментально в 1971 г. Вердман [9], а также Степа-
Степанов и др. [10].
Хотя наша основная цель состояла в том, чтобы показать роль
фазового сопряжения, решение A3.4.12) позволяет выявить некото-
некоторые новые особенности. Заметим, что в области
A3.4.15)
мы имеем
и зеркало, осуществляющее фазовое сопряжение, действует как уси-
усилитель. При этом усиление по мощности оказывается равным
tg2|K|L.
A3.4.16)
На рис. 13.4 приведены результаты измерений усиления при от-
отражении (вплоть до 300%) в ячейке из дисульфида углерода (серо-
0 5 10
Энергия на входе, мДж
РИС. 13.4. Нелинейный коэффициент^ отражения в зависимости от энергии накачки
(в мДж); точки соответствуют экспериментальным данным; сплошная кривая по-
построена подгонкой формулы /? = tjrae по методу наименьших квадратов к экспе-
экспериментальным данным.

600
Глава 13
Накачка
<t * ' ^NDS NDR;
Рз I I Pi / 0 < 0 < X/4
CS,
40 см
М,
I
I
R = 0,5 м f3
/? = 4m
Задержка 40 не
Рубиновый лазер
с модулир.
добротностью
(~ 8 мДж; ~ 5 не)
РИС. 13.5. Экспериментальная установка для измерения нелинейного коэффициента
отражения (все зеркала являются полностью отражающими).
углерода) с использованием излучения (X = 0,6943 мкм) рубинового
лазера с модулируемой добротностью. Соответствующая экспери-
экспериментальная аппаратура схематически показана на рис. 13.5.
Из выражения A3.4.13) также следует, что для одной падающей
волны Л4@) поле в плоскости z = L дается выражением
1
A3.4.17)
Отсюда мы видим, что AA{L) всегда больше чем Л4@), т. е. устрой-
устройство действует как усилитель для любых значений к при любом
уровне накачки.
Квантовомеханический анализ четырехволнового взаимодейст-
взаимодействия показывает, что усиление прямой волны АА и генерация обрат-
обратной волны А3 происходят за счет энергии волн накачки Ах и А2.
Для каждого фотона, добавляемого к А3, один фотон должен быть
добавлен к А4, тогда как одновременно по одному фотону отнима-
отнимается от каждой из волн Л, и А2.
На рис. 13.6 показано распределение поля внутри среды при вы-
выполнении условия большого усиления х/4 < I к IL < ж/2.
Если интенсивность накачки (т. е. произведение 1Л,Л21) возрас-
возрастает до \к\Ь — х/2, то из выражений A3.4.16) и A3.4.17) следует,
что
= 00.
Оптика фазового сопряжения
601
Л3@)
A4 @)
*
>
<
15
52 "
'¦)l
vl^3 B)|
\
At (i)
О L
РИС. 13.6. Распределение поля внутри нелинейной среды в условиях большого уси-
усиления.
Это означает, что исчезающе малое значение входного сигнала
АА@) приводит к конечным значениям выходных амплитуд A^(L) и
Л3@). Устройство, которое генерирует излучение в отсутствие сиг-
сигнала на входе, называется генератором. Таким образом, мы теоре-
теоретически установили возможность генерации в резонаторах без зер-
зеркал, что напоминает нам генерацию в лазерах с распределенной об-
обратной связью, описанных в гл. 11. Аналогия с лазером с распреде-
распределенной обратной связью является совершенно четкой. В этом лазе-
лазере взаимодействие между прямой и обратной волнами осуществля-
осуществляется благодаря пространственному периодическому возмущению
среды с периодом, равным половине некоторого нечетного числа
РИС. 13.7. Распределения мощности />4 входного сигнала и мощности Р сопряжен-
сопряженной волны в зависимости от величины \k\z вблизи условия генерации (\k\L = тг/2).
(Из работы [1].) Мощности Р} и />4 нормированы на полную мощность Р , а зна-
значения \k\z отнесены к \k\L. полн
39-631

602
Глава 13
Измеритель
мощности
Ячейка из
СиС12:Н2О
fr
R = 2м
Рубиновый лазер
' с модулир-
R = 4м
Задержка 40 не добротностью
(~8мДж; -15 не)
изв.
о
о.
С
/"V
/ Ч
1
1
Л
/
20 не/дел
РИС. 13.8. Экспериментальное устройство, использованное для наблюдения генера-
генерации при четырехволновом смешении. (Из работы [1].) На оси ординат отложена от-
относительная мощность (по отношению к Я ).
ПОЛИ7
длин волн генерируемого излучения в этой среде. В четырехволно-
четырехволновом генераторе волны А2 и АА модулируют показатель преломле-
преломления (или потери). Образующаяся при этом решетка показателей
преломления отражает волну Ах в направлении волны Av Одновре-
Одновременно волны Аъ и Ах образуют решетку, которая отражает волну
А2 в направлении Аг Нетрудно показать, что при использовании
схемы, показанной на рис. 13.3, условие Брэгга автоматически
удовлетворяется для обеих решеток. На рис. 13.7 представлены
распределения интенсивности внутри нелинейной среды при выпол-
выполнении условий генерации.
Схема экспериментальной установки, в которой наблюдалась ге-
генерация, приведена на рис. 13.8. Следует заметить, что волны на-
накачки А{ и А2 (волна А2 создается отражением волны А1 от зеркала
Mj) поляризованы ортогонально возбуждаемым волнам. Это обу-
обусловлено тем, что CS2, а также все изотропные среды характеризу-
характеризуются не равными нулю компонентами тензора
13.4.1. ОЦЕНКА ПОСТОЯННОЙ СВЯЗИ к
В большинстве практических случаев в соответствии с выражения-
выражениями A3.4.11) требуются достаточно большие интенсивности накач-
Оптика фазового сопряжения
603
ки, так что kL ~ 1. В настоящее время многие устройства по фазо-
фазовому сопряжению выполнены на основе CS2. Поэтому представляет
интерес вычислить значение постоянной связи к для этого материа-
материала. Мы имеем
Хухку(-ш, со, со, -со) * 3,57-Ю-13 ед. СГСЭ = 4,41 -Ю2 ед. МКС
[здесь мы использовали следующее соотношение: уй), =
- ,.В) „о ,. ш,8)] Из A3 4 9) и выражения Л^с
Г
А, =А,=
получаем
C>
= 2,03-Ю-31 ед. МКС,
пео\
Используя значения
^cl2 = 6хухху(-и, со, со,'гсо)
X = 10m, n = 1,62,
находим
к (м-1) = 0,21/j (МВт/см2).
Чтобы получить величину кЬ ~ 1, например при L = 10 см, требу-
требуются интенсивности порядка десятков мегаватт на квадратный сан-
сантиметр, которые можно получить только от импульсных лазеров.
Требуемую интенсивность можно уменьшить, если брать большие
значения хC), которые можно получить в случае, когда частота па-
падающего сигнала близка к некоторой частоте перехода в среде. О
такого рода экспериментах по резонансному усилению посредством
четырехволнового смешения в парах атома Na сообщается в работе
Для более детального изучения данной области, включающей
такие приложения, как обработка изображений, частотная фильт-
фильтрация и сжатие импульса, читатель может обратиться к соответст-
соответствующей литературе [12, 14]. В работе [14] содержится обзор мно-
многих статей по оптическому фазовому сопряжению.
ЗАДАЧИ
13.1. Рассмотрим среду, диэлектрическая проницаемость которой
зависит от интенсивности поля следующим образом:

604
Глава 13
е(г) = eo(r) + E2(r)|?|2 ,
где Е — полная комплексная амплитуда монохроматическо-
монохроматического поля в точке г. Покажите, что волновому уравнению
=0
удовлетворяет решение
Е = [ф{т)е''к2 + af{r)eikz]eiat + компл. сопр.
при условии, что
Это справедливо для любой среды без потерь, поскольку
е — вещественная величина. При доказательстве мы отбра-
отбрасываем члены с e±likz, которые не синхронизованы в про-
пространстве. С помощью более полного доказательства можно
было бы показать, что фазово-сопряженная волна может
компенсироваться обратной волной не только в случае ста-
статических неоднородностей показателя преломления [ео(г)],
но и при зависящих от интенсивности неоднородностях
[e2l?!2].
13.2. Пусть имеется экспериментальное устройство, схематически
показанное на рис. 13.9. Покажите, что пороговое условие
для генерации волн в направлении, перпендикулярном пло-
плоскости зеркала, имеет вид
k\L\ = arctg(l/r),
где R = \г\2 — коэффициент отражения зеркала.
Зеркало
-/
РИС. 13.9.
Оптика фазового сопряжения
605
13.3. Покажите, что если нелинейная среда, используемая в экспе-
экспериментальной установке, схематически показанной на
рис. 13.3, обладает затуханием, то уравнения связанных мод
A3.4.8) принимают вид
где а — коэффициент поглощения интенсивности и
Решите эти уравнения при граничных условиях А3(Ь) = 0 и
данной амплитуде А4@). Покажите, что коэффициент отра-
отражения дается выражением
г =
А;@)
где
aL _ (SL\
[2!
2к
эфф
13.4. Решите уравнения A3.4.8) в случае, когда частота входной
волны А4 небольшой интенсивности не равна частоте волны
2, w4 * wi)- Постройте зависимости
накачки (т. е.
функции
со, = ш
Л =
S)
от отклонения частоты 6. Здесь со — частота накачки, а
со — 5 — частота входной волны. [Указание: учтите фазовый
множитель к, + к2 — (к3 + к4) в выражении
(к,+ k2)-r+(*3l + *4l)z,
который при 5 Ф 0 не равен нулю.]

606
Глава 13
13.5. Покажите, используя рассуждения, аналогичные тем, кото-
которые приводились при получении выражения A2.2.7), что в
случае атома, для которого наведенная поляризация являет-
является однозначной функцией электрического поля (мгновенный
отклик), восприимчивость xijki (-«р «2» шз> ~Ш4) в A3.4.2) та
же самая, что и в выражении A3.4.1).
13.6. Покажите, что резонансные частоты лазерного резонатора,
в котором одно из зеркал заменяется фазово-сопряженным
зеркалом, не зависят от расстояния между зеркалами.
13.7. Сопряженные волны. Вектор электрического поля монохро-
монохроматического излучения записывается в виде
где амплитудная функция Е(г) удовлетворяет уравнению
V X (V X Е) - оз2цеЕ = 0.
а) Покажите, что сопряженная волна
Е2(г, 0 = Е*(гУ*"
также удовлетворяет записанному выше уравнению при
условии, что величина це вещественная (т. е. для сред
без потерь).
б) Пусть электрическое поле имеет вид
Е(г) - A(r)e'*w,
где А и ф — вещественные функции координаты г. По-
Покажите, что волновые фронты (поверхности постоянной
фазы) волн Е, и Е2 даются выражениями
ф(г) + «/ = С,,
- ф(г)
С2,
где С, и С2 — постоянные величины. Поскольку С1 и
С2 — произвольные постоянные, в любой момент време-
времени t эти волновые фронты можно записать в виде
ф(г) = const.
Оптика фазового сопряжения
607
Иными словами, во всем пространстве г волновые фрон-
фронты у волн Ej(r, t) и Е2(г, t) являются одними и теми же.
б) Пусть волновой фронт распространяется в пространстве
в течение интервала времени (t, t + dt). Покажите, что
смещения волнового фронта V0(r) волн Ej и Е2 даются
соответственно выражениями
dxx • v*(r) + «dt = 0, -dr2 • v<Kr) + wdt = O.
Отсюда следует, что волновой фронт сопряженной вол-
волны движется в противоположном направлении по отно-
отношению к исходной волне.
г) Пусть
Е(г) = JB(k)e'k"d3k.
Покажите, что каждая фурье-компонента сопряженной
волны распространяется строго в противоположном на-
направлении по отношению к фурье-компоненте исходной
волны.
13.8. Состояния поляризации сопряженных волн. Пусть имеются
следующие волны:
Е^г, 0 = Ее«"'-к2), E2(z, t) = EV<*"+*Z>,
E3(z, t) = Ee'<a'+k'\
где Е — комплексная постоянная, а к — постоянная распро-
распространения.
а) Покажите, что если волна Е, является линейно поляри-
поляризованной, то волны Е2 и Е3 будут также линейно поля-
поляризованными.
б) Покажите, что если Ej является волной с правой круго-
круговой поляризацией, то такую же поляризацию будет
иметь и сопряженная ей волна Е2. Пусть Е3 является
волной с левой круговой поляризацией. Физические сооб-
соображения здесь следующие: спин фотона переворачивает-
переворачивается при отражении от зеркала, осуществляющего фазовое
сопряжение, в то время как спиральность (проекция спи-
спина на направление распространения) остается неизмен-
неизменной.
13.9. Собственная модуляция показателя преломления. Пусть в
среде, характеризующейся сильным эффектом Керра, рас-
распространяется интенсивный оптический пучок.

608 Глава 13
а) Покажите, что комплексная амплитуда поляризации
может быть записана в виде
РГ = еоХиЕ; + Ъхик,Е?ЕГЕ;,
где EJ — комплексная амплитуда электрического поля.
б) Предполагая, что электрическое поле поляризовано
вдоль направления х, покажите, что показатель прелом-
преломления, связанный с полем пучка, можно записать в виде
3Х
пп
И ЧТО П2=
В некоторых средах эта величина п2 вызывает самофоку-
самофокусировку лазерного пучка.
ЛИТЕРАТУРА
1. Yariv A., Phase conjugate optics and real time holography. — IEEE J. Quant, Elec-
Electron., QE-14, 650 A978).
2. Giuliano C. R., Applications of optical phase conjugation. — Phys. Today, April
1981, p. 27.
3. Зельдович Б. Я., Поповичев В. И., Рагульскип В. В., Фапзуллов Ф. С. О связи
между волновыми фронтами отраженного и возбуждающего света при вынуж-
вынужденном рассеянии Мандельштама — Бриллюэна. — Письма в ЖЭТФ, 1972,
т. 15, вып. 3, с. 160.
4. Носач О. Ю., Поповичев В. И., Рагульскип В. В., Фапзуллов Ф. С. Компенса-
Компенсация «фазовых искажений в усиливающей среде с помошью «бриллюэновского
зеркала». — Письма в ЖЭТФ, 1972, т. 16, вып. 11, с. 617.
5. Yariv A., Three-dimensional pictorial transmission optical fibers.— Appl. Phys.
Lett., 28, 88 A976).
6. Yariv A., On transmission and recovery of three-dimensional image information in
optical waveguides. — J. Opt. Soc. Amer., 66,301 A976).
7. Hellwarth R. W., Generation of time reversal wavefronts by nonlinear refraction- —
J. Opt. Soc. Amer., 67, 1 A977).
8. Hellwarth R. W., Third-order optical susceptibilities of liquids and solids. — Proc.
Quant. Electr., 5, Pergamon Press, 1977, pp. 1—68.
9. Woerdman J. P., Formation of a transient free carrier hologram in Si. — Opt. Com-
mun., 2, 212 A970).
10. Степанов Б. И., Ивакин Е. В., Рубанов А. С. О регистрации плоских и объем-
объемных динамических голограмм в просветляюшихся веществах. — ДАН СССР,
1971, т. 196, № 3, с. 567.
11. Liao P. F., Bloom D. М., Есопотои N. Р., CW optical wave front configuration
by saturated absorption in atomic sodium vapor. — Appl. Phys. Lett., 32, 813
A978).
12. Phase Conjugate Optics (ed. R. Fisher), Academic Press, New York, 1983.
13. Dunning G. J., Lind R. C., Demonstration of image transmission through fibers by
optical phase conjugation. — Opt. Lett., 7, 558 A982).
14. Pepper D. M., Nonlinear optical phase conjugation.— Opt. Engineer., 21, 156
A982). В этом специальном выпуске содержится много статей по оптическому
фазовому сопряжению.
Предметный указатель
Автокорреляционная функция 436
Акустические волны 343, 347, 376
Акустический резонанс 284
Акустооптика 343
— поверхности 384, 390
Акустооптическая модуляция 393
в одноосных кристаллах 407
коллинеарная 408
неколлинеарная 407
Акустооптические анализаторы спектра
428
— дефлекторы 410
— корреляторы сигнала 431
— материалы 348, 370, 371, 401
— модуляторы 393
— перестраиваемые фильтры 419
угловая апертура 424, 426
ширина полосы пропускания
421, 426
Акустооптический эффект 343
— вода 347
— германий 353
— LiNbO3 389
Акустооптическое взаимодействие 354
— LiNbO3 376
Ампера закон 10
Амплитудная модуляция 260, 270, 310
акустооптическая 393
показателя преломления 271
электрооптическая 260
Амплитудные модуляторы 260, 307
акустооптические 339
Фабри — Перо 311, 312
электрооптические 260
GaSe 275
Анизометрические молекулы 286
Анизотропная среда 63, 78
с кручением 156
Антисимметричный тензор 107, 127
ABCD-закон 38, 42
Бесселя функция 264
Бистабильность 321
Бистабильные резонаторы Фабри — Пе-
Перо 321, 323, 325, 340
— электрооптические устройства 321,
325
Блоха теорема 170
Блоховские волны 169, 183
в периодических слоистых средах
170, 185
затухающие 185, 226, 518
— моды 173
Елоховский волновой вектор 170
Елоховское волновое число 174
в периодических волноводах 435
Бриллюэна зоны 210
— рассеяние 543
Брюстера угол 187, 212
Брэгга режим 381, 395
Брэгговская дифракция
акустооптическая 356
в анизотропной среде 358, 360
одноосных кристаллах 360
встречных волн 375, 378
попутных волн 375
теория связанных мод 362
электрооптнческая 495
Брэгговские дефлекторы 414
— отражатели 191, 209, 235
Брэгговское отражение 189
в периодических волноводах 463
Вектор Пойнтинга 14, 89, 219
блоховских волн 220
— — направляемых волн 444
плоских волн 21
поверхностного плазмона 540
усредненный по времени 16, 21, 221
— решетки 170
Внутриатомное поле 241
Вода, акустооптические свойства 370,
371
— акустооптический эффект 347, 369
— коэффициенты фотоупругости 353
— показатель преломления 370, 371
— постоянная Верде 114
Керра 281
Волновая матрица 119
— пластинка 133
матрица Джонса 135
преобразование состояния поляри-
поляризации 162
Волноводный лазер 521, 528
Волноводы асимметричные 450
— диэлектрические 438
моды 450
общие свойства 438

610
ортогональность 442
передача Энергии 444
планарные 447, 538
с вытекающими модами 521
— модовое условие 518
— на брэгговском отражении 516, 519
металлической подложке 511
затухание 513
Волновое уравнение 17, 18, 440
для магнитного поля 18
электрического поля 17
Волновой вектор 18
— пакет 25, 89
— фронт 37, 41, 333,592
Волны Рэлея 384
Восприимчивость
— линейная 543
— нелинейная 543
— свойства симметрии 587
Встречная связь 203, 378, 465, 510
брэгговская 375
Гармонический осциллятор 47, 50
Гауссов пучок 18, 320
в линзоподобной среде 38
среде однородной 34
с квадратичным профилем
показателя преломления 47
комплексный радиус q(z) 42, 45, 47
модуляция 338
моды высшего порядка в однород-
однородной среде 46
преобразование 42
линзой 60
угловое расхождение 38
радиус кривизны волнового фрон-
фронта 40, 45
радиус перетяжки 40, 45, 60
фокусировка 45
Гепзенберга соотношение неопределен-
неопределенностей 28
Гельмгольца уравнение 32
Генерация второй гармоники 557
в кварце 558
кристаллах KDP 563, 569
гауссовыми пучками 568
фазовый синхронизм 560
эффективность преобразования
558, 569
— третьей гармоники 543
Геодезические линзы 431
Предметный указатель
Гидродинамическое уравнение движения
27
Гирация, вектор 107, 113
— тензор 109, 112
Гиротропная среда 130
Гистерезис 324
Глана призма 126
Голография 590
— в реальном времени 590
Гофрированная поверхность 459
Градиентное волокно 38
Граница полосы 176
Групповая скорость 21, 24, 25, 30
дисперсия 25, 30, 330
направляемых волн 445
необыкновенных волн в одноосных
кристаллах 125
света в среде анизотропной 89, 125
периодической 218
Гюйгенса принцип 385
Дву лучепреломление 132
в одноосных кристаллах 99
графический метод нахождения
углов преломления 98
жидкие кристаллы 288
циркулярное 104
Двулучепреломляющие брэгговские де-
дефлекторы 414
— оптические системы 132
— фильтры 143
Дефлекторы:
— акусюоптические 410
— электрооптические 333
Динамическое рассеяние 290
Директор 288
Диспергирующая среда 19, 22, 328
Дисперсия 19
— аномальная 26
— групповая скорость 25, 54, 328
— модовая 53, 54
— нормальная 26
Дифракционная эффективность:
акустооптические модуляторы 395,
398
Романа — Ната рассеяние 383
электрооптические решетки 384
Диэлектрическая проницаемость 10
комплексная 511, 533
отрицательная 511,528
Диэлектрический тензор 10, 78
Предметный указатель
611
анизотропная среда 78
антисимметричная часть 107
симметричный 80
Эрмитов 81
Диэлектрическое возмущение 115, 195
в волноводах 459
однородное 460
Жидкий кристалл 78
директор 288
нематический 288
с кручением 156, 158, 289
смектический 287, 288
холестерический 287
электрооптический эффект 286
Жира — Турнуа эталон 313
Запрещенная зона 176, 191, 215, 471
одномерная периодическая среда
185,232
Золото 511, 534
Импеданс 21
Импульс гауссов 28, 54
— искажение 26
— лоренцев 28
— распространение 21
— сжатие 328, 590
— уширеиие 53, 61
— форма 340
— ширина 54
Интегральная оптика 438
Ионная решетка 239
Квадратичные электрооптические коэф-
коэффициенты 277
в условных обозначениях 277
Квадратичный электрооптический эф-
эффект 275
Кварц 78, 434
— акустооптические свойства 370, 401
— генерация второй гармоники 558
— коэффициенты фотоупругости 348
— нелинейная оптическая восприимчи-
восприимчивость 552
— показатель преломления 92, 370, 595
Керра постоянная 281
некоторых веществ 281
Комплексная амплитуда 14
Коэффициент отражения 236
— связи 201
— — для плоских волн 201
Кристалл двуосный 91, 93
— изотропный 91, 93
— одноосный 95
— отрицательный 94
— положительный 94
Кулона закон 10
Кюри температура 243, 282
Лазер
— рубиновый 558, 586
— с распределенной обратной связью
474, 601
Левовращающее вещество 105
Лед, показатель преломления 92
Линзоподобная среда 32, 47
гауссовы моды 47
пучки 38
Лио фильтры 132
Лио — Эмана фильтры 143, 163
угловая апертура 166
ширина полосы пропускания 164
Лоренца сила 27
Лучевое уравнение 42
для линзоподобной среды 42
Магнитооптический эффект 113
Максвелла уравнение 9, 170, 439
в импульсном пространстве 82, 90
Материальная дисперсия 57
Материальные уравнения 10
Матрица Джонса 135
— поворота 135
— унитарная 135
Метод вариации постоянных 197
Модовая связь 459
в диэлектрических волноводах 459,
483
Мбдовый фильтр 516
Моды излучения 449
подложки 449
Модуляторы:
— акустооптические 393
— бегущих волн 318
— электрооптические 261
Модуляция амплитудная 260, 310
— высокочастотная 316
— глубина 274,-318
— индекс (глубина) 264, 301, 383
— фазовая 262, 266
Монохроматические излучение 31

612
Мультиплексирование по длине волны
507
Направленная связь 495
электрооптнческая 502
Направленные ответвители 496
на решетках 510
со знакопеременными А0 502
частотная избирательность 510
Нелинейная оптика 543
Нелинейное взаимодействие 5?5
Нелинейность 321, 544
Нелинейные оптические материалы 551
Необыкновенный луч 96, 562, 563
поляризация 96
Нормальные моды распространения 47,
88, 197
среда анизотропная 81
гиротропная 122
оптически активная 119
периодическая 170
Обработка изображения 590
Обращение времени 591
Огибающая функция 24
Одноосные кристаллы 95
распространение света 95
Омические потери 515, 531, 533
Оператор проектирования 162
Оптика фазового сопряжения 590
Оптическая бистабильность 321, 325
Оптические выключатели 327
— осн 82, 93
Оптический дифференциальный усили-
усилитель 327
Ориентацнонный эффект, жидкие кри-
кристаллы 288
Оси распространения 265
в кубических кристаллах 294
Параболическое приближение 198
Параметрический генератор 578
порог 579
самосогласованный анализ 575
условие генерации 577
Параметрическое усиление 571
Передача изображения 590
в волокнах 592
Периодическая прямоугольная функция
207
фурье-разложение 233
Предметный указатель
— слоистая среда 179
Периодические волноводы 463
.Периодическое возмущение 149, 601
Плавленый кварц, акустооптические
свойства 371, 401
— — коэффициенты фотоупругости 347
показатель преломления 20, 370
Плазменная частота 540
Плотность электрического заряда 10
— энергии 14, 89
Поверхностная акустооптнка 384
Поверхностные волны акустические 384
электромагнитные 225, 528, 533
— состояния 226
Поверхностный плазмон 528, 540
Поверхность нормалей 82
Поглощения коэффициент 127, 603
Показатель преломления 19
в среде анизотропной 93, 94
изотропной 19
комплексный 511, 532
металлы 511, 533, 534
некоторые кристаллы 92
Пойнтинга теорема 13
Поккельса эффект 239
Полное внутреннее отражение 450
в планарных волноводах 456
Поляризационное состояние 64, 71, 74
Поляризационные интерференционные
фильтры 143
Поляризация 63
Поляризованный свет 63
Постоянная связи 199, 201
акустооптическое взаимодействие
366
моды в направленных ответвите-
лях 499
фильтрах Шопьца 208
Поток энергии 14
¦ в анизотропной среде 85
скорость 89
Приближение геометрической оптики
456, 525
Романа — Наша акустические модулято-
модуляторы 434
— дифракция 380
— режим 381, 394
Решетки 354
Сапфир (А1,О,) 243
Предметный указатель
613
Сдвиговые волны 354
Сегнетова соль 242
Сигнальная волна 571, 572
Скорость звука 356, 401
Соотношение ортогональности 196
моды волноводные 444
нормальные 196, 444
собственные 85
Сопряженные волны 30, 591, 606
Сохранение заряда 26
— энергии 14
в анизотропной среде 130
Сохранения законы 13
Спектральный диапазон 164
Стекло 413
— акустооптические свойства 401
— показатель преломления 401
— постоянная Верде 114
Спюкса теорема 12
Температура перехода 243, 285
Тензор упругости 343
Теория связанных мод 195
Тонкая линза 43
— структура 161
Трансляционная симметрия 169
Турмалин 92
Угловая апертура 424, 426
— настройка 580, 581
Угловое расхождение 38, 396
Угловой момент 66, 68
Уравнение непрерывности 12, 26
Уравнения связанных моя 117, 201
Фазовая модуляция 262, 313
— решетка 382
— скорость 19, 217
блоховской волны 218
звука 354, 401
необыкновенной волны в одноос-
одноосном кристалле 125
света 19, 25
Фазовое сопряжение 594
Фазовый модулятор 263, 313
— синхронизм 149, 200, 506
Фонон 357
Фотон 66, 68
— угловой момент 66, 68, 75
Фурье-спектр 23
Харриса фильтр 435
Холестерическая фаза 286, 287
Холостая волна 571, 572
Цинковая обманка 308
Частота отсечки 454
Ширина запрещенной зоны 176 188 215,
216
Шопьца фильтры 205
Электромагнитная поверхностная волна
225, 528
Электромагнитное поле 9
Эрмитово сопряжение 136, 162
Эффективный показатель преломления
458,473,490, 514

ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 7
Глава 1. ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ 9
1.1.Уравнения Максвелла и граничные условия 9
1.2.Теорема Пойнтинга и законы сохранения 13
1.3.Формализм комплексных функций 14
1.4.Волновое уравнение и монохроматические плоские волны .... 17
1.5.Распространение лазерных импульсов; групповая скорость .. 21
Задачи 26
Литература 30
Глава 2. РАСПРОСТРАНЕНИЕ ЛАЗЕРНЫХ ПУЧКОВ 31
2.1.Скалярное волновое уравнение 31
2.2.Гауссовы пучки в однородной среде 34
2.3.Фундаментальный гауссов пучок в линзоподобной среде; за-
закон ABCD 38
2.4.Моды гауссова пучка высшего порядка в однородной среде .. 46
2.5.Моды гауссова пучка в среде с квадратичным распределени-
распределением показателя преломления 47
Задачи 60
Литература 62
Глава 3. ПОЛЯРИЗАЦИЯ СВЕТОВЫХ ВОЛН 63
3.1.Что такое поляризация? ; 63
3.2.Поляризация монохроматических плоских волн 64
3.3.Представление комплексного параметра 70
3.4.Вектор Джонса 71
Задачи 73
Литература 77
Глава 4. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В АНИ-
АНИЗОТРОПНЫХ СРЕДАХ 78
4.1.Диэлектрический тензор анизотропной среды 78
4.2.Распространение плоских волн в анизотропных средах 81
4.3.Эллипсоид показателей преломления 86
4.4.Фазовая скорость, групповая скорость и скорость переноса
энергии 89
4.5.Классификация анизотропных сред (кристаллов) 93
4.6.Распространение света в одноосных кристаллах 95
4.7.Двойное лучепреломление на границе раздела 98
4.8.Распространение света в двуосных кристаллах 100
4.9.Оптическая активность 104
4.10.Фарадеевское вращение 113
4.11.Анализ распространения волн в анизотропных средах мето-
методом связанных мод 114
4.12.Уравнение движения для состояния поляризации 120
Задачи 124
Литература 131
Глава 5. ИСЧИСЛЕНИЕ ДЖОНСА И ЕГО ПРИМЕНЕНИЕ ДЛЯ РАСЧЕ-
РАСЧЕТА ДВУЛУЧЕПРЕЛОМЛЯЮЩИХ ОПТИЧЕСКИХ СИСТЕМ 132
5.1.Формализм матриц Джонса 132
5.2.Интенсивность излучения, прошедшего через оптическую си-
систему 139
5.3.Поляризационные интерференционные фильтры 143
Оглавление
615
5.4.Распространение света в анизотропной среде с кручением .... 156
5.5.Учет френелевского отражения и фазового сдвига 160
Задачи ]6i
Литература 168
Глава 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПЕРИ-
ПЕРИОДИЧЕСКИХ СРЕДАХ 169
6.1.Периодические среды 169
6.2.Периодические слоистые среды 179
б.З.Брэгговское отражение 189
6.4.Теория связанных мод 195
6.5.Теория связанных мод для фильтров Шольца 205
6.6.Теория связанных мод для брэгговских отражателей 210
6.7.Фазовая скорость, групповая скорость и скорость переноса
энергии 217
6.8.Двулучепреломление за счет формы 222
6.9.Электромагнитные поверхностные волны 225
Задачи 232
Литература 237
Глава 7. ЭЛЕКТРООПТИКА 238
7.1.Электрооптический эффект 238
7.2.Линейный электрооптический эффект 241
7.3.Электрооптическая модуляция 257
7.4.Распространение волн в электрооптических кристаллах 264
7.5.Квадратичный электрооптический эффект 275
7.6.Физические свойства электрооптических коэффициентов 283
7.7.Электрооптические эффекты в жидких кристаллах 286
Задачи 290
Литература 296
Глава 8. ЭЛЕКТРООПТИЧЕСКИЕ УСТРОЙСТВА 297
8. ЬЭлектрооптические модуляторы света 297
8.2.Электрооптические модуляторы Фабри — Перо 310
8.3.Некоторые конструктивные особенности модулирующих
устройств 316
8.4.Бистабильные электрооптические устройства 321
8.5.Электрооптический сдвиг частоты и сжатие импульса 327
8.6.Электрооптическое отклонение светового пучка 333
Задачи 336
Литература 342
Глава 9. АКУСТООПТИКА ..'. 343
9.1. Фотоупругий эффект 343
9.2.Основные представления об акустооптическом взаимодейст-
взаимодействии : 354
9.3.Корпускулярная картина акустооптических взаимодействий . 357
9.4.Брэгговская дифракция в анизотропной среде 358
9.5.Брэгговская дифракция и теория связанных мод 362
9.6.Дифракция Рамана — Ната 380
9.7.Поверхностная акустооптика 384
Задачи 389
Литература 391

616 Оглавление
1 Глава 10. АКУСТООПТИЧЕСКИЕ УСТРОЙСТВА 393
1 10.1-Акустооптические модуляторы 393
] Ю.2.Акустооптические дефлекторы 410
Ю.З.Акустооптические перестраиваемые фильтры 419
10.4.Акустооптический спектр-анализатор 428
Ю.5.Акустооптические корреляторы сигнала 431
Задачи 434
Литература 437
Глава 11. НАПРАВЛЯЕМЫЕ ВОЛНЫ И ИНТЕГРАЛЬНАЯ ОПТИКА 438
11.1 .Общие свойства диэлектрических волноводов 438
] 11.2.ТЕ- и ТМ-моды в асимметричном волноводе 450
11.3.Возмущение диэлектрической проницаемости и взаимодейст-
взаимодействие мод 459
11.4.Периодический волновод; брэгговское отражение 463
11.5.Встречная связь в периодическом волноводе 471
П.б.Лазеры с распределенной обратной связью 474
11.7.Электрооптическая модуляция и модовая связь 483
11.8.Направленная связь 495
11.9. Частотные мультиплексоры 507
П.Ю.Другие планарные волноводы 510
] 11.11.Диэлектрические волноводы с вытекающими модами 521
11.12.Поверхностные электромагнитные волны (поверхностные
плазмоны) 528
Задачи 534
Литература 541
Глава 12. НЕЛИНЕЙНАЯ ОПТИКА 543
12.1.Введение 543
] 12.2.Нелинейные явления второго порядка; общая методология .. 544
12.3.Электромагнитная формулировка нелинейного взаимодейст-
взаимодействия 555
12.4.Генерация второй гармоники в оптическом диапазоне 557
12.5.Генерация второй гармоники при наличии обратного воз-
воздействия 566
12.6.Генерация второй гармоники гауссовыми пучками 568
12.7.Параметрическое усиление 571
12.8.Параметрическая генерация 574
12.9.Настройка частоты в параметрических генераторах 579
12.10.Повышение частоты 581
Задачи 586
Литература 588
Глава 13. ОПТИКА ФАЗОВОГО СОПРЯЖЕНИЯ 590
13.1.Введение 590
13.2.Распространение чере,з неоднородную среду 590
13.3.Передача изображения в волокнах 592
13.4.Теория фазового сопряжения при четырехволновом смеше-
1 нии [7] 594
Задачи 603
Литература 608
Предметный указатель 609