7. ПРИНЯТИЕ РЕШЕНИЙ В РАСПЛЫВЧАТЫХ
УСЛОВИЯХ »)
Р, Беллман и JI. Заде
1.	ВВЕДЕНИЕ
На практике во многих случаях принятие решений
происходит в таких условиях, когда цели, ограничения
и последствия возможных действий точно не известны.
Для обращения с неточно известными величинами
обычно применяется аппарат теории вероятностей, а
также методы теории принятия решений, теории упра¬
вления и теории информации. Таким образом, интуи¬
тивно принимается допущение, что неточность (impre¬
cision) независимо от ее природы может быть отожде-
ставлена со случайностью (randomness). Это, как нам
представляется, является спорным предположением.
По нашему убеждению, необходимо различать слу¬
чайность (randomness) и расплывчатость (fuzziness),
причем последняя является основным источником не¬
точности во многих процессах принятия решений. Под
расплывчатостью подразумевается тот тип неточности,
который связан с расплывчатыми множествами2) [20,
21], т. е. с классами, в которых нельзя указать резкую
границу, отделяющую элементы, принадлежащие к
данному классу, и элементы, не принадлежащие к не-
') Bellman R. Е., Zadeh L. A., Decision-Making in Fuzzy En¬
vironment, Management Science, 17, № 4, 141—164 (1970).
2) Термин «fuzzy sets», введенный в научный обиход Л, Заде,
в отечественной литературе переводится по-разному — как «раз¬
мытые», «нечеткие», «нечетко определенные», «расплывчатые» и
Т. д. множества. Мы сочли целесообразным остановиться на по¬
следнем термине, как наиболее близко передающем смысл, кото¬
рый вкладывается в это понятие в современной литературе,—
Прим. ред.

7. Принятие решений в расплывчатых условиях
173
му. Например, класс зеленых предметов есть расплыв¬
чатое множество. Расплывчатыми являются также
классы объектов, характеризуемых такими часто ис-
полмуемымй прилагательными, как «большой», «ма¬
ленький», «существен н ы й», «значительный», «важ¬
ный», «серьезный», «простой», «точный», «приближен¬
ный» и т. п. Фактически большинство классов в реаль-
ном мире, в 'ТГр'отивоположность понятию класса или
множества в математике, не имеют четких границ, ко¬
торые отделяли бы входящие в класс объекты от объ¬
ектов, не входящих в него. В связи с этим важно от¬
метить, что в разговоре между людьми расплывчатые
утверждения, такие, как: «Джон на несколько дюймов
выше Джима», «х значительно больше г/», «У корпора¬
ции X прекрасные перспективы», «На фондовой бирже
наблюдается резкий спад», все же несут значительную
информацию, несмотря на неточность выделенных
курсивом слов. Более того, на наш взгляд одно из
основных различий между человеческим интеллек¬
том и «искусственным интеллектом» ЭВМ заклю¬
чается в том, что в отличие от современных ком¬
пьютеров люди обладают способностью оперировать
расплывчатыми понятиями и выполнять расплывчатые
инструкции.
В чем состоит различие ме^ду случайностью и
расплывчатостью? По сути дела, случайность связана*
с неопределенностью, касающейся принадлежности
или непринадлежности некоторого объекта к нерас-^
плывчатому множеству. Понятие же расплывчатости
относится к классам, в которых могут иметься различ¬
ные градации степени принадлежности, промежуточ¬
ные между полной принадлежностью и нёпринадлеж-
ностыо объектов к данному классу.
Например, расплывчатое утверждение «Корпора¬
ция X придерживается прогрессивных взглядов» яв¬
ляется неточным вследствие расплывчатости выраже¬
ния «прогрессивные взгляды». В то же время утвер¬
ждение- «Вероятность того, что корпорация X рабо¬
тает в убыток, равна 0,8» содержит информацию о
мере неопределенности относительно принадлежности
корпорации X к нерасплывчатому классу корпораций,

174
Р. Веллман, JI. Заде
работающих в убыток. Аналогично утверждение «Сте¬
пень принадлежности Джона к классу высоких муж¬
чин равна 0,7» является «невероятностным» утвержде¬
нием относительно принадлежности Джона к расплыв¬
чатому классу высоких мужчин, а утверждение «Ве¬
роятность того, что Джон женится в течение года,
равна 0,7»—«вероятностное» утверждение, характери¬
зующее неопределенность наступления нерасплывча¬
того события (женитьбы).
Это различие приводит к тому, что математические
методы теории расплывчатых множеств совершенно не
похожи на методы теории вероятностей. Они во мно¬
гих отношениях проще вследствие того, что понятию
вероятностной меры в теории вероятностей соответ¬
ствует более простое понятие функции принадлежно¬
сти в теории расплывчатых множеств. Кроме того,
вместо обычных операций а + Ь и ab, где а я b — дей¬
ствительные числа, используются более простые
операции Мах (а, Ь) и Min (а, Ь). По этой причине
даже в тех случаях, когда расплывчатость в про¬
цессе принятия решений может быть представлена
вероятностной моделью, обычно удобнее оперировать
с ней методами теории расплывчатых множеств без
привлечения аппарата теории вероятностей.
Процессы принятия решений, в которых тем или
иным образом присутствует расплывчатость, могут
изучаться с различных точек зрения [22, 9, 14]. В на¬
стоящей статье основное внимание уделяется введе¬
нию трех фундаментальных понятий — расплывчатой
цели, расплывчатого ограничения и расплывчатого ре¬
шения, а также исследованию их применения к много¬
шаговым процессам принятия решений, в которых
цели или ограничения могут быть расплывчатыми,
а управляемая система может быть либо детермини¬
рованной, либо стохастической, но не расплывчатой.
Это, однако, не накладывает существенных ограниче¬
ний на применимость концепций и методов, описаннйх
в последующих разделах.
Вообще говоря, под дасплывчатой целью подразу¬
мевается цель, которую можно описать как расплыв¬
чатое множество в соответствующем пространстве. Так,"

7. Принятие решений в расплывчатых условиях 175
простым примером расплывчатой цели, связанной с
вещественной переменной х, может служит цель: «х
должно быть существенно больше 100». Со своей сто¬
роны, ограничение «х должно находиться приблизи¬
тельно в интервале 20—25» является простейшим при¬
мером расплывчатого ограничения. Источниками рас¬
плывчатости в этих утверждениях являются слова, вы¬
деленные курсивом.
Менее тривиальным примером может служить де¬
терминированная система, работающая в дискретном
времени и описываемая уравнениями состояния
хп+\ = хп-{- ип, /1 = 0, 1, 2, ...,
где хп и ип обозначают соответственно переменную
состояния и входную переменную в момент времени п
и для простоты предполагаются вещественно-значны¬
ми. Расплывчатое ограничение, наложенное на вход¬
ную переменную, могло бы здесь иметь вид
где волнистая линия под символом означает «опера-'
тор размытия», который переводит нерасплывчатое
множество в приблизительно равное ему расплыв¬
чатое множество. В этом случае выражение
ип Ssj 1 читается следующим образом: «ип должно
быть приблизительно меньше или равно 1», и резуль¬
татом действия оператора размытия будет перевод не¬
расплывчатого множества —1 ^ ип ^ 1 в расплывча¬
тое множество —1 ип ^ 1. Способ, которым послед¬
нему множеству можно придать более точный смысл,
будет рассмотрен в разд. 2.	j
Предположим, что расплывчатая цель состоит в
том, чтобы сделать х3 приблизительно равным 5, на¬
чиная с исходного состояния Хо= 1. В этом случае
задача заключается в нахождении такой последова¬
тельности входов и<>, щ, и2, которая будет как можно
более близко реализовать установленную цель с уче¬
том наложенных ограничений на входы ио, ии и2.
Ниже мы более подробно рассмотрим несколько
характерных задач этого типа. Следует подчеркнуть,

176
Р. Беллман, Л. Заде
что в данной статье мы ставим перед собой ограничен¬
ную цель—привлечь внимание к задачам, включающим
многошаговые процессы принятия решений в расплыв¬
чатых условиях, и предложить возможные пути их ре¬
шения и отнюдь не претендуем на построение общей
теории процессов принятия решений, в которых рас¬
плывчатость и случайность могут входить самыми
, разнообразными способами и в виде различных ком¬
бинаций. В частности, мы не будем заниматься вопро¬
сом о приложении к задаче принятия решений поня¬
тия расплывчатого алгоритма [22], которое может ока¬
заться полезным в задачах, плохо поддающихся коли¬
чественному анализу.
Для удобства читателя в следующем разделе дает¬
ся краткий обзор основных свойств расплывчатых
множеств.
2.	краткое введение в теорию
РАСПЛЫВЧАТЫХ МНОЖЕСТВ
Вообще говоря, расплывчатое множество есть класс
объектов, в котором нет резкой границы между теми
объектами, которые входят в этот класс, и теми, ко¬
торые в него не входят. Более точное определение мо¬
жет быть сформулировано следующим образом.
Определение. Пусть X = {х} — совокупность объ¬
ектов (точек), обозначаемых через х. Тогда расплыв¬
чатое множество А в X есть совокупность упорядочен¬
ных пар
А = {х, Цд(х)}, xs=X,	(1)
где цл (*) представляет собой степень принадмжнд-
сти х к А, а рА:Х-*-М— функция, отображающая X
в пространство М, называемое пространством принад¬
лежности. Когда М содержит только две точки 0 и 1,
А является нерасплывчатым и его функция принад¬
лежности совпадает с характеристической функцией
нерасплывчатого множества.
В последующем мы будем предполагать, что М
есть интервал [0,1], причем 0 и 1 представляют соот¬
ветственно низшую и высшую степени принадлежно¬

7. Принятие решений в расплывчатых условиях 177
сти. (В более общем случае М может быть частично
упорядоченным множеством и, в частности, решеткой
[15, 6].) Таким образом, наше основное предположение
состоит в том, что расплывчатое множество А, не¬
смотря на нечеткость его границ, может 6ыгь~точно
определено путем сопоставл ения каждому "объекту X
числа, лежащего между 0 и 1, которое представляет
суепень его принадлежности к А.
Пример. Пусть X = {0, 1, 2, ...}—совокупность
неотрицательных целых чисел. В этом пространстве
расплывчатое множество А «нескольких объектов» мо¬
жет быть определено (субъективно), скажем, как на¬
бор упорядоченных пар
А -{(3; 0,6), (4; 0,8), (5; 1,0),
(6; 1,0), (7; 0,8), (8; 0,6)},	■	(2)
причем считается, что- в (2) перечислены только те
пары (х, pa(*))i для которых ца(*) положительно.
Замечание. Следует заметить, что во многих
практических ситуациях функция принадлежности ца
должна быть оценена исходя из частичной информа¬
ции о ней, скажем такой, как значения, принимаемые
ею на конечном множестве опорных точек Хи ..., Xn.
Когда А определено таким образом неполностью — и,
следовательно, лишь приблизительно, — мы будем го¬
ворить, что оно частично определено с помощью «пояс¬
няющего примера». Задача оценки ца по известному
множеству пар ((хи pA(*i)), ..., (xN, ца(*я)) есть
задача абстрагирования — задача, играющая цен¬
тральную роль в распознавании образов [4, 18]. В на¬
стоящей статье мы не будем заниматься решением
этой задачи, а всюду будем предполагать (если толь¬
ко не оговорено противное), что Ца(*) задано для
всех х в X.
Для рациональной записи удобно было бы иметь
средство для указания того, что расплывчатое множе¬
ство А получено из нерасплывчатого множества А за
счет «размытия» границы множества А. Для этой цели
мы будем использовать волнистую черту под симво¬

178
Р. Беллман, Л. Заде
лом (или символами), определяющими А. Например,
если А есть множество действительных чисел между 2
и 5, т. е. А = {х 12 ^ х ^ 5}, то А — {х 12 ^ х ^ 5}
есть расплывчатое множество действительных чисел,
которые заключены приблизительно между 2 и 5. Ана¬
логично А = {х\х “ 5} или просто 5 будет обозначать
Л/У
множество чисел, приблизительно равных 5. Сим¬
вол — будет называться оператором размытия
(fuzzifier). Перейдем теперь к 'определению несколь¬
ких основных понятий, которые понадобятся нам
в следующих разделах.
Нормальность. Размытое множество А нормально
тогда и только тогда, когда 5иржрА(х) = 1, т. е. су¬
премум p,A(*) на X равен единице. Расплывчатое
множество субнормально, если оно не является нор¬
мальным. Непустое субнормальное расплывчатое
множество может быть нормализовано делением каж¬
дого рА(*) на величину Sup*p,A(*). ^Расплывчатое
множество пусто тогда и только тогда, когда рА(х)г=
= 0.)
Носитель. Носитель расплывчатого множества А
есть такое множество 5(A), что хе5(Л) <=Ф рА(х)>
> 0. Если рА(х) = const на 5(A), то А нерасплыв¬
чато. Отметим, что нерасплывчатое множество может
быть субнормальным.
Равенство. Два расплывчатых множества равны
(что записывается как А = В) тогда и только тогда,
когда рА = Рв, т. е. ра(*) == Рв(*) для всех х в X.
(В дальнейшем мы для упрощения записи будем опу¬
скать аргумент х, когда равенство или неравенство
имеет место для всех значений х в А.)
Включение. Расплывчатое множество А содер¬
жится в расплывчатом множестве В, или является
подмножеством В (записывается как Ас=Д), тогда
и только тогда, когда рА ^ рв- В этом смысле рас¬
плывчатое множество очень больших чисел есть под¬
множество расплывчатого множества больших чисел.

7. Принятие решений в расплывчатых условиях
179
Дополнение. Говорят, что А' есть дополнение к А
тогда и только тогда, когда рл, = 1 — рл. Например,
расплывчатые множества А = (Высокие люди} и
А' — {Невысокие люди} являются дополнениями друг
к другу, если отрицание «НЕ» понимается как опе¬
рация, заменяющая ра(*) на 1—ра(*) для каждого
х в X
Пересечение. Пересечение А я В обозначается
А Г) В и определяется как наибольшее расплывча¬
тое множество, содержащееся как в А, так ив В.
Функция принадлежности для АПВ определяется
следующим равенством:
^апв (*) = Мт(рл (*)>	М)>	х<=Х,	(3)
где Min (а, Ь) = а, если а ^ Ь, и Min (а, 6) = 6, если
а > Ь.
Если использовать вместо символа Min знак конъ¬
юнкции Л, можно переписать условие (3) в более
простом виде:
^ Л Рв-	(4)
Понятие пересечения имеет близкое отношение к
понятию соединительного союза «И». Так, если А —
класс высоких людей и В — класс полных людей, то
А[\В — класс людей, которые одновременно высокие
И полные.
Замечание. Следует заметить, что отождествле¬
ние союза «И» с операцией (4) означает, что «И» по¬
нимается в «жестком» смыслу, т. е. отсутствует воз:
можность какой-либо «компенсащии» имеющихся зна¬
чений Ца(*) какими-либо значениями рв и, наоборот,
«компенсации» рв(х) за счет значений ра(*)> по_
скольку мы I имеем дело с ситуацией либо ра(х) >
> рв(х), .(ибо рв(х)>рЛ(х)- Например, если
Ра(х) =0,8 и рв(х) = 0,5, то рАпв(*) = 0,5, по¬
скольку ра (я) >0,5. В некоторых случаях ближе к
подразумеваемому смыслу союза «Й» может ока¬
заться более «мягкая» интерпретация союза «И», со¬
ответствующая образованию алгебраического-Произ¬
ведения ра(*)рв(*)> а не пересечения Ра(*)Л рв(х).

180
Р. Веллман, JI. Заде
Как с математической, так и с практической
точки зрения более предпочтительно отождествлять
союз «И» с операцией пересечения Л, а не с опера¬
цией произведения, за исключением тех случаев,
кода операция Л совершенно не передает требуемого
смысла «И». По этой причине в дальнейшем «И»
будет пониматься в «жестком смысле», если только
особо не оговорено противное.
Объединение. Понятие объединения множеств
двойственно понятию пересечения. Объединение А и
В обозначается A U В и определяется как наимень¬
шее расплывчатое множество, содержащее как А,
так и В. Функция принадлежности для AUB опре¬
деляется соотношением
М'лив(л:) = Мах(^л(х)> М*)) хеХ, (5)
еде Мах (а, Ь) — а, если а^Ь, и Мах (а, Ь) = Ь, если
а<.Ь. Используя вместо символа Мах знак дизъ¬
юнкции V, можно записать условие (5) в более про¬
стом виде:
^лив^Рл V Рв*	(6)
В отличие от пересечения, операция объединения
имеет близкое отношение к соединительному союзу
«ИЛИ». Так, если множества А п В имеют прежний
смысл, то A U В = {Высокие или Полные люди).
Можно также различать «или» ,в «жестком» смысле,
соответствующее операции (6), от «или» в «мягком»
смысле, “соответствующего алгебраической сумме А
и В, обозначаемой как АфВ и определяемой соотно¬
шением (9).
Несложно проверить следующее тождество, свя¬
зывающее операции пересечения и объединения:
AUB = (A'f]B')'.	(7)
Алгебраическое произведение. Алгебраическое про¬
изведение расплывчатых множеств А и В обозна¬
чается через АВ и определяется равенством
Илв (х) ~ Рл (■*•) Рв М»	х е= X.	(8)

7. Принятие решений в расплывчатых условиях 181
Алгебраическая сумма. Алгебраическая сумма А
и В обозначается через А®В и определяется равен¬
ством
Ра ф в (*) — Ра (*) +	(*) — Ра (*) Рв (*)•	(9)
Легко проверить, что	'
А@В = {А'В'У.	(10)
Замечание. Необходимо отметить, что опера¬
ции V и Д ассоциативны и дистрибутивны по отно¬
шению друг к другу. В то же время операции • (про¬
изведения) и ® (суммы) ассоциативны, но не дис¬
трибутивны. Заметим также, что операция ■ (произ¬
ведение) дистрибутивна по отношению к объедине¬
нию V, но не наоборот. Вообще говоря, таким свой¬
ством обладает любая операция *, монотонно не¬
убывающая по каждому из своих аргументов. В сим¬
волической записи
если b’^b'=^a*b’^a*b' и а"^ а' =^а*Ь^а' *Ь,
то
a* {by с) — (а* Ь)У (а* с).
Большинство полученных ниже результатов остается
справедливо при замене операции А на операцию *,
которая является ассоциативной и дистрибутивной
относительно операции V.
Выпуклость и вогнутость. Пусть А — расплывчатое
множество в пространстве X = Rn. Тогда А является
выпуклым расплывчатым множеством в том и только
в том случае, если его функция принадлежности для
каждой пары точек х, у из X удовлетворяет нера¬
венству
Рл(и + (1 -А)г/)>Мт(цл(х), цА{у)) (11)
для ijcex 0<;А,<;1. Соответственно А является вог¬
нутым, если его дополнение А' выпукло. Нетрудно по¬
казать, что если два расплывчатых множества А и В
выпуклы, их пересечение А[\В также выпукло. С дру¬
гой стороны, если А и В вогнуты, то вогнутым будет
и их объединение AUB,

182
Р. Веллман, Jl. Заде
Отношение. Расплывчатое отношение R на пря¬
мом произведении пространств Xy^Y ={(х, у), х^Х,
у е= Y] есть расплывчатое множество в X X У, харак¬
теризуемое функцией принадлежности рд, которая
сопоставляет каждой упорядоченной паре (х, у) ее
степень принадлежности yR(x,y) к R. В общем слу¬
чае n-арное расплывчатое отношение на декартовом
произведении X = Хг X Х2 X • • • X есть расплыв¬
чатое множество в X, описываемое зависящей от п
переменных функцией принадлежности р,д(.*п,... ,*п)>
Х{<=Хи t = 1, П.
Пример.	Пусть X = Y = R',	где R' — действи¬
тельная	прямая (—оо, оо). Тогда	условие х^$>у	за¬
дает расплывчатое отношение в R2, функция принад¬
лежности которого может иметь, например, такой вид:
(	0,	если х^.у,
И-Я (Х> у) ~ 1 /. . ,	V.
(Д1-И* — у) ) .	если х>у.
Расплывчатые множества, порождаемые отобра¬
жениями. Пусть f:X-*-Y — отображение из X = {х}
в Y — {(/}, причем образ элемента х обозначается
через y~f(x), и пусть А — расплывчатое множество
в пространстве X. Тогда отображение / порождает
расплывчатое множество В в пространстве У с функ¬
цией принадлежности, задаваемой соотношением
Рв(У)= SuP М*)>	(12)
X е f 1 {у)
причем супремум берется по всем точкам, составляю¬
щим прообраз f~l (у) в X точки у.
Условные расплывчатые множества. Расплывча¬
тое множество В (х) в пространстве У = {у} назы¬
вается условным по х, если его функция принадлеж¬
ности зависит от переменной х как от параметра. Эта
зависимость выражается записью ув{у\х).
Предположим, что областью изменения параметра
х является пространство X и при этом каждому х из
X соответствует расплывчатое множество В (х) в У.
Таким образом, мы имеем дело с отображением из X
в пространство расплывчатых множеств в У, характе¬

7. Принятие решений в расплывчатых условиях
183
ризуемым функцией рв(у\х). Посредством этого
отображения любое заданное расплывчатое множе¬
ство А в X порождает расплывчатое множество В в
У, определяемое соотношением
Рв(у) = Sup Min (цл (ж), цв (у \х)),	(13)
где ца и рв — функции принадлежности множеств
А и В соответственно. Используя операции Д и V,
можно переписать условие (13) в более простом виде:
Рв(«/)= \МРл(х) А Цв{у\х)).	(14)
Отметим, что это соотношение аналогично — однако
не эквивалентно—выражению для маргинального рас¬
пределения вероятностей совместного распределения
двух случайных переменных, причем \тв{у\х) играет
роль, аналогичную условному распределению.
Разложимость. Пусть X = {х}, У = {у} и пусть
С — расплывчатое множество в пространстве Z —
= ХХ^ с функцией принадлежности рс(х,у). Тогда
С называется разложимым по X и У в том и только
в том случае, если С допускает представление С =
.= АС\В, или, что эквивалентно,
г/) = Ид(*) А Рв{у),	(15)
где А и В — расплывчатые множества с функциями
принадлежности ца(х) и рв(у) соответственно. (Та¬
ким образом, А и В — цилиндрические расплывчатые
множества в Z.) Этй! определение справедливо для
расплывчатого множества, заданного в декартовом
произведении любого конечного числа пространств.
Вероятность расплывчатых событий. Пусть Р —
вероятностная мера в Rn. Расплывчатое событие [23]
А в Rn определяется как расплывчатое подмножество
А пространства Rn, функция принадлежности кото¬
рого, рА, измерима. Вероятность события А задается
интегралом Лебега — Стилтьеса:
Р(Л)= $ рл(*МР.	(16)
Rn
Иначе говоря, Р(Л) =ЕрА, где Е — оператор мате¬
матического ожидания. В случае нормального нерас-

f84	P.	Беллман,	Jl.	Заде
4	          .
^лывчагого множества (16) сводится к общеприня¬
тому определению вероятности случайного события.
Этим завершается краткое введение в основные
понятия теории расплывчатых множеств. В следую¬
щих разделах эти понятия будут использованы в ка¬
честве основы для важных определений цели, ограни¬
чения и решения в условиях «расплывчатости».
3.	РАСПЛЫВЧАТЫЕ ЦЕЛИ, ОГРАНИЧЕНИЯ
И РЕШЕНИЯ
В общепринятом подходе главными элементами
процесса принятия решения являются: а) множество
альтернатив, б) множество ограничений, которые не¬
обходимо учитывать при выборё~мёжду различными
альтернативами, и в) функция предпочтительности,
ставящая каждой альтернативе в соот вето гвие выиг¬
рыш (или проигрыш), который будет получен в рё”*
зультате выбора этой альтернативы.
При рассмотрении этого процесса с более общих
позиций принятия решений в расплывчатых условиях
естественной представляется другая логическая.схе¬
ма, важнейшей чертой которой является симметрия
по отношению к целям и ограничениям. Эта симмет¬
рия устраняет различия между целями и ограниче¬
ниями и позволяет довольно просто сформировать на
их основе решение.
Действительно, пусть X {х} — заданное множе¬
ство альтернатив. Тогда расплывчатая цель, или про¬
сто цель, G будет отождествляться с фиксированным
расплывчатым множеством G в X. Например, если
X = R1 (действительная прямая), а расплывчатая
цель формулируется как «х должно быть значительно
больше 10», то ее можно представить как расплывча¬
тое множество в R1 с функцией принадлежности,
имеющей, скажем, такой вид:
Г	0,	х	<	10,
^W = \(1 + (X_io)-2)-‘, *>ю.	(17)
Аналогично цели «х должно быть в окрестности 15»
может быть поставлено в соответствие расплывчатое

7. Принятие решений в расплывчатых условиях
185
множество с функцией принадлежности
М*) = (1+(*-15)4Г'.	(18)
Отметим, что оба эти множества выпуклы в смысле
(11).
При обычном подходе функция предпочтительно¬
сти, используемая в процессе принятия решения,;слу¬
жит для установления линейной ^упорядоченности на
множестве альтернатив. Очевидно,'что функция при¬
надлежности цв(х) расплывчатой цели выполняет ту
же задачу ‘) и, конечно, может быть получена из функ¬
ции предпочтительности с помощью нормализации,
сохраняющей установленную линейную упорядочен¬
ность. В сущности, такая нормализация приводит к
общему знаменателю различные цели и ограничения
и позволяет, таким образом, обращаться с ними оди¬
наковым образом. Как мы увидим, это является важ¬
ным аргументом в пользу того, чтобы в качестве одно¬
го из основных компонентов в логической схеме приня¬
тия решений в расплывчатых условиях пользоваться
понятием цели, а не функции предпочтительности.
Подобным же образом расплывчатое ограничение,
или просто ограничение, С в пространстве X опреде¬
ляется как некоторое расплывчатое множество в X.
Например, в случае X = R1 ограничение «х должно
находиться приблизительно в диапазоне 2—10» мо¬
жет быть представлено расплывчатым множеством с
функцией принадлежности, скажем, вида:
Рс (*) = (1 +а(х~ 6)т)-1,
где а — положительное число и m — четное положи¬
тельное число, выбираемое так, чтобы передать
смысл, в котором следует понимать «приближение» к
интервалу [2, 10]. Если, в частности, положить m — 4
и а — 5~4, то в точках х = 2 и х = 10 функция при¬
надлежности равна рс(х) = 0,71, в то время как при
х = 1 и л:=11 pc(x)=0,5, а при х — 0 и х — 12
Рс(х) = 0,32.
') Предполагается, конечно, что принимаемые функцией р<з
значения образуют линейно упорядоченное множество,

186
Р. Беллман, Л. Заде
Важным аспектом приведенных выше определений
является то, что и цель и ограничение рассматри¬
ваются как расплывчатые множества в пространстве
альтернатив; это, как будет показано ниже, дает воз¬
можность не делать между ними различия при фор¬
мировании решения. В противоположность этому при
традиционном подходе к принятию решений множе¬
ство ограничений считается нерасплывчатым множест¬
вом в пространстве альтернатив X, тогда как функция
предпочтительности является функцией перехода из
X в некоторое другое пространство. Но даже и в этом
случае использование множителей Лагранжа и
штрафных функций делает очевидным существование
некоторого внутреннего сходства между функциями
предпочтительности и ограничениями (см. [17], гл. 15).
Это сходство — а на самом деле тождественность —
становится совершенно естественным при нашей фор¬
мулировке.
Действительно, предположим, например, что рас¬
плывчатая цель G и расплывчатое ограничение С
заданы следующим образом:
G: х должно быть значительно больше 10 и
С: х должно быть в окрестности 15.
[ро(*) и рс(*) задаются соответственно формула¬
ми (17) и (18).] Заметим, что цель G и ограничение
С соединены между собой союзом «И», причем, как
было указано в разд. 2, «И» соответствует пересече¬
нию расплывчатых множеств. Это означает, что в рас¬
сматриваемом примере совокупное влияние расплыв¬
чатой цели G и расплывчатого ограничения С на вы¬
бор альтернатив может быть представлено пересече-
-нием GflC. Функция принадлежности для пересече¬
ния задается соотношением
И1 q п с	== 11 о W A (-'•)
или, в разрефнутой форме,
пс М =
f Minftl +(х-10Г2)"1, (1 +(х-15)4)-1) Для х>10,
1 0	длях<10.

7. Принятие решений в расплывчатых условиях
187
Отметим, что в силу выпуклости расплывчатых мно¬
жеств G и С множество G[)C также является вы¬
пуклым.
Обратимся теперь к понятию решения. Интуитив¬
но ясно, что решение — это по существу выбор одной
или нескольких из имеющихся альтернатив. Преды¬
дущий пример наводит на мысль, что расплывчатое
решение, или просто решение, следует определить как
расплывчатое множество в пространстве альтерна¬
тив, получающееся в результате пересечения задан¬
ных целей и ограничений. Следующее определение
уточняет эту мысль.
Определение. Пусть в пространстве альтерна¬
тив X заданы расплывчатая цель G и расплывчатое
ограничение С. Тогда расплывчатое множество D, об¬
разуемое пересечением G и С, называется решением.
В символической форме
D = Gf]C	(19)
и соответственно pi> = це Л цс- Взаимосвязь между
G и С показана на фиг. 1.
В более общем случае, если имеется п целей и пг
ограничений, то результирующее решение опреде¬
ляется пересечением всех заданных целей и ограни¬
чений, т. е.
Z) = G,nG2n ... ПС„ПС,ПС2П ... ПСт (20)
и соответственно
Л Рс2 Л ... А А Ню, А 9с2Л ... ЛрСт- (21)
Заметим, что в приведенном определении расплыв¬
чатого решения цели и ограничения входят в выраже¬
ние для D совершенно одинаковым образом, что и
доказывает утверждение о тождественности целей и
ограничений в сформулированной нами логической
схеме процессов принятия решений в расплывчатых
условиях.
Замечание. Определение решения как пересе¬
чения целей и ограничений соответствует пониманию
союза «И» в «жестком» смысле формулы (4). Если

188	Р.	Веллман,	Л.	Заде
вопрос об интерпретации союза «И» остается откры¬
тым, мы будем говорить, что решение — понимаемое
как расплывчатое множество — является слиянием
целей и ограничений. Таким образом, «слияние»~пр5-
обретает смысл «пересечения» или «алгебраического
произведения» в зависимости от интерпретации союза
«И» в смысле (4) или (8); кроме того, ему может
быть приписано какое-либо другое конкретное значе¬
ние, если возникает необходимость в специальной
Фиг. 1.
интерпретации союза «И» [см. замечание после фор¬
мулы (10)]. Коротко обобщенное определение реше¬
ния можно сформулировать следующим образом:
Решение = Слияние целей и ограничений.
В качестве иллюстрации к соотношению (21) рас¬
смотрим простой пример, в котором X = {1, 2,..., 10},
a Gi, G2, Ci и С2 определяются табл. 1. Образуя конъ¬
юнкцию pCi, fiC!, pCi и рСг, получим таблицу значений
для цр(х) (табл. 2).
Решение в этом случае есть расплывчатое мно¬
жество
£> = ((2; 0,1), (3; 0,4), (4; 0,7), (5; 0,8),
(6; 0,6), (7; 0,4), (8; 0,2)}.
Заметим, что ни одно х из X не принадлежит реше¬
нию D полностью (т. е. со степенью принадлежности,
равной 1). Это, конечно, является следствием того,
что заданные цели и ограничения вступают в конф¬
ликт друг с другом, исключая тем самым возмож-

7. Принятие решений в расплывчатых условиях
189
Таблица I
X
1
2
3
4
5
6
7
8
9
10
UG,
0
0,1
0,4
0,8
1,0
0,7
0,4
0,2
0
0
Рв,
0,1
0,6
1,0
0,9
0,8
. 0,6
0,5
0,3
0
0
йс,
0,3
0,6
0,9
1,0
0,8
0,7
0,5
0,3
0,2
0,1
Vc,
0,2
0,4
0,6
0,7
0,9
1,0
0,8
0,6
0,4
0,2
Таблица 2
X
1
■ 2
3
4
5
6
7
8
9
10
Й£>
0
0,1
0,4
0,7
0,8
0,6
0,4
0,2
0
0
ность существования альтернативы, которая бы пол¬
ностью им всем удовлетворяла.
Понятие решения как расплывчатого множества
в пространстве альтернатив может поначалу пока¬
заться несколько искусственным. На самом деле оно
совершенно естественно, поскольку расплывчатое ре¬
шение может рассматриваться как некоторая «инст¬
рукция», расплывчатость которой является следствием
неточности формулировки поставленных целей и огра¬
ничений. Так, в приведенном примере Gu G2, Ci и С2
могли бы быть выражены следующими фразами:
«х следует взять близким к 5», «х следует взять близ¬
ким к 3», «х следует взять близким к 4», «х следует
взять близким к 6». Тогда решение состоит в том,
что «следует взять» «х, близкое к 5». При этом точное
значение слова «близко» определяется в каждом слу¬
чае значением соответствующей функции принадлеж¬
ности.
Как следует выполнять расплывчатые инструкции
типа «х следует взять близким к 5»? Хотя на вопросы
такого типа не представляется возможным дать уни*

190
Р. Беллман, Л. Заде
версальный ответ1), во многих случаях все же ра¬
зумно выбрать те альтернативы, которые имеют мак¬
симальную степень принадлежности к Д. В нашем
примере этому соответствует х = 5.
В общем случае примем, что D — расплывчатое
решение с функцией принадлежности ци. Пусть К —•
множество тех точек в X, в которых функция pD до¬
стигает максимума (если он существует). Тогда не¬
расплывчатое, но, вообще говоря, субнормальное
подмножество DM из D, определяемое условиями
( Мах Цд (х) для х еД,
РдмМ | о для остальных х,
будет называться оптимальным решением, а каждое
х из носителя множества DM — максимиризующим
решением. Другими словами, максимизирующее ре¬
шение— это любая альтернатива в пространстве X,
которая максимизирует функцию рр(х) (скажем, как
х = 5 в предыдущем примере). Отметим, что в Rn
достаточным условием единственности максимизи¬
рующего решения является сильная выпуклость рас¬
плывчатого множества D, т. е. выпуклость D и нали¬
чие у него унимодальной функции принадлежности.
В определении расплывчатого решения D как пе¬
ресечения или, в более общем смысле, как слияния
целей и ограничений подразумевается, что все вхо¬
дящие в D цели и ограничения имеют в некотором
смысле одинаковую важность. Однако встречаются
ситуации, в которых некоторые цели и, возможно, не¬
которые ограничения являются более важными, чем
остальные. В таких случаях решение D может быть
выражено выпуклой комбинацией целей и ограниче¬
ний с весовыми коэффициентами, характеризующими
относительную важность составляющих элементов.
Таким образом, рв(х) может быть записано в виде
п	m
Pd (ж) = S щ (х) рс. (х) + £ р/ (х) цС/ (х),	(22)
‘) По поводу использования • «расплывчатых инструкций»
см. [22].

7. Принятие решений в расплывчатых условиях
191
где а; и Pj — функции принадлежности, такие, что
п	m
(=1	;=1
С учетом этого ограничения функции аДя) и |ЗДа')
могут быть подобраны так, чтобы передавать относи¬
тельную важность целей Gи G2, ..., Gn и ограниче¬
ний Си С2, ..., Ст. В частности, если т = п=\,
нетрудно проверить, что из выражения (22) можно
получить любое расплывчатое множество, содержа¬
щееся в G U С и включающее G Г) С. Отметим, что
формула (22) напоминает известный способ сведения
векторного критерия к скалярному с помощью обра¬
зования линейной комбинации компонент векторной
функции цели.
До сих пор мы ограничивались рассмотрением си¬
туаций, в которых цели и ограничения являются рас¬
плывчатыми множествами в пространстве альтерна¬
тив X. Практический интерес представляет более об¬
щий случай, когда цели и ограничения — расплывча¬
тые множества в разных пространствах. Пусть / —
отображение из X = {*} в У = {у}, причем перемен¬
ной х обозначено входное воздействие (причина), а
переменной у— соответствующий выход (следствие).
Предположим, что цели заданы как расплывчатые
множества Gь G2 Gn в У, в то время как ограни¬
чения— расплывчатые множества Си С2, ..., Ст в
пространстве X. Имея расплывчатое множество Gt в
У, можно найти расплывчатое множество G{ в X, ко¬
торое индуцирует Gi в У. Функция принадлежности
G, задается равенством
И-о. (*) =	. (/ (*)),	/ = 1, • • •, п. (23)
После этого решение_0 может 6j>iTb выражено пере¬
сечением множеств Gu С2, ..., Gn и Си С2, ..., Ст.
Используя соотношение (23), можно записать рх>(*)
в развернутом виде:
Рв(х) = рс,(/(а)) Л ...
А (/ (*)) А Рс, (*) А • ■ • Л УСт М, (24)

192
Р. Беллман, Jt. Заде
где f:X-+Y. Таким образом, случай, когда цели и ог-
раничения задаются как расплывчатые множества в
разных пространствах, может быть сведен к случаю,
когда они задаются в одном и том же пространстве.
Соотношение (24) является весьма полезным при ана¬
лизе многошаговых процессов принятия решений.
4.	МНОГОШАГОВЫЕ ПРОЦЕССЫ ПРИНЯТИЯ
РЕШЕНИЙ
В качестве приложения введенных в предыдущих
разделах понятий мы рассмотрим несколько основных
типов задач, связанных с многошаговым принятием
решений в расплывчатых условиях. Необходимо, од¬
нако, подчеркнуть, что основная задача последующего
изложения — иллюстрация понятий расплывчатых це¬
лей, ограничений и решений на ряде примеров, а не
развитие общей теории многошаговых процессов при¬
нятия решений, в которые тем или иным образом вхо¬
дит расплывчатость.
Для простоты будем предполагать, что управляе¬
мая система А является инвариантной по времени де¬
терминированной системой с конечным числом со¬
стояний. Именно, каждое состояние Xt, в котором
система А находится в момент времени t, t — 0, 1,
2, ..., принадлежит заданному конечному множеству
возможных состояний X = {ои ..., On}; при этом
имеющий место в момент i входной сигнал u(t) яв¬
ляется элементом множества U — {ось ..., ат}- Эво¬
люция системы во времени описывается уравнением
состояния
xt+i = f(xt, ut), t = 0,1,2,...,	(25)
в котором / — заданная функция, отображающая
XX U в X. Таким образом, f(xt, ut) представляв1!
собой последующее состояние для xt при входном
сигнале щ. Если f является случайной функцией, тщ
А — стохастическая система, состояние которой в м(Й
мент t + 1 характеризуется распределением вероятна
стей P(xt+i[xt,ut) на X, условным по xt и щ. Анала
гично если расплывчатая функция, то А являете

7. Принятие решений в расплывчатых условиях
193
расплывчатой системой [21], состояние которой в мо¬
мент t + 1 есть условное по xt и щ расплывчатое мно¬
жество, характеризуемое функцией принадлежности
вида \x,(xt+\\xt,Ut)x). Так как подобные системы в по¬
следующих разделах рассматриваться не будут, то
функция / будет считаться нерасплывчатой, если
только особо не оговорено противное.
Предполагается, что в каждый момент времени t
на входную переменную наложено расплывчатое ог¬
раничение С1, являющееся расплывчатым множест¬
вом в U с функцией принадлежности рДщ). Кроме
того, считается, что цель — расплывчатое множество
GN в X, определяемое функцией принадлежности
рйлт(%), где N — время окончания процесса. Эти
предположения являются общими для большинства
рассматриваемых ниже задач.
ЗАДАЧА 1. Предполагается, что система описы¬
вается уравнением (25), в котором / — заданная не¬
случайная функция. Считается также, что заданы на¬
чальное состояние Хо и фиксированное время оконча¬
ния процесса N. Задача заключается в нахождении
максимизирующего решения.
Применяя уравнение (20), можно записать реше¬
ние, рассматриваемое как разложимое расплывчатое
множество в (/ X ^ X ... ХУ,в виде
R^COQC'fl ... (\CN'lVGN,	(26)
где Gn — расплывчатое множество в U X U X • • • X U,
индуцирующее GN в X. Для функций принадлежности
имеем
рл (н0, ..., «лг_ i) =
— И0(«0) Л ••• Л Рдг-i (уц-1) Л РдМ (хм)>	(27)
где xN может быть выражено как функция от ии ...
..., Ндг_ 1 и хй путем последовательного применение
соотношения (25).
’) Следует отметить, что, говоря о расплывчатых условиях,
мы имеем в виду, что расплывчатыми являются цели и (или)
ограничения; однако это не означает, что управляемая система
обязательно является расплывчатой.
у27 Зак, 837

194
Р. Веллман, JI. Заде
Задача сводится к нахождению последовательно¬
сти входных воздействий и0, ..., uN-it максимизи¬
рующей p,D в формуле (27). Как обычно в многоша¬
говых процессах, целесообразно представить решение
в виде
ut = nt(xt)	t = 0, 1, 2, ..., N— 1,
где nt — принятая «стратегия», т. е. принятое правило
выбора входного воздействия ut в зависимости от
реализовавшегося xt. После этого для получения как
щ, так и максимизирующего (оптимального) реше¬
ния uff, ..., можно применить метод динамиче¬
ского программирования. Действительно, используя
(26) и (25), имеем
Н (ио <-«)=* Мах Мах (l*o («о) А • •.
“о	“N-2	“JV-1
... Л 1*^-, («ЛГ-i) A Hn(f(x^v «„_,))).	(28)
Если у — константа, a g — произвольная функция ар¬
гумента uN-1, то справедливо тождество
Мах (у Л g («jv-i)) = у Л Max g (и*-,).
“jv-i	UN~	1
Следовательно, (28) можно переписать в виде
•••» <-i)= Мах (ц0 (ыо) Л ...
и0. •••• им~2_
... Л И'^-гС^лг-г) А И-вЛГ— i (^лг_х))»	(29)
где	г	ч_
= Max(p/tf_1(MJV_i) Л р0лг (/(%_!, ы^_[))) (30)
“лг—1
может рассматриваться как функция принадлежности
расплывчатой цели в момент t = N— 1, индуцирован¬
ной заданной целью GN в момент t = N.

7. Принятие решений в расплывчатых условиях
195
Повторяя процесс обратных итераций, получаем
систему рекуррентных уравнений
PaW-v—
= Max (p„_v (u„_v) Д (xflV-v+i (*w_v+1)),	(3i)
N-v
^AF-v+1 == /	v> v)>	Т7=1,	N,
которая дает решение задачи. Таким образом, макси¬
мизирующее решение получается последовательной
максимизацией величин uN-w в (31), причем u^_v
определяется как функция от xN-v, v = 1 N.
Пример. В качестве простой иллюстрации рас¬
смотрим систему с тремя состояниями <xi, аг, аз и дву¬
мя входными сигналами оы и а2. Пусть для простоты
N = 2 и расплывчатая цель в момент t — 2 опреде¬
ляется функцией принадлежности ц0„ принимающей
значения
=== 0»^» И'дг (°г) = 1 > М'о* (^з) ~ О»®-
Пусть, далее, расплывчатые ограничения в моменты
t = 0 и t = 1 задаются функциями
1 p0(ai) = O,7; р0(а2)=П Pi(ai) — 1; р, (a2) = 0,6.
Предположим, что таблица изменения состояний,
задающая функцию f в формуле (25), соответствует
табл. 3. Используя (30), находим функцию принад¬
лежности расплывчатой цели в момент t == 1:
== 0,6, Р <31(^2)	М' о1 (^з) ==
Таблица 3
xt
о,
<Jl
<Ь
u<
«1
CTi
03
а2
02
01
<*3
lh7*

196
Р. Веллман, 'JI. Заде
и соответствующее максимизирующее решение имеет
вид
я, (о,) = а2;	n1(a2)	= ai; Jt1(a3) = a2.
Аналогично для t = О имеем
^G«(ai) = 0>8;	^C»(a2)	= 0>6> Нч5» (аз) = °>6
И
л0 (ст,) = a2; п0 (а2) = а, или а2; я0 (ог3) = а, или а2.
Итак, если начальное состояние (в момент времени
t = 0) есть о,, то максимизирующим решением будет
а2, а,, причем соответствующее значение функции
принадлежности pQ2 равно 0,8.
Обратимся теперь к более общему случаю много¬
шагового процесса принятия решений, в котором
управляемая система является стохастической, а цель
и ограничения — расплывчатыми.
5.	СТОХАСТИЧЕСКИЕ СИСТЕМЫ
В РАСПЛЫВЧАТЫХ УСЛОВИЯХ
Как и в предыдущей задаче, предположим, что
время окончания процесса N зафиксировано и задано
начальное состояние х0. Предполагается также, что
система характеризуется условным распределением
вероятностей p(xt+\\xu ut). Задача заключается в
максимизации вероятности достижения расплывчатой -
цели в момент N при условии, что должны быть выч
полнены расплывчатые ограничения С0, ..., С^-1.
Если расплывчатая цель GN рассматривается как
расплывчатое событие [23] в пространстве X, то услов¬
ная вероятность этого события при фиксированных
Xjv-i и u,v_ 1 выражается формулой
Prob (Gn | ATV_J, идг_,) = Ерслг(хлг) =
— Р (XN I XN-1> UN-1) P‘aN (XN) >	(32),
XN
где E — оператор условного математического ожида-(
ния, а — функция принадлежности расплывчатой
цели.

7. Принятие решений в расплывчатых условиях
197
В формуле (32)условная вероятность Prob GN(xN~,,
Hjv-i) [или Ёцслг (*дг)] выражена в виде функции пере¬
менных Xjv-i и Ujv-i, точно так же как в предыдущей
задаче (xN) было представлено в виде функции от
Xjv-i и Hjv-i посредством соотношения (25). Это озна¬
чает, что проделанные в детерминированном случае
выкладки для р0лг (xw) справедливы и для Ец0лг (XN)>
т. е. рассматриваемая задача сводится к предыдущей.
Рекуррентные соотношения (31) заменяются сле¬
дующими:
PflW-V (^Ar<-v) =
= Мах (м-^—v (mjv—v)> Eiigjv-'’+1'(a4v-v+i))>
N—v
Ердлг-v+i (-%_v+1)
= S p(%_v+i |%_v> mjv-v) Pg'V-v+I (xjV-v+l)>
XN-V+1
где p.Gw-v (XN-V) по-прежнему обозначает функцию
принадлежности расплывчатой цели в момент t =
— N — v, индуцированной расплывчатой целью в мо¬
мент t = N — v+1, v=l, ..., N. Эти уравнения по¬
зволяют получить искомое решение задачи, что ил¬
люстрируется приведенным ниже примером.
Пример. Как и в предыдущем примере, счи¬
тается, что система имеет три состояния ai, а2, сг3 и
два входных сигнала ои, а2. Время N принимается
равным 2, а распределение вероятностей p(xt+l\xt, ut)
задается табл. 4 и 5 для ut = cci и ut = а2. В таблицах
Таблица 4
“<“°1
о,
о2
а,
ai
0,8
0,1
0,1
о2
0
0,1
0,9
Оз
0,8
0,1
0,1

198
Р. БеллМчн, Л. Заде
Таблица 5
ut = a2
xt
0,
0,
0,1
0,9
0
02
0,8
0,1
0,1
03
0,1
0
0,9
представлены величины p(xt+\\xt,ut). Например,число
0,1 в положении (<ть аг) в табл. 4 означает, что
если в момент времени t система находится в состоя¬
нии щ и на вход поступает сигнал ой, то в момент
/+1 система с вероятностью 0,1 будет находиться в
СОСТОЯНИИ 02.
Пусть по-прежнему расплывчатая цель в момент
t — 2 определяется функцией
H'G*(<Ti) = 0,3; О^г) == ^ ’ И-ог (®з) = 0)8
и ограничения остаются теми же:
Po(ai) = 0,7; Цо(а2)=1; M-i («i) = 1; ц1(а2) = 0,6.
Применяя (33), получим Ец0,(л:2) как функцию от
*i и «ь см. табл. 6. Далее, используя (33) при v = 1
и вычисляя ц0, (Xj), находим
1*0. Oi) = °.6; Ц01 (<Т2) = 0,82; цо,(о3) = 0,6.
Соответствующая оптимальная стратегия имеет вид
я, (от,) = 02; n1(o2) = ai; л,(о3) = а2.	(33а)
Результаты последней итерации для v = 2 приведены
в табл. 7. Имеем также
M-Go (О[) = 0,8,	pG0(o2) = 0,62,	ро„(а3)=0,62,	(336)
я0 (Oi) = ос,, Яо(о2) = а! или ctj, no(a3) = a!. (ЗЗв)
Значения функции Цд, в (336) представляют собой
вероятности достижения поставленной цели в момент

7. Принятие решений в расплывчатых условиях
199
t = 2 в предположении, что процесс начинается с со¬
стояний аь 02 и аз соответственно и что входные сиг¬
налы выбираются в соответствии с оптимальной
Таблица 7
*1
Но
<П
о.
0,
а,
0,62
0,62
0,62
а2
0,80
0,62
0,60
стратегией щ, которая задается соотношениями (33а)
и (ЗЗв), т. е.
ut = nt{xt), (* = 0,1; Xt — ai, о2, о3; «г = аь а2).
Замечание. Необходимо отметить, что в тех
случаях, когда расплывчатая цель в момент N задана
таким образом, что вероятность ее достижения мала
для всех значений xN-i и 1%-ь может возникнуть не¬
обходимость в нормализации расплывчатой цели, ин¬
дуцированной в момент N—1, прежде чем отыски¬
вать ее пересечение с Сдт-р, в противном случае огра¬
ничения могут перестать влиять на решение. Вообще
говоря, подобная нормализация может потребоваться
на каждой стадии процесса принятия решений. Хотя
в данной статье мы не будем больше касаться этого
аспекта задачи, следует подчеркнуть, что вопрос этот
вовсе не является тривиальным и требует более тща¬
тельного анализа.

200
Р. Беллман, Jl. Заде
6.	СИСТЕМЫ С НЕЯВНО ОПРЕДЕЛЕННЫМ
ВРЕМЕНЕМ ОКОНЧАНИЯ ПРОЦЕССА
В рассмотренных задачах предполагалось, что
время окончания процесса управления N фиксировано
заранее. В этом разделе мы обратимся к более об¬
щему случаю, в котором время окончания определено
неявным образом, посредством дополнительного ус¬
ловия вида xN е Т, где Т — заданное нерасплывчатое
подмножество пространства X, называемое финаль¬
ным множеством1). Таким образом, процесс прекра¬
щается, как только управляемая система в первый
раз перейдет в состояние, принадлежащее заданному
подмножеству пространства состояний. В этом случае
цель определяется как расплывчатое множество О
в Г, а не во всем пространстве X.
Итак, пусть управляемая система А является де¬
терминированной системой, характеризуемой уравне¬
нием состояния вида
xt+i = f(xit щ), t = 0,1,2,...,	(34)
где xt принадлежит множеству X — {щ, ..., щ,
«Т/+1, ..., On}, а Т — [oi+u On} —финальное мно¬
жество. Как и прежде, / считается заданной функ¬
цией, осуществляющей отображение из X X U в X,
где U = {а 1, ..., ато} — область изменения ut, i = О,
1, 2 Отметим, что если щ является поглощаю¬
щим состоянием, т. е. состоянием из множества Т, то
можно записать /(с,-, а,) = аг- для всех а,- в U.
Предположим, что расплывчатая цель есть под¬
множество множества Т, определяемое функцией при¬
надлежности pg(*iv), где N — тот момент времени,
для которого имеет место	тогда при t < N
имеем xt ф Т. Что касается ограничений, наклады¬
ваемых на входную переменную, то для простоты бу¬
дем считать, что они не зависят от времени, но могут
зависеть от состояния. Таким образом, если система
*) Эта задача в такой традиционной постановке (когда «рас¬
плывчатость» полностью отсутствует) играет важную роль в тео¬
рии оптимального управления и марковских процессах принятия
решений (см. литературу в конце статьи).

7. Принятие решений в расплывчатых условиях 201
А в момент t находится в состоянии а,-, то расплывча¬
тое ограничение на ut задается расплывчатым множе¬
ством С(Ог) [или С(хг)] в U, условным по а. Функ¬
ция принадлежности этого множества будет обозна¬
чатся как \xc(Ut\xt)-
Пусть х0 — начальное состояние х0 е Т, где V —
=5 {ел, ..., сгг} — дополнение Т до X. Каждому та¬
кому начальному состоянию будет соответствовать
решение D(x0)r определяемое формулой
D (х0) = С (а:0) П С (*,) П ... ПС (**_,) П G, (35)
в которой последовательные состояния Хи ..., xN мо¬
гут быть выражены в виде функций от х0 и «о, • • •
..., uN-1 в результате последовательного применения
уравнения состояния (34). Итак,
*L==f(*o. «о),
х2 = f(x 1, -и,) = f {f (х0, м0), «i).	(36)
X3 = f(f(f(Xo, Uo), и,), и2).
Отметим, что так же, как и в уравнении (26), мно¬
жества С в (35) следует рассматривать как расплыв¬
чатые множества в декартовом произведении прост¬
ранств U X U X • • ■ XV XT. Кроме того, нужно от¬
метить, что соотношением (35-) D (х0) определяется
однозначно для каждого Хо, причем считается, что
D(x0) пусто, если не существует конечной последова¬
тельности входных сигналов «о uN-\, переводя¬
щей систему из начального состояния х0 в состояние
из Т. В этом случае мы будем говорить, что Т недо¬
стижимо из начального состояния.
Из (35) несложно получить более простое неявное
уравнение, которому удовлетворяет D(x0). Действи¬
тельно, вследствие инвариантности по времени Систе-
мгл А и независимости от времени цели и ограниче¬
ний из (35) вытекает
D (xt) = С (xt) П С (xi+1) П • • • П С (*,+*-,) П G (37)
для t = 0, 1,2, ... .В частности,
D(x(+1) = C(xt + 1)П ... ПС(х<+^_1)ПО,	(38)
8. Зак. 837

202
Р. Беллман, JI. Заде
и, следовательно, (37) можно записать как
D (xt) — С (Xf) П D (xi+l),	(39)
или, используя (34), в виде
D(xt) = C(xt)[\D(f(xt, и*)), t = 0,1,2	 (40)
что и является искомым неявным уравнением. Для
функций принадлежности рассматриваемых множеств
уравнение (40) приобретает вид (для t = 0)
•••> «ЛГ-1 \хо)~
= Не (ыо 1*о) Л Ро («1. •••, Wtf-ilf(*o, «о))>	(41)
где время окончания N также является функцией от
х0, «о, «1, «2> •••и определяется с помощью уравнения
состояния и дополнительного условия xN е Т при
хо фТ, ..., xN—x ф Т.
Предположим теперь, что последовательные вход¬
ные сигналы «о, Щ, ■■■, «лг-1 выбираются на основе
принятой стационарной (не зависящей от времени)
стратегии я, я:	т. е. правила, сопоставляю¬
щего с каждым состоянием xt в Т' входной сигнал
щ, который нужно подать в систему А, когда она на¬
ходится в состоянии xt. Таким образом,
w* — я(Xf), t = 0, ..., N — 1, Xt £ Т'.	(42)
Поскольку но, • • •, uN-1 определяются по х0 и я
с помощью (42) и уравнения состояния (34), то функ¬
цию принадлежности для D(x0) можно записать как
Рв(хо|я). Аналогично pc(u0|x0) можно представить
как рс(я(х0) 1*о)> а Рп(мь , Mjv-1 lf(xo, "о))—как
Рс(/(*о, я(%о))|я). В этих обозначениях (41) приоб¬
ретает более компактный вид:
Рд (х01 я) = рс (я (х0) | х0) Л
Д рд (/ (х0, я (х0)) | я), х0 е Т',	(43)
что по существу является системой I уравнений (по
одному для каждого значения х0) относительно ро.
Эта система уравнений определяет pd как функцию;
от Хо для каждой стратегии я, причем считается, что-
pD = о, если при стратегии я процесс не заканчи-;

7. Принятие решений в расплывчатых условиях 2()3
вается, т. е. не существует конечного числа N, такого,
что xN е Т. Кроме того, считается, что pD = Pg для
состояний из Г.
Легко показать, что (43) имеет единственное ре¬
шение. Действительно, если разложить множество со¬
стояний V = {оч, ..., 0;} на непересекающиеся под¬
множества Т\,	, Т'к, где Т\ — совокупность со¬
стояний, из которых Т достижимо за К шагов, то,
как легко видеть, уравнения (43), соответствую¬
щие тем *о, которые принадлежат Т\, дают одно¬
значно значения рд. С учетом этого обстоятель¬
ства уравнения в системе (43), соответствующие со¬
стояниям х0 е Т'2> однозначно определяют величины
рл для Хо из Т'2. Действуя аналогичным образом,
можно однозначно определить все функции ря, по¬
следовательно решая подсистемы уравнений из (43)
для блоков переменных из Т[, ..., Т’к.
Для решения задачи удобно представить страте¬
гию я в виде вектора стратегии
я==(я(01), ..., я(ог)),	(44)
/-й компонентой которого, /'=1, ..., I, является
входной сигнал, который должен быть подан, если
А находится в состоянии ог-. Отметим, что областью
изменения я (о,) является множество U = {оси ...,ат}
и, следовательно, существует т1 различных стратегий.
Имея в виду систему уравнений (43), введем
n-мерный вектор
Ро (я) = (ро (о, | я), ..., pD (0„ | я)),	(45)
называемый вектором достижения цели, компонен¬
тами которого являются значения функции принад¬
лежности расплывчатого множества D в точках о{...
• 0П (при стратегии я). Естественно установить
предварительную упорядоченность на множестве
стратегий посредством условия
я/>я"4Фрл(я')>Рв(я"),	(46)
которое означает, что стратегия я' не хуже стратегии
п' в том и только в том случае, если рл(о<|я') ^
8*

204
Р. Беллман, Л. Заде
&£Цо{о{\п") для i = 1, п. Стратегия п будет
называться оптимальной тогда и только тогда, когда
она не хуже любой другой стратегии из рассматри¬
ваемого множества стратегий.
Существует ли оптимальная стратегия для рас¬
сматриваемой задачи? Ответ на этот вопрос является
положительным. Это утверждение может быть строго
доказано [12], однако для наших целей достаточно
считать его следствием принципа «чередования»
[13] — весьма общего принципа, справедливость кото¬
рого в каждом конкретном случае может быть непо¬
средственно доказана.
Действительно, пусть я' и я" —два произвольных
вектора стратегии, причем рг>(я') и pD(ft") являются
соответствующими векторами достижения цели. По¬
строим с помощью я' и я" вектор стратегии я со¬
гласно правилу
__(■<» если
П‘ “ [ я" если рл (ot | я') < Рд (огг | я")	^
для каждой компоненты Я{ вектора я, i = 1, ..., I.
Тогда в соответствии с принципом чередования я^я'
ия^ я", т. е. стратегия я не хуже как я', так и я".
Из этого факта и из конечности множества стратегий
следует существование оптимальной стратегии.
Пользуясь соотношением (43), нетрудно получить
функциональное уравнение, которому удовлетворяет
вектор достижения цели, соответствующий оптималь¬
ной стратегии. Пусть
Ро = Мах рд (я)	(48)
Я
и пусть Я (я) — матрица размером п Х«, состоящая
из нулей и единиц, (i,j)-й элемент которой равен
единице в том и только том случае, если О} =
= [(о{, я(0()), т. е. состояние о, непосредственно сле¬
дует за Oi, когда принята стратегия я.
Пусть, далее, через рс (я) обозначен вектор, I-й
компонентой которого является рс (ft (сг4) | щ). Взяв

7. Принятие решений в расплывчатых условиях 205
максимум от обеих частей равенства (43), получим
Рд = Мах (рс (я) Д Р (я) р").	(49)
Данное выражение и является искомым функцио¬
нальным уравнением относительно Рд. Уравнение
(49), отличаясь в деталях, имеет тот же общий вид,
что и функциональные уравнения, возникающие в тео¬
рии марковских процессов принятия решений [17]. Од¬
нако его решение может быть получено значительно
проще вследствие дистрибутивности операций Мах
и А.
Действительно, пусть я1, ..., лг, где г — tnl, обо¬
значают т1 различных векторов стратегии. Тогда, за¬
меняя в (49) Мах на V, получаем
Ияв(Мя-)ЛЯ(я')|*о) V •••
... V (р (rtr) Л Р (яг) р^).	(50)
Воспользовавшись дистрибутивностью V и Л и при¬
водя подобные члены, можно представить уравнение
(50) в гораздо более простой форме —в виде системы
уравнений относительно компонент р^:
Vd (<*/) e V, (Рс (a, J от,) Л Р^{f (а,, «/))),	(51)
I 1, . . ., Я, /	1, «.., их,
где cty — я (<Ту) — входной сигнал при стратегии я в со¬
стоянии о,; Рд(Оу)~ i-я компонента оптимального
вектора достижения цели; f (, aj) — последующее
состояние для ог при входном сигнале а/'), причем
f(aу ау) = 0у для t = /-fl, ..., п (т. е. для о у из фи¬
нального множества Г); Рс(«/[(Ту) — значение функции
принадлежности ограничения С в состоянии аг для
входного сигнала af, причем цс (ау | 0у) = 1 для / =
= /+1 л; и, наконец, р^(0г) = ро(0;) —значе¬
ние функции принадлежности заданной цели G в состоя¬
нии оь i = I -|- 1; ... f п. Таким образом, неизвестными
') Заметим, что последующие состояния, фигурирующие в
(49), определяются с помощью матрицы Р(я).

206
Р. Беллман, Jl. Заде
в уравнении (51) являются Цд(стг), г = 1,	в	то
время как Цд(аг), г' = /+ 1, п и цс(а;.|ст,),
г = 1, п, /= 1, /п — заданные константы.
Чтобы облегчить поиск решений уравнений (51),
полезно упростить обозначения, введя новые неизве¬
стные =	(о,.),	г = 1,	/.	Заменим	также
символы Л и V знаками произведения и суммы.
Тогда в матричной записи уравнение (51) примет
следующий весьма компактный вид:
со = J3cd-J-у,	(52)
где а = (а,, ..., со;), у = (уь • • •, Y/)> В = {bik), причем
bik = 0, если ок не следует непосредственно за ot\
bik=V apV-ci^Gi), где ар — входные сигналы, пе¬
реводящие оi в ак; и
Yf — V/(lie (“у I ot) A Ho (f (<4> ay)));	(53)
при этом считается, что jag((T;) = 0 для состояний,
не входящих в финальное множество Т.
Представив (51) в виде линейного уравнения
(52), легко показать, что решение (53), а следова¬
тельно и (51), может быть найдено с помощью ите¬
ративного процесса. Действительно, пусть со0 =
= (0	0)	и
ms+i = ^tos -f у, s = 0, 1, 2, ... .	(54)
Тогда методом индукции можно доказать, что после¬
довательность а0, со1, со2, ... является монотонно не¬
убывающей. Действительно, допустим, что для неко¬
торого k cofe+1 ^ coft; тогда, согласно (54), имеем
<й&+2 = Bak+1 + у ^ Вак + у == coft+1, (55)
а поскольку со1 ^ со0 = 0, то, следовательно, cds+1 ^
^ со8 для s = 0, 1, 2, ... .
Поскольку последовательность а0, а1, ... моно¬
тонно не убывает и ограничена сверху величиной
а = (1, ..., I), она сходится к решению (52), т. е.
к первым I компонентам оптимального вектора до¬

7. Принятие решений в расплывчатых условиях
207
стижения цели '). Более подробный анализ пока¬
зывает, что процесс (54) дает решение уравнения
(52) не более чем за I итераций. Этот факт является
непосредственным следствием следующей леммы.
ЛЕММА. Пусть В = [Ьц] — квадратная матрица
порядка I, состоящая из вещественных элементов.
Пусть также В8 — s-я степень матрицы В, причем
знаки суммы и произведения везде обозначают опе¬
рации V и А соответственно. Тогда для всех целых
s ^ I
В + В2+ ... + BS = B + B2 + ... +В1	(56)
и
/ + В + В2+...+В5 = / + В + В2 + ... +В1~\ (57)
где I — матрица тождественного преобразования.
Доказательство. Справедливость леммы ста¬
новится довольно очевидной, если интерпретировать
(56) в рамках теории графов. Именно, пусть G(B)
обозначает граф с I вершинами, причем Ьц, i, / = 1,
2, ... представляет «прочность» дуги между верши¬
нами i и /. Пусть через yj ^ обозначена цепь из s
дуг в графе 0(B):
^г./, ц = (6/v \v	Ч+i•/)’
начинающаяся в вершине i и оканчивающаяся в вер¬
шине /. Индекс р служит меткой рассматриваемой
цепи и изменяется в пределах от 1 до М, где М —
число различных цепей длины s, соединяющих вер¬
шины i и /.
Определим прочность о (у) f цепи ys( ; как проч¬
ность самого слабого ее звена, т. е.
0(Yb.Je4A V,A' ••• A\+Vr (58)
Из определения произведения матриц (с заменой
суммы и произведения на операции V и А соответ-
’) Остальные п — I компонент р£? определяются через соот¬
ветствующие компоненты р0-

208
Р. Веллман, JI. Заде
ственно) ясно, что (i,/)-й элемент b*tj матрицы
В3, s ^ 1, может быть представлен в виде
ЬИ = а W.1.1) V а W. /. 2) V • • • V<t(yI 1, м)> (59)
или, в более компактной форме,
(м)
где Vn обозначает супремум по всем цепям длины s,
соединяющим вершины i и /. Иными словами, вели¬
чина b\j представляет собой прочность самой прочной
цепи среди всех цепей длины s, соединяющих вер¬
шины i и /.
Согласно данной интерпретации элементов мат¬
рицы В3, каждый (£,/)-й элемент В + В2 + ... -j-Bs
можно рассматривать как прочность самой прочной
цепи среди всех Цепей длиной не более s, соединяю¬
щих вершины i и /.
Таким образом, утверждение леммы эквивалентно
следующему:
Если В — матрица порядка / и s ^ I, то прочность
самой прочной из всех цепей с длиной s, соединяю¬
щих вершины i и равняется прочности самой проч¬
ной цепи среди всех цепей с длиной, меньшей или
равной /, соединяющих вершины i и /.
Лемму, сформулированную в таком виде, легко
доказать. Во-первых, очевидно, что для s^s I
В+ ... +BS>B+ ... +В1.	(61)
Следовательно, для окончания доказательства доста¬
точно установить справедливость противоположного
неравенства В + • • • + В3 В + ... + В1.
Пусть у? / — Цепь из 1 в / длины s > I. Очевидно,
что в каждой такой цепи по крайней мере одна вер¬
шина должна встречаться более одного раза, т. е.
каждая цепь длины s > I должна иметь один или не¬
сколько контуров. В результате отбрасывания этих
контуров получается цепь у£. / Длины г ^ I. Тогда

7. Принятие решений в расплывчатых условиях
209
из определения прочности цепи (58) имеем
/)	(62)
и, следовательно, супремум от	a (yfпо всем цепям
длины	s(s>/) не превышает	супремума от	а(у1 j)
по цепям длины Таким образом,
BS<B+B2 + ... -\-В‘,	s>l,	(63)
откуда
В + В2+ ... +BS<B + B2+ ... +Bl, s>l, (64)
что вместе с (61) доказывает соотношение (56).
ау 0,6
Фиг. 2.
Что касается равенства (57), то заметим, что при
i ф / (62) справедливо для s ^ I — 1 и г ^1—1.
Без ограничения i ф j (62) имеет место для s^l — 1
и г ss: / — 1, если Ьц ^ Ьц для i, / = 1, ..., /. Послед¬
нее условие удовлетворяется при замене В на I + В.
Это означает, что показатель I в (56) может быть
заменен на I — 1 при замене В на / + В. В результате
получается формула (57).
Возвращаясь к решению уравнения (52), заметим,
что s-я итерация имеет вид
1Г = (в*-1+ ... +В + /)у.	(65)
Применяя лемму, получим
Ws = Wl, s > I,	(66)
откуда следует, что процесс (54) дает решение урав¬
нения (52) не более чем за I итераций.

210
Р. Беллман, Jl. Заде
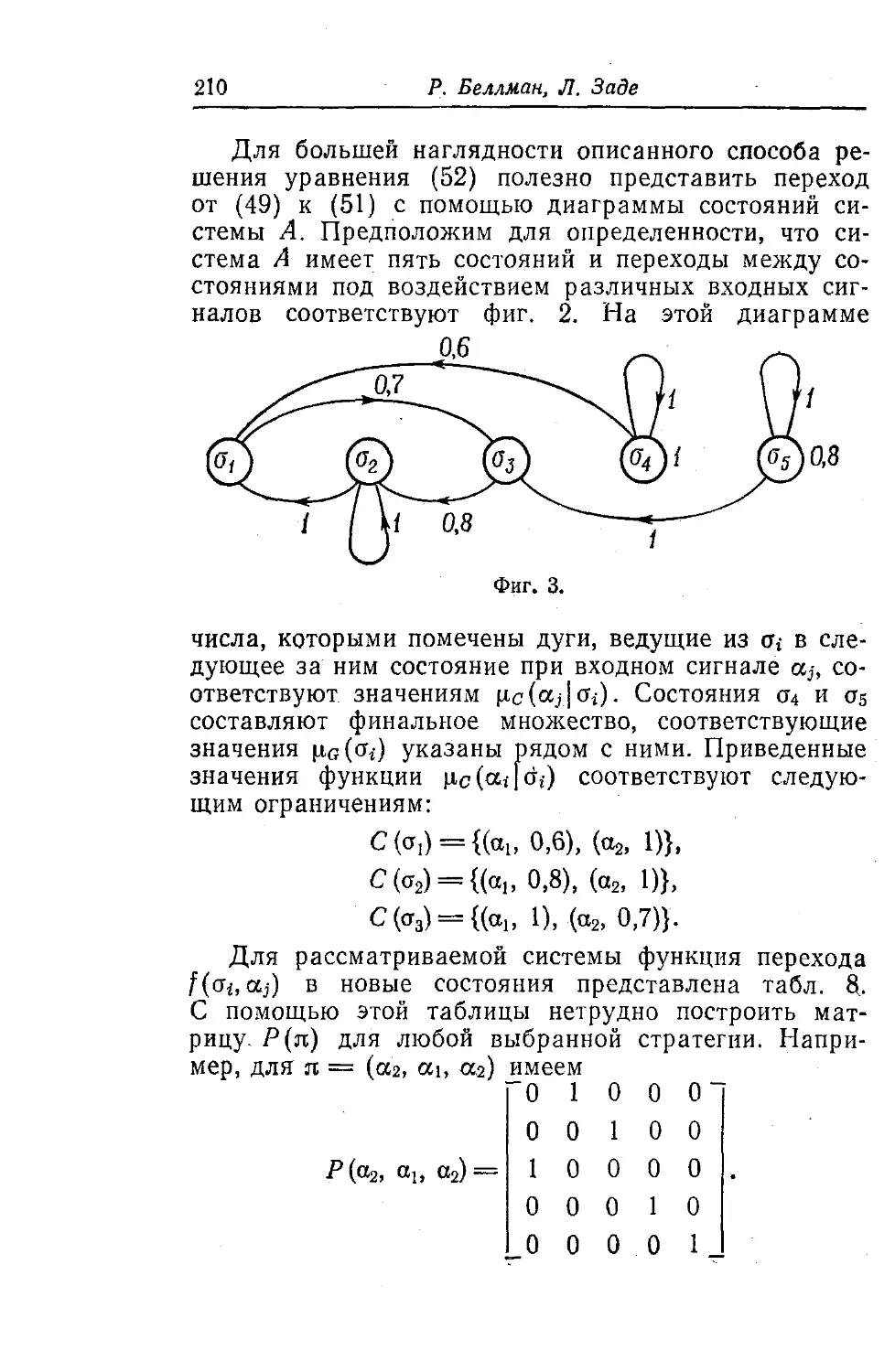
Для большей наглядности описанного способа ре¬
шения уравнения (52) полезно представить переход
от (49) к (51) с помощью диаграммы состояний си¬
стемы А. Предположим для определенности, что си¬
стема А имеет пять состояний и переходы между со¬
стояниями под воздействием различных входных сиг¬
налов соответствуют фиг. 2. На этой диаграмме
числа, которыми помечены дуги, ведущие из щ в сле¬
дующее за ним состояние при входном сигнале а3-, со¬
ответствуют значениям pic (otj | сТг) - Состояния о4 и 05
составляют финальное множество, соответствующие
значения щДо*) указаны рядом с ними. Приведенные
значения функции рс(аг|аг) соответствуют следую¬
щим ограничениям:
С(а,) = {(а1; 0,6), (а2, 1)},
С (ог2) = {((*!, 0,8), (а2, 1)},
С (<т3) = {fa, О, (а2> 0,7)}.
Для рассматриваемой системы функция перехода
f(ai, <Xj) в новые состояния представлена табл. 8-
С помощью этой таблицы нетрудно построить мат¬
рицу. Р(я) для любой выбранной стратегии. Напри¬
мер, для я = (а'г, ось «2) имеем
"0
1
0
0
0"
0
0
1
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
1 _

Т. Принятие решений в расплывчатых условиях
211
Система уравнений (51) получается при измене¬
нии направления перехода по каждой дуге на
обратное (фиг. 3), причем состояния о4 и as из Г
рассматриваются как источники, а состояния о и ог
и аз из Т' — как приемники (стоки). Пользуясь диа¬
граммой, представленной на фиг. 3, можно сразу на¬
писать уравнения системы (51):
Pd (ад ~ С0»6 Л Рд (a4)) V (1 Л P# (<тг)),
Vd (*2) = (°>8 А P# Оз)) V (1 А Рд (а2)),	(67)
А р%(а6)) V (0,7 Л I*# (*!)),
^(а4) = ^(а*) = 1'
1*о(*В) = 1*оЫ=0>8-
Таблица S
“/
о,
Ог
0,
at
as
а,
а4
о3
Оз
ot
Os
а2
о2
02
Ot
ot
Os
Применяя систему упрощенных обозначений, в ко¬
торой операции Л и V заменены произведением
и суммой, и полагая юг = Рд(сг()> i— 1. 2, 3, можно
привести систему уравнений (67) к виду
ш = В(й + у,	(68)
где
•o
1
0 '
■0,6'
B =
0
1
0,8
. Y —
0
-0,7
0
0 -
-0,8 -
Полагая со0 = (0,0,0), получаем первое приближение
ю1 = (0,6, 0, 0,8). Последующие итерации дают
со2 = (0,6, 0,8, 0,8),	©3	=	(0,8, 0,8, 0,8),
со4 = (0,8, 0,8, 0,8).

212
Р. Беллман, Л. Заде
Следовательно, со3 = (0,8, 0,8, 0,8) есть решение
уравнения (68).
Чтобы наглядно представить процесс итераций,
предположим, что каждый из источников на фиг. 3
(являющихся поглощающими состояниями на-фиг. 2)
порождает шарики различных диаметров, причем для
источника ои i = 1+\, ..., п, диаметры шариков ме¬
няются в пределах от 0 до p,G(cri). Представим себе
далее, что дуга на фиг. 2, соответствующая переходу
из состояния Oj при входном сигнале от,-, является
трубой диаметром рс(от?[о,), которая в обратном на¬
правлении, т. е. в направлении, показанном на фиг. 3,
может пропускать шарики диаметром не более
Рс(а./|стг-). Следовательно, диаграмму на фиг. 3 можно
интерпретировать как сеть труб указанных диамет¬
ров, которые могут пропускать шарики меньшего или
такого же диаметра в указанных направлениях. Со¬
стояния 04 и os, принадлежащие финальному множе¬
ству, играют роль источников шариков диаметров не
более pg(o4) и щз(05) соответственно, а остальные
состояния (о], ог и сгз) являются приемниками. По¬
скольку поглощающие состояния действуют как ис¬
точники, описанный метод решения будет называться
методом обратного потока.
Предположим теперь, что на переход шарика из
одной вершины сети на фиг. 3 в другую затрачи¬
вается одна единица времени. Если в момент времени
t = 0 шариков в вершинах щ, о2 и а3 нет, то в мо¬
мент t — 1 максимальные диаметры шариков в о\,
02 и аз будут соответственно равны ©{, со' и ©], где
и1 ==(©*, «>>, Ц) —первая итерация, получаемая с по¬
мощью уравнения (68). В момент t = 2 максималь¬
ные диаметры шариков будут задаваться величиной
со2, а в момент t = 3 — величиной to3. Так как для
перехода любого шарика из порождающего его ис¬
точника в любую вершину сети требуется не более
трех единиц времени; то при новых итерациях не бу¬
дет происходить дальнейшего увеличения размеров
шариков в каждом источнике.^Таким образом, вели¬
чина со3 определяет максимальный диаметр шариков

7. Принятие решений в расплывчатых условиях
213
в каждом стоке и, следовательно, является искомым
решением (68).
Переходя к иллюстрации уравнений (43) и прин¬
ципа чередования, рассмотрим вектор стратегии я —
= (аьаьон). Для этого вектора система (43) при¬
нимает вид
рд (ст, | л) = 0,6 Л Рд (<х41 л),
Рд (о21 я) = 0,8 Д pD (о31 я),	(69)
Цд(а3|я) = 1 Д рд(ст5|я).
В этом случае- состояния Oj и о3 принадлежат к Т[,
а о2 — кТ'2. Замечая, что рд(о4[я) = pG(cr4) = 1
и	pd(<T5|jt)	= pg(o5) — 0,8, сразу находим	искомое
решение:	pD(cn |я) = 0,6; рв(02|я) = 0,8;	рс(оз|я) =
= 0,8.
Результаты, полученные с помощью аналогичных
вычислений для других возможных стратегий, приве¬
дены в табл. 9.
Таблица 9
я
о,
а.
Os
(оц, аь а4)
0,6
0,8
0,8
(«1, аь а2)
0,6
0,6
0,6
(alt a^ ai)
0,6
0
0,8
(aj, а2, ct2)
0,6
0
0,6
(а2, ab aj)
0,8
0,8
0,8 .
(а2, а4, а2)
0
0
0
(а2, а2, сц)
0
0
0,8
(а2, а2, а2)
0
0
0
Для проверки принципа чередования возьмем
я' = (аь<%ьа2) и л" = (<%ь а2, оц). Применение пра¬
вила (47) дает л = (ai,ai,ai). Отметим, что л ^ л'
и л> я". Согласно данным табл. 9, оптимальной
стратегией будет (аг, ai.ai), что совпадает с резуль¬
татом итераций.
Описанный в настоящем разделе подход к реше¬
нию задач с неявно определенным временем оконча-

214
Р. Беллман, JI. Заде
ния может быть распространен на более общие про¬
цессы принятия решений в расплывчатых условиях.
В частности, метод решения функционального урав¬
нения (49) может быть легко обобщен на случай
расплывчатых систем в расплывчатых условиях.
Кроме того, по аналогии с разд. 4 уравнения (43)
и (49) можно обобщить на случай стохастических си¬
стем с конечным числом состояний.
7.	ЗАКЛЮЧЕНИЕ
Создание общей теории принятия решений в рас¬
плывчатых условиях является чрезвычайно сложной
и трудной задачей. Приведенные в настоящей статье
результаты следует рассматривать лишь как первую
попытку построения логической схемы такой теории.
Многие аспекты теории принятия решений в рас¬
плывчатых условиях требуют более тщательного ана-.
лиза. К ним относятся такие вопросы, как осуще¬
ствление расплывчатых решений, способ объединения
целей и ограничений в случае их неодинаковой важ¬
ности или взаимозависимости, управление расплыв¬
чатыми системами и реализация расплывчатых алго¬
ритмов, понятие расплывчатой обратной связи и ее
влияние на принятие решений, управление системами ■
в расплывчатых условиях, частично определенных
с помощью «поясняющего примера», и, наконец, при¬
нятие решений в смешанных условиях, в которых не¬
точность является следствием как случайности, так
и расплывчатости.
ЛИТЕРАТУРА
1. Athans М., Falb P., Optimal Control, Me Graw-Hill, New York,
1966.
2. Bellman R. E., Dynamic Programming, Princeton Univ. Press,
Princeton, 1957; русский перевод: Беллман P., Динамическое
программирование, ИЛ, 1960.
3. Bellman R. Е., A Marcoffian Decision Process, J. Math. a.
Mech., 6, 679—684 (1957).
4. Bellman R. E., Kalaba R., Zadeh L. A., Abstrcation and Pat¬
tern Classification, J. Math. Anal. a. Appl., 13, 1—7 (1966). ,'
'5. Болтянский В. Г., Гамкрелидзе Р. В., Поптрягпн Л. С., К тео¬
рии оптимальных процессов, Изв. АН СССР, 24, 3—42 (1960).

7. Принятие решений в расплывчатых условиях 215
6. Brown J. G., Fuzzy Sets on Boolean Lattices, Rep. № 1957,
Ballistic Res. Labs., Aberdeen, Maryland, Jan. 1969.
7. Bryson A. E., Jr, Ho Y. C., Applied Optimal Control, Blaisdell
Co., Waltham, Mass., 1969.
8. Chang C. L., Fuzzy Topological Spaces, J. Math. Anal. a. Appl.,
24, 182—190 (1968).
9. Chang S. S. L., Fuzzy Dynamic Programming and the Decision
Making Process, Proc. 3d Princeton Conf. on Information Sci¬
ences and Systems, 1969, pp. 200—203.
10. Derman C., Marcoffian Sequential Control Processes — Denu-
merable State Space, J. Math. Anal. a. Appl., 10, 295—302
(1965).
11. Derman C., Klein М., Some Remarks on Finite Horizon Marcof¬
fian Decision Models, Operat. Res., 13, 272—278 (1965).
12. Eaton J. H., Zadeh L. A., Optimal Pursuit Strategies in Dis¬
crete-State Probabillistic Systems, J. Basic Eng. (ASME), 84,
Ser. D, 23—29 (1962).
13. Eaton J. H., Zadeh L. A., An Alternation Principle for Optimal
Control, Automation a. Remote Control, 24, 328—330 (1963).
14. Fu K. S., Li T. J., On the Behavior of Learning Automata and
its Applications, Tech. Rep. TR-EE 68-20, Purdue Univ., La¬
fayette, Indiana, Aug. 1968.
15. Goguen J., L-fuzzy Sets, /. Math. Anal. a. Appl., 18, 145—174
(1967).	)
16. Howard R. A., Dynamic Programming and Marcoff Processes,
М. I. T. Press a. Wiley, Cambridge, Mass. a. New York, 1960.
17. Wagner H. М., Principles of Operations Research, Prentice-
Hall, 1969; русский первод: Вагнер Г., Основы исследования
операций, т. I, 1972, тт. II и III, 1973.
18. Wee W. G., On Generalisation of Adaptive Algorithms and App¬
lication of the Fuzzy Set Concept to Pattern Classification,
Tech. Rep. TR-EE 67-7, Purdue Univ., Lafayette, Indiana, Ju¬
ly 1967.
. 19. Wolfe P., Danzig G. B., Linear Programming in a Marcoff
Chain, Operat. Res., 10, 702—710 (1962).
20. Zadeh L. A., Fuzzy Sets, Inform, a. Control, 8, 338—353 (1965).
21. Zadeh L. A., Toward a Theory of Fuzzy Systems, ERL Rep.
№ 69-2, Electronics Res. Labs., Univ. California, Berkeley, June
1969.
22. Zadeh L. A., Fuzzy Algorithms, Inform, a. Control, 12, 99—
102 (1968).
23. Zadeh L. A., Probability Measures of Fuzzy Events, /. Math.
Anal. a. Appl., 23, № 2, 421—427 (1968).