Текст
COMBINATORY ANALYSIS
BY
MAJOR PERCY A. MACMAHON, F.R.s, D.Sc, LL.D.
(late royal artillery)
of st john's college, Cambridge
VOLUME II
Cambridge :
at the University Press
1916
PRINTE» IN GREAT BRITAIN
INTRODUCTION
Τ 70LUME I of this work will not be found to overlap Netto's Combi-
* natorik to any considerable extent.
The latter excellent treatise treats for the most part of combinations of
objects which are all different, and deals with many special investigations of
interest concerning them. It is particularly good in the historical treatment,
and the reader who desires a comprehensive account of combinatory analysis
should read the Combinatorik, as well as the present book. Investigations
by, amongst other writers, Weyrauch, Longchamp, Tait, Cantor, Terquem,
Weiss, Metzler, Sprague, Scheck, Schroder, Steiner, Reiss, Moore, De Vries,
Heffter, Kirkman, Lucas, are given by Netto, which are valuable, but are
not within the scope of the task undertaken here. This has in view the
presentation of processes of great generality, and of new ideas, which have
not up to the present time found a place in any book in any language.
This second volume commences with a detailed account of what is known
concerning the algebra of the Theory of Partitions of Numbers, the point of
view being that of Euler, and the first Section overlaps the Combinatorik to
some extent. It does not include the investigations of Sylvester and Cayley
in regard to expressions for the general coefficients in the enumerating
generating functions. These are omitted as being arithmetical rather than
algebraical. The reader is recommended to consult the original memoirs,
and also a short account in the work of Netto.
New ideas will be found in Section VII in regard to:
(i) the transformation of certain series by a graphical method ;
(ii) the discussion of Ramanujan's important identities;
(iii) the transformation of certain generating functions by means of
symmetric functions;
(iv) the connexion of the theory of partitions with other combinatory
theories.
The most important part of the volume, Sections VIII et seq., arises from
basing the theory of partitions upon the theory of Diophantine inequalities.
This method is more fundamental than that of Euler, and leads directly to
a high degree of generalization of the theory of partitions, and to several
VI
INTRODUCTION
investigations which are grouped together under the title of "Partition
Analysis." A partition of a number consists essentially of an assemblage of
integers whose sum is equal to the number partitioned. There is a priori
no definite order amongst the integers (parts of the partition), and it
therefore becomes possible to import a new idea into the definition of a partition
by regarding a descending order of magnitude amongst the parts as essential.
A partition thus becomes a series of integers in descending order of
magnitude, and the problem of enumeration is transformed into the enumeration
of the solutions of a set of Diophantine inequalities. In fact, a part of
a partition is considered to have the attribute of position as well as of
magnitude, the position being determined by relative magnitude.
The ordinary partitions of Section VII are regarded, from this point of
view, as essentially belonging to space of one dimension with a graphical
representation in two dimensions. One generalization, taken up in Sections
IX and X, considers partitions which appertain essentially to space of two
dimensions, with a graphical representation in three dimensions.
The complete solution of this problem is given. After fruitless researches
extending over many years it finally yielded before the invention of the
lattice function and its derivatives. This function, which is otherwise of
much intrinsic interest, is formed from the lattice permutations of a given
assemblage of letters through the medium of the index of a permutation.
The assemblage of letters spoken of arises from the Ferrers graph, which
involves the points or nodes at which the parts of a partition, subject to
Diophantine inequalities, are placed. The lattice permutations, and the
theory of the indices, were studied in Section III of Vol. I.
The subject of partitions in space of three dimensions is also broached,
and the complete solution in regard to the summits of a cube is reached.
There is here no convenient graphical representation, and the general
question appears to bristle with difficulties.
In Section XI an account is given of the Theory of the Symmetric
Functions of several systems of quantities. A knowledge of this subject
must be of service in further researches in Combinatoiy Analysis. It is
here shewn to yield a second brief and elegant solution of the question of
the Latin Square and its generalizations.
In conclusion, I would say that I am aware that the reader will probably
find imperfections in these volumes, but I shall be satisfied if they arc found
to contain ideas which are new and fresh, and such as are likely to prove
starting-points for further investigations in an exceedingly interesting field
of pure mathematics.
I wish to express my thanks to the Cambridge University Press for the
care they have taken in producing the work, and to Mr H. В. С Darling, of
the Standards Department of the Board of Trade, for his kindness in reading
the proofs of both volumes.
INTRODUCTION
Vll
Note on Waking's Formula for the Sum of the Powers
of the Roots of an Equation
In the work Grundzuge der Antiken und Modemen Algebra von Ludwig
Matthiessen, Leipzig, 1878, there appears, p. 62, the following statement:
"Der niederlandische Mathematiker Albert Girard hat in einer
1629 verfassten Schrift fur die Potenzsumme die Forme!
angegeben. Sie wird zumeist Waring zugeschrieben, der sie erst 1782
und zwar ohne Beweis mittheilt";
with a foot-note:
"Girard, Invention nouvelle en VAlgebre, Amsterdam, 1629."
This statement is absolutely incorrect, as I will now shew. I was
unfortunately misled by it to ascribe the formula in Vol. I of this work to
Girard.
Girard, in the pamphlet quoted by Matthiessen, gives the formula*
Aq-B2
АсиЪ-АВЗ + СЗ
A(jq - AqBk + ACk + Bq2 - i)4
for the sums of the first, second, third and fourth powers of the roots. He
gives no formula for the general coefficient, and there is no sign whatever
that he knew of the existence of such a formula.
So much for Matthiessen's first statement.
In regard to Waring, the theorem in question forms the subject of the
first problem in Chapter τ of the Meditationes Algebraicce, which was
published at Cambridge in 1770, and therein is given a complete proof by
mathematical induction.
Compare Matthiessen's second statement to the effect that Waring first
gave the formula in 1782, and then without proof. It appears, therefore,
that the theorem is due to Waring, and I much regret having failed to verify
Matthiessen's references before adopting his view.
I am indebted to Dr R F. Muirhead for drawing my attention to this
subject, and for giving me the reference to his paper, " A proof of Waring's
Expression for £ar in terms of the Coefficients of an Equation/' Broc. Edin.
Math. Soc. Vol. xxiii., wherein the matter is discussed.
Vlll
INTRODUCTION
Note on the Greater Index of a Permutation and the Number
of Inversions of a Permutation
It is shewn in Vol. II, Sect. IX, p. 206 that, in regard to any assemblage
of letters, if ρ be the greater index of a permutation and we take %xp, the
summation being in regard to every permutation of the assemblage,
Sr, (l)(2)...(i + j + k+...)
Ш -(l)(2)...(i).(l)(2)...(j)(l)(2)...(k)....'
where the assemblage of letters is taken to be
01*^7*....
Netto and other investigators have on the other hand considered the
number of inversions of a permutation, say v.
I have recently shewn in Proc. L· M. S. 1916 that while ρ and ν are
different numbers for the same permutation, the assemblage of numbers ρ is
identical with the assemblage of numbers v. Hence
and the properties of the numbers ν are comprised in the algebraic expression
of Ί,αοΡ given above.
Compare Netto's Combinatorik, p. 92, and this work, Vol. I, p. 135.
To the original papers reference is made in regard to:
Section VII. Sylvester, Collected Mathematical Papers, Vol. in.:
pp. 249-51, " Note on continuants" ;
pp. 653-S, " On Crocchi's theorem ";
pp. 658-60, "On the fundamental theorem...5';
pp. 661-3, "Note on the paper by Mr Durfec...";
pp. 664-6, " Note on Dr Franklin's proof...5';
pp. 667-71, " On the use of cross gratings...";
pp. 677-9, " Proof of a well-known development...";
pp. 680-2, " On a new theorem in partitions ";
pp. 683-4, " Note on the graphical method in partitions";
pp. 685-6, "An instantaneous graphical proof...";
and in Vol. iv.:
pp. 1-83, "A constructive theory of partitions... ."
Cayley, Collected Mathematical Papers, Vol. IT. pp. 235-49, 506-12,
" Researches in the partition of numbers."
The Author, Phil. Tram. Pi. S. 1896, a, " Memoir on the theory of the
partition of numbers —Part i."
S. Ramanujan.
INTRODUCTION
ix
Section VIII. Phil. Trans. R. S. 1899, a, " Memoir on the theory of the partition of
numbers—Part и." and 1905, a,—Part Ш.
Camb. Phil. Trans. Vol. xyin. " Application of the partition analysis to
the study of the properties of any system of consecutive integers."
Camh. Phil. Trans. Vol. xix. Part i. " The Diophantine inequality \x ^ /u#."
Section IX. Phil. Trans. R. S. 1911, a, "Memoir on the theory of the partition of
numbers—Part v. Partitions in two-dimensional space."
Section X. Phil. Trans. R. S. 1911, a, "Memoir on the theory of the partition of
numbers—Part vi."
Camh. Phil. Trans. Vol. xvn. Part ii. "Partitions of numbers whose graphs
possess symmetry."
Section XL Phil. Trans. R. S. 1890, a, " Memoir on symmetric functions of roots of
systems of equations."
P. A. M.
April 1916.
a 5
TABLE OF CONTENTS
SECTION VII
THE PARTITION OF NUMBERS
CHAPTER I
THE THEORY OF EULER
ART. PAGE
238—240. The intuitive basis of the theory. Partitions into a given number of
parts. Algebraic identities 1
241. Partitions whose parts are limited both in number and magnitude . 5
242, 243. Interpretation of the generating function #*/(1)(2) ...(j) ... 5
244, 245. Interpretation of algebraic identities. A formula of transformation . 7
246. Expansion of a finite product 9
247. Partitions into uneven parts and connexion with partitions into
unequal parts . 10
248, 249. Algebraical and graphical proofs of the correspondence after Glaisher
and Sylvester 11
250. Sylvester's more refined correspondence 14
CHAPTER II
GEOMETRICAL AND OTHER TRANSFORMATIONS
251. Durfee's dissection of a graph and its applications . . . . 15
252, 253. Sylvester's dissection into angles of nodes, and its applications to the
enumeration of symmetrical and other graphs . . . . 16
254, 255. Another investigation of the generating function of symmetrical graphs 18
256. Euler's expansion of (1) (2) (3)... ad inf. Franklin's proof. . . 21
257—262. An identity of Jacobi and its particular cases 23
263—265. Expansions of the reciprocals of certain continued products . . 24
266—275. The transformation of certain series. Examples from the Funda-
menta Nova of Jacobi 26
TABLE OF CONTENTS
XI
CHAPTER III
ramantjjan's identities
ART. PAGE
276. Statement of Theorem I. Connexion with partitions which involve
neither repetitions nor sequences of parts. Connexion with other
partitions 33
277. Second statement of Theorem I 34
278. Statement of Theorem II. Connexion with partitions which have no
part less than 2, and which involve neither repetitions nor sequences
of parts 35
279. Connexion of Theorem II with other partitions 36
280. Second statement of Theorem II 36
281—285. Connexion of the theorems with certain groups of partitions . . 36
286—293. The two Ramanujan series when the magnitudes of the parts occurring
in the partitions are restricted 40
294. Two complementary theorems 45
295. Connexion with the Theory of Continuants 46
296. Connexion with the Theory of Compositions 47
CHAPTER IV
PARTITIONS WITHOUT SEQUENCES
297. The difference equations satisfied by the generating functions . . 40
298. Investigation when the number of parts is given .... 52
299, 300. Determination of the enumerating generating functions ... 52
301, 302. The partitions of multipartite numbers 54
303. Connexion between the partitions and divisions of numbers . . 57
CHAPTER V
PARTICULAR STUDY OF THE FUNCTION
(i-*0(i-**)...(i-*0
304—306. Cay ley's transformation 59
307—310. Transformation by symmetric functions 61
311—319. Generalization of the foregoing 65
320, 321. Ettect of the relations between the quantities «;, hi . . . . 70
322, 323. Connexion with a limited double product after Sylvester . . . 71
324—326. Further examination of the limited double product .... 75
327—333. The methods and processes of Gauss 78
Xll
TABLE OF CONTENTS
CHAPTER VI
CONNEXION OF THE THEORY OF PARTITIONS WITH OTHER
COMBINATORY THEORIES
ART. PAGE
334. The graphical representation of two partitions in the cells of a complete
rectangular lattice . 84
335. Connexion with the compositions of bipartite numbers ; with the
compositions of unipartite numbers; with permutations involving two
different letters 85
336, 337. Particular theorems arising from the correspondences ... 86
338. The "line of route" and the "zig-zag graph" 89
SECTION VIII
A NEW BASIS OF THE THEORY OE PARTITIONS.
PARTITION ANALYSIS IN SEVEN CHAPTERS
CHAPTER I
THE METHOD OF DIOPHANTINE INEQUALITIES
339. New definition of a partition. The symbol β 91
340. "Stepping back" from the intuitive generating function of Eulcr.
Numerical examples 93
341. Further applications to enumerating functions 95
342. Application to real generating functions. Connexion with the graphical
representation of Ferrers. Crude and ultra-crude forma of functions 97
343, 344. Euler's intuitive form of generating function when the parts are
restricted both in number and magnitude. Extension of Euler's
result 98
345. The case in which the two highest parts are separately restricted in
magnitude 100
346. The partitioning of a number into j or fewer uneven parts . . 101
347—354. Study of the Ω operations. The relations between Diophantine
equalities and inequalities 101
CHAPTER II
A SYZYGETIC THEORY
355. The fundamental solutions of a system of Diophantine inequalities or
equalities after Hubert. The syzygetic theory of the solutions . 107
356, 357. Examples of syzygetic theories 109
358, 359. Linear homogeneous Diophantine Analysis after Ε. Β. Elliott.
Examples Ill
TABLE OF CONTENTS xiii
CHAPTER III
THE DIOPHANTINE INEQUALITY Μ^Ιβ
ART. PAGE
360—362. Two lemmas which yield a process of reduction 115
363—365. The fundamental solutions as depending upon the ascending series of
intermediate convergents to the fraction ajb 118
366, 367. Expression of every solution of the inequality in terms of a consecutive
pair of intermediate convergent numbers 121
368—373. Examples of the foregoing 121
374. Derivation of a syzygetic theory 125
CHAPTER IV
THE SIMULTANEOUS DIOPHANTINE INEQUALITIES
375—377. Reduction of the given inequalities to a standard form . . .126
378. Numerical example of the reduction 131
379. The complete solution of the inequalities 131
380. A numerical example 132
381. The allied theory of two simultaneous equalities . . . .133
CHAPTER V
ON THE FORM OF ENUMERATING FUNCTIONS
382, 383. Form of the factor of a generating function. Formulation of the
problem presenting itself for solution 136
384, 385. Determination of the Diophantine conditions 138
386—388. The cases of orders two, three and four. The generating functions
and the syxygics 139
389. Simplification of the work by the imposition of a new condition . 141
390 -396. The solutions as far as the order eight inclusive . . . .141
397, 398. Proof that a particular standard form of generating function of great
generality is always Unite and integral when expanded in ascending
powers of its argument ......... 145
CHAPTER VI
ON ΤΓίΕ ALGEBRAIC FORMS OF INTEGERS
399. Formulation of a problem which is a generalization of the fact that the
product of any m consecutive integers is divisible by factorial m.
Connexion of the problem with that discussed in the previous chapter 131
400, 401. Formation of the Diophantine conditions. Solutions for the orders
two and three 132
402. Solution for the order four. Appearance for the first time of un-
symmetrical solutions 153
403. Discussion of the order five. The thirteen fundamental solutions.
The unsymmctrical fundamental forms of orders six ;md eiglit . 134
xiv
TABLE OF CONTENTS
CHAPTER VII
THE THEOEY OF MAGIC SQUARES
ART.
404.
405.
406—409.
PAGE
410—412.
413-415.
416-419.
The application of the method of Partition Analysis to the study of
magic squares and other configurations of integers in piano and
m solido. Definition of a "general magic square" . . .157
General magic squares of order two 158
The syzygetic theory of general magic squares of order three. The
Diophantine equalities. The squares when the two diagonal
properties are not in evidence. The six fundamental squares connected
by one simple syzygy. Derivation of the enumerating function
from the real generating function. Squares in which the principal
diagonal alone shares the properties of the rows and columns. The
five fundamental squares connected by one simple syzygy. The
theory when the secondary and not the principal diagonal is in
evidence. The five fundamental squares connected by one simple
syzygy. The enumerating functions. Theory of the general magic
square. The five fundamental squares connected by two first
syzygies and one second syzygy. The enumerating function.
Derivation of eight ordinary magic squares
The enumeration of general magic squares from another point of view.
Connexion of the theory with the squares enumerated in Section V.
Derivation of a new function AWt8 from the homogeneous product
sum of degree m, km. Formal solution of the problem of
enumeration. Some particularly simple examples by way of elucidation .
The solutions for the general even order and for the general uneven
order .
Some verifications. The simplification of the necessary calculations .
159
164
166
169
SECTION IX
PARTITIONS IN TWO DIMENSIONS
CHAPTER I
INTRODUCTORY NOTIONS
420. Partitions on a line. Representation of the generating function by
algebraic fractions placed at points on a line . . . .171
421—423. Definition of "partitions in two dimensions" or "partitions in a plane."
The unit Ferrers graph as a partition in a plane. Anticipation of
a particular result, and representation of a generating function by
algebraic fractions placed at the points of a two-dimensional lattice.
A solid graph of nodes or of units 172
424. A general observation which connects graphs with successive orders of
figurate numbers 175
TABLE OF CONTENTS
XV
ART. PAGE
425—428. The interpretation of solid graphs. The six ways of reading. Identity
of enumeration. Cases in which the six readings degenerate to one,
two or three readings. The graphs of thirteen nodes which have
two readings. Really distinct graphs of a given number of nodes . 176
CHAPTER II
THE METHOD OF DIOPHANTINE INEQUALITIES
429. The enumeration of solid graphs regarded as a question of unipartite
partition in two dimensions. Anticipation of a general result. The
symmetry of the generating function. The different ways of
exhibiting it 182
430—433. Investigation of the simplest cases of partitions in a plane . . 183
434, 435. Formation of the crude generating function for the general case. Six
representations of the anticipated pure generating function by
means of algebraic fractions placed at the points of a
two-dimensional lattice. Particular example of the system (3 ; 2 ; 1) . . 186
CHAPTER III
THE METHOD OF LATTICE FUNCTIONS
436, 437. Permutation functions and lattice functions. Derivation of the lattice
function from the lattice permutations. Connexion between lattice
functions and generating functions of plane partitions . . .189
438, 439. Study of simple cases leading up to the general theory of the
connexion spoken of in the previous article 192
440—442. The sub-lattice function of given order. Utilization of the sub-lattice
function in denning the lattice function for a restricted part
magnitude. Theory of the lattice function for a restricted part
magnitude 194
443, 444. Generalization of a well-known formula in line partitions . . .197
445, 446. Study of sub-lattice functions. Determination of the highest order of
such a function. Algebraic expression of the sub-lattice function
of highest order 198
447—450. Proof that in La for every term xv there is a corresponding term λλ>μ"Ρ.
Result of writing l/д? for χ in Ze. Theorems concerning the lowest
and highest exponents of χ that occur in L8. Proof that ZM-8 ai^
L8 only differ by a factor which is a j.K)wer of ./.*. Proof that sub-
lattice functions do not alter when we pass from a lattice to its
conjugate 199
451. Relations between generating functions and sub-lattice functions.
Algebraic expression of L\ 203
452. Expression of Lx in the form of a series 204
XVI
TABLE OF CONTENTS
CHAPTER IV
EXCURSUS ON PERMUTATION FUNCTIONS
ART. PAGE
453—455. Expression of the function. The sub-permutation functions of different
orders. A restriction placed upon the part magnitude. Algebraic
expressions of the sub-permutation functions .... 206
456—461. A remarkable expression of the permutation function. Results for a
complete lattice. Some examples. A remarkable simplification in
a particular case. Elegant properties of the sub-permutation
functions 208
462, 463. A certain summation to infinity which involves the permutation
functions. Some identities 211
SECTION X
COMPLETION OF THE THEORY OF SECTION IX
CHAPTER I
PLANE PARTITIONS WITH UNRESTRICTED PART MAGNITUDE
464—466. The difference equation for L{pu p»; oo). Its algebraic expression
established by induction 213
467, 468. Factors of the lattice function termed the Outer and Inner lattice
functions respectively. The factors not unchanged when tlic lattice
is changed to its conjugate .216
469, 470. The functional equations satisfied by the generating function, the
lattice function and the inner lattice function respectively.
Derivation of a new functional equation satisfied by the generating
function 217
471—473. Symbolic expression of the functional equation 220
474. The corresponding relation between lattice functions . . . .221
475, 476. The corresponding relation between inner lattice functions . . 222
477—483. Algebraic expressions of the inner lattice functions for the cases of two
and three rows. The fundamental solutions of the functional
equations in these simple cases. Expressions of the inner lattice
functions in terms of fundamental solutions and in determinant
form 223
484, 485. The twenty-four fundamental solutions in the case of the fourth order.
Expression of the inner lattice function as a determinant of the
fourth order 230
486, 487. Verification of the expression in particular cases . 232
488, 489. The expression of the inner lattice function in the case of the general-
order m. Summary of results 233
TABLE OF CONTENTS
XV11
CHAPTER II
PLANE PARTITIONS WITH RESTRICTED PART MAGNITUDE
ART. . ... PAGE
490, 491. The factorization of the lattice function into outer and inner lattice
functions. The functional equation satisfied by the generating
function. The functional equation for the lattice function. Its
symbolic expression. The functional equation for the inner lattice
function. Its symbolic expression 235
492. The fundamental solutions for the order two. Expression of the inner
lattice function in terms of them 236
493. The six fundamental solutions for the order three. Expression of the
inner lattice function in terms of them and in determinant form 238
494, 495. The complete solution in the case of the order four. The general case
and the final resulting expression. Summary of results . . 239
496. The identities derived from conjugating the lattice. General remarks
upon this subject 243
497, 498. Application of the foregoing results to line or one-dimensional
partitions 245
CHAPTER III
PARTITIONS IN SOLIDO
499. Definitions. Partitions in three dimensions. Solid lattices and lattice
functions. Coincidence of partitions in solido, the part magnitude
being restricted to unity, with partitions in piano . . . 247
500—505. Solid lattices in which not more than two nodes appear in the direction
of either axis. Study of the particular cases leading up to the
lattice specified by the summits of a cube . . . .· 248
506, 507. The one-to-one correspondence between the solid lattice permutations
and the arrangements of different integers placed at the nodes of
the lattice. Detail of the correspondence in the case of the eight
summits of a cube. The complete solution of the problem of the
cube 252
508. Some remarks upon the further theory of these partitions, and some
particular results 256*
CHAPTER IV
THE SYMMETRY APPERTAINING TO PARTITIONS
509, 510. The graphs which have only one reading. Enumeration of the graphs
which have i nodes along each axis and every node upon one of the
coordinate planes. In particular when /=oo 258
511, 512. Another method of enumeration leading to an identity . . , 259
513. Representation by solid angles of nodes. Derivation from any one
graph of an infinite number of others which possess symmetry of
the same kind 261
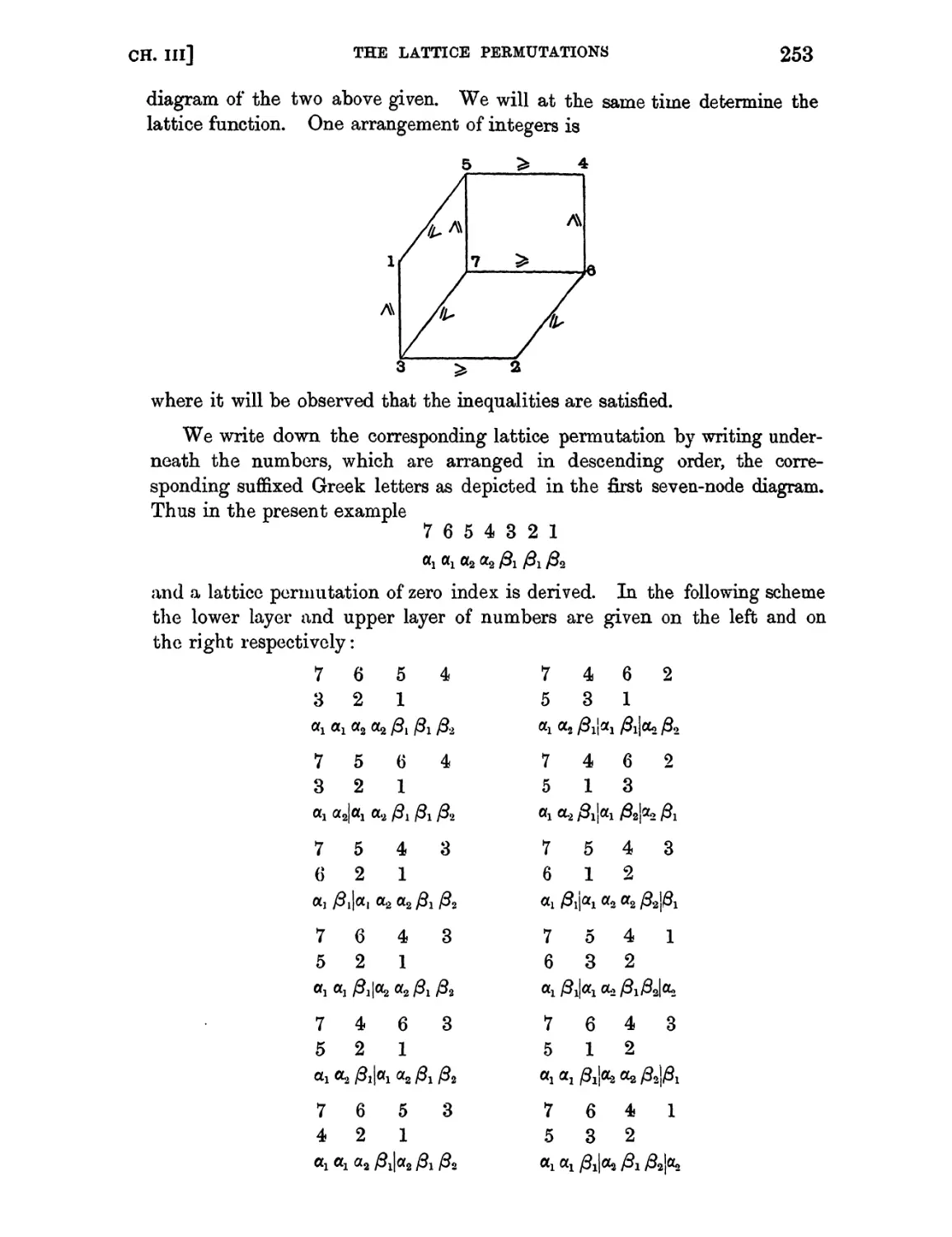
xviii
TABLE OF CONTENTS
ART. PAGE
514—519. Graphs which possess symmetry in relation to the axes of χ and y.
Investigation by the method of Diophantine inequalities.
Formation of the crude generating function. The complete syzygetic
theory in some simple cases 262
520—526. The probable form of the generating function in the general case. The
deduction of some interesting consequences and some verifications
in particular cases. Some correspondences with line partitions . 267
527. The graphical representation of the generating function upon the major
half of a plane lattice 270
528—533. The graphs which possess two readings. The fundamental property
of the derived partitions. The enumerating generating function in
certain cases. The construction by solid angles .... 271
534. Remarks upon the aspects of solid graphs 277
SECTION XI
SYMMETRIC FUNCTIONS OF SEVERAL SYSTEMS OF
QUANTITIES, WITH SOME APPLICATIONS TO DISTRIBUTION
THEORY
CHAPTER I
ELEMENTARY THEORY
535, 536. Preliminary notions and the, notation employed 280
537. The partitions with one bipart. Relations between these partitions
and the elementary functions 282
538, 538 bis. The definitions of hm and kpq. Reciprocal relation between km and
aM. Relation between кш and spq 283
CHAPTER II
THE THEORY OF SEPARATIONS AND THE ALLIED
THEORY OF DISTRIBUTIONS
539. Study of the theory of separations by means of three identities
connected by one relation 285
540. A new theory of distributions. Objects and parcels of given types. A
distribution function. Type of a distribution. Interchange of
parcels and objects. Effect of this upon the type of the
distribution 286
541. Method of ascertaining the number of distributions of given type when
the types of the objects and parcels are given .... 288
542. Intuitive proof of a law of symmetry 290
543. Theorem of expressibility 291
543 015—546. Resumed discussion of the three identities. Generalization of the
formula of Girard and Waring. Its dual character. Its statement
for multipartite symmetric functions. Particular example. A
convenient notation for expressing the general result . . . 292
TABLE OP CONTENTS
XIX
CHAPTER III
THE DIFFERENTIAL OPERATIONS PAGE
ART.
547—549. Extension of the idea and notation of the linear operator gv of Section I.
Notation for successive and symbolic multiplication of operators.
The obliterating operator Gm. Correspondence of Gpu) gm with am,
spq respectively. Mode of operation of Gw. Replacement of
symbolic products by products which denote successive operations . 297
550—555. The operators which correspond to other symmetric functions. An
operator invariant of the transformation denoted by the Three
Identities. Substitution of operators for symbols of quantity.
Various laws of symmetry 302
CHAPTER IV
THE LiNEAR PARTIAL DIFFERENTIAL OPERATORS OF THE THEORY OF
SEPARATIONS AND THE PARTITION OBLITERATING OPERATORS
556, 557. The separates as independent variables. Definition of the linear
partition operator. Expression of the linear part operators in
terms of linear partition operators 311
558, 559. Properties of linear partition operators. Their importance in the
calculation of symmetric function tables 313
560, 561. Definition of the partition obliterating operators. Their connexion
with part obliterating operators 315
562—564. Connexion of linear partition operators with partition obliterating
operators. Formula analogous to Waring's 316
565. The inverse relations 319
566. Replacement of multiplications of operators which denote successive
operations by multiplications which are symbolic .... 320
567. Use of the operators in the multiplication of symmetric functions . 321
568. The construction of symmetrical tables 322
CHAPTER V
FURTHER THEORY OF THE LATIN SQUARE
569. The choice of operator and operand so as to produce diagrams of the
desired character. Examples of diagrams. The law of symmetry
or reciprocity that arises by rotating the diagrams . . . 323
570. The condition for the diagrams to be free from empty compartments.
The complete solution of the problem of the Latin Square . . 325
571. New solution of the generalized Latin Square previously investigated
in Vol. I, Section V 325
TABLES
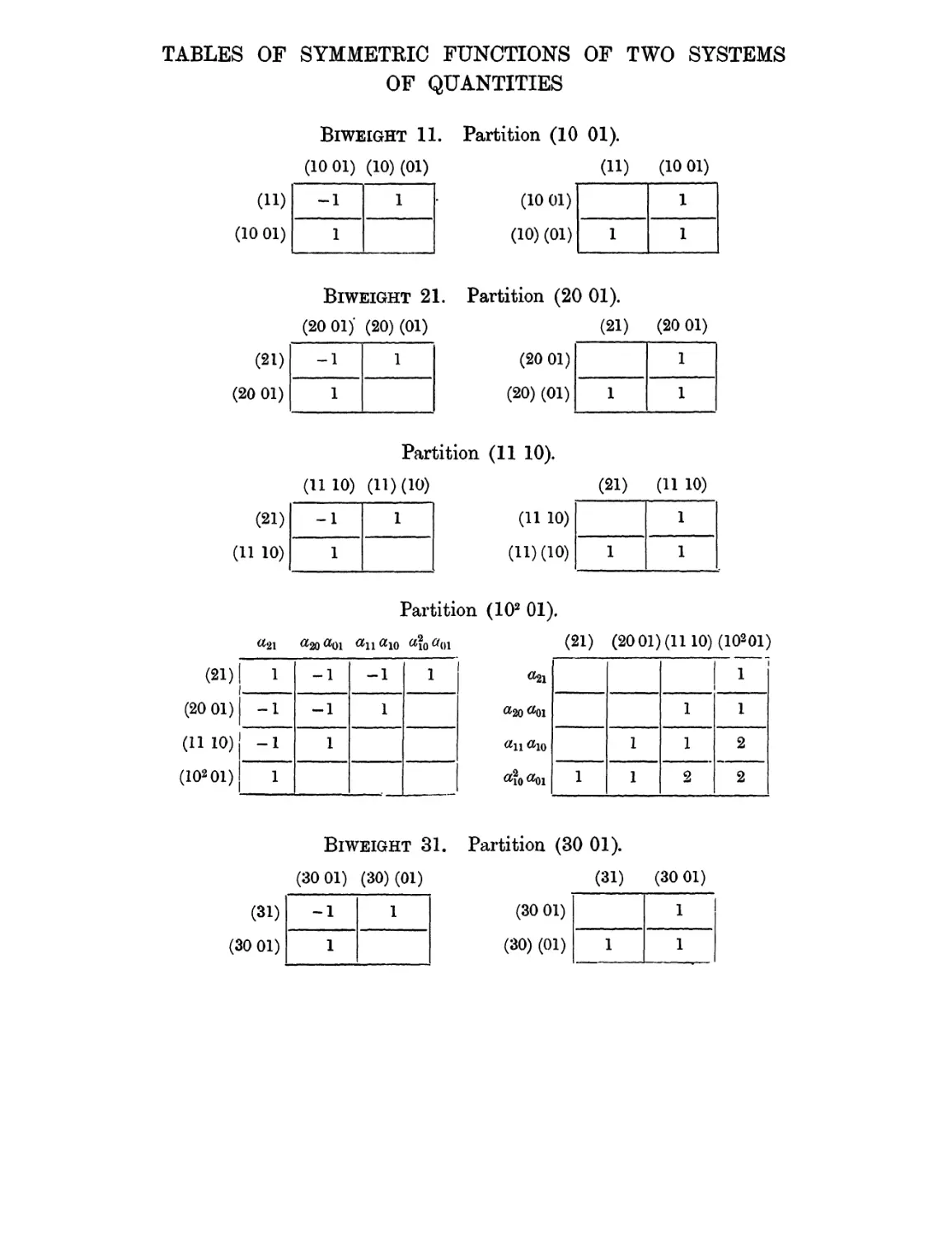
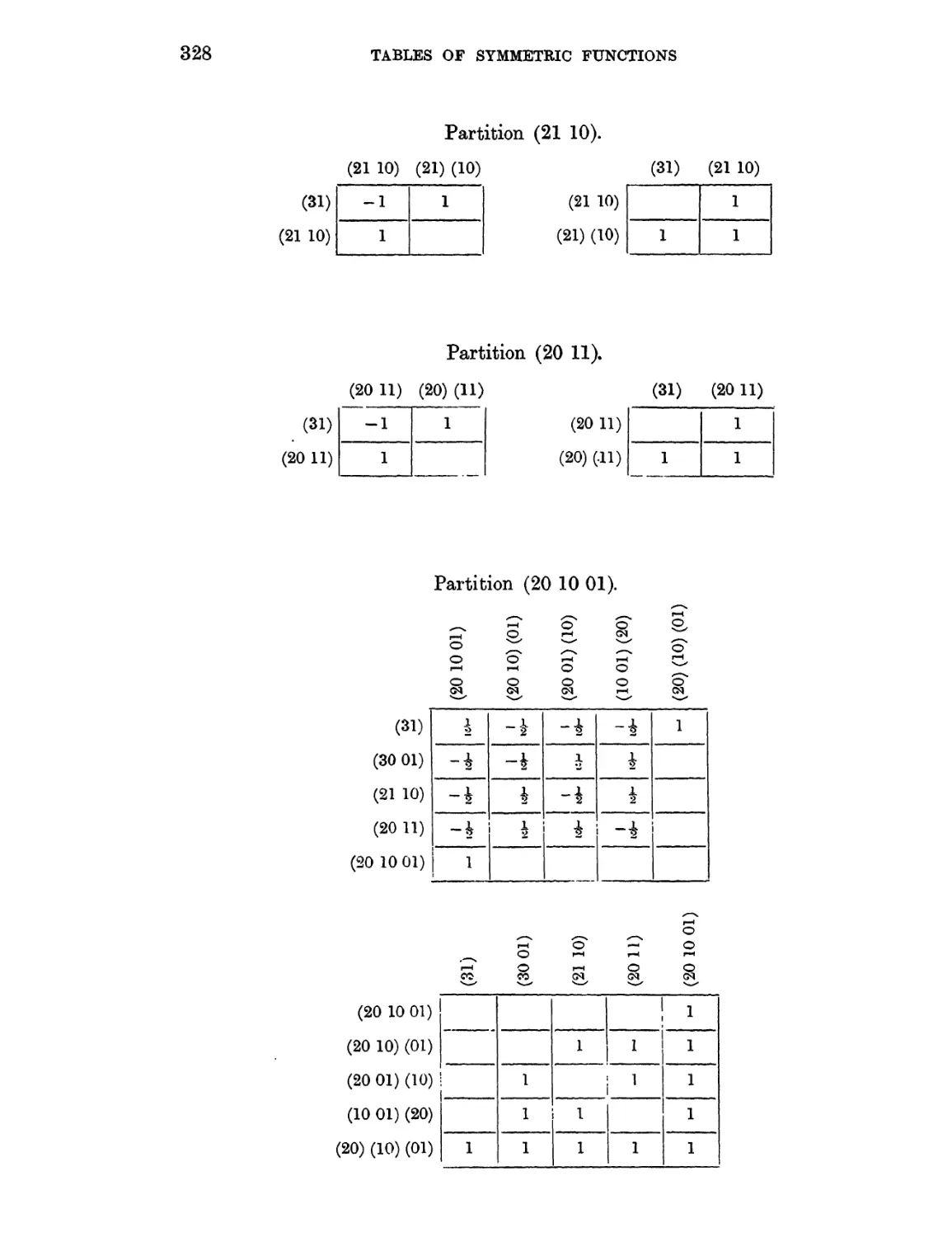
Symmetric Functions of two systems of quantities . . . 327—331
Enumeration of Solid Graphs 332
Index to the Two Volumes 333
SECTION VII
THE PAKTITION OF NUMBERS
CHAPTEE I
THE THEORY OF EULER
238. We have now to consider in interesting detail the division of an
integer into other integers of which it is the sum. The integers last
mentioned are the parts of the partition of the first mentioned integer.
These parts may be drawn from the whole series of natural numbers or they
may be drawn from a system of integers which is duly specified; thus the
system may be that which involves the uneven integers or the even integers
exclusively, or the actual numbers which may appear as parts may be
particularly specified as being any integers agreed upon. Further the number of
times which each integer or the whole of the integers may appear as parts
may be fixed and also the whole number of the parts of the partition. The
part magnitude may also be fixed and a host of other conditions may be
imposed upon the partitions.
Euler's theory proceeds from the fact that algebraical multiplication of
integral powers of the same numerical magnitude is equivalent to the
arithmetical addition of the powers; thus
x91. xP2. xVz.... = xPl+:P2+Ps + ···.
It thence follows at once that the whole number of partitions of an
integer η is equal to the coefficient of x11 in the expansion of the function
1
(1-#)(1 -ж2) (1-я3) ...ad inf.*
Ex. gr. expanding each factor into an infinite series and then multiplying
them together we find that the term 7#5 arises made up in the multiplication
in the manner
дД+1+l+l+l _|_ #1+1+1+2 + #1+2+2 + #1+1+3 + #2+3 + #1+4 + #5
due to the expansion
(1 -xr)~l = 1 + xr + x* + a?r + ...,
where r has all values not exceeding in this instance 5.
Μ.Δ. II. 1
2 PARTITIONS INTO A GIVEN NUMBER OF PARTS [SECT. VII
The above written algebraic fraction we call the enumerating generating
function (G.F. for brevity) of the partitions of n. It is also clear that if the
part magnitude be restricted to not exceed j, the enumerating generating
function will be
1
(1 _ x) (1 -a?) (1 - a?) ... (1 - ^) *
If the condition of partition be that there are to be exactly i parts the
number of partitions of η will be equal to the coefficient of а1хп in the
expanded fraction
1
(1 - ax) (1 - ax*) (1 - aa?) ... ad inf. *
This fraction may be expanded in ascending powers of a in many ways;
one of the simplest is to write it as a function F(a) of α and to put
F(a) = 1 + афг (χ) + α*φ2(χ) + α*φζ(χ)4-...,
from which we derive
F(ax) = 1-f αχφχ (χ) + α?χ*φ2 (χ) 4- α?χ*φζ (χ)+ ....
Now, from the g.f.,
F(ax) = (l-ax)F(a),
so that
1 + αχφχ (χ) + α2χ-φ2 (χ) 4- ... = (1 - αχ) {1 4- αφΎ (χ) + α2φ2 (#)+...}.
Herein equating coefficients of like powers of a we find
χφχ (χ) = фг (χ) — χ,
χ2φ2 (χ) = φ2 (χ) - χφλ (χ),
α?φζ (χ) = φ3 (χ) - χφ2 (χ),
etc.
from which φλ (χ) =
φ20) =
and in general
leading to the algebraical identity
1
(1
-x'
x*
-*)(i
-хГ
X1
Φι («) - (ί _^у(1-_-^у;-(1 _ χί).
1
(ϊ — αχ) (1 — см;2) (1 — αχ3) ... ad in£
_ Ί αχ ей»2 сЛв*
" +Γ^ + (1-Λ!)(1-^)+·'· + (1-Λ!)(1-^)...(1-Λ;ί) + *'*'
сн. ι]
CONJUGATE GRAPHS
3
and to the conclusion that the enumerating g.f. for partitions into exactly i
parts is
#*
(1-#)(1-#2)...(1-а;У
the number required being given by the coefficient therein of xn.
239. Moreover this coefficient is equal to the coefficient of xn"1 in the
expanded fraction
1
(l-aO(l-#2)...(l-#V·
a fact which demonstrates that η has as many partitions which involve
exactly i parts as η — i has partitions in which the part magnitude is limited
so as not to exceed i. This theorem is not obvious immediately a priori
but becomes so on further consideration. Ferrers (and after him notably
Sylvester) denoted a partition of a number graphically. The parts being
arranged in descending order of magnitude from left to right, corresponding
rows of dots or nodes are placed in succession, each row starting from the
same line parallel to the long edge of the page; thus the graph of a partition
7521 will be
wherein it will be noticed that, in general, the number of rows is equal
to the number of parts in the partition while the number of columns is equal
to the highest part. If we now rotate this graph so that the rows become
columns wc find the graph
which now denotes the partition 4322211 of the same number 15. The two
partitions are said to be conjugate; and so also the two graphs.
It is clear that if a graph denote a partition having a highest part j and
exactly г parts, the conjugate graph will denote one which has a highest
part i and exactly j parts. Hence these two sets of partitions are equi-
numerous. Moreover if we have a set of partitions in which the highest
part is limited not to exceed j, the conjugate set of partitions will be such
that the number of parts is limited not to .exceed j. We thus see clearly
1—2
4 EXPANSION OF AN ALGEBRAIC FRACTION [SECT. VII
that the partitions having a highest part not exceeding j have the same
enumerating g.f. as the partitions in which the number of parts does not
exceed^'. The theorem which gave rise to this discussion may therefore be
stated in the form: " A number η has as many partitions involving exactly
г parts as the number n — г has partitions which do not involve more than
г parts/' In this form its truth is seen at once, for if we diminish each of
the parts of the former partitions by unity we obtain each of the latter
partitions.
Ex.gr, n=ll, г = 3.
The sets of partitions are
911 821 731 722 641 632 551 542 533 443
8 71 62 611 53 521 44 431 422 332
Conversely reasoning in this manner leads at once to the expansion of the
reciprocal of (1 — ax) (1 — ax2) (1 — aa?)... ad inf. in ascending powers of a.
240. We can obtain a different expansion of the same fraction from the
following consideration. The G.F. of the partitions which have exactly г parts
and a highest part precisely equal to j is clearly
αχί
(1 - ax) (1 - ax2) ... (1 - art)'
the number of partitions being given by the coefficient of aV*.
Hence giving j all values
(1 — ax) (1 — ax2) (1 — ax3) ... ad inf.
" +1-ая +(1 - ax)(l - ax*) + (1 - ax) (1 - ax2)(\ - ал·3)
The partitions which involve not more than г parts are given by the
coefficient of alxn in the G.F.
1
(1 — a) (1 — ax) (1 - ax2) ... ad inf.
~ +Г^+(1-ж)(1~^ + (1~^)(1-^)(1-^)
This series is obtained as before from the consideration that writing ax
for a is equivalent to multiplication by 1 — a.
The number in question is the coefficient of xn in
1
(1-*)(1-0»)...(1-^'
verifying a previous conclusion.
CH. I] THE HIGHEST PART AND THE NUMBER OF PARTS BOTH LIMITED 5
241. We now come to the important G.F. which enumerates the partitions
in which the number of parts and the highest part are limited by the numbers
i, j respectively. The number is clearly given by the coefficient of afx71 in
the fraction
1
(1 - a) (1 - шс)(1 -ая2)... (1 - aaf)m
Writing ax for a is equivalent to multiplication by
1-q
hence as before we are at once led to the expanded form
!-*>** , (l-**')(l-g*") <(1-^)(1-^...(1^
+ ...,
establishing that the enumerating G.F. is
(1-^)(1 -a?***)... (l-afo)
(1-я) (1-я2)...(I-**) '*
which may be also written
(l-aQ(l-a?)...(l--a^)
(1 -a?) (1 - я8)... (1 -a*). (1 -a?)(l -л»)... (1 -xj)'
This is symmetrical in i and j, as should be the case from the consideration
of conjugate graphs*.
Cayley, in his researches on partitions, adopted a very convenient notation.
He wrote
1 - χ™ a (m),
thus the above generating function would be written
(j+l)(j + 2)...(i + j)
(1) (2)... (i)
242. It is important at this stage to examine the G.F.
x*
<l)(2)...(j)
in some detail so as to become familiar with a method of interpretation in the
theory of partitions.
We take the particular case
x9
<1)<2)<3)·
The highest part of a partition exceeds the next highest part by one of
the numbers 0, 1, 2,... n. This will be called the "first excess"; similarly the
* An arithmetical proof of this theorem has been given by Franklin, Amer. Journ. of Math,
Vol. iv. p. 18.
6 INTERPRETATION OF AN ALGEBRAIC FRACTION [SECT. VII
second highest part (which may be equal to the highest part) exceeds the
next occurring part by some number which we shall call the "second excess/'
and so on.
Take any partition of 9 into three or fewer parts and express it graphically;
thus suppose we take the partition 333
• ••ooooo
• · · о о
• · · о
and continue it by any graph of three rows represented by hollow dots or
nodes. We may suppose the g.f. to represent such graphs where the filled
nodes are fixed and the hollow nodes can be written down at pleasure so as
to constitute the regular graph of a partition. The partitions represented by
the combined graph are specified, by the statement that " there are exactly
three parts and no part is less than three." If instead of 333 we take the
partition 531 we find
• ••••ooooo
• · · о о
• о
and the hollow nodes must be regarded as moved to the left as far as
possible so as to form the combined regular graph
• · · о о
• о
We look upon the filled-in nodes as fixed and the hollow ones to be
assigned at pleasure. We have here exactly three parts with the conditions
(i) the first excess must be at least 2,
(ii) the second excess must be at least 2.
These partitions are therefore also enumerated by the G.F.
The conditions in regard to the first two excesses shew that the partitions
under view are those in which there are no repetitions or sequences of parts.
In fact consecutive parts such as ρ, ρ; ρ + 1, ρ; are clearly ruled out.
Bringing under view the successive partitions
1, 31, 531, 7531, 97531,...,
we see that the partitions of numbers which involve neither repetitions nor
sequences are enumerated by the series
χ x4 x° x1(i
+ {T) + (ΪΓ(2) + (1) <2) (3) + (1) (2) (3) (4) + ··'
the powers of χ involved in the numerators being the successive square
numbers.
CH. i] PARTITIONS WITHOUT REPETITIONS OF PARTS 7
Again if we take the partition 72 of 9 the partitions enumerated will be
those into not less than two nor more than three parts subject to the
condition that the first and second excesses must be at least 5 and 2
respectively.
Generally, in respect of the fraction
at
(l)(2)(3)...(j)'
considering the partition pip2p$ ...p8 of i the partitions enumerated will be
those which involve not less than s nor more than j parts subject to the
condition that the μύι excess must be at least ρμ—ρμ-ι, μ having all values
from 2 to 6*.
243. Another interesting series is obtained by consideration of the
successive partitions
1, 21, 821, 4321, etc
This is
# я? я? x10
+ (Ϊ) + ЩЩ + (1) (2) (3) + (1) (2) (3) (4) + -'
the exponents that occur in the numerators being the triangular numbers.
The series clearly enumerates the partitions in which no part is repeated; in
other words partitions into unequal numbers. Moreover such partitions are
obviously enumerated by the infinite product
(1 + x) (1 + л·2) (1 H- Xs) (1 + an) ... ad inf.
Hence the identity
(1 + x) (1 + x') (1 + a?) (1+ tf4)...
~1 + Ш + (1И2) + (1)(2)(3) + (1)(2)(3)(4)+···
244. An important identity is
-i- = (1+ x) (1 + 0(1 + «0(1 +*a) (1 + °°w) ■■■■
χ —~ Χ
This is obvious as soon as we multiply up by 1 — x.
On interpretation it establishes that every integer can be partitioned in
one and only in one way into parts which are different powers of 2.
There is thus one partition uniquely connected with every integer. The
parts are different powers of 2. The reader will have no difficulty in
establishing that a particular power of 2, say 2a, will or will not be a part in
this special partition of an integer η according as the greatest integer in
η/2Λ is uneven or even.
8 A FORMULA OF TRANSFORMATION [SECT. VII
For example, since the greatest integer in 73/8 is 9, an uneven number,
23 will be one part in the special partition of 73. The partition in question
is in fact 64 +8-fl.
Stated in another way we may say that
22* = ?г,
where the summation is for every integer α such that
En/2a
is uneven.
Writing xm for χ we find
—!-^ = (1 + am)(l + хш)(1 + atm) (1 + x*m) ...,
X -~* ОС
a formula of use in the transformation of generating functions. Thus
1
(1)(3)(5)(7)...
= (1 + χ ) (1 + tf ) (1 + я?4) (1 + a?)...
χ (1 +#3)(1 +а?) (14-0 (1 +Я24)...
χ (1 +afi)(l + x10)(l +0(1 +Я40)...
χ (1 + x7) (1 + xu) (1 +#28)(1 +Я56)...
»(1+л)(1+^)(1+д?)(1+«*)...
because every integer is uniquely expressible as the product of an uneven
number and a power of 2.
If we apply the transformation to the G.F.
1
<1)<2)<3)<4)...*
it becomes (1 + χ ) (1 -f a? ) (1 + x4 ) (1 + x8 ) (1 -k#16)...
х(1 + ^)(1+я*)(1+а?)(1 + я16) ...
χ (I + x*)(l + x«)(I + x1*) ...
x(l + x*)(l + a*)(l+x™) ...
х(1+я5)(1-Ь#10)...
χ ...
and in this infinite product 1 -f xm occurs with an exponent 1 + ρ where 2^ is
the highest power of 2 which is a factor of m.
We may therefore write the G.F.
(1+ «?)(!+ Λ^)·(1+β^(1+^)·(1 + ^)(1+^)β(1+«»)(!+л·)*...,
сн. ι]
EXPANSION OF A FINITE PRODUCT
9
and interpret it to mean that the whole number of partitions of η is equal to
the number of partitions into the parts
1, 2U 22, 3, 41? 42, 43, 5, 6l9 62, 7, 8b 82, 83, 84, ...
where 4>l9 42, 43, for example, denote the number 4 in three different colours
and the partitions are such that no number occurs twice as a part with the
same colour. The seven partitions of the number 5 are
5, 4Д, 4,1, 433, 32b 322, 2^1.
245. The identity
_L_=: (1 + я) (1 + af)(l+al·) (1 +a?) + ... ad inf.
X *~ X
may be put into the form
1 _!_*
(1 + χ) (1 + χ2) (1 + я4) (1+ a?) ... ad inf. '
from which expansion of the left-hand side shews that every number greater
than unity when partitioned into repeatable parts which are powers of 2
has as many partitions involving an even number of parts as partitions
involving an uneven number. As an example, the number 12 has the
partitions
Even number of parts Uneven number of parts
84, 8212, 4222, 4214, 42312, 822, 814, 43 , 42212, 424,
4216, 26 , 2414, 2218, l12 , 42214, 418, 2612, 231\ 2110,
the number being ten in each case.
246. The expansion of the finite product
(1 - ax) (1 - oaf) ... (1 - ax1)
can bo derived from the expansion of its reciprocal by the following
considerations. The coefficient of a^x11 in the former is equal to the number of
partitions of η into exactly j unequal parts, none greater than г; the same
coefficient in the latter is equal to the number of partitions of η into exactly
j parts, equal or unequal, the part magnitude as before being limited so as
not to exceed i.
Now if one of the latter partitions written in ascending order of part
magnitude be
Pi>p*,p*> —Pj,
where jft + ft +ft + ... + |ty = Щ
it is clear that
Pi + 0, ft + 1, jft + 2, ...jft+j'-l
is a partition of w+(o) into exactly j unequal parts, the limit to the part
magnitude being i +J — 1.
10 PARTITIONS INTO A GIVEN NUMBER OF UNEQUAL PARTS [SECT. VII
Conversely from any partition of ^ + (0) ^nto exactty j unequal parts,
ho part being greater than г +j — 1, we can by subtracting the numbers
0,1, 2, ... j — 1 from the successive parts reach a partition of η into exactly
j equal or unequal parts, no part greater than i. There is thus a one-to-one
correspondence between the system of partitions of η into exactly j equal or
unequal parts, no part greater than i, and the system of partitions of η + Κ j
into exactly j unequal parts, no part greater than г +j — 1. Therefore we
pass to the coefficient of a? in the expansion of
(1 - ax) (1 - ax2)... (1 - ax1)
from the coefficient of ai in the expansion of
1
(1 - ax)(l - ax*)... (1 - oaf)
(J)
by changing i into г — j + 1 and multiplying by xK2\
Since therefore
(1- ow?)(l- ax2) ... (1- oaf')
a(l-d*)a? a2(l-^)(l-^+1)^
+ 1-я + (1-я)(1-0 + ·"
о*' (1 - of) (1 - #*+1)... (1 - a?i+bi) agi
+ (i-tf)(i-#2)...(i-^') + **"
we find that (1 - ax) (1 — ал?2)... (1 - а#{)
1-я + (1-#)(1-я2)
+ ( } (1-д?)(1->)...(1-^) "" +·*··
The generating function for partitions into exactly j unequal parts none
greater than г is therefore
(i-j + l) (i-J + 2)·.. (i) №)
(if® ... (j) X '
or as it may be also written
(j+l)(i + 2)...(i) (*?)
(l)(2)...(i-j)
247. Let us next consider partitions into uneven parts.
The αι. is clearly ^^_l____ .
CH. i] PARTITIONS INTO UNEVEN PARTS 11
Multiplying numerator and denominator by
(2) (4) (6) (8) (10)...,
we obtain (2) (4) (6) (8) (10) ...
(1)(2)(3)(4)(5)... '
which is (1 + x) (1+ я2) (1 4- хг) (1 +0 (1 + я5) ...,
which is none other than the a. P. for partitions into unequal parts. We thus
find the theorem: " Any number can be partitioned into uneven parts in
the same number of ways as it can be partitioned into unequal parts/'
Cf. Art. 243.
Again, putting
^^"(l-oo?) (1 -ax*)(l - ax6)(l -ax1) ... ad inf.'
we find that F (a#2) = (1 - ax) F (a),
and we are led to the expansion
This shews that the g.f. which enumerates the partitions into exactly i
uneven integers is
xl
(2)14Γ(6)ΓΠ(2Ϊ) '
a result which might have been predicted, because considering г nodes placed
in a column
if we place to the right of it the graph of any partition which involves г even
parts and no uneven parts we find that the combined graph exhibits a
partition composed of exactly i uneven parts.
248. In a precisely similar manner we are led to the expansion
1
(1 - ax) (1 - aa?)... (1 - ао^"л)
-1 + αββ» + α.β.^Μ4+2), ^(2j)(2j + 2)...(2i + 2j-2)
-l + a*(2)+a* (2)(4) +...+aw (2) (4) ... (2i) +* '
establishing that the g.f. for partitions into uneven numbers such that the
highest part does not exceed 2j — 1 while there are exactly г parts is
(2j)(2j + 2)...<2i+2j-2)
(2)(4)...(2i)
12 ALGEBBAICAL PROOF OF ONE-TO-ONE CORRESPONDENCE [SECT. VI
The fact that the partitions into uneven parts are equi-numerous witl
those into unequal parts has been shewn by Glaisher in an ingenious manner
He establishes a one-to-one correspondence between the two sets of partitions
Writing a partition into uneven numbers in the form
<*υ <*3> «5, α7ί ·.. denoting repetitions of parts, he expresses these numbers α ir
the binary scale; thus
сь+1~2Ая + 2АЧ-2АЧ-...>
and thence proceeds to the partition
1 χ (2^ + 2*°+ ...) + 3 x (2Al + 2β21 +...)+ 5 x (2fe + 2fe + ...) + ...,
the parts being
gfto 2&0, ... 3.2й1, 3.2*1, ... 5.2βι\ 5.2fe, ...,
and asserts that these parts are all different because any integer is onb
expressible in one way as the product of an uneven integer and a power of 2
The correspondence in the case of the number 9 is
9 7l2 531 514 З3 3213 31е l9 parts uneven,
9 72 531 54 63 621 432 81 parts unequal.
In this connexion it should be observed that the function which enumerate,
partitions into uneven parts, viz.:
(1)(3)(5)(7)...'
may be put into the form (by Art. 244)
(l + #)(l + #2 )(l+a?) (1 + a* )...
χ (1 + Λ·)(1 +#*·2) (1 + я3'22) (1 + a»·*)...
χ (ΐ+^)(ΐ +^-«χι + ^-'χι+ «··*)...
χ (1 + χ7) (1 + #7·2) (1 + a?·*) (1 + a?-*)...
χ
wherein the 5th row of factors is equal to ,~ ■■ . .
Considering now the partition into uneven parts
12>13*з5Рб ...(25~1)г?28-1...,
it is clear that the factor хы~г {2s"1]
of the term ял.1+л.8+л.б+...+А|.1(2.-1) + ...
is obtained from the 5th row of factors in the form
(2s-1) (2*42*42*4...)
CH. I] GRAPHICAL EXHIBITION OF ONE-TO-ONE CORRESPONDENCE 13
and that we thus arrive at a partition of i>2s-i(2s— 1) into unequal parts
Moreover varying 5 so as to obtain similarly a partition of
ίι.1+^.3 + ρβ.6+··.+1^ι(2*-1)+...
into parts we see that no two parts can be equal since we know otherwise thai
the enumerating function is identically the same as
(1 + x) (1 + x*) (l-h^)(l -Ьл?4)....
Hence the form of enumerating function written above involves necessarilj
the one-to-one correspondence under discussion. It is also the analytical
expression of the fact that a number is only expressible in one way as the
product of an uneven number and a power of 2.
249. Another method of exhibiting a one-to-one correspondence is due to
Sylvester. It is valuable as shewing the power of the graphical
representation. The correspondence differs from that obtained by Glaisher. In the
discussion of self-conjugate partitions (Art. 252) it will be shewn that the graph
may be composed by means of angles of nodes, each angle containing an
uneven number of nodes, and it will thus appear that the number of
self-conjugate partitions of a number η is equal to the number of ways of
composing η with unequal uneven numbers. In the present case we are
given a partition of η into repeatable uneven numbers and we may form an
angle graph, but it will not be regular.
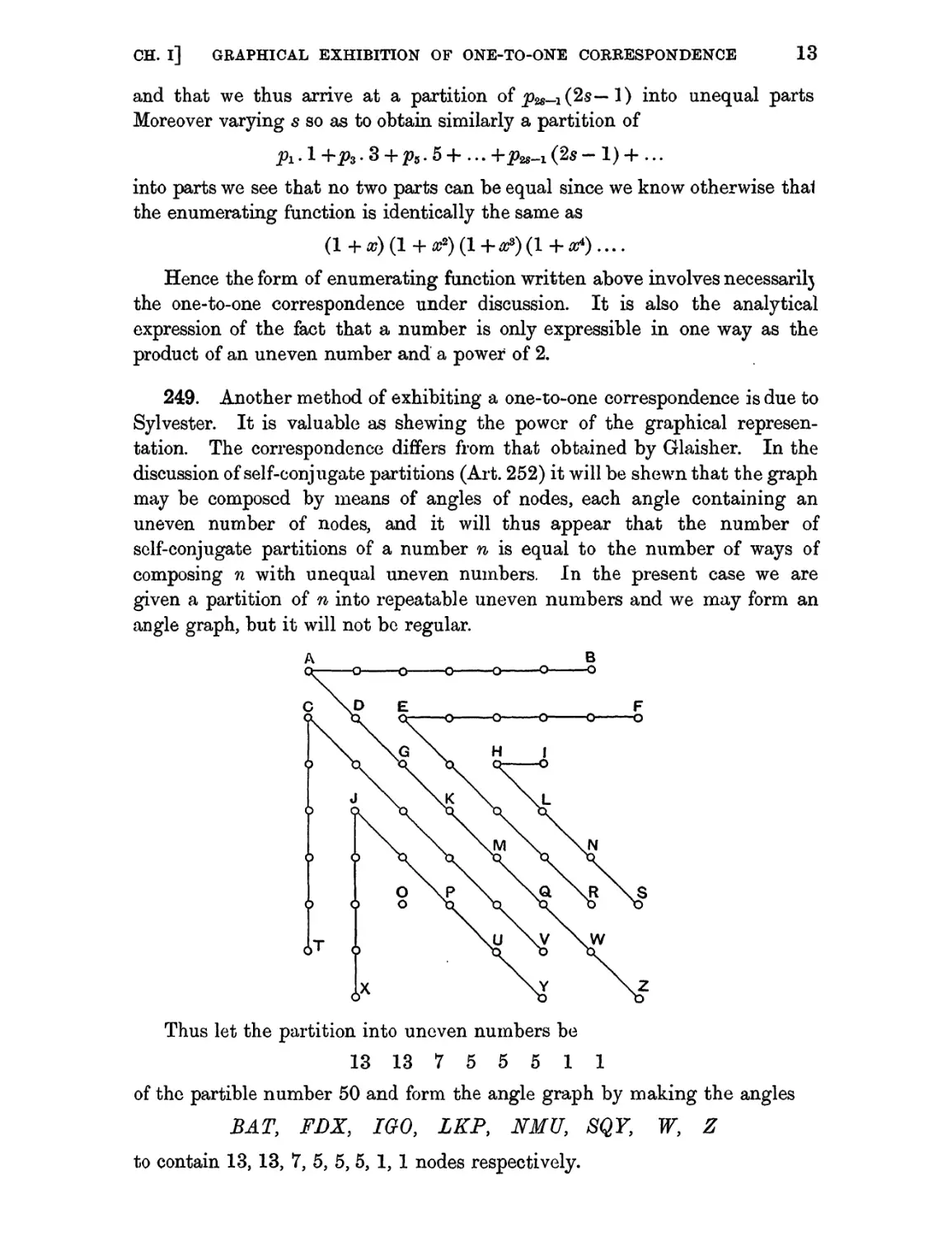
Thus let the partition into uneven numbers be
13 13 7 5 5 5 1 1
of the partible number 50 and form the angle graph by making the angles
BAT, FDX, IGO, LKP, NMU, SQY, W, Ζ
to contain 13, 13, 7, 5, 5, 5, 1, 1 nodes respectively.
14 THEOREM IN REGARD TO SEQUENCES [SECT. VII
The graph is now to be read in the manner
ZAB, VCT, REF, YJX, SHI} 0,
yielding the partition into unequal numbers
14, 11, 10, 9, 5, 1
of the partible number 50.
Slight consideration shews that the process must produce a partition into
unequal numbers.
The correspondence in the case of the number 9 yields
9 712 531 514 3s 32ls 316 1·
54 63 531 72 432 621 81 9
which should be contrasted with that reached by the method of Glaisher.
250. There is also a more refined correspondence arising from this
point of view. A partition into unequal parts may involve s consecutive
numbers. This is termed a sequence of order s. If a number is not
accompanied by the next highest or the next lowest number this would be
called a sequence of order one. This is obviously the same as no sequence
at all, but in what follows it counts as a sequence. A partition into s unequal
parts may therefore involve 1, 2, 3,... or s sequences. For example the
partition
14, 11, 10, 9, 5, 1
involves four sequences, viz.:
14; 11, 10, 9; 5; 1.
This partition was derived, by Sylvester's graphical method, from the
partition
13, 13, 7, 5, 5, 5, 1, 1
which is composed of four distinct uneven numbers.
The correspondence to be noticed here is that between the partitions
which are composed of s distinct uneven numbers and the partitions into
unequal parts which involve s sequences.
Thus for the number 9 we have for
s = l, 9, 33, l9 uneven parts,
54, 432, 9 unequal „
5 = 2, 712, 514, 3313, 31* uneven „
63, 72, 621, 81 unequal „
5 = 3, 531 uneven
531 unequal „
The proof of the theorem, too long to be given here, will be found in
Sylvester's Collected Mathematical Papers, Vol. iv. p. 45.
CHAPTER II
GEOMETRICAL AND OTHER TRANSFORMATIONS
251. One of the most important methods of studying the graph of a
partition is due to Durfee*. He fixed attention upon the square of nodes
that appertains to every graph. Consider the graphs of the partitions
32, 662, 4431, viz.:
о о · о о · · · · о о о ·
оо о о · · · · о о о ·
• · о о о
•
where the square of nodes is specified in each case. The reader will observe
that if the mth part of the partition is at least equal to m, and the (m -f- l)th
part less than m +1, the graph involves a square of nodes having m nodes
in the side. It follows at once that every graph of i rows and j columns
can be dissected into three pieces:
(i) a square containing m2 nodes,
(ii) a lateral graph of m rows (at most) and j — m columns,
(iii) a subjacent graph of г — m rows and m columns (at most).
The number m may be as large as the least of the numbers i, jy and may
have any lesser value.
If the content of the graph be n, and there is a square of m2 nodes, we
may distribute η — m3 nodes into two groups, one of which involves m or
fewer rows and exactly j — m columns, and the other exactly i — m rows and
rn or fewer columns. The corresponding partitions will have in the one case
m or fewer parts and a highest part equal to j — m, and in the other exactly
г - rn parts and a highest part not greater than m.
* Johns Hopkins University Circulars, n. (1883); Sylvester's Collected Mathematical Papers,
Vol. in· p. G61.
16 dubfee's dissection of a graph [sect, vii
Many applications may be made of the dissection above described.
Consider in the first place a self-conjugate partition; that is to say, one
whose graph reads the same by columns as by rows.
в
о о о о ·
о до о о ·2)
о о jgro о %q
О 0 О OJ
• F· Ι·
Obviously we can dissect it into a Durfee square and two perfectly
similar appended graphs, lateral and subjacent respectively. If the square
involve m3 nodes, the lateral graph may have any number of columns but
not more than m rows; similarly the similar subjacent graph may have
any number of rows but not more than m columns.
The lateral graph may be appended in as many ways as the number
£ (n — m2) possesses partitions into not more than m parts.
We are therefore concerned with the coefficient of
JHn-щв)
in the development of the fraction
or of xn in the development of
(l-#2)(l-ar%..(l-#2™)·
It follows, giving m all possible values, that the function which
enumerates self-conjugate partitions can be expressed by the series
- x_ a? a?
:+..
n (l-#2)(l-^)...(l-#2m)
252. Another expression is obtainable from the circumstance that the
symmetrical graphs which appertain to these partitions can be dissected in
another manner, viz. into a succession of angles of nodes fitting into one
another. Each such angle involves an uneven number of nodes, and no two
angles involve the same number.
Thus in the graph depicted which denotes the self-conjugate partition
85543111 of the number 28, the successive angles are ABO, DEF, GHI and
J, involving 15, 7, 5, 1 nodes respectively.
сн. и]
SELF-CONJUGATE PARTITIONS
17
We find in fact that every symmetrical graph denotes a partition into
unequal uneven numbers, and we are led to the identity
(1 +x) (1 + я8) (1 + x5) ... ad inf.
_ χ x4 x9
+ T^~x~* + (l-a*)(l-a«) + (l-x2)(l-x*)(l-x«) + "·
because the left-hand side infinite product enumerates the partitions into
unequal uneven parts.
Moreover, if there be a square of m2 nodes, the partition involves exactly
m unequal uneven numbers; it follows that the coefficient of amxn i
infinite product
(1 + ax) (1 + ax2) (1 + ax5)...
is equal to the coefficient of xn in the development of
(1 -x2) (1-х4) ...(1- x™)'
a fact which establishes the identity
(l + ax)(l + ax*)(l +aa?) ... (1 + ax2m"1) ...ad inf.
χ о #4 ^ xm2
= 1 + а ч 9 -f a2 jz -r-7z - + ... + cT
1-х2 (1-я2)(1-0 (1-а?)(1-я«) ...(1-я2™)^ ""
This is a well-known result, but it was obtained in the above manner by
Sylvester. It is a good example of the application of graph dissection to
obtain results in algebraic series.
253. In a similar manner the reader will have no difficulty in dealing
with the finite continued product and in establishing the formula
(1 + сив)(1 + ax3) (1 + ax5) ... (1 + ax2*"1)
1-х21 n (I - of*4*) (I - aF) t
1-х2 (1 — x2)(l — x4)
(1 - x*~2™+2) (1 -«*-*»+*) ... (1 -a*')
(1-^)(1-#<)... (1-я;1™)
The number of self-conjugate partitions which involve exactly i parts
may be similarly discussed. If a symmetrical graph involve a square of m2
nodes the subjacent graph will involve exactly г — m rows and not more
than m columns; it will denote a partition of the number \ (n — m2) into
exactly i—m parts, no part exceeding m in magnitude. The subjacent
graphs will therefore be enumerated by the coefficient of аг~т x*^l~m~' in
the expansion of
(1 - ax) (1 - ax2)... (1 - axm)'
M.A. II.
18 SELF-CONJUGATE PARTITIONS [SECT. VII
or by the coefficient of ar *7l~w ' in
^(i-^)(i-^I)---a-*<-1)
(1-л?)(1-^)...(1-д^*-т) '
or by the coefficient of xn~m% in
(1-л;2)(1-л;4)...(1-^-2^) '
or by the coefficient of xn in
+**** (i-Q(i-^).--(i-**-').
(1-х~)(1-а?)...(1-х*-™) '
and now giving m the values 1, 2, 3, ... in succession the enumerating
function is found to be
„· , ы 1 - я2*""2 „-4., (1 - x*~4) (1 - #2i~2)
x +x 1_^ + * (1-^(1.^)
(1-д^)(1-я^)(1-д^)
Corresponding to these parti fcions we find from the dissection of the
graphs into angles that we have partitions into unequal uneven parts which
involve a highest part exactly equal to 2г — 1.
The number of these partitions is equal to the coefficient of xn in the
finite product
a?-1 (l+a')(l+ic3)(lH-^)...(l+ x^-%
that is to say, in
„. , ,, 1 - #2i-2 (1 - я8*-4) (1 - а!*-*) л
1-х2 (1 — #2)(1 — яг1)
a verification.
(1 - а^-6) (1 - д^4) (1 - а*-») ^ |
4 (1-#2)(1-χ4)(1--^) * }'
254. There is another way of investigating the generating function of
conjugate partitions which leads to its expression by another series.
• o·
Consider this graph of a self-conjugate partition 664322.
CH. II] INVESTIGATION BY GRAPHS 19
It is symmetrical about the diagonal ABC, to the right of which we find
an irregular graph of three rows, viz.:
If there are s nodes in the diagonal the irregular graph under view must
have either s — 1 or 5 rows. If we transform the irregular graph by shifting
the second, third, etc. rows to the left, so as to bring the left-hand nodes of
those rows underneath the left-hand node of the first row, we obtain a
regular graph
which has the property that no two rows can be of the same length. Now the
function which enumerates such graphs is either the product
(1+я)(1 + <)(1+&·») + ...,
or the series (which is algebraically equal to it)
χ a? #°
/Η-ι\
(1Γ(1) (2) <1)(2)(3) "'-'-<1)<2)...<β)ΊΓ·'··
In the series the term
аЛ 2 /
(T)(2)...(s)
enumerates the partitions into exactly s parts.
Suppose now that the irregular graph, and therefore the derived regular
graph also, has s rows exactly. Then the diagonal of nodes ABC... may
have s or s +1 nodes. There is a corresponding graph consisting of s
columns below the diagonal of nodes. These are also enumerated by
(l)(2)...(s)*
Hence considering the combined contents of the graphs to the right
of and below the diagonal of nodes we see that the enumerating function is
found by writing #2 for χ in the above function. It is
X*(s+1)
(2) (4) ...(2s)
That is to say that the number w of nodes can be arranged in a pair
of irregular graphs, competent to be the right-hand and lower graphs of
2-2
20 INVESTIGATION BY GRAPHS [SECT. VII
a self-conjugate partition, in a number of ways given by the coefficient of
xw in
(2) (4) ...<2s)'
the right-hand graph having s rows.
Containing only the two graphs the self-conjugate graph is so far
invertebrate. It has no diagonal of nodes. Since this diagonal may have $ or $ + 1
nodes, we must multiply by
afi + af+^af^,
to make the graph complete.
Hence as regards exactly $ rows in the right-hand irregular graph, we
have the enumerating function
* (?) „ ^1
* (1) (2) (4)7.. (2s)
Hence the generating function for self-conjugate partitions is
Г (1) (2) (4) ...(2s)
а? а? ж15 д,(«+р»-1
" + X + (lj+ (1) (4)+ (1) (4R6) + · · + (1) (4) (6) .T7(2s) + · ·'
and the term
(l)(4)(6)...(2s)
enumerates those of them which have s rows in that portion of the graph
which lies to the right of the diagonal of nodes. The series obtained is
therefore equal to the product previously found
(1 + x) (1 + a?) (1 + x") ... ad inf.
and to the scries
χ x4 x° xs*
1 + Й+Щ + «1Щ + "'+12|(4)...(Й) + "''
255. We are also led to the identity (by dividing each side of the identity
which involves the old product and the new series by 1 -f x)
(1 + Xs)(1 + я8) (1 + χ7) ... ad inf.
0* Xs X15 x(s+D*-i
+ (2) + (2)14) + (2И4И6) + * + (2) (4) (27) + ""
The truth of this result can be seen from a priori considerations. For
since ($+ l)2 —1 is equal to $ terms of the series
3 + 5 + 7 + 9+ ...
CH. II]
AN IDENTITY OF EULER
21
we can write down the graph of the partition
(25+1,25-1, ... 5,3)
and join it to the graph which denotes a partition into 5 or fewer even
numbers and thus obtain a graph which denotes a partition into $ uneven unequal
parts, no one of which is less than three. Such partitions are therefore
enumerated by the (s 4- l)th term of the above series. The whole series is
therefore equal to the product concerned . which obviously enumerates all
partitions into uneven unequal parts, no one of which is less than three.
256. The general term in the expansion of the infinite continued
product
(1 - x) (1 - of) (1 - of) ... ad inf.
was obtained by Euler and is a celebrated result.
He shewed that the expansion is
2 (-)'V2 .
The coefficient of xn in the expansion denotes the excess of the number
of partitions of η into an even number of unequal parts over the number into
an uneven number of unequal parts.
Many proofs of the theorem exist. One of the most interesting is that
given by Franklin in the Comptes Rendus of the Institut (1880).
Suppose a partition into unequal parts written in ascending order of
magnitude. Its graph consists of rows of nodes which continually increase in
length. Consider the particular graph
л в
о
υ
ε
of the partition 23567. In particular fix the attention upon the nodes A, B
at the summit (of the graph) and upon the nodes С, D, Ε which form a slope
line at the base (of the graph). We can remove the nodes A, B from the
summit and place them so as to form a new slope line at the base in the
manner
·λ
в
This is also the graph of a partition into unequal parts. The process,
which has been termed " contraction," can be applied, with exceptions to be
22
AN IDENTITY OF EULER
[SECT. VII
specified later, whenever the nodes in the summit are equal to or less than
the number of nodes in the slope line.
When this is not the case we can reverse the process, viz. remove the
nodes in the base line and place them so as to form a new summit. For
example, take the graph
ABC
which now becomes
the process being termed " protraction." This also produces a partition into
unequal parts.
Subject to exceptional cases, when neither contraction nor protraction can
be applied, contraction or protraction can be applied and the number of parts
in the partition (always into unequal parts) is thereby changed from an even
to an uneven number or vice versa.
Hence, subject to elimination of the exceptional cases, there is a one-to-
one correspondence between the partitions into an even number of parts and
those into an uneven number.
The exceptional cases arise when the summit meets the slope line and
contains either the same number or one more than the number of nodes in
that line, for then neither contraction nor protraction is feasible. To explain
this statement observe that to the graph
in which the summit meets the slope line and contains the same number of
nodes, neither contraction nor protraction can be applied. Also that to the
graph
contraction cannot be applied, for it produces the graph of a partition with two
parts equal; protraction is obviously out of the question.
CH. II]
JACOBl'S IDENTITY
23
The exceptional cases therefore arise when the graphs correspond to one
or other of the partitions
j, j + 1, j + 2, ...2j-l,
j + 1, j + 2, j + 3, ... 2j,
where j may he unity or any larger numher.
The contents of the two partitions are
H%*2-i)> i(3j2+j) respectively,
and each involves j parts; when j is even in each case there is no
corresponding partition into an uneven number of parts obtainable by contraction
or protraction, and therefore the number of partitions of \ (3j2 — j) or \ (3j2 + j)
into an even number of unequal parts must exceed the number into an
uneven number of unequal parts by unity. Further if j be uneven the
number of partitions of £(3j2 — j) or of ?(3j2+j) into an uneven number of
parts must be in excess by unity. These facts are all summed up in the
identity
(l-#)(l-#2)(l-#3)...adinf.= X {-Ух 2 ,
/я-00
the numbers J(3j2 — j) and £(3f+j) being the direct and retrograde
pentagonal numbers.
Jacobi's Identity.
257. An important theorem in this subject is derived by Jacobi from his
researches in elliptic functions*, viz. it has the two statements
(1 + xn~m) (1 + xn+m) (1 - x271). (1 + x*n~m) (1 + ajsn+m) (1 - x4n)
χ (I + xfm~m) (1 + a^+m) (1 - xm)...
+ 00
-00
(1 - a*»-*) (I - a*»+») (I - a;»1) . (1 - x*n-™) (1 - a»*'») (1 - x*n)
χ (1 - a^-») (1 - я**+») (1 - л·™)...
+α>
= Σ (-)* 0nii+wi,
- 30
wherein n and m arc not necessarily integers.
258. The important particular cases are:
(i) In the second formula put ?ь = §, m = £, deriving Euler's formula
discussed in the last Article.
* Crelle, Vol. xxxii. p. 1G6.
24 JACOBl's IDENTITY [SECT. VII
259. (ii) In the first formula put η = £, m = |, deriving a series given by-
Gauss*, viz.:
(lH-ic)(H-^)(H-^)...x(l-a?2)(l-^)(l-^)...
the left-hand side of which may be also written
(l-fljP)(l-a*)(l-fl?)...
260. (iii) In the second formula put w= f, m = §, obtaining
(1 -ж)(1-^)(1-^). (1-<*)(1-<*)(1 -л;10).(1-^)(1-#14)(l-#15)....
~l-(* + afi) + (a? + aP)-(aP + c^+...(-)*(***-** +
the exponents on the left-hand side being numbers of the form
0, 1, 4 mod 5.
261. (iv) In the second formula put η = f, m — \> obtaining
(1 -я»)(1 -я3)(1 - x5). (1 -л?*)(1 -00- -#10). (1 -#12) (1 -#13) (1 -^1S)....
the exponents on the left-hand side being numbers of the form
0, 2, 3 mod 5.
262. (v) It has been shewn by Sylvesterf that, taking the second
formula and making n = ^> m — \-\-e where e is an infinitesimal, another
formula of Jacobi may be deduced, viz.:
(1-х)Ц1-а?У(1-х*)К..=1-Зх+5х*-7а?> + ...(-У(21 + 1)хУ 2 '....
This celebrated result is justly considered to be one of the most remarkable
in the whole range of pure mathematics.
263. There is an important expansion of
1
(1 - ax) (1 - a?x) (1 - άΛχ) ... ad inf.'
for if we suppose that it can be expanded in the form
Ί Λ Τ) *^ Π
\ — ax (1 — ax) (1 — a?x) (1 — ax) (1 — α8&·)(1 — α3л;) '"'
where Л, Д (7, ... etc. do not involve x, we substitute ax for x. This has
the effect of multiplying the algebraic fraction by 1 — ax while the series
becomes
.ax д а2з? ~ α*χ*
+ T^tfx* (l-a;2x)(l-a*x) (1 - a*x)(1 - a*x)(1 -a4x)+ "*'
* Gottingen Commentaries for the years 1808-11.
t Collected Mathematical Papers, Vol. iv. p. 60.
CH. II] EXPANSION OF AN INFINITE PRODUCT 25
Hence this series must be equal to
(1 - ax) jl + A T^- +Bt. ^= -.
' { 1 - ax (1 — ax) (1 — a?x)
+ o — + I
^ (l-ax)(l-a*x)(l-aax)^ J '
Comparing these two series in regard to powers of χ we find without
difficulty
а
A =
JB =
C =
1-a'
a*
(1-α) (1-α3)
0
a?
(Ι-αχί-α^χΐ-α·)'
and thence the formula
= 1 +
(1 - ax)(l - a2x) (1 - a?x) ... ad inf.
χ a4 я2
1-a'I-ax (1 - a) (1 - a2)' (1 - ax) (1 - аЯя)
а9 я3
(1 - а) (1 - а2) (1 - а3) * (1 - ах) (1 - а*я?) (1 - а3#)
264. Putting herein χ = 1 and а = ж we have
+ .
(1 _ я) (i _ дв) (χ _ ^3)(ΐ _ я*) ... ad inf.
(1 - xf + ("l - xf (1 - я2)3 + (1 - x)2 (Y^~aff\l - χ*)* + '"'
a new form of the function which enumerates the unrestricted partitions of
numbers.
The expansion can be at once interpreted by means of the Durfee square
of nodes. The (i + l)th term of the series enumerates all the partitions whose
graphs involve a Durfee square of i2 nodes. For the lateral appendage to the
square may be the graph of any partition of any number into not more than
г parts, the part magnitude being unrestricted; and the subjacent appendage
may be the graph of any partition of any number where the part magnitude
is restricted not to exceed i, and the number of parts is unrestricted. Each
appendage may involve partitions enumerated by
(l)(2)...(i)
26 TRANSFORMATION OF SERIES [SECT. VII
Hence the whole of the partitions which involve a Durfee square of i2
nodes when graphically considered are enumerated by
{(l)(2)(3)...(i)r
and therefore the whole of the partitions of all numbers by
?{(l)(2)(3)...(i)p'
which is the theorem in question.
265. Similarly it is easy to find the corresponding theorem when the
number of denominator factors is limited. Thus
(1 - ax) (1 -a2#)(l - a?x) ... (1 - alx)
1 - α* χ A (1 - a*"1) (1 - of)
= 1 + a - . ζ + a4 Ц= Γ7Γ 5Γ- ·
Xй
l-a'1-ая (l-a)(l-a2) л (l-ax)(l-a*x) '
a series possessing i +1 terms.
Putting herein χ — 1, a — x, we find
1
(1-я?) (1 -x2)(l -a?)... (1-я*)
а?(1-а?) ^(l-fl^1)^-^) #°(1 -a?~*) (1 -&*-1)(1 -x{)
"" (1 - .г·)2 + (1 - a)8 (1 - a?)* + (1 - xf (1 - &)* (1 - ж3)9 + * * *'
and the reader will have no difficulty in observing that the (,s4-l)th term
enumerates partitions whose graphs involve a Durfee square of .v2 nodes, and
whose part magnitude is limited by the number i.
The Transformation of certain Series.
266. We consider a square lattice of nodes where there is no limit to the
number of nodes in the side of the square.
At these nodes suppose numbers to be placed in such wise that they are
in arithmetical progression alike in each row and in each column. Such an
arrangement involves in general four parameters, and has the representation
r r + s r + 2s r + 3s
r+ t r + s+t+w r + 2s + t + 2u r + 3.9H- t + 3u ...
r + 2t r + s + 2t + 2u rH-2.9 + 2i + 4u r-|-3s + 2£ + 6w ...
г + Ы r + $+3t + 3u r + 2s + 3t + 6u r + %s + 3t + 9u ...
the common differences being
s, s + u9 s + 2u, $ 4- Згг, ...
сн. π]
FOUR METHODS OF SUMMATION
27
in the successive rows, and
t, t + щ t + 2u, t + 3u, ...
in the successive columns respectively.
Let Xpq be a function of χ and μρα a numerical coefficient; we then
construct the tableau
μ^Χψ μ*Χ#***« /^ХЙГ2^2* /^Й""4*"11 ...
/faXS* /^Χ^+2ί+2" μ*Χ$*+"*** μνΆΐ*8™*6" ··.
/%^ίί3ί Μ42^2+δ+3ί+3Μ μ„Χ^+η+6η μαΣϋ****** ···
The transformation which we consider is concerned with the sum of this
infinite number of functions and depends upon the circumstance that in
certain cases the summation may be performed in a variety of different ways.
This arises because the exponents in each row and in each column are in
arithmetical progression, and in consequence the functions Xpq" in each row
and in each column are in geometrical progression.
267. There are four methods of summation which are principally
effective:
(i) We may be able to sum the functions in each row of the tableau.
(ii) We may be able to sum the functions in each column.
(iii) We may be able to sura, firstly, the functions in the first row;
secondly, the remainder of the functions in the first column; thirdly, the
rcmaindor of those in the second row; fourthly, the remainder of those in
the second column, and so forth.
(iv) We may sum, firstly, the functions in the first column; secondly,
the remainder of those in the first row; thirdly, the remainder of those in
the second column; fourthly, the remainder of those in the second row,
and so forth.
Denote these modes of summation by Д G, BO and CR respectively, so
that geometrically
•—·-
• f
• i
• <
1 <
RC
t—· · <
ь— ■· · ■ <
■ ϊ ~ '
> i
t <
> <
CR
> <
• ι
As one of the simplest cases put
(r, s, t, u) = (1, 1, 2, 2),
28 APPLICATION TO JACOBl'S FORMULA [SECT. VII
the tableau is
X
Xs
x6
X7
X2
X6
x"
χ14
я3
χ9
χ15
χ*
χ4
χ™
χ20
χ™
and the summations R, С, RC, OR lead to the identically equal series
+ ...,
1-х \-a? 1-oP 1-аР
χ Xй x* x1
X Xs X6 X10
T^x +Ь^+Ь^ + Г^*
Χ Χ2 Xе . Χ9
1-х2 '1-х 1-я4 1-я3 '"'
or, as they may be written,
/»M-l\
X*™~1 __ ^ X™ _ ^ дЛ 2 /
T' 1 _ aP-i "71-i«»"il. x™
g>m{-2m—ι) ^(w-Ы) (2wi—ι)
= il- a*3*1 + ι 1 - л^-1 '
268. The identity between the first and third of these scries is
interesting in the theory of partitions. The first clearly enumerates the
number of ways of partitioning a number into parts which arc repetitions
of a single uneven number. The general term of the third may be written
дД+2+...+Wl ι Д.2+3+...+7П+1 _j_ дЛ+4+...+МЦ-2 -L . #
and we gather that the series enumerates the ways of partitioning a number
into parts which form a single sequence. We have thus the simplest case
of the theorem which states that a number may be partitioned into parts
which are repetitions of г distinct uneven numbers in as many ways as it
may be partitioned into parts which form г distinct sequences. We have
proved the theorem for i = l.
It will be observed that the first series also enumerates the uneven
divisors of numbers.
269. In a similar manner it is easy to establish Jacobi's formula
χ x3 x5 x7
1 4- x 1 + x? 1 + χ5 1 + x7
X Xs Xе X10
' TTx ~" 1 + X2 + Г+яГ3 ~ l+x4'
+ ..
CH. II] EXAMPLES OF TRANSFORMATION 29
For this purpose we put as before
(r,s,t,u) = (1,1, 2, 2),
Xvq = x, but аьм = (-)*+3;
the tableau is then
χ — x2 Xs — x4 ...
-ж* x£ -я9 x12...
#* — я10 #16 —я20 ...
-л?7 л?14 -л?21 х^ ...
and we find that the summation R gives
1+я 1+я3 1-far5 1 + #7
and the summation i?(7 yields
χ χ* χ6 χ10
establishing the formula.
Observe that the summations G and (722 give respectively
X X2 X* X4
l+#2 l+#4 1+&л 1 + я8
ί(/ Χ" Χ/ Χ
1+я8 1+д? l+я4 1+а?
270. If in the general tableau we put
**- pq == ^> f^pq == ■*
wc find that the modes of summation give respectively the series
af ivr+t xr+2t я?+и
"*"* Ί ~j(-!-m "«"···>
1 _ лл τ ι _#«+<* l - aJri-w 1 _ #»+»»
a^ af*· жг+2* #г+3*
1 -^ + Γ- #i+w + 1 - #i+2W + 1 - x*+**"
1 - #* i - a;' 1 - af14* 1 - #i+w
: + η . + ^ 7X„ + ·
1-х1 1-х8 1-^+" T l-^+w
/gH-2ff+2t+4tt ^r+3SH-2t+6t6
30 CERTAIN TRANSFORMATIONS [SECT. VII
so that they are equal to one another. If we take pm = (—)#+я the first series
becomes
xr xr+b xr+2t л?г+зе
l + a?~~ ί + x*+u + 1 +л^+ш ~ 1 4 0·+**+'"'
and the other three are similarly altered as to signs.
271. If we take (r, s, t, u) = (1, 1, 2, 1)
Xn = x and μΜ=ί>#,
we find the tableau
ж 2л?2 Зл·3 4л?4 ...
2л?3 4л?5 6л·7 8л·9 ...
Зл?5 6л8 9л11 12л;14...
4л;7 8л;11 12л?15 16л;19...
and the R and G summations give us the relation
χ 2x* Зл·5 4л·7
(l^xf + (1 -л?2)2 + (1 -л?)2 + (1 -л?4)2"4" "··
л? 2л?2 Зл?3 4л4
_| ^ J. -, Г" +~, Г 4" ...
~(1-л*)2 (1-л?3)2 (1-л?4)2 (1-л?5)2
Similarly, when fim = ίΡ 9 ) ί « ) ' we reach ^e identity
л; Зл?3 6л;6 Юл?7
ι _^ ^ _L . J. -, h .. .
» · /t . ο\·ι · /τ .«A«t ' /ι ..^\·ί ' ···
(1-л?)3 (1-л;2)3 (1-л?3)3 (1-л?4)3
χ Зл,·3 6л3 Юл·4
~ (1-л;3)3 + (1 -л3)3 + (1 - л;4)3 + (1-л;5)3 +'"'
and in general when
_/p + m-lWg + ro--l\
^A ™ А ш /'
we obtain
л? /m +1\ л?3 /m-+2\ a?
(b^)^1 4\ 1 / (1 - л2)ш~' + V 2 J (1 - л-0ш+1
га -Ь 3\ л?7
/ra + 3\ л?7
A 3 / (1 - л?4)ш+1
Η- ...
л? /m 4-1\ л?2 /m + 2\ л?3
i + lN\ Д?2 /m + 2\ л^_
' + ' 1 / (1 - л,·3)™*1 + { 2 У (1-дг*у*+1
(l-#-)w+1 V 1 /(Ι-λ·3)™*1 V 2 /(1-л·4)''
+ (т + 8\ ^_ +
v з д1-^5)^1
men ^-(-^(^ГОГГ1).
the signs in all the denominators are changed and also the signs of alternate
fractions on both sides.
СЫ. II] EXAMPLES FROM THE FUNBAMENTA NOVA 31
272. Other identities given by Jacobi in the Fundamenta Nova Theoriae
Functionum Ellipticarum are as follows:
(г,М,м)-(1э2,2,4)
gives by the summations R and G
χ a? x? x7
i + i -7л-^ -T.+ ...
1-a? 1-я? 1-х10 1-х14
χ a? a? x7
1 + #2 1+#β 1 + #10 1 + #14
This is the identity of Jacobi, but if we take the summations RG and CR
we obtain two other forms of the series
χ a·3 xQ x15 a?25 x?5
, + T-T—« + :
1-я2 1+a? 1-я6 ' 1+#« 1-я10 1+ж10
# я3 #° #15 я26 я85
: + :
l-h#2 1-я2 1 + я6 1-я6 1+#10 1-х10 ""
273. Again if (r, 5, i, и) = (1, 1, 1,1)
•^ PQ == *^>
and yLtpg numerically equal to ρ but with the negative sign, if both ρ and q are
even, we find by the R and G summations
χ 2л,·2 За? 4л·4
1-я; 1 + ж2 1 — &3 1 4- x*
χ
//j2 /ι.·8
(1 - ;/;)2 + (1 + off + (1 - (x?f + (1 + #4)2 + ''
(see Zoc. cit § 40).
274. Again if (r, s, i, w) = (1, 2, 2, 4)
Xpq = л?, /^ = 2p — 1,
the R and 0 summations give
χ Зхл 5я? 7x7
■ + ϊ r« + ς—л + n~-τ, + ···
1-я2 1-я* 1-я10 1-я*
д?(1 + р д?»(1+^) яб(1+^10) Д7 (1 + ^,14)
(1-я2)2 + (1-я6)2 + (1-я;10)2 + (1 -х·14)2 + '"
(see loc, cit § 40).
32 EXAMPLES FROM THE FUNDAMENTA NOVA [SECT. VII
275. Similarly (r, s, t, u) = (1, 1, 2, 2)
ΙΛ = ^ ^ = (-^(2ρ-1)»
л? 9л?3 . 25л?5 49л·7
&уе* 1 + л? 1+#3 + ϊ+#5 1+λ?7''"
_ д?(1 - 6а2 + а?4) х2(1 -№ + а?) л*Ч1-6ав + #12)
(14-л;3)3 (1+а?4)3 + (1 + ару
and (r, 5, *,м) = (1, 2, 1,2)
A jp^r — Л', ^£од ==ί?
л? 8л?2 27л?3 64л?4
gives _ + _ + _ + _+...
= #(1 + 40 + 0») ж3(1+4л?3 + л?6) л?5 (1 + 4а8 4- л;10)
(1 -л?)4 (1 - л?3)4 + (1 - а*)* + '
CHAPTER III
RAMAN UJAN'S IDENTITIES
276. Mr Ramanujan of Trinity College, Cambridge, has suggested a
large number of formulae which have applications to the partition of
numbers. Two of the most interesting of these concern partitions whose parts
have a definite relation to the modulus five. Theorem I gives the relation
+ I^+(l-#)(l-a;y) + (1-я)(1-я?) (1-я8) + ***
""^"(l -x){i -of') ...(1- а**)+ '"
__ 1
~" (T- x) (1 - of) (1 - a?11) ... (1 - a*»+1)...
1
X (T-0(L -лл)(1-я?14)... (1 -iCBW+4)... '
where on the right-hand side the exponents of χ are the numbers given by
the congruences == 1 mod 5, ξ 4 mod 5.
This most remarkable theorem has been verified as far as the coefficient
of ;l*° by actual expansion so that there is practically no reason to doubt its
truth; but it has not yet been established.
The series on the left-hand side can be interpreted in the theory of
partitions. In fact it has been discussed in a previous article (Art. 242).
The circumstance that i2 is equal to the sum of the first i uneven numbers
shews that the algebraic fraction which has xi2 for numerator enumerates the
partitions of all numbers into exactly г parts between which there are neither
repetitions nor sequences. Hence the whole series enumerates all partitions
of any given number which involve neither repetitions nor sequences of parts.
The theorem asserts that the partitions, whose parts are limited to be of the
forms 5m+1, 5m + 4, are equi-numerous with those which involve neither
repetitions nor sequences.
M. А, И, 3
34 INTERPRETATION OF FIRST THEOREM [SECT. VII
Thus the six-to-six correspondence for the partitions of ten is
Parts of the forms 5m ±1 No repetitions or sequences
91 10
64 91
614 82
4212 73
41е 64
l10 631
By a previous article the fraction aPfcl — x) (1 -#s) ... (1 — χ1) also
enumerates the partitions into exactly i parts, no part being less than i,
so that the series enumerates partitions such that the smallest part is not
less than the number of parts. These six partitions of the number ten are
10, 82, 73, 64, 55, 433.
277. The right-hand side of the identity can be put into the form of the
product of two series because, starting with the known expansion
1
(l-a)(l-ax)(l-ax2) ...ad inf.
-1+Λ + . w, * + ■ *
1-я? (1-аО(1-яО (!-*)(!-^)(1-^) "'
we put a = x and x=af simultaneously and find
1
(1-я?) (1-х6) (1 - x11) (l-o?16)...
a? x2 a?3
" +(l-tfV (1-я5) (1-я10)4 (1-#δ)(Ί -#10)(1-#15)+ ""
Similarly if we put a = x\ x~x* simultaneously we find
1
(1 - of) (1 - a?) (1 - xu) (1 - x1Q) .V.
(1 -^) + (1 -<)(1 - a?°) + (Г- ^)(1 -x10)0.-x") + **' '
We can see almost intuitively that these results are true; take for instance
the fraction xz/(l - a?) (I —x10) (1 —x15). We can realise the partitions which
it enumerates by taking a vertical column of three nodes
and placing to the right of it the nodal graph of any partition into three or
fewer parts of the form 5m. Hence the partitions enumerated have exactly
three parts, each part of the form 5m -f 1.
Similarly the fraction #13/(1 — a^)(l — л?10)(1-я;15) enumerates the partitions
having exactly three parts, each part of the form 5m 4- 4.
CH. Ill] INTERPRETATION OF SECOND THEOREM 35
Another statement of Ramanujan's First Theorem is therefore
χ x4 я?
1 - x + (1 - x) (1 -tf)+ (1 -x) (1 -я?) (1 -я*)+ ·"
~ 1 + 1 - x"+ (1 - я»)(1 - x") + ''e J \ * 1 - a? (1 - я5) (1 - л;10) j '
278. Theorem II gives the relation
a? x6 x12
+ Т^Ъ + (1 - x) (1 - ¥) + (1 - β) (1 - я») (1 -a?) + 'e'
1
(1 - #2)(1 ~ж7)(1 -ж12)... (1- #™+2)...
1
(1~^)(1-^)(1 -a?*)...(l -я6"**3) ...'
the exponents of χ on the right-hand side being of the form 5m + 2 and
5m + 3.
This relation has also been verified by actual expansion to a high power
of x} but it has not been established.
To interpret the series on the left-hand side we observe that the number
i2· 4- i is the sum of the first i even numbers. In particular when г = 3, since
12 = 6 + 4 4- 2 we form the graph of the partition 642 of the number twelve
and find that if we place to the right of it the graph of any partition which
has three parts the combined graph clearly denotes a partition which has
exactly three parts, no part less than two, and which involves neither
repetitions nor sequences of parts.
Hence we at once infer that the whole series enumerates partitions of all
numbers which are such that no part is less than two and which involve
neither sequences nor repetitions of parts.
Ramanujan's Second Theorem thus states that of any given number such
partitions arc equi-numcrous with those whose parts are all of the forms
5m + 2, 5m + 3. Thus for the number ten the four-to-four correspondence is
Parts of the forms 5»4±2
82
73
3*23
25
No
repetitions or sequences
and no part < 2
10
82
73
64
3-2
36
ANOTHER INTERPRETATION
[SECT. VII
279. The series on the left-hand side has another interpretation due to
the circumstance that i2 4- i is the product of the numbers i + 1, i.
Thus when i = 3, since 12 = 4 4- 4 + 4 we take the graph of the partition
444 of the number twelve.
and place to the right of it the graph of any partition which has three parts;
the combined graph denotes a partition into exactly three parts and no
part less than four. In general the combined graph denotes a partition into
exactly i parts and no part less than г + 1.
Thus the whole series enumerates partitions such that no part is less than
the number which exceeds the number of parts by unity.
For the number ten these partitions are
10, 73, 64, 55.
280. We may also obviously write Ramanujan's Second Theorem in
the form
x2 x{i -12
1 + Л ч +74 w^ on +
(l-x)^(l-x)(l-a?y (l-x)(l-x*)(l-a?) '"
_ L x2 xA яР__ _
I (l-^) (1-я5) (1-я?15) + (1 - x5) (1 - χ^ΰϊ~-χιτ)
( 0$ Xе Я?
X J + (1 - of) +(1 - a*) (1 - aF) + (1 -<)(1 -a10) (1 - я") + '"
Ramanujan himself deduces other results, of great interest and beauty,
from these, but they are not given here as they are not directly connected
with the combinatory analysis.
The circumstance that the two theoi-cms given still await demonstration
adds greatly to their interest for the student and stamps them as being very
remarkable.
281. There is a correspondence between the whole of the partitions of a
number and those particular partitions which involve neither repetitions nor
sequences of parts.
If we consider the graph of any partition of any number, say the graph
A
в
• · ιι· ·σ
• F·
С·
CH. Ill]
A PARTICULAR CORRESPONDENCE
37
of the partition 64'221 of the number seventeen, and read the graph by-
enumerating the nodes in the angles
ABC, DEF, GH,
we obtain the partition 10, 5, 2 of the same number which necessarily has
neither sequences nor repetitions. But this is not a one-to-one correspondence
because several other partitions are made up of angles which, looking only to
the numbers of nodes which they contain, are precisely the same and lead to
the same partition 10, 5, 2.
Ex. gr. the partition 34213 having the graph
leads by angle-reading to the same partition 10, 5, 2.
There is thus a group of partitions each member of which leads to the
same partition which possesses neither repetitions nor sequences. Further,
corresponding to every partition which possesses neither repetitions nor
sequences, there will be a group of partitions and there is a one-to-one
correspondence between the groups and the special partitions.
The problem of enumerating the special partitions is the same as that of
enumerating the groups, of the nature considered, into which the whole of
the partitions may be separated.
For the number six there arc three groups, the correspondence being
groups (6, 51, 412, 3P, 214, Iе), (42, 321, 2-P), (33, 2a),
special partitions 6 , 51 , 42 .
It is, in fact, evident that of the number m the; group which belongs to
the special partition (m) comprises the m members
s\m-\
where s has values 0, 2, 3,... m.
It is not difficult also to establish that corresponding to the sjjecial
partition (т^щ) the group has
(m1—'m.2 — l)7n.2
members.
38 PROOF OF THE CORRESPONDENCE [SECT. VII
282. It will now be proved that corresponding to the special partition
(mxm2... m8) the group has
(m! - m2 -1) (ma - m8 -1)... (тм - ms -1) m8
members.
This will be accomplished by comparing the series
a; a? a?
1 + (Ϊ) + (ΪΗ2) + (1)(2)(3)+··'
the first series of Ramanujan which enumerates the partitions without both
repetitions and sequences, hereafter termed special partitions, with the series
i+ (l)l+(1)42)" (1)42)43)*+ "'''
which is one form of the function which enumerates the whole of the
partitions.
The whole of the partitions, whose graphs involve precisely $ angles, are
enumerated by
(l)»tSy...(B)« = S (?1 + 1) (?2 + 1)...(q8 +1)rf.^+...+«.+*
where under the sign of summation the numerical magnitudes
Si, ?2, ...&
may, each of them, have all values from zero, to infinity.
If we write herein
wiM = qs^ + q8 + 3,
ms_2 = qs-2 + gM + J« + 6,
then m! + m2+ ... + ms = qi + 2q2 + 3q3 + ... + *g> +A
and (mlm2m3 ...ms)
is a special partition involving precisely s parts.
Also q8 + l =ms,
gV-i + l=Wi-i-me-l,
gs_2 +1 = me-t - wig-! -1,
52 + l =7?г2 — ra3-l,
<fr + 1 = Wx - wi2 — 1.
Hence
(1)42)* (s)2 = ^mi"'m2""1)(?w2"W3"1)···(т*->""m*- x)m*^^+Wl^-+Ms
CH. Ill] THE SAME FOR THE SECOND THEOREM 39
the summation being for every special partition which involves exactly $
parts.
But from the first series of Ramanujan
a**
Hence to every special partition
corresponds a group of
(m1-m2-l)(?n2~m3 — l)...( ?ηδ_! — mn - 1) ms
partitions drawn from the whole of the partitions.
283. It is thus seen that the number of partitions of η is
2 (Щ - w2 -1) (m2 - ra3 - 1) ... (ms-! — ms -1) m*,
the summation being for every special partition
(га1иг2...т5)
of the number n.
284. If we realise the number mY physically by a chain of щ beads
connected at equal intervals by threads, and so also the other numbers
why '»h> · ·· m«> tbe s chains can be placed in angles in
(wT — m2 — 1) (m2 — m3 — 1)... (m^ — ms — 1) m8
different ways to form different regular graphs of the number n.
285. The special partitions enumerated by the second theorem of
Hainanujan are included in those enumerated by the first theorem. The
same group of partitions is in correspondence with the same special partition
in each case. In the case of the second theorem, however, the whole of the
unrestricted partitions are not involved because those partitions which give
rise by angle reading to a part 1 are necessarily omitted. If a graph involves
a square of s2 nodes an angle will consist of a single node if the lateral graph
has at most s — 1 rows and the subjacent graph at most s -1 columns.
The graphs to be omitted are therefore enumerated by
of
(l)42)*...(s--l)s
Hence giving $ all values not less than unity the whole of the omitted
graphs are enumerated by
&A #9 cf_
40 RESTRICTION OP THE PART MAGNITUDE [SECT. VII
and subtracting this function from that which enumerates the unrestricted
graphs, viz.
χ & χ9
ffi2+ WW + iiwW+
we reach the function
S=co С д& (8+1) /ρβ(β+1) |
as that which enumerates the partitions which compose the groups associated
with the special partitions of the second theorem.
286. The left-hand side of the identity which constitutes Ramanujan's
First Theorem has been shewn to be the function which enumerates the
partitions which are without repetitions and sequences of parts.
If we wish to restrict the part magnitude we may proceed in the following
manner:—Consider the partition into three parts
When the part magnitude is unrestricted we construct the graph of the
partition 531 of the number 9 and join to it any partition into three parts.
If however the part magnitude is restricted not to exceed m, the partitions so
added must be such that the part magnitude does not exceed m — 5. These
are enumerated by the function
(m - 4) (m - 3) (m - 2)
(1)(2)(3)
and give rise to the term
(m-4)(m-3)(m-2)
a>(2)(3)
in the sought function.
When the partitions have i parts, the part magnitude of the added
partitions must have a part magnitude not exceeding 2г —1 and we are
similarly led to the term
.,(m-2i + 2) (m-2i + 3) ...(m- i+ 1)
* (l)(2)...(i)
Hence the function required is
1 + г И . ,,(m-2)(m-l) (m - 4) (m - 3) (m- 2)
Η- ... to μ terms.
The series evidently does not extend to infinity because when the part
magnitude is restricted there is a limit to the content of the partitions, and
CH. Ill] A CONDITIONED INFINITE PRODUCT 41
also to the number of parts. When m is even the partition, of the nature
considered, which involves the greatest number of parts is m, m —2,
m — 4, ... 2, and this has \m parts. When m is uneven the partition in
question is m, yn — 2, rn — 4, ... 1 and this has J (m 4-1) parts. Hence г has
the limit \m} or % (rn -f 1) according as m is even or uneven, and therefore μ
the number of terms to be taken of the series has the value
Hm + 2), °* i(«* + 8)
according as τη is even or uneven.
287. We may expand the general term of the series
i2 (m - 2i + 2) (m - 2i + 3)... (m - i + 1)
(l)(2)...(i)
by means of the theorem
(1 - xP) (1 - x"+1)... (1 - «*+«->)
(1-*·) (l-«)(l-<*) (1-в?)(1-а?)(1-в»)
+ ... to q + 1 terms,
and wo arc led to the identity
(m) ,(т-2)(т-1), ,(т-4) (т-3) (m-2)
1+вШ+*■ —1#) +ж (Wi + "t0 μ terms
" 1+(f) + (W+(I)|n3)+---t0/iterms
/g.m+1
IT
{г г*4 #9 )
l + ci) + (T^^i)W(3)+-t0/A-ltermsi
,/;»№+l Г д. дЛ /р»
+WWi1+^+um + (iM2)l3)+-t0^-2terras
+<->s (im^s)!1 +щ+(ΪΜ2)+oT(2ji3j+-to^-sterms
+ ,
a scries which involves μ rows of terms.
288. The same function is also that part of the expansion of the product
(1 + x) (1 + я?) (1 + ж3). ·. (1 + xm)
which presents itself when from the product of consecutive factors
(l + **)(l+«»«)
the term λ·μ+ι is deleted.
42 THE SAME FOR THE SECOND THEOREM [SECT· VII
This deletion insures that the partitions, which necessarily involve no
repetitions, do not contain any sequence of parts.
We denote such a product by
Jf (1 +«) (1 + 0(1 +o»)... (I +#m).
289. In Ramanujan's Second Theorem regarded in connexion with the
enumeration of partitions which possess no repetitions, no sequences and no
part less than two, we similarly restrict the part magnitude. For partitions
into three parts we take the graph of the partition (642) of the number
twelve, viz.
and add to it the graph of a partition which has three parts and no part
greater than m — 6. We thus obtain the graph of a partition of the desired
character and a term
(m-5)<m-4)(m-3)
(1) (2) (3)
of the enumerating function.
In general when there are i parts the term of the function is
Mi+1) (m-2i+l)(m-2i + 2)...(m-i)
(l)(2)...(i)
leading to the enumerating function
1|дД(ш-1), ^(ш-3)(ш-2) (m-5)(m-4)(m-3)
1+Л (1) +X (1)(2) +X (1)(2)(3)
+ ... to v terms,
where ν has the value J (m ■+- 2) or £ (m +1) according as m is even or
uneven.
This series can be put into the form
дЛП+1 С rjfi дЛ дЛ2 ]
- ИГ t1 + Щ + <T)T2) + ЩЩЩ + - *«» - 1 terms}
+йщ{1+й) + (1Ш + ам2йз) + ···t0 v~2 termsl
+ ,
a series which involves ν rows of terms.
СЯ. 1П] A GENERALIZATION 43
The same function is also that part of the expansion of the product
(l+#2)(l+^)...(l-b#m)
which presents itself when, from the product of consecutive factors,
(l + a»)(l+a·**),
the term a?2**1 is deleted.
290. Let V8fm denote the function which enumerates partitions without
repetitions and sequences and having no part less than s nor greater than m.
Then
■4«-l + * (1)+* (1)(2) +x (1)(2)(3) +-'
V -1 ι r«(m~l) ,^(m-3)(m-2) (m-5) (m-4) (m - 3)
V2,m-i + * (1) + * (1)(2) +<* (i)(2)(3) H"···,
S'M"~1+^ (1) +^ (1)(2) + * (1)(2)(3) + ···'
etc.,
and considering the expressions
M(l+x)(l+x*)...(l+x™)}
M(l +a?)(l +a?) ... (1 + xm)}
if (1 +^)(1+ж4) ... (1 Ч-л·™),
we see that
Μ (I + x) (I + x*) ... (I + x™)
= if (1 + .г·2) (1 + .г·3)... (1 + д?'л) + л?Л/(1 + .га) (1 + я3) ... (1 + ят),
and moreover хМ{\ -Ь ,г*2)(1 + яг*) ... (1 -t-#m) is effectively equivalent to
that is Vh ш = T7^, μ + # ^ m
and in general V8t m = VB+lt w + я" V*+* m,
relations readily verified from the series expressions.
291. From this result it is manifest that we can express F4>m as a linear
function of Vhm, V2tm. We obtain the series of results
л '4,m==~~ ^1,т"Ь(1 "b^O '2,m>
a*VGfm= (1 +#4J) Г1|Я1-(1 + β + я2) F2,w,
etc.,
and observing that the last written equation may be written
44 GENEEAL FOEMUL^l [SECT. VII
it is natural to assume that, as far as the integer $,
with the object of proving that the formula holds when s +1 is written for s.
We require the theorem
v s,m — * gjUir-i τ^ «^ K a,m—2·
Writing Fs<m in the form of the conditioned product
if (1 +cc8)(l + xs+1) ... (1 +Я™-1) (1 4- xm)
= M(l+a?)(l + #*+1)·.· (1 + ^nv"1) + ^m-3f(l + О (1 + ^+1) ··· (1 + xm~l)
=if(i + ^)(i +^+i)...(i+^m-o+^w^(i + ^0(1+^H"1)--(i + ^m-2)>
we see that ^m^ "^,т-1 + #т^5, m-2-
Now я*-1 l^+i,w = V8-1)7)l - Fe>m,
and substituting for V8-hmi VSym the assumed expressions linear in Vhm, V2jm
we find on reduction
or *Q F,+1>m = (-)·+> (FM_2Flim - FM_2F2,W).
Hence if the theorem be true for the integer s and lower integers it
is equally true for the integer s + 1. It is thus established by induction.
292. The theorem is better written in the form
/*VW, m = (-nV^V^n- FMF2,,„),
and in particular, when m = <x>,
In utilizing the formulae the particular cases
^ wi,m— χ τ* л , r m-f-i, m — A>
must be noted and it further appears that in the formula we must suppose
that
V = Λ-Υ71 V , —О
The particular case
is interesting since the left-hand side has a very simple expression. It may
be verified in the simplest cases.
It will be noticed that the two Ramanujan series when modified so as
to shew a maximum part magnitude are the only fundamental series in this
branch of the theozy of partitions.
СЫ. Ill] ARITHMETICAL INTERPRETATIONS 45
293. The Generating Function V3)O0 which enumerates partitions
without repetitions or sequences which have no part less than three has, by
Ramanujan's results, the simple expression
и. 1 l
:.b
χ ((1) (4) (6) (9) (11) (14)... (2) (3) (7) (8) (12) (13)
which, by previous theorems, can be thrown into the form
(1) (2) - x« (2) (4) + ж17 (3) (6) - x* (4) (8) 4- Xs* (5) (10) - ...
(1) (2) (3) ...ad inf.
where the general numerator term is
(_)· + ! ^<"l>(*+2)W(ae)>
294. The two theorems
.1/1)
,m—ι "Ь* &т У e,m—2>
are complementary and ariso from reasoning in regard to the beginning and
end of the conditioned product respectively.
From them we derive the two series
Vhm = V%m + ^4,m + ^V{]y7n + tf>V8>m + ... + «*TVhM» + ... ,
+ ...,
and we can interpret each term in both series.
The partitions enumerated by the 5th term in the first series arc those
which, while involving no repetitions or sequences, have
(i) no part equal to 2s - 1;
(ii) the parts 1, 3, 5,... 2s - 3;
(iii) other parts equal to or greater than 2s and not greater than m.
Those enumerated by the 5th term in the second scries are those which,
while involving neither repetitions nor sequences, have
(i) no part equal to m — 2s -I- 2;
(ii) the parts m — 2s -h 4, m — 2s 4- 6,... m;
(iii) other parts equal to or less than m — 2s-f 1.
Complementary to the formula
/s+2\
*< 2 ^m,m = (-)4^,sFliW- Vh8V2ym)}
we establish in the same manner the formula
l(*-l)(2m-.« + 2)-pr _/ γ/ττ V V V \
л r itm-s — \ ) iKw-s+3,m-i^i,m"" У w-s+3tw v iym—v-
46 CONNEXION WITH " CONTINUANTS" [SECT. VII
We can also obtain formulae by reasoning in regard to a factor of the
conditioned product which is not the first or last factor.
Thus since
Ff>w«Jf(l + of)... (l+a?-l)(l H-^+1) ... (1 + аГ)
+ Jf(l +я») ... (1 + rf-1) я* (1 + «*+»)... (1 +#w),
we have V8>m = FM_a Fi+1>w+^Fs,^2Fi+2im,
an inclusive formula; for if
(l) t=S, Г8>т~ Ч+],»» "Ь * u+2,m>
(ii) t = m, Vs>m = Fs>m_! + #M Ks,w_2.
295. It is a remarkable circumstance that the present theory is connected
with the theory of continuants in the subject of determinants.
Sylvester shewed in 1879, "Note on Continuants," Messenger of
Mathematics, Vol. vni., that the number of terms in a continuant (a^ ... an) is
1+( 1 Μ 2 Μ 3 )+-
and that this series has the value
Now recalling the result
^»-i+*w+«· (1)(2) +^ (1)(2)(3) + "·'
we find, by putting χ equal to unity, that the whole number of partitions of
all numbers which have no repetitions, no sequences and no part greater
than m, is
1 +
fm\ /m — l\ , /7>i-2\
(l) + ( 2 ) + ( 3 ) + -·
which is equal to the number of terms in a continuant of the order m -+· 1,
and has therefore the value
1_
V5
[δΨ»Π-(Η"Π·
Similarly, from the expression for VStm> we find that the whole number
of partitions of all numbers which have no repetitions, no sequences, and no
part less than s or greater than m, is
i+CTVCiX"".·"1)*·-
CH. Ill] CONNEXION WITH " COMPOSITIONS " 47
which is equal to the number of terms in a continuant of the order m - s + 2,
and has therefore the value
1 f/1 1 ,Λ™-*+* /1 1 /tf\1tl-*+8l
V5{(2 + 2Vo) -(l-2V5) }·
In this enumeration the absolute term unity which commences the series
is always included, so that the true enumeration is obtained by subtracting
unity from the above expression.
When s = m, the only partition satisfying the conditions is m, and we
find that the expression has the value 2 on development. So also when m = 2,
s = l, the expression has the value 3 corresponding to the two partitions 1, 2.
However, when 5=1 it is, exceptionally, correct to regard the absolute
partition of zero content as included, and then the expression given above is
exact.
296. There is another correspondence with the enumeration of the
compositions (partitions in which account is taken of the order of the parts)
of numbers into parts from which unity is excluded. The function which
enumerates such compositions which have exactly $ parts is
x*8
(<* + & + <*+.„Y ОГ —p,
and the coefficient of xw in
x2 x4, x*
, , fw-3\ , /w-4\ , (w-b\ ,
which is identical with the series
1+(lH 2 ) + ( 3 ) + -'
when w = m H- 3.
Hence we may say that the partitions of all numbers which have no
part greater than m} and no repetitions and no sequences, are equi-numerous
with the non-unitary compositions of the number m -f 3.
For m = 3, the fivc-to-five correspondence is
0 1 2 3 31 partitions,
6 42 24 33 222 compositions.
There is, in fact, a more intimate correspondence still, because the number
of the partitions above defined which have t parts is
cr1).
48 CONNEXION WITH " COMPOSITIONS" [SECT. VII
while the number of the compositions above defined which have s parts and
a content m -h 3 is
fm - s + 2\
V «-1 J'
Hence the partitions without repetitions or sequences, ajbdghest part not
greater than m and exactly $ parts, are equi-numerous with the non-unitary
compositions of the number m-f 3 which have exactly s +1 parts.
Thus for m — 7, $ = 2 the correspondence is
31 41 42 51 52 53 61 62 63 partitions,
532 523 352 325 253 235 622 262 226 compositions,
64 71 72 73 74 75 partitions.
442 424 244 433 343 334 compositions.
(Compare Cayley, Messenger of Mathematics, Vol v. (1876), pp. 166, 167.)
CHAPTER IV
PARTITIONS WITHOUT SEQUENCES
297. Just as we represented the enumerating functions of partitions
without repetitions or sequences by the conditioned product
$, m being the lower and upper limits of the part magnitude, so in the case
where repetitions are allowed but not sequences we can represent the
enumerating function by
τ —Μ -
*>w (1 - af) (1 - #*+1) ... (1 - xmY
the condition of the product being that in the multiplication of any two
consecutive factors
1 - a' · 1 - xl+l'
ЛТЛ7 1 J- 1 -1
1 1-е» 1-^+1 *(1-««)(1-
χ2ΐ+1
tnc last term (1 - **) (1 - «"«)
is to be deleted.
It is best to write
τ -м(л , * Wi , **+1 \ (
■ «*+»)'
ι , *m
and it will be observed that the conditioned multiplication permits
repetitions but forbids sequences.
Wo find T„m = Μ (l + fi£-) ... (l + ^)
+ Γ^^(1 + ΓΓϊ«)···(1+ϊ^=)'
or
Μ. A. II.
&
J- 8, m — ■* e-f-i,m + . л ■* β+2,
50 GENERAL FORMULAE [SECT. VII
v,m
X
Similarly TSitn = Т8уШ^ + τ^τ Т8>1П^У
the two complementary formulae.
In particular Tly7n = T^m + -τγτ Т3>т,
(т)
1 and m being now the lower and upper limits of the part magnitude.
An inclusive formula is obtained by writing
when we find
We can express Т8)Ш as a linear function of Т1)Ш and Т2,т-
л?
^ Τ - X 7» (3) φ -
(1)(2)(3)^*- (2)-1·"1 (1)(2)
and noticing that the last result may be written
™ rp __ rp rp ψ Τ
(1\ (Q\ /31 *»ш — 2»2 xi»w ""* -*1»2 J-2,mt
it is natural to assume the formula
with the object of establishing it by induction.
We assume it to be true for the first s integers.
Then X Τ Χ (Τ -Τ Ϊ
and substituting for Ts~ltm and T8t.m from the assumed formula we readily
find that
(J)
completing the proof.
CH. IV] GENEBAL FOBMULjE AND INTERPBETATIONS 51
Similarly we can obtain the complementary result; that is, we can
express Thm^8 as a linear function of T1%m and Thm^.
Thus in succession
fp>Yl
^_ rp rp rp
/mv -*■ ι,in—2 — * i,m ""* ■* l, m—ι >
(m - 1) (m) '>™-3" ^ш + (m) i 1'm~1'
77 _ 1 m (230U " 1) rp
(m- 2) (m - 1) (m) 1>т~4 (m- 1) 1M (m - 1) (m)
and noticing that the last formula may be written
лЛт—3
~ φ rp rp rp rp
(m - 2) (m - 1) (m) hm^ " *»-*.«-ι·4ι* " ^«-i,»·2 l*
it is natural to assume a formula
д.4(*-1)(2»1-* + 2)
-*1,Я
(m- s + 2) (m - s + 3)... (m) ",'m-s
== v / С* »л—*+3,»»—1 * 1,«г *m—e+з, ?иД iym—i/>
with the object of proving it by induction.
There is no difficulty in thus establishing it.
of
From the formula l\m = TWtm + rr Ts+^m,
there is no difficulty in establishing the result
i'.»-J«.« + (8)i·^^+(β)(β + 2)lf^m + (в)(в + 2)(β + 4)if47·яl + ,
and from the formula
the result
Τ = 7T -1- _ T7
*stm — ■* #,иг— ι π # * -*■ s,m—2
7Т — Τ -4- Τ 4- Τ
■*■ s, m—7 τ · · · ·
(m - 4) (m - 3) (m)
In the first series the pth term enumerates partitions which contain the
parts $3 $ + 2, ... 5 -t- 2p — 4, but not the part s H- 2p — 2.
In the second series the £)th term enumerates partitions which contain
the parts m, г/г — 2, ... m — 2p -f 4, but not the part ?>г — 2p + 2.
4—2
52 RESTRICTION ON THE NUMBER OF PARTS [SECT. VII
298. If we put the number of parts in the partition in evidence we
introduce the symbol g and consider the coefficient of gp in the function
Such coefficients enumerate the partitions which have exactly ρ parts.
Putting 5=1 and m = χ , it is easy to calculate the coefficients of the
earlier powers of g. These are found to be
χ
x* 1+x3
ЩЩГ+~х'
a? 1+x3 1 + ofi
(1)(2)(3)1 + ж Ί+χ*'
я? 1+я? 1+я? 1 +о?
(1) (2) (3) (4) Ί + χ Ί+ο?Ί+α?'
suggesting that the coefficient of gp is in all probability
x* 1 + af 1+g? l+x*-*
(1)(2)...(р)1 + ж Ί+ο?"Ί + χΡ~1'
an expression which may be put into the form
ж* (6) (12) (18)...(6p- 6)
(p) (2) (4) (6)... (2p - 2). (3) (6) (9):.. (3p - 3)'
This shews that the function which enumerates partitions without
sequences may probably be represented by the series
χ | ω | .^ (6) t β» (6) (12)
(1)τ(2)(2) (3)Ί(3)(2)(4).(3)(6)
In general
+ «L (6) (12) (18)
+ (4) "(2) (4) (6). (3) (6) (9)
*(-τ^)(^τ^.)-(1+τ^)--ιω
χ8 ., χ** (6) ч я?8 (в) (12)
+ ΰ (1) +g (2) (2). (3) + 9 (3) · (2) (4). (3) (6)+ ·· ·
299. Partitions without sequences may be looked at from another point
of view. Suppose
{A1A<iAi... Αρ-χΑρ)
be a partition in which the parts are arranged in ascending order of magnitude.
Denote the differences between successive parts by <x0> u1}...,
0f0 Α χ <Χλ A 2 #2 A 3 . . . Ap—i Op_! Ap.
CH. IV] THE THEORY PROM ANOTHER POINT OF VIEW 53
If there are to be no sequences, oc0 which is equal to Аг may be any integer
but aly ag,...^-! may each of them be zero or any integer except unity.
We have
■^2 = a0 + «i,
A3 = «o + «1 + «2,
Ap = ao + «i + . -. 4- Op-i,
and 1Л =pa0 + (jp - 1) e^ + ... + 2otp_a + V-i.
The enumerating function is
the summation being in regard to the values of ct0, a1} «2j ... αν^χ above
specified. Now
~1 + (1) (2) (2)(3)'
71 + (2) (4) (4) (β)'
?>-D«i = 1 . ^ _l+a^^ (6p-6)
(p-1) (2p-2) (2p-2)(3p-3)'
^ "Ίρ) (ρ)'
so that the function is
(6) (12) (6p-6) J_
(2) (3) (4) (6) - (2p - 2) (3p - 3) · (p)
In this summation the smallest part may be zero. If zero be excluded as
one of its values we have exactly ρ parts and
-<P)·
Hence the function which enumerates partitions without sequences and
exactly ρ parts is
«* (6) (12) (6p - 6)
(p) (2) (3) * (4) (6) · (2p - 2) (3p - 3)'
confirming the result of the previous article.
300. If the smallest part is not to be less than two, if it be not zero,
у-imp -ι , «P (6P)
-1+(p)-(2p)(3p)'
so that the summation gives
(6) (12) (6p)
(2)(3)·(4)(6)··(2ρ)(3ρ)'
54 PARTITIONS OF MULTIPARTITE NUMBERS [SECT. VII
which enumerates partitions of the nature under consideration which have ρ
or fewer parts.
Putting ρ equal to oo we find now the noteworthy result that the
partitions, without restriction as to the number of parts, are enumerated by the
function
(1) (7) (13) ...x (5) (11) (17)...
(1)(2)(3)...
Also those which involve precisely ρ parts are enumerated by
*lL @L (12) (6p - 6)
(p) · (2f (3) * (4) (6) · · · (2p - 2) (3p - 3)'
for this is equal to the expression
(6) (12) (6p) {6)_ (12)^ _<6p-6)_
(2) (3) (4) (6) · ·· (2p) <3p) (2) (3) * (4) (6) " (2p - 2) (3p - 3)'
and we reach the algebraic identity
,.£.«£ J6)_ , * J6)_ (12χ *_ (6)_ (12^ (18)
+ (1)+ (2) (2) (3) + (3) (2) (3) (4) (6) + (4) (2) (3) (4) (6) <6)~ (9) +""
(1) (7) (13) ...x (5) (11) (17)...
(1)(2)(3)...
1
" (2) (3) (4) (6). (8) (9) (10) (12) (14) (15) (16) (18)....
The Partitions of Multipartite Numbers.
301. In regard to the function which enumerates the partitions of
multipartite numbers in general there is not very much to be said. For the
bipartite number щщ if we wish to find the number of partitions which
possess i or fewer parts we seek the coefficient of αϊχ'^χζ* in the expansion of
1
(1 — a) (1 — ахг) (1 — ax2) (1 — axf) (1 — ахгх2) (1 — α#1) · · ·'
wherein 1 — αχψχψ- is a factor of the denominator, plt p2 being given all
integer (including zero) values.
More generally for the multipartite number щщ...пш the enumerating
function is
1
(1 — a)(l —αχχ) ...(1 —ахш)(1 — аа%) (1 — α#!#2)... (1 — ас^1Ь)...'
wherein 1 - αχ^χψ ... χ*™ is a factor of the denominator, pl9 p2> ...рш being
given all integer (including, zero) values.
CH. IV] PARTICULAR CASE OP BIPARTITE NUMBERS 55
In order to expand it in ascending powers of a we write it
F(a; xlf x2, ... xm),
and also 1 4 афщ1 + а2фЩ2 + а*фщз + ...,
where фшл> фт>2> etc. do not involve a.
If we write axm for a we find at once the relation
F(axm; xlt x2, ... xm)F(a; xlf x2> ... xm^) = F(a; xu x2, ...xm\
leading to
(1 + ахтфщ1 + а2а?тфт>2 + a*xz^m%2 + ...)
Χ (1 + афт-ι,ι + <*>2фтг-1,2 + а8фт-1,з + ...)
== 1 + афЩ1 + а2фт,2 + а?фЩъ + ....
Comparison of coefficients of like powers of a then yields the relations
%тфт,1 + фт-ι,ι = фюг,1>
%in Фт, 2 + #т фт—ι, ι фт, ι Η" фт—ι, 2 = фт, 2 >
#тфт,з + хтфт-\у\фт,2 + хтфт-1,2фт,1 + фт~1,з = фга,з>
etc.,
and we deduce the relations
(1 d?™) фт>1 = фт—i,i,
(1 - #m) (1 - л&) фт,2 = av»^.lfl + (1 - ж») ψ^-ι,2,
(1 - л») (1 - a&) (1 - xl) фШ|3 = я&ф^ы + От + a& - 2x*m) фт-мфт-1,2
+ (1-я?»,)(1-л4)фя|-1,3,
etc.,
and thence
*"M=(ΐ-^χι-βο-α-^)>
__ 1 + Sa?!^ + %χλχ2χ^χ4 + Σ#ι^μ8^#β&<ι + ...
^а~(1-^)(1-^).(1-^)(1-^....(1-Жи|)(1-л?ш)'
where in the last fraction the elementary symmetric functions of even order
Df the magnitudes x1} лл», ... xm appear.
The functions фт,:{, etc. are very complex and lead to no interesting
results.
The result in the case of фтл is of a trivial character.
302. The case of фт>2 is however worth a moment's consideration.
It enumerates the partitions of all multipartite numbers into two or fewer
parts. Its form is such that the enumeration is made to depend upon the
enumeration of the partitions of unipartite numbers into two or fewer parts.
56 A VERIFICATION [SECT. VII
1^ Βηχ-Пъ...Пт,
denote the number of partitions, into two or fewer parts, of the multipartite
number щп2... nm. Then the form of фт,2 shews that
^ni%...nm ~ &ПХ&Щ, · · · -&П
+ Σ-Β^-ι Вщ-ι Вщ-1 Вщ-i B<ns · · · 5П))1
+ ,
the symmetric function in the .9th line involving f 9 9 J terms.
We shall verify this result for the case
щ = щ = ... = nm = n.
This particular case is convenient because we can predict the result with
ease. If a partition into two parts be
(ιίι>2... yw)(i/iW ... i/m),
the constituent ^. may be any one of the numbers
0, 1, 2, ...я
and z/.9 4- v8' = ?&.
The case in which ^ = v2 = ... = *>w = 0 is included, because then in fact
we have a partition into one part included in the enumeration. Hence vs
may have η + 1 different values and the value of vH determines the value of
v8\ It follows that
may have (n +· l)m different values and this fact leads to
or £(n-|-l)m + £
partitions into two parts according as η is uneven or even.
The reader will notice that when η is uneven every partition occurs twice
in the above process, but that when η is even one of the partitions occurs
only once. This happens when
v& = Vb = hl
for all values of $.
We now observe that
according as s is uneven or even.
CEL IV] RELATION BETWEEN PARTITIONS AND DIVISORS 57
The formula therefore gives
Case I. η uneven:
υ(» + ΐ))-+(™)ΐ4(«+ΐ))·"(Η«+ι)),+(ΐ)(Κ'·+ΐ))"-,[Η«+ΐ))'+···
-^<-И1+(™)+(:)Ч
=40 + 1)™,
which is correct.
Case II. η even: the number is
Й (n 4- 2)}« + Q H (я + 2)}— {*η}» + (™) {* (n + 2)}«~ Цп}* + ....
Herein we write
(£){i(» + 2)i«~ftnl·
-(&){*(« + 2)^»}{i(» + 2)--lj*
and it is now an easy task to shew that the expression is equal to
i |(я + 2)'» - Q (n + 2)^ + (™) (л+ 2)·" - ... (-)*» 1 + ll,
or to £{(n + 2-l)m+l}, or to £(л + 1)»л + £.
For consider the identity
put successively л? equal to +1 and to — 1 and add, obtaining
(2p - l)« + l _ 2 |j>» + (™) p-2(i> - 1У + (^У*-Ч*> - I)4 + ···} ,
and now putting ρ = £ (д + 2) we have proved as required.
303. The connexion between the partitions and divisors of numbers was
established by Euler*.
He proceeds from his formula
(1-я) (1-^)0- -л^)... = 1-ж-л? + жв+яд-л;12-ж1в+....
Differentiating logarithmically and multiplying throughout by — x we
find
χ 0 хй 0 я3 # + 2#2 - 5л·5 - 7л·7 + 12л12 Η-15я?15 - ...
+ Δ ^ ■ -f Ο j +... = ■
1-я? 1-я2 1-#»τ*" (1-я?) (1-я2) (1-я8)...
* "Observatio de summis divisorum," Opera Minora Collecta, Vol. i. pp. 141—154.
58 PABTITIONS AND DIVISORS [SECT. VII
On the left-hand side the coefficient of xn is equal to the sum of the
divisors of n. Denoting it by σ (η) and the number of partitions of η by
Ρ (n) we have
σ(1)χ + <τ(2)α?+σ(3)χζ+...
= (χ + 2αβ - эя5 - 7x7 +12#12 + 15#1δ + ...)
х(1 + Р(1)я + Р(2)я2 + Р(3)^+...),
and by equating coefficients of like powers of χ
σ(η)«Ρ(Λ-1) + 2Ρ(η-2)-δΡ(η-5)-7Ρ(η-7)
+ 12P(n-12) + 16P(n-15) + ...,
the two general terms on the right-hand side being
(-y+i £r (8r + l) Ρ {η - £r (8r 4-1)}.
Writing the intermediate formula in the form
{σ(1)0+σ(2)^ + σ(3)Λ?+...}(1 - л? - ^ + л?6 + л?7 ~ ж12 - #» + ...)
= л? + 2#2 - 5я? - 7л?7 -I- 12#12 + Ιδχ15 + ...
we obtain another of Euler's results
σ (η)- σ (n -I)- <r (n -2) + <r (n - 5) + σ (n — 7) - ... =0 or (-)r+1??,
according as η is not or is a pentagonal number
£r(3r±l).
CHAPTER V
PARTICULAR STUDY OF THE FUNCTION
(1 -& + 1) (1 -#'+2)... (1 -x>'+i)
(1-я)(1-я8) ...(!-«*)
304. The study upon which we now enter has for its object the
transformation of the enumerating generating function of partitions limited both
as to number of parts and as to part magnitude, so that it may be conveniently
expanded.
We first have to note the method of Cayley, whose purpose was to
transform it so that it might be dealt with by breaking it up into partial
fractions.
Cayley*s Transformation*,
We take the equation
(1 + ал?)(1 + а^)...(1 + ax{)
(1-е*) t ,(1 - x1'1) (1 - of)
= l + o«S J + a2x*K— r-^f ir + ...,
1 — χ (1 — x) (1 — χη
where the general term is
„. ,a «с+1) (L-1^) (i-^g+2)-(i-^)
(l-x){l-x*)...{\-a?)
rfhe series is finite, having i + 1 terms, the last term being
We now write — x> for a and obtain the identity
(1 - жЯ-i) (l _ χί+η ... (1 - χ}**)
(1— &·) (1— λ·)(1 — л·2)
- *S ( У,и-^'^1) (1 -^-8+1) (1 ~ **-*) - (1 ~ «0
,V ' ' (1-*)(1-Λ»)...(1-«·) '
* PMt Ггапл Й. S. London, Vol. oxlv. 1855.
60 cayley's transformation [sect, vii
Dividing both sides by (1 ~ x) (1 — a?) ... (1 — xl) we find
(1 - x^) (1 - x^) ... (1 - a№)
st0K } (1-х){1-я*)...(1-х*).(1-х)(1-а?)...(1-я*-°)'
The function under examination is thus presented in the form of a sum
of i H-1 fractions each of which can be dealt with by the method of partial
fractions.
305. For full particulars of the way in which Cayley employs partial
fractions the reader may consult the paper quoted. It is convenient here to
explain the notation in which he exhibits his results.
The function jz r-r= r-4
(1 - x) (1 - x2)
is in the ordinary manner thrown into the form
1_L_+1JL + 1JL·
2(l-#)2^4 1-# 4 1+#'
and supposing that the coefficient of xw in the function is required, he
denotes this coefficient by
Ρ (1, 2) w.
He then expands each of the three fractions and finds that the coefficients
of xw in the first and second fractions are
\ (w -f-1) and I respectively.
To expand the third fraction he writes it
1 1-х
4 Ϊ - я *'
and denotes the coefficient of xw by the notation
i (1, - 1) per 2W,
wherein the portion (1, — 1) has reference to the numerator coefficient,
per means "prime circulator," and the combined expression
(1,-1) per 2*
indicates the way in which the coefficient of xw is actually obtained by
expansion.
He thus gives the formula
о,, оч If 2^ + 3 }
^>2)- = 4J+(l,-l)pcr2J>
and in a precisely similar manner he obtains the formula derived from
1
(1-я) (1-я*) (1-я·)'
CH. V] TRANSFORMATION BY SYMMETRIC FUNCTIONS 61
This is
ί 6м2 + 36w + 47
Ρ (1, 2, 3) w = ^ + 9 (1, - 1) per 2W
" 1+8(2, -1,-1) per 3*
wherein (2,-1,-1) per Sw
2 + χ 2 — x — %2
is derived from
1+я + я2 1-я3
306. The notation is convenient, but a very slight consideration will
convince the reader that the method does not always exhibit results in the
simplest form.
For example, Cayley applies the method to the simple fraction
1
1-я2'
and finds Ρ (2) w (viz. the number of ways of partitioning w into parts when
2 is the only part allowed) to have the expression
2 |+(1,-1) per 2»}·
Now wc know that with the notation explained
Р(2)ш = (1,0)рсг2ад,
so that clearly the ordinary method of partial fractions cannot be relied upon
to give the result invariably in the simplest (and therefore the best) form.
Transformatio'ib by Symmetric Functions.
307. We commence by observing the two identities
1 1 1 1 1
(1 _д.)(1 _^) 2 (1 -#)2 + 2 (1 -a;2)'
(1-л-)(1-л»)(1 -О 6(1-л?)8 2(1-я)(1-д;а) 31-ж3'
which we will also write in the illuminating notation so often employed:
1 1 1 1JL_
(1) (2) 2 (1)* 2 (2)
11 11 .11
. + ;
(1) (2) (3) 6 (Ι)* 2 (2) (1) 3 (3)
The observation leads to the conjecture that we are in the presence of
partial fractions of a new and special kind. We note that in the first identity
we have a fraction corresponding to each of the partitions (l)2, (2) of the
62 A GENERAL FORMULA [SECT. VII
number 2 and in the second fractions corresponding to and derived from each
of the partitions· (l)s, (21), (3) of the number 3. The coefficients of the
fractions also remind us of numbers which arise in symmetric function
formulae, and we are led easily to the symmetric function view of the matter
which is now given.
Consider symmetric functions of the powers of x, infinite in number, viz.
1, x9 x\ x\ ....
Let Si denote the sum of the ith powers of these quantities. Then
clearly
Now if hi be the homogeneous product sum of weight i of the quantities
а, Д γ, ..., we have
(1-α*)(1-£*)(1-7*)...
Putting herein 1, χ, χ*, ... instead of α, β, у, ... we have
1 ζ ζ* ζ1
(1-5)(1-«)(1-^)..."XT(1)T(1)(2)T-T(1)(2)...(I)
Hence if hi denote the homogeneous product sum of order г of the quantities
Χ, X, X j X у ...
We&et **■(!) СТ...Ц'
Having obtained expressions for $i and A* we recall that we can express hi
in terms of sl9 s2, s3> ... (see Vol. I, Section I, Chapter I, Art. 6). The
formula is
(i) k = t
*fl8f*8f» ...
where (1*»2**3A...) is a partition of г and the summation is in regard to all
partitions of г.
Substituting herein
(1) (2). ..<i)' (1)' (2)' (3) ·-
for hi, sly 6\2, 6'3, ...
respectively we find
1 :-S
(1)(2) ... (i) 1л.2л.3*»...#!^!;рь!... (1)*>. (2)^ (3)^
where (1*»2*»3*» ...) is a partition of i and the summation is in regard to all
partitions of г.
CH. V]
PARTICULAR CASES
63
308. This remarkable result shews the decomposition of the generating
function into as many fractions as the number г possesses partitions. The
denominator of each fraction is directly derived from one of the partitions
and is of degree г in x. The· numerator does not involve χ and the coefficient
is the easily calculable number
1
1Λ.2Λ.3Λ ...^l^!#,!...'
The general formula, on proceeding to the coefficient of xw, takes the form
in Cayley's Notation
Ρ(1,2,3,...^ = Σ1Ρι 2Д3,з _pilp>ps[ mmm.
We have used the two symmetric functions Si, hi.
For г = 2 we get
1 1111
(1) (2) 2 (1)= 2 (2)
and we are led, in Cayley's notation, to the result
P(l)2)W=-li W + 1
Also for i = 3 we have
1
2 (+(1,0) per 2 J
1 1 1
; + ;
+ o
1 1
or making use of the decomposition of
(1)(2)(3) 6(1)» 2 (2) (1)^3(3)'
1
(1)(2)'
11 11
+ 777П+;
leading to
(1)(2)(3) 6(1)3 4<1)*T4(2)^3(3)>
P(l,2,3)w-jg
(w + 1) (w + 5)
+ 3 (1, 0) per 220
[ + 4 (1, 0, 0) per 3,
expressions which are simpler than those given by Cayley.
Of the order 4 similarly
1!+l
-.+ ;
ι ι
\2 + ;i
1 1
(1) (2) (3) (4) 24 (1)* 4 (2) (1)^ 8 (2)* 3 (3) (1) 4 (4)'
As is well known the sum of the coefficients on the right-hand side is
unity. This serves as a verification.
Of these fractions jj^, -т^гт, j^r are immediately dealt with.
64 A SECOND FORMULA [SECT. VII
Moreover, —Lj-, = щ \\± + \ ^
(2)
1J_ 1111
: 2 (l)3 + 4 (l)2 + 4 (2)'
1+* + a;S = (l,l,l)pcr3?t
(3) (1) (3)>
and the expression of P(l, 2, 3, 4) w is readily written down.
It thus appears that the Transformation by Symmetric Functions is a
valuable first step towards the expansion of the function. Particular fractions
that thence arise may require breaking up by the same or some other process
as a second step.
309. The fraction
1
(I -«)(1 -a?)... (1 -of). (1 -a?)(l -<*) ... (1 -eh*)'
which presents itself in Cayley's Transformation, is seen to be
and is therefore expressible in terms of
J_ J_ Jl
<1>' (2)' (3) "
by the above formula. Each fraction thus obtained will have a denominator
of weight i
310. The function ai} that is to say, the sum of the quantities г and i
together of the quantities
1, x, #2,...,
is obtained from the formula
(1+^(1+«)(1+<)а+^...-1+^+^ + (ТГ^+....
yielding αί= ____..,
and now the three functions give rise to six formulae, of which one has already
been given. The five others are :
(ii) Si = Σ (-)2*-1 ί*£ζΐϊ1!± Ар ι AfAp...,
w ч У ^1!р2!р3!.··
which, if we denote
for brevity by
(l)(2)-(i) "'Ή'
leads to X -Sf y^^P-1)" * 1 I
leads to w -Σ(-) ^,^, ___ [1]Λ ρ]Λ [J}]
CH. V] SIX FORMULAE OF TRANSFORMATION 65
where (1*» 2** 3Рз...) is a partition of i, and the summation is for all partitions
of г;
leading to
(1) (2) ... (i) 1л. 2л. 3»з... Pl\p2\p3\... · (1)г>. (2)?= (3)*>*
(iv) Si = ^ (-)*+* V?1)1' арфа*...,
leading to
i = sr-v+* (^p-1)'» JJLV"ijlI2''/_£.Γ3 .
(i) ^ ' ihlp.!p,!...|[l]i Ш Ш '""
(v) A, - S (_)«* pi,^·,^ φφφ...,
leading to
[i] ^ ; ftlftlftl... l[l]f 1M) l[3]J "·'
(vi) at = 2 <-)<+* ι-**; др. A№...,
(Sp)'
leading to
= 2 (—)*+2*'
These all involve noteworthy theorems in partitions.
The formula in (iii) above may be expressed in the form
P(l,2,8,...i){«-i<(i-l)}-2(-^ *0* ****->«
311. We have next to extend these results by considering the
symmetric functions of the finite number of powers of x,
1, x, я2, ...aA
w « j 1 - ^+i W±i)
We find "-T3? -IT·
Ί
The formula
(1-*)(1-λ*)(1-λ?*)...(1--0Ϊ*)
-i + * (1) +. (1)(a) + ...
shews that A< = ^ '" " ;
M.A. II.
66 EXTENSION OF PREVIOUS RESULTS [SECT- VII
and the formula
(1 +z)(l +жг)(1 + x*z)... (1 +a&)
-1+* (1) + *л (1)(2) +^ (1)<2)<3) +"·'
that α _^(f-i)(j-i + 2)<j-i + 3)...(j + l)
№at Ul X (l)(2)...(i)
We are accordingly led to the formulae
312· (1) (l)(2).(i)
...ftiftip»!...! (i) I 1 (2) \ \ (3)" I -■
Here the left-hand side enumerates partitions which are limited to
involve not more than j parts, and no part greater than i.
The product
i(J + i)I* J(?)+?)]ft i(3j + 3)^3
I (i) i I (2) J 1 (3) J ""
which is typical of those on the right-hand side, enumerates partitions whose
parts may be
ones of рг different kinds
twos „ jo2
threes „ p2
but in which no part of a particular kind occurs more than j times.
The simplest cases of the formula are
(j + l)(j+2) l(j+l)* 1β] + 2)
(1)(2) 2 (1)* +2 (2) '
(j + 1) (J + 2) (j 4- 3) 1 (j + l)> l(2j + 2)(j + l) 1 (3J + 3)
(1)(2)(3) ■ "β (1)> +2 ~(2)(1) +3 (3) '
and if, extending Cayley's notation, we denote the coefficient of xm in
(j + l)(j + 2)...(j+i)
(if(2)...(i)
by P(l,2,3,...»;j)w,
and the coefficient of xw in
(1+ΐ)Γ f(2j + 2)]g* ;(3j + 3))^
(1) I t (2) j \ (3) } -
by •^(1"'. 2л, 3» ...)«;,
we have the relation
_ PiCli"' 2^ 3"' . W
P(l,2,3,-i;i)№ = S1^3^;^;>J
in itself a noteworthy theoreman partitions.
CH. V] SIX NEW FORMULA
If in the formula we put χ = 1, we obtain the arithmetical relation
(j H- 1)pi+p*+p»+ -
67
V i J 1ft.2*.3ft...ρι!^!^!...'
a theorem which expresses the binomial coefficient
en
as a linear function of powers of the integer j + 1.
The simplest cases are
(j^2)=i(i+i)2 + *0'+i),
(J33)=Hi + i>3+iO'+imO'+D·
313. (ii) Writing for brevity
(j + l)(j + 2)...(j + i) П_+Л
(l)(2)...(i) L * J*
we obtain
w+*) _ « /_v^_x _<&»_rj)!* П_±11л Г1±2?а Γί±?
"w" ^; &p,w... L ι J L 2 J L a
The product
(4 + 1> П + 2> [j + 3>>
L i"J L a J L 3 J -
ΠΰΊ 'ΙΊ2ΓΙ ΐΊ3Γί ·-
If we put χ equal to unity we have the arithmetical relation
•which expresses the integer j + 1 as a linear function of certain definite
products of binomial coefficients.
The simplest cases are
314. (iii)
*i (i -1) (j-i + 2)(j-i + 3)...(j + l)
(l)(2)...(i)
№±2№ Ιί?Γ±ΜΛ f(3j + 3)|ft
= £ (-V+iP I CI·) it (2) И (3) f -
Λν > 1л.2й.ЗР»...^!р8!^!...
5—2
68 THE SIX FOKMULJE [SECT. VII
The factor
(j-i + 2)(j-i + 3)...(j + l)
(l)(2)...(i)
may also be written in the form
(l)(2)...(j + l)
(l)(2)...(i).(l)(2)...(j-i+l)·
It is obvious that, since аг· refers to the quantities
1, x} a?y...xi,
i must be equal to or less than j 4- 1.
The factor enumerates partitions into parts limited in number to j - г + 1
and in magnitude to г or partitions limited in number to i and in magnitude
to j — г-f 1.
We may therefore write
P(l,2,3,..,t;j-t+l){fi;-ii(i-l)}
ш У (-Y+*p Pj(l»,2»,8y..)t0
w^ > lPi.2P*.3P°....p1\p2\p.i\...'
involving a noteworthy theorem.
The simplest cases are
„. U)(j+1) _ 1 (j + l)1 _ 1 (2j+2)
(1)(2) 2 W' 2 (2) '
(1)(2)(3) " 6 (1> 2 (2) ' (1) 3 (3)"
Putting χ equal to unity we have the arithmetical relation
of which the simplest cases are
fg^^O' + D'-iO' + i^ + ^u + i)·
315. (iv) We have
ιιϊγι 1(2)1 ι (3) i -·
Рз
CH. V] THE SIX FORMULAE 69
Putting x equal to unity we have the arithmetical theorem
J K ' Px\W-Pb\..\ 1 ) \ 2 ) \ Ζ ) -'
with the simplest cases
Putting χ equal to unity we have the arithmetical result
with the simplest cases
317. (vi) We have
Putting ж equal to unity we have the arithmetical result
with the simplest cases
318. It is to be observed that these several transformations are not only
intermediate steps but are in themselves noteworthy theorems in partitions.
Each of the partial fractions that is obtained is in itself an enumerating
generating function in the theory. This is not the case in the ordinary
70 FORMULA OF TRANSFORMATION [SECT. VII
method of partial fractions that has been developed in this connexion by
Cayley and Sylvester.
The breaking up into partial fractions of the fraction
(j + l)(j + 2)...(j+i)
(l)(2)...<i)
has one important property that must not be overlooked.
The function as it stands is not visibly a finite integral function and in
order to express it as a product of finite integral functions it is necessary to
know the actual values of i and j so as to find the irreducible factor of the
various numerator and denominator factors. In the transformations before
us in this chapter the partial fractions which present themselves are such that
each is visibly a product of finite integral functions and consequently itself a
finite integral function.
319. Speaking in general we may in any relation which connects the
quantities Si, ai} hi substitute either
(i) &i =
(i)'
«,,· =
Шг-1)
X1 v '
or (ii) Si =
(l)(2)...(i)
1
(l)(2)...(i)'
(ij+i)
(i)
„ _ JJ (i-D <j-i + 2) (j-i + 3) .. (j + 1)
(l)(2)...(ij '
h _(J+l)(j+2)...(J+i) .
(l)(2)...(i)
and since each of these expressions is an enumerating generating function in
partition theory it follows that every such relation involves a theorem in
partitions.
320. In particular the relations between the quantities ait hi are
interesting because in any such relation, as we have seen in an earlier
section of this work, we may interchange the symbols a, h.
Moreover there is an infinite number of functions of the quantities a such
that each function remains unaltered when h is written for a. In fact %+i
when expressed in terms of аг> а.>, a3, ... has this property and sw merely
changes sign.
CH. V] INTERCHANGE OF SYMBOLS 71
In order therefore to form such functions we may take any product
$^s%*s§*sf*...y
such that p2 ■+- p4 +p6 +...
is even.
Every linear function of such products has the desired property.
As one of the simplest examples we have
έ(βί-*8) = θιθ2-«ί,
leading us to the relation
аг a2 — a3 = hlh2 — h3j
and thence to
x__ a? _ 1 1
(1)^(2) " (1) (2) (3) " Щ^Щ - ОШШ '
which we may write in Cayley's Notation
Ρ (1,1, 2) (w - 1) - Ρ (1, 2, 3) (w- 3)
= P(1, 1, 2)w-P(l, 2,3)w,
or in another form
P(l, 2, 8)ur- Ρ(1,2, 8) (w-8)
= P(1, 1, 2)w-P(l, 1, 2)(w-l),
a relation which, in this simple case, is obviously true because each side is
equal to
Ρ (1, 2) w.
321. Again taking the second set of expressions for «;,«$, hi we have
r (J)(i + i)8 _ ,* (i-i)(j)(3 + i)
*" (1) (2) (1)(2)(3)
_ Q + l)'Q+2) _ 0 + 1)0 + 2)0 + 3)
(1)42) (1)(2)(3)
a relation which is not immediately obvious.
It leads us to
2P(l;i)(W-S)P(l,2;i-l)(S-l)-P(l,2,3;i-l)(W-3)
= SP(1; j) («/-*) Ρ (1, 2; j)*-P(l, 2, 3; j)w.
322. The method of partial fractions and other methods have been
applied to the actual evaluation of the coefficients in the expansions of
enumerating functions in the theory of partitions. The reader is referred
to the original researches of Cay ley* and Sylvester f, and to a very good
short summary in Netto's Combinatorik%.
* Coll. Math. Papers, Vol. п., pp. 235, 506.
+ Math. Papers, Vol. п., p. 90.
.t Lehrbuch der Combinatorik, Leipzig, 1901, p. 146 et seq.
72 A LIMITED DOUBLE PRQDUCT [SECT. VII
323. The function
(j+l)(j + 2)...(j+i)
(l)(2)...(i)
is intimately connected with the limited double product
(1 + ax) (1 + ax*) ... (1 + ax*-1)
Mathematicians have almost invariably considered the case of the double
product in which j = i and have thus not directly connected it with the
function which we are studying.
Sylvester only considers the special case, but his quasi-geometrical method
of demonstration is equally available for the general case and is the one to
which attention will now be drawn.
The coefficient amxw in the first part of the product denotes the number
of ways of composing w with m unrepeated uneven numbers none of which is
greater than 2i— 1. Similarly in the second part the coefficient of a"mxw
gives the number of ways of composing w with m unrepeated uneven
numbers none of which is greater than 2/ — 1. The product is not symmetrical in
a and - unless j is equal to i, but observe that it is unchanged by the simul-
taneous substitution of - for a and interchange of i and j. It results from
this remark that the coefficients of am and a"™ in the double product are
derivable the one from the other by merely interchanging i and j. The
coefficient of am in the double product is obtained by multiplying the
coefficient of am+e in the first part of the product by the coefficient of α~θ in the
second part, giving θ all values from zero to j (so long as m + θ does not
exceed i) and adding the results. The coefficient of am+9 in the first part is
a function of χ which enumerates the partitions of numbers into m + θ
unrepeated uneven parts none of which is greater than 2г — 1. In this
function of χ the power of x, viz. #M\ occurs with a coefficient GWl indicating
that there are 0Щ such partitions of the number wx. Let one of these
partitions be
the parts being, as usual, written in descending order of magnitude. Also,
in the second part the coefficient of a~"exw* gives the number of ways of
partitioning the number w2 into θ unrepeated uneven parts none of which is
greater than 2j — 1. Let one of these partitions be
(λχ, λ2, ... λβ),
the parts being written in descending order of magnitude.
CEL V]
CONSIDERED GRAPHICALLY
73
We now form a graph from the two sets of numbers
in the following manner.
Calling г the major half of the uneven number 2% — 1, we form an angle of
nodes
where the number of nodes in the line A^ is the major half of lm+l and the
number of nodes in the line A& is the major half of λ^ The number of
nodes in the angle is thus
\ (w-i + W
Similarly we form angles of nodes Β2Α202) В3АйС3) ... ΒθΑθΟθ involving
numbers of nodes equal to
4 V"m+2 + λ.ο), φ (^w+ίί + \t)t · · · 4" (lm+θ Η" λβ)
respectively, and then fit the angles together in the manner
A,
-в*
so as to form a regular graph of content
\ \hn+i + iwn-a + ... + Ι,η+θ + λ-ι + λ* -f ... + λθ).
The number of nodes in the first row of the graph is
and the number in the first column is
H^ + i).
Since k :f> 2% - 1, L $ 2г- 3, ... lw+1 :\> 2i- 2m -1,
λ**2/-1,
it is clear that the first row and the first column are limited to contain not
more than г — m and j nodes respectively.
74 A LIMITED DOUBLE PRODUCT [SECT. .VII
Now form a second graph of m rows containing
i \<"m—ι "~ 3),
i(/m-i)
nodes respectively.
The content of this graph is
H7i + Z2 + ... + C~'m2),
and the rows are limited to contain not more than i — m nodes.
If we now superpose this graph to the former (as we may, because
i^m —i>iWi + i) we obtain a graph of content
J (Zi + k + ... + lm+β + λ1 + λ8+...+λβ- m2),
which is % (Wi +· w2 — m2)
or £ (w — m2) where w = w1 + w2.
The number of nodes in the first row is
i(Zi-2m + l),
and in the first column
«w+ 4(^ + 1),
numbers which are limited not to exceed
г — m, j + m respectively.
The graph that has been constructed is specified by the content £ (& — m3)
and by the two limiting numbers г — w,^ + m.
The number 0 does not enter into the specification.
By varying θ and the two sets of numbers
&!, 62, ... 69714.4 J Αχ, Λ2, ... Лд
we arrive at all graphs which have the defined specification.
This is so because from any graph so specified the numbers
ό \ l1} Iqj ... lm+Q J Αχ, A2, ... л>0
can be recovered for a given value of the integer m.
It follows that the coefficient of amxw in the double product is equal to
the coefficient of the function which enumerates partitions limited
by the two numbers
г — m, j -f w.
CH. V] CONSIDERED GRAPHICALLY 75
This function is
(l)(2).„(i + j)
(l)(2)...(i-m).(l)(2)...(j+m)·
The coefficient herein ofx^b0-™*) js equal to the coefficient of xw in
(2)(4)...(2i + 2j)
(2) (4)... (2i-2m). (2) (4)... (2j + 2m)
Hence the coefficients of am and a-™· in the double product are
(2)(4)...(2i-2m).(2)(4)...
(2)(4)...<2i + 2j)
(2)<4)...<2i + 2m).(2)(4)..
respectively.
We have thus the identity
(1 + ax) (1 + сит3) ... (1 + ал?1'-1)
*ЮЮ-(1+?)
(2)(4)...(2i + 2j)
(2j + 2m) *
■«1-
ywtf
-2т)Ж
(2)(4)...(2i).<2)<4)...(2j)
+ Σα« (2)(4>...(2i + 2j)
» (2) (4)... (2i - 2m). (2) (4)... (2j + 2m) *
- (2)(4)...(2i + 2j)
+ t (2)(4)...(21 + 2т).(2)(4)...(25-2т)ж '
324. We now make an important transformation.
Observing that if we write ax for a, each side of the identity becomes a
function of xa, we so write and subsequently write χ for x-.
Wc thus obtain the identity
(1 + ax) (1+ ax*) (1 + ax3)... (1+ ax1)
*K)K)K)-(1+i?)
= (l)(2)...(i+j)
(l)(2)...(i).(l)(2)...(j)
+ Se» (l)(2)...(i+j) _i»(* + i
(l)(2)...(i-m).(l)(2)...(j + m)
+ * a-m (l)(2)...(i+j) im{m- 1)
(1)(2)..а + т).(1)(2)...(]-т)Ж
76 VARIOUS FORMULAE [SECT. VII
(l)(2)...(i+j)
(l)(2)...(i).<l)(2)...(j)
I (J + l) (ι + 1)α
+ (j + l)(j + 2)*a+(i + l)(i + 2)a*
(i-2)(i-l)(i) (j-2)(j-i)(j) «»
+ (j + 1) (J + 2) (j + 3) Xa+ (i+ 1) (i + 2) (i + 3) a»
+
}'■
325. The limited double product may be dealt with in another manner
which will lead to an important identity.
For
(1 + αβ)(1 + ω»)... (1+α^-1) * (l +£) (l + f) ··· (l +^)
- 1 | ar'2i> | aV<2i-2)<2i) ι aV(2i-4)(2i-2)(2i)
1 + β*(2)+βί? (2) (4) +ttx (2) (4) (6) +···'
into 1 , * (2j) a* (2j - 2) (2j) tf (2j - 4) (2j - 2) (2j)
α (2) a2 (2) (4) α3 (2) (4) (6) + "'
and by simple multiplication
_ι + „ьШШ , rJ2i-2)(2i).(2j-2)(2j)
"1 + Α"ΐ27~+Λ5 (2Й4> +-
+
ν α» L-. (2i-2m + 2)...(2i) 1)2+l2 (2i-2m)...(2i) (2j)
-a Г (2) (4)... (2m) +* (2) (4)... (2m + 2) (2)
, r^1+t,<21-2m-2)...(gl) (2j-2)(2j)
(2) (4)... (2m+ 4) · (2) (4)
+ a*****+ (2i-2m-4)...(2i) (2j -4) (2j - 2) (2j)
+
(2)(4)...(2m + 6) · (2) (4) (6)
1
+ S a-™ L»* <gJ-g» + g)-(gJ) , ж ,**■,).+,. (2j-2m)-(2j) (2i)
+ Λα Γ (2) (4) ...(2m) -+X (2) (4) ...(2m+ 2) (2)
,m4,^(2j-2m-2)...(2j) (2i-2)(2i)
(2) (4) ...(2m+ 4) · (2) (4)
+
* See Sylvester, Coitected Matliematieal Papers, Vol. iv., "A Constructive Theory of
Partitions," where the particular case j=i is considered.
CH. V] DERIVED FROM THE DOUBLE PRODUCT 77
Now put ax for x, and subsequently write χ for a?, obtaining
(1 + ax) (1 + a«?)... (1 + aw*) χ (l + ^ (l + ^ ... (l + ^
-lixWW ^<i-D(i) <3-l)(J) ,
-i + * (1)3 + * (1)2(2)2 +...
.«-« Li* (m+i)(i-m+ 1) · (i) *{я»+8»+8) (i-m)(i-m + l)...(i) (j)
+ Xa Г -йЙЙй15)" + · (i)(2)...(m+i) (ϊ)
i(w*+5»+8) (i - m - 1) (i - m)... (i) (j - 1) (j)
(1)(2)... (m + 2) * (1)(2)
*(m^7»t+i8) (i -m - 2) (1 -m - 1) ... (i) (j - 2) (j - 1) (j)
(l)(2)...(m + 3) ' (1)(2)(3)
+ }
* («»+8»»+8) (j-m-l)(j-m)...(j) (i - 1) (i)
~(l)(2)...(m + 2) (1)(2)
4K+s»'+i8) (j-m-2)(j-m-l)...(j) (i - 2) (i - 1) (i)
+ (1)(2). (m + 3) · "(1)(2)(3)
+ .
326. Now looking to the prior result and equating coefficients of like
powers of α we find, after striking out common factors, the identities
(i) ι + ,ЙЙ, «-(i-D(i).(j-D(j) ^(i-2)...(i).(j-2)...(j)
W Α+*(1)3^* (1)2(2)3 + * (l)*(2)*(3)· +"·
. (l)(2).(i + j)
(l)(2)...(i).(l)(2)...(j)'
which is hereafter reached from a consideration of Permutation Functions;
W *+* (m+l)(l)+ib (m+l)(m + 2) · (1) (2)
(i-m-2)(i-m-l)(i-m) (j -2) (j - 1) (j)
+ г (m+l)(m + 2)(m + 3) (1) (2) (3)
+
_(j + m+l)(j+m + 2) ...(j + i)
(m+l)(m + 2)...(i)
derived by comparison of the coefficients of am.
78 THE METHODS OF GAUSS [SECT. VII
Comparison of the coefficients of a~m gives the same formula with the
mere interchange of i and j.
327. In the concluding articles of this chapter it is proposed to give
some of the methods and processes of Gauss in the study of partition series.
They are highly ingenious and no student would find his equipment complete
without them. The notation is to a large extent altered to be in accordance
with that used in this work.
Consider the product of two infinite products
(1 + ax)(1 + ax>)(1 + ож5) ...
and suppose multiplication to produce
R.Q
• ~z Η—
a2 a
Writing ax2 for a has the effect of multiplying the product by
ax 1
1 + ax ax'
hence
(i+«.)(i+^)...(i + l)(i+i)(i+i)(i+g...
= · · · + -π+—.+F + Q^ + в***4 + · · ·
a* or aw-
aix a2x αχ χ χ
the last line but one being derived by writing ax2 for a, and the last line by
multiplication by —.
Comparison gives ... = R = Qx? = Px4 = ...,
and thence the right-hand side
...+-s + ^ + P + Qa + i2a2+...
ай а ^
of the above assumed identity may be written
and it only remains to calculate Ρ which is the term independent of a in the
given product.
СЫ. V] THE METHODS OF GAUSS 79
328. He shews by precisely the same method that if the square of the
last considered product be written
... + ^ + P+Qa + ...,
then
(1 + axni + crtYQ. +aa,*y ... (l +£f (l +£)*(l + ^f ...
+ Q|(e+I)+^(* + i)+^(rf+i)+^(tf+i)+...},
the exponents of χ in the Ρ series being the doubles of the square numbers
and in the Q series the quadruples of the figurate numbers of the third
order.
329. Write
D - xn I-#2n+1 хш l-#2?l+2 l-xn+1
1+0**1 +a*»+;L ι + лл · ι + дл+1 · ι + хп+*
дЯП 1 _ дувИ·» 1 _ дЛ1+1 1 _ ^П+2
+ 1 + л?» ' 1 + #η+1 Ч+#n+2'l+#,г+3"l"''',
У - 1"5Г5»+ i + лл · rqr^n+i+ 1 + ^'1 + ял+1 · Г+ЖП+2 + ···»
ρ = ρ~ρ.
We first of all calculate R by subtracting the terms of Q from those of Ρ
in order. We find
n = 1_ xn (1 - a?n) ^»(l-a»)(l-a?*+1) , .
""l+^ + (l +a»)(l+^H-i)+(1 + ^)(l+an+i)(i+a^+i)+ — - 9(*>л>
But if we find R by adding the first term of P, the difference between the
second term of Ρ and the first of Q, between the third term of Ρ and the
second of Q and so forth, we find
R - ι _ ^2η+1 _ ^+ί(1-^+ι) #*η+* (1 - ^n+1) (1 ~ а,?г+2)
1 + αη+1 (1 + ^+1) (1 + лл+2) "" (1 + α^+i) (1 + χη+*) (1 +"*»+») ~~ "'
= 1-^*+ΐφ(^Η + 1),
or φ (л?, η) = 1 - л*14"1 φ (ж, η + 1),
true when τι is an integer greater than unity; and with this restriction we
are led to the identity
φ {χ, η) = 1 - x2n+1 + χ411** —л*»+» + a*n+M _ # #
80 THE METHODS OF GAUSS [SECT. VII
When η = 0, the last term of Q must be taken into account. Calling it
Q' the second series for R is greater than the first series for R by ty. Thus
ι-*Φ(*,ΐ)-Φ(*,ο) + ρ/,
leading to
φ(χ,0) = 1-χφ{χ,1)-$=\-χ + αϊ·-χ» + χ™-...-$.
Now φ (xy 0) = -£ by putting η = 0 in the first series for R, and from the
series for Q
ff_l (!-*)(!-*)(!-<*)...
v 2(1 + «)(1+^)(1 + ^)...'
Hence
(1-а?)(1-д?)(1-д?)...
= 1 - 2# + 2#4 - 2л9 + 2л;16 - ...,
(1+л?)(1 + ^)(1+л?)-
an important result first obtained from elliptic function theory.
The left-hand side of the identity may be written
(1)^(2)(3)44)(5)M6)...,
so that writing 1 - 2# + 2л4 - 2л9 4- ... -F{x\
we find FQc) F(-x) = [F(x2)\K
330. In a similar manner by considering the two series
1 - x™+* xn(l -а^+4)(1 - xn+*) x2n (1 - я2^6) (1 - #п+3) (1 - #*+*)
Γ-^+ϊ" +"" (1 - χη+1) (Ι -Ί^Τβ)" + (1 - a«+i) (1 - χη+2) (1 - ^*+·)~+ ·"'
а?п(1-а^) ^(l-a^XJ -a>>n+4) я?" (1 - χη+2) (1 - зЯ+4)(1 - a*+«)
1 - #η+1 (1 - λ*»+1) (1 - α?**) + (1 - л^+0 (1 - #η+3) (1 - «»*+»)" +'''
it is shewn that
(1 — ж) (1 — ж3) (1 - л·5)...
and thence by changing the sign of χ
(1-а?)(1-а?«)(1--0«)..,
(Ι+λΧΙ+^ΧΙ+λ·)...
Putting 1 — a? - a? + x6 + &ло — ... = φ (χ),
and as before 1 - 2a? + 2x* - 2x» + ... =F(ai),
it is easy to shew that
ψ (л) φ (- χ) = φ (л?) ί7 (л?4).
= 1 — л? — χ3 + я6 4- χ10 —
CH. V] THE METHODS OF GAUSS 81
331. In the result of Art. 327 if we put a«l, comparison with the
expression that has been obtained for
1 ~2# + 2#4-2#9 + ...
shews that
(l+«)(l + o^(l+a^)...(l + ^(l+^)(l+|)...
_ 1 + (a + a-1) a: + (a2 + ατ*)αή 4- (α3 + or3) я° + ...
~ (1-Λ·2)(1-.^)(1-^β)(1-^)...
If herein we write x* for χ and — χ for a we find
(4) (10) (16)...(2) (8) (14)...
1 - a? - x* + xw + xH - at» - Xй + ...
(6) (12) (18) (24)...
or multiplying up and writing χ for x2 we get
(1)(2)(3)(4) ... = l-x-x* + x5 + x'7-x12-xl5+...,
an interesting way of arriving at this celebrated identity.
If on the other hand we write x* for χ and «f x for a we find
(3) (6) (9) (12) (15) (18)...
1 + χ + a? + Xs + x1 + x12 + xK +... =
(1) (5) (7) (11) (13) (17) (19)...·
332. Following Gauss wc denote the function
—1(1<)(У).:(1)а+- ьу «+^> °r o,+^>
Since (i +j, г + 1) = (г Ч- j - 1, г 4- 1) Ч- л?·7'"*1 (г + j - 1, г),
(г'+j-l, г + 1)=(гЧ.?'-2, t41) + ^(t4i-2,i),
(г + 2, г + 1) = 1 + χ (г + 1, г),
it is easy to shew that
(i+j, i+l)= 1 +я?(г+ 1, г)-Ь я2 (г* + 2, г) + ... + χ^λ(гЧj -1, г).
Now consider the series
η* *=ι 1"a?y+11 д-*од-**+1) а-^-г)(1-^)(1-^+1),
J\*>3) l-w + (l-x)(L-x*) (1-л?)(1-а?)(1-а?») *'
j being of course a positive integer. The series has j 4- 2 terms, the last term
being + 1 according as j is uneven or even.
m. а. и. 6
82 THE METHODS OF GAUSS [SECT. VII
Writing
/(«i#«l-(j + l,l) + (.7 + l,2)-0-+l,3)+...
we have 1 = 1)
-04i,i) —(j,iW,
+ 0 + 1, 2) = + 0*. 2) + a-* (j, 1),
-0 + 1,3) = -0,3)-^0,2),
etc.,
leading to
/(*, j) = (1 - xi) - (1 - *>-) (j, 1) + (1 - ^-2) 0*. 2) - · · ·,
but (1 - of-*) (j, s) = (1 - «0 0 ~ 1. «).
so that f(x, j) = (1 - «9/(«, j - 2).
Now Д*,0)-0, Дя,1) = 1-Ж, Д«,2)=0,
and we find f(x, 1) = 1 — x,
f(x,3) = (l-x)(l-x>),
/(^δ)-(ΐ-*)(ΐ-«·)(ΐ-βθ,
etc.,
and when j is uneven
/(χ,ί) = (1-χ){1-3?)(1-χ*)...(1-χη.
Clearly, when j is even, /(ж, j) = 0,
and it is manifest that the terms destroy one another in pairs.
333. Next consider the series
^ (ΐ-^)(ΐ-Λ·2)(ΐ-Λ·3) "*■"·'
or 1+«*0Ч1, l) + «(j+l,2)+a*(j + l, 3) + ....
Reversing the series, it may be written
F(xJ)^xi^+1)^x^ (j^l>l) + xi^-l)(j + l>2) + x^^^(j + l1S)^....
Multiply this series by x^ ^ + 2) and add it, terra to term, to the first series,
obtaining
=»l+«*(j + l, l) + *0' + l, 2) + ^0'+l,8) + ^(j + l,4) + ...
+ л?*.^+1 + л?.я^0' + 1, l) + «*.a^-1(j + l, 2) + #2.^-2(j + l, 3) + ....
сн. ν]
THE METHODS OF GAUSS
Now by the last article
so that
Moreover
so that
and in general
(j + 1, l)+^+» = (j + 2, 1),
(j +1, 2) + ^(j +1,1) = 04-2,2),
(j + 1,3) + a»-"1 (j + 1, 2) = (j + 2, 3),
etc.,
{1 + x\ (i+2)j ρ (ж> j) = ^(a!> j + χ).
J?>,-1) = 0,
^(ж, 0) = 1+^,
.Ffo 1)=(1+я*)(1 + я),
^ (a;, 2) = (1 + ж*) (1 + x) (1 + a#),
83
F(x,j) = (1 +я*)(1 + ж)(1 + al)... (1 + аЭ'+*).
Writing a? for χ we have
1 | a.(2J + 2) , ^(2J)(2J + 2) , ^(2j-2)(2j)(2j + 2)
1+* (2Γ +Я" (2) (4) +^ (2) (4) (6) +
= (1 + x) (1 + a*)(l +a?)... (1 +Ж-Н-1).
CHAPTER VI
CONNEXION OF THE THEORY OP PARTITIONS WITH OTHER
COMBINATORY THEORIES
334. It has been shewn that the partitions of unipartite numbers into
parts limited as to magnitude by ρ and as to number by q can be graphically
represented by nodes or units placed in the cells of a rectangular lattice
formed by cutting ρ +1 vertical lines by q +1 horizontal lines.
d ___ в
+
+
+
1 ь
+
+
о
+
с
+
+
-
о
о
о
+
О
О
о
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О
о
о
о
о
А
As a particular and representative case take ρ = 7, q = 6 and construct
the lattice. On it depict by crosses the unipartite partition 32211 of the
number 9. If the unoccupied cells be filled by noughts we obtain a
complementary partition 766554 of the number 33, where
9 + 33 = 42 = 7x6 =pq.
Now separate these two partitions by the path marked in black.
The whole lattice denotes, by Sect. IV, Ch. H, the graph of the bipartite
number pq and the blackened path is a line of route through it. This line of
SECT. VII, СЯ. Vl] CONNEXION WITH COMPOSITIONS
85
route denotes a principal composition of the bipartite pq and also by Sect. IV,
Ch. I, it is the zig-zag graph of a composition of the unipartite number
p + q + 1.
The line of route also denotes a permutation of the letters
335. It follows that partitions of unipartite numbers are closely
connected with
(i) the compositions of bipartite numbers;
(ii) the compositions of unipartite numbers;
(iii) permutations involving two different letters.
In the above diagram we have
(i) the composition (θϊ Ϊ2 Ϊ2 Π 4θ) of the bipartite Тб,
(ii) the composition 23321111 of the unipartite 14,
(iii) the permutation βχββαββαβαααα of α7/3β.
The compositions of the bipartite number pq which are under examination
are those in which consecutive figures of successive biparts are both greater
than zero. There is one such defined by each line of route and they are
called principal compositions. Their enumeration therefore coincides with
that of the lines of route.
To each unipartite partition which has no part greater than ρ and not
more than q parts corresponds a line of route. It has been shewn in Sect. IV,
Ch. II, that the number of lines of route through the lattice is
ΓΛ
Ρ
Hence the correspondence gives the theorem:
" The number of partitions, of all numbers, into parts limited in magnitude
to ρ and in number to q is
This number is also by Euler's intuitive theory given by the coefficient
of aqaPq or of {aaP)q in the expansion of
1
(1 _ a) (1 - x) (1 - ax) (1 - aa?) .'.'. (1 - aa?)'
Hence that portion of this expansion which involves powers of axp is
or (1 - ae*)-*-».
86
DERIVED THEOREMS
[SECT. VII
The number of different parts in the unipartite partition (denoted by-
crosses) is equal to the number of left-bends J in the line of route, and the
number of lines of route which possess s left-bends (or $ right-bends ~~|) has
been shewn in Sect. IV, Ch. II, Art. 145, to be
ш·
Hence the theorem is:
" The number of partitions of all numbers into $ different parts limited in
magnitude to ρ and in number to q is
This number is the coefficient of μ8ΌΡβ^ in the product
(α + μβ)Ρ(ζ+β)<1,
and therefore also by the Master Theorem of Sec. Ill, Ch. n in the
expansion of
1-α-/3 + (1-μ)α/3'
which may be written
^ <*& ,
* (1-α)Η-ΐ(ΐ_ βγ+ιμ'
Hence the function
ο?β8
(1_α)*+1(1 _£)*+!
enumerates the lines of route, which possess s left-bends or s right-bends,
*n all bipartite reticulations. When the lattice is of the bipartite pq we
merely seek the coefficient of α?β«.
It also enumerates all unipartite partitions into s different parts limited
in any desired manner in number and magnitude.
336. If we form the product
('♦£-.№+£>)-('♦£..)'
we find that the general term in the development is
bx^.hx2c\...bxV(T»,
σ1} σ2,... σρ having any integer values from 0 to oo. If s of these
magnitudes be greater than zero this is equal to
and consequently the coefficient of b8xn in the product denotes the number of
ways of partitioning η into parts limited in magnitude to ρ and of exactly $
different magnitudes, the number of parts being otherwise unrestricted.
CH. VI] DERIVED THEOREMS 87
If we modify the product in the manner
/, abx \ /, abx2 \ /, abac* \
and take the coefficient of аЯЪ9хпу the partitions possess the further property
that the total number of parts is exactly q. If we add the additional factor
- the partitions enumerated by the coefficient of аЯЪ*хп possess the
property that the total number of parts is q or fewer.
Again if we also multiply the product by the factor - , the coefficient
JL — X
of aqb8xn enumerates the partitions of all numbers equal to or less than n9
where the part magnitude is restricted so as not to exceed p, exactly $ of
the parts are different and the total number of parts is q or less. Hence the
partitions of all unipartite numbers into exactly s different parts, limited in
magnitude to ρ and in number to q, are enumerated by the coefficient of
a*b8xpv
in the development of the product
abx \ л abx2 λ Λ abxv
1-х' 1 —α
1 + l-ax) VI- aW '" \ 1 - a*) '
This may be regarded as the intuitive solution of the problem after
Euler.
This coefficient is equal to that of {axvy in
(1 _ x) (i _ a) (1 - uaT1) (1 - ax4) ... (1 - ааГ<)
where klf Ly ... Z?.s. are any s different numbers drawn from the series
1, 2, Ζ,.,.ρ,
and the summation is in respect of all such selections.
Inasmuch as we know from the reticulation theory that the coefficient is
equal to
ш·
we find that the effective portion of the above generating function is
00<·->·+(ϊ)(*ί1)<-^"+-·άΜ
\$J (1 - ax?)8+1
88
THEOREMS DERIVED FROM
[SECT. VII
Here we have regarded ρ and s as constant and q as variable; but if we
take ρ and q to be constant and $ variable we know that the coefficient of
{ace*)* in the product
1 / dbx \f abx2 \ / aba? \
(1 -a?)(l -a) V + 1 -ax) { 1 - ax*) '" { 1 - aW
Ш+©е>+"+©(Р*
A line of route with $ left-bends has either $— 1, s or $ + 1 right-bends.
If it commences by tracing an α-segment and ends by tracing a /3-segment
the number is s — 1. If it commences by tracing an α-segment and ends by
tracing an α-segment or if it commences and ends by tracing ^-segments the
number is s. If a β-segment begins and an α-segment ends the line of route
the number is $ -h 1.
To obtain the correspondence with partitions we remark that if an
α-segment begins the line, the partition (marked with crosses) has exactly
q parts; if an α-segment ends, the highest part is less than ρ; if a /3-segment
begins, the number of parts is less than q; if a /3-segment ends, the highest
part is equal to p. It can moreover be readily shewn by the method pursued
in Sect. IV, Ch. II, Art. 144, that the enumeration of the lines of route
possessing $ left-bends and $ — 1, $, 5 + 1 right-bends respectively is given by the
numbers
6:ϊ)0*:ί)·
the sum of these numbers being of course rj Ρ ].
337. Hence the following theorems :
" The number of partitions of all numbers which have exactly q parts,
a highest part equal to ρ and s different parts, is
j - 1 )\s - 1) *
" The number of partitions of all numbers which have exactly q parts,
a highest part less than_p and s different parts, or which have less than q parts,
a highest part equal to ρ and s different parts, is
r.X-lW-W;1
CH. VI] THE LINE OF ROUTE 89
" The number of partitions of all numbers which have less than q parts,
a highest part less than p, and s different parts, is
ГЛГЛ
Ex. gr. If ρ = q = 3, s = 2, the partitions enumerated by these three
theorems are
(311), (331), (322), (332);
(31), (211), (32), (221);
(21);
respectively.
It is clear that identical relations between binomial coefficients yield
results in the theory of partitions.
Thus the relations
admit of immediate interpretation.
By Euler's intuitive theory the enumerations in the three cases are
given by
(i) the coefficient of a*-1^-1^-^ in
1 -χ γ + ι -αχ] Iх + ϊ -ααή - \ι + ι -αβΗ" \ + 1 -αχ») '
(ii) the coefficient of a^b8x^"1)q in
ί- «( +l-4l !" α^ '""fl- α^1] '
plus the coefficient of αΡ^Ι^ω*®"1* in
1_ f aba? ) J aba? ) L o*?^1 I fi ^
(1-я?)(1-"а) Г + 1-ал?[ ( l-o^J '" \ 1-ах^]\ + 1 - ax?
(iii) the coefficient of afl-tyx (р-1) ίί"""1) in
(1
1 ( аЬ* | [ _oftg Ϊ L abx^ ]
- a?)(l - а) Г + 1 - ад?! Г + 1 - o^J "'" Г + 1 - ая^1] *
338. When the line of route is regarded as the zig-zag graph of a
composition of the unipartite number ρ 4- q -Ы, it is convenient to rotate
the figure clockwise through a right angle. The reading of the graph then
shews ρ +1 parts, no part being greater than q + 1.
90 COMPOSITIONS OF UNIPARTITE NUMBERS [SECT. VII, CH. VI
The number of the compositions so defined we know by the
correspondence
This is verified because the number is given by the
Coefficient of ^+«+1 in {% + я2 4- ... + ^+1)^+1,
or of afl in (1 - %)-p-\
and this is (P + q).
In order from a composition of the unipartite to proceed to the uni-
partite partition, we write down the composition, say,
2 3 3 2 1111 as in the diagram,
2 2 ]
1 2 3
and form a second row by subtracting unity from every part except the first,
and then a third row of the natural numbers in order underneath the
numbers in the second row; then the partition is formed by taking a
number in the third row, repeated a number of times shewn by the number
in the second row immediately above it; thus in the above case the
partition is
31 2212.
Generally if the composition be ττχ тг2... тгр+1 we form the scheme
77*! 7Г2 7Гз 7Г4 ... 7Γρ—ι 7Γρ Tfp+l
7Г2 — 1 7Г3 — 1 7Г4 — 1 ... 7Гр—ι .— 1 ТТр — 1 ТГр^ — 1
1 2 3 ... р-2 р-1 ρ
and the corresponding partition is
рЯуи-i ю —1**""* г) — 21Гр_1~1 .. зт4-1 21Гз~'1 1х2""1
Omitting the first part of the composition, if of the remainder there be
s parts greater than unity, the partition will have s different parts. The
total number of parts is Σ·7τ — irl — ρ or q 4- 1 - тгг.
SECTION VIII
A NEW BASIS OF THE THEORY OF PARTITIONS.
PARTITION ANALYSIS IN SEVEN CHAPTERS
CHAPTER I
THE METHOD OF DIOPHANTINE INEQUALITIES
339. In this Section we no longer rest upon the intuitive observation of
Euler, but penetrate deeper into the Theory of Partitions.
A partition of a number may be regarded as any collection of positive
integers whose sum is equal to the number. There is no specification of
order amongst the numbers which are the parts of the partition, and that
being so, we may import into the definition any particular order or
arrangement that is convenient. There are only two arrangements that are
universally applicable. We may in all cases arrange the parts either in
descending or in ascending order of numerical magnitude. We choose the
former of these and make a new definition of a partition of a number, viz.:
" A partition of a number is any collection of positive integers arranged
in descending order of magnitude whose sum is equal to the number."
The problem now is to find successions of numbers in descending order
of magnitude where the numbers enjoy some other property which may be
that their sum is to be equal to a given number. This is, in fact, the
question immediately before us, but it is clearly not the only one that may
present itself.
Consider i numbers in descending order of magnitude
alta»t α:ι?.·.α/.
The order is defined by the Diophantine relations
αϊ ^ α2,
a2 > «3,
Οί_! ^ 0Lit
92 EXPLANATION OF THE OPERATIVE SYMBOL [SECT. VIII
and subject to them we consider the sum
V rai + <*2+a3 + · · · + ai
Now observe that the algebraic fraction
1
(i-M(i-£.)(i-*.)...(i-£.)'
when expanded in ascending powers of x, has the general term
or A^l ~ «2 ^a2 ~ α3 φ φ Χ?ί-1 ~ αίX** #ai + «2 + a3+ ··· + аг
and that if the Diophantine relations are to be satisfied this must be free
from negative powers of Xb λ2, λ3, —
It is thus evident that we have only to expand the fraction
1
<l-»*)(l-£.)(l-£.)...(l-£.)'
reject all the terms involving negative powers of λ^ λ2, Хз, ..., and
subsequently put
Aj = Aq = A3 = ... = A$ = 1
to obtain the desired sum
V „,al + a2 + а3 + · · · + аг
The performance of these operations upon the fraction we shall denote by
prefixing the symbol ίϊ, so that
»<i-»*>(i-£.)(i-£.)...(i-£.)
It will be noted that \ is retained although it may be immediately put
equal to unity.
In regard to the operation of Ω we have the easily established result
>
> (1 - λ, A^) (l - ^) ^ - A^ & ~ ^A^^j'
leading to fl«
> (1 - \A^) (l - ^*A (l - £«*)
(1 - Λ^ΧΙ - A1A2x^+^-) (1 - АгА2Агх^+^+^)'
CH. I] STEPPING BACK PROM EULER'S FUNCTION 93
and to the similar general result involving any number of denominator
factors.
In reaching this it will be observed that the auxiliaries λ are successively
eliminated.
We thus find that
У./Л + α2 + a3 + · · · + ai
~(l-#)(l~^)(l-<)...(l--#ί),
the generating function which with Euler was intuitive. The investigation
above shews how the Theory of Partitions may be enlarged because we may
vary the Diophantine relations, and also the linear function of the parts
which above was taken to be the simple sura.
340. It has been shewn that we can step back from the generating
function of Euler
1
(l)<2)<3)...(i)
to the crude generating function
1
ft.
M-*..)(i-£.)(i-£.)...(i_£.)·
and it will become evident that we can step back further still to a more
crude generating function. This arises from the circumstance that
δ· Χ l
><,-,m>(i-*)(i-*)...(i-£) (1-*>"
because Ω
>(,-„*)(,-&)
й х '
>0-л.>(1- £)(>- S)
(1-я)2(1-ум?У
and so on by successive elimination of μΐ9 μ2, ... .
With two sets of auxiliaries we have therefore for the sum
λ μ Ί
an .
> > (ί -λ^*) (ι - Jf-2) (ι - ¥±£) (i - x^)... (ι - ^ht*\
μ
Eliminating μχ> μ2,... μι bv the operation of il this becomes
>
λ 1
Vv.)(,-b.)(,_£.)... (!_£.)■
the function already considered.
94 INTERPRETATION OF CRUDE GENERATING FUNCTIONS [SECT. VIII
To interpret the ultra-crude generating function above we form the
general term
which is
^αχ -2θ2 4- α3^«2 - 2α3 + α4^α3 ~2α4 + α5 \*ί-2 ~ 2αι-ι + αΐ\?ΐ-ι " ^4-χ^ί „αι ~ α2„α2 ~ α3 φ.
a^j-a^ α^ αχ
and since the exponents must be non-negative we have the Diophantine
relations
«1 + «3 > %<*2 \
a.2 + a4^ 2a3 [
I
cti-2 + <*·%> 2а^г
сц-i ^ 2o^
in connexion with the sum %хак
If then aly a2, ... cti be any г integers, which satisfy the above set of
relations, 2#as the sum being in respect of each set of integers, is equal to
1
(l)(2)(3)...(i)·
This shews that the number of ways of choosing the integers, the number
ax being fixed, is equal to the number of partitions of ax into г or fewer parts.
Ex. gr. take <хг = 4, г = 4, the sets of integers are
«ι α, σΆ α4
4
4
4
4
4
0
1
2
2
3
0
0
0
1
2
0
0
0
0
1
in each of which the Diophantine relations are satisfied. They are five in
number, because the number four has five partitions into four or fewer parts.
In fact, to make the one-to-one correspondence between the sets and the
partitions of four we have merely to take the numbers
In general we may bake a set of integers enumerated by the ultra-crude
form to be
A + &+...+A, & + A+...+&, &+...+&,...£*.! + &, ft,
CH. I] EXAMPLES OF CRUDE FORMS 95
which plainly satisfies the Diophantine relations, and then the corresponding
partition of ax is
βι> Aj> β3>··Ά·
341. As another example the generating function
1
of the partitions composed of uneven parts not exceeding 2i — 1 in magnitude
may be exhibited in the crude form
XI
►<i-M)(i-£,)(i-£.,)...(i-£,)'
which is equal to the sum
^ αϊ + 2<X2 + 2<x3+... + 2α$
subject to the Diophantine conditions
«i > a2 ^ «з^ ··· > «г-ι ^ a*.
Ex. gr. for i = 3, «i + 2a2 + 2a3 = 6, it enumerates the partitions
22, 211, 41, 6,
equi-numerous with the partitions of 6 into uneven parts.
We further proceed to the ultra-crude form
λ μ
пи.
since the elimination of the auxiliaries μ leads to the crude form.
This is the sum 2a?ttl + ea,
for sets of integers au ct2, a,,... ai}
which are subject to the Diophantine relations
*i 4- *, > 2*2
er3 + α4 ^ 2a3
<*г-2 + «г > 20Гг_!
«{-ι ^ 2аг·
αϊ > «2 ^ «з > ··· >«i-i ^ «{·
The number of such sets of integers for which аг + cx2 has a given value
is equal to the number of partitions of <χΎ + a2 into uneven parts, no part
exceeding 2г — 1 in magnitude.
96 EXAMPLES OF CRUDE FORMS [SECT. VIII
Similarly the function
(1 - x) (1 - xs) (1 - a?u)... (l - я*-<)
has the crude form
λ 1
Ω-
>(1->.-)(ΐ-^)(ΐ-^)...(ΐ-^)'
which denotes the sum
subject to the conditions
and the ultra-crude form
λ μ 1
?Vw>(i-^«0(i-^)(i-*£)...(i-5^)'
which denotes the sum 2#*ι+**2
for sets of integers al} a2) a3, ... аг·,
which obey the conditions
«! -h а3 ^ 2*2,
ff2 + a4^ 2«3>
аг-_2-Ьаг^2аг-.1,
аг·-! ^ 2аг·,
The number of such sets of integers for which аг + 4а2 has a given value
is equal to the number of partitions of аг 4- 4a2 into parts of the form 5m + l,
no part exceeding 5г — 4 in magnitude.
In general we find the crude form of the sum
where θ1} θ2, ... #$ are positive or negative integers, subject to the Diophantine
relation
σ^ 4- σ2α2 4- ... 4- <τ%&% ^ 0,
where σΎ} σ2, ... σι are positive or negative integers, to be
n I
^ (1 -Л^лЛ) (l-\*»a*) ... (1 - Xf<^<)'
If we have an additional Diophantine condition
tj «! + T2or2 + ... + τ< α< > 0,
CH. I] PASSAGE TO EEAL GENERATING FUNCTIONS 97
we intercalate another auxiliary λ2, making the function
1
Λ:
> (1 - XfiXia*)(I - λ**λ^) ... (1 - λ^λ^*) '
and so forth, a new auxiliary appearing for each additional Diophantine
relation.
342. The generating functions which have been considered above
enumerate the partitions specified. They are enumerating generating
functions. We can form real generating functions which put in evidence
the partitions enumerated in the following manner.
The general term in the expansion of the fraction
1
<ι-»Λ>(ι-**.)(ι-**.)...(ι-£*~)(ι-£*)
^■*£*·Γ£*·Γ···(&*»Γ(ά*Γ·
is
or x?1 - α2λ2α2 -аз... xtii1 - ^χρχρχ?... 2гйда.
If the numbers al9 a2) ... o^ are subject to the Diophantine relations
«i ^ Oa > «3 > ··· > «i-i > «г,
it is clear that the product
x?x?x?...x?
indicates a partition (а^а^... а$) of the number αΎ 4- а2 + <Ч + · · · 4· α*, and
гх?х?х?...х?
can be represented in the crude form
λ 1
?(1-«(1-^-)(1-^')-(1-&л'-)(1-хЬл)'
which by a previous Article has the expression
1
(1 - Xx) (1 - XA) (1 - J^Z,*,)... (1 - ХгХ*Х%... Z<)'
We observe herein that
Xti"a*(XlX2)aa"as(XlX2X9)^"ai... (XjX* ...Xi-y-i-'i&X,... Xi)ai
= X?X?X?...Xt\
and that the denominator factors establish that the partitions under
consideration are uniquely composable by means of the partitions
1, 11, 111, .,.111...г units.
M. A. II. 7
98 PAETS LIMITED IN MAGNITUDE [SECT. VIII
Ex. gr. To obtain the partition
a^ocs... aiy
we take 1, αλ — a^ times; 11, a2 — a3 times, and so on.
We have thus the algebraic indication of the Ferrers' graphical
representation of a partition in which the nodes are replaced by units, and we
further learn that the partitions 1,11, 111,... are the fundamental or ground
partitions from which all others of the nature considered may be derived by
addition.
These remarks may appear, in the present instance, to be of a trivial
character, but they involve an idea which will be found to be of great
importance as the theory advances.
We can also proceed to an ultra-crude form
\ μ. ι
the first of an infinite series of ultra-crude forms. The next one is
λ μ ν l
and succeeding ones are written down without difficulty.
Each one is interpretable in terms of Diophantine inequalities by
constructing the general term.
343. We pass on to the consideration of the partition of numbers into
parts limited not to exceed j in magnitude.
It is merely necessary to restrict the highest part and we are led to the
crude enumerating function
a ι - (λ^ν+1
►α-»..>(ι-*.)...(ι-£)'
the partitions possessing at most i parts.
Instead of at once evaluating this expression we notice the identity
ι j%" , ι - (λ^ν*1
(1 - g) (1 - g\x) уГ0 9 1 - \x '
and observe that the crude function is equal to the coefficient of gi in
о i
·α-#-Μ(ι-^)(ι-^)...(ι-^'
1
orm (l-g)\i-g*)(i -sO ...(i -~g£y
the well-known intuitive result of Euler.
сн. ι] a generalization 99
We apply the same method to reach results which are generalizations of
the foregoing.
Let us restrict the magnitudes of the successive parts, written in
descending order, by the numbers
We are led to the crude enumerating function
/-<^Ч-й'Н-4-£Г
? (1-Х,-) (l-£.) -. {!-£) '
which we notice is the coefficient of
in the function
> (1 -<*)(! -Л) - (1 ~9i)a Si\«) (l -*£*) - (l ~^хУ '
and this function is
1
(l-0i)(l-#a)...(l-#)(l-^
We have therefore to expand this function and take the coefficient of
9\ xffi2 · · · ΰΐi- There are two remarks to be made here.
344. Firstly the function lends itself to intuitive interpretation after
Euler. For clearly the factor g-J* of g^gij2... g{1 points out that parts not
less than $ in magnitude occur in the partitions j8 or fewer times. This is
seen at once by merely looking at the denominator factors which involve g8.
Hence by the intuitive interpretation the partitions enumerated are those
in which the part magnitude in the whole partition is restricted not to
exceed i and parts not less than s in magnitude occur js or fewer times, where
$ has any of the values 1, 2, 3, ... i.
The same function also enumerates, by this investigation, partitions into
i or fewer parts, any part s occurring at most js times, where s has any of the
values· 1, 2, 3, ... i.
We have thus a theorem of reciprocity the generalization of that in
regard to partitions restricted as to part magnitude and as to number of
parts.
The reader will notice that this generalized reciprocity is made evident
by the graph of a partition. It simply depends upon the circumstance that
the graph may be read either by rows or by columns.
7—2
100 SPECIAL CASE OF THE TWO HIGHEST PARTS [SECT. VIII
Secondly the function, in the form to which it has been brought, is still
crude because the numbers^, j2} ...# are necessarily in descending order and
we require therefore only those products of powers of glf g2i ... gi which arise
in the expansion for which this descending order is in evidence.
Taking a new set of auxiliaries vl9 v2, ... v^i the true generating function
may be written
Ω 7 r г-1 ·
> (1 -Mi) (l -^flr.) ... (l -^(1-Mi«)(l-Mift^)..-.(1-M«···^^
Eliminating νΎ we find
and we can continue to eliminate v2, ν$, ... in succession. By doing this,
however, we rapidly arrive at very complicated expressions. We can,
however, eliminate vz now without difficulty. The function becomes
(l - Уг&дъх) [l - ^ g^gig^j
V^<l-^4l-©(l->)(l-^)...(l-;g;)
x (1 - gxx) (1 - рфдлх) (1 - v2gxg2&) (1 - дгд2д^)
(1 - vtgxg2gzg±x%) (1 - v^gxg2gzg^x)
and z/6, v7, ... can be eliminated without trouble.
The even suffixed auxiliaries however introduce complexity.
345. The case in which the two highest parts are the only ones restricted
is worth a moment's attention.
The true generating function is then
i-gig*x
(1 - 9i) (1 - 9ιχ) (1 - 0ιΛ) (l - ΰιΰ*00) С1 - 9Ф&) . -. (1 - д&а?)'
The coefficient of g{xgb in the part
1
(i -gig*) (i - 9ιθ*χ) ..·(!- 9ig*rf)'
(i + l)(i + 2)...(i + j2)
(1) (2)...(j2)
and thence the coefficient of the product gtgt in the whole fraction is
(i+l)(i + 2)...(i+JJ(J,-J. + l) r(l+l)(H-2)...(l+J>>l)(J1-JJ
(I)2 (2)... (« (1)42).. (J,- 1)
-fi+1)(i)t^;;;^J,"1)№+3J«'-j»+i)-«(Ma-jjb
IS
CH. I] THE XI OPERATIONS 101
a function which reduces when j2—ji =j to the well-known enumerator
(i+l)(i + 2)...(i + j)
(l)(2).(j)
346. The function which enumerates the number of ways of partitioning
a number into j or fewer uneven parts, no part being greater than 2i — 1, is
by intuition
1
{l-g){l-gx){\-ga?)...(l-gx*-y
in which we have to seek the coefficient of gK
This function is
il ί
►0-й(1-М(>-^)(1-^)...(1-а'
and herein the coefficient of gi is
»<ι-Μ,(ι-^)(ι-^)...(ι-£)-
This denotes the sum
5* αϊ + 2tt2 + 2a3 + ... + 2<ц
subject to the Diophantine relations
This summation, in consequence, depends upon partitions into uneven
parts limited both in number and magnitude.
The Ώ operations.
347. The operations that are of chief use in connexion with the
Diophantine equalities and inequalities which present themselves in many of the
ensuing chapters of this book are il, XI, XI; but to these wo may add as
> = >
occasion arises Ώ, XI, XI.
< < $
The operation XI has been already defined as cancelling all terms of
>
expansions which involve negative powers of certain auxiliary quantities and
in the remaining terms, which involve positive or zero powers of such
quantities, putting each of the quantities equal to unity.
The operation XI retains only terms which involve zero powers of such
quantities.
The operation XI retains only positive powers and then puts each quantity
>
equal to unity and so forth.
A short study of these operations is essential.
102
FORMULA
[SECT. VIII
The operation Ώ.
>
In connexion with the inequality
we have already found that the sum
1 1
depends upon il
>(ι_λ*)(ι_£) (ΐ-·)(ΐ-«*)'
348. We may add conveniently the easily verifiable results
>(1_хж)(1_|)(1_£) <ι—)(ΐ-«*)<ι-~>·
a I \^уа
>(i-x,)(i-xy)(i-|) a—)(i-y)d-«)(i-y)'
n 1 - 1
(i-x*)(i-g)
1
Ω * ί+Ж
ii
1 + xyz — а? у ζ — Λ'ί/2£
>(ΐ-λ.)(ΐ-^)(ι-§) 0-)(i-y)(i-^)d-^)'
η
>a-x.)(i-g) α—>α—■*>·
1 - w"-1
0 1 1 + #?/ + л?-2г + xyz
>
(1_χ.β)(ι-|)(ι-ί) α—)(1-чГ)(1-«V
~ 1 \+xz — xyz — xyz2
><i-v.)(i_xy)(i-£) d—Xi-yXi-yXi—O·
CH. I] SOME USEFUL PRINCIPLES 103
Ω 1
>α-λ*)(ΐ-λ0)(ΐ-λ*)(ι-ΐ?)
__ 1 — xyw — xzw — yzw H- xyzw 4- xyzvP
~ (1 — x) (1 — y) (1 — #) (1 — xw) (Ϊ — yw)(l — zw) '
?(i-x«)(i-xy)(i-i)(i-f)
_ 1 — xyz — #yw — xyzw -f xy2zw + a? yzw
~ (1 - a) (1 - 2/) (1 - a?*) (1 - aw) (1 - y*) (1 - yw)'
349. A very useful principle is that of adding an inequality which is
ά fortiori true. Thus considering the inequality
«ι > 2θ2,
which leads to il ,
»a-»-)(i-i)
we may add the inequality ατ ^ a2,
which is ά fortiori true if the former be true, and thence we are led to
о 1 .
><1-^>(1-jfc)
Eliminating μ this is
. ?c-4-f)'
and now eliminating λ this is
1
<l-«0(l-aty)'
obtained by two applications of the simplest theorem of the subject.
Similarly any number of inequalities which are ά fortiori true may be
added with the object of reducing the problem to one of greater simplicity.
Other useful principles present themselves as the subject advances.
350. Every Diophantine inequality is expressible as a Diophantine
equality. For it is clear that
is equivalent to Лаг + Ba2 = Ca3 ■+- a4,
it being postulated that a1} c^, a8, a4 are positive integers or zero.
Moreover every Diophantine equality is expressible in the form of two
simultaneous Diophantine inequalities. For
Ааг -+- Ba2 = Colz -f Dct4
104 EQUALITIES AND INEQUALITIES [SECT. VIII
is clearly equivalent to the pair of inequalities
Λαλ -hBot^ Ca3 + Da4>
Cas + Da^A^ + Baz.
Thus X^xpxp for the inequality
is il - ,
and %%*1Х$*я%*яр for the equality
Аъ + Въ^Сссз + ъ
1
is . Ω
(1-λ^)(1-λ^)(ΐ-§.)(ΐ-ξ)'
which is the same as the former with the additional factor in each term
gyd&i+Itau—Ca3
Also il ·
(ΐ-λ^κι-λ^ι-^ι-^)
= Ω·
351. In general, if the operand be F(\), it is easily seen that
> > νλ/
Q.F(\) = Q.f(\\,
< > \Л7
F(l) = ilF(\) + D, F(\) - il F(\),
> <
and thence il F(\) = Π F(\) + Ω ί7 (~) - .F(t),
a result of much service.
Also ilF(X) = ilF(^Y
il F(\) = il F(K)-a F(X) = F(l) -QF(l),
> > > \λ/
Ω^(λ) = ί1^(λ).
CH. I] FOEMULS 105
Making use of these theorems we obtain, the formulae
1 1
Ω-
(i-x*)(i-Q
Ω
У\ У-иву'
1
(1-лж)(1-|)(1-£) a-4f)(i-«)·
1 1
ω
(»-M(i-J) '-^'
1 н-яу*
-(l-X^-i^l-.*) (1-ЧГ)(1--0·
Ω
(1-λ·)(1-λ*)(1-λ,)(ΐ-ϊ) (1-^)(1-^)(1-^)'
0 1 1 — xyzw
-(ΐτλ*)(ΐ-λ^)(ι-ί)(ι-ξ)~(1-β»><1—ιβ>(1-»,)(1-^>"
352. Also in connexion with ^ + a2 > а.л
1
Σίβαι2/α,^α3 = ί1
> (l-7u)(l-Xy)(l-i)
= Ω·
1
λ
363. Ω
>(l_jUB)(l_Xy)(l_0
_ x + y — xy — xyz
{l-x){\-y){l-xz){\-yzy
1 ж
>(ΐ-λ^)(ι-|)(ι-?) (i-*)(i-*y)(i-«*)·
Ω
>
1 л· (1 — 2/*)
^i-x^i-lp1-^1-^1-^)'
О 1 х(1 Л-у + z + xyz)
106 FORMULiE [SECT. VIII
354. To these results may be added
il
1_
X8 of
>(1_x.)(i_g a—)d--y)·
>(1_^)(l_Q"(1-^)(1-2/)(l-^)'
corresponding to ax ^ or2 + 5,
«i + 5 > or2,
respectively.
CHAPTER II
A SYZYGETIC THEORY
355. The simple theory of unipartite partitions has been made to depend
upon $ Diophantine inequalities
s being an arbitrary integer.
We enlarge the theory by making the integers al9 o^, Og,... depend upon
a number of inequalities
Афа1 + АРал + ...+АЫа9>о,
Афъ + Αψα, + ...+ Αφα, > О,
which involve at most rs numerical magnitudes A> each of which may be
positive, zero, or negative; but in each inequality it is clear that one at
least must be positive.
For all sets of numbers α1} α2> ··· a$ which satisfy the inequalities we seek
the sum
By a theorem of Hubert it appears that there is in every case a finite
number of ground or fundamental solutions of the inequalities, viz.:
φ 4!) <4υ ...α?»,
αψ «<?> αψ ...α<2>,
a{m) a(m) e4m)...aim),
such that every solution alt c^, a3,... <x8
is of the form
«i = erf* + св?> + ... + ста(Г>,
a* = Ci41, + C242,+ ...H-Cmaiw,>
Си ^2, c3, ...cw being positive integers.
108 EXPLANATION OF "A SYZYGETIC THEORY" [SECT. VIII
This arises from the circumstance that every term
of the summation is found to be expressible as a product
{xfxfxf...xfb
x{xfxfxf...xfY>
X
х\Х? Χ? Χ? ...if* / m.
Denoting this product by
the sum (or generating function of solutions) takes the form
i-{QP + QP + W + .■■} + №»+W+W + ...}-№) + Qg» + Qg> + ...} + ...
and we have what is termed a syzygetic theory.
When a number of algebraic expressions which involve the same numerical
magnitudes are not linearly independent, but are connected by a linear
relation, they are said (borrowing a word from Astronomy) to be in syzygy.
In the above sum the expressions
■* 11 Ρ2) -*3j · · · *m
are all different, but it might happen that
This would be termed a syzygy, and clearly the sum we are seeking
cannot have the form
1
(l-P1)(l-l\)(l-Ps)...(l~Pmy
for this would sum the term (or expression) РгРц twice over. The syzygy
before us shews that 1 — РгР9 must be a portion of the numerator of the
sum, so that the term ΡλΡζ may be only accounted for once in the sum. The
syzygy is called further a first syzygy. There may be more than one, and
they account for the numerator terms
— «I11 —Q?1 —Q^ —....
Moreover, these first syzygies may themselves not be independent.
Writing a first (or simple) syzygy
as 8X = 0,
CH. II] FUNDAMENTAL SOLUTIONS AND SYZYGIES 109
and other simple syzygies
&«0, £3 = 0,...,
it may happen that P\S1 = P2'S2,
where P/, P2' are any products of the members of the set P1} P2,... Pm.
This is termed a second syzygy, and necessitates a term
+ Р/ЛР»
in the numerator of the generating function; if we did not get this the term
Р^РгРг would be omitted from the summation.
In the same manner we may have third, fourth, etc., syzygies. It follows
that when the sum is presented in the form
i-[W + W + ...} + № + <№+■·.}-№+<№ + · ·.} + ■■■
(ΐ-ροσ-ΛΗΐ-ι^.-.α-Λ»)
Рь Р2,... Pm denote the m ground or fundamental solutions,
Q{i\ Q¥\... „ first syzygies,
Qi\ Q{i\... y> second syzygies,
QP> QS\... „ third syzygies,
and we have what is termed a complete syzygetic theory of the solution of
the proposed Diophantine inequalities.
356. Some examples will now be given of simple syzygetic theories.
Consider the system of inequalities
«1 >«2,
«! > «3.
We find
1
tx*lx?xlz=&
>(i-V^)(i-^.)(i-^,J
= Ω
>(1-μΧ1)(1^μΧ1Χ2)(ΐ^^Χ3)
which for the inequality <χλ + α2 ^ as denotes the sum
= {\-xl)(i-xlx^{\l-xX)(i-xxx,xy
a result which shews that there are four fundamental solutions, viz.
«i = 1, «2 = 0, o3 = 0,
«i = l, «2=1, «* = 0,
«1 = 1, «2 = 0, «8=1,
«χ = 1, «2=1, «3=1·
110 EXAMPLES [SECT. VIII
The numerator term — X\X2XZ indicates the single first syzygy
JLi. Jii-Л.2-Л-3 — JLjJiz, л^з12 О.
In fact the solution «1 = 2, 02 = 1, а3=1,
can be formed either by adding the first and fourth or the second and third
fundamental solutions.
The general solution may be written
ax = Ci + c2H-o34-C4,
a2 = c2 + c4,
a* = c3 + c4,
ία, c2, Сз, с4 being arbitrary positive integers.
The enumerating generating function is, by putting Xx = Z2 = Z3 = %}
l + cc2 (4)
(1-ш)(1-л?)(1-^)-(1)(2)МЗ)·
357. Next consider the system
Using three auxiliaries λ, μ, ν we find
1
%χ*ιχ?χΐζχ?=ςι
>(ι4ι1)(ΐ.νΐ2)(ι^ΐ3)(ι^ι4)'
We may eliminate λ, μ, ν in any order we please, and consideration will
in most cases indicate the best order to select. In the present instance the
order makes little difference. Eliminating λ we find
Ω ! Γ-,
> (1 - μΧ,Ζύ (1 - μΧ*) (l " Ι Χ)) (l " \ Χ)
/which for the inequalities o^ +■ α2 > ая, α3 > α4 denotes the sum
Now, eliminating v, we find
> (1 - μΖ,Σύ (1 - Μ (1 -1 X3) (1 - i X3X4) '
^which for the inequality «i + or2 > a3 + ff4 denotes the sum\
Finally eliminating μ by a formula given ante Art. 348 we find
ι - xxx*xt - ххх\хгхА - χ,χίχιχ, + ζ,ζ?ziZq + дг?α:;ζ;дг4
(1 - Х,Х2) (1 - Ζ2) (1 - ХгХ2Хл) (1 - ΖβΧ8) (1 - Ζ2Ζ3Ζ4)(l - ^Ζ,Ζ,Ζ,)'
the real generating function of the solution of the inequalities.
СН. П] THE METHOD OF ELLIOTT 111
We have thus six fundamental solutions, viz.
«1 = 1,
«1 = 0,
«1 = 1,
«1 = 0,
«1 = 0,
«1 = 1,
«2 = 1,
«2=1,
a2= 1,
a2=l,
«2 = 1,
a2=l,
«3=0,
«3=0,
«3=1,
a3=l,
a3=l,
«8 = 1,
«4 = 0,
«4=0,
«4 = 0,
«4 = 0,
a4=l,
«4=1,
shewn by the denominator factors; also three first syzygies given by
Jl2 · -S-i ^2^3 ~ Xl Λ'2 . 2L22L'% =s ^1 = 0,
Jl2 · -3li-3l2^3-^4 ~" -^1-^2 · -^2^3^4 = £>2 = 0,
2L%2L<b. -Л-!JL2X.^2L^ — Х.\&22±.ъ · ^2-^3-^4 = &з = 0,
and two second syzygies given by
-л2А3-д4 . JLi-ZI-X^j — -5l2X3 . Αχ ^£2-5Γ3.Χ4 = 0,
JL1-3l2-3l3 . X\ JC2J£32C4 — Χ12ί2 · -^1-Λ-2·^-3-^·4 == 0.
The general solution of the inequalities is
OLx = Cx + C:i + C6,
a2 = Cj + c2 ■+ c3 4- c4 -1- c5 + c6,
a3= c34-c4+c6 + Ce,
«4 = 05 + C6.
358. The reader who is interested in the subject of linear homogeneous
Diophantine analysis should, as regards equalities, study a valuable paper by
Ε. Β. Elliott*. It has been shewn in Art. 350 that every Diophantine
Inequality is a particular case of a Diophantine Equality, so that there is
necessarily much that is common to the two theories. They are not
however quite parallel because the Inequality, being a particular case, lends itself
to particular treatment which is not available for the Equality in general.
Thus although Elliott gives a discussion of the Equality
αα = 1β + су,
he does not make the solution depend upon the ordinary theory of continued
fractions because this dependence only arises, for the particular case c= 1,
when the Equality merges into the Inequality
aa ^ Ъβi
which is fully discussed in a subsequent chapter of this work.
* " On Linear Homogeneous Diophantine Equations," Quarterly Journal of Pure and Applied
Mathematics, No. 136, 1903.
112 THE METHOD OF ELLIOTT [SECT. VIII
Some examples of his method are now given in the notation employed in
this book.
Taking the Equality to be
A& + A2ct2 + ... + AiOi
-ДА + ДД^.-. + ад,
where the numerical magnitudes A, B are integers which have no common
divisor and the magnitudes α, β are integers to be determined. He shews
that
is expressible in the form
Ω I
= (1 -λ^)(1 - ХА*яъ) ... (1 - \А<аь). (1 - λ--%+1) ... (1 -\-Bixi+j)'
with an auxiliary quantity λ.
To reduce this expression he makes use of the equation
I . ι ( ! .+ _J Λ
(1 - xs\A°) (1 - xt\-Bt) 1 - x8xt\A°~Bt Vl - Ха\Аш 1 - аь\-в* J '
choosing A8 and Д to be the greatest of the quantities At В respectively.
The generating function is thus expressed as the sum of three fractions, each
with either ± 1 for numerator. Each of the three fractions is on the whole
simpler than the original. The process is continued with each fraction but
it cannot be indefinitely applied. Eventually the original fraction will be
replaced by a sum of fractions each with either ± 1 for numerator, in none of
which is there in the denominator both positive and negative powers of λ.
The factors of a denominator will either involve both factors without λ and
with positive powers of λ or both factors without λ and with negative powers
of λ. No single denominator will involve both positive and negative powers
of λ. Putting all factors, which involve positive or negative powers of λ,
equal to unity in these fractions gives the completion of the operation Λ and
the remaining denominator factors indicate the fundamental solution of the
equality.
As an example consider the Equality
За! = Д + 5Д.
The crude generating function
a ι
β (1 - λ3^) (1 - λ"1^) (1 - λ~5^)
is reduced by the method to the expression
1
(1 - хго$) (1 - ^2#з) (1 - а\(%) (1 - #?#sA) 1 - х\хгх.6'
CH. II] THE METHOD OP ELLIOTT 113
indicating the fundamental solutions
(«i,A,&)« О, 3,0), (5,0, 8), (2, 1, 1).
The Equality considered is in fact equivalent to the Inequality
3(4 >5&,
and is fully considered in the subsequent chapter to which reference has been
made above.
359. In particular consider the Equality
Αα=Β1βχ + Β*βί + ...+Β&,
for which the crude function is
a
= (L-XAx1)(l-\~Blx2)(l-\-B2x3)...(l-\'-:B>'xj+1)'
First when A = 1, suppose that
<?(*) = J0 + J1* + ia*i+...,
a power series free from negative powers of z. We take G (z) to be the series
itself or the function of which it is the formal expansion.
Write the function under the operation Ω
which is (1 4- 7щ + Х2я? + ...) (b0 + Ъ^-1 + δ3λ~2 +...),
shewing that Ώ -—— G (λ"1) = G (^)>
= J. — A.CCj
and that the generating function is
1
(1 - «*'aO (1 - afrab) ... (1 - *?Ч'«) '
Secondly when A > 1, the terms free from λ in
are 1 +#1δΑ + <«ϊδ2λ+ ···>
which has the expression
where pA = 1 and the summation is for each root ρ of this equation.
This however is not a convenient solution. It is better to multiply
numerator and denominator of G^"1) by such factors that the denominator
becomes an integral function of \-A. For we can then write λ for λ^ and
the case can be dealt with in the same manner as when .4 = 1.
M. A. II. 8
114 EXAMPLES OF ELLIOTT'S METHOD [SECT. VIII
For example—for the Equality
6а.=:2/31 + 3/32 + 12/Зз
- have Ω„ >6 W1 , . * ,_, ,,, λ „ v
= (1 - λ6^) (1 - X -x2) (1 - λ 3#3) (1 - λ"12^)
-which we may write
(1 + λ-2#2 + λ-^j) (1 + \-»ccs)
" (1 - Х6хг) (1 - λ-«<4) (L - λ"64) (1 - λ-12#4) '
wherein we may put the numerator function equal to unity because the
remaining terms plainly contribute nothing to the terms of the whole
expression that are free from λ. Doing this and then putting λ for λ6
we find
1
Ω
(1 - λ^) (1 - X~l4) (1 - λ-1^) (1 - \~2χ4)
1
(1 - α^αξ) (1 - α^αξ) (1 - φ4)'
indicating the fundamental solutions
(α, A, A, A) = (1, 3, 0, 0), (1, 0, 2, 0), (2, 0, 0, 1).
In the above process after multiplication of numerator and denominator
by certain factors we retain in the numerator only terms which involve
integral powers of λ""6.
One particular case is for the Equality
Α<χ1 = ηιΑβι + Ρβ2,
where Ρ is prime to A.
Elliott gives the generating function
1
(1-*Глз)(1-^)
and the reader will find that it is at once established by applying the above
principle to the crude function
1
Ω
(1 - \ла?,) (L - \~mAx2) (1 - λ-ρΟ '
CHAPTER III
THE DIOPHANTINE INEQUALITY αα^Ββ
360. The Inequality is equivalent to the Equality αα = 6/3 + 7.
The problem is to obtain the fundamental solutions by forming the sums
'Zaf-yP, Xaflyfi^aa""bfi for every pair of numerical magnitudes α, β which satisfy
the inequality.
>
If Ε
denotes the smallest integer which ^ the quantity which follows it, we may
>b
carry out the summation by first summing α from В - to 00 and then summing
β from 0 to 00. The result of this procedure is
1 + a? *у + л? а у2 + ...+a? а y*"1
(l-*)(l-aV)
which certainly proves that the fundamental solutions are included in the
exponents of the x, у products in numerator and denominator; but it does
not specify them. The true method leads to a sum of algebraic fractions and
is essentially connected with the Theory of Continued Fractions.
Wc have %xayp = Ω ,
><l_X«*)(l-iy)
and we suppose a, b to be relatively prime positive integers.
We require two lemmas.
361. Lemma I. " The relation
aoL^Ъβ
may be made to depend upon a similar relation in which a is unchanged and
а>Ы
8-2
116 TWO LEMMAS [SECT. VIII
For suppose a :|> b; if jp be the greatest integer in - the given relation
implies the relation
α>ρβ>
and introducing a second auxiliary we may write
1
Sa-y = β -
Eliminating /г we find
taf-y* = il -
»<i-x-)(i-^)·
which denotes the sum
ttf (xPyf = l^+Myt,
where α, β are connected by the inequality
αα^(δ—_pa)j8.
We have therefore reduced the sum
2лл/. for the relation cm ^ 6y3
to the sum 1хл+№у(* „ „ αα ^ (δ —ρα) /3.
This proves the lemma.
362. Lemma IL "The relation
αα ^ &/3,
where a > b} may be made to depend upon a similar relation in which b is
unchanged and a < b."
The relation aa ^ bβ) in which a > b} may be broken up into the two
simultaneous sets of relations
aa > bβ} aa ^ bfi,
β^α, α > /3,
and the second simultaneous set
aa > 6/3,
a>/3,
may be replaced by the single relation
a>/3
because, a being > 6, the relation
aa > Ъβ
is implied thereby.
CH. Ill] TWO LEMMAS 117
We therefore separate a portion of the sum corresponding to α > /3, viz.
12 or
>(i-.3UB)(i_g a—xi-y)·
and consider the remaining portion due to the first set
This portion is Ω τ—τ
= il
>(i-b-6*y)(i-jpy)'
which gives the sum Σ (яуУу1* or 1af-ya+p
for the relation (a — 6) a ^ δ/3.
If a — b< b we have done what was required, but if a — b > b we may-
repeat the process; and just as we have found
Ω 1 — = -- £- 4 + ί1· Ί
><i-x'*)(i-£y) ^-Х1-*) >(l-^)(l-iy),
we shall find that
Л - г-т-я & * + <*■
>(i-*·>*) (i-£y) α-^Χΐ-^ >(i-x~V)(i-£y)'
. α
Moreover if g be the greatest integer in γ we obtain finally
>(l-V*)(l-±y)
Ж1/ жг/f-1
+ л χ-л τ? + ··· +
(1-х) (I-coy) (l-xy)(\-anf) (1 - ху^) (1 - хуЯ)
1
+ Ω
>(l-X-*ey«)(l-^y)'
118 REDUCTION OF THE CRUDE FUNCTION [SECT. VIII
where the last written portion of the sum represents the sum
2(а#9аз/э or 2#а2/*а+э
for the relation (a - gb) О 6/3.
This proves the second lemma.
363. The two lemmas evidently yield a process of reduction which can
be pushed to the last extent.
In what follows a will be considered > 6. If b > a it wi}l merely be
necessary to write b — pa for b and x*y for у where ρ is the greatest integer
. b
in -.
a
The reduction depends upon the convergents of the continued fraction
to r·
τ , α 1 1 1 1
b (ι* + a3 + a4 + ... 4- an
where η is uneven; this is always possible because an may be written
(α^-1)+-.
Take as the first two convergents
1 g-i* 0 ge'
and write down the convergents of uneven order
P^i Pi Ps Pn
q-iy gi1 q*''" qn'
Now form the ascending series of intermediate convergents, viz.
д./ g-,+ίο' g-1 + 2g0, '" g_! + (^ - 1) g0'
Pi Ρι±ρ* Ρΐ±?Ρΐ Pi + fa-l)Pa
g,' gi + g,>' gi + 2g,' *** gx 4 fa- 1)g2'
ff/>-2 f>n-2 + pn-1 Pn-2+2j)n^ Ρη-2 + (αη-1)ρη-ι
gn_a' qn-2 + qn-i' gn_8 + 2gn_1' "' gn_2 + (an - 1) gn_x'
where of course ~ = r .
g^ t>
СЫ. Ill] REDUCTION OF THE CRUDE FUNCTION U9
Applying now the second lemma to the crude generator
1
Ω.
1 \ *
we obtain
Ω 1 =—- + 2
Oy X^"1
> (i - х»-м*Г.) (i - Ιή » <x - "***> <l - «*-> *
where in the expression last written the summation is in regard to a^.
Now
xy**-1
(i - a?^-1) (i - #гл)
' (1 - л?1 у0) (1 - #1+y+1) (1 - &·1+<γ+1) (1 - #ι+2.<γ+2.ι)
дЛ+2.0^0+2.1
(1 - ^+2·γ+2.1) (1 - ^1+3.0^0+8.1)
^1+ {βγ—ΐ). ο ^ο+(αϊ—ι). ι
"*" {1 — aji+№i-i)oy)+{«i-i)i| Π — д-ι+Λι.««/>+■«! -11
(1 -**-^-*)(1 -**-*+^~1+Л)
<7-ι + <?ο,„ί>-ι+2>ο
+-- ^——
(1 _ #ff-i+ ffo^l>-i +Po\ ft _ αί-ι + 2q0yP-i + 2ρ0\
Η - h .
(1 _ a.flf-i + 2ϊο.Μ + 2i>0) (ι _ χ4-ι + 3?ο 2>-ι + 8ρ<^
#<M + («ι -1) ЯоуР-1 + f«i " 1)Λ>
+ {1 - а*-1 + (Λι" Х) ^V"1 + К ~1)Ро}{1~ xqxyVl]'
wherein the exponents are derived from the intermediate convergents to
—-, -- inclusive of these principal convergents.
364. The remaining part must now be subjected to the process of the
first lemma and we find that
а. г
>a-x-%v«y)(i-^
-Ω Χ
>(1-λ^^)(ΐ-^-;)
120 COMPLETION OF THE REDUCTION [SECT. VIII
Now the second lemma yields
il-
> {1 — \а-а1Ь-аз№*ъ~4*а)х$1+азЯ*ур1+азР«\ Μ X "У ' \
Яз ФуР\ (#&уЛу*з-1
+ χ {1 ~ Фур* (а&у**уь-1\ {1 - Фу* (я&уА)«ь}
-Ω. 1
Х^\уР\ <jc<2i+byP\+Pz
(1 -aflxyv.) (i _#ii+fcyft+ft) + (Γ- авН-ЛуЛ+л) (i - Λ4.+«δ^ϊι+ν.) + * · *
^ffi+ (o»-i) fry 2>i+ («3-D ft
{1 — Ж^+^з-1)?^^4-^-!)^} (1 — хЯ*уРз) '
and we have before us a new portion of the generating function corresponding
to the intermediate convergents to the principal convergents — , —, the latter
both included.
365. The portion remaining,
Ί
> (1 - λ^-^yft) (ι _ ^Щ '
is now subjected to Lemma i", and the lemmas operate alternately until the
final result is reached.
The last remaining portion must be
Ω 1 ,
> τ / Λ-lJn-l \ '
(i - λ*·Λ-Α**ν·) ι - -^-/—
which since qna — pnb = 0 is
1
1 - xqnyVn'
or 1 Η 2
1 — xqnyVn
Hence the complete generating function is
(1 - a·) (I - xy) '" (1 - xrhfl) (1 - /y*) "" 1 - дг^уР»'
wherein there is a term corresponding to every pair of consecutive members
of the ascending intermediate series of convergents to γ, viz.
fi £2
Г л ' Го '
CH. Ill] SOLUTIONS OF THE CORRESPONDING EQUALITY 121
From well-known properties of the convergents every xy product that
appears in the function yields a ground or fundamental solution of the
relation
ad ^ Ιβ.
Hence the ground solutions are
α = r, β = s,
where - is in its lowest terms and is, at pleasure, any member of the ascending
intermediate series of convergents to r .
366. Moreover every solution of the inequality is expressible in terms of
a consecutive pair of intermediate convergent numbers.
Thus the general solution may be written
α = ολτλ + c2r2, β = c1sl + c2s2>
where cb <% are arbitrary positive integers.
367. If we have before us the Equality
au = 6/3 + 7,
the sum ΣοΡί/ζύ for the whole of the solutions is formed by multiplying each
xy product
xry*
by zar"bsy
and the general solution is
a = c^! + c2r2, β = c^ + c2$2i 7 == α {ρχτλ -l· c2r2) — Ъ (с^ + c2s2).
Observe that we may also write
7 = cx (m\ — foj) + c2 (ar3 — bs2).
368. As an example take the inequality
779a > 2()7y8,
, 779 0 1 1 1 1 1 1
where _.8 + T + 5+i + 2 + i + i.
The principal convergents are
0 1 3 4 15 64 143 636 779
1 ' 0' 1' 1' "4 ' 17' 38 ' 169' 207'
and the ascending intermediate series
0 1 2 3 7 11 15 79 143 779
1' 1' 1 ' 1 ' 2 ' "3 ' 4 ' 21 ' 38 ' 207"
If the principal convergents are 2m + 3 in number, the number in the
intermediate series is
1 + θ! + α3 + a5 + ... + a2w+1.
122 PABTICULAR EXAMPLES [SECT. VIII
Here 2,0? y&
χ xy_ xy2
+ (l-x)(l-xy) + (l-xy)(l-xf) + (l-xy>)(l-xy*)
xyz x2y* x?y11
+ (l-xy*)(l-x2f) + (\-x*y7)(\-xAyu) + (1 -а?уи)(1-а*&*)
any16 ^y79 x®y™
^7^
,779
Г(1-#20У79)'
and the fundamental solutions of the relation are
α
1
1
1
1
2
3
4
21
38
207
γ having reference to the equality 71
β
0
1
2
8
7
11
15
79
143
779
7
779
572
365
158
109
60
11
6
1
0
79α =207/9+γ.
The successive pairs of values of α, β are
gradually increasing approxi-
raations to the simplest solution of the equality
779<
χ = 207/3.
369. It appears that the ordinary theory of numerical continued fractions
is coincident with the simplest case of Partition Analysis.
It is a theory concerned with, in the first instance, two relative prime
integers. It is clear that the fundamental solutions of simultaneous Dio-
phantine Inequalities involving many unknowns will give properties of л set
of numbers and constitute л generalization of the Theory of Continued
Fractions.
370. As another example, take
77a > 104/9.
The operation of Lemma I shews that we have to sum
to? (xyf
for the relation 77α > 27β.
СН. Ш] PARTICULAR EXAMPLES 123
α· 77 0 1 1 1 1
Since 27 = 2 + ϊ + 5 + ϊ + 3'
the principal convergents are
0 1 2 3 17 20 77
1' 0' 1' 1' 6 ' 7 ' 27'
and the ascending intermediate series
1' 1' 1' 2' 3' 4 ' 5 ' 6 ' 13' 20' 27 '
leading to the result Σ#* (xyf
= 1, # х.ху_ a^Jjcyf ■
+ (1 -a?) (1 -я.яу) (ΐ -л?.л?у)"(1 -х.я?у*) + ··* ^ 1-^7 (^)ττ ·
The operation of Lemma I is however not necessary, for we have merely
to form the ascending intermediate series of convergents to 77/104 in
connexion with the sum
1xayfi.
пч. 77 Λι111111
lhus _=0 + ϊ + 2 + ϊ+5 + ϊ + 3.
The principal convergents are
0 1 2 3 17 20 77
1' 1' 3' 4' 23' 27' 104'
and the intermediate series
0 12 5 8 11 14 17 37 57 77
1* 2' 3' 7' 1] * 153 19* 23' 50' 77' 104*
The generating function is now at once written down.
371. For the Equality 77a = 104β + у
we have merely to multiply each product хлу& by гПа~ш^ and then
1*хау*гУ
xf[ tfysP
(1 - ivz11) (1 - xHjzm) + (1 - a*ysP) (1 - aty9 s»)
xsyizt^ x7yr,z™
+ (I - a?tfz*) (I - x'tfz") + (1 - x4fz™) (1 - a;11?/8*15)
а?" у8*» x™ynzn
+ (I - &JY*«) (1 - a:lByuzn) + (1 -^^(l-a-'yV)
+ (1 - a*y V) (1 -лу7) + (1 - ж2У V) (1 - aPy*&)
алоу2722 al"tf*z хшу17
(1 - aPy"z*) (1 - x^y^z) (1 - а:7у7г) (1 - a;loy7) 1 - #10У7 '
124
PROPERTY OF CONSECUTIVE SOLUTIONS
[SECT. VIII
establishing the fundamental solutions
a.
1
2
3
7
11
15
19
23
50
77
104
β
0
1
2
5
8
11
14
17
37
57
77
7
77
50
23
19
15
11
7
3
2
1
0
372. The reader will notice a peculiarity in this example because if we
omit the highest value of α and the lowest value of 7, the α numbers read
downwards are the same as the 7 numbers read upwards. He will find it
interesting to investigate this coincidence.
373. It appears from the form of the generating function that every
solution (α, β, у) of the Equality must be derivable from at most two of the
fundamental solutions, say
(α<'·>, βν, 7W), (α*»*1», /3<r+1\ 7<r+1>),
and these must be consecutive solutions, viz. we must have
a = craw+<V4-i«(r+1),
β = ^+ον+1β^,
7 = cr7i"+cr+i7tr+l),
where cr and cr+1 are positive integers.
Eliminating these magnitudes we find
α
/β 7
aW β(Τ) γ (Г)
a(r+i) β(Η-ΐ) (r+i)
= 0,
a linear relation between η, β, у which must be identical with
αοί — Ιβ - у = 0;
hence
β(τ) β(ν+ΐ)
с
= a,
I (r) a(r+i)
1 (r) β(Η-ΐ)
гу(Г) л/(Н-1) I
«и a(f4-i) \
= 1
)
CH. Ill]
THE SYZYGETIC THEORY
125
the latter verifying an elementary property of intermediate convergents. The
two former may be verified from the examples given.
Thus in connexion with the Equality 77a = 104/3 4- γ we find
50
1
23
2
= 77,
23
3
19
7
= 104.
374. To arrive at the syzygetic theory it is necessary to express the
generating function as a single algebraic fraction.
Thus in the case of the Equality
7α = 3β + 7,
„ Ί ^ a „ 1 — x2y-z8 — x4y7z7 — x^y^z4, 4- x*y8zn -f х*у*2р
we find ЪРуРзР- -/Γ" 7V7i—^νΓΓ .wi—^л" >
** (1 — χζ7)(1 —осуг*){1— xy2z)(l — x*y7)
where, the fundamental solutions being indicated by the denominator factors,
the first syzygies are
#i = (*у*У - (ooz7) {xifz) = 0,
S2 = (xz7) (x*y7) - (xyz*) (anfzf = 0,
S* « fay*4) (aY) - (xtf-zy = 0,
and the second syzygies
(atfzf & + (я?уж*) £2 - (**») & = 0,
(«Y) $ + (xfz) S2 - (лу^) 8t = 0.
Denoting a solution by (a; /3, 7) the first syzygies shew the relations
(1; 0, 7)-2(l; 1,4) + (1; 2,1) = 0,
(1; 0, 7)-(l; 1,4)-3(1; 2,l) + (3; 7,0) = 0,
(1; 1,4)-4(1; 2, 1) + (3 ; 7,0) = 0,
from which are deduced the relations
(1; 2,1) = -(1; 0,7)+2(1; 1,4),
(3; 7,0) = -4(l; 0,7) + 7(l; 1,4).
It will be observed that fundamental solutions are such that every
solution is expressible in terms of them by means of a linear function in
which the coefficients are positive integers. If negative integers be admissible
a certain number of the fundamental solutions cease to be fundamental. In
the above example the fundamental solutions (1; 2, 1) and (3; 7, 0) are
linear functions (negative coefficients being admissible) of the solutions
(1;0,7), (1; 1,4).
CHAPTEE IV
THE SIMULTANEOUS DIOPHANTINE INEQUALITIES
375. We assume au bx to be relatively prime integers and also a2> b2.
If the given relations can be satisfied by other than zero values of the
magnitudes α, β we must have
αϊ α, Ι
Oi 02 \
Assume that ^>αλ.
The first step is to prove that the relations may be reduced to other
relations in which simultaneously ax > hu b2 > a2.
The crude expression for 2#ау,
the sum being for every solution of the simultaneous inequalities, is
n. l
>
^ be d(
h
first step is to write
If the fraction — be developed in the form of a continued fraction, the
Οχ Οχ
where cY = аг and c2 < Ci and then α^πι1β.
The crude expression may then be written
1
which by elimination of ν is
(ι-^ή(ι-^'ή
'('-S-X1-^*)
SECT. VIII, CH. IV] BEDUCTION OF THE CRUDE FUNCTION 12 7
Herein if i>2 — тга2< 0, the whole expression is equal to unity, indicating
that the only solution is the singular one α = β = 0.
If Z>2 — m^o = 0, we must have a.2 = 1, b2 = mb and the whole expression is
il i ,
which is unity, except when Ьг — w^Oi = 0; in this case αΎ = 1 the Inequalities
become
α > f>i& bi>S ^ or,
equivalent to α = Ιχβ,
and the generating function is
Assume therefore ba — m1a2>0 and put α2 = с/, f>2 — w?a<x2 = &/ so that the
expression is
Ί
^-S-N'-S"·')
If now c2' > c/ we have effected the reduction because d > a2 and we have
the two relations
connected with the sum %яа+т^уР.
If c2' = c/ or 62 = (т!-1-l)a2, we must take Oo = l because 02, &2 &re
relatively prime and i>2 > aa.
The expression then becomes, by elimination of c/, connected with a single
inequality. Putting this aside as a case already dealt with when the single
inequality was under discussion, we are left with
η l
Ч1-£·)('-S~»)'
μ*
in which d > c2, cJ < c/ and the expression must be further reduced.
Since h> — тгсил > 0 and a! < c/ or h> — mva>> < a2,
it is clear that mx is the greatest integer in—·, and
C£2
— =ш + -,.
Write now — = тг Η , —,,
α2 tw3 -l· Co
where т?^ н is the second convergent to — and of course c3' < c2'·
??i2 ^2
128 REDUCTION OF THE CRUDE FUNCTION [SECT. VIII
Since %==Ш2^.\)
c3 c2
we may take for the expression
Ί
V μ^ν™* )\ λ°* V
from which eliminating ν we obtain
Ω. Χ
b α
Since — = mx + — where c2< C! we may write
C\ , C3
C2 ^2
whenever Cj —m^ is positive, and then
δι 1 c3
— =01!+-- -,
aj 7иа + Cg
where c3 is no£ necessarily < c2.
If c3 be zero, c3' must be zero also and the generator is simply
1
corresponding to the Equality
m2cc = (m^z + 1) /3.
If c3 be not zero we must have
Сз > as ОГ < C2.
If C3 ^ Co the reduction is complete because also a/ > c3'.
In this case πιλ + — is the second convergent to ~ but is not the second
7/ϊ2 &2
convergent to —.
#1
If c3 = Co we can at once eliminate λ and obtain an expression that has
been already dealt with. In such a case it is clear also that m2 simply
becomes w2 + 1.
If c3 < c2, w^ Λ is the second convergent to both — and — and a further
m2 & ax a2
process of reduction is necessary.
CH. IV] REDUCTION OF THE CRUDE FUNCTION 129
376. To sum up the results so far reached :
(i) If ax > blt a2> b2}
the inequalities are already in the desired form.
(ii) If Z>2 -m1a2> a2t ax > Ьг - тгс^,
C2 > C\ у С\ > C2)
the final reduced form is
•(■-S-X1-^)'
wherein — = rax + - , ρλ = щ, qx = 1, and m1 = — is the first convergent to
—; also - = jwi + -, and чщ is not the first convergent to — .
(l\ Ct2 C\ &2
h h
(iii) If m1 is the first convergent to both ~ and — ,
Qj\ СЬ2
C$ > C2, C2 > C3 ,
and the final form is
1
>(i-£*pv)(i-^**trf'
where — = mj Λ— - ,
αλ m2 4- c2
b2 1 c3'
— = mY + — — ,
a2 m2 4- c2
and mi Η is the second convergent to -- but is not the second convergent
m2 ь а,2 °
to К
Ί h h
When mY Η is the second convergent to both ~ and 2 we write
m2 ° di Oq
b, 1 1 c4
a! ra2 + m3 + c3
b, 1 1 c/
си m2 -t- m:l 4- c3
wherein, if c3 > c4, c/ > c/,
1 1 P*
w2 4- ra3 j3
is the third convergent to — but is not the third convergent to — .
M. A. II. 9
130 COMPLETION OF THE REDUCTION [SECT. VIII
The final reduced form is then
Ω . 1 __,
which denotes the sum
for the relations c3cc ^ c4/3, c//3 ^ с3'сс
7 λ
But if —, — have the same third convergents, a further reduction is
necessary.
377. We proceed in this manner to establish the following general
results:
7 Λ
We develop —, — to the point where they fail to have the same con-
vergents. We have then two cases.
Case I. If
аг пц + Щ ■+- ... + тп 4- сп
α2 д т2 + тй + ... + яги + сп' '
wnere с<п > c?i+i, c^, < с п+д,
so that — is the nth convergent to - but not to — ; the final reduced
form is
V£-*V~)(i-g-V)'
which represents the sum
for the inequalities cna ^ cn+1/3,
С 71+1P ^ ^tt а)
wherein cn > cn+1, c',i+1 > cn'.
Case II. If cn < cn+1> cn' > cfn+u
then — is the nth convergent to — but not to —; the final reduced form is
qn a2 a-!
Ω : 1 „
4ι-%ί+ή(}-ι&-'~)
μ
CH, l.V] THE FUNDAMENTAL SOLUTIONS 131
which represents the sum
2(a?*y*)*(^-y»-%
for the inequalities Cn+i«^cn/8,
wherein cn+1 > cn> cn' > c'w+1.
We have thus shewn how in every case to reduce the given inequalities
to a standard form
12β>α*α,
wherein аг > Ъг, b» > a2.
378. As an example take the simultaneous inequalities
64a ^275/3,
142/3:* 33a.
We find that У = 4+| + 1 + ?>
142 114
33 +3 + 2 + 3·
This falls under Case I and we observe that
4 ,13
ϊ and Τ
30
are the first and second convergents to both fractions, but that -y is the
275 142
third convergent to -τητ but not to -^ .
The problem thus presents itself in the form of finding the sum
for the relations 7α ^ 5/3,
4/3 ^ 3a.
379. We are now able to give a complete solution of the problem of
finding the fundamental solutions of the Diophantine system
Oia^ib/3,
Ья/8 ^ ад
wherein аг > Ъх, h>> α2.
For we can break up the system into the three systems
I II III
аха^Ьф а^а^Ьф αΎα^^β
63/3 ^ α2α 62/3 ^ α2α Κβ ^ α3α
/3^α α^/3 α = β
9—2
132 EXAMPLES [SECT. VIII
in such wise that if FY (x, y), F2 (x, y), F2 (x, y) be the generating functions
concerned with the three systems respectively, the sum that we seek is
Fl (x, y) + F2(x, y) - Fs (x, y\
for clearly when we add the systems* I and II we count the system III twice
over, and since α may be > = or < /3 so long as the other conditions are
satisfied the sum must be as stated.
We can now reject as superfluous the second relation of I (because
b2 > Og), the first relation of II (because ax > Ъг) and the first and second
relations of III. They thus become
I II III
с^а^/З 62/3>α2α α = /3
β>α *>β
Hence FY {χ, у) + F2 (x, у) - Fz {x, у)
= Ω- } + Q. Ύ 1
*{>-*·)(*-&) *(·-£■)('-?»)
λ£ \ 1-ху
= Ώ · + Ώ
>(1-λ^^)(ΐ-^) >(1-λ^^)(ΐ-^;)
1-ху
We have now only to apply the theorem of the single inequality to the
two β expressions by forming the ascending intermediate series of con-
, , Oj — i>! , b2 — a2
vergents to —;— and .
We can thus determine the complete generating function and by inspection
ascertain the fundamental solutions of the inequalities.
380. As an example we will continue the case of the system
64a > 275/3, 142/3 ^33a,
which has been reduced to finding the sum
Ъ{оРу*У(а?*уУ
for the system 7 a > 5/3, 4/3 ^ 3a.
The sum Σ&Λ^ for the system is
Ω - - + Ω. * λ
>(l-V4f)(l-i) >(l-X^)(l-g) X-»
CH. IV] THE ALLIED SIMULTANEOUS EQUALITIES 133
2
The ascending intermediate series to ■= is
0 12
1* 3' 5'
andto§ j, 3.
Hence
ZXy ~ (1 - xy) (1 - attf) + (1 - a*y*) (1 - a»jf) + L - tff
+ 1+,-, ^—^+,^
(1 - ay) (1 -#Y) 1 - #y 1 - «у
_ 1 xy_ xAyz xzy* ору1
+ (1 - жу)~(1 - я-у) + (1 - xy) (1 - я4*/3) + (1 - a?if) (1 - x4f) + 1 - #y
This shews that of the system
7a ^ 5/3, 4/3 ^ 3a,
the fundamental solutions are
(a,/3) = (l, 1), (4, 3),(3,4), (5,7).
Also writing xl3y3 for χ and aPy1 for у the sum ЧяГу? for the system
64a ^275/3, 142/8» 33a
&i4V° л·142-?/38
(1 - x™y10) (1 - юшу") (I - a*yo) (1 - xl*y*>)
+ (Γ^^^ίΙ-Λ*5^) + 1-^5^04 >
establishing the fundamental solutions
α I /3
43
159
142
275
10
37
33
64
381. Allied to this theory is that of the simultaneous equalities
α1α=&1)8 + 7,
Ь2/3 = α2α + δ.
In the sum just obtained it is merely necessary to multiply each хлу&
term by ярхь-ъ^уЪьР-*** in order to obtain the sum
^xay^zyus
for all solutions of the simultaneous equalities.
134
PROPERTY OF CONSECUTIVE SOLUTIONS
[SECT. VIII
It will be observed that every solution is composed of at most two
fundamental solutions. The latter present themselves in two sets which are
derived from two series of ascending intermediate convergents and every
solution is derived from two consecutive fundamental solutions of one or
other of the sets.
Denoting consecutive solutions by
eW, £(>·>, 7W, £('·> ; aH-1)^ 0(г+1)? 7(r-fi)> gir+1)^
and by cry cr+1 undetermined positive integers we have
u^CraM + c^aW,
(H-i)
whence
7 = cr7w + c,.+i7
B^CrB^ + c^B^,
α β
a(r+l) β(Η-ΐι
tfM
Jr+l)
= 0,
/3
βϋτ+ΐ)
jW
АГ+l)
в
g(r+i)
= 0,
and also two other relations, which are not linearly independent of these,
γ И
β
βΜ
В
gc>
= 0,
α γ δ
α(Η-ΐ) 7(r+i) g(r+i)
= 0.
а(Г+1) β(Τ+1) g(r+l)
These must be practically identical with the four relations
axa = bi/3 + 7, («ib2- <^2ί>ι) β = <vy + аД
Ьо/8 = а2а + δ, (α2 62 — α2&ι) α = ^>7 + ^δ,
so that on comparison we find
a(r+\) βρ+ΐ)
β*
/И
}(Г+1) у(Г+1)
= ±1,
= + а,,
α(/·>
а(Г+1)
/3(г+1)
у(Г+1)
ξ (г)
g(?'+l)
= + δι,
= ± α2,
a(r)
α(τ+ΐ)
γ И
γ(»·+υ
g И
g(H-i)
δ(^
gir+D
= ±δ,,
г±(«1&а —«Л)>
the upper or lower sign being taken according as the consecutive solutions
arise from the first or the second of the given equalities.
For the equalities 64a = 275)8 + у; 142/3 = 33а + В the solutions are
а
43
159
142
275
. β
10
37
33
64
У
2
1
13
О
δ
1
7
0
13
CH. IV] PROPERTY OF CONSECUTIVE SOLUTIONS 135
of which the second and fourth arise from the first equality and the first and
third from the second. Hence the results shew that
1 43
j 159
1 43
1 159
1 43
159
10
37
1 10
37
2
1
10
37
2
1
1
7
2
1
1
7
1
7
159 37
275 64
159 1
275 0
159 7
275 13
37 1 !
64 0 1
37 7 1
64 13 |
1 1 7 |
1
о is I
= 1;
= -275;
= 142;
= -64;
= 33;
= 13;
43 10
142 33
43
142
43
142
10
2
13
1
0
2
33" 13
10
33
2
13
1
0
1
0
= -i;
= 275;
= - 142;
= 64;
= -33;
= -13;
the value of αΑ-α-Λ here being 64.142-33.275 = 13. These are
properties of consecutive solutions analogous to the property of successive
convergents in the theory of simple continued fractions.
The next step -would be apparently to work out the theory of the
inequality
ал > Ιβ + су
This has not yet been accomplished.
CHAPTEE V
ON THE FORM OF ENUMERATING FUNCTIONS
382. The problem we take up in this chapter is one of considerable
interest. The enumerating generating functions that are met with at the
outset in the theory of the Partition of Numbers are such as are formed by
factors of the form
-, — written for brevity , '.
1 — or (s)
If such a function, involving a finite number of factors, appears as an
enumerating generating function it necessarily follows that it is expressible
in a finite integral form. The reasoning is precisely the same as that which
may be employed to shew that
n!
si (ft -s)\
is an integer. This follows as a matter of course directly it is shewn that
the numerical magnitude in question enumerates certain combinations. In
many difficult cases of enumeration of partitions it is natural, after some
calculations, to attempt to conjecture the form of the generating function.
In one research the function
(n+1) f(n + 2)V (n + 3)
(1) I (2) J (3)
appeared as the enumerating function. It is therefore necessarily expressible
in a finite integral form whatever be the magnitude of the positive integer
я. As the research proceeded certain calculations in a more general problem
might have led the investigator to conjecture, guided by analogy, that the
form he was seeking was
(n+1) f(n + 2)V Γ(η + 3)γ (n + 4)
(1) I (2) И (3) J (4) '
but it had to be rejected forthwith because .it does not happen to be
expressible, for all values of ft, in a finite integral form.
SECT. VIII, CH. V] FORMULATION OF THE PROBLEM 137
It is therefore natural, as well as important and interesting, to seek the
general expression of functions, formed by factors such as those here
considered, which possess the property of expressibility in a finite integral form
It is moreover conceivable that the study will indicate promising paths of
future research.
It will be seen that there is a syzygetic theory of such expressions.
383. Consider the function
/<n+ill"1 ί(η + 2)Γ ί&±9\°* /<ϋ±±>Γ
1(1) J I (2) J I (3) / I (s) J '
and write it, for short,
ΧΐιΧ?Χ?...ΧΪ.
We investigate the sum
ъх?х?х?...х?
for every set of numerical magnitudes
«1> a2> °k> ··· a8>
which renders the expression under the sign of summation expressible in a
finite integral form/or all values of the integer n.
Let ξt be that factor of 1 — xl which, when equated to zero, yields all the
primitive roots of the equation
1-^ = 0.
Then if 1, di, d2, ... t be all the divisors of t,
l-0i=*fi&1&i...ft,
as shewn in works on Higher Algebra.
If the product X?1 XT X?3... X?
be now expressed in terms of
ζΐ> ?2> ζ'Λ) ··· ζη+8>
there will be a numerator and a denominator, and if the function be integral
the whole of the denominator will divide out into the numerator, leaving a
finite integral algebraic expression.
We have therefore to ascertain the circumstances under which every
expression ξι will occur at least as often in the numerator as in the
denominator.
For example
(5)(6)M?) ШЩ,6,)»6&
(1)(2)M3) MfcWffc
is in this manner seen to be finite and integral.
In general we pay no attention to ξι because, at sight, it occurs with
equal frequency in numerator and denominator.
188 THE DIOPHANTINE CONDITIONS [SECT. VIII
With regard to ξ2 it cancels out in the case of every factor of the form
(n + 2m)
(2m)
if η be even, and does not occur at all in the factor
(n+2m + l)
~(2m+l)
if η be even.
But if ?i be uneven, it occurs a2m+i times in the numerator for every
numerator factor (n + 2m+l)a'2m+1 and аш times in the denominator for every
denominator factor (2m)a2m.
Hence we have the single condition expressed by the Diophantine
inequality
(Χι + α3 + «s + · ·. > «2 + «4 + ас 4- · ·· ·
For |n if m = 0 mod. 3 there is no condition;
if m = 2 mod. 3 we must have
α1 + α4 + α7+ ... ^ α3 + αΰ + α9 + ···,
and if m = 1 mod. 3
«2+«5 + α8+...^«3 + «6 + θ9+···.
384. Proceeding in this manner we have the conditions:
for fa αχ + α3 4- α, + ... > «a + *4 + «в + ···
[α, + 0Г4 + a7 + -.·> «a + <*<; + Of» + ...
l«2 + «8 + «8 + . . . > Я.1 + вГв + «9 + · · ·
fo + α6+ or» + ... ><*+ + «8 + ^i2+ ·-
for f4 job+ «в+а1в+ ... >«*+ a8 + a13+ ...
U:{ + a7 + au + ... > a4 + «я + «i2 + · · ·
for &
for fs-2
i«i + a.v
a*-2
for fM
f'j in number.
a*-i
ОН. V] TFIE SECOND AND THIRD ORDERS 139
385. All the conditions are included in the inequality
a<r 4* 0L2ff+r + вщг+2г + · · · ^ ^σ+τ + &&σ+2τ + 0^ Дог Η" · · ·,
σ and τ being any positive integers.
In the case of the gth inequality arising from ξρ the values of σ, τ are q
and ρ — ^ + 1 respectively.
The next step is to construct an fl function which shall expreo
conditions and lead practically to the desired summation.
386. First take 5 = 2; there is but one condition
«i > ct2,
and the function is Ώ
> (1-^^0(1-^2:.)
1
-(1-*0(1-*!*,)'
We may call Хг> ХгХ2 the fundamental forms, the general form being
There are no syzygies.
387. For 5=3 the conditions are
αϊ + «a > a2>
leading to the summation formula
Ω Ϊ ,
»(ΐ-νΛ)(ι-£*.)(ι-,£*,)
\lt λ-j, Хл being the auxiliaries connected with the inequalities respectively.
Eliminating Xg we find
η i . ,
> (1 - λ,λ,Ζ,) (l - £ Z.) (1 - i Za X;()
which denotes the sum Slf'i^IJ,)*8
for the inequalities a, > a2, ai > a,.
Writing А'гА'з for Xs in the sum is equivalent to writing a2 + a3 for a2 in
the inequalities.
140 THE FOURTH ORDER [SECT. VIII
We now eliminate λ2 and proceed to
1
П-
> (1 - λ,Χ.) (l -1X2) (1 - λ,Χ,Ζ,Ζ,)'
which denotes the sum
for the inequality а! + а$>а2, so that clearly writing ΧλΧζ for X3 in the
previous sum is equivalent to writing ^4- or3 for a3 in the connected inequality.
On the whole so far we have substituted ΧτΧ2Χζ for Хг in the sum and have
changed the original three inequalities by writing o^ -f a, for аг and α2 + α3 for
a2, thus reducing them to the single inequality a1 + α3 ^ α2·
Making use now of a formula on a previous page we obtain finally
(i - хг) (i - x,x2) ci -Vlzll^i^fх"2да'
the complete solution.
The denominator factors yield the fundamental forms
in addition to those previously met with, and the general integral form is
ν% + w2 + m3+m4 хгм2+Щ + 2w4 vmz + w4
The numerator term — Χ\Χ\ΧΆ indicates the simple syzygy
X!. Х-^Х^Хъ — -STi A 2. -3Γ ι X^X-i = 0.
The form ХгХ2Х^ occurs in simple partition theory, whilst
AlA* *{== (i-^)(i-^)2(I-^)
is connected with another kind of partition which is dealt with in this
volume.
388. Passing to the case $ = 4, the conditions are
«2 ><*4>
of which we neglect the fifth as it is implied by the third and sixth.
These lead to
a ! .
>(1-^a,)(i-^,)(i-gi,)(i-^i,)
CH. V] MODIFICATION OF THE PROBLEM 141
Eliminating λ5, λ4, λ3 and \ in order, this becomes
> (1 -λ,ΖΟ (1 - Х^Х2) (l - ±Z2X3) (1 -λ,Χ^Ζ,Ζ,) '
and, making use of a formula on a previous page, this is
ι - x?xjx3- x^xjx4- x\x\x\x,+z;zsz; jj+z*z42z33z4
(1-Ζ1)(1-Ζ1Ζ2)(1-Ζ1Ζ2Ζ3)(1-Ζ1Ζ1Ζ3)(1-Ζ1Ζ2Ζ3Ζ4)(1-Ζ1Ζ22Ζ23Ζ4)'
indicating the new ground forms ΧΎΧ^ΧζΧΑι ΧΧΧ\ΧΙΧ^ both of which are
known in the theory of partitions.
We have the first syzygies
(-л) = JC12l2· X1X^XZ — Χι, ΧτΧ2Χ$= 0,
(Β) = ΧτΧ2Χζ · ΧχΧ^ΧζΧ^ — Χ\ · ZiZ2Z|Z4 = 0,
(G) = X1X2Z3 . X1X2Z3Z4 — ZJZ2.ZJZJJZ3Z4 = 0,
and the second syzygies
X1(G)^X1X2(B) = 0>
ΧΎΧ2ΧΖ (С) - X,X\XZ (В) - 0.
389. There is no difficulty in continuing the series. The obtaining
however of the reduced forms soon becomes laborious.
Moreover there is obviously a waste of energy because in each case we not
only determine the new forms but also all of those that have previously
presented themselves. It will be advantageous to adopt some method that for
each order only causes the forms of that order to emerge. The whole of the
fundamental forms so far met with, as well as all of those that have so far
presented themselves in the theory of partitions, are such that if
Χΐ*Χ?...Χΐ°
be the form, then am = «e+i-m·
We will therefore for any order impose this condition which clearly
eliminates all forms of lower order. It is possible that by this method
some fundamental forms will escape notice, but those that are most likely to
occur in the theory cannot escape detection.
For use with the added condition we put
XiihX»+i-m = Yni, but Xm = Fw when 2m = e + l,
and examine the sum X Y?1 F2a2I?3....
390. For s = 2 we have simply
142 THE THIRD, FOURTH, AND FIFTH ORDERS [SECT. VIII
391. For s = 3 the conditions become
2a1>a2^or1,
and lead to Ω -
'i^-b^-M
which on reduction is
1
392. For s = 4 we have the same conditions as for 5 = 3, viz.
and we produce the same Υ function, viz.
(г-вда-таг
but since now ΥΊ = ΧΎΧ4> F2 = X^Xt this is
1
(1 - XiXzXzX*) (1 - X.XIXIXd'
and we have thus found the fundamental forms that have already been found
by the first method. · Observe that no syzygies have so far presented
themselves.
393. For 5 = 5 the conditions are
αλ + a2 > a3 > a2,
2a1^a2>a1,
leading to
l
wherein 7,-Ζ,Χ., Fa = Z2Z4, F3 = Z3.
Eliminating 7ц, λ4 and λι in order, this becomes
ΠΓ
Ρ 1
» (1 - λ, F, F2F3) (l - I F2F3) (1 - λ, F, F2Fj)'
l-F!F!Fi
(1 - F,F3F3) (1 - YWi) (I - Υ,γ-iYl) (I - FF^l)
(l~2ί1X2ZзX4XΓ))(l-Z1Z2Z|Z4Z5)(l-X1Z:i^^U^)(l-A^Z^·ЗZ42Z5),
indicating the new fundamental forms
Χ1Χ2ΧζΧ4Χ6, ХгХъХъХ^Хъ, XiX\X\X\Xs, Х1Х\Х1Х\ХЪу
CH. V] THE SIXTH AND SEVENTH ORDERS 143
connected by the simple syzygy
ХгХлХ9Х4Хй. X, X\X\X\X, - ΧΎΧ2Χ\Χ,Χ,. ХХХ\Х\Х\ХЬ = 0.
The new forms either have been or will be met with in this work with the
exception of
X1-5-2 X\ X±Xb ·
This is associated with partitions whose parts are placed at the points of
the incomplete and dislocated lattice
Ά . ^
V
'
w
> >
the magnitudes of the parts being governed by the symbols > placed upon
the lines between the points. The reader who has understood this chapter
will have no difficulty in proving this by forming the Diophantine inequalities
and examining the associated Ω sum.
394. For s — 6, the conditions are
2*3 ^ «! 4- as,
2oCj > a2,
a, >a„
leading to
ν^Κ1-^1-^)'
which quickly reduces to
1
(l - Y, Y,Y:) (l - WiYl) (l - YrYiYl)'
yielding the fundamental forms :
X j X 2 Χχ X 4 X 5 X (J)
А Дз-лзА jA^A,;,
X^lXlXiXlXa,
unconnected by any syzygy.
The reader will notice that the results are more simple for the even
orders.
395. For s = 7 the independent conditions are
2^ η- 2a3 > 2cc.> + o4,
2α2^α4>α3^α2^ al9
2*i > cx2)
144 THE EIGHTH ORDER [SECT. VIII
which finally lead to the function of which the numerator is
(l-7lYlYtYi)0-Y\YlYin),
and the denominator
(1 - YJ-J-,Υϊ (l - ГгВДП) (1 - YJ*Y%Yb
χ (l - Y,Y\Y\YX) (l - YJ-WIYX) (I - YWYIYi),
establishing the fundamental forms
Χ ιX%X 3X* X 5 Χ β X7,
Χ ι X2 X 3 X 4 X 5 ^ б Χ γ,
ХУ "Г2 V2 V2 V у
ХгХ 2Х^Χ^Χ^Χ^Χ7ί
ΧιΧ$ΧζΧ\Χ'δΧ6Χ7}
у уз уз у4 уз У2 у
connected by the simple syzygies
{A)=YXY%Y%YA. YJ\Y\Y\- YiY*YlY\. Y*YIYIYI = 09
(Β) = ΥΧΥ*Υ9Υ<. Υ,ΥΙΥΙΥί - YlY2YiYlY1YlYlYl^0y
and the second or compound syzygy
(вдга. ΓχΠΡ,Γΐ) <ii) - (y,y*yiy\. YiYiYtYb (B)=о.
396. For $ = 8 the conditions are
«2 + «3 ^ «1 + «4>
«1 + ^2^ a3>
a4 > аз > «a,
and the reader will have no difficulty in establishing the fundamental forms
X ^ъХъХ^ХьХвХтХы
Χλ Χ 2 Χ ζ Xl Χ 5X^X7 Χ 8 >
XlX^XzXlXbX(iX1Xii
XjX2X ^Χ^Χ^Χ^ΧηΧξ,
ΧΧΙ\Χ\Σ\Χ\Ι\Χ\Χ»
Ύ Υ'2 V3 У4 у4 уз γι у
connected by three simple and two compound syzygies.
We may now conveniently take stock of the results so far obtained.
We have not so far met with any fundamental form which is not
exponentially symmetrical, and the second method of investigation has effectually
eliminated such from consideration.
This must not be forgotten.
CH. V] EECTANGULAR SYSTEM OF FORMS 145
All the forms that have emerged have the property that the exponent of
Xl9 viz. otj, is unity. Assuming that no fundamental form exists in which
Ъ = 0 it is clear that every form, satisfying the conditions, that has αλ = 1 is a
fundamental form.
397. A large number of the forms are seen to be such that the factors
X1} X2, ... can be arranged in the form of a rectangle such as
ΧΎ X% X-6 X4 ...Χι,
X2 Хг X4 Xs ...-ij+1,
in which tableau the suffix of any X exceeds by unity the suffix of the X
immediately above it or immediately to the left of it.
Ira factors X are involved and the product of them all appears, from the
results hitherto reached, to be a fundamental form.
The product for m ^ I is
ХгХ2Хз.. · X{Zi (Α χΧι+ι... Xm) Xm+iXw+z... Aw+j_2 Ат+г_1,
and we can establish that it is a fundamental form by simply proving that it
is finite and integral for all values of the integers m, L
This will be the next step.
Comparing the form with
ХрХ?...Х?*, *«m + i-l,
it will be seen that
oip^p for I >p,
ap=l for ρ > I and < m 4-1,
amH_p = l — p for I — 1 ^ p.
It has been already remarked that all the Diophantine conditions may be
resumed in the single formula
«<r 4- α2α+τ 4- aa<r+2r 4- ... > «σ+τ + α2σ+2τ 4- flW+w 4- ...,
σ and τ being any integers.
We must first find how many terms of the series
Of or + #2σ-|-τ 4* 0£.4σ+2τ 4* · · ·
appear in the first portion
Z72 уз γι-ι
of the form.
If the first к terms appear, then
к + (Ы)т<г-1,
τ Ι+τ-Ι
or
Μ. Α. II. 10
146 ESTABLISHMENT OF THE [SECT. VIII
we may therefore take к to be the greatest integer contained in the numerical
fraction
Ζ + τ-1
σ + τ ' '
and write it Ix or 1г for brevity.
Again if the first к terms appear in the first two portions
ΧχΧ2 ··· «^l-l (XlXl+i ··· X-m) у
then ka + (k - 1) τ < m,
or & is the greatest integer in
uLzLr
σ + τ '
and we write it J2 or /2 for brevity.
с + τ
Again for the whole form
&σ Η- (A? - 1) τ = m + Ζ - 1,
and к may be written I3 or 7"3 for brevity.
σ + τ
We can now sum the series
«σ + «8σ+τ Η" «3σ+2τ + · ··
for the given product.
We first take Ix terms, remembering that each α is here numerically equal
to its suffix. The sum is
ΚιΟ^+Ιισ + ΙχΤ-τ),
or *Л(«т+τ)+ϋ"ι(σ-τ).
We now take the next /2 — Ix terms, remembering that here each α is
numerically equal to I. This is clearly
Finally we take the next ΙΆ —12 terms, remembering that each a, viz. ap}
is equal to l + m — p. The series to be summed is
«(/2+1)σ+/.ι· + α(/2+2)σ+(/ί+1)τ + · · · + «/3σ+(/3-1)τ,
or
(7,-Ι,)(Ζ + ίη)-{(7,+ 1)σ + Λτ^^
or (/3-72)(/ + т)-4(/3~/2){(/2 + /з + 1)^ + (/2 + /3-1)т}.
Assembling the three portions of the sum and simplifying we find
= ^(7? + /1-/Ι)(σ + τ)
- £/ц (2ί - σ + τ) - £/2 (2иг - <τ + τ) + J /3 (2ί + 2m - <r + τ).
CH. V] RECTANGULAR SYSTEM 147
Next in regard to the series
Яг+т + #2<г+2т Н" а3<г+3т 4" · · ·
we have, analogous to Il9 T2J Ja,
Jx = Ji = greatest integer contained in ,
σ + τ σ + τ
r Ζ + m — 1 _ r l + w-1
σ+τ σ + τ
and we find for the sum of the series
α<τ+τ + α2σ+2τ Η" α3σ+3τ + · · · >
the three portions \J\ (σ + τ) + ^ Jx (σ + τ),
(Л -Л) г,
(/.-/,)(ϊ + ι»)-1(/3-Λ)(Λ + Λ + 1)(σ + τ).
Adding and simplifying we find
Н</! + Л-Л)(<г + т)
-£Λ(2Ζ-σ-τ)-£^2^-σ-τ) + £/3(2ί + 2^-σ-τ).
The general Diophantine inequality therefore assumes the form
*α!+/5-/»(«τ+τ)
- \ Ιλ (21 - σ + τ) - £ /2 (2m - σ + τ) + \I3 (21 + 2m - σ + τ)
^(J* + j;j- J») (σ + τ)
-iJΓ1(2г-.σ-τ)-iJ2(2ш-σ-τ) + JΛ(2г + 2m-σ-τ),
and we must shew that it is satisfied by the values of IXl I2l J3, Ju J2, J&
given above in terms of Z, m, σ, τ.
Since ΙΎ is the greatest integer in and Jx the greatest integer in
it is clear that Ιλ is either equal to Jx or to Jx +1.
σ+τ χ
Similarly L2 must be either equal to X2 or to J2 +1 and /3 to e/"3 or to
Λ+1.
Also Д + I2 = Ii h Z> must be either equal to
σ + τ - σ + τ
Tl+т+т-1 г -
/s . or to i3 +1,
σ + τ
10—2
148 ESTABLISHMENT OF THE [SECT. VIII
and Ji 4- J2 =5 Jx h J2 —— must be either equal to
σ + τ σ + τ ^
rZ+m —1 Γ Ί
j3 or to J3 — 1.
σ + t
We have therefore the relations
Ix = Jj or Ji + 1, Д + I2 = J3 or J3 H-1,
/2 = ^2 ОГ «^2 +1, Jl 4" J2 = J» 0Г e/3 — 1,
/3 — ^s ОГ J"3 + 1.
All of these alternatives are not simultaneously possible; for instance if
I\ = J\> I* = «^2, £> = Λ) we cannot have Λ 4-12 = /3 4- 1 because that would.,
lead to Jx 4- J2 = Jz 4- 1, a relation which is barred.
There are just ten possible sets of alternatives, viz.:
Case I
1χ = ϋ1> 12 = J2} Jt3 = t/3J li 4* 12 — i3, t/j 4" e/2 = «/3.
Substituting in the inequality we find
/з^Л + Л,
which is satisfied because Ix 4- J2 = /3.
Case /J
Jti = t/i + 1, ·Χ2==«/2> ■*3=S<^3J ·*1 4" -*2 == ^3> wi + W'2 = W3 — 1
leads to J^ > ,
<T 4" Τ
and Ji being the greatest integer in , where σ 4- τ is at least unity, the
relation is satisfied.
Cose III
ii = Ji 4-1, 12 = J2, i3 = t/85 ij 4- J-2s=: *з 4- 1, t/i + t/г = «/»
leads to Jx > ,
σ + τ
satisfied because σ ^ 1.
Cow /F
J-l β t/i, Jt2 == «A 4" lj -*3~<^3? A 4" Jt2 = Jt3, «/1 4" «^2 == *^3— 1
leads to Ja ^ 1,
*r 4- τ
which is true by the definition of /2-
CH. Vj RECTANGULAR SVSTEM
Case V
I\ = J\y 12 = «/2 "Ь 1> *8 = t/3 J -Μ + Ζ2 = 13 + 1? «/χ + t/2 = t/s
leads to Λ > >
which is obviously satisfied.
Case VI
1г = ^ +1, /2=/2 +1, i*3 = /3; /i +12 = /3 +1, j; + j"2 = js
ι л 4. r -. l + m-σ
leads to J3 ^ ,
*r -t- τ
which is clearly satisfied.
Case VII
Ii = Ji + 1, /2 = f/2, ί} β J-i + 15 Λ H- /2= *з, «m 4-1/2 = «/й
leads to «72 ^ —■— ,
σ + τ
which is right.
Case VIII
II = */i, i2 = t/2 + 1, /3 = t/3 + 1 j ij ·+- i2 = i 3, Ji + «/2 = «/3
leads to J^ ^ ,
σ* + τ
which is satisfied.
Case IX
/^./i + i, /2 = /2 + ι, /3»·7"3 + ΐ; λ + ι^/*, j; + /2 = j3-i
leads to a relation of equality between the two sides.
Case X
/,β-Λ + 1, Ι2 = Λη-1, Ι,—Τ, + ΐ; Λ+Ζβ-Λ + ΐ, J^J^Js
leads to σ + τ^Ο,
which is correct.
Hence the inequality is in every case satisfied.
398. This proves that the form
X\X\X\ ··· -3-zll (-3Γг-ЗГг-bi ··· -^m) -^w+i-^»7+2 ··· Щ-^л-^Хг-ил-х
is finite and integral and also a fundamental form.
This form plays an important role in a later section of this work.
It may be regarded as a First Standard Form.
150 FORMS WHICH ARE OUTSIDE THE SYSTEM [SECT. VIII
The fundamental forms, that have emerged so far, not included in the
tandard are
u£\ Л 2 Л s Л 4 2l 5 A e Ji 7 ,
γ γ γζγζγζγ γ
Χι Χ2 Χ ζ Х-Ь Χ$ Χ β Χ7 Χ* у
XV2 Υ2 ]Γ3 V3 Υ2 V2 Υ
and it may be desired to obtain information concerning them.
In the standard form if Op = Op+1 no exponent Op+q is greater than ctp. We
may therefore eliminate the standard forms from consideration by imposing
other Diophantine relations such as
ctp = Op+i < а^+2
upon the conditions to which the exponents are subject.
In this way there is no doubt that other Standard Forms can be obtained,
but for the purpose of this work it is not necessary to carry the investigation
any further.
CHAPTER VI
ON THE ALGEBRAIC FORMS OF INTEGERS
399. We may apply the method of the preceding chapter to another
question which is not directly connected with the subject of partitions. In
the binomial and multinomial expansions, the exponent being a positive
integer, every coefficient is an integer. This fact depends analytically upon
the circumstance that the product of any m consecutive integers is divisible
by factorial m; we have
n-f 1 n + 2 n + m
1 * 2 ■■* m
an integer for all values of n.
The present question is the determination of all values of alt cr2, ... aw for
which the expression
(n + 1 \αι /n + 2 \a* in + m\am
{ 1 ) { 2 J '"[ m )
is an integer for all values of n. In particular the discovery of the finite
number of fundamental products of this nature, for a given value of m, from
which all the forms may be generated by multiplication; and the complete
syzygetic theory.
We write the expression in the notation
and observe that it is derived from the product
Ttix?...xtr
discussed in the previous chapter by putting χ equal to unity. All the
algebraic products which are finite and integral give rise in this manner to
arithmetical products which are integers. This however is as much as can
be said, for beyond this the two theories proceed upon widely divergent lines.
As might be expected, the arithmetical products form a more extended
system than the algebraical.
152 FORMS OF ORDERS TWO AND THREE [SECT. VIII
400. To commence with the Order Two or
(η + l\e» (n -f 2\a*
(Ч-ЧТ-г?-^·
the product is an integer when η is even, but when η is uneven we must
have
oti > ot2.
Hence S Ν? 2V> = Ω - r
>(l-XiT1)(l-iJyi
shewing the trivial result that ¥x and ΝΊ¥2 are fundamental forms.
401. For the Order Three, where
we have to consider the divisibility of the numerator numbers by powers of
2 and 3, and since if η be uneven one of the numbers η -Ь1, w + 3 must be
divisible by 4 it is necessary to investigate the conditions according as η is
of the forms 4m +1, 4m + 3, 3m + 1, 3m 4- 2, the forms 4w, 4m + 2, 3m
yielding no conditions.
When η is of the form condition is auxiliary
4m +1 oil 4- 2as ^ α2 λ·ι
4??г + 3 2α2 -f α3 ^ α2
3m -h 1 α2 ^ α3 Хз
3??ι +2 ^ ^ α:ι λΛ
It will be noted that these inequalities are not independent since addition
of the first and fourth produces the second. We therefore omit the second
as superfluous and assign auxiliaries \1} λ2, λ^ as shewn. We have therefore
1
1Νΐ>ΝρΝρ = Ω·
Eliminating \ this is
1
a-
(1 -λ^ΛΓ,)(l-i jyt) (l-hN2N3)
and eliminating λ,
ι
a.
> (1 - XXN,) (1 - £ 2Vt) (1 - WiN.K)'
and this by a formula on a previous page is
(1 -#,)(! -JMW -Ν,Ν,Ν,)^ - ^ЩЩ'(1 - ΝΧ№Ν3)'
CH. VlJ FORMS OF ORDER FOUR 153
establishing the new fundamental products
-МЛГ,, ΉΛ№ ЯгЩ^,
connected by syzygies as shewn by the numerator terms.
We observe one form NiNlNs which is not derivable from the algebraic
theory of the previous chapter.
402. The forms are exponentially symmetrical. On proceeding to the
Fourth Order unsymmetrical forms appear for the first time. A few
experiments shew that the unsymmetrical forms are of the form
so that we may divide the investigation into two cases.
Case I. The form ΝρΝ&ΙΓρΝ?.
Case II. The form NpNpNp.
The conditions for the general form JSFpNpiTpNi*, obtained by discussing
η in the forms 4m -f 1, 4w Η- 2, 4m + 3, 3m -f 1, 3m + % are
αϊ + 2α, ^ α2 4- 2α4,
α2 ^ α4,
2αχ -f α.Λ ^ α2 + 2α4,
α2 ^ α»,
«ι 4- α4 ^ α8.
For Case I these become
«2 > «11
2α! ^ α2,
leading to Ω
>(1-^ад)(1-^ад)
-Ω. *
* (1 - \N,KzWi) (1 - ^-ВД>)
1
" (i - лГхУ.-ад) (i - л^маг,)'
and we have merely the fundamental forms derivable from the algebraic
theory.
For Case II the conditions become
αχ > Oj + 2a4>
otj ^a4,
164
FORMS OF ORDER FIVE
[sect, лап
leading to
η I
>(i-W(i-^)(i-^)
= Ω
> (i -χ,лто (ι - £ж) (l- ^-ВД)
1
- (i - no (i - iw (i - ж?^2ж4) ·
establishing the new fundamental form
Forms of this species occur in the case of every even order but never
present themselves for an uneven order.
The general form is
NpN?M?N?>... Л>.
403. For the case of the Order Five there is a very complicated system
of fundamental forms. They appear to be, by an investigation which is too
long to reproduce here, thirteen in number, viz.
N.NlNlNiNr,,
four which are derivable from the previous algebraic theory;
two which are symmetrical but do not appertain to the algebraic theory;
NlNlNtN\Nt,
and seven which are unsymmetrical.
It will be useful to verify these forms a posteriori.
With the first four we need not deal.
As regards the next two which are symmetrical we note that the conditions
that MpN^NfsN^Nf* may be an integer, obtainable by discussing w in the
Cfl. VI] FORMS OF ORDER FIVE 155
forms 4ra +1, 4m 4- 2, 4nn + 3, 3m 4-1, 3m, + 2, 5m + 1, 5m + 2, 5m + 3, 5m + 4
are
αχ + 2a3 + a6 > «2 + 2a4,
2a! 4- a3 + 2a5^a24- 2a4,
aa + a6^a3,
ai + a4 ^ и»>
«4 > «б>
a3 > «б>
that corresponding to 5m + 3 being implied by the remainder.
Putting herein a5 ~аг> α4 = α2 and further Oj = olx -f a2 in order to find the
form N\N\N\N\N\ and to exclude some of the others, we find
4αι>α2, 5α1>2α2, a2 ^ аг
for the form
and we are led to
η 1
>(1-^^ад)(1-^вд^)
= il
> (1 - λ?λ^ К2Щ^Щ (l-^| ЛГ.*,^)
1 + Х^ЩЩЩЯ, + ± ЪЩЩЯИГ.
= il _±L
> (1 - λΙΝ,Ν,ΝΙ^Ν,) (l - ^i-^Al-W»)
_ (i - ν,νΜ^ν,) (ι - mmNiNim) ·
establishing the form ЩЩЩЩЩ.
If we take the special condition «3 = c^ instead of a, = at + a.2 the conditions
become
and we are led to
1
= Ω
(l-^iMT^l-bA^)
> (i -х^щя^щ (ι - 2j #2i\r4)
1
" (1 - Ν,Ν,Ν,Ν,Ν,) (1 - ЩЩЩЩЩ)'
establishing the form ЩЛГ1ЩЩЩ.
156 SOME HIGHER FUNDAMENTAL FORMS [SECT. VIII
For the unsymmetrical forms, it will be observed that as regards the first
five of them «5 = 0^, <x2>ct4; and in the last two a1>a6} α2 = α4. Making
use of these special conditions the forms are readily established.
For the Order Six we will examine the form
= (n + * V1 (n + 2 V8 {ό^±*Υ4 (n+Jiy*
The conditions are easily seen to be
«! > a2 + 2a4 4- ae,
«2 + «6 ^«4,
η being of the forms 4m + 1, 4m H- 2, 3m 4-1, 3m + 2 respectively.
Obviously the fourth condition is superfluous.
We find
»α-χΛ)(ι-^.)(,-^Α)(ι-^.Λ)
-β-
» (i - if,) (ι - λ,λ,ϋτ,Λ·,) (ι - J- дгглг.) (ι - ~ jv.jv.)
= ίϊ
» (ΐ - лт.) (ΐ - мда (ι - £<ВД) (i - >№.ВД)
establishing the fundamental forms
H\NtirtN„
Similarly for the Order Eight it is easy to find the fundamental forms
CHAPTER VII
THE THEORY OF MAGIC SQUARES
404. The method of Partition Analysis is applicable to all arrangements
of integers which are defined by homogeneous linear 'Diophantine Equalities
or Inequalities; and when the properties which result from the definition
persist after addition of corresponding numbers a syzygetic theory results.
Many instances of configurations of integers in piano or in solido will occur to
the mind as having been subjects of contemplation by mathematicians and
others from the earliest times. Amongst these are those of the nature of the
magic square. The properties of such squares are usually stated in terms of
the sums of the numbers which appear in the rows, columns and diagonals.
In an ordinary magic square of order n} the square is divided up into n2
compartments; the n2 compartment numbers are all different, being usually
the first n2 natural numbers, and the arrangement is such that every row,
every column and each diagonal contain numbers which have the same sum.
As distinct from an ordinary magic square a "general magic square" is
defined to consist of ri1 integers arranged in the compartments in such wise
that the numbers in the rows, columns and diagonals add to the same
number, zeros and repetitions of the same number being permissible among
the integers.
We may regard general magic squares of the same order η as numerical
magnitudes. To add two such magnitudes we add together the numbers in
corresponding positions or compartments to form a new magnitude which
obviously is also a " general magic square." We can form a linear function of
such magnitudes, of the same order, the coefficients being positive integers,
and it also will be a general magic square. An ordinary magic square is a
particular case of a general magic square, but the particular property of an
ordinary magic square that it must involve different integers in the
compartments prevents the formation of new squares by addition, so that within
the group of such squares there is no syzygetic theory.
158
THE SYZYGETIC THEORY
[SECT. VIII
405. We proceed to investigate the syzygetic theory of general magic
squares of the Third Order. Such squares do not exist in the case of the
Second Order except in the trivial case
a a
a a
but there are squares in which the row and column but not the diagonal
properties are in evidence.
For let such a square be
"1
«3
This must clearly have the form
where if a5 be some integer
and we find
%xpxpx%s = Ω
α3 + c*2 = α5,
(ΐ-λΛοα-λ^ι-^)'
wherein we recall that'the symbol fl denotes that in the ascending expansion
of the function to which it is prefixed we are to retain only those terms which
are free from the auxiliary λ.
The expression clearly has the value
1
{l-xYxb){l-x2xb)'
the denominator factors denoting the fundamental solutions
αϊ
1
0
«2
0
1
αδ
1
1
Thus we have the fundamental squares
10 0
0 1 1
and the most general square of the type
I1 °
0 1
+ «s
0 1
ι o:
«1
a,
a trivial result.
a
СН. VII] THE THIRD ORDER 159
406. Passing to the third order let the square he
ax a2 «3
«4 α5 «β
Oj <x8 Og
and let the number associated alike with the sura of each row, each
and each diagonal be aI0; we then have the eight equalities
Λΐ + «2 + «3 = «4 + «5 + <*6 = «7 + «8 + «9 = «10,
<*1 + «4 + «7 = «2 + «6 + «8 = ЛЗ + «6 + «9 = «10»
а! + аБ + а9 = «s + аБ 4- а7 = а10.
We require the sum
for all sets of integers satisfying the equalities.
Associate with the equalities the auxiliaries
Aj Λ»2 λ^
λ4 λ»5 Лб
λ? \8
respectively, each equality having а10 on the dexter, so that λ^ is associated
with α4 + α5 + α6 = α10.
The sum is
1
(1—λ1\4\α;ι)(1-\1Χ6χ2)(1—\1\β\8χ3)(1—λ2\χ4)(1—λ2Χ5λ7\8χ6) j #
(1-\2\χ6)(1-\ζ\4\8χ7)(1-ΧΛ\5χ8)(1-\,\ΰ\7χ^ ( 1 - —;-_-__._- χΛί
\ Л,1Л2Л3Л4ЛбЛ6Л7Л8 /J
Eliminating \l9 λ2, Хз, λ4, λ5, λ6 in any convenient order, this is found to
have the expression
Ω _J -
1(1 - Х^/ад,^) f 1 - z-XoXbXvXho) ( i - ^-oc^x4x8xlo\\
(1 — \§χ-όχ6χ7χϊ()) II — — x2x4x^x^ J
+ Ω
j (1 - Х\хххьхъх^) (1 - — akWtuCjXn j ( 1 - - а?8я4я?8л?10 j
Ι ί 1 - г- #2#·Α#ιο JΙ 1 - Г2 Х1%гХ4ХвХ6Х»х(0) \
"~ Л?jXqХ8d?jQ ^± Х^Х^Х^Х^Х^Х^Х7X8XqXjq)
(1 - Χ?χΎχ5χ9χ1ύ) ί 1 - — x»x6x7xl0) ί 1 - — χ^χ&χΛ
Λ Γ
Ι (1 - \lx3Xsx7XlQ) ( 1 - — Я?1Й?вА%Я?ю) ί 1 ~ д2 #ι#*#Λ#8#9#ιο) j
and we may pause to draw some deductions.
+ ft
160 SQUARE WITHOUT DIAGONAL CONDITIONS [SECT. VIII
407. If the general magic squares we are considering are deprived of the
properties of the two diagonals we have merely now to put \ = λ8 = 1.
The real generating function then reduces to
Jl "~" ΧγΧ%Χ§Χ4Χ§Χ§ΧγΰΟ%Χ$Χ]β
((1 - a\x6x9x1Q) (1 - %iX6xQx10) (1 — #2#Λ#ιο)| '
((1 - #2#6#7#io) (1 ~ #3#4#8#1θ) (1 — X^u^h^lQJ )
indicating the fundamental products
#1#5#9#10 #l#e#8#10 %2X4XS%10
connected by the simple syzygy
XjX^XqXiq . ^2*^6^7*^10 · %3^4*^8*^10 — *% 1^6*^8*^10 · ^^^^lO · ^Z^b^7^l4 = ">
corresponding to the fundamental squares
^аздЯю
10 0
0 10
0 0 1
XiXqX^Xjq
10 0
0 0 1
0 10
я^хцянх^
0 10
0 0 1
10 0
XqX^XqXiq
0 10
10 0
0 0 1
Χ$Χ±Χ$Χ\§
0 0 1
10 0
0 10
X% Χ$ΧηΧ\§
0 0 1
0 10
10 0
(the exponent of x10 being unity shewing that the number associated with
the rows and columns is unity)
connected by the simple syzygy
10 0 0 1
0 10 + 00
0 0 1 10
0 0
1 + 1
0 0
0 1
0 0
1 0
10 0
0 10
0 0 1
= 001 + 100 + 010
0 10
each side being equal to
111
1 1 1
0 0 1
10 0
— X\ #2 X% X4 X5 Xq X7 Xq Xq X\q ·
1 1 1
This is the complete syzygetic theory of these squares.
CH. VII] THE PRINCIPAL DIAGONAL ALONE INVOLVED 161
+ Ω
To obtain the enumerating generating function we put
ос1==%2 = а}8 = х4 = хб==осв==(1с7 = хв = а;9~а} and #ιο = 2Λ
when we find τ- -^-.
(1 - a?y)«
In this the coefficient of a?nyn represents the number of squares such that
in each column and in each row the sum of the numbers is n. It has the
-"-'Civet1)·
408. Resuming the discussion of Art. 406 we' eliminate Xy and find
(1 - XixsXsXtXio) 11 - — x2x^9x10 j j
-— ΧιΧ6Χ$Χ10 ул. — Х^Х^ЩХ^ЩХ^Х^ЩХ^Хх^)
Л>8
(1 - ΧχχΙχΙχ^Ιχ^) (1 - ΧχχΙχ^χ^χΙο) \ '
1(1 - Χ&όχ6χ7%10) ί 1 -— ΧχΧβΧβΧχο) ί 1 — --2 x^oX^XqXs^xIojI
and the reader should observe that the second fraction of Art. 406 has the value
zero and contributes nothing to this result. But if we wish to discuss the
squares which have the principal diagonal property but not that associated
with the secondary diagonal, we do not omit the second fraction referred to
but add it to the two just obtained and then put λ8= 1. We then get on
simplification
ί —~ ΧγΧ^Χ^Χ^Χξ^Χ^Χ^X^XqX·^
f(l - ^aVVlo) (1 - #2#Α#1θ) (1 - #3#5#7«1θ)1 '
( (1 - x^x^xlx^x^) (1 - х^^х^х»^) j
establishing the five fundamental products
X\ Xq X% Xiq, X2 X± Xq Χι ο, №ц 00ъ ^7 &ιο >
ΧιΧ\χ*> x\ x\ Χϋ #ιο, Χι x\ x\ #6 Щ, xv #ϊο >
connected by the simple syzygy
(χιΧ6χ8χ1())2 (%>>x4Xi}Xiof (%#5#7#ιο)2 = {χ^χ^χΐχ^χ^) (χΛ xi%iXbXlxdx%)}
corresponding to the fundamental squares
10 0
0 0 1
0 1 0
1
0
2
0
1
0
2 0
1 2
0 I
1
0
0
ΰ
0
1
1
2
0
0
0
1
0 2
1 0
2 1
0 1
1 0
0 0
Μ. Α. II. 3 1
162
THE SECONDARY DIAGONAL ALONE INVOLVED [SECT. VIII
connected by the simple syzygy
1 0
0
0 0 1+2
0 1 0
=
0 1
0
1 0 0 + 2
0 0 1
1 2 0
0 12 +
2 0
1
0 0 1
0 10
10 0
10 2
2 10
0 2
1
squares, all of them, such that the principal diagonal is associated with the
same number as the rows and columns.
Similarly if it is the secondary diagonal that is to be associated with
the rows and columns we arrive at the real generating function
JL —~ X^X^X^X^X^X^X^X^X^X·^
f (1 - Я^вЯоЯю) (1 ~ #2#β#7#ιο) (1 - #3#4#8«%))) '
( \Д — ^^s^B^^V'k'a^ao/ ν Ι — ^г^'з^^5*^7*^9^10) )
from which the fundamental squares and the syzygy connecting them can be
written down.
In both cases of the one diagonal theory the enumerating function is
1 - x^y6
(1-а?уУ(1-х»у*)2)
in which the coefficient of иРъуп must be sought in order to enumerate the
squares such that each row, each column and one selected diagonal are to be
associated with the number w.
409. Resuming the discussion we finally eliminate λ8 and arrive at the
real generating function
1 - 2xi
2 li 4 /)X& 7**"8 9 10 ·* Х\ХчХ'1Х^Х^ХяХ'7Х^Х[)Х\{)
|(1 - х^х^х^х^) (1 — х^а^х^я^) (1 - а?1а^х^х7о^с^{М
[ \L Х^ХцХ^Х^Х^Х^ХЦ)) \L XiU'sXxXiXuXqCCjXuXhXiq) j
indicating the fundamental products
X\ Xo X5 Xq X4 Xq Хщ ,
ι .j 4Χ§ΧκΧ$Χ\{))
Χ ι Χ$ Χ5 *&β &h Я 8 *^ιυ »
Χ 2 & у Χ ι Χζ Χγ Χ§ Χ\ο j
Χ γ ff О Χ·£ Χ^ it g itftXy XqX^ X^Q j
connected by the first syzygies
Хл ОСуХщ/ЬцХуХдХц) . Х^Х^Х^Х^Х^ХуХцу
= ΧιΧ^ΧζΧβΧγΧχΧι^. Χ^Χ^Χ^Χ6Χ7Χ^Χ'ι^
~ {^XiX^X^X^XqXqXjX^X^Xi^) ,
CH. VII] PROPERTIES OF BOTH DIAGONALS IN EVIDENCE
and writing these
AB=CD = E\
we have the second order syzygy
E* (AB - Я2) + AB (CD - E*) = 0,
corresponding to the fundamental squares
163
1 2
0 1
2 0
0
2
1
1
2
0
0
1
2
2
0
1
1
1
1
1
1
1
2
0
1
1
1
1
0
1
2
1
2
0
0 2 1
2 10
10 2
111
111 =
111
2 0 1
0 12 +
12 0
0 2 1
2 10
10 2
in which both diagonals share in the property of the rows and columns.
The first syzygies connecting them may be written
12 0 110 2
0 12+210=2
2 0 1 I 0 2 1
The enumerating function is
(l-#18yff)2
(l-afitff '
in which the coefficient of xmyn must be sought.
Moreover η must be of the form 3m so that we have to seek the coefficient
oia?mymin
(1-*У)2(1-Л/)-5,
and this is in fact ma H- (m + l)2.
The ordinary magic squares, the component integers being 1, 2, 3, 4, 5, 6,
7, 8, i), arc eight in number. Calling the fundamental squares as written
above
А В С D
Ε
these are
+ 30 + 2? =
+ W + E =
8
1
6
2
7
6
3
5
7
9
5
1
4
9,
2
4
3,
8
SA+C+E =
, 34+D + 2?-
6
1
8
4
3
8
7
5
3
9
5
1
2
9
4
2
7
6
11—2
164
ANOTHER VIEW OF GENERAL MAGIC SQUARES [SECT. VIII
B + BC + E =
B + SB + E =
8
3
4
2
9
4
1
5
9
7
5
3
6
Ϊ,
2
6
1,
8
3B + C + E =
8B + I) + E =
6
7
2
4
9
2
1
5
9
3
5
7
8
3
4
8
1
6
There is no theoretical difficulty in dealing with the squares of higher
orders, but even in the case η = 4 there is practical difficulty in handling the
Ω, generating function.
410. Apart from the syzygetic theory the enumeration of general magic
squares of given order and given number associated with the rows, columns
and diagonals may be viewed in the following manner·
If we are not concerned with diagonal properties the squares have already
been enumerated in Section V.
If hm denotes the sum of the homogeneous products of degree m of the
η magnitudes
αι> a2> ··· an>
and hm be raised to the power η and be developed so as to be a linear function
of monomial symmetric functions, the coefficient of
is the number of squares of order η which have the property that the sum of
the numbers in each row and in each column is m. (See Section V, Art. 199.)
Thus if τη = 3, η = 2,
Ц = («ϊ + «S + οία, + αιαϊ)»= ... + 4ю?«5 + ...,
the coefficient 4 enumerating the four squares
30 03 21 12
0 3 3 0 12 2 1
411. To introduce the diagonal properties, let кт>ы denote hm when in it
<xs, orn_s+1 are replaced by \ccSi μοίη_8+1 respectively.
Form the product
and it will be found that the coefficient herein, after development, of
is the number of general magic squares of order n, associated with the
number m
CH. VII]
PARTICULAR EXAMPLES
165
To see how this arises take η = 4, m = 1 and form a product
(λ^ + eta + a3 4- μα4)
χ ( аг + λα2 -f μα3 + a4)
χ ( αλ + μα2 + λα3 4- α4)
χ (/*«! 4- я2 + «3 + λα4)·
When we multiply out in order to obtain the term involving
λ,μ»α1α2α3α4,
we must take one portion of the term from each of the four factors and
regarding the elements of the four factors as corresponding to the
compartments of a square of order 4, this means that in picking out the product
X/ta^OgGt* we take an element from each row of the square. Again since
аь «2, аз> a4 only occur in the first, second, third and fourth columns of the
square respectively we must also take an element from each column of the
square. Finally in order to obtain λμ, we must choose elements from each
diagonal of the square.
Ex. gr. If we were to select in the multiplication o^, μα3, ctlf λα4 from the
first, second, third and fourth factors respectively, the selection would
correspond to the square
10 10 0
0 0 10
10 0 0
Ι ο ο ο ι
412. Again take η = 4, m = 2. We form the product
[λ2α2 + Χμα^ + /Λ| 4- (каг + μαΑ) (α2 4- α,) + α%+ α^ + <*з}
χ {λ2α! + λμα»03 4- μ2α! + (λα2 + μα*) («ι + «*) 4- α'ϊ 4- α^ 4- α*}
Χ {λ2α| 4- λμα2α3 4- μ*ά% 4- (λα3 4- μα2) («ι + α*) + «? + «ι«ι 4- α4}
χ {\*aj 4- λμα, α4 4- μ2α? 4- (λα4 4- //tfi) (α2 4- α3) 4- οξ + «2«з + «з}·
In forming the term which involves the product
λ η η О ·> О f>
2μ,2α{α2α3α!,
we regard the successive factors as corresponding to the successive rows of
the square; the suffix of the a as denoting the column, and λ, μ as
corresponding to the diagonals. The exponent of the α represents the number
which is to be entered in the compartment of the square, this compartment
being specified by the suffix of the a and the factor in which the a occurs.
Thus if in performing the multiplication we select the terms
λ-α'ί, μα&9 μ<ζ2<χ4, α2α3,
166 ENUMERATION OF CERTAIN SQUARES [SECT. VIII
from the four factors respectively, we have the corresponding square
2 0 0 0
0 0 11
0 10 1
0 110
In whatever manner we select the factor elements we have in
correspondence a general magic square.
These examples suffice to establish that the number which enumerates
the magic squares is identical with the coefficient of
λ>Λ(βΛ...Οη)«,
which arises from the product
If we wish to make any restriction in regard to the numbers that appear
in the 5th row of the square we have merely to strike out certain terms from
the function
For example if no number is to exceed t we have merely to strike out all
terms which involve exponents which exceed t.
If the 5th row is to involve numbers which collectively are included in
certain specified partitions of m we merely strike out from hmy8 all terms
whose exponents do not collectively correspond to one of such partitions.
If the 5th column of the square is not to include the number t we must in
each factor strike out every term which involves aj. In fact each and all of
the n2 numbers in the square can be restricted in any desired manner.
If ordinary magic squares are under consideration we must from hm)S (for
all values of s), m having now a fixed value in relation to n, strike out all
terms which involve a repetition of exponent. Also in picking out the η
elements which form \ηημηι<χψοξι... α™ we must take care that ct8 (for all values
of s) never appears twice with the same exponent. In both cases zero counts
as an exponent. Also neither λ nor μ in the elements must occur twice with
the same exponent, zero being counted as an exponent.
413. To resume the general subject we will now consider the enumeration
of the squares which are such that the sum of the numbers in each row and
in each column is unity, the sums of the numbers in the λ and μ diagonals
being any given numbers.
Observe first that if the numbers occurring in the diagonals are immaterial
the number of the squares is η ! because
К
CH. VII] CONNECTED WITH UNITY 167
Consider an even order 2n and form the product
(λα! + <X2 + Os + ... + «2n-2 + a«i-i + M«2n)
X ( <*! + XOs + O3 + ... + «271-2 + ^271-1 + «31»)
χ ( θ! + «a + λα3 + ... Η- μα2η-2 + «sn-i + ctm)
Χ ( «ι + «2 + μ<*3 + · · · + λα^-β + «2λ-ι + am)
Χ ( «1 + /&«£ + 03 + ... + 0С2П-2 + λ*2»1-1 + «2η)
χ (μαΎ + α2 + αη Η- ... 4- о^-г Η- ««λ-ι + Xam).
When the multiplication has been performed we require the complete
coefficient of
а1 «Л · · · ^271—2 а2П—1 **2Я·
Writing 2o = A, the £th factor of the product is
h + (λ - 1) at + (μ - 1) α2η-ί+ι,
and since we only require the quantities a with unit exponents the product
of the complementary factors
h + (λ - 1) «ί + (μ - 1) Ojn-i+b
h + (λ - 1) α2η_ί+1 Η- (/α -1) αί?
the second of these being the (2n — £ Η- l)th factor of the product, is effectively
Α2 + (λ + μ - 2) (at + α2η_ί+1) Α + {(λ - Ι)2 + 0* - I)2} ъ<ь^+19
and the complete product may now be written
П* [A» + α + Μ - 2) (α, Η- a2n_t+1) A + {(λ - Ι)2 + (μ - 1)а} *t *2n_t+1].
Consider these я factors of degree 2. Each one of them involves explicitly
two of the quantities a, say at and or2n_i+1, neither of which occurs explicitly in
any of the other η — 1 factors. In the product of the η factors therefore each
of the quantities α occurs explicitly to the power unity. Hence if we write
the product in the form
hm + AJi™-1 + ЛаА3*-» +...+Am,
Am is a linear function of products of the quantities a, each of which contains
m different quantities a, each with the exponent unity.
In particular the reader will readily observe that
4i = (\ + /a-2)So,
Λ2η « {(λ - Ι)8 + (μ - Ι)8}* «!«,... α2η-ι«2η.
Now Am = ...+m!Saia2... «m-iOre + ···>
as is evident by operating with the differential operator Д of Section I
m times successively.
168 THE SYMBOLIC SOLUTION [SECT. VIII
This is the only portion of the development of hm in which the exponents
of the a's do not rise above unity. Hence for the present purpose
hm = m 1 Xsj a.2... ofm_! a,n effectively.
The co-factor of hm in the product is A.2ii—m which is a sum of products of
the quantities a, each of which contains Ъг — m different quantities a (each
with exponent unity) and has a certain function of λ and μ as a coefficient.
Each of the α products which occurs in Am^n can be multiplied into one of
the members of the sum
%αχα2... (V.!^
to form the product αλα2... o^n-i^n because for this purpose we associate an a
product occurring in Am-.m with that member of Σα^... аш^ат which does
not contain any α which occurs in the α product. That particular a product
will not be multiplied into any other member of Sa^... вт-Лп because that
would produce an a with an exponent 2.
The result of the multiplication
Л hm
•П-271—т'1'
is to produce as many effective terms as Am^.m contains a products.
414. We may therefore, to obtain the desired coefficient, put in
each quantity a, that occurs explicitly in -4зл-»л> equal to unity and hm equal
to m !. Hence therefore in
h?n + A^-1 + Ash*»4* + ... + Am,
we may put each a, occurring explicitly in the quantities A} equal to unity
and km = m ! where m ranges from 2n to unity.
It is thus established that in the product
Π [Λ2 + (λ + μ - 2) (at + α2η_ί+1) h + {(λ - Ι)2 + (μ - Ι)2}
ί = 1
we may put each explicitly occurring α equal to unity and regard h as a
symbol such that on completing the multiplication any power of h, say hm,
is to denote m !.
Thus the desired coefficient is expressed by
{}1/> + 2(\ + μ-2)}ι + (\-1)* + (μ-1)%
or by {A2-4A + 2 + 2 (λ + μ) (A -1) 4-λ2 Η-μ/2}η,
where, after development, A™ is to be put equal torn!.
The coefficient is by this means represented symbolically as an 72th
power.
CH. VII] VERIFICATION OF RESULTS 169
415. Putting A2 — 4Д H- 2 = η2, h - 1 = ηγ it is more conveniently written
[η* + 2(Κ + μ)ηι + \* + μ*}η.
For an even order 2n the coefficient herein of
\ιμ™
enumerates the squares which have one unit in each row and in each column,
I units in the λ diagonal and m units in the μ diagonal.
For an uneven order 2/i-fl, the (n + l)fch factor corresponding to the
(n -b l)th row of the square is
Ιι+(Χμ-1)οίη+1}
and thus the product of the 2n + 1 factors may be written
if [Α2 Η- (λ + μ - 2)(at Η- α2η_ί+2) h + {(λ - Ι)2 + (μ - Ι)2} a^n-t+J
*=ι
χ{Α + (λ^~1)αΛ+1},
and now the coefficient of α^... ^ma2n+i is, by the same argument, represented
by the symbolic form
[η2 Η- 2 (λ 4- /г) ^ + λ'2 Η- μ2}η Oh Η- λμ),
the complete solution in respect of the uneven order 2w + 1.
416. We may test the truth of these results in two ways.
(i) If we put λ = μ = 1 the coefficient is (2n)! for even order and
(2n + 1)! for uneven order. This is verified because our symbolic expressions
become in this case
hm and hm+1 respectively.
(ii) If we put λ = 0, μ = 1, the coefficient is equal to the number of
permutations of e^oto ...a^ or of ахай... α2η+1 such that every quantity <xs is
displaced. Our symbolic expressions become
(h - l)m and (h - l)m+1 respectively,
equivalent to
(2n)!-(2n)(2»-l)! + (^)(2n-2)!-...,
(2η + 1)!-(271)(2,0!+(271)(2η-1)!-...)
which agree with the results of Section III, Chapter Ш, Art. 69.
417. To find the number of general magic squares corresponding to the
sum unity we require the coefficient of \μ and this is found to be
for even order 2n
for uneven order 2?г Ч-1 8 L·
170 FORMULA FOB CALCULATION [SECT. VIII, CH. VII
Those squares which have only zeros in the diagonals are enumerated by
rfl and rfivi according as the order is even or uneven, while those which
involve the maximum number of units in the diagonals depend merely upon
the expressions
(λ*+/*)η, (λ2 + μψ\μ.
418. The calculation of products of powers of щ and ητ is simplified by
the consideration that since
η2 = h* - 4th + 2, щ = h - 1,
we have η2 = η\ — 2ηχ — 1
and η*ήξ= η***η*-1 - 2η^1ηΓ1 - V\vV,
a convenient formula because the numerical values of powers of ηΎ are known.
L19.
Vi
vl
vi
vi
v\
vl
vl
vl
The
V2
V\V2
v\v*
ViV*
V1V2
V1V2
V1V2
following table
2
vi
ViVl
2 *>
v\v\
v\v\
vl
ViVl
vivl
vi
gives
the values of simple η
0
1
2
9
44
265
1854
14833
0
0
4
24
1C8
1280
10860
4
16
116
920
8132
products:
80
672
6176 <
4752
Each column is derived from the column to its left.
Thus by the formula
Vivl = v\v* - 2η\ν* - ViV*>
920 = 1280-2 χ 168-24.
SECTION IX
PARTITIONS IN TWO DIMENSIONS
CHAPTEE I
INTRODUCTORY NOTIONS
420. In this Section we take up a particular generalization of the Theory
of Partitions which arises directly from the improved definition of a partition
of a unipartite number due to the importation of an assigned order, viz. the
descending order, among the parts and the consequent basing of the theory
upon that of linear Diophantine Inequalities.
The Definition regards the parts of the partition as being placed at points
of a line
and the symbol > as regulating the magnitudes of the parts at any two
adjacent points. It is important to realise that the partitions may be regarded
as partitions on a line or in one dimension of space. Moreover the enumerating
generating function
(i + l)(i + 2)...(i + j)
(l)(2).(j)
when the number of parts is limited by the number . and the part magnitude
by the number \, can also be associated with either i or j points upon the
line. For example we take i points in a line
(j+l) (J+2) (j+3) (j + i)
(1) (2) (3) (i) '
172 DEFINITION OF PARTITIONS IN TWO DIMENSIONS [SECT. IX
and place the algebraic fractions
(j + l) (3 + 2) (3+3) (j+i)
(1) ' (2) ' (3) ' (i)
at the successive points from left to right, and we observe that the continued
product of such fractions is in fact the generating function. Instead of so
proceeding we may take j points in a line and again we find the generating
function as the product of j algebraic fractions each of which is placed at one
of the j points, viz.
(i + l) (i + 2) (i+3) (i+j)
(1) "(2) (3) - (j) ·
421. We are about to see that we may have partitions in two dimensions
of space and it is interesting to observe that the Ferrers-Sylvester graph of
a partition of a unipartite number is in reality a partition in two dimensions.
Such a graph of the partition 4311 is
and we have already seen that for many purposes it is advantageous to
replace the nodes by units, leading to the unit graph
1111
111
1
1
which as we shall see is a two-dimensional partition of the number 9 in
agreement with the definition which is now given.
Consider the points of a two-dimensional lattice
0 · ^ · ^ · > · > · χ
V V V V V
V V V V V
ν ν ν ν ν
У
and let the first row and first column be axes of χ and у respectively.
Suppose the parts of the partition to be placed at these points so that a
descending order of magnitude is in evidence in each row in direction of the
#-axis and also in each column in direction of the y-axis.
CH. I]
PRELIMINARY CONJECTURE
173
The arrangement of numbers thus reached is defined to be a two-
dimensional partition of the number partitioned.
Clearly the unit graph of a partition is a two-dimensional partition in
which the part magnitude is limited not to exceed unity.
422. In the case of a partition in two dimensions we are concerned with
three limiting numbers, for we may limit
(i) the number of rows,
(ii) the number of columns,
(iii) the part magnitude.
Suppose for a moment that there is no restriction upon the rows and
columns but that the part magnitude is limited by the number I.
Guided by the results reached in the case of partitions on a line we may
conjecture that the form of the enumerating generating function of the
partitions will be
(1+1^ (t + 2)** (f + 3^
(1)4 (2)** ' (3)*> ""
If this be a right conjecture the function, on putting £= 1, is
1
(ϊ)«ι (2)**-*i (3)s~s* (4)*-* ... ad inf. *
But if I = 1, the two-dimensional partitions enumerated are those of the
nature
1111
1 1 1
1
1
where there is no restriction upon the rows and columns. These are the unit
graphs of the one-dimensional partitions of all numbers and therefore are
enumerated by
1
(1) (2) (3) (4) ...ad inf.*
Comparison now gives
*i = l, *з=2, *8 = 3, ... sp = p, ...,
establishing that, on the assumption as to form, the generating function
which enumerates two-dimensional partitions, with the single restriction that
the part magnitude is not to exceed I, is
(t + l) (t+2)a (1+ЗИ (i + 4)'
(1) · <2)* · (3)' · (4)* •ааш1·
This is, in fact, the result which will be rigidly established later.
174 CONNEXION OF THE RESULT WITH A GEAPH [SECT.. IX
423. It is to be particularly noted that this result also can be depicted
upon the lattice in the manner following:
О (Ul) (i + 2) (1 + 3) (1 + 4) χ
(1) ~(2) (3) "(4) * *
(1 + 2) (1-^3) (£+4) (1 + 5)
(2) (3) (4) » * *
(ί + 3) (1 + 4) (ί + 5) (l+JJ)
(3) (4) (5) (6)
• · · ·
У
We place · , . at the origin and give a unit increase whenever we
advance a segment in the direction of either axis.
In future we shall speak of a plane partition instead of using the
combined word two-dimensional.
As an example of a plane partition take
3 3 1-х
2 2
1
I
у
Note that we may replace each part by a pile of nodes in the direction of
the s-axis and that we thus arrive at a solid graph analogous to the Ferrers-
Sylvester plane graph.
The enumeration of plane partitions is the same as the enumeration of
the solid graphs. In the graph the three restricting numbers limit the
numbers of nodes that may appear along the three axes of the graph and we
have a more direct symmetry, which is at once apparent in plane partitions. If
Z, 4)i, η be the three restricting numbers we must expect the general generating
Junction to remain unaltered when.Z, m, η are subjected to any permutation;
just as in line partitions the numbers limiting the number of parts and the
part magnitude are interchangeable.
In the solid graph we may substitute units for nodes and thus realise a
solid partition in which the part magnitude is limited by unity. We may say
that there is a one-to-one correspondence between plane partitions and solid
partitions in which the part magnitude is limited by unity. The plane
partition arises by projection of the solid partition upon one of the coordinate
planes, just as the line partition arises by projection of the plane partition
(with which it is in correspondence) upon one of the coordinate axes.
сн. ι] further conjectures as to " form " 175
424. The reader will find it interesting at this point to make the
following observation. Consider for a moment solid partitions unrestricted
in regard to the three axes but such that the magnitude of the part at the
origin is limited not to exceed k. The descending order of magnitude is to
be in evidence in the direction of each axis, so that it is only necessary to
restrict the magnitude of the part at the origin.
Assume the form of the enumerating generating function to be
(1)'T (2y* (3)r> ""
This for к = 1 becomes
(l)n (2)'2-n (3)^'*... ad inf.'
and enumerates the solid graphs in which the part magnitude does not
exceed unity; and these, being equi-numerous with plane partitions which are
absolutely unrestricted, are enumerated by
J.
(l)(2)M3)T(4)4...adinf.
Hence by comparison
n = l, r2 = 3, r3 = 6, ...r^^J1),
and on the assumption as to form the generating function of the solid
partitions we are considering must be
(k+l) (k + 2)' (k + ЗГ (k + p)^"') . .
(1) · <2)> · <3)« -■ (p)("f) ■mim-
Moreover, we notice again that this expression can be depicted on the
points of the solid graph just as in the plane case.
Гц the cases of line, plane and solid partitions the enumerating functions
appear to be associated with the series of numbers
line 1, 1, 1, 1,...
plane 1, 2, ii, 4, ...
solid 1, 3, 0, 10, ...
viz. with the successive orders of figurate numbers.
If we go back a step to point partitions it is clear that the function is
(t + i)
(1) '
yielding the series of numbers
1, 0, 0, 0,... ,
This assumption as to form is shewn later not to be justified.
176 INTERPRETATION OF SOLID GRAPHS [SECT. IX
which is the series of figurate numbers prior to
1, 1, 1, I,.···
It may be remarked that the function
(k + 1) (k + 2)3 (k + 3)6 (k + p)V Д )
~ (i) * (2Y · (sr -■ (р)('Г)
may be also written as the product of
ad inf.
(l)(2)M3)«...(k)
and
1
en
(k+l^(i+5l(k+2^(l+5)(k + 3)*'|H7)...adinf.'
425. Before broaching the formal study of the enumeration of plane
partitions we must look into the properties of the solid graphs to which they
give rise and enquire into their interpretation.
The graph of a partition of a unipartite number, say
viz. the partition 642 of the number 12, may be also regarded as the graph of
the multipartite number 642.
For present purposes we will regard it as being such.
If we take the successive layers, in the plane ocyt of a solid graph we obtain
a succession of multipartite numbers in correspondence. This succession
may be regarded as constituting the successive parts of the partition of a
multipartite number. Reading the graph by successive layers in either of
the three coordinate planes we thus obtain a partition of a multipartite
number.
Moreover in each of the three coordinate planes the layers may be read in
the direction of either of two axes, so that there are altogether six (3!) ways
in which the graph may be read and in each case we arrive at a partition of
a multipartite number.
But conversely it is not true that every partition of a multipartite number
may be represented by a regular solid graph.
For suppose
сн. ι] six headings of a regular graph 177
to be a multipartite partition. In order to arrive at a regular solid graph
the series of numbers
<h> (h) &з> ··· Αι» Οι, Cx, ...
bit b2) b3, ... a2, b2, c2, ...
Cij C'2, C3, ... #3, t>3, C3.. ...
must all be in descending order of magnitude.
It follows that the multipartite partitions that are in evidence in the
greater part of the present investigation are those which are representable by
regular solid graphs.
Consider now the solid graph
Or-r - -r—- ■*
333322
s 3221
321
у
the axis of ζ being perpendicular to the plane of the paper.
We read as follows:
Planes parallel to the plane xy and in direction Ox
(643, 632, 4ΪΪ) a partition of (l6, 8, 6).
Planes parallel to the plane xy and in direction Oy
(333211, 332111, ЗТШО) a partition of (976422).
Planes parallel to the plane yz and in direction Oy
("333, 33Ϊ, 32Ϊ, 2ΪΪ, ΪΪΟ, ΪΪ0) a partition of (13, 11, б).
Planes parallel to the plane yz and in direction Oz
(333, 322, 321, 310, 200, 200) a partition of (16, 8, б).
Planes parallel to the plane xz and in direction Oz
(333322, 322100, 321000) a partition of (976422).
Planes parallel to the plane ooz and in direction Ox
(664, 431, 321) a partition of (13, 11, б).
The graph is representative of three multipartite numbers and of two
partitions of each. The readings that give partitions of the multipartite
16, 8, 6 are those (i) in plane xy and in direction Ox, (ii) in plane у ζ and in
direction Oz. It will be noted that in both instances the specification of the
plane and the direction in the plane involve the letter у once only. It is for
M. A. II. 12
178 PLANE GRAPHS IN THE SAME THEORY [SECT. IX
this reason that the two readings are associated with the same multipartite
number. So also the readings (i) in the plane xy and in direction Oy, (ii) in
the plane xz and in direction Oz, involving in their specifications the letter χ
once only, refer to the same multipartite number 976422. The remaining
two readings involve the letter ζ once only and refer to 13, 11, 6.
In regard to the six partitions, if one of them contains a highest figure
equal to p, is r-partite and has q parts and we say that r, p, q are its
characteristics, then the other five partitions will have the characteristics
Ρ
я
r
Ρ
Я
г
г
Я
Я
Ρ
Я
Ρ
Ρ
г
г
derived from the permutations of ρ, q, r.
The two partitions which are r-partite appertain to the same multipartite
number; similarly for the pairs which are p-partite and g-partite respectively.
Hence the three multipartite numbers involved correspond to the three pairs
of permutations so formed that in any pair the commencing symbol of each
permutation is the same.
426. The consideration of graphs formed with a given number of nodes
now leads to the theorem:
" The enumeration of the graphically regularized r-partite partitions into
q parts and having ρ for the highest figure gives the same number for each
of the six ways in which the numbers p, q, r may be permuted/'
The six-fold conjugation of the characteristics may obtain even though
there may be equalities between the numbers p, q} r.
It is interesting to view the plane graphs of unipartite numbers from the
point of view of the solid graph.
Take the graph
у
which in the unipartite theory denotes the partition 3211 when read in
direction Ox and 421 when read in direction Oy.
CH. i] A PARTICULAR ILLUSTRATION
In the present theory there are six readings:
Plane xy Direction Ox (3211) p} q, r = 3, 1, 4
179
., soy ■
.. yz
„ yz
, zx
» zx
Oy
Oy
Oz
Oz
Ox
(421)
(421)
(nil noo ϊοοδ)
(3211)
(m Ш ϊοό Too)
»
>»
»
?»
»
= 4, 1, 3
= 4, 3, 1
= 1, 3, 4
= 3, 4, 1
-1, 4, 3
The three multipartite numbers (7), (421), (32] 1) appear each in two
partitions.
In general if the plane graph is of a partition involving a highest part
ρ and q parts, we establish a 6-fold correspondence between
(i) a unipartite partition having a highest part ρ and q parts.
(ii) „ „ „ >, q „ ρ ,.
(iii) a ^-partite partition „ .,
(iv)
(v) a ^-partite partition „ „
V*I/ » » » »
427. It has been shewn that a graph admits in general of six readings.
In other words we may say that a graph has six aspects depending upon the
position from which it is viewed. Thus, denoting by the integer m a pile of
nodes (or units) m nodes high, the graph examined in Art. 425 is denoted by
333322
3221
321
and the other five aspects it can assume arc
1
<1
Ρ
1
»
»
»
»'
9 »
1 part.
1 „
ρ parts.
333211
332111
3111
333
331
321
211
11
11
333
322
321
31
2
2
664
431
321
643
632
411
A graph however does not always admit of six different readings or
assume six different aspects.
Thus the graph
Θ
.or 21
1
12—2
180 DIVISION OF GEAPHS INTO FOUR CLASSES [SECT. IX
admits of only one distinct reading, viz.
(21 10),
and has no other aspect. It is in fact completely symmetrical.
This is also obviously the property of the graph which consists of a single
node, and these two are the earliest of an infinite series of completely
symmetrical graphs.
Again, the graph
• · or 11
admits of three distinct readings, viz.
(Щ (2), (11),
and of three aspects. This is the first of an infinite series of graphs which
have three different readings and three aspects.
428. There is also an infinite series of graphs which have two distinct
readings and two aspects. The simplest of these involves thirteen nodes
and is
331
211
2
the other aspect is
322
31
11
and the two readings are
(33Ϊ 2ΪΪ ilO), (322 3Ϊ0 Ш).
Each of the solid graphs therefore belongs to one of four classes according
as it has 1, 2, 3 or 6 distinct readings and can assume 1, 2, 3 or 6 aspects.
Graphs which are different aspects of the same graph are not essentially
different. Ex. gr. of two nodes there are three graphs
11, 1, 2
1
but they are all aspects of any one of them, so that of two nodes there is only
one essentially distinct graph.
In examining or tabulating the graphs appertaining to a given number of
nodes we may or may not take account of the essentially distinct graphs.
Thus the thirteen different graphs that can be formed of four nodes may
be written down by noting that the really distinct graphs are
1111, 111, 21, 11
1 1 11
CH. I]
and we find
Graphs
Readings -
EXAMPLES OF GRAPH-READING
Г 1111
| W
1 (1111)
(1111)
111
1
(31)
(31)
(211)
(211)
(ffi Ш)
(Πϊοϊϋ)
21
1
(2ΪΪ0)
11
11
(22)
(22)
(ϊϊϊϊ)
181
or we may write down the whole of the graphs and interpret each by reading
in the plane xy and in the direction Ox. Thus
rllll
Graphs J
Readings (4)
/ 22
Graphs A
ι
111
1
(31)
1
1
1
1
211
(31)
2
1
1
11
1
1
(Ш)
3
1
21
1
(21 10)
2
2
11 31
11
(22) (211)
4
Readings (22) (1111) (111 100) (11 10 10) (11 11) (1111)
Some remarks will be made later as to the nature of the symmetry which
results in a graph possessing one, two or three aspects.
No one, so far, has succeeded in enumerating the number of really distinct
graphs that appertain to a given number of nodes.
Omitting the trivial graph of unity every plane graph can be read in
three or six ways. Those which have three readings may be
(i) those which have a single line or a single column of nodes,
(ii) those which are self-conjugate.
The remainder have six readings.
CHAPTER II
THE METHOD OF DIOPHANTINE INEQUALITIES
429. The problem of the enumeration of solid graphs may be regarded
as a question of unipartite partition in two dimensions. It may be given the
following statement.
Integers limited in magnitude to n, zero being included, are arranged in
a rectangle of m rows and I columns in such wise that in each row and in
each column there is a descending order of magnitude. It is required to find
the number of ways in which a given number w can be partitioned into
integers which satisfy these conditions.
As soon as we import the idea of the descending order of magnitude into
ordinary or line partitions this generalization to plane partitions at once
comes into view.
We denote by GF(Z; ra; n)
a function of χ such that the coefficient of xw gives the number of
arrangements.
It will be convenient to give at once the result that will be established
later:
QF(l;m;n)
(l-a-n+i) (ΐ-α«**γ (1 - χη+ι-iy-i
~ (1-я?) " (1-х2)2 "" {l-x1-1)1-1
f(1 - xn+l) (l-a?"+*+1) (l-xn+m))1
Xj(i-^) * (l-^1) ··" \\-&*)]
X "TT^^+iy-^ * (1-хт+2У~2 "" "(l-a^-1) '
wherein m is supposed to be ^ I.
This supposition does not affect the generality of the formula because it
is symmetrical in the three magnitudes I, m, n. These therefore can be
arranged in any desired order. The reader will have no difficulty in
establishing the symmetry referred to.
The expression a,bove written involves Im factors in numerator and in
denominator. It may also be written as a product of mn or of nl factors, by
permuting the numbers I, m, n.
SECT. IX, CH. II] PARTITIONS IN TWO DIMENSIONS 183
In the usual notation 1 — Xs = (s) it may also be written
j(n+JL) (n + 2fr (n + m + I - 1))
I (1) · (2) ·- (m+l-1) Г
f(n + 2) (n + 3) (n + m + I-2»
(2) · (3) ·-· (m+l-2)j
3) (n + 4) (n + m + I-3)
1 О)
(3) - (4) ·- (ш+1-З)
x ... to I factors in brackets { }.
430. To begin with the most simple case. The numbers are placed at
the corners of a square
V W
θ2ΐ · > · a22
subject to the descending orders as shewn. If there is no limit to the
magnitude of the numbers this is the case (I; m; n) = (2 ; 2; oo ) and we find,
employing the auxiliaries \b Xs, λ3, λ4,
β^(*;2;2) = Ω L _- ,
> (l-V^*,)(l-g<*J
wherein subsequently we are to put #! = #2 =#3 = ж4 = χ.
Eliminating \λ and λ3 this is
Ί
χ (1 - λ2λ4Λ;1Λ·3) ί 1 — —- χ2χλ
and eliminating \4 and \2 in succession we find
(1 - χλ) (1 - χγχ2) (1 — хгх3) (1 — хгх2х9) (1 - χ1χ2χζχ4)*
a real generating function shewing the fundamental partitions
10 11 10 11 11
00 00 10 10 11
from which all partitions can be obtained by addition, and the syzygy
10 1 1 _ 1 1 10
00 + 10~0 0 + 10
Putting ^=«2=^ = «4=iKwe obtain the enumerating function
1
GF(2;2;oo) =
(1)(2)M3)
184
431.
SOLUTION OF THE SIMPLEST CASE
Also
<НЧ2;2;»)-П 1-(W)"+'
[SECT. IX
* (i-x,a,*).(i-g«)
ι =l η ι - (λ,λ.*)»+»
{\—g){\—g\lXsx) о 1—λιλ^Λ '
we require the coefficient of gn in
and since
a-
>(1-9)(1-9Χ1\,χ)(ΐ-^
which is readily seen to reduce to
l + дя?
(1 -g)(l -gx)(l-gx*)(l - <^)(1 -g*Y
Now we know from the Section on line partitions that
1
(1 - g) (1 - gx) (1 - go?) (1 - go?) (1 ->·)
-1 „,>+l)fo+2)fr + 3)(n + 4)
-f5' (1)(2)(3)(4)
Hence the expression becomes
* «· ί <*_+ l)(n + g)(a + 3)(a + 4) (n)(n+l)(n+2)(n + 3)
fM~ (1)<2)(3)(4) +Ж (1)(2)(3)(4)
_ ? an (n+l)(n+2)2(n + 3)
7* (1)(2)M3)
and we have the result
(n+l)(n+2)2(n + 3)
GF(2\2;n)~
(1)(2)M3)
432. We shall now obtain this result in another manner by considering
the graphs (oo ; 2 ; 2) and (n; 2 ; 2). In the case of the former we have two
rows of infinite length and a part magnitude not exceeding 2. The partitions
are such as
2222111.,.
22111...
CH. II]
A PARTICULAR GENERALIZATION
185
which have the property that in the first row the number of twos is equal to
or greater than the number of twos in the second row, and also that the
number of twos added to the number of ones in the first row is equal to or
greater than the similar sum in the second row- If λ4 and \a be the auxiliaries
appertaining to these inequalities respectively we are led to the crude
enumerating function
Ω 1
> (1-λ,*)(ΐ-£*)
χ (1 - λολ4#2) (l - r-r- oA
and this leads by the foregoing article to the same result as before.
If the rows are not to contain more than η numbers the crude function on
expansion must not involve \ to a higher power than η in the portion
1
of the function. We are therefore led to the function
1
Ω-
in which we take the coefficient of gn.
This leads to the result already obtained.
433. Instead of dealing with the numbers 2 and 1 in the two rows we
may more generally deal with the numbers ρ and q, and if there be no
restriction on the length of the rows this leads to the function
a l
(l-W^l-^)
which is readily expressed in the form
1 _ xp+w
(1 - xp) (1 - sfi) (1 - λ*ρ) (1 - χρ+t) (1 - 30)'
In particular if ρ = q = 1, this becomes
(3)
(1)42)»'
which on development = 1 + 2% + бос2 4- 9л?3 + 18#4 + ....
The partitions enumerated involve two rows of units of two different
kinds.
186 CRUDE SOLUTION OF THE GENERAL CASE [SECT. IX
Ω
Let и and ν denote these units, then of the content three the nine
partitions given by the formula are
uuu uu uuv uu uv uv uvv vvv vv
и ν и ν ν
the и unit, when it is present, always precedes the ν unit in row and in
column.
433ш. Now consider the system of partitions (3; 2; n).
An investigation carried out in the same manner as that above results in
the generating function
(n+l)(n + 2)s(n + 3)2(n + 4)
(1)(2)M3)2(4)
and also in the formula
So> CF(* ■ 2. n) _ Σαη fr + 1) (* + 2)2 fr + 3)2 (a + 4)
Ъд Ы!{о,2,п)-Ъд (1) (2)43)2(4)
_ 1 4- g (a? -fa;3 -ffl4) + ff2^6
" α-^α-^χι"^2) (i - ^з) (i - 9&) (i - ^5) (i - <p6)'
a result which is particularly recommended to the reader's attention for the
reason that it is fundamentally connected with much that is given later in
the work and is fully generalizable.
434 There is no difficulty in forming a crude generating function for the
general case (Ι; τη; η). The denominator is a rectangle of either Zm, ran or
nl factors at pleasure. The most convenient course is to choose the rectangle
corresponding to the smallest of these three numbers. We choose to take, let
us say, Im factors and form the rectangle of I columns and m rows. There
will then be (I — 1) m auxiliaries in the crude function if we form it according
to the second method employed above. Observe that using the first method
there would be (I — 1) m + (m — 1)1 auxiliaries of which {rn —1)1 could be
eliminated at sight. The crude function is
1
α-w^)(i-^-v) (i-^A... (i3-^-^-v)(i- _-1—A
\ λ1μ1ΐ'ι /\ \2^v2 / \ λ,^μΐ-^νι^ζ /\ Лг_! μΐ-iVi-! J
It enumerates the partitions (I; m; oo ).
CH. II] REPBESENTATION AT THE POINTS OF A LATTICE 187
To obtain the enumeration of the partitions (I; τη; n) it is merely necessary
to write instead of the first column of factors, the column
(1 - g\xx)
(l-g\fJh.a?)
(1 - дХф^а?)
{1-д\ф1...х™\
and also to take the additional factor 1 — g. The generating function is the
coefficient of gn in the crude function.
Our knowledge of the Ω operation is not sufficient to enable us to establish
>
the final form of result. This will be accomplished by the aid of new ideas
which will be brought forward in the following chapters.
435. In the meantime it is necessary to impress upon the mind the
nature of the result by shewing how it is directly connected with complete
lattices. It is formed as a product of factors placed at the points of a lattice
I nodes in breadth and m nodes in depth in the following manner:
(n+1) (n + 2) (n+3) (n + I-1) (n + i)
(1) (2) (3) <t-l) (О
(n+2) (n+J3) (n + 4) (μ+ί) (n + I+1)
(2) (3) (4) (i) (t+1)
(n+J) (n + 4) (n+5) (n + l+1) (n + I + 2)
(3) (4) (5) (t+1) (i + 2)
(n + m-1) (n + m) (n + m+1) (n + m +I- 3) (n + m + I-2)
(m-1) ~M~ "(ni+1) (m + l-3) (m + i-2)
(n + m) (п + ш+l) (n+m+2) (n + m+t-2) (n + m + ϊ-Ι)
(m) "(m+1) (m + 2) (m+I-2) (m+l-1)
In this tableau of factors the magnitudes Ι, τη, η may be permuted in any
manner so that there are six representations at the points of a complete
lattice, two for each of the dimensions Ι χ τη, τη χ η, η χ I. Of these six, only
three are essentially different, the remaining three being mere rotations of
them. Whenever one of the numbers I, m, η is unity the partitions can be
denoted by plane partitions composed entirely of units as well as by two line
188 EXAMPLE OF MANIFOLD REPRESENTATION [SECT. IX
partitions. Thus the system (3; 2; 1) has a generating function represent-
able in the three ways:
(2) (3) (4)
(1) · (2) · (3)
(ι) ; I = 3, m = 2, η = 1,
(3) (4) (5)'
(2) · (3) · (4)
W (1) · (2) ' (3)' «-e>"*-A.»-4
(Ш) jfj · j||; г-2,да-1,п-8,
(4) (51
the resulting product being -. 'y. : in each case.
CHAPTEE III
THE METHOD OF LATTICE FUNCTIONS
436. For the further discussion of the subject of the last chapter we
introduce ideas derived from Vol. I, Sect. Ill, Chs. ν and VI.
Therein we defined Lattice Permutations and shewed their connexion
with the different ways of placing different numbers at the nodes of a Lattice,
complete or incomplete, in such wise that the descending order of magnitude
is in evidence in each row and in each column in the direction of the axes
Ox, Oy of the lattice.
It was established that the lattice permutations of the assemblage
a?1 a?* ...aPm,
Pi,p»>··- being in descending order of magnitude, arc enumerated by the
number
(Pi+Ps+...+ff^ + Ы·1 U(ri „ _, . ,ч
(Pl + m-l)l(p2 + m-2)\...(pm_1 + l)ipmrl{P* Pt & + ^
where $< t and the product Γ1 has reference to every pair of numbers pS3 pt
that can be selected from the assemblage
Pi,p<z, ...J>».
In the succeeding chapter the idea of the greater index of a permutation
ρ was introduced and it was stated, but not proved, that the sum
extended to every permutation of the assemblage, has the expression
(l)(2)...(Pl + p2+... + pm)
(1) (2)... (Pl). (1) (2) ... <p2) (1) (2) ... (pmj'
We may call this the Permutation Function. It will be established
presently*. In the meantime we observe that we may form the sum %%?,
extending it merely to every Lattice Permutation of the assemblage. We
thus obtain a Lattice Permutation Function, or briefly a Lattice Function,
which is of fundamental importance. F^om the manner of formation it is a
* Post Chapter iv.
190 DEFINITION OF THE LATTICE FUNCTION [SECT. IX
finite and integral function of χ with positive terms and integral coefficients.
The coefficient of x* denotes the number of lattice permutations which have
the same index ρ and the sum of the coefficients must be equal to the
number of lattice permutations.
The assemblage α^α^2... α^1 gives rise to the incomplete Lattice
containing pitjk, ---Pm nodes in the successive rows as well as to the Lattice
Permutations and the Lattice Function.
Consider the assemblage αδ/32γ and with it the lattice
Ол χ
I · * *
У
It was shewn that we can place the first six integers at its nodes so that
there is descending order of magnitude in the directions Ox, Oy in just as
many ways as the assemblage possesses lattice permutations.
Taking any such arrangement of numbers
641
53
2
we form the corresponding lattice permutation by commencing with α because
6 is in the first row, we follow with β because 5 is in the second row; then
with a because 4 is in the first row and so on, and finally reach the
permutation
αβαβγα
2 5
Here the 2nd and 5th letters precede letters which are prior in alphabetical
order, so that the greater index is 2 + 5 = 7.
The complete calculation for the Lattice Function is as follows:
654
32
1
0ί<χαββ*γ
X»
652
43
1
ααββ\<Χ4
χ4
654
31
2
αααβγ\β
χ5
652
41
3
αα/3γ|α/3
χΑ
653
42
1
αα/3|α/3γ
χ9
651
43
2
αα/3/3γ|α
ж5
653
41
2
ααβ\ατ
Xs
651
42
3
ααβγ|^
χ9
CH. Ill] ITS CONNEXION WITH THE GENEBATING FUNCTION 191
631
52
4
632
51
4
641
52
3
642
51
3
α/3γ|α/3|α α/3γ|αα/3 α/3|αγ|/3|α α/3|αγ|αβ
χ8 χ3 χ11 χ6
641
53
2
643
51
2
642
53
1
643
52
1
αβ\αβ^\α αβ\αα^\β οίβ\οίβ\α^ αβ|αα/3γ
χ1 χ7 χ* χ2
For a reason that will appear we write the Lattice Function L (3, 2, 1; oo )
so that
Z(3, 2, 1; oo)=l +#- + 2#3+ 2^ + 2#5 + 2a·6 + 2x7 + 2л·8 + л·9 + #n.
The contacts which contribute to the index have been indicated, above,
by dividing lines. In the present instance we have either 0, 1, 2 or 3
dividing lines, and putting the terms which arise from the same number of
lines together we may write
X(3, 2, 1; oo) = l + (х°+%ъ* + 2х4 + 2а?) + (2х6 + 2х'7+2а?+х*) + х11.
When the lattice is complete with I columns and m rows we will write the
lattice function formed in this manner
L (I; m; oo );
when the lattice is incomplete with successive rows involving pl9 p2i ...jpm
nodes we will write it
ZO^o...^™; oo).
437. It is a remarkable fact that the enumerating generating function of
the plane partitions of the system (I; m; oo ) has the expression
and here we can anticipate the generalization appertaining to the incomplete
lattice; for denoting the enumerating generating function of the plane
partitions, appertaining to successive rows involving plt p.2) ...pm nodes, by
GF{plp.1... pm, oo ), the part magnitude being unrestricted, it will be shewn
that
^4Ρ^.·.ρ«>,«υ- (i)(2)...(2p) *
We establish these results before considering a restriction upon the part
magnitude.
192 PROOF IN THE SIMPLEST CASE [SECT. IX
438. In the simplest case take alf a2, βτ> β2 numbers at the corners of a
square and subject to descending orders along the rows and columns
«! a2
fix A
These numbers can be arranged collectively in two descending orders, viz.
«i> «2» βι> A, and al9 /3b a2, /32; and we may say that these numbers must
satisfy one or other of the conditions
These conditions do not overlap, because we must have either <x2 ^ βι or
βι>α2. To obtain 2ж*1+м*1+Эв for the first condition we put
βι=β*+Α, α2 = β2 + Α+Β, ^«A+^+jB+O,
where А, В, С are arbitrary integers, zero not being excluded.
Hence ^-нх^+э* = 2^+84+ад+,сг,
and since /32, -4, Б, О may each assume any value from 0 to со the result is
1
(1) (2) (3) (4)
For the second condition we put
ог2 = /32-ьЛ &=& + -* +-В+ 1, α^Α+4+Β + σ+Ι,
and thence 2ίϋ*ι+<4+Ρι+0ι β 2^4*ά+8*+ο+2
__ χ1
-(1)(2)(3)(4)·
By addition we find that the enumerating function for the system
(2 ; 2 ; oo ) is
1 +a? __1
(1)(2)(3)(4) υΓ <1)<2)«(S)'
When we compare the conditions
Ηι^α^βιΖ A
<*ι^βι>«2^β2
with the lattice permutations of the assemblage ααβ/З, viz.
ααββ
αβαβ
we notice a connexion between them and observe also that each condition
gives rise to a portion of the enumerating function
X»
(1) (2) (3) (4)'
where ρ is the greater index of the corresponding lattice permutation.
7ι>
A,
7i>
A,
72>
72,
72,
72,
CH. Ill] THE ROLE OP THE LATTICE FUNCTION 193
The whole enumerating function is
X(2; 2; oo)
(1)(2)(3)(4)·
439. Again consider a case which is not quite so simple, vi
«ι α2
A A
7i 7a
a plane partition of the system (2; 3; oo ).
Here the numbers may be in five descending orders when taken
collectively, viz.
«i, «2, A, A,
«1, «2, A> 7l>
αϊ, A» «2, A,
«1, A, «2, 7l>
«1, A, 7l> ^2, A, 72,
corresponding to the five lattice permutations of the assemblage α2β2*γ% viz.
ααββη,
a<*Ay|Ay>
αβ|α/3γ7,
oANAy,
aAy|<*Ay,
and we may say that the numbers must satisfy one or other of the five sets
of Diophantine inequalities
*l> «2 ^ A ^ A ^ 7l ^ 72,
αϊ ^ a2 > A > 7i > A ^ 72,
<*1>A> <*2>β*> 71^72,
«!^A> «9^ 7l>A>72>
<*ι>βι> Ъ> a2 ^ A ^ 72,
conditions which do not overlap.
Comparing them with the lattice permutations which are lined, as a
preparation to finding the index, we notice the correspondence between the
places where the symbol > occurs, and the lines in the permutations.
If wc now take any one of these sets of inequalities we find that it gives
rise to a portion cvp/(l) (2)... (6) of the enumerating function, where ρ is the
index of the corresponding permutation. To see how this is observe that if
the symbol > occurs between the sth and (s -f l)th letters of the set of
inequalities, we put
6-th letter = (s -H l)th letter -f N+ 1
M.A. II. 13
194
THE SUB-LATTICE FUNCTION
[SECT. IX
to find the corresponding portion of the enumerating function, and this unit
necessarily persists in the expressions of each of the first s — 1 letters of the
inequalities. When these come to be added together as we added them in
the case of the system (2; 2; oo) it is clear that the integer s will be
outstanding in the exponent of χ in the numerator of the function. The
occurrence of this particular symbol > after the 5th letter thus contributes s
to the exponent referred to. On the whole the symbols > in the set of
inequalities will contribute a sum of numbers to the exponent of χ in the
numerator; and this sum of numbers we have defined to be ρ the greater
index of the corresponding permutation.
Hence taking all the sets of inequalities the enumerating function is seen
to be
(1)(2)...(6)'
£(2;3;qo)
<1)(2)...(6)·
Looking at the lattice permutations as lined, it is seen at once that the
lattice function is
l + (x* + x* + x4) + x*,
so that
/зет/о о \ l+^+^ + ^ + tf6 1
GF(2; 3; oo) =
(1)(2)...(6) (1)(2)43)2(4)'
since 1 + #2 + #3 + ^ + #6 = 7o[tJ .
The reasoning is quite general and establishes that
sy-η,Ί \ L(l: m: со)
a very interesting result.
Precisely the same argument applies to the incomplete lattice, so that
also
WiPiftPB-fti, «>) (1)(2)...(Σρ) '
establishing beyond doubt that the method of investigation includes in its
purview the subject of plane partitions at the nodes of any incomplete
lattice.
440. In obtaining the lattice function the index of a permutation arises
as the sum of s numbers when s has values from zero to μ where μ is a
number to be determined. To use a phrase employed elsewhere in this
work, such a permutation involves s major contacts. If we restrict attention
to these permutations we arrive at what is termed a
Sub-Lattice Function of Order s.
СН. Ш] THE PART MAGNITUDE RESTRICTED 195
This is written
L8(l;m;<x>) or L8(pxp2...pm; oo),
so that
L(l;m; oo) = Z0(Z;m; oo)+ L1(l;m; oo ) + L2(l;m; oo ) + ... + Βμ(1;ιη; oo ).
In particular we see that L0(l;m; oo ) or L0(p1p2... pm] oo ) is always
unity. Thus we have shewn that
i0(3;2; oo) = l, Д(8; 2; оо) = а5»+я? + я*, £2(3;2; 00) = ^.
The sub-lattice functions possess elegant properties. One of the most
elegant is that which enables us to define a new lattice function
L(l;m;n) or L(pYp2 ...рт; n)
appertaining to plane partitions in which the part magnitude is limited by
the number n. The definition of L (pip2... p<m',n) is given by the relation
L(pip2...pm\ n)= (n + 1) (n+ 2)... (η+Σρ)Ζ0(ίΜ>2·..ί>™; <*>)
+ (η) (n+ 1)... (η + Σρ - 1) 1г(ргрй... рт\ oo )
+ (n-l)(n)... [п + Яр-2)Вя(р1р2...рт', 00)
+
+ (n-/i+l) (n-/i + 2) ...{η-μ+Σρ)Σμ(ρ1ρ2...ριΛ; оо).
The new sub-lattice function is
LtiPiPi —Pml w)« (n-s+ 1) (n-s+2)... (n-s+Σρ) 18{ργρ.2 ...pm\ 00 ).
We are now ready to investigate the expressions of
GF(l;m; n) and GF(pipa...pm; n).
We have to modify the previous work so as to take account of the
circumstance that the part magnitude is now restricted not to exceed n.
441. Recalling the simple case of the plane partition
«1 «*
A A
7i 72
we had the five distinct parts of the summation:
(i) «i ^ ora > A ^ A* ^ 7i > 7a giving 2я5ву.+^+4Я+зс+ич-^
(ϋ) «ι > α« > A > 71 > A > 72 „ 2^+5Л+4*+зС+20+*+4,
(Ui) Л! > A > «2 > A > 7l > 72 » ^«У2Н-5Л+4В+ЗС+20+ЬЧ2?
(iv) ^ ^ A > *« ^ 71 > A > 7a » 2^^5'1+4fi+3CV+2D+^+(i,
(v) «! ^ A > 7i > «2 ^ A > 72 » 2я«уИ-^+4^зсч-2я+№
In dealing with the set of inequalities (i) we put
71=72 + J., A=72 + -4+A А=7а+^+Я + <?, Ъ^Уъ + А+В + С+В,
Ъ^ъ + А+В+С + В + Е,
13—2
196 THE ROLE OP THE SUB-LATTICE FUNCTION [SECT. IX
and since ax cannot exceed n, so also γ2 + A 4- В Ч- G + D + Ε cannot exceed n.
We have therefore
where y2> А, Д C, D, Ε may assume any integer values, including zero,
subject to the condition that 72+ A+B+ 0 4-D + E^n.
This is equivalent to enumerating line partitions composed of η or fewer
parts, no part exceeding 6 in magnitude. The set of inequalities (i)
therefore leads by a known theorem in line partitions to
(n+l)(n + 2)...(n + 6)
(1)(2)...(6)
For the set of inequalities (ii) similarly we find
α!=γ2 + A + B + C + D + E+l,
so that y2 + A+B+C + D + E cannot exceed n — 1 in magnitude and the
sum 2яву*+54+4в+зс+20+я+4 j[s cieariy
(n)(n+l)...(n+5)
(1)(2)...(6)
V.
So also in the case of each set of inequalities that is associated with the
sub-lattice function of order 1
y2+A+B + C+D+E
cannot exceed η — 1 in magnitude.
Therefore sets (ii), (iii) and (v) contribute altogether
(1)(2)...(6) M2,3,oo).
The remaining set (iv) involves putting
a1 = y2 + A+B + C+D + E+2J
because the set is associated with the sub-lattice function of order 2, and this
leads us to the final portion of the enumerating function
<n-l)(n)...<n + 4)
(Γ) (2)77(6) A (2' 3' °° *
X2 (2; 3; 00) being here а;2+4 = aA
Hence GF(2;3;n)
(n+l)-(n+6)£0(2;3;oo) + (n)...(n+5)4(2; 8;оо)+(п-1)...(Щ-4)1»(2;3; oo)
(1Γ(2)...]6)
= X(2;S;n)
(1)(2)...(6)
CH. Ill] GENERALIZATION OF A WELL-KNOWN FORMULA
442. The reasoning is quite general and establishes the results
GF(l,m,n)-{im (im),
443. From the result
GF(p1p2...pm;n)
(n+l)(n + 2)...(n+6)
- —(i)(2)...(sp)— A(ftft-p«; ·>
in)(n+l)... (n + 5) _
+ (ΐ)(2)...(Σρ) b(plP*...Pm;*>)
+ ■
, (n-/t+l)(n-/«+2)...(n-/t + Sp) , ,
+ — ЩЩ:~(Щ Up**-*.;*)
we can immediately derive a valuable theorem.
Multiply each side by gn and then sum each side from η = 0 to η = oo .
The term
* n(n-s+l)(n-s+2)...(n-s + Sp) r 7 ч
which thus arises on the right-hand side, is equivalent to
$ n (n-s+l)(n-s + 2)... (n-s + Σρ) r / ч
У (1)(2)...(Σρ) ШЬ(Р*-1Ы*>).
or to
.г, ч d (2p + l) (Σρ+1)(Σρ + 2) 0
^.(P,ft-Pm;oo)|i + ^ p(1) ;<y + *p (1jj2|—V
(Σρ + 1)(Σρ + 2)(Σρ + 3)
(1)(2)(3) ^+··
= g*Ls(p,p2...pm; oo)
(1 -flr)(l -^)(1 - ^;... (1 -^)
by a well-known summation in connexion with line partitions.
OO
Hence 2 GF(ргр2...pm;n).gn
о
U{pxp2...pm\ QO)+ff£i(piP9...jpw;oo)+... +fl^Q>iP9...;Pm; 00 )
(1 - #) (1 -£*) (1 -^) ... (1 - <^)
198 STUDY OF THE SUB-LATTICE FUNCTION [SECT. IX
a noteworthy result which is a generalization of the well-known formula in
line partitions
1
% (l)(2)...(m + n)
79 (l)(2)...(m).(l)(2)...(n)
It is thus noticeable that the sub-lattice functions play an important role
in the Theory of Plane Partitions.
444. It is convenient, when no confusion can arise, to write
Ls(PiP*~-Pm\ °° ) = -£»·
Then writing χ for g we obtain the result
(1)(2) (Σρ+1) -Σ* GF(plPi ...pm; η),
the generalization of the formula
1 =|^ (l)(2)...(m + n)
(1) (2) ... (ш+ 1) 7 (1) (2)...(m).(l) (2)...(n) *
445. We now make a further study of the sub-lattice functions and the
first step is to find the value of μ, the highest order of sub-lattice function in
the case of a complete lattice.
For a lattice of m rows and I columns form the rectangular scheme
/
«! аг αΎ ... аг
a2 α2 α2 ... α2
or, α3 α3.··«8
#m am am · · · ^m
where there are I columns.
Reading this parallel to the arrow commencing at the origin we obtain
the lattice permutation
<Χι βφχ α3|α2|«ι ··· α»»|α«&-ι|*«ι-2 «m|««n-i am·
This is the permutation which involves the maximum number of major
contacts and corresponds to the sub-lattice function of highest order. There
is only one such permutation, so that the associated sub-lattice function is a
single power of oc.
* See ante Art. 343.
CH. Ill] THE SUB-LATTICE FUNCTION OF HIGHEST ORDER 199
We may without loss of generality suppose I ^ m and then the number of
major contacts is
l + 2 + 3 + ... + m-2 + (Z-m + l)(m-l) + (wi-2) + (m-3) + ... + S + 2 + l
-(|-l)(m-l).
Hence for the complete lattice the maximum value of μ is (Ι— 1)(τη — 1).
The same method is applicable in the case of the incomplete lattice, but
no convenient expression for μ is apparently obtainable.
446. The next step is to determine the expression of
J/0-u (m_i) (l; ra; oo)
as a power of x.
The dividing lines which mark the major contacts of the permutation
occur
(i) Inm-2 groups involving 1, 2, ... m —2 lines respectively.
(ii) In I — m +1 groups involving each m — 1 lines.
(iii) In m — 2 groups involving m — 2, m - 3, ... 2, 1 lines respectively.
Let the sought exponent of χ be πλ + 7г2Ч-7г3; 7Г!, 7г2, 7г3 corresponding
respectively to (i), (ii) and (iii).
Then
7r1=2 + (4 + 5) + (7H-8-i-9)+... + {i(m2~3m + 4)+...-|-i(m2--m-2)}
= Η1·2* + 2.32 + 3.42+... tom-2 terms)
= ъ\т(т-1)(т~2)(Вт- 1),
7г2 = £(m- l)m2-f£(m — l)m(m-h 2) + £(m — l)m(m + 4)+ ... to Z — m + 1
terms
= \ (m -1) Zm (I — m H-1),
7r3 = (Zm-2) + (Zm-4 -Ияг-5) + (Zra - 7 -f lm — 8 + lm - 9)+ ... tom-2
terms
= £Zm(ra- l)(m-2)-^?m(m-l)(m-2)(3m- 1),
whence τγί + тт2 + тг3 = \l (I - 1) m (m - 1),
and £(,_!> (m_1} (Z; w; oo ) = #*««-« m (m-D.
It will be noticed that the exponent of χ may be written
\1ηΐμ,
ОГ Ιηημ - \ Ιίημ.
447. We next establish that in Ls for every term x* there is a
corresponding term ocl™-p. These two terms, as shewn above, coalesce when
8= μ.
200
PROPERTIES OF
[SECT. IX
If, in the permutation
considered above, we fix upon a dividing line and arrange the letters to
the right of it in alphabetical order (or in ascending order of suffix), thus
obliterating the lines to the right of the one fixed upon, we obtain a lattice
permutation involving (suppose) s lines which yields χ to the lowest power
that occurs in L8. In fact we thus obtain a maximum condensation of $ lines
towards the origin of the permutation. If on the other hand we fix upon a
dividing line which is the sth from the end of the permutation and arrange
the letters to the left of it in alphabetical order, we obtain a lattice
permutation involving $ lines which yields χ to the highest power, that occurs in L$.
In iact we thus obtain a maximum condensation of s lines towards the end of
the permutation.
When the lattice is complete we may in any derived lattice permutation
write Om-e+i for a$ and invert the order of the whole of the letters. We thus
obtain another lattice permutation, and the latter has the same number of
major contacts as the former and thus contributes to the same sub-lattice
function. For a succession
*iK (р>я)
in the former, ap being the Jcth letter from the left of the permutation,
becomes
«m-№|am-p+i (m-g + l>m-p + l)
in the latter, Om-q+ι being the {Ira — k)th letter from the left of the
permutation.
Hence if in the former the components of the index are
in the latter the components of the index are
lm — к1у Ira — k2> ... lm — k8.
If the index of the former be p, that of the latter must be
Ims — p.
It is therefore proved that in Ls (I; m; oo) there are corresponding terms
x? and xlms~i>,
and thence we conclude that Ls is centrically symmetrical both as regards the
powers of χ and the coefficients. In fact
a* and х1ш~Р
occur with the same coefficients.
If e be the lowest power of χ in L8 determined as above directed, the
highest power will be Iras — €.
CH. Ill] SUB-LATTICE FUNCTIONS 201
Ex. gr. For the system (3; 3; oo)
A = l,
Lj = x2 + 2a? + 2x4 + 2л6 + 2#β + x\
Z2 = 2 (#б + #7+ 2л8 + № + 2#10 -f #и + я12),
X3 = #" + 2л?12 + 2^3 + 2л;14 -f 2л?15 + #1δ,
Z4 = #18,
verifying the above relations.
The permutation connected with L4 is
α/3|αγ|/3|αγ|/3γ
2 4 5 7
where the components of the index are entered.
It will be noted that 2, 2+4, 2 + 4+5, 2 + 4 + 5+7 give the lowest
powers of χ that occur in Ll9 L2, LS,L4, respectively and that the highest
powers are given by 7, 7 + 5, 7 + 5 + 4, 7+5 + 4 + 2; in conformity with
the above theory.
The result of writing - for χ in Ls is to convert it into %-lmsL8.
448. If e8 be the least exponent of χ that occurs in Ls we can find a
relation between es and eM_s.
In the permutation connected with Σμ, viz.
&m\ &m—i I Я?л—2 am\ am—ι &m >
e8 is equal to the sum of the components due to the first s major contacts—
say
6* = &ι + &2 + ... +&e,
βμ-8 is equal to the sum of the whole of the components minus the sum of
the last 6' components. Now the last s components are
Ion — /»'s, lm — к8-г, ... lm — kj,
therefore e^s = #M — Ims + e9,
or eM_s — е6. = \ hi ι μ — Ims = \ lm (μ — 2s).
Moreover if f8 be the highest exponent of χ that occurs in L8} the
symmetry of the permutation shews that
Λ~*-/· = ε*™ 0* - 2s),
and we deduce that
„V* + ^-, = ^™ (A - 2,) (λα + χΐ%
a result which foreshadows the theorem
which will be presently established.
202 RELATION BETWEEN L* AND ZM_* [SECT. IX
Combining the above with the relation
we find «*+/,»-* = 4 Jm/*,
so that 0S +^*-g does not vary with $.
449. To prove that Ζμ_β and L8 only differ by a factor which is a power
of χ we suppose that ^ is a term of Ls derived from any s of the lines
appertaining to the permutation connected with Σμ; the remaining μ — $
lines can be obliterated by arranging the letters in alphabetical order between
the chosen lines. Thus
ρ = ττ + r2+ ... +rs suppose.
If instead we retain only those lines which we have just obliterated we
obtain a term in Σμ_8 in which the exponent of χ is \1τημ —ρ because the sum
of the components due to the whole of the lines is ^Ιπίμ. Hence if Ls = %хр,
we have
Now it has been shewn (Art. 447) that if L8 — *S,xp, it follows that
1,χ-Ρ=χ-ι™%χΡ,
so that
Σμ-8 = χ¥7ημ Sx~p = χ¥Μ{μ " 2s) Xxp = x¥m {μ " 2s) is.
450. If a lattice be read by columns instead of by rows its specification
changes from a certain partition to its conjugate. It is a trivial remark that
the generating function which enumerates the associated plane partitions is
not altered by the change. That is to say that if
be conjugate unipartite partitions
GF(Plp2... ; n) = GF (q,q2... ; n),
a relation which we can express in the form
L(p1p2...; n) Z(ftg8...; n)
(1)(2)...(Σρ) (l)(2)...(2q)'
wherein 2p = 2g. Hence
L (ргр2...; n) = L (q,q2...; ri),
establishing that changing the lattice into its conjugate does not alter the
lattice function for any value of n.
Moreover the last relation may be written
(n + l)(n + 2) ...(η + Σρ)Ζ0(Μ>2-..; oo)
+ (n)(n + l) ... (n + Sp-lJAiftjp,...; «>) + ...
= (n+l)(n + 2) ... (n + Sq)Z0(y1g2...; oo)
H-(n)(n+l) ... (n + Sq- l)L1(q1qt...; oo )+....
CH-IIl] EXAMINATION OP A FUNDAMENTAL FORMULA 203
Putting herein η = 1, 2, ... in succession we establish that
ItsipiPi—l oo )«£,(£#...; oo ),
and thence £*(PiP2···; я) = L8(q1q2..*l n)9
proving that the sub-lattice functions do not alter when we pass from a
lattice to its conjugate.
451. The fundamental relation
GF{1> m' n) ~ (l)(2)...(Im)
exhibits GF (I; m; n) as a linear function of the sub-lattice functions. By
giving η the special values 0, 1,2,... in succession we obtain the relations
ОР(1;т;0)-£,(1',т;ао) = 1,
GF (I; m; 1) = ^^^ + A (i; m; oo ),
tri (£, m, .i) = m(2j + —(Ϊ)— г + 2'
GF{l,m^)- ^-^ + Щ...^.!) A + -+A.,
W(i,»»,M + *)- (1)(2)...(/t + s) + (l)(2)..> + s-l) A+-
(hn-H)...(Im + s)r
(1) (2) ... (s) *"
and thence
£» = 1,
Д-^(«;„;1)-1Ь»^11,
Ι,-^(ί;«;2)-^+1>^(ί;«»;1) + .^^1>,
X„ = OF (l; m; μ) - ®η^OF (I; m; μ -1)
^{^^OF(l;m^-2)-...
(1) ... (К)
, Ψ Λ(μ-ΐ)μ(ίια-μ + 2)...{ίιια+1)
This series may be continued, the left-hand side becoming zero.
204 STUDY OP THE SUB-LATTICE FUNCTION Ц. [SECT. IX
We then get a number of difference equations satisfied by the function
GF (I; m; n).
From the first series we at once find the general expression of Lx (I I m; oo ),
viz.
А(г'т)0О) (l)(2)...(m) (ΪΓ~·
because we know the expression of the line-partition generating function
GF(l;m;l).
452. Another method of investigation leads to another expression forix.
Taking the assemblage of letters
and observing that the index of the lattice permutation with which we have
to deal has only one component, let the index arise from the conjunction.
oivOiu, where v>u. The whole permutation will be
A)av\au(B>
where in the space A there is any succession of letters in ascending order of
subscripts to ν and in the space В any succession such that the subscripts are
in ascending order from u.
The least index is obtained when the permutation is
αί«2... «1-ι«ι*««+ι ··· α»-ι) Ыаи (<~4ΐι ·.· а1-\<~Ч+1 ... «L>
because no one of the letters al9 α2, ...α^ can be in the space В without
introducing another dividing line and the letters au, au+1)... av_x must each
occur at least once in the space A to satisfy the lattice condition.
This gives the index ν + (l— l)u— l + l, and the term
The greatest index is derived from the permutation
because no one of the letters av+1, av+2, ... am can be in the space A without
introducing another dividing line and the letters au+li ctu+2i... <xv must each
occur at least once in the space В to satisfy the lattice condition.
This gives the index (I — l)v + u— 1 and the term
x(l—i)v+u—ie
In regard to the space A and the letter av, to the immediate left of the
dividing line, we have to determine all the successions ranging from
«гЛ+ι · ·. α*-ι α» to αίτ1 ofcji ... a[z\ «i"2»
that can be placed between the succession
and the dividing line, in order to form a permutation of the desired nature.
CH. Ill] NEW EXPRESSION FOE Lx 205
Suppose that one such succession is
ti, t2, ... to-u+г may be any succession of ν — и + 1 numbers in descending
order of magnitude, such that no number is greater than I — 1 or less than
unity. Or, subtracting unity from each number we may say that the
succession
t\ — 1, i2 ~" 1> · · · ^г?~и+1"""" l
is a partition at the points of a one row lattice of ν — и + 1 nodes such that
no part exceeds I — 2 in magnitude.
The generating function enumerating such partitions is
(l-l)(I)...(t + v-u-l)
(l)(2)...(v-u+l) *
Denote by Lhm that portion of Lx which arises from the major contact
<xv<xu. Then
4~-* (l)(2)...(v-u+l) '
leading to
Put herein # = w + j; then for a constant value of j we have
Lx (I; m; <x>)} = {ж>'+1 + жЯ-г+ι + ... + a*»-«-» <·>+■>}
(l)(2)...(j + l)
_ (im-ij) (f-l)(f)...(I+j-l)
(i) · (l)(2)...(j+l) '
and consequently giving j all values from 1 to m— 1,
£,(*;«; oo) = rf-^—. (1)(2)
„(lm-2l) (I-!)(()({+!)
+ * (I) · (1)(2)(3)
+
(J) (f-l)(I)...((+m-2)
+ a ({)· (l)(2)...(m)
a result which, as not depending upon the enumerating function GF(l; m\ oo ),
is more interesting than the one reached in the previous Article.
CHAPTEE IV
EXCURSUS ON PEEMUTATION FUNCTIONS
453. If we had dealt with the whole of the permutations instead of
merely with the lattice permutations, we should have similarly arrived at
an enumerating function
PF(lhP*Ps — Pm', QQ )
" (1)(2)(3)...(Σρ) '
but what arrangements should we have enumerated ?
Taking the last particular case examined above (Art. 441) we should have
written down the 90 permutations of αα/3βγγ and the corresponding 90 sets of
Diophantine inequalities in which ctlf β1} уг would always precede a2) β2> <y2
respectively, but there would be no further restriction of order between the
letters otlt сц, βλ) β2, ylf <y2- Consequently in the plane partitions we should
retain the descending order of magnitude in the rows while abolishing it in the
columns. We are thus in the general case dealing with arrangements at the
nodes of a lattice, complete or incomplete, the only condition being that
a descending order of magnitude is to be in evidence in each row. Now in
a row containing ps nodes we can place any line partition of any number so
long as the number of the parts does not exceed ps. The generating function
for these is
1
(l)(2)...(Ps);
and, regarding all the rows, we find that the arrangements in view are
enumerated by the function
(1) (2) ... (Pl). (1) (2) ... (P2) (1) (2) ... (Pm)
Honcc
PF(PiPi—Pm', °0)
(1) (2) (3)... (Σρ) (1) (2)... (Pl). (1) (2) ... (P2) (1) (2)... (Pm)
^^-^■>-(i)»...W.Sg.
the result anticipated in Vol. I, Sect. Ill, Ch. vi.
or PF(ot> r> -co \- (1) (2)(3) ... (ΣΡ)
(i,lP2··^ )_(l)(2)...(Pl).(l)(2)...(P2) |1|W...W'
SECT. IX, CH. IV] LIMITATION OF THE PART MAGNITUDE 207
The expression should be compared with the number which enumerates
the permutations of the assemblage
α W3. aPm.
12 3 m *
The former becomes equal to the latter in the limit when ω approaches
unity.
454. When the part magnitude in the partitions is limited by the
number η the partitions as defined in the last Article are enumerated by the.
expression
(П+ 1) ... (n + pj. (n + 1) ... (n + p2) (n + 1) ... (n + Pm).
(l)...(Pl).(l)...(P2) (l)...(Pm)
but employing the same reasoning as we did in the case of the lattice
permutations, if PF8(p1p2...pm; oo) be the sub-permutation function derived
from the permutations which possess s major contacts, the enumerating
function is also
(η+1)...(η+Σρ)Ρ^0+(η)...(η^^
" (1)<2)... (Σρ)
Hence
fp+l)...(n+2p)PF0+(n)...{n+-Sp-l)PF1+... + (ii-p+l)...(n-v+Vp)PFv
= {(n + l)... (n + Pl) .(n+ 1)... (n + P2) (n + 1)... (n + pm){
y (1)(2)...(Σρ)
(ϊ)...(Ρι).(1)...(Ρ2) (l)...(Pin)
= {(n+l)...(n + Pl).(n + l)...(n + P2) (n + l)...(n + Pm)}
xPF(p1pt...pm; oo);
ν is equal to the maximum number of major contacts that can occur in a
permutation of the assemblage. This was found in Vol. I to be 2p — 2>ι·
When the lattice is complete and has as usual I columns and m rows
v=l(m — 1).
455. Equating the two expressions for the generating function and giving
η the values 0, 1, 2, 3, ... in succession, wo find
PF = i,
(Σρ+l) , „„ _ (Px+lKPu+ll-tem+l)
(i) ' (l)"·
(ΣΡ + 1)(ΣΡ + 2) (ΣΡ+1)
(Щ2) +—^~1F1+PF.1
_(Pi+l)(Ps+l)-"(Pm+l) (Pi+2)(P2 + 2)-(Pm + 2)
(1)'" (2)m
etc.,
from which the general expression for PF, is readily obtainable.
208 EXPRESSIONS OP THE SUB-PERMUTATION FUNCTIONS [SECT. IX
In fact
PFt = l,
pip « tPi+l)ftM-l)··· (Pm+1> _ (ΣΡ + 1)
(i)m (i) '
Pr.=(Pl+1)(p2+l)-(Pm+l) (Pi+2)(p2 + 2)...(pm+2)
2 (l)m * (2)m
(ΣΡ+1) (Pi+ 1) (P2+ D - (Pm + 1) , _ (Σρ) (Σρ + 1)
(1) * (1Г (1)(2) '
and in the expression of PFS the last term is
/-V Λ(s"4s (Σρ-3 + 2)(Σρ-8 + 3) ... (Σρ + 1)
^ ' (D(2)...(s)
456. If now from these formulae we write down
PFo + P^-h...+Ρ^ where v^llp-p1
we obtain a remarkable expression of PF(pip2...pm; oo) which we know
otherwise has also the expression
(1)(2)...(ΣΡ)
(1) (2)...(Pl) .<1)<2) ... (P2) (1) (2)... (pm) *
457. Putting, for a complete lattice, рг =p2= ··. =pm— I, we find
ffa.,r;0) (l)(2)-(tm).
(n+1)... (n + lm) P/'0+(n.)(n+l)...(n + Im-l)PJPJ + ...
+ (n+ 1 - im +1)... (n + I) PFlm_{
= {(*+ 1) (n+ 2)... (n + I)}-. ^Ш^-^
- I(P+l)(n + 2)-(n + I))" ... m .ш .
-{ (l)(2)...(l) J (1И2)-(М,
and thence
ΡίΌ=ι,
pff._j(t+1HM (fo+i)
^"1 (D(2) } ~-(ϊΓ"ΐΊΪΓί + (1X2)"'"'
PP - ΐα + 1)(ί+2)(ί + 3)1'" (jm + 1) [(l+l)(l + 2))»
^'"l (1)(2)(3) } " (1) { (1)(2) f
I'd)}
. (im)(Im+l) \(ί + 1)Γ ,3gm-l)(tm)(tm + l)
+ * <1) (2) J1ΪΓ) " (1) (2) (3)
etc.
CH. IV] INTERESTING ALGEBRAIC IDENTITIES
458. As an example put I = m = 2, so that
(1)(2)(3)(4)J3)(4).
{(1) (2)}·" (1) (2)'
209
PP(2;2;oo) = i
ν is here 2 and
рЫМ8_Ф
1 l(i)J (i)'
PP2 =
leading to the identity
(3)(4))
(l)(2)j
Г (5)((3)j2. (4)(5)
(1)1(1)1 + (1Н2Г
ИГ, , i(3)i2, j
(3) (4)1*
(1) (2)1 J
(5)
(1)L
1 +
i(3H2l+iK(4M5)
ml
(1)(2)"
469. Again putting I = m = 3, so that
(1)(2)...(9)
PP(3;3;oo) =
we find the identity
-1+1(ϊ)}+{(ϊ)(2,
, f(6)(7)(8)
+ 1(1)(2)(3)ί +1(1)(2)(3)
{(1)(2)(3)}»'
(l)(2)-(9)
{(l)(2)(3)j»
(4) (5) (6)1» i(5)(6)(7)
(1) (2) (3)1 + 1(1) (2) (3)
(7) (8) (9)
<^Г1 + |Щ3+ ■ ((6>(7>(8)r
(1) L (Wi +- + |(l)(2)(3)i.
(9) (10)
(1) (2)
J(8) (9) (10)
' (1)(2)(3)
Nlf-
+
1 +
fl»'--t
(5) (6) (7)
(1) (2) (3)] J
(4) (5) (6) Η
(1)(2)(3)ί
+
(5) (6) (7) (8) (9) (10)
+ " (1)(2)(3)(4)(5)(6) '
indicating clearly that the identities that arise from this theory are
noticeable.
460. Then j is a remarkable simplification when m = 2, for then it can be
shewn that
^.(i;2;oo)-*-i«<I-1>-«i-+-^
leading to the. identity
(1) (2)
1(1) (2)
(l)(2)...(s)
·· (20 _ %l - ((O(t-l)-(t ^s + 1)1*
...(ί)}»-.ί,* 1 (l)(2)...(s)" Γ
Μ. Λ. II.
14
210 SIMPLIFICATION IN A PARTICULAR CASE [SECT. IX
which may be also written
In fact, more generally, it will be found that
pr./^ . ^ ν ^fa) (Pi - l) - (ft -B+ 1). (p2) (p,- 1) ... (p2-s+ 1)
^.(ЛЛ,оо)-^ {(l)(2)...(s)}*
It has been shewn elsewhere (Vol. I, Sect. IV, Art. 146) that the number
of permutations of the assemblage α& β** which possess s major contacts
is given by the coefficient οΐ\*αν*βν* in the product
(α + \β}*(α + β)Λ.
From this product we can derive a function of x, viz.
(α+\βχ)(α + \βα?) ... (α + \βχ*) .(# + «)(β + αχ) ... (β + axft-%
and herein the coefficient of \*aftfi** is
**(Pi)(Pi-l) ..(p1-s+l).(p2)(p2-l)...(p2-s + l)
{(l)(2)...(s)r
For the first рг factors of the function of χ may be written
aft + Xaft-^x Щ + X'aft-^1^ , *f* Τ ^ + ...
I1) I1) (2)
+ P (l)(2)...(s) +·"·
and the last p.z factors
β* + α/Зйг-' Щ + *β*-* χ (Ρ2)(Ρ2" 1} + ...
Ρ (1) (2) ... (s)
so that the coefficient of αρ,βρ* is seen to bo
1+λΛ κι»2 +λΛ Rim? +-
, λΒ./Λ* (Ρι) - (Pi-s+ 1)■ (Ρϋ) - (Ρ2 -s+ 1) .
{<1)(2)...(β)}« +··"
461. For the complete lattice the functions PFS possess further elegant
properties. Thus starting with the relation
(n+l)(n + 2)...(n + I))Ml
(l)(2)...(l)
(п+1)...(п+1т)Р^0+(п) ...(n+lm-l)PF1 + ... + (n+l-lm+i)...(n+l)PFim..l
(l)(2)...(Im)
CH. IV] FURTHER PROPERTIES OF THE SUB-FUNCTIONS 211
if in the left-hand side we substitute — η — I — 1 for η we find that the effect
is merely to multiply it by
-1тп-%1т(1 + 1)
X ,
whilst on the right-hand side the coefficient of PFS is multiplied by
- lmn + J lm (Im - 21 - 2s -1)
SO
An identity thence arises and, putting therein η = 0,1,2, ... in succession,
we find the relations
PFlm+s = x*m{m-l^-lmPFs;
giving noteworthy algebraic identities.
462. We can find an expression for the sum
| „n(n+l)-..(n + I>i)-fo+l)-fr + Pj (n+l)...(n + Pn,)
79 (l)(2)...(pj).(l)(2)...ftg (1) (2) ...&>,„)
for this is
f я(п + 1)-(п+2р)Р^о+(п)-(п + 2р-1)Р^Н-... + (п-у+1)...(п-У+2р)Р^
ο9 (1)(2)...(Σρ)
Now for
5 ,„(n-s+l)(P-B + 2)--(n-s + Sp) pf
t9 ' (1Η2)...(Σρ)
we have only to sum from η = s to η = <x> and the result is
fPF,
(1 - g) (1 - gx) (1 - gsfi) ... (1 - go**) '
Hence the sum required is
ΐ + gPF, + g*PFt + ...+ g'PF,
(1 -g)(\ -gx){\-ga?) ... (1 -</*·-*)'
463. The foregoing investigation establishes the identities
(i)Jj) (i+l)(j + l) _ (i + j + 1).
(1)" (I)2 (1) '
(i -1) (i). (j -1) (j)
(1)42)*
_ (i+l)(i + 2).(j+l)(j + 2) _ (i+j + 1) (i+ 1) (} + 1)
(Ι)2 (2Υ (1) (1)»
(i + j) (i + j + 1).
+ * (1)(2)
14—2
212 FURTHER IDENTITIES [SECT. IX, CH. IV
and (i-2Hi-l)(i).(j-2)(j-l)(j)
_(i+l)(i+2)(i+3).(j + l)(j + 2)(j + 3)
(1)M2)M3)2
(i+j + l)(i+l)(i + 2).(j+l)(j + 2)
(1) (I)2 (2)2
(i + j)(i+j + l) (i+l)-(j + l)
(1)(2) (1)·
^ (i + j - 1) (i + J) (i -b J +1>
(1) (2) (3)
etc.;
and thence denoting
(i+l)(i + 2)...(i + s).(j+l)(j + 2)-(j + s)
(l)M2)2...(s)2
we obtain
0 + 1)0 + 2) ...(j+i)
(l)(2)...(i)
+ Д(1Ч-Л2 + 44+...+Л21,_4)
by Л*,
where ν is the smallest of the numbers i}j.
SECTION X
COMPLETION OF THE THEORY OF SECTION IX
CHAPTER I
PLANE PARTITIONS WITH UNRESTRICTED PART MAGNITUDE
464. In this Section we determine the actual algebraic form of
L{p1p2...pWl\n).
We first consider the particular case
Lip^.^pmi oo),
the lattice derived from the most general incomplete lattice. These
determinations will of course lead to the expressions of
GF(p1p2...pm)n) and GF(p,p2... pm; oo).
An incomplete lattice is the graph either of the partition of a unipartite
number or of a multipartite number. The partitions we enumerate are such
that the parts, limited in magnitude to n, are placed at the nodes in such wise
that there is a descending order of magnitude in each row and in each
column. It is the most general case of plane partition as defined in this
book.
As leading up to the method employed we will commence by determining
the lattice function derived from two unequal rows, say
L(pip2; oo).
The first step is to establish the relation
L(p№\ oo)
=Z(pi,i)2-l;oo) + #^^^ oo)
+ ...+a^*Z(^,p,-l; oo ).
214 THE FUNCTIONAL EQUATION SATISFIED BY L{pl9p2; oo) [SECT. X
Consider the lattice permutations of the assemblage
α'Ριβρ* where pi>p2.
By reason of the fundamental property of a lattice permutation the letter
α cannot occur more than p1 —p2 times repeated at the end of the permutation.
Every permutation must terminate in one of the following ways:
β; β\α; /3|α2; ...0\α*-**9
the dividing line as usual marking a major contact in the permutation. From
these terminations components of the greater index arise, viz. :
0; pi+ik- l; P1+P2-2; ... ty%
respectively.
These give rise to factors in the power of χ associated with a permutation,
viz.:
respectively.
In particular when the terminating letters are
β\α\
the factor xPi+p*.~8 arises; the remaining letters are
and they may appear in any lattice permutation and produce a lattice
function
£(Pi-*,i>a--l; oo).
Hence all permutations which terminate with #as(,9 >0) contribute
χΡι-Ннг-я I (pi _ ,9) p2 - 1 ; oo )
to the lattice function L (ρι,ρ*; oo ).
When $ = 0 the contribution is simply L (pl9 ρ2 — 1\ oo ) since the power
of χ which is the factor is x° or 1.
We therefore have the relation
L(Pi>P*;*>) = l<(PuP*-i;<x>)+ Σ x'^^sL{pl-s>p,-\\<x>).
1
465. Now assume that
Ζίρ,,Λ-Ι;·). (l)(2).-(Pl + P2-l) (Pi+^iPA^J)
W'P* > ) (2)(3)...<Pl+l).(l)(2)...(P!!-l)· (1)
for all values of ρτ.
CH. I] SOLUTION OF THE FUNCTIONAL EQUATION 215
Then the functional equation leads to the relation
(l)(2)...(p1 + p2-l) (Pi+l)-*(p2-l)
(2)(3)...(p1+l).(l)(2)...(p2-l)· (1)
,„,+„„., (1) (2) ...(^4-ft-2) (Pj-^foi-l)
+ X - (2){3)...{Ρι).(1)[2)...{ρ2-1)- (1)
,„„.+„-, (l)(2)-(Pl + p2-2) fo-l)-^-!}
(2)(3)...(p1-l).(l)(2)...(p2-l)· (1)
+
(l)(2)...(2p2-l) (р2+1)-Ж(р2-1)
+ a" (2)(3)...(p2+l).(l)(2)...(p2-l)· (1)
The right-hand side has pi — p2 + l terms; assume that the sum of the
last к terms may be written
^ (D(2)...(2p2 + k-l)
* (l)(2)...(p2 + k).(l)<2)...<p2)<K''
an assumption which it is easy to see is justified when к = 1.
The (k + l)th term from the end is the (px —p2 — к -f l)th from the
beginning and this is
^м* <1)(Й)...(2рИ-Ь-1) (р2 + к+1)-Ж(р2-1)
(T)(2)...(p2 + k-l).(l)(2)...(p2-l)· (1)
Adding this to the sum of the last к terms we find on simplification
(l)(2)...(2p2 + k)
* (l)(2)...(p2 + k+l).(l)(2)...(p2)tK+lb
a result which justifies the assumption.
Hence putting к=рг — p2 we find
(lM2)...(Pl+p2-l) (р1+1)-*(р2-Г)
(2)(3)... (p1+l).(l)(2)...(p2-l)· (1)
ы,,. (ЧИ-htft-H ( ,
(l)(2)...(Pl + P2) (Р1+1)-Ж(р2)
-(2)(3)...(p1+iy.(l)(2)...(p2)· (1)
This result being true when p2 = 0 is established universally.
466. It must reduce when χ is put equal to unity to the number which
enumerates the lattice permutations of the assemblage
216 DEFINITION OF OUTER AND INNER LATTICE FUNCTIONS [SECT. X
This number is
-i*^ (ft-*+!>,
(ih + l)Iftl
and the resemblance between the algebraic function and the enumerating
number at once strikes an observer.
467. We therefore seek in· the general case to always have this
resemblance in evidence. This idea leads to a very interesting arrangement of
the work.
The number which enumerates the lattice permutations of the assemblage
«?«?·■·«£·
may from Sect. Ill, Ch. ν be written
(l)(2)...(lp)
(m)...(^14-m-l).(w-l)...(i?2 + m~2) (l)...(pw)
H(ps-pt+t-$)
wherein t>$ and the continued product has reference to every pair of
numbers that can be selected from the first m natural numbers.
We now say that we shall express the lattice function
Црф%...рт\ oo)
in the form
(1)(2)...(Σρ)
(m)... (pj + m- 1). (m - 1)... (p2 + m - 2) (1)... (pm)
xIL{^p2...pm\ oo),
where the algebraic fraction first written is a fixed factor of the lattice
function and the remaining factor has to be determined.
The fixed factor before us is called the Outer Lattice Function and
written
OL(p1pi...pm; oo).
The remaining factor is called the Inner Lattice Function and is written
IL(p1pi...pm; oo ).
The expression of the outer lattice function is in every case known.
That of the inner function is unknown and has to be determined.
We have
LilhPi—Pm', <*>) = 0L(p1pv...pm; <x>)xIL(p1pt...pm; oo).
Above we have arrived at our first result
TT / \ (Pi+ l)-«(pj
IL{pxpo\ οο)=ΠΏ 1 "ч*.
CH.l] RELATION BETWEEN GENERATING AND INNER LATTICE FUNCTIONS 217
468. A principal object of this Section is the determination of the
algebraic expression of the inner lattice function for the general incomplete
lattice. A particular object is to prove that in the case of the complete
lattice the inner lattice function is unity, viz.:
IL (I; m; oo )= 1.
In that case the outer lattice function is identical with the lattice function.
It has been already proved that if we substitute for a lattice the
conjugate lattice, the lattice function as well as all of the sub-lattice functions
are unchanged. This is only true of the outer and inner lattice functions in
special cases. As a general rule they both change when such a change is
made in the lattice. The product of the outer and inner lattice functions,
being equal to the lattice function, necessarily remains unchanged under
the circumstances stated.
We have as a consequence of the new arrangements
where OL (pxp,... pm; oo )
(1)(2)... (Σρ)
(m)...(p1 + m-l).(m-l)...(p2 + m-2) U).(Pm)'
so that OF{'px2h · ·· Pm '·> oo )
= IL{p,p.1...pm) oo )
(m) ... to + m- 1) .(m- 1)... (p2+m- 2) (1)... (Pm)'
The only general fact we at present know about the inner lattice
function is that the sum of its coefficients is equal to
nP«-pt + t-s ^
When this question has been completely answered, the next step will be
to consider the problem when the part magnitude is restricted.
469. So far we have established the formula
(Pi+1)-*(P2)
<1)
(2)(3)... (p1+l).(l)(2)...(p2)5
and its particular case
GF(VP;cc) = GF(P;2^) = {1){(2){3) ..1(ρ))2<ρ+1} -
by considering the derivation of the lattice function from lattice
permutations. We found a functional equation connecting lattice functions and
we might have then proceeded to form a functional equation connecting the
corresponding inner lattice functions. We might adopt the same procedure
218 FUNCTIONAL EQUATION SATISFIED BY GENERATING FUNCTION [SECT. X
in the further study of the subject, but there is an alternative. We may
proceed from the solid graph of a plane partition to form a functional equation
between the generating functions which enumerate plane partitions and
thence deduce equations connecting the lattice and inner lattice functions.
This is the more convenient course. Suppose that the lattice, at the nodes of
which the parts of the partition are placed, has three unequal rows
comprising ρλί p2 and pz nodes respectively, where of course px ^p2 ^p*.
For a moment we suppose the part magnitude to be restricted by the
number n.
Subject to the parts being in descending order of magnitude in each row
and in each column, in every plane partition each node is either occupied by
zero (that is, is unoccupied) or by some number greater than zero and not
greater than n.
In certain partitions every node is occupied; such partitions may be
constructed by
(i) placing a unit at each node,
(ii) superposing every partition enumerated by GF(pip2pz; ?i— 1).
Such partitions will be termed " full-based " partitions.
They are clearly enumerated by
ял+л+л GF(p1p2pz) η -1),
the factor #л+л-ня» arising from the presence of the base which has every node
occupied by a unit.
Every lattice that can be formed from a given lattice by obliterating
nodes may be said to be " contained" in the given lattice. Among such
contained lattices is reckoned the given lattice itself.
Now suppose that a lattice having rows containing pi, p2', pz nodes is
contained in the given lattice ; it is obvious that some of the plane partitions
we seek to enumerate will be full-based upon such contained lattice and will
be enumerated by
^Pl'+ft'+p.' QF fa'pjjb' · η - 1).
Speaking of lattices contained in a given lattice is equivalent, since a
lattice is the graph of a line partition, to speaking of line partitions
contained in a given line partition.
We thus find that
OF(Plp2ps] n^^'+rt+b'QFfa'pfa'; τι-1),
the sign of summation indicating every lattice piplpl contained in the
lattice pxp2p^
сн. ι] equations satisfied by lattice functions 219
470. This relation shews the derivation of the generating function when
the highest part is η from generating functions when the highest part is n— 1.
When there is no restriction upon the part magnitude
eF(PlpiPs; oo) = %xrt+rt+r* GF (Pl'p*%'; oo),
and generally
GF(plPi ...Pm; χ )-bP'+»'+-+*'»GF(pl'pa' -pV, oo),
leading to
Xfofl,—.ft»; oo)_? ^Lfa'pi ...p'm; <*>).
(1)(2)...(ΣΡ) ~** <1)(2)...(Σρ') '
JZ(ffiff2---;Pm;oo)
(ш)...{р1+ш-1).(ш-1)...(р2 + ш-2) (f)...(Rm)
= Syv ILjp/p,' ...p'm; oo) ·
(m)...(p1' + m-l).(m-l)...(p2' + m-^ (l)..(p'm)'
It must not be overlooked that in these relations the lattice ρλρ2 ---Pm is
included under the sign of summation on the right-hand side. Also in using
the last formula that m may be 1, 2,... m — 1 orm, according to the number
of rows in the contained lattice. Also that unity arising from the absence
of nodes is included under the sign of summation as usual in all partition
formulae.
As an example we find that
^l - X) (1) (2)* (3) ~ * (1) (2) (3) + X (1) (2) +X (1) (2)
(1) +l'
and since
IL (21; со ) = 1 + &·'-, IL (11; oo ) = IL (2; oo ) = IL (1; oo ) = 1,
we verify that
IL(22; oo)=l.
In this case the lattices contained in
are
and the zero lattice counting as unity under the summation sign.
If from the plane partitions enumerated by
GF(PiP*P*'> n)>
we subtract those enumerated by
xPi+Pi+p3GF(p1p2p.i;n-l),
220 SYMBOLICAL EXPRESSION OF FUNCTIONAL EQUATION [SECT. X
we have remaining, in the case of three unequal rows, partitions whicihinclude
those enumerated by each of the three generating functions
GF{px -1 p2p3; n\ GF (рг p2 -1 ps; n), GF(p,p2 pz -1; n),
and these, by a well-known principle of the combinatory analysis (see Whit-
worth's Choice and Chance, Fourth Edition, pp. 73 et seq.), are enumerated by
GFfa-1 p2pz\ η) Η- GF(p,p2-1 ps; η) + GF(p,p2pz-l;n)
- GF^-l p>-1 jp,; n)-GF(px- 1 #2 #,-1; n) - Gi1^ #2--1 pz-1; л)
The reader will see without difficulty that in the functions of the first line
of this expression the partitions enumerated by each of the functions in the
second line are enumerated twice over. We therefore subtract these functions
each once, but in doing so we find that the partitions enumerated by the
function in the third line have been omitted altogether. We therefore add
once the function in the third line.
Hence the functional equation
GF(plP2pz; n) - дЛ+А+А GF(p,p2pz) η -1)
= GFfa-1 p2p3; n) + GF(Plp2-lpz\ n) + GF(Plp2 p3-l;n)
-GF(p1-lp2-lps;n)-GF(p1-lp2pz~l; n)-GF(Plp2-lp3-l;n)
+ GF(p1-lpu-lp9-l; n).
471. In the general case of m unequal rows we have the functional
equation which is elegantly expressed in the following manner:
Let θ8 be a symbol such that
θ8 GF(pxp2 ...p8...pm',n)= GF(p1p%...pt- 1 ...pm\ n),
then
(1 -00(1 -θ2) ... (1 - вш)GF(Plp2...pm', n) = x» GF(Plp2...pm) л-1).
472. The formula may be modified in the direction of simplification
when the rows are not all different.
For suppose pz =_p2
we must see how many nodes may be singly obliterated so as to leave a
contained lattice. It is clear that in this case the right-hand nodes of the
first and third rows may be detached but no other node. Reasoning as
before we are led to the functional equation
GF(PM; n) - xPl+2p* GF(Plp2Pi; η -1)
= GF(Pl - 1 p2ps; Λ) + GF(ριΡΐ p,-l;n)
-GF(Pl-lp2p2-l;n),
сн. ι] corresponding relation between inner lattice functions 221
which may be compared with the equation appertaining to a lattice of two
unequal rows:
GF(plPl; n) -^l+i,i GF{Plp2- n-1)
= GF(Pl - 1 p2; n) + GF(Plp2- l;n)~ GF(Pl-lp2-l; n).
Similarly we derive the equations
GF(PlplP2; n)-o&i+p* GF(plPlPi; n-l)
= GF(px Pl-lpt;n) + GF(plPlpi-l;«)- GF{Pipx-lps-\; n);
GF(plPlPl; n) - a?*1 GF (ρ,ρ,ρ,; n-l)=GF (plPl p, - 1; n);
and also
GF(pf; п)-л"» GF(pT; n-l)= GF(p\*->Pl-1; n).
473. When the part magnitude is unrestricted we have
(Px + P2) GF(plP3; <x>) = GF(p1-lp2;co)+GF(Plp,-l;x>)
- GF(p,- 1 p2-l; oo);
(Pi + P2 + P3) QFfaPtP*, <* )
= GFfa- 1 p2p3; 00 ) + GF(pxp2-1 p3; 00) + GF(plPiPa-l: χ)
-GF(pl-lp2-lp3;cc)-GF(Pl-lp,p3-l; <x>)-GF(p1 Pl-lp3-l; 00)
+ GF(p, -1 p2 -1 ps -1; 00 );
(Σρ) GF(Plp2...pm; со ) = {1 -(1 - 0.) (1 - θ3)...(1 - вш)} GF(plPi...pM; 00).
In general when a lattice has some equal rows so that pj' appears in the
specification of the lattice the symbol Θ, acts in the manner
0sGF(Pl...2?J·... pm; cc) = GF(Pl ...pj'^p,- 1...pm; χ),
s<» that, whatever equalities of rows may exist the symbolic expression is
available.
474. The next step is the deduction of the corresponding relation
between lattice functions.
Substitution from the relation
ηιρ, λ L(Plp2...pm;cc)
GF(Mh...Pni; 00)- (1)(2)...(Σρ) »
£ives
L(pp; 00 ) =Ζ(£ψ-1; oo );
L(PiP2\ <*>) = L(p1-lp2\ co)+L(p1p2-l: «)
~(Pi + P2-1)i(Pi-1i)^1'oc);
L{ppp\<x>) = L(ppp-l; oo);
Lip^p^ <x>)=L{plpl-lp<>\ oo) + £(ριί>ιΡ*-1; *>)
222 CORRESPONDING RELATION BETWEEN INNER LATTICE FUNCTIONS [SECT. X
£(ftftft>; oo) =£(ft-lftft; χ ) + L(p1p2 ft- 1; oo)
~(Pi + 2p2- l)£(ft-lftft-l; oo);
£(ftftft; <x>) = L(pL-lp2p3;oQ) + L(p1p2-lp2') oo) + L(p1p2 ft-1; x)
-(Рх + Рг + Рз-1)^^!-1^-!^; oo)
+ Z(ft-lft jp»— 1; <x>) + L(p1 ft-lft-Γ, oo )}
+ (Pi + P2 + P3-1)(Pi + P2 + P3-2)i(Pi-1P2-lp3-l;oo).
In the case of m unequal rows if 6S be the symbol before defined and X
a new symbol such that
(Zp)(tp-l)...(tp-s + l) = X*,
we have in general
(l-X)L(p1p2...pm; oo )
= (1-в1Х)(1-в2Х)...(1-втХ)1(р1р2...рт;х>).
475. "We now proceed to the equation satisfied by the inner lattice
functions. Substituting from the relation
£(ftft...ftn; oo )
β <l)(2)...Ep).f£(ftft..,p«;oo)
(m) ... (Pl + m- 1). (m- 1) ... (p2 + m- 2) (1) ... <pm)'
we find
(2p) IL (pp; oo ) = (p) IL (2> ρ - 1; oo );
(Pi+p2)^(m>2; °°)
= (px+ 1) /X (ft - 1 ft; oo ) 4- (p2) /X (ft ft- 1; χ )
- (Pi+1) (P2) Z£ (ft -1 ft -1; χ);
<3p) IL {ppp; oo ) = (p) IL (pp ρ - 1; oo ) ;
(2p!+pJiX(ftftft;oo)
= (px + 1) IL (ft ft - 1 p,; χ ) 4- (p2) /£ (p.ft ft- 1; χ )
- (Pi + i) (p2) ^ (ft Pi -1 ft - ι; χ);
(Pi + 2P2)/X(ftftft; oo)
= (px + 2) IL (ft - 1 ftft; χ ) 4- (p2) /i (ftft ft - 1; oo )
- (Pi + 2) (P2)IL (ft ~ 1 ft ft2 - 1; oo );
(Pi + P2 + Рз)IL (ftftft i °° )
= (p1 + 2)/X(ft-l ftft; oo)+ (p2+ l)IL(ft ft-1ft; oo )
+ (Рз) IL (ftft ft - 1; oo ) - (px + 2) (p2 + 1) IL (ft - 1 ft - 1 ft; χ )
- (Pi + 2)(p3) IL (ft - 1 ftft- 1; oo) - (p2+ 1) (p3) IZ (ft ft- 1ft- 1; oo )
+ (Pi + 2) (p2 + 1) (p3) IL (ft - 1 ft - 1 ft -1; χ).
CH. I] INNER LATTICE FUNCTIONS OF THE SECOND AND THIRD ORDERS 223
476. In general, for m unequal rows, if φ8 be a symbol such that
falL (ргр2...pm; oo )= (ps +m - s) IL(ргр2... ps - 1 ...pm; oo ),
x^IL (pxp2...pm\ oo) = (1 - фг) (1 - ф2)... (1 - фт) IL (p,p2 ...pm;cc).
When the specification of the lattice involves repetitions of letters the
equations satisfied by the lattice and inner lattice functions are
= (1 - Θ,Χ)(1 - ΘΛΣ)... (1 - втХ) L (p?p? ... jp5-; oo),
where
esLip^K^pl^i^^Lip^pP^.p^Ps-l^.p^l^l
and a& IL(pppp... pi» ;ao)
- (i - фг) α - Л)... α - Фт) /х (р№ ... pi*; ω),
where фа L (pi1 pi2... plm; oo )
= (Ps + ^s+i + ^s+2 + ... + 7rm)JZ(^
The reader should verify the validity of the general formulas in the case
of the particular examples m = 1, m = 2 and m = 3 given at length above.
He may be reminded also that throughout the investigation we employ the
notation 1 - a?= (s), the letters or figures in the bracket being in Clarendon
type.
477. The following investigation into the form of the inner lattice
function has reference in the first instance to lattices with unequal rows.
Later the results will be shewn to be applicable to lattices in general. In
the case of the lattice of two unequal rows we have established the theorem
JJ (,)i} ■ CQ4-<Pl+1) JP2>.
the sum of the coefficients of this integral algebraic function is visibly
P\ — Pi + 1 as it should be.
Now we know that the sum of the coefficients in IL (prfhps; oo) is
(Pi -p-2 + 1) (lh —p* + 2) (p2-2h + 1) аи<1 it might be conjectured that the
form of IL (ΡιΡ·>Ρζ; со) is
i(Pi+ 1) JP2)! ((Px + 2) (p3)l i(p2+ 1) <Рз)1
but this function is quickly seen neither to satisfy the functional equation
nor to be verifiable in simple cases.
It must also be noticed that the lattice function L (P1P2 · · · Pm \ °o )
becomes equal to L (pip2 · · · Pm-i; 00) on putting pm = 0, but that we have
no reason to conclude that the inner lattice function IL(p\P* ··· Pml °o )
becomes IL (pxp2 · · · Pm-ι; oc ) on putting pm = 0.
224 INNER LATTICE FUNCTION OF THE THIRD ORDER [SECT. X
In fact it does not do so, as can be verified at once by comparing
(l) x (i) '
the expression of IL (pip2 \ oo), with unity which is the expression of
IL (рг; oo ).
Now we know also that GF(p1p2... pm; oo ) becomes GF(p!p2... pm-x; oo )
on putting pm = 0 and we find that if we take the formula
rF, . ч IL (P1P2P2; °o )
KPlP2l?Zi °° ;""<3) (4) ... (Pi+ 2). (2) (3)... (p2+ l).(l) (2)... (Рз)'
and substitute for IL (P1P2P2I 00 ) the product of three factors above written,
the putting of рг = 0 does produce the correct expression of GF{pxp2) 00).
We gather from this fact that we are justified in concluding that we may
put
IL (ριρφ; со )
i(Pi+l) r(P2)l j(Pi + 2> хЛъ)} 1(Р2+1> г(Рз)1 , ы F(nnn . „\
~ \Щ~ " ОТ) ("ТаГ" W) VW " Ш <Рз) {Plplpi' )}
because ρΆ = 0 causes (p3) to vanish.
F(piP*ps *, 00 ) is a function to be determined.
We further conclude, by working out a few particular cases, that a probable
result is
F (ргрф J CO ) = JL {tflVM (Pl - p2) _ Д.А+. (p, - pj},
and on trial it is found, the work being too tedious to reproduce here, that
the expression
(Pi+ 1) _ r Ы) j(Pi + 2) _ ДРзИ ((P2 + I) _ r (Pj)
(l) KdI {"Тар (2) 11"йГ (i)
+ ^ {**+» (Pl - p2) - *·*·+2 (p2 - pj)}
docs, as a fact, satisfy the functional equation.
478. The actual forms of the inner lattice functions for the cases of two
and three rows will prove of much advantage in the investigation to which
we now proceed.
In the equation (px + p2) IL (ρλρ.>; oo)
- (Pi+ 1) d>2)IL(Pl - ift- 1; χ )
put
x-^{lL{pxp,\ go)-(Pi+ l)IL{pl-lp9; 00)}= V.ip.p.; 00),
сн. ι] inner lattice function of second order 225
then (Pi + PJ^i(ftft;oo)
β (pi+i) Pi (α- ι л; *) + (p2) vi (ftft-1; «>)
- (Pi+1) (p2) К (ft-1 p.- ι; oo),
an equation of the same form as that satisfied by IL (ftft; oo ).
Hence we conclude that if IL (ftft; oo ) is a solution of the equation,
#-*>* {IL (ftft; oo ) - (px + 1) Ji (ft - 1ft; oo )}
is also a solution.
It is convenient to exhibit the new solution by means of an operation
performed upon the original solution.
We therefore write
0Pl IL (ftft; oo ) = ντ (ftft; oo ).
479. Again put
лгл {IL (ftft; oo) - (pg) IL (ft ft -1; oo)} = 7, (ftft; oo),
and we find that
(P1 + P2) 72(ftft; 00)
= (Pi + 1) "^(ft-lft; oo)+(p2) F2(ftft-1; 00).
- (Pi+ 1) (P2) ^2(ft- lft- 1; 00 ),
again an equation of the same form as that satisfied by 7X(ftft; 00 ).
Therefore another solution is V2 (ftft; 00 ) which we may represent by
0PJL(Plp2] со).
Further suppose that 0PlP2 is an operation such that
Qpift IL (ftft^ °°)
= x-p>-p*{IL(plP,; oo)-(Pl + l)JZ(ft-lft; 00) - (P2) JX(ftft-l; 00)
+ (px + 1) (Рз) IL (ft -1 ft - 1; 00 )},
so that from the functional equation itself
°j>u>*IL (ftft; °°)=IL (ftft; °°)»
or 6W2=1·
Moreover if we operate with On upon Fi (ftft; 00) we reproduce
/X (ftft; 00 ), as may be verified in two lines; so that we have the relations
We now apply these operators to the known solution of the functional
equation which, discarding the non-essential factor щ, we may take to be
(Pi+lJ-^Pa)
M.A. II. 15
226 TWO FUNDAMENTAL SOLUTIONS [SECT. X
We find
0* {(ft +1) - * Wl - <pi + υ - *2 <P2>>
giving us another solution (px+ 1) - x2 (р2); we can now operate again, and
operating $ - 1 times successively we obtain
о8р;г hpx+i) -* w}« o?i+ΐ)-*· w.
Similarly operating with 0P2 we find
0P2 {(Pi + 1) - * (Рз)} - (Pi + 1) - (P2>>
and operating 5+1 times successively
0;2+1{<Pi+ l)-*(P2>} = <Pi+ l)-«-W·
It is therefore abundantly clear that two fundamental solutions of the
functional equation are
<px+l) and <p2);
and we still obtain a solution if we multiply by any function of χ which does
not involve рг or p2.
Putting the fundamental solution in evidence we find that we have the
expression of IL (ргр2 \ °o ) given by the formula
IL{P№\ °°) =
(Pi + 1) (Pg)
(1) ' (1)
χ , 1
in determinant form.
In the above investigation we have only been concerned with integer
values of plt p2 such that p^p2 because only in that case is IL {ρλρ2\ oo)
an inner lattice function according to definition; but the investigation is
equally valid as regards the functional equation when ρλ)ρ2 are any numerical
magnitudes; they need not be integers and there is no necessity for them to
be in descending order of magnitude.
If in the functional equation
(Pi + p2)^Gm>2; *>)
= (p1+l)IL(p1-lp2] oo)+(p2)/Zr(pIpa-l; 00)
-(pi+i)(pJ/-£(jPi-1a-i;qo)
we put p2=pi we find
(2pj) IL {plpl; 00 )
- (Pi+ 1) (Pi) ILip^lp, - 1: 00 ),
CH. I] INNER LATTICE FUNCTION OF THIRD ORDER 227
wherein IL {рг — 1 рг; oo) is not an inner lattice function, but still the
solution we have obtained is valid. Combining the equation just written
with
(2px) IL (рхрг; oo ) = (рг) IL (p^ -1; oo),
we find IL(Pi-lpi'9 oo) = (p1)7X(p1-lp1-l; oo),
which is true as a result of the formula
Hence our investigation implies the formula
(2pj) IL (ргрг; oo ) = (рг) IL {ρΎρτ - ] ; χ )
and we see that
IKjhfr; oo) = щ {(px+ 1) -λ·(Ρι)} = unity.
480. Passing to the Third Order, the functional equation is written in
the form
IL (ргр2ръ; oo) - (p2 + 1) IL (ргр.2 -1 рй; ос ) - (p3) IL (ргр2ръ - 1; oo )
+ (Рг + l) (Рз)IL(PiP* - ii?a-1; oo)
= χρ>+ρ*+ρ»Μ(Ριρ2ρ3; <x>) + (v1 + 2)IL(p1-lp2ps;co)
-(p2+ 1) !L{pY~ 1 p2-lp3; oo)
- (Рз) IL(Pi ~ li>2 Рз - 1; oo ) Η- (p2+ 1) (p3) IL {p, - ljp2 — 1рз -1; oo ).
Writing
^ (jPiftft; oo ) = аг^-л [ JZ (pj^; oo ) - (p2 + 1) IL (ft ,p2 - 1 p2; oo )
- (Рз) ^ (pijp* i* - 1; oo) + (p2 + 1) (p3) IL (p,p2 - Ip, -1; oo )},
we derive the relation
(P1 + P2 + P3) ViPiPtP*'**)
= (Pl + 2) VQh - 1 p,p,) 00 ) + (p2+ 1) V(Plp2 -lp,; со )
+ (Рз) V(PiP*P*-l'> *>)
-(Pi + 2)(p2 + l) V{p{-lp,-l<p,- co)-(v1 + 2)(pz)V(p1-lp2p,-l; 00)
-(Рг + ^Рз) ^Oftib-lpi-l; °°)
+ (Pi + 2) (p2+l) (p3) Fdh-lft- lph-1; oo).
Comparing with the functional equation it is clear that V (рхр2р^\ со ) is
a solution if IL (pijhp-a; 00 ) be one.
481. Proceeding similarly we find six solutions which are exhihited as
operations performed upon IL (pip2ps; 00) as follows:
(i) OpJLuhptpt; 00)
= х-* [IL dhjhpt; 00) - {рг + 2) IL (pi - 1 p2p3; 00 ){;
15—2
228 INNER LATTICE FUNCTION OF THIBD ORDEB [SECT. X
(ii) 0ftIZr(#tfM>8; °°)
= лгл {IL(ptfzps; oo)-(p2 + l)/£(i>ijpa-ljp»; со)};
(iii) OpblLfjMfap^cc)
= лг-л {IL (ргр2р,; oo ) - (pg) iX (p^p, -1; oo )};
(iv) 0Pli?2 IX (pip&i; oo )
= Л-Л-*» 17X (ρ^,ρ*; oo ) - (Pl + 2) /Z (Pl - 1 p2p3; oo )
- (p2 + 1)IL(p^-lp*; oo) + (px + 2) <p2 + 1) IL(p, -lp2-lps; oo)};
(v) 0Р1Л1Х(рдр*р*;оо)
«βτΛ-^ΙΙΧΟΡχΡ^; oo)-(ft + 2) JZfo-lpift; oo )
- (p3) 77 (^р2 p3- 1; ос) + (Pl + 2) (p3) IL (p, - 1р2рг- 1; oo)};
(vi) Олл IL (ргр2р,; oo)
= яг**-*» {7£ (i)ip2p3; oo ) - <p2 + 1) IL {ргр2 -1 рь; со )
- (p3) IL (р^2р3 - 1; со ) + (р2 + 1) (р3) IL (р,р2 - 1 ра - 1; оо )}.
То these may be added for the sake of symmetry
0PlP2p3IL(p1p.2pb; oo)
= агъ-ъ-ъ {IL (prftps; oo ) - (px + 2) IL (Pl -lp2ps;co)
-(PzHLiptfzPs-l] oo)+ {p1+2)fa2 + l)IL(pl-lp2-lp,) oo)
+ (Pi + 2)(p3)JX(^1-lp2p3-l;oo) + (p2+l)(p3)JrX(pli)2-li9a-l;oo)
- (Pl + 2) (p2 + 1) (p3) JXfo- 1л- 1 p3~ 1; oo)},
and it is easy to establish the operator relations
Upi Ц»2 ЧР8 = ■* »
Opx Up2 = Ц,1Р2, uPl Op3 = Ц>1Рз, Op2 (JPs = Op2i,8,
VpxUpzPa = 0ρ2^Ριί>8 = VpsOpiPi = ^ί>ιί>22>3 == *·
482. We now perform these operations upon the known solution of the
functional equation. Clearing it of fractions, by multiplying throughout bj
(l)2 (2), this may be written :
(1) - x^+1 (2) (p2 + 1) - я*-" (pj + 1) + «л+* (p2) + ял+**ы (Pl - P2)
- χ {(2) + x*+* (1 + «) (Pa - P2 - 1) ~x^* (2ft - 2P2){ (p3)
+ *» 1(1) + **+* (Pi - ft)} (ft - 1) (p3)
Operating s times successively with 0Pi we obtain the function
(1) - #*>>+1 (2) (p2 + 1) - xp^ (Pi + 1) + a?*+* (p2) + **+*»+« (px - Рз)
- *« {(2) + «ft+» (1 + a?) (Pl - p2 - 1) - afP^ (2Pl - 2P2)} (p3)
+ *-+» {(1) + x^ (Pl - P2)) (ft - 1) (Рз),
CH. I] SIX FUNDAMENTAL SOLUTIONS 229
and since s is any integer at pleasure we conclude that the functions
P, = (1) - жл+1 (2) (p2 + 1) - жр.+2 (Pj + 1) + tf*>>+* (p^ + «ft·****· (ft - p,),
P2 = {(2) + «*+· (1 + ») (Pl - p2 - 1) _ a*P>+* (2^ - 2P2)} (pj),
P, - {(1) + **« (Ρα - P2)} (P$ - 1) (P3),
are solutions of the functional equation.
These results are easily verified by shewing that
0РгР^Ри 0РгР2 = х~*Р2, 0ρ>Ρ9-ατ*Ρ9.
We now operate with 0P2 s times successively upon P19 when we obtain
(Pi+ 1) (Pi + 2) (P2+ 1)-*-e+1(P2) (P2+ 1) (Pi + 2),
leading to the conclusion that the functions
(p1+l)(p1+2)(p2+l), (p2)(p2+l)(P! + 2)
are solutions of the functional equation, and moreover they are fundamental
solutions since no simpler functions can be produced from them by means of
the operations.
Again operate with 0P2 $ times successively upon P2 and we find
*· (Pi + 1) (Pi + 2) (P3) - x-8+> (P2) (P2 + 1) (Рз>>
and wc conclude that the functions
(Pi + l)(Pi + 2)(Ps), (р2)(Р2 + 1)(Рз>
are fundamental solutions.
Finally operating with 0P2 upon P3 we obtain
- χ (p3 - 1) (Рз) (р2 + 1) +a? (p3 - 1) (p3) (Pl + 2),
establishing that the functions
(Рз - Μ (Рз) (ft + *)> (Рз - !) (Рз) (ft* 2)
arc fundamental solutions.
We have thus six fundamental solutions
(Pi + l)(Pi + 2)(p2+l), (P2)(P2+1)(Pi + 2), (p3) (p3-1) (Pi+2),
(ft +1) (Pi + 2) (p3), (Рг) (Р2 + 1) (p3), (Рз) (Рз - 1) (P2 + 1),
and no more are obtainable.
483. The known solution of the functional equation, which is the inner
lattice function we require, can now be expressed in terms of these. Since
it has been found that
O;, (l)2 (2) IL (Plp2pz; oo ) = Л - **-ipf + ar*+*P>,
by putting s = 0 we find
(1)* (2) IL (plP$Pt; χ ) = P1 - xP2 + a*P*;
230
INNER LATTICE FUNCTION OF FOURTH ORDER
[SECT. X
also putting s = 0 in the results
ОкРг - (Pi + 1) (Pi + 2) (p2 + 1) - x~'» (P2) (p2 + 1) (pa + 2),
0£aP2 = «· (Pi + 1) (Pa + 2) (p3) - ar·* {pj (p2 + 1) (Рз),
0£2P3 ж (pj - 1) (ρ,) (p2 + 1) + *· (p3 - 1) (Рз) (ft + 2),
it appears that
Pi = (Pi + 1) (Pi + 2) (p2 + 1) - χ Ы (p2 + 1) (ft + 2),
P* = (Pi + 1) (Pi + 2) (p3) - з? (P2) (p2 + 1) (p3),
P3 χ (p3- l)(p8) (p2+ 1) + (p3- 1) (Рз) (Pl + 2);
whence, substituting,
(l)M2)/Z(PlAft;oo)
= (Pi+ 1) (Pi+ 2) (p2+ 1) -«(Pj) (p2+ 1) (px + 2) -ж(рх+ 1) (Ρχ + 2) (p3)
+ * (P2) (P2 + 1) (Рз) + ^ (Ps " !) (Рз) (Pi + 2) - «* (P3 - 1) (Рз) (Рг+ 1)»
(Рз-1) (Рз)
or
Ι1(ρφ,ρ3; οο) =
(1) (2)
(Рз)
(Pi+1) (Pi+ 2) (pj (p2+l)
(1) (2) (1) (2)
r(Pi + 2) (p2+l)
(1) (1) (1)
X* X 1
an elegant expression of the inner lattice function in determinant form.
Reasoning as in the case of the second order it is not difficult to see that
this expression of the inner lattice function is valid whatever equalities
exist between the numbers p1} p2y p3.
It is to be noticed that if it is convenient for any purpose we may take
; and since
1 1
out the factor
(1)42)
(l)'-(2) =
χ
χ 1 1
Xs χ 1
we may express the inner lattice function as the quotient of two
determinants.
484. Passing now to the Fourth Order IL (Pip2psP4 \ <*> ) and guided by
the foregoing results put
A=l, 4i = <Pi + 3), ^2=<Ρι+2)(Ρι + 3), Λ = (Ρι+1)(Ρι + 2)(Ρι + 3),
Б0 = 1, Д = <р2+2), Я2=(р2+1)(р2+2), ЯзНр2)(р2+1)(р2+2),
<70 = 1, С1=(р3+1), С2=(р3)(Рз+1), <?з = (Рз-1)<РзМРз+1)>
А> = 1, А=(Р4>> А=(Р4-1)(Р4>, А=(Р4-2)<Р4-1)(Р4)>
TWENTY-FOUR FUNDAMENTAL SOLUTIONS
CH. I]
and consider the twenty-four products
AqBiC2D$ A1BqC2jDs
231
A0BiCsD2
A0B2G1D3
A0BzO1D2
A0B$C2Di
AxBqGsDz
A.iB20qD$
AiB2(j$±)q
AlBscol)2
Α2Β0ΟχΌζ
A2BQGsDi
A2B1G0DB
A2BiCs-L/q
A2BbGQDi
A2BsGxDq
,AbB$GiD2
A$B0C2Di
A$Bi GQD2
A$BiGiDo
ASB2G0D1
AAOlD.
in which every permutation of the numbers 0, 1, 2, 3 is in evidence.
We shall shew that each of these products is a solution of the functional
equation
X*> IL (ptftPsP* ; 00 ) » (1 - ψ0 (1 - ф2) (1 - ф3) (1 - ф4) IL (ргРъРзР* \ 00 )
where, as above,
ф811(р1р2...рт; <x>) = (pa + m-s)IL(p1p2...p8-l ...pm; 00),
for if i,j, k, I be any permutation of 0, 1, 2, 3
ФИ^АА=ВДА<М*·
Now
Mi = <Pi + 4-1)(Pi + 2) = (Pi + 2)^i = <Pi-1 + 3)^li>
and in general φλΑι = (рг — i + 3) Ait
so that φ,ΑίΒ^Βι = {рг - i + 3) AiBjGhDb
and similarly φ^ΑιΒ^Ώι = (p2- j + 2) AiBjGkDh
φΜΒβ^ = (p3 - к + 1) AtfyCbDu
φιΑϊΒ,ΟΑ = (p4 - Ϊ) AiBsCkDi.
Hence (1 - φ,) (1 - φ2) (1 - φ,) (1 - φ4) -^ВДЛ,
= {l~(Pl-i + 3)}{l--(p2-j + 2)}{l~<P3--k+l)}{l-.(p4-i)|^^i7,A
= xPi-i+z+Pf-j+z+Pi-k+i+Pt-l AiBjGjcDi
= ***AiBsChDu
since i4-j4-A? + Z = 0-bl + 2 + 3 = 6.
485. It is thus established that each of the twenty-four products is a
solution of the functional equation. Hence the determinant which is a linear
function of these products, viz.:
-*3
xA2
x*Ax
x«
&г
в,
xBx
a?
l>3
c2
Ог
Χ
±>ъ
xD,
А
1
232 THE DETERMINANT EXPRESSION [SECT. X
is also a solution; and we shall shew that when divided by (l)3 (2)2 (3), which
in determinant form is
1 1 a a?
ω 1 1 χ
Xs χ 1 1
χ6 χ? χ 1
it is the actual expression of IL (ftftftft; oo).
The expression is
<Pi+l>(Pi+2)(Pi+3> Ы(р2+1>(Р2+2) *(Рз-1)(Рз)(Рз+1) *(ρ4-2)(Ρ4-1)(Ρ«)
(1) (2) (3)
(1)(2)(3)
(1)(2)(3)
(1)(2)(3)
(1) (2)
«*(Pi + 3)
(1)
(P2+l)(P2+2)
(1)(2)
ж(р2 + 2)
(1)
(Рз)(Рз+!)
(1) (2)
(Ps+1)
(1)
Ж(Р4-1)(Р4)
(1) (2)
(рЛ
(1)
Χ6
Xs
486. We first take the test of the sum of the coefficients.
Putting χ as 1 it becomes
(ft+lXft + 2Xft+3), ft(ft+l)(ft+2), (ft-l)(ft)(ft + l), (ft-2Xft-l)(ft)
(ft + 2Xft+3) , (ft+l)(ft + 2), (ftXft + 1) , (ft-lXft)
(ft + 3) , (ft+ 2) , (ft+1) , (ft)
1,1,1, 1
wherein of course (ft + 1) denotes the number ft + 1 and not 1 — x^+l.
Now if, herein, we put separately
ft-pe + 1, ft-ft+ 2, ft-ft + 3, ft-ft+1, ft-ft+ 2, ft-ft + 1
equal to zero, we find that in each case two columns become identical and the
determinant vanishes. Each of these numbers is therefore a factor of the
determinant and the expression is easily seen to be
TV (Pi - P* +1) (Pi - P* + 2) (Pi - P* + 3) (p2 - ft +1) (ft - ft + 2) (ft - ft +1)
which we know otherwise to be the sum of the coefficients in the inner
lattice function.
сн. ι]
TESTS OF THE RESULT
233
487. Also on putting px = p2 = p3 = jp4 = p} the function ought to become
equal to unity. Apart from the factor . . . 2 . the expression becomes
(p+l)(p+2)(p+3), <p)(p+l)(p+2), <φ-1)(ρ)(ρ + 1), tf3(p-2)(p-l)<p)
я(р-1)<р)
(P)
1
*(p + 2)(p + 3) , (p+l)(p + 2), (p)(p + l) ,
яЧр + 3) , я(р + 2) , (p+1)
a? , #8 , χ .
Transform this by taking—
For New First Row:
1st Row + ^Lx 2nd Row + x^1 jjj χ 3rd Row + л^+3 х 4th Row;
For New Second Row:
2nd Row +aP LJ χ 3rd Row + a?»*1 x 4th Row;
For New Third Row:
and it becomes
3rd Row + vP χ 4th Row;
1 1
χ 1
я3 χ
χ a?
1 χ
1 1
x° a? x 1
which is an expression of (1)* (2)2 (3).
Hence the value of the determinant expression for IL (pppp; oo) is
unity.
It can also be shewn that putting pY = p2 =ρΆ =p, p^^p — 1 makes the
expression equal to 1 + aP + x2? + x^ and this can be verified in particular
cases.
488. All of the above processes are valid when applied to the functional
equation of order m and lead to a determinant expression of IL (piPz...pm\ oo ).
The constituent of the determinant which is in the rth row and cth column
apart from the power of χ which appears explicitly is
(Pc+r-e+ 1) (Pc + r-c + 2) ... (pc + m- c)
<1)(2)... (m-r)
The part which involves χ explicitly presents exponents of χ which are
figurate numbers of the third order.
234 THE GENERAL RESULTS
It is exhibited in the determinant
1 1 χ xs ...x
/m- \
x 1 1 x ... лЛ 2 '
/m-3\
χ* χ 1 1 ...аЛ 2 /
[SECT. X
,(V)
/m\ /ire—1\ /m-2\ /m-3\
x\2l x\ 2 ) χ\ 2 / a;\ 2 / ...
489. The results obtained for the second and third orders are now set
forth:
(Pi+1) (Pi
IL(p1pi; oo ) =
(1) (1)
χ 1
L{p№; oo) =
GF(plPi; oo) =
7X 0\р,р,; oo ) =
L(piPip3; oo ) =
(l)(2)...(p1 + P2)
(l)(2)...(Pl+l).(l)(2)...(P2)
1
(l)(2)...(p1+l).(l)(2)...(p2)
(Px+1)
X
(Pi+1)
(Рг)
1
<P2>|
1
(Pi+1) (Pi+ 2) (P2>(P2+1) г(Рз-1НРз)
(1)(2) (1)(2) Ж (1)(2)
χ
(P! + 2) (p2+l)
(1) (1)
Xs X
(l)(2)...(p1 + p2 + p3)
(Pi
(1)
1
(1) (2)... (p1+ 2) <1) (2) ... (p2+.l). (1) (2)... (p8)
(Pi+l)(Pi + 2) (P2)(P2+1) *(Рз-1)(Рз)
« (Pi + 2) (p3 + 1) (Ps)
ж3 ж 1
6Jff(2W3; °° } = (1) (2) ... (Pl + 2). (1) (2) ... (p2 + 1).(1)(2)... <p3)
(Pi+l)(Pi+2) (P2)(P2+1) ^(Рз-1)(Рз)
^(Pi + 2) (P2+1) (Рз)
χ3 χ 1
The results for the fourth order are similarly written down.
In particular GF (pm; oo )
1
~(m) (m+ 1) ... (p + m- 1). (m- 1) (m)... (p + m~ 2) ... (1) (2) ... (p)'
the inner lattice function being unity.
CHAPTER II
PLANE PARTITIONS WITH RESTRICTED PART MAGNITUDE
490. When the part magnitude is restricted not to exceed the number
η we have the formulae
GF(Plp2...pm,n) = <1)(2) /(Σρ) ,
L (ргр2...pm; η) = (tl+ 1) (n + 2) ... <η + Σρ)Ζ0
+ (n)(n+l) ... (η + Σρ -1)1, + ...,
wherein for brevity L8{pxp2... pm; oo ), the sub-lattice function of order $,
is written L8.
The inner lattice function, for a restricted part magnitude, is defined
by the relation
(n + m)<n + m+l)...(n + p1 + m-l)(n + m-l)...(n + p2+m--2) (n+ l)...(n + pm)
(m) (m+ 1) ... (Pl + m- 1). (m- 1) (m) ... <p2 + m- 2) (1) (2) ... (Pm)
(1)(2)...(Σρ)
= OL (pYp2 ...pm; n) .IL (p,p2 ...pm\ n\
where the outer lattice function, for a restricted part magnitude, is of fixed
form, and we have before us the inner lattice for investigation.
We are guided in fixing the form of the outer function by analogy
with the case η = oo. We have not the sum of the coefficients in
L(pxp2 ...pm\ n) before us.
491. We take as the point of departure the functional equation of
Art. 471,
(1 - вг) (1 - θ2) ... (1 - θη) GF(PiP*... Рш\ η) = sflp GF(plP2 ...pM', η- 1),
where θ8 is a symbol which operates as explained above.
236 THE FUNCTIONAL EQUATIONS [SECT. X
Converting this into a functional equation for the lattice function we
find for the order two
L (ргр2; η) - χΡ****L (ргр2; η - 1)
= (Ρι + Ρϋ) iL (Ρι - Ί-Ρ** η) + L(pxp2 - 1; η)}
- (Ρι + Ρ2- ЖР1 + Рг) l(pi- 1?2-1; η\
and for the order three
L (ΡιΡΦ I n) ~ хрх+м* L {pip2pz; η - 1)
= (Pi + P2+ Ps) iL (Ρι-ΊρζΡ*'* n) + L(plp2-lpz; n) + L (p1p2pz-l; n)\
~(Pi+P2 + p3-i)(p1+P2+P3)i^(pi-ip2-i?>8;^) + i(Pi--ip2i)3--i;w)
+ £(ί>ι:Ρ2-1^3-1;^)}
+ (Pi + P2 + Рз " 2) (Pi + Рг + Рз - !) (Pi + Рг + Рз) ^ OPi - χ ί>2 --1 i>s -1; я),
and in general for the order m
(l-01X)(l-02X)...(l-emX)L(p1p2...pm;n) = x*PL(p1p2..^
where symbolically
Xs = (Σρ) (Σρ - 1) ... (Σρ - s + 1).
Also passing to the inner lattice function we have, for the order two,
ар**** (η) (η + 1) IL (pxp2; η - 1)
= (η + pj + 1) (η + Pg) IL (рхр2; η) - {рг + 1) (η + р2) IL (ρ, -1 #>; η)
- (η + Ρ!+ 1) {p^IL(p1p2- 1; η) + (ρχ + 1) (pj /Ζ^-Ιρ,-Ι; η).
For the order three
а^-НРз+Рз(n) (n + χ) (n + 2) IL(pip2ps;n-l)
= (n + px + 2) (n + p2 + 1) (n + pg) IL (ргр2р.л; η)
- (Pi + 2) (η + p2 + 1) (η + ρ3) IL (рг - lptpz; η)
- (η + ρχ + 2)(ρ2 + 1)(η + Рз) IL(ргр2-1рз; η)
- (n + Pi + 2) (n + p2+ 1) {pz)IL(Plp2p»-l; n)
+ (Ρι + 2) (ρ2 + 1) (η + ρ3)ΙΧ(ί>ι-1ρ2-1^; η)
+ (Ρι + 2) (η + ρ2 + 1) (ρ3) IL (ρ,- Ιρ,^- 1; я)
+ (η + Ρχ + 2) (ρ2+ 1) (ρ3) IL(p1p2-lp,-l; я)
- (Ρι + 2) (р2+ 1) (р3) ILipb-lρ,- 1ft- 1; *')·
In general, if χ8 be a symbol such that
tt / \ (Ρβ + m-s) TT , Ί
%s Л (Plp2 ...рш\ η) = —-^—-—J—IL (p,p2 ...jpf-l...jp«; л),
then #2*>(n) (n+ 1) ... (n + m- Ι) ΙΙ(ρλρ2 ...ftw; ?i- 1)
= (n + p1 + m-l)(n + p2 + m-2)...(n + pln)Kl--%1)(l-%2)...(l--xw)}
xJX(ftp2...^m;n).
CH. II] INNER LATTICE FUNCTION OF SECOND ORDER 237
492. Taking first the order two, it is convenient to examine several
particular cases in order to find the probable form of the inner lattice
function. Doing this, the conclusion is that the function is probably
i + * (l)(n + p1+l)·
Observe that this reduces to the right expression when η = oo. Also it
is found to satisfy the functional equation. Moreover, it may be written
rr, ч 1 [(Pi+1) (P2)
wit*> / (l)(n + Pl+l) J Ж(П) (n+i)
which, in the light of previous results, is very suggestive of truth.
To obtain the fundamental solutions we recall the case of η = oo, and seek
solutions of the form
(Pi+1) w (P2) ρ
(α + Α+1)**' (η + Ρι+1)^'
where Fn is a function of η to be determined in each case.
and find
We substitute 7-^ I— Fn for IL {ΡιΡ2 \ n) in the functional equation
(n + pj + 1)
Hn + P1+l)(n + PJ(^
which is equivalent to (n) Fn = (n + 1) Fn-U
from which we deduce Fn = (n + 1), and we have a fundamental solution
(p1 + l)(n+l)
(n + Pl+l)
Similarly, when we substitute ·. ———-τ Fn in the functional equation,
we find
(n-l)^n = (n)^b
giving us Fn = (n) and the fundamental solution
(a + p1+l)'
and in terms of these we find
lL(Plp2,n)-(1)^ (n + pi+1) V + ft+D
238 THE THIRD ORDER—SIX FUNDAMENTAL SOLUTIONS [SECT. X
493. This simple exposition for the order two points out the path of
investigation for the order three; for, guided by the six fundamental solutions
when η = oo, it is natural to seek for solutions of the functional equation of
the six types:
(Pi + l)(Pi + 2)(P2+l) F (Pi+l)(Pi+2)(P3) F
(n + Pl+l)(n + Pl + 2)(n + p2+l) n' (n + pj+lMn+p^Hn+p^l) n>
(P2)(P2+l)(Pi+2) F (P2HP2+IHP3) rr
(n + Pl+l)(n + Pl + 2)(n + p2+l)^ni (n + Pi+lXn+^+^Xn+^+l) n'
(Рз"1)(Рз)(Р1+2) (Рз-1)(Рз)(Р2+1) F
(n + Pl+l)(n + Pl + 2)(n + p2+l) n' (n + Pl+l)(n+Pl+2)(n+p2+l) n'
where Fn is a function of η to be determined in each case.
Substituting these successively for IL (piP^Ps; n) in the equation we find
for the six cases respectively:
F - fo+l)fo + 2> F . F _
fc + 2)
(n-1)
(n + 2) F , v (n)(n + 2)
(n-1) iM' '""(n-aXtt+l)·
ρ _ (n)(n+l) » . » _ MJ.) -,
n_ (n-1)8 n_1' "~ (5^2) *'
The solution of the functional equation
is clearly Fn =/„/„-,/„-2...,
so that if Λ=(η+ΐ;^ + 2).
then
j, _(n + l)(n+2) (n)(n + l) (n-l)(n) (n-2)(n-l) _,n+lWn+2>
*n (n^ · (n"^TF ' (n-2)^ · (n-3)° - — (4+1) РИ-2)
and similarly; so that we have the six results:
Fn = (n + 1У (n + 2), Fn - (n) (n + 1) (n + 2),
.F» = (n) (n + 1) (n + 2), Jf№ = (n - 1) (n) (n + 2),
Fn = (n)* (n + 1), Fn = (n - 1) (n) (n + 1),
respectively.
We are thus led to the six fundamental solutions:
(i) (ft + iltei + gXft+iKa+iPfo + a)
(n + p1 + l)(n + p1 + 2)"(n + p2+l) '
(ii) ^l+JL) (Рх + 2)(Рз)И(п+1)(п + 2)
w (n + Pi+l)(n + P! + 2)(n + p2+l) '
CH. II]
THE DETERMINANT EXPRESSION
239
(iii)
(iv)
(v)
(vi)
(Ps) (P2+ 1) <Pi + 2) fo) fr + 1) fr+ 2)
(n + p1+l)(n + pi + 2)(n + p2+l) '
Ы(Р2+1)(Рз)(п-1)(п)(^ + 2)
(n + Pi+1) (n + Pl + 2) (n + p2+ 1)'
(Рз-1)(Рз)<Р1 + 2)(п>а(п+1)
(n + p1+l)(n + Pl+2) (n + p2+1)'
(Рз - 1) (Рз) (Р2 + 1) fr ~ 1) fo) (Ц + 1)
(n + p1 + l)(n + p1 + 2)(n + p2+l)
Guided by previous work we form ΙΣζριρ^; η) Ъу taking a fraction
with numerator
(Pi+ 1) (Pi + 2) (P2+ 1) (n+ l)*(n + 2)
-«(Рг) (Р2+ 1) (Pi + 2) (n) (n+ 1) (n+2)
-*(Pi + 1) (Pi + 2) (Рз) (η) (n + 1) (n + 2)
+ *» (Рз - 1) (Рз) (Pi + 2) (η)' (η + 1)
+ я» (Рг) (Р2 + 1) (Рз) (η - 1) (η) (η + 2)
- *л (Рз" 1) (Рз) <Р2 + 1) (η - 1) (η) (η + 1),
and with denominator
(1)« (2) (η + Pl +1) (η + Pl + 2) (η + ρ2 + 1),
and we find that we may write
(l)2 (2) (n + Pi + 1) (n + P! + 2) (n + p2 + 1) IL (ρ,ρ,ρ,; η)
(Ρα +1) (Pi + 2) (Pa) (P2 + 1) * (p3 - 1) <Рз)
β (Pi + 2) (η) (ρ2 + 1) (η + 1) (Рз) (η + 2)
а? (η- 1) (η) χ (η) (η+ 1) (η + 1) (η + 2)
an elegant result which suggests the general formula.
494 We may also take the following view:
Recalling a previous notation for the order four
A> = (Pi + 1) (Pi + 2) (Pi + 3), etc.
and taking a product
where i,j, k91 denote some permutation of the numbers 3, 2, 1, 0 and Fn is
a function of η to be determined, we substitute
AiBjCbDi.F*
(η + ρ1+1)(η + ρ1+2)(η + ρι + 3).(η + ρ2+1)(η + ρ2 + 2).(η + ρ3 + ϊ)
240
INVESTIGATION OF THE FOURTH ORDER
[SECT. X
for IL(p1p2pzpi; w).in the functional equation and find a result which
on reduction is
(n)(n+l)(n+2)(n + 3)
Fn (n + i - 3) (n + j - 2) (n + к - 1) (η +1)
so that Fn =fnfn-ifn-z ....
Now write
fo) (n-l) (n-2)
J?n—ι —Jn-^n
(n + i-3) (n + i-4) (n + i-5)
(n + j-2)> + j-3)> + j-4)
(n + 2) (n+1) (n)
= Фаг*
• = Фъэ,
• = фск,
• = φαι,
(n + k-l)(n + k-2)(n + k-3)
(η + 3) (η + 2) (η+1)
(η + Ι) (η + Ι-1)(η + ί-2)
Fn ~ фаъфуфскфсИ-
We then have
(^(^(SXn + ^ + lXn + Pi + ^tn + Pi + ^.in + Pjj+lXn + p^^
χ (η + p3 + 1) IL (ргрфр*; η)
Ацфаг В-аФы юСьфсъ Χ^Ώζφ^
X Л2фа2 Вафъ2 С2фс2 ® ·Α}φά*2
Λΐιφαι хВгфъ Сгфс1 D^dl
ХеЛ0фа0 Я?В0фъо хС0фс0 Ώοφάο
where
фаз = фы = фея = фаз = 1,
фа2=(п), фЬ2=(п + 1), ф<,2 = (п + 2), фф2 = (п + 3),
фа1-<п-1)(п), фЬ1=(п)(п+1), фс1 = (п+1)(п + 2), фй1 = (п+2)(п + 3)
фа0= (п- 2) (п- 1) (п), фЬ0= (п- 1) (п) (п+ 1),
фс0 = (η)(η + 1)(η + 2), фй0 = (п+1)(п + 2)(п + 3),
so that the determinant is
(Pi+l)(Pi+2)(Pi+3) (p2) (p2+ 1) (p2 + 2) я(р3-1)(р3)(Рз+1) ^(Р^Ир^Ш)
x(n) (Pl+ 2) (p!+ 3) (n+l)(p2+l)(p2+2) (n + 2) (Рз) (p3+ 1) *(n+3)(p4- l)(p4)
.^(n- 1) (n) (p!+ 3) #(n) (n+ 1) (p2+ 2) (n+l)(n+2)(p3+l) (n+ 2) (n+ 3)(p4)
л» (n- 2) (n-1) (n) ^(n- 1) (n) (n+ 1) x(n) (n+1) (n + 2) (n+ l)(n+2)(n + 3)
CH. II] THE FINAL DETERMINANT 241
This is evidently a general process and suffices to establish that a solution
of the functional equation of order m is a determinant of order ra in which,
to a power of xprh, the constituent in the rth row and cth column is
(pc + r-e + l)...(pc + m-c). (n-r + c + 1)... (n + c- 1),
the associated power of χ being лЛ 2 / when the constituent is below the
principal diagonal and яЛ 2 ' when above; the determinant being divided by
(l)™-1 (2)m~*... (m- 1) (n + Px+ 1)... (n + Pi + m - 1)
x(n + p2 + l)...(n + p2 + m-2) (n + pm-x + l).
This is the expression of IL (ргр2... pm; n).
It clearly reduces to IL (ргр2 · · · pm I °°) as previously found when
71= 00.
To illustrate the properties of the determinant we will consider either
the determinant of order three or that of order four.
If we put Pi = p2z=z ··· =Pm = h the expression of IL(plp2...pm; n)
should become unity. It is then in fact
IL(l; m; n),
and is concerned with a lattice in which the nodes in the directions of the
axes x7 y, ζ do not exceed I, m, η in number respectively.
GF(l; m; n\ L (I; m; n) and IL (I; m; n) are each of them symmetrical
as regards the numbers I, m, n. In particular the determinant portion of
IL (I; m; n) is symmetrical in the numbers Z, n.
In the determinant of order three put px — p2 = p3 = I, and we find
I (i+l)(I + 2) (i)(l+l) ^(1-1) (Ϊ) 1
a(n)(l + 2) (η+1)(ί+1) (η + 2)(ί) ,
I ar» (η- Ι) (η) χ (n) (n+ 1) (n+ 1) (n + 2) J
which must be symmetrical in l7 n.
The associated denominator is
(l)2(2)(n+I+l)2(n+I + 2),
and we have to shew that the determinant is equal to it.
If we put η = oo , the determinant becomes (l)2 (2); that is to say, η and
I disappear together. It follows from this remark that the determinant must
be a function of η + I. We therefore put I = 0 in the determinant in order
to find it as a function of n. If then we substitute η +1 for n, we must get
the expression of the determinant.
M. A. II. 16
242
SUMMARY OF RESULTS
[SECT. X
For example, putting I = 0, the determinant becomes
(1) (2) 0 0
β (n) <2) (n+l)(l) 0
ж»(п-1)(п) ж(п)(п+1) (n + l)(n+2)
which is (l)a (2) (n + l)2 (n + 2).
Thence writing η + I for n, we see that the former determinant is
(l)2(2)(n+I+l)2(n + l + 2),
and thus IL (I; 3; n) = 1.
The reasoning is general, and establishes the result
IL(l; m; n) = l.
This may be verified in numerous special cases, and suffices to confirm
the expression obtained for
IL(p,p2...pm;n).
495. The results that have been established may now be set forth as
follows:
IL(ргр2; n) =
(l)(n + Pl + l)
L(plp,;n)=(l)(2)...{p1 + ]
(lMn + Pi+l)
(Px+1) (P2)
a?(n) (n+1)
(n + 2)... (n + P!+ 1). (n+ 1)... (η+Ρϋ)
(2)...(p1+l).(l)...(p2)
(Pi+1) (Рг)
χ (η) (η + 1)
GF(Plp2,n)- й___.)___
(Pi + 1) (Рг)
χ (η) (η + 1)
(1)(η + Ρι+1)
IL(U;n) = IL(l;2;n) = l;
GF(ll;n) = GF{l-2;n)J^V ^^ί)·. (ί)+ ■ V^'
Observe that we may also write
bJripfr.n) (l)...(p1+l).(i).T(pl) I eW (n+i)
a form which has some advantage.
CH. II] CONJUGATE RESULTS
We have yet another form, viz.:
243
GF(p1pt;n) = -
(l)...(n + Pl)
(D-.fo-t-Ps)
(1)... (пч^). (1)... &+I)'(1)... (n). (1)... (Pa)
(Pi + 1) Ы
ж(п) (n+1)
(^-(n + P!) (l)...(n + P2) (1)...(п + Рз)
(1)...(п + 2).(1)...(р1 + 2)(1)...(п+1).(1)...(Р1!+1)(1)...(п).(1)...(Рз)
(Pi+l)tPi + 2) <Ρ2)(Ρ2 + 1) ^(P3-l)(Ps)
^(11)^ + 2) (n+l)(p2+l) (п + 2)(рз)
a»(n-l)(n) ж (η) (n+1) (n+l)(n + 2)
ΛΓ.//.ο.,Λ-(η + 3)···<η + ϊ + 2) (η+2)...(η+Ι+1) (η+1)...(η+ί).
W^d.nj- (3)..(l+2) · (2)...(l+l) * (1)... (I) '
СМ*(1;»»;п)
(n + m)...(n + l + m-l) (n+m-l)...(n+t + m-2) (n + l)...(n+l)
" (m)...(I + m-l) * (m-1)... (t + m-2) " (1) ... (I) ;
1
GF(l;m; co)«
QF (I; oo;oo) =
(m)... (I + m- l).(m- 1)... (I + m-2) (1)... (I)'
1
(1)(2)... (I). (2) (3)... (1+ 1).(3) (4)...(I+ 2) adinf.;
(?F(oo;oc;co)=(1)(2).2(3)3(4)4 ^ .^ .
496. The expression of GF{pxp2 ...pw; n) is not altered by substituting
for Pip2---Pm the partition conjugate to it; though the form is changed.
Interesting identities therefore present themselves.
In general, the solid graphs with which GF{pvp2... pm; n) deals are those
contained in the graph
0 χ
η η η η η ρλ nodes in breadth
η η η η рг „
η η η η ρΆ „
η η ρ4
η η
У\ η η рт
where η denotes a pile of η nodes in direction of the axis of z.
16—2
244 CONJUGATE RESULTS [SECT. X
This graph has six aspects which may be exhibited in the following
manner, so as to put in evidence the numbers Z, m, n.
Instead of the partition р^.2... рш adopt the notation
M2 ··· Zm,
and let rn^in^ ...mi be the partition conjugate to it, so that
Ζχ = Z, mx = m.
If we rotate the above .graph about the axis of у through a right angle
we get
Zj Zi k lY Ιλ η nodes in breadth
V2 *2 '2 *2 ^2 »
h h h Z3 lz „
Z4 Z4 Z4 64 64 „
I'm "m "in "m I'm -
which is a graph, uniformly η nodes in breadth, parallel to the axis of #, and
standing on a plane graph, m nodes long, parallel to the axis of у; the sth
row being uniformly of height Z8, parallel to the axis of z. Rotating to obtain
the other aspects we find that
enumerates plane partitions specified by
(i) rows ll} Z2, ... ^n.in length respectively with a limit of part
magnitude η;
(ii) rows mlt ηι2)... mi in length respectively with a limit of part
magnitude n\
(iii) η columns and m rows, the part magnitudes in the rows being
limited by the numbers l1} Z2, ... Zm respectively;
(iv) η columns and I rows, the part magnitudes in the rows being
limited by the numbers mb rn2,...mi respectively;
(v) m columns and η rows, the part magnitudes in the columns being
limited by the numbers Zb Z2, ...Zm respectively;
(vi) Ζ columns and η rows, the part magnitudes in the columns being
limited by the numbers ml9 m2> ...rrii respectively.
CH. II] APPLICATION TO ORDINARY PARTITIONS 245
497. Valuable information concerning line or one-dimensional partitions
is furnished by putting η = 1 in the general formula.
The partitions which are then enumerated are those in which every part
is unity, there being not more than pr units in the rth row:
11111
111
1 1
1
In fact each partition is derived from the graph of a unipartite line
partition by substituting units for nodes, and the number of units in each
row is limited not to exceed a certain number appertaining to the row.
If we add up the units in each row we obtain a line partition
(P1P2P3 ...jO»
in which Ps'^P*,
Pi, p2> ---Pm being given numbers in descending order of magnitude. The
partition (pip* ---Pm) may be said to be "containedv in the partition
(P1P2... Pm)> and the formula shews how many partitions of given content are
contained in the given partition (ρλρ2 .--Pm)-
Putting w = 1 in the expression of GF(plp2p^'i n) we find after a slight
reduction
(Pi+1) (P2)(P2+1)
"(m*;!)-^},
and denoting
{fj(P2+l)
ж (p3 - 1) (Рз)
(2M3)
Tl) (2)
U)(2)...(P)
U)(2)...(q).(l)(2)...(p-qr·' * *
by Xn ОГ Χρ,ρ-q,
we may write
QFiw, l) = (f^
^•OWftiD-fjJ^
-<1)(2)(3)(4)
(Pi + 1) (P2)
О! Хщ
(Pi + 1) (P2) (P2 + 1) * (Рз - 1) (Рз)
(p2+l) Хм(Рз)
О но Х&
QF (ргрфр^, 1)
(Pi+1) (P2XP2+1) ^(Рз-1)(Рз)(Рз+1) *!(Р4-2)(р4-1)(Р4)(Р4+1)
ее Х21(р2+1) Х»Ы<Рк+1) ^«(р4-1)(Р4МР4+1)
(Рз+1) ^г(Р4)(Р4+1)
0 0 « Х«(Р4+1)
246 EXAMPLES [SECT. X
In this formula of the order four the factor (p4 + 1) has been entered
in the last column of the determinant so that the law may be the more
apparent to the reader, χ appears in each constituent in the minor diagonal
which lies below the principal diagonal. In the minor diagonals which lie
above the principal one the powers of χ are x°, χ, χ О, eG),..
. etc., the
figurate numbers of the third order appearing as exponents.
Ex. gr. GF(Plp,; 1) = (1.^)(1,^(1 + *p>+1 -*Pi+1 -^+%
and we find particularly that
&F(42; 1) = 1 + x + 2x* + 2я* + 3x* + 2x* + x*,
the partitions enumerated by the coefficients being
zero; 1; 11, 2; 21, 3; 22, 31, 4; 32, 41; 42,
viz. all those that are contained in 42.
498. To enumerate the partitions contained in (pip2··· Pm) is the same
as to find the sum of the coefficients in the expanded expression of
W(PiP*-~Pml 1)·
We have therefore to put χ = 1 in the above formula. This is done by
putting every bracketed number (s) equal to s and Xpq = ( J ·
Thus for the order two we find the number \{p2 -fl) (2px — p2 + 2).
These results are unchanged when for (pip* ---Pm) is substituted the
conjugate partition.
OHAPTEE III
PARTITIONS IN SOLIDO
499. In this chapter we make a preliminary investigation concerning
solid partitions where the parts are placed at the nodes of a solid graph and
descending order of magnitude is insisted upon in the directions of the three
axes of the graph.
The remark may be made that if a unit he placed at each node of a solid
graph and the graph be projected upon either of the coordinate planes by
addition of units we thus obtain a plane partition in the plane of projection.
In fact plane partitions are in theory coincident with solid partitions in
which the part magnitude is restricted not to exceed unity. It will be
remembered that similarly it was found that plane partitions in which the
part magnitude is restricted not to exceed unity are coincident in theory
with line partitions.
The enumeration of solid partitions is also connected with permutations
derived from a solid lattice and with lattice functions. If we consider the
three-dimensional system of nodes we regard it as a system of layers of
nodes parallel to the ^-plane, each layer being the graph of a unipartite
partition. If a particular layer, the 5th from the #y-plane, be the graph
of the partition {sxs2... sm) we associate with it the assemblage
Thus taking the whole of the layers we get an assemblage of Greek letters
involving as many suffixes as layers. Of such an assemblage we form lattice
permutations. These are such that (i) looking merely at a particular suffix s
the permutation must be a lattice one, (ii) looking merely at a particular
Greek letter, say Θ, the permutation must be a lattice one. In forming the
lattice functions from these permutations we note (i) a letter which comes
immediately before another which is prior to it in alphabetical order, (ii) a
suffix which comes immediately before a suffix prior to it in numerical order
provided that both suffixes are attached to the same Greek letter.
248
THE LATTICE LAW
[SECT. X
500. If we restrict attention to the cases in which not more than two
nodes appear in the direction of either axis the distinct solid graphs are
©. ΘΘ ΘΘ ©Θ ΘΘ
Θ · Θ Θ
otherwise denoted by plane partitions
21 22 22 22 22
1 1 11 21 22
Taking the first of these we have four nodes, shewn in the diagram
in perspective, at which numbers are to be placed so as to obey the
inequalities indicated. The two layers parallel to the #y-plane have the
specification 21 and 1 read parallel to the ж-axis. We associate with the
ζ
>—.*
У
solid graph the assemblages <*Ύ<χ.ιβι> α2 for the layers respectively and
consider the lattice permutations of the assemblage ад&Яз- The lattice law
must be obeyed by each of the triads α1α1β1) a^a^. We find that the
permutations are six in number, viz.:
Index
*i&|«i«2 2
α1α1α2β1 Ο
«iAW^i 5
ai^iajA 2
«i«2Al<*i 3
leading to the lattice function
1 + (2#2 4- 2#3) + a*f
the sub-lattice functions being indicated.
Λ\
СН..Ш] THE LATTICE PERMUTATIONS 249
501. Denote by GLF(21; 1; «)
the function which enumerates the partitions when the part magnitude
is restricted by the number n. Then the principles established in preceding
chapters give the results:
0*421, 1, »)- (1M2)(3M4) .
GF (21; 1; n)
(η+1)(η+2)(η+3)(η+4) + (2^+2^)(η)(η.+ 1)(η+2)(η+3)+^(η-1)(ηΜη+1)(η+2)
(1) (2) (3) (4)
±g Ы(Л, 1>Ю-{1_дП1_9в.)(1„да^{1_9вгП1_дв11у
502. In fact the assemblage of Greek letters must be regarded as
connected with the solid lattice in the manner shewn
in the figure, and the property of a lattice
permutation of the assemblage is that if a line be drawn
between any two letters the nodes which
correspond to the letters to the left of the line con- aA αχ
stitute a complete or incomplete lattice. Thus
the permutation cannot commence with β1 or a2
because neither of the nodes corresponding thereto л ,
constitutes a lattice. The letter αΎ must be at
the origin of the lattice. In the present instance every permutation which
commences with щ forms progressively a system of nodes which always
constitutes a lattice. It is clear that, fixing the attention upon the nodes which
lie in any plane parallel to one of the coordinate planes, the corresponding
letters must occur in a lattice permutation of those letters. If the nodes lie
in ξ planes parallel to the ^г-plane, η planes parallel to the 2#-plane, and
ζ planes parallel to the #jr-plane, the whole assemblage of letters must
satisfy ξ-\-η + ζ conditions; for that number of collections of letters drawn
from the assemblage must be in a lattice permutation. In the above simple
case
f-2, i? = 2( Г=2,
but the six conditions practically reduce to one only, viz. that associated
with either of the planes ccy, zx. It is easy to see that in any solid lattice
each layer of nodes parallel to a coordinate plane must be a plane lattice and
that if, in proceeding from left to right of the permutation of the assemblage,
at any moment any such plane lattice be deficient, then the solid lattice will
be deficient and cannot be in correspondence with a lattice permutation of
the assemblage. The full number of conditions for a lattice permutation,
viz. ξ + η 4- ζ, will most frequently suffer some reduction, as those conditions
250
SIMPLE PARTICULAR CASES
[SECT.X
may be either trivial or not independent. In the above case the planes
which contain the single nodes au βΐ9 щ, give three trivial conditions and the
planes yz, xy conditions implied by that given by the plane zx.
The lattice permutations are then connected, as in the case of plane
partitions, with non-overlapping Diophantine inequalities and the
investigation proceeds with the results given.
603. Passing now to the solid graph
we consider the system
A\
Э
Θ
•
α
A\
<*1
•2
_ 22
1
>
> \
and in forming the lattice permutations of the assemblage α1α^α2α2β1 we have
only to take care that the letters in the plane zx are in lattice permutations
There are eight lattice permutations:
Index
0
2
4
6
«ιβι&αΛ
«1«2βΐ«1«2
αι/3ι<*ια2α2
«ιβι^αιΟο
Index
3
3
2
5
α1α2α1α2β1
*ι«2«ιΑ«β
and the lattice function is
1 + (2x* + 2л?3 4- x4) +X5 + x\
yielding the results
1 + (2&·2 + 2x* + x4) + (x5 + x6)
(1)(2)(3)(4)(5)
GF (21; 2; oo) =
GF (21; 2; n)
(n+l)...(n+5)+(2^2+2^+^)(n)...(n+4)+(^+^)(n--l) ..
(n + 3)
(1)(2)...(5)
1 + g(2x2 + 2х* + х*) + д2(х* + х«)
(l-g)(l-g*)(l-ga!)(l-gaV(l-g*)(l-gafi)'
tgn GF (21; 2; n) =
CH. Ill] SIMPLE PARTICULAR CASES
504. Next we come to the solid lattice
Θ Θ = 22
• · " 11
and consider the system
251
[ndex
4
6
8
7
5
10
7
8
«ιαιΑ«ί<%Α
αιβ1α1<^αίβ1
α1α1αίβ1(^β1
βιΑ^α^Α
αΐ«2βΐΑα2^1
«lOifta^A
«ιβι^β^Α^
α,^^α^,/δι
Index
3
2
4
δ
6
3
0
2
The lattice permutations of the assemblage α^ο^^βχβχ must involve the
collections «Л АД, a^c^c^ in lattice permutations and we do not attend
to other conditions. We have sixteen permutations :
αι«ιΑΑ«№
αιβΛ α2/3ιθ2
«ι&ββΟιΑα,
and the lattice function
1 H- (2л?3 + 2#3 + 2#* H- я5) + (^ -f 2л·6 + 2л;7 + 2л8) + л?10.
When we come to examine these permutations we find that those which
terminate with βτ give rise to a portion of the lattice function which is
equal to the whole lattice function derived from the permutations of the
assemblage α^ο^βι, and necessarily so because no component of the index
can arise by the contact of any letter with the terminating &. Also as
regards those which terminate with a2 the permutations are of two kinds.
Those lattice permutations of the collection α1α1β1β1α2 which terminate with
a2 pass on the same index when another Oj is added, but those which
terminate with β1 add the number 5 to it when a2 is added.
The reader will now have no difficulty in realising the relation which
follows from these observations, viz.:
£(22; 2; oo) = Z(21; 2; oo)+aftb(21; 1; ос)+л*Х(22; оо ),
252 PARTS Αϊ THE SUMMITS OF A CUBE [SECT. X
because those permutations, written out above, which terminate with βιΟ^,
are the whole of the lattice permutations of the assemblage ал/З^; and
those which terminate with a^ are the whole of the lattice permutations of
the assemblage а^Д Д, the factor xi appearing because of the conjunction
of β1 with the penultimate a2.
The formula for OF (22 ; 2; oo ), QF(22 ; 2; л) and tgnGF (22; 2; n)
are written down as in the other cases and need not be particularly given.
505. The remaining cases for consideration are the solid lattices
Θ Θ _ 22
© . ~ 21'
Θ Θ _ 22
Θ Θ ~ 22
and they are so intimately connected that it is convenient to consider them
together.
The assemblages of letters are ο^αιΑ&ο^Α and «ιΟ^Α^ο^α^Α
respectively. If we write down any lattice permutation of the first of these we
can obtain a lattice permutation of the second by the addition of β2 as last
letter, and since every lattice permutation of the second must end with
/32 it is clear that each assemblage has the same number of lattice
permutations. Moreover the addition of β2 to the lattice permutations of the first
introduces no new component to the index. Hence the two solid lattices we
are considering lead to the same lattice function and we have
£(22; 21; oo) = £(22; 22; oc).
506. There is a one-to-one correspondence for a solid lattice of w nodes
between the arrangements of w different integers placed at the nodes so as
to satisfy the inequalities marked between adjacent nodes and the allied
lattice permutations. We will illustrate this in the case of the seven nodes,
which form seven out of eight summits of a cube, shewn in the left-hand
CH. Ill]
THE LATTICE PERMUTATIONS
253
diagram of the two above given. We will at the same time determine the
lattice function. One arrangement of integers is
5^4
where it will be observed that the inequalities are satisfied.
We write down the corresponding lattice permutation by writing
underneath the numbers, which are arranged in descending order, the
corresponding suffixed Greek letters as depicted in the first seven-node diagram.
Thus in the present example
7 6 5 4 3 2 1
«1 «1 «2 <*2 βΐ βΐ β*
and a lattice permutation of zero index is derived. In the following scheme
the lower layer and upper layer of numbers are given on the left and on
the right respectively:
7 6 5 4
3 2 1
«! «1 «2 «2 Α βΐ A
7 5 6 4
3 2 1
θ! aje, а„ Α βι β.,
7 5 4 3
6 2 1
<*ι Α|α. α2α2Α A
7 6 4 3
5 2 1
«iOift|«2«a&&
7 4 6 3
5 2 1
αιαίβ1\αια3β1βί
7 6 5 3
4 2 1
«1«1«аАКАА
7 4 6 2
5 3 1
a,a,Alai&l«sA
7 4 6 2
5 13
«ι α* £ι|αι&|ο.Α
7 5 4 3
6 12
βΐ Α|«1 «2 «2 A|ft
7 5 4 1
6 3 2
«ι АЦвгААК
7 6 4 3
5 12
«ι<*ι ΑΚ«β&|&
7 6 4 1
5 3 2
«ι«! Al«9 A Ah
254 THE LATTICE PERMUTATIONS [SECT. X
7632 7463
5 4 1 5 12
αϊ «ι A A|*i <h A «i«aA|«i«»A|A
7362 7461
5 14 5 3 2
«i «a A Ah «a A Oi«»A|«iAAh
7652 7653
4 3 1 4 12
«ι «ι α2 A Ah Α αϊ α, α, Ah A|A
7652 7631
4 13 5 4 2
<*ι «ι α2 A Ah Α «ι«! A Ah Ah
7654 7361
3 12 5 2 4
α, «J α2 α2 & ΑΙΑ «! «s A AK Ah
7651 7651
4 3 2 4 2 3
αϊ αϊ «2 A A Ah «i«i*aAA|Ah
7453 7452
6 2 1 6 3 1
«ι Ahh α4 Α Α α! Ahh Ah A
7563 7452
4 2 1 6 13
<*i «sh Ah A A «i Ahh Ah A
7532 7453
6 4 1 6 12
«j Ah Ah ог Α αϊ Ahh as ΑΙΑ
7352 74 5 1
6 14 6 3 2
αϊ Ah Ah α2 Α «ι Ahh A Ah
7562 7563
4 3 1 4 12
αϊ ^h A Ah A ai «ah Ah A|A
7562 7531
4 13 6 4 2
αϊ «ah A Ah A «i Ah Ah Ah
7542 7351
6 3 1 6 2 4
ax Ah «2 Ah Α «χ Ah Ah Ah
CH. Ill] GENERAL RESULTS FOR THE CUBE 255
7542 7561
6 13 4 2 3
<h A|«l «2 A|«2 Α βΐ Oj«l A A|A|«2
76 4 2 7541
5 3 1 6 2 3
«ι «ι ft|«2 Ala, & «i A|«i «2 A|A|«2
7642 7641
5 13 5 2 3
«1 Λΐ A|«2 &|«2 A «! «a A CbfiJlA|*2
7564 7461
3 12 5 2 3
«i a2|«i a2 A A|A «i «2 Al«i AlAk
7561 7451
4 3 2 6 2 3
«i «2|«i A A Al«2 «i AW«iAIA|«2
507. There are 48 permutations. The dividing lines shew the order of
the associated lattice function. Forming the lattice function in the ordinary
way we find that
X(22; 22; oo)
= 1 +(2л?+ 2л?3 + Зл?4 + 2л?5 + ЪР)
4- (ά5 4- 3α?β + 4л·7 + 8z* + 4#° -f За?10 + л;11)
+ (2ж10 + 2л?11 Η- 3#12 Η- 2&α3 + 2л?14) + xl(i
= Z(22; 21; oo);
and thence writing
L (22 ; 22 ; oo ) = L0 + L, + L2 +L3 + X4,
wc obtain
grr22-22-oo-) -Z(22;22;0O)-
W(^,22,oo)_ (1)(2) (8) ,
gJ'(22-21-co'>-£(22;21;00)·
W (22, 21, oo)- (1)(2) (7) -
/?r./gg.go.1,4_SXt(n-t+l)(n-t + 2)...(n-t + 8).
fltf(22,22,ii) (l)(2)...(8) '
Ар/а,. gi .1)v_2Xt(n-t+l)(a-t + 2)...(q-.t + 8).
(M (22, 21, и) (1)(2)...(7) '
S>#Fi22 · 22 · «Л - Д + gA + g*Д» + g"£8 + 9*А ш
Σ9 ^(22,22,η)-(1_^)(1_^)(1_^) (1_^);
Za*GF№· 21- гЛ - А + gA + g* A + g* A + g1 A
2g ^(22,21,re)-(1_^)(1_^)(1_^)^(i_^).
256
FURTHER SHORT DISCUSSION
[SECT. X
508. This completes the results up to the point where the number of
nodes along each axis does not exceed two. It suffices to establish that by
the method pursued we have potentially the complete solution of the problem
of Solid Partitions. The discovery of the algebraic form of the lattice
function in the general case has not been made. It appears to be a
complicated and difficult question. A short discussion, however, may be given.
When we were speaking of solid lattices it was shewn that such a lattice
might be read in either one, two, three, or six different ways, according to
the degree of symmetry possessed by the lattice. It follows that the
specification of a lattice by layers of nodes may be in one, two, three, or six
different forms. Thus the notation GF (21; 1 ; n) is unique ; but the three
forms
GF(22; 1; n\ GF(21; 2; n), GF(21; 11; n)
are equivalent because each is associated with the same graph
Θ Θ _ 22
1 '
which has three aspects.
In particular the equivalence
GF(p^2\qiq2\ n) = GFip^; p2q2; n)
should be noted.
We have already met with one or two instances of relations between
lattice functions of the new kind, so that it is not surprising to find that
lattice functions and generating functions are connected by functional
equations. By the same reasoning as was employed in a previous chapter
we establish equations of the type
(Pi + P2 + qi) GF{p,p2\ qx\ oo)
« GF(th - 1ft; «ι; χ) + GF(p1p2- 1; ?i; ») + GF(Plp2; ?l - l; «)
-GF(p1-lp2-l;q1;n)-GF(p1-lp2,ql-l]cc)-GF(plP2-l;q1-l;tt)
+ QF(pj-lpt-l; j!-l; oo ),
and transforming to lattice functions
= X(pi-lft;ii; οο) + £(ρι#,-1; &; *>) + L(plpi;ql-i·, oo)
-(Pi + p2+qi-i){£(pi-ift-i;?i; °°) + -£(i>i-ift;?i-i; <»)
+ £(Pil>a-i;?i-i; oo)}
+ (Pi + P2 + qx - 2) (px + p2 + qx - 1) L fa -1 p2 - 1; q 1 - 1; oo ),
сн. πι]
GENERATING FUNCTION IN A PARTICULAR CASE
257
with the usual modifications when there are equalities between the numbers
Pn Pt, ?ι· As a particular case
i(a;l;oo)=X(Z-ll;l;oo)+2X(il;oo)-(I+l){2i(i-ll;oo) + X(i;oo)}
+ (i)(I+l)Z(i-l;oo).
Since
we find that
X(il;oo)-l+*»fi^; Z(i;»)-1,
L(ll; 1; oc ) = L(l -1 1; 1; oo) + d»(l + «) (-Ш^ - 2^+*,
and now it is readily shewn that
(l)3 L (11; 1; oo ) = (t + 1) (i + 2) - 2x (1) (I + 2) + *»(1) (2)
(1 + 2) (t + 2)-cc(2)
M. Л. IIt
17
CHAPTER IV
THE SYMMETRY APPERTAINING TO PARTITIONS
509. It has already been observed in Art. 428 that the
three-dimensional graphs of plane partitions have either one, two, three, or six aspects,
leading to one, two, three, or six different readings. There are thus four
classes of graphs and partitions, and although their complete theory has not
yet been discovered, the subject may be usefully discussed up to a certain
point. Taking an origin and three coordinate axes, the graphs which permit
of only one reading are symmetrical about the
line through the origin equally inclined to the
three coordinate planes (or axes). Upon that
line, which may be called the diagonal of the
solid graph, there must be one node, at the
origin, and there may be any number. First
consider the symmetrical graphs which have
only the origin node upon the diagonal. Then
the whole of the nodes must lie in one or other
of the three coordinate planes. For every node
upon the axis of χ there must be corresponding
nodes upon the axes of у and z. For every node, not upon an axis, that lies
in the plane xy there must be corresponding nodes in the planes yz and zx.
The nodes that lie in any one of the three coordinate planes constitute a
self-conjugate graph in two dimensions. We thus obtain three perfectly
similar self-conjugate graphs, but they are not quite distinct, because there
is overlapping due to the circumstance that the origin node lies in each of
the three planes, while every node which lies upon one of the coordinate
axes necessarily lies in each of two of the coordinate planes. We may
therefore separate the nodes into three lots: (i) the origin node, (ii) nodes
which lie upon the axes, the origin node excepted, (iii) the nodes which do
not lie upon an axis. The nodes in (ii) occur in threes. The nodes in (iii)
constitute in each coordinate plane the same self-conjugate graph, and
therefore these nodes also occur in threes. The whole number of nodes must
consequently be of the form 3m + 1.
SECT. X, CH. IV] GRAPHS WITH ONLY ONE READING
259
510. Let us now enumerate the graphs which have i nodes along each
axis (the origin node included on each axis). We have then as a minimum
Ы — 2 nodes. In the plane xy we may have any self-conjugate graph which
involves exactly i nodes in the direction of each of the axes of χ and y, or, if
we omit those nodes which lie upon those axes in the plane xy, we have any
self-conjugate graph which involves i — 1 or fewer nodes in the direction of
the axes of χ and y. These graphs are enumerated by the function
(1+л0(1 + ^)(1+^...(1+а^),
since we have seen that the nodes may be separated into angles of nodes,
symmetrical about their origin, which involve numbers of nodes which are
unrepeated uneven numbers. Clearly the external angle of nodes involves a
maximum of 2г — 3 nodes.
Hence, since, as remarked, the nodes occur in threes, and there are Зг — 2
nodes upon the axes, we find that
^•-2 μ + a») (i + #9) (χ + дл«) ... (l + a!*-*)
is the function which enumerates the solid graphs which have only one
aspect, i nodes along each axis, and every node upon one of the coordinate
planes. This leads us to the function
to enumerate the graphs when there are г nodes or fewer upon each axis.
Also when г = oo to the function
1 + я + л'(1+лл) + л'(1+^)(1+^)+ ad inf.
511. By viewing the matter in another manner we can obtain another
form of the function which gives an interesting identity.
Suppose that in the plane xy we have four nodes along the diameter О A.
This implies that the square OA is full of nodes, and, by symmetry, also each
of the squares OB, 00 must be full of nodes. (For diagram, see p. 260.)
Altogether we must have at least 4 χ 32 ■+-1 or 37 nodes, and 37 = 43 — 3s.
Without increasing the number of nodes upon the diameter О A, we may
add nodes in the plane xy which constitute a plane graph made up of rows
which do not exceed four nodes in length, the rows being taken parallel to
the axis of у and terminating in the axis of x. But if we do this, symmetry
demands that we add a similar graph in the plane xy, the rows being
parallel to the axis of χ and terminating in the axis of y; similar graphs
also
in the plane yz, with rows parallel to the axis of y, and terminating in
the axis of ζ;
in the plane yz, with rows parallel to the axis of ζ and terminating in
the axis of у;
17—2
260 ANOTHEB SOLUTION AND AN IDENTITY [SECT X
in the plane zx, with rows parallel to the axis of z, and terminating in
the axis of χ;
in the plane zx, with rows parallel to the axis of я?, and terminating in
the axis of z.
These six graphs are not quite distinct; there is overlapping due to the
nodes that are added upon the axes. Thus a row of four nodes added in each
of the six half-planes adds not 6 χ 4 or 24 nodes, but 24 — 3 = 21 nodes. So
rows of three, two and one add 6 χ 3 — 3 = 15, 6 χ 2 — 3 = 9, and 6x1-3=3
nodes respectively.
* χ x x
7
χ /
x/
в
у
ν
Χ ,
/
/
/
γ.
/
/
/
/
/ο
7
/ / /
/ / .
/ / /
с χ
χ
Λ
χ χ
Χ
Χ
χχχ
The case of a row of four nodes is indicated by crosses in the diagram.
Hence our addition resolves itself into lots of 21 nodes, 15, 9, 3 nodes
each any number of times repeated. We see then that if there are exactly
four nodes along the diameter OA wc have an enumerating function
x^f_
(1 - a?) (1 - x») (1 - x15) (1 - a")'
and generally, if we have exactly k — 1 nodes along the diameter О A, we
have an enumerating function
ж(*-1)3-{*-2)3
(1 - я») (1 _ да) (χ _ χιη ... (1 _ дл*-») ·
512. Thence we conclude that the graphs which have one reading only
and every node in one of the coordinate planes, are enumerated by the series
a? x"
1+-
7,19
+
а? (1-аз»)(1-яР) (1-л»)(1-я?)(1-ж»)
#{*-l)S-(fc-2)S
+ ...
(1-я»)...(1-а?*-*)
+ ...
CH. IV] ONE GRAPH GIVING RISE TO AN INFINITE NUMBER 261
which, on expansion, must be identically the same as that previously found,
viz.:
1 +x + я4(1 +я*) + a?(I +0(1 + #9) + ... + ^-2(1 + a?) ... (1 -f я6*"9) + ....
We thus establish an interesting identity.
513. These partitions the nodes of whose graphs lie all upon the
coordinate planes are represented by solid angles of nodes which are perfectly
symmetrical in respect to the three coordinate planes. All other partitions
which possess this #i/#-symmetry are formed by fitting into one another two
or more symmetrical solid angles of nodes so as to produce a regular solid
graph. So far we have merely enumerated the external solid angles of
nodes or boundary partitions. It is not difficult to construct a crude
generating function arising from a number of Diophantine inequalities, but
effectively the enumeration has not, up to the present time, been earned
any further.
One further remark however may be made. From any one of these
graphs we can immediately derive an infinite number of others of the same
symmetrical nature; for if we take a square of nodes having г nodes in
a side and form a symmetrical three-dimensional graph in the left-hand top
corner, we may conceive the square
2 1
1
completed into a cube of г3 nodes. The graph in the corner if now
subtracted from the cube leaves a solid graph which if rotated through· 180°
presents a symmetrical graph. The two graphs are in fact supplementary
the one of the other qua a cube of г3 nodes. Hence a symmetrical graph of
г3 — w nodes in the general case where the graph of weight w has г or fewer
nodes along each axis.
In the case above the graph of weight 4 gives rise to the graphs whose
generating function is
л,·4 + з/~* + я*3-4 + a?3-4 + ... + af-A + ....
Exceptionally in this case when г — 2, the graph itself is reproduced.
Thus from the partition
321
21
1
262
GRAPHS WHICH POSSESS ^-SYMMETRY [SECT. X
we produce
332 4444 55555
321 4443 55555
21 4432 55554 etc. ad inf.
4321 55543
55432
514. Certain graphs possess symmetry in relation to the axes of χ and у
and do not possess symmetry in regard to the three coordinate planes. If
we enumerate all the graphs which possess ^-symmetry we include those
which possess ля/г-symmetry. Those which possess #y-symmetry only have
three aspects and give rise to plane partitions which read the same by rows
as by columns. We therefore attempt the enumeration of plane partitions
which have this property and understand that those which are perfectly
symmetrical are included. Each layer of nodes parallel to the #2/-plane
is a self-conjugate graph. We may regard the whole graph as arising by
superposing, when possible, such layers. This would be one method of
attacking the problem, but it gives rise to Diophantine inequalities which
are not easy to deal with. The method now given is preferable. Every
plane partition possessing ^-symmetry naturally has successive rows of
numbers of the same lengths as the successive columns of numbers. It is of
the form
an «i2 au...
«21 «22 #23 ...
«31 «32 «33 ···
where a8t = au.
Consider the portion of the partition
«11 «12 «13 ···
«22 «23 · · ·
«33 ...
where the numbers are subject to the inequalities
«11 ^ «12 ^ «13 ^
V V
022>«23>..·
V
«33 ^ · · ·
CH. IV]
and seek the sum
THE CRUDE GENERATINi
Stfn11 *Sa «S1
Χ Λ?22 ^23
X я?зз
263
for all systems of such numbers.
We are led to the crude function
Ω-
>(1-λη^)(ΐ^^^2)(ΐ-^^)... '
\ μιι J \ λ22^12 У
V /^22 /
wherein the auxiliary Xrc refers to arc > ar.c+i, and /i,rc refers to ar.«+i > «r+i.«+i-
Since in the enumeration in order to obtain the content or weight of the
partition we have to double the parts which lie above the principal diagonal,
to obtain an enumerating function we must put xrr = χ for all values of r
and xrc = x2 whenever с > г.
We thus find the function
a I ,
1-
(
M22
the crude expression of the sum
2#απ + «22 + a.33 +... + 2 (ai2 + an + ... + a2:i + ...)^
The coefficient of xw in the sum is equal to the number of plane partitions
of content w which possess #y-symmctry.
Suppose that the first row of the partition involves % numbers. We
then have only to consider the first i columns of factors in the denominator
of the crude function.
For г= 1, we have , which is clearly correct, for the partition consists
for each weight of a single number (equal to the weight) at the origin of the
graph or partition.
264 INVESTIGATION OF THE SIMPLEST CASE [SECT. X
515. For г = 2, we have
ι
>(l-X,,«)(l-g«.)(l-i,)'
as the crude function which enumerates partitions of the form
«11 «12
«21 «22
Eliminating μη it is
Ί
^1-ΧΜ1^^){1'1/Ϊ
and this is γζ r-rz tt-jz -zr ОГ ,_. iov ,л\ >
(1 _ д) (1 _ я*) (1 - д?*) (1) (3) (4)
the correct enumerating function.
516. If we had required a real generating function we should have dealt
with
Ω I - ,
> (1 - ХцЯп) (l - ^ ΧηχΔ (l хЛ
and have found
(1 - #ll) (1 - #11#12#2ΐ) (1 - #11#12#21#22) '
shewing that the partitions can all be obtained from the partitions
1 . 11 11
• ·; ι .' ι r
by adding A times the first or to В times the second or ^ and
С С
to С times the third or ~ p', thus producing the partition
A+B + C, B + C:
B+C , С ,
Ay В, С being arbitrary positive integers. This is the general form of plane
partition of the nature considered and there is no overlapping. There are
no syzygies.
517. If we wish to restrict the part magnitude we proceed as on a
former page, Art. 431, and write gxn for #n, at the same time introducing the
additional denominator factor I — g. The generating function for a part
CH. IV] THE CASE OF г=3 265
magnitude not exceeding η is then equal to the coefficient of gn in the
expanded function. We are thus led to the algebraic fraction
1
(l-if)(l-^)(l-^)(l-^)'
and herein the coefficient of gn is readily found to be
(1 - xn+1) (1 - xn+*) (1 - a?*4)
(l_#)(l_tf3)(l_#4)
518. Proceeding to the case i = 3, we find the crude function
a г-2 .
> (1 -\nxn)(l - -~W) (l - g*i»*fc)
\ Mil / \ λ22Α6ΐ2 /
(1 χΛ
which successively exhibits the forms which follow, in which for brevity and
convenience xrcxcr is written xrcr:
a 1 . .
> (1 - xn) (1 - λ12μη#η#121) (l - *~xmJ
1 -χΔ (1-ς οοοΔ
Κ μη у \ λ22^12 /
1
and thence
and thence
> (1 - xu)(l -Х12а?,1Я?ш) (l ~ — xm)
(I — ApjA^^'n^'isi^W I -*· ~~ л -Г~ #131 #232 J
\ *Ί2 >Ч>2 /
v1 ~~ \7\T>^^^J
fl
> (1 -.*n)(l -'Х1ажпа?ш) il - £~#т)
\J- A.io«^'ji^',ji>i«'2?21i/ \A #11 #121 #22 #131 #23
(J — #п#121#22#ш#232#зз)
and finally by the formula given in Art. 348,
-l· — #ίι#i2i #22#i:n
J(l - #ll) (1 - #ll#l2l) (1 - #11 #121 #22) (1 ~ #ll#121#13l) (1 - #H#l21#22#13l))
( Χ (1 — Xj! #?l21 #22#131 #23г) (1 -~ #11 #121 #22#131 #232#3з) J
266 GEOUND-FORMS AND SYZYGY WHEN г = 3 [SECT. X
This result shews that the fundamental products are
^-i = #m 53 = Λ?ιι ^12^21, CA = #π#ι2#2ΐ#22> A = #n #ΐ2#2ΐ#ΐ3#3ΐ>
Д> = Жц^^^^з^з!, F6 = ^ii^2%«22^13^1^23 #32, ^9 = #И #12 #21 #22 #13 #31 #23#32#33,
connected by the syzygy
The associated fundamental partitions from which all others can be
derived by addition are
1 . . 11. 11· 111
Аг = ..., Д = 1.., C4=ll·, A=l·.,
• · · ··· ··· 1··
111 111 111
E6=l 1 ., .Ρ8 = 111, (?9 = 1 1 1.
1 · · 11· HI
These are connected by the simple syzygy
221
04 + Д = Д + #в=21·.
1 · ·
The general form of ^-symmetrical plane partition of order 3 is therefore
A+B+C+D+E+F+G B+C+D+E+F+G D+E+F+G
B+C+D+E+F+G G +E+F+G F+G
D+E+F+G F+G G
where A, B, C, D, E} F, G are arbitrary positive integers.
519. The derived enumerating function is
1
(1 - x) (1 - я3) (1 - я5) . (1 - О (1 - of) (1 - ar4)'
the numerator term disappearing.
Proceeding to restrict the part magnitude in the usual manner, we find
the algebraic fraction
1 - g2xd
in which we have to seek the coefficient of gn.
This, with some little trouble, is found to be
(1 - xn+1) (1 - xn+s) (1 - χη+δ). (1 - Λώη+4) (1 - хт+6) (1 - я^+8)
(1 - χ) (1 - Xs) (1 - χ5) . (Τ^) (1-я*) (1-я8) '
CH. IV] CONJECTURE OF RESULT IN THE GENERAL CASE 267
520. If we were to proceed to the next case, г ~ 4, we should find the
work very laborious; too much so to be given here in detail; but the result
that would emerge would be
(1 -xn+1)(1 -xn+*) (1 -a?"+8)(l-a?"+y). (1 -д*»+«) (1 -#*"+«) (1 -a2"**)^! -#*"+">)(1 -д***»)
Guided by the circumstance that for the ith order the generating
function must reduce for η = 1 to the function which enumerates self-
conjugate partitions in the Theory of Line Partitions, we may construct
the enumerating function for the order г. It is, written in Cayley's notation
1 - oc8 = (s), an algebraic fraction, of which the numerator is
(n+l)(n+3)(n + 5) (n+2i-l)
χ (2n + 4) (2n + 6) (2n + 8) (2n + 4i-4)
x(2n+8)(2n+10)(2n + 12) (2n + 4i-8)
χ
χ (2n+4s)(2n + 4s+2) (2n + 4s + 4) (2n + 4i-4s)
χ
wherein if г be even there are, omitting the first row, \i rows the last of
which is
(2n + 2i);
and if г be uneven there are \{i — 1) rows, the last of which is
(2n + 2i - 2) (2n + 2i) (2n + 2i + 2);
and the denominator is obtained from the numerator by putting η = 0, viz.
it is
(1)(3)(5) <2i-l)
x(4)(6)(8) (4i-4)
χ (8) (10) (12) (4i-8)
χ
χ (4s) (4s + 2) (4s + 4) (4i - 4s)
χ
the last row being (2i) or (2i — 2) (2i) (2i + 2) according as i is even or
uneven.
521. The reader must be warned that, although there is little doubt
that this result is correct, its truth at present rests upon the fact that it
represents faithfully every particular case that has been examined, and that
some consequences deduced from it also appear to be correct. The result has
not been rigorously established. Nor has the expression when multiplied by
gn been summed into the form of an algebraic fraction. Further
investigations in regard to these matters would be sure to lead to valuable work.
268 DEDUCTION OP SOME CONSEQUENCES [SECT. X
622. We proceed to deduce some consequences from the result.
When the number of layers of nodes is unrestricted we put η = oo , and
then the numerator becomes equal to unity. The function in that case may
also be written
(1 + д?)(1+0»)(1 + а») (1+d*-1)
(2) (6) (10)... (4i - 2). (4) (6) (8)2 (ΙΟ)2 (12)3 (14)*
the last factors in the denominator being determined from the formula.
Here the numerator is precisely the enumerating function of self-conjugate
line partitions of at most i parts. It is, in fact, precisely what the whole
expression, in the general formula, becomes when η is put equal to unity.
If is at once seen to be
(2)(6)(10)...(4i-2)
(l)(3)(5)...(2i-l) '
which is (1 + x) (1 + ж3)... (1 + аР'1).
523. On putting η = 2 we obtain a very interesting result.
We find
(2i+l> (2i + 4)(2i + 6)...(4i-2)(4i)
(1) · (4)(6)...(2i-2)(2i)
which may be written
(2i + 2) (2i + 4)... (4i - 2) (4i)
<2)<4)...(2i-2)(2i)
(2i + 4)(2i + 6)...(4i-2)(4i)
+ X' (2)(4)<6)...<2i-2)
This expression enumerates plane partitions which possess the properties:
(i) they have ^/-symmetry;
(ii) the part magnitude does not exceed 2;
(iii) there are not more than i parts in the direction of either axis.
For an even weight 2w we have to take the coefficient of x-w in
(2i + 2)(2i + 4)...(4i-2)(4i)
(2)(4)...(2i-2)(2i)
or of *" in <i+l)(i + 2)...(2i-l)(2i)
<l)(2)...(i-l)(i)
This function, as we have seen, enumerates in the Theory of Line
Partitions those partitions of the number w in which both the part
magnitude and the number of parts are limited so as not to exceed i.
CH. IV]
SOME CORRESPONDENCES
269
524. Hence a correspondence between the plane partitions of 2w, for
which there is ^-symmetry, the part magnitude does not exceed two, and
there are not more than i parts in the direction of either axis; and the line
partitions of w, for which the part magnitude and the number of parts are
both limited so as not to exceed i.
Or we may state the correspondence in another manner.
It is between the at most two layer ^-symmetrical graphs, of weight 2w,
restricted as to nodes along the χ and у axes by the number i\ and the
graphs in two dimensions of weight w restricted as to nodes along the axes
by the number i.
Ex. gr. for w = 4, i = 3, the correspondence is
111
1
11
11
11
1
гЧ
221
2
1
22
22
111
111
11
525. For an uneven weight 2w + l we similarly take the coefficient of
d*in
(i + 2) (i + 3)...(2i-l)(2i)
(l)(2)»...(i-2)(i-l) '
and this enumerates partitions of w limited as to part magnitude by i+ 1,
and as to number of parts by г — 1.
526. Hence a correspondence between the plane partitions of 2w + ly
for which there is #?/-symmetry, the part magnitude does not exceed two,
and there are not more than г parts in the direction of either axis; and
the line partitions of w, limited as to part magnitude by г ■+-1, and as to
number of parts by г — 1.
As before, we have the alternative statement of the correspondence.
Ex. gr. for w = 5, г = 4, we have the five-to-five correspondence
Ш11
1111
111
111
ГЧ
1111
1
2111
111
11
1
the generating
111
11
2211
21
ГЧ
I-H
111
1
1
221
211
11
function becomes
1 +cc
11
11
1
222
21
2
(l-^2)(l-^)(l-^)---adinf.
This result shews that the whole number of plane partitions of w which
possess #y-symmetry and no part greater than two, is equal to the whole
number of partitions of \w or \ (w — 1), according as w is even or uneven.
270 GRAPHICAL REPRESENTATION OF GENERATING FUNCTION [SECT. X
Ex. gr. Since the number 5 has seven line partitions we must have
precisely that number of plane partitions, of the nature considered, of the
number fifteen. These are
111
1
1
1
1
1
1
1
11111 111
111
111
1
1
1
2111111
11
111
211111
111
11
1
1
1
11111 1111
1111 1111
in
11
1
I
1111
111
21111
1111
11
11
1
527. There is one circumstance which gives a high probability to the
conjectured enumerating function of icy-symmetrical graphs. It will have
been remarked in a previous chapter that the function which enumerates
plane partitions in which no particular symmetry is in question is composed
of factors of the type (n+s)/(s) when the corresponding lattice of nodes is
complete. Further it was seen that one such factor being placed in regular
order at each node the whole function was the product of such factors.
Now in the present case take, not a complete lattice of nodes, but that
portion which involves the principal diagonal and all nodes to the right of it.
If г is the number which limits the part magnitude and the number of parts,
the successive rows of such a triangular lattice involve г, г— 1, i — 2,... 1 nodes.
The factors of the enumerating function can be placed at these nodes in the
following manner:
(n+1) (2n + 4) (2n+6) (2n + 8)
(1)
(4)
(n + 3)
(3)
(6)
(2n + 8)
(8)
(n+5)
(5)
(8)
(2n+10)
(10)
(2n+12)
(12) *
(n+7)
(7) '
(2n + 2i)
" (2i)
(2n+2i + 2)
" (2i + 2)
(2n + 2i + 4)
' (2i + 4)
(2n+2i + 6)
(2i + 6)
(2n + 4i-4)
(4i-4)
(n + 2i - 1)
(2i-D
CH. IV] GRAPHS WHICH HAVE TWO READINGS 271
Proceeding from the left-hand node always to the right or downwards
till we arrive at (say) the 5th node, we place a factor , v or -—^r-r—-
4 J; r (s) (2s)
according as the node is on or not on the principal diagonal.
In #y-symmetry a node not on the diagonal represents (or may be taken
to represent) the two nodes which are symmetrically situated in regard
to the diagonal. In this case we see that the letters in the factor are
doubled.
This property of the enumerating function is of great beauty and
mathematical elegance.
528. There is one more nature of symmetry that occurs in solid graphs.
We have seen in a previous chapter (Art. 428) that graphs may have two
aspects and be therefore capable of supplying two readings. Such occur for
the first time at weight 13. They are in plane partition form
322
31
11
331
211
2
the first reading by rows as the second does by columns.
We have two distinct plane partitions associated with two solid graphs
which are in reality the same graph under different aspects.
The graphs are
(©)
Θ Θ (Θ) (©) ·
Θ
Θ
However they be viewed they invariably give one of these two aspects.
The fundamental property which is possessed by the corresponding plane
partitions is this. The line partitions which constitute the successive rows
are the conjugates of the line partitions which constitute the successive
columns, and also the line partitions in question are not all self-conjugate,
so that the plane partition does not read the same by rows as by columns.
The latter condition is necessary, for if it were not complied with the plane
partition would possess #y2-symmetry and the associated solid graph would
have only one aspect.
272 DERIVATION FROM FIRST ROW OF PARTS [SECT. X
Φ
We now construct the solid graph of the left hand of the two partitions
above written. Projecting perpendicular
to the plane xy we obtain the
partition.
The reader will observe that every
node is in one of the coordinate planes.
This fact follows as a matter of course
from the circumstance that in the
partition the second number along the
principal diagonal is less than 2.
Further make the observation that
the plane graphs in each of the three
coordinate planes, if suitably read, are
graphs of the line partition 322 which
is the first row of the plane partition.
In the plane xy we read parallel to the axis of #,
yz
zx
z.
It thus appears that the whole plane partition is dependent upon the first
row of parts.
This first "row has a highest part which also designates the number o\
parts in the row. Moreover the first row partition is not self-conjugate.
If we treat in this manner a partition having г parts and a highest part
equal to г we obtain, so long as the partition is not self-conjugate, a plane
partition associated with a solid graph which has precisely two aspects
To make this evident take the line partition
4332
and form a solid graph by placing the corresponding plane graph in eacr
of the coordinate planes according to the above rule:
CH. IV] THE GENERATING FUNCTION IN A PARTICULAR CASE 273
This solid graph denotes the plane partition
4332
411
311
11
and if we had started with the line partition 4431 we should have arrived at
4431
3111
311
2
It thence appears that we can at once enumerate all plane partitions
which are derived from solid graphs which have:
(i) two aspects,
(ii) every node in one of the coordinate planes.
Because we can derive such a plane partition uniquely from every line
partition which has the two properties:
(i) the highest part is equal to the number of parts,
(ii) it is not self-conjugate.
529. Consider the case where the highest part and number of parts arc
both equal to i.
If the highest part and number of parts are both conditioned not to
exceed г the enumerating function is
(1) (2) ... (2i)
fli) (2) ...(I)}»'
Hence the enumerating function we require is
(l)(2)...(2i) (l)(2)...(2i-l) (l)(2)...(2i-2)
{(1) (2)... (i)}' (1) (2)... (i). (1) (2) ... (i - 1) + {(1) (2) ... (i-1)}2'
which reduces to ,*- ^ jg - g^,.
We must subtract from this the function which enumerates the partitions
which are self-conjugate. This is
л3*-1 (1 + x) (1 + tv>) (1 + a5)... (1 + A·2*"3).
Hence the required enumerating function is
^~1\^ΐ)%'.'.{'{ί-^γ-{1 + χ)(1 +0(ΐ+*5)·-(ΐ +^"s)j,
and summing for i we obtain
ДУ" [{(1)((2)'.'.'. fl^ff}'" (1 + X)(1 +Ж3)(1 +XS) - (1 +X*~3)] ·
M. A. II. 18
274 SIMPLE EXAMPLES [SECT. X
630. The function enumerates for a given weight of first row all the
plane partitions derived from solid graphs with two aspects and having
every node upon one of the coordinate planes.
Thus for г = 2, the enumerator for a given value of i gives zero.
For i = 3, we get
*ρ#$β-α+.>(ΐ+->]
= а?(1 + х + 2сс2 + а? + а?--1-а)--я?--я?)
= 2#7,
verifying the two line partitions (322), (331).
631. So also for i = 4, we arrive at the expression
2(α? + χ1« + χ1ι+χι*+αϊ* + χ1*) or ^Ш,
verifying the partitions
4221 4311 4222 4411 4322 4421
4332 4431 4333 4441 4433 4442-
and establishing that each is the first row of a plane partition which enjoys
the stated properties. These are in fact
4221
31
11
1
4332
411
311
11
4222
41
11
11
4333
411
411
111
4322
411
21
11
4433
4111
411
211
and the six others formed by taking the columns of these as rows.
632. Similarly for i=5 the function which enumerates the first rows is
found to be
(1)(2)·
It will be clear on consideration that if w be the weight of the first row,
the weight of the associated plane partition is
3(w-i) + l.
CH. IV]
CONSTRUCTION BY SOLID ANGLES
275
We now derive the function which enumerates the plane partitions of
given weight from that which enumerates the first rows of given weight by
performing successively the operations:
(i) multiply by ar*
(ii) write x* for x}
(iii) multiply by x}
and we obtain
and in particular for i = 3, 4>, 5 the functions
г#9 A& (3) , ix (3)(6) .
533. These plane partitions which possess the peculiar symmetry we
are investigating form, from the graph point of view, solid angles since
every node is upon one of the coordinate planes. Every partition must
involve one of these solid angles in its graph. In other words these solid
angles of nodes constitute the boundaries, so far as the coordinate planes are
concerned, of the graphs of all of the partitions under examination. From
these boundary partitions we can construct others by fitting into the solid
angles, when possible, graphs which have either one or two aspects. Thus
from the boundary partition
322
31
11
we can derive the partition
322
32
11
by fitting into the solid angle graph a single node which of course is a
one-aspect graph. We of course could not fit in the next most simple
graph, viz.:
Θ · 21 ,.
= of one aspect,
because that would make
which is not a partition at all.
322
331
12
The general expression appears to be 2#3i+4 L-' . J,L f \ \\ ' ·
(3) (6) (9)... (31—9)
18—2
276 ONE GRAPH GIVING RISE TO AN INFINITE NUMBER [SECT. X
So if we choose, of the order four, the boundary partition
4442
4111
3111
31
we can fit into the solid angle either of the graphs of
to the partitions
1 21 311 22 22 321 331
1 ί 21 22 21 211
1 12
thus constructing the partitions
4442
4211
3111
31
4442
4331
3331
31
4442
4321
3211
31
4442
4432
3321
32
4442
4422
3211
32
4442
4442
3322
33
4442
4331
3321
31
4442
4442
3332
33
each of which possesses the symmetry we are examining.
We thus see that the enumeration of the solid angle or boundary
partitions is only the first step towards the enumeration of the partitions
before us. The enumeration has not yet been carried any further. The
relation of the graphs to a cube of i:i nodes is the same as that which we
found in the case of #?/2-symmetrical graphs. The supplementary graph also
has exactly two aspects. Thus from
322
31
11
we immediately deduce
322 4444
32 4433
11 4431
4221
and an infinity of others.
This fact must be of importance in an investigation into the form of the
complete enumerating function.
nodes equivalent
331
221
2
CH. IV] ASPECTS OF REGULAR GRAPHS IN THREE DIMENSIONS 277
534. It is necessary to make some further remarks upon the different
aspects of regular graphs in three dimensions. Consider first of all the
graph in two dimensions of the partition (31)
and construct it in another manner by means of four square plates fastened
A
together so as to form one piece. Suppose that the two faces of the piece
are lettered A and B. Observe that the piece cannot be made to represent
the conjugate partition (211) so long as the face A is exposed to view, but
that if it be turned over so as to expose the face В we can place it in the
required manner, viz.:
ω
Because we can expose either face of the graph at pleasure the graphs
are not essentially different. If we are restricted to the face A of the graph
we can only represent the partition (211) by regarding the reflection of the
graph last depicted about its left-hand edge as a proper representation. Thus
we may agree to so regard the piece with the A face exposed as under:
>
When we come to graphs in three dimensions we may similarly construct
the graph in another manner by means of cubes fastened together. Instead
of vertical piles of nodes we have vertical piles of cubes raised upon the
plane xy. If the graph be also a graph in two dimensions we may treat the
piece, composed of blocks all in one plane, as above, and, by turning it over,
cause it to represent one, three, or six multipartite partitions as the case
may be. Thus a single cube may be placed in one position; two cubes
joined together in three positions, viz., with the greatest length along either
of the three axes; the piece above depicted, when composed of four cubes, in
six positions, viz., in two positions in each of the planes xy, yz,zx.
278
THE EEFLECTION OF A GEAPH
[SECT. X
When however the graph is essentially three-dimensional the case is
different. Consider the graph of the partition (31, 10) of the bipartite
number (41):
о
Θ
where at the origin there is a pile of two nodes in the direction of the axis
of z. If we replace the nodes by cubes and fasten them together we can
place the piece in a second position:
®
which is the graph of the partition (21, 10,10), but we cannot place it in the
third remaining position, which is the graph of the partition (211, 100).
Turning the piece over is of no service, and we can only realise the missing
position by adopting the first position, after rotation clockwise through a
right angle,
Θ
Q
Θ
as a proper representation of the partition. This graph Q is the reflection of
the real graph Ρ in the plane yz.
The two graphs
Θ
Θ
when formed of cubes fastened together are essentially different pieces, but
they are reflections of one another.
CH. IV] NUMBERED SQUARE PLATES VERSUS CUBES 279
In the theory of partitions discussed in this book they are regarded as
being essentially graphs which are convertible the one into the other. We
have two alternatives. We must either admit the principle of reflection, or
we must denote the graphs by numbers written in space of two dimensions,
so that they may be turned over. For example, we may denote the above
graph by
211
1
so that we may turn it over and give it'the position
21
1
1
The vertical pile of two nodes at the origin is regarded as a flat number
two for the purpose in hand. It ceases to be so when we come to the graph
31
1
In every case the representation by nodes in three dimensions is replaced
by a plane partition in two dimensions; this is then regarded as composed
of square plates numbered on both faces so as to be reversible. At any
moment, however, we may pass back to the representation in solido. Thus
the two plane partitions
322 331
31 211
11 2
are not essentially different when constructed of square plates numbered on
both faces, but they are so when made up of cubes piled up on the plane xy;
they are in that case not convertible the one into the other except by
reflection.
In fact, in regard to the representation by cubes fastened together,
every form, which is essentially three-dimensional, has either one or three
aspects; every form, which is really two-dimensional, has one, three, or six
aspects. The above two forms, for instance, have each only one aspect when
composed of cubes; but when made up of square plates numbered on both
faces they are identical, and each has two readings in the theory of partitions.
SECTION XI
SYMMETRIC FUNCTIONS OF SEVERAL SYSTEMS OF
QUANTITIES, WITH SOME APPLICATIONS TO DISTRIBUTION
THEORY
CHAPTER I
ELEMENTARY THEORY
535. For certain parts of the Theory of Distributions a knowledge
required of the Theory of the Symmetric Functions of several systems
quantities.
It will be sufficiently illustrative of the general theory to consider men
two systems of quantities
«1, «2> «3,··· >
A, /3o, /33,... .
For the single system we wrote
(1 + <vr) (1 + ol2x) (1 4 a:ix)...
= 1 4-2a1.A, + 2a1a2..T2 + 2aiaia3.#3 + ...,
= 1 4- агх + α2χ* + α.όχ3 4- ... ,
= l+(l)<* + (lQ)rf + (lB)tf+...,
and considered symmetric functions
ta?*a$*ap ...=(№№ ...).
So now we write
(1 + αΎχ + Ду) (1 + a2x + /3,y) (1 + α,χ 4- β,ν)...
= 1 + Σα,. χ + Σ/3ι. у + Σα,«о. χ- 4 Σα,β,. xy 4- Sft/32. у2 4-...,
== 1 + а10х + а01у 4- a2Qx2 + аиху 4· а^у* + а30л^ + а21х-у 4- а12#у2 4- а^у* -4 ... ,
^14-(Ю)ж+(01)2/+(10 10)#24-(10 01)#у+(01 01)у2+(103)^+(10201)^+...
[SECT. XI, CH. I] DEFINITIONS AND NOTATION 281
The most general symmetric function before us is
tcp№*t*№ot*№...,
denoted, symbolically, by
The summation is in regard to the expressions obtained by permutation
of the η suffixes 1, 2, 3,... but as a rule it is not necessary to specify the
value of n, and it may be regarded as being as large as may be necessary.
The generalization of the nomenclature and notation for three or more
systems of quantities is evident.
The weight of the symmetric function is bipartite, and depends upon
the numbers
ίι + ?2 + ?3 +...=%
We speak of the biweight (2p, %q) of the symmetric function.
The expression (pi#ii>2?si>3?3 ··.) is a partition of the bipartite number
%p} ?q. The sum %p 4- %q is the weight of the number w if Xp 4- %q = w.
associated with any number w there is a biweight corresponding to every
composition of w into two parts, zero counting as a part.
Repetitions of biparts are denoted by exponents; thus
(Λβί) = ΟΡι?ιΡι?ι).
In the relation above
aP(? = (10*>01*),
and apq is an elementary symmetric function; it is also said to be " single-
unitary ," because each bipart of its partition contains but a single unit. The
expression "unitary" is reserved for those symmetric functions whose partitions
involve only units and zeros, such as the tripartite partition (111 110) for
instance.
536. The number of partitions of the bipartite number pq is the
coefficient of xvy(i in the ascending expansion of the algebraic fraction
1 m
1 — ,r. 1 — у. 1 — χ1.1 — xy. 1 — y-. 1 — x*. 1 — xly. 1 - xy". 1 — ys...'
for the general term of the expansion is
which is equal to xvy4 if
m10 + 2??г20 + mn 4- 3m:l0 -|- 2?п.л -I- m12 Η-... = p,
*Woi + mu + 217*02 + m2i + 2m12 + Зягю + ... = q;
and this will be the case if pq possesses the partition
(10wi,0Olwo"20^oHinuo2»«o230m^2l^il2w,^03w?''3...).
282 PARTITIONS SYMBOLIZED BY ONE BIPART [SECT. XI
The number of times xpyQ appears in the expansion, or in other words the
coefficient oix*yq, is equal to the number of partitions oipq.
The number of partitions of pq into exactly μ parts is, by similar
reasoning, equal to the coefficient of ar-aPy* in the expansion of
1
1—ax. l-ay. I—ax*, l — axy. 1—ay2, l-ax* А — аяРу Л—аху2.1 —ayz...'
This function is, when expanded to a few terms and omitting terms which
are simple powers of χ or of y,
(a+a2)xy + (a 4- 2a2 + as) (afy + xy*) + (a + 3a2 + 2a3 + a4) (x*y -f xys)
+ (a + 4a2 + 3as + a4)^2y2+...,
and the corresponding partitions are
Number 11
(11)
(10 01)
Number 31
(31)
(21 10)
(30 01)
(20 11)
(20 10 01)
(11 10=)
(10301)
Number 21
(21)
(20 01)
(И 10)
(10=01)
Number 22
(22)
(21 01)
(12 10)
(20 02)
(IP)
(20 01=)
(02 10=)
(1110 01)
(10= 01=)
Number 12
(12)
(10 02)
(0111)
(10 01=)
Number 13
(13)
(12 01)
(03 10)
(02 11)
(02 10 01)
(11 01=)
(10 013)
537. The partitions with one bipart correspond to the sums of the
powers in the single system or unipartite theory. We will express them in
terms of the elementary functions. We will write (p,^) in the form .<?mi,
just as with a single system we write (pi) in the form sPl.
Taking logarithms of both sides of the relation
(1 + alx + fi1y)(l + a2x + /?,y)... = 1 + a10x + aoly +... + apqx*>yq + ...,
and remarking that
Σ («!# + /3i2/) = sl0x + s01y, Σ {щх + β^)2 = s.J0#2 + 2suxy + s^y2, etc.,
there results
(s10x + «01 y) ~ Ь (*2o#2 + %8цху Η- s02y*) + £ (si0oc? + 3s21x2y + S$12xy2 + s03ys) + ..
= log(l +а10# + а01у+ ... + apgxPy* + ...);
GENERALIZATION OF WARING S FORMULA
283
CH. I]
leading to 1 4 a^x 4 a01y 4 ... 4- apqxpy* 4 ...
= exp {(swx 4 s01y) - \ (saotf2 4 2snxy 4 5o22/a) + ...};
and now expanding the logarithm and exponential functions in these
identities, we find by comparison of like powers of χ and у:
$ю — Cti0
(Sen = a01
$20 =S #10 """ ^#20
! == #01 "~ <^#02
$30 = aj0 — За^Ою 4 Зазо
$21 =s #10 #01 #20 #01 — #11 #10 "» #21
2
$12 — #01 #10 — #02 #10 — #11 #01 4 #i<
\$03 = #01 "" 3^02^01 4 3&03
ί α10=*ί
*10 ~ «10
#01 = $01
2θ20 β $10 ~~ $20
#11 β $10 $01 *"~ $11
-^#02 ^ $01 — $02
/ бЯзо = $jf0 — 3$20^10 + 2$30
I ^>&21 =s $10 $01 — $20 $01 •«$11 $10 "T* ^$21
j A&12 — $01 $10 — $02$10 ""$11 $01 "·" ^$12
\OC&03 =S $01 — "$02 $01 "T* ^$03
and by an application of the multinomial theorem we find
!л!
F?
7Г! ! 7Г2 ! -
V\ Я\ №г
(-)2'-1
Ρι «ι Р-Ч-.
the summation, in each formula, being for all partitions
(Piiffft??···)
of the bipartite number (pq).
538. In the case of the single system we denoted the sum of the
monomial symmetric functions of weighty by hp. In the present instance,
if hn denote the corresponding sum for the biweight pq, we find that
i+*^+*..y+*^+*n^+^i^----(1_^)(1_at<B)...1(1_Ay)(1_J8iy)...;
and, since the right-hand side is
(1 4 Лю#4 Λοο#2 4 ...)(l + A«y + Aosys+ ···)»
it is clear that hpq = h^h^.
538 bis. A more interesting function kpq is defined by the relation
1 4 a10x 4 aoly 4 ... 4 apqxVy* + ...
1 - k10x - k01y 4 ... 4 (-)'p+qkpqx*y<i 4 ...'
284 CONNEXION OF kpq WITH CLpq AND Spq [SECT. XI
for then
^-^+^ + -+^^+- = (1_а1Ж_Ау)(11_агЖ-^)...»
and ^ = 2f + ^)f + ^...(MlM2...).
Moreover, 1 + &10# Η- &0ι2/ + ·. · + кмосРу* Η-...
1
1 - α10# - апу + ... + (-)*+*aw#*y* + ...'
so that, ia any relation connecting the functions apq with the functions kpq>
we are always at liberty to interchange the symbols a and к.
We have the formula
and the similar one with a and к interchanged.
From Art. 537
*io0 + «oi2/ - h (*2o#2 + 2*ияу + s^y2) + ...
= - bg {1 - few* - *toy + ... + (~)p+qkpqx^ + ...},
and this, by the multinomial theorem, leads to
and it will be remarked that, if we multiply the left-hand side by (—)^+^-1,
we may replace the symbol к by the symbol a on the right-hand side.
Thus spq remains unchanged when к is replaced by a, except for a change
of sign when ρ + q is even.
CHAPTER II
THE THEORY OF SEPARATIONS AND THE ALLIED
THEORY OF DISTRIBUTIONS
539. What has been said by way of definition and explanation
concerning the separations of a partition applies equally in the general case
of multipartite partitions. Thus of a partition (р^р^р&ъ), a separation
might be (jPiJiPsiftHpaie) composed of separates (p^prfs) ana (p2?s); its
specification is
(Pi +Ps> ϊι + ?з> i>2?2),
a partition of the same bipartite number as the separated partition. The
separation theory must now be connected with a Theory of Multipartite
Distribution. Consider three identities
1 + alQx + tt01y + ··· +<hqxPVq+ ··· =(1 + *i *> + &' У) (1 + °* « + &' y)...,
1 + 610л; + 6иу + ... + ЪрдяРу* Η- ... = (1 + «χ'7 л· + βχ" у) (1 + α2"χ + Д"у) ...,
1 4- с10л; + coiy Η- ... + Ср^'у* + ... = (! + α/''я + Д'"у) (1 + сь'"х + fi2"'y) ....
Assume the various coefficients of л? and у in the two first identities to be
given and those in the third to be connected with them by the relation
A'
ξ and η being undetermined quantities.
Multiplying out the right-hand side and denoting by partitions symmetric
functions of the quantities a/, cr2', a/,...; /3/, ДД ДД... we find by
comparison of coefficients of like powers of ξ and η the series of relations:
Сю = (10) b10,
Coi=(01)b01,
ο»«(20)δ* + (10*)%,
cu = (11) 6„ +(10 01) Ь10Ь01,
(?M = (02)bM + (0P)%,
cw = (30) ft» + (20 10) ^ b,o + (103) 6?0f
^ = (21)^+ (20 01)M« + (H 10)6ηδ10 + (10201)^0601,
ο·12 = (12) Ь18 + (02 10) Ьо2 Ью + (И 01) bn bQ1 + (OP 10) % δ10,
Co, = (03) bo, + (02 01) 6ϋ2 Ъп + (OP) 6Jb
etc.
Cpq= 2 (Piji ftjaftj» ·..) 6Λίι &Α«Α.ί,...,
the summation being for every partition of (pq)·
286 A NEW THEORY OF DISTRIBUTIONS [SECT. XI
It will be observed that, when the quantities bpq are each of them put
equal to unity, cpq becomes hpq and splits up into the product hpohn'}
moreover when Ью = boi = 1 and the remaining quantities bpq are put equal to zero,
Cpq becomes apq.
540. In order to establish comprehensive laws of symmetry in analogy
with those appertaining to the unipartite case we now require a new theory
of distributions.
Let parcels of type (p^i P2?2i>s?s ···) be denoted by
Af* B^ A»* Bp Af· B«*...,
that is to say there are
px similar parcels each denoted by Aly
?1 >y » » -k>li
P2 » >t » A2y
*±2 » » » ·&2>
jPs }) i> » -&-3>
?3 f> it » -t>2>
let objects of type (г^т^^А ···)> where %ν = Σρ = η1, %s=Xq = n2} be
denoted by
of»bf»of» bpaj» !§»....
The number of objects is equal to the number of parcels and we define a
distribution of the objects into the parcels, one object into each parcel, in the
following manner:
"A distribution of objects of type (^A^^A ···) into parcels of type
(Р1Я1Р2Я2Р2& ···) is su°b that denoting the objects and parcels by
of»if»aj«δ?aj>6f»..., A^B%ΑφΒ&АрΒρ... respectively,
the objects of· of* aj>... are to be distributed into the parcels ΑρΑξ*Αξ*...
and the objects bp b^bf/ ... into the parcels Б?· В$*Вр ...."
The number of these distributions is clearly equal to the product of two
numbers, one denoting the number of ways of distributing objects of type
OWs...) into parcels of type (ρφ2ρ$ ...)> and the other the number of ways
of distributing objects of type (м2$3...) into parcels of type (дчдъф···)·
From the unipartite theory the one number is given by the coefficient of
OWs ···)· iQ *he expansion of hPi0hPi0ftPa0... and the other by the coefficient
of (*A*s··-)* in the expansion of h^h^^.... Hence the number of
distributions is given by the coefficient of
(η*νν··)«(*ι*Α ·..)*>
in the expansion of hPx4y hM% кМз..., since hpq = АрЛ«.
CH. Il] TYPE OP A DISTRIBUTION 287
These distributions are considered to be unrestricted since the condition
of the distribution that objects a and b must be placed in parcels A and В
respectively is fundamental and does not count as a restriction.
We may write the unipartite functions 0ν2τ8...)α, (We···)^ ^п fc^e
bipartite forms
(rfir20rfi ...), (Os, 0s20s3...)>
and, multiplying them together, we see that the enumeration is given by the
coefficient of the bipartite function (rl8ir2s2rz$s...) in the development of
From the reciprocity that has been established in the unipartite case we
see that we may interchange the partitions (r^r^ ...), (pip2ps ·..) and also
similarly the partitions ($ιΜθ···)> (ίι?2?»···)· Thus the enumeration is
given in either of four forms:
(i) as coefficient of (r^ r2$2 rs$b ...) in hPtqihMihMi...y
(ii) „ » (PiSi p2s2 Ps$* ···) Ь Kxqx Artft hr3q3 ...,
(iii)
(iv) „ „ (Pi?iPi?8jPs?3 -О^'Ч·.^^ ····
The last of these is derived at once from the bipartite distribution by a
simple interchange of objects and parcels or of capital and small letters
in the literal distribution scheme. The development of hPiqi кРйЯйhM3...
enumerates the distribution of objects of all types into parcels of type
(PiiiPi<hP*4* ···) and is therefore the "Distribution Function," the
distributions being unrestricted.
As in the unipartite case every distribution has itself a type specified by
a partition of the original bipartite number. If, in the distribution, we
observe
objects <;г£ in parcels АЦВ%,
where sl} s2 arc any integers and σ1} σ2 are integers one of which may
be zero, we are given one part σΎσ2 of the partition which specifies the type
of the distribution.
Ex. gr. For the distribution of objects of type (22) into parcels of type
(11 10 01) we find only one distribution shewn by
<h bi ax Ζ),
Here for $г = $2 = 1 we have σχ = 1, cr2 = 1,
^i=l, 52=2 „ ^ = 1, <t2=0,
$i = 1, $2 = 3 „ σλ = 0, cr2 = 1,
shewing that the distribution is of type (11 10 01).
288 THEOEEM OF ALGEBRAIC SYMMETRY [SECT. XI
If we interchange capital and small letters we find
Аг Аг A A
and we observe that the type of the distribution has not changed; it is still
necessarily (11 10 01).
In general the interchange of capital and small letters does not alter the
type of the distribution. This circumstance is of first-rate importance
because it leads directly, as will be seen presently, to a theorem of algebraic
symmetry.
The interchange of capital and small letters may be denoted by the
substitutions
(Aa)(Bb).
Looking merely to the effect of the substitutions upon the type of the
distribution we have
(Aa)(Bb) = l.
If we merely interchange the symbols A} a the types of both the objects
and parcels connected with the distribution are changed and, in general, the
type of the distribution is also changed. That this is so is seen at once
from the definition; for when objects αζι b*2 occur in parcels A J1 Βζ% giving
rise to a part σχσ* in the partition specifying the type, it is clear that if
A, a be interchanged the part σλσ2 does not arise unless $г =&>. Similarly
also for the interchange of the symbols B, b.
We find however that the interchange (Act) produces a distribution of
the same type as the interchange (Bb). This is so because if we first make
the substitution (Act) and second the substitutions (Aa)(Bb) the latter
has no effect upon the type of distribution. Accordingly
(Aa) = (Aa). (Act) (Bb) = (Bb),
since (Aa)(Aa) = 1.
The effect of (Aa) upon the type of the distribution is therefore the same
as that of (Bb).
541. The distribution function hPlQi hPi(hhVa<b ... is precisely the same as
cP\<hcPiQ2CPiQa ··· when the whole of the quantities bpq arc put equal to unity.
If we retain these quantities bpq and use the product оРх<1хс1Ч(нсРзЯ.л ... we are
able to single out the distributions which have any given type. For consider
the relation
c*(fcK21)(01)bta&M + (2001)^
and make the observations:
(i) the symmetric function product attached to any 6-product is a
separation of the partition which specifies the Ь-product;
(ii) the symmetric function product in every term is a separation of
specification (21 01), (21 01) being the partition which specifies the c-product.
. II] DISTRIBUTIONS IN A PARTICULAR CASE
If we further develop the right-hand side of the relation we find
C21C01 = {(22) + (21 01)} M01 + {(21 01) + (20 02) + 2 (20 01 01)} b*> b20l
+ {(12 10) + 2 (1111) + (1110 01)} ЪцКК
+ {(11 10 01)+ (10 10 02)+ 2 (1010 01 01)} %%.
We will now exhibit the whole of the distributions involved.
Parcels of type (21 01).
Type of Objects
(22)
(21 01)
(21 01)
(20 02)
(20 01 01)
(20 01 01)
(12 10)
(11 11)
(11 11)
(11 10 01)
(11 10 01)
(10 10 02)
(10 10 01 01)
(10 10 01 01)
The Distribution
4,iA Bt
«! Ol 6l &i
АгАгВг Д
Οχ αχ Ьг b2
АгАгВг B2
Ог ах Ъ2 Ьг
АгАгВг Д>
аг <Хг b2 Ь2
АгАгВг В2
<h <hb2 bz
АгАгВг Д>
«ι αΎ bz Ъ2
АгАгВг В2
СЬг СЬ2 Ьг Ьг
АгАгВг В2
ах а2 Ьг Ь2
АгАгВг В2
аг Оа Ь2 Ьг
АгАгВг В2
«ι С12 Ьг Ъг
АгАхВг В2
αλ а2 Ь3 Ьг
АгАгВг В.2
ага2 Ь8 Ь3
АгАгВг В2
а>1 а* Ъь ЪА
АгАгВг В2
<Хг CCi 64 Ьз
Type of
Distribution
(21 01)
(21 01)
(20 OP)
(20 ΟΙ2)
(20 ΟΙ2)
(20 ΟΙ2)
(11 10 01)
(11 10 01)
(11 10 01)
(11 10 01)
(ΙΟ2 ΟΙ2)
(ΙΟ2 ΟΙ2)
(ΙΟ2 ΟΙ2)
(ΙΟ2 ΟΙ2)
Μ. Α. II.
290 INTUITIVE PROOF OF A LAW OF SYMMETRY [SECT, XI
It will be observed that the type of the distribution is invariably the
same as that which specifies the 6-product to which the symmetric function,
denoted by the same partition as the type of the objects, is attached. To
explain this consider for a moment the terms
(2101)6*6^, (2101) 6*6&
in the expression of c21c0i, and therewith the second and third distributions
set out above. The term (21 01)621601 arises from the development of the
term (21) (01) 621601 and thus (21 01) arises from the product (21) (01);
therefore it must be possible to distribute the objects of type (21 01) in such
wise that the type of the distribution is (21 01). Similarly (21 01) 620 Z>oi
arises from the development of (20 01) (01)6206^; (21 01) comes from the
product (20 01) (01) and thus it must be possible to distribute objects of
type (21 01) in such wise that the type of the distribution is (20 01 01).
Hence if
CP&CMiCP>q* ... = ». + 0 fa*i Г^ЗД...) 6i|ttl Ькщ bt,uz ... + ... ,
there are θ ways of distributing objects of type (r^ r2s2rss:i...) into parcels
of type {р^р^РзЦз .··) so that the distributions are of type (^щ t2u2 ttiu3...).
We have shewn also that we may interchange the types of the objects and
parcels without the type of the distribution being affected. Hence also
Crltl <V2s2cVih ... = ... + θ(^ρ&ρφ...) btlUi ЪкщЬ(зЩ ... + ....
542. We have therefore an intuitive proof of a law of symmetry. If we
write
CV\ <i\ CP2<]2 ci>87s ··· = ···+ PbtlUl btiU2 6is?,3 ... 4- ...,
Ρ is a linear function of separations of the function {t^ t,it2t<iu-lt...), each of
which has a specification (piqiP^Psfy ···)· ^ Ρ be developed so that
P= ... +i(?*1e1ra&ir8si...) + ... ,
we have seen that the number θ remains unchanged when the partitions
(i>i?ij9a?2i>»?3 ···)> O'jS, r2s.2i\ds.0...) are interchanged, while the partition
(Ъщ t2u2t:ius...) remains constant. Hence the whole of the functions
(?"!«! r2s.2rr% ...) that arise by multiplying out the various functions Ρ must
be the same as the various specifications of the separations of (^щ £/м.2£3^3...).
There is therefore a one-to-one correspondence between the functions Ρ
and the functions (r^ r2s2 r.0,% ...), and we may form a table which possesses
row and column symmetry, by expressing the different functions Ρ
appertaining to the various specifications (pi qi p-^q-i p^ .··) of the separations of
(Ъщ 12и2^щ ...) in terms of the equi-numerous functions (г&г.ь·* r:is:}...)
which in some order are identical with the functions (ρ& 2WJ*Р»Я* ···)·
There is a symmetrical table in connexion with every partition of a given
bipartite number. There will also be the inverse tables expressing the
CH. II]
THEOREM OF EXPRESSIBTLITY
291
monomial functions whose partitions are specifications of the separations in
terms of the members of the system of functions, each member being a
definite linear function of the separations which have a particular
specification.
The inverse tables will also be symmetrical. This may be established
by making use of the operators as in a previous chapter, or it may be
regarded as necessarily following from the known properties of determinants.
In the direct tables the corresponding distributions are all of them of
tyPe (Ъщ Ъи2ЪЩ ...)· When in particular the chosen partition is (10# (Ш)
we find that the whole of the monomial functions are expressible in terms
of the separations. Each separate is an elementary function, and the
corresponding distributions are such that into a set of parcels ΛζιΒζ2 are placed
objects, no two of which have the same suffix. The combinations atat} atbt
are not permissible.
As in the unipartite case we have a theorem of expressibility, which may
be enunciated as follows :
Theorem of Expressibility.
543. "If any partitions of the bipartite numbers p^i, p2q2> p$qz> ... be
selected, and all of the parts assembled so as to form another partition of the
same biweight as {'PiqiPi^p·^ ···)> the symmetric function {p^p^p^qz...)
is expressible as a linear function of the separations of the partition thus
formed."
There is also the theory of Groups of Separations, and in the inverse
tables the sum of the coefficients of the separations of a group is zero,
according to the theorem:
" In the expression of a symmetric function
(ΡιϊΓ'ΑίίΜΐ···)
by means of separations of
(t^i? fc»wj»fc,wf» ...),
the algebraic sum of the coefficients in each group will be zero if the partition
possesses no separations of specification
(ti^i, тгии т2£.>, T2tt2, т^у, т3щ, ...)."
The law may be verified in the ease of the table of separations of (102012)
for the symmetric functions (22), (21 01), (12 10), (ll2), (11 10 01), for none of
these five functions can be separated with a specification (20 02). On the
other hand, the law does not obtain for the functions (20 02), (20 012), (02 102),
(102 012), for each of these four functions .can be separated with a specification
(20 02).
19—2
292 THEORY OF THREE IDENTITIES LSECT· XI
It must be observed that in the unipartite case there is no group theory
when the replaced partition is (ln), and the separates are elementary
functions. In the bipartite case there is no such exception, because the
separated partition (ΙΟ** 01?) does not consist of repetitions of a single bipart.
Hence the group theory exists when functions are expressed in terms of the
elementary functions. On the other hand, an exception occurs when the
separable partition does consist merely of a single bipart repeated.
Ex. gr. Exceptions occur for the separated partitions (ll2), (21s), etc.
543 bis. In order to examine more closely the subject of multipartite
separation we recall the identities
1 + a^x + a01y + ... + амх*>уя + ... =(1 + α/ χ + /3/ у) (1 + < χ + &' у) ...,
1 + b10x + b01y + ··· +bj*«*y*+ ... = (1 + «ι" χ + β "у) (1 + ai'x + A"y) ···,
1 + с10х + с01у + ... + CpqaPtf Η-... = (1 + al"x + Д'"у) (1 + α2'"# + Д'" у) ...,
and the connecting relation
The right-hand side of this relation is, from the second of the three
identities, if we put therein χ = α8'ξ, у = β8'η in succession for all values of s}
equal to
Π Π (1+ «/«/'£ +/3//3/Ч),
s t
so that Π (1+ α/"ξ + β/"η) = Π Π (1 + α/α/'ξ + β.'&"ν),
$ s t
or taking logarithms
X log (1 + α,'" ξ + jS/"^) = Σ Σ log (1 + «,V£ + /З/уЗ/^).
S 5' if
We now expand each side in ascending powers of ξ and η} and observing
that
where symmetric functions of quantities α', β*; α", β"; α'", β"', arc denoted
by partitions in brackets ( )1} ( )2, ( );{ respectively, we find by comparison of
coefficients of £pvq the noteworthy identity
This important result may be written in the two forms
Λ „\„_\ C»tff. W ^*A Г 7Г,! «-J . .. °Ρι1ι °P
РгЯх Patfe 4^17ί ^ тг/i 7Γ2! ..
1>\Я\ PiQ*
CH. Il] EXTENSION OF WARING'S FORMULA 293
In fact, the connecting relation is unaltered when the singly dashed
quantities a', /3',... are severally interchanged with the doubly dashed
quantities α", β", ....
Taking the latter form of the result the next step will be to compare the
coefficient of the term
Vх Ьщ ...,
on the dexter with the coefficient of the same term when the sinister is
developed by means of the relation
cpq = S (ρι4ι№*Ρ*<1* ···) КЧх ЪМйЬМз
of Art. 539.
When the left-hand side is multiplied out each symmetric function
product which multiplies the term
Vх Vе* ...
is necessarily a separation of the symmetric function
The result of the comparison will be therefore the expression of the
function (pq)i in terms of such separations.
Let (-P-M^-l)!^, c* ^
be a term of the left-hand side of the identity.
Since the coefficient herein of
v* v* ...
is a linear function of separations of
(ftiPftii·—)
of specification (r^f» r2$$>...),
it is clear that we are only concerned with those terms in the expression of
which involve symmetric functions which are separates of separations of
(i>iSTlP2?22···)·
In other words, we need only to attend to the terms which involve
exclusively symmetric functions composed of the parts pxqu p»q2) ....
If we do this there is no necessity to attend to the Ь-products at all.
294 EXTENSION OF WARING'S FORMULA [SECT. XI
Let us denote then by
w,w,...(Jo,(Ja
various separates of separations of
and suppose that the effective part of cri8l is
(Ji) + W + ...,
andofcr2S2 0Л') + (<Л')+...,
etc.
Then the effective part of
is
(->»-'&>-i)j s-£lL_- w,„(j0ft....^__(/1>(j0..
wherein of course
This may be written
pu\ pV2\ ...poi! />»!
№*» (J*)**... №*№)*" ,
wherein 2 />1ί? 4- Σ ρ28 + ... = ρ;
and the symmetric function product
(;>(^»...(Л>№>...
is a separation of (PiffiP^q? ···)
of specification (r, sf· r2$i*...).
From this result, in order to proceed to the effective part of
(-)^-4Σττ-1)ί
we must consider all terms of the sum which involve a c-product
cf" <f* ... ,
(r^sf"?eas£* ...) being a partition of the bipartite number p</, and also a
specification of some separation of
(Р1?Г,Л??а·..)·
We find that the required effective part is necessarily
J У1 · У2 · · · ·
CH. II] DUAL CHARACTER OF THE GENERALIZATION 295
where the summation is in respect of every separation
of the partition (p1 qp p2q%*...).
Hence the formula
7ΓΧ! 7Γ2 ! ... j Ji \ J2 · · · ·
where the summation is in regard to a particular symmetric function
(ЛЗГРгЗ?3···)» and t° every separation of it.
544. This important result is a generalization of the Waring formula
for the expression of the sums of the powers of a single system of quantities
in terms of the elementary symmetric functions. The generalization is of a
dual character because there are two systems of quantities and the expression
is in terms of separations of an arbitrary partition of the bipartite number.
The like reasoning at once extends the theorem to any number of systems
of quantities, and the reader will have no difficulty in realizing the truth of
the formula
t£=^W ...>-^--^MW да...,
7Ti! 7Г2! ... j ]Ύ\ J2\ ...
where the summation is for every separation
WW··.·
of the partition {ρ^\ ...7Γι ρ^τ2 ...ν*...) of the multipartite number
(pqr...).
545. Ex. gr. To express (31) by means of separations of (20 10 01).
Here ^ = ^2 — ^ = 1, Σ·7τ = 3,
and we find
2 (31) = (20 10 01) - (20 10)(01) - (20 01)(10) - (10 01) (20)4-2(20) (10) (01).
Again to express (333) by means of separations of (311 011 011).
Here 7Γι = 1, 7г2 = 2, Σπ = 3, and
(333) = (311 011 011)-(311011)(011)-(0112)(311) + (3tl)(011)2.
546. The formula that has been reached may be written in the form
Η^-ΗΣ*·-!)! (-)^(Sj-l)!
,γ,Ιιγ,Ι... Λ(Λίι*Λ7."...)"7 filj,]... WW-·
the notation being such that
296 NEW STATEMENT OF THE THEOREM [SECT. XI
denotes Spq or (pq) when expressed in terms of separations of the symmetric
function
In this notation, recalling a previous formula, viz.:
since aPlQl = (10*1 01^) and the formula expresses Spq as a linear function of
separations of the symmetric function
(10* 015),
the formula is equivalent to
<-)-- (J^ffP V..·. -? <-)*-' И' w w ■··■
CHAPTEK III
THE DIFFERENTIAL OPERATIONS
547. The elegant properties of these symmetric functions are most easily
established by means of the differential operations which we now consider.
The theory is completely parallel to that of the single system discussed
in Section I.
Starting with the identity
(1 + «ι# 4- βχν) (1 4- <x2x 4- /32y)... (1 4- 0LnX + βην)
= 1 4- a10cc -Ь a01y + α20^ + <hi®y + а^У2 + ... + apqa?y<i +
where η may be as large as we please, and multiplying each side by
(1+μχ + vy\ the right-hand side becomes
1 + Ою + μ)% + (α01 + ν) у 4- (α» 4- μ,^ο) я? 4 (au + μα0ι 4- уа10) д?у 4- ...,
and in general apq becomes converted into
ttpq 4" pCbp—i, q 4" Vdpt q—χ.
Write now
#10 = va10 4- C^oidail 4- ... 4· &p-i,q Vwpq 4* · · ·,
#01 = Ъщц + ^ιο9αι14-... 4 <*>ptq-i dapq 4 ....
Then any rational integral function of a1Q, a01} O20, αη, ^o2> ···> <fyg, ··· say
J\CLio> &оь ^2o> &ib a02, ... <Xpg, ···)—/>
becomes /(βίο + μ> αοι + ν, ..., <% 4 /иОр-ι, ? 4- νθρ, ?-ι, · · ·)
which is by Taylor's Theorem
/ + (μ#ιο + ^oi)/+ g-j (a*0u> 4 vg0iYf+ 3-, (W10 + ^oi)3/+ ·.. = ёхр (щи 4- j/#oi) ./,
where the bar of exp denotes that the multiplication of operators is symbolic
as in Taylor's Theorem.
Moreover - (^10 4 vg*Y = 2 -^—] {g% gi) μΡ ν*,
the summation being subject to p + q = $ and the placing of gfigfa in a
single bracket denotes symbolic multiplication of the operators.
298 THE OPERATOR WHICH OBLITERATES A BIPART [SECT. XI
Therefore if we write
we obtain
= exp(^10 + ^oi)·/
Observe that as regards quantity we may write
1 4- μα10 + ναύ1 + /Лг*, + μνα^ι + Л»ю + ... + μρν^αΡ4 Η-... = exp (jjau + vs01)
if we agree that on the right-hand side there is a symbolism according to
which
— (sf04) = cW
This is important from the point of view by which there is throughout
this subject an exact correspondence up to a certain point between the
algebras of quantities and differential operations.
We are about to see that in these algebras
correspond to Gpq, gpq respectively.
548. Now suppose that the function / is a symmetric function which
when expressed in terms of oclf β1} α2, /3S, α3, /33,... is
(i>l3i;P2?2ft?8...)·
The introduction of the new quantities μ, ν results in the addition to
0>i?ii*?aft?8···)
of the new terms
μρ*ρ** (p2q2РъЪ · · ·) + μν*ν<1* (Pi ?i РФ · · ·) + Ζ*****3 (Pi Ь V*b ...) + ··· ·
Hence
(I + μσιο + νθ01 + ... + μ^ Gpq+ ...)f
=/+ μ**Φ (p^Pzb ···) + A^MPiffiftffs ···) + ···>
and equating coefficients of like products μνν^ we find
unless the bipart rs occurs in, the expression of/,
врхях CPi?ift?2i>.?. ..·) = (ft?»A?8 .··),
6p,i,(Pl?lJPl?8i>8?8...)=s(Pl?lP8?8.·-)»
б!м(рд)-1,
ffftf, блл бл«, ··· (PiqiV*bP*b ···)= 1·
CH. Ill] SYMBOLIC PRODUCTS AND SUCCESSIVE OPERATIONS 299
From these relations we gather the important feet that the effect of QPq
upon a symmetric function symbolized by a partition is to obliterate one
part pq when such part is present and to cause the function to vanish when
no part pq appears in it.
549. Returning to the relation of operators, now written without
specification of an operand,
1 + μ(?ι0 + vGoi + ... + μΡν*Θρς+ ... = exp fag10 + vg01)
we recall that on the right-hand side the multiplications of operators are
symbolic. We now seek to replace the right-hand side by an expression
which involves products of linear operators which are not symbolic products
but on the contrary denote successive operations.
To the two linear operators
#w = 3al0 + ^io3a2o + <hfiau + · · ·
#oi = 3a01 + Cl0idaoi + ОиЭв|| + · - -
we add a general linear operator including them and defined by the
statement
ffpq ==r Uapq *+* &io dap+if« ~^~ aoiVap,q+i + · · · + &r$(7ap+r,q+8 + ....
We will establish the relation
exp (m1Qff10 + m01gQ1 + m^g» + mugu + ... + %уй + ...)
= exp (ϋί10#10 + Moi#01 + ^20#20 + Mngu + .. . + Afpgfttf +...),
where if £, τ; be undetermined algebraic quantities, the numerical magnitudes
Mpq are given in terms of the numerical magnitudes mpq by the relation
exp(Jf10f+Jf01i7 + ... +Л/^р^+ ...) = 1 + Μιοξ + 7ηνιη+...+*ηρ9ξΡη*+....
First observe the well-known relation
(ft*) (0·*) = (ft* ft··) + ffp+r, q+S
where on the left-hand side the multiplication denotes successive operations
and the second term on the right-hand side is obtained by operating with
gvq upon gr8 where grs is considered to be a function of algebraic quantities
only and the differential inverses are not subject to operation. The reader
should verify the simple case
(#ιο)(#οι) = (#ιο#οι) + #ιι.
Put щ = m10g10 + m01#oi + · · · + MpqSlpq + · · ·
and observe that if 7)ipqgpq be written symbolically mpqg, we obtain
^ = (m10 + m01 + ··· +Щч+ ...)#·
Two successive operations of ult written (г^)2, result in two terms, one of
which is an operator of the second order, written (и*), and the other a linear
operator, formed by simple differentiation as above explained, which we will
write щ:
(Ujy = (Ul*) + м2.
300 AN IMPORTANT CALCULUS OF OPERATIONS [SECT. XI
Also щ = %7пРЯтГ8др+г,д+8, and if we write mPqrnr8gp+rtq+8 in a symbolic
form
mpqWrsg
it is at once seen that
Щ = Ow + ^01 + ... + rnpq + .-.fg.
Similarly (щ) (щ) = (щщ) Н- г^,
where щ = (% + % + ... + mM -ь . ..)*д;
leading to ^ = (% + Woi + ... + *Λρβ4· ···)*#>
and (ws) (щ) = (г^г) ч- wg+i.
Moreover it has been shewn in Volume I that for any series of linear
partial differential operators щ, щ, α3,... enjoying the property
we have exp (щ) — exp (щ — \и% 4- \иг — ...),
the multiplications which arise on the development of the right-hand side
being non-symbolic.
Hence on substitution for u1} u2> щ,...
exp (mio#io + ™oi#oi + ·.. + ЩЯдРЯ + . ·.)
= exp {(wim + m01 + ...)g - £(w10 H- m01 + ...)lg + J(m10 + m01 + ...)3# - ...j.
If the right-hand side be written in the form
exp (M1Qg10 -f- MQ1g01 + ... + Mpqgpq + ...)
we must have, for undetermined multipliers ξ, η,
exip [(ιη10ξ + m01v + ...)- H*Hio? + Moi*? + ...)2 + ?Ою£ + ™oi*? + ...)- ...}
= exp (M10g10 + JfM #oi + ... + ϋί^^,κ/ + ···);
and since the left-hand side is
exp log(1 + τηιοξ + ukiV + ··· +%Рч, + ...),
we have the identity
exp(Jf,of+ ATwiy + ...+Jlfw^ + ...)
= 1 + 7№ю| + moi*7 + ... + ?/yy f*V + .. .
for the determination of the magnitudes Mpq when the magnitudes mvq are
given and vice versa.
The relation is clearly otherwise written
= log (1 -f m10£ + me# + ... + т^фф + ...).
CH. Ill] RELATIONS BETWEEN gpq AND Gpq 301
Comparing Art. 537 it is evident that mpq and Mpq are connected in the
same way as
<* .ad (-)>*-&t£zI>J
,!
p\ q\ "Spq'
Thence the formulae of the same Art. give
Mpq = 2(-)2*-1 (ST^t1)! ηΐ* m* .
7Γχ 1 7Γ2 Ι
mpg = S . * . Μ* Μ** ...,
tf 7Γχ ! 7Γ2 ! ... Λ ft РъЧъ J
the summation in each case being for all partitions
(Ρι?ΓιΜ?2...)
of the bipartite number pq.
The particular case of this theorem that we require now is obtained by
putting % = μ, mQi = v> mpq = 0 in other cases.
Thus
exp fag10 + vgn) = exp (M10gl0 + MQ1g01 + ....+ Mpqgpq + ...),
where Μ10ξ + MolV + ... + Мтф<ф Η-... = log(l + ^ + ^).
We derive the relation
j/pg=(-)^-^+g-1)Vyg,
so that exp (μ#10 Η- vg01)
= exP {0#ю+^#01) -£0*sflto + 2μζ/#η +ϊ>2#02) +^^30+3^^81 + 3^^ + 1^08)+...}.
Thence from Art. 547
(дом+vgoi) - i (t*g* + 2aw#h + vVob) + 4 <У#ш + 3/Λ#2ι + 3|«ty12 + ^oa)
= log(l + μθ1ϋ + i/ffoi + ...+/^^6>g+..·).
Expansion of the right-hand side, and subsequent comparison of like
terms in μ, ν, yields the relations:
#10 = $10 ^10 = #10
#01=$01 $01=#01
#20 = GJo ~ 20* 20* =^0 - ^
gn = (?10 $0i "" $ii $ii = #io#oi - #n
#02 = $01 - 2$02 2$02 = gi - #02
#30 = $?o - 3$20 $io + 3$зо 6$30 = #?o - 3#?0#io + 2#зо
#21 = $?0$01 - $20 $01 ~ $11 $10 + $21 26?21 = #?0#01 ~ #20#01 " 2#ц#10 + 2^
#12 = $01 $10 - $02 $10 - $11 $01 + $1* 2#12 = ^^10 - <702#10 " 2#n#01 + 2#12
#03 = $2i - 3$o2$oi + 3$оз 6$оз = #b\ - 3#02#oi + %03
etc. etc.
relations to be compared with those of Art. 537.
302 OPERATIONS IN CORRESPONDENCE WITH SYMMETRIC FUNCTIONS [SECT. XI
The corresponding general formulae are
<_.)«-.{P + «-1)lgM = %(-у-г0ρ*1!<?;· g*> ...,
the summation being for every partition
(ΡιβΡΛβΡ—)
of the bipartite number pq.
In the second formula the multiplications of linear operators denote their
successive performance.
550. By comparison of these relations with the corresponding algebraic
ones to which reference has been made, it is found that gvq and Gpq are in
co-relation with spq and apq respectively. In other words, these operations
correspond to the partitions (pq) and (10p 01?). It is necessary to find the
operations which correspond to the remaining partitions which symbolize
symmetric functions. We easily derive the relations
(ffPiQi) (9P2Q2) * (УР1Я1 9Р2Я2) + 9pi+P2, <7i+9a »
(W2 = (&)+#*>> *? >
((ffpiQi) (9p<tte) (#Рз<7з) ~ (9piQi 9p*Q2 9pbQs) + Ч/piQi 9р2+Рй> <?2+<?з) + \ffP2Q* 9pi+Pu> 7i+<73)
+ \9р$Чз9Р1+Р2> Ql+W + 9Pl+P2+Pu> 7l+02+'/S »
(dPiQif (9P2<22) = \9plQi9p2Q2/ "+" ^ (&>i7i 9pi+P2* <h+Q2/ + (/fen. *1ι9Ρ242/
+ fel+i>2, 2V1+V2»
and comparison with the algebraic formulae
(Pi?i)(P*?a)asa(jPiiift?») + 0,i + P*» Ϊι + ί/ti).
(PiJi) (Р»?2> (Pa?») = 0>i?iP2(73pS2s) + (pi(/i ^, + jft, </a + (/») + 0>a</a jp, + |>3, ft + </3)
+ OV/a pi + Pa, У1 + ?3) + (p, + p, + p3, </, + ?3 + ?,),
('Pi<liY(M*) = 2 (# ϊϊ ?λ^Α) + 2 0>i tfi Pi + V*> Ъ + ft) + (2Pi 2?i Paft)
+ (2pi + p3,2jI+iA),
0>гУ = 6 (F/) + 3 (2p, 22 pff) Η- (ty, Зг),
shews that the operators
2~j \5w> 2"] (Λίϊι 9p*q*/> 3] №i)
are produced according to the same law as the symmetric functions
(Ρϊ1). (ΡιίϊΡΛίΛ (Pi3)·
CH. Ill] PARTICULAR RESULTS 303
In general the operator
1т-(/1 <f2 ..·)
7Гг ! 7Г2 I ..
corresponds to the symmetric function
(ftff'ftiP —)■
There is thus complete correspondence between quantity and operation,
and any formula of quantity may be at once translated into a formula of
operations.
Observe that a product of symmetric functions
(ΑβΓΑί? —) (ri«fir»#—)
is in correspondence with the operation
= (a** ащ ) - (aPl aPi )
7Γλ ! 7T2 ! ... Pl ^ №* " pi I />2 -1 · · · ,il 2*2 '' *
the notation indicating that the two operations
1 /«-Ι Q** ...) and (qpl qp,i ...)
are to be successively performed.
Ex. gr. From the formula
(31 01) = - £ (21 10) (01) + \ (21 01) (10) + \ (10 01) (21) - \ (21 10 01)
we derive
(#31 #0ΐ) = - i (921 9ΐθ) (#0l) + i (#21 #0l) (#1θ) + i (#10 #0l) (#2l) - £ (#21 #10 #0ΐ).
551. Since every symmetric function
(ΑϊΡΑίϊ1—)
is expressible in terms of the elementary functions o^, we may express every
operator
щ ! 7T2 ! ... ^PiQ^lM* '"'
in terms of the operators C?^.
The operation therefore may be performed upon a function symbolized
by a partition by simply operating independently with the successive G·
products and adding together the results.
As a particular result observe that since
{ Г p\q\ &* *l J τγ,Ιτγ,Ι... *'.«■**·'''
\a\
we have fe = (-)*+g-i (p*g^1}1 ^ + · · · ,
304 FUBTHEB SYMMETRICAL RELATIONS [SECT. XI
and therefore gm svq = (-)*+«?-* ( *' qJ f;
and from a theorem of symmetry established in Art. 542,
(AffMP .·.) - (-)-+*+< (p.ffi-1), (|r^1: «■»+···.
from which we derive the result
552. Referring to the three identities of Art. 543 bis, and the relation
we see that in the relation
1+ Сю? + ο01η + ... + CpgpV + ...
= Π (1 + а/Ью?+ i8;M + ... + оС*0*Ъ„&1А + ...)
we can interchange the singly dashed quantities a/, /3/ with the doubly
dashed quantities α/', β8".
Let the differential operators
9pq Gpq
9pq Wpa
ypq Wpq
refer to the sets of quantities with one, two, and three dashes respectively
and write the relation
1 + c10? + c01i) + ... + c^ip + ...
= Π (1 + «/&„£ + j8;bwi? + ... + οίνβ'^ξνψ + ...)
in the abbreviated form
U = tt'a^ ^'a2/J2 W'*303
The performance of the operation
Яге" = Ча+ ^Ч+ы + 6«Э*л.«+1 + · * *
upon both sides of the relation yields
9m ^ = OWu'o.^y) и'а2в2иа3Эз + ...;
and since g^ u'a^ = α'νβ'1 ϊ?ψιι'% ^ ,
it follows that gpq" U = (pq^pv* U.
If we now substitute 1 + ο10ξ + c0iv + ... for £f, and compare coefficients,
we find that
9pq crs — CP?)i C>—P. «~9 *
CH. Ill] AN OPERATOR INVARIANT 305
We can now connect the operators gpq'ftg^"t for regarding the coefficients
bpg as functions of the coefficients Cpq only
9pq = (W Cpq) Ъст + ... + (gVq Cr8) 3Cyg + ...
= (Ρϊλ (Зсм + с10ЭСр+17Н- c019Cpa+1 + ... + cr^^9Cre + ...)
Similarly, or as a result of the symmetry that has been established,
9pq'=(P<l)2 9pq">
and since (pq% = (pq)2(pq)i, we may write down the relations
(Ρϊλ flW = (РЯ% 9m = (Ρίλ ft*'"·
If then we regard the relation
1 +Cio? + colV+ ... + cM£^ + ...
= Π(1+α/610£ + &Λι *? + ..·)
= Π (1+«."ααξ + β*"αΛη + ···)
as defining a transformation of the set of quantities
clo> Coi> ··· Gpq ···
into ейДег of the sets of quantities
^10i ^Ob ··· Vpq ···
the operation {pq)z9pqn
is an invariant of the transformation.
Expressing the operators g in terms of the operators О by Art. 549, we
obtain the system of relations
G10" = (10).GV"
(?„," = (01), (?„'"
G„" = (20), <?,"' + (10*), <Э»И"
0„" = (11), <?„'" + (10 01), <?,„'"(?„,"'
(?„/' = (02), G№r + (OP), <?iV"
which should be compared with the relations set forth in Art. 539 between
the quantities cm and bvq.
553. In general we may take the following view:
We have
log(l + £<*," + n&u" + ... + Ρ*Θ„" + ...)
= Ы' + 49» ~ * (?0* + 2^.." + *9ηΊ + -
= %hg(i +«8'θω"'ξ+β8'σ01"'ν + -+^'iOPq,41,vj + ...);
Μ. Α. II. 20
306 OPERATORS AND SYMBOLS OF QUANTITY [SECT. XI
by making use of the relations
we find log (1 + f GV" + ηθ^" + ... + £*^GW" + · · ·)
= &/' + W ~ i (Г <b'" + 2fWu " + 4V« ") + · · · ·
Hence 1 + #?„" + ч <?и" +... + PV Gpq" + ...
= π (i +«; <V"£+β/ вп'" v + ...+α'ρβ'ι бу" *V +···),
and comparing this with the relation of Art. 539, viz.
s
we arrive at the following important theorem :
" In any relation connecting the quantities cpq with the quantities bpq we
can obtain a relation between operators by substituting Gpq\ Gpq" for cpq,
bpq respectively."
It is established in the same manner that in any relation connecting the
quantities cpq with the quantities apq we can obtain a relation between
operators by substituting Gpq, Gpq" for cpq, ap(J respectively.
In fact, ξ, τ) being undetermined quantities in the assumed relation which
connects the magnitudes in the three identities, we are able to express any
product, or sum of products, of the quantities c10, c01, ... cm,... in terms of
products of the quantities 610, b01,... bpqi... and of symmetrical functions of
the quantities a/, /3/, a2'> A7,...—or in terms of products of the quantities
Οίο> «οι» ··· apq> ··· ancl of symmetrical functions of the quantities a/', /3/',
a2", /32", The substitutions before us can be carried out in any equation
thus formed.
It must be borne in mind that in any relation connecting the three sets
of quantities
«* > β81 α*"> β*"\ as'"> A?"';
we may interchange the two sets
я/> fis'l as", fit'-
We can now establish various laws of symmetry in regard to symmetric
functions of several systems of quantities.
554. In view of the equality
(pq)*=(pq)i(pq)2,
it is clear that any integral symmetric function of the system
CH. Ill] A LAW OF SYMMETRY 30*7
which is expressible in brackets ( )3, can be expressed as a linear function
of products of symmetric functions, each of which is of the form
( ). ( X,
and that in that expression we can interchange the brackets ( )19 ( )2.
We may therefore suppose an identity
(А) (гг^гл8р...\
= ... + J"{fob? α2δ? ...)ι (ΑβΓ Α3Τ· ...)1 + (а1^аа^...)|(А5Г»Адр...)1},
wherein the functions
foef raep ...), («Α» α2ί>? ...), (Piq?p2q? ···)
are all of the same weight.
Moreover, any product of the quantities c10, cw, ... cw,... can be expressed
as a linear function of expressions, each of which contains a monomial
symmetric function of the quantities α/, β8\ and a product of the quantities
^10> ^0i> ··· Vpq, ....
Assume then the relations
(0) c«',». «£*, ··· = ···+ Μ(ftif. i>3??...X b>U &£,,... + ....
It will be shewn that the numerical coefficients J, L, Μ are equal to one
another.
For from the relation (B) is derived the operator relation
and performing each side upon the opposite side of relation (A) we obtain
after cancelling (afy a2b^ ...χ,
LG'Z\ &:%- ('·.**·,* ··· W<%, G%k...(Plq?M?...%,
no other terms surviving the operations.
Hence L = J.
In a similar manner from the relations (A) and (C) we prove that
M = J.
As a particular verification observe the relations
(103 01), = ... + 3 {(20 Ιΐχ (103 01>, + (ΙΟ3 Οΐχ (20 11)2} + ...,
С2ос;и = ...4-3(10301)Ь?оЬ01н-.,.,
c?0c01=...+3(2011)b?0b01 + ....
We have, therefore, another proof of the Law of Symmetry which was
established in Art. 542 by the method of Distributions.
20—2
308 SECOND LAW OF SYMMETRY [SECT. XI
Since it has been shewn above that in any relation connecting the
quantities cpq with the quantities bn we are at liberty to substitute GPq\
&pq" f°r °Mi> ^P7 respectively, it follows from Art. 550 that in any relation
which connects the monomial symmetric function
(ΑίΓΆίΡ—λ
with a linear function of products of the quantities bvq we are at liberty to
substitute
Wil 7Г2!... ^ΡιΖι^Μ* '
for (АзГ'лдр·.·)
and Gpq'" for Ъм.
555. This fact leads at once to a second law of symmetry, for if we
derive, from the three initial identities and the relation assumed to exist
between the quantities involved, a relation
(й?Г1М? ...)з = ... +PbpiSib*H ... + ...,
wherein Ρ is some symmetric function of the first system of quantities ag\ β8\
we are led to an operator relation
Now assume a second relation
fatf ra«f ...)3=... + Qb£qx b^ ... + ...,
and utilise the operator relation in the manner
and we find Ρ = Q, since no other terms survive the operation.
We thus have before us
A Theorem of Symmetry.
"If (Α8Γ" Α9Γ·...)ι = ...+-Ρ*?1#1δ?Λ..· + ...,
the co-factor symmetric function Ρ is unaltered when the partitions
(ρ,ίΓΆ??·.·)* (Vfa*?*···)
are interchanged."
The function Ρ presents itself; in the first place, as a linear function of
separations of the partition appertaining to the 6-product to which it is
CH. Ill]
TABULAR REPRESENTATION
309
attached. The theorem furnishes linear functions of separations of any two
partitions
respectively of the same biweight, which are algebraically equal to one
another.
To elucidate the matter we can form a table of biweight 21 as follows:
b2i O20 h\ ЪпЬ10 ό?0δ0ι
(21)8
! +(21)
-(21)
-(21)
+ (21)
+(20 01)
-(20) (01)
-(20 01)
-(20) (01)
-(2001)
+(20) (01)
+ (2001)
+(11 10)
-(11) (10)
-(1110)
+ (11) (10)
-(11 10)
+(U 10)
+ (102 01)
"(ΙΟ2) (01)
-(10 01) (10)
+(Ю)2 (01)
-(102 01)
-(ίο2) (oi)
+ (10 01) (10)
-(ΙΟ2 01)
+ (102) (01)
+(102 01)
(20 01)3
(11 10)з
(Ю201)з
which is to be read by rows.
The table possesses certain properties :
(i) Each term in a column is a separation of the partition of the
Ь-product at the head of the column.
(ii) The separations in any line of terms as written possess the same
specification.
(iii) A row of terms possesses at most four lines, because the partitions
prefixed to the rows, viz. (21), (20 01), (1110), (10201), are four in number
(the same of course as the number of rows). In any row of terms the
specifications of the separations in the first, second, third and fourth lines are
equal respectively to the partitions (21), (20 01), (1110), (10201).
(iv) The separations which appear in the same line are affected by the
same coefficients.
(v) The Theorem of Symmetry shews that algebraically the table
possesses row and column symmetry.
The block of terms in the rth row and cth column is algebraically
equal to the block of terms in the cth row and rth column.
310 NEW STATEMENT OF A LAW [SECT. XI
A block of terms in the rth row and cth column may be briefly and
suggestively defined to be
" A linear function of separations of the partition of the Ь-product at
the head of the cth column formed according to the law of the function
prefixed to the rth row."
We may then state the Theorem of Symmetry in the form: "The
assemblage of separations of
formed according to the law of the function
is algebraically equal to the assemblage of separations of
formed according to the law of the function
CHAPTER IV
THE LINEAR PARTIAL DIFFERENTIAL OPERATORS OF THE THEORY
OF SEPARATIONS AND THE PARTITION OBLITERATING OPERATORS
556. We have seen that if the biparts of a monomial symmetric function
θ are themselves partitioned in any manner into biparts so that when they
are all assembled in a single bracket they are represented by the partition
the symmetric function θ is expressible as a linear function of certain
assemblages of separations of the symmetric function (г^т,^...). We
have moreover actually so expressed the functions whose partitions comprise
but a single bipart. For the calculation of other functions in terms of
separations of a determined function it is necessary to find the adaptation
of the linear operators gWt g01>... gpq>... so that they may be performed on a
function when it is expressed in terms of separations. Of any partition
(r^nsg2...) separates are formed by taking all possible combinations of
its parts one, two, etc. at a time. There are thus (рг + l)(/o2+ 1) ... — 1
distinct separates which must be regarded as independent variables. Let
any such separate be
ΠΟΊο+Ριο ΟΙ""01 +p°l ... Г$">«+р™ ...),
where (10*'· Ol^»'... rsnrs...)
is some partition of (pq).
Then by a known theorem of transformation in the differential calculus
9vq= Σ {gm (IO'w+^OI'oi+p*! ... rs*"*·'» ...)}d(10*io+9»0i*n+hi_„*„+*»...),
where -7- has been written in the notation dx and the summation on the
right-hand side is in regard to every distinct separate of the partition
(гг8(хгй$^...). Unless however a separate contains some partition of (pq) the
operation of gpq will cause it to vanish. We can immediately transform
the expression of gpg because
(-^fe^-'ft.-a<;C',<8V.1)'«»»-«»·-
Ρ · Ч- π·ιο! 7Γ01! ... 7ГГ8\...
312 SEPARATES AS INDEPENDENT VARIABLES [SECT. XI
and
#н>10 Go?1 ·· · Gr?tra · · · (107Γι°+<)ι« 01π»ι+ρ°ι... rsT"l·**...) — (10p"> 01Po1... r$**...)·
Hence (-)P^(PMz^} ,pq
Ρ' 4L ·
= % S : : : " (10p,° 01Po' ... Τ&*· ...) 3/10«·ιβ+Ριο (««Όι+Ροι r$vrt+f>rs ) ,
„ ρ 7Γ10Ι 7Γ0ι! ... 7ГГЯ\... *
the summation being in regard to (i) every partition (ΙΟ7"10ΟΙ*·1 ... г$ж™...)
of (pq), (ii) every separate (101Γιθ+Ριο017Γοι+Ρο1... rsv»+fin...) of the partition
(r^pr^p...). The right-hand side of this relation may be regarded as the
sum of a number of portions in each of which the numbers тгю, 7г01,... тгг89...
are constant.
In fact writing
X (10Pl° 01Pm ... TfPn ...) Э/цую+Рю o^oi+Poi _ j.^rs+Pj-e # \ =#(107Γι0017Γ»1 ... PS*™ ...)>
Ρ
we have
/ 4^-,(Ρ + 9-1)ί _^(-)5'-ΜΣτγ-1)! .
(_) ρ!3! ^9 -^1о!^1!...^!...^10№010,-и"-)'
a formula which should be compared with the two
н·***^'*. -*£C'(*',"1)'<»<»-*-;
jpi qi η- *лг101 7Γ«ιϊ ··· тгг8\ ···
jP ί 9 ! π 7Γ10 ! 7Γ01 ! ... ττ.η : ... "
the summation in each formula being for every partition (lO^Ol""»1... rsVr*...)
of the bipartite number (pq).
The operator g{10*luQlm „*«...) is of biweight до. It is equal to
2(10^01^ ... Г&» ..ОЗ^ю + Ртох-.п+Ро^^^^+Рг....).
Ρ
where (10*io+p,001ff°1+Pul ...rsw™+p»·*...) is a separate of the given separable
partition. If this separable partition be written in the form
(lCK10 010"01... rs°>»...),
the expression of #(10*ίο01*-οι ша#гя*«_) wiU involve the term 3/107no01ffol _„»«_]
and also a term corresponding to every separate of
and thus altogether it will involve
(σ10 - 7г10 + 1) (σ0ι — тг01 Η- 1) ... (<rr$ — я>, + 1) ... terms.
CH. IV] PROPERTIES OF PARTITION OPERATORS 313
557. The operator g(pq) is a linear function of the operators
5f(107Γ10017r0l...n·'г,·ί...),
and in the general case this linear function may be regarded as involving as
many partition operators as the number (pq) possesses partitions
(ΙΟ*10 ΟΙ"01... re"*·»...);
but for particular operands some of these partition operators will be
necessarily absent, for a given separable partition may not contain every
partition of {pq).
In particular we have in the simplest cases
#10 = #(10),
#01 = #(01),
#20 = #(l02) ~ 2#(20)>
#11 = #(1001) —#<n)>
#0Э = #(012) — 2#(02)>
#30 = #(10») — 3#(2010) + 3#(30)>
#21 = #(10*01) —#(2001) —#(1110) + #<2lb
etc.
Some developed expressions of partition operators are
#do) = Э(10, + (10) дт + (01) doom, 4- (20)дто) + (102) Э(103)
-ΚΠ)9(ΐιιο)+(Ю01) <7(W201) tfttooi2) -г ··· >
#(2001) =9(2001) + (10)3(201001) + (01) 0(2001*) + (20)Э (20'2О1) + (102) 0(2010-01)
+ (И) 0(201101) + (10 01) θ,,,,,β, + (02) 3 (200201)
+ (01»)Э
(2001а) "Г
558. It will be seen that the operators #/10πιο01τοι Τ8π„ \ are readily
performed upon a separation but their importance lies mainly in important
properties which they possess, to which we now proceed. Denote any two
operators of the same or different weights
by #и, 9ip) respectively and #(107Γ111+ρ1„01π01+Ρο1 г^гв+рг, } by glir+p)> we have
#(ir) #<P) = iff Μ #(Ρ)) + #(*+P) I
because g(V+P) is the result of operating with gM upon the algebraic portion
of #(p), the differential inverses being regarded as coefficients.
Thence we find
#(t)#(p) — #w#(»> =o;
establishing that any two partition operators are commutative.
The same fact is expressed by saying that the alternant of any two
partition operators vanishes.
314 CALCULATION OF TABLES OP SEPABATIONS [SECT. XI
We learn therefrom that if φ be an operand such that
9m Φ = 0>
then also g(ir) {g^ φ] = 0; in other words if φ be a solution of the equation
giir) = 0, then also is #(p) φ a solution.
If the right-hand side of the relation
1 ; 2>!?! fe ^тг10!7г01!...7гг,!... 0(io*»oi«*...r·*"...)
be performed upon a linear function of separations of the function
(lO^Ol0"01... rs°>*...),
which satisfies the equation gpq = 0, the effect of the particular partition
operator
#(107Г1°017г°1...г/г™...)
is the production of terms each of which is a separation of the function
(10σιο~7Γι0ΟΙ0"01"*01... rs*™-*™ ...) ;
and separations of this partition cannot be produced by any other partition
operation included under the sign of summation. In consequence the terms
in question must vanish identically and the function which satisfies the
equation gm = 0 must also satisfy the equation
5Г(107Г10017Г°1... г*"*»...)" ®'
559. We thus obtain the theorem :
"If a function, expressed in terms of separations of a given monomial
symmetric function, be annihilated by a certain biweight linear operator, it
must also be annihilated by every linear partition operator of the same
biweight."
This is the cardinal theorem for use in the calculation of tables of
separations of symmetric functions.
Ex. gr. We will calculate the function (31 01) as a linear function of
separations of the partition (21 10 01). The law of expressibility shews that
this is possible because (21 10) is a partition of (31). Observing that the
separation (21) (10) (01) cannot present itself because it is the only separation
which on multiplication produces the function (32) we put
(31 01) = A (2110) (01) + В (21 01) (10) + С (10 01) (21) + D (2110 01).
Now a monomial symmetric function vanishes by the operation of g{pq) if
no partition of the weight pq is comprised amongst its parts. Therefore the
only operators which do not annihilate (3101) are g01, g31 and д& and the
annihilating operators are g10, g-i, .... Hence the partition operators
#<10)> #(21),
cause the function to vanish and are sufficient for the purpose.
CH. IV] PARTITION OBLITERATING OPERATORS 315
Retaining only significant terms
{Эй» + (01) d(mi) + (21) 3(2110) + (2101)
V (211001) J (8101) «0,
{Эй + (ίο) 3,3Uo) + (oi) э(2Ш> + (ίο oi) a
(211001) }(3101) = 0,
leading to А+С=0, J? + Z) = 0, C4D = 0, 4+5 = 0,
or Z) = -C=-£ = A
Hence
(3101) = 4{(2110)(01)-(2101)(10)-(1001)(21) + (211001)b
and now it is easy to see that A = — |.
2%e Partition Obliterating Operators.
560. In the foregoing a generalization has been made, in the case of the
linear operators <7ю,#0ъ ··· 9pq, ·.· from a number to the partition of a number.
We proceed pari passu with the theory regarding a single system of quantities
and now seek the like generalization in regard to the obliterating operators
6?io > Gr0i,... Gpq, .... Consider a symmetric function
J\aw> ^oi» •••Ярд» •••)=/
to be the product of w functions and write
Supposing a.m to be changed into am4- μαν-Ύ>4 + ναν>4-λ we have from
previous work
(Ι +μΟιο + ΐ'6οι + — + PPvqGn+ .·.)/
= (1+Д„ + ^„ + ...+/*¥(?м-|....)/1
χ (1+ μ(?10 + ι/(?οι + ... + /**i* ffw +...)/*
X
Kxpanding the right-hand side and then equating coefficients of like
products of powers of μ and ν we obtain the relations
Gwf = S ( Cr Ю./1Х/2/3 '"fm>
β20/ = 2 (β»Α){0»/№...fm + t(0»f1)ft .../„,
β„/= 2 «?„/.) (<?»/0/. ···/» + Σ (Gu/i>/« ···/«·
G«/ = 2 «?,./,) (0«Д) (<?»/»)/* · · -A + 2 (<?«/,) (£o/2)/3 · · ·/«
G„/ = 2 (Cr.o/0 (GWi) (Яа/ЛЛ · · ·/» + 2 (<?„/.) (<?I0/2)/s · · ·/»
+ 2 ((?„/,) «?„/,)/, · · ./„ + 2 (©и/О/. ···/«.
etc.
316 CONNEXION WITH PART OBLITERATING OPERATORS [SECT. XI
Herein the summations are in regard to the different terms that may
be obtained by permutation of the m functions fif2 ..-fm and there is no
diminution in the number of terms arising from any equalities between the
m functions. Regarded in another manner we may consider the m functions
to be fixed in order and the sum to arise by distributing the operators in all
possible ways.
Generally in the expression for Gpqf there will occur a summation
corresponding to every partition of pq. If such a partition be (piqi, P2<lz>---P$qs)
the summation is
561. Thus when performed upon a product of functions the operation
Gpq breaks up into as many distinct operations as the weight pq possesses
partitions. We write therefore
^ (bpiiiA) (4M2/2) · · · (Gpsqsfs/fs+i · · -fm = G(Piqi ίλ>?2...ρβ<?β)>
and call ©(^^^...ρ^) a partition obliterating operator.
In this notation we have
©10 = ©do),
©20 ^ ©(20) + ©(102),
©11 — ©(11) + ©(1001),
©30 = ©(:ш) + ©(20Ю) + ©(юз)?
©21 = ©(21) + ©(НЮ) + ©(2001) + ©(102 01),
etc.
and generally
where the summation is in regard to every partition of pq.
This is a theorem for operating with Gpq upon a product of functions
and is strictly analogous to that obtained for a single system of quantities.
The reader will have no difficulty in seeing that when there are more than
two systems of quantities
562. The next step is to connect the linear partition operators
yipiqiPzQf.Paqs) with the partition obliterating operators ©(a^^,...^^).
We have the three relations
pi ?1 " 9vq ~ 7 7г10!тг01!...7г,П... W'-oi'" ... *·«...,,
p\q\ 9n Г7г10!7г01!...тггв!...1о(Го1 --—'
VTpq = Σ©(3 0πι° 01,Γϋ1 ... rs*™ ..)>
CH. IV] CONNEXION WITH LINEAR PARTITION OPERATORS 317
the summation in each case being for every partition (10**>01*η ...rs"**...)
of pq. From these we can eliminate the two operators gpq, Gpq. Thus the
first two relations yield
ιγ7Γ101 7Γ01Ι ... 7TrsI ... V ' η 7Γ10ί 7Γ0ιΙ ... 7TrifI ...
and with this we have now merely to combine the third relation. The
simplest particular cases are
( #(10) = "10 = "'(ΙΟ)»
1 #(01) = "01 = "(01) >
' #(102) — 2^(20) = Сг10 — 2(?20 = {"(10) "" 2ff(l03)} — 2(r(20)>
#(1001) ""#(11) = "10 "01 — "11 == {"(10) "(01) — "(1001)} ~ "(11),
w #(01-) — %(02) = "01 "" 2(?02 = {"(01) ~" 2(?(oi2)} — 2(?(02)>
/ #(10») ~~ %(20 10) + %(30) = "10 — 3(?2o "10 + $"30
= l"Uo) ~" 3&(ΐΦ) "(ίο) + 3G(103)} — 3 {&(.Λ) ff(10) — (t(2oio)} + 36г(30),
#(ισ·ΐοΐ) ~" #(20 0i) "■ #(u io) + #(21) = "10 "01 "" "20 "01"" "11 "10 + "21
— {"flO) "(01) "" "(102) (?(()i) — (?(10 01) "(10) + "(10201)} "- {"(20) #(01) *~ "(20 01)}
— {#(ll) #(10) — #(ц 1С)} + "(21)>
and we learn much from their examination.
563. Take the result
#(io2) — 2<7(20) = {(?f10) — 2(τ(10·2)} — 2G(ao)
into consideration.
Suppose that the operand is a linear function of separations of a given
partition.
Upon it the two sides of the operator relation must produce identically
the same function; but the terms produced by gm), Crf10) and Gm are
separations of one partition, and the terms produced by gm and 6r(20) are
separations of one partition different from the former. Hence for the given
operand the relation breaks up into the two relations
#(κβ = "(Ίο) — 2Gr(102),
#(20) = #(20)·
This reasoning is applicable in general and gives us the relations
#(10) = "(10))
#(11)2) — G(10) — 2 СГ( ю-.»),
w#(20) = #(20) >
{;
318
OPERATOR FORMULA ANALOGOUS TO WARING'S
[SECT. XI
{#(1001) ~ ©(10) ©(01) ~ ©(Ю01)>
#(11) = ©(11)>
9m = ©ao)~~ 3(?(io2) ί?(ΐο) + 3(?(10з),
#(20 10) = ©(20) ©(10) — ©(2010)>
#(30) == ©(30) >
#(10*01) = ^(10) ©(01) ~ ©(10*) ©(01) — ©(10 01) ©(10) + ©(10201)»
#(20 01) = ©(20) ©(01) ~~ ©(20 01)>
#(11 10) — ©(11) ©(10) "~ ©(11 10) >
#(21) = ©(21)·
564. The general formula that will be established is
(-^-MStt-I)!
7Г101 7Г01 ; ... ik r8; . . . ^
where the summation is for every separation
(ΙΟ*10 01πο1... τ$π™ ...).
We proceed from the formula
WW
of the partition
2(-)*-1
фг-1)1
Mo! TToi 1 · ·. 7rrs
_ V / \2л—1 V^77" ·*·) · β7™ ft*01
7Γ10!7Γ0ι! ... 7ГГ8\
g:
and we have to substitute for ©w, ©0i,... ©rs> ··· tbe sums of the partition
operators of weights 10, 01,... rs>... respectively. We have then to collect
on the right all the © operator products which are associated with separations
of the same partition and to equate them to the corresponding g operators on
the left.
Suppose (σΟ, (σ2), ...
to be the several partitions of (rs); we find that
τι rs · ^rs ·
*"* 7Γσ, ! 7Γ„J... '
leading to the relation
where
#(ΐοπι° οι"'01.
.. Г**" ... - * V-; · . · , "Γ/,η ""/ тл · · ·
ЗгЫ
Vl) №
WW*..
CH. IV] THE INVERSE FORMULA 319
is a separation of the symmetric function
and the summation is in regard to the whole of such separations.
This formula is to be compared with that which expresses spq in terms of
separations of any partition
(lO^Or^.-.r^™...)
of the bipartite number pq, viz. :
_λς>-ι_
(->
(Sir-1)1
Διγ„\
7Г10! 7T01I...7rrS!
1 ^(ю71"10О!""01 ... rs1
.я .«^(-^-iSL^'iJiy^j^....
л» л
565. From the above relations we can express the partition G operators
in terms of the partition g operators. Thus
£(10) = #(10)>
f 2! (?(102) = #fi0) ~ #(102),
#(20) = #(20)>
#(io oi) — #(ю) #(oi) — #(iooi)>
#(ιι) =#(ΐΐ)»
( 3 ! 6τ(10·ΐ) = #(\o) — 3#(102) #(ιο) + 2<7(ltfi),
#(20 10) = #(20) #(10) "~ #(20 10)»
#(зо) — #(зо) >
2#(io3oi) = #fio) #(oi) ~~ #002) #(oi) — 2#(iooi)#(io) *+· 2#(10201)>
#(20 01) = #(20) #(01) -" #(20 01)»
#(n ίο) — #(ii) #(io) ~~ #(ii io)»
#(21) = #(21)·
The general formula that is established follows the law by which any
symmetric function is expressed in terms of the one-part symmetric functions.
Thus the first of the last batch of formulas is in correspondence with the
formula
Δ (J 0" 01) = $ΐ0$οι ""* $20^01 "~ ^'ll^lU + ^21,
and it will be noted that
takes the place oig(PiqiP2q2PBqs...) on the right-hand side.
It will be noted that the partitions associated with the right-hand side
of the algebraic formula, viz.:
(10201), (20 01), (1110), (21),
320 FORMULA INVOLVING SYMBOLIC MULTIPLICATION [SECT. XI
are the specifications of the separations
(10)2(01), (102)(01), (10 01) (10), (10201),
which are associated with the right-hand side of the operator formula.
The formula which expresses any monomial symmetric function in terms
of functions with a single part in their partitions is
(_)27r-l(lQ7r10 01*oi ... rS"rs ...)
= <( pi-i fipi-l)!(Sfr-l)!... i, h
^ } ii!js!.../hi!pi.!...p*i!p»! WW"·
where (Ji) = (pujfi'ftrfS* ···)> W = (Αιίϊ1 ЛИ1 -λ
and (t/i)7*1 (/2У2... is a separation of
(lO^Ol1*1... rs*>«...).
If (/χ), (/a),... are of weights Piqup2q2,··· respectively, s(Jj, sw> ... are
equal to 8Ρι9ι, sMl,... respectively.
The corresponding operator formula will be found to be
(_)2тг-1 (?(χοπιο017Γοι _ r^r*...)
= S( ^'-Ί (Σ/>ι-1)!(2/>2-1)!... j, л
k ' Λ!Λ!...ριι!ρι«!...Λι!ρ«! ^^W"'
but here of course we are not at liberty to substitute piqi, 2>2?2>··· f°r
(Jj), (J2),... respectively in the formula.
566. In these formulae the multiplications of operations denote
successive operations. The products of g partition operators are readily transformed,
so that the multiplications may be symbolic; for, denoting symbolic
multiplication by external brackets as usual, we find
2 ! СГ(102) = (#(Ю))>
#(10 01) = \9(Щ9(01))>
3 ! <9(10з) = (#fio))>
and in general
7Г10! 7Г()1! ... 7Ггв! ... G^io 0liroi _ 7V«...) = (#U0) 9m · · · ffjrs) · · ·) >
and this is to be compared with a previous result
p!i!Gj*-(fltofl*).
These results are readily generalizable for multipartite symmetric
functions in general. Thus
(-^φτ-Ι)!
Γ— j Z i 9(100..."м-.. 010...""0!0"· rst...*««···)
_^(-)^(Σ?·-ΐ)!^·, «a
7 ji!;.!... V,)^-'
CH. IV] THE MULTIPLICATION OF SYMMETRIC FUNCTIONS 321
where («Tiy» (JQy*... is a separation of (100..."*»··· 010.. .7Г01°- rst...*«*... ...),
and the summation is in regard to the whole of the separations.
The reader will have no difficulty in reversing this formula.
Also
7i"ioo..J ^οιο.,.ϊ ··· ^rst... * ··· ^(100..71(Ю-"010...7Г°10··· ret...***···...)
= (a"100'" <y"m'" cTrst~ )
Vi/noo...) У (Οία j · · * ί/(,·Λ„.) * * * /·
These relations are of importance in the studies of combinations on a
chess board or lattice, which will be taken up in the next chapter. In that
theory it will be found that certain enumerations are determined in the forms
(jtu an, Cr\n am, (г1Ш «ЦП,
and generally in the form GgJ?^"· affit"*"".
In feet these expressions, on evaluation, are integers, and severally
enumerate interesting combinations on a chess board.
567. We have above the results that have been, or are likely to be, of
the greatest service in Combinatory Analysis. An example may be given of
the use of the operators in the multiplication of symmetric functions.
Suppose that we require the coefficient of (ll2) in the product
(102)(01)2.
Put (10s) (0l)2= ... + A (IP) + ....
When wc operate with G'ii on the right-hand side the result is A> since
every other term is caused to vanish.
Hence A «0b (10·) (01)*.
Now Gu = G{n) + G{lQoi)>
and since the operand involves no part (11) we find
A = ^ooi,(1Os)(O1)^ = 20(1OO]) (10) (01)- 2.
Again, to find the coefficient of (11 10 01) in the product
(10 01) (10) (01),
wc have to evaluate
<?n #io G«i (10 01) (10) (01)
ξ σ,ιβ .1)^0,0^,(10 oi) (ίο) (οι)
«^(ιοβι) »(ю) {(10 01) (10) +(ΙΟ)3 (01)}
= β(,ο οι) 1(10 01) + (10) (01) + 2 (10) (01)},
and remembering that (ruooD (10 01) = 0, since in operating with G&ooi) the
parts (10), (01) must be taken away from separate factors of a product, we find
the result
Goool). 3(10) (01) = 3.
M.A. II. 21
322 CONSTRUCTION OF SYMMETRICAL TABLES [SECT. XI
The Construction of Symmetrical Tables.
568. It has been established in Art. 542 that it is possible to form two
symmetrical tables in connexion with every partition of every biweight.
Certain representative tables are given as far as weight 4 inclusive. Of that
weight we neglect the biweights 40, 04 as they are practically the same as
the weight 4 for a single system of quantities. Of the remaining biweights
31,22,13, it is only necessary to give the two former, because the biweights
31,13, are practically the same.
There are seven partitions of biweight 31, viz.:
(10301), (11 102), (2010 01), (2011), (2110), (30 01), (31),
and nine of biweight 22, viz.:
(1020P), (1110 01), (IP), (20 OP), (20 02), (2101), (22).
(02102), (1210),
Of these the tables for (20 012), (21 01) give those for (02 102), (12 10)
respectively by transposing the elements of the biparts, and the four
corresponding to (31) and (22) are mere identities, so that the number is
reduced from 32 to 24.
The earlier tables which are necessary are those of the partitions (10 01),
(20 01), (1110), (103 01).
Each table is read horizontally, or as may be said, by rows and not by
columns.
CHAPTER V
FURTHER THEORY OF THE LATIN SQUARE
569. The question of the Latin Square can be regarded from another
point of view. Let us consider the symmetric functions of many systems
of quantities and the associated differential operators. Three systems of
quantities may be taken as typical of the general case. As operand we may
have the product
оХлГ1 aW2... aWf = (100λ> 010* 001*0 (100λ* ОКУ» 001"»)·· ·(100Ч>10*001"·)
and as operator
(\ιμ1ν1\2μ2ν2...\8μ8ν8) and (р^ЛМг^'з ··· Рь&п) being partitions of the
same tripartite number.
It will be remembered from Chapter ш that
"W = ^~j T] f\ \9ioo9ow 9m)>
where gm = Sap-i q r <W >
^ooi = ^<%<?r—ι "аде?·
Moreover it was proved that if on multiplication
Η- Л (ί?ι?ιПjp2^2r2 ...ptqtrt) + . ■.,
then ^Ριί,»-! Ьр^п ·· · ^fptqtrt ^λιΑΑ, μ, <^\2μ2ν2 - · · α\μ8^ = Λ ·
We must carry out the operation upon the function
(100λ· 010* 001"·) (100λ* 010* 001"*) ... (100λ* 010* OOP*)
and then determine the nature of the diagrams enumerated by the number
A. Consider first the operation of GPiqirr It operates through the
partitions of (ρι?ιΛ) upon the operand. The only effective partition is
(100* 010*' 001r«),
and its parts must be picked out from the factors of the operand in all
possible ways subject to the condition that only one part must be taken
from any one factor. The operation breaks up as usual into a number of
minor operations and each of these yields a first row of a lattice of s columns,
21—2
324 THE LATIN RECTANGLE PROBLEM [SECT. XI
s being the number of factors of the operand, and of t rows, t being the
number of factors composing the operator. The first row comprises $
compartments and in ply ql} гг of these will occur the tripartite numbers 100, 010,
001 respectively, px + q1 4- rx compartments being occupied and s —px — qx — rx
unoccupied.
Read from left to right these tripartite numbers constitute a composition
into parts 100, 010, 001 of the tripartite number (pi^ifi). Similarly a minor
operation of GMir2 gives in each case a second row involving the numbers
100, 010, 001, p2} ?2> ?\j times respectively, and these numbers read from left
to right constitute a composition into parts 100, 010, 001 of the tripartite
number (рг^г)·
We finally arrive at a diagram such that the tripartite numbers in the
successive rows read from left to right constitute compositions into parts
100, 010, 001 of the tripartite numbers (pig^), (р2?Л)> ··· (ptqtn),
respectively; and in the successive columns if the reading be from top to bottom,
we have compositions into parts 100, 010, 001, of the tripartite numbers
(λιμιΐ/ι), (λ2^2^2), ... (\8μ8ν*) respectively. To give the proposition a purely
literal form wc write 100, 010, 001 equal to a, b, с respectively, and the
diagrams are then such that there are s columns and t rows, the products of
letters in the successive rows being
a^b^c^, α*·δ«ν»,... a*t¥t<f%9
and in the successive columns
a^b^c"1, αλ*№*ον*, ... α뻥-Βθν*.
The number of these diagrams is therefore
Vfpxqxri bptfin '" ^Xptton αλ,μ,ι/, α\2μ2ν2 ··· Q>kaV*V8m
In this distribution not more than one letter occurs in each compartment
and there may be empty compartments.
Ex. gr. With the operator Gm Gm Gm and the operand a110 От «ою аш we
obtain the integer 7 which enumerates diagrams of four columns and three
rows such that the products of letters in the successive rows are abc, ac, abc
and in the successive columns ab, etc, i>, ac\ The seven diagrams are
b
0
a
a
с
0
0
0
b
с
a
с
! °
1
a
b
a
0
с
b
0
0
с
с
a
a
0
b
0
с
a
■ b ' с
0
0
a
с
a
0
b
0
a
с
Ь
0
с
с
0 ; a
0
a
b
с
0
a
b
0
0
a
с
с
b
a
0
с
0
a
0
0
b
a
с
с
b
0
a
с
a
0
0
0
b
a
с
с
and they are the only ones satisfying the conditions.
CH. V] EXAMPLES OF LATIN EECTANGLES 325
If we rotate these diagrams we obtain those derivable from
^"110 ^101 ^010 ^102 &111 #101 &1U>
which therefore necessarily has the value 7. In general we thus prove that
@pxqxrx Grpuq2r2 ··· ^Ptqtrt αλχμχνχ a\uw2 ··· ^λβ/ιβ^β
= ®λχμχνχ ^λβ^νβ ··· ^λβ^β ap^rx ар,&г2 ··· aptqtrtf
involving a law of symmetry already established in this Section, Art. 542.
570. If we require diagrams with no empty compartments we must
have
Pi + ?i + rx = p2 + q2 + r2 = ... =pt + qt + rt = s,
and \ + fa + vi = Xg + fc + J>2 =* ... ~ λβ + μβ + νβ = ί.
Thus G211 #121 αιιο ^ιοι αοιι °^ю
leads to the three diagrams
b
a
a
с
с
b
a
b
a
b
с
a
b
с
a
b
a
b
a
с
с
b
b
a
possessing the property that the letters in the successive rows make the
products a?bc, ab2c and in the successive columns the products ab} ac, be, ab.
These diagrams when rotated correspond to the same integer 3, viz.:
^110 ^"101 ^"011 ^110 ^211 ^121 ·
Further if the diagrams arc to be squares we must have s = t Moreover
if the diagrams are to bo Latin Squares the product connected with each
row and each column must be abc and for the third order we find that the
Latin Squares arc enumerated by
^111 "ΊΙΙι
and for the order η by
Cr4 ft4
^111 ...1 "'111... 1>
a very simple expression for the numbers.
571. Again corresponding to
QX + fL+μ aP + q + 1*
•pqr \μ.ν
wc have diagrams such that there are λ + μ 4- ν rows and p + q + r columns
with a product d»WcT corresponding to each row and axbllcv to each column.
Ex. gr. The expression 0%^ a\n gives diagrams such as
a
с
b
b
a
с
a
с
b
с
b
a
с
b
a
b
a
с
326 SOLUTION OF GENEEALIZED LATIN SQUARE [SECT. XI
which have the property that each row gives the product a2b*c2 and each
column the product abc.
In particular
λμν λμν
gives square diagrams of order \ + μ + ν such that the product акЪ^ср is
given by each row and each column.
In general
/-γλ+μ + !>+... „λ+μ+ν + ...
gives square diagrams of order Х + /л + ^+... such that the product
corresponding to each row and each column is a^c"....
This is the generalization of the Latin Square previously met with in
Section V, Art. 219.
TABLES OF SYMMETRIC FUNCTIONS OF TWO SYSTEMS
OF QUANTITIES
(И)
(10 01)
BlWEIGHT 11
(10 01) (10) (01)
-1
1
1
. Partition (10 01).
(И)
(10 01)
(10) (01)
1
(10 01)
1
1
(21)
(20 01)
(21)
(11 10)
Biweight 21. Partition (20 01).
(20 01)' (20) (01) (21)
(20 01)
(20) (01)
-1
1
1
Partition (11 10).
(U10) (11) (10)
(11 10)
(11) (10)
-1
1
1
Partition (102 01).
(20 01)
1
1
1
(21) (11 10)
1
1 1
(21)
(20 01)
(11 10)
(10201)
α2ι
ι
-1
-1
1
«20 #01
-1
-1
1
au αϊ0
-1
1
«ίο "οι
1
(21) (2001)(1110)(10201)
«21
«20 «01
an a10
«10 «01
1
1
1
1
1
2
1
1
2
2
(31)
(30 01)
Biweight 31. Partition (30 01).
(30 01) (30) (01) (31)
(30 01)
(30) (01)
-1 1
1
(30 01)
1
1 1
328
TABLES OF SYMMETRIC FUNCTIONS
(31)
(21 10)
Partition (21 10).
(21 10) (21) (10) (31) (21 10)
(21 10)I
(21) (10)
-1 1
1
1
1 1
(31)
(20 11)
Partition (20 11).
(20 11) (20) (11) (31) (20 11)
(20 11)I
(20) (11)
-1 1
1
1
1 1
Partition (20 10 01).
(31)
(30 01)
(21 10)
(20 11)
(20 10 01)
о
о
о
о
о
о
о
о*
-
-4
-4
1 ■"-
| ι
-4
-4
4
4
-4
1
-4
4
-4
4
4
-4
1
О
о
(20 10 01)
(20 10) (01)
(20 01) (10)
(10 01) (20)
(20) (10) (01)
'г-Н
00
1
о
о
00
1
1
1
г-ч
СМ
1
г-1
i
1 !
1
: 1
I
1
1
1
OF TWO SYSTEMS OF QUANTITIES
329
Partition (11 102).
(31) (2011) (2110) (11102)
(31)
(20 11)
(21 10)
(11 102)
1-1-1 1
-1-1 1
-11
1
(11 102)
(102) (11)
(11 10) (10)
(11) (10)2
1
1
1
1
1
2
1
1 '
2
2
Partition (10301).
#31 #JJ0#01 #21 #10 #20#11 #20 #10 #01 #11 #10 #10 #01
(31)
(3001)
(21 10)
(20 11)
(2010 01)
(11 102)
(10301)
-1
1
1
1
-2
-1
1
1
2
-1
-1
-1
1
1
-1
0
-1
1
1
-1
-1
1
-2
-1
1
-1
1
1
«31
#30 #01
#21 #10
#20 #11
#20 #10 #01
#11 #10
#10 #01
о
о
со
о
о
1
1
1
1
1
3
1
1
2
3
1
1
1
3
3
1
1
2
3
4
6
1
1 1
3
3
3
6
6
21-
330
TABLES OF SYMMETRIC FUNCTIONS
Biweight 22. Partition (21 01).
(22)
(21 01)
о
ι—I
CM
©q
-ι | ι
1
(21 01)
(21) (01)
о
I—I
CM
I
1
1
(22)
(20 02)
(20 02)
-1
1
(20) (02;
1
Partition (20 02).
(20 02)
(20) (02)
1
ι 1
1 1
(22)
(11*)
(11*)
— 2
1
Partition (ll2).
(11)*
1
(11*)
(11)*
(22)
1
(11»)
1 |
2
Partition (20 OP).
(22)
(20 02)
(21 01)
(20 012)
о
о
CM
^^^
о
CM
о
о
CM
о
о
1
-1
-1
1
-1
-1
1
-1 Ι ι
1
I
1
!...
(20 0l2)
(20) (01*)
(20 01) (01)
(20) (01)2
1
1
1
1
1
2
1
1
2
2
OF TWO SYSTEMS OF QUANTITIES
331
Partition (1110 01).
о
о
о,
о*
о
о
о*
(22)
(21 01)
(12 10)
(И2)
(11 10 01)
s~'
Ϊ
~ь
— 1
— 1
4
1
ч-'
2
-ь
ϊ
i
^
-ь
i
-ь
ι
см
-i
i
ϊ
-i
s—'
1
05
05
01)
1-4
(Μ
о*
CM
О
о
Ξ
(11 10 01)
(11 10) (01)
(И 01) (10)
2 (10 01) (11)
(11) (10) (01)
Partition (ΙΟ2 ΟΙ2).
1
1
2
1
1
0
2
1
2
2
0
2
ι 1
1
1
2
1
(22)
(21 01)
(hi 10)
(20 02)
("*)
(20 012)
(02 102)
(11 10 01)
(К)" ОГ-5)
«22
— 2
3
2
3
2.
3
2
3
1
3
2
3
_2
3
_ 4
3
1
«21 «01
2
3
1
3
— 2
3
— 2
3
1
3
— 1
3
2
3
1
3
«12 «10
2
3
__ 2
3
1
3
_2
3
_ 1
3
2
3
- 1
3
1
3
«20^02
2
3
2
3
2
3
10
3
_ 1
3
_ 4
3
__ 4
3
4
3
«11
1
3
__ 1
3
_ 1
3
__ 1
3
1
3
1
3
1
3
- 1
3
«20ifc01
__ 2
3
— 1
3
2
3
_ 4
3
1
3
1
3
1
3
_ 1
3
«02 «10 «11«10«0
__2
3
2.
3
_ 1
3
_ 4
3
1
3
1
3
1
3
1
3
4
3
3
3
4
3
_ 1
3
— 1
3
— 1
3
L «10«01
1 1
1 >
8 1
«22
«si«m
«12%
«a» «02
a
«20 «01
«и «io «oi
о
r-t
О
О
S
о
о
о
о
■Μ
о
1
1
1
2
1
0
1
2
1
0
0
1
1
1
2
2
2
2
4
1
0
2
0
1
2
2
1
0
0
2
1
0
2
2
1
1
1
2
2
2
3
4
1
2
2
1
4
2
2
4
4
332
ENUMERATION OP SOLID GRAPHS
Enumeration of Solid Graphs.
Number
of
Nodes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Number of
Distinct
Graphs
having
one aspect
1
0
0
1
0
0
2
1
0
2
1
0
2
1
0
3
Number of
Distinct
Graphs
having
two aspects
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
1
Number of
Distinct
Graphs
having
three aspects
0
1
2
2
4
6
6
11
16
20
28
41
51
70
93
122
Number of
Distinct
Graphs
having
six aspects
0
0
0
1
2
5
11
21
39
73
129
226
388
659
1100
1821
Total
Number
of
Distinct
Graphs
1
1
2
4
6
11
19
33
55
95
158
267
442
731
1193
1947
Total
Number
of
Graphs
1
3
6
13
24
48
86
160
282
500
859
1479
2485
4167
6879
11297
If we add together the 2nd, 3rd, 4th and 5th columns we obtain the 6th column.
Also adding the 2nd column, twice the 3rd, three times the 4th, and six times the 5th
we obtain the 7th column.
The graphs are unrestricted in regard to the numbers of nodes that may be placed
along the three axes.
INDEX TO THE TWO VOLUMES
[Volumes are indicated by Roman numerals.
Pages are indicated by Arabic numerals.]
Abbreviation: (s) for !-#*, i, 136; xrw for xrcxWy π, 265
Addition: magic squares and other configurations which may be added, и, 157
Algebra: connexion with Arithmetic, I, Introduction; of operators, I, 30-32, 79-80
Analysis : partition analysis, n, 91-170
Angle: of nodes, n, 13; of nodes in the case of a symmetrical graph, II, 16-18; solid
angles of nodes, и, 261-262
Arrangements: Probleme des rencontres, i, 99; of cards, i, 187; upon a chess board,
I, 224-241; Latin squares and rectangles, I, 246-260; Probleme des menages, I,
253; magic squares, и, 157-170; in two dimensions, π, 171-246 ; in three
dimension, II, 247-257; of functions prior to multiplication, II, 187, 270
Arrays: two-dimensional array of numbers, i, 125
Ascending : ascending specification of permutations of different integers, 1,188 ;
arrangement of parts of partition in ascending order, n, 91
Aspect: of a graph, и, 179, 271, 277-279
Assemblages: of letters, i, 87
Auxiliaries: in generating function, и, 183
Average: values of indices of permutations, of greater index, of equal index, of square
and higher powers of greater index, I, 141-144; of sums of powers of components
of index, i, 145; of class of a permutation, i, 14C; values connected with the equal
index, I, 147; of major, equal and minor contacts in random dealing of playing cards,
i, 149
Axis: of plane graph, i, 172; of solid graph, i, 176
Binomial Coefficients: calculus of, i, 74-77; certain permutations enumerated by the
sum of the ?*th powers of, i, 116 117; application of Master Theorem to sums of
powers of, I, 119-122
Binomial Theorem: linear function of squares of binomial coefficients, i, 120
Bipart: the term, I, 264; и, 281 ; partitions with one bipart, и, 282-284
Bipartite: the term, I, 264; enumeration of bipartite numbers, i, 265-276; theory of
bipartite partitions, ir, 280 et seq.
Biweight: the term, i, 281
Boundary partitions: π, 275
Branch: of a tree, the term, i, 181
Calculus: of finite differences, I, 75; n, 213-231; n, 241-242; of binomial coefficients,
I, 74-77
334
INDEX TO THE TWO VOLUMES
Cards: random dealing of playing cards, i, 149; Simon Newcomb's game of
"patience," i, 187; ascending and descending specifications of a pack of, i, 188,
197
Cayley: writes (s) for 1 — #*, i, 136; I, Introduction; on Latin square, I, 247;
transformation of generating function, n, 59-61, 71
Cells: of a lattice, i, 225
Characteristics: of a separation, i, 46
Chess board: arrangements upon, I, 224-245; Latin square, I, 246-260
Circulator: Cayley*» prime circulator, и, 60-63
Clarendon type: the notation (s) for 1 - #*, i, 136
Class: distribution of a series of elements into a series of classes; species of; type of;
of unarranged objects; of arranged objects, i, 8; of a permutation qua major
contacts, I, 135 ; qua equal contacts, qua minor contacts, I, 136; average value of,
I, 146
Column: of a lattice, i, 124; of a chess board, i, 190; of a graph, H, 3; (see also
Conjugate and Reciprocation)
Combinations: enumeration of, i, 87; restricted combinations, i, 89; identity of
enumeration of combinations and permutations in certain cases, I, 90-92; of order
к in respect of ρ units and in general, I, 180-186
Compartments (see Cells)
Complete lattice (see Lattice)
Components: of index, i, 145; average value connected with, ib.; connexion with class
of permutation, I, 148; properties of, ib.
Compositions: of numbers, the term, I, 9; of unipartite numbers, I, 150-154; graphical
representations by black and white nodes, and by zig-zag graph, I, 152-154;
conjugate, inverse, self-inverse, ib.; of multipartite numbers, the generating function,
I, 155; connexion with the theory of permutations, i, 159; graphical representation
of bipartite compositions, I, 165 ; principal compositions, I, 171; inverse bipartite,
I, 172 ; of tripartite numbers in particular, i, 178; generalization of the idea and
correspondence with " Trees," i, 180; connexion with Simon Newcorab's problem,
I, 187
Compound denumeration: the term after Sylvester, i, 264
Conditioned product: the term, n, 41, 49
Configuration: arithmetical, the term, n, 157
Conjugate: graphs and lattices, n, 3; partitions, ib.; compositions, I, 151-154; self-
conjugate permutations, i, 118; inverse conjugates, I, 153
Contact: major, equal and minor contacts, the terms, i, 132; in the compositions
of multipartite numbers, I, 176; in permutations, i, 177-183; species of, in
bipartite compositions, I, 168
Continuants: connected with partitions, n, 46
Continued fractions: in connexion with Diophantinc inequalities, n, 118-125
Contraction: the term, n, 21
Convergents: in connexion with Diophantinc inequalities, n, 118-125
Crelle: π, 23, foot-note
Crude generating function: the term, n, 93; ultra-crude, the term, n, 94
Cube: solid graph formed by the summits of, n, 252; partitions in solido, ib.;
corresponding lattice permutations, lattice functions and generating functions, n, 252-
257
Degree: of a separation of a partition, the term, i, 46
Denumeration (see Compound denumeration)
INDEX TO THE TWO VOLUMES
335
Descending: descending specification of permutations of different integers, I, 188;
arrangement of parts of partition in descending order, n, 91
Determinant: guiding determinant of the Master Theorem in permutations, the term,
I, 100; in solutions of problems, n, 213-234
Diagonal properties: of magic squares, n, 157
Diagram: in theory of arrangements on a chess board, and in denoting minor operations
into which differential operations may be dissected, I, 224-263
Differential Calculus: applied to theory of distributions on a line, i, 26 et seq.; to
arrangements on a chess board, I, 224 et seq.; to theory of permutations and
combinations, i, 87 et seq.; to compositions of numbers, i, 160, 174; to enumeration of
multipartite partitions, I, 225 et seq.
Diophantine: analysis, n, 91; inequalities and equalities, ib. et seq.
Discordant permutations: the term, i, 253; with any given permutations, i, 254-255
Displacements : theory of, i, 99
Dissection: of differential operations into minor operations, I, 224-263
Dissimilar: objects, i, 8; parcels, ib.; parts, n, 9-14
Distributions: theory of, i, 8-18; operators in the theory, i, 26-44; restricted, I, 49;
derived from partitions with zero parts only, i, 76; concerning more than two sets
of objects, I, 83; upon a chess board, i, 224 et seq.; applied to the multipartite
partitions which appertain to a given group, I, 264 et seq.; in the theory of separations
of multipartite partitions, n, 285-296
Divisors: of numbers connected with partitions, n, 57-58
Dixon: cubes of binomial coefficient, I, 121
Durfee : his square of nodes appertaining to a graph, n, 15; square of г2 nodes, II, 25
Elementary symmetric functions: the term, i, 2
Elliott: on linear homogeneous Diophantine analysis, II, 111-114
Elliptic functions: Jacobi's identity in, n, 23
Equal index (see Index)
Equality: Diophantine, connected with Diophantine inequalities, n, 103-104
Essential nodes : upon a line of route, the term, i, 167
Euler: I, Introduction, v; on the Latin square, I, 240; on partitions of numbers, n, 1;
his celebrated formula in partitions, n, 21 ; upon divisors of numbers, n, 57
Expressibility: theorem of, i, 53 ; it, 291
Ferrers: his graph of a unipartite partition, it, 3
Figurate numbers: appear as exponents, n, 175
Finite Differences (see Calculus)
Fractions: }_>artial, after Cayley, Л, 59 ; partial, derived from symmetric fmiction
transformation, n, 61-71
Franklin: n, 5, foot-note : graphical proof of theorem in Comytes Itendus of the Institut,
и, 21
Fundamenta Nova of Jacobi, n, 31
Fundamental forms: in various theories derived from partition analysis, n, 91-170
Gauss: a series of, n, 24; methods and processes of, n, 78-83
General magic square: the term, и, 157
Generating function: I, Introduction, and throughout both volumes (see Crude, Real,
Redundant, Ultra-crude)
Girard: n, Introduction, Note
Glaisher: I, Introduction, viii; proof of theorem in partitions, n, 12
336
INDEX TO THE TWO VOLUMES
Gbttingen Commentaries, it, 24, foot-note
Graeco-Latin square: of Euler, i, 246-248
Graph: line graph of composition, i, 151-153; zig-zag, i, 153-154; representation of
compositions of bipartite and multipartite numbers, i, 165 et seq.; of partition, n,
3 et seq.; transformation of, n, 13; square of, after Durfee, n, 15; in
transformation of series, n, 26; functions placed at the nodes of a rectangular graph, it, 145,
270; solid graph, n, 258; aspects of, in three dimensions, n, 27*7
Greater index (see Index)
Ground forms (see Fundamental forms)
Group: in theory of distributions, the term, i, 8; of separations, the term, i, 47
Guiding determinant (see Determinant)
Hammond: i, Introduction, ix ; his operators d, D, i, 27 et seq.; proof of laws of
symmetry, I, 40-41
Hilbert: solutions of inequalities, и, 107
Homogeneous product sums: expression in terms of other symmetric functions, i, 3-4,
7 ; connexion with the theory of distributions, i, 10-15 ; derivation of the functions t,
i, 14; connexion with distribution into groups of type (lm), ι, 17-18 ; connexion
with distribution in general through the derived functions By I, 19-22 ; derivation
of the operator δ, ι, 36-37 ; in enumeration of permutations and combinations, i, 87-
92 ; connected with Simon Newcomb's problem, I, 197 et seq. ; derivation of a new
function haic..., I, 200; connected with arrangements on a chess board, I, 234 ;
connected with multipartite partitions, I, 277-287; connected with generating
functions of partitions, II, 62 et seq. ; of several systems of quantities, II, 283 ; in
multipartite distribution, n, 287; connected with magic squares, n, 166; (see also Tables)
Identity: theory of Three Identities, I, 79-86
Incomplete lattice: the term, и, 191
Indeterminate equations: in partition analysis, ir, 91-170
Index: of permutation, I, 135-149 ; in the study of lattice functions, n, 189 et soq. ; in
the theory of permutation functions, π, 206-2Ι2; in the study of solid lattice
functions, II, 247-257 ; (see also Multiplicity)
Inequality (see Diophantine)
Inner lattice function (see Lattice)
Integer: consecutive integers, properties of algebraic forms of, n, 151-156
Integral: finite and integral character of a standard form of generating function, n,
145-150
Intermediate (see Convergents)
Intuitive : generating function of Euler (see Eulcr)
Invariant: arising from the theory of Three Identities, i, 79-80
Inverse : compositions, I, 152 ; self-inverse, ib.; inverse conjugates, 153 ; inverse line of
route through a graph, the term, 1,172 ; bipartite compositions, ib. ; inverse principal
compositions, i, 173 ; of a permutation of different integers, I, 188
Jacobi: elliptic function identity, II, 23-24; Fundamenta Nova, и, 31
Knot: of a tree, the term, I, 181 ; terminal knot, ib.
Laplace : i, Introduction, vi
Latin square : of Euler, theory of, i, 246 et seq.
Lattice : permutation, the term, τ, 124-125 ; correspondence with two-dimensional arrays
INDEX TO THE TWO VOLUMES
337
126 ; enumeration of, 127-134 ; incomplete, the term, n, 213 ; factors at the points
of, II, 187 ; lattice function, the term, n, 189 ; sub-lattice function, II, 194 et seq. ;
Outer and Inner lattice functions, the terms, n, 216 ; lattice, lattice permutations and
lattice functions in solido, II, 247-257
Lemma: in theory of Diophantine inequality, n, 115-116
Lesser index (see Index)
Letters: in envelopes, i, Introduction, ix (see Probleme des rencontres)
Limited double product: studied by Sylvester, и, 72-77
Line : partitions on a line, the term, n, 171 ; line of route, the term, i, 167
Linear operator (see Operators)
London Mathematical Society's Proceedings : Hammond in, I, 27
Lots: grouping of compositions in, i, 188
Lucas: on Probleme dcs mcnages, i, 253
4 (see Modified multiplication)
Magic square: theory of, ir, 157 ; general magic square, the term, ib. (see also Chess
board)
Major: contact (see Contact); index (see Index)
Master Theorem : in permutations, i, Introduction, vii; I, 93-98 ; applied to theory of
displacements, i, 99-114 ; to powers of binomial coefficients, etc., I, 115-123
Maxima and Minima: in connexion with sub-lattice functions, и, 198-200
Menages: Probleme des, i, 253
Metzler: n, Introduction, ν
Minor: contact (нее Contact); index (see Index)
Modified multiplication: denoted by J/, u, 42, 49
Modulus: greater index of permutation in respect of a prime modulus, I, 140
Modus operandi: concerned with arrangements on a chess board, i, 228
Monomial symmetric function: the term, i, 7
Muirhead: on Waring*» theorem, n, Introduction, Note
Multinomial theorem: applications of, i, 7; symmetric function expression of, I,
231
Multipartite : numbers, ι, L, 155, 204 ; symmetric functions, n, 280; representation by
graphs of nodes, n, 170 ; generating function, n, 54
Multiplicity: of a separation, i, 40
Netto: (Joinbinatorik, n, Introduction, 71
Newcomb's problem in patience, ι, 187
Node: of graph or lattice (see Graph, Lattice)
Non-unitary: symmetric function or partition, [, 2; n, 28L
Notation: (7ay ley's writing (s) for I -& (see Clarendon type, Cay ley); exp (see Operators)
Objects: in theory of distributions, I, 8
Obliterating operator: the term, i, 28 ; π, 298-299
Omega: operative symbol Ω, n, 92, 10L
Operation: й (see Omega)
Operators : Hammond's, i, 27; notation for symbolic multiplication, ib. ; algebra of, I,
28; the notation exp, [, 31 ; upon a product of symmetric functions, I, 32;
obliterating, i, 28 ; partition obliterating, i, 33 ; applications of, I, 38; of the theory of
separations, i, 62 ; the operator J)0 and its properties, i, 74-77 ; applied to enumerate
permutations and combinations, I, 87-90 ; in theory of displacements, I, 99 ; in
enumeration of multipartite compositions, I, 160, 206, 213 ; in arrangements upon
338
INDEX TO THE TWO VOLUMES
a chess board, i, 224 ; dissection of, ib.; connected with diagrams, I, 225 ; of Calculus
of Finite Differences, I, 241 ; in theory of Latin square, i, 248 ; in enumeration of
bipartite and multipartite partitions, i, 267 et seq. ; in theory of symmetric functions
of several systems of quantities, n, 297; in further theory of Latin square, u, 323-326
Order: of algebraic forms of integers, n, 152
Ordinary magic square: n, 157
Outer lattice function: n, 216
Parcels : in theory of distributions, i, 8 et seq.; type of, ib.
Parity: of greater index of a permutation, i, 139
Part: of partition, the term, I, 1 ; partition into different kinds of, II, 1 et seq.
Partial fractions (see Fractions)
Partitions: definitions connected with, i, 1, 45 ; operators, i, 66 ; of zero, i, 77 ; perfect,
the term, I, 217; sub-perfect, the term, ib. ; Ferrers graph of, I, 236 ; of zero leading
to distribution, I, 242; bipartite and multipartite, i, 267 et seq.; Euler's theory, n,
1-58 ; Cayley's transformation, ir, 59-60 ; transformation by symmetric functions, n,
61-71; processes of Gauss, n, 78; connexion of theory with other combinatory
theories, II, 84-90 ; new basis of, n, 91; partition analysis, n, 91-170 ; in two
dimensions, Π, 171 et seq. ; in solido, ir, 247-257
Patience: Simon Newcomb's game of, i, 187
Perfect partition: the term, i, 217
Permutations: as particular case of distributions, i, 9 ; enumeration of, I, 90; Master
Theorem in theory of, I, 93 ; displacements, I, 99 ; Theory of Substitutions, I, 112 ;
enumeration by powers of binomial coefficients, I, 115 ; lattice permutations, I, 124-
133 ; prime and composite, ib. ; reduudant generating function, I, 128 ; indices of,
I, 135-148; index components of. I, 146 ; connexion with compositions of
multipartite numbers, i, 157 ; with given number of major contacts, i, 181-186 ; discordant,
i, 254; permutation function, n, 189, 206-212 ; derivation of lattice function, II,
189 et seq.
Plates: representation of regular graphs by, n, 277
Point: of graph or lattice (see Node)
Prime lattice permutation (see Permutations)
Prime circulator (see Cayley, Circulator)
Principal composition: ι, 171
Probabilities : I, Introduction ; I, 133, 149, 187
Probleme : des rencontres, I, 99, 247 ; des menages, I, 253, 255
Projection: of solid graph, и, 246
Protraction: applied to a graph, the term, n, 22
Quarres magiques: of Euler, i, 246
Ramanujan: identities of, и, 33-48
Reading: of graph, n, 176
Real generating function: the term, и, 97
Reciprocation: method of, ι, 232-233
Rectangle: Latin, ι, 251
Reduced Latin squares: the term, i, 248
Redundant generating function: the term, i, 128
Reflection: of graph, n, 277
Rencontres (see Probleme)
Repetitions: partitions without, n, 33 (see Unequal parts)
INDEX TO THE TWO VOLUMES
339
Restricted distribution: i, 49; on a chess board, r, 234
Reticulation (see Lattice)
Roots: primitive of unity, и, 137
Rotation: of graph or lattice (see Reciprocation)
Rothe: on self-conjugate permutations, i, 118
Route: line of, the term, i, 167
Row: of graph or lattice (see Graph, Lattice)
Self-conjugate: permutations, i, 118; partitions, и, 13-18; graphs, и, 18-20, 179-181
Self-inverse compositions: i, 152-153
Separate: of a partition, the term, i, 45
Separations: of a partition, theory of, i, 45-54; characteristics of, I, 46; groups
of, i, 47, 58 ; multipartite, n, 285-296; the connected differential operators, i,
62-73
Sequences: of numbers in a partition, ir, 14; partitions without sequences or
repetitions, ii, 33; partitions without sequences, n, 49-54
Simultaneous Diophantine inequalities: ir, 126-135, 138 et seq., 152 et seq.
Single-unitary: symmetric function and partition, n, 281
Solid graph: the term, n, 177; partitions in solido, и, 247-257
Space: in enlarged idea of composition, I, 181; blank space as a symbol, ib.
Specification: of a separation, the term, i, 46; of a bipartite separation, и, 285 ;
ascending and d&scending of a permutation or composition, i, 188
Square (see Magic square, Latin square)
Standard forms: of generating functions, n, 150
Stepping back: to a crude form of generating function, n, 93
Steps: between points of a graph, the term, I, 164
Sub-lattice function: n, 194
Sub-perfect partitions: the term, i, 217; theory of, i, 223
Sub-permutation function: π, 207
Substitutions: theory of, in the Theory of Displacements, i, 112
Summits: of a cube, certain partitions, n, 252-255
Sums: of homogeneous products, I, 3; of powers of elements, i, 4; of powers of binomial
coefficients, I, 119-121
Sylvester: I, Introduction; i, 32; n, 13, 14; in Johns Hopkins University Circulars^
ii, 15; in Collected Papers, ib.; on Jacobi's identity, n, 24; on continuants, II, 46;
on expansion of enumerating functions, n, 71; on a limited double product, n,
72, 76
Symbolic form: of an enumerating expression, ι, 273
Symmetric functions: ι, 1-86; π, 280 et seq.
Symmetry: laws of, 1,11, 14; Hammond's proof of second law, ι, 40; proofs by operators,
I, 42-43; generalization of laws, ι, 51 ; concerning binomial coefficients, r, 76; further
laws, ι, 79; и, 290; of arrangements on a chess board, I, 236
Syzygy: syzygetic theory of Diophantine equations, n, 107 et seq.
Tables: I, 201-202, 288-300; П, 327-332
Transformation: geometrical of certain series, u, 26-32 ; of generating functions by
(Jayley, и, 59-61; by symmetric functions, n, 61-69
Trees: the mathematical forms so called, I, 181-182
Tripartite: numbers and partitions, I, 277-287
Type: of classes, parcels, groups, and objects, i, 8; of a distribution, i, 50
340
INDEX TO THE TWO VOLUMES
Ultra-crude generating function: и, 95
Unequal parts: of partition, и, 11-14
Uneven parts: of partition, и, 13-14
Unipartite number: the term, i, 1
Unitary symmetric functions: the term, i, 2
Values: average, connected with indices of permutations, i, 139-147
Waring: n, Note following Introduction; formula of, i, 5; generalization of formula,
I, 5, 57; И, 283, 295
Weight: of a symmetric function, the term, i, 3; of a separation, i, 46
Whitworth: GJioice and Chance^ i, Introduction; n, 220
Cambridge: printed by j. b. peace, m.a. at the university press