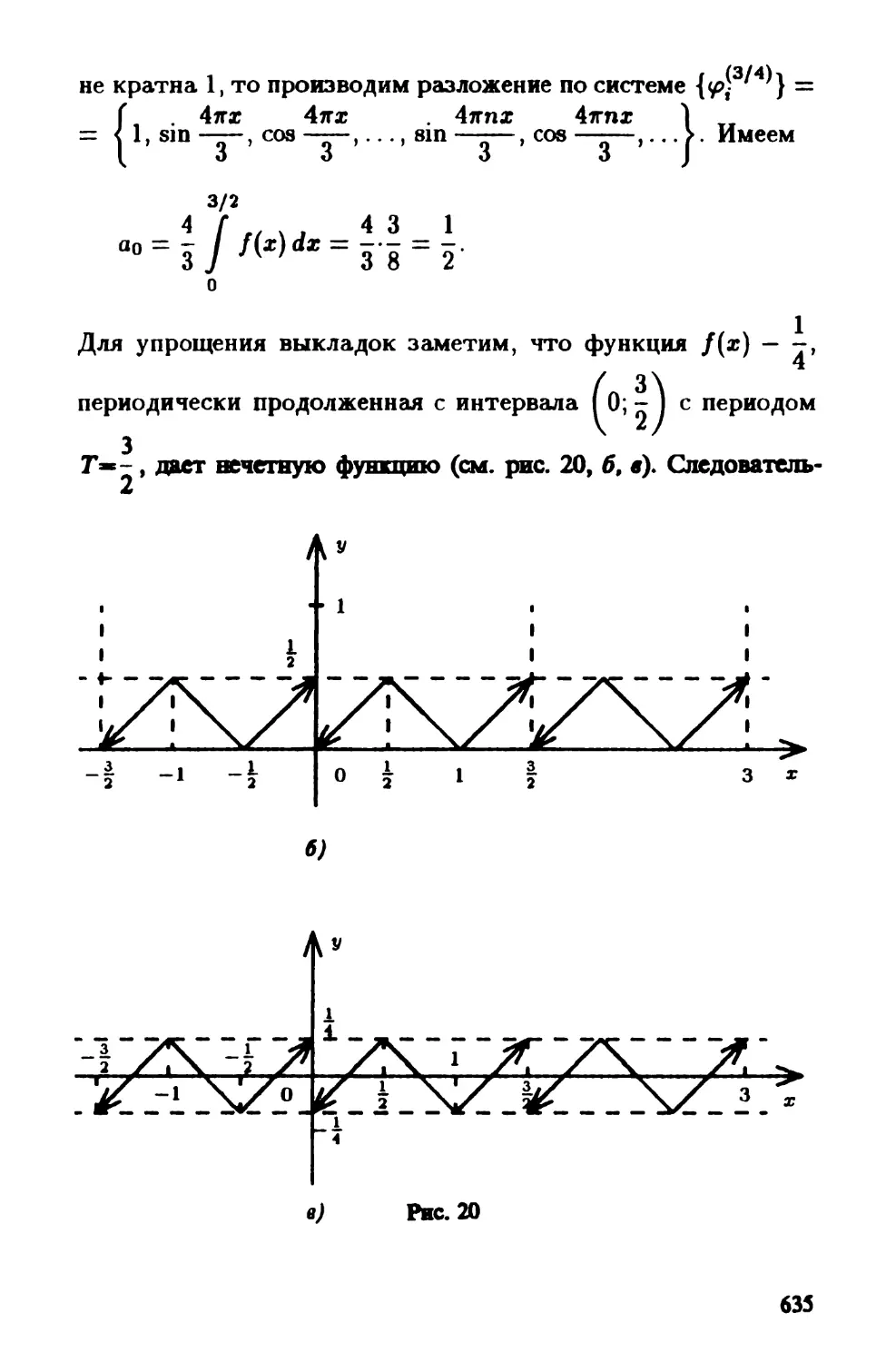
Автор: Олехник С.Н. Виноградова И.А. Садовничий В.А
Теги: анализ математический анализ функциональный анализ задачи по математике высшая математика учебное пособие
ISBN: 5-7107-4295-3
Год: 2001
Текст
И.А. Виноградова
С.Н.Олехник
В.А. Садовничий
ЗАДАЧИ
И УПРАЖНЕНИЯ
ПО МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ
Часть 2
РЯДЫ, НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ,
РЯДЫ ФУРЬЕ, ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Издание третье, исправленное
Рекомендовано Министерством образования
Российской Федерации
в качестве учебного пособия для студентов
высших учебных заведений,
обучающихся по направлениям и специальностям
физико-математического профиля
эрофа
МОСКВА • 2001
УДК 517.1(075.8)
ББК 22.161
В49
Рецензенты:
чл.-кор. РАН Л. Д. Кудрявцев, академик РАН В, А. Ильин
Серия «Высшее образование: Современный учебник»
основана в 2001 году
Виноградова И. А., Олехник С. Н., Садовничий В. А.
В49 Задачи и упражнения по математическому анализу: Пособие для
университетов, пед. вузов: В 2 ч. / Под ред. В. А. Садовничего. — 3-е изд.,
испр. — М.: Дрофа, 2001.— Ч. 2: Ряды, несобственные интегралы, ряды
Фурье, преобразование Фурье. — 712 с.: ил. — (Высшее образование:
Современный учебник).
ISBN 5-7107-4295-3(4.2)
ISBN 5-7107-4296-1
Учебное пособие (2-е изд. — 2000 г.) соответствует программе курса математиче¬
ского анализа для студентов механико-математических и математических факультетов
университетов, педагогических и технических вузов. Задачник отражает современные
тенденции развития математики. Большинство задач в пособии сопровождается решения¬
ми, поэтому оно может быть полезно при самостоятельном изучении предмета. В книге
содержатся следующие разделы: ряды и бесконечные произведения; несобственные инте¬
гралы и интегралы с параметрами; ряды Фурье; преобразование Фурье.
Для студентов университетов, педагогических вузов, вузов с углубленным изучением
математики.
УДК 517.1(075.8)
ББК 22.161
Учебное издание
Вино1радова Ирина Андреевна,
Олехник Слав Николаевич, Садовничий Виктор Антонович
ЗАДАЧИ И УПРАЖНЕНИЯ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Часть 2
Зав. редакцией Н. Е. Рудомазина
Ответственный редактор Ж. И. Яковлева
Художник Т. Е. Добровинская
Корректор JI. А. Александрова
IIj.i. inn Ni' 061622 ш 07.10.97.
Подписано и печать 10.04.01. Формат 6()х‘>()'/1(1. liyMai a т mioi рафская. Гарииiура «Таймс».
Печать офсетная. Уел. нем. л. 44,5 Тираж 10 000. Закач № 3966.
ООО «Дрофа». 1270IS, Москва, Сущевский пал, 49
По вопросам приобретении продукции lii/uncviucuta «Дрофа»
обращаться но адресу: I2701X, Москва. Сущевский вал. 49
Тел.: (095) 795-05-.50. 795-05-5 I. Факс: (095) 795 05-52.
I орговын дом «Школьник». 109172, Москва, ул. Малые Каменщики, д. 6, стр. I Д.
Тел. (095)91 1-70-24. 912-15-16. 91 2-45-76.
011 юча 1 ;шо в полном соотнегсшии
е качеи ном предоставленных дпапозптвов
в ОАО «Мо/канскип полиграфический комбинат»
143200. I. Можайск, у л Мира. 93
ПРЕДИСЛОВИЕ
В России исторически сложилось так, что представление об
образовании включает в себя органичное единство школы как
системы приобретения знаний, фундаментальной науки как пока¬
зателя уровня подготовки специалистов и гуманитарной культуры
как основы духовного богатства человека.
В предисловии к первой части этого задачника приведены сло¬
ва Н. И. Лобачевского, который на протяжении всей своей препо¬
давательской и научной деятельности размышлял о целях и прин¬
ципах математического образования, о пользе новых учеоных
книг. С удовлетворением отмечая успехи своих учеников, он пи¬
сал, что «они тверды в правилах, понимая все, совершенно увере¬
ны в своих знаниях, отвечают со рвением на вопросы с намерени¬
ем даже сысканные, решают их легко, не подозревая, чтоб в них
можно скрываться затруднение, достойное занять взрослых». Эти
слова по существу отражают основные творческие устремления
каждого преподавателя по отношению к своим ученикам.
Во второй части учебного пособия «Задачи и упражнения по
математическому анализу» представлен материал по теории ря¬
дов, несобственным интегралам и интегралам с параметрами, рас¬
смотрены теория рядов и преобразование Фурье. Оно позволяет
реализовать указанные выше принципы преподавания математики
и служит достижению поставленных целей.
Третье издание задачника, так же как и его второе издание,
выходит в двух частях. Часть 1: «Дифференциальное и интеграль¬
ное исчисление». Часть 2: «Ряды, несобственные интегралы, ря¬
ды Фурье, преобразование Фурье».
Серия «Высшее образование: Современный учебник», в кото¬
рой он выпускается, кроме практической ценности, призвана по¬
двести некоторые итоги раооты российских ученых и педаго-
гов-математиков по созданию базовых учебников по математике.
Академик
Российской Академии наук
В. А. Садовничий
Глава I
РЯДЫ И БЕСКОНЕЧНЫЕ
ПРОИЗВЕДЕНИЯ
i 1. ЧИСЛОВЫЕ РЯДЫ
Определение 1. Последовательность чисел (вообще го¬
воря, комплексных) {ап}, соединенных знаком плюс, ах + а2 +
4- аз + • + ап + • • • называется рядом (числовым рядом) и
обозначается ^ ап
п= 1
Определение 2.
которого являются все члены ряда ап, начиная с (fc-f 1) -го,
п = I
взятые в том же порядке, что и в исходном ряде, называется
оо
остатком к -го порядка ряда ап и обозначается г^, т. е.
п= 1
Определение 2. Ряд а*+1 +а*+2 + - • -f-afc+m + - • членами
гк — ^ * ап — ^ ] Я|с+т-
гг=Ас 4-1 m = 1
Определение 3. Сумма а\ + а о + • • • + а* первых к членов
оо
ряда а„ называется к-ой частичной суммой или частичной
п = 1
суммой порядка к этого ряда и обозначается S*, т. е.
к
Sk = вп
п = 1
оо
Таким образом, каждому ряду ап соответствует по-
п= 1
следовательность {5*} его частичных сумм. Обратно, ка-
оо
ждой последовательности {А^} соответствует ряд ай, где
п = 1
а\ = Л\, ап — Ап — Лп_ь п 6 N, тг ^ 2, частичными суммами
которого являются члены данной последовательности По¬
этому каждое свойство последовательностей перефразирует¬
ся в некоторое свойство рядов заменой характеристики чле¬
4
нов последовательности соответствующей характеристикой
членов ряда.
оо
Определение 4. Ряд ап называется сходящимся, если
п = 1
сходится (имеет предел) последовательность Sk его частич¬
ных сумм.
оо
Ряд ап называется расходящимся, если последователь-
П = 1
ность Sk расходится.
оо
Если ряд 7 ап сходится, то число S = lim Sk называется
4 fc—►оо
П = 1 оо
его суммой, при этом пишут: S = ап •
п — 1
Если ряд расходится, то и его остаток любого порядка
расходится. Если ряд сходится, то и его остаток к-го по¬
рядка г к при любом к сходится, в этом случае остаток г к
записывается в виде г к = S — Sk и lim Гк = 0.
к-+ оо
Если члены ряда — комплексные числа ап = огп + Л.
где {t>n} и {/?п} - действительные последовательности, то
по оо
сходимость ряда ^ а„ = ^^(rvn + i/3n) эквивалентна одно-
п = 1 п = 1
оо оо оо
временной сходимости рядов ^ лп, 0п и 5 = ап =
00 ОО П = 1 П=1 п = 1
= ^ тп + i ^2 @п Таким образом, исследование свойств ря-
n = 1 п = 1
да с комплексными членами сводится к исследованию свойств
рядов с действительными членами, поэтому в дальнейшем, в
основном, рассматриваются ряды с действительными члена¬
ми.
Приведем несколько примеров, показывающих взаимоот¬
ношение понятий ряда и последовательности, суммы ряда и
предела последовательности.
Пример 1. Рассмотрим ряд
ОО
1 +q + q2+ -+qn + • •• =
П = 1
5
где q — комплексное число и |д| ф 1. Частичная сумма Sk
2 к- 1 1 — Qk
этого ряда есть 1 + q + q + • • -f <7 = "Г ^ак как
1 - q
lim = 0 при \q\ < 1 и lim Igl* = -foo при |<?| > I, то
к-+оо к-+оо
lim Sk = при |g| < 1 и lim Sk = оо при |g| > 1. Сле-
к—¥оо 1 — q к-too
оо
довательно, ряд ^^qn~l при |^| < 1 сходится и его сумма
п — 1
равна , а при |g| > 1 расходится.
1 - q
Записав q в виде q = \q\eta = |gr|(cos or -h isin а), получаем,
что
qn 1 = ^ |^|n(cos na + г sin na) =
n=l n=0
1 1 — |</| cos a + t|g| sin a
1 — \q\ cos a — z|qr| sin a 1 — 2|</| cos a -I- \q\2
и, следовательно, для действительного числа р, — 1 < р < 1,
имеем равенства:
оо оо ,
Еп-1 / n v' п 1 - pcosa
р cos(п ~ \ )(У — > р COS net - —
' „ 1 — 2р cos а + р2,
п—1 п=0 г
оо
psin a
' sm па —
П = 1
1 — 2р cos a + р2.
Пример 2. Рассмотрим ряд 1 — 1 + 1 - 1 + = ^ (— 1 )п 1.
п — I
Поскольку для этого ряда .$2т-1 = 1, *S'2m = о при любом
натуральном т, то последовательность {5*} не имеет предела
оо
при к —У оо. Следовательно, ряд ]^(-1)п~1 расходится.
П=1 *
Пример 3. Рассмотрим последовательность Лк =
& + 1
fc € N. Членами соответствующего ряда, частичными сумма-
ми которого являются числа Аь, будут числа а„:
, 1 I
а' = Л‘ = 2 = Г2'
71 11 ~ 1 1 V41 о
ап = Ап- Лп-1 = —— = —-тт, п G N, п^2.
п + 1 п п(п + 1)
оо со J
Гак как lim
fc—►оо
Л* = 1, то ряд У^ап = У~] ——гг сходится и
fx п^Т‘(П+1)
сумма его равна 1.
Пример 4. Рассмотрим последовательность {А*}: А* =
1 °°
= —, к 6 N. Соответствующим ей рядом будет ряд а„,
№ ;
П = 1
где ai = А\ = 1, ап = Ап - Л„_, = — - -——п € N,
П? (П+1)?
п ^ 2. Так как последовательность {Л*} сходится при q ^ 0 и
о° °о , 1 J \
расходится при q < 0, то и ряд У] a„ = 1+V ( — - — )
^ ("-I)9/
сходится при ООи расходится при q < 0.
°° 71
Пример 5. Рассмотрим ряд —. Чтобы решить вопрос
п=i2\ !
о сходимости последовательности {.$*}: .Sfc = 1 + 2 - +
-f3 g-f +&преобразуем выражение .b* следующим обра¬
зом:
Sk = G + ? + ' +i) + (i + §+ +^) + ' +
+ (2*-1 + 2*) + 2* ** (l ~ 2*) + 2 (* ~ 2fc_ 1) +
+ ?(1_2^)+ ' +2^t(1_0=2“2^_^-
CO
Отсюда получаем, что lim Sk = 2, следовательно, ряд —
fc-foo 2n
сходится и сумма его равна 2. n=1
00 1
Пример 6. Рассмотрим ряд V* --——-——. Для уп-
^ п(п+ 1)(п + 2)
I*ИЩС||им 'НМ ГИЧ1П.1Х ( VMM
I I
I f . +
w> :\ 2X4 к(к + \)(к + 2)
иргмЛц.иугм выражение для члена ряда ап. разложив его на
щнм п ишиг дроби:
= 1(1. _н_ + _!_л =
(n + 2) 2 \7* /1+1 л -1-2/
. п(п + 1)(
_ П 1 1_ 1 \
2 \ п п + 1 71 + 1 п + 2 )
Отсюда получаем, что
1 / 1 I 1\ 1 /1 I 1 1\
~ 2 \~2 + 3~2,/2 \2_3^4 3/^
\ (\_ 1_ 1 I \ _ 1 / 1
+ 2 \к k+l+k+2 k+l)~2\ 2 +
- 1 1 ( 1 1 \
~ 4 + 2 \к + 2 * + I/
• +
*+2 *+1/
1 ^ ]
Следовательно, lim .S* = т. е. ряд У] ~7—TTw—схо"
/с-►со 4 п(п + 1)(Я + 2)
1
дится и сумма его равна
4
В приведенных примерах последовательность {,Vn} части¬
чных сумм соответствующего ряда или задавалась заранее,
или выражалась достаточно просто, так что существование и
величина предела Sn устанавливалась непосредственно. Та¬
ким образом, в силу определения одновременно устанавли¬
вались и сходимость, и величина суммы рассматриваемого
ряда. В основном, непосредственный анализ последователь¬
ности {.Vn} не представляется возможным, поэтому основны¬
ми задачами в теории числовых рядов являютс я установление
сходимости или расходимости данного ряда без вычисления
величины его сумм и оценка зависимости остатка ряда гп от
номера 7i (скорость сходимости ряда).
В силу равенства S = Sn + rn, оценка гп дает оценку гю-
8
грешности при замене суммы ряда S = ап частичной сум¬
мой 5„. n=1
Перефразируя критерий Коши сходимости последователь¬
ности, получаем оо
Критерий Коши сходимости ряда. Ряд ^ ап схо-
п = 1
дится тогда и только тогда, когда для любого положительно¬
го числа в найдется такой номер N = N(e)t что для любых
натуральных чисел р и n, п > N(e), справедливо неравенство
п+р
к=п
< е.
Приведем формальную запись критерия Коши сходимости
ряда:
со
ап сходится <=> Ve > 0 ЗМ(е) £ N :
п = \
Vn€N, п>М(е),:
п+р
YLak
к—п
< €.
Заметим, что, как и при анализе последовательностей,
критерий Коши редко применяется для доказательства схо¬
димости конкретного ряда из-за технических трудностей.
Область применения критерия Коши — как правило, или ут¬
верждения, в которых из сходимости одного ряда выводится
сходимость другого, или установление расходимости ряда.
Пример 7. Покажем, пользуясь критерием Коши, что
всякая бесконечная десятичная дробь 0,(11 сдоз .. .а„ ... =
п = 1
определяет действительное
число а, т. е. ряд
EQ п
10п
п = 1
сходится.
му
Возьмем произвольное натуральное число п и оценим сум-
п+р
ак
при любом р £ N. В силу условия 0 ^ ^ 9
к =п
10*
9
получаем, что
°<E£<’£iiFT-i54' + ra + -" + I5;)-
/с=п fc =
J ^ ~ 10»>-П <
10n"‘ 1 - 10й-1’
Для произвольного положительного числа е положим Ые =
= max 11, |lg -J | + 2, тогда из полученной оценки следует,
что для любых натуральных р и n, п > Afe, имеем:
^ а* 2 2
0 ^ 2^ ю* < Ю"-1 < То^--1 < *'
к —п
<Х>
Итак, в силу критерия Коши ряд Т^п ’ ^ ^ (1пв ^ гхоДит*
п = 1
ся.
11 J ^ 1
Пример 8. Ряд 1 + - + -4 \ - называется
2 л л ' п
п = 1
гармоническим рядом.
Пользуясь критерием Коши, покажем, что гармонический
ряд расходится. Для :ггого надо указать такое число £<) > 0,
что для любого номера N и некоторой пары натуральных
п+р j
чисел р и п, ?i > Л/\ имеет место неравенство ~ ^ So¬
le г:п
Возьмем произвольное натуральное число п. Тогда
V - - - __L_ J_ 2L - 1
n + 1 2п 2и 2
к—п
Таким образом, для ео = - и произвольного номера Л/* найде¬
ны натуральные числа 7t = Л/* 4 1 > Л/* и р — /i, для которых
п+Р j 1
- > - = fo, что и требовалось установить, Следователь-
к =п пи j
но, гармонический ряд - расходится.
п — 1
10
Из критерия Коши непосредственно следует
Необходимое условие сходимости ряда. Если ряд
оо
Еап сходится, то lim ап = 0.
П-+ ОО
П = 1
Гармонический ряд является примером расходящегося ря¬
да, для которого lim а„ = 0. Следовательно, условие
п—>оо
lim ап = 0 недостаточно для сходимости ряда.
п-*оо
по
Пример 9. Ряд ^sinn расходится, так как последова¬
ла
тельность {sin п} не является бесконечно малой (эта последо¬
вательность не имеет предела)*)
Пример 10. Как было показано (см. пример 2) ряд А:
оо
1 — 1 + 1 — 1 + 1 — 1Н— =
п — 1
расходится. Рассмотрим ряд В.
(,_ !) + (,_!) + (!_!) + ...+ (!_]) + ....
. Если в ряде В опустить (раскрыть) скобки, не произво¬
дя сложения внутри них, то ряд В превратится в ряд А. В
таких случаях принято говорить, что ряд В получен груп¬
пировкой членов ряда А. Если же сделать сложение внутри
скобок ряда В, то получим, что
Ои
В . 0 + 0 + 0Н +0+ =£о.
п = I
Все частичные суммы Sk этого ряда равны нулю, следова¬
тельно, ряд В сходится и его сумма равна нулю.
Пусть njf = [27г/с], к 6 тогда 2пк < n* + 1 < 2этк -f 1 и, следо¬
вательно, sin(n* + 2) — sin пд. = 2sin,1 cos(n* + 1) > 2 sin 1 cos 1 = sin 2.
Таким образом, для e = sin 2 и любого числа М найдутся натуральные
числа п* > Мир = 2 такие, что |sin(7i*. -f 2) -sinu*l > f, следовательно,
в силу критерия Коши последовательность ап = sin?i не имеет предела.
11
Итак, группировка членов ряда может превратить расхо¬
дящийся ряд в сходящийся. ! )то утверждение было доказано
го
на примере ряда ^(— 1)п-1, не удовлетворяющего необходи-
Т| =Г 1
мому признаку сходимости - последовательность {( — 1)п-1}
его членов не является бесконечно малой. Покажем, что груп¬
пировка членов может превратить расходящийся ряд в сходя¬
щийся и в том случае, когда последовательность членов ряда
является бесконечно малой
Примсф 11. Ряд
. 1 1 1 1 II I
А : 1 — + 1 К• • • Н
2 2 2 2 п п п
^ ^ ^
ti раз
11 11
... -| -}-■••
71 71 П 71-f-l
у >
и раз
расходится. Докажем .»то, пользуясь критерием Коши.
Действительно, для любого натурального V существукгг
такие натуральные числа > /V и р, что
1 1 1
И Л f 1 — ~ 1 Ия + 1 — (ln + И — ~ *
V V Р
И +Г
следовательно, ап = I. Условие Коши не выполнено,
к = ii -f-1
поэтому ряд А расходится.
Рассмотрим ряд
»= C-4+(j + 5-5-i)+ +
/11 111 1\
4 “ + » +
\П 71 7} 1) 71 п J
полученный группировкой членов ряда А. Поскольку каждый
член ряда В равен нулю, то ряд В сходится и его сумма равна
нулю.
Проанализируем проблему группировки членов ряда в об-
12
щем виде. Пусть дан ряд ^^ап. Сгруппировать члены этого
п = 1 оо оо
ряда — это значит вместо ряда ^ ап рассмотреть ряд
пк-\ n=l *=1
где Ак = ^2 а" ’ * = п° < 711 < 712 < • < Пк < .т. е.
П=П*_ 1
Ак для каждого к есть сумма к-ой группы (скобки) членов
со
ряда. Пусть Sn — частичные суммы ряда ^ ап и Sk — ча-
оо п = 1
стичные суммы ряда Ак- Для конечных сумм раскрытие
к = 1
скобок законно, следовательно,
Sk = ^ i + Л 2 + • • * + Ак =
П|-1 П 2 — 1 flfc — 1
= а„ + ^ а„ Н + ^ а„ =
П — 1 п = П] п=П*_1
= а 1 + «2 + ' ■ ■ + (lnk- 1 = 'b'rifc-l,
т е. последовательность 5* есть подпоследовательность по¬
следовательности 5п, именно, Sfc = Snk-1-
Из теории пределов последовательностей известны следу¬
ющие утверждения:
1. Если сходится последовательность 5П, то последова¬
тельность SUk-1 сходится и lim 5n = lim Snk-\.
n-+r\) к-too оо
Для рядов это означает, что если сходится ряд ап, то
СК> 71= 1
сходится и ряд ^ Ли суммы обоих рядов равны.
k=1
2. Сходимость последовательности Snfc-i, вообще говоря,
не влечет сходимости последовательности .Sn.
оо
Для рядов это означает, что если сходится ряд Ак, то
оо к = 1
ряд ап может и расходится, это и показывают примеры 10
п — 1
и 11.
13
Утверждение. Пусть дан ряд ^ап. Пусть далее
п — 1
п*-1
Ak = ^ Лтп 1 = ^0 < «I < Т12 < ■ • • < Пк < . . .
и ряд Ак сходится. Тогда для того чтобы сходился ряд
к- 1
оо
£«п, необходимо и достаточно, чтобы
п = 1
Jim (max Л £ а.
Докажем это утверждение, используя критерий Коши.
Для произвольного числа е > 0 в силу условия найдутся на¬
туральные числа /\' и <2, такие, что
гпах
II ± -
' m — п »
, пк-1 ^ п $: пк - 1
m=n*_,
для всех натуральных А: > К и
<?+р
И
5>
k-q
е
<2
для всех натуральных р и g > Q.
Для натуральных п > 1 и р положим
ко = max{Ar п > Пк} и к] = max {к : п + р п*},
тогда ко ^ к\. Используя эти обозначения, эаиишем
+р
nfcl -1
п-1
Р+п
>2 ат =
Е
ат - 53
ат +
Е
1=П
яа=п*()
т=пк
О
т=пк
ki
п-1
Р+п
- Е
Ак ~
53 °т +
Е«
т •
Дс =Дс0-|-1
m=n*0
m=nfc
14
Так как из определения ко и к\ следует, что я*0 < п ^ п*0+]
и я*, ^ п + р< пк,+1 , то
п+р
|Цат| ^ | £ ^1 +
т = 1 к — к0 + 1
п п
+ max 7 ат + max } ат .
nfco^n<nfc +i I ' I п* <п^п*1 +1 I ' I
0 0 m=nfc0 1 1 т=п*,
Положим N = тах(71#, tiq). Тогда, если п > /V, то ко + 1 > Q
и fci + 1 ^ /:о + 1 > Л', следовательно, в силу определения К
и <2 получаем, что
п+р
Е| £ 6 £
Ч<2 + 4 + 4=£
Итак, ряд ^а„ удовлетворяет условиям критерия Коши и,
П= 1
следовательно, сходится.
оо
С другой стороны, если ряд сходится, то условие
lim max
к—too пя_ | <Cn^nfc — 1
lim г-* = 0, так как
к —► оо
У! am
m=nfc_,
£
n= t
= 0 следует из соотношения
= |r„t., - г„|.
Пк~ 1
Следствие 1. Пусть дан ряд ^ an и Ак = а"-
П = 1 П = П*_,
1 = no < 7ii < 712 < •• Если lim ап = 0 и sup(7i^ — n/c_i) <
n —► оо
оо
< -f ос, то ряды ^ ап и ^ Л* сходятся или расходятся
п — 1 Ac = 1
одновременно.
ОО Пк-\
Следствие 2. Пусть дан ряд ^ an и Л* = а„,
n = l n=nfc_i
1 = no < 7ii < П2 < — Если для 7ifc_i ^ 71 ^ тг* — 1 все
числа ап имеют одинаковый знак (нуль будем считать с лю-
15
ou ou
бым знаком), то ряды ^ «„ и Аь сходятся или расходятся
п — 1 к — 1
одновременно.
Следствие 3. Пусть дан ряд Обозначим через
П = 1
{6Г1} последовательность, содержащую все те и только те чле¬
ны последовательности {ап}, п = 1,2,..., которые отличны
от нуля, перенумерованные с сохранением порядка. Тогда
пи оо
ряды ап и ^ Ьп сходятся или расходятся одновременно.
п=1 п = 1
Если два ряда ап и 6„ сходятся, то для любых по-
п = 1 п = 1
(X- оо
стоянных muff ряд ^(аап+/?6п) сходится и ]^(аап+/?Ьп) =
оо оо п = 1 п = I
= а^Гап +Р^1Ьп'
п = 1 п = 1
Таким образом, множество сходящихся рядов представля¬
ет собой линейное пространство.
Отсюда получаем следующее утверждение.
оо
Пусть члены ряда ^ ап представлены в виде суммы: а„ =
= с<"+с!,г>+ ■■ .+С?Г
Тогда
<х> оо
I. Если все ряды ^ с^1\ 1 ^ t ^ А, сходятся, то ряд ^ ап
n = 1 П=1
сходится.
оо
2. Если среди рядов 1 ^ i ^ ку только один расхо-
п = 1 оо
дится, а все остальные сходятся, то ряд а„ расходится.
оо П= 1
Если среди рядов ^ \ 1 ^ t ^ fc, расходится более,
оо п = 1
чем один, то ряд ^ ап может как сходиться, так и расхо-
п = 1
16
диться — такое представление не информативно в вопросе о
сходимости ряда.
Приведем соответствующие примеры.
^ 2Л + 5П
Пример 12. Рассмотрим ряд ^ —• Так как ап =
1 1 „ ^1^1
= ^ — и каждый из рядов 2^ 5^ и 2^ 2" сходится (см*
П=1 П = 1
v-k 2П + 5П
пример 1), то и ряд — сходится.
П=1 ОО О
2 “I" п
Пример 13. Рассмотрим ряд 2"”~ ^аК КаК вп =
п = 1
1 п °° п °° 1
= - + сходится (см. пример 5), а ряд У] -
п z I п
п=1 п=1
/ о \ ^ + П2
расходится (см. пример 8), то ряд > — расходится.
п-2п
П = 1
00 1
Пример 14. Рассмотрим ряд } —7 -г-. Так как ап =
" n(n -1- 2)
= Н»~;гт2)’то
*‘-Ki-i)+sG-0+-+Ki-m)-
-1 (1 1 1 1 ^
” 2 ^ + 2 * + 2 k+l)’
следовательно, lim S* = ^, т. е. ряд У* - ---- - сходится и
k->OQ 4 "п(п-1-2)
3 Л °° 1
его сумма равна -. В то же время, каждый из рядов —
оо J П = 1 п
и V] расходится — расходимость первого установле-
т) 4- /
П=1
на в примере 8, расходимость второго следует из равенства
Sk = S*+2 - 1 ~ где S* — частичные суммы гармонического
17
ряда, a Sk — частичные суммы ряда 2^ ^
п = I
~ ^ -1
Пример 15. Рассмотрим ряд ^ . 1ак как
п = 1 П
1 2 , \/й — I 111
—т= ^ - для п ^ 4, то = —7= - - ^ - для /г ^ 4.
>/п п п у/п п п
Пользуясь этими неравенствами, получаем, что для любых
натуральных п ^ 4 и р
а ,/1-1 itri Й I ,У?|
Е —
fc=n АС — п Ас — п к—п
Пользуясь критерием Коши и установленной в примере 8 рас¬
ходимостью гармонического ряда, отсюда получаем, что ря-
00 . 00 /—.
Е1 Vn “ * II
-т= и расходятся. Итак, расходятся все
п = 1 * П = 1
оо . сю , оо /— . сю / 1 V
п = 1 n = l v п = 1 п = 1 4 v '
Свойство ряда быть сходящимся или расходящимся не за¬
висит от изменения любого конечного чис ла его членов (это
следует, в частности, из критерия Коши). Поэтому всюду в
формулировках условий сходимости или расходимости ряда
можно требование “для всех членов ряда” заменить на “для
всех членов ряда, начиная с некоторого номера”. В даль¬
нейшем такая замена будет подразумеваться без специальной
оговорки.
Определение. Ряд ап называется абсолютно сходя-
п = 1
оо
щимся, если сходится ряд ^ |ап|. ,
п = 1
СХ)
Если ряд ап сходится абсолютно, то он сходится. Если
п — 1
оо оо
же ряд ап сходится, а ряд ^ |ап| расходится, то говорят,
п = 1 п = 1
18
оо
что ряд ап сходится неабсолютно.
N = 1
Пример 16. Ряд
, , 1111 ^ (~l)n+1
+ 2 2 + 3 3+ [=*Ч
сходится неабсолютно.
Действительно, мастичные суммы S2n этого ряда с четны¬
ми номерами равны нулю, частичные суммы .S^n-i с нечет¬
ными номерами равны —. Последовательность Sn сходится
71
к нулю, следовательно, и рассматриваемый ряд сходится к
нулю.
ся, ис-
Покажем, что ряд ^ |ап| = ^ r'n+П РасхоДИТ(
п = 1 п — 1 I- 2 J
пользуя критерий Коши. Для произвольного нечетного чи¬
сла 71 = 2g - 1 возьмем р = п + 2 = 2g + 1, тогда получим,
что
n+p Aq ^
Z>*i = Е тщ
к-п k = 2q— 1 L 2 J
k = 2q-
111 1 112 q t
— Н Ь т г Н ~т 4- • + -—
Я Я Я + I q + 1 2q Zq 2q
Итак, для = 1 и любого номера 7V нашлись такие натураль-
п+р
ные числа п = 2 N -1-1 >ДОир = л + 2, что |а^ | > fo, т. е.
к =п ос
критерий Коши не выполнен и, следовательно, ряд |ап|
п = 1
расходится.
Определение. Ряд называется безусловно сходящимся,
если для любой перестановки ip(n) натурального ряда (<р есть
оо
биекция 14 на N) ряд ^[2av(n) схоДится-
п = 1
оо
Теорема. Ряд ап сходится безусловно тогда и только
п — 1
тогда, когда он сходится абсолютно.
19
Теорема. При любой перестановке абсолютно сходящего¬
ся ряда сумма полученного ряда равна сумме исходного.
Часто используется краткая формулировка этой теоремы:
сумма абсолютно сходящегося ряда не зависит от порядка его
членов. Такая формулировка удобна, если речь идет о сумме
некоторого счетного множества чисел, нумерация которого
еще не установлена или устанавливается произвольно.
В силу вышесказанного, для числовых рядов принято вме¬
сто термина “неабсолютная сходимость” использовать тер¬
мин “условная сходимость”.
оо
Теорема Римана. Если ряд ^ ап с действительными
п = 1
членами сходится условно, то для любой точки А расширен¬
ной числовой прямой найдется такая перестановка натураль¬
ного ряда (р(п), что для последовательности Sn частичных
оо
сумм ряда Vs a^in) имеем: lim Sn = А.
' V ' П-¥ ОО
п = 1
Пример 17. Рассмотрим ряд
Последовательность хп = 1 + - + - + Н *n п имеет
_ 2 3 п
предел. Обозначим этот предел через 6^, тогда
, 11 ' 1 .
2 3 Ь — = In п + + £п,
где lim еп = 0. Для частичной суммы четного порядка
П —4 ОО
ОО
отсюда получаем равенство:
1 11
п = 1
, 1 1 1 1 1
52*-1_2 + 3"4+ ' +2Г~1~2к =
= (1 + I + I + ...+ l)-(l + I + i + ...+ l):
= In 2Аг -|- Сэ + б2к — (In к + (?j + €k) = In 2 + €2к — £*
20
и, следовательно, lim .$2к = In 2. Так как S2*+i =52*+ а; , '7»
/с-foo 2к + 1
то
lim S2*+i — lim 62* = In 2,
к-* оо /с—►оо
откуда получаем, что lim Sn = In2, т. е.
п-*оо
5= У" — = In 2.
" П
(-1ГИ _
п=1
Сделаем перестановку членов этого ряда таким образом,
чтобы за двумя положительными членами шел один отрица¬
тельный, тогда получим ряд
1 11111 А
1 + 3-2 + 5 + 7_4 + "‘-2>"’
П = 1
где аз*-2 = 4рз* азк-‘ = 4ГГТ’аз* = -h’k* R 0б°-
значим через Sn частичные суммы этого ряда, тогда для лю¬
бого натурального к справедливы соотношения
$3к— 1 = Ssk + 7ГГ, $3к - 2 = $3к + 7ГГ
24, -г 2jb
Следовательно, полученный ряд будет сходиться, если схо¬
дится последовательность и при этом справедливо ра¬
венство
S = lim Sn = lim S3*.
n-foo к —f 00
Так как
5,11111 i i i
■ 3* “ 3 2 5 + 7 4 4*- 3 + 44-1 2* “
= l + I + ...+l-i(i + I + ... + ±)_I(i + i + ...+^ =
= In +63+64* — - (In 2k+Cj+£2k)-m 2 (In Л+Сэ+£*) =
3
то lim 5з/с = ;rln2. Итак, сумма S переставленного ряда
к — оо 2
3
равна - In 2 и не совпадает с суммой S — In 2 исходного ря¬
да. Это, как показывает сформулированная выше теорема
Римана. есть следствие неабсолютной (условной) сходимости
Ы)п+1 ^ 1
данного ряда. Действительно, ряд > = > - есть
Т1 г П
п- 1 п=1
гармонический ряд, расходимость которого уже была уста¬
новлена в примере 8. оо
Как указывалось выше, сходимость ряда ^(ап + *Ьп) с
П = 1
комплексными членами эквивалентна одновременной сходи-
оо оо
мости двух рядов с действительными членами: и ^ 6„.
п=1 П=1
Из неравенств
. /п+р П+р \ П+р П+р П +р
\k—n к =n / kzzn k=n k—ti
в силу критерия Коши следует, что и абсолютная сходимость
оо
ряда ^^(an ibn) эквивалентна одновременной абсолютной
п = 1 (X) оо
сходимости двух рядов ап и 6„ с действительными чле-
П — 1 П = 1
нами.
Приведем несколько примеров анализа абсолютной и не¬
абсолютной сходимости рядов с комплексными членами.
оо
Пример 18. Ряд ^ гг^- сходится абсолютно, так
П = 1 ' (X)
71 П г-л П
^ = 2^» а сходимость ряда ^ 5- установлена в
п = 1
примере 5. Так как
-5—4:0-0--
как
(l+i)2n 22"
= 2^ +«Х(-1)'СС-2п"1) .
\К=1 Лс=1 /
22
оо
V V ' Tt
то из абсолютной сходимости ряда, > — -г— следует схо-
“ (1 + *)
п = 1
димость рядов £а„ и £б„, где
П = 1
П = 1
а,г -
22п
Ё(-о*сй
/с=1
" ‘"=2*7
* = 1
Пример 19. Рассмотрим ряд
” (-i)"+,(>+>+»■)
г
п = 1
тг(п + 1)
Сходимость (абсолютная сходимость) этого ряда эквивалент¬
на одновременной сходимости (абсолютной сходимости) ря¬
дов
£ „(„+,) Л. „
1
-П»+1
(-1)
п(п + 1)
1
п(п + 1)
(-l)n+1
и ряд У] ———Г сходится (см. пример 3), то ряд У/-; ■
^in(n + 1) ^n(n+1)
сходится абсолютно. Ряд 2 , как показано в приме-
п= 1
ре 17, сходится условно (неабсолютно). Итак, ряд
(-l)n+1(l + i+m)
п = 1
сходится условно
п(п + 1)
овно.
~ in
Пример 20. Рассмотрим ряд 2^ —. Так как
п= 1
п = 4к,
п = 4к -I- 1,
Tt — Ак -|- 2,
n = 4* + 3, *GN,
(0n
i_
n
i
n ’
n 9
i
’ >
n
23
то сходимость (абсолютная сходимость) данного ряда экви¬
валентна одновременной сходимости (абсолютной сходимо¬
сти) рядов
—, п = 4к,
п
]Гап, где а„ = ^ _ 1 п _
п ’
О, п = 2к + 1
4 к + 2,
п = 1 I 71
]Гб„, где Ь„ = <
П=1
n = 4fc + 1,
71
п = 4* + 3,
71
О, п = 2к.
Следствие 3 утверждения о группировке членов ряда (см.
00
стр. 17) говорит, что сходимость ряда ^а„ эквивалентна
оо / n = 1
сходимости ряда ' Л» ' > а сходимость ряда Ьп эквива-
LK
оо / j\* n = l
лентна сходимости ряда ^Сходимость рядов
^ ——— и 2^ ы 1 устанавливается так же, как и схо-
к=1 к=1 ~
00 (_1)" + 1 00 i"
димость ряда в примере 17. Итак, ряд ^ —
п — 1 П п = 1 П
00 tn 00 1
сходится. Ряд же ^ расходится - это гар
П = 1 П=1 ОО .п
монический ряд (см. пример 8). Следовательно, ряд ^ —
сходится условно. п"1
У J . ч П
Пример 21. Рассмотрим ряд ^ . Гак кар
л 2n/2 n=1
= = 1, то данный ряд расходится - для не
1+|
1 - г
24
го не выполнено необходимое условие сходимости. Так как
то, следовательно, расходится, по крайней мере, один из ря-
ОО 1 / п \ оо
дов ]Га„, где а„ = — ( ), или где 6П =
n = l \1г = 1 / п—1
Поскольку из абсолютной сходимости ряда следует его
сходимость, начнем с изучения исследования сходимости ря¬
дов, члены которых действительные неотрицательные числа.
Заметим еще, что для ряда, члены которого, начиная с не¬
которого номера, не меняют знака, сходимость эквивалентна
абсолютной сходимости.
Все дальнейшие утверждения относятся только к действи¬
тельным последовательностям {ап}, поскольку в этих утвер¬
ждениях явно или неявно используются условия, содержащие
неравенства.
Ряды с неотрицательными членами
оо
Если все члены ряда ^ ап неотрицательны, то последо-
п — 1
вательностъ {/?*} его частичных сумм не убывает. Для не¬
убывающей последовательности ее сходимость и ограничен¬
ность эквивалентны. Поэтому для рядов с неотрицательны¬
ми членами — и только для них! — вместо слов “ряд сходит¬
ся” и “ряд расходится” употребляют соответственно символы
IX) оо
]Рап<+оо и У^ап = +оо.
П = 1 П = 1 ОО
Теорема сравнения. Пусть даны два ряда А : ^ ап,
оо п = 1
<*п ^0 VnGN, и В : бп^О Vn€N. Если ап ^ 6n Vn € N,
п = 1
то из сходимости ряда А следует сходимость ряда В, из рас¬
ходимости ряда В следует расходимость ряда А.
25
Следствие 1. Если ап О, Ьп ^ 0 Vn £ N и ап = 0(6П)
оо
при п -> оо, то из сходимости ряда следует сходимость
со ^
ЕТ1 — 1
flfl.
nr 1
Следствие 2. Если ап ^ 0, Ьи ^ 0 Vn 6 N и ап ~
(X) оо
при п -> оо, то ряды а„ и 6„ сходятся или расходятся
п = 1 п = 1
одновременно
оо
Внимание! Если в ходе анализа ряда ап, ап ^ 0, полу-
п = 1
чена оценка ап ^ 6П, или ап = 0(6П), п —► оо, или ап — о(Ьп),
оо
тг -> оо, где ряд Ьтх расходится, то такие оценки не дают
п~ 1 оо
возможности сказать, сходится или расходится ряд ап -
71 — 1
О.)
они не информативны в вопросе о сходимости ряда ап.
п — 1
Пусть {^п} и {6П} -- неотрицательные бесконечно малые
последовательности. Тогда из теоремы сравнения получаем
следующие утверждения.
Если ап и Ьп бесконечно малые одного порядка, т. е.
со со
ап = 0(Ь„) и 6П = 0(ап) при 71 —► оо, го ряды ам и 6П
П — I п=1
сходятся или расходятся одновременно.
Если последовательность {ап} стремится к нулю быстрее
последовательности {6yt}, т. е. ап = о(Ьп) при п -> ос», то из
сходимости ряда ^ Ьп следует сходимость ряда ^ ап, а из
п= 1 п = 1
'Х; оо
расходимости ряда ^ ап следует расходимоггь ряда ^ 6П.
П = 1 П - I
Таким образом, сходимость ряда с неотрицательными члена¬
ми связана со скоростью стремления к нулю его членов.
К сожалению, не существует такой “граничной” последо¬
вательности {ап}, а„ ^ 0 Утг 6 N, lim ап — 0, для которой
п—*оо
26
все ряды, члены которых стремятся к нулю быстрее, чем аП}
сходятся, а все ряды, члены которых стремятся к нулю мед¬
леннее, чем ап, расходятся (см. задачи 9, 11, 13 и вывод из
них, стр. 314)
Сама формулировка теоремы сравнения показывает, что
для ее применения необходимо наличие достаточно широко¬
го запаса “эталонных” рядов, сходимость или расходимость
которых известна.
оо
Ряд сходится при О $ q < 1 и расходится при
п = 1
q ^ 1. Используя такой ряд, из теоремы сравнения можно
вывести:
Признак Даламбера. Пусть дан ряд с положительными
оо
членами ^ ап, ап > 0 Vn Е N, тогда
п= 1
Г— ап + 1 |
если Inn = q < 1, то ряд сходится,
n-юо ап
если - -*1- ^ 1 Vn £ N, в частности, если Um —q}> 1,
ап п—►оо dri
то ряд расходится.
На практике, в основном, применяется более слабое усло-
оо
вие: если все члены ряда У ап положительны и lim = g,
t'l n^°° a"
то ряд сходится при q < 1 и расходится при q > 1.
Признак Коши (радикальный). Пусть дан ряд с не-
оо
отрицательными членами: а„, ап ^ 0 Vn € N. Тогда
П = 1
если lim ?/а^ < 1, то ряд сходится,
п-юо
если lim > 1, то ряд расходится.
п-юо
На практике, в основном, применяется более слабое усло-
оо
вие: если все члены ряда Y44 ап положительны и lim </a^=g
п-юо
п= 1
то ряд сходится при q < 1 и расходится при q > 1.
В теории последовательностей доказывается, что для по¬
следовательности {an} с положительными членами из суще-
27
r an+l
ствования предела lim следует существование предела
п—♦ со ап
lim v/a^ и равенство этих пределов. Следовательно, если для
п—►оо
ряда с положительными членами выполняется одно из условий
признака Даламбера, то обязательно выполняется и соответ¬
ствующее условие признака Коши. Но на практике отноше-
^п+1
ние часто аналитически проще, чем радикал с перемен-
an
ным показателем \/an, поэтому проще применить признак
Даламбера. В то же время область применения признака Ко¬
ши шире, чем область применения признака Даламбера. В
частности, для выполнения каждого из условий признака Да¬
ламбера необходима монотонность последовательности {an},
а условия признака Коши не требуют сравнения друг с дру¬
гом соседних членов последовательности {an}.
Приведем характерные примеры исследования рядов при¬
знаками Даламбера и Коши.
^ 2п + и2
Пример 22. Рассмотрим ряд > — . Для членов
' Зп + 71
п= I
этого ряда имеем:
(2+ 1^) (1 + JL)
3«+1 + (n+ lT 2» + »2 ” (з+:Ш.) (1 + |2) '
an+1 2n+l+ (»»+!)* 3" + n
3 V 1 +
n ’
с. I • ^Tl *f 1 ^
откуда легко получаются оба равенства: urn —= - и
2 п^по ап 3
lim уап -
п—юо J
Итак, данный ряд достаточно просто анализируется как
признаком Даламбера, так и признаком Коши.
^I\2
Пример 23. Рассмотрим ряд ^ : . |. Для этого ряда
П = 1 ' '
г- (п!)"
исследование последовательности уап = —■-—-—г существен¬
ен)!]^
<*n+i (п + I)2
но сложнее, чем последовательности —— = —-—- .
an (2 + 2n)(2n + l)
28
то в силу признака Даламбера данный ряд сходится.
Замечание. В теории последовательностей доказывается
неравенство < п! < е■ (^) » откуда следует,
(n!)± ^ ei-f _ е1+±
НТО
((2п)!)* < ¥ 4
и, следовательно, lim \/а^ < <1. Таким образом,
n-fOO \ 4/
данный ряд можно было исследовать и с помощью признака
Коши, но при этом пришлось бы использовать более сложные
соотношения.
°° n"-i
Пример 24. Рассмотрим ряд У По-
^ (2n2 + n+ l)“t"
скольку члены ряда аналитически записаны в виде степени с
переменным показателем, то следует ожидать, что исследо¬
вание последовательности будет проще, чем последова¬
тельности в--1. Действительно, вычисление
ап
lim fe±! = lim ("+■)’(*■» + ■■+iff
n-юо ап п->оо Пп-1(2П2 + 5п + 4)“11-
явно громоздко и проводить его не будем. Применим для
анализа данного ряда признак Коши: так как
П’П »
</Оп = Щ
(2+±+£)■*■•»•»*
то lim v/a^ = -^= < 1, следовательно, данный ряд сходится.
Л-ЮО у/2
/ 2 + (—1)л \п
Пример 25. Рассмотрим ряд ^ (^5 + ( 1)"+1/ ^ока~
жем, что признак Даламбера непригоден для анализа этого
ряда. Так как
а„-и _ /2 +(-!)"+'у>+‘ /5 + (-l)n+1 \"
а„ V5 + H)n+V V 2 + (—1)" )
*n + l.ftn i /Q\n + 1
, п = 2к — 1,
4n+Mn 6 V 4
1 Ц\"
.6^nF = 6leJ • ” =
то lim = -i-oo и lim - = 0 < 1. Таким образом,
п-*оо ап П —>00 On
ни то условие признака Даламбера, из которого следует схо¬
димость исследуемого ряда, ни то, из которого следует его
расходимость, не имеют места.
Попробуем применить признак Коши. Из равенства у/а^=
2 -|- ( — 1)п 3
= т;n г 1 получаем, что lim \/а^ — Следова-
5 + (— l)n+ Ti —► оо 4
тельно, в силу признака Коши, данный ряд сходится.
Итак, вопрос — каким из признаков — Даламбера или
оо
Коши исследовать данный ряд ^ ап решается в зависимо¬
го!
сти от конкретного вида последовательности {ап}. Однако,
поскольку оба эти признака основаны на сравнении иссле¬
дуемого ряда с геометрической прогрессией, то ни тот, ни
оо
другой не дают ответа на вопрос о поведении ряда ап,
п = 1
члены которого стремятся к нулю медленнее, чем последо¬
вательность вида {gn}, О < q < 1. Для таких рядов нужна
другая эталонная шкала.
Выделим новую серию эталонных рядов, используя ре¬
зультат примера 2. В этом примере было показано, что ряд
У2 (- —I )
(п + 1 )Я)
сходится при q > 0 и расходится при q < 0. Оценим скорость
/г 1 1
стремления к нулю последовательности {ап}, ап = ——
30
при q ф 0. Имеем
1 1 _ 1 / / А
гг** (гг -h 1 п(* у \ п)
= JL (Vi + ^+of-^Y) - —
Т\Ч V 71 \п J/ пЧ
, п -> оо.
В силу следствия 2 теоремы сравнения (см. стр. 27) получаем,
°° 1
что ряд ^ — сходится при р = q + 1 > 1 и расходится при
п = 1
р < 1; если же р = 1, то перед нами гармонический ряд,
расходимость которого установлена в примере 8. Отсюда
следует
Признак сравнения. Если для последовательности по¬
ложительных чисел {ап} существуют такие числа р и С > 0,
что
On ~ П -»• ОО, (1)
ОО
то ряд а« сходится, если р > 1, и расходится, если р ^ 1.
г» = 1 °° 1
Сравнением с тем же рядом ^ — получается
П = 1
Признак Гаусса. Если ап > 0 и существует такое число
е > 0, что
*•±1 = 1 + ^ + 6>(-1_Л, п-юо,
о„ п V” + /
(2)
ОО
то ряд ^ ап сходится, если ц < -1, и расходится, если
п-1
Ц ^ -1.
Заметим, что условие признака Гаусса часто формули¬
руется для обратного отношения ——. Приведенная здесь
Дп + 1
формулировка подчеркивает связь признаков Гаусса и Да-
ламбера. Оба эти признака основаны на анализе отноше¬
ния ——. Признак Даламбера рассматривает тот случай,
an +1
31
когда это отношение отделено от единицы снизу или свер¬
ху, и сравнивает последовательность {ап} с геометрической
прогрессией. Признак Гаусса рассматривает тот случай, ко¬
гда lim —— = 1, и сравнивает последовательность {ап} с
п->оо ап
последовательностью {п~ **}.
Вопрос — каким из признаков - - сравнения или Гаусса —
00
исследовать данный ряд ап решается в зависимости от
п = 1
того, какое из представлений (1) или (2) легче получить. В
ап + 1
частности, если ап или отношение являются достаточно
ап
гладкими функциями от п, необходимое представление полу¬
чается применением формулы Тейлора.
Рассмотрим характерные примеры.
ОО J ^
Пример 26. Рассмотрим ряд 7 —sin —.
п
п=\
П
Так как ап ~ , п —> оо, то этот ряд сходится при
nP+1
р > 0 и расходится при р 0 в силу признака сходимости.
Пример 27. Рассмотрим ряд
Для последовательности {ап}, ап = -- \/1п ——, как от-
\/п V п
ап +1 ,—
ношение , так и радикал ?/ап имеют достаточно СЛОЖ¬
ЕН
ный вид. Выделим главную часть переменной ап следующими
преобразованиями:
32
Апу/п
^о(') , п
п \ Пу/П )
оо.
Итак, ап — —у, п —> -foo, следовательно, в силу признака
4пз
со
сравнения ряд ап сходится.
П = 1
Пример 28. Рассмотрим ряд
р > О, q > О, г > 0.
ОО / J. . J. \
Е/ I. 0 * + Г * 1
(»■-— j.
Для последовательности {а„}, ап =
Рп о—
, как от-
^п + 1 /
ношение , так и радикал уап имеют достаточно слож¬
ен
ный вид. Для того, чтобы выделить главную часть перемен¬
ной ап, запишем а„ в виде
- = |,+v-K, + v + 1 + v)+e(i)|-
= i.|21np_ln,_lnr| + C)(^) =
In— n-4oo.
qr j \n2J
2n
1 I «2,
Переменная — In — является главной частью a„ при
2n j qr|
2
n —► оо, если In — ф 0, т. e. p ф y/qr. При этом усло-
qr
вии an — —
« 2 n
In
оо, и в силу признака сравнения
/ 1 \
ряд ^ ап расходится. Если же р = v/gr, то an = О I — ),
п = 1 со j \п )
п —► оо. Поскольку ряд > —X сходится, то в силу след-
' 71
П=1
ствия 1 из теоремы сравнения получаем, что в этом случае
33
W -i- . J-
1 ^" T Гп 2
an сходится. Так как pn = ап, если р > qr,
n= 1
-L , i
1 0 " + Г » 2 ^
л pn = —аП1 если p ^ qr, то данный ряд сходится,
если р2 = gr, и расходится, если р2 ^ qr.
Заметим, что формула Тейлора позволяет получать точ-
-L , X
х. q п ~т г*
ную величину константы ь в равенстве ап = рл
~ С-“, р2 = qr, п -> оо. Но следствие I теоремы сравнения
п
позволяет обойтись без этой величины, что часто упрощает
ход решения.
оо п|еп
Пример 29. Рассмотрим ряд ^ . В формулу об-
п= 1
щего члена входит функция п!. В таком случае естественно
ал+1 (п + 1)!<?л+1пл+р ^
рассмотреть отношение = 7 rr-v-vi- ,—• Так как
ап (п + 1)п+Р+1п!еп
3 3
то данный ряд сходится при р > - и расходится при р ^ -
в силу признака Гаусса.
Пример 30. Рассмотрим ряд
с»
£(2 - ,)(2 - **)(2 (2 - ,*). д > 0.
П = 1
Прежде всего заметим, что если q = 2m, m G N, то, начиная
с некоторого номера, все члены данного ряда обращаются в
нуль, следовательно, ряд сходится. Если же q не является
целой степенью двух, то, начиная с некоторого номера, все
члены данного ряда не меняют знака. Поскольку
an+1 = (2 - q)(2 -q*)... (2 - ?-)(2 - 9^т) = an(2 -
вп+1 „ *
то естественно рассматривать отношение —— = 2 — q**7.
то данный ряд сходится при In q > 1 и расходится при Inq ^ 1
в силу признака Гаусса. Окончательно получаем, что данный
ряд сходится при дг = 2идг>е,а расходится при 0 < q < 2 и
2 < q ^ е.
Две основные элементарные функции — показательная ех
и логарифмическая 1пх — при х —> +оо не являются беско¬
нечно большими степенного порядка, т. е. для любого а > О
имеем соотношения ха = о(ех) и 1пх = о(ха)> х —> +оо. По¬
этому ряды, в формулу общего члена которых входят эти
функции с бесконечно большим при п —> +оо аргументом,
не анализируются с помощью признака сравнения. Однако,
иногда возможно получить оценку общего члена такого ряда
через степенную функцию и, пользуясь теоремой сравнения,
сделать вывод о поведении этого ряда.
о°
Пример 31. Рассмотрим ряд ^ п2е_>^. Так как
П = 1
lim Vn2e~^ = lim = 1,
n—f 6о n—► оо
то ни радикальный признак Коши, ни, тем более, признак
Даламбера не решают вопрос о сходимости этого ряда.
Функция епри п —► оо убывает быстрее, чем любая
отрицательная степень показателя у/п, т. е. = о(п~*)
0° j
при п —>* оо (а > 0). Если ао > 6, то ряд сходит-
ся.'В силу теоремы сравнения отсюда делаем вывод, что ряд
оо
^п2е~^* сходится.
Заметим, что оценка п2е~^ = о^п2~^ верна и для
О < оо < 6, но, как указывалось выше, такая оценка не инфор-
оо
мативна в вопросе о сходимости ряда ^ п2е'~^1 поскольку
оо J п=1
ряд ^2 2 —ао ’ а° ^ 3’ Р^ХОДИТСЯ.
п - 1 °° III п
Пример 32. Рассмотрим ряд ^ , q > 0. Из неравен-
П — 1
35
In n 1
ства > —, n > 3, q > 0, в силу теоремы сравнения сле-
п** п?
дует, что данный ряд расходится при 0 < q ^ 1. Пусть q > 1.
Так как In п = о{па) при п -> оо для любого а > 0, то для ка-
кП - 'П П ^
ждогоа > 0 найдется номер Л (а), такой, что - - для
всех п > М(а). Чтобы из этого неравенства сделать вывод о
сходимости рассматриваемого ряда, необходима сходимость
°о 1
ряда ^а для этого, в свою очередь, необходимо усло-
п— 1
вие q — а > 1. Итак, для каждого фиксированного q > 1 берем
зависящее от q значение а = —, тогда для всех п > Af(a)
Inn 1
справедливо неравенство < , откуда в силу теоремы
пя п 2
°° In п
сравнения сделаем вывод, что ряд сходится. Оконча-
п— 1
тельный результат таков: данный ряд сходится, если q > 1,
и расходится, если 0 < q ^ 1.
Поскольку и признак сравнения, и признак Гаусса осно¬
ваны на сравнении членов исследуемого ряда с последова-
/ 1 \
тельностыо вида < — >, то ни тот, ни другой не дают от-
1”р J
вета на вопрос о поведении ряда, члены которого стремятся
к нулю быстрее, чем —, но медленнее, чем —для любо-
п п1+£
°° 1
го е > 0. Рассмотрим, например, ряд ——. Так как
' п In п
1 fl\ 1 f 1 \
—— = о - I, но ----- = о I —— I при п —► оо для любого
п\пп \п / п1+с \n\nn/
е > 0, то признак сравнения не решает вопрос о поведении
этого ряда. Точно так же отношение
(n+1) 1п(п+1) 1 I л/1\
= 1 гт-.-.х+О т , п-»оо,
(*)■-
(л-f 2) ln(n + 2) п п ln(n + 2)
не представляется в виде (2). Итак, данный ряд не анализи-
. / 1 \
руется сравнением со шкалой < — >.
1"р J
Интегральный признак Коши. Если/: [1, +оо) -» Я —
36
неотрицательная, невозрастающая, непрерывная функция, то
оо
ряд f(n) сходится или расходится одновременно с инте-
п = 1
+ оо
/w
f(x) dx\ если ряд /(п) сходится, то
i "=1
+00 +00
Jf(x)dx^rn^ J f(x)dx,
где r„ = f(k).
/c=n 4-1
00 j
Пример 33. Рассмотрим ряд ^ —j—p—, p > 0. T;
n = 2
~T~r— = o(-), p > 0, HO = of I1 - ), p > 0, для
n III7 71 \n / П \ П In' 71/
любого e > 0 при 7i -> оо, то признак сравнения не реша¬
ет вопрос о поведении этого ряда. Не должен давать ответ
на этот вопрос и признак Гаусса; действительно, отношение
(71 + 1) IIIР(П +1) 1 1 / 1 \
(71 + 2) 1пр(п + 2) п рт?1п(7?+2) + \П2 / не ПРеД
ставляется в виде (2). ^
Положим f(x) = — —р—, х ^ 2. Функция f(x) удовлетво-
х lnF х
ряет всем условиям интегрального признака Коши. Так как
4-00
интеграл / -■ —dx сходится при р > 1 и расходится при
J х hr х
2 V" 1
р ^ 1, то ряд > —г~б— сходится при р > 1 и расходится
пиг п
п — 2 оо
при р ^ I. Таким образом, мы выяснили, что ряд 7 ——
71 In П
п — 2
расходится.
00 i
Пример 34. Найти сумму рядаУ^ — с точностью до 10“’*
. п
п = 1
Решение. Задача поставлена корректно, так как данный
ряд сходится. В силу интегрального признака Коши получа¬
37
ем, что
+оо
л - ( dx 1
гп — S — Sn $ I 4 —
J X4 3(п -
п — 1
I)3
00 I
Следовательно, для вычисления S = ^ —j с заданной по-
п = 1 П
грешностью достаточно взять сумму
1 1 1 1 1 1 1
- + 24 + 34 + 44 + + g4 + 7< + .
так как jL = jij <
Ряды с членами произвольного знака
оо
Признак Абеля. Пусть дан ряд ^ апЬп. Если после до-
П = 1 ОО
вательность {ап} монотонна и ограничена, а ряд Ьп схо-
ОО П = 1
дится, то ряд ап6п сходится.
п— 1 оо
Признак Дирихле. Пусть дан ряд ^ап6п. Если по-
п п = 1
следовательность {Bn}> Bn = ограничена, апоследова-
1 ОО
тельность {ап} монотонно стремится к нулю, то ряд ^ апЬп
п = 1
сходится.
Следствие (признак Лейбница). Если последователь-
ность положительных чисел {ап} монотонно стремится к ну-
ОО
лю, то ряд —1)л+1ап сходится и его остаток гп удовле-
П=1
творяет неравенству |rn| ^ an + i-
~ (-l)n+1
Пример 35. Рассмотрим ряд - . Так как ап =
п — In и
] 1 («1)п+1 - J
= : , п -> ОО, ТО ряд > = > :
п —Inn П “ п — Inn ' тг — In п
п = 1
38
расходится. Итак, если данный ряд сходится, то он сходится
условно. Последовательность {ап} положительна и стремит¬
ся к нулю при п —► оо. Так как (г — In х)' = 1 ^ О,
х
х ^ 1, то эта последовательность монотонна. Итак, данный
ряд удовлетворяет условиям признака Лейбница и, следова¬
тельно, сходится условно.
Пример 36. Рассмотрим ряд V(—l)"*1 arctg .
^ ("+1)2
Так как In(n + 1) < у/п+1 для п > 2, то
ln(n-hl) ln(n -I- 1) 1
0•= TTmF < -(TTiF< (TTi)T’ ">2
Из этого неравенства в силу признака сравнения следует, что
* ln(n +1)
ряд > arctg —у сходится, следовательно, данный ряд
п = 1 \п ^ )
сходится абсолютно.
00 .
ЕЧ п ( П -f 1 ) / CI \
(—1) * (cos — J .При
п = 1 П
любом а для достаточно больших п имеем, что cos — =cos —.
Ini n
оо пз
Для исследования сходимости ряда ^|cos“| используем
п=1 П
радикальный признак Коши. Так как
lim п2 (cos — — l) = — lim п2-^Ц- = —
n-юо \ п / n-юо 2гк 2
то
lim {/(cos-V*’ = lim еп3 *n(cos f) =
n—fOO у V Ц/ n-fOO
lim na(cosJ-l) аз
— gn-ЧОО — £> T #
00 . .„3
El fl I
cos — сходится при аф 0. Бели же
I п I
п=1
/ а \п3
а = 0, то ^cos — J =1 для всех n G N, т. е. не выполнен
не-
39
V^/ ,x2l2±^ / a\n
обходимым признак сходимости и ряд > (— * ) 2 I COS — 1
П = 1
расходится. Итак, данный ряд абсолютно сходится при а ф О
и расходится при а — 0.
Пример 38. Рассмотрим ряд tg — . Так как
4пя
4 n't ’
п -> со, то данный ряд сходится абсолютно при q > 1. Так
f j \П + 1 ^
как tg = ( — 1)<п+1) tg-— и положительная после-
6 4пя v ; * 4п?
1Г
довательность tg (q > 0) монотонно стремится к нулю
при ti —у оо, то в силу признака Лейбница данный ряд схо¬
дится условно при 0 < q ^ 1. Если же q ^ 0, то данный
ряд расходится, гак как не выполнено необходимое условие
сходимости.
Замечание. Условия ^ 1 и lirn а„ > 1 расход и мо-
ап п--юо
сти ряда соответственно в признаках Даламбера и Коши, как
это видно из их доказательств, являются условиями наруше¬
ния необходимого условия сходимости ряда. Поэтому, если
оо
ряд |ап| удовлетворяет этим условиям, то не только он,
п = 1
оо
но и ряд ^ а„ расходится, так как последовательность {ап}
п = ]
не является бесконечно малой при п —> оо.
°° n 71!
Пример 39. Рассмотрим ряд ^. Начнем с иссле-
n~* Iqr 1*^ • п!
дования абсолютной сходимости. Пусть ап — —, тогда
ап+1 kl(n+ 1)пп \q\
-ST = КЛЯГ = (ITif- 1,1 < “ с"')'
неравенства lim = — < 1 признак Даламбера показы-
п-юо ап е
вает, что данный ряд сходится абсолютно.Если \q\^e, то для
40
любого натурального п верно неравенство
«п+1 ы
О + *)*
> I,
п *
следовательно, в силу сделанного выше замечания данный ряд
расходится.
“ (-1)п+1Пп+»
Пример 40. Рассмотрим ряд > —- г-^й—. Я > 0.
\Яп + k)
Намнем с исследования абсолютной сходимости. Так как
/ Пп+* п1 + ^ ,г. г 1 _
\/7 ГТЯ- = ГТ> то lim V е» = - В силу ради-
V \Яп + £) + n n_f°° ?
кального признака Коши данный ряд сходится абсолютно при
q > 1 и в силу сделанного выше замечания расходится при
О < q < 1. Осталось выяснить поведение данного ряда при
q — 1, поскольку радикальный признак Коши не дает в этом
случае определенного ответа. Рассмотрим поведение после-
довательности |ап| = при п —у оо. Из соотноше-
(» + £)
НИИ |а„| = "* n = п»е-п|п(1+-*) H-nln ~
0 + £) V nV »
п —у оо, следует, что lim |ап| = 1. Итак, последователь-
п—►оо
ность {ап} не является бесконечно малой при п —> оо и, сле-
оо
довательно, ряд ап расходится. Объединяя все сказанное,
П=1
получаем, что данный ряд абсолютно сходится при q > 1 и
расходится при q ^ 1.
Абсолютная сходимость ряда, как уже говорилось при рас¬
смотрении рядов с неотрицательными членами, обусловлива¬
ется скоростью стремления членов ряда к нулю. Это хорошо
видно в формулировке критерия Коши: при условии, что все
п+р
слагаемые неотрицательны, малость суммы а*
к=п
малости каждого из слагаемых. Если же слагаемые имеют
п+р
разные знаки, то малость суммы
требует
J2ak
к=п
может быть обязана
41
не малости каждого слагаемого, а взаимной интерференции
положительных и отрицательных слагаемых. Перестановка
членов ряда меняет порядок этой интерференции - в этом
суть теоремы Римана. Этот факт позволяет ожидать, что
условие ап ~ 6П, п оо, не гарантирует одновременную
по со
сходимость или расходимость рядов ^ ап и ^ 6п, если чи-
п=1 п=1
ела ап (следовательно, и 6п) меняют знак. Покажем, что это
действительно так.
™ /(_Пп + ] 1 \
Пример 41. Рассмотрим ряд ^ [ -= Ь “ ) • Ряд
v" п/
(-i)n+1
сходится в силу признака .Лейбница, гармониче-
Е
П= 1
у/п
1
ский ряд — расходится, следовательно, данный ряд расхо-
_ 71
(-i)n+I 1 (-i)n+1
дится. В то же время ■= Ь — ~ ■=—, п —► оо. Итак,
у/П 71 у/П
последовательность членов данного расходящегося ряда экви¬
валентна последовательности членов сходящегося ряда.
Внимание! Делать вывод о сходимости или расходимости
оо оо
ряда ^ап по поведению ряда где ап — 6„, п —У оо,
П=1 П=1
возможно только для рядов с неотрицательными членами!
Тот же эффект интерференции положительных и отрица¬
тельных слагаемых лежит в основе признаков Абеля и Ди¬
рихле. Хотя в отличие от признака Лейбница в формулиров¬
ках этих признаков формально не указано, что рассматрива¬
емые ряды имеют члены разных знаков, но область их приме¬
нения — именно такие ряды. Действительно, в силу условия
монотонности члены последовательности {ап} в обоих этих
признаках могут без ограничения общности считаться поло¬
жительными. Если и члены последовательности {6П} неотри¬
цательны, то ограниченность последовательности Вп — Ьк
оо к-1
и сходимость ряда Ьп эквивалентны, а так как при этом
42
<in6n = 0(bri), n —► оо, то сходимость ряда anbn следу-
n = l
ст просто из признака сравнения. Если же в основе сходи-
оо
мости ряда Ьп или ограниченности последовательности
П П = 1
Вп = ^6^ лежит интерференция положительных и отрица-
fc=i
тельных членов последовательности {Ьп}» то именно призна¬
ки Абеля и Дирихле позволяют установить сходимость соот¬
ветствующих рядов, чаще всего условную.
На практике в признаках Абеля и Дирихле в качестве по¬
следовательности {Ьп } чаще всего берется или последователь¬
ность {(— 1)^п)}, или одна из последовательностей {cos па} и
{sinпа}. Ограниченность последовательности
при данной функции <р(п) устанавливается непосредственно.
Рассмотрим последовательности
п
Вп = cos a + cos 2a + • • • + cos na = cos qa
<7=1
И
n
Bn = sin a + sin 2a H 4- sin na = ^ sin qa.
9=1
Так как
. a _ 1 / . 3a . a\ 1 / . 5a . 3a\
Sm 2Bn = 2 ГП T ‘ Sm 2 J + 2 iSm T ' 8Ш T J +
1 / . 2n + 1 . 2n-l \
1 / . 2n+l . a\ /
= 2 1“ —2—a ~ Sm 2 J ~ cos(n + l)<*-sinna,
то для любого a ^ 2тгЛ, к 6 Z, получаем, что
id I |cos(n + l)a sinna| 1
l^nl = -г-ъ $ t-г—т.
sin y I |sin •
43
Точно так же получаем, что
sin(п + 1)а sin па
\Вп\ =
^ I . „I, а Ф 2тгк, к 6 Ъ.
Итак, установлено, что последовательности Вп и Вп огра¬
ничены при любом а ф 2жк, к 6 2. Поэтому, если при ис-
ОО ОО
следовании рядов вида f(n) cos па или /(n) sin па про-
П=1 П=1
стейшая оценка | cos па| ^ 1, | sin na| ^ 1 не дает возможности
сделать вывод об абсолютной сходимости, то обычно проще
начать исследование сходимости, а уже потом перейти к ис¬
следованию абсолютной сходимости.
оо
Пример 42. Рассмотрим ряд —7=~ Простейшая оцен-
ка
ОО
£
П — \
COS П
у/п
cos п
у/п
< —= не дает информации о поведении ряда
у/П
Покажем, что данный ряд сходится. Положим
1
bn = cosп и ап = —т=, тогда \Вп\ -
у/п
а последовательность
{Js}
cos к
к — 1
1
1 1
Sm 2
монотонно стремится к нулю
при п —> оо. В силу признака Дирихле данный ряд схо¬
дится. Для исследования абсолютной сходимости этого ря¬
да удобно воспользоваться оценкой |cosn| ^ cos2 п. Име-
COS п
" “А
ем:
у/п
1 cos 2 п
2у/п 2у/п
_ cos 2 п
Ряд У ' '/=- так
п = 1 v
же, как и исходный ряд, сходится в силу признака Дирихле,
°° 1
а ряд = расходится. Следовательно, расходится ряд
Ly/П
n = l v
ОО 9 ОО
cos п
Е COS2 71
—а в силу теоремы сравнения и ряд >
n=l П = 1
оо
ECOS 71
—j=r сходится условно.
» = 1 '/и
у/а
. Итак,
44
Пример 43. Рассмотрим ряд
п = 1
cos п ■ arccos -
7= —. Простеи-
у/п
шал оценка
cos п arccos ~
п
у/а
2 у/п
не дает информации о по¬
ведении ряда У]
П = 1
cos n- arccos -
у/п
Покажем, что данный ряд
cos п 1
сходится. Положим Ьп = —т=- и ап = arccos —. Условная схо-
у/П п
оо оо
Е. г—' cos п
Ьп = 2^ Установлена в предыдущем
монотон-
п = 1
примере. Так как последовательность
1 7Г
на и ограничена, 0 ^ arccos — ^ —, то в силу признака Абеля
п 2
00 I cos п* arccos —•
< arccos — >
El ииа u* —
7=
n=l I V"
следует из неравенства
cos n- arccos -
y/n
Icosn 1 ,
^ —7=— arccos - (n ^ 2)
yn 2
и расходимости ряда ^
n=l
сходится условно.
cosn
V cos n- arccos
. Итак, ряд > 7= ^
r-^ cos n • arccos ^
Заметим, что сходимость ряда > — можно
^ V"
было обосновать и признаком Дирихле. Но если выполнение
П
условий ограниченности последовательности Вп = cos /: и
1 к — 1
arccos -
стремления к нулю при п оо видим непосредствен-
arccos -
п
но, то проверка монотонности последовательности
у/п
достаточно громоздка. В данном случае проверка выполне¬
ния условий признака Абеля существенно проще.
_ _ sin n(l — sin п)
Пример 44. Рассмотрим ряд > .
П = 1
45
Простейшая оценка
иии о поведении ряда У
П=1
sin n( 1 — sin п)
sin n(l - sin ?i)
п
sin n( 1 — sin n)
^ — не дает информа-
n
Представление
в виде произведения апЬп, где ап = sin п и
п
1 - sin п
Ьп = также не дает информации о сходимости этого
п
п
ряда, поскольку хотя последовательность {Лп}, Лп = aq,
<7=1
ограничена и lim Ьп = 0, но последовательность {6П} не мо-
П—ЮС
нотонна; таким образом, условия признака Дирихле не вы¬
полнены. Покажем, что этот ряд расходится. Действитель-
оо
но, ряд сходится в силу признака Дирихле. Так как
. 71
п = 1
sin2 п 1 cos 2п ^ cos 2п
= , ряд > — сходится в силу при-
п In In in
п ~ 1
оо - оо.?
\-л 1 г-л sin п
знака Дирихле, а ряд > — расходится, то и ряд >
' 2 п ' п
П —1 П=1
расходится, откуда следует расходимость и данного ряда, no-
sin n(l — sin n) sinn sin2 n
скольку = .
п п п
°° cos /па
Пример 45. Рассмотрим ряд ^ . Последова¬
ла 1
тельность ап = cos у/па не является бесконечно малой (доста¬
точно рассмотреть подпоследовательность апа), откуда сле¬
дует, что данный ряд расходится при q 0 и любом а. При
любом а и q > 1 данный ряд сходится абсолютно. Если а = О,
то данный ряд расходится и при 0 < q ^ 1. Итак, осталось ис-
ОО /—
Ecos у/па . „
при о ^ 0 и 0 < q ^ 1 •
п = 1
Имея в виду формулу Тейлора
Ф(п + 1)-Ф(п) = Ф'(п) + Ф"(п+вп), 0 < 0„ < 1,
46
_ / f соs\/ia
рассмотрим функцию Ф(д?) = / ———at, производная ко-
1
торой при х — п равна CQS . Приведенная выше формула
ос
Тейлора показывает, что если ряд Ф"(п +0П) сходится, то
п = 1
сходимость рассматриваемого ряда эквивалентна существо¬
ванию предела Ф(п) при п —► оо.
Начнем с оценки Ф"(п + 0П). Из равенства
„ , -asinv/xa qcosy/xa
Ф"(*) =
я**1
, к
получаем, что |Ф (х)| ^ —-г-, где к зависит только от q и а.
5
Следовательно, для q 6 Г 1| ряд ^ Ф"(п + 0П) абсолютно
' ** П=1
сходится.
Покажем, пользуясь критерием Коши, что для этих значе¬
ний q существует и lim Ф(я). Действительно, пусть £ > 0.
г—f+OO
Интегрируя по частям, получаем
1*(* + 0-♦(*)! =
2 sin уДа
at4~h
x+i 2 ( 1\ Xf
sin уДа
dt
*
2 2 2 / 1\ mf dt ^ 8
- 1 + a(9 2j J -1 "
^a(x + £),-i ® \ 2/7 ^
откуда и следует существование lim Ф(я). Итак, данный
X-f + OO
ряд сходится для а^0и~<д^1.
Пусть теперь а^0и0<^|. В таком случае при¬
веденные выше рассуждения не позволяют утверждать, что
47
ряд ^ Ф"(тг 4- Эп) сходится. Напишем для функции Ф(х)
п — 1
формулу Тейлора второго порядка
Ф(п + 1) — Ф(п) =
cos y/nat a sin y/nat q cos у/ппс ш
= JS 2пЯ+\ Й5+5 + n)’
0< 0„ < 1.
Из равенства
— a2cosy/xa a (g -f sin y/xoi
4x9+1 2х«+?
aq sin y/xa q(q -f 1) cos y/xa
+ 2*«+i + ^ ’
к
получаем, что ^'"(х)! ^ ~j-, где к зависит только от а и q,
оо
следовательно, ряд Фт(я+0п) абсолютно сходится. Заме-
П= I X
_, . _ . ч / sin \/tor
нив функцию Ф(х) на функцию v(x) = / ———си, такими
1 ОО . /—
Ear sin v™*
—
n = . 2n?+5
сходится. Таким образом, сходимость рассматриваемого ря-
, Л Л 1
да при q f 0 и 0 < q < ^ эквивалентна существованию пре¬
дела Ф(п) при п —> оо. Интегрируя по частям, получаем ра¬
венство
- / v 2 . /- 2 (? — i) /* sin >/ioc .
Ф(п) = —7i2 9sm \/7ia sma+ — / — dt.
a tt 2a J *</+2
l
. [ 81\\\Да . Л 1
Существование предела lim / :—dt, 0 < a ^
x-> + oo J iq+2 2
1
устанавливается точно так же, как и существование предела
lirn Ф(х) при q £ (^,1 Поскольку о ^ 0, то последова-
х—► -Ьоо \ 2
48
телыюсть Ьп = sin у/па не имеет предела (достаточно рас¬
смотреть подпоследовательность 6пз при а ф пку |&| £ N, и
подпоследовательность 6пз+п при а = як, |fc| £ N), то и по¬
следовательность Ф(п) не имеет предела. Итак, данный ряд
при а^ОиОсд^- расходится.
Для исследования абсолютной сходимости при - < q ^ 1
воспользуемся стандартной методикой — используем нера¬
венство
|cos<y/nar| cos2 у/па 1 cos 2у/па
пЯ ^ пЯ ~ 2пЧ+ пч
^11
Так как ряд > -—, - < q ^ 1, расходится, то из этого нера-
п = 1 оо о /— .
Ecos* у/па 1
q ’ 2 < ^
п = 1
E|cOSv/™*| 1
, 2 ^ ^ ^
П = 1
Сведем вместе все полученные выводы. Данный ряд схо¬
дится абсолютно при q > 1 и любом а; сходится условно при
-<^1иа^0; расходится при всех остальных комбина¬
циях значений q и а.
Гораздо чаще, чем для рядов с неотрицательными члена¬
ми, при исследовании рядов, члены которых меняют знак,
оо
используется разложение членов ап ряда ^ап в сумму:
ап = Сп^ + сп^ + ’ Ь Сп^*
Это связано с тем, что оценка скорости стремления последо¬
вательностей {с^}, 1 ^ i ^ к, к нулю обычно ничем не легче,
чем последовательности {an}, а интерференция положитель¬
ных и отрицательных членов в каждой из последовательно¬
стей {с£>}, 1 ^ i <С fc, может быть существенно более про¬
стой, чем в последовательности {ап}. Напомним, что опреде-
оо
ленный ответ о сходимости ряда ап при таком разложе-
П — 1
49
нии возможно дать только тогда, когда среди рядов с^,
1 ^ t ^ к, расходится не более чем один. n_1
Будем считать, что ап достаточно гладко зависит от п.
Если последовательность {ап} не является бесконечно малой,
оо
то в силу необходимого условия ряд ^ ап расходится. Если
п = 1
lim ап = 0, то, пользуясь формулой Тейлора, можно ПОЛу-
n-f 00
чить представление ап в виде суммы:
с1,п . с2,п ск,п .
а"-^г + ^ + '" + ^г + Гк’п>
где или rfc n = 0(^7). или г*,„ = О п 00 > и
or 1 < аг < ... < otk < orfc+i- Главная трудность здесь — ис-
оо
следование ряда ^г*>п. Практически применяется два спо¬
соба: n=1
1. Если otk+\ > 1, то представление г*|П = О
п —у оо, показывает, что ряд г*(П сходится абсолютно.
п = 1
2. Если последовательность {с*п} положительна, то ряд
£ (^7 + »•*.") = £ (^7 + ° (;?£)) является ряд°м с
П=1 П=1
неотрицательными членами и, следовательно, сходится или
оо
Ск п
расходится одновременно г рядом > —
п = 1
ОО п
Пример 46. Рассмотрим ряд ^ g > 0.
п = 1
Так как |\/п ^1 - е (~^ ^ ——г, п —► оо, то данный ряд
расходится при q ^ -, поскольку не выполнено необходимое
условие сходимости, и абсолютно сходится при q > ^ в силу
50
признака сравнения. Используя формулу Тейлора, получаем,
что
а„ = у/п (l — eL$1) = i_ + 0f l ) ,
V / и*-* 2n2q~i \n«-ij
q > 0, n —> oo.
00 (— l)n+1 1
Ряд ^ ? Я > 2 ’ сходится в силу признака Лейбница.
г» = 1 ^
РяД £ (^гт + 0 (^гт) ) ■ п °°' «°Д™ при Я > I
3
и расходится при q ^ в силу признака сравнения. Объ¬
единяя все сказанное, получаем, что данный ряд расходится
3 3 3
при 0 < q ^ сходится условно при - < q $ - и сходится
3
абсолютно при q > -.
00
Пример 47. Рассмотрим ряд > : , q > 0. Про-
" 2пя + sin п
п = 1
стеишая оценка
sinn
^ показывает, что при
2п« - 1
1
<
2пя + sin п
q > 1 данный ряд сходится абсолютно в силу признака срав¬
нения. Для q € (0,1] начнем с исследования сходимости. Ис¬
пользуя формулу Тейлора, получаем, что
sin г ' 1
°п “ 2пя
inп _ sinп / sinn\“ _
-fsinn 2пя \ 2пя )
sinn/ sinn /sinn\\
= 2^+4**vJ =
sin n sin2n /sin 2n\
= 2^-- 4^r+4^7’
OO
_ V-^ Sin n
Ряд 2nq' > ^ > » сходится в силу признака Дирихле. Ряд
/ sin2 n / sin2 п \ \
/ , I ^2q~ 0 I ~~n2q~ ) ) ’ 11 00’ схоДится или раСХОДИТСЯ
n = 1 ' \ / /
51
00 • 2 -2 1
sin П „л sin 71 I
Esin n
- - £ •' • *aK KaK
n = l
oo
4^2 q /\n2q gn2 q
cos2 n y^cos2ti
и ряд > 2~ при q > 0 сходится в силу признака
Sn2q Sn‘2q
n = l
—> I
Дирихле, а ряд ^ 2 сходится тогда и только тогда, когда
, 8п2ч
П = 1
■Л
1 ^(нт2п /sin 2п\\
q > то и ряд ^ I ^ + о II I, п -+ оо, сходится
П—1 ' ' ' '
1 1 I,
ПРИ Я > 2 и РасхоДится ПРИ 0 < Я ^ 2 Используя соотноше
ние
I sin2n 1 /1 о \
ап ^ ^ : = — (1 ~ COs2n)
2п? -f sin п АпЯ + 2 sin п
оо
так же, как и выше, получим, что ряд расходится
п— 1
при 0 < q ^ 1. Объединяя все сказанное, получаем, что дан-
1
ныи ряд расходится при 0 < q ^ ", сходится условно при
- < q ^ 1 и сходится абсолютно при q > 1
оо
°°^ / /_ПП"И\
Пример 48. Рассмотрим ряд sin n* In ( 1 4- 7=— ).
£1 \ v* ;
( .(_!)"+! \ 1
Простейшая оценка sinn In I 1 + — < не дает
V у/п ) у/п
00 / ( l)n+1 \
информации о поведении ряда sin п- In I 1 + -—~— ) .
t[ \ >/» /
Используя формулу Тейлора, получаем, что
( (-1)Л+1\
ап = sin п In ^1 Н —j=~—J =
=s”n ^+° (^)) ■" -*”•
ОО / gju
Так как (— l)n sin n = sin(l+7r)n, то оба ряда —=.
nZ\ vn
52
и V сходятся в силу признака Дирихле. Ряд V Ьп, где
. 2п ,
П г. | п = 1
сходится в силу признака сравнения. Следова
n I I I Sin 711
ли ряд сходится. Далее, \ап \ — —^=—, п —у оо, \
у/ 71
Isinnl sin2 п 1 cos2n ^>cos2n
—т=~^ ^ —7=“ = *r“F= гг^ • Гак как ряд > - _ с
у/п у/п 2у/п 2у/п 2у/п
^ 1
дится в силу признака Дирихле, а ряд N —7= расходится в
пЫ 2V^
хо-
силу признака сравнения, то ряд ^|ау|| расходится. Итак,
п- 1
данный ряд сходится условно.
^ (-1)1^1
Пример 49. Рассмотрим ряд ^ —. Пось
скольку
?!'/
Л = 1
1
п?’
то данный ряд сходится абсолютно при q > 1 в силу призна¬
ка сравнения и расходится при q 0, гак как не выполнено
необходимое условие сходимости. Пусть q Е (0, 1]. Члены
последовательности {ап|, ап = , меняют знак то-
71
гда, когда номер тг переходит от значения т2 — 1 к значе¬
нию m2, т Е N. Отсюда можно вывести, что последователь-
п
ность Вп — (— неограничена, но поскольку этот
т= 1
факт ничего не дает в решении вопроса о сходимости дан¬
ного ряда, не будем проводить его доказательство. Восполь¬
зуемся следствием 2 утверждения о группировке членов ряда
(см. стр. 16). Если
^ пЯ v ; ^ п<1
п—к2 n—k'J
53
то в силу этого следствия ряд ^ Ак сходится или расходится
fc=i
одновременно с данным рядом. Из неравенств
2 п( 1 А _ 2* +1 Дv 1
+ Ук2*) к2* < 2^ пч
1 п=к2
2* + 1 2 1 \ ,
(&Tw = k^+0{i&)'
следует, что Ак = (-1 )к + ■ гДе *>к = О ( — ), к -* оо.
-М
Л2* / ’
/ I 1 °°
Отсюда видно, что при q € ( 0, - ряд ^ Л* расходится, по-
' " J t=i
скольку не выполнено необходимое условие сходимости. Если
же q Е ( l], то ряд сходится в силу (бедствия 1 из
50 2
теоремы сравнения, а ряд (— 1)* ргтг сходится в силу при-
* а: ~Я 1
к = 1
знака Лейбница. Итак, ряд сходится при q € l| и
Ы] “
расходится при q €
. Объединяя все сказанное, полу-
“(_!)[•/*] 1
маем, что ряд > расходится при q ^ сходится
" пЯ 2
условно при q £
П = 1
е в-']
и сходится абсолютно при q > 1.
[Заметим, что из полученного вывода о поведении ряда
следует, что последовательность Вп = D-
п = 1 т = 1
неограничена, ибо в противном случае в силу признака Ди¬
рихле этот ряд сходился бы при q > 0.
Произведение рядов
ОО оо
Пусть даны два ряда ^ ап и ^ Ьт. Рассмотрим все
n=1 m=1
возможные пары произведений (an-6m), п 6 М, т € N, т. е.
бесконечную матрицу:
(a\b\ 0261 03^1
а\^2 <*2^2 <*3^2
а\Ьт а^Ь
т <*з Ьп
апЬ\
апЬ2
<*пЬг,
(3)
Занумеровать члены этой матрицы можно многими спо¬
собами; таким образом получим множество рядов, составлен¬
ных из этих чисел, например:
Al: Я1&1“НД2&1+а2&2+а1&2+вЗ&1+вЗ&2+аЗ&3+Д2&3+а1&3 + ' * *
или
А.2 : ci\b\ + 0162 + CI261 + a36i -f- 0262 + ai^3 + * ■ *
00
Каждый такой ряд называется произведением рядов ^ ап и
оо
Х>-
П = 1
тп= 1
Если один из рядов А\, Аг> • • • сходится абсолютно, то и
все остальные также сходятся абсолютно и суммы всех таких
рядов равны. Таким образом, в случае абсолютной сходимо-
оо
сти полученного ряда значение произведения рядов ап и
оо гх — 1
bm определено однозначно, хотя представляется это про-
m= 1
изведение различными рядами.
оо оо
Теорема Коши. Если каждый из рядов ^2 ап и 6т
п=1 т=1
сходится абсолютно к Аъ В соответственно, то произведение
этих рядов сходится абсолютно к АВ.
55
Если члены матрицы (3) не образуют абсолютно сходяще¬
гося ряда, то и сходимость, и величина полученного из нее
ряда зависят от способа нумерации этих членов. Одним из
распространенных методов рассмотрения произведения ря
дов является его представление в форме Коши.
ведением этих рядов в форме Коши.
В силу теоремы Коши из абсолютной сходимости двух ря¬
дов следует и сходимость их произведения в форме Коши.
Как- показывает следующая теорема, произведение в форме
Коши сходится и при более слабых условиях на сомножители.
Теорема Мертенса. Если из двух сходящихся рядов
оо оо
ап и Ьт хотя бы один сходится абсолютно, то их про-
П — 1 ТП— )
изведение в форме Коши сходится и его сумма равна произ¬
ведению сумм сомножителей.
лютно, первый — к 1, второй — к 2 (см. стр. 8). Следова¬
тельно, их произведение абсолютно сходится к 2. Записывая
это произведение в форме Коши, получаем равенство
оо
ОС)
Определение. Пусть даны два ряда ^ ап и ^ 6т. Ряд
сп, где сп = а\Ьп + «2^п-1 + • • • + dnb] называется произ-
п = 1
Пример. Оба ряда
оо
расходятся. В то же время
сходится абсолютно,
56
Таким образом, теорема Коши дает только достаточное,
но не необходимое условие абсолютной сходимости произве¬
дения рядов в форме Коши.
Точно так же и теорема Мертенса дает только достаточ¬
ное, но не необходимое условие сходимости произведения ря¬
дов в форме Коши даже при условии сходимости каждого из
сомножителей.
Пример. Рассмотрим произведение неабсолютно сходя-
щегося ряда 7=— на себя. В этом случае
n=l V"
сп = = + 'гг , == + • • • +
\\/п у/2-s/n — 1
+ 1 _1_Л
у/ку/п — к -f 1 >/я/
Поскольку > -7=-—7=5 ( П > 1) И ЧИСЛО СЛаГав-
VVn - * + 1 у/^у/^ 9
оо
мых в сумме равно п, то \сп\ > 1 и, следовательно, ряд ^ с„
п = 1
расходится.
Пример. Рассмотрим произведение неабсолютно сходя-
°° ( — 1 )п
щегося ряда ^ на себя. В этом случае
11 I 1
h — — + • • ■ H 1 гг 4 • 4 --
I n 2(n— 1) Я\п' (1+ч 7L
1 / 1\ 1/1 1 \
Г I ^ ) H г ( 4 г 4 • 4
n-fl\ n J ?i 4 1 \ 2 n — ] J
= (-1)п-4т(Ьп + ^ + о(1)).
n 4 1
Полученное соотношение показывает, что lim |cn| = 0.
п—юс
Так как |с„| > и |сп+,| = |с„| + —j— ( —- |г„|),
/14 1 п 4 2 \ п 4 2 /
то последовательность |с„| монотонна. Таким образом, в си¬
ро
лу признака Лейбница ряд ^сп, т. е. произведение ряда
~ (_П" + 1 n = 1
2_\ на себя в форме Коши, сходится.
п = 1
/_ ПП+1
Сумма ряда ) равна In 2 (см. стр. 22). Теорема
f п
п = 1
Мертенса не применима к произведению
^ЫГ1 ^(-I)n+1
п — I п = 1
ОО
Равенство сп = In2 2, где сп = (-l)”*1 V' уста-
навливается следующей теоремой:
ОО оо
Теорема Абеля. Если оба ряда £а"и £ 6,„ схо-
п — 1 т= 1
дятся и их произведение в форме Коши ^Г\*Г1 сходится, то
ОО ОО ПС
53Cn = •
п — I
n — 1 n — 1 m = l
§ 2. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
Определение. Пусть дана числовая последовательность
{рп}. Символ Р\ Р2 РЗ• • 'Рп • называют бесконечным про-
оо п
изведением и обозначают рп. Число Рп = называ-
п~ 1 <j= 1
ется n-ым частичным произведением.
оо
Определение. Бесконечное произведение рп называ-
п = 1
ется сходящимся, если последовательность Рп имеет предел,
отличный от нуля, в противном случае это произведение на¬
зывается расходящимся. Если lim Рп = 0, то говорят, что
ОО П—>CXJ
произведение рп расходится к нулю. Если бесконечное
п - 1
произведение сходится, то число Р = lim Рп называют зна-
n -f оо
оо
чением этого произведения и пишут: Р = рп.
п — 1
Пример 1. Рассмотрим бесконечное произведение
п(-^
Так как
^ _ 6 _ (я -• 2)(п 4- 3)
п(п + ]) п(п + 1)
2 7 п(» + 5)
4-5 "(п + 2)(п + 3)’
1 *2*3 п 6-7 •••(п +5)
1 6 2 7 п(п + 5)
то Рп = Т7 77 ''' 7—Г~о\7"" ,"?i' откУЛа получаем, что
3 4 4-5 (п + 2)(п + 3)
Рп ~ 3 4-5 • • (п + 2) 4-5 (п + 3) ~
_ 1 2 (n+4)(n + 5) _ 1 (п + 4)(п+5)
~ (п+ 1)(п + 2)-4-5 _ 10 (п + 1)(п + 2)
Из полученного равенства видим, что lim Рп = —, т е.
п-^оо 10
данное бесконечное произведение сходится и
59
Пример 2. Рассмотрим бесконечное произведение
П 4^ГТТ Имеем:
П=1
Рп =
(2-4-6 • • -2п)2
1 3 3 5 (2т* — l)(2n + 1)
(2п)!!
.(2n- 1)!!.
1
2n+ 1
Для нахождения lim Рп поступим следующим образом. Me-
п—►ОО
тодом математической индукции проверяется, что
2
/
' (т - 1)!! 7г
yj т = 2к} к Е N,
771
(m- 1)!!
тП
, т — 2к — 1,
Из этого равенства и неравенства
w п
7 2 2
J sin2n + 1 xdx < J sin2n xdx < J sin2n 1 x dx% n E N,
0 0 0
получаем следующие соотношения:
(2n)M (2‘n— 1)!! ж (2n — 2)!!
(2n+l)!! (2п)!! 2 (2и-1)!Г
/ (2п)\\ \'2 1 ^ тг ^ / (2п)!! \2 1
\(2п — 1)!!/ 2п+1 < 2 < \(2п-])!!/ 2^’
2 71 + 1
/ (2n)!! VI / (2n)!! V
\(2п — 1)!! / 2 я \(2и — 1)!! /
1 ( (2т») М Л2 1 тг
“ 2n V(2п - 1)!!/ 2п + 1 < 4тг
Л .. / (2n)!! \2 1 тг
Отсюда следует, что lim — -—— = -, т. е.
л) . 9 n-юи\(27i — 1)!!/ 2тг + 1 2
Я* ТТ 471
2 = 11 4 [ то Равенство называется формулой* Вал-
гг = 1
лиса.
Из формулы Валлиса можно получить следующие равен¬
ства:
СК>
60
и Л _ —±—\ = п 2п(2я+2) = 1
11Д (2*1+ 1)=»^ 11 (2П+1)2 4
Действительно, для первого бесконечного произведения име¬
ем:
1
Р(.) =
Ад
и, следовательно
П
11 4q2 — 1
q= 1
lim P<‘* = — 1
Для второго бесконечного произведения имеем:
Р(2) _ 4-2-6-4 • • • (2п + 2)-2п
" “ 3-3-5-5-(2n + l)(2n+ 1) ”
_ 2 [4-4 б-6 • • • (2п - 2)-2п-2п] (2п + 2)
[3-5 • • • (2n + I)]2
_ 2п + 2
2(2n -f- 1)
и, следовательно,
( (2»)!! У 1
\(2п - 1)!!/ 2п 4- 1 ’
(((2^Лй) -5Гм) = Г
п-+оо
Пример 3. Рассмотрим бесконечное произведение
. Используя равенство
п = 1
1 + ^ + 7Г 4* * * * + — — In П + Сэ + о( 1)| п—> оо,
Z 6 п
где Сд — постоянная Эйлера, получим, что
n!el+*+ +n eino+c,+o(i) с п
Рп “ (В +1)! “ ~_е ,ТТТ(1 + о(1))’
п —► оо.
Следовательно, lim РЛ = eCj.
61
Отбросив в бесконечном произведении JJp„ первые т чле-
п = 1
оо
нов, получаем остаточное произведение J"J рп.
оо n = m+1
Если произведение рп сходится, то сходится и любое
П = 1 оо
остаточное произведение рп; обратно, из сходимости
n=m + l оо
любого из остаточных произведений рп и условия р* ф О,
ПГШ+1 ОО
I ^ к ^ т, следует сходимость произведения р„. Другими
П = 1
словами, отбрасывание или присоединение в начале бесконеч¬
ного произведения конечного числа множителей, отличных
от нуля, не влияет на его сходимость.
Прежде чем формулировать основные свойства бесконеч¬
ных произведений, заметим, что из сходимости бесконечного
произведения следует, что, начиная с некоторого номера, его
сомножители не должны менять знака. Поэтому в дальней¬
шем будем всегда предполагать, что все числа рп положитель¬
ны. оо
Утверждение. Если бесконечное произведение п Рп
ОО П = 1
сходится, то lim ТТ р„ = I.
m-юо АХ
п=т+1
Следствие. (Необходимое условие сходимости бес¬
конечного произведения.) Если бесконечное произведе-
оо
ние 1| рп сходится, то lim рп = 1.
■*>А п-юо
П = 1
Пример 4. Рассмотрим бесконечное произведение
ТТ п + * о л + 1 тпг Я + 1
II Здесь рп = и lim pn = 1; Рп = I I =
П П а—►оо ха, q
п- 1 <7=1 4
— п -f 1 и lim Рп = 4-оо, т. е. данное бесконечное произведе-
п—►оо
ние расходится.
Таким образом, условие lim pn = 1 является необходи-
п—^оо
62
мым, но не достаточным условием сходимости произведения
оо оо
рп (сравните с условием ап 0 для ряда ^ ап).
п=1 п=1
Основным утверждением в теории бесконечных произве¬
дений является оо
Теорема. Сходимость бесконечного произведения п Рп,
оо п=1
рп > 0, эквивалентна сходимости ряда ^1пр„. При этом,
00 оо п = 1
если ^ 1пр„ = S, то рп = es.
п—1 п=1
Пример 5. Исследовать сходимость бесконечного произ>
ведения
ЙЫ>
n=1 ( 1 \ 1
1ение. Так как In I 1 + — I ~ — при х > 0, п
/ , ч V " / "
E'-O-i).
то ряд 2^I 1 + ~ }» соответствующий данному произве-
п = 1 ' '
дению, сходится при х > 1 и расходится при 0 < х ^ 1. Если
же х ^ 0, то рп = ( 1 + — ) не стремится к 1 при п оо.
V п* / ОО у j \
Следовательно, произведение ТТ (1 4- —) сходится при х > 1
nVi V "V
и расходится при х ^ 1.
Пример 6. Исследовать сходимость бесконечного произ¬
ведения П(»+о.
п=0
Решение. Если а ^ 0, то рп = 14еа^п ^ не стремится к 1
при п —► оо, следовательно, данное произведение расходится.
оо
Пусть а<0. Тогдаln(l+een) ~ е-*®'", п -► оо, и ряд ^ е~^п
п=0
сходится, откуда следует сходимость ряда ^^1п(1 4- еап) и,
п=0
00
следовательно, сходимость произведения JJ(1 4 еап).
п=0
Как видно из этих примеров, при исследовании сходи-
63
мости бесконечного произведения J"J рп удобно представить
п= 1
его сомножители рп в виде р„ = 1 4- ап. Тогда произведем
оо
ние и соответствующий ему ряд принимают вид По+«•.),
ОО п = 1
^^1п(1 + ап) и условие рп -* 1, п оо, эквивалентно усло-
п = 1
вию оп —>> 0, п —► оо. Если ап —> 0, г? —> оо, то 1п(1 + ап) =
о2
= а„ 4- о(а2), п оо. Применяя основную теорему,
получим следующие утверждения:
I. Если рп = 1 + ап и последовательность ап локально
оо
сохраняет знак, то сходимость произведения Д рп эквива-
ОО П = 1
лентна сходимости ряда ап.
П”1 00 оо
И. Если pn = 1 4- <*п и оба ряда ^ ап и ^ а2 сходятся,
оо п = 1 п=1
то произведение J~J рп сходится.
n = 1 сю
Заметим, что если ряд ^ а„ сходится абсолютно, то ряд
оо п = 1
<*п сходится (см. задачу 25, стр. 317).
n = 1 оо оо
III. Если один из рядов ^ ап и ^ от2 сходится, а второй
п = 1 п = 1
оо
расходится , то произведение рп расходится.
п — 1
Пример 7. Исследовать сходимость бесконечного рроиз-
т-г п3 4- 4п 4- 8
ведения I I г-——
j 71 + 1
_ гтл и3 + 4п 4- 8 , 4п 4- 7
Решение. Так как 0 < = ; 1 = -=—-, п £ N, и
гг5 4- 1 п3 4- 1
4п 4- 7 4 ^4п + 7
■ о - ~ -т, п ч оо, то ряд у ——- сходится и, следова-
71° 4” 1 7lz ' TV* 4" 1
П — 1
64
■pr n + 4n + 8
тельно, сходится произведение I I = —.
AJ: + 1
n = l
Пример 8. Исследовать сходимость бесконечного произ¬
ведения ТТ cos -7=.
„=1 ^
Решение. Так как cos -4= — 1 < 0, n Е N* и 1 —cos -L= ~ ,
у/п у/п 2п
п —У оо, то ряд (cos "4= “ 1) расходится и, следователь-
п=1 ' ^ п ^
1
но, расходится произведение ТТ cos—
nVi Vй
Пример 9. Исследовать сходимость бесконечного произ¬
ведения
y-r / п -I- sin п \
„УД-" )'
n + sinn
Решение. Здесь последовательность ап — 1 =
п
sin п
не сохраняет локально знака, поэтому необходимо
п оо оо оо оо . о
Sin 71 ч 9 ч Sin П
рассмотреть оба ряда: > an = > и > a* = > —^ .
n=l n=l n=l n=l
Так как первый ряд сходится в силу признака Дирихле,
а второй — в силу теоремы сравнения, то произведение
п(^)
сходится.
Пример 10. Исследовать сходимость бесконечного про-
оо
изведения
Решение. Так же как и в предыдущем примере, необхо-
Й(*+ЗД-
[ие. Так же как и в
* V44 (~1)П+1 V44 ^ гт
димо рассмотреть оба ряда: > у=— и > —. Первый
П=1 П=1
ряд сходится в силу признака Лейбница, а второй — гармо¬
нический ряд — расходится. Следовательно, произведение
00 / (_1)л+1\
ТТ [ 1 + -—4=— ) расходится.
п=1 V V» ;
Пример 11. Исследовать сходимость бесконечного про-
65
~ / (_l)[log2n)4
изведения М I 1 Н I.
п= 1 ' 71 /
Решение. Опять необходимо рассмотреть два ряда:
- (_l)[log,n] 1 _ Т *
> и > —т. Второй ряд сходится. 1аким обра-
“ п п1
п=1 п=1
зом, сходимость данного произведения эквивалентна сходи-
мости ряда у . Покажем, что он расходится, поль-
1 71
п = 1
эуясь критерием Коши. Так как [log2n] сохраняет знак, если
2m < п < 2m+1, т € N, то
от + 1 _ 1
_ ^ 1 2т _ 1
2-J п > 2т+1 ~ 2
п=2т
п=2т
В силу произвольности m € N полученное неравенство по¬
следовательно,
~ "J
казывает расходимость ряда 2^ - и,
ТТ Л (-1)[,ок'п1\
расходимость произведения 11(1-1- 1 •
»=1 v п >
Пример 12. Исследовать сходимость бесконечного про-
ОО
изведения а„, где
П = 1
02т-1 = ( 1 + "4= ) . «2т = ( 1 7= + ~ ) > Ш G
\ ут / \ у/т т /
Решение. В этом случае
{-4=, n = 2m — 1,
j vm. т G N »
=, п — 2т,
т ут
оо оо
и оба ряда ^ап и ^ расходятся, поэтому ни одно из
П=1 п= 1
вышеприведенных утверждений не позволяет сделать вывод
о сходимости или расходимости данного произведения. Рас-
66
смотрим непосредственно последовательность Рп = JJay.
Соотношения Я~1
показывают, что сходимость последовательности Рп эквива¬
лентна сходимости последовательности РД = ТТ (1 + —— ),
q= 1 ' Яу/Я )
т. е. произведения ТТ f 1 4- —\ Так как ряд У^ —^т=
V ту/т) " ту/т
m=l v v ' m=l Y
сходится, то и произведение ТТ (1 + —”7= ) > и, следова-
АА \ ту/т)
оо m=l 4 V /
тельно, произведение J"J ап сходятся.
п = 1 ОО
Теорема. Бесконечное произведение п Рп, Рп>о, расхо-
П = 1
т
дится к нулю тогда и только тогда, когда lim Ylnpn = — оо.
m—►оо
т—►оо 4
п = 1
Следствие. Бесконечное произведение JJ( l4on), ап > — I,
П = 1
п (Е N, расходится к нулю, если
оо
1. lim ап = 0, -1 < an < 0, ?i € N, и ряд У^ an расхо-
П —► ОО А—^
П = 1
дится;
оо оо
2. ряд ^ ап сходится, а ряд ^ а2 расходится.
П=1 П=1
Пример 13. Исследовать сходимость бесконечног о про-
00 2п + 2
ПАП f- *
2п"+~3'
П = 1
т> 2п + 2 -1
Решение. В этом случае а„ = — 1 = < О,
2п + 3 2п + 3
67
ОО ОО J
lim ап = 0 и ряд ап = - расходится. Следо-
п—►оо ' 2п 4-
, 2п + 3
п = 1 П=1
вательно, данное произведение расходится к нулю.
Точно так же расходятся к нулю и бесконечные произве¬
дения из примеров 8 и 10 (стр. 66). ^
Определение. Бесконечное произведение fjpn, Рп > 0,
ОО Г1=1
п — 1
сходится абсолютно тогда и только тогда, когда абсолютно
о
п = 1
Пример 14. Исследовать на абсолютную и условную схо-
сходится абсолютно, если ряд In рп сходится абсолютно.
П = 1
оо
Бесконечное произведение Рп, рп >0, сходится условно,
со п = 1
если ряд In рп сходится условно.
п = 1
Критерий абсолютной сходимости бесконечного
оо
произведения. Бесконечное произведение JJpn, Рп > 0,
сходится абсолютно тогдг
оо
сходится ряд £>„ - 1).
П = 1
Пример 14. Исследовг
димость бесконечное произведение Д П + ■ оТТ JT )>
. п п t V ^ П|П "Ь / /
Q > 0. П~1
Решение. Так как —— — > 0 для всех п £ N, то
па In(71 -+■ 1)
сходимость этого произведения может быть только абсолют¬
ная. Согласно критерию абсолютной сходимости, рассмо-
ОО
трим ряд ^ —— —. Так как в силу интегрального при-
' па 1п(п + 1)
П=1 > %
знака этот ряд сходится (абсолютно) при а > 1 и расходится
при 0 < а ^ 1, то и данное бесконечное произведение абсо¬
лютно сходится njJli а > 1 и расходится при 0 < а ^ 1.
Пример 15. Исследовать на абсолютную и условную схо-
тт ( (“l)n+1 А
димость бесконечное произведение ТТ ( 1 + —г—г гг I,
, \ иа ‘п(п 4- 1) у
а > 0. "=1 4 v ;/
68
Решение. Так как
па 1п(п -I- 1)
1
, то дан-
иа1п(п + 1)
ное произведение сходится абсолютно одновременно с беско¬
нечным произведением, рассмотренным в предыдущем при-
°°ч (—l)n+1
мере, т. е. при а > 1. Далее, ряд ~ша у } гг сходится при
п= 1 ' '
оо
всех а > 0 в силу признака Лейбница, а ряд ^
1
" In (п+ 1)
1 л 1
сходится при а ^ - и расходится при 0 < а < - в силу инте-
Z Z
трального признака. Итак, данное произведение абсолютно
сходится при а > 1, условно сходится при - 1 и расхо¬
дится (к нулю) при 0 < а <
Рассмотрим некоторые приложения.
, „ №+ 1) •••(£ + п)
I. Докажем, что пт ; = 0, если
п->оу + 1) • • • (а + п)
О < р < а. Действительно, выражение
+ 1) • • • (а + п)
можно рассматривать как частичное произведение Рп+\ бес-
Y7 [Р +п) п Р + п ,
конечного произведения I I г. Поскольку 1 =
~ (<* + я) + п
11=0 4 '
/3 — а а — /3
= < 0 и ряд > расходится, то произведение
а + п J а + п
+ п
п а + п
п —О
п
П = 1
расходится к нулю, а это означает, что
|im /?(/?+ О • • ■ (/?+«) = о (о < ^ < Q).
п-юо ог(а+1) • • (а+п)
1)п+1пп
И. Исследуем поведение ряда 2_^ — . Этот
п !е"
П = 1
ряд
знакочередующийся, причем
Дп+1
_ (тг + l)n+1 w!en = (1 + £)"
(n+l)!en+1 nn е
ап
т. е. последовательность |ап| монотонна. Следовательно, схо-
69
длмость этого ряда эквивалентна выполнению равенства
lim — = 0. Введем обозначения: Ьп — —г—> Рп — ?*-■ и
п->оо п\еп п\еп оп
1 °°
рассмотрим бесконечное произведение Р — - ТТ Рп- Так как
е
п = 1
г> I ^П + 1 I
частичное произведение = -р\р2 Рп = —г— = &п+1> то
Пп е e&i
равенство lim —:— = lim 6п = 0 есть расходимость к нулю
п—►оо п\еп п—юо
этого бесконечного произведения, а эта расходимость экви-
оо
валентна условию 1прЛ < 0, n € N, и ряд ^ 1пр„ расходится.
Так как n=1
, 6п+1 , (n + l)n+1 , (1 + £)”
In Рп = 1п -г— = 1п ■ ■■ ■ ■■■; - = 1п 2 ,
6п е(п + 1)пП е
Л
то первое из этих условии следует из неравенства I 1 + — 1 < е,
п 6 N, а второе ---- из соотношения ' п'
(—l)n+1nn
Итак, ряд > : сходится.
' п\сп
п = 1
111. Выведем важную формулу представления функции
sinx бесконечным произведением.
Из формулы Муавра (cos z + i sin^)m = cos mz + isinmr,
применяя формулу бинома Ньютона и приравнивая коэффи¬
циенты при мнимой единице в левой и правой частях, полу¬
чаем равенство *
sin mz —
m_1 mini — 1 )lm - 2) a . о
= m cos z sin z ^ cos z sin z + • •
Бели m нечетно, то все степени cos z в правой части этого ра¬
венства четные, следовательно, sin(2n + 1 )z = sinz-P(sin2 z),
1 J-, n oo.
In
70
где Р(у) — многочлен степени п. Если sinzo ф 0, а
sin(2n+ l)zo = 0, то, как видно из полученного равенства, чи¬
сло у = sin2zo является корнем многочлена Р(у). Непосред¬
ственно проверяется, что таким свойством обладают числа
о тптг
yk = sin m = 1, 2,..., п, причем все они различны.
2п ■+■ 1
(Следовательно, многочлен Р(у) имеет п различных действи¬
тельных корней, ни один из которых не равен нулю, и, тем
самым, представляется в виде произведения
Р(у) = А(у - yi)... (у - у„) =
где В = Р(0). Значение В находится из соотношения
sin(2n+l)*
Р(0) = lim —v . J- = 2n + 1.
*-+o sinz
Итак,
sin(2n + l)z = (2 n + 1) sin x
или
£
sinx = (2n + l)sin
2n ■
аму
■ n('-SS)
Пусть x ф жк, к E Z. Фиксируем число g такое, что
|x| < (g + 1)^г Для n > g запишем полученное равенство в
виде sinz = U^ V^n\ где
t/<n) = (2n + 1) sin ;
2n+1ii V s*n2 2птт /
, »— . -2n+
m=<j+l \ Sin 2п + 1 /
Для рассматриваемых х, g, п имеем: U^ ф 0 и, следователь-
71
Так как при этих х и q имеем
lim t/in) =
■.“Я,(Р" + ,)-5ТтЙ(‘-5^))-
m=l 4 7
то существует и предел
sin х
V4 = lim K/n> = —.
П-fOO * Uq
Итак, для x ф жку к Е и любого q, удовлетворяющего
неравенству |х| < (q -f 1 )тг, имеем равенство
sin* = ия уч = * (д (] - да))
Из выпуклости вверх функции у = sin я на |о, —J следует,
2 / 7Г\
что — (р < sin <р для у? Е (О, — !, откуда получаем, что
ж \ 2 /
7ГШ 47Г2Ш2
Sin
2n -f 1 7г2(2п + 1)
и так как sin
2n + 1 (2n -f I)2,
ПО-етИ"*'-
m=<j+1
(X) о
Гак как ряд « при любом х сходится абсолютно, то
' 4тг
т= 1 оо / о ч
х М
бесконечное произведение ( 1 - Т~~2 ) сходится
т=</+1 ' 171 '
72
n / ^2 \
абсолютно. Так как последовательность jQ f 1 — J
m=<j+l ' 171 '
убывающая, то отсюда получаем неравенство
к,-< П (• - £?) < К,'"' < I
т=<7+1
Переходя в нем к пределу при п —> оо, получаем, что V* ^
00 / 2 \
<: Vq ^ 1. Так как lim V* - lim ТТ ( 1 - ) = 1,
q—¥oc> 4 q-юо V 4mz У
т=</+1 4 7
то, переходя в последнем неравенстве к пределу при q —► оо,
получаем, что lim VQ = 1, и, следовательно,
q-¥oo
sin а: = lim f/c- lim VQ = lim a: TT^ ( 1 ^ ) .
q-+oo q-юо q-*oo 11 V 7Tzmz J
m=l x '
Итак, получаем формулу:
л
■*пО-та)-
m = l 4 7
Заметим, что это равенство было выведено при условии,
что х ф irk% к Е Z. Но если т = коп, А:0 Е то левая его часть
равна нулю и правая часть также равна нулю, поскольку один
из сомножителей в бесконечном произведении обращается в
нуль. Таким образом, полученная формула верна для всех
х Е Ш.
s 3. ФУНКЦИОНАЛЬНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ.
РАВНОМЕРНАЯ СХОДИМОСТЬ
Отметив в предыдущем параграфе взаимосвязь рядов и
последовательностей, мы рассматривали только свойства чи¬
словых рядов, поскольку соответствующие свойства число¬
вых последовательностей изучаются ранее. В этом же пара¬
графе центральное место занимает новое понятие — равно¬
мерная сходимость, и поэтому свойства последовательностей
и рядов будут рассматриваться параллельно.
Определение. Пусть дана последовательность функций
{/„(х)}, х 6 X. Точка хо Е X называется точкой сходимости
этой последовательности, если все функции /п(я) определены
в точке х0 и числовая последовательность {/п(^о)} сходится.
оо
Определение. Пусть дан функциональный ряд ип(я)
п = 1
Точка хо Е X называется точкой сходимости этого ряда, если
все члены ряда функции ип(х) определены в точке хо и
пи
числовой ряд 5>«(*о) сходится.
п = 1
Определение. Совокупность всех точек сходимости по¬
следовательности {/п(*)} называется множеством сходимо¬
сти последовательности {/п(я)}-
Определение. Совокупность всех точек сходимости ряда
~Ю по
У] ип(я) называется множеством сходимости ряда un(^)
П=1 п = 1
Аналогично определяются множества абсолютной и услов¬
ной сходимости ряда.
На множестве М сходимости последовательности (ряда)
оо
определена функция /(х) = lim /п(х) (.S'(x) = wn(x)).
n-+(XJ *
п = 1
Фактически мы уже находили множество сходимости по¬
следовательности (ряда), когда исследовали последователь¬
ность (ряд), члены которой зависели от некоторого параме-
74
тра. Так, множество сходимости последовательности
будет множество М = {х : х > 1}, множеством сходимости
о° j
ряда ^ п-^-у будет множество М = {х : |х| > 1} и т. д.
х"
п = 1
Рассмотрим еще два примера.
Пример 1. Последовательность {/п(я)Ь /п(*) = n* Inn,
имеет своим множеством сходимости множество М =
= {х : х < 0} — отрицательную полуось — и сходится на М
к нулю. оо п
Пример 2. Рассмотрим ряд V] г-. Если |х| < 1, то
~ 1 -f- в
п = 1
,im (/_!£!!_= iim w_ = w<i.
n-foo V 1 + я «-►оо л/l +
\/l + x^n
Если |x| > 1, to
lim Ш1-. lim рт f/j-
n —► оо V 1 + x2n n-^oo X V 1
1 =A<>.
|x| V 1 + *“2n 1*1
rn
Если |x| = 1, to
1 Л
» = В силу радикального признака
1 Н- xzn 2
Коши и необходимого условия сходимости ряда получаем, что
множеством сходимости (абсолютной) данного ряда является
множество М = {х, |х| ф 1} — числовая ось с выколотыми
точками 1 и —1.
Пусть М есть множество сходимости последовательности
(ряда) и Е С М, тогда будем говорить, что последователь¬
ность (ряд) сходится поточечно или, короче, сходится на Е.
Определение. Пусть последовательность {/»»(*)} сходит¬
ся на множестве Е и /(х) = lim fn(x)> х € Е. Последователь-
п —►оо
ность {fn(x)} называется равномерно сходящейся на множе¬
стве Е, если для любого положительного е можно указать
такой номер Л/\ что условие |/п(*) — f{x)| < £ выполнено для
всех х £ Е и всех п > М.
В этом случае употребляются также выражения: “после¬
довательность {/п(х)} равномерно сходится на Е к /(х)”,
“сходимость последовательности {/п(*)} к /(х) на Е равно¬
мерна” .
75
Если последовательность {/п(я)} сходится на множестве Е}
но не удовлетворяет приведенному выше определению, то го¬
ворят, что эта последовательность сходится неравномерно
на Е. Выражение “последовательность {/п(*)} не является
равномерно сходящейся на множестве Е” принято употре¬
блять тогда, когда последовательность или сходится нерав¬
номерно на Е, или расходится хотя бы в одной точке множе¬
ства Е. Равномерная сходимость последовательности {/п(я)}
к f(x) на множестве Е обозначается: /п(я) /(*) на Е.
Приведем формальную запись этого определения.
(/„(*) =* /(*) на Е) *=> Ve > 0 ЗУ(е) :
Vn 6 N, т» > АГ, V* е Е =>\fn{x) - /(*)| < е.
ОО
Определение. Ряд ип(х) называется равномерно схо-
п= 1
дящимся на множестве Ел если последовательность 5п(х) его
частичных сумм равномерно сходится на Е.
оо
Другими словами, ряд ип(х) является равномерно схо-
п=1
дящимся на множестве Е, если последовательность его остат-
оо
ков {гк(х)}} Гк = сходится к нулю равномерно
на Е. n=*+1
Так же, как и для последовательности, для ряда исполь¬
зуются термины: “ряд сходится равномерно на Е'\ “сходи¬
мость ряда на Е равномерна”, “ряд сходится неравномерно
на множестве и “ряд не является равномерно сходящимся
на множестве Еп.
Приведем формальную запись равномерной сходимости
со
ряда ^ ип(я) на Е
Т1= 1
( Url(x) -3 на <==^ ® ЗМ(е) :
л — 1 '
Vn 6 N, л > ЛГ(е), Vx е Е => \Sn{x) - 5(х)| < £
76
или
Г £ un(x) 4 S{x) на е) <=► Ve > 0 ЭУ(е) :
' П = 1 '
Vn € N, п > Л/(бг), Ух 6 Е ==>• |гп(х)| < е.
00 ( 1 Л
Пример 3. Рассмотрим ряд ^ х2п на интервале -, -J.
Во всех точках этого интервала ряд сходится как геометри-
^ х2к+2
ческая прогрессия, и его остаток т> = 2^ х^п равен
( J JV П=* + 1
Из того, что для всех х Е I - ) справедливо неравенство
1 1
О ^ г* ^ тгтг и *1т тгтг = 0» следует, что данный ряд схо-
3-4* к-+ оо 3-4*
дится равномерно на множестве Е=|х:
оо
Пример 4. Рассмотрим ряд х2п на интервале (—1,1).
П = 1
Как и в предыдущем примере, во всех точках этого интер-
x2Af+2
вала ряд сходится и его остаток г* = г. Покажем, что
1 — xz
последовательность г*(х) неравномерно сходится к нулю на
Е = {х : |х| < 1}, т. е. данный ряд неравномерно сходится
на Е. Для этого надо указать такое положительное число £о,
что для любого номера N найдутся натуральное число ко > N
и точка хдг £ Е, для которых г/с0(хдг) > £о- Действительно,
для произвольного N положим к = Л/* + 1 и xjy = 1 - а(Л0,
О < ol(N) < 1. Тогда, используя неравенство Бернулли*),
получаем, что
Г, , (1.-а(Л0)2^4 (2^ + 4)a(AQ
»>Лм(*лг)- !_аа^ ^ 1 — а2 (Л/-) '
Отсюда видно, что если a(Af) = —Д—-, то 7*^+1 (х) ^ i что
•/V ~I- 1 2
и требовалось доказать.
*)Если а > — 1, то для любого натурального п имеем', что (1 + а)п >
> 1 + па.
77
(-l)n + l*
Пример 5. Рассмотрим ряд ^ ~7=f===5 на интеРва"
п = 1 V 71 + Х
/ 2 \n+i
ле (0,1)- Для каждого х0 € (0,1) ряд V] —зна-
V«2 + *o
*0
кочередующиися и последовательность —==== монотонно
у/п2 + х2
стремится к нулю при п —> оо. Следовательно, в силу теоре-
ОО / 1 \ ^ ]
мы Лейбница, для любого х Е (0,1) ряд — ■ _, ^ сходит-
^ V п2 +
ся и его остаток гп(хо) удовлетворяет неравенству |гп(хо)| <
< — —— Итак, для всех х Е (0,1) справедливо
у/{п + I)2 + xl ^ ^
неравенство |гп(х)| < - , откуда, если
у(п + I)2 + I2 П+1
1
учесть соотношение lim = 0, следует, что данный ряд
n-*oo п + 1
равномерно сходится на интервале (0,1).
Критерии Коши равномерной сходимости последо¬
вательности. Для того чтобы последовательность {fn(x)}
равномерно сходилась на множестве Е, необходимо и доста¬
точно выполнение условия: для любого положительного
числа е можно найти такой номер N, что неравенство
Ifn(x) — fm{x)I < £ справедливо для всех точек х множества Е
и любой пары натуральных чисел* п и т при условии п > N,
т > N.
Приведем формальную запись критерия Коши равномер¬
ной сходимости последовательности:
ifn(x) z* f(x) на Е) *=> Ve > 0 ЗМ(е) :
Vn, mEN, n>N(e), т>М{е), VxE£=> |/n(x)-/m(x)| < e.
Критерии Коши равномерной сходимости ряда.
оо
Для того чтобы ряд £>„(*) равномерно сходился на мно-
п = 1
жестве Е, необходимо и достаточно выполнение условия: для
любого положительного числа е можно найти такой номер N,
78
что неравенство
< е справедливо для всех точек х
п+р
к=п
множества Е и любой пары натуральных чисел пир при
условии n > Af.
Приведем формальную запись критерия Коши равномер¬
ной сходимости ряда:
( jr un(x) z* S(x) на е\ Ve > 0 3Af(e) :
П — 1 '
Vx € E} Vp € N, Vn £ N, n > Af(e)
n+p
k=n
< e.
Необходимое условие равномерной сходимости ря-
оо
да. Если ряд ип(х) сходится равномерно на множестве Е}
п = 1
то последовательность {ип(х)} сходится к нулю равномерно
на Е.
Как и для числовых рядов, это условие не является доста¬
точным даже для того, чтобы множество Е входило в множе-
оо
ство сходимости ряда ^п„(х), как показывает следующий
пример. п = 1
°° 1
Пример 6. Рассмотрим ряд на интервале (О, I).
п = 1
Неравенство 0 < —-— < -, х G (0,1), n G N, показывает,
х + n п
Г 1 \
что последовательность < > сходится к нулю равномер-
L х + п J
но на (0,1), но в то же время для любого значения Хо £ (0,1)
1
ряд расходится.
' Хо + п
п = 1
Пример 7. Рассмотрим ряд — на интервале (1,2).
п= 1
С одной стороны, неравенство 0< — < —, х € (1,2), п £ N,
пх п
79
J 11
показывает, что последовательность < — > сходится к ну-
[п* J
лю равномерно на (1,2). С другой стороны, применяя ин-
оо ^
тегральную оценку остатка ряда ^ — при фиксированном
п — 1
+оо
/ ч [ di 1
г Е 11,2), получаем, что rk(x) > J - = —_ .
* + 2
Для произвольного N положим к = Af + 1 и хм = 1 + ^,
ЛГ 1 ^ 1
тогда глг+1 хдг) > 7-т——г > т, т. с. ряд > — сходится
(У + 3)*г 4 71
неравномерно на (1,2).
На практике удобно пользоваться следующим критери¬
ем -фактически переформулировкой определения равномер¬
ной сходимости последовательности.
Последовательность {fn(x)} равномерно сходится на Е
к /(х) тогда и только тогда, когда
lim sup | fn(x) - f(x)| = 0, x € E.
11—¥OQ
Пример 8. Рассмотрим последовательность {/n(z)},
7ГХ
/п(х) = xarctgnx. Если x > 0, то lini fn{x) = —; если
n —► Ou 2
7ГХ
x < 0, to lim fn(x) = ——, /n(0) = 0 для всех п. Следова-
п—юо 2
тельно, множеством сходимости последовательности {fn(x)}
является вся числовая ось IR и /(х) = lim fn(x) — тг|х|.
n->CXJ 2
Оценим sup |^|х| — хarctgnx|, х G К В силу четности
„ 7Г - . . . 7Г
функции у — х arctg пх, у = — |х| и неравенств | arctg пх\ < —,
| arctg а| ^ |а| имеем, что
sup ^|х| — х arctg пх = supx (77 - arctg пх) =
r€R*2 \2 /
1 1
= sup(x arcctg пх) = sup х arctg — ^ —.
х>0 r>0 flX П
Отсюда получаем, что lim sup \fn(x) - /(*)| = 0 и, следова-
n“>°°reR
80
тельно, последовательность {/п(я)}, /п(х) — х arctg пх, рав-
_ 7Г
номерно сходится на Ш к — |х|.
Пример 9. Рассмотрим последовательность {/п(я)},
fn(x) = arctgпх. Как и в предыдущем примере, получаем,
что эта последовательность сходится на всей числовой оси Ш
и /(х) = lim arctg nx = — signx. Так как
п —►оо 2
I *■ . I (* \ ^
sup arctg nx — — sign x = sup I — - arctg nx) ^
rER I 2 I x>0 '
7Г / 1 \ 7Г 7Г Я
> 5-„ctg(„.-) = 5-? = -
то последовательность {/n(z)} неравномерно сходится к
7Г .
— sign х на К.
Обратим внимание на то, что равномерная сходимость по¬
следовательности (ряда) на множестве Е является глобаль¬
ным свойством, характеризующим поведение последователь¬
ности на множестве “в целом”, т. е. множество рассматрива¬
ется как единый объект. Поэтому недопустима формулиров¬
ка локального типа: “последовательность (ряд) равномерно
сходится в точках множества Еп или “последовательность
(ряд) сходится неравномерно в точках множества Еп. В то
же время определение равномерной сходимости имеет смысл
и для множества Е, состоящего из одной точки: Е = {хо}, и
эквивалентно в этом случае сходимости последовательности
(ряда) в точке хо. Если мы хотим говорить о равномерной
сходимости в таком случае, то формулировка должна быть
следующей: последовательность (ряд) сходится равномерно
на множестве Е = {хо} (т. е. не в точке хо, а на множестве,
состоящем из одной точки Хо).
Следующие утверждения немедленно следуют из опреде¬
ления равномерной сходимости.
1. Если последовательности (ряды) {fn{z)} и {^„(х)}
/ ОО ОО ч
I ип(х) и v"(x)) равномерно сходятся на множестве Е,
П —1 п = 1 '
то любая их линейная комбинация {а/л(х) + /Здп(х)}
81
I ^((*un(x) + /:/vn(x))J, где а и fi - постоянные, равномерно
П — 1 '
сходится на Е.
2. Если последовательность (ряд) сходится равномерно на
множестве Е} то сходимость будет равномерной и на любом
множестве Е\ С Е.
3. На всяком конечном подмножестве множества сходимо¬
сти последовательности (ряда) эта последовательность (ряд)
сходится равномерно.
4. Если последовательность (ряд) равномерно сходится на
каждом из множеств Е\ и £*2, то на множестве Е = Е\ U Ё2
эта последовательность (ряд) сходится равномерно.
Внимание! Это утверждение не переносится на бесконеч¬
ное объединение множеств, как показывает следующий при¬
мер.
Пример 10. Рассмотрим последовательность {/п(х)},
ffx(х) = arctgnx, на множестве Ет —
i-H»)
т )
при фикси¬
рованном m £ N. Так как для х £ имеем lim /п(я) = —■
П —► ОО 2
I 7Г I 7Г 71
и sup I— — arctgnx = — — arctg У 0, п —> оо, то на Ет
X12 12 т
последовательность {arctg nr) сходится равномерно. Но, как
7Г
I *
было показано в предыдущем примере, sup — — arctgnx
r>0 ' 2
оо
т. е. на множестве (0, + оо) = Егп эта последовательность
т~ 1
сходится неравномерно.
5. Понятие равномерной сходимости на множестве пред¬
полагает, что рассматриваемая функциональная последова¬
тельность (функциональный ряд) определена на данном мно¬
жестве. Иногда удобно рассматривать числовую последова¬
тельность (числовой ряд) как последовательность (ряд) функ¬
ций, каждая из которых есть константа на данном множе¬
стве. Сходимость такой последовательности (ряда) на любом
множестве равномерна.
Как и в случае поточечной сходимости, при исследовании
равномерной сходимости ряда непосредственный анализ по-
82
ведения последовательности {Sn(x)} или (гп(х)} в подавляю¬
щем большинстве заменяется косвенным — применением при¬
знаков равномерной сходимости, выраженных через свойства
членов ряда.
Признак Вейерштрасса (мажорантный признак).
Если для функционального ряда ^Ptin(x) существует схо-
~ п = 1
дящийся числовой ряд Vj ап такой, что |tin(x)| ^ а„ для
п = 1
всех х £ Е и п £ N (мажорантный ряд), то ряд цп(д)
сходится абсолютно и равномерно на Е. п=1
Область применения признака Вейерштрасса — исследо¬
вание абсолютно сходящихся, в частности, знакопостоянных
рядов. Но множество, функциональных рядов, для которых
на множестве Е существует сходящийся мажорантный чи¬
словой ряд, уже множества рядов, абсолютно и равномерно
сходящихся на Е. Дело в том, что при применении призна¬
ка Вейерштрасса остаток г^(х) = ^ ип(х) ряда ип(х)
пгЛ + 1 оо П = 1
оценивается неравенством sup|rfc(x)| ^ sup |г£п(х)|, а
«/- Г ^ _ г- Е»
n=fc+lJ
такая оценка может оказаться слишком завышенной, т. е. по-
оо
следовательность {nt}, f* = yZ suPlun(x)| может не стре-
п=/с + 1г€£?
миться к нулю, в то время как последовательность {г^(х)}
равномерно сходится к нулю на Е.
Приведем соответствующий пример.
оо
Пример 11. Рассмотрим ряд ^^un(x), где
П = 1
ип{х) =
О,
X €
— sin 2п7гх, х£
п
О,
°,f).
- —1
[2n ’ 2П“1
(JL
\2П-1 ’
83
В каждой точке х0 € [0,1] все члены ряда, кроме, может быть,
1
эдного, обращаются в нуль (в точках х* = j-r все члены ряда
2*
равны нулю). Отсюда получаем, что
»*(*) = £ и"(х) =
n=fc-f 1
о,
— sin22nJTJC, а: €
п
I 1_
2" ’ 2n_1
следовательно,
sup |г*(г)| =
«-€[0,1]
1
j-—r, lim sup |r/c(a:)| = О,
*+ 1 к-*°°тф,\]
т. е. ряд £>„(х) сходится равномерно на отрезке [0,1].
П = 1 J оо
С другой стороны, Мп = sup |ti„(x)| = т. е. ряд ) Мп
*610.11 " ^
расходится. Итак, для абсолютно (поскольку и„(х) ^ 0 для
всех х .Е [0,1]) и равномерно на [0,1] сходящегося ряда
оо
У] ип(х) не существует сходящегося числового мажорантно-
П=1
го ряда.
оо
При анализе функционального ряда ^un(x) методом
п = 1
Вейерштрасса оптимальным — с наиболее точной оценкой —
оо
мажорантным рядом является ряд SUP lwn(*)| Однако ча-
сто бывает достаточно более грубой, но легче получаемой
оценки для |м„(х)|. Приведем несколько характерных приме¬
ров. оо
Пример 12. Проверим, что ряд \ ~:(хП + Зх~п) равно-
мерно сходится на
п = 1
84
Решение. Первое слагаемое в сумме хп + Зх п прини¬
мает наибольшее знамение в точке Х\ = 2, второе - - в точ¬
ке х2 = Следовательно, для всех х £
имеем, что
1 _ 4*2П
О $ —г(хЛ + Зх п) ^ ——, и в силу признака Вейерштрасса
п! п!
получаем, что данный ряд сходится равномерно на
Замечание. Точная оценка
[И-
i(*n + 3r-"K sup (Ч(*"+3*-п))
n! *6[i,2]\n! /
^ 3 2”
дает мажорантный ряд 2^ —р. члены которого имеют тот
П=1
же порядок малости, что и полученный.
оо
_ . _ Sin ПХ
Пример 13. а) Проверим, что ряд > 17= Р^вно-
_ Vn4 + х4
мерно сходится на М. п-'
ОО г
Esin —2
■ ■ 'г'.ггг.: равномерно сходится
1 VH2 + х2
на R. ” = 1
Для любых а имеем неравенство |sino| ^ min{ |r>|, 1}. От¬
сюда видно, что, желая получить лучшую оценку для |sina|,
надо брать оценку |sina| 1, если а принимает значение вне
отрезка [-1, 1], и оценку |sina| ^ |а|, если а € [—1, 1].
В пункте а) при х ф 0 аргумент синуса принимает сколь
угодно большие значения, поэтому удобна оценка | sin пх\ ^ 1.
Итак,
sin пт
Уп* + X4
1
\/пЛ -}- X4
для всех х £ IR, следовательно, в силу признака Вейерштрасса
оо
Esin ПХ
сходится равномерно на 1R.
n = l V» +*
X
В пункте б) для любого х £ R имеем —► 0 при п —► оо,
85
поэтому удобна оценка |sin ■— | < (“■(. Итак,
|и (аЛ| = lsin£l < и < _!_
П у/п2 + X2 ^ п2у/п2 + X2 Л2
для всех х £ R, следовательно, в силу признака Вейерштрасса
ОО х
Esin £
t . ■■■ .: сходится равномерно на К.
п = 1 V п + X2
Проверьте, что в пункте а) оценка | sin пх| ^ |пх|, а в пунк¬
те б) оценка |sin ^ 1 не дают сходящихся мажорантных
рядов.
Внимание! При анализе ряда в пункте б) использовалось
неравенство |sina| ^ |а|, а не соотношение эквивалентности
sin a ^ a, a —► 0. Из соотношения u„(x) ^ vn(x), п -* оо,
вообще говоря, не следует одновременная равномерная или
оо оо
неравномерная сходимость рядов ^^un(x) и ^^vn(x) даже
П=1 П=1
при условии 1in(x) ^ 0, г„(х) ^ 0.
Приведем соответствующий пример.
оо оо
Пример 14. Рассмотрим ряды —— г- и У —,
'' п(хг + п*) ' п3
11 = 1 ' ' п = 1
XX
х £ R. С одной стороны имеем, что —г - ~ —, п —► оо.
ПХ1 + 71 71
С) другой стороны, неравенство
X _ 1 |x7l| I
7l(x2 -f 7l2) 712 X2 + II2 ^ 2n2 X ^
в силу признака Вейерштрасса показывает, что ряд
оо
е-ч X
у "V o гг сходится равномерно на Ш1, а соотношение
' 711 х -f п^)
п гг 1 ' 7
|х| г х л
sup —^ = +оо —- что последовательность < — > неравномерно
reR п ’■«' >
ПО
сходится к нулю на 1 и, следовательно, ряд — неравно-
" 71
мерно сходится на R. П-1
по
Пример 15. Проверим, что ряд ^^х2е~пх равномерно
п = 1
86
сходится на [0,1].
Решение. Поскольку sup г2 = 1 и sup е~пх = 1, то
*e[o,i] *e[o,i]
оценка sup х2е-п* ^ sup х2- sup e_n* = 1 не дает сходя-
*€[0,1] *€[0.1] *€[0,1]
щегося мажорантного ряда. Найдем sup x2c~nz. Поскольку
*€[°,1] /оч2
(аг2е п*У = хе п*(2 - пх), то sup х2е п* = (
*€[0,1] \п/
е~2 =
4 ~ - _2п* - 4
*€[0,1]
, следовательно, 0 ^ х2е-п* ^ ,* ,, х G [0,1], и в
с »- в П
силу признака Вейерштрасса данный ряд сходится равномер-
но на [0,1]. <*,
— - (пЧхТ
„ + х2 п4 + а:4
п=1
Пример 16. Проверим, что ряд 3 % ln
сходится равномерно на №.
Решение. Найти sup —А т In -— — технически сло-
хекп*+х7 п4+х4
жно, поэтому попробуем провести оценки каждого из сомно¬
жителей. Используя неравенства 1п(1 4- а) $ а, а > 0, и
2\ху\ ^ х2 + у2, получим, что
, (п2 + х2)2 _ (х . 2п2х2 ^ ^ 2п2х2 ^ ,
4, 4 — In 11+ . 4 ) ^ 4 . 4^^*
П4 + 14 \ n4 + r4/ n4 -f X4
/ X V n4 — X2 I
Так как I -т—T ) = ГГГ 2Т2» то ГТ
\n4 + x2/ (fl4 + X2)2 |n4
n2 1
n4+x2
(n2 + x2)2 ^ 1
n4+n4 2n2
и, следовательно, —A rln—-; — < —Итак, в си-
n4 + x2 n4 + x4 2n2
лу признака Вейерштрасса, данный ряд сходится равномерно
на R.
Определение. Последовательность {/п(я)} называется
равномерно ограниченной на множестве ЕУ если существует
такая константа А/, что неравенство |/n(x)| ^ М справедливо
для всех п 6 М и всех х G Е.
Признак Дирихле. Бели члены функционального ряда
оо
и„(х) могут быть представлены в виде tin(x) = an(x)6n(x),
n = l
87
где m
а) последовательность сумм ^|^ап(х) равномерно ограни¬
чена на множестве Е, n = 1
б) для каждого х(, £ Е последовательность Ьп(хо) моно¬
тонна ({Ьп(я)} монотонна относительно параметра п),
в) последовательность {6п(я)} сходится к нулю равномер¬
но на Еу оо оо
то ряд ^un(x) = ^ап(х)6п(х) сходится равномерно
на Е. n=1 n=1
Признак Абеля. Бели члены функционального ряда
оо
£>„(х) могут быть представлены в виде ип(х) = ап(х)6п(х),
П=1
где оо
а) ряд ап(х) равномерно сходится на Еу
п = 1
б) для каждого х0 6 Е последовательность {Ьп(хо)} моно¬
тонна (последовательность {Ьп(я)} монотонна относительно
параметра гг),
в) последовательность {6„(х)} равномерно ограничена
на Е} оо оо
то ряд 2>„(х) = ^ап(х)6„(х) сходится равномерно
на Е. n=1 n = 1
Так же, как и для числовых рядои, область применения
признаков Абеля и Дирихле — неабсолютно сходящиеся ря¬
ды. При исследовании конкретных рядов с помощью этих
признаков монотонность последовательности {6п(х)} относи¬
тельно п часто не требует особого анализа — она очевидна.
Но грубой (и частой!) ошибкой является пропуск указания
на то, что это условие выполнено. Отметим, что именно при
применении признаков Абеля и Дирихле иногда возникает
необходимость рассматривать числовые последовательности
или ряды как равномерно сходящиеся на данном множестве.
оо
Пример 17. Рассмотрим ряд }
, п
п = 1
а) на интервале (е, 2тг - е), 0 < е < тг;
б) на интервале (0, 2тг).
а) Так как
s>
sin пх
п = 1
|sinf
для х G (е,27г — е) имеем, что
Последовательность
Ш
2>
П=1
sin ПХ
1C
монотонно сходится к нулю при
п -> оо. А поскольку эта последовательность числовая, то
сходимость равномерна на любом множестве, в том числе и
на {бу2п — е). Итак, в силу признака Дирихле на интерва¬
ле (€у2ж — б), 0 < е < тг, ряд У
мерно.
sinnx
сходится равно-
п = 1
б) На интервале (0,2тг) приведенное в пункте а) рассу ж де-
m ^
ние уже неприменимо, так как оценка
sm пх
п = 1
|®1П 2 I
не дает возможности равномерно ограничить последователь¬
ность < ^sinnx > на (0,27г). Эта оценка дает только воз-
п = 1 '
можность утверждать, что для любого фиксированного
сю
sin ПХ
П
чен при рассмотрении числовых рядов), т. е. интервал (0,2л*)
входит в множество сходимости рассматриваемого ряда.
Пользуясь критерием Коши, покажем, что на (0,2тг) ряд
оо
sm пх
сходится неравномерно, т. е. можно указать такое
. г~л sm пх .
х £ (0, 2ж) ряд у сходится (этот результат был полу-
*■ ^ п.
п = 1
Esm п
п
П = 1
число е > 0, что для любого номера N найдутся такие зна¬
чения р, п ь N, п > М, и хп £ (0,2тг), что
п+р . ,
X—ч sm кхп
к =П
> е.
Прежде всего подберем х„ £ (0,2тг) так, чтобы на достаточ¬
но большом промежутке изменения к: п ^ к ^ п + р вели-
I гл Ж
чина sin кхп была отделена от нуля. Если взять х„ = —, то
^ 6п
для п ^ к ^ 5п имеем, что sin кхп ^ Для произвольного
89
номера Af положим n = N + 1, тогда
5»
El
Sn .
Esin kxn
I
k=n
11 2
>Jta'4"=5'
Esin nx
сходится неравномерно на
(0, 2jt). n=l "
Замечание 1. Еще раз обращаем внимание на то, что
признаки равномерной сходимости Вейерштрасса, Абеля и
Дирихле — достаточные. Для утверждения, что данный ряд
сходится неравномерно, обычно опираемся или на критерий
Коши, или на его следствие — необходимый признак равно¬
мерной сходимости. оо
Замечание 2. Сходимость ряда на (0,2тг) мо-
* ^ п
Я = 1
sin ПХ
П
1 = 1
оо
/ I Л I \
на ка-
/1 I \
жно обосновать и так: (0,2тг) = III —}2тг ) ;
\m ml
( 1 1 \ m" „
ждом интервале I —,2л* ) данный ряд сходится (даже
\т т)
равномерно), следовательно, этот ряд сходится и на (0,27т) =
00 ( 1 1 \
= I I [ —, 2л- 1. Здесь отчетливо видна разница между
^ V га т)
m= 1
глобальным (рассматривающим множество “в целом”) свой¬
ством равномерной сходимости и локальным (рассматриваю¬
щим множество как совокупность точек) свойством поточеч¬
ной сходимости. Локальное свойство естественно сохраняет¬
ся при объединении множеств -- оно имеет место в каждой
точке каждого множества, следовательно, и в каждой точке
их объединения, — а глобальное свойство при таком объеди¬
нении может и не сохраняться, что и имеет место в данном
примере.
00
Замечание 3. Из того, что ряд на (0,2тг) схо-
‘ ^ и
п = 1
дится неравномерно, следует, что последовательность
m
{£>»*}
п — 1 J
не является равномерно ограниченной на (0,27т).
Более глубокий анализ, выходящий за обычный объем нашего
90
курса, показывает, что оценка
х>
sin пх
п=1
1
завыше¬
на, но отражает качественную характеристику
т
ченныи рост sup
r€(e,2ir-c)
sin nx
n=l
при £
oo
неограни-
04- и m —► +оо.
w л (cos nx) sin x arctg nx
Пример 18. Проверим, что ряд > :
“ Vn2 + х2
У] -(sin(n 4- 1)х — sin(n — l)x) =
сходится равномерно на М.
Так как
Dcos nx) sin х
n = l
1 3
= -|sin(m + l)x 4- sinmx — sinx| ^ -,
то достаточно показать, что последовательность
Г arctg пх
I \/п2+х2
}
монотонна относительно п и равномерно сходится к нулю
на IR. Второе утверждение следует из неравенства
arctg пх
\/п* + :
а первое требует более глубокого анализа. Поэтому приме-
^ Л cos nx sin х
ним другой способ. Рассмотрим сначала ряд > —. ■ .
~ х/п2+Х2
Из полученных выше соотношений следует, что этот ряд удо¬
влетворяет условиям признака Дирихле, если ап = (cos nx)sin х
1
и Ьп = -т- у ■ следовательно, сходится равномерно на IR.
vn2 -f х2
Последовательность {arctg пх} монотонна относительно п
(на это достаточно указать) и равномерно ограничена:
| arctg пх| < —, п € N, х € К. Следовательно, в силу призна-
. ^ (cos nx) sin х arctg пх
ка Абеля ряд 2^ Г'^ 2 сходится равномерно
на®. "=l vn +г
Внимание! Иногда при применении признака Дирихле из
неравенства 0 ^ Ьп(х) ^ jJ„, х 6 £, где /?п — монотонная
бесконечно малая последовательность, делается совершенно
91
необоснованный вывод о монотонности последовательности
Ьп(х) относительно п. Это является грубой ошибкой.
(1 - cos пх) cos пх
Пример 19. Рассмотрим ряд ^
п = 1
всех I G R члены последовательности
| 1 — cos пх |
Для
удовле-
1 — cos пх 2
творяют неравенству 0 ^ ^ следовательно,
1 — cos пх
п
z^O на Ш. Если бы эта последовательность была и мо-
_ (1 “ cos пх)cos пх
нотонна относительно п на К, то ряд 2^
сходился бы равномерно на
7Г ЗТГ
4’Т
(1 — COS ПХо) cos ПХ о
Так как ряд 53
к = 1
-2
4*+ 2
k ( 1 — COS ПХо) COS ПХо
О, п = 4 к,
О, n = 4к -|- 1,
— —, V = 4к 4- 2,
п
О, п = 4* + 3.
расходится, то расходится и ряд
Итак, хотя последовательность
п = 1
7Г ЗТГ
4’Т
и последо-
< 53 cos пх г Равномерно ограничена на
П = 1 '
{1 - cos пх 1
> равномерно стремится к нулю на
(1 — costij) cos пх
вательность
Гтг Зтг1 ^
4-Т ’РЯД£
*■ J П=1
не только не сходится рав¬
номерно на
п Зтг
4’Т
, но даже расходится, по крайней мере, в
одной точке этого отрезка. Признак Дирихле в данном слу¬
чае не применим, поскольку нарушено условие монотонности
92
{1 — cos nx \
I
Из критерия Коши выводится следующее утверждение.
оо
Пусть члены ряда ^ип(х) непрерывны на замкнутом
п = 1
множестве F и ряд сходится равномерно на множестве вну¬
тренних точек F. Тогда этот ряд сходится равномерно на F.
Это утверждение позволяет в некоторых случаях устано¬
вить неравномерную сходимость ряда. Именно, если рассма¬
тривается ряд, члены которого непрерывны на замкнутом
множестве F, но ряд расходится в некоторой граничной точ¬
ке множества F, то тогда ряд сходится неравномерно на мно¬
жестве внутренних точек F.
Приведем соответствующий пример.
Пример 20. Рассмотрим ряд агсР^ а) на ЛуЧе
л л
П = 1
(е, +оо), е > 0, б) на луче (0, +оо).
а) Если х 6 (е, +оо), е > 0, то
arcctg nx 1 111
О ^ = - arctg — ^ -у- ^ -у,
71 71 пх п х пге
_ „ ^ arcctgnx
следовательно, по признаку Веиерштрасса ряд > -—
-\ п
сходится равномерно на (е, Ч-оо) , е>0. "-1
б) В силу произвольности числа е > 0 и неравенства
л ^ arcctg пх ^ 1
п пге
заключаем, что луч (0, Ч-оо) входит в множество сходимости
Е°° arcctg пх _
. Поскольку все члены этого ряда непре-
п
п = 1 оо J. п ОО
гЛ ч arcctg 0 я
рывны на [0, Ч-оо) и ряд 2^ = 2^ 2~~ РасхоДится> то
П=1 П = 1
ч arcctg nx
делаем вывод, что на луче (0, Ч-оо) ряд 2^ ”— сходится
неравномерно. П”1
Свойства равномерно сходящихся
последовательностей и рядов.
Теорема о непрерывности предела последователь¬
ности (суммы ряда). Если все члены последовательно-
ке хо 6 Е и последовательность (ряд) сходится равномерно
на Е, то предельная функция (сумма ряда) непрерывна в точ¬
ке хо € Е относительно множества Е.
Обратим внимание на сочетание локальных и глобальных
свойств последовательности (ряда) относительно множества
в формулировке этой теоремы. Равномерная сходимость —
глобальное свойство, а непрерывность в точке — свойство
локальное. Разумеется, если члены последовательности (ря¬
да) непрерывны относительно Е в каждой точке х 6 Е, то
при условии равномерной сходимости этой последовательно¬
сти (ряда) на Е предельная функция (сумма ряда) непрерыв¬
на на Е относительно этого множества.
Теорема о почленном интегрировании последова¬
тельности (ряда). Если все члены последовательности
сходится равномерно на [а,6], то функция /(х) = lim /п(х)
сти (ряда) непрерывны относительно множества Ев точ-
оо
интегрируемы в смысле Римана на
отрезке [а,6] и последовательность {fn(x)} (ряд ^tin(x))
п = 1
интегрируема на [а, 6] и для любого
п = 1
X
г
на [а, 6]
Функция /(г) непрерывна относительно множества — это значит,
что сужение функции на это множество непрерывно.
94
Теорема о почленном дифференцировании после¬
довательности (ряда). Если все члены последовательности
оо
{/„(г)} (ряда $>(*)) дифференцируемы на [а,6], после-
П = 1 ОО
довательность {/^(х)} (ряд У^ц^(х)) сходится равномерно
П= 1 OCJ
на [а,6], последовательность {/п(*)} (ряд ^Гип(х)) сходит-
п = 1
<*я хотя бы в одной точке хо (Е [а,Ц то последовательность
оо
ifn(x)} (ряд£«„( х)) сходится равномерно на [а, 6] к диффе-
n=1 / \/
ренцируемой на [а,61 функции и ( lim /п(я)) = lim f'n(x)
\П-¥ ОО / П—►ОО
a^un(x)J = £<(*)) для всех х € [а,6].
П — 1 ' П — 1 '
Условие равномерной сходимости последовательности (ря¬
да) производных в теореме о почленном дифференцировании
естественно потребовало существования этих производных
на всем отрезке [а, 6]. Таким образом, хотя эта теорема и
говорит о локальном свойстве — дифференцируемости пре¬
дела последовательности (суммы ряда), но условия ее более
глобальные, чем условия теоремы о непрерывности.
Отметим еще, что все три теоремы — о непрерывности,
интегрируемости и дифференцируемости предела последова¬
тельности (суммы ряда) дают только достаточные условия
того, что предельная функция (сумма ряда) обладает соот¬
ветствующими свойствами (см. задачи 60, 61, 62, 63
стр. 324-325).
Обращением (с некоторыми дополнительными условиями)
теоремы о непрерывности предельной функции (суммы ряда)
является теорема Дини.
Теорема Дини для последовательности. Если все
функции последовательности {/п(я)} непрерывны на компак¬
те К у последовательность монотонна относительно п и функ¬
ция f(x) = lim fn(z) определена и непрерывна на К, то
п-юо
fn{x) =*/(*) на К.
95
Теорема Дини для рядов. Если все члены ряда
оо
ип{х) непрерывны и неотрицательны на компакте К и на
п — 1
этом компакте ряд сходится к непрерывной функции 5(х), то
оо
на К.
П = 1
Пример 21. Определим область существования функции
оо
f(x) = ^un(x), где ип(х) = п2х2е~п х , и исследуем ее не-
п — 1
прерывность.
Так как для всех п £ N функция ип(х) четная и un(0) = О,
а для х ф 0 имеем
lim \/ii2x2e~nJx2 = lim п*х*е пх = О,
то функция f(x) определена на всей числовой прямой явля¬
ется четной функцией и /(0) = 0. Так как
sup ип(х) ^ ип (- ) = е'\
r€R \п/
то на Ш не выполнено необходимое условие равномерной схо-
оо
димости ряда ип(х) - последовательность {t/n(x)} нерав-
п — 1 оо
номерно сходится к нулю на 1R. Следовательно, ряд tin(x)
П = 1
сходится неравномерно на Ш и его сумма f(x) не обязана быть
непрерывной на IR.
Рассмотрим луч Ет — ( —, +ос*\ т £ N. Так как
\тп )
v!n(x) — Ъг2х(\ - п2х2)е~п х ,
то для п > т и х £ Ет имеем, что 0 ^ ип(х) ^ ип (— ) =
п2 _
= —re т7, следовательно, на луче Ьт ряд из непрерывных
m оо
функций £«*(*) сходится равномерно. Отсюда получаем,
п= 1
96
что функция /(х) непрерывна на каждом луче Ет и, тем са-
оо
мым, на их объединении луче (0,+оо) - (J Ет. Осталось
т.— 1
невыясненным поведение f(x) в точке Хо = 0.
Так как 0 ^ ип(х) для всех г 6 R и n G N, то / | -j >
-i 1
> щ I - 1 = е , т. е. существует последовательность х„ — - ,
\Ч/ Я
сходящаяся к нулю, для которой значения f(xq) > е 1 не схо
дятся к /(0) = 0. Это показывает, что точка х0 = 0 есть
точка разрыва функции f(x).
Замечание. Разрывность f(x) в точке х0 = 0 можно было
установить и на основании теоремы Дини. Действительно, в
рассматриваемом ряде члены непрерывны и неотрицательны
оо
на отрезке [—1,1]; если бы функция f(x) = ип(х) была
п — 1
непрерывна на этом отрезке, то ряд сходился бы на [—1,1]
оо
равномерно. Но было показано, что ряд ^ип(х) сходится
п -1
неравномерно на [—1, 1], а других точек разрыва кроме хо = 0
функция f(x) на [-1, 1] не имеет.
Пример 22. Определить область существования, исследо¬
вать непрерывность и дифференцируемость функции f(x) =
°° 1
= 5Z М"(Х)> ГДе = 2 arCtS К**1'
п = 1 71
Решение. Все функции ип(х) непрерывны и дифферен¬
цируемы на R. Так как |i/n(x)| ^ -^-г для х £ R, то ряд
оо 2 п г
У] ип(я) сходится равномерно на IR, следовательно, функция
п = 1 оо
f(x) = определена и непрерывна на IR. Рассмотрим
п~\ ~
‘‘формально продифференцированный ряд”: \Jv?n(x), где
2х n=1
у?п(х) = и^(х) = ———. Так как ^п(О) = 0 для всех n £ N,
1 + их *
97
*>n(*) = и lv>n(*)l = , ~ ^3’ n -»• °°- ДЛЯ
oo
всех x ф 0, то ряд ^у?п(я) абсолютно сходится на Ш к не-
n=i 1 1
четной функции (р(х). Пусть < х ^ —, п £ N. Тогда
п + 1 п
для п ^ к ^ 2п справедливы неравенства:
<кх^ 2; 1 + А4!4 ^ 17;
п + 1
Ч2' / v 2 2п 1
j£ £17(»+!) > 17(”+1) > 17
Отсюда получаем, что, во-первых, в силу критерия Коши
сю
ряд сходится на [—1,1] неравномерно, во-вторых,
п — 1
у?(х) > — для всех х > 0 и <р(х) < — — для всех х < 0. Итак,
на отрезке [—1,1] не выполнены условия теоремы о почлен-
оо
ном дифференцировании ряда ^un(x). Возьмем луч Ет =
п=1
Для всех х € Ет справедливо неравенство
= (^+~)
2х 2п2х2 1 т
^ ^п(*) 1 " 7 I I * 4~4 * 2 ^ о1
1 + П4Х4 1 + П4Х* П^Х П*
оо
откуда следует, что ряд ^^у?п(х) на Ет сходится равномер-
п = 1
но. Итак, на Ет выполнены условия теоремы о почленном
дифференцировании ряда, следовательно, функция /(х) =
оо оо
= ^Un(ar) дифференцируема на Ет и /'(х) = ^<рп(х) =
П=1 П=1
= ф(х) для всех х £ Ет. Пользуясь локальностью дифферен-
оо
цирования и равенством (0, +оо) = /?т, получаем, что
т=1
/(х) дифференцируема и /'(х) = <р(х) для всех х > 0, а в силу
четности /(х) и нечетности у?(х) это равенство верно и для
х < 0.
98
Теперь можно показать, что f(x) не дифференцируема в
точке го = 0. Действительно, в противном случае f(x) была
бы дифференцируема на интервале (-1,1), причем
f'(x) = <р(х) для i/O. Но функция f'(x) как точная про¬
изводная должна обладать свойством Дарбу — ее значения
должны заполнять промежуток между любыми двумя значе¬
ниями f'(xi) и /'(хг), хь *2 € (-M)i а это условие проти¬
воречит полученным выше неравенствам: f‘(x) = у>(х) > —,
0 < х < 1; /'(х) = <р{х) < -1 < х < 0.
§ 4. СТЕПЕННЫЕ РЯДЫ.
РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННОЙ РЯД
ОО
Определение. Ряд ^ an(z — 20)п, где {ап} — числовая
п=0
последовательность, называется степенным рядом с началь¬
ной точкой zo. Числа ап называются коэффициентами дан¬
ного степенного ряда.
Линейная замена £ = z — zq переводит степенной ряд с
оо
начальной точкой z0 в степенной ряд ^ ап£п с начальной
п=0
точкой в нуле. Те свойства степенных рядов, которые не ме¬
няются при линейном переносе, удобнее формулировать для
оо
рядов вида 53 *п-
п=0 оо
Первая теорема Абеля. Бели степенной ряд ап zn
п=О
сходится в некоторой точке го, |zo| Ф 0, то он сходится абсо¬
лютно для всех z таких, что \z\ < |го|. ^
Следствие. Каждому степенному ряду ^ anzn соответ-
п=0
ствует действительное число R ^ 0 или символ +оо так,
что для всех z : \z\ < R этот ряд сходится абсолютно и для
всех z : \z\ > R этот ряд расходится (более того, при этих
значениях z члены данного ряда не представляют бесконечно
малой последовательности).
Число или символ R называется радиусом сходимости дан-
ного степенного ряда. Радиус сходимости является основной
характеристикой степенного ряда.
оо
Если радиус сходимости ряда ^ anzn равен нулю, то мно-
п=0
жество сходимости этого ряда состоит из единственной точ¬
ки 2 = 0. Таким образом, этот ряд определяет единственное
число do. оо
Если радиус сходимости степенного ряда есть
п=0
100
символ Ч-оо (Я = Ч-оо), то множеством сходимости этого ря¬
да является вся комплексная плоскость. Таким образом, этот
ряд определяет функцию S(z) = для любого ком¬
плексного числа. п=о
оо
Если радиус сходимости ряда ^anzn есть число Я > О,
п=0
то множество сходимости этого ряда представляет собой вну¬
тренность круга радиуса Я с центром в нуле, т. е. множество
{z: \z\ < Я} с возможным добавлением точек, лежащих на гра¬
нице этого круга. Как будет показано ниже, множество то¬
чек сходимости данного ряда на окружности \z\ = R может
быть пустым, может быть правильной частью этой окруж¬
ности, может полностью совпадать с ней. Таким образом,
оо
этот ряд определяет функцию £(г) = Для всех ком-
п=о
плексных чисел, удовлетворяющих условию \z\ < Я, и, может
быть, для некоторых или всех чисел, удовлетворяющих усло¬
вию \z\ = R. оо
Если радиус сходимости ряда ^^an(z — zo)n есть число
п=0
R > 0, то открытый круг {z : \z — zq\ < Я} называют кру¬
гом сходимости этого ряда. Если радиус сходимости ряда
оо
У] - *о)п есть символ -foo (Я = Ч-оо), то в целях едино¬
го
образия формулировок кругом сходимости этого ряда назы¬
вают всю комплексную плоскость. Еще раз обратим Внима¬
ние на то, что круг сходимости степенного ряда обязательно
входит во множество абсолютной сходимости этого ряда, но
не обязательно совпадает с этим множеством и, тем более, со
множеством сходимости.
Радиус сходимости Я степенного ряда связан с его коэф¬
фициентами формулой Коши-Адамара:
I = */Kj. (1)
Если lim 1 ^ — А, то А — lim \/\ап\. следователь-
n-*+oo |an| п-*+оо
101
ю, в таком случае
R =
(2)
Если А = 0, то R = +оо).
Какой формулой — (1) или (2) — пользоваться для вы-
шсления радиуса сходимости конкретного степенного ряда,
шределяется видом зависимости ап от п. Приведем харак¬
терные примеры.
Пример 1. Найти радиус сходимости и множество схо¬
димости ряда
нить формулу (2), поскольку в выражение |ап| входит п!. Так
как
по радиус сходимости данного ряда R = е2. Для окончатель-
юго определения множества сходимости исследуем поведение
этого ряда на окружности круга сходимости, т. е. на множе-
|gn+iz"+1| = (п + 1)а(яа+1)"еа
|а„гп| (я2 + 2n + 2)n+I
102
=(1+оШ)(1+^+о(^))‘
= i + \+0{h)'
Отсюда следует, что положительная последовательность
|an2n|, \z\ = е2, по крайней мере, начиная с некоторого номе¬
ра, возрастает и, тем самым, не является бесконечно малой.
, . 2 ^ (п!)2*П
Следовательно, для любого z,\z\ = e , ряд 2^ |2п +’(п2
расходится в силу необходимого условия сходимости. Таким
образом, множество М сходимости данного ряда совпадает
с его кругом сходимости: М = {z : \z\ < е2}.
Пример 2. Найти радиус сходимости и множество схо¬
димости
(3 + 4«)"*п
ряда 2^
“ \/пи + 1
5п
Решение. Имеем |а„| = —. . Здесь удобно приме-
Vn2n + 1
нить формулу (1). Так как
lim \/|а„| — lim г* = 5,
„ 1 „
то радиус сходимости данного ряда R = Для окончатель-
5
ного определения множества сходимости исследуем поведение
этого ряда на окружности круга сходимости, т. е. на множе-
стве \z\ — Бели |г| = то
5 5
I П. 1 1 1
К* = -ундин»,. = г ~ ~5> п -»■ оо.
^n2n + 1 »a(l + s4a-)* "
Отсюда видно, что данный ряд сходится и притом абсолютно
во всех точках окружности |г| = -. Таким образом, множе-
5
ство М сходимости данного ряда является замыканием его
круга сходимости: М = : \z\ ^
Заметим, что в данном примере можно было вычислить R
и по формуле (2), но это вычисление технически сложнее.
103
Пример 3. Найти радиус сходимости и множество схо
^ (1 - уДi)nzn
димости ряда ^
2П
Решение. Имеем: |«„| = —— ;———Здесь последо-
la I »Ф+М)П)
вательность -——т не имеет предела (проверьте!), поэтому
K+ll
если в предыдущем примере выбор формулы (1) для вычи¬
сления R был сделан из соображений удобства, то в дан¬
ном примере формула (2) просто не применима. Так как
2 2
v < v/|ariI ^ —?=1 тс) lim v/|tt„| = 2 и, следователь-
v/4n vn n-» + oo
„ 1 „ . . I
но, радиус сходимости данного ряда R — Если |г| = то
~ — lj(c(xi‘P + isin^), <р € [0,2л-) и
(2 " ^*) + * sin f)n
а,,г" = »(3 + (-1П =
[(cos - - »sin tJ-) (cos <p + isin y>)]"
= n (3 + (-I)") =
[cos (ip - I) + «sin (y> - f)]"
n(3 + (-i)»)
и но формуле Myanpa получаем, что
» _ cos [я (у - §)]+« Sin [»(»>-§)]
n(3+ (-!)»)
Таким образом, исследование сходимости данного ряда на
окружности круга сходимости состоит в исследовании сходи-
^ cos [п (у?—^)] ^ sin [тг (<р- ^)]
„ост. р»до. Y. -п „ •£ л|3 + (_||„) »» (0,2*);
П — 1 ' \ ' П = 1 \ \ / /
именно, если для <р\ € [0,27т) оба эти ряда сходятся, то ряд
°° 1
^anzn сходится при г = r(cos</?i + tsin )» если Для ^2 £
n = l
€ [0,2тг) хотя бы один из этих рядов расходится, то ряд
104
2^ 1
^ап2л расходится при z — -(cos<p2 + * sin у?2)-
n = l
Ряд
cos [п (<р - I)]
'Ч »(3+ (-!)»)
(3)
а = 1
представим как сумму двух рядов
°о [ О,
cos [m (р ~ ^)] . *>т = Я 1
m=1 I 4m ’
и
Г21
V'cmcos L cm = < m’
i^i L v 3/J [ 0,
oo
Отсюда видно, что если оба ряда А :
n “cos Г(2д- 1)(<^-5)] 7=1
В : > —- сходятся, то сходится и ряд (3),
<7=1 2я “ 1
если один из этих рядов сходится, а второй расходится, то
расходится ряд (3), а если расходятся оба эти ряда, то вопрос
о сходимости ряда (3) остается открытым. Из соотношений:
§“К*-т)]|<1=бЬ1Я-
Q I I 2Q
^cos[(2?- !)(*>- |)] $ 53cos [m (*- J)]
rn = 2n — 1,
m — 2n
rn = 2 n - 1,
m — 2 n.
cos[</(2y>- ^)]
bq
lm = 1
SC“KV^)]|
lsin(f-f)l Ип(^~з)|
в силу признака Дирихле следует сходимость рядов А и В
, п / 4тг _ ~ чч
для v? ^ и (р ф — (мы рассматриваем только ip Е [0,27г)).
и О
105
« п 47Г
При у? = — и (р = — ряды А и В становятся расходящимися
рядами:
оо . оо 1
-5* В:5^;
ip -
7Г
3’
4тг
ip -
т
оо оо
А
я
поэтому при этих значениях <р рассматриваем непосредствен¬
но ряд (3). Если <р = —, то ряд (3) принимает вид
о
оо J
Sn(3 + (-!)")
1 1
и неравенство ■— — -—^ — показывает, что этот ряд
_ 4тг
расходится. Если у? = —, то ряд (3) принимает вид
о
(-1)"
S»(J + (-i)")'
Поскольку члены этого ряда стремятся к нулю при п —► оо,
то его сходимость эквивалентна сходимости ряда
оо
£ (й - £)
111
(см. стр. 16). Неравенство —— — - -— > -— покаэыва-
2(2т — 1) 8т 8т
ет расходимость этого ряда и, следовательно, расходимость
ряда (3).
^ COs[n(y?-^)l 7Г
с, ряд 2^ д сходится при <р€ [0,2Я-),
. 4jt n_1 к 4л
<р ф —, и расходится при <р = — и (р = —. Совершенно ана-
^ sin [п (<р - §)]
логично доказывается, что ряд 2^ ——7—г^г сходится
Итак,
106
, 7Г 47Г 7Г 47Г
при <р е [0,2тг), ^ ф -, ip ф —, в точках же^=-и^>=у
все члены этого ряда равны нулю. Окончательно получаем,
00 1
что ряд ^ anzn сходится во всех точках окружности \z\ = -
n = 1 l + v/5. -I -л/5|
кроме двух: z\ = и г2 = . 1аким образом,
4 4
множеством М сходимости данного ряда является множество
М
Ряд вида ап [/(г)]а называют обобщенным степенным
п = 0
рядом. Множеством сходимости такого ряда является мно¬
жество М = {z : /(z) £ £’}, где Е - множество сходимости
оо
ряда У1ап*П
п=О
Пример 4. Найти множество сходимости ряда
^ (*+*г
[(5 + 6 (-1)")“ (z -0Г
Решение. Положим t = ~~ и найдем множество сходи-
^ t" _ , . 1
мости ряда > т-————-т-. Так как а„ = т- ———-г—.
^[5 + 6(“1)п]п [6+ (—1)п-5]п
то
— 1
^=|
1
lim v/|an| = lim -———-г- = 1
П —► 4“00 n-f-foo 6 5*(—1)п
и, следовательно, Я= 1. Если |<| = 1, то |an<n| = jjj"+ ^ (-1)п]п
и так как lim тт—— = 1, то последовательность
n-f-foo [6 + 5.(_l)njn
|а„<п| не является бесконечно малой. Следовательно, в си-
оо
лу необходимого признака ряд ^ antn расходится во всех
п=0
точках окружности \t\ = 1. Итак, множество Е сходимо-
107
00 tn
гти ряда V 77 7П—ГГ"совпадает с его кругом сходи-
“ (5 + 6(-1)п)
мости: Е = {/ : |*| < I}. Множеством сходимости ряда
у U + 0"
[(5 + 6-(—1)п) (г — *)]”
является множество
М
-ЖИ'
т. е. множество тех комплексных чисел г, для которых рассто¬
яние до точки г больше расстояния до точки —г (см. рис. I).
Рис. 1
Таким множеством является комплексная полуплоскость, ле¬
жащая ниже действительной оси: М = {г : г = а + 6i\ а £ R,
ft £ R, 6 < 0}.
Вопрос о свойствах суммы степенного ряда имеет смысл,
если эта сумма определена более, чем в одной точке, т. е. если
радиус сходимости этого ряда не равен нулю. Не углубля¬
юсь в теорию дифференцирования и интегрирования функций
комплексного переменного, заметим только, что проиэвод-
нюй степенной функции zn, п £ N, является функция nzn~l
((производная f'(zo) функции комплексного переменного f(z)
определяется как производная функции действительного пе-
1108
ременного равенством
гы = lim Я*. + А») - !Ы
V Az-+0 Az
при условии, что этот предел существует), и, соответственно,
первообразной степенной функции zn, п £ N, является функ-
zn + l
ция . Определение равномерной сходимости ряда непо-
п + 1
средственно переносится на ряды в комплексной плоскости;
теоремы о почленном интегрировании и дифференцировании
рядов также справедливы в комплексной области.
Из формулы Коши-Адамара немедленно следует, что ряды
00 °° a zn
А : В : ^ — р (почленно проинтегрированный
п=0 ^ п=0 П +
ряд А), С : ^>2nanzn~l (почленно продифференцированный
п = 1
ряд А) имеют один и тот же радиус сходимости.
Теорема. Если R > 0 есть радиус сходимости ряда
оо
^T^anzn, то для любого г, 0 < г < Я, этот ряд сходится
п =0
равномерно на множестве {z : \z\ ^ г} (на любом круге с
центром в нуле, лежащем строго внутри круга сходимости
данного ряда).
Следствие. Сумма S(z) степенного ряда беско-
п= О
но дифференцируема в круге сходимости, при этом
оо
S(m)(z) = ^ п(п- I)...(n-m+l)a„2n~m;
функция F(z) = Га„—— является в круге сходимости
П + 1
П=0
первообразной для S(z), принимающей нулевое значение при
z = 0.
Определение. Функция f(z) называется аналитической
оо
в точке z0 6 С, если существует степенной ряд ^ ап(2г-г0)п,
п=о
109
сходящийся к f(z) в некоторой окрестности U(zo) точки zq\
оо
f(z) = ^ an(z — z0)n, Vz £ C/(zo). Точка zq в этом случае на-
п=0 оо
зывается точкой аналитичности функции /; ряд ^Pan(z—z<j)n
п=0
называется рядом, представляющим функцию / в U(z0).
Из определения немедленно следует, что сумма степенно-
оо
го ряда ^ an(z — zo)n, РаДиус сходимости которого не равен
п=0
нулю, является аналитической в точке zq. Более глубокое
утверждение теории функций комплексного переменного со¬
стоит в том, что каждая точка круга сходимости степенного
ряда есть точка аналитичности его суммы.
Если zo — точка аналитичности функции /, то эта функ¬
ция бесконечно дифференцируема в точке zq (как сумма сте¬
пенного ряда) и коэффициенты степенного ряда, представля-
/(п)ы
ющего эту функцию, определяются равенством ап — \—-.
00 f(n4zо)
Ряд ^ j—(z — z0)n называется рядом Тейлора функ-
п=0 П' 1
ции / в точке Zq .
Итак, с одной стороны, каждый степенной ряд есть ряд
Тейлора для своей суммы; с другой стороны, существует
оо
единственный ряд вида ^ an[z — z0)n, представляющий дан-
п=0
ную функцию в некоторой окрестности точки zo, именно, ряд
Тейлора этой функции.
Как уже говорилось, степенной ряд *о)п, радиу-
п= о
сом сходимости которого является положительное число Я, в
круге сходимости К = {z : |z-zq| < R} определяет функцию
Я(г) = ]Гап(г-гоГ.
п=0
оо
Предположим, что два ряда ^оп(^ — z0)n = Si(z) и
п=0
НО
оо
У bn(z—zo)n = 5г(^) имеют частично пересекающиеся круги
п=0
сходимости К\ и соответственно, и их суммы совпадают
на общей части этих кругов: Si (z) = £2(2), Vz £ К\ П AY То¬
гда каждая точка части окружности одного круга, лежащей
внутри другого, является точкой аналитичности функции
pi(4 г€А'ь
Ы(*). г € К2.
Определение. 1. Точки £ окружности круга сходимости
оо
ряда — z0)n, обладающие такой окрестностью
п=0
в которой существует аналитическая функция f(z), совпада¬
ющая с суммой данного ряда на пересечении его круга схо¬
димости с t/(£)> называются правильными или регулярными
точками данного ряда.
2. Точки £ окружности круга сходимости, не обладающие
такой окрестностью, называются особыми точками данного
ряда.
Теорема. На окружности круга сходимости степенного
ряда находится, по крайней мере, одна особая точка этого
ряда. оо
Пример 5. Найти регулярные и особые точки ряда zn.
ОО 71 = 0
Решение. Радиус сходимости ряда zn равен 1, и для
оо п=0
всех z, |z| < 1, имеем равенство ^ zn = Функция
| п=0 *
fiz) — j определена для всех z ф 1. Покажем, что для
любого а ф 1 функция f(z) представляется степенным рядом
в некоторой окрестности точки а.
Обозначив t = z - а, получим, что
1 _ 1 _ _1_ 1 _ 1 Г
1 — z 1 — а — t 1—а 1 — ~ 1 —а (1 —а)п
1-а n=0v 7
111
Итак, все точки окружности \z\ = 1 кроме точки z0 = 1 явля-
оо
ются регулярными точками ряда Поскольку в силу
п = 0
приведенной выше теоремы на окружности \z\ = 1 должна
быть хотя бы одна особая точка этого ряда, то таковой явля¬
ется точка zq = 1. оо
Обратим внимание на то, что ряд ^ ztl расходится во
п = 0
всех точках окружности \z\ — 1 как в особой точке, так и
в регулярных. Выше был приведен пример степенного ряда,
сходящегося во всех точках окружности круга сходимости
также независимо от того, особые это точки или регуляр¬
ные. Таким образом, сходимость степенного ряда в точках
окружности круга сходимости, вообще говоря, не связана с
регулярностью его точек.
Для функций комплексного переменного справедливо ут¬
верждение: если функция / дифференцируема в каждой точ¬
ке области G, то каждая точка этой области является точкой
аналитичности функции f*K
Степенные ряды в действительной области
Си
Если все коэффициенты степенного ряда ^ an(z — хо)п и
п = 0
точка хо действительны, то его сужение на действительную
оо
ось дает степенной ряд ^ ап(х - х0)п. Теперь в дальнейшем
71 = 0
будем считать числа ап действительными, не оговаривая это¬
го специально.
Вместо круга сходимости {z: \z\< R} на комплексной плос¬
кости на действительной оси получаем интервал сходимости
оо
{х : |х| < R). Множество сходимости ряда ^ап(х — хо)п
71 = 0
Можно было обосновать аналитичность функции /(г) =- —-— в лю-
1 - г
бой точке z ф 1 ссылкой на эту теорему, но мы предпочли дать прямое
доказательство этого свойства J(z).
112
или совпадает с интервалом сходимости, или получается до¬
бавлением к нему одной или обеих концевых точек.
Пример 6. Найти множество сходимости ряда
J2- / кп сп \
(<»" + — + ^2 ) х". <* > 0, 6 > 0, с > 0.
П=1 ' '
Решение. Положим М = шах{а,6,с}. Тогда
В силу неравенства
1 / о \» 1 / Ь 1 / с\» , 1 1 „
^Пм) +п{м) +^\М) <1 + п + ^^3
отсюда получаем, что
/ 6"с"
lim \ ап + h — = М
П-++00 V п п1
и, следовательно, Д = Осталось исследовать поведе-
М
ние данного ряда в концевых точках интервала (—Д, Д) =
/ i 1 \ п
= I — —, — I. В зависимости от соотношения величин а, 6,
с возможны три случая.
I. М = а. Тогда Л = - и для |г| = - имеем:
|(аП+^+^)х"|=1+« Ш ~*1,
п —> -f оо,
откуда следует расходимость данного ряда как в точке
х\ — -Д, так и в точке х2 = Д.
И. М = Ь > а. Тогда Д = | и0< -^ < 1. Для х = — 7
о М о
имеем равенство
113
Ряд с членами (-1)п + "j? (]^) | схоДится абсо¬
лютно, ряд V"4 -—сходится условно. Следовательно, в
, п
п = 1
точке х\ = -R данный ряд сходится условно.
Для х = - имеем равенство
о
( п bn сп\ п 1 Г / \ п 1 / с \п
Iе + =п + [(м) +^Ы .
1_
п ’
-1-00.
Следовательно, в точке х2 = Я данный ряд расходится.
III. М = с > шах{а,6}. Тогда Я=-иО<-~<1,
b 1 с
О < — < 1. Для |я| = - имеем равенство
М с
( п 6" с"\ п\ ( а \п 1 ( Ь\П 1 1
(в+7^)т® +пЫ
п —> -foo.
Следовательно, данный ряд абсолютно сходится как в точке
х\ = -Л, так и в точке х2 = R
Итак, окончательно получаем, что
а) если тах{а, 6, с} = а, то множество М сходимости дан¬
ного степенного ряда совпадает с его интервалом сходимо¬
сти: М — ( —, — );
\ а а)
б) если тах{а,6,с} = 6 > а, то множество М сходимости
данного степенного ряда есть полуинтервал
LI I)
Ь'Ъ)'
т. е.
интервал сходимости этого ряда с добавлением левого конца;
в) если тах{а,6,с} = с > тах{а,6}, то множество М схо-
1 ]1
димости данного степенного ряда есть отрезок I —, - , т. е.
L г с\
интервал сходимости этого ряда с добавлением обоих концов.
Предлагаем читателям проверить, что эти три случая ис¬
черпывают все возможные взаимные соотношения между чи¬
слами а, 6, с.
114
Из равенства |ап(-Я)п| = |алЛп| следует, что абсолют-
оо
нал сходимость степенного ряда ап(х — жо)Л на одном из
п=0
концов интервала сходимости влечет абсолютную сходимость
его и на другом конце этого интервала. Таким образом, мно¬
жество сходимости степенного ряда может быть полуинтер¬
валом только тогда, когда в соответствующем конце этот ряд
сходится условно. Из этого же равенства видно, что если рас-
оо
ходимость ряда ^ ап(х — xo)Ln на одном из концов интервала
п=0
сходимости следует из того, что последовательность {апЯ”}
не является бесконечно малой, то и на другом конце интер¬
вала сходимости этот ряд расходится по той же причине.
Из формулы Коши-Адамара следует, что
lim \/\ап№\ = 1.
П-++00
Отсюда видим, что ни радикальный признак Коши, ни при¬
знак Даламбера не дают возможности установить сходимость
оо
степенного ряда аЛ(ж — хо)п в концевых точках Интерва¬
ла
ла сходимости. Однако, расходимость этого ряда в концевых
точках иногда устанавливается с помощью этих признаков в
допредельной формулировке. оо |ч2 п
Пример 7. Найти множество сходимости рядаУ^ --—у- .
Решение. Так как п=0
,.m JoJ Вт (2n + 2)(2» + l)
n-++oo |an + i| п-*+оо (71 Н- 1)^
1 4п(п!)2
то R = Положим Ьп = ■ ■ - ■■*■■■■ . Тогда, если х = 4, то
4 со (2л)!
ОО
£«„*" = £<>„, аесли х = -4, ТО £а„а:п = £(-1)п6„.
п=0 п=0 п=0 п=0
rp ^n + l 2(п+1) L V"4/ | \n l
Так как -j— = -----у > 1, то оба ряда 2_^Ьп и Ьп
п п=0 п=0
расходятся.
Таким образом, множество М сходимости данного ряда
совпадает с его интервалом сходимости: М = (—4,4).
115
Пример 8. Найти множество сходимости ряда
со
Е
П = 1
Решение. Если последовательность {ап} имеет предел,
то для любой последовательности {/?п} имеем равенство:
lim otn&n — lim an lim f3n.
n —► +00 n—► + 00 n —► -f - 00
Пользуясь этим свойством, получаем, что
Ш "Л4+(~1)п]п'= 1ПЙ[4+(-1)п] = 5.
п—► +оо V 71 п—►оо
следовательно, R= Положим
5
Ьп =
О j п и1]
2т — 1
J ОО 00
Если х = то апхп = ^ 6П. Пусть
П=1 П — 1
О, п = 2m — 1.
г" = < 1
Расходимость ряда ^ сп и неравенство Ьп ^ сп ^ 0 покаэы-
ОО П = 1
ваюг, что ряд ^ 6П расходится.
п = 1
Если х = - то
5
ОО ОО оо ОС)
^a„z” = ^P(~l)n6n = - У^»,
Tl — 1 П = 1 П “ 1 n = I
где
О, п — 2т - 1,
*n=<-L n = 2т
. 2т
116
О, п = tm,
I \ 2т — 1
г 1 , п — — 1.
>/
1 /3'
п- Г \5>
С» оо
Так как ряд ^ гп сходится абсолютно, а ряд ^ qn расхо-
П=1 П=1
оо
дится, то ряд 1)ПЬП расходится.
гг — 1
Таким образом, множество М сходимости данного ряда
МЛ
совпадает с его интервалом сходимости: М — I —- 1 .
Пример 9. Найти множество сходимости ряда
у (2п -!)!!„
к (**>«
Решение. Так как
(2п+ 1)!!(2п)!! 2n + 1
n-1+oo (2n + 2)!!(2п - 1)!! ~ «■!+"« 2п + 2 ~ ’
то К - 1.
i (2п — 1)!!
Положим Ьп = -^Г'
ОО ОО
Если х = 1, то ^ апхп = ^ 6П. Так как
П=1 П=1
6n+, 2n+ 1 , 1 - / 1 \
~Т^~ ~ 2п4-"2 — 2п \п*/ ’ П"++°°’
ОО
то в силу признака Гаусса ряд 6П расходится.
п = 1
ОО оо
Если х = —1, то ]Г^апЯп = £(-1)п6п. Из неравенств
П=1 п=1
1^2 3 4 2п - 3 2п - 2 2п - 1
2 < 3 ’ 4 < 5 ’ ' ’ 2п - 2 < 2» - Г 2п <
117
получаем, что
1-3 • • • (2п - 1) 2-4 •••(2п-2) 1
Ьп = —л z— < -
2-4 • 2п 3-5---(2п-1) 2п-6„ ’
откуда следует, что 0 < 6„ < I—, т. е. lim Ьп = 0. Со-
6n+1 2n+l , »-+~
отношение —— = < 1 показывает, что положитель-
Ь„ 2п + 2
пая последовательность {&„} монотонна. Следовательно, ряд
ОО
]Г^(-1)П&„ сходится в силу признака Лейбница.
п = 1
Таким образом, множество М сходимости данного ряда
есть полуинтервал [—1,1).
Пусть Хо — точка действительной оси и функция
оо
f(z) = £ап(г — хо)" аналитическая в некоторой окрестно-
псО
сти (/(хо) точки хо. Сужение этой функции на действитель¬
ную ось дает аналитическую, т. е. представимую как сумма
оо
степенного ряда, функцию /(х) = ^Рап(х - х0)п.
п=0
Теорема о единственности степенного ряда. Если
функция / в некоторой окрестности U(xо) точки Хо предста¬
вляется как сумма степенного ряда:
00
f(x) = '%2ап(х ~ хо)п, x€U(xo),
п=о
то эта функция бесконечно дифференцируема в Г/(хо) и ко¬
эффициенты ап однозначно определяются равенством
_ /{п)ы _ _ 0 ,
ап — , п — 0,1,...,
п\
т. е. единственным рядом, представляющим функцию /(х) в
окрестности точки х0, может быть ее ряд Тейлора в этой
точке.
Следствие. Для того чтобы функция / представлялась
степенным рядом в окрестности точки хо, необходимо, что¬
бы в некоторой окрестности этой точки функция / имела
производные всех порядков.
118
В отличие от функций комплексного переменного диффе¬
ренцируемость функции действительного переменного в не¬
котором интервале (а, Ь) не влечет се аналитичности в этом
интервале. Действительно, существует функция /, непрерыв¬
ная на К, но не дифференцируемая ни в одной точке х Е К
(см. задачу 68, стр. 327). Функция /j, первообразная для /
на R, является непрерывно дифференцируемой на R функци¬
ей, не имеющей ни в одной точке х € R второй производной.
Беря последовательно первообраэную /2 от /1, первообраз¬
ную /3 от /2 и т. д., получим для любого п Е N функцию,
имеющую п непрерывных производных на R, но не имеющую
производной порядка п + 1 ни в одной точке действительной
числовой прямой.
Покажем, что и условие / 6 С°° (U(x0)), где U(x0) — не¬
которая окрестность точки хо, только необходимо, но не до¬
статочно для того, чтобы функция / была аналитической в
точке хо- Пусть f(x) = е“^, х ф 0. Так как lim /(х) = 0, то,
полагая /(0) = 0, получим функцию /, непрерывную на всей
числовой прямой. Для х ф 0 имеем:
24 1 36 l. 8 1
= —=*е ** ** 4- —е **.
X' X9
продолжая операцию дифференцирования, получим, что
А 1
ф 0, есть сумма выражений вида — е~^, т Е N.
j хт
Из равенства = 0, m Е N, и непрерывности
функции / в нуле следует, что /' в нуле существует и равна
нулю и, таким образом, непрерывна; точно так же получаем,
что /" в нуле существует, равна нулю и непрерывна. Продол¬
жая эти рассуждения, получим, что функция / имеет в любой
точке х Е R производные всех порядков, причем в нуле все ее
производные равны нулю. Следовательно, ряд Тейлора функ-
ОО 00
ции / в нуле представляет собой ряд ^ апхп = ^ 0*хп, все
п=0 п=0
119
коэффициенты а„ которого равны нулю. Радиус сходимости
:»того ряда R = +оо, т. е. ряд сходится при любом х 6 К (это
видно и непосредственно), но сумма его есть тождественный
нуль и ни в какой точке, кроме нуля, не равна f(x). А по¬
скольку единственным степенным рядом, представляющим в
некоторой окрестности нуля функцию /, может быть только
ее ряд Тейлора в точке хо = 0, то, следовательно, функция /
не представляется степенным рядом в окрестности нуля, т. е.
не является аналитической в точке хо = 0.
Еще один пример неаналитической в нуле функции / €
€ С°°(М) приведен в задаче 75, стр. 329. Для приведенной там
функции / ряд Тейлора в нуле представляет степенной ряд
ЭО
]Г^апхп с нулевым радиусом сходимости, т. е. не существу-
п = 0
ет такой окрестности нуля, в которой этот ряд представлял
бы какую-нибудь функцию. Поскольку другого степенного
ряда, представляющего / в окрестности нуля, не существу¬
ет, то эта функция в окрестности нуля не представляется
степенным рядом, т. е. не является аналитической в точке
х0 = 0.
оо
Если радиус сходимости ряда ^ап(г — хо)п есть число
оо п=0
R > 0, то функция 5(г) = ^ an(z — хо)п не может на круге
п=0
сходимости совпадать с функцией, аналитической в области,
включающей замыкание круга сходимости, поскольку хотя
бы одна точка окружности {z : \z - z01 = R) должна быть
особой точкой рассматриваемого ряда. Но эта точка не обя¬
зательно лежит на действительной оси. Так что в отличие от
функций комплексного переменного функция действительно-
оо
го переменного 5(х) = ^ап(х — хо)п может совпадать на
п=0
интервале сходимости этого ряда (-R, R) с функцией f(x),
аналитической на интервале (а, 6) Э [—Я, Я].
ОО
Пример 10. Рассмотрим ряд У^(—1)пх2п.
п=0
120
Радиус сходимости его равен 1, и
СО 1
£(-1)ni2n = TT^ (4)
1
1 + х2
п=0 - + Х
для всех ху \х\ < 1. Покажем, что функция f(x) =
является аналитической в каждой точке а > 0.
Положим I = х — а, тогда х = t + а и
_1 1 1 1 _
1 + х2 1 + а2 + t(t + 2а) 1 -f а2 \ л.
п=0 ' 7
t(t + 2a)
Полученный ряд сходится абсолютно, если ^
т. е. для t Е (—а — \/2а2 + 1, -а + \/2or2 + 1). Если t Е
Е (0, —аЧ-\/‘2а2 + 1), то все слагаемые в многочлене [t(<+2a)]n
положительны, следовательно, ряд, полученный после рас¬
крытия всех скобок, также сходится абсолютно для t Е
Е (0, -аг+ \/‘2а2 + 1) (см. стр. 16). Делая перестановку членов
этого ряда и группируя члены с одинаковыми степенями мы
получим ряд вида
< 1,
5>ntn = ^а„(*-а)п,
п=0 а=0
абсолютно сходящийся при t Е (0, —а + \/2аг2 -f 1), сумма ко-
торого равна —— — = —Выпишем несколь-
у 1 + а2 + t(t + 2а) 1+ х2
ко первых членов этого ряда:
1 2аI <2(3а2 - 1) <3(4а3 - 2а)
1 + а2 (I + а2)2 (1+а2)3 (1 + а2)4
<4(5а4 — 10а2+ 1)
+ (1 + а2)5 + '"
ОО
Итак, для любой точки а > 0 существует ряд —с*)п,
п=0
121
радиус сходимости которого Я ^ \/2а2 + 1 - а, а сумма рав¬
на —т. е. функция /(х) = -—аналитична в точке а.
1 + хг 1 + х1
Аналитичность / в нуле установлена равенством (4), а анали¬
тичность в точках отрицательной полуоси следует из четно¬
го
сти /. Таким образом, сумма ряда ^(-1)пх2п не определена
п=0
вне интервала ( — 1, 1) и в то же время всюду в этом интер¬
вале совпадает с функцией f(x) = =•, аналитической в
1 4- хг
каждой точке действительной числовой оси.
Полное объяснение подобного поведения степенных рядов
для действительного переменного получается только в тео¬
рии функций комплексного переменного. Если для действи¬
тельного аргумента функция f(x) = |е ’ х ^ ® бесконеч-
{ 0, х = О
но дифференцируема в нуле, то для комплексного аргумента
нуль является неаналитической — особой — точкой функции
f(z) = Если все точки действительной оси аналитиче¬
ские для функции f(x) = г, то в комплексной плоскости
1 + х1
точки z\ = г и z2 = являются неаналитическими точками
1
функции f(z) = - и> соответственно, кругом сходимо-
оо
сти ряда ^(—l)nz2n, представляющего эту функцию для г,
п =0
\z\ < 1, естественно является круг {z : \z\ < 1}, на окружно¬
сти которого лежат эти особые точки.
Представление функции f(x) в виде £]ап(х - х0)п,
п=0
х £ (/(х0), называют разложением /(х) в степенной ряд в
окрестности точки хо.
Сравнивая представление функции /(х) в окрестности
точки хо многочленом Тейлора и ряд Тейлора с центром в хо
этой функции, видим, что стремление к нулю при п —► оо
остаточного члена формулы Тейлора г„(/, х, хо) является не¬
обходимым и достаточным условием разложения /(х) в сте¬
122
пенной ряд с центром в хо- Из представления остаточного
члена в форме Лагранжа
rn(f,x,xо) = - 'р^;Х (x~*o)n+1, о < 0 < 1,
получаем следующее утверждение:
Теорема. Если для некоторой окрестности U(xо) точ¬
ки хо функция /(х) £ C°°(U(xq)) н существуют такие чи¬
сла Мид, что |/<п)(х)| ^ Mqn для всех п = 0, 1, 2,... и всех
х Е U(xо), то функция /(х) раскладывается в ряд Тейлора в
окрестности точки хо:
п -О
и интервал сходимости этого ряда включает U(xо).
Если функция / удовлетворяет условиям этой теоремы, то
задача: разложить / в степенной ряд в окрестности точки Хо
/(п)(х0)
сводится к вычислению коэффициентов Тейлора ап = \—-
п\
этой функции в точке хо- ^
Обратно, если степенной ряд ^ ап(х - х0)п представляет
п=О
функцию / в окрестности точки хо, то значения производ¬
ных /(п)ы вычисляются через коэффициенты этого ряда:
/(П)Ы = п!о„.
Пример 11. В примере 10 был получен степенной ряд,
представляющий функцию /(х) = ^ в окрестности точ-
ки г = а: 1 + 1
*, ^ 1 2а , , За2-1 . ч2
~ 1 + а2 (1 + а2)2 (1 + а2)з(г а)
2а(2а2-1), , 5а4 - 10а2+1, ч4
--(ГТ^г (*~а) (ГТ^р (г “а) ~
2а(3а4 - 10а2 + 3) , ч5
- (1-Ьа2)6 >-«)*+■•■•
123
Следовательно,
tn \ _ -2“
/(0t) “ (1 + О2)2 ’
2(За2-1).
f {а) ~ (i + e*p
*>"/■, л — ~ 12(2а3 —а)
* И " (1 + о2)4 1
_ 24(5а4 — 10а2 + 1)
; (1 + а2)5
m ч_ 240а(3а“ - 10а2 + 3)
7 (а) “ (1 + а2)6
Разложение функций в степенной ряд
Возможность почленного дифференцирования и интегри¬
рования степенного ряда внутри его интервала сходимости,
а также относительная простота степенной функции делают
степенные ряды незаменимыми как в теоретических, так и в
практических исследованиях. Естественно, встает вопрос о
разложении функции в степенной ряд и исследовании области
его сходимости. Существуют различные методы разложения
функции в степенной ряд. При этом основными здесь явля¬
ются следующие утверждения:
1) Каким бы образом функция f(x) ни была разложена в
степенной ряд, этот ряд будет для нее рядом Тейлора (т. е.
единственность разложения функции в степенной ряд).
2) Если функция f(z) (комплексного переменного z) ана-
литична в точке z = а, а £ М, и zq — хо + *Уо — ближайшая к а
особая точка функции f(z), то функция f(x) (действитель-
оо
ного переменного) разложима в степенной ряд ^ сп(х — а)п,
п=о
сходящийся к f(x) в интервале (а — /?,а+ Я), радиус R кото¬
рого равен расстоянию между точками а и zq (особая точка
функции f(z) — точка, в которой /(г) не является аналити¬
ческой) .
124
С помощью этих утверждений гарантирована возмож¬
ность применения различных приемов разложения функции
в степенной ряд в интервале (а — \zo - а|,а + |го — a|) без до¬
полнительного исследования остаточного члена соответству¬
ющей формулы Тейлора и применения других достаточных
условий сходимости полученного ряда к функции f(x).
Перейдем к конкретным приемам разложения функции в
степенной ряд.
а) Непосредственное разложение функции /(х) в
ряд Тейлора. В этом случае, находя f^(xо), формально
составляют ряд
£££!)„_ „г.
п = 0
находят область сходимости этого ряда и анализируют, для
каких значений х из области сходимости этого ряда справед-
П \ \П
ливо равенство /(х) = ^ j—Iх “ *о) ■
п=0 П’
Пример 12. Разложить функцию /(х) = ех sin х в степен¬
ной ряд с центром в точке хо = 0.
Решение. Применяя формулу Эйлера
sin х =
2г ’
получаем
Р** _ е-**\ е(1+*> _ е0-*)*
/(*)
2i
и для п-ои производной имеем
/1")(х) = (1 + t)"<'(1+')x ~ (1 ~ г)пг(1~,)т =
2 г
ех ((1 + i)ne'x - (1 - i)np-r)
_ _
В силу формулы Муавра
(1 + t)n = (V2)n (cos Jn + tsin Jn) = (у/2)пе**п,
125
(1 - i)n - (\/2)n ^cos ^ + tsin =
/ /“xn ( 7tt . . 7n \
= (v2) I cos —n + i sin —n 1 =
= (V2)n ^cos +isin (“™)) = (%/2)”е~^\
поэтому
»(т"+*)* _ е-(тп+1)*
/<">(х) = с*(ч/2)" 2.
= (\/2)пег sin (х 4- ~п^
И
/(">(0) = (v/2)"sin™.
Оставим для функции /(я) ряд Тейлора:
(V2)"sin^
1ГП
п
о '*
п =0
Поскольку для радиуса сходимости Я этого степенного
ряда имеем
-^г = lim \/|an| = lim — Г, / — 4 . = 0,
R п—►+<» V 1 1 п-^+оо ' -
ф*п£)п(\ + о{\))
ТО ряд сходится при любом X.
Выясним, для каких знамений х найденное разложение схо¬
дится к функции ersinx. Рассмотрим произвольный проме¬
жуток [—а, а]. Для х из этого промежутка имеем:
|/<">(*)| < (х/2)пе“,
откуда следует, что выполнено достаточное условие вида
|/(п)(г)| ^ Ап при любом п 6 N, |х| ^ а (см. стр. 124).
Отметим, что метод разложения функции f(x) в степен-
оо
ной ряд ^а„(х — х0)п непосредственным вычислением ее
п=0
производных /(л)(х0), п = 1, 2,..., в основном, позволяет
126
найти, как правило, только любое конечное число членов это¬
го ряда, поскольку найти общую формулу для /*п)(х0) бы¬
вает затруднительно, не говоря уже об исследовании сходи¬
мости ряда к функции /(х). Разумеется, вычислив конечное
число коэффициентов ряда Тейлора, можно утверждать, что
это есть коэффициенты степенного ряда, представляющего
функцию в окрестности данной точки, только опираясь на
общие теоремы, сформулированные выше, именно, на теоре¬
мы существования и единственности степенного ряда.
Пример 13. Написать три члена разложения функции
/(х) = хг, х > 0, в степенной ряд с центром в точке хо = 1.
Решение. Поскольку хх = вг|пх, х > 0, то для производ¬
ных этой функции последовательно имеем
(гг|пг)' = е.т |пг(1 + 1пх),
(<■*|п *)" = ' *1п ' (1 + 2 In * + In2 х + I j ,
(f*■"*)'" = ^1 + 3lnr + 31n2z + ln3x +
In x 2 2 In x 1
_|_ -f 1 r
XX X X1
Значения этих производных в точке х = 1 соответственно
равны 1, 2, 2, откуда получаем, что для данной функции сте¬
пенной ряд с центром в точке х = 1 имеет вид
1 + + (5)
Заметим, что поскольку z = 0 — особая точка функ¬
ции гг1п то разложение (5) представляет /(г) в интерва¬
ле (0,2).
В некоторых случаях для нахождения значений f^(x0)
совсем не обязательно искать производные функции у = f(x)
в точке х0, дифференцируя /(х), затем f'(x) и т. д. Иногда
значения /^(хо) находятся из соотношения, связывающего
функцию, ее производные и некоторые известные функции.
Дифференцируя затем последовательно это соотношение, по¬
лучаем другие соотношения, из которых последовательно на¬
ходятся значения производных высшего порядка.
127
Пример 14. Написать пять членов разложения функции
у = earccte* в степенной ряд в окрестности точки хо = 0.
Решение. Производная функции у = earccter и сама функ¬
ция у связаны соотношением
у, = -унЬ’
т. е.
1/(1 + х2) = -у, (6)
поскольку у' = — е"00*®*--—!—Так как у(0) = е'j', то у'(0) =
1 4" х
= -е *. Дифференцируя равенство (6), учитывая, что у — у{х\
имеем
у"(1 + х2) + у'-2х = -у', (7)
откуда
у"(0) = у' (0) = е*.
Далее, дифференцируя равенство (7), имеем
у'"( 1 + х2) + 2ху" + у"-2х + 2 у' = -у",
откуда
j/"(0) = -у"(0) - 2у'(0) = -е* + 2г» = е*.
Аналогично находим
y<,v>(l +х2) + 6у" + 6ху"' = -у"',
откуда
y^)(0) = -J///(0)-6y/,(0) = ~7r^;
y(v) (l +Х2) + 8xj/<,v> + 121/" = -y{lv\
откуда
y(v)(0) = — 7е% + 12с^ = 5е^.
Применяя метод математической индукции, находим, что
у(п)(х)(1 + х2) + 2(п - 1)ху(п-‘)(х) + (я - 2)(я - 1 )у(п -2)(х) =
= - у*п-1)(х), откуда
у(">(0) = -у(п-1)(0) - (я - 2)(п - 1)у(п-2>(0),
•1 л ' }
п = 3, 4,....
128
Итак, для нахождения з/п)(0) полумили рекуррентную фор¬
мулу (8), причем
У(0) = с*. 1/(0) = -у(0) = -е*. у"(0) = у(0)
и разложение данной функции в степенной ряд с центром в
точке х = 0 имеет вид
arcctgх f § .Х+Ц.х* + —x3_ ]_eix4+ Ц j.5 + . .
2! 3! 24 24
б) Использование основных табличных разложе¬
ний. Как уже указывалось, на практике выразить зависи¬
мость ап от п непосредственно дифференцированием функ¬
ции /(х), т. е. найти явное выражение гпЦхо) как функции п,
чаще всего не удается. Для разложения конкретной функ¬
ции f(x) в степенной ряд с центром в точке хо = 0 пользуют¬
ся разложениями основных функций:
_2L хп т2 т3 тп
е‘= ■£-;= 1+г+- + - + ■■+-+ - ,\г\<с*,
п=0
Ж2п + 1
sin”S(^TiT(',r =
X3 X5 X2n + 1
= * “ ¥ + 5Т + ''' + (”1)П (2n + 1)! + ' ’' ’ ,i|<00’
00 Х2п
X2 X4 , *2п
п= 0 ' '
2! ’ 4! ' ’ ' v (2п)
in(i + x) = f;^(-i)'-i =
■ ■n
n = l n
X2 X3 xxn
= *-y + y- ■•• + (-i)n"1 — + •••. -i<*£ 1,
129
и+,г = I+f; "‘t’" - ?■>'Jm ~" =
П= 1
m(m - 1) 2
- 1 + mx + x + • • • + ^
m(m — 1)-... (m — n + 1) _
+ —1- 1 г ~x + ‘ ‘ *'
n!
m E IR, -1 < x < 1.
Приведем некоторые частные случаи последней формулы:
1 = 1 + |х|<1,
1 + *
* = 1 + х + х2 + х3 Ч hxn Н , |ar| < 1,
1 — х
1 ,1 13 2 13-5 о
= 1 — -X + -—X - ■—--X + h
у/Г+1 2 2-4 2-4-6
П,(2п-1)М ,
(2п)!! ’
1 ,1 1 3 2 13-5 з
= 1 + -х + —X2 + —— X3 + • • • +
vT^x 2 2-4 2-4-6
+ (2г^т
(2п)Н ■
г- ,1 1 1 2 113 3
^П=1 + -х--х +—X ---.+
I ( 1)” 1)!!хп+1 | |х| < 1
+ [ > (2п + 2)!! + ' 1 К ■
л . 1 11 2 113 з
V1- X = 1 - -х - —х - ——— X
2 2 4 2-4-6
(2п - l)!! »+i I I < 1
(2п + 2)!! + ’
Пример 15. Разложить функцию f(x) = е1"-2*3 в степен¬
ной ряд с центром в точке xq = 0.
130
Решение. Поскольку е1"2** = е е”2а? , то, полагая -2я3 =
= у и используя табличное разложение (9) для функции еу,
имеем ряд
е(1 + (-2,з) + Ь|!)I + ...+fc*2l + ...).
„ , 22е в 23е 9 - ,Чп2"е Зп
= е - 2ех + —х6 - —х9 + • • •+ (-1)"—х3" + • • .
Так как разложение в ряд функции еу имеет место для
всех у, то и разложение в ряд данной функции справедливо
для всех |х| < оо.
Пример 16. Разложить функцию f(x) = --- в степен-
1 + Xя
ной ряд с центром в точке хо = 0.
Решение. Полагая х4 = р используя формулу (9) для
функции z = , имеем ряд
, * -4 = 1 - х4 + X8 - х12 + • • • + (~1)пх4п + • .
1 + хн
Этот ряд представляет данную функцию для х таких, что
\у\ < 1, т. е. |х4| < 1 и, значит, для х из промежутка — 1 < х < 1.
Заметим, что на первый взгляд кажется странным тот
факт, что функция f(x) = j является бесконечно диф-
1 + я
ференцируемой на всей прямой, а разлагается в степенной
оо
ряд 1+^(—l)nz4n только для х из промежутка |х| < 1. Дело,
п=1
однако, в том, что соответствующая функция комплексного
переменного f(z) = —^ ^, сужением которой на действи¬
тельную ось является функция f(x) = —j, имеет особые
1 Ч- х
точки z\ = i и zi = —t, и поэтому разложение f(z) в степен¬
ной ряд верно для \z\ < 1, что соответствует |х| < 1 (сравните
пример 10).
131
в) Использование сложения и вычитания рядов и
умножение ряда на многочлен и ряд. В некоторых слу¬
чаях разложение функции в степенной ряд можно получить,
суммируя табличные разложения или ранее найденные. Так,
например, для разложения функций у = х2гх, y=(x2-f 1) sin х3
достаточно разложение функции ех умножить на х2, а разло¬
жение функции sinx3 умножить на (х2 + 1). При :>том ино¬
гда надо аналитическое представление функции преобразо¬
вать так, чтобы представить ее в виде удобной комбинации
функций, разложения которых известны.
Так, например, для разложения функций у = 5Г, у = sin2 х,
У = "о : У — 1пП + х + х'2 + я3) в степенной ряд
х1 — 4х 4- 3
оо
^^апхп достаточно преобразовать их соответственно к
n=0 rln5 1 cos2x 1/1 1 \
.иду у = е ,у=
1 — X4
у = In = In(1 - х4) - In(1 - х).
1 — X
Помимо перечисленных выше утверждений законность та¬
кого метода разложения функций в степенной ряд основыва¬
ется на следующих результатах.
Рассмотрим два ряда:
оо
^апж" = а,, + сцх 4- а2х2 + ■ • + а„х" + (10)
п — 0
с радиусом сходимости R\ и ряд
оо
= 6о + Ь\х + 62х2 + • • • + Ьпхп + ■■■
п=0
С радиусом СХОДИМОСТИ /?2
Пусть R = min{/Zi, R2)
Тогда для |х| < R эти два ряда можно складывать, вы¬
читать и перемножать, причем в результате опять получим
132
соответственно степенные ряды:
оо оо
£(an+6n)x", £(ап-6п)х",
п=0 п = 0
оо
-I- а\Ьп-\ 4- а2&п-2 4- • • • 4- о.пЬо)*п-
п=0
Такое приведение подобных членов в произведении степен¬
ных рядов является представлением этого произведения сте¬
пенных рядов в форме Коши (см. стр. 57). Ясно, что степен¬
ной ряд (10) на интервале сходимости |я| < R можно возво¬
дить в любую натуральную степень шив результате опять
оо
получится степенной ряд коэффициенты которо-
n = U
го находятся путем перемножения ряда (10) самого на
себя rn раз и приведением любым способом подобных чле¬
нов ахп, п - 0, 1, 2 ....
Пример 17. Разложить функцию }(х) = —— в
х — 2х — 3
степенной ряд:
а) с центром в точке xq = 0,
б) с центром в точке хо = 4.
Решение, а) Представим данную функцию в виде
л,) = = L_U
х2 — 2х — 3 4 \х — 3 х + 1 /
11 11
12 1 - § 4 х + Г
Применяя известные разложения для функций у =
,
и у = , имеем
I — х
х , (х\ (х\п i-' I
-1 + з + (з) +"'+(з) + "’ Ы<1
1-| ' 3 \3/ V3/ 43
1 х . Iх\2 ,/Х\п IхI
1
- = 1 - х + х2 - х3 + 1- (-1)"х" н , |х| < 1.
*+ 1
133
Следовательно, получаем:
/(х) = пН1+!+(!)+ +(f)+ "■)“
- ^(1-* + г2-х3 + - +(-1)пхп+-) =
12 7 ,
(- -X X2 + h
Q Q 07
ч^г-моу-
(11)
Поскольку первый ряд сходится к функции у =
1
|х| < 3, а второй — к функции у =
ряд (11) представляет функцию у =
Итак,
(-1)П + 1
1
1 — £
1 3
при
X + 1
1
х2 - 2х - 3
при |х| < 1, то
при |х| < 1.
6) Представим данную функцию в виде
„.11 11 1 1 1
/(*) = 7
1
4 г-3 4 г + 1 4 г - 4 + 1 4 х-4 + 5
1 1 1
1
4 1 + (* - 4) 20 1 -h Н4 ’
откуда имеем
n=0 п =0 4 '
т. е.
Полученное разложение верно при х таких, что одновре-
х — 4
менно выполняются неравенства |ат — 4| < 1 и < 1, т. е.
5
при \х — 4| < 1.
134
Пример 18. Разложить в степенной ряд функцию /(х) =
= ln( 1 + х 4- х2).
Решение. Представим функцию у = ln( 1 + х + х2) в виде
1-х3
у = In или так у = 1п(1 — х ) — 1п(1 — х). Раскладывая
1 — х
теперь в степенной ряд каждую из функций у = 1п(1 - х ) и
у = 1п(1 - х), имеем
/—6 -»9 г3п
1п(1 - х3) = -х3 - - — + ■■ ■,
|х3| < 1, т. е. |х| < 1,
х2 х3
1п(1 - х) = -х - — - y 1*1 < 1
Следовательно,
1п( 1 + X + х2) = -х - у - ^1 + ^ х3 -
-Т-Т-ИУ-Т-
Отметим, что предложенное преобразование функции у =
= 1п(1 + х + х2), определенной на всей действительной оси,
/1 -х3\
к функции у = In ( — 1 не сужает области разложимости
функции у = 1п(1 + х + х2) в степенной ряд, поскольку разло¬
жение функции у = 1п(1 + х + х2) возможно до первой особой
точки функции у = ln(l + z -f z2) = f(z). Особые же точки
1 .V3 1 .V3
этой функции есть точки z\ = — - 4-1— и z2 = — - — t — ,
£ & L л*
которые находятся на окружности \z\ = 1, т. е. кругом схо¬
димости степенного ряда с центром в нуле, представляющего
функцию /(*), является круг \z\ < 1. Его сужение на дей¬
ствительную ось есть интервал (—1,1), поэтому интервалом
сходимости степенного ряда с центром в нуле, представляю¬
щего функцию у(х), является именно этот интервал, в кото¬
ром функция у = 1п(1 + х + х2) тождественно равна фуцкции
у = 1п(1 — х3) — 1п(1 — х).
Для разложения функции /(х) в степенной ряд с центром в
точке Хо Ф 0 чаще всего применяется следующий метод: вво¬
135
дится новая переменная t = x — xq и ищется разложение функ¬
ции f*(t) = f(t + xо) в степенной ряд по степеням t (с центром
сю
в точке t = 0) f*(t) = ^2 antn, |(| < R. Откуда получаем, что
n =0
ОО
/(*) = а,%(х ~ х°)п’ Iх ~ ж°|< Л’
п=0
Пример 19. Разложить функцию f(x) = cos4 х в степен-
7Г
нои ряд с центром в точке хо = —.
Решение. Поскольку
7 1 -h cos 2х
С08 X — ,
ТО
+cos4х
а \ (1 + со® \ 11 г, 1
/(*)=( 2 j =4 + 2COS2x+"
8
3 1 1
= - + - cos2x + -cos4x.
Обозначим t = x — тогда x = t + cos2x = -sin2t,
4 4
cos4x = — с os 4t. Следовательно,
/(*) = /*(<) = | - ^sin2t - ^cos4(.
Применяя разложения (9), имеем
f() - 3 1 V (-l)n22n+,<2n+1 1 (—l)n42n<2n
fW-8 2 " (2п + 1)! 8^-; (2n)! ’
n=0 4 n=0 4 7
|t| < OO.
Возвращаясь к x, получаем
n=0 4 '
+ £■ (2n)! Л-?) >W<CO-
n = l 4 7
Остановимся более подробно на сложении бесконечного
множества степенных рядов.
136
Пусть дана последовательность степенных рядов
оо
Y^anmxn, т = 0, 1, 2,....
п=0
Из них составим повторный ряд
оо / оо \
£ ( £ “nm*n j
т=0 \п=О /
(12)
Бели при значении х, равном хо, сходится ряд, полученный
заменой всех членов их абсолютными величинами, т. е.
£ (x>«~ikiY
т=0 \п=0 /
то сходится и ряд (12), причем сумма
его 5(х) может быть представлена степенным рядом просто
оо
путем приведения подобных членов: А(х) = £^Лпхп, где
оо п=0
Ап - ^ ^ flnmi П = 0, 1, 2, . . ..
m — О
Пример 20. Разложить функцию
/<*) = £ ("dl - 1 1*1 < 1, 0 < а < 1,
т=0
в степенной ряд с центром в точке х = 0.
Решение. Поскольку
— оо
= £(-1Гат(2п+1)г2п, |*| < 1,
1 + а2тх2
п=0
то, подставляя это выражение в /(х), получаем
(E(-ir«m(2n+1)*2n) =
m=0 \п=0 /
°° °° ( 1\тЛ(2п+1)т °°
= E(-1),*’n Е ( 1 = £<-»"«- *г"-
п=0 т=0 п=0
Перестановка суммирования законна, поскольку ряд
оо . оо
V4 J_ Y^„(2n + l)rn 2п
сходится:
оо 1 / о° \ оо , г
т=0 \п=0 / т=0
1 _ еа
< 1 - х2 ". т! 1-х2
т
—г <
Пример 21. Разложить в степенной ряд с центром в точ¬
ке хо = 0 функцию у = ctgx.
Решение. Используя результаты задачи 80 п. 1 (стр. 330),
имеем соотношение
°°s 2х2
хctg* = 1 + V -? г—хфкк, к = 0, 1, 2....
Лшш\ хс — ir*mz
т= 1
Если |х| < 1, то для любого т — 1, 2, 3,...
2 X2 оо / „2 \п
* _ тг5т2
xz - n*mz 1 -
п*тл
оо / о v п
П= 1 4 '
поэтому
00 / оо / 2 \ п\
■-*Е ЕШ )-
т = 1 \п = 1 4 ' /
оо оо / 2 \ п
—*eeU0 -
, ^12л
~ 1 2И^гГ2п*
(13)
. *■
п = 1
°° 1
где г2п = V] —or-, п = 1, 2,.... Отметим, что если искать
~ 171*"
т=1
разложение функции /(х) = xctgx в виде ряда
у = а0 4* atx -f а2х2 + h anxn Н
13*
(см. пункт г) настоящего параграфа), то коэффициенты а*
можно найти из равенства х соех = sin х, т. е.
Л *2 *4 *6 / ,чп *2" ^
* ( 2! + 4! 6! И (2п)! + ' j ~
/ X3 хь х2п~1 \
Ч'-¥+5Г--' + '-1>"''(5ГГТ)? + ''')><
х (а0 4* Л\Х 4* а2ж2 4- h апхп 4* • • •)
Приравнивая коэффициенты при одинаковых степенях х как
в левой, так и в правой частях этого соотношения, последо-
1 п 1 1
вательно находим а0 = 1, а\ = 0, аг - — = т. е.
о 2 6
л 1 ао «2 1 ^
аз = 0, — = — - — 4 а4, т. е. а4 = Сопоставляя
коэффициенты при х2 и а?4 в разложении (13) со значением а2
и сц, получаем
оо , 2 оо , 4
Е1 _ JT ^ 1 _ *
т2 б ’ ~ т4 90
т=1 т=1
г) Метод неопределенных коэффициентов. В неко¬
торых случаях для нахождения разложения функции в степен¬
ной ряд используется метод неопределенных коэффициентов.
Суть его состоит в следующем: ищется разложение функ-
ОО
ции /(я) в виде затем составляется некоторое соот-
к=о
ношение, связывающее функцию f(x) или ее производные с
другими функциями, и из условия тождественного равенства
нулю степенного ряда на некотором множестве приравнива¬
ются к нулю его коэффициенты. В результате получаются
соотношения, связывающие числа а*, из которых они последо¬
вательно могут быть все или в достаточном количестве (нам
необходимом) найдены. Этот метод полезен при разложении
в ряд функций у = у = 1п/(х) и т. д., и, кроме того,
при решении обыкновенных дифференциальных уравнений,
нахождении у(п)(х0) с помощью рядов и т. д.
Отметим еще, что в этом методе существенно можно об¬
легчить вычисление, пользуясь тем, что степенной ряд с цен¬
139
тром в точке х = 0, представляющий четную функцию, имеет
оо
вид у а соответствующий ряд для нечетной функции
/с=0 оо
Е2к-\
CkX
к = )
Рассмотрим некоторые примеры.
Пример 22. Разложить в степенной ряд с центром в точ¬
ке хо = 0 функцию у = earctgr.
Решение. Дифференцируя функцию у = earctsx имеем
./ _ arctg х 1
1 -f хг
откуда (1 + х'2)у' = у.
Будем искать разложение функции у = eai4‘tgx в виде у =
= ао + а\Х + а2х2 -f • • • + апхп + • • •. Тогда имеем
(1 + x2)(aj + 2а2х + За3х2 + • • • +
+ 7ianxn"'1 + (ti + l)an + 1xn + •••)= (14)
= a0 + (iir -f a2x2 -I- h anxn + • •
Приравнивая свободные члены и коэффициенты при оди¬
наковых степенях х как в левой, так и в правой части (14),
находим
ai = a0,
2a2 = ai,
1 aj + За.з = a2,
2a2 -|- 4a^ = аз,
(n - 1 )a„_i + (n + l)an+i = °n,
Поскольку при x = 0 имеем earctg* = 1, то а0 = у(0) = 1.
Следовательно, ао = 1, а тогда а\ = 1, а2 = аз =
7 5 2 6
°4 24’ “5 120 “ Т Д
140
Итак,
1 2 1 3 7 4 1 5
»=l + « +-j. -я. +я« +■•••
Заметим, что разложение для функции у = е*1"01** можно
получить, зная разложение функции у = earcctex (См. при¬
мер 14), поскольку
^ arctg х _ ef-arcctgx _ f §-(ir-arcctg(-x)) = § >earcctg(-x) _
= e'I,eI 1 + ,+ 2* Г ~ 24* + 24* +
д) Подстановка ряда в ряд. Пусть функция у = /(х) в
оо
промежутке (-Я, Я) разлагается в степенной ряд ^Panxn, a
п=0
оо
функция (р(у) разлагается в степенной ряд (р(у) = бту1
,т
>тУ
т=О
для у €(-*>,*>).
Если ао = 1/(0) | < р, то при достаточно малом г будет
верно неравенство |/(х)| < р и имеет смысл функция <р (/(ж)).
Справедлива следующая
Теорема. Если |ао| < р, то функция <p(f(x)) разлагается
в окрестности точки х = 0 в* степенной ряд, который можно
оо
получить, подставляя в ряд для (р(у) вместо у ряд апхп и
п=0
производя возведение в степень и объединяя затем подобные
члены хр, р = 0, 1, 2,....
Заметим, что область изменения х, для которых обеспе¬
чивается возможность разложения функции (p(f(x)) в ряд по
степеням х, можно, например, определить из условий |х| < Я
оо
и неравенства ^ |апхп| < р. Если представляет интерес вся
п=О
141
область, в которой возможно разложение <р (/(*)), то этот
вопрос требует отдельного исследования.
Пример 23. Рассмотрим функции
оо
/(*) = -2х - х2, R = +оо, и <р(у) = ym, р = 1.
т=0
Функция ^ (/(*)) = ) + 2Х + X2 = (Г^)2 ИМееТ СМЫСЛ
при —1 < — 2х — х2 < 1, т. е. при —1 - \/2 < х < — 1 + \/2,
х ф — 1. Ее разложение по степеням х есть
1 - 2х + Зх2 - 4х3 + • • • + + • • •.
Этот ряд сходится при |х| < 1. Равенство
ОО
]Г (-2* - х2)т = 1 - 2* + Зх2 - 4х3 + • (15)
т=О
имеет место при условии -1 < х < -1+ч/2. Согласно же при¬
веденной выше теореме и замечанию, разложение (15) имеет
место во всяком случае для таких х, что 2\х\ + х2 < 1, т. е.
1 — у/2 < х < — 1 -f у/2. Следовательно, равенство (15) верно
в более широкой области.
Пример 24. Разложить функцию
fln^
1 o'
sin Я
. __j , х ф О,
я*) = * -
о
в ряд по степеням х.
Решение. Так как при любом х
д.3 Ть _2 *-1
х х ' *\к-\ х
sinx = x- — + —-•• + (-!)*
3! 5! у ' (2к — 1)!
ТО ДЛЯ X Ф О
2 -4 „6 -2к — 2
-1-Ч7 + 77~^Г + ' + (_1)
3! 5! 7! ' ' (2*- 1)!
142
sm X
а тогда для функции у = In получаем
х
. 8Ш X ( X2 X4 X6 \
(“I + 120 ~ 840 + 'j ~
2 V 6 120 840 )
X2 X4
Т~ 180 +
Поскольку полученный ряд при х = 0 сходится и его сум¬
ма равна нулю, то этот ряд представляет функцию /(х) для
всех х. Отметим, что с другой стороны имеем (см. стр. 74)
(17)
Разлагая этот ряд по степеням х и приравнивая коэффициен¬
ты соответственно при х2, х4,... в (16) и (17), находим
1 f 1 1 ^ 1 7Г
^Е^=6-откуда х^=Г’
П=1 П=1
1^1 1 ^ 1 л-4
2ir4 ^ п4 “ 180’ откуда „4 ~ go’
П = 1
имер 25. Найти первь
_ |(1 +х)*, х Ф 0,
\ е, х = 0
П=1 П=1
Пример 25. Найти первые пять членов разложения функ¬
ции у = ^ в степенной ряд в окрестности
точки х = 0.
Решение. Перепишем функцию в виде
_Ге^Щ(1+*)1 хф0
Поскольку для |х| < 1 имеем
X2 X3 , X"
143
то
!in(i+*) = i-f+т-••+Н)П_,^+" , o< |*|< 1.
x 2 6 n
Подставляя это выражение в данную функцию, получим, что
у = е1-! + т-- + (-1)п-1£^+- =
= ее_2 + Т + (-l)n"‘V- + ---, 0<|*|<1.
Используя ряд для еу и предыдущую теорему, находим
1 / X X2 X3 1гП~1 \2
+ 2!Г2 + Т"Т+ +(_1) ~ + ‘") +
1 / X X2 X3 J ХЛ_1 \3
+ 3!Г2 + Т"Т+'"+("1) ~ + ' ) + +
+ ^(~?+Т~Т + • + (-1)"_l£v~ + - ) +• ••)=
+ (Ьт? + § + ^ + 24Г1б)х4+ ) =
/ X 11 2 7 з 7341 4 \
С V 2 241 1бХ + 17280Z + J
Пример 26. Разложить бесконечное произведение
оо
/(«)= П 0+ «"**>. \я\< 1,
то = 1
в степенной ряд с центром в точке х = 0.
Решение. При |х| < 1 произведение сходится и /(х) > 0.
Рассмотрим логарифм /(х):
оо
ln/(*)= £ln(l+ ,"*).
m=l
144
Для |z| < 1 имеем
In/(Г) = f; (,”> - \q2m r2 + l-i3mx3 -•••).
Так как этот ряд сходится при замене всех членов в скоб¬
ках их абсолютными значениями, то In /(г) в окрестности
нуля разлагается в степенной ряд, а тогда в силу теоремы на
стр. 142 в степенной ряд можно разложить и функцию еХп^х\
Итак, для достаточно малых х имеем
f(x) = 60 + Ьхх + Ъ2х2 + h bnxn + • •
Поскольку
f(x) = (1 +gz)(l + g2x)(l + <73r)... =
= (l + 9x)[(l + ЯЯх)(1 + Я2 Я*) ...] = (!+ Ях)' (/(ях)) ,
то имеем
Ь0 + bi* + Ь2х2 + h Ьпхп + • • =
= (1 4- Ях)(Ьо + b\qx + b2q2я2 + • • • + bnqnхп + •■•),
откуда, замечая, что 6о = /(0) = 1, имеем
Ь\ = яЬо + b\q, b2q2 + biq2 = 62, • •,
bnqn + 6П_1*Л = Ьл,
т. е.
= б2= ’3
6п =
1-?’ (1-*)(1-92Г
п(п-|)
(1-д)(1-д2)...(1-д")'
Итак,
з
/(*) = 1 + 1 + 71 гг. 2Т*2 +
1 -Ч (1-?)(1-?2)
145
Заметим, что поступая формально, получаем:
/(*) =
= (l+9r)(l+g2a:)(l+03z)(l+fl4x) . ,(l+gnx)... =
= 1 + (Я + Я2 + Ч3 + ' • + Чп + ••■)* +
+ (Я Я2 + (Я + Я2)Я3 + (Я + Я2 + Я3)ЯА +' • ) *2 + • • =
= 1 + у(1+? + 72 + •• •) х +
+ я2 (я + {я + Я2) + (я + я2 + Я3) + • ) *2 + • • =
= 1 + Y^-x + (q(q2 + q3 + qA + ■■■) +
+ я2(я3 + яА + я5 + ■ ■) + я3(я4 + яъ +•••)+••• +
+ яп(яп +' + яп + 2 + • • + ят + • •) + • • -)*2 +
+ (я я2 я3 + • )*3 +••■• =
= 1 + Т^—Х + (?3( 1 + я + Я2 + •• •) +
1 - q
+ яЧ 1 + я + я2+ •••) +
+Я7(\+Я+Я2+ ••)+•• )х2 + (яя2д3+ ■ ■ )х3+ • • =
= 1+ *
х + + -i— + Л х2 +
\\-q 1 - Я 1-Я )
1 - q
+ (?6 + • • )х3 + • • • =
а3
= 1 + х + (1 + q2 +я4 + ■■ -)х2 +
1-q 1-q
+ (Я6+ ■■ )х3 + • =
= 1 + -г1-* + т^- Т-1—х2 + •••.
1 — q 1 — q 1 — q2
е) Деление степенных рядов. Важным применением
теоремы о подстановке ряда в ряд является деление степен¬
ных рядов. оо
Рассмотрим степенной ряд ^Рапяп, где ао Ф 0, х Е
е(-я,,я,). п=0
146
Представим этот ряд в виде
а0
Л , ах а2 2
1 + —X + —Z
\ do <*0
+ —х"+-
ао
+ у)>
где
®1 - а2 2 . I e*» п |
У =—Х +—X Н 1- X +
во во а0
Тогда
1
1 1
(18)
а0 + а\Х Н (-о„хп + - - а0 1 + у
= 1 -у + у2 + (-l)mym+-
«о
ОО
Радиус сходимости ряда ^(—l)mJ/m есть 1.
т=0
Подставляя вместо у соответствующий ряд в (18), полу-
чаем в силу общей теоремы выражение 1 в ви-
а0 + <их + • • •
де степенного ряда с центром в точке xq = 0 для достаточ¬
но малых значений х (например, для таких, что — |х| +
«о
02
1 i2 • ■
On
\ху + • • ’ +
ао
ао
1
|х|Л 4 < 1), т. е.
= с0 + С\Х + 1- спхп 4-
ао + а\х 4- а2х2 +
оо
Пусть есть еще ряд ^Г^Ьпхп с радиусом сходимости Яг- По¬
может быть записано
гда частное
п=0
Ьо *+■ ^ix + • • * 4- Ьпхп 4- •
ао + aix 4- h апхп 4-
в виде
(Ьо + b\x 4- •' +bnxn 4 ) (со +cix 4- С2Х2 4- • • -4-спхл + • • •),
т. е. представлено степенным рядом
do 4* d\x 4- cf2x2 4- • • • 4* dnxn 4- • • •
147
Коэффициенты dt, i = 0, 1, 2,..., можно определить, напри¬
мер, методом неопределенных коэффициентов, исходя из ра¬
венства
(ao+ai£+ • • • +an*n + • • + ■ +dnxn + • •) =
= 60 + b\x + • • ■ + bnxn + • • •,
производя перемножение рядов и приравнивая коэффициен¬
ты при одинаковых степенях х в левой и в правой частях
равенства.
Пример 27. Написать несколько членов разложения фун-
/ т.{ 1, г = О
Решение. Для |х| < 1 имеем
х = О
Поэтому
х
148
ж) Почленное интегрирование ряда. Пусть f(x) пред¬
ставляется в виде
х
/(х) = /(*<>) + J <p(t) dt,
где разложение <р(х) — ап(х — жо)Л известно или доста-
п=0
точно легко получается. Тогда в силу общей теоремы (см.
стр. 110) равенство
л*)=/(*„)+£; а-(д~+1)--~ (2°)
п=0
справедливо внутри общего интервала сходимости рядов
V"' ( \п ап(х “ хо)Л + 1
х;в»(*-*о)я и n+i—•
п=О п=0
Вторая теорема Абеля. Пусть Я — радиус сходимости
степенного ряда и S(x) — его сумма для х 6 (—Я, Я). Если
ряд сходится в точке х = R (х = —Я), то его сумма является
функцией непрерывной в точке х = Я ( х = —Я), т. е.
lim У2апхп = У2апНГ
г—►Я—0 i
п=0 п=0
(ji. £>«*=£>.(-« г).
\ п=0 п=0 /
Из этой теоремы следует, что если ряд ^ аЛ(х-хо)Л или ряд
^ап(*-*0)"+1
> сходится в одном или обоих концах проме-
л п + 1
п=0
жутка (—Я, Я), то и равенство (20) имеет место при соответ¬
ствующих значениях х (х = Я, х = — Я).
Пример 28. Разложить функцию у = arctg х в степенной
ряд с центром в точке xq = 0.
149
Решение. Поскольку arctgx = J , то, разлагая
функцию ■ -~-^2 в степенной ряд с центром в точке хо = 0 и
1 „ 0
1 -f* х
интегрируя почленно полученный ряд, имеем
arctg х =
х
= j (l - х2 + х4 - х6 + • • • + (-l)"_1x2n-2 + • • •) dx =
0 X3 X5 X7 (-l)n_1x2n-1
“ * 3 + 5 7 + '+ 2n - 1 + " ’'
Разложение функции ——- справедливо для x, удовлетворя-
1 -h X2
ющих условию |х| < 1. Для этих же х верно и разложение
г3 г5 (-Пл”1ж2п“1
+-■ (2,)
Отметим также, что одновременно получено разложение в
степенной ряд с центром в точке хо = 0 функции у = arcctg х,
7Г
так как arcctg х = — — arctg х, т. е.
ж х3 х5 (-l)nx2n_1
иссЦ,,= --«+у-т + ...+ 2п1 +.... (22)
Заметим также, что в силу сходимости ряда (21) в точ¬
ках х = +1 и г = - 1из второй теоремы Абеля (стр. 150)
следует, что разложения (21) и (22) справедливы и для этих
значений х, т. е.
хз (-1)п~1х2п“1
arctg* = *-_ + ... + i—i——j + • • • для |x| ^ 1,
* х3 (-1)пх2"-' , , ,
arcctg х = -- х + у+ -+ —2п^~1— + для |*| ^ 1.
Пример 29. Разложить функцию у = arctg2 х в степенной
ряд с центром в точке хо = 0.
Решение. Возводя в квадрат ряд для у = arctgx, имеем
2 / х3 хб х7 (-1)п-1х2"-1 \2
„а, ,= ^-т+т-т +—-Я | +...j ,
W ^ 1.
ISO
т. е.
*б+
|х8+- +
arct8»i = .“+(-?) гЧ(1 + 5 + 0
+Н-Ж4МН)>
+,,_(1 + 5)V+(l + 5 + 0V"
"(, + 5 + Ё + 0т+ +
+(-,)“" (1 + j + s+ " + 2^r)v + ""
Итак,
■"V* = D-i)-1 (' + 5 + • + 2^гт) V'w < L
п = 1 х '
Для доказательства формулы общего члена полученного
, 1 1
ряда ап = 1 + -Н |- - г можно воспользоваться методом
о In — 1
математической индукции (проверьте!).
х
Пример 30. Разложить функцию J f(x)dx, где
1п(1 + X)
■{'
хфО,
/(*) = { х
1, х = О
в степенной ряд с центром в точке хо = 0.
Решение. Разложение функции /(х) в степенной ряд с
центром в точке Хо = 0 есть
Н-7 + Т +
-1 < х < 1, х ф 0,
т. е. есть
X X2 — I
/« = 1-J + T+ tf-T-'—+ .
131
Это разложение верно и в точке х — 0, т. е. для всех х из
промежутка -1 < х 1. Следовательно,
X
1
о
Предложенный способ находит широкое применение при
приближенном вычислении определенных интегралов, когда
найти первообразную в конечном виде не представляется воз¬
можным (см. далее гл. II § 2).
Пример 31. Разложить функцию у = ln(x -f \/l + *2) в
степенной ряд с центром в точке хо = 0.
Решение. Для производной данной функции имеем
у' =(1
Эта функция разлагается в степенной ряд
(i+x2)-i = i + f;(-i)"(-2”^!!x2n, i*i <i.
n = l
Интегрируя почленно этот ряд от 0 до х, имеем
х
. . г. ( dx
1п(х +
\/1 + X2) = J
%/гг
Поскольку этот ряд сходится и в точках х = ±1 (проверьте!),
то по второй теореме Абеля отсюда имеем, что полученное
разложение справедливо для всех |ж| ^ 1 В частности, полу¬
чаем, что
1 13 1
+
+ (-|>‘1fcw-STr + - +
X
о
г
2
152
2 4-... (2n) 2n + l
+ - =1п(^2 - 1).
з) Почленное дифференцирование ряда. Суть мето¬
да состоит в следующем. Пусть надо найти разложение неко¬
торой функции в степенной ряд. Если удается найти такую
функцию д{х)у что /(аг) = д'(х), то, разложив функцию ^(х) в
степенной ряд и продифференцировав его почленно, получим
разложение в ряд функции /(х). При этом полученное раз¬
ложение верно всюду, где соответствующее разложение было
верно для функции д{х).
Пример 32. Разложить функцию у = ———~ в степен-
(1-х)2
ной ряд с центром в точке хо ~ 0.
= 1 + 2х + Зх2 + h пхп 1 Н
Так как при дифференцировании интервал сходимости сте¬
пенного ряда не меняется, то найденное разложение имеет
место при х, удовлетворяющих условию — 1 < х < 1.
и) Представление степенным рядом неявно задан¬
ной функции. Пусть функция у(х) определяется уравнени¬
ем F(x,y) = 0 и условием у(х0) = уо (числа х0 и уо должны,
естественно, удовлетворять равенству jF(xo,#(xo)) = 0).
Теорема. Пусть функция F(x,y) в окрестности точки
(х<ь Уо) разлагается в ряд по степеням х —хо и у—уо и коэффи¬
циент при у — уо этого разложения отличен от нуля
(^у(х0,у0) Ф 0). Тогда функция у(х), определяемая уравне¬
нием F(xty) - 0 в окрестности точки хо, разлагается в ряд
по степеням х — хо
Решение. Поскольку
(1-X)2
= (1 + X + х2 + х3 + ■ ■ ■ + хп + • • •)' =
133
Другими словами, эта теорема означает, что если F(x, у)
аналитическая в некоторой окрестности точки (хо, Уо) такой,
что F(xo, Уо) = 0, то функция у = у(х), определяемая уравне¬
нием F(x,y) = 0, также будет аналитической в окрестности
точки хо, если Fy(x0,yo) ф 0.
Без ограничения общности будем считать, что хо = уо = 0.
оо
Пусть F(x,y) = ^2 сц,х*зЛ- Так как F(x,y(x)) = 0 в
i,*=0
некоторой окрестности точки (0,0), то, следовательно,
53 ci**V = 0
• ,Д=0
Если выделить член с первой степенью у, то, перенося его в
другую часть и деля на коэффициент при нем, можно данное
уравнение переписать так:
У = С\фХ + С20у + Сцху + С02У2 + СэоХ3 + С2IX2 у +■■■. (23)
Ряд для функции у(х) будем искать в виде
у(х) = а\х + а2х2 + азх3 + • • •.
Подставляя это выражение у в (23) и приравнивая коэф¬
фициенты при одинаковых степенях х, после возведения со¬
ответствующих рядов в степень и приведения подобных чле¬
нов, получим систему уравнений, из которой последовательно
найдем коэффициенты а;:
at = сю, а2 = C20 + Cuaj +c02Oi и т. д.
Заметим, что сформулированная теорема носит лишь локаль¬
ный характер и устанавливает только возможность
разложения у по степеням х — хо вблизи хо. Определение
точного промежутка сходимости этого разложения требует
особого исследования.
Известно, что если для F(x, у) ее разложение в ряд по сте¬
пеням х и у справедливо для |х| < г и |у| < р, то ряд для у(х)
сходится, по крайней мере, для |х| < п, где г} = г
И |c,*|rV't < М.
154
Пример 33. Найти пять членов разложения в степенной
ряд функции у(х), являющейся решением уравнения
у = 1 4 хеу и удовлетворяющей условию у(0) = 1.
Решение. Функция еу является аналитической в окрест¬
ности любой точки, в частности, в точке у = 1. Поэтому на
основании предыдущей теоремы из уравнения у = 1 4- хеу и
условия у(0) = 1 функция у(х) определяется как функция х,
аналитическая в точке х = 0:
у = 1 + ахх 4 а2х2 -f • • • 4 апхп -f • •
Подставляя из последнего равенства выражение у — 1 в
уравнение у — 1 = хеу~1е, получаем, что
а\Х -I- а2х2 + а3х3 + Ь а„хЛ 4 • • • =
= хеев|Х+аз*3+ = хе ^(1 + ахх + а2х2 4 азх3 4 • • •) 4-
]■
(<цх + а2х2 + ■ - )2 (air + a2x2+•• )3
2! 3!
откуда
ai = е, а2 = <ме = е2,
а? С а 3 о
a3 = a2e4-f-=e3 + y = -e3,
а?е 34 4 14 114
а4 = а3е + aia2e 4 -у- = -е’ + е’4- -еч = —ея и т. д.
Следовательно, в некоторой окрестности нуля имеет место
представление
у = 1 4 сх 4 е2х2 4 ^е3х3 4 -тт*4*4 4 • ■ •
I о
Пример 34. Рассмотрим уравнение
у = a 4 ху>(у), (24)
где функцию <р(у) будем предполагать аналитической в точ¬
ке у = а. Тогда из предыдущего следует, что в окрестности
точки х = 0 можно определить у как функцию х, аналитиче¬
скую в точке х = 0, такую, что у(0) = а. Пусть и = /(у) —
любая функция от у, аналитическая при у = а. Если вместо у
подставить в функцию и = f(y) функцию у(х), определяемую
155
из (24), то и также будет аналитической в точке х = 0. Най¬
дем разложение ti(x) по степеням х. Заметим, что у = у(х, а).
Дифференцируя соотношение (24) по х и по а, находим
у'х = ¥>(у) + Х(РуУх
Уа = х,РуУа + !.
т. е.
*4)^ = *(»)• =
откуда
ду , ч ду
Поскольку у = у(х, а), то и и - f(y) - / (у(х, а)) и
ди df ду Of ду ди
Tx^Tydi^di^Ta^^lT* (й)
Для любой функции F(y) имеем
Е ('«я) = к Ня)
Справедлива формула
дх" <9an~'
В самом деле, при п = 1 это следует из (25). Если при
п = к она верна, то при п = к + 1 имеем
дк+
<9xfc+1
д_
дх
у-1 д
дап~1 да
* — ® _
kl U дх \dx* /
(^K))*£isK) =
156
Поскольку
и = Щ + X
+
/#ti\ х2 / ди V
W ,=0 + 2! \di)
Х-(д^)П\ +••..
»! W Lo
x=0
и при x = 0 имеем
«(0) = /(у(0)) = Да) = и0,
дпи
дх"
(Г-
<ian
Г»)/»),
ТО
/М = /<«) + +
+ 2Г^И«>т+
х" rf
in — 1
(26)
n! dan
Такой ряд называется рядом Лагранжа.
При f(y) = у получаем
у = а + хг(а) + ^~(?2(а))+-+^£—[(<рп(а))+--.
Пример 35. Для уравнения Кеплера
Е = М + е sin £*,
где # — эксцентрическая аномалия планеты, М — средняя
аномалия, е — эксцентриситет планетной орбиты, сообразно
вышесказанному имеем
е2 d
Е = М + € sin М + ;г7 777 (8*п2 Н ^
А\ ам
+
tn dn~1(smn М)
n! dMn~x
(Лаплас установил, что для этого ряда сходимость имеет ме¬
сто при 0 < е < 0,6627...).
к) “Обращение степенного ряда”. Пусть функция
у = /(х) в некоторой окрестности точки х = хо представля¬
ется рядом по степеням х — хо, т. е.
у = a0 + ai (х - х0) + а2(х - х0)2 + • ■ • + ап(х - х0)п + • • *
157
Ясно, что ао = у(хо) = уо, поэтому имеем
У - Уо = <м(х “ *о). (27)
Предположим, что а\ ф 0 в окрестности точки уо- Тогда
х определяется по предыдущей теореме как функция у, при¬
чем х(у) разлагается в ряд по степеням у — уо
Вывод: Если у является аналитической функцией от х
в точке хо, то в соответствующей точке уо = /~ЧХо) (при
условии у;(хо) Ф 0) обратная функция также будет аналити¬
ческой.
Если хо = уо = 0, то из (27) имеем
х = огу + /?2х2 -I- /?3х3 + • • (28)
и коэффициенты искомого разложения х = Ь1у+Ь2У2+6зУ3Н—
последовательно определяются из соотношения
<*У + 0ъ(1>1У + Ь2у2 4* • )2 + 0з(Ь\у + Ь2у2 + • • )3 + • • • =
= Ь\у + Ь2у2 4- 63у3 + • * • *
т. е.
6j = а, Ь2 = 02Ь\У 63 = *202Ь\Ь2 + /?з63 ■+• • • • и т. д.
Пример 36. Используя разложение функции у = arctg х в
степенной ряд
arctg г = х - i*3 + - i*7 + ir9 ,
найти разложение в степенной ряд функции
* = tg у = у + а3у3 + а5у5 + а7у7 + а9у9 + •• •.
(Выписаны только нечетные степени у, так как у = tg х есть
нечетная функция.)
Решение. Из уравнения
^ 3 , 1 5 1 7 . 1 9
+ 5* ~7* 9 ""
имеем
Подставляя в это соотношение вместо х ряд
у + а3у3 + as у5 + а7у7 + а9у9 + ■,
получим равенство
У + «з у3 + a5y5 + a7y7 + a9y9 + • •• =
= У + ^(у + «зУ3 + а5у5 + «7У7 + )3 -
- ^(у + азу3 + а5у5 + • • )5 +
0
+ ^(у + аз у3 + asy5 + • • )7 + • • •,
откуда
1 112
а3=з, a5 = --3a3-- = T5,
1 „ 1 « 2 1 г 1 2 1 17
07= --3a5 + j'3a3 — ~5аз + - = a5 + a3 — a3 + - —
Итак,
1 з 2 s 17 7
* = l*» = »+3# +,5» +ш» + •••.
т. e.
1 з 2 5 17 7
v = te x = x 4- -x -f —x 4 x H
У 8 3 15 315
Задача разложения в степенной ряд функции у, определяе¬
мой уравнением (24) (см. стр. 156), и обращения ряда связаны
между собой. Если предположить, что <^(а) ф 0, то урав-
у — a
нение (24) можно переписать в виде х = ——■ и ясно, что
<Р(У)
нахождение разложения в степенной ряд функции х(у) равно¬
сильно обращению степенного ряда функции <р(у) с центром
в точке а.
Обратно, если надо обратить ряд
у = aix4- a2x2 4- h апхп Н (<*i ф 0),
то перепишем это соотношение в виде
у = х(а\ 4- a2x Н ) = хф(х)
159
и придем к уравнению типа (24)
1
X = у
ф(х)
= О + у-у?(х).
Тогда имеем в силу соотношения (26)
1 !Г ( А 1
X = у-
+
. £ (±-L-)
V'(0) 2! \dx\i>7(x)J
tL (<fn~1 1 ^
n! \dxn~1 v>n(x) /
r = 0
Пример 37. Рассмотрим уравнение
у з= х(а + х), а ф 0.
Перепишем его в виде х = у-
1
а + х
Так как
d^
dx
— (—V =
n“1 \a + x J
n(n + I)... (2n - 2)
то получаем разложение
У У , I / 1 \
х = з + • •+(-])
(a + x)2n_ 1
»-,Г2п-2)! у"
(н — 1 )!n! a2n“1
+
Пример 38. Рассмотрим уравнение
у2 = ay + х
1
Здесь у?(у) = Полагая /(у) = у , по формуле Лагран¬
жа (26) находим
1 1 к х2к(к + :\)
у*
a*+2 2! a*+4
г3 fc(A + 4)(* + 5) х4 к(к + 5)(* + (>)(* + 7)
3!
4!
г» Ас +8
С другой стороны, у = ^ + + х (у(0) = а). Отсюда
160
получаем, например, при а = 2, что
к
2
1 + у/ГТх
к(к + 4)(к + 5) /ж \ 3
+
л) Разложение функции в обобщенный степенной
ряд. Иногда возникает необходимость разложить функцию
не по степеням х - ж0) а по степеням некоторой другой функ¬
ции, т. е. в обобщенный степенной ряд. При этом можно поль¬
зоваться всеми рассмотренными выше приемами и, конечно,
табличными разложениями функций в степенные ряды.
Пример 39. Разложить в ряд по степеням у/х функцию
у = arcsin(l — х) при х }> 0.
Решение. Для производной функции у = arcsin(l — х)
имеем у1 = . Применяя разложение для бинома
(1 + z) ~ получаем
1 1 1 Л 1 3 2 \
у" ^хфТГх~ ^(1 + 41+ 32х + ) -
= З2^(ч/х)3~ " =_ж + у?(г)'
1 3
Функция (р(х) = --^=\/х - представляет
собой равномерно сходящийся ряд на [0, а], 0 < а < 2. Поэто¬
му первообразная для функции = есть —\/2х, а для функ-
у/2х
2 з 3 5 7Г
Ции Ч>(х) есть -^гдх* ~ • Поскольку у(0) =
Отметим, что получить разложение данной функции по
положительным степеням х невозможно, иначе, основываясь
на теореме о том, что внутри промежутка сходимости сте¬
пенного ряда функция, его представляющая, имеет проиэвод-
161
ную, получили бы, что ее имела бы в точке х = 0 и исходная
функция, что не так.
IX I
cos -1 в ряд
по степеням cosx.
х I 1 1
Решение. Поскольку In COS2| = 2^* +cosx) 2^П^’
то полагая у = cosx и разлагая в степенной ряд функцию
у = ln(l + у)} получаем
In |cos ||= Iln(l+y)-i|n2 =
Ч У2 t У3 , , (-l)n"V , 11в0.
= j(,*-T+j + -+—;— + -j-5ini-
= -5ln2+5E(-|>"'lJv5- ***<“-'), »ez.
П = 1
Пример 41. Функция y(x) задана уравнением
x - у - arctg у.
Выделив главную часть вида (7xrt, С ф 0, функции у при
х —► 0, найти три ненулевых члена разложения этой функции
в ряд по степеням ха.
Решение. Из равенства
. У3 У* У1 У9 .
*гсц„ = !,-у + --т + - +
(см. пример 28) следует, что у ^УЗх1^3, х —► 0. Итак, будем
искать три ненулевые члена разложения функции у(х) в ряд
по степеням х1/3. Замечая, что из уравнения х = у — arctg у
следует нечетность функции у(х), делаем вывод, что коэффи¬
циенты у хп/3 при четном п должны равняться нулю. Итак,
представим функцию у в виде
у(х) = \/Зх1^3 + а\х + a-jx5^3 + • • •
и будем искать коэффициенты аь а2 так же, как при “обра¬
щении"’ степенного ряда (см. стр. 157). Из соотношений
у = V^3x1/3 + а\х + а2х5/3 + •
получаем:
у3 = Зх + З^х5'3 + З’УЗа?*7'3 + З^9х7'3 -
у5 = З^9х5/3 + 15^3а,х7/3 + • •,
у7=9^х7/3+ - •,
х = х + Х5/3 ^v^9ai - +
+ х7/3 ('УЗа? + \/За2 - З^За, + ^^ +
3 9\^9
Откуда следует, что а\ = -, а2 = -ттг- Итак,
5 175
§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ
Пусть задано счетное множество числовых последователь¬
ностей
<*11, 012, 013, • • • , <*1 п, • • •
<*21, а22, <*23, • , «2п, • • •
(1)
aml ? ат2, ЛтЗ, • • ■ , атп, • ••
Можно считать, что элементы этих последовательностей рас¬
положены в виде матрицы с бесконечным числом
строк и столбцов.
Элементы матрицы (1) можно многими способами пред¬
ставить в виде последовательности
«1, U2,---, Up,...
и составить из нее простой ряд
<2)
Р=1 Я>г= 1
Бели просуммировать каждую строку матрицы (1) от¬
дельно, то получим бесконечную последовательность рядов
оо оо оо
5Zairi - - (3)
Г = 1 Г — 1 Г — 1
Запишем формальную сумму
оо оо
(4)
9=1 г =1
Эту сумму принято называть повторным рядом.
Если сначала просуммировать элементы каждого столбца,
то получим последовательность
оо оо оо
^
<7=1 <7=1 <7=1
164
Суммируя эту последовательность, пэлучим другой повтор¬
ный ряд
оо оо
£(£<v). (в)
г=1 <7=1
Определение. Повторный ряд (4) называется сходящим-
оо
ся, если сходится каждый из рядов (3) и сходится ряд Ая,
оо <7=1
где Ая = 53 аяг — сумма </-го ряда (3). В этом случае сумма
оо г= 1
^^Ач называется суммой повторного ряда (4).
<7=1
Определение. Повторный ряд (6) называется сходящим¬
ся, ('(‘ли сходится каждый из рядов (5) и сходится ряд Аг,
го г = 1
где Аг = 53 аяг сумма г-го ряда (5). В этом случае сумма
оо <7=1
Аг называется суммой повторного ряда (6).
г=\
Как показывает следующий пример, суммы обоих повтор¬
ных рядов не обязаны совпадать; более того, сходимость од¬
ного повторного ряда, вообще говоря, не влечет сходимости
другого.
Пример 1. Рассмотрим матрицу
/I _ 1 1 _ 1 1 _ 1 ч
'2 2^ 2^ 2^ 2^ 2* '
1 i (1 ~тг) (*~?г) _0zikl (1-jM _1Llh1
2 2 2s 2J 23 2s 2*
i.-L (*~ jr)* ('~jr)-1 ('~^)3 ('-jr)* (‘~jr)2
•j 22 2* 22 2Л 23 24
1 i (*~ft)* (*~O-A)3 0-jr)3
2 2* 2s 22 23 23 2«
\ /
Каждый из рядов по строке сходится абсолютно и суммы
I II 11
их равны: первого второго -третьего - ^ и т. д. Эти
165
суммы образуют сходящийся ряд, сумма которого равна
1 1 1 11 _ 1 1
2 + 22 + 2 22 + '" “ 21 - i “
Рассмотрим теперь ряды по столбцам. Для первого полу¬
чаем сумму
1 Л 1 1 1 1
2 V 2 + 2^+ +2^ + ' j-1
Для второго
-М'*('-»*Н)’* *('-«'* )■
Для столбца с номером 2q + 1 сумма равна
2^(1+(1_2^) + (1_2^) + '" +
+ (1_2^) + •'•) = 2^T'2i^= '■
Для столбца с номером 2q сумма равна
'25^(' + ('"2Гг') + (1"2Гг') + ' +
+ ('-55W)
Поскольку ряд 1 — 1 + 1 — I Н h ( - l)n+L + расходится, то
повторный ряд вида (6) расходится, в то время как повтор¬
ный ряд вида (4) сходится и сумма его равна 1, причем как
все внутренние, так и внешние ряды сходятся абсолютно.
Определение. Пусть дана бесконечная матрица (I). Сим¬
вол
оо
£ V (?)
<7=1,г=1
называется двойным рядом.
166
Определение. Частичной суммой двойного ряда (7) на-
m п
зывается конечная сумма Smn = т. е. сумма тех
<7=1Г=1
элементов матрицы (1), которые находятся в прямоугольнике
из ее первых п столбцов и тп строк:
( ап
021
а\2
<*22
а\п
«2 п
От2
<*ln+l
Л2п + 1
Отп+1
^ат+11 ат+12 am1-ln ат+1п + 1
Заметим, что множество 5mn, гл = 1, 2, ..., n = 1, 2,...
представляет собой опять бесконечную матрицу.
Определение. Двойной ряд называется сходящимся, если
при независимом стремлении переменных т и п к бесконеч¬
ности существует предел
lim Smn.
m—f+oo
N—►+00
Значение этого предела называют суммой двойного ряда (7)
оо
и пишут S = ^ aqr. Если предел Smn при m —> оо, п -> оо
я>г—1
не существует, то ряд (7) называется расходящимся.
оо
Пример 2. Ряд ^ хку1 является сходящимся для |х| < 1,
k=\,i=i
|у| < 1. В самом деле,
*=i/=i *=1 1=1
1 - zm+1 1 - yn+1
х I - у
fc = l ’ *
Поскольку
/=1
lim
1 - xm+l
m—►-foo 1 — X
1
1 - X
. kl < i-
167
I _ «"+• I
lim —j = , |y| < 1,
n-++oo 1 — у 1 - у
TO
1 _ xm+l 1 - v" + l 1
lim
m—►+oo 1 — X 1 — у \ — X 1 — у
n—►-f-oo
Значит, сумма исходного двойного ряда хку1 равна
1 1 *',=1
1-х 1 - у
Естественно поставить вопрос о взаимосвязи сходимости
рядов (2), (4), (6) и (7).
Теорема. Если простой ряд (2) абсолютно сходится к
сумме и, то каким бы образом ни расположить его члены
в виде матрицы (I), сходятся оба повторных ряда (4) и (6) и
их суммы равны и.
Отметим, что эта теорема формулирует важные резуль¬
таты сочетательного и переместительного свойства абсолют¬
но сходящегося ряда: для такого ряда его члены можно пе¬
реставлять произвольным образом и объединять в любом ко¬
личестве в скобки, составляя таким образом новый ряд, и
суммы всех таких рядов равны между собой. Так, например,
сумма ряда
iIiJ.i_J_i_i.JLJL
+ 2 + 3 + 22 + 22 + З2 + З2 + 23 + З3 + 42 + ’
ОО | °0 |
т. е. ряда, где перемежаются члены рядов
П=1 П=1
ОО j 00 - 00 - 00-
Е з^> равна °умме +
П = 1 П=1 П — 1 П = 1
Теорема. Пусть дан повторный ряд (4). Если после заме¬
ны его членов их абсолютными величинами получается сходя¬
щийся ряд, то сходится не только сам повторный ряд (4), но
и простой ряд (2), состоящий из тех же членов, что и ряд (4),
расположенных в любом порядке, и притом к той же сумме.
168
Следствие. Пусть дана матрица (1). Если после замены
всех членов повторного ряда (4) их абсолютными величина¬
ми получится сходящийся ряд, то сходятся оба повторных
ряда (4) и (6) и их суммы равны.
Отметим, что предположения об абсолютной сходимости
рядов по строкам (или по столбцам) н об абсолютной сходи¬
мости ряда, составленного из их сумм, не может заменить
требования сходимости повторного ряда для матрицы абсо¬
лютных величин.
Пример 3. Рассмотрим матрицу
1-1 О О О Д
0 1-10 0
0 0 1-1 0 • ’
/
аяя = 1, <*<7<7+1 = -1} aqr =0, если г/диг^ + 1. Для
этой матрицы все ряды как по строкам, так и по столбцам
являются конечными суммами и, следовательно, сходятся аб¬
солютно. Сумма в каждой строке и во всех столбцах, начи-
оо оо
ная со второго, равна нулю. Оба ряда = ^Ро = 0
оо оо <?=! Я— 1
и Лг = 1 + 0 = 1 сходятся абсолютно; однако, сум-
г — 1 г = 2
мы повторных рядов (4) и (6) не равны. Если же заменить
все члены данной матрицы их абсолютными величинами, т. е.
рассматривать матрицу
110 0 0
0 110 0
CLqq = Clqq+l = 1, dqr = 0, вСЛИ Г^ИГ^+1,ТО ВСв СуММЫ
по строкам и суммы по всем столбцам, начиная со второго,
равны 2, следовательно, в этом случае оба повторных ряда (4)
и (6) расходятся, как и надо было ожидать.
169
Основные свойства двойных рядов:
оо оо
1. Если ряд ^ адг сходится к сумме 5, то ряд ^ Аадг
<7,г= 1 7>г = 1
сходится к сумме А5, где А — константа.
оо оо
2. Если ряды ^ а9Г и ^ 67Г сходятся, то сходится ряд
оо <7.г— 1 7*г=1 оо оо
(а?г + Ь,г) и его сумма равна ^ а,г + ^ 6gr.
7,г = 1 7ir=l <7, т* = 1
оо
3. Если ряд V' а«г сходится, то lim aqr = 0 (необходи-
1-++0О
9<г-1 г —► -j- оо
мое условие сходимости двойного ряда).
4. Если все члены двойного ряда адг неотрицатель-
<7,г=1
ны, то ограниченность множества {Smn} его частичных сумм
есть необходимое и достаточное условие сходимости этого
ряда.
оо
5. Если ряд ^2 аяг с неотрицательными членами схо-
7,r=1
дится и существует такое число С, что 0 ^ bqr ^ Caqr, то
оо
ряд bqr также сходится (теорема сравнения для двойных
<7.г= 1
рядов).
6. Если члены двойного ряда определены равенством aqr —
оо оо оо
= bqcr И ряды Ev Е* сходятся (ряд aqr получен
7=1 г= 1 7»г = 1
оо оо оо
произведением рядов и 5^сг), то двойной ряд aqr
7=1 г = 1 7.г — 1
оо оо
сходится и его сумма равна ^ bq• ^ с*г.
7=1 г=1
~ (_l)n+m
Пример 4. Рассмотрим ряд > . Так как
' т п
тп
п,т = 1
170
(_l)«+m (_l)n + l (_l)m+l ^(_1)«+1
- - - - - - - и > 1 = m2, то, еле-
m n n m ■■ ■ ^ Tk
771 1
n— 1
довательно, данный двойной ряд сходится и его сумма рав¬
на in 2. оо ^
Пример 5. Доказать сходимость ряда ^
m,n = l
Решение. Поскольку для любых пит справедливо нера¬
венство
1 1
£
п4 -|- т4 ^ 2т2п2 ’
то для сходимости данного ряда достаточно установить схо-
°° 1
димость ряда У^ —г—« . Так как члены этого ряда получе-
* т1п1
m>n — 1 оо ^ оо 1
ны умножением двух сходящихся рядов > —г- и > —то
т1 п1
оо m= 1 п = 1
ряд У* ——- сходится, а значит, сходится и данный ряд.
' 7177Z
m»n=1 ^
Пример 6. Рассмотрим двойной ряд =. . Ра-
rrwT^l Vnm
(-l)n+m (-l)n+1 (-l)m+1
венство jr. — = — -=— показывает, что этот
у/пт у/п у/т
двойной ряд представляет собой произведение сходящегося
f 1 \n +1 j\n+m
ряда т=—на себя. Следовательно, ряд > -—
" у/п ' у/пт
n = l m,n = 1 v
v>(-i)n+1
сходится и его сумма равна квадрату суммы ряда > 7=—.
tl ^
В то же время, как показано в примере на стр. 58, произ-
(— 1 )п+1
ведение ряда 7=— на себя в форме Коши является
расходящимся рядом. Этот пример показывает, что опре¬
деленное выше (стр. 171) представление произведения рядов
в виде двойного ряда не эквивалентно ранее рассмотренно¬
му (стр. 57) представлению этого произведения в форме
Коши.
171
Теорема. Если сходится двойной ряд aqr и сходят-
Я,г-\
оо
ся все ряды по строкам (или столбцам) Я — 2,...
г — 1
схэ оо оо
(^а^г, г = 1, 2,...), то сходится и повторный ряд
</=1 <7=1 Г=1
оо оо
(Е(Е адг^ и его сумма равна сумме двойного ряда.
г = 1 д=1
Заметим, что условие сходимости всех рядов по строкам
не следует из сходимости двойного ряда, т. е. это условие не
может быть пропущено в формулировке теоремы.
Пример 7. Рассмотрим ряд, определяемый матрицей:
(~i)n+l ^
(-•г •
1
-1
1
-1
-1
1
-1
1
1
1
1
1
2
ICS
1
2
2
1
1
1
1
2
2
2
2
1
1
1
1
т
т
т
Ш
1
1
1
1
т
т
га
га
НУ
(-0"
йг
НУ
V
•/
Каждый ряд по строке этой матрицы имеет вид
ОО
±5>1)"с и является расходящимся. Покажем, что двой-
п = 1
ной ряд сходится к нулю.
п п
Действительно, поскольку ^a2m-ir + ^a2mr = 0 для
г — 1 г — 1
любых т и п, то 52m п = 0; точно так же Sm 2п — 0 для
172
любых тип. Далее,
S2m+1 2п + ! “
/1111 l\ 1 1
= *$2т2п+1 + ( Ь 1 Ь —) ~
\ 7?1 т т т тп) т т
^ у ^
2п членов
Полученные равенства показывают, что lim 5mn = 0.
n—►+оо
оо m—►+оо оо
Пусть для ряда апт сходятся как все ряды апт
П, ТП — 1 оо 171=1
по строкам, так и все ряды ^ апт по столбцам. Тогда в
П = 1
силу приведенной теоремы условие сходимости и равенства
оо оо оо оо
сумм повторных рядов ^ПШ ) и £(£а"'п) необ-
n = l m = l т = 1 п = 1
оо
ходимо для сходимости двойного ряда ^ апт. Однако,
п,т=1
как показывает следующий пример, это условие не является
достаточным.
Пример 8. Рассмотрим ряд, определяемый матрицей:
/ 1-1 0 0 О- Л
<*2a-lm = < m ^ 92.fl2q-lm = ~“,g2< ™ < 1),
<7 Я
a2q-1 m — 0 для всех остальных индексов m, a2qm = ~ a2<?-i m-
Каждая строка и каждый столбец этой матрицы содер¬
жат только конечное число отличных от нуля членов; полови¬
на из них положительны, половина — отрицательны, причем
абсолютные величины этих членов равны. Итак, все ряды
оо оо
аптп и ^ anm сходятся к нулю, откуда следует, что и
т=1 п = 1 оо оо оо оо
оба повторных ряда flnm) и ^ (X>anm) схоДятся
n = l т=1 т=1 п = 1
и суммы их равны нулю. ^
Покажем теперь, что двойной ряд ^ anm расходится.
n,m= 1
Действительно,
m (m+02 (m + *)2
(m+1)2 — ( 53 a2<7~ 1 r + a2?r^ — 0,
9=1 r = l r = 1
^2m-f 1 (m+1)2 —
11 1
- *b2m (m+ 1)H — H — + 1- — - 1 •
m-fl m-f 1 m-fl
v v "
(m+l) членов
Полученные равенства показывают, что предела Snm при
п —► -fоо, m —> оо не существует.
оо
Определение. Двойной ряд amn называется абсо
m,n = 1 о©
ЛЮТНО СХОДЯЩИМСЯ, если СХОДИТСЯ ряд |amn|-
m,n = 1
Как и для простых рядов, из абсолютной сходимости
двойного ряда следует его сходимость.
оо
Если двойной ряд ^ amn сходится абсолютно, то лю-
m,n = l
бой простой ряд, составленный из чисел amn> также сходит¬
ся абсолютно. Отсюда следует, что amn стремится к нулю
174
не только при одновременном возрастании обоих индексов т
и п, но и при возрастании хотя бы одного из этих индексов.
Отсюда же следует, что множество {amn} ограничено. Если
оо
же ряд ^2 атп сходится неабсолютно, то множество {amn}
m,n = 1
может быть и неограниченным.
Пример 9. Рассмотрим ряд, определяемый матрицей:
/0
1
2
3
4
п
1
-1
-2
-3
-4
—п
2
-2
0
0
0
0
т
—т
0
0
0
0
\
Для этого ряда Smn = 1, когда т + п > 2, следовательно,
он сходится к 1, но множество {amn} его членов неограничен
но.
Обратим внимание на то, что в силу сходимости двойного
оо
ряда атп имеем, что lim amn = 0; таким образом,
* m,n—»+оо
m,n=l
для множества {amn} чисел, занумерованных двумя индекса¬
ми, существование предела lim атп не влечет ограничен-
m-f+oo
п—►+оо
ности этого множества в отличие от множества чисел {an},
занумерованных одним индексом.
Как следует из вышесказанного, данный ряд не сходится
абсолютно. Покажем это непосредственно. Действительно,
m п
Smn - ЕЕ 1®*'! Г
— (1+2+-** + (п-“ l))-|-(l-h 1 + 2 + • • • -j- (п — 1))”1"
*|- 2*2 -f- • • * -f* 2(m — 1) —
= (п — 1)(гс - 2) + 1+2 (2 + 3 + • • * -Ь (т — 1)) =
= (п - 1)(п - 2) — 1 + (m - 1 )т —У -f оо
при п —у -fоо, т —У оо.
175
Теорема. Пусть дан двойной ряд ^ апт. Составим
оо п,т=1
каким-либо образом простой ряд ^ Uk, состоящий из тех же
к = ]
членов. Тогда абсолютная сходимость одного из этих рядов
влечет за собой абсолютную сходимость другого и равенство
их сумм.
Теорема. Рассмотрим четыре ряда: два повторных (4),
(6), двойной (7) и простой ряд (2). Если хотя бы один из этих
рядов сходится при замене всех его членов их абсолютными
величинами, то все четыре указанных ряда сходя гея и имеют
одну и ту же сумму.
Следствие. Если все числа атп ^ 0, то из сходимости
(X) оо оо оо
одного из четырех рядов: (53amn)’ XI(amn)5
оо оо пг = 1 n = 1 n = 1 m — 1
amn, ( uq есть произвольно занумерованное од
т,п — 1 <7=1
ним индексом множество {amn}) следует сходимость осталь¬
ных трех и равенство сумм всех четырех рядов
Пример 10. Доказать сходимость и найти сумму ряда
ОО j
^ (2n)m+1
n,m=l 4 7
Решение. В силу вышеприведенного утверждения для от¬
вета на заданный вопрос достаточно доказать сходимость и
CXJ ОО J
найти сумму повторного ряда То"lm+i ) ' * ак как
п = 1 m = I '
оо оо . оо , v
SS = £ + (2п)3 + ‘=
ОО 1 оо .
_ (2п)> _ 1
, 1 — , 2п(2п - 1) ’
п = 1 2п n = i V /
то этот ряд сходится. Для вычисления его суммы проведем
176
следующие преобразования:
я J я J Я J
= Е 2п(2п — 1) " ^ 2л - 1 “ ^ 2п ~
n=l v 7 п=1 П=1
= (1 + 5+ +5тЬ)"5(1 + 5+ ' +0 =
2? . <? ,
= Е1-Е1 =
= In2g + С3 - lng - + о(1) = 1п2 + о(1), п оо.
Отсюда получаем, что
ОО ОО . ОО -
£(£ (йг?т) = Е 5^гп) = Д™*.=1п2
n= 1 m=1 4 7 n=1 '
00 j
с’ ряд 12 ?2пГ+Т схоДится к |п2-
n,m=l *
Итак,
Пример 11. Исследовать на сходимость ряд
^ 1
^ (т + п)"
т,п=1 '
, а > 0.
Решение. Матрица, соответствующая данному ряду, есть
/11 1 1
(1 + 1)“ (1+2)“ (1+3)" " (1 +п)а "
s s S
111 1
(2 + 1)" (2+2)“ (2 + 3)« (2 + п)а
i /* /
111 1
(3+1)" (3 + 2)" (3 + 3)“ (3 + n)“
\
177
Составим простой ряд, расположив его члены так, как ука¬
зано стрелками (по диагоналям).
1 1 1
(1 + 1)“ (1 + 2)® (2+1)«
1 1 1
(8)
+
+
(3+ 1)" (2 + 2)“ (1 +3)“
Так как все члены этого ряда положительны, то он сходится
одновременно с рядом
1/1 I
+
4-
=)
(1 + 1)“ 4(1+2)° (2+ I)
I 1 1
(3+1)“ (2 + 2)" (1+3)"
1
+
-I-
1+2)“ (1+п)“
полученным его группировкой (см. стр. 16). Итак, сходи¬
мость рассматриваемого двойного ряда эквивалентна сходи-
* • и - 1 1
^гг н +°°
Т1а 1
МОСТИ
оотношение
п = 2
показывает, что этот ряд и, следовательно, ряд (8), сходится
при а > 2 и расходится при а ^ 2. В силу теоремы о сходи¬
мости двойного ряда с неотрицательными членами, получаем
оо J
отсюда, что ряд } - —, rv > 0, сходится при о > 2 и
, (т + и)"
п,т= 1 v '
расходится при 0 < г» ^ 2.
Пример 12. Рассмотрим матрицу
_L J_ _L J_
V2 5Гз 1Г4 Tb
1111
Л =
1-2-3
2
234
2
3-4-5
2
4-5-6
2
1
?Гб
1
5~67
2
а<|Г —
12 3-4 2 3-4-5 3 4-5-6 4 5 6-7 5 6 7 8
(V-1)! _ (г-1)!
r(r+l)...(r + ?) q(q + l)...(q + r)'
178
Сумма членов q-ой строки этой матрицы равна
у* (Я-1У-
f^r(r+l)...(r + q)
l/l 1 \
^ ^ ^ 9\г(г+1) • (г+?-1) (г+1) - (г+?)У
,д ПД 1 _ (g — I)- _ 1
1-2-... -g qq\ q2'
CO J
Следовательно, сумма ^ -j есть сумма повторного ряда
ОО ОО
Ей»- (»)
q=1 г=1
Ясно, что поскольку agr = arq, то сумма и второго повторно-
°° 1
го ряда также равна ^ -j. Рассмотрим теперь матрицу В:
г=1
/Чгг + гЗ + з^'1 ) 0 0 00 Д
ТТз (гЗТ+зТв "*"4Т<И ) ® 00 •••
ОО
1 2 34 234 5 Ц?(?ИН9+-2)(7+3) 0 0 ' ‘
д=3
т. е. в m-ой строке ( m = 1, 2,...) до ее диагонали сохраняем
члены предыдущей матрицы, на диагонали ставим сумму всех
членов m-ой строки предыдущей матрицы, начиная с m-го, а
остальные члены заменим нулями.
Для такой матрицы суммы по ее строкам останутся рав¬
ными суммам по тем же строкам предыдущей матрицы, т. е.
оо оо
сумма повторного ряда также будет равна
00 1
n = l m=1
п = 1
179
Найдем теперь суммы по столбцам матрицы В. Для этого
сначала упростим выражения диагональных членов Ьтт этой
матрицы:
(т-1)!
,.=«+1 ф+1)..(« + т)
_ у' (т- 1)! (т- 1)!
(т — 1 + д)... (2т— 1 +q) т2(т+1)... (2т— 1)
Теперь найдем сумму оставшихся членов m-го столбца.
Она равна
^ (т-1)! ^ (т-1)!
i£?+1 + 1) ••■(* + т) ^ (т + *)... (2т + *)
' (т-1)!
т(т -hi)... (2т)
Следовательно, сумма: всех членов m-го столбца равна
(т - 1)! + (т ^1)!
т2(т -|- 1)... (2т — 1) т(т + 1) • • (2т)
_ (т - 1)! 2т + т _ ((т - I)!)2
т(т + 1)... (2т) т (2т)!
Суммируя теперь эти числа, получаем сумму повторного ря¬
да, которая в силу приведенной выше теоремы, должна со¬
впадать с суммой повторного ряда (9) (см. стр. 180). Итак,
используя равенство, выведенное на стр. 140, получаем
,2 » , ~((т_!)!)2
Ч. (2т)! •
к = 1
Отсюда следует, что
1 I2 (2!)2 (п!)2 тг2
L L L 1 ' 1
2! 4! 6! (2n + 2)! 18
Пример 13. Рассмотрим ряд ^ хтуп. Поскольку он
т,п=0
оо оо
получен умножением рядов хт и ^ уп, каждый из кото-
т = 0 п=0
180
рых абсолютно сходится соответственно при |х| < 1 и |у| < 1,
то для этих же знамений х и у абсолютно сходится и двойной
ряд. Если |х| > 1 и |у| > I, то хтуп не стремится к нулю и
данный ряд расходится.
Рассмотрим множество {(x,t/) : |х| = 1, \у\ < 1}. При
х = 1 матрица (хтуп) принимает вид
Л =
/1 У У2
1 У у2
1 У у2
г
уп
Л
а при х — — 1
ВИД
в =
Сумма рядов по строкам равна
(~1)9+1
1 - У
для матрицы А и
, где q — номер строки, для матрицы В; таким обра-
оо оо
зом, повторный ряд cimn^ расходится как для матри-
m = 1 п = 1 оо
цы А, так и для матрицы В. Если бы двойной ряд хтуп
m,n=О
был сходящимся, то в силу теоремы на стр. 173 эти повтор¬
ные ряды сходились бы. Итак, рассматриваемый ряд рас¬
ходится на мнбжестве {(х,у) : |х| = 1, |у| < 1}. В силу
симметрии переменных х и у этот ряд расходится и на мно¬
жестве {(х,у) : |х| < 1, |у| = 1}. Таким образом, множе-
оо
ством сходимости ряда хтуп является открытый ква¬
драт (-1, 1) х (-1, 1). m'n=0
181
00 I
^r—^ X
Пример 14. Рассмотрим ряд > а, , где а* — про
1 — х%
i=l
извольные числа. Справедливо утверждение, что этот ряд
оо
сходится, если сходится ряд ^а, х* и \х\ ф 1 (см. задачу 78,
• = 1 оо
стр. 330). Пусть радиус сходимости ряда х* не мень‘
оо . «= 1
\ v—n а%'Х
ше 1, тогда функция у?(х) = > т определена для всех х,
1 — х
t=i
|х| < 1. Для х, |х| < 1, справедливо равенство
t 00
х _» . _21 . . „mi . _ \ s _m*
г = X + X + h X + •••=> X
1 — X
т= 1
Составим матрицу
Л :
(а\х
ajx2
aix3
4
а\х
aix5
aix6
ajx7
ajx8
diX9
д
0
о2х2
0
а2х4
0
а2х6
0
а2х8
0
0
0
азх3
0
0
азх6
0
0
аз*9
0
0
0
а4х4
0
0
0
в4Х8
0
0
V....
0
0
0
а5х5
0
0
0
0
/
Повторный ряд по строкам будет
(aix + а\Х2 + • • • + aix* + •••) + (a2x2 -f a2x4 + ■ •) +
+ (a3x3 + a3x6 + )+•• =
<цх a2x2 amxm
1 — X 1 — X2 1 — xm
«=1
OO
Так как повторный ряд сходится к ^(ж)> а РЯД
1 — X*
оо t = l
сходится при тех же х, что и х*’ то после замены х
1 = 1 оо
на |х| и а, на |а»| получим, что вместе с рядом ^ |а,*||х|ш схо-
»=1
182
00 Ixl*
дится и ряд |а,| г-р. В силу теоремы на стр. 177 мож-
1 “ 1ХГ
но просуммировать элементы матрицы вначале по столбцам;
тогда получим разложение в степенной ряд функции у?(х):
оо оо
<р{х) = ^anxn, где ап = Значок i\n условно означа-
п = 1 «|п
ет, что сумма распространяется лишь на делители г числа п.
Если взять cii = 1, то получим, что
ОО ,• оо
i=l
n = 1
где т(п) —7- число делителей п.
Если взять а, = г, то получим, что
£тз^ = 5>(п)*п’
1 - х
где <г(п) — сумма делителей числа п.
Рассмотрим еще матрицу
В
/ aix
2
a\xz
а\х3
aixn
a2x2
4
а2хч
а2х6
а2х2п
акхк
акх2к
а*х3*
a*xfcn
Суммы по строкам матрицы В те же, что и матрицы А;
оо
суммируя же по столбцам, получим: в первом: ряд ^ amxm,
оо
во втором: ряд ^ атх2т.
т=1
т— I
w w сю
Итак, повторный ряд ^ (E*mn) имеет ВИД Л1").
т — 1 n = l m = 1
оо
где /(г) = ^ атхт. В силу равенства сумм повторных ря¬
183
ах
ах ’
дов имеем равенство:
оо
?(*) = £/(*")• (10)
п = 1
Полагая а,- = а*, |а| ^ 1, получим, что
1 — I
к = \
поэтому в силу (10) имеем
оо I ч. оо п
Е(ах)* я* , , , ,
Ь^ = ^ТГ^Г' w «'.!*!<>
1=1 п = 1
1 1
В частности, при а — - и х — - получаем равенство
оо сю ,
^ 2«Г2* - П = ^
^ 2* (2* - 1) 2n+1 - I
1 4 П -1
Определение. Степенным рядом с двумя переменными х
и у называется двойной ряд вида
оо
атпхтуп. (И)
т,п=0
Множество всех тех точек (хо,2/о), для каждой из которых
оо
сходится ряд ^ атпх™у%} называется областью сходимо-
т,п = 0
сти ряда (11).
Пример 15. Найти множество сходимости ряда
оо
Е_ „т т,п
атпХ У ,
т,п=0
где аоо = о, а0„ = ап0 = n!, п € а]т = ат1 = - т!, т G N,
атп = 0, если или т ^ 2, или п ^ 2.
Решение. Для частичных сумм 5mn данного ряда имеем
равенство
m п
Smn = (1 -у)^у!х9 + у+(1 -*)]Гг!уг. (12)
q=1 Г — 1
184
Отсюда видно, что *Vmn(0,0) = 0 и *Smn(l,l) = 0 при лю¬
бых тип, следовательно, рассматриваемый ряд сходится в
точках (0, 0) и (1,1).
Покажем, что этими двумя точками и исчерпывается мно¬
жество сходимости данного ряда. Действительно, применяя
формулу Коши-Адамара, получим, что радиус сходимости
оо
степенного ряда n\tn равен нулю, следовательно, для лю-
п = 1
бого t > 0 имеем:
lim V a! tq — -fоо.
i—юо
п —f ОО
<7=1
Далее, при t ф 0 и q > справедливо неравенство
(2? - 1)! К|2,-1(2?|<| - 1) > (2q - 1)! |<|2?_1,
откуда для t < 0 и п > п0 =
2 п п
LHJ
-I- 1 получаем, что
<7=1 <?=1
2по п
>£?!<’ + £ (2?- 1)!|<|2’-1.
<7=1 <7=п0 + 1
оо
Радиус сходимости ряда £(2q - 1)! r2<,_1 равен нулю, сле-
<7= 1
П
довательно, для г > 0 имеем: lim У^(2о - l)!r2,_l = +оо,
п —► оо '
<7 = 1
откуда получаем, что и
2п
lim q\t4 ~ +оо, t < 0.
п—►оо '
<7=1
Таким образом, если (х,у) ф (0,0) или (х, у) ф (1,1), то либо
одно, либо оба слагаемых в сумме (12) неограниченно растут,
185
когда тип четны и возрастают. Следовательно, в :>том
случае
lim 52m,2п(ж, у) = ОО.
Ш.Т1-
Зтот пример показывает, что для двойных степенных ря¬
дов нет аналога первой теоремы Абеля и структура мно¬
жества сходимости двойного степенного ряда существенно
сложнее структуры множества сходимости простого степен¬
ного ряда. В то же время имеет место
оо
Теорема. Если ряд ^ атпхтуп сходится в некоторой
m, п = О
точке Мо(хо,уо), обе координаты которой отличны от нуля,
И множество {<1тпт\Х™Уъ) ограничено, то этот ряд сходится
абсолютно во всех точках М(х,т/), координаты которых удо¬
влетворяют неравенствам: |х| < kol, Ы < |уо|, т е- во всех
точках открытого прямоугольника с центром в начале коор¬
динат и вершиной в точке Mq.
Как показывает эта теорема, причиной разно! о поведения
двойных и простых рядов является то, что имеющая предел
lim ап последовательность {<*пЬ занумерованная одним ин-
п —►по
деке ом, обязательно ограничена, а имеющая предел liin
m,n->oo
последовательность {c*mn}, занумерованная двумя индекса¬
ми, не обязана быть ограниченной (см. стр. 175).
оо
Следствие. Если ряд атпхтуп абсолютно сходи гея
т,п=О
в точке Afo(xo, Уо), обе координаты которой отличны от нуля,
то этот ряд сходится абсолютно во всех точках Л/(х,у), ко¬
ординаты которых удовлетворяют неравенствам: |х| < |хо|,
М < Ы
Пример 16. Найти множество абсолютной сходимости
(m + 7i)!
ряда mlfi I Х У
*—4 mlfil
т, n = О
Решение. Покажем, что множество абсолютной сходимо¬
сти данного ряда совпадает с множеством сходимости ряда
186
оо оо (ffi -J- Ti) ^
У^(|х| 4 |у|)п. Действительно, пусть ряд У* j—— xmyn
П — 0 т,п = 0
сходится. Занумеруем числа атп = -——-Д"|х|т|у|п, чтобы
т!п!
полученный простой ряд принял вид
1 + (|х| + |у|) + (|хр + 2|х||у| + |у|2) +
+ (|х|3 + 3|х|2|т/| + 3|х||у|2 + |у|3) + • • •,
т. е. упорядочение идет по возрастанию суммы (т + п), а
для членов an q-n — по возрастанию степени \у\. Такое упо¬
рядочение есть нумерация членов соответствующей матрицы
“по диагоналям”. Так как все члены ряда неотрицательны,
то сходимость этого простого ряда эквивалентна сходимости
ряда
t(t^z^М"-‘1#) = Х>1+МГ
п— 0 <7=0 ' п=О
(см. стр. 176).
ОО
Обратно, если сходится ряд ^(|х| + |у|)п, то сходится и
п=0 оо / . \J
ряд (13), откуда следует сходимость ряда
т'п'
т,п=0
оо
V- (т + п)!
т. е. абсолютная сходимость ряда > ——х у .
' т\п\
m,n=О
Применяя признак Даламбера, получаем, что множеством
ОО
сходимости ряда ^Г^(|х| -I- |у|)п является открытый квадрат
п =0
|х| + |у| < 1. Итак, множество абсолютной сходимости ряда
есть М = {(х,у) : |х| + |у| < 1} (см. рис. 2).
Пример 17. Найти множество абсолютной сходимости
оо
ряда ^2 *ту".
п=0,
т^п
Решение. Для абсолютной сходимости двойного ряда не-
187
Рис. 2
обходимо, чтобы сходился каждый из рядов ^ \х\т\у\п =
ОО ТП — П
= \х\п\у\п ^ |х|д, отсюда получаем необходимость условия
<,=о
|х| < 1. При этом условии имеем, что
Е |*Г1уГ = кПуГу^
И'
m=n
Так как далее необходима сходимость ряда
I*
то, следовательно, необходимо условие \ху\ < 1. Обратно,
оо
если |х| < 1 и |ху| < 1, то сходятся все ряды |x|m|y|n
оо оо
и сходится ряд £(£ |х|т|уГ), следовательно, сходится
двойной ряд с неотрицательными членами |x|m|t/|n, т. е
п = 0,
m>n
188
Рис. 3
ряд хту11 сходится абсолютно.
п=0.
т>п ^
Итак, множество абсолютной сходимости ряда хтуп
п = 0,
т>п
есть М = {(x,J/) : |х| < 1, \ху\ < 1} (см. рис. 3).
со
В силу абсолютной сходимости ряда хтуп оба по-
п=0,
т>п
189
h У
со оо
(гу)п I 1
1 — Г 1 — X 1 — XV
п =0 m=n п=0
ПЕ *v) сходятся к одной сумме, если \х\ < 1, \ху\ < 1.
m = U п=0
Следовательно, для таких значений х и у имеем равенство:
1 + х(1 + у) + *2(1 + у + у2) Н 1-
+ хт(1 +у+ ■ + ут) + ■■■= —^?—
1 — х 1 — ху
Откуда получаем, что
°о
Е"*" ■ (1 -«)>■1,1 < '■
т = О * *
{ 6. УПРАЖНЕНИЯ
1. Числовые рады
В следующих примерах, рассмотрев предел частичной сум¬
мы ряда, установить его сходимость и величину суммы или
расходимость.
п=0
°° 1
^ ^ (а + п)(а + п + 1)
оо оо
9)S »(»+!)(» + 2)' 10)S^'
оо J
11) У'' т — г: -г, с ф —п, п € N.
^ (с + П - 1)(с + п)(с + п + 1)
ОО
12) У" 2n+1 13) V3n2 + 3n + 1
j^n2(n+l)2 2^ n3(n+1)3 •
n= 1 ' 7 П=1 '
oo 1 OO
H> E 4^-4„ -3 l5)£(-№+2-2WTfT+tf;).
П=1 П=1
OO
16) ~
n
OO
2>(. + ±). ">£-(■-£)
п=1 4 ' n=2 4 7
Io4^, ^n2 + 3n + 2^ n3 + 1
18)Eln(-nT^-3n--j 19)Eln^3T
n=l 4 7 n-2
191
'8"
22) ^2 n V. Ы < 1 23) ]Г arctg ^.
п =1 п—\
оо 2 00
24) ^2 wctg —. 25) ^2 arcctg(n2 -f n + 1).
я>£(*г=*)’
2») £) ((„ + 1)»^- (» + 2)SiM
Tl — 1
29) X! ‘2n rtg — ’ 0< 1 < 2 ^ 1 + x2—‘
r. = l z g 2" Z „ = ] 1 + 1
00 ~2n_1 00 ~3u , i
адЕЬ' здЕ»--*1 +'
f»= 1
1 - x2n 7 ^ x2" ч I
В следующих примерах, не находя явной зависимости ма¬
стичной суммы ряда Sn от п, проверить, что последователь¬
ность Sn не является ограниченной.
оо - оо
ЭДЕгтг 34>£
П — 1
1
Ты v^* rf^t v/(»*+ 1)(" + 2)
оо ^ ОО j
35) > ==. 36) > arcsin-7=.
; ^ v/з^ГТТ + v/Зп^Т ^
Установить расходимость следующего ряда, используя не¬
обходимое условие сходимости.
37) 1-1-1+1+1+1—1—I—1—1+.
3*)Е!тг 39)fysin 1
. - + 1 , П2 + П + 1
п—I п=1
40)
П
192
ЁШГ
п=1 х ' п=1
«)£
(n + 1) In n! — 2 ln(2! -3! • • •«!)
n2 + n
f»= 1
46) ^T^sinna, афжm, m£Z. 47) ^^cosn2.
n=1 n=l
Следующие ряды удобно исследовать, применяя признак
Даламбера.
оо
(2п - 1)!! ,п^п!(2п-Ц)!
п! ' ^ (Зп)!
п — 1 v '
4-7-13-... (Зп + 4) “ (2п-1)«! 1
—' 3 7 11 ... (4« + 3) ' ^ (2п)!! п-2"+1
П-1 4 ' П= 1 4 '
00 Ч fi 1 оо П (Зк + 1)
и> L |„ , 1)1 - 8 V- ъ3) Е —2„уГ~
п=1 v ’ п=1 4 '
ОО п • Т ОО -1
М)Е^Л. 55,Е;Л_.
п=1 п=1
Следующие ряды удобно исследовать, применяя радикаль¬
ный признак Коши.
оо оо
56) ^2(-1Г+п. 57) ^2^_1>"_п.
62)
Следующие ряды удобно исследовать, применяя теорему
сравнения или нриэнак сравнения (см. стр. 26 и стр. 32).
ОС) ОО j
Ь4)Ё(п + 2)2" 65>п5 v4« + 2)'
™ V' 1 V' п'2 + ап + 2
^ + 2)(п2 + 1)' ’ ~ «И + 6п3 + 2п + Г
°о
68) Г а > 0.
^ 1 + ап
п. = 1
ОО J
7°)Ё^г 71>ЕйЬ
п4 + Зп3
п = 1 п = 2
00 «2
и> ,
П =11 П — 1
ОО 1 оо 1
74)Е'ь^- 75) Е (1пп)|п1пп'
n = l v Я-2 4 '
оо J °° 1
76^ Е (Inn)inn- 77) Е (1п lnn)lnn
л—2 я-4
78) £(х/п + 1 - \/п + 2)" In jj" * |
П — 1
оо
I 1 uu
. х' Л т 1 .л. v' 7ГП
79) > arctg —7=- 80)} arcsin _
f-; 1/Ъп7 + Зп3 + 1 ^ п2^п + п+1
194
Следующие ряды удобно исследовать, применяя признак
Гаусса.
оо) У' (2п ~ *)" 1 031 у' ((2п^1)И\ Л
(2п)!! 2п + 1 }^V (2п)!! )
П — 1 4 ' П = 1 4 4 ' '
84, у (JWLY.1
’ V(2n - 1)!!7 »’
»(«» +J) (^+!)...(„>+12=^)
П = 1
ОО
2"-(п!)2 2-5-8 (Зп- 4)
} 2^4 11 -(2n2 + n + l)' } ^ Зп-п!
П = 1 V ' П — 1
“ (2n- l)!!sin& ™ (“ п \
88) ^ —, р > 0. 89) у I ТТ cos ■ .j:I .
it, »nw siU,1, v*+v
Применяя различные признаки сходимости, исследовать
сходимость знакоположительных рядов.
Д2п + 3 2П
^П+Г 91) Е 1+22п-
П=1 П=1
»>Ез^
П —1 П = 1
_°° on 1 „10 00 w
94) Е 3" + П2 95) 12 7П _ 5п
П — 1 П=1
1 00 1
96) 5(3+(-!)")” ' 97)S^’
00 7" °° 1
98) Y" . 99) —т=.
' 5"-n n Vn
П—1 n=l v
10°) Ё |г- 101) Ё
»=1 п ™=х
оо оо
102) 5; V^555- ЮЗ) £
v"3 + 4r*2 + 1
195
104i У* .====. 105) V tga
1 Vn4 + 6n - 2 ^ П + 2
00 1 1
106) V sin tg a > 0, /? > 0.
^ n<* * n?
n = l
107) £>" In" (l + i;) .
n = l 4 7
108) V (»!)3
’ ^518-47 ... (n3 + 2n2 + 2)'
10.) т±Ц*.
n=l e n=l 1
3 + (-l)n ^2n + (-!)"
112)52
n = 1 n = l
n = l 4 '
114) f <3^-.
ll4; A; (n+ l)3"
П = 1 4 '
°° 1 1 °° 1 1
115) -7=sin —. 116) Vlj-L- —.
||7)r!lti^il UgjV^r-.
k1, 2" й^1)1
OO , OO , |4o
«•JEsrb-
П=1 П=1 V 7
00 / \n 00 / . о \ n2
“i£ stt)
n=l n=l
1231 f (fr»-1»» 124) f >
123 J 1, n.(2n)!! ' 124> 1, (2„_ l)(5^n- 1)
196
,10
00
125)Е^г- 126)Е2чЛг
n=l n=l
127)fVtg‘-^, 128) £
t?\ V»5 <" + 2)!
00 n2n ~ n3
J29)Z(sp- |3»IE?T
П=1 V '
1 e
n = l
131) E m e N- 132> Ё f1 - cov) ■ p > °-
n=l n=l
„ = 1 ^ ’ ^n(ln3n+l)'
00 n' °° 3"
135) V' ——, a > 0. 136) У' —-X-.—, a > 0.
> Z_rf nn+a ’ > (2n)!n“
n=l П—1 v >
W±^(l±\),P> 0.
1381 v 1391 v
s(5 + i)"' s;
°° ft" ОП+1 00
14°) E —•. ■■ - ---.. 141) y>5e-^.
^3n(3n~1) ("+l)!
00 / . 1 \ n3 OO
142) У (H±±) -3-". 143) ]T -7
п^Л n ' ^ >/”(”+ !)(" +2)
0° OO
1441
,ln n
146) E (in „)n • 147) E 2"
n vn
oo / 2 . i \ n 00
148)E(C08^n) • 149)E
n = 2 4 ' n= 1
n = l
n3+l
£ (<+*)■'
197
1
OO J оо
150)^-2^% 151) £ ^ln'nln'lnn'
TX — Z П = 1 и
152) £ "7 ТТ^“7 Г» * > °-
^ Я(.Я + 1) • • •(? + ")
■»>Х>дат7- ■«ifHsrr)-
П=1 v П=1 V '
“Ч£(*ЯТ5)’’ ^g^-C-V.-
m±WT. ш)±^.
r»=l n-3 n
~ ГпП2 22n ^2, 1
161) S p > °' 162) 5 0°&^'
1fi4\ V'i In2ln3-ln(n + 1)
n ’ln<2 + P)' M3 + P)'' • ln(" + 1 + P) ’
°o 1 OO J
164) 52 arcsin3 —, « > o. 165) £ arcsin ^3^4-
П=1 n=l
00 1 00 П3
166) X) "CCOS 167) £ arccos .
П=1 n=l
OO OO
168) arccos n П о• w+v^)i a > 0.
n=1 n=l
OO
170) ^сова сов2а • • cos2na.
•")£§*££ -)£Ш”
n=l n=l N '
198
173
175
177
179
180
181
182
183
184
185
187
189
190
ОО/ \”l 00 / \П
^ 1И> E (“““ ;rTj)
П—1 4 7 n =1 v '
DO / 9 \ 2n OO /, 1 \2n
|76>Е|т7т^
П = 1 4 7 n = l 11 +
^(2n-l)!f ' ^ nn
П — 1 V ' n=l
(1-4-7 • • • (3n - 2)) (5 8 11 ■ • (3n 4- 2))
n! (n 4- 1)! -9n
П = 1
OO .
^_n!_
3" («!)”
11 -84 • • (3n4 4- 4 n3 + 4)
1-n3
E“**n + 4
n = 1
V~^ (a(e 4- 1) • • (a + n - 1)V .
2^{b(b + i)...(b + n-i)) ' > •
n! np
, a > 0.
^ (l + a)(2 + a)...(n + a)
£ arcctg 186) £ arctg 2_i.
П=1 n=l
£45-3-2n' 188) £ ln”(n4- 1)
n=4 n=1 v 7
oo / ч n
/ 2-5-8 -(3n-1) у 1
^ \2-712 - (5п-3)У nP
199
ОО / /— \ +Зп+2 ОО / .ч ,
,91) £ (^) l94) £ Н" «О
Ш) £ ^(«+l)-j» + —')y , о > о,
1И) у~(“+ ')Р»+ ‘) ('"»+') (Р\п „>0 0>о
'^(0+0(2/9+!)...(»/*+О U; ’ >U’^>U-
а(} а(а +!)/?(/?+!) а(а+ 1)(аг+2)/?(/?+1)(/?+2)
1-7 1-2-7-(7+1) 1-2-3-7(7+1)(7+2)
а(а+1) .. .(а + fc-l)... (а+п)/?(/?+1)... (Р+п)
+ (п+1)! 7(7+1)... (7+п)
7 > 0.
Л(2а+1)(2а + 3)...(2« + 4п-1)22п
(2-4 • • 2п)(2а + 2)... (2а + 2п) ’ ^
201)|2!ЬМ:^
205)£(1_^г) • 206) Jn(v^-1).
ОО ОО .
207)£(tf5-l), в>0. 208) Е-^т-
nt 4 n=l v
оо ОО 3 I 1
215) 4-а“ * — 2^ , а > 0. 216) па In ^—•
217) £>(е*->).
n=l n=l
оо оо , ,
тгп v-^ Inn!
219) У cos 220) V --i-,—.
' 2n + 5 ' *-rn ln(n")
n=l n=4 4 7
m|Svsrfr+~gV
223) f;0 + ■*"
n=2 ,0^n!
225) f;»•( VS- V2). 226) £) "°P5(11+"^I°"1’
r» = 1 n = l
227) ^(чЛГТТ- v^)'. 228) f2)j2-\l2+\/2+ -'fi
n = 1 n = ls
n корней
P
oo oo ✓ - v
229) (a± - a*‘n ±) , a > 0. 230) £(ch--l)
n=l N ' n=l x л'
»>£(«?-*?)', *>o, p •
201
234) £; ri
ch f-1
235) 52,n
ne n
n = 1
236)
n = l \
- 1 +
, a > 0, 6 > 0.
237) £ | ^±1-1 | ,«>0.
n= 1
OO
713 -f П -f 1
n = 1
238) 52 ^arccos ^1 -
oo / \
239) 52 (arctg I - arctg J y/Z.
oo n
240) ^ ^arcsm - - arctg ^
:)>
21„ X>” 1^+1' +
n = 1
n = l
(1 + з^гг) ~{] + h
3 n
243) 52(^n + 1 - \/n)pln
n = 2
1 +
1 —-у/л
>«> £^ (»=**■- 0 *«) X>" (v^-
n = l n=1 \ /
о,1я\ * n + 2 7i4 + 3;i2 + 4
246) > arccos — • arccos .247) > arccos ———- -.
; n n 1 n4 + 3n2+n+l
*■> ХУ К'♦;)"->]'
П = 1
202
252) f”TTrl , а > 0, 6 > 0.
n=i 'П
+ ь)
оо оо
253) £nfc (а» - l)P , аф 1. 254) ^ [(np-l)r - nj , р>0.
П = 1 П=1
255) Yis/n* -f an + 6 — у/п2 + ain -I- 6i)a.
n = l
2581 Е(^г{^)А 2“) £(""; + “•;) •
n = l 4 / n = l 4 '
260) ^ na In fnsin — ^ . 261)^)Pn^tg — ^
n=l ' ' n=l
oo 1 oo
262) У" ■■—■■ 263) V ■■ . ■
h'x ^l + 2»-(--D" ^ Vl + 2n<-,)n
-IЁ(ms)”"" -.£(*j*|F
>»Ё('-(=ет)-лЬ)
n*o
OO
267) Y (n(n<,) - ')
П — 1
(•* I ln (n “ 2 (,n 0 + l8 «))) \
m 2-12+ —— I
269) f:n-lnchi.
П
» ~ i„п+1
271) £272> £, о/я ,ч-
’ ^ (2п)! ln"(n + 1)
П— 1 4 ’ П — 1
203
273) £>(n2 + e~2n) - ln(n3 + e*")]-ne.
П= 1
OO
274) £[ln(n2 + e2n) - ln(n3 + e")]ne.
U= 1
OO
275) ^ (In In(n + l)a - In lnna), a ф 0.
n= 5
/ l+sin-7
1 V»
n = 1
a
arcsin (e - (l •+ £)")
ln“(l + 7i2)’'
27б) E —T~e4 277>£
„=л »+tg7e /
278) ^ jln ^ ^arccos-^ +sin
279)E(1-(ln(1-t^)+eS,n")n )
o° / / л 1 \ 2n \a OO -1
™>E (£* -■) ».»D.**.)h-=f.
n=l \ 4 n ' / n=l n
00 /1 1 \
282) sin ( arctg — j .
«,£(,*-*-„1.1)*
°° / 1 I \ ^
284)£(ch--oos-J
n = l x 7
285) £ (arctg - In (1 + tg Л \
П=1 ' \ / /
“•SK -o°
oo
287) E(\/n2+2-V«J+ U‘arctg.
71= 1
204
00 / 1 \а
288) V -J—-e*rct*£ )
'jfeVnsml )
289) У" arctg° +sin — \ ^e1_cos» — lj
n = l \ n nJ
oo .
290) Y2 ( 1 “ si
П = 1 '
2 \ а
—r np sin arcsin arctg
2n2 + 1) V "
r.
;)
oo .
291) sin2 ^rr\/n2 -f nj • tg
n = l ^
292) ^^^nsh--ch-j
OO
293) ^ (ln(n2 + 1)- 21nn)a | cosn|.
n = 1
OQ
294)^
n = 1
In n + In sin
^ctg(i/n+T-'/n) _
295) nsin(27rn! e).
n = 1
OO
296) Y^n + arctg na — y/n).
n = 1
297) f; ((„««*
298) ^ In cos ftg — - arctg —^
n = l ' ^ ™'
OO
299) ]T(ensin^-ne-l).
П = 1
OO
300)E(c~(' + ",)7(I + .^).
n=1 (1-cosi) \ П/
205
302)
303)
304)
°o / 4 or ,
E( 1Г nn\ 1
I ^^ — COS ) in cos —.
V 2n + 2 2n -h 2 / n
n = l 4
|(^r-
305) ^ (in ( 1 4 tg2 — In cos , a > 0, P > 0.
306) fj|(co. (cosI) -'OS (chi)) (b^l5-)
OO
Исследовать сходимость ряда an со следующим общим
членом ап. п=\
X 1.
307) а1
" “ / 1 + хЗ dx 308) °" - / 1
+ г3'
о о
тп+ir 2
309) а„ = -— *■ —. 310) а„ = / —dx.
J v^l +x3dx пп Х
о
1ГП + 1Г rn + ir
311) an = J °-QS g dx. 312) а„ = j С°--^ Х dx} q> 0.
1ГП тгп
n+1 £
313) а„ = J e~V*dx. 314) an = J ^
sin3 X .
dx.
315) an = lnn^ n а, a > 0.
+ x2
0
206
316) ап — 2
In П
П+1
п2 + 1
[ sin х ,
/ dx
. 317) ап =
/ sin ii2 du
J *
J
п
n2
318) ап =
п + 10
J sin и3
du
2 n
320) an = n2 J ^x
n + l
319) an = n2 J у
n
n2
321) an ~ n f —
+ x
■ dx.
dx.
' n+l
322) an =
Xх dx
323) an =
(£i
(2n + 2)!
Рассматривая an как члены соответствующего ряда, по¬
казать, что данные последовательности {an} сходятся.
п'*
324) а„ = —.
330) а„ -
332) а„ =
334) ап =
n5
2”
325)
an —
5n
n!
an
n\'
327)
an —-
bgon
nk
, *€N.
naqn, k|< 1.
329)
an =
(2n)!!
n"
(2n)»
331)
n"
(2n+ 1)!‘
cin —
3"n!"
(n!)n
nn!
333)
an =
(2n)!
(2")!
nn
335)
(2 n
-1)!!
(2 гг)!
an —
(2n)!!
(2n+ 1)
(n!)"
*1 n
337)
an =
n"*
\П •
Рассматривая 5П как частичные суммы соответствующе¬
го ряда, показать, что данные последовательности сходятся.
338) sn = 1 +*
п п+1 3 п
207
339) S„ — 1 H—+ • • • + —f= — 2\/Ti.
У2 Vn
340)S" = uT^ + Jlbi+ +^“1л1л"
Mi)S. = tln* '"2’“
к 2
Ac = 1
Ea\ 11)
——, a > 0, где a(n) —
число цифр числа п. п={
343) Пусть Ап — последовательные положительные корни
°° 1
уравнения tgx — х. Исследовать сходимость ряда ^ .
п = 1Л^
344) Исследовать сходимость ряда ^^r(n)an, а >0, где т(п)~
п = 1
число делителей числа п.
п-1
345) Исследовать сходимость ряда где (р(п) = j.
т
346) Исследовать сходимость ряда
к'
п — 1 к — 1
- Е in2* по Е {-
) ft >°; б)Ц^!г-а>0-
гг
п — 1 п=1
347) Найти все значения а, для которых сходится ряд } ——,
“ п2
п— 1
где <р(п) --- число нулей в десятичной записи числа п.
Последовательность {an} задана рекуррентно. Исследо-
оо
вать сходимость ряда ап.
п = 1
348) в1 = 1. <in + i = —.
п
Q Л(\\ 1 П°"
349) ai = an+i =
2’ n+1 n + 2
350) ax = an + i = a„ - na
208
351) di — 1, On+i —
352) ai = 1, fln+i — , .
1 -f nan
353) ai = 1, a2 = 2 - \/3, an+2 — 4a„+i + a„ = 0.
1 n
354) ai = 1 = Si, an+1 = —, где Sn = ^ a*
*=i
Доказать сходимость ряда и найти его сумму.
356) 1 + 2_4 + 8+16~32 +
357) 1 _I + I_I + I_I+...
358) I-1-Ih-I-I-I + I- ^L-^-h -..
„гм ,111111 1 11
^ +‘3 + 5 2 4 + 7 + 9 + 11 б 8 +
11111111 11
360) 3 + 5 + 7"3 + 9 + ТГ“5 + 1з + 15~7 + ' '
361) l + \-\ + l+l7-\+ ' + 4*^з + 4-Г^Т"4 + ' '•
„„„ч ,111111 1 1 11
’ 2 4 6 8 3 10 12 14 16 5
Применяя признак Лейбница, показать, что данный ряд
сходится условно.
n^J Vn2 — 4n + 1 Vn20 + 4n3 + 1
(-l)nln25n f (-l)nn
366)S(»+.)^
n=l n=1
209
369) У>п(тгуУ + а).
п ~ 1
Применяя признаки Абеля или Дирихле, показать, что
данный ряд сходится условно.
ОО Оо Л
cos In
37°) Е о О’ 371) El,
^ Зп + 2 ' In Inn
n = 1 я —4
^ sin in + J) л/п
372) V Кг-~- ■ 373) V(-l)"X_.
n — ln'(n + 2) ^ Inn
^)f'<-'l"sln:l'1 375) V(" + 2> *"("+;)
^ N/n^TT n2 — n + 1
n = l n =4
Исследовать сходимость (абсолютную и условную) ряда.
«•1 377,S^
(-l)n + 1 ln2(n+ 1)
oto\ V' I-1) In (n-f 1) „n4 • (* . \- 1
378) E 379) 2^sin^-+7rnjsm-.
П=1 n=l
OO oo
380) Y^jro/n* + n). 381) Yj sin(7rv^n2 + n).
n=l n=l
3»2
OO
384) У^(-1)п(\/n2 -f 3n 4- 1 — \/n2 — 3n 4- 1).
П — 1
38,, EH);
n = 1 v n-1 n2 + sin2n
388) D-1)“+Il„(l + I).
П 1 4 ' n — 1 4 '
„^(n + 1)a n=1
210'
390
391
393
395
397
399
401
403
405
407
409
410
411
\П — 1
Y ( nn lnn 392) У HH"*1)"
> nlnlnn > ^ (271 + 3)"+! '
n = 10 n=1 4 '
n = 1 ' ' n = l
396i D-! r^n.
£<-1)n(iw' 3981
n=l ' ' n=l
f I (-1)" 400) £(-l)"+18in l—r.
^ (n+ l)(Vn+T- 1) ^ n + v/n
(-1)" „no> v' (-1)"
S nlnpnln,ln(n+ 1)
n»2 n=10 4 '
ghlttir.
n = l n = l
00 00 In (l + t~UnV)
^oosnU-^. 406) £
n=l n=l
00 / l\n CO
£<$-•
n = l V n = l
p>°-
n = l
f-( nn in ln(n 4- 2)
„T^o nln(n+ l)ln*(n + 2)
D-r(£±i)-. ->£<-■>" (|ЙГ
n=1 4 x n=l 4 7
211
(-1)
}Ln.-.U
3n
\n- 1
4M)j;fcip(i + l + i + ...+i-h.).«>o.
n = 2 4 7
(-i)n
4I5'E£
In n
416
417) jT(-\)n2+ (~ir. 418
П = 1
OO
419)2
n= 1
ИГ1 • Л
sin .
2 П+ 1
421) Ё
(-1)
1)
423)2
^ v/2n + 1
(-1) *
1 +
I)'
420
422
n + In n
7Г П
T'
425) n3e n sin
n = l
n = l v
424
426
428
429) y^sin(7r\/n-f l) sin—. 430
n = 1
431) Ё
(-1)
Tl — 1
n = 1
oo
433) sin(gy/na + 10).
+ 1)
n= 1
oo
435)53
П = 1
3n n
432
434
436
E
n = l
oo
E
n — 1
oo
E
(2n>! ■
“ (-!)"+>
^ 2n - ^/n
n = l v
(—l)n arcctg n
пЧ
E
П= 1
oo
2nVl)n+1
Tl!
n=4 '
oo ! 2
Em n 7ГП
COS —.
n 4
n = 2
E
n = 10
(~i)n+1
n — In3 71
00 j
y>in(Wn + 2) - cos —.
n = 1 ”
00 ros
LCOS 1+Г»
- 3/
n-2
oo
(-l)n
n=1 n Inn + v^ln3 n
4" + (-5)n
V-
Z_,
+ (~5)n
212
437)
n = 2
OO
439) £(-1
n = l
441) £
(-
fl = l
443) £(-1
fl = l
445) jr(-1
n = l
OO
446) £(-1
П — 1
OO
447) £(-1
n= 1
448)
nln n
n2 -f 4
438) £(-1)
n = l
narctgn
arctg
n + 4
Inn 7r(n2 -f 1)
44°) V^cos^—
b; ^
Гсо.;
n2 4 4
442) У] п 8ш(тг\/n2 4- 2).
( sin n\
n = l
OO
"„cctg^. 444)
"(,~5i"5STr)1,>0
П |п°^1 + У , Q>0.
449) >T
sin П
«0) E ^
n = l
OO q
<52>E^
nrl v
.„г'»-! 2?rn
451) > cos ——.
1 4 1 3
n = 1
V'"4 (—l)ncos2n Sin Ш'
453>E,>0 454)£—’ ■
n=I v n=2
(n 4 1) cos 2n
sin 2n lna n
/ikk\ 4 1
455) £^2^С08П
n= 1
456) £
457) £
sin
n3 - In Tl
r*2nP + Sin SL
. In n . 7ГП
458) sm
n = 2
n = l
П
213
» „ ~ (-l)"sin2(a)
459) V sinnarccos 460) V —.
' ^ n + 5 n-lnn
n = 1 n = l
4б1)Г(-1)пГгг". 462)f;i^i2±i.
“ y/n ^ у/n + 3n + 2
463) 464)f;^iL_
n In2 n " 2n - sin 3n
n^z n=l
oo oo
COS n Sinn
465) 7 . 466) } —- :—, a > 0.
" n — COS n " 3na + sin n
n=l n=l
V'' (—1)" sin n sin4 n - 4
467) > -v g > 0. 468) >
si vsttt s;
469) f;
cos n - cos n
n = 1
(без исследования абсолютной сходимости).
оо -2
— sinn-sin 7Г
470) £
n=l
(без исследования абсолютной сходимости)»
47!) £ "■ (■ + *>. 472) V “£+£>.
lnn + 5 ■‘Ч Ч/п + 2
П=1 П=1 v
v / . 4 3\ ._ *v (■—l)nsin4n
473) 2J (sin п “ 5 ) arcctgn. 474) 2_, —7-," •
8' n=2 '/п1пп
475>f:(‘*(?+1isr)-i)'»>o-
n=l N х 7 7
476) £>(
П = 1 '
ИГЛ
пя
1 + sin -—J , д > 0.
ОО
479) 53tg(7r</n4 + (-l)"-n? + 4).
П = 1
214
<»»> f> (■+ > 0
481) £ («Ц5Р 0. 482 )g;
n = l n=l
П — 1
^ COS Я- (n + -M n
S'8 ^ (» + l)V» + 2'
“ an ir (n + i) , Л (-l)IW
;:7i ■y-,~ 4861 £ -
-)£-»" ьют
o° , m[:f] 00 n
488) ^ —. 489) ^ («п(»^Щ))
n= 1 n = I
oo
490) Y^n + (~l)n — y/n) arcctg nq, g > 0.
n= 1
491) УЛу/п^ -f (—l)™*1 — v^), <7 ^ 0.
n = 1
oo
«2) £(-ir»,ein n4"o»'+l
n = 1
.°°s / l\n
493) -f 1 — y/n^) arctg — , q > 0.
fl — 1
oo
E- cos (n arccos - ) / 1\
K— aZ. 495) £(-l)»lnefl + tg-).
n=1 n —1 ' '
n=1 n—1
oo
sin n
n2 + 2
n= 1
496) У sin3 n- arctg
215
COS у/пТТ - cos у/п
49?) Е ^——■ р > °-
(_n[lnnl cos*5 па
498) V * ]- . 499 У — .
' п *—*1 п - 2 sin па
п=1 п=2
500) _
:1
ОО
Е^-^Ч—'—-cosiV
h \nsm± ”/
,,n /sinn /sinn\\
“‘)Е(-чЧда“5,пЫ))
°°^ / J J \
502) E(-])n (arctg ~7f= ~ arcsin ~7Г= I
\ vlnn V In 71 /
503) E(-Dn E
n = 1 \k = \
2 n
oo £ COS/г
k—n
rt VrvM-* ,
504) V -
1' 71 -f COS .>77
n = 1
oo (El) sin 3rt
505) V ^fc=‘ ' .
’ ^ 3n + 1
n = l
oo (Ef) cos2n
506) V = l .
' In n
n = 1
507) V(-|)"-' + C>) а > 0.
np n!
n = 1
В задачах 508 5*22 для исследования условной сходимости
использовать группировку ряда.
^ +2+3~4~5_6+7+8+9
ГЛЛч ,11111111
',09) 1 + 2“3+4 + 5“б + 7 + 8_9+ " ■
216
г,ПЧ .11111111 1
^ + 2 + 3 4 5 + 6 + 7 + 8 9 10 +
1111111
2In2 ^ 3In3 4In4 5In 5 61пб + 71n7 + 8In8
Р1П1 ,11111 11
512) + + + ' +7ё~¥ + '
513) 1~72~7г + 7л~75~7б*" +
1 1 i_
\/3 п — 2 у/Ъп — 1 \/Зп
1 1 1 1
514) —р: — — 1- — — —т= + • • • +
л/5-1 х/2 + 1 V§- 1 V3+ 1
1 1_
\/п — 1 Уп + 1 ^
С1С. ,111111 1 1
> +v/3 у/2 + у/5 + у/7 ^+У9 + УЙ v6 + "
„ 1 1_ }_ \_ \ 1 1 1 1
> 22 З2 + 42 + 52 + 62 72 82 92 102 +
с* ,1111111
* 2 + 3 4 + 5 + 6 + 7 8 + "’
здесь знак минус имеют члены вида 2~*, к 6 N.
J 1 1_ _1_ J 1 1_ J_ J_
1 +х/5 V4 + Vb + V6 л/7“у/8 + %/9 + 7Ш + '
,111111 1
^ + ЗР 2р + 5Р + 7Р ~ 4»" + 9р + 11Р
520) 1 + — - — + — + - + — + — - + •••.
’ У 1р 5р 7Р Зр 9р 1 1р 5Р
co1, 111111
521 ) 1- (- I- .
’ I р 2« ЗР 4» 5р б?
Со«ч ,21121121
522) 1 h 1 1- 1 1 1 .
’ 2ч Зр 4р 59 6р 7р 89 9р
523) \ап\ = —7='> знаки расставлены следующим
г^2 П^П
образом: два плюса, пять минусов, два плюса, пять
минусов и т. д.
217
/ 1 1 \ S{n an / __ | | _
524;£(l + - + ---+J—, «.#2»*, *GZ.
n = l 4 '
ror V"' n'<’n • 71,71 со/?ч V"' (-1)”-cos an
525' > —r^sin—. 526 > ’...
^ nn+2 4 7 ^
П — 1 n=1 VI
527; V(-I)1-^—1 1
Ч«Ч1 ,1 V" sinfffv^n3 + ft2) „
52«) *> Ъ i^rj , 6) ъ —^—•« > »•
n — 2 n=3
y-co.(c,h.); уЦ«И
'1 71 In Tl 71 In 71
n=2 n=2
00 i 00 L
530) ^2 I xs*n nxdx. 531) X>1)"W xn arctg —dx.
n=l0 n=l Q
1 "r
532) J arctg nx dx
n= 1 0
n
00 1 f
534 £(-1 r^je-‘dI
n-1 0
™>D->r- 7S*?*- /^b
П — 1 П
00 ’m+,r . 00 »"+*
M6»E / ^ “7)£ /
COS X
dx.
хя
n=l *n
1
tip n
OO
538) У (1 - x2)n sin n rfx. 539) ^ j dx.
oo n + * оо wn
и2> £'<-!»"*' / гаг *«) £<-»•/*=*•
n_10 п п-1 о
°° 1
544) Евп’ ГДе а1 =_1> а2 = 2 >
П = 1
(n -f 2)а„^_2 + 2(n + l)an+i + пап = 0.
Исследовать абсолютную и условную сходимость ряда.
И5,£(-)". ш,£(40*’
п=1 ' n=l N
00 п 0° / • , \ п
">ЕШ ■
п=1 4 7 п = 1 4 '
549)
00 ;п °° /II V\n
551lE^
n = l
2. Бесконечные произведения
Выяснить, сходится или расходится бесконечное произве¬
дение, и в случае сходимости найти его значение.
оо
1 / 1 \
“»> П ;гтт 5И) п (> -
555)Й(, + (0!") 5561
557)JI(1+*JV 55») П
с,° 2п + 1
n+1
/, , 1 \п сю JL
559) П 560) П у^Х
п=1 ' п = 1 " ^
оо оо
561) П™5^" 562) ПсЬ^.
П=1 П=1
219
563
565
567
569
571
573
574
575
577
579
581
583
585
/
nh
n = l 4
OO
П
2 +3n + 2,
3 n 3 n
n = 2
) se4>П('-;?)•0<I<1
n = l
3n — 1 3n + 1
00 2
n=3
- 1
П—. «>/»
n = l
OO
П (2„)!!
П = 1 4 '
OO
a( ^ , a > 0.
a + n
(2n- 1)!!
566) Й (' ■ isW) •
“»П(' + 5ГЬ)
n = l 4 7
570,n(2" + 1,(2" + 7)
A1 (2n -f 3)(2n -f 5)
4 n -
4r/ +
OC’ ,4 1
П HI
n = 1
n = 1
П ■ +
, «1 = 1, a«+i = (n + 1)(I + a„), \ .
Исследовать сходимость бесконечного произведения.
ОО
1
П^т
йда-
п = 0
тг + 1
п -1- 2
п
n2- 1
г2+ 1
п
П — 1
™>n*(££)
П — 1 4 х
оо
580) Д п±.
п = 1
1 \
a • , a > 0.
п — 1
оо
cos (arcctg n).
n = l
Ш) Д v +
OO
584) Да^, a> 0.
M = 1
00 I 1 \ °
586) ( nsin - J , a > 0.
220
587
588
589
590
591
592
593
594
595
596
597
598
e>0-
о° а
JJ |п (е » - l)j , о > 0.
П=1
00 а.
ПттТ' “>°
П = 1 п
ТТ (п<* - Л
1 I arccos , а > 0.
й V »- )
оо " + 1
П/
^ е* > 6 > 0, а фЬ + к, /: £ N.
SO**)-
оо
JJ (l + е~ » , аф -к, к € N.
П = 1
ОО
\/ln(n -fa) - Inn, а > 0.
П = 1
х2 dx
\ + х2
5(-^)
п= 1
оо
Ш'+ЦгЧ.-»-
п=1
оо / • а \
п(^).
п=1 4 П /
а ф пк, к £ Z.
221
60°) Д (l - ^е(^+^), а ф \/к, /: € N.
оо оо
601) П tg (j + ап) , |а„| < Я-/4, ^ |а„| < +оо.
П=1 П=1
602) f[sin[i (1 + ^)Ь Р>°
п=2 L 4 7 J
п—2
Исследовать абсолютную и условную сходимость беско¬
нечного произведения.
604) ft (■ + 605) Д (l +
п—2 4 п=2
оо оо
608) JJ 609) JJ
П = 1 П — 1
бю)П(1-*п)- ^ЙО + Й-
П = 1 П=1 ' '
613) Ц tgw/4 (l + , * > 0.
ОО
614) Д а„, где ап :
П=1
, 1 1 1 1 \
а2т — 1 77=) а2т-1 —11 + ~Гг= + ~^7=~г — I , Ш Е N.
\ У™ Ут? гп)
222
оо
615) JJ ап, где а„ :
П = 1
«2т = 1 Г", Ос > 0, а2т-1 =
та
*('-^)(1 + ;7з) "
6171 (1+f)('-.f) (1+f)(1+^)(‘-^) (1+f)--
ОО •
стр. 74), получить равенство cosx =
п = 1
619) Используя рассуждения, аналогичные рассуждениям при
представлении функций у = sinx и у = cosx бесконечным
произведением, получить равенства
sh» = «n(l + j|l),
<*~iiO+<dw)-
3. Функциональные последовательности и ряды-
Равномерная сходимость
Найти предельную функцию для последовательности
{fn(х)} и построить ее график.
620) /„(*) = 621) /„(*) = х{\ + е-"*).
1 •+- X
622) /„(*) = 623) fn(x) =
624) fn(x) = \/xn + x2n + !. 625) /„(*) = \/x2n + 4r" + 3.
1 *—)
V (2n-l )**>)■
618) Используя представление sinx = x
n = l
( 1 + — + —L- ) , m € N.
\ ma m2a J
)(1 + 7f) (1_7^)x
223
626) fn(x) - cos n ^\An2 + nij .
627) /n(x) = sin ^7г\/n2 + x2) .
628) /„(x) = sin ^тг^п2 + ^ + x2j .
629) fn(x) = sin (2тгУ^Т nx -f x2^ .
/2 \2n"‘
630) /„(x) = f - arctg nx)
631) fn(x) = lim cosm(n!2тгх).
m—►co
632) /„(*) = ne~nx‘.
633) /„(x) = nxe~n*\
634) /„(x) = xsign |sin2(n! ;rx)|,
xtg2"^ + y^
tg2n 22. + Г
X Г X
636) /„(x) = cos - cos - • • cos —.
637) /„(x) = (x - 1) arctg xn.
638) f„{x) = \jx + \fi + y/x -f • *, X > 0.
n корней
x"+2 x2n
639) /n(x) - (ЛТТ)! + {^+2y. + " ' + (2n)!
Исследовать равномерную сходимость последовательнос¬
ти /п(х) на заданном множестве Е.
640) /„(*) = х2", а)Е =
, б)Е = [0; 1].
641) /„(*) = xn - xn+1, а )Е= [0; 1], б )Е= [1; 2].
642) /п(х) = -ji—, Е — (0; + оо).
х п
643) /„(») = а)Е = [1;+оо), б)Я = [0;1].
х ■+• fix 4" 1
224
644) /„(*) = __, а) £7 = [0; 1], б)Я = [1;+оо).
I -|- 71 + X
645)/„(*) = х"-х2", а.) Е = [0; 1], б)£=[1;10].
О ПТ
646) /„(*) = ——, а)Е = [0;1], 6) £ = [1; +оо).
1 + п х
Оп^т
647)/п(1) = ТТ^' £ = (-°°;+00)-
648) /„(г) = ^х4 + Е = (-оо;+оо).
649) /„ (х) = п ^^х2 + ^ - х/х2^ , Е = (0; + оо)
650) fn(x) = S‘n WI, а) Е = [—А; А), 6) £ = (-оо; +оо).
П
651) /п(*) = sin —, а) Е = [—>1; А], 6) Е = (—оо; +оо).
п
652) /n(z) = v^cos" х + sin" х, Е = ^0; .
653) fn(x) = \/l + arctg" x, E = [0;+oo).
654) /„(*) = e"(r-2)| e = [0;4).
655)/„(*) = 4 »n-1 £? = (0;1).
n* n*
656) fn(x) = Vl +x2n, a) E = [0;4], 6) E = (4;+oo).
657)/„(x) = nln(l + ^), a) £7 = [0; A], 6) E = (0; +oo).
658) /„(*) = n In (l + ^ , a) E = (0; 2), б) E = (2; +oo).
659) /„(*) = - a)E= [0; 1], 6)E= (0; +oo).
Tl -f X t V nx
660)/n(x) = nin+2”2J~2j2, E = [0; 1].
661) /„(x) = sin2”x + —r, a)E = [0;jt], 6)E- [J;7Г — J], <J > 0.
n*
I 4 2
662) /»(*) = -4 . 2 ■ E = (0;+oo).
21n n + x2 + xln n
225
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
226
/п(х)
fn(x)
fn(x)
fn(x
fn(x):
/»(*)
/»(*)
a )E
Ш
fn(x)
fn(x)
U(X)
fn(x)
/»(*)
fn(x)
fn(x)
fn(x)
/»(*)
fn{x)
- \/x sinx, E - |o; .
= \/cos x, E =
ТГ 7Г
2’ 2
sinx
= E - (0;я-), где <p(x) - { x ’ x ^
1, x = 0.
(arctg x
■Г
> * Ф 0,
X — 0.
: arctg 3nx — arctg 2nx, a)E = (0;l), 6)E = (l;+oo).
TlX — 1
: arcctg ——, a) E = (0; 1), б) E = (1; +oo).
n X -f 1
= n4 fchx" ^^ ,
V i + *ny
= [0;J], S > 0, 6)E=(6; l-S), 0 < S < 1, в)Я=[0;1).
= 24?Z1F^=M.
= n(l — x)xn_1, E ■ [0; 1].
= n2(l -x)xn-', E = [0; 1].
= tix(1 -x)n, E = [0; 1].
1
1 4- nx
, a.) E = [0; 1], 6)E = [l;+oo).
= In (\ + , E= [0;3].
V nVn+lJ
n + i
, a) E-[0; 1], 6) E — [ l;+oo) в) E =
nx -I- 1
= 1 - (I -X2)", E=[-y/2\y/2].
n „ r,
= n arcctg—, F=[l;-foo).
n* tg-, £7= [0; 1].
1 + n2x2 ° n
= nsin —, a) E = [1; -fсо), 6) E = (0;+oo).
nx
681) /„(х)
682) /я(х)
683) /„(*)
684) /п(х)
685) /п(х)
686) /„(*)
687) /„(*)
688) /„(*)
689) /п(х)
690) /«(*)
691) /»(*)
692) /„(*)
а )Е
693) /„(*)
694) /„(*)
695) /„(х)
а) £ =
696) /„(*)
697) /„(*)
698) /„(х)
arctg пх _ Гл ч
; Е= [0;+оо).
4- п
:|п(1 + Пб"+Сеа») ’ £ = [°;+00)-
: а)Е=[-1;1], 6) Е = (—оо; +оо).
п4-х
пх2
—, а) Е = [1; -foo), б)Я=[0;2].
п4-1
: у/пхе~^^, Е — [0;4оо).
: пх2е~пх, а) Е = [2; 4оо), б) Е = [0; 2].
: sin(n2e“nx), a) F = (0; 4-оо), б) Е = [1; 4оо).
: я) Е — [1; +оо), б) Е = (0; 1).
у/ПХ
:х2е-пх, Е = (0; +оо).
n ^-^=-arctg-^=^ , а)£=(0;1), б)Я=(1;+оо).
: sin (е'“ + тг) ■
(а; +оо), а > 0, б) Е = (0; +оо).
: COS (frix2) ’ ^ Е ~ б)Е= +0°^'
- , a) Е = (0; а), б) Е = (0; +оо).
= |п (*' + i).
(0; +00), б) Е = (а; +оо), а > 0.
; cos > a) Е — (0; а), а > 0, б) Е= [0; +оо).
=”с,‘гт!^'*)г=(о:0'в)£=0;|)-
= - cos Л a )Е = (0; 2), б) Е = (2; +оо).
X п
227
6") /»(*) = ’а) Е=(0; 1]| 6)Е=[1;+^-
4 -|- In (п + 1)х
700) /„(*) = (* - 1) arctg i2n, Е = (0;+оо).
701) /„(*) = VI + Е = (0;+оо).
пх3
702) /„(х) = -j- —, Е = [0; +оо).
X* + ПХ -т п
703) /„(*) = п2 (х* - l) , Я=[1;10).
704) /п(х) = *e""**-ln3n, £ = [0;+оо).
705) fn(х) = sin ) ■ Е = (-оо; +°°)
706) /„(*) = e-2lJ-3ni, а) Е = (0; 1), б) Е = (1;+оо).
707) /п(х) = п4 (е* — cosx"^ ,
а.) Е — (0; 1), 6)Е = [0;*),0< S < 1.
708) /„(x)=sin2(\/l + пх2-Упх), а)Е = (0;1), б)Е = (1;+оо).
709) /„(*) = v/nx+ln(nx)-%/nx, а)Е=(0;1), б)Е=(1;+оо).
710) /„(x) = arcsin »)^=[0;а), 0<а< 1, б)£ = [0; 1).
711) /„(*) = arcsin , Е = (0; 1).
I 4- пх
’12) /•(*> = "’(л*"-ГТрг),
a) Е = [0; 1), б)Е = (0; а), 0 < а < 1.
713) /п(х) = (l + “) > а) Е = (а; 6), 0<а<6, 6) Е = (—оо; +оо).
714) /«(*)= (1-“) - а)^ = (-а;а), а>0, 6) Е = (-оо; +оо).
716)/„(«) = ,", ^={1;!;!}.
716)/„(*) = *", Е= (о,0 и {1}.
717) /п(х) = х2п — xn, £={^}-
228
718) /„(*) = *2n - a) E = {0; 1}, б) E = (0; 1).
719) /„(*) = n*e-"lr|,
a) E = [-10; -9] U [1; 2], б) E = [-2; -1] U [0; 1].
720) fn(x) = arctg nx, a) F = [-5; —3]U{0}, 6) E = {-5} U[0; 1].
721) fn(x) = - — ry—,
(ni — 1)л(х — n)1 + 1
а)Я = [0; 1], б)Е= [1; 2], в) E = [2; -hoc).
Для следующей функциональной последовательности
{/n(*)},*e Е,
1) установить ее сходимость и исследовать ее равномерную
сходимость на множестве Е\
2) выяснить, справедливо или нет равенство
lim ( lim /n(*)j = lim ( lim /n(*)j, xo € E.
X—►Xn \n —► CXJ / n-4 00 \X —►Xq /
722) f„(x) = rn, £’ = [0; 1], a)x0 = 0; 6)x0 = 1; в) x0 =
723) /„(*) = -*(*), £ = (-ooj+oo),
n
{0, x — иррациональное число,
1, x — рациональное число
а) Хо ~ 1; б) х0 = л/2-
724) fn(x) =
1
х + п5
, Е = [0; +оо), х0 = 1.
[п/(х)1
725) /п(^) = , Е - [а;6],/(х) — произвольная функ¬
ция, определенная на[а; 6], a) xq = а; 6) Xq =
а + 6
п2х,
726) /„(*) - 1 п*( I-xV -<*<-, Я = [0;1], *о = 0.
\п J 71 71
0,
2
71
пт I
727) /„(*) = , , 2 ,, Е = [0; 1], а)*0 = 0; 6)х0 =
1 + n*xz 2
229
728)/„(*)= V1 + х", Е = [0;2] а)хо = 0; б)х0 = 1; в)х0 = 2.
Для следующей функциональной последовательности
{/„(х)}, х € [а;<*],
1) установить ее сходимость и исследовать ее равномерную
сходимость на множестве х G [а; 6];
2) выяснить, справедливо или нет равенство
ь 6
lim [ f(x)dx= /(lim fn(x))dx.
n—► oo J J n—► oo
a a
729) /„(*) = x", [a;6] = [0; 1].
730) /„(*) = nxe~nx\ [a;b\= [0; 1].
731) /„(x) = naxe~nt, [a; 6] = [0; 1].
732) fn(x) = nx(l - x)n, [a;b] - [0; 1].
nx
733) fn(x) = l+n2x4> [e;6] = [0;l].
734) fn(x) = nxae~ni, a > 0, [a; 6] = [0; 1].
735> = [°;!]-
1 4- nx
736) /„(x) = nx(l - x2)n, [a; 6] = [0; 1].
737) /„(x) = n2 sinx cos2" x, [a; 6] = [0;jt/2].
738) /n(x) = v/”sin * c°s2n x, [a; 6] = [0;тг/2].
739) /n(x) = 2n2xe-n2*\ [a;6] = [0; 1].
nx
740) /n(x) = t +ri2r2, M] = [0; 1].
Для следующей функциональной последовательности
{/«(*)}, хеЕ,
1) установить ее сходимость и исследовать равномерную схо¬
димость последовательности {/^(х)} на Е\
2) выяснить, справедливо или нет равенство
( lim /п(*))'| = lim /' (х0), х0 €
П-ЮО lx=r0 n-fOO
741) /п(х) = ^ arctg xn, Е f [0; 1], х0 = 1.
230
742) /„(х) = х2 + ^sin (п (х + , Е = (-оо;+оо), хо € Е.
Sin пх
743) fn(х) = —JZT-, Е - (—оо; +оо), х0 € Е.
у тг
744) /п(х) = Х Е = (—оо; +оо), х0 € Е.
1 4- пх
745) fn{x) = e-n2*\ Я = [- 1J2], а)хо = 0; б)*0 = 1.
Найти множество сходимости (абсолютной и условной) ря¬
да.
00 00 /_ 1 \п
™> £ 7«> £ Уг-
П—1 п=1
ОО ■* ОО ofl fl
'г—л 1 _ ^ \ г—' 3 • sin X
1 7 9) Е „(п + 2) '
П=1' ' П=1 ' '
^ 2ncos’1 х ^ 1
75°) Е „4 751) Е п2(х + ЦП'
" п2 + п 4 1 " (х -1- п)3
п=1 п=1 4 '
(-!)” ,«х V2' nl
™>Е^пЬ' ™>£(1_3)„
п=1 п=1 4 7
ОО 1^1 оо
™) £ 2^. 757) £
п=1 п = 1
ОО - оо г—
758)^—759) V
; ^ х + 2" ^ х2 + п2
П=1 Л = 1
760> Е rfeiw 761' Е
х2 4- п2/3 х2 4- п2
П =г 1 п=1
n=l
80)
«>Ё££- ™>E^.
n = l П n = 1
">±g£-
»>W n.»E(^)'
n=l n=l x
00 i 1
n + 1
xn*
n = l
OO Г— OO -
74) £ 3nr 4- 2' 775) £ 7Z
3n* + 2' 7 ^ 1 + 4" x1
n — 1 v
(2*)"
7fi'V -1 (2»)“
£l+X2" Tly/n + I2
П — 1 n=l
°° I 1 °° onr
78) — - 779) У .
7 2n nx ^ nx
n=l n=l
(-1)" sin
°0 /о _2\n 00
E 4^ "»E
n=1 4 У n=l
n cin JL
ХП
n + 1
8o\ v _LD1 7m у (-0й
^lin v'n2 + I2Inn
П=1 n=l
OO
84) V sinrt —-—, a > 0, a > 0, x > 0, — > - > 0.
' a + n 2 a
n = l
OO
85) У tga —, a > 0, x > 0, ^ > - > 0.
' a + n 2 a
n = l
00 1 00 / . \n
86) £ —— • 787)
xn ter z-' nn+x
П= 1
Xn tg X
88,l^
232
7Э0) f *2П 791) f V"( 2« У
Zw i -|_ j.2n+i iyi) 2^ (2n)!l Vl+*V ‘
n=1 n=l
79 ~ a,ct8n»»si.. 793 y- *(*+1). ..(. + ■.)
h '^I+? t, n!
oo
sin x sin nx ^ (—l)flxn
794) У /I . 795) V 2 ..
^E^rby- 797)f>".n"(l-^).
n=l 4 ’ n=I
798) ^2 sin яnx. 799) ^ Q) (e - - 1)" .
П=1 n=l
S„0 ) £ (-£)"’ «ЧЁЛ--.
802) £
£^(l+x)(l+ar:2).. .(l+xn)
00 40
COS™ П
«ИЧЕ^Г1- 8M)E:
, . ,2 + iJ“'
n=1 n=l
oo
8°5) 52(l + -)nn-*. 806) ^e"”3*cosn*.
n=l n=l
00 2 00 • 4n
n^i лллЧ sin X
“7>Етпй? “«IE—■
n = l n=J
Ь " '^ЛПТТ,-:
OO
813)^
^(1 + пг)(1 + (п+1)г)
233
In xn
. V—> 111 n
8.6) Ё
arcsin x 4- n
8,8) f\p&L.
1 + n2X2
n = 1
820) J2
COS 71X
n = 1
00 i..n
71 lnr(n 4- 1 )
822)
824) У
arctgn x
n = I
n= I
oo
n — 1
830)
sin nx
rt \/n2 + 1
n - 1
832) f;
^ Пп -Xй
815) £
TT. — 1
817) £
П = 1
np sin 7ii
\ + n4 '
(-1 r
arccos x + n
q > 0.
819) £
71 = 1
У*
1 + xn
, x 0.
823) £
cos nx
Tf V^n2 4- 1
n = 1
X2nt-nx
8251
n = 1
826) £ + (-l)n)n. 827) ]T
COS П J?
1 = 1
(■ +
828> Ш TT^cos nx' 829)
n = l
831) £
n = 1
n sin П2Г
n2x2 4- 1
(- l)n sin nx
^ '
834) ]T
sin n- sin n‘
n = l
7i 4 уг
835) ^sin 7г(\Jyt2 4- у2)-
n = l
7-; (1 4х2)(24х2). . .(n + z2)
п= 1
837) n v^sin” х.
838) £
77 4- sin X
234
(z + l)2n COS и
839) V
" 9" lnJ n
n = l
ПХ
1 1 A3'"'
84°)E(1+2 + 3 +'"+nj~
fl = l N
nmV (-1)" (-1)"
h + Sin(*”) ' ^2 «*»* + ^
oo . 2 O 00 3
лллч r-^ sm nicos3ni ft_,4 v > cos°nx
W)S пн.*» ■
845) V 846) V ”У" + Ч».
^^10(0 + 1) v/n3 +1
m±=t£&.
m m±*&-
П=1 n=l
or 1 \ Y' COslW1 П* ОСОЛ V (nx + y2)" n!
851) Ъ „«/< • 852) 2- SS •
n=l n n=l
853)f;tg"(*+-^). 854) f;
00
sinnx
nr+V
Исследовать равномерную сходимость ряда на множест¬
ве Е.
оо
п = 1
оо
п = 1
П=1
858) £ £ = [0; 1г].
V"7+1
235
859) jP , , , E = [0; +00).
’ ^ v^ + fn+l)*
8 ^(x+O^nx E = (_3;0]
' nyn + 1
n = l
00 / 1 \n - 1
861) У" V-;- У, E = [0; +00).
\/n + v/X
n = l
n = l
863)^x2e-rn, E = [0; +00).
П -1
n = l
00
n4 + 1
866) ^TV", a) E= (-0,2;0,75); б) E = (-0,2; 1).
n = l
00 1
867)E~ 2 2- £ = (0;10).
' ^n2 + nr + I2 v
n = l
OO
868> 5 3’VH-(2n+ •)*’ E = ,°;+00)
«и) f; 2!li±2, £ = №+<»).
n — 1
OO 9 .
T-л П Sin ПХ
87°) E 9^ ’ b = (-oo;+oo).
fl — 1
00 1
871) — sin E = (-00; +00).
ГК 71
n = 1
236
872
873
874
875
876
877
878
879
880
881
882
00 e-n2rs
n = 1
£V"S, a) E = (0; 5); 6) E - (1; -too).
П = 1
OO I—
a)t' =
П — 1
»4
; 6)£ =
i='
ES1I1 ИХ л V г-, ГЛ л 1
——, 0 < a ^ 1. а)£ = [0; 2тг];
n = l
б) E = [<f; 27Г — S], 0 < <$ < 7Г.
OO / .4
E, / Sin ПХ \ „
( + ’ a >0- = (_oo;+°o)-
n= 3 4 7
oo
£(2*"-*2"), E = [0;1).
g(G--')4b")> *=**'•
oo
У" xe~nx cos nx, E = [0; тг/2].
n= 1
£
n = 1
E=(0;ir/2).
^^x2e ni cos nr, Е = [0;тг/2].
z,„-(r„L,r *=<m.
n = 1
oo
У x sin
I + n5x3
, E = (-oo; +00).
237
885) —е пг cos пх, Е = [0; 7г/2]
п = 1
886, £; ™L»“)
а > 0; a) Е =
п = 1
6) Е
2тг
б; б
0;-
а
888) £
sin пх <р(п, х)
п — 1
у>(п,х) = |
889) £
П — 1
п + П2Х2
890) Y, ~
cos2 а:
П = 1
891) £
3 епх
X cos nz
n = 1
n2x2 + n ’
1, 0 ^ х < п,
sin пх, х > п,
, Е={ 0; тг/2).
Е = (-оо; +оо).
Е=(0;х/2).
892)
П=1
п4 + х
, Е — [0; +оо).
893) V 2 * ■ , Я=[0;1].
'' nzxl + п
п = 1
894) £
п = 1
оо
895) £
-j-—Г, Е = (-оо;+оо).
гк + х1
cos пх
, 0 < е < -;
а
Е — (0; +оо).
п = 1
10п + cos пх
, a) Е = (0; 7г/2], б) Е — [тг/2; я-).
896) £
Sin I - cos nx
, Е - (-оо; +оо).
238
00 (— Пп
897> Е 2 1 ■ = (0; 1].
* Т>*Т!г -I- п
71^2^ + П
П = 1
ч ( 1 )П П 71 Г 1
£ 7 ’ ~ [1; +оо).
п + *
ОО , v "(" + 1)
899) У" 1~ /_ 57, £=[0;+оо).
' ^ п + х - 1п(п2 + х2) 1 ’
71 = 1 '
оо ( у pjM-.U . 2
(—1) 2 Sin I „
900) Е ^гт^2 Е = (-оо;+оо).
П= 1
°°^ е—п 81П 2*
901> Е пз/2 ■ ! ■ Е = (-°°; +°°)
П=1
°° ч/1 _ т2п
902> Е on > Е = [-1;Ч-
2"
П = 1
П = 1 v
£=i-1;4
П= 1
905) Е d* ~ по ’ ^ = [1;3].
(2п - 1)2П 1 J
°° 2х
906) ^ arctgЕ — (—оо; +оо).
П = 1
ОО
X
907> Е 1+п4ж2’ ^ = (-оо;+оо).
П— 1
ОО
908) YI *2е_'/"-*) Е = [0; +оо).
П = 1
СО
909) S + ПХН1 + (п + 1)*) ’ а) Е ~ ^ +°°^ 5 > °’
б) Е = (0; +оо).
239
оо п
Ч
X
X sin ПХ
00 2 2
910) У — e~*z~, £ = (0;+оо).
■ ■ ^ 3*
п = 1
оо
л -v V"* X S1I1 ПХ _ , ч
911) > . . : —, Е = (—сю; +оо).
^ л/п*+Т + е"1г1
912) У](-1) (*~ 1 arcctg(x2 + п3), Е = (-оо;+оо).
П = 1
X
X л
913)£-f=—Е = (-оо;+оо).
^Г, vn3 + | arctgпг|
914) У" /|П:С2 , Е = (0;+оо).
; п2 + cos2 х '
П= 1
ОО 1
In X
915>Е;?Т^' е = №+“1
^gln^n + 2)^ £ = (_1;+оо).
п — 1
cos2n(x-2”)
*17) Е=(0;+оо).
ОПХ
П = 1
918) ^^ , а.) Е = (0; 1); 6) Е = (1; 2).
П
п = 1
Определить область Е существования функции /(г) и ис¬
следовать ее на непрерывность.
оо оо .
919) /(*) = Y, хе~ПХ- 92°) Я*) = Е -ГГ-2 •
п =0 п = 1
оо оо -
921) /(*) = ErVnt 922> Я*) = Е ^
n=0 n=1
оо п оо
923) /(*) = Е „2- 924> Я*) = Е»'Г1*,’‘.
П = 1 п— 1
925) /(*) = £ arcsin 926) /(*) = £
n=z 1 n = 1
240
927)
OO
n = l ' 7
OO
928) f(x) = £
n = 1
929)
оо . о
. sm nx
^ ~ ^ n In2 П
П — 2
930)
OO |
w-E,(1+nV). °
n = l 4 '
>0.
931)
n
1
932)
<.».Ё(.+1)‘
n — 1 x '
933)
(«) = f; (*n *n+1)
tM "+1/
934)
(«) = £У'"Ч
n-l
OO
935) /(*) = £
n = l
936)
H
II
“M8 !
'
937) /(*) = f;
n = l
938)
м-V (_1)"
x2 + П + 2'
n = l
OO
939) /(*) = 52'
n = l
940)
941)
942)
943)
sin nx
+ n(-l)*
X7 + n2
X + n
= y 2 .
(1 + 2x2)(l + 4x2)...(1 + 2nz2)
OO
= ^[nxe-"‘ - x(n - IJe-t""1)*].
n = l
= E(-i)
П + 1
(*-2)
2 n
n = l (n+ l)2ln(n+ 1)
= £(l-*)(3*-l)".
n = 1
241
944) /W-E(V?+n)(v/5;+;t+1)-
OO
945) /(X) = 5 0 +*2)0 +2*2)- (1 +n*2)'
00 1
946) /(«) = ^-_e-n*.
n=in n
OO
947) f(x) = e~nx sin nx.
n = 1
OO
948) /(x) = e~ v/”x cos nx.
n = l
Определить область E существования функции и иссле¬
довать ее на дифференцируемость во внутренних точках Е.
949) /(*) = £ Т-
г» = 1
00 • / ч
/ ч Sin пх
951) /(*) = E-^rJ.
п= 1
оо
953) Пх) = ^\*Г1-
П = 1
955) f(x) = j; 1
(-1)"
П= 1
+ X
2 *
950) /
952) /
954) /
956) /
958) /
957) /(х) = ^ х4е
п = 1
959) /(х) = ^2 зГУ^П- 960)/
^ п31п (п+ 1)
ОО
961) /(*) = £-
ОО 2
п(п -f 1)
п — 1 '
оо . / V
ул Sin(nx)
п= 1
П!
к2' 1*1
= J2 arctg
п-1
П = 1
= £
п — 2
П In П
2 -f X2
sin(2n7rx)
3s
n = 1
242
Показать, что данный ряд допускает почленное интегри¬
рование на [а; 6] и написать полученный при этом числовой
ряд.
962) [а;Ь] = [0)2;5].
П!
п = 1
[а;Ч = [-1;б].
п — 1
\2п
k4 = (-i;2]-
П = 1
965) Ет. (•;*] = [-2; 5]-
П = 1
ОО
966) 53 (*'^ ~ 155^т) • [а; 6] = [0; 1].
П = 1
4. Степенные рады
Найти множество сходимости ряда.
ОО ОО
967) 53 п*" 968) 53('/”*)П-
п = 1 п = 1
“ *“ ... ^ I"
969) £ - ЭТО) Е ^
П=1 П=1
971) 53 972) J *L,".
П=1 П=1
°о ОО п
973) 53( -2)"х2п. 974) 53
п = 1 Я_2
^ х2п _°°. Гп I П"/3_2п
975»Е^- —
я—2 п = 1
00 I п 00 I п
978) 53 "•*
7 п^(2п-I)!!'
243
оо
979) У ^—гх2п. 980) У
п\ yjAn -I- 1 -5П/2
fl = 1
п = I
оо
оо „ оо , 1 V п
98|»Е^. »>» 982)E(1 + ;J *”■
СО 2 п 00 п
983) ;^(-1)П3"(п + 1)3/2' 984)Ё^ТГ-
00 / 1 \n _3п 00 1
985) У ( з/■ 986) У -тг-^—г*".
^ 5nv/nrTT , 2[|о83")
п— 1 V П = 1
987) |>"(j+ !)*". 988)|>"(^±i)"
989) f; 990) f; n‘(’+4}™
nlnn ' n + 1 !
n=2 n=l V '
П=1 ' * n=l
993) f НИ;-l)". 994)f;(-,).-'fc-i
n=1 n=l
М7)Е-‘)”(^тг)" <'+')*”
^Е^+ч’"- 999)£;<1±Щ>:
'°°»>Ё(ШЙ"(‘+ЗГ
.оо^МШ^)”-"
n = 0
244
2n — 1
1
(x+l)n.
~ (2+5(-1)=!т!1)“
'»«2> Е
л-2
1003) £*.^.(.-2)". .004) f
n=0 n=l v
oo / \n 00
>“») E^ (згтт) 1006)E<”»V(‘+-)"
w±(*±Z)'
n —1 4 ' n = 2 4 7
io°9) 1010) f;
„=2 "Vlnn ^ n2
OO n3 00
1011>£^Г- Ю12) ^5" x"3.
n = 1 nil
OO Qo n 2
1013) £ 5»’(x + 2)"’. 1014) J2
,o,5>£(1+H+...+iy. ”='
n —1
1016) Yl xn.
n = 1 ^
Найти круг сходимости ряда.
!0I7)EV-
п= 1
Ю18)
^—4 п\
П —1
-»ёсгг-
п -1 4 7
п = 1
1022) V
' п! (1 — г)1
п = I 4 7
оо
1023) Г /о "л г"-
^(2 + ,)"
Пг 1 7
(z-i)".
(2 + 2)".
245
'°”>Ш
п—1 4 ' п—1
1028) У ? 1029) V - ,-)».
^>/(Зп-2)2“ ^
(3-4*)" „ lMnf(* + <1h
юзо) У" ;n, V;*"- 1031)У//о ч„ •
' ^ 5n(m - 1) 7 ^ (3 + t п
П=1 4 7 П=1 4 ’
Ю32) £ iilig^L ,033)£iiM.
^(!->/3*)п 3"(n — i)
Ю34) f; ^~-2t)TT- 1035) E ,■ (гГ1)Пп2-
2n(n + 1) 2n 4 (n — l)i
n=l 4 7 n=l 4 ’
«ив) Е(^)" (* + *■)-■
П=1
Вычислив значения производных /^(х0), написать п от¬
личных от нуля членов разложения функции f(x) в степенной
ряд с центром в точке хо-
1037) /(х) = 2^, х0 = 4, п = 4.
1038) /(х) = tgx, хо = тт/4, п = 4.
1039) /(х) =
I
с* - Г
О
N
1,
Н
II
О
, sin х
In
X
х Ф 0
0,
н
II
о
1040) /(х) = t х ’ ^ , х0 = 0, п = 3.
[ 0, х = 0
1041) /(х) = 1п(\/х 4 1), х0 = 16, п = 4.
1042) /(х) = sin \/х, хо = —1, п — 4.
1043) /(х) = е'/ТТ*\ ю = -1, п = 3.
1044) f(x) = -г-—, *о = ^/2, п — 3.
sin X
246
1045) f(x) — —^—, xq = 1, n - 3.
arctg x
1046) f(x) = —-—, Xq = 0. n — 4.
cos x
Разложить функцию f(x) в степенной ряд с центром в
точке xq = 0, используя разложения основных элементарных
функций. Указать радиус сходимости полученного ряда.
1047) f(x) = е~2х. 1048) /(ж) = sin5*.
х3 1
1049) f(x) = cos —. 1050) f(x) = In -——.
о 1 — 2x
Ю51) f(x) ,= rln ^1 + . 1052) /(x) = ■j~ZT^2
1053) f(x) =Vl + x. 1054) f(x) = s/l - Ax.
1055) f(x) = ch (-|) . 1056) f(x) = sh(-3x).
1057) f(x) = arctg 2x. 1058) /(x) = arcsin ^x.
о
Разложить в степенной ряд с центром в точке хо функ¬
цию /(х), преобразовав ее при необходимости так, чтобы
можно было применить формулы стр. 130-131. Указать ра¬
диус сходимости полученного ряда.
1059) f(x) = с‘г/2, а) х0 = 0; б) х0 = 10.
1060) /(х) = 2х, х0 = а.
1061) f(x) = 2Г З'х, х0 = 0.
1062) f(x) = (2 -I- xje*-1, а) х0 = 0; б) х0 = 1; в) х0 = -2.
1063) /(х) = sin(a + х), хо = 0.
1064) /(х) = cos(a + х), х0 = 0.
1065) /(х) = cos3 х, а) хо = 0; б) хо = п/2.
1066) /(х) = sinx cos Зх, х0 = 0.
1067) /(х) = sin х cos х, а) х0 = 0; б) хо = тг/6.
{cos х — 1
i ’ , *0 = 0.
0, 1 = 0
247
1069) f(x) = lnx, a) x0 = 1; 6)x0 = e2.
1070) f(x) = ln(4 + 3x - x2), x0 = 2.
1071) f(x) = ln(l + x + a:2), xo = 0.
1072) /(*) = sh3x, x0 = 0.
1073) /(x) = ch2x, xo = 0.
1074> '<*> = *rhrr *»=0
IC75) /w = -Гз a|ro =0; 6111 = 1/2
1076) /W = + ~ix + 8' 10 = ~2
1077) f(x) = ^x, a) xo = -8; 6)x0 = 125.
Используя методы дифференцирования либо интегриро¬
вания степенного ряда, разложить функцию /(х) в степенной
ряд с центром в точке х<> = 0 и указать его радиус сходимо¬
сти.
1078) f(x) = arctgx. 1079) /(х) = arcctg x
1080) /(x) = (x+l)ln(x+l)-x. 1081) f{x) = ——-——.
(1 - х)л
1082) /(х) = arcsinx. 1083) /(х) = arccosx.
1084) /(х) = arcsin ,.-f ■■■■■. 1085) /(х) = arccos(l - 2х2).
\/1 + х2
10861 1087)/(»)= /^ Л.
О о
1088) /(*) = j Л. ,089) f(x) = j
1090)
о о
х *
/(*) = / 'п |г7 Л. 1091) /(х) = J Л.
о о
1092) /(*) = j 1 tC2°s2< Л. 1093) /(х) = J ^5^1 dt.
248
Применяя различные методы, разложить функцию /(х) в
степенной ряд с центром в точке х0. Указать радиус сходи¬
мости полученного ряда.
1094) /
1095) /
1096) /
1097) /
1098) /
1099) /
1100) /
1101)/
1102) /
1103) /
1104) /
1105) /
1106) /
1107) /
1108) /
1109) /
1110) /
1111)/
1112) /
1113)/
1114)/
1115)/
1116)/
= 1п(1 — х2), хо = 0.
1 j, *о = 0.
1 + X4
1
= . *о = 0.
</\ + х3 ’
= (1 - Х2)“1/2, х0 = 0.
= ех_\ а) х0 = 0; б)х0 = 4.
= е3х - 2е~г, х0 - 0.
= хе~£ , хо = 0.
1
Г, Хо = -1.
23г_2'
= 2*ех“\ х0= 1.
= sin3x, а) хо = 0; б) хо = —.
4
X . 7Г
= cos а) х0 = 0; б)х0 =
= ^(er -f е~* 4- 2 cos г), х0 = 0.
= sin2 г, а) го = 0; б) х0 =
4
= cos2 х, а) х0 = 0; б) х0 = в) х0 =
I 4
• 4 *
= sin4 X, Х0 = —•
4
= sin X сов2 X, Хо = 0.
= cos х cos 2х, х0 = 0.
= х cos3 2х, хо = 0.
= (х — tg х) COSX, Хо = 0.
= xsin2x cos3x, хо = 0.
= 1п(4 4- х2), х0 = 0.
= х ln( 1 4- х2), х0 = 0.
= xlnx, а)х0 =1; б)х0 = 4.
249
1117
1118
1119
1120
1121
1122
1123
1124
1125
1126
1127
1128
1129
1130
1131
1132
1133
1134
1135
1136
1137
1138
230
/(х) = ln(2x + 3), a) xo = 0; 6) x0 = -1; в) xo = 4.
f(x) = ln(3 - 4x), x0 = —2.
f(x) = ln(2 - 7x), x0 = -1.
2x + 1
f(x) = In , a) Xo = 0; 6) x0 = 1.
x + 1
f(x) = In 7ГТТ~ > a) xo — 0; 6) x0 = 1 •
2 + Sx
f(x) - ln(x2 + 5x + 6), x0 = 0.
2 + x2
f(x) = In , Xq = 0.
1 - X
fw ~In ^ - L+6' ~1
f(x) = In \/ *0 = 0.
/(x) = ln(2 + x)(3 + x)(l + x), a) Xo — 0; 6) x0 = 1.
/(x) = ln(l - x + x2), x0 = 0.
/(x) = ln(l + x + x2 4- x'*), x0 = 0.
/(x) = (x2 + x + 1) ln(2 + x), x0 = -1.
/(x) = (x2 + 5)In j——2, x0 = 0.
4 — xJ
/(*) = 2Г+3' ^X° = °’ 6^° = 2'
f(x) = a)x0 = 0; 6)x0 = -1.
Zt I
f(r) = X5, a) x0 = 0; 6)x0 = -1.
f(x) = x6 — 2x2 + 4x, a) xo = 0; 6) Xo = 1.
1 i
/(x) = - + 2x , x0 = 1.
X
/(I) = I= °-
Пх) = S-L + 2’’° = 0
1139) f(x
1140) f(x
1141) f(x
1142) f(x
1143) /(x
1144) f(x
1145) f{x
1146) f(x
1147) f(x
1148) f(x
1149) f(x
\
1150) f(x
1151) f(x
1152) f(x
1153) f(x
1154) /(x
1155) f{x
3 — 8z
, x0 = 0.
1 — 5x + 6x2
5 — x
12 — x — x2
1 — x + x2
, xo = 0.
1 + x + x2
1
, xo = 0.
, x0 = 0.
X4 + X3 + X2 + X + 1
(1+x)2’ 10 = °-
xo = 0.
(2 + x2)2 ’
(i 10 ~ °'
(ГГ^’1» = 0
(T^I)5' 10 = 0
X 1
X + 1 X2 — 1
1
x3 + x2 + 5x + 5
2 — x + x2
, xo = 0.
, xo = 0.
(1-x)3
3x + 8
, x0 = 0.
, X0 = 0.
(2x - 3)(x2 + 4)
x2 + x + 1 _
(x - l)2(x — 2) ’ •
v^+T Xo = 1‘
л/l -2x’ Xo = ~L
2x - 3
VbT+4' *°
251
1156) /
1157) /
1158) /
1159) /
1160) /
1161) /
1162) /
1163) /
1164) /
1165) /
1166) /
1167) /
1168) /
1169) /
1170) /
1171)
1172) /
1173) /
252
1
\/х2
- 12х + 40
х -|- 3
\/х2
-6х + 18’
( 1
— у/\ — х2
, *o = 6.
j Хо — 3.
, x ф 0,
X
О, х = О,
arctg(x +1), х0 = -1.
а — х
arctg , хо = 0.
а + х
1 х
3
Хо = 0.
- arctg j + - arctg х, х0 = 0.
I 1 j
1
1 — X'
ху/2
75*гс‘81-г’
, х0 = 0.
2- 2х
= arctg — . ■, , хо = 0.
= arctg
= arcctg
1 + 4х
2 + х2
2-х2
х
уГ—X
, х0 = 0.
==, х0 - 0.
= х arctg х — In У1 + г2> *о = 0.
= ln(x + л/l + z2), хо = 0.
1 , x2 + Ху/Ъ + 1
In — ^ , х0 = 0.
2уД
г^З+1
1 , 1 + 2х + х2
= 3'" *° = 0
= х ln(x -f \/х2 4- 2), х0 = 0.
= х2 arccos 2х, хо = 0.
2х
= arcsin
1 -f х:
г, Хо = 0.
= х arcsin(x + \/1 - х2), хо = 0.
1174) /(
1175) /(
1176) /(
1177) /(
1178) /(
1179) /(
1180) /(
1181) /(
1182) /(
1183) /(
1184) /(
1185) /(
1186) /(
= x arccos(x — s/l — x2), x0 — 0.
= x arccos
v/4 + x4
3 x r. г 1
= -- + -Vl - x2 + - arcsin x, x0
, x0 = 0.
1
sj 1 - X2 arcsin X
= 1 , x ф 0, /(0)
X
— j df, xo = 0.
о
r
= J cost3, dt, xo — 0.
0
x
/sint ,
-y- dt, x0 = 0.
о
f dt
~ J NГГТ*' xo ~
0
r
= J cos Vtdt, xo = 0.
о
x
= J >/Г+7*л, xo = o.
0
r
/arcsint ,
—j A, x0 = 0.
о
Г
= J t2 sh t dt, xq = 0.
X
4'-
— e
“72"
■ xq = 0.
Используя функции комплексного переменного, найти
разложение функции /(х) в степенной ряд с центром в точ¬
ке хо = 0 и указать радиус сходимости полученного ряда.
1187) /(х) = ех sin х. 1188) f(x) — tx cos x.
1189) f(x) — e3x sin 2x. 1190) f(x) = e~x cos 3x.
1191) f(x) = ch xcosx. 1192) f(x) — sh xsin x.
1193) f(x) — erctgQr cos x. 1194) f(x) - errosor cos(x sin a).
1195) f(x) = arctg(x 4* 1).
1196) a)/(x) = -=—l——, 6) f(x) = '
x2 — X + 1 ’ ' 4 ' X2 4 X + 1
Используя метод неопределенных коэффициентов, напи¬
сать п первых ненулевых членов разложения функции f(x) в
степенной ряд с центром в точке хо = 0.
1197) /(х) = tg х, п — 5.
( J. J_
1198) /(х) = < sinx х’ Х п = 2.
[ 0, х = 0,
1199) /(*) = п = 3.
COS X
X
1200) f(x)
I
= < Sin X П = 4.
I 1, x=0,
1201) /(x) = ■ ■, n — 3.
2 + sin x
1202)
Г xctgx, x^0,
/г) = < 71 — 4
\ * = 0,
x2
T 0
ln(l+x)2’ F ’ n = 4.
0, x = 0,
71 — 5.
\/l + x2 ’
254
X2
х Ф О,
1206) /(*) = { char - Г г ’ п = 3.
2, х = 0,
1207> я*) = п = 3-
Г г, х ф О,
1208) /(х) = < ех — \ г п = 4.
I 1, х = О,
1209) /(х) = ег 1п(1 + х), п = 4.
х
Ф
1210) /(х) = ^ 1п(1 — х) ’ л = 4.
1211) f(x) =
Используя умножение степенных рядов, написать п пер¬
вых ненулевых членов разложения функции /(х) в степенной
ряд с центром в точке хо = 0.
1213) = л = 7.
1 — X
1214) }(х) — ех 1п(1 - х), п = 6.
1215) /(х) = arCtg Х, п - 6.
1 - X
1216) /(х) = arctg х-cosх, п — 4.
1217) /(*) = -^L, n = 5.
V1 + х
1218) /(х) - е_г cos у/х, п = 4.
1219) /(х) = п = 4.
1 — X1
1220) f{x) = -£—, п = 7.
\/1 + X2
1221) f(x) = sinx-ln(l — x2), n = 4.
255
1222) f(x) = (a + bx + cx2 + dx3 + /х4 + кхъ -1- • • )2, n = 6.
Проверить равенство.
/1 i \
1223) ln2( 1 — x) = 2 У ^ ( 1 + “ 4" • * • -f — j ^ ^ ^ , —■ 1 ^ x < 1.
n = l '
1224) arctg2 x =
(1 + >+... + _LT).^lW<1.
= Ё('-* + Н + - +S1) H<‘
n = l '
1226) (£>") = l + j£>+l)(n + 2)*", |*| < 1.
\n=0 / n=0
1227) (£>") (£>+1)*"] =l + if](n+l)(n + 2)*".
\n=0 / \n=0 / n = l
>«) w<~.
\n=0 / n=0
*«>(f:SV=£^w<-
\n=0 / n=0
4nj»n Snrn /цп «
”»» EtE(-'IV = E Чг-• 1*1 < “
л п! " П\ ' n\
n = 0 n=0 n=0
Найти произведение двух рядов.
оо t оо
п=0 п=О
ОО 00
1232) £д", |д|<1
п=0 п=0
256
1233)
OO
n = l
oo
£
n= 1
чп
n(n + 1)
°° 1
V' 1
00
1
1 J
1)’
Ь (2« -
l)(2n+ 1)
1235)
v (-i)n
-1
1)!’
v(-ir
h (2">!
I
1236)
00 on
n = 0
00 r
£-
n = 0
-5)”
n!
1237)
Доказать
, ЧТО
(si)
'‘±1?
k = 1
делителей числа к.
Используя деление степенных рядов, написать п первых
ненулевых членов разложения функции /(х) в степенной ряд
с центром в точке хо = 0.
1238) /(*) = ln*1 + g), п = 4.
COS X
I
/ arctg х
I !-
,1^0,
1239) f{x) = < arctg х r п = Ь.
* = 0,
1240) /(*) = thx, n = 3.
1241) f(x) = -i—, n = 4.
cos X
1242) /(*) = —V, n = 4.
lnbh
1243) /(*) = , а0фО, n = 4.
E «n*n
n=0
Проверить равенство.
^(-l)"2nxn ^,7"*" ,,
) E -^r: E —^— = E 1*1 <
n=0 n=0 n=0
257
1245) ]Г(п+1)(п + 2)(п + 3)х" : ^ xn =
11 = 0 n=0
оо
= 6+3^(n+l)(n+2)zn, |х|<1.
n = 1
n =0
n = l
1247) |l +5 £(" + »)("+ 2)*-
11 = 1
■} £>-=
) n = 0
= + i)*n, kl < l.
n=0
Используя метод обращения ряда, найти п первых нену¬
левых членов разложения в степенной ряд с центром в точке
х0 = </(0) функции /(я), обратной к функции #(х).
1248) ^(х) = е* - 1, п = 3 (/(х) = ln(l + х)).
1249) <7(х) = sinx, п = 3 (/(х) = arcsinx).
1250) д(х) = х -f sin х, п = 3.
1251) <z(x) = х — е“х, п — 4.
1252) д(х) = 2х - ^1 +х2, п = 3.
1253) <z(x) = х - ln(l -f х2), п — 4.
Используя метод подстановки ряда в ряд, найти п первых
ненулевых членов разложения функции f(g(x)) в степенной
ряд с центром в точке хо = 0, если известны разложения в
степенные ряды функций /(х) и д(х).
1254)
/(*)
= sin(sin х), п — 3.
1255)
/(*)
= 1п(1 + ег), п — 4.
1256)
/(*)
= — In cos х, n = 3.
1257)
fH
= ln(l 4-sinx), n = 3
1258)
/(*)
= \/l + sinx, n = 4.
1259)
/(*)
= 2co,Jr, n- 4.
1260)
я*)
= In tg(x + jt/4), n =
258
1261) /(г) = \/Г+4*ТТ2*2, п = 4.
1262) /(х) = 1п(х2 - х + 1), п = 4.
Получив соотношение между у и у', последовательным
дифференцированием установить соотношение между функ¬
цией у и ее производными до порядка fc. Исходя из полу¬
ченных равенств, написать п отличных от нуля членов раз¬
ложения в степенной ряд с центром в точке х0 = О функ-
ции у
= /(
*)
1263)
/(*)
er5inr, п = 4.
1264)
/(*)
ecosх, п =4.
1265)
/(*)
е1*х, п = 6.
1266)
/(*)
-
earctgI, п = 5.
1267)
/(*)
=
esinr, Ti — 8.
1268)
/(*)
=
(1 + х)т, 71 = 5
1269)
/(*)
=
е со«* , 71 = 4.
1270)
/(*)
=
^arcs.n г ^ п = 4
1271)
/(*)
=
tgX, 71 = 3.
1272)
/(*)
—-—, п — Ь.
COS X
Составив дифференциальное уравнение, которому удовле¬
творяет функция /(х), доказать справедливость равенства.
|етз)Щ1±£)=,-+ _!_W +
' (1 +х)" ’ \п п+ \) 2!
+ „(,, + 1И„+2|.(1 + _1т + _±_)|! + ....
/ х^ 2 х^
1274) у 1 - I2 arcsin х = х
' 3 3 5
— — _
ЗЙГТ
2 х5 2-4 х7
1275) \Л + x2ln(x + \/l + х2) = г+у-з У + ^-7
“"’Ж’-Ч^От+О^От--
■) -5"(1 + 0j+(I + 5 + 0t-'
259
ГЛ8) ^ arctg xln(l + т2) -
I \ х3 ( 1 I 1 \ г5
1 + 2) (1 + 2 + 3 + 4Jy +
. гп2 2 m2(m2 — 4) л
1279) cos (га arcsin х) = 1 2Г 4! Х ^
m2(m2 - 4)(m2 - 16) 6
+ _1 л _2,•+....
1280) sin(m arcsin х) =
m(m2 — 1) ^ m(m2 — l)(m2 — 9) ъ
= mx зГ х' + 5| *' -
1281) cos(m arccos х) =
7ГШ ( тп1 9 77/2 (т2 - 4) л \
= —-2- (' - IT' + —iHL* - ) +
7Г//1 ( m{m2 - 1)
+ sin — I mx —- -x*5 +
Разложив функции у - sin(m arcsin x) и у = cos(rn arcsin x)
в ряды no степеням буквы m, получить разложение в ряд но
степеням х функции
1282) }(х) = arcsin х.
1283) /(х) = arcsin2 х.
1284) f(x) = arcsin3х.
1285) f(x) = arcsin4 x.
Доказать справедливость разложения.
,286) = г - (l + I) x2 f (, + I + i) x3 -
1 1 1
1 + 2 + 3 + iK+ W<L
1287) — ln(l + x)ln(l - x) = x2 + ^1 - ~ + 0 у +
/, I I I l\i6 , , ,
+ {l~2 + i~^b) T+ "' |X|<L
260
1290) In 1 + ^ * =
1 x 1-3 x2 13 5 x3
~ ~2 2 ~~ 24 T ~ 2Тб У
1*1 < 1
1291)
1 x *1 3 x2 13 5 x3 , , ,
— • — -|- — — -!-•••, x I 1 .
2 2 2-4 4 2-4-6 6 11
л /"2(1 ~ n/1 ~ x) \ m x m . 0ч/х\2
,292) (-±_* [j =l + T4 + 2!{m + 344) +
-f
»i(m +_4|(mjf5) (I)3 + ^| < (
Написать n ненулевых членов разложения в степенной ряд
с центром в точке хо = 0 функции у = f(x), являющейся
аналитической ветвью кривой F(x,y) = 0.
1293) F(x, у) = у3 + ху - 8 — х2. п = 3.
1294) F(x, у) = 2у - sm у - х, п - 2.
1295) F(x, у) = у7 - ау - х, у(0) = 0, а ф 0, п - 4
1296) F(x, у) = у - a + ху5, а ^ 0, п = 5.
1297) F(x, у) = у4 - 4у - х, п = 2.
1298) F(x, у) = х’5 - Зху +у3, п - 2.
1299) F(x, у) = 4(х — 1)у5 + 2ху3 — Зх3у + х4, п — 2.
оо
1300) Пусть /(х) = ^ апхп Написать разложение функции
п = 0
с/ \ Я*) - п
F(x) = в степенной ряд с центром в точке хо = 0.
1 — х
1301) Доказать справедливость разложения
1 _
1 — х — х2 — X3
= 1 4- X + 2х2 + 4х3 + 7г4 + 13х5 + 24х6 + • + апхп + ■■■,
где а„ = а„_1 + а„_2 + а„_3, я ^ 4, |г| < <5, S > 0.
1302) Доказать справедливость разложения
п=0
где коэффициенты ап есть последовательные числа Фибонач¬
чи 1, 1, 2, 3, 5, 8, 13,. . каждое из которых равно сумме двух
предыдущих
1303) Разложив в ряд по степеням х обе части тождества
1
1 - X — X2
1
1
v/5-И
+
1
+ X
/5-1
2
найти формулу, выражающую числа Фибоначчи ап.
1304) Доказать, что если справедливо равенство
1 +р,* + р2Г2 + р3Х3 + - = • - г,
1 + Ьх + ахг
то справедливо также и равенство
1 + ах
1 -j- Р\Х Р2Х 4 Рз^ 4 • • • —
(1 — ах)[(1 4- ах)2 — 62х]
Пользуясь разложением функции /(х) в степенной ряд,
найти значение производной /^(хо) указанного порядка п.
1305) /(*) = е“£, /(1О)(0).
1306) f{x) = /<6>(0).
1307) /(х) = х6 arctg х, /(18^(0).
1308) f(x) = х2 >УГТ?, /(5)(0).
1309) /(х) = cosx chx, /<7>(0).
262
1311) /(*) = x3ln(l-x + x2-x3), /(8,(0).
1312) /(*) = x5cos|, /(,1)(0).
1313) /(*) = - 2 ■ ‘ - a)/(38>(-l); 6)/<1,,0,>(-l).
xz + Ix -f о
1314) /(x) = (x -2)2ln(3x + 2), /(7)(2).
1315) f(x) = х2е2г, /(20)(1).
1316) /(*) = *+L, /(10°)(0).
V 1 — x
,3i7) '<*>=
1318) /(*) = In (ab ф 0), /<">(0).
a — bx
Разложить функцию у = f(x) в обобщенный степенной
ряд относительно функции д(х) и указать множество сходи¬
мости полученного ряда.
1319) f(x) = ——, д(х) =
I — X X
1320) f(x) = lnx, ^(х) = Г
х 4- 1
1322) /(i) = х, ,(j,)=Tif-j.
1 4- xz
1323) f(x) - —g{x) = cos
cos- x 2
1324) /(x) = x, <j(x) = sinx.
1325)/(x) = x, g(x) = ctgx.
1326) f(x) = —, g(x) = cos2x.
Z COS X
1327) f(x) — arccos(l — x), g(x) = y/x.
263
С)
13*29) f(r) = arcsin ^ ^ ^, g(x) = y/x.
1329) f(x) = arcsin
Выделив главную часть вида сх", с ф 0, функции у(х)
при т. —> О, наити л ненулевых членов разложения :>той функ¬
ции в ряд по степеням х°.
1330) х ~ у — 1 +<~у, п = Л.
1331) х — у -- 1п(1 4- у), п ~ 4.
1332) х = у - sin у, п — 3.
1333)- х = tgy - у, п = 3.
у2
1334) х = —— 14 ros y, п = 3.
Проверить равенство.
^ • 9
Г sin ь
1335) / — А = С + In |*| +
1
X
0 < |х| < 1.
0 < |х| < 1.
0 < х < 1, 1 < х < оо.
1340)
X
/
dt ... . In x In2 x
— = 1ц|1ц,|+—+ —+
ln"x
+ j- +
nn!
5. Двойные ряды
Для данной матрицы рассмотреть соответствующие по¬
вторные ряды и двойной ряд и выяснить их сходимость.
1
2 3
1341)
/JL JL
f 12 2 3
0
о о
0 0
\
1342)
1
1
1
34
4 5
5 6
1
1
1
34
4 5
5 6
1
1
1
3 4
4 5
5 6
0
1
4 5
1
5 6
-х3
х2
2(1^г2)
х2
((1-<г2)
(1-<г2)3
гх2
(1-х2):
'(I-*2)2
'х2
0-*3Г
-г3(1 -чс3)3 г3(1-*3)3 •
\
О < X < 1.
1343)
( 1
-1
1
-1
-1
1
-1
1
1
1
1
1
3
3
3
3
1
1
1
1
3
3
3
3
1
1
1
1
4
4
4
4
1
1
1
1
4
4
4
4
265
Исследовать сходимость следующего ряда, используя в
случае необходимости результаты задач 105, 107, 108, 113
стр. 336, 337.
1344) Ё -4-S> ^ > 0, /? > 0.
' тапР
т,п = 1
°о
1345) ————, а > 0.
(ш + п)<*’
m,n = 1 4
°о J
1346) Е (Ат2 + 2Втп + Сп2)“ ’ “ > °’
m,n = ! v 1
АС - В2 > 0, А > 0, С > 0.
/ 1 \™+п
1347) V 7 Г“. а>0*
; ^ т| п)а
т,п = 1
-2L /_пт+"
1348) V ( /т п.
1349) V
’ та + п&
m,n = 1
,350) V ■”*? + ">.
тп2 + 5т
т,п = 1
,351) у tlT~.
' та +п0
т,п — 1
>«> Ё
(пт)!
т, п—2
Inm^lnn
1353) V 77-7 ■
(1п(ш + п))т+п
m,n = l v
1354) J] cos тх sin пу
m,n = 1 l+^2nJ
266
Найти сумму ряда.
1355> Е i-
л тгг
т,п = 2
т,п=2
оо
1357) V
„.■Ь., <2">
1358) £ (4п - 1)2т+1'
m,n = 1 4
,3591 £ (3^2F
m,n = l v 7
т,п = 1 4 7
также гм. пример Г) на стр. 8. 22) Указание. Ис-
' 1 - W
ОТВЕТЫ К ГЛАВЕ I
3 2 I
1) 2) 3) Расходится. 4) Расходится. 5) —.
2 1] 1 — In 2
6) Расходится 7) И. 8) ~ 9) 1. 10) g. II) _J_.
12) 1. 13) 1. 14) ^ 15) 1 - \/2. 16) Расходится. 17) - In2.
18) 1пЗ. 19) In 3/2. Указание. Sn = -In--- ^ас“
ходится. 21) -—-—— Указание. Рассмотреть Sn - Sn q, а
(1 - <7)
•ни (/(1 + Я)
<1):]
пользовать результат и метод решения задачи 21. 23) 7г/4.
Указание. Воспользоваться соотношением
с г с
arrtg „ arct,g - arrtg .
а + п—1 а-\-п с-+ (а + ида + п—1)
71 3 7Г 7Г
Sn = arctg . 24) —. Гм указание к задаче 23. 25)
п -+ 1 1 4
26) 1. Указание. Проверить, что .S'Tl = I . 27) —Т)
(71 + 2)! sin j*
I I / 1 х 2
Указание. Проверить, что Sn - ——- - -—:——
«г sin" х \2nsin^r
28) —3/2 29) ctgj*. Указание Рассмотреть функцию
х
П г х х sinx
(-Г) = cos - cos — • • ■ COS
2 22 2n 2n sin ~
и найти Y[ (x)' Доказать. что частичная сумма данного ря-
П (х) 1 X X
да равна-=^—, т е. равна — ct.g —-ctgx. 30) . Ука-
Цп(х) 2п 2п 1 - х
х 2п х2" о ч х
зание. Проверить, что .Ъп = — . 31) при
1-х 1 — х2 1-х
|х| < 1 и S = при |х| > 1. Указание. Прологарифми-
х — 1
268
n
ровать и продифференцировать равенство ^1 4- х2 ^ =
к = 1
1-Х2" ,1 1
= . Проверить, что STl ^ 32) Расхо-
1 — х ] — х \ —х£
дится. 33) Указание. Sn = 1 Н -= 4 • • 4 —7= ^ —т= = у/п.
у/2 у/п у/п
34) Указание. . 35) Ука-
у/гГ+1 >ДТ2 у/п7 4- Зп 4- 2 2п
1 111
зание. ■ -- > 7= •—= .
\/3п 4- 1 4- V^3n — 1 2\/Зп 4- 1 2\/3 >/w 4- 1
36) Указание, arcsin —у= ^ —-=. 45) Указание. In п! = 0(п In п),
Vn vn
n —> 00.
(n 4- 1) In n! — 2 ln(2!*3!... n!) 1
lim 5 =
n-H-oo 71 4* n 2
47) Указание. Предположив, что cos n2 -4 0 при n —У 4-oo
придти к противоречию, рассматривая разность cosn2 —
— cos(n4-l)2 и используя то, что последовательности cos(n+ I)
и sin(2n 4- 1) не являются бесконечно малыми при п —► 4-оо.
48) Расходится. 49) Сходится. 50) Сходится. 51) Сходится.
52) Расходится. 53) Сходится. 54) Расходится. 55) Сходится.
56) Расходится. 57) Сходится. 58) Расходится. 59) Сходится.
60) Сходится. 61) Сходится. 62) Расходится. 63) Расходится.
64) Сходится. 65) Расходится. 66) Сходится. 67) Сходится
при а ф 0, расходится при а = 0. 68) Сходится при а > 1,
расходится при 0 < а ^ 1. 69) Сходится при b > 0 и s > 1, рас¬
ходится при 6 > 0, 0<$^1и6=0, s любом. 70) Сходится.
71) Расходится. 72) Сходится. 73) Расходится. 74) Расхо¬
дится. 75) Расходится. Указание. — rr—t— = -77-:—>
7 (1пп),п,пп e(in in п)2
> -г— = 76) Сходится. Указание. Тл—~— = —г-^.— <
е\пп п / « (1пп),пп П1п1пп
< 1. 77) Сходите. Указание. (|п ^^
78) Сходится при а > 0. Расходится при а ^ 0. 79) Расходит¬
ся при 6 = 0, сходится при 6 ф 0. 80) Сходится. 81) Сходится
при а > 0, расходится при а ^ 0. 82) Сходится. 83) Сходится
269
при а > 2, расходится при а 2. 84) Сходится при р < 12,
расходится при р ^ 12. 85) Расходится при любых а. 86) Рас¬
ходится. 87) Сходится. 88) Сходится при р > -, расходится
при 0 < р ^ 89) Сходится. 90) Расходится. 91) Сходится.
92) Сходится при а > 1, расходится при а ^ 1. 93) Сходится.
94) Сходится. 95) Сходится. 96) Сходится. 97) Расходится.
98) Расходится. 99) Расходится. 100) Сходится. Ю1) Рас¬
ходится. 102) Расходится. 103) Сходится. 104) Расходится.
105) Сходится при q > 1, расходится при а ^ 1. 106) Сходит¬
ся при а + 0 > 1, расходится при a -f 0 ^ 1. 107) Сходится.
108) Сходится. 109) Расходится. 110) Сходится. 111) Схо¬
дится. 112) Сходится. 113) Сходится при а > 1, расходится
при а ^ 1. 114) Сходится. 115) Сходится. 116) Сходит¬
ся при а > 1/2, расходится при а ^ 1/2. 117) Сходится.
118) Сходится. 119) Сходится. 120) Сходится. 121) Сходится.
122) Сходится. 123) Сходится. 124) Расходится. 125) Сходит¬
ся. 126) Сходится. 127) Сходится. 128) Сходится. 129) Рас¬
ходится. 130) Сходится. 131) Расходится. 132) Сходится при
р > 1/2, расходится при р ^ 1/2. 133) Сходится. 134) Схо¬
дится. 135) Сходится. 136) Сходится при любом а > 0.
137) Сходится при р > расходится при р ^ -. 138) Сходит-
ся. 139) Сходится при а > 1, расходится при а ^ 1. 140) Рас¬
ходится. 141) Сходится. 142) Сходится. 143) Расходится.
144) Расходится. 145) Расходится. 146) Сходится. 147) Схо¬
дится. 148) Сходится. 149) Сходится. 150) Сходится при
а > 1 и при Of — 1, 0 > 1, расходится при а ^ 1 и при а - 1,
0^1. 151) Сходится при а > 1, при а = 1, р > 1, при а = 1,
р = 1, q > 1; расходится при а < 1, при а = 1, р < 1, при
а = 1, р = 1, q < 1. 152) Сходится при q — р > 1, расходится
при q -р ^ 1. 153) Сходится. 154) Сходится. 155) Сходится.
156) Сходится. 157) Сходится. 158) Сходится. 159) Сходит-
3
ся. 160) Сходится. 161) Сходится при р> - расходится при
3 2
р ^ 162) Расходится. 163) Сходится при р > 1, расходится
при р ^ 1. Указание. ап(р) — монотонная функция, и для
270
р > 1 ^ “г™—, п ^ No{p,e), где 6n = nlnp £ я при лю-
бом е > 0 (см. также задачу 22 стр. 316). 164) Сходится при
а > расходится при а ^ -. 165) Сходится. 166) Расхо-
о о
дится. 167) Сходится. 168) Расходится. 169) Расходится при
любом а ф 1. 170) Сходится при а ф тгк, к € Z. Расходится
sin 2п+1а
при а = 7гЛг, к 6 Z. Указание. ansina = — . 171) Рас¬
ходится. 172) Расходится. 173) Сходится. 174) Расходится.
175) Сходится. 176) Сходится. 177) Сходится. 178) Схо¬
дится. 179) Расходится. 180) Расходится. 181) Сходится.
3
182) Расходится. 183) Сходится при р > расходится при
3
2' 184) Сходится при а —р > 1, расходится при а — р ^ 1.
185) Сходится. 186) Расходится. 187) Сходится. 188) Рас¬
ходится. 189) Сходится при а < 1, расходится при a ^ 1.
190) Сходится при а > 0, р любом, расходится при a = 0,
р ^ 1 и при a < 0, р любом. 191) Расходится. 192) Схо¬
дится. 193) Сходится. 194) Расходится. 195) Сходится при
р( 1 — а) < 1, расходится при р(1 — a) ^ 1. 196) Сходится при
a — (3 — а(3 > 0, расходится при а — (3 - а/3 ^ 0. 197) Сходится
при 7 — а — /? > 0, расходится при 7 —a —/? <С 0. 198) Сходится
при всех а ^ 0. 199) Расходится. 200) Сходится. 201) Схо¬
дится. 202) Расходится. 203) Сходится. 204) Сходится при
а > 1, расходится при а $ 1. 205) Расходится. 206) Расхо¬
дится. 207) Расходится при а ф 1. 208) Сходится. 209) Рас¬
ходится. 210) Сходится при р > расходится при р ^ -.
4 4
211) Сходится при а > 2, расходится при а $ 2. 212) Сходит¬
ся при a < —1/2, расходится при а ^ —1/2. 213) Расходится.
214) Расходится. 215) Сходится при любом а > 0. 216) Схо¬
дится при а < 2, расходится при а ^ 2. 217) Расходится.
218) Сходится. 219) Сходится. 220) Расходится. 221) Расхо¬
дится. 222) Расходится. 223) Расходится. 224) Сходится при
(3 — За > 3, расходится при /3 — За ^ 3. 225) Сходится при
а < 2, расходится при а ^ 2. 226) Сходится при (3 — a + 1 > 0,
расходится при /? — a+ 1 ^ 0. 227) Сходится при а = 1, Р > 2,
271
расходится при а ф 1 и любом р и при а = 1, р ^ 2. 228) Схо¬
дится. Указание. V2 = 2cos7r/4. 229) Сходится при любых
а > 0. 230) Сходится при р > -, расходится при р ^ 1/2.
231) Сходится при р > -, расходится при р 232) Рас-
и О
ходится. 233) Сходится при х = 0 и любом р и при х ф 0
и р < —. 234) Расходится. 235) Сходится. 236) Расходит-
3 к
ся при любых а > 0 и 6 > 0. 237) Сходится при а > 1/2,
расходится при a 1/2. 238) Расходится. 239) Сходится.
240) Сходится. 241) Расходится. 242) Расходится. 243) Схо¬
дится при р > 3/4, расходится при р 3/4. 244) Сходится
при а < 2, расходится при a 2. 245) Сходится при а. < 1 /2,
расходится при а ^ 1/2. 246) Расходится. 247) Сходится.
248) Сходится при q > 1, расходится при q ^ 249) Сходит¬
ся. 250) Сходится при а > 6, расходится при а ^ 6. 251) Схо¬
дится при р— к > 1, расходится при р - к <. 1. 252) Сходится
при к < —1, расходится при к ^ -1. 253) Сходится при
р — к > 1, расходится при р — к <С 1. 254) Сходится при р > 2,
расходится при 0 < р 2. 255) Если а ф сц, то сходится
при а < 0 и расходится при а ^ 0, если а = аь 6 ^ 6i, то
сходится при а < 1 и расходится при а ^ 1, если а = сц,
6 = 6], то сходится при любом а. 256) Сходится при а — 2,
расходится при а ^ 2. 257) Сходится при а = —, расходится
7Г
при а ^ . 258) Расходится. 259) Расходится. 260) Сходится
7Г
при а < 1, расходится при а ^ I. 261) Сходится йри а > 2/3,
расходится при а ^ 2/3. 262) Расходится. 263) Расходит¬
ся. 264) Сходится. 265) Сходится при а > 1, расходится
при о? 1. 266) Сходится. 267) Сходится при а < — 1, рас¬
ходится при а ^ — 1. 268) Расходится. 269) Сходится при
а < I, расходится при а ^ 1. 270) Сходится. 271) Сходит-
пп\
ся. Указание. 0 < ап ^ . 272) Сходится при а > 1,
(2п).
расходится при а ^ 1. 273) Сходится при а < — 1, расходит¬
ся при а ^ —1. 274) Сходится при or < —2, расходится при
а ^ — 2. 275) Расходится при любом а ф 0. 276) Сходится.
272
277) Сходится при а > 1, расходится при а <С 1. 278) Схо¬
дится при а > расходится при а ^ 279) Сходится при
1
а < 2, расходится при а ^ 2. 280) Сходится при а > рас-
О
1 3
ходится при а <С - 281) Сходится при а > -, расходится
о *
3
при а -. 282) Сходится при а < 2, расходится при а ^ 2.
283) Сходится при а > расходится при а ^ - 284) Схо¬
дится при а > расходится при а $ 285) Сходится при
а > ^, расходится при а ^ 286) Сходится при а > 1,
3
расходится при а ^ 1. 287) Сходится при а > — расхо-
3
дится при а ^ — -. 288) Сходится при а > 1/2, расходится
при (х ^ 1/2. 289) Сходится при 2/? + а > 1, расходится при
2(3 + а ^ 1 290) Сходится при 4а - /? > -2, расходится при
5
4а-/? ^ -2. 291) Расходится. 292) Сходится при а > рас-
8
5 1
ходится при а ^ 293) Сходится при а > расходится при
8 2
а ^ 294) Сходится при а > 1/4, расходится при а ^ 1/4.
295) Расходится. Указание. Найти предел ап при п —у +оо.
296) Сходится при а < — -, расходится при а ^ . 297) Схо¬
дится при а < 1, расходится при а ^ I. 298) Сходится при
а > -, расходится при а <С - 299) Сходится при а < — 1,
6 6
расходится при а ^ — 1. 300) Сходится при а > 5, расхо¬
дится при а ^ 5. 301) Сходится при а > расходится при
ос ^ 302) Сходится при <*>—-, расходится при а ^
Z Z Z
303) Сходится при а < — 1, расходится при а ^ — 1. 304) Схо¬
дится при а < 1, расходится при а ^ 1. 305) Сходится при
min(a,/?) > расходится при min(a,/?) ^ 306) Сходится
273
при а + (3 > расходится при а + /? $ -. 307) Сходится.
308) Расходится. 309) Сходится. 310) Расходится. Указание.
Сравнить ап и 311) Расходится. Указание. Срав¬
ни + 1)
нить ап и -— -. 312) Сводится при q > 1, расходится при
7Г(71 + 1)
0 < q ^ 1. 313) Сходится. 314) Сходится. 315) Сходится
при а > 1, расходится при 0 < а <С 1. Указание. Последова-
n ^ j
тельность -— Inn имеет конечный предел константу
' к
к = \
Эйлера. 316) Сходится. Указание. Для оценки интеграла
п+1
dx применить формулу интегрирования по частям.
х
J
317) Сходится. Указание. Применить формулу интегриро-
a+J
[ 2usinir „
вания по частям к интегралу / аи. 318) Сходится.
J 2 и
а
Указание. Применить формулу интегрирования по частям к
а+6
/3t* sin tz
—^—du. 319) Сходится. 320) Расходит-
о
ся. 321) Сходится. 322) Сходится. 323) Сходится. Указание.
п
к\ ^ (п + 1)! 342) Сходится при а > I, расходится при
к = 1
0 < а 1. 343) Сходится. 344) Сходится при 0 < л < 1,
расходится при а ^ 1. 345) Сходится при а > е, расходится
при а < е. См. указание к задаче N 315. 346) а) Сходится при
а > 2, расходится при 0 < а <С 2. См. указание к задаче N 45.
б) Сходится при а > 1, расходится при 0 < а ^ 1. См. ука¬
зание к задаче N 315. 347) Сходится при |а| <С 1, расходится
при |а| > 1. 348) Сходится. Указание. Применить признак
Даламбера. 349) Сходится. Указание. Применить признак
Гаусса. 350) Сходится. Указание. Методом математической
1 2
индукции доказать, что справедлива оценка — < ап < —г-.
пг п1
274
351) Сходится. Указание. Доказать методом математиче-
1 2
ской индукции справедливость неравенства 0 ^ — < п .
ап
352) Сходится. Указание. Доказать методом математиче-
1 2
ской индукции справедливость неравенства 0 ^ — < п .
ап
353) Сходится. Указание. Найти такие постоянные Сид,
что ап = Cqn. 354) Расходится. Указание. Показать, что
условия: Sn ограничена и ап —> 0 не могут выполняться од-
2
новременно. 355) Указание. Представить члены ряда ап
(-1)"п (-1)"
в виде ап — Ь ——— и воспользоваться методом ре¬
шения примера 5 на стр. 8. 356) —. Указание. Предста-
j j n ^ j
вить 5з„ в виде S3n = ^ 357) In2. Указание.
*=о к=0
j | I
Представить 52п в виде ,V2n = £ - - El' ^58) - ln2.
*=i fc=i
Указание. Представить 6з„ в виде 5зп = — —
Ас — 1 Ае = 1
1 ХП ^ 1 1
- - ^ 359) 2 Указание. Представить Ssn в виде
к- 1
бп 1 ] 3n 1 1 2П 1 1
Se„ = 360) 1 + - 1п2. Указание.
Ас — 1 Ac=I *=]
2n j j n 1 4n+4 j
Представить 53„ в виде 53n = I ~ Е £ + 2 53 I + Е I ~
Ас = 1 /с — 1 Ас = 1
1 1 3
- - г 361) -In2. Указание. Представить 53п в виде
2 fc=i * 2
4n j 1 2n 1 1 " ]
5зп= El~ 2E1-9E1 362) °- Указание- Предста-
*=1 к=1 *=1
| | n ^ j | j
вить S5n в виде 55п= Сходится
Ас = 1 Ае = 1 Ае = 1
275
условно для всех а ф 0. Указание. Представить выраже¬
ние sin 7Г\/п2 + а в виде (- l)n sin(7r\/п2 + а - тгп). 376) Схо¬
дится условно. 377) Расходится. 378) Сходится абсолютно.
379) Сходится условно. 380) Сходится условно. 381) Расхо¬
дится. 382) Сходится условно. 383) При р > 2 сходится абсо¬
лютно, при 0 < р ^ 2 сходится условно, при р ^ 0 расходится.
384) Расходится. 385) Сходится абсолютно. 386) Сходится
абсолютно. 387) Сходится абсолютно при \а\ > 1, сходится
условно при |а| = 1, расходится при |а| < 1. 388) Сходится
условно. 389) Сходится абсолютно. 390) Сходится условно.
391) Сходится условно. 392) Сходится абсолютно. 393) Схо¬
дится абсолютно. 394) Сходится условно. 395) Сходится аб¬
солютно. 396) Сходится условно. 397) Сходится абсолютно.
398) Сходится условно. 399) Сходится абсолютно. 400) Схо¬
дится условно. 401) При а > 1 сходится абсолютно, при
а = 1, 0 > 1 сходится абсолютно, при а = 1, (5 ^ 1 схо¬
дится условно, при 0 < а < 1 сходится условно, при а — 0,
/3 > 0 сходится условно, при а = 0, 0 ^ 0 расходится, при
о < 0 расходится. 402) При р > 1 и любом q сходится аб¬
солютно, при р — 1, q > 1 сходится абсолютно, при р — 1,
q ^ I сходится условно, при 0 < р < 1 и любом q сходится
условно, при р ^ 0 и любом q расходится. 403) Сходится абсо¬
лютно. 404) Сходится абсолютно. 405) Сходится абсолютно.
406) Сходится абсолютно. 407) Расходится. 408) Сходится
абсолютно. 409) Сходится абсолютно при р > 1, сходится
условно при р ^ 1. 410) Сходится абсолютно. 411) Сходит¬
ся абсолютно. 412) Расходится. 413) Сходится абсолютно.
414) Сходится абсолютно при а > 1, сходится условно при
а ^ 1. 415) Сходится условно. 416) Сходится абсолютно.
417) Расходится. 418) Сходится условно. 419) Сходится абсо¬
лютно. 420) Сходится абсолютно при q > 0, сходится условно
при -1 <<7^0, расходится при <7 <1 -1 421) Сходится услов¬
но. 422) Расходится. 423) Сходится условно. 424) Сходится
абсолютно. 425) Сходится абсолютно. 426) Сходится условно.
427) Сходится условно 428) Сходится условно. 429) Сходит¬
ся условно. Указание. Сравнить с примером 45 на стр. 47-50
430) Расходится. Указание. Рассмотреть а^+к- 431) При
276
Q > 1 сходится абсолютно, при 0 < (* ^ 1 сходится условно,
при а $ 0 расходится. 432) Сходится условно. 433) Сходит¬
ся условно. 434) Сходится условно. 435) Сходится условно.
436) Сходится абсолютно. 437) Расходится. 438) При q > 1
сходится абсолютно, при 0 < q ^ 1 сходится условно, при
q <С 0 расходится. 439) Расходится. 440) Сходится услов¬
но. 441) Сходится условно. 442) Расходится. 443) Сходится
условно. 444) Сходится условно. 445) Сходится абсолютно
1 Л 1
при а > -, сходится условно при 0 < о ^ расходится при
а <С 0. 446) Сходится абсолютно при q > 1, сходится условно
при q ^ 1. 447) При а > I сходится абсолютно, при а ^ 1
сходится условно. 448) При а > 1 сходится абсолютно, при
а ^ 1 сходится условно. 449) При а > 1 сходится абсолютно,
при 0 < а ^ 1 сходится условно. 450) При а > 1 сходится
абсолютно, при 0 < а ^ 1 сходится условно. 451) Расходится.
452) Сходится условно. 453) При q > 2 сходится абсолютно,
при q ^2 сходится условно. 454) При 0 > 1 и любом а и при
Р = 1 и а < — 1 сходится абсолютно, при (3 = 1 и а ^ — 1
сходится условно, при 0 < Р < 1 и любом а сходится услов¬
но, при /? = 0, а < 0 сходится условно, при /9 > 0 и а ^ 0
расходится, при (3 < 0 и любом а расходится. 455) Сходится
условно. 456) Сходится абсолютно. 457) Сходится абсолют¬
но при р > 1, сходится условно при 0 < р ^ 1, расходится
при р ^ 0. 458) Сходится условно. 459) Сходится условно.
460) Сходится условно. 461) Сходится условно. 462) Сходится
абсолютно. 463) Сходится абсолютно. 464) Сходится условно.
465) Сходится условно. 466) Сходится абсолютно при а > 1,
сходится условно при - < а I, расходится при 0 < а ^
1 1 sin п „
Указание. —— :— = - —— г—г. 467) При
3 па + sin п 3 па 3na(3na + sin п)
q > 2 сходится абсолютно, при 0 < q <С 2 сходится услов¬
но. 468) Расходится. 469) Сходится условно. 470) Сходит¬
ся условно. 471) Сходится условно. 472) Сходится условно.
473) Сходится условно. 474) Сходится условно. 475) Сходит¬
ся абсолютно при q > 1, сходится условно при ^ < q ^ I, рас-
277
ходится при 0 < q ^ 476) Сходится абсолютно при q > 1,
сходится условно при ^ < g ^ 1, расходится при 0 < q ^
477) Сходится абсолютно при р > 1, сходится условно при
О < р ^ 1, расходится при р 0. 478) Сходится абсолютно
при р > сходится условно при max (- — 1,0) < р ^
Я \Я ) Я
расходится при р ^ max ( 1,0^. 479) Сходится услов¬
но. 480) Сходится абсолютно при а > 1, сходится условно
при а ^ 1, 481) Сходится абсолютно при р > 1, сходится
условно при 1/2</><1.482) Сходится условно. 483) Сходится
условно. 484) Сходится условно. 485) Сходится абсолютно.
486) Сходится абсолютно при q > 1, сходится условно при
2 2
расходится при q ^ 487) Сходится абсолютно
3 3
при а > 1, сходится условно при 0 < а ^ 1, расходится при
а < 0. 488) Сходится абсолютно при а > 1, сходится условно
при 0 < а <С 1, расходится при а $ 0. 489) Сходится абсо¬
лютно. 490) Сходится абсолютно при q > —, сходится услов-
1
но при q ^ - .49!) Сходится абсолютно при q > 2, сходится
2 2
условно при - < q ^ 2, расходится при g ^ 492) Сходится
о
условно. 493) Сходится абсолютно при всех q > 0. 494) Схо¬
дится условно. 495) Сходится абсолютно при а > 1, сходится
условно при 0 < а ^ 1, расходится при а $ 0. 496^ Схо¬
дится абсолютно. 497) Сходится абсолютно при р > схо-
1 2
дится условно при 0</><-. 498) Расходится. 499) Сходит-
, 2тгАг 2тг
ся условно при а ^ , к 6 расходится при а = ,
3 3
к Е Z. 500) Сходится абсолютно. 501) Сходится абсолютно.
502) Сходится условно. 503) Сходится условно при любом к.
п n + i 1
504) Сходится условно Указание. cos к = :
28*П2
505) Сходится условно. Указание. Показать, что последова-
278
но. См. указание к задаче N 505. 507) Сходится абсолютно
при Р > а+1, сходится условно при а < /3 ^ а+1, расходится
при р ^ а. 508) Сходится. 509) Расходится. 510) Расходится.
511) Расходится. 512) Сходится абсолютно. 513) Расходится.
514) Расходится. 515) Расходится. 516) Сходится абсолютно.
517) Расходится. 518) Сходится условно. 519) Сходится абсо¬
лютно при р > 1, расходится при р < 1. 520) Сходится абсо¬
лютно при р > 1, сходится условно при р = 1, расходится при
р < 1. 521) Сходится абсолютно при р > 1, q > 1, сходится
условно при 0 < р = q ^ 1, при остальных значениях параме¬
тров расходится. 522) Сходится абсолютно при р > 1, q > 1,
сходится условно при 0 < р = q 1, при остальных значениях
параметров расходится. 523) Сходится абсолютно. 524) Схо¬
дится условно. 525) Сходится абсолютно. 526) Сходится
условно при а ф 2тгк + тг, к £ Z, расходится при а = 2жк + тг,
к G Z. 527) Сходится абсолютно. 528 а) Сходится условно при
а > 0. 528 б) Сходится абсолютно при а > 1, сходится услов¬
но при а ^ 1. 529 а) Сходится условно при а ф 0. 529 б) Схо¬
дится условно при а ф 0, сходится абсолютно при а = 0.
Указание. Сравнить с примером 45 на стр. 47-50 (см. также
задачу 42 на стр. 321). 530) Сходится условно. 531) Схо¬
дится абсолютно. 532) Расходится. 533) Сходится условно.
534) Сходится абсолютно. 535) Расходится. 536) Сходится
абсолютно при q > 1, сходится условно при 0 < q ^ 1, расхо¬
дится при q ^ 0. 537) Сходится абсолютно при q ^ 0, сходит¬
ся условно при —1 < q < 0, расходится при q ^ — 1. Указание.
Применить формулу интегрирования по частям к интегралу
о
тонно стремится к нулю при п —> оо и проверить справедли-
/
—— dx и использовать результат задачи 536. 538) Схо¬
дится условно. Указание. Показать, что
j(1 — х2)п dx
моно-
279
вость оценок J~ х2)П ^ ~ ~ ^2^ ^ Ъ>п' П ^
0
539) Сходится условно Указание Проверить справедливость
зш п
п
/sin х , sin п . / 1 \
—— dx hО I I, п -+ +оо. 540) Сходит-
о
ся абсолютно. 541) Сходится условно. 542) Сходится услов¬
но. 543) Расходится. 544) Сходится условно. 545) Сходит¬
ся абсолютно. 546) Сходится абсолютно. 547) Расходит¬
ся. 548) Сходится абсолютно. 549) (’ходится абсолютно.
550) Сходится абсолютно. 551) Сходится условно. 552) Схо¬
дится условно. 553) Расходится к нулю. 554) -. 555) 2.
556) 2. 557) — при |r| < 1, расходится при |х| ^ 1.
1 — х
558) Расходится. 559) Расходится к нулю. 560) ес\ ('у —
константа Эйлера. 561) 562) 563) -. 564) Рас-
2 Х Х
ходится к нулю. 565) 5(56) —. Указание. Восполь¬
зоваться формулой Валлиса. 567) -. 568) 2. 569) Расхо-
3
дится к нулю. 570) -. 571) Расходится к нулю. Указание.
1 (2п)!!
0 < Рп ^ . Умножить Рп на — —. 572) Расхо-
у/ЪгТТ (2л + 1)!!
дится к нулю. 573) а“1п2. 574) 2. Указание. Проверить, что
ап = 2(п!) и Рп = —. 575) Расходится к нулю. 576) Рас-
а\-п\
ходится к нулю. 577) Сходится. 578) Сходится. 579) Сходит¬
ся. 580) Расходится. 581) Сходится. 582) Сходится. 583) Рас¬
ходится. 584) Сходится. 585) Сходится. 586) Сходится при
а > расходится при 0 < ос ^ 587) Сходится при ос > 1,
расходится к нулю при 0 < а ^ 1. 588) Сходится при ос > 1,
расходится при 0 < а ^ 1. 589) Сходится. 590) Сходит¬
ся. 591) Сходится при а > 1, расходится при 0 < q 1.
592) Расходится к нулю при 0 < а ^ 2. 593) Сходится.
280
594) Сходится. 595) Сходится при ja| < 2, расходится при
|а| ^ 2. 596) Сходится. 597) Расходится. 598) Сходится при
| а | > е. 599) Сходился. 600) Сходится. 601) Сходится. 602) Схо¬
дится при Р > \> расходится к нулю при 0 > р <
603) Расходится ж. нулю. 604) Сходится условно. 605) Схо¬
дится абсолютно при р > 1, сходится условно при
\ К р ^ 1
606) Расходится. 607) Расходится. 608) Расхо¬
дится. 609) Сходится условно. 610) Сходится абсолютно при
|х| < 1, расходится при |х| ^ 1. 611) Сходится абсолютно
при |х| < 2, расходится при |х| ^ 2. 612) Сходится условно.
613) Сходится абсолютно при х > 1, сходится условно при
- < х 1. 614) Сходится условно. 615) Сходится абсолютно
при a > 1, сходится условно при ^ < a 1. 616) Расходится.
617) Сходится абсолютно при a > 1, сходится условно при
1 f _, sin 2х
- < (у 1. 618) Указание, cosx = —:—.
° 2 sin х
621) f(x) = х, х ^ 0.
622) /(*) = 0. 623) /(*) = \х\.
Г 1 I I <г I (1, (К И < 1.
624) f(x) = | х2 625) f(x) = < 1, *=1,
|*|> 1.
7ГХ
626) /(х) = cos —. 627) f(x) = 0.
628) f(x) = 1 629) f(x) = sin тгх.
f'~ , x > 0,
630) f(x) — ^ *<0,
0, x = 0.
631) /(«) = ( '■ 1 p*“"0"MbU0'''
^ 0, x иррациональное.
x2, Ixl > 1.
281
(532) f(x) = 0, x ф 0.
633) J(x) = 0.
•534) /(х)
0, г рациональное,
х, г иррациональное.
635) Дх) = <
у/х, 0^х<1и4&— l<x<4fc+l,
х, 4А- — 3 < х < \к — 2 и
4Аг - 2 < х < 4* - 1,
~(\/х + х)’ х = ‘2к — 1,
к = 1,2,....
636) /(*)
sinx
• X ф О,
х
1, х = 0.
(
0, -I < X $ 1,
638) /(г) = i( 1 + vT+ 4х). 639) /(х) = 0.
640) а) ( 'ходи гея равномерно, б) Сходится неравномерно.
641) а) Сходится равномерно, б) Расходится. 642) Сходит¬
ся равномерно. 64.4) а) Сходится равномерно, б) Сходится
неравномерно. 644) а) Сходится равномерно. 6) Сходится
неравномерно. 645) а) Сходится неравномерно, б) Расходит¬
ся. 646) а) Сходится неравномерно, б) Сходится равномерно.
647) При а ^ 2 расходится всюду кроме х — 0, при а > 2
сходится равномерно. 648) Сходится равномерно 649) Схо¬
дится неравномерно. 650) а) Сходится равномерно, б) Схо¬
дится равномерно. 651) а) Сходится равномерно, б) Схо¬
дится неравномерно. 652) Сходится неравномерно. 653) Схо¬
дится равномерно. 654) Сходится неравномерно 655) Схо¬
ди гея равномерно. 656) а) Сходится равномерно б) Сходит¬
ся равномерно 657) а) Сходится равномерно 6) Сходится
неравномерно. 658) а) Сходится неравномерно, б) Сходит¬
ся равномерно. 659) а) Сходится равномерно, б) Сходится
неравномерно. 660) Сходится равномерно. 661) а) Сходит¬
ся неравномерно, б) Сходится равномерно. 662) Сходится
неравномерно. 663) (!ходится неравномерно. 664) Сходится
282
неравномерно,
неравномерно,
ся равномерно
ся равномерно
ся равномерно
неравномерно
665) Сходится неравномерно. 666) Сходится
667) а) Сходится неравномерно, б) Сходит-
668) а) Сходится неравномерно, б) Сходит-
669) а) Сходится равномерно, б) Сходит-
в) Сходится неравномерно. 670) Сходится
671) Сходится неравномерно. 672) Сходится
неравномерно. 673) Сходится неравномерно. 674) а) Сходит¬
ся неравномерно, б) Сходится равномерно. 675) Сходится
равномерно. 676) а) Сходится неравномерно, б) Сходит¬
ся неравномерно, в) Сходится равномерно. 677) Сходится
неравномерно. 678) Сходится неравномерно. 679) Сходит¬
ся равномерно. 680) а) Сходится равномерно, б) Сходится
неравномерно. 681) Сходится равномерно. 682) Сходится
равномерно. 683) Сходится неравномерно. 684) а) Сходит¬
ся равномерно, б) Сходится неравномерно. 685) а) Сходит¬
ся неравномерно, б) Сходится равномерно. 686) Сходится
неравномерно. 687) а) Сходится равномерно, б) Сходится
равномерно. 688) а) Сходится неравномерно, б) Сходится
равномерно. 689) а) Сходится равномерно, б) Сходится не¬
равномерно. 690) Сходится равномерно. 691) а) Сходится
равномерно, б) Сходится неравномерно,
равномерно, б) Сходится неравномерно,
неравномерно, б) Сходится равномерно,
равномерно, б) Сходится неравномерно,
неравномерно, б) Сходится равномерно,
равномерно, б) Сходится неравномерно,
равномерно, б) Сходится неравномерно,
неравномерно, б) Сходится равномерно,
ся неравномерно, б) Сходится равномерно. 700) Сходит¬
ся равномерно. 701) Сходится равномерно. 702) Сходится
неравномерно. 703) Сходится равномерно. 704)
равномерно. 705) Сходится равномерно.
Сходится равномерно.
692) а) Сходится
693) а) Сходится
694) а) Сходится
695) а) Сходится
696) а) Сходится
697) а) Сходится
698) а) Сходится
699) а) Сходит-
неравномерно
неравномерно
неравномерно
неравномерно
равномерно.
равномерно.
б)
б) Сходится равномерно,
б) Сходится равномерно
б) Сходится равномерно
б) Сходится неравномерно.
Сходится
706) а) Сходится
707) а) Сходится
708) а) Сходится
709) а) Сходится
710) а) Сходится
711) Сходится не-
712) а) Сходится неравномерно, б) Сходится
283
равномерно. 713) а) Сходится равномерно, б) Сходится не¬
равномерно. 714) а) Сходится равномерно, б) Сходится не¬
равномерно. 715) Сходится равномерно. 716) Сходится рав¬
номерно. 717) Сходится равномерно. 718) а) Сходится рав¬
номерно. б) Сходится неравномерно. 719) а) Сходится рав¬
номерно. б) Сходится неравномерно. 720) а) Сходится равно¬
мерно. б) Сходится неравномерно. 721) а) Сходится неравно¬
мерно. б) Сходится равномерно, в) Сходится неравномерно.
722) Сходится неравномерно, а) Да. 6) Нет. в) Да. 723) Схо¬
дится равномерно, а) Нет. б) Нет. 724) Сходится равномер¬
но; да. 725) Сходится равномерно; а) и б), если существу¬
ет lim /(я), то “да”, в противном случае “нет”. Указание.
X—fro
п/(х) - 1 ^ [л/(х)] ^ nf(x). 726) Сходится неравномерно; да.
727) Сходится неравномерно, а) Да б) Да. 728) Сходится
равномерно, а) Да. б) Да. в) Да. 729) Сходится неравно¬
мерно; да. 730) Сходится неравномерно; да 731) Для а > 1
сходится неравномерно и равенства нет; для -1 ^ а 1 схо¬
дится неравномерно, равенство есть; для а < — 1 сходится
равномерно и равенство есть. 732) Сходится неравномерно;
да. 733) Сходится неравномерно, нет. 734) Для а > 1 схо¬
дится равномерно и равенство есть; для 0 < а ^ 1 сходится
неравномерно, равенство есть. 735) Сходится неравномерно;
да. 736) Сходится неравномерно; нет. 737) Сходится нерав¬
номерно; нет. 738) Сходится неравномерно: да. 739) Схо¬
дится неравномерно; нет. 740) Сходится неравномерно; да.
741) 1) Сходится равномерно. 2) Нет. 742) I) Сходится рав¬
номерно. 2) Нет. 743) 1) Сходится равномерно. 2) Спра¬
ведливо всюду, кроме нуля. 744) I) Сходится равномерно.
2) Справедливо всюду, кроме нуля. 745) 1) Сходится неравно¬
мерно. 2) а) Нет б) Да. 746) Сходится абсолютно при х = 0.
747) Сходится абсолютно при '2тгк < х < (2к + 1)7г, к G Z.
748) Сходится абсолютно при i > е и 0 < i < -. 749) Схо-
е
дится абсолютно при пк - arcsin - $ х <С пк + arcsin -, к £ TL.
v и
7Г 27Г
750) Сходится абсолютно при —\- тгк х Ь тгк, к Е Ъ.
3 3
751) Сходится абсолютно при т 0 и х ^ —2. 752) Сходится
284
абсолютно при — ^- + тг/:<Сх^^ + пк, к £ 7L. 753) Сходится
абсолютно при х ф -к, к £f$. 754) Сходится абсолютно при
2
х > 1, сходится условно при - < х ^ 1. 755) Расходится при
о
всех х ф 3. 756) Сходится абсолютно при 2пк < х < (2к + 1 )7г,
к £ Z. 757) Сходится абсолютно при |х| > 1. 758) Сходится
абсолютно при х ф —2П, п £ N. 759) Сходится абсолютно
при |х| < оо. 760) Сходится условно при |х| < оо. 761) Схо¬
дится абсолютно при |х| ^ 1/2. 762) Сходится условно при
|х| < оо. 763) Сходится абсолютно при х ф 0. 764) Сходится
абсолютно при |х| < оо. 765) Сходится абсолютно при х > 1.
766) Сходится условно при 0 < х ^ 1, сходится абсолютно при
х > 1. 767) Сходится условно при —п/2+2пк < х < п/2 + 2пк,
к £ Z. 768) Сходится условно при пк < х < пк + п/2,
к £ TL. 769) Сходится абсолютно при |х| < оо. 770) Схо¬
дится абсолютно при |х| < оо. 771) Сходится абсолютно при
|х| < оо. 772) Сходится абсолютно при \х\ < оо. 773) Схо¬
дится абсолютно при х > 2. 774) Сходится абсолютно при
х ^ 0. 775) Сходится абсолютно при х ф 0. 776) Сходит¬
ся абсолютно при |х| > 1. 777) Сходится абсолютно при
|х| ^ 1/2. 778) Сходится абсолютно при |ж| < оо. 779) Схо¬
дится абсолютно при х < 0. 780) Сходится абсолютно при
\х\ < оо. 781) Сходится абсолютно при х ф 0. 782) Сходит¬
ся условно при х ф —к} к £ N. 783) Сходится условно при
|х| < оо. 784) Сходится абсолютно при а > 1, расходится при
О < а ^ 1. 785) Сходится абсолютно при а > 1, расходится
при 0 < а ^ 1. 786) Сходится абсолютно при 1 < |х| < п/2
я пк < |х| < пк 4- п/2, к £ N. 787) Сходится абсолютно при
х > 1. 788) Сходится условно при |х| ^ 1. 789) Сходится
абсолютно при х ^ 0. 790) Сходится абсолютно при |х| < 1.
791) Сходится абсолютно при \х\ ф 1, сходится условно при
х = — 1. 792) Сходится абсолютно при |х[ < оо. 793) Сходится
абсолютно при х ^ — 1, х = 0. 794) Сходится абсолютно при
х = пк, к Е Z, сходится условно при х ф пк, к £ Ъ. 795) Схо¬
дится абсолютно при |х| ^ 1. 796) Сходится абсолютно при
|х| < оо. 797) Сходится абсолютно при |х| < 1. 798) Схо¬
дится абсолютно при х £ Ъ. 799) Сходится абсолютно при
285
|х| < 3. 800) Сходится абсолютно при х ф 0. 801) Сходится
абсолютно при х > 0. 802) Сходится абсолютно при |х| < оо,
х ф — 1. 803) Сходится абсолютно при х > 1. 804) Схо¬
дится абсолютно при \х\ ф 1. 805) Сходится абсолютно при
х > 1. 806) Сходится абсолютно при х > 0. 807) Сходит¬
ся абсолютно при |х| < оо. 808) Сходится абсолютно при
х ^ 1их^7г/2 — як, к £ N. 809) Сходится абсолютно при
—тг/4+7гк ^ х ^ п/4+пк, к £ Ъ. 810) Сходится абсолютно при
X > 1 и -1 < х < 0, сходится условно при |х| = 1. 811) Схо¬
дится условно при х ф 2пк, к £ 7L. 812) Сходится абсолютно
при |х| < оо. 813) Сходится абсолютно при х ф —, п £ N.
п
814) Сходится абсолютно при х < -1. 815) Если р < q - 1,
то сходится абсолютно при |х| < оо, если q - 1 ^ р < q, то
сходится условно при х ф пк, к £ Z, и абсолютно при х = тг&,
к £ Ъ, если р ^ qt то сходится абсолютно при х — ттк,к £Ъ.
816) Сходится условно при |х| ^ 1. 817) Сходится условно при
|х| ^ 1. 818) Сходится абсолютно при |х| < оо. 819) Сходится
абсолютно при х > 1 и х = 0. 820) Сходится абсолютно при
х > 1, сходится условно при х ^ 1 их / 2тг к} к £ 7L. 821) Схо¬
дится абсолютно при |х| < оо. 822) Сходится абсолютно при
- < х < е, сходится условно при х = -. 823) Сходится
е е
условно при х ф 2пк, к £ Ъ. 824) Сходится абсолютно при
|х| $ tg 1. 825) Сходится абсолютно для х таких, что х2 < ех.
826) Расходится при любом х. 827) Расходится при любом х.
828) Сходится абсолютно при |х| < 1. 829) Сходится абсо¬
лютно при х = 7г/г, к £ Z, сходится условно при х ф irk, к £Ъ.
830) Сходится абсолютно при х = тг/с, ik £ 7L, сходится услов¬
но при х ф пку к £ 7L. 831) Сходится абсолютно при х = пк,
к £ Ъ, сходится условно при х ф жк, к £ Ъ. 832) Сходится
абсолютно при |х| > -. 833) Сходится абсолютно при |х| < 1.
с
834) Сходится условно при х ^ 0. 835) Сходится абсолютно
при х = 0, сходится условно при х ф 0. 836) Сходится абсо¬
лютно при х > 1, сходится условно при 0 < х ^ 1. Указание.
2
Для 0 < х $ 1 показать, что |ап| = 0(п х ), п —> оо, рас¬
смотрев 1п|ап|. 837) Сходится абсолютно при х ф пк 4* — >
286
к £ Ъ. 838) Сходится абсолютно при |х| < 1, сходится услов¬
но при х = 1. 839) Сходится абсолютно при — 4 < х < 2,
« ходится условно при х = 2 и х = —4. 840) Сходится условно
при х ф жк, к £ Z, сходится абсолютно при х = тгк, к £ It.
841) Сходится условно при всех х. 842) Сходится условно при
х ф п(2к И- 1), к £ Ъ. 843) Сходится абсолютно при х = 7гк,
8тг к
к £ Z, сходится условно при х ф —к £ TL. 844) Схо-
5
2ттк
дится условно при х ф ——, к £ Z. 845) Сходится условно
о
при х ф (2к + 1)тг, к £ Ъ. 846) Сходится абсолютно при
7Г 7Г к
х = — (2к + 1), к £ Z, сходится условно при х ф —, к £Ъ.
847) Сходится абсолютно при х = сходится
тгк
условно при х ^ —, к £ 7L. 848) Сходится абсолютно при
х > 1, сходится условно при 0 < х ^ 1. 849) Сходится абсо¬
лютно при х > 1, сходится условно при 0 < х $ 1. 850) Схо¬
дится абсолютно при х > 3, сходится условно при 0 < х ^ 3,
27Г
х ф —. 851) Сходится абсолютно при х > 4, сходится услов-
о
но при 1^х<2,3^х<4. 852) Сходится абсолютно при
|х| < е. 853) Сходится абсолютно, если существует к £ N та¬
кое, что |х — жк\ < 854) Сходится абсолютно при х = пк>
к £ N, или х + у > 1, сходится условно при х ф тгк, к £ Z, и
0 < х + у ^ 1. 855) Равномерно. 856) Равномерно. 857) Рав¬
номерно. 858) Равномерно. 859) Равномерно. 860) Равно¬
мерно. 861) Равномерно. 862) Неравномерно. 863) Равно¬
мерно. 864) Равномерно. 865) Равномерно. 866) а) Рав¬
номерно. 6) Неравномерно. 867) Равномерно. 868) Равно¬
мерно. 869) Неравномерно. 870) Равномерно. 871) Равно¬
мерно. 872) Равномерно. 873) а) Неравномерно, б) Равно¬
мерно. 874) а) Неравномерно, б) Равномерно. 875) а) Не¬
равномерно. б) Равномерно. Указание. См. пример 17 на
стр. 89. 876) Равномерно. 877) Неравномерно. 878) Неравно¬
мерно. 879) Неравномерно. 880) Равномерно. 881) Неравно¬
мерно. 882) Равномерно. 883) Равномерно. 884) Равномер¬
но. 885) Равномерно. 886) а) Равномерно, б) Неравномерно.
287
887) Равномерно. 888) Неравномерно. > казание. Расемо-
2к .
треть У />(п, хи, гл*‘ J'k = 2i*-f 1. лг G FI. 889) Неравно-
' 71
п—к
мерно. 890) Равномерно. 891) Равномерно. 892) Равномерно.
893) Равномерно. 894) Равномерно. 895) а) Неравномерно.
6) Равномерно. 896) Равномерно. 897) Равномерно. 898) Рав¬
номерно. 899) Равномерно. 900) Равномерно. 901) Равно¬
мерно. 902) Равномерно. 903) Равномерно. 904) Равномер¬
но. 905) Равномерно. 906) Равномерно. 907) Равномерно.
2к
908) Равномерно Указание. Рассмотреть xlr~^Tk, где
| п = к
Хк = ^ ^ ^ *^9) а) Равномерно. 6) Неравномер¬
но. 910) Неравномерно. 911) Равномерно. 912) Равномер¬
но. 913) Неравномерно. Указание. Проверить, что ап —> 0,
тг —> оо, неравномерно. 914) Неравномерно. Указание. Про¬
верить, что ап —> 0, 71 -> оо, неравномерно. 915) Неравно¬
мерно. Указание. Проверить, что ап —> 0, п —> оо, неравно¬
мерно. 916) Неравномерно. 917) Неравномерно. 918) а) Не¬
равномерно. 6) Равномерно. 919) Е — [0;ос); разрыв в нуле.
920) Е — К, непрерывна. 921) Е - [0; -h-^о), непрерывна.
922) Е - (1;+оо). непрерывна. 923) Е - [—l;-fl], непрерыв¬
на. 924) Е — (-1/3; 1/3), непрерывна. 925) Е ~ К, непре¬
рывна. 926) Е = 'Ж. непрерывна. 927) Е = К, разрыв в нуле.
928) Е = Ш \ {2лк, к £ Z}, непрерывна. 929) /? = 1R, непре¬
рывна. 930) Е — К при а > 1. Е - R \ {0} при 0 < «г $ 1;
непрерывна. 931) Е = (— оо; —2) U (2;-hoc) U {1}, непрерывна.
932) Е — (—1;+1), непрерывна. 933) Е — [—1; + 1], непрерыв¬
на. 934) Е - (0;+оо), непрерывна. 935) Е = IR, непрерывна.
936) Е - ,|РПР°Р|ЛВНа- 937) Е - {х ф. - 71, 7i £ Z}}
непрерывна. 938) Е — И'., непрерывна. 939) Е -- К, непре¬
рывна. 940) Е — Ш\ {0}, непрерывна. 941) Е — IK, непрерыв¬
на. 942) Е = [ 1; 3], непрерывна 943) Е = (—oo;log32)U {1},
непрерывна. 944) Е = (0,-hoo), непрерывна. 945) Е = М,
разрыв в нуле. Указание. Рассмотреть / (±-V Использо¬
288
вать неравенство 1 + кх2 ^ 1 + —. Доказать, что \f{x)\ >
п е
946) Е = [0;+оо), непрерывна. 947) Е = [0;+оо), разрыв в
нуле. Указание. Вычислить /(х), перейдя к комплексным пе¬
ременным. 948) Е = (0;+оо), непрерывна. 949) Е = [—1; 1),
дифференцируема на (-1; 1). 950) Е = [—1; 1), дифференци¬
руема на (—1; 1). 951) Е = R, дифференцируема. 952) Е = IR,
дифференцируема. 953) Е = (—1;1), дифференцируема при
х ф 0. 954) Е = R, дифференцируема. 955) Е = R, диф¬
ференцируема. 956) Е = 1R, х ^ 7гАг, к £ Ъ, дифференци¬
руема. 957) Е = [0;+оо), дифференцируема. 958) Е = R,
дифференцируема при х ^ 0. 959) Е = R, дифференцируе¬
ма. 960) Е = R, дифференцируема. 961) Е = М, в нуле не
дифференцируема. Указание. Рассмотреть при
1
п = 1
оо
964) £
П = 1
1 (1 — (—2)2n+l)
п-9" 2п+1
00 1
965) Е^Г^С082п — cos3n).
п=1
оо
967) |х| < 1. 968)i = 0. 969) -1 ^ х < I.
970)-1 ^*^1. 971) х = 0. 972) |х| < оо.
973) |х| < 4=. 974) -1 < с < 1. 975) |х| < 1.
V2
976) |х| < оо. 977) |х| < оо. 978) |х| < 2.
289
979) |х| < 980)-^Ux<^.
981) |х| ^ 1 при а > 1, \х\ < I при а ^ 1.
982) |х| <
€
983) |х| ^ уД. 984) |х| < 2.
985) -\/b < х $ \/Ъ. 986) — 1 ^ х < 1.
987) |х| < 1. 988) |* + 3| < 3/2.
989) 0 ^ х < 2. 990) |х| < оо. 991)-10^х<0.
992) \х\ < оо. 993) |х — 1| < 3. 994)|х-1|^4.
995) |х - 2| < \/3. 996) -1 ^ х < 0. 997) |х + 1| < </2.
998) |* + 2| ^
16'
999) |х + 1|< 1
1000) |х + 3| <
1001)-1^х<1
1003) 1 ^ X ^ 3.
1004) х ^ —3, х > — 1.
1002) -I <х-3< I
1005) х>-1 *<~\-
,лл.ч 1 л/2 11 л/2 1
Ю06) — — — С х С —, --<Х<—
1007) |х| < оо.
1009) — — + жк ^ х < — + тгк, к £ Z.
4 4
1010) — arcsin -^= -f жк ^ х ^ arcs in -^= + тг/:, к £ Z.
1011) | х ] < 1.
1014) |х| < е.
1017) |г| < 1.
1020) г € С.
1023) \z\ < у/1.
уД
1012) |х| < 1.
1015) И < 1.
1018) г G С.
1021) |г| < е.
1024) |г + 2| < 2.
1013) ~<х<~
5
1016) |х| < 1.
1019) \z\ < %/2.
1022) |г+ 1| < —.
е
1025) |г-2|< -L.
290
СЛ | СО
у/2
1026) \z- 1| < 1. 1027) |*| < 1. 1028) |z — 1| <
1029) \z-i\ < 1. 1030) |аг| <1. 1031) \z +1| < -УТО.
1032) |z + 4*| < 1. 1033) \z + 1 + «| < 3.1034) \z - 2i| < 2.
1035) \z- 1| < 1. 1036) |z + i| < -^=.
v2
1037) 4 + ln2(x — 4) + In 2(2 In2 — l)(x — 4)2 +
10
4 In3 2 — 6 In2 2 + 3 In 2 .
+ ш («-4)» + ...
X2 X4 x6
1040) — +
] 6 180 2835
1 24
1041>1"3+5!2<I-le>-9™48<*-16>, + ""
1042) -ein 1 + |coel (* + 1)+ ~ 5 е0*1) ^ ^ ^ +
1046)l + i.1+A«' + ^«< +.
1047) ^ R = oc
n=0
1019) f'(-1)"-52n+1i^1 Л лл
-a ~(2пТТ)Г >Я-°°-
n=0
291
n=0
oo
2nrn 1
•050) E— .*=2-
n=1
/_i\n_3r.+l
1051)ЕЧт-'й=^
n=l
OO
1052) Yi*2"' R=l
n= 0
1053) l + lg + f^-l)"-1^^*", Я = 1.
n=2 '
4_ . ^4"-25-(3n-4)_n
1054) 1 - -x + 2^ 3^j * , Я - 1.
n=2
-22- x2n
'»“)Epr(boT'R=“'
n=0 ' ’
_°° o2n+l_2n+l
,o“)-i:-^+ir,B=00-
n=0 4 7
°° ( i\n-lo2n-l i
Ю57) V i x2-1, Я = i
' 2n - 1 2
n = l
inro4 x ^(2n-l)!! x2n+1 „ ,
3+S (2n^!! (2n+^32n+i
00 f—Плгп
1059)*) л=о°-
fiw"-* ^(-1)п (*-10)" p-^
б)е yT—• H-°°
n=0
1060) 2вУ'^(*-а)п, Я =00.
^ n!
00 1 / 2\n
Ш)Е/ |пз , Я = oo.
n=0 ' 7
292
1062) а) - ^ f~T~) гП) ^ = °°
п=0 ' '
П = 0 ' 7
, 1 ^-(*+2)"« „
■)?Z- nf ' R = °°
n=0
°° / 1 \n _2n °° /_ i \n _2n + l
1063)sin«g (2n), +cosa.g—— —r, R= oo.
1,|пж2п 1)пдт2п + 1
Юм) с».. £-553;—“••E-jsrnr'я=”'
n=0 ' ' n=0 ' '
3 (-l)n(l + 32r*-1)
x2n, R= oo.
n=0
oo
v 3 ^ (-l)n + 1(32n - 1) / Я-\2"+1 „
«> l*"*) ’й = 0°-
,nfiBv 1 y- (~i)n(4«)3"+1 i (-1H2*)2"*1
2S (2n + 1)! 2^ (2,1 + 1)! ’
OO
«£й(-Г
(2п+1)!
l)n2n /
n^0{2n+l)!lI 6>
- (_ir2?.-i (,_.)*•
V3L, щх л-°°-
rv=0 ' 7
Ю68) £ r '2n), , « = ~
n=0 '
— (-1)"!2"-1
(2n)!
юб9),)|;(-')'1~'п(,-|)',д=1,
293
1070
1071
1072
1073
1074
1075
1076
1077
1078
1079
1080
1081
294
n = l v
(-l)"-1*3" _ у (-1)»-^" R=l
n ’
n = 1 n = 1
q _°° qn _ i
6 У 1 -2n + l D
4„^(2^ТШ* 'Л-“-
, A 22n-lx2n
> + Е-(здг. * = »•
n = l v '
” (-l)n(4»-H-3n-n)jn
12"+i
a) -2 + 2f;-^ '2(43пП-2)(» + 8Г, Д = 8.
n = l
00 / МП-1
» Y' (-l)""1*2"-1
2 " 2n — 1
f» = l
n(n + l)
..(n + 1)
П = 1 ' '
if>+!)(„ +2)*", Д= 1.
n=0
2.
= 125.
Ю | CO
infl'M I У"1 ^2n ~ x2n+1 r— i
1082) x + ^ R - 1.
П = 1 ' '
,лллх П (Z71 - 1
(2n — 1)!! x2n+1
R=\.
f — llnx4n+2
■«■«igpLnVi^i)’ я=о°
д,2п+1
'»87)ЕнГр^,я='.
П=0 ' 7
“ ~ x17n+1
1088) 1—L , R=l. 1089) £ pjj-j-p Я=1.
~ (.nn-Un 1 ~ x2n
!°90)Е4г-'й=1 1091)-2^M^j!’ Д=°°
n = 1 n=l v 7
— (-l)n4n*2n-1
1094) - jP —- Д= 1. Ю95) jPf-1)"*4". Д= 1.
n=l n=0
1ллл\ i (— l)n(4-7 • (3n — 2)) 3n _
1096) 1 + £ 3n,n; ■ « = 1.
n=l
00
x2n, Д= 1.
295
1098) a) Д = оо; б) е3 £ il-i)
п=0 п=0
">")f~ У *
п=О
1100) Ц^~*2п+1. я = оо-
п=О ***
1101) 32^^T-(*+l)n. я = 0°-
п=0
1102) 2^ *1п2^ 1Г{Ж. 1)", Я = оо.
п=0
110»Ч ^ V'(_1)"'32n+1x2n+1 Ft - ею
ПОЗ) а) ^ р»+1у; *
п=0 '
V^^-(-l)"3S” ( TN»-
n=0
Y' (-l)n32n+1 / JT\2"+1
2 ho (2n+l)! ' 4'
(-1)"*2"
11°4)») Е^ГЩТ’ s=o°
n=0 4 9
\2 n
n=0
oo*
fi\ /oV^ (-l)n(x + Я-/3)1-
6> V3L—p^rn—+
+ £ (2n + l)!2ln+1 iX +
1 ^ 1 + 4-(—1)"
no«)«)
n=0
296
n
—, Я = oo.
Я = oo.
= oo.
= oo.
I со «2"
1107) a) (-1)* —-г2-1, oo.
1 ^(-l)"2"-4x-V2)2"
*>2-E (йГЙ)! 'я-~'
1,08)b£wnF<I-'/4),’+,+
n=0
oo
(_l)" + 1.24n 3 /4Ч2П n_
+ 2^ Torn (*-*/4) - д-°°-
n=l
oo
(2n)!
1109) Ei^(l + 3J"+1)l2n+1> Д=0°-
11|0>5£<-1»"((2Ь+1пт)*,”-я=~
Я = оо.
n=0
“ 2n*3n+l it
ш2> + »»,*€ z.
5!"+l”‘I,"«, R = oo.
X2 X4 X6
1114),n4+2^-2^ + 3^- - * = 2
1H5) E —----- , Я= 1.
П = 1
297
in6).)Lizia£ziz^+f н)г^, я=1.
n=l n = l
~ (— 1)Пшт1(х — 4^n+1
6) 4 In 4 + (r — 4) In 4 + фГп +
n = l
T» = l
1117) a) ln3 + £-———n~3--- , R=\-
(-"lj"-12" „ D_1
fiv ^(-l)"-1^- „ 1
6) ^—-—* , Я--.
n = l
oo / о \ " + 1
(A) *=t-
n..,ta.-£(l)-fc±i£. «[-£?)■
n=1 N ' L 7
,,„nl .^(-l)n-12n _ ^(-l)n-1xn „ 1
П20) a) £ !—i- *» - £ i—L- , R =
n = l 4 ' n — 1
«4
n = l x ' n — 1 4 7
6) _in5+f;^(*-i)" +
+£4%<->". *4
П= 1 4 '
298
cs ico
1123) ln2+52a„xn,
n=l
On =
1
2*—1’
1 ■ И)*"1
2 к 2* к
n = 2Jk- 1,
, n = 2k,
2n+l
n=0
1127) 52
fl = l
n
»
Д = 1
•
(-
l)»-1
f-U
1
n 1
\2n
3n
(-
■I)""1
(- +
l
n
\2n
3n
53"
oo
V
ИГ
V
n
00 *"+i
fl = l
1128) V'i—Я = 1.
£5"+1 «»"+1
H29) l)I+"
91
-E
fl = 1 fl = 1
00 / I i\n
+E
(-l)»-l(« +1)"
Д= 1.
n=l
—HI "‘1У+£’Ч1
N ' n=2 N
+ ^|-j-(41-n - 9*-")^ , Л = 2.
R = 2.
Я= 1.
: = 2.
|x", д = 1.
-)(*-l)n, Д = 2.
Д = 1.
x(x+l)n+1 (
n
-(4-n — 9-n) +
299
I,*I,-,iD-,)-(!)V. «л.
«ijD-O-(|)’(*-гг. я=5-
n=0 ' '
И32)а) 1-£(-1)"£, Я = 2.
n=0
оо
б) 1-2£(-1)"(1+х)", Я = 1.
п=0
1133) а) г5, Я = оо.
б) — 1+5(х+1) + 10(х+1)2 +10(х+ 1)3+5(х+I)4 + (х+1)®,
R — оо.
1134) а) г6 - 2х2 + 4х, R = оо.
б) 3+6(х-1)+13(х-1)2+20(х-1)3+30(х-1)4+6(х-1)5+
+ (х-1)6, Я = оо.
ОО
1135) 52(-1)"(*-1)п+2+6(х-1)+6(х-1)2+2(х-1)3, Я= 1.
п=0
п=0
у/ь- 1 1 -л/5 . 1 + у/Ь
1136) 4fE(*n+1-en+1)*n-
^ п =
1137)Ё(1_гят)*’' К=1
,138)„?.(('0"+1_2"+‘)т' я4
00 1
1139) 52(2"+1 + 3")хП- R - к
п=О
1140) + Я = 3.
7 ^ V 21 Зп 28 4" )
г»—П 4 '
п=0
300
1141) 1 - 2х + 2х2 - 2х4 + 2х5 + апхп + • • •,
= 0, аз^_1 = 2, а3^_2 = —2, /: Е N, Я = 1.
л, *уч 1 2х 2х2
Указание, /(х) = 1 - -——^ + г.
1-х3 1 - х3
00
1142
1143
1144
1145
1146
1147
1148
1149
1150
1151
1152
Е*5" “ Ех5П+1> Я=1‘
п=0 п=0
оо
£(-1Г(п+1)*п+2, Д = 1.
п ~0
оо
5>+1)х3", Д = 1.
п=О
оо
n=0
53 nx", Д = 1.
n = l
OO
2 " 2 ,
n=0 n=l
1 1 ~2n + l i op ~2n
5 E<-»*«" - 5o'E(-T— + 50 D-‘) V'
n=0 n=0 n=0
Д = 1.
jT((n+l)2+l]x", Д = 1.
-gor-sf^-en
X
*4
Ё(3-3"-упт)*”’ я=‘
301
ПСЙ\ 1 I V' (“1Г(2п- 1)"/ />\2п р_
456) 2 + 2^ jT!23n+i (*-6) ■ R-
П= 1
11 vn 2 J- if* - 41 -4- - V' (~0"(2n ~ O-'/j.
1157) 2+ 3(x 3)+ 3 2^ 32n(2n)!! ^
fl = l 4 7
. о Y' (~ 1)"(2« - 1)!! 2„
+ 22w 32” (2«)!! (I_3) 1 R-
n = l ' '
~ (2n-3)!! 2n_,
1158)2-, (2n)!! * ft_1
n= 1
"“tD-Tp^rr+J. *-w.
fl = 1 ' 7
„ 6n + 1 ^ 6n + 5
n=0 n=0
1182>1, 4n +1 +^„ 4„ + 3 ■ Л
n=0 n=0
= 2.
- 3)2n+1 +
;3.
I = 1
= 1.
°° ( i \no2n— 1 i i
1163) arctg2+J]) ЦЬ-j— г2""1,
n = l
_ 00 ГГ4п + 2
»“>4+В«=^-
|1в5>?-2',-|ет2!"м',п+г' я=^
П = 1 ' 7
МЯ7у f*(2n-l)!! х2"*1
,,6Т)2^ (2л)!! 2п + 1 ’
п—О
°° /т6п+1 г6п+5 \
П^В-.Г (вггт - SJ+») ■ R=1
п = 1
°° / _Зп+1 _Зп+2 \
11«11:<-,>*(5Гм-5Гп)- *=■'
„«,.^^+ffca^g^j}^. я=л
— (2п)! *г"« „ 1
' 2
1171) J*2 - 2х3 - 2 52 ^
' 2 ^ (n!)2 2n+ 1
П= 1 х '
П72)У'^1Их2"+') Д=1.
’ ^ 2n + 1
п=0
1173И I ** I У'Г(2П_1)!! *2П+2^ д-1
1 + — + 2^ \(2п + 2)!! 2TTTl)' R -1
303
117<?\ (2n-3)!! 2n+i
1176) 2 6 ^ (2n+l)(2n)!!
n ~2
1 ,77\ (2(n ~ •))" 2n p_i
1177)2. (2n + I’jli" ’ R~l
П= 1 ' '
™ f _ I \nT2n+4
11-78) \n > A. , , R = oo.
} ^ (2n + 4)n!
n =0
E- r_n^j.6n + l
,[ } ,wo R= oo.
(6n+l)(2«)!
2n+l
n=0
°° X
OO
xn + l
"м>£нг<^П)№ x>0-
11831 i I *6 (2"-Wxs»+1
1183)x+12 + ^ 2"n!(5n + l) 1 •
1184) x + Y' (2n~1)!! r2n+i Я=1
I io4) x + 2_^ 2".n!(2n + l)2 ’
n = l ' '
^ r2n+4
U85) S 2(2n + 2)(2n+ 1)!’ Я = °°
им,я.
л—П * ' '
п=0
с»
« = *
П!
п=0
1191) Ё(-1Г^“, Я = оо.
п=О
оо
“ЧЕЖ-"-—
v~'4 cos (па) хп , л ^
1193) > —г— г, sina ^ О, Я = оо.
9 ^ sm ап! ^
п=0
,194) f)S2f2f4^, Я = оо.
п!
п=0
1196) a) f;(-l)"-l,-»„2lr<"+1). Я
п=0
1 2 2 5 17 , 62 9
1,97), + 5*’+1Г‘ + +
498) *- + J^«3 + - , **»*,*€ г.
‘>99) 1 + y + 5J*" + - •
,200) 1+|^ + ^+51|5««+.--.
>»» 5 +**+*«’ + ■--
Ш2),
ОО.
= 1.
= 1.
305
1203
1204
1205
1206
1207
1208
1209
1210
1211
1212
1213
1214
1215
1216
1217
1218
1219
1220
SC Л 1 о 1 л
2 + Т ~ 12* “12х + “''
X 1 о 1 » 1 4
- + -х х Ч х + ■■■.
2 4 24 48
1 з 1 4 3 5
+ 3* +5Х “lo1 +
2 - -х2 Н—— х4 + • • •.
6 120
тгх jtx2 / Зтг3 + 4лД з
~2 4 ( 24 jХ +" ■
х 1 , 1 4
1 1 х х -f • • •
2 12 720
х2 2х3 9х5
* + 2! + 1Г + "5Г + " ’
, 1 1 2 1 3
- 2х + 12* +Й* + -•
1 гг2 -I- 46 г6 -I-
1-1 +3* ~ 45 + "•
11 1 3 1 5
-2 + Т2Х" 720Г +46^!Х +
, „ 5 , 8 з 65 4 163 5
1 + 2*+-х2+-х*+-х4 + —х5
3 , 4 , 4 89 5 409
X Н X -I- —г -4- X + X -+■ 2
2 3 120 720
, 2 з 2 4 13 5 13 6
х + х +зх +зх +ТГ +!Г
_ ^_3 . ^9 5 _ 1301 7
6 + 120 5040 +
, 1 1 2 1 з 49 4
1 х х — —х Н х + ■ • •
2 8 16 384
, 3 25 , 331 з
'-Г+24* _ 720* + -•
5 , 101 , 4241 ,
х + -х + х Н х + • •.
6 120 5040
1 2 1 з 7 4 7 5
,+ж+в* "6Х +72Х +40Х “
1957
+ ~720
* + •••■
481 6
6480
~ 3 120" 252
1222) а2 + 2а6х + (62 + 2ас)х2 4- (2ad + 2Ьс)х3 +
+ (с2 + 2а/ + 2bd)x4 + (2ак + 26/ + 2cd)x5 +
1231) 1.
ОО |
1232) £(п+1 )," = 7Г—-
n=0 V
П=1
,И4) ‘+JL + ...+
(l 2 (2n- l)(2i> + 1) + +n(n+ I)-,!,) +
°° / i \n- 1 o2n —2 °° / o\n
1^) E (2„ — 1)! • 1236> E = e'3'
n=l v 9 n=0
1238) x - ~x2 + |*3 - ~x4 + • • •
1239) ^ -5*4 + Ш*в + ”-
,240),-£+!,• + ....
, *2 5x4 53x6 921 о 23513 10
1241) l + y+_ + _ + _x +-fir* + •••
1251
1252
1253
1255
1257
1259
1260
1261
1262
1263
1264
1265
1266
1267
1268
1269
1270
1271
+ 1) + + I)2 + + »)3 + + П4 + '
I(*+l)+l(*+l)2+i(*+l)3+. .
ry ~ 9 a 4 x3 x5
X + X2 + 2x6 + -X4 + • • .1254) X - — -f — + • •
xx2 x4 x2 x4
ln2+2 + T~84!+ ' 1256) Y + T2 +
X2 X3 X X2 x3
*-y + T + "- 1258) , + 2 "¥“48 +
2 - (2ln2)x + ^ln 2 + - In 2j x + • •.
4 з 4 c
+ 3 + 3 +
1 + 2x + 4x2 - 8x3 + - • •
x2 2x3 x4 x5
~X + T + 1_ + T“T+ '
l+l!+y + Bol6 +
/ x2 4x4 31x6 \
4 ^ + ^T"^60+" 7'
x x2 3x3 9x4 29x5 129x6
Т+2Г + 'зГ + 1Г + “sT + ~бТ~ +
x2 x3 7 4
1+*+T“T"24* +"-
x2 Зх4 8x5 3xe 56*7 119x8 440x9
+ ;E+2! 4! ~5! бГ 4 7Г 8! 9!~
1 + X + ^x2 + ?x3 + • •.
X2 X3
T + y + ' '
*3 4 5
•+T + T6* +--
3
5x4 5
1272
1282
1283
1284
1285
1293
1294
1295
1296
1297
1298
1299
1300
1303
1305
1308
с2 5х4 53х6 921а:8
1 + 2! + 4! + 6!
(2 п)!
8!
j \ 2п + 1
_п (n!)2(2n + 1)
п=0
(I)
2 (2т»)!
n=0 v ’
(2х)
2 п
(2п)!
6^5 (n!)2 2n+ 1
П = 1 ' '
6^4"-М(п-1)!]2.2п
1 + 32 +
(2
п = 2
(2п)!
.2
1 1
i+ 22 + 32 +
(п - I)2
х х
~ 6 + 12 +
У = х-у +
2г3 5х4
а а° а° а'
,5. , cJJ ir 13 3
у — а а х •+■ 5а х - 15а1 V* + 35а1'х4 +
4
х х
V — j. h * * • •
У 4 1024
s' = r, + 8T‘s+ •
vl-l (У3-,Г
У 2 24
оо п
F(z) = '£snxn, S„=£afc.
n=0
Wn =
-945.
105
16 ’
у/Ъ
(MVS)"
n + 1
, n <= N.
1306) 0.
1309) 0.
1307) 0.
1310) -16! (l + ^).
309
1311)-^. 1312) —-г--
5 4
?(!)’
1313) а) - в; б) о. 1314)
1315) 220-116е2. 1316)
1317)Ц^,п[(п + 1)|].
1318) /<”>(0) = 0 при п = 2*. Jfc G N;
/(">(0) = 2- (п - 1)! при п = 2к - 1, * € N.
w>'
1320) —2z — \г3 ---- г2"-1 , 0 < х <+оо.
3 2п — 1
iooi\ - | 1 -2 , 1*3 _3 . | (2П ~1)!! а+1 , ^ 1
1321) г + -г +—, +...+ (2п),, , +...,
1323) ]Г^(л + 1)2Л cos2n 7 + < а? < + 2тг£, к £Z.
п=0
Указание. —=— = — разложить по степеням
сов X у2
у + 1 = сов х -I- 1 = 2 сов2 —.
Z
1324) sinx + лгчм/о i\ (8*п s)2"*1-
^ (2n)!!(2n+ l)v ;
Указание. Применить формулу х = arcein(sinx).
1325) | + £^3T(ctg*)2n"‘.
n = l
Указание. Применить формулу
х = arcctg(ctgx) = - - arctg(ctgx).
ОО
1326) 5^(-1Г-1 ^"-‘(гх), X Ф | + irk, kez.
310
1327) v/2V?+^=(v^)3 +^^(л/^)5 + - -. (К г <2.
1328) j(V^)3 ~ "*■ ■ "*"
I ( П"-1 + I 0 < х < 1
+ < 1> (а+1)„+ ’
1329) \/2 ^\/*+^(V*)3-g(\/*)5-y(v^)7+ • ) . <К*<1.
1330) у = Л,'» + ‘ * + + _|_*> + ....
.33i)» = ^,,2 + r + ^W-I'J+ "
1333) у = ^Зг>/3 - \х - :^*5/3 + • - -.
1Ж),= »Я^+^« + ^^+....
1341) Сходятся ряды по столбцам и по строкам. Оба по¬
вторных ряда и двойной расходятся. 1342) Сходятся ряды по
строкам и по столбцам. Один из повторных рядов сходится,
а другой повторный и двойной ряды расходятся. 1343) Все
ряды по строкам расходятся, все ряды по столбцам сходятся.
Соответствующий повторный ряд и двойной ряд сходятся.
1344) При а > 1, /? > 1 сходится, при а ^ 1 или /? ^ 1 рас¬
ходится. 1345) Сходится при а > 2, расходится при а ^ 2.
1346) Сходится при q > 1, расходится при а ^ 1. 1347) Схо¬
дится абсолютно при а > 2, сходится условно при 0 < а ^ 2.
1348) Сходится условно. 1349) Сходится абсолютно при а > 1
и в > 1, расходйтся при а ^ 1 или 0^1. 1350) Сходится
условно. 1351) Сходится абсолютно при а > 2 и 0 > 2, схо¬
дится условно при 0<а^2и0</?^ 2. 1352) Сходится.
1353) Сходится. 1354) Сходится условно. 1355) 1. 1356)—-—.
р+ 1
1357) In2. 1358) ^ - In 2. 1359) 1360) iln2.
8 2 8 4
311
s 7. ТЕОРЕТИЧЕСКИЕ ЗАДАЧИ
1. Числовые ряды*1
ОО
1. Пусть а„ > 0 и ряд ^ а„ сходится. Доказать, что
lim ап п — 0. n=l
П-ЮО ОО
2. Пусть ап > 0 и ряд ^ ап сходится. Доказать, что
ОО с П — 1
Е^п
— расходится.
П = 1
3. Привести пример сходящегося ряда с ненулевыми чле-
ОО ОО Q
а„, для которого ряд У — сходится.
П = 1 П = 1 оо
4. Привести пример сходящегося ряда ^ а„ с положи-
оо п = 1
тельными членами, для которого ряд ^ гп расходится.
п= 1 оо
5. Привести пример сходящегося ряда ап с положи-
оо П = 1
тельными членами, для которого ряд гп сходится.
п = 1
6. Доказать, что для монотонной последовательности {а„}
из сходимости ряда ^ а„ следует, что ап = о ( — V п -* оо.
п = 1 '
7. Пусть вп 4- 0, р > I и ряд У^вп' I — I сходится.
П = 1 \П / СЮ
Используя результат задачи 6, показать, что ряд а„ схо-
П = 1
дится.
оо
8. Привести пример сходящегося ряда ^ап с положи-
п = 1
тельными членами, для которого lim пап > 0.
п—*оо
Всюду 5П обозначает n-ую частичную сумму, а гп — n-ый остаток,
рассматриваемого ряда.
312
9. Пусть ряд ап с положительными членами сходится.
П = 1
оо
Доказать, что ряд сходится.
n=l v'r"-1
10. Последовательность {ап} задана условиями а\ = 1,
2 00 °° Д
a„+i = у. Доказать, что ряд £ а„ сходится, а ряд ^ —==
П=1 П=1 V П
расходится.
оо
11. Пусть ряд ^ап с положительными членами расхо-
п = 1 оо
дится. Доказать, что расходится ряд
П=1 ОО
12. Положим ап = 2П . Доказать, что ряд ^ а„ расхо-
ОО п = 1
— СХОДИТСЯ.
n=l n+1
13. Пусть {ап} и {6П} — две последовательности положи¬
тельных чисел, причем последовательность {ап} монотонна,
ОО
ряд ^Ьп сходится и ап = o(6n), п оо. Доказать, что
П = 1
существует такая монотонная последовательность {/?п}, '«то
00
а„ = о(/Зп), п -> оо, и ряд Р” сходится.
П = 1
Вывод из задач 9, 11, 13. Пусть {ап} — произвольная
ОО
монотонная последовательность. Бели ряд сходится,
п=1
то существует такая монотонная последовательность {ЬЛ}>
ОО оо
что ап = о(Ьп), п -4 оо, и ряд ^ Ьп сходятся. Если ряд ^ ап
П = 1 П=1
расходится, то существует такая монотонная последователь-
00
ность {Ьп}, что Ьп = о(ап), п —¥ оо, и ряд ^ Ьп расходится.
п=1
14. Доказать, что для любой бесконечно малой последова¬
тельности {ап} найдется последовательность bn = (— l)v^n\
313
<p(ri) =1,2, такая, что ряд а.пЬп сходится.
п= 1
15. Пусть последовательность {ап} бесконечно малая и
оо
ряд \ап \ расходится. Доказать, что 1) для любого числа А
п-1
найдется такая последовательность Ьп = (— 1)^п\ <р(п) =1,2,
оо
что ряд ^^ап6„ сходится к А, 2) найдется такая ПОСЛеДОВа-
ri = 1 т
тельность Ьп = (— 1)^п), <^(п) = 1,2, что lim 7 6„а„ = -f оо
т-¥оо ^
п = 1
(сравните с теоремой Римана).
оо
16. Пусть для ряда ап существует такая перестановка
nr 1
00
</?(n):N <—► N, что ряд av>(u) сходится. Доказать, что
п= 1
оо го
ряды ^^(|an| -f an) и ^(|an| — an) сходятся или расходятся
п=1 п — 1
одновременно оо оо
17. Пусть ряд ап сходится, а ряд \ап\ расходится.
р
Доказать, что lim —= 1, где Рт = V'fan + |а„|) и Nm =
т~*оо /Vm “
т n= 1
= £(lanl ~ а")-
п = 1
18. а) Доказать, что если последовательность положи-
оо оо
тельных чисел {an} монотонна, то ряды ап и 2та2*»
П=1 П=1
сходятся или расходятся одновременно.
б) Пусть {г*п} — монотонно возрастающая последователь¬
ность положительных чисел. Доказать, что ряды
■>£('-£:) “ «ЁОГ-О
сходятся, если эта последовательность ограничена, и расхо¬
дится, если она неограничена.
п — 1
т
314
19. Пусть {ап} и {6n} — Две последовательности положи¬
тельных чисел и существует такое число N € N, что ^
^ для всех п > М. Доказать, что из сходимости ряда
оп
оо оо
6П следует сходимость ряда ^ ап.
n = 1 us 1 оо
20. Пусть ап > 0 и ——1 = l-an. Доказать, что ряд ^ ап
П=1
q
сходится, если, начиная с некоторого номера, an > —, где
91
q > 1, и расходятся, если, начиная с некоторого номера,
an < —, где q < I (признак Раабе).
Я оо
21. Пусть ап > 0 и ^ciп ~ 1 —an. Доказать, что ряд ^ ап
п = 1
7 Uin
сходится, если, начиная с некоторого номера, ап > ,
91
где q > 1, и расходится, если, начиная с некоторого номера,
q Inn
or„ < , где q < 1.
fl
22. Пусть {an} — последовательность положительных чи¬
сел и lim \п ( -^2 1 ) — 1 Inn = Ь. Доказать, что ряд
п-юо [ \an+i J J
оо
У] ап сходится, если 6 > I, и расходится, если 6 < 1.
п = 1
23. Привести пример двух последовательностей {an} и {Ьп}
оо
таких, что ап ^ 6П для всех 91 6 N, ряд ^an сходится, а
оо П = 1
ряд ^2 ьп расходится.
п = 1
24. Привести пример двух последовательностей {an} и {&„}
оо
таких, что |а„| > |ЬП| для всех n € N, ряд а„ сходится, а
оо П = 1
ряд расходится.
П= 1
315
25. Доказать, что из сходимости ряда ап с неотри-
п = 1
оо
цательными членами следует сходимость ряда для
п — 1
любого £ > 0.
26. Привести пример монотонной последовательности по-
оо
ложительных чисел {а„} такой, что ряд а2 сходится, a
оо п = 1
ряд ^ ап расходится.
п= 1
27. Доказать, что ряд
11 111 1 1
1п2 ~ 2ln2 ~ 21п2 + ЬГз ~ 31п3 ЗЙГЗ “ зТпЗ + +
_1 1 1 1_+ _ у'д
Inn nlnn nlnn nlnn " n’
П — 1
n членов
где
an =
1 m + m — 4
i ’ n= о ’
In m 2
1 m2 + m - 4 m2 + 3m - 2
—^ < n < ,
m In m ’
oo
сходится, а ряд |a„|^signan расходится при любом q ф 1.
n = 1
28. Пусть {an} — последовательность неотрицательных
оо
чисел. Доказать, что из сходимости ряда а„ следует схо-
П=1
димость рядов.
оо
1) Y ; 2) V ;
й 1+а" ^1 + па"
оо
3) 53max(an, ап+ь ап+2);
п = 1
316
4) ^тт(ап, an+l)..., a2n-i);
«n + Gn + 1 + h 02n-l .
n = l
oo
•>£
П
n = 1
oo oo
6) У ^ 'dn + 1 i 7) ^ ^ >/anan + l • • -a2n-l*
n — 1 n = l
29. Пусть {bn} — последовательность неотрицательных
oo
чисел. Доказать, что из расходимости ряда 6„ следует
п = 1
расходимость рядов:
°о . оо
5Imax(6n’6n+1’ ^-0.
30. Пусть
ГО, пф 2*,
Ьп = < 1 fc
W' "=2*’
Доказать, что ряд ^ 6п сходится, а ряд
п — 1
оо
^тах(Ьп, 6п+ь.... Ь2„-|)
П= 1
расходится (ср. с п. 4) задачи 28 и с п. 2) задачи 29).
31. Пусть
{0, п = 2* — 1,
1 кеы.
-к, п = 2к,
ОО
Доказать, что ряд 6„ расходится, а ряды
п-1
l) £n/M^, 2) 5^min(6n, 6п+1,., 62n-i)
п = 1 п = 1
сходятся (ср. с пп. 4), 6) задачи 28 и с п. 2) задачи 29).
317
32. Пусть
[О, пф 2\
6" = Ь
к£П.
СО оо
Доказать, что ряд ^ 6П расходится, а ряд ^ схо-
n = 1 п — 1 П п
дится (ср. с п. 2) задачи 28).
оо оо
33. Доказать, что из сходимости рядов а2 и ^
П=1 П=1
следует сходимость рядов:
Iе*» I
П=1 П= 1 П = 1
1)£|ап6„|, 2) £>» + 6»)2.
34. Пусть /(х) — непрерывная, строго возрастающая на
[0; -foo) функция, /(0) = 0, lim /(х) = -foo, и д(х) — функ-
х-ч+оо
цця, обратная к /(г). Доказать, что для любых положитель¬
ных чисел а и 6 справедливо неравенство Юнга
а о
аЬ ^ / f(x) dx + Jg(x)dx.
о о
В частности, получить неравенство:
ah ^ Аа1^ + /i-б1^, а>0, 6 > 0, 0<А<1,/1=1 — А.
35. Пусть /(х) — непрерывная, строго возрастающая на
[0;-foo) функция, /(0) = 0, lim f(x) = +00, и д(х) — функ-
х —► 4”Оо
ция, обратная к /(х). Доказать, что если последовательно¬
сти {ап} и {Ьп} неотрицательны, то из сходимости обоих ря-
оо оо оо
дов Y2 a„f(a„), Ьпд(Ьп) следует сходимость ряда ^ апЬп
П = 1 П = 1 П — 1
36. Пусть {ап} и {6П} — две последовательности положи¬
тельных чисел, 0<А<1,/1=1 — А. Используя результат
задачи 34, доказать неравенство Гельдера:
318
1) для любого m Е N справедливо неравенство:
£а„6п<(ЕаЛЛ(х;бЛ';
п = 1 \п = 1 / \п = 1 /
оо °° JL
2) если ряды ^ ап и ^ сходятся, то сходится ряд
П=1 П=1 /°° ЛХ /°° Л"
ап6п, и его сумма не превосходит I a* I I W 1 •
п = 1 \п = 1 / \г»=1 /
37. Пользуясь результатом задачи 34, доказать, что при
q > 1 для любых положительных чисел а и 6 имеет место
неравенство:
аЬч~1 <; -(а9+ (?- 1)6’).
Я
38. Пусть {ап} — последовательность положительных чи-
L Л L а1 + °2 + ^ Лп П
сел, 6о = 0, Ьп = . Пользуясь результатом
п
задачи 37, показать, что для q > 1
6* - тЬ6Г,а" * т~г[(п -
m m
2>
П=1 V П=1
39. Пусть {ап} — последовательность положительных чи-
оо
сел, g > 1 и ряд сходится. Пользуясь результатами
П = 1
задач 36 и 38, доказать неравенство Харди-Ландау:
40. Пусть {а„} — последовательность положительных чи-
оо
сел и ряд ^а„ сходится. Пользуясь результатом задачи 39,
П = 1
доказать неравенство Карлемана:
оо оо
\/ах аг-.. -ап ^ е У"\ап.
П=1 П=1
319
41. а) Пусть последовательность {ап} монотонна, но не
бесконечно малая. Доказать, что ряды
ОО '"О
У] а„ sin па, ап cos па
п=1 п гг О
расходятся при любом а ф тгк, к Е Ъ.
б) Пусть последовательность {ап} монотонна, бесконечно
малая и ряд ап расходится. Доказать, что ряды
П=1
го оо
^«„sinna, ал
П=1
оо
k cos 7i а
п = 1 « = I
сходятся условно для любого а ф пк, к Е /£•
Вывод из задачи 41. Для рядов
со оо
^arlsinna и an cos na,
n = 1 n = 1
где последовательность {an} монотонна, ус ловия I) lim an =0
n —► го
го
и 2) 5^|rtn| < -boo не только достаточны, но и необходи-
п = I
мы соответственно для сходимости и абсолютной сходимости
этих рядов при а ф пк, к Е Ъ.
+ СО
4*2. Пусть / Е С^Г.+оо) и интеграл J f'(x)dx сходится
I ГО
абсолютно. Доказать, что сходимость ряда ^^/(70 зквива-
+ СХ) " = 1
лентна сходимости интеграла I /И dr.
I
43. Доказать, что хотя бы одна ил точек 0 или 1 является
предельной точкой последовательности {тгп — [тгп]}, п Е Н
44. Пользуясь результатом задачи 4.4, привести пример
последовательности {an}, являющейся бесконечно малой,
оо
ДЛЯ которой ряд ^2 ап s*n п сходится абсолютно.
П — I
320
45. Положим
„ -А - Н)П + '
fln — bfi — J—
у/й
оо оо
Доказать, что ряды ^ ап и ^ Ьп сходятся, а их произведе-
П=1 П=1
, оо
ние по Коши, т. е. ряд ^ сп, где ст = ai&m_i -f a2&m-2H 1-
П = 1
-f ат _ 1Ь1 расходится.
2. Функциональные ряды и
последовательности
46. Пусть последовательность непрерывных на М функ¬
ций /п(я) сходится равномерно на М. Доказать, что эта по¬
следовательность сходится равномерно на М.
оо
47. Привести пример ряда ^tin(x), равномерно сходя-
«=1
оо
щегося на [0; 1] такого, что ряд ^ |ип(я)| сходится на [0; 1]
п = 1
неравномерно.
48. Как показывает результат задачи 47, из условий:
оо
1) ряд 5>n(z) сходится на Е равномерно,
п = 1
2) последовательность {vn(x)} ограничена в совокупности
на Еу оо
вообще говоря, не следует, что ряд vn(x)un(x) равномер-
п = 1
но сходится на Е. Какие дополнительные условия достаточно
наложить: а) на последовательность {un(x)}; б) на последо¬
вательность {гп(х)}, чтобы можно было гарантировать рав¬
номерную сходимость ряда vn(x)un (х) на Е?
оо п= 1
49. Пусть ряд ]>>2(х) сходится на множестве М к огра¬
n = 1
321
ниченной функции. Доказать, что из сходимости ряда а2
ОО П = 1
следует равномерная сходимость на М ряда ^ |anun(x)|.
П-\
50. Может ли последовательность разрывных на [а; Ь] фун¬
кций /п(х) равномерно сходиться на [а; 6] к функции /(х),
непрерывной на [а; 6]? Если да, то привести пример, если
нет, то объяснить, почему.
51. Может ли последовательность непрерывных на [а; 6]
функций {/п(я)} равномерно сходиться на [а; 6] к функции,
разрывной на [а; 6]? Если да, то привести пример, если нет,
то объяснить, почему.
52. Привести пример последовательности {/п(я)}> равно¬
мерно на [0; 1] сходящейся к неограниченной функции /(х).
53. Пусть последовательность {/п(я)} равномерно сходит¬
ся на М к функции /(х), ограниченной на М. Доказать, что
существуют такие числа А > 0, N Е N, что |/п(я)| ^ А для
всех п > М и всех х 6 М.
54. Пусть две последовательности {un(x)} и {vn(x)} рав¬
номерно сходятся на М к ограниченным на М функциям и(х)
и v(x) соответственно. Доказать, что последовательность
{u„(x)vn(x)} сходится равномерно на М.
55. Привести пример двух последовательностей {un(x)} и
{г?п(х)}, равномерно сходящихся на [0; 1] таких, что последо¬
вательность {tin(x)t>„(x)} сходится на [0; 1] неравномерно.
56. Привести пример последовательности {/n(z)}, Удо¬
влетворяющей условиям: 1) все функции /п(х) непрерывны
на (0; 1); 2) для любого хоЕ (0; 1) последовательность {/n(*o)}
монотонна; 3) последовательность {/п(я)} сходится к непре¬
рывной на (0; 1) функции /(х) неравномерно на (0; 1). Какое
условие теоремы Дини нарушено?
57. Пусть последовательность непрерывных на [а; +оо)
функций /п(х) сходится к непрерывной на [а;+оо) функции
/(х) и при этом:
1) существуют lim /(х) — А и lim /n(z) = Ап, Vn E N;
X —► -f- OO X —► -f- oo
2) lim An = A\
n—►oo
322
3) для любого хо € [а;+оо) последовательность {/п(хо)}
монотонна.
Доказать, что последовательность {/п(х)} сходится рав¬
номерно на [а; +оо).
58. Пусть последовательность непрерывных и монотон¬
ных на [а; Ь] функций /п(х) сходится к непрерывной на [а; 6]
функции /(х). Доказать, что последовательность {/п(х)}
сходится на [а; 6] равномерно. Верно ли будет аналогичное
утверждение на компакте К?
59. Пусть последовательность непрерывных на (а; /?) фун¬
кций /п(х) сходится на (а;/?) к /(х). Доказать, что для не¬
прерывности / на (а;/?) необходимо и достаточно следую¬
щее условие: для любого отрезка [а; 6] С (а; /?) и любых чи¬
сел е > 0 и N 6 N существует конечный набор интервалов
Uq С (от; 0) и чисел nq 6 N, 1 ^ q ^ Q} таких, что
2) п, > Я, 1 s: q ^ Q;
3) |/п,(*) - /(*)I < е для всех * € Uq, 1 ^ q ^ Q.
60. Привести пример последовательности непрерывных
на [0; 1] функций /п(х), сходящейся на [0;1] к функции / ?
61. Привести пример последовательности непрерывных
на [0; 1] функций /п(х), сходящейся к непрерывной на [0; 1]
функции, и такой, что
62. Привести пример последовательности непрерывных
на [0; 1] функций /п(х), сходящейся к непрерывной на [0; 1]
функции /(х), и такой, что
Q
1)
9=1
5 Л[0; 1].
О
о
323
63. Привести пример неравномерно сходящейся к /бС[0;1]
последовательности непрерывных на [0; 1] функций /п(я) та¬
кой, что
1 1
lim [ fn{x)dx= f f(x)dx.
n-*00 J J
Вывод из задач 60-63. Условие равномерной сходи¬
мости интегрируемых на [а; Ь] функций существенно, но не
необходимо для возможности перехода к пределу под знаком
интеграла.
т
64. Занумеруем множество чисел ^>1 ^ т 2Ч — 1, £ N,
/z mn
и обозначим через элемент этого множества с номером п.
Положим
/п(х) =
1,
0,
х =
( тп 1
■е |^-оо;
U
U[^ + 2^;4°°)’
(тп 1 mn \
\2^п 2<*"~1 1 2?" /
(х-—х ^ + ——\
\ 2?" 2*"-1/ \2^п ’ 2^ 29"-1/
(см. рис. 4).
Показать, что последовательность {/п(я)} расходится в
1
каждой точке отрезка [0; 1], но J /^(х) dx -> 0, п —► оо.
о
65. Показать, что последовательность гладких функций
/п (х) = -7= sin пх равномерно сходится на IR, а последова-
у/П
тельность ffn(x) расходится при любом х £ №.
66. Пусть
1 - (х — \)2п
/п(х) = * х G [0; 1],
324
fn(x)
Рис. 4
fn(x) = ~, х>1,
fn{x) = -fn(-x), X < 0.
Показать, чт?
1) fn E для любого n E N;
2) /„(x) =3 /(x) = 0 на отрезке [—1; 1] ,
3) /^(1) = f'(-l) = 0 для любого n E N;
4) /40) = 0 / iim /„(О) (см. рис. 5).
n—юо
67. Пусть
<Pn(x) =
0,
/„ [2’+' (« - ,&.)! + i , 1
2ч+1
n2«’
n’
x ^ 0,
x€
I
\2e ’ 2«-1
?€N,
*> 1,
где fn(x) — функции, определенные в задаче 66. Показать,
что
1) 'Рп Е C!(IR) для любого n Е N;
325
Рис. 5
2) <pn(z) =4 ¥>(*) = 0 на К;
3) последовательность 'р'п(х) сходится на R;
4) для любого q € N имеем <р' (^jj =0 ф <р'п
68. Функция /о(х) определена условиями:
( *■ [°:^1 ■
.) /„(«>= '
[l х, х € ^2, lj ,
2) периодична с периодом 1.
/о(4я*)
Положим /„ (*) =
(см. рис. 6) и /(*) = £ /nW-
4 It-о
nAAAM/V.
_3_
4»
j L_
4W 24"
1 J_ 3 2_
2 4* 4» 2 4* 4n
Рис. 6
326
Показать, что /(х) непрерывна на R и не имеет производной
ни в одной точке iGM-
69. Показать, что последовательность
равномерно сходится на К к функции /о(я) из задачи 68.
Пользуясь этим, доказать, что непрерывная, нигде не диффе¬
ренцируемая функция /(х) из задачи 68 может быть предста¬
влена как предел равномерно сходящейся последовательности
функций класса С°°(М).
Вывод из задач 65 и 69. Условие равномерной сходимо¬
сти последовательности производных существенно для диф¬
ференцируемости предельной функции даже при условии, что
все функции этой последовательности бесконечно гладкие и
последовательность сходится равномерно.
°° (х 1)
70. Пусть /(х) = ^ —. Показать, что
п = 1
а) /(х) определена на [1;+оо*);
б) /(х) £ С°°(1; +оо);
в) 1 < /(х) < х для всех х 6 (1;+оо);
г) liraI f(x) = 1 Ф /(1);
Г-П +
д) прямая у = х — 1 является правой асимптотой графика
функции у = /(х).
71. а) Пусть последовательность {6П} монотонна и Ьп =
оо. Доказать, что последовательность 5т(я) =
=°G>"
= ^ bn sin пх ограничена в совокупности на [0; 2тг].
п = 1
б) Пусть последовательность {frn} монотонна. Доказать,
что условие 6„ = о п —► оо, необходимо и достаточно
оо
для равномерной сходимости ряда ^P6nsinnx на [0;2тг].
п = 1
327
72. Пользуясь результатом задачи 71, привести пример
оо
равномерно сходящег ося на [0; 7г] ряда Ьп sin х такого, что
оо П-1
ряд £|‘ yisin7ix| расходится при любом х £ (0; 7г).
73. Пусть
<Рп{х) =
0, х = 0,
1
1 У" V " г-
sinnx ч /8
у/п
Показать, что
1) у?п(х) =4 0 на [0;2тг];
2) для любого хо 6 [0;27г] найдется такое п0 € что
последовательность у?п(хо), п ^ По, монотонна;
оо
3) ряд ^ <р„(х) sin nxsin х сходится на [0;27г] неравномер¬
но.
74. Пусть ряд cos пх + 6n sin пх) сходится на Отрез¬
ав
ке [«;/?]. Доказать, что lim (|ап| + |&п|) = 0 (ср. с задачей 44).
п —* оо
оо
75. Показать, что функция /(х) = e_fl cos п2х имеет
гг = 1
производные всех порядков в любой точке х € IR, а ее ряд
Тейлора с центром в нуле имеет нулевой радиус сходимости.
оо
76. Показать, что радиус сходимости ряда ^ п,ппхЛ pa¬
ri = 1
оо
вен 1 и для любого натурального q ряд Ьп,?*"*9, получен¬
ий
ный (/-кратным почленным интегрированием данного ряда,
расходится при |х| = I.
77. Доказать, что если |х| < 1, то из сходимости ряда
оо оо
Х>п(х) следует абсолютная сходимость ряда ^ tin(x)xn.
п = I п = 1
328
78. Доказать, что если ряд ап сходится, то ряд
п = 1
°о а хп °°^
—-—- сходится при всех х, |х| ^ 1; если же ряд ап
гг=1 1 “ ХП п = 1
оо
расходится, то на множестве {х : |г| ф 1} ряды £апхп и
п — 1
ОО п
Еапх
одновременно сходятся или расходятся.
оо
79. Пусть М\ — множество сходимости ряда и
п = 1
П=1
оо .
п!а„
М2 — множество сходимости ряда . .
^*(х+1)...(* + п)
Доказать, что
М2 = Mi -{0, -1, —2,..., —т,...}, теП.
80. Используя равенство
оо
sin X
-п(-£)
п = 1 4 '
(см. стр. 74), получить равенства:
00 л 1 0°
1^2* 1 ~ / 1 1 \
1. ctg х = - + V -г 5-г = - + V + — )
X ' х^— 7Г*П* X V® — *ГП Х + 7ГП У
п=1 п=1 4 '
х ^ 7гА: , к 6 Z.
2х
п — 1 х
2. tgX— 2 (2п-1)»>а
3.^- =-4^-1)”—*
sin X х —
п — \
оо
= 7 + £Н)п(-^ + ;гггг). ****• keZ'
X V X — 7ГП X 4“ 7Г71 У
n = l v '
329
1___L ^ f 1 1 \
l2 x ~ x2 + " \ (x — 7m)2 (x + тгп)2 / ’
fl = 1 7
4.
sin
x ф 7гАг, к € S.
81. Используя равенство
sin £ тт x л*
= I 1 cos —, 0 < x < —
x 11 2" 2
n = 1
(см. задачу 561 стр. 220), доказать, что
ОО 1 ,
El X I ТГ
2^ 2" = I — gх’ 2
П=1
82. Используя равенства
оо оо / 2 \
sh* = х Л (l + ^5^2) > х = П ( I + -(2^1)а,2 )
п~\ п=1 \ 4 /
получить равенства
1 °°
1. cth х — —Ь
2х
X XZ + 7Г2П2 ’
2 1 = 1 I у-У1)"2*
shx х X2 + ТГ2П2
п = 1
3. Суммирование числовых рядов методами
(С, 1) и Абеля
ОО
Пусть дан ряд ап. Сопоставим ему последователь-
Si + S2 + • • ■ + Sn ж
ность сгп = средних арифметических его
п
частичных сумм. Если существует lim <тп = 5, то говорят,
п- —
что ряд ^ ап суммируется методом (С, 1) (методом средних
п = 1
арифметических) к числу S или, короче, (С, 1)-суммируется
оо
к 5; если величина S несущественна, то говорят: ряд ап
(С, 1)-суммируем. n=1
330
Пусть дан ряд а„. Если ряд ^ апхп 1 сходится на ин-
п=1 п=1
оо оо
тервале (0; 1) и lim апхп~1 = S, то говорят, что ряд У] а„
п=1 п=1
суммируется методом Абеля к числу 5; если величина 5 несу-
оо
щественна, то говорят: ряд ап суммируем методом Абеля.
п = 1
оо
83. Доказать, что ряд сходящийся к числу S,
п = 1
(С, 1)-суммируется к тому же числу S (регулярность
(С} 1)-суммирования). оо
84. Доказать, что если для ряда } а„ имеем lim Sn = +оо,
' п—юо
П=1
то lim <тп = -fоо.
71 *Т W | »•
85. Показать, что 5П — <тп = — (гп — 1)ат.
т=2
оо
86. Доказать, что из сходимости ряда ^а„ следует, что
m n = 1
пап = о(т), т —► +оо.
П=1
87. Привести пример последовательности {ап}, не являю-
оо
щейся бесконечно малой, для которой ряд ап (С, 1)-сум-
п = 1
миру ем. оо
88. Доказать, что из (С, 1)-суммируемости ряда ^ ап
п = 1
следует, что an = o(n), n —► -f оо.
89. Пусть ряд (С, 1)-суммируем и ап = <>(-)>
п=1 \п /
п —у оо. Пользуясь результатом задачи 85, доказать, что
этот ряд сходится.
90. Привести пример бесконечно малой последовательнос-
оо
ти {ап}, для которой ряд ^ап расходится, но (С, 1)-сумми-
п=1
руем.
331
91. Доказать, что ряд ^^ап, сходящийся к числу 5, сум-
п = 1
мируем методом Абеля к тому же числу S (регулярность сум¬
мирования методом Абеля).
оо
92. Показать, что если ряд ^an^n_1 сходится на (0; 1),
п— 1
то для х € (0; 1) справедливы равенства
оо оо
1) ^2апхп-' = (1 -
П — 1 П = 1
оо оо
2) ^a„xn_I = (1 -х)2У^п<тпд"~1.
П=1 П=1
93. Пусть последовательность {an} такова, что ряд
оо т
Еапхп сходится на интервале (0; 1) и lim / ап — +оо.
т—юо
п=1 п=0
Пользуясь результатом задачи 92, доказать, что
оо
lim ) anxn~l = -foo.
I —► 1 — *
П—\
94. Пользуясь результатом задачи 92 и равенством
оо
1 = (1 -х)2^пхп'\ х € (0; 1),
П= 1
оо
доказать, что ряд а„, (С, 1)-суммируемый к числу 5, сум-
п = 1
мируется методом Абеля к тому же числу S.
95. Пользуясь результатом задачи 88, привести пример
оо
ряда , суммируемого методом Абеля, но не суммируе-
П=1
мого методом (С, 1).
оо
96. Доказать, что если ряд ап суммируем методом
п = 1
Абеля, то ап = о(1 -f е)п, п —► оо, при любом е > 0.
оо
97. Доказать, что если ряд ап суммируется методом
п = 1
332
Абеля и ап = о ( — j, п —> оо, то ряд ^ ап сходится.
00 п —1
98. Доказать, что если ряд ^ап суммируется методом
ОО П=1
Абеля и ап ^ 0, то ряд ап сходится.
п — 1
4. Бесконечные произведения
99. Пусть {рп} и {gn} — последовательности положитель¬
ных чисел, для которых сходятся бесконечные произведения:
оо оо
Рп и JJ qn • Что можно сказать о сходимости бесконеч-
П —1 П-1
OO OO OO 1
ных произведений: 1) П(р«+?");2) Прп-а>°;3) П —;
п = 1 п = 1 п = 1
4) пПт1’
П-l П — 1
100. Доказать критерий Коши сходимости бесконечно¬
го произведения: условие — для любого € > 0 найдется чи¬
сло Af(e) £ N такое, что для любых натуральных чисел т
п+т
и п > Af(e) справедливо неравенство
(П*)
<7=п
необходимо и достаточно для сходимости бесконечного про-
оо
изведения рп, если рп > 0, Vn £ N.
П= 1
101. Пусть последовательность {рп} монотонна. Дока-
оо оо
зать, что бесконечные произведения П Рп И П p\l сходятся
п = 1 </=0
или расходятся одновременно.
102. Пусть последовательность {рп} монотонна, рп > О,
оо
Vn £ N, и произведение Рп сходится. Доказать, что
оо
103. Пусть рп ^ 1, Vn £ N, и произведение рп сходится.
п = 1
Доказать, что lim nlnp„ = 0.
n-f оо
104. Привести пример последовательности {рп} такой,
оо
что рп ^ 1, произведение рп сходится и lim nlnpn > 0.
п = 1
5. Двойные ряды
Для последовательности с двумя индексами ат п, го, n £ N,
введем обозначения:
Al,o(flm,n) — <*т,п ^т + 1,п,
^0,1 (®m,n ) — ®m,n ®m,n + l j
Al,l(®m,n) — ®m,n ®т+1,п Ят,п+1 ®m+l,n+l =
= Ai,o(am,n) — Ao,i(am+i,n)-
Последовательность атп называется убывающей, если
Ai,o(am,n) ^ 0 и До,1(ат п) ^ 0 для всех m, п £ N. Последо¬
вательность am n называется убывающей в строгом смысле,
если Ai,o(am,n) ^ 0, A0(i(am>n) ^ 0 и Aitl(am|n) ^ 0 для всех
771, п £ N.
Для двойных сумм имеет место преобразование Харди,
аналогичное преобразованию Абеля простых сумм:
т п т— 1 п — 1
« = 1 j = 1 i = l j = 1
m— 1 n — 1
“Ь ^ ^ ,n&\,o{b% ,n) 4“ ^ ^ ^n(j Aq,1 (bm,j ) "Ь 5тпЬтп ,
»=1 J=1
» J
где *•.; = YlYlaP4
q=1p=l
105. Пусть am n > 0, m,n £ N, и существует g < 1 такое,
am,n+1 . am +1,1 /T
что ^ q и ^ g для всех m,n £ N. Доказать,
am,n am,l
oo
ЧТО ряд am,n СХОДИТСЯ.
m,n = 1
334
i тт _ л I _ n am,n +1 ^ ^m,n + l a>m+1,1 ^
106. Пусть am n > 0, 6Ш|П > 0, —2 ^ t~ , ^
®m,n *m,n Am, 1
^ -Г1'1 для всех m, n G N. Доказать, что из сходимости
°т, 1
оо оо
ряда ^
bfixtix следует сходимость ряда ®ш,п •
m,n = l m,n = l
107. Пусть am n ^ 0, m, п Е N, и существует такое g < 1,
что m+^/amn ^ q для всех m, n G N. Доказать, что ряд
оо
am,n СХОДИТСЯ.
m,n = 1
108. Пусть /(х,у) > 0 на [а;+оо) х [6;+оо). Доказать, что
из условий
1) при любом хо G [а; +оо) функция f(xо, у) убывает;
2) при любом уо G [6; +оо) функция /(х, у0) убывает;
3) при любом х G [а; +оо) определена функция
+оо
♦(*) = J f(x,y)dy,
ь
+оо
4) интеграл j Ф(х) dx СХОДИТСЯ,
а
оо
следует сходимость ряда /(a + m,Hn).
m,n= 1
109. Пусть атп > 0, m,rr G N, и последовательность
am,n — убывающая. Доказать, что ряды
оо
У am „ и 2 2р+<?а2»,2«
m,nrl Р,<7=0
одновременно сходятся или расходятся.
110. Пусть {а„} и {Ьп} — две неотрицательные после-
р
довательности, р > 1, q = -. Пользуясь результатами
Р- 1
оо
задач 39 и 36, доказать, что из сходимости рядов а£ и
п = 1
335
°° °° Q b
bqn следует сходимость ряда ———.
n — 1 m,n = l
111. Пусть последовательности am n и bm n удовлетворяют
условиям:
1) существует такое число А, что
т п
£Х>.;
»=ij=1
всех m, n Е
2) последовательность Ьт п — убывающая в узком смысле.
т п
Доказать, что ^ Ab\ti для всех m,n Е N.
;=1j=i
112. Пусть последовательность ат п — убывающая в уз¬
ком смысле. Используя результат задачи 111, показать, что
если ат 1 -4 0, т —У + оо, и ain 4 0, n -) -foo, то ряд
оо
^2 (--l)m+"am,n СХОДИТСЯ.
m,n = 1
ИЗ. Пусть последовательность атп — убывающая в уз¬
ком смысле и lim am i =0, lim a\ n = 0. Доказать, что
m—юо ’ n—foo ’
ряды
oo oo
1) am n cos na cos n(3} 2) am n cos na sin n/?;
m,n= 1 m,n = l
oo
3) £ am n sin nar sin n(3
m,n= 1
сходятся при любых а ф nk, /3 ф nq, k,q E Z.
114. Пусть радиус сходимости каждого из степенных ря-
оо оо
ДОВ ЕЯпхП и £ 6пхп равен 1. Доказать, что для всех х,
П — 1 п=1 СО оо оо оо
|х| < 1, сходятся оба ряда ^ an Ьтхтп и ^ 6m anxnm
п — 1 т= 1 т= 1 п = 1
и суммы их равны.
оо
115. Пусть ряд am nxmt/n сходится в точке (хо,уо)-
m,n= 1
Обозначим через Rn и Ят радиусы сходимости рядов
336
оо ои
ат пхгп и ат,пуп соответственно. Положим
т— 1 n = 1
а = min(|xo|, inf Яп), b — min(|yo|, inf Ят).
Доказать, что ряд <im,n*myn абсолютно сходится в точ-
m,n = 1
ке (х,у) G (-а; а) х (-Ь\Ь).
ОТВЕТЫ, РЕШЕНИЯ, УКАЗАНИЯ
3. Например, a2q-i = a2q = —, q Е М.
Я Я
+оо
1 „ f dx 1
4. Например, ап = -х. Здесь гп ^ / — = ——
J х* п -f 1
п + 1
+ 0О
1 / dx I
5. Например, а„ = Здесь 0 < гп ^ / — = —
п
п
6. Указание. Для произвольного п 6N рассмотреть а,.
Н*1
'(»)
' = О , п ->оо, т- е. a„f = о . п
7. Решение. Так как последовательность
монотонна, то из сходимости ряда anp I — I следует,
Ел!
Умножая обе масти этого соотношения на anp , получаем, что
/ EzlL / 1 \ Р \
ап = о \ апр - , п —> оо, откуда и следует требуемое
утверждение.
1 2 1 2
8. Например, an = —г, пф тп , an = —, п = m , n, m Е N.
гк п
оо
9. Сходимость ряда ■ ■ п- следует из неравенства
О <; -g!L- = r?-LT.Гл =
у/Тп— 1 -^/Гп— 1
_ / /Z /Г“\ \/Ггг“1 ^ о/ /Г /Г~Л
— (y/rn — 1 л/гп)' у ^ 2(>^ГП _ 1 у/гп).
Vrn- 1
10. Решение. Из условия следует, что для любых п Е N
an
и р Е N имеем неравенство: an+p ^ Отсюда получаем,
338
1 00
во-первых, что 0 < ап ^ -- и, следовательно, ряд ап
п=1
сходится, во-вторых, что
rn^al (j + \ + - +2^Г+ •) = а«
оо
и, следовательно, —= ^ 1, поэтому ряд у, “7= расходится.
V*» „=1 vr"
11. Решение. Из соотношения
ат , ®го+1 , , х Sg Sm—q , ы . м
+ > -3—~m€N,fl€N)?>m,
*^m+l
oo
и расходимости ряда ап следует, что при фиксирован-
П=1
ном тп
lim + M ^ 1,
!-*•+«> \bm ья/
q-f+oo y^m
откуда в силу критерия Коши вытекает расходимость ряда
ОО
Ет
П=1 Л
12. Указание: Sn+i >an*2n.
13. Решение. Положим no = 1 и определим числа пя,
q € N, условием nq = min{n : п > ng_ 1, Ьп < Ьт^-Л- Так
как Ьп —► 0+ при п +оо, то числа nq определены для всех
q 6 N и nq | -foo. Положим рп = 6n^, nq ^ n < ng+i. Если
пя^п< п9+1) то справедливы неравенства 0 ^ /?п = ЬПя ^ 6П
в 0 ^ ~ ^ -г"1* Первое из них показывает, что ряд
Рп оп
ОО 4 9
ЕРп сходится, а второе — что lim = 0.
П—►ОО рп
П—1 ОО Нп
14. Указание. Если ряд |an| сходится, то bn = 1 для
П = 1
всех п 6 N; если этот ряд расходится, то утверждение дока¬
зывается аналогично теореме Римана.
15. Утверждение доказывается аналогично теореме Рима*
на.
339
17. Утверждение следует из соотношений:
lim Рт - lim Nm = +00, Sm = Рт - Nm.
m—►+00 m—►+<»
18 а). Указание. Сравнить последовательности и Sq,
п п
где 5„ = У^ач, Sn = У^2га2г.
<7=1 г=1
18 6). Решение.
1. Из условий следует, что для любых натуральных тир
справедливо соотношение
m+p / v т+р
ttm+p + 1 ~ um ^ / j _ tin \ _ цп+1 ~ Цп ^
«т+р+1 n=m V «п + 1 / п=т «п + 1 (1)
^ ttm+p+1 ~ um ^ ^т+р+1 ~ ит
s s •
«т+1 Щ
Если последовательность {un} неограничена, то при фикси¬
рованном m
lim “m+p+1 ~Um = 1,
р-юо ит+р + 1
откуда в силу соотношения (1) и критерия Коши следует рас¬
ходимость ряда } (1 ]. Если последовательность
{un} ограничена, то она сходится, следовательно, в силу кри¬
терия Коши для любого е > 0 найдется такое N{£) € N, что
О < tim+p+i — tim < £-u\ для всех натуральных рит> М(£),
откуда в силу соотношения (1) следует, что для этих р и т
т+Р ✓ ч
имеем: 0 ^ [ 1 — ) < £ и в силу критерия Коши ряд
“п + 1/
Ef1-—)
h'l v u«+i)
сходится. Пункт 2) доказывается аналогич-
\ un + l/
но.
19. Утверждение следует из неравенства
аПо+ч ^апо -!Г±1> ?€N.
®п0
340
20 Указание. Использовать результат задачи 19 и при¬
знак Гаусса.
21. Решение. Из условия следует, что ап = ел|п^1_ап^,
q In п t . . л ч
1 — ап > 0. Если ап > , q > 1, то имеем: п 1п(1 — ап) <
71 ^
< — пап < —q\nn, откуда следует, vto 0 < ап < —, q > 1,
п*
оо .
Е_ q\nn
ап сходится. Если 0 < осп < , 0 < q < 1, для
п
п — 1
п > УУо, то ап —► 0, п -* +оо, и, следовательно, найдутся та¬
кие числа </1, 0 < </1 < 1, и N] € N, что 1п(1 — а„) > —
71
для п > N\. Отсюда получаем, что ап > —0 < q\ < 1,
п?1
оо
тг > N1, и ряд ап расходится. Если же существует бес-
71=1
конечная подпоследовательность пи, для которой аПк ^ 0, то
оо
расходимость ряда ап следует из того, что lim ап ^ 1.
. п —► оо
П — 1
22. Решение. Проведем доказательство для случая Ь < 1.
Доказательство для Ь > 1 проводится аналогично.
Из условия
п __ \ 1
In 71 = 6
lim
n —► + оо
„(-5Ъ--Л-1
. Van +1 /
1
следует существование таких чисел £, 0 < 5 < —, и /Vj,
iV] 6 что для п > N\ справедливо неравенство
71 ^ — 1^ - lj 1ПП $ 1-1
и, следовательно, ^ 1 + — + — , n > N\ Положим
an+i n nlnn
1 00
n iV n ^ 2. Так как ряд } a„ расходится, то в
n(lnn)1 '
v ’ n=2
силу результата задачи 19 для доказательства расходимости
341
ряда ^ ап достаточно найти такое число /V, N £ N, что при
п = 1
п > N справедливо неравенство
ап ^ _ап_ (2)
«п+1 <*п + 1
Возьмем такое N2 £ N, чтобы для п > N2 выполнялось нера¬
венство In ^1 + ^ ^ (l - ^ Тогда для п > N2 имеем,
что
-Въ^Л + Г) ('iHtLtll')1'* =
orn+i V п) \ \пп J
-ИХ'-^Г >
1 1 - е
> 1 н— н .
п п In п
Отсюда следует справедливость неравенства (2) при
п > max(Ni, N2), что и завершает доказательство.
23. Например, ап = Дг, 6П = —
71 П
(-1)П + 1 1
24. Например, ап = — , Ьп =
) - Т1 « •
п п-f 1
26. Например, ап = —.
п
27. Решение. Так как для данного ряда
Sma+m_, =0, т- 2, 3,...,
——
1 m2 + m — 4 m2 + 3m — 4
0<S"<i^' 2 <л< 2 '
го этот ряд сходится и его сумма равна нулю.
Так как ап —> 0, п -* оо, то для q ^ 0 последовательность
{|an|9signa„} не является бесконечно малой, таким образом,
оо
ряд ^lanl’signan расходится. Пусть q > 0, q ф 1, пт =
П = 1
m2 -f т — 6 • / ч
= , т = 2, 3,..., и — соответствующая ча¬
342
стичная сумма ряда ^ \ап\я sign ап. Записав в сумме 5^
П = 1
сначала все положительные, а затем все отрицательные сла¬
гаемые, получим:
т < тп гм 4 / « \
“ 5Z „9 ln« п = (* “ ^Т) '
п = 2 п = 2 п=2 4 7
Для любого q > 0, д ^ 1, разность 1 ^у, п = 2, 3,..не
1- 1
„9-1
> Сq
меняет знака и существует такое Ся > 0, что
для всех п = 2, 3, Следовательно,
m 1
m=2'3
n=2
°° 1
откуда в силу расходимости ряда ^ г—^— при любом q > О
' lnv п
п = 2
следует, что lim \Sft | = +оо при любом q > 0, q ф 1, что
т—>■ -f-oo т
оо
и доказывает расходимость ряда \<*п\я signan при q > О,
П = 1
q ф 1. ^
28. 1) Следует из неравенства 0 ^ -—-— ^ ап. 2) Сле-
а °п
дует из неравенства 0 ^ -—-— ^ ап. 3) Следует из нера-
1 + пап
венства max{an, an+1, an+2} < an + «п-i-i + <»n+2- 4) Следует
из неравенства min{an, an+i,..., a2n-i} ^ an- 5) Обозначим
через 5„ последовательность частичных сумм ряда
Е
П=1
Тогда
+ <*n + l + 1- 02*1 — 1
5 , 02 + 03 , fl3+a4 + a5
«. = «■ + —j—+ j
an-f an+i-f • • •-f в2п-1 ^
343
^ а, + °Л + °3(\ + \) + 04 Q + ■ ■ +
+ а’(^ + ^т + "+тгт)+ "+
+ агп~1{ъЬт+2^2+'"+1) < Е
х ' g = 1
Я
Полученное неравенство показывает, что ряд
Efli + оз + • • • + q2n-l
п
П = 1
сходится. 6) Следует из неравенства между средним геоме¬
трическим и средним арифметическим. 7) Следует из п. 5 и
неравенства между средним геометрическим и средним ариф¬
метическим.
29. 1) Так как -—= 1 , то для сходимости ряда
1 + bn 1 -|- Ьп
°° 6
необходимо, чтобы 6„ -* О, п —У +оо, а при этом
ЬПуп —у -foo, и расходимость ряда > — следует
1 + Ьп ^ 1 + 6„
оо
из расходимости ряда 6„. 2) Следует из неравенства
п — 1
max{ bn у bfi ,.. •) ^2n—i} ^ bn.
30. Решение. Если 2* + 1 ^ п ^ 2/с+1, то
2*+1 + 1 ^ 2n- 1 2*+2 - 1,
следовательно,
^^х{ dfi, An -f-1) • • • ) &2п — 1 } 2^ 1
для 2* + 1 ^ п ^ 2* + 1. Отсюда получаем неравенство:
г^ 2 к j
У! max{an, an^i,..., a2n-i} = 2^+7 = 2 ’
п = 2* + 1
344
что и доказывает расходимость ряда
оо
^ ^ шах{ап, Дп+1) • • •) а2п—i}-
п = 1
33. 1) Следует из неравенства |ап6п| ^ ^2) Сле¬
дует из неравенства (ап + 6П)2 ^ 2(а2 -f 62). 3) Следует из
п. 1).
34. Решение. Построим график функции у — f(x) (см.
а
рис. 7). Величина S\ = J f(x)dx представляет собой пло-
о
щадь фигуры, ограниченной полученной кривой, осью ОХ и
ь
прямой х = а; величина S2 = J д(х) dx представляет собой
V0
площадь фигуры, ограниченной полученной кривой, осью OY
и прямой у = 6. Нужное неравенство вытекает из того, что
площадь прямоугольника со сторонами а и 6 не превосходит
суммы площадей S\ + S2- Полагая /(г) = получим по¬
следнее неравенство.
345
а
35. Утверждение следует из неравенств J f(x)dx^.af(a),
Ь °
Ь д(Ь) и результатов задачи 34.
о
36. 1) Решение. Пусть ап = — г- и /?„ = ■ Л
/ m . \ ^
Тогда
(§■*)* (£*0”
апЬп а / Ао„/Л цЬп **
= <*П Рп ^ + т
1/А у-* »1 //1
(1л4) (М £*
m i
m / m \^/т 1 \ ^ ^ ^
£ “n^n ^l£a") ' ( £ ) т 1 , +
п = 1 \п = 1 / \п = 1 / ап
У* Ьп \г» = 1 / \п=1 /
+ -
£
п = 1
2) Следует из п. 1).
37. Указание. Применить последнее неравенство из зада
чи 34, положив А = и = 1 .
Я Я
39. Решение. Из п. 2 задачи 38 получаем, что
k я
^Ql + <*2 + 1- д|»у
z-u^:L_±±,y
’-‘is \ » J
для любого натурального т. Полагая А = — 1 —
Я Я
346
отсюда в силу неравенства Гельдера получаем, что
Так как
Е(а,+а2! • +апУ>0>
Я1 + а2 + ' * ‘ + ап
то отсюда следует требуемое неравенство.
40. Указание. Применить утверждение задачи 39 к ряду
41. а) Решение. При любом а ф тгfc, к £ Z, последова¬
тельности {sinпа}, {cos па} не являются бесконечно малыми
(доказательство этого факта проводится так же, как дока¬
зательство в сноске на стр. 12). Так как из условия следует,
что последовательность {ап} отделена от нуля, то и после¬
довательности {an sin па} и {aacosna}, а ф irk, к £ Z, не
являются бесконечно малыми, следовательно, данные ряды
расходятся.
б) Утверждение следует из соотношений:
|an sin па| ^ |an|sin2 па = ^—^(1 — cos2na);
|ап cosna| ^ |аа| cos2 па = + cos2na).
42. Решение. Положим Ф(х) = I f(t)dt. Сходимость ин¬
теграла f (х) dx эквивалентна существованию предела Ф(х)
при х —► -foo. Применяя формулу Тейлора, получаем, что
ап и перейти к пределу при q -foo.
п= 1
X
П + 1
Ф(п + 1) - Ф(п) =/(п) + J + 1 - t)dt
П
347
Неравенство
n+1 П+1
J f'(t)(n+l-t)dt ^ j \f'(t)\dt
показывает, что при заданных условиях ряд
со » + ‘
X; / f(t)(n+i-t)dt
П — I ~
сходится абсолютно, откуда следует, что из условия суще¬
ствования предела Ф(я) при х -> +оо следует сходимость ря-
оо
Да
П — 1
СХЭ
Обратно, если ряд ^ f(n) сходится, то из предыдуще¬
го
го рассуждения вытекает существование предела Ф(п) при
п —у +оо. Для х 6 (0; 1) в силу формулы Тейлора имеем
п+аг
|Ф(п + я) - Ф(п)| = \xf(n) + J f (t)(n + х - t) dt\ ^
П
n+1
В силу сходимости ряда f(n) и абсолютной сходимости
+оо П = 1
интеграла J f (х) dx отсюда следует, что Ф(п + х) — Ф(п) —>> 0
1
при п —У оо равномерно на (0; 1), что и показывает одновре¬
менное существование пределов lim Ф(п) и lim Ф(х).
п—ЮО X—► -f-OO
43. Решение. Обозначим через а минимальную, в че¬
рез 6 — максимальную из предельных точек последователь¬
ности {тгп - [тгп]}, n £ N, тогда 0 ^ а ^ b ^ 1. Предположим,
что 0 < 1 — Ь ^ а, тогда найдется такое натуральное число т,
348
1
что или 1)1 — 6= — или 2) 0 < 1 — п(1 — 6) < а. Возьмем
тть
такую последовательность n* t +°°» 1ТО {ппя “ t7171?])
q -> Ч-оо. В первом случае получаем, что
lim т(тгп* — [тгп*]) = mb = m — 1.
Jim (тгтп9 - т[тгп7] — т -4 1) = О,
откуда следует, что для последовательности {(irmnq—[fl*mn<j])}
либо нуль, либо единица являются предельной точкой. Так
как последовательность {(тгтпд — [7гтл^])} есть подпоследо¬
вательность последовательности {(7гп — [*гп])}, то получен¬
ное утверждение противоречит принятому предположению.
Во втором случае, не ограничивая общности, можно считать,
что неравенство 0 < 1 <£ m(l — (nnq — [я*п9])) < Q справедливо
для всех q € N, откуда получаем, что m-1 < m(irnq-[nnq]) < т,
т. е. [nmnq] = m[irnq] + т — 1. Следовательно,
lim (irmnq — [тгтп^]) =
= lim (m(imq — [тги^]) — m 4- 1) = 1 - m(l — 6) < a,
g-f+oo
что противоречит определению a. Итак, предположив, что
О < 1 — Ь ^ а, мы пришли к противоречию. Аналогично дока¬
зывается, что предположение 0 < а < 1 — 6 также приводит
к противоречию. Следовательно, верно хотя бы одно из ра¬
венств: а = 0, 6=1.
44. Решение. В силу утверждения задачи 43 существует
1
последовательность nq t +оо, для которой |smnJ < —.
Я
Последовательность
<7—► +оо
т. е.
удовлетворяет требованиям задачи.
45. Указание. Так как \/к(т — к) ^ —, l^Ar^m—1,то
2 2
|ст| ^ —т = 2.
349
46. Указание. Написать условие критерия Коши равно¬
мерной сходимости последовательности {/п(х)} на М и пе¬
рейти в нем к пределу при х хо, где х Е Л/, хо 6 М.
47. Например,
«„(*) = (-1)в[*"-*п+1].
оо
48. а) Ряд |tin(x)| сходится равномерно на Е.
п = 1
б) Последовательность {«„(ж0)} монотонна при любом
го € Е.
ОО
49. Решение. Для ряда ^^|апип(х)| выполнено условие
П — 1
критерия Коши равномерной сходимости на М. Действитель-
оо т+9
но, пусть А = sup ^2 ип(х) + тогда 0 ^ и2(х) < А
Х^М п=. 1 п=т
любых натуральных m, q и А ^ 1. В силу критерия Коши
оо
и сходимости ряда а2 для любого числа е > 0 найдется
п = 1
такое число N Е что для всех натуральных q и т > N вер-
m+g ^2
но неравенство ^ а2 < —. Отсюда, применяя неравенство
п=т
Коши-Буняковского, получаем, что
1
< е
™+q /т+q \ I /т+<7 \ 2
|a„un(x)| ^ I unix) ) ( £ a" )
n=m \n=m / \n=m /
для всех натуральных q и m > TV, что и требовалось доказать.
г/ч п г / ч D(x)
50. Да, например, /п(х) = х + -, где
о(*> - {J:
х рационально,
х иррационально
функция Дирихле. Здесь каждая функция /п(х) разрывна во
всех точках отрезка [0; 1] и в то же время /„(х) на [0; 1].
350
51. Нет. Это предположение противоречит теореме о не¬
прерывности предельной функции.
52. Например,
/„(*) = 1- i х^О, /п(0) = 0.
X п
54. Указание. Использовать равенство
UnMM*) - ti(r)v(jc) =
= u„(x)[t>n(x) - v(x)] + t>(x)[un(x) - u(x)]
и результат задачи 53.
55. Например,
п2х2
vn{x) ^ _j_ nx^2n — x) ’
u„(x) = - - X Ф 0, u„(0) = 0.
X In
56. Например, fn(x) = яп- Нарушено требование ком¬
пактности множества, на котором заданы все остальные ус¬
ловия.
57. Решение. Возьмем произвольное число е > 0. Из
условия 2) следует существование такого числа N\ Е N, что
\Aj\fl — Л\ < -, а из условия 1) — существование такого числа
£ £
Ь> а, что |/(х) - А\ < - и |/лг,(х) - Л*,| ^ - для всех х ^ Ь.
Для всех х € [Ь; +оо) и любого натурального числа п > Ni из
условия 3) следует, что
\fn(x)~f(x)\ ^ |fNl(x)-f(x)\
$ l/jVi(*) - + I-An, - A\ + \ A - f(x)| < e.
На отрезке [a;6] последовательность fn(x) удовлетворяет ус¬
ловиям теоремы Дини, следовательно, существует такое чи¬
сло N2 Е N, что \ fn(x)—f(x)\ < е для всех х 6 [а; 6] и всех*нату¬
ральных п > ЛГ2. Отсюда получаем, что \fn(x) — f(x)\ < е для
всех х Е [а;+оо) и всех натуральных n > N = тах{ЛГь #2},
что и требовалось доказать.
351
58. Решение. Не ограничивая общности, можно считать,
что каждая из функций /п(х) неубывающая, тогда и функция
/(х) — неубывающая на [а; 6] Положим
а(Ь — а)
Хат - а + , 0^7$ т, m Е N.
771
Для любого числа е > 0 в силу непрерывности f(x) существу¬
ет такое гп Е N, что \f(xqm) - f(xq_] m)\ <-,!$?$ m,
а в силу сходимости fn(x) и f(x) на [а; 6] существует такое
N 6 N, что 0 5$ \fn{Xq n\) /(*<f,m)| < - для всех (/, 0 ^ q ^ 7Г1,
и всех натуральных п > N. Если х Е x7>m], 1 ^ <? ^ т,
то, используя неубывание функций fn(x) и f(x), получаем,
что
|/п(х)-/(х)К
^ | fn(Xq,m) ~ f (Xq- I ,т)\ ~ f{xq,rn)\ $
$ |/п(л>(7,т) “ /(^<7,т)| + |/(^q,rn) — /(г^--1,т)| +
+ \fn(Xq- \ tin) ~ f(xq- 1,т)| 4 \ f {Tq- \ ,т) ~~ 7(^)1 < £
для любого натурального п > N. Так как
т
[(J,6] — [x(f- 1 m , X<j,m],
q-\
то неравенство |/n(x) - /( *)l< e при 7J > N справедливо для
всех x E [a; 6], что и требовалось доказать. На компакт К
доказательство переносится дословно.
59. Решение. Необходимость. Пусть [а; 6] С (с*;/?). Для
произвольных фиксированных чисел е > 0 и N Е N положим
Ет =•- {* : х € («;/*), |/(*) - /л/+га(*)| < е}, тп £ N. Из сходи-
мости /п(х) к f(x) на (or;/9) и непрерывности функций /п(х)
и /(х) на (а;/Я следует, ч го каждое из множеств Ет) m Е N,
является объединением интервалов и совокупность всех этих
интервалов представляет покрытие отрезка [а; 6]. Выбрав
из полученной совокупности интервалов конечное покрытие,
обозначим полученные интервалы через (Jq и соответствую¬
щие им числа вида N + т через nq, 1 ^ q ^ Q. Полученный
набор интервалов и натуральных чисел удовлетворяет требу¬
емому условию.
352
Достаточность. Пусть хо € (<*;/?)• Возьмем произволь¬
ное число е > 0. В силу сходимости /а(хо) к /(хо) найдется
такое ЛГ £ что |/п(х0) — /(х0)| < - для всех натураль-
и
ных п > N. Возьмем отрезок [а;6] С (<*,/?)> содержащий
внутри себя точку xq. Пусть набор интервалов Uq и чисел
nq £ N, 1 ^ q ^ Q, соответствует отрезку [а; 6] и числам
N. Обозначим через Uq интервал Uq> содержащий точ-
и
ку х0, и через по — соответствующее натуральное число. В
силу непрерывности функции /По(х) на (а;/?) существует та-
кое числоS > 0, что (х0-<5; х0+<5) С U0 и |/п0(х)-/„о(х0)| < ^
для всех х € (*о — <5; хо + <$)• Отсюда для х € (хо — 6\хо + 6)
получаем соотношение: |/(х0) - /(х)| ^ \f{x0) - /00(^0)! +
+ 1/п0(хо) - /«„(*) I + !/«„(*) - /(*) I < 3 - = е, что и дока¬
зывает непрерывность функции /(х) в произвольной точке
353
Го € (а;/?).
60. Например,
fn(x) =
1
/ X п
\п2х, 0
-^х<С 1,
п
0<х< i
(см. рис. 8).
61. Например,
2п ^"х,
2п
/п(х) = ^ -2п п( 1)П (г - £-) , < а; < -
п 2тг п
О,
(см. рис. 9а, б).
- I
п
У =
1
1
4fc+2 2* + 1
в;
62. Например,
4 п2х,
/„(*)= < _4п2(*-1),
О,
0^х<-,
2т» ^ < гг’
- $*<: 1
п
(см. рис. 10).
1
354
Рис. 10
63. Например,
2 nx,
fn(x) = < —2n - i) ,
0,
2n ’
1 ^ 1
^ X < -,
2n n
- ^ X ^ 1
n
(см. рис. 11).
64. Решение. Из определения /п(х) получаем, что
и так как </„ -* +оо при п —► оо, то, следовательно,
1
[ fi(x)dx = 0.
n-юо J
Пусть хо € [0; 1]. С одной стороны, существует такая под*
последовательность nj f +оо, что /п,(хо) = 0, а с другой
355
Рис. 11
стороны, существует такая бесконечная последовательность
m„t 1 тп% 1
Щ t Ч-OO, ЧТО Xq £
1
24ni 29п* ’ 29п« 2Япг
и, следователь¬
но, /П|(хо) ^ откУДа и следует расходимость последова¬
тельности /п(х о).
65. Указание. Использовать то, что последовательность
{cosnx} не является бесконечно малой ни при каком х £ IR.
68. Решение. Так как 0 ^ /о(х) ^ х £ R, то 0 ^ /п(х) <
< тДтГ) х £ IR, и непрерывность функции /(х) следует из
оо
2-4"
равномерной сходимости ряда /п(х) на IR. Для любой точ-
п = 0
ки хо £ Ш найдется последовательность вложенных отрезков
Яп 1 Яп ^ ^ содержащих xq. На отрезке Дп
Ап =
2 4п ’ 2-4п
1
4n+i
. Если т > п, то
возьмем точку хп, отстоящую от хо на
число ^ является периодом для функции /т(х), следова¬
тельно, — -Х-п -—= 0. Если т ^ п, то функция /т(х)
Хп Хо
линейна на Дп и ее угловой коэффициент по модулю равен 1.
356
Поэтому
/(*n) - /(жо) _ у fm{xn) - /т(=о) _ у'/ nv>(m)
*»“*«> ^ X"-r0 Ьi
где <р(т) равно 0 или 1 и, следовательно,
f(xn) — /(хо) __ Г четному целому числу при нечетном п,
хп — хо \нечетному целому числу при четном п.
^ /(^п)-/(х0)
Отсюда видно, что отношение не имеет преде-
хп Хо
ла при п —у +оо. Так как при этом хп —У хо, то, следователь-
/(х) - /(хо)
но, и отношение не имеет предела при х -* хо-
х - Хо
70. Решение. Пункты а) и б) следуют из определения /(х)
и равномерной сходимости при любых фиксированных к
00 In* п
и е > 0 ряда ^ —— на [б:;+оо). Запишем функцию /(х) в
_ TL
п — 2
оо X 1
виде /(х) = х — 1 -f ——. Из неравенства
о 71
п=2
/ — л<£—< I —Л= 1, Х> 1,
2X_1 J tx J Iх
2 n=2 1
получаем правую часть неравенства в). Так как In2 <1,
In 2
то ^ ” 2^-1 > ® Д*®* х ^ откуда следует, что функция
х ~~ 1 + 2* -1 монотонно возрастает на [1; -|-оо), и следова¬
тельно, для всех х > 1 имеем неравенство х — 1 4- > ^
Пункт г) следует непосредственно из п. а) и п. в). Соотноше¬
ния
1 00 1
х — 1 х — 1
2* ^ п1
п=3
+оо
n V- X -1 /■*-!., 1
0 < > < / dt — -—- х > 1,
пх J t* 2r_1
п=3
357
показывают, что lim [f(x) — (x — 1)] = 0, т. е. справедливость
т —► -f- оо
П. д).
71. а) Решение. В силу периодичности и нечетности фун¬
кций Sm(x) достаточно найти такое число М, что |5m(x)| <С М
для всрх х £ (0; 7г) и всех т £ М. Пусть С — sup|n6„|. Для
х £ (0; 7г) положим /1 = j. Если m ^ /i, i
|5т(х)| ^ £ \bn sin пх | |^6пх| ^ С fix ^ Стт.
П=1 П=1
Если же m > /1, то
frnsii
I'S'mlx)! < l”6nXl +
n = l
m
53 ft"si
UZZfJi + 1
sm nx
n = *i+l
Для оценки суммы ^ 6n sin nx применим к ней преобра¬
зование Абеля:
6n sin пх
п=р + 1
гтг- 1
^2 (bn-bn+i)B„(x) + bmBm(x)-b„+lB„{x)
n = *i-f 1
где Bq{x) = Г sin пх. Так как
П — 1
|5,(х-)| ^ х G (0; тт), ?GN,
X
(см. стр. 44- 45) и последовательность {6П} монотонна, то от¬
сюда получаем, что
Ьп sin пх
п = ц~f 1
^2|Ьй+1| - + 2|Ьт| - ^ < 78-^п-
X XX x(/i + 1)
358
Из определения числа р, следует, что — < /1 + 1, откуда окон-
х
чательно получаем для т > р оценка:
|5ш(х)[ ^ Сп + 8Стт = 9С7Г,
что завершает доказательство.
6) Указание. Для доказательства необходимости рассмо-
2т
треть V 6„sinxm, где хт = -—. Доказательство доста-
' 4 т
П—ТП
точности проводится аналогично доказательству в решении
предыдущей задачи.
sin пх
72. Например, > —7—7 —.
nln(n+ 1)
73. Указание. Для любого m <Е N рассмотреть
2т
У <^„(xm)sinnimsinxm>
n=m
2
где хт =
у/т
74. Решение. Запишем ряд cos пх -h bn sin пх) в виде
П-\
оо
Урп cos[n(r - <рп)), где рп = + Ь*. Надо доказать, что
п = 1
lim рп — 0. Если это не так, то найдутся такая последова¬
ть—юо
тельность натуральных чисел nq f +00 и такое число С > 0,
что \рпя\ > С для всех q € N. Пусть mi — первый член по-
2тг
следовательности nqy большии, чем — . Тогда на отрезке
[а;/?] функция cos[mi (х — <ртх)] принимает все значения от —1
до 1, следовательно, существует отрезок [а\\Р\] С [<*;/?], на
котором cos[mi(x — y>mi)] ^ и тем самым
Рассуждая аналогично, найдем число m2 и отрезок
[(*2,02} С [ai;/?i] такие, что
| pm2 cos [m2 (х - х € [си2,02]-
Продолжая этот процесс неограниченно, получим возраста¬
ющую последовательность натуральных чисел т*, к £ N, и
последовательность вложенных отрезков [or*;/?*] таких, что
С
\ртк cos[t»*(x — ipmk )]| > —, х G [c*fc; /?*] Для точки £ G
€ Р|[а*;/?*] имеем
к = 1
с
lim |рп cos[n(4 - v?n)]| ^ — > О,
П—ЮО I
и, следовательно, ряд ]T^/>nCOs[n(£ — <£>п)] расходится, что
п = J
противоречит условию.
оо
75. Решение. Ряд e-n cos п2х сходится при х = 0; все
п= 1
его члены tin(x) бесконечно дифференцируемы на IR; для лю¬
бого натуральног о q имеем: (ип(х))^ = е~п-n2q cos (ri2x-
00 00
и в силу сходимости ряда ^ е~пп2д ряд ^^(un(x))^ сходит-
п=1 П=1
ся равномерно на IR. Следовательно, / £ C°°(1R). Ряд Тейло-
00 х2 q 00
ра /(х) с центром в нуле имеет вид ^ -- -- е~пп4д.
п=0 ' п = 1
Итак, для доказательства утверждения задачи достаточ¬
но показать, что
\
1 °°
Х]6-"”49 +°°- (3)
Используя неравенство п! < е , получаем,
— У e~nnAq > = I (
(2^)- ' eq2<*eA<* е \ е2 ) ’
что
2 q
360
откуда и следует соотношение (3).
76. Следует из равенств
f jjln П
lim п“ = 1 и lim — — — ; = оо
п-¥00 п-юо п(п + 1 )(п + 2) . . . (п + Я)
для любого натурального q.
77. Следует из неравенства:
|Un(z)*"| ^ |l|nSUp|«„(l)|.
П
оо
78. Решение. Если ряд сходится, то радиус сходи-
П= 1
оо
мости степенного ряда ])^anxn не меньше 1, следовательно,
П = 1
оо
ряд Е апхп сходится абсолютно для любого х, |х| < 1. Если
п = 1
оо
|х| < 1, ТО
^ Кхп\ ^ апхп
1 _ ХП ^ 7ГТЛ* следовательно, ряд ^ у—;
' ' П = 1
сходится абсолютно. Если же |х| > i, то сходимость ряда
^ апхп апхп ап (£)п
> следует из равенства = -ап - - fr-fi
1 - хп 1 - хп 1 - (I)
П=1 \т)
оо
и вышеприведенного рассуждения. Пусть теперь ряд ап
П = 1
оо^
расходится. Если |х| < 1 и ряд —2—- сходится, то,
П = 1 1 ~~ *П
77 п «П«П
применяя результат задачи 77 и равенство апх =
1 — хп
а хп °°
- ^—п'хП' получаем, что сходится ряд У^апхп. Обратно,
1 х
п = 1
оо
пусть |х| < 1 и ряд ^ апхп сходится. Так как последователь-
п = 1
1
ность ^ монотонна и ограничена, то в силу признака
о° а хп
Абеля сходится и ряд ^ п . Опять применяя результат
п=\1~х П
361
00 л
anxn
EUfj X
- —, откуда в
1 x
n = 1
силу равенства
anxn an anxn
1 — xn 1 — x2n 1 — x2n
00 „
anjc
получаем, что сходится ряд . Осталось показать,
1 х
п = 1
сю
что из расходимости ряда ап следует расходимость ряда
п = 1
оо п
ЕЛ X
—-—- для всех х : |х| > 1. Действительно, если |х| > 1 и
П — 1
0° п п
Еапх апх ап
х _ — сходится, то из равенства у—^ уЦп и
п=1
СЮ / 1 \ п
ап \х)
результата задачи 77 следует, что сходится ряд 2_^ тугй ,
п — 1 * ~ Vi/
«п ф"
откуда в силу равенства а„ = следует
оо
сходимость ряда что противоречит принятому усло-
п = 1
ВИЮ.
79. Решение. Равенство
апп\ ап п\пх
х(х + 1 )...(x + n) пг х(х + 1)... (х + п)
показывает, что в силу признака Абеля для доказательства
данного утверждения достаточно показать, что для любо¬
го х ф 0,-1, —2,..., —m, т £ N, обе последовательности
_ п\пх 1
Рп = гг : г и — ограничены и локально моно-
х(х + 1)...(х + п) Рп
тонны. Так как
Рп+1 (п + !)*+»
Рп пх(х +
утверждени
Рп — ^1 + — ^ локально сохраняет
то это утверждение эквивалентно тому, что последователь-
L }х+1 / • 1\ ”1
ность ~
362
знак и произведение Рп сходится, а это утверждение сле-
П = 1
дует из соотношения
1 -
г2г,2
80. Указание. 1) Показать, что ряд In |*|+]Г^ In
П = 1
допускает почленное дифференцирование в окрестности лю¬
бой точки х ф 7гАг, к Е Ъ. 2) Использовать равенство tgx =
= ctg - *) . х Ф ^ + **'. к £Z. 3) Использовать равенство
1 XX
= tg — -h ctg —, х ф тгку к Е Z. 4) Показать, что ряд из
sin х 2 2
п. 1 допускает почленное дифференцирование в окрестности
любой точки х ф 7гАг, к Е Z.
оо
81. Указание. Показать, что ряд In cos —, 0 < х < —,
П = 1
допускает почленное дифференцирование в окрестности лю¬
бой точки х Е ^0; ^ .
82. Указание. Обоснование этих равенств полностью ана¬
логично обоснованию равенств I) и 3) в задаче 80.
83. Решение. Возьмем произвольное е > 0 и найдем такое
число iV Е N, что для n > N имеем |5 — 5П| < -. Пусть
т > N. Представив разность Sm — S в виде
(S1-S) + (S2-S) + ..-+(5Ar-S) (
т
[Sn+ 1 - S) 4- h(Sm — S) т - N
m-N т ’
363
видим, что
N
- S)
km - •*>! ^ —
771
q= 1
e(m - N)
+ L:
откуда следует, что существует число N\ 6 N, N\ > TV, обла¬
дающее свойством: для всех тп > N\ имеем |<тт — 5| < £, что
и завершает доказательство.
84. Доказательство аналогично доказательству утвержде¬
ния задачи 83.
86. Следует из результатов задач 83 и 85.
87. Например, ап = ( — 1)п_и.
88. Следует из соотношения:
ап - п сгп + (п - 2)сг„_2 - 2(n -
90. Например,
s \ - n -1-11 _1 \
“п 2 ’ 2 ’ 2’ г’З’З'З’ 3’ 3’ 3
т. е.
ал = —, m(m— 1) < п ^ш2, ап = — —, тп2 <п<^ 771(771 + 1)
т т
95. Например, ап = (— 1)п п.
96. Указание. Использовать формулу Коши для определе¬
ния радиуса сходимости степенного ряда.
97. Решение. Применяя результат задачи 83 к ряду
оо 1 Ш
Е(1П<*Г»1 - |(» — l)<Jn-i|), получим, что lim — У^|па„|=0.
т—Юо ГП
п=1 п=1
Возьмем произвольное е > 0 и найдем такое N £ N, что для
всех m > N' имеем:
771
п= 1
Пусть хт = 1 , тогда в силу неравенства Бернулли для
771
/ J \ п -1 fi — \ л
любого п £ N имеем 1 — я"-1 = 1 — ( 1 ) <С < —.
\ 771/ 771 771
364
Таким образом, для т > N получаем:
£
- «Г1
^5>n|(l-C-‘)+ £
n = l n=m + l
т оо
1 '' • ^ 1
1 v—> . , £ ^ п.—1 £ £ 1
^ m^|n“n| + b Е *•» <2 + 2^'Т^=£’
п= 1 п=т+1
откуда в силу соотношения lim хт = 1 следует требуемое
m-foo
утверждение.
98. Следует из результата задачи 94.
99. 1) Расходится, так как не выполняется необходимое
условие сходимости бесконечного произведения.
2) Сходится к (п
3) Сходится к
П Рп
П = 1
4) Сходится к
Й
Pnj q”j
5) Сходится к (п Pnj : ^ri9nj*
оо
100. Заметим, что как из сходимости рп, так и из
п = 1
условия критерия Коши следует существование таких чисел
а > 0, Л > a, N £ N, что
п
а < Пр9 < А’ (4)
<7 = 1
m > N и п > N, поэтому будем использовать это соотноше¬
ние как в доказательстве достаточности, так и в доказатель¬
стве необходимости условия критерия Коши.
Достаточность. Из соотношения (4) получаем, что для
365
п > N -1-1 и любого натурального т справедливо неравенство
n+m п — 1
П р* - П р* =
к~\
к = \
п— 1
П р*
fr = l
откуда в силу условия критерия Коши вытекает, что после-
п
довательность частичных произведений Рп = J"J рк удовле-
к-1
творяет критерию Коши сходимости последовательности и,
следовательно, сходится.
Необходимость. Возьмем произвольное число б > 0 и по¬
ложим е 1 = а£, где число а определено в соотношении (4).
В силу критерия Коши сходимости последовательности Рп =
п
- Рк найдется число Ni 6 N такое, что для любых нату-
/с = 1
ральных 771 и п > /V справедливо неравенство |Pn+m—Рп-\ I < ^1
Отсюда для 71 > max{7Vi, TV} получаем, что
^n+m
. , у 1 > а ( ТТ Ро ) — 1
Kq = n
/п+m
1
е, = ае > |P„_i|
т. е. неравенство
\ * ' \
(П р*) -1 >мПм
^ q = n гл—п '
l+m ч
Пр.)
Г7 —п '
< справедливо для любых
натуральных тп и п > N2, где N2 = max{7Vi, ЛГ}.
2* fc
101. Указание. Сравнить П Р» н 11 Р23 •
t=l j=o
102. См. решение задачи 6.
104. Например,
Рп =
п, m £ N
(ср. с задачей 8).
366
105. Следует из неравенства 0 < am n ^ a\ iqm^n 2 и
оо
сходимости ряда gm+n.
m,n = l
106. Следует из неравенства 0 < ат „ ^ Ьт п-т^--
107. Следует из неравенства 0 ^ am n ^ gm+n и сходимо-
оо
сти ряда gm+n.
m,n = 1
108. Решение. В силу интегрального признака сходимо-
оо
сти простых рядов ряд ^ /(a + т, 6 + п) сходится и его сум-
п = 1
ма 5(т) удовлетворяет неравенству 0 ^ S(m) ^ F(a -f m).
Из условия следует, что F(x) — неотрицательная убываю¬
щая функция на [а; +оо). Снова применяя интегральный при-
оо
знак сходимости простых рядов, получаем, что ряд ^ S(m)
т= 1
сходится. Так как последовательность /(а + т,Ь -+ п) нео-
оо
трицательная, то сходимость повторного ряда 5(ш) =
m= 1
оо оо
= f(a + т, Ь + п) эквивалентна сходимости двойного
m=l n = 1
оо
ряда 53 /(a + m,6 + n).
т,п = 1
2* 2J * j
109. Указание. Сравнить ^ ^am n и ^ ^ 2р+<7а2р,2«
m=l n = l р=0д=0
и использовать то, что сходимость ряда с положительны¬
ми членами эквивалентна ограниченности множества его ча¬
стичных сумм.
110. Решение. Равенство
ОО , ОО.ОО,
m + n " m + n ^ m + n
m,n = l ,
m = l n = l
l^n<m l^m^n
367
ОО , Oj ,
,, amVn ,1 ат&п
и симметрия рядов ,Sj = > и ^ = >
' 7П + 71 ' 7П -J- 71
m = 1 n = 1
l^n^m l^m^n
показывают, что достаточно провести доказательство схо¬
димости только для ряда S^. Положим Ап — а\ -+Я2 + • * * + ап,
оо ^ °° /\
тогда 52 ^ > --- -п- = > —Ьп- Неравенство Харди-Лан-
' 71 ' 71
. п=1
п = 1
n^m ^
дау (см. задачу 39) показывает, что ряд ( — ) сходится,
ед
п=1 4 7
а неравенство Гельдера (см. задачу 36), — что сходится ряд
°° л °о ,
Е. am&n
6„, откуда и следует сходимость ряда > .
71 ' m-f-n
n = l п,т=1
112. Указание. Записать разность Sm+Pin+q — 5m n в виде
V Я ГП д
EE(-i)m+n+,+>am+<1n+i+££(-i)r+n+v»+i +
i = 1 J = 1 *=lj = l
m+t
i = l 5=1
и применить результат задачи 111.
113. См. указание к задаче 112.
114 Указание. Использовать неравенство
|an6m*mn| <: |anxn| |6mxm|, m E N, п E N, m > 1, n > 1,
и свойства абсолютно сходящихся рядов.
115. Указание. Доказать, что для (х,у) Е (—а; а) х (—6; 6)
последовательность ат пхтуп ограничена.
Глава II
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
И ИНТЕГРАЛЫ С ПАРАМЕТРОМ
§ 1. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
Определение А. Пусть и> — собственная или правая
несобственная (+оо) точка числовой прямой и функция
f:[a\u) —> Ш интегрируема в смысле Римана на каждом от¬
резке [а; 6] С [а\и>). Тогда, если существует предел
6
lim [ f(x)dx, (])
b-+u>— J
a
u>
J f(x) dx и
то его величина обозначается j f(r) dx и называется несоб
a
ственным интегралом функции / по промежутку [а;и>) и фун¬
кция / называется интегрируемой в несобственном смысле на
[а;ы).
Сам символ I fix) dx также называют несобственным ин-
.//<«
тегралом. Если предел (1) существует, то говоря'г, что дан¬
ный интеграл сходится или является сходящимся интегралом.
Если предел (1) не существует, то говорят, что данный ин¬
теграл расходится или является расходящимся интегралом.
Таким образом, вопрос о сходимости несобственного интс-
ы
грала J f(x)dx есть по сути дела вопрос о том, является ли
а
и
символ J f(x)dx определенным чис лом пли но г.
а
Ь
Точно так же, рассматривая lim I f(x) dx, можно oilре-
(1 ->-Ы 4- J
a
делить сходимость и величину пли расходимость нссобствен-
369
ь
ного интеграла J /(х) dx, где и — собственная или левая пе-
и>
собственная (—оо) точка числовой прямой.
Поскольку оба определения симметричны, то все утверж-
ш
дения в дальнейшем приводятся для интеграла вида J f(x)dx.
а
Если ы есть собственная точка числовой прямой и / Е
6
€ Я[а;ы], то / G R[a\b] для всех b Е (а;ы) и lim I f(x)dx =
b—tuj — J
a
и/
= J /(*)<**• Это свойство выражают так: несобственный
а
интеграл есть обобщение интеграла Римана, и эти интегралы
неп роти вореч ивы.
Рассмотрим, насколько расширилась область применения
операции интегрирования с введением понятия несобственно¬
го интеграла.
Во-первых, появляется возможность интегрирования по
+оо
бесконечному промежутку. Символ J /(х) dx не может быть
а
определен конструкцией Римапа или Дарбу, поскольку в эти
конструкции входит длина промежутков разбиения проме¬
жутка интегрирования, что подразумевает конечность этих
промежутков и, следовательно, всего промежутка.
Во-вторых, появляется возможность интегрировать неог¬
раниченные функции.
Согласно определению А для того, чтобы ставить вопрос
о сходимости интеграла J f(x)dx, необходимо, чтобы функ-
а
ция / была интегрируема в смысле Римапа на каждом отрезке
[в; 6] С [а;и;). Пусть {е,,} — монотонно возрастающая пос ле¬
довательность: е] ^ а и lim £„ — ы. Тогда в силу критерия
370
Лебега*) функция / ограничена на каждом отрезке [а:е„]
и множество Мп точек разрыва / на [а;£„] есть множество
меры нуль. Следовательно, функция / может быть неограни-
чена 'голько и левой полуокрестности точки ш и множество М
оо
точек разрыва / на [п\и) п силу равенства М — Мп есть
П = 1
множество меры нуль.
Обозначим символом (а, 6) собственный или несобствен¬
ный промежуток, не уточняя, является ли он интервалом, по¬
луинтервалом или отрезком, с возможным исключением ко¬
нечного множества точек. Точки а и b будем называть конце¬
выми точками промежутка (а, 6) независимо от того, являют¬
ся ли они собственными или несобственными точками число¬
вой прямой. Несобственную точку числовой прямой и такую
собственную точку, что в любой левой или любой правой по¬
луокрестности ее функция / неограничена, будем называть
особыми точками функции /.
Пользуясь введенными терминами, заметим, что опреде¬
ление А есть определение несобственного интеграла функ¬
ции / на промежутке (а^и) в том случае, когда особой точ¬
кой функции / является только правая концевая точка про¬
межутка (а,о;); а затем определен несобственный интеграл
а
ff(x)d х, если особой точкой функции / является только ле¬
ей
вая концевая точка промежутка {и), а).
Определенно В. Пусть функция /:(а,/?) —► R имеет на
промежутке (а , /3) конечное число особых точек и
Т : а = ао < ai < ... < ап = /?
такое разбиение промежутка (а,/?), что на каждом из
j, а,), 1 ^ ?*, особой точкой функции / является толь¬
ко одна из концевых точек. Тогда
•^Функция / Е Я[а;Ь] тогда п только тогда, когда она ограничена
на |п;6] и множес тво се точек разрыва на [о; 6] ость множество мери
нуль.
371
“ >
а) если каждым из интегралов j f(x)d.r. \ f i ^ п,
р
сходится, то интеграл J f(x)dx называется сходящимся (ин-
0 а
теграл J f(x)dx сходится), его величина полагается ранной
(X
" ?
I f(x)dx и функция / называется интегрируемой в не-
»=1Л
а. — I
собственном смысле на (а,/?);
<>•
б) если хотя бы один из интегралов J f(x) dx расходится,
интеграл J f(x) dx называется расходящимся (интеграл
Р
то
(3
J f(x) dx расходится).
а
Это определение корректно, т. е. ни сходимость или расхо-
Р
димость интеграла J f(x) dx, ни его величина в случае сходи-
Ог
мости не зависят от выбора разбиения Т, удовлетворяющего
сформулированному условию.
Обратим внимание на то, что выражения “функция / не
интегрируема в несобственном смысле па (а,/?)” п “иите-
Р
грал J f(x)dx расходится” не полностью тождественны.
« р
Именно, говоря “интеграл J f(x)dx расходится", мы Пред¬
ок
полагаем и конечность множества особых точек функции /
на (а,/?), и интегрируемость в смысле Римана функции / на
любом отрезке \и\Ь] С (п,/?), не содержащем особых точек, и
372
утверждаем только го, что хотя бы один из пределов. входя
iii.liх и определение несобственного интеграла по промежутку
(о,_]:п,) с концевой особой точкой, не существует. Пмра-
желне “функция / не интегрируема на (а;/?) и несобствен¬
ном смысле” может, кроме того, обозначать и то, чгго мно¬
жество особых точек функции / на (а;/?) бесконечно, и то,
что / не интегрируема в смысле Римаиа па некотором от¬
резке [ci\b] С (а;/?), не содержащем особых точек функции /
(в силу критерия Лебега это эквивалентно тому, что множе¬
ство точек разрыва / на [а; 6] и, тем более, на (or;/?), не есть
множество меры нуль).
+ оо
/dx
- Функция
1 + хг
1 0
/(х) = - на (0;-foo) имеет одну концевую особую точ-
1 -f х1
ку - несобственную точку ы = -foo. Так как
6
lim / —^—rdx= lim arctg 6=^.
b—► -foo J 1-fX2 6-k+oo ° 2
0
+00
dx
то по определению интеграл / ^ сходится и его вели-
тг У 1 + х2
чина равна —. о
+оо
Пример 2. Рассмотрим иитеграл J sin xdx. Функция
о
f(x) = sinx на (0;-foo) имеет только одну концевую особую
точку - несобственную точку и = -foo. Так как
о
о
lim / sinхdx — lim (—cos6)
-►-foo J 6-++CO
I sili xdx pa i
+ CO
не существует, то no определению интеграл / sm xdx рас¬
ходится.
373
Пример 3. Рассмотрим интегралы:
4-оо 1 -f со
а)
1 о о
+ OU 1 + оо
f dx Г dx [ dx
^ J XT' J хР’ ./ хР’
Начнем с пункта а). На промежутке (1;+оо) функция
/(х) = — имеет одну особую точку — несобственную точ¬
ку (+оо). Так как
6
dx
_ |т^(*1_р-а1_р). рФ 1,
In-, р= 1,
+оо
/dx f dx
— = lim I — сходится при p > 1 и pac-
XP 6->+oo J xP
l l
ходится при p ^ 1.
Переходим к пункту б). Ha промежутке (0;1) функция
f(x) = — интегрируема в смысле Римана при р < 0 и имеет
хр
особую точку хо = 0 ири р > 0. Пользуясь приведенным выше
равенством, получаем, что
Г & 1^(1-*•->), рф 1,
{ хР \ -In6, Р= 1,
1
откуда следует, что интеграл / — сходится при р < 1 и
f dx
J
расходится при р ^ 1. 0
Переходим к пункту в). Разбиение 7' : (0, 1, +оо) предста¬
вляет промежуток (0; +оо) как объединение двух промежут¬
ков (0; 1) и (1; +ос), на каждом из которых функция fix) — —
имеет не более одной особой точки, причем эта точка коиеч-
4-со
n f dT
ная. Согласно определению И интеграл / —сходится тогда
J *г
о
374
1 4 оо
f dx ( dx
и только тогда, когда сходится оба интеграла I --- п I
О 1
Первый из этих интегралом расходится при р ^ 1, ivropoii —
при р ^ 1, таким образом, одновременно оба. птн интеграла
+ оо
м / dx
не сходятся ни при каком значении р. Итак, интеграл / —
расходится при любом значении р. 0
+ ОС>
_ Г х cos х — sin х
Пример 4. Рассмотрим интеграл / ах.
J т2
X cos X SD1 X ^
Функция /(х) = — г на промежутке (0; +оо) имеет
X
две особые точки — собственную точку хо = 0 и несобствен¬
ную точку (+оо). Разбиение Т : (0,7Г, +оо) представляет про¬
межуток (0;-foo) как объединение двух промежутков (0; 7г)
и (7г;+оо), на каждом из которых функция /(х) имеет толь-
ко одну концевую особую точку.
Так как
х cos х —sin х . ,/sinx\
=
TO
6
/xcosx —sinx . /sin 6 sina\
? *=(—-—). 0<.<K+oo.
a
Отсюда получаем, что
[ lim f<l(-1)=
J x1 /'-ю+j \ x J V b J
0 b
и
-f PO -J-OCi
/xcosx -sili. v , f ./sin x\ sin 6
dx — lim I dI — Inn —-— = 0.
X 6-» + cxj J \ X J b-> + со I)
375
+ C4j
[ x cos x — sin x
Итак, по определению В интеграл / г ах схо-
J х1
о
дится, поскольку сходятся оба интеграла
гг 4-оо
/xcosx —sinx Г х cos х—sin х
—р—•>* » j —
О 7Г
+оо
/х cos x — sin x , f
dx — —J -f 0 — —1.
x2
о
2
f dx
Пример 5. Рассмотрим интеграл / Па проме-
J I - хг
1 0
жутке (0;2) функция /(х) = имеет одну, но уже не
1 — х1
концевую особую точку Хо = 1. По определению В для схо-
2
[ dx
димости интеграла / необходима сходимость обоих
J 1 ~ х1
1 0 2
f dx f dx
интегралов: / ~ и /
J 1 - xl J 1 — xz
b]
f dx 1 — 6
Если 0 < 6 < 1, то I = In Так как функция
J 1 — xl 1-1-6
1-6 °
F(6) = In- не имеет предела при 6 —> 1 —, то, следова-
1 + 6
1
телыю, интеграл / расходится. Итак, независимо от
J \ - х1
О 2 2
f dx
J 1-х'2
О 2
f dx f dx
поведения интеграла / т интеграл / расходит-
J 1 — х1 J 1-х-
СЯ. 1 о
ч 1 — Я
Замечание. Функция F(x) = ln определена при х = ()
1 + х
и х = 2 и ^(2) — F(0) = In Если не обратить внимание па
о
то, что функция f(x) = —-—- неограниченна и, тем самым,
1 — тг
376
нгинтсгрируема на (0;2), то, формально применив формулу
Ньютона Лейбница, можно сдрлать неверный вывод: ипте-
f dr 1
грал / сходится и его величина равна In
J 1-г 3
о
Внимание! Прежде нем применить формулу Ньюто-
ъ
на Лейбница к интеграл}' I /(х) с/х, необходимо убедиться,
что функция f(x) интегрируема в смысл Римана на (а; 6).
Пример 6. Функция Дирихле
щ*) = (?’
v 7 [ J, х — рационально
х — иррационально,
не интегрируема в смысле Римана ни на каком отрезке [а; 6] С
С [0; 1]. Следовательно, функция D(x) не интегрируема и в
несобственном смысле на (0; 1).
Множество функций, интегрируемых в несобственном
смысле на промежутке (а; 6) (собственном или несобствен¬
ном), обозначим через Л(а;Ь). Еще раз обратим внимание,
что для собственного промежутка (а; Ь) множество Я[а; Ь] ин¬
тегрируемых в смысле Римана на [а; Ь] функций есть подмно¬
жество R(a;b).
Основные свойства несобственного интеграла.
1. Если / € R(a;b) и д £ Л(а;6), то для любых постоян¬
ных а, Р функция а/ + 0д Е Л(а; 6) и
6 ь ь
J(af(x)+Pg(x))dx = a jf(x)dx+/3Jg(x)dx (линейность).
а a a
Другими словами, несобственный интеграл есть линейный
функционал на линейном пространство R(a;b).
Следствие. Если /(х) = /i(x) -+ ••• + fq(x) и ингегра-
ь ь
лы J fi(x)dx, 1 ^ i ^ q — 1, сходятся, а интеграл / /<?(*) dx
а а
377
ь
расходится, то интеграл j f(x) dx расходится.
а
2. Если / £ R(a\b) и г £ (я; 6), то / £ Я(я;с), / £ R(c\b) и
ebb
J f(x)dx + J f(x)dx = J f(x)dx (аддитивность).
аса
3. Если / £ R(a\b)} g £ R(a\b) и f(x) ^ ^(x) для всех
x £ (a; 6), то
6 6
J /(*)dx ^ J з(х)dx (монотонность интеграла).
a a
Следствие. Если / £ R{a\b) и |/| £ Я(а;6), то
6 6
|У Д*М*| ^ J\f(x)\dx-
а а
4. Если ш — единственная особая точка функции / на
(а;ы) и / £ Л(а;ы), то для любой строго монотонной и непре¬
рывно дифференцируемой на [от;/?) функции [а,Р) [а;и;)
функция (/ о <р)<р' £ Я(а; /?) и
Р
J /(*) dx = j f((p(t))ip'(t)dt
(замена переменного в несобственном интеграле).
5. Если функции /:[a;u>) К и <;:[а;ы) -> R непрерывно
дифференцируемы на [а;ы) и существует lim /(х)р(х), то
6->ы -
мепно схо-
интегралы J f{x)sf(x)dx и / /'(х)^(х) dx одпоиро
a a
дятся или расходятся, и в случае их сходимости имеет место
равенство
W
J f(x)g'(x)dx = f{x)g(x)^ - j f'(x)g(x)dx,
378
ГДР
/(*).</(*) = lim if(x)9(x))-f(a)g(a)
la b-+u> —
(интегрирование по частям в несобственном интеграле).
Из рассмотренных выше примеров видно, что если перво¬
образная функция F:(a\b) —»• К для функции f:(a;b) —» R
аналитически представлена как элементарная функция, то
исследование сходимости и вычисление несобственного ин¬
теграла I f(x)dx сводится к ранее изученному вопросу су¬
ществования и вычисления предела элементарной функции.
Поэтому основным вопросом в этом разделе является иссле¬
дование сходимости несобственного интеграла в том случае,
когда такое представление первоообразной или невозможно
или достаточно громоздко.
Заметим, что условие: множество точек разрыва функ¬
ции / на промежутке (а; Ь) есть множество меры нуль — не¬
обходимо и достаточно для того, чтобы функция / была ин¬
тегрируема в смысле Римана на любом отрезке [or; /?] С (а; Ь),
не содержащем особых точек /. Поскольку функции, не обла¬
дающие этим свойством или имеющие бесконечное множество
особых точек на (а; 6), заведомо не интегрируемы в несоб¬
ственном смысле на (а;6), то в дальнейшем изложении, не
оговаривая этого специально, будем считать, что все рассма¬
триваемые функции имеют на промежутке интегрирования
конечное множество особых точек и что множество точек
разрыва этих функций на данном промежутке есть множе¬
ство меры нуль. ь
Поскольку несобственный интеграл / /(.г) dx сходится
тогда и только тогда, когда сходятся все составляющие его
я, —,
на являет» и только одна из точек a,_i, я,-, а схо¬
димость несобственного интеграла этог о вида симметрично
6
а
а
особой точкой функции /
379
определяется как для левой, так и для Ираном концевой точки,
'го дальнейшие у тверждения и соотношении и целях просто-
да I /(.г) <1х,
ты изложения формулируем для nirra рала ви
гДе / € Н[а,Ь] для всех [а; 6] С [н;^), если специально пе ого¬
ворено противное. ^
Так как сходимость несобственного интеграла /(.г) dx
b о
есть существование предела функции F(b) = J /(х) dx при
, то условия сходимости интеграла
j f(x) dx, в <
ном, получаются иерефразировкой условий существования
предела функции. В частности, если функция / иеотрица-
моногонпа
тельна на [а;ы), то функция F(b) = / /(.г ) f/г:
а
на [я;и>) и существование предела lim F(b) эквивалентно ог-
6—H*J —
раниченности F на [а;и>).
Критерий Коши сходимости несобственного инте-
и>
грала. Интеграл j f(x)dx сходится тогда и только тогда,
а
когда для любого положительного числа е > О можно указать
такое Число /У > <7, что для любых чисел b\, Ьп, удовлетворя¬
ющих условию В < Ь\ < 62 < w, справедливо неравенство
Ь-2
\J f(x)dx
Ьг
< Е.
Пример 7. Покажем, пользуясь критерием Коши, что ин-
f sign sin nr
теграл I —r/.г сходи'гсн.
J x 4 2
1
1мми x E [?i; ?i + 1], С N, to sign sin л\г — (-l)”. (’ледова-
380
тел ы го, если [b\] ^ [h] ~ 2, то
&2
Sign Sill 7ГХ
/sign sii
X +
„ dx =
’ + 2
'J7t^iz+tb£
J я + 2 fri., J i; + 2 у a;+ 2
ь, «=[6,1+1 „ [6j]
если [6j] =: [62] — 1, TO
62 [63] 62
r signsinir£Jt_ >(--■£.1Л+ / (-I)W
J x + 2 J x+ 2 J x+ 2
b 1 61 [6a]
если же [6j] = [62], т. e. тонки 6i и 62 лежат на одном полуин¬
тервале с целочисленными концами [n;n+ 1), п £ N, то
63
7si|nshurxdz= f(-l)[b']dx
J х + 2 j i + 2
Ь| Ь,
Так как
[Ь.1+1
х + 2
ь2
1 1
< 77-Т—И <
[6j] -Ь 2 61 -|-1
/
1 1
< 7ГТТТ <
[62] + 2 61 + I
х + 2
б2]
и
М-1 1 \ц , I М-1
■£7£Н-Г£ «-г..(.+^)|<
-=[*.1+1 „ 1 п=[Ь|]+1 V 7 1
<2|п(1+гатз)
< б, + 1,
ТО
Ь2
I j sign dx^ <
sign sin nx 4
+ 2 * 61 + 1
381
4 I f sign sin жх
Итак, если - < b\ < 62, то / ax
£ \J x + 2
^2
< e. Таким
+00
ySlgll SHI 71 JT
— dx выполнены условия
l
критерия Коши и, следовательно, этот интеграл сходится.
Пример 8. Покажем, пользуясь критерием Коши, что ин-
+°°
/ sign sin (л* In х) ,
^ dx расходится.
1
Начнем с формулировки отрицания критерия Коши. Надо
найти такое число ео, что для любого В > 1 можно указать
пару чисел 61, 62, для которых В < Ь\ < 62, но
Ьз
sign sin (тг In ж)
оценивается сни-
К!
62
_ I / signsin(Trlnx) .
Поскольку интеграл / dx
Ьг
зу, то естественно взять такой промежуток интегрирования
[61 ;6г], па котором подынтегральная функция не меняет зна¬
ка. Определим числа 61 и 62 равенствами: In 6] = 2п, In 62 =
= 2n + 1, п € N; тогда для любого числа Л > 1 условие
В < bi < 62 выполнено, если взять достаточно большое п.
Для х G (61162) имеем signsin(Trln х) = 1, следовательно,
bj 63
/sign sin (я-In г) f / dx , . /B
«+2 '<b = Jrn = Hh + 2)-HI>, + 2) =
b\ 61
= lnfe-llil, +ln (' + ^) -ln(l + ^) > ' - ^ > 5
Итак, если e = -,то для любого числа В > 1 находится такая
2 б2
II sign sinfjr 111 х)
пара чисел oj, 62, что В < < Ьп ч / ох > 6.
У х + 2
bi
382
-f оо
f signsin(jr In x)
Следонательно, интеграл / ax расходится.
J x H- 2
l
Пример 9. Покажем, пользуясь критерием Коиш, что ин-
+ ОЭ
теграл J я| cos 7гя2| sin2^ ^ пх2 dx сходится.
1
Пусть 1 < &1 <62. Так как подынтегральная функция
неотрицательна, то для целых чисел </гу^2 таких, что 1 ^ q\ ^
^ Ь2 < Ь\ ^ (72, имеет место неравенство
ь2 у/я?
О ^ J x|cos7rx2|sin2^^27rx2dj: ^ J х\cos irx2\sin2^3^7rx2 dx.
y/qT
Так как
>А+Г v/H+T
J x\cosnx2\sin2^2irx2 dx = j x\cosnx2\ein2n*nx2 dx =
Г y/K
n + 1 ir/2
= \ J lCOS7r^l8*n2n ^ J sin2n% <f(sin 2) = 27п~2’
n
TO
1 1
I x|cos>ra;2|sin2^37rx2 dx = -—- < — —.
J & 2?rn2 2»г(д, - 1)
"=**
Итак, если \l-J- h 2 < 6j < 62, то
V 27Г5
6?
0 ^ J XI COS 7ГХ21 sin2^ J 7ГХ2 dx < 6,
bi
слсдоиательно, n силу критерия Коши, интеграл
+ Ou
J x| cos 7гх*2| sin2tx ^ nx2 dx
]
сходится.
383
Обратите внимание на то, что подынтегральная функция
f(x) = х\cos irx2\ sin2lr ^ пх2 в данном сходящемся интеграле
не стремится к нулю при х —> -+оо и даже не ограничена на
[1; +оо).
Предлагаем читателю самостоятельно сформулировать
утверждение критерия Коши сходимости несобственного ин¬
теграла и его отрицание в том случае, когда единственной
особой точкой подынтегральной функции является левая кон¬
цевая точка промежутка интегрирования.
Из критерия Коши немедленно следует, что сходимость
или расходимость интеграла J f(x) dx зависит от поведения
а
функции / только в левой полуокрестности точки и) - проме¬
жутке вида (с;ы). Будем говорить, что функция / локально
слева (справа) в точке ш обладает некоторым свойством, если
существует такая левая (правая) полуокрестность точки ы, в
которой / обладает этим свойством. Например, выражение
“функция / монотонно локальна слева в точке и/’ обозначает,
что / монотонна на некотором промежутке (с; и;).
Как уже не раз отмечалось при исследовании существо¬
вания предела, применение критерия Коши для исследования
сходимости конкретного несобственного интеграла, по боль¬
шей части, технически сложно. Поэтому, в основном, при
решении этого вопроса используются достаточные условия,
в совокупности имеющие большой объ^м применения.
Теорема сравнения. Пусть функции f:[a\u>) ч R и
д:[с\ш) —»• Ш удовлетворяют неравенству 0 ^ f(x) ^ д(х)
локально слева в точке ш. Тогда из сходимости интеграла
Ul и,
/g(x)dx следует сходимость интеграла I f(x)dx, я из рас-
Ы J U)
ходимости х следует расходимость интеграла jg(x)dx.
а с
Следствием этой теоремы является
Признак сравнения. Пусть функция /: [а;ы) —> IR нео¬
трицательна, функция д: [с; w) —> 1R локально слева неотрица¬
тельна в точке ш и f(x) ~ д(х) при х —У ш. Тогда интегралы
384
Uf ш
J f(x)dx и J g(x)dx сходятся или расходятся одновременно.
а с
Заметим, что для локально неотрицательных слева в точ¬
ке и функций /:[а;и>) -* Ш ограниченность функции F(b) =
6
= J f(x)dx на [а; и;) эквивалентна сходимости интеграла
w а
/f(x)dx. Поэтому для таких — и только для таких! —
и/
функций вместо выражений “интеграл I f(x)dx сходится”
ш J
и “интеграл J f(x) dx расходится” применяют соответствен-
а
ш ш
но символы: J f(x) dx < оо и J f(x) dx = оо.
а а
Применение теоремы и признака сравнения для анализа
сходимости несобственных интегралов требует, как и для ря¬
дов, набора “эталонных” функций, сходимость или расходи¬
мость соответствующего интеграла для которых установле¬
на. Наиболее употребительным таким набором является се¬
мейство степенных функций: д(х) = — для анализа интегра-
+0О Хр
лов вида j f(x) dx и <7(х) = ^ ^ для анализа интегралов
6 *
вида J f(x) dx, где особой точкой функции } является точка
а
Ь (—оо < а < 6 < +оо).
+оо
f dx
Как было показано выше, интеграл / — сходится при
J хр
1
р > 1 и расходится при р ^ 1. Дословно повторяя ход анализа
1 ь
f dx Г dx ,
интеграла J — получаем, что интеграл J — ^ (—
оо <
385
< а < b < + оо) сходится при р < 1 и расходится при р ^ 1.
В силу линейности для любого с > 0 получаем, что инте-
+00
/cdx t ^ i
сходится при р > 1, расходится при р ^ 1, а
хР
1 6
/cdx , ,
— — (—оо < а < о < +оо) сходится при р < 1
(6 - х)*
а
и расходится при р ^ 1.
Обратим внимание на то, что хотя в теореме сравнения и
признаке сравнения есть условия как сходимости, так и рас¬
ходимости интеграла J /(ж) dx, однако ни то, ни другое не
а
являются критерием сходимости. Дело в том, что нет та¬
кой универсальной (зависящей только, может быть, от про¬
межутка [а; о;)) функции д: [а; а;) —► R, чтобы из неравенства
О ^ f(x) ^ £(*)’ х € [в'»*4*)) следовала бы сходимость, а из
неравенства /(х) > ^(ж), ж € [a;w), — расходимость интегра¬
ла
J f(*)dx (или из неравенства 0 ^ /(х) < д(х) сходимость,
а из неравенства /(х) ^ у(х) расходимость).
Признаки Дирихле—Абеля сходимости несобст¬
венного интеграла.
I. Пусть функции /: [а; и) —► К и д: [а; и/) —► R удовлетво-
ряют условиям:
ш
а) интеграл J f(x)dx сходится,
б) функция д локально монотонна слева в точке и/ и огра¬
ничена на [а; о;).
W
Тогда интеграл J f(x)g(x) dx сходится.
а
II. Пусть функции /: [а;ы) R и д: [а; и/) -► Ш удовлетво¬
ряют условиям:
386
о
а) функция F(b) = J f{x)dx ограничена на [а;и),
о
схо-
б) функция д локально монотонна слева в точке и и
lim д(х) = 0. ш
X —► Ы — г
Тогда интеграл I f(x)g(x) dx сходится.
J ш
Теорема. Если интеграл I \f(x)\dx сходится, то HHTe-
oi^ У
грал I f(x) dx сходится.
«/ и>
Определение. Если интеграл I \f(x)\dx сходится, то ин-
и> J
теграл J f(x)dx называется абсолютно сходящимся. Если
a w w
интеграл J\f(x)\dx расходится, а интеграл J f(x)dx
а а
дится, то этот интеграл называется условно сходящимся.
Пользуясь этими терминами, предыдущую теорему мож¬
но сформулировать так: мабсолютно сходящийся интеграл
сходится” или “множество абсолютно сходящихся интегралов
есть подмножество сходящихся интегралов”.
Для функций, локально сохраняющих знак в соответству¬
ющей полуокрестности особой точки, сходимость несобст¬
венного интеграла, очевидно, совпадает с абсолютной схо¬
димостью. Таким образом, теорема и признак сравнения го¬
ворят по сути об абсолютной сходимости несобственного ин¬
теграла. В формулировке признаков Абеля—Дирихле огра¬
ничений на знак подынтегральной функции нет, так что они
могут применяться как к интегралу от функции, локально
сохраняющей знак в левой полуокрестности точки ы, так и к
интегралу от функции, не обладающей этим свойством. На
деле, признаки Абеля и Дирихле существенно используются
именно для установления сходимости, чаще всего условной,
интегралов от функций, не являющихся знакопостоянными
в левой полуокрестности точки ы. Действительно, из усло¬
вия, что сомножитель д(х) — локально монотонная и огра¬
387
ниченная слева в точке ш функция, следует, что д локально
сохраняет знак слева в точке ы. Бели произведение f(x)g(x)
локально сохраняет знак слева в точке и, то, не ограничивая
общности, можно считать, что обе функции д и / локаль¬
но неотрицательны слева в точке ы, поэтому ограниченность
Ь w
функции F(b) = J f(x)dx и сходимость интеграла J f(x)dx
а а
эквивалентны. Из всего этого следует, что при выполне¬
нии условий признаков Абеля и Дирихле сходимость интегра-
ла I f(x)g(x) dx следует из теоремы сравнения и сходимости
J ш
интеграла J f(x)dx. Проверка же того, что для данной по-
а
дынтегральной функции выполнены условия теоремы сравне¬
ния, обычно проще проверки выполнения условий признаков
Абеля или Дирихле.
Чаще всего признаки Абеля—Дирихле применяются для
-foo
установления сходимости интегралов вида I /(x)sinxdx и
-foo -foo ~
J /(ж) cosx dx, если интеграл J \f(x)\dx расходится. В та-
а а
ком случае проще начать с установления сходимости инте¬
грала, а для анализа абсолютной сходимости широко исполь¬
зуемым приемом является оценка:
|/(x)sinx| ^ |/(х)| sin2 х = — cos2x);
|/(x)cosx| ^ |/(x)|cos2x = Щ—^-(1 + cos2x).
Распространенной ошибкой при применении признаков
Абеля—Дирихле является пропуск установления монотонно¬
сти сомножителя <j(x). Часто она происходит из-за очевид¬
ности этой монотонности, но всегда необходимо отмечать,
что это свойство выполнено. Иногда считают достаточным
написать оценку 0 ^ д(х) ^ где функция <р(х) монотон¬
388
но стремится к нулю при х -¥ +оо. Следует ясно понимать,
что из этой оценки следует только равенство lim д(х) = О,
®-++оо
но никоим образом не монотонность д(х). Заметим, что ал¬
гебраическая (в частности, рациональная) функция локально
монотонна слева в +оо: этим фактом будем в дальнейшем
пользоваться.
Пример 10. Исследовать сходимость интеграла
+оо
' - 2х2 - 1
ах.
/
х6 -|- 4х3 -|- 3
о
Решение. Прежде всего заметим, что поскольку функция
х* - 2х2 - 1
f(x) = —-——-—- рациональна, то ее первообразная выра-
х -f* 4х 3
жается в виде элементарной функции. Найдя это выраже¬
ние, можно было бы не только решить вопрос о сходимости
данного интеграла, но и в случае положительного решения
найти его величину. Но вычисление первообразной здесь тех¬
нически громоздко, а задача определения величины интегра¬
ла не ставится, поэтому вместо нахождения и исследования
первообразной воспользуемся признаком сравнения. Так как
единственной особой точкой функции /(х) = ^^ на
х 4х -j- 3
-foo
dx
д
х4 — 2х2 — 1 1 1
сходится и — —Z—- ~ — при х —У -foo, то в силу призна-
xb + 4xJ -|-3 х1
-foo
f х4 - 2х2 - 1 ,
ка сравнения интеграл I "з~д dx сходится.
о
Пример 11. Исследовать сходимость интеграла
+оо
dx
+оо
(0; +оо) является несобственная точка -|-оо, интеграл J
/
\/хА + 8х9
шение. Фу
жутке (0; +оо) две особые точки: 0 и +оо. Следовательно, не¬
Решение. Функция /(х) = --==L=== имеет на проме-
ух4 -|- 8х9
389
обходимо отдельно рассмотреть сходимость каждого из ин-
о +оо
/dx f dx
—====. и I --7======: для некоторого a £
\/х< + 8х9 J да
О а
€ (0;+оо).
Пользуясь признаком сравнения и соотношениями
-foo
[ dx
получаем, что интеграл / —===== сходится, а интеграл
а У vx4 + 8x9
/dx ®
■у:.:. . == (0 < а < +оо) расходится. Таким образом,
Vx4 + 8х9
0 +оо
/* dx
интеграл / = расходится
У \/х4 + Л
8fc9
Пример 12. Исследовать сходимость интеграла
+оо
/
dx
\/х -|- X3
Решение. Функция имеет на промежутке (0;+оо)
VX+x3
две особые точки — собственную хо = 0 и несобственную
точку (+оо). Следовательно, необходимо отдельно рассмо-
[ dx
треть сходимость каждого из интегралов / —== и
+00 J VX + X3
[ dx 0
I ■ ... для некоторого а 6 (0; +оо).
J vх + х3
а
Пользуясь признаком сравнения, из соотношений
11 11
у-■ "ч ~ -7= при х -» и+, /=—*■ зТо ПРИ х +°°
vx + х3 vx \/х + х3 х3'2
*ем
/
получаем, что каждый из этих интегралов сходится, т. е. схо-
+°°
dx
дится
yjx + Х^
о
390
Пример 13. Зависимость периода колебаний Т матема¬
тического маятника от его длины L и начального угла откло¬
нения от вертикали <ро выражается формулой
Показать, что этот интеграл сходится при 0 < <ро < тт.
Решение. На промежутке (0; тг) функция
1
сходится.
Если представить маятник как невесомый стержень, один
конец которого закреплен в шарнире без трения, а второй,
с закрепленной на нем точечной массой, свободен, то можно
говорить и о начальных углах <ро = 0 и <ро = л- При этом
маятник качаться вообще не будет, ибо в первом случае он
находится в устойчивом, а во втором — в неустойчивом рав¬
новесии. Если (ро -+ О-f, то Т -> 0, а если <ро —У тг-, то
Т -4 -+оо, т. е. по мере приближения начального положения
маятника к состоянию неустойчивого равновесия период его
колебаний неограниченно растет.
Пример 14. Исследовать сходимость интеграла
ке (0;-foo) одну особую точку (+оо). Поскольку функция
имеет одну особую точку (р = <ро. Так как
то в силу признака сравнения интеграл
+оо
О
Решение. Функция f(x) = имеет на промежут-
391
/(х) = е 'f* при х —► +оо не эквивалентна никакой степен¬
ной функции, то применяем не признак сравнения, а теорему
сравнения. Для любого а > 0 неравенство 0 < e_v^ < —
ха
справедливо, если х > #(а) (обратите внимание, что значе¬
ние В зависит от а). Если а ^ 1, то такая оценка неинформа-
+оо
f dx
тивна — интеграл / — расходится, а этот факт ничего не
1
говорит о поведении интеграла от меньшей функции. Зна-
+оо
чит, нужно взять такое значение а, чтобы интеграл
1
[ dx
J ха
! 1
сходился, тогда оценка 0 < < — будет информатив-
ха
на. Поскольку единственное ограничение на а есть условие
а > 0, то имеем право взять а = 2, и тогда из неравенства
е~'S* < —, х > В(2), в силу теоремы сравнения получим, что
интеграл /Vv* * сходится.
О
Пример 15. Исследовать сходимость интеграла
п/2
In sin х dx.
о
Решение. Подынтегральная функция f(x) = In sin х непо¬
ложительна и имеет на /о; одну особую точку Хо = 0. В
п/2
силу линейности сходимость интеграла j In sin xdx эквива-
0
лентна сходимости интеграла от неотрицательной функции
п/2 п/2
j | In sin х| dx = — j In sin xdx. Так как аргумент логариф-
0 0
ма при х —► 0 является бесконечно малой величиной, то функ¬
ция | In sin х| не эквивалентна никакой степенной функции ар-
392
гумента логарифма, т. е. функции вида . Поэтому
sin х
применим не признак сравнения, а теорему сравнения. Для
любого числа а > 0 неравенство |lnsinx| < -г-j— справедли-
sin X
во, если 0 < х < В(а) (величина В зависит от а). Если а > 1,
1 1
то из соотношения ~ —, х —> 0, и признака срав-
sin х ха
тг/2
нения следует, что интеграл / :— dx расходится — эта
J sin х
о
оценка неинформативна, поскольку расходимость интеграла
от большой функции ничего не говорит о поведении интегра¬
ла от меньшей. Значит, надо взять такое значение а, чтобы
п/2
f dx , - , 1
интеграл / -r-z— сходился, тогда оценка |lnsinx| < -r-j—
J sin x sin X
0
будет информативна. Поскольку единственное ограничение
на а есть условие а > 0, то имеем право положить а = -.
1 1
Тогда из соотношения ~ —7=, хчОи признака срав-
ysinx yjx
п/2
Г dx
нения получим, что интеграл / . ; сходится, а из не-
1 0
равенства |lnsinx| < —- и теоремы сравнения получим
п/2
окончательно, что сходится интеграл j In sin xdx.
о
Обратим внимание на то, что в ходе решения использо¬
валось соотношение эквивалентности sinx ~ х, х —У 0, а не
In sin х ~ lnx, х 0+. Из соотношения <j(x) ~ f(x), х —► а,
вообще говоря, не следует соотношение Л(^(х)) ~ Л(/(х)),
х —» а; такое утверждение в каждом конкретном случае тре¬
бует обоснования. Соотношение In sinx ~ lnx, х —► 0+ верно
(проверьте), но его обоснование было бы излишним усложне-
•)lna = о » Q Д-*1* любого а > О.
393
нием решения примера.
Пример 16. Исследуем сходимость интеграла
+9°
Ж COS X
/
40 + х2
о
dx.
X COS X
Функция /(ж) = — - имеет на (0;+оо) одну особую
40 + х
точку (+оо) и не сохраняет знак локально слева в этой точ¬
ке. Теоретически надо было бы начать с анализа абсолют-
X 1
нои сходимости данного интеграла, но так как — ~ ,
40 + х1 х
х —► +оо, то простейшая оценка |/(х)| — не дает воз-
40 + х1
+оо
можности утверждать, что интеграл J \f(x)\dx сходится.
о
Как уже говорилось, в данном случае проще начать с про¬
верки выполнения условий признаков Абеля—Дирихле. Дей-
, функция F(b) = J cos xdx = sin b ограничена
ствительно
на [0;+оо), рациональная функция у(х) = — локаль-
40 + х1
но монотонна слева в точке (+оо) {д{х) монотонна на луче
х ^ \/40) и lim #(ж) = 0. Итак, в силу признака Дирихле—
+оо
А. f xcosx
Абеля интеграл / ^ dx сходится.
о
Для исследования абсолютной сходимости данного инте¬
грала применим указанную выше оценку |cosx| ^ cos2 ж.
Имеем
X cos X
40 + ж2
ж cos2 ж
40 + ж2 40 + ж2
Дословно повторяя приведенные выше рассуждения, получат
+оо
/ж cos 2ж . _
5Т сходится. Соотношение
2(40+ж2)
о
394
1
—, х —>• +оо, и признак сравнения показывают,
2(40 + х2) 2х
+ 00
что интеграл J х~лп~Г~2~\ РасхоДится. Следовательно,
2(40 + х2)
/Xcos^ X
— z- dx расходится, откуда в силу теоремы
40 + х£
+ оо 0
0 +0О
/
0
/X COS X
— г' dx сходится условно.
40 +
сравнения следует, что расходится интеграл
+ оо
X COS X
40 + х2
dx,
о
Пример 17. Исследуем сходимость интеграла
+оо
sin х ,
: dx.
I
у/х3 +
х°
Решение. Функция /(х) = имеет на (0;+оо)
у/х3 -f х5
две особые точки Хо = 0 и (+оо), следовательно, необходи¬
мо отдельно рассмотреть сходимость каждого из интегралов
а +оо
/sinx . Г sinx _ /Л ч
, .= ■■■■: : ахи / . ■ : dx для некоторого а € (0; -foo).
у/х3 + х5 J vx3 + x5
0 а
U - гтл sin х 1
Начнем с простейших оценок. Так как —===. ~ при
у/ X3 + X5 у/х
х —>> 0 и подынтегральная функция неотрицательна, то в силу
а
/sinx
- .. _= ах сходится абсо-
V Я ”f" я
о
лютно.
Так как
sinx
у/х3 + х5
1 1 1
И jrrr при
\/х^ + Xs у/х3 + X5 Я5/2
х —► +оо, то в силу теоремы и признака сравнения инте-
+оо
sinx
грал
а
/
у/х3 + хь
dx сходится. Следовательно, интеграл
395
-f оо -f-сю
/sin x . f sin x
—===== ax сходится, т. e. интеграл / —===== dx
y/x3 + x5 У У X3 + X5
O ' 0
сходится абсолютно.
l
Пример 18. Исследуем сходимость интеграла I dx
cos - 0
/ !!2?1
J *3/2
Функция /(х) = —jjy на (0; 1) имеет одну особую точ¬
ку хо = 0. Начнем опять с проверки условий признаков
cos - 1
Абеля—Дирихле, поскольку простейшая оценка - - ■~ < —т-
хх •
не дает возможности утверждать о сходимости (абсолютной)
данного интеграла.
Особой точкой подынтегральной функции является левый
конец промежутка интегрирования, поэтому и условия в при¬
знаках Абеля—Дирихле симметрично изменяются. Функция
1
/11 1
— cos — dx = sin - — sin 1 ограничена на (0; 1),
х1 х b
ь
функция д(х) — у/х монотонна на (0; 1] и lim д(х) = 0, следо-
1 i
Г cos ~ Г 1 1
вательно, интеграл / ■■;■■■ dx — / ух •—г- cos — dx сходится.
J xd'z J хл х
о о
I cos - I cos2 - 1 + cos -
Применяя оценку > "жз/2 = 2x^2 ' видим’ что ин~
1 i 1
f\cos т , 1 f008 * J
теграл I I —з^2 РасхоДится» так как интеграл - I -щ- dx
0
I f dx
сходится, а интеграл - / —расходится. Итак, интеграл
Г1
—3f% dx сходится условно.
Замечание. При исследовании сходимости интегралов
ш ы
вида j f(x)sin(<p(x))dx и *)cos(y>(r))rfi:, где <р(х)
ло-
396
кально монотонна слева в точке ш и <р(х) —> +оо при х —► ы—,
часто делают замену: <р(х) = t с тем, чтобы прийти к инте-
+оо -foo
грату “стандартного” вида: J f* (t) sin tdt и J f* (0 cos * dt.
a a
В данном примере можно было, сделав замену t = —, перейти
+оо *
/cost .
"vT
к интегралу J —тт®*» но поскольку проверка выполнения
1
условий признака Дирихле—Абеля оказалась несложной, осо¬
бой Необходимости в этом преобразовании нет.
Пример 19. Исследовать сходимость интеграла
+оо
_2
/
о
sin(x — х) dx.
Решение. Функция t = х2—х монотонна на луче
но обратная функция х = г + \ А + т на соответствующем
2 V 4
луче (“tJ+ooj имеет неограниченную производную. По-
(5;+°°)'
(4Н
скольку непрерывность производной х\ является одним из
условий замены переменного в несобственном интеграле (см.
пункт 4 в основных свойствах несобственного интеграла), то
2 1 L Г j dt
замену t = х — х, х = - + \/* + 7, dx = ^ сделаем
+оо 2 V 4 >/4* +1
в интеграле J sin(x2 — x)rfx, так как на луче [1;+оо) уже
1
все условия замены переменной выполнены. Так как функ¬
ция sin(x2 — х) непрерывна на [0; 1], следовательно, интегри¬
руема в смысле Римана на [0; 1], то сходимость интеграла
+оо -foo
J sin(x2 — х) dx и сходимость интеграла J sin(x2 — х) dx =
397
+oo b
= J -J^!j!J=dt эквивалентны. Функция F(b) = j sin tdt =
О О I
= 1 — cosb ограничена на [0; -foo), функция g(t) — . - мо-
V41 + 1
нотонна на [0;-foo), lim <;(<) = 0, следовательно, интеграл
t —► -f-OO
+oo
sinf
dt сходится в силу признаков Дирихле—Абеля. Так
/
л/4*+1
о
как
sin t | sin21 1 cos 21
IV4F+TI" y/4t + i 2V4TT1 2y/AtTi'
-foo +00
f dt f cos 21 .
интеграл J _ расходится, а интеграл J Jj. \
о 0
-foo -foo
сходится, то интеграл / / | sin(a?2—x)| dx pac-
0 +oo
ходится. Итак, интеграл J sin(x2 — x) dx сходится условно.
Пример 20. Исследуем сходимость интеграла
+оо
(sin х) In х
/
у/х2 + 1
1
dx.
Функция F(b) = J sin х dx = cos 1 — cos b ограничена на
l
/t v „ lnx yfx 1
(1; oo). Неравенство - показы-
V^TT у№П
вает, что функция g(x) — ^ПХ--- стремится к нулю при
у/х2 + 1
х —► +оо, но ничего не говорит о монотонности и(х). Так
как ^(х) не является алгебраической функцией, локальную
монотонность которой слева в (+оо) мы считаем известной,
то в решении данного примера проверка монотонности </(х)
необходима.
398
_ w ,/ v 1 - *2(lnx — 1)
Действительно, соотношение g (x) = no-
x(x^ + 1 yt1
называет, что g(x) монотонна на [e2; +oo). Итак, все условия
признаков Дирихле—Абеля выполнены, следовательно, инте-
+оо
/ (In г) sin х
грал I —гг- dx сходится. Из соотношении:
J у/х2 + 1
1
I (In х) sin х
у/х2 + 1
^ (In х) sin х _ lnx (lnx) cos 2х
^ у/х2 -f 1 2у/х2 -+ 1 2у/х2 + 1
> т: (О1)
4х
+0О
следует, что интеграл
/
%/^тт
+оо 1 +оо
(In х) sin х I ,
1 ах расходится, ибо ин-
/<dx f (lnx)cos2x ,
— расходится, а интеграл / г:-г?.- dx схо-
4x J 2vxM- 1
1 -foo 1
f (In x) sin X
дится. Итак, интеграл / —- - dx сходится условно.
J yjx2 + 1
l
Пример 21. Исследуем сходимость интеграла
+оо
/(xsinx — cosx) ,
- 1 cos x ax.
X2
1
6
Функция F(b) = J cos xdx = sin 6 — sin 1 ограничена на
, [xsinx — cosx
(l;+oo). Неравенство -
1 1
< —(- — показыва-
x sm x cos x
ет, что функция g(x) = — ^ стремится к нулю при
х —► +оо, но функция <у(х), очевидно, не является локаль¬
но монотонной слева в (+оо). Таким образом, представление
подынтегральной функции в виде произведения
х sin х — cos х
cos х г
399
не дает возможности применить к данному интегралу при¬
знаки Дирихле—Абеля. Испробуем другой путь: представим
подынтегральную функцию в виде суммы:
cosx(xsinx — cosx) sin2x cos2 х
х2 2х х2
Из неравенства О <С C°S ■ Х ^ ~ (х ^ 1) следует, что интеграл
+оо X X 4-оо
/cos^ х f sin 2х
-— dx сходится абсолютно. К интегралу / —— dx
х2 J 2х
1 1
уже легко применяются признаки Дирихле—Абеля. Предла¬
гаем читателю самостоятельно доказать, что этот интеграл
сходится условно. Следовательно, интеграл
+оо
cos х(х sinx — cosх) .
dx
/
сходится условно.
Читатель, наверное, обратил внимание, на параллелизм
многих понятий и методов в теории рядов и несобственных
интегралов, как, например, условная и абсолютная сходи¬
мость, теоремы сравнения, признаки Абеля—Дирихле и т. д.
Эта взаимосвязь есть отражение взаимосвязи понятий пре¬
дела последовательности (сумма ряда) и предела функции
(несобственный интеграл). Как предел последовательности
есть предел функции, определенной на множестве натураль-
00
ных чисел, так и ряд ап является интегралом I f(x)dx,
п = 1 {
где /(х) = аП1п^х<п + 1,пбК. В свою очередь, оиределе-
ь
ние Гейне предела lim / /(х) dx приводит к утверждению:
Ь-*ш- J
а
если / € Я[а;6] для любого [а;6] С [а; и;), то для сходимо-
и>
сти интеграла J f(x)dx необходимо и достаточно условие:
400
для любой монотонной последовательности 6П —► w—, а = &о,
оо Ь"
п Е N, ряд ^ I f(x) dx сходится.
*='bL
Существенное — но не принципиальное! — отличие тео¬
рии рядов от теории несобственного интеграла — как и от¬
личие теории предела последовательности от теории предела
функции, — это то, что в первом случае параметр перехода
к пределу меняется по дискретному множеству натуральных
чисел с единственной предельной точкой (-foo), а во втором
этот параметр меняется непрерывно и предельной (односто¬
ронней) точкой может быть любая точка расширенной чи¬
словой прямой. Не имеют аналогов в теории несобственного
интеграла те методы исследования сходимости рядов, кото¬
рые существенно используют свойства натурального ряда —
признаки Даламбера, Коши, Гаусса. В свою очередь, спе¬
цифика несобственного интеграла проявляется при исследо¬
вании
интегралов вида j f(x)dx} где / Е Я[а; 6] для любо-
функции: [ -—необходимым и достаточным является
J {и - гЧп
го [а; 6] С [а;а>) и ы — собственная точка числовой прямой.
Так, в этом случае для сходимости интеграла от степенной
w
dx
~х)Р
а оо j
условие р < 1, а для сходимости аналогичного ряда — —
я — 1
условие р > 1. Обратим еще внимание на то, что из сходи-
+0О
даже абсолютной — интеграла J f(x)dx (см. при-
а
мер 9) не следует, что функция f(x) стремится к нулю при
х —► +оо, в то время как условие lim ап = 0 необходимо для
n-f оо
сходимости ряда.
Необходимо ясно и четко понимать как общность, так и
особенности теории рядов и теории несобственных интегра¬
лов и не допускать ложных аналогий и неверных переносов
утверждений из одной в другую.
мости
401
§ г. СОБСТВЕННЫЙ ИНТЕГРАЛ,
ЗАВИСЯЩИЙ ОТ ПАРАМЕТРА
ОО
В функциональном ряде un(z) член ряда представляет
п = 1
собой функцию двух переменных: натурального числа п —
индекса суммирования и параметра х из некоторого мно¬
жества X. Параллельным понятием в теории несобствен¬
ных интегралов является несобственный интеграл от функ¬
ции двух переменных /(x,f), из которых одно является пере¬
менным интегрирования, а второе — параметром из некото¬
рого множества Т. Такой интеграл определяется предельным
переходом в интеграле Римана от /(х,<) так, как сумма ря¬
да — предельным переходом в последовательности конечных
сумм {Sn(x)}. Поэтому прежде, чем рассмотреть свойства
несобственного интеграла, зависящего от параметра, необ¬
ходимо рассмотреть свойства интеграла Римана, зависящего
от параметра.
Определение. Пусть для каждого t Е Т функция /(х,<)
интегрируема в смысле Римана на отрезке [a(f);6(<)]. Тогда
6(e)
функция F(t) = I f(xyt)dx называется собственным Инте¬
ле)
г ралом, зависящим от параметра t.
Замечание 1. Термин “собственный интеграл, завися¬
щий от параметра” принят вместо термина “интеграл Рима¬
на, зависящий от параметра” в целях однородности термино¬
логии.
Замечание 2. Собственным интегралом, зависящим от
МО
параметра, называют и сам символ
a(t)
ной областью изменения t в таком случае является совокуп¬
ность тех значений to, для которых /(х,<о) € Я[а(<о); &(<о)]-
Теорема о непрерывности собственного интегра¬
ла, зависящего от параметра. Пусть D = {(х, t): а ^ х ^
J /(x,£)cfx. Естествен*
402
^6, с ^ t ^ d}, функции a(t) и /3(1) непрерывны на [c;d]
и a[c;d\ С [а;Ь], /?[с;</] С [а;6]. Тогда, если /(х,<) £ C(D),
т
то функция F(J) = j f(x,t)dx определена и непрерывна
на [c;d].
Теорема об интегрировании собственного интег¬
рала, зависящего от параметра. Пусть D = {(x,f):a ^
ь
^ х ^ 6, с ^ J ^ d}. Если f{x,t) £ С(/)) и F(t) = J f(x,t) dx,
a
TO
d b d
J F(t) dt = J (J f(x,i) a) dx.
В силу предыдущей теоремы функция F(t) непрерывна и,
тем более, интегрируема на [c\d\.
Теорема о дифференцировании собственного ин¬
теграла, зависящего от параметра. Пусть D = {(x,t):
а ^ х ^ 6, c^t^.d}n функции a(t), f3[t) непрерывно диф¬
ференцируемы на [c;d], причем a[c;cf] С [а;6], P[c\d\ С [а;Ь].
«О
Если / £ С7(1>) и ^ € C(D), то функция F(f) = J f(x,t) dx
непрерывно дифференцируема на [с; d] и
т
F'(t) = mt),ty•^(о-/ио,<)•«'(<) + f ^(*,t)dt.
«(О
з
Пример 22. Найти lim - / sin<x\/x2 + f2 + fx - 1 dx.
t-+o+ t J
l
Решение. Функция
{sin tx
~г
^ f - \/x2 + t2 +tx - 1, < Ф 0, x e [l;3],
/(*, *' - 7 *
x\/x2 - 1, < = 0, or € [ 1; 3],
403
непрерывна на прямоугольнике [1; 3] х [0; ]]. Следовательно,
в силу теоремы о непрерывности интеграла, зависящего от
параметра,
з з
lim - I sintx \/x2 -f t2 + tx — 1 dx = lim I f(xA)dx =
->o+ t J t->o+ J ' 1
t—► O-f-
l
3
16 уД
= J f(x,0)dx = J x\/x2 — 1 dx = ^(x2 ~ 1)3/2|' —
1 1
1
f dx
Пример 23. Найти lim / ; гтг.
*-*+«> J 1+ l_£)n
0
Решение. Для того, чтобы применить теорему о непре¬
рывности интеграла, зависящего от параметра, введем функ¬
цию двух переменных:
И-(!-<,)■/■■ *<ПО;1],1€(0;1),
/(*.0 =
1 X е [0; 1], * =0.
1 + е-*’
Функция f(x,t) непрерывна на прямоугольнике [0; 1] х [0; 1]
(проверьте!), следовательно, в силу указанной теоремы:
1 1 1
t|im J /(*, t)dx = j f(x, 0)dx = j = >n(l + e).
0 0 0
Так как
l
0
TO
1
lim f [ f dx =
"-><»./ l-f(l-J) п-юоу \ n J
0 V П / (J
1
= lim [ fix,/) dt = ln( 1 -+ e).
t-*o+y
404
Пример 24. Функции
тг/2
\/] — к2 sin2 <р
dp
о
о
где О < к < 1, называются полными эллиптическими инте¬
гралами. Доказать, что
для любого к £ (0; 1).
Решение. Для любого к Е (0; 1) существует такой от¬
резок [о;/3] С (0; 1), что к £ (о;/У). На прямоугольнике
|0; X [nr; ft] функция /(у?, к) = —======== удовлетворяет
1 \/] ~ к2 sin <р
условиям теоремы о дифференцировании интеграла, завися¬
щего от параметра, следовательно,
Алгебраическими преобразованиями из этого равенства по¬
лучаем следующее:
«.„ _ т
к Л(1 - к2)
т
к
«/2
к ^2 J (1 — A*2 sin2 у>)3/2
о
*■/2
1 [ к sin2 (р
/
d<p +
к2 J (] — к2а\п2 <р)3/2
О
/
к J \Л — Аг2 sin2 \р
*12
*0
где к £ («;/?), откуда выводим, что
я/2
(J -k2)P'k = kF(k)— J cos<р
О
405
Так как ——^ о/о = d ^—jJL===^, то
dz
(1 ~J)3/7
w/2
/d(k sin <p)
COS^(l — fc2sin2 ip)3/2 ~
0
w/2
к cos pain ip I*/2 f ksin2<p
v/T^fe^sin^'0 J yj\ — A*2 sin2 <p
я/2 ir/2
=i Jтшт' i *e (ei л
0 v ^ 0
и следовательно,
А(1 - k2)FL = fc2F(fc) - F(fc) + F(t), к € (a; /?) С (0; 1),
откуда и получаем, что для любого к £ (0; 1) верно равенство
Е(*) _ £(*)
* *(1-*2) к '
§ 3. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ,
ЗАВИСЯЩИЙ ОТ ПАРАМЕТРА
Определение. Пусть для каждого/ Е 7’функция /(.г,/) Е
Е 7?(а;/>), причем /(я,/о) € Я(а;6) хотя бы для одного to Е Т.
ь ь
Тогда функция 7#,(/.) = J f(x11)dx и сам символ J f(x,1)dx
<1 а
называются несобственным интегралом, зависянщм от пара¬
метра i.
Замечание 1. Необходимость исследовать несобствен¬
ный интеграл, в котором от параметра зависят не только по¬
дынтегральная функция, но и пределы интегрирования, воз¬
никает крайне редко. Поэтому здесь будем рассматривать
только несобственные интегралы, зависящие от параметра
такого вида, как определены выше.
Замечание 2. Требование неинтегрируемости в смысле
Римана на (а; Ь) функции f(x, t0) хотя бы для одного значения
10еТ существенно, поскольку в противном случае мы имеем
дело с уже рассмотренным собственным интегралом, завися¬
щим от параметра. В то же время в целях удобства формули¬
ровок и применений соответствующих утверждений не стоит
вводить жесткое условие: для всех t Е Т функция /(х,/) не
интегрируема в смысле Рпмана на (а; 6).
Определение. Пусть задан несобственный интеграл
6
F{1) = j f(x,t)dx.
а
Множеством сходимости (абсолютной сходимости, условной
сходимости) этого интеграла называется множество М тех
значений /, при которых он сходится (абсолютно сходится,
условно сходится).
+оо
__ _ Г sin х ,
Пример 25. Для интеграла / —— dx из признаков Абе-
о
ля—Дирихле и теоремы сравнения получаем, что луч t > О
есть множество сходимости и луч t > 1 - множество абсо¬
407
лютной сходимости, полуинтервал (0; 1] — множество услов¬
ной сходимости.
По тем же соображениям, как и для несобственных пито
гралов, пс зависящих от параметра, будем и дальнейшем из-
U'
ложении рассматривать только интегралы вида J f(j-, I) <h\
а
где f{x,t) £ K[a\b] для всех [а\Ь] С [и; и;), если не оговорен
специально другой вариант.
Определение. Функцию определенную на множе¬
стве X х У1, называют семейством функции, зависящих от па¬
раметра £, если переменная i выделена и называется параме¬
тром. Множество Т в таком случае называется множеством
значений параметра.
Семейство f(x,t) функций, зависящих от параметра /,
иногда записывают в виде /*(х), явно выделяя параметр.
Определение. Пусть /(х,£), х £ Лг, t £ 7’, — семейство
функций, зависящих от параметра t, а хо предельная точ¬
ка множества X. Множество М С Т тех значений I £ 1\
для которых существует предел lim /(х,/) = у>(0> налыва-
ется множеством сходимости семейства f(x,1) при х —У Хо-
Функция ip(t), t £ М, называется предельной функцией или
пределом семейства f(x,t) при х х*о.
В дальнейшем для любого множества Е С М будем ко¬
ротко говорить: семейство /(х,/) сходится на Е при х —У х()
к <р(1)> и записывать <p(t) = lim /(.г, £), / £ Е, или /(х, I) —у tp(1)
Х~¥Х0
при х —У хо, t £ Е.
Пример 26. Рассмотрим семейство функций
f{x,t) — sin(/;r), х ^ 0, t ^ 0.
Рхли 0 <С t < 1, то при х —► -foo имеем, что Iх -> 0 н, сле¬
довательно, f(x,t) —у 0. Если / = 1, то при любом х ^ 0
имеем, что f(x,t) = sin 1. Если t > ], то при .с —> -foo ар-
гумент синуса неограниченно растет и функция sin(£T) при
этом не имеет предела. Итак, множеством сходимости се¬
мейства f(x,l) = sin(Jr), х ^ 0, t ^ 0, при х —> -foo является
отрезок [0; 1].
408
Определение. Пусть семейство /(х,/) сходится на Е при
л: —> хо к <^(0* Если выполнено з'словиг: для любого положи¬
тельного числа е найдется такая окрестность U(xq) точки хо,
о
что для всех х Е и(хо) П X и всех / Е Ё справедливо нера¬
венство \f(x,t) — ip(t)| < е} то говорят, что семейство /(х,/)
сходится равномерно к <p(t) на множестве Е при х —> хо-
Если семейство f(x,t) сходится на Е при х —► Хо к (p(t),
но не удовлетворяет приведенному выше определению, то го¬
ворят, что это семейство сходится к у?(<) неравномерно на Е
при х -> Хо-
Равномерная сходимость семейства f(x,t) к функции <p(t)
на Е при х —у Xq обозначается символом /(х,<) :=£ tp(t) на Е
при х -> Хо-
Приведем формальную запись сходимости и равномерной
сходимости к tp{t) семейства /(х,<) на Е при х —► хо в слу¬
чае, когда хо — собственная точка числовой прямой и функ¬
ция /(х,<) при всех i Е Е определена в некоторой, может
быть, проколотой, окрестности точки хо:
/(х,<) -* (p(t) при X —> Xq на Е <=>
V* Е Е Че > 0 36 = 6{t,e): Vx: 0 < |х - х0| < S =>
\f(x,t)-<p(t)\<e-,
f(x, t) <p(t) при * -* x0 на Е <=>
Ve > 0 35 = S(e): V*: 0 < \х - х0| < <5, Vt € Е =>
|/(*,|)-у>(<)| < е.
Предлагаем читателю самостоятельно записать в таком
виде определение сходимости и равномерной сходимости на
множестве Е семейства /(х,/) к <р{1) при х -* -foe.
Пример 27. Семейство функций
/(*.*) = 737^, *€(0;1), <€(0;2),
1 + Х
на интервале (0; 2) сходится при х —► 0+ к функции <p(t) = 3.
Покажем, что а) на интервале (1; 2) семейство /(х,/) сходит¬
ся к <p(t) равномерно; б) на интервале (0; 1) семейство /(х,/)
сходится к <p(t) неравномерно.
2х
Для любого 1 Е (0; 2) имеем, что f(x,l) = 3 , т. е.
t -f- х
409
If(x,t) - p(<)| =
2x
t ■f I
2x
4- x
< 2x,
откуда следует, что если 0 < х <
то для всех t Е (1; 2)
Начнем с пункта а). Если 1<£<2их>0,то —
I ■
е
Г
выполнено неравенство |/(x,f) — <р(1)\ < т- е* /(*>0
на (1; 2) при х -* 0+.
Переходим к пункту б). Нужно указать такое положи¬
тельное число £о, что для любого S > 0 найдутся значения
х6:0 < xs < 6 и is Е (0;2), для которых \f(x6,ts)-<p{U)I ^ £(>•
Возьмем хь — - и is = х$, тогда = 1, откуда и сле-
2 ^ х<*
дует, что /(х,<) неравномерно сходится к v?(f) на (0; 1) при
х —► 0+.
Следующие утверждения немедленно следуют из опреде¬
ления равномерной сходимости семейства функций.
1. Если два семейства /i(x,<) и /2(x,t) равномерно схо¬
дятся на множестве Е при х -> хо, то любая их линейная
комбинация a/i(x, t)+ /?/г(х,<), где а и /? — постоянные, рав¬
номерно сходится на Е при х —* хо-
2. Если семейство f{x,t) равномерно сходится на множе¬
стве Е при х —У хо, то это семейство равномерно сходится
при х -4 хо на любом подмножестве Е.
3. Если семейство /(x,f) равномерно сходится на каждом
из множеств Е\ и Е2 при х -* хо, то это семейство при х -* Хо
сходится равномерно на множестве Е\ U Е2.
Внимание! Это утверждение не переносится на бесконеч¬
ное объединение множеств, как показывает
Пример 28. Рассмотрим семейство
sintx л m
f{xj) = , х > 0, t Е К.
х
Для любого < Е К имеем: lim /(x,t) = t. Из неравенства
0-f-
= |*3х2| следует, что если n £ N, е > 0,
sin tx
t3X3
t
<
X
X
|t| ^ ?г и 0 < х <
\/^то
зом, на множестве Еп = {/,
sin tx _
< < е. Таким обра-
<| ^ п} семейство f(x}t) схо-
410
дится к <p(l) = t при х —> 0+ равномерно. Покажем, что на
оо
множестве Ш = Еп семейство f(x,t) сходится к <р(1) при
71—1
х —> го неравномерно. Для этого нужно указать такое по¬
ложительное число fo, что для любого числа S > 0 найдутся
числа xs} 0 < х$ < <5, и is Е М, для которых верно неравенство
sin t6xs ^ 7I v
^ €q. Действительно, пусть xs
ts -
Х<5
2
is = —, тогда имеем, что
Х<5
= min{|; 1} и
sin tsxs tsxs — sintsxs 2-sin 2 1
* S — — x ^ 1 •
Xs Xs XS Xs
sin tx
Итак, семейство f(x,t) = сходится при x —> 0+ к
x
<p(t) = t равномерно на каждом из множеств Еп = {<: |1| ^ п}
оо
и неравномерно на множестве К = Еп.
П = 1
На практике удобно пользоваться следующим критери¬
ем — фактически переформулировкой определения равномер¬
ной сходимости: семейство /(x,J), х Е Xtt Е 2?, сходится при
х —> хо равномерно на Е тогда и только тогда, когда
lim sup |/(х, *) — (p(t)| = 0.
х-^хо t£E
Критерии Коши равномерной сходимости семей¬
ства функций. Семейство /(х,<), х Е X, t Е Т, равномерно
сходится при х —> хо на множестве Е С Т тогда и только
тогда, когда для любого положительного числа е > 0 найдет¬
ся такая окрестность [J(xо) точки Хо, что для любой пары
о о
X] Е 1/(хо) П X, х2 Е U(xо) П X и всех i Е Е справедливо
неравенство |/(xi, t) — /(х2, <)1 <
Если критерий Коши не выполнен для семейства /(х,/),
х Е X,i Е Е, при х —► х0, т. е. можно указать такое положи¬
тельное число еу что для любой окрестности U(xо) точки Хо
о
найдутся точки xj, Х2 из проколотой окрестности £/(хо) и
значение /q Е Е, для которых верно неравенство |/(xj,<o) —
411
— /(#2iMI ^ то говорят, что семейство J(x,t) не сходится
равномерно на E при x —» хо-
Обратите внимание, что говоря “семейство f(x,t) сходит¬
ся неравномерно при х —У хо на Еп мы утверждаем существо¬
вание предела lim /{х,1) = ip(t) для всех t Е Е. Говоря же
X—►Го
“семейство f(x}t) не сходится равномерно на Е при х —> хо”,
мы не утверждаем, что множество Е входит в множество
сходимости семейства /(я,<) при х -* х0- Только, если сходи¬
мость f(x,t) при х хо иа Е заранее известна или доказана,
утверждения “ f(x,t) при х —> Хо сходится на Е неравно¬
мерно” и “ f(x,t) при х —> хо не сходится равномерно на Е”
эквивалентны.
Теорема о перестановке двух предельных перехо¬
дов. Пусть f(x,t) — семейство функций, х £ X, t. Е 71, хо —
предельная точка ЛТ, to — предельная точка Т. Если
1) для любого х Е X существует lim f(x,t) = ф(х),
t—bl о
2) при х —> хо семейство f(x,t) сходится равномерно иа Т
к <p(t),
то существ}'ют оба предела lim ф(х) = lim (lim /(х,/)) и
X—►lo X—ЬТу t—Но
lim (p(t) = lim ( lim /(x,/)) и справедливо равенство
t-^^0 t*4to Г*4Го
lim ф(х) — lim <p(t).
x-f.ro t-w0
Следствие 1. Пусть семейство функций /(х,<), х Е X,
I € удовлетворяет условиям:
1) для любого х £ X функция f(xti) непрерывна на Т\
2) семейство /(х,<) при х —> хо сходится равномерно на Т
к <p(t).
Тогда функция <p(t) непрерывна на Т.
Следствие 2. Пусть семейство функций /(х,/), х Е X,
t Е [а; 6), удовлетворяет условиям:
1) для любого х £ X функция f(x,t) непрерывна иа [а; 6);
2) семейство f{xyi) при х —> хо сходится на (а]Ь) к
Тогда, если предел функции /(х,а) при х -> хо не суще¬
ствует или не существует предел <p(t) при 1 —> а-}-, или оба
предела существуют, но lim f(xya) ф lim ^(/), то семсй-
х—>хо t—► <*+
ство f(x,t) сходится неравномерно на {а\Ь) при х —> х0.
412
Так, например, в силу следствия 2 семейство /(х, /.) =sin
х £ 0, * £ О, рассмотренное в примере, сходится на интерва¬
ле (0; J) и. тем более, на отрезке [0; 1] неравномерно, посколь¬
ку при любом х ^ 0 функция sin/x непрерывна на [0; 1], а
предельная функция
Ч>{1) = ( °’ ° ^ 1 < г’
\sinl, *=1
разрывна на (0; 1].
Пример 29. Рассмотрим семейство функций
I(x,t) — ext cos x(t + 1), x E £ E IK.
При любом х Е Ш функция ex*cosx(J + l) непрерывна на [0; 1].
Если х —У —оо, то при i £ (0; 1) имеем, что ext 0, и, сле¬
довательно, <p(t) = lim ext cos x(t + 1) = 0. В то же время
X—► — оо
функция /(х, 0) = cos х не имеет предела при х —оо. Следо¬
вательно, в силу следствия 2 семейство /(х, t) =: eTl cos x(/-f 1)
сходится при х —у —оо на интервале (0; 1) неравномерно.
Если семейство /(x,J), х £ X, t Е Т, сходится при х —У хо
к непрерывной на Т функции tp(t) и для любого х £ X функ¬
ции f(xyt) непрерывны на Т1, то сходимость может быть как
равномерной, так и неравномерной.
Пример 30. Рассмотрим два семейства fi(x,t) = te~xt,
х ^ 0, t Е [0; 1] и /г(х,*) = xte~xt, х ^ 0, £ Е [0; 1]. Так как
/i (х, 0) = /г(х, 0) = 0, Vx ^ 0, а для £ > 0 при х —> +оо имеем,
что t — o(e~xt) и xt = o(e“rt), то как семейство /i(x, <), так и
семейство /г(х, f) при х —»> +оо сходятся к функции = 0,
t Е [0; 1]. Покажем, что сходимость семейства fi(xyt) на от¬
резке [0; 1] равномерная, а семейства /г(х,/) — неравномер¬
ная.
Действительно, гак как для любого х > 0, /) (х, 0) = 0,
lim fi(x,t) = 0 и (fi)'t — е xt(l — xt), то при х > 1 име-
t —► -|-оо
ем, что sup |/i(x,/)| = /1 (х, —] = —, и соотношение
*€[0,1] \ х/ хе
lim sup |/i(x,<)| 0 показывает, что fx(xyt) = ie~xt 0
т-ч+оо t6[0;l)
при х —у +оо на [0; 1].
413
(*'*)
= - не
с
Функцня /г(®, t) = ixe 1х при любом х > 1 принимает
максимальное на [0; 1] значение также и точке I = ~. Но
г.
в этом случае величина sup |/2(®»01 — f: ‘
«€[0,1]
является бесконечно малой при х —> +оо, откуда следует, что
f2(x,t) = txe~ix ► 0 при х -У -foo на [0; 1] неравномерно.
Теорема Дини. Пусть семейство функций /(х, / ), х £ X,
t £ Т, удовлетворяет условиям:
1) множество Т есть компакт;
2) для любого х £ X функция f(x>t) непрерывна на Т;
3) для любого t £ Т функция /(х,/) монотонна на Х\
4) предельная функция <p(t) = lim /(x,t) определена и
непрерывна на Т.
Тогда f(xyt) ^ <p(t) при х —> х0 иа Т.
Пример 31. Рассмотрим семейство функций
/(*, t) = arctg —, х > 0, t € [0; 1].
I X
Отрезок [0; 1] — компакт. Для любого х0 > 0 функция
f(zyt) = arctg непрерывна на [0; 1]. Для любого <о € Т
i + х0 j
функция f(x,to) = arctg монотонна на луче х > 0.
+ х j
Так как при t ф 0 lim /(х,<) = arctg - и lim /(х,0) =
1 it г‘ч0+
= lim arctg — = —, то при х -> 0+ предельной функцией
х-*о+ х 2
семейства /(х,<) является функция
{arctg j, <е(0;1],
2’ < = 0’
определенная и непрерывная на [0; 1]. Итак, все условия те¬
оремы Дипи выполнены и, следовательно, f(x,t) =3 ¥*(0 ПРИ
х —> хо на [0; 1].
Теорема Дини не является полным обращением теоремы
о непрерывности предельной функции равномерно сходяще¬
гося семейства функций — в ней введены дополнительные
414
требования компактности множества значений параметра и
монотонности функции /(х,/), определяющей семейство, от¬
носительно переменной х. Эти условия существенны. Так,
например, семейство /(х,/) — xte~xl, рассмотренное и при¬
мере 30, сходится при х —> +оо к непрерывной на [0; 1] функ¬
ции <p(t) = 0 неравномерно. Здесь множество значений пара¬
метра — компакт, функция /(хо,/) непрерывна на [0; I] при
любом хо ^ 0, предельная функция p(t) = 0 определена и
непрерывна на [0; 1]. Нарушено только условие 3 теоремы
Дини — функция f(x,1c) при любом /о G (0; 1] не монотонна
на положительной полуоси.
Пример 32. Рассмотрим семейство функций
= rhi' °0, ^°'
Для любого хо ^ 0 функция f(xо, t) = -— непрерывна на
I + Хо t
Т = {l:t 0}. Для любого *о^0 функция f(xjo) = —
1 -fa;/о
монотонна на X = {х:х 0}. Предельная с}>ункция <£>(/) =
= lim /(х, £) ~t непрерывна на Т. Покажем, что /(х, /.) -* <£>(/)
х~*0 +
при х 0+ на Т неравномерно. Действительно, при каждом
* *о*2
хо > 0 разность t — - = неограничепа на поло-
1 + x0t 1 -+ х0/
жительной полуоси, т. е. условие lim (sup |/(х,/) — <£>(01) — 0
л-->о+ teT
не выполнено. Здесь нарушено условие 1 теоремы Дини —
множество значений параметра не компакт.
Заметим, что на любом отрезке [0; а] выполнены уже все
условия теоремы Дини, следовательно, f(x,t) =£ ip(t) при
х -> 0+ на [0; а].
Если множеством значений переменной х является множе¬
ство N натуральных чисел, то семейство /(х,/) представляет
собой последовательность /(п,/).
В дальнейшем для краткости вместо “несобственный ин¬
теграл, зависящий от параметра” гам, где это ясно из кон
текста, будем говорить просто “интеграл”.
Определение. Пусть множество Т есть множес тво сходи¬
415
мости интеграла f[x,t.)dj- и E С 7I'/C.in для любого 110-
<7
ложнтелыюго числа 5. существует такое число В. а < В < и),
что для всех Ь: В < b < lj ч всех / Е У:’ справедливо неравен¬
ство
/(г, /) dx есть равномерная сходимость семейства функций
6
—^ uj— на Е
| ^ f(x.l)dx < е, то говоря'г, что интеграл J f (х, I) dx
Ь а
сходится равномерно па Е.
Заметим, что равномерная сходимость на Е интеграла
и>
/
а
/г(6, /) = J J(x,t) dx к J[t) — J f(x)t}dxnpi\b
a a
Следующие утверждения являются перефразировкой
свойств равномерно и неравномерно сходящихся семейств
функций, рассмотренных выше, на случай несобственного
интеграла, зависящего от параметра.
Критерий Коши равномерной сходимости интег-
IV
рала. Интеграл j f(xyt)dx сходится равномерно на миоже-
а
стве Е гогда и только тогда, когда для любого положитель¬
ного числа е найдется такое число В, а < В < w, что для
любой пары чисел 6], 62, удовлетворяющих неравенству В <
< 6] < 62 < и* и любого t Е Е справедливо неравенство
ь7
И* f(r, i) dx < f.
ь,
Как и при рассмотрении семейства функций, следует от-
o'
личать утверждения “интеграл I f(j,t)dx сходится неравно-
J ы
мерно на множестве Е” и “интеграл J f(r,1)dx не сходится
а
равномерно на множестве Е”. Первое утверждение нодразу-
416
мевает, что Е ость подмножество множества сходимости ин¬
теграла, а второе допускает, что в некоторых (может быть, и
w
всех) точках множества Е интеграл J /(#,/) dx расходится.
а
Следующие утверждения непосредственно следуют из оп¬
ределения равномерной сходимости интеграла.
Ы и)
Если интегралы j S\(x,i)dx и J f2(x,t)dx равномерно
а а
сходятся на множестве Ег то и интеграл
(afi(x,t) + 0f2(x,t))dx,
где а и /? — постоянные, равномерно сходится на множе¬
стве Е. w
Если интеграл J /(х, t) dx равномерно сходится на миоже-
а
стве Е1 то он равномерно сходится на любом подмножестве Е.
и)
Если интеграл J f(xyt)'dx равномерно сходится на каж-
а
дом из множеств Е\ и Е2, то он равномерно сходится на мно¬
жестве Е = Е\ U Е2.
Это утверждение не переносится на бесконечное объеди¬
нение множеств.
+оо
Пример 33. Рассмотрим интеграл J с~х% dx.
° ( 1 1
а) Покажем, что на множестве Еп = \t:t> — п Е N,
этот интеграл сходится равномерно. Действительно, если
/ > —, то для любого 6 > 0 имеем неравенство
-г»
о </
-foo
e“*f dx = < nc" п.
ь
417
Так как lim не » = 0, то для любого е > 0 существует
6-* + оо
такое В > 0, что для всех Ь > В верно неравенство 0 <
4 оо + оо
< J e~xi dx < £, т. е. по определению интеграл J e~xt dx
ь г, о
сходится равномерно на Еп.
оо
б) Покажем, что на множестве IR+ = {/: / > 0}, М* = Еп,
п — 1
интеграл сходится неравномерно. Для этого нужно указать
такое положительное число £, что для любого В > 0 при не¬
которых значениях 6 > В и to > 0 справедливо неравенство
+оо
/e~xt° dx ^ е. Возьмем 6 = 1,6 = тах(£ + 1, е) и to =
+оо 6
0 [ 16
Тогда I e~xto dt — —e~bt° = - 1, что и требовалось про-
J t0 е
ь
верить.
Теорема о непрерывности несобственного интег¬
рала, зависящего от параметра. Если семейство функ¬
ций /(г,<), х Е [а;ы), t Е Т, удовлетворяет условиям:
!)/(*,0 еС([а;ы)хТ),
ш
2) интеграл I f(xyt)dx сходится равномерно на 7’,
в г
функция J(t) = I f(x,t)dx непрерывна на Т.
а
Эта теорема является переносом следствия 1 теоремы о
перестановке двух предельных переходов. Переносом след¬
ствия 2 является следующее утверждение.
Если семейство функций /(х,<), х Е [a;u^), t Е [с; с/], удо¬
влетворяет условиям:
!)•/(*. 0 €С([а;ы)х [с; </])►
Ы
2) для любого ( Е (с; с/) интеграл / /(я,/) dx сходится,
и> J
3) интеграл J f(x,c)dx расходится, или он сходится, но
то
418
на [c\(f] разрывна функция J(t) = J f(xyt)dx, тогда интс-
ш а
грал J /(x, t) dx сходится неравномерно на (c\d).
а 4-оо
/dx
t Е [2; 10].
1 + xl
о
Покажем, пользуясь критерием Коши, чтоэт.от интеграл схо¬
дится равномерно на [2; 10]. Действительно, для любой па¬
ры 6], 62, 1 < 61 < 62, и любого I Е [2; 10] имеет место нера¬
венство
6з 6а
f dx Г dx
0< J ТТ? ^ J 1+^2 =arctg62-arctg6,.
61 Ьг
Поскольку функция arctg z имеет предел при z -> +00, го
в силу критерия Коши для любого е > 0 найдется такое
число В > 1, что для любой пары fci, 62 из неравенства
В < bi < 62 следует неравенство 0 < arctg 62 — arctg 61 < е,
Ьа
т. с. О < / -—< е для В < Ь\ < Ь2 и всех < Е [2; 10]. Так
J 1 -I- х1
bi 2
как функция /(х, t) = непрерывна на множестве [2; 10]
1 + х1
+оо
/dx
- 7 сходится равномерно на [2; 10], то на
!+** +оо
и f dx
отрезке [2; 10] функция J(t) = / непрерывна.
j 1 + а?
0 +оо
тт «е г» ( e~txcostx
Пример 35. Рассмотрим интеграл / dx.
J *
Для
х
1
1с '■*
cos tx <С
X
С ~ J
^ < —=■ для всех х > х*о(/). Следовательно, в силу теорс-
X X1 4-00
cos tx
dx сходится абсолютно
х
419
+ сх> 1 сю
f с °'rcosO-x f dx
для всех i > 0. Интеграл же / ах = / — рас-
J х J х
+~ „ 1
ходится. Следовательно, интеграл / — dx сходится
J *
1
на луче О 0 и на любом интервале (0; а) неравномерно.
Пример 36. Рассмотрим интеграл
+оо
"trsinJx ,
dx, t> 0.
Для любого t > 0 существует такое xq(/), что
с tx sintx
с 1
< < — для всех х > хо(0- Следовательно, в силу теоре-
х х£
+ сх>
/еГ sin tx
dx сходится абсолютно
1
для всех t > 0. В отличие от предыдущего примера интеграл
-foo -foo
f е.-° х sinO i J /•
I dx = I 0 dx
1 0
■foo
/С ^ Sill tx
— dx раз
x
l
рывна на [0;+oo), откуда следует, что интеграл
+ 00
[ С tXS\ntx
I
J *
1
сходится на (0; Ч-оо) и, тем более, на [0;+ос) неравномерно.
Как уже установлено, ./(0) = 0. 15с л и / > 0, то
-foo 1
т/,4 f e“usinti . f e”“sinw .
m= J ~^~dv= j dv + h'
420
+РО
f с. usinii
где К — I du (гходимость этого интеграла уже
J w
1
установлена). Функция
(_t. si n w
е , и > О,
и
1, U = О
интегрируема на [0; 1] в смысле Римана, откуда полу магм, что
1 -foo
,/.» Г е и sill и j rr f е u sin и .
J(t) - / du+ К = / du.
J и J и
lim
t-+0+
o о
Итак, для доказательства разрывности функции J(t) па [0; 1]
(точнее, справа в нуле) осталось показать, что
+ оо
f е и sin и . . Л
/ —
о
Применяя теорему о среднем, получаем, что для любого на¬
турального п имеет место равенство
2ir(n + l)
>~~и «in
du —
/
и
2 яп
ж(2п+1) 2ir(n + l)
/ e_tisinu . /*
= J w J
c-(i f-b
■ du = 2— 2
u 6 6
2irn ir(2n+l)
где 6 E (27rn; 7r(2n-f 1)) и £2 € (тг(2п + 1);27г(п + 1)). Так как
e_z
функция монотонно убывает и £1 < £2) то
Z
2w(n-f1)
*“u fiin
■ du > 0
/
Ti
2*n
для любого п Е N.
e"w
Так как функция не определена при и = 0, то оцен-
v
421
2тг
ку интеграла J du проведем другим способом. Из
о
sin у 2и
неравенств ^ 0, и £ (0;тг), и sin и ^ —, и £ (0;яу2),
получаем, что1 п
7Г ТГ 7Г/2
/c“usinu , _ [ sin и _ / sin и .
du > е / du > сГп / du ^ е~\
О 0 0
2п 2п
_ I /* e~usinti _ __ /* rfit
Так как / аи ^ е / — := е In 2, то оконча-
7Г 1Г
тельно имеем, что
2п it 2*
/e“usint/ , /* e“u8inu . I f e“u sin ti ,
du =± / t/w - / du >
w J и \J и
0 0 IT
> е“ж(1 — In2) >0.
Объединяя все полученные неравенства, выводим, что
+оо 2ir +оо
/e“usinit . f c_usinu , f e“usinu ,
dv = / dt/-f / du =
ti J и J и
0 0 2*
2n 2*(п + 1)
/* e u sin и f e u sin и
=j——d“+E j ——*■>».
0 n”1 2irn
что и требовалось установить.
Замечание. Неравномерную сходимость на [0,-foo) ин-
+°° .
J е trsin tx
теграла / dx можно было доказать и с помощью
1
критерия Коши, но в данном примере главной целью было
+о°
/с sin tx
dx, а за-
о
ключение о неравномерной сходимости интеграла есть след¬
ствие этого основного факта.
422
Теорема Дини. Если семейство функций /(j:, /), х Е [я; и;),
I £ удонлетворнет условиям:
1) множестио 7' петь компакт,
2) функция /(■!*,/) непрерывна и неотрицательна на
[о;ы) х 7’, *
3) функция J(/) = I f(x,l)dr определена н непрерывна
на 7’, и. '
тогда интеграл / /(а*,/) r/х сходится равномерно на Т.
а tdx
Пример 37. Рассмотрим интеграл / -г г, £ Е [0:1].
J t2 + х2
1
Множество значений параметра t есть компакт. Функция
г/ ч *
f(x,t) = — непрерывна и неотрицательна на множестве
1- 4" х1
[];+оо) х [0; 1]. Функция
+9° . (тг 1
= о
ни выполнены, следовательно, интеграл / — сходится
л 'х2
определена и непрерывна на [0; 1]. Все условия теоремы Ди-
+оо
f t dx
J <2 + x:
равномерно на [0; 1]. 1
Переходим к свойствам несобственного интеграла, зави¬
сящего от параметра, не являющимся перефразировкой сфор¬
мулированных выше свойств семейства функций. Рекоменду¬
ем читателю сравнить все рассматриваемые свойства инте¬
грала с соответствующими свойствами функциональных ря¬
дов.
Достаточные признаки равномерной
сходимости несобственного интеграла,
зависящего от параметра
Признак Вейерштрасса (мажорантный признак).
Пусть семейство функций /(ж,/), х Е [а;ы), t € 7\ удовле¬
творяет условиям:
423
1) для любого [а;6) С [а;ш) функция /(x,f0) £ R.[a\b) при
любом /о £ Т\
2) существует функция д:[а\и) -* Ш такая, что при всех
х £ [a;u;], t £ Т справедливо неравенство |/(х,/)| ^ 9ix)
(мажорантная функция семейства f(x,L) на 7 ) и интеграл
/
д(х) dx сходится.
а ы
Тогда интеграл J f(x,t)dx сходится абсолютно и pastic¬
ci
мерно на множестве Т. I
f dx
Пример 38. Показать, что интеграл / ; ■■■
и и J () +12/2)х/Г^
о
сходится равномерно на положительной полуоси.
Решение. Функция f(xyto) = : — непре-
Vl - х2(1 -|- х2Ц)
рывна на множестве [0; 1) при любом to £ [0;+оо), следова¬
тельно, для любого 6, функция f(x,to) £ /?.[0;6]. Так
как 0 < 77Т~Т^Г7г==Ч ^ л Лля любого t € [0; +00)
(1 + x^)vl - xl vl - ®
1
f dx
и интеграла / ■ сходится, то в силу признака Всйер-
J vl — х2
о
штрасса данный интеграл сходится равномерно на положи¬
тельной полуоси.
Признак Вейерштрасса представляет собой аналог теоре¬
мы сравнения для несобственных интегралов, независящих от
параметра. Существенное отличие этих двух утверждений
состоит в то, что в теореме сравнения требовалось выпол¬
нение неравенства \/(х)\ ^ </(х) локально слева в точке и>, а
в признаке Вейерштрасса требуется выполнение неравенства
|/(х, t)\ ^ д(х) как для всех t £ Т, так и для всех х £ [а; Де¬
ло в том, что если д(х) £ Я[а;а;) и неравенство |/(х, / )| ^ </(*)
для каждого I € 'Г выполнено для *о(0 < * < и, т. с. левая
полуокрестность точки и;, в которой это неравенство спра¬
ведливо, зависит от значения t, то интеграл может сходиться
неравномерно. Приведем соответствующий пример.
424
1
Пример 39. Рассмотрим интеграл [ -dx, если
J Vх
о
а) Т - (0; Л), 0 < А < +оо, и б) Т = (0;+оо).
Покажем, что в случае а) данный иитеграл сходится рав¬
номерно, пользуясь признаком Вейерштрасса. Действитель¬
но, из неравенства 0 < t < А следует, что
|lnx|f ^ шах{1, |1пх|л}.
_ ж 1 +1\пх\А
Таким образом, функция д(х) = 7= является мажо-
Vх
I Inх\*
рантной функцией семейства /(х,/) = -—-jJ- для t Е (0;Л).
Vх j
Так как существует такое X, что 1 + |1пх|л < —7= для х Е
V*
Е (0;Х), то функция д(х) локально справа в точке Ч) удовле-
творяет неравенству 0 < д(х) < следовательно, схо
1 Х
дится интеграл Jд(х) dx, и в силу признака Вейерштрасса
1 0
f 11пя|* /л
интеграл / —у=г- ах сходится равномерно на (0\А).
J у/х
о
Покажем, что в случае б) данный интеграл сходится не¬
равномерно. Действительно, сходимость этого интеграла для
любого t Е (0;+оо) показана в пункте а). Далее, для любой
пары 6i, из неравенства 0 < Ь\ < 62 < - следует неравен-
Ьа.
ство
ь
[ 11ПТ1. fix > 2|1пб2|с(\/^2 — \/^i)- Если числа bi и 62
ь
фиксированы, то lim 2| — \/bi) = +°°» следова-
f —>сю
тельНо, для любого М > 0 и любой пары b\, Ь2, удовлетворя¬
ющей неравенству 0 < 63 < 62 < -, найдется такое значение
h е
t
t Е (0;+оо), что J dx > М. В силу критерия Коши
425
f IM'
отсюда, следует, что интеграл / —=- ах сходите н неравно
J Vх
мерно на луче (0; -Нею). 0
Теперь обратим внимание на то, что для любого JE(0; -foo)
л IM* 1
неравенство 0 < —j— < -т-гт верно, если 0 < х < хо(и, т. е.
\Jx х*5/4
Inx* 1
для каждого 1 Е (0; -foo) оценка 0 < =- < —т- справед-
у/Х х*5/4
лива локально справа в точке 0. Но, как было показано, из
этого факта и интегрируемости функции </(х) = на [0; 1]
х •
[ |1п*|‘
не следует равномерной сходимости интеграла / —-=- ах на
луче (0;-foo). 0
+00
Г dx
Пример 40. Рассмотрим интеграл / -z , если
J (x-t.y + 1
a) t € (0; А) и б) t G (0; +00). 0
Покажем, пользуясь признаком Вейерштрасса, что в слу¬
чае а) данный интеграл сходится равномерно. Если t\ < t2}
1 1
то неравенство — < верно только на
(х - ti)2 -f 1 (х -*2)2 + 1
луче х > c(*i,/2), где t\ < c(t\yt2) < <2 (см. рис. 12). Таким
образом, функция 0i(x) = 7 77= не является мажоран-
(х — Ay -f 1
той семейства f(xyt) = ——- для t Е (0; Л). Поскольку
(х tj ~f 1
для любого t € (0; -foo) имеем, что 0 ^ /(х, /) ^ 1, то функция
02(х) = 1 является мажорантой семейства /(х, t) для t Е (0; А)
-foo -foo
и для t Е (0; -foo), но интеграл J </г(^) dx = J dx расходит-
о о
ся. Возьмем функцию
1, О^х^Л,
1
я(х) =
х > А.
(х - A)2 -f Г
Эта функция уже удовлетворяет обоим условиям: онаявляет-
426
Ршс. 12
ИНТ
ся мажорантой семейства f(x}t) — —- для < Е (0; И) и
+оо Vх “ Ч + 1
еграл J д(х) dx сходится, так как д(х) ~ при х —► +-оо.
о
Покажем, что в случае 6) данный интеграл сходится не¬
равномерно, пользуясь критерием Коши. Действительно, схо¬
димость этого интеграла для любого t Е (0; -foo) показана в
пункте а). Далее, так как максимальное значение функция
/(x,f) = ——- принимает в точке х = t, то для того,
(х — t)z + 1
ь2
чтобы получить интеграл J ——^ большой величины
естественно взять числа 6i, 62 так, чтобы b\ < t < Ь2. Пусть
61 = t — 1, 62 = t + 1, тогда
ь2 1
/dx _ [ dz _ ж
{г-<)2 + 1 ~ J z2 + 1 ~ 2
Ьх -1
Итак, для любого В > 0 найдется значение t = В + 2 на лу¬
че (0; -foo) и числа &i = t — 1 = В -f 1, 62 = * + 1 = В + 3
427
Г) L I f n
такие, что И < b\ < 62 и / -г^ = т. с. инте-
J (х - ty + 1 2
+°° 6,
( dx
грал I сходится неравномерно на луче (0;-foo).
J (х -ty -hi
о
В обоих приведенных примерах неравномерная сходи¬
мость интеграла на соответствующем множестве доказыва¬
лась с помощью критерия Коши.
Разумеется, если интеграл j f(x,t)dx сходится неравно-
а
мерно на множестве 71, то никакая мажорантная функция ^(х)
семейства /(х, /), t £ Т, не интегрируема на [о; w). Но неинге-
грируемость наиболее точной мажорантной функции ^(х) =
= sup|/(x,J)| на [а;о>) еще не обозначает, что интеграл
/
/(x,/)dx не сходится равномерно на Т. Во-первых, если
ш
интеграл J f(x,t)dx при некоторых t £ Т сходится услов-
а
но, то его равномерная сходимость заведомо не может быть
установлена с помощью признака Вейерштрасса, поскольку
из выполнения условий этого признака следует абсолютная
сходимость рассматриваемого интеграла на Т. Во-вторых,
даже в случае абсолютной и равномерной сходимости на мно-
и>
жестве Т интеграла I f(x,t)dx функция #(х) = sup|/(x,/)|
J teT
а
может не интегрироваться на [a;u>). Приведем соответству¬
ющий пример. +оо
Пример 41. Рассмотрим интеграл J
Ы
t dx
(tx — I)2 — In/1
0
Множество значений t не является компактом.
Доопределим функцию f{x,t) = т , х ^ 0, t €
(tx — 1 у — 111 t
, положив /(х,0) = 0 для всех х > 0. Тогда к инте-
К]
428
\ оо
гралу I J
f(z,t)dj‘ применима теорем* Дипн. Действительно.
множество значений / отрезок
°s5
сеть компакт, фун-
0;
кция f(x, t) неотрицательна па множестве [0: +оо) х
неравенство 0 < /(x,f) ^ j—- показывает, что f(xyt) непре¬
рывна па :>том множестве, функция
+ ос
./(/•) = J f(r,t) dr =
О
/
dz
I
J 22-l 11/ x/fTnTj ^ 2
0,
7Г 1
- + arcl.g
\/n^lJ’,ev0;2
/ = 0,
Следовательно, инте-
определена н непрерывна на
+ oc
грал I f(x, t) dx сходится равномерно на
J +OU
t dx
интеграл / — :— сходится равномерно на I 0;
1-ГХ.
/
a
и, тем более,
Г
(tx — l )2 — In t
В то же время для x > 2 имеем неравенство
т. е. функция д(х) локально слева в -foo совпадает с фупкцп-
+ оо
еп — , и, так как
х 111 х
хо-
f dx
с интеграл / —: расходится, то расх
+cw J *ln*
дится и интеграл J g(x)dx.
О
Признак Аболя- Дирихле равномерной сходимости
интеграла, зависящего от параметра. Пусть функции
f(x,t)'- х £ [о;cj), t е 7\ и д(я\1): х € [о:w), i £ 7\ при кн-
429
ждом / £ Г интегрируемы и смысле Римты пл любом отрезке
[л;Ч С [«;^). Если при этом выполнена одна ил следующих
пар условий: ь
ai) функция F(b,l) = J /(х,/) r/х ограничена ил [г/;и;) ж 71.
а
6]) при любом t Е 7* функция <7(х,/) монотонна па [о:и;) и
<7(х, t) =£ 0 при х -* и;— на 7';
и>
а«2) интеграл j f(x,t)dx сходится равномерно па 71,
а
62) функция ^(х,/) ограничена 11а [a;u>) х Т и при любом
/ Е Т монотонна иа [а;и>).
w
Тогда интеграл / /(х, t)g(x, t) dx сходится равномерно
наТ. {
Так же, как и для несобственных интегралов, независящих
от параметра, область применения признака Абе¬
ля—Дирихле, в основном, неабсолютпо сходящиеся интегра¬
лы. При этом иногда одна или обе функции /(х,/), g(x,t)
не зависят от t. Тогда соответствующая сходимость, есте¬
ственно, является равномерной на рассматриваемом множе¬
стве значений параметра /. +ос
_ _ [ /sin/x .
Пример 42. Показать, что интеграл / ", \у- -■ dx схо¬
дится равномерно на [0; 1]. о ^ *
Решение. Положим /(х,/) = / sin tx и g(x,t) —
\/х2 + 1
Функция g(x,t) монотонна на [0; +оо) и, поскольку эта функ¬
ция не зависит от /, g(xyt) 0 при х —► foe па [0; 1]. Далее,
6 6
|| /(х,/) </х| = tsmtx dx
Итак, выполнены условия а) н б) признака Абеля - Дирих-
+ оо
Г . ош I ..
ле и, следовательно, интеграл / — dr сходится райпо
мерно на [0; 1].
f /sin/.г
J \/x2-f 1
о
430
•foo
/t2cosix
тг-dx cxo-
x + tl
дится равномерно на [0;+oo).
Решение. Положим f(x,t) = tcostx и g(x,t) = ——
x | I
Функция <](x, /) монотонна на [1; -foo) при любом t £ [0; +00),
а неравенство 0 ^ g(x,t) < ;г7=> z 6 [l;-foo), t E [0;+oo),
2y/x
показывает, что g(x,t) 0 при x —> -foo на [0; foo). Далее,
ь
I
I cos txdx
1
= I sin bt — sin t\ ^ 2, <E[0;+oo), 6e[1;+oo).
Итак, выполнены условия а) и б) признака Абеля—Дирихле и,
+°°
/t cos tX
— dx сходится равномерно
х + t2
на [0; -foo).
+00
/cos X
- - arctg tx dx
2x — t
сходится равномерно на [0; 1].
tx
Решение. Если положить f(x,t)=cosx и g{x,t) = — —,
2x — t
го неравенство I/ f(x, t) dx 1 = 1/ cos xdx
^ 2 верно для всех
l l
t E [0; 1] и b E [l;+oo), но монотонность функции g(x,t) не
очевидна — и числитель, и знаменатель при t > 0 растут
с ростом х — следовательно, требуется дополнительное ис¬
следование. В данном случае проще представить подыите-
COS X
тральную функцию в виде произведения arctg tx и про-
2 х — /
верить выполнение второй пары условий признака Абеля—
Дирихле. Действительно, поскольку, как уже установлено,
ь
функция F(b,t) = J cos xdx ограничена на [1; -foo) х [0; 1] и
431
неравенство —-— ^ —-—-, х £ [1;+оо), t £ [1; 2], показы ва-
2 х — t 2х — 1
ет, что функция монотонна и равномерно сходится к
2х — г
+оо
/cos х dx
— сходится
2 х — t
1
равномерно на [0,1]. Функция g(xyt) = arctg tx ограничена
на [1; +оо) х [0; 1] и при любом t Е [0; 1] монотонна на [1; +оо).
+оо
Следовательно, интеграл / — arctg txdx сходится рав¬
номерно на [0; 1].
/cos х
2 x-t
1
+оо
/t sin (x + -J
- flx
X
сходится равномерно на [0; 1].
t sin (x + f)
Решение. При любом t ф 0 функция /(х, t) = —
х
на (0; -f оо) имеет две особые точки — 0 и (+оо). В таком слу¬
чае, как и для интеграла, независящего от параметра, про¬
межуток интегрирования разбивается на два так, чтобы на
полученных промежутках только одна и при этом краевая
точка являлась особой для подынтегральной функции, инте¬
грал сходится равномерно тогда и только тогда, когда рав¬
номерно сходятся интегралы по каждому из полученных про¬
межутков.
Следуя этому правилу, представим данный интеграл в ви¬
де
*4*оо 1/2 оо
11.1.[‘jjiktilь +
J X J X J X
о 0 1/2
и проверим, что каждое из слагаемых есть равномерно схо¬
дящийся на [0; 1] интеграл.
1/2
Интеграл
/t sin (х + -)
dx, в свою очередь, представля-
432
1/2 # 1/2
ется
// sin jr cos 7 / / cosx sili £
-dx+ I —dx.
X J X
о 0
Рассмотрим каждое слагаемое отдельно. Неравенство
(о; 0 . < € [0; 1],
t sin х cos -
i
X
t cos —
X
X
1/2 • <
/t sin X cos -
— dx сходится равно-
х
о
г
t smxeos-
мерно на [0; 1J (заметим, что — Е Я
х
°’ 2
для всех
< £ [0; 1], но равномерная сходимость интеграла является след¬
ствием ограниченности функции двух переменных g(x,t) =
femxcoe- /_ l\ __
Подынтегральную функцию во
(0; х [о;!1)-
втором слагаемое представим как произведение следующим
t cos х sin ~ t t
образом: — = —^-sin — *хcosx. Так как д(хЛ) =
х хг х
= xcosx не зависит от £, то g(x,t) :=£ 0 при х —> О-f на [0; 1],
а неравенство (xcosx)' = cosx — xsinx > 0, х Е ^0; , по¬
казывает, что ^(х) монотонна на £о; . Функция F(btt) =
1/2
= j* ■—2 sin — dx ограничена на ^0; ^ х [0; 1]. Итак, инте-
ь
1/2
f t sin (х + i)
грал I — dx как сумма двух равномерно сходящих-
о
ся на [0; 1] интегралов сходится равномерно на [0; 1].
+ос • / t\
Г / sin (х + £)
Интеграл / —dx тоже разобьем на два слага-
J х
1/2
смых '
433
+°° +со
//sinxcos^ Г ( cos х sin- .
^r/x + / z-dx
1/2 1/2
и будем рассматривать каждое из них.
Так как
t cos х sin -
^:+оо^ , I € [0; 1],
f ОО #
// COS X sin ^
dx
1/2
сходится равномерно и абсолютно на [0; 1].
В первом слагаемом подынтегральную функцию удобно
sin £ I ,
представить как произведение / cos - (если же взять
t хх
t cos -
произведение sin х то придется дополнительно прове-
+оо J при 1 е [0; 1]).
х
I
^;-|-оо) х [0; 1] и монотонна на
cos -
рять монотонность функции — на
х
+оо
Интеграл j ---- dx сходится в силу признака Абеля—Ди-
1/2
рихле, а поскольку подынтегральная функция не зависит от /,
то эта сходимость равномерна па [0; 1]. Функция g(x,t) =
t
= t cos - ограничена на
х
-foo
1 \ ft sin х cos ^
-foo 1 при любом t £ [0; 1]. Итак, интеграл I dx
i
сходится равномерно на [0; 1], следовательно, интеграл
+ (Х> • / / ч
f t sin (х + М
I dx сходится ранномерно на [0; 1].
1/2
Объединяя все вышесказанное, получаем, что интеграл
+°° . / * \
Г tsin (х + М
I dx сходится равномерно на [0; 1].
434
Сравнивая формулировки признаков Абеля—Дирихле для
сходимости несобственного интеграла, независящего от па¬
раметра, и для равномерной сходимости несобственного ин¬
теграла, зависящего от параметра, видим, что требование ло¬
кальной монотонности слева в точке ш функции </(х) заменено
требованием монотонности функции g(xyt) при фиксирован¬
ном t на всем промежутке [а;ы). Если же функция g(xyt)
монотонна на промежутке [6(f);и;), где а ^ b(t) < ы, то рав-
и>
номерная сходимость интеграла Jf(x,t)dx на Г и ограни-
а
ченность g(xyt) на [а; о;) х Т не гарантируют равномерную
U)
сходимость интеграла J /(х, t)g(x% t) dx на Т. Приведем со-
а
ответствующий пример.
Пример 46. Для t 6 (0; 1] найдем натуральное число n(t)
n(t) j j
такое, что - > -. Положим
(x,i) =
siatx, ^ ’ 1 G ^0;
тг(4п + 5) п(Ап + 5)
х> 2i—’ 'е(0>1]l
0, X ^ 1, t = 0,
где п = п(<), и
tsintx
/(х,0 = __.
Тогда получим, что
1) так как функция F(6,t) = Jtsintxdx = cost — cosbx
0 1
ограничена на [1 ;+oo) x [0;1], функция — монотонна на [l;+oo)
x +oo
и =£ 0 при x —► +oo на [0; 1], то интеграл J /(х, t) dx
схо¬
435
дится равномерно на [0; 1];
2) функция д(х, () непрерывна и ограничена на [1 ;4-оо)х[0;1]
и при каждом t £ [0; 1] локально монотонна слева в -boo.
Следовательно, при каждом фиксированном / Е [0; 1] иите-
+ оо
грал I /(х, t)g(x, () dt сходится в силу признака Абеля - Ди-
1
рихле. Покажем, пользуясь критерием Коши, что сходимость
этого интеграла на [0; 1] неравномерная.
п * - м «I » 2тг 2тг(п(1) -f 1)
Пусть t Е (0; 1], &! = —, 62 = , тогда
sin2 tx
f f tsin tx . f sill ix
I f(x,t)g(x*i)dx= I dx = t I dx.
6, 6, 9=1 lUL
1 I
Так как подынтегральная функция неотрицательна, то
3»(g+l) 2шЯ + Эу/Л
r sin2<x
dx.
I /
4
Г 9.7Г/1 -4- 7Г IЛ *).1ГП 4- .Чтг !А
X
2wq+w/4
_ .2 1 Г27г<7 +тг/4 2тгд 4-37г/4
Так как sin «х ^ - для х £ 1
2 | / ’ t
то
2w«43ir/4
I
/
sin2<x 1 27Го + Зл74 1 тг 1
dx > - In —^> — >
2 27гд -f 7г/4 2 47г<7-Ь7г/2 10^’
3f*W4.
е
Объединяя все полученные неравенства, имеем, что
Ь? n(t)
/
0=1
Итак, для любого Б > 1 возьмем такое /о Е (0; 1], что — > 77;
27Г 27г(п(<) 4- 1) °
тогда числа о\ = — и 62 = —— удовлетворяют нера-
to
436
и2
Kciirriiy Н < b\ < bj и j f{r,ta)g(x,lu)dx > -j^, откуда еле-
-foo k,
дуст, ЧТО J I(x.t)g(-r J)dx сходится неравномерно на [0; I].
l
Теорема об интегрировании несобственного инте¬
грала по параметру. Пусть семейство функций
х 6 [a; u;), t G [с; с/] удовлетворяет условиям:
1) f(x,l) £ (7([«;ы) х [с; </]);
LO
2) интеграл J(t) = J/(х, ^)</х сходится равномерно на [г; с/].
а
Тогда справедливо равенство
d ы и> d
/ (//(х-, i) rfx) dt = J f(x,t) dt'j dx.
с a a c
Заметим, что функция J(t) в силу теоремы о непрерывно¬
сти несобственного интеграла непрерывна и, следовательно,
интегрируема на [г; </].
/arctg х
—ах, пользу-
XV1 - х2
„ arctg х f dt
ясь формулой = / X > 0.
X J 1 1
1 о
dt
+ х2/2’
о
Решение. Запишем данный интеграл в виде
[([ * , ) dx.
J \J (1 + x2t2)y/\ - xz)
о о
Покажем, что функция f(x,l) = ; ==^ удовлетво-
(I -f x2/-)v 1 - х2
pRi'T условиям теоремы об интегрировании несобственного
интеграла по параметру и, следователыю,
/ ^7Г=£ = / (/л*, о л)* = /(//(*. 0*) л.
437
Функция У(д", ^) = — -^-^-^==== пепрерыина на [0: 1) >: [0: I].
Для i Е [0; 1] имеем, что
тг/2
[ * = f -
J (1 +хЧ2)х/Г^ J 1
dz
(1 -f x'2t2)y/\ — х1 J 1-M2sin2z
о о
+ оо
du тг
/г
+ /2 + u2 2\/l + t2'
О
1
dx
(1 + х2Ь2)\Д~- х2
Таким образом, интеграл J — сходится для
о
любого t Е [0; 1]. Поскольку множество знамений t есть ком-
1
пакт, функция : неотрицательна и непрерыи-
(1 + a?2l2)vl —*2
/dx
(1 + r2^)VT^P =
К непрерывна на [0; 1], то в силу теоремы Дини
2y/T+t*
1
/dx
r ■■ сходится на [0; 1] равномерно.
(1 + x2t2)y/\ — х2
о
Итак
1 i
Г arctg х dx = f f f \ И1 _
J xy/\ — x2 J \J (1 + x2i2)\J 1 — x7 )
0 0 0
1
= / -Д=*Л = >(1 + >/2).
J 2VTTF 2 '
H'OD
Пример 48.
a G Ift.
i-сю
dx, /?>(),
я
438
Решение. Запишем данный интеграл в виде
-f оо а
J е Рх cos txdt^jdx.
о о
Покажем, что при любых 0 > 0 и а Е 1R функция /(х,*) =
= е~Рх costх удовлетворяет условиям теоремы об интегри¬
ровании несобственного интеграла по параметру и, следова¬
тельно,
+оо -foo а
J = j (/ /(.,ол)л =
а 0 0
а +оо а +оо
0 0 0 0
Функция f(x,t) = с~^х cos tx непрерывна на (0;-foo) х [0;а),
+оо
*
схо-
а G М. Так как для любого 0 > О интеграл J е &х dx
о
дится, то неравенство \f(x,t)\ ^ е“^*, < Е [0;а], показывает,
+оо
что интеграл J е~^х сов txdx сходится равномерно на [0;а]
о
в силу признака Вейерштрасса. Итак,
+оо а +оо
р-Р*
j s_in_a.£e_:!: dx=д j t-» cos <х л=
о
а
= / /?2 + <2
0 0 0
а
0 О
dx = arctg —, 0 > 0, а Е R.
а Е
+°о
/sin ах
dx,
х
о
439
Решение. Воспользуемся результатом предыдущего при-
+°°
/sin ах а
е dx = arctg-, t > 0. Интеграл
х t
-l-оо О
/
sin ах
-l-oo
/
dx сходится равномерно на множестве [0; 1]
х
о
в силу признака Абеля—Дирихле, поскольку интеграл
+°°
sin ах , Гл ..
ах сходится равномерно на [0; 1J, функция е мо-
х
о
нотонна на [0; -foo) при любом t Е [0; 1] и 0 < e~tx <С 1 для всех
х Е [0;-foo), t Е [0; 1]. Следовательно, в силу теоремы о не¬
прерывности интеграла, зависящего от параметра, функция
+°°
/sin ax
e~tx dx непрерывна на [0; 1], откуда получа-
о
ем, что
+9°
sin ax
/
dx — J(0) = lim J(t) = lim arctg — = ■— sign a.
x v ; v ' t->0+ b t 2
о
Внимание! В приведенных примерах вычисления несоб¬
ственных интегралов проверка выполнения условий теоре¬
мы об интегрировании несобственного интеграла по параме¬
тру — существенная часть решения. Отсутствие такой про¬
верки — грубая ошибка, и формальное вычисление никоим
образом не представляет решения.
Приведем пример, показывающий, что условие равномер¬
ной
сходимости интеграла J(t) = Jf(x,t)dx на [c\d\ суще-
а
ственно для справедливости равенства
d ы d
J J{t) dt= f{x, t) d?j dx.
с ас
2 x2t2
Пример 50. Функция /(x, /) = t arcctg tx2 — —- onpe-
1 -f tlx4
440
делена и непрерывна на множестве [0; -4 оо) х [0; 1]. Так как
+ оо +оо
■7(0= I f(x,1)dx= j (t arcctg tx2 - t ^2^.4 )dx ~
n 0
= lim 6/ arcctg b2t = 0
b-¥- l-ro
]
для всех t 6 [0; 1], то J J(t) dt = 0. Функция
о
l l ^
¥>(*) = J f(x,l)di = J (t arcctg tx2 - ■—{ ^) dt =
0 0
1 1
/2 11 i r #2«2 r j.2/2
= — axcctg((i )\+-JT-jspHt-2j ТТрр* =
0 0
= 5»ссЧ!.!-^/(1-тт^)л =
о
] 2 3 ..I1 3
= 2arCCtg* +2^arctg<X lo'2^ =
1 2 3 3 ,
= - arcctg * - 2x2 + 2?f arct8 * • x # °-
непрерывна на [0;+oo), если y>(0) = так как
4
im ( arctg x2 - = 0.
-*o\2x4 b 2 z2 J
lim t Л .
x->o \2x4
Найдем первообразную F(z) функции <p(x) на произвольном
отрезке [а; 6] С (0;+оо).
Так как х не обращается в нуль на [а; 6], то
= I .гг*, P + i + ,,, ,1
f dx x 2 3 1 M
+ i *>(!+,«) = 2arCC‘S* + & “ •,,••■' '*" +
/* dx f x 2 dx
+J ^+2J rr^ =
x , 1 1 , „ f x2 dx
- r> arcclg x + — - arctg x +2 1
2 b 2x 2a:3 b J 1 + x4
Так как lim (-7 ^ arctg x2 ) = 0, to
*-ю\^2х 2x3 /
+ OO +OO ^
I ip(x) dx = 2 / —J dx + lim ( — + - arc ctg 62 -
J ^ ’ J 1 +*4 b-ц-оо 2 Б
о
+ oo 1
263
В теореме об интегрировании несобственного интеграла
по параметру речь идет об интегрировании функции J(t) =
и>
= I /(я, t) dx в смысле Римана. Если же рассматривается не-
а ^
собственный интеграл J J(t)dt, то обычно используют тер-
с
мин “перестановка двух несобственных интегралов”.
Теорема о перестановке двух несобственных инте¬
гралов. Пусть семейство функций f(xyt), х £ [a\cj),t £ [<*;£>),
удовлетворяет условиям:
1) f{x,t) € С([а;и)) х (с;й>));
U)
2) интеграл F(t) — I f(x,t)dx сходится равномерно па
а ^
любом отрезке [c\d] С [с;cZ;), интеграл Ф(а:) = J f(x,t) dt схо-
с
дится равномерно на любом отрезке [а;Ь] С
442
3) существует хотя бы один из двух интегралов
ш ш ш ш
/ (/ dt) dx ИЛИ / (/l-rt*»*)!dx) dt'
ас с а
Тогда справедливо равенство
ш ш
j Ф(х)dx = / F(t)A
а
ИЛИ
w UJ
/(/= Jf(x,t)dx^dt.
а с
Используя теорему Дини, получим следующее
Следствие. Пусть семейство функций /(х,<), х € [a;u>)i
/ Е [с; о>), удовлетворяет условиям:
1) функция /(Xyt) непрерывна и неотрицательна на
[a;w) х [с;ы); ш й
2) функции F(t) = J f(x,t)dz и Ф(я) = J f(x,t)dt не-
а с
прерывны на [с; о)) и [a;w) соответственно;
ы ш
3) существует один из интегралов J F(t) dt или J Ф(ж) dx.
с а
Тогда существуют оба эти интеграла и
й) U)
J F(t)dt = j Ф(г)с/аг
или
ш ш
/(/ /(*,<) dxj dt — J f(x, t) dtj dx.
с a a с
Пример 51. Вычислить интеграл Эйлера—Пуассона
+оо
используя перестановку двух несобственных
о
443
интегралов.
-foo
Решение. Положим ip(t) = J le ^Tt>l dx, тогда ф(0) — О
о
-foo +00
и ф(1) = J te~(xl^ dx — J с~и du — J при / > 0. Следова-
0 о
тельно,
-foo -foo +00
J ^ dx^j dt = j еГ{ ip(t) dt=
00 о
-foo -foo
= J c~t2 J dt — J £ e~t2dt = J2.
о 0
Функция f(x,t) — <e~(1+r ^ непрерывна и неотрицательна
-foo
на [0;+oo) x [0;+oo). Функция Ф(х) = J tc~(]+x ^ dt =
0
-foo
= — г- непрерывна на [0; -foo) и интеграл I Ф(х) dx =
2(1 |r) J
0
-foo
1 f dx it
— - I ——- = — сходится. Функция же F(t) =
о
-foo
rr J te~^l*x ^ dx = e~l 1p(t) непрерывна только на луче
о
[б;+оо), где е > 0. Таким образом, условия следствия теоре¬
мы о перестановке двух несобственных интегралов выполне¬
ны для семейства /(х,<)> х € [0;+°°)» * £ [е; -f-oo), при любом
е > 0, т. е.
-foo -foo -foo -foo +00
/(«,!)*)*=/(/л., 1)dfS)j dx = J G(x,e)dx
€ 0 0 с 0
444
при любом в > О, где G (х, ^ f(x,t) Ж, х е [0; +со),
в е [0; 1).
+ ®
Неравенство 0 < G (х, е) < j* f(x, t) Ж = Ф (х), е ^ О,
О -|-в9
показывает, что в силу признака Вейерштрасса J G(x,e) dx
о
сходится равномерно на [0; 1], следовательно,
+оо ^ -foo v +оо ^ +оо
J2
= J ^ J f(x}t)dx^J dtzz lim J f(xyt) dx^j dt =
0 0 с *0
+oo -foo
= lim J G(x,e)dx= J G(xy0)dx =
о о
+ oo -foo
= /(/ /(*,*)<*)
0 0
Отсюда получаем* что J =
Пример 52. Вычислить интеграл Френеля
-|-oo -foo
Jc«,Sdt=\ J
0 0
+oo
] 2 f v
пользуясь формулой —j= = —I c~xt dt, x > 0.
x/х Х/7Г У
0
+•0
/COS X
—7=- dx сходится в силу признака
у/i
1
1
/COS X
—т=- с/х сходится в силу нера-
\/х
о
445
венства
(*08 X
I
< —= и теоремы сравнения, следовательно,
у/X
sfz
t>P<
> -+
-^= J cosxc~Tt (li^dx.
интеграл Френеля сходится. Запишем его в виде
-foo +OG
+ 00
Интеграл J cosxc~xt di расходится при х — 0, следова-
о
тельно, сходится неравномерно на (0; а] при любом а > 0;
+ оо
интеграл / cosxe_xt dx расходится при t — 0, следователь-
о
но, сходится неравномерно на (0; с] при любом с > 0. Таким
образом, теорема о перестановке двух несобственных инте-
-f оо -foo
г рал о в непосредственно к интегралу к/ cosхс xt dt'j dx
о о
неприменима. Поскольку именно нулевые значения х и / дали
расходящиеся интегралы, рассмотрим интеграл
-foo -foo
Id cos xt xt dt'j dx
6
для e > 0 и 6 > 0. Покажем, что для такого интеграла усло¬
вия теоремы о перестановке двух несобственных интегралов
выполнены.
Функция f(x,t) =cosxe~xt непрерывна на [£;+оо)х[£;+оо).
Если I G ;с], то |/(х,/)| ^ с~т6 , и из сходимости инте-
+оо
г рал а I е~т6 dx и признака Вейерштрасса следует равно-
J -foo
мерная сходимость интеграла /г(£,/) = J f(x}t)dx па [<J; г].
£
Если х £ [е;я], то |/(г./)| ^ и и.» сходимости ннтегра-
446
+ СЮ
ли I e~€t dt н признака Вейерштрасса следует равномерная
6 +со
сходимость интеграла Ф(х, J) = J f(x, t) dt на [г; а]. Так как
6
|/(я,01 < е~Х^ Дл>1 х £ [е; Ч-оэ), / Е [£;+оо), то
+ °о +оо 2
О ^Ф(1)= J \f{x,t)\dx $ J е~хС* dx =
и в силу теоремы сравнения интеграл
Ч-СО +оо -f ОО
у (/ ^г,<)|d^jdi- J №)dt
6 е S
-f oo -f-oo
сходится. Итак, J Ф(x)S)dx— J I* (с, t) dt для любых £ ^ 0,
S > 0. e 6
+ OC
Функция F(e}t) = J cosxe~xt dx = e~xt
tit2 cose — sine
1 +*4
<2
для б > 0 и t £ [0;+oo). Если положить F(0,t) = -
1 -f-1
t E [0;-foo), то получим функцию F(£,£), непрерывную на
[0; 1] х [0;+оо). Покажем, что
-foe -f ОО
lim^ J F(e,t)dt= J F(0,t)dty S > 0.
Для этого достаточно установить равномерную сходимость
+оо
интеграла J F(e1t)dt на [0; 1], что следует из неравенства
6
/2 -f 1
7ГГТ’" Е [0; 1], t Е [£;+оо), и сходимости иите-
t -f- 1
447
+ °° о
f * * rl4 и
грала I t4^j at. Из всего вышесказанного следует, что
6
+оо 2 +оо +оо
/ ^ТЛ= / ^(0,<)Л = Дт I F(e,t)di =
it i
+00 +00
= lirn^ J Ф(х}6)<1х = J Ф(x1S)dx.
€ 0
+ OO
/2 2 coe x
cosxe~xt dt = —7= —7=-, т. e.
y/x
0
+00
подынтегральная функция в интеграле J Ф(х, 0) dx имеет
о
на (0;+оо) две особые точки. Поэтому отдельно докажем,
что
1 1
J Ф(x,6)dx = J Ф(х,0) dx
о о
+оо +оо
lim I Ф(x,6)dx = I Ф(х,0Ых.
£—►(>+ J J
1
Так как функция х ^ 0, t ^ 0, неотрицательна, то
для S ^ 0 справедливо неравенство
+оо +оо
|Ф(МЖ J J е xt’dt=-?==,
6 О
откуда в силу признака Вейерпгграсса следует равномерная
1
сходимость интеграла f Ф(г ,8)dx на [0; 1]. Так как функ-
448
ция Ф(я,Л) = j cosxe ** ell непрерывна на (0; I] x |0; J]. to.
* 1 1
следовательно, lim / Ф{x,8)dx — I Ф(хЛ))(1.г.
<J-*o+ J J
о 0
-foo foo
Интеграл J Ф(я, <5) dx запишем в ниде J <p(x,fi) <7 .г,
\ i
-foo
где (р(х,6) = / у/хс xi dt. Соотношение
о
f-оо foo
0^y>(x,£) = J e~z dz ^ J с~г dz
&Jx о
показывает, что функция у>(х, Л) ограничена на [1; +оо) х [0; 1]
и монотонна на [1; -foo) при любом S 6 [0; 1]. Функция *
-foo Vх
/COS X
—-=-dx сходится раи-
Vх
1
номерно на [0; 1]. Отсюда следует, что в силу признака Абс-
-1-00
ля—Дирихле интеграл / —j=-ip[x, <S) dx сходwгея рапномор
/
1
но на [0; 1]. Так как функция Ф(х,£) непрерывна на [1; Н-оо) х
foo -foo
х [0; 1], то J Ф(x1S)dx= j Ф(а:,0)с/з:.
l *1
Объединяя все вышесказанное, получим, что
foo -foo foo
О С) О
foo foo ^ foo ^
= lim I Ф(x,S)dx — lim f — dt — f — dt,
^Of J v ; *->0f Jt4 f ] J tA + j
449
откуда следует, что
-foo f оо
/2 ] f COS X
cos х dx — - I —dx =
2 ./ Vх
о о
-foo -foo
0 0
Теорема о дифференцировании несобственного
интеграла по параметру. Пусть семейство функций
/(х,<), х Е [a; u;), t Е [с; rf], удовлетворяем условиям:
1) функции /(х,<) и //(х>0 непрерывны на [a;u;) х [с;</];
U)
2) интеграл J f(xyt)dx сходится хотя бы при одном зна-
a
чении t Е [с; cf] ;
ш
3) интеграл J fl(x}t)dx сходится равномерно на [с;</].
a ы
Тогда интеграл J J(x,t) dx сходится равномерно на [с; d\ к
а
непрерывно дифференцируемой на [c;rf] функции с/(<) и J'{t) =
w
= j fl(x,t)dx.
а
В силу локальности существования и величины производ¬
ной получаем
Следствие. Пусть семейство функций /(j:,/), х Е [a;w),
t Е [c;d], удовлетворяет условиям:
1) функции /(ж,*) и //(ж,/) непрерывны на fa;с^) х [r;d];
U)
2) интеграл J f{x,t) dx сходится равномерно на [c\dj] для
а
любого с/j, с < d\ < d,
U)
3) интеграл J f[(xj)dx сходи тся ранномерно на любом
а
отрезке [7;^] С (с.](1).
450
ы
Тогда функция J(t) — j f(x,t)dx непрерывна на
а и>
дифференцируема на (сг; с/) и «/'(/) = J f[(x,t)dx для всех
*<ЕМ).
Это следствие позволяет применить дифференцирование
ш
по параметру для вычисления таких интегралов /
а
для которых функция J(t) не является непрерывно диффе¬
ренцируемой на соответствующих отрезках изменения пара¬
метра, и, тем самым, семейство /(х,/) заведомо не удовлетво¬
ряет условиям теоремы о дифференцировании но параметру.
Пример S3. Вычислить штгры J,—' cost «Л,« > О,
t его. 0
Решение. Функции
/(х,<) = е~ах* costх и //(х,<) = —хе~ах sin tx
непрерывны на [0; -foo) х ГО. Бели t = 0, то интеграл
•foo -foo -foo
J e“ar cos txdx= J e~ax2 dx = J e~z dz
0 0 0
есть интеграл Эйлера—Пуассона, вычисленный в примере 51.
Таким образом, выполнено второе условие теоремы о диффе-
+°° ^
ренцировании по параметру и J(0) = J е~ах dx =
-foo -foo И
Интеграл J xt~ax* dx = ^ J e~az dz сходится, поэтому не-
о о
2
равенство |//(х,<)| ^ хе~ах , t е ГО, показывает, что в силу
признака Вейерштрасса интеграл
-foo -foo
J f[(x,t) dx = — J xe ar sin tx dx
451
сходится равномерно на любом отрезке [с; d] С М. Итак, в с с
условия теоремы о дифференцировании по параметру выпол-
4-00
нены, следовательно, функция J(i) — J с ах cos (х dx, а > О,
о
непрерывно дифференцируема на любом отрезке [с; d\ С
т. е. J(t) £ С1 (К) и для любого t £ R
+00
г,0 -/
О
Первообразная функции хе~ах sin tx относительно х, если
ни а, ни t не равны нулю, не выражается в элементарных
функциях, но из равенства
+оо
Г 2 1 2 1+00
— I хе ах sin tx dx — —е ах sin*x —
2 а 1о
/,
о
+оо
— [ е~ах cos tx dx — — I е~ах costxdx
2а J 2а J
+00 4-00
О О
следует, что функция J(t) удовлетворяет дифференциально¬
му уравнению J'(t) = — — J(f). Из этого уравнения и началь-
2а
1 т, ч 1 /я7 _il
ного условия j(0) — ~\1 получаем, что J(<) = -\ — е «« .
2 у а 2 у а
Если аналитическое выражение функции f(x,t) или //(х,£)
не определено при некоторых значениях х £ [а;^), но эти
функции могут быть доопределены так, чтобы получились
функции, непрерывные на [а;о;) х [с;</] (или [а;ы)*& [с; с/)), то
такое доопределение всегда подразумевается. При вычисле¬
нии конкретного интеграла в таком случае проверка возмож¬
ности доопределения функции “по непрерывности” — обяза¬
тельная часть решения.
+ °° 2 I 2
/с~ах —
2~
О < а < 6. 0
452
е *J — е
Решение. Рассмо'грим функцию f(xj) — ,
хг
I Е 1R . 10с аналитическое выражение не имеет смысла при
х = 0. ( ледоиателыю, необходимо проверить возможное!'!»
определения значений /(0,/) так, чтобы функция f(x,t) стала
непрерывной на [0;+оо) х Ш. Соотношение
С-Ь«а
Inn = b — t
*-►0 + X2
показ1лвает, что, положив /(0,<) = b — t, получим функцию,
непрерывную на [0;+оо) х IR. Итак, возможность доопре¬
деления “по непрерывности” функции f(x,t) 11а [0; + оо) х К
проверена. Далее, непрерывность функции //(х,/) = e~tx
следует из ее аналитического выражения. Так как а > 0,
+оо
то интеграл J е~ах dx сходится. Отсюда и из неравенства
о
О < е~'г < /Гах , t Е [а; 6], в силу признака Вейерштрас-
+оо
са следует равномерная сходимость интеграла I e~tx dx —
о
+ °° +00 з 2
f f c~tx - е~
— — I ft(xi t) dx на [a; 6]. Наконец, I - dx — 0
о о
при I = b. Итак, все условия теоремы о дифференцировании
по параметру выполнены для семейства /(х,/), х Е [0;+оо),
e~tx2 — c~bx2
I Е [а; 6], где функция f(x,t) = , х ф 0, и доонре-
х1
делена “по непрерывности” на множестве [0; +оо) х [я; Ь]. Сле-
+/°е~^2 - еГЬх2
дователыю, функция J(t) = / dx непрерывно
о
дифференцируема на [я; 6] и удовлетворяет равенствам:
J(b) - О
453
(гм. пример 51). Отсюда получаем что J(t) = \Лг6 — \/nl.
Окончательно,
+ <*> 2 • 2
- е-аг _е-Ьх
/
dx = J(a) = \/7r(v^ - у/й) (() < а < 6).
+ CXJ
/cos ах
г> dx.
] -f х2
о
_ _ _/ ч cos*x ... ч —xsin ix
Решение. Функции /(х,<) = - и /*(х,/) = —- —
1 + xz 1 ^
cos tx
1 -I- х
,2
1
1 -f X2
непрерывны на [0; -foo) х R. Неравенство
-foo
сходимость интеграла J ——^ показывают, что в силу при-
0 + 00 -foo
знака
Г dx
J 1+х2
о
/г cos tx
f(x,l)dx — I ~2^x
о 0
сходится равномерно на 1R. При любом е > 0 функция F(6, i) =
6
/I sin bt гЛ \ f \
sinlxax = —-— ограничена на |0;-foo) х |£,+оо); функ-
о
х
ция g(x,t) = г- не зависит от <, монотонна на [1; + оо) и
1 -\~х
lim д(х} t) = 0. Следовательно, в силу признака Абеля—Ди-
х —► -f-oo
+оо
[ • х I
рихле интеграл / sinfx ax сходится равномерно на
J 1 -f х2
1
[е;+оо) при любом е > 0. Применяя критерий Коши, ви-
-foo
дим, что равномерная сходимость интеграла / sin 1.x dx
J
]
на [е;+оо) эквивалентна равномерной сходимости интеграла
Ч-oo
—х r v roalx
^ sin/х ax на [fj+oo). Итак, семейство f(xy1) — - -,
1 + X- J
о
х £ [0;+оо), < £ [0; +оо), удовлетворяет всем условиям слсд-
454
ствия теоремы о дифференцировании несобственного инте¬
грала по параметру, следовательно, функция
+оо
cos tx ,
dx
+ X2
о
непрерывна на [0; +оо), дифференцируема на (0;+оо) и
+оо
О
для t > 0.
При любом t G К интеграл
+оо / +оо
f f xsinix\ J f X2COS tx J
J \TT^)t x- J
о 0
, xsin^x
расходится, поэтому семейство <j(x,i) = =- не удовлетво-
1 + х1
ряет условиям теоремы о дифференцировании несобственно¬
го интеграла по параметру. Используем равенство
+°°
7г С sin tx ,
2 = J — **, *>°
0
(см. пример 49). Складывая его с равенством
+оо
О
+°°
т// ч * Г smtx . , А
получаем, что J it) + — = I —т: тгг dx для i > 0. Ана-
2 J х(1+х2)
о
sin tx л
литическое выражение —г; не имеет смысла при х = 0,
х(1 + х2)
г sin*x ^ ^
но соотношение пш — гт- = t показывает, что функция
х-»0+ х(1 + х )
sin tx
<p(x,t) = — — доопределяется “по непрерывности” на
х(1 + х2)
455
[0;+оо) х [0; + оо) равенством у?(0,/) — t. Функция v?J(.r,/)
cos (х
= непрерывна на [0;4-оо) х [0; -|-оо), интеграл
1 + х1
f по -1-00
f , V . ( sin/а: f
J *>(*.')«<«= J
сходится при / = 0, неравенство
-1-00
COS /х
1 + j:
,2
димость интеграла J - ---- показывают, что в силу при-
0 -foo foo
знака
f dx
>ала J тт^
о
Вейерштрасса интеграл / <p't(x,t)dx - im
о о
сходится равномерно на [0;+оо). Итак, семейство <p(x,t)}
х Е [0; -f-oo), t Е [0;+оо), удовлетворяет всем условиям те¬
оремы о дифференцировании несобственного интеграла по
параметру, следовательно,
foo f-oo
j"(t)=(j'(t)+^)' = j <p't(x,l)dx= f ^dx = j{t)
0 0
для t > 0.
Итак, функция J(t) удовлетворяет следующим условиям:
1) J(t) — четная непрерывная функция па IR;
2) J"(i) = J(t) для 1 > 0;
foo
3)^0)=/^ = ^
0
foo
/dx 7Г
j + х2 - 2 АЛН |,ссх 1
436
Из дифференциального уравнения J”{f)=J(t) (условие 2)
следует, что J(t) = Cl е*+С2е~1 для г>0. Из ограниченности J(t)
на IR (условие 4) следует, что = 0. Из непрерывности J(t)
расходится. Этот факт показывает, что теорема о дифферен¬
цировании несобственного интеграла по параметру дает только
достаточное, но не необходимое условие дифференцируемости
функции.
Внимание! При вычислении несобственного интеграла с
помощью дифференцирования или интегрирования по пара¬
метру проверка выполнения достаточных условий со отвеет-
вующих равенств является существенной частью решения. От¬
сутствие или неполнота такой проверки грубая ошиб¬
ка. Формальное вычисление в таком случае не представляет
решения.
на {R и равенства У(0)= (условия 1 и 3) следует, что
2
Из честности /(/) (условие 1) следует, что
j(t)=K е~т, /е
2
Следовательно,
+ 00
О
Заметим, что функции
о
дифференцируема при всех f >0, хотя интеграл
о
о
457
ЭЙЛЕРОВЫ ИНТЕГРАЛЫ
(БЕГА- И ГАММА-ФУНКЦИИ)
1. Бета-функция. Так называется интеграл Эйлера пер¬
вого рода
1
В(х,у)= (1)
О
где х > 0, у > 0.
Данный интеграл равномерно сходится по х и у на мно¬
жестве х ^ Хо > 0, у уо > 0 соответственно.
В области х > 0, у > 0 функция В(х.у) непрерывна и
бесконечно дифференцируема. Делая в интеграле (1) замену
z
t = , получаем другое аналитическое выражение функ-
1 + z
ции В(х,у):
+°° х_ х
в^»|=/ п+,).+, <2>
0
Непосредственно из определения Бета-функции следует (если
положить t = 1 — г), что
В(х,у) = В(у,х),
а с помощью формулы интегрирования по частям получаем,
что
В(х + 1, у) = В(х,у),
уУ (3)
В(х,у+ 1) = —— В(х,у).
х + у
Если у есть натуральное число, то, последовательно применяя
формулу (3), получим равенство
-w ч 71—1 71 — 2 1
В(х, п) = ... 1),
x-f-n - 1 x + n- 2 x+J
и поскольку
1
458
то
В(п,х) = В(х, п) = —{4)
х(х -f 1) • • • (я + п — 1 )
Полагая в формуле (2) у = 1 — я, 0 < х < 1, имеем
+°о х ]
В(х,1-х)= J
О
2. Гамма-функция. Так называется интеграл Эйлера вто¬
рого рода
+оо
Г(*)= J tx-le~ldt. (5)
О
Данный интеграл сходится равномерно в области х ^ Хо > 0.
В области х > 0 функция Г(х) непрерывна и бесконечно диф¬
ференцируема, причем
+оо
Г<п>(*) = J Indt.
О
Положив в (5) t = In —, получаем другое аналитическое вы¬
ражение функции Г(х):
1 х— 1
Г(*)
=/ Н) *• («>
Поскольку In — = lim n(l — z*) и выражение n(l — z*) при
Z n-+oo
возрастании n стремится к своему пределу, возрастая (рас-
1
смотрите производную функции по а), то аналогично
О'
утверждению задачи № 51 гл. I § 5 из (6) следует, что
1
I»= lim га1-’ [(I — z'* )г~* dz
п-юо J
459
Полагая z — tn, имеем
l
Г(х) = lim и* f t”~'( 1 - О3-"1 dt.
n-> OO J
0
Применяя формулы (1) и (4), получаем
i
J<n-1(l - t)1-1 dl = B(n,x) =
0
Следовательно,
г/ * г x 1 -2-3 •••(« — 1)
1 (x) = lim n
1 2 3 - - (7i — 1)
x(x +])••• (x + 71 — 1) ’
0
n-¥0о x(x + 1) • • • (x + П — 1 ) ’
Из этого равенства следует, что
T(x-fl) пх
■ р/ V = 1*т ■ ■■■■— = X,
I (х) n-Юо X Ч- 1 + п
откуда получаем формулу приведения
Г(х + 1) = хГ(х), х > 0. (7)
Из этой формулы, в частности, следует, что
Г(п+1) = п!, п£М, (8)
так как
+ OG
€~х dx = 1.
о
"г оо
Г(1)=/
Для любых х > 0 и у > 0 справедлива формула, устанавли¬
вающая связь между эйлеровыми интегралами Г-функцией и
5-функцией:
д( _ Г(*)Г(к)
J 00 (1 _|_ 1)Г
Рассмотрим функцию G(x) = - , х ф 0, х ф z,
Х п= 1 п
z — целое отрицательное число.
460
Поскольку
- ,1+х(п“^)+^+оШ] *
п —> ОО,
то бесконечное произведение сходится абсолютно для любого
х ф 0. 'Гак как п-ое частичное произведение есть
Итак, функция С(х) совпадает с функцией Г(х) для х > 0,
и, следовательно, получено разложение функции Т(х) в бес¬
конечное произведение
Так как :>то произведение сходится для всех отрицатель¬
ных нецелых х, то молено принять равенство (10) за опреде¬
ление функции Г(я) для таких значений х.
Используя связь Т('х) и G(x), можно непосредственно про¬
верить, что для отрицательных нецелых х справедливо ра¬
венство
1 (1 + 1)*р + 1)г...(1 + !)-_ (B+i).
* (1 + *) (1 + §) • • • (1 + f) +
то
= Г(х), X > 0.
(10)
л-Г(ж) = Г(* + 0-
461
График функции у — Г (я) приведен на рис. 13.
Прамер 56 . Вычислить
Рис. 13
+ 00
м
J (1 +
+ х)2
О
Решение. Используя представление
+оо -1-00
/ 7Г^Ъ<Ь= I —~~1—г dx,
J (1 + *)2 J (]+r)s+«
dx.
462
получаем, что
+ °° _ +°° 6
■-v-4*kH'GK)-
= ir (-4) Г (\ - -4) =• -—— = -
5 \ь) V Ь) 5 sinf 5
Применим формулу представления функции sinx бесхоиеяным
произведением (см. с. 73). Имеем
sinx = 111 (1-^2)- 1*1 < 00
ТП—\ ' '
Полагая здесь пх вместо х, получаем
sin 7ГХ = 7ГХ ТТ ( 1 — ) , |х| < ОО.
iiA
Поскольку
1 00 f1 + I^x
И*) = - П V , Г(х+1) = хГ(х),
П = 1 п
00 (I + -М-*
г(1 - *) = -*г(-*) = п Lr_4".
п=1 п
ТО
Значит,
Г(«)Г(1-х) = -£Х
XSin 7ГХ
т. е.
г(х)г(1-г) =-Д-, nez. (in
Sin 7ГХ
Положив здесь х = получим Г
463
Из формул (2), (9) и (И) следует, что
Т Jll j, = B(1,1 - г) = г(ЧН| - , -JL-,
У (] + Z) Г(1) Sin 7TJT
0
О < X < 1.
Првмер 57. Определить область существования и вычи-
+ OCJ
[ хт
слить интеграл / - ; r~dxy п > 0.
F J (а + Ьхп)Р
о
Решение. Введем новую переменную t, полагая " = £,
тогда — ( " у dt = dx, поэтому
п V 6 / 6
-foo rnf 1 -1-00 , .
f x™dx = (§) " f£±^_dt =
J (a + bxn)P naP J (1 + <)P
0 0
m f I foo _ . .
_ (f)" f Jf
пая J (i +<)=^+Р-=±г-
1 /m + ] m+l\
= (5) J-
Следовательно, данный интеграл сходится при условии
О < ^-— < р. Заметим, что подобные преобразования явля-
тг
ются обратимыми, поэтому из сходимости последнего инте¬
грала следует сходимость исходного.
Таким образом, при решении задач подобного рода можно
не выяснять предварительно сходимость заданного интегра¬
ла, поскольку она эквивалентна определенности полученных
Бета- или Гамма-функций.
Пример 58. Определить область существования и вычи-
п/2
слить / = j sinm х cosn х dx.
о
Решение. Положим sin х = \Д, t ^ 0. Тогда cos х dx =
1 ,
= —г А,
2уД
464
1 1
1 f m — 1 л-1 1 f m +1 | u41 i
1=2 J t-r~(\-t)— dt = - J H^-*( 1
di.
Следовательно, данный интеграл сходится при условии
m-fl Л п + 1
—-— > 0 и —-— > 0 и его значение равно
Пример 59. Найти площадь области, ограниченной кри¬
вой (*2 + у2)’б = *У.
Решение. Поскольку х и у входят в данное уравнение в
четной степени, то кривая симметрична относительно обеих
координатных осей. Следовательно, достаточно найти пло¬
щадь |Di| области Di, ограниченной этой кривой и осями
координат и лежащей в области х > о, у > 0. Введем поляр¬
ную систему координат, совмещенную с декартовой систе¬
мой, и сделаем замену х — г cos у?, у — rsin<^>, тогда уравне¬
ние кривой в полярной системе, ограничивающей область D\,
запишется в виде г12 = г6 cos4 у? sin2 у?, т. е. г6 = cos4 <psin2 ip,
0 ^ <р . Следовательно,
л-/2
\°\\=\ j cos^sin» tpd<p = (JT“,'3T“):=
= I«?7 5>\ 1ГШГ(1) _
2 \6’ 6/ 2 Г(2)
= ir (' + g) Г (I) = 15r (ff) г (I) =
= ±r(T)rM') = i
12 \6J V 6/ 15
1Г
V2s\nn/6 6’
и площадь всей области, ограниченной данной кривой, есть
. 7Г 2тг
4- — , т. е. —.
6 3
+°° ^ 2
Пример 60. Вычислить 1 — I - jdx.
J 1 + X4
463
Решение. Полагая хл = t, получаем, что
1 Г Г3/“1п2<
“64 J 1 + t
dt.
о
+оо
+оо
ЯВЛЯ-
Интеграл / — at равен / ——-г at и
J i+< J м + оН1-!)
0 о ' 7
ется второй производной функции В(р, ] — р), вычисленной в
1 „
точке р = Поэтому
64 \dp2 \sin7rp//
*> \'
7Г“ COS 7Гр \
р= 1 64 \\ S»4 /Р>
7Г2 /— 7Tsin3 пр — 27Tsin 7TpCOS2 7гр\
64 \ sin4 пр )
_ 7Г3 sin2 ^ + 2 cos2 7 7Г3 1 + (^) _ Зл-3У2
“ 64 ^in3 5- “ 64 ^^3 “ 64
Пример 61. Доказать формулу Лежандра
Г(*)Г(*+0 = 2^ГГ(21)-
Решение. Преобразуем интеграл
1
В(х,х) = j <*-'(1-<)*->
dt
следующим образом:
1
lt2r
*<*■*>=/ИН ■"=2/ ?-(!-')
о L J о L
1 , 1 Г
н сделаем в нем замену - — / -- -у/и, тогда получим
г- 1
dt
466
1
в (х- J* 1/2(l В Q, xj
О
Вьфажая функцию В(х, у) через функцию Г(х), имеем
Г(х)Г(х)^ 1 Г (1/2) Г (х)
Г(2х) 22*-1 Г(1/2+х) ’
откуда получаем искомое соотношение.
Пример 62. Доказать, что
r(:)rC)-r(v)-^”^
п натуральное.
Решение. Обозначив данное произведение через Е, рассмот¬
рим его квадрат
ак
ШЫ,-
Tax как
Г
то
2_
Е2 =
тт .
Для вычисления [[ si11— рассмотрим тождество
рш 1 Л
*"-• nY пр ■ ■
=П U-c°s--ism — I.
г-l л " )
В пределе при z-> 1 имеем
откуда
я—1
=2"-1 П sin
я-i
nil пр • • 2*п
Л= 1 — 008 — — !ЯП —
.1 Л Л
р-1 I
467
П-l /o X n-1
II TT . Р7Г fl 2тг 2
Поэтому I I sm — = -—г и, значит, E = ~=—.
'11 n 2”-1 Jn
p=l e v
a*f 1
Пример 63. Вычислить 1(a) = J 1пГ(х)</х, a > 0.
a
Решение. Заметим, что функция 1пГ(х) непрерывна как
функция двух переменных на (х;а) = (0; -|-оо) х (0;+оо). Та
а+1
ким образом, при любом a > 0 интеграл J h\T(x)dx есть
a
собственный интеграл, подынтегральная функция в котором
непрерывна как функция двух аргументов х и а, а пределы
интегрирования — непрерывные функции параметра а. Нре-
1
дельное значение этого интеграла — интеграл J In Г(х) dx -
о
является уже несобственным интегралом, так как подынте¬
гральная функция 1пГ(х) является неограниченной на (0; 1).
м Г(х+1) г/ . 1
Из равенства Г(х) = — получаем, что Г(х) ~ -,
х ^ х
х -> 0-Ь, откуда из равенства In Г(х) = 1пхГ(х) -f In следу-
х
1
ет, что 1пГ(х) ~ In -, х —> 0+, и следовательно, J 1пГ(х) dx
сходится. о
Дифференцируя данный интеграл по параметру а, имеем
/'(а) = 1п Г(1 + а) - In Г(а) = 1п(аГ(а)) - In Г (а) = )п а,
откуда
1(a) = a(lna- 1) + С, (13)
где С - константа.
а+1
Интеграл J 1пГ(х)</х стремится к нулю при а —> 0 как
1
непрерывная функция переменной а. Следовательно, для лю¬
468
бого е > 0 существует S > 0, такое что для любого а, удовле¬
творяющего условию 0 < а < <$, а < 1, имеем
1 а+1 а
| J In Г(х) dx — J 1п Г(х) dx | ^ || hi Г(х) dx
О а О
I а+1
+ / in Г(х) dx < е,
1
т. е.
а+1
linri^ J 1пГ(х)с/х = J\nr(x)dx.
а О
1 *
Для вычисления интеграла I — I In Г(х) dx заметим, что
1 J
I = J In Г(1 — х) dx. Тогда
0 1 1
/ = 1- [ 1п(Г(*)Г(1 - *)) dx = I / In dx =
2 J I J Sin 7ГХ
0 0
1 1
If 11 f
= - I (In 7Г — In sin 7Tx) dx — — In 7Г — — I In sin 7ГХ с/х =
о 0
n rc/2
— - In 7Г — — I In sin x dx — - In 7Г I In sin xdx.
2 2тг J 2 7Г J
о 0
Для вычисления этого интеграла положим х = 2<, тогда
тг/2 тг/4
Д = J lnsinx<fx = 2 J In sin 2tdt —
о о
тг/4 тг/4
= ~ In 2-f2 J \ns\ntdt + 2 J In cos t dt.
Подставляя в последнем интеграле t = — — и, приведем его
469
п/2
к виду 2 J In sin u chi, откуда I) = ^ In 2 + 27j, и значит,
тг/4
1\ = — — In 2. Поэтому
Z
1
I = f In Г(1 — х) dx = ^ In 7Г — — (— ~ In 2) = In VS.
J 2 тг V 2 /
о
Переходя к пределу при а —> О-f в (13), имеем
lim а(1п а — 1) + С = In л/27г,
а-*о+ v 7
откуда С = 1пл/27г, и следовательно, /(а) = In \/27г+а(1п а —1).
При вычислении многих интегралов большую роль игра¬
ет так называемая логарифмическая производная функции
Г(х) — функция
<йпГ(х) _ Г'(*)
dx ~ Г(х) ’ Х>"’
именно, важны различные ее представления в виде интеграла.
Рассмотрим тождественное равенство при х > 0, у > 0
= Г(у)у Г(« + у)-Г(«) = Г(1 + у) Г(д + у) — Г(х)
Г(* + у) у Г(* + у) у
Если перейти к пределу при у —> ОН- в этом равенстве, то в
силу дифференцируемости функции Г(х) и ее непрерывности
получаем, что
+оо -foo
О О
470
Поскольку Г (у) = J ty хе 1 dt, В(х,у) = J dt.
то
£М= U™ 7*-'=
Г(лт) у+о+J \ (1+<)х+»у
= 7(е~1--L-H
J V (1 + ty) f
(14)
Для обоснования законности предельного перехода заметим,
что функция
а*.») = (е (i+<)*+y)’
{ х + у-1,
1ф о,
t = О,
непрерывна как функция двух переменных на мнржестве
+°°
[0;/] х [0; -foo) и интеграл J ty~] \ е~ь - • — ^g+y) dt сх°-
1
дится равномерно на ^0; , так как при t ^ 1 и у £ [^’^]
1
справедливо неравенство
1
t^~ • |е -
-foo
(1 + *)*+у
(1-И)а
— е
Из формулы (14) получаем, что (полагая t = eu — 1)
-foo -foo
г ' - • -
Г(
цт/ [ Cl*- f dt \ -
'(*) »-*0+\У < J <(1+/)*J
е с
-foo -foo
= lim ( / — du- [ g “*■ du\ =
r-m+\ J и J 1 - e-u J
f ln(l+f)
In(l-fe)
471
Поскольку ДЛЯ 0 < £ < X
е-их е-их
<
;n(i+o
1 — е~и е~и(еи — 1) e“(*-i)(eu - 1) (l+e)*-1^’
f е~их e-ln(l + e) е
J 1 — е~и U < е(1 + е)*-1 < 2(1 + е)*"1’
€
е2 f е~их
1п(1+е) = е-—+ о(е2), е —► 0+, то lim^ / —du —
ln(l+e)
и,значит,
ЕМ-Т(е—- e~UX \ Аи
Г(х) J \ и l-e-“j
О
Полагая в (14) х = 1, имеем
+оо
Ш
Г(1)
Ш) _r4u_T(-t 1 \dt
m-r{i)-J [е ~ш)т
о
Вычитая это равенство из (14), получим
m _ га) = 7 (-1 i *
Г(х) 1 > J \l+t {! + *)•) t
Введя новую неизвестную - - - = z, получаем формулу Гаус¬
са ^
Н«)
Г(х)
/1 — 2х*1
~Y=7~dz- (15)
Поскольку —^— = 1 + z -f z2 Н , Ы < 1, то
1 - z
1 х—1 1
/ ~ Т~Г~ ^ = /(1”z*"1)( i + * + *a + ---M* =
о о
| оо
= / -*т+,-‘)||*.
472
(16)
При любом х > О члены ряда, стоящего под знаком интеграла,
являются непрерывными и знакопостоянными на [0; 1] фуик-
1-Z*-1
циями, причем сумма ряда, равная — , непрерывна на
[0; 1] при любом х. Следовательно, этот ряд в силу теоремы
Дини сходится равномерно на [0; 1] и его можно интегриро¬
вать почленно.
Итак,
/ ^ = Е f-Ч - —)
У 1-2 " Vm + 1 ТП + X/
о т-и
v ' т=0 х '
Отсюда получаем, что
d2 In Г(х) _ у. 1
dx2 (ш + х)2
т=О v '
и вообще
т=0 v '
Дифференцировать почленно ряды по х можно, т. к. они схо-
1 1 ™
дятся равномерно вследствие оценки — < . Инте-
(m + x)n mn
грируя почленно ряд (16) по х от 1 до х > 0 (это законно в
силу его равномерной сходимости), имеем равенство
т=0 х '
Полагая здесь х = 2 и учитывая, что In Г(2) = 0, получаем
равенство
оо
г/(1) = -у;
“о 1 m + l'
473
т. е.
m=l '
ггичная сумма Sn этого ряда равна
-(' + i + I+ +
Следовательно, в силу равенства
(1 + 5+"+^~Inn)=Сэ
lim
г»->Ч-оо
где Сэ — постоянная Эйлера, получаем, что
Г'(1) = —Сэ, (Сэ~ 0,577). (17)
+оо
Пример 64. Вычислить J е~х In2xdx.
о
Решение. Полагая х2 = t, перепишем исходный интеграл
+ 00
в виде 2 It 1/2е 1 In2 tdt. Рассмотрим функцию Г(ж) =
+°° J
= J t*~le~l dt. Последовательно имеем
О -foo -foo
Г'(х) = J Int tx~lc~l dt, r"(ar) = J In2 14х~1с~1 dt,
о о
и следовательно, данный интеграл равен 2Г" . Значение
Г" выводится из формулы (16):
d2\nT(x) /Пх) У Г"(х)-(Т'(х))2 А 1
dx2 \Г(Х))Х Г2(х) £j(n +
1
При х = - имеем
Г2Ш п^0(2^1)2’
474
хУ
Поскольку по формулам (15) и (17)
г(±) J i-t J y/ip + y/i)
О О
= Сэ — 2 In 2,
то
г> (0=^(сэ_2,п2)-
Поскольку
00 1 _2 00 ( 1 \ п — 1 00 1 00 1 -.2
Е — = —• V ' ’ —У" =
п2 б ’ " п2 “ п2 “ (2п)2 12’
П = 1 П = 1 П = 1 П —1 v
то
сю
У' 1 _ 1 /ТГ2 ТГ2\ _ *2
(2n- l)2 “ 2 V 6 + 12/ 8
И
r„m ^Г2(1) + (Г(1))2
Ц" г(1)
= у\А+ (у^)2(Сэ-21п2)2 = * + (Сэ-21п 2)2^ .
Пример 65. Вычислить интеграл
/(, .,1- / (1 -«”)<1 - *■").
О
а > -1, /? > — 1, 7 > — 1, or + /? > — 1, а + 7 > -1,
/? + 7>-1, ar + /J + 7>-l.
Решение. По формулам (15) и (17) имеем, что
dx J- 1 — i
Значит,
1
475
f (1 -r)(l -/*)(! -Г) .
Рассмотрим интеграл 1 = J ————- аI
о
dl f t°(\-1p)(l-P)J
производная по а равна — = — / а
da J ] — /
о
скольку
<"(1 - ^)(1 - р) = (ta - ta+p) - (1а+1 -
то
dl /din Г(а +1) <ЛпГ(а+])
'■)
da \ da da
f <ЛпГ(о + 0 + 7+1) _ tfln Г(а + 7 + 1)\ _
\ da da )
_ d Г(а + 1)Г(а +/3 + 7 + 1)
~ da П Г(а + 0 + 1)Г(а + 7 + 1)
и а \ 1 Г(а + 1)Г(а +/? + 7 + 1)
/(«,Лтг) = 'п r(a + g+|)r(tt + 7 + 1) + C(ft7)•
При а = 0 имеем 7(0, /?,7) = 0, следовательно,
Г(1)Г(/? + 7 + 1)
С(/9,7) = -1п
7) = In
Г(/?+1)Г(Т+1)
Г(а + 1)Г(а + /3 + 7 + 1)
— In
Г(а + /? + 1)Г(а + 7+1)
Г(/? + 7+1)
Г(/?+1)Г(7+1)
Г(а + 1)Г(/? + 1 )Г(7 + 1)Г(а + 0 + 7 + 1)
" Г(а + ^+1)Г(а + 7+1)Г(/? + 7 + 1) '
. Его
I. Но-
§ 4. УПРАЖНЕНИЯ
Несобственные интегралы,
независящие от параметра
В следующих примерах непосредственно установить схо¬
димость интеграла, и в этом случае наитн его величину, или
установить расходимость.
-f-oo 10
. f dx лч f dx
"/?• “>l 2)/^
a 0
6 b
. f dx v f dx
) J (x-a)*' ] J (Ь-х)“'
a a
1 -f oo
5)/(1-»K2»-I) 6)/(T
1 0
2
0 OO
— oo 3
3 -foo
f 2xdx 1ЛЧ [ dx /л f //4
J J (*s- I)2' J J 7F+iw' *
-3 0
foo -foo
Г xdx Г
' j i2 + 4i + 3 ' У *2 + 4* + 3
о
f-oo f СО
U) / ^ -tr-nr ,/
f x dx
!5) J . ,v^> . 0
(x'2 + a2)2
-foo
All
+ СЮ
,7>/i
dx
(l+*2)3‘
+ <v
/ d.v
'») ./ (,:П-7н
-foo
■ 9)/
0
-foo
x 2 dx
2o>/(^
0
-foo
21)/
(x2 + а2)(х2 + 62)' а2 + Ь^°
dx
»)<*’ + *)• “M°'
dx
1 + x
l
25
22>Ш
dx.
25)
27)
29)
z
/
1
1
/
</x
2<1) /
-1
dx
vT — x2
x\/3x2 — 2x — 1
201 Jr.
Vs
dx
(x — 1 )\/x2 -- 3
dx
\Л(1 - *)
o f dx
28) J (a - .r)x/T^
. IX — a
30) I x\l с/х,
/ a <6'
a u
31) f ■ , a < b. 32) f
J yj(x - a)(b - x) J \/(x - a)(b - r
b — £
x dx
“>/(?
х"1 (lr
(x2 + 1)v/l-—- *'
, a > ].
a < b.
, a < b.
478
34)
I I "Г
У \/l - 2ax + a2\/l — 2fix + /32
0<a/?< 1, |a|< 1, Щ < 1.
+oo
35) J e1-2* dx.
-2
fe*
37) j ^dx.
-1
+oo
sin 2x Ac.
In xdx.
l
4*oo
39) J si
0
Ч-oo
41)/
1
4-0.
с
45) / —
У xln
0
«>/£*•
с/х
ГГ
«>/
-i
arccos х
dx.
511/тот
Varcsin:
cosax dx.
+00
36) J x2 b~xdx.
0
38)/eig.
-1
4-00
40)/
0
1
42) J In xdx.
о
44)/
0
1
46)/
dx
x In2 x
dx
x lnx
0
4-00
48) [ Дт sin — dx.
J x2 x
i
w
l
so, f
J v 1 — x
479
* • я я
53) f 7^Ш *. dx. 54) f tg xdx.
J v cosr> x J
о о
1 +oo ^
^ I л/1 - x2(] — a2x2) ^ I Vx2 — l(a2x2 — 1)
о 4 i
-foo -foo
"> / ^ »> /
1 ]
+9° 2 +9°
1 0
1 -foo
61) J x In j-— » dx. 62) J e~ax cos fix dx> a > 0
о о
-foo -foo
63) J e“arsin ftxdx, a > 0 64) J xe~x sin x dx.
о о
2
65) J ^2xsin — — cos dx.
о
-foo
66) J xc~x (2x4 — 1).
Исследовать сходимость интеграла от неотрицательной
функции.
-foo . -foo
Г х5/2 Г ха~1
67) / — гтг- dx. 68) / dx.
J (1 +х2У ’ J 1 + х
о о
2 1 2
69) / rdx. 70) f jz— , dx.
'У |1-х| } J |1 — х|«
о о
480
71
73
75
77
79
81
82
84
85
87
89
. +?■ з
f dx f *3 + *
J (x3-\y ' ’ j x' + x* -\-
1 0
+ co -foo
/ f-5j+l dx. 71) /
J xA -f I8x + 100 J tv + 2
0 0
j x^-'O-xf-'dx. 7(5) j *-у^у2-
0 I)
-f OO +oo
[ ^X f ^X
J xVTTW J x2 4- \/хл + l
1 2
f , Jx . . 80
J v/(4 — я2)2 J \/x — x3
</.C.
2
4-00
Q' > /? > 5.
y(4 - *2)2
)
у dx
J y/x(x - a)(x - 0)’
4-ос 1
/ /* 8.1) ,/*
J ?A^T\ Ч УПГЙ
1 v * 0
/ dx 1.1 s 1
I V(1 _ *a)(l-tV)’
4-00 + oo
/ ЁЛ*. », / i^SJ
dx.
1 0
-foo -fro
I" y/xc~r dx. 88) J c-^dx.
о 0
-hCVj
J xae-fixdx, a>0, 0>O.
0
481
-f oo -f oo
90) / 91) J
0 0
+ oo +oo
92) / **** . 93) [ ;ne“(r4^) dx, n > 0.
i vc31-! J
0 -oo
+oo -f oo
94) J Xхe~*' dx. 95) j .'2n"V
ex dx.
96>/£- 97>мши
2 0
, 0 < b < 2тг.
98)/</,(Л,-.)
") / t —--
У V cos a: — с
о
w/4
/ /cos0 — вт0\р
100) J (гггрлд) |,>0-
-ir/4
+00 _ »/
101) J Yrhdx- 102> /(t6I)PdiC
0 0
ж/2
103) J 8\na xcos? xdx, a>—1, /?>—1.
о
1Г 1Г
/ 1 \ di /"1 - cosx
104) Jm\^)7S' 1051J
0 0
■f oo 1
106)/-&*,„> a 107)/^*-
482
108
110
112
114
116
118
119
121
123
125
127
+0О -foo
/ 109) /
J y/x* + 2x3 ' J x2
о 0
-foo -foo
У I J s/4 + ж"
о 0
1/8 -foo
/ "3) [ , f 4, <fe.
J xln(l+x) J |tr2-x2|
0
+oo
dx
f -U - I dx. 115) /
У x2 | ex — e * 2 J xy/i_ |n2
ТГ 1
/1+ COS X ллп\ f dx
1 \^dx. 117) I : .
(7Г — X)P J X — Sin X
0
dx, or > 0, P > 0.
x^-x""1
lnx
0
1
IГ xa 1 (1 —x)^ ^lnxldx. 120) xp Inq-dx.
о 0
+oo 1
dx 0 v f |lnx|
dx.
/ xPln9*' 122) / л/(1 - *2)3
1 о v 4 7
+oo -foo
f dx f dx
J x|lnx|a J x In x| In In x|
0 100
foo -foo
/ttt==f- *>/£*■
0 1
2
/ jkf*- 128»/
dx
x\/lnx
1
483
129
131
133
135
137
139
140
142
144
146
148
484
+оо
f JnO
J №
ln(l H- x)
0
+oo
/
+ 3x5
In X
dx.
dx.
ху/х2 — 1
dx.
m
0
+/* In cos ^1
132) J d*•
1
n -foo
J |lnsinx|</x. 134) j Ij
In COS
n/2
/|lnsinx|
\/x(n -
\/x(n — 2x)5
dx.
|lnx|
[ Jin
J JS
dx.
о
n/2
i
/
0
+oo
ln(l -|~ xa)
yjX + \fx
dx.
и x 4- sin x ,
X : dx.
x — sin x
y1n(l -f x)
COS X
/
1
J 1-'
0
1
-foo
/ In (l + 8in —^ dx.
ir
136)/
|nsin x\
clg — dx.
X
dx.
о
-fOt
y/smx
2
J |In|sin2<p — k?\\dip,
mf
|*| <1.
IM
l+x2
dx.
'?«•}
1411/i?i
o
l
/dx
-x—
:* - CO
COSX
145)
J si
Je* - 1
dx.
sin x
о
+C
M7> /^ ('*-■)*•
1
-f 0
H9)/( 1 — cos —^ dx.
,50, J
+00
>У.г3 + Зх2 - X
> dx.
у/^П
о
i _ i v | у/х2 + 2х - \/х3 4- Зх2
151) / s dx.
[ ^
J X 111 X
о
+ оо
152) J ^ у/ х3 4- Зх2 — \/х4 4- 4х3^ dx.
о
+ оо
153) J (1и(лг2 +1) — 2lnx)dr.
О
+оо -foo
155) /(c'S
О
4оо
/
\/х
о
■foo -foo
j I — -г Kltl - Г t 1 г г\\ Я X dx
[ c~x**'"2xdx. 158) [ , 0 .
J ./14- xn sin x
о 0
/ l+Jw* ,60) / (' (*+1))rfl
0 0
l(il> / ?(‘+ г)’л- ч/г(ё1)!'''
1 1
-foo r -foo
f хг + X + 1
/ (^3+3)' ,
165, r_*u 1M)
J xr + хя J (1 + I)«V*
163) f*2±i±±dr. m [JZ+nLb.
{ (е*3 + з)* / V*V?TT
+ 00 -foo
(/x.
485
Исследовать сходимость (абсолютную и условную) инте¬
грала.
-foo -foo
[ xain ах , f cosx ,
167) / 168) ] 7ndx’ ”>0'
О о
-foo +00
f sinx . f cosx ,
,б9) J ~^rdx 17°) J ~dx■
О о
-foo +00
f cos ах , л [ cos2x
17,1 J \T^ix‘ “s0- l72) J 7^Tudl-
0 0
+00 +00
f sin3x _ ... f x+1 .
173) I dx. 174) I sin xdx.
J VPTl ’ J xa
0 0
+00 +00
.—4 f * cos я . f xp sin xdx
175) / dx. 176) / — , q> 0.
' J xP + x4 ’ J 1 + ХЧ 4 "
W
+OO
,77)/
+9°
Wxcosx _
T7T<*X.
x + 10
0
+00
f 8m x гЛе ^m(x) и Pn(x) — целые многочле-
J *nl*)
0
ны и Pn(x) > 0 при x ^ 0.
+00 +00
1?9) J у + dx, 0. 180) J (lnx)A^^ dx.
0 100
+00 +00
181) j eeing .s*n^g fix ig2) J arctg xdx.
1 0
+00 +00
^о«ч f sin3x , f exsinx ,
183) I e*** dx. 184) / —7 rrdx.
; У x* * J x(ex + 1)
486
185
187
189
191
193
195
197
199
201
203
205
/sin хч [ cos -j—-
0 0
+oo -f oo
j sin(x2)dx. 188) J cos(x3) dx.
о о
i i i
/' cos - f sin -
-f-ь.
0 0
я/2 4-oo
J sin(sec x) dx. 192) J x2 cos(ex)dx.
n 0
+ oo -foo
J (ex -h x) sin e2r dx. 194) J |x|a sin eT dx.
0 -со
4-oc +oo
f cos(x -h x3) dx. 196) [ CQS^-—-— dx.
J J ot£ -f x
о 0
+°° о +°°
J 198) J
/ J V
J ^ x■ dx. 200) J x cos(x3 — x) dx.
0 0
-f oo +00
J sin | In *|«~, q > 0. 202) j rf*-
0 0
+00 +oo
d,. 204) /«—._!inf-j,.
У X \ x J J X 4 Sin X
1 l
+oo 4-oo
J sin(x2 4-sin x) </x. 206) J cos(x34-sin2x)di.
487
+ 00
207) J e
0
При помощи сравнения с рядами исследовать сходимость
следующих интегралов.
4 оо ^
208) J f(x)dx, /(х)=^~^П , «е[п-1;»], п е N.
О
+°° 4-оо
209) J (-1)1**1</*. 210) J Г dx.
О 1
211) Jtip.j,. 212) J
dx.
о
+оо
О
4-00
ха dx
1 + х.Р\ sin х*) ’
213) J , о > 0, /3 > 0.
214) / 'Д , а>0, /?>0.
У 1 + Х.Р Sill х
п
+ °° . Г*1 + °° Г*12
/sin L J х / costw J X
5 dx. 216) / 5 dx.
1 -1- lll2(x + 1) J 1 + lll2(x + 1)
0 0
Установить, собственным или несобственным является
интеграл, и, если он несобственный, то исследовать его схо¬
димость.
1 4-е»
2,71 / а — ctg2x^ dx. 218) j — arcctgx^ dx.
0 1
219) —4 ctgJ~~ dz'
J sm(x - a) у a
0
488
-l-oo ]
220) / ^ln-—\dx. 221) I -—^
J x x + 5 J xsm x
10
1/3
222) f |П(1 + X+^lVn{]rX±- —dr.
x3/2(ex — I)
2231 I WTW - 0 *•
0
1 2
/1 f cx — e~x — 4x
a: In In -dx. 225) / : dr.
X J X — Sill X
о 0
^dt 221)
J y/x-smy/x J tfx- SIM tfx
0
2
228) J
0
+ oo
c&* - e-У* - 2tfx ,
тл— dx.
x2/3 _ gjn x2/3
0
1
229J f tgfrg - (1 - 6x2 -f 4a;3) sin nx
J X4 In4 X
0
dx.
l
230) j ^—r~ a 1 -.l.r:—Z fix.
tg 7ГХ — (1 — 6x2 -f 4x3) sin 7ГХ
x4ln3
0
1
tgnx - (1 — 6x2 + 4x3)sin тгх
ax.
2311 /
0
5
9?9 f sin(sin ж) — x^l — x2
’ J y/x" + llX19
0
233) j sin(si',;r) “ xv/1 “ *2
у/х13 + 1 lx19
0
dx.
489
mf
5
sin(sinx) — x\/l — x2
л/х10 -f 1 lx19
0
+ oo
dx.
о
2
sin(sinx) — xV\ — x2
y/x] 1 -f 1 lx19
235) J , 7,-—- rfx.
\/x2 — x + 1 — v^e*3-1
236) [^-X+ 1
4 (e*3 — e) In ^ x
-f OO
237) I
J (ex — e) In ^ x
•foo .
238) f
J (e*2 — e) In ^ x
>/x2 — x + 1 — v^ex2“1
239) J
dx.
24°,/
(e*2 — c) In2 x
о
(ln(l -f 3x + 3x2)2 + 3(x — ])2 - 3)\/x3 -f 4
== ax.
\/x13 -h x15
(In(1 + 3x + 3x2)2 + 3(x - l)2-3)y9T4
о
+oo
241^ / ^xlS + X15
0
10
242) j (ln(] + 3x + 3x2)2 + 3(x - l)2 — 3)\/x3 + 4
*>)/
^X12 + X13
0
-foo
(In( 1 -f 3x + Зх2)2 -f 3(x — l)2 — 3)y/x^ + 4
dx.
о
^x12 + x13
'У ln(]+X2) ' ./ ln3/2(l +*2)
0 0
490
1
*•)/
2^+5
(1 + *2)
ln4/3(l + X2)
■dx.
Доказать справедливость неравенств.
+оо -foo
dx > 0. 248)
+00
247) I
cos ax
1 +x2
dx
<
x J 1
dx <
ЮОтг
■foo +oo
Л f cosxdx 1 , , л f cos.
249)° <J 250) 0 < у —
ж lOOir
1
251) 0 < f ^^-dx< 2*+ 2^2-2.
J XyJX
0
-foo 1
252) 0 < / — d*<^r- 253) fSU\^~X^dx> 0.
J x 50я- ’ J v^l — x
0
1/2
1 f dx 3
255) 2</7P??<5' n€
lOOtr
-foo
254) 0 < j
x2 dx
1
2x* + x + 2<5'
N.
■"Wtt^s+s-
1
20 Tl+x- 20 1
^ 19 < J 1 +z40 < 19 + 20'
0
Ч-oo
258) 1 — - < f t~x"dx< 1 + i, n>l.
n J n
0
-foo -fc
259) 0 < J
t ~ dx < —.
n
260) 0 < j e-*'‘dT<±.
491
2 f
26,1 !штЬj<w):i' ш,о</G'
1,9
foo
263) j e~x cosx4 dx
-foo
<(5
21
20-1)/
e‘x 1
100+ x > Too'
-foo
265) V < f < f
\/l + (n+l)PirP l-fx^siir a: ^
/? > 2(q + 1)-
foo -foo
/Sill 7ГХ /*
dx < 0,01. 207) I sin 7r.rJ r/.r < 0,01.
100
Вычислить.
1
268) f ri
J (nz — ж
100
dx
-1
f (ЧЭ
(f>2 — x2)y/\ — x
f , «.> 1.
269)
f dx
J (x2 - tt2)V
(x2 — a<2)\/x2 — 1
dx
, 0 < r* < 1.
270^/(x2- |-а2)%/Г^2’ a>0'
dx
l
fro
=r. a > 0.
-71) ./
f XJ
/ с/х
272) / 7=--==, a > 0.
492
Применяя формулу интегрирования по частям, получить
рекуррентную формулу для интеграла /п, v G N, и найти его
значение.
ОО -f ОС)
273) /„ = Je~xxndx. 274) 1п = J < -х\2п dx.
О о
+оо
275) /„ = J с~ах sin” х dx, а > 0.
о
1
276) 1п(тп) = J xn\Wnxdx, т Е N.
о
1
277) 1п(т) = j хп-\\-х)т-х dx, т Е N.
о
+оо + оо
278) 1п — j xne~xs\nxdx. 279) /п = J xnc~xcosxdx.
0 о
1
280) In = f{l-x2)ndx.
о
+oo
/dx
, , ■> . о., . AC-B2>0.
[Ax2 + 2Dx + C)n'
-OO
ж/2
282) /„ = cosxcos2nx dx.
о
283) A, =
J cos X
0
+ oo
284) In = f </x, a > 0.
J cos X
— qx2 C°s(?n - ])r
493
1
/х2и + х f
-^=— dx. 286) In = J (111 •'■)" dx.
О n
1 +(X)
-2n r dx
т)'-Чл
289)/„= J
•h',+ 11
0 0
+ oo
dx
x(l f ж) ... (n -f x)
1
290) Доказать, что существует M > 0, такое, что при а > М
справедливо равенство
+оо
[ e~xdx 1 1 12 1-2-3
I — м Н о й 1 -\~
J х + a a a2 ad aq
Доказать равенства.
п/2 п/2 п/2
291) / In sin xdx— I In cos xdx — — I dx.
J J J tgx
0 0 0
о 0
1 1
Г In x f arcsin x ,
293 / - 7=^- dx — — I dx.
' J J x
о 0
+oo +oo
f sinx , f cosx ,
m) J _Л = _у _Л.
п/2 п/2
+оо 1
295> / ТТР''« = -/rfP"*
494
+оо +оо -foo
___ч f х2 dx f dx 1 f 1+x*2
J 1 + хл ~ J 1 + sc4 ~2J 1 +хл X'
0 0 0
rr/2 tt/2 +oo
297»/^5=/^ = 2/tIf
0 0 0
1 я/2
298) / 7ПТ* 4*m J’dx'
0 0
-foo 1/>/®о
o f dx n f d
299) J ^/x(x - l)(x - k*) =2 J s/(l - x*)(l - k*x2)'
To 0
-foo 1
/81П £ /*1 2?
y-j-—4 dx = 0. 301) I cos ж• In y--j-—dx = 0.
-oo -1
302) =
0 0
303) = =
dx
Используя разложение подынтегральной функции в ряд и
равенства
r2 ~ 1 „2
_ ^(2п+1)2 _
п=1 п=0 ' п = 1
вычислить следующие интегралы.
v 1 - ж2 v 1 - *2 v(-1)n_1 - *2
^п2_ 6’ ^ (2п + I)2 ~ 8 ’ ^ л2 “ 12 ’
dx.
30<) + 305) | M1
о о
1 -foo
306) J In у—— 307) J In Cx — | dx.
495
+ ео
Г х Нх
■т) j
О
+ 'Х,
310) / ——.
/ ГПХ ... г-.м
О
1
V /* 1п.Т .
о
:,м,
О
я/2
316) ^ hrtgxdx.
fcv
Вычислить.
00
[ xlnx
*wJW+7W"-
1
»>/
3") /
и
и
3,5, /|„1±£
J 1 — л: х
и
1
317) J 1пх-1п(1 -*■)&.
п/2
319) j In |sin2 | a2<Cl.
о
+ oo
И0) [ ' t .
’ J s/7^ 7
0
я /2
.422) I s/lg<pdip.
0
я/2
4 f dx
”1)./ 7Я7-
321) j \/l - jr2 h
0
»>
dx.
dx.
о
я/4
325) I v^ctg
496
326)
/
О
-1-00
oos±*
\/2(ros т — cos ip)
dx. 3*27)
/;
c os i.r
/‘2 (cos x — cos 9)
dx.
x f xm\nx ,
J 1 + x2,n+2 dX■ 771 > _
0
*/2
In sin x dx.
x I11 sin x dx.
329) J In sir
0
я
mf;
0
1
arcsinx .
:ш) J ~r~dx-
0
335)
330) /
0
+00
Ш) /
In COS x с/х.
332) I
x2\/x
337)
i
/
0
rr/2
(i + *2)2
(1 -X2):j/2
— 2x
0
+00
338) f
dx.
x dx
Y'
dx f 1
f 7Г — 2x , 4Ъ^Ч f sin nx cosx ,
339) I —================ dx. 340) I ; dx, n £ N.
J vsin x cos3 x J ^
0 0
7Г
341) J In sin x cos ?jx dx, 7? £ H.
0
-foo
-1-00
v /* cos o x — cos/Ух , f e. “ r — с
m J —a«) J j»-
dx.
0
+00
*«) /
In( 1 -I- q2xj) - ln( 1 4 /*~x”)
dx.
497
4-оо +оо
345) / 5Щ±4,. 346) / 5^Jx.
J Ху/Х J у/X
0 0
+oo
/С1ПП X
^jdx, пбР), /i€N, n£2#i+l.
0
+?° • 2П + 1 • \"
1 Sin T px t л _4 / /sinx\
348) I dx, p > 0. 349) I ( J dx.
350) Доказать теорему Фруллани:
а) если существует lim f(x) и для любого а > 0 имеем
Г-+0+
fix) ~ [ /(ах) - /(/?х)
■ Е /ца,+оо), то I —— 5—-ах сходится для лю-
х J х
о
бых а > О, Р > 0 и равен /(0+) In ^ ;
б) если существует lim f(x) — А и для любого а > О
г—►-foo
ДХ) n/л \ f f(QX) — f(PX) J
имеем —— £ n(0,a), то / —— 1—-dx сходится для
x J x
о
Ol
любых а>0и/?>0и равен А• In —.
Р
Используя теорему Фруллани, вычислить интегралы.
+оо л
/е-ах _е-Рх
dx, a > О, р > 0.
о
+оо
352) [ , р > 0, ? > 0, a > 0, /? > 0.
У p+qe-P* х
о
+оо
353) J tt>0li9>0.
498
foo
f cos ax — cos Qx , л л
354) j dx, a > 0, P > 0.
/
о
+oo
“S> / - 0 §
о
-foo
356) J - — Q > 0> P > 0.
е~ат - е-^+ф - /?)е"^х
о
foo
357)/
sin ax — sin Px
dx, a > 0, P > 0.
x
о
foo foo
„ . f sin ax —or sin x , rtl^v /* ax cos x —sin ax
358) J ~2 d*' 359) J ~2 ^X.
0 0
foo
Г sin ax sin вх , л л _
360) I dx, a > 0, P > 0, ot Ф P.
о
foo
/1 — COS flfl
cos Px dx, a > 0, /? > 0, ос ф p.
0
1
362) J
xa-l_xp-l
lnx
0
foo
dx, a > 0, P > 0.
A /?sinax — asintfx . _ л
363) I ^ dx> « > 0, p > 0.
о
foo
364)/
P ln(l + ax) — a ln(l + Px)
dx, a > 0, P > 0.
о
foo
365) j (e~ax - e~ptf a > 0, /? > 0.
499
36G) Доказать формулу:
+ СО
/
A j c os а 1 х + А'2 cos о *>х + • • 4 Л „ cos c*r, j•
dx -
х
= -(,4j In a j -I- A2 1» a2 + h A„ Iji o„),
(\i > 0, i= \, 2,..., ii, Л] -f -42 4 •••■+■ l/j ~ (I
Вычислить.
f sin2n ax — sin2” fix
367) I dx, a >0, /У > 0, 6 M.
о
+oo
368) J
cos2”-1-1 ax — cos2n+1 /Зх
dx, a > 0, /? > 0, ?i 6 H.
cos2n orx — cos2*" /?x
0
+ ОЭ
369) J C~- — dx, a > 0, /? > 0, ?i e M.
0
-1-00
/SI II (>2*
cos /Зх dx, a > 0, /? > 0.
о
-foo
57,1 /2
0
+a
372) j
373) f "
sin ax sin fir. sin yx
dx,
x
0 a > 0, (3 > 0, 7 > 0, a - max(o, /У, 7)
+90
sin ax sin/?x . л _
—dx, a > 0, /3 > 0.
X X
0
+00
sin ax sina )X sin Qnx
x x
0
a > 0, «,•>(), ? = 1, 2,.. , ??. a > a t
t — 1
+03
/« dx
(sin ax — sin (3x)1—^.
500
Собственные интегралы,
зависящие от параметра
Мсследонать равномерную сходимость относительно мно¬
жества -Y семейгтпа функций /(х,у) при у-*уо-
375) /
376) /
377) /
378) /
379) /
380) /
381) /
382) /
383) /
384) /
385) /
386) /
387) /
а
388) /
389) /
а
х,у)=.г2 + у2, Х = [-1;1], у -> 0.
2 2
■с’у)=Г‘;—* = (0;+оо), у-> + оо.
I -f a- tr
2 2
Х'У) = Г+Х2у2' *=(1;+оо), у-> 0+.
х2-у2
Х'У) = -Г~, 2“2> ^=(1;+Оо), у-» +00.
1 + х2уг
2 2
у) — i-7—^Ц-i ^ = 0;Л), у —> о-f .
1 4- х у
ху
х, у) = ~2~, 2> ^ = (1;+00), у-^+ОО.
X2 + J/2
ху
X2 + у'1
ху
ж-у) = -2 . -2 ’ * = (0; + °с), У~¥ 0+.
д.у) = ,2 , 2 . * = (1;И), у->+оо.
Х’У) = ~Г1~2' * = 0;+°°)> .v-*o + .
4- у
х,у) = ln(l - y2cosx), X = ^0; ^ , у-»• 0.
*,У) = ln(I+y2tg2 ж), Л ~ (0; ^) ’ У-^0-
х, у) = 111 sill2 х^ , X — |о; ^| , у -ч- +оо.
х, у) = yln(r2 + у2), X ~ (0; 1),
у -> 0; 6) .7 —> 1.
X, у) = У./,, -V = (1:2), у->+оо.
1и(х- + ул)
у arclg(xy)
*,У)= г-г—. * = (0;+оо),
у + 1
у —> 04-; б) у —> 4 °о.
501
392)/(«,|,)= * У X = (1;+оо),
390)Д*,Й=^М, Х = |1;+»),
а) у —» 0+; б) у -> +оо.
39.) /(.,„) = ?И£1±Д X = (,;+„),
а) у —> +оо; б) у 0 + .
xycosfx2 + у2)
х2 + у2
а) у ->■ +оо; б) у -► 0 + .
393) /(х,у) = — (егу — 1), X = (0; -foe),
X
а) У -+ 0+; б) у -► О—; в) у -+• -оо; г) у -> -I; д) у
1ГГ
394) Дх,у) = tg—, ЛГ = (0; 1), а) у-И+; б) у -► 2.
1ГХ
395) /(х, у) = (х — 1) tg —, А- = (0; 1).
а) 2-Ь; 6) у —> 3.
Проверить, выполняется или нет равенство
ь ь
lim / /(x,y)dx= I lim f(x)y)dx
y-*vo J J v-^yo
a a
для следующей функции /(x,y).
396) /
397) /
398) /
399) /
400) /
401) /
502
Х,у) = x2\/x2 + y2, [a; 6] = [0; 1), y0 = 0.
x,y) = [a;6] = [0; 1], уэ = 0.
2xv2
Х'У) — ^2 _|_ y2 J2 ’ [a» fc] = [0; 1], y0 = 0.
x3 *1
х'У)=у2е * ' [a;6] = [0; 1], y0 = 0.
e-xy
x,y) = --fc+y2 » = [°; 2], 1/0 =+00.
x,y) = arctg [<i;6] = [—1;3], y0 = 0.
402) f(x, у) = / я s,n у ’ х^0’ [a;ft] = [о; ^j , у0 =+00.
[ 0, х = 0,
Найти следующие пределы.
3 1/2
403) lim J х2 cos(xy) dx. 404) lim J \Jx2 + у2 dx.
о -1/2
>/з+у »r/2
405) lim f - ^ 2. 406) lim f ===.
ИО j 1 -I- X2 + y2 У-+0 J Vl - yl sin2 if
у о
ж/2
407) lim f ф — у2 sin2 <р dip.
о
х
408) lim - f [f(t + у) - /(<)] dt,
V-*0 у J
a
где f(x) непрерывна на [Л; B\, А < а < х < В.
2 */2
409) lim / ,l"^ + gL dx. 410) lim [ e~n*in* dx.
y-> +00 J ln(x^-fjr) n-400 у
1 0
411) lim f 412) lim [ ^-^dx.
' n^ooj l + (l + £)n n-юо J 1+x2
0 0
Исследовать на непрерывность функцию
6
Ну) = J f(x, У) dx, yEY.
а
1
413) F(y) = J f(x,y)dx, /(*, у) = | J'
о
У = (—oo; +oo).
x < У,
X^y,
503
]
414) /•’(.'/) — J h'(у, t)v(x) dr. V = (-00; +oo),
1
415) F(y) - J arctg —f/ar, Y = {у: у > 0}.
0
1
416) F(y) = J\x\(x7 + y2)dx, Y = {y:y^ 0}.
о
i
417) F(y) = J xy dx, Y = {у: у ф 0}.
о
l
418) F(y) = J dx, Y = {y: |y| < oo}.
о
i
419) F(y)= [ jd^Ldx, feC[ 0; 1], Y = {»/: |y| < oo}.
J x* + yz
0
1
420) F(y) = J xi*y2 dr' Y = Ы < oo}.
0
]
421) F{y) = f (lX lx + y' Y = {y y>{i)
0
1
422) F(y) = J (I +x)Ty dx, Y = (-oo;+oo).
о
ir/2
423) F(y) = f ——r, Y = {»:» > 0}.
J xy- sms + 1
504
424) F(y) = J *cos(xy)rfx, Y = {y:y> 0).
>/v
Можно или пет вычислить по правилу Лейбница произ¬
водную функции F(y) в точке уо = 0?
1
425) F(y) = J In sjx1 + у2 dx.
о
l
426) F(y) = J f(x, y) dx,
0
У ХУ
arctg 0 < z ^ 1, O^y^l,
/(«,»)=< %■
X xz + yz
r = 0, 0 ^ у ^ 1.
2’
i
427) F(y) = J f(x, y) dx,
J. (arctg-,
428) F(y) = / f(x,y)dx, f(x,y) = < „ У
io I 2’
1 Вычислить производную функции F(y).
» , 0 ^ x 1, 0 < у ^ 1,
f(x,y) = <
0 ^ x <: 1, у = 0.
уф 0,
y = 0.
6
/ i*
У
t
429) F(y) = 1 e*,+y* dx.
430) F(y) = / (x + xy)10
J
J
a
0
2
r
V*
r
431) F(y) = I y/xysinxydx.
432) F(y)= 1 e~*3 dx.
J
У
У
у2
6+y
43$) F(y) = f e~x*y dx.
J
4*)>M = /
V
л+У
305
cos у у
435) F(y) = J cos y/iydz. 436) F(y) J - * уХ^ dx.
sin у 0
У
437) F(y) = J f(x + y, x -y) dx,
0
f(x,y) € ^((-ooj+oo) x (-oo;+oo)).
i/y
438) F(y) = J dx, y> 0.
0
у3 Х+У
439) F(y) = J dx J sin(x2 + z2 — у2) dz.
0 x-y
У3
440) F(y) = J exp(-y(x + y)2)dx.
у
l
441) F(y) = J /(*) sign (sin ys)<fz, у > 0, / G (^([O; 1]).
о
у У*
442) F(y) = J ( j ***** dz) dx, у > 0.
0 -yx
Вычислить вторую производную функции F(y).
}
443) F(y) = I (x + y)ex dx.
о
у
444) F(y) = J(x + y)f(x)dx,
о
где /(я)— дифференцируемая на (—оо; +оо) функция.
506
445) F(y) = j /(x)\x - y\dx,
a
где f(x)— непрерывная на [a; 6] функция.
У
446) F(y) = J f(x)(y - x) dx,
0
где f(x)— непрерывная на (—оо; -boo) функция.
a a
447) F(y) = J d£ J f(y + Z + t]) dr), a > 0,
0 0
где f(x)— непрерывная на (— oo;+oo) функция.
448) Найти F"y, если F(x,y) = / (x - yz)f(z) dz,
х/У
где f(z) — дифференцируемая функция.
449) Проверить, что функция F(y) удовлетворяет уравнению
^"(у) = -«(у). У € [0; 1],
I
I i
где F(y) Ц j K(y,x)v(x)dx] К(у,х) = J J *’
о
и v(x) — непрерывная на [0; 1] функция.
л
450) Проверить, что функция щ(г) =
j еnrccHVdp удовле-
] 0
творяет уравнению и" -|—и' — п2и = 0.
г
ж
451) Проверить, что функции у = хп J cos(x cos <р) sin2n <р d<p
/П о
cos(ny> — х sin <р) dip удовлетворяют уравнению х2у" +
+ ху* + (х2 - п2)у = 0.
507
452) Проверить равенство F^n\x) — (п — 1)!/(х), где
д;
п*) = / f(y)(x ~ dy.
О
Применяя дифференцирование по параметру, вычислить
следующие интегралы.
п/2
453) J ln(a2 — sin2 <р) dip, |а| > 1.
о
п/2
454) J 1п(1 + (т2 — J) sin2 х) dx, т > 1.
о
п/2
455) J In (а2 sin2 х -f b2 cos2 х) dx, ab * О
о
456) j ln(l -f 2acosx + a2) dx. 457) J — dx.
о о
п/2
f 1 1 + a sin х dx , ,
458 / In- : г—, а <1.
J 1 — asm х sin х
о
п/2
/\ l+acosx dx , ,
459) / In- , а < 1.
J 1 — a cos х cos х
о
п
460) J еасовх cos(asinx) rfx, а > 0.
о
1г/4 п/2
461) J arctg(a^/1 — tg2 х) dx. 462) J —dx.
о о
463)
sjnx
о
508
тг
ч f ln(1 + a cos я) .
464) / dx, 0 < а < 1.
J cos х
о
я/2
. f l*i(l -f а cos ж) ,
465) / — -dx, 0<а<1.
J cos х
о
f ln0 + asinх)
466) / ; dx, 0<а<1.
J sin х
о
«7> i'"<>+«*ь.
1 +12
о
468) Функцию f(x) = г2 на промежутке [1; 3] приближенно
заменить линейной функцией а + Ьх так, чтобы интеграл
з
/(а, 6) = J(,а + Ьх — х2)2 dx
1
принимал наименьшее значение.
Выяснить, справедливо или нет равенство
d Ь Ь d
J dy J f(x, y)dx = J dx J f(x, y) dy
с a a с
для следующих интегралов.
i 1
т) Sdi! ^rwis-
О О
mj**} (£-£)«■*■'»■
о о
т!Чт5*'-
о О
509
473) f dy f ■ dx. 474) f dy f - arctg - dx.
J J wx2 + y2 + l J J У у
— iff л 0 V 0-1
Применяя интегрирование иод знаком интеграла, вычи¬
слить следующий интеграл.
/1 хь — ха
— dx, а > 0, 6 > 0.
In X
о
/( 1 \ хь — Xй
sin (in - J •—j dxy a > 0, 6 > 0.
о
l
477)
/ cos
J
0
ir/2
478)
/,п
0
479)
я
[
J 0
0
dx
а > 6 > 0.
sin2f> xdx ™ , v . .
n£N,i) |a| < 1,6) |a| > 1.
2a cosx + a2)"'
Несобственные интегралы,
зависящие от параметра
+оо
f dx
480) Показать, что интеграл / —
а) сходится равномерно на промежутке 1 < ао ^ а < +оо;
б) сходится неравномерно на промежутке 1 < a < -foo.
i
f dx
481) Показать, что интеграл / — сходится неравномерно на
промежутке (0; 1). 0
510
-foo
482) Показать, что интеграл J - "у
о
а) сходится равномерно на промежутке J < ar0 ^ а < -foo;
б) сходится неравномерно на промежутке 1 < о < -foo.
foo
483) Показать, что интеграл J ас~ах dx
о
а) сходится равномерно на промежутке 0 < а ^ о ^ 6,
а в R, b е R;
б) сходится неравномерно на промежутке О^а^б, 6 € М.
Исследовать равномерную сходимость интеграла на мно¬
жестве М.
■foo
ш) j rhdx' = б)л/=(-1;о).
О
-foo ^
xdx j
485> / т
+ (х - а)4 ’
о
a) М = (-оо;а], а > 0; /б) А/ = [0;+оо).
+оо
486) j ! + £+«*’ М = (-00’+0°)-
— ОО
-foo
487) / a)M = (-1;1); б)"=*-
i
■foo
4881 / " = |0;Ч
1
+ oo
'2-Х2
511
1
491^ / Vx(a2 + i2)2 dx' M = (0;J)‘
0
492) f - ■ dx =,
J \/(l — a?)(l - ax)
a) M = (0; q0), oro < ] i б) M — (0; 1).
+ oo
493) f — — Ж ■■■■ = dx, M = (0;+oo).
' J (а2 + *2)>Л*2 + *2 V ;
з 7
■f°°
494) / 1+ “«* + «»)»'*' M = [0;+00)-
0
+00
495)/ (a+l^4dX> " = (5;+°°)-
3
+ oo
496)/гн?Ь?' "=№+“>•
0
497^ / ТТЛ2’
1
а) M = [1;3]; 6) A# = [l;+oo); в)М = [0;3].
l
4981 /" = №+“)•
0
1
499>/jS^iF’ »)" = (»'I)' «)" = (»;')■
0
500) J *^-dx,
0
а) M ^ (-oo;or0), 0 < an < 2; 6) M = (-oo;2).
512
501) / dx' а) м = (_2; I); б)м=(_1;!)-
о
+ оо
502) jtgaib,„>2,
О
а)М= (о;£); б) М = (0;п-1).
+ 00
503) [ a^CtgX dx, а) М = (0; А); б)М = (0;+оо).
у хЧа
о
+ о°
-ar л «.2
504) j е ar arctg ах2 dx,
о
а) М — (a0;-foo), a0 > 0; 6) М = (0;+оо).
+ оо
505) J e^x~Q^dx, а) М = (—оо; а], а > 0; 6) М = [0; +оо).
о
+ оо
506) J —Х dr, M = [0;-foo). |
о
+оо
507) J ае~ахdx,
0
а) М — [а; 6], 6 > а > 0; б) М = [0; 6], 6 > 0.
1
508) У xa_1e'x dx, М = [а; 6] С (0; -foo), а < 1.
о
+ оо
509) J xa-1e-Tdx, Л/ = [а; 6] С (0; -foo).
1
-foo
510) J хае х dx,
о
а)М = (0;Л); 6) М = (0; +оо); в) М = (-1; Л)
513
а) М = (а0;+оо), оо >0; б) М = (0;+оо).
+оо
512) J {а3 + х)е~ат3 dx, a)Af = (l;5); б) М = (0;5).
0
+оо
513) J хаех° dx, a.) М = (1/2; 2); б) М = (0; +оо).
1
+ 00
514) J у/ЕеГа*а dx, М = (0; +оо).
О
+оо
515) J хе~х (1+Qr ) dx, М = [а; 6] С (0;+оо).
о
+оо
516) J ac-o2(<'+*2Ux% M = [c;d\C (0;+оо).
0
1
517) J dx, a) M = (—1;0); б) M = (-9/10;0).
о
0
1
519) J i°-‘lnmxdx,
0
a) M = [u0; +oo), o0 > 0; б) M = (0; +00).
+ OO
/I Q ^
</*, a) M = (0; 10); б) M = (0; +00).
-boo
ln(l + ax)
ax,
0
а) M — (a0; -foo), a0 > 0; б) M = (0; -foo).
2
522) / n^F’ a) M = [1/2;2/3]; 6) M = {0;!)-
1
+oo
523) / /“ ,, 2 2 y
J ух 1 + a2x2
l
+oo
/sin ct«c
■ -y=- dx, а) Л/ = (а0;+оо), ao>0; б) M — (0; -foo).
о
+oo
f x sin ax , .
525) / T dx, А/ = [a0; -foo), a0 > 0.
J 1 -f xz
о
+oo
/x • cos ax
j-—-д— <fe. а) M = (1; 10); б) M - (0; 10).
0
+°°
/sin ax
j - xi dx, a) M = [a0;+oo), ao>0; 6) M = (0;+oo).
0
+oo
528) f cos(a x) dx M = [l;+oo).
J X -f a
о
i
«• 1 a
sin — ax,
x
529) J x
0
а) M = [—2 -f e\ -foo), f > 0; 5) M = (-2;-foo).
+00
i sin ax
530) j -j===dz, а) M = [ao', +00), ao>0; 6) M = (0;+oo).
*0
515
531
532
533
534
535
536
537
538
539
540
541
516
J пгсов(а^х) dx a)M = (1;10); б) M = (0; 10).
I
+oo
J cos(ax3)dxy M = [l;+oo).
l
M=[1/2.+00).
о
+oo
J ж" sinx3dx, а) M — (0; 1); б) M = (0;2).
0
+00
/sinx . в # /л 4
■ ■■■-- dx, M = (0; +oo).
0
+oo
f xcoewxd* t a) M - (0;Л), Л>0; 6) M = (0;+oo).
J (я — a)* + 1
о
/ ттЬЛх' M = (°;+00)-
о
+oo
J sinxctdxi а) M = (A; +00), Л > 1; б) M = (1; +oo).
о
+oo
J sinx sin ^ dr, Af = [0;l].
0
+o°
/sin(a2x) , 4
—arctg or xdx y M = [1/2; +oo).
1
+oo
J sin x2 arctg axdxy M = R.
+0О
542) J sin(aex)rfaj, а) M = (1; +oo); 6)Af = (0;l).
о
+оо
ах cos ах dx
о
а) М = (0;+оо); б) М = (а0; + оо), а0 > 0.
+оо
544) j ein(x2 -f ах) dx, Af = (0;+oo).
о
+oo
545) J e“axsin xdx, M = (aro; -foo), a0 > 0.
о
+ 00
546) J e~x ) sin xdx, M = R.
0
+°°
547) J f^e-agdz, M = [0; +00).
0
1
548) J i sin -2er <te, M = (-00; 1].
0
+00
- -«v f sin ax , _ _ r
549) I cos x dx, M — [a, 6]
о
и отрезок [a; b] не содержит точек a = ±1.
+oo -foo
550) J e~X€tf(x)dxi Af = [0;+oo), если J /(x) dx сходится.
a a
551) M = [0;+cc), если //(,)rfx сходив.
517
552) j(l + x+ - +xn-l)yJbJdx, M = {0,1,2,...}.
0
+ оо
553) J ^e'&dx, M = {1,2,3....}.
1
+ oo
554) f \l ~TT~dx' a)M = (0;l); 6)M=(l;+oo).
J V ~T X
0
Исследовать равномерную сходимость интеграла относи¬
тельно параметра а на множестве М.
1
555) Jxa-l(l-x)l>-idx, М — [а0; +оо), а0 > 0.
о
1
556) J x^"l{\ — x)a~l dx, М = [с*о; +оо), ао > 0.
о
5571 /
+ оо
558) [ ■■■/" — ■ dx, М = (- 1;1),0>О.
J х/*2-/?2
+оо
/COS X
е~*аlcP~dxJ 0</?< *’ М = [°;+°о)-
о
+°°
/х sin ах
— dx, Р > 0, М = [а0; -foo), Q0 > 0.
/7* -f JT
о
+oo
561) / cos.*? dx, 0 < ft < I,
X0
0
a) M = [a0;+oo), a0 > 0; б) M — (0;+oo).
518
Доказать равенства.
2 dx
\)у/х
562) lim f —з2 f^ = 1 •
a->oJ (qj;3 +
О
■foo +оо
563) lim [ 1^e-asdx= [ ^dx.
а_ю+ J yjx J y/x
о 0
■foo *foo -foo
564) lirn^ Je~arf(x) dx= Jf(x)dx, если Jf(x)dx сходится.
о
-foo
565) lim [
a—►O-f J
0
f-oo
566) lim f
a-*0+ J
0
+o
.. Г COSX dx
567) lim I —7=^~—5 2 =
a-^+oo J y/X 1 + Ck2X2
1
f-oo +00
568) lim J sin(x2) arctg ax dx = ~ J sin x2dx.
о о
-foo
.. Г axctg ax , л*
569) lim I —-==== dx = -.
a—►-foo J fpy/x — 1 2
0
+9°
c”°'x8in x dx — 1.
о
f-°o
e“a*cos xdx — 0.
о
f-oo
l
f-OO
. f cosax , к
570) lim / ——2 dx —
7 or—f0-f J 1 +x2 2
0
-foo
c„n .. f dx In
571) lim I - ; rrr = -—t= .
; *-+(>+ J 1 + (a + x2)^ 2 x/2
0
+oo
572) ,im / = JL..
<x-+o+ J l+(a + x2)2 2\/2
о
519
-foo -foo
573) lim f — (] + -Yn dx= f —e-xdx.
n-*-foo J x \ n/ J X
0 0
-foo -foo
,• f 1 — e~nT • , [ sin® ,
5741 lim I smiax= / dx.
»W+oo J X J X
0 0
1 1
/ xn f sinn irx ,
575) lim I .■ dx — 0. 576) lim I dx = 0.
n-++ooj */\ - X n-++ooJ y\n2x
о 0
w/2 -foo
577) lim f C08"* xdx = 0. 578) lim f ■1~ ~ = 1.
n-foo J J\\^x\ »-►« J 1 + *2n
О VII 0
-foo
579) lim f e~x* dx — \ .
' a—►-foo J
0
-foo
580) lim I a2e~a x sinxdx=:0.
<*-+ o+ J
0
-foo
581) lim f a2e~a7x* sinxdx = 77.
«-►-foo J 2
0
-foo
, .л lim /(x + o)+ lim f(x — a)
Ж 4- U) , _ tt-+(TV ' a->crV ;
582) lim a f ^ du = it
a—»-0 у a2 -f u2
— oo
-foo
583) lirn^ a J c~ax arctg x dx =
о
Исследовать на непрерывность в указанном множестве Л/
следующую функцию F(a).
-foo
584) F(») = / М = (2;+оо).
520
585) F(a)
586) F(a)
587) F(a)
588) F{a)
589) F(a)
590) F{a)
591) F(a)
592) F(a)
593) F(a)
594) F(a)
595) i^c*)
+oo
/cos ax
—, M = K.
y/\ + Xs dx
0
ir/2
/COS —
■pTfcb, M = (0;2).
—/2
/ M = №+oo).
1
+oo
J sin(ax2) dx, M = (0;-foo).
о
+oo
/sin x , я ж ^
- - Tidx, M =R.
1 + (x + a)2
0
-foo
/lnxdx w ^
7 ТГТТ’ w=®-
(x -а)Ч1
1
4*oo
J are-*0'3 dx, Л/ = R.
0
4*00
; J ae~*a dx, M = [0;-foo).
о
+oo
J e~ax sin yfxdx, Af = (0;-foo).
о
Ч-oo
f -^Le~axdx, M = [0; -foo).
J v2 + x
о
f M = [0; 1).
У sin x
0
521
596) /•'(о)
597) F(«)
598) F(a)
599) F(a)
600) F(a)
601) F(a)
602) F(a)
603) F(a)
604) F.(q)
605) F(a)
1
/SH1X , .ж /л
—— dx, M = (0; 2).
о
l
= J lna(l + x2) dx, M = (-1/2;+oo).
о
+oo
= J e"ai? sinx2dxy M = [0;+oo).
о
-foo
= J sin In xdx, M = R.
0 v
/■ sin £
-J-^rdx. Af-(0;2).
0
+°°
/sin(l — az)x . ^
— — cfx, M = R.
о
-foo
: J e-<x-a)3 <fcc, Л/ = R.
0
1
J y/x(x2 + a2 + 1) ’
3ln(e“J* + 1)
0
r -foo
dx
M = R.
/• ln(e“ * + 1) J
J x2+<*’ dx, а ф0 M_K
In 2, nr = 0,
522
606) F(о) = <
гг/2
I
-ж/2
+00
¥*dx , Q
arctg(x2 + a2) sin x1 M = R.
0,
/ ч Г a sin x , _
607) F(a) = I -dx} M = R.
J sa -f 1
0
Найти производную функции F(a).
+°°
60,8) F(a) = J
sin ax
, a > 0.
1
+00
609) F(a) = j U™la)2dx, |ar| < oo.
0
+00
610) F(a) = J e~*2 cos axdx, |a| < 00.
0
+00
611) F(a) = j a) a > 0; 6) |a| < 00.
0
612) F(a) = J dx, |a| < oo.
0
+00
613) F(a) = J e~ax dx, a > 0.
a
+00
614) F(a) = J e~ax dx, a > 0.
a
+°°
ч f sin ax t
615) F(a) = j j—idx.
523
Найти множество М точек дифференцируемости функ-
6
ции F(a) = J f(x,a)dx и проверить, справедливо
а Ь
равенство F'a = J f'Q(x,a)dx для а € М.
а
2
/е~ха 1
—-=- sin — dx.
yjx x
о
l
/1 dx
cos—————.
x2 x3 + a + 2
-l
+oo
618) F(a) =
/sin axdx . Л
о
0, a = 0.
a
619) Пусть 1(a) = f dx, где функция <p(x) непрерыв-
J yja- x
о
на вместе со своей производной на [0;а]. Доказать, что при
Л г/ ^(0) [ <pf(x)dx
0 < а < а справедливо равенство 1а — - - ' + / ■ >■ ■■.. ■■■ .
у/а J у/а — х
о
+оо
620) Пользуясь равенством / e"at dt = —, a > 0, вычислить
J ос
о
+00
интеграл J х2е~ах dx.
о
1
621) Пользуясь равенством / х"”1^; = —, вычислить инте-
J п
1 о
грал J xn~l\nm xdx.
о
524
+°° ^
622) Пользуясь равенством / —= = 7—7=, а > 0, вычи-
J х1 + а 2у/а
+оо О
слить интеграл J ^ ^ , п € N.
О
623) Пользуясь равенствами
-foo -foo
/ е "* сое /?х dx = а , / с “* sin уЗх dr =
У а* + р* J
Р
а2 + ’
вычислить интегралы:
-foo +ОО
a) J хе nxsinxdx; б) J хе пх coa xdx\
о о
-foo +00
в) J z2e~n* sinxdx; г) J х2е~пх coaxdx;
о о
-foo -foo
д) J х*е~пх sinxdx; е) j х3е~пх сое xdx.
о о
1
624) Пользуясь равенством I xn~l dx = —, вычислить инте-
J «
о
гр&лы:
61/(^- £)'*'
о о
1
В)
о
625) Пользуясь результатами задачи 624, вычислить интегра¬
лы:
+оо
a) J d.г;
О
525
О
+ оо
. Г (п2еГт п 1 -е~пх\ ,
■> / + )d'
о
Используя значение интеграла Дирихле
+оо
/sin ах тг .
ах ~ ~ sign а
х 2
о
(см. пример 49, § 3), вычислить интеграл.
+°° ч . 4
Г sin аж . f sin ах ,
626) I dx. 627) / 2—
о о
+°о . 5 +0О
Г sin ах , ч /* sin ах .
628) I з— dx. 629) I g— с/х.
о о
!° • a
ах
+°° 3 +?° -4
dx.
/* sin ах , _ ч /* sin (
630) J —^3—63|> J —
о о
+оо +оо
632) у 633) у г
О о
+00 -f-oo
*0,1 \ / sin ах cos/?х /* sin ах sin (Зх cos 7Х
' J iJ J ?
о о
+°° . . +°°
( sin ах sin (Зх sin ух f sin ах cos (Зх cos ух
636) I ах. 637) I ах.
о о
-foo
f sin х cos ах ,
638) / dx.
о
526
+?° • 2 +?° • 2
Г sin ах-sin х , л,лЧ Г 81 п х cos ах .
639) J р dx. 640) J -j dx
о о
+оо +оо
л,, ч [ х — sin X , л , Г 81П X — X сое X ,
641) / з—dx. 642) / з dx.
о о
Используя знамение интеграла Пуассона
+°°
о
(см. пример 51) § 3), вычислить интеграл.
+0О
643) J еГ**** dx, а > 0.
о
+оо
644) j xlne~ct^s2 dx, п£ N, а > 0.
о
+оо
645) j x2n+1e~atgt dx, a > 0.
0
+00
646) J е“^а* +2^r+c^cfx, а > 0, ас — /?2 > 0.
— сю
+оо
647) J (ai*J +2ft* + С!)e-(°*a+^*+c)<f*, а>0, ас-02 > 0.
О
+оо
648) J e'^'^dx, а > 0, р > 0.
О
+оо
549) J е~ах* ch 0xdx\ а > 0.
527
•foo
650) j xe a x sh (3xdx, a > 0.
о
foo
651) j x2ne~x ch 2Pxdx.
о
foo
652) J x2n~lc~x sh2/3xdx.
о
foo
653) J e~a x cos 2fixdx, a > 0.
о
foo
654) J e~ax sh((2y/x) dx, a > 0.
о
foo
655) J x2e~x cos 2xdx.
о
foo
656) J x2ne~x* cos2/?z dx, n 6 N.
о
-foo
657) J xe~az sin(3xdx, a > 0.
о
-foo
658) J x2n~1e~* sin2/?jtdx, n £ N.
о
Используя значение интеграла Лапласа
foo
/
cos ax , 7Г
] +x2 2
0
528
(см. пример 55, § 3), вычислить интеграл.
+оо
_2 ,
О
Ч-оо
ein гът. Г гплгут
*(1 +л*) ' J (1 +х*)' *'
О
+оо
( cosax
663) / —=—— <
J ах2 + 26х + с
— оо
+оо
‘ Л,2
+°°
660)
f х sin ax
J 1 + x2
0
+oo
662)
f cos ax
J (1+x2)-
0
0, ас
- 62 > 0.
f X —а 8inx _
664) / -г-—г dx, a > 0.
J i4a2 х
о
+°°
sin ax .
dx, a > 0.
/ пт
X2)2
О
Используя значение интегралов Френеля
+оо +оо
J aia(x2)dx=^yj^ и J cos{x2)dx=^^,
О о
(см. пример 52, § 3), вычислить интеграл.
+оо +оо
666) J sin(ax2 + 26х + с) dx. 667) J cos(x2)cos2axdx.
—оо —оо
+оо
668) J sinx2-сое 2axdx.
-оо
Применяя метод дифференцирования по параметру, вы¬
числить интеграл.
/* ха~1 - хр~1
669) / — с/х, a > 0, (3 > 0.
о
529
+ 00 _ 2
670) ~ А, „ > 0, ?>0.
о
+оо
/1 - е'пх
cos х dx, n > 0.
о
-foo
/с~ах - е'Р*
cosmx <fx, а > 0, /? > 0.
о
+оо
* 1 - />-"*
sin х с/х, п > 0.
673) J -
X
о
+о°
- р — ах _ р-/9х
/е-ах _ е~рх
sin тх dx, а > 0, Р > 0.
о
+оо
675) J \е~$ -е~&) dx, а > 0, /? > 0.
О
+оо
/р-ах _ е-^г
dx, а > 0, р > 0.
X
о
-foo
/с~ах — с”^х
<fx, а > 0, р > 0.
о
+ °° 2 «2
/• ^ ах — ^ /?х
678) / dx, а >0, 0> 0.
о
■fOO п
/ f с~а* - е~Рж\
679) / ( — J dx, а > 0, /? > 0.
о
+0О
680) J
_sin Зх cos *7Х , л л
! </х, а > 0, Р > 0, 7 > 0.
530
+оо
681) | dXt „ > 0, „ > 0, 7 > 0.
0
+oo
Ш) J q > 0, 0 > 0, 7 > 0.
0
+oo
/1 — e“ax
—— dx, a > 0.
xex
о
+oo
684) j
/
0
+?°£ л,е_0,,х «
685) J dx, ^2 А{ = 0, a, > 0.
o •-1
+00
v f e~P* -e~ax -х(а-в)е-а* ,
686) I ^ dx, a>/?> 0.
e""*** sin2 (3x
о
+oo
687) / dx, л > 0.
x
0
688) J
+o°
e arsin2/?x
5 dx, a > 0.
о
+oo
689) / „ > o, „ j T > 0.
0
+00
690) J e agS*n dx, c* > 0, /? > 0.
о
+00
691) J e ax3-1~fX dx, a > 0, /7 > 0.
531
692
693
694
695
696
697
698
699
700
701
702
532
f ln(l — a2i2) j .j
J
0
f In(I - »2*2)
J ,v/l'“UI-
0
/• ln(l - a2*2) , .
/-^r1*. wo-
0
j-HS + zp n.(H-.V)
’ J VT^X* ’ J v/T^2
о 0
/* ln( 1 -I- cr2x2)
0
+oo
/
ln(l + a2x2)
dx, a > 0, /3 > 0.
/?2 + JC2
о
foo
/* ln(a2 + x2)
J *x, a >0,(3 >0.
0
+oo
arctg ax
/
x2y/x^ — 1
1
dx.
+oo
/
0
x(l + /?2X2)
dx, a > 0, P > 0.
arctg ax
x|
+oo
, a > 0, /? > 0.
о
+oo
ln(l + ar2x2) arctg /?x
J 1 dx, a > 0, /? > 0.
ln(l -f Of2r2)- ln(l + P2X2)
+оо
703) J -
arctg ax- arctg fix . л _
b 2 dx, a > 0, /? > 0.
x
0
+o° _
/6 + X
In “5 ^ cos ax dx, a > 0, b > 0, с > 0.
+ x^
о
-f-oo
f sin ax
705) J ,(H-«y‘fa-‘>>0-
0
+00
„ллЧ /* cosax ,
706) J {TT^dx' a>0-
0
foo
707) J 1 ~"^~e-a«ds, a > 0, /? > 0.
708) J
1 - cos fix _ax
*2 C
0
foo
2х/?8Ш2/?£ + СОв2/?Х — 1 _aara
dx, a > 0, p > 0.
о
foo
709) J e arein y/mxdx, a > 0.
о
l
/wctt f
—^ dx следующими способами:
xv 1 — x2
о l
,x arctg х Г da
1) используя равенство = / —
х J 1 + а2х2
о
1
/arctc хо'
dx И ПрИМб-
XV 1 — X2
о
нить метод дифференцирования по параметру.
533
711) Рассматривая производные функций, стоящих н правой
и левой частях, проверить справедливость равенств:
.г foo
) J el dt = е* J e~l su\2xtdt\
а)
о о
/Г * \2 7г f е-*3(«3+1)
б)(/e_t dt) =4 -j-^TTdv'
о 0
+oo
. f ln(l+ar) 7Г, 2x f In/ .
4 l+,>' '1=4l'|lt,)'J
о 0
r +oo
v /* t7 . 1 f _#asin2/x f
4 7? Уe" i
о 0
712) Используя равенства
■foo foo
TTF =/'""*mxix’ щг=/
о 0
доказать равенства
foo -foo
v / sin xdx /* e_at ,
*>У трг=./
0 0
foo +oo
v / cos xdx f tc~at ,
б) I = I - — d/,a>0.
J i + a J 1+/2
о о
Преобразование Вейерштрасса Ф(р) функции /(f) опреде¬
ляется формулой
foo
4>(p) = -L J e~^f(t)dt.
-OO
Найти преобразование Вейерштрасса функции /(f).
713) /(/) = 1. 714) /(/) = t2.
715) /(/) = e2ort. 716) /(/) = cosnt.
534
Преобразование Лапласа F(p) функции f(t) определяется
формулой
+оо
F(p)= J e~plf(t) dt.
о
Найти преобразование Лапласа функции /(<).
717) f{t) = 1. 718) f{t) = е°".
719) fit) = sin fit. 720) fit) = сов fit.
721) fit) = tn, neN. 722) fit) = Vt.
723) f{t) = te~at. 724) /(t) = sin(av/t).
725) fit) =
= (LT-’ ‘*0’
I 1, 1 = 0-
726) Пусть f(x) ограничена на IR и интегрируема на любом
конечном отрезке. Доказать, что при х > 0 функция
+оо
f *f(z) , п
и = J ■ 2 ^ ^ dz удовлетворяет уравнению Лапласа
д2и д2и _
+ W ~
727) Пусть f(x) абсолютно интегрируема на (—оо;+оо). До¬
казать, что интеграл
+оо
ди 1 д2и
удовлетворяет уравнению теплопроводности — = — г- и
at а1 ох1
начальному условию u(jc, /) = /(х).
Пусть ы — особая точка функции / и ы Е (а; Ь). Тогда
6
(Ит+ ( / /(*) dx + J fix) dx'j,
W + ff
535
если он существует, называется главным значением интегра-
6 6
ла J f(x)dx в смысле Коши и обозначается v.p. J f(x)dx.
а а
+ оо
Главным значением в смысле Коши интеграла J f(x) dx, если
— оо
А
f Е R[—Л\ А] для любого А Е К, называется lim I f(x) dx
Л-Ч+оо J
-А
+оо
и обозначается v.p. J f(x)dx.
— OO
6
Найти v.p. J f(x)dx для следую!цих интегралов.
а
j ^TZ~C' а<с<ь- 729) / (х - с)2п+1' п € N.
а а
Я/2 2 а— 1
730) [ —, 0 < к < 1. 731) / ^—dx, а > 0.
J к — sin J 1 — х
о о
■foo -foo
7521/ Hfhr 7331 /
О о
2 -foo
7341 735>/iTPdl
1/2 -oo
-foo +oo
736) J arctg x dx. 737) J
— oo —oo
-foo -foo
738) J sinxdx. 739) J coaxdx.
536
Используя значения интегралов Эйлера, вычислить следу
ющис интегралы.
1 1
740) J \Jx-x'ldx. 741) J xz\/Y~x}4r.
о о
1 -foo
f dx f tfx
4_/W7?F3' 743) J or»)5
foo -f-oo
f Jx dx f x2 dx
744> / fe?- 74S> / T??
о 0
foo f-oo
f dx f xdx
746) J TT?' 747> J
0 0
1 -f-oo
748) J{ 1 - *2)n dx, n G N. 749) /o^ лр *»eN, n£2.
0 0
a a
750) J x2\J a2 — x2 dx. 751) J x2n \/a2 — x2 dx, n G И.
о о
1 1Г/2
-2n
752) f— —.= dx, nEN. 753) [ sin6 xcos4 x dx.
7 </x(l - x2) У
0 v 0
w/2 ir
754) f sin3^2 xcos1/2xdx. 755) f -=£f===.
У У V3 — cos x
0 n
foo -foo
756) J tbe~atdt. 757) J 1ье~ы' dt.
0 0
foo foo
/■ tflnx . [ III X f
758) J TT^dx- 759) J TT^dx-
о 0
537
760) j
sinnxlncosxdx, n> — 1.
о
tr/2
761) / sin" x In sin xdx, n>-1.
0
1
762) J In r(x)sin TTx dx.
0
1
763) J In Г( x) cos2n7Tx dr, ri6N.
Определить область существования и выразить через ин¬
тегралы Эйлера следующие интегралы.
+°° - +°° „2т
/хт Г х
ТТ*"1**' ">0 765) / TTF"
0 — оо
7“> / (ГТ^г
о
+оо
/* хт dx
767> J
о
7“’/^'
о
1
769) J хр_1(1 -хт)ч~Чх, т> 0.
о
г хР-'а - х)?_1
™»У "So. 0>»,г>о.
О
538
0
6
772) / If-AZVzSFdx, 0<:c<b,c>0
(x + c)m+"+2
a
[( l+x)2m-4i-x)2" —!
m)J (1+X2)m+"
-1
+oo
[ arctg г
774) J
0
-foo foo
775) f 776) / '“<l^a,) Д.
0 0
ir/2 w/2
777) a) J sma~lxdxi 6) J cosQ~lxdx.
о 0
7Г/2
778) J tg® x dx.
о
/sinn x
(H-tcos»)"^ ° < W •= '
0
я/4
f ( cos x -f- sin x \ cos a
780) / : dx.
J \ cos x — sin X J
— п/Л
Я31ПХ \a~} dx |
TTIotiJ ТП^П1 0<t<l
0
+ 00 1 p
782) J xme~r" dx. 783) j ^ln ^ dx.
, a > 0.
539
+°° -
7вЛ\ f ХР 1 In X . Г X* InX
784) / — dx. 785) / - 5-dx.
J 1 + х J 1 + х2
О
+ 00
786) j Х { .‘"■ ~dx. 787) / ~ dx.
сР-Чп2! /•,«,„2
+ х
+ 00
г
785)
/
0
+оо
г
787)
/
0
-x-р
[хр-1-х-г
788) Проверив, что / dx, О < р < 1,
У 1-х
о
lim (£(р, £) — В(1 — р, £)), вычислить этот интеграл.
равен
с-Ю+
+ оо
Г t*-1 7Г
789) Используя равенство В(х, 1 — х) = / dt = — ,
J t + 1 sm 7гх
+оо О
гР-1 -тч-1
, /• ХР-1-!"'1 J
проверить, что I = / — — ах равен
J (1 + х)1пх
р 0 <7
J В(х, 1 — х) dx- j B(x,\ — x)dx (0 < р < 1, 0 < 7 < J).
1/2 1/2
Найти величину интеграла I.
Вычислить.
■foo -foo
f sh ах , Л _ Г ch их ,
790) J 0<а<1)- 791)У 55^*, »<,<,.
о о
Доказать.
+оо
792) „И™, fe-'dx=l.
0 +°°
J е-*'Л*) =-Г1 (I).
О
Проверить равенства.
1 1
/dx [ х2 dx п
у/\ — х4 J Vl-x4~ 4'
540
1 ir/2
795) f — . f \/sin2xdx =
j J </(l-*4)3 J 2
0 V 0
] 1
0
1
0
1
798) J
о
\/l — x2n J
0
y/l - x2n
1
dx f
x 2 ^
y/l-Xn J
0
VI - xn
l
л/1 — Xn dx-
/ Vi -
2nn
J
0
7Г
.ч Ctg ,
тг/2 ir/2
0 0
800) /<-'*• У A-,*=5^j.
0 0
+oo +oo
801) J are-** rfz- J e-** <fx =
о о
+oo +oo
802) J e~x* xm~l dx- j e~B"xn-m~l dx =
о о
JT 1 - .
- Vm> n > 0> 0 < m < n.
П sin 22* ’
+oo +oo
/dx Г dx
1 -foo
805) J (\—x3)~l^2dx = y/^J(x3—\)~l^2dr.
— oo
-foo
/
oft« , x” 3/2 Ar - \Z* r(p- V2)
806> J (x2 + ax + b)P 2v^ + 2#-'/2' Г(р) ’
— OO
6 > 0, a + 2л/б > 0, p > 1/2.
-foo
V-*r rf/, J* > (); И
1 1 f
Используя равенство = ——- I tm~lt
xm Г(m) J
о
возможность перестановки интегралов, вычислить интегра¬
лы.
•foo -foo
/sin ax . Л /* cos qx .
—^-dx, 0<m<2. 808) / —- dx, 0<m<\.
о 0
Обосновав возможность дифференцирования по параме¬
тру интеграла задачи 807, вычислить интегралы.
•foo -foo
f sin х , Г sin X . 9
809) I lnxcfx. 810) I In xdx.
о о
811) Используя соотношение Г;(1) = —Сэ, Сэ — константа
-foo
Эйлера, и дифференцируя по х формулу Г(х) - J Ьт~х е~1 dt,
о
вычислить интегралы:
-foo 1
а) J е~х \пх dx\ б) J In(— In x)dx\
о о
-foo -foo
в) J e~l In tdt; г) J е~г1п2 х dr\
о
+°о
~2tdt.
Д) / е ‘’in2
542
812) Используя формулу Лобачевского (см. задачу 39 § 5 гл. П),
-foo
/sinpx _
ах, где р есть рациональная
о
дробь с нечетным числителем и знаменателем.
813) Используя формулу Гаусса (гл. II формула 16), вычи-
1
/хр - Xя
— cfx, p-h 1 >0, 1 >0.
1-х
о
814) Используя результат задачи 813, вычислить следующие
интегралы:
Г (1 - х )(1 - х?) dx а+1 > 0 > о, a-f/?+] > 0;
J (1-х) lnx
о
1
,/
хв(1-**)(1 -х?)
(1 — х) lnx
о
а + /? + 7 > -1;
в
dx, а > -1,а + /?> —1, o-f*7 > —1,
/ха~ — х^”1
п ■ vi dx, а > 0, р > 0;
(1 + х) lnx
о
]
/Д. Of-1 _ х-ОГ
>« _Г- Г] dx, 0 < а < 1.
(1+х)1пх
о
*г/2
f 2а— 1 . \А Г(ОГ)
815) Используя формулу J ат1а 1 <pdip = —
Р
ir/2
а > 0, вычислить интеграл J sin2n In sin
о
816) Найти площадь области, ограниченной кривой
(х2 + у2)4 = ху3.
817) Найти площадь области, ограниченной одной петлей кри¬
вой rm = ат cos т<р, т Е N, и длину этой петли.
543
818) Найти объем тела, ограниченного поверхностью хп +
+ уп + zn = ап, п > 0, и координатными плоскостями, нахо¬
дящегося в первом октанте х ^ 0, у ^ 0, z ^ 0.
819) Исходя из определения функции Т(х) для х < 0, z ф — п,
n G N (гл* И* с* 461), проверить равенства
их
б) Г(1 + *)Г(1 - х) = , О < \х\ < 1;
Исследовать сходимость интеграла.
-l-оо -foo
-foo
-foo
ОТВЕТЫ К ГЛАВЕ П
1) При а > 1 сходится к —а1'®, при а ^ 1 расходится.
а — 1
2) Сходится при а < 1 к 101-а, при а ^ 1 расходится.
1 — а
(Ь -а)1"*
3) При а < 1 сходится к — , при а ^ 1 расходится.
1 — 0
(6 — а)1 ~а
4) При а < 1 сходится к —, при а > 1 расходится.
си — 1
5) Расходится. 6) 7) 8) 9) Расходится. 10) -г ~.
2 2 8 ab 2
11) Расходится. 12) Расходится. 13) 14) Расходится.
уб
и, JL. „) н ф |6|; jL, И = |ц. ,7,
iS) __ - arctg-. 19) j-|^. 20) 2 |а6|(|а| + |Ь|)'
25) ^ — arcsin j. 26) —^=. 27) я. 28) ■ . 29) ^
7 2 4 ' 2\/2 у/а2 — 1 2
30) £(6-а)(а+36). 31) тт. 32) 33) £(^2-1).
oi\ J_In l + ^ Ы L* Ы __L j. L_
* V5P 1 - 2 In 5 (ln5)2 (In5)3
37) —26*"1. 38) Расходится. 39) Расходится.
40) Расходится при всех а. 41) Расходится. 42) —1.
43) Сходится при а>1 к расходится при а^.1.
а —1
1 4
44) —. 45) Расходится. 46) Расходится. 47) 48) 1.
я*2 3 /7Г\^/^ я2 49
49) 50) 2. 51) - (-J 52) у. 53) —. 54) Расходится.
55) Сходится при \а\ < 1 к —т , расходится при |а| ^ 1.
2v 1 — а2
56) Сходится при |а| > 1 к — расходится при |а| ^ 1.
4\/а2 — 1
57) у. 58) Расходится. 59) т - + ^1п2. 60) 61) 1.
4 4 16 z о
545
“> 63> 64> 165>2Л 66) i
67) Сходится.
68) Сходится при 0 < а < 1, расходится при а ^ 0 и при а ^ 1.
69) Расходится.
70) Сходится при а < 1, расходится при а ^ 1.
71) Сходится при - ^ р < 1, расходится при р ^ 1.
и
72) Расходится. 73) Сходится.
74) Сходится при р > 1, расходится при р ^ 1.
75) Сходится при а > 0, Р > 0, расходится при а ^ 0, Р —
любом и при Р ^ 0, а — любом.
76) При любом а расходится. 77) Сходится. 78) Сходится.
79) Сходится. 80) Сходится. 81) Сходится. 82) Расходится.
83) Сходится. 84) Сходится.
85) Сходится при а > 1, расходится при а ^ 1.
86) Сходится. 87) Сходится. 88) Сходится. 89) Сходится.
90) Сходится.
91) Сходится при 1<а<2, расходится при а^1 и при а ^2.
92) Сходится. 93) Сходится.
94) Сходится при n > 1, расходится при п ^ 1.
95) Расходится. 96) Сходится. 97) Расходится.
98) Сходится. 99) Сходится.
100) Сходится при р < 1, расходится при р ^ 1.
101) Сходится при а ^ 0, расходится при а < 0.
102) Сходится при \р\ < 1, расходится при |р| ^ 1.
103) Сходится. 104) Сходится.
105) Сходится при а < 3, расходится при а ^ 3.
106) Сходится при 1 < р < 2, расходится при 0 < р ^ 1 и при
p'Z 2.
107) Сходится. 108) Сходится. 109) Сходится.
110) Сходится, если аР > 0.
111) Сходится при т > —2, — — т > 1, расходится в против¬
ном случае.
112) Расходится. 113) Сходится. 114) Сходится.
115) Сходится.
116) Сходится при р < 3, расходится при р ^ 3.
117) Расходится. 118) Сходится.
546
Сходится при а > 0 и Р > — 1; расходится при а <С 0 и
любом /? и при ^ — 1 и любом а.
Сходится при р > — 1, любом q и при р = —1, q > — 1;
расходится при р = — 1, g ^ — 1 и при р < —1 и любом q.
Сходится при р > 1, q любом и при р = 1, q > 1; расхо¬
дится при р = 1, q ^ 1 и при р < 1 и любом q.
Сходится. 123) Расходится при любом а.
Сходится при а > 1, расходится при а <С 1.
Расходится при любом а. 126) Сходится.
Сходится при р < 1, расходится при р ^ 1.
Сходится. 129) Сходится.
Сходится при 1 < а < 2, расходится при а ^ 1 и при
а ^ 2.
Сходится.
Сходится при р > — 1, расходится при р ^ — 1.
Сходится. 134) Расходится. 135) Расходится.
Расходится. 137) Сходится. 138) Сходится.
Сходится.
Сходится при а < —расходится при а
Сходится при /? < 1, аг — любом и при /? = 1, от < — 1,
расходится в противном случае.
Сходится при к < — 1, расходится при & ^ -1.
Расходится. 144) Расходится. 145) Сходится.
Сходится. 147) Сходится. 148) Расходится.
Сходится. 150) Расходится. 151) Сходится.
Расходится. 153) Сходится.
Сходится при 2 < а < 3, расходится при а 2 и а ^ 3.
Сходится.
3 3
Сходится при а > расходится при а <
4 4
Сходится. Указание. Использовать соотношение
+СЮ ™ wn
J f{x)dx = jp f f(x)dx.
n «=!_/- * \
ir(n-l)
158) Сходится при n > 4, расходится при n 4. См. указание
к № 157.
159) Сходится. См. указание к № 157. 160) Расходится.
547
161) Сходится. 162) Сходится. 163) Сходится.
164) Сходится.
165) Сходится, если min(p, q) < 1 и max(p, q) > 1, расходится
в противном случае.
166) Сходится.
167) Сходится условно при всех к и а ф 0, сходится абсолютно
при а = 0.
168) Сходится условно при всех а > 0.
169) Сходится абсолютно при 1 < а < 2, сходится условно
при 0 < а ^ 1, расходится при а <С 0 или а 2.
170) Сходится условно при 0 < а < 1, расходится при а ^ 0
или а ^ 1.
171) Сходится условно при а/0и0<а^1, сходится аб¬
солютно при а > 1 и любом а; расходится при а = 0 и
любом а и при а ^ 1 и а = 0.
172) Сходится абсолютно. 173) Сходится условно.
174) Сходится абсолютно при а > 2, сходится условно при
1 < а <С 2.
175) Сходится абсолютно при max(p, q) > 2. Сходится услов¬
но, если 1 < max(p, q) ^ 2, расходится, если шах(р, q)
^ 1.
176) Сходится абсолютно, если q > р + 1 ир > —2, сходится
условно, если р<д<Ср+1,р> —2; расходится, если
р ^ q или р ^ —2 при любом q.
177) Сходится условно.
178) Сходится абсолютно при п > m-fl, сходится условно
при т < п ^ т + 1, расходится, если т ^ п.
179) Сходится абсолютно, если р>—1и0>р+1, сходится
условно, если р> —1 и р < q ^ р + 1, расходится, если
р>-1ир^;д или р ^ — 1 при любом q.
180) Сходится абсолютно, если Л < — 1. Сходится условно,
если А ^ -1.
181) Сходится условно. 182) Сходится условно.
183) Сходится условно при 0 < а <С 1, сходится абсолютно
при ot > 1; расходится при а ^ 0.
184) Сходится условно.
548
185) Сходится абсолютно при —1 < -—- < 0, сходится
Я
1 — р
условно при 0 ^ < 1, расходится при q = 0 и лю-
Я
1~р ы.
бом р или при
186) Сходится абсолютно при р < 1, сходится условно при
1 ^ Р< 2.
187) Сходится условно. 188) Сходится условно.
189) Сходится условно.
190) Сходится условно при р < 2; расходится при р 2.
191) Сходится абсолютно. 192) Сходится условно.
193) Сходится условно.
194) Сходится условно при а > —1; расходится при о ^ — 1.
195) Сходится условно.
196) Сходится условно при а ф 0; расходится при а = 0.
197) Сходится условно при —1 < р <С 1; расходится при
р <С — 1 или р ^ 2; сходится абсолютно при 1 < р < 2.
198) Сходится условно при 0 < р <С 1, сходится абсолютно
при р > 1.
199) Сходится условно при 0 < р < 2. 200) Сходится условно.
201) Сходится условно при q > 1, расходится при 0 < q ^ 1.
202) Сходится абсолютно. 203) Сходится условно.
204) Сходится условно.
205) Сходится условно. Указание. См. задачу 48 гл. I § 5.
206) Сходится условно. Указание. См. задачу 48 гл. I § 5.
207) Расходится. Указание. Показать, что функция
X
F(x) = j eslnrsinx(/x удовлетворяет условию С\х ^
о
^ F(x) ^ С2х для х > 27г, где 0 < С\ < С2.
208) Сходится условно. 209) Сходится условно.
210) Сходится условно при 0 < а ^ 1, сходится абсолютно
при а > 1, расходится при a 0.
211) Сходится условно. Сравните с предыдущим примером.
212) Расходится.
549
213) Сходится абсолютно при ft > о -f 1, расходится при
^ л + 1.
214) Сходитгя абсолютно при ft > 2(а 4- 1), расходится при
/?^2(а+1).
215) Сходится условно. Указание.
к /2 тг / 2
1 [ . ' [ 2
—< / sinfl л dx — I cos” х dx < —7===.
2х/?Г=Т ^ У J ^ УгГ^ПГ
о 0
216) Сходится абсолютно. См. указание к № 215.
217) Собственный. 218) Сходится. 219) Сходится.
220) Сходится.
221) Расходится при а ^ 1, сходится при or < 1.
222) Сходится. 223) Сходится. 224) Сходится.
225) Собственный. ^226) Сходится. 227) Собственный.
228) Расходится. 229) Расходится. 230) Сходится.
231) Собственный. 232) Сходится. 233) Расходится.
234) Собственный. 235) Сходится. 236) Сходится.
237) Сходится. 238) Расходится. 239) Собственный.
240) Сходится. 241) Сходится. 242) Собственный.
243) Расходится. 244) Собственный. 245) Расходится.
246) Сходится. 268) —7=L=. 269) arcsmQ
ay/a2 ~ 1 ау/\ — а2
1п(а + \/1 + а2)
ау/1 4* а1 а\/\ 4- а1
Лгточ 1п(а 4* л/or2 - 1) t _
272) при а > 1; 1 при а = 1;
а у а2 — 1
arccos а
—7=== при 0 < а < 1.
ау 1 “ а
273) 1п = п/п_ь /„ = м!.
2ii-lf f (2n- 1)!! ^
274) /п = —-—Л*-ь /п = —2гГГ\—^казаиио Приме¬
нить результат примера 51 гл. I § 3.
550
n2 -f a2 ’ a ’ 1 -f a2 ’
, (2*-!)!
2fc_1 (1 + a2)(32 + a2)... ((2* - J )2 + a2]'
, (W
2fc “ a(a2 + 22)(o2 + 42)... (о2 + (2Jfc)2) ‘
276) /„(m) = - 1), /n(m) = •
277) In(m) = 278) /„ = sin(n + 1)J.
279) /„ = -^j-cos(n + 1)£. 280) 22" ^
2Sp. — v”-r^4- —; (2n + l)2
oon (2»-3)H «гЛ"-1 (-1)"-'*
281) (2п-2)!!'(ЛС-В2)"+*' 1 '
2*4) (-.)• Д (-1 + 285> (2^7)П
286) (-D-.nl. 287)
oopx F _ (**“ ON n_ OL. . _(»-!)!! _ Ojf. ,
288) In — |f тг, n — 2A?, Jn — , я — 2A. 1.
n!! ?i!!
n 2 2
289) n!^(-l)fc+1C£ln(* + J). 304) 305) 306) 1.
k=l 12 6
307) 308) £. 309) £ 310) 31.) 312)
313) -j. 314) -*1. 315) j. 316) 317) 2 -
318) ln(l + \/5).
319) —jrln2. Указание. sin2</? — si»2 u> = sin(v? — w)-sin(v? + w),
a = sin u).
320) 77 In 2. Указание. Сделать замену In -— = x и проинте-
2 sin/
грировать по частям.
551
321) —. Указание. Сделать замену х — sin / и проинтегриро¬
вать по частям.
" -L. ^+1
7Г -f 111
322) 323) J. 324) —=. 325) '
\/2 2' v/2' 2v/2
казание. Обозначить cosy
cosy? = z и (1 — z)/ = ^/(z — t/)(l — z)
у?. Указание. Обозначить cos <p
НЫ cosy? = z и (1 — z)t = \/(z — u)( 1 — z).
n/2- 1
326) Указание. Обозначить cosy? = и и сделать замены
СО!
327) ~ cosy?. Указание. Обозначить cosy? = ии сделать заме-
+оо
/х™ In х dx
■ сделать замену
j + + ^
*= -. 1
У
329) —^ In 2. 330) — ^ In 2.
7Г2
331) — — In 2. Указание. Сделать замену 7г - х = у.
332) . Указание. Проинтегрировать по частям.
333) — In 2. Указание. Сделать замену х = sin у.
Z
334) — ^1п2. Указание. Сделать замену x = siny. 335)
336) 0. 337) -2 In 2.
338) тг1п2. Указание. Сделать замену ar = tg у. 339) 7г\/2.
340) 0 при п нечетном, ж при п четном. Указание. Выразить
я
/sin(n — 2) cos х .
—-—: dx.
341) 0 при п нечетном; при п четном.
7Г 71
342) ^-(№1 ~ М)« Указание. Проинтегрировать по частям и
применить результат примера 49 гл. 1 § 3.
343) у/тг(\Ь\ — \а\). Указание. Проинтегрировать по частям и
применить результат примера 51 гл. I § 3.
344) тг(|а| — \Ь\). Указание. Проинтегрировать по частям.
345) Указание. Проинтегрировать по частям.
552
346) 2^2 ^каэание‘ Проинтегрировать по частям.
347)
(-l)^ ж
(2i/ + I)2" - {2и + l)(2i/ - I)2" +
,n = 2i/+l,i/6N;
22^-i (2/i)!
2j/(2j/- 1)
+ 1-2
348) "• (2r»~ t)!»
J 2 (2n)!! '
(2t/)2" In 2v - 2u(2u - 2)2" ln(2i/ - 2) +
(2i/ - 4)2/i ln(2i/ - 4) -
, n = 2i/, j/ £ N.
"-1 - n(n - 2)"-1 + n(".-1}(n - 4)n_1 -
349) 2^=TjT
351) In —. 352) ln( l + i ) .i„£. 353) £ln^. 354) ln^.
or \ p J or 2 'a
355) --In 2. Указание. Рассмотреть тождество
p (г^-s)-■’Ч+
+ i(_! ±+ie-.\_I(_! 1 + I.--V
x \ er — 1 2jc 2 / x \e2x — 1 2x 2 /
356) /f—a+aln - • Указание. Использовать равенство
+ООГ
/
О +оо
-г-
е-р* + ^(а — /?)е
-arr _ р-Р*
dx =
+оо
dx +
(a-^) j —dx
+00 о
e-ax_e-f)x
и преобразовать / 2
мастям. о *
357) 0. 358) a In | а | > 0
3591a ln|a| — a. Указание. Использовать равенство
ax cos x — sin ax = ax (cos x — cos ax) -f- ax cos ax — sin ax.
360) In 361) In v/|a^a| 362) lnfi . 363) a/?ln
dx интегрированием no
553
в 26 2а
364) с*Р In —. 365) 26 In - + 2а In
а а + 6 а + 6
366) Указание. Полагая Ап = —А\ — Аг — • • • — Дг-ь рассмо¬
треть интегралы
+оо
А{ cosaiX — Ai cosanx , . _ а,
" dx — i4j In ■■ ■
X ttn
-t-oo
/
(2n — l)!! p
3^7) ; — In—. Указание. Свести интеграл к интегралу
(2п)!! &
Фруллани, заменив sin2fl х на
. 2п l 2n(2n - I)... (г* + I)
sm х - - —г
2П I *2 ... 77
368) In-.
а
369) [I — -' ) In —. Указание. Свести интеграл к ин-
V (2n)!! J а
тегралу Фруллани, заменив cos2n х на
2п _ l 2п(2тг-1)...(п + 1)
2 I-2 ... 71
370) — при Р < а; — при Р = а; 0 при Р > а.
371) ^ при а < Р + 7; ^ при а = Р + 7; 0 при а > Р -1- 7.
372) ^р при Р ^ а; при /? ^ а.
373) ^oria2 •• -<*„.374) ^|а —/?|. 375) Равномерно.
376) Неравномерно. 377) Неравномерно. 378) Равномерно.
379) Равномерно. 380) Неравномерно. 381) Неравномерно.
382) Равномерно. 383) Равномерно. 384) Равномерно.
385) Неравномерно. 386) Равномерно.
387) а) Равномерно, 6) равномерно. 388) Равномерно.
389) а) Равномерно, б) неравномерно.
390) а) Неравномерно, б) равномерно.
391) а) Неравномерно, б) равномерно.
392) а) Неравномерно, б) равномерно.
393) а) Неравномерно, б) неравномерно, в) неравномерно,
г) равномерно, д) равномерно.
394) а) Неравномерно, б) равномерно.
554
395) а) Неравномерно, б) равномерно. 396) Да. 397) Нет.
398) Нет. 399) Нет. 400) Да. 401) Да. 402) Да. 403) 9.
404) 1 405) 406) J. 407) 1. 408) /(*) - /(а). 409) ^
л О Z L
410) 0. 411) In 412) 0. 413) Непрерывна.
414) Непрерывна. 415) Непрерывна. 416) Непрерывна.
417) Непрерывна. 418) Непрерывна.
419) Если /(0) ф 0, то разрывна в точке у = 0; если /(0) = 0,
то непрерывна при |у| < оо.
420) Разрывна в точке у — 0. 421) Непрерывна.
422) Непрерывна. 423) Непрерывна. 424) Непрерывна.
425) Нет. 426) Нет. 427) Нет. 428) Нет.
Ь у
429) J 2уех +v dx. 430) (у2 + у)10 + J х(х + ху)9 dx.
а 2 0
431) —|y|siny2 + J Q^^sinzy + xy/xycosxy^j dx.
У
432) 2уе“у4 — е~у2.
у2
433) 2уе“5 — е~у — j х2е~х у dx.
у
434) ( - 4- —J siny(y 4-6) - (-4- —j—) sin у(а + у).
\У У + Ь) \у а 4- у/
435) — cos(y/cosyy) sin у — cos(\/sin у у) cos у —
cosy
— J ^/xsin(\/xy)dx.
sin у
436) -ln(l + у2).
У
4 У
437) f(y, -у) + 2 J f'u{u,v)dx, и = х + у, v = х - у.
а
1/У
У2 1 + У ' / * (1 + У)2(1 + ху)
555
У +У
439) 2у J sin(z2 + уЛ — у2) dz 4- 2 J sin 2z2 cos 2yz dz —
ул-у
у- *+у
„2 , ^2 2
2у /■'*/ cos(x2 4 -г2 — yJ) dz.
0 x-y
У
440) - J((x 4 у)2 4 2y(x 4 у)) exp(-y(x 4 у)2) dx 4
у
4 2yexp(-y3(l 4 у)2) - yexp(-4y3).
l
1 1 Г
441) -/(1) sign (sin у) I f(x) sign (sin xy) dx —
У У J
l о
I x/'(x)sign(sin yx)dx, у ф ттп, n6Z,
У У
о
если /(1) =0, то F'(y) существует всюду на К.
у2
442) J exp(y4z3) dz 4
~у2у У*
4/ |я3 J exp(x3z3y)z3 dz4-z ехр(у4х4)+х ехр(—y4x4)|dx.
0 -ух
443) Зеу 4 2уе*. 444) ЗДу) 4 2у/|(у).
445) F"(y) = 2/(у), у G (а;6); F"(y) = 0, yG (а;6).
Если /(а) = /(6) = 0, то F"{a) = F"(6) = 0;
если /(х) ф 0 для х = а и х = 6, то существуют од¬
носторонние производные ^+(а) = ^/(а), F|'(6) = 0,
F"(a) = 0, Fl'(b) = 2/(6).
446) /(„). 447) +
аг
448) F'Jy{x,y) = x(2-3y2)/(zy) + -^-/ (-'j + х2у(1 -y2)f'(xy).
У \ У J
453) тг1п 1°1 + *. 454) я-In —.
|а| 2
SS6
455) *ln |a|+|61. 456) 2тг1п |а|, |а| > 1; 0, |а| ^ 1.
457) ^signaln(l + |а|). 458) п arcsin а. 459) 7Г arcsin а.
460) 7г. 461) ^ ^arctga\/2 — arctg -^=
462) ^-(1 — elal)signa. 463) ^ 1п(а + \/1 + а2). 464) 7Г arcsin а.
465) — . 466)^-—агссов2а. 467)^ arctgaln(l+a2).
468) у = Ах - 469) Нет. 470) Нет. 471) Нет. 472) Да.
О
473) Да. 474) Нет. 475) In 476) arctg t.
1 ь2 + 26 + 2 6
477) - In —г— -. 478) я-arcsin-.
’ 2 а2 + 2а + 2 ’ а
(2п — 1)!! я- . (2п — 1)!! я- _2
479) а) (2п)ГГ""2* б) (2я)!! 2а~ ' Укаэание Дока*
зать, что I удовлетворяет уравнению
Г (а) + ———/(а) = 0.
а
484) а) Неравномерно, б) равномерно.
485) а) Равномерно, б) неравномерно. 486) Равномерно.
487) а) Равномерно, б) равномерно. 488) Равномерно.
489) Равномерно. 490) Неравномерно. 491) Неравномерно.
492) а) Равномерно, б) неравномерно. 493) Равномерно.
494) Равномерно. 495) Равномерно. 496) Равномерно.
497) а) Равномерно, б) равномерно, в) неравномерно,
498) Неравномерно. 499) а) Равномерно, б) неравномерно.
500) а) Равномерно, б) неравномерно.
501) а) Равномерно, б) неравномерно.
502) а) Равномерно, б) неравномерно.
503) а) Равномерно, б) неравномерно.
504) а) Равномерно, б) неравномерно.
505) а) Равномерно, б) неравномерно.
506) Неравномерно. 507) а) Равномерно, б) неравномерно.
508) Равномерно. 509) Равномерно.
557
510) а) Равномерно, б) неравномерно, в) неравномерно.
511) а) Равномерно, б) неравномерно.
512) а) Равномерно, б) неравномерно.
513) а) Равномерно, б) неравномерно. 514) Неравномерно.
515) Равномерно. 516) Равномерно.
517) а) Неравномерно, б) равномерно. 518) Равномерно.
519) а) Равномерно, б) неравномерно.
520) а) Равномерно, б) неравномерно.
521) а) Равномерно, б) неравномерно.
522) а) Равномерно, б) неравномерно. 523) Равномерно.
524) а) Равномерно, б) неравномерно. 525) Равномерно.
526) а) Равномерно, б) неравномерно.
527) а) Равномерно, б) равномерно. 528) Равномерно.
529) а) Равномерно, б) неравномерно.
530) а) Равномерно, б) неравномерно.
531) а) Равномерно, б) неравномерно. 532) Равномерно.
533) Равномерно. 534) а) Равномерно, б) неравномерно.
535) Неравномерно. 536) а) Равномерно, б) неравномерно.
537) Равномерно. 538) а) Равномерно, б) неравномерно.
539) Равномерно. 540) Равномерно. 541) Равномерно.
542) а) Равномерно, б) неравномерно.
543) а) Неравномерно, б) равномерно. 544) Равномерно.
545) Равномерно. 546) Равномерно. 547) Равномерно.
548) Равномерно. 549) Равномерно. 550) Равномерно.
551) Равномерно. 552) Неравномерно. 553) Равномерно.
554) а) Неравномерно, б) неравномерно. 555) Равномерно.
556) Равномерно. 557) Равномерно. 558) Неравномерно.
559) Равномерно. 560) Равномерно.
561) а) Равномерно, б) неравномерно. 584) Непрерывна.
585) Непрерывна. 586) Непрерывна. 587) Непрерывна.
588) Непрерывна. 589) Непрерывна. 590) Непрерывна.
591) Непрерывна всюду, кроме а = 0.
592) Непрерывна всюду, кроме а = 0. 593) Непрерывна.
594) Непрерывна. 595) Непрерывна. 596) Непрерывна.
597) Непрерывна. 598) Непрерывна. 599) Непрерывна.
600) Непрерывна. 601) Непрерывна.
602) Непрерывна всюду, кроме а = ±1. 603) Непрерывна.
604) Непрерывна. 605) Непрерывна всюду, кроме а = 0.
558
606) Непрерывна всюду, кроме а = 0. 607) Непрерывна.
1 +О0 0
610) F'q = - j же”** sin crx dx.
0 +оо +00
Ml) •) П = - / =*£*■, 4 n = - / *0.
0 0
в нуле F(a) не имеет производной. Указание. Предста-
+оо +оо
Т?п \ Л f 3™QX J [ sin ах
вив F(а) для а Ф 0 в виде / — тг: dx— / dx,
J ж(1 + ж2) У х
о о
найти lim F' и lim F'(a).
СГ-+0+ cr-+0-
^// ч /* ж2 cos аж .
612)F-(“)=y
о
+оо
613) F; = - f xe~ar dx-e-*1 = -2e~a'-\e~a\ У:
J 1 a -foe
Для любого a > 0 имеем F(a) = J e~QX dx+ J e~ax dx.
a 1
Второй способ. Вычислив интеграл, найти явно функ¬
цию F(a) и продифференцировать ее.
+00
614) F^(a) = — jх2е~ах dx — е~а . См. указание к зада¬
че 613. а
+9° 2
п// ч / ж cos аж . sina^
615) Fa(ot) = / — г-аж — См. указание к зада-
J 1 + ж3 1+а3
че 613. а
616) Равенство справедливо. М — R.
617) Равенство справедливо. М = Ш.
618) Равенство несправедливо. М = (-оо; 0) U (0; +оо) или
+оо
®\ {0}- Указание. J f,a(x}a)dx расходится.
559
620) 4 62') «22) '
’ a3 ’ nm+‘ ’ 2 (2n)!!
2n н2 — 1 . 2(3n2 — 1) 2n(n'2 — 3)
J a) (n2 + l)2’ 6) (n2 + l)2 ’ U) (n2 + l)3 ’ Г) (n2 + I )3 ’’
24n(n2 — 1) 6(n4 - 5)
л) (n2 -f I)4 ’ e) (n2+ l)4'
»2 3
624) a) In n; 6) n)nn-n; в) — In n — -n2.
625) a) In n\ 6) n Inn — 7i; в) In n - ^n2. 626) ^sign q.
627) ![h!. 628) 629) ^тга3|«|. 630) Ци«1
631) ^|o|3- 632) j. 633) у при a > /3; у при а ^ 0.
7Г 7Г
634) 0 при H < |/?|; —signa при |а| = \0\, -signо при
и > \р\.
635) ^0 при а ^ 0 + 7; ^(а + 0 - у) при \0 - 7| ^ а ^ 0 + 7;
при 0 > 7, л ^ 0 - 7; 0 при 0 < 7, а ^ 7 - /?.
636) ^*7?7 при л ^ /? + 7; ^(2а0 + 2а-7 + 20ч - а2 - 01 - yJ)
L о
при а (3 + 7.
_ . 7Г Зтг 7Г
637) - при а > р + 7; j при а = /9 + 7; - при
\0 - 7| < от < 0 + 7; ^ при а = \0 - 7|; 0 при а < \0 - 7|.
638) y при |а| < 1; ^ при |а| = 1, — ^ при 1 < |аг| ^ 3, 0 при
4 8 8
М > з.
639) ^ при |а| < 2; ^ sign а при |а| ^ 2.
640) ^(2 - |а|) при |а| ^ 2, 0 при |а| > 2. 641) j. 642) j.
"» £ •«> «•> dU
646)
(л + 202)а\ - 4а/?/?1 + 2а2С] [ж _
6471 2^ *
560
ас— р
648)
2а^ Указание. Представить (0; -foo) как
2а
(0;\/1)и [\/1:+0°)'в интеграле по (0: vf)
0
поло¬
жить X = .
at
649) yi«£. 650) ^5ei6. 651) ^ ^(е'>1).
655) 656) 657) ^,-ё.
“8)
659)^'-^.
4 а
660) lalsigna. 661) —(I — е а). 662) ^-(1+ \а\)е 1в1.
2 2 4
663)
-7==f« ^VeC fc:,cos^- 664) f(2e “-O'
Vac — b2 a I
665) -j-e~a•
4
666)
ПГ . fac-b2 n . \
л / 7—7 sin I h — sign a 1. Указание. Сделать
V M V a 4 /
заме-
/— с?
ну vax + —= = <, a > 0.
\/a
667) у/п8\п (a2 -I- 668) y/ncos (a2 + ^. 669) In
670) 67i) jin(i+n2). 672) iin^:m;.
I I I a4, + тп
673) arctgn. 674) arctg ^ (/? — or)\/7r. 676) ln~.
677) Itaf. 678) rtrf-VS>. 679)
a(/? - 7)
a
680)1
a
.681) arctg
a2 + £7
682) Iln^b. 683) ln(l+a). 684) £(/?-*).
561
11 Я [ Л
685) — Ai In or*. 686) а — Р -f /?1п —. 687) In \/l -h ——.
a у
688) parctg M _ £ ]n + .
P + 7 a 7Г7
689)__arctg__ + _
690) ^ I* + arctg ^ - 3arctg ~
„. о2 + 9/?2 a
6911 S^lSTW + 4
, 3/i /)
arctg 3 arctg —
a or
2
692) 7r(\/l — a2 — 1). 693) — (arcsin o)2. 694) 7г1п^-^ ^ .
695) .) “ + VTT? 6) ,,, HvfftT
z z
696) ^ In ^1 + ^ . 697) ^ ln(l + a/?). 698) ^ ln(a + /?).
699) ^signa(l -f |a| — \/l + a2). 700) ^ln ^1 + - j.
701) —[a/? -f (or2 — p2) ln(or + P) — or2 In a + /?2 In p\.
o_
702) — [a/?(a + P) - (or3 -|- /?3) ln(ar -f p) + or3 In ae + p3 In /?].
TO>?'n(<,^tl’704> -«-"*)■
705) ^(2 - ac-a - 2e~a). 706) ^(a2 + 3a + 3)e-".
4 16
707) p arctg - - gin 708) 2a^ (l -irSY
a 2 or \ )
709) У-^Le-S. 710) jMH-v^).
lay/a I
712) Указание. Рассмотреть
-foo-foo foo foo
// e (a/+bx+ir,)sin xdxdi, J Je (at+bT+zl\:osx dx <lt, 6>0.
oo oo
713) 1. 714) P2 + 715) e2o,P+a\ 716)
717) p > 0. 718) ——, p > or. 719) , p > 0.
p /> - n -f /7Z
562
720)
722) -^L, р > 0.
1
^Ру/Р
СГл/п _з1 п
е 4f, р> 0.
723) 7 1-TV. Р > -<*■ 724) л л-
(р + <*)■* 2 psfp
725)ln(l + ^, - Ь~С
1
р > -1. 728) In
1 1
а — с
2 п
729) 2п [(а - с)2"
(1 -*)“-1 -(1 +t)“_1
(6-с)
. 730)
1
l-VF-I2
731)/
v/ППк2к
di. 732) - In 2. 733) 0. 734) 0.
735) jr. 736) 0. 737) 0. 738) 0. 739) Не существует.
п
8‘
741)
2тг
9>/3
п
2\/2
744)
7Г
3'
2тг
27Г
ЗуТ
747)
{К/З
743)
746)
749)
(2п — 2)!! 2’
751) J*»-1)» ■
; (п + 1)!22"+2
3 я-
7В> 5Т2
755) '
2jr
742)^3
JT
745)
748)
2уД'
(2 п)!!
(2n+ I)!!’
1ХСГ
750) 1Г.
,2п + 2
7Г.
752)
754)
1 *4*... (Зп — 2) 7г
3*6 ... Зп v/3
тг\/2
~4~
-*т
Указание. Сделать замену cos х = 1 - 2у/й.
756)
Г(6+1)
>6+1
757)
^(Ч1)
2а^
758) ^-тг2
27
759)
3jt3
32>/5'
К(» + Л Г'фГ(п+1)-Г'(п+1)Г(1)
т 4Г l—J (i>7T)P
1 /1\ Г>+ 1) Г Ц) - г'(1) Г(и + 1)
' 4 V2/ (Г(п + I))2
563
762) —• ^1 + 1п^. Указание. Сделать замену х = 1 — t и
применить формулу дополнения для функции Г(х).
763) Указание. Сделать замену х = 1 - t и применить
4 п
формулу дополнения для функции Г(х). Представив интеграл
1
J In sin пх cos 2п7гх dx в виде
о 1/2 1
j In sin пх cos 2ппх dx + J 1 n sin nx cos 2nnx dx,
° ^ 7Г
в первом интеграле сделатьзамену = У, а во втором —
п
™-2=У-
764) 0 < тл + 1 < п, , .W
nsm * п■^
765) -j <m<n--1
766) 0 < ш + 1 < n, B(n - m - 1, т + 1).
т + 1 а“р (а\^ о (т + 1 ™+1\
767) 0<-г- <„, — (j) В(— ,Р-— j
7Мч >/* Г (а)
7“)“>0' “ГСТПУ
1 Г(£)Г(я)
769) Р>0, 4>0,
770) Р > 0, q > 0, г—• Указание. Сделать замену
7 (а + 7)р(Р + 7Г
(g + 7)z _f
az + /?(1 - z) + 7
771) п < 1, — В (—,1 - п).
’ т \т /
(к — а\т+п + 1
772) -— , т > -1, п > -1. Указание. Сде-
(a + c)n+1(6 + c)m+1
х - а Ь — a
латъ замену = т—■—г.
X + с 6+ с
564
773) m > 0 n > 0. 2m+n-20(m,n). Указание. Сделать замену
1 (1 + х£
2l + x> ' t
7«) I < m < 2.
sin -j-
7Г 1
775) 0 < m < 1. ^ —г • —ssr
7 2(1 — m) an -y
am_1
776) 1 < m < 2. TB(2 - m,m - 1)
771—1
778) LK1.!-^.
2n“1 (n n\
779) n > 0, ——^2jn/2^ \ 2 ’ 2/' ^казание Сделать замену
x
< = tg-.
_om /Г7Г , __ ТГ
7oUJ a ф —Д: € N. s—г. Укаэание. В интеграле
2 2sm(7rcos2 a)
задачи 773 положить n = 1 — m, 2m — 1 = cos 2a и сделать
подстановку / = tgs.
20-1 р2 /а\
781) а > 0, 7* ,,о-'Г7о' \ • Указание. Сделать подста-
(1 — А:2)®/2 Г(а)
Л* 2!
новку =
\-й
m + 1 1 _ /т + 1\
782) >0, т—гГ (
n |n| V п )
783) р > — 1, Г(р+1).
ТГ2 COS ТГ
784) 0 < р < 1, -- —. Указание. Данный интеграл
sin пр
является производной по р от функции В(ру 1 — р).
7Г2 sin ^
785)1*1<1’Т^'
716) 0 < р < 1,
81П 7Гр
565
7Й7Л II i *3 1 +Sin2 ЧГ
7°7) а < L 2_
1 1 ^ ’ 8 cos3 ^
788) тг ctg тгр. Указание. Доказать возможность предельного
перехода при е —У 0+ под знаком интеграла
1
-x-r)(l-x)-l+'dx.
о
1
/
Использовать формулу Г(е) = ~ и
применить правило
Лопиталя.
г Т
789)
tg»
tg
*£
2/3 ^ 2/? ^кaзaнIle• Сделать замену е 2^т = t и исполь¬
зовать результат задами 788 .
791) f 1
792) Указание. Сделать замену хп — t, использовать формулу
дополнения и непрерывность функции Г(х), £ > 0
804) Указание. Полагая хп = доказать, что
п +°° п
пin«■(=)■
m=l « m=l
Записывая произведение Г в прямом и обратном по-
m= 1
рядке и применяя формулу дополнения для функции Г (ж), по¬
лучить, что
П'(=)-
у/пп~1
к-1
п — 1
Для вычисление произведения ТТ sin — разложить двучлен
х± п
к=1
zn - 1 на множители (z — l)(z - Z\) ... (z — zn_\), zk =
fc = 1, 2,..., n — 1, и использовать равенства
566
lim = n = lim TT (* - <**) = П (l - «“*) .
~iz-l ’ iJv
1 — e,fc^| = 2sin —.
I n
805) Указание. Положить
1 +oo о
h=j{x*-l)-l'3dx, J3=j(l-x3ri/2dx
0 1 -*°°
и применить к этим интегралам соответственно подстановки
х3 = “з = t, ТТТ ~
X X -f“ 1
IT Qm_1 1 7Г Otm~ 1
807) 2'^f ГИ' 808) 2 TR
809) -|Сэ. 810) |С.| +
811) а) -СЭ; б) -Сэ\ в) -^-(Сэ + 2In 2); г) Г"(1) = С£+
4 6
г21
(С7э+21п2)2 + ^-
Г(^-И) Г(р+1)
Г(, + 1) Г(р+1)
*$[
•* f Vfij- ад
8цч \ I Г(®+!)Г(^+1) -ч , Г(о + 7 + 1)Г(о + ^+1)
,14) *> Т(о +0 + if б) Г(а + i)T(a 4 /?+ 7 + I)'
r(efI)r(f) ajr
в) In 7 ч * г) Указание. В интеграле п. 6)
г(1)г(г±1) 2
сделать замену х = <2, положить ,7 = |. В интеграле п. в)
положить Р — \ — а.
о1«ч * (2п — 1)!! / 1 1 I Л
^ 2 (2п)!! ( ~2 + 3 217“” )
Указание. Продифференцировать по а данную формулу.
К полученному результату применить формулу Гаусса (см.
формулу (16) гл. III) и положить 2а - 1 = 2п.
567
тгл/2
т
817) -^ -тттт; —-2™-1 Йгт • Указание. Использовать
Vi Г*(±У т r(i)
формулу Лежандра (см. пример 12 гл. 11J § 5).
а3Г3(-)
818) \jlL
} Зп2Г (£)’
820) Сходится. 821) Сходится. 822) Расходится. 823) Схо¬
дится. 824) Сходится. 825) 1 826) 1 (а).
§ 5. ТЕОРЕТИЧЕСКИЕ ЗАДАЧИ
Интегралы, независящие от параметра
1. Пусть
я*) =
V(n)» X = П, 77 £
1 °°
О, л: ^ (J [» + £„_]-1;п-£п],
П=]
о ^ <*п < 2’ 71 6
линейна на [л — 6п; п] и [п; п + Jn]
(см. рис. 14).
При каких условиях на (р(п) и <5п справедливы утвержде¬
ния:
а) функция / неограничена на [0;+оо), а интеграл
-1-00
J f(x)dx
О
абсолютно сходится;
569
+оо
б) интеграл I f(x)dx расходится, a lim f(x) = 0.
J х-*+оо
О
2. Пусть 0 — единственная особая точка функции / на
1
(0; 1) и lim xf(x) > 0. Доказать, что интеграл I f(x)dx
x-fO+ J
о
расходится.
3. Пусть функция / монотонна на (0; 1] и lim f(x) = оо.
г->0+
1
Доказать, что из сходимости интеграла J f(x) dx следует,
что lim xf(x) =0. 0
Г-+0+
4. Привести пример непрерывной и неотрицательной на
(0; 1] функции / Е R(0; 1), для которой lim xf(x) > 0.
г-+0+
5. Пусть функция / монотонна на [а;+оо), а ^ 1, и инте-
1
грал I xqf(x)dx сходится. Доказать, что lim xq+l f(x) = 0.
J x-foo
0
6. Пусть функция / монотонна на (0; 1) и интеграл
1
J f(x)dx сходится. Доказать, что
О 1 п-1 / ’ \ /*
lim - ^2f[-)= / f(x)dx-
n-*oo n f-' \nj J
»_1 о
7. Пусть функция / монотонна на (0; 1) и только один из
концов этого интервала является особой точкой /. Доказать,
что из существования lim — f (следует сходимость
П—Юо — ^ 1 “
1
интеграла
=£'(=)
J f(x)dx.
0 11
8. Показать, что функция f(x) = — + монотонна на
х х—1
п — 1
1 / ^ \
(0; 1) и существует предел lim — > / [ - ),
n-foo п 4 \п J
i=i х
хотя интеграл
570
i
j f(x) dx расходится.
о
9. Пусть функция / монотонна на (0; 1) и интеграл
1
J f(x) dx сходится. Доказать, что
•-1 о
10. Пусть функция / монотонна на [a; -foo). Доказать, что
оо
условие: “для любого Л, 0 < h ^ 1, ряд /(a-f nh) сходится
ОО П=1
и существует предел lim h /(a -f nh) = А” необходимо и
h-+ 0-f 4
n = 1 +00
J f(x) dx и
J f(x)dx = A.
a
11. Пусть и) — единственная особая точка функции /
на (а;ш) ((u>;a)). Доказать, что условие “для любой после¬
довательности {хп}: а — хо < xi < х^ < ... < хп < и/
°о у
(а = х0 > xi > х2 > ... > w), lim х„ = ы, ряд / /(<) Л
п—>оо * /
П — 1 . J
хп-\
сходится” необходимо и достаточно для сходимости интегра-
п = 1 +оо
достаточно для сходимости интеграла f Дх) dx и при этом
-foo
ла
J f(x)dx (J f(x)dx).
х
12. Пусть /(х) = sin —, х G [тгп(п — 1); жп(п -f 1)],
п п
п G N, (см. рис. 15). +00
Показать, что интеграл J f(x) dx расходится, а ряд
7ГГ»(п + 1) ®
ОО Г
I /(х) dx — сходится.
п=1 /
7гп(г» — 1)
571
Рис. 15
13. Пусть функция /(х) неотрицательна на [а;ы) и ы —
единственная особая точка / на (а;и). Доказать, что, если
найдется хотя бы одна последовательность, удовлетворяющая
условиям
1) а = х0 < xi < х2 < ... < хл < x„+i < ... <и>\
2) lim хп = и;
п-юо
оо *•
3) ряд ^ I /(х) dx сходится,
п=1г
и>
то интеграл J f(x)dx сходится.
а
14. Пусть ы — единственная особая точка функции /
на (а;ы) и последовательность {хп} удовлетворяет условиям:
1) а = х0 < xi < х2 < .. . < т.п < xn + i < .. . < ы;
2) lim хп — иг,
п—юо
3) на отрезке [xn_i ;x„], п £ N, функция / не меняет знака;
572
оо у
4) ряд / /(х) dx сходится.
Доказать, что интеграл J f(x)dx сходится.
а
15. Пусть / Е Л(а;6). Доказать, что для любого £ > О
существует функция деу удовлетворяющая условиям:
1) де равна нулю в некоторой окрестности каждой особой
точки функции / на (а; 6);
2) де € С(а; 6);
3) |/(/(0-*(<)) л
< е для любого х Е (а; 6).
16. Пусть / Е R(a\b) и |/| Е Я(а;6). Доказать, что для
любого £ > 0 существует функция де, удовлетворяющая усло¬
виям:
1) де равна нулю в некоторой окрестности каждой особой
точки функции / на (а; 6);
2) (/feC(a;A);
3) У \f(x) - gt(x)\dx
< е.
17. Пусть / Е Я(а;6) и |/| Е Л(а;6). Доказать, что для
любого промежутка (а; /?), а < о < /? < 6,
Р
lim J |/(х + Л) - /(х)| dx = О
а
(интегральная непрерывность функции /).
18. Пусть / G Д(а; +оо) и |/(i)| G Я(а;+оо) , а > —оо.
+оо
Доказать, что lim / /(х) sin nx dx — 0.
п-»оо у
a
19. Пусть 0 — единственная особая точка положительной
х
функции / на (0; 1), / Е Я(0; 1) и Ф(х) = J f(t) dt. Доказать,
573
20. Пусть 0 — единственная особая точка положительной
1 i
функции / на (0; 1), Ф(х) = J f(t)dt и интеграл J f(x)dx
о
1
/f (^)
——- dx
Ф(х)
о
21. Привести пример двух функций / и д, для каждой
из которых 0 — единственная особая точка на (0; 1), таких,
1
что /(*) ^ д(х), х Е (0; 1], интеграл I f(x)dx сходится, а
f
интеграл I д(х) dx расходится.
о
22. Привести пример двух функций fug, для каждой
из которых 0 — единственная особая точка на (0; 1), таких,
1
что |/(х)| ^ |</(х)|, х Е (0; 1], интеграл I f(x)dx сходится, а
1 п
Г 0
интеграл I д(х) dx расходится.
о
+оо
sin X
23. Доказать, что интеграл I ~ dx расходится,
J у/х- sin х +оо
sin х sin х 1 f sin x
хотя —= : ~ —t=- при x —> +oo, и интеграл / —т=г dx
y/x — smx y/x J yjx
x 1
сходится.
~Г\ , ^ ' ' 'I, " . ’ ,что
+00
удится. _ r
24. Пусть / E Я(0; +oo) и Ф(х) = I f(t)dt. Доказать,
7°Ф(2х) - Ф(х) , 0
интеграл / dx сходится.
J х
о
25. Пусть а> 1 и /Е Я(а; -foo), #Е Й(а; +оо), /2Е Я(а; +оо),
<72 Е Я(а;-foo). Доказать, что сходятся интегралы
+оо +00 -foo
\) j \fg\dx-, 2) J(f + g)2dr, 3) J
574
26. Пусть неотрицательная функция / £ Л(0; 1). Дока-
1
зать, что J dt = о ^, х 0+.
х
27. Пусть неотрицательная функция / £ С\е\ 1] для лю-
1
бого б, 0 < е < 1, и д(х) = J ^p-dt. Доказать, что, если
X
1 1
/ € R(0; ]), то д € Л(0; 1) и jg(x)dx - J f(x)dx.
о о
28. Пусть неотрицательная функция / £ С[е\ 1] для лю-
х
бого е, 0 < е < 1, / £ #(0;1), F(x) = J f(t)dt и интеграл
1 о 1
——dx сходится. Доказать, что интеграл / /(x)|lnx|dx
о 1 о
Г F{*) ,
сходится и равен / —-— ах.
J *
о
Обозначим через Rq(a;b) класс функций /, для которых
6
интеграл J f(x)dx сходится абсолютно и \f\q £ R(a;b).
а
29. Пусть q > 1 и функции / £ Rq(a;b) и (7 £ Д«^т(а;6)
неотрицательны на (а; 6). Доказать, что /# £ Д(а;6) и спра¬
ведливо неравенство Гельдера:
6 b ± Ь я—1
f \f(*)-9(x)\dx^. |s(x)|J^<f*J
а а а
30. Пусть неотрицательная на (0; 1) функция / принадле¬
жит классу Rq(0; 1), q > 1. Доказать, что
X
j f(t) dt = о(х*Т~), X -> 0 -f .
575
31. Пусть неотрицательная на (о; -foo) функция / принад¬
лежит классу Rq(a;+ оо), q > 1. Доказать, что
X
J f(t)dt = о(хЯ^~)1 X -* -f оо.
а
32. Пусть 0 — единственная особая точка функции /
1
на (0; 1) и интеграл J xf2(x)dx сходится. Доказать, что
1
J f(t)dt = o(sJ\ lni|),
X -+ О +
. Пусть / G C[0;-foo), F(x) = I f(t)dt и интегралы
+°o J
/ /*(*)<** ■ J x2F2(x)dx сходятся. Доказать,
v , ri r , что
о о
-foo +oo J y2 -foo
I F2(x) dx <L 2^ J x2F2(x)dx| | J /2(x)c/xj^
0 0 0
-foo
34. Пусть / G C(—oo; Ч-oo) и интеграл I — I f(x) dx
сходится. Доказать, что
-foo
— oo
-foo
//X д \ dx
f ( 1 J
\a xJ x
//x &\ In x dx ^
/ ( —I— I сходятся. Доказать, что J-2 =
\a £/ x
о
= I\•In a.
576
36. Пусть / Е С[0; +оо) и интеграл I = / f(x2)dx схо-
0
+/° \( &\21
дится. Доказать, что I = а / / (аг J dx, а > О,
6 > 0. о ^ ^ -I
+оо
37. Пусть / 6 £7(0; -foo) и интеграл I = J / ^ах +
о
+оо
а>0, 6> 0, сходится. Доказать, что /= — I f(yx2+4ab)dx.
/ п-Л
О
38. Пусть / 6 С(0;+оо) и у(х) = /(хр -f х“р)1пх, р > 0.
/у(х) [ д(х)
dx и / —-—- dx схо-
х J lfxj
дятся, то они равны нулю. 0 0
39. Пусть для функции / Е С[0; -foo) выполняется тожде-
+°°
/I (х) sin X
— dx
сходится. Пользуясь равенством 0
+ —1. х/о,
81П X X |х + 7ГП X — 7ГП I
n=l *" J
ж/2
доказать, что / = I f(x) dx (формула Лобачевского).
« 00
40. Пусть 6 R[a;b] при любом n E N и ряд }u„(x)
n = l
сходится равномерно на [a; 6] к 5(х). Доказать, что если ин-
6
теграл J д(х) dx сходится абсолютно, то
41. Пусть последовательность {<fn} обладает следующими
свойствами:
1) <рп Е Я[—А] А) при любом А > 0;
2) фп 0 на R \ (—<5; — <5) при любом S > 0;
А
3) I <fin(x) dx 1, п -+ оо, при любом А > 0;
4) при любом А > 0 последовательность / |у?„(х)| dx огра¬
ничена. £ -а
Доказать, что если интеграл / /(х) dx сходится абсолют-
а
но и хо Е (а; Ь) — точка непрерывности /, то
6
lim [ f(t)<pn(t - хо) dt = /(х0).
n-юо J
а
42. Пусть
1 х
f(x) = д(х) = cos X £ [ят»(п- 1);я-п(п+1)), n 6 N.
n П
Показать, что хотя / монотонна на [0; + оо) и lim /(х) = 0,
г—>+оо
+оо
но интеграл J f(x)g(x) dx расходится. Какое условие при-
о
знака Дирихле нарушено?
v sign(cosx) л „
43. Пусть /(х) = ~=—-, х > 0Т Показать, что хо-
Vх
v Г
тя lim /(х) = 0 и функция Ф(х) = / cos tdt ограничена
r-юо I
+оо «/
на [l;-foo), но интеграл J /(х) cos xdx расходится. Какое
1
условие признака Дирихле нарушено?
44. Пусть функция / монотонна на [а; +оо) и интеграл
+оо
/
/(x)einxdx сходится. Доказать, что lim f(x) = 0.
х->+оо
578
45. Пусть функция / монотонна на [a; -foo) и интеграл
+оо
J f(x)sinxdx сходится абсолютно. Доказать, что
|/|ЕЯ(а;+оо).
46. Привести пример непрерывной, неотрицательной, не¬
ограниченной на [0;-foo) функции /, для которой интеграл
-foo -foo
J f(x)sinxdx сходится абсолютно, а интеграл J f(x)dx
о о
расходится.
47. Пусть функция / монотонна на [а;+оо) и Hm f(x) =0;
функция д £ Я[а;а -f Т\у Т > 0, и периодическая с пери-
а+Т
одом Т. Доказать, что если J у(х) dx = 0, то интеграл
а
+оо а+Т
J f(x)g(x) dx сходится, а если J д(х) dx ф 0, то интегралы
а а
4-оо 4-оо
J f(x)g(x)dx и J f(x)dx одновременно сходятся или рас¬
ходятся. а
48. Доказать, что если / Е С1 [a;-foo), /' монотонно воз¬
растает на [a; -foo) и lim f'(x) = -foo, то интегралы
foo 4-оо
J cos(f(x))dx и J sin(f(x))dx
a a
условно СХОДЯТСЯ.
Интегралы, зшешще от параметра
49. Задана функция f(x,y) = 0 ^-^V1 ~ у ’ По-
l.2z,
казать, что функция /(х, у) разрывна на [0; 1] х [0; 1], а функ-
579
ция
1
П») = / /(х, у) dx непрерывна на [0; 1].
о
50. Пусть уо — предельная точка множества Е\ /(х, у) Е
Е R[a;b] при любом у Е Е\ /(х,у) =£ (р(х) на [а;6] при у -* у0,
j Е Я(а;6) и |^| 6 Д(а;6). Доказать, что ^ 6 Л(а;6) и
6 6
lim / f(xy j/)<7(х) dx — / <р(х)$(х) dx.
У-^Уо j J
51. Пусть уо — предельная точка множества £; /(х,у) Е
Е Д[а; 6) при любом 6 > а и любом у Е /(х, у) ^>(х) при
У Уо иа[а; 6] для любого 6 > а;
|/(х>у)1 ^ ПРИ любом
у Е Е и F Е Я(а; +оо). Доказать, что
+оо -foo
lim I f(x,y)dx = I <p(x)dx.
у-*уо У У
а а
52. Пусть / Е С([а;6] х [c;d]), Е Л(а;6>, |<р| Е Я(а;Ь).
ь
Доказать, что функция F(y) = J <p(x)f(x,y)dx непрерывна
на [c\d\. а
53. Пусть / Е С[0; 1]. Доказать, что
1
Ит f \e~**f{x)dx = /(0),
V-fOy у1
О
т. е. равенство
1
lim [ \е ** f(x)dx = [ lim ( 4ге у7/(хм dx
у-*0У !/ У у-ю \у2 /
о о
имеет место только тогда, когда /(0) = 0.
54. Пусть 6 > 1. Доказать, что
-foo +оо
1) lim I е~ах cosxdx = 0;2) lim I c~ax sinxdx=l
a-> 0+ у a-> 0+ У
0 0
(сравните с задачей 50).
580
55. Пусть / £ C([a]b\ х [c;<f]), д € R(a\b) и |#| £ R(a;b).
Доказать, что
d ь Ь d
J dy J f(x,y)g(x)dx = Jg(x)dx J f(x, у) dy.
с a a с
56. Задана функция
f{’~\x2, y2^x^ 1.
Показать, что функция / разрывна на [0; 1] х [0; 1]; функция
1
Пу) = J f(x,y)dx определена и непрерывна на [0; 1]; для
о
любого у £ [0; 1] функция /(х,у) интегрируема на [0; 1];
1 11 11
J F(y)dy = J f(*,y)dySj dx = J dx j f(x,y)dy.
0 0 0
57. Задана функция
1
Показать, что функция F(y) = J f(x,y)dx определена и не-
о
прерывна на [0; 1]; для любого х £ [0; 1] функция /(х, у) инте-
1 1 1
грируема на [0; 1], но J F(y)dy£ J dx J f(x,y)dy.
О 0 0
58. Доказать, что
/sin я У1 f ( 7ГП\
{—) Jv С<*(у+Т)<1у
о
/sin х\ ^1 1
Пользуясь этой формулой, показать, что ( ) < ,
V х ) п + 1
х £ R \ {0}. 4 7 I
581
59. Пусть функции /(х,у) и /'(ж,у) непрерывны на
у ь
[а; 6] х [c]d\,g Е Л(а;6), \д\ 6 Я(а;6), F(y) = f g(x)f(x,y) dx.
ь J
Доказать, что F Е С1[а;Ь] и F'(y) = Jg(x)f'y(х,у)dx.
а
60. Задана функция
/х arctg 4, *#0,-1 <у^1;
/(*.») = < 1
t 0, х = 0, -1 < у ^ 1.
Показать, что / Е С([0; 1] х [—1; 1]); функция /у(х, у) опреде¬
лена на [0; 1] х [—1; 1]; для любого уо € [-1; 1] функция /у(х, уо)
1
интегрируема на [0; 1], а функция F(y) = J /(х, у) dy опреде-
о
лена и непрерывна на [—1; 1], но не дифференцируема в нуле.
61. Пусть функция /(х, у) непрерывна на [а;а;) х [с; d] и ин-
U1
теграл J /(x,y)dx сходится равномерно на (c;d). Доказать,
а
что этот интеграл равномерно сходится на [с; d].
62. Пусть /(х,у0) Е R[a\b] для любого у0 Е М и любо¬
го 6, а < 6 < ы. Доказать, что из равномерной сходимо-
ш
сти на М интеграла / |/(x,y)|dx следует равномерная схо-
J W
димость на М интеграла J /(x,y)dx.
а
63. Задана функция
[0, у = 0, х ^ 0,
/(х, у) = ^ li У > 0, 0 ^ х ^
0, у > 0, х > -.
У
+оо
/
/(х,у) sinx
Показать, что интеграл / dx сходится равно-
582
+оо
Г f(xiV)Isinxl .
мерно на [0; 1J, а интеграл / ах сходится не¬
равномерно на [0;'1]. 0
64. Как показывает результат задачи 63, из условий
-foo
1) интеграл J /(х, у) dx сходится равномерно на Л/,
а
2) функция д(х,у) ограничена на [а; +оо) х М
+оо
вообще говоря не следует, что интеграл / f(x,y)g(x,y) dx
а
равномерно сходится на М. Какие дополнительные условия
достаточно наложить а) на функцию /(х, у), б) на функцию
у(х,у), чтобы можно было гарантировать равномерную схо-
+оо
димость интеграла J /(х, у)у(х, у) dx на М?
а
65. Пусть / Е R[0; а] для всех а > 0 и интеграл J ху f(x) dx
о
сходится при у = сиу = </, с<</. Доказать, что этот инте¬
грал сходится равномерно на [с;</].
66. Задана функция
+оо
/(*,у) =
О, У — 0, X ^ 2,
ysinirxy 2 3 Л
—j , -<*<-, 0<у^1,
lnx у у
0, 0<у^1, 2$х^-и-^х.
У У
Показать, что функция /(х,у) неотрицательна на [2;+оо)х[0;1]
-foo
и интеграл J f(x,y)dx сходится равномерно на [0; 1], хотя
2
для любой функции ^>(х), х ^ 2, удовлетворяющей условию
-foo
/(х,у) ^ <р(х), X € [2; -foo), у € [0; 1], интеграл / (р(х) dx
расходится. 2
583
67. Задана функция
г 0, у = О, х ^ О,
sin х
А*.У) = <
1
, 0<у^1,0^х<-,
1 У
о, о < у ^ 1, - < X.
У
Показать, что для любого у0 Е [0; 1] функция /(х, уо) локаль¬
но монотонна в правой несобственной точке -f оо, /(х, у) 0
1
на [0; 1] при х —> -foo, а интеграл J /(х, у)sin xdx сходится
неравномерно на [0; 1]. 0
68. Задана функция
У) =
г 0, у = 0, х ^ 0,
1
Показать, что при любом уо Е [0; 1] функция /(х, уо) монотон-
+оо
на на [0;-foo) и lim /(х, уо) =0, а интеграл / /(х, у) sin xdx
х—► -foo /
О
сходится неравномерно на [0; 1]. Какое условие признака Ди¬
рихле нарушено? +со
69. Пусть интеграл J /(х, у) sin xdx сходится равномер-
о
но на М и для любого уо Е М функция /(х,уо) монотон¬
на на [0; +оо) и стремится к нулю при х —► -foo. Доказать,
что /(х,у) при х —> -foo сходится к нулю равномерно на М.
70. Пусть для любого уо Е М единственной особой точ¬
кой функции /(х,уо) на (a;cj) является точка ы. Доказать,
что условие “для любой последовательности {х„}, а = Хо <
< xi < х2 < ... < х„ < х„ + 1 < ... < и, linvi-юо х„ = ы,
0° г
ряде /
»=>, .
dt сходится равномерно на М” необходимо
584
и достаточно для равномерной сходимости интеграла
/(х, у) dx на М.
/
а -foo
71. Показать, что интеграл J е~ту coaxdx сходится не-
о
2 пп7
°°^ Г
равномерно на (0; 1), а ряд I е~ту cos х dx сходится
равномерно на (0; 1). n=1 2*(n-i)a
72. Пусть для любого уо Е Л/ единственной особой точ¬
кой функции /(х,з/о) на (а;ы) является точка и. Доказать,
что если /(х,у) неотрицательна на (a;w) х М и хотя бы для
одной последовательности {х„}: а = х0 < х\ < х2 < • • • <
со у
< хп < х„+1 < ... < и, Нт„_»оо Хп = ы, ряд Е / f(t,y)di
П=1
Я»_1
Ы
сходится равномерно на М, то интеграл J /(х, у) dx сходится
а
равномерно на М.
73. Пусть для любого уо € М единственной особой точкой
функции /(х,уо) на (а;ы) является точка а; и последователь¬
ность {хп}, а = х0 < xi < х2 < ... < х„ < xn+i < ... < а/,
lim хп = ы, такова, что функция /(х, у) не меняет знака на
П-ЮО Тп
[хп_1,хп] х М, n е N, и ряд I f(t,y)dt сходится рав-
п=1 ^ .
номерно на М. Доказать, что интеграл j f(x,y)dx сходится
равномерно на М. а
74. Обосновать возможность перестановки двух несоб¬
ственных интегралов в интеграле
ОТВЕТЫ, РЕШЕНИЯ, УКАЗАНИЯ
ОО
1. a) lim у>(п) = оо и <5п|у>(п)| < -foo;
П—►ОО ^
п=1
оо
б) lim у?(п) = 0 и ряд расходится.
п = 1
3. Указание. Рассмотреть J f(t)dt, 0 < х < 1.
4. Например, г/2
' 2msin (|(22mx-2m +1)), х е [2_m—4_m; 2-m+4"m],
.... m e N, m > 1,
+oo
o, xeU[2~m-4"m;2_m+4-m]-
m=2
2r
5. Указание. Рассмотреть J tqf(t)dt, если / не возраста¬
ет и I tqf(t)dt, если / не убывает.
аг/2
6. Решение. Бели функция / не убывает на (0; 1) и ин-
1 1
-L
П
/ «одится, то J /(х) dx = j f(x) dx £
0 J. 1=2 iz_L
*"£ //<->«*- = '/’/w*.
« — 1 « — 1 i 0
n — 1 / . \ n — 1
откуда сле-
o
n
дует требуемое утверждение. Для невозрастающей функции
доказательство аналогично.
7. Решение. Если функция / не убывает на (0; 1) и ее осо-
1
бой точкой является 1, то сходимость интеграла I f(x)dx
i_i. J
я О
и ограниченность последовательности J f(x)dx эквивалент-
о
586
ны. Таким образом, из неравенства
i-х ± ^
/ /(*м* = £ / J(x)dx ^
0 •=» Л •=• V 7
п
следует требуемое утверждение. Все остальные варианты до¬
казываются аналогично.
8. Указание. Использовать равенство f(x) = -/(1 — я).
9. Решение. Бели функция / не убывает на (0; 1), то
1-* п-1 ^ п-1 . V
1 /(,)* = £ /
L ‘=1 « = » 4 7
*
it
Отсюда получаем, что
1-3t
* ,_i
V±W
Используя результат задачи 3, имеем, что lim — / ( — ) = 0.
л-юо п \ 2п )
Аналогично доказывается, что lim — / f 1 — ) =0. Из по-
п-Юо п \ 2п)
587
лученных соотношений следует требуемое утверждение. Для
невозрастающей функции доказательство аналогично.
10. Решение. Из результата задачи 5 следует, что f(x) -*0
при х —► -foo, поэтому, не ограничивая общности, можно
считать, что функция / положительная и невозрастающая
на [a; -foo). Тогда для 0 < Л ^ 1 имеют место неравенства
а+(т+1)Л а+(п+1)Л
J /(«)& = £; j /(*)&<
»+Л П~1 а+пЛ
т т e+пЛ а+тЛ
< Л53/(а + пЛ) ^ / f(*)d*= J f(x)dx.
П * П 1 а+(п —1)Л -
В силу неотрицательности / отсюда следует эквивалентность
+оо
сходимости ряда ^ /(а+пЛ) и интеграла J f(x) dx, а также
неравенство n=1 в
+~ со +“
J f(x)dx < Л^/(а + пЛ) J f(x)dx,
а+Л n=1 а
из которого следует требуемое утверждение.
а/
11. Решение. Необходимость. Пусть интеграл J f(x)dx
а
сходится и {х„} — произвольная последовательность, удо¬
влетворяющая условию. Возьмем произвольное е > 0. В си¬
лу критерия Коши сходимости иптеграла, существует число
В > а, такое, что для любых 6i и 62, В < Ь\ < 62 < си, имеем
Ьа
I/
/(*)<**
< е. Так как хп —> u>, п —У оо, то существует
6i
такое число N Е N, что для любых р Е N, ш Е N имеем
В < xm_i < жт+р < ы. Отсюда получаем, что
хп xf*+p
m+p у у*
£ у = у лол
< £
588
oo *n
и, следовательно, в силу критерия Коши ряд ^ I f(t) dt
п=\ J
СХОДИТСЯ. *п-1
ш
Достаточность. Предположим, что интеграл J f(t) dt pac¬
ts
хо дится. В силу критерия Коши сходимости интеграла су¬
ществует такое число ео > 0, что для любого В > а най¬
дется пара чисел Ь\ л b2l В < Ь\ < b2 < w, для которых
ь2
I/
f(t)dt
> £о,
е0- Пусть сп — некоторая возрастающая после-
bi
довательность, со = a, lim сп = ш. Пусть В\ — ci, найдем
П-ЮО (,)
2
числа
г Для которых I £ /(0 ^ I
6<,,)
и положим «1 = 6^, х2 = bi1*, хо = а. Для В2 = max(x2tc2)
,(1) ,(2) ,(1) ,(2)
найдем соответствующие Ь2 Ь2 ' и положим х$ = Ь2 , х4 = о2 .
Из построения видно, что а = хо < х\ < Хъ < хз < х+ < и>
и ci < х\ < «з < и>, с2 < хз < Х4 < U). Продолжая этот про¬
цесс неограниченно, получим последовательность {хп}, удо¬
влетворяющую условиям
1) а = х0 < хх < х2 ... < хп < х„+1 < ... < ы,
2) Сп < Х2п — \ < Х2п < ы, п 6 N,
*3*
3)
/ /«)
dt
> ео-
*a»-i
Условие 2) показывает, что lim х„ = cj, а условие 3)
П-ЮО
оо
что ряд / /(0 dt расходится, так как не выполнено не-
**-1
обходимое условие сходимости. *
Итак, предположив, что интеграл J f(x) dx расходится,
а
мы построили такую последовательность {хп}: а = хо < х\ <
589
оо *-
Е / л*)Л|
n=l ,J
< *2 < ... < r„ < w, lim = ш, что ряд > / /(<) Л рас-
П-ЮО
п — 1
1«-1
ходится, что противоречит требованию сходимости такого
ряда для любой последовательности {х„}: а<х0 < х\ < ... <
< хп < ... < u>, lim хп = ы. Полученное противоречие
П—ЮО
показывает, что при выполнении этого требования интеграл
/
/(х) dx сходится.
13. Указание. Если xn_i < 61 < 62 < xm, то
Ьэ т х*
о^J/(*)j f(t)л-
■ I — fl e
Ь|
14. Указание. Бели x„_i < fti < 62 < xm, то величи¬
на
на I f(x) dx заключена между наибольшей и наименьшей из
5, т х2 m—1 ж2 т-1
величин
j /(*)<** заклю
,ин Е / ЛОЛ. j f(t) dt, ^ f f(t) dt,
t. »="-И **_, ‘-"+1 *i_, «'=»
E / ло*.
•=n.
15. Решение. He ограничивая общности, можно считать,
что единственной особой точкой функции / на (а; 6) является
точка а. Зададим число е > 0. Найдем такое ft > а, что
л
f(t) dt < - для всех г), а < г) ^ h. Так как / 6 Я[Л; Ь], то
а
найдется такое разбиение
Т : {А = хо < х\ < х2 < ... < xn_i < хп = 6},
для которого
I/
V
о *:£(/, г)- J f(x)dz<j,
590
ж*
где5(/,Т) = y^M,(x, -x,_i), А/, = sup/(x), х € —
I
1Я сумма
=(°’
\л*,
верхняя сумма Дарбу. Положим
Ч>€
Так как - /(х) ^ 0 и х Е (Л; 6)
* € (в; Л],
* € 1 ^
X О
о ^ IЫО - /(<)] dt $ S(f, T)-J /(*) dx < £~, X 6 [Л; 6].
Л A
Пусть A — диаметр разбиения T и М = sup|/(x)|, х Е [Л; 6].
Бели 6=m\n , то отрезки [х*—rf; xt*+<f], [xj — 6]Xj+S\t
0^i^.n10^.j^nii^ j, не пересекаются. Пусть
п— 1
1 = 1
всех
.линейна на [ft;/i+rf] и [xt — S; Xj+£], l^t^n—1.
Функция де отлична от функции (ре только на п отрезках
[Л; h -|- J], [х,- - 6] Xi + Л], 1 ^ f ^ п — 1, причем
Ы*) - v>e(*)| ^ 2А/. х € [Л;*],
X
следовательно, J |<7е(<) — <pe(t)\dt ^ П-2&-2М ^ ^ для
х G [А; А]. *
Покажем, что функция д€ удовлетворяет всем требовани¬
ям задачи. Условия а) и б) выполнены в силу определения де.
X X
Если х е (а; А], то |/(/(<) -$(*)) *| = f(t)dt
а а
X € [Л; 6], то
< -. Если
4
X П X
/(/(<) - л (0) Л = j № dt + j(f{t) - Л (0) л =
591
П X X
= JЛ0Л + -<Р'(*))Л + JfaW-bitydx.
ah h
Применяя полученные выше оценки, получаем, что
I/
(/(*)-*(*)) л
е е е
<4 + 4 + 2~е-
Итак, условие в) выполнено.
16. Указание. Если а — единственная особая точка /
на (а; 6), то для любого е > 0 найдется такое h > а, что
/
|/(t)|<ft < 7 для всех I/, а < т) ^ Л. Далее доказательство
4
дословно повторяет решение задачи 15.
17. Решение. Не ограничивая общности, можно считать,
что единственной особой точкой функции / на (а; 6) явля¬
ется точка а. Возьмем число е > 0. Используя результат
задачи 16, найдем непрерывную на (а; 6) функцию д, рав¬
ную нулю в некоторой окрестности точки а, для которой
6
/1/(*) - 9(x)\dx < Если с = inf{x, х € (а;6), д(х) ф 0},
а
то —оо < с и а < с. Так как а < а < /? < 6, то найдется
такое »у > 0, что а < с — т) и а < а — q < 0 + т) < Ь. Так
как функция д непрерывна на [с — 17; 6], то найдется такое
А > 0, что |у(х!)-^(х2)| < тгтт ;—Г для любой пары ХЬ Х2>
Z(b— c + i/J
Е [с — 6], |xi — X2I < А. Положим S = min тогда
для любого A, |А| < j, имеем
Р Р
0 ^ J |/(x + /»)-/(x)|dx^ J \f(x) - g(x)\dx +
a a
P P
+ f \f{z + h)-g(x + h)\dx + J |0(x + h)-0(*)|dx<£
592
Ь Ь-Г)
^2 J\f(x)-g(x)\dx + J \g{z + h)-g(x)\dx <
a c—rj
< 2 + (6_c)2[b-c + rj\ <£>
P
откуда следует, что lim I |/(x + A) - /(x)| dx = 0.
« +00
18. Указание. Сделать в интеграле J f(x) sin nx dx за-
a
мену x — t и воспользоваться свойством интегральной
п
непрерывности (см. задачу 17).
19. Решение. Возьмем число е > 0 и найдем такое h > 0,
Г 4е2
что 0 < / f(x) dx = Ф(т)) < — для любого т), 0 < q < h.
J 25
о
Пусть 0 < 6i < 62 < Л. Т&к как / Е R[b\\bi]j то найдется та¬
кое разбиение Т : {61 = х0 < < ж2 < ... < x„_i < хп = 63},
что
ба
0^5(/,Г)- ff(x)dx<*M,
ь,
п
где S(f,T) = =sup/(x), x e [*i-i;x,-],—
» = 1
верхняя сумма Дарбу функции /. Положим
6а 4
тогда Jд(х) dx =S(f,T). Так как д{х) ^ /(*), х G [fri; Ь2],
gt* г€(ь*;*^
\Л#<» * G (*j_i;xt], 2 ^ ^ п,
Ьа
ТО
Ьх
отсюда получаем, что
Ьа
ф(М
0 < JШ - /(«)) Л < /*(<) Л -1 № <Ь<Ц
593
для всех х £ [Ь\; 62]. Так как функция д на [Ь\; 62] имеет только
конечное число точек разрыва, то функция
I
G(z) = Ф(6,) - J g(t)dt
является первообразной для д на [61; 62]. В силу монотонности
функции Ф отсюда получаем, что
о < о(х) - ♦(*)=jт - л*» & < *£>1 <
Ь' хе[Ь,;62],
g
и, следовательно, 0 < G(x) < 7Ф(х), х £ [61; 62]. Из всех
4
полученных соотношений имеем, что
< 41 ж. & < 41 * =
/ \/*И 2 У ^/аЩ " 2 У
о\ ог Ьj
= >/5(х/С(Ы - v/G(M) < ^%/Ф(Ы < е.
Отсюда в силу критерия Коши следует сходимость интеграла
Я*) Hr
—7=s= ах.
о v v 7 р
20. Указание. Рассмотреть поведение интеграла
/
/(x)rfr
Ф(х)
при фиксированном /?, 0<а<]5<1,иач 0+. а
21. Н&прнмер, /(*) = -Ij, х € (0; 1], ${*) = х € (0; 1].
ХЛ X
22. Напрвмер, /(*) = (-l)n(n+ 1), х € (“
J \п+1 п
, п G1
23. Указание.
sinz sinx 1 coe2x sin3x
+ —+
у/х — sin x yfx x 2x x(y/x — sin x)
594
24. Решение. Так как Ф Е С[0; -foo), то для любого отрез¬
ка [а; 6] С (0; -foo) имеем
6 ь/2 ь
J Ф(2х) - Ф(х) = J Ф(р dt j Ф(х) ^ =
а а/2 <*
= j ^-dx- J^ldx = 1п2 [Ф(6) - ф(6)],
а/2 6/2
где 6 G (|;«). 6 G (^2’^' Так как имеет предел
при х —> -foo, то для любого е > 0 найдется такое С, что
|Ф|Х|) - Ф(*2)| < Т-r для все* *ь *2. *1 > с, х2 > С; следо-
In Z ь
I f ф^2х) ф/jpj
ва гельно, если а > 2С и Ь > 2С, то / —— dx
< £.
В силу критерия Коши отсюда следует сходимость интеграла
J♦<**>;*<*> Л. Схода-осгь .тгегр*,. }*<г*>-ф<*> dz
1 О
доказывается точно так же.
/2 + Я2
25. 1) Следует из неравенства \fg\ $ —-—;
2) Следует из неравенства (/ -f д)2 ^ 2(/2 -f 02);
3) Следует из 1).
26. Решение. Возьмем число е > 0 и найдем такое А,
л
0 < А < 1, что 0 ^ J /(*) < ^ для всех 0 < i] ^ Л. Если
о
0 < х < mini Л, —р^ I, то
V 2 Jf(t)dJ
л
л
0 ^xjyp-dt = zjttp-dt+xjftp-dt< Jf(t)dt+^e.
595
Следовательно, lim х f dt = 0.
х-*о+ J t j
27. Указание. Применить к интегралу J g(x)dx, 0<£<1,
€
формулу интегрирования по частям и использовать резуль¬
тат задачи 26.
28. Решение. Равенство
1 1
J dx = ,F(a)|lna| + J f(x)\lnx\dx, 0 < а < 1,
а а
показывает, что требуемое утверждение эквивалентно вы¬
полнению условия lim F(a)|lna| = 0. Для любого е > 0
а-+0+ 1
f F(*) Л - к
в силу сходимости интеграла / —-—dx найдется такое л,
А О
/F(x) Е
—— dx < - для всех iy, 0 < г) < Л, а в си-
х 2
ч
лу непрерывности F на [0; 1] найдется такое 0 < S < 1, что
F(jc)| 1пЛ| < - для всех г, 0<х<6. Бели 0<a<ao = min(h,6),
то в силу монотонности F на [0; 1] имеем
h
е> f Ei*ldx^ F(a)(lnA-lna) =
I» J X
a
= F(a)| lnor| — F(a)\InД| ^ F(a)| lna| —
Отсюда следует, что 0 ^ In a| < e для всех a, 0 < a < aro,
т. e. lim Ffa)!Inal = 0.
ar—*0+ V 71 1
p
29. Решение. Покажем сначала, что если р > 1 и q =
Р-1’
a? bq
то для любых а > 0, Ь > 0 имеем неравенство ab < — -f —.
Р Я
Действительно, функции v = ир 1 и и = Vя 1 взаимно обрат-
ны; площадь фигуры, ограниченной осью Ои, кривой v = up~l
аР
и прямой и = а, равна —, площадь фигуры, ограниченной
Р
596
Ь*
осью Ov, кривой ti = vq и прямой v = 6, равна —, сумма
Я
этих площадей не меньше площади прямоугольника [0;а] х [0;6]
(см. рис. 16).
Положим а —
!/(*)! 6_ 1д(*)1
Из неравенства ао ^ 1 (q — 1) получаем, что
Ч 9
Это неравенство показывает, что \f(x)g(x)\ £ Д(а;6). Инте¬
грируя по промежутку (а;Ь), получаем:
ь
а
* {/{/ W*)!5*1*'!
/ 6 ч 1 / 6 \
30. Решение. Возьмем число е > 0 и найдем такое А,
*?
0 < Л < 1, что j \f(x)\4dx < еч для всех ?у, 0 < т) < h. Если
о
0 < х < ft, то применяя неравенство Гельдера (см. задачу 29),
X г 1
получаем, что J 1 f(t)dt < У |/(*)|»<**}’ •zV < e.,v.
о о
х
Таким образом, lim+ х^• J f(t) dt = 0.
о
31. Указание. Провести рассуждение, аналогичное реше¬
нию задачи 30.
32. Решение. Возьмем число е > 0 и найдем такое ft,
л
0 < ft < 1, что J xf2(x)dx < е2 для всех 1/, 0 < tj ^ ft. Если
о
0 < х < ft, то, применяя неравенство Гельдера (см. задачу 29),
получаем неравенство
Таким образом, lim f f(t) dt = 0.
v *-o+vThTiJУ JK>
33. Решение. Так как F(x) E C[0; +oo), то из неравенства
x2F2(x)
0 ^ F2(x) ^ 2“^» x ^ следует сходимость интеграла
+oo
/F2(x) dx. Отсюда следует, что lim xF2(x) = 0 (срав-
r-f+oo
0
ните с задачей 2). Обозначим через {а*} такую монотон¬
но возрастающую неограниченную последовательность, что
ak F2(ak) —> 0, —> оо. Из равенства
J F2(x)dx = xF2(x) |о -2 J F(x)f(x)x dx
о о
получаем, что
«* в/к
O^J F2(x)dz^akF2(ak) + 2 J F(x)\f{x)\x dx.
О о
Применяя неравенство Гельдера (см. задачу 29), получаем от-
сюда, что
Ofc в* ^ в* ^
J F2(z)dx <a*F2(a*) + 2{/x2F2(*)dr| -|у /*(*М*} ,
0 0 0
и, переходя к пределу при fc —► оо, получаем требуемое нера-
венство. +°° , j v
34. Указание. Представить I fix J dx в виде
— оо
и в первом слагаемом сделать замену х = — j.
35. Указание. В обоих интегралах сделать замену х = аег.
36. Решение. Так как функция f(x2) четная, то
+оо
I=\ J /{**)<**■
—оо
ь
Сделав в этом интеграле замену х = at — -, получаем
+оо
1
/
=!//(«<-*) («+£)■*=
= г//((--‘))Л + 5 *)Г/((*‘-0)р-
6
Сделав во втором интеграле замену t = , получим
аи
и в силу четности подынтегральной функции имеем требуе-
7/(“+i)
f { ь\ 0 6
+J f I ax + — I dx, где ®o — точка минимума функции axH—,
*• 6 п,
■ в каждом из слагаемых сделать замену ах + — = y/i2 + 4a6.
X
38. Указание. Представить луч (0; -foo) в виде (0; 1) U
U [1; -foo) и в интеграле по промежутку (0; 1) сделать замену
*=i.
х
мое равенство /:
J \\ х/ /
—оо ' /Го
37. Указание. Представить / в виде / / ( ах + 7 ) dx +
+оо
600
39. Решение. Представим интеграл 1 в виде
ж/2
w/2
=il
f(a»-i)
/(x) sin x
n—1 0
Так как функция f(x) sin x ограничена на [в; ~ j, то ряд
9i~l
сходится равномерно на ^0; , следовательно,
Ё /[jtjs+r^d /(*)"**=
Л— 1 Q
v/2 ^
= / Е(-Ч* (rns + ГПй;) '<*'Л * *•
П П-1
и в силу равенства
оо
-Д- = ± + 5>1)» [—^—+ —?—] , хфо,
8\пх х [х + тгп х — irnj
получаем
f/2, - ж/2
/=Д/(.) л, х +D-4" [г^+7^]]) *
601
40. Указание. Показать, что S(x) Е Я[а;6] и g S Е Я(а;Ь),
ь „6
затем
оценить ||g(z)S(z)dx — ^ Jg(x)ui(x)di
а 1=1 а
41. Решение. Пусть А > 0 и [—Л; Л] С (а - хо;Ь - хо).
ь
В силу условия 1) несобственный интеграл J f{t)<pn (t — xq) dt
Ь — Xq
определен для любого Xq E (a; b) и равен J f(t + xq)<pn(i)dt.
a—аr0
6
В силу абсолютной сходимости интеграла J f(x) dx и усло-
а
вия 2) имеем
-А 6
I [ f{t+*o)<pn(t)<U ^ sup |у>„(*)| f \f(t)\dx = o(l),
I J te[as0,-A] J
а—хо a
П —> OO,
6-*0
J f(t + *o)y>„(f) dt = o(l), n
OO.
Следовательно, достаточно доказать, что
л
lim f /(t + *o)v>n(*) А = /(*<>)•
П—¥00 J
-А Л
Из условия 3) получаем, что J<Pn(t) dt = 1+€„, где бп -*■ 0,
J f(t + *o)<Pn(i) dt - f(xо) =
-A
A
= J(/(< + *o) - /(*o))y»n(0 dt - e„ /(x0).
->4
602
Возьмем число е > 0. В силу непрерывности / в точке хо
найдется такое 6, 0 < S < А, что |f(t + х0) - /(хо)| < -ГТ7
А 4ЛГ
для всех t, \t\ ^ S, где М = eup J |y?n(x)| dx (см. условие 4)).
-л
Отсюда получаем:
А
|/(/(< + *о) - f{*o))<Pn(t) dt ^
-6
< | /М* + ~ Я*»))<М*) Л| +
А
+ |/(/(* + *о) - /(*o))v>n(0 dt +
+ У 1/(< + *о) - /(*о)|у>»(*) Л <
-в
ь
4 вир |у>„ (*) | [ |/(*) | dx + |.
[-Л;Л]\МЯ J 4
-6
€
В силу условия 2) и условия е„ —► 0, л —* оо, найдем такое
N € N, что |е„/(х0)| < n > 7V, и
eup lv>n(*)l < —g— . п> N.
[-л^1М-<Л 8 /1/(*)| dx
Для п> N получаем окончательно
А
|/ f{i + zo)<pn{t)dt - f(z0)
е е е
<4 + 2 + 4~С’
-Л
чем и завершается доказательство.
603
42. Не выполнено требование ограниченности функции
wn(n-f 1)
Gi*) = J 0(0 Л Указание. Рассмотреть / f{x)g(x) dx
О frn(n-l)
1Гп(п +1)
и J д(х) dx.
xn(fl — 1 )
43. He выполнено требование монотонности /. Указание.
*rn+f
Рассмотреть J /(х) cos х dx, n Е N, и использовать резуль-
ЖП— 5
тат задачи 11.
44. Решение. В силу монотонности /, не ограничивая
общности, можно считать, что /(х) ^ 0, х ^ а. Если не
выполнено условие lim f(x) = 0, то найдутся такие числа
г-»-foo
с > 0 и С > а, что /(х) > с, х ^ С. Если 27гЛг > С, то
/
/(х) sin х dx > 2с. Отсюда в силу критерия Коши следу-
-1-00
2*» г
ет расходимость интеграла / /(х) sin х^х. Полученное про-
а
тиворечие показывает, что lim /(х) = 0.
45. Решение. Из результата задачи 44 следует, что
lim /(х) = 0. Не ограничивая общности, можно считать,
г—►-foo
что /(х) > 0, х ^ а. Так как в силу признака Дирихле
-foo
интеграл J /(x)coe2x<fx сходится, то соотношение /(х) ^
а
, ч . . ,/Ч.2 /(х) /(x)cos2x
^ |/(х)81пх| ^ /(x)sin х = — показывает,
-foo -foo -foo
что интегралы J If{x)\dx = J f(x) dx и J |/( x) sin t\dr
a a a
одновременно сходятся или расходятся.
604
46. Например,
n, х = 2пп, п € N,
h" -
^2jto; 2itn + , n € N
лиыеина на отрезках
;2irn ,
e+T
47. Решение. Бели J g(x) dx = 0, то функция G(x) =
X e foo
= J ijr(<) dt ограничена на [а; -Нею) и интеграл J f(x)g(x) dx
a afT a
сходится в силу признака Дирихле. Бели I д(х) dx = А ф 0,
то равенство
+оо
J f(x)g(*) dx = ji J /(*)dx + J f(x) [*(*) ~ dx
a a
foo foo
, что интегралы / f(x)g(x) dx я I f(x) dx одно-
показывает
временно сходятся или расходятся.
48. Решение. Из условия следует существование тако¬
го х0 > а, что функция / строго возрастает на [хо;+оо) и
Lim f(x) = +00. Пусть x(t) — функция, обратная к / на
хч+оо
[/(х0); +оо), тогда х(*) монотонно возрастает на [/(хо); +оо),
lim x(t) — -foo и x't монотонно стремится к нулю при t—► +оо
на [/(хо); +оо). Делая замену х = х(<), получаем, что
foo Хо foo
I соs(f(x))dx = j coe(/(x)) dx + J (cos t)x[dt
a a f(xo)
605
-1-00 Го -foo
J ein(/(ar)) dx = j sin(/(*)) dx + J (sin t)x'tdt,
Л a /(xo)
откуда в силу признака Дирихле следует сходимость этих ин¬
тегралов. Так как
+9°
x'tdt = lim х(/) — хо = -foo,
/
t->+oo
/(* о)
то, применяя результат задачи 45, получаем, что
+оо +оо
j |coe(/(x))|<fx = +оо и j |ein(/(x))|dx = +оо.
л а
50. Указание. Показать, что выполнены все условия тео¬
ремы о переходе к пределу под знаком несобственного инте¬
грала. +00
51. Указание. Проверить, что интеграл J f(xiy)dx схо¬
дится равномерно. а
52. Следует из результата задачи 50.
53. Указание. Доказательство данного равенства анало¬
гично доказательству в решении задачи 41.
54. Решение. Пункт 1. Интегрируя по частям, получаем,
что
+оо +оо
/« = J coex {fx=e~ax*sin х|^ +6 J ахь~1е~АХ* sin xdx.
о о
Функция /(х) = ахь~1е~а*Ь неотрицательна на положитель¬
ной полуоси, и для любого а > 0 существует такое ха > О,
что / монотонно возрастает на [0; ха] и монотонно убывает
на [хо;+оо). В силу второй теоремы о среднем
х« *•
J ахь~1е~аж* в\пх dx = J /(х) sinxdx =/(х„) J sinxdx,
о о е»
6 € (0; xe)
606
и
■foo +00
J axb~1e ** e\nxdx = J /(x)sinxdx =/(xe)^sinxdx,
Г. X.
6 € (**;+<»).
Отсюда получаем, что
*• +oo
|/e| = \b j /(x) sin xdx + b J f(x) sin x dx
0 X.
(2
= 6/(xe)|y sin xdx I ^ 26/(xe) =
(1
= 2ba*(a*xa)k-1e-(et**) 2ba*K,
где постоянная if = max^*1^"* не зависит от а. Полученное
t>o
неравенство показывает, что lim Ia = 0. Решение в пункте 2
проводится точно так же. 6
55. Указание. Показать, что интеграл J f(x%y)g(x)dx
сходится равномерно. а
58. Указание. Применить метод математической индук¬
ции.
59. Указание. Показать, что выполнены все условия те¬
оремы о дифференцировании несобственного интеграла по
параметру.
61. Указание. Написать условие критерия Коши равно¬
мерной сходимости интеграла на (c;<f) и перейти к пределу
при уЧс+иу->d—.
63. Решение. Возьмем число е > 0. Так как интеграл
+оо
sinx „
dx сходится, то найдется такое число В > 1, что для
/
О . ь-3
любой пары чисел Ь\, 6?, В < Ь\ < 6*, имеем | J dx| < е.
607
Бели 1 ^ У ^ тт или у = 0, то для любой такой пары
В
Ч8Н1Х _
f(*,y)-^-dx = 0\
если же 0 < у < , то для любой такой пары или В < Ь\ < —,
В у
тогда
0».i)
Ь1 Ьг
<
Ьа
или 5 ^ 6i, тогда / /(д?,.у)—1— dx = 0. Следовательно,
У J *
bi
+°°
в силу критерия Коши интеграл J f(xfy)^-^-dx сходится
о
равномерно на [0; 1]. Для доказательства неравномерной схо-
+°°
димости на [0; 1] интеграла J дх прежде всего
о
заметим, что при любом у Е [0; 1} этот интеграл сходится,
так как подынтегральная функция отлична от нуля только
на конечном интервале. Пусть у„ = n € N, тогда
4лТ1
Лжп 4irn я
[ | sin яг| / | sin х| 2п Г . 1
У /(*.*)-7“л = У —r-dx>A^j |8,n*|d* = ^
2irn 2ж n О
что в силу произвольности п Е N и показывает неравномер¬
ную сходимость рассматриваемого интеграла на [0; 1].
+оо
64. а) Интеграл J |/(х, у)| dx сходится равномерно на М;
а
б) Функция у(х, уо) монотонна на [а; +оо) для любого уо Е М
на [а;/?].
608
65. Решение. Интегралы
1 1
J ху f(x) dx = j xy~c(xcf(x)) dx
0
и
•foo foo
J xyf(x)dx = J xy d(xdf(x))dx
l l
сходятся равномерно в силу признака Абеля.
66. Решение. Неотрицательность /(х, у) следует из ее
5 1
определения. Бели х ^ 5, то 0 < — ^ г и
2х 2
Следовательно, если f(x,у) ^ <р(х), х 6 [2;+оо), у £ [0; 1],
•foo
то (р(х) ^ -—-— для х ^ 5 и интеграл / у>(х) rfx расходит-
2Х1ПХ -foo '
ся. Покажем, что интеграл J f(x,y)dx сходится равномер-
2
но на [0; 1]. Возьмем число е>0и найдем такое В > 2, что
1 3 2
In В ^ Пусть В <Ь\ < bj. Если 1 у ^> — или 0<У^ 7-,
5 6i 02
Ь-2
/2 3
/(х, у) dx = 0. Если же — < у < —, то
ь,
ба i i
J f{*,V) < J yal**V dx ^ jysin nxydx
61 max(6i,J) J
ПГв* /“'
Зяг
^ г-^ - I aiotdK
2ir
Итак, в силу критерия Коши данный интеграл сходится рав¬
номерно на [0; 1].
609
67. Решение. Локальная монотонность функции /(х,уо),
Уо Е [0; 1], в правой несобственной точке +оо следует из опре¬
деления; равномерное стремление /(х,у) к нулю при
х -* -foo — из неравенства |/(х,у)| <С —, у Е [0; 1]. Пусть
х
1
Уп = —, пбК, тогда
4irn
Ажп Ажп к
[ sin2 х 2п / . 2 1
I /(х, у) sin х ах = I —-—ах ^ / sin хах= - ,
2пп 2жп О
что в силу произвольности п Е N и показывает неравномер¬
ную сходимость рассматриваемого интеграла на [0; 1].
Функция <7у(х) = /(х,у) монотонна на (6(у),+оо), и Ь(у)
зависит от у (ср. с примером 46 гл. I § 3).
68. Решение. Монотонность на [0; +оо) и стремление к ну¬
лю /(х, уо) при х —> +оо для любого уь € [0; 1] следует из опре-
+ 00
деления. В силу признака Дирихле интеграл / /(х, у0) sin xdx
о
сходится при любом уо € [0; 1]. Положим В\ — 2пn, В2 =
= т(2п + 1), уо = ■ у1-:-;т, n Е N, тогда Вх < В2 < —
2п(п + 1) уо
и, следовательно, /(х,уо) = 1 для х Е [BijSj]. Отсюда по-
Ва *(2п+1)
как
лучаем, что J /(х, у0) sin х dx = J sin xdx — 2. Так
Bi 2*n
Уо G [0; 1], a #1 может быть сколь угодно большим за счет
выбора п, то полученное равенство показывает, что
+оо
/
/(х, у) sin х dx сходится неравномерно на [0; 1],
о
Функция /(х,у) неравномерно стремится к нулю на
[0; +оо).
69. Решение. Не ограничивая общности, можно предполвг
гать, что /(х, у) ^ 0 на [0; -foo) хМи, следовательно, /(х, уо)
монотонно не возрастает на [a;-foo) при любом уо Е М. Ес¬
ли /(х, у) при х -4 -foo сходится к нулю неравномерно на [0; 1],
610
то существует число £о > 0 такое, что для любого п £ N най¬
дутся уп £ М и хп > п(2п -f 1), удовлетворяющие условию
/(ящ Уп) > £о- Так как /(х,уп) монотонно не возрастает, то,
не ограничивая общности, можно считать, что /(х,уп) > во
для всех х ^ тг(2п + 1). Отсюда получаем, что
21ГП + 7Г
J f(x,y„)sinzdx ^ е0 J siaxdx = 2е0,
2жп
откуда следует неравномерная сходимость интеграла
+оо
/
/(х,у)sinxdx на М. Полученное противоречие доказы¬
вает, что /(х, у) 4 0 на М при х -> Н-оо. +оо
70. Решение. Необходимость. Пусть интеграл J f(x)y)dx
а
сходится равномерно на М и {хЛ} — последовательность,
удовлетворяющая данному условию. Возьмем число е > 0 и
найдем такое В > а, что для любой пары 61,62, В < 61 < 62,
6з
имеем I/ f{x,y)dx
< б для всех у £ М. В силу монотонно-
ь 1
сти последовательности {хга} и условия lim хп— и найдется
n—foo
такое N £ N, что xm_i > В для всех m £ N, т > 7V. Тогда
для всех у Е М и любых натуральных чисел р и т > N имеем
оо
и в силу критерия Коши ряд ^ / /(t,y)oft сходится рав¬
номерно на М. п=1 Гл_, ^
Достаточность. Предположим, что интеграл J f(x,y)dx
а
сходится неравномерно на Af. Построим такую последова¬
тельность {хп}, удовлетворяющую заданным условиям, что
611
ряд ^ / /(*,у)Л будет также сходиться неравномерно
п—1 J
*т-1
на М. Возьмем некоторую последовательность {сп}: а = со <
< ci < С2 < ... < сп < ... < ы, lim с„ = ш. Так как интеграл
п—юо
ш
J
/(х, у) dx сходится неравномерно на М} то существует та-
а
кое число ео > 0, что для любого В > а найдутся числа 6], 62,
В < bi < 63 < о;, и yi Е М, для которых I/ f{x,y)dx
> £о-
Ь1
Положим хо = а и найдем Xi, х2, а < xi < х2 < и/, yi Е М так,
*2
ЧТО |у /(<, у) Л
,> Со- Положим = max(x2,ci) и найдем
*1 г4
*з,*4, Bi < х3 < х4 < и, У2 е М так, что | J f{i,yi)dt
*3
> б0.
Продолжая этот процесс, получим последовательность {х„}
и последовательность уп такие, что
1) Уп € Л/ для любого n Е N,
2) а = X0<X1<X2<X3<X4< ... <х2т-1<я2т< ••• <ы>
3) Cm-1 < Х2т-1 < *2т ДЛЯ ЛюбОГО Ш Е N,
>3»
4) J /(<,Ут)
dt
> £0 для любого т Е
*2т-1
Свойства 2) и 3) показывают, что lim хп = о/, т. е. после-
П-ЮО
довательность {х„} удовлетворяет условиям формулировки
оо у
задачи, а свойства 1) и 3) — что ряд ^ / /(<, у) dt схо-
п — 1 ,■*
*«1-1
дится неравномерно на М. Итак, получено противоречие с
требованием равномерной сходимости этого ряда при любой
последовательности {хп}, удовлетворяющей этим условиям.
Полученное противоречие заканчивает доказательство.
<612
+оо
71. Решение. Сходимость интеграла J е~ух cos xdx на
о
(0; 1) следует из признака Дирихле, а неравномерная сходи¬
мость на (0; 1) — из расходимости этого интеграла при у = 0
(см. задачу 61). Так как функция <p(t) = te~kt, к ф 0 на [0; 1]
неотрицательна, принимает наибольшее значение — при
, 1 С
*=кЛ
2tna
/e-V* i2irn
t у* сое xdx — -(sio х - у со8х) =
1 "Ь У l2*(n — 1)а
2»(п—1)а
= _2L_e-a«rt»- 1)а(1 _ е-з^зп-!)^ у ф 0
то
2irna
0
2ir(n—1)а
< ( coexdx < ие~,я^п~^2 < -
^ j е совхах ^ уе ** 2we{n - I)*'
У€(0;1).
В силу признака Вейерштрасса полученное неравенство дока-
„ 2irna
зывает, что ряд I е~у* сое х dx сходится равномер-
n=1 2w(n—1)а
но на (0; 1).
72. Указание. Если xn_i < 6i < 62 < xm> то
Ь2 т *i
о ^ J /(*. у) dx ^ J f{t, у) dt.
73. Указание. Если a?n_i < &i < 62 < хт, то величи¬
на
на I/ /(х, у) dx
6l
заключена между наибольшей и наименьшей
613
величинами:
If /я.,.)*. \1 7Л..»)
dt
*.-1
m—1
» I II»— ж -
X) J /(*•»)Л • IE J я**у)
dt
t=n +1
*i-l *.-1
74. Указание. Обоснование производится так же, как обо¬
снование перестановки двух несобственных интегралов при
вычислении интеграла Френеля (см. пример 52 гл. II § 3).
Глава Ш
РЯДЫ ФУРЬЕ.
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
$ 1. РЯДЫ ФУРЬЕ
Определение. Функция /: [а; 6] —► R называется функци¬
ей с интегрируемым квадратом на [а; 6], если / Е Я(а,6) и
/2 Е Я(а,6). Множество функций с интегрируемым квадра¬
том на [а; 6] будем обозначать Я2(а, 6).
Отметим, что множества Я(а,6) и Я2(а, 6) частично пе¬
ресекаются. Действительно, если неограниченная функция
/ Е Я(а,6), то /2 не обязательно интегрируема на [а; 6], на¬
пример, f(x) = —р= на (0; 1). Для ограниченных на (а, 6)
Vх
функций из интегрируемости / на [а; Ь] следует интегриру¬
емость /2 на [а; 6], но из интегрируемости /2 на [а; 6] не сле¬
дует интегрируемости / на [а; 6], например, f(x) = - — D(x)
ГЛ ч f 1. х — рационально,
на [0; 1], где D(x) = < — функция
' ^ 0, х — иррационально
Дирихле.
Множество Я2(а,6) представляет собой линейное прост-
6
ранство. Интеграл J f(x)g(x) dx определен для любых двух
а
функций из Я2(а, 6). Его можно рассматривать как скаляр¬
ное произведение в Я2(а, 6) и ввести соответствующую норму:
1/2
(/
11/11= / / (*) dx
Отметим, что фукционал fz(x)dxj не удовлетво¬
ряет всем требованиям, предъявляемым в определении нормы
линейного пространства; именно, если / Е Я2(а, 6) и множе¬
ство М = {х, х Е [а; 6], /(х) ф 0} является множеством меры
615
о
нуль, то J f2(x)dx = 0. Таким образом, из условия ||/|| = 0
а
не следует, что / есть нулевой элемент пространства Л2(a, b)t
т. е. /(х) = 0, х G [а; 6], а следует только то, что /(х) = 0 для
х G [а;Ь] \ Af, где М — множество меры нуль. Будем назы¬
вать две функции / G Я2(а, Ь) и д G Л2(а, 6) эквивалентными,
если они отличаются только на множестве меры нуль; тогда
1/2
можно сказать, что функционал (/ /2(ж) dx ) есть норма
в пространстве (линейном), элементами которого являются
классы эквивалентных функций из Л2(а, 6).
Определение. Система функций {ф^х)}, ф{ G Я2(а, 6),
называется ортогональной на [а; Ь], если
6
/*<*)*(*)*={ «>0. !=>!
а
Определение. Система функций {^«(*)Ь V’e 6 Я2(а, 6),
называется ортонормированной на [а; 6], если эта система ор¬
тогональна на [а; Ь] и
lhMI= ФН*)<ь^ =1
для всех ».
Если {ф{ (х)} — ортогональная система на [а; Ь\, то система
1 7м”ГГ Г ортонормированная на [а; 6].
I IIrill J
Пример 1. Рассмотрим функции и(х), являющиеся реше¬
ниями уравнения ti" + q(x)u — Ли, где функция q G С"00[а, 6] и
А — некоторое число.
Если при некотором А существует отличная от тожде¬
ственного нуля на [а; Ь] функция и\(х) Е С2[а, 6], удовлетво¬
ряющая этому уравнению и условиям и (а) = и(Ь) — 0, то таг
кое число А назовем собственным значением задачи, а функ-
616
цию и\ — собственной функцией задачи, соответствующей
собственному значению А. Предположим, что существует по¬
следовательность {А,} различных собственных значений за¬
дачи. Покажем, что система и,(ж) = маДя) соответствующих
собственных функций ортогональна на [а; 6].
Действительно, во-первых, из непрерывности и отличия
от тождественного нуля функции следует неравенство
ь
J u?(x)dx > 0. Во-вторых, интегрируя по частям, получаем
а
равенство
6 ь
А< JIti(x)uj(x)dz = J(«" + qtii)tij dx =
a a
6 6 6 ^
= J guiuj dx + - J u'iiij dx = J qu;uj dx - +
a a a
6 6 6
+ J Uittj dx = J u,(u" + quj) dx = Xj J UiUjdx
a a a
6
и так как А,- ф Aj, то отсюда следует, что JUiUj dx = 0.
а
Пример 2. Пусть 0 < & < & < (з <•••<& < • • • —
последовательность корней уравнения ctg х =■ х. Покажем,
что система {cos(£,ac)} ортогональна на (0; 1].
1
Действительно, во-первых, J соa7(fjx)dx > 0. Во-вто¬
рых, если i ф ;, то 0
О
617
Определение. Пусть {0,} — ортогональная система на
[в;6] и /6 Й2(а,6). Числа
6
С. = с<(/) = jj^jp J f(x)1>i(x)dx
» а
называются коэффициентами Фурье функции / по системе
м-
Определение. Пусть {^«} — ортогональная система на
оо
[а;6), f € R2{a,b). Ряд £с^(я), где с, = с<(/) - коэффи-
1=1
циенты Фурье функции / по системе {^i}, называется рядом
Фурье функции / по системе {ф{}.
В дальнейшем, говоря о коэффициентах или ряде Фурье
функции / по системе {^ч}, постоянно будем иметь в виду,
что /6^2(a,6) и система {^*} ортогональна на [а; 6], не ого¬
варивая этого специально.
Бели функция / представляет собой многочлен по орто¬
гональной на [а; 6] системе {^«}- / = то» очевидно,
c‘=isr//w*wHo: !>:""'
а
Таким образом, любой многочлен по ортогональной систе¬
ме -является своим рядом Фурье по этой системе, все коэффи¬
циенты С{ которого равны нулю, если t > п, где п — степень
рассматриваемого многочлена.
Для коэффициентов Фурье с, = c%[f) функции / по систе¬
ме {fa} справедливо неравенство Бесселя:
6
£с,?-|№1|2 < ll/ll2 = f f2(x)dx.
«=1 .
Бели для системы {V\} выполнено условие inf ||^t*|| > 0, в
частности, если система {ф{} ортонормированная, то из нера-
венства Бесселя следует, что последовательность с*(/) коэф¬
фициентов Фурье функции по системе {^i} бесконечно малая.
618
Определение. Последовательность {/п}, fn € Я2(а,6),
называется сходящейся по норме, или сходящейся в среднем,
к функции / Е Я2(а, 6), если ||/„ — /|| —0, п —► оо, т. е.
ь
j CM*) - f(x)Ydz -*■ О, П -> оо.
а
Пусть {/п} — последовательность, сходящаяся в среднем
к /i {cn,t}» {й} соответственно — коэффициенты Фурье функ¬
ций /п и функции / по системе {V't}- Из неравенства Бесселя
следует, что
lim сП){ = Ci (1)
п —► оо
для любого I.
Определение. Ортогональная система {ф*} называется
полной в Я2(а, 6) (или полной на [а; 6]), если для любой функ¬
ции / Е Я2(а, 6) и любого числа е > 0 существует такой поли-
п
ном Tn(ipi) = по системе {V*.}, что ||/ - Т„(^,)|| < е.
«=1 _
Бели система {^,*} полна в Я2(а, 6), то неравенство Бесселя
превращается в равенство Парсе валя
1>?М2 = II/II2 =
»=1
Бели выполнено равенство Парсеваля и все коэффициен¬
ты Фурье функции / по системе {V>t} равны нулю, то полу¬
чаем, что Ц/ll = 0; следовательно, функция / эквивалентна
тождественному нулю на [а; 6]. Итак, если ортогональная си¬
стема {^i} полна в Я2[а, 6], то каждому классу эквивалентных
функций из Я2[а,6] взаимно однозначно соответствует после¬
довательность {с,} коэффициентов Фурье этих функций по
системе {V>t}
Коэффициенты Фурье с*(/) = с, функции / по систе¬
ме {^} обладают экстремальным свойством: для любого по¬
линома Тп(ф{) степени не выше п по системе {^t} имеет место
п
неравенство ||/ -Tn(V>,)|| ^ ||/ - У^с,У»,||. Отсюда следу-
t=l
619
ет, что если система {ф{} полна в Я2[а,6], то ||/ — Sn\\ —► О,
п
п -> оо, для любой функции / G Я2[а, 6], где Sn = ^ct^» —
i=l
частичная сумма ряда Фурье функции / по системе {V\}> т- е-
ряд Фурье функции / по системе {^,} сходится в среднем к /.
Простейшей полной ортогональной системой является
тригонометрическая система
{y?,}=:{l,smx,cosx,sin 2х,cos 2х,... ,sinnx,cosnx,...}, n£N,
на отрезке [—7г; 7г].
В силу периодичности входящих в нее функций эта си¬
стема является ортогональной и полной также на любом от¬
резке [а; а + 27т]. В основном, тригонометрическую систему
рассматривают на отрезках [—тг; тг] и [0;27г].
/х
Линейная замена t — — переводит тригонометрическую
7Г
систему в полную ортогональную систему
{ТГПХ
cos ——, 1 = 2 п— 1,
п Е N
. 7ГПХ
sin—, г = 2п,
на отрезке [—/;/] или [0;2/]. Ряд Фурье функции / 6 Я2[—/,/]
по системе записывается в виде
ао ( тгпх , . тгпх\
/ ~ у + 2Дап cos ~ + 6п 8Ш ~ J ’
п=1
где
ап = у J f(x)cos dx, b„ = jj f(x)sin dx,
-l -l
n = 0,l,2,...,
и обозначается 04(f) ( crn(f) будем одозначать просто or(f)
так же, как систему — просто {y>i}). Равенство Пар-
620
севаля для системы {<^} имеет вид:
J- + £(ап + 6п) = у J f2(x) dx-
n=l
Как и для любой ортогональной системы, многочлен
N
v <*о ( лпх л . 7Г7гх\
т(х) = — + 22, (а"cos ~j~ + sm “т-)
П — 1
.(Oi
по системе {<р\ '} является своим рядом Фурье по этой систе¬
ме. Из ограниченности тригонометрических функций следу¬
ет и более общее утверждение.
Если тригонометрический ряд
оо
ао / 7ГXXX _ 7ГТ1Х \
у + 2Да"cos ~Г + Р"sin ~Г)
п = 1
сходится равномерно на [—/;/] к функции /(х), то этот ряд
является рядом Фурье функции / по системе
Будем говорить, что функция f(x) на отрезке [а; 6] пред¬
ставляется тригонометрическим рядом или раскладывается в
тригонометрический ряд по системе если существуют
такие две последовательности {ап} и {&„}, что
г/ ч ао / ттях _ . 7ГПХ\
/(*) = у + 2^ \ап сов ~ + bn sin “)
п=1
для х € [а; b] \ М, где М — конечное множество.
В силу полноты системы в Я2[—/,/] для любой функ¬
ции / G Д2[—/,/] справедливо равенство
Jjs. | /(/(*> ■ (?+Н“"cos Т+*■“ ))) =
= /(*> - (т + £ (■■" cos + *” ”п )) I = “■
где а, и есть коэффициенты Фурье функции / по систе¬
ме Это свойство формулируют так: любая функция
621
/ E R2[—l, /] представляется своим рядом Фурье, <т/(/), в смы¬
сле сходимости в среднем. Однако, поскольку сходимость в
среднем последовательности {Л»}, /п € Я2[а,6], к функции
/ Е Я2[а,6] не влечет поточечной сходимости /п(х) к /(я)
на [а;6], даже если все функции /„ и / непрерывны на [а;Ь]
(см. задачу 1 гл. III § 5), то вопрос о поточечной сходимости
ряда <т/(/) требует специального исследования.
Определение. Точка Хо из множества определения функ¬
ции / называется регулярной точкой этой функции, если су¬
ществуют пределы:
lim /(х) = /(хо + 0), lim f(x) = /(х0 - 0)
X—►Го+ T—*Iq -
и 1 (2)
Я*о) = ^(Яяо + 0) + f(xо - 0)).
Все точки непрерывности функции, очевидно, являются
ее регулярными точками.
Определение. Функция /, определенная на отрезке [а; 6],
называется кусочно гладкой (или кусочно дифференцируе¬
мой) на [а; 6], если
1. множество М точек разрыва функции / на [а; 6] конечно
и каждая точка хо Е М есть точка разрыва первого рода
функции /;
2. функция / дифференцируема во всех точках [а; 6] \ Л/1,
где М1 — конечное множество (очевидно, М1 DM);
3. для каждой точки хо Е М1 существуют пределы
lim |im 0)-/<«. -.?) (3)
/*—►0+ h Л—►o-j- h
(если хо Е М1 \ Л/, то существование этих пределов есть
существование односторонних производных /+(хо) и /1(х0)).
Теорема (признак Дини поточечной сходимости
тригонометрического ряда Фурье). Пусть хо £(—/;/) —
регулярная точка функции / Е Л2[-/,/]. Если для некоторого
S > 0 сходится интеграл
s
j \f(x0 + «) + f(x0 - «) - 2/(*o)|^,
О
622
то ряд Фурье cri(f) (по системе {^[^}) функции / сходится в
точке хо К /(хо).
Из этой теоремы вытекают следующие утверждения.
1. Принцип локализации Римана. Если функция / Е
Е R2[—/,/] равна нулю в некоторой окрестности точки Хо Е
Е (—^;/), то <ri(f) сходится в точке хо к нулю.
Отсюда следует, что для двух функций / Е Л2[—/,/] и
9 Е Я2[—/,/], совпадающих в некоторой окрестности точ¬
ки хо Е (—/;/), ряды <Ti(f) и 0i{g) в точке хо одновременно
сходятся или расходятся.
Принцип локализации часто выражают в такой форме:
сходимость тригонометрического ряда Фурье функции f Е
Е Я2[—/;/] в точке хо Е (—/;/) зависит от поведения / только
в окрестности этой точки.
2. Если функция / непрерывна на [—/;/] и в каждой точке
интервала (—/;/) имеет односторонние производные /1 и Д,
то <т/(/) сходится к /(х) для всех х Е (—/;/)
3. Если функция / кусочно гладкая на (-/;/), то для лю¬
бой регулярной точки Хо Е (—/;/) этой функции ряд <Tl(f)
СХОДИТСЯ к /(хо).
В силу периодичности тригонометрических функций ряд
Фурье 0"/(/), представляющий функцию /(х) на [—/;/]> пред¬
ставляет в каждом отрезке [а;6] Э [—/;/] функцию /*(х), по¬
лученную 2/-периодическим продолжением функции /(х) с
интервала (—/;/) на всю числовую прямую за исключением
точек /(2m + 1), т Е Z. Значения /*(/(2т + 1)), т Е вы¬
бираются произвольно. Если определены значения /(/ — 0)
и /(—/ + 0) (см. (2)), то обычно полагают
Г(1(2т + 1)) = !(/(/ - 0) + /(/ + 0)), т € Z.
Тогда при выполнении условия признака Дини для функции
/*(х) в точке х = /, в частности, если функция /Ф(х) удо¬
влетворяет условию (3) в точке х = /, ряд <Ti(f*) сходится в
точках х = /(2m + 1) к /*(/(2т -f 1)), т Е Z.
Для определенности все формулы и утверждения были за¬
писаны для системы на отрезке [—/;/]. Заменяя всюду
промежуток (—/;/) на промежуток (0;2/), получим соответ-
623
ствующие формулы и утверждения для системы на от¬
резке [0; 2/].
Итак, для достаточно широкого класса функций задача
представления функции тригонометрическим рядом по си¬
стеме решается с помощью ряда Фурье по этой си¬
стеме. Для сравнения рассмотрим представление функции
степенным рядом Тейлора. Для определения коэффициентов
ряда Тейлора функции / в окрестности точки хо необходима
бесконечная дифференцируемость / в этой точке. Если по¬
лученный ряд Тейлора сходится в некоторой точке, отличной
от хо, то, как степенной ряд, ряд Тейлора сходится на целом
интервале. Однако сумма этого ряда может и не совпадать
с порождающей функцией /. Разложение в ряд Тейлора или
представление степенным рядом имеет место только для ана¬
литических в некотором интервале функций, а этот класс уже
класса функций, бесконечно дифференцируемых на этом ин¬
тервале. Таким образом, величина коэффициентов ряда Тей¬
лора есть локальное, а сходимость этого ряда к порождающей
его функции есть глобальное свойство функции.
В отличие от степенных рядов принцип локализации Ри-
мана показывает, что сходимость тригонометрического ряда
Фурье к порождающей его функции есть локальное свойство;
в то время как величина коэффициентов Фурье — глобальное
свойство. Поэтому, с одной стороны, исследовать сходимость
тригонометрического ряда Фурье приходится в полном смы¬
сле “поточечно”, — в каждой точке независимо от других;
а, с другой стороны, представление функции тригонометри¬
ческим рядом Фурье возможно для гораздо более широкого
класса функций, нежели аналитические. В частности, одним
из примеров непрерывной нигде не дифференцируемой функ¬
ции является именно функция, представимая равномерно схо¬
дящимся к ней тригонометрическим рядом Фурье.
Если представление функции тригонометрическим рядом
является частью решения другой задачи, то система и
соответствующий отрезок определяются условиями этой за¬
дачи. Поскольку здесь разложение в тригонометрический
ряд рассматривается как самостоятельная задача, то необ-
624
ходимо указание, по какой именно системе и на каком
отрезке требуется получить представление данной функции
тригонометрическим рядом. Формулировка “найти разло¬
жение в тригонометрический ряд Фурье функции / на от¬
резке [—/;/] (или [0;2/])” и будет обозначать, что ряд Фурье
образуется по системе и рассматривается на соответ¬
ствующем отрезке. Вопрос о сходимости полученного ряда
к данной функции при этом не возникает, так как все рас¬
сматриваемые функции удовлетворяют условию Дини всюду
на (—/;/) ((0;2/)) за исключением, может быть, нескольких
особых точек.
Пример 3. Найти разложение в тригонометрический ряд
Фурье функции /(х) = х3 4* х2 — х — 1 на отрезке [—1; 1].
Формулировка показывает, что ряд Фурье образуется по
системе
= { 1 ,COS 7ГХ, sin 7TX,COs27TX, Sm2TTX,. . . ,COS П7Г2, sin 717ГХ,. . .}.
Таким образом,
1
<*0
- J(x3 + x2-x- l)dx=
-1
1
ап = J (х3 -f х2 — х — 1) cos П7гх dx —
1 / I1 f
— I (x2 — l)sin7rnx — 2 I xsir
rnV I- -i
-1
-nf-
7Г ft 1
X COS 7ГПХ
4 (-1)", n#0.
7T27l2
i
bn = J (x3 + x2 — x — 1) sin ТГ71Х dx =
-l
625
Так как функция /(х) = х3 4- х2 — х — 1 дифференцируема
на (—1; 1), то равенство
3 2 , 2 4 ^ /(-1)" 3-(-1)" . \
х-\~х —х— 1 = ——Н—Г ) (-—cos пх Н -т- sin пх)
3 7Г2 “ V п *п )
n=l N '
имеет место для всех х £ (—1; 1). Так как /(—1) = /(1) = О,
то 2-периодическое продолжение функции f(x) на всю чи¬
словую прямую дает непрерывную на всей числовой прямой
функцию /*(х). Легко проверить, что
/;(2* + 1) = 0, /1(2*+1) = 4
(см. рис. 17). Следовательно, в силу признака Дини равенство
ч 2 4^. /(-1)" 3.(-1)" . \
1 <х) = -»+ Й Г
П = 1 х '
имеет место на всей числовой прямой.
Пример 4. Найти разложение в тригонометрический ряд
Фурье функции /(х) = еог, а ф 0, на отрезке [0; 1].
Формулировка показывает, что ряд Фурье образуется по
системе {^^(*)}: {1, sin27rx, соз2тгх, зт4тгх, cos4ttx,...,
sin 2птгх, cos 2птгх,...}. Таким образом,
1
ао = 2 J еах dx — ^(еа - 1);
626
■»-2 J
"(
а„ = 2 J елв сое 2жпх dx =
о
*.<** + 4ffar»s
1
bn = 2 J еав ein 2im* dx =
о
(a coe 2nnx + 2nn sin 2irnx)
)C-s
-1).
4 *ran3 ’
-=2/'
о j
= (aa +4ffan* ”П ^nnx 2ffn 008 j =
4тгп
a3 + 4тгапа
Так как функция /(*) = ea® дифференцируема на (0; 1), то
равенство
«~ = £^i +
а
+2<'*-1)£(?+Wc"2’ra*-5TO?™8’”1)
627
имеет место для всех х Е (0; 1). 1-периодическое продолже¬
ние функции f(x) = еаг дает функцию /*(я), разрывную в
точках х = к, к £ Z (см. рис. 18). Так как
/(1 - 0) = lim еах — еа,
х-*1 —
/(0 + 0) = lim еах = 1,
v 7 г—ю+
еа + I
то положим f*{k) = —-—, к Е Z. Так как
-П> + » nt + ,),||m£^1 = ai
л-*о+ h h-* o+ A
/*(* + Л)-/*(* + 0) e«(»+*)-e“
lim — - - = lim : = ae .
h-* о- Л л-чо- A
то в каждой точке x = I, t E 2, условие признака Дини
выполнено. Следовательно,
ев±1 ев - 1
/*(*) == +
+ Е cos2,rot+ffiiw "n2",t)=
П = 1
628
Пример 5. Найти разложение в тригонометрический ряд
Фурье функции /(х) = sin 2х + cos Ъх на отрезке
а) [-*;*]; б) [—»г/2; Я-/2].
Отрезку [—тг; 7г] соответствует система
{^>,(x)} = {l,sinx,cosx,sin2x,cos2x,..., sinnx, cosnx,...}.
Поскольку данная функция является многочленом относите¬
льно этой системы, то, следовательно, этот многочлен и пред¬
ставляет собой соответствующий ряд Фурье, т. е.
(т(/) = sin 2х + cos 5х.
[тг тг 1 ( п \
— —соответствует система {^>t- (х)} = {1,
Z Z J
sin2x, cos2x, sin4x, cos4x,..., sin2nx, cos2nx,...}. Относи¬
тельно этой системы данная функция уже не является мно¬
гочленом, так как функция cos5x не входит в систему. Вы¬
числим коэффициенты Фурье /(х) по системе стан¬
дартным способом:
тг/2
2 Г
in = — I (sin2x + cos5x)cos2nxcfx =
-тг/2
ж/2
= — J [cos(5 + 2n)x + cos(2n — 5)х] dx =
-п/2
_ 1 Tsin(5-f 2n)x sin(2n — 5)1
тг I 5-1-2п 2п — 5
= ?нг
— я/2
тг 7 4п2 — 25 ’
ж/2
6П = — J (sin2x + cos5x) sin 2nx dx = 0, n ф 1.
— n/2
Я-/2
b\ = — j (sin2 2x + sin 2x- cos 5x) dx = 1.
-1Г/2
629
Функция f(x) = sin 2x-fcos5x дифференцируема на •
Так как / ^ ^ = 0, то ее 7г-периодическое продол¬
жение дает функцию /*(х), непрерывную на всей числовой
прямой. Легко проверить, что
</•(*»;и+„»=з, (/•(«))'-!„.
\+*к
= -7
(см. рис. 19).Следовательно, применяя признак Дини, получа¬
ем, что равенство
r(*) = _5^ + sin2x + T2-
ж ^ 4п2 - 25
П= 1
cos 2пх
справедливо для всех значений х. Обратим внимание на то,
что функция /* (х) равна sin 2х + cos 5х на отрезках + 27гт;
+ 2ятп|, т G Z, а на интервалах (—у + 2тгт; ^ -f 2irm^j ,
тЕ2, равна sin(2(x — 7г)) + cos(5(x — 7г)) = sin 2х — cos 5х.
630
Бели рассматривается отрезок [—/;/], симметричный от¬
носительно начала координат, то для четной функции / Е
Е Я2[—/,/] имеем
Ьп = 0, n Е N;
/
2 f ,, ч этих . Л Л
а„ = у / /(х) cos —— dx, п = 0,1,2,...,
(4)
о
а для нечетной функции у Е Я2[—/,/]
а„ = 0, п = 0,1,2,...;
i
» 2 /* . . тгпх .
6„ = у / /(х) sin -у- dx, n Е N.
о
(5)
Пример 6. Найти разложение в тригонометрический ряд
Фурье функции /(я
Отрезку
= х cos х на отрезке [—7г/2; 7г/2].
соответствует система = {1,
sin 2x,cos2x,sin4x,cos4x,..., sin2nx, cos2nx,...}. В силу не¬
четности функции / получаем, что ап = 0, п = 0,1,2,...,
и
ir/2
х cos х sin 2nx dx =
0
ж/2
2 f
= — / x(sin(2n + l)x + sin(2n — l)x) dx =
о
2 f Г /cos(2n - l)x cos(2n + l)x\l I
-*\K 2n-l + 2n+l jj[
n/2 */2 .
+ I cos(2n-bl)x dx -f I cos(2n—l)xdx > =
2n+l j 2n—1 у I
_ 2 (—1)" [1 1 1 _ 16-(—I)*-1»
n [(2n+l)2 (2n — 1)2J — тг(4п2 — 1).
|*/2
+
631
Периодическое с периодом тг продолжение функции /(х) =
— xcosx с Дает функцию /*, непрерывно дифферен¬
цируемую на всей числовой прямой (проверьте!). Следова¬
тельно, равенство
х cos
16
х- — >
тг Z—*
(-1)
П = 1
4п2 - 1
sin 2пх
7Г ТП
2’ 2J
имеет место на веем отрезке
Z ZJ ТГ тг
Справедливость этого равенства в точках — — и — видна и
непосредственно, так как в этих точках обе его части обра¬
щаются в нуль. Но хотелось обратить внимание на общий
принцип исследования поведения тригонометрического ряда
Фурье в концевых точках рассматриваемого отрезка.
Пример 7. Найти разложение в тригонометрический ряд
, . , тг я*
Фурье функции fix) = xsm2x на отрезке — —; — .
4 4
Отрезку соответствует система {^-^^(ж)} = {1,
sin4x,cos4x,sin8x,cos8x,... ,sin 4nx,cos4nx,...}. В силу чет¬
ности функции / получаем, что 6П = 0, п (Е N, и
тг/4 тг/4
х sin 2х dx
4 ( ir/4 г \ 2
= ( х cos 2х — / cos2xdx) = —;
п \ о J ) тг
х sin 2х cos 4nx dx =
8 /
а0 = -
* J
о
тг/4
О
тг/4
4 /*
= — / x[sin(4n -|- 2)х — sin(4n — 2)х] dx =
тг У
17
4п - 2
4n 2
тг/4 \
/sin(4n — 2)х sin(4n-f2)x\ I _
V (4n — 2)2 (4n + 2)2 Jo j~
_ (—l)n-2(4n2 + 1)
тг(4п2 — l)2 ’
neN.
632
Периодическое с периодом ^ продолжение функции
/(х) = xsin2x с Дает функцию /*, непрерывную на
всей числовой прямой*), но не дифференцируемую в точках
7Г пк . г_ _
Xk = — + —, к ЕЪ. Равенства
lim г(^ + * + *)-/*(*г + 1)_
л-*о+ h
/И + М-/Н) , • о V
= lim 3 —— = (xsin2x)
o-f h
lim r (¥ + f + fr)-r(¥ + ?) _
Л—► 0 — /l
= ,im tii±4^m=(isin2l).
Л-+0- /l
= -1,
x=-n/4
= 1
x = rr/4
показывают, что в этих точках условие Дини выполнено.
Итак, равенство
1 8 ^ (-1)"+1п
xsm2x = —|— > ——т: cos4nx
п — \
Ап2 — 1
Г 7Г 7Г "I
имеет местб во всех точках отрезка ^ J
Поскольку аргументы всех функций системы {<р\1\х)}
кратны аргументу — второй и третьей функции этой систе-
п| 1 w . *х
мы, то минимальныи период 2/ функции sin — и cos — явля¬
ется и минимальным общим периодом всех функций системы
{^•^(ж)}. Поэтому, если функция / имеет период Т = 21 и
/ € R2[—/,/], то при отсутствии других условий естественно
рассматривать разложение / в ряд Фурье по системе
на отрезке [—/;/]. Как следует из результата задачи 10 гл. И
§ 5 коэффициенты ряда
оо
/ гч а0 V' / п7ГХ I П1ГХ\
°д/) = у + 2Да"cos ~j~ + n sin
* '
*) Для непрерывных и четных на [-/; /] функций 2/-периодическое про¬
должение с [-/;/) всегда непрерывно на всей числовой прямой.
633
не зависят от того, является ли Т = 21 минимальным пери¬
одом функции или нет, т. е. этот ряд есть ряд Фурье функ¬
ции / по любой системе
/ (m/)i f, • ПХ WX 2пх <llZX \ г- тм
>= 75r'c“-ST"-j' m£N
Поэтому, если Т = 21 — минимальный период функции / Е Я2
и в условии задачи не указан отрезок, на котором ищется
разложение / в тригонометрический ряд Фурье, то это раз¬
ложение производится по системе на отрезке [—/;/].
Если же отрезок [—а; а] (или [0;2а]) указан, то необходи¬
мо различать два варианта. Первый — 2а пс является крат¬
ным Т — в таком случае разложение производится согласно
общему правилу по системе (см. пример 5 гл. 11 § 1).
Второй вариант — 2а является кратным Т, т. е. 2а = кТ,
к 6 N. В таком случае, как указано выше, достаточно вы-
(?)
числить коэффициенты Фурье функции / по системе {<pt- '},
и полученный ряд будет одновременно и рядом Фурье по си-
стеме {^в)} =
Пример 8. Символ (х) обозначает расстояние от числа х
до ближайшего целого числа. Найти разложение функции
f(x) = (х) в тригонометрический ряд Фурье
а) на [0; 3/2],
б) на [0; 8].
Решение. Функция / имеет минимальный период 1 (см.
рис. 20, а). Поскольку длина отрезка И] , заданного в п. а),
а) Рис. 20
634
не кратна 1, то производим разложение по системе =
{, . 4пх 4тгж . 4ппх 4irnx 1 „
1, sm —, cos —,..., sm —-—, сое -у-,... У Имеем
3/2
4 f ft W 43 1
Для упрощения выкладок заметим, что функция fix) — —,
4
периодически продолженная с интервала
с периодом
Г*-, даст нечетную функцию (см. рис. 20, б, *). Следователь-
!\у
— — - — ~ —— — —-
~ 4
Рис. 20
635
но, ап = 0, n G N. Вычисляем коэффициенты Ьп:
1/2 1
4 f . 4тгпх . /V ч . 47ГПХ .
= - I х sin —-— dx + / (1 - х) sin —-— dx +
о 1/2
3/2
/, ч . 4тгпх . 1 Г 47ГПХ11/2
(х — 1) sin —-— dx = — — х cos —-— +
v ' 3 тг п[ 3 1о
1
1/2
4тгпх , v 4ТГПХ11
/4тгпх , ч
cos —-— dx — (1 — х) cos
3 11/2
о
1 3/2
/47гпх , , 4тгпх|3/2 Г 47гпх ,
cos—-—dx—(х—ljcos—-— + I cos—-—dx
О oil У о
1/2 1
1 Г 1 27ГП 3 . 27ГП 1 27ГП
= — X COS ——Ь -— sin ——|- - cos —
7гп [ 2 3 4тгп 3 2 3
3 . 4тгп 3 . 2тгп 1
— -— sin ——Ь -— sin — cos 2тгп +
4тгм 3 47гп 3 2
3 . 3 4тгп
+ Sin 2тГП — -— sin ——
4тгп 4тгп 3
3 9 2тгп
вял 4тг2п2 П 3
Так как во всех точках интервала (0; 3/2) функция / удовле¬
творяет условию признака Дини, то равенство
п \ 1 V' 3 Л 6 • 27ГГЛ •
fix) = - — > I 1 Sin —— I Si
4 " 8тгп V тгп 3 )
n=l 4 '
4тгпх
sin —-—
верно для всех х Е (0; 3/2).
В пункте 6) формально надо было производить разложе¬
ние по системе
г f4b Г, пх пх wnx ппх }
tei / = sin_4'> COS—,..., sin-^-, cos—
но так как длина отрезка [0; 8], заданного в этом пункте крат¬
на 1 — минимальному периоду /, то требуемым тригономе¬
трическим рядом будет ряд по системе = {1, sin2Trx,
636
cos 27гх, sin 47ГХ, cos 47ГЖ,..., sin 2irnx, cos 2wnx}. В силу чет¬
ности функции f(x) получаем, что Ьп = 0, п Е N, и
*
a0 = 4J f{x)dx=
О
1
а
ап = 4 I f(x) cos 27ГПХ с/х = — [
J ™\
о
— [ sin27r nxdx) =
У / 71^71
О,
2
х sin 2ж пх
COS 27ГПХ =
п = 2т,
п = 2т — 1,
тп £ N.
тг2(2га — I)2 ’
Так как функция / 1-периодическая и в каждой точке чи¬
словой оси удовлетворяет условию признака Дини, то равен¬
ство
1 2 cos(2m — 1)2тгх
= ^ (2m - I)2
т=1
верно на всей числовой оси.
Используя связь показательной и тригонометрических
функций, можно получить тригонометрический ряд Фурье
аналитической относительно cos х и sin х функции / на от¬
резке [—7г; 7г], не прибегая к интегральному вычислению коэф-
t2 + 1
фициентов. Для этого положим t = etr, тогда cosx = ———
£1
t2 ~ i
и sina: = —-—. После разложения функции / в степенной
ZI
ряд по t обратным переходом к функциям cos пх и sin пх по¬
лучается тригонометрический ряд по системе {y>i(x)}. Из
аналитичности функции / следует равномерная сходимость
этого ряда на [—7г; тг] к /, откуда в силу приведенной выше
теоремы следует, что полученный тригонометрический ряд
есть именно ряд Фурье <r(f) по системе {^(г)} функции /.
637
Пример 9. Найти разложение в тригонометрический ряд
Фурье функции /(х) = ln(l — 2gcosx + q2) (\q\ < 1).
Функция f(x) = ln(l - 2</cosx + q2) имеет минимальный
период Т = 2я\ Поскольку в условии не указан отрезок, на
котором производится разложение, то, как сказано выше, бе¬
рем отрезок [—7г; 7г] и соответствующую систему {y?j(x)}. По¬
лагая / = е*х, получаем, что
In(1 - 2q cos х + q2) = In ^1 - q =
= In ((1 - qt) (l - I)) = ln( 1 - qt) + In (l - I) .
Так как |g<| = |?e,r| = |ge-,*| = |~| = |g| < 1, то для любого
t = e,x, x G [—it; тг] , имеем равенства:
°° ЛП4П , °° „ПЛ — П
П = 1 П — 1
00 n
ln(l - qt) + In (l - I) = - £ 4-(t" + t~n).
n = l
Отсюда следует, что для любого х Е [—7г; 7г] имеем равенство
°° Яп
ln(l — 2</cosx + q2) = —2 — cosnx (\q\ < 1),
1 71
n = 1
и поскольку этот ряд сходится равномерно на [—7г; 7г], то он
есть тригонометрический ряд Фурье своей суммы. Таким
образом, разложение функции f(x) = 1п(1 — 2^cosx + q2) в
тригонометрический ряд Фурье получено.
Заметим, что из полученного разложения для любого на¬
турального п следует равенство
тг
/
irqn
1п(1 — 2*7cosx + g2)cosnxdx = (|<7| < 1).
о
Пример 10. Найти разложение в тригонометрический
IX
sin- (хф2пк).
Функция /(х) = In |sin имеет минимальный период 27т,
следовательно, разложение производится по системе {y>j(x)}
638
на [—7г; 7г]. В данном случае полученная заменой t = егх функ-
1 ~ 1 не является аналитической. Заметив, что
ция f(t) = In
2 уД
lim ln(l — 2gcosx + q2) = ln2(l — cosx) =
= In 4 -f 2 In |sin , хф2кк, к £ Z,
постараемся найти связь коэффициентов Фурье функций
fq(x) = ln(l — 2<jcosx -|- g2) и /(х) = In jsin ^ . Обозначим
для краткости ln(l — 2<7Cosx + <72) = fq(x) и In4sin2 ^ = /i(s),
^ Z
тогда /(х) = — In 2 4- -/i(x). Пусть a9f„ — коэффициенты
_ _ / ч Л 2<jrn
Фурье fg(x); как показано в примере 9, agn = .
_ ' п
Функция /i(x) £ jR2[—7г, 7г]. Если семейство fq{x) сходит¬
ся при q —> 1— к /i(x) не только поточечно на (—тг; тг) \ {О},
но и в среднем на [—7г; 7г], то в силу соотношения (1) числа
2
ап = lim aq n — являются соответствующими коэффи-
<7-41- ’ П
циентами Фурье функции /i(x) и, следовательно, ряд
_,п2-£^
" п
COS ПХ
п = 1
есть тригонометрический ряд Фурье функции f(x) = In jsin
по системе {v?i(x)}. В силу 27г-периодичности функции / и ее
дифференцируемости для всех х ф 2тгк> к £ Z, равенство
1п
XI V—ч cos пх
sin — = — In 2 — >
2 1 п
п=1
справедливо для всех х ^ 2тгk £ Z.
Для полноты решения осталось проверить, что семейство
{Д(х)} сходится при g 1— к Д(х) в среднем на [—7г; 7г],
поскольку это утверждение не следует из поточечной сходи¬
мости fq(x) при q 1— к /i(x) для х ф 2пк, к £ Z. Функция
2 1 — 2q cos х + g2
¥>(*. ?) = [/*(*) - Л(*)]2 = In2 -—
4sm f
639
непрерывна на [5; тг] х [0; 1] при любом <$, 0 < S < тг; следова¬
тельно,
1Г п
lim I <p(x,q)dx = I lim <p(x,q)dx = 0, 0 < S < it.
Я-+1-J J q-+l-
6 6
X 4. 2 3
Если cos — ^-и-<д<1,то
Z О 4
2^1— 2gcosx + g2 = (1 — gcosx)2 + g2 sin2x ^
v j 2 • 2 ® *2®
^ V Sin-* 2 008 2 ^ 81 2 ’
следовательно,
, 1 1 -2gcosz + g2
In ^ In ■ ■ ^ - In 4,
2 sin | 4 sin |
откуда получаем неравенство
Л ^ / ч , 1 ” 2g cos i + g2 2 1 f 2 ^
= 2 ^ln r~TV + ln 4
4 2 sin161
Так как функция In2 ^5 h In2 4 интегрируема на [0; тг]
2 sin4* §
в смысле несобственного интеграла, то отсюда следует, что
для любого числа е > 0 найдется такое 6> 0 < S < 7г, для
6
которого неравенство J <p(x1q)dx < ^ верно при любом д,
о
3 „ 3
*7 < д < 1. Зафиксируем такое S, найдем такое до > т> что
4 4
4
Окончательно, для g G (go; 1) в силу четности функций
640
/9(х), О ^ q < 1, и f\{x) имеем:
tr тг
J {Mx)-Mx))2dx = 2 J <p(x,q)dx =
-п О
S к
-2 J <р(х, q)dx + 2j <р(х, q) dx < | + | = е,
о в
что и показывает утверждение о сходимости в среднем На
[—тг; я*] семейства fq(x) к fi{x) при q -> 1—.
Замечание. Равенства
К 1Г
2 f 2 [
ап = — I fi(x)coe.nx dx= lim — / fq(x) cos nx dx= lim ая%пу
ТГ J q-+l- П J q-+\-
0 0
n£ N,
можно было получить и переходом к пределу под знаком ин¬
теграла, но обоснование законности такого перехода требу¬
ет рассуждений, схожих с проведенными. В данном случае
хотелось обратить внимание на связь сходимости в среднем
последовательности функций и сходимости соответствующих
коэффициентов Фурье.
V
Пусть функция / 6 Л2[— я-, ж], I f(x)dx = 0 и F(x) =
X J
= J/(tydt, х € [—тг; тг]. Тогда коэффициенты ап, ЬП} n € N,
о
ряда <r(f) и коэффициенты АПу ВП1 п G N, ряда <r(F) связаны
равенствами:
А — — В — - —
П П
оо
Так как в силу равенства Парсеваля ряд +62) сходится,
то сходится и ряд £(1^г1+|тг|)- ***
оо
J^(an сое nx + Ьп sin nx)
n=l
641
сходится к /(х) в среднем на [—тг; л*], а ряд
Ао ^ п ап . \
Ь > [ — cos пх sin пх )
2 " )
уже равномерно на [—тг; л*] сходится к F(x). Таким образом,
получаем, что ряд Фурье по системе {^>,(х)} независимо от
того, сходится он равномерно на [— 7г; тг] или нет, допускает
почленное интегрирование. Обратно, если 2тг-периодическая
функция F(x) является обобщенной первообразной функции
f{x) £ Я2[-тг, 7г], то ряд Фурье a(f) является почленно про¬
дифференцированным рядом Фурье <t(F). Так как коэффи¬
циенты Фурье функции / образуют бесконечно малую после¬
довательность, то в этом случае коэффициенты Фурье функ¬
ции F имеют порядок о ^ , п —> оо. Продолжая это рассу¬
ждение по индукции, получаем утверждение:
Если функция F Е С,ш""1[— тг; тт], т £ N, F^ £ Я2[-тг,тг]
и F(j\-ir) = F{j){ir)y О ^ j ^ m - 1, то коэффициенты ряда
Фурье <r(F) имеют порядок о , п —► оо.
Аналогичное утверждение имеет место и для любой си¬
стемы {^^(я)}-
Пример 11. Напишем тригонометрический ряд Фурье
функции f(x) = х на отрезке [—/г, я*]. В силу нечетности дан¬
ной функции получаем, что ап = 0, п = 0,1,2,..., и
х sin пх dx =
I }
I —xcosnx + I <
\ о
2 / Г f j 1 2(-l)n+1
— I —xcosnx| + I cosnxdx | = , n E N.
icn
Так как для любого х £ (—тг; тг) условие признака Дини вы¬
полнено, то равенство
„vM-l)n+l •
i = 2> sin пх
, п
П = 1
642
верно для любого х Е (—я*; я*). Непосредственно видно, что
в точках хт — (2m + 1)п, т G Z, ряд 2 V' sin пх
f(*-0) + f(-n + 0) n "=1
СХОДИТСЯ к —1 ———: = 0.
Z
X2
Функция F(x) = — является первообразной для f(x) = х
Z
на [—тг; тг]. Следовательно, как разобрано выше, ряд
Ао , 0 (~1)п
T + 2E"^“cosnx
п = 1
является рядом <r(F), равномерно сходящимся к 2я*-периоди-
ческой функции F*, совпадающей на [—я*; я*] с F. Значение
коэффициента Ао находится по общей формуле
* -2
Л 2 t* Л *
A° = *JTJx = T
о
Итак, для всех х Е [—я*; я*] имеем равенство
«.2 -я-2
п = 1
,а ж2 ~(_1)«
т=т+2£—
1Г
/
Очевидно, функция <р(х) = — — удовлетворяет условию
2 6
<р(х) dx = 0 и одной из ее первообразных является нечетная
/ х3—я*2г •
функция Ф(х) = . Следовательно, ряд 22_^“—3 sin пх
п=1
является рядом <г(Ф) (Ло = 0 в силу нечетности Ф). Так как
тг2х
к2 00 / |\п+1
ряд — У2 ein пх есть ряд а(у), где у = —, то ряд
6 . п о
п=1
00 Цп Г 7Г2П21 X3
[2—з~ j8inn*есть ряд где = у-
Функция Ф Е С°°[—тг; я*] и удовлетворяет условиям Ф(—я-) =
= Ф(тг), Ф;(—7г) = Ф'(7г); согласно вышеприведенному утверж-
643
деаию, ее коэффициенты Фурье имеют порядок о п 00
Хотя функция G также бесконечно дифференцируема на
[—ir; яг], но на концах этого отрезка принимает различные зна-
чеаия. Этим обстоятельством и объясняется, почему коэф¬
фициенты Фурье функции G имеют порядок о (—), п —> оо,
/ i \ W
а ее о I — J, п —► оо.
Непосредственно проверяется, что каждая из систем:
<Pi(x) = cos (i- 1)х,
ф*(х) = sin ix, i G N,
ортогональна на [0; 7г]. Бели функция / е Я2[0,тг], то для
функции д, совпадающей с / на (0; л*] и являющейся четным
продолжением / с (0;яг] на [—тг; 0), тригонометрический ряд
Фурье имеет вид ап cos пх.
2
Из сходимости в среднем этого ряда на [—тг; тг] к д следует,
что на [0; *г] этот ряд сходится в среднем к /, т. е.
что показывает полноту системы <pi(x) — cos(i — 1)х, « £ N,
в Я2[0, тг]. Точно так же, только используя нечетное продол¬
жение функции с (0; тг] на [—тг;0), показывается полнота си¬
стемы ф%(х) = sintx, • € N, на Я2[0,тг]. Одновременно вид¬
но, что для рядов Фурье по каждой из этих систем сохра¬
няет силу условие Дини поточечной сходимости. Коротко
задачу разложения функции в ряд Фурье по этим системам,
а также и полученных из них линейным переносом на от¬
резок [0;/], формулируют так: найти разложение функции
/ € Я2[0,/] в ряд Фурье по косинусам (синусам) кратных
углов. При этом коэффициенты искомого ряда находятся по
формулам (4) или (5) соответственно, а четное или нечетное
продолжение подразумевается.
644
Пример 12. Найти разложение функции у = 2х ~ х2 по
косинусам кратных углов на отрезке [0; 2].
По общему правилу получаем, что
верно для всех х £ (0;2). Из вышесказанного вытекает, что
сумма равномерно сходящегося на всей числовой прямой ря-
функции f(x) = 2х — х2 сначала четным продолжением на
[—2; 0), а затем периодическим с периодом 4 продолжением
на всю числовую прямую (рис. 21).
Пример 13. Найти разложение функции у = cos х по си¬
нусам кратных углов на отрезке [0; тг].
По общему правилу получаем, что для пф 1
о
2
О
2
arsm
1.
В силу условия Дини равенство
ч /I I | И
х) cos —- + / cos —— dx
.2 i
жnx I Жnx
ж nx
равна функции f*(x)} полученной из
IT
о
645
Рве. 21
1Г
= ^ J[ein(n + l)x + sin(n - l)x] dx =
о
_ 1 Гсов(п+1)х coe(n — l)xl
n +1 n — 1 J
-{■
0, n = 2*-l,
2/1 IN 4n n. *6]
я- U + l + »»-lJ “ я-(»а - 1)’ ’
2 t
b\ = — J cosx* Bine dx = 0.
_ w 8 ^ n sin 2nx
В силу условия Динн равенство сое х = — > т"3—Г веР“
тг ^ 4ni — 1
nsl
но для всех х € (0; «г); если х = пк, к 6 Z, то непосредственно
видно, что сумма полученного ряда равна
п _ сов(0 + 0) + coe(jr — 0)
2
В заключение скажем о некоторых вопросах, выходящих
за рамки курса математического анализа. Мы рассматри¬
вали представление интегрируемой с квадратом функции /
рядом Фурье по системе, состоящей из тригонометрических
функций. Справедливо утверждение, если тригонометриче-
646
<*0 ( ЯПХ , . ппх\
скии ряд — 4* 2^ ^ап с°8 ——1“ Ьп вш —J сходится к функ-
п=1
ции / £ Я2[-/,/] для всех х £ [—/;/] \ М, где М — не более
чем счетное множество, то этот ряд есть ряд 04(f) функ¬
ции /. Таким образом, на множестве кусочно гладких функ¬
ций представление функции ее рядом Фурье по системе
является единственно возможным представлением этой функ¬
ции тригонометрическим рядом. В то же время сумма сходя¬
щегося всюду на [— яг; тг] тригонометрического ряда
оо
^(агп сое пх 4* sin пх) может быть функцией не интегри-
п=1
руемой с квадратом на [—7г; яг] (и даже не входящей в класс
Я[— яг, я*]; см. задачи 22 и 23 гл. II § 5), т. е. такой ряд не явля¬
ется рядом Фурье никакой функции / £ Я2[— тг, тг]. Вопрос о
характеристике класса функций, являющихся суммами всюду
сходящихся тригонометрических рядов до сих пор не имеет
полного решения.
Как показывает результат задачи 19 гл. II § 5, даже для
непрерывных функций / ряд o(f) может расходиться в неко¬
торых точках. Более того, известны примеры непрерывных
функций /, для которых ряд o(f) расходится на множестве
мощности континуума. В то же время известно, что для всех
функций / 6 Я2[—тг, тг], в частности, для всех непрерывных
на [— тг; тг], ряд o(f) сходится к / для х 6 [—тг; тг] \ М, где М —
множество меры нуль. Но известны также примеры триго-
оо
нометрических рядов ^(arncosnx 4- /?n8innx), содержащих
п=0
отличные от нуля коэффициенты и сходящихся к нулю всю¬
ду, кроме некоторого множества меры нуль. Таким образом,
если требовать в задаче представления функции тригономе¬
трическим рядом поточечную сходимость этого ряда к дан¬
ной функции всюду или за исключением не более чем счетного
множества, то задача не имеет решения даже для некоторых
непрерывных функций. Бели же ограничиться требованием
сходимости всюду, кроме множества меры нуль, то задача
решается неоднозначно.
647
} 2. СУММИРОВАНИЕ
ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
С ПОМОЩЬЮ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Пусть ряды
j оо оо
2«о + ^2 Ят cos тх, Ят sin тх (6)
т=1 т=1
сходятся на отрезке [0; 2тг] соответственно к /(х) и д(х), кро¬
ме быть может конечного множества точек. Рассмотрим сте¬
пенной ряд с теми же коэффициентами, расположенный по
степеням комплексной переменной z:
J?o+f(7)
m= 1
На окружности \z\ = 1, т. е. при z = е,г, этот ряд сходится,
кроме, быть может, конечного множества точек. Следова¬
тельно, ряд (7) сходится всюду при \z\ < 1 и его сумма
W(z) ~ W{reiT) = + ^2 4mZn
m=1
при 0 ^ \z\ = г < 1 есть аналитическая функция. Тогда по
второй теореме Абеля, если ряд (7) сходится, то
/(х) + ig(x) = lim Wirt*) = W(eis). (8)
Найдя функцию W в явном виде и вычислив ее значение
1У(е’*), тем самым найдем и суммы рядов (6).
Пример 1. Найти сумму рядов
Е°° cos тх A sin тх
и
m=1 т= 1
Решение. Первый ряд сходится для х ф 2пят, п € Z, вто¬
рой сходится для всех х G К, Оба ряда являются рядами
Фурье для определяемых ими функций /(х) и д(х).
648
00 zm
Рассмотрим ряд ^ —. Его сумма <p(z) равна — 1п(1-г),
т=1
т. е. равна In , \z\ < 1. Следовательно,
/(х) + ig{x) = In YLeis » x € (0; 2л*)’
Поскольку
1 _ 1 _ 1 — cos x + i sin x __
1 — eix 1 — cos x — i sin x (1 — cos x)2 -f sin2 x
_ 1 sinx _ 1 . cos | _
2 % 2(1 — cos x) 2 * 2 sin |
1 / . x x\
= т sin - + : cos — =
2sin | V 2 2/
TO
1 1 i _ , X . 7Г — X
In — = — In 2 sin — -f i—-—.
1 - e'x 2 2
Таким образом,
oo
#*/ \ V—' C08 nx . _ . X /л _ x
/(*) = 2J = - In2sin —, x € (0; 2тг),
n=l ” Z
/ 4 sin nx 7Г — X . л .
я(*) = = —2~“’ * G (0;2*r).
n = l
Отметим, что для применения изложенного выше метода
обязательно надо быть уверенным в сходимости рядов (6),
чтобы определять их сумму с помощью предельного перехо¬
да (8). Одно существование предела в правой части равен¬
ства (8) еще не позволяет сделать заключение о сходимости
рядов (6). Для иллюстрации этого утверждения рассмотрим
ряды
J оо оо
- + ^ cos тх и sin mx.
m=l т—1
649
Эти ряда расходятся при 0 < х < 2л*, однако для соответ¬
ствующего ряда
оо
- + T,zm = -!--!
2 1-2 2
т—1
при стремлении точки z = retx по радиусу к точке ехх на
окружности имеем
.. 1 1 .. 1 — г cos х — ir sin х 1
lim : = lim — = =
r-*i\ — rexx 2 r-fi (1 _ rcosx)2 + r2sin x 2
_ Г / 1 — r cos x 1 \ ir sin x
r-¥ i [д 1 + r2 — 2rcos x 2 J 1 + r2 — 2r cos x
.. Г 1 — г2 isinx
= lim
r-¥ i [ 1 -f r2 — 2r cos x 1 + r2 — 2r cos x
i sin x t ctg f
= Tj \2 = ^ 2*’Г> * 6
(1-cosx)2 2
Пример 2. Найти сумму рядов
/м=f;(-ir-
n=l
И
П=1
Решение. Рассмотрим ряд
E(-1)n"1£rT- */±i-
n = l
В теории функций комплексного переменного выводится, что
сумма этого ряда равна arctg z. Функция w = tg z не прини¬
мает значений ±i (проверьте!). Применяя формулы Эйлера,
получаем, что при z ф ^к -f ^ j яг, к £ Z,
sinz 1 ezi — t~iz 1 e2zl — 1
tgZ ” cosz ” i e2i + e~iz " t e2z* + 1 ’
65(0
1 e2,i - 1
Уравнение w = т 2W ^ разрешимо относительно г:
Лгх _ 1 + »*' . _ 1 т _ 1 + «>*'
““ л • 1 •“ _ , lv П , .
1 — гсл 2t 1 — г/л
т. е. получено выражение обратной многозначной функции
Arctg w.
Если для логарифма взять его главное значение, то полу¬
чится главное значение арктангенса
arctg w = ^ In ., w ф ±i, (9)
Zt 1 XJUl
которое характеризуется тем, что его вещественная часть со¬
держится в промежутке (—7г/2, п/2). Положим в формуле (9)
w = е,х, О^х^тг, х ф —, тогда имеем
Z
1 + itxx 1 — sin x + i cos x
1 — ie,r 1 + sin x — г cos x
(1 — sinx -|- icosx)(l + sinx 4- * cosx) _ г cosx __
(1 + sinx)2 + cos2 x 1+sinx
Так как модуль этого числа равен |tg ^ ^ |, а аргумент
ТГ ТГ ТГ ТГ
равен —, если х < —, и ——, если х > —, то
Z А X А
Следовательно,
{7Г 7Г
* <г
И
5(ar) = ^ln|tg(^-|)|, 0^х^тг,г^|.
651
§ 3. ИНТЕГРАЛ ФУРЬЕ
И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Определение. Функция /(х) называется абсолютно ин¬
тегрируемой на (—oo;-foo), если /(х) интегрируема по Рима-
ну на любом отрезке [—/;/], / > 0, и существует несобствен-
+оо
ный интеграл f \m\dx.
В этом случае будем говорить, что функция /(х) при¬
надлежит на прямой ( —оо;+оо) классу Д1 и писать /(х) Е
£ Я1 (—оо, -foo)*).
Определение. Пусть /(х) € Rl{—oo,-foo). Интеграл
+ 00
J (a(A) cos Ax-f 6(A) sin Ах) с/А, |х| < оо, (10)
о
где
+ оо
а(А) = — J f(t)cos\tdt (11)
+оо
6(Л) = — У /(<) sin Xtdt, Ае[0;+оо), (12)
— оо
называется интегралом Фурье функции /(х) для любой /(х) £
е Я1(—оо, +оо).
Отметим, что оба интеграла а(А) и 6(A) существуют для
любой функции /(х) £ Л^—оо,-foo). Подставляя в (10) вы¬
ражения (11) и (12) для а(А) и 6(A), получим, что функции
/(х) G Rl( —оо, -foo) сопоставляется интеграл Фурье
4-00 +оо
/(*) ~ 1 / <fA J f(t) cos А(/ — х) dt. (13)
Аналогично определяется класс функций Я1 [О, +оо)
652
Как и в теории рядов Фурье, так и в теории интегралов
Фурье основная проблема — это указать условия на функ¬
цию /(х), при выполнении которых интеграл Фурье сходится
к /(х) или к ^[/(х+0) +/(аг-0)].
Теорема. (Признак Дини сходимости интеграла
Фурье). Пусть /(х) G/r(—оо,-foo) и в точке xoG (—оо,+оо)
существуют конечные односторонние пределы /(хо±0) =
= lim /(х). Если в точке хо выполнены условия Дини,
x-fr0iO
т. е. существует h > О, такое, что несобственные интегралы
J f(xo + u)-f(xo+0) и у f(xp-u) -f(xo-O)
О о
сходятся, то интеграл Фурье (13) для функции /(х) сходится
в точке х0 к — [/(л:0 + 0) + /(х0 - 0)].
Итак, теорема утверждает, что при выполнении условия
Дини
+оо +оо
^ J dX j f{t) cos А(/ — Xo) dt —
0
— [/(дго + 0) + /(x0 — 0)], если xo — точка разрыва
1 рода функции /(х);
/(хо), если х0 — точка непрерыв¬
ности функции /(х).
Следствие. Пусть /(х) G Я*(—оо,+оо) и кусочно непре¬
рывна на любом конечном отрезке. Пусть для любого х G
G (—oo;-foo) либо существует конечная производная, либо
существуют конечные односторонние производные. Тогда
интеграл Фурье (13) для функции /(х) сходится всюду на
( оо,-f-oo) к функции ~[У(х + 0) + /(х - 0)].
Следствие. Пусть /(х) G Я1 (—оо, +оо) и /(х) G
G С!(—оо,+оо), тогда интеграл Фурье (4) для функции /(х)
сходится к /(х) на (-оо, +оо).
653
Заметим, что для четной функции f(x) £ Я1(—оо, -foo)
•foo -foo
dt
a(A) = i / /(<) cos Xt dt = — / Л0 cos А/ i
— oo 0
-foo
6(A) = ^ J f(t) sin A< dt = 0,
— OO
следовательно, ее интеграл Фурье имеет вид
-foo -foo
f(x) ~ ^ / cos Ах dX j f(t) cos Xt dt, |x| < oo;
о 0
для нечетной функции /(x) соответственно имеем
оо -foo
f(x) ~ ^ / sm Ах dX ^ Уsm Xt dt, 1*^1 ^ оо.
(14)
(15)
(16)
Если функция /(х) определена в промежутке [0;-foo), /(х) £
£ /£*[(),-foo), то ее интеграл Фурье можно представить как
в виде (15), так и в виде (16), доопределив на луч х < 0 в
первом — четным, а во втором — нечетным образом.
Теорема. Пусть функция /(х) £ Д^—оо,-foo), /(х) £
£ С(—оо, +оо) и для любого х £ (—оо; -foo) выполнены усло¬
вия Дини, тогда
1) если функция /(х) четная, то
-foo -foo
Я*) = \ / cos Ах dX j f(t) cos Xt dt, x £ (—oo; -foo);
о о
2) если функция /(x) нечетная, то
-foo -foo
Д*) = \ / sinAxdA J f(t)s\nXtdt, x £ (—oo;-foo).
о 0
Определение. Пусть функция f(x) определена на отрез-
ке [a; 6] и Т = {a = хо < xi < ... < xm = 6} — любое раэбие-
654
ние отрезка [а; Ь]. Тогда величина \J f(x) = sup ^ |Д/*|. где
а Т к-\
Afk = f(&k) — f(xk-1), называется полной вариацией функ
ь
ции f(x) на отрезке [а; 6]. Если \J f(x) < -foo, то в этом
а
случае говорят, что функция /(х) имеет в промежутке [а; 6]
ограниченное изменение (или ограниченную вариацию).
Примером функции с ограниченным изменением может
служить любая монотонная на отрезке [а; 6] функция. Ука¬
жем, кроме того, пример непрерывной функции
{. я*
xsm —,
*
О,
, хеш-, 0 < х ^ 2,
/(*) .
х = О,
которая не является функцией с ограниченным изменением
(проверьте!).
Классы функций с ограниченным изменением:
1. Если функция /(х), заданная на промежутке [а; Ь] тако¬
ва, что этот промежуток может быть разложен на конечное
число промежутков [a*;a*+i], к = 0,1,2, 1, ао = а,
ат = 6, в каждом из которых /(х) монотонна (такая функ¬
ция называется кусочно-монотонной), то /(х) имеет на [а;Ь]
ограниченное изменение.
2. Если функция /(х) в промежутке [а; 6] удовлетворяет
условию Липшица |/(xi) — /(хг)! ^ Ь \х\— хг| (L —константа,
*1» *2 € [а; Ь])у то /(х) имеет ограниченное изменение, причем
ь
V /(*) < 1(ь - °)*
a
3. Если /(х) в промежутке [а; 6] имеет ограниченную про¬
изводную: \f'(x)\ ^ L, х Е то она имеет ограниченное
изменение.
4.. Если /(х) в промежутке [а; Ь] представима в виде инте¬
грала г
/(х) = С + f ¥>(0*.
655
где y>(t) предполагается абсолютно интегрируемой (хотя бы и
в несобственном смысле) на [а; 6], то f(x) имеет ограниченное
изменение, причем
к г
\//(*к /мои-
{
Свойства функций с ограниченным изменением:
1. Функция с ограниченным изменением ограничена.
2. Сумма, разность и произведение двух функций с огра¬
ниченным изменением на [а; 6] есть функция с ограниченным
изменением на [а; 6].
3. Если f(x) и <7(х) — функции с ограниченным измененн¬
ую)
ем на [а; 6] и |<7(х)| ^ а > 0, то и частное —-f есть функция
9\х)
с ограниченным изменением на [а; 6].
4. Если f(x) имеет ограниченное изменение на [а;Ь], то
X
для любого х Е [а; Ь] функция д(х) = \J f(t) будет монотонно
а
возрастающей функцией, ограниченной на [а; 6]; если f(x) не¬
прерывна в х = хо, то и <7(х) непрерывна в х$.
Критерий для функций с ограниченным измене¬
нием. Для того, чтобы функция /(х) имела в промежут¬
ке [а; 6] ограниченное изменение, необходимо и достаточно,
чтобы она представлялась в этом промежутке в виде разно¬
сти двух монотонно возрастающих функций.
Для функции /(х) с ограниченным изменением в проме¬
жутке [а; 6] в любой точке Хо этого промежутка существуют
конечные односторонние пределы.
Отметим, что непрерывная функция с ограниченным из¬
менением представима в виде разности двух непрерывных
возрастающих функций.
Теорема. (Признак Дирихле—Жордана сходимо¬
сти интеграла Фурье). Пусть /(х) абсолютно интегриру¬
ема на всей прямой и в некотором интервале [х0 - А;х0 + А],
А > 0, функция /(х) имеет ограниченное изменение, тогда ин-
656
теграл Фурье функции /(х) сходится в точке хо к -[/(*0+0)4-
+ /(*о - о)].
Пример 1. Найти интеграл Фурье функции
[ 1, 0 ^ х ^ 1,
/(х) = < 0, 1 < х < +оо,
[ 0, -оо < х < О
и нарисовать его график (рис. 22, а).
Решение. По определению интеграл Фурье F(x) функ¬
ции f(x) равен:
+оо
F(x) = /( а(A) cos Ах 4- 6(A) sin Ах^ dX,
о
где
-foo 1
/ 1 /* -, v .. 1/* « I sin А
а(А) = — I /(х) cos At dt = — I cos Atdl = —— ;
я J it J тгА
— oo 0
-l-oo 1
6(A) — — f f(x) sin Xt dt = — f sin А/ dt = —r(l — cos A),
тг J 1Г J wX
— oo 0
Следовательно,
+9°.
me \rein \ /1 — me W
dX
^./ > f ГсовАязшА (1 — cos A) . ,
fW = y l^r- + L^r-L”"A*
0
является искомым интегралом Фурье. Согласно общей тео¬
реме F(x) имеет график, представленный на рис. 22, б.
Пример 2. Найти интеграл Фурье функции
'«={£ “5Г1,
а) продолжив ее четным образом; б) продолжив ее нечетным
образом.
а) Если продолжение функции /(х) четное, то имеем
+ оо 1 +оо
ч 2 Г х шх f х. 2 [ cosAxsinA
F(x) = — I cosXxdX I cos Xtdt = — I dX.
657
Л»
График f(x)
а)
}\У
о 1
Рис. 22
График интеграла Фурье
функции /(х)
б)
Следовательно, в силу теоремы о сходимости интеграла Фу¬
рье имеем, что
+оо
/
сое Ах sin х
[ */2,
dx=l я/4,
I о,
я/2, при |А| < 1,
при |А| = 1,
при |А| > 1.
б) Если продолжение нечетное, то
■foo 1 -f-oo
ч 2 f - х f • -и 2 /* sinAx(l-cosА)
F(x) = — I sm Ax dA I sin At dt = — I ^ dA,
0 0 0
откуда в силу теоремы о сходимости интеграла Фурье полу¬
чаем, что
О, при |А| > 1,
+оо
/
sin Ах(1 — cosx)
ах = <
1
2’
при |А| = -1,
— 1, при - 1 < А < О,
0, при А = О,
1, при 0 < А < 1,
при А = 1.
Определение. Пусть функция /(х) определена на
(—оо;+оо) и интегрируема на любом отрезке [-/;/], / > 0.
т
Если существует ^lim j f(x) dx — А,
-т
то он называется гла-
658
+9°
вным знамением интеграла
+ 00
J f(x)dx.
В этом случае пишут:
■foo Т
v.p. J f(x)dx — ^lim J f(x)dx.
-oo -T
Заметим, что из существования несобственного интеграла
-foo -foo
I f(x)dx следует, что существует v.p. / f(x)dx и
— ОО —ОО
чения совпадают.
Однако, обратное утверждение не имеет места, например,
■foo -foo
их эна-
(1 — cosx)
интегралы J xdx, J - dx не существуют как не-
— оо —оо
собственные, но в смысле главного значения существуют и
равны нулю.
В дальнейшем будем рассматривать комплекснозначные
функции вещественного аргумента: tu(x) = u(z) + iv(x). Пре¬
дел и непрерывность таких функций определяется обычным
образом. Производная такой функции и/(х) определяется
формулой
и/(х) = и'(х) + lV(x).
Аналогично определяются интегралы: Римана, несобствен¬
ный и интеграл в смысле главного значения, например,
ь ь ь
J w(x)dx = J u(x)dx + i J v(x)dx.
a a a
Функция называется абсолютно интегрируемой, если абсо¬
лютно интегрируемы каждая из функций и(х) и v(x). Спра¬
ведливо неравенство
6 ь
J w(x)dx < J\w(x)\dx.
659
Теорема (формула Фурье для интеграла Фурье d
комплексной форме). Пусть функция f(x) абсолютно
интегрируема на (—оо;+оо), / Е (7(-оо,+оо) и для любог о
х € (—оо; +оо) выполнены условия Дини.
Тогда интеграл Фурье для функции }{х) сходится к функ¬
ции }{х) всюду и имеет место формула Фурье в комплексной
форме:
(-foo -foo \
v p-/ [ / /(<)e“,A(t'l)^]rfA| , W < ос. (17)
— oo — oo /
Заметим, что если кроме перечисленных выше условий на f(x)
функции
+оо -f-oo
I f(t) cos А(< — х) dt и J /(/) sin Л (t-x)dt, |х| < оо,
— оо —оо
абсолютно интегрируемы на ( —оо; +оо), то внешний интеграл
в (17) понимается в обычном смысле.
Преобразование Фурье
Пусть функция f(x) абсолютно интегрируема на (—оо; +оо)
и f(x) непрерывна на (—оо;+оо). Тогда, если для любого
х Е (— оо;-f оо) выполнены условия Дини, то существует не¬
собственный интеграл
+о°
Л( dt
— оо
и в силу формулы Фурье из теоремы Фурье имеем равенство
/(i)=^(vp7F(A,e'x'"
для любого х Е (—оо;+оо), где несобственный интеграл по¬
нимается в смысле главного значения.
660
Определение. Пусть /(х) абсолютно интегрируема на
(—оо; +оо), тогда функция
w, / л')е"Л‘
dt
называется преобразованием Фурье функции /(х) и обозна¬
чается F[f\ или F(\). Отметим, что хотя преобразование
Фурье определено для абсолютно интегрируемой функции, но
ее преобразование Фурье совсем не обязательно будет абсо¬
лютно интегрируемой функцией.
Пример 3. Найти преобразование Фурье функции
1*1 ^ <*.
\х\ > а.
Решение. Пусть А ф 0, тогда
-foo а
/<*>
1
— oo
e-«A* |«
л/2тг -iA |_e
sin A a
1
л/2тг
е“*Лв - e
— a
iAa
-«a
l
:-2-
sin A a
\/2fr A
Если A = 0, to
'M-vbJ “Л-
Итак,
л/] =
.^/§, л = о.
Как известно, эта функция не является абсолютно интегриру¬
емой на (—оо; +оо). Выше было отмечено, что если /(х) абсо-
661
лютно интегрируема на (—оо; +оо), непрерывна на (—оо; +оо)
и для нее выполнены условия Дини в любой точке х Е
6 (—оо; +оо), то из формулы Фурье получается формула об¬
ращения для преобразования Фурье:
^ = (v p / F(A)e‘Ax<fAj ’ lxl<°°-
Надо отчетливо понимать разницу между “формулами”
+оо
F[f]=-^= J f(t)e-iX4t, |А| < оо,
— ОО
И / +00 \
/(*) = -^= I V.p. j F(A)e'Xr d\ j , |s| < oo.
Эти “формулы” различны по существу (а не знаком минус
в показателе expz). Первая из них является не формулой, а
определением, в котором несобственный интеграл существу¬
ет в обычном смысле для f(x) Е Д^—оо, -foo), вторая - явля¬
ется формулой, которая доказывается при некоторых допол¬
нительных условиях на f(x) (например, f(x) Е С(—оо,+оо)
и удовлетворяет условию Дини) и в ней несобственный инте¬
грал понимается в смысле главного значения.
Преобразование Фурье определено для функций, задан¬
ных на всей прямой. Иногда в физических задачах исполь¬
зуют преобразование Фурье функций, заданных на [0;-foo).
Заметим, что если /(х) Е ДЧ”оо, -foo), /(х) Е С(-оо,+оо) и
/(х) удовлетворяет условию Дини для всех х Е (—оо; -foo), то
в случае четной функции /(х) имеет место формула Фурье
■foo -foo
/(*) = \ / COS \xd\ j f{t) cos Atdi, |x| <
oo,
а в случае нечетной функции /(х) имеет место формула
-foo +00
/Г) ; ; о°.
о о
-f ОО -1-00
/(*) = I J sin Ах с/A j f(t) sin Xtdt, |x| <
662
Поэтому, если непрерывная на [0; + оо) функция /(х) Е
Е Я1 [0,-foo), то ее можно непрерывно продолжить Четным
образом на (—оо;0) по закону /(—х) = /(х), а если /(0) = 0,
то и нечетным образом на (—оо; 0) по закону /(-х) - — f{x).
Тогда при выполнении еще и условий Дини имеем для одной
и той же функции формулу
о
называется косинус-преобразованием Фурье функции /(х) и
называется синус-преобразованием Фурье функции /(х) и
обозначается F9[f] либо Fs(А).
Немедленно из этих определений и теоремы Фурье по¬
лучаем формулы обращения для коси нус-преобразования и
синус-преобразования Фурье.
Теорема. Пусть /(х) £ Я^+оо), /(х) £ С^О.+оо) и для
любой точки х £ [0; -foo) выполнены условия ДиНи. Тогда
имеет место формула обращения для косинус-преобразования
Фурье:
о
о
или
о
о
Определение. Пусть /(х) Е Я^О.+оо). Функция
обозначается Fc[f] либо Fc(Л).
Определение. Пусть /(х) Е Я1^,-foo). Функция
4-гш
О
х Е [0; -foo),
о
663
и *слн /(0) = 0, то имеет место и формула обращения для
синус-преобразования Фурье:
Отметим, что если /(0) ф 0, то формула обращения для
синус-преобразования Фурье имеет место для х £ (0;+оо).
Сформулированные результаты используются для нахожде¬
ния значений определенных интегралов.
Пример 4. Найти косинус- и синус-преобразование Фу¬
рье функции /(х) = e"^r, Р > 0, х ^ 0.
Решение. Согласно определению косинус-преобразова¬
ния Фурье для функции /(х) = е~Рх имеем:
Согласно определению синус-преобразования Фурье для фун¬
кции /(х) = е~^х имеем
Таким образом, получаем значения следующих интегралов
о
о
о
Из полученных результатов следует, что
о
о
О 0,
о
о
х > 0.
Лапласа:
664
Пример 5. Рассмотрим интегральный логарифм
l,(i)
О < X < 1.
int
о
Отметим, что этот интеграл является собственным при лю¬
бом х Е (0; 1).
Положим z = еГх, х > 0, и t = e“u, тогда
-foo
X
Отсюда видно, что функция Li(x) непрерывно дифференци¬
руема на (0; 1) и функция
f(x) = Li(e”x) Е С1(0, +оо).
+оо
f du _
Поскольку при х > 1 имеем / —- < е *, а при 0 < а: < 1
1 J ие
имеем
/с/ti х
—- < |1пя|, то f(x) — Li(e“x) абсолютно интегри-
ис
х
руема на (0;+оо).
Значит, справедливы обе формулы Фурье (18) и (19).
Найдем косинус-преобразование Фурье функции
у = Li(e“*):
__ f _kxBinax . а n .
Поскольку I e dx = arctg—, a > 0 (см. пример 48
J X к
0
гл. I § 3), to
p.[ Li(e~)] =»>0.
Применяя теорему обращения, находим знамение интеграла
+оо
/arctg z я тг „
coBzxdz = — — Li(e ), х > 0.
о
Аналогичным образом, использовав синус-преобразование
Фурье, найдем знамение интеграла
+°°
Г ln(l + z2) . J
/ — -Binzxdz = -тг1л(е ), x > 0.
о
Пример 6. Найти косинус-преобразование Фурье функ-
ЦИИ у = In ^1 + ^2^
Решение. Рассмотрим косинус-преобразование Фурье
1 — е~р*
функции /(х) = , /? ^ 0. Имеем
X
+оо
р2 [ I — е~рх
Fc(А,/?) = у — I cos Axdx.
о
Для вычисления этого интеграла применим дифференциро¬
вание по 0 под знаком интеграла:
откуда
Fc(\, = l M/?2 + A2) + С’, p ф 0.
Так как Fc(А,/?) непрерывна в точке /? > 0 и при /? = 0
Fe(A,0) = 0,ToC = -y^~JnA2. Итак,
Отсюда при (3=1 находим
'Fc(A,1)= (1 + а*)'
Используя теорему обращения косинус-преобразования Фу¬
рье при А ^ 0
I +00
f(x) = J| f FC(A) cos Хх dX,
О
находим, что косинус-преобразование Фурье функции у =
равно V^/(А,1), т. е. равно \/27Г-——.
Для обоснования законности применения теоремы обращения
косинус-преобразования Фурье и теоремы дифференцирова¬
ния по параметру заметим, что функция
{1 - е~Р*
—, *#0,
-/?, X = 0,
абсолютно интегрируема на [0; +оо), непрерывна и имеет не-
+оо
прерывную производную и интеграл J е~&х cos Хх dx схо-
о
дится равномерно на множестве /? ^ е > 0. Следовательно,
дифференцирование по параметру законно для любого /? > 0.
667
Определение. Пусть ^>(х) определена на (-оо;+оо). Об¬
ратным преобразованием Фурье функции ^>(х) называется
функция
если главное значение несобственного интеграла существует.
Обратное преобразование Фурье функции у?(х) обознача¬
ется F”1^].
Заметим, что если у?(х) абсолютно интегрируема на
(—оо;+оо), то обратное преобразование Фурье существует
И -foo
(несобственный интеграл существует в обычном смысле).
Теорема обращения (для преобразования Фурье и
для обратного преобразования Фурье). Пусть f(x) £
£ Rl(—оо, +оо), /(х) ЕС(—оо, +оо) и для любого х£ (—оо; +оо)
выполнены условия Дини. Тогда имеют место равенства
Справедливы следующие свойства преобразования Фурье:
1. F[a\fi + 0:2/2] = <*i^[/i] + о2^[/2] — линейность пре¬
образования Фурье.
2. Пусть Ср — множество непрерывных на (—oo;-foo)
функций, абсолютно интегрируемых на (—оо; +оо) и удовле¬
творяющих условию Дини в любой точке х £ (—оо; +оо); то¬
гда
F[fi] = F[fi) *=> /1 = /2, U € CD, i = 1,2.
3. Пусть f(x) 6 Д^-оо.+оо), тогда
1) F(\) £ C(—00, +00);
2) lim |F(A)| = 0;
|A|—>00
— OO
668
4. Пусть f(x) € й’(-оо,+00), f'(x) € Л^-оо.+оо), тогда
F[f) = *'AF[/].
5. Пусть f(x) € Dk{-oo,+oo), 1У/(х) G Я^-оо^оо),
1/г G N, тогда
T-’[/(,)] = (»'A)'F[/], Isj/O.
6. Пусть f(z) G Dk(—oo, +00) и D1 f(x) G Д1(—oo,+oo)
для всех 1 ^ I ^ к] тогда при |A| oo
И*м-(иг)-
7. Если /(ж), f'(x) и /''(ж) абсолютно интегрируемы на
(-00; foo), то F[f] абсолютно интегрируема на (—00;-foo).
8. Если /(ж) Е С°°(-оо, *fоо) и & f(x) Е Rl{ —00, -foo) при
любом /, то
F[fM] G Я1 (-00,+00)
при любом /, причем |F[/^^]| убывает при |А| —► +оо быстрее
любой степени 777т» к Е N.
|А|
9. Пусть /(г) и xf(x) абсолютно интегрируемы на
(-00; -foo). Тогда
Ff/leCV-oo.+oo), lim |(F[/])'|=0,
|A|-»oo
причем
(ППУх = F[-ixf(x)).
10. Пусть х1 /(яг) Е R}(—00, -foo) при / = 0,1,2,.. То¬
гда
F[/]EC*(-оо,+00), lim |D'F[/]| = 0, / = 0,1,2,...,*,
|А|—too
причем
(F[/])(0 = F[(-ixYf(x)), I = 0,1,2,..., к.
669
i 4. УПРАЖНЕНИЯ
Разложить функцию /(х) в тригонометрический ряд Фу¬
рье на заданном отрезке. В примерах 3, 8, 9, 10, 11, 28, 29,
32, 34 указать функцию ^(х), к которой сходится полученный
ряд.
1) /(х) = xsinx на [—тг;тг]. 2) f(x) = xcosx на [—тг; тг].
9\ г/ \ -тг < х ^ 0, г .
3) /(*) = { на [-тг; тг].
^ОХ, U х X х ТГ,
( х, 0 < X ^
4) /(*) = \ тг 2 на [0; я-].
l*-1’ 2<х<*,
5>'<*> = {>-*, о'^Г
"•«-‘-U'l. o«fst0, н*Н;11'
7) /(х) = х2 на [—тг; тг]. 8) /(х) = х2 на [0; 2тг].
9) /(*) = х2 на [0; тг].
Iм \ Г X2, 0 < * < тг,
10) /(х) = < - „ на [—тг; тг].
' Jy ’ , -тг < х < 0, 1 J
/ 0, -тг < ж < 0, . .
= < , _ на I—тг; тг.
\х2, 0 < х < тг, 1 1
(а, |х| < Л,
= л « , ^ . на I—тг; тг .
\0, Л ^ |х| ^ тг,
И) f{x
12) fix
13) fix
14) fix
15) fix
16) f{x
■ft
-{
{7ГХ
8,nT’
o,
0 < x < Л,
Л <C x 2tt,
008 S’
на [0;2тг].
Л ф —, п е N, па [—тг; тг].
О, Л |х| ^ тг, 2"
тгх л
О < х < Л, тг г - «1
h ф —, п £ N, на [0; 2тг].
Л <С х <С 2тг, п
== sign (sin х) на [-тг; тг].
670
17) /(*)
18) /(*)
19) /(*)
20) /(*)
21) /(*)
22) /(*)
23) /(*)
24) /(*)
25) /(*)
26) /(x)
27) /(*)
28) /(*)
29) /(x)
30) /(*)
31) /(*)
32) /(*)
33) /(*)
34) f(x)
35) /(*)
■{
■I
■I
•(
О, -7Г ^ X ^ 0,
на[~тг;тг].
smx, 0 < x ^ тг,
sin ^x, 0 ^ x ^ тг,
^ ^ на [0; 2тг].
1 -I- COS -X, 7Г < X ^ 2тг,
0. \ ^ M <
;. я- Ha [-*•; 4
cosx, |x| < -,
— sinx, — тг < x < 0, r ,
л на [-тг; л- .
х, 0 ^ х ^ тг,
—х, —jt ^ х ^ 0,
j.2 на [—jr;я-].
[ —, 0 < х ^ ж,
4 Л*
=• sin5 х на [—тг; тг].
= сов4х на [—тг; тг].
= arcsin(cosx) на [—Ютг; Ютг].
= arcsin(sinx) на [6тг;20тг].
= chx на [—тг; тг].
= shx на [—тг; тг].
= sinх на
Г * *1
= cosx на — —; — .
L 2 2 J
= cosx на [0; тг].
-1, -с < х ^ 0>
на [—с; с].
1, 0 < х < с,
0, -с < х ^ 0,
* л на [-с; с].
1, 0<х<с, 1 1
- х на [—с;с].
|х, 0 < х ^ с,
■Г
■{
О, -с<««0,
: |х| на [—с; с].
671
36) f(x) = x — [x] на [0; 3]. 37) f(x) = x2 на [-1; 1].
38) /(x) = x2 на [0; 2]. 39) f(x) — с2 — x2 на [—с; с].
40) f(x) = x(c2 — x2) на [—с; с]. 41) f(x) = (с2 — х2)2 на [—с; с].
{cos х, х е |0;~] ,
/JT 1 на [0; тг].
cosх, х € ^2;7rJ ’
43) /(i) = евх, а ф 0, на [-тг; тг].
44) /(*) = cosax, а — не целое, на [—тг;тг].
45) /(х) = x2cosx на |о; .
Разложить функцию /(х) в ряд Фурье на заданном отрез¬
ке по косинусам кратных дуг.
46) /(х) = sin х на [0; тг]. 47) /(х) = х cosx на [0; 7г].
(0, 0^х^1-,
I 2 на [0; /].
2х-/, - <х^/,
49)/(х) = {1 2Л’ °^x^2h’ на [0;тг].
{ 0, 2Л < х ^ тг,
50) /(х) = ев* на [0;тг]. 51) /(х) = sin ах на [0; тг].
52) /(х) = chax на [0; тг].
Разложить функцию /(х) в ряд Фурье на заданном отрез¬
ке по синусам кратных дуг.
53) /(х) = cosх на [0; тг]. 54) /(х) = xsinx на [0; 7г].
55) /(«) =
hx
—, О^х^с,
Л с 0 < с < /, на [0;/].
(l-х), с< х ^ /,
1-с
56) /(х) = еа* на [0; тг].
57) /(х) = sin ax, a — не целое, на [0; тг].
58) /(х) = shax на [0; тг].
672
Пользуясь формулами
cosx = ^(f,X + e~'X)i sinx — Y'it%X ~
разложить в тригонометрический ряд Фурье следующую
функцию
59) у — cos2m х, т Е N.
1 — 2(7cos х + Я
6|)»=Г^Т?' WO-
62)»=, \-'т‘ „ |,|<1.
1 — 2q cos х + Я
Разложить в тригонометрический ряд Фурье следующую
неограниченную периодическую функцию
63) у = In |со8||. 64) у = In jctg ||.
б5)у=/1пуМ
66) Как следует продолжить заданную в интервале ^0; ^ не¬
прерывную функцию /(х) в интервал (—тг; 7г), чтобы ее раз¬
ложение в ряд Фурье имело вид
оо
/(х) = ^2 ап cos(2n — 1)х, —ТГ < X < тг.
п = 1
67) Как следует продолжить заданную в интервале ^0; ^ не¬
прерывную функцию /(х) в интервал (—тг; тг), чтобы ее раз¬
ложение в ряд Фурье имело вид
ОО
/(х) = ^ bn sin(2n - 1)х, —тг < х < тг.
п=1
68) Пользуясь разложением функции у = signx, —тг < х < тг,
в тригонометрический ряд Фурье, найти сумму ряда
ОО
1
} 2п — 1
П = 1
673
69) Пользуясь разложением функции у = х2 в ряд Фурье
1) по синусам кратных дуг,
2) по косинусам кратных дуг,
3) в интервале (0;2тг),
наити суммы
00 1 00 (_1\п+1
П = 1 п = 1
Г^(2п-1)2'
70) Пользуясь разложением функции f(x) = — — в триго-
нометрический ряд Фурье на промежутке (0;27г), получить
разложения
оо
v тг ^ sin(2& — 1)х
«)т = Е «_■; ■»<«<«■
4 ^ 2к — 1
fc = l
71) Найти сумму ряда, используя результат задачи 70:
*) 1 - 3 + 5 “ 7 + ' 1
Ql+l-i-Ti+h+T,-
4,11 1 1
5 + 7 11+13
72) Написать равенство Парсеваля для функции
= 1*1<а-
\0, 0 < 1*1 < п,
и, исходя из этого равенства, найти сумму ряда
оо . 2 оо 2
ч v-л sin па . v-л cos* па
а)
п=1 ” п=1
73) Исходя из разложения
, sin пх
-1 yw,J
п=1
674
и результатов, изложенных в примере 11, почленным инте¬
грированием получить разложение в тригонометрический
ряд Фурье на интервале (—тг; тг) функции
а) х2 + 2х; б) х3 + х2; в) х4.
74) Доказать справедливость равенства
£ CO(2fc- l)1** = ^('-^М»^2**-2*3). *€ [0;ж].
75) Используя разложение функций у — х и у — х2 и ряд
Фурье по косинусам кратных дуг, получить формулу
Зх2 — 67ГХ + 2тг2 ^ cos пх Г#1 Л .
- = 1^—2-, хе[0;2ж].
12
П = 1
__ TV — X Г-Л bill пх
76) Исходя из разложения —-— = 2^ » 0 < х < 2л-,
П— 1
получить формулу для — ОО < X < +оо
х — Е(х), х — нецелое,
1
х — целое,
2’
где Е(х) — целая часть числа х.
77) Исходя из разложения функции у = cosax в ряд Фурье
(см. задачу 44), получить формулу
ал--(—1)"
sin ал* an (ал-)2 — (лгп)2 ’
\ 1 1 of
а) = h 2 > Г——г=-, а не целое;
flin Л1Г Л1Г
б) j- = I + £(-1)" М- + ——
smz z " |z — л-n z + ffn
n=i u J
1 f r 1 1
B)ctgz=- + g[7-^: +
7ГП Z + Л*П ^
78) Исходя из разложений функций у = ch ax и у = sh ax в
ряд Фурье (см. задачи 26 и 27), получить формулу
Z
675
1 00
6) cth z = - + ^
2z
Z «—J Z2 + 7T2n2 *
n = l
79) Доказать формулы:
4 cos 5л: cos7x cos llx
a) cos x 1 — h
11
5Л-
7Г _ 7Г
4^!’ I-3’
7Г 2тг
3<*<y
7Г _ 27Г
~4>/f ’ x_ T’
7Г 2?r
rivr т<г«'
. sin5x sin7x sin llx
6) sin x — 1 — 77т; h
52
2^*’
6v^’
r2 ll2
о ^ X $ J,
тг 2тг
з <J:< T’
в) - sinx -f ~^-j-8innx = sinx-In2cos|x
(-1)"
n=2
ч 1 1 Г4' 1 — 1 ГП . _
r) - — - COS X -I- > —2 Г cos nx = COS X * 2 COS
Z 4 _ П 1
n=2
Найти сумму ряда.
. . . C08X cos2x cosnx
80) a) 1 + —— + —7-^— + • • • + — + •
12
1-2-... n
. sinx sin2z sinnx
6) —7— + -rz- + • • • + — +
1-2
1-2
I < n.
676
ю| H
л«ч ч cosx совЗх cos5x . sinx sin3x sin5x
”11 3! 1 5! ’ 6>~ii 3! 5!
ч . cos2x cos4x v sin2x sin4x sin6x
82) 1 2Г + —4Г ’ б)-2! «-+~V.
M).) D-.r^. «> £м>*ггт
n=2 n=2
oo oo
85) а) ^(“^"^гТГТ00801’ 6) E(_1)"^aTT8inna:-
n=2 n=2
87) *)?.
n=l
ллЧ ч COS nx Д cos nx
S8)a)S(^' 6)S(-'H-+.)-
901 Ve ir-lC08(2n- 1)x
Si (2--D2» -
4 lcos3x 1-3 cos 5x 1-3*5 cos 7x
90) .) со., + j— + __ + —— + • •
. Isin3x 1*3 sin 5x
.inz + j j h ^ g I .
cosx lcos3x 1-3 cos 5x 1-3-5 cos 7x
91) *'ТГ + 2ir + 23"M-+ ТГ + " ■
^ sinx f lsin3x t 1-3sin5x
* T2~+ 2 3 4 + 24 5-6 +
Доказать равенства.
ллЧ cos2x cos4x совбх 1 тг .
92)ТГ + ТГ + -57- + ' »<*<'
677
sinx sin3x sin5x тгх . ,
93> ^3- + -p- + -53-+ - =0<*<*-
94) S‘n^n — sin2y> — (тг — 2y>) sin2 <p —
»(»+!)
— sin cos (p- ln(4sin2 <p), 0 < x < тг.
лг.к ^ cos(2n -I- l)<p rt/ л v .
95> E ~^27^+ i~)2- = 2(* ~ 2^) 8Ш У +
П=1 ' '
-f — 2тгу> + 2y?2 — 3^ cos ip, 0 < x < тг.
cos3x cos5x cos7x тг 2 1
I Тз1Г-‘з5Т+Т75' = ?“* г~асо"' »<*<»
cos nx 1 cosx ТГ — X .
97)Е^ггт = 2 + 1 r-sm*’ 0<1<2,r-
n=2
^ sin nx (I , / . x \ \
98> X3 = sina? ( 4 ~ln (2sm 2) ) * 0<x<2n-
n=2 ' '
00 1
ч г-л Sin ПХ I r . ill
99) > —7—г гг- = т—л|тг — x — тг ch ex -f" тг cth втг* sh clx\ ,
n(n2 -I- a2) 2a2
r» = l 4 '
0 < x < тг.
(—l)n sinnx 1 (nshax x\
10°) / a , 2\ = ~2 ( TT O ) > < x <
; n(n2 + a2) a2 V2shTra 2/
n=l \ / \ /
. (—l)ncosnx _ 1 Г тг cos(x>/5) тг ch(x\/2)
“ n4 — 4 8^ уД 8т(тг>/2) \/2зЬ(тг\/2)
—тг < х < тг.
Разложив функцию /(х) в ряд Фурье, вычислить интеграл
ъ
/(х) dx. Использовать следующие разложения:
а
1 —асовЬх , , V"' „ 1 it
-— : г = 1 + > a cos nbx, a < 1;
1 - 2acos6ar + a2 ' 1 ’
П=1
О
/
678
a sin Ьх _ . . . .
; ~ = > a sin по*. а < 1;
] - 2а cos Ьх + а2 ^ ’ 1 1
П = 1
1 - а2 °°
-— j——у = 1+2 y'oncosn6i, |а|<1.
1 - 2а cos Ьх + а2 "
П = 1
п
102) J Ь(1 — 2о cos х -|- а2) dx.
о
fr
103) f cos nx ln(l — 2а cos x + a2) dx, n £ N.
J
о
it 2*
/* lnsinxdx /* si
l04> j 105)/
0
Ж
106^ / l-2acosar + a2
2*
sin mi dx
2 a cosx-ha2 ’
о
°2 dx.
— ж
+00
/* xdx sin6x
J J T+"** 1 — 2acosbx + a2 ’ 6 > °‘
0
IT 1Г
/* 1—acosx , /*
108) I -— r dx. 109) I -—
У 1 — 2a cos x + a2 J 1-
2a cos 2x -f a
о о
2* 2ir
x2 sin x dx f x cos mx dx
. f x2sin xdx f x<
J 1 — 2a cos x -I- a2 J 1—2a cosx-fa2 ’
о 0
IT IT
/* einmxsinxdx . /* In sin xdx . .
112 / 7^5 Г7' meN* 113 / 1 ’ a
у 1—2acosx+a2 J 1 —acosx
о 0
1Г
f cosmxdx * |
114) / , m £ N, a < 1.
J 1 — a cos x
m£N.
m£N.
< 1.
679
„ «I ^ * f COS тХ .
1151 / 1 — 2асо»д + ад ""SFJ, Ы<1-
— Ж
21Г
f sinmxdx ™ , ,
116) / , m £ N, а < 1.
J 1 — а cos х
о
ж
/" xsinxdx , ,
117) / , а <1.
J 1 — а cos х
о
1Г
118) Jln(l — aco8x)dx, |а| < 1.
о
ж
119) Jсовпх \п(1 — acosx)dx, |а| < 1.
о
1201 < *•
о
2ir
/* xcosmxdx , ,
121) / — , а <1, m6N-
J 1 — a cos х
о
2*
/ r2sinxdx . .
122 / Т“^7’ “ < L
j 1 — a cos х
о
ж
Г sinmx sinxdx м , ,
123 / 1 л т.» ’ "»€N, а <1.
у 1 — a cos х
о
+оо
+ f xsinbxdx , , , ,
124 / /1 д 2ui ГТ> Н<1. Ь>0.
У (1-f х2)(1 - acostx)
о
+оо
125) / /Гл. гиГ ГТ> 1«1 <1, * > О-
у (1 + х^)(1 — асозбх)
680
Найти интеграл Фурье F(x) функции /(ж). Построить
график функции F(x).
lOrtW/,!-/1* W^1' to,» ,/.» _ /«в11*.
126) /(«)- (о, W>i. 0_ w>)
130) /(X) = 3—3, «>0. 131 )/W = 3—з, а > 0.
аг + хг ' J + х2
{sinx, |х| < тг, (cosx,
" 133)/(*) = <
0, |х| > JT. [о,
134) f(x) = sign(x — а) — sign(x — 6), 6 > а.
{. . , ( 2пп
ylsinwx, |х| ^ ,
„ ,, *"» "€N
0, |х| > ,
и)
136) /(х) = е_0,,г|, а > 0.
(е—*, х>0,
137) /(х) = ■] 0, х = 0, а > 0.
1-е“, г < О,
138) /(х) = е~аМ cos0х, а > 0.
139) f(x) = e~“^sin/?x, а > 0.
140) f(x)=e~x\
141) f(x) — xe"*J.
Найти преобразование Фурье функции /(х).
■«>/<*>={£
< х < 0 U 1 < х < +оо.
1*1 ^ f.
|х|>§.
681
146) f(x) = <
i .< I,к 2, и»» я.»‘Л1:
.0, |x|>2.
(e~x cosx, x^>0,
\ 0, x<0.
150) f(x) = e-a|r|, a > 0. 151) f(x) = хе~а^, a > 0.
148) w<;:.44/(.)
152) f(x) = e 1*1 coswx.
154) f(x) = e-“3*3.
156) f(x) = e-2lr-,l.
158) f(x) =
160) /(x) --
(1+X2)2'
sin x
1 + x4
153) f(x) = e lxlsinu>x.
155) /(x) = xe~x .
157) /(*) = (2x + l)p-|r|.
x 2
359) f(x) —e~~ cosax.
i6i) /(*) =
X COSX
(1+X2)2'
Найти синус-преобразование Фурье функции /(х)
1
162) /(*) =
163) /(*) =
4х — 1, 0 <С х <С
0,
1
Х > 4
(1, О^х^а,
2’ * = “•
. 0, х > а.
т /„) = {-•
165) /(х) = 5-г.
166) fix) =х~а, 0 < a < 1.
168) Дх)=хе-*Ч
■«IW-jsrrГ ,70)/м=^ГТ-^
1711 /w = sW- ™ = srF7U -4f'
173) /(x)=max((2x-x2), 0).
0<,<*
I 0, x^n.
175) /(*) = ТГТТ2\2- 176) /(*) = 1
(1 + x2)2 a2 + jc
177) Л*) = ./.2\ Мч- 178) /(*) = 1
2 *
179) f(x) =
x(x2 + 62) x(x2 + 62)2
1 — COS X
X
sm jc
0<a<l.
Найти косинус-преобразопапие Фурье функции f(x).
181)/W-| 0j i>3/2
j"COS X, 0 ^ X ^ 7Г,
X > 7Г.
__ Jsinx, 0 ^ x ^ 7Г,
X > 7Г.
184) /(r) = 2-x. 185) /(*) =*■", 0 < а < 1.
186) /(*) = ----- , p > 0. 187) /(*) = е-Л
X
188) = 189)/(i) = '
183) /(,) = l Qi
192) /(*) = ——j
1 — X*
1 +хл'
1 v v sinx
а* + х*
X sin 7ГХ
19°) /(*) = 1аХЛ- 191> Л*) =
683
ОТВЕТЫ К ГЛАВЕ Ш
1 °°^ f—1)П
1)1 — “ cos х — 2 -Ц—— cos пх.
’ 2 ^П2-1
п—2
2) -- sin х + 2 ^ 2 i sin пх■
£ 2 ^ 1
n=0 v ' n — 1
6x, — 7Г < X < 0,
ax, 0 ^ x < 7Г,
a — b
—2—7r’ * ~ ±7r*
7Г 2 cos(4n + 2)x
' 4 " тг (2n
g{x) =
■hi (2" + »! ’
4 — тг 2 ^ cos(2n -+ l)x ^ (—l)n 1 sin n
4 тг (2n -f I)2 n
n=o v ' n—1
1 1 ^ l + 3(-l)n+1 .
1 v — зттгпх.
•I * E
2 7Г “ n
n = l
о OO
r* — , cos nx
7)т-4Е(-!Г1:
n=l
oo
4тг2 , (cos nx Trsin nx\
»)—+4Sw—H’
л/„\-/х2’ xG(°;2,r)-
g{x)~\2n\ x = 0,x = 2x.
пл x“^/cos2 nx 7rsin2nx\
T+S(—-—)
x"
9)^Г+>. -Г5 1 >$(*) = < 1
2*
2
. (—l)n"^* sin nx 8 sin(2n -j-1 )x
10)2*^ ;2^"(2„ + 1). •
n=l n=0 4 1
( x2, x G (0; тг),
g(x) = < -x2, xG(-7r,0),
( 0, X — ТГ, X = 0, X — —7Г.
l)n Jsinnx
X € (0;тг),
X = 0, Х = 7Г.
684
И) /м = *± - 2f; (-|)"~!,oos"j: -t ,£;м>" У"пт -
П = 1
4 ^ sin(2n + l)x
n — 1
П
*S (2- + 1)3 И
. 9{x) =
П = 1
0, — 7Г < * ^ 0,
_ J X2, 0 < X < 7Г,
Г2' х = ±ж-
12
13
14
15
16
17
18
19
20
21
22
23
ah
an v 2a
1- > — sin rm
тг 1' тгп
n=l
«л a r/
-—I- > —[(1 — cosnn) sinni + sm nh cos nx].
2тг тгn
cos nx.
n=l
2h cos nh
П — 1
A v f fesi
тг2 \TT2 — h2n2
fl— 1 x
4 sin(2n — l)x
7Г ^
sinn/i Л(1 + cosn/i)
sin nx H —- о— cos nx
7Г2 - h2n2
)
n = l
2n — 1
1 1
- + -sinx-^
cos 2nx.
- !)
1 2 A / 2cos(2n — 1)г sin(2n — l)x \
2 ~ n ^ \(4n — 3)(4n - 1) “ (4n-3)(4n-2)(4n- 1)) ‘
1 1
- + -cosx-^
cos2nx.
5 г-л
" ;r(4n2 — 1)
n=l 4
08 X +
-i)n+1-i\
Тг(п2-1) J
ТГ 1 1 . 2
— H sm x cos x +
+E*[(fcU^i+('1)Г‘:Л с», +!
cos nx
12 j ятИ
n=l n=l
5 5 1
- sin x — — sin 3x -f — sin 5x.
8 16 16
3 1 л 1
- + — cos 2x + - cos 4x.
8 2 8
4 sin(2n — l)x
“ 2-, тг2(2п- l)3 ’
685
м> Ес“(2” + 1,1
25»E^TTPsln(2"+i)*
п=0 4 '
J COS ПХ.
2 s^ + 2shjr^(-ir
ТГ ТГ ' 1 + П
п — 1
л . 2sh тг V—\. 4._ 1 п
2?)— £(-i)" гг^8Шпа:
п=1
28> J £ _ i sin2nx- »(*) = |
sin х, |х| <
О, 1*1 =
оо
л/чч l 4 (—l)ncos2nx , ч , , ТГ
29> " - * £ 4п2 -1 ’ = С°8Г’ W ^ 2'
П = 1
8 nsin 2пх
' тг ^
п = 1
4п2 — 1
>1 00
J 2п + 1
1 (2п+1)тгх
sm —.
п=0
оо
2 тг 2n -|-1
п=0
1 (2п + 1)тгх
sin —,
X — —с.
!0, — с < х < О,
1, 0<«<с,
2 > * = 0, * = с,
чоч 2с 'Г' (~1)п+1 • п*х
33) — > sin .
тг “' п с
П — 1
л ОО (2n + l)lTX ОО тгпх
ч с 2с ^ COS *—— C^sm2—5-
<?(*) =
^ (2n +1)2 .. ,
г»=0 ' ' п=1
'О, —с < * < О,
*, 0 ^ * < с,
С~, х = ±е.
686
(2n + \ )nx
ок\ c V44 * (2n
35)2_?1;(5гп)5е“—;
n=0 v '
1_1 Asin^mx
0. 7Г ‘ ^ n
fl = l
о,ч 1 4(-])n
37>3+i:wcos’"1'
n=1 4 7
4 cos7гпаг /2 1 \ . 1
38)q+2/I —o”l ( з~з ) smnnx .
3 ; 7Г П \7ГП nJ7Tdy I
n=l N x J
оЛч 2 o 4c2 ^ (-1)"-1 jrnx
39 + — 5Z a cos •
3 тгг ' n2 с
n=l
(—1)Л“1 . 7Г71Ж
■; Sin .
n=l
(-1)
41) +
’ 15 + JT4 ^ n<
n = ]
n— 1
7ГПХ
V n=1
[a cos nx — n sin nx]
i
sinaTT 2a . ч, ,4fl cos nx
45) 7f2~8 + y4 17 192"2 + 4 1_Л cos 4nz -
27Г ^[U(16"2-l)3 16n2 — 1/
-(
8n 128n3 + 24n\ .
(16n2 — l)2 + тг(16п2 - l)3) "
sin 4nx .
,лЧ 2 4 cos2nx
«)^-;Е5?Г7
fl = l
. 1 W 2 ^
47) 1- — cosx >
1Г J. 7Г '
4n2 + 1
7Г ' (4n2 — l)2
fl —1 v '
cos 2 nx.
•il-SE
oo тг(2п+1)л
COS ^ i 1
4 я2 n (2n+l)2 7Г2 " (4n + 2)2
n=0 v ' n=l v 7
Oi ГЛ
+ гЕ
r(4n-f2)д
687
2h [ 1 ^ /sinhn\2 \
^T\2 + ^{—)
ee* - 1 2a ^ (—l)n eeir - 1
50 ) 1- —У] гг"2 cos nx-
АТГ 7Г 'f a2 4- n2
n = l
51) Если a целое, то при a = 2m
8m cos(2n — l)x
» ^(2m)2-(2n-l)2’
при a = 2m — 1
. . 2 Г Л/Л ^cos2nx
a„(2m -l)* = -|l + 2(2™ - 1) £ (2ro_i),_(2„)1
если a не целое, то
1 — cos тга I ^ cos %nx
„„„ = |1 + 2a g al _ (2„); +
A cos(2n -1)г I
“J e2 — (2n - l)2 J
Л 1 + cos тга
-f 2a—
sh атг „ чn a
52) |-2shaTr } (-l)n-r ^ cos nx.
тга ' a2 -f n2
n=1
Л oo
8
“tjEs^rr8'”2"1'
n=l
8
54) -1 sin x - - £ 74n2-^-T)2 sin 2nx.
a=l ' '
r 4 2 hi2 1 тгпс . тг nx
55) "TTi \ z_^ “7 sln “7” sm “T“*
irzc(l — c) nl I I
v n=l
56) - ^[1 - (—l)ne’ro] -y " 2 sin raz~
тг 1' a^ +
n=l
„ 4 2 sin атг <4rlnsinnr
57 У. (-1) ~2 2-
тг " a2 — n2
f»=l
oo
__v 2shатг v^/ ,чi n
58) } (— 1) -5 r sin nx.
’ n ' a2 + n2
n — \
2m 2m“
n = l
688
60) £ gn sin пх. 61)1 + 2 ^ qn cos пх.
П=1 П=1
V'' п _„ч l)n+1 COSTJX
62) ^9 cos пх. 63)— In 2 +2^ — •
n=0 n=l ”
O V" cos(2n + !)* 2^vsin(2n + l)x
64>22_. 2„ + 1 • ,2„+1)2 •
n=0 n=0 '
66) /(-х)=/(х),/(7Г-х) = -/(х).
67) /(-x) = -/(x), /(?r - x) = /(x).
ллч 7Г xr 4 sin(2n — l)x
68) —. Указание, у = — > —J-
4 тг «' 2 n — 1
n = l
\ 71,2 *r\ 71,2 Л2
69) *> T; 6) 12; ■> T M
,, ТГ — X x^s^nnx л л v
70) Указание. —-— = ^? 0 < x < 2тг; а) в разло-
n = l
7Г — X
/I — л
жении функции t/ = —-— заменить x на 2x; б) вычесть
из разложения функции у = ——— разложение функции
тг х 2
y=4’2-
_-ч ч тг тг тг
7,) 114 ’6) г-в) т
п)») у + 4D-D”5=?£ + 4f:(-i)"=v£;
п=1 п=1
о оо оо
б) у + + 2,’£(-!)"+• ^ +
П=1 П=1
+ 12D-1Г^;
ч * 4 о 2^/ ^чп0087^
в) -тг4 + 8я- ]Г(-1)" -JJ5- + 48 £ —jpj— cos пх.
689
74) Указание. Разлагал в ряд Фурье функцию, приведенную
в правой части, при повторном интегрировании по ча¬
стям учесть, что значения ее производной в точках 0 и 7г
равны 0. о о
_ v _ _ _ :\х2 - бжх + 2тг2
75) Указание. Получив разложение функции —
на [0; тг], доказать, что обе части полученного равенства
не меняются при замене х на 2тг — х.
80) а) ecosx- cos (sinx); б) ecosx sin(sin х). Указание. Рассмо¬
треть у?(е,х), где <p(z) = е2.
81) a) sin(cosx) ch(sinx); б) cos(cos х) sh(sin х). Указание. Рас¬
смотреть tp(cos х 4 i sin х), где <p(z) = sin z и использовать
формулу sin(a + fit) = sin a ch ft -I- i cos a sh /?.
82) a) cos(cos x)-ch(sin x); 6) sin(cos x) sh(sin x). Указание.
Рассмотреть y>(cos x 4 isin x), где <p(z) = cos z и использо¬
вать формулу cos(a -I- fii) = cos a ch /3 — i sin a sh /?.
x 1 ]
83) а) (1 + cosx) In 2cos — 4 -xsinx, |x| < тг; 6) -x(l-j-cosx) —
z z z
—sin x In ^2 cos , |x| < тг. Указание. Рассмотреть <^(е|Х),
пользовать равенства
n(n 4 1) n n 4 1
n2 — 1 2 \n — 1 n 4 1 / Pa(
2 4 / X ^ • Указание. Приме-
x = кж.
)■
рассмотреть
функцию <p(z) = ln(l -h z).
X 1
85) a) sinx-In2cos — — - sinx, |x| < ж\
£ *
x 1 1
6) cosx-In2cos - — - 4 - cosx, |x| < 7Г.
X 1
2 2 4
X X
86) a) (cos x + cos 2x) In 2 cos — 4 — (sin x 4 sin 2x) - cos x;
z z
690
Указание. Рассмотреть функцию ip(z) — — In(1 + z2).
88) а) (1 — cos х) In 2 sin — — ■—■ sin x + cos x, 0 < x < 2iz\
z z
x 3 1
6) (1 — cos x) In 2 sin — -f- - cos x — -, 0 < x < 2я\
Z л z
Указание. Использовать равенства -—■ = — —;
(n — 1 )n n—1 n
(„-!)„(„+!) = iirb -; + 5VTT
функцию y?(z) = ln(l — z).
\ v ( 1 . i , \ л ТГ
89) — — -(cosx In2cosx + xsinx), 0 ^ x < —;
7Г 1 , i | ( / \ \
— — — -(cosx In 2| COSX| -f (x — 7Г) Sin x), — < X ^ 7Г.
т z z
Указание. См. пример 2 гл. II § 2 и задачу 87.
Л/ч\ Ч . COS X
90) a) arcsin —====, 0 ^ х ^ 7г;
VI + sin х
б) In (\/1 + sin х + Vsin х), 0 ^ х ^ 7г. Указание. Рас-
/ \ V' (^п ~ 3)!! z2n_1
смотреть функцию <p(z) = ^ Т^п- 2)" 2п - 1 = аГС8Ш
п = 1 '
проверить формулу
arcsin егх = arcsin SX = + i.ln(v^l + sin x + VsirTx).
л/l + sin x
Л, 4 v cos X /7Г~^ (x *r \
91) a) arcsin —===== + V2 sinx cos — И- — — cosx,
' ; Vl + sin x V2 4/
0 ^ x ^ 7г ;
6) ln(\/l -f sinx + VsirTx) — >/2sin xsin + sinx,
0 <C x ^ 7Г. Указание. Рассмотреть функцию
у>(г) = arcsin z + —(\/1 — z2 — 1) =
Г 1 г3 1 3 г5 1-3-5 z7 1
— \ Z 4- — * — *4- — • — -J- ——— • — -J- • • ■ / —
L 2 3 2 4 5 2-4-6 7 J
1 Г 1 2 1 1 4 1-1-3 6 1 1-3-5 8 I
~1{Г +2~4Z 4 2*6*+2Ш*1* + -} =
г 1 г3 1-3 г5 13 5 г7
" 1-2 + 2 3-4 + 24 5-6 + 2-4-6 7-8 + "'
102) 0 при |а| < 1, 2тг1п|а| при |а| > 1. Указание. Продиффе¬
ренцировать по а.
103) ——ап при |а| < 1, — при |а| > 1. Указание. Продиф-
п пап
ференцировать по а.
тг , 1 — а2 , , , тг , а2 - 1 . ,
104) ln~Y~ при ^ ~2аг 1фИ ^ >
Указание. Разложив функцию — г в ряд,
1 — 2а cos х + а
проинтегрировать по частям.
105) 0. 106) 2тг.
107) — -г-— при \а\ < 1, при |а| > 1. Указание.
7 2 еь - а 2а аеь - 1
« sin Ьх г •, л
Разложить в ряд по системе \ sin nbx}
1 - 2а cos Ьх + а2 1 J
и использовать значение интеграла Лапласа (см. при¬
мер 55 гл. I § 3).
108) тг при |а| < 1, 0 при |а| > 1.
2 2
109) 2(1 — а2) ПР" |а| < *’ 2(а^~—TJ ПРИ |а| > L
4тг2 4тг2 ( 1 \
110) 1 n(1 - а) при |а| < 1, In [1 ] при |а| > 1.
а а \ a J
о_2 ат 2тг2
1П) ПрИ |а| < 11 ПрИ ,а| > 1
112) ^am~l при |а| < 1, ~при |а| > 1.
тг у/l — а2
113) - у In . Указание. Положив а = sin а,
; у/ГГа2 1 + ч/ГГ^2
692
1J4
115
117
118
119
120
121
122
123
124
125
126
128
130
2 а
привести знаменатель к виду 1 — 2Acosx + А , А = tg —.
а
Восстановить а из уравнения А = -===.
1 + л/П^г
у--Т... [ f :■■■■= ) . См. указание к задаче 113.
ат
2тг 116) 0. См. указание к задаче 113.
1 — а2
2тг ( а \
— In ( 1 Н . -- 1. См. указание к задаче 113.
а V 1 + у/\ - a2 J
1 + >/ПГ^2
Tj-Jn _ указание к задаче 113.
— — ( в.) См. указание к задаче 113.
nVl + ч/П^/
2тг2
-^===. См. указание к задаче 113.
2 л-2 ( а \т
. ■■■■ . ( . (Jm. указание к заднче I \л.
V - ТТТГ^У с“' ук““ие “ “даче 113'
7Г ( а \m
— ( -з.---:-— ) . См. указание к задаче 113.
а VI + л/1 - а2/
я
... ■ . См. указания к задачам 113 и 107.
е*(1 +УГ^2)-а
7г 1 1*4- \Л — а2 + ае-6
——.. . ут -:.г . См. указания к зада-
2 у/Т^а? ] -|- — ае~ь
чам 113 и 107.
-foo -foo
2 Л sin А . 2 f 1— cos А .
— / —г—cosAxdA. 127) — / г smAxdA.
7Г J А тг J X
о о
-foo * -foo
1 /* /?cos Ax+Asin Ах 2h f 1—cosaA 4 1%
-J —dA '29)™У А*л
0 0
+QP -foo
— j e~aX cosAx dA. 131) J e”aA sin Ax dA.
693
132
134
135
136
138
139
140
142
144
145
146
147
149
694
+°° +“ Air
2 Г зтАя- . . 2 f cos^
— I - r^sinAxdA. 133)— I £TcosXxdX.
к J 1 — Хг n J \ - X2
о о
+°о
2 f sin А(х — а) — sin А(х — Ь)
*] Л "•
2Аш 7°sin^ . х J4
/ ^ sin Ах аЛ.
7Г J X1 —
о
•foo -foo
2а / cosAx 2 /" AsinAx ..
— / .2 . 2rfA. 137 - / ■■ dA.
я- у А2 + а2 )г У А'' + о
о о
•foo
7 / [(А->)2 + а2 + (А + /?)2 + а2] °OS А*dX'
о
+оо
4а/? f AsinAx
~ J [(А — /?)2 4- «2][(А + 0)2 + а2] •
О
■foo -foo
-4= f е“^~ cosXxdX. 141) ^ f Хе~ ^ sinAxrfA.
>А J 20F J
о о
v^- '">&*?-*■
1 Г2(sin 2А — sin A) 4 cos A /2 4 \ .
vsl л + ~ + {\-T>)sm\
1 ^sin2A — sin A . A cos A —sin A ^
7^1 A +* A* J
,— . 148) \/—ie'x cos 1.
V^(l + iA) V 7Г
1 2 - ЗА2 + t(4A - A3) /2 a
^ 4 + Л< ‘^VfAHa2
151) -i/f
152) л/2тг
aA
(Л2 + о2)2
1
+
1
153)
(A-w)2 + l (A + и)2 + 1
1 1
154)
|o|
156)
А\/2тте~
A2+ 4
(A-w)2 + l (A + u/)2 + 1
iA
~Ж
2\/2я-(А2 -4A+ 1)
1EC\
155)-ТГ •'
»A
158) -
‘^Exe-\
l57) (A’ + 1)S
159) e ^ chaA.
iso» -j [«*«« (V+?) (w+i)]-
,.1,^-‘,л*.-*1).
,63) 1M|
165)
/L_
V it (In'
A
In 5
'“'Уж*-’
(In2 5 +A2)'
167) y|ln(l + A2).
,69) ^ (x - щ)- w""e ab = i+Ё jnS
168) Ae 2.
170)
1
gVti’FA — 1 %/2jtA
mjib^-i).
2 *%/2
173)(1-С082Л-А sin2A)
•у/лЛ*
171)
v/2tt
thA.
695
174) -2-^-2 ^ап ^ —япла).
/
1,5>i
178) ^ (2—(2+1АЯ |) е”|И|) sign А.
179)^, 0«Л<1; iy|.
180) ■ - ^ (|1+ АГ-11-АГ).
2V2 Г (а+1) sin у
/, 2 (cos 3i
181)
Я=1; 0, А>1.
183)
185)
Ь!0~т-1) /2.^
V Я Я* V* 1-Аа
/ 2 1+совяА / 2 In 2
1 / 184) / -
v« 1-Л1 V Я to1 2+Аа
/я в1'1 /2 VP+Zt1
/ г. 186) /-In —
V 2га>совт V" *
’ Г (Л) cos у
ф.
14!
187) —= в” 4. 188) е 2.
,ад>/1/лЧИ)- *-»£•-
0<А<1; А=1; 0,А>1.
/* 1
2 008 А,
191)
192) / - cosA, 0<А<я; 0, А>я.
§ 5. ТЕОРЕТИЧЕСКИЕ ЗАДАЧИ
т
1. Занумеруем множество чисел —, 1 ^ т ^ 2я — 1,
гм П1П
q € П, и обозначим череп элемент этого множества с
номером п. Пусть /п = 1 в точке /п(я) = О
(-^i^-2^ri]U[^ + 2^;+°°) "fn{x)
(см.
на
линеи-
на на отрезках
рис. 23).
тп
2 Яп
1 ТПп
2Яп~]' 2я»
Показать, что последовательность {/п(я)} расходится в
каждой точке отрезка [0; 1], но
1
J f'*(x) dx 0, п +оо.
о
2. Пусть {^п} — ортонормированная система на [а; 6];
/ € Я^(а, 6) и Sn (я) — частичная сумма порядка п ряда Фурье
697
функции /по системе {^п}« Функция Kn(t, х) = ijjj(i)ipi(z)
называется ядром порядка п системы {фп}- 1=1
Показать, что
ь
Sn(x) = j f(t)Kn(t,x)dt.
а
3. Система Хаара состоит из следующих функций: Хо^ = 1;
Хо1} = ^ °> х ~
-1, х е
для m€Nnl^i)^2m
. т
2“, х 6
1, х G
О;*).
(И
У 2т ’ 2т / ’
xL4)(*) = 4-2^, хе(^-,^у
х ^ ^ 2т ’ 2"*) ’ г^9.1^г^2 ,
хй}(0) = х&} (2^2)- хЙ}(1) = *т (J - ^2)- в Тех Т04-
ках интервала (0; 1), где значение не определено преды-
д у щи ми условиями, это значение равно полусумме значений
на прилегающих интервалах. Проверить, что система
Хаара ортонормирована на [0; 1].
4. Пусть
Кт(*>х) = Хо0)(*)Хо0)(*) + Хо^ОХо^О*) +
+ xiI>(<)xiI)(*) + • • • + хЙ)(0хЙ)(1).
где Х^(х) — функции Хаара, определенные в задаче 3, т. е.
ядро системы Хаара соответствующего порядка. Обозначим
698
через Q квадрат [0; 1] х [0; 1]. Разделим его горизонтальны¬
ми и вертикальными прямыми на 22п равных квадратов ,
] ^ i ^ 2n, 1 ^ j2П, занумерованных первым индексом сле¬
ва направо и вторым — снизу вверх. При этом считаем, что
квадраты, не прилегающие к границе Q, открытые, а при¬
лежащие к границе Q включают соответствующий интервал
этой границы (например, квадрат Q^l включает интервал
{I<(< I- *=°} ). Таким образом, при любом фиксиро¬
ванном п каждая точка Q либо принадлежит одному из
1 ^ i <Z. 2n, 1 ^ j ^ 2П, либо лежит на общей границе двух
или четырех этих квадратов.
Показать, что
а) K^0)(t,x) = l, (t,x)e Q;
б)Kj£P(t,z) =
Ь",
I i=1
{ 0, \t, x) 6 gjj, 1 ^ i ^ 2", 1 ^ j ^ 2”, * Ф j,
а значение K„_x в точках общей границы двух или четырех
квадратов равно среднему арифметическому ее значе¬
ний на этих квадратах;
в) функция 1 ^ q ^ 2П, совпадает с функцией ^
во всех точках Q, не принадлежащих замыканию квадратов
1 ^ ^ 9» лежащих на главной диагонали Q; если
(<,х) е Q^, 1 ^ i ^ то
KP(t,x) = 2п41] (Jt- -2"; (х - -2") ;
x-v(n + l)
в тех точках, лежащих на границах квадратов Q]j , где
значение К^ не определено предыдущими условиями, это
значение равно среднему арифметическому значений К^ в
прилегающих квадратах.
699
5. Пусть / £ л (О, 1). Пользуясь результатами задач 2 и 4,
доказать, что в любой точке хо непрерывности функции / ее
ряд Фурье по системе Хаара сходится к J(xо).
Многочлен Рп(х) = ~ *2)" называется
v n!2n+1/2 rfxn
нормированным многочленом Лежандра порядка п.
6. Показать, что нормированные многочлены Лежандра
Рп(я) образуют ортонормальную систему на [-1; 1].
7. Доказать, что система нормированных многочленов
Лежандра полна на [—1; 1].
8. Обозначим через Ап множество всех многочленов Па(х)
степени п со старшим коэффициентом 1. Доказать, что
Г / n;w = (2»)!((г1("!>1)!]>
-1 -1
9. Обозначим через Вп множество всех многочленов Г1п(х)
1
степени не выше п, удовлетворяющих условию / Г12 (х) dx ^ 1.
п J
Доказать, что тахП2(0) = (0).
к=О
10. Пусть 2/-периодическая функция / £ Я2(-/,/). Для
q £ N обозначим через апд, 6пд коэффициенты Фурье функ¬
ции / по системе {<р^} и через аШ|<?, bm q — по системе
Доказать, что если т — nq, то am g = anj, 6Ш|<7 = 6пд, а если
m не кратно д, то am>g = 0, 6m q = 0; т. е. ряд <т/(/) совпадает
с рядом <Tqi(f).
11. Пусть функция /, определенная на IR, удовлетворяет
условиям: / £ Я2[—тг, 7г]; /(х + 7г) = — /(х). Показать, что
/ является 2тг-периодической, и найти, какой особенностью
обладают ее коэффициенты Фурье an, bn по системе {<£>,}.
12. Пусть / — периодическая функция / £ Я2[—тг, 7г] и а„,
6П — ее коэффициенты Фурье по системе {<р, }. Какими осо¬
бенностями обладают последовательности {an} и {6П}, если
график / симметричен
а) относительно оси OY и точки
700
б) относительно оси OY и прямой х = -~?
13. Показать, что системы {cos2nx} и {sin(2n — 1)х},
п £ N, являются полными ортогональными системами соот¬
ветственно на [0; тг] и [0; 7г/2].
14. Пусть / — 2тг-периодическая функция, / £ Л2[—тг,тг].
Функция w\(6У /) = sup I \f(x+h) — f{x)\dx называется
0^|Л|^<5-тг J
— п
интегральным модулем непрерывности /. Доказать, что
где an, 6n — коэффициенты Фурье / по системе {^»}-
15. Пусть / — 2тг-периодическая функция с ограниченным
изменением на [—7г; 7г] и V --- ее полная вариация на [—тг, тг].
Доказать, что
|вп1 < 2п> \Ь»\ ^ 2^.
где an, 6П — коэффициенты Фурье / по системе {<Pi}.
16. Доказать, что семейство функций Фп(х) = s*n ^
ограничено в совокупности на [—тг; тг]. Л=1 *
17. Пусть
ч cosnx cos(n-fl)x cos(2n — 1)х
Q(x>» = —— + ; + • • • + —S—- -
n n — I J
f cos(2n + l)x ( cos(2n -|- 2)x ( t cos3nx^
1 + 2 +■"+ ~ )■
Используя результат задачи 16, доказать, что существует та¬
кая постоянная С, что |Q(x, п)| ^ С для всех х £ [—тг; 7г] и всех
п £ N.
18. Пусть <p(x,Q) обозначает сумму любого числа пер¬
вых слагаемых тригонометрического полинома Q(x, ?i), опре¬
деленного в задаче 17. Доказать, что для любого 6 > 0
существует такое число Ms, что |<p(x,n)| ^ Ms для всех х:
S <С |х| ^ тг и всех п £ N.
2
19. Пусть Qm(x) = Q(x, 2m ), где тригонометрический по¬
лином Q(x,n) определен в задаче 17. Доказать, что функция
701
°o J
/(г) = —*Qm{z) непрерывна наМ, а ряд <т(/) расходится
т—1
при X = 0.
20. Доказать, что для любой функции / 6 Я(—тг, 7г) и всех
n Е N определены числа
ж п
а„ = — J fix) cos пх dx, bn — — J* /(x) sin nx <fx, n = 0,1,2,—
— 1T — 7Г
21. Функция / определяется на [—7г; 7г] следующими усло¬
виями:
/(*) = 3nsin4nx, ^ е , « 6 N,
/(0) = 0,
/(х) = -/(-х), х£[—7Г;0).
Показать, что
а) / Е С[е, 7г] для любого е > 0;
б) / € Л(-тг, л-); ,
в) lim 6„ = оо, где 6„ = — / /(x)sinnxdx (ср. с зада-
n—f оо 7Г J
чей 18 гл. I § 5).
оо
t ч v—> 81П ПХ .
22. Пусть /(х) = 2^ "' Показать, что / Е Я(—тг, тг),
но / £ Я2[—тг, тг]. n_1
ЛП „ ,, ч v-л sin пх ^
23. Пусть fix) = > — . Показать, что
i Inn
г»=2
/ Е С([-тг; тг]\[-е;г])
при любом е>0, но/е Л <— п, п).
24. Пусть / Е С[—7г; тг] и ряд a(f) сходится к функции д(х)
для всех х Е (—тг; 7г). Доказать, что /(х) = д(х) для всех
х Е (-тг;тг).
25. Пусть 2тг-периодическая функция / Е С[-тг;тг] и а„,
6„ — ее коэффициенты Фурье по системе {у?,}. Доказать, что
ап = о ,bn=o , п -> оо, то <т(/) =£ / на [-тг; тг].
если
702
ОТВЕТЫ, РЕШЕНИЯ, УКАЗАНИЯ
1. Решение. Из определения /п(х) получаем, что
1
о ^ J ft(x)dx ^
О
и так как q„ —> +00 при п —> оо, то, следовательно,
]
lim / f2(x) dx = 0.
n—foo ^
О
и, следователь-
Пусть хо € [0; 1]. С одной стороны, существует такая под¬
последовательность rij | -foo, что /пДхо) = 0; а с другой
стороны, существует такая бесконечная последовательность
ж , ^ Гшп. 1 ™П1 1
nit+00, нтохоб [^--^7 + 2^
но, /п,(хо) ^ откуда и следует расходимость последова¬
тельности {/п(я)Ь
4. Указание. Пункт а) проверяется непосредственно.
Пункт б) доказывается по индукции. Для доказательства
пункта в) воспользоваться равенством
A^)(<,x) = ^2_7‘)(t,x) + f;x'i)(<)xli)W, 1 0<2".
«=1
5. Решение. Пусть хо G (0; 1) и не является двоично раци¬
ональным числом. Тогда, применяя результаты задач 2 и 4,
получаем, что
1
&Ч*о) = [ /№%Ч*,*о)А = -i_ f f(t)dt, (*)
о ' m
1 тп
где I$ есть интервал длины или . Если же хо €
Z Z
£ [0; 1] -- двоично рациональное число, то либо K$(t,x0)
равно 2m+1, 2m или 2т-1 на интервале включающем хо, и
703
ДЛЕНЫ ^тг, ^ ИЛИ -Aj- соответственно; либо h х0) =
на ин-
= '2т на интервале /$ = ^хо - —^; х0^ и 2т 1
тервале Jm = (*о\хо+ В первом случае для
справедлива формула (*), а во втором — равенство
/&> W
(см. рис. 24). В силу непрерывности / в обоих случаях имеем
704
равенство
lim S$ (аг0) = /(x0).
TTl—foo
6. Решение. Интегрируя п раз по частям, получаем ра¬
венство
1
J Pn(x)Pm(x)dx =
-1
=^^^(D-ir4(i-*a)"](n-,)-[(i-*an(m+,-I)+
i 4
+ (-!)" J(1 - X2)n[(l - *»)•»]<"»+«> dx).
-1
Так как —1 и 1 — корни порядка п многочлена (1 — х2)п, то
отсюда получаем, что
1 1
J Pn(*)Pm(x)dx = t£^+p. J (l-s2)n[(l-*2)m](m+,,)<fx.
-1 -1
Если т < п, то степень многочлена (1—х2)т меньше, чем m+n,
и следовательно,
1
j Рп(х)Рт(х) dx = 0.
-1
Если т = п, то поскольку старший коэффициент многочлена
(1 — х2)п равен (—1)п, то
1 1
/ «(*)*= даят/(■—')’* =
-1 -1
(2 п + 1)!
(п!) s23n+iJ
__ (2»+1)! / 1\_ (2п+1)!
V 2/ 2"»!(2л + 1)!!
7. Указание. Если / € Я?[— 1,1], то для любого е > 0
существует тригонометрический полином
т
Тт(х) = -j- + СОВ Я71Х + Ьп sin тг пх),
f/ = l
705
приближающий / в среднем с погрешностью не больше, чем
а тригонометрический полином на [ — 1; 1 ] равномерно при¬
ближается алгебраическим многочленом с погрешностью не
больше, чем
8. Решение. Представим многочлен Пп(х) Е Ап в ви-
п
де Пп(х) = атРт(х)- Так как степень многочлена Рт(х)
т=О
равна т, старший коэффициент П„(х) равен 1, а в Рп(х) стар-
- ^ (—1)п(2п + 1)!! 1 D
шии коэффициент а0 = у /о > то ап = —. В силу
(п!)22п+1/2 а0
полноты системы {Р,(х)} справедливо равенство Парсеваля:
/ = Л + 53
_] ^ ТП — О
1
откуда видно, что интеграл / II* dx принимает минималь-
[ I^(x)dxr
-1 П-1
ное значение на множестве А, если °т = 0, т. е.
П„(г) = -Рп{х).
ао
9. Решение. Представим многочлен Пп(х) Е В в виде
п
Пп(х) = ^ ^ PmPт(^)- В силу неравенства Коши—Буня-
т=0 n п
ковского имеем: п’(0) < £ ^ РД(0). Так как систе-
т—0 т=0
ма {Pi} полна, то, используя равенство Парсеваля и условие
)
П„ G В, получаем, что 1 = / П^(х) dx = ^ Рт> откуда сле-
-1 "*=0
дует, что П2(0) ^ Е РД(0) для всех Пп(х) С В. В то же вре-
т=О
МЯ ДЛЯ многочлена П}/2(х) = ^т(О)} • ^ Рт(0)Рт(х)
706
ft 1/2
справедливы соотношения ПД С В, (II* )2(0) = Лп(0)^ ,
т=0
что и завершает доказательство.
10. Указание. Равенства amq = anj, 6m><7 = 6П|1 для
m — nq проверяются непосредственно, а равенство нулю всех
остальных коэффициентов следует из равенства Парсеваля.
11. а2п-\ = ^2n—1 = 0, п £ N.
12. а) 6П = 0, а2п = 0, л £ N; б) = 0, a2n-i = 0, п £ N.
13. Указание. Продлить функцию / с отрезка [0; тг] или
[0; 7г/2] на [—7г; п) таким образом, чтобы в ряде <r(f) коэф¬
фициенты при функциях, не входящих в рассматриваемые
системы, равнялись нулю (ср. с задачей 12), и использовать
полноту системы {у>,} на [—тг;тг].
14. Указание. В интеграле, определяющем ап и 6П, сделать
тг
замену t — х —.
п
15. Указание. Проверить, что неравенство
dx
— tr
< пх < nxX < 1.
справедливо для любого к £ Z, и сложить эти неравенства для
к = 1,2..., 2п. То же самое рассуждение проводится для 6П.
16. Решение. Пр любом п £ N функция Фп(х) нечет¬
ная, поэтому достаточно доказать ограниченность в сово¬
купности семейства Фп(я) на (0; тг]. Для х £ (0; 7г] положим
nr = J. Если п ^ пх, то
к = 1
Если п > пх, то представим Фп(х) в виде
_ , ч sin кх sin kx
ф„м=£ — + E —
kzzl k=nx + l
Первое слагаемое, как и выше, по абсолютной величине не
превосходит 1. Второе слагаемое преобразуем:
sin кх Вп (1 1 ^ ВПх
.4, *U"*+Tj_iCTT'
/с=пх+1 fc=nx+l
707
^ . cos I - cos (m + i) I
где Bm = 2_^ sin fcx = -——— — (проверьте). Сле-
fc=1 S111 2
довательно,
I чАч sin kx I 2 1 2тг
> —-— < — < 2тг,
I ^ A: I nx + 1 sm § x(nr + 1)
fc=flx + l * ' '
и окончательно,
|Ф„(х)| ^ 1 + 2ж.
17. Указание. Получить равенство
r\t \ о • f sin тх
У(х, п) = 2sin пх- > .
т=1
18. Указание. К сумме членов y>(x,Q) с положительными
коэффициентами и к сумме членов с отрицательными коэф¬
фициентами (если они присутствуют) применить преобразо-
I N 1
вание Абеля и оценку ^^совпх ^ — — (см. решение
п=1 |sinx/ |
задачи N 16).
19. Указание. Показать, что ряд, полученный раскрытием
00 1
скобок в ряде —j(Qm(x)), есть <r(f) и этот ряд при х = О
ТП= 1
не удовлетворяет критерию Коши.
21. Указание. При m = 4n, п £ N, имеем:
,»-i
6m = ^ J /(х) sin 4nx dx = ^ ^ ^ 3n J sin4nxsin4/cx с/х +
О * = 1 тг/2*
2п—1
+ 3n j sin2 4nxdx + ^ 3n I sin4nxsin4*xdx +
*/2» *=» + * ir/2k
оо
+ 3n I sin4nxsin4*xdxY
le—On . . '
к~2п ir/2*
708
Показать, что первое и третье слагаемые равны нулю, че¬
твертое является бесконечно малым, а второе — бесконечно
большим при п —У -foo.
^ 8*п 11 х
22. Решение. Ряд у, —7=^“ сходится равномерно на ка-
П = 1 ^
ждом из отрезков [2kw -f е;2(к -f 1)тг — е], к £ Z, при любом
. . ^ cos пх _
е € (0; 7г). Ряд > ■=- сходится равномерно на R, сле-
, nvn
n = l v оо
. r-^ COS ПХ
довательно, функция .г (х) = — > -=• непрерывна на IR
П=1 ^ ж
и F'(x) = /(ж) для всех х ^ 2тгАг, к £ Z. Тогда J f(x)dx =
с
= F(n) — F(e) для любого е £ (0; тг), и в силу непрерывности F
ж
существует linri^ J f(x) dx = F(tt) — F(e). Так как функция f
с
нечетна, то отсюда следует, что / £ Я(—тг, тг). Посколь-
оо
ECOS ПХ
7=- сходится равномерно, то этот ряд есть
»=1
<t(F). Из равенства F'(x) = /(г), х ^ 2жЛ, следует, что если
ОО
. . г—> Sin ПХ
/ Е Я (—тг; тг), то ряд > —j=- есть <т(/), что противоречит
, л/П
n=l v оо / j ч 2
равенству Парсеваля, так как ряд ( —■= ) расходится.
00
_ _ _ тл Sin nx
23. Решение. Ряд 2^ “j сходится равномерно на ка-
п—2
ждом из отрезков [2тгА: + е\ 2тг(к + 1) — е] при любом е £ (0; тг).
оо
_ г-' COS ПХ
Ряд > —- также сходится равномерно на каждом та-
1 п in п
п=2 оо
Г-Л COS ПХ
ком отрезке. Следовательно, функция F(x) = — > —:
' n In п
п=2
на каждом интервале (2тг*;2(Аг + 1)тг), к £ Z, является пер-
. _ sin пх
вообразнои функции /. Ряд — > —гг сходится равномер-
; п-* In п
п=2
709
но на М, следовательно, его сумма Ф(х) непрерывна на Ш и
этот ряд есть о'(Ф). Функция F непрерывна на множестве
М = [—7г; тг] \ {0}, и Ф'(х) = F(x) для всех х Е М. Пред¬
положим, что lim F(x) = Л. Так как функция F четна,
г-+0+
то в таком случае lim F(x) = Л, функция F ограничена на
г->0—
г 1 cos пх /
[—тг; 7TJ и ряд — у —: есть <r(F). В таком случае в силу
п In п j п ^
теоремы Фейера последовательность <тп = > *9т, где
т 1 71 + т—2
Sm = должна сходится к —Л, а так как 7im Sm =
' Af In А: т-юо
/с=2
= + оо, то и lim <гп = +оо. Полученное противоречие
п—►+оо
показывает, что функция F не имеет предела при х —У 0+,
к
а так как J f(x) dx = F(tt) — F(e) для любого е Е (0; тг), то
е
тг
интеграл I f(x)dx расходится. В силу нечетности / отсюда
о
следует, что / Е Я(—тг, тг).
24. Решение. Пусть
•SoW = у, 5„(х) = у + ^(amcosmx + 6msinmx)
m=l
*n(*) — п _|_ I ^m(X)’
m=0
В силу теоремы Фейера lim <тп(х) = f(x) для всех х Е (—тг; тг).
п —► оо
Так как из равенства lim Sn(x) = <7(х), х Е (—тг;тг), следует,
п —► оо
что lim <гп(х) = у(х), х Е (—тг; тг), то /(х) = д(х) на (—тг; тг).
п—* оо
25. Решение. Пусть
So(z) = у, 5„(Х) = у + (am cos mx + 6m sin mx)
2
710
В силу теоремы Фейера lim сгп(т) = f(x) для всех х£ (—7г; 7г).
П-ЮО _
] “Л
Из равенства Sn(x) — <тп(х) = —-j-y ^ m(am cos mx-f-6m sin mar)
m=l
1 П
получаем, что 0 ^ |5„(х) - <г„(х)| ^ m[|am| + |6m|],
п + I “
m=l
откуда в силу условия ат — о ( — ). Ьт = о ( — ), тп —> оо,
\mj‘ \тп)
следует, что lim (^(х) — <т(х)) = 0. Отсюда получаем, что
П —► ОО
lim Sn(x) = lim <тп(х) = /(х) для всех х £ (—7г; тг).
ОГЛАВЛЕНИЕ
Предисловие
Глава I. Ряды я бесконечные произведения
§ 1. Числовые рады ...
§ 2. Бесконечные произведения
§ 3. Функциональные последовательности и ряды. Равномерная схо¬
димость ♦
§ 4. Степенные ряды. Разложение функции в степенной ряд . . . .
§ 5. Повторные и двойные ряды
§ 6. Упражнения
1. Числовые ряды
2. Бесконечные произведения
3. Функциональные последовательности и ряды. Равномерная
сходимость
4. Степенные ряды ...
5. Двойные ряды ... .... . . .
Ответы к главе I . . .
§ 7. Теоретические задачи
Ответы, решения, указания
Глава П. Несобственшй интеграл ■ интегралы с параметром
§ 1. Несобственный интеграл
§ 2. Собственный интеграл, зависящий от параметра
§ 3. Несобственный интеграл, зависящий от параметра
§ 4. Упражнения
Ответы к главе II
§ 5. Теоретические задачи
Ответы, решетя, указания
Глава Ш. Ряды Фурье. Преобразование Фурье
§ 1. Ряды Фурье
§ 2. Суммирование тригонометрических рядов с помощью аналити¬
ческих функций комплексного переменного
§ 3. Интеграл Фурье и преобразование Фурье
§ 4. Упражнения ....
Ответы к главе III ...
§ 5. Теоретические задачи
Ответы, решения, указания
3
4
59
74
100
164
191
Ч
219
223
243
265
268
312
338
369
402
407
477
545
569
586
615
648
652
670
684
697
703