Автор: Гартман Т.Н. Клушин Д.В.
Теги: информационные технологии вычислительная техника обработка данных химическая технология химическая промышленность микропроцессоры химические производства компьютерные технологии
ISBN: 5-94628-268-9
Год: 2006
TH ГАРТМАН, Д& KMWH!
основы
КОМПЬЮТЕРНОГО
МОДЕЛИРОВАНИЯ
хиглико-технологичосхих
процессов
УЧНМОГ ЛООО*Ч£ ДЛЯ ЖУЭОв
УДК 004+66.0
ББК 32.97-В6+35
Г20
Рецензенты:
доктор технических наук, профессор А.Э. Софиев
доктор технических наук, профессор В.Ф. Корнюшко
Гартман Т.Н.
Основы компьютерного моделирования химико-технологических про-
цессов : Учеб, пособие для вузов / Т.Н. Гартман, Д.В. Клушин. — М. :
ИКЦ «Академкнига», 2006. — 416 с. : ил.
ISBN 5-94628-268-9
Рассмотрены основные подходы к компьютерному моделированию химико-техно-
логических процессов (ХТП). Особое внимание уделяется изучению методологии рас-
четов и построения математических моделей типовых процессов химической техноло-
гии, их идентификации с использованием экспериментальных данных и решению за-
дач оптимизации. Это позволяет рассматривать данное учебное пособие как руководство
по созданию компьютерных моделей ХТП и их использованию для исследования, мо-
дернизации, диверсификации, оптимизации и управления процессами химической тех-
нологии специалистами, применяющими пакеты моделирующих программ ASPEN,
HYSYS, PRO-II и ChemCad.
Книга предназначена для обучения студентов химико-технологических вузов, а также
для повышения квалификации инженеров-химиков и химиков-технологов для реше-
ния задач расчетно-технологического проектирования и управления химическими про-
изводствами, может быть полезной для специалистов в области нефтехимической, га-
зоперерабатывающей промышленности, в производствах органической и неорганичес-
кой химии, использующих современные автоматизированные системы проектирования
(САПР) и системы научных исследований (АСНИ), и для инженеров химических пред-
приятий, решающих задачи автоматизированного управления технологическими про-
цессами (АСУТП), основу которых составляют статические и динамические компью-
терные модели производственных процессов.
ISBN 5-94628-268-9
© Т.Н. Гартман, Д.В. Клушин, 2006
© ИКЦ «Академкнига», 2006
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ.....................................................................И
ВВЕДЕНИЕ.......................................................................13
ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
ХИМИЧЕСКИХ ПРОИЗВОДСТВ.........................................................16
1.1. Системный анализ химико-технологических процессов......................17
1.2. Построение систем уравнений математического описания химико-
технологических процессов...................................................20
1.3. Разработка и реализация расчетных модулей и моделирующих алгоритмов
химико-технологических процессов............................................22
1.4. Идентификация математических описаний химико-технологических процессов.23
1.5. Оптимизация химико-технологических процессов...........................24
1.6. Анализ, оптимизация и синтез химических производств —
химико-технологических систем...............................................28
1.6.1. Анализ химико-технологических систем..............................29
1.6.2. Оптимизация химико-технологических систем.........................30
1.6.3. Синтез химико-технологических систем..............................30
ГЛАВА 2. ПРИНЦИПЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ХИМИКО-
ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ......................................................32
2.1. Математическое описание химико-технологических процессов с помощью
физико-химических моделей...................................................33
2.1.1. Математическое описание зоны потока, движение фазы в которой
представляется гидродинамической моделью идеального смешения.............35
Динамическая модель....................................................35
Статическая модель.....................................................38
2.1.2. Математическое описание зоны потока, движение фазы в которой
представляется гидродинамической моделью идеального вытеснения...........38
Динамическая модель......................................................39
Статическая модель.......................................................40
2.1.3. Математическое описание зоны потока, движение фазы в которой
представляется однопараметрической диффузионной моделью..................40
Динамическая модель....................................................41
Статическая модель.....................................................42
2.2. Компьютерное моделирование химико-технологических процессов с помощью
физико-химических моделей...................................................43
2.3. Компьютерное моделирование химико-технологических процессов с помощью
эмпирических моделей........................................................47
2.4. Алгоритмическое обеспечение решения задач компьютерного моделирования. 50
ГЛАВА 3. ЧИСЛЕННЫЕ МЕТОДЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ...............................................55
3.1. Анализ погрешностей приближенных вычислений............................55
3.1.1. Учет погрешностей арифметических операций.........................56
Оценка погрешностей арифметических действий............................57
Решение обратной задачи теории погрешностей............................58
3.1.2. Технический подход к учету погрешностей арифметических действий..*.... 60
3.1.3. Оценка погрешностей компьютерной арифметики.......................60
3.2. Решение систем конечных уравнений......................................63
3.2.1. Системы линейных алгебраических уравнений.........................64
Элементы матричной алгебры.............................................64
Матричные операции..................................................66
Анализ систем линейных алгебраических уравнений........................68
Анализ трех вариантов решения неоднородных систем линейных
алгебраических уравнений............................................69
Анализ двух вариантов решения однородных систем линейных
алгебраических уравнений............................................70
Обусловленность задач решения систем линейных алгебраических уравнений.73
Прямые методы решения систем линейных алгебраических уравнений.........76
4
Метод обратной матрицы......................................77
Метод Гаусса................................................78
Метод Гаусса—Жордана........................................79
Анализ прямых методов решения систем линейных алгебраических
уравнений.......................................................80
Итерационные методы решения систем линейных алгебраических
уравнений.......................................................81
Метод простых итераций......................................81
Метод Зейделя...............................................83
3.2.2. Нелинейные уравнения.......................................84
Понятие об отделении корней.....................................84
Уточнение корней................................................85
Метод половинного деления...................................86
Метод простой итерации......................................87
Метод Ньютона (касательных).................................90
Метод хорд..................................................92
Комбинированный метод.......................................94
3.2.3. Системы нелинейных уравнений...............................94
Метод простых итераций..........................................95
Метод Ньютона—Рафсона...........................................95
3.3. Интерполяция и аппроксимация функций............................98
3.3.1. Интерполяция...............................................101
Интерполяционный полином Лагранжа............................. 101
Конечные разности и их свойства............................... 103
Разделенные разности и их свойства.............................. 105
Интерполяционные многочлены Ньютона........................... 106
Погрешности интерполяционных формул............................. 109
Обратное интерполирование..................................... 109
Сплайн-интерполяция ............................................ ПО
3.3.2. Аппроксимация............................................ 112
Линейное приближение по методу наименьших квадратов............ ИЗ
Полиномиальное приближение функций............................ 114
Определение обусловленности задачи аппроксимации функций многочленом
(полиномом) произвольной степени с помощью матрицы Гильберта.. 117
Аппроксимация многочленами Чебышева........................... 119
Замечания о выборе аппроксимирующей зависимости............... 122
3.4. Приближенное дифференцирование и интегрирование................123
3.4.1. Численное дифференцирование.............................. 124
Понятие о графическом дифференцировании......................... 125
3.4.2. Численное интегрирование ................................ 125
Метод прямоугольников......................................... 127
Метод трапеций ............................................... 128
Метод парабол. Формула Симпсона............................... 129
Квадратурная формула Ньютона—Котеса........................... 131
3.4.3. Понятие о приближенном вычислении несобственных интегралов. 133
3.5. Решение систем дифференциальных уравнений..................... 133
3.5.1. Обыкновенные дифференциальные уравнения.................. 134
Постан овка задачи Коши и краевой задачи..................... 134
Явные и неявные методы численного решения................... 136
Явный метод Эйлера........................................ 137
Неявный метод Эйлера...................................... 137
Модификации явного метода Эйлера...........................138
Явный метод Рунге—Кутта................................... 140
Погрешности численных методов решения обыкновенных
дифференциальных уравнений.....................................141
Обусловленность численных методов решения обыкновенных
дифференциальных уравнений.....................................143
Численная устойчивость явного метода Эйлера................143
Численная устойчивость неявного метода Эйлера..............144
5
Обусловленность задачи решения системы обыкновенных
дифференциальных уравнений. Стационарные точки решения.
Устойчивость решений дифференциальных уравнений по Ляпунову....... 145
Определение условий устойчивости в смысле Ляпунова для двух
обыкновенных дифференциальных уравнений...................... 148
Жесткие системы обыкновенных дифференциальных уравнений......... 150
Неприемлемость явного метода Эйлера для решения жесткой системы
из-за возможной ее «раскачки» и отсутствия сходимости........ 152
Приемлемость неявного метода Эйлера для решения жестких систем
обыкновенных дифференциальных уравнений...................... 152
Решение краевых задач........................................... 153
Итерационный метод решения краевой задачи.................... 154
Решение линейной краевой задачи методом конечных разностей... 155
3.5.2. Дифференциальные уравнения в частных производных............ 156
Сущность разностного метода..................................... 158
Решение уравнений первого порядка............................... 160
Решение эллиптического уравнения ............................... 160
Решение гиперболического уравнения.............................. 162
Решение параболического уравнения............................... 163
Метод прогонки для нахождения решения неявной схемы
дифференциальных уравнений в частных производных................ 164
3.6. Оптимизация ......................................................166
3.6.1. Геометрическая интерпретация задачи оптимизации............. 167
Особые точки и овраги целевой функции........................... 169
Глобальный и локальный оптимумы................................. 170
3.6.2. Методы оптимизации, основанные на классическом математическом
анализе............................................................ 170
Необходимые условия существования экстремума функции одной
переменной...................................................... 170
Достаточные условия существования экстремума функции одной
переменной.......................................................171
Необходимые условия существования экстремума функции многих
переменных...................................................... 172
Достаточные условия существования экстремума функции многих
переменных...................................................... 172
3.6.3. Методы оптимизации для решения экстремальных задач
с ограничениями типа равенств...................................... 174
Метод неопределенных множителей Лагранжа........................ 175
3.6.4. Численные методы оптимизации без ограничений ............... 176
Прямые методы поиска экстремума функции одной переменной...... 179
Метод сканирования........................................... 179
Метод локализации экстремума................................. 180
Метод золотого сечения....................................... 181
Метод поиска с использованием чисел Фибоначчи................ 182
Метод Дэвиса, Свенна, Кемпи (ДСК) и метод Пауэлла.............183
Прямые методы поиска экстремума функции многих переменных,
не использующие производные (методы нулевого порядка) .......... 185
Метод сканирования........................................... 185
Метод поочередного изменения переменных (метод Гаусса—Зейделя). 186
Метод пробных движений....................................... 186
Поиск по деформируемому многограннику.........................187
Методы случайного поиска..................................... 188
Прямые методы поиска экстремума функции многих переменных,
использующие производные (методы первого и второго порядка)..... 189
Метод градиента.............................................. 189
Метод наискорейшего спуска................................... 190
Метод релаксаций............................................. 191
Метод Ньютона................................................ 192
3.6.5. Численные методы оптимизации при наличии ограничений........ 193
6
Методы штрафных функций........................................ 193
ГЛАВА 4. ЭМПИРИЧЕСКИЕ МОДЕЛИ. ОБРАБОТКА РЕЗУЛЬТАТОВ
ПАССИВНЫХ ЭКСПЕРИМЕНТОВ И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ.....................196
4.1. Основные понятия теории вероятностей и математической статистики.
Обработка результатов измерений одной случайной величины..............197
4.1.1. Выборочный метод............................................200
4.1.2. Оценки параметров распределения случайной величины..........203
Определение доверительного интервала для математического ожидания .... 204
Применение стандартного нормального распределения (большие объемы
выборок)....................................................207
Применение распределения Стьюдента (малые объемы выборок)....208
Метод максимума правдоподобия...................................209
Оценка параметра показательного распределения................210
Оценка параметров нормального распределения..................210
Метод моментов..................................................212
4.1.3. Проверка статистических гипотез.............................213
4.2. Обработка результатов пассивных экспериментов и построение эмпирических
моделей...............................................................213
4.2.1. Элементы корреляционного и регрессионного анализа...........214
4.2.2. Основные этапы построения эмпирических моделей..............218
4.2.3. Определение вида приближённого уравнения регрессии..........218
4.2.4. Определение параметров эмпирических моделей (коэффициентов
регрессии) для линейных моделей с одной независимой переменной.....223
4.2.5. Определение параметров эмпирических моделей (коэффициентов
регрессии) для нелинейных моделей с одной или многими независимыми
переменными...................................................... 225
4. 2.6. Определение выборочных (эмпирических) коэффициентов регрессии
для линейных по параметрам моделей при произвольном числе входных
переменных.........................................................226
Регрессионный и корреляционный анализ экспериментальных данных,
описываемых линейными и линеаризованными эмпирическими
моделями........................................................228
Определение дисперсии и ковариаций для элементов вектора наблюдений
выходной переменной у........................................230
Определение дисперсии и ковариаций для элементов вектора
коэффициентов регрессии а....................................231
Определение оценок дисперсии выходной переменной уравнения
регрессии S2....................................................233
4.2.7. Определение значимости коэффициентов регрессии..............236
Процедура исключения незначимых коэффициентов регрессии.........237
4.2.8. Проверка адекватности уравнения регрессии — адекватности эмпирической
модели ............................................................238
Оценка совместной доверительной области коэффициентов регрессии.239
4.2.9. Метод множественной корреляции для определения коэффициентов
корреляций между входными и выходной переменными процесса.
Определение коэффициентов множественной коррелляции................241
4.2.10. Метод множественной регрессии Брандона для построения нелинейных
эмпирических моделей ..............................................246
4.3. Обработка результатов активных экспериментов и оптимальное планирование
экспериментов.........................................................250
4.3.1. Полный факторный эксперимент и обработка его результатов....251
Определение кодированных коэффициентов регрессии в случае
проведения ПФЭ..................................................253
Определение значимости кодированных коэффициентов регрессии
в случае проведения ПФЭ.........................................254
Проверка адекватности уравнения регрессии в случае проведения ПФЭ .... 255
4.3.2. Ортогональный центральный композиционный план эксперимента
и обработка его результатов........................................256
Определение кодированных коэффициентов регрессии в случае
проведения ОЦКП ................................................258
7
Определение диагональных элементов информационной
и корреляционной матриц...........................................258
Определение значимости кодированных коэффициентов регрессии
в случае проведения ОЦКП.............................................260
Проверка адекватности уравнения регрессии в случае проведения
эксперимента ОЦКП....................................................260
Определение экстремума функции отклика............................260
4.3.3. Экспериментально-статистический метод оптимизации Бокса—Вильсона.261
Алгоритм движения к экстремуму.......................................262
Уточнение положения экстремума в «почти стационарной области»........265
ГЛАВА 5. ФИЗИКО-ХИМИЧЕСКИЕ МОДЕЛИ. ПОСТРОЕНИЕ МОДЕЛЕЙ.
ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И ОПТИМИЗАЦИЯ
ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ..............................................267
Общие принципы построения физико-химических моделей процессов.............268
Математическое описание процессов системами конечных нелинейных
уравнений.........................................................268
Математическое описание процессов системами с обыкновенными
дифференциальными уравнениями.....................................268
Информационные матрицы систем уравнений МО и блок-схемы
алгоритмов их решений................................................269
Информационная матрица системы конечных нелинейных уравнений...........270
Блок-схема алгоритма решения системы конечных нелинейных
уравнений.........................................................271
Информационная матрица системы с обыкновенным дифференциальным
уравнением........................................................272
Блок-схема алгоритма решения системы с обыкновенным
дифференциальным уравнением.......................................273
5.1. Математические модели движения жидкости в простых гидравлических
системах...................................................................274
5.1.1. Математические модели стационарных режимов движения жидкости
в простых гидравлических системах.......................................274
Система уравнений математического описания стационарных режимов
движения жидкости в простой гидравлической системе...................276
Построение и анализ информационной матрицы системы уравнений
математического описания стационарного режима движения жидкости
в простой гидравлической системе.....................................277
Блок-схема алгоритма расчета стационарного режима движения жидкости
в простой гидравлической системе.....................................279
5.1.2. Математические модели нестационарных режимов движения жидкости
в простых гидравлических системах.......................................280
Построение и анализ информационной матрицы системы уравнений
математического описания нестационарного режима движения жидкости
в простой гидравлической системе.....................................282
Блок-схема алгоритма расчета нестационарного режима движения жидкости
в простой гидравлической системе.....................................283
5.2. Математические модели стационарных режимов процессов теплопередачи
в поверхностных теплообменниках............................................284
5.2.1. Математическая модель стационарного режима процесса теплопередачи
в теплообменнике типа «смешение—смешение»...............................285
5.2.2. Математическая модель стационарного режима процесса теплопередачи
в теплообменнике типа «смешение—вытеснение».............................289
5.2.3. Математическая модель стационарного режима процесса теплопередачи
в прямоточном теплообменнике типа «труба в трубе» (решение задачи Коши) 292
5.2.4. Математическая модель стационарного режима процесса теплопередачи
в противоточном теплообменнике типа «труба в трубе» (решение краевой задачи).294
5.3. Математические модели химических превращений в реакторах..............297
5.3.1. Микрокинетика сложной химической реакции.........................300
Выбор ключевых компонентов химической реакции........................302
5.3.2. Математическая модель стационарного режима политропического процесса
в реакторе с мешалкой и рубашкой (произвольная кинетическая схема
химической реакции).....................................................304
8
5.3.3. Математическая модель нестационарного режима политропического
процесса в реакторе с мешалкой и рубашкой (произвольная кинетическая
схема химической реакции)............................................307
Преобразование системы уравнений математического описания
нестационарного режима процесса в реакторе с мешалкой и рубашкой
с целью её решения................................................308
5.3.4. Устойчивость тепловых режимов политропических реакторов с мешалкой ..311
Оценка тепловой устойчивости динамического режима политропического
реактора с мешалкой и с экзотермической реакцией первого порядка.....312
Оценка тепловой устойчивости стационарного режима политропического
Й актора с мешалкой и с экзотермической реакцией первого порядка.314
нтерпретация физического смысла тепловой устойчивости стационарного
режима политропического реактора с мешалкой, в котором протекает
экзотермическая реакция первого порядка...........................315
5.3.5. Математическая модель стационарного режима политропического процесса
в трубчатом реакторе с прямоточным и противоточным режимами движения
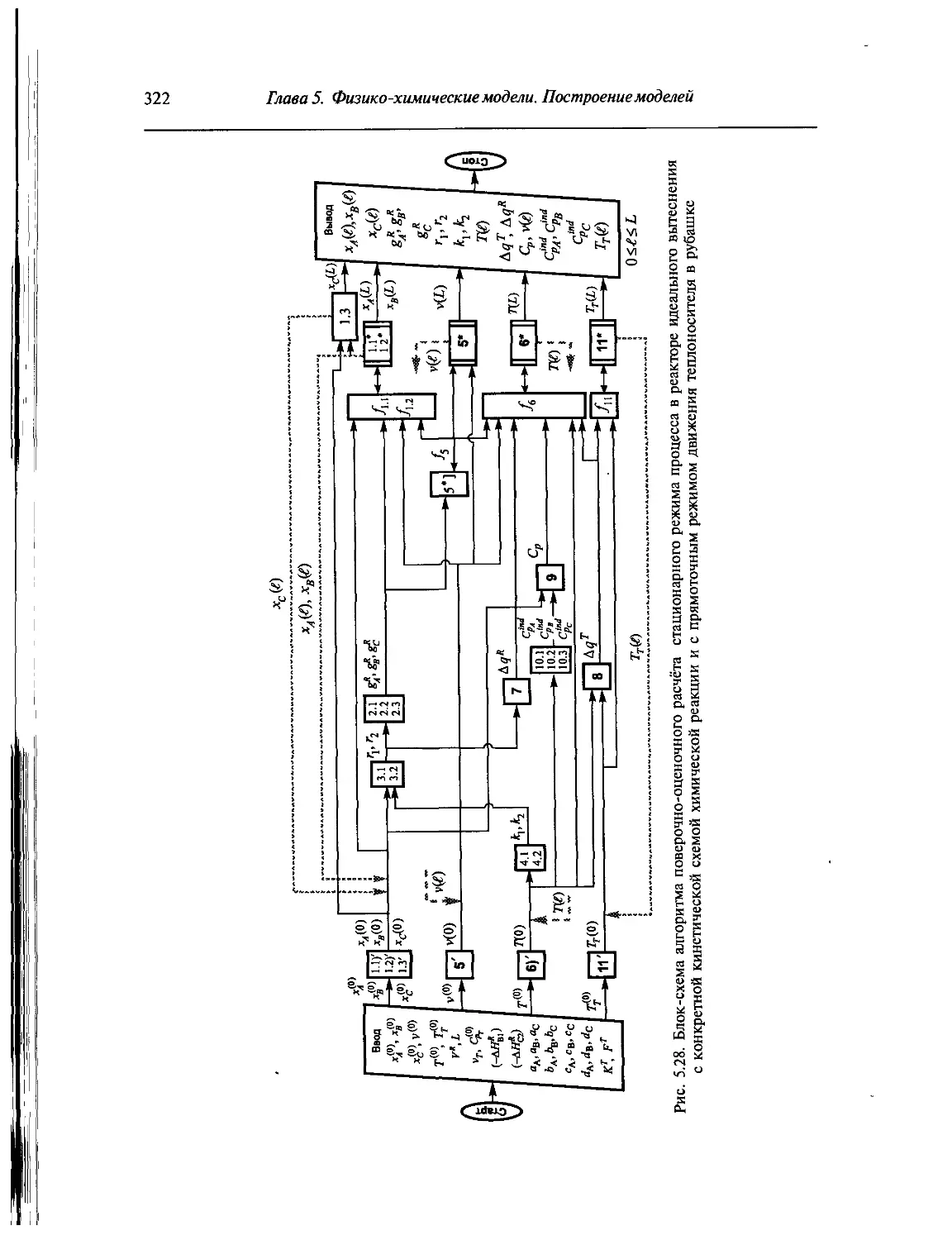
теплоносителей в рубашке (конкретная кинетическая схема химической реакции).317
Описание микрокинетики процесса в реакторе........................318
Построение математической модели стационарного режима процесса
химического превращения в реакторе идеального вытеснения
с прямоточным движением теплоносителя (решение задачи Коши).......318
Построение математической модели стационарного режима процесса
химического превращения в реакторе идеального вытеснения
с противоточным движением теплоносителя (решение краевой задачи).323
5.3.6. Математическая модель нестационарного режима процесса химического
превращения с простейшей кинетической схемой реакции в изотермическом
трубчатом реакторе..................................................326
5.4. Математические модели процессов разделения: ректификации и абсорбции.. 330
5.4.1. Математическая модель процесса непрерывной многокомпонентной
ректификации в тарельчатой колонне..................................332
Математическая модель фазового равновесия жидкость—пар...........333
Математическая модель процесса многокомпонентной массопередачи
на тарелке..................................................... 335
Математическая модель стационарного режима процесса в колонне...339
5.4.2. Математическая модель процесса непрерывной многокомпонентной
ректификации в насадочной колонне...................................344
Математическое описание процесса в насадочной секции колонны....345
Математическое описание процесса в кипятильнике..................346
Математическое описание процесса в полном конденсаторе...........346
Математическое описание условий сопряжения между секциями
насадочной колонны...............................................347
Разработка модели процесса в насадочной ректификационной колонне ... 347
5.4.3. Математическая модель процесса многокомпонентной абсорбции
в насадочной колонне................................................353
Математическое описание процесса в насадочной секции колонны....354
Разработка модели процесса в насадочной абсорбционной колонне...357
5.5. Идентификация и оптимизация химико-технологических процессов.....360
5.5.1. Решение задачи идентификации математического описания.......360
Общая стратегия решения задачи идентификации в единичном аппарате .. 363
Статистический подход к идентификации...........................365
5.5.2. Решение задачи оптимизации...................................366
Формулировки задачи оптимизации при использовании
для её решения математических моделей различных типов...........367
Оптимизация объектов с сосредоточенными параметрами.............369
Оптимизация объектов с распределёнными параметрами..............373
Анализ экономических критериев оптимальности............374
ГЛАВА 6. ПАКЕТЫ МОДЕЛИРУЮЩИХ ПРОГРАММ...........................379
6.1. История создания пакетов моделирующих программ..........380
6.2. Принципы функционирования моделирующей программы........381
6.3. Режимы работы моделирующей программы....................384
6.4. Этапы работы моделирующей программы и основные модули, обеспечивающие
их выполнение................................................400
ЗАКЛЮЧЕНИЕ..........................................407
ПРИЛОЖЕНИЕ.......................................410
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА............................413
СОКРАЩЕНИЯ И ОБОЗНАЧЕНИЯ
АИС АОС АС АСНИ АСУ АСУП АСУТП ГВС (WAN) дек ИДЕНТ ИИ ИМ ИТ кпд ЛВС (LAN) МА мив мис мм мнк МО НЛП НУ НФЗ одм опт оцкп ПК пмп по ПФЭ САПР САР СДУЧП СКУ СЛАУ СНУ СОДУ ФЗ ФХС хтп хтс ЭВМ эс — автоматизированная информационная система — автоматизированная обучающая система — автоматизированная система — автоматизированная система научных исследований — автоматизированная система управления — автоматизированная система управления предприятием — автоматизированная система управления технологическими процессами — глобальная вычислительная сеть — Wide Area Network — метод Дэвиса, Свенна, Кемпи — идентификация — искусственный интеллект — имитационное моделирование — информационные технологии — коэффициент полезного действия — локальная вычислительная сеть — Local Area Network — моделирующий алгоритм — модель идеального вытеснения — модель идеального смешения — математическая модель, математическое моделирование — метод наименьших квадратов — математическое описание — нелинейное программирование — нелинейное уравнение — неформализованная задача — однопараметрическая диффузионная модель — оптимизация — ортогональный центральный композиционный план — персональный компьютер — пакет моделирующих программ — программное обеспечение — полный факторный эксперимент — система автоматизированного проектирования — система автоматического регулирования — система дифференциальных уравнений в частных производных — система конечных уравнений — система линейных алгебраических уравнений — система нелинейных уравнений — система обыкновенных дифференциальных уравнений — формализованная задача — физико-химическая система — химико-технологический процесс — химико-технологическая система — электронно-вычислительная машина — экспертная система
alg ВР сР D g • АН — алгоритм расчёта — Bubble Point метод расчета процесса многокомпонентной ректификации — теплоёмкость при постоянном давлении — коэффициент продольного перемешивания — суммарные интенсивности источников компонентов смеси в потоке — локальные интенсивности источников компонентов смеси в потоке — тепловой эффект элементарного процесса
10
к L t m n bQz A? r T t V* V X У — коэффициент массо-, теплопередачи; константа фазового равновесия — длина рассматриваемой зоны — координата пространства — число элементарных стадий в сложной химической реакции — число компонентов в многокомпонентной системе — суммарная интенсивность источников теплоты в потоке — локальная интенсивность источника теплоты в потоке — скорости стадий химической реакции — температура потока — координата времени — объём рассматриваемой зоны потока фазы физико-химической системы — расход потока — состав потока — состав контактирующей фазы при изменении агрегатного состояния при фазовом переходе
a — стехиометрические коэффициенты компонентов в реакциях ИНДЕКСЫ ВЕРХНИЕ
(0) R M A П T И (*) — признак поступающего в зону потока — химическая реакция — массопередача — изменение агрегатного состояния при фазовом равновесии — подпитка от «внешнего» потока — теплопередача — теплоизлучение — термодинамическое равновесие — зона потока, контактирующая с рассматриваемой
допуст расч ср табл эксп min — допустимое значение — расчётное значение — среднее значение — табличное значение — экспериментальное значение — минимальное значение
max opt — максимальное значение — оптимальное значение ИНДЕКСЫ НИЖНИЕ
ср i — среднее значение — компонент
J (0 p — стадия химической реакции — распределённость параметра — образующийся компонент (продукт) на элементарной стадии химичес- кой реакции
min — минимальное значение
max — максимальное значение
ПРЕДИСЛОВИЕ
Более 40 лет вычислительная техника широко применяется в химической техно-
логии для решения всевозможных научно-технических задач, автоматизации про-
ектных работ и управления производственными процессами. В настоящее время
химикам-технологам различных специальностей в своей повседневной практичес-
кой деятельности приходится сталкиваться с применением компьютеров, а также с
автоматизированными компьютерными системами научных исследований (АСНИ),
системами автоматизированного проектирования (САПР), автоматизированными
системами управления технологическими процессами (АСУТП) и автоматизиро-
ванными системами управления предприятиями (АСУП). Основу этих автоматизи-
рованных систем составляют компьютерные модели конкретной предметной обла-
сти, с которыми имеют дело химики-технологи, в частности, компьютерные моде-
ли химико-технологических процессов (ХТП).
Бурное развитие индустрии аппаратных средств и программного обеспечения
компьютеров требует постоянной модернизации методологии компьютерного моде-
лирования ХТП. С этой целью ведущими мировыми фирмами по программному
обеспечению разрабатываются коммерческие пакеты моделирующих программ, в
которые постоянно включаются новейшие достижения в области компьютерных
систем и химической технологии.
Авторы учебного пособия убедительно показывают, что современный взгляд на
компьютерное моделирование ХТП не ограничивается только их математическим
моделированием, но и теснейшим образом связан с решением задач идентификации
и оптимизации химических производств. Совершенно справедливо акцентируется
внимание на том, что задачи компьютерного моделирования нельзя рассматривать
как исключительно формализованные задачи, во многих случаях их более правильно
относить к неформализованным задачам выбора вариантов, методов и алгоритмов
решения.
Все это нашло отражение в учебном пособии «Основы компьютерного моделиро-
вания химико-технологических процессов», которое в этой связи является своевре-
менным и актуальным как для студентов высших учебных заведений, так и для спе-
циалистов, занимающихся расчетами ХТП с применением для этой цели пакетов
моделирующих программ.
В Российском химико-технологическом университете им. Д.И. Менделеева
30 лет тому назад стало ясно, что знания в области вычислительной техники не
должны быть прерогативой только узких специалистов в этой области. Поэтому уже
тогда в учебные программы всех специальностей университета были включены такие
курсы, как «Моделирование и основы оптимизации», «Применение ЭВМ в химичес-
кой технологии» и в настоящее время — курс «Компьютерное моделирование хими-
ческих процессов». С этой целью в 1975 году в институте была создана кафедра
вычислительной техники, которая в настоящее время преобразована в кафедру ин-
форматики и компьютерного моделирования.
Первый автор настоящего учебного пособия — заведующий кафедрой информа-
тики и компьютерного моделирования Российского химико-технологического
12
Предисловие
университета им. Д.И. Менделеева Т.Н. Гартман, профессор, доктор технических
наук, который с первых дней создания кафедры вычислительной техники принимал
активное участие в становлении и модернизации названных выше курсов, является
известным специалистом в области разработки алгоритмов и процедур решения фор-
мализованных и неформализованных задач компьютерного моделирования хими-
ческих производств и более 10 лет занимается применением и адаптацией для этих
целей пакетов моделирующих программ (ПМП), в частности для автоматизирован-
ных систем научных исследований (АСНИ), систем автоматизированного проекти-
рования (САПР) и автоматизированных систем управления технологическими про-
цессами (АСУТП). В связи с этим излагаемый в книге материал рассчитан и на
специалистов, занимающихся внедрением перечисленных автоматизированных ком-
пьютерных систем на предприятиях.
Книга написана языком, доступным студентам химикам-технологам, с подроб-
ным изложением основных понятий компьютерного моделирования, вычислитель-
ной математики и математической статистики и не требует специальных знаний в
области компьютерных систем и математического моделирования. Настоящее учеб-
ное пособие может быть также рекомендовано для специалистов химиков-техноло-
гов и инженеров-химиков, которые решили углубить свои знания в области приме-
нения компьютеров и расчетных методов для компьютерного моделирования ХТП.
Президент Российского химико-технологического университета
им. Д.И. Менделеева,
академик РАН, профессор П.Д. Саркисов
ВВЕДЕНИЕ
Одной из характерных черт начала третьего тысячелетия являются интеграционные
процессы в мировой экономике и, одновременно, устойчивые тенденции роста цен на
энергетические, материальные и другие природные ресурсы, необходимые для раз-
личных производственных процессов. Для химической, нефтеперерабатывающей, неф-
техимической, газоперерабатывающей и многих других смежных отраслей промыш-
ленности задача снижения затрат на получение требуемых продуктов является перво-
степенной. Важнейшим условием успеха при этом является выбор, эксплуатация и,
при необходимости, создание высокоэффективных энерго- и ресурсосберегающих тех-
нологий химических процессов. Для этого требуется реализация целого комплекса
мероприятий и одним из важнейших из них является применение достаточно точных
методов расчета химико-технологических процессов (ХТП), что невозможно без при-
менения современных компьютеров и средств вычислительной техники.
Традиционные методы расчета ХТП, основанные на учете при вычислениях уп-
рощенных механизмов их протекания, абсолютно не удовлетворяют современным
требованиям. Только компьютерное моделирование дает возможность учесть наи-
большее число факторов и явлений, влияющих на протекание реальных процессов,
и обеспечить высокую точность предсказания их поведения при расчетах. В резуль-
тате коэффициенты запаса, которые необходимо было вводить раньше при проекти-
ровании для обеспечения надежности оборудования химических производств, могут
быть существенно уменьшены, что должно привести к требуемой экономии энерге-
тических, материальных и других ресурсов.
Поэтому при оценке параметров технологических регламентов производств, спро-
ектированных ранее и эксплуатируемых в настоящее время, необходим их критичес-
кий анализ и, возможно, пересчет их значений с учетом результатов применения
современной методологии компьютерного моделирования. Эта задача важна как при
решении задач проектирования (САПР), так и управления действующими произ-
водствами при комплексной автоматизации химических предприятий с использова-
нием современных достижений в области информационных технологий, в частности
при интеграции автоматизированных систем управления предприятиями (АСУП) с
автоматизированными системами управления отдельными технологическими про-
цессами (АСУТП).
Для достижения поставленных целей необходимы достоверные и надежные ком-
пьютерные модели ХТП, среди которых наибольшее распространение получили два
типа моделей — физико-химические и эмпирические. В книге подробно излагается
методология построения указанных типов моделей, решение задач идентификации и
оптимизации с их использованием. Показаны возможности совмещения двух подхо-
дов при компьютерном моделировании ХТП.
При построении физико-химических моделей используются модельные представ-
ления о механизме реально протекающих процессов химической технологии. Мето-
дологические принципы для создания таких моделей основаны на признании того
факта, что различные ХТП базируются на одинаковых законах физики и химии, в
частности, на знании закономерностей, так называемых элементарных процессов
(гидродинамики, массо- и теплопередачи, химической кинетики, процессов фазо-
14
Введение
вых переходов и т.д.). Обобщение этих закономерностей дает возможность с единых
позиций подходить к разработке компьютерных моделей ХТП с учетом блочного
принципа анализа и учета моделей отдельных элементарных процессов. Они, как
правило, справедливы для описания поведения реальных процессов в более широ-
ком диапазоне изменения режимных и конструкционных параметров, чем эмпири-
ческие модели, и поэтому более пригодны для решения задачи оптимизации хими-
ческих производств.
Эмпирические модели применяются, когда закономерности элементарных про-
цессов химической технологии мало изучены или недостаточно известны. Для мате-
матического описания реальных процессов используется известный кибернетичес-
кий принцип «черного ящика» и анализируются экспериментальные данные о вход-
ных переменных системы (условно независимых) и выходных переменных системы
(зависимых). При этом обрабатываются результаты либо пассивного, либо активно-
го эксперимента методами корреляционного и регрессионного анализа.
Следует отмстить, что в последнее десятилетие широкое применение получили
так называемые пакеты моделирующих программ (ПМП) для компьютерного моде-
лирования химических производств. Они используют физико-химические модели
отдельных процессов химической технологии, позволяют решать большое разнооб-
разие задач компьютерного моделирования, включая задачи идентификации и опти-
мизации, и для их применения необходимы специальные знания в области матема-
тического моделирования и оптимизации, излагаемые в настоящей книге. Среди
известных ПМП наиболее распространены следующие комплексы программ — ASPEN,
HYSYS, PRO-II и ChemCad.
С использованием компьютерных моделей химических производств решаются
задачи как автоматизированного проектирования химико-технологических процес-
сов (САПР), так и управления химическими процессами (АСУТП) и предприятиями
(АСУП).
Применение этих моделей в САПР дает возможность успешно решать целый
комплекс задач расчётно-технологического проектирования химических производств,
в частности, определять оптимальные значения параметров технологических режи-
мов и показатели эффективности функционирования производств, в том числе свя-
занные с экономическими аспектами (стоимость необходимых ресурсов на проведе-
ние процесса и цена целевых продуктов) и экологическими аспектами (выход вред-
ных примесей).
При оперативном управлении химическими предприятиями компьютерные мо-
дели позволяют:
• в рамках решения задач АСУТП определять оптимальные параметры уставок
систем регулирования;
• в рамках решения задач АСУП рассчитывать технико-экономические показатели
процессов, необходимые для правильного принятия управленческих решений;
• организовать эффективный обмен информацией между уровнями АСУТП и
АСУП для оптимального управления работой всего предприятия.
В рамках одной книги не представляется возможным рассмотреть всё многообра-
зие компьютерных моделей ХТП, протекающих в различных аппаратах (единицах
оборудования) химических производств. Однако единые методологические принци-
пы, необходимые для компьютерного моделирования ХТП, излагаются в полном
объеме и включают следующие этапы:
• математическую формализацию задачи для описания ХТП;
• анализ численных методов вычислительной математики, положенных в основу
решения уравнений математического описания ХТП;
Введение
15
• построение вычислительных алгоритмов для решения задач компьютерного
моделирования ХТП.
Задача настоящей книги состоит в ознакомлении читателя с общими принципа-
ми построения компьютерных моделей отдельных процессов химической техноло-
гии, их идентификации и оптимизации без излишней детализации, связанной, на-
пример, с полным представлением в математической модели выражений расчета
физико-химических коэффициентов и подробным учетом конструкционных харак-
теристик оборудования, в котором протекают реальные процессы. При необходимо-
сти указанные модели могут быть дополнены требуемыми соотношениями, что, бе-
зусловно, приведет к получению более точных количественных результатов компью-
терного моделирования.
В то же время в книге уделяется серьёзное внимание общим принципам постро-
ения и анализа систем уравнений математического описания ХТП, выбору и разра-
ботке наиболее эффективных алгоритмов расчета отдельных процессов химической
технологии, решению задач идентификации ХТП, применению статистических ме-
тодов для обработки результатов экспериментов с целью выбора адекватных моделей
химических производств и решению задачи оптимизации с различными целевыми
функциями (критериями оптимальности) — технологическими и экономическими.
Авторы считают своей обязанностью выразить благодарность своим коллегам,
которые принимали участие в обсуждении содержания настоящей книги и прежде
всего Г.С. Ривину — профессору кафедры информатики и компьютерного моделиро-
вания Российского химико-технологического университета имени Д.И. Менделеева
за полезные советы, касающиеся изложения материала третьей главы.
Знание материала, излагаемого в настоящей книге, позволит химикам-технологам:
• корректно ставить и решать задачи построения компьютерных моделей хими-
ческих производств, решать задачи идентификации и оптимизации химико-
технологических процессов;
• правильно анализировать результаты расчетов, получаемые при компьютерном
моделировании реальных процессов химической технологии;
• грамотно пользоваться пакетами моделирующих программ (ПМП) для реше-
ния задач проектирования и управления химическими производствами.
Книга написана на опыте более чем 25-летнего чтения лекций по одноименному
курсу для студентов общих потоков Российского химико-технологического универ-
ситета им. Д.И. Менделеева, а также на опыте применения ПМП ChemCAD для
компьютерного моделирования химико-технологических процессов.
1
'лава
ОСНОВНЫЕ ПОНЯТИЯ
КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
ХИМИЧЕСКИХ ПРОИЗВОДСТВ
Современные достижения в области компьютерного моделирования химических
процессов дают возможность более строго и с большей точностью решать задачи
проектирования и управления химическими производствами. При этом широко ис-
пользуется методология системного анализа, с применением которой успешно ре-
шаются задачи анализа, оптимизации и синтеза новых и реконструируемых техноло-
гий. Рассчитываемые в этом случае оптимальные (наилучшие) режимные и конст-
рукционные параметры процессов составляют основу технологических регламентов
производств, позволяют наиболее эффективно управлять ими и в наибольшей степе-
ни удовлетворяют требованиям энергоресурсосбережения.
Развитие и широкое распространение информационных технологий (ИТ-техно-
логий), внедрение локальных (ЛВС) и глобальных (ГВС) вычислительных сетей,
интернет-технологий дают возможность развивать и совершенствовать современные
системы прикладной информатики — автоматизированные (компьютерные) систе-
мы (АС).
К ним относятся:
• автоматизированные информационные системы (АИС);
• системы автоматизированного проектирования (САПР);
• автоматизированные системы научных исследований (АСНИ);
• автоматизированные системы управления (АСУ);
• автоматизированные обучающие системы (АОС).
При применении указанных АС для решения задач химической технологии пред-
полагается использование компьютерных моделей реальных процессов и производств,
в частности, результатов компьютерного моделирования химико-технологических
процессов. При этом автоматизированные системы, в соответствии с требованиями
к новым информационным технологиям, должны включать в себя методологии реше-
ния задач с применением прикладных систем искусственного интеллекта (ИИ) и
экспертных систем (ЭС), с использованием которых удаётся моделировать некото-
рые интеллектуальные функции специалистов в конкретной проблемной (предмет-
ной) области, а соответственно, и увеличить надёжность принимаемых решений не-
формализованных задач (НФЗ).
В отличие от формализованных задач (ФЗ), для решения которых требуется реа-
лизация вычислительных алгоритмов на компьютерах, рациональные решения для
НФЗ получаются в результате творческой деятельности специалистов, которая тре-
бует, прежде всего, переработки большого количества смысловой (семантической)
информации и непосредственно не связана с проведением каких-либо вычислений.
Для поиска семантических решений НФЗ необходимо применять не вычислитель-
ные алгоритмы, как в случае с ФЗ, а эвристическо-эволюционные процедуры.
Экспертные системы (ЭС) — это интеллектуальные системы, которые способны в
диалоге с квалифицированным пользователем — лицом, принимающим решение, на
основе накопления и переработки специальных знаний и правил принятия решений
проводить экспертизу, консультировать и давать рекомендации по выбору действий
1.1. Системный анализ ХТП
17
(операций), распознавать ситуации; ставить диагноз и обосновывать заключения при
поиске решений НФЗ некоторой проблемной (предметной) области. ЭС можно рас-
сматривать как своеобразные программно-технические усилители интеллектуальной
творческой деятельности лица, принимающего решение. Такие интеллектуально-ди-
алоговые системы представляют собой сложные человеко-машинные системы, так
называемые системы эргатического типа, применение которых обеспечивает полу-
чение наиболее надёжных результатов решения задач химической технологии.
В настоящей главе представлены основные понятия, связанные с компьютерным
и математическим моделированием реальных процессов.
Компьютерное моделирование химико-технологических процессов предполагает
решение следующих основных задач:
• построения математической модели процесса и её реализацию на компьютере;
• идентификации (отождествления) разработанной математической модели с
моделируемым процессом с целью обеспечения её адекватности, т.е. качествен-
ного и количественного соответствия модели реальному процессу;
• оптимизации процесса с использованием его математической модели, т.е. оп-
ределения оптимальных (наилучших) режимных и конструкционных парамет-
ров процессов, которые обеспечивают наибольшее или наименьшее значение
выбранного критерия оптимальности (целевой функции), характеризующего
эффективность реального процесса.
1.1. Системный анализ химико-
технологических процессов
Для решения задач компьютерного моделирования применяется системный подход,
в соответствии с которым химико-технологический процесс (ХТП) рассматривается
как некоторая функциональная система («объект» на рис. 1.1), характеризующаяся
следующими основными совокупностями переменных:
X ~ вектором входных переменных, которые влияют на состояние процесса и, в
общем случае, определяют его состояние;
у — вектором выходных переменных, которые характеризуют состояние процесса и
зависят от входных переменных X .
Системный подход даёт возможность осуществить математическую формализацию
задачи при построении математических моделей как процессов в отдельных аппаратах
(типовой ХТП), так и в их совокупности
(химических производств), обеспечивая
возможности познания физико-химических
механизмов протекающих процессов и по-
лучение широких обобщений и количе-
ственных закономерностей.
Любая система состоит из взаимосвя-
занных и взаимодействующих между со-
бой и с внешней средой частей и, в опре-
делённом смысле, представляет собой зам-
кнутое целое.
Объект, представляющий собой один
аппарат или секцию аппарата (типовой
ХТП), в котором протекают физико-хи-
мические процессы, называется физико-
химической системой (ФХС).
Рис. 1.1. Схематическое представление
ХТП как функциональной системы
18 Глава 1. Основные понятия компьютерного моделирования химических производств
Объект, являющийся совокупностью соединённых между собой аппаратов (хи-
мическое производство), в частности, для производства некоторого целевого продук-
та, называется химико-технологической системой (ХТС).
Принципиальная технологическая схема процесса получения произвольного це-
левого продукта Р*, представляющая собой ХТС и включающая различные ФХС,
приведена на рис. 1.2.
Для отображения зависимости выходных переменных у от входных переменных
X используется физико-химический оператор (для ФХС) или химико-технологи-
ческий оператор (для ХТС) £2:
у=й(х)- (1-1)
В (1.1) оператор £2 отображает пространство входных переменных X в простран-
ство значений выходных переменных у.
Отображение (1.1) отражает все реально протекающие процессы и представляет
собой отображение объективной реальности, для которой требуется построить при-
ближённую математическую модель процесса. При этом к входным переменным X
относят не только собственно входные переменные, как, например, свойства перераба-
тываемого сырья — его расход, состав, температуру, а также возмущающие переменные
(значения которых изменяются случайным образом во времени и по тем или иным
причинам не могут быть измерены) и компенсирующие их управляющие переменные
(которые могут быть измерены и имеется возможность на них воздействовать в соот-
ветствии с теми или иными требованиями). Для нестационарных режимов объектов
одним из компонентов вектора X может быть время, от которого могут зависеть и
другие компоненты вектора входных переменных X .
Важнейшим этапом построения адекватной математической модели химических
процессов является анализ структуры химико-технологического или физико-хими-
ческого операторов £2 (1.1). При этом осуществляется декомпозиция сложной систе-
мы на более простые подсистемы в соответствии со следующими принципами:
• определения иерархической структуры системы, т.е. выделения её иерархических
ступеней и взаимосвязей между ними на основе фундаментальных знаний, эк-
спериментальных данных и опыта специалистов;
• реализации принципа иерархической соподчинённости при формализации знаний
об изучаемых элементах системы и принятии разумных допущений, что выра-
жается в учёте наиболее важных (приоритетных) процессов, протекающих на
Рис. 1.2. Принципиальная технологическая схема получения целевого продукта Р*:
1 — реактор с мешалкой; 2 — теплообменник; 3 — отстойник; 4 — ректификационная
колонна; 5 — делитель потока
1.1. Системный анализ ХТП
19
низких ступенях иерархии сйстемы и оказывающих влияние на процессы на
верхних уровнях иерархии (при этом для выявления учитываемых процессов
низких уровней иерархии необходимо их тщательное изучение с целью выявле-
ния наиболее приоритетных из них);
• комплексного исследования отдельных процессов с учётом влияния переменных
не только на рассматриваемом уровне иерархии системы, но и на низших уров-
нях, и на более высоких ступенях иерархии системы.
В химической промышленности целесообразно выделить 5 ступеней иерархии
системы.
1. Микроуровень — процессы и явления рассматриваются без учёта влияния за-
кономерностей движения потоков фаз в аппаратах.
2. Макроуровень — ФХС — представляет собой секцию аппарата (например, слой
насадки или тарелку) или отдельный аппарат. Все процессы рассматриваются
с учётом движения материальных и тепловых потоков.
3. Уровень химического производства — ХТС — представляет собой совокуп-
ность аппаратов, связанных между собой материальными, тепловыми и ин-
формационными потоками.
4. Уровень предприятия — это несколько производств, составляющих предприя-
тие, при анализе работы которого необходимо учитывать экономические и
управленческие закономерности протекания бизнес-процессов функциони-
рования предприятия.
5. Уровень компании или объединения — это несколько предприятий, объеди-
нённых в компанию (Газпром, Лукойл, Сибур и др.).
Следует отметить, что на каждом из перечисленных уровней иерархии совместно
решаются задачи оптимизации технологических процессов и автоматизации управления
производством.
Рассмотрим первые три уровня иерархии химического предприятия на примере
получения продукта Р* (см. рис. 1.2) по следующей кинетической схеме реакции:
А + В -> Р*.
При этом основные стадии химической реакции получения целевого продукта Р*
с учётом образующихся побочных продуктов можно условно описать уравнениями:
А + В-> С;
В + С -> Р* + Е;
С + Р*-> G.
Целевой продукт Р* образует с компонентом Е азеотроп с максимальной темпе-
ратурой кипения, в результате чего часть его попадает в куб ректификационной ко-
лонны. Чтобы снизить потери целевого продукта Р* при технологическом оформле-
нии процесса его получения необходимо организовать рециклический (обратный)
поток в реактор.
Принципиальная технологическая схема получения продукта Р* в промышлен-
ных условиях представлена на рис. 1.2. При этом химическое производство рассмат-
ривается как химико-технологическая система (ХТС), а процессы в отдельных аппа-
ратах — как физико-химические системы (ФХС).
Химико-технологическая система (ХТС) — это технологическая схема процесса,
которая рассматривается как совокупность тесно связанных подсистем (процессов в
отдельных аппаратах, или химико-технологических процессов - ХТП), имеющих
единую цель функционирования и подчиняющихся основным принципам систем-
ного анализа, в частности комплексности, иерархичности и иерархической соподчи-
ненное™.
Физико-химическая система (ФХС) — это сплошная многофазная многокомпо-
нентная среда в отдельном аппарате или секции аппарата, распределённая в про-
странстве и переменная во времени, в каждой точке гомогенности которой и на
границе раздела фаз происходит перенос вещества, энергии и импульса при наличии
их источников (стоков).
20 Глава 1. Основные понятия компьютерного моделирования химических производств
Рис. 1.3. Схематическое представление
модели ХТС, технологическая схема
которой представлена на рис. 1.2, в виде
совокупности ФХС
На рис. 1.2 подсистемами ХТС явля-
ются ФХС — реактор, теплообменник, от-
стойник, ректификационная колонна, де-
литель потока. Каждая из подсистем име-
ет цель функционирования — проведение
химического взаимодействия, нагревание
(охлаждение) потоков, выделение компо-
нентов из потока и т.п. Подсистемы ХТС
(отдельные аппараты) связаны между со-
бой технологическими потоками (трубо-
проводами), что обеспечивает получение
целевого продукта Р* — т.е. достижение'
единой цели функционирования всей
ХТС.
Схематически изображение ХТС (см.
рис. 1.2) в виде совокупностей ФХС пред-
ставлено на рис. 1.3. На вход ХТС посту-
пают потоки, характеризующиеся векто-
ром входных переменных X (например,
•Д.). В
составы потоков на входе в аппараты, температуры и давления в аппаратах и т
пределах ФХС входные переменные X претерпевают целенаправленное физико-хи-
мическое превращение в вектор выходных переменных у.
1.2. Построение систем уравнений
математического описания химико-
технологических процессов
Так как структура химико-технологического или физико-химического оператора
досконально не известна, то вместо него пользуются функциональным оператором
Ф (1.2), являющимся приближением истинного оператора Q (1.1).
Превращение входных переменных X в оценки выходных переменных у может быть
отображено с использованием функционального оператора Ф:
у=ф(х,о), (1-2)
где Ф — функциональный оператор, который отображает пространство входных пере-
менных X в пространство оценок выходных переменных у, а ~ коэффициенты урав-
нений, описывающих физико-химические процессы.
Соотношение (1.2) представляет собой систему уравнений математического опи-
сания (МО) химико-технологического процесса (ХТП) с начальными и граничными
условиями. Для синтеза функционального оператора Ф для ХТС необходимо на ос-
нове системного анализа ХТС идентифицировать функциональные операторы всех
ФХС, составляющих её (находящихся на более низких уровнях иерархии).
Математическое описание процессов в отдельных аппаратах химического произ-
водства может быть теоретическим или эмпирическим, в соответствии с чем получа-
ются теоретические или эмпирические модели (рис. 1.4).
Математическое описание фундаментальных комбинированных моделей ХТП — это
сложные интегро-дифференциальные уравнения, детально описывающие процессы,
в том числе и на атомно-молекулярном уровне.
п
1.2. Построение систем уравнений математического описания ХТП 21
Математическое описание физико-хи-
мических блочно-структурных марелей
ХТП — это модельное описание «элемен-
тарных» процессов, в основе которого ле-
жат балансовые уравнения, записываемые
с учётом гидродинамических закономер-
ностей движения потоков фаз и включа-
ющие интенсивности источников массы,
теплоты и импульса соответственно в урав-
нениях балансов массы, теплоты и им-
пульса.
Математическое описание эмпирических
вероятностно-статистических моделей XTJ1
может быть получено в виде полиномиаль-
ного представления зависимости выходных
Рис. 1.4. Типы моделей ХТП (ФХС)
переменных урасч от входных X в явном
виде при обработке опытных данных.
Математическое описание (МО) теоретических моделей строится на основе зна-
ния механизмов протекания процессов химической технологии:
• для фундаментальных комбинированных моделей — это детальное описание меха-
низмов процессов;
• для физико-химических блочно-структурных моделей — приближённое описание
процессов, базирующиеся на модельном представлении гидродинамических, массо-
и теплообменных процессов, а также процессов химических превращений, называе-
мых в этом случае «элементарными» процес-
сами.
В результате получаются системы урав-
нений математического описания большой
размерности для фундаментальных комбини-
рованных моделей и менее сложные системы
уравнений — для физико-химических блочно-
струк- турных моделей.
Как правило, для моделирования химичес-
ких производств используются физико-хими-
ческие блочно-структурные модели, которые
по функциональным возможностям вполне
удовлетворяют точности, необходимой для
расчётов технологических схем реальных про-
изводств. Основные описываемые в этом слу-
чае «элементарные» процессы представлены
на рис. 1.5.
Для совокупности этих «элементарных»
процессов получаются три основных типа урав-
нений математического описания.
1. Системы конечных уравнений (СКУ):
системы линейных алгебраических урав-
нений (СЛАУ) или системы нелинейных
уравнений (СНУ).
2. Системы обыкновенных дифференциаль-
ных уравнений (СОДУ).
3. Системы дифференциальных уравнений в
частных производных (СДУЧП).
Рис. 1.5. Основные «элементарные»
процессы при построении физико-
химических блочно-структурных
моделей ХТП
22 Глава 1. Основные понятия компьютерного моделирования химических производств
Для получения зависимости выходных переменных у расч от входных X системы
уравнений МО (1.2), используемые для физико-химических моделей, должны быть
решены относительно выходных переменных. В этом случае решается так называе-
мая прямая задача математического моделирования, когда известен вид уравнений
МО (оператор Ф) и значения его коэффициентов а (1.2). Из-за того, что эти модели
основываются на знании физико-химических механизмов протекающих процессов,
они могут использоваться для экстраполяции свойств реальных объектов за пределы
диапазонов изменения переменных, в которых проводилась их экспериментальная
проверка и определение коэффициентов моделей а.
Для эмпирических моделей не требуется решение уравнений математического опи-
сания процесса. Для этих моделей зависимости урасч (число этих зависимостей равно
размеру вектора урасч) от X и а получаются в явном виде путём непосредственного
решения задачи аппроксимации экспериментальных данных, т.е. при решении так
называемой обратной задачи математического моделирования, когда по опытным
данным определяется и вид уравнений математического описания (МО) (структур-
ная идентификация), и значения их коэффициентов а (параметрическая идентифи-
кация). Эти модели, как правило, лишены физического смысла и справедливы толь-
ко в том диапазоне изменения параметров реального процесса, где был поставлен
эксперимент. За пределами этого диапазона экстраполяция поведения процессов с ис-
пользованием эмпирических моделей не желательна.
1.3. Разработка и реализация расчетных
модулей и моделирующих алгоритмов
химико-технологических процессов
Для физико-химических блочно-структурных моделей алгоритм решения системы
уравнений МО (1.2) отображается с использованием вектор-функции следующим
образом:
y^"=f?(X,a), (1.3)
где <р — вектор-функция, которая отражает последовательность аналитического или
численного (приближённого) решения системы уравнений (1.2), определяемой фун-
кциональным оператором Ф.
Отображение (1.3) помимо того, что задаёт количественные соотношения между
входными и выходными переменными процесса, несёт в себе ещё очень важную
информацию о способе получения решения, т.е. об алгоритме решения задачи.
По существу, вектор-функцию <р можно рассматривать как формальное пред-
ставление алгоритма решения системы уравнений МО химико-технологического
процесса (1.2). Этот алгоритм, называемый моделирующим алгоритмом (МА) или
алгоритм математического моделирования (alg ММ) и представляет собой комбина-
цию известных алгоритмов (в простейшем случае — один алгоритм) вычислительной
математики, функции (1.2) для которых записаны с учётом физико-химических меха-
низмов протекающих реальных процессов.
В дальнейшем будет показано, что для разработки оптимального МА (1.3) целесо-
образно провести анализ системы уравнений МО (1.2) с использованием её информа-
ционной матрицы, а сам алгоритм представлять в виде блок-схемы алгоритма расчёта
ХТП.
Реализацией на компьютере МА завершается этап построения математической
модели — первый этап компьютерного моделирования ХТП.
1.4. Идентификация математических описаний ХТП
23
Рис. 1.6. Этапы построения математической
модели ХТП
Основные этапы построения физико-
химической блочно-структурной матема-
тической модели ХТП изображены на
рис. 1.6 и включают в себя следующие пос-
ледовательные стадии.
1. Построение системы уравнений ма-
тематического описания ХТП (МО).
2. Разработка моделирующего алго-
ритма (МА).
3. Реализация моделирующего алго-
ритма решения системы уравнений
математического описания ХТП на
компьютере, в результате чего получается математическая модель (ММ) про-
цесса или её расчётный модуль (расчётный модуль ФХС/ХТС).
В результате можно привести два определения математической физико-химичес-
кой блочно-структурной модели ХТП [21, 46]:
1) математическая модель — это реализованный на компьютере алгоритм реше-
ния системы уравнений математического описания;
2) математическая модель — это система уравнений, которая связывает между
собой входные и выходные переменные реального процесса (МО), для про-
гнозирования свойств которого необходимо с помощью специального ал-
горитма решить эту систему уравнений, а сам алгоритм должен быть реали-
зован на компьютере.
Следует упомянуть о важной разновидности компьютерных моделей, так называ-
емых имитационных моделях. Имитационное моделирование, как правило, связано с
моделированием динамических процессов, т.е. нестационарных режимов работы ре-
альных объектов. Изменение ситуаций во времени — тот феномен, который изучает-
ся с использованием имитационных моделей. В результате могут быть получены
новые знания и выработаны разного рода решения для управления реальным дина-
мическим процессом. Разработка таких моделей обычно сложнее разработки мате-
матических моделей, описывающих стационарные режимы работы объектов. Это
связано с тем, что уравнения МО нестационарных режимов объектов включают в
себя обыкновенные и частные производные функций переменных процессов по вре-
мени, а соответствующие алгоритмы их решения — МА — требуют реализации эф-
фективных методов решения систем обыкновенных дифференциальных уравнений и
систем дифференциальных уравнений в частных производных.
1.4. Идентификация математических
описаний химико-технологических процессов
Разработанную математическую модель процесса необходимо использовать для
исследования и прогнозирования поведения реального объекта, т.е. её свойства и
поведение с определённой степенью приближения должны совпадать с моделируе-
мым процессом. Это свойство ММ называется свойством традуктивности, или пере-
носимости результатов расчёта, получаемых с помощью ММ, на поведение реальных
ХТП. В результате вместо анализа свойств реальных объектов или их физических
моделей, реализуемых обычно на пилотных или полупромышленных установках, боль-
шинство исследований можно проводить с применением разработанной ММ, что
существенно дешевле, быстрее и безопаснее.
Для корректного решения этих задач необходимо, чтобы математическая модель
была адекватна реальному процессу.
24 Глава 1. Основные понятия компьютерного моделирования химических производств
Под адекватностью математической модели понимается соответствие её реально-
му объекту как качественное (тенденции изменения переменных в модели и в объек-
те должны быть одинаковы), так и количественное (экспериментальные данные дол-
жны совпадать с расчётными).
Адекватность ММ проверяется с помощью с выражения (1.4), включающего нор-
му вектора рассогласования
-Расч
<£,
(1-4)
где у расч — значения выходных параметров, рассчитанные по ММ; у’ксп — значения
выходных параметров, полученные экспериментально на реальном объекте при тех
же значениях входных переменных х (1.3), что у расч; е - погрешность модели, кото-
рая должна быть близка к погрешности экспериментальных измерений.
Если адекватность ММ не достигнута, необходимо решать задачу идентификации,
т.е. отождествления МО объекта моделирования с описанием закономерностей ре-
ально протекающих процессов.
Процедура решения задачи идентификации математического описания объекта
моделирования — это поиск наиболее подходящего вида уравнений МО — структуры
оператора Ф (1.2) и коэффициентов (параметров) этих уравнений а с использовани-
ем экспериментальных данных и алгоритмов идентификации (alg ИДЕНТ), т.е. алго-
ритмов оптимизации, когда определяется наименьшее значение критерия рассогла-
сования ||урасч — уэксп||;
min ||урасч-уэксп||,
ф€фдапуст ||-' J ||
(1.5)
где Флопуст и адопуст — область допустимых значений структуры уравнений МО и их
коэффициентов.
Идентификация может быть структурной — это определение вида уравнений МО,
описывающих реальный процесс (1.2) и параметрической — определение коэффици-
ентов (параметров) а уравнений МО (1.2) процесса.
Адекватная ММ ХТП подвергается исследованию, в ходе которого анализируется
параметрическая чувствительность модели, т.е. определяется влияние различных пере-
менных и коэффициентов, в том числе и физико-химических моделей, на выходные
переменные процесса. В результате выявляются наиболее подходящие ресурсы для уп-
равления реальным процессом и его оптимизации. Одновременно ХТП моделируется
(симулируется) на компьютере, т.е. проводятся его расчётные исследования с целью ана-
лиза поведения процесса при различных условиях и всевозможных режимах работы.
Это позволяет с использованием адекватных компьютерных моделей определять «узкие
места» химических производств и возможности их совершенствования и модернизации.
1.5. Оптимизация
химико-технологических процессов
Объективная тенденция к проведению химико-технологических процессов в оп-
тимальных (наилучших) условиях — важнейшая задача химической технологии. Это
соответствует современным требованиям к технологическим процессам, в том числе
1.5. ОптимизацияХТП
25
с позиций энерго-ресурсосбережения, экологической безопасности, противоаварий-
ной работы и др. Успешное решение задачи оптимизации определяется, прежде все-
го, правильным выбором критерия оптимальности или целевой функцией, которая в
полной мере должна характеризовать эффективность технологического процесса с
учётом требований, являющихся наиболее приоритетными при решении конкрет-
ной задачи.
Это связано с тем обстоятельством, что результат решения задачи оптимизации
может зависеть от вида математического выражения критерия оптимальности (целе-
вой функции). Поэтому на практике часто приходится решать задачи многокритери-
альной (многоцелевой) оптимизации с использованием весовых коэффициентов не-
скольких критериев (целевых функций), объединённых в один критерий оптималь-
ности. В результате определяемые оптимальные условия обеспечивают требуемые
наилучшие (в соответствии с выбранной многоцелевой функцией) условия проведения
технологического процесса.
При этом критерий оптимальности (целевая функция) R обязательно должен ха-
рактеризоваться некоторым числовым показателем, т.е. быть количественным, и за-
висеть от переменных процесса, в частности, от выходных (зависимых) переменных
производства (у).
Вид функциональной зависимости критерия оптимальности (целевой функции)
от выходных (зависимых) переменных имеет вид:
Я = Я(у), (1.6)
зависит от типа выбранного критерия (технологического, экономического, технико-
экономического, термодинамического и т.п.) и, как правило, задаётся специалистами.
В свою очередь, для определения значений выходных переменных в зависимости
от входных (X ) в критерии (1.6) используется математическая модель процесса (1.3):
У1”" =<р(х,й,а). (1.7)
В этом случае входные переменные процесса X рассматриваются как некоторый
вектор, состоящий из двух подвекторов:
(1.8)
где х — собственно входные переменные процесса, влияющие на процесс, но на
которые нельзя воздействовать, вследствие чего они не могут быть ресурсами опти-
мизации; й — оптимизирующие (управляющие) переменные процесса, которые под-
даются целенаправленным изменениям, и определение оптимальных значений ко-
торых является целью решения задачи оптимизации.
Для корректного решения задачи оптимизации ММ процесса (1.7) должна быть
адекватной, по возможности, в широком диапазоне изменения режимных и конст-
рукционных параметров, т.е. для неё должны быть однозначно определены:
• вид уравнений математического описания (МО);
• коэффициенты уравнений МО (а).
Одновременно для ММ должен быть выбран наиболее эффективный алгоритм
(моделирующий алгоритм — МА) решения системы уравнений МО.
В связи с тем, что собственно входные переменные х не могут быть ресурсами
оптимизации, а коэффициенты уравнений МО а определены при решении задачи
идентификации, в частности, задачи параметрической идентификации, то с пози-
ций решения задачи оптимизации процесс решения системы уравнений МО (1.7)
может быть представлен в виде зависимости (1.9) с вектор-функцией (1.3), учитыва-
ющей влияние на значения выходных переменных у расч только оптимизирующих или
управляющих переменных «:
26 Глава 1. Основные понятия компьютерного моделирования химических производств
у ^ = ^(11).
(1.9)
Рис. 1.7. Преобразование
входных переменных и управ-
ляющих воздействий в выход-
ные переменные моделирую-
щим алгоритмом (alg ММ)
системы уравнений математи-
ческого описания
Более эффективным для решения задачи оптимизации является применение
теоретических моделей, в частности физико-химических блочно-структурных, в общем
случае справедливых в широком диапазоне изменения параметров процессов, но
требующих реализации достаточно сложных вычислительных алгоритмов.
В этом случае с учётом подстановки выражения (1.9) в (1.6) задачу оптимизации
можно рассматривать как математическую задачу на поиск экстремума функции
многих переменных R = R(u) с использованием алгоритма оптимизации (alg ОПТ).
Менее привлекательным для решения задачи оптимизации является применение
эмпирических вероятностно-статистических моделей, которые обычно представляют
собой простые линейные относительно коэффициен-
тов зависимости (1.7), в частности, полиномиального
вида, и позволяют достаточно просто определять вы-
ходные переменные при известных значениях соб-
ственно входных переменных х и оптимизирующих
или управляющих переменных й. Однако из-за того,
что эмпирические модели, как правило, справедливы
в достаточно узких диапазонах изменения параметров
процессов, и для их определения требуется постанов-
ка специальных экспериментов (пассивных или актив-
ных), которые обрабатываются статистическими ме-
тодами (см. главу 4), то задачу оптимизации для таких
моделей решают так называемыми вероятностно-ста-
тистическими методами. В этом случае при решении
задачи оптимизации вычисления чередуются с постановкой экспериментов, статисти-
ческой обработкой последних и расчётом экстремумов целевых функций, т.е. с помо-
щью так называемого экспериментально-статистического метода оптимизации или
оптимального экспериментирования.
Для физико-химических моделей отображение вектора входных переменных х и
вектора управляющих воздействий й в вектор выходных переменных урасч может быть
представлено с помощью вектор-функции <₽ (1.3), как показано на рис. 1.7.
Реализация alg ММ в соответствии с соотношениями (1.6) и (1.7) необходима
каждый раз при расчёте критерия оптимальности (целевой функции) в процессе
выполнения alg ОПТ.
Формулировка задачи оптимизации химико-технологического процесса для мно-
гих переменных выражается следующей записью:
opt 7?(w), (1-Ю)
где opt (оптимум) — глобальный экстремум (минимум или максимум в зависимости
от характера целевой функции R).
При этом уравнения МО процесса (1.2) обязательно должны иметь решение. Это
требование можно рассматривать как обязательное ограничение при решении зада-
чи оптимизации.
Результаты решения задачи оптимизации сокращенно могут быть записаны:
й4”
alg ОПТ,
(1.И)
т.е. оптимальные значения оптимизирующих переменных uv и соответствующее
минимальное или максимальное (оптимальное) значение критерия оптимальности
целевой функции л”'”, полученные с помощью алгоритма оптимизации (alg ОПТ).
1.5. Оптимизация ХТП
27
В общем случае задача оптимизации формулируется следующим образом: необхо-
димо найти такие значения оптимизирующих переменных й°р' из области их допус-
тимых значений [ й и т<и] (й т1п, йтшс - границы области допустимых значений
оптимизирующих переменных), которые обеспечат оптимальную (наибольшую или
наименьшую) величину критерия оптимальности (целевой функции) процесса R"p‘.
Решение задачи оптимизации для одной переменной (одномерная оптимизация) с
областью допустимых значений [ й т‘", й т<и] можно представить, как показано на рис. 1.8.
В данном случае оптимизация — это поиск оптимального значения критерия оп-
тимальности как функции управляющей переменной и (значения и находятся в ин-
тервале от w"" до if'ax):
opt R(u) . (112)
umin<u^umaJC
Результат решения задачи одномерной оптимизации:
a/g ОПТ. (1.13)
Для двух оптимизирующих переменных оптимальное значение в параметричес-
кой плоскости можно изобразить графически с помощью линий постоянного уров-
ня, каждая из которых состоит из точек с одинаковым значением целевой функции,
как представлено на рис. 1.9.
Задача двумерной оптимизации формулируется следующим образом:
opt R(ux, и2)
,,min <итах .
“1 > (1 14)
и™” <«2
Результат решения задачи двумерной оптимизации:
a/gOnT. (1.15)
Задача оптимизации ХТП с использованием компьютерной модели может быть
сформулирована как задача нелинейного программирования (НЛП) с ограничениями
первого рода, накладываемыми на оптимизирующие (управляющие) переменные, и
j^min
u°pt,u°2pt
n°Pt
Рис. 1.8. Графическое изобра-
жение решения задачи оптими-
зации по одной переменной
Рис. 1.9. Графическое изображение решения
задачи оптимизации с двумя оптимизирую-
щими переменными
2 8 Глава 1. Основные понятия комп ыотерного моделирования химических производств
Рис. 1.10. Блок-схема процедуры компьютерного моделирования ХТП
второго рода, накладываемыми на физико-химические переменные и параметры про-
цесса, зависимость которых от других переменных (собственно входных, оптимизи-
рующих-управляющих и выходных), в общем случае, носит нелинейных характер:
Поиск opt R(u)
ограничения первого рода: й"*“ <й <и"“ (1-16)
ограничения второго рода: Ф(х, й, у) < 0,
где ф — заданная вектор-функция технологического процесса.
По аналогии с (1.10) здесь также математическое описание процесса (1.2) следует
рассматривать как обязательное ограничение при решении задач НЛП.
Алгоритмы оптимизации и решение задач оптимизации ХТП подробно описаны
в разд. 3.6 и 5.5 соответственно.
Итак, процедура компьютерного моделирования химико-технологического процесса
состоит из семи следующих основных этапов (рис. 1.10).
1. Анализ и исследование ХТП — экспериментальное и теоретическое.
2. Построение математической модели (ММ).
3. Идентификация математического описания (МО) ХТП с использованием опыт-
ных данных, полученных на объекте моделирования.
4. Проверка адекватности ММ.
5. Анализ параметрической чувствительности ММ.
6. Расчётные исследования (симуляция) ХТП.
7. Оптимизация ХТП.
1.6. Анализ, оптимизация и синтез
химических производств - химико-
технологических систем
При решении задач компьютерного моделирования необходимо более детальное
представление математической модели химико-технологического процесса всего
производства — химико-технологической системы (ХТС), которая учитывает топо-
логические особенности технологической схемы, конструкционные особенности от-
дельных аппаратов и их размеры, типы аппаратов, а также физико-химические спо-
собы проведения отдельных процессов, например, на стадии разделения или в реак-
торном узле.
1.6. Анализ, оптимизация и синтез химических производств
29
В результате адекватная ММ ХТП с учётом (1.3) с помощью вектор-функции <р
может быть записана следующим образом:
ypm=q(x,T,K,S,A,v), (1.17)
где х — вектор собственно входных переменных, аналогичный х в (1.7) и (1.8); т —
вектор режимных (технологических) переменных; к — вектор конструкционных
переменных, характеризующих размеры конструкций аппаратов; s — вектор, харак-
теризующий топологические особенности технологической схемы производства
(сколько аппаратов включает производство, как они соединены между собой и т.д.);
А — вектор типовых аппаратов для реализации конкретных технологических про-
цессов; V — вектор, характеризующий физико-химический способ технологической
реализации процессов химических превращений, разделения, изменения агрегатных
состояний потоков химических производств и т.д.
В общем случае для характеристики совершенства производства используется
коэффициент эффективности производства к,, который зависит от перечисленных
ранее переменных:
K, = K,{x,T,K,s,A,v). (1.18)
Коэффициент эффективности производства — это некоторый количественный
показатель, по которому оценивается степень приспособленности химико-техноло-
гических систем к выполнению поставленных целей функционирования. Его следу-
ет рассматривать в более широком плане, чем просто как характеристику технико-
экономических показателей производства, как, например, в случае критерия опти-
мальности R. При его определении должно быть учтено влияние технологического
процесса на экономические, природоохранные и социальные факторы окружающей
среды и прилегающего региона.
Именно такие компьютерные модели химических производств (ХТС) позволяют
наиболее рационально подойти к решению задач проектирования и управления хи-
мико-технологическими процессами.
1.6.1. Анализ химико-технологических систем
А
i i
ХТС
I I г
Анализ ХТС — это операция определения выходных переменных (урасч) и коэф-
фициента эффективности производства (К,) при варьировании значений остальных
переменных и параметров производства х,T,K,S, когда известны значения вектора
типовых аппаратов (А) и вектора физико-химического способа технологической ре-
ализации процессов (V ). Учитывая, что в данном случае моделируется не отдельный
процесс, а химическое производство, включающее множество потоков и аппаратов,
добиться корректной постановки и наилучших результатов решения задачи возмож-
но с использованием пакетов моделирующих программ (ПМП), таких как ASPEN,
HYSYS, PRO-II и ChemCAD (см. главу 6).
Для расчёта урасч и К, используется алго-
ритм математического моделирования (a/g ММ),
получаемый при построении компьютерной
модели химического производства (ХТС).
В общем случае задача анализа ХТС мо-
жет быть сформулирована следующим об-
разом (рис. 1.11):
• Дано: x,f,K,S.
• Известно: v,A.
• Определить: у1”’, К,
• Необходим: alg ММ.
Т К S
Рис. 1.11. Схематическое изображение
процедуры анализа ХТС
30 Глава 1. Основные понятия компьютерного моделирования химических производств
1.6.2. Оптимизация химико-технологических систем
Оптимизация ХТС — это операция определения оптимальных значений векторов
Т"1", К*, Sv' при выбранном виде выражения для определения критерия оптималь-
ности (целевой функции) R и заданных значениях векторов х,у, а
В общем случае задача оптимизации ХТС может быть сформулирована следую-
щим образом (рис. 1.12):
• Дано: x,v, А.
• Известно: вид выражения для критерия оптимизации R.
• Определить: f°'”, K‘rl, S^'.
• Необходимы: alg ММ, alg ОПТ.
Математическая формулировка задачи оптимизации в этом случае имеет вид:
Рис. 1.12. Схематическое изображение
процедуры оптимизации ХТС
opt R(T, K,S), (1.19)
у gуДОПуСТ
5 с S ДОПУСТ
т.е. определяются оптимальные значения
режимных (технологических) г*, конст-
рукционных К'"’1 параметров и компонен-
ты вектора S °'”, характеризующие тополо-
гические особенности технологической схе-
мы производства из области их допустимых
значений Т""'уст, к 5»^ соответственно, которые обеспечивают оптимальное зна-
чение выбранного критерия оптимальности (целевой функции) R.
Как бьию показано, критерий оптимальности R зависит от урасч, т.е. для его опре-
деления при очередных приближениях оптимизирующих переменных т, к, S , генери-
руемых алгоритмом оптимизации (alg ОПТ), необходимо каждый раз рассчитывать
значения выходных переменных урасч с использованием алгоритма математического
моделирования (alg ММ). Поэтому будет справедливо считать, что во внешнем цикле
процедуры решения задачи оптимизации химико-технологической системы использу-
ется alg ОПТ, а во внутреннем — alg ММ.
1.6.3. Синтез химико-технологических систем
Синтез ХТС — это операция её создания для производства заданной химической
продукции с учётом определённых требований к функционированию ХТС, а также
различных физико-химических и технологических ограничений на их выполнение.
Поскольку процедуры синтеза ХТС включают как формализованные задачи (ФЗ),
так и неформализованные задачи (НФЗ), то наряду с алгоритмом математического
моделирования (alg ММ) и алгоритмом оптимизации (alg ОПТ) для их решения не-
обходим также алгоритм синтеза (а/^СИНТ), широко использующий эволюционно-
эвристические процедуры и тесно связанный с применением методов искусственного
интеллекта и экспертных систем.
В общем случае задача оптимизации ХТС может быть сформулирована следую-
щим образом (рис. 1.13):
1.6. Анализ, оптимизация и синтезхимическихпроизводств
31
Рис. 1.14. Взаимосвязь постановки
Рис. 1.13. Схематическое изображение и решения задач анализа, оптимизации
процедуры синтеза ХТС и синтеза ХТС
• Дано: х, у.
• Известно: физико-химические и технологические ограничения.
• Определить: v4”, А°р', Т°р’, к°р', s°pl, к,.
• Необходимы: alg ММ, alg ОПТ, alg СИНТ.
Все перечисленные определяемые переменные при решении задачи синтеза на-
ходятся с учётом ограничений первого и второго рода (1.16), накладываемых из фи-
зико-химических и технологических соображений как на искомые переменные (ог-
раничения первого рода), так и на вычисляемые с их помощью переменные, харак-
теризующие качество проведения ХТП (ограничения второго рода).
Задачи анализа, оптимизации и синтеза ХТС тесно связаны между собой (рис. 1.14).
Анализ ХТС позволяет определить ресурсы оптимизации и поэтому предшествует
решению задачи оптимизации производства (ХТС). Задачи анализа и оптимизации
ХТС являются необходимыми этапами решения ФЗ синтеза ХТС и необходимыми
для реализации эволюционно-эвристических процедур решения НФЗ синтеза ХТС.
Комплексное решение задач анализа, оптимизации и синтеза химических произ-
водств является важнейшим этапом проектирования новых и модернизации дей-
ствующих производств и широко используется в системах автоматизированного про-
ектирования (САПР) в химической промышленности.
ПРИНЦИПЫ КОМПЬЮТЕРНОГО
МОДЕЛИРОВАНИЯ ХИМИКО-
ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
В общем случае для моделирования химико-технологических процессов (ХТП) на ком-
пьютерах необходимо знание физико-химических закономерностей их протекания, а так-
же данных лабораторных и/или полупромышленных (реже промышленных) эксперимен-
тов для подтверждения справедливости (адекватности) моделей.
Однако для сложных гетерофазных процессов, сопровождающихся химическими
превращениями в различных фазах, эти закономерности не до конца известны, и их
дальнейшее изучение требует существенных инвестиций в научные исследования, что
не всегда оправдано. В этих случаях приходится разрабатывать так называемые
эмпирические модели ХТП, в которых, в отличие от физико-химических моделей, не
учитываются закономерности протекания реальных процессов, и построение которых
базируется на формализованном описании данных экспериментальных исследований.
В результате для каждой выходной (зависимой) переменной эмпирической модели
получается достаточно простая функциональная (чаще всего, аппроксимационная) её
зависимость от входных (условно независимых) переменных процесса. Вид и коэффи-
циенты этих зависимостей, как правило, определяются методами регрессионного и
корреляционного анализа по результатам обработки данных пассивных или активных
экспериментов. К недостаткам таких моделей, кроме необходимости проведения боль-
шого числа уточняющих опытов, относится также то обстоятельство, что, строго гово-
ря, они справедливы только в том диапазоне изменения параметров технологического
процесса, в котором были проведены экспериментальные исследования.
В этом плане физико-химические модели являются более привлекательными, так как
они основаны на учёте действительных закономерностей протекающих процессов, и
поэтому могут применяться для прогнозирования поведения промышленных произ-
водств в достаточно широких диапазонах изменения параметров. При их построении
сначала изучается теория процесса, исходя из чего строится система уравнений
математического описания (МО), после анализа которой разрабатывается
моделирующий алгоритм (МА) её решения. Последний, чаще всего, представляет собой
комбинацию известных численных методов решения стандартных задач вычислитель-
ной математики (см. разд. 3.2, 3.5 и 3.6). В результате реализации моделирующего
алгоритма (МА) на компьютере одновременно вычисляются все выходные перемен-
ные технологического процесса при известных значениях входных переменных, т.е.
решается так называемая прямая задача математического моделирования.
Не менее важным является также и решение обратной задачи математического
моделирования, когда на основе экспериментальных данных определяются как
вид уравнений, описывающих физико-химические закономерности протекающих
процессов (гидродинамики, химических и фазовых превращений, массо- и теп-
лопередачи и других), так и значения параметров (коэффициентов массопередачи,
теплопередачи, констант фазовых равновесий и др.) этих уравнений. Только при
успешном решении обратной задачи удаётся добиться адекватности математичес-
кой модели (ММ) и использовать её для исследования поведения реальных про-
цессов.
2.1. Математическое описание ХТПс помощью физико-химических моделей
33
Обратные задачи математического моделирования тесно связаны с задачами иден-
тификации МО ХТП. Идентификация МО объектов заключается в определении вида
уравнений системы (структурная идентификация) и её коэффициентов (параметри-
ческая идентификация) на основании ограниченной выборки (статистики) экспери-
ментальных данных. С практической точки зрения однозначного решения задачи
идентификации не существует в том смысле, что при различных наблюдениях экспе-
риментальных данных получаются отличающиеся друг от друга результаты. Для
эмпирических моделей задача идентификации решается при их построении статис-
тическими методами. В случае физико-химических моделей для решения задачи иден-
тификации приходится реализовывать специальные оптимизационные алгоритмы,
которые минимизируют отклонения между расчётными и экспериментальными
параметрами ХТП (см. разд. 1.4).
Решение задачи оптимизации процесса также отличается при применении эмпири-
ческих или физико-химических моделей для описания поведения процессов.
При использовании эмпирических моделей из-за ограниченности диапазона изме-
нения их параметров в процессе описания поведения реальных процессов расчёт
оптимальных условий приходится сочетать с дополнительной постановкой экспери-
ментальных исследований — реализуются так называемые экспериментально-стати-
стические методы оптимизации. В этом случае оптимальные условия проведения
процессов из-за простого вида функциональных зависимостей моделей могут опре-
деляться с использованием необходимых и достаточных условий экстремума функ-
ций многих переменных.
Д ля решения задачи оптимизации с использованием физико-химических моделей при-
меняются численные методы одномерной и многомерной оптимизации. Проведение допол-
нительных экспериментов при этом не требуется, так как модели справедливы в широ-
ком диапазоне изменения параметров процессов и допускается возможность экстрапо-
ляции их свойств. Рассчитываемые оптимальные условия проведения процессов при
условии адекватности используемой компьютерной модели обычно соответствуют дей-
ствительности.
2.1. Математическое описание химико-
технологических процессов с помощью
физико-химических моделей
Химико-технологические процессы обычно протекают в движущихся потоках фаз
(паро-газовых, жидкостных и твёрдых), гидродинамические закономерности пере-
мещения которых оказывают влияние на эффективность химических производств.
Выбор конструкций аппаратов химической технологии во многом связан с необхо-
димостью обеспечения требуемых гидродинамических условий проведения процес-
сов. Поэтому основу уравнений МО ХТП составляют балансовые уравнения для по-
токов вещества (массы), теплоты (энтальпии) и импульса (количества движения),
записанные с учётом гидродинамических закономерностей их движения.
Характерной особенностью перечисленных балансовых уравнений является то
обстоятельство, что они должны включать выражения, описывающие интенсивнос-
ти источников (стоков) веществ, теплоты и импульсов, характеризующих скорости
их образования (выделения) и расходования (поглощения) в потоках за счёт различ-
ных «элементарных» физико-химических процессов — химических реакций, массо-
передачи, фазовых переходов и т.д.
Принципиально можно построить гидродинамические модели потоков различ-
ной сложности, наиболее отвечающие используемым конструкциям технологичес-
3-4544
34
Глава 2. Принципы компьютерного моделирования ХТП
кого оборудования. Для этой цели при построении физико-химических моделей ре-
альных процессов применяются так называемые комбинированные гидродинамические
модели движения потоков. Они представляют собой комбинации описаний зон ап-
паратов с более простыми гидродинамическими моделями движения потоков, в ча-
стности, комбинации моделей идеального смешения, идеального вытеснения и однопа-
раметрической диффузионной модели. Основная особенность этих моделей состоит в
том, что они содержат минимальное число параметров:
• модель идеального смешения — объём;
• модель идеального вытеснения — объём и длину;
• однопараметрическая диффузионная модель — объём, длину и коэффициент
продольного перемешивания.
Химико-технологические процессы обычно сопровождаются перемещением не-
которых материальных потоков жидкости, газа (пара) или твёрдых частиц. Потоки
могут быть однофазными, т.е. целиком состоять из частиц одной фазы (например
жидкости), которые перемещаются в некотором объёме аппарата, и многофазными
(в частности, двухфазными), когда процесс проходит в условиях взаимодействия не-
скольких фаз, например, газ—жидкость, жидкость—твёрдое вещество, газ—твёрдое
вещество и т.д. В связи с этим основу уравнений математического описания ХТП
составляют балансовые уравнения движения потоков.
Уравнения гидродинамики реальных потоков обычно очень сложны (например,
уравнения Навье—Стокса) и часто не могут быть записаны в общем виде (например,
для многофазных потоков из-за отсутствия возможности задания граничных усло-
вий на нестационарной поверхности раздела фаз). Поэтому на практике при состав-
лении математических описаний обычно используют приближённые (модельные)
представления о структуре движущихся потоков отдельных фаз — гидродинамичес-
кие модели идеального смешения, идеального вытеснения и однопараметрические
диффузионные модели.
Для зон потоков, описываемых этими приближёнными моделями, составляются
балансовые уравнения гидродинамики в соответствии с рис. 2.1. В общем случае
балансовые уравнения гидродинамики записывают отдельно для
• массы;
• веществ (компонентов) многокомпонентной смеси;
• теплоты (энтальпии);
• импульса
и распространяют на всю движущуюся систему с учётом её полного объёма и дли-
ны (для модели идеального вытеснения и однопараметрической диффузионной мо-
дели).
Под потоком массы понимают общую массу многокомпонентной смеси, протека-
ющую в единицу времени в рассматриваемой системе. Единица измерения потока
массы, например, [кг/час] или [кг/сек].
Скорость
накопления
количества
массы,
вещества,
энтальпии
(теплоты)
или импульса
в единице
объема
Поток массы,
вещества,
энтальпии
(теплоты)
или импульса,
поступающий
в единицу
объема
Поток массы,
вещества,
энтальпии
(теплоты)
или импульса,
отводимый
из единицы
объема
Суммарная интенсивность
источников (стоков) массы,
вещества, энтальпии
(теплоты) или импульса
за счет различных
физико-химических
процессов в рассматриваемой
зоне, включая дополнительный
подвод (отвод) указанных
потоков от (к) внешних
источников в единице объема
Рис. 2.1. Общий принцип составления балансовых уравнений для идеальных
гидродинамических моделей движущихся потоков фаз
2.1. Математическое описание ХТП с помощью физико-химических моделей 35
Поток вещества (компонента) является частным слу-
чаем потока массы. Термин относится только к массе выб-
ранного z-го компонента. Единица измерения потока ве-
щества (компонента), например, [молей z-го компонента
смеси/час] или [молей /-го компонента смеси/сек]. Из
определения закона сохранения массы следует, что внутри
системы сумма потоков компонентов равна потоку массы.
Поток теплоты или энтальпии в инженерных расчётах
является энергетической характеристикой системы. Под
этим термином понимают поступающее (отводимое) в
единицу времени в (от) систему (системы) количество
теплоты (энтальпии), отнесённое к стандартному состоя-
нию. Единицы измерения потока теплоты или энталь-
пии, например, [ккал/час] или [ккал/сек].
Поток импульса (количества движения) характеризу-
Рис. 2.2. Объект с сосредо-
точенными параметрами
ется значением подводимого (отводимого) в единицу вре-
мени к (от) системе импульса. Единица его измерения, например, [кг-м/час2] или
[кг-м/сек2].
Следует отметить, что уравнения балансов импульса при МО ХТП используются
достаточно редко. Это связано с тем, что они существенно усложняют процедуру ре-
шения систем уравнений МО, в то время как дополнительная информация, получае-
мая при их применении, как правило, не столь важна. На этом основании уравнения
балансов импульса в дальнейшем не рассматриваются.
2.1.1. Математическое описание зоны потока,
движение фазы в которой представляется
гидродинамической моделью идеального смешения
Объекты, описываемые моделью идеального смешения, относятся к объектам с
сосредоточенными параметрами. Для них характерно, что все переменные и парамет-
ры процесса одинаковы во всём объёме зоны идеального смешения (рис. 2.2).
Динамическая модель
В соответствии с табл. 2.1 и табл. 2.2 уравнения покомпонентного баланса для
динамической модели объекта с сосредоточенными параметрами записываются сле-
дующим образом.
(л|) Уравнения покомпонентных балансов [и уравнений обозначаются („,) ]:
4сЧ) = _vx Gz = ! }
dt ‘
2) Уравнение общего баланса массы (Хл> =1):
Z=I
dV R (0) xVr1
= v<’-v + ^Gf . (2.1)
dt i=i
3) Уравнение теплового баланса:
- vCpT+дех.
dt
36
Глава 2. Принципы компьютерного моделирования ХТП
Таблица 2.1. Уравнения балансов гидродинамических моделей
Класс уравнений Покомпонентного баланса
Вид модели Динамическая Статическая
пленными параметрами Однопараметрическая диффузионная модель м с. 4 £ * d ) dt L де2 де ,ю 1=1 п С К 43 к а; Чз Q 5 с г 7 ^3
О О. с о га О. О Модель идеального вытеснения м 4 2 \l) dt де w i = 1, .... п 1 м 1 de “° i = 1 п
С сосредоточенными параметрами Модель идеального смешения ; 4 с, © к а: тз V Л: УЛ: Л- V/, Л i = 1,.... п 0= 'о + 'ХЛ- , 'X, .Л о т (о) <0>
Общего баланса массы Теплового баланса
Динами- ческая Стати- ческая Динами- ческая Стати- ческая
w
О)
<
4-
о
М 5 II
о о w
и O) <
4- 1 4-
г© | го 1 <0 eJ w <1“Э‘
e 1 й- 1
Q «J 1 ro
II ft; Q < b- a.
D L dt II 2(VRC de1
33 1
QN
у 1
w
O)
<
4-
'H's U to w O)
dv “~э74 Ф' n 1 II < II £?
%
1 •X3 1 “53
1-Г
CX
<
4- о
II
о о cT M 04
'И* 4- II I © < 4-
1 © lT
© + c
©
II 1 о
о II
о
зз| и
©
a; ^3
2.1. Математическое описание ХТПс помощью физико-химических моделей 3 7
Таблица 2.2. Основные интенсивности источников элементарных процессов
в потоках
Источники элемен- тарных процессов Тип источников Интенсивность источников в зоне
С сосредоточенными параметрами С распределен- ными параметрами Локальная
Суммарные Компонентов 1 v + Е * .. Г 1 «+ v II с .. н . <0 W + G.w = GW +G“) + + G.<o +G<n> i = 1, n
Теплоты A(2I=Aes+AC*' + + ЛвЛ+ЛвТ+АвИ + + AQn + Cd) + Д2(о + Д|2(И() + +e<">
Химическая реакция в объеме VR Компонентов G* = V* g* i = 1,п rS Vя к Gi(l)= — g. i = 1,n m gi =Ъа:>г> i = 1, n
Теплоты &QS =VR&qR АПК R AQ(t) =
Массо- передача через поверхность площадью FM Компонентов Gt =F g, i = 1,л r* M Г M Gw i = 1,n j=l i = 1, n
Теплоты &QU =FMbq“ bQ“,=^-bqu <=)
Изменение агрегатного состояния при фазовом равновесии Компонентов GA = -v x,’** i -1,..., n Gxo- Lxi i = 1,n x,<*> = yp i = 1, ...,n
Теплоты AQa = -V ДНЛ ДНА = f=l
Теплопере- дача через поверхность площадью Теплоты AQ' = FTAq ^qT=KT(f-Ty
Теплоизлу- чение с поверхности площадью Р1 Теплоты AC1* = FKAqK ^q" =KK(f* -T*)
38
Глава 2. Принципы компьютерного моделирования ХТП
Система (п + 2) обыкновенных дифференциальных уравнений (СОДУ) (2.1) — см.
разд. 3.5.1 — используется для математического описания нестационарных режимов
процессов с сосредоточенными параметрами. В систему уравнений (2.1) дополни-
тельно должны быть включены выражения для определения интенсивностей источ-
ников всех компонентов G,£ (/= 1.л) и теплоты А (Г (см. табл. 2.2).
Результатом решения системы уравнений (2.1) должны стать функции, отражаю-
щие зависимость от времени концентрации компонентов реакционного объёма Vя
и температуры потока Т.
х' =x‘(t) о = 1.л), vs,=Vs’(<), Г =Г(/). (2.2)
Статическая модель
Статическая модель объекта с сосредоточенными параметрами описывается систе-
мой конечных уравнений (СКУ): либо линейных (СЛАУ), либо нелинейных (СНУ) —
см. разд. 3.2.
В соответствии с табл. 2.1 уравнения покомпонентного баланса для статической
модели объекта с сосредоточенными параметрами записываются следующим обра-
зом (производные в уравнениях (2.1) равны нулю).
Т (л)) Уравнения покомпонентных балансов:
у10>х\0> — vxt + Gf = 0 (i = 1,..., п) .
п
2) Уравнение общего баланса массы (Хл< =1):
«=1
v(0) -v + ^Gf =0. (2.3)
i=l
3) Уравнение теплового баланса*.
v<0)C'>0)7’<0) -vCpT + \Ql =0.
Система (и + 2) конечных уравнений (СКУ) (2.3) используется для описания
стационарных режимов процессов с сосредоточенными параметрами. В эту систему
уравнений должны быть включены выражения для определения интенсивностей ис-
точников всех компонентов G,1 (1 = 1, ...,л) и теплоты AQy (см. табл. 2.2).
Результатом решения конечной системы уравнений (2.3) должны стать расчётные
значения концентраций, расхода реакционного потока и температуры:
х\ v*, Т*. (2.4)
2.1.2. Математическое описание зоны потока,
движение фазы в которой представляется
гидродинамической моделью идеального
вытеснения
Объекты, описываемые такими моделями, относятся к объектам с распределён-
ными параметрами. Для них характерно, что все переменные и параметры процесса
изменяются вдоль пространственной координаты зоны идеального вытеснения.
Схематическое изображение объекта с распределёнными параметрами приведено на
рис. 2.3. Такой поток представляется совокупностью бесконечного числа зон, опи-
сываемых гидродинамическими моделями идеального перемешивания.
2.1. Математическое описание ХТП с помощью физико-химических моделей 39
Динамическая модель
Приведём вывод уравнения покомпонентного баланса для динамической модели
объекта с распределёнными параметрами.
Уравнения покомпонентных балансов для произвольной зоны идеального сме-
шения ДУ" в данном случае можно представить так:
Л<^> _ v((>x(())+ Gz (/ = L , (2 5)
dt L
где
ДУ*=$-ДЛ (2.6)
При этом площадь поперечного сечения потока 5 при допущении о цилиндри-
ческой форме трубы с постоянным сечением выражается:
s = vr!l.
(2.7)
После подстановки выражения (2.6) в уравнение (2.5) получаем:
Ldt ~ Ы + L
(2.8)
При стремлении интервала д£ к нулю (д£ _> о) получаем уравнения покомпонен-
тных балансов (см. табл. 2.1).
!(„)) Уравнения покомпонентных балансов:
d(v*x() Э(гх() „у у у ,
Г д. -----+ ’ Где GW = Gi /L =
L-dt dt
2) Уравнение общего материального баланса (£х, =1) имеет вид:
1 dvR
L dt
(2.9)
3) Уравнение теплового баланса записывается подобно уравнениям
покомпонентных балансов с учётом замены х, на СрТ:
a(vRc„r) a(vc„r) д г Е/
В результате получена система (п + 2) диф-
ференциальных уравнений в частных произ-
водных (2.9). В эту систему уравнений должны
быть включены выражения для определения
интенсивностей источников всех компонентов
(i = l,...,n) и теплоты де(^ (см. табл. 2.2).
Таким образом, для описания нестационар-
ных режимов процессов с распределёнными
параметрами, движение потока фаз в которых
представляется гидродинамической моделью
идеального вытеснения (трубчатый аппарат),
используется система дифференциальных урав-
нений в частных производных (СДУЧП) (2.9) —
см. разд. 3.5.2.
bVR«S-M
Рис. 2.3. Схематическое изображение
движения потока, представляемого
гидродинамической моделью идеально-
го вытеснения (бесконечным числом
ячеек идеального перемешивания)
о
40
Глава 2. Принципы компьютерного моделирования ХТП
Результатом решения системы уравнений (2.9) должны стать расчётные значения
концентраций х, расхода реакционного потока и/' и температуры Т‘ в зависимости
от двух независимых координат — времени t и длины реактора с.
х’=x’(t,l\ i = l,.... л;
у/’=У*'(1,Л (2.10)
Статическая модель
Уравнения покомпонентных балансов в данном случае можно представить в сле-
дующем виде (см. табл. 2.1) — так как производные по времени для стационарных
режимов процессов в системе (2.9) равны нулю.
!(„))Уравнения покомпонентных балансов:
d(vx,) т т ,
Где G*() = Gf]L (i - 1,..., п).
2) Уравнение общего материального баланса (j^x, =1) имеет вид:
3) Уравнение теплового баланса записывается следующим образом:
— d? )=дб(о, гае =деЕ/ь.
Для описания стационарных режимов процессов с распределёнными параметра-
ми, движение потока в которых представляется гидродинамической моделью иде-
ального вытеснения, когда изменение переменных происходит вдоль одной про-
странственной координаты I, используется система обыкновенных дифференциальных
уравнений (СОДУ) (2.11) — см. разд. 3.5.1. В эту систему уравнений должны быть
включены выражения для определения интенсивностей источников всех компонен-
тов G*o (i = l, ...,л) и теплоты Д2(Е() (см. табл. 2.2).
Решением данной системы уравнений математического описания должны стать
зависимости концентрации х", расхода реакционной смеси v* и температуры Т* от
пространственной координаты I:
r=<W (i = 1,.V* = v*(f), 7’*=T*(f). (2.12)
Другими словами, решением системы (2.11) являются изменение температуры,
концентраций, расходов вдоль длины реактора.
2.1.3. Математическое описание зоны потока,
движение фазы в которой представляется
однопараметрической диффузионной моделью
Объекты, описываемые этими моделями, как и моделями идеального вытесне-
ния, относятся к объектам с распределёнными параметрами. Схематическое изобра-
жение потока, в котором движение фазы представляется однопараметрической диф-
фузионной гидродинамической моделью приведено на рис. 2.4.
В этом случае наряду с конвективными потоками компонентов (/ = 1,... , п) на
2.1. Математическое описание ХТПс помощью физико-химических моделей 41
входе в бесконечно малую ячейку с ко-
ординатами и потоками компонентов
на выходе (v('+A,)x,('+")) из неё, как это было по-
казано для гидродинамической модели идеаль-
ною вытеснения, существуют и обратные диф-
фузионные потоки [vx]™* (со знаком «минус»
на рис. 2.4.) как на входе в бесконечно малую
А(,)
ячейку (-DSWтак и на выходе из неё
)
df. ’
Частичное перемещение фазы навстречу
конвективному потоку (так называемое «обрат-
ное перемешивание») описывается уравнени-
Рис. 2.4. Схематическое представление
однопараметрической диффузионной
гидродинамической модели движения
потока
см, аналогичным уравнению молекулярной диффузии (закон Фика):
[VX]*=-DS^. (2.13)
Коэффициент D называется коэффициентом продольного перемешивания и являет-
ся эмпирическим параметром, который определяется из экспериментальных данных.
Он в совокупности учитывает и молекулярную диффузию, и турбулентность, и неравно-
мерность поля скоростей в потоке; принимается постоянным для всей зоны потока,
описываемой однопараметрической диффузионной гидродинамической моделью.
В то же время площадь поперечного сечения потока S может изменяться в раз-
личных сечениях. Поэтому на входе в элементарную ячейку 5 определяется так:
5(')=v*(0/L, (2.14)
а на выходе из неё:
(2.15)
В результате для многокомпонентной системы вместо обыкновенных производ-
ных следует использовать частные производные, и с учётом равенств (2.14) и (2.15)
величина диффузионного потока на входе в элементарную ячейку с координатами
f + ле] будет равна:
D Э(Ук(,)хФ)
а на выходе из неё:
L де
(2.16)
D Э(у"('+А,)х’'+А,))
L де
(2.17)
Динамическая модель
Уравнение покомпонентного баланса для элементарной ячейки (см. рис. 2.4) с
координатами [м + Д^] в соответствии с (2.16) и (2.17) может быть записано:
d(bVRX,) D d(VR{‘^x^
dt
L де
D d(VR(,)x^)
L де
(2.18)
-(v('+A,)x)'+A') _ v(')xw) + Gf^- (i = 1, ..., л), где дVs = 5 ле.
42
Глава 2. Принципы компьютерного моделирования ХТП
После чего будет справедливо:
a(Ks('>x('>)
d(VRXi) D м у
Ldt L Д/
0 =1, п).
bf + L
(2.19)
В результате после перехода к частным производным с учётом д/’ 0 для описа-
ния динамического режима рассматриваемого объекта с помощью покомпонентного
баланса применяется следующее уравнение (см. табл. 2.1).
1J„)) Уравнения покомпонентных балансов:
Э(Уях,) £>Э2(Уях,) Э(их ) z j. v/
------эГ+с''-гае C*> = G> fL <; = 1....">
n
2) Уравнение общего материального баланса ( V х,. = 1):
dVR _ D Э2У* Эу z
Ldt ~ L Э£2 ,(<) ’
3) Уравнение теплового баланса записывается подобно уравнениям
покомпонентных балансов с учётом замены х, на СрТ:
(2.20)
Э(УяСрГ)
Ldt
Од2(УкСрГ)
L df
d(vCT) _ _ _ .
+ где = \Q*/L.
В результате для математического описания зоны потока, которая может быть
представлена однопараметрической диффузионной гидродинамической моделью,
может использоваться система (п + 2) дифференциальных уравнений в частных произ-
водных второго порядка (СДУЧП) (2.20) — см. разд. 3.5.2. Полученная система долж-
на быть дополнена уравнениями для интенсивностей различных элементарных
физико-химических процессов для всех компонентов (/=1,...,л) и теплоты Дб^
(см. табл. 2.2) в рассматриваемой зоне, а также зависимостями для физико-химичес-
ких коэффициентов элементарных процессов.
После этого СДУЧП (2.20) может быть решена одним из известных методов
(см. разд. 3.5), и полученные решения, как и для процессов, движение потоков фаз
которых описывается гидродинамической моделью идеального вытеснения, являют-
ся функцией двух независимых переменных — времени t и пространственной коор-
динаты г (2.10).
Однако, в отличие от модели идеального вытеснения, процедура решения здесь
оказывается более сложной по двум причинам:
• в данном случае приходится решать СДУЧП второго порядка, тогда как в слу-
чае модели идеального вытеснения решается СДУЧП первого порядка;
• для решения требуется определить коэффициент продольного перемешивания D,
что связано с проведением специальных экспериментальных исследований.
Статическая модель
При описании стационарных режимов объектов, движение потока фазы которых
представляется однопараметрической диффузионной гидродинамической моделью,
производные по времени в системе уравнений, описывающей динамические режи-
мы (2.20) равны нулю. Поэтому для случая однопараметрической диффузионной
модели полученная СДУЧП (2.20), для описания стационарных режимов преобразу-
2.2. Компьютерное моделирование ХТП с помощью физико-химических моделей 43
с гея в систему обыкновенных дифференциальных уравнений с одной независимой
переменной — пространственной координатой I (см. табл. 2.1).
(я)) Уравнения покомпонентного баланса:
РЛ2(Уях,.)
l de2
dtyXi) L
---------t-G/,, = 0 (i = l,...,n).
d£ '<(>
2) Уравнение общего материального баланса (^х, =О;
Dd2VK dv £
L d£2 d£ h w
= 0.
(2.21)
3) Уравнение теплового баланса:
DdW^T) d(VCpT)
L d£2 d£
Так как объекты, движение фаз которых описывается однопараметрическими диф-
фузионными гидродинамическими моделями, также относятся к объектам с распреде-
ленными параметрами, общий вид решений системы обыкновенных дифференциальных
уравнений (СОДУ) (2.21) — см. разд. 3.5.1 — не будет отличаться от решений, получае-
мых при описании гидродинамики процесса моделью идеального вытеснения (2.12).
Однако, поскольку в этом случае решается СОДУ второго порядка, алгоритм
решения оказывается более сложным, и, как упоминалось выше, возникает задача
определения коэффициента продольного перемешивания D путём проведения спе-
циальных экспериментальных исследований.
Из изложенного выше следует, что для решения прямых задач математического
моделирования ХТП необходимо располагать тремя основными алгоритмами решения:
• алгоритмом решения С КУ: СЛАУ или СНУ;
• алгоритмом решения СОДУ;
• алгоритмом решения СДУЧП.
2.2. Компьютерное моделирование
химико-технологических процессов
с помощью физико-химических моделей
При компьютерном моделировании химико-технологических процессов с при-
менением физико-химических моделей необходимо руководствоваться следующими
основными принципами.
1. Движущийся поток рассматривается как многофазная, многокомпонентная си-
стема (число компонентов = п), для каждой из фаз которой записывают уравнения
балансов, базирующиеся на принятой гидродинамической модели движения потока:
• модели идеального смешения (МИС);
• модели идеального вытеснения (МИВ);
• однопараметрической диффузионной модели (ОДМ).
2. Реальный поток движущейся фазы может быть представлен в виде комбиниро-
ванной гидродинамической модели идеального смешения, состоящей из зон МИС,
МИВ и зон, соответствующих ОДМ, причём для каждой зоны записывается своя
система уравнений балансов.
44
Глава 2. Принципы компьютерного моделирования ХТП
3. Для каждой зоны записываются следующие уравнения балансов:
• уравнения покомпонентных балансов, которые характеризуют изменение кон-
центраций компонентов в зоне; число уравнений — п;
• уравнение общего материального баланса, характеризующее изменение расхо-
да потока в зоне; число уравнений — 1;
• уравнение теплового баланса, которое характеризует изменение температуры в
зоне; число уравнений — 1;
• уравнение баланса импульса (количества движения), которое характеризует из-
менение давления в зоне (в этой книге не используется).
Поэтому общее количество балансовых уравнений для отдельной зоны без учёта
уравнения баланса импульса (количества движения) составляет (п + 2).
4. Если уравнения балансов включают производные по времени, то строятся ди-
намические математические модели, которые описывают нестационарные режимы
движения потока фазы. Если в системе уравнений нет производных по времени, то
строятся статические математические модели, которые описывают стационарные
режимы движения потока.
5. Основу уравнений математического описания составляют гидродинамические
уравнения балансов для движущихся потоков, перечисленные в табл. 2.1, в которые
включаются интенсивности источников вещества (компонентов) — см. табл. 2.2 — в
уравнения покомпонентных и общего материального балансов, а также интенсивно-
сти источников теплоты (см. табл. 2.2) — в уравнение теплового баланса.
6. Интенсивности источников веществ характеризуют скорости образования или
расходования компонентов в потоке за счёт отличных от гидродинамики элементар-
ных процессов.
7. Интенсивности источников теплоты характеризуют скорости выделения или
поглощения теплоты' в потоке за счет отличных от гидродинамики элементарных
процессов.
8. К основным элементарным процессам относятся:
• химические превращения или реакции, для которых интенсивность источников
вещества обозначается G," (/ = 1, ...,л), а интенсивность источников теплоты — \qr ;
• массопередача, для которой интенсивность источников вещества обозначается
G," (; = 1, ...,п), а интенсивность источников теплоты — Ag";
• изменение агрегатного состояния или фазовые переходы, для которых интен-
сивность источников вещества обозначается G,4 (/ =1.п), а интенсивность ис-
точников теплоты — Agx;
• поток подпитки, для которого интенсивность источников вещества обозначает-
ся G/I(; =l,...,n), интенсивность источников теплоты — Ag";
• теплопередача, для которой интенсивность источников теплоты обозначается Agr;
• теплоизлучение, для которого интенсивность источников теплоты обозначается Ag11.
9. Общая суммарная интенсивность источников вещества обозначается
G,1 ((= 1, ...,п), суммарная интенсивность источников теплоты — Agz. Суммарные ин-
тенсивности источников веществ и теплоты определяются как аддитивная сумма
(см. табл. 2.2):
Gz = G* + G," + G. + G,n (Z = 1.n) (2.22)
де1 = де" + де" + АеЛ+де" + дег+деи. (2.23)
Для совмещённых процессов в этих суммах присутствуют два и более слагаемых,
например, для процесса хемосорбции - G,“, AgM (описание процесса массопереда-
чи) и G,s, Ags (описание химической реакции).
2.2. Компьютерное моделирование ХТП с помощью физико-химических моделей 45
10. Различают объёмные интенсивности источников элементарных процессов, для
локальных интенсивностей которых (/ = ],...,«) и Ас/, отнесенных к «минимальному
локальному» объему, записываются физико-химические зависимости с соответству-
ющими коэффициентами, и поверхностные интенсивности источников элементар-
ных процессов, для локальных интенсивностей которых g, л) и A<?, отнесен-
ных к «минимальной локальной» поверхности, также записываются физико-хими-
ческие зависимости с соответствующими коэффициентами.
Например, для химической реакции локальные интенсивности источника веществ
(/ = 1,и источника теплоты д</" относятся к единице объёма рассматриваемой
юны (см. табл. 2.2):
Gg=Vgg* = (2.24)
Д2" = Vs Ас/. (2.25)
В этом случае g. (i = l, ...,п) — локальная скорость химической реакции по компо-
ненту i (скорость, отнесённая к единице объёма), i\qg~ локальная скорость выделе-
ния или поглощения теплоты за счёт химической реакции (также отнесённая к еди-
нице объёма).
Для процесса массопередачи локальные интенсивности источника веществ
х," (i = l, ...,л) и источника теплоты д^" выражаются через поверхность рассматрива-
емой зоны массопередачи (см. табл. 2.2):
G," (i = l,...,«); (2.26)
AQ“ =FMbqM. (2.27)
В этом случае g" (/ = 1,...,л) — локальные скорости массопередачи по каждому
компоненту, отнесённые к единице поверхности, FM — поверхность массопередачи,
~ локальная скорость выделения или поглощения теплоты за счёт массопереда-
чи, отнесённая к единице поверхности.
11. Записываются выражения для локальных интенсивностей элементарных про-
цессов, зависящих от различных переменных процесса.
Например, локальная скорость химической реакции по компоненту i в уравне-
нии (2.24) для реакции с т «элементарными» стадиями определяется следующим
выражением (см. табл. 2.2):
?." = = (2.28)
где г} — скорость J-й стадии химической реакции; % — стехиометрический коэффи-
циент i-го компонента на j-й стадии реакции, когда стадия реакции является «эле-
ментарной»; и — число компонентов многокомпонентной системы; т — число эле-
ментарных стадий сложной химической реакции.
Выражение для скорости стадии «элементарной» химической реакции в соответ-
ствии с законом действующих масс имеет вид:
=*уПх? (/ = 1> т), (2.29)
(=1
где kj — константа скорости j-й стадии химической реакции, определяемая по урав-
нению Аррениуса; П - обозначение произведения, а принимает значения: ча = -а,у
(если / — реагент j-й стадии реакции) и ч,7 =0 (если i — продукт j-й стадии реакции
или отсутствует на этой стадии).
46
Глава 2. Принципы компьютерного моделирования ХТП
В свою очередь локальная скорость выделения или поглощения теплоты за счёт
химической реакции в уравнении (2.25) определяется следующим выражением
(см. табл. 2.2):
(2.30)
где АН* — тепловой эффект элементарной стадии реакции, перед которым стоит
знак минус, так как его величина рассматривается относительно движущегося пото-
ка, а не окружающей среды, как общепринято в химии; он относится к одному молю
продукта р на этой стадии.
Локальная скорость массопередачи по компоненту i в уравнении (2.26) определя-
ется следующим выражением (см. табл. 2.2):
g“ <'=1’(2.31)
где К," — коэффициент массопередачи; х’ — равновесная концентрация компонента j.
В свою очередь, локальная скорость выделения или поглощения теплоты за счёт
массопередачи определяется (см. табл. 2.2) с помощью следующего соотношения:
(2.32)
1=1
12. Записываются выражения для коэффициентов элементарных процессов, за-
висящих от различных переменных процесса (коэффициентов теплопередачи К7,
констант скоростей реакций к} и т.д.).
Например, для химической реакции нужно включить в систему уравнений мате-
матического описания выражение для к} — константы скорости на J-й стадии хими-
ческой реакции в соответствии с законом Аррениуса в уравнение (2.29), а для про-
цесса массопередачи — выражение для К" — коэффициента массопередачи в урав-
нение (2.31).
13. Записываются уравнения ограничений на конструкционные параметры про-
текающих процессов [например, длина трубы от 0 до L (где L — длина зоны)] и на
физические переменные процесса (например, суммы долей компонентов реакции).
В результате выполнения п.п. 1 — 13 получается система уравнений математичес-
кого описания процесса (МО).
14. Проводится анализ полученной системы уравнений МО процесса, который
состоит в следующем:
• исключаются зависимые уравнения, которые можно получить комбинацией
других уравнений системы;
• проверяется совпадение размерностей физических величин левых и правых ча-
стей уравнений МО;
• по возможности, уравнения системы заменяются более простыми, например,
уравнения покомпонентных балансов для потоков веществ в химических реак-
торах выражаются через потоки других веществ (их составы) с использованием
стехиометрических соотношений, вытекающих из кинетической схемы конк-
ретной реакции.
15. Выбираются переменные системы уравнений МО, относительно которых она
решается, и определяется — к какому математическому типу задач относится решае-
мая система уравнений. Если в число определяемых переменных включаются пере-
менные размеров аппаратов и их конструкционные параметры, реализуемое реше-
ние рассматривается как проектный расчёт. При отсутствии указанных параметров
среди определяемых при решении систем уравнений МО, т.е. когда они заданы,
процесс решения считается поверочно-оценочным расчётом.
2.3. Компьютерное моделирование ХТПс помощью эмпирических моделей
47
16. В зависимости от того, к какому математическому типу уравнений относится
математическое описание (МО) процесса, выбирается моделирующий алгоритм для
решения системы уравнений МО.
17. Моделирующий алгоритм (МА) представляет собой либо известный численный
алгоритм решения системы уравнений МО, либо комбинацию численных алгорит-
мов. При разработке МА пользуются специальными приёмами для сокращения раз-
мерности решаемой задачи и уменьшения числа итерационных процедур решения.
Для этой цели используется метод декомпозиции решаемой задачи, который реализует-
ся с использованием информационной матрицы системы уравнений МО (см. разд. 5.1).
Для обеспечения сходимости расчётов важно правильно выбирать ограниченный набор
итерируемых переменных, начальные приближения для них и условия сходимости с
предварительно задаваемой точностью, связанной с завершением вычислений.
18. Разработанный МА реализуется на компьютере в виде расчётного модуля ХТП.
19. Проводится анализ параметрической чувствительности разработанной матема-
тической модели, и выявляются те её параметры (переменные и коэффициенты), ко-
торые наиболее сильно влияют на свойства и поведение технологического процесса.
20. Проверяется соответствие разработанной модели данным экспериментальных
исследований, оценивается так называемая адекватность математической модели,
и, в случае отрицательного результата, решается задача идентификации математи-
ческого описания ХТП с целью обеспечения адекватности модели (см. разд. 5.5).
21. Решается задача оптимизации ХТП, и определяются оптимальные режимные
и/или конструкционные параметры, обеспечивающие оптимальность процесса в
смысле выбранного критерия оптимальности (целевой функции) (см. разд. 3.6 и 5.5).
Следует отметить, что отдельные из перечисленных этапов компьютерного моде-
лирования ХТП с использованием физико-химических моделей могут быть пропу-
щены в силу различных причин. Например, если известна приоритетность и степень
влияния различных переменных на поведение процесса, анализ параметрической чув-
ствительности модели не проводится или если нет необходимости в решении задачи
оптимизации, то определение оптимальных параметров процесса не проводится.
Однако, для комплексного решения задач компьютерного моделирования ХТП же-
лательно выполнение всех перечисленных выше этапов.
2.3. Компьютерное моделирование химико-
технологических процессов с помощью
эмпирических моделей
Эмпирические модели применяются в тех случаях, когда либо нет информации о
механизме протекающих процессов, либо они плохо поддаются описанию с исполь-
зованием физико-химических блочных моделей. В этом случае объект (ХТП) пред-
ставляется в виде так называемого чёрного ящика (рис. 2.5) — кибернетической сис-
темы, в которой единственно доступной информацией являются её входные (х) и
выходные (у) переменные: где х = [хр..., хт] — вектор входных переменных, влияю-
щих на состояние системы и её свойства, у = [уР ..., уг ] — вектор выходных пере-
менных, характеризующих состояние системы.
В общем случае эмпирические модели строятся для каждой отдельной выходной
переменной из всех у, (/ = 1, ..., () в зависимости от всех входных переменных х,
(1 = 1, ..., т), т.е.
у = /(х1,...,хт,а), (2.33)
где « = — (т + 1) коэффициентов эмпирической модели.
48
Глава 2. Принципы компьютерного моделирования ХТП
—*
Уе
Рис. 2.5. Изображение ХТП в
виде «чёрного ящика»
Конкретный вид функциональной зависимости (/)
и значения коэффициентов (а) определяются из опыт-
ных данных, т.е. эмпирически.
Так как результаты опытных измерений являются
случайными величинами, то для их обработки исполь-
зуется один из наиболее распространённых методов
математической статистики — метод регрессионного и
корреляционного анализа.
В соответствии с методом регрессионного анализа
Усчитается случайной величиной, распределённой по
нормальному закону распределения, а компоненты
вектора х — детерминированными (неслучайными) ве-
личинами. Поэтому, согласно закономерностям теории вероятностей, при каждом
фиксированном значении вектора х величина У является случайной величиной с
определённым (зависящим от х) условным распределением вероятностей.
В связи с этим для описания функции (2.33) используется зависимость условного
математического ожидания случайной величины У (М[У |г]) от х. Зависимости та-
кого типа принято называть уравнениями регрессии:
Л/[У|:]=/(х,а), (2.34)
а коэффициенты уравнения (2.34) а = [а„,а,,..называются теоретическими
коэффициентами регрессии.
Так как коэффициенты (а) определяются по ограниченной выборке (статистике)
экспериментальных данных, то их значения отличаются от истинных (теоретических)
и обозначаются а (так называемые выборочные коэффициенты регрессии). В результате
пользуются приближённым уравнением регрессии, в котором вместо условного матема-
тического ожидания величины У Л/[у |-] фигурирует её оценка у и выборочные коэф-
фициенты регрессии а:
у = /(х,«). (2-35)
Для приближённого уравнения регрессии — эмпирической статистической моде-
ли — на выборке экспериментальных данных необходимо решить три основные за-
дачи (см. главу 4):
• определить конкретный вид функции (2.35), т.е. решить задачу структурной
идентификации;
• определить выборочные (эмпирические) коэффициенты регрессии д, т.е. ре-
шить задачу параметрической идентификации;
• провести статистический (регрессионный и корреляционный) анализ полученных
результатов с целью оценки погрешностей полученной модели.
Таким образом, задача идентификации математического описания процесса в этом
случае, в отличие от физико-химических моделей, решается уже при построении эм-
пирической модели и не является отдельной задачей компьютерного моделирования.
В то же время оптимизация процесса с использованием эмпирической модели
выполняется с применением уравнений регрессии, выходные переменные которых
являются критериями оптимальности (целевыми функциями) технологического про-
цесса. В результате упрощается процедура решения задачи оптимизации, так как
явный вид зависимости целевой функции от входных (в данном случае оптимизиру-
ющих) переменных позволяет определять оптимальные условия проведения процес-
са с использованием необходимых условий экстремума функции многих перемен-
ных. Это позволяет свести решение задачи оптимизации к решению систем конеч-
ных (линейных или нелинейных уравнений).
2.3. Компьютерное моделирование ХТП с помощью эмпирических моделей
49
Следует отметить, что редко удаётся решить задачу оптимизации с применением
эмпирических моделей без постановки дополнительных экспериментов. Это связано с
тем, что определяемые расчётным путём оптимальные условия проведения процессов
оказываются за пределами диапазонов изменения их переменных, в которых эмпири-
ческие модели справедливы, т.е. адекватны реальному процессу. В этих случаях, как
правило, следует провести дополнительную серию экспериментов, чтобы уточнить (скор-
ректировать) параметры эмпирических моделей с учётом новых обстоятельств.
Конкретный вид эмпирических моделей (2.35) определяется по результатам экспе-
риментов — активных или пассивных.
Активный эксперимент проводится в соответствии со строгим планом опытных
исследований. Согласно этому плану устанавливается количество экспериментов и
значения переменных процесса, в которых они должны проводиться, а также ис-
пользуются специальные приёмы, позволяющие упростить процедуры обработки
результатов опытных исследований. К таким типам экспериментов относятся, на-
пример, полный факторный эксперимент (ПФЭ) и ортогональное центральное ком-
позиционное планирование эксперимента (ОЦКП).
Уравнения, описывающие результаты ПФЭ (эмпирические модели) имеют вид:
без учёта взаимодействия входных переменных (факторов) процесса
У = (2.36)
7=1
с учётом взаимодействия входных переменных (факторов) процесса (например,
двойных)
у = а0+ХаЛ7+ЁЁа7"хА’ U>J, (2.37)
;=1 j=l u=2
где учёт двойного взаимодействия факторов в уравнении (2.37) представлен их про-
изведением с коэффициентом aju.
Приведённые модели (2.36) и (2.37) справедливы в ограниченных областях фак-
торного пространства, располагающихся вдали от оптимальных значений целевых
функций (у).
В областях, «близких» к оптимальному значению целевых функций — «почти ста-
ционарных областях», проводятся опыты в соответствии с ОЦКП, результаты кото-
рого описываются также линейным относительно коэффициентов уравнением сле-
дующего вида (учитываются только двойные взаимодействия факторов):
hvtwELW' U>j, (2.38)
j=l j=l u=2 j=l
где 5 — расчётный коэффициент, обеспечивающий выполнение свойства ортого-
нальности матрицы планирования ОЦКП и позволяющий упростить обработку его
результатов.
В пассивном эксперименте (план эксперимента составляется, исходя из опыта и
знаний специалистов) могут использоваться эмпирические модели, имеющие доста-
точно сложный вид и справедливые в более широких диапазонах изменения факто-
ров. Они могут быть не только линейными относительно коэффициентов, как в
активном эксперименте (2.36)—(2.38), но и нелинейными.
Такой нелинейной моделью является, например, эмпирическое уравнение (2.39),
представляющее собой произведение многочленов различных степеней (mJ для каж-
дого фактора (i = 1, ..., ту.
> = аооПЁаох/ (2.39)
,=1 7=0
При правильном выборе приоритетности факторов, влияющих на процесс, с его
помощью может быть успешно решена как задача структурной, так и параметрической
идентификации.
50
Глава 2. Принципы компьютерного моделирования ХТП
Результаты пассивного эксперимента в узких диапазонах изменения факторов
могут быть представлены также линейными относительно коэффициентов моделями
с учётом (2.37) и без учёта взаимодействия факторов (2.36). В особенности это отно-
сится к обработке результатов промышленных экспериментов, когда вследствие необ-
ходимости получения продукции требуемого качества требуется исследовать стабиль-
ные, близкие к стационарным, режимы производств. В этом случае колебания режим-
ных параметров непрерывных производств несущественны, и их изменения могут
быть описаны линейными моделями.
Коэффициенты эмпирических моделей определяются, как правило, методом
аппроксимации, в частности, методом наименьших квадратов (МНК).
Статистический анализ эмпирических моделей в соответствии с методологией
регрессионного и корреляционного анализа предполагает определение значимости
коэффициентов регрессии с использованием критерия Стьюдента t, адекватности
уравнений регрессии с применением критерия Фишера F и совместных доверительных
областей для коэффициентов регрессии. Одновременно определяются коэффициенты
корреляции и коэффициенты множественной корреляции для линейных по факторам
моделей и корреляционные отношения для нелинейных по факторам моделей. Также
оцениваются экстраполяционные возможности эмпирических моделей.
Задача оптимизации с использованием эмпирических моделей обычно решается с
применением необходимого условия экстремума функции многих переменных вида:
|^ = 0, i = l,...,m. (2.40)
Зх,
Путём решения получаемой в этом случае, чаше всего, системы линейных урав-
нений (реже нелинейных уравнений) удаётся определить оптимальные условия про-
цесса. В этом случае дифференцирование, как правило, удаётся выполнить аналити-
чески, что упрощает реализацию алгоритма решения задачи. Следует отметить, что
корректное решение задачи оптимизации в такой постановке требует проверки дос-
таточных условий экстремума целевой функции.
Для эмпирических моделей, справедливых в широком диапазоне изменения факторов
и получаемых по результатам пассивного эксперимента, получаемое таким способом
решение задачи оптимизации (2.40) можно считать достоверным.
Для эмпирических моделей, справедливых в узких диапазонах изменения факторов и
получаемых по результатам активного эксперимента, например ПФЭ и ОЦКП, не-
обходимо реализовать процедуру определения новых ограниченных областей прове-
дения опытов по планам ПФЭ и ОЦКП с целью определения оптимальных эмпири-
ческих моделей типа (2.38). Например, в оптимизационной процедуре Бокса—Вильсо-
на для этого применяется экспериментально-статистический метод, который основан
на методе градиента (см. разд. 4.3.3). В результате, несмотря на то, что при активном
эксперименте описываются ограниченные области факторного пространства, соче-
тание экспериментов со статистической обработкой их результатов и с использова-
нием направления вектора градиента для «продвижения» к оптимуму в факторном
пространстве приводит к определению оптимальных условий протекания процесса с
требуемой точностью.
2.4. Алгоритмическое обеспечение решения
задач компьютерного моделирования
Для алгоритмического обеспечения решения задач компьютерного моделирова-
ния используются стандартные алгоритмы приближенных численных методов реше-
ния задач вычислительной математики (см. разд. 3.2, 3.5~3.6). При построении
2.4. Алгоритмическое обеспечение решения задач компьютерного моделирования 51
эмпирических моделей XTVI зависимости выходных переменных от входных определя-
ются аппроксимацией экспериментальных данных (см. разд. 3.3.2) путем решения
задачи идентификации — структурной и параметрической. В этом случае решение
прямой задачи компьютерного моделирования сводится к простому вычислению
выходной переменной с использованием получаемой аппроксимационной формулы
и реализация моделирующего алгоритма (alg ММ) для решения систем уравнений
маге магического описания процесса, как для физико-химических моделей, не тре-
буется.
При компьютерном моделировании ХТП с применением физико-химических мо-
делей может потребоваться реализация трех типов вычислительных алгоритмов:
• моделирующего алгоритма (alg ММ) для проведения поверочно-оценочного
и/или проектного расчетов процесса путем решения уравнений его математи-
ческого описания (МО), составленного в соответствии с предполагаемой мате-
матической моделью;
• алгоритма идентификации (alg ИДЕНТ) реального процесса, который исполь-
зует метод оптимизации (минимизации) для обеспечения адекватности (соот-
ветствия) поведения предполагаемой математической модели с эксперимен-
тальными данными, полученными при наблюдении за реальным объектом;
• алгоритма оптимизации (alg ОПТ) (минимизации или максимизации), исполь-
зование которого для адекватной математической модели позволяет определить
оптимальные (наилучшие) параметры реального процесса в смысле выбранно-
го критерия оптимальности (целевой функции).
Все указанные алгоритмы реализуют процедуры вычислений в соответствии с
выбранными методами математического моделирования (ММ), идентификации
(ИДЕНТ) и оптимизации (ОПТ). Как правило, эти вычислительные процедуры явля-
ются приближенными, реализуются на компьютерах и представляют собой извест-
ные численные методы вычислительной математики или их комбинации. При этом
задача состоит:
1) в правильном выборе численного метода (комбинации численных методов);
2) в корректном составлении функции для выбранного численного метода (фун-
кций для комбинации численных методов), исходя из физико-химических
и/или эмпирических закономерностей протекающих процессов;
3) в обеспечении сходимости выбранных численных методов к правильному
физически обоснованному решению задач ММ, ИДЕНТ и ОПТ.
В случае построения физико-химической математической модели процесса (рис. 2.6)
важно выбрать метод решения задачи и правильно сформировать функцию f (функ-
ции /) для численного метода (комбинации численных методов). При этом, как
правило, решаются системы конечных уравнений (СКУ), системы обыкновенных диф-
ференциальных уравнений (СОДУ) и системы дифференциальных уравнений в частных
производных (СДУЧП). В общем случае, в результате решения прямой задачи матема-
тического моделирования получаются приближенные решения урасч указанных выше
систем уравнений, а сама процедура решения является повторяющейся пошаговой
или итерационной, реализующей различные методы последовательных приближе-
ний к физически обоснованному окончательному (правильному) решению.
Для эмпирических математических моделей, получаемых не представленным выше
способом (решением систем уравнений МО), а на основании результатов экспери-
ментальных измерений параметров реальных процессов путем описания аппроксима-
ционными (интерполяционными) ф°РмУлами в явном виде зависимостей выходных
(зависимых) переменных у^4 от входных (условно независимых) переменных X,
изображенный на рис. 2.6 пунктирной линией итерационный алгоритм численного
метода отсутствует. В этом случае результаты математического моделирования получа-
ются прямым расчетом по аппроксимационным (интерполяционным) формулам.
52
Глава 2. Принципы компьютерного моделирования ХТП
Рис. 2.6. Процедура построения математических моделей на основе знания физико-химичес-
кой сущности протекающих процессов и их математического описания
Алгоритм
численного
метода
Задача идентификации решается с использованием экспериментальных данных,
полученных на объекте моделирования, путем минимизации критерия рассогласова-
ния между рассчитанными по математической модели выходными (зависимыми)
переменными урасч и такими же данными уЭ1ССП, полученными из экспериментов при
одинаковых с расчетом значениях входных (условно независимых) переменных X.
Основная цель решения задачи идентификации — получение адекватной (соответ-
ствующей действительности) математической модели. При этом алгоритм иденти-
фикации представляет собой один из методов оптимизации, который должен обес-
печить наименьшее, в частном случае минимальное, значение упомянутого выше
критерия рассогласования (невязки).
В общем случае этот критерий может быть представлен в виде нормы вектора
урасч _ -wen -
/=||урзс,-у’“пй, (2.41)
которая при выбранном численном методе оптимизации (минимизации) должна стре-
миться к наименьшему значению /, в частном случае к локальному минимуму:
f -> min. (2.42)
Успешное решение задачи идентификации (рис. 2.7) и, соответственно, адекват-
ность математической модели обеспечивается путем определения наименьшего зна-
чения функции — критерия (2.42) — за счет выбора наиболее достоверного вида
уравнений МО процесса структурной идентификацией, и определения оптимальных
значений коэффициентов — параметров уравнений МО — параметрической иденти-
фикацией.
Необходимо отметить, что при решении задач структурной [определяется Ф в
(1.2)] и параметрической [определяются коэффициенты а в (1.2)] идентификации
(1.5) следует учитывать три существенных обстоятельства:
а
Рис. 2.7. Процедура решения задачи идентификации реального процесса
2.4. Алгоритмическое обеспечение решения задач компьютерного моделирования 53
• способ расчета минимизируемой нормы вектора рассогласования (2.41) может
быть различным и, соответственно, вид критерия, с применением которого ре-
шается задача идентификации, также должен отличаться, что может сказывать-
ся на получаемых результатах; в свою очередь, финальное значение рассогласо-
вания (2.41) не должно значительно отличаться от ошибки экспериментов при
измерении значений уЭ1КП;
• при решении задачи идентификации реализуется метод последовательных при-
ближений (последовательных итераций), причем на каждой итерации осуществ-
ляется расчет по физико-химической математической модели процесса с исполь-
зованием соответствующего моделирующего алгоритма (МА) — см. рис. 2.6;
• так как результаты расчетов зависят от выборочных экспериментальных дан-
ных уэксп (2.41), то задача идентификации является статистической и для оцен-
ки достоверности полученных результатов следует провести их статистический,
в частности, корреляционный и регрессионный анализ.
Для решения задачи оптимизации (1.10) (рис. 2.8) используется алгоритм оптими-
зации, целевой (оптимизируемой) функцией которого является выбранный крите-
рий оптимальности (технологический, экономический, термодинамический и т.д.) с
наибольшим или наименьшим оптимальным значением, получаемым в результате
решения.
f -> к оптимуму: наименьшему или наибольшему значению. (2.43)
При этом именно численный метод оптимизации путем последовательного изме-
нения значений оптимизируемых (управляющих) переменных процесса (ресурсов
оптимизации) и (1.8) должен обеспечить оптимальное (наибольшее или наимень-
шее) значение критерия оптимальности — целевой функции f Ресурсы оптимизации
й выбираются из числа входных переменных процесса X , которые в наибольшей
степени приемлемы для оптимизации управления и к которым наиболее чувствите-
лен критерий оптимальности (целевая функция) /.
Следует отметить, что при каждом новом приближении оптимизирующих (уп-
равляющих) переменных й в процессе решения задачи оптимизации проводится
расчет по адекватной математической модели, для которой предварительно успешно
решена задача идентификации реального процесса (см. рис. 2.7).
К решению задач компьютерного моделирования, как с использованием физико-
химических, так и эмпирических моделей, предусматривающих применение трёх
типов алгоритмов — построения математической модели (ММ), идентификации
(ИДЕНТ) и оптимизации (ОПТ), можно подойти с единых позиций. На самом деле,
каждый из перечисленных алгоритмов, по существу представляет собой эвристичес-
ки эволюционную процедуру решения неформализованной задачи выбора вариан-
тов, используемую при получении решений в экспертных системах.
Рис. 2.8. Процедура решения задачи оптимизации
с использованием математической модели процесса
54
Глава 2. Принципы компьютерного моделирования ХТП
Рис. 2.9. Обобщённая блок-схема алгоритма
решения задач
компьютерного моделирования
В общем случае всегда должна ста-
виться неформализованная задача выбо-
ра как численного алгоритма (возможно,
их комбинации), так и функции, исполь-
зуемой численным алгоритмом для полу-
чения решения (рис. 2.9).
Как правило, численный алгоритм
решения является итерационным (пунк-
тир на рис. 2.9), который предполагает
многократный и повторяющийся расчёт
функции с изменяющимися значениями
аргументов. Выбор конкретного вида функции для обобщённого алгоритма опреде-
ляется физико-химическими механизмами протекающих процессов и спецификой
решаемой задачи. От правильного выбора численного алгоритма или их комбинации
зависит принципиальная возможность получения физически обоснованного реше-
ния и скорость сходимости численного метода.
При построении физико-химической модели — ММ — функция представляет собой
систему математических зависимостей, описывающих взаимосвязь выходных и вход-
ных переменных процесса и достоверно отражающих физико-химическую природу
протекающих процессов. Численный алгоритм решения в этом случае (см. разд. 2.1) —
это либо алгоритм решения системы конечных уравнений (СКУ): системы линейных
алгебраических уравнений (СЛАУ) или системы нелинейных уравнений (СНУ), либо
алгоритм решения системы дифференциальных уравнений', обыкновенных (СОДУ) или
в частных производных (СДУЧП). Возможна также комбинация этих алгоритмов, а так-
же использование в них алгоритмов численного дифференцирования и интегрирования.
При построении эмпирических моделей — ММ — функция (см. рис. 2.9) представля-
ет собой суммарное рассогласование экспериментальных и расчётных значений вы-
ходных переменных процесса (например, в виде критерия метода наименьших квад-
ратов — критерия МНК) при одинаковых значениях входных переменных. При этом
расчётные значения выходных переменных получаются из уравнения эмпирической
модели. В качестве численного алгоритма в этом случае обычно используется алго-
ритм решения СЛАУ и, реже, — СНУ, позволяющих определить минимальное рас-
согласование критерия, например, МНК в соответствии с необходимым условием
экстремума функции многих переменных.
Задача идентификации — ИДЕНТ — решается при построении физико-химичес-
ких моделей также путём минимизации критерия рассогласования эксперименталь-
ных и расчётных значений выходных переменных процесса при одинаковых значе-
ниях входных переменных. В этом случае критерий рассогласования (2.41) и (2.42)
является обобщённой функцией структуры уравнений МО процесса и входящих в
них коэффициентов (1.5), а численный алгоритм является алгоритмом одномерной или
многомерной оптимизации, определяющей минимум функции — критерия рассогла-
сования.
При решении задачи оптимизации — ОПТ — в качестве функции обобщённого алго-
ритма (см. рис. 2.9) используется критерий оптимальности (целевая функция) в виде
технологического, или экономического, или технико-экономического и т.д. показа-
теля эффективности функционирования процесса. Численный алгоритм в этом слу-
чае представляет собой алгоритм, в общем случае, многомерной оптимизации, опре-
деляющей максимальное или минимальное значение целевой функции, в зависимо-
сти от физического смысла критерия оптимальности.
ЧИСЛЕННЫЕ МЕТОДЫ
КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
ХИМИКО-ТЕХНОЛОГИЧЕСКИХ
ПРОЦЕССОВ
Численные методы вычислительной математики широко используются для реали-
зации алгоритмов расчёта химико-технологических процессов (ХТП). Для расчёта кон-
кретных технологических процессов может потребоваться не один численный метод, а
несколько, связанных между собой и выполняемых совместно. При современном под-
ходе к реализации этих методов в виде объектно-ориентированных модулей компью-
терных программ предполагается применение дружественного интерфейса для пользо-
вателей, который позволяет наиболее удобно вводить исходные данные для расчётов и
представлять результаты вычислений с использованием таблиц, графиков и диаграмм
процессов. Наиболее эффективно это проявляется в пакетах моделирующих программ
(ПМП) (см. главу 6), в которых все вычисления выполняются в единой операционной
среде с применением управляющей программы, использующей кроме расчётных модулей
отдельных численных методов и фактографические базы данных по физико-химичес-
ким свойствам веществ и их смесей, необходимые для вычислений.
К расчётным модулям, реализующим алгоритмы вычислений по различным чис-
ленным методам, предъявляются следующие требования:
• надёжность в смысле получения решения, т.е. обеспечение сходимости вычис-
лений к решению задачи с требуемой точностью;
• физическая обоснованность получаемого решения;
• простота задания исходных данных для итерационных (меняющихся) в процес-
се расчётов переменных — желательна автоматизация этой процедуры;
• простые и эффективные способы изменения итерируемых переменных и пара-
метров алгоритмов в случае отсутствия сходимости, т.е. когда требуемое реше-
ние не получается;
• экономия ресурсов компьютера — минимальное время расчётов и минималь-
ный объём используемой оперативной памяти.
Приходится констатировать, что для моделирования ХТП могут использоваться
различные численные методы и соответствующие им расчётные модули (алгоритмы).
Не существует универсальных численных методов решения конкретных задач вычис-
лительной математики, например, систем нелинейных уравнений или систем обыкно-
венных дифференциальных уравнений и, строго говоря, каждый раз с учётом специ-
фики решаемой задачи надо выбирать соответствующий вычислительный метод. Это
приводит к тому, что при изучении и анализе численных методов решения задач ком-
пьютерного моделирования ХТП необходимо рассматривать и исследовать несколько
методов, приемлемых для решения одной и той же вычислительной задачи.
3.1. Анализ погрешностей приближенных
вычислений
При численном (приближенном) решении прикладных задач компьютерного мо-
делирования ХТП возможно появление следующих четырёх типов погрешностей.
I. Погрешности задачи. Они связаны с приближенным характером математического
56
Глава 3. Численные методы компьютерного моделирования ХТП
описания поведения реального процесса вследствие неучета или неправильного учета
целого ряда существенных факторов, влияющих на результаты решения задачи. Эти
погрешности считаются неустранимыми (безусловными), хотя постановщик задачи, в
некоторых случаях может изменить (уточнить) математическое описание процесса.
2. Погрешности исходных данных, используемых для расчетов. Эти погрешности
обусловлены тем обстоятельством, что на практике исходные данные для расчетов, в
частности, входные переменные модели и ее параметры-коэффициенты, чаще всего
определяются из экспериментальных данных, измеряемых с определенной точнос-
тью. Увеличение точности измерений возможно, но имеет ограничения, связанные с
методикой измерений и точностью измерительных приборов. Поэтому эти погреш-
ности относят к условно-устранимым.
3. Погрешности методов решения задач. Как правило, существует несколько мето-
дов решения одной и той же задачи, из которых стремятся выбрать наиболее эффек-
тивный, приводящий к получению правильного решения наиболее надежным и бы-
стрым способом. Эту погрешность относят к устранимой (или условной).
4. Погрешности алгоритма реализации численного метода решения задачи, которые воз-
никают при реализации метода решения задачи. Возможные численные алгоритмы и их
комбинации, которые применяются для расчётов по выбранному методу решения при-
кладной задачи, могут обеспечивать различную сходимость к правильному решению из-за
различного количества вычислений, влияющих на их суммарную погрешность.
В свою очередь этот вид погрешности складывается из следующих погрешностей:
переходной погрешности вычислительного процесса при пошаговой реализации
выбранного алгоритма. Она связана с тем обстоятельством, что большинство
алгоритмов численных методов являются пошаговыми и/или итерационными,
которые реализуются путем последовательных приближений (итераций) к ис-
комому решению. Погрешности, возникающие на каждом шаге (итерации), могут
передаваться (переходить) от шага к шагу (итерации к итерации), в результате
чего и получаются переходные погрешности. В некоторых случаях при реализа-
ции численных алгоритмов от шага к шагу (итерации к итерации) может проис-
ходить уменьшение погрешностей и их устранение. В этом случае численные
алгоритмы называются самоисправляющимися',
погрешности бесконечных вычислительных процессов. Например известно, что
выражение для вычисления синуса угла в радианах представляет собой беско-
нечный ряд. Все члены бесконечного ряда использовать для вычислений невоз-
можно. Чтобы завершить процесс вычисления за конечное число шагов, оста-
навливаются на некотором члене последовательности. Отброшенные члены
последовательности вносят в результат вычислений погрешности, которые на-
зывают остаточными погрешностями',
погрешности округления. Этот тип погрешностей обусловлен необходимостью
выполнять арифметические операции над числами, усеченными до количества
разрядов, характерных для аппаратуры применяемого компьютера;
погрешности действий. Они возникают при выполнении действий с прибли-
женными числами, чаще всего при выполнении арифметических операций.
Все четыре описанные типы погрешностей позволяют оценить полную погреш-
ность результата решения прикладной задачи на компьютере.
3.1.1. Учет погрешностей арифметических операций
Пусть А и a — два «близких» числа; причем А — точное значение некоторой вели-
чины, а а — её приближенное значение.
Величина ЛА = | А — а | называется абсолютной погрешностью приближенного
„ Ла &а „ ,
числа а, а За = -р-р или За = — — относительной погрешностью приближенного числа а.
3.1. Анализ погрешностей приближенных вычислений
57
Различают также абсолютные и относительные ошибки, которые определяются по
приведенным выше соотношениям, но без знаков модулей и поэтому они, в отличие
от погрешностей, имеют знаки.
Числа Д и 8 такие, что Д„ > Да и 8„ = > 8а, называются оценками или границами,
соответственно, абсолютной и относительной погрешностей.
К величинам До и 8а часто применяют термин предельные погрешности, а так как
истинные абсолютные и относительные погрешности (Да и За) неизвестны, то пре-
дельные погрешности Да и 8я часто называют абсолютными и относительными погреш-
ностями, соответственно.
При грубом оценивании погрешности результата вычисления значения дифференци-
руемой функции и =flxl,..., хя) с приближенными аргументами хр ..., хп будем считать,
что известны границы их абсолютных погрешностей А Ах соответственно. В
этом случае точные значения аргументов х',,...,х' лежат, соответственно, на отрезках:
[х,-ДхРХ| +Лх,]...[х„-Дх„,х„ + Дх„].
При этом абсолютная погрешность результата и = Дхр ..., хя) равна
Ди = |/(х,,..., х„) - /(х,',..., х*)|
и представляет собой модуль полного приращения функции.
Главной (линейной) частью этого приращения является полный дифференциал
du, который имеет вид:
п
\и =| du |= X
По этой причине за границу абсолютной погрешности результата приближенно
может быть принята величина
п
“7 ох;
(3.1.1)
В соответствии с этим равенством получается формула приближенной оценки гра-
ницы относительной погрешности дифференцируемой функции и:
(3.1.2)
Оценка погрешностей арифметических действий
Оценка погрешностей арифметических действий проводится с применением фор-
мул (3.1.1) и (3.1.2).
Сложение {вычитание)
Пусть « = х1+... + х„. Тогда =1 и абсолютная погрешность операции сложения
(вычитания) по формуле (3.1.1) будет равна
АццгЁЧ = 2Х ,
Г=1 1=1
т.е. при сложении и вычитании приближенных чисел их предельные абсолютные
погрешности складываются.
58
Глава 3. Численные методы компьютерного моделирования ХТП
При оценке относительной погрешности суммы и положительных приближенных
чисел х1,х2,...,х„, имеющих границы относительных погрешностей Sy ,5^ соот-
ветственно, будет справедливо:
б(х,+...+Хп)===
= 5\
где 5‘ =тах5л (1 < / <„).
В результате можно сделать вывод, что относительная погрешность суммы поло-
жительных приближенных чисел не превосходит максимальной относительной по-
грешности слагаемых.
Для оценки относительной погрешности разности будет справедливо
А,, А. + ДГ
5
что указывает па возможность сильного возрастания погрешности при л, -х2 -хО. В
этом случае принято говорить о потере точности при вычитании близких чисел.
Умножение (деление)
В соответствии с формулой (3.1.2) при умножении положительных сомножителей
и = х, — хп будет справедливо:
Э1пи 1
In и = Inx, + ...+ Inx И —— = —
’ " Эх( х,
в результате чего получается:
5 а
гь
При делении двух чисел и = —, где , х, > 0, in и = Inx. - In %,,
у
Л2
и, соответственно, с учетом (3.1.2):
Э1пи
Эх,
1
X,
Таким образом, при умножении
Д А
8,,, = — + -— = §„ + \
' ’ х, х.
и делении приближённых чисел предельная от-
носительная погрешность результата равна сумме предельных относительных по-
грешностей сомножителей.
Решение обратной задачи теории погрешностей
В отличие от представленной в предыдущем разделе прямой задачи оценивания
погрешности результата вычисления значения функции при заданных оценках по-
грешностей аргументов обратная задача заключается в оценивании величин Дх;
(и 5х,) по известной величине Ди. С физической точки зрения необходимо опреде-
лить, какой точности нужно подать данные на вход, чтобы на выходе получить ре-
зультат заданной точности.
Для случая дифференцируемой функции одной переменной грубое решение
обратной задачи тривиально: если y = f(x), то Ду = |dy| = |/(х)|Дх, откуда
3.1. Анализ погрешностей приближенных вычислений
59
Для функции большого числа переменных нужно использовать дополнительные
условия, формируемые, например, в соответствии с принципом равных влияний.
ди
Он состоит в предположении, что частные дифференциалы в (3.1.1) оди-
наково влияют на погрешность значения функции.
В результате получается, что в соответствии с (3.1.2):
Эи
Д. =пч~дх,,
ОХ-
откуда решение обратной задачи имеет вид:
Другим вариантом формулировки дополнительных условий является допущение
О равенстве относительных погрешностей всех аргументов, т.е. принимается, что
А,
5 =у^ = 5 (i = l,...,п).
Тогда А, = SjjcJ и в соответствии с (3.1.1):
л xV
Из последнего равенства можно получить величину 8, характеризующую относи-
тельный уровень точности задания аргументов:
5 = ——,
уЧ Эи
Эи
' дх,
откуда легко записываются выражения для определения границ абсолютных погреш-
ностей аргументов:
д
п).
OXj
Рассмотренный выше аналитический (классический) способ учета погрешностей
действий предполагает точное оценивание погрешностей и основан либо на приве-
денных правилах расчета погрешностей арифметических действий, либо на парал-
лельной работе с верхними и нижними границами исходных данных.
Для него характерно два существенных недостатка. Во-первых, этот способ чрез-
вычайно громоздок и не может быть рекомендован при массовых вычислениях.
Во-вторых, он учитывает крайние, наихудшие случаи взаимодействия погрешнос-
тей, которые допустимы, но маловероятны. Очевидно, что, например, при суммиро-
вании нескольких приближенных чисел (полученных в результате измерений, округ-
лений или каким-либо другим путем) среди них будут как слагаемые с избытком, так
и с недостатком, т.е. произойдет частичная компенсация погрешностей.
Следует отметить, что при больших объемах вычислений вступают в силу уже
вероятностные или статистические законы формирования погрешностей результа-
нт арифметических действий, которые в этой книге не рассматриваются. В то же
время прямое применение вероятностно-статистических оценок погрешностей так-
же является достаточно сложным и не может быть рекомендовано для массовых
вычислений.
60
Глава 3. Численные методы компьютерного моделирования ХТП
3.1.2. Технический подход к учету погрешностей
арифметических действий
Применение вероятностно-статистических оценок погрешностей позволило сфор-
мулировать практические правила работы с приближенными числами на основании
принципа А.Н. Крылова.
Согласно этому принципу, приближенное число должно записываться так, чтобы
в нем все значащие цифры кроме последней были верными и лишь последняя была
бы сомнительна, и притом в среднем не более чем на одну единицу. Напомним, что
значащими цифрами числа в его позиционной записи называются все его цифры,
начиная с первой ненулевой слева. Значащую цифру приближенного числа называ-
ют верной, если абсолютная погрешность числа не превосходит единицы разряда, в
котором стоит эта цифра (или половины единицы: в этом случае иногда применяет-
ся термин верная в узком смысле).
Чтобы результаты арифметических действий, совершаемых над приближенными
числами, записанными в соответствии с принципом А.Н. Крылова, также соответ-
ствовали этому принципу, нужно придерживаться следующих правил.
1. При сложении и вычитании приближенных чисел в результате следует сохранять
столько десятичных знаков, сколько их в приближенном данном с наименьшим
количеством десятичных знаков.
2. При умножении и делении в результате следует сохранять столько значащих
цифр, сколько их имеет приближенное данное с наименьшим количеством знача-
щих цифр.
3. Результаты промежуточных вычислений должны иметь один—два запасных знака
(которые затем должны быть отброшены).
Таким образом, при техническом подходе к учету погрешностей приближенных
вычислений предполагается, что в самой записи приближенного числа содержится
информация о его точности. И хотя прямая выгода от применения приведенных
правил работы с приближенными числами может быть получена лишь при ручном
счете (не нужно оперировать с цифрами, не влияющими на информативную часть
приближенного результата), их знание и понимание помогает правильной интерпре-
тации компьютерных расчетов, а иногда и самой организации таковых.
3.1.3. Оценка погрешностей компьютерной
арифметики
Основу запоминающего устройства (памяти) компьютера составляют однотип-
ные физические устройства — базисные элементы, имеющие г устойчивых состоя-
ний (где г соответствует r-ичной системе исчисления и, как правило, г = 2, 8, 16 и
т.п.). Каждому числу ставится в соответствие одинаковое количество к базисных
элементов, и, кроме того, с помощью таких или более простых базисных элементов
фиксируется знак числа.
Упорядоченные базисные элементы образуют разрядную сетку машинного слова’, в
каждом разряде может быть записано одно из базис-чисел 0, 1, ..., г — 1 (одна из
приведенных г цифр г-ичной системы счисления) и в специальном разряде отобра-
жается знак «+» или «—».
Для представления вещественных чисел в компьютере применяют, в основном,
два способа: с фиксированной (fix) и с плавающей (fl) запятой (точкой).
При записи числа с фиксированной запятой кроме упомянутых г параметров (осно-
вания системы счисления) и к (количества разрядов, отводимых под запись цифр чис-
ла) указывается еще количество t разрядов, выделяемых под дробную часть числа.
3.1. Анализ погрешностей приближенных вычислений
61
Таким образом, положительное вещественное число а может представлять собой
в г-ичной системе счисления дробь и отображается следующей конечной последова-
тельностью:
где а, е (0; 1;г —1}т.е. реализуется приближенное равенство:
а ~ fix(a) = a,r‘+ а,г‘^2 + ...+ ak_tra + ал_(+1г‘' +...+ .
Диапазон представляемых чисел с фиксированной запятой определяется числами с
наибольшими цифрами во всех £ разрядах, т.е. наименьшим числом — (г-1)(г-1)...(г-1)
и наибольшим числом (г-1)(г-1)...(г-1).
Абсолютная погрешность представления числа в этом случае есть оценка величи-
ны |a- yix(a)| зависящая от способа округления:
г' при простом отбрасывании «хвоста» числа а:
at+;r-('+1, + at+2<<,+2, + ...;
половина величины г' при правильном округлении, т.е. при увеличении а, на еди-
ницу, если а1+/ > г/2.
Абсолютная точность представления вещественных чисел с фиксированной за-
пятой одинакова в любой части диапазона. В то же время относительная точность,
т.е. оценка величины
a - fix(a) I а - fix(a)
а | fix(a)
может значительно различаться в зависимости от того, берется а близким к нулю
или к границе диапазона.
Значительно чаще употребляется представление вещественных чисел с плаваю-
щей запятой, которое записывается в экспоненциальной форме в следующем виде:
а = +М гр,
где г — основание системы счисления; р — порядок; м — мантисса числа, такая, что
г~‘ <М <1( = г°).
Если под мантиссу выделяется I r-ичных элементов, а под порядок — т, то в
системе записи с плавающей запятой вещественное число а представляется конеч-
ным числом fl(a) (от англ, floating — «плавающий»):
а = fl(a) = ±(Р, г-1 + р2г-2 +... + IV' )гт,
где у - целое число из промежутка [-r",r”-l]; ₽,е [1;...; г-1]; р, е {0; 1;г -1} = ,
т.е. машинное слово имеет структуру, как показано на рис. 3.1.
Числа ± г'" определяют границы допустимого числового диапазона. При этом ди-
апазон представления положительных вещественных чисел составляет промежуток
V’] Левую и правую границы этого отрезка называют соответственно машин-
ным нулем и машинной бесконечностью, так как числа из промежутка [-г"',
компьютер заменяет нулем, а числа, лежащие за пределами промежутка V1],
он не воспринимает.
Знак порядка Порядок Знак мантиссы Мантисса
т разрядов / разрядов
Рис. 3.1. Структура машинного слова
62
Глава 3. Численные методы компьютерного моделирования ХТП
Важной характеристикой является число е, называемое машинным эпсилон и обо-
значаемое обычно идентификатором macheps. Эта характеристика определяется как
расстояние между единицей и ближайшим следующим за ней числом системы ма-
шинных чисел с плавающей запятой. Так как
1 = (1г-1 + 0г“2 +... + 0г"' + ...)/,
а следующее за 1 машинное число есть
(1г+ 0г 2 + ... + 0г " 11 + 1<')г’ = Д(1 + £),
то за macheps можно принять величину
е = = г1-' •
Это число непосредственно связано с относительной погрешностью представле-
ния чисел в системе с плавающей запятой. Имеем:
|«~Л(«)| = P^r-(M)+p<t2r-^>+- < I t-' < = е
I « I РТ-* +Р2г2 +...
Таким образом, машинный эпсилон* служит мерой относительной погрешности
представления вещественных чисел, причем эта точность одинакова в любой части
числового диапазона и зависит лишь от числа r-ичных разрядов, отводимых под
мантиссу числа. В то же время оценка абсолютной погрешности
I a-ftia) | <| а | А'
показывает, что расстояние между вещественными числами и конечными прибли-
жениями к ним в системе с плавающей запятой неодинаковы в разных частях число-
вого диапазона.
Заметим, что величина macheps служит оценкой относительной точности пред-
ставления вещественного числа а при условии, что |а|>г
Если же ае[-г"'", г_г'],то /Ца) = О и значит относительная погрешность
|а-Л(а)1_1
I а I ’
т.е. является постоянной достаточно большой величиной, в то время как абсолютная
погрешность не превосходит величины г'".
Приведем значения введенных выше теоретических параметров для нескольких
типов компьютеров (реальные параметры, естественно, могут незначительно отли-
чаться от приводимых).
Так, например, для записи числа в 48-разрядном машинном слове 40 двоичных
разрядов выделяются под мантиссу, 6 — под порядок и 2 — под знаки мантиссы (т.е.
числа) и порядка. Отсюда, принимая г = 2, t = 40, т = 6, получаем, что точность
представления чисел с плавающей запятой не хуже 2"39 10“12), граница машинного
нуля 2~ы (=10~19), машинной бесконечности 263 (=1019).
Если машинное слово имеет 32 двоичных разряда, из них под мантиссу выделяет-
ся 24, а под порядок 7. Зная параметры г = 2, I = 24, от = 7, получаем macheps = 2~2i
(=10-7), машинные нуль 10~38 и бесконечность =10+38.
* Если трактовать macheps как минимальное положительное действительное число,
прибавление которого к 1 дает следующее за 1 число с плавающей запятой, то, очевид-
но, при правильном округлении значение macheps будет в два раза меньшим. Действи-
1 г ( А
тельно, полагая е =-г* 1*'= ~г“(г+1)г‘, получаем 1 + е= 1тч +0т-2 -i-... + 0-r-' + ^г_('+') г1
и значит + е) = 1 + г1-< > 1. «Мера дискретности» множества машинных чисел при
этом остается той же: Г~(.
3.2. Решение систем конечных уравнений
63
Когда используется представление вещественных чисел по основанию г= 16, эти
машины имеют относительную точность представления = 10-7 и диапазон для поло-
жительных чисел = 10~77 + 1076.
Практически любой компьютер рассчитан на то, чтобы выделить под запись чис-
ла двойное машинное слово, что позволяет более чем вдвое увеличивать точность пред-
ставления. Поэтому двойная точность и предусматривается многими языками про-
граммирования.
В заключение обратим внимание на возможность возникновения больших слу-
чайных погрешностей, которые обусловлены следующими основными причинами:
• методом округления, принятым в компьютере;
• потерями значащих разрядов при вычитании;
• потерей разрядов при превышении допустимой разрядности представления чи-
сел (например, при делении на малые числа).
Весьма важным является также понятие устойчивости численного (приближенного)
метода, под которым подразумевают несущественное отклонение получаемых при-
ближенных результатов от точного решения. Строгому определению устойчивости
численного метода соответствует утверждение: численный метод называется устойчи-
вым, если для любой погрешности е > 0 в исходных данных существует такое 8 > 0, что
максимальная погрешность результатов будет меньше е при максимальной погрешнос-
ти ввода, меньшей б.
Основной задачей при реализации численных методов (комбинации численных
методов) для решения задач компьютерного моделирования является обеспечение
их устойчивости, т.е. минимизации всевозможных погрешностей.
3.2. Решение систем конечных уравнений
Система конечных уравнений (3.2.1) включает функции от искомых аргументов
(неизвестных) и, в отличие от дифференциальных уравнений, не содержит произ-
водные. Задача решения этой системы конечных уравнений заключается в нахожде-
нии таких значений аргументов функций, которые обращают все конечные уравне-
ния системы в тождества. Найденные при этом значения аргументов функций (чис-
ла) называются корнями (решениями) системы уравнений.
В общем случае систему конечных уравнений можно представить в виде:
/(х,,х2,...,х„) = 0;
/2(хрх2>-->х»)= о; (3 21)
Д(х1,х2,...,х„) = 0,
где п — число неизвестных; т — число уравнений (т*п)', f^,..., х„), i = 1,..., т —
линейные или нелинейные функции неизвестных аргументов х,,...,х„; х........ — аргу-
менты функций, которые становятся корнями уравнений после их успешного решения.
Корни (решения) конечных уравнений обозначаются в виде ..., с„ или х’,..., х‘ и
при подстановке их в (3.2.1) будут справедливы следующие тождества:
-,^„) = о (i = l,...,m) или /Хх,',... ,x*)sO (1 = 1,.,.,т). (3.2.2)
Если т > п, то система называется переопределенной’, если т < п, то система недооп-
ределена. В дальнейшем будем рассматривать только определённые (нормальные) си-
стемы, когда т = п.
Системы конечных уравнений (СКУ) можно разделить на два класса — линейные
и нелинейные, в зависимости от того, являются ли функции в (3.2.1) линейными
или нелинейными функциями аргументов х,,х2,...,х„.
64
Глава 3. Численные методы компьютерного моделирования ХТП
Системы линейных уравнений содержат алгебраические функции с искомыми ар-
гументами в первой степени во всех уравнениях системы (3.2.1) и называются систе-
мами линейных алгебраических уравнений (СЛАУ).
В случае СЛАУ из двух уравнений она имеет, например, следующий вид:
Системы нелинейных уравнений (СНУ) также можно разделить на два класса
— алгебраические и трансцендентные.
Алгебраическими уравнениями называются уравнения, содержащие только алгеб-
раические функции (целые, рациональные, иррациональные). Алгебраическое урав-
нение в общем виде можно представить с помощью функции, являющейся много-
членной п-й степени с действительными коэффициентами (a0,at,-,a„):
f(x) = аохп + «,х” ' +... + а„ = 0. (3.2.4)
Пример такого уравнения: х5 + х2 + Зх = о.
Трансцендентными называются уравнения, содержащие показательные, логарифмичес-
кие, тригонометрические и другие функции, не являющиеся многочленами, например:
5x-3sinx = O. (3.2.5)
При изучении методов решения нелинейных уравнений целесообразно раздельно
рассматривать решения одного нелинейного уравнения (НУ) и решение системы нели-
нейных уравнений (СНУ).
3.2.1. Системы линейных алгебраических уравнений
В общем случае нормальная неоднородная система линейных алгебраических
уравнений (СЛАУ) может быть записана в виде:
%аЛ=Ь, (i=\, ...,п), (3.2.6)
J-1
где av — известные вещественные значения коэффициентов СЛАУ (У, у = 1,...,«); Ь, —
известные свободные члены СЛАУ (г = 1,..., п).
Принято считать, что 75% всех расчетных математических задач приходится на
решение СЛАУ. Это не удивительно, так как математические модели тех или иных
явлений или процессов либо сразу строятся как линейные алгебраические, либо сво-
дятся к таковым посредством дискретизации и/или линеаризации. Поэтому трудно
переоценить роль, которую играет выбор эффективного (в том или ином смысле)
способа решения СЛАУ. Современная вычислительная математика располагает боль-
шим арсеналом методов, а математическое обеспечение компьютеров — многими
пакетами прикладных программ, позволяющих решать различные возникающие на
практике линейные системы. Чтобы ориентироваться в этом море методов и про-
грамм и в нужный момент сделать оптимальный выбор, нужно разбираться в осно-
вах построений методов и алгоритмов, учитывающих специфику постановок задач,
знать их сильные и слабые стороны и границы применимости.
Элементы матричной алгебры
Приведем некоторые сведения из матричной алгебры, необходимые в дальнейшем.
Будем рассматривать как квадратные матрицы, т.е. такие, у которых число строк
равно числу столбцов (т = п):
"12 -
Я22 " а2п
Рп1 ап2 •” а>
3.2. Решение систем конечных уравнений
65
так и прямоугольные матрицы, у которых число строк т не равно числу столбцов п tm/ny.
ап а12 ... а1п
Я21 а22 а2п
... а,
ж1 ml !
Квадратная матрица называется треугольной (В), если все элементы, располо-
женные ниже или выше главной диагонали, равны нулю; диагональной (D), если все
ее элементы, кроме элементов главной диагонали, равны нулю; единичной (Е) назы-
вается диагональная матрица, все элементы главной диагонали которой равны еди-
нице:
Матрица, полученная из исходной путем замены элементов строк элементами
соответствующих столбцов, называется транспонированной. Так, для квадратной мат-
рицы А транспортированная ей матрица Ат имеет вид:
Pin а2п ’ ’ ’ ai
Для сравнения матриц между собой используют следующие их числовые характе-
ристики: определитель, норму и ранг матрицы.
Определитель — числовая характеристика квадратной матрицы, которая обознача-
ется det А или А . Одним из способов вычисления определителя является разложение
по строке или столбцу: определитель матрицы А равен сумме произведений элемен-
тов строки (столбца), взятой для разложения, на их алгебраические дополнения Akl, т.е.
detA = atlAtl+a,2AJ2+... + abAb = £а„А„ ( (3.2.7)
где к — номер строки разложения; Ак/ = — алгебраическое дополнение', MtJ —
минор, который равен определителю подматрицы А после вычеркивания k-й стро-
ки и у'-го столбца.
Порядок определителя равен числу строк (столбцов) квадратной матрицы.
Если определитель квадратной матрицы равен нулю, то она называется вырожденной.
Пример. Вычислить определитель матрицы А и указать его порядок, если
103
4 5 0 .
0 8 9
5-4544
66
Глава 3. Численные методы компьютерного моделирования ХТП
▼ Путем разложения этой матрицы по первой строке получаем сумму трёх опре-
делителей второго порядка (миноров) с соответствующими коэффициентами
- 1, 0, 3 (3.2.7):
з
о
9
45 + 3-32 = 141.
Порядок исходного определителя равен З.А
В отличие от определителя матрицы |а| , минора Мц и алгебраического дополне-
ния AkJ, которые могут быть рассчитаны только для квадратных матриц, норма мат-
рицы И и ранг матрицы г= определяются как для квадратных, так и для прямоу-
гольных матриц.
Нормой матрицы А (Евклидовой нормой) называется число а, поставленное в соот-
ветствие данной матрице и определяемое для квадратной матрицы следующим образом:
“ = Н=^ЁЁ<. (3.2.8)
По аналогичной формуле определяется и норма прямоугольной матрицы. При
этом верхняя граница первой суммы заменяется на т, так как (т * п).
Например:
1 о 3
4 5 0
= V1 + 9 + 16 + 25 + 64 + 81 = J196 = 14.
0 8 9
Ранг матрицы г= — наивысший порядок минора, отличного от нуля.
Пример. Определить ранг прямоугольной матрицы А, если
▼ Составим квадратную подматрицу 2x2 из элементов первого и второго столб-
цов. Минор этой подматрицы равен нулю. Составим другую подматрицу из
элементов первого и третьего столбцов; минор ее отличен от нуля; порядок
этого минора равен 2. Следовательно, ранг матрицы А равен 2, т.е. г= = 2. А
Матричные операции
Матрицы можно сложить (вычесть), если они имеют одинаковое число строк и
число столбцов. Результатом является матрица того же размера, каждый элемент
которой равен сумме (разности) соответствующих элементов матриц.
Чтобы умножить матрицу на число, надо каждый элемент ее умножить на это число:
A = ?.А; а9=1ая, j = I,2,...,n.
Если матрица А имеет размер mxn, матрица В -п/.р, то размер матрицы произ-
ведения С - А В будет тяр, причем каждый элемент ее вычисляется по правилу:
с,;=ЕаА’ i = l,2,...,m, j = l,2,...,p,
т.е. элементы i-й строки матрицы А умножаются на соответствующие элементы у-го
столбца матрицы в, а произведения суммируются, например:
3.2. Решение систем конечных уравнений
67
1 1 1
2 2 2
3 3 3
1 4
2 5
3 6
(1 + 2 + 3)
(2 + 4 + 6)
(3 + 6 + 9)
(4 + 5 + 6)
(8 + 10 + 12)
(12 + 15 + 18)_
6 15
12 30
_18 45
Таким образом, при перемножении матриц необходимо расположить их в пра-
вильной последовательности: число столбцов первой перемножаемой матрицы (со-
множителя) должно быть равно числу строк второй перемножаемой матрицы (со-
множителя).
Поэтому при перемножении матриц перестановка местами матриц-сомножите-
лей может привести к невозможности выполнения этого действия.
Обратной матрицей к квадратной матрице А называется такая матрица А , при
умножении на которую как слева, так и справа получается единичная матрица:
А А = Е; А-а'=Е.
Обратная матрица существует лишь для невырожденных квадратных матриц (det А * 0).
Рассмотрим два метода нахождения обратных матриц.
Классический метод обращения матрицы А состоит из следующих этапов:
1) вычисление определителя матрицы det А;
2) вычисление алгебраических дополнений А:] (3.2.7) для всех элементов матри-
цы А и построение матрицы алгебраических дополнений АА;
===== =Т
3) транспонирование матрицы алгебраических дополнений АА в АА , т.е. полу-
чение присоединенной матрицы А , равной АА ;
4) нахождение обратной матрицы А путем деления всех элементов присоеди-
ненной матрицы на определитель det А :
A-1 =(l/detA)-A .
Метод Жордана для обращения матрицы А заключается в построении расширен-
ной матрицы, содержащей исходную матрицу А и единичную Е. Левая часть расши-
ренной матрицы А-.Е
а11 а12
. • а21 а22
А.Е =
_Я»1
с помощью допустимых элементарных преобразований (умножение строки на кон-
станту и сложение ее с другими строками) приводится к единичной матрице. Парал-
лельно те же самые преобразования делаются над правой частью расширенной мат-
рицы, в результате которых и получается обратная матрица, т.е. А-Ё-> Ё:А~'.
Пример. Для матрицы а =
найти ей обратную методом Жордана.
▼ Составим расширенную матрицу, а затем вычтем из первой строки вторую и
умножим ее на —‘/4:
4 2'1:Г1 о]
8 2j.:|_0 Ij
I 0]: Г-1/4
8 2_]:|_ 0
+ 1/41
1 J
68
Глава 3. Численные методы компьютерного моделирования ХТП
Умножим вторую строку на 1/2 и затем вычтем из нее элементы первой строки,
умноженные на 4:
Г1 0]: Г-1/4 +1/4~|
[о ij;|_ 1 -1/2J’
Слева получена единичная матрица, а справа — обратная, т.е.
Т-1 _ Г-1/4 1/4] А
L1 -1/2J*
Анализ систем линейных алгебраических уравнений
Система уравнений называется совместной, если существует хотя бы одно реше-
ние этой системы, в противном случае система несовместна.
Частным, но весьма важным в практическом отношении является случай линей-
ной системы уравнений, когда функции /,(х„ л^,...,х„) (/ = 1,2,...,п) в (3.2.1) являются
линейными функциями неизвестных. Именно для этого случая широко разработаны
как аналитические, так и численные методы решения, причем для последних хоро-
шо развит аппарат анализа существования решения и процесса сходимости методов.
Система линейных алгебраических уравнений записывается в виде:
+ а12х2 + ...а1лх„ = 6,;
ct2]x, + а22х2 + ...а2лх„ = Ь2,
................................................. (3.2.9)
апЛ1 +“„2х2 + ...а„„х„ =Z>„.
Она называется неоднородной, если найдется хотя бы один свободный член ь, * 0;
если все Ь. =0, i = 1,2,..., п, то система называется однородной. Очевидно, что однородная
система всегда совместна; так, при х, =0, j = 1,2,..., п, ее уравнения обращаются в тожде-
ства. Вопрос о совместности неоднородной системы решается по следующей теореме.
Теорема Кронекера—Капелли. Для того чтобы система линейных неоднородных
уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы коэф-
фициентов А был равен рангу расширенной матрицы коэффициентов А (расшире-
ние — за счет столбца свободных членов ь,).
Проверка условия единственности решения выполняется в соответствии с теоремой.
Теорема. Для того чтобы неоднородная система из п уравнений с п неизвестными
имела единственное решение, необходимо и достаточно, чтобы определитель матри-
цы коэффициентов был отличен от нуля. В противном случае неоднородная система
не имеет решения либо имеет их бесчисленное множество.
Пример 1. Решить систему уравнений:
ixj-zx2 = и;
1 + 4x2 =
▼ Для проверки совместности составим матрицу А из коэффициентов системы
и расширенную матрицу коэффициентов А. Определим их ранги (ранг матрицы
равен максимальному порядку минора, отличного от нуля):
Ч/ Ч-'г ;2
Так как г= trt, то система несовместна, т.е. не имеет решения.А
3.2. Решение систем конечных уравнений
69
Пример 2. Решить систему уравнений:
[Х1 + 2х2 “ 3'
▼ Проверим совместность:
Здесь , поэтому система совместна.
По сформулированной выше теореме определим, сколько решений имеет си-
стема, для чего вычислим ее определитель: det а = +з. Определитель системы отли-
чен от нуля; следовательно, система уравнений имеет единственное решение.
Найдем решение системы уравнений по правилу Крамера согласно следую-
щей формуле:
х, - det A,b I det A, t = l,...,n, (3.2.10)
где Alb ~ матрица, полученная из исходной матрицы А путем замены в ней /-го
столбца столбцом свободных членов. Если 1 = 1,2, то получим:
4» =
О -1
3 2 ’
1 О
1 3
detA14=3; det A2b = 3; х, =3/3 = 1; х2 =3/3 = 1. А
Анализ трех вариантов решения неоднородных систем линейных алгебраических уравнений
1. Решение системы уравнений существует и является единственным. Например,
(3.2.11)
Решение этой системы х, = 1 и х2 = 2, никакие другие значения х, и х2 не способ-
ны одновременно удовлетворить этим двум уравнениям. Геометрически эта система
уравнений представлена на рис. 3.2, где видно, что
две прямые линии, образующие между собой доволь-
но большой угол и соответствующие двум уравне-
ниям, пересекаются в одной и только в одной точке.
Координаты этой точки как раз и представляют со-
бой искомое решение.
2. Система уравнений вообще не имеет решения.
Например,
4х, +6х2 =10;
2х, + Зх2 = 6.
(3.2.12)
На рис. 3.3 показаны прямые линии, соответству-
ющие этим двум уравнениям. Две прямые парал-
лельны, они нигде не пересекаются, и система урав-
нений не имеет решения.
3. Система уравнений имеет бесконечное мно-
жество решений. Например,
4х, + 6х2 =12;
2х1 + Зх2 = 6.
представление системы двух
(3.2.13) линейных уравнений, имеющей
единственное решение
70
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.3. Геометрическое пред-
ставление системы двух линейных
уравнений, не имеющей решения
Рис. 3.4. Геометрическое пред-
ставление системы двух линей-
ных уравнений, имеющей
бесконечное множество решений
Как видно из рис. 3.4, эти два уравнения описывают одну и ту же прямую линию.
Любая точка, лежащая на этой линии, является решением такой системы уравнений,
например: х, = 0, х2 = 2; х, =1, х, =4/3 и т.д.
Системы уравнений типа (3.2.12) и (3.2.13) называются вырожденными, так как оп-
ределители матрицы коэффициентов А равны нулю, т.е. являются вырожденными. Иногда
непосредственно из поставленной задачи бывает ясно, что система уравнений не может
быть вырожденной. Если же, как это бывает в большинстве случаев, соответствующая
информация отсутствует, то приходится или проверять вырожденность системы уравне-
ний в процессе решения, или исследовать такую возможность непосредственно.
Анализ двух вариантов решения однородных систем линейных алгебраических уравнений
В общем случае однородную СЛАУ можно представить:
или
(3.2.14)
Первый вариант решения этой системы существует всегда и является тривиаль-
ным (нулевым), когда ^ = (§р^2,=[о,О,..,о]г и располагается в начале «-мерной
системы координат.
Второй вариант соответствует бесконечному множеству решений и может быть
найден, когда определитель матрицы А коэффициентов системы (3.2.14) равен 0, т.е.
detA = |A| = 0. (3.2.15)
Например, для системы двух уравнений вида
для которой И =0, бесчисленное множество решений, например:
AJ L-1.
3
-3
И т.д.
4, 1
3.2. Решение систем конечных уравнений
71
располагается на прямой, пересекающей на-
чало системы координат (рис. 3.5).
Если определитель матрицы коэффициен-
тов системы (3.2.14) не равен 0, т.е.
det А = |а | Ф О,
то для однородных СЛАУ существует только
тривиальное нулевое решение, т.е.
"О'
ь ° •
О
Например, это будет справедливо для сле-
дующей однородной СЛАУ:
Рис. 3.5. Графическое представление
бесчисленного множества решений
системы уравнений (3.2.14) располага-
ется на прямой АВ
%! + 2х, = о,
2х, + х, = О,
(3.2.17)
определитель матрицы коэффициентов которой:
1
2
2
1
det А = |а| =
= -3*О.
На практике представляют интерес однородные СЛАУ с нетривиальными решени-
ями. В этом случае для обеспечения равенства нулю определителя матрицы коэффи-
циентов однородных СЛАУ (3.2.14) можно использовать собственные числа (значе-
ния) исходной матрицы A-Х, значения которых вычитают из ее диагональных эле-
ментов. При этом получается преобразованное однородное СЛАУ, включающее соб-
ственные числа (значения) X матрицы А:
(А-ХЕ)х = О
(3.2.18)
или
Й11 - °12
Й21 °22 -
ап\ ап2
Собственные числа (значения) матрицы А - ХЕ определяют из условия равенства
определителя матрицы коэффициентов преобразованной системы (3.2.19) нулю, тем
самым обеспечивая получение нетривиальных решений.
Эта задача эквивалентна задаче исследования однородной СЛАУ с параметром X:
при каких X система (3.2.18) имеет нетривиальные решения.
Теоретически эта задача легко решаема: нужно найти корни так называемого
характеристического, или «векового» уравнения
|а-Хе| = о (3.2.19)
и, подставляя их поочередно в (3.2.18), получать из соответствующих однородных
систем уравнений искомые решения х (бесконечное множество) — собственные век-
торы матрицы А.
Практическая реализация этого подхода сопряжена с рядом трудностей, возрастаю-
щих с ростом размерности решаемой задачи. Эти трудности обусловлены развертывани-
ем «векового» определителя (3.2.19) det (А-ХЕ) и вычислением корней получающегося
’ll
Глава 3. Численные методы компьютерного моделирования ХТП
многочлена (полинома) n-й степени X, а также поиском линейно независимых реше-
ний вырожденных СЛАУ (3.2.19) — х — собственных векторов матрицы А.
В действительности, из сказанного следует, что характеристическое уравнение (3.2.19)
можно переписать в виде равенства нулю характеристического многочлена Р(Х):
Р(Х)= det^ - Хе)= |а - ХЁ| = (-X)” + b,(- X)"1 +. . + Ьп_, (- Х)+ Ьп = 0 , (3.2.20)
где ь,,...,Ь„ — известные коэффициенты получающегося характеристического много-
члена.
Отсюда можно сделать вывод, что матрица А порядка п имеет п собственных
чисел (собственных значений) Хр Х2,.., Хл, если каждый корень считать столько раз,
какова его кратность.
Рассмотрим пример определения собственных чисел (собственных значений) и
собственных векторов следующей матрицы А:
1 2
2 1
А =
(3.2.21)
Для этого записывается характеристическое уравнение в виде (3.2.19) или (3.2.20):
1 —X 2
^)= 2 1Х=Х2-2Х-3 = 0. (3.2.22)
Корни этого характеристического уравнения — собственные числа (значения) —
соответственно равны: X, = -1 и х2 = 3.
При нахождении собственного вектора для первого корня (X, = — 1) следует запи-
сать однородное СЛАУ (3.2.14):
1-(-1) 2 2 1-(-1) < *2. = 0‘ 0 , (3.2.23)
в результате чего получается система: (2х, + 2х, = 0;
[2х, + 2х2 = 0 (3.2.24)
ИЛИ X, + х2 = 0. (3.2.25)
Таким образом, для этого собственного числа (собственного значения) X, =—1
один из собственных векторов (бесчисленного множества решений однородной СЛАУ)
может быть представлен как
I,
1
-1
(3.2.26)
Для второго собственного числа (собственного значения) Х2 =3 по аналогии име-
ем однородное СЛАУ:
что дает
или
1-3 2 Го'
2 l-3j[_x2J [о
- 2х, + 2х2 = О,
2х, - 2х2 = О
(3.2.27)
(3.2.28)
(3.2.29)
х, - х2 = 0,
3.2. Решение систем конечных уравнений
73
откуда второй собственный вектор, соответствующий второму собственному числу —
Х2 =3, и являющейся одним из множества решений однородного СЛАУ имеет вид:
1
1 '
(3.2.30)
Оба эти решения (3.2.26) и ^2 (3.2.30) могут быть умножены на произвольные
скалярные множители, в результате и получается множество решений однородных
СЛАУ (3.2.24) и (3.2.28).
Рассмотренный непосредственный подход к решению алгебраической проблемы соб-
ственных чисел (собственных значений) обычно применяют лишь при очень малых
размерностях матриц коэффициентов А (п = 2,3); уже при п > 4 на первый план выходят
специальные численные методы решения задач о собственных числах и собственных
векторах, в соответствии с которыми разработаны многочисленные алгоритмы, в том
числе и для решения однородных СЛАУ, которые в книге не рассматриваются.
Обусловленность задач решения систем линейных алгебраических уравнений
Трудность понимания природы вычислительных ошибок впервые была осознана
для линейных систем, а это та область, где такие трудности возникают часто. Однако
вычислительные ошибки существуют повсюду в численных расчетах.
Ответом задачи может быть единственное число, множество чисел (для линейной
системы), функция (для дифференциального уравнения) или их сложная комбинация.
На рис. 3.6 показано геометрическое представление процесса решения задачи. Мы
имеем «истинные данные» d' и «истинный ответ» х . Также имеем «возмущенные
данные» d и соответствующий «истинный ответ для возмущенных данных» х. В чис-
ленных расчетах мы почти никогда не получим истинного ответа, поэтому должны
быть также рассмотрены «вычисленный ответ для точных данных» х‘ и «вычисленный
ответ для возмущенных данных» у.
На самом деле процесс заканчивается вычислением х вместо х , и поэтому жела-
тельно оценить ||х’ -х||. К сожалению, часто это совершенно невозможно сделать кон-
структивным способом, и в этом состоит трудность в понимании существа ошибок.
Теория обусловленности представляет собой попытку систематического изучения
этого вопроса. Говорят, что задача или вычисление плохо обусловлены, если они
чрезвычайно чувствительны к ошибкам или к неопределенности исходных данных.
Обусловленность является качественным
свойством, хотя ее и стараются оценивать
количественно.
Прежде всего, мы оговорим различие
между плохо обусловленной задачей и плохо
обусловленными вычислениями. Все плохо
обусловленные вычисления являются резуль-
татом применения численно неустойчивых
алгоритмов. Четыре возможные комбина-
ции «плохой» и «хорошей» обусловленно-
сти показаны на рис. 3.7. Ключ к понима-
нию существа дела состоит в следующем:
если задача плохо обусловлена, то никакие
усилия, потраченные на организацию изощ-
ренных вычислений, не могут дать правиль-
ных ответов, исключая случайности. решении задачи
Истинное
Л^^нное
Иипинное __
Вычисленное
Ответы
Рис. 3.6. Геометрическое представление
влияния неопределенности исходных
Данные
d**
d*
данных (d вместо d ) и вычислительных
ошибок (х вместо х и х‘ вместо х‘) при
74
Глава 3. Численные методы компьютерного моделирования ХТП
Поэтому [см. рис. 3.7, в] можно добиться того, чтобы х было ближе к х, а х* —
ближе к х*, но вычисления не могут повлиять на расстояние между х и х .
В случае плохо обусловленной задачи решения линейной системы незначительные
возмущения (изменения) элементов матрицы А и/или вектора Ь (3.2.9) могут приве-
сти к существенным изменениям результатов решения, т.е. определяемые коэффици-
енты (константы и параметры физико-химических моделей) будут сильно отличаться.
На практике это всегда возможно, так как опыты могут проводиться разными экспе-
= _ ГО.550
“ |о.484
риментаторами, с различной точностью и
в отличающихся опытных точках.
Для иллюстрации плохо обусловленной
системы (задачи) целесообразно рассмот-
реть СЛАУ (3.2.9) с матрицей коэффицен-
тов А и правой частью Ь (3.2.31) вида:
0.423П - ГО.1271
0.372 J’ -[о.112/
(3.2.31)
Рис. 3.7. Четыре комбинации плохой и
хорошей обусловленности задачи и вычис-
лений при решении этой задачи: а —
хорошо обусловленные задача и вычисле-
ния; б — хорошо обусловленная задача,
плохо обусловленные вычисления; в —
плохо обусловленная задача, хорошо
обусловленные вычисления; г — плохо
обусловленные задача и вычисления
Точное решение системы уравнений
(3.2.31) есть;
При возмущенной правой части (gb):
0.127071 - Г0.00007
• 8х =
0.11228J’ [0.00028
(3.2.32)
точным решением становится вектор:
х+8х =
1.7
-1.91
• 8х =
1
0.7
-0.91 '
(3.2.33)
Видно, что относительное изменение
решения намного превышает относитель-
ное изменение правой части Ь.
Можно варьировать элементом а21 мат-
рицы А [вместо числа 0.484 в матрице
(3.2.31) использовать число 0.483 в мат-
рице (3.2.34)] так, чтобы
0.550 0.423
0.483 0.372
(3.2.34)
При этом точное решение возмущен-
ной системы, округленное до четырех зна-
ков, выглядит следующим образом:
-0.4535
0.8899
(3.2.35)
И здесь относительное изменение ре-
шения намного превышает относительное
изменение исходных данных (матрицы А).
Г
3.2. Решение систем конечных уравнений
75
Объяснение в обоих случаях одно и то же — плохая обусловленность системы
(3.2.9) с параметрами (3.2.31). Следует подчеркнуть, что представленный анализ воз-
мущений проводился в терминах точных решений и, значит, касался только внут-
ренних свойств системы уравнений (3.2.31). Плохая обусловленность была определе-
на безотносительно к проблемам вычислений с конечной точностью и по сути дела
представляет собой исключительно характеристику математической задачи решения.
Для количественной оценки обусловленности задачи используют числа абсолютной
и относительной обусловленности.
Чтобы получить аналитические выражения для расчета чисел обусловленности,
следует воспользоваться матричной формулой для точного решения (3.2.48):
х= А Ь. (3.2.36)
Точным решением системы с возмущенной правой частью Ь + 5Ь будет вектор
т + 8х, удовлетворяющий равенству:
а(х + 8х)= b + 5Ь. (3.2.37)
В соответствии с (3.2.36) решением (3.2.37) можно представить:
х+5х=а'^ + 5ь} (3.2.38)
а так как справедливо (3.2.36), то возмущение решения определяется по формуле:
8х = А8й. (3.2.39)
Для оценки 8х можно воспользоваться векторными и матричными нормами (3.2.8),
в результате чего выражение (3.2.39) преобразуется к виду [7, 26]:
М’ (3.2.40)
где при некотором ёЬ возможно равенство.
Таким образом, возмущение точного решения может превосходить возмущение
правой части не более, чем |а | раз. Эта величина называется числом абсолютной
обусловленности и определяется по формуле:
^=|р’,|- (3-2.41)
Для определения числа относительной обусловленности необходимо преобразо-
вать СЛАУ (3.2.9) по аналогии с (3.2.40) с использованием норм векторов и матриц (3.2.8):
II^RI'R (3-2.42)
С учетом последнего неравенства из неравенства (3.2.40) легко получить соотно-
шение для определения числа относительной обусловленности:
При этом число относительной обусловленности определяется по формуле:
^=|4Kl (3.2.44)
Аналогичный результат можно получить и при возмущении элементов матрицы А.
Число относительной обусловленности часто называют числом обусловленнос-
ти матрицы А — обозначают conJ^) Это число характеризует максимальный эффект
16
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.8. Геометрическое
представление системы двух
линейных уравнений, которая
является почти вырожденной
(определитель матрицы ее
коэффициентов равен рулю) и
плохо обусловленной
от возмущений в Ь и А при решении СЛАУ {3.2.9). Из
выражения (3.2.44) следует, что при большом точ-
ное решение системы может существенно изменяться
даже при малом изменении данных, что является при-
знаком «плохой» обусловленности задачи решения СЛАУ.
В качестве конкретного примера рассмотрим сис-
тему уравнений:
[5х, +7х2 = 12;
[TXj+lOx, =17. (3.2.45)
Эта система имеет единственное решение:
х, =1, хг = 1. Теперь рассмотрим пару значений неиз-
вестных х, =2.415, х2 =0. При подстановке этих зна-
чений в исходные уравнения получаем:
5х, + 7х2 = 12.075;
7х,+10х2 = 16.905. (3.2.46)
После округления до двух значащих цифр правые части равенств (3.2.46) совпада-
ют с правыми частями исходных уравнений. А так как исходные уравнения были
заданы только с точностью до двух значащих цифр, то решение (3.2.46) так же хоро-
шо отвечает условиям поставленной задачи, как и решение х, =1, х2 =1.
Дело в том, что две прямые линии, описываемые двумя уравнениями этой систе-
мы, почти параллельны, как это показано на рис. 3.8. Точка х, = 2.415, х2 =0 хотя и не
лежит ни на одной из этих прямых линий, но очень близка к ним.
Системы типа (3.2.45) являются плохо обусловленными. В любом случае, когда
две линии (либо плоскости и гиперплоскости) почти параллельны, система уравне-
ний становится плохо обусловленной. В этом случае найти численное решение сис-
темы трудно, а точность его весьма сомнительна.
Прямые методы решения систем линейных
алгебраических уравнений
Все методы решения линейных алгебраических задач (наряду с задачей решения
СЛАУ, это и вычисление определителей, и обращение матриц, и задачи на собствен-
ные значения) можно разбить на два класса: прямые и итерационные. Здесь будут
рассмотрены как прямые методы, т.е. такие методы, которые приводят к решению за
конечное число арифметических операций [если операции реализуются точно, то и
решение также будет точным (в связи с чем к классу прямых методов применяют
еще название «точные методы»)], так и итерационные методы, т.е. методы, в которых
точное решение может быть получено как предел единообразно получаемых после-
довательных приближений.
Условимся говорить о численном решении таких СЛАУ, у которых число уравне-
ний совпадает с числом вещественных неизвестных (так называемая система нор-
мальных уравнений), причем будем предполагать наличие единственного решения,
если существование и единственность не следует из каких-либо условий.
Такое ограничение здесь довольно естественно, так как решение и недоопреде-
ленных, и переопределенных систем, а также систем с комплексными коэффициен-
тами и переменными, в конечном счете, сводится к решению однозначно опреде-
ленных вещественных систем нормальных уравнений.
Рассмотрим прямые методы.
3.2. Решение систем конечных уравнений
77
Метод обратной матрицы
С использованием понятия матрицы и матричных операций система уравнений
(3.2.9) может быть записана в матричном виде:
Ах = Ь, (3.2.47)
где А — матрица коэффициентов системы вида
Д11 fl12
а21
_ап1 ап2
(х, Ь ~ вектор неизвестных и вектор свободных членов, соответственно).
Например, система
2х, + Зх2 = 5;
Зх, + 4х2 = 7
в матричном виде записывается в соответствии с (3.2.47):
Ах = Ь ’
где
Методом обратной матрицы решение системы может быть получено в результа-
те умножения слева правой и левой частей уравнения (3.2.47) на обратную матрицу
от матрицы коэффициентов системы (при перемножении матриц порядок располо-
жения в произведении матриц-сомножителей имеет значение — см. выше разд. «Мат-
ричные операции»):
А Ах = А Ь-
Учитывая, что произведение обратной матрицы на прямую дает единичную мат-
рицу е, получаем
Ёх = А Ь или х=А Ь. (3.2.48)
= -1
Таким образом, решение системы сводится к нахождению обратной матрицы А
и затем вычислению произведения этой матрицы на вектор Ь.
Этот метод удобно применять в тех случаях, когда несколько раз решается систе-
ма с разными правыми частями. В этом случае достаточно один раз вычислить об-
ратную матрицу А и затем умножать ее на разные векторы Ь.
Недостатком метода являются трудности вычисления обратной матрицы, особен-
но если матрица большой размерности, либо если ее определитель близок к нулю.
Пример. Методом обратной матрицы решить систему
5х1 - Зх2 = 2;
х, - 5х2 = -4.
▼ Решение ищется в виде х = А Ь . Вычислим обратную матрицу А классичес-
ким методом согласно алгоритму (см. выше разд. «Матричные операции»):
1) det А =-25 + 3 =-22;
2) А., =
-1
5
3'
5
3) А =
78
Глава 3. Численные методы компьютерного моделирования ХТП
1 -5
22|_-1
4)А ‘
3]_Г5/22 -3/22'
5 ~ 1/22 5/22
Теперь найдем вектор решения:
5/22 - 3/22] Г2 1Г10/22+12/22'
1/22 - 5/22 -4 - 2/22+ 20/22
'1
1
т.е. х, =1; хг =1 (решение). ▲
Метод Гаусса
Этот метод известен также как метод исключений, поскольку на первом этапе
метода («прямой ход») происходит поочередное исключение одного из неизвестных
во всех уравнениях, кроме одного. Результатом «прямого хода» является приведение
матрицы коэффициентов исходной системы к верхнетреугольной (см. выше разд.
«Матричные операции»).
Второй этап («обратный ход») состоит в отыскании неизвестных путем последо-
вательной подстановки определяемых значений неизвестных в уравнения, начиная с
последнего, в вышерасположенные.
Существует несколько модификаций этого метода. Рассмотрим один из них, из-
вестный под названием «решение по компактной схеме Гаусса». Пусть имеем систе-
му вида:
йцХ,+арх2+а13х3 =/>,;
- #21'^1 + «22^2 + «23^"3 = />2;
Я31Х| + «32Х2 + «33х3 — i3,
в которой а„ *0. Если «н^О, то переставим уравнения так, чтобы коэффициент при
х, в первом уравнении был не равен нулю.
Прямой ход. Последовательным исключением неизвестных из уравнений приво-
дим систему к треугольному виду. Умножая первое уравнение по очереди на коэф-
фициенты (-а21 /аи) и (-д31 / а,,) и складывая соответственно сначала со 2-м, а затем
с 3-м, получаем систему
ОцХ, + OjjXj + OjjXj = ip
°22Х2 + a21’X3 =
<$’*2 + ag’x3 = Лз11
где а*" = ц,-(а,!/а,,)^, A,"’ = Ь, -(а,, /а^)^; i = 2, 3, j = 2, 3, в которой неизвестное х,
исключено из всех уравнений, кроме первого. Последовательность аналогичных пре-
образований, примененная к полученной системе, позволяет привести ее к треуголь-
ному виду уже при втором преобразовании:
anXj + а12х2 + я13х3 = fy;
а^хг + о23 х3 = 62";
ат = ьт
1°зз Лз из
Здесь а® = а33 - (а™ / a"’ )а<", i<2’ = b?> - (а£ / a™ )&<*>.
В общем случае для СЛАУ произвольной размерности расчет коэффициентов
при k-м преобразовании проводится по формулам:
а? = -(«Г> /«Г= Г 2, п);
/а^-1’)^*^ (к =1,2,..., л-1).
3.2. Решение систем конечных уравнений
79
Обратный ход. Вычисление неизвестных (элементов вектора решения системы)
проводится по формуле
х, =(1/ц(/-,))(г>Г1,-Х;=,+1хХ' ”), < = «, л-1, .... 1.
Пример. Методом Гаусса решить систему
х, + х2 + х3 = 4;
• 2х, + Зх2 + х3 =9;
х, - х2 - х3 = -2.
▼ Прямой ход. На первом шаге умножаем первое уравнение сначала на —2 и скла-
дываем его со вторым (получаем преобразованное второе уравнение), затем пер-
вое уравнение умножаем на —1 и складываем с третьим (получаем преобразован-
ное третье уравнение):
X, + х2 + х3 = 4,
• х2 - х3 = 1;
- 2х2 - 2х3 = -6.
На втором шаге полученное преобразованное второе уравнение умножаем на 2 и
складываем с третьим (получаем заново преобразованное третье уравнение):
х1 + х2 + х3 = 4;
• х2 - х3 =1;
-4х3 = ^4.
В результате преобразований получили треугольную систему уравнений, рав-
носильную исходной решаемой системе уравнений.
Обратный ход. Из последнего уравнения определяем, что х3 = 1. Из второго и
первого уравнений находим:
х2 = 1 + х3, х2 =1 + 1 = 2; х, = 4 - х2 - х3, х1=4-2-1 = 1.А
Метод Гаусса—Жордана
В основе метода лежат алгоритм Жордана обращения матриц и стратегия метода
_ ==-1_
исключения (метод Гаусса). Однако для получения решения системы х= А Ь, соглас-
но этому методу, обратная матрица не ищется в явном виде, а сразу находится произ-
ведение обратной матрицы на вектор свободных членов А Ь. Поэтому алгоритм Жор-
дана применяется к расширенной матрице В результате элементарных преобра-
зований слева получается единичная матрица, справа — вектор неизвестных : у).
Расширенная матрица
путем вышеописанных преобразований приводится к виду
о о
Ь,
Ъг
ъ.
80
Глава 3. Численные методы компьютерного моделирования ХТП
что соответствует системе уравнений
х2=Ь2,...,хп=Ь„.
В этом случае отпадает необходимость вычисления значений неизвестных при
«обратном ходе», которые оказываются равными значениями свободных членов в
преобразованной матрице.
Пример. Методом Гаусса—Жордана решить систему уравнений
|2х, -7х2 = 3.5 ;
[Зх, -х2 = 10.
▼ Составляем расширенную матрицу из коэффициентов системы и столбца сво-
бодных членов размера 2x3:
Г2 -71 Г3.51 Г1 -3.51 ! Г1.751 Г1 -3.51": Г1.751
[з -ij [югЬ -d ' L10 J-*L° 9-5J; I_4-75j
Далее все элементы первой строки, включая свободный член, умножим на 1/2. В
преобразованной матрице I из второй строки вычтем элементы первой строки,
умноженные на 3. Левый нижний элемент стал равен нулю, а левый верхний —
единице (II). Разделив элементы второй строки на 9.5 (III преобразование) и
затем, умножив их на 3.5, сложим с элементами первой строки (IV преобразова-
ние). В результате получаем слева единичную матрицу, а справа — преобразо-
ванный столбец свободных членов, значения которых соответствуют искомым
корням системы:
________Ш________ _______IV_____
ГТ -3.5^ : Г1.751 Г1 ofT r3.5'
[о 1J ; [ 0.5 ] ДО d : 1.0.5
Таким образом, х,=3.5; х2=0.5. А
Анализ прямых методов решения систем линейных алгебраических уравнений
Эффективность прямых методов решения во многом зависит от структуры и свойств
матрицы А: размера, обусловленности, симметричности, заполненности (т.е. соот-
ношения между числом ненулевых и нулевых элементов), специфики расположения
ненулевых элементов в матрице коэффициентов СЛАУ и др.
Так, размерность системы (т.е. число п) является главным фактором, заставляю-
щим вычислителей отвернуться от весьма привлекательных в теоретическом плане и
приемлемых на практике при небольших п (2 или 3) формул Крамера (3.2.10): Ъ
х, = det A, /det А (; = 1, 2,..., п),
позволяющих находить неизвестные в виде дробей, знаменателем которых является
определитель матрицы системы, а числителем — определители матриц д, получен- •
ные из А заменой столбца коэффициентов при вычисляемом неизвестном столбцом
свободных членов. Если при реализации этих формул определители вычисляются
понижением порядка на основе разложения по элементам какой-нибудь строки или
столбца матрицы, то на вычисление определителя п -го порядка будет затрачиваться
«! операций умножения. Факториальный рост количества арифметических операций
(и вообще, очень быстрый рост) с увеличением размерности задачи называют «про-
клятьем размерности». Что это такое, можно представить, зафиксировав, например,
п = 100. Оценив величину 100! =10158 и прикинув потенциальные возможности разви-
тия вычислительной техники, приходим к выводу о том, что в обозримом будущем к.
системы сотого порядка в принципе не могут быть решены по правилу Крамера.
3.2. Решение систем конечных уравнений
81
Заметим при этом, что, во-первых, правило Крамера будет неустойчиво, т.е. погреш-
ности округлений будут катастрофически нарастать, во-вторых, размерность л = 100
для современных задач не так и велика: довольно часто решаются системы с сотнями
и с тысячами неизвестных.
Если осуществлять вычисление обратной матрицы через алгебраические дополне-
ния (3.2.7), то нахождение решения векторно-матричного уравнения по формуле (3.2.48):
х = А 'ь
фактически равнозначно применению правила Крамера и также практически не-
пригодно по упомянутым выше причинам для вычислительных целей.
Итерационные методы решения систем линейных алгебраических уравнений
При решении СЛАУ любым из итерационных методов можно выделить три пос-
ледовательных этапа.
1. Приведение исходной системы вида Ах = Ь к преобразованной (итерационной)
форме х = Сх + d.
2. Анализ системы на сходимость метода.
3. Решение преобразованной системы одним из методов последовательных при-
ближений, в основе которых лежит та или иная стратегия получения вектора
решений по его предыдущему приближению.
Рассмотрим два итерационных метода.
Метод простых итераций
Метод простых итераций — один из наиболее распространенных методов реше-
ния СЛАУ, который отличается простотой вычислительного процесса и во многих
случаях дает хорошую сходимость.
Представить систему из трех уравнений вида (3.2.9) в итерационной форме мож-
но путем записи каждого его уравнения в виде решения относительно одного из
неизвестных, например:
+ С12Л2 + С13*3 +dt',
(3.2.49)
или, в матричном виде,
х = Сх + d,
(3.2.50)
где
х,
хг
хз
4
d2
С =
d =
Элементы матрицы С и вектора d вычисляются по формулам:
д,=Ь, /а„, /, у = 1,2,3.
При использовании итерационного метода решения необходимо оценить сходи-
мость метода для данной системы, которая зависит только от матрицы коэффициен-
тов с Процесс сходится в том случае, если норма матрицы с меньше единицы, т.е.
(3.2.51)
Это условие является достаточным для сходимости метода. Для его выполнения
82
Глава 3. Численные методы компьютерного моделирования ХТП
необходимо, чтобы на этапе приведения к итерационной форме (3.2.49) каждое урав-
нение системы (3.2.9) решалось относительно той неизвестной переменной, которая
имеет наибольший по модулю коэффициент. Поэтому порядок расположения урав-
нений в системе имеет важное значение.
Стратегия метода простых итераций основана на последовательном приближе-
нии к искомому решению системы, при этом каждое следующее (к +1) приближение
получается в результате подстановки в правую часть преобразованной системы (3.2.49)
приближения, полученного на предыдущей к-й итерации, т.е.
_<<+1)==-<4)+-^ (3.2.52)
В качестве начального приближения обычно принимают вектор-столбец свобод-
ных членов преобразованной системы: х<0) = d . Условие окончания итерационного
процесса для получения решения принимает вид
(,=1,2,3) (3.2.53)
ИЛИ
тах|х,<‘+,)-х)‘’|^е (,= 1,2,3). (3.2.54)
Пример. Методом простых итераций с точностью s = 0,1 решить систему
-7х, -2х2 + х3 =1;
8xj + Зх2 + Зх3 =2; (3 2 55)
х3 +6х2 -х3 = 3.
▼ Для получения преобразованной системы уравнений необходимо сделать до-
пустимые преобразования над исходной системой (3.2.55) с тем, чтобы диаго-
нальные коэффициенты матрицы были максимальными по модулю. Для этого
второе уравнение сделаем первым и в качестве второго используем третье. Сло-
жив первое и второе уравнения исходной системы, получим третье: х, + х2 + 4х3 = 3.
Тогда в итерационной форме имеем систему
х, = - (3/8)х2 - (3/8)х3 + 2/8;
х2=-(1/6)х, + (1/6)х3+3/6;
х3 = —(1/4)х, — (1/4)х2 +3/4.
Проверяем условие сходимости (3.2.51):
|с| = V(-3/8)2 + (-3/8)2 + (-1/6)2 + (1/6)2 + (1/4)2 + (-1/4)2 = л/266/576 < 1;
так как ||С||< 1, то решение может быть получено методом простых итераций.
Результаты расчета представлены в табл. 3.1. *
Таблица 3.1. Значения приближённых решений, получаемых на последователь-
ных итерациях при решении СЛАУ (3.2.55) методом простых итераций
_________________________________________________________________ %
Итерации х2 х3 тах|х,<<+1) - x,w|
0 0.25 0.5 0.75
1 -0.125 0.583 0.75 0.13
2 -0.217 0.583 0.575 0.18
3 -0.308 0.632 0.559 0.09
Таким образом, для получения решения с заданной точностью s = 0,1 потребова-
лись три итерации: х, = х’3) =-0.308, х2 = xf’ =0.632, х3 = х33' =0.559. А
3.2. Решение систем конечных уравнений
83
Метод Зейделя
Метод Зейделя представляет собой модификацию метода простых итераций.
В этом методе при вычислении (к + 1)-го приближения неизвестной х, использу-
ются уже рассчитанные на текущей итерации (к + 1)-е приближения неизвестных
х., х2,..., х, и к-е приближения неизвестных х,,х,н,...,х„. Расчетная формула Зейделя
имеет вид
%<‘+1>=di+£Ci;%<‘+1>+£Cvxj‘>, / = 1,2,...,п. (3.2.56)
Метод Зейделя в большинстве случаев дает более быструю сходимость, чем метод
простых итераций.
Пример. Методом простых итераций и методом Зейделя с точностью s = 0,003 ре-
шить систему
5х, - 4х2 - х3 = -2;
4х, + х2 - 2х3 = 8;
Зх, + х2 -5х3 = 10.
▼Вначале рассмотрим решение системы методом простых итераций и обеспечение
достаточного условия сходимости этого метода. Система в исходном виде не может
быть решена методом простых итераций, ибо простой перестановкой уравнений
нельзя получить систему, в которой по диагонали стояли бы максимальные значе-
ния коэффициентов (здесь нет ни одного уравнения, в котором коэффициент при
х2 был бы максимален по модулю по сравнению с другими коэффициентами того
же уравнения). Преобразуем систему. Вторым уравнением возьмем уравнение, по-
лученное как разность первого и второго уравнений. Третье уравнение остается
неизменным. В качестве первого уравнения возьмем второе уравнение исходной
системы. Представим преобразованную таким образом систему (по диагонали будут
коэффициенты с максимальными по модулю значениями) в итерационной форме:
х, = 0 - 0.25 х2 + 0.5х3 + 2;
• х2 = O.lx, + 0 + 0.2х3 + 2;
х3 = О.бх, + 0.2х2 +0 - 2.
Проверяем условие сходимости:
Достаточное условие сходимости для метода простых итераций выполнено.
Результаты расчета по методу простой итерации (3.2.52) и по методу Зейделя
(3.2.56) представлены в табл. 3.2 и 3.3, соответственно (в первых трех строках
указаны приближения, в последней — решение).
Таблица 3.2. Значения приближённых решений, получаемых на последовательных
итерациях при решении СЛАУ методом простых итераций
Итерации л, х3 max|x,<i+1> - x,(t)|
0 2 2 -2
1 0.500 2.000 -0.400 1.600
2 1.300 2.020 -1.300 0.900
11 0.999 2.000 -0.999 0.003
84
Глава 3. Численные методы компьютерного моделирования ХТП
Таблица 3.3. Значения приближённых решений, получаемых на последователь-
ных итерациях при решении СЛАУ методом Зейделя
Итерации X, х2 •*3 maxjx*1*" -x,(t>|
0 2 2 -2
1 0.500 1.700 -1.360 1.500
2 0.895 1.907 -1.082 0.395
6 1.000 2.000 -1.000 0
Решение показывает большую скорость сходимости метода Зейделя. ▲
3.2.2. Нелинейные уравнения
В общем случае уравнение с одним неизвестным имеет ввд
/(х) = 0 (3.2.57)
или
/,W = /2W, (3.2.58)
где /(х),/;(х),/2(х) — заданные функции, определенные на данном отрезке [а, б].
Всякое число (действительное или мнимое) на отрезке [а, б], обращающее лю-
бое из этих уравнений в тождество:
f&^0 (3.2.59)
или
Ш = (3.2.60)
называется корнем уравнения или его решением.
Решение задачи приближенного определения корней уравнения состоит из двух
этапов:
1) отделение корней, т.е. нахождение подынтервалов [а, Р) на отрезке [а, 6],
которые содержат только один корень уравнения;
2) уточнение корней, т.е. непосредственное вычисление значений корней на
найденных подынтервалах [а, Р] с заданной точностью г.
Понятие об отделении корней ф,
Графический способ отделения корней заключается в построении графика функ-
ции f(x) (3.2.57) либо графиков двух функций /,(х) и /2(х) (3.2.58) на отрезке [а, б].
В первом случае точка пересечения графика функции с осью абсцисс, а во втором —
абсцисса точки пересечения двух функций дают приближенное значение корня урав- V
нения (3.2.57) или соответственно (3.2.58). Найденные таким образом приближен- <
ные значения корней позволяют выделить отрезки [а, Р] (на рис. 3.9, а их три, на
рис. 3.9, б — два), в которых при необходимости можно выполнить уточнение кор-
ней.
При отделении действительных корней расчетным путем для непрерывных функ-
ций / (х) можно руководствоваться следующими соображениями:
если на концах отрезка [а,/>] функция имеет разные знаки f (a)f(b)<0, то меж-
ду точками а и б на оси абсцисс имеется нечетное число корней; если же
f (a)f (b) > 0, то между а и б имеется четное число корней или их совсем нет; ь
3.2. Решение систем конечных у равнений
85
• если f(a)f(b)<0 и либо f'(x), либо
f"(x) не меняет знака на этом
отрезке, то уравнение имеет един-
ственный корень на отрезке [а, Ь].
Пример. Отделить все действительные
корни уравнения х5 - 4х - 2 = 0 на от-
резке [-2, 2].
▼ Находим значения функции f(x)
на концах отрезка: /(-2) = -2б;
/(2) = 22. Так как функции имеют
разные знаки, то на отрезке [-2, 2]
имеется нечетное число корней.
Первая и вторая производные от
функции f(x),
/'(%)= 5х4-4 И У"(х) = 20х3,
меняют знак на отрезке [-2, 2], по-
этому корней будет несколько и от-
резок надо разделить пополам.
Рассмотрим два отрезка [-2, 0] и
[О, 2J отдельно; так как /(0) = -2, то
Рис 3 9. Графический способ отделения
корней: а — график построен для одной
функции; б — график построен для двух
функций
/(-2) /(0) >0, а /(0) • /(+2) < 0. На первом отрезке [-2, 0] либо не содержится кор-
ней, либо их четное число, а на втором [0, 2] — их нечетное число. На втором
отрезке первая производная меняет знак, вторая — не меняет, поэтому он содер-
жит единственный корень. Таким образом, отделен один корень уравнения — на
отрезке [0, 2J.
Первый отрезок делится пополам и получается два отрезка [-2, -1] и
[-1, 0]. Так как /(—1) = 1, значения функций на концах каждого из отрезков раз-
личны: /(-2) /(-1)<0 и /(-1) •/(0) < 0; эти отрезки должны содержать нечетное
число корней. На отрезке [—2, -1] первая производная не меняет знака, а на
отрезке [-1, 0| вторая производная не меняет своего знака. Отсюда можно зак-
лючить, что на отрезках [—2, -1] и [-1,0] имеется по одному корню.
Таким образом, на отрезке [-2, 2] для уравнения х! - 4х-2 = 0 отделено три
действительных корня на отрезках [-2, -1], [-1, 0] и [0, 2]. ▲
При решении задач всегда следует руководствоваться физическими соображени-
ями при отделении корней. Это дает возможность существенно сузить диапазон по-
иска корней, а часто и локализовать их физически допустимые значения.
Уточнение корней
Численный приближённый метод решения задачи, при котором уточняется пер-
воначальное заданное приближение решения, называется итерационным методом или
методом последовательных приближений. Каждый шаг этого метода носит название
итерации.
Если при последовательных итерациях (к = 1,2,3,...) получаемые величины xw все
ближе приближаются к истинному значению корня , то итерационный процесс будет
сходящимся, в противном случае — расходящимся. При этом различают монотонную или
колебательную сходимость (расходимость) в зависимости от того, с одной или с разных
сторон осуществляется приближение (удаление) к (от) искомому (-го) решению (-я).
86
Глава 3. Численные методы компьютерного моделирования ХТП
Для реализации итерационного процесса должны быть заданы начальное при-
ближение х(0) и точность е, с которой требуется найти решение уравнения.
Первоначальное грубое приближение х'°’ следует задавать из физических соображе-
ний и по результатам отделения корней. Все остальные приближения получаются из
итерационной формулы, соответствующей используемому методу решения уравнения.
Условие окончания итерационного процесса (нахождения значения корня с точ-
ностью е) имеет вид:
k =0,1,2,3,.... (3.2.61)
При этом согласно тождеству (3.2.59) для приближения х<1+1), принимаемого за
решение уравнения (3.2.57), должно также выполняться и неравенство
|/(х<‘+1))|<е . (3.2.62)
Итерационные методы являются самоисправляющимися, так как отдельные ошиб-
ки расчетов не приводят к искажению конечных результатов. Это обусловлено тем,
что каждое очередное приближение корня при последовательных итерациях можно
рассматривать как новое начальное приближение.
Метод половинного деления
В основе лежит деление отрезка [а, д], на котором отделен корень уравнения,
пополам; итерационная формула для вычисления последовательных приближений
имеет вид:
х<1> =(а + Ь)/2, £=1,2,3,.... (3.2.63)
На каждой итерации отрезок [а, Ь] уменьшается в два раза и выбирается та его
половина, на концах которой функция /(х) имеет разные знаки:
если /(а)/(х<‘>)>0, то а = х<‘);
если /(Z>)/(x(‘)) > 0, то Ь = х“’;
если /(х(1,) = 0, то х'** = ^, т.е. корню (решению) уравнения.
Процесс деления каждого нового отрезка проводится по аналогии и продолжается до
тех пор, пока длина последнего отрезка не станет сравнимой с заданной точностью е:
|«-&|<2е. (3.2.64)
Появление сомножителя 2 в правой части неравенства по сравнению с (3.2.61) объяс-
няется тем, что в качестве решения всегда принимается середина последнего отрезка:
^~(а + Ь)12. (3.2.65)
Пример. Методом половинного деления найти корень уравнения х2 — 0.6 = 0,
локализованный на отрезке [0, 1], с точностью е = 0.025.
▼ Имеем /(х) = х2-0.6; при а = 0^> f(a) = а1 - 0.6 = -0.6;
И при ь = 1 ->/(£) = 62-0.6 = 0.4.
Таким образом, на концах отрезка [а, Ь] функция /(х) имеет разные знаки.
Первое приближение определяется по итерационной формуле (3.2.63):
х(1) = (0 + 1)/2 = 0,5; /(х01) = -0,35, выбирается правая половина отрезка [0.5, 1.0].
Значения всех приближений представим в табл. 3.4, в которой к — номер итера-
ции.
3.2. Решение систем конечных уравнений
87
Таблица 3.4. Значения приближённых решений уравнения х2 — 0.6 = 0, получае-
мых методом половинного деления
к а Ь f(a) f(b) x(i) (х<‘>)2 /СО
1 0.00 1.00 -0.6 0.4 0.5 0.25 -0.35 1.00>2е
2 0.50 1.00 -0.35 0.4 0.75 0.563 -0.037 0.50>2е
3 0.75 1.00 -0.037 0.4 0.825 0.681 0.081 0.25>2е
4 0.75 0.825 -0.037 0.081 0.788 0.620 0.020 0.075>2е
5 0.75 0.788 0.038<2е
Искомое приближение корня находим по формуле (3.2.65): (0.75+ 0.788)/2 = 0.769.
При этом функция ЛЛ) = 0.59136 - 0.6 = -0.008639, а точность е = 0.038 / 2 =
= 0.019 < 0.025, т.е. выполнено условие завершения итерационного процесса.Л
Для нахождения количества итераций, необходимых для обеспечения требуемой
точности определения корня, находим выражение для отрезка [а, Ь] на k-й итерации:
b-a = (b-a)mJ2t ,
где (6-а)„„ — длина исходного отрезка [а, />]. Подстановка этого соотношения в
(3.2.64) приводит к неравенству (б-а)исх <2‘+1е или, после логарифмирования,
* “ lg2lg^Z’”a)“x/^_1 °3’3 •
Число итераций в этом методе зависит от предварительно задаваемой точности е
и длины отрезка [а, Ь] и не зависит от вида функции f (х). При заданной высокой
точности е расчетов метод сходится медленнее, чем другие известные методы.
Метод простой итерации
Уравнение /(х) = 0 (3.2.57) должно быть преобразовано к виду:
х = Ф(х), (3.2.66)
который является частным случаем уравнения (3.2.58) - см. рис. 3.9, б, когда /, Сх) = х
и f2(x) = q(x). Поэтому корень уравнения (3.2.66) при графической интерпретации
соответствует абсциссе точки пересечения прямой х с кривой <р(х) (рис. 3.10).
Сущность этого метода заключается в следующем. Задается начальное приближе-
ние х<0) (один из концов интервала [а, />] либо точка внутри него) и подставляется в
правую часть уравнения (3.2.66). В результате получается приближение корня на
первой итерации:
х(1) =<рС/°>).
На второй итерации полученное значение х*1' опять подставляется в правую часть
(3.2.66) и вычисляется второе приближение
хт = <р(х<1>).
Эти соотношения будут справедливы и для всех последующих итераций, включая
и произвольную (к + 1)-ю:
Х^‘> =ф(х“»), * = 0,1.................... (3.2.67)
88
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.10. Графическая интерпретация метода простых итераций' а — сходящиеся процессы;
б — расходящиеся процессы
Итерационный процесс завершается, когда будет выполнено условие (3.2.61).
Графическая интерпретация метода представлена на рис. 3.10. Приведены случаи
сходимости (см. рис. 3.10, а) и расходимости (см. рис. 3.10, б), причем оба этих
процесса могут происходить как монотонно, так и колебательно. В соответствии с
этим сходимость или расходимость метода зависит от того, каким образом распола-
гается кривая <р(х) относительной прямой х, т.е. как преобразуется уравнение вида
(3.2.57) к виду (3.2.66). Например, из уравнения igx-x2+3 = 0 можно получить следу-
ющие формы уравнения (3.2.66):
а) х = ^/lgx + З = ф(х); б) х = (1g х + 3)/х = ф(х); в) х = 10х'-3 = ф(х).
Предпочтение следует отдавать тому виду функции <р(х), при реализации которой
обеспечивается сходимость, по возможности монотонная.
При выборе вида функции <р(х) следует руководствоваться достаточным условием
сходимости, которое справедливо для непрерывных функций <р(х), имеющих непре-
рывную производную. Это условие формулируется следующим образом: итерацион-
ный процесс обязательно сходится, если для всех значений х отрезка [а, б] выполняется
неравенство:
|ф'(х}) < 1, хе [а,б]. (3.2.68)
В соответствии с этим неравенством тангенс угла наклона кривой <р(х) в точках
х'1’ (см. рис. 3.10) не должен превышать величины, равной единице. При этом при-
нято различать три вида сходимости:
|<р’(х)|<0.1 — хорошая сходимость;
3.2. Решение систем конечных уравнений
89
0.1 < |<р’(л)| <0.5 — удовлетворительная сходимость;
0.5 < |<р’(х)| <10 — плохая сходимость.
Пример. Методом простых итераций решить уравнение lgx-x2+3 = 0 с точнос-
тью 6 = 0 001, принимая в качестве начального приближения х,о' = 2.0.
▼ Из рассмотренных выше способов выражения функции <р(х) выберем следующий:
1g е
<?(Ь) = фёх + з, тогда <?'М = 2х/ёх+з-
Определим значения ф’(х) в различных точках х:
<₽ ’(2.0) = 0.06, Ф ’(1.8) = 0.067, ф ’(1.6) = 0.076 .
Здесь ф’(х)<0 1, поэтому есть основание ожидать хорошей сходимости.
Итерационная формула будет иметь вид
х'‘И) = y/lgxw+3, к = 0,1,... .
На первой итерации имеем:
х'°> = 2.0; х<” = 71g 2.0 + 3, х<1) =1.817;
|х<,)-х<0,| = 0.183; 0.183 >0.001.
На второй итерации имеем:
X2 = Vlgl.817 + 3; х<2) = 1.8052;
|х<2)-х<1)|=|1.8052-1.817| = 0.0118, 0.0118 > 0 001.
На третьей итерации вычисляется следующее значение:
х<3) = 71g 1.8052 + 3; х<3) = 1.8046,
|х(3) -х<2)| = |1.8046 -1,8052| = 0.0006; 0 006 < 0.001.
Так как в соответствии с (3.2.61) точность достигнута, то = 1.8046 .Л
В том случае, когда уравнение (3.2.57) не удается привести к виду (3.2.66) таким
образом, чтобы в процессе решения выполнялось достаточное условие сходимости
(3.2.68), то вместо уравнения /(х) = 0 берут равносильное уравнение
VW = 0.
где X — некоторое число. К левой и правой частям прибавляют х и получают урав-
нение в форме (3.2.66):
х = х + V(x) = ф(х).
Достаточное условие сходимости (3.2.68) для последнего уравнения имеет вид:
|l + V’(x)|<l. (3.2.69)
В этом случае параметр X следует подбирать таким образом, чтобы условие (3.2.69)
всегда выполнялось.
Точность приближений х<‘+1', т.е. близость их к истинному значению корня
оценивается по формуле
|x‘i+*> -?| > (g /(1 - g))|x<t+,) -х‘*>|, (3.2.70)
где g определяется как наибольшее значение функции производной ф’(х), удовлет-
воряющей неравенству (3.2.68) на отрезке [а, £]:
|q>'(x)|<g <1. (3.2.71)
90
Глава 3. Численные методы компьютерного моделирования ХТП
Из этого условия следует, что если g близко к 1, то г*'1' далеко от даже тогда,
когда х(1> близко к x<i+1), так как g/0-g) велико. Поэтому получаемое по условию
(3.2.61) приближенное значение корня х(‘+1) в этом случае будет неточным.
Достоинство метода простых итераций состоит в том, что при удачном выборе
вида функции <р(х) он обеспечивает быструю и надежную сходимость. Однако для
сложных уравнений получение такого вида функции связано с большой предвари-
тельной работой, а иногда и вообще не представляется возможным.
Метод Ньютона (касательных)
Итерационная формула этого метода получается, если разложить функцию f(x)
уравнения (3.2.57) в окрестности точки х'*’ (£-го приближения) в ряд Тейлора, огра-
ничившись линейными членами:
/(х<Л) + Дх<‘)) = /(х<‘,) + Дх<‘)/'(х<‘))- (3.2.72)
Окрестность Дх(‘’ выбирается таким образом, чтобы следующее приближение стало
корнем, т.е.
/(х<<+1)) =/(х**’+ Дх*’) = 0 и Ах'" =х"*,'-х<<|.
Использование этих соотношений и (3.2.73) приводит к итерационной формуле
метода Ньютона
х<^1> = (*>_/О( *) Л = 0,1,2,3,... . 13 2 731
/’(х'")
Геометрическая иллюстрация итерационного процесса этого метода представле-
на на рис. 3.11 (а — сходимость, б — расходимость). Значение каждого нового при-
ближения (3.2.73) на графике получается, если к кривой функции /(х) в точке х*"
провести касательную до пересечения с осью абсцисс:
О.г.74)
В качестве начальных приближений обычно принимается либо один из концов
отрезка [a, Z>] (на рис. 3.11, а — точка Ь), либо точка внутри него (рис. 3.11, б).
Достаточное условие сходимости процесса расчета определяется для непрерыв-
Рис. 3.11. Геометрическая иллюстрация сходимости (а) и расходимости (6) метода Ньютона
(касательных)
3.2. Решение систем конечных уравнений
91
ных функций с непрерывными производными при условии, что /'(х)*0 и /”(х)*0
на отрезке [а, 6]. В этом случае <р(х) = х-/(х)>/'(х) [см. (3.2.66)], поэтому условие
сходимости (3.2.68) имеет вид:
|<р’(х)| =
[/•’(X)]2 -/”(х)/(х) _|/(х)/"(х)|
[/'(X)]2 [/’(х)]2
(3.2.75)
Для выполнения этого условия необходимо, чтобы:
начальное приближение выбиралось достаточно близко к корню уравнения;
вторая производная не становилась очень большой;
первая производная по возможности больше отличалась от нуля.
Отсюда также следует, что если при последовательных итерациях будет выпол-
няться условие:
/(х)/"(х)>0, (3.2.76)
то приближение к значению корня г, будет происходить с одной стороны. Поэтому в
качестве начального приближения в методе касательных рекомендуется использо-
вать тот конец отрезка [а, Ь\, где выполняется условие (3.2.76).
Пример. Найти действительный корень уравнения lgx-x2+3 = 0 с точностью
е = 0.002 на отрезке [1.5, 2.0].
▼ Определяем производные функции /(х) = lg(x) - х2 + 3:
/' (X) = (1g е) / X - 2х, /"(х) = -(1g е) / х2 - 2.
Находим значения функции и ее производных на концах отрезка:
/(1,5) = 0.9; /'(1.5) = -2.71; /" (1.5) = -2.19;
/(2) = -0.70; /’(2) = -3.78; /"(2) =-2.11.
В качестве начального приближения принимается правый конец отрезка, так
как /(2) • /"(2) > 0, т.е. х<0) = 2.0. Далее расчеты выполняются в такой последова-
тельности:
/(2.0) =-0.699; /’(2.0) = -3.783; х® = 2.0-0.699/3.483 = 1.815;
|x<‘> -х<°>| = |1.815 - 2.0[ > 0.02;
/(х®) =-0.03535; /’(х®) =-3.391; х<2> =1.815-0.03535/3.391 = 1.80457;
|х<2> - х(1) = |1.80457 -1.815|| < 0.02.
В качестве корня следует принять х<2) =1.80457, так как функция при этом
значении аргумента близка к нулю: /(х<2,) =-0.00723. Ответ: ^ = 1.80457. ▲
Скорость сходимости оценивается с помощью разложения функции /(х) в окре-
стности приближения х*’ в ограниченный ряд Тейлора:
/(£) = /(Х(‘>) + /'(х*’)^ - х“’) + (1 / 2)/" (n)(§ - , (3.2.77)
где л заключено между £ и /*>; так как /(£) s о, то
/(х“>) / /' (х<‘>) = х<‘> - (^ - х“> )2
2 f U )
ИЛИ
Х<‘> - /(Х<‘>)/ /Чх“>) - ij = | (ij - Х<‘> )2. (3.2.78)
2 / (х ') v '
Если принять, что т = ^nitj|/’ (х)|, а м = тах[/"(х)|, и левую часть равенства (3.2.78) взять
с учетом итерационной формулы этого метода (3.2.73), то будет справедливо неравенство:
92
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.12. Графическая иллюстрация
сходимости модифицированного
метода Ньютона (касательных)
(3.2.79)
Неравенство (3.2.79) гарантирует быст-
рую сходимость метода Ньютона, если вы-
полняются достаточные условия сходимос-
ти (3.2.75) для всех приближений.
Наибольшее распространение получила
модификация метода Ньютона, когда про-
изводная в формуле (3.2.74) вычисляется
приближенно по результатам двух преды-
дущих итераций
/(Л-ЛЛ1’)
J ' x(k> - У’0 ’
и итерационная формула (3.2.73) принимает вид:
- /(/‘>)-——— (з.2.80)
J / J \Л /
или
(3.2.81)
Итерационная формула (3.2.80) предполагает задание некоторого начального шага
поиска Л = |х"' - У’|, т.е. практически в этой модификации метода Ньютона следует
задавать два начальных приближения: хт и У’ (рис. 3.12), а модифицированный
метод Ньютона называется методом секущих.
Метод хорд
Сущность этого метода заключается в аппроксимации функции f(x) на отрезке
[а, 6] хордой, стягивающей значения функции на концах отрезка (рис. 3.13). Точка
пересечения хорды с осью абсцисс представляет собой приближение к искомому
корню уравнения.
Итерационная формула метода получается из подобия треугольников x<M>aL и х<ы>МЬ;
= af(b)-bf(a)
f(b)-f(a) ’
Рис. 3.13. Графическая иллюстрация
вывода итерационной формулы метода
хорд
Л =0,1,2,3,.... (3.2.82)
Из сравнения последнего выражения с
(3.2.81) следует, что новое приближение в
модифицированное методе касательных
представляет собой точку пересечения хор-
ды, стягивающей функции, соответствующие
значениям приближений на двух последних
итерациях, с осью абсцисс (см. рис. 3.12).
После каждой итерации длина отрезка
[а,б] уменьшается, причем оставляется та
его часть, на концах которой функция имеет
разные знаки. При этом изменяется либо
а, либо b в формуле (3.2.82) (рис. 3.14):
если /(а)/(У+1)) >0, то а = У+|’;
если > 0, то b = У+1).
3.2. Решение систем конечных уравнений
93
Рис. 3 14. Графическая иллюстрация сходимости метода хорд: а — сходимость итерационно-
го процесса при изменении правой границы (Ь) интервала поиска; б — сходимость итераци-
онного процесса при изменении левой границы (а) интервала поиска
Пример. Найти корень уравнения х3 - 2х2 + Зх - 5 = о на отрезке [1.8, 1.9] с точностью
с = 0.005.
▼ Вычисляем значения функции f(x) на концах интервала: /(1.8) = -0.248;
/(1.9) = 0.339. Далее по формуле (3.2.82) определяем первое приближение:
х<” = (1.8 • 0.339 -1.9(-0.248))/(0.339 - (-0.248)) = 1.842; /(1.842) = -0.01009.
Отсюда получаем, что /(а)/(х(”) >0, поэтому а = 1.842 и корень следует искать
на отрезке [1.842,1.9]. Второе приближение определяется также по формуле (3.2.82):
хт =(1.842 0.339-1.9(-0.01009))/(0.339 + 0.01009) = 1.8437;
|х<2)-х(1)| = 0.0017 <0.005;
поэтому q = 1.8437 .▲
Условие сходимости метода хорд (3.2.61)—(3.2.62) оценивается для непрерывных
функций f(x) (3.2.57) с непрерывными первыми и вторыми производными, которые
не меняют знака на отрезке [а, Ь] и не равны нулю на нем.
Для таких функций f(x) при реализации итерационного процесса один конец
отрезка [а, Ь] будет неподвижным, причем тот, где /(<?) /"(<?)> 0 [с = а (см. рис. 3.14, а)
либо с = Ь (рис. 3.14, б)]. Итерационная формула для этого случая имеет вид
хо^-х^> f(x(4} x<t>~c _cf(x(t))-Z7(c) to) _ (а,еслмс = Ь
f(x'k>)-f(c) f(x(t>)-f(c) ’ [b, сслис = а
Условия сходимости и его скорости оцениваются так же, как и для метода Нью-
тона (3.2.73). Если принять в этом случае:
/’(х) = (/(х)-/(с))/(х-с),
(3.2.83)
то можно показать, что условия сходимости (3.2.75) в случае непрерывных функций
/(х) всегда выполняются, а скорость сходимости оценивается с помощью неравенства
| х“+” -^|<(3//(2m))|5-c
где М и т определяются с учетом (3.2.79). По сравнению с (3.2.79) здесь в
первой степени и сомножитель |£, - с| не уменьшается от итерации к итерации.
Этот метод применять отдельно нецелесообразно, но желательно в комбинации с
другими методами.
94
Глава 3. Численные методы компьютерного моделирования ХТП
Комбинированный метод
В этом методе одновременно используются
методы касательных и хорд. Целесообразность
совмещения этих двух методов обусловлена тем,
что для непрерывных функций f(x) в уравне-
нии (3.2.57) с непрерывными производными, не
меняющими знака на отрезке [а, 6], приближе-
ние к корню производится с разных сторон.
В этом случае на каждой итерации полу-
чаются два приближения х/41’ и х'141' соот-
ветственно по формулам метода хорд и мето-
Рис. 3.15. Графическая иллюстрация да касательных, между которыми находится
сходимости комбинированного метода точное значение корня
Графическая иллюстрация этого метода
представлена на рис. 3.15. Касательные проводятся к тем точкам графика функции
/(х), где согласно (3.2.76) /(х<1))-/"(х<‘,)>0. Тогда итерационные формулы (3.2.73) и
(3.2.82) используются в следующем порядке:
х<1) = а - = af(b)-bf(a).
‘ f'ia)’ ' fib)-Да) ’
х<2)_х<» Ж0) . xVf(x?)-x?f(x?).
* k fXx^y 1 ДхУ)-ДхУ) ’ (3.2.84)
<4я> _ r<o _ Ж*1) . r(t+.) _ x^f(x^)-x^f(^)
‘ ‘ - fXW)’ c ~
Вычисления продолжаются до тех пор, пока выполняется неравенство
|ха+,,-х<‘+1,|>£-
Как только это неравенство не выполнится, находится приближенное значение
корня £ по формуле
$ = (х?+,’+х<‘+,,)/2.
3.2.3. Системы нелинейных уравнений
Пусть задана система нелинейных уравнений вида:
f (х1,х2,...,хп) = 0, i = l,2,...,n, (3.2.85)
где / — некоторые действительные функции от аргументов х,.х„, причем одна, или
несколько, или все являются нелинейными относительно одного (или нескольких,
или всех аргументов х.,х„).
В матричной форме эта система уравнений имеет вид:
fix)
f(x) = 0, где х =
f"(x)
Требуется найти такую совокупность значений х,, i = l,2,...,n, которая удовлетво-
ряет всем уравнениям системы.
В общем случае решение системы нелинейных уравнений не может быть получе-
но в аналитическом виде; решение, как правило, ищется численными методами, для
3.2. Решение систем конечных уравнений
95
которых анализ сходимости оказывается значительно сложнее по сравнению с ли-
нейными системами, а порой становится практически невозможным. Кроме того,
следует отметить, что сходимость методов существенно зависит от задания начально-
го приближения, т.е. от того, насколько начальное приближение близко к искомому
решению. Поэтому при выборе начального приближения необходимо использовать
максимум имеющейся информации об искомом решении.
Метод простых итераций
При использовании этого метода система (3.2.85) приводится к итерационной
форме вида:
х, = <р,(х1;х2,...,х„), ( = 1,2,...,п, (3.2.86)
для которой используется расчетная формула
х<м> = <р,(х<1), х<‘>.х(”), i = 1, 2,..., п,
где выражения для функции фДх,,х2,..., х„) получаются из системы (3.2.85) аналити-
ческим решением каждого уравнения относительно соответствующего неизвестного
х,, 1 = 1, ...,п; х,“+1>, x,(t> — значения (£ + 1)-го и k-ro приближений z-ro неизвестного.
С использованием матричной формы записи расчетная формула метода имеет вид:
-пи, --<*). -<*+!>
х = <р(х ), где х
Процесс итераций заканчивается при выполнении на очередной итерации условия
ШаЛ Л — X. | — с
l<z<n I
для i = 1,2, ..., п, где е — заданная точность решения.
Метод Ньютона—Рафсона
Вывод итерационной формулы метода Ньютона—Рафсона выполним для систе-
мы двух нелинейных уравнений [сравн. с методом Ньютона (касательных) для реше-
ния одного уравнения (3.2.73)]:
/i(-W2) = O, /2(х,,х2) = 0. (3.2.87)
Допустим, что имеется k-е приближение к решению х]*’, х?’. Величина поправки
Дх,й’, Дх)*’ для получения нового (к +1) -го приближения может быть определена из условия,
что новое приближение будет соответствовать решению — функции (3.2.87) равны нулю:
/.(х]*’ +Дх1<2,,х<‘) + Дх<‘>) = 0, f2(x^ + Дх<‘>,х<‘> +Дх<‘>) = 0. (3.2.88)
Полагая, что Дх^’.Дх^*’ — величины малые, функции уравнений системы (3.2.88)
можно представить в виде разложения в ряд Тейлора по степени Дх с точностью до
членов первого порядка малости:
Ла;\хГ)+^ф^^ Л(^2Х = 0;
OXj ох2
x<‘h arzx**’ xw4 (3.2.89)
/2(x1(t),x<t)) + Л( 1 ’ 2 )Дх1+ Л( 1 ’ 2 Дх2=0.
Эх, Эх2
Перенеся первые слагаемые в уравнениях в правую часть, запишем систему в
матричной форме в виде СЛАУ (3.2.9):
96
Глава 3. Численные методы компьютерного моделирования ХТП
J(xt>)&x(t'1 =-f(x(t\
где
(3.2.90)
of,(x ) dj\(x )
Эх, дхг
of2(x ) of2(x )
Эх, Эх2
(3.2.91)
— матрица частных производных, называемая матрицей Якоби (определитель этой
матрицы называется якобианом).
Обозначим:
.-<*)
Дх
Дх,*’
Дх<‘>
----(*)
fix ) =
f2(x«\xp)
(3.2.92)
откуда с применением метода обратной матрицы (3.2.48) СЛАУ (3.2.90) имеет следу-
ющее решение:
дх<‘)=-7’'а(‘))-7(х<‘,)’ <3-2-93)
где j (xw) — матрица, обратная матрице частных производных 7(xw).
С учетом того, что Дх'*+1) =х<м> -x(t>, соотношение для определения очередного
приближения может быть записано в виде:
-(itl) = -(o _y-1(-<*>) --Ш) (3 2 94)
Такой итерационный метод решения систем нелинейных уравнений принято на-
зывать методом Ньютона—Рафсона.
В качестве критерия окончания решения используется условие:
тах|х,(‘+|) - х,(*)| < е для/ = 1,2. (3.2.95)
Для улучшения сходимости метода можно использовать корректирующий пара-
метр X. Тогда расчетная формула модифицированного метода Ньютона—Рафсона
приводится к виду
Г’1’ =х'‘’ -U '(х'‘’)7(х"'), где О < х < 1. (3.2.96)
Процесс итераций заканчивается при выполнении того же условия (3.2.95).
Иногда применяется другая модификация, которая отличается от выше рассмот-
ренного метода Ньютона—Рафсона тем, что матрица Якоби и обратная ей вычисля-
ются только для начального приближения. Рассчитанная таким образом обратная-
матрица частных производных используется затем на всех последующих итерациях.
Такая модификация сокращает объем вычислений на каждой итерации, однако схо-
димость итерационного процесса при этом может замедлиться и оказаться медлен-
нее, чем в двух предыдущих методах.
Последовательность решения системы нелинейных уравнений по методу Ньюто-
на—Рафсона состоит в выполнении следующих этапов:
1) выбор вектора начального приближения х<0);
2) вычисление матрицы Якоби j и якобиана 7 ;
3) нахождение обратной матрицы J ;
4) расчет очередного приближения по формуле (3.2.94);
5) проверка условия окончания итераций (3.2.95).
Если заданная степень точности еще не достигнута, то процесс вычислений по-
вторяется начиная с п.2.
3.2. Решение систем конечных уравнений
97
Пример. Методом Ньютона—Рафсона решить систему нелинейных уравнений
х3 + х2 - 4 = 0;
х, + х2 - 28 = 0
при заданном значении вектора начальных приближений х<0)
(3.2.97)
с точностью е = 0.005.
▼ Используем формулу (3.2.94), т.е. вычисление обратной матрицы производных
Якоби проведем для каждого приближения. Для начального приближения по соот-
ношениям (3.2.92) и (3.2.91) вычисляем f(x'0’), 7(х(0)),|7(х<0))|;
7(Х<“>) =
f(x ) =
АСМ)
3(х]га’)2 1
.1 3(х™)2
Определим обратную матрицу классическим методом с использованием ал-
гебраических дополнений (см. разд, выше «Матричные операции») и вектор не-
известных на первой итерации:
=-1
J
1 12
143 -1
-1
12
-со
х
21_ 1 Г12
2У йзЬ-1
-f) Г б"|_Г1.371
I2J |_isj —1_3.552
Дальнейшие вычисления выполняются аналогичным образом до момента вы-
полнения условия окончания итераций. Результаты расчета представлены в табл.
3.5, из которой видно, что для получения решения заданной системы нелиней-
ных уравнений требуются четыре итерации.
Таблица 3.5. Получаемые приближения при решении системы (3.2.97) методом
Ньютона-Рафсона
№ итера- ции -(*) X /(х*’) J 1’1 =-1 J шах|хУ*^-х^1 £ 1<»<Л 1 1
0 1 1 tN) N)| ' 6 -18 Г12 Г 1 12 143 1 143 12 -fl -1 12J
1 '1.371' 3.552 ' 2.129' 18.187 5.64 1 1 37.85 212.4 1 212.4 '37.851 -Г -1 5.64 1.552 >е
2 1.077 3.079 0.328 2.266 '3.48 1 1 28.44 97.971 1 28.44-1 ' -1 3.48 0.473 > е
97.971
3 '1.005' 3.002 '0.017' 0.059 '3.030 1 1 27.036 80.919 1 '27.036 -1 “I -1 з.озо] 0.077 > е
80.919
4 '1.000' 3.000 0.005 = е
7-4544
98
Глава 3. Численные методы компьютерного моделирования ХТП
3.3. Интерполяция и аппроксимация функций
Одной из наиболее важных проблем численного анализа является проблема при-
ближенного описания неизвестной функциональной зависимости по известным ее
значениям в некоторых точках, называемых узловыми. Наиболее распространенны-
ми способами такого приближения функций являются методы интерполяции и апп-
роксимации. Принципиально в качестве приближенной функции может быть выбрана
любая из функций, однако чаще всего, исходя из соображений простоты и удобства
решения задачи, выбираются многочлены (полиномы) произвольной степени т:
Рт(х) = а0+щх + а2хг +- + атхт , (3.3.1)
где а = [а0, а,.«„Г — коэффициенты многочлена (полинома).
В этом случае задача интерполяции и аппроксимации заключается в определении
значений коэффициентов а приближенных функций, в частности функции много-
члена (полинома) Рт(х) по дискретной таблице данных с N = п + 1 известными
точками Х'.У' (i = 0,l,..,n) - табл. 3.6.
Практически необходимо решить обратную задачу, по известным табличным дан-
ным и известному виду приближенной функции [в данном случае — многочлен сте-
пени т (3.3.1)], требуется определить элементы вектора коэффициентов этой функ-
ции — а (для многочлена (3.3.1) — (т + 1) коэффициентов а0,а1,...,а„).
В прямой задаче все коэффициенты а известны и вычисляются значения функ-
ций yt по формулам типа (3.3.1), исходя из данных х,(< = 0,1,...,п).
В соответствии с методом интерполяции коэффициенты а (3.3.1) определяются
из условия совпадения результатов расчетов по интерполирующей зависимости в уз-
ловых точках х,, в данном случае Рт(х,), с известными табличными данными у, т.е.
Л.и,) = У, (< = 0,1, ...и). (3.3.2)
Так как путем решения этой определенной (нормальной) линейной относитель-
но а системы уравнений [с учетом выражения для многочлена (3.3.1)] вычисляется
(т + 1) коэффициентов а , то требуемое число табличных значений у, (< = 0,1,...,«),
равно (w + i), т.е. при решении задачи интерполяции многочленом степени т долж-
но выполняться условие (см. табл. 3.6):
m + l = n + l, (3.3.3)
или
т = п. (3.3.4)
Первая узловая точка (х0) имеет индекс 0, а последняя (xj — индекс п, а степень
интерполирующего многочлена (3.3.1) принимается равной п вместо т.
Таблица 3.6. Данные о приближенной функции в узловых точках
Номер точки № Узловые точки X Значения приближенной функции у
0 *0 Уо
1 Xj У1
2 Уг
п Уп
3.3. Интерполяция и аппроксимация функций
99
При требовании точного совпадения в узловых точках функции и ее приближе-
ния (задача интерполяции) число определяемых параметров интерполирующей за-
висимости равно числу точек. При выборе такого критерия задача сводится к пост-
роению интерполяционных многочленов. Доказано, что задача полиномиальной
интерполяции имеет единственное решение при построении по (т + 1) узловым точ-
кам многочлена степени т. Построенный интерполяционный полином в дальнейшем
используется для определения значений функции между узлами, и процесс расчета
называется интерполяцией.
Если интерполирующую зависимость вычисляют вне интервала, в котором рас-
полагаются узловые точки, то процесс расчета называется экстраполяцией.
В соответствии с методом аппроксимации коэффициенты а (3.3.1) определяются
из условия наибольшей близости (но не совпадения) результатов расчетов по аппрок-
симирующей зависимости в узловых точках х,, в данном случае Р„(х,), с известными
табличными данными yt(i = 0,1,..., п) (см. табл. 3.6).
Можно использовать три различных критерия для оценки степени близости рас-
четных и табличных значений у:
— критерий метода наименьших модулей
я = Ё1л.и.)-у.|; (3.3.5)
- критерий метода наименьших квадратов (МНК)
я = ЁЬРДх.)-?.]2; (3.3.6)
— критерий «минимаксного» метода Чебышева
/? = max^(x,)-zi. (3.3.7)
При определении коэффициентов методом аппроксимации стремятся к тому, чтобы
эти критерии принимали в результате решения задачи наименьшие значения (отсю-
да и название, например, метода с критерием (3.3.6) — МНК).
Следует отметить, что наибольшее распространение при решении задач аппрок-
симации получил метод наименьших квадратов с критерием (3.3.6), так как он обес-
печивает наименьшее значение средней квадратичной ошибки. В то же время при
применении этого метода могут наблюдаться большие ошибки в отдельных точках. В
тех случаях, когда требуется уменьшить экстремальную ошибку, допуская большое
среднее квадратичное отклонение, целесообразно для аппроксимации использовать
критерий Чебышева (3.3.7).
При решении задачи аппроксимации число определяемых коэффициентов а может
быть существенно меньше количества узловых точек. Таким образом, количество
узловых точек табл. 3.6 в этом случае не ограничивается числом определенных коэф-
фициентов многочлена (полинома) (3.3.1), как при использовании метода интерпо-
ляции (3.3.2).
Применение многочленов Р„(х) для приближенного описания функциональной
зависимости от одной переменной f (х) может быть обосновано с помощью теоремы
Всйерштрасса. Если функция f(x) является непрерывной на конечном замкнутом ин-
тервале [а,4>| изменения независимой переменной, то для любого е>0 можно найти
такой многочлен Р(х), что |Дх)-Р(х)|<е при всех х на интервале [а, Ь].
Другим важным моментом при решении задачи приближения функции является
выбор критерия согласия (3.3.5)—(3.3.7) — критерия соответствия аппроксимирую-
щей функции и аппроксимируемой, вид которого определяет математический аппа-
рат, используемый при решении задачи.
100
Глава 3. Численные методы компьютерного моделирования ХТП
В действительности, наиболее общим подходом к решению задачи интерполяции
является решение определенного (нормального) неоднородного СЛАУ следующего вида:
а0 + а,х0 + а2х02 +... + а„х0” = У о
аа + OjX] + а2х2 + ... + а„х" = у,;
............................................ (3.3.8)
а0 + а,х„+а2х2+... + аХ = у,
или в матричном виде:
1 х0 х„ • 1 X, х} • п х6 < ао ai = Уо У1 , (3.3.9)
_1 х„ х2 • х“. а._ У„_
где искомым решением является вектор а = [а0,а1,..„ атГ.
В тех случаях, когда значения функции в узлах определены с некоторой погреш-
ностью или количество узловых точек велико, требование точного совпадения в уз-
лах излишне.
Аппроксимирующая зависимость должна быть близка к исходной функции лишь в
смысле некоторого критерия. В этом случае задача о приближении (задача аппроксима-
ции) ставится следующим образом. Требуется данную достаточно сложную функцию
f (х) заменить (аппроксимировать) полиномом так, чтобы рассогласование или откло-
нение функции от полинома на заданном множестве X = {х} было минимальным.
Если множество X состоит из отдельных точек х0,х,,...,х„, то приближение назы-
вается точечным; если же X представляет собой отрезок а < х < Ь, то приближение
называется интегральным.
Задачу аппроксимации, по аналогии с системой (3.3.8) или (3.3.9), можно рассмат-
ривать как задачу решения переопределенного неоднородного СЛАУ (нумерация узловых
точек соответствует табл. 3.6):
«о + ал + а2хо +-+а„х" = У0;
а0 + а,х, + агх2 + ... + апх( = у,;
а0 + а,х, + агх, + ...+ а„х" = у2; (3.3.10)
а0 + ал + ал +... + а„х" = У„,
где n + l>m+l и искомым решением является вектор а^а^а,......
Для получения этого решения (решения задачи аппроксимации) переопределен-
ную систему (3.3.10) необходимо преобразовать в определенную {нормальную) систему
(3.3.11) путем использования необходимого условия экстремума функции — крите-
рия, например, МНК (3.3.6):
Др Ё(ао + а1*. + а2х2 +...+ ал ~У,)2
— = зй---------------------------= 0, где j = 0,1,..., т+1. (3.3.11)
да, да,
Полученная система (т + 1) определенных (нормальных) уравнений включает (т + 1)
коэффициентов а0, а,,.... ат, которые могут быть найдены одним из известных мето-
дов решения неоднородных СЛАУ.
3.3. Интерполяция и аппроксимация функций
101
3.3.1. Интерполяция
Задачи интерполяции часто возникают в практике инженера-химика, например
при:
I) интерполировании табличных данных;
2) получении аналитической зависимости по экспериментальным данным, пред-
ставленным в табличной или графической форме;
3) замене сложной с вычислительной точки зрения функции более простой за-
висимостью, хотя и с некоторой ошибкой;
4) приближенном дифференцировании и интегрировании;
5) численном решении дифференциальных уравнений.
Задача интерполирования может быть сформулирована следующим образом. Пусть
на отрезке [a,Ь] заданы л + 1 точек х0,х„...,хя, которые называются узлами интерполя-
ции, и значения некоторой интерполируемой функции f(x) в этих точках, т.е.
Уо = /Uo);yi = /Ui);-;y„ = /(*„)• (3.3.12)
Требуется построить некоторую интерполирующую зависимость F(x), которая в уз-
лах интерполяции принимает те же значения, что и интерполируемая функция f (х), т.е.
F(x0) = f(x0) = у„,
.................................. (3.3.13)
Нх,) = /(Х„) = К.
При решении задачи интерполирования обычно принимается, что:
1) интерполируемая функция непрерывна на отрезке [в, Ь] и в каждой точке име-
ет конечные производные любого порядка;
2) узлы интерполирования отличны друг от друга.
Графически решение задачи интерполяции заключается в том, чтобы построить та-
кую интерполирующую функцию, которая бы проходила через все узлы интерполяции.
Интерполяционный полином Лагранжа
Пусть на отрезке [а, 6] заданы п +1 значения функции /(х) в точках х„, х„..., х„, т.е.
у, =/(х,), i = 0,1,2,.... п. (3.3.14)
Требуется построить полином Р„(х) степени не выше п, имеющий в заданных
узлах те же значения, что и функция /(х), т.е.
Л(х,) = /(х,) = у,, / = 0,1,2,..., л.
Решение ищется в форме
(3.3.15)
Л(*)=ЁуД(*)>
(3.3.16)
где у, — значения функции в узлах интерполяции; £,(х) — некоторый полином, при-
нимающий значения
[1, если / = j,
лс*.)=L
[О, если i Ф ].
Этому условию удовлетворяет многочлен, имеющий вид
(3.3.17)
£,(*) =
(3.3.18)
102
Глава 3. Численные методы компьютерного моделирования ХТП
тогда
(х-х0)(х-х|)...(х-х,.1)(х-х,4,1)-(х-х,)
У‘ (х, -х0)(х, -х,)...(х, -х,_,)(х, -х,+1)...(х, -х„)
(3.3.19)
— многочлен Лагранжа. Для практических целей формулу (3.3.19) целесообразно
преобразовать следующим образом. Если положить
' (х, -х0)(х, -Х^-Лх, -х.^Хх, -Х1+1)...(Х, -Х„) ’
ТО
п Л я я и л. Л
= (3-3.21)
1=0 Vх Xi' J=0 J=o i=O(X xt)
Пример 1. Построить интерполяционный многочлен Лагранжа по заданным зна-
чениям (представлены в таблице) некоторой функции:
i 0 1 2
xi 0 1 2
У, 0 1 2
Решение ищем в виде (3.3.21):
J=o 1=0 У А (х-х,)‘
Вычислим коэффициенты A,, i = 0,1,2:
4> = 1 /[(*0 -*1)(х0 -х2)1 = 0.5;
4 =1/[(х1-^)(х,-х2)] = -1;
А2 = 1 /[(х2 - х0 )(х2 - х,)] = 0.5,
тогда
Р2 (х) = (х - 0)(х - 1)(х - 2)[ ° 1 5 + 2LA
Цх-0) (х -1)
Интерполяционный многочлен имеет вид у = х.А
2-0.5
(х-2) J
Пример 2. Построить интерполяционный многочлен Лагранжа для заданной за-
висимости молярной теплоемкости Ср метана от температуры t и определить
значение Ср при t =420К:
i t, К Ср, Дж/(моль-К)
0 273 35.61
1 373 39.58
2 573 47.65
▼ Сначала вычислим значения А0,А,,А2:
. д —. д •
(^о ^iX^o ~^г) (Л — А)ХЛ ~G) ^2 — Л)Х^2 —Л)
Ао =------5-----= 0.3 104; А. =----!----= -0.5 10’4;
(-100)-(-300) 1 100(-200)
Полином второй степени находим по формуле
f С Ao С А,
А, =-----5---= 0.16 10’4.
300-200
С А,
Рг 2
а-*0) а-о а-о Г
3.3. Интерполяция и аппроксимация функций
103
Р2(?) = (I - 273)(/ - 373)0 - 573) • 10"* ( - 61 0,3 - 3958 °-5 + 47.65-0.1б\
2 0 - 273) 0-373) 0-573) )
P2(t) = 10-4(2.09 10’2 ?2 + 390.38? + 35.6 • 104).
Для того чтобы определить значение теплоемкости при t = 420 к, надо вычислить
значение полинома Р2 (?) при ? = 420 К:
Р2(420) = 10-4 (2.09 • 10 2 • 4202 + 390.38 • 420 + 35.6 • 104) = 41.38,
поэтому Ср =41.38 Дж/(моль-К). ▲
Конечные разности и их свойства
Пусть задана функция у = f(x) на отрезке [х0,х„], который разбит на п одинако-
вых интервалов Дх = h. Для каждого узла:
х0,х, = x0 + h,...,x, =х0 +nh (3.3.22)
определены значения функции в виде:
/(х0) = у0, /W = У1> •••> f(x„) = у„. (3.3.23)
Выражение:
ДУ, =/U,) = /(x,+1)-/(x,) (3.3.24)
называется конечной разностью функции первого порядка в точке.
Аналогично определяются конечные разности высших порядков, например:
Д2у, = Д(Ду,)=Д(у1+1-у,) = Ду,+1-Ду, = у,+2-y,+i-(y,+i “У,)= У,+2 ~2у,+1+у,. (3.3.25)
Значение функции для любого узла можно выразить через начальное значение
функции и через конечные разности. Например, значение функции в точке х, через
значение ее в точке определится следующим образом:
/(X) = /(Хо + h) = /(х0) + Д/(х0) = (1 + Д)/(х0). (3.3.26)
Аналогично для точек х2 и х„ соответственно имеем:
/(Х2) = /(х0 + 2Л) = /(х,) + Д/(х,) = (1 + Д)/(х,) = (1 + Д)2/(х0); (3.3.27)
/(х,) = /(х„+лЛ) = (1 + Д)’/(х0). (3.3.28)
Раскрывая выражение (1 + д)" по формуле бинома Ньютона, получаем соотношение
/(х0 + лЛ) = £с„"Д”/(х0), (3.3.29)
где с" — число сочетаний из п по т, удобное для практического использования и
позволяющее по значению функции в исходной точке и значениям конечных разно-
стей для этой же точки определять значения функции в других точках.
Решение обратной задачи, т.е. нахождение значений конечных разностей через
последовательные значения функции, позволяет получить формулу, согласно которой
дл№>) = £(-i)”+" с;/(х0+mh). (з.з.зо)
Для конечных разностей строят таблицы двух типов: горизонтальные и диаго-
нальные (треугольные). Наибольшее распространение получила диагональная таб-
лица конечных разностей (табл. 3.7).
Анализ таблицы показывает, что для этой функции разность второго порядка
постоянна для всех точек, а разность третьего порядка равна нулю.
Свойство разностей полиномов иметь во всех точках постоянное значение разно-
сти, порядок которой равен степени полинома, позволяет определять порядок ин-
терполирующего полинома, т.е. порядок полинома равен порядку той разности, ко-
торая имеет постоянное значение в таблице разностей.
104
Глава 3. Численные методы компьютерного моделирования ХТП
Таблица 3.7. Диагональная таблица конечных разностей
i х, У, Ьу, Д2у, Д3у, Д4у;
0 *0 Уо
ДУ0
1 xi У\ Д2Уо
Ду, Д’Уо
2 Х2 Уг Д2у, Д4у0
Ду2 Д3у,
3 Х3 Уз Д2у2
Ду3
4 Х4 У<
При составлении таблицы разностей возможны случайные ошибки. В табл. 3.8
показано распространение ошибки, допущенной при вычислении функции в чет-
вертой точке (+е). Наглядно видно, что даже незначительная ошибка в значении
функции приводит к значительным ошибкам в ее разностях высокого порядка. При-
чем максимальная ошибка для четных разностей находится в той же горизонтальной
строке, что и ошибочное значение функции, для нечетных разностей — в верхней и
нижней соседних строках.
Таблица 3.8. Диагональная таблица конечных разностей функции у = х2 с распро-
странением ошибки £
i X У, ^У, д2у, Д3У,
0 0 0
1
1 1 1 2
3 0
2 2 4 2
5 0(+£)
3 3 9 2(+е)
7(+£) О(-Зе)
4 4 16(+£) 2(—2е)
9(+е)
5 5 25 2(+е)
11 0(-е)
6 6 36 2
13
7 7 49
3.3. Интерполяция и аппроксимация функций
105
Кроме того, можно заметить, что для каждой k-й разности сумма ошибок равна
нулю, а сумма их модулей равна 2*|е|, т.е.
ЁЕ.=°- £|е.1=1е1-2 3‘- (3.3.31)
|=о 1=0
Рассмотренный закон распространения ошибки в таблице конечных разностей
дает возможность в некоторых случаях установить наличие и место ошибки, ее чис-
ловое значение, а также исправить значение функции.
Разделенные разности и их свойства
В тех случаях, когда значения функции /(х) на интервале заданы через неравные
промежутки, т.е. х, - х,_, * const, строят таблицы разделенных разностей.
Разделенной разностью первого порядка называется отношение вида:
k„x,]=J'№1~J'' 0 = 0,1,.., л-1). (3.3.32)
х.+.-х.
Аналогично определяются разделенные разности второго порядка:
Г 1 (Х|+2’ Х< 1 (Х<+1 > Х, 1 /" Л 1 т ттч
1-*,+2> *,+1> х. 1=-2------ 0 = 0,1,..., л-2). (3.3.33)
Xi+2 Xi+1
С помощью следующего рекуррентного соотношения определяются разделенные
разности и-го порядка через разности (п — 1)-го порядка:
к.х„-....,ха]=[х"’х-" -х°Нх--х^.--хо]_ (3.3.34)
Отметим, что разделенные разности являются симметрическими функциями ар-
гументов (не меняются при перестановке элементов), например:
[х,, ^] = 7тт- = *>]• (3.3.35)
Разделенные разности удобно записывать в таблицу (табл. 3.9).
Таблица 3.9. Таблица разделённых разностей
i xt У, к >х0] k.xpxj [x,,X,_l,Xl,X0]
0 х0 Уо
1 Х1 Уз 1*1, х0 ]
2 х2 У1 Lx2 ’ Х0 J kj.XpxJ
3 хз Уз bwoJ [x3 , X], Xq ] [x3 , X2 , X,, x0 ]
Приведем пример заполнения таблицы разделенных разностей для заданных зна-
чений аргументов х, и функции у, (табл. 3.10).
Таблица 3.10. Формирование таблицы разделённых разностей по конкретным
данным
t х, У, > Х0 1 [-xi>xl>xol к ’ Х2» Х| ’ Х0 ]
~о о 1
12 3 1
2 4 13 3 1
3 17 6 -5 2
106
Глава 3. Численные методы компьютерного моделирования ХТП
Интерполяционные многочлены Ньютона
При построении интерполяционного многочлена Лагранжа степени п использу-
ются значения функции в (и + 1)-м узле интерполирования. При добавлении новых
узлов необходимо заново вычислять полином, так как увеличивается число слагае-
мых и число сомножителей. Это является серьезным недостатком использования
полинома Лагранжа, так как такие ситуации часто возникают при построении поли-
нома по данным еще не завершенного эксперимента, а также при выборе располо-
жения и числа узлов для достижения заданной точности интерполирования. От ука-
занного недостатка свободны интерполяционные многочлены Ньютона.
Интерполирующий многочлен ищется в виде:
Р„ (х) = аа + а, (х - х0) + а2 (х - ха )(х - ) + ... + а„ (х - х0 )(х - х, )...(х - х,ч),
или в компактной форме:
р„(х) = £й,П(х-х;). (3.3.36)
i-0 j~O
Задача построения многочлена сводится к определению коэффициентов из условий
Р.Ы = а0 = у0-,
рАхд = ао + ai(xi ~хо)= УГ>
Р.(х2) = а0 + в1(*2 -х0) + а2(х2 -х0)(х2 -х,) = у2; (3.3.37)
Л ПЭ = «о + а, (х„ - х0) + аг (х„ - х0 )(х„ - х,) +... + а„ (х„ - х0).. (х„ - х„.,) = у„.
Используя метод индукции, можно получить следующие соотношения:
= у0;
X, -х0
а2 =----;
(х2 х0 )(х2 X,)
________У, - У-i______.
(х, -х0)(х, -Х|)...(х, -Х,_,)’
(3.3.38)
а =__________У. - У„-1______
(x^XoXx.-xJ.-.Cx.-x,.,)’
которые удобно записать через разделенные разности (3.3.32):
«о ~ У о* ф
(к =[*>
^=[_Х2, *4=^,
[х Х_2, ..., X, Xol-fx, Х,_2, ..., X., Х)1 г ,
а, = _ 11 —- = [*„ х,.!, .., х„ х0]; (3.3.39)
_ [л, Х„_2, ..., X,, хо] [x„_j, х„_2, .., Х|, Хо]_г 1
ап - х _х - |Лм Лл-1» •••» *1» Ло]-
3.3. Интерполяция и аппроксимация функций
107
Тогда интерполяционный многочлен Ньютона примет вид:
Л(*) = Ё1л..(3.3.40)
i=0 j=0
В таком виде формулой удобно пользоваться для интерполяции функций, задан-
ных через неравные интервалы аргумента, т.е. для неравноотстоящих узлов.
Если узлы интерполяции находятся на равном расстоянии друг от друга, т.е.
х, =xa+ih, / = 0,1,...,л, (3.3.41)
где h — шаг интерполяции, то выражение (3.3.41) можно упростить за счет более
компактных формул расчета коэффициентов а,, полученных из соотношений (3.3.38):
а0 = у0;
а. - АУ° .
4 1 h 1 Л ’
Уг А^°(х2 Хр) У0 = y2_2yl+y0 = ^Уо _
(Xj-XjXXj-x,) 2'й2 2'й2’
(3.3.42)
а, = &‘y0/(i'.h‘).
Тогда интерполяционный многочлен Ньютона для равноотстоящих узлов при-
нимает вид:
л Д* V
= (3.3.43)
,-О ЦП J=o
откуда для и = 2 получаем:
f2(x) = Уо + ^2-(х-хо) + ^-^-(х-хо)(х-х1). (3.3.44)
h 2\h
Если при интерполировании полиномом второй степени точность окажется не-
удовлетворительной, то при добавлении еще одного узла интерполяции полином
третьей степени Р3(х) строится с использованием рг(х) в соответствии с соотноше-
нием
Р3(х) = Л(х) + Р3(х),
где
А (х) = (X - х0 )(х - X, )(х - х2).
(3.3.45)
(3.3.46)
Пример 1. Построить многочлены Ньютона второго и третьего порядков по
следующим значениям равноотстоящих узлов интерполяции при Л = 1 и
i = 0,1, 2,3:
Х! 0 1 2 3
У, -1 0 3 10
▼ Строим таблицу конечных разностей (табл. 3.11).
108
Глава 3. Численные методы компьютерного моделирования ХТП
Таблица 3. II. Таблица конечных разностей, построенная по данным задачи
i X У, ДХ д2У, д3У,
0 0 -1
+1
1 1 0 +2
+3 +2
2 2 3 +4
+7
3 3 10
При построении р2(х) используем первые три узла. По формуле (3.3.44) имеем
Р2(х) = -1 + у^(х-0) + ^у(х-0)(х-1) = х2-1.
Для построения многочлена третьего порядка определим слагаемое р'(х) по (3.3.46):
Р/ = (х-°Хх“1Хх-2) = ^х3 ~х2 + |х-
Тогда многочлен Ньютона третьего порядка будет иметь вид:
Р3(х) = Р2(х) + Р3' (х) = х2 -1+ (1 /З)х3 -х2 +(2/3)х = (1/3)х3 +(2/3)х-1.А
Пример 2. Построить интерполяционный полином Ньютона для заданной за-
висимости поверхностного натяжения <т раствора азотнокислого натрия от тем-
пературы Т и определить значение <т при Т = 285 К:
т, К 278 293 323
<т, Н/м 72.1-103 74.4 10"3 79.8 10’3
▼ Значения функции даны в неравноотстоящих узлах, поэтому для построения
полинома используем соотношение (3.3.44); строим таблицу разделенных раз-
ностей (табл. 3.12).
Таблица 3.12. Таблица разделённых разностей, построенная по данным задачи
/ X, У, Iх,, Хо1 Iх,. Х1> хо]
0 278 72.1 10’3
1 293 74.4 10'3 (74.4-7_2Л)-10^ 0.153. 10-з 293 - 278
2 323 79.8 10“3 (79.8 - 72.1) • 10'3 0171.10-з (0.171 - 0.153) 10 3 _ 0 0006 10_3
323- 278 *“ 323- 293
Построение полинома Ньютона по заданным узлам с использованием получен-
ной таблицы разделенных разностей сводится к расчету по формуле
Pl (.X) = V0 + [xi, хо ](х - Х0 ) + [Х2 , Х1, Х0 ] (Х - Х0 Xх - Х1);
Р2(х) = 10“3 (72.1 + 0.153(х - 278) + 0.0006(х - 278)(х - 293)) = 10'3(0.0006х2 + 0.138х + 71.395).
3.3. Интерполяция и аппроксимация функций
109
Определим значение вязкости при т = 285 К, для чего вычислим:
/>2(285) = 73.9-1О‘3; следовательно, о285К = 73.9 10’3[Н/м]. ▲
Погрешности интерполяционных формул
Значения интерполяционных многочленов Лагранжа и Ньютона в узлах интерпо-
ляции полностью совпадают со значениями интерполируемой функции, для проме-
жуточных точек их значения отличаются от точных значений функции. В связи с
тем, что интерполяционные многочлены используются именно для вычисления зна-
чений функции в промежуточных точках, необходимо сделать оценку максимально
возможной погрешности при интерполяции, т.е. необходимо оценить значение ос-
таточного члена:
Я„(х) = /(х)-Р„(х), (3.3.47)
где /(х),р„(х)- значения функции и полинома п-й степени в точке х. Остаточный
член равен нулю в узлах интерполяции и в общем случае не равен нулю в точках,
расположенных между узлами, т.е.
[= Опри х = х,,i = 0,1,..., п,
(3.3.48)
0 в остальных точках. ' '
Для оценки максимальной погрешности можно воспользоваться формулой:
1 " 1 [(п + 1)!]
П(х-х,)
(3.3.49)
где Мп+1 = max /n+1(x) — максимальное значение по модулю производной (п — 1)-го
порядка для интерполируемой функции на заданном интервале.
Следует отметить, что результаты расчётов по интерполирующим многочленам
Лагранжа и Ньютона совпадают друг с другом во всех точках. Поэтому их погрешно-
сти одинаковы.
Пример. Оценить погрешность интерполяционной формулы Лагранжа при вы-
числении функции у = х1/2 в точке х = 10, если выбраны узлы интерполяции
х„=4, х, =12, х2 =15.
▼ Вычислим максимальное значение третьей производной в узлах интерпо-
ляции. Для этого вначале получим ее аналитическое выражение:
у",(х) = (1/2)х1'2; ,у<2>(х) = -(1/4)х’2/3; у3(х) = (3/8)х‘5'2.
Третья производная на интервале принимает максимальное значение по моду-
лю в точке х0 = 4 .
maxly<3) (х)| = М3’ (4)1 = --Д= = 3 • 2’8.
Максимальная погрешность при интерполяции для точки х = 10 определяется
выражением (3.3.49)
|я2 (х)| < (3 • 2 -’ / 3! )|(10 - 4)(10 -12)(10 -15)| = 0.12. ▲
Обратное интерполирование
Задача обратного интерполирования заключается в том, чтобы по значениям мо-
нотонной функции /(х), заданной таблично, определить соответствующее значение
аргумента х. Эта задача для случая неравноотстоящих значений аргумента решается
110
Глава 3. Численные методы компьютерного моделирования ХТП
непосредственно с помощью интерполяционных формул Лагранжа или соответству-
ющей формулы Ньютона. Если у — независимая переменная, то формулы, выража-
ющие х как функцию у, имеют вид
у (у-У1)(у-Уг)-(у-у,-1)(у-у»1)-(у-у.) .
(У, - У1)(У, - У2)-(У. - У,-1)(У, - У,+1)—Су, - у,)’
(3.3.50)
X = Хо +[у1,уо](у-у[|) + [у2,у1,уо](у-Уо)(у-у1) + ... + [ул, ..^УоКУ-УоМУ-У,,-!) ,
где [ур у0], [ур у„_р..., ур у0] - разделенные разности.
При использовании интерполяционных формул для равноотстоящих значений
аргументов (формула Ньютона) задача обратного интерполирования решается с ис-
пользованием итерационных методов.
Сплайн-интерполяция
Интерполяция на больших отрезках, т.е. с относительно большим количеством
узловых точек, связана с дополнительными трудностями. С одной стороны, при боль-
шом количестве узловых точек и соответственно высоких степенях многочленов точ-
ность очень мала, а, с другой стороны, интерполяционные многочлены высокого
порядка вблизи концов отрезков могут приводить к возрастанию погрешностей, что
существенно искажает поведение функции и нежелательно при решении задачи чис-
ленного дифференцирования.
Отчасти при решении таких задач оказывает помощь кусочная интерполяция более
низкого порядка: интерполяция осуществляется по небольшому количеству узловых
точек отрезка, и затем многочлены объединяют в общую интерполяционную функ-
цию. При этом в точках стыковки обычно терпит разрыв уже первая производная.
Для получения интерполяционных формул с гладкими производными применя-
ют сплайн-интерполяцию, когда интерполирующую функцию между узлами ищут в
виде, чаще всего, многочленов третьей степени 5/х).
В этом случае задача формулируется следующим образом: пусть заданы (п + 1)
узловых точек на замкнутом интервале [а, Ь], т.е. а = х0 <х, <...<х„ =Ь. Интерполируе-
мой функцией является /(х), а интерполирующими функциями на /-ом замкнутом
интервале — кубические многочлены (полиномы) $,(х) (j =0,1,..., п-1), которые прово-
дят через каждые две соседние точки х;, х;+1:
Sj(x) = at +bJ(x~ х.) + сt (x-Xj)2 + </;(х-х;)3, / = 0,1,..., л-1.
(3.3.51)
Сплайн формируется из вышеприведенных кубических многочленов (3.3.51).
Таким образом, сплайн представляет собой следующую совокупность кусочно-
кубических многочленов (полиномов) (3.3.51), значения которых на концах каждого
/-го интервала [х;, х;+1] совпадают с функциями/(х):
5(х) =
5Дх), х0<х<х,;
5/х), х,<х<х2;
S„Jx), хп_}<х<х„.
При этом для них должны также выполняться следующие условия:
(1) Sj(x) с различными наборами коэффициентов описывает поведение функции
/(х) на всех замкнутых подынтервалах [х;,х;+1] для всех j = 0,1,..., п-1;
(2) S(xJ) = f(xJ') = aJ, j = 0,1, ...,л;
(3) SJ+1(x;+1) = S/x;+1), у = 0,1,...,л-2;
3.3. Интерполяция и аппроксимация функций
111
(4) S;+1(xJ+1) = 5/x;rt), 7 = 0,1,..., л-2;
(5) S^,(x7+1) = S,'(x,tl), j = 0,1,...,п-2.
Последние условия, относящиеся к
равенству производных, позволяют ре-
ализовать переход от сплайн-функции,
описывающей функцию на отрезке
[xr ^+1], к сплайн-функции на соседнем
отрезке [х;+1, xJ+2].
Кроме этого должны выполняться
еще два граничных условия:
S’(xo) = O и S'(x,) = 0, (,)
либо
S(x0) = /(x0) И 5 (х„) = /(х„). («)
Рис. 3.16. Графическая иллюстрация процедуры
кубической сплайн-интерполяции
Кривизна сплайна S(x) при указанных условиях является минимальной — свой-
ство, которое приближенно реализуется упругой линейкой (от англ, spline), закреп-
ленной в узлах интерполяции (рис. 3.16).
Так как используемый полином (3.3.51) включает на каждом отрезке четыре оп-
ределяемых коэффициента (a^b^c^d^, они должны находиться из четырех приве-
денных условий (2), (3), (4), (5).
Условие (2) в соответствии с функцией (3.3.51) имеет вид:
SJ(xJ) = aJ =/(х/), 7 = 0,1,...,и. (3.3.52)
Условие (3) с учетом функции (3.3.51) может быть записано:
а;+1 = 5 J+1 (х;+1) = SJ(xJtl) = а, + 6, (xJ+1 -xI) + Cj(xj+i - х; )2 + dj(xJ+I -х;)2, j = 0,1,..., п- 2. (3.3.53)
Если обозначить:
/1;=хуИ-х;, 7 = 0,1,...,п-1
и принять (3.3.52), что а„ = f(x„), то уравнение (3.3.53) принимает вид:
а/+1 = а: + b/hJ + erf + drf ( j = 0,1,..., n-1). (3.3.54)
Аналогичным образом можно определить
b„=sXx„)
и представить 5/х) следующим образом:
5;(х) = bj + 2с)(х-Xj) + 3d^х-х7)2. (3.3.55)
Принимая, что SJ(xJ) = bl для j = 0, 1, ..., л — 1 и с учетом условия (4), а также
предыдущего обозначения для Л, в этом случае будет справедливо:
bJtt = bj + 2с rf + 3drf ( 7 = 0,1,.. .,»-!) (3.3.56)
В соответствии с условием (5) для второй производной можно записать
Sj(x) = 2сt + bdj (х - Xj) (3.3.57)
и, определяя
с 2 ’ (3.3.58)
в этом случае будет справедливо:
С;+1 =с1+ 3d)hj. (3.3.59)
112
Глава 3. Численные методы компьютерного моделирования ХТП
Выражая из последнего соотношения dt и подставляя его в формулы для ау+1
(3.3.54) и />;+1 (3.3.56) можно записать:
+су«) (3.3.60)
и
*7+1 = bt + ht(С1 + с;+1) (у = 0,1,...,п-1). (3.3.61)
Из уравнения (3.3.60) можно выразить bt:
1 Л,
b, =~h'(ajt'~a,}~'3'(2c,+Cj^ (3.3.62)
и по аналогии — b t:
1 h.,
= Ч + <•,). (3.3.63)
Подставляя полученные выражения в уравнения (3.3.51), получаем следующую
систему (п — 1) линейных уравнений:
3 3
+ 2<h,_, + h, )с, + h,c„ = —(а7+1-а,)-—(а,- а,.,), j = i ; „ _t (3.3.64)
с (п — 1) неизвестными элементами вектора с =[с„...,с,_1]т.
Поэтому система (л — 1) линейных уравнений (3.3.64) дополняется еще двумя
уравнениями, вытекающими из граничных условий (<) и (и) для нахождения с0 и <?„
(в частности, из условий (г) следует, что <?0 = <?„== 0). В этом случае эта система
(3.3.64) становится определенной и легко решаемой относительно коэффициентов
с/; = 1,...,п-1).
Исходя из полученных значений определяются и остальные коэффици-
енты кубических многочленов (3.3.51): сначала по формуле (3.3.62) с учётом усло-
вия (2), потом dJ по формуле (3.3.59).
Таким образом, при сплайн-интерполяции (см. рис. 3.16) путем решения систе-
мы уравнений (3.3.64) относительно с„ и расчетам по формулам (3.3.62) и
(3.3.59), получаются конкретные значения коэффициентов для п кубических мно-
гочленов S0(x), 5,(х).(3.3.51), с применением которых на соответствующих
подынтервалах [*;,х;+1] (у = 0,-1) могут вычисляться значения интерполируе-
мой функции f(x) .
3.3.2. Аппроксимация
Пусть имеется совокупность (л + 1) пар величин
у,,х,, i = 0,1,.... п.
Требуется построить зависимость f(x,a0,ax,...,am), являющуюся функцией одной
независимой переменной х и параметров а0,at,a2,...,am и близкую к заданной сово-
купности значений в смысле минимума квадратичного критерия R(a0,at,...,am):
R(a0, at,..., а„) = '£(f(xl, а0, а,.а„)-у,)2. (3.3.65)
у=О
3.3. Интерполяция и аппроксимация функций
113
Аппроксимирующая функция Дх, а0, а,, ат) наиболее часто ищется в классе
полиномов и в общем случае имеет вид
f(x, а0, at,.... ат) = a0 + atx + a2x2 +...+ ayxJ +... + amx" . (3.3.66)
Задача состоит в выборе такой совокупности параметров а„, а„..., а„, при которых
значение критерия R является минимальным.
В задачах аппроксимации всегда п > т. В случае п = т решается задача интерполя-
ции, в которой значение критерия R равно нулю.
При этом различают два метода решения задачи аппроксимации — прямой и
косвенный. В случае прямого метода для определения коэффициентов а0,ах,...,а„
используется один из методов многомерной оптимизации (см. разд. 3.6): сканирова-
ния, симплексный, случайного поиска, градиентный и др., и находится наименьшее
значение квадратичного критерия R и соответствующие ему оптимальные величины
параметров, например, многочлена (3.3.66) — a0,at,...,am.
Задача аппроксимации может быть представлена как задача оптимизации с огра-
ничениями 1-го рода [см. главу 1 — (1.10)]:
min R(a), (3.3.67)
—min —max '
a <a<a
т.е. определяются такие значения параметров d из области их допустимых значений
а”“], которые обеспечат наименьшее значение критерия R при реализации одно-
го из перечисленных алгоритмов оптимизации для поиска наименьшего значения R.
Прямой метод применяется, в основном, для нелинейных по коэффициентам а
функций Дх,а). Однако возможная многоэкстремальность целевой функции R, ее
часто овражный характер и, как следствие, большое число шагов поиска при опти-
мизации приводит к тому, что этот метод является весьма трудоемким.
Косвенный метод используется для линейных по коэффициентам функций /(%, а),
как в случае (3.3.66), когда искомые коэффициенты а определяются из необходимо-
го условия экстремума функции многих переменных Л = Л(а0,а1,...,а„) (3.3.65).
Необходимым условием минимума критерия (3.3.65) является равенство нулю
всех частных производных функции R по параметрам а0,а,,...,ап, т.е.
dRIda, =0, J = 0,1,..., т . (3.3.68)
Решая полученную систему (т + 1) уравнений одним из известных методов реше-
ния систем конечных уравнений (чаще всего линейных), можно найти вектор неиз-
вестных параметров а (а0, а,, ,а„).
Линейное приближение по методу наименьших квадратов
Пусть искомая функция Дх, а) является линейной относительно х. В этом случае
задача сводится к отысканию двух параметров о0 и а, в зависимости
/(х, а) = а0 + а,х . (3.3.69)
Критерий (3.3.65) примет вид
R = '^<~Д*., и0, а,Д у,)2 . 1=0 (3.3.70)
Условия минимума этого критерия таковы: ^ = 0; ^ = 0. Эа0 Эа, (3.3.71)
114
Глава 3. Численные методы компьютерного моделирования ХТП
Система уравнений (3.3.71), получаемых дифференцированием выражения (3.3.70),
имеет вид
2£(Ц) + “\Х, - у,) = 0; 2£(ц, + а,х, - у,)х, = 0 (3.3.72)
<=0 1=0
или, после преобразований,
(п + Оао + а^х, =Хх: aj^x, + а^х~ = '£х1у,, (3.3.73)
1-0 1=0 1=0
(п + 1)£х,у, -£х,£у,
------------=?. (3.3.74)
(„ + 1)Х^2-d>)2
i-b ?-0
Пример. Требуется определить зависимость растворимости хлорида бария ВаС12
в воде (у) в присутствии хлорида кальция (х) при 343 К по следующим экспе-
риментальным данным (г — номер опыта):
откуда
1 0 1 2 3
•*СаС1г % 0 5 10 20
УваСЦ % 32 25 17 5
▼ Зависимость растворимости хлорида бария в воде от хлорида кальция най-
дем в виде полинома первой степени:
у(х, а) = а0 + аре.
Экспериментальные данные и результаты расчета представим в табл. 3.13.
Таблица 3.13. Данные для решения задачи аппроксимации для конкретной задачи
1 X, У, х,У, 2 Xi
0 0 32 0 0
1 5 25 125 25
2 10 17 170 100
3 20 5 100 400
S 35 79 295 525
Используя полученные в таблице значения, определяем:
О] = (4 395- 35 79)/(4 • 525 - 352) =-1 37; ц, = (79 - (-1.37) • 35)/4 = 31.45 .
Тогда искомая линейная зависимость будет
у = 31 45-1 37х. ▲
Полиномиальное приближение функций
В тех случаях, когда линейное приближение оказывается неудовлетворительным,
т.е. дает значительное отклонение расчетной зависимости от аппроксимируемой,
используется приближение полиномами второй степени и выше (т > 2) вида:
т
f(x,a) = '^a1xl ,
(3.3.75)
3.3. Интерполяция и аппроксимация функций
115
Рассмотрим вывод матричной формулы для определения коэффициентов много-
члена второй степени (т = 2).
Определение параметров а0,а„ а2 по методу наименьших квадратов сводится к
нахождению минимума критерия (3.3.70) как функции трех переменных а0,апа2:
R = £[/(х,, а) —у,]2 = У(а„ + а,х, +а2х2-у,)2 (3.3.76) <=0 1=0
Необходимые условия минимума этого квадратичного критерия имеют вид:
= 2Х (“о + а|Х, + а2х2 - у,) = 0; ^0 г=О ~ = 2У («o + «jX, + а2х,2-у,)х, =0- (3.3.77) da, 1=0 ' 7^- = 2£(ао +«1Х, +а2х2-у,)х2 =0 da2 ZS
или
1п + 1)а0 + (^1х,')а2 + (^х2)а2=^1у, ;
1=0 /=0 1=0
(Xx,)ao + (X^2)ai + (Xx’)a2 = ^y,x, ;
»=0 1=0 i—0 »=0
(3.3.78)
(Xх,2 )а0 + (£ х,3 )«, + х* )а2 = У у,х2 .
Линейная относительно искомых параметров а0,а1,а2 система уравнений (3.3.77)
может быть записана в матричной форме:
Аа =Ь
где
(3.3.79)
п
^У,
/=0
п
Ь,х,
:-0
(3.3.80)
Для удобства выполнения матричных операций введем матрицу Ф размера (п +1) х 3,
элементы которой определяются через значения независимых переменных
х,, i = 0,l,..., п, следующим образом:
(3.3.81)
1 х х2
L -*Я -*Л _
Тогда нетрудно проверить справедливость равенств (3.3.80):
-1Г 1 *0 *0
г 1 X, X?
(3.3.82)
116
Глава 3. Численные методы компьютерного моделирования ХТП
(3.3.83)
Знание элементов матрицы Ф (3.3.81) позволяет легко вычислить матрицу коэф-
фициентов А и столбец свободных членов Ь в системе линейных уравнений, в резуль-
тате чего неоднородное СЛАУ в развернутом виде записывается так:
фТфа = фТу. (3.3.84)
Для решения системы уравнений (3.3.84) с учетом равенств (3.3.82) и (3.3.83)
можно использовать рассмотренные ранее методы решения СЛАУ (см. разд. 3.2),
например метод обратной матрицы:
а = А b 115111 а = (ф Ф)-1Ф у (3.3.85)
Соотношения (3.3.75)—(3.3.85), полученные для аппроксимации полиномом вто-
рой степени, можно использовать и при аппроксимации полиномами высших по-
рядков. В этом случае размер матрицы Ф будет равен (n + l)x(m + l), где т — порядок
полинома, (п + 1) — число опытов:
Размеры и элементы матрицы А и вектора b определятся по соотношениям
(3.3.82)—(3.3.83).
В результате можно перечислить основные шаги общего алгоритма решения за-
дачи аппроксимации для линейных по коэффициентам функций /(х, а):
• ввод массивов данных (х,, у,), i = 0,1,.., п;
• формирование матрицы Ф;
• транспонирование матрицы Ф;
• определение произведения транспонированной матрицы на исходную и
= =т=
получение квадратной симметричной матрицы а = Ф Ф;
=-1 =т —
• определение обратной матрицы А =(Ф Ф)~';
=т _
• определение произведения матрицы Ф на вектор данных у и получение
вектора ь=Ф у;
• решение неоднородного СЛАУ Аа = Ь и определение вектора коэффициентов
а = [а0,а,,...,аДт.
3.3. Интерполяция и аппроксимация функций
117
Пример. Построить аппроксимирующий полином второй степени по методу
наименьших квадратов. Значения аргументов и функций приведены в табл. 3.14.
Таблица 3.14. Исходные данные для решения задачи аппроксимации полино-
мом второй степени
i 0 1 2 3
X 1 1 2 3 4
У, 2 2 4 5
▼ Для аппроксимирующей зависимости вида у = а0 + а1х + а2хг и по данным
таблицы строим матрицу Ф размера 4x3:
Вычисляем элементы Ф и вектора Ь:
А = ФТФ = 1 2 3
1 4 9
4 10 30
10 30 100
30 100 300
13
38
126
Решением системы уравнений
4а0 + 10а, + 30а2 = 13;
10ао + 30а, + 100а2 = 38;
ЗОао + 100а, + 300а2 = 126
будут значения параметров
0.4
1.2
-0.02
Тогда аппроксимирующее уравнение, описывающее данную совокупность то-
чек наилучшим образом, будет иметь вид:
у = 0.4+1.2х-0.02х’ • Л
Определение обусловленности задачи аппроксимации функций многочленом
(полиномом) произвольной степени с помощью матрицы Гильберта
Как было показано выше, задача аппроксимации функции с использованием
многочлена произвольной степени сводится к решению неоднородной СЛАУ (3.3.79).
Поэтому надежность получаемых коэффициентов зависит от достоверности реше-
ния СЛАУ и, соответственно, обусловленности задачи ее решения, которая опреде-
ляется формулами (3.2.41) и (3.2.44).
118
Глава 3. Численные методы компьютерного моделирования ХТП
Показатели абсолютной (3.2.41) и относительной (3.2.44) обусловленности задачи
решения СЛАУ, по-существу, позволяют оценить влияние на результаты решения
малых изменений (возмущений) элементов матрицы коэффициентов А и вектора
свободных членов ь. Если влияние всевозможных возмущений (незначительных
изменений) на результаты решения невелико, то задача аппроксимации хорошо обус-
ловлена и показатели абсолютной (3.2.41) и относительной (3.2.44) обусловленности
СЛАУ характеризуются «небольшой» величиной. В противном случае, когда абсо-
лютная (3.2.41) и относительная (3.2.44) обусловленность СЛАУ является относи-
тельно «большой» величиной, то задача аппроксимации плохо обусловлена.
Следует отметить, что при решении задачи аппроксимации элементы матрицы А
и свободного члена СЛАУ Ь определяется из набора данных, которые, чаще всего,
являются экспериментальными. Известно, что опытные данные, как правило, под-
вержены всевозможным возмущениям и измеряются с различной точностью, т.е.
являются источником возмущений. Для получения надежного решения задачи апп-
роксимации (соответственно, СЛАУ), т.е. нахождения достоверных а (это могут быть
константы физико-химических моделей реальных процессов), необходимо миними-
зировать влияние возмущений, в частности экспериментальных измерений, на по-
лучаемые результаты, т.е. решать хорошо обусловленные задачи.
Оценим обусловленность задачи аппроксимации с использованием многочлена
произвольной степени.
Для аппроксимирующего многочлена произвольной степени т (3.3.75) квадрат-
ная симметричная матрица а с учётом (3.3.86) и (3.3.82) при решении задачи апп-
роксимации имеет вид:
(3.3.87)
„ + 1 t*. - tx!
i=0 1=0
а = Xх- - Xх"
(ж+1><(т+1) »=0 i=0 1=0
элемент которой aJS определяется по формуле:
а,, = £х,'х’ =Х*/+' , j, s =0, 1, ... , т.
|=о 1=0
(3.3.88)
Нормы матрицы || А || (3.3.87) и ее обратной матрицы || А ' || определяют величи-
ны абсолютной (3.2.41) и относительной (3.2.44) обусловленности СЛАУ (3.3.79) и,
соответственно, задачи аппроксимации.
Покажем, что эта матрица А может быть сведена к квадратной матрице Гильберта
Н, приведенные выше нормы которой с возрастанием ее размера (порядка) резко
возрастают. Соответственно с увеличением степени аппроксимирующего многочле-
на наблюдается также резкое возрастание чисел абсолютной и относительной обус-
ловленности (3.2.41) и (3.2.44).
Для этой цели преобразуем матрицу А (3.3.87) в матрицу А , нумерация строк и
столбцов которой будет начинаться с 1 (в отличие от А, где нумерации начинаются
3.3. Интерполяция и аппроксимация функций
119
с 0), т.е. элементы матрицы А определяются:
< =Ё<1-2, у, s = 1, ..., m + 1. (3.3.89)
г=О 1=0
Умножая и деля каждое слагаемое полученной суммы (3.3.89) на Дх, (принимая
допущение: h = Дх = л*! = ... = Дх„) и, переходя к определенному интегралу с предела-
ми от 0 до 1, получаем элемент матрицы Гильберта — HJa, умноженный на 1//г.
• 5? W-2 АТ. 1 Г ,+,-2 j 1 1 ,+,-1 ' 1 1 1 „
aj.=Zx' Т-STJ* Л = Т~Т—(х j,s =0,1,...,т + 1. (3.3.90)
ZZ Ах, Л о h j + s-1 0 h j + s-1 h v '
В общем случае квадратная и симметричная матрица Гильберта порядка дхд
имеет вид:
н = 1/1 1/2 1/2 1/3 - 1/Р - 1/(P + 1) (3.3.91)
У/р 1/(р + 1) • 1/(2р-1)
Таким образом, для оценки обусловленности задачи аппроксимации многочле-
ном произвольной степени может использоваться матрица Гильберта НР*Р (3.3.91),
умноженная на 1/h (3.3.90), вместо матрицы А (3.3.87) или А (3.3.89), при этом ее
порядок определяется по формуле р = т + 1. Как уже указывалось, число относитель-
ной обусловленности матрицы НР резко возрастает с ростом ее порядка. Так, уже
== =-1
при р = 8 cond(Hs)>10'° и обратная матрица Ни , полученная на компьютере с точно-
стью представления чисел порядка 10-8, может не содержать ни одного верного знака.
Поэтому к решению задачи аппроксимации функций многочленами (полиномами)
высоких степеней (выше пятой степени) следует подходить очень внимательно из-за
возможно плохой ее обусловленности.
Аппроксимация многочленами Чебышева
При построении аппроксимирующей зависимости в классе многочленов увели-
чение степени полинома требует выполнения всех вычислительных операций (3.3.76)—
(3.3.85) сначала, но уже с новой (увеличенной) матрицей А . Этого можно избежать,
если матрица А будет диагональной, что возможно при условии ортогонализации
матрицы Ф . Для этой цели необходимо решать задачу аппроксимации в классе орто-
гональных функций.
Две функции называются ортогональными, если они удовлетворяют условию:
£/,(х,)-/2(х,) = 0. (3.3.92)
»=0
Тогда решение системы (3.3.79) относительно определяемых параметров а0, а,,..., а„
находится по формуле:
а;=ЁЛи.)У./ElAU,)]2. y = 0,l,...,m. (3.3.93)
1=0 1=0
120
Глава 3. Численные методы компьютерного моделирования ХТП
В этом случае матрица Ф (3.3.86), с размерностью (n+l)x(m + l), имеет вид:
/О(*о) /lUo) Л(*о) Л,(*о)
= = Л(*1) А<*1) ••• ЛСч)
./о(-Ч) f№ fi(x,) fm(x„)_
В качестве ортогональных функций наиболее часто используются полиномы Че-
бышева, которые относятся к классу ортогональных многочленов и для которых вы-
полняется условие ортогональности:
£РДх,)Р/х,) = 0 (k,j = O,l, -,т). (3.3.94)
Аппроксимирующая зависимость, использующая многочлены Чебышева, ищется
в виде:
/(х,^,^,.. ,а„) = ^а;Р/х), (3.3.95)
J=°
где
(3.3.96)
|=о 1=0
Общий вид многочлена Чебышева у-го порядка представляется в виде:
Р/х) = х’ + k^x^ + k^x(J-2y +...+ к™. (3.3.97)
Тогда
Р0(х) = 1;
p1(x) = x+t1<1’;
Р2(х) = х2 + к™х + к<2},
причем эти полиномы удовлетворяют рекуррентному соотношению, которое позволяет
по двум предыдущим полиномам Рю(х) и Рт_х(х) строить новый многочленР„+1(х):
Л,+1 W = U + Р„+1)Л. W + (3.3.98)
Коэффициенты р и у выбираются таким образом, чтобы для всех трех многочле-
нов Рт(х), P„_t(x) и Р„+1(х) выполнялись условия ортогональности (3.3.94):
X^,tiU,)/’„-1U,) = XU,+pm+1)Pm(x,)Pml(x,) + £ym+1P„_1(x,)Pm_,(x,) = O. (3.3.99)
i=0 1=0 1=0
Учитывая, что р„+1£Р„(х,)Рт.,(х,) = 0 (3.3.94), получаем выражение для уя+1:
1=0
y„+i = ~Yx.pjx,)pm . (з.з.юо)
1=0 1=0
Из соотношения:
Ёл.+1(*,)Л,и,) = Та*. +Pm+i)[^U,)]2 + =0
1=0 1=0 1=0
с учетом у„+1£р„(х,)Р„.1(х,) = 0 (3.3.94) определяем величину:
Р„., =-X^,[Fm(x,)]2 /£[Р„(х,)]2.
(3.3.101)
3.3. Интерполяция и аппроксимация функций
121
Значение коэффициента kJ'1 (3.3.97) определяется из условия ортогональности
многочленов Ра(х) и /’(х):
£ро(х,)Р,(х,) = 0, т.е. =
r=0 i=0 i=O 1=0
откуда
1 п
(3.3.102)
п + 1,,0
С помощью формул (3.3.97)—(3.3.101) можно получить выражение для многочле-
на второго порядка Р2(х), которое, в свою очередь, используется для вычисления
многочлена третьего порядка Р3 (х) и т.д.
Пример. Построить аппроксимирующую зависимость первого и второго поряд-
ков с использованием многочленов Чебышева для зависимости степени диссо-
циации а йодистого водорода от температуры Т, если известны следующие эк-
спериментальные данные:
т, к 553 573 633 673 733
а 0.178 0.182 0.196 0.207 0.228
▼ Для удобства вычислений сделаем следующую замену переменных для Ти
для а:
Х = (Т-533)/2О-, у = 1000(а —0 178).
Полученные значения х и у, а также промежуточные расчеты будем записы-
вать в табл. 3.15.
Согласно формуле (3.3.95), аппроксимирующую зависимость многочленов
первой степени найдем в виде:
f(x,a0,al) = a0P0(x) + alPl(x),
где р0(х) = 1, P1(x) = x-kJ”. Вычислим значение коэффициента kJ11 по формуле
(3.3.102) и найдем Р^х):
1 и
= ; ^’-т=“5’ РМ=*~5.
5 <=о Ь
Таблица 3.15. Данные для решения задачи аппроксимации с использованием
многочленов Чебышева
i х, У, [ВД]! УЛ y,pSx)
0 1 0 -4.0 16.0 0 0
1 2 4 -3.0 9.0 4 -12.0
2 5 18 0 0 18 0
3 7 29 2 4 29 58
4 10 50 5.0 25 50 250
S 54 101 296
122
Глава 3. Численные методы компьютерного моделирования ХТП
Продолжение табл. 3.15
i х,[Л(х,)]2 W [ВДР у№)
0 -4.0 16 8.31 69.06 0
1 -6.0 18 12.52 157 50.1
2 0 0 -10.6 114 -191
3 14 28 -8.4 70.5 -243.5
4 50 250 10.2 102 510
S 54 312 512.6 125.6
Коэффициенты а0 и а, определим по формуле (3.3.96):
а0 = ^ = 20,2; а, = ^ = 5,49
5 '54
Найдем аппроксимирующую зависимость многочленом первой степени:
у = а0Р0(х) + atPt(x) = 20.2 + 5.49(х-5.0) = 5.49х-7.2 .
Аппроксимирующую зависимость второй степени будем искать согласно соот-
ношению (3.3.95) в виде
У = а0Р0 (х) + aj\ (х) + а2 Р2 (х),
где Р2(х) = (х + р,)/’1(х) + у2Р0(х). Коэффициенты у2 и р, рассчитываем по форму-
лам (3.3.100), (3.3.101), принимая Pm=Pt и Рт_, = Р0:
у2 = -54/5 = -10,8; Р2 = -312/54 = - 5,79.
Тогда
Р2 = (х - 5.79) (х - 5.0) - 10.8) -1 = х2 - 10.79х +18.1.
Коэффициент а2 рассчитываем по формуле (3.3.96), полагая Р, = Р2:
а2 =125.6/512.6 = 0,244.
В результате получаем следующую аппроксимирующую зависимость (много-
член второй степени):
у = 5.49х-7.2 + 0.244(х2 -10.79х+18.1) = 0.244х2 + 2.87х+ 2.79. А
Замечания о выборе аппроксимирующей зависимости
Если имеется набор значений аппроксимируемой зависимости в (п + 1)-й точке, то
порядок аппроксимирующего полинома всегда должен быть меньше числа этих точек.
Чем меньше значение т, тем проще эмпирическая зависимость, однако при малых т
ошибка аппроксимации может быть существенной. Чрезмерное завышение т приводит
к неоправданному увеличению вычислительных операций. В качестве рекомендаций по
выбору аппроксимирующей зависимости можно использовать одно из свойств таблицы
разделенных разностей (см. табл. 3.9). Рекомендуется брать такое значение степени ап-
проксимирующего полинома, которое равно порядку тех разделенных разностей, значе-
ния которых мало отличаются между собой в разных точках. Другими словами, линей-
ная эмпирическая формула оказывается пригодной лишь в тех случаях, когда первые
разделенные разности мало отличаются друг от друга. В тех случаях, когда имеется таб-
лица конечных разностей с постоянным шагом (см. табл. 3.7 и 3.8), аналогичный вывод
можно сделать и по этой таблице, не вычисляя разделенных разностей.
3.4. Приближенное дифференцирование и интегрирование
123
Так, если конечные разности первого порядка изменяются от 0.97 до 7, тогда как
разности второго порядка колеблются в сравнительно небольших пределах (табл. 3.16),
то пригодна квадратичная аппроксимация.
Таблица 3.16. Таблица конечных разностей для конкретной задачи
X У А у д2 У д3 У А4 у
0 0.03
0.97
1 1.0 2.01
2.98 0.04
2 3.98 2.05 -0.12
5.03 -0.08
3 9.01 1.97
7.00
4 16.01
В заключение следует отметить, что методы аппроксимации для описания зави-
симостей переменных, как правило, являются более предпочтительными, чем мето-
ды интерполяции. Интерполяция обычно применяется при ограниченном наборе
исходных данных, которые необходимо описать. В некоторых случаях рассмотрен-
ные в этой главе методы интерполяции и аппроксимации многочленами (полинома-
ми) являются явно недостаточными, и приходится выбирать другие типы интерпо-
лирующих и аппроксимирующих функций.
3.4. Приближенное дифференцирование
и интегрирование
Под задачами численного дифференцирования и численного интегрирования
понимают приближенное вычисление значений производных различных порядков
ь
fk(x) (где к — порядок производной) и значения определенного интеграла jf(x)dx
при условии, что функция /(х), от которой берется производная и которая при ин-
тегрировании является подынтегральной, задана конечной последовательностью пар
значений [х,,/(х,)]. Этот случай часто встречается на практике, когда аналитическое
взятие производных и точное вычисление интегралов не представляется возможным.
В результате приходится ограничиваться приближенными (численными) методами,
которые позволяют решать задачи численного дифференцирования и интегрирова-
ния с приемлемой точностью.
124
Глава 3. Численные методы компьютерного моделирования ХТП
3.4.1. Численное дифференцирование
Задача численного дифференцирования возникает в тех случаях, когда диффе-
ренцируемая функция /(х) имеет сложное аналитическое выражение для непосред-
ственного определения производных или же задана таблично. В этих случаях вместо
функции /(х) используют соответствующую интерполирующую зависимость. Если
интерполирующая зависимость с достаточной степенью точности совпадает с задан-
ной функцией, то считают, что производные от этих зависимостей отличаются не-
значительно.
Приведем формулы численного дифференцирования при использовании интерполи-
рующей зависимости в виде интерполяционного полинома Ньютона с равностоящи-
ми узлами. Пусть для функции у = /(х) на отрезке [a, Z>] в равноотстоящих точках
заданы значения у, = /(х,). Заменив функцию у = f(x) на отрезке [а, Ь] интерполяци-
онным полиномом Ньютона, выраженным через конечные разности (3.3.43),
у - у.(3.4.1)
где 9 = —= х,+1--г, ('= 0,1,2,; можно показать, что формула вычисления произ-
водной k-го порядка имеет вид:
^-г = -т^-г- (3.4.2)
dxk hk dq
В частности, для первой (%) и второй (% ) производной при подстановке (3.4.1)
в (3.4.2) имеем:
, 1 Г. 2<у — 1 2 3q2-6q+2 3
Уо = т ЛУо + Д Уо + ——73 Л Уо + - ,
Л 2 о
(3.4.3)
, 1 Г» 2 / .. .э 6<?2 - 18о + 11 .4
Уо =р- Д Уо + (9-1)Д Уо+-^2 -дУо + - •
Изложенную методику можно использовать для вычисления производных функ-
ции у ~ f (х) любого порядка при условии, что степень интерполирующего полинома
будет достаточно высокой. Приведенные формулы численного дифференцирования
используют лишь односторонние значения функции при х > х0. Относительно боль-
шую точность имеют симметрические или центральные формулы дифференцирова-
ния, учитывающие значения данной функции у = /(х) как при х > х0, так и при х < х0,
которые здесь не рассматриваются.
Оценка погрешности формул численного дифференцирования определяется по
формуле:
г(х) = /'(х)-Л(х) = 7?’(х),
где R(x) = f(x) - Р(х), т.е. погрешность производной интерполяционного полинома рав-
на производной от погрешности этого полинома.
Следует отметить, что приближенное дифференцирование представляет собой
операцию менее точную, чем приближенное интерполирование. Поэтому при чис-
ленном дифференцировании необходимо выбирать расстояние между узлами интер-
поляции достаточно малым, чтобы функция между ними, по возможности, не имела
экстремумов. В противном случае может оказаться, что разность между значениями
функции и интерполяционного многочлена мала, а значения производных значи-
тельно отличаются друг от друга.
3.4. Приближенное дифференцирование и интегрирование
125
Пример. Методом численного дифференцирования найти первые две производ-
ные в точке х = 1 функции у = /(х), заданной таблицей:
X 1 2 3 4
У, 11 28 57 104
▼ Составим таблицу конечных разностей:
i X У, дт, дД, д3У,
0 1 И
17
1 2 28 12
29 6
2 3 57 18
47
3 4 104
Шаг этой таблицы Л = 1, a q = 0. Используя формулы (3.4.3), определяем значе-
ния первой и второй производных:
X = т[дл -|д2л + |д3хД у'о =17-^ 12+ | 6 = 13;
ЛI 2 о J хи
Уо = l?^y° “ЛЗК); = 12~6 =6 ж
Понятие о графическом дифференцировании
Задача графического дифференцирова-
ния состоит в построении по заданному
графику функции у —f(x) графика ее про-
изводной У = fix').
Для построения графика производной в
натуральном масштабе поступают следую-
щим образом. На оси аргумента выбирают
точку М с координатами (—1, 0). Из этой
точки веерообразно проводятся прямые,
параллельные касательным к функции
v =Дх) в заданных точках 1, 2, 3, 4, 5. На
рис. 3.17 точки пересечения этих прямых с
осью Оу обозначены соответственно, Г, 2’,
3', 4’, 5'. Точки графика производной нахо-
дятся как точки пересечения горизонталей,
проведенных к точкам Г, 2', 3', 4', 5'и вер-
Рис. 3 17. Иллюстрация графического
дифференцирования функции у — f(x)
I икалей, проведенных через точки 1, 2, 3, 4, 5; соединяя их, получаем график у = f’(x)
т.е. ординаты точек 1", 2", 3", 4", 5".
3.4.2. Численное интегрирование
В основе способов вычисления интегралов численными методами лежит пред-
ставление определенного интеграла как некоторой суммы:
I =\f<~x)dx = ^_lI, = £ J/(x)<Zx, (3.4.4)
« ,=1 '1
126
Глава 3. Численные методы компьютерного моделирования ХТП
где [х,_1;х,]- п замкнутых интервалов, на которые разбивается отрезок интегрирова-
ния [а, Ь\, причем а = х0 и ь = х„.
В предельном случае, когда maxfx, -х,.,] -»о, формула (3.4.4) преобразуется в соот-
ношение для расчета определенных интегралов:
/= (3.4.5)
тах(х,-х|_1)—'
где — некоторая точка в замкнутом интервале [х,ч,х,].
Задача приближенного интегрирования по формуле (3.4.4) практически сводится
к эффективному разбиению отрезка [а, Ь\ на соответствующие интервалы [х.^.х,] и
правильному описанию вида подынтегральной функции /(х).
Наиболее удобным оказывается разбиение интервала [а, 6] на интервалы [х,_,,х,]
одинаковой длины h, которую принято называть шагом интегрирования:
, Ь-а , ,
h =---, х, = а + in, 1 = 1, ,п .
п
Подынтегральная функция /(х) на интервале описывается интерполяционным
многочленом степени т:
/(x) = Pm(x) + R(x),
где Л(х) — функция ошибок интерполяции.
Тогда интеграл на интервале [х,_1;х,] определяется по формуле
I, = JPm(x)dx+ JR(x)dx = I, + S, (i = 1,.. ,n),
1 *.4
Рис. 3 18 Графическое представление
интеграла I,
(3.4.6)
где 7, — вычисляемое приближенное зна-
чение интеграла на интервале длиной h;
S, — величина ошибки интегрирования
(остаточного члена) на этом интервале.
Графически интеграл I, представляет
собой площадь криволинейной трапеции
(рис. 3.18). Интеграл (3.4.4) на отрезке [а, Ь]
также равен площади криволинейной тра-
пеции, полученной путем суммирования
всех интегралов /, на этом отрезке.
При подстановке равенства (3.4.6) в
(3.4.4) получаются обобщенные (состав-
ные) формулы для приближенного вычис-
ления определенного интеграла на отрез-
ке [а, £>]:
Z=X/,=Sj^(x№,
(3-4.7)
/ = 1 !
(3.4.8)
где 1 = 7 + 5; I — вычисляемое значение интеграла; S — величина ошибки (остаточ-
ного члена). Для снижения ошибки S необходимо стремиться к более точному опи-
санию вида подынтегральной функции.
3.4. Приближенное дифференцирование и интегрирование
127
В простейших случаях для интерполяции подынтегральной функции на интер-
вале [х,.,,*,] используются многочлены:
Р0(х) = а0
/’1(х) = а0+а1х
Рг (х) = а0 + а(х + а2х
(метод прямоугольников);
(метод трапеций);
(метод парабол)
(3.4.9)
(3.4.10)
(3.4.11)
В действительности, вид подынтегральной функции обычно значительно слож-
нее, и приведенные простые функции могут удовлетворительно применяться только
на небольших интервалах [х, „х,]. Отсюда следует, что для достижения требуемой
точности надо задаваться как можно меньшим шагом интегрирования. Однако это
может привести к существенному увеличению вычислительных затрат, что также
нежелательно.
Можно рекомендовать следующую стратегию приближенного вычисления интег-
рала Г. В начале задаются сравнительно большим шагом интегрирования. Далее его
последовательно дробят до тех пор, пока различие между двумя последующими значе-
ниями интегралов 1, рассчитанными при различном шаге, не станет незначительным.
Метод прямоугольников
Подынтегральная функция/(х) на интервале [х1Ч,х,] интерполируется многочле-
ном нулевой степени. Для определения единственного коэффициента а,, может ис-
пользоваться любое значение функции на этом интервале. Чаще всего применяют
три значения функции: в начале интервала, в середине и в конце (рис. 3.19), т.е.Дх)
принимается равной одной из следующих констант Р0(х) = const'.
Ро(х) = /(х1Ч),
Ро(х) = /(х,),
Д>(х) -'2 'j
В соответствии с этим получаются три формулы метода прямоугольников:
7, =/(х,.1)й; (3.4.12)
Л = Дх,)Л;
Л = /((х,-1 +х,)/2) h.
(3.4.13)
(3.4.14)
Название метода объясняется тем, что величины в правой части последних соотно-
шений равны площадям прямоугольников со сторонами h и Дх,.,) — см. рис. 3.19, а,
h и /(х,) — см. рис. 3.19, ба h и —J — см- Рис- в'
Из рис. 3.19 видно, что величина ошибки S, представляет собой площадь криво-
линейного треугольника и в каждом конкретном случае зависит от вида подынтег-
ральной функции и шага интегрирования.
128
Глава 3. Численные методы компьютерного моделирования ХТП
Рис 3 19 Графическая иллюстрация метода прямоугольников для вычисления определен-
ных интегралов по формулам а — (3 4 15), б - (3 4 16), в — (3 4 17)
Для всего отрезка интегрирования [a, Z>] расчетные формулы метода прямоуголь-
ников в соответствии с (3.4.7) и (3.4.12)-(3.4.14) имеют такой вид:
/=1/(х,_,)Л;
«=1
7 = £/(х,)й;
1=1
7 = £/((х,ч+х,)/2)й.
• (3.4.15)
(3.4.16)
(3.4.17)
Пример. Вычислить приближенно методом прямоугольников интеграл
j(3x2-4x)<&, если Л = 02.
о
▼ По формуле h = (b-a)/n находим п = (1-0)/02 = 5. Если воспользоваться тре-
тьей формулой метода прямоугольников, то подынтегральная функция рассчи-
тывается в следующих точках:
1-1 1 Х,-1 + х, 2 / Д-i —5 1 1 2 )
0 1 0.1 -0 37
1 2 0.3 -0.93
2 3 0.5 -1 25
3 4 07 -1.33
4 5 0.9 -1.17
Ответ: 7 = о.2(—5.05) = -1 01, / = -101. А
Метод трапеций
В этом случае для интерполяции подынтегральной функции используется много-
член первой степени (3.4.10). При этом необходимо знать значение функции /(х) в
двух точках: в начале интервала — /(х,.,) и в конце интервала — /(х,).
3.4. Приближенное дифференцирование и интегрирование
129
Для построения интерполяционного многочлена
используется полином Лагранжа при т = 1 (3.3.21).
Р,(х) = /(х,.,)-------- + /(х,)
Тогда, согласно (3.4.6), получаем:
I, = J ^(х)<£с =
1
= f(x, д J -^—^—dx + /(х,) ) ^^dx =
? х<_1 ~x, J x, ~x,_l
Рис 3 20 Графическая иллюст-
рация метода трапеций для
вычисления определенных
интегралов
(3.4.18)
= ) + /(x,)) = ^ (/(x,_,) + f(x,))
— формулу трапеции, поскольку значение интеграла 7,
(3.4.18) приближенно полагается равным площади
трапеции с высотой h и основаниями /(х,.,) и /(х,) — рис 3.20.
Для приближенного определения интеграла Т во всем интервале интегрирования
используется формула (3.4.7).
= h |/(x0)+£/(x,) + |/(x,) .
£ |«1 £
(3.4.19)
Пример. Вычислить приближенное значение интеграла / = J(3x2-4x)4x по фор-
0
муле трапеций при h = 0 1.
_ ТТ 1-0 .г. Л. ,
▼ Находим п = -^—= 10, и функция /(х) = 3х -4х в различных точках деления
отрезка [а, 6] принимает следующие значения:
1 х, Дх) 1 X Дх)
0 0 0 6 06 -1 32
1 0 1 -0 37 7 07 -1 33
2 02 -0 68 8 08 -1 28
3 0 3 -0 93 9 09 -1 17
4 04 -1 12 10 1 0 -1 0
5 05 -1 25
По формуле трапеции (3.4.19) получаем.
1 =0 1[1/2(0-1)-9 45] = -0 995, / = -0995- А
Метод парабол. Формула Симпсона
Подынтегральная функция на интервале [х,ч,х,] заменяется интерполяционным
многочленом второй степени (3.4.11), совпадающим с /(х) в трех узлах — на концах
( х.-1 + х,
и в середине —-— интервала:
9-4544
130
Глава 3. Численные методы компьютерного моделирования ХТП
х1=~7;—L = xo+/l; х2=х, = х0 + 2й, (3.4.20)
где й =(х,-х,_1)/2 = й/2 ИЛИ (3.4.4) й =(й-а)/(2п).
С учетом принятых обозначений подынтегральная функция /(х) может описы-
ваться многочленом Лагранжа:
Р2М =
(х —х,)(х —х2)
(х0-Х1)(х0-х2)
Л*о) +
(х х0)(х х2)
(х,-х0)(х,-х2)
Тогда получается формула для приближенного вычисления интеграла (рис. 3.21):
2й
(х-х0)(х-х,) _
x0+2h
2Й
-h
/(х,)
й2
2Й
-2h
й
3
2
3
p-[|A7(2o)+^7(x.)+|*7(x2)]=
Рис. 3.21. Графическая иллюстра-
ция метода парабол для вычисле-
ния определённых интегралов
= ||/(хо) + 4№) + /(х2)], (3.4.21)
которая называется формулой Симпсона.
С учетом (3.4.20) формула Симпсона прини-
мает вид
I, = J/’2(x№ = -^(x,_1) + 4^-^-^J+/(x,)j. (3.4.22)
Аналогичный результат получится, если через
три точки /(х.-ДДх,, +х,/2) и /(х.) (см. рис. 3.21)
на отрезке [х, ,,х,] провести параболу и опреде-
лить площадь под ней. Так как для описания па-
раболы используем выражение р,(х) = Ах2 + Вх + С,
причем коэффициенты А, В я С считаются извест-
ными величинами, то вместо (3.4.21) получается
формула
х' ( 3 — 3 1 ( 2 — X2 1
f (Ах2 + Вх + C)dx = А ——+ В Х‘----------------------— + С(х, - х j) =
j 3 2
Х‘ Х,‘ [2А(х2 + х,х,_, + х.2.,) + 3Д(х, +х,_,) + бс]=Х' Х"‘[Ах,2 + Вх, +С +
6 6
+ + Ях,., + С + А(х( + 2х(х(1 + Х7_|) + 2Z?(x( + x(_j) + 4С] —
(3.4.23)
/(v.l + V +/U)
3.4. Приближенное дифференцирование и интегрирование
131
Отсюда этот метод называется также и методом парабол.
Если принять во внимание, что согласно (3.4.20) число интервалов разбиения в
этом случае уже равно 2и, а длина каждого из них h = h/2, то формулу (3.4.21) можно
представить в виде
Xj+1 h
j P2(x)dx = + 4f(x,) + /(x?+1)] (3.4.24)
Тогда формула для приближенного вычисления определенного интеграла (3.4.7)
примет вид
7 = Jp2(x)dx+...+ |p2(x)dx (3.4.25)
или, с учетом (3.4.24)
/ = (h/3)[/(х0) + 4/(х,) + 2/(х2) + 4/(х3) + 2/(х4) + ...+ 2/(х2„.2)+ 4/(х2„_,)+ /(х2я)]. (3.4.26)
После соответствующей перегруппировки членов с учетом формулы для шага ин-
тегрирования (3.4.20) получается формула Симпсона для приближенного вычисле-
ния определенного интеграла на отрезке:
I = f f(x)dx = {f(xa) + 4[/(х,) + /(х3) +... + f (x2fl_l)] +
6п (3.4.27)
+ 2[/(х2) + /(х4) + ...+ /(х2„.2)] + /(х2„)}.
Пример. Вычислить приближенно по формуле Симпсона значение определенно-
С ах
го интеграла I з/—- при h = 0.3
▼ В соответствии с формулой (3.4.20):
h = й/2 = 0.15; п = (й-а)/й = (1.2-0)/0.30 = 4,
подынтегральная функция Дх) = 1/Vx+l вычисляется в следующих точках:
i X Лх) i х, Лх,)
0 0 1 5 0.75 0.830
1 0.15 0.954 6 0.90 0.807
2 0.30 0.917 7 1.05 0.787
3 0.45 0.883 8 1.2 0.769
4 0.60 0.855
По формуле (3.4.27) имеем:
I = 0.05[1 + 4(0.954 + 0.883+0.830 + 0.787) + 2(0.917 + 0.855 + 0.807) + 0.769] = 1.037; 7=1.037. ▲
Квадратурная формула Ньютона-Котеса
Эта формула является обобщением рассмотренных методов, когда подынтеграль-
ная функция на отрезке [х,_,,х,] описывается многочленом Лагранжа Р„(х) (3.3.21)
произвольной степени т:
= (3-4.28)
А=0 ;=0 % к %]
132
Глава 3. Численные методы компьютерного моделирования ХТП
где х0 = хм и х„ = х,. При этом принимается, что узлы интерполяции располагаются
на одинаковом расстоянии друг от друга и тогда по аналогии с (3.4.20) будут справед-
ливы равенства
а для всех узлов — равенство
xt=x0+hk, к = 0,1,..., т.
Если теперь перейти к непрерывной переменной t, определяемой с помощью
соотношения
x = x0+ht, t = 0 + m;
то зависимость (3.4.28) можно переписать так:
о < \ *о +ht— x0—hj ~ у. A-1- j
р~ W = 111 т—№) = 2Л1—f<X,)
4=0 J=Q хо + пк — XQ — hj к=0 j-О к J
или с учетом переменной t вместо х, т.е. dx = hdt\
7 т т t — 1 —
(3.4.29)
О 4=0 j=0 К J
После перегруппировки членов в последнем равенстве получается квадратурная
формула Ньютона— Котеса:
(3.4.30)
4=0
где хк — узлы квадратурной формулы (узлы интерполяции); <uk — веса квадратурной
формулы, определенные согласно (3.4.29) по формуле
=й|П-^-^-А. (3.4.31)
Обычно более удобным оказывается применение последней формулы в преобра-
зованном виде:
-x.-jf (r-0)(r-l)...[r-(4-l)][r-(4 + l)]...(r-m)
---- -------------------------------------------dt
т {(k- 0)(k -1)...[k -{k-1)][Л - (k +1)]...(k - m)
. /По - dt =
mk'. iyj [(4 +1) - k]...(m - k)
V — v ”1 m
(3.4.32)
mk'.(m -k)!J0 ,=*«
С помощью квадратурной формулы Ньютона—Котеса (3.4.30), где определяет-
ся по (3.4.31), можно получить выведенные выше формулы метода прямоугольников
(3.4.15)—(3.4.17) при т = 0, метода трапеции (3.4.19) при т = 1, метода парабол (3.4.22)
при т = 2.
Для приближенного вычисления интеграла 7 на всем отрезке [a, Z>] следует вос-
пользоваться формулой (3.4.7):
i=l 4=0
Следует отметить, что погрешность приведённой (обобщённой) составной формулы
(3.4.8) на порядок ниже, чем погрешности S: на каждом частичном интервале (3.4.6).
3.5. Решение систем дифференциальных уравнений
133
3.4.3. Понятие о приближенном вычислении
несобственных интегралов
Несобственными называются интегралы, у которых
один или оба предела интегрирования бесконечны:
+~ ь ъ
j f (x)dx = Inn j f (x)dx, j f (x)dx = hm j f (x)dx.
a a /»—>+« «
Если пределы в правых частях равенств существуют,
to интегралы называются сходящимися, в противном
случае — расходящимися.
Геометрически (рис. 3.22) для неотрицательной по-
дынтегральной функции несобственный интеграл
f f(x)dx представляет собой площадь криволинейной Рис- 3-22- Графическое
„ представление несобственного
1рапеции, ограниченной графиком подынтегральной интеграла
функции, осью абсцисс и прямой х = а.
В основе приближенного вычисления несобственных интегралов лежит их пред-
ставление в виде:
J/(x)dx= jf(x)dx + jf(x)dx + ]f(x)dx. (3.4.33)
При этом в случае сходящихся интегралов решение задачи заключается в следующем:
а) нахождение пределов интегрирования [а, Ь], при которых значения первого и
I рстьего интегралов несущественны;
б) приближенный расчет второго интеграла в найденных пределах [а, Ь] любым
и < рассмотренных выше методов.
Практически алгоритм определения несобственного интеграла включает итера-
ционную процедуру расчетов. Сначала задаются одни пределы интегрирования и
вычисляется значение среднего интеграла (3.4.33), затем более широкие пределы [a, Z>]
и снова рассчитывается его значение. Так происходит до тех пор, пока два последо-
вательных значения интеграла j f(x)dx при различных пределах [a, не будут несу-
щественно отличаться друг от друга.
Необходимо отметить, что практические расчеты при компьютерном модели-
ровании ХТП часто сопровождаются расчетами производных и интегралов, аналити-
ческое вычисление которых не представляется возможным. Поэтому на первый план
выходят представленные в этой главе приближенные методы, которые находят ши-
рокое применение.
3.5. Решение систем дифференциальных
уравнений
Различают системы обыкновенных дифференциальных уравнений (СОДУ) и системы диф-
ференциальных уравнений в частных производных (СДУЧП). Основное отличие между ними
состоит в том, что обыкновенные дифференциальные уравнения включают производные
от одной независимой переменной, так называемые обыкновенные производные, а диф-
134
Глава 3. Численные методы компьютерного моделирования ХТП
ференциальные уравнения в частных производных — частные производные функций с
несколькими независимыми переменными (как минимум с двумя). Соответственно, в
результате решения получаются функции с одной независимой переменной — для обыкновен-
ных дифференциальных уравнений и функции с нескольких независимыми переменными —
для дифференциальных уравнений в частных производных.
К обыкновенным дифференциальным уравнениям относятся уравнения, включаю-
щие производные различных порядков и функции только от одной независимой
переменной. Функция, которая при подстановке в дифференциальное уравнение
превращает его тождество при всех возможных значениях независимой перемен-
ной, и представляет собой решение обыкновенного дифференциального уравнения.
Таких функций (решений), как правило, бесчисленное множество, т.н. общее решение
дифференциального уравнения. Для определения одной из функций решения, которая
имеет практическое значение, необходимо задать дополнительные условия — на-
чальные (решается задача Коши) и краевые (решается краевая задача). В результате
при решении может быть получено требуемое частное решение обыкновенного диффе-
ренциального уравнения — одна функция для одного уравнения или конечное число
функций для системы уравнений.
Для обыкновенных дифференциальных уравнений характерно, что как одна функ-
ция решения для одного обыкновенного дифференциального уравнения, так и конеч-
ное число функций для СОДУ зависят только от одной независимой переменной. По-
этому производные функций, включаемые в решаемое или решаемые дифференциаль-
ные уравнения, являются обыкновенными производными, а не частными производны-
ми функций. Этим СОДУ принципиально отличаются от СДУЧП, которые содержат
частные производные от функций с несколькими независимыми переменными.
3.5.1. Обыкновенные дифференциальные уравнения
Постановка задачи Коши и краевой задачи
Обыкновенным дифференциальным уравнением я-го порядка называется выра-
жение
у, у, у", (3-5.1)
устанавливающее взаимосвязь между одной независимой переменной х, неизвест-
ной (искомой) функцией у и ее производными у’, у".у'"-”.
Решением дифференциального уравнения является некоторая функция у(х), которая
при подстановке в уравнение обращает его в тождество. Существует множество ре-
шений (частных решений) дифференциального уравнения (3.5.1), которые могут быть
объединены и записаны в виде общего решения:
у = у(х,С1,С2,...,С„), (3.5.2).
где С„С2, -, С„ — произвольные постоянные.
Для выделения одного частного решения уравнения (3.5.1) необходимо задать п усло-
вий, которые единственным образом определяли бы постоянные С1,С2,...,СП. Если эти
условия заданы в одной точке х0 и представляют собой совокупность значений искомой
функции у(х) и всех ее производных до (п -1 )-го порядка включительно в этой точке:
yUo) = у 0;
у'(х0) = у';
(3.5.3)
У("’1>(х0) = у<"-”,
3.5. Решение систем дифференциальных уравнений
135
то задача интегрирования дифференциального уравнения (3.5.1) называется задачей
Коши, а условия (3.5.3) называются начальными условиями.
Дифференциальное уравнение и-го порядка (3.5.1) может быть представлено как
система дифференциальных уравнений первого порядка:
у'= уДх);
y; = y2W;
у'п-2 = Ул-iU);
Л-1= У’ у№
(3.5.4)
При этом начальные условия по аналогии с (3.5.3) могут быть записаны:
у(х0)= у0;
У1'(л0) = у';
(3.5.5)
У("-1>(х0) = уГ1>
Для решения СОДУ первого порядка используются методы, которые являются обоб-
щением методов решения одного дифференциального уравнения первого порядка.
Дифференциальное уравнение первого порядка [(3.5.1) при п = 1] имеет вид:
dyldx = f(x,y(x)). (3.5.6)
Геометрически его можно интерпретировать как задание семейства кривых у(х)
(рис. 3.23) через их производные, при этом каждая кривая является решением (3.5.6).
Это семейство кривых и характеризуется общим решением:
у = у{х,С). (3.5.7)
Для выбора одной кривой из семейства (частного решения — у = у(х, с), где с —
одно из конкретных значений С) необходимо задать начальное условие:
у(х0) = у0, (3.5.8)
I .с. одну точку на искомой кривой решения (см. рис. 3.23). Как правило, практическое
шачение имеет всегда частное решение дифференциального уравнения.
Приближенные методы интегрирования обыкновенных дифференциальных урав-
нений позволяют решить задачу Коши и найти некоторую функцию у(х), близкую к
искомой функции у(х) — истинному решению.
В случае решения краевой задачи дополнительные условия (краевые условия) типа
(3.5.3) или (3.5.5) задаются как минимум при двух и, возможно, большем числе значений
независимой переменной, например, х0 и х„.
Поэтому для получения частных реше-
ний обыкновенных дифференциальных
уравнений при заданных двух краевых
условиях необходимо решать как мини-
мум систему двух дифференциальных
уравнений первого порядка:
dyjdx = fi{x УМ, У2(х));
dyjdx = /, (х, у,(х), у2(х))
с краевыми условиями
У1(Хо) = Л<»;
У2(х„) = У2(„>.
*о х
Рис. 3.23. Геометрическая интерпретация
решений задачи Коши
(3-5.9)
(3.5.10)
136 ГлаваЗ. Численные методы компьютерного моделирования ХТП
I
Рис. 3.24. Геометрическая интерпретация краевой задачи
Геометрическая интерпретация получаемых частных решений краевой задачи пред-
ставлена на рис. 3.24 (сравните с частным решением задачи Коши - см. рис. 3.23).
Следует отметить, что решение краевой задачи на компьютере представляет со-
бой более сложную процедуру, чем решение задачи Коши и, как правило, включает
дополнительный цикл (циклы) решения, которые обеспечивают выполнение всех
краевых условий.
Основные характерные особенности численного (приближенного) решения обык-
новенных дифференциальных уравнений на компьютерах состоят в следующем:
• всегда определяются частные решения уравнений путем решения задачи Коши
или краевой задачи;
• при решении дифференциальных уравнений высоких порядков их можно све-
сти к системам дифференциальных уравнений первого порядка;
• в процессе пошагового решения обычно происходит накопление погрешнос-
тей, т.е. процедура решения в отличие от итерационных методов решения ко-
нечных уравнений не является самоисправляющейся (см. разд. 3.2).
Явные и неявные методы численного решения
Большинство методов решения основано на том, что замкнутый интервал [х0, хп]
для независимой переменной х, на котором определяется искомая функция решения
у =у(х) для дифференциального уравнения первого порядка dy/dx =fix, у) разбива-
ется на п равных частей (отрезков). На каждом отрезке, длина которого равна
h = (хП —х0)1п (h — шаг решения: шаг сетки), а концы отрезков являются узлами
сетки, по формуле одного из численных методов рассчитываются приближенные
значения искомой функции у =у(х). При этом первый шаг решения в соответствии
с методологией решения задачи Коши выполняется с учетом данных (3.5.8) о на-
чальных условиях в точке х0 и в результате решения получаются приближенные зна-
чения функции у( в точке xt — (х,, у) (/ = 1, ..., п). Значения искомой функции на
последующих шагах решения (вплоть до их значений в последней точке хп, ул) опре-
деляются из приближенных результатов, которые были получены на каждом преды-
дущем шаге. В результате с увеличением числа шагов могут накапливаться погреш-
ности, что весьма нежелательно.
Описанная процедура решения относится к явным методам решения обыкновен-
ных дифференциальных уравнений. Метод называется явным, если приближенные
зависимости для определения решения (значений искомых функций) на каждом шаге
могут быть записаны непосредственно в виде расчетных формул для вычисления
значений функций у( в узлах сетки (z = 1, ..., и), где п — количество узлов сетки.
Метод называется неявным, когда для приближенного определения значений искомой
функции в узлах сетки необходимо решать систему линейных или нелинейных уравнений.
Проиллюстрируем явные и неявные методы на примере использования извест-
ного алгоритма Эйлера для решения задачи Коши в общем случае для нелинейного
обыкновенного дифференциального уравнения первого порядка:
3.5. Решение систем дифференциальных уравнений
137
^ = /(х,у(х)), (3.5.11)
с начальным условием
у(х0)=у0. (3.5.12)
Явный метод Эйлера
В явном методе Эйлера первая производная для дифференциального уравнения
(3.5.11) представляется в виде конечной разности (см. разд. 3.3.1), а её правая часть f
находится для (*,.,. y,_i):
V1" " = У' ~Л‘ = h=bx„ i = 1,..., л, (3.5.13)
dx Дх, h ’ ’ ’ ’ ' ’
причем по аналогии с (3.5.12):
у, i = y(x,,), < = 1,...,л. (3.5.14)
Отсюда формула явного метода Эйлера для решения обыкновенного дифферен-
циального уравнения первого порядка имеет вид:
у, = у,_[ + Л/(Х,_1,у,_1), 1 = 1,...,и. (3.5.15)
Отметим, что на первом шаге определяется приближенное значение у, по форму-
ле (3.5.15) с использованием начальных условий (3.5.12). При каждом из п шагов
решения вычисляется правая часть дифференциального уравнения (3.5.13) f(x,_„
исходя из данных х,_, и приближения решения у,.!.
Неявный метод Эйлера
В неявном методе Эйлера первая производная для дифференциального уравне-
ния (3.5.11) также представляется в виде конечной разности, однако правая часть f
находится для (х,, у,):
Отсюда уравнение для определения приближений искомой функции в узлах сет-
ки неявным методом Эйлера принимает вид:
2L“-/(x,,y,) = 0, , = i.п. (3.5.17)
h
Так как в общем случае правая часть дифференциального уравнения может быть
нелинейной функцией независимых переменных х; и искомых значений прибли-
женных функций у то для определения значения последней на каждом шаге реше-
ния (i = 1,п), возможно, потребуется использовать один из итерационных методов
решения нелинейного уравнения (см. разд. 3.2.2).
На практике большее распространение получил неявный метод трапеций, кото-
рый представляет собой модификацию неявного метода Эйлера и для которой значе-
ния искомой функции у(/ = 1, ..., и) в узловых точках определяются путем итераци-
онного решения нелинейного уравнения следующего вида:
У' ,У'~‘ -^l7(x,-i,y,-i) + /(x,,y,)]=0 i = l,...,п. (3.5.18)
h 2
Следует отметить, что рассмотренные неявные методы решения одного дифферен-
циального уравнения первого порядка достаточно просто могут быть распространены
для решения систем обыкновенных дифференциальных уравнений. При этом для
138
Глава 3. Численные методы компьютерного моделирования ХТП
определения приближенного решения на каждом шаге — вектора у = у(х,) (г = 1, п)
необходимо итерационным методом решать, как правило, систему нелинейных уравне-
ний.
Несмотря на большую трудоемкость неявные методы численно более устойчивы
и допускают достаточно широкую вариацию величины шага решения, не приводя к
существенному отклонению от точного (аналитического) решения. Будет также по-
казано, что они более пригодны для решения жестких СОДУ.
Модификации явного метода Эйлера
Явный метод Эйлера относится к классу численных, и поэтому функция, пред-
ставляющая собой приближенное решение дифференциального уравнения, получа-
ется в виде таблицы чисел
х0 X,, ..., х,-1, х„ ..., х„;
У о Ур У.-и У<> У,.
(3.5.19)
где х0 и у0 задаются заранее в виде начальных условий (3.5.8). Расчетная формула
выводится из исходного дифференциального уравнения (3.5.6), если производную
заменить ее разностным представлением
Рис. 3.25. Графическая иллюстрация
получаемого решения явного метода Эйлера
Ф' _ АУ, _ У, ~ У,.
dx Дх, h
(3.5.20)
У. =y,-i+W,-i-y.-i)! < = 1,-,и, (3.5.21)
где h — шаг интегрирования. При этом первое
значение функции у1 в точке х, =x0+h рассчи-
тывается с помощью предварительно заданных
начальных условий (3.5.8), а все последующие (у,) —
по предыдущим (у,.,) в соответствии с (3.5.21).
Графической иллюстрацией получаемого
решения является ломаная линия у(х), при-
ближенно описывающая истинное решение
у(х) уравнения (3.4.6) - рис. 3.25 (tga =J{x<), у0) ~
~ (у{~ y0)/h ДЛЯ i = 1).
Пример. Найти приближенное решение дифференциального уравнения у'= у - 2х/ у на
отрезке [0, 1], если начальное условие у(0) = 1, шаг h = 0.2.
▼ Если х0 = 0 и у0 = 1, то
у, = у0+ й/(х0,у0); у =1 + 0.24 = 1,2 И x1=x0+/i; х, = 0 + 0.2 = 0.2; /(х,, у,) = 0.866 .
Дальнейшие расчеты производятся аналогичным образом и представлены в таб-
лице:
/ X У, 2х/у, Дх„ У,) йДх, у,)
0 0 1.0000 0 1.0000 0.2000
1 0.2 1.2000 0.3333 0.8667 0.1733
2 0.4 1.3733 0.5928 0 7805 0.1561
3 0.6 1.5294 0.7846 0.7458 0.1492
4 0.8 1.6786 0.9532 0.7254 0.1451
5 1.0 1.8237
3.5. Решение систем дифференциальных уравнений
139
Ответ:
X 0 0.2 0.4 0.6 0.8 1.0
У 1 1.2 1.3733 1.5294 1.6786 1.8237
Для оценки погрешности метода формула (3.5.21) сравнивается с разложением в
ряд Тейлора в окрестности точки х.^:
у, = у,-1 + йу.ч + У,'1 + у,'1 + - • (3.5.22)
С учетом (3.5.22) формула (3.5.21) согласуется с разложением в ряд Тейлора вплоть до
членов первого порядка (Л) и ошибка метода (5) пропорциональна й2, т.е.
S = Kh\ (3.5.23)
где К — некоторый коэффициент.
Увеличения точности метода Эйлера можно достигнуть уменьшением шага ин-
тегрирования, что, однако, увеличивает объем вычислений.
Различные модификации метода Эйлера (3.5.21) позволяют увеличить его точ-
ность, в результате чего ошибка (5) становится пропорциональной й3.
В соответствии с первой модификацией (рис. 3.26, а) функция у,.,) в формуле (3.5.21)
заменяется функцией f ’ (х,_>+h П, у'_,), т.е. значение этой функции рассчитывается в точке
(x,_t+h/2, у*.,), причем у\ определяется в этой же точке по формуле Эйлера (3.5.21):
у' 1 = у, i+^h/2)f(,x,_„y,.t). (3.5.24)
На рис. 3.26, а представлена геометрическая интерпретация этого метода. Вместо
3^1эйл, получаемого по методу Эйлера на прямой , в этом случае значение у, опре-
деляется на прямой Д, которая согласно приведенным соотношениям параллельна
L2 и пересекает точку начального условия (х0, у0).
Во второй модификации (рис. 3.26, б) функция /(х^.у,^) в формуле (3.5.21) заме-
няется функцией /'(х,.,, у,.,), определяемой следующим образом:
/'(V,, у,ч) = (1/2)[/(х,.„ у,_,) + Ж, у,*)], (3.5.25)
где у' вычисляется по формуле Эйлера:
у’ = y,-i +hf(x,.t, у,.,). (3.5.26)
Рис. 3.26. Геометрическая интерпретация модифицированного метода Эйлера:
первая (а) и вторая (б) модификации (/ = 1)
140
Глава 3. Численные методы компьютерного моделирования ХТП
Так как согласно (3.5.21) и (3.5.25) /(х,_1,у,.1) характеризует средний угол накло-
на прямых и l2 , то первая точка решения у, (см. рис. 3.26, б) будет лежать на
прямой Lt, параллельной L, и выходящей из точки начального условия (х0, у0).
Явный метод Рунге—Кутта
Это тоже численный метод; его применением достигается согласие получаемого
решения с разложением в ряд Тейлора вплоть до четвертого порядка (3.5.22). Расчет-
ная формула метода имеет вид:
У, ~ y,-i +cikl + c2k2 +cjk3 + ('АкА, (3.5.27)
где ct и kt согласно (3.5.21) определяются так:
<?! = !; /с, = Л/(х,_1,у,_1); (3.5.28)
а остальные k2,k},kt ~ по формуле (3.5.29):
k, =hf(x,_, +a,h,y,^ + Ylbllkl) . (3.5.29)
1=1
Неизвестные коэффициенты c2,c,,c,,a2,a,,al,h2l,b,jl,b32TAl-.bt2,bi, определяются
из условия согласия с формулой разложения в ряд Тейлора (3.5.22).
В результате формула Рунге—Кутта (3.5.27) принимает вид:
У, = У,-1 + + 2Л‘“1> + 2к^1> + I = 1, 2, 3,.... п, (3.5.30)
где к{-1)
h к(,'п
kr)=hf(x,_1+^ у,-1 + ^-);
h Г0-1’
kf" =hf(x._t+^, у,_,+—;
к:Г'’ = hf(x,_,+h,yl_l+k^l>).
Из-за предпосылок, положенных в основу вывода этой формулы, ошибка метода
пропорциональна Л5.
Пример. Найти решение уравнения у’=0.25у2 + х2 с начальным условием у(0) = -1
на отрезке [0, 0.5], приняв шаг Л = 0 1.
▼ Уравнение (3.5.30) представляется в виде:
У, = У.-i + дУ,-1, где Ау,-! = - (Ау)!’ + AyS + Дуй + Дуй) •
6
Уравнение решаем с помощью рабочей таблицы, заполнение которой произ-
водим следующим образом:
1) записываем в первой строке х0 = 0, у0 = -1;
2) вычисляем /(х0,у0) = 0.25, тогда к'°’ =0.1 0.25 = 0.025;
3) записываем во второй строке хо + й/2 = 0.05, у0 + *J0) /2 = -0.9875;
4) вычисляем /(х0 + й/2, у0 + к™ / 2) = 0.24629, тогда к^ = 0.024629;
5) записываем в третьей строке х0 + h/2 = 0 05, у0 + к‘°’ /2 = -0.98769;
6) вычисляем (х0 + h/2, у0 + к{0)/2) = 0.24638, тогда к!? = 0.024638;
7) записываем в четвертой строке х0 + h = 0.1; у0 + к^ = -0.97536;
3.5. Решение систем дифференциальных уравнений
141
8) вычисляем f(x„ + h,ya + Л3<0)) = 0.24783, тогда к(°' = 0.024783;
9) заполняем столбец Ду:Ду*” =Л1(0); Ду*2’ = 2А)0); Ду„3) = 2Л3(О); Ду‘4) = к(°>;
10) вычисляем Ду0 =(1/6)-0.148317 = 0.02472;
11) получаем на первом шаге yj = у0 + Ду0 = -0-97528;
12) значения xt = 0.1 и у, = -0.97528 заносим в строку с индексом г — 1 = 1 и продол-
жаем вычисления аналогичным образом.
Результаты вычислений представлены в таблице:
1 -1 X У 0.251/ k = hf(x, i) Ду
0 0 -1 -0.25 0.025 0.025
0.05 -0.98750 -0.24688 0.024629 0.049258
0.05 -0.98769 -0.24692 0.024638 0.049276
0.1 -0.97536 -0.24384 0.024783 0.024783
S 0.02472
1 0.1 -0.97528 -0.24382 0.024779 0.024779
0.15 -0.96289 -0.24072 0.025429 0.050858
0.15 -0.96257 -0.24064 0.025413 0.050826
0.2 -0.94987 -0.23747 0.026557 0.026557
X 0.02550
2 0.2 -0.94978 -0.23745 0.026553 0.026553
0.25 -0.93650 -0.23413 0.028176 0.056352
0.25 -0.93569 -0.23392 0.028138 0.056276
0.3 -0.92164 -0.23041 0.030236 0.030236
X 0.02824
3 0.3 -0.92154 -0.23039 0.030231 0.030231
0.35 -0.90642 -0.22661 0.032790 0.065580
0.35 -0.90514 -0.22629 0.032732 0.065464
0.4 -0.88881 -0.22220 0.035743 0.035749
S 0.03284
4 0.4 -0.88870 -0.22218 0.035745 0.035745
0.45 -0.87083 -0.21771 0.039209 0.078418
0.45 -0.86910 -0.21728 0.039134 0.078268
0.5 -0.84957 -0.21239 0.043070 0.043044
X 0.03925
5 0.5 -0.84945
Ответ: у(0.5) = -0.84945. ▲
Погрешности явных методов решения обыкновенных дифференциальных уравнений
Основным недостатком явных методов является накопление ошибок в процессе реше-
ния. Погрешности, допущенные при определении первоначальных значений у{, уг, у3 в
соответствии с (3.5.21) или (3.5.30), вызывают систематическое нарастание ошибок при
дальнейших вычислениях, причем порядок роста может оказаться довольно большим.
142
Глава 3. Численные методы компьютерного моделирования ХТП
Как было показано, погрешность метода Эйлера пропорциональна й2, модифи-
цированных методов — й3, метода Рунге—Кутта — й5. Однако с оценкой значения
коэффициента пропорциональности (3.5.23) на всём отрезке решения дифференци-
ального уравнения дело обстоит значительно сложнее. Значения этих коэффициен-
тов зависят также от величины шага интегрирования и характера искомой функции.
По аналогии с методами приближенного вычисления интегралов здесь также можно
оценить границы погрешностей. Однако при большом числе шагов фактическая по-
грешность оказывается значительно меньшей, чем дают эти оценки.
Применяя численные методы, целесообразно вычисления проводить так, чтобы
каждый раз можно было сравнивать приближенные значения функции у„ i = 1,..., п,
полученные с различными шагами. Расчет заключается в следующем. Сначала бе-
рется достаточно большой шаг интегрирования и определяется значение функции в
первой точке по формулам (3.5.21) или (3.5.30) — у,0’. Затем шаг h уменьшается
(обычно в 2 раза) и снова находится значение функции в этой же точке у'2’. Эти
итерации повторяются до тех пор, пока будет выполняться неравенство
|у.“+,’-У,“’|>е, (3.5.31)
где с — предварительно заданная точность; к — номер итерации для первой точки.
После этого приведенная процедура реализуется для следующих точек: у2, у3 и т.д. В
результате искомая приближенная функция представляется в табличном виде:
X х0 х2 Х„
У Уо тГ’' (й+1) Уг У^
причем у,'141’ - приближенное значение функции в точке х,, полученное путем (к +1)
итераций. Следует отметить, что для различных точек у<1*'> число итераций (к +1) мо-
жет быть разным.
Графическая иллюстрация возможных ошибок (как указано в разд. 3.1, ошибки в
отличие от погрешностей имеют знаки), которые возникают при решении обыкновен-
ных дифференциальных уравнений явным методом Эйлера, представлена на рис. 3.27.
Предположим, что получено приближённое реше-
Рис. 3.27. Графическая иллюст-
рация ошибок при численном
решении обыкновенных
дифференциальных уравнений
явным методом Эйлера
ние уравнения, например, методом Эйлера, в точке х,
при котором переменная у, соответствующая точному
решению s, имеет значение, представленное на рис. 3.27
точкой а. Мы хотим получить решение на следую-
щем шаге для момента времени х + h, где точное ре-
шение s соответствует точке d. Если использовать яв-
ный метод Эйлера, начиная из точки а, то достигнем
точки е. Ошибка de называется ошибкой метода на
шаге для случая явного метода Эйлера. Для этой ошиб-
ки легко получить оценку путем разложения в ряд
Тейлора переменной у(х + Л). При этом очевидно, что
желательно иметь маленькую ошибку метода на шаге,
но, как будет показано при дальнейшем рассмотре-
нии, этого недостаточно для того, чтобы быть уверен-
ным в том, что явные методы типа Эйлера и Рунге-
Кутта являются удовлетворительными.
Вследствие ошибок метода на шаге и соответству-
ющих ошибок округления, решение в точке х достиг-
нет значения в некоторой точке Ь, а не а. Разность ab
представляет собой остаточную ошибку, на рис. 3.27
3.5. Решение систем дифференциальных уравнений
143
она увеличена для более четкого представления. При использовании любого метода
ошибка ab должна быть мала.
Точное решение системы дифференциальных уравнений, соответствующее точке
b, представлено кривой Ьс. Приближенное решение системы уравнений явным ме-
тодом Эйлера изображено прямой bf. Величина ef представляет ошибку в момент
x + h, получающуюся вследствие наличия ошибки ab в точке х при решении задачи
явным методом Эйлера. Эту величину (ef) называют ошибкой, обусловленной ошибкой
начальных данных на шаге.
Как было указано, при расчетах на компьютерах получаются также ошибки из-за округ-
ления. Вследствие этого при переходе от решения в точке х к решению в точке х + Л
определяемое значение при x + h будет соответствовать не точке f, а точке g. Полная
величина ошибки dg в точке x + h может быть представлена в виде суммы трех слагаемых:
dg = de + ef + fg , (3.5.32)
т.е. полная ошибка равна сумме ошибки метода на шаге (de), ошибки, обусловленной
ошибкой начальных данных на шаге (ef) и ошибки округления (fg). Полная ошибка dg
для следующего шага вычислений является остаточной ошибкой.
По аналогии, для последнего шага решения его полная ошибка является оценкой
погрешности найденного значения приближённой функции в точке х„(3.5.19).
Обусловленность численных методов решения обыкновенных дифференциальных
уравнений
Как было показано при рассмотрении систем конечных уравнений (см. разд. 3.2),
хорошо обусловленный численный метод приводит к несущественному отклонению
получаемых приближенных решений от истинных. С позиций теории погрешностей
(см. разд. 3.1) в этом случае говорят об устойчивости применяемого численного (при-
ближенного) метода. В любом случае исследование устойчивости численных мето-
дов оказывается весьма полезным и позволяет, как будет показано, дать рекоменда-
ции по выбору величины шага при решении дифференциальных уравнений.
Численная устойчивость явного метода Эйлера
Точное решение у‘ (i = 0,1,..., п) обыкновенного дифференциального уравнения пер-
вого порядка (3.5.20) с начальным условием (3.5.8) в Z-м узле сетки независимой перемен-
ной с учетом необходимых требований для разложения в ряд Тейлора имеет вид (3.5.22):
у.н = У.* + Ziy,''+~y,1 = 0,1,..., л-1. (3.5.33)
В качестве приближения точного решения используется формула явного метода
Эйлера (3.5.21):
у,+1 = у, + hf(x,, у,), i = 0,1,..., л-1. (3.5.34)
С учетом общего выражения дифференциального уравнения (3.5.11) для беско-
нечного ряда Тейлора может быть записано:
У,*’= f(x„y’). (3.5.35)
Для определения ошибки численного метода в сравнении с точным решением
(3.5.33) вычитаем из (3.5.34) значение (3.5.35), пренебрегая членами разложения со
второй и более высокого порядка производными и опуская х,:
У.+1 - у,Я ~У. ~у' + Л[/(у,)“/(/)], (3.5.36)
144
Глава 3. Численные методы компьютерного моделирования ХТП
обозначая ошибки:
s.+i = Z+1 - Уж и S, =У, -у' (3.5.37)
и для простоты рассматривая модельное уравнение (3.5.35), устойчивое по Ляпунову
(см. раздел «Обусловленность задачи решения системы обыкновенных дифференци-
альных уравнений. Стационарные точки решения. Устойчивость решений диффе-
ренциальных уравнений по Ляпунову») вида (3.5.66):
у’=—ау (а > 0), (3.5.38)
где а — некоторый постоянный коэффициент, в соответствии с формулами (3.5.34)
и (3.5.33) (с учётом того, что f(x, у) = -ау) будет справедливо:
Уж = У, + Л(-ау,) = (1 - »Wy, J (3.5.39)
с учётом (3.5.33) и (3.5.36):
y.+i - Уж = у, - у,' + Му, - у,’); (3.5.40)
учётом (3.5.37):
Е,+1 = s, -hae, = (l-ha)e,. (3.5.41)
Достаточное условие устойчивости численного метода следующее: ошибка каж-
дого следующего шага решения s,tl меньше или равна ошибки предыдущего шага s,:
|1-/ш|<1. (3.5.42)
Раскрывая это неравенство:
-1 < (1-йа) < 1
и учитывая, что а>0, получаем:
ha<2- (3.5.43)
Таким образом, для определения величины шага в случае модельного уравнения
(3.5.38) можно применять следующую формулу:
h<2/a. . (3.5.44)
Отсюда следует, что при больших значениях коэффициента а величина шага ре-
шения дифференциального уравнения явным методом Эйлера должна быть весьма
незначительной.
Аналогичные выводы справедливы и для других явных методов типа Эйлера и
Рунге—Кутта, что сужает области их широкого применения.
Численная устойчивость неявного метода Эйлера
Формула неявного метода Эйлера для приближения точного решения имеет вид
(3.5.16):
Уж = У, +¥(х,+1,у,+1), 1=0,1,...,Л-1. (3.5.45)
Или для выбранного модельного уравнения (3.5.38):
Уж = У, + Л(—ау,+,)
Если преобразовать последнее уравнение к виду
у,+1(1 + ah') = у, (3.5.46)
и вычесть из него выражение для точного решения (3.5.38) с учётом соотношений
для ошибок (3.5.37), будет справедливо:
еж=гАг (3.5.47)
1 + ha v '
Отсюда вытекает следующее достаточное условие устойчивости неявного метода
Эйлера (3.5.42):
|1 + Ла| > 1.
(3.5.48)
3.5. Решение систем дифференциальных уравнений
145
Так как величина шага решения h>0 и величина коэффициента а>0 (3.5.38),
для выбора величины шага в неявном методе Эйлера для выбранного модельного
уравнения следует использовать неравенство:
ha>o, (3.5.49)
из которого следует, что при любом шаге решения h и для любых положительных
коэффициентов а для модельного уравнения (3.5.38) неявный метод Эйлера будет
численно устойчивым.
Аналогичные выводы будут справедливы и для других неявных методов решения
обыкновенных дифференциальных уравнений.
Поэтому в большинстве случаев, несмотря на трудоёмкость, неявные методы счи-
таются более надёжными, чем явные методы.
Обусловленность задачи решения системы обыкновенных дифференциальных
уравнений. Стационарные точки решения. Устойчивость решений
дифференциальных уравнений по Ляпунову
Рассмотрим систему дифференциальных уравнений первого порядка:
ф- = /,(х, у,(х),..., У„(х)) 1 = 1,..., л (3.5.50)
ах
с начальными условиями
у,(хо) = у,о, < = 1,л.
В результате ее решения могут быть получены функции со стационарными точками
решения, так называемые решения устойчивые в «большом», когда после некоторого
значения независимой переменной х, например xs, величина искомой функции-ре-
шения становится константой, т.е.
у,(х) = const10 (| = 1, ..., л) (3.5.51)
и, соответственно:
^ = 0 п) (3.5.52)
при всех x>xs.
Таким образом, устойчивые решения дифференциальных уравнений (кривая 1 на
рис. 3.28) представляют собой функции, состоящие из двух частей:
• области стационарности (I), в которой они не
меняются и их значения равны соответствую-
щим стационарным точкам решения;
• области нестационарности (II) (так называемые
области «переходного процесса»), в которой зна-
чения функций изменяются с изменением ве-
личины независимой переменной х.
Неустойчивые решения (кривая 2 на рис. 3.28)
не содержат стационарных точек решения и всегда
изменяются с изменением независимой перемен-
ной х.
Очевидно, что больший интерес представляют
устойчивые решения дифференциальных уравнений
(решения, устойчивые «в большом»), которые с из-
менением независимой переменной х достигают
областей стационарности. Эти области соответству-
ют областям нормальной эксплуатации большей ча-
сти химико-технологических процессов в непрерыв-
ных режимах.
Рис. 3.28. Графическое изобра-
жение устойчивых и неустойчи-
вых в «большом» решений
обыкновенных дифференциаль-
ных уравнений
146
Глава 3. Численные методы компьютерного моделирования ХТП
Поэтому анализ обусловленности задачи решения систем дифференциальных урав-
нений (устойчивости «в малом»), в большинстве случаев, выполняется для систем с
устойчивыми «в большом» решениями и в двух областях решений — области стаци-
онарности (чаще всего) и области нестационарности (реже). По-существу, в этом
случае речь идет о влиянии незначительных возмущений (поэтому говорят об устой-
чивости в «малом») на результаты решения задачи. Если результаты решения (иско-
мые функции) изменяются также незначительно, то задача решения обыкновенного
дифференциального уравнения считается хорошо обусловленной, в противном случае —
плохо обусловленной.
Хорошо обусловленные системы называются устойчивыми в смысле Ляпунова. В этом
случае каждое частное решение системы (3.5.4) может быть истолковано как координата
движущейся материальной точки в «-мерном пространстве, зависящая от времени х.
В результате анализируемая СОДУ записывается в виде
^- = Х(х, У1, ..., у„), i = i, ...,п. (3.5.53)
Пусть функции f(i = 1,2,..., п) имеют непрерывные частные производные 1-го по-
рядка. Обозначим через у, = у,(х, х^у,'0',..., у'0’), 1 = 1,..., л решение данной системы с
начальными условиями у,0 при х = х0, т.е.
У,о=У,(^о, Ую. •••, Ум) ('=1> -, ”) (3.5.54)
В результате можно привести строгое определение устойчивости в смысле Ляпу-
нова: движение точки с координатами у, = у,(х, х0, yj0’,.., у'0>) называется устойчивым
в смысле Ляпунова, если для каждого s>0 можно найти такое 5>0, что для всех
|у10 - у,0| < 8 (1 = 1,..., л) в промежутке х„<х<~ будет справедливо неравенство:
|у,(х> Т10, -, Ло)~У,(х, У10- ••• Ло)| < е , 1 = 1,-, л. (3.5.55)
Каждое движение, которое не является устойчивым, называется неустойчивым.
Решение у, = у^х^у!01,...^) называется невозмущенным, а у, = у,(х,х0, у'°\-, у\") ~ воз-
мущенным решением.
Геометрически устойчивость означает, что в каждый момент времени х > х0 точка
траектории возмущенного движения (решения) лежит в достаточно малой окрестно-
сти соответствующей точки невозмущенного движения.
Для вывода условий устойчивости в смысле Ляпунова запишем для возмущенно-
го решения (у) равенство в векторном виде (для простоты выкладок умышленно
опускаем переменные в скобках):
у — у’ + Ду, (3.5.56) ч
где у" — вектор невозмущенного решения, Ду — вектор возмущения решения, физи-
чески обоснованный колебаниями, например, режимных параметров реальных про-
цессов. Тогда для невозмушенного решения будет справедливо:
^ = 7(П, (3.5.57)
dx
а для возмущенного:
^(у-+Ду)=7(_.+ду) (3.5.58)
dx v
Раскладывая правую часть последней системы в ряд Тейлора и ограничиваясь
членами с первыми производными, можно записать:
J, df
f(y +Ду) = f,(y ) + £^-(у W, / = (3.5.59)
3.5. Решение систем дифференциальных уравнений
147
или в виде матриц:
7,(Г + ду)‘ /„(у’ + Ду). 1—— ——1 *>. PS 4^1 4^1 fO | г© го' | г© *>> <'£?|г©'‘ Ду/ Ьу,_ + Л(у*)' Л (у*). , (3.5.60)
или в векторно-матричной форме: Лу" +Ду) = А(у*)Ду+ /(у’) (3.5.61)
где А(у*) — матрица частных производных с элементами:
Э/,
ач ~ ду (У \ i = l,...,п, j = l,...,n. (3.5.62)
Если невозмущенные значения функций неизвестны, то приходится рассчиты-
вать производные при их возмущенных значениях.
Подставляя линеаризованную правую часть (3.5.61) в (3.5.58) с учетом (3.5.57) вводим:
^ + ^) = Л(Г)Ду + /(Г) (3.5.63)
dx dx
и, как результат, получаем однородное дифференциальное уравнение, решаемое от-
носительно Ду, следующего вида:
= (3.5.64)
(зависимость элементов матрицы А от у* (3.5.62) для простоты выкладок опущена).
Условием устойчивости в смысле Ляпунова является стремление всех элементов
вектора Ду к нулю, т.е. с использованием понятия нормы вектора должно быть спра-
ведливо:
||Ау|| —(3.5.65)
Система (3.5.64) имеет аналитическое решение. Однако, прежде чем его привести
рассмотрим аналогию: вместо вектора Ду рассмотрим Ду, а вместо матрицы А — число X:
= (3.5.66)
Общее решение (3.5.64) имеет вид:
Ду = Се'‘ , (3.5.67)
где С — произвольная постоянная, а X — некоторое число.
Из последнего равенства следует, что для того чтобы уравнение было устойчивым
в смысле Ляпунова, вещественная часть X, т.е. Re(X), должна быть меньше 0:
Re(X)<0. (3.5.68)
Решение системы уравнений (3.5.64), по аналогии с (3.5.67), может быть записано:
Ду = Се‘х, (3.5.69)
и для обеспечения устойчивости в смысле Ляпунова для всех X,,..., Х„ по аналогии с
(3.5.68) необходимо выполнение условий:
Re(X,)<0, (3.5.70)
т.е. вещественные части всех X, (/ = 1,..., л) должны быть меньше нуля.
148 Глава 3. Численные методы компьютерного моделирования ХТП
Для определения значений X подставим выражение для решения (3.5.69) в исход-
ное дифференциальное уравнение (3.5.64):
лсХ = ЗсХ, (3.5.71)
в результате чего получается однородная система линейных алгебраических уравне-
ний (см. разд. 3.2.1):
(я-ХГ)с=б. (3.5.72)
Ее решениями являются собственные векторы матрицы А — векторы С, число
которых не ограничено.
Для получения бесчисленного множества нетривиальных решений С необходи-
мо выполнение условия, в соответствии с которым определитель матрицы (a-XZ-J
должен быть равен нулю (3.2.19):
|а-ХЁ| = О. (3.5.73)
Это условие рассматривается как уравнение для определения X,,..., Х„ и называет-
ся характеристическим уравнением матрицы А, а определяемые конкретные величи-
ны (элементы вектора X) называется собственными значениями или собственными
числами матрицы А.
Следует отметить, что левая часть характеристического уравнения представляет
собой многочлен (полином) степени п (3.2.20). Определение всех его корней, среди
которых могут быть кратные и комплексные корни, часто непростая задача.
Поэтому был предложен критерий Рауса—Гурвица, который путем анализа коэф-
фициентов упоминаемого многочлена позволяет установить, будут ли все веществен-
ные части собственных чисел X, (i = l, ...,п) отрицательными.
Для использования критерия Рауса—Гурвица характеристическое уравнение пред-
ставляется в следующем виде:
/>„Х" + Ъ„_у' +... + Ь.Х + = 0, (3.5.74)
где Ьо >0 и условия отрицательной действительной части всех его корней (устойчи-
вости в смысле Ляпунова) будут выполняться тогда и только тогда, когда станут
положительными все определители вида:
Ь, Ьг 0 0 ... о
ь, ьг ь, о ... о
61П-1 62„_2 Ь2п-3 62„_4 ... Ьп
(3.5.75)
Определение условий устойчивости в смысле Ляпунова для двух обыкновенных
дифференциальных уравнений
Запишем выведенную выше систему (3.5.64) дифференциальных уравнений для
возмущений (Ду„Ду2):
3.5. Решение систем дифференциальных уравнений
149
4(Ду,)
°и °а
dx
dx
°21 “аЛЛ'г
(3.5.76)
и в соответствии с (3.5.69) будем искать решения в виде:
Подстановка этих решений в исходные уравнения приводит к следующим соот-
ношениям:
XC,e'J =а11С1е“ + а12С2Сх;
ХС2е^ = a21C,eu + а22С2е\
(3.5.78)
в результате чего получается однородная система линейных алгебраических уравнений:
(а., -Х)С, + а,,С, = 0;
Г П (3.5.79)
а21С, + (а22 -Х)С2 =0, v ’
которая может быть записана в матричном виде:
а„-Х а12
0
0
(3.5.80)
Для получения нетривиальных решений этой системы — собственных векторов мат-
рицы А необходимо, чтобы определитель матрицы ее коэффициентов был равен нулю:
ан —X а12
аи а22~^
= 0.
(3.5.81)
Полученное уравнение называется характеристическим уравнением и решается
относительно неизвестных X, и Х2, в результате чего устанавливается отрицатель-
ность или не отрицательность действительных частей корней X, и х2, т.е. определя-
ется выполнение условия устойчивости СОДУ в смысле Ляпунова (3.5.70).
Получим выражение для определителя (3.5.81):
(я,! Х)(а22 X) я12я21 — 0
(3.5.82)
и запишем характеристическое уравнение (3.5.82) в виде квадратного уравнения
X2 +[-(а„ + а22)]Х + апа22 -а12а21 =0.
(3.5.83)
С учетом принятых обозначений р и q решение квадратного уравнения можно
представить в виде:
=-р + з/р2-9; ^2=-р~^р2-q
(3.5.84)
С учетом принятых обозначений р и q и сравнивая с (3.5.83), для полученных
решений будет справедливо:
(Х-Х,)(Х-Х2) = Х2 +[-(Х, +Х2)]Х + Х,Х2 = 0.
(3.5.85)
Условие отрицательности вещественных частей корней X, и х2 может быть уста-
новлена путем сравнения уравнений (3.5.83) и (3.5.85).
150
Глава 3. Численные методы компьютерного моделирования ХТП
Рассмотрим три случая:
1) если q<0 и р<0, то X, и х2 являются вещественными числами и имеют раз-
ные знаки;
2) если q> о и р <0, то X, и х2 являются или вещественными положительными чис-
лами, или комплексными числами с положительными вещественными частями;
3) если q>o и р>0, то X, и х2 являются или вещественными отрицательными
числами, или комплексными числами с отрицательными вещественными час-
тями (что соответствует условию устойчивости в смысле Ляпунова).
Таким образом, как следует из уравнения (3.5.83) для двух обыкновенных диф-
ференциальных уравнений, система будет устойчива в смысле Ляпунова, если для ее
коэффициентов будут выполняться два неравенства:
0^11 + ^22 ) >
“ п (3.5.86)
flllfl22 fl12fl21 > 0-
Отметим, что коэффициенты в этих неравенствах для произвольных правых час-
тей дифференциальных уравнений (3.5.76) определяются как частные производные
(3.5.60) по искомым функциям (у, и у2), и их величины зависят от значений функ-
ций-решений, при которых производные рассчитывались.
Можно легко проверить, что полученные условия устойчивости в смысле Ляпу-
нова для двух обыкновенных дифференциальных уравнений полностью соответству-
ют условиям Рауса—Гурвица (3.5.75).
Жесткие системы обыкновенных дифференциальных уравнений
Сущность явления жесткости для систем дифференциальных уравнений состоит
в том, что существуют решения (искомые функции), которые меняются медленно и
которые нужно определять", однако одновременно существуют и очень быстро меняю-
щие (затухающие) решения (функции). Наличие последних затрудняет получение мед-
ленно меняющихся решений численными методами.
Сильно меняющиеся компоненты решения называются жесткой компонентой
решения и их считают переходной частью решения. Медленно меняющиеся компонен-
ты часто называются непереходными или гладкими. Термин «гладкие» используется в
том смысле, что производные от этих компонент решения значительно меньше про-
изводных от переходных компонент решения.
Свойство жесткости является свойством системы дифференциальных уравнений
и для неоднородных линейных систем вида:
^ = Ау(х) + г(х) (3.5.87)
ах
может быть установлено путем анализа собственных значений матрицы ее коэффи-
циентов А.
Задачу можно назвать жесткой, если среди собственных значений матрицы А:
• существуют X,, для которых Re(X,)« 0;
• существуют X, умеренной величины, чьи абсолютные величины малы по срав-
нению с абсолютными величинами собственных значений, удовлетворяющих,
предыдущему условию;
• не существует X, с большой положительной вещественной частью;
• не существует X, с большой мнимой частью, для которых не выполняется усло-
вие Re(X,)«0.
На практике, для определения жесткости СОДУ обычно используется первое из
перечисленных условий. Можно показать, что выполнение этого условия соответ-
3.5. Решение систем дифференциальных уравнений
151
ствует матрице коэффициентов системы А (3.5.64) с сильно различающимися по
модулю элементами (на 3 и более порядков).
На примере исследования кинетики последовательной реакции:
A—(3.5.88)
с кинетическими константами л1 =1000 и к2 =1 покажем, что применение явного мето-
да Эйлера приводит к появлению жесткой компоненты решения и, соответственно,
искажению («раскачке») гладкой компоненты решения.
На самом деле применяемый при решении жестких систем уравнений численный
метод должен быть в состоянии подавить эти возмущения. Применение неявных методов,
в частности, неявного метода Эйлера, позволяет успешно справиться с этой проблемой.
В соответствии с представленной кинетической схемой последовательной реак-
ции и заданными значениями констант скоростей к. и к2 СОДУ, которая описывает
скорости образования (расходования) компонентов А (соответствует компоненте 1)
и Р (соответствует компоненте 2), имеет следующий вид:
с начальными условиями:
^- = ^У1-А2)’2
ах
sl;
ТгС^о) = Уго ^0.
(3.5.89)
(3.5.90)
При этом у, =ух(х) и у2 =Уг^х'> — искомые переменные (функции решений), соот-
ветствующие изменению концентраций компонентов А и Р, т.е. = [А] и у2 =[Р].
Аналитическое решение этой системы имеет вид:
(3.5.91)
Исследуемая система может быть представлена в матричном виде:
дУ1 ' ’-*1 0
dx йУг . dx . = л -*2. У1. (3.5.92)
Собственные числа матрицы коэффициентов системы определяются из характе-
ристического уравнения:
откуда следует, что
-к,-к о
к, -к2-к
(к, + к)(кг + А.) = 0.
(3.5.93)
(3.5.94)
Результатом решения характеристического уравнения являются собственные числа:
X, =-А, =-1000 и к2=-к2=-1,
т.е. для одного из собственных значение будет справедливо:
(3.5.95)
Re(XI)«o. (3.5.96)
Таким образом, выполняется первое из приведенных выше условий жесткости
системы дифференциальных уравнений. Легко установить, что остальные три условия
152
Глава 3. Численные методы компьютерного моделирования ХТП
жесткости также справедливы для этого случая, и поэтому СОДУ (3.5.89) с коэффи-
циентами А, = 1000 и к2 = 1 можно считать жесткой.
Неприемлемость явного метода Эйлера для решения жесткой системы из-за воз-
можной ее «раскачки* и отсутствия сходимости
Явный метод Эйлера (3.5.15) для решения систем двух обыкновенных дифферен-
циальных уравнений может быть записан:
д <*ч
л
М‘+,)
h
(3.5.97)
^У^ку^-к^,
где к — номер шага решения; h — величина шага решения.
С учетом значений кинетических коэффициентов (кх = 1000 и к2 = 1) эти уравнения
принимают вид:
у'4*” = у(‘> + A(_i000j,(‘>) = _ ЮООЛ];
у‘4+,) = у‘‘> + Л(1000у‘4>-у'‘)) = 1000/!у1(4)+(1-Л)у[4), (3.5.98)
жесткая
компонента
Рис. 3.29. Схематическое представление
функций решения явным методом Эйлера
для жесткой системы дифференциальных
уравнений
На рис. 3.29 схематически представлены
функции-решения [сплошные линии — точ-
ные решения (3.5.91), а пунктирные линии
получены явным методом Эйлера (3.5.98)].
«Раскачка» решения, а затем и отсутствие
сходимости численного явного метода Эй-
лера при получении приближенного реше-
ния Ь = Уг<Х) (пунктирная линия на рис. 3.29)
обусловлены наличием ее жесткой компо-
ненты во втором уравнении явного метода
Эйлера. Эта жесткая компонента становит-
ся все «жестче» при переходе к каждому сле-
дующему шагу решения, так как в соответ-
ствии с первым уравнением (3.5.97)
у;4) = у10(1-1000й)‘, (3.5.99)
а подстановка ее во второе уравнение приводит к следующему результату:
у<‘41) = 1000/1(1-1000/1)* у10 + (1 - Л)у<‘> 3 5
жесткая компонента
Из-за степенного выражения в жесткой компоненте приближенного решения
явным методом Эйлера становится понятным отсутствие сходимости и его непри-
годность для решения жестких систем дифференциальных уравнений.
Приемлемость неявного метода Эйлера для решения жестких систем обыкновенных
дифференциальных уравнений
При решении жесткой системы уравнений (3.5.89) неявным методом Эйлера можно
записать соотношение (3.5.17):
3.5. Решение систем дифференциальных уравнений
153
п
Av(*+1>
=Л ОТ > > уГ >) = - к2УГ> •
п
(3.5.101)
С учетом значений кинетических коэффициентов (it, = 1000 и кг = 1) эти уравнения
принимают вид:
[у'**0 =у1“)+Л(-1000у,“+'));
И+1) =Уг} +Л(1000у,<<+1) -у‘‘+1)), (3.5.102)
путем преобразования которых получается:
(1 + 1000Л)
мм, _ У1У , ЮОО/оГ0 - У? , юоо^Р (3.5.103)
У1 1 + Л 1 + Л 1 + Л (1 + Л)(1 +1000Л) ’
Второе уравнение в системе (3.5.103) — представление приближенного решения
Уг = У2(х) неявным методом Эйлера, может быть записано в следующем виде:
Таким образом, это решение у2 = Уг(х) уже не содержит жесткой компоненты [в
отличие от явного метода Эйлера (3.5.98)], тем более что с учетом пошаговой реали-
зации метода из первого уравнения (3.5.103) следует:
v(0)
у<‘> = ___Z1______
1 (1+1000Й)*’
(3.5.105)
и после подстановки в (3.5.104) уравнение для расчета приближения у,*’1' на
(к + 1) шаге принимает вид:
мм, =к01+ уТ
(1 + Л)(1 + ^1)(1 + 1000Л)‘ 1 + й
h
(3.5.106)
Таким образом, неявный метод Эйлера при решении жестких систем дифферен-
циальных уравнений из-за степенной функции в знаменателе первого слагаемого в
(3.5.106) не допускает «раскачки» решения у2 = у2(.х) в сравнении с явным методом
Эйлера [см. (3.5.100) и рис. 3.29]. Этим объясняется его пригодность для решения
жестких систем обыкновенных дифференциальных уравнений.
Решение краевых задач
В краевых задачах для нахождения частного решения дифференциальных уравне-
ний и-го порядка (3.5.1) на искомую функцию и ее производные до (и — 1)-го порядка
включительно накладываются условия не при одном значении независимой перемен-
ной, как в задаче Коши (3.5.3), а при нескольких — в частном случае при двух, т.е. эти
условия задаются при двух значениях а и Ь независимой переменной х. Последнее
означает, что получаемое решение — функция у(х) и ее производные — должно удов-
летворять в общем случае системе нелинейных уравнений (см. разд. 3.2.3):
<рДу(а), у'(а),..., у*"'1’(а), у(Ь),..., у("-1)(/>)] = 0, 1 < j < п, (3.5.107)
154
Глава 3. Численные методы компьютерного моделирования ХТП
которые называются краевыми условиями. В результате задача решения дифференци-
альных уравнений (3.5.1) существенно усложняется.
Целесообразно рассмотреть два основных метода решения краевых задач:
• итерационный метод, являющийся универсальным и позволяющий решать
как нелинейные, так и линейные краевые задачи;
• метод конечных разностей, в основном применяемый для решения линейных
краевых задач.
Итерационный метод решения краевой задачи
Этот метод удобно рассмотреть на примере решения системы, в общем случае,
двух нелинейных уравнений первого порядка (3.5.9):
dyjdx = fl(x, у,(х), у2(х));
dy-Jdx = f2(x, у2(х), у2(х))
(3.5.108)
с краевыми условиями:
(3.5.109)
Рис. 3.30. Схематическое представле-
ние частных решений краевой задачи
и краевых условий
= Л(0);
Уг(х,) = у2(л).
Геометрическая интерпретация искомых ча-
стных решений У1 = У1(х) и уг = уг(х) с приве-
денными краевыми условиями схематически
представлена на рис. 3.30.
Так как краевые условия (3.5.109) задаются
при различных значениях независимой пере-
менной х х0 и х„, то пошаговое решение сис-
темы дифференциальных уравнений не может
быть выполнено из-за отсутствия данных обо
всех значениях функции решения на любом из
концов замкнутого интервала [х0,х„].
Поэтому первый шаг этого метода состоит в
том, что задается отсутствующее в исходной по-
становке задачи значение условия, накладыва-
емое на искомую функцию у2 = у2(х), напри-
мер — у2(0), при той же величине независимой переменной, например — х0, при
котором задано известное краевое условие (3.5.109) — у|(0). Отсутствующее в исход-
ной постановке условие:
У2(Л) = ?2т (3.5.110)
задается как некоторое приближение (поэтому над ней специальный знак), которое .
будет уточнено в процессе решения задачи во внешнем цикле расчетов.
На втором шаге решения во внутреннем цикле расчетов решается система диф-
ференциальных уравнений (3.5.108) с дополнительными условиями:
з'1(хо) = Л(о);
У2(*о) = Уг(о>-
(3.5.111)
Эта система уже может быть решена, так как все дополнительные условия, накла-
дываемые на искомые функции у, = у/х) и у2 = у2(х) заданы при одном значении
независимой переменной х0 (как при решении задачи Коши). При этом может быть
применен любой из рассмотренных численных (приближенных) методов — см. (3.5.15),
(3.5.21)—(3.5.30) или (3.5.17), (3.5.18).
3.5. Решение систем дифференциальных уравнений
155
В результате получаются функции решений у/х) и у2(х), которые отличаются от
искомых, так как дополнительное условие у2(0) задано как некоторое приближение и
влияет на результаты.
Полученные решения можно представить как:
У1 = 71 W{72(0)} >
у2=72«{72(о)} (3.5.112)
или графически на рис. 3.30 — пунктирными линиями. Очевидно, что они зависят от
дополнительного условия — приближения у2(0), что отражено в формулах (3.5.112) в
виде фигурных скобок за знаками функций.
Для получения правильного решения необходимо выполнение второго краевого
условия исходной постановки задачи (3.5.109), т.е. должно быть выполнено равенство:
у2(^){у2(о) 1 = У2<п> (3.5.113)
На рис. 3.30 выполнение этого условия соответствует попаданию конечной точки
пунктирной кривой решения уг(х) в точку у2(я) на правом конце интервала [xo,xj.
Поэтому на третьем шаге расчетов проверяется выполнение условия:
Уг(хп) = у2^, (3.5.114)
которое зависит от того, правильно ли определено приближение у2(0), влияющее на
значение у2(х„) (3.5.113).
Таким образом, для определения приближений у2(0) в соответствии с (3.5.114)
необходимо решать в общем случае нелинейное уравнение следующего вида:
У2(^){У2(О)}-У2(П) =°- (3.5.115)
Это уравнение решается во внешнем цикле расчетов — во внутреннем цикле рас-
четов при каждом приближении у2(0) решается СОДУ (3.5.108), одним из рассмот-
ренных методов их решения — см. (3.5.15), (3.5.21)-(3.5.30) или (3.5.17), (3.5.18).
В результате решения уравнения (3.5.115) будет определено корректное значение
у2(*о) = Уад, и рассчитанные с его применением функции решения СОДУ с краевы-
ми условиями будут правильными.
Этот метод может быть легко распространен на решение краевых задач с любым чис-
лом дифференциальных уравнений и краевых условий. Однако необходимость во внеш-
нем цикле расчетов итерационно решать нелинейные уравнения или их системы во мно-
гих случаях приводит к большим сложностям при практической реализации метода.
Решение линейной краевой задачи методом конечных разностей
Решение линейных краевых задач удобно рассмотреть на примере дифференци-
ального уравнения второго порядка
y"+p(x)y'+g(x)y = г(х) (3.5.116)
с линейными краевыми условиями
аоу(а) + аху\а) = А; „
РоХй) + Р.у'(*) = В, (3.5.117)
где |я0| + |aj * 0, |Ро| + |Р,|* 0, р(х), g(x), z(x) — заданные функции независимой пере-
менной х; А, В,ао,а„ро, р, — известные константы.
156
Глава 3. Численные методы компьютерного моделирования ХТП
Решением этого уравнения будет такая функция у(х), которая одновременно удов-
летворяет как дифференциальному уравнению (3.5.116), так и системе краевых усло-
вий (3.5.117).
Предполагается, что краевые условия (3.5.117) заданы на концах отрезка интег-
рирования [a,й], который делится на и равных частей с шагом h = (b-a)/n. В резуль-
тате получаются точки:
х, =a + ih, i = 0,(3.5.118)
в которых требуется найти искомые значения у, = у(х,) — решение.
Все производные в дифференциальном уравнении (3.5.116) заменяются их ко-
нечно-разностным выражением (см. разд. 3.3). При этом первая производная у' = у'(х,)
рассчитывается с помощью среднего арифметического первых конечных разностей:
а вторая — через вторую конечную разность:
/=(у,+1-2у, + у,_1)/Л2. (3.5.120)
При подстановке соотношений (3.5.119) и (3.5.120) в дифференциальное уравне-
ние (3.5.116) получается система:
~ + У'~' + Р(Х‘}+8(х')у‘= г(х'1 ' = (3.5.121)
Если преобразовать эту систему уравнений и дополнить ее краевыми условиями (3.5.117),
причем соответствующие производные в них заменить с помощью соотношений .
- У" ~ , (3.5.122)
то получится система (п + 1) линейных уравнений:
(Оой-а^Уо+^у, = Ah;
1 -[2-g(*,)h2]y, +|\ +|д(х,)^у„) = г(х,)й2, 1= 1, ..., п - 1; (3.5.123)
(0ой + 01)К -31К-1 = Ж
которая решается относительно неизвестных у0,у„...,у„ любым из рассмотренных
методов решения систем линейных уравнений (см. разд. 3.2). В результате получает-
ся таблица приближенных значений искомой функции у, = у(х,).
Таким образом, решение краевой задачи для дифференциального уравнения
(3.5.116) с краевыми условиями (3.5.117) сводится к решению системы линейных
уравнений (3.5.123). Чем меньше приращение h, т.е. чем больше уравнений в систе-
ме (3.5.123), тем точнее должно быть получаемое решение при соответствующих
условиях для р и g (3.5.117).
3.5.2. Дифференциальные уравнения
в частных производных
Дифференциальные уравнения в частных производных составляют в настоящее
время одну из наиболее быстро развивающихся направлений вычислительной мате-
матики. Области науки и техники, где решаются уравнения в частных производных,
весьма многочисленны и важны. К ним относится и химическая технология. Кроме
того, возможности современных компьютеров позволяют эффективно решать эти
3.5. Решение систем дифференциальных уравнений
157
уравнения практически любой сложности благодаря бурно возрастающим показате-
лям их производительности.
Математическое описание целого ряда процессов химической технологии пред-
ставляется дифференциальными уравнениями в частных производных второго по-
рядка вида:
. д2и „ п д2и „д2и 'ди ди _ „ _
А—- + 2В—— +С—- + D — + Е—+ Fu + G = 0
дх2 дхду ду2 дх ду
где А, В, С, D, Е, F, G являются функциями только
независимых переменных х и у, что удовлетво-
ряет условию линейности уравнения (3.5.124).
Функция и=и(х, у), которая определена внутри
плоской области G переменных х, у (рис. 3.31),
непрерывна, имеет непрерывные производные и
удовлетворяет уравнению (3.5.124), является реше-
нием дифференциального уравнения в частных
производных.
Если функция и зависит от одной переменной,
то уравнение (3.5.124) представляет собой обык-
новенное дифференциальное уравнение, имеющее
семейство решений.
Выбор единственного решения становится воз-
можным при наличии начальных условий.
Аналогично при решении уравнений в частных
производных получение единственного решения свя-
зано с заданием некоторых дополнительных усло-
вий на границе Г области G, внутри которой опре-
делена функция и(х, у), называемых граничными.
(3.5.124)
Рис. 3.31. Графическое представле-
ние функции решения дифферен-
циального уравнения в частных
производных второго порядка
Граничные условия могут накладываться на функ-
ции (граничные условия первого рода), на ее производные (граничные условия второго рода)
или одновременно на функции и производные (граничные условия третьего рода). Гра-
ничные условия третьего рода или смешанные граничные условия задаются в виде:
+ =F, (3.5.125)
где а и р — заданные функции в некоторой точке контура Г, F = F(x, у, и) — некоторая
функция, значения которой в точках границы известны, ди/дп — производная иско-
мой функции по нормали к границе Г в рассматриваемой точке. Граничные условия
первого рода являются частным случаем уравнения (3.5.125) при [3=0, граничные
условия второго рода — при а = 0.
Задание таких граничных условий дает возможность сформулировать три различ-
ные задачи с граничными условиями в зависимости от типа кривой контура Г обла-
сти G. Граница области, вдоль которой известны граничные условия, может быть
как замкнутой, так и незамкнутой, или «открытой» (рис. 3.32).
Уравнения в частных производных вида (3.5.124) принято классифицировать по
трем типам в зависимости от знака определителя, составленного из элементов урав-
нения (3.5.124):
А В
В С
(3.5.126)
При АС-В2 <0 уравнение (3.5.124) называется гиперболическим, при АС-В2 =0 —
параболическим, при АС-В2 >0 — эллиптическим.
158
Глава 3 Численные методы компьютерного моделирования ХТП
Решить задачу с граничными условиями означает найти такую функцию и(х, у),
которая удовлетворяет уравнению (3 5 124) и граничным условиям (3 5 125) Точные,
или аналитические, методы решения краевых задач применимы лишь в некоторых
частных случаях, и область их использования ограничена Поэтому большое значе-
ние на практике имеют приближенные методы, которые разделяются на две группы
• методы, в которых возможно получить приближенные аналитические выраже-
ния для искомой функции (здесь не рассматриваются),
• численные методы, в которых аналитические выражения для функций отсут-
ствуют
Вторая группа методов наиболее универсальна, так как пригодна для решения
уравнений всех типов
Сущность разностного метода
Основная идея решения СДУЧП разностным методом заключается в том, что
решается не исходное дифференциальное уравнение в частных производных (3 5 124),
а соответствующее ему уравнение в конечных разностях (см разд 3 3), получаемых
путем замены частных производных их выражениями через конечные»разности При
этом осуществляется переход от поиска решения в виде непрерывной (интеграль-
ной) поверхности и(х, у) к поиску значений сеточной функции и(х,, у7) в дискретно
расположенных точках (х,, у), образующих прямоугольную сетку (рис 3 33)
Для такого разбиения области определения G выбираются постоянные шаги раз-
биения h в направлении х, / в направлении у При этом точки имеют координаты
х, = х0 + ih,
У^Уо + J^ (3 5 127)
i,j = 0, +1, ± 2, ,
где х0 и у0 — координаты начальной точки, i и j — номера узлов по направлениям
х и у
Значения функции в узловых точках обозначаются с указанием координат
u(x0+ih,y0+j£) или сокращенно с помощью индексов
«01 = «(*0, у„ + (),
ин = и(хо + h уа +1), (3 5 128)
= “(ха + 'Л. Уо + Д)
Рис 3 32 Графическое изображение
границы области известных граничных Рис 3 33 Графическое представление
условий значений сеточной функции
3 5 Решение систем дифференциальных уравнений
159
Первые производные в сеточной области заменяются отношениями разностей
между значениями функции в соседних узлах к величине шага сетки Замена может
быть выполнена тремя способами Так, первая частная производная функции и в
узле (х0,у0) выражается через конечные разности в направлении х в виде
а) разностного отношения «вперед»
ди
дх *
u(x0+h, у0)-и(х0, у0)
h
(3 5 129)
б) разностного отношения «назад»
Эи| u(x0,y0)-u(x0-h,y0)
Эх г h
в) симметричного разностного отношения
Эи1 _u(x0+h, у0)-и(х0-й, у0)
Эх > 2h
(3 5 130)
(3 5 131)
Аналогичные выражения получаются и для производных по у
Вторые частные производные в сеточной области определяются как отношения
разностей первых производных (3 5 129)—(3 5 130) к величине шага сетки Напри-
мер, вторая производная для узла (х0, у0) по направлению х определяется
Э2и
Эх2
X Хо
У Уо
и(х0 + Л, у0) - «(Хр, у0) _ и(Хр, у0)-ц(Хд-Й, у0)
ujxg + h, у0)-2и(х^, у„)+ц(х0-й, у0)
(3 5 132)
й2
Для производной по направлению у выражение аналогично
д2и
Эх2
и(х0, у0 + л-2и(хо, у0) + и(х0, у0 - л
е2
(3 5 133)
дующим образом
д2и
дудх х
= 1/й{1/ф(х0 + й, у0 + е)-и(х„ + й, у0)]-1 /ф(*о, Уо + () - и(х0, у0)]} = (3 5 134)
= П/(^)][«(Х0 + Й, Уо + О - и(Хо + й, Уо)-«(Хо, у0+О + и(Хр, у0)]
Предположим, что область G, на которой определена функция и(х, у), прямо-
угольна (рис 3 34)
На этой области строится сетка с параметрами й и I и узлами по горизонтали
i = о, 1,2, , п и по вертикали j = о, 1,2, , т Разностные уравнения связывают значения
искомой функции в узлах сетки, число которых равно (» + \)(т +1) Решение задачи с
граничными условиями заключается в отыскании этих значений при заданных зна-
чениях функции в граничных узлах Таким образом, в замкнутой прямоугольной
области остается (п - 1)(/и -1) неизвестных, для которых составляется и решается сис-
тема (п- \)(т -1) разностных уравнений
160
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.34. Графическое представление области, на
которой определена функция
Рис. 3.35. Соседние умы сеточной
функции
Решение уравнений первого порядка
Запишем дифференциальное уравнение в частных производных первого порядка:
Аппроксимация производных осуществляется по разностному соотношению
(3.5.129) и уравнение для узла с координатами (i, j) имеет вид:
и(х , У,х1 1 — и(х , у,) и(х У')-и(х, у,)
D ' + Е = о, (3.5.136)
i = 1, 2,..., п -1; j = 1,2,...,т-1
Для простоты примем, что DI Е = 1 и fjh = l. Тогда значение функции в узле (1, j+1)
выражается (рис. 3.35):
ulx,, yJ+1) = 2u(x,,yJ)-u(xl+1, у,). (3.5.137)
Решение уравнения (3.5.135) заключается в отыскании значений и(х,у), т.е. дис-
кретных значений «(х,,у;) при 1=1,2,...,п и j = 1,2,....т — см. (3.5.136), (3.5.137), по
заданным граничным значениям и(х,, у0) при i =1,2,..., п.
Решение эллиптического уравнения
Одним из часто используемых дифференциальных уравнений эллиптического типа
является уравнение Лапласа:
S+0=o- <з-51з8)
дх ду
Аппроксимация производных выполняется с использованием формул (3.5.132) и
(3.5.133), которые для узла (i, J) принимают вид
ч(х^, у/)-2и(х„ у^ + и^, у/) u(x„y^)-2u(xl,yJ) + u(x„y/_i) _
Л2 (2 ’ (3.5.139)
i = 1, 2,..., п -1; j = 1, 2,..., т -1.
Тогда значение функции в узле (i, j) при Uh = 1:
и(х,, У;) = -^[«(*,+!> У7) + «(х,_!, у,) + «(*,, у;+1) + «(х,., у,.,)]. (3.5.140)
3.5. Решение систем дифференциальных уравнений
161
Таким образом, значение функции в каждом внутреннем узле сетки равно сред-
нему арифметическому значений функции в четырех соседних узлах (рис. 3.36). На-
чало координат сетки (рис. 3.37) совпадает с точкой (х0, у0). Граничные условия
(3.5.125) в разностной форме принимают вид:
а) для нижней границы «,0 = Fl0 = F(x,, у0); i = 0,1,2,..., п ;
б) для верхней границы
- Р(Х, • Ут ); ‘ = о, 1,2,..., п;
в) для левой границы и0, = FOl = F(x0, у,); j = 0,1,2,.... т;
г) для правой границы unj^= Fnj = F(xn, у;); j = 0,1,2,т.
Решается краевая задача с условием первого рода. Решение начинается с первого
(нижнего) «слоя» сетки j = 1; i = 1,2,...,n-l:
U(X1 ’ УI) = 7 [“<*2 • УI) + “C*i > У г) + F(x0, у,) + F(x,, y0)];
4
У1) = [«(*э, У1) + »(x2, y2) + u(x,, y,) + F(x2, y„)]; (3.5.141)
“(-«„-i. У,) = 7 [F\x„, У1) + «(-«„-i > Уг) + “(x„_2, y,) + F(x„_,, y0)].
4
Для второго слоя узлов сетки j - 2; i = 1, 2,..., n-l:
“(х,, У2) = 71“(x2 < У2) + “(*i - Уз) + Г(х0, у2) + и(х,, у,)];
4
“(Х2>У2) = 7["(ХЗ.У2) + “<Л2>>'з) + “(Л1.>'2) + “(Л2.>'1)]; ,, , , ...
4 (3.5.142)
. У2 ) = 7 ’ Уз ) + - Уз ) + "(Л-2 , У2 ) + • У1 )] •
4
Подобным образом запишутся системы уравнений до слоя j = т -1. Доказано, что
такая система, состоящая из (п - 1)(т -1) линейных неоднородных уравнений с (п - l)(m -1)
неизвестными, всегда совместна и имеет единственное решение. Так как большая
Рис. 3.36. Значения функций, определяю-
щие значение функции во внутреннем
узле сетки
х
Рис. 3.37. Графическое изображение границ
сетки при решении эллиптического
уравнения
11-4544
162
Глава 3. Численные методы компьютерного моделирования ХТП
часть коэффициентов системы равна нулю, то для ее решения наиболее целесообраз-
но использование итерационных методов, в частности, метода Зейделя. Запишем часть
уравнений системы (3.5.141) в приведенном виде, где верхний индекс показывает но-
мер итерации. Все значения неизвестных в начале счета примем и,™’ = 0. Тогда значе-
ния функции в узловых точках на первой итерации будут следующими:
,,<!> _ 4- J. Г j. Г 1-
М11 — . 1М21 + м12 + Г01 + Г10],
4
4
«',-)1.l=7[T„1+u<0)12+M<1-)2.1 + T„_l,0]1
4
^)=|[«g’+«1? + F02 +«<«];
4
u<‘> 4^+«<?];
4
“ “1.2 = + и'ч.З +“i-2 О ]’
4
(3.5.143)
(3.5.144)
Доказано, что при h 0 и f -> о решение разностного уравнения (системы линей-
ных алгебраических уравнений) сходится к решению исходного дифференциального
уравнения в частных производных без ограничений на величину отношения Uh.
Решение гиперболического уравнения
Уравнение гиперболического типа можно получить из уравнения (3.5.124), если
переменную у трактовать как временную координату t, а переменную х — как про-
странственную координату
д U д U с л лс\
(3.5.145)
Граница области, вдоль которой заданы краевые условия для уравнения (3.5.145),
незамкнута по временной координате, и граничные условия представляются в виде:
u(O,t) = F(I)(Z); u(L,z) = F(2)(z); z>0- (3.5.146)
Граничные условия по временной координате относятся к фиксированному мо-
менту времени и носят название начальных условий:
и(х, 0) = /(х); 0<x<L,
= F(a); 0<x<L. (3-5-147)
dt
Таким образом, имеем смешанную краевую задачу. Для численного решения урав-
нения (3.5.145) строится прямоугольная сетка в полуполосе z>0, 0<x<L, которая в
направлении положительных значений простирается неограниченно (рис. 3.38) и
позволяет искать решение для сколь угодно далекого момента времени.
Решение явной разностной схемы для уравнения (3.5.195) можно найти по следу-
ющей формуле:
U(x,, Zytl) = 2(1 - Л2)«(х,, tj) + Х2[и(х,+1, Q + uix^, z7)]-u(x,, tj_i);
X = t/h; z = l, 2, ..., n , J = l, 2, 3, ... . (3.5.148)
3.5. Решение систем дифференциальных уравнений
163
Граничные и начальные условия представляются в
разностной форме:
“о, ^^ОоЛД:
en,=F^ = F^\Xn,tl), у = 1,2,... (3.5.149)
и
и,о =f,o =f(x„t0) 1 = 1,2,..., л-1; (3.5.150)
1/t[u(x,, Zj -u(x,, Zo)] = F(x,, z„). (3.5.151)
Подставляя уравнение (3.5.150) в (3.5.151), получим
) = f(x,, z0) + CF(x, ,tQ). (3.5.152)
Далее из уравнения (3.5.150) определяются все зна-
чения функции и для нулевого слоя сетки при j = 0. Зна-
чения функции и для первого слоя при j = 1 определя-
Рис. 3.38. Иллюстрация
границы области при
решении гиперболического
уравнения
ются из уравнения (3.5.152). Значения функции и,2, со-
ответствующие второму слою сетки, получаются из разностного уравнения (3.5.148)
для j = i:
u(xt, t2) = 2(1 - X2)zz(x,, Z,) + X’[zz(x,+1, z,) + zz(x,_,, Zl)]-zz(x,, Zo). (3.5.153)
Таким образом, значения функции в каждом следующем слое вычисляются по
шачениям функции в двух предыдущих слоях. Существенно, что использование этой
схемы не требует решения системы уравнений, так как значения искомой функции
вычисляются в явном виде. Вычислительный процесс сходится при (<h или ?,<1.
(3.5.154)
(3.5.155)
Решение параболического уравнения
Дифференциальное уравнение параболического типа имеет вид
Э2и ди _
Эх2 ду
Разностное уравнение для узла (z, j) представляется в виде
yj)-2u(x,, уД+ zz(x,,, у,) zz(x,, yJ+t)-u(,x„ УД
h1 t ~ '
£/h2=k; z = 1, 2,..., n — 1; J = l,2,....
Приведем уравнение (3.5.155) к форме (3.5.140):
и(х,, у^) = Хи(х„,, уД + (1 - 2Х)и(х,, уД + Мх,_,, уД . (3.5.156)
Отсюда следует, что значение функции в узле (z, j +1) рассчитывается по трем значени-
ям функции в соседних точках (/ +1, j), (z, j\ (z-1, j) предыдущего слоя сетки (рис. 3.39).
Таким образом, решение параболического уравнения сводится к решению систе-
мы линейных алгебраических уравнений. Граница области, вдоль которой заданы гра-
ничные условия для уравнения этого типа, незамкнута, поэтому независимая перемен-
ная у трактуется как временная координата t. Тогда уравнение для узла имеет вид:
zz(x , Z,..) = Xzz(x,.,, Z,) + (1- 2X)zz(x,, Z,) + Xzz(x,, Z,),
z = l,2,...,«-l; ) = 1,2......... ' <3-5-157>
Граничные условия:
zz(O, Z) = F(o);
u(i,z) = F4 z>0. <3-5-158)
164
Глава 3. Численные методы компьютерного моделирования ХТП
Начальное условие:
Рис. 3.39. Графическое изображение
соседних узлов сетки при решении
параболического уравнения
«(x,0) = /(x), 0<x<L.
(3.5.159)
Решается краевая задача с граничными услови-
ями первого рода (3.5.125). Строится прямоуголь-
ная сетка в полуполосе t > О, о > х < L (см. рис. 3.38).
Граничные и начальные условия в разностной
форме принимают вид:
и(х0,Г;) = F{0\x0,tt);
, , . г.(1), , . , п (3.5.160)
u(x„,tj) = F{ ’(x^tj), j = l,2,...; v '
u(x,,tB) = f(x,,t0), i = 1,2,...,n-l. (3.5.161)
Значение функции вычисляется в явном виде
u(x,,tJ+l) по уравнению (3.5.157) аналогично слу-
чаю гиперболического уравнения. Решение для нулевого слоя j = о известно из гра-
ничных и начальных условий. Решение для первого слоя j = 1 получается из уравне-
ния (3.5.157) при j = 0:
и(х,, tt) = Xu(x,+l, z0) + (l-2X)u(x,,t0) + Xu(x,_,, z0), 1 = 1,2,—, n-l, (3.5.162)
и так далее для каждого следующего слоя сетки решения находят по предыдущему
слою. Доказано, что при решении параболического уравнения вычислительный про-
цесс устойчив и сходится при (<h2 / 2 или Х<1/2.
Метод прогонки для нахождения решения неявной схемы дифференциальных
уравнений в частных производных
Решение гиперболических и параболических уравнений разностным методом свя-
зано с выбором величины шага £ по временной координате в зависимости от вели-
чины шага h по пространственной координате. Точность решения оказывается тем
выше, чем меньше выбран шаг h. Это приводит к малой величине шага по времени,
что значительно затягивает процесс решения краевой задачи.
Существует другая более устойчивая вычислительная схема — неявная, для кото-
£ £
рой величина отношения - и не является ограниченной сверху, и поэтому шаг
по временной координате £ = Az7 может быть выбран сравнительно большим. Рас-
смотрим её на примере уравнения параболи-
ческого типа (3.5.154). Построим в области G
Рис. 3.40. Изображение неявной схемы
для замены уравнений в частных
производных их конечно-разностным
представлением
прямоугольную сетку, величина шага £ в ко-
торой не зависит от h. Для замены уравнения
(3.5.154) конечно-разностным соотношением
воспользуемся неявной схемой, показанной на
рис. 3.40.
Эи _ Ц,,Л1 ~и,!
dt £ ’
(3.5.163)
(3.5.164)
Тогда, полагая л2/£ = X (число 1/Х принято
называть числом Куранта), имеем систему ли-
нейных алгебраических уравнений:
3.5. Решение систем дифференциальных уравнений
165
И1Ч,Л1 - (2 + Х)И, J+1 + u,+1J+1 = -Хи,, i = 1, 2,п -1; j = 0,1, 2,....
(3.5.165)
Рассмотрим уравнения этой системы для первого слоя сетки при J = o:
и0, -(2 +A)u„ +и2, = -Аи,0;
“п — (2 + X)u2, + u3, = -Xu20i
(3.5.166)
“л-2,1 — (2 + Х)ИЯ_,, + «„ = — X22„_, о,
где на основании граничных и начальных условий:
“oi=v(fi): “,i =4>(Q; и,о=?(х„0); 2 = 1,2.п-1. (3.5.167)
Ненулевые элементы матрицы коэффициентов системы (3.5.166) расположены
па трех диагоналях симметрично относительно главной диагонали. Матрица коэф-
фициентов системы (3.5.166) такого типа называется трехдиагональной.
Изложенный ниже метод решения системы такого типа принято называть мето-
дом прогонки. Он заключается в следующем.
Из первого уравнения определяется и„:
= X“10 т“°‘+“21 =an<z,1i+ц2!), где ач=т~7- *n = 4o+“oi. (3.5.168)
С использованием полученного значения решается второе уравнение:
+л>1). (5 5 169)
2 т Л 2 т Л — i
где 2^2, = 1/(2+Х-Оц); Ь2, = 22,,*,, + Аию и так далее:
и,, =a,,(b,, + и,+11), Где а,, = 1/(2 + Х-а,_11); Ьа =а,^,Ь,_1Л + Хи10, (3.5.170)
и»-1,1 = 1 *“»!) > ГДе <2л_,, = 1/(2 + Х —ал_21); ЬпЛ, = ап_21Ьп_2, + Х22л_,о. (3.5.171)
Необходимо отметить, что выражения для коэффициентов aa,blt зависят только
от значения X, значений коэффициентов в предыдущей точке и значений искомой
функции на предыдущем слое. По формуле (3.5.168) последовательно вычисляются
коэффициенты данного слоя сетки:
22,, 222, ... 22л_,д
Z?,, Ъ2} ... Ьп_]} .
Далее с использованием значений а,„ ЬЛ и граничного условия ил1 =у(г,) с помо-
щью «обратного хода» осуществляется расчет значений искомой функции и на пер-
вом слое сетки:
“-л =а-1,Д-1,1 +<₽(',));
Un-2,1 ~ ал-2,1(^»-2,1 + “л-1,1)'.
“и =an(fcii+a2i);
L“oi =V(6)-
(3.5.172)
166
Глава 3. Численные методы компьютерного моделирования ХТП
Таким образом, шаг за шагом строится решение исходного дифференциального
уравнения во всех точках сетки (x,,z7). Такой метод нахождения решения на (j +1)
слое (см. рис. 3.40) принято называть методом прогонки, а коэффициенты аЛ и ЬЛ —
прогоночными.
Данная схема решения устойчива при любом значении отношения ’k = h2l(.
В заключение следует отметить, что математические описания большинства ХТП
представляют собой системы дифференциальных уравнений, решение которых при
компьютерном моделировании требует знания рассмотренных в этой главе особен-
ностей применяемых вычислительных алгоритмов, как например, приемлемости их
для решения задач с жесткими системами уравнений, с неудовлетворительной обус-
ловленностью по Ляпунову, а также умения оценить численную устойчивость при-
меняемых при этом расчетных методов.
3.6. Оптимизация
Важнейшей задачей применения расчетных методов при компьютерном модели-
ровании химико-технологических процессов (ХТП) является определение оптималь-
ных, т.е. наилучших условий их функционирования.
Решение этой задачи возможно при выполнении трех условий:
• выборе критерия оптимальности функционирования ХТП — целевой функции R;
• выявлении ресурсов оптимизации — независимых переменных оптимизации
х = [х,,.... х„], оказывающих, по возможности, наибольшее влияние на величину
целевой функции;
• реализации метода оптимизации, обеспечивающего определение оптимального
(наилучшего) значения целевой функции путем целенаправленного изменения
независимых переменных оптимизации.
С математической точки зрения задачи оптимизации следует отнести к типу эк-
стремальных задач.
В общем случае при оптимизации ХТП различают два класса экстремальных задач:
• решение представляется как совокупность оптимальных значений конечного чис-
ла независимых (управляющих) переменных (в основном, для процессов с сосредо-
точенными параметрами и описываемых системами конечных уравнений)',
• решение представляется как совокупность неизвестного вида функций от пере-
менных либо по времени (для динамических процессов, так называемых распре-
деленных во времени процессов), либо по пространственной или пространствен-
ным координатам (для распределенных в пространстве процессов).
В настоящем разделе рассматриваются методы и алгоритмы решения экстремаль-
ных задач первого класса. Методы решения экстремальных задач второго типа пред-
ставлены в разд. 5.5.2.
Решение экстремальной задачи первого типа заключается в нахождении совокуп-
ности значений независимых (оптимизирующих или управляющих) переменных,
при которой заданная целевая функция этих переменных имеет максимальное или
минимальное значение. Для решения таких задач разработано достаточно много ма-
тематических методов, отличающихся стратегией поиска экстремума. Как правило,
нельзя рекомендовать какой-то один универсальный метод; для решения конкрет-
ной задачи следует учитывать ее особенности и опыт применения различных мето-
дов. При поиске экстремума функции многих переменных наибольшее распростра-
нение получили методы шагового поиска, реализация которых осуществляется пос-
ледовательными шагами. Все существующие методы при этом различаются лишь
стратегиями выбора направления и величины шага поиска.
3.6. Оптимизация
167
В дальнейшем будем полагать, что всегда ищется экстремум, являющийся мини-
мумом заданной целевой функции многих переменных. Задача на поиск максимума сво-
дится к задаче на поиск минимума простым изменением знака функции.
В результате задача оптимизации в узком смысле (экстремальная задача) может
быть записана как
min R(x). (3.6.1)
— min <—<—max ' '
В этом случае отрезок [х”п,х”“] представляет собой ограничения 1-го рода, на-
кладываемые на независимые переменные, и соответствует области допустимых зна-
чений независимых переменных оптимизации, в которой определяются их опти-
мальные величины (с”'”), обеспечивающие минимум целевой функции R""":
< Я”“=Я(Г/И). (3.6.2)
Задача оптимизации в широком смысле (задача нелинейного программирования) зак-
лючается в отыскании экстремума целевой функции при заданных ограничениях в
виде равенств и (или) неравенств. Ограничения могут быть линейными и (или) не-
линейными.
Пусть непрерывная функция R(x) представляет собой целевую функцию;
Ф,(х),...,ф„(х) задают ограничения в виде равенств, a ...,qp(x) - ограничения в
виде неравенств.
Переменные х(х>,. .,х„) могут быть конструкционными параметрами, параметра-
ми режимов, уставками регуляторов и т.п.
Формально задача нелинейного программирования может быть сформулирована сле-
дующим образом:
минимизировать R(x), хеХ" (3.6.3)
при т линейных и (или) нелинейных ограничениях в виде равенств
ф;(х) = О, ] = \,...,т (3.6.4)
и (р-т) линейных и (или) нелинейных ограничениях в виде неравенств
<7;(х)>0, у = т + 1,..., р. (3.6.5)
Решение этой задачи соответствует отысканию множества х" = [xf,..., х*], удовлет-
воряющего соотношениям (3.6.4) и (3.6.5) и составляющего экстремум функции Я(х).
По аналогии с экстремальной задачей (3.6.1), задачу нелинейного программиро-
вания можно представить следующим образом:
min7?(x).
—min —max
Ч>,(£)=0, у=1, ,т (3.6.6)
<?,(*)> О, _/=т+1, ,р
Здесь появляются ограничения 2-го рода в виде предпоследних равенств и после-
дних неравенств, что может существенно усложнить решение задачи оптимизации.
3.6.1. Геометрическая интерпретация задачи
оптимизации
В соответствии с соотношением (3.6.3) значение критерия оптимальности R мо-
жет рассматриваться как функция, определенная в «-мерном пространстве перемен-
ных х7 (/ = 1,..., п). Поскольку наглядное графическое изображение «-мерного про-
странства отсутствует, далее используется следующий прием представления функ-
ции 7?(х) на плоском чертеже.
168
Глава 3. Численные методы компьютерного моделирования ХТП
Предположим, что через точку х^' в п -мерном пространстве, соответствующую
оптимальному решению задачи, например, минимуму целевой функции, проведена
двухмерная плоскость Р. Тогда при удалении от точки х°р' по этой плоскости в лю-
бом направлении значение R(x) увеличивается. Если Я(х) является непрерывной
функцией в области X, то вокруг точки х°р' в данной плоскости всегда можно прове-
сти замкнутую линию, вдоль которой значение R(x) постоянно (рис. 3.41, а). Таких
замкнутых линий, называемых линиями постоянного уровня функции R(x) и отвечаю-
щих различным значениям R(x) = ck, можно провести в плоскости Р вокруг точки х°р'
сколько угодно, причем каждая из этих линий для точки минимума будет целиком
охватывать любую линию, для которой значение функции R(x) меньше. Форма ли-
ний постоянного уровня, соответствующих разным значениям ct, при этом может
существенно различаться.
При наличии ограничений типа равенств (3.6.4) рассмотренный прием изображе-
ния целевой функции также можно использовать, если принять во внимание, что
каждое из уравнений (3.6.4) определяет в л-мерном пространстве (л — 1)-мерную
поверхность, пересечение которой с двухмерной плоскостью Р имеет вид некоторой
линии t (см. рис. 3.41, б), вдоль которой и ищется оптимальное решение. Правда,
случай, когда число ограничений типа равенств больше 1, пересечения поверхности,
например, двумя ограничениями
<р,(х) = О,
<p2w=o
(3.6.7)
может иметь с плоскостью Р только некоторые общие точки. Однако в большинстве
случаев для наглядной иллюстрации метода оптимизации при наличии ограничения
типа равенства (3.6.4) достаточно чертежа, изображенного на рис. 3.41, б.
Ограничения же типа неравенств (3.6.5) независимо от их числа наглядно пред-
ставляются описанным способом на рис. 3.41, в.
Очевидно, что рассмотренный способ изображения функции R(x) с ограничени-
ями или без них не является однозначным, так как форма линий постоянного уров-
ня функции R(x) (и форма ограничений) может существенно изменяться в зависи-
мости от ориентации плоскости Рв л-мерном пространстве. Тем не менее, изложен-
ный прием во многих случаях позволяет наглядно представить различные принцип
действия алгоритмов решения задач нелинейного программирования, вследствие чего
он и применяется в дальнейшем.
?2W = О
Рис. 3.41. Геометрическая интерпретация задачи оптимизации: а - без ограничений; б - с
одним ограничением в виде равенства; в — с двумя ограничениями в виде неравенств
3.6. Оптимизация
169
Особые точки и овраги целевой функции
Рис. 3.42. Линии постоянного
уровня в окрестности седловой
точки
Как известно, необходимым условием экстремума функции многих переменных
является выполнение системы равенств:
^ = о, ; = (3.6.8)
Поскольку условие (3.6.8) — лишь необходимое, но еще не достаточное, могут
представиться случаи, когда при его выполнении в некоторой точке хм, экстремума
функции R(x) в ней не будет.
Примерами подобных точек целевой функции
служат точки, в которых функция Я(х) по одно-
му или нескольким направлениям имеет мини-
мум, в то время как по остальным — максимум.
Такие точки называются седловыми точками фун-
кции R(x). Для случая двух переменных пример
функции с седлом представлен на рис. 3.42.
Линии постоянного уровня на плоскости Р,
проведенной через седловую точку х(1), изобра-
жены на рис. 3.42, где стрелками показаны на-
правления уменьшения значений функции Я(х).
Другим типом особенностей целевой функции
являются так называемые овраги, при наличии
которых вдоль определенных направлений вели-
чина данной функции изменяется очень слабо.
В качестве примера можно привести функцию
а Ь
(3.6.9)
у которой при выполнении условия а > Ь имеется
овраг, причем его «дно» расположено вдоль оси
л,. На рис. 3.43 изображены линии постоянного
уровня этой функции.
В общем случае линия «дна» оврага может не
совпадать по направлению с осями координат и,
кроме того, существенно отличаться от прямой,
т.е. возможны также криволинейные овраги.
Функции многих переменных могут иметь
овраги с размерностью, превышающей 1. Нагляд-
ное графическое изображение таких случаев от-
сутствует, однако формально многомерный ов-
раг можно определить как область значений не-
Рис. 3.43. Характер линий постоян-
ного уровня у функции, имеющей
овраг
зависимых переменных в л-мерном пространстве,
в котором целевая функция вдоль некоторых направлений имеет малую скорость
изменения, тогда как вдоль остальных направлений скорость изменения этой функ-
ции сравнительно высока.
В качестве примера функции с многомерным оврагом приведем функцию
(3.6.10)
которая при выполнении условия at > bt для всех at и bt имеет овраг размерности q.
170
Глава 3. Численные методы компьютерного моделирования ХТП
Как показано ниже, наличие оврагов у оптимизируемой функции затрудняет отыс-
кание истинного положения экстремума, и для точного его нахождения приходится
использовать специальные методы поиска.
Глобальный и локальный оптимумы
При отыскании оптимума целевой функции R(x) (3.6.1) задачей, как правило,
является определение совокупности значений независимых переменных х], соответ-
ствующей не какому-нибудь экстремуму функции R(x), а наибольшему или наи-
меньшему значению /?(Х) в допустимой области X, описываемой соотношениями
(3.6.6). В дальнейшем обычно предполагается, что оптимум отвечает наименьшему
значению функции R(x), т.е. совокупность оптимальных значений независимых пе-
ременных х°р' {j = 1,..., п) при этом удовлетворяет условию:
R(x°p') < R(x), (3.6.11)
х е X
которое выполняется для любых допустимых значений х.
Оптимум, для которого справедливо условие (3.6.11), обычно называется глобальным.
Кроме него функция R(x) может иметь один или несколько локальных оптимумов в
точках х^ (Л = 1,.., р), для которых можно также записать соотношения типа (3.6.11),
выполняющиеся в окрестностях точек xk е Хк.
Поскольку заранее число локальных оптимумов р целевой функции не известно,
становятся очевидными трудности, которые могут встретиться при отыскании гло-
бального оптимума, так как для этого необходимо найти и проверить все без исклю-
чения локальные оптимумы, имеющиеся у целевой функции решаемой задачи. Од-
нако и для определения положения оптимума целевой функции даже в том случае,
когда заранее известно, что функция имеет только один оптимум, являющийся гло-
бальным, отыскание решения часто представляет собой задачу далеко не тривиаль-
ную, поскольку это связано с операциями поиска в л-мерном пространстве.
3.6.2. Методы оптимизации, основанные
на классическом математическом анализе
Необходимые условия существования экстремума функции одной переменной
В основе методов, рассматриваемых в этом разделе, лежит учение классического
математического анализа об экстремумах функций одной переменной.
Говорят, что функция R(x), определенная на промежутке [«,£>], имеет в точке
х = х0 максимум (минимум), если эту точку можно окружить такой окрестностью
(х„ — б, х0 +е) , содержащуюся в промежутке [а, Ь\, что для всех точек этой окрестности
выполняется неравенство:
R(x) < R(x0) или R(x)>R(x0) для всех х^х0. (3.6.12)
В первом случае максимум — наибольшее значение, во втором минимум — наимень-
шее значение.
Понятия «максимум» и «минимум» объединяются в одном понятии — экстремум —
крайнее (значение).
Необходимое условие существования экстремума функций одной переменной фор-
мулируется следующим образом: в точках экстремума производная dR(x)/dx либо
3.6. Оптимизация
171
обращается в нуль, либо не существует. Это условие
является только необходимым, но не достаточным, т.е.
производная dR/dx может быть либо равной нулю, либо
ис существовать, а экстремума может и не быть.
На рис. 3.44 показан случай, когда необходимое усло-
вие выполняется (производная не существует в точке х0),
а экстремума нет. Таким образом, используя необходи-
мое условие существования экстремума, мы можем лишь
определить те точки на промежутках, в которых, в прин-
ципе, возможен экстремум — «подозрительные» точки.
Итак, чтобы исследовать функцию /?(х) на экстре-
мум, надо воспользоваться еще и достаточными усло-
виями существования экстремума.
Рис 3 44. Случай отсутствия
экстремума при выполнении
Достаточные условия существования экстремума необходимого условия его
функции одной переменной существования (производная
не существует в точке х0)
Первое достаточное условие. Исследуют поведение
функции в с-окрестности «подозрительной» точки, для чего вычисляют:
/?(х0 - 5) и R(xfj + 5), где 5 < е .
Если при этом выполняются соотношения:
R(x0 -8)<R(x0);
Я(х0+8)<Я(х0),
то х0 есть точка максимума (М).
Если:
Л(х0-8)>Л(х0);
7?(х0 + 8) > 7?(х0),
(3.6.13)
(3.6.14)
(3.6.15)
то х0 есть точка минимума (т).
Если условия (3.6.14) и (3.6.15) не соблюдаются, то экстремума в точке нет.
dR
Второе достаточное условие. Исследуют поведение первой производной — = R в
е-окрестности «подозрительной» точки. Если знак Я'(х0-8)* знаку /<(х0 + 8), то экст-
ремум в точке х0 есть. При этом, если R'(x0 -5) > 0, a R'(x0 + 8) < 0, то в точке х0 макси-
мум; если 7?’(хо-8)>0, а /?'(хо+8)>0, то в точке х0 минимум. Если знак R’(x0+8)
совпадает со знаком R'(x0 -8), то в точке х0 экстремума нет. Этим правилом следует
пользоваться, когда R’ вычислить легче, чем R.
Третье достаточное условие. Исследуют знак высших производных непосредственно
в точках, подозреваемых на экстремум. Правилом можно воспользоваться, если /?(х)
- непрерывная функция и имеет непрерывные производные высших порядков. Тог-
да, если 7?"(хо)>0, то в точке х0 имеем минимум, если Л"(хо)<0, то в точке х0 имеем
максимум, если Я"(хо) = о, то необходимо исследовать знаки высших производных.
При этом применяется следующее правило: если первая, не обращающаяся в нуль
производная нечетного порядка, то в исследуемой точке нет ни максимума, ни ми-
нимума; если же эта производная четного порядка, то имеется максимум, при усло-
вии, что она отрицательна, и минимум, если она положительна.
172
Глава 3. Численные методы компьютерного моделирования ХТП
Пример. /?(х) = х3;/?'(х) = Зх2; таким образом, точка х0 = 0 - «подозрительная» (по
необходимому условию).
▼ Вычисляем: при х = О R'(x) = 6х = 0,- R'(x) = 6; R' * 0, следовательно, экстрему-
ма нет, так как порядок производной 3 — нечетный. Пусть теперь
/?(х) = х4;Л’(х) = 4х3 =>х0 =0 - «подозрительная» точка. Вычисляем: при х = О
К"(х) = 12х2 =0; К"'(х) = 24х = 0; Kiv(x) = 24 *0- Порядок производной четный и
Rlv > 0, следовательно, в точке х = 0 имеем минимум. ▲
Однако в конкретных задачах химической технологии не всегда бывает необходи-
мо проверять достаточные условия существования экстремума. Иногда достаточ-
ность следует из законов химии и химической технологии.
Необходимые условия существования экстремума функции многих переменных
Функция многих переменных Я(х,,х2,...,х,) имеет в точке (х°,х°,...,х°) максимум
(минимум), если существует такая окрестность этой точки, взятая из области опре-
деления функции, что для всех точек этой окрестности справедливо следующее не-
равенство:
R(xt, х2,.... х„) < R(x° х°,..., х°)
или (3.6.16)
R(x„ х2, х„) > R(x° х°,..., х°).
Необходимым условием существования экстремума функции многих перемен-
ных является равенство нулю частных производных первого порядка по всем пере-
менным, т.е.
В этом случае полный дифференциал дифференцируемой функции R равен нулю:
dR(x,, х2,.... х„) = 0. (3.6.18)
В самом деле, так как
ч dR , dR dR dR
dR(,xx, x2,.... xn) = —dx} + —dx2+ ...+ — = >—dx,
vXj C/%2 VXn ,=i vXf
и —— = 0 по условию (3.6.17), следовательно, dR(x., хг,x„) = 0.
ox,
Достаточные условия существования экстремума функции многих переменных
формулируются значительно сложнее, чем для функции одной переменной.
Достаточные условия существования экстремума функции многих переменных
Разложим функцию /?(х,,х2,...,х„) в окрестности точки (х°,х°,...,х°), исследуемой
на экстремуме, в ряд Тейлора по степеням Дх,:
R(x° + Дх,, х° + Дх2,.... х° + Дх„) = R(x°, х°,..., х°) +
(3.6.19)
Но по необходимому условию (3.6.17) имеем:
3.6. Оптимизация
173
А Эя
(3-6.20)
л я Э2/?
Далее, если выражение У У--------Дх.Дх сохраняет один и тот же знак для любых
7^ 7^ Эх, Эх,
приращений Дх, и Дх,, то экстремум есть. Обозначая
Э2К
— = а„; Дх, =z,; Дх,=г„ (3.6.21)
это выражение примет вид:
(зад
1=1 ;=1 <JX,OXj |=1 ;=1
При этом полученное выражение для определения zm называется квадратичной
формой.
Если при любых значениях z, и z,, z(2), кроме z, = 0 и z, = 0, величина z<2) > 0, а в
точке z, =0 и z, = 0 величина z(2) =0, то квадратичная форма zm (3.6.22) называется
положительно определенной, что соответствует минимуму целевой функции К(х„хг,.... х„).
Условие положительной определенности квадратичной формы (3.6.22) формули-
руется следующим образом.
Квадратичная форма будет положительно определенной в том случае, если все
определители, составленные из элементов а,,, положительны, т.е.
а„ > 0;
°11 °12
а21 агг
>0;
011
а21
o„i
012
а22
а„2
а,„
а2и
(3.6.23)
Условия (3.6.23) носят название условий Сильвестра, а определители в этих нера-
венствах называются определителями Сильвестра.
Итак, если все определители Сильвестра положительны, то имеет место минимум
целевой функции; если определители Сильвестра нечетного порядка отрицательны, а
четного порядка — положительны, то имеет место максимум целевой функции; а если
последовательность чередования знаков у определителей Сильвестра иная, то экст-
ремума у целевой функции нет.
Для случая 2-х переменных определим условия минимума и максимума целевой
функции, а также отсутствие экстремума с помощью определителей Сильвестра
(3.6.23).
Если:
^>0
Эх2
Э2/? Э2/?
Эх2 Эх,
Э2/?
Эх^х,
=> минимум.
(3.6.24)
Если:
Эх,
Э2/? Э2/?
Эх2 Эх,
э2/? Y
SxjSxj I
=> максимум.
(3.6.25)
174
Глава 3. Численные методы компьютерного моделирования ХТП
Если:
а2/? а2/? Г э2/?
Эх2 Эх2 I Эх, Эх,
=> экстремума нет.
(3.6.26)
3.6.3. Методы оптимизации для решения
экстремальных задач с ограничениями типа равенств
Пусть требуется найти экстремум функции R(x,, х2,..., х„) с п переменными, причем
эти переменные связаны между собой дополнительными условиями вида:
<Р2(х,, х2,.... х„) = 0, j = 1, 2,..., m .
(3.6.27)
(Это часто встречаемая задача оптимизации процессов химической технологии, для
которых Я(х,,х2,...,х„) является критерием оптимальности, а уравнения вида (3.6.27)
представляют собой уравнения математического описания.)
Для данной постановки задачи должно быть выполнено условие m < п. В против-
ном случае, т.е. при m > п, если система имеет решение, то это решение представляет
собой набор дискретных точек, причем решение оптимальной задачи сводится в
этом случае к проверке значений R, вычисленных в этих точках, и экстремальная
задача решается обычным перебором.
Экстремум функции /?(х,,х2,...,х„) с ограничениями вида (3.6.27) носит название
условного экстремума [(экстремум при условии, что выполняются соотношения
(3.6.27)].
Для определения условного экстремума (при т < ri) наиболее просто применить
следующий прием: выразить т переменных (так называемых зависимых перемен-
ных) через остальные (n-т) переменных, т.е. получить соотношения вида:
= ft (Tm+l>Tm+2,-,Х„).
(3.6.28)
Затем подставить эти зависимости в выражение функции Л(х,,х2,...,х„) и полу-
чить функцию:
= хп), /2(х„+1, ..., Х„),..., А,(хт+1, ..., х„), х„+1, хт+2,..., х„] =
= /?'(хт+1,х„+2,...,х„),
(3.6.29)
в которой переменные х„+1,х„+2,...,х„ являются уже независимыми.
Далее находится экстремум функции R’ с (п — т) независимыми переменными
обычными способами, т.е. определяются значения х°+1, х°+2,..., х°, составляющие эк-
стремум функции R" или, что то же самое, R. По известным значениям х°+1, х°+2,..., х°
и по формулам (3.6.28) определяются остальные значения переменных в точке экст-
ремума х°,х°,...,х°. Таким образом, задача определения условного экстремума
R(x„ х2,..., х„) сведена к задаче определения экстремума функции Л*(х„+1, xm+2,..., х„), в
которой переменные хш+1,х„+2,...,х„ являются независимыми.
Однако этот способ решения задачи отыскания условного экстремума обычно
бывает неприменим из-за трудности или невозможности разрешить систему (3.6.27)
относительно переменных в виде (3.6.28). Тогда задачи на условный экстремум ре-
шаются методом неопределенных множителей Лагранжа.
3.6. Оптимизация
175
Метод неопределенных множителей Лагранжа
Пусть 5° = (х°, х°,х°) есть экстремум функции R(xt, х2,х„) при наличии связей
между переменными вида (3.6.27):
<р/х,, х2, х3,..., х„) = 0 (у = 1,.... ти < п), (3.6.30)
т.е. является условным экстремумом.
Запишем необходимое условие существования экстремума функции многих пе-
ременных (3.6.16), предполагая дифференцируемость функции R по всем перемен-
ным:
=0- (3.6.31)
При этом не все дифференциалы dx, являются независимыми, так как на перемен-
ные х, наложены дополнительные условия (3.6.27).
Далее, предполагая, что функции <₽, также дифференцируемы по всем перемен-
ным, запишем полный дифференциал функции ср, в точке экстремума:
d<?, = vL| dx' =0 О' = 1> ••>"’), (3.6.32)
,=1 I dx, 1-о
причем очевидно, что полный дифференциал функции <7<р, равен нулю, так как пра-
вая часть соотношения (3.6.32) равна нулю.
Сделаем следующие конструктивные построения. Умножим каждое из получен-
ных равенств (3.6.32) на некоторый множитель и сложим с соотношением (3.6.31).
При этом получим:
л'=0 (3.6.33)
»-1 I "X, l-о у=1 »=1 I ОХ, 1-о
ИЛИ
*-» <3-6-34’
<=i I dx, dx, dx, dx, l-o
Так как правые части соотношений (3.6.31) и (3.6.32) равны нулю, то и в правой
части соотношений (3.6.33) и (3.6.34) должны стоять нули.
Как мы уже подчеркивали ранее, дифференциалы dx, не все являются независи-
мыми, а только последние (п-т) дифференциалов. Попытаемся исключить т зави-
симых дифференциалов из выражения (3.6.34) таким выбором множителей X,, что-
бы коэффициенты при этих дифференциалах обратились в нуль. Это условие запи-
шется следующим образом:
f—+ Х Эф^ Эф^ Эф/| < = 1,2,...,т. (3.6.35)
I dx, dx,
Левая часть соотношения (3.6.35) представляет собой коэффициент при i-м зави-
симом дифференциале. Очевидно, что соотношение (3.6.35) представляет собой си-
стему из т уравнений, по которой могут быть определены т множителей (если
они существуют).
Из соотношения (3.6.34) исключим нулевые члены (3.6.35). Тогда в этом соотно-
шении останутся только независимые дифференциалы dx, (i = m + l,..., п):
176
Глава 3. Численные методы компьютерного моделирования ХТП
£(|*+Xi|pl + X2|pl + + Л,=о. (3.6.36)
j=/n+ll 0Xt дх, vX| 0Х{ J-o
Но для того чтобы сумма в левой части (3.6.36) равнялась нулю при независимых
(произвольных) dx, (i = m+l,m+2,...,n) достаточно, чтобы коэффициент при каждом
независимом дифференциале был равен нулю, т.е.
^- + Z1^- + Z2|B2- + ... + Zm^| =0; i = т + 1, т + 2,п (3.6.37)
OX, OX, OX, OX, J-c
co значениями А,, определенными по соотношению (3.6.35).
Объединяя равенства (3.6.35) и (3.6.37), получим
3£+х ^L + x ^. + ... + х =о; , = 12,..., л. (3.6.38)
Эх, 1 Эх, 2 Эх, ” Эх, J,-»
Системе (3.6.38) должны удовлетворять как А, (j = 1,2,..., т), так и х° (i = 1,2,..., п).
Кроме того, х° должны удовлетворять системе (3.6.27).
Таким образом, мы получаем систему из (п + т) уравнений для (n + m) неизвест-
ных (т значений и л значений х°).
Для удобства полученную систему (3.6.38) с учётом (3.6.27) запишем в форме
Лагранжа, для чего введем функцию Лагранжа
ф = л + ЕЧч>,. (3.6.39)
Тогда система уравнений (3.6.38) и (3.6.27) примет вид:
Эф'!
— =0, 1 = 1,2,...,л;
Эх,
ЭФ) п . (3.6.40)
--- =0, j = 1, 2,..., т.
ЭЛ. _
Используя данный прием, задача на условный экстремум снова сводится к задаче
определения экстремума функции ф вместо R. При решении системы (п + т) уравне-
ний с (п + т) неизвестными (т значений А, и п значений х°), получаются опти-
мальные значения х° (г = 1,...,л) с учетом ограничений в виде равенств (3.6.27).
3.6.4. Численные методы оптимизации
без ограничений
Если целевая функция не является унимодальной (т.е. имеющей один экстре-
мум), то могут существовать различные типы решений (локальный и глобальный
экстремумы). Для задач, соответствующих действительным физическим параметрам
процессов, целевая функция обычно является приемлемой, так как обладает един-
ственным экстремумом. Поэтому для большинства практических целей локальное
решение задачи не является существенным недостатком. В случае множественных
оптимумов полезны понятия вогнутости и выпуклости при определении того, при
каких условиях локальное оптимальное решение является также глобальным опти-
3.6. Оптимизация
177
мумом. Функция R(x) называется выпуклой в области G, если для любых двух векто-
ров х, и х2 е G
/?(0х, +(1-0)12)<0/?(х,) + (1-0)/?(?2), (3.6.41)
где 0 — скалярная величина, изменяющаяся в диапазоне 0 < 0 < 1. Функция Rix) яв-
ляется строго выпуклой, если для х, *х2 в выражении (3.6.41) не используется знак
равенства.
На рис. 3.45, а изображена строго выпуклая функция одной независимой пере-
менной; выпуклая функция не может принимать значения большего, чем значения
функции, полученной линейной интерполяцией между R(x,) и /?(х2). Если имеет
место неравенство, обратное (3.6.41), то функция называется вогнутой (рис. 3.45, 6).
Дифференцируемая выпуклая функция обладает следующими свойствами:
1)
/?(х,) - /?(х2) > VT/?(x,)(x, -х2)
(3.6.42)
для всех х,,х2, где VR(x,)— градиент функции /?(х) в точке х,:
v/?(x‘)
dR(x')
Эх,
dR(x’)
Эх,
(3.6.43)
2) матрица вторых частных производных /?(х) по х [матрица Гесса — Я(х’)] поло-
жительно определенная (или положительно полуопределенная) для всех х, если /?(х)
строго выпуклая (или просто выпуклая):
Э2/?(х*)
Эх,Эх„
Э2/?(х*)
Эх2
V2/?(x") = Н(х’) =
d2R(x')
дх„Эх,
3) в области G функция /?(х) имеет только один экстремум.
Требование унимодальности функции является значительно более слабым, чем
требование вогнутости или выпуклости, поскольку унимодальность не требует ни
непрерывности, ни единственности производной.
В нелинейном программировании большое внимание уделяется определению не-
обходимых и достаточных условий того, чтобы некоторый вектор решения х’ являл-
ся локальным экстремумом.
Рис. 3.45. Строго выпуклая функция вниз (а) и строго выпуклая функция вверх (б) от одной
независимой переменной
178
Глава 3. Численные методы компьютерного моделирования ХТП
При отсутствии ограничений необходимыми условиями того, что х* — точка ло-
кального минимума, являются:
1) функция /?(х), дифференцируемая в точке х*;
2) v/?(x*) = o, т.е. существование стационарной точки в х*.
Достаточные условия того, что х’ — точка локального минимума (максимума),
кроме условий 1 и 2 включают следующее:
3) v27?(x*)>0 (V 2/?(х*) < 0), т.е. матрица Гесса положительно определенная (отри-
цательно определенная).
Непосредственное использование этих условий связано зачастую со значитель-
ными трудностями и поэтому оптимизационные процедуры носят характер поиска
по следующей общей методике:
1) выбирается некоторая начальная точка х° = (х°, х°,..., х°); выбор этот произво-
лен, зависит от интуиции исследователя и существенно влияет на скорость решения
задачи;
2) по какому-нибудь признаку выбирается направление, в котором ожидается
найти оптимальную точку;
3) в выбранном направлении делается либо один шаг, либо множество шагов в
зависимости от степени их успешности.
Направление в л-мерном пространстве задается с помощью вектора, содержаще-
го л координат, т.е. с помощью л чисел.
( 1 П Г 1 Л
Например, на плоскости пары чисел определяют направления - L ”4’ ~ 2 Г
[i’i] и т'п’ (рис' 3-46).
Таким образом, для любого направления существует пара чисел, которая един-
ственным образом его определяет.
Аналогично определяется направление в л-мерном пространстве как л-мерный
вектор.
Пусть задан некоторый л-мерный вектор s = (s{,s2, . ,s„) и начальная точка
х° = (х“, х°,..., х"), тогда сделать шаг величины L в направлении ? из точки х0 — значит
определить новую точку х1 = (xj, х'2,.., х‘), которая находится от х0 на расстоянии L:
х1 = х° + Ls (3.6.45)
или
х,1 = х,° + Ls, , ; = 1, 2,..., п . (3.6.46)
Существует два подхода при движении по заданному направлению. •
Первый: по заданному направлению делается шаг произвольной длины и, если
полученная точка успешная (движение происходит в направлении оптимума), то в
новой точке определятся новое направление и процедура повторяется (градиентный
метод, релаксационный и т.д.).
Второй: в заданном направлении ищется минимум целевой функции /(х), т.е.
решается задача mmL f (х° + Ls). В найденной новой точке х1 определяется новое на-
правление, и процедура повторяется (метод крутого восхождения, метод Гаусса и т.д.).
Все существующие методы безусловной оптимизации отличаются друг от друга
способом выбора направлений и методом определения необходимого движения в
принятом направлении. По способу выбора направления они разделяются на гради-
3.6. Оптимизация
179
Рис. 3.46. Задание различных направ-
лений поиска при реализации алго-
ритма оптимизации
Рис. 3 47. Графическая иллюстрация
проблемы, связанной с определением
экстремума при поиске оптимума
функции с криволинейным оврагом
ентные и методы поиска, т.е. не использующие градиент. Такое обилие методов
объясняется тем, что все они имеют разную скорость сходимости, и их выбор суще-
ственно зависит от вида оптимизируемой функции.
Так, например, простая на вид функция (полином 4-го порядка)
/(х,, х2) = 100(х2 - х, )2 + (1 - х, )2
имеет следующий вид (рис. 3.47), где сплошные линии (линии уровня) обозначают
точки, в которых /(х,,х2) = const. Пунктирная линия обозначает «дно» оврага, вдоль
которого функция убывает очень слабо, зато на стенках она убывает сильно, что
создает значительные трудности при отыскании экстремума. Поэтому любой метод с
применением поиска в одном направлении «скатывается» на «дно» оврага и медлен-
но движется вдоль него.
Прямые методы поиска экстремума функции одной переменной
Прямые методы в качестве критерия движения к экстремуму используют сравни-
тельную оценку величины целевой функции, вычисленной в соответствующих точ-
ках. Следует отметить, что прямые методы поиска экстремума функции одной пере-
менной имеют не только самостоятельное значение, но и широко используются как
вспомогательные методы при поиске экстремума функции многих переменных.
Метод сканирования
Интервал поиска [х„„,х„„] разбивается на п равных участков, длина каждого из
которых равна шагу поиска h (рис. 3.48). Далее последовательно определяется значе-
ние функции во всех точках разбиения и в точках х,„т и х„„ и запоминается наи-
меньшее значение. Таким образом, экстремум может быть найден с точностью до
шага поиска. Основным достоинством метода является его простота и возможность
нахождения глобального экстремума. Недостатком метода является большой объем
вычислений, которые необходимо выполнять при его реализации.
180
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.48. Графическая иллюстра-
ция метода сканирования
Рис. 3.49. Графическая иллюстрация
метода локализации экстремума
Метод локализации экстремума
Метод локализации представляет собой модификацию метода сканирования. При
его использовании существенно снижается количество выполняемых вычислений.
Весь интервал поиска как и в методе сканирования, разбивается на
несколько частей (подынтервалов) точками xt,x2 и х3, но более крупных размеров
(рис. 3.49).
Вычисляется значение критерия /?(х) во всех точках разбиения и в точках х„„„ и
хт<а. Все значения /?(х) сравниваются между собой и из них оставляется наименьшее,
если ищем минимум, и наибольшее, если ищем максимум. Далее выбирается новый
интервал поиска, равный двум подынтервалам, с наименьшим (наибольшим) вычис-
ленным значением R на их общей границе (на рисунке это соответствует интервалу
[х„,„,х2]). Этот интервал меньше исходного, и в нем локализован экстремум. Затем
поступают следующим образом. Интервал, в котором локализован экстремум, делят
на несколько подынтервалов (на рисунке точками 7 и 2) и снова вычисляют значе-
ния критерия оптимальности в точках деления. Сравнивают их между собой, нахо-
дят наименьшее, локализуют экстремум в меньшем интервале (на рисунке в интер-
вале 7—2) и т.д. до тех пор, пока экстремум не будет локализован в интервале, размер
которого соответствует заданной точности поиска.
Наилучшие результаты поиска получаются в том случае, когда первоначальный
интервал х„„] разбивается на четыре подынтервала (и = 4). При этом каждый
последующий подынтервал делится пополам, и вычислять значение функции нужно
только в двух новых точках, так как ее значения на концах нового интервала и в его
середине известны из предыдущих расчетов.
Абсолютная ошибка в нахождении экстремума в этом случае определяется выра-
жением:
д = (т„„-^т,л)-2 2 , (3.6.47)
где s — количество точек, в которых вычисляется значение критерия оптимальности.
Так, при 5 = 21 относительная ошибка составит:
--------= 2"10 = 0,001. (3.6.48)
3.6. Оптимизация
181
Метод золотого сечения
а
^88888
b с
Рис 3 50. Графическая
иллюстрация правила
золотого сечения
В основе этого метода лежит правило геометрического
отношения или золотого сечения:
а b ,
- = - или ас = Ъ , (3.6.49)
о с
где а — длина всего отрезка; b — длина его большей части;
с — длина его меньшей части.
В соответствии с этим законом определяются точки ис-
следуемого интервала, в которых необходимо производить
вычисление целевой функции R.
Из рис. 3.50 следует, что:
с = а-Ь- (3.6.50)
Тогда, подставляя в (3.6.49) соотношение (3.6.50) получим:
a(a-b) = b2. (3.6.51)
Обозначив отношение Ыа = к и подставив его в (3.6.51), получим:
а2к2 + а2к-а2 =0, (3.6.52)
откуда следует:
*2+*-1 = 0. (3.6.53)
Решение этого уравнения дает:
Й88888|88888888888888888|
Поскольку к > 0, то его значение принимается равным:
Л = ~1^ = 0.62. (3.6.55)
Порядок поиска экстремума методом золотого сечения будет следующий.
На исследуемом интервале определяются две точки (рис. 3.51):
Xi = хтт + к2 а:
х2 = х„„ + ка,
где а - длина интервала .
В точках %, и х2 рассчитываются значения
целевой функции R. По найденным значени-
ям /?(х,) и R(x2) определяется подынтервал, в
котором локализован экстремум. Этот подын-
тервал состоит из двух подынтервалов не рав-
ной длины.
На рис. 3.51 минимальное значение будет
/?(%,) в точке х,. Подынтервал, в котором ло-
кализован экстремум, будет [х„„,х2]. Далее
внутри большего подынтервала (в нашем при-
мере внутри [л,,»,,*,]) находится точка, отстоя-
щая от общего конца интервала на расстояние
(3.6.56)
Рис. 3.51. Графическая иллюстрация
метода золотого сечения
182
Глава 3. Численные методы компьютерного моделирования ХТП
кгЬ, где b — длина подынтервала, в котором локализован экстремум [хт,„, х2], причем
Ь = ка.
В нашем примере это будет
= хт,„ + к2(ка) = хтт + к'а (3.6.57)
Нетрудно заметить, что величина интервала [х,, х2] также равна к3а. В самом деле,
величина х2]) равна ка, тогда величина (х, -х,) будет определяться:
ka-k1a = ka{i-k) = k3a, (3.6.58)
так как (1-Л) из уравнения (3.6.53) равно кг.
Таким образом, (х2 -х,) = (х3 -х„„), следовательно, рассчитывать длину интервала
[х„„„,х3] нет необходимости.
Далее вычисляется Я(х3), и сравниваются значения Л(х2), Я(х,) и Л(х3). Находит-
ся минимальное [в примере Я(х3) ] и процедура продолжается до достижения требу-
емой точности.
Абсолютная ошибка в определении экстремума после 5 вычислений будет:
А = (3.6.59)
2 I 2 I
и для 5 = 21 относительная ошибка есть:
--------= 1-0.6218=0.9 10-4) (3,6.60)
X max X тт ~
т.е. точность расчета значительно превосходит точность расчета по методу локализа-
ции при одном и том же количестве вычислений.
Метод поиска с использованием чисел Фибоначчи
Последовательность чисел Фибоначчи, определяемая реккурентным соотношением
Г = TO = F,=1, (3.6.61)
может быть использована для организации поиска экстремума функции одной пере-
менной. Причем абсолютная погрешность, возникающая при поиске этим методом,
не превышает величины
А = , (3.6.62)
где Fs — s-e число в последовательности чисел Фибоначчи.
Таблица этой последовательности до 5 = 12 приведена ниже:
5 1 2 3 4 5 6 7 8 9 10 11 12
F 5 1 2 3 5 8 13 21 34 55 89 144 233
При выполнении 5 = 21 вычислений точность определения экстремума составляет
% jr- = y-S0.56.10\ (3.6.63)
лтах Лтт 1 21
т.е. оказывается еще более высокой, чем в методе золотого сечения.
3.6. Оптимизация
183
Ниже приведен порядок поиска эк-
стремума с использованием чисел Фи-
боначчи.
1. По заданной точности Д поиска рас-
считывается вспомогательное число:
= (3.6.64)
2. Находится число Фибоначчи Fs,
такое, что:
FS,<N<FS. (3.6.65)
3. Определяется минимальный шаг
поиска:
Рис. 3.52. Графическая иллюстрация метода
с использованием чисел Фибоначчи
hmm = Х""":. Х"“" . (3.6.66)
4. Рассчитывается значение R в точке, определяемой соотношением:
=хт„ +hm,„Fs_2. (3.6.67)
5. Рассчитывается значение R в точке, определяемой соотношением:
x2=x,+hm,„Fs_3. (3.6.68)
6. Если шаг оказался удачным, т.е.
R(x2) < R(x,), (3.6.69)
то рассчитывается значение R в точке, определяемой соотношением
• (3.6.70)
Если шаг оказался неудачным, т.е. r(x2)>R(xt), то х3 определяется по соотно-
шению
хз ~ •’>1 ~ V.C 4. (3.6.71)
Процедура продолжается последовательно до тех пор, пока не будут исчерпаны
все числа Фибоначчи в убывающей последовательности.
На рис. 3.52 показана процедура поиска при д = 21 (s = 7), что отвечает точности
поиска порядка 5%.
Метод Дэвиса, Свенна, Кемпи (ДСК) и метод Пауэлла
В отличие от известных методов (золотое сечение, числа Фибоначчи и т.д.) наи-
более эффективными оказываются методы, в группе которых текущая точка х вбли-
зи х" (оптимальная точка) определяется с помощью экстраполяции и интерполяции.
В качестве примера рассмотрим два алгоритма: Дэвиса, Свенна и Кемпи (алгоритм
ДСК) и метод Пауэлла.
При одномерном поиске по алгоритму ДСК проводятся возрастающие по величи-
не шаги до тех пор, пока не будет пройден минимум, а затем выполняется квадра-
тичная интерполяция.
Алгоритм поиска следующий.
Шаг 1. Вычислить R(x) в начальной точке х,.. Если R(x0 + Дх) < R(x0), то возврат на
шаг 2, в противном случае Дх = -Дх.
Шаг 2. Вычислить х(Л+1) = х„ + Дх.
Шаг 3. Вычислить R(x(t+1)).
Шаг 4. Если R(x(1+I)) R(xJ, удвоить Дх и вернуться к шагу 2 при k = k+l. Если
184
Глава 3. Численные методы компьютерного моделирования ХТП
Рис. 3.53. Графическая иллюстрация метода ДСК
Л(х(4+,))>Л(х4), обозначить x(t+1)
через х„,хЛ=х„_1 и т.д. Умень-
шить Дх пополам и вернуться к
шагам 2, 3 для еще только одного
вычисления.
Шаг 5. Из четырех равностоя-
щих значений х = {х„+,, х„, х„_,, х„_2}
исключить либо х„, либо х„_2 в
зависимости от удаленности зна-
чения К(х) от наименьшего зна-
чения К(х). Пусть х“,хь и хс ос-
тавшиеся три значения х, где
х‘ - центральная точка, а
х“ =х‘ -Дх; Xе =хь +Дх.
Шаг 6. Провести квадратичную интерполяцию для определения х*, обеспечива-
ющей минимум параболы, проходящей через х“,х‘ и хе:
। Дх[Я(х“)-Я(хг)]
2[R(x“)-2R(x‘) + R(xc)] ’
На этом заканчивается первый этап метода ДСК. При желании процедуру можно
повторить из точки х‘ или хе, если R(xc)<R(x'), уменьшив Дх (рис. 3.53).
В алгоритме Пауэлла квадратичная аппроксимация проводится путем использо-
вания первых трех точек, полученных в направлении поиска. Затем определяется
точка у’, соответствующая минимуму квадратичной функции. Такая квадратичная
аппроксимация продолжается до тех пор, пока с требуемой точностью не обнаружи-
вается экстремум К(х).
Алгоритм Пауэлла строится следующим образом (рис. 3.54).
Шаг 1. От начальной точки х(,) нужно перейти к х(2) =х(1) +Дх.
Шаг 2. Вычислить Л(х(”) и /?(х(2>).
Шаг 3. Если К(х(1)) > Я(х<2)), положить х<3) =х(1)+2Дх.
Если R(x(1’)< Я(х'2’), положить х(3) = х(1) - Дх.
Шаг 4. Вычислить R(x<3)).
Шаг 5. Вычислить приближенное значение х в точке минимума R(x) по следую-
щей формуле:
_ 1 [(х(2>)2 - (Х(3>)2]/?(х(1>) + [(Х(3>)2 - (х(|))2]/?(х(2>) + [(х(1))2 - (х(2>)2]R(x(3))
Х ~ 2 (хт -x(3,')R(x(',) + (x(3’ -x('>)R(x(2>) + (x(', -xm)R(x(3>')
Шаг 6. Если и любое из значений х = {х(1), х(2), х<3)}, соответствующих миниму-
му R(x), отличаются друг от друга меньше, чем на заданную точность, то закончить
поиск. В противном случае, вычислить R(x*) и исключить из множества {х(1),х(2),х(3)}
то значение х, которое соответствует наихудшему (наибольшему, см. рис. 3.54) зна-
чению R(x), однако если, при этом не будет потерян интервал, в котором находится
3.6. Оптимизация
185
экстремум Rix). В этом случае сле-
дует исключить х так, чтобы со-
хранялся этот интервал. Перейти
к шагу 5.
Наиболее эффективной оказа-
лась комбинация методов ДСК и
Пауэлла. Комбинированный алго-
ритм ДСК—Пауэлла состоит из
одного этапа (шаги с 1 по 6) алго-
ритма ДСК, на котором опреде-
ляется интервал, включающий эк-
стремум Rix), шага 6 алгоритма Рис. 3.54. Графическая иллюстрация метода
Пауэлла и затем, если это необ- Пауэлла
ходимо, шагов 5 и 6 алгоритма Пауэлла.
Прямые методы поиска экстремума функции многих переменных,
не использующие производные (методы нулевого порядка)
Метод сканирования
Как и в случае одной переменной, метод сканирования для случая многих пере-
менных заключается в последовательном просмотре значений критерия оптималь-
ности в ряде точек, принадлежащих области изменения непрерывных переменных, и
нахождении среди них такой, в которой критерий оптимальности имеет минималь-
ное (максимальное) значение. Точность метода определяется тем, насколько плотно
располагаются выбранные точки.
Метод заключается в следующем. Исследуется целевая функция вдоль одного
выбранного направления (вдоль одной из координатных осей) с шагом h,. В каждой
точке вычисляется и запоминается значение целевой функции. После того как весь
диапазон изменения этой переменной исследован и для него найдено минимальное
(максимальное) значений целевой функции, изменяется значение другой перемен-
ной на величину шага и опять исследуется диапазон первой переменной, в кото-
ром снова определяется искомый экстремум, и т.д. После нахождения всех экстре-
мумов находится искомый глобальный экстремум.
Графическое представление поиска экстремума для случая двух переменных при-
ведено на рис. 3.55.
Для произвольного числа переменных
шаг по каждой следующей переменной
производится после того, как завершен
цикл по предыдущей.
Если имеются ограничения, то точки,
которые не удовлетворяют уравнениям
(или неравенствам) ограничений исклю-
чаются, и в них не вычисляются значе-
ния критерия R. Однако каждую точку
требуется проверять относительно огра-
ничения. Если переменных много, то та-
кого рода проверка также требует д литель-
ного времени. Прием проверки ограни-
чений типа равенств может быть пред-
ставлен в следующем виде:
Рис. 3.55. Графическое представление
поиска экстремума для случая двух перемен-
ных методом сканирования
186
Глава 3. Численные методы компьютерного моделирования ХТП
х, = f(.xl,x1,...,x1_l,x^l,...,xj, (3.6.72)
при этом поиск ведется по (п-1) переменной, а значение рассчитывается из соот-
ношения (3.6.72). Разумеется, что х, должно проверяться на допустимый диапазон
его изменения.
Если относительная точность поиска равна е по каждой из переменных, то количе-
ство вычислений целевой функции, необходимых для поиска экстремума, составит
S=(l/s)“, (3.6.73)
где п — число переменных.
Этот метод имеет существенный недостаток, связанный с тем, что число вычис-
лений при определении положения оптимума очень велико и возрастает в показа-
тельной степени от размерности решаемой задачи. Преимущество метода — просто-
та, возможность определения глобального экстремума. Метод может быть использо-
ван для грубого анализа областей расположения экстремумов.
Метод поочередного изменения переменных (метод Гаусса—Зейделя)
Рис. 3.56. Путь поиска методом поочередно-
го изменения переменных
В этом методе движение к оптимуму
происходит по каждой из осей до част-
ного экстремума. Они чередуются. Путь
поиска показан на рис. 3.56.
Первая ось, по которой осуществля-
ется поиск минимума (максимума), вы-
бирается произвольно. Частный экстре-
мум (по одной переменной) может быть
найден любым из методов поиска экст-
ремума функции одной переменной.
После того как найден частный мини-
мум (максимум) по первой оси, начинает-
ся поиск минимума (максимума) по вто-
рой оси при условии, что значение первой
переменной равно найденному минимуму
(максимуму) на первой оси. Далее определяется минимум (максимум) на второй оси и, с
учётом изложенного, осуществляется поиск по третьей, четвертой и т.д. оси. Процесс
последовательно продолжается до тех пор, пока не будет достигнута заданная точность
локализации экстремума, т.е. если шаг по каждой из осей приводит к возрастанию функ-
ции, а величина шага меньше или равна заданной точности поиска, то расчет закончен.
Метод пробных движений
В этом методе дается приращение по всем переменным
хГ' = х/+Дх/+1, (3.6.74)
где i — номер переменной; у — номер шага, и вычисляются значения целевой функции.
Из всех опробованных направлений выбирается то, в котором уменьшение (увели-
чение) целевой функции наибольшее. В этом направлении делается рабочий шаг h,
больший Дх/*1, и находится новая точка, из которой делаются пробные движения.
Процедура повторяется до достижения заданной точности поиска.
3.6. Оптимизация
187
Поиск по деформируемому многограннику
Поиск по деформируемому многограннику (метод Нелдера и Мида) основан на ис-
пользовании нерегулярных многогранников (деформируемых симплексов). Для случая
двух переменных регулярный симплекс — равносторонний треугольник (три точки); в
случае трех переменных — тетраэдр (четыре точки) и т.д. (рис. 3.57).
При поиске минимума целевая функция может быть вычислена в каждой из вер-
шин симплекса: из вершины, где целевая функция максимальна (точка А) проводит-
ся проектирующая прямая через центр тяжести симплекса. Затем точка А исключа-
ется и строится новый симплекс, называемый отраженным из оставшихся прежних
точек и одной новой точки В, расположенной на проектирующей прямой на задава-
емом расстоянии от центра тяжести.
Наличие оврагов и хребтов целевой функции приводит к необходимости изме-
нять размеры и форму симплекса в процессе поиска.
В методе Нелдера и Мида минимизируется функция п независимых переменных
с использованием (л + 1) вершин деформируемого многогранника. Каждая величина
идентифицируется вектором х. Вершина, в которой значение R(x) максимально,
проектируется через центр тяжести оставшихся вершин. Улучшенные значения це-
левой функции находятся последовательной заменой точки с максимальным значе-
нием R(x) на более «хорошие» точки, пока не будет найден минимум R(x).
Алгоритм метода Нелдера—Мида является следующим.
Пусть х,<4) =[x'*),...,л-'*,,...,Д*,]т, i = l,..., п + 1 является /-й вершиной (точкой) в
л-мерном пространстве Е" на Л-м этапе поиска k = 0,1,..., и пусть значение целевой
функции в х,<4) равно R(x,"’). Кроме того, отметим те векторы х многогранника,
которые дают максимальное и минимальное значения R(x).
Определим
R(^’) = max(R(x1(l,),...,R(x<V1)}, где 1</г<п + 1, (3.6.75)
И
R(x/,) = mm{R(x,w),...,R(x„<‘;)}, где 1<(<п + 1- (3.6.76)
Пусть — центр тяжести всех вершин, исключая xf’. Тогда координаты этого
центра тяжести определятся формулой:
;=1> о-6-77)
п I" I
где j — координатное направление.
Начальный многогранник обычно выбирается в виде регулярного симплекса с
точкой 1 в качестве начала координат. Процедура отыскания minR(x) состоит из
следующих операций.
1. Отражение — проектирова-
ние х(^ через центр тяжести в
соответствии с соотношением
^=е2+а(^-хГ), (3-6.78)
где а > 0 — коэффициент отраже-
ния; х^г — центр тяжести (3.6.77).
2. Растяжение. Если
R(x„®)^R(x,<‘)), то вектор
(x^3_x'4j) растягивается в соот-
ветствии с соотношением
Центр тяжести Центр тяжести
Рис. 3.57. Графическая иллюстрация определения
новых точек при поиске по деформированному
многограннику
1
188 Глава 3. Численные методы компьютерного моделирования ХТП
= (3-6.79)
где у>1 — коэффициент растяжения. Если К(х!„к^) < Rix',1''), то %<*’ заменяется на х^ и
процедура продолжается снова с операции 1 при k = к +1. В противном случае
заменяется на х£’3 и также осуществляется переход к операции 1 при к = к +1.
3. Сжатие. Если R(x‘„l,3) > Я(х,(‘’) для всех то вектор (х[к’-х^2) сжимается в
соответствии с формулой
Ж = Ж +Р(^’-^), (3-6.80)
где о < р < 1 — коэффициент сжатия. Затем х'1’ заменяется на и происходит воз-
врат к операции 1.
4. Редукция. Если К(х^)>/?(%/’), все векторы (x,<J:) -х)*1) для / = 1,...,л + 1 умень-
шаются в два раза с отсчетом от по формуле
х^ = х)1’+ 0.5(х/’- x,'l)), z=l,..., п + 1. (3.6.81)
Затем осуществляется переход к операции 1. Критерий окончания поиска, использо-
ванный Нелдером и Мидом, имеет следующий вид:
где е — произвольное малое число.
Деформируемый многогранник адаптируется к топографии целевой функции, вы-
тягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых
впадинах и сжимаясь в окрестности минимума.
Методы случайного поиска
В основе методов случайного поиска лежит стратегия нахождения экстремума
функции путем перебора совокупностей случайных значений независимых перемен-
ных. Эти методы, получившие общее название методов Монте-Карло, успешно при-
меняются с использованием вычислительных машин для решения задач обращения
матриц, нахождения собственных значений и собственных векторов матриц, реше-
ния систем алгебраических уравнений и целого ряда других задач. Общим для всех
методов случайного поиска является генерирование и использование случайных чи-
сел в процессе поиска, отличием — стратегия движения к экстремуму.
Из методов случайного поиска наибольшее распространение получил метод
случайного направления. При использовании этого метода очередное приближение
определяется соотношением
х)‘+” =х,(‘’+/г<‘,р;‘’, /=1,2,..., л, (3.6.83)
где й<4) — параметр шага; р, — компонент случайного вектора р.
Если значение функции /(х<л+1)) в новой точке оказывается меньше предыдущего
/(х<Л)), то в качестве очередного приближения принимаются последние значения
неизвестных х(М>, в противном случае остаются предыдущие значения х(*’. Проце-
дура генерирования случайного направления (вектора p(t)) повторяется до тех пор,
пока не будет найден экстремум функции.
Известно несколько модифицированных методов случайного поиска. Так, на-
пример, метод случайных направлений с обратным шагом рекомендует при неудач-
ном шаге делать сразу же шаг в обратном направлении, равном — hwpw, что позволя-
I
3.6. Оптимизация
189
ст существенно сократить время поиска. Если и обратный шаг окажется неудачным,
то можно из предыдущей точки сделать новый шаг, сгенерировав новый случайный
вектор направления, или перейти к поиску с меньшим значением шага.
Прямые методы поиска экстремума функции многих переменных,
использующие производные (методы первого и второго порядка)
Методы оптимизации с использованием производных, как правило, более эф-
фективны в смысле скорости сходимости, чем методы, не использующие производ-
ные. Они делятся на методы первого и второго порядка, в которые соответственно
используются первые и вторые производные. Проблема, однако, состоит в том, что
на практике редко удаётся аналитически вычислить первые, не говоря уже о вторых
производных. В свою очередь, приближённый расчёт производных численными ме-
тодами (см. разд. 3.4) трудоёмок и трудно оценить погрешность полученных при
этом результатов.
Метод градиента
К градиентным методам относится совокупность методов, стратегия движения к
экстремуму в которых основана на вычислении значений частных производных це-
левой функции й(л1,х2,...,х„) и которые являются компонентами градиента:
_ ___ dR - dR-.
VR(x) = gradR(x~) — + + эх (3.6.84)
где 7 — единичные векторы для соответствующих осей координат.
Известно, что градиент (3.6.84) является вектором, который определяет направление
наискорейшего возрастания целевой функции Л(х)( в противоположность антиградиенту,
определяющему направление наискорейшего убывания целевой функции R(x)).
Координаты новой точки в результате шага, выполненного по направлению век-
тора градиента из точки с координатами х* =(x1,,xj,...,x'), определяются:
X,=X,+hdT(x ); 7 = 1’"’л (3.6.85а)
или с учётом нормировки с использованием нормы градиента ||v/?(x)||:
ЭЯ
—(X )
х =x’+h-$=r——j = l, ...,п, (3.6.856)
|v«(x)||
где h и h - факторы шага.
При этом норма градиента ||vK(x)|| определяется по формуле:
||v/?(i)|| = ||gr^(I)|| = +^2+...+^ ) (3.6.86)
dR dR dR
где и^“ _ компоненты градиента.
Одним из важных свойств градиента функции gradR(x) является то, что он на-
правлен по нормали к линиям постоянного уровня целевой функции Я(х) (рис. 3.58).
Поскольку градиент функции дает направление, в котором функция возрастает с
максимальной скоростью, то направление градиента применяется для поиска экст-
190 Глава 3. Численные методы компьютерного моделирования ХТП
*0
Рис. 3.58. Траектория поиска экстре-
мума методом градиента
ремума в методах, использующих вычисление
частных производных целевой функции.
В этом методе поиск экстремума функции
осуществляется последовательно — шагами в
направлении градиента.
Алгоритм поиска имеет вид:
х/+1=х/+Л2^-, (3.6.87)
Эх,
где индекс i — номер переменной; индекс j —
номер шага поиска.
Итак, в начальной точке поиска
х° = (х°, х°,...,х°) вычисляется градиент функ-
ции, а затем находятся координаты положе-
ния точки х1 = (х!,х2,.... х'„):
1 0 . , /-о\
х, = %1 + ” Эх” ’
1 0 . г. dR /—0)
х2 = х2 + п——tx I;
Эх,
(3.6.88)
В полученной точке х* = (х‘, х'г,..., х^) снова вычисляется градиент функции и находит-
ся точка х2 = (х2, х2.х2), координаты которой получаются по тому же алгоритму (3.6.87):
2 1 , ЭК \
х, =%1 +АэГ''%
2 1 , ЭК
х2 = х2 + н-^-\х );
Величина h обычно выбирается либо постоянной, либо пропорциональной зна-
чению производной в данной точке и носит название фактора шага. Траектория
поиска показана на рис. 3.58. Процесс продолжается до тех пор, пока экстремум не
будет найден с достаточной точностью, т.е. пока не будут выполнены неравенства
К(х1<+1,х'+1,...,х'+1)<К(х1',х',...,х');
I (3.6.90)
где е, — заданная точность поиска.
Метод наискорейшего спуска
Метод наискорейшего спуска напоминает метод градиента, т.е. в исходной точке
определяется направление наискорейшего возрастания функции (градиент). Затем
вдоль этого направления делается не один шаг, как в методе градиента, а продолжа-
3.6. Оптимизация
191
ется движение до нахождения максимума вдоль
этого направления. Затем в точке максимума
вновь определяют градиент, и осуществляется
движение в направлении этого градиента до
частного максимума и т.д. до тех пор, пока не
находится абсолютный максимум функции
цели (путь движения к максимуму изображен
на рис. 3.59).
Направление, противоположное нормиро-
ванному (единичному) градиенту й(х), т.е. на-
правление наискорейшего спуска, определяется
в точке x(i> по формуле:
х0
Рис. 3.59. Путь поиска экстремума
методом наискорейшего спуска
||VX(x“>)|| ’
(3.6.91)
где — единичный вектор в направлении градиента V/?(x<l>) и, соответственно, Дх1*’.
На к-м этапе переход из точки x(i> в точку х(‘+1> описывается как:
x(t+1> = x(t> - Дх“> = = I(i> -Vfl(xrt)) • (3.6.92)
Подстановка (3.6.91) в (3.6.92) дает следующее соотношение для метода наиско-
рейшего спуска:
)|WW)| ’ ( }
но поскольку выражение ||v«(x(t’)|| скалярная величина, то оно может быть заме-
нено некоторым числом к*'1*, т.е.
X“+1> = х(Л> - k‘mVR(xm) • (3.6.94)
Поиск в соответствии с (3.6.94) осуществляется многократно, причем для каждо-
го направления градиента осуществляется минимизация функции K(x(i>). Это может
осуществляться формально также [см. (3.6.91) — (3.6.93)] путем вычисления x(i> из
уравнения:
(3.6.95)
dk
Но чаще используют тот или иной метод одномерного поиска для определения вели-
чин V1' или г'1’, минимизирующей на к-м шаге поиска целевую функцию.
Метод наискорейшего спуска позволяет найти экстремум при минимальном объеме
вычислений. Метод особенно выгодно использовать в том случае, когда градиент
функции изменяется не резко. Очевидно, что вблизи экстремума метод наискорей-
шего спуска вырождается в метод градиента. В качестве критерия окончания поиска
можно использовать те же критерии, что и в методе градиента.
Метод релаксаций
Метод также использует производные, в частности, первые производные целевой
функции и состоит в нахождении осевого направления, вдоль которого целевая фун-
кция возрастает наиболее быстро. Для этого в начальной точке поиска определяются
производные функции по всем переменным Эй/Эх,. По той оси, вдоль которой про-
192
Глава 3. Численные методы компьютерного моделирования ХТП
изводная наибольшая, и производится движение до частного минимума одномер-
ным методом поиска. Затем анализ производных вновь повторяется. Критерием окон-
чания поиска может служить следующее положение: если при движении из очеред-
ной точки не наблюдается дальнейшее возрастание целевой функции, то максимум
найден.
Алгоритм поиска при методе релаксаций имеет вид:
, ,, (dR
xl = х/+й;-^ — I (3.6.96)
где х/ — значение переменной, по которой происходит оптимизация на данном шаге
у =
1, если у > 0;
0, если у = 0;
-1, если у < 0,
(3.6.97)
a h1 — фактор шага, величина которого изменяется в процессе поиска.
Обычно шаг выбирается так: вначале он принимается равным числу Л1 = 8, затем
делается еще один шаг в этом направлении h1 = Л1; если шаг оказался успешным, то
он удваивается h3 =2h2. Если же следующий шаг оказался не успешным, то из пре-
дыдущей точки, в которой был удачный шаг, делаются шаги в 2 раза меньше, чем
последний удачный. Уменьшение величины шага в области максимума производит-
ся до заданного значения, определяемого желаемой точностью.
Метод релаксаций можно рассматривать как комбинацию методов, использую-
щих производные.
Метод Ньютона
Направление поиска, соответствующее наискорейшему спуску, можно интерпре-
тировать как следствие линейной аппроксимации целевой функции. С другой сторо-
ны, методы вторых производных (метод Ньютона) возникли из квадратичной апп-
роксимации К(х), определяемой следующим уравнением:
/f(x(‘t,)) = /f(x(‘>) + VT/f(x(‘))^<‘) + |(Ax(‘>)TV2/f(x‘‘))Ax(‘>. (3.6.98)
Используя (3.6.98), минимум «(х) в направлении &х(к> определяется дифферен-
цированием R(x) по каждой из компонент Дх и приравниванием к нулю полученных
выражений, что приводит к следующему уравнению:
Г=2 Т1 —
дг<‘> =- V «(х(‘>) VR(x(t>), (3.6.99)
где [vW4’)?1 — матрица, обратная матрице Гесса H(x<4>) (3.6.44).
Подставляя (3.6.99) в (3.6.92), получаем:
х“И) = x^-Jv'/fCx»’] V«(x<4>). (3.6.100)
Здесь и направление, и величина шага точно определены. В случае, если й(х) —
квадратичная функция, то для достижения минимума достаточно одного шага. Но в
общем случае минимума достичь за один шаг нельзя, и поэтому уравнение (3.6.100)
обычно приводят к виду (3.6.93) путем введения специального параметра длины шага:
х(‘+,) = . (3.6.101)
3.6. Оптимизация
193
Отношение Х<4) /|[V2R(xa))] 1[VJ?(x<*,)]|| — некоторая скалярная величина , поэто-
му (3.6.101) чаще приводят к виду:
х“+,) =x<t>-r<t,H"l(x<i>)VR(xw). (3.6.102)
Здесь направление поиска задается вектором:
= -н ‘(х(‘>)VK(x“>). (3.6.103)
Применение подобных методов, использующих для определения экстремума вто-
рые производные, довольно затруднительно, хотя они и обладают при прочих рав-
ных условиях очень высокой эффективностью.
Необходимо отметить следующие недостатки метода Ньютона.
1. Необходимо обращать матрицу Гесса Н(х), и поэтому используемая процедура
решения должна обеспечивать положительную определенность обратной матри-
цы (3.6.23).
2. Требуется аналитическое вычисление вторых частных производных целевой
функции.
Анализ методов решения задач нелинейного программирования при отсутствии ог-
раничений приводит к выводу, что градиентные методы и методы, использующие
вторые производные, сходятся быстрее, чем методы поиска экстремума, не исполь-
зующие производные. Тем не менее, применяя на практике методы, использующие
производные, приходится сталкиваться с двумя главными препятствиями.
Во-первых, в задачах с большим количеством переменных довольно трудно или
практически невозможно получить производные в виде аналитических выражений,
необходимых для алгоритмов, использующих градиент или вторые производные.
Хотя вычисление аналитических производных можно заменить вычислением с
помощью разностей, возникающая при этом ошибка может ограничить применение
подобной аппроксимации в случаях оврага и в окрестности минимума.
Во-вторых, градиентные методы требуют регулярности и непрерывности целевой
функции, т.е. существования непрерывных частных производных.
К недостаткам градиентных методов по сравнению с методами поиска можно
отнести количество затраченного времени при подготовке задачи к решению.
Вследствие вышесказанного, методы прямого поиска нулевого порядка, не ис-
пользующих производные, оказываются зачастую более удовлетворительными с точ-
ки зрения их использования, чем градиентные.
3.6.5. Численные методы оптимизации
при наличии ограничений
Все методы оптимизации при наличии ограничений делятся на два класса: мето-
ды сведения к задаче безусловного экстремума без ограничений и методы прямого
решения задач с ограничениями.
Среди методов, сводящих задачу с ограничениями к безусловной оптимизации,
наиболее широко распространены методы штрафных функций.
Методы штрафных функций
При решении задач оптимизации химико-технологической системы существует,
как правило, как ряд ограничений типа равенств (например, значения потоков в
местах разрывов в схемах с обратной связью), так и ограничения типа неравенств
(например, технологические ограничения по диапазону концентраций, температур,
давления и т.д.).
13-4544
194
Глава 3. Численные методы компьютерного моделирования ХТП
Тогда в общем виде задачу можно сформулировать следующим образом:
минимизировать
Я(х),
тш
при ограничениях
(3.6.104)
4>(x) = 0, i = l, т;
g,(x) >0, i = т + 1, ..., р
В основу методов штрафных функций положена идея преобразования общей нели-
нейной задачи (3.6.6) в последовательность задач без ограничений (3.6.1) путем добав-
ления к целевой функции одной или нескольких функций, задающих ограничения с
тем, чтобы ограничения, как таковые, в задаче оптимизации не фигурировали.
Например, необходимо минимизировать функцию
R(x) = ах + Ь, где х0 < х < х,.
(3.6.105)
Графически это изображено на рис. 3.60. Ясно, что ограничение х, должно сдер-
живать любой шаговый метод поиска, такое ограничение называется активным.
Одним из наиболее простых методов штрафа является изменение целевой функ-
ции с тем, чтобы образовать локальный экстремум в окрестности активного ограни-
чения. С этой целью формируется новая целевая функция (штрафная функция):
Р(х) = ах + Ь + (х-х,)2 •
(3.6.106)
Тогда целевая функция будет иметь вид, показанный на рис. 3.61, и методом
Рис. 3.60. Графическая иллюстра-
ция целевой функции (3.6.105) при
поиске оптимума без использова-
ния метода штрафных функций
прохождения безусловного экстремума можно оп-
ределить точку оптимума. Однако, как видно из
рис. 3.61, получается точка, отстоящая от грани-
цы и, следовательно, от точного решения на ве-
личину (х, -х*), что не всегда удовлетворяет точ-
ности решения задачи.
Для того, чтобы удовлетворить точности, не-
обходимо ввести некоторый множитель ц, кото-
рый называется весовым коэффициентом (ц>1).
Тогда целевая функция примет вид как пока-
зано на рис. 3.62, из которого видно, что с увели-
Рис. 3.61. Графическая иллюстра-
ция целевой функции (3.6.106) при
поиске оптимума с использованием
метода штрафных функций
чением ц х' —► х,, т.е. выполняется наперед задан-
ная точность.
Аналогично можно ввести штрафную функ-
цию для ограничений в виде равенств, тогда обоб-
щенный критерий оптимизации для задачи типа
(3.6.104) примет вид:
P(x) = R(x) + ^,tf(x) + £u,g?(x), (3.6.107)
/=1
где и,, i = l,2,..., р — весовые коэффициенты, а
и — оператор Хевисайда, который принимает зна-
чения 0 и 1, если в точке xt gSxky>0 и 1, если
£,(**) <0 .
Таким образом, вводя штрафную функцию, мы
тем самым выделяем своеобразную «стену» на
границе области и чем больше р,, тем она «кру-
че». Однако на этой же границе образуется овраг,
который резко замедляет скорость сходимости
3.6. Оптимизация
195
любого метода, а для некоторых он непро-
ходим. Поэтому выбор весовых коэффици-
ентов тоже является своеобразной задачей,
и от удачного выбора во многом зависит
время решения задачи.
Теория штрафных функций достаточно
хорошо разработана и основана на идее
изменения целевой функции таким обра-
зом, чтобы последовательность точек, по-
лучаемых в результате применения какого-
либо метода безусловной оптимизации, од-
новременно сходилась и к выполнению всех
ограничений и к минимальному значению
целевой функции.
Необходимо отметить, что оптимизация
ХТП в большинстве случаев связана с ре-
шением сложных задач нелинейного про-
граммирования (НЛП) часто с овражными
целевыми функциями и необходимостью
Рис. 3.62. Графическая иллюстрация
целевой функции (3.6.107) при поиске
оптимума с использованием метода
штрафных функций с различными
значениями весовых коэффициентов
использования при вычислениях ограничений первого и второго рода, что, в свою
очередь, требует реализации специальных алгоритмов, позволяющих вести поиск не
только локальных экстремумов, но и глобального оптимума.
ЭМПИРИЧЕСКИЕ МОДЕЛИ.
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПАССИВНЫХ ЭКСПЕРИМЕНТОВ
И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
Эмпирические модели строятся на основе данных пассивных и активных эксперимен-
тов. По-существу, эмпирическая модель представляет собой уравнение, точнее, аппрокси-
мационную зависимость (см. разд. 3.3.2), описывающую всевозможные опытные данные.
Следует иметь в виду, что все измеряемые величины и данные лабораторных
анализов являются случайными величинами. Поэтому в соответствии с закономернос-
тями теории вероятностей и математической статистики обработку как результатов
каждого отдельного измерения, так и совокупности данных, необходимых для постро-
ения эмпирических моделей, следует проводить статистическими методами.
При обработке результатов пассивных экспериментов получаются линейные и нели-
нейные по параметрам эмпирические модели, достаточно точно описывающие всю
совокупность опытных данных. Основные трудности в этом случае заключаются в
правильном выборе вида модели — уравнения (задача структурной идентификации) и
определения параметров моделей — коэффициентов аппроксимирующих уравнений
(задача параметрической идентификации). Для решения задач структурной и парамет-
рической идентификации нелинейных объектов в своё время был предложен метод
Брандона, который представлен в этой книге (метод множественной регрессии).
В последнее время подобные задачи в химической технологии успешно решаются
с применением метода нейронных сетей (НС), и их относят к так называемому классу
задач распознавания образов. Распознаванием называют процесс обработки инфор-
мации об объекте, в результате которого последний относится к тому или иному
образу (классу). Процессу распознавания образов всегда предшествует процесс обуче-
ния. Основная задача теории распознавания образов состоит в выработке решающих
правил, позволяющих относить опознаваемые объекты к тому или иному образу (клас-
су). Исходной информацией для построения решающих правил являются обучаю-
щие выборки, которые содержат репрезентативные (представительные) наборы свойств
объектов разных классов. Существуют различные способы построения эмпиричес-
ких моделей процессов методами НС, которые в этой книге не рассматриваются.
В общем случае с использованием моделей, построенных на основе данных пас-
сивных экспериментов, может быть решена важнейшая задача компьютерного моде-
лирования — задача оптимизации.
Для описания результатов активных экспериментов используются простые линейные
по коэффициентам уравнения определённого вида, описывающие ограниченную об-
ласть факторного пространства, т.е. часть опытных данных, необходимых для решения
задачи оптимизации. Определение коэффициентов аппроксимирующих уравнений при
этом максимально упрощено (они вычисляются по формулам), а сами уравнения ис-
пользуются для планирования экспериментов в новых областях факторного пространства,
более близких к оптимальной, так называемой «почти стационарной области» [см. (2.38)],
где также проводится серия экспериментальных исследований для получения решения
задачи оптимизации. Таким образом, активное экспериментирование представляет собой
процедуру оптимального планирования экспериментов, конечной целью которой является
определение оптимальных условий проведения химико-технологических процессов.
4.1. Основные понятия теории вероятностей и математической статистики 197
4.1. Основные понятия теории вероятностей
и математической статистики.
Обработка результатов измерений
одной случайной величины
Любые практические исследования связаны со сбором информации о функцио-
нировании объектов с последующим ее представлением в форме таблиц, графиков
или математических зависимостей, характеризующих свойства этого объекта. Полу-
чение информации при этом связано с организацией различных измерений на ис-
следуемом объекте, которые неизбежно искажаются случайными неучитываемыми
факторами, например, погрешностью измерительных приборов, погрешностью ис-
пользуемой методики измерений, колебаниями параметров окружающей среды, вли-
яющих на точность измерений, и т.п. Поэтому для оценки достоверности только
одного измерения физической переменной следует использовать статистические мето-
ды, связанные, как правило, с необходимостью проведения повторных измерений
значений тех же самых физических величин.
Несколько другие задачи, также требующие применения статистических методов,
возникают при построении математических зависимостей, описывающих наблюдае-
мые изменения свойств исследуемого объекта. Эти зависимости обычно строятся в фор-
ме некоторых выражений, отражающих связь одной или нескольких величин (пере-
менных), характеризующих свойства объекта с одной или несколькими величинами
(переменными), которые определяют состояние объекта. Первая группа переменных,
характеризующих свойства объекта, может быть названа выходными или зависимыми
переменными, а вторая — входными или независимыми. Практически всегда существуют
неизвестные для экспериментатора или не поддающиеся измерениям факторы, кото-
рые не включаются в искомую зависимость, однако влияют (возможно, слабо) на вы-
ходные переменные. Флуктуации этих факторов, а также случайные погрешности из-
мерений наблюдаемых входных и выходных переменных приводят к тому, что получа-
емая зависимость также может оказаться недостаточно точной, и для проверки ее
достоверности также приходится использовать статистические методы, требующие
дополнительной информации, т.е. дополнительных измерений.
Статистические методы оперируют со случайными величинами и позволяют оце-
нивать погрешности измерения физических величин, а также достоверность зависи-
мостей, построенных на их основе.
Величина, которая может принимать различные значения при некотором комп-
лексе одинаковых условий, называется случайной величиной. Для характеристики слу-
чайной величины недостаточно иметь набор ее допустимых значений. Для полной ее
характеристики необходимо указать так же, как часто случайная величина может
принимать те или иные значения. Если случайная величина X может принимать в
результате повторяющихся опытов дискретные значения х1г х^, ..., х„, то отношение
числа опытов т, в результате которых случайная величина X приняла значение х„ к
общему числу п произведенных опытов называется относительной частотой т/п
появления события X = х,. Относительная частота зависит от количества произведен-
ных опытов п, и при увеличении п она стремится к некоторой постоянной величине
р„ называемой вероятностью события X = х;.
р, = Р(Х = х,) ~ т!п. (4.1)
Если событие достоверное (обязательно должно произойти), его вероятность рав-
на единице. Вероятность невозможного события равна нулю. Поэтому вероятность
случайного события находится в пределах о < Р < 1 •
198
Глава 4. Эмпирические модели. Обработка результатов экспериментов
В результате опыта случайная величина обязательно примет одно из своих значе-
ний, поэтому
£л=1-
(4-2)
Эта суммарная вероятность распределена некоторым образом между отдельными
значениями х, (i = 1, ... , п):
Л[ Л2 ...
Р1 Р1 Рз Pi
Соотношение, устанавливающее связь между возможными значениями случай-
ной величины и соответствующими им вероятностями, называется законом распреде-
ления вероятностей случайной величины.
Распределение непрерывной случайной величины (такой, которая может принимать
любое значение внутри некоторого интервала) нельзя задать с помощью вероятнос-
тей отдельных значений. Поэтому для непрерывных случайных величин рассматри-
вается вероятность того, что в результате опыта случайная величина принимает зна-
чения меньшие некоторого заданного вещественного числа х. Эта вероятность явля-
ется функцией от х
(4.3)
(4.4)
F(x) = Р(Х < х) = Р(-°° <Х <х)
и называется функцией распределения случайной величины.
В соответствии с этим определением значения функции распределения при пре-
дельных значениях аргумента х будут F(-°°) = 0 и F(+°°) = 1.
Отметим некоторые функции распределения, имеющие важное практическое значение:
F(x) = -J^
— нормальное распределение (имеет два параметра тх и в2х);
F(x) = l-e-x* длях>0,
F(x) = 0 для х < 0
— показательное распределение (содержит один параметр X).
Для непрерывной случайной величины используется также производная функции
распределения — функция плотности распределения случайной величины fix). Если Дх)
непрерывна и дифференцируема, то
/(x) = F'(x). (4.7)
Приведем выражения функции плотности распределения для показательного и
нормального законов распределения:
/(х) = Хе~и для х > 0;
Лх)=75Ьге""р!/<2°и- <4-9>
По известной плотности распределения в соответствии с (4.4) и (4.7) функция
распределения может быть найдена следующим образом:
(4.5)
(4.6)
(4.8)
(4.Ю)
Для дискретных случайных величин, так же как и для непрерывных (4.4), вводится
функция распределения дискретной случайной величины, определяемая соотношением:
п
F(x) = P(X <x) = ^p(Xl),rpex„<x_ (4.Ц)
1=1
4.1. Основные понятия теории вероятностей и математической статистики 199
Функция распределения в этом случае представляет собой разрывную ступенча-
тую зависимость (рис. 4.1).
Вместо функции плотности распределения (4.7) иногда используется распределе-
ние вероятностей дискретной случайной величины (4.3), представленное на рис. 4.2.
Случайные величины часто определяют с помощью следующих числовых харак-
теристик, выражающих особенности случайных величин.
Математическое ожидание тх случайной величины характеризует центр рассея-
ния случайной величины и определяется выражениями:
тх = Л/[Х] =
J=1
| xf(x)dx,
если X дискретна;
если X непрерывна.
(4.12)
Дисперсия ох характеризует разброс значений случайной величины относительно
ее центра (математического ожидания тх)'.
а2х =М[(Х -тх)2]
и определяется следующим образом:
£(х, -тх)2р,, если X дискретна;
(=1
J (х - тх)г f(x)dx, если X непрерывна.
(4.13)
(4.14)
Следует иметь в виду, что для нормально распределенной случайной величины
тх и сх являются параметрами функции распределения вероятности (4.5).
Обобщением указанных числовых характеристик являются значения моментов слу-
чайной величины. Принято различать начальные и центральные моменты. Для диск-
ретной случайной величины начальный момент k-го порядка определяется формулой
Рис. 4.1. Функция распределения
для дискретной случайной величины
Рис. 4.2. Распределение вероятностей
дискретной случайной величины
200
Глава 4. Эмпирические модели. Обработка результатов экспериментов
для непрерывной случайной величины — формулой
mk = §xkf(x)dx. (4.16)
Начальный момент первого порядка (£ = 1) соответствует математическому ожи-
данию случайной величины (ш, = тх). Центральный момент k-го порядка для диск-
ретной случайной величины определяется формулой
Hi =Е(*,, (4-17)
1=1
для непрерывной случайной величины — формулой
Hl = f (x-mx)k f(x)dx. (4.18)
Первый центральный момент всегда равен нулю. Второй центральный момент
соответствует значению дисперсии (4.13) и (4.14).
4.1.1. Выборочный метод
При изучении законов распределения случайной величины о характере закона
судят по значениям, принимаемым случайной величиной. Предположим, что прово-
дятся повторные измерения некоторой случайной величины. Назовем исходом опы-
та результат одного такого измерения. Тогда совокупность исходов опытов при бес-
конечном их числе представляет собой так называемую генеральную совокупность
значений случайной величины. Числовые характеристики случайной величины, по-
лученные по генеральной совокупности и определяющие параметры их функций
распределений, называются генеральными параметрами.
Совокупность значений случайной величины, полученная при любом конечном
числе п опытов, при этом называется выборкой объема п из генеральной совокупнос-
ти.
Любая выборка должна давать достаточное представление о генеральной совокуп-
ности, т.е. быть представительной (репрезентативной). Если о генеральной совокуп-
ности ничего не известно, то единственной гарантией репрезентативности является
случайный отбор результатов наблюдений для выборки. Для имитации случайного
отбора можно использовать таблицу случайных чисел, равномерно распределенных в
интервале [0, 1] (табл. 4.1). Все значения, приведенные в таблице, увеличены в 10s раз.
Таблица 4.1. Равномерно распределённые случайные числа в интервале [0, 1],
увеличенные в 105 раз
10097 32533 76520 13586 34673 54876 83491 25624 88685 40200 86507 58401
37542 04805 64894 72496 24805 24037 35273 88435 99594 67348 87517 64969
08422 68953 19645 09303 23209 02560 22109 40555 60970 93433 50500 73998
99019 02529 09376 70715 38311 31165 50725 68248 29405 24201 52775 67851
12807 99970 80157 36147 64032 36653 13716 70078 18475 40610 68711 77817
80959 09117 39292 74945 66065 74717 36766 67951 90364 76493 29609 11062
4.1. Основные понятия теории вероятностей и математической статистики 201
20636 10402 00822 91665 31060 10805 91826 08928 93785 61368 23478 34113
15953 34764 35080 33606 85269 77602 65481 17674 17468 50950 79335 51748
88676 74397 04436 27659 63573 32135 80124 35635 17727 08015 82391 90324
98951 16877 19171 76833 73796 45753 74350 99817 77402 77214 50024 23356
34072 76850 36697 36170 65813 39885 69915 26803 66252 29148 24892 09994
45571 82406 35303 42614 86779 07439 09893 20505 14225 68514 83647 76938
02051 65692 68665 74818 73053 85247
05325 47048 90553 57548 28468 28709
03529 64778 35808 34282 60935 20344
11199 29170 98520 17767 14905 68607
23403 09732 11805 05431 39808 27732
18623 88579 83452 99634 06288 98083
Пусть, например, имеется совокупность наблюдений, состоящая из 100 замеров.
Требуется сформировать репрезентативную выборку объемом в 10 элементов. Для этого
перенумеруем наблюдения от 0 до 99. Из таблицы случайных чисел, начиная с любого
места (например, начиная с пятого числа в первом столбце) выпишем две последние
цифры идущих подряд 10 чисел: 07, 59, 36, 53, 76, 51, 72, 71, 51, 25. Полученная после-
довательность указывает, какие номера наблюдений надо взять для выборки.
Из случайного характера выборок следует, что суждение о генеральной совокупно-
сти также является случайным. Функция распределения, получаемая по выборке объе-
ма п, называется выборочной, или эмпирической, функцией распределения и определяет-
ся соотношением, вытекающим из (4.4) и (4.11) для дискретных случайных величин:
Fn(x) = nxln, (4.19)
где х — некоторое значение случайной величины (некоторая точка на оси х); пх —
число выборочных значений этой выборки, меньших х.
Относительная частота попадания случайной величины в /-й интервал есть
р* — п,! п. (4.20)
Результаты обработки удобно представить в виде табл. 4.2, в которой / обозначает
интервал, h — длину интервала, х' — середину интервала, л, — число точек в интервале,
р’ — относительную частоту.
Таблица 4.2. Обработка данных выборки случайной величины X объёмом п для
построения гистограммы
i h X* n p*
1 ^\= Xl~ Xmm X1‘ «1 Pi
2 Й2 = X2 — X, x2’ «2 Pl
i A, = x, — X,_, p'
k hk = xk - x*-i xk "k Pk
202
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Зависимость p’/h от х* (рис. 4.3), построенная по данным табл. 4.2, называется
гистограммой выборочного распределения.
По этим же данным можно построить выборочную функцию распределения', по оси
х надо отложить значения х' и длины интервалов ht (рис. 4.4), по вертикальной оси
отложить значения выборочной функции распределения, которые вычисляются для
каждого х* следующим образом:
Л.а.') = Ё^. (4.21)
По выборке могут быть рассчитаны выборочные статистические характеристики,
которые являются оценками соответствующих генеральных параметров. Приведем
формулы для расчета оценки математического ожидания (выборочного среднего) тх
и оценки дисперсии бгх:
юх = * = ; (4.22)
«=1
^x=Dx=^J(x,l-x)2 Р: . (4.23)
»=1
Пример. Дана выборка объема п = 50 со следующей таблицей распределения:
X 1 2 3 4
nt 20 15 10 5
Найти выборочное среднее и выборочную дисперсию.
▼ Для вычислений используем формулы (4.22)-(4.23). Учитывая, что Р,=п,1п,
получаем формулу для расчета выборочного среднего:
Ёп-х' 20-1 + 15-2 + 10 3 + 5-4 _ 2
= “20 + 15 + 10 + 5 “ ’
п
Оценку выборочной дисперсии вычисляем по формуле (4.23), а также с учётом (4.20):
^и,(х,-х)2 20(1 — 2)2 +15(2 —2)2 + 10(3-2)2 +5(4-2)2 , .
п - 1 Dx =---------------------------= 1. А
Dx---------- 50
Рис. 4.3. Гистограмма выборочного
распределения
Рис. 4.4. Выборочная
функция распределения
4.1. Основные понятия теории вероятностей и математической статистики 203
4.1.2. Оценки параметров распределения
случайной величины
Из случайного характера выборки следует, что определяемые на ее основе значе-
ния параметров функции распределения также являются случайными величинами и
служат лишь статистическими оценками истинных значений параметров распреде-
ления.
Рассмотрим оценки параметров распределения, зависящие от выборки п значе-
ний случайной величины X.
Точечной оценкой называется статистическая оценка, определяемая одним значе-
нием (числом). К точечным оценкам, рассчитанным по выборке, предъявляются тре-
бования состоятельности, несмещенности и эффективности.
Оценка называется состоятельной, если с увеличением объема выборки п она
стремится (по вероятности) к оцениваемому параметру: Jim® = 0. В этой записи 0 —
истинное значение оцениваемого параметра, в качестве которого могут использо-
ваться математическое ожидание т*, дисперсия огх и т.п.; 0 — точечная оценка
параметра.
Оценка называется несмещенной, если ее математическое ожидание при любом
объеме выборки равно оцениваемому параметру: Л/[0] = 0.
Среди всех несмещенных оценок параметров, полученных по выборкам одинако-
вого объема, эффективной называется оценка с минимальной дисперсией.
Эффективность оценок генеральных параметров для различных несмещенных
оценок одного и того же параметра при фиксированном объеме выборок обратно
пропорциональна дисперсиям этих оценок. Так, например, если дисперсии двух то-
чечных оценок 0 и ш удовлетворяют неравенству £>[й] > £>[0], то эффективность
оценки 0 выше, чем <в.
Понятие интервальной оценки связано с понятием доверительной вероятности и
доверительного интервала.
Доверительной вероятностью р называется вероятность того, что истинное значе-
ние оцениваемого параметра 0 заключено в интервале
Р = Р(0-ер <0<0 + ер) (4.24)
или
Р = Р(|о-0|<ер. (4.25)
Границы этого интервала 0-ер и 0+ер называются доверительными границами, а
сам интервал — доверительным интервалом. Для определения границ доверительного
интервала необходимо найти точечную оценку параметра 0 и точность этой оценки
, т.е. разброс оценки 0 вокруг истинного значения параметра 0.
Точечные оценки параметров распределений X, тх,о2х (4.5), (4.6), (4.8), (4.9) оп-
ределяются различными методами, чаще всего методом максимума правдоподобия.
Точность оценки зависит от закона распределения случайной величины, числовой
характеристикой которого служит параметр 0, и заданной доверительной вероятнос-
ти р. Доверительная вероятность р характеризует надежность оценки 0 и определяет
величину доверительного интервала. С использованием формул (4.4) и (4.7), опреде-
204
Глава 4. Эмпирические модели. Обработка результатов экспериментов
ляющих функции распределения и функции плотности распределения, в результате чего
соотношение (4.25) можно представить в виде:
р =/’(-Ер < 0-9 < ер) = - FC-Cp) = j f(x)dx . (4.26)
Отсюда следует, что чем больше значение р, тем больше должно быть значение
этого интеграла и тем шире доверительный интервал, т.е. больше £р и меньше точ-
ность оценки. С другой стороны, чем меньше надежность р для оценки 0, тем уже
доверительный интервал и больше точность оценки. На практике обычно значения р
принимают равными 0.9, 0.95, 0.99.
Часто вместо р используют другую величину, называемую уровнем значимости, и
обозначают ее р = 1-р. Уровень значимости определяет вероятность того, что ис-
тинное значение не попадает в доверительный интервал.
Определение доверительного интервала для математического ожидания
Рассмотрим построение доверительного интервала для одного из параметров нор-
мального распределения (4.9) — математического ожидания тх. Точечная оценка ма-
тематического ожидания тх в этом случае определяется выборкой объемом п (4.22)
при р*=Уп (i = l,...,n) и х* = х, (i = l,...,n):
тх =х = (^х,)/п. (4.27)
Эта оценка тх также является нормально распределенной случайной величиной,
так как она получена на основе случайной выборки из генеральной совокупности и
выражается через сумму значений случайных величин х„ i = 1,..., п, распределенных
по нормальному закону.
Оценки параметров распределения т-у: и д~х случайной величины X определя-
ются в соответствии со свойствами суммы математических ожиданий и дисперсий и
с учетом того, что все х„ i = 1, ..., п являются значениями одной и той же случайной
величины X, т.е. справедливы равенства:
™ „2 _ „2
тх ~ тх — — ™Х 1 & х — &X
= ст
Тогда генеральные параметры тх и определяются так:
(4.28)
(4.29)
(4-30)
В этом случае соответствующая оценка тх рассчитывается по формуле (4.27), а
оценка 6^ — по формуле (4.23) при р' = 1/п (i = 1,...,п) и х* = х, (i = 1,...,п):
-*)
1=1
(4.31)
4.1. Основные понятия теории вероятностей и математической статистики 205
Далее будет показано, что полученная оценка дисперсии не является несмещен-
ной, поэтому вместо нее используется несмещенная оценка S2X;
Ё(х,-х-)г
S2X=-^--------, (4.32)
(n-l)
где число степеней свободы этой оценки дисперсии определяется как v = п-1.
Различие между оценками дисперсий несущественно при больших объемах вы-
борки (л), однако оно значительно для малых выборок.
При определении доверительного интервала для математического ожидания со-
отношение (4.25) принимает вид:
Р = Р(\х-т7| < Ер) , (4.33)
и от случайной величины х следует перейти к нормированной случайной величине X :
X = (^-т7)/с?, где = тх,а-= 7<тГ. (4.34)
Если разделим и левую и правую часть неравенства в (4.33) на <тх и обозначим
ер /стх через , то с учетом (4.4) и (4.10) получим:
Р = Р([Х |<Кр), (4.35)
ИЛИ
о о о о
Р = Р(-Кр<Х <Кр) = Г(К^-$f(x)dx, (4.36)
~к,
о о
где F(x) — функция распределения нормированной случайной величины; f(x) —
функция плотности распределения нормированной случайной величины.
Величина называется квантилем распределения нормированной случайной ве-
личины. Квантиль Хр есть такое значение нормированной случайной величины, для
которого значение функции распределения равно доверительной вероятности Р, т.е.
для определения квантиля при заданной доверительной вероятности надо ре-
шить уравнение
Г(х) = р. (4.37)
Для того чтобы привести вероятностные соотношения (4.35) и (4.36) в соответствие
с определением (4.37), рассмотрим симметричное относительно нуля распределение
о О
нормированной случайной величины (согласно (4.29) и (4.30), М[X ] = О, D[X ] = 1). В
этом случае площади под кривой функции плотности распределения слева и справа от
оси ординат (рис. 4.5) равны друг другу, а площади под кривой, соответствующие
уровню значимости р = 1 - р , также равны (они равны р/2 — на рисунке не заштрихо-
ваны). При этом соотношение (4.36) с учетом (4.37) принимает вид:
Р = / /(x)<fo = F(K1.„2)-F(K,/2), (4.38)
К р/1
ИЛИ
Р(Кр/2 < X < К1_„2) = р. (4.39)
206
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Я*)
Рис. 4.5. Симметричное относительно нуля распределение нормированной случайной
величины
В соответствии с рис. 4.5 значение Кр/2 отрицательно, однако для симметричных
относительно 0 распределений будет справедливо равенство:
Кр1г=-К._р12, (4.40)
где Кх_р12 является всегда положительным.
Эта замена позволяет использовать таблицы квантилей распределений, состав-
ленные только для их положительных значений, и получить вероятностное соотно-
шение (4.39), определяющее доверительный интервал для математического ожида-
ния в виде:
Р(-7С1_р/2<Х<1С1_(,/2) = р (4.41)
или, с учетом того, что X = (х -тх)/сх и тх=тх (4.29),
_ < х-тх
Ki-p/2- (4.42)
° X
При подстановке оценок х (4.27) с учётом (4.29) и 6^ (4.30) в эти неравенства
доверительный интервал для математического ожидания имеет вид:
и п
Ki_pl2^<mx<^+K (4.43)
п----------------------------------------------у/п п к у]п
Значение квантиля Ki_p/2 определяется по специальным таблицам как решение
уравнения:
F(x) = l-p/2, (4.44)
где р - уровень значимости, задаваемый обычно равным 0.05.
Значение оценки дх , называемое средним квадратичным отклонением (стандартом),
либо задается, если известно значение генеральной дисперсии, либо рассчитывается
по выборке объемом п по формулам (4.31) или (4.32). При этом очевидно, что
4.1. Основные понятия теории вероятностей и математической статистики 207
(4.45)
Из анализа неравенства (4.43) следует, что с увеличением числа экспериментов
уменьшается величина доверительного интервала, т.е. возрастает точность оценки.
Если надо уменьшить возможную ошибку в два раза, необходимо увеличить число
наблюдений в четыре раза.
Величина доверительного интервала также зависит от квантиля распределения
случайной величины Ktp/2, т.е. в соответствии с (4.44) от задаваемого уровня значи-
мости р и характера закона распределения.
При оценке доверительного интервала для математического ожидания использу-
ются два закона распределения нормированной случайной величины: нормальное,
называемое в этом случае стандартным, и распределение Стьюдента.
Применение стандартного нормального распределения (большие объемы выборок)
Стандартное нормальное распределение используется либо когда известно значе-
ние генеральной дисперсии , либо когда оценки х тх (4.27) с учётом (4.29) и
дисперсия 6^ (4.31) определяются по выборке большого объема (и >50). В этом
случае для нормированной случайной величины U:
U =
х-тх
4п
(4 46)
функция стандартного нормального распределения имеет вид:
(4-47)
а график функции её плотности распре-
деления приведен на рис. 4.6, при этом
число степеней свободы дисперсии (4.32)
стремится к бесконечности (v —э °°).
Как следует из вида этой функции,
результат решения уравнения (4.44) в
данном случае зависит только от задан-
ной доверительной вероятности р = 1- р.
Соответствующие квантили стандартно-
го нормального распределения их_р/2 в
зависимости от (1 - р/2) (4.43) приведе-
ны в табл. 1 Приложения.
При заданном значении 1 - р/2 в поле
таблицы (см. табл. 1 Приложения) иско-
мая величина U находится в первом стол-
бце и первой строке. Если значение ге-
неральной дисперсии задано, то довери-
тельный интервал для тх в соответствии
с (4.43) определяется как:
Рис. 4 6 Графическое представление функ-
ции плотности распределения Стьюдента для
нормированной случайной величины при
различных степенях свободы дисперсии
(4.32) - v (v = °° — стандартное нормаль-
ное распределение)
208
Глава 4. Эмпирические модели. Обработка результатов экспериментов
- 2х.
< -_ + (/ (4.48)
п yjn п у/п
Пример. По девяти проведенным опытам определено среднее значение, равное
50. Известно среднее квадратичное отклонение этой величины дх =1.01. Найти
с надежностью 95% (Р = 0.95) границы доверительного интервала, внутри кото-
рых лежит истинное значение измеряемой величины.
▼ Полагая, что случайная величина ^распределена нормально, доверительный
интервал определяем по найденной формуле. Величина (1- р/2), при которой
следует искать квантиль нормального распределения, равна 0.975. По табл. 1
Приложения находим Ох_р12 = 1.96, тогда имеем
50-1.96(1.01/3) < тх < 50 + 1.96(1.01/3) .
Следовательно, истинное значение измеряемого параметра с доверительной ве-
роятностью р = 0.95 будет 49.35 < тх > 50.65. ▲
Применение распределения Стьюдента (малые объемы выборок)
Данный закон распределения используется, когда значения оценок х и сх опре-
деляются по выборкам, объем которых меньше 50 (п < 50). Оценки параметров нор-
мированной случайной величины X- х и дх в этом случае проводятся по формулам
(4.27), (4.32) (оценкой ох служит Sx , так как п мало):
t = ((х - тх) /Sx)-Jn , (4.49)
где t — случайная величина /-распределения Стьюдента.
Знаменатель выражения (4.32) для 5 * определяет число степеней свободы выбор-
ки объемом л:
v = n-l, (4.50)
где 1 — число уравнений связи между элементами выборки — уравнение (4.27) для
определения среднего значения х .
Функция распределения Стьюдента имеет более сложный вид, чем функция стан-
дартного нормального распределения, и ее значение зависит от числа степеней сво-
боды дисперсии (4.32), т.е. (4.50). Графики функций плотности распределения Стью-
дента для различных степеней свободы v приведены на рис. 4.6 (при v = °° функция
плотности распределения Стьюдента совпадает с нормальным распределением).
В этом случае результат решения уравнения (4.44)
Ж-р/2) = 1-Р/2 (4.51)
зависит не только от уровня значимости р , но и числа степеней свободы (верхний
индекс v при /). Квантили распределения Стьюдента приведены в табл. 2 Приложе-
ния. При заданных значениях v (в таблице первый столбец) и (1- р/2) в поле табли-
цы определяется соответствующий квантиль /2.
4.1. Основные понятия теории вероятностей и математической статистики 209
Соответствующее выражение (4.43), определяющее доверительный интервал для
малых выборок, имеет вид:
п п
____Л ^-<т <— + Л
I--------------"‘Х - т*1-р/2 ’
П yjn п у/п
где Sx находится по формулам (4.32) и (4.45), a v - по формуле (4.50).
(4.52)
Пример. Определить доверительный интервал, в котором с доверительной вероят-
ностью 0.95 располагается истинное значение измеряемого параметра, по резуль-
татам восьми титрований х, см3: 76.48, 76.25, 76.43, 76.48, 77.20, 76.48, 76.45, 76.60.
▼ Имеем функцию распределения Стьюдента:
л
х - —— ; х = 76.546 см3; v = 8 -1 = 7 .
п
По табл. 2 Приложения находим zj975 = 2.365, а по формуле (4.32) —
f п Л
S2X = £(х,-х)2 /V =0.5543/7 = 0.079 см3.
I '=! J
Подставляя эти величины в (4.52), получаем:
75.546-2.365V0.079/8 < тх < 76.546+2.365л/0.079/8
или
76.55 - 2.36 • 0.099 < тх < 76.55 + 2.36 • 0.099.
В результате определен доверительный интервал, в котором с доверительной
вероятностью 0.95 располагается истинное значение результата титрования:
76.31 см3 < тх < 76.79 см3 • А
Метод максимума правдоподобия
Метод максимума правдоподобия получил широкое применение для нахождения
точечных оценок параметров распределения. Сущность этого метода заключается в
определении таких оценок неизвестных параметров, для которых функция правдо-
подобия принимает наибольшее значение. Расчетные соотношения для отыскания
значений параметров в общем случае получаются из следующих соображений.
Пусть известен общий вид функции плотности вероятности теоретического распре-
деления f (х, 0), где 0 — вектор неизвестных параметров, входящих в выражения зако-
нов распределения, например (4.5) и (4.6). В результате опытных исследований получе-
на выборка значений случайной величины х = [хр..., х„]т. Обозначим вероятность по-
падания величины х, в интервал (х, -е/2, х( +е/2) через /(хр 0)е (4.4) и (4.10).
Если произведено п наблюдений, то вероятность того, что одновременно первое
наблюдение попадает в первый интервал, второе — во второй и т.д., есть вероятность
совместного осуществления независимых событий и равна произведению вероятностей:
Р(х, 0) = /(х„ 0) /(х2,0),..., /(х„, 0) Б". (4.53)
Так как это событие произошло при первом же испытании (получена выборка х),
то его вероятность максимальна. Таким образом, оценка параметров 0 должна под-
бираться так, чтобы обеспечить максимум этой функции.
210
Глава 4. Эмпирические модели. Обработка результатов экспериментов
При решении задачи нахождения максимума функции Р(х, 0) по параметрам
0;, j = 1,к можно пользоваться любыми методами — численными или аналити-
ческими. При использовании аналитических методов удобнее искать максимум не
функции (4.53), а ее логарифма:
1пР(х, 0) = 1пе" + ^1п/(х,,0). (4.54)
i=i
Однако в этом случае выкладки оказываются более простыми, поскольку произ-
ведение в выражении (4.53) заменяется суммой в выражении (4.54).
В результате параметры определяются из условия максимума функции правдопо-
добия (4.54):
£(х, 0) = ^1п/(х,,0). (4.55)
«=1
Система уравнений, определяющая оценки параметров 0;, j = 1,..., к , в соответ-
ствии с необходимыми условиями экстремума функции многих переменных при
этом имеет вид (3.6.17):
дЦх, 0)/Э0; =0, J = 1,..., к. (4.56)
Поскольку система (4.56) представляет собой лишь необходимые условия экстре-
мума, после ее решения иногда может возникнуть необходимость проверки типа
найденного экстремума, для чего следует воспользоваться достаточными условиями
максимума (3.6.25).
Оценка параметра показательного распределения
Функция плотности распределения имеет вид (4.8):
Дх, X) = Хе^'. (4.57)
Определение оценки параметра X проводится по выборке х = [jq,..., хл ]т, тогда
функция правдоподобия (4.55) примет вид:
Цх, X) = ^in(Xe “’) = zilnX-^Xx, . (4.58)
,=1 i=i
В соответствии с уравнением (4.56) оценка параметра показательного распреде-
п
ления находится из уравнения nfk - \ х( = 0:
<=1
п
Х = 1/х,где х = —— (4.59)
п
есть среднее выборки.
Оценка параметров нормального распределения
Функция плотности распределения случайной величины X имеет вид (4.9):
_ 2 , 1 (х - тх)
/(х, тх, ох) = _ exp - ( - /
V2™x I 2ox
(4.60)
4.1. Основные понятия теории вероятностей и математической статистики 211
Оценка двух параметров распределения — математического ожидания и диспер-
сии — проводится по выборке х = [х,,х„]т. Функция правдоподобия (4.55) в этом
случае формируется так:
Цх, тх, а2х) = -^1п2л-Jlno2 "wx)2.
^0 у .=]
(4.61)
Тогда система уравнений (4.56) для определения оценок параметров х — тх и
д2х — представляется в виде:
dL(x,mx,o2x)=_2_^(x_Ax) = 0_
дтх 26х
анх m Д +- ^ >=о.
Эс2х 262 2(62А.)2^
(4.62)
Определяя из первого уравнения тх, а — из второго (после подстановки в
него тх), получаем оценки параметров нормального распределения, аналогичные
(4.27) и (4.31):
Для проверки несмещенности полученных оценок следует вычислить их матема-
тические ожидания:
М[тх] = М
п
1 п 1 л
= -^A/[x,] = -^/nx = т
П ,=1 п ,=1
(4.64)
т.е. оценка математического ожидания является несмещенной.
При проверке несмещённости дисперсии с учетом (4.13) получаем:
£(\ -х)2
£=1
п
М[с52х} = М
= -М[^[(х, -mx)-(x-mx)]2 =
П ,=1
*
I
I п
= -М[У (х, ~тх)2 -2(х, -тх)(х-тх) + (х~тх)2] =
п ,=1
= -М[]Г(х, - тх)2 - 2(х - тх)(^х1 -птх) + п(х-тх)2] = (4.65)
П ,=1 Z=1
= -XMt(x,-/«x)2]-nM[(x-/Wx)2] = -(Xo2x -no2) =
и J=1 п I=1
, / 2 \ л
1 2 *2
= — П(5У-П---- =----Оу
п J п ’
т.е. полученная оценка дисперсии д2х оказывается смещенной.
Для того чтобы получить несмещенную оценку, вместо сх (4.63) рассмотрим оценку:
212
Глава 4. Эмпирические модели. Обработка результатов экспериментов
S* ~*)2, (4.66)
которая связана с &х соотношением:
9 По
$х=—(4.67)
Определим математическое ожидание с учетом (4.65):
= = < (4.68)
т.е. дисперсия (4.66) является несмещенной оценкой истинного параметра. Поэтому
в качестве выборочной оценки дисперсии используют выражение для Sx (4.32).
Метод моментов
Этот метод получения точечных оценок параметров распределения целесообраз-
но применять в том случае, когда система уравнений (4.56) в методе максимума
правдоподобия представляет собой нелинейную систему уравнений относительно
искомых параметров. Сущность метода состоит в следующем. Для функции (4.7)
плотности распределения вероятностей, содержащей к параметров, по формуле (4.15)
или (4.17), (4.16) или (4.18) записываются выражения для вычисления первых к-х
моментов случайной величины, как функции параметров распределения. Получен-
ные соотношения приравниваются соответствующим значениям выборочных мо-
ментов, которые определяются из экспериментальных данных. В результате получа-
ется система к уравнений, из которой найти оценки параметров распределения 0Р..., 0t
проще, чем по системе (4.56) методом максимума правдоподобия.
Метод моментов можно проиллюстрировать на примере показательного закона
распределения с одним определяемым параметром X. Согласно формуле (4.8), пер-
вый начальный момент (4.16) представляет собой математическое ожидание, кото-
рое можно представить в виде:
тх = kjxe^dx. (4.69)
о
Интегрирование этого выражения по частям приводит к соотношению:
(4-70)
С другой стороны, выборочный начальный момент первого порядка (выборочное
среднее) определяется по формуле (4.63):
тх = ±х.'п. (4.71)
i=i
Приравнивая правые части двух последних равенств, получаем уже известную
формулу для оценки параметра показательного распределения:
X = п / у1, xt _
(4.72)
4.2. Обработка результатов пассивных экспериментов
213
4.1.3. Проверка статистических гипотез
Под статистическими гипотезами понимаются некоторые предположения отно-
сительно распределений генеральной совокупности той или иной случайной вели-
чины. Во всех предыдущих параграфах закон распределения случайной величины
считался известным и проводились лишь оценки значений параметров этого закона.
Однако во многих случаях самый вид закона является гипотетическим и нуждается в
статистической проверке.
Проверка гипотезы заключается в сопоставлении некоторых статистических по-
казателей, критериев проверки (критериев значимости), вычисляемых по выборке,
со значениями этих показателей, определяемых в предположении, что гипотеза вер-
на. Если расхождение этих показателей (критериев) превосходит надлежаще уста-
новленный предел, то гипотеза бракуется как несостоятельная, в противном случае
считается состоятельной. Для того чтобы дать правило проверки, следует выбрать
уровень значимости: 0.10, 0.05, 0.02, 0.01, 0.001. Уровню значимости соответствует
доверительная вероятность 0 = 1 - р. По этой вероятности находят квантильные до-
верительные границы 0р/2 и 6/-Р/2- Значения Qp/2 и 0;_р/2 называются критическими
значениями гипотезы. Если рассчитанное по выборке значение критерия 0О попадает
в доверительный интервал, то данная гипотеза принимается. Если же найденное
значение 0О окажется за пределами доверительного интервала, т.е. в критической
области, то гипотеза отвергается.
При проверке гипотез можно совершить ошибки двух типов.
Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле
верна. Вероятность такой ошибки не больше принятого уровня значимости. Напри-
мер, при р = 0,10 можно совершить ошибку первого рода в десяти случаях из ста.
Ошибка второго рода состоит в том, что гипотеза принимается, а на самом деле
она неверна. Вероятность ошибки второго рода тем меньше, чем выше уровень зна-
чимости, ведь при этом увеличивается число отвергаемых гипотез. Более точную
оценку сделать трудно, так как ошибка второго рода зависит от типа проверяемой
гипотезы, от способов проверки и ряда других причин.
Для подробного ознакомления с методикой проверки статистических гипотез
можно рекомендовать следующую литературу: [1, 6, 53].
4.2. Обработка результатов пассивных
экспериментов и построение эмпирических
моделей
В разделе 2.2 (2.35) указывалось, что эмпирические модели в общем виде могут
быть представлены в виде приближённых уравнений регрессии'.
y = f(x,a). (4.73)
Для определения конкретного вида приближённого уравнения регрессии [эмпи-
рической модели (4.73)] необходимо:
1) найти конкретный вид функции f в уравнении (4.73), в частности, линейна
или не линейна ли она относительно коэффициентов а ;
2) определить значения коэффициентов а модели — коэффициентов регрессии;
214
Глава 4. Эмпирические модели. Обработка результатов экспериментов
3) провести статистический анализ полученных результатов.
Статистический анализ, как правило, проводится методами регрессионного и
корреляционного анализа.
4.2.1. Элементы корреляционного
и регрессионного анализа
Для иллюстрации метода корреляционного анализа рассмотрим две случай-
ные величины X и Y, для которых известны законы распределения. Предполо-
жим, что для них будет справедливо простейшее приближённое уравнение регрес-
сии (4.73):
y = a0+ai*- (4-74)
Представим поле корреляции Y, X в виде чертежа с результатами опытов, отмечен-
ных точками в соответствующей системе координат (рис. 4.7). Поле корреляции яв-
ляется графической формой систематизации опытных данных.
Наличие корреляционной зависимости часто можно определить интуитивно по ре-
зультатам опытов. Наличие такой зависимости характеризует некоторую тенденцию
изменения у от х. При установлении зависимости между этими параметрами возни-
кает задача определения тесноты связи.
Рассмотрим два поля корреляции величин Yn X(см. рис. 4.7 а, б). Пусть линии
регрессии в обоих полях расположены одинаково. Однако точки поля рис. 4.7, б
значительно ближе примыкают к линии регрессии (4.74), чем точки поля рис. 4.7, а.
Очевидно, что чем сильнее влияние неконтролируемых факторов на У, тем больше
отклоняются экспериментальные точки от линии регрессии и тем слабее проявляет-
ся зависимость у от х. И, наоборот, чем слабее влияние неконтролируемых факторов
на У, тем менее отклоняются экспериментальные данные от линии регрессии и тем
теснее связь между у и х.
Если теснота связи мала, то влияние х на у обнаруживается лишь в среднем по
уравнению регрессии. В каждом же отдельном наблюдении оно перекрывается дей-
ствием неконтролируемых параметров.
Эмпирическое корреляционное отношение, характеризующее тесноту связи между У
и X, определяется следующим образом:
Рис. 4.7. Изображение поля корреляции: а — с меньшей теснотой связи; б — с большей
теснотой связи
4.2. Обработка результатов пассивных экспериментов
215
n= ,
V («-ж2’
(4.75)
При этом остаточная дисперсия, характеризующая погрешность уравнения рег-
рессии (4.73) и (4.74) рассчитывается по формуле:
£(уГ-х)2
S^= —-----------, (4.76)
п-р
где р — число значимых коэффициентов регрессии, а общая дисперсия (дисперсия
относительно среднего значения по экспериментальным данным) определяется по
формуле:
(у,экс"-у)2
, (4.77)
л-1
Здесь среднее значение по экспериментальным данным определяется как:
п
У =
(4.78)
Корреляционное отношение (4.75) характеризует связи между случайными вели-
чинами Хи Y. Чем больше величина т| (4.75), тем сильнее связь.
Величина п находится в пределах:
О < г| < 1. (4.79)
Между случайными величинами обычно существует такая связь, при которой с
изменением одной величины меняется распределение другой. Такая связь называет-
ся стохастической. Изменение случайной величины У, соответствующее изменению
величины X, разбивается при этом на две компоненты: функциональную (связанную
с зависимостью У от X) и случайную. Если первая компонента отсутствует, то вели-
чины У и X независимы. Если отсутствует вторая компонента, У и X связаны функ-
циональной зависимостью. При наличии обеих компонент соотношение между ними
определяет силу (тесноту) связи. Существуют показатели, оценивающие те или иные
стороны стохастической связи. Из них важнейшими являются корреляционное отно-
шение (4.75) для нелинейных моделей и коэффициент корреляции для линейных мо-
делей.
Если две случайные величины независимы, то дисперсия суммы равна сумме
дисперсий этих величин:
D{X + У}= £>{х}+ Г>{У}. (4.80)
Из определения дисперсии (4.13) и математического ожидания (4.12) следует:
D{X + У} = М[Х + Y - М(Х + У)]2 =
= М[Х-М(Х)]2 +2М{[А'-Л/(А')][Г-М(Г)]} + Л/[Г-Л/(Г)]2 = (4.81)
D(X) + 2М {[X - М(X)] [У-Л/(У)]}+Л(У).
Зависимость между Хи У вытекает из неравенства
М[(Х -mx)(Y-mr)]*0. (4.82)
216
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Величина (4.82) называется корреляционным моментом, моментом связи или кова-
риацией случайных величин Хи У и обозначается: СОИ[ХУ}, COVXY.
Безразмерная величина
Л/[(Х-ОТх)(Г-тг)]
гхг=------------------ (4.83)
называется коэффициентом корреляции. Для независимых случайных величин коэф-
фициент корреляции равен нулю, но он может быть равен нулю и для некоторых
зависимых величин, которые при этом называются некоррелированными. Для случай-
ных величин, имеющих нормальное распределение, отсутствие корреляции означает
и отсутствие всякой зависимости.
При этом выборочный коэффициент корреляции ?XY вычисляется по формуле:
п
^(у^-т^у,-mY)
1=1____________
(n-\)SxSY
Здесь тх, mY, Sx, определяются согласно (4.27) и (4.32) по формулам
=-£*,> sx = _/”х)2;
п ,=i V п -1 ,=i
mY = -£у,, Sr = р— ^(у,~тг)2 .
п ,=i у л -177
(4.84)
(4.85)
(4.86)
Коэффициент корреляции характеризует не любую зависимость, а только линей-
ную. Линейная вероятностная зависимость случайных величин заключается в том,
что при возрастании одной случайной величины другая имеет тенденцию возрастать
(или убывать) по линейному закону. Коэффициент корреляции характеризует сте-
пень тесноты линейной зависимости. Если случайные величины Хи У связаны точ-
ной линейной функциональной зависимостью у = а0 + а,х, то гхг = ±1; причём знак
соответствует знаку коэффициента а,. В общем случае, когда величины Хи Усвяза-
Рис. 4.8. Изображение полей корреляции: а — со слабой отрицательной корреляцией между
Хи У; б — с сильной положительной корреляцией; в — без корреляции
4.2. Обработка результатов пассивных экспериментов
217
ны произвольной стохастической зависимостью, коэффициент корреляции может
иметь значение в пределах
-1<гет<1. (4.87)
При rXY > 0 существует положительная корреляционная связь между величинами
У и У, при гхг < 0 — отрицательная.
Коэффициент корреляции, существенно отличный от ± 1, характеризует и слишком
большую долю случайности, и слишком большую криволинейность связи между слу-
чайными величинами. Зависимость Хи Yможет быть строго функциональной, а коэф-
фициент корреляции всё ещё будет меньше единицы. О наличии или отсутствии корре-
ляции между двумя случайными величинами качественно можно судить по виду поля
корреляции.
На рис. 4.8 приведены корреляционные графики для двух величин % и У. Каж-
дая точка показывает значения х и у для некоторого объекта. Рис. 4.8, а соответ-
ствует слабой отрицательной корреляции между % и У (гхг =-0.3); рис. 4.8, б —
сильной положительной корреляции (гхг =+0.99); рис. 4.8, в — отсутствию корре-
ляции (fry = 0).
Регрессионный анализ проводится после того, как определён вид уравнения рег-
рессии (4.73) и найдены значения его коэффициентов. Этот анализ состоит в следу-
ющем: проверяется значимость всех коэффициентов уравнения регрессии и устанавли-
вается адекватность уравнения.
При проведении регрессионного анализа принимаются следующие допущения:
1) входные переменные х измеряются с пренебрежимо малой ошибкой. Появле-
ние ошибки в определении у объясняется наличием в процессе невыявленных пере-
менных и случайных воздействий, не вошедших в уравнение регрессии;
2) результаты наблюдений выходной переменной уэкс" представляют собой неза-
висимые нормально распределённые случайные величины;
3) при проведении экспериментов с объёмом выборки п при условии, что каждый
опыт повторён одинаковое число раз, выборочные дисперсии S,2,..., S„ однородны.
Первое допущение означает, что входные переменные х можно рассматривать
как детерминированные величины. В соответствии со вторым допущением с экспе-
риментальными значениями выходных переменных следует оперировать как с неза-
висимыми нормально распределёнными случайными величинами. Согласно третье-
му допущению оценки дисперсий S2 (i = 1,..., п), получаемые по различным выбор-
кам экспериментальных данных, могут усредняться и будут справедливы для всего
рассматриваемого пространства входных и выходных переменных.
Следует отметить, что существуют статистически обоснованные критерии про-
верки как справедливости нормального закона распределения для выходных пере-
менных у',ксп, так и критерии оценки однородности дисперсий S2 (z = 1,..., п), кото-
рые в настоящей книге не рассматриваются.
Важным условием проведения регрессионного анализа является хорошая организа-
ция опытных исследований. В любом хорошо организованном эксперименте необходи-
мо предусмотреть меры для обеспечения независимости ошибок измерений. Одной из
важнейших мер такого рода является рандомизация (от англ, random — беспорядочно,
случайно). Рандомизация заключается в том, что планируемые опыты выбираются слу-
чайным образом, и именно в таком случайном порядке опыты производят. При этом
важно, чтобы при наличии параллельных опытов каждому из них присваивался свой
номер, и номера всех опытов, включая параллельные, рандомизировали совместно.
218
Глава 4. Эмпирические модели. Обработка результатов экспериментов
4.2.2. Основные этапы построения
эмпирических моделей
Построение эмпирических моделей вклктчает следующие этапы:
• выбираются входные переменные, влияющие на протекание процесса, — так на-
зываемые факторы',
• определяется выходная (зависимая) переменная, характеризующая состояние про-
цесса, его эффективность, которую можно рассматривать как критерий оптимально-
сти (целевую функцию), — так называемая функция отклика',
• определяется вид приближённого уравнения регрессии;
• вычисляются коэффициенты регрессии;
• определяется значимость коэффициентов регрессии с использованием крите-
рия Стьюдента г,
• устанавливается адекватность уравнения регрессии с применением критерия
Фишера F;
• определяется совместная доверительная область для коэффициентов регрессии.
4.2.3. Определение вида приближённого
уравнения регрессии
В общем случае необходимо анализировать графики зависимостей эксперименталь-
ных данных выходных переменных (функции отклика) у от входных переменных (фак-
торов) х и по их виду выбирать конкретную форму функциональной зависимости (4.73).
Для случая одной входной переменной х по опытным данным рекомендуется пост-
роить эмпирическую линию регрессии (рис. 4.9) и с её помощью выбирать конкрет-
ный вид функции (4.73).
При этом весь диапазон изменения х разбивается на s равных интервалов Дх. Все
точки, попавшие в данный интервал Дху, относят к его середине х/. После этого
подсчитывают частные средние у/ для каждого интервала:
Рис. 4.9. Построение эмпирической
линии регрессии по опытным данным
у^ = —--, 7=1,..., 5, (4.88)
nj
где — число точек в интервале Дху.
В результате объём выборки определяется
по формуле:
£«>=«• (4.89)
7=1
Эмпирическая линия регрессии у по х по-
лучается в виде ломаной линии путём после-
довательного соединения отрезками прямой
линии точек
U’.y’)’ J = (4.90)
Для определения вида приближённого урав-
нения регрессии для случая одной входной пе-
ременой желательно привести его к линейному
виду путём преобразования осей координат в
соответствии с табл. 4.3.
4.2. Обработка результатов пассивных экспериментов
219
Таблица 4.3. Преобразования к линейному виду функций одной переменной
Уравнение Координаты прямой Уравнение прямой Замечания
ОСЬ X ось у
1) — = а + р • х У X £ У 1 — = а + р-х У Асимптоты: x = --,y = 0 P
2) у = а Д X 2 X У р у = а + — X Асимптоты: x = 0, у = a
3) — = а + рх У X ИЛИ у - а + рх или Д-+Р У х X j. X X У £ У ч: |- 1н II II X |Я 2 i £ Асимптоты: a 1 x = —, у = - p p
~ ч X За)у = + у а + рх X X - Xj У-У1 ’ где (х,, у,) — любая точка на эксперимен- тальной кривой Х-Х, L = а + рх, + У-У1 + — (a + pxjx а Асимптоты: a 1 x = —,y = - + y P P Та же кривая, что и в 3), сдвинутая вверх или вниз на расстоя- ние у
4)у = а-х? log X logy logy = logo + piogx Если р > 0, кривая имеет вид параболы и проходит через начало координат и точку (1, а); если р < 0, кривая является гиперболой с осями координат в качестве асимптот и проходит через точку (1,а)
4а) у = а • х*' + у log X log(y-y) log(y-y) = logd + + p log X Сначала аппроксими- руют у по формуле т- У.Уг-Уз У1 + Уг~2Уз ’ где у3 = а xj + у, хз = у]ххХ2 , а (ХрУДСХг, у2)- экспериментальные точки
220
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Продолжение таблицы
Уравнение Координаты прямой Уравнение прямой Замечания
ось аг ось у
4h) у = у 10а> log X log(logy-logy) log(log у-log у) = = loga + plogx После логарифмиро- вания исходного уравнения поступают, как в 4д)
5) у = «₽' X logy logy = logo + xlogp Кривая проходит через точку (0, а)
Уравнение 1 (см. рис. 4.10, а): — - а + Р х
А Б в г
— = -0.1+0.3х - = 0.1 + 0.3х — = -0.5 + 0.3х - = 0.5 + О.Зх
У У У У
Уравнение 2 (см. рис. 4.10, б): у = а + —
х
А Б в Г
у = Ч).1 + ^ X 9 о.з у = 2 + — Л 0.3 у = 4 +— , 0.3 у = 6 + —
Уравнение 3 (см. рис. 4.10, в): — - а + Р • х
А Б в г
— = -0.1 +О.Зх У — = 0.1 + 0.3х У — = -0.4 +О.Зх У - = 4 + 0.Зх У
Уравнение 4 (см. рис. 4.10, г): у = а-хр
А Б В Г
у = 4х0'5 у = 4х03 у=4х"°'3 у = 4х"°'5
Уравнение 5 (см. рис. 4.10, б): у = а-0*
А Б В Г д Е Ж
у = 2(0.2)" У = 2(0.3/ У = 2(0.8/ у = 2(0.95)" у = 2(1.02/ у = 2(1.04/ У = 2(1.3/
4.2. Обработка результатов пассивных экспериментов
221
Рис. 4.10. Изображение зависимостей у от х для уравнений 1 (а), 2 (б), 3 (в), 4 (г), 5 (д)
Вид функции одной переменной может быть выбран (решение задачи структурной
идентификации) путём анализа графиков функций (рис. 4.10), оси координат кото-
рых преобразованы в соответствии с табл. 4.3. В результате преобразованные функ-
ции у становятся линейными не только по коэффициентам регрессии, но и по пре-
образованным переменным х.
222
Глава 4. Эмпирические модели. Обработка результатов экспериментов
При выборе вида функции (4.73) для случая нескольких входных переменных
х = (хрхт) задача определения вида приближённого уравнения регрессии суще-
ственно усложняется.
В общем случае различают два вида уравнений регрессии (эмпирических моде-
лей) — нелинейные по параметрам а , статистический анализ которых осуществляется
методом «нелинейной регрессии» и линейные по параметрам а , статистический ана-
лиз которых проводится методом «линейной регрессии».
Линейные по параметрам модели могут быть представлены в следующем виде:
У = Еа;(Р/^)’ (4.91)
7=0
где q>j (х) (j = 0,1,..., т) - линейные или нелинейные функции входных перемен-
ных (Хр..., хт); у — верхний символ над выходной переменной у обозначает её оце-
ночное (приближённое) расчётное значение, так как коэффициенты а получаются
по выборкам из генеральной совокупности, т.е. по экспериментальным данным.
Определение параметров (коэффициентов) а линейных моделей и их регресси-
онный анализ существенно проще, чем для нелинейных моделей. Поэтому нелиней-
ные модели, по возможности, стараются линеаризовать и привести к виду (4.91).
Частными случаями уравнения линейной регрессии с одной независимой перемен-
ной х являются:
• полиномиальная регрессия, когда
Ф7(х)=х7, у=0,1,..., т, (4.92)
и её разновидности — линейная регрессия от одной переменной (т = 1):
у = а0+а1х (4.93)
и параболическая регрессия (т = 2):
у = а0 + агх + а2х2; (4.94)
• трансцендентная регрессия и её разновидности
в виде зависимости показательного типа'.
У = , (4.95)
которая линеаризуется путём логарифмирования:
1п5' = 1па0 + х1па1, (4.96)
и дробно-показательного типа'.
у = аох“', (4.97)
которая также линеаризуется путём логарифмирования:
lny = lna0 4-aJnx. (4.98)
Частным случаем уравнения линейной регрессии (4.91) с многими независимыми
(входными) переменными х является:
• множественная регрессия, когда число входных переменных больше единицы,
т.е. (ф/х) = х,):
y = a0 + a1x1+... + amxm
при х0 = 1 .
(4.99)
4.2. Обработка результатов пассивных экспериментов
223
4.2.4. Определение параметров эмпирических
моделей (коэффициентов регрессии) для линейных
моделей с одной независимой переменной
Параметры (коэффициенты) эмпирических моделей могут определяться методом
наименьших квадратов {МНК) и методом максимума правдоподобия.
В соответствии с методологией регрессионного анализа решается задача аппрокси-
мации экспериментальных данных МНК (см. разд. 3.3.2).
На рис. 4.11 приведена графическая интерпретация МНК для случая регрессии от
одной переменной х (у— экспериментальные данные, урасч — расчётные данные
по уравнению регрессии, i = 1, ..., л). При этом результаты экспериментов приведе-
ны в табл. 4.4.
Таблица 4.4. Таблица проведения экспериментов для случая определения пара-
метров уравнения регрессии с одной входной (независимой) переменной
В этом случае для простейшей линейной модели (4.93) задача формулируется
следующим образом.
Пусть требуется определить параметры а0 и ах для линейной зависимости вида
у = а0+а1х (4.100)
по выборке объемом л:
Эту задачу можно решать двумя методами:
рекомендуемым методом наименьших квадратов
и методом максимума правдоподобия.
В методе МНК параметры определяются из
условия минимума критерия:
Л = -Z)2 =SU -а0-аЛ)2 . (4.102)
<=1 < = 1
При использовании необходимых условий
экстремума функции двух переменных а0 и ах
(3.6.17) получается система нормальных урав-
нений вида:
Рис. 4.11. Графическая интерпретация
метода наименьших квадратов для
случая линейной регрессии (4.93) от
одной переменной
224
Глава 4. Эмпирические модели. Обработка результатов экспериментов
п п
Ez ~^(aQ + alxl)=O;
1=1 1=1
или
п п
na0+(^Jxt)al = '^Jy, ;
1=1 1=1
и п
Tjy>x‘~^ («о + «1х, )х, = 0 (4.103)
1=1 1=1
п п п
(£ х, )«о + <Х *,2 )«i = X х, У,. (4.104)
1=1 1=1 1=1
Метод Крамера для решения системы линейных уравнений (3.2.10) приводит к
следующим формулам для искомых параметров:
п
«о
X* X
Ъ.У.
а! =
« X
1=1
л л
X*. X
и, после вычисления определителей, получаем:
л л л л
Х^.Х^-Х^Х^ь
«0="^-----4^—; ах
п£х* -(Xх,)2
"Х^-Х^Х?.
4>2-(Хх.)2
(4.105)
(4.106)
п
X
2
2
В методе максимума правдоподобия аппроксимирующая зависимость (4.100) рас-
сматривается как функция математического ожидания случайной величины (услов-
но среднего значения) от неслучайного аргумента х:
mr=a0+a1x. (4.107)
При этом принимается, что случайная величина подчиняется нормальному зако-
ну распределения. Поэтому в выражение для функции правдоподобия нормального
закона распределения (4.61) вместо математического ожидания следует подставить
выражение для mY из (4.107):
, . -п, „ и, 2 1 -A z >2
L(x,y,or,fl0,a1) = —1п2л--1пог-—5-2^(>’._ао-а1х,) . (4.108)
Z у |=1
При выводе этого соотношения предполагается, что все дисперсии у равны, т.е.
=оп = —= <3г • В этом случае нахождение максимума функции правдоподобия со
знаком минус (4.108) соответствует поиску минимума критерия МНК (4.102), и ре-
зультаты определения параметров эмпирических моделей совпадают. Когда диспер-
сии для выходных переменных у (aj) различны и зависят от коэффициентов регрес-
сии, задача поиска параметров моделей существенно усложняется, и необходимо
минимизировать следующий критерий:
V (Z-«o-«ix,)2
Cr = Z------~2-----• (4.109)
1=1 ° г
4.2. Обработка результатов пассивных экспериментов
225
Для известных оценок дисперсий в каждой опытной точке о2 критерий (4.109)
можно рассматривать как критерий МНК с заданными весовыми коэффициентами:
Сг = ^АУ, ~ао -ДЛ)2, (4.110)
1=1
где весовые коэффициенты определяются следующим образом:
а, =1/с2 (/ = !,...,«). (4.111)
На практике редко удаётся в полном объёме воспользоваться критериями (4.109)
и (4.110), и поэтому чаще всего ограничиваются обычным критерием МНК:
" / ?
Сг = ^{уГч-УГ) . (4.112)
i=i
где урасчи у’ксп рассчитываются при одном и том же значении элементов вектора
х, (/ = 1,..., л), а л — общее число опытов или объем выборки.
4.2.5. Определение параметров эмпирических
моделей (коэффициентов регрессии)
для нелинейных моделей с одной или многими
независимыми переменными
Согласно уравнению регрессии (4.73), записанному в общем виде, эмпирическая
модель может быть и нелинейной по параметрам и тогда, в предположении, что
урасч = у, критерий МНК Сг (4.112) следует рассматривать как функцию многих
переменных от параметров a = (а0, ар..., am):
Сг = Cr(a0, a,,..., am). (4 113)
Для определения (подгонки) коэффициентов (параметров) модели (4.73) необхо-
димо, чтобы критерий Сг (4.112) стал наименьшим, т.е. чтобы сумма квадратов вер-
тикальных отрезков на рис. 4.11 (например, х, :[у1р*с’, yf®"] и х„ :[урас’, у’“"])
(см. разд. 3.6.4 и 3.6.5) стала наименьшей.
Поэтому задача определения коэффициентов модели (4.73) сводится к реализа-
ции одного из алгоритмов оптимизации (см. разд. 3.6) для определения минимума
критерия (4.112):
™ф.УГ-уГ), (4.114)
где адоп — допустимая область изменения параметров a .
Именно так решается задача параметрической идентификации для нелинейных
моделей.
В данном случае возможно также воспользоваться необходимым условием экст-
ремума функции многих переменных Сг (4.113), (3.6.17):
ЭСг _ дСг _ дСг
да0 ’ да, ’ дат
(4.115)
15-4544
226
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Для определения искомых коэффициентов система в общем случае нелинейных
уравнений (4.115) должна быть решена относительно коэффициентов а0, at,ат.
Однако, как показывает практика, решение систем нелинейных уравнений (см.
разд. 3.2.3) ничуть не проще, чем прямое решение задачи оптимизации (4.114).
4.2.6. Определение выборочных (эмпирических)
коэффициентов регрессии для линейных по
параметрам моделей при произвольном числе
входных переменных
Таблица 4.5. Таблица прове-
дения экспериментов при про-
извольном числе входных пере-
менных
\р п \ *1 Х2 хг уЭКСП
1 *11 х12 Х1г у ЭКСП
2 . *21 х2г Д1ЭКСО Л2
п Х„1 хп2 хпг у-ЭКСО
При определении элементов вектора наблюде-
ний у’*0" (/ = 1,..., и) зависимых (выходных) пере-
менных (табл. 4.5) при постановке п эксперимен-
тов для произвольного числа г факторов
Xj(j = 1,..., г) матрица входных (независимых) пе-
ременных х размером п х г может быть представ-
лена: х,г = [xd, х,2, ..., х„] (1 = 1, ..., и).
Для линейных или линеаризованных по пара-
метрам моделей необходимо выражение (4.91) под-
ставить в критерий МНК (4.112):
и, воспользовавшись необходимым условием экстремума функции многих перемен-
ных (3.6.17), (4.115), решать полученную систему линейных алгебраических уравне-
ний (СЛАУ):
1>,Ф,(х,)-УГп Фо(х,) = 0;
oaQ l=i \^J=Q J
r)Cr n ( m '
“2X X^(x,)-y- Ф1(х,) = 0;
oa, ,=i J
.'|ГГ л ( m A
4— = 2E x л,Ф, (x,) - зГ" Фт (x,) = о.
dam <-l 7=0 j
(4.117)
Перегруппировав члены в системе уравнений (4.117), можно записать СЛАУ в виде:
m n п
Ха;Ефи(х,)фу(х,)=Х(Р«(^)>'’'“:п. j,u = 0,l,...,m. (4.118)
j=0 1=1 1=1
И, если ввести в рассмотрение информационную матрицу IU] (J = 0, 1,..., т и
и = 0, 1,..., т):
п
IUJ =Ефи(х,)ф/х,), 7 = 0,1,...,/и, и = 0,1,...,т, (4.119)
1=1
4.2. Обработка результатов пассивных экспериментов
227
то она окажется квадратной, симметричной и значения её элементов зависят только
от входных переменных и конкретного вида функций Ф7 (х) (j = 0,1,т).
В матричном виде информационную матрицу I можно представить в виде про-
изведения транспонированной и исходной матрицы входных переменных Ф :
7 = фГф. (4.120)
При этом матрица Ф размерностью п х (т +1), зависящая от входных перемен-
ных и конкретного вида функций % (х) (j = 0,1,т), имеет вид:
’фо(*1) фД) • • Ф„Д)
ф = лх(т+1) Фо(^) Ф1(*2) • • Фт(*г) (4.121)
Фо(*„) Ф1(*„) • • <Рт(х„)
Соответственно правую часть СЛАУ (4.118) по аналогии с (4.119) можно записать:
^=5ф«(х,)уГ, и = 0,1,...,т, (4.122)
или в матричном виде:
Ь=фТу^т. (4.123)
В результате СЛАУ (4.118), решаемая для определения коэффициентов эмпири-
ческой модели, может быть представлена:
и =0,1,..., т, (4.124)
j=o
или в матричном виде:
!а=Ь. (4.125)
Если для определения коэффициентов а (4.91) воспользоваться методом обрат-
ной матрицы (3.2.48), то получается:
717а = 7‘* (4.126)
и, так как произведение I1 I равно единичной матрице Ё (см. разд. 3.2.1), т.е.
Е = Т'1 (4.127)
то
E=a = T'b, (4-128)
или
a=7-1F. (4.129)
Матричная формула для определения коэффициентов линейной регрессии (па-
раметров эмпирической модели) получается после подстановки в (4.129) матричных
равенств (4.120) и (4.123):
а=(ф ф^ ф уэжсп (4.130)
228
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Таким образом, для определения коэффициентов линейной или линеаризованной
регрессионной модели необходимо выполнить следующую последовательность действий:
• сформировать вектор наблюдений у’*0" и вычислить его элементы (только для
линеаризованных моделей);
• сформировать и рассчитать элементы матрицы, зависящей от входных пере-
менных Ф и конкретного вида функций Фу(х) (j = 0,1,т);
— =т
• транспонировать матрицу Ф => Ф ;
= = =т =
• перемножить транспонированную матрицу Фт на исходную матрицу Ф: Ф Ф;
• выполнить обращение информационной матрицы — (ФТФ)-1;
• умножить полученную обратную матрицу на матрицу фт;
• умножить полученный результат на вектор наблюдений уэксп и получить выбо-
рочные коэффициенты регрессии а (4.130).
Регрессионный и корреляционный анализ экспериментальных данных,
описываемых линейными и линеаризованными эмпирическими моделями
Определение коэффициентов линейной или линеаризованной модели вида (4.91):
У = 5Хфу(*)
7=0
методом аппроксимации (конкретно МНК) приводит к матричной формуле (4.130):
где значения элементов матрицы независимых переменных Ф зависят только от
входных переменных х и вида функций ф(х) (4.121):
Ф0(*1) Ф101) - Фи(*1)
Ф0(х2) Ф1(х2) ... q>m(x2)
ФоСч.) Ф1(^л) - фЖ).
а вектор экспериментальных значений (вектор наблюдений) _уэксп присутствует в этом
матричном соотношении в качестве линейного сомножителя.
Поэтому целесообразно ввести матрицу L :
=т=\-1=т
ф ф ф .
После чего можно записать матричную формулу МНК для определения коэффи-
циентов модели (4.130) с учётом того, что их значения являются оценками их истин-
ных значений (поэтому обозначаются д ) и получены по выборке вектора наблюде-
ний выходной переменной _уэкс":
а=1ужп. (4.131)
L =
4.2. Обработка результатов пассивных экспериментов
229
Если принять, что расчет по этой формуле происходит при конкретной реализа-
ции элементов случайного вектора наблюдений выходной переменной у (уэксп), то
элементы вектора коэффициентов регрессии а в соответствии со свойством линей-
ности нормального закона распределения также будут случайными величинами, оп-
ределяемыми по аналогии с (4.131) по формуле:
а = Ly. (4.132)
Статистический анализ результатов вычисления а необходим, так как вектор
у’ксп, который влияет на значения а в соответствии с (4.131), является реализацией
случайного вектора у (это приводит к тому, что а — также случайный вектор).
Причины случайного характера вектора у, полученного в результате опытных
измерений, следующие:
• используется случайная выборка для определения вектора наблюдений уж“;
• результаты измерения каждого у',|‘с" (z = 1,..., л) — реализации случайных ве-
личин.
Один из видов статистического анализа — регрессионный анализ — предполагает,
что элементы вектора уэксп — реализации независимых случайных величин у, рас-
пределённых по нормальному закону распределения, т.е. для плотности распределе-
ния у, (z-го измерения) будет справедливо (4.5):
1 G,-"ч. У
2 <
i = l,
п,
(4.133)
и числовыми характеристиками случайной величины у будут:
ту — математическое ожидание;
cP — дисперсия;
cv = среднеквадратичное отклонение или стандарт.
Допущение о нормальном законе распределения элементов вектора у — это
первое допущение регрессионного анализа. Второе допущение регрессионного анализа —
о не случайности элементов вектора х , т.е. х, (i = 1,..., г) — не случайные величины.
Из этих двух допущений следует, что, как уже указывалось, в соответствии со
свойством линейности нормального закона распределения (4.132) элементы вектора
а также являются случайными величинами со следующими числовыми характери-
стиками (4.5):
та — математическим ожиданием,
а2а - дисперсией,
о„ — среднеквадратичным отклонением или стандартом.
Третье допущение регрессионного анализа заключается в допущении об однород-
ности дисперсии случайных величин у. Свойство однородности дисперсий предпо-
лагает несущественное отличие дисперсий у, что позволяет усреднять их оценки
или значения, полученные по ограниченным выборкам, и распространять на всю
исследуемую область изменения входных и выходных переменных (условие одно-
230
Глава 4. Эмпирические модели. Обработка результатов экспериментов
родности дисперсий проверяется с помощью специальных критериев, которые здесь
не рассматриваются).
В соответствии с регрессионным анализом всегда рассчитывается оценка коэф-
фициентов а (оценка обозначается Л) (4.131), в результате получается приближенная
зависимость (4.91):
У = (4.134)
7=0
Для получения строгой зависимости, и так как у — случайная величина, необхо-
димо строить зависимость условного математического ожидания ту\_ (при условии
известных экспериментальных значений х) от факторов х , с помощью теорети-
ческого уравнения регрессии:
т,\.=ЪаГ*№ (4.135)
7=0
где а] — истинные значения коэффициентов регрессии, называемые теоретически-
ми коэффициентами регрессии; ту = т^ — условное математическое ожидание слу-
чайной величины у (2.34).
При этом регрессионный анализ экспериментальных данных включает три этапа.
1. Определение оценок коэффициентов регрессии методом наименьших квадра-
тов по формуле (4.130).
2. Определение значимости коэффициентов регрессии, т.е. существенного отли-
чия их от нуля с помощью критерия Стьюдента t (табл. 2 Приложения).
3. Определение адекватности уравнения регрессии (4.134) с помощью критерия
Фишера F (см. табл. 3 Приложения).
Определение дисперсии и ковариаций для элементов вектора наблюдений выходной
переменной у
Обозначим вектор математических ожиданий для п экспериментов как ту = М |_ .
Соответственно, для дисперсий у, (I = 1,..., л) для л случайных величин будет
справедливо (4.13):
%. = М[(у, —ту)21, 1 = 1,...,л. (4.136)
Ковариация двух случайных величин у, и у, равна математическому ожиданию
произведения (у, - ту )(уу - ту/) (4.82):
COVyy = M[(yt-ту )(у7-ту )], t = 1,..., л; у = 1,...,л; i*j. (4.137)
Для независимых нормально-распределённых случайных величин
(у, ~ту )(у; ~ту):
COVyy=0. (4.138)
Для нормально-распределённых случайных величин вместо размерной величины
COVy ъ целесообразно пользоваться безразмерным коэффициентом корреляции (4.83):
4.2. Обработка результатов пассивных экспериментов
231
Для независимых случайных величин у, и yt: Гуу —>0 (i = l,...,zi; j = l,...,n).
Для дисперсий oj в и экспериментальных точках создаётся специальная матрица
дисперсий-ковариаций размерностью пхп следующим образом:
COV- = Л/[(у-отДу-й^)т ]=
Л/[(У] - тЛ )2] Л/[(у] - ту )(у2 - ту2)]
м [(у„ “ ту. )(У1 - ™yt)] м [(к - т,. \У1 ~ тУ2 )]
Л/[(У, -«Л)(У„
w[(v„ У]
(4.140)
В результате матрица дисперсий-ковариаций для экспериментальных значений
ужен _ j, , имеет вид:
COVj = < covyiyi cov^ • < • •• covyty; •• cov^ (4.141)
C0Vy.yl C°Vy.y2 • o2
Если принять два допущения регрессионного анализа для п случайных величин
у , соответствующим элементам вектора наблюдений у’ксп (i = 1,п):
• о независимости измерений (COVyy =0, i * j);
• об однородности дисперсии, т.е. несущественном отличии о2 (z=l, ...,п) и их
равенстве о2,
то получается диагональная матрица дисперсий-ковариаций для измеряемых значе-
ний уэксп с одинаковыми дисперсиями о2:
СОУ-=о2Е .
(пхп) (zixzz)
(4.142)
Определение дисперсии и ковариаций для элементов вектора коэффициентов
регрессии а
Так как а — случайная величина, распределённая по нормальному закону,
та = м[а]. По аналогии с (4.140) составим матрицу дисперсий-ковариаций для а :
COV3 = M [(a - ma \a - ma )T]= C0V^ cov^ • < • •• cov^_ (4.143)
cov^ cov^ •• <
В соответствии с (4.132): ma - Lmy. (4.144)
Для определения элементов матрицы дисперсий-ковариаций необходимо под-
ставить (4.132) и (4.144) в матричную формулу (4.143).
232
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Если в результате подстановки матрица (4.143) получится диагональной, то по
аналогии с (4.142) коэффициенты регрессии можно считать статистически независи-
мыми.
Z==y =т=т
Выполним эту подстановку, пользуясь тем, что (ЛВ] =В А (см. разд. 3.2.1):
= Л/ ь(у-ту}(у-туУ L
= LM[(y-mv)(y-mv)TF =LCOV-L =
(4.145)
= Lo2EL
Е
Согласно (4.142), COV- =с2уЕ, а так как матрица (Ф Ф) симметрична, то
COVs=c2
(4.146)
Назовём обратную матрицу (Ф Ф) 1 корреляционной матрицей С :
с ^00 Col СОт
Сю С» с1и
Ст0 СИ1
(4.147)
Тогда
Qo СОт со^
COV-a = <с = Сщ С„ • С1и = <
Сио Ст1 .. с ^тт _ cov^ cov^
откуда следует:
для дисперсий коэффициентов регрессии
covata_ , (4.148)
2
G
ат
для ковариаций коэффициентов регрессии
C0Va,a, = °2,Су, , Л 1 = 0, 1- ' * j-
(4.149)
(4.150)
Таким образом, в соответствии с (4.149) и (4.150) независимость коэффициентов
определяется тем, будут ли недиагональные элементы в матрице корреляции С (4.147)
равны нулю.
В соответствии с (4.148) и (4.121) значения элементов этой матрицы определяют-
ся экспериментальными величинами х и видом функций <р(х), т.е. зависят от того,
как поставлен (спланирован) эксперимент.
4.2. Обработка результатов пассивных экспериментов
233
В случае активного эксперимента (например, полного факторного эксперимента
или ортогонального центрального композиционного плана эксперимента) его про-
водят так, чтобы матрица С стала диагональной, т.е. коэффициенты регрессии
будут статистически независимы.
В случае произвольного пассивного эксперимента матрица С оказывается недиа-
гональной, и поэтому коэффициенты будут статистически зависимы.
Матрица С (4.147) называется корреляционной, так как с помощью её элементов
в соответствии с (4.139) и (4.148)—(4.150) можно рассчитать корреляции коэффици-
ентов регрессии:
^,=-^==. у, । = 0,1,..., от. (4.151)
Определение оценок дисперсии выходной переменной уравнения регрессии S2
Оценка дисперсии выходной переменной у (4.142) - <з2у в формулах (4.149) и
(4.150) важна для определения оценок дисперсий и ковариаций коэффициентов рег-
рессии. Эта оценка определяется из различных экспериментов и обозначается S2 (4.32).
Пусть выходная переменная у зависит от г входных переменных хг - хр..., хг
(независимых переменных хг).
Для оценки дисперсии проводятся два типа экспериментов:
• в различных опытных точках xIr(j = 1, ..., п) (см. табл. 4.5) для определения
параметров уравнения регрессии {параметров эмпирической модели), а также дисперсий
адекватности и остаточной дисперсии Sj,;
• в одних и тех же опытных точках (так называемые параллельные опыты) с целью
определения дисперсии воспроизводимости S2.
I. Определение оценок дисперсий с различным числом параллельных опытов
в каждой экспериментальной точке
Число параллельных опытов в каждой z-й экспериментальной точке при проведе-
нии п опытов в различных экспериментальных точках (хр...,хп) обозначается как
kt (i = 1,..., п).
а) Определение остаточной дисперсии Sr.
определяется из экспериментов с из-
меняющимися значениями х, (i = 1,..., п)
(пассивный эксперимент). Таблица проведе-
ния экспериментов представлена в табл. 4.6.
о 2 _ t-j ц-1_________
V,’ (4.152)
Lk‘~P
i=i
где р — число значимых коэффициентов
регрессии, в частном случае (когда все ко-
Таблица 4.6. Таблица проведения эк-
спериментов с изменением независимых
переменных с различным числом парал-
лельных опытов в каждой точке
6 / (к / |н/ / с Х1 хг у ЭКСП
\...кх Хц-.Хц ... ХК...Х1Г v эксп v эксп Л1 ”’zu1
\...кп Х„1...Х„1 xw...xw -у ЭКСП у эксп Л|1 ’"^пкп
234
Глава 4. Эмпирические модели. Обработка результатов экспериментов
эффициенты значимы) р =т + 1 — см. (4.134); SR ~ остаточная дисперсия, характе-
ризующая погрешности уравнений (или моделей) и погрешности экспериментов;
у, (i = l,..., п) — значения, определяемые расчетным путем с помощью уравнения
регрессии (4.134) в п различных опытных точках; у™" (i = l, ...,п; и = 1, ...,£,) —
значения, определяемые экспериментально в nxk: (i = l.п) различных опытных
точках, включая различное число параллельных опытов kt (i = 1,..., п) в каждой опыт-
ной точке; SSR — сумма квадратов остаточной дисперсии равная числителю формулы
(4.152); vR — число степеней свободы остаточной дисперсии равно знаменателю
формулы (4.152); п — число опытных измерений при проведении экспериментов в
различных точках, в каждой из которых ставится kt параллельных опытов (i = 1,..., п).
Сумма квадратов остаточной дисперсии 88R (4.152) равна сумме квадратов диспер-
сии адекватности SSad, характеризующей погрешность уравнения регрессии, и сумме
квадратов дисперсии воспроизводимости SSe, характеризующей погрешность экспери-
ментов:
SSR=SSad+SSe. (4.153)
Соответственно, для числа степеней свободы остаточной дисперсии SR (4.152)
будет справедливо:
P=v^+ve. (4.154)
1=1
б) Определение дисперсии воспроизводимости S?.
Дисперсия воспроизводимости 8? определяется из параллельных опытов, когда
их число в каждой экспериментальной точке различно и равно kl (i = 1,..., n):
i=i
где среднее экспериментальное значение результатов параллельных опытов в каж-
дой опытной точке определяется следующим образом:
эксп* _ И=1 — 1 и
При этом числитель формулы (4.155) равен сумме квадратов дисперсии воспроизводи-
мости 88 г, а знаменатель — числу степеней свободы дисперсии воспроизводимости ve.
в) Определение дисперсии адекватности S^d.
88
В этом случае в соответствии с приведёнными ранее равенствами: 8<и1 =—
где, как следует из равенств (4.153) и (4.154), сумма квадратов дисперсии адекватно-
сти 88 ш1 и число степеней свободы дисперсии адекватности vad определяются:
4.2. Обработка результатов пассивных экспериментов
235
SSad = SSR-SSe;
=vR-vf-
(4.156)
(4.157)
IL Определение оценок дисперсий с одинаковым числом параллельных опытов в каж-
дой экспериментальной точке
Возьмём z-ю строку из табл. 4.6 пассивного экспери-
мента и повторим в ней опыты к раз (табл. 4.7). При
этом полная таблица эксперимента получается при из-
менении i от 1 до п.
В этом случае дисперсия воспроизводимости для каж-
дой экспериментальной точки определяется как:
(4.158)
Таблица 4.7. Таблица
проведения эксперимен-
тов в z-й опытной точке с
к параллельными опытами
п \ хп xir уЭКСП
1 хч Х1Г рЭКСП •'ll
к хп xir эксп ?ik
при ЭТОМ у’™'
к -1 v„ ’
к
к
(i = 1,..., п) ,
где S„ — дисперсия воспроизводимости, характеризующая погрешность экспери-
мента в z-й опытной точке; у,™™ — экспериментальные значения, полученные в па-
раллельных опытах в z-й точке; у’ксп* — усреднённое экспериментальное значение в
z-й точке; SSCI — сумма квадратов дисперсии воспроизводимости в z-м эксперименте;
v„ = к -1 — число степеней свободы дисперсии воспроизводимости в z-й точке; к —
число параллельных опытов в z-й экспериментальной точке.
Если к параллельных опытов проведены во всех экспериментальных точках таб-
лицы эксперимента (см. табл. 4.7), то в соответствии со свойством однородности
дисперсии с учётом (4.158) дисперсия воспроизводимости вычисляется:
s * = (4.159)
zz^-1)
м
так как Sd = —-- и v, = п(к -1).
п
Для одинакового числа параллельных опытов в каждой экспериментальной точке
(к) дисперсия адекватности в соответствии с (4.156) и (4.157) определяется как:
к±(у.-уГ'1 „
~, при этом у’"0"* = ------------------ (z = 1,..., zi). (4.160)
П~Р Vad ’ к
236
Глава 4. Эмпирические модели. Обработка результатов экспериментов
III. Определение оценок дисперсий при постановке параллельных опытов в одной
экспериментальной точке по отдельной серии экспериментов
Если опыты проведены без параллельных, и для получения дисперсии воспроиз-
водимости проведена отдельная серия из к параллельных экспериментов в одной
опытной точке, то дисперсия воспроизводимости вычисляется по формуле:
л у Г"
где у’ксп' --------
v к
* е
(4.161)
В этом случае остаточная дисперсия sR равна дисперсии адекватности S2^:
-хэксп) „„ „„
S2R = S2, = ---------= -S°d = (4.162)
« - Р ad VR
Для оценки дисперсий а2 в (4.142) целесообразно использовать S2, а при отсут-
ствии параллельных опытов — S2d.
Для определения оценок дисперсий коэффициентов в соответствии с (4.149) ис-
пользуют следующие оценки а2 (по представленному приоритету) — дисперсию вос-
производимости S2, дисперсию адекватности S2ud или остаточную дисперсию S2R.
4.2.7. Определение значимости
коэффициентов регрессии
Для определения значимости коэффициентов регрессии (4.134) используется нор-
мированная случайная величина (4.34):
а ~та
t=—-------7=0,1.......т, (4.163)
°-,
подчиняющаяся 1-распределению Стьюдента (4.49) (табл. 2 Приложения).
Воспользовавшись оценкой дисперсии воспроизводимости S2 и принимая во
внимание, что в соответствии с (4.149): S2 = S2Cn (j = 0,1,..., т), и с учетом того, что
, можно записать следующее вероятностное соотношение для коэф-
фициентов регрессии а (4.35):
хтабл.
Ж)
= ₽, 7=0, 1,
(4.164)
..., т .
В этом случае табличное значение t определяется при доверительной вероятности 0
(чаще всего 0.95) и числе степеней свободы дисперсии воспроизводимости 5е2 — vf.
Если предположить, что математическое ожидание коэффициента т = 0 (т.е. истин-
ное его значение равно нулю), то условие незначимости коэффициента о имеет вид (4.164):
4.2. Обработка результатов пассивных экспериментов
231
t^= N j = O,l,...,m. (4.165)
В противном случае коэффициенты регрессии значимы.
Если раскрыть вероятностное неравенство (4.164), для коэффициентов регрессии
получается следующий доверительный интервал:
а^б^-^т^ <а] + 8еу[с~-^}, j = 0,1,..., т. (4.166)
Это означает, что вместо оценки коэффициентов регрессии можно пользо-
ваться их критическими (крайними) значениями в соответствии с (4.134). Это, в
свою очередь, приведёт к различным величинам у в уравнении
7=0
В результате на графике (рис. 4.12) вместо одной кривой, полученной по оценоч-
ным значениям коэффициентов регрессии, получается три: одна — минимальных
значений ар вторая — максимальных значений at и третья — сплошная, для оценоч-
ных значений коэффициентов регрессии.
Процедура исключения незначимых коэффициентов регрессии
В соответствии с (4.165) незначимые коэффициенты следует исключать из урав-
нения регрессии (4.134). Однако так как корреляционная матрица С (4.147) в общем
случае недиагональная и коэффициенты статистически зависимы, то после исклю-
чения одного коэффициента необходимо пересчитать оставшиеся и рассчитать
сумму квадратов остаточной дисперсии SSR (4.152). Если она не ухудшилась (не стала
больше), то исключение было правомочным. В противном случае исключение было
неправомочным.
В случае незначимости нескольких коэффициентов
всегда исключается только один (так как существует
статистическая зависимость коэффициентов), при-
чём тот, для которого отношение (4.165):
является наименьшим.
Остальные коэффициенты пересчитываются, и,
как указывалось выше, определяется дисперсия вос-
производимости SSe.
Исключение незначимых коэффициентов по од-
ному производится до тех пор, пока сумма квадра-
тов остаточной дисперсии SSR (4.152) не ухудшается.
В случае незначимости нескольких коэффици-
ентов в активном эксперименте из-за диагональнос-
ти матрицы С (4.147) можно одновременно исклю-
чать все незначимые коэффициенты.
Рис. 4.12. Кривые уравнений
регрессии, полученные при
оценочном и критических
(крайних) значениях коэффици-
ентов регрессии
238
Глава 4. Эмпирические модели. Обработка результатов экспериментов
4.2.8. Проверка адекватности уравнения регрессии -
адекватности эмпирической модели
При определении вида приближённого уравнения регрессии (4.134) и коэффици-
ентов регрессии (4.130) практически решаются задачи структурной и параметричес-
кой идентификации эмпирической модели.
В результате успешного решения задачи идентификации (параметрической и струк-
турной) должна получиться адекватная математическая (эмпирическая) модель (ММ).
Под адекватностью Л/Л/понимается:
1) качественное и количественное соответствие поведения ММ и объекта моде-
лирования;
2) выполнение этого соответствия как при одном наборе режимных параметров
(адекватность состояния), так и при различных наборах режимных параметров
(адекватность поведения);
3) возможность интерполяции и экстраполяции свойств реального объекта с по-
мощью ММ.
Качественное соответствие поведения модели и объекта моделирования опреде-
ляется путём установления приближённого совпадения тенденций изменения пере-
менных процесса в модели и объекте.
Для количественной оценки адекватности уравнения регрессии необходимо определить
отношение дисперсии адекватности S2rl к дисперсии воспроизводимости :
Fpac4=5i/Sj. (4.167)
Это отношение сравнивается с табличным значением распределения Фишера F
при доверительной вероятности р (0.9, 0.95, 0.99) и двух числах степеней свободы —
дисперсии адекватности (v0(/) и дисперсии воспроизводимости (ve), т.е. с величиной
(табл. 3 Приложения).
При использовании статистического распределения Фишера всегда рассматривает-
ся отношение (4.167) большей дисперсии (в данном случае - 5^)к меньшей (в дан-
ном случае — S2), равное F, и для адекватной модели её рассчитанное значение должно
быть не больше стандартного (табличного) значения распределения Фишера:
р табл
Pl».!.»,)"
(4.168)
В противном случае модель считается неадекватной.
Если нет параллельных опытов, то либо для моделей сравнивают остаточные дис-
персии (4.162):
2
(4.169)
_____________________________________________
п-р
либо сравнивают эту величину с оценкой разброса опытных данных относительно
п v
,.ср _ v У,
среднего значения У - Л, — дисперсией среднего:
2
S2 = &----
ср п-1
ssm
(4.170)
4.2. Обработка результатов пассивных экспериментов
239
Так как последняя дисперсия больше S2R, то для критерия Фишера рассматрива-
ют отношение Sк SR, и условие адекватности будет иметь вид:
S2
(4-171)
Оценка совместной доверительной области коэффициентов регрессии
При рассмотрении доверительных интервалов для каждого коэффициента рег-
рессии (4.166) было показано, что следует оценивать и доверительные интервалы для
функции отклика — выходной переменной модели (4.134) — см. рис. 4.12. Однако,
если требуется определить, описывает ли экспериментальные данные линейная по
коэффициентам модель, необходимо оценивать совместную доверительную область
для всех коэффициентов регрессии.
Для этой цели экспериментальные данные по выходным переменным (у’ксп) срав-
ниваются с их математическими ожиданиями (т^), получаемыми по теоретическо-
му уравнению регрессии (4.135).
При этом формируется количественный критерий, который включает в себя:
• У™" ~ экспериментальные значения случайной величины уа, полученные в у-м
параллельном опыте z-ro эксперимента;
• т- — математическое ожидание, рассчитанное по модели величины выходной
переменной у для значений входных переменных х, в z-м эксперименте.
Если также ввести среднее значение в z-м эксперименте у' и рассчитанное по
математической модели (уравнению регрессии) это же значение у,, полученное при
тех же величинах входных переменных х,, что и в эксперименте, дающем у*, то
будет справедливо:
ЭКСП ( эксп эксп* \ . ( ЭКСП* Л \ I (Л \
y.j -т9,=\уу -у. )+\У, -y,)+\y,-m9i).
' s’ ' si ' s’ ' ’
Оценкой первых разностей будет дисперсия воспроизводимости S2 (4.155), кото-
рая характеризует ошибку экспериментов.
Оценкой вторых разностей будет дисперсия адекватности S2d (4.160), которая
характеризует ошибку уравнения (модели) в сравнении с экспериментальными вели-
чинами ут (если нет параллельных опытов в каждой экспериментальной точке — это
не среднее значение, а просто измеренная величина).
Оценкой третьего слагаемого является дисперсия рассчитанного значения вы-
ходной переменной (определяемая по аналогии с S2 и SR).
п . .2
SS
S2=-sl__________Л (4.173)
у „ „
Р Р
где р — число значимых коэффициентов уравнения регрессии.
240
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Аппарат дисперсионного анализа указанных выше трёх дисперсий З2, 32rf , и З2
позволяет решить две задачи:
• оценить адекватность уравнения регрессии (S°d / S2) с использованием крите-
рия Фишера (4.167) и (4.168);
• определить совместную доверительную область для коэффициентов регрессии
s2y/s2ad.
Отношение дисперсии рассчитанной величины выходной переменной у S2 к
дисперсии адекватности S2d подчиняется распределению Фишера с доверительной
вероятностью Р, и условием их малой различимости является:
S2
< 77табл
~ ₽(v,,v^)’
аа
В соответствии с логикой рассматриваемого анализа граница области, где это
условие выполняется, задаётся уравнением:
S2y
(4.174)
у _ ртабл
’’ - ЧЬ v„r
(4.175)
или, с учётом (4.173) и (4.162),
^у _ Р ртабл
SSad п — р ₽<v>”v")’
(4.176)
Величина SSad = ^(у, - у^")2 - значение критерия (4.112), полученное при реа-
1=1
лизации программы минимизации.
Значение SSy (4.173) можно заменить матричным произведением (см. разд. 3.2.1):
SSy = (у-т-У(у-т.)= -д)У
_\т=т=, v (4.177)
= (а - a J Ф Ф(д - а )
так как в соответствии с эмпирическим и теоретическим уравнением регрессии (4.134)
и (4.135) для всех расчетных значений выходной переменной будут справедливы сле-
дующие матричные равенства:
у = ф« и т - = Фа .
Подставлением выражения (4.176) вместо 33у в (4.177) получается квадратичная
форма (см. разд. 3.6) вида:
(а-а)ТфТф(а-«)= SS^-P-F^. (4.178)
Геометрической интерпретацией этой квадратичной формы (3.6.22) является
= =т =
эллипсоид, оси которого пропорциональны собственным значениям матрицы А = Ф Ф,
определяемой из характеристического уравнения вида (3.2.18)—(3.2.20):
|а-ХЁ| = 0. (4.179)
4.2. Обработка результатов пассивных экспериментов
241
Для двух коэффициентов а0 и ау, напри-
мер, простейшей линейной модели (4.100), по-
лучается эллипс, как показано на рис. 4.13.
Получена совместная доверительная об-
ласть для коэффициентов (здесь а0 и а.) в
линейной модели. Её можно сравнить с пря-
моугольником, образованным оценками дове-
рительных интервалов коэффициентов регрес-
сии (4.166).
Длинная, вытянутая доверительная область
Рис. 4.13. Совместная доверительная
область для коэффициентов регрес-
сии а0 и at линейной модели
(собственные значения матрицы А существен-
но отличаются) указывает на то, что коэффи-
циенты сильно коррелированны и значения
коэффициентов плохо оценены.
Результатом высокой корреляции коэффи-
циентов является то, что неправильно оцененное значение одного из коэффициен-
тов можно сбалансировать при проведении подгонки компенсирующим исправлен-
ным значением другого параметра. При этом поверхность суммы квадратов (Сг)
отклонений расчетных значений у от истинных для совместной доверительной обла-
сти коэффициентов с учетом (4.176) задаётся уравнением (4.112):
Cr - SSad + - SSad 1 +
Р у-табл
п — р
(4.180)
4.2.9. Метод множественной корреляции
для определения коэффициентов корреляций
между входными и выходной переменными
процесса. Определение коэффициентов
множественной коррелляции
Коэффициенты корреляции (4.83) характеризуют линейные вероятностные зави-
симости между двумя случайными величинами. На практике необходимо оценивать
эти зависимости между выходными переменными процессов и многими входными,
а также зависимости между различными входными переменными. Для количествен-
ной характеристики таких связей используют коэффициенты множественной корре-
ляции.
Для установления корреляционных связей между многими переменными исполь-
зуется метод множественной корреляции, основанный на использовании линейного
уравнения вида (4.99):
у = а0+аЛ+... + атхт, (4.181)
где Xj,...,входные переменные, влияющих на состояние процесса; у — расчет-
ное значение выходной переменной, которое характеризует состояние протекающе-
го процесса; а0,а1,...,ат — определяемые из экспериментов коэффициенты регрес-
сии.
242
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Для определения коэффициентов (4,181) может использоваться таблица резуль-
татов пассивного эксперимента в натуральном масштабе (табл. 4.8).
Таблица 4.8. Результаты пассивного эксперимента на действующей установке
в натуральном масштабе переменных
Номер опыта *1 х2 Хт У
1 хч *2! Хт1 У,
2 *12 Х22 хт2 У2
п Х2п У„
Для большего удобства обработки результатов экспериментов и определения корре-
ляционных зависимостей между переменными в соответствии с методом множествен-
ной корреляции производится нормировка всех переменных процесса по формулам:
(i = 1,...,п);
О _
£ (i = l,..., п; j = l,...,m).
В этом случае:
Е(л-/р)2 Ex
С = 1 _Е1_________ w „СР - -!=1_
(4.182)
(4.183)
(4.184)
Ж-*?)2
5 =1-^------ и
’ » п-1
(J = 1,..., ш).
(4.185)
В результате получается уравнение регрессии (4.181) между нормированными
переменными в безразмерном масштабе, которое не имеет свободного члена и мо-
жет быть представлено в виде:
*0 ~ о , ~ о , , ~ о
у =alXl +а2х2+... + атхт,
(4.186)
где at,..., ат — нормированные коэффициенты, а данные пассивного эксперимента
для нормированных переменных представлены в табл. 4.9.
Таблица 4.9. Результаты пассивного эксперимента для нормированных
переменных в безразмерном масштабе
Номер опыта X» х° Л2 х° т У°
1 Л Х2\ У°
2 ^2 Л22 х°, m2 У°2
п А, Х° 2л х° тп У„
4.2. Обработка результатов пассивных экспериментов
243
Для переменных процесса в натуральном масштабе выборочные коэффициенты
корреляции определяются по формулам (4.84):
ух
- У4’)».
(n-l)SyS
(7=1,...,/и);
(4.187)
Ж -<P)
(£, и = 1,..., m; l>u).
(4.188)
При этом уср и х‘р (J = 1, ..., т) рассчитываются по соотношениям (4.184) и (4.185).
В случае нормированных переменных в безразмерном масштабе у ° (г = 1,..., п)
(4.182) и х° (i = 1,..., n; j = 1,..., ш) (4.183), следует определять следующие величины
для вычисления выборочных коэффициентов корреляции:
^(y, -y^) cp cp
ocp = = y^n-nyV = 0.
n5„ nS„
(4.189)
.Оср _ i-1_____
J n5
nx. -nx;
nSr
(4.190)
и с учетом (4.184), (4.185) и (4.189), (4.190):
Ж-/ср)2
^=f=152(n-l) H
Ж)2 t(y,-ycp)2 i 1ДГ—^7 5
= У ) =5l = 1; (4.191)
sj n-l 5„
п-1
S>-1)
Ж.
.Оср \2
Ж.)2
п-1
ЖЖСР)2
t-1______
52 (п-1)
В
1
ЖЖ)2 5
~у~ = 1- U = 1- т).
(4.192)
п-1
В результате для нормированных переменных в безразмерном масштабе форму-
лы для выборочных коэффициентов корреляции записываются следующим образом
[см. (4.84), (4.187) и (4.188)]:
у0^,-х0^
(j ~ 1,..., т);
(и -1)5 „5
(4.193)
244
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Ё<4 ~4Р)(4 -х?Р)
г „ „ = —------------------- (£, и = 1,..., т; I > и) (4.194)
ХЛ (п-1)5л„5л;
и, принимая во внимание полученные равенства (4.189), (4.190), (4.191) и (4.192),
выборочные коэффициенты корреляции между всеми входными переменными и
выходной переменной определяются как
(7 = l,...,w); (4.195)
у 1 п-1
Ё44
r00=-^------ (4w=l,...,m; t>u). (4.196)
x'x- n_{
Для определения коэффициента множественной корреляции между выходной пе-
ременной у и всеми входными переменными х, (J = 1, ..., т) также используют нор-
мированные переменные (4.182) и (4.183) и одновременно с выборочными коэффи-
циентами (4.195) рассчитывают нормированные коэффициенты регрессии уравне-
ния (4.186).
Для этой цели используется таблица экспериментов (см. табл. 4.9) и критерий
наименьших квадратов вида (4.112):
п п т
Сг = £(у?-уУ =Х(£2,х°~У?)2, (4.197)
»=1 i=l ]=\
который минимизируется с учетом необходимого условия экстремума функций мно-
гих переменных:
^ = Е<Е2Л =° (И = 1,..., W1). (4.198)
В результате получается система нормальных неоднородных линейных уравне-
ний с симметричной матрицей коэффициентов (4.119):
(Ё(4,)2)21 + (Ё44)22 +---+(Ёх°4)2т = Yx°y°’
1=1 1=1 1=1
<Ё + (Ё <^2,)2)а2 +...+ (Ё xlx°JSm = Ё 44
/=! »=1 /=! »=!
...................................................... (4.199)
(Ё 44,)21 + <Ё (Х2,)2)22 + - + (Ё Х2-Х°^ = Ё&У‘’
1=1 1-1 i=l J=1
(Ё 44. )«i+(Ё 44 )а2+-+(Ё (4 УЧ = Ё 44
,=1 ,=1 <=1 i=i
Для преобразования элементов матрицы коэффициентов этой системы и элемен-
тов вектора свободных членов в выборочные коэффициенты корреляции (4.195) и
(4.196) необходимо ее левую и правую части разделить на (и — 1) и принять во
внимание, что в соответствии с равенствами (4.183) и (4.185) диагональные элемен-
ты матрицы коэффициентов системы (4.199) равны:
4.2. Обработка результатов пассивных экспериментов
245
Ж)2 , 52
=4"------------= TF = 1 (J = 1, ..,«)• (4.200)
п-1 S2X] п-1 52
В результате получается линейная система уравнений с выборочными коэффи-
циентами корреляции, при решении которой определяются нормированные коэф-
фициенты регрессии а1га2, ...,ат уравнения (4.186):
а, + (.г. ° )а2 +... + (г о о )ат = г. .;
-*1 -*2 Л1К У Л1
(г „ „ )а, + а2... + (г,. )ат = г „ „;
Л2-*1 Л2л-и У -*2
о О )^1 + (г„о О )л2-.. + — То о •
Лтд1 лтл2 У лж
(4.201)
В этой системе уравнений перекрестные выборочные корреляции равны между собой, т.е.
(и,£=1,..., ш), (4.202)
и значения т нормированных коэффициентов уравнения (4.186) определяются пу-
тем решения линейной системы уравнений (4.201) методом обратной матрицы (3.2.48).
По найденным значениям нормированных коэффициентов регрессии коэффициент
множественной корреляции вычисляется по формуле:
R = + «1га» +-+5"г« , (4.203)
он служит показателем силы связи для множественной регрессии и значения кото-
рого располагаются в замкнутом интервале о < R < 1
Нормированные коэффициенты регрессии , а2,..., ат также могут использоваться
для прогнозирования поведения процесса с использованием линейного уравнения
регрессии (4.181):
y = a0+Y,a1X]_ (4.204)
7=1
Для определения коэффициентов регрессии а0, а1г.... ат уравнение (4.186) с нор-
мированными коэффициентами регрессии а1, а2,..., ат записывается с учетом систе-
мы нормировки переменных (4.182) и (4.183) в виде:
в результате чего коэффициенты регрессии уравнения (4.204) определяются по формулам:
(4.206)
7=1
Метод множественной корреляции позволяет определять не только коэффициен-
ты множественной корреляции (4.203), характеризующие линейную зависимость
между выходной переменной и множеством входных переменных. Он также позво-
ляет оценить линейную связь между двумя любыми переменными: входные — вход-
ные (4.196) и выходная — входная (4.195), что имеет важное практическое значение.
246
Глава 4. Эмпирические модели. Обработка результатов экспериментов
4.2.10. Метод множественной регрессии Брандона
для построения нелинейных эмпирических моделей
Применение этого метода позволяет определять как вид уравнения регрессии
(структурная идентификация), так и его коэффициенты (параметрическая иденти-
фикация). При этом вид, в общем случае, нелинейного уравнения регрессии пред-
ставляется произведением многочленов различных степеней от каждой входной пе-
ременной. Большой объём экспериментального материала и правильный выбор при-
оритетности построения многочленов для различных входных переменных могут
обеспечить удовлетворительный результат при построении эмпирических моделей.
Ставится задача определить зависимость одного основного параметра системы у
(выходная переменная) от г других параметров х,, х2, х3,..., х, (входные переменные),
т.е. необходимо найти функцию (4.73):
у = F(xn х2, х3,..., хг). (4.208)
Необходимо решить задачи структурной и параметрической идентификации. Эти
задачи решаются, исходя из опытных данных, получаемых в результате проведения
пассивного эксперимента, в том числе и промышленного. При этом эксперимен-
тальные данные представляются в виде табл. 4.10 (и — общее число опытов).
В рассматриваемом методе множественной регрессии предполагается, что функ-
ция F является произведением некоторых функций отдельных параметров:
У = К • Л (X,) • f2 (х2) • /з (Х3) •... • Л (хг), (4.209)
где К — некоторый коэффициент.
Предполагается, что каждая функция/(х,) описывается многочленом произволь-
ной степени т;
=a0,+ahx,+a2X+-+am,x^ f (4.210)
2=0
причем конкретная степень многочлена т и его коэффициенты aOl, аи,..., ат опреде-
ляются из экспериментальных данных.
Таким образом, по экспериментальным данным табл. 4.10 определяются:
• К— общий коэффициент уравнения (4.209);
• т, — степень многочлена для каждой из г функций/ (х,) (/ = 1, ..., г);
• ар — соответствующие коэффициенты для каждой из п функций (/ = 0, 1, ..., т;,
i = 1, ..., г).
В результате одновременно определяется вид функций /(х,) — путем нахождения
оптимальных степеней многочленов т„ а также значения соответствующих коэффи-
циентов регрессии ар, и только после этого определяется параметр К.
Таблица 4.10. Результаты экспериментальных исследований
№ Х2 X г У
1 *11 х12 У1
2 х21 Х22 X2,r-l Х2г У2
п -1 *„-1,1 Лп-|,2 Хп-1, Х„-1
п х,а Х„г у„
4.2. Обработка результатов пассивных экспериментов
247
Обязательным условием реализации рассматриваемой стратегии множественной
регрессии является последовательное определение коэффициентов регрессии и оп-
тимальных степеней многочленов/(х,), соответствующих параметрам х„ по мере убы-
вания их влияния на выходную переменную у. Поэтому в таблице эксперименталь-
ных данных целесообразно входные переменные х1;х„ располагать в порядке убы-
вания степени их влияния на выходную переменную у.
т
На первом этапе определяются коэффициенты линейной регрессии У~'^а1х‘
J=0
методом наименьших квадратов по экспериментальным данным у-х,, т.е. данные
для входных переменных берутся из первого столбца табл. 4.10.
Ставится задача как определения степени многочлена /и, (4.210) путём увеличения
т в (4.211) последовательно до тех пор, пока критерий Сг (4.211) уменьшается, так и
определения коэффициентов регрессии а . При этом вектор х считается равным .
Критерий аппроксимации в соответствии с методом наименьших квадратов имеет вид:
п т
Сг = £(£а//_^)2. (4.211)
,-1 7=0
Коэффициенты регрессии определяются путем минимизации этого критерия с
использованием необходимого условия экстремума функции (в данном случае кри-
терия Сг многих переменных):
Cr= Cr(aQ, ах, ...ат). (4.212)
В результате получается:
^^Ё2(Уа;х/-у,)х;=0 (5 = о, 1, ..., ш). (4.213)
oas J=Q
Перемножив соответствующие члены уравнений
и т п
ЕЕа№=2Х>’- (5 = 0, 1, ..., т) (4.214)
<=1 у-О 1=1
и выполнив перегруппировку слагаемых их левой части, получим систему линейных
алгебраических уравнений относительно коэффициентов регрессии аа, а,, ..., ат:
Yai^x‘+S>> = Yx'y' (5 = 0,1,...,»г). (4.215)
7=0 1=1 |=1
В развернутом виде система линейных уравнений для определения коэффициен-
тов регрессии записывается в виде:
««о + (Ё + <Ё х^аг + •• + <Ё ХГК = Ё Уб
i=l i=l 1=1 »=!
(Ё х,)а»+(Ё х-2ч+<Ё х’ч+-+<Ё х"'+1)а„ = Ё х'Уб
«=! /=! »=! /=! 1=1
• (Ёх2ч+(Ёх-3ч+(Ёх-4ч+-+(ЁхГ+2Чп = Ёх.2ч (4.216)
1=1 /=! (=1 <=1 1=1
(Ё хГ ч+(Ё +(Ё <+2х+-+(Ё х2тк=Ё х”у-
/ = 1 1 = 1 ! = ! 1=1 1=1
248
Глава 4. Эмпирические модели. Обработка результатов экспериментов
или в матричной форме:
п
п
п
1=1
. 1=1
п
1У.
i^y.
1=1
1=1
(4.217)
В этом случае матрица коэффициентов этой системы уравнений получается сим-
метричной и для ее решения используется метод обратной матрицы.
Если обозначить матрицу коэффициентов через А с размером
(т + 1) х (т + 1), вектор определяемых коэффициентов регрессии через а с разме-
ром (т + 1), а вектор свободных членов через b , то матричная формула для опреде-
ления коэффициентов регрессии методом обратной матрицы имеет вид (3.2.48):
~х = Ть (4.218)
Задача выбора оптимальной степени многочлена у = решается на отдель-
но
ном (в данном случае первом этапе, так как х = xj решается путем постепенного
увеличения т: 1, 2, 3 и т.д. и определением для каждого его значения коэффициен-
тов регрессии по матричной формуле (4.218).
Выбор оптимального значения т на отдельном этапе осуществляется путем оцен-
ки значения двух факторов:
• остаточной дисперсии S2R;
• числа относительной обусловленности матрицы коэффициентов А в линейной
системе уравнений - cond(A).
Остаточная дисперсия S2K характеризует точность уравнения регрессии (в данном
случае уравнения многочлена) и определяется по формуле (4.162):
Ео-г-зГ”)2
с 2 - 2d______
п-р
(4.219)
где у^4 находится с помощью рассчитанных значений коэффициентов регрессии
по формуле:
урасч = ; j = 1, .... И , (4.220)
7=0
ар — количество коэффициентов регрессии при выбранной степени многочлена.
Число относительной обусловленности матрицы коэффициентов А характеризу-
ет максимально возможный эффект от возмущений при расчете ее элементов и эле-
ментов вектора свободных членов на результат решения линейной системы (4.217),
4.2. Обработка результатов пассивных экспериментов
249
т.е. на значение коэффициентов регрессии. Чем меньше это число, тем надежнее
получаемые значения коэффициентов регрессии (см. разд. 3.2). Оно определяется с
использованием норм прямой и обратной матриц коэффициентов линейной систе-
мы уравнений (4.216) по следующей формуле (3.2.44):
cond = \\A || || А ||. (4.221)
В результате оптимальная степень многочлена и его коэффициенты на первом
этапе построения эмпирической модели (тх) определяются при наименьших значе-
ниях 5* и cond(A). Таким образом, на первом этапе построения эмпирической
модели получается конкретное выражение для функции/(x,) в уравнении регрессии,
которое имеет вид:
/1(ч) = Еалх/ =aoi+«n^+- + am,i^r . (4.222)
7=0
На втором этапе построения эмпирической модели аналогичным путем опреде-
ляются конкретный вид f2(x2) и оптимальная степень многочлена ти2:
/г<>2) = ЕаРх2 =ат+а12хг+... + ат1гх2г . (4.223)
7=0
При этом обрабатываются экспериментальные данные второго столбца (Xj) табл. 4.10,
а элементы вектора выходной переменной у вычисляются по формуле:
=
(4.224)
L, 1 =
7=0
На третьем этапе по аналогичной схеме определяются конкретный вид функции
Уз(х3) и оптимальная степень многочлена ту.
т3
/з(хз) = ^а1^ = аоз + а1зхз+- + атззхз! . (4.225)
7=0
Для этой цели используются экспериментальные данные третьего столбца табл. 4.10,
и элементы вектора выходной переменной у вычисляются по формуле:
(^х'Х^х//
7=0 7=0
(4.226)
На г-этапе расчетов для получения конкретного вида функции _4(хг) и оптималь-
ной степени многочлена ту
= aOr + alrxr + amrx"r (4.227)
7=0
повторяется та же процедура расчетов, что и на предыдущих этапах.
Из табл. 4.10 берутся элементы вектора последнего столбца хг, а элементы вектора
выходной переменной у вычисляются по формуле:
у(г) =--------------—-------------=---------------------—------------------, i = 1, ..., п
7=0 7=0
(4.228)
Последним определяется значение К в уравнении эмпирической модели (4.208)
по следующей формуле:
250
Глава 4. Эмпирические модели. Обработка результатов экспериментов
к=.У' п• (4-229)
Л (х,1fr (х1Г)
В результате получается конкретный вид функции (4.209) с известным значением
коэффициента К, а также коэффициентов функций/(х,), fr(xr) с оптимальными
порядками многочленов для них - т„ тг (4.210).
Полученная функция представляет собой в общем случае нелинейную эмпиричес-
кую математическую модель технологического процесса, для которого были проведе-
ны экспериментальные исследования, представленные в табл. 4.10.
4.3. Обработка результатов активных
экспериментов и оптимальное планирование
экспериментов
При проведении опытных исследований различают пассивный и активный экс-
перимент.
Методология пассивного экспериментирования предполагает проведение большой
серии опытных исследований с поочередным варьированием значений входных пе-
ременных х и анализом результатов измерений выходной переменной у (лабора-
торный эксперимент и эксперимент на пилотной установке). К пассивному экспери-
менту принято относить также и сбор опытных данных в режиме эксплуатации про-
мышленной установки — так называемый промышленный эксперимент.
Обработка результатов пассивного эксперимента проводится методами регресси-
онного и корреляционного анализа, и выбор вида эмпирической модели (уравнения
регрессии), т.е. решение задачи структурной идентификации, является достаточно
сложной задачей. Это связано с тем, что вид уравнения регрессии необходимо опре-
делять по характеру изменения переменных на графике эмпирической линии рег-
рессии (см. разд. 4.2.3), полученной по выборке экспериментальных данных.
Для решения этой задачи для одной входной переменной х предложены эффек-
тивные методы (см. табл. 4.3), в которых предусматривается преобразование систе-
мы координат как для входной х, так и для выходной переменной у. При большем
числе входных переменных х1;..., хт надёжных методов определения вида уравнения
регрессии (вида эмпирической модели) в настоящее время не существует.
Активный эксперимент проводится по заранее составленному плану, в соответ-
ствии с которым ставится задача не только определения оптимальных условий прове-
дения эксперимента, но и оптимизации процесса (эти две задачи принято относить к
задачам оптимального планирования экспериментов). При этом уравнения регрес-
сии (эмпирические модели) описывают данные активного эксперимента, в основ-
ном, в двух ограниченных областях изменения переменных, характеризующих про-
цесс, и имеют следующий вид:
* вдали от экстремального значения выходной переменной у.
т /л-1 т
у1 = ао++Е X а!их,хи (и > j); (4.2зо)
2=1 7=1 «=2
вблизи экстремального значения выходной переменной у («в почти стационарной
области»):
т т-l т т
Уа =a0+^a1xJ+Y^alux1xu+^aix21 (u>j). (4.231)
j=l u=2 j=l
4.3. Обработка результатов активных экспериментов
251
Приведённые уравнения являются линейными относительно коэффициентов рег-
рессии а и имеют достаточно простой вид.
Они включают слагаемые с двойным взаимодействием входных переменных
EEVA (4.232)
j=l и=2
и не учитывают взаимодействия более высоких порядков (тройные, четверные и т.д.),
вероятность которых существенно меньше.
Последнее уравнение включает слагаемые с квадратами входных переменных
т
7=1
коэффициенты которого получаются при обработке результатов активных экспери-
ментов П-го порядка (верхний индекс II при у: у") ~ например, ОЦКП — ортого-
нального центрального композиционного плана эксперимента (см. разд. 4.3.2).
Уравнение (4.2.230) не включает слагаемые с квадратами входных переменных, и
его коэффициенты получаются при обработке результатов активных экспериментов
I-го порядка (верхний индекс I при у: у1) — например, ПФЭ — полного факторного
эксперимента (см. разд. 4.3.1).
При определении оптимальных условий проведения процесса с использованием
эмпирических моделей (например, методом Бокса—Вильсона [см. разд. 4.3.3)] выходная
переменная у11 (4.231) является критерием оптимальности или целевой функцией.
В теории активного экспериментирования выходную (зависимую) переменную
принято называть функцией отклика, а входные (независимые) переменные —
факторами. Соответственно — координатное пространство с координатами ..., хт
называют факторным пространством, а геометрическое изображение функции от-
клика в факторном пространстве — поверхностью отклика.
Активный эксперимент планируется таким образом, чтобы упростить обработку
его результатов методами регрессионного и корреляционного анализа.
Ортогональные планы экспериментов, используемые при активном эксперимен-
тировании, обеспечивают диагональный вид корреляционной матрицы С (4.147) при
регрессионном анализе и, соответственно, статистическую независимость коэффи-
циентов регрессии COVaa = Q:j^ i (j, i = 0,1,..., m) — cm. (4.150).
К другим достоинствам активного экспериментирования относятся:
• возможность предсказания количества опытов, которые следуют провести;
• определение точек факторного пространства, где следует проводить опыты;
• сокращение объёма опытных исследований;
• отсутствие проблем, связанных с выбором вида уравнения регрессии;
• упрощение процедуры обработки результатов эксперимента.
4.3.1. Полный факторный эксперимент
и обработка его результатов
ПФЭ относится к экспериментам I-го порядка, так как описывающее его урав-
нение у1 не включает факторы в квадрате.
Для двух факторов (%, и х2) и без учёта их взаимодействия соответствующая
эмпирическая модель (4.230) может быть записана:
у1 = а0 + арс, + агхг. (4.233)
252
Глава 4. Эмпирические модели. Обработка результатов экспериментов
В соответствии с теорией ПФЭ при проведении опытных исследований каждый
из факторов варьируется только на двух уровнях — минимальном (кодированное
значение —1) и максимальном (кодированное значение +1).
При этом реализуются возможные комбинации минимальных и максимальных
значений факторов, в результате чего общее число опытов (и) в ПФЭ равно 2т и
полный факторный эксперимент обычно называется ПФЭ типа 2т.
Для определения числа опытов применяется формула:
п = 2т. (4.234)
В последнее уравнение (4.233) включаются кодированные значения факторов z,
вместо х}, значения которых получаются по следующей схеме кодирования:
х -х(0)
г7=~Г" О = 1>(4-235)
где
х(? = 0.5(т7 + х™) (j = 1,..., т); (4.236)
Дх, = 0.5(х"“ - х;,п) (j = 1,..., т). (4.237)
В результате план проведения эксперимента с учётом вышесказанного и кодиро-
вания факторов имеет вид, представленный в табл. 4.11 (число факторов т = 2,
число опытов п = 2т = 22 = 4).
При этом уравнение регрессии, описывающее эти опытные данные, записывает-
ся с использованием кодированных факторов zy (/ = 0, 1, 2) и, соответственно,
кодированных коэффициентов регрессии а0, ах, а2 :
у = aozo + а,г, +a2z2, (4.238)
где кодированный фактор z0 всегда равен единице, т.е. z0 = 1.
В кодированном факторном пространстве в соответствии с указанным планом
проведения эксперимента проведённые опыты представляются точками вершин квад-
рата (рис. 4.14).
Для параметрической идентификации кодированного уравнения регрессии (4.238) —
определения коэффициентов регрессии, используется метод регрессионного анали-
за, включающий три этапа:
• определение кодированных коэффициентов уравне-
Таблица 4.11. План про-
ведения полного фактор-
ного эксперимента для
двух факторов без учёта
взаимодействия факторов
\р п \ zo г1 г2 У эксп
1 +1 -1 -1 ^уЭКСП
2 + 1 +1 -1 д;ЭКСП У1
3 + 1 -1 + 1 У эксп уъ
4 +1 +1 + 1 Т,ЭКСП Л4
ния регрессии а методом наименьших квадратов (4.130);
• оценка значимости кодированных коэффициентов
регрессии с использованием критерия Стьюдента t
(4.164);
• проверка адекватности кодированного уравнения
регрессии с использованием критерия Фишера F(4.168).
Реализация двух последних этапов возможна при
выполнении свойства однородности дисперсий (одно из
требований регрессионного анализа) и проведении па-
раллельных опытов, например, в точке с координатами
Z] = 0 и z2 = 0 (центр плана, на рисунке — тёмная точка).
При проведении к параллельных опытов в центре
плана (у’“п, s = 1,..., к) среднее значение у’*'"* опреде-
ляется как среднее арифметическое результатов изме-
рений во всех параллельных опытах:
(4-239)
4.3. Обработка результатов активных экспериментов
253
Определение кодированных коэффициентов
регрессии в случае проведения ПФЭ
В этом случае используется применяемая при
линейном регрессионном анализе матричная фор-
мула метода наименьших квадратов (МНК), кото-
рая с учётом кодирования факторов имеет вид (4.130):
г = т = у1 = т
. а , = . Ф Ф ,Ф У > (4.240)
(m+l)xl (и+1)хп лх(т+1) (m+l)xn '
где кодированная матрица ф, зависящая от незави-
симых переменных, включает только +1 и —1 и для
двух факторов имеет вид (см. табл. 4.11):
Рис. 4.14. Опытные точки ПФЭ
в кодированном факторном
пространстве для двух факторов
2]0 2П 212 г+1 -1 -1
Ф =z = 2 20 г21 2 22 +1 +1 -1
(4x3) 2зо г31 2з2 +1 -1 +1
_Z40 ^41 242 _ +1 + 1 +1
(4.241)
Матрица Z при активном экспериментировании называется матрицей планиро-
вания и в случае ПФЭ обладает тремя оптимальными свойствами:
• симметричностью — сумма элементов всех столбцов матрицы кроме первого
и
(точнее, нулевого) равна нулю: X S = 0 (7 = 1’ > тУ
i=i
• ортогональностью: скалярное произведение двух любых столбцов матрицы рав-
но нулю: гХ = гуг,„ = 0 (у, и = 0,1,..., т и* j);
1-1
• нормировкой: скалярное произведение двух одинаковых столбцов матрицы рав-
но л: = « U = 0,1,т). В ПФЭ п = 2га (4.234).
i=i
Благодаря перечисленным оптимальным свойствам матрицы планирования Z ,
информационная матрица в ПФЭ при т = 2 равна [см. (4.119) и (4.120)]:
I =ф ф = z т z =
(3x3) (3x4) (4x3) (3x4) (4x3)
л 0 0
0 п 0 ’ (4.242)
0 0л
т.е. она является диагональной с одинаковыми элементами на главной диагонали,
равными п = 22 = 4. _
Соответственно, корреляционная матрица С также будет диагональной (4.147) и
с одинаковыми элементами главной диагонали:
= /=Т =
С = Ф Ф
(3x3) I
л"1 0 0
0 п’1 0
0 0 п'
(4.243)
254
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Результатом подстановки последних соотношений в матричную формулу для оп-
ределения кодированных коэффициентов регрессии (4.240) будет простая формула:
(4.244)
При учёте взаимодействия двух факторов и z2 кодированное уравнение рег-
рессии (4.244) принимает вид:
У = аого + 2^ + a2z2 + 212ztz2,
(4.245)
(где z0 si), и в матрицу планирования Z включается ещё один дополнительный
последний столбец, каждый элемент которого равен произведению элементов столб-
цов, соответствующих взаимодействующим факторам:
Z10 ^11 г12 ^11^12 +1 -1 -1 +1
II IIN II || Ю 2 20 ^21 ^22 ^21^22 +1 +1 -1 -1
(4x4) ^30 Z3l ^32 ^31^32 +1 -1 +1 -1
>40 >1 2 42 г41г42. + 1 +1 +1 +1
(4.246)
При этом матрица планирования (4.246) сохраняет все три оптимальных свойства
(4.241) — симметричности, ортогональности и нормировки, а кодированный коэф-
фициент уравнения регрессии при члене, характеризующем взаимодействие факто-
ров, определяется по формуле (4.244):
% =£(z,;z,Jy,’Kcny«- j,u = l,...,m u>j. (4.247)
В теории ПФЭ доказывается, что при увеличении числа факторов (т >2) матрица
планирования Z строится с использованием рассмотренной методики, в том числе
и с учётом взаимодействия факторов (не только двойного, но и тройного, четверного
взаимодействия и т.д.), где р — число коэффициентов регрессии с учётом взаимодей-
ствия факторов.
В этом случае число столбцов р матрицы Z (4.246) зависит от числа учёта взаи-
модействий факторов (п = 2т), и матрица планирования сохраняет перечисленные
оптимальные свойства. Поэтому для определения кодированных коэффициентов
регрессии используются приведённые выше формулы (4.244) и (4.247).
Для расчёта натуральных значений коэффициентов в кодированные уравнения
регрессии (4.233) и (4.245) вместо кодированных факторов z2 (J = 1, ..., т) следует
подставить выражения для последних через натуральные значения факторов
(/ = 1,..., т) в соответствии с приведённой выше схемой кодирования (4.235)—(4.237).
Определение значимости кодированных коэффициентов регрессии
в случае проведения ПФЭ
Незначимость кодированных коэффициентов регрессии определяется с использо-
ванием квантиля t — распределения Стьюдента при помощи неравенства (4.165):
Ini 6
(4.248)
где Р — доверительная вероятность (в инженерных расчётах равная 0.95); ve — число
степеней свободы дисперсии воспроизводимости [при одной серии параллельных
опытов в центре плана эксперимента — чёрная точка (рис. 4.14)], равное (к — 1).
4.3. Обработка результатов активных экспериментов
255
Выборочное значение квадратного корня дисперсии кодированного коэффици-
ента регрессии определяется по формуле (4.149):
(4.249)
где Se — квадратный корень из дисперсии воспроизводимости, определяемой по к
параллельным опытам в центре плана эксперимента (4.161):
1(уоТ-уГсп*)2 „
S2 = (4.250)
е к-1 ve ’
Здесь SSe — сумма квадратов дисперсии воспроизводимости; ve — число степеней
свободы дисперсии воспроизводимости; у’ксп* — определяется по формуле (4.239).
Как было показано выше, диагональные элементы корреляционной матрицы
(4.147) в ПФЭ при кодировании факторов одинаковы и равны 1/л (4.243), вследствие
чего формула (4.249) видоизменяется:
S5i=sJ^. (4.251)
В результате условие незначимое™ кодированных коэффициентов регрессии при-
нимает вид (4.165):
laj г 6
0 = 0,1,...,«). (4.252)
Так как корреляционная матрица С (4.243) в этом случае является диагональ-
ной, то кодированные коэффициенты регрессии статастически независимы, и при
одновременной незначимости нескольких кодированных коэффициентов регрессии
они [в отличие от процедуры обработки пассивного эксперимента] могут быть сразу,
все вместе, исключены из кодированного уравнения регрессии (4.245).
Проверка адекватности уравнения регрессии в случае проведения ПФЭ
Проводится так же, как и при проведении пассивного эксперимента, с использова-
нием табличного значения критерия Фишера [см. (4.167), (4.162)], выбранного при
доверительной вероятаосш (3 (чаще всего равной 0.95) и числе степеней свободы оста-
точной дисперсии vR и дисперсии воспроизводимое™ ve (табл. 3 Приложения).
Условие адекватное™ с учётом того, что проводится отдельная серия параллельных
опытов в центре плана и = Sfld (4.162), проверяется с использованием неравенства:
У2
fp>c4=£l<f^ (4.253)
^2 - p(vs V,)’ ' ’
где остаточная дисперсия (4.162), характеризующая точность уравнения, определяет-
ся по формуле:
Х^.’-уГ)2 „
S? _ ,=1__________ (4.254)
n-p v/; '
При этом \’R — п —р, где п — число экспериментов при различных значениях факто-
ров; р — число значимых коэффициентов регрессии.
256
Глава 4. Эмпирические модели. Обработка результатов экспериментов
К недостаткам ПФЭ относится резкое увеличение числа опытов при возрастании
количества факторов больше, чем 5 (п = 25 = 32 при т = 5).
Для проведения регрессионного анализа при пренебрежении целым рядом несу-
щественных взаимодействий факторов достаточно проводить меньшее число опы-
тов. В этом случае можно реализовать часть ПФЭ, так называемый дробный факторный
эксперимент, который здесь не рассматривается.
4.3.2. Ортогональный центральный композиционный
план эксперимента и обработка его результатов
ОЦКП эксперимента относится к экспериментам П-го порядка, так как описы-
вающее его уравнение у11 включает факторы в квадрате и поэтому может описывать
поверхности функций отклика в окрестности их экстремальных значений.
Для двух факторов (х1 и х2) с учётом только двойного взаимодействия факторов
соответствующая эмпирическая модель может быть записана:
у11 = a0 + OjXj + а2х2 + а12Х]Х2 + anxf + а22х2. (4.255)
В соответствии с методикой ОЦКП здесь также как и для ПФЭ, осуществляется
кодирование факторов по приведённой выше схеме (4.235)—(4.237), и для обеспече-
ния ортогонального свойства матрицы планирования эксперимента в уравнение рег-
рессии _уп включается некоторая постоянная Л1.
В результате уравнение регрессии при m = 2 принимает вид:
У = aozo + a1zI+a2z2+a12z1z2+a11(z12 -s)+a22(z2-s). (4.256)
Для определения большего числа кодированных коэффициентов, чем при обра-
ботке ПФЭ, и описания поверхности функции отклика вблизи её экстремума («по-
чти стационарной области»), количество опытов увеличивается.
При этом опыты, проводимые по плану ПФЭ (n = 2”), дополняются опытами в
«звёздных» точках факторного пространства na = 2m и опытами в центре плана с
координатами Z] = 0 и z2 = 0, число которых равно пс.
«Звёздные» точки в факторном пространстве располагаются на осях координат на
расстоянии +а и —а от центра плана эксперимента; причём величина а называ-
ется «звёздным» плечом и её значения, так же как величина S, определяются из
условия ортогональности матрицы планирования Z (4.241) для ОЦКП.
Общее число опытов Nb ортогональном центральном композиционном экспери-
менте определяется по формуле:
N=n + n6+nc, (4.257)
или, с учётом приведённых выше равенств,
N=2m + 2m + nc. (4.258)
Для случая двух факторов (т = 2):
N=8 + nc. (4.259)
Расположение опытных точек в факторном пространстве для случая двух факто-
ров в приведённой ранее кодированной системе координат может быть представле-
но, как показано на рис. 4.15.
План проведения экспериментов в этом случае может быть представлен, как по-
казано в табл. 4.12.
4.3. Обработка результатов активных экспериментов
257
Матрица планирования Z представля-
ет собой часть плана проведения экспери-
мента без горизонтальных и вертикальных
заголовков таблицы и вектора наблюдения
-эксп (Правого столбца).
Определение величины «звёздного плеча» а
и значения постоянной S из условия орто-
гональности матрицы планирования
эксперимента ОЦКП
Матрица планирования Z [см. (4.241),
(4.246)] является ортогональной (4.242),
если выполняются следующие равенства:
Рис. 4.15. Опытные точки ОЦКП-экспе-
римента в кодированном факторном
пространстве для двух факторов
zj eJ-5j = O 0 = 1, 2)
(4.260)
и
fe2-s)Tfe-s)=0. (4-261)
Раскрывая первое равенство, можно получить (см. табл. 4.12):
^0T(o2-S) = £^0^= п + 2а2= о о = 1, 2),
1=1 1-1
(4.262)
откуда
(4-263)
Раскрывая второе равенство (4.261), с
учётом (4.262) получаем (см. табл. 4.12):
0-5)’0-5) =
=О)’?-О)т^-^+^-
= п - (п + 2а2) S - S (п + 2а2) + NS2 =
= п - 2NS1 + NS2 = n- NS2 = 0, (4.264)
из которого
5=^. (4.265)
Последнее выражение используется для
определения S.
Приравнивая правые части двух вы-
ражений для S (4.263) и (4.265), можно
получить формулу для определения а:
Таблица 4.12. План проведения
ОЦКП для двух факторов с учётом толь-
ко двойного взаимодействия факторов
п \ zo zi Z2 Z1Z2 zf-S zj-S у ЭКСП
< 1 + 1 -1 -1 +1 1-S 1-S у эксп
2 +1 +1 -1 -1 1-S 1-S рЭКСП z2
3 +1 -1 +1 -1 l-S 1-S ..ЭКСП Л
4 +1 +1 +1 +1 1-S 1-S рЭКСП Л
< 5 + 1 -а 0 0 a2-S -s ..ЭКСП О
6 + 1 +а 0 0 a2-S -s ..эксп Уб
7 + 1 0 -а 0 -s a2-S У, ЭКСП Л
8 + 1 0 +а 0 -s a2-S УГ°
< 9 +1 0 0 0 -s -S ..эксп ^9
N + 1 0 0 0 -s -s -.эксп Уц
п + 2а2 _ Гп~
N~ V7V
(4.266)
17-4544
258
Глава 4. Эмпирические модели. Обработка результатов экспериментов
«2=|(V^-«)=^ (4.267)
В результате «звёздное плечо» а можно определить по формуле:
<4-268>
• к 7
Определение кодированных коэффициентов регрессии в случае проведения ОЦКП
В соответствии с МНК эти коэффициенты определяются по матричной формуле
(4.240), (4.241) и (4.247):
a =CZTy3Kcn, где C=^ZTZ^ . (4.269)
Из-за свойства ортогональности матрицы планирования Z необходимо опреде-
лить только диагональные элементы информационной матрицы [см. (4.242) и табл. 4.12]:
7 = ZTZ, (4.270)
а затем диагональные элементы корреляционной матрицы (4.243):
В=Г. (4.271)
Определение диагональных элементов информационной и корреляционной матриц
Обобщая уравнение регрессии на случай т факторов и учитывая только все
двойные взаимодействия факторов, число которых определяется по формуле опреде-
ления числа сочетания из т по 2:
2 _
2! ’
общее число коэффициентов р уравнения регрессии для т факторов равно:
р = \ + т+ '+т, (4.272)
Диагональные элементы информационной матрицы I (4.119), (4.120), (4.242)
определяются следующим образом (см. табл. 4.12):
Тм= N — число таких элементов равно 1;
1^п+ 2аг (/= 1, ..., т); (4.273)
. . . т(т-1)
I/u = п (и> J) ~ число таких элементов равно —-—.
Для определения 7л при квадратах факторов можно записать:
=n(l-s)2+2(a2-s)2+(w-n-2)s2 =
= л-2п5+«52+2a4-4a25 + 252 + NS2-nS2-2S2 =
= 2a4+n-25 (n + 2a2s) +NS2=2a4+ n^NS^ = 2a4. (4.274)
из равенства (4 263>.W "3 равеисгаа (4 264>0
Количество таких диагональных элементов равно т.
4.3. Обработка результатов активных экспериментов
259
Диагональная матрица I имеет размер (4.270):
(4.275)
что соответствует числу определяемых параметров р.
В результате диагональная корреляционная матрица С =1~' размером р хр для
т факторов и с учётом их двойных взаимодействий, а также (4.272)—(4.275) имеет
вид (4.271):
W
(п + 2а2)'
(п + 2а2)'
С =
т (т — 1)
(4.276)
М-
Кодированные коэффициенты регрессии определяются с помощью (4.276) по
матричной формуле (4.269):
~ 7 Т — ЭКСП
а = CZ у
(4.277)
В результате для вычисления отдельных коэффициентов регрессии кодированно-
го уравнения (4.256) можно записать следующие формулы:
Д'
Z > Л
(4.278)
(4.279)
»=i
и> j (число коэффициентов —-----у
(4.280)
,=1
(J = l,..., т).
2а4
(4.281)
Для пересчёта полученных коэффициентов регрессии в натуральные значения
необходимо вместо кодированных факторов (j = 1,...,т) подставить их натураль-
ные величины х (j = 1, ...,/n) в соответствии с приведённой схемой кодирования
(4.235)—(4.237).
260
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Определение значимости кодированных коэффициентов регрессии
в случае проведения ОЦКП
В отличие от ПФЭ значимость коэффициентов регрессии определяется по раз-
ным формулам для различных коэффициентов, так как диагональные элементы кор-
реляционной матрицы С отличаются друг от друга.
С учётом общей формулы для определения незначимости коэффициентов рег-
рессии (4.248) — см. табл. 2 Приложения:
1 -/1 .табл „ (4.282)
и, соответственно, незначимость каждого вида коэффициентов регрессии определя-
ется аналогично (4.252):
^пасч / * г ^табл ° = s^ (4.283) ^^Ил/Л + 2а2<Г^)(у- = 1,...,т); (4.284)
расч _ | * = Se' Г , таб, эт(/Л-1) ^-r₽(vj (число коэффициентов , и>/); (4.285) |~ ।
• ,рас, s < £36» (у = j, , т) (4 286)
Проверка адекватности уравнения регрессии в случае проведения
эксперимента ОЦКП
Проверка адекватности уравнения регрессии в случае проведения эксперимента
ОЦКП выполняется так же, как и в случае с ПФЭ — с использованием критерия
Фишера (4.253) — см. табл. 3 Приложения.
Определение экстремума функции отклика
Задачей проведения активного эксперимента с применением ОЦКП является
определение экстремального значения функции отклика у11. С помощью получен-
ной модели второго порядка, описывающей почти стационарную область фактор-
ного пространства (4.256), удаётся рассчитать координаты экстремальной точки с
использованием необходимого условия существования экстремума функции мно-
гих переменных.
В этом случае для уравнения регрессии с т факторами вида:
Уп =20+£Н/;+ХЕ%г/„+£гг(г;2-$) («>у) (4.287)
7=1 7=1 «=2 ;-1
могут быть применены соотношения, характеризующие необходимое условие суще-
ствования экстремума функции многих переменных (3.6.17):
4.3. Обработка результатов активных экспериментов
261
3^-0 (4.288)
Полученная система линейных уравнений (СЛАУ) позволяет расчётным путём
определить z^' (j = 1, ..., т) и после подстановки их величин в исходное уравнение
уп — получить максимальное или минимальное значение функции отклика.
Полученный результат считается справедливым, если оптимальные значения фак-
торов располагаются в интервале:
|<|<1 (J = 1,...,т).
При невыполнении этого неравенства рекомендуется повторить представленную
процедуру построения модели (4.256), описывающей почти стационарную область с
найденным центром плана z°f‘ (j = 1,..., т).
4.3.3. Экспериментально-статистический метод
оптимизации Бокса-Вильсона
Этот метод применяется, когда построение математической модели процесса для
всей области факторного пространства, где необходимо решать задачу оптимизации
(см. разд. 3.6), невозможно. В соответствии с методом активного эксперимента путём
обработки определённой совокупности опытных данных получают эмпирические мо-
дели, описывающие ограниченные области факторного пространства — вдали от оп-
тимальных значений факторов х (модели I-го порядка, полученные на основании об-
работки данных ПФЭ) и вблизи оптимальных значений факторов х (модели П-го порядка —
на основании обработки данных ОЦКП). В этом методе определение ограниченных
областей факторного пространства вдали от оптимума функции отклика у, где следует
производить очередные экспериментальные исследования и обрабатывать их результа-
ты, происходит с использованием градиента этой функции. Вектор-градиент в фактор-
ном пространстве указывает направление наискорейшего возрастания функции отклика
у, а антиградиент — наискорейшего убывания функции отклика у (3.6.85) и (3.6.105).
Такой способ планирования опытных исследований со статистической обработкой их
результатов (см. два предыдущих раздела) позволяет сократить объём экспериментов
при решении задачи оптимизации экспериментально-статистическим методом.
При решении этой задачи известны лишь факторы х (оптимизирующие пере-
менные) и выходная переменная у (критерий оптимальности), значение которой
определяется из опытных данных.
Формулировка задачи оптимизации в этом случае такова (1.10):
opt у(х). (4.289)
хел“0”у"
Так как выходная переменная определяется из опытных данных, для поиска её
экстремальных значений необходимо реализовать оптимальную стратегию экспери-
ментирования.
Функция критерия оптимальности (функция отклика) у = у(х1,х2,...,хт) в этом слу-
чае может быть представлена в виде поверхности отклика, одинаковые значения которой
262
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Рис. 4.16. Решение задачи оптимизации для
двух переменных экспериментально-
статистическим методом
для двух факторов (х1; х2) изображаются
линиями постоянного уровня (у = const). Эти
линии являются проекциями сечений по-
верхности отклика на плоскость факторов
(см. разд. 3.6.1). Искомая экстремальная
точка поверхности отклика соответствует
точке «О» (рис. 4.16). В этом случае исполь-
зуется «шаговый» метод движения по по-
верхности отклика с целью определения
её экстремального значения.
При этом выделяются два этапа пла-
нирования эксперимента:
• движение в факторном пространстве к
экстремуму (так называемой «почти ста-
ционарной области») методом крутого
восхождения в случае максимума или наи-
скорейшего спуска в случае минимума
(3.6.113);
• уточнение положения экстремума в
«почти стационарной области».
Алгоритм движения к экстремуму
Движение к экстремуму осуществляется по направлению градиента в случае по-
иска максимума функции отклика у или антиградиента в случае поиска минимума
функции отклика у.
Вектор градиента определяет направление наискорейшего возрастания функции
и для у1 = уЧхр х2,..., хт) [см. (4.230)] равен:
где
—j , Эу1 - Эу1 - Эу1 _
grady = —1+ — J + ... +—т, (4.290)
dx, дх2 дх„ v
ду1 г-1 -а
единичные векторы в направлении осей координат; —
проекции вектора градиента на оси координат (хг, х2,хт).
Для т = 2 движение методом крутого восхождения можно представить на рис. 4.17.
Последовательные координаты поиска экстремума в факторном пространстве
определяются по формуле (3.6.105):
х,<5+|) = х^ ± h
dy,W
(i = l,..., т s =0,1,2,3...),
(4.291)
где z — номер координаты вектора-градиента; h — задаваемый фактор шага по
направлению вектора-градиента; s — номер точки экспериментирования; ± — дви-
жение к максимуму (+) или к минимуму (—).
Величина у1 в (4.290) определяется из уравнения регрессии, которое является
линейным относительно факторов и коэффициентов (4.233):
т
У1 =ao+YajXJ .
7=1
(4.292)
4.3. Обработка результатов активных экспериментов
263
Это уравнение используется для локаль-
ного описания поверхности отклика в об-
ластях, далёких от её экстремального зна-
чения.
Ограниченная область факторного про-
странства, где справедливо это уравнение
регрессии, задаётся центром области —
центром плана эксперимента:
х<0) =0.5(%7" +%7), j = l,...,m (4.293)
и интервалом (точнее, полуинтервалом)
варьирования факторов:
Ах, = 0.5(,х^ - х™), j = 1,..., т . (4.294)
Для локальной области факторного
пространства уравнение регрессии запи-
сывается с кодированными факторами
(4.292):
У1 ,
7=1
Рис. 4.17. Графическое изображение
движения к экстремуму функции двух
переменных методом крутого восхождения:
— центры планов эксперимента
первого порядка (ПФЭ); j(2> — центр
плана эксперимента второго порядка
х -х(0)
где z = J 1 (j = 1,..., т). (4.295)
Ах,
(ОЦКП)
В результате минимальному значению фактора соответствует z} = ~ 1, макси-
мальному — Zj = 1, а центру плана эксперимента — точка с координатами z} = О,
J = 1, т .
Коэффициенты уравнения регрессии с кодированными факторами а, отличают-
ся от коэффициентов уравнения регрессии с натуральными значениями факторов х}
и определяются из ПФЭ, проведённого в рассматриваемой ограниченной области.
Одним из таких свойств является свойство ротатабельности, которое характери-
зует равную предсказательную способность уравнения регрессии с кодированными
факторами на одинаковом расстоянии от центра плана.
Для характеристики предсказательной способности уравнения регрессии исполь-
зуется оценка дисперсии выходной переменной у1 -S2, которая из-за статистичес-
кой независимости коэффициентов а, и их одинаковой дисперсии в случае ПФЭ
определяется по формуле:
т
Sy=Sl+t^Sl = S*(l + p2),
7=1
где S2s
одинаковая для всех коэффициентов оценка дисперсии а,:
Sl=S2Jn.
(4.296)
Здесь п — число опытов ПФЭ; S2 — дисперсия воспроизводимости выходной
переменной у, определяемая по параллельным опытам; р2 — квадрат расстояния из
центра плана до рассматриваемой точки факторного пространства:
т
2 V' 2
Р = 1^
(4.297)
264
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Величина, обратная S*, принимается за меру точности уравнения регрессии.
Точность уравнения для S2 убывает пропорционально квадрату радиуса сферы р2 и
одинакова для всех эквидистантных точек. Поэтому в факторном пространстве нельзя
выделить ни одно предпочтительное направление, и вектор градиента (grad у1) не
хуже, в смысле предсказания величины выходной переменной у , чем любое другое
направление. Однако так как вектор-градиент (grad у1) характеризует направление
наискорейшего возрастания функции у , в этом смысле движение по нему является
наиболее предпочтительным.
Для определения координат вектора-градиента (grad у1) используется адекват-
ное уравнение регрессии, полученное по результатам ПФЭ (4.295):
У1 =aozo+YiajZj. (4.298)
Задаётся фактор шага h , и из центра плана ПФЭ (х^ — начальное приближение)
выполняется шаг по градиенту в сторону экстремального значения функции откли-
ка, определяются координаты нового центра плана в факторном пространстве — х^.
После этого вновь проводится ПФЭ, обрабатываются его результаты, вычисляется
новое направление вектора-градиента:
---- -t ду т ду - ду _
s,ady =аГХ'+ '^.т' <4'299)
по которому выполняется шаг
x,(s+1) = х,(5) ± h , fl| (i = l,...,m; s = 0,1,2,3...) (4.300)
[ ni
JW
V 7=1
в сторону экстремума (h — задаваемый фактор шага по направлению вектора-гра-
диента в кодированной системе координат).
Процедура последовательного экспериментирования продолжается до тех пор,
пока не будет достигнута область, близкая к экстремальному значению функции
отклика, т.е. к «почти стационарной области».
Близость «почти стационарной области» может быть установлена с помощью
критерия Стьюдента t путём оценки значимости различия между эксперименталь-
ными у’ксп* и расчётными у0 величинами в центре плана:
(4.301)
у0=Н0. (4.302)
Условие близости экстремума функции отклика имеет вид:
kcn’-“oi та6л
где ve = k — 1 — число степеней свободы; к — число параллельных опытов; 0 — заданная
доверительная вероятность.
4.3. Обработка результатов активных экспериментов
265
Уточнение положения экстремума в «почти стационарной области»
Для определения (уточнения) оптимальных величин факторов, обеспечивающих экст-
ремальное значение выходной переменной у“ (4.287), решается система уравнений, ко-
торая вытекает из необходимого условия экстремума функции многих переменных (4.288):
^- = 0; ^- = 0; ...; ^ = 0. (4.303)
Эгг Эг2 6zm
В данном случае также удобнее пользоваться кодированными факторами zr
Для описания области, близкой к экстремуму, можно использовать уравнение
второго порядка с двойными взаимодействиями факторов (4.287):
уп =aozo +YSJZJ + +5ХЖ2 ~S^’ zo=l; u>j (4.304)
j=l j=l u=2 j=l
Рис. 4.18. Блок-схема алгоритма экспериментально-статистического метода оптимизации
Бокса—Вильсона
266
Глава 4. Эмпирические модели. Обработка результатов экспериментов
Введение величины 5 обеспечивает ортогональность матрицы эксперимента, ко-
торый проводится с целью определения коэффициентов (а}, aJU, а») этой модели.
Для вычисления этих коэффициентов уравнения для у" реализуется ОЦКП экспе-
римента в «почти стационарной области».
Результат решения задачи уточнения положения экстремума нельзя считать удач-
ным, если не выполняется условие:
|<'|<1 (j = 1,..., т), (4.305)
так как уравнение регрессии справедливо только в диапазоне кодированных факто-
ров -1<z7<1 (j = 1, ..., т), где был поставлен эксперимент. При невыполнении
условия рекомендуется снова реализовать ОЦКП эксперимента с новым центром
плана, в частности, в точке тГр (j = 1,..., т) или в точке xc°r (j = l,...,m) (4.293) в
натуральной системе координат (4.236).
Процедуру последовательного экспериментирования в окрестности экстремума
рекомендуется продолжать до тех пор, пока условие приведённого выше неравенства
(4.302) не выполнится.
Блок-схема алгоритма экспериментально-статистического метода оптимизации
представлена на рис. 4.18.
Глава-
ФИЗИКО-ХИМИЧЕСКИЕ МОДЕЛИ.
ПОСТРОЕНИЕ МОДЕЛЕЙ.
ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКОГО
ОПИСАНИЯ И ОПТИМИЗАЦИЯ
ХИ МИ КО- ТЕХНОЛОГИЧЕСКИХ
ПРОЦЕССОВ
Физико-химические модели строятся на основе знания механизмов протекания ре-
альных процессов. Важнейшим условием применения этих моделей является обес-
печение их адекватности путём решения задачи идентификации. Основной целью
применения физико-химических моделей является решение задачи оптимизации, в
результате чего определяются оптимальные (наилучшие) условия проведения хими-
ко-технологических процессов (см. главы 1 и 2).
При построении физико-химических моделей сначала составляется система уравне-
ний математического описания процессов (МО), затем проводится анализ получен-
ной системы уравнений МО с целью выбора наиболее эффективного алгоритма её
решения и, наконец, разрабатывается моделирующий алгоритм (МА) решения сис-
темы уравнений МО, который должен быть реализован на компьютере.
С позиций математического моделирования химико-технологических процессов
объекты моделирования принято разделять на объекты (процессы) с сосредоточенны-
ми параметрами и объекты (процессы) с распределенными параметрами.
Объекты с сосредоточенными параметрами характеризуются одинаковым значе-
нием свойств (параметров и переменных) во всем объеме (на всей поверхности)
единицы технологического оборудования или его секции. Как правило, стационар-
ные режимы этих объектов описываются системами конечных нелинейных (линей-
ных) уравнений — СКУ: СНУ (СЛАУ) (см. разд. 3.2), а нестационарных режимов —
системами с обыкновенными дифференциальными уравнениями — СОДУ (см. разд. 3.5).
Чаще всего, для описания гидродинамической структуры движущихся потоков фаз в
этом случае используются модели идеального перемешивания (см. табл. 2.1).
Объекты с распределенными параметрами характеризуются изменением параметров
процессов, как минимум, вдоль одной пространственной переменной. В этом случае
для описания гидродинамической структуры движущихся потоков фаз используется либо
модель идеального вытеснения, либо однопараметрическая диффузионная модель (см.
табл. 2.1), и математическое описание стационарных режимов процессов может быть пред-
ставлено системой обыкновенных дифференциальных уравнений — СОДУ (см. разд. 3.5).
При изменении параметров процессов вдоль двух и более пространственных координат
МО стационарных режимов процессов записывается с помощью системы дифференци-
альных уравнений в частных производных — СДУЧП (см. разд. 3.5). Нестационарные
режимы объектов (процессов) с распределенными параметрами всегда описываются сис-
темами дифференциальных уравнений в частных производных — СДУЧП.
Для построения математического описания (1.2) объектов (процессов) с сосредо-
точенными и распределенными параметрами используются табл. 2.1. «Уравнения
балансов гидродинамических моделей» и табл. 2.2. «Основные интенсивности источ-
ников элементарных процессов в потоках».
Решение задач идентификации (1.5) МО объектов с сосредоточенными парамет-
рами обычно сводится к определению вида и коэффициентов систем конечных урав-
нений, а объектов с распределенными параметрами — к определению вида и коэф-
фициентов систем дифференциальных уравнений.
268
Глава 5. Физико-химические модели. Построение моделей
В равной степени отличается и процедура решения задач оптимизации [см. разд. 3.6,
(1.10)]: для объектов с сосредоточенными параметрами — это решение задач не-
линейного программирования (1.16), а для объектов с распределенными парамет-
рами — это решение вариационных задач (см. разд. 5.5). При этом решение задачи
оптимизации для объектов с сосредоточенными параметрами представляет собой
совокупность оптимальных значений конечного числа переменных (1.11), а для объек-
тов с распределенными параметрами — совокупность оптимальных функций.
Общие принципы построения физико-химических моделей процессов
Системы уравнений МО химико-технологических процессов представляют со-
бой, в основном, системы конечных (обычно нелинейных) уравнений (СКУ) и системы
дифференциальных, чаще всего, обыкновенных дифференциальных уравнений (СОДУ).
Системы конечных {обычно нелинейных) уравнений описывают процессы с сосредо-
точенными параметрами, в которых переменные и параметры процессов не изменя-
ются ни по пространственной координате (процессы с идеальным перемешиванием
среды), ни во временной координате {стационарные процессы).
Системы дифференциальных уравнений описывают процессы:
с изменяющимися во времени параметрами — так называемые распределенные во
времени процессы {динамические процессы);
с изменяющимися по одной или нескольким пространственным координатам па-
раметрами — так называемые процессы с распределенными параметрами.
Следует отметить, что разделение объектов на объекты с сосредоточенными и
распределенными параметрами в известной степени является условным, и четкое раз-
граничение этих процессов невозможно. Тем не менее, с методической точки зрения
при разработке физико-химических математических моделей ХТП такое разделение
является весьма полезным.
Математическое описание процессов системами конечных нелинейных уравнений
В общем случае система конечных (обычно нелинейных) уравнений (можно пред-
положить, что она описывает стационарный режим некоторого процесса) с пятью
определяемыми переменными х = [хр х2, х3, х4, х5] в неявном виде может быть запи-
сана в следующем виде (см. разд. 3.2.3):
1 fi(xl,x2,x5) = Q;
2 /2(Х1,х3,х5) = 0;
3 /з(хрх2,х4) = 0; (5.1)
4 Л(хРх5) = 0;
5 Л(*3’ *<)=0-
Математическое описание процессов системами с обыкновенными дифференциальны-
ми уравнениями
Предположим, что обыкновенное дифференциальное уравнение первого порядка
(можно доказать, что уравнения более высоких порядков можно привести к системе
дифференциальных уравнений первого порядка), записанное в явном виде, с незави-
симой переменной t (производная по у — dxjdt) описывает нестационарный ре-
жим некоторого процесса. Система уравнений МО, включающая такое уравнение
для пяти определяемых переменных х =[хр х2, х2, х4, х5] (5.1) имеет вид:
Общие принципы построения физико-химических моделей
269
1 = fi(x^x2,x5)-
at
1 /2(хрх3,х5) = О;
3 /}(х1,х2,х4) = 0; (5.2)
4 /4(х1,х5) = 0;
5 Л(*3>*4)=0-
Для получения частного, физически обоснованного, решения дифференциально-
го уравнения 1 в (5.2) необходимо задать дополнительные условия, например, на-
чальное условие при t = в виде:
Г х^0}) = х<°>. (5.2')
Системы уравнений МО (5.1) и (5.2) составляются с использованием таблиц ба-
лансовых уравнений гидродинамических моделей и основных интенсивностей ис-
точников элементарных процессов в потоках, куда включены выражения для описа-
ния движения потоков и выражения для определения интенсивностей различных
элементарных процессов в потоках (см. табл. 2.1 и 2.2).
Информационные матрицы систем уравнений МО
и блок-схемы алгоритмов их решений
Для выбора эффективного алгоритма решения систем уравнений, например, систем
уравнений (5.1) и (5.2) используются соответствующие им информационные матрицы.
Информационная матрица системы уравнений МО (для системы (5.1) — табл. 5.1,
а для системы (5.2) с начальным условием (5.2) — табл. 5.2) представляет собой
квадратную матрицу, строки которой соответствуют номерам уравнений, а столбцы —
обозначению определяемых переменных. Информационная матрица формируется
следующим образом: на пересечении z-й строки, соответствующей z-му уравнению, с
j-m столбцом ставится знак плюс, если z-e уравнение включает j-ю определяемую
переменную. Эта процедура повторяется для всех независимых уравнений и опреде-
ляемых переменных системы.
При построении информационных матриц используются следующие условные
обозначения:
а) для левого столбца информационных матриц — номеров уравнений:
1 — конечное уравнение 1 в (5.1) (см. табл. 5.1);
дифур ~ обыкновенное дифференциальное уравнение первого порядка 1 в (5.2),
представленное в конечно-разностном виде (5.4) для нахождения функции
x/z) (z<°* < t < z(4)) (см. табл. 5.2);
10 - система конечных уравнений 10 (здесь не приводится); _
И — система обыкновенных дифференциальных уравнений первого порядка 11,
Диф ур
представленная в конечно-разностном виде 11 (здесь не приводится);
5 — корректирующее уравнение 5 в системе (5.1) для нахождения определяемой
Кор УР
переменной х1 (см. табл. 5.1);
12 — система конечных корректирующих уравнений (чаще всего нелинейных)
Кор УР _
12 для нахождения определяемых переменных (здесь не приводится);
270
Глава 5. Физико-химические модели. Построение моделей
| + | - задание начального приближения
- определение значения переменной
©- использование значения переменной,
полученное из предыдущих расчетов
/X- коррекция значения переменной,
заданной как приближение для расчетов
Рис. 5.1. Условные обозначения, применяемые
для построения информационных матриц
уравнений математического описания
б) для правого столбца информаци-
онных матриц:
№ — последовательность вычисле-
ний согласно выбранному алгоритму
решения.
В поле информационных матриц
применяются условные обозначения,
представленные на рис. 5.1.
Разработка алгоритмов решения зада-
чи — моделирующих алгоритмов {МА) —
выполняется с применением блок-схем
алгоритмов расчётов, реализующих выб-
ранный метод или методы решения за-
дачи.
При этом предлагается пользоваться условными обозначениями графических бло-
ков (рис. 5.2).
Информационная матрица системы конечных нелинейных уравнений
Для выбора алгоритма решения системы конечных нелинейных уравнений МО
(5.1) используются табл. 5.1.
Анализ информационной матрицы проводится следующим образом. Каждое из
пяти уравнений содержит по 2 и 3 определяемые переменные, поэтому ни одно из
уравнений не может быть решено самостоятельно.
Для получения решения этой системы уравнений необходимо задать начальное
приближение по одной переменной (в табл. 5.1 — по jq в уравнении 4), которое в
- начало вычислительного процесса
Старт
- конец вычислений
- блок обмена информацией: ввод и вывод
данных и результатов расчетов
- вычислительный блок: блок вычислительного
процесса, не использующий стандартные
вычислительные процедуры и алгоритмы
- алгоритмический блок: блок предопределенного
вычислительного процесса, в том числе со сложными
численными алгоритмами и процедурами проверки
условий окончания приближенных расчетов
- блок расчета, связанный с алгоритмическим блоком
и используемый предопределенным алгоритмом
для расчета функций с решении конечных уравнений,
записанных в неявном виде, либо для расчета
правых частей обыкновенных дифференциальных
уравнений, записанных в явном виде
Рис. 5.2. Изображение основных блоков в блок-схемах алгоритмов расчёта
Общие принципы построения физико-химических моделей
271
дальнейшем будет уточняться с использованием
некоторого корректирующего уравнения (в табл.
5.1 — уравнение 5).
В действительности, в соответствии с этой
таблицей (см. правый столбец табл. 5.1, где ука-
зана последовательность расчётов — №), после
того как по уравнению 4 задано приближение по
определяется переменная х5, которая стано-
вится известной для всех уравнений системы (5.1).
После этого вычисляется х2 из уравнения 1 (шаг 2),
х3 - из уравнения 2 (шаг 3) и х4 — из уравнения
3 (шаг 4).
В результате в уравнении 5 обе переменные
известны из предыдущих расчётов — х3 и х4. Они
Таблица 5.1. Информационная
матрица системы конечных нели-
нейных уравнений (5.1)
зависят от начального приближения х,, заданного на шаге 1, т.е. справедливы зави-
симости х3 = х3{х,} и х4 = х4{х1}.
Критерием получения решения xj является превращение уравнения 5, включаю-
щего х3{х,} и х4{х,} в тождество.
Поэтому уравнение 5 является корректирующим уравнением для х(, т.е. для него
будет справедливо:
/5(х3{х1},х4{х1}) = 0.
(5.3)
Это означает, что каждое новое приближение по х, должно получаться путём
реализации итерационного алгоритма решения уравнения с одной неизвестной (5.3)
(см. разд. 3.2.2). Когда результат решения уравнения (5.3) х3 будет получен, одно-
временно рассчитаются и оставшиеся четыре переменные — xj,x3,x4 и х, [они по-
лучаются на последней итерации решения уравнения (5.3)].
Таким образом, систему из пяти конечных нелинейных уравнений удалось ре-
шить путём реализации алгоритма решения одного уравнения (5.3) с одной итериру-
емой переменной Xj. В результате удалось снизить размерность решаемой задачи —
для определения значений пяти переменных итерационным путём вычислялась ве-
личина одной переменной. Такой способ решения систем уравнений называется де-
композиционным, для его применения и проводится анализ информационной матри-
цы системы уравнений МО.
Блок-схема алгоритма решения системы конечных нелинейных уравнений
Блок-схема алгоритма расчёта строится в строгом соответствии с правым столб-
цом информационной матрицы (см. табл. 5.1), где указана последовательность вы-
полнения расчётов (рис. 5.3). Корректирующему уравнению 5 системы (5.1) соответ-
ствует алгоритмический блок 5 с выбранным численным методом решения одного
уравнения с одним неизвестным и блок расчёта функции f5, определяющей на каж-
дом шаге итерационного процесса левую часть уравнения (5.3).
272
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.3. Блок-схема алгоритма решения системы конечных нелинейных уравнений (5.1)
декомпозиционным методом
Процесс последовательных приближений (итерационный процесс) для итери-
руемой переменной х,, приводящей к решению корректирующего уравнения (5.3)
и соответственно всей системы (5.1), отображается пунктирной линией, направ-
ленной в противоположную сторону от основного направления последовательнос-
ти расчетов.
Информационная матрица системы с обыкновенным дифференциальным уравнением
Для построения информационной матрицы системы уравнений (5.2) её целесо-
образно записать, используя конечно-разностное представление производной
(см. разд. 5.3) в уравнении 1 (5.2), и с учётом начального условия 1 '(5.2') на отрезке
z(°) и z(*) будет справедливо:
1’ --------------— fi (.X,, х2, х5) ;
2 /2(х,,х3,х5) = 0;
3 /3(х1,х2,х4) = 0; (5.4)
4 /4(х3,х5)=0;
5 fs (*з > х4) — 0,
Г х,(г(°)) = х<°).
Результат решения - функция х, = х, (г) на отрезке [z(0), и, так как от неё
зависят другие переменные х2, х*, х4 и х*, то они также будут зависеть от времени. В
действительности, искомая функция х, (г) будет получаться при расчётах в дискрет-
ном виде — х1(/|)), х,(/2)),..., х,)/^), число точек функции определяется шагом реше-
ния дифференциального уравнения — А/. В информационную матрицу (табл. 5.2)
включаются величины хДг^) и хд/*)) и, в конечном счёте, задача решения заклю-
чается в определении хД/^) и всех предыдущих дискретных значений этой функ-
Общие принципы построения физико-химических моделей
ТП
ции (без этих значений величина xj/*)) не мо-
жет быть определена).
После выполнения шести шагов последова-
тельности, приведённой в правом столбце ин-
формационной матрицы, определяется значе-
ние х( (/*)), которое является последней точ-
кой кривой х,=х,(/) на заданном отрезке
[z<°), /*>], а это означает, что все предыдущие
дискретные точки функции — решения х, = х, (/)
также рассчитаны в соответствии с величиной
шага решения Дт
Блок-схема алгоритма решения системы
с обыкновенным дифференциальным уравнением
Таблица 5.2. Информационная
матрица системы (5.2) [соответ-
ственно, (5.4)] с обыкновенным
дифференциальным уравнением
первого порядка
Блок-схема алгоритма решения (рис. 5.4) со-
ставляется в соответствии с правым столбцом информационной матрицы (см. табл.
5.2). Алгоритмическому блоку будет соответствовать дифференциальное уравнение Г
(5.4), в котором определяются значения х, (/')), xft^),..., х,(?(Л)), а блоку расчёта фун-
кции — правая часть дифференциального уравнения 1* (5.4). Цикл решения диф-
ференциального уравнения для различных ? = z(0),z<l) = /0) + Дг, z<2) =/*0) + 2Д? и т.д.
также изображается пунктиром, направленным в противоположную сторону от ос-
новного направления последовательности вычислений, однако рядом с изменяю-
щимся на каждом шаге значением х, при последовательных вычислениях в скобках
указывается независимая переменная дифференциального уравнения — в данном
случае t.
Необходимо отметить, что применение информационных матриц систем уравне-
ний для анализа математического описания процессов и графическое изображение со-
ответствующих алгоритмов их решения в виде блок-схем расчётов позволяет наибо-
лее рационально решать проблемы сокращения размерностей решаемых задач и
выбора эффективных моделирующих алгоритмов при построении физико-хими-
ческих моделей ХТП.
Рис. 5.4. Блок-схема алгоритма решения системы (5.2) [соответственно, (5.4)J
с обыкновенным дифференциальным уравнением первого порядка
ПА
Глава 5. Физико-химические модели. Построение моделей
5.1. Математические модели движения
жидкости в простых гидравлических
системах
К простым гидравлическим системам относятся технологические схемы трубо-
проводов, для которых принимаются следующие допущения:
• во всех трубах протекает однофазный поток жидкости, температура которого
одинакова на всех участках;
• все трубы располагаются на одном уровне, в системе нет рециклических (обрат-
ных) потоков, или рециклов, не учитываются местные сопротивления и пере-
пады давлений в трубах, т.е. рассматриваются, так называемые короткие трубо-
проводы;
• системы включают только клапаны (вентили) с постоянными, не изменяющи-
мися коэффициентами пропускной способности и закрытые емкости (аккуму-
ляторы), давление газа в которых подчиняется идеальным законам.
Реальные гидравлические системы включают насосы, компрессоры и другие еди-
ницы оборудования; в них наряду с жидкостью могут перемещаться потоки газа,
газо- и парожидкостной смеси. Тем не менее, изучение общих принципов построе-
ния математических моделей простых гидравлических систем позволяет получить
представление о стратегии их математического моделирования.
5.1.1. Математические модели стационарных
режимов движения жидкости в простых
гидравлических системах
Для построения статической модели представленной гидравлической системы (рис. 5.5)
необходимо выполнить три последовательных этапа:
1) изучить и/или ознакомиться с теорией протекающих процессов;
2) построить и проанализировать системы уравнений математического описания
(МО) процесса;
3) выбрать и реализовать на компьютере моделирующий алгоритм (МА) решения
системы уравнений МО гидравлического процесса.
Изучение теории процесса осуществляется с целью построения системы уравне-
ний МО гидравлической системы, которая включает:
• балансовые уравнения;
• уравнения для определения скоростей движения жидкостей через клапаны (вен-
тили);
• уравнения, определяющие давление жидкости на дне закрытой емкости и дав-
ление газа над поверхностью жидкости в этой же емкости.
Для системы, изображенной на рис. 5.5, будут справедливы два уравнения массо-
вого баланса (третье возможное балансовое уравнение — уравнение общего баланса —
получается сложением двух других, т.е. будет линейно-зависимым):
- v3 - v5 = 0; (5.1.1)
v2 + v5-v4 = 0. (5.1.2)
Формула для определения скорости v протекания жидкости через клапан в соот-
ветствии с уравнением Бернулли для суммарной удельной энергии элементарной
струи идеальной жидкости при установившемся движении и с учетом допущений о
простой гидравлической системе имеет вид:
5.1. Математические модели простых гидравлических систем
275
v = kyjPm-P^, (5-1.3)
где к — коэффициент пропускной способ-
ности клапана; Рт, Рвых — давления жид-
кости на входе и на выходе из клапана.
Более строгая запись формулы (5.1.3)
имеет вид:
V = к sgn(P„ - Рвых )V| Р„ -Рвых I ,(5.1.4)
где sgn(x) — функция знака и может при-
нимать только три значения: —1, 0, +1 в
соответствии со схемой:
Рис. 5.5. Схема простой гидравлической
системы
sgn(x) = — 1, если х < 0;
sgn(x) = 0, если х = 0;
sgn(x) = +1, если х > 0.
(5.1.5)
В соответствии с формулой (5.1.4) знак скорости потока жидкости становится
отрицательным, если направление ее движения будет противоположным направле-
нию на рис. 5.5.
Так как гидравлическая система содержит 5 клапанов, то приведенных формул
(5.1.3) в системе уравнений МО должно быть 5.
По аналогии, должно быть две группы уравнений, определяющих давление жид-
кости внизу закрытой емкости и давление газа над поверхностью жидкости. При
этом принимаются допущения:
• об идеальном поведении газа в емкости;
• о цилиндрической форме закрытой емкости с площадью поперечного сечения
5 и геометрической высотой Я0;
• об одинаковом давлении газа РК в емкостях, не заполненных жидкостью.
В соответствии со следствием из закона Паскаля давление жидкости Ржидк внизу
емкости определяется по формуле:
Р^ = P„3 + Pg# (5.1.6)
где Ргаз — давление газа над поверхностью жидкости; р — плотность жидкости; Н —
уровень жидкости в емкости.
Для определения давления газа Ргаз используется соотношение для идеального газа:
ЛазКа3 = PNV* = const, (5.1.7)
где V* — объем емкости, не заполненный жидкостью, V^= SH°; — объем газа в
закрытой емкости, V^= 5 (Я° — Н).
В результате будет справедливо:
PmS{H°- Н) = PNSH°
или
N HG-H
(5.1.8)
Формулы для определения давления жидкости Р (5.1.6) и давления газа Ргаз
(5.1.8) используются для описания поведения двух закрытых емкостей в гидравли-
ческой системе, изображенной на рис. 5.5.
276
Глава 5. Физико-химические модели. Построение моделей
Система уравнений математического описания стационарных режимов движения
жидкости в простой гидравлической системе
Система независимых уравнений (5.1.9), приводимая ниже и описывающая пове-
дение простой гидравлической системы в стационарном состоянии, состоит из сле-
дующих уравнений:
а) определения скорости потоков жидкости через клапаны (5.1.3) — при програм-
мировании используется строгое уравнение (5.1.4):
1 V1 = k{ (Р, - Р5)|/2;
2 v2 = &2 (Р2 — Р6)1/2;
3 v3= &3 (Р5 — Р3)|/2;
4 Vi=k<(Pb-P^-
5 v5= k5 (P5 - P^
б) расчета балансов (5.1.1) и (5.1.2):
6 v, — v3 — v5 = 0; (5.1.9)
7 v2 + v5 - v4 = 0 ;
в) определения давления жидкости (5.1.6) и газа (5.1.8) в закрытых емкостях:
8 Р5 = Р7 + pgH,;
10 P6=P8+pgtf2;
11 P^ = Pn HG -Н '
Так как система конечных уравнений (5.1.9) включает 11 независимых уравнений
(в дальнейшем используется последовательная нумерация уравнений от 1 до 11), она
может быть решена, в принципе, относительно любых 11 переменных, которые на-
зываются определяемыми переменными. Все остальные переменные системы (5.1.9),
соответствующие числу степеней свободы, должны задаваться.
Кроме этого, должны быть специфицированы коэффициенты (например, коэф-
фициенты пропускной способности клапанов — вектор к), а также постоянные в
системе уравнений (5.1.9) — геометрические высоты емкостей HG, Н°, давление в
незаполненной жидкостью емкости PN и плотность жидкости р.
Исходя из физических соображений, при гидравлическом расчете систем трубо-
проводов (см. рис. 5.5), представляющем собой решение системы 11 уравнений (5.1.9),
определяемыми переменными выбираются:
• расходы жидкости на всех участках (у): 5 определяемых переменных;
• промежуточные давления в системе Р5, Р6, Р7, Р8 (Р): 4 определяемых переменных;
• уровни жидкости в двух ёмкостях (Н): 2 определяемые переменные.
Всего: 11 определяемых переменных.
Давления на входе в систему Р и Р2, а также давления на выходе из системы Р3 и
Р4 задаются и их число (в данном случае 4) соответствует числу степеней свободы
системы уравнений (5.1.9), которое определяется как разность числа переменных —
5.1. Математические модели простых гидравлических систем
277
числа независимых уравнений и равно: 15 — 11 = 4. Эти четыре переменные могут
задаваться независимо в соответствии с физическим смыслом решаемой задачи. Это
означает, что если предполагается движение жидкости в соответствии со стрелками,
изображенными на рис. 5.5, давления на входе в систему Р{ и Р2 должны быть боль-
ше давлений на выходе Р} и Р4.
Система 11 конечных уравнений (5.1.9), решаемая относительно следующих 11
определяемых переменных
V„ V2, v3, V4, V5, P5, P6, P7, P&, Hv Hv (5.1.10)
является системой нелинейных уравнений.
Для ее решения наиболее целесообразно использовать декомпозиционный метод,
который позволяет существенно снизить размерность решаемой задачи и определять
все искомые переменные путем решения системы (или систем) уравнений значи-
тельно меньшей размерности, чем размерность исходной системы.
Размерность исходной системы уравнений (5.1.9) равна 11. Для выбора алгорит-
ма декомпозиции, который позволит определить 11 искомых переменных (5.1.10) пу-
тем последовательного решения одного нелинейного уравнения размерностью 1 и
одного квадратного уравнения, необходимо построить и проанализировать инфор-
мационную матрицу системы уравнений МО (5.1.9).
Построение и анализ информационной матрицы системы уравнений математического
описания стационарного режима движения жидкости в простой гидравлической
системе
Для выбора оптимального алгоритма расчетов при решении системы уравнений
(5.1.9) необходимо проанализировать информационную матрицу (табл. 5.3).
Каждое уравнение системы (5.1.9) содержит несколько определяемых перемен-
ных: как минимум две. Начальные приближения для итерационных расчетов при
Таблица 5.3. Информационная матрица системы уравнений математического опи-
сания стационарного режима движения жидкости в гидравлической системе (рис. 5.5)
л\ V1 v2 ъ V4 v5 ps p6 я2 №
1 © 3
2 © 7
3 © 4
4 © 8
5 © 6
6 © © 5
7 Кор ур © © 9
8 © © 2
9 □ 1
10 © 10,11
11 10,11
278
Глава 5. Физико-химические модели. Построение моделей
решении нелинейных уравнений следует задавать в тех уравнениях, которые содер-
жат наименьшее число определяемых переменных (в данном случае две) и могут
быть хорошо обоснованы из физических соображений. Например, значение прибли-
жения Я( может быть задано в интервале [О, Я ° ], так как высота емкости Н° задана
в условии задачи.
Для обозначения задания начального приближения итерационного процесса вы-
числения в информационной матрице ставится знак плюс, соответствующий задава-
емой переменной в конкретном уравнении, и обводится квадратом.
Первым шагом вычислительной процедуры будет определение переменной Р1 в
уравнении 9 (см. число 1 в правом столбце информационной матрицы). Для обозна-
чения переменной, которая определяется в уравнении 9, соответствующий ей плюс в
строке 9 обводится ромбом. Заданное значение приближения Нх и найденная пере-
менная Р7 справедливы для всей системы уравнений, и поэтому эти величины долж-
ны использоваться и другими уравнениями системы (см. строку 8 в информацион-
ной матрице). Для обозначения распространения значений переменных на все урав-
нения системы соответствующие им плюсы в столбцах обводятся окружностями. В
уравнении 8 окружностями обведены плюсы, соответствующие Я, и Р7, что позволя-
ет решить это уравнение относительно Р5 на шаге 2 вычислительной процедуры.
Дальнейшие последовательные шаги расчетов дают возможность определить только
приближенные значения vp v3, v5, Р6, v2, v4, что связано с выбором в самом начале
реализуемой процедуры вычисления приближения величины Я,.
Таким образом, определение корректного значения Я1 приведет, соответственно,
к получению корректных значений и Р7, Р5, vp v3, v5, Р6, v2, v т.е. 9 из 11 искомых
переменных.
Для коррекции Я, должно использоваться уравнение 7, в котором все пере-
менные известны из предыдущих расчетов (соответствующие им плюсы обведены
окружностями) — шаг 9. Когда система уравнений МО решена, то уравнение 7
вида:
у2{Я,} + у5{Я,} - у4{Я,} = 0 (5.1.11)
должно превратиться в равенство. Переменная Я3 в фигурных скобках в этом случае
означает, что каждое слагаемое этого уравнения зависит от переменной Яр и оно
должно быть решено относительно Я3 для получения ее корректного значения.
Реализацию алгоритма решения уравнения 7 можно рассматривать как процеду-
ру коррекции переменной Нх и, соответственно, определение значений переменных
Pv Р5, Vp v3, v5, Р6, v2 и v4. Для обозначения того факта, что уравнение 7 является
корректирующим для Яр в строке 7 информационной матрицы в позиции, соответ-
ствующей переменной Яр стоит пустой ромб.
Наиболее эффективным алгоритмом для коррекции переменной Я1 и решения
уравнения 7 является метод половинного деления, с нижней границей интервала
поиска — 0 и верхней границей (Н°) -1.0 • 10-5, так как только в этом случае знамена-
тель уравнения 9 системы уравнений МО (5.1.9) не станет равным нулю при подста-
новке в него верхней границы Н°
При решении уравнения 5 в итерационном цикле на шаге 6 необходимо опреде-
лить Р6. Так как на предыдущих этапах расчетов v5 может получиться как положи-
тельным, так и отрицательным, выражение для определения Р6 должно учитывать
это обстоятельство — используется функция знака sgn(x) (5.1.5) для решения уравне-
ния 5:
5.1. Математические модели простых гидравлических систем 279
Р6 =/’s-sgn(v5)
(5.1.12)
Для определения двух оставшихся переменных Р8 и Н в уравнение 10 подставля-
ется Р8 из уравнения 11 системы уравнений МО (5.1.9). В результате получается
квадратное уравнение относительно Н2 (Р6 известно из предыдущих расчетов):
н G
po=PN 2U +PgH2. (5.1.13)
Л 2 «2
Для определения значения Н2 используется алгоритм вычисления корней квадратно-
го уравнения и выбирается тот из корней, который располагается в интервале [0, Н2 ].
Блок-схема алгоритма расчета стационарного режима движения жидкости
в простой гидравлической системе
В блок-схеме алгоритма расчета стационарного режима гидравлической системы
(рис. 5.6) используются два алгоритмических блока, в которых реализуются два чис-
ленных алгоритма:
• алгоритм метода половинного деления: алгоритмический блок (7) для опреде-
ления Яг
• алгоритм вычисления корней квадратного уравнения: алгоритмический блок
(10, 11) для определения Н2 и Р8.
После вычисляются три коэффициента функции fl0 представляющей собой мно-
гочлен 2-й степени, получаемый после соответствующего преобразования квадрат-
ного уравнения (5.1.13). Алгоритмический блок (10,11) реализует стандартный алго-
ритм решения квадратного уравнения с конкретными значениями коэффициентов
(fw п), в результате чего определяется высота жидкости во второй ёмкости Я2.
Топология гидравлической системы отображается вычислительными блоками слева
от алгоритмического блока (7). Результатом расчета по вычислительным блокам (9),
(8), (1), (3), (6), (5), (2), (4) является значение величины функции:
/z=V2+V5-V4’ (5.1.14)
которая используется стандартным модулем метода половинного деления (см. разд. 3.2.2)
в алгоритмическом блоке (7) для определения уровня жидкости Я, в первой емкости.
Рис. 5.6. Блок-схема алгоритма расчёта стационарного режима движения жидкости
в гидравлической системе (рис. 5.5)
280
Глава 5. Физико-химические модели. Построение моделей
5.1.2. Математические модели нестационарных
режимов движения жидкости в простых
гидравлических системах
При построении динамических моделей конечные балансовые уравнения 6 и 7 в
системе уравнений МО (5.1.9) превращаются в обыкновенные дифференциальные
уравнения вида:
(5.1.15)
(5.1.16)
dV.R
----= vi _ _ ;
dt 1 3 5 ’
dVR
—— - V2 + v5 - v4,
dt
где y R и V2r — объемы жидкости в верхней и нижней ёмкостях гидравлической сис-
темы, представленной на рис. 5.5.
Если эти ёмкости являются цилиндрическими, то объем жидкости в них опреде-
ляется как
VR=SH (5.1.17)
(S — площадь поперечного сечения цилиндра), и вышеприведенные обыкновенные
дифференциальные уравнения (5.1.15) и (5.1.16) принимают следующий вид (в ну-
мерации системы (5.1.9) — это будут уравнения 6 и 7):
t/Я, _ у,-v3-v5 .
dt S,
dH2 _ у2 + у5 - у4
dt S2
Для решения системы дифференциальных уравнений на компьютере (см. разд. 3.5),
т.е. получения соответствующего частного решения необходимо задать начальные
условия, в нумерации системы (5.1.9) — это будут уравнения 6'и 7':
6’ Я^(0)=Я,(О = Я,<0);
= Я2(Г(0)) = Я<0>. (5.1.19')
При этом решается задача Коши или задача с начальными условиями, и получа-
емые частные решения представляют собой функции Ht(t) и рассматриваемые
в замкнутом интервале [/0), /ч], которые являются приближениями истинных функ-
ций решения Н*(Г)и H2(f)
Более общее представление систем двух дифференциальных уравнений (5.1.18) и
(5.1.19) имеет вид:
6
(5.1.18)
7
(5.1.19)
(5.1.18')
7'
(5.1.20)
(5.1.21)
^ = А(Н„Н2);
at
at
где fb{Hv Н2) и/7(Я|, Н2) — правые части дифференциальных уравнений первого
порядка, записанные в явном виде.
Существуют два подхода при интегрировании дифференциальных уравнений —
явный и неявный (см. разд. 3.5).
Для явного метода Эйлера систему дифференциальных уравнений на каждом к-м
шаге решения представляют с использованием конечно-разностной схемы в виде:
5.1. Математические модели простых гидравлических систем
281
—— = f6{Hy ,НУУ, (5.1.22)
txt
AH(k>
—^- = У(НУ,НУ), (5.1.23)
где txt=h — шаг решения (интегрирования); к — номер шага решения (интегрирования);
ДН,<‘) = 7/,(‘+1) - НУ (1=1,2).
В этом случае, зная ну, НУ, в том числе и Н'У, НУ, можно легко рассчитать
Н'У'! и НУ'У по простым формулам:
Н(У1) =НУ+hf6(H<y, НУ); (5.1.24)
Н(2М) = Н(У + hf7(H(y, НУ). (5.1.25)
При этом необходимо располагать алгоритмом расчета правых частей дифферен-
циальных уравнений f6(Hy, НУ) и У(Н(У, НУ) при известных значениях нУ,Н(У-
Для неявного метода Эйлера соотношения (5.1.22) и (5.1.23) принимают вид:
-^ = /уну\нУУ- (5.1.26)
—^- = У{НУ'\НУУ. (5.1.27)
В этом случае уравнения (5.1.24) и (5.1.25) для определения Н'У'' и 7/*‘+1) запи-
сываются в виде:
Н *‘+1) = Н(У + hf6 (НУ1), Н У"); (5.1.28)
Н(У'} = нУ + hf7 (НУ", нУГ>). (5.1.29)
Сравнение (5.1.20) и (5.1.21) с (5.1.18) и (5.1.19), а также учет зависимостей сис-
темы уравнений (5.1.9) позволяет установить, что функции f6 и /7 являются нелиней-
ными относительно определяемых на каждом к-м шаге интегрирования н[М} и НУ".
Отсюда следует вывод, что определение нУ'} и НУ{) на каждом очередном к-м
шаге интегрирования сводится к решению системы двух нелинейных уравнений
(5.1.28) и (5.1.29). Это в свою очередь усложняет расчеты и делает их более длитель-
ными. Поэтому неявные методы относят к классу медленных методов и применяют,
когда быстрые явные методы, например (5.1.24) и (5.1.25), не дают удовлетворитель-
ных результатов.
Опыт показывает, что для большинства простых гидравлических систем явные
методы обеспечивают требуемую сходимость.
Математическое описание динамики простой гидравлической системы представ-
ляет собой систему уравнений (5.1.9), в которой балансовые уравнения 6 и 7 замене-
ны на дифференциальные уравнения (5.1.18) и (5.1.19), и в систему включены два
начальных условия (5.1.18') и (5.1.19) для получения частного решения на компью-
тере (общее решение обыкновенных дифференциальных уравнений, как правило,
получают аналитическими методами).
В результате необходимо решить систему уравнений (5.1.9), из которых два 6 и 7 явля-
ются дифференциальными (5.1.18) и (5.1.19) с начальными условиями (5.1.18') и (5.1.19).
282
Глава 5. Физико-химические модели. Построение моделей
Построение и анализ информационной матрицы системы уравнений математического
описания нестационарного режима движения жидкости в простой гидравлической системе
Для построения информационной матрицы для решения дифференциальных урав-
нений (5.1.18) и (5.1.19) целесообразно представить их в конечно-разностной форме,
аппроксимирующей исходные дифференциальные уравнения (в нумерации системы
(5.1.9) - это будут уравнения 6* и 7‘):
r (5119+)
Дг S2
Если интервал интегрирования равен [Л”, rw], то правые части дифференциаль-
ных уравнений 6* и 7‘, а также соответственно (5.1.18*) и (5.1.19*), вычисляются при
/°>, г(1), ..., В результате конечно-разностных преобразований 6* и 7* система
уравнений МО нестационарного режима движения жидкости в гидравлической сис-
теме (5.1.9) — см. рис. 5.5, представленная в конечно-разностной форме, имеет вид:
1 Vj = Л, (Pi ~ Р^
2 v2 = (Р2 - Р6)1/2 ;
3 v3=A:3(P5-P3)‘/2;
4 v4=fc4(P6~ Р^~
5 v5= fc5 (Р5 - Р6)‘/2 ;
W1(O-#1('<0,)_v1-v3-v5
6 Дг ~ S, ~Л’
6' Н1(?(0)) = Н1(0); (5.1.30)
H2(t^-H2(t^ у2+у5-у4 = f .
Д/ s2 ’
7' P/2(r(0J) = ;
8 P5=P7+pgtf,;
Ю P6=P,+ pgH2\
Информационная матрица системы уравнений МО, соответствующая системе
уравнений (5.1.30), приведена в табл. 5.4.
Так как при решении системы двух дифференциальных уравнений (5.1.18) и (5.1.19)
необходимо определить функции Ht(f) и H2(t) [/0), /*>], т.е. и H[k) = H^t^) и
=H2(r(t)) при заданных начальных условиях (5.1.18’) и (5.1.19’) - Н,0’ и Н*0),то
конечным результатом расчетов должны быть указанные функции, представленные
в дискретном виде, при t = t(0), tw, ..., z(t-1), t{k}. Последними значениями искомых
функций являются определяемые на 12 и 13 шаге вычислений Н2}
5.1. Математические модели простых гидравлических систем
283
Блок-схема алгоритма расчета нестационарного режима движения жидкости
в простой гидравлической системе
Блок-схема алгоритма расчёта простой гидравлической системы (см. рис. 5.5) при
нестационарном режиме движения жидкости изображена на рис. 5.7.
Таблица 5.4. Информационная матрица системы уравнений математического описа-
ния нестационарного режима движения жидкости в гидравлической системе (рис. 5.5)
н.б)
Рис. 5.7. Блок-схема алгоритма расчета нестационарного режима движения жидкости
в простой гидравлической системе (рис. 5.5)
284
Глава 5. Физико-химические модели. Построение моделей
5.2. Математические модели стационарных
режимов процессов теплопередачи
в поверхностных теплообменниках
В теплообменных аппаратах (теплообменниках) часть энтальпии более тёплой
среды передаётся более холодной среде. Для этой цели используются различные типы
теплообменников, которые широко распространены в химической промышленнос-
ти. Теплообменники применяются для нагревания и охлаждения веществ, находя-
щихся в различных агрегатных состояниях, испарения жидкостей и конденсации
паров, перегонки и сублимации, абсорбции и адсорбции, расплавления твёрдых тел
и кристаллизации, отвода и подвода теплоты при проведении экзо- и эндотермичес-
ких реакций и т.д.
По способу передачи теплоты различают поверхностные и смесительные тепло-
обменные аппараты. В первом случае передача теплоты происходит через разделяю-
щие твёрдые стенки, во втором — непосредственным контактом (смешением) нагре-
тых и холодных сред (жидкостей, газов, твёрдых веществ).
Поверхностные теплообменники подразделяются на рекуперативные и регенера-
тивные.
В рекуперативных теплообменниках чаще всего теплота от горячих теплоносите-
лей к холодным передаётся непрерывно через разделяющую их стенку с определён-
ной площадью поверхности теплообмена. В некоторых случаях рекуператоры могут
работать и в периодическом режиме.
Регенеративные теплообменники являются аппаратами периодического действия, в
которых оба теплоносителя попеременно соприкасаются с одной и той же стенкой, нагре-
вающейся (аккумулируя тепло) при прохождении горячего потока и охлаждающейся (от-
давая аккумулированное тепло) при последующем прохождении холодного потока.
В теплообменниках может изменяться агрегатное состояние одного или обоих
теплоносителей, теплообмен может происходить между различными потоками: жид-
кость-жидкость, жидкость—газ и газ—газ.
Теплообменники могут изготавливаться из различных материалов: металлов, теф-
лона, стекла и др.
По конструкционным характеристикам они подразделяются на кожухотрубные,
трубчатые, пластинчатые, змеевиковые, спиральные и др.
Корректный расчёт теплообменников принципиально важен при разработке энер-
го- и ресурсосберегающих технологий различных химических производств. В этом
плане особенно неприемлемо получение завышенных результатов вычислений при
определении режимных (температура теплоносителей и их расходов), а также кон-
струкционных параметров. Такого рода неточности могут привести к неоправданно
большим коэффициентам запаса при проектировании и, как следствие, к снижению
показателей технологического процесса по энерго- и ресурсосбережению.
Движение потоков теплоносителей в теплообменниках для целей компьютерного
моделирования представляется идеальными гидродинамическими моделями, что
позволяет получать адекватные компьютерные модели без излишнего усложнения
математического описания (МО).
Гидродинамическую модель идеального смешения и идеального вытеснения для
потоков теплоносителей можно применять для поверхностных теплообменников
следующих типов:
• кожухотрубных теплообменников (рис. 5.8, а);
• трубчатых теплообменников (рис. 5.8, б);
• аппаратов воздушного охлаждения;
• пластинчатых теплообменников;
• змеевиковых теплообменников (рис. 5.8, в).
5.2. Математические модели поверхностных теплообменников
285
Рис. 5 8. Поверхностные теплообменники, кожухотрубный (а), трубчатый (б),
змеевиковый (в)
В настоящем разделе рассматривается методология поверочно-оценочного расчё-
та основных типовых фрагментов промышленных теплообменников, когда конст-
рукционные параметры считаются известными. Варианты проектного, точнее, про-
ектно-конструкционного, расчёта реальных теплообменников с выбором их типо-
размеров в соответствии с известными нормативами и отраслевыми стандартами не
приводятся. Представлены алгоритмы поверочно-оценочного расчёта стационарных
режимов типовых фрагментов поверхностных теплообменников, в которых учитыва-
ются только процессы теплопередачи.
5.2.1. Математическая модель стационарного
режима процесса теплопередачи в теплообменнике
типа «смешение-смешение»
Построение компьютерной модели теплообменника в соответствии с принципа-
ми, изложенными в главе 2, включает следующие этапы:
• изучение и/или ознакомление с теорией процесса теплообмена для данного
типа теплообменных аппаратов;
• построение математического описания (МО) конкретного процесса теплообмена;
• выбор и реализация алгоритма (моделирующего алгоритма — МА) решения урав-
нений МО модели данного теплообменника.
Представленная на рис. 5.9 схема теплообменника включает в себя два потока тепло-
носителей — например, охлаждаемый поток с начальной температурой (на входе в аппа-
рат) конечной температурой (на выходе) 7], расходом у(, теплоёмкостью Ср1
286
Глава 5. Физико-химические модели. Построение моделей
и нагреваемый поток с начальной температурой (на входе в аппарат) , конечной
температурой (на выходе) Т2, расходом v2, теплоёмкостью Ср2. Поверхность тепло-
обмена имеет площадь FT. Коэффициент теплопередачи обозначен Кт.
Рис. 5.9. Схематическое изображение теплообменника типа «смешение—смешение»
Для упрощения построения математического описания рассматриваемого про-
цесса принимаются следующие допущения:
рассматривается стационарный режим теплопередачи;
оба потока теплоносителя описываются моделью идеального смешения;
происходит только процесс теплопередачи.
Так как рассматривается стационарный режим, следовательно, уравнение тепло-
вого баланса для потока первого теплоносителя для рассматриваемой гидродинами-
ческой модели идеального перемешивания записывается следующим образом (см.
табл. 2.1) — производная по времени равна нулю:
1 v^C^T^-v}Cp2Tx+FT^ (5.2.1)
где Agf — локальная интенсивность теплопередачи.
В систему уравнений МО в соответствии с принципами построения компьютерных
моделей, сформулированными в главе 2, необходимо включить выражение для локаль-
ной интенсивности теплопередачи для первого потока теплоносителя (см. табл. 2.2):
2 =Кг(Г2-7'1). (5.2.2)
Уравнение теплового баланса для потока второго теплоносителя для рассматри-
ваемой гидродинамической модели идеального перемешивания записывается анало-
гично (5.2.1) — производная по времени также равна нулю:
3 v2yC{p2T2a) - v2Cp2T2 + FTbqT2 = 0. (5.2.3)
Выражение для локальной интенсивности теплопередачи для второго потока теп-
лоносителя также включается в систему уравнений МО:
4 ixqT2=KT(7\-T2). (5.2.4)
Учитывая, что локальные интенсивности теплопередачи обоих потоков совпада-
ют по величине, но различны по знаку, можно записать:
A/=Agf=-Ag[. (5.2.5)
Это даёт возможность сократить количество уравнений (см. главы 1,2), входящих
в систему линейных алгебраических уравнений (СЛАУ) математического описания
для данной модели теплообменника. В результате эта система записывается следую-
щим образом:
1 + Fr Ag7' = 0 ;
2 v<O)C<°2)r2(0)-v2Cp27’2 + Fr(-A/)=O; (5.2.6)
3 ^т = Кт(Т2-Т,).
5.2. Математические модели поверхностных теплообменников
287
Рассмотрим следующие частные случаи.
Первый частный случай — принимается допущение о том, что константа теплопере-
дачи через поверхность теплообмена постоянна (А7 = const). Это означает, что, в
частности, теплоёмкости потоков Ср1 и Ср2 постоянны и не зависят от температуры.
В этом случае система из трёх уравнений (5.2.6) позволяет найти три определяе-
мых переменных. В качестве определяемых переменных выбираем температуры по-
токов на выходе из теплообменника Т{ и Т2 и локальную интенсивность теплопере-
дачи tsqT.
Найдём решение системы уравнений МО рассматриваемой модели теплообмен-
ника (5.2.6).
Для этого преобразуем систему (5.2.6) путём подстановки в уравнения 1 и 2 выра-
жения для локальной интенсивности теплопередачи A<?r:
1 (v,Cpl7] + АГАГ)7] + (-FtKt)T2 = v1<0,Cj;,T1(0) ; (5.2.7)
“и
2 {-FTKT) 7] + (v2C,2 + FTКт) T2 = у!»С$Т™ .
«21 «22 4
Обозначив коэффициенты перед переменными Т\ и Т2 как «а» с соответствующи-
ми индексами и свободные члены уравнений 1 и 2 системы (5.2.7) как «Ь» с соответ-
ствующими индексами, получаем возможность записать СЛАУ (5.2.7) в матричном
виде:
Ах=Ь;
«11 «12 ^1 _
«21 а22_ _^2_ _^2
(5.2.8)
т-
откуда методом обратной матрицы (см. разд. 3.2) находим значения температур по-
токов на выходе из теплообменника
т; =
к
После определения температур потоков на выходе из теплообменника из уравне-
ния 3 системы (5.2.6) определяется значение локальной интенсивности теплопереда-
чи AqT. Таким образом, определяются все три искомые переменные.
Второй частный случай — константа теплопередачи непостоянна и зависит от
температур, теплоёмкостей и расходов потоков (КТ Ф const), также учитывается за-
висимость теплоемкостей потоков (Ср1,Ср2) от температуры.
В этом случае к уравнениям 1, 2 и 3 системы уравнений МО (5.2.6) должны быть
добавлены уравнения (5.2.10), (5.2.11) и (5.2.12), являющиеся выражениями для кон-
станты теплопередачи и теплоёмкостей потоков:
Кт =КТVi,v2, Ср1, Ср2)~ (5.2.10)
Ср1 = О] +&1Г1 + с17'12 + <717'13; (5.2.11)
Ср2 = а2 + b2l2 + с2Т2 + d2T2 , (5.2.12)
где а, Ь, с и d — константы для конкретных теплоносителей, значения которых дос-
тупны в справочной литературе.
В результате система уравнений МО теплообменника типа «смешение—смеше-
ние» (5.2.6) записывается следующим образом:
288
Глава 5. Физико-химические модели. Построение моделей
1 - vxCpJ\ + FTbqT = 0;
2 v'o)C'02Y2(0’-v2Cp27'2+Fr(-A97)=O;
3 &qT =КТ(Т2-7]); (5.2.13)
4 KT =KT Vi,v2,C pl,C p2);
5 C^a'+b^+crf+drf-,
6 Ср2 ~ ^2 ~^b2T2 + с2Г2 + d2T2;
В данном случае из шести уравнений системы уравнений МО (5.2.13) возможно
найти шесть определяемых переменных. В качестве решения этой системы в соот-
ветствии с информационной матрицей (табл. 5.5) следует выбрать температуры по-
токов на выходе из теплообменника 7\ и Т2, локальную интенсивность теплопереда-
чи Д</, константу теплопередачи К7 и теплоёмкости потоков Ср1 и Ср2:
Т2, Д/, Кт, Ср1, Ср2. (5.2.14)
Таблица 5.5. Информационная матрица системы уравнений математического опи-
Шаг 1 решения системы уравнений (5.2.13) — задание начального приближения,
в данном случае — произвольное задание температуры первого потока на выходе из
теплообменника Г, и определение теплоёмкости первого потока Cpi по уравнению 5.
После этого на втором этапе вычислений (шаг 2) определяется значение локальной
интенсивности теплопередачи &qT по уравнению 1. Шаг 3 — задание начального
приближения по температуре второго потока на выходе из теплообменника Т2 и
определение теплоёмкости второго потока Ср2 по уравнению 6. Шаг 4 — определе-
ние во внутреннем итерационном цикле точного значения температуры второго пото-
ка на выходе из теплообменника Т2 по уравнению 2 (коррекция значения Т2):
А =^С^-г2Ср2{Г2}Г2 + ГгД/{Г2}=0^ А, (5.2.15)
где f2 - функция уравнения (5.2.15), решаемого относительно Т2.
Следующий шаг (шаг 5) — определение значения константы теплопередачи № по
уравнению 4. Последний, 6 шаг решения — определение во внешнем итерационном
5.2. Математические модели поверхностных теплообменников
289
цикле точного значения температуры первого потока на выходе из теплообменника
7]* по уравнению 3 — коррекция значения 7\:
/3 - V{t;}-^{7'1} (7'2{7;}-7;) = 0) (5.2.16)
где /3 — функция уравнения (5.2.16), решаемого относительно 7].
Блок-схема алгоритма расчёта в соответствие с информационной матрицей (см.
табл. 5.5) изображена на рис. 5.10.
Рис. 5.10. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима
процесса теплопередачи в теплообменнике типа «смешение—смешение» с переменным
значением коэффициента теплопередачи
5.2.2. Математическая модель стационарного
режима процесса теплопередачи в теплообменнике
типа «смешение-вытеснение»
Рис. 5.11. Схематическое изображение
теплообменника
типа «смешение—вытеснение»
Расположение змеевиков в резервуаре
змеевикового теплообменника может быть
различным, например таким, как это показа-
но на рис. 5.8, в, схематически же змеевико-
вый теплообменник можно изобразить как по-
казано на рис. 5.11.
Эта схема включает в себя два потока теп-
лоносителей — поток в резервуаре с началь-
ной температурой (на входе в аппарат) 7'/°\
конечной температурой (на выходе) Т\, рас-
ходом Vj, теплоёмкостью Ср1 и поток в змее-
вике с начальной температурой (на входе в аппарат) , конечной температурой (на
выходе) T2(L), расходом v2, теплоёмкостью Ср2. Длина змеевика обозначена L.
Для построения математического описания данной модели примем следующие
допущения:
• поток, проходящий через резервуар, описывается гидродинамической моделью
идеального смешения;
• поток в змеевике описывается гидродинамической моделью идеального вытес-
нения;
• рассматривается стационарный режим работы теплообменника;
19-4544
290
Глава 5. Физико-химические модели. Построение моделей
• коэффициент теплопередачи считается постоянным;
• никаких процессов кроме теплопередачи не происходит;
• теплоёмкости теплоносителей одинаковы и не меняются с изменением температуры.
Уравнение теплового баланса для потока теплоносителя в резервуаре для рассмат-
риваемой гидродинамической модели идеального перемешивания записывается следу-
ющим образом (см. табл. 2.1):
1 - ^Ср2Т\ + FTbqTx = 0. (5.2.17)
Выражение для локальной интенсивности теплопередачи для потока теплоноси-
теля в резервуаре:
2 (5.2.18)
Уравнение теплового баланса для потока в змеевике (гидродинамический режим
идеального вытеснения):
dT, FT
3 V2Cp2l£=~L^2' (5’219)
Выражение для локальной интенсивности теплопередачи для потока теплоноси-
теля в змеевике:
4 =KT(Tt-T2). (5.2.20)
С учётом равенства (5.2.5) выведем уравнение общего теплового баланса:
Г(°)С(0)Г1(0) _ V) CpiT + [Fr]ср = 0 (5.2.21)
В уравнении (5.2.21) произведение [FrAgr]cp представляет собой усреднённую по
длине змеевика скорость теплопередачи.
Уравнение теплового баланса для потока в змеевике (5.2.19) записывается через
\qT с учётом (5.2.5) следующим образом (см. табл. 2.1 и 2.2):
Рис. 5.12. Зависимость функции
[FrAgr] от длины змеевика
_ dT2 FT / r\
V2 "2~М=~Ь^^ ’ (5-2’22)
Для того чтобы определить усреднённую ско-
рость теплопередачи в рассматриваемой модели
теплообменника, необходимо найти площадь
криволинейной трапеции под линией [FrAgr]
на рис. 5.12, т.е. проинтегрировать функцию
[FrAgr] по длине змеевика и разделить на дли-
ну змеевика, в результате чего получается усред-
ненное значение скорости теплопередачи
[^Л/]сР:
[FrAgr]cp=ljFrV^- (5-2-23)
L о
При интегрировании (5.2.23) с учетом (5.2.22) будет справедливо:
[Fr^r]cp =-v2Cp2lj^-de = -v2Cp2[T2(L)-T2(0')\ (5.2.24)
Подставляя выражение для функции [FrAgr]cp (5.2.24) в (5.2.21), получаем урав-
нение общего теплового баланса для змеевикового теплообменника:
5.2. Математические модели поверхностных теплообменников
291
" v2Cp2 [Т2 (L)- Т2 (0)]+ - v, CpJ\ = 0. (5.2.25)
Система уравнений МО рассматриваемой модели теплообменника таким обра-
зом будет состоять из следующих уравнений:
" уравнения общего теплового баланса (5.2.25)
1 + =0;
обыкновенного дифференциального уравнения в явном виде для
потока теплоносителя в змеевике
FT ( т\
2 ’• (5Л26)
выражения для локальной скорости теплопередачи
з V = /Г(г2-7;).
Кроме этого, для решения дифференциального уравнения 2 (вычис-
ления частного решения на компьютере), к данной системе уравнений
МО необходимо добавить начальное условие:
2' 7’2(0) = 7’2(0).
В качестве определяемых переменных для решения системы уравнений (5.2.26)
выбираются: функция зависимости температуры теплоносителя в змеевике от длины
змеевика (рис. 5.13), температура теплоносителя в резервуаре, локальная скорость
теплопередачи и начальная температура теплоносителя в змеевике:
т2=тМ т;, д/, т2(о).
(5.2.27)
В данном случае дополнительное условие 2' задаётся при одном значении неза-
висимой переменной, т.е. решается задача Коши. Решение Т2 = T2(f) дифференци-
ального уравнения 2 схематически показано на рис. 5.13.
Уравнение 2 для решения на компьютере представляется в конечно-разностной
форме. Согласно нумерации системы (5.2.26) это будет уравнение 2*:
где f2 — правая часть дифференциального
уравнения (5.2.22) и конечно-разностного урав-
нения (5.2.28), расчет которой необходим для
определения дискретных значений функции
Т2 = TjW - см. рис. 5.13.
В информационной матрице системы урав-
нений МО стационарного режима процесса
теплопередачи в теплообменнике типа «сме-
шение-вытеснение» (табл. 5.6) уравнение 1
(корректирующее уравнение) — это внешний
цикл решения задачи; уравнение 2* (цикл ре-
шения дифференциального уравнения) — это
внутренний цикл решения задачи.
Рис. 5.13. Зависимость температуры
теплоносителя в змеевике от длины
змеевика
292
Глава 5. Физико-химические модели. Построение моделей
Таблица 5.6. Информационная
матрица системы уравнений ма-
тематического описания стацио-
нарного режима процесса тепло-
передачи в теплообменнике типа
«смешение—вытеснение»
Корректирующее уравнение 1 представляется
в следующем виде:
Л -V, CplTt -v2Cp2[Т2(Lfo}-Т2(0)] = 0,
(5.2.29)
где - функция уравнения (5.2.29), решаемого
относительно 7].
В соответствии с выбранным алгоритмом ре-
шения задачи (рис. 5.14) во внешнем цикле реше-
ния может быть применен, например, метод
половинного деления для решения одного урав-
нения (5.2.29). Во внутреннем цикле решается диф-
ференциальное уравнение (5.2.22) или, соответ-
ственно, (5.2.28) (например, методом Эйлера) при
каждом очередном приближении Tv
Рис. 5.14. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима
процесса теплопередачи в теплообменнике типа «смешение—вытеснение»
5.2.3. Математическая модель стационарного
режима процесса теплопередачи в прямоточном
теплообменнике типа «труба в трубе»
(решение задачи Коши)
Представленная на рис. 5.15 схема прямоточного теплообменника типа «труба в
трубе» включает в себя два потока теплоносителей — например, охлаждаемый поток
Рис. 5.15. Схематическое изображение
прямоточного теплообменника типа
«труба в трубе»
с начальной температурой (на входе в аппа-
рат) 7'1(0), конечной температурой (на выходе)
Т2 (L), расходом vt, теплоёмкостью Ср1 и на-
греваемый поток с начальной температурой
(на входе в аппарат) Т2(о), конечной темпера-
турой (на выходе) Т2(Ь), расходом v2, тепло-
ёмкостью Ср2. Поверхность теплообмена име-
ет площадь Fr. Коэффициент теплопередачи
обозначен Кт.
5.2. Математические модели поверхностных теплообменников
293
Для построения системы уравнений математического описания процесса тепло-
передачи в прямоточном теплообменнике типа «труба в трубе» принимаются следу-
ющие допущения:
рассматривается стационарный режим процесса теплопередачи;
• кроме процесса теплопередачи никаких других процессов не происходит;
коэффициент теплопередачи постоянен и известен (решение прямой задачи);
теплоёмкость потоков теплоносителей постоянна;
• поверхность теплообмена равномерно распределена вдоль участка длины теп-
лообменника;
движение первого и второго потоков теплоносителей описывается гидродина-
мической моделью идеального вытеснения.
Уравнение теплового баланса для принятой гидродинамической модели идеаль-
ного вытеснения и выражение для локальной интенсивности теплопередачи для пер-
вого потока теплоносителя записываются следующим образом (см. табл. 2.1 и 2.2):
ЛТ тТ
1 VlCpl~M=~L^’ (5-2’30)
2 Д91г=/Г(т2-7;). (5.2.31)
Уравнение теплового баланса и выражение локальной интенсивности теплопере-
дачи для второго потока теплоносителя записываются следующим образом:
з = (5.2.32)
4 Д92г=ЛГг(7’1-7’2). (5.2.33)
С учётом равенства (5.2.5) система уравнений МО модели прямоточного теплооб-
менника типа «труба в трубе» записывается как СОДУ в конечно-разностном пред-
ставлении (5.4) с начальными условиями, заданными при значении пространственной
координаты t -
1
или
1*
0:
dT] _ F
dt ~
Aq
Wpl
Л(^)-Л(о)_ F
2
или
2*
3
1'
2х
dT2 _ F
dt Lv2Cp2
(5.2.34)
t2(l)-t2(o)_ ft
At Lv2Cp2
AqT =Кт(Тг-Т\У,
Т$)=Т^
т (п\=т^
t = 0.
Поскольку начальные условия задаются при одном и том же значении независи-
мой переменной t, в данном случае решается задача Коши.
294
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.16. Изменение температур
теплоносителей по длине теплооб-
менника типа «труба в трубе»
(прямоток)
Таблица 5.7. Информационная матрица систе-
мы уравнений математического описания стацио-
нарного режима процесса теплопередачи в прямо-
точном теплообменнике типа «труба в трубе»
Эту систему можно решить аналитически точно. Задание начальных условий и
изменение температур теплоносителей по длине теплообменника для данного случая
показано на рис. 5.16.
Информационная матрица системы уравнений МО стационарного режима про-
цесса теплопередачи в прямоточном теплообменнике типа «труба в трубе» приведена
в табл. 5.7, а блок-схема алгоритма поверочно-оценочного расчёта по этой информа-
ционной матрице — на рис. 5.17.
Г1Ю
Рис. 5.17. Блок-схема алгоритма поверочно-оценочного расчета стационарного режима
процесса теплопередачи в прямоточном теплообменнике типа «труба в трубе»
5.2.4. Математическая модель стационарного
режима процесса теплопередачи в противоточном
теплообменнике типа «труба в трубе»
(решение краевой задачи)
Представленная на рис. 5.18 схема противоточного теплообменника типа «труба в
трубе» включает в себя два потока теплоносителей — например, охлаждаемый поток
5.2. Математические модели поверхностных теплообменников
295
с начальной температурой (на входе в аппа-
рат) конечной температурой (на выхо-
де) 7\ (L), расходом v,, теплоёмкостью Ср1 и
нагреваемый поток с начальной температу-
рой (на выходе из аппарата) Т2^, конечной
температурой (на входе) Т2(0), расходом v2,
теплоёмкостью Ср2. Поверхность теплопере-
дачи имеет площадь FT. Коэффициент теп-
лопередачи обозначен К7.
Основные допущения для построения этой
модели нужно принять такими же, как в слу-
Рис. 5.18. Схематическое изображение
противоточного теплообменника типа
«труба в трубе»
чае прямоточного теплообменника «труба в трубе».
Уравнение теплового баланса для принятой гидродинамической модели идеаль-
ного вытеснения и выражение для локальной скорости теплопередачи для первого
потока теплоносителя записываются относительно координаты I следующим обра-
зом (см. табл. 2.1 и 2.2):
1
2
— =----------Д?Г-
М LVlCpl ’
= лгг(т’2-т;).
(5.2.35)
(5.2.36)
Уравнение теплового баланса и выражение локальной скорости теплопередачи
для второго потока теплоносителя записываются относительно координаты р следу-
ющим образом:
3
dTl рТ Л г
М Lv2Cp2
(5.2.37)
4
(5.2.38)
При этом l'= L-1, откуда следует, что М'= -М.
С учётом равенства (5.2.5) и того, что М'= -М, система уравнений МО теплообмен-
ника типа «труба в трубе» записывается как СОДУ в конечно-разностном представле-
нии (5.4) с краевыми условиями, заданными при разных значениях пространственной
координаты I = 0 и I = L (система приведена к единой системе координат £):
1
t/т; ft •
---- = --------Д<7'
Л £v,Cpl
или
Л(^)-Л(о)_ FT т
Ы LViCpl
или
(5.2.39)
2*
T2(l)-T2(0)_ FT т
Ы Lv2Cp2
296
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.19. Изменение температур
теплоносителей по длине теплооб-
менника «труба в трубе» (противоток)
3 А/ = КТ(Г2-Т1);
Г 7’1(О)=7’1(о);
2' Т2 (L)= Т2(о).
Дополнительные условия Г и 2', заданные
при разных значениях пространственной коор-
динаты I называются «краевыми условиями».
Задача получения частного решения системы
обыкновенных дифференциальных уравнений в
таких условиях называется краевой задачей.
Задание краевых условий Г и 2' (•) и на-
чального условия Т2(о) в этом случае и измене-
ние температуры теплоносителей по длине теп-
лообменника представлены на рис. 5.19.
Алгоритм решения системы уравнений МО (5.2.39) в рассматриваемом случае таков.
Шаг 1 — задаются все дополнительные условия при одном значении независимой
переменной, например, I = 0, в том числе и отсутствующие в исходной постановке
задачи. Последние задаются как начальное приближение Т2(о).
Шаг 2 — решение системы обыкновенных дифференциальных уравнений Т\(£) и
Т2(Г) во внутреннем цикле решения задачи. Однако полученное решение будет невер-
ным, т.к. одно из дополнительных условий — Т2(о) — было задано как приближение.
Шаг 3 — проверяется выполнение краевого условия 2', т.е. превращение его в
Таблица 5.8. Информационная
матрица системы уравнений матема-
тического описания стационарного
режима процесса теплопередачи в
противоточном теплообменнике типа
«труба в трубе»
равенство
^2 (^)^2 (0)}= 7^(0)
Если это равенство не выполняется, реализу-
ется шаг 4.
Шаг 4 — краевое условие 2' рассматрива-
ется как корректирующее уравнение для вы-
бора нового приближения Т2(о), т.е. по суще-
ству реализуется процедура решения уравне-
ния:
f^T2{L^2{G)}-T2^=G, (5.2.40)
где /2. - функция уравнения (5.2.40), решае-
мого относительно Т2(о)
Так определяется решение во внешнем
цикле решения задачи:
тДо)’. (5.2.41)
5.3. Математические модели химических реакторов
297
Т2(0)
Рис. 5.20. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима
теплопередачи в противоточном теплообменнике типа «труба в трубе»
Шаг 5 — как только будет получено решение последнего уравнения (5.2.41) во
внешнем цикле решения задачи, задача будет решена, и результаты решения уравне-
ний 1 и 2 во внутреннем цикле решения задачи будут корректными.
Информационная матрица системы уравнений МО процесса теплопередачи в про-
тивоточном теплообменнике типа «труба в трубе» (5.2.39) приведена в табл. 5.8, а
блок-схема соответствующего алгоритма расчёта стационарного режима — на рис. 5.20.
5.3. Математические модели химических
превращений в реакторах
Химические реакторы являются одними из самых важных и распространённых
аппаратов химической технологии. Именно в них в результате химических превра-
щений из исходного сырья получают необходимые продукты. Многообразию хими-
ческих реакций, описываемых микрокинетическими закономерностями, соответствует
большое число различных типов реакторов, для математического описания которых
используются макрокинетические закономерности.
Наиболее распространены следующие признаки классификации химических ре-
акторов и режимов их работы:
• режим движения реакционной среды (гидродинамическая обстановка в реакторе);
• условия теплообмена между реактором и окружающей средой;
• метод организации теплообмена;
• фазовый состав реакционной смеси;
• метод организации процесса;
• характер изменения параметров процесса во времени;
• конструкционные характеристики.
По режиму движения реакционной среды реакторы разделяются на реакторы вы-
теснения (трубчатые реакторы) и реакторы смешения (ёмкости с устройствами для
перемешивания).
Идеальные смешение и вытеснение недостижимы в реальных реакторах, поэтому
при применении математических моделей идеального смешения и идеального вы-
теснения для описания процессов в реальных реакторах необходимо вносить по-
правки на неидеальность.
298
Глава 5. Физико-химические модели. Построение моделей
В зависимости от условий теплообмена между реактором и окружающей средой
можно выделить изотермические реакторы (температура в реакторе постоянна, не-
смотря на тепловые эффекты проходящих в нём процессов), адиабатические реакто-
ры (теплообмен с окружающей средой отсутствует) и реакторы с промежуточным
тепловым режимом при наличии теплообмена с окружающей средой, в том числе
реакторы, снабжённые рубашками.
По методу организации теплообмена реакторы подразделяют на реакторы с вне-
шним теплообменом, внутренним теплообменом, комбинированным теплообменом и ав-
тотермические реакторы (необходимая температура процесса поддерживается без
использования внешних источников энергии). Автотермические реакторы являются
наиболее предпочтительными с точки зрения энергосбережения.
В зависимости от фазового состава реакционной смеси реакторы подразделяют на
аппараты для реакций в газовой фазе и жидкой фазе (гомогенные процессы). Аппа-
раты для гетерогенных процессов подразделяют на газожидкостные реакторы, реак-
торы для систем газ—твердое вещество, жидкость—твердое вещество и др., а также
реакторы для гетерогенно-каталитических процессов.
Существуют следующие методы организации химического процесса в реакторе:
• периодический;
• непрерывный;
• полупериодический.
Применение периодического метода организации процесса подразумевает подачу
реагентов в реактор перед началом реакции и отведение продуктов реакции после её
завершения. В этом случае время пребывания реагентов в реакторе и время реакции
совпадают.
Непрерывный метод организации процесса в реакторе характеризуется одновре-
менным и параллельным осуществлением стадий подачи реагентов, химических ре-
акций, отвода продуктов. Поскольку время пребывания частиц реакционного потока
в непрерывно действующем реакторе не совпадает со временем полного химическо-
го превращения и является, в общем случае, случайной величиной, то средняя глу-
бина химического превращения является функцией распределения времени пребы-
вания частиц реакционного потока в реакторе. В то же время непрерывно действую-
щие реакторы являются самыми высокопроизводительными, поскольку не требуют
затрат времени на загрузку реагентов и выгрузку продуктов, этим обусловлено их
широкое применение в крупнотоннажных современных химических производствах.
Полупериодический метод организации процесса в реакторе подразумевает поступ-
ление одних реагентов непрерывно, а других — периодически, либо периодическое
поступление реагентов и непрерывный отвод продуктов реакции, либо непрерывную
подачу реагентов и периодический отбор продукта.
В зависимости от характера изменения параметров процесса во времени реакторы
могут работать в стационарном и нестационарном режимах.
Режим работы реактора называют стационарным, если протекание химической
реакции в произвольно выбранной точке характеризуется одинаковыми значениями
концентраций реагентов или продуктов, температуры, скорости и других параметров
процесса в любой момент времени. Стационарный режим возможен в непрерывно
действующих проточных реакторах.
Режим работы реактора называют нестационарным, если в произвольно выбран-
ной точке происходят изменения параметров химического процесса во времени по
тому или иному закону. Нестационарными являются все периодические процессы.
Стационарные проточные реакторы проще для моделирования, поскольку они
описываются более простыми уравнениями, протекающие в них процессы легче ав-
томатизировать.
Нестационарность процесса в реакторе усложняет описание реактора и управление
его работой, однако во многих случаях нестационарные режимы технологических про-
цессов, протекающих в химических реакторах, легче приблизить к оптимальным.
5.3. Математические модели химических реакторов
299
Химические реакторы различаются по конструктивным характеристикам, оказы-
вающим влияние на расчет и конструирование аппаратов:
• емкостные реакторы (автоклавы; реакторы-камеры; вертикальные и горизон-
тальные цилиндрические конверторы и т. п.);
• колонные реакторы (реакторы-колонны насадочного и тарельчатого типа; ката-
литические реакторы с неподвижным, движущимся и псевдоожиженным слоем
катализатора; полочные реакторы);
• реакторы-теплообменники;
• реакционные печи (шахтные, полочные, камерные, вращающиеся печи) и т. д.
Реакторы с мешалкой представляют собой резервуары, снабжённые перемешиваю-
щими устройствами (мешалками или насосами). Как правило, перемешивание осуще-
ствляется настолько интенсивно, что обеспечивает равномерность состава и температу-
ры в объёме реактора. В тех случаях, когда процесс сопровождается значительным теп-
ловым эффектом, реакторы снабжают теплообменными устройствами: рубашкой, окру-
жающей стенки аппарата, внутренними или внешними змеевиками. Это позволяет под-
держивать определённую, наиболее благоприятную температуру реакционной смеси.
При непрерывном процессе обычно целесообразно применение многоступенча-
тых реакторов с мешалкой. Такой реактор можно выполнить в одном корпусе, разде-
лённом на секции, или в виде ряда отдельных аппаратов.
При принятии допущения об идеальном перемешивании реакционной смеси реактор с
мешалкой рассматривается как объект с сосредоточенными параметрами, и задача
математического моделирования заключается в определении параметров выходного
потока в стационарном и нестационарном режимах (так называемый поверочно-оценоч-
ный расчёт). Проектный расчёт реактора в книге не представлен, так как, с одной
стороны, он требует выбора стандартных типоразмеров аппаратов из соответствующих
баз данных по конструкциям реакторов с мешалкой, а с другой, его реализация пред-
полагает многократное повторение варианта поверочно-оценочного расчёта с учётом
выбранных стандартных конструкционных параметров реакторов с мешалкой.
Трубчатые гомогенные реакторы представляют собой полую трубу или систему из
таких труб, через которые непрерывно проходит реакционная смесь. Такие реакторы
можно выполнить в адиабатическом варианте, т.е. без теплоотвода (теплоподвода),
или с их применением (политропический режим), если требуется определённое рас-
пределение температуры в реакционной зоне. В последнем случае труба с реагирую-
щей смесью нагревается или охлаждается каким-либо теплоносителем.
Гомогенные реакторы с теплообменом выполняются как змеевиковые теплооб-
менники или в виде трубчатых теплообменников, т.е. труб, в которых протекают
химические реакции и которые снабжены рубашкой с теплоносителем. В некоторых
случаях их конструктивно оформляют в виде кожухотрубных теплообменников, где
реакционная смесь проходит по параллельным трубам, а теплоноситель — по меж-
трубному пространству. При этом для математического описания движущегося реак-
ционного потока используется либо модель идеального вытеснения, либо однопара-
метрическая диффузионная модель (см. табл. 2.1).
Реактор идеального вытеснения представляет собой длинный канал, через кото-
рый реакционная смесь движется в поршневом режиме. Каждый элемент потока,
условно выделенный двумя плоскостями, перпендикулярными оси канала, движется
через него как твёрдый поршень, вытесняя предыдущие элементы потока и не пере-
мешиваясь ни с предыдущими, ни со следующими за ним элементами.
Идеальное вытеснение возможно при выполнении следующих допущений:
• движущийся поток имеет плоский профиль линейных скоростей;
• отсутствует обусловленное любыми причинами перемешивание в направлении
оси потока;
• в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры
процесса (концентрации, температуры и т.д.) полностью выровнены.
Следует отметить, что строго эти допущения в реальных реакторах не выполняются.
300
Глава 5. Физико-химические модели. Построение моделей
Поэтому более предпочтительным является использование однопараметрической
диффузионной модели для описания движения потока реакционной смеси в трубча-
тых реакторах. В отличие от модели идеального вытеснения, в этой модели учитыва-
ется наличие перемешивания реакционной среды в осевом направлении, вызванно-
го продольной диффузией.
В настоящей главе представлены варианты поверочно-оценочного расчёта стаци-
онарных и нестационарных режимов гомогенных трубчатых реакторов.
Так как трубчатые реакторы относятся к объектам с распределёнными (вдоль
пространственной координаты) параметрами, то для стационарного режима рассмат-
риваются два варианта теплообмена:
• с прямоточным движением теплоносителя (задача решения системы обыкно-
венных дифференциальных уравнений (СОДУ) с начальными условиями или
задача Коши);
• с противоточным движением теплоносителя (задача решения СОДУ с краевы-
ми условиями или краевая задача).
При этом движущиеся потоки реакционной смеси и теплоносителя описываются
моделью идеального вытеснения.
Описание нестационарного режима трубчатого реактора представлено однопара-
метрической диффузионной моделью для изотермического режима с простейшей
кинетической схемой реакции (задача решения дифференциального уравнения в
частных производных с начальными и граничными условиями).
Для моделирования процессов в химических реакторах применяются два вида
уравнений математического описания — макрокинетические и микрокинетические.
Макрокинетические уравнения (см. табл. 2.1) — это уравнения балансов, записан-
ные с учётом гидродинамической модели движения потоков (уравнения покомпо-
нентного баланса, общего баланса массы, энергетический (тепловой) баланс), кото-
рые включают в виде слагаемых выражения для интенсивности источников (скорос-
тей) различных «элементарных» процессов, как например, химических превращений,
массо- и теплопередачи, фазовых переходов и т.д.
Микрокинетические уравнения (см. табл. 2.2) записываются для элементарного
объёма, вне зависимости от того, в каком потоке протекает процесс (например, урав-
нения скорости протекания химических реакций для каждого компонента, уравне-
ния скорости выделения и поглощения теплот за счёт химической реакции). Эти
уравнения скоростей называются интенсивностями источников компонентов в эле-
ментарном объёме или локальными интенсивностями источников теплот и включа-
ются в уравнения покомпонентных балансов, уравнение общего баланса массы, а
также в уравнения теплового баланса.
В настоящем разделе освещены вопросы построения математических моделей
стационарных и нестационарных режимов непрерывных гомогенных реакторов с
мешалкой и трубчатых реакторов. Предполагаются кинетические модели, в общем
случае, произвольных одновременно протекающих необратимых реакций, скорости
которых определяются константами, рассчитываемыми по закону Аррениуса. Коли-
чество компонентов реакционной смеси и число стадий реакций не ограничено.
5.3.1. Микрокинетика сложной химической реакции
Для построения математических моделей процессов в гомогенных химических ре-
акторах, в общем случае, с участием п компонентов в т стадийной химической
реакции на микрокинетическом уровне необходимо решить две задачи (см. разд. 2.1.1):
1) определить локальную (отнесённую к единице объёма) скорость химической
реакции по каждому компоненту — вектор скоростей химической реакции по каждо-
му компоненту gR:
5.3. Математические модели химических реакторов
301
g* О'=
где п — число компонентов в сложной химической реакции;
2) определить локальную (отнесённую к единице объёма) скорость выделения
или поглощения теплот в химической реакции:
\qR.
Для решения первой задачи моделирования процесса на микрокинетическом уровне
скорость химической реакции по произвольному Z-му компоненту определяется
следующим образом (см. табл. 2.2):
(1 = 1,..., п), (5.3.1а)
7=1
где г — скорость у-й элементарной стадии химической реакции, определяемая по
закону действующих масс; аа — стехиометрический коэффициент Z-го компонента
на у-й стадии, причём если / является продуктом на у-й стадии, то а/у > 0, если i
является реагентом на у-й стадии, то а1у < 0, если компонент i отсутствует на у-й
стадии, то = 0; ти — число элементарных стадий сложной химической реакции.
Если скорость реакции по компоненту положительна (gR > 0) — компонент i в
реакции образуется; если скорость реакции по компоненту отрицательна (gR < 0) —
компонент i в реакции расходуется.
В матричном виде выражение для скорости химической реакции по компоненту
(5.3.1а) записывается следующим образом:
Г=а-г (5-3.16)
или
где а — матрица стехиометрических коэффициентов; г — вектор скоростей элемен-
тарных стадий химических реакций (компоненты вектора г всегда положительны).
Рассмотрим следующую схему химических превращений (химическую реакцию):
1А+В < / > 2С —> D.
В этом случае число компонентов п = 4, число стадий т = 3.
Скорость у-й элементарной стадии химической реакции в жидкой фазе г, опре-
деляется по закону действующих масс:
п
(у = 1,...,/п), (5.3.2)
«=1
где , если компонент i — реагент нау-й стадии; х,; =0, если компонент i —
продукт на у-й стадии или отсутствует на у-й стадии.
Для рассматриваемого уравнения реакции выражения для скоростей стадий (5.3.2)
записываются следующим образом:
П = к1хАхвхсх°о = k1xAxB;
г _ л г° г° г2 v° — V -г2 •
'2 — Л1ЛАЛВЛСЛО ~Л2ЛС’ (5.3.3)
, 0 0 2 0 >2
r3 — k3xAxBxcxD — k3xc.
302
Глава 5. Физико-химические модели. Построение моделей
Тогда, если выражение для скоростей реакций по компонентам представить в
матричном виде, оно выглядит следующим образом (5.3.1в):
Sa
gRB
gc
,gRD
-2 2 0 ' 2
-1 1 0
2 -2 -2
0 0 1 к2хс
(5.3.4a)
откуда по правилу матричного перемножения (см. разд. 3.2.1) можно записать выра-
жения для скоростей реакции по всем компонентам:
(5.3.46)
g& ='~2к1хЛхв + 2к2хс-,
gB = —кххАхв + к2хс\
gc = '2к1хАхв -2к2хс — 2к2хс,
gD — куХс.
Для решения второй задачи моделирования процесса на микрокинетическом уровне
локальную (отнесённую к единице объёма) скорость выделения или поглощения
тепла в химической реакции можно выразить следующим уравнением (см. табл. 2.2):
(5-3.5)
где (-1ГН*) — тепловой эффект у-й стадии, отнесённый к одному молю продукта р.
Для рассматриваемого уравнения реакции, с учётом приведённых выше выкладок
для скоростей стадий реакции (5.3.3), выражение (5.3.5) записывается следующим
образом:
V = 2(-ДЯД) + 1(-ДЯА) Vc + 1(-ДЯ*3)^. (5.3.6)
При этом константы скоростей стадий реакции в соответствии с законом Арре-
ниуса выражаются следующим уравнением:
£у=Ауехр(-Еу/Ят); у = 1,...,3, (5.3.7)
где Ау — предэкспоненциальный множитель для у-й стадии реакции; Еу — энергия
активации на у-й элементарной стадии реакции.
Выбор ключевых компонентов химической реакции
Среди компонентов химической реакции любой сложности можно выделить клю-
чевые и не ключевые.
Ключевые компоненты — это компоненты, задание которых однозначно характе-
ризует состояние процесса, сопровождаемого химической реакцией, в любой мо-
мент времени. Уравнения математического описания с учётом гидродинамических
условий и микрокинетических закономерностей записываются только для ключевых
компонентов, в то время как расчёт остальных (не ключевых) компонентов произво-
дится по стехиометрическим соотношениям.
Процедура выбора ключевых компонентов сложной химической реакции связана
с понятием ранга матрицы стехиометрических коэффициентов а (5.3.1), который
характеризует максимальное число линейно независимых строк или столбцов этой —
в общем случае прямоугольной — матрицы.
Число ключевых компонентов химической реакции равно рангу матрицы стехи-
ометрических коэффициентов (5.3.1).
5.3. Математические модели химических реакторов
303
Рангом матрицы называется максимальный порядок её минора, отличного от нуля
(см. разд. 3.2.1). Для прямоугольной матрицы стехиометрических коэффициентов
размера п х т определитель квадратной подматрицы 5-го порядка называется мино-
ром 5-го порядка матрицы стехиометрических коэффициентов (5.3.1). Если матрица
стехиометрических коэффициентов а имеет минор порядка 5, который отличен от
нуля, а любой другой минор порядка (5 + 1) и выше равен нулю, то ранг матрицы
равен 5. Очевидно, что ранг матрицы может быть определён как для квадратной, так
и для прямоугольной матриц.
Для построения математической модели нужно определить скорость реакции по
каждому компоненту. Если удаётся выразить скорости образования одних компо-
нентов через скорости образования других — ключевых компонентов — сокращается
количество сложных, в общем случае, нелинейных кинетических уравнений, необходимых
для описания всего процесса. В результате по концентрациям ключевых компонентов
через стехиометрические соотношения можно рассчитать состав всей реагирующей
смеси в любой момент времени.
Матрица стехиометрических коэффициентов а для рассматриваемого уравнения с
компонентами А, В, Си D {п — 4) и тремя элементарными стадиями (т = 3) имеет вид:
2 О'
° L
Задача выбора числа ключевых компонентов реакции сводится к нахождению
ранга матрицы стехиометрических коэффициентов (5.3.8). Ранг матрицы и число
ключевых компонентов определяют методами матричного исчисления (см. разд. 3.2.1).
Определим ранг матрицы стехиометрических коэффициентов (5.3.8):
и равны 0. Для матриц 2x2 есть миноры не равные 0. Поэтому наивысший (макси-
мальный) порядок минора матрицы (5.3.8) равен 2. Значит, ранг матрицы стехио-
метрических коэффициентов а равен 2, и число ключевых компонентов трёхста-
дийной реакции с четырьмя компонентами А, В, Си D равно 2.
Для выбора ключевых компонентов конкретной химической реакции с матрицей
коэффициентов (5.3.8) запишем выражения для скоростей химической реакции по
компонентам, исходя из микрокинетических соотношений (5.3.46):
gR=\gR‘, (5.3.9)
Sc=-gR-lgRD, (5.3.10)
откуда
J?p=-|G?a+J?c). (5.3.11)
В результате для рассматриваемой реакции в качестве ключевых (как показано
выше, их число равно 2) выбираем компоненты АиС. Скорости химической реак-
ции по компонентам Ви Dвыражаются через скорости реакции по компонентам А и
С через стехиометрические соотношения следующим образом:
304
Глава 5. Физико-химические модели. Построение моделей
• для компонента В
dx 1 dxA
8в ~~dt~~2~dT
или в конечно-разностной форме (см. разд. 3.3.1)
^в-40) = |(хл-4));
• для компонента D
к _ ^Хл + ^Хс
8d dt ~ dt dt
или в конечно-разностной форме
(5.3.12)
(5.3.13)
5.3.14)
XD-*D} =“|[(ХЛ -40))+(хс -40))]- (5.3.15)
Таким образом, окончательный вид системы уравнений для описания скоростей
химической реакции по компонентам включает два микрокинетических уравнения (вместо
первоначальных четырёх) для двух ключевых компонентов Аи С (1 и 3) и два стехиомет-
рических соотношения для определения концентраций компонентов Ви D (2 и 4):
1 = -2к,х2лх„ + 2к2х1;
М /1 1/10 X С, '
(5.3.16)
gc = 2ktxAxB - 2к2хс - 2к}хс;
5.3.2. Математическая модель стационарного
режима политропического процесса в реакторе
с мешалкой и рубашкой (произвольная кинетическая
схема химической реакции)
Для построения математической модели химического превращения в реакторе с ме-
шалкой (рис. 5.21) в стационарном состоянии принимаются следующие допущения:
• движение потоков реакционной смеси в реакторе (основной поток) и теплоно-
сителя в рубашке (вспомогательный поток) представляется гидродинамическими
моделями идеального перемешивания;
• параметры потока теплоносителя в рубашке (обозначаются нижним индексом
Рис. 5.21. Схематическое
изображение реактора с
мешалкой и рубашкой
«у») неизменны, кроме температуры потока теплоноси-
теля в рубашке.
• реакции в реакторе гомогенны, без фазовых пере-
ходов;
• все процессы происходят в жидкой фазе, все реак-
ции протекают одновременно;
• тепловые эффекты стадий химической реакции не
зависят от температуры;
• при теплообмене между основным и вспомогатель-
ным потоками учитывается только теплопередача;
• коэффициент и поверхность теплопередачи между
основным и теплоносителя вспомогательным потоками
являются постоянными и не изменяются.
5.3. Математические модели химических реакторов
305
Уравнения материального и теплового балансов (5.3.17) для потока реакционной
смеси в реакторе (основного потока) (1, 2, 3) и для потока теплоносителя в рубашке
реактора (вспомогательного или теплового потока) (4) записываются следующим
образом (см. табл. 2.1):
1 v(0)x,(0)-vx, + VRgR =0 (i = l,...,n);
2 v^-v + V^g, =0; (5.3.17)
3 yWcft® - vCpT + VRAqR + FT&qT = 0;
4 - vTCpTT + FT(- V)= 0,
где \qr — интенсивность локальной теплопередачи через поверхность F\ AqR —
интенсивность локального источника тепла химической реакции в объёме К; gR —
интенсивность локального источника компонента за счёт химической реакции; ниж-
ний индекс «у» — признак потока теплоносителя.
С учётом изложенного выше (5.3.17) и выражений для локальных интенсивнос-
тей источников массы и тепла система уравнений МО процесса химического пре-
вращения в реакторе с мешалкой и рубашкой в стационарном состоянии записыва-
ется в виде системы нелинейных уравнений:
v(0)x,(0) - та, +VRgR=0 (/ = 1,...,л);
2(л) 0 = 1, -,«);
7=1
3(т) (7 = 1, -,'”),
1=1
|-а <= i - реагент нау-й элементарной стадии,
= п .
[ 0 <= i - не реагент нау-и элементарной стадии;
4(m) =A]exp(rE]/RT) (у = 1,..„т);
5 г(0)-г + УЛ£^,Л = 0; (5.3.18)
6 -vCpT + VRAqR + FTAqT = 0;
7 V=£|aw|(-AW:)ry;
7=1
8 Aq =KT(TT -T);
«=1
i0(„> C'p^ =al+blT + clT2+d,T3 (i = l,...,n);
(ap bt, cp d: — коэффициенты зависимостей теплоёмкостей
индивидуальных веществ С1™' от температуры)
11 v(0)C<0)Tr(0) - vTC ТТ +FT(-AqT\=Q.
i Рт 1 1 Рт 1 \ “ /
306
Глава 5. Физико-химические модели. Построение моделей
Информационная матрица системы уравнений МО (5.3.18) приведена в табл. 5.9.
При выборе приведённой в ней совокупности (Зп + 2т + 6) (первая строка табл. 5.9)
определяемых переменных выполняется поверочно-оценочный расчёт стационарно-
го режима процесса в реакторе (рис. 5.22 на стр. 310).
В соответствии с предлагаемым алгоритмом решения во внутреннем итерацион-
ном цикле расчётов решается система нелинейных уравнений 1 из системы (5.3.18)
относительно х вида:
yi=v(°)x(0)_VXi+V«{jf}.^{j} = 0, i = l,...,n. (5.3.19)
Во внешнем итерационном цикле расчётов решается одно уравнение 11 из системы
(5.3.18) относительно температуры в реакторе Т:
/и = -vtCPtTt{T}+ Ft(- V{n)=0. (5.3.20)
Таблица 5.9. Информационная матрица системы уравнений математического опи-
сания стационарного режима процесса химического превращения в реакторе с ме-
шалкой и рубашкой
\р п \ х(л) *(Л) Г(Л1) т txqT &.qR СР VR f,ind ^Р(п) №>
1(и) Кор УР ф © © 6
2(П) © 4
3(т) 1 + 1 <+> © 3
4(т) 1 + 1 1
5 © 5
6 © © © © 9
7 © 8
8 © © <+> 10
9 © © 7
10(л) © 2
И Кор УР © © 11
5.3. Математические модели химических реакторов
307
5.3.3. Математическая модель нестационарного
режима политропического процесса в реакторе
с мешалкой и рубашкой (произвольная кинетическая
схема химической реакции)
С учётом основных допущений, принятых для стационарной модели реактора с ме-
шалкой и рубашкой (см. рис. 5.21), и с применением всех рассуждений, приведённых
выше для случая стационарного режима модели реактора с мешалкой, система уравнений
МО этого процесса в нестационарном состоянии записывается следующим образом:
dfy^ = v(0)x(0) _ VXi +vRgK (i = ! n).
2(„) g, =Yaurj (i = i,-,n);
7=1
ri = ^fl^’ (> = 1,•••.»»):
1=1
|-au <= i - реагент на j-й элементарной стадии,
%, = „ .
[0 <= I - не реагент на у-й элементарной стадии;
4(и) *,=А,ехр(-Е,/Ят) (у = 1,...,т); (5.3.21)
5 ^i = v0)_v + y«£^.
dt Tt
6 d(y Срт) = (o)c(o)r(o) _ vC т у r^r
dt ” p
7 д«л = Й%|(-дя£к;
7=1
8 bqT = Кт(Тт-Т);
9 cp^c'>.;
1=1
10(„) Cp‘‘ =at +b,T + c,T2 +dlTi (i = l,...,n);
n d^T^rr) = v(0)c ^(0) _ VtC^ Tt + FT (_ )
Для определения условий описания непрерывных, полупериодических, периоди-
ческих, стационарных и нестационарных режимов процессов в реакторе с мешалкой
рассмотрим различия в МО этих процессов на примере системы уравнений поком-
понентных балансов 1<„)ИЗ (5.3.21) (выделив в ней для реакционного потока в реак-
торе члены I, II, III и IV):
= v®x® -vx,+VRgR (i = 1,...,n).
---' п ш TV
308
Глава 5. Физико-химические модели. Построение моделей
Итак,
• процесс будет периодическим, если члены II и III равны 0;
• процесс будет полупериодическим или полунепрерывным, если член либо II, либо
III равен 0;
• процесс будет непрерывным, динамическим {нестационарным), если присутству-
ют все члены уравнения;
• процесс будет непрерывным, статическим {стационарным), если член I равен 0.
Преобразование системы уравнений математического описания нестационарного
режима процесса в реакторе с мешалкой и рубашкой с целью её решения
Для того чтобы решить систему уравнений МО на компьютере, нужно выполнить
преобразования дифференциальных уравнений с учётом допущения о том, что теп-
лоёмкость Ср , а также произведение Сне меняются со временем:
d{vx,) dx, dv
----— = V—- + X —
dt dt dt
d{VRCpT) V^dT^ T dVR
dt Cp dt C p dt
(5.3.22)
d{VRCpTT) dTT
dt T PI dt
С учётом этих преобразований дифференциальные уравнения в (5.3.21) могут
быть записаны:
!(»))
5)
6)
11)
dx, у(0)х,(0) -vx, R х, dVR _
~dt v~R + 8‘ vR'Jir=
f,
(i = l,...,n);
^L=vv_v+V*^g* = f5\
dt 1 5
dT _ A^-vCpT ! ! FTbqT T dVR
dt CpVR Cp CpVK VK dt
dTT _v^C^-vtCpT Ft , .
(5.3.23)
В этом случае величина f5 =---- определяется как правая часть дифференци-
dt
ального уравнения 5 системы (5.3.21). Кроме того, нужно задать начальные условия
для получения частного решения системы (5.3.21) - решение задачи Коши:
5.3. Математические модел и химических реакторов
309
I)' х^}=х^\
5)' V л(?0))= Ул(н);
6)' т(г(0))=Т(н); (5.3.23х)
11)' ТТ^)=Т^.
Таким образом, в системе уравнений МО (5.3.21), описывающей нестационар-
ный режим процесса в реакторе с мешалкой и рубашкой, дифференциальные урав-
нения , 5, 6 и И заменяются на дифференциальные уравнения l^j), 5), 6) и 11)
системы (5.3.23) с начальными условиями 1)', 5)', 6)' и 11)' (5.3.23х).
Для построения информационной матрицы для преобразованной системы диф-
ференциальных уравнений (5.3.21) с учётом (5.3.23) и (5.3.23 х) производные в них
представляют в конечно-разностном виде (см. разд. 3.3.1):
т. xl(t(i))-xl(t(0>)_v(<”^0)-vxl
"" Д? ~ Vх
n
5’] f5=v[0}-v + VRYg?-’
1=1
х, dVR
(i = l,...,n);
(5.3.24)
_ v(0)C<°)T<0) - vC7 ! ! FTbgr T dVR
At CpVR Cp CpVR VR . dt
11’
TT(t^)-TAt{0}) _
& CPTVTR
+/-(-д/),Л1.
^РтТ
В связи с тем, что в правые части дифференциальных уравнений 1<„)) —
f\ (1 = 1,..., л) и 6) - f6 (5.3.23) входит производная dVR/dt, которая равна правой
части дифференциального уравнения 5) — /5 (5.3.23), то в алгоритме расчётов снача-
ла должна вычисляться величина /5 [текущее значение производной dVR/dt ~ 5)] в
(5.3.23), и она включена как дополнительная переменная в информационную матри-
цу системы уравнений МО рассматриваемого процесса (табл. 5.10). Величина /5
вычисляется по формуле 5’] (5.3.24), а дифференциальное уравнение представляет-
ся в виде 5* с правой частью /5 (5.3.24).
Результатом решения системы (п + 4) в общем случае нелинейных дифференци-
альных уравнений первого порядка (5.3.23) с начальными условиями (5.3.23х) будут
следующие функции в заданном интервале z(0) < t <
x,=x,(t) (i = l,...,n); VR=VR(t); T = T(t); TT=TT(t).
Блок-схема алгоритма поверочно-оценочного расчёта нестационарного режима
процесса в реакторе с мешалкой и рубашкой изображена на рис. 5.23.
Рис. 5.22. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима процесса химического превращения
в реакторе с мешалкой и рубашкой
х(0
Ввод
j* (H) j4a)
V® V
j'CO j>(0)
_Crt
а, я, т
Ё,А
(.-лнр.с™
а, Ь, с, d ^(и)
11)
fW пул
j/A(h)
.(н) । _ |
5*
rr(O
Вывод
х(О
gs
к
T{t)
&qT
&qR
Ср
ИО
^fad
LP
rT(t)
Fjm
p*(t)
310 Глава 5. Физико-химические модели. Построение моделей
ЛО
fbitsv
Рис. 5.23. Блок-схема алгоритма поверочно-оценочного расчёта нестационарного режима процесса в реакторе с мешалкой и рубашкой
5.3. Математические модели химических реакторов
311
Таблица 5.10. Информационная матрица системы уравнений математического
описания нестационарного режима процесса химического превращения в реакто-
ре с мешалкой и рубашкой
V п \ 'к' |>Г 1И т & h, «S’ < а; «S’ < § у о ЕЛ" №
5ч © © © © 14
2(") © 8
3(т) © © 7
4(т) А © 5
5* Яиф ур © © 13
5*] © © 12
6* ДН УР © О © © © © 15
7 © 10
8 © © 9
9 © © 11
© 6
11* Ц*Ф УР © © 16
W 1
5)' 2
6)' 3
П)' 4
5.3.4. Устойчивость тепловых режимов
политропических реакторов с мешалкой
При оптимизации и управлении химическими реакторами, в которых протекают
экзотермические реакции, одним из основных вопросов является определение их
тепловой устойчивости.
Понятие устойчивости систем обыкновенных дифференциальных уравнений (см.
разд. 3.5.1) впервые сформулировал А.М. Ляпунов: система называется устойчивой,
если после наложения какого-либо возмущения она возвращается в прежнее состояние
при снятии этого возмущения.
В общем случае политропических реакторов с мешалкой при описании движения
потоков в них моделью идеального перемешивания необходимо исследовать устой-
чивости различных динамических режимов, которые и описываются системами обык-
новенных дифференциальных уравнений.
312
Глава 5. Физико-химические модели. Построение моделей
Оценка тепловой устойчивости динамического режима политропического реактора
с мешалкой и с экзотермической реакцией первого порядка
(5.3.25)
Для простейшей экзотермической химической реакции А—динамический
(-д«)
режим процесса в политропическом реакторе с мешалкой с учётом принятых ранее
допущений и с учётом теплообмена с окружающей средой, ограничиваясь только
теплопередачей, может быть описан системой двух обыкновенных дифференциаль-
ных уравнений вида (5.3.21):
V«^ = v(x(0)_x)_bV«;
dt
VRC— = vC (Г(о) -Т) + Vк(-txH)kx + КтFT(Тт-Г),
dt
где х = [А], то есть х соответствует концентрации компонента А в смеси.
Если воспользоваться временем пребывания в реакторе т = VR / v, то система урав-
нений (5.3.25) может быть записана в явном виде:
dx х^ -х ,
— =---------кх = ^{х,Т}\
dt т
dT Т<9)_Т (-ДН), KTFT
— =--------+ -----кх + —в---(Тт-Т) = f2{x,T},
dt х С VRC т ' ’ ’’
(5.3.26)
где J\{x, Т}, f2{x, Г) — правые части дифференциальных уравнений, зависящие от
концентрации х и температуры Т.
Для получения частных решений этой системы можно решать задачу Коши со
следующими начальными условиями:
х(Г(°>) = х(в).
El? <0)) =
в результате чего получаются функции от одной независимой переменной — времени t.
х = x(t\,
т = T(t),
(5.3.27)
Рис. 5.24. Достижение стационарного
состояния в политропическом реакторе с
мешалкой, в котором протекает экзотерми-
ческая реакция l-ro порядка А—
(-ЛЯ)
где № <t <t^.
В реальных условиях рассматривае-
мый динамический процесс проводят
таким образом, чтобы он достигал ста-
ционарного состояния, так называемых
стационарных точек решений, которые
изображены на рис. 5.24.
В непрерывных производствах про-
цессы стремятся проводить в областях,
близких к стационарному состоянию. Од-
нако различные возмущения, особенно
в процессах с экзотермическими реакци-
ями (изменения расходов поступающих
потоков, ухудшение теплоотвода, флук-
туации состава исходной смеси и т.д.)
могут вывести процесс из стационарно-
го состояния, если он не является устой-
чивым в смысле Ляпунова.
5.3. Математические модели химических реакторов
313
В соответствии с методикой проверки условия устойчивости системы в смысле
Ляпунова СОДУ (5.3.26) должна быть представлена с возмущением решений (Дх и
ДГ) и с линеаризованной матрицей коэффициентов atj (i = 1, 2; j = 1, 2) (3.5.64):
</(Лх)
Дх
Л
d{AT)
dt
В этом случае элементы линеаризованной матрицы коэффициентов системы
(5.3.28) определяются как частные производные правых частей дифференциальных
уравнений системы (5.3.26):
°11 °12
_°21 °22. ЕТ _
(5.3.28)
а Л-
12 дг’
п
а„ =--
22 дт
а Л-
11 дх’
а Л-
21 дх ’
В разделе 3.5.1 были выведены условия устойчивости в смысле Ляпунова для
системы двух обыкновенных дифференциальных уравнений, которые имеют вид
(3.5.86):
(5.3.29)
(5.3.30)
апа22 - апа21 > 0. (5.3.31)
Аналитическое определение выражений для расчета коэффициентов af(i= 1, 2; j= 1, 2)
осуществляется с учётом (5.3.26) и (5.3.29) и известного выражения для константы ско-
рости реакции согласно закону Аррениуса k = Ae~EIRr, в результате чего получается:
1 , , Е
а 1 =---к: л т = -хк т;
Т RT2
(-ДЯ), 1 (-ДЯ), Е
021 = ^ к; а-п = — ч-2——'-кх-
1 т Ср RT2
К1 F1
VRCp ‘
Подставляя полученные выражения (5.3.32) в (5.3.30) и (5.3.31), получаем:
2 , KTFT {-/АН)
- + к + —^—-К
т VRCp
С„
Е
RT
(5.3.32)
(5.3.33)
1 К1 F1
т+ VRCp
Последнее неравенство (5.3.34) может
1 {-АН) , Е
--2——’-хк т>0 .
т Ср RT2
быть преобразовано к виду:
(5.3.34)
(1 + Н) - + ^-
v 'I т VRCp
{-АН) . Е _
-—-хк =- > 0 .
Ср RT2
(5.3.35)
Сформулируем обязательное условие выполнения первого неравенства (5.3.33),
обеспечивающего выполнение условий устойчивости в смысле Ляпунова (5.3.30) и
(5.3.31), когда верно второе неравенство (5.3.31) и (5.3.35):
1 , KTFT
->кх—-—
т VRCp
(5.3.36)
1
t
314
Глава 5. Физико-химические модели. Построение моделей
Выполнение этого условия позволяет оценивать устойчивость динамической си-
стемы (5.3.25) в смысле Ляпунова только по одному неравенству (5.3.31) и, соответ-
ственно, (5.3.35) — другое неравенство (5.3.30) и соответствующее ему неравенство
(5.3.33) будут при этом автоматически соблюдаться.
Оценка тепловой устойчивости стационарного режима политропического реактора
с мешалкой и с экзотермической реакцией первого порядка
(5.3.37)
(5.3.38)
(5.3.39)
В соответствии с системой уравнений (5.3.25) математическое описание этого
процесса в стационарном режиме имеет вид:
х(0) - х
-----------------------------------~-кх = Ь-
т
Z^+<z^fa+^(rr_r)=0.
т Со vRco Т
р р
Условие применимости только одного неравенства (5.3.35) для оценки устойчи-
вости стационарного режима с учётом уравнения (5.3.37) может быть получено, как
описано ниже.
Так как из (5.3.37) следует, что
, х®-х х'°> ,
kt =-------------------------------=------1,
х х
и степень превращения х компонента А определяется формулами:
х(0) - х X
Х-—(оГ или1-Х = ту,
то
(5.3.40)
(5.3.41)
х(0)_ 1
х 1-Х ’
После подстановки (5.3.40) в (5.3.39), получаем
kt = ^.
1-х
Подстановка последнего равенства (5.3.41) в условие применимости только одно-
го неравенства (5.3.36) для оценки устойчивости в смысле Ляпунова (5.3.35) приво-
дит к неравенству:
1-Х
X KTFT
(5.3.42)
или
1-х
(5.3.43)
KF х
При выполнении (5.3.43) устойчивость динамической системы в смысле Ляпуно-
ва может быть оценена с применением только одного неравенства (5.3.31), которое в
данном случае целесообразно записать в виде (5.3.35):
1 KTFT (-&Н) k Е
т VRCp Ср Х (1 + ktyRT*
(5.3.44)
5.3. Математические модели химических реакторов
315
Из первого уравнения описания стационарного режима (5.3.37) следует, что:
х(0>
х = ---,
1 + kt
поэтому условие устойчивости (5.3.44) имеет вид:
(5.3.45)
т VRCp Ср (1 + kt)2 RT2
Принимая во внимание, что т = VR / у, последнее неравенство может быть записано:
у KTFT (-ДЯ) fcx(0) Е
VR VRCp Ср Q + kt)2 RT2 ’
что при приведении к общему знаменателю даёт следующее условие устойчивости
стационарного режима реактора (5.3.35) в смысле Ляпунова:
x^k F
vCp+KTFT >VR(-&H)-------Т(5.3.46)
р (1 + fcr)2 RT2 ’
Следует отметить, что полученное неравенство (5.3.46) гарантирует устойчивость
стационарного режима при выполнении условий (5.3.36) и, соответственно, (5.3.43).
Интерпретация физического смысла тепловой устойчивости стационарного режима
политропического реактора с мешалкой, в котором протекает экзотермическая
реакция первого порядка
(5.3.47)
(5.3.48)
Второе уравнение математического описания стационарного режима рассматри-
ваемого реактора (5.3.38) с учётом (5.3.37) может быть записано:
т С 1 + & VRC
р р
После замены т = VR /у и соответствующей перегруппировки членов этого урав-
нения оно принимает вид:
VR Ср 1 + kt VR VRCp
После элементарных преобразований (5.3.48) получаем:
, ч Х<°>
уС Т + КТFT(Т-Тт) = уС Т(о) + VR(-&H)k----,
р 1 + £т
и окончательный вариант его представления может быть записан:
-(KтFт)Tт+(vCp + KтFт)T = vCpT^'0)+VR(-^H)^-j^x^f,'^
Так как рассматривается экзотермическая реакция в реакторе, то
• левая часть уравнения (5.3.49) соответствует скорости отвода теплоты Д(2ОТВ и
графически изображается некоторой прямой в системе координат Д0ОТВ = Д7)
(рис. 5.25):
(5.3.49)
(5.3.50)
деога= -{KTFT)FT + iyCp + KTFT}T-,
правая часть уравнения (5.3.49) соответствует скорости подвода (прихода) теп-
лоты за счёт поступающего потока (первое слагаемое) и теплоты экзотермичес-
316
Глава 5. Физико-химические модели. Построение моделей
(5.3.51)
(5.3.52)
(5.3.53)
(5.3.54)
Рис. 5.25. Графическое представление
возможных решений уравнения
(5.3.49), описывающего стационарный
режим политропического реактора с
мешалкой и с экзотермической
реакцией первого порядка
кой реакции (второе слагаемое), а так как константа скорости реакции к опре-
деляется по закону Аррениуса (к = Ae~E/RT), то графически зависимость Д (2|фих =
Д7) изображается 5-образной кривой (см. рис. 5.25):
до = уС T<f,)+VR(-AH) —— х(й}
Уприх р 1 + кх
Для оценки тепловой устойчивости возможных трёх решений уравнения (5.3.49) —
1, 2 и 3 (точек пересечения прямой Д(20ТВ с кривой Д(2прих, где Д(20ТВ = ДО рих) необхо-
димо воспользоваться полученным выше условием устойчивости (5.3.46).
Как следует из равенств (5.3.50) и (5.3.51), левая и правая части условия устойчи-
вости системы в смысле Ляпунова (5.3.46) соответственно равны:
^(AQ0TB) = у(? ktft
dT р
К ________к___х(о) Е
dT \\ + кх)2 RT2
В результате условие устойчивости рассматриваемой системы в стационарном
состоянии в смысле Ляпунова (5.3.46) принимает вид:
<WOT.) ; ^(А6прих
dT dT
Последнее условие (5.3.54) позволяет физически интерпретировать тепловую ус-
тойчивость политропического реактора с мешалкой, в котором протекает экзотерми-
ческая реакция первого порядка А—: в системе координат AQ—Tусловием ус-
(-М)
тойчивости решений в стационарном режиме (точках пересечения линий Д(20ТВ = j(T) и
Д0прих = /(7), т.е. Д(20ТВ= ДСприх) является следующее — наклон прямой скорости отвода
теплоты d^Q^/dT должен быть больше наклона кривой скорости прихода теплоты
‘KMZwJ/dT.
Из рис. 5.25 следует, что из трёх возможных решений рассматриваемой задачи
только решение 2, соответствующее температурному режиму 71, не удовлетворяет
условию устойчивости (5.3.54), поэтому оно
считается неустойчивым, и незначительные
возмущения режимных или других параметров
могут привести к тому, что процесс перейдёт в
другое, но уже устойчивое стационарное со-
стояние 1 или 3.
Как было показано выше и в разд. 3.5.1 ус-
тойчивость стационарных состояний процесса
в полной мере может трактоваться с позиций
устойчивости решений СОДУ в смысле Ляпу-
нова. Очевидно, что реальные промышленные
процессы не следует проводить при неустой-
чивых режимных параметрах (в рассматривае-
мом случае неустойчивым режимным парамет-
ром была температура Т2).
Таким образом, на примере реактора с ме-
шалкой показано, что с применением матема-
тических моделей возможно выявление неус-
тойчивых тепловых режимов промышленных
процессов.
5.3. Математические модели химических реакторов
317
5.3.5. Математическая модель стационарного
режима политропического процесса в трубчатом
реакторе с прямоточным и противоточным
режимами движения теплоносителей в рубашке
(конкретная кинетическая схема химической
реакции)
При описании построения компьютерной модели политропического реактора в ста-
ционарном режиме будут рассмотрены два варианта движения потока теплоносителя*:
а) теплоноситель движется в режиме прямотока (решение задачи Коши) —
рис. 5.26, а;
б) теплоноситель движется в режиме противотока (решение краевой задачи) —
рис. 5.26, б.
х(0) -----------► х(£) х(0) ---------► х(£)
0</<£
L-1
Рис. 5.26. Схематическое изображение политропического реактора с прямоточным (а)
и противоточным (б) движением потока теплоносителя
Для построения модели политропического трубчатого реактора примем следую-
щие допущения (см. разд. 2.1.2):
• рассматривается двухстадийная трёхкомпонентная химическая реакция, проте-
кающей по схеме 2А—Ь—>ЗВ—к-2—>С;
(-Д//,) (-дн2)
• движение основного потока (реакционной смеси) в реакторе и вспомогатель-
ного потока (теплоносителя в рубашке) представляется гидродинамическими
моделями идеального вытеснения;
• параметры потока теплоносителя в рубашке (обозначаются нижним индексом
«j») неизменны, кроме температуры потока теплоносителя в рубашке;
• реакции в реакторе считаются гомогенными, без фазовых переходов;
• считается, что все процессы происходят в жидкой фазе, все реакции протекают
одновременно;
• тепловые эффекты стадий химической реакции не зависят от температуры;
• при теплообмене между основным и вспомогательным потоками учитывается
только теплопередача;
* Все параметры потока теплоносителя (вспомогательного потока) обозначаются с
нижним индексом ; L — длина зоны контакта теплоносителя с основным (реакцион-
ным) потоком; 0<£ < L ~ обозначение основной системы координат; £=L-t ~ обо-
значение противоположной системы координат.
318
Глава 5. Физико-химические модели. Построение моделей
• коэффициент и площадь поверхности теплопередачи между основным и вспо-
могательным потоками являются постоянными и не изменяются.
Описание микрокинетики процесса в реакторе
Для заданной схемы химической реакции:
2А—Ь->ЗВ—
необходимо определить gR, gR, gR, &qR [см. (5.3.1)].
Выражение для скоростей химической реакции по компонентам записывается в
следующем виде (см. табл. 2.2):
Я о
8 а = -2г, ;
gf =3-Г1-Зг2 ; (5.3.55а)
8с=Г2
или в матричном виде:
gK=a-r (5.3.556)
или с учётом (5.3.2) и (5.3.3):
8л ’-2 0 ' ~ 1 2 -
8в = 3 -3 = ЗЛ,Хд - ЗЛ2х| (5.3.55в)
8с _ 0 1 _'v2 В _ &2хв
Ранг матрицы (см. разд. 3.2.1) стехиометрических коэффициентов й равен 2
(rang(5) = 2), поэтому следует выбрать 2 ключевых компонента А и В. При этом
скорость реакции по компоненту С выражается в соответствии с (5.3.55а) через ско-
рости реакций по компонентам Ан В следующим образом:
К 1 К 1 к
8c=--8a--Sb . (5.3.56)
Стехиометрическое соотношение для неключевого компонента С записывается
как
Интенсивность локального источника теплоты за счёт химической реакции в дан-
ном случае выражается таким образом (см. табл. 2.2):
2 . . . .
=£|а»|гДЯ«)г/ =з(-ЛЯД)г1+1(-Д^с2)г2. (5.3.58)
2=1
Построение математической модели стационарного режима процесса химического
превращения в реакторе идеального вытеснения с прямоточным движением
теплоносителя (решение задачи Коши)
Математическое описание данного процесса для конкретного случая описанной выше
химической реакции (5.3.55) включает в себя в соответствии с табл. 2.1 и 2.2 (л + 3)
дифференциальных уравнений.
5.3. Математические модели химических реакторов
319
1 Уравнения покомпонентного баланса для компонентов А, В и С [кон-
центрация компонента С выражается через концентрации компонентов
А и В, т.к. он не является ключевым] - см. (5.3.23):
1.1 d(yxA) _ dv dxA _ VR R dxA VR R xAdv ,, = , gA И 1.1) = gA \ at at at L at vL v at
1.2 d(yxB) _ dv dxB VR R dxB VR R xB dv dt -X’ dC’ d<‘ LS- " dt~ LS’~ . dt''
1.3 xc =40)-|(a4-40))-|ta-4°0-
2. Уравнения для скоростей реакций по компонентам А, В и С
[см. (5.3.55а)]:
2.1 R о . Sa =-^,
2.2 SR =3r\ -3r2;
2.3 gR =г2.
3. Уравнения для скоростей стадий химической реакции [см. (5.3.2),
(5.3.3) и (5.3.55в)]:
3.1 n = k,x2;
3.2 r2 = к2хв
4. Уравнения для констант скоростей стадий химической реакции
в соответствии с законом Аррениуса [см. (5.3.7)]:
4.1 = A! exp(- E1 / RT);
4.2 k2 = А2 ехр(- Е2 / RT).
5. Уравнение общего баланса массы:
5 (5.3.59)
at L
6 Уравнение теплового баланса для потока реакционной смеси:
, d(vT) VR . R FT . T dT VR R FT . T T dv
6 =----Д/+-------Д/ ---------=------Д/+--------AqT-------
dt CL CL и dt vCL vCL v df
p p p p
7. Выражение для локальной интенсивности выделения или поглоще-
ния теплоты в химической реакции [см. (5.3.58)]:
7 AqR=3(-AHRB1)ri + (-AHR2)r2.
8. Выражение для локальной скорости теплопередачи:
8 AqT =КГ(ТТ-Т).
9. Выражение для теплоёмкости потока реакционной смеси [см. (5.3.18)]:
9 С = С'^х. + С^хв + .
Р Ра А Рв ° Рс с
10. Выражения для индивидуальных теплоёмкостей компонентов А, В и С
[см. (5.3.18)]:
10.1 С^ =aA+bAT + cAT2+dAT3.
10.2 С% =aB+bBT + cBT2+dBT3.
10.3 С? =аг + beT + сгТ2 + dcT3.
Рс с с с с
320
Глава 5. Физико-химические модели. Построение моделей
11. Уравнение теплового баланса для потока теплоносителя (см. разд. 5.2.3):
Для определения частного решения системы обыкновенных дифференциальных
уравнений (5.3.59) необходимо решить задачу Коши, при этом задаются следующие
начальные условия:
1.1)' хд(0)=4>;
1.2)' хв(0)=40);
1.3' хс(о)=4О); (5.3.59')
5' v(o)=v(o);
6)' г(о)=7’(о);
И' 7’7.(0)=Т}(0).
Задание начальных условий и изменение определяемых переменных по длине
реактора представлены на рис. 5.27.
Рис. 5.27. Изменение концентраций компонентов, расхода потока и температур
реакционного и вспомогательного (теплового) потоков по длине реактора
Для включения дифференциальных уравнений в информационную матрицу сис-
темы уравнений (5.3.59) их представляют в конечно-разностном виде (см. разд. 3.3.1):
хл(Л)-хл(0) _ V*R _^_dv =
М vL 8а v М Л1 ’
. хв(L) - хв(0) _ VR к _*B_dv_ =
М vL8b v М
"а
5. v(L)-v(0)
(5.3.60')
5*1 Г ( К , к , к)
] fs ~ V? а + 8 в + 8 с Л
T(L)-T(0) Vs bqR FT&qT Т dv
о ----------=--------1-----------
IXt vL Cp vCpL v M
T
n. Tr(L)-Tr(0)
FT
LC PiVT
5.3. Математические модели химических реакторов
321
По аналогии с системой уравнений, описывающей нестационарный режим про-
цесса в реакторе с мешалкой и рубашкой (5.3.21) с учётом (5.3.24), правые части
дифференциальных уравнений 1.1), 1.2) и 6) содержат производные dvjdf [в (5.3.24) —
dVR/dt], которые определяются из выражения 5’] (5.3.60) и обозначаются /5. По-
этому информационная матрица (табл. 5.11) системы уравнений (5.3.59), которая в
этом случае представляется в конечно-разностной форме (5.3.60), включает в себя
переменную /5 с соответствующим уравнением 5*] (5.3.60).
Результатом решения системы (и + 3) в общем случае нелинейных дифференци-
альных уравнений первого порядка (5.3.59) с начальными условиями (5.3.59') будут
следующие функции в заданном интервале 0 < £ < L-.
xa=xaW xb=xbW хс =хс(£); v = v(£); т = Т(1); Тт = Тт(£).
Информационная матрица системы уравнений МО, описывающая рассматрива-
емый процесс в реакторе идеального вытеснения, и соответствующая блок-схема
алгоритма его расчёта приведены в табл. 5.11 и на рис. 5.28.
Таблица 5.11. Информационная матрица системы уравнений математического
описания стационарного режима процесса химического превращения в реакторе
идеального вытеснения с конкретной кинетической схемой реакции и с прямоточ-
ным режимом движения теплоносителя в рубашке
Р п 5 'S § * з S' * o' "с и" 3 Do tSq iVо у* у* у* Ч1 o' S' S' < a; < о 3 Ч- А? 2 Na
1.1*, 1.2* Диф ур © © © © © 13
1.3 © © © О © 14
2.1,2.2,2.3 © 7
3.1, 3.2 © © © ф © 6
4.1,4.2 © 5
5* Диф УР © © 15
5‘] © и 8
6* Диф УР © © © © © © 16
7 © 9
8 © © 10
9 © © © © 12
10.1, 10.2, 10 3 © 11
11* Диф УР © © 17
1.1)', 1 2)', 1 3' 1
5' ф 2
6)' 3
11’ 4
21-4544
1 2'
2^1! XD
IxJ—
6*
7W
-j—lxJL)
1.3 —►
t
xb(L)
W
) Вывод
XA^XB^
pR nR
*>А’*В’
8c
r,,r2
fcpfcj
T®
&qT, &qR
q,,v0
,~,ind ^ind
PA’^Pg
ind
cPc
TT(e)
o^e<.L
Рис. 5.28. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима процесса в реакторе идеального вытеснения
с конкретной кинетической схемой химической реакции и с прямоточным режимом движения теплоносителя в рубашке
Глава 5. Физико-химические модели. Построение моделей
5.3. Математические модели химических реакторов
323
Построение математической модели стационарного режима процесса химического
превращения в реакторе идеального вытеснения с противоточным движением
теплоносителя (решение краевой задачи)
Математическое описание данного процесса для конкретного случая описанной выше
химической реакции (5.3.55) включает в себя в соответствии с табл. 2.1 и 2.2 (и + 3)
дифференциальных уравнений.
1. Уравнения покомпонентного баланса для компонентов А, В и С [кон-
центрация компонента С выражается через концентрации компонентов
А и В, т.к. он не является ключевым — см. (5.3.23)]:
1.1 d(yxA) dv dxA VR R <Ьа r xAdv dt A dt dt L8a ' ’ dt vL 8a v dt’
1.2 + = и 1.2) = dt dt dt L dt L v dt
1.3 xc =40)-|(хл -40))-|(*s -40)).
2. Уравнения для скоростей реакций по компонентам А, Ви С [см. (5.3.55а)]:
2.1 ^=-2Г];
2-2 gB=3rt-3r2;
2-3 gR=r2.
3. Уравнения для скоростей стадий химической реакции [см. (5.3.2),
(5.3.3) и (5.3.55b)]:
з.1
3.2 r2 = k2xB-
4. Уравнения для констант скоростей стадий химической реакции в со-
ответствии с законом Аррениуса [см. (5.3.7)]:
4 .1 kt = А, ехр(- EJRT)',
4 2 ^2 = А2 ехр(- Е2 / RT)
5. Уравнение общего баланса массы:
(5.3.61)
л т Т dv
Aq--------
v dt ‘
5 = + ^ + g?)-
at L
6. Уравнение теплового баланса для потока реакционной смеси:
• , d(yT)_ VR . R FT . T dT VR . R FT
6 -----—-----Aq H-----Aq и -------—------Aq H------
dt CpL 4 CpL и dt vCpL vCpL
7. Выражение для локальной интенсивности выделения или поглоще-
ния теплоты в химической реакции [см. (5.3.58)]:
7 \qR = з(-ДН*)г1+(-ДН*2)г2.
8. Выражение для локальной скорости теплопередачи:
8 AqT =КТ(ТТ-Т).
9. Выражение для теплоёмкости потока реакционной смеси [см. (5.3.18)]:
9 С =C‘"dxA+C‘^lxB+C‘”dxc.
Р Рл Л Рв а Рс С
324
Глава 5. Физико-химические модели. Построение моделей
10. Выражения для индивидуальных теплоёмкостей компонентов А, В и С
[см. (5.3.18)]:
10.1 C^=aA+bAT + cAT2+dAT3'
10.2 C^=aB+bBT + cBT2+dBT3'
10.3 C'£=ac+bcT + ccT2+dcT\
11. Уравнение теплового баланса для потока теплоносителя (см. разд. 5.2.3):
tZTL FT . T
11 —L = bq. dt C„ LvT Pt 1
По сравнению со случаем политропического реактора с прямоточным движением
теплоносителя, рассмотренным выше (5.3.59) в данной системе уравнений матема-
тического описания (5.3.61) изменилось только уравнение 11 (см. разд. 5.2.4).
В этом случае для определения частного решения на компьютере необходимо
решить краевую задачу, при этом задаются следующие краевые условия'.
1.1)' ХЛ (9) — XA(0) >
1.2)' хв Ф) = XB(0) ,
1.3' xc(°)=xc(o); (5.3.61')
5' v(o)= v(0);
6)' 7’(o)=t(o);
11' 7^ (/.)= T’rjo).
Для включения дифференциальных уравнений в информационную матрицу сис-
темы уравнений (5.3.61) по аналогии с (5.3.60) их представляют в конечно-разно-
стном виде:
. xA(L)-xA(0) _Vr ~r xAdv_f
Ы vL8a vdt Л”
, xB(L)-xB(0) _ VR R xBdv
А Л “ T J„- J12’
vL v ctt
. v(L)-v(0) _ , .
bt
5*] fs =~~(,8a + ?b +8c)’
T(L)-T(0) VR bqR FTbqT T dv
6 ----------=----------1------------
M vL Cp vCpL v dt
(5.3.62)
5.3. Математические модели химических реакторов
325
Рис. 5.29. Изменение концентраций компонентов, расхода потока и температур потоков
по длине реактора
Все рассуждения, приведённые для уравнений (5.3.60) являются справедливыми
и для представленных уравнений (5.3.62).
Результатом решения системы (и + 3) в общем случае нелинейных дифференци-
альных уравнений первого порядка (5.3.61) с начальными условиями (5.3.61 ’) будут
следующие функции в заданном интервале о < (. < L:
xa=xaW хв=хв(О хс = МО; v = v(O; т = т(О; тТ=тТ(£).
Задание краевых условий и изменение определяемых переменных по длине реак-
тора представлены на рис. 5.29.
Алгоритм решения краевой задачи в этом случае подобен алгоритму расчёта про-
тивоточного теплообменника (см. разд. 3.2.4). Однако здесь в одном из потоков на-
ряду с процессом теплопередачи протекает конкретная химическая реакция (5.3.55).
При задании начального приближения Г; (0), после представления системы диф-
ференциальных уравнений в конечно-разностном виде (5.3.62), краевое условие 11*
превращается в уравнение, путём решения которого можно корректировать величи-
ну ТТ (0), т.е. величину температуры теплоносителя на выходе из реактора.
В этом случае решением уравнения 1Г будет значение температуры потока теп-
лоносителя, движущегося противотоком, на выходе из реактора (/ = 0) — Г;(0)’ •
Уравнение 1Г при этом имеет вид:
/и- = Тт (L)[TT (0)}- ТТ(0) = 0. (5.3.63)
Информационная матрица системы уравнений МО описывающая рассматривае-
мый процесс в реакторе идеального вытеснения, и соответствующая блок-схема ал-
горитма его расчёта приведены в табл. 5.12 и на рис. 5.30 (стр. 327).
326
Глава 5. Физико-химические модели. Построение моделей
Таблица 5.12. Информационная матрица системы уравнений математического
описания стационарного режима процесса химического превращения в реакторе
идеального вытеснения с конкретной кинетической схемой реакции и с противоточ-
ным режимом движения теплоносителя в рубашке
р п >4 S; * 2 "s- o' 5 "с Ьс Ьс Ьс «г* о4 К' К" <3 а; < о в и С1, з и 3s S' 3 Ns
1.1*, 1.2* Диф. ур. © © с+> © © © 12
1.3 © © 0 © © 13
2.1,2.2, 2.3 © 6
3.1,4.2 © © © © 5
4.1, 3.2 © 4
5* Диф. УР- © <+> © 14
5‘] © <-О 7
6* Диф. ур. © © © © © © 15
7 © <-Л 8
8 © <+> E 9
9 © © © <+> © 11
10.1,10.2,10.3 © A 10
11* Диф Ур. © © 16
1.1)', 1.2)', 1.3' <+> 1
5' 2
6)' <+> 3
11' Кор. ур. A © 17
5.3.6. Математическая модель нестационарного
режима процесса химического превращения
с простейшей кинетической схемой реакции
в изотермическом трубчатом реакторе
Для построения математической модели процесса в трубчатом реакторе, схемати-
ческое изображение которого показано на рис. 5.31, в случае нестационарного режи-
ма принимаются следующие допущения:
• аппарат представляет собой трубу цилиндри-
*( (0 ческой формы постоянного диаметра;
/ = 0
t = L
Рис. 5.31. Схематическое изображе-
ние трубчатого реактора
• реактор является изотермическим;
• движение потока описывается однопарамет-
рической диффузионной моделью (см. табл. 2.1).
Уравнение покомпонентного баланса для рас-
сматриваемого простейшего уравнения реакции
записывается в данном случае следующим обра-
зом (см. табл. 2.1 и 2.2):
*с(0
ХВ^
гт(0)
Рис. 5.30. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима процесса в реакторе идеального вытеснения с
конкретной кинетической схемой химической реакции и с противоточным режимом движения теплоносителя в рубашке
5.3. Математические модели химических реакторов 327
328
Глава 5. Физико-химические модели. Построение моделей
DVr д2
при этом х = [а} 5 =
д£2 Vdl А(/)’
VR
(5.3.64)
L dt L
yR
GR(t) =^~gA = -——kx', v = S -W , где W— линейная ско-
L L
L
рость потока.
Учитывая вышеизложенное, уравнение МО модели трубчатого реактора в неста-
ционарном режиме будет иметь следующий вид:
1 <5Л65>
Уравнение 1 (5.3.65) является дифференциальным уравнением в частных произ-
водных второго порядка параболического типа (см. разд. 3.5.2) с двумя независимы-
ми переменными t и t и описывает нестационарный режим трубчатого реактора, в
котором протекает единственная простейшая реакция при условии представления
движения потока однопараметрической диффузионной моделью.
В качестве решения необходимо определить значения выходной переменной х (кон-
центрация компонента А), которая зависит от двух независимых переменных t и t.
x = x{t,l), (5.3.66)
изменяющихся в следующих пределах:
Q<t<L. (5.3.67)
Решение этой задачи требует задания начальных и граничных условий (см. разд. 3.5.2):
• начальное условие:
Г x(r(0),Z
• граничные условия:
(5.3.68а)
(*)
1
(5.3.686)
Для решения полученного дифференциального уравнения в частных производ-
ных (СДУЧП) (5.3.65) может быть использован метод конечных разностей [(3.5.129)
— (3.5.131)1, в соответствии с которым производные представляются в конечно-раз-
ностной форме в определённом интервале Д*’] и/или [О, L] в результате чего
уравнение 1 (5.3.65) с начальным Г и граничными 1' условиями (5.3.68) превраща-
ется в систему обыкновенных дифференциальных уравнений (СОДУ) и/или в систе-
му конечных уравнений (СКУ) (см. разд. 3.2).
Для этого уравнения можно использовать три варианта представления производ-
ных с помощью конечных разностей (см. разд. 3.3.1).
1. По независимой переменной I:
(5.3.69а)
В результате получается СОДУ первого порядка с независимой переменной t.
2. По независимой переменной Г.
дх х,,« — х,
-^- = -4—С/ = 1,-,т-1). (5.3.696)
Эг Аг
В результате получается СОДУ второго порядка с независимой переменной £.
3. По независимым переменным £ и t.
5.3. Математические модели химических реакторов
329
Эх _ х,+1 - х,
де= де
(i = 1,п-1) ;
Эх _ ~ х}
dt ~ AZ
т-1).
(5.3.69b)
В результате получается СКУ.
Детально рассмотрим первый вариант применения метода конечных разностей
по независимой переменной I (рис. 5.32).
....... 1|с.гг.фм..|
п = 0 1 2 • •• л-2 л-1 п
Рис. 5.32. Дискретизация по длине реактора
При о < I < L [см. (5.368а)] конечно-разностное представление производных имеет вид:
• производная «по недостатку»:
Эх, _ х, - х,(
де ,_ы де ’
dxt ~ х,+! - х,
• производная «по избытку»:
(5.3.70)
• вторая производная:
Эх, Эх,
х, ~ де де
де “ де
де
В результате из одного уравнения в частных производных вследствие дискретиза-
ции получается система (п — 1) обыкновенных дифференциальных уравнений с не-
зависимой переменной t (5.3.65) и начальным условием Г (5.3.68а), представленным
в дискретном виде.
В этом случае граничные условия 1' в соответствии с (5.3.686) таковы:
i; x(z,o)=xo(z) t^<t<t^-
rL x(z,t)=xL(z) t^<t<t^
(5.3.71)
В частном случае можно допустить, что на границах (е = 0 и е = L) стационарные
условия и х0 = const а, а х, = constL.
Если для конечно-разностного представления производной использовать «произ-
водную по избытку» (5.3.70), то СОДУ 1 с начальными условиями Т имеет вид:
1 = 2а, + *-i. _ w х^ х, _ ц (i = 1,..., п — 1);
dt (д^)2 де '
Г x,(z(0))=x,(0) (i = l,..., n-l).
(5.3.72)
Граничные условия 1' (5.3.686) и соответственно (5.3.71) легко включаются в
СОДУ (5.3.72).
330
Глава 5. Физико-химические модели. Построение моделей
Преобразуя систему уравнений 1 (5.3.72) и предполагая, что их параметры явля-
ются константами (D, Wvi к), можно получить следующую СОДУ:
dx: _ dt D 1 х<-1 + (А0 ^-k 2D (AO2 J x, + D [(AO2 _ W_ M *,+l , J = l,. „п-l (5.3.73a)
ИЛИ dxv dt dx2 At b c a b 0 ••• c ••• 0 0 0 O’ 0 0 1" x2 - ax0 0
D где а = ; М II I 1 1 II -ft 0 0 .° 0 2D 0 ••• 0 ••• D a 0 Г ' b c a b V Xn-2 LX»-1 + 0 _CXn_ (5.3.736)
Из изложенного следует, что система уравнений (5.3.72), включающая граничные
условия 1„ и 1' (5.3.686) и, соответственно, (5.3.71), в матричном виде может быть
представлена в следующем виде:
- dx = ~
1 — = Ах + 8
dt
Г х(/°>) = х<°>,
(5.3.74)
где 8 — вектор с граничными условиями (5.3.686) и, соответственно, (5.3.71), а на-
чальные условия 1' (5.3.74) являются дискретным представлением начального усло-
вия 1' (5.3.68а) х(0)(0> 0<не-
полученная система неоднородных обыкновенных дифференциальных уравне-
ний (5.3.74), аппроксимирующая дифференциальное уравнение в частных произ-
водных (5.3.65), может быть решена любым из известных методов [например, мето-
дом Эйлера или Рунге—Кутта (см. разд. 3.5.1)]. Следует отметить, что матрица её
коэффициентов А является трёхдиагональной.
5.4. Математические модели процессов
разделения: ректификации и абсорбции
Процессы массопередачи (ректификация, абсорбция и т.п.) относятся к важней-
шим процессам разделения в химической, нефтехимической и газоперерабатываю-
щей промышленности. Так, например, ректификационные колонны и абсорбцион-
но-десорбционные комплексы широко используются на разных этапах получения
целевых продуктов: при очистке сырья, при улавливании целевых и побочных про-
дуктов, а также непрореагировавшего сырья химических процессов и, наконец, при
выделении целевых продуктов. Характерной особенностью этих процессов является
то обстоятельство, что при их использовании можно осуществить наиболее глубокое
5.4. Математические модели процессов разделения: ректификации и абсорбции 331
(«тонкое») разделение многокомпонентных смесей различных веществ. Одновременно
ректификация — один из наиболее энергоёмких процессов (более 70% энергозатрат
при производстве продуктов основного органического и нефтехимического синтеза
приходится на подсистему ректификации) химической технологии. Поэтому точно-
сти расчётов процессов массопередачи следует уделять пристальное внимание, так
как неточности вычислений могут приводить к увеличению энергозатрат и, соответ-
ственно, к снижению энергосберегающих показателей процесса.
Разделение жидких смесей при ректификации на практически чистые компонен-
ты или на фракции различного состава является широко распространённым процес-
сом химической технологии. Разделению подвергаются смеси, состоящие из компо-
нентов с неограниченной и ограниченной взаимной растворимостью, в том числе и
взаимно нерастворимые. Каждому классу этих смесей соответствуют характерные
условия равновесия кипящей жидкой фазы и образующихся из неё паров, отобража-
емые диаграммами фазового равновесия жидкость—пар.
Как правило, компоненты жидких смесей имеют при одинаковом внешнем дав-
лении различные температуры кипения, а при одинаковой температуре они кипят
при разных внешних давлениях. Благодаря этому, в процессе испарения жидкой
смеси её компоненты проявляют различное стремление к переходу в парообразное
состояние, то есть обладают различной летучестью. Очевидно, самым летучим явля-
ется компонент с наименее низкой индивидуальной температурой кипения — низко-
кипящий компонент. Поэтому при испарении жидкой смеси концентрация низкоки-
пящего компонента в образующихся парах больше, чем в жидкой фазе. Это позволя-
ет разделить исходную жидкую смесь с любым числом компонентов на любое число
фракций различных составов путём частичного испарения этой смеси и конденсации
образующихся паров. Такой процесс называется дистилляцией, а получаемые конден-
саты — дистиллятами. Неиспарившаяся часть жидкой смеси называется кубовым ос-
татком.
При частичной конденсации паровой смеси путём её охлаждения будут в боль-
шей степени ожижаться высококипящие компоненты, а остаток пара будет обогащать-
ся низкокипящими компонентами. Такой процесс разделения паровой смеси на фрак-
ции различных составов называется конденсацией.
На практике для чёткого разделения жидких смесей на индивидуальные компонен-
ты или фракции из индивидуальных компонентов прибегают к чередованию процессов
испарения и конденсации, используя при этом каждый раз теплоту конденсации паров
для испарения соответствующего количества жидкости.
Этот сложный процесс, называемый ректификацией, осуществляется чаще всего в
аппаратах колонного типа с различными типами тарелок и насадок. При этом восходя-
щий поток пара при каждом контакте со стекающей жидкой смесью обогащается низ-
кокипящими компонентами за счёт частичной конденсации высококипящих и час-
тичного испарения низкокипящих компонентов. При достаточном числе таких кон-
тактов на поверхности тарелок или насадки пар будет уходить вверху колонны с преиму-
щественным содержанием низкокипящих компонентов, а жидкость уйдёт из нижней
части колонны с преимущественным содержанием высококипящих компонентов.
Ректификация относится к классу массообменных процессов, скорости которых про-
порциональны разностям равновесных концентраций компонентов в паровой фазе
(по отношению к их действительным концентрациям в жидкой фазе) и рабочим
(действительным) концентрациям компонентов смеси в паровой фазе. Интенсив-
ность (скорость) массопередачи также пропорциональна и коэффициенту массопере-
дачи при ректификации.
В отличие от ректификации, абсорбцией называется процесс поглощения индиви-
дуального газа, а также избирательного поглощения одного или нескольких компо-
нентов газовой смеси жидким поглотителем — абсорбентом. Процессу абсорбции
соответствуют диаграммы фазового равновесия газ — жидкость, когда поглощение газа
происходит только за счёт его растворения в абсорбенте (физическая абсорбция).
332
Глава 5. Физико-химические модели. Построение моделей
В книге рассматривается только физическая абсорбция, которая является также
массообменным процессом, интенсивность (скорость) которого пропорциональна
разности концентраций поглощаемого компонента в газовой фазе и в равновесном
состоянии над раствором. Степень интенсивности (скорости) массопередачи также
пропорциональна и коэффициенту массопередачи при абсорбции.
5.4.1. Математическая модель процесса
непрерывной многокомпонентной ректификации
в тарельчатой колонне
Одним из наиболее эффективных способов разделения жидких смесей является
процесс непрерывной ректификации, характеризующийся чередованием процессов
испарения и конденсации, рассмотренных в предыдущем разделе. Несмотря на зна-
чительное потребление энергии при проведении процессов ректификации, их при-
менение обосновано тем обстоятельством, что часто благодаря их использованию
удается обеспечить требуемую четкость разделения, необходимую для промышлен-
ного применения. Тарельчатые ректификационные колонны (рис. 5.33) широко рас-
пространены на практике, так как их эксплуатация является наиболее удобной и
надёжной для широкого спектра разделяемых жидких систем.
Принятые обозначения для тарелок ректификационной колонны (см. рис. 5.33):
• нумерация тарелок производится сверху вниз;
• тарелка 1 является конденсатором или дефлегматором;
• тарелка N является кипятильником куба.
Для построения математической модели процесса непрерывной многокомпонен-
тной ректификации в тарельчатой колонне необходимо принять следующие допуще-
ния:
• в колонне контактируют только две фазы — жидкость и пар;
• рассматривается стационарный режим процесса;
• дополнительных отборов потоков с промежуточных тарелок, кроме куба и кон-
денсатора, не происходит;
• в межтарельчатом пространстве нет контакта между фазами;
• межтарельчатый унос жидкости отсутствует;
• на тарелках колонны протекает только процесс массопередачи.
a б
Рис. 5.33. Тарельчатая ректификационная колонна (а) и её схематическое изображение (б)
5.4. Математические модели процессов разделения: ректификации и абсорбции 333
Необходимо отметить следующие характерные особенности рассматриваемой модели:
• рассматривается «-компонентная смесь, например, концентрация жидкости на
тарелке i может быть представлена как ху О' = 1,N; j = 1,.... п):
• на каждую тарелку может подаваться поток жидкого питания F с концентра-
цией ху О = 1,..., N; j = 1,п);
• на каждую тарелку может подводиться или отводиться поток теплоты AQ",
I = 1,...,л (если Ag,n- положительно, то теплота подводится, если А()п — отри-
цательно, то теплота отводится);
• эффективность массопередачи на тарелке оценивается с использованием моди-
фицированного КПД Мерфри для многокомпонентных смесей:
0 = 1,..,АО ; = 1,(5.4.1)
Уу Ji+lj
где y,j — состав паровой фазы в долях, покидающей тарелку I; у|+1 — состав паровой
фазы в долях, поступающей на тарелку i с тарелки i + 1; у'*’ — равновесный состав
паровой фазы в долях на тарелке /;
• равновесный состав паровой фазы на тарелке i определяется по формуле:
0 = 1,-.АО j = l,...,«), (5.4.2)
где К — константа фазового равновесия на г-й тарелке для у-го компонента; ху —
состав жидкой фазы в долях на тарелке /.
Таким образом, для построения модели необходимо построить:
• модель фазового равновесия жидкость—пар (5.4.2);
• модель процесса разделения на тарелке с учётом её эффективности (5.4.1), т.е.
с учётом многокомпонентной массопередачи;
• модель тарельчатой ректификационной колонны, т.е. каскада тарелок с потока-
ми питания Ft и потоками подводимой (отводимой) теплоты AQ/1 (i = 1,..., п).
Математическая модель фазового равновесия жидкость—пар
Фазовая диаграмма жидкость—пар бинарной системы при изобарических услови-
ях (Р = const) представлена на рис. 5.34.
Задачей математического моделирования равновесной системы жидкость—пар
является определение равновесных условий в экспериментальной точке, то есть со-
ответствующей выраженной в долях концентра-
ции компонентов в жидкости х или паре у при
известном общем давлении Р, то есть при задан-
ных х, Р определить у, Т при равновесных усло-
виях (см. рис. 5.34).
В общем случае данная модель строится не для
бинарной (л = 2), а для многокомпонентной сис-
темы с числом компонентов п, и для её построе-
ния необходимо составить:
• математическое описание (МО) процесса;
• информационную матрицу системы уравне-
ний МО,
• блок-схему алгоритма решения системы урав-
нений МО.
Рис. 5.34. Фазовая диаграмма
жидкость—пар в бинарной системе
334
Глава 5. Физико-химические модели. Построение моделей
Математическое описание фазового равновесия жидкость—пар в многокомпонен-
тной системе включает следующие уравнения:
1) описывающее объединённый закон Дальтона—Рауля с учётом неидеальности
жидкой фазы с помощью коэффициентов активности у, (j = ), то есть прини-
мается допущение об идеальности паровой фазы:
Ру? = р1х)У1’ j = (5-4-3)
2) зависимости давления насыщенного пара индивидуального вещества j Р° от
температуры Т по уравнению Антуана:
2(")
/ в
Р° =ехр А, +----—
1 1 С,+Т
где — известные константы, справедливые в определённом диапазоне
изменения температур и, соответственно, давлений;
3) известные зависимости коэффициентов активности компонентов системы от
состава жидкой фазы х, температуры Т и известных констант бинарного взаимодей-
ствия молекул многокомпонентной смеси а , также справедливых для определённо-
го диапазона температур и давлений в системе:
3(») У1=У](х’Т’а\ i=^-,n-
4) стехиометрическое соотношение для мольных долей равновесной паровой фазы:
4 5>Г> = 1-
7*1
В результате получена система (Зи + 1) уравнений (5.4.3), и в качестве определяе-
мых переменных должны быть выбраны: y/’j — мольные доли равновесной паровой
фазы; Р(°) — давления насыщенных паров индивидуальных веществ; У(„; — коэффи-
циенты активности компонентов смеси; Т — температура. Остальные переменные и
константы должны быть заданы.
Таблица 5.13. Информацион-
ная матрица системы уравнений
МО фазового равновесия жид-
кость-пар в многокомпонентной
системе при постоянном давле-
нии
Информационная матрица рассматриваемой
системы уравнений (5.4.3) и соответствующий
алгоритм её решения приведены в табл. 5.13 и на
рис. 5.35.
Задание температуры Т в качестве начально-
го приближения расчётов позволяет по уравне-
ниям 2, 3 и 4 определить функцию корректиру-
ющего уравнения 4 в системе (5.4.3).
Корректирующее уравнение 4 имеет следую-
щий вид (рис. 5.35):
4)
(5.4.4)
f(T^ iy?{T}~ 1 = 0- <5А5>
7’1
5.4. Математические модели процессов разделения: ректификации и абсорбции 335
Рис 5.35 Блок-схема алгоритма расчёта фазового равновесия жидкость—пар
в многокомпонентной системе при постоянном давлении
Результат решения уравнения — равновесная температура 7’(’> или температура
кипения смеси. При этой температуре определяются равновесные концентрации у''
из уравнений 1 (5.4.3):
Р°х У
у? = 1 р 1 и = 1,->п).
Для идеальной жидкой фазы (у, = 1, j = 1,...,п) и будет справедливо:
Р°
yT=y-xj О = 1......")• (5.4.6)
В результате константа фазового равновесия (5.4.2) определяется как:
K^Pf/P 0 = 1,..., п) (5.4.7)
и зависит от давления и температуры, что следует из уравнения Антуана 2 из (5.4.3)
(Р° зависит только от температуры).
Таким образом, для вычисления равновесного состава паровой фазы использует-
ся формула:
у^=К1Х1 (у = !,...,«). (5.4.8)
*4...
» » к
Математическая модель процесса многокомпонентной массопередачи на тарелке
Для построения математической модели процесса многокомпонентной массопе-
редачи на тарелке ректификационной колонны с учётом гидродинамики движущих-
ся потоков (рис. 5.36) принимаются следующие допущения:
• процесс протекает в стационарном режиме;
• движение потока жидкости может быть представлено
моделью идеального смешения, а потока пара — моде-
лью идеального вытеснения;
• на тарелке протекает многокомпонентная массопере-
дача;
• перекрестными эффектами матрицы коэффициентов мас-
сопередачи можно пренебречь;
• потоки жидкости (Z) и пара (V) на тарелке постоянны.
Уравнения для описания движения жидкой фазы на тарел-
ке (см. табл. 2.1) записываются в предположении идеального
перемешивания жидкости, поэтому для покомпонентных ба-
Lx,
Рис 5.36 Схемати-
ческое изображение
потоков на тарелке
ректификационной
колонны
336
Глава 5. Физико-химические модели. Построение моделей
лансов и выражений для определения локальных скоростей массопередачи будет
справедливо (см. табл. 2.2) — в связи с тем, что у, и g*^ зависит от высоты паро-
жидкостного слоя на тарелке Я (5.4.11) и (5.4.12), а в соответствии с (5.4.13) g'^L>
связано с g^'r>, то в модели идеального перемешивания для g*^ необходимо ис-
пользовать среднее значение
Lx^-Lxj+[FMg^Lhcp=0, j = l,..„ п- (5.4.9)
g“W = J^)(x'*’-x5) j = l,...,«, (5.4.10)
5=1
где «('•)» — верхний индекс, позволяющий отнести переменную к жидкой фазе; рм
— матрица коэффициентов массопередачи; FM — площадь поверхности массопере-
дачи; xs(,) (s = 1,..., п) — равновесный состав жидкости.
Уравнения для описания движения паровой фазы на тарелке записываются в
предположении справедливости зависимостей для моделей идеального вытеснения
(см. табл. 2.1), а для определения локальных скоростей массопередачи используются
выражения, аналогичные (5.4.10) (см. табл. 2.2):
= (5-4.11)
ah Н
g^ = tK^(y(p-ys} j = п, (5.4.12)
5=1
где «09» — верхний индекс, позволяющий отнести переменную к паровой фазе; h —
текущая координата высоты парожидкостного слоя на тарелке колонны (о < h < Н )
В процессе ректификации при массопередаче предполагается перенос частиц ком-
понентов потока из жидкой фазы в паровую и будет справедливо:
-g^L) = g^(V), J = l,-..,n. (5.4.13)
Для определения [FMg“(i)]cp в уравнении (5.4.9) воспользуемся соотношениями
(5.4.13) и (5.4.11):
[FMg7(L)]cp = FM^—„—
П
\g^dh
рм _____
н
(5.4.14)
= -[v^-dh = -v(y^-
J dh
Подстановка (5.4.14) в (5.4.9) приводит к уравнению покомпонентного баланса
следующего вида:
Lx^-LXj+Vy^-Vy^^O, 7 = 1,..„л. (5.4.15)
Далее воспользуемся уравнением локальной скорости многокомпонентной мас-
сопередачи из табл. 2.2 в терминах паровой фазы — верхний индекс «(v)» (5.4.12):
g-^=K 1V-A
(5.4.16а)
5.4. Математические модели процессов разделения: ректификации и абсорбции 337
где у(,) — равновесный состав паровой фазы, или в матричной форме:
>r(v)
^(v)
^(v)
ЛЛ1
Л]2
Лл2
^A/(V)
Л1л
vM(V)
nn
УГ-У1
уГ’ - Уп
(5.4.166)
Недиагональные элементы матрицы коэффициентов массопередачи называются
её перекрестными эффектами, а так как они на 2—3 порядка меньше диагональных
элементов, ими пренебрегают, вследствие чего матрица коэффициентов массопере-
дачи становится диагональной:
=M(V) к -K^v} 0 0 Л. 22 0 0 (5.4.17)
0 0 J
В результате уравнение (5.4.12) для локальных скоростей массопередачи прини-
мает вид:
^М = ^(г)(у(.)_уД 7=1,...,и. (5.4.18)
Таким образом, система уравнений, описывающая многокомпонентную массо-
передачу на тарелке, может быть представлена в виде системы Зи уравнений (5.4.15),
(5.4.11) и (5.4.18):
1<л) Lx^-LXj+Vy^-Vy^^O (j =!,...,«);
2(„) = O = 1.(5-4.19)
ah H
После подстановки третьего выражения системы (5.4.19) во второе, получается
система 2п уравнений:
1<„) Lx^-LXj+Vy^-Vy^O (у = 1,...,л);
2(„) = (5-4.20)
Рассмотрим аналитическое решение дифференциальных уравнений системы 2(л)
из (5.4.20) (у = !,...,«):
f dy>
j») У', ~ У>
Т?М н
F к“ [dh
VH {
(5.4.21)
в результате чего получается:
,Ю
Г
Л> У:~У
FM KM(v)
JJ
V
(5.4.22)
где у® и у^ (у = 1,..., п) — концентрации компонентов в паровой фазе, когда они
поступают на тарелку (верхний индекс «(»)») и покидают её (верхний индекс «(*)»).
После взятия определённого интеграла в левой части (5.4.22) получаем:
338
Глава 5. Физико-химические модели. Построение моделей
~Й)---^у = ехр-----
У) - У) v )
(5.4.23)
Для определения эффективности тарелки Ej (5.4.1) запишем:
у?-у? _/‘Мо)
Ej 1 У^-У? У®-У? У? - У(Р ’ (5.4.24)
С учётом равенств (5.4.23) и (5.4.24) эффективность тарелки по каждому компо-
ненту может быть определена как
E]=l-exp(-FM K^v}/v\ j = l,...,n, (5.4.25)
а состав паровой фазы, покидающей тарелку с учётом (5.4.23) рассчитывается по
формуле:
У^У^ + Е^-у®), у = 1,...,и , (5.4.26)
где в соответствии с (5.4.25) эффективность массопередачи на тарелке для у-го ком-
понента зависит от площади поверхности массопередачи FM , соответствующего ему
диагонального элемента матрицы коэффициентов массопередачи A'“(v\5.4.17) и рас-
хода парового потока на тарелке V.
Для теоретической тарелки, где устанавливается термодинамическое равновесие
жидкость—пар и протекает процесс массопередачи, Е = 1 и у'^ = у^ .
В результате МО процесса массопередачи на тарелке имеет следующий вид.
Уравнение баланса для жидкой фазы:
Kn) Lx^-Lxj+Vy^-Vy^ = O (у = 1,...,«).
Уравнение баланса для паровой фазы:
2(л) У{Р = У{°} + Е^-У^) (у=1,...,и).
Уравнение для эффективности тарелки по компоненту:
3(л) E,=l-exp(-F^(v)/v) (у = 1,...,л).
Уравнение для равновесного состава паровой фазы:
4(") уГ = кЛ = (5-4.27)
При условии идеальности паровой и жидкой фаз константа фазового
равновесия выражается как:
5(л) К^Р'/Р (у = 1,...,л).
В этом случае давление насыщенного пара индивидуального вещества
определяется по уравнению Антуана:
6W
Р® = ехр А; +
В1 '
С,+Т
1 У
где — известные константы.
г
5.4. Математические модели процессов разделения: ректификации и абсорбции 339
Уравнения (5.4.27) обычно дополняются стехиометрическими соот-
ношениями для составов фаз, выражаемых в долях:
7 ^=1;
7=1
7=1
Математическая модель стационарного режима процесса в колонне
Тарелка i
р;+1у,+1(Дя,+1)
Рис. 5.37. Схематическое изображение
потоков на (-Й тарелке ректификацион-
ной колонны
V (Ah,)
Одну i-ю тарелку (i = 1,..., N) ректифика-
ционной колонны в случае многокомпонен-
тной смеси с п компонентами (j = l,...,n )
можно изобразить, как показано на рис. 5.37
(см. также рис. 5.33).
Принимаются допущение о том, что пи-
тание является жидкостью (F — расход пи-
— F
тания х — состав питания) и следующие
обозначения: Д()п — внешние потоки теп-
лоты (в конденсаторе «минус», в кипятиль-
нике «плюс»); АН'(Ah,) — энтальпии паро-
вой (жидкой) фазы; N — число тарелок; г — номер тарелки = );J — номер
компонента (у = !,...,«).
При составлении МО процесса уравнения (1(л), 2(п), 3(п), 4(п), 5(п), 6(п), 7,8) систе-
мы (5.4.27) для тарелок надо повторить #раз (первый индекс «/» меняется от 1 до Л)
и добавить для всех тарелок уравнения теплового баланса.
В результате получается система уравнений математического описания стацио-
нарного режима процесса непрерывной ректификации в тарельчатой колонне (5.4.28).
Система уравнений МО стационарного режима процесса непрерывной ректифи-
кации в тарельчатой колонне с учётом сказанного выше имеет следующий вид:
i(N.„) +Ll_lxl_lJ-Llxil+Vl+lyl+lJ-V,yIJ=O 0 = 1,-Л, j = 1,...,ti);
2(n.„) yy = y,+o + £y(y,,*)-yI+1J = j = 1,...,h);
3(n.„) Ey = l-exp(-F/£"(v)/v,) 0=1,...,N, j = l,...,n);
4(n.„) y^ = Kyxy (i = l,...,N, j = l,...,7i);
S(N.n} Ky = Py/Pl (i = l,...,N, j = !,...,«);
340
Глава 5. Физико-химические модели. Построение моделей
Стехиометрические соотношения для паровой и жидкой фаз записыва-
ются как:
7(л-) 0 = 1,-,#); (5.4.28)
7=1
IX =1 о=1,-л).
7=1
Уравнение теплового баланса:
9(Л>) F,A/z,f + L^lAh^ - L,Ah, + Vl+lAH,+l - V,АН, + A2,n =0 (i = 1,..., N).
Выражения для энтальпий газового и жидкого потоков записываются
следующим образом:
10(7V) Ah,=Y^x, 0 = 1,-, У);
7=1
11М АН,=^АН^х,} 0 = 1,-,#).
7=1
Выражения для энтальпий индивидуальных компонентов паровой и
жидкой фаз:
12(77.„) Ah^1 =a^+bfT,+c^Tl2+d^T3 0 = 1,-Л; j = 1,...,и);
=а^+b^T,+cvJT,2+d^T3 0 = 1, ...,#; j = l,...,n),
где aL,bL,cL, dL,av,bv,cv,dv - известные константы
для жидкой и паровой фаз.
Для удобства расчётов необходимо сложить уравнения системы (5.4.28) с
учётом стехиометрических соотношений 7(ЛГ) и 8(л>), в результате чего получаем урав-
нение баланса потоков на каждой тарелке 8^), а соотношения 8^) исключаем из
системы (5.4.28):
8(;, F,+L,_1-L,+l/+1-)/=0 0 = 1,-,#).
Таким образом, получается система (5.4.28) из (8#*тг + 5N) независимых уравне-
ний:
- 8 уравнений: ^.n), ^.л), 3(Л,.п), 1(Лг.л), 12(Лг.„), 13(Лг.л);
- 5 # уравнений: 7(N), 8JN), 9(N), 10(N), 11(n),
и в качестве определяемых переменных выбираются также (8#*тг + 5N) переменных:
= == = = =(о) _ _ _ _ _ = =
Х(л?«л); y^N,„yE(N.„y, у #(л,.„); Р^у, T^NyL^Ny Ah^; AH^Ny Ah^,ny AH^,^,
т.е. получена система нелинейных уравнений (5.4.28), для решения которой мето-
дом декомпозиции можно использовать приведенную ниже информационную мат-
рицу (табл. 5.14).
При решении уравнений 7^,9^) происходит коррекция определяемых в
них величин.
5.4. Математические модели процессов разделения:ректификации и абсорбции 341
Таблица 5.14. Информационная матрица математического описания стационар-
ного режима процесса непрерывной ректификации в тарельчатой колонне
Во внутреннем итерационном цикле решается система нелинейных уравнений l(W.n)
системы (5.4.28) относительно х :
i = l,...,N, j = i,...,n. (5.4.29)
Во внешнем итерационном цикле решается система нелинейных уравнений 7 от-
носительно температур Т:
£yy{f}-l = O, i = l,...,N (5.4.30)
7=1
В самом внешнем итерационном цикле решается система нелинейных уравнений 9
относительно расхода потока паровой фазы V :
+L, , {v }- A, {v {v }+ {v {v }- V, {v {v }+ Д<2,П =0
(1 = 1,... Л). (5А31)
Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима тарель-
чатой ректификационной колонны ВР-методом (bubble point) изображена на рис. 5.38.
342
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.38. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима
тарельчатой ректификационной колонны ВР-методом
Для решения системы уравнений МО во внутреннем итерационном цикле для
теоретической тарелки, уравнение (5.4.29) с учётом 2(JV,nj и из (5.4.28) может
быть записано:
i = j = l,...,n (5.4.32)
или
i = у = 1,...,п. (5.4.33)
Последнее уравнение можно записать п раз относительно концентрации каждо-
го компонента в жидкой фазе (например, компонента у):
i = l,...,N, j = l,...,n (5.4.34)
или для каждогоу-го компонента на Nтарелках с учётом того, что тарелок с номером
I = 0 и i = N + 1 не существует:
5.4. Математические модели процессов разделения: ректификации и абсорбции 343
1 fl ("Ч.; ’ X2,j )— 0;
2 /2Ur'x2/^J=°;
1 fn-1 \XN-2,J ’ XN-1,J ’ XN,.
№ fn{XN-1,j’ XN,j)= 0 •
Таблица 5.15. Информационная мат-
рица системы уравнений, решаемой во
внутреннем итерационном цикле ВР-
методом для произвольного компонента
(5.4.35)
)=0;
Последняя система уравнений решает-
ся п раз для каждого компонента, для чего
используется метод решения трёхдиаго-
нальных систем уравнений, отраженный в
информационной матрице (табл. 5.15).
При решении корректирующего урав-
нения 1 в (5.4.35) относительно xN:
fi(xi{xA 0 (5.4.36)
определяется распределение произвольно-
го компонента (например, у) по высоте
колонны:
Xi, -^2 » • ’ "^V •
Для всех компонентов при «-кратном
решении получается искомая матрица кон-
центраций жидкой фазы на каждой тарелке:
Реш.1 Реш .2 Решп
Комп. 1 Комп.2 Компл
Хц *12
XN*n ~ х21 Х22 • Х2„
XN1 XN2 XNn
(5.4.37)
После этого производится нормировка состава жидкой фазы на каждой тарелке:
• для тарелки 1
норм
Л1;
(5.4.38)
• для тарелки N
x"r=xNJ/tx^’ 7 = (5-4.39)
Полученные нормированные значения исполь-
зуются для дальнейших расчётов (см. рис. 5.38).
Если при парожидкостном равновесии жидкая
фаза неидеальна и константа равновесия зависит
от состава жидкой фазы, то решение системы урав-
нений, решаемой во внутреннем итерационном
цикле рассмотренным методом, повторяется до тех
пор, пока нормированные значения
хкорМ (J = i J = 1,...,п) на двух последующих
итерациях не совпадут.
Рис. 5.39. Схема итерационных
циклов решения системы уравне-
ний МО стационарного режима
тарельчатой ректификационной
колонны ВР-методом
344
Глава 5. Физико-химические модели. Построение моделей
В результате схема итерационных циклов решения системы уравнений (5.4.28)
имеет вид, показанный на рис. 5.39.
5.4.2. Математическая модель процесса
непрерывной многокомпонентной ректификации
в насадочной колонне
Схематическое изображение простой насадочной ректификационной колонны с
одним потоком питания F и двумя потоками отбора — дистиллята D и кубового
продукта Wпредставлено на рис. 5.40.
Создаётся математическая модель стационарного режима этого процесса. При
этом принимается допущение о том, что питание в колонну подаётся в виде жидко-
сти при температуре кипения с известным составом х'. Количество отбираемого
дистиллята D и величина орошения (флегмы) L заданы.
Принимается также допущение о равенстве скрытых теплот испарения и тепло-
емкостей компонентов, что позволяет считать постоянными величины потоков пара
и жидкости в отпарной и укрепляющей секциях насадочной колонны, высоты кото-
рых соответственно равны Й''1 и Й2\ Поэтому нет необходимости включать в состав
математического описания уравнения тепловых балансов и стехиометрическое соот-
л
ношение для состава жидкой фазы (^lx] = 1).
7=1
В результате для описания процесса достаточно использовать уравнения поком-
понентных балансов и стехиометрическое соотношение для состава равновесной
паровой фазы =1 (см. табл. 2.1).
7=1
Поскольку количество отбираемого
дистиллята D задано, количество кубо-
вого продукта W определяется из урав-
нения общего материального баланса
колонны:
W=F~D. (5.4.40а)
С учётом заданной величины ороше-
ния (флегмы) L и принятых допущений
величина потока пара одинакова в от-
парной (верхний индекс «(1)») и укреп-
ляющей (верхний индекс «®») секциях
колонны и равна:
V = 0» = 0» = D + L. (5.4.406)
При этом поток жидкости в укрепля-
ющей секции колонны равен Lm, а в от-
парной (см. рис. 5.40):
£(1) = £(2) + /7 (5.4.40b)
В этом случае также принимается, что
в пределах секций колонны движение
потоков может быть описано гидроди-
намической моделью идеального вытес-
I Конденсатор |
Ь(2)хд | | Уу^
Укрепляющая ГуР>'(Я®)Т
секция ! Н''2’
£<2>х<2)(0) (2) И/2>(0) j
Зона питания
Отпарная
секция
(1)
L(1)0O) ,, ^Vy%
ч 'w
I Кипятильник
Рис. 5.40. Схематическое изображение
простой насадочной ректификационной
колонны
^’(я^Т'й,
5.4. Математические модели процессов разделения: ректификации и абсорбции 345
нения, а в кипятильнике и конденсаторе — моделью идеального смешения, причём
конденсатор является полным, а не парциальным.
Допускается, что при описании фазового равновесия жидкость—пар паровую и
жидкую фазы в колонне можно считать идеальными и жидкость в колонне находит-
ся при температуре кипения.
Предполагается, что массопередача является эквимолярной (5.4.13), матрица ко-
эффициентов массопередачи многокомпонентной смеси — диагональная (5.4.17) и
что коэффициенты массопередачи одинаковы в пределах секций колонны и равны
— для отпарной и j^WXz) — ддя укрепляющей секции, а площади поверхно-
сти массопередачи и /?м(2) соответственно в отпарной и укрепляющей секциях
равномерно распределены по их высоте.
Математическое описание процесса в насадочной секции колонны
При описании движения потоков паровой и жидкой фаз в произвольно выбран-
ной секции колонны (отпарной или укрепляющей) гидродинамическими моделями
идеального вытеснения с учётом принятых допущений можно записать следующие
уравнения покомпонентных балансов (см. табл. 2.1 и 2.2):
а) для паровой фазы
V^- = —g/00, j = i (5.4.41)
dhH J v '
где локальная скорость массопередачи для паровой фазы (верхний индекс «(И*»):
g^> = K^v>(y^-yj), j = (5.4.42)
б) для жидкой фазы
dx, FM и,,,
L—r =------g“(\ j = l,...,n, (5.4.43)
dh Н 1
где локальная скорость массопередачи для жидкой фазы (верхний индекс «*°»):
g“(L> = _XjY j = 1,п. (5.4.44)
С учётом того, что для локальных интенсивностей источников массопередачи в
случае процесса ректификации будет справедливо (5.4.13):
= (5.4.45)
а также принимая во внимание, что уравнения покомпонентных балансов записаны
в разной системе координат — huh', имеющих противоположное направление из-за
противоточного движения жидкой и паровой фаз (сравн. с разд. 5.2.4):
h=H~h', (5.4.46)
где Н - высота слоя насадки, h,h'~ текущие координаты;
и, соответственно:
dh = — dh',
уравнения покомпонентных балансов с учётом выражений для локальных.скоростей
(5.4.42)—(5.4.44) могут быть записаны в единой системе координат й:
dv
V—d- =---j = l,...,n- (5.4.47)
dh H 1 1 1 ’ v ’
dr
Ь^~К“т(у^-У]), j = l,...,n. (5.4.48)
an H
346
Глава 5. Физико-химические модели. Построение моделей
Учитывая равенство правых частей уравнений (5.4.47) и (5.4.48), последнее диф-
ференциальное уравнение можно записать конечным уравнением следующего вида:
v(y,-y,(0))=L(x,-x,(0)) j = \,...,n, (5.4.49)
где у(0), .х(О) — составы соответственно паровой и жидкой фаз при значении теку-
щей координаты слоя насадки й = О(о</г<Я).
Таким образом, для секций насадочной колонны при условии стационарности
процесса будут справедливы следующие уравнения:
Я-у
= K"V'(y<:'' >,Д j = 1’-’п; (5А5О)
V(y} -у}(О)) = ь(х} -х/0)) j = 1,...,л, (5.4.51)
уравнения фазового равновесия (5.4.6) и 2(л) и 4 из системы (5.4.3):
У1: = 1 j = Р (5.4.52)
Р° = ехр ' В] , 7 = 1,- (5.4.53) (5.4.54)
J С,+Т к 1 > 7=1
Последние (4п +1) уравнения должны быть повторены в общей системе уравне-
ний математического описания рассматриваемого процесса два раза с разными верхни-
ми индексами для отпарной и укрепляющей секций ректификационной колонны.
Математическое описание процесса в кипятильнике
Так как для процесса в кипятильнике принята гидродинамическая модель иде-
ального перемешивания с учётом интенсивностей источников, связанных с измене-
нием агрегатного состояния при фазовом переходе (см. табл. 2.1 и 2.2), уравнение
покомпонентного баланса будет иметь вид:
- Wxwj -Vy$ =0, j = l,...,n. (5.4.55)
Система уравнений дополняется уравнениями фазового равновесия (в данном
случае идеальной жидкой и паровой фаз):
Уч = Р4Х4/pw, j = i, ,*; ( в, '\ (5.4.56)
Рч = ехР 14,+ w , 7=1,...,п; С.+Т \ } 7 (5.4.57)
£у£=1. (5.4.58)
Математическое описание процесса в полном конденсаторе
С учётом принятой модели идеального смешения для процесса в полном конден-
саторе будут справедливы следующие уравнения покомпонентного баланса:
Vy(S = Dy» + - j =1--« • (5.4.59)
5.4. Математические модели процессов разделения: ректификации и абсорбции 347
Для процесса в полном конденсаторе может быть записано равенство:
yoj=xDj’ j = (5.4.60)
и, с учётом общего баланса для потоков колонны (5.4.59), математическое описание
процесса в полном конденсаторе принимает вид:
^’"^=0, j = i,...,n. (5.4.61)
Математическое описание условий сопряжения между секциями насадочной
колонны
В соответствии со схематическим изображением насадочной колонны (см. рис. 5.40),
условия сопряжения должны быть записаны между пятью основными её секциями:
• кипятильником;
• отпарной секцией (секцией с верхним индексом «(1>»);
• зоной питания;
• укрепляющей секцией (секция с верхним индексом «®»);
• конденсатором.
Уравнения, описывающие условия сопряжения между кипятильником и отпар-
ной секцией, имеют вид:
x^ = x^(0), j = l,...,n; (5.4.62)
уУ’(О) = у<;;, j = \,...,n. (5.4.63)
Уравнения, описывающие условия сопряжения между отпарной секцией и ук-
репляющей секцией в зоне питания:
L(2>^2if0)+Fx'’ = Д1)х<1)(Я(1)), J=l,...,n; (5.4.64)
у'2’(0) = у(1’(Я(1’), J = l,...,n. (5.4.65)
Уравнения, описывающие условия сопряжения между укрепляющей секцией и
полным конденсатором:
xDj=x<2W2)), 7 = 1,...,п; (5.4.66)
= У? W2)), J=l,...,n. (5.4.67)
Разработка модели процесса в насадочной ректификационной колонне
Как было установлено, система уравнений МО стационарного режима процесса
непрерывной ректификации состоит из (18w + 3) уравнений, среди которых есть как
обыкновенные дифференциальные уравнения, так и конечные линейные и нели-
нейные уравнения. Дополнительные условия (начальные и краевые) для получения
частных решений дифференциальных уравнений сформированы, в основном, из
уравнений, описывающих условия сопряжения между секциями насадочной колон-
ны [(5.4.62)—(5.4.67)] и уравнения, описывающего процесс в полном конденсаторе.
В результате система уравнений математического описания включает:
• (3w + 1) уравнений для кипятильника [(5.4.55)—(5.4.58)];
• (4w + 1) уравнений для отпарной секции [(5.4.50)-(5.4.54)];
• (4w + 1) уравнений для укрепляющей секции [(5.4.50)-(5.4.54)];
• п уравнений (5.4.61), описывающих полный конденсатор;
• 6п уравнений [(5.4.62)—(5.4.67)], описывающих условия сопряжения между сек-
циями колонны.
348
Глава 5. Физико-химические модели. Построение моделей
С позиций выбора алгоритма решения производные в дифференциальных уравне-
ниях целесообразно представить в виде конечных разностей между начальной {h = 0)
и конечной (Я = й) точками их решения.
Таким образом, система уравнений математического описания этого процесса с
учётом конечно-разностного представления производных (5.4.50) [сравн. с (5.3.60)]
принимает вид:
1(л) L«4>-W^-%’=0 (у = 1,...,и);
2(„, у^р^/р” (j = !,-,«);
п).
5
4 Е^) = 1;
i=i
5(„, 4,М’(0) (j = 1,...,»);
6(„) уУ’(О) = у« (j = !,...,«);
7(„) Дй _ FMl^ £-M(v)(i)/ (.)(1) _ (i)\ - у(1)Я(1) » VJ yj ' (7=1,...,п);
8(„) V(1)(yW(^(1)) - yW(0)) = Ь(1) (xj0 (Я(1)) -х<‘>(0)) (j = !,...,«);
’w р( vwa) О 1 (i 1 «V
У1 р(1) <7
10(„) 11 Ру0(1) = ехр 7=1 ' в 4'+с,А"> (1’' ); \ 7 У 1;
(5.4.68)
12(„) L(2)x'2>(0) + Fxf = Д(1)х«(Я(1)) (j = 1,...,п);
13(„) у<2’(0) = у(1’(Я(1)) 0 = 1,...,и);
у<2)(Я(2’)-/2’(0) _ F1 14 W дй - v Р) 15(„, V%^(H^)~y(p(0)) = р°(2)г(2) 1б(-) f D 4 17/ \ р°(2) _ РУП л J- 7 0 = 1 £(2’(х(2’(Я(2))-х'2)(0)) (у=1,...,п); 0; (У=1 п);
1/(н) г, ехр ду I < 7
5.4. Математические модели процессов разделения: ректификации и абсорбции 349
18 5Х)(2) = 1;
7=1
19(„) xD]=x^\h(2>) (j=1,...,«);
20(„) 4) = y?’(w(2)) (j = l,-,«);
21(„) Уо?-^=0 0=1,-,и).
Представленная система (18и + 3) уравнений математического описания (5.4.68)
решается относительно следующих (18и + 3) определяемых переменных:
в кубе колонны — х§\ xw, у$\ P^,TW;
в первой — отпарной секции — х^(0), х^\н^), у^(0), у(,)^\ Р°®, Т^\
во второй — укрепляющей секции — х(2\0), х(2\я(2'), у(2\0), у(2\я(2'), у(')(2\ р°(2\т(2Х
в полном конденсаторе — xD, у $
Все остальные переменные и константы, в том числе и коэффициенты физико-
химических зависимостей, например, коэффициенты уравнения Антуана для расчё-
та давлений насыщенных паров индивидуальных веществ (5.4.53) и (5.4.57) и диаго-
нальные элементы матрицы коэффициентов массопередачи (5.4.17) и (5.4.50), долж-
ны быть заданы.
Таким образом, при такой постановке задачи выполняется поверочно-оценочный
расчёт стационарного режима процесса в насадочной ректификационной колонне.
При этом для каждой из секций (1) и (2) решается система 1п дифференциальных
уравнений покомпонентного баланса (5.4.50) и (5.4.51), последние п из которых для
определения х заменены конечными уравнениями (5.4.51), что существенно упро-
щает процедуру расчётов.
В результате для переменных у(1),х(2\ у(2* получаются не только конечные
точки решения, такие как х(1)(0), х(1)(Я(1)), х(2)(0), х(2)(Я(2)), но и профиль изменения
составов фаз для каждой из секций x(1)(/i), y(1)(/i), x(2)(/i), y(2)(/i) (где 0< h< H ), т.е.
получаемые решения имеют вид:
х^\0)<х^<х^{Н^У,
у^(0)<У1(й)<у^(Н(1));
х<2)(0) < x2(h) < х®(Н(2)); (5.4.69)
у'2)(0)<у2(Л)<у'2’(Я(2)).
Одновременно с изменением указанных определяемых переменных изменяются
и остальные определяемые переменные (ут,Р°,Т) вдоль пространственной коор-
динаты h в циклах решения задачи, связанных с решением конечно-разностных урав-
нений 7(п) и 14(п), аппроксимирующих соответствующие дифференциальные урав-
нения, и конечных уравнений 8(л) и 15(„).
Информационная матрица системы уравнений (5.4.68) и соответствующий алго-
ритм её решения приведены в табл. 5.16 и на рис. 5.41.
В соответствии с выбранным алгоритмом расчёта в самом внешнем итерацион-
ном цикле решения задачи задаётся начальное приближение по составу кубового
350
Глава 5. Физико-химические модели. Построение моделей
продукта .хи, (блок ввода на рис. 5.41), после чего при заданном приближении тем-
пературы в кипятильнике Tw (блок ввода на рис. 5.41) по уравнениям 3(„j, 2(л)И
системы (5.4.68) в итерационном цикле расчёта фазового равновесия жидкость—пар
определяется температура Т" и состав равновесного пара в кубе колонны у'^'.
После этого по уравнениям покомпонентного баланса для процесса в кипятиль-
нике!^ вычисляется состав жидкости jffl, поступающей в куб колонны, а по урав-
нениям 5(„) и 6(„) соответственно — начальные условия решения системы дифферен-
циальных уравнений 7(„) и 8(„j для первой отпарной секции колонны, образуя цикл
Таблица 5.16. Информационная матрица системы уравнений математического
описания стационарного режима непрерывной ректификации в насадочной колонне
”\ (0)- 1^ t-ч J4, Т;? о ©я io. J5, о ечО s о. о е'с |>Г S 10. м4 №
1(л) © © 4
2(Л) □ © 2
3(л) и 1
4 Кор.ур © 3
5(л) © 5
6(л) © 6
© © 10
8(л) © © © 11
9(л) © © 8
10(л) □ 7
и Кор.ур. © 9
12(л) © 12
13(л) © 13
© © 17
15(«) © © © 18
16(л) • © © 15
Цл) □ 14
18 Кор.ур. © 16
19(л) © 19
© 20
© © 21
*1
Ввод
XW^ i
/ЧО /’(2)
Z(2>, Lm
/4 />)
Lm, Lm
^(1) fX2)
p(l) p(2)
P* ДЛ
A, B,C
-
К^(Ю(2)
i<2>(A)
х(1)(Л)
x(1)(//(I))
ж
7*(1)
y('\h}
f(2)
x<2)(0)
ТЪ(2)(0)
13
16 7*d
mJ—*L_ie
: ^(2)
>-<2’(Л)
х<2’(Я<2))
w
Вывод
X x<°>
xw xw
>(0), p°
J’W w
У(”(0)
х(1)(Я(1))
x(1)(0)
/•)(')
p'o(i) r(i)
у<2>(Я<2))
>'®(0)
x,2>(//(2))
x(2)(0)
j;CM2)
/>0(2) 7<2)
y(0) у
yD ' XD
Рис. 5.41. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима насадочной ректификационной колонны
5.4. Математические модели процессов разделения: ректификации и абсорбции 351
352
Глава 5. Физико-химические модели. Построение моделей
решения этих дифференциальных уравнений по высоте слоя насадки в секции (|):
О < h < Н® [изменение составов жидкой и паровой фаз представлены в этом цикле
пунктирными линиями и обозначаются соответственно и у^(Л)]. Следует
отметить, что, хотя уравнения 8(л) и не являются дифференциальными, они равно-
сильны им, и с их использованием более просто получается профиль изменения
состава жидкой фазы по высоте насадки х, (й), где о < h < Н
Внутри цикла решения дифференциальных уравнений 7(л) (блок ввода на рис. 5.41)
и 8(„) при заданном начальном приближении температуры Т® с помощь уравнений
10(л), и ii(„) решается задача определения равновесного состава паровой фазы
и температуры кипения . Эта задача определения Pai'\ yw®, Т® решается
для каждого шага решения дифференциальных уравнений, то есть указанные вели-
чины равновесных составов зависят от пространственной координаты — высоты слоя
насадки h. В соответствии с принятыми допущениями так определяется профиль
изменения температуры по высоте слоя насадки в отпарной секции (1).
В результате решения системы дифференциальных уравнений 7(л) и 8(л) кроме
определения изменения равновесной температуры по высоте слоя насадки находят-
ся также изменения концентраций жидкой и паровой фаз — соответственно х(1\й)
и у (1\й), где 0 < h < Н(1).
Далее по уравнениям 12(л) и 13(„), описывающим условия сопряжения между
секциями с индексами «(1)» и «<2>» колонны в зоне питания определяются начальные
условия х(2>(0) и у(2)(0) для решения системы дифференциальных уравнений 14(л) и
15(„) для укрепляющей секции.
Процедура расчёта процесса в укрепляющей секции (верхний индекс «<2>») полно-
стью совпадает с вычислениями, проведёнными для отпарной секции (верхний ин-
декс «<п»). Во внешнем цикле решения системы дифференциальных уравнений 14^
и 15(„) определяется профиль изменения состава жидкой и паровой фаз соответ-
ственно по высоте слоя насадки у^2\й) и x^\h), где 0<й<//(2). Во внутреннем
цикле на каждом шаге решения системы дифференциальных уравнений 14(„) и 15(л)
вычисляются р0<2>*? у<*)(2), (уравнения Г7(„), 16(л) и 18(л)), то есть условия фазово-
го равновесия жидкость—пар (сначала задаётся начальное приближение f в блоке
ввода).
В результате для укрепляющей секции получается (по аналогии с отпарной сек-
цией) профиль изменения равновесных температур по высоте слоя насадки
0<h< Н(2).
После этого по уравнениям 19(я) и 20(л), описывающим условия сопряжения
между укрепляющей секцией и полным конденсатором, определяется состав пара,
поступающего в конденсатор у£> и состав дистиллята xD. Компоненты этих двух
векторов зависят от состава кубового продукта xw , заданного приближённо в самом
5.4. Математические модели процессов разделения: ректификации и абсорбции 353
внешнем цикле решения задачи вначале рас-
чётов, то есть для них будет справедливо:
(5А70)
При подстановке алгоритмических зависи-
мостей (5.4.70) в уравнения 21(„), описываю-
щие полный конденсатор, получается нели-
нейная система уравнений для коррекции xw
в самом внешнем цикле решения задачи сле-
дующего вида:
j = l,-,n. (5.4.71)
Решение системы (5.4.71) относительно
состава кубового продукта х£} означает, что
получено решение всей системы уравнений
МО (5.4.68) стационарного режима процесса
непрерывной ректификации в насадочной
колонне.
Схема циклов решения этой задачи, соот-
ветствующая информационной матрице МО
процесса (см. табл. 5.16) и блок-схеме алго-
ритма расчётов (см. рис. 5.41), приведена на
рис. 5.42.
Таким образом, при реализации повероч-
но-оценочного расчёта стационарного режи-
ма насадочной ректификационной колонны
получается профиль изменения составов па-
ровой и жидкой фазы, а также температур по
высоте колонны.
Рис. 5.42. Схема циклов поверочно-
оценочного расчёта стационарного
режима насадочной ректификационной
колонны
5.4.3. Математическая модель процесса
многокомпонентной абсорбции в насадочной
колонне
Для построения математической модели процесса многокомпонентной абсорб-
ции (рассматривается процесс физической абсорбции) в насадочной колонне рас-
смотрим непрерывный процесс в стационарном режиме на рис. 5.43. В данном слу-
чае h — текущая система координат; h' — текущая обратная система координат; Н —
высота слоя насадки; h'= Н -h.
Входные потоки жидкости L(0) и газа G(0), а также их составы х,(0), у,(0) (г = 1,...,п)
заданы. Температура по высоте колонны постоянна и равна заданному значению,
вследствие чего из уравнений МО процесса исключены уравнения тепловых балан-
сов. Содержание абсорбируемых компонентов в газе относительно мало, и допуска-
ется, что условия фазового равновесия могут быть описаны для всех компонентов с
использованием закона Генри:
у^=К,х,, !=1,...,л, (5.4.72)
где Kt — постоянная Генри для каждого компонента.
23-4544
354
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.43 Схематическое изображе-
ние процесса многокомпонентной
абсорбции насадочной колонне
В качестве гидродинамических моделей дви-
жения жидкости и газа в колонне принимаются
модели идеального вытеснения. Предполагается,
что массопередача при абсорбции происходит
только в направлении от газа к жидкости, что
приводит к изменению как расхода газа G, так и
расхода жидкости L по высоте колонны Н. Коэф-
фициенты массопередачи компонентов при
выражении движущей силы процесса абсорбции
в концентрациях газовой фазы (5.4.12)-(5.4.18)
предполагаются известными и постоянными по
высоте колонны. Недиагональными элементами
матрицы коэффициентов многокомпонентной
массопередачи (5.4.16) можно пренебречь (5.4.17).
Определяются расходы газа G и жидкости L, ухо-
дящие из колонны, и их составы соответственно
У и X •
Математическое описание процесса в насадочной секции колонны
В соответствии с принятыми допущениями для каждой из фаз можно записать сле-
дующие уравнения покомпонентного баланса и общего баланса массы (см. табл. 2.1, 2.2
и рис. 5.43):
• для газовой фазы в системе координат о < h < Н
. = 1.». <5.4.73)
где локальная скорость абсорбции вычисляется по формуле:
^^К.^Чу^-у,), (5.4.74)
[причём, равновесные концентрации газовой фазы у**’ (i = !,...,«) определяются по
закону Генри (5.4.72)] и
в данном случае краевые условия для решения системы (п + 1) дифференциальных
уравнений имеют вид:
Х(О) = у,(о), г (5.4.76)
G(O) = G(o); (5.4.77)
• для жидкой фазы в системе координат о < h' < Н :
d(Lx) F , . = р , 1 =: dh' Н ' (5.4.78)
(5.4.79)
dL FM уЦ M(L) dh H (5.4.80)
5.4. Математические модели процессов разделения: ректификации и абсорбции 355
• краевые условия для решения системы (п + 1) дифференциальных уравнений в
данном случае имеют вид:
х,(О) = х,(о)> ! = и);
(5.4.81)
MO) = L(o). (5.4.82)
Учитывая то обстоятельство, что в процессе абсорбции при массопередаче осу-
ществляется перенос компонентов газовой фазы в жидкую и будет справедливо:
i = !,...,л, (5.4.83)
и для перехода к единой системе координат 0 < h < Н [см. (5.4.46)] можно восполь-
зоваться уравнением:
h = H-h', (5.4.84)
откуда следует, что
dh = -dh'. (5.4.85)
В результате чего вместо уравнений (5.4.78) и (5.4.80), описывающих поведение
жидкой фазы, можно записать:
и
dh н
dL
dh
р.м
Н
£^(С)
i=i
(5.4.86)
(5.4.87)
При этом краевые условия для жидкой фазы (5.4.81) и (5.4.82) в системе коорди-
нат о < h < Н с учётом (5.4.84) принимают вид:
х,(Н) = х,(0), г = 1,...,п; (5.4.88)
t(H) = t(o). (5.4.89)
Таким образом, в систему уравнений МО процесса включаются уравнения для
газовой фазы (5.4.73), (5.4.74), (5.4.72) и (5.4.75) с краевыми условиями (5.4.76) и
(5.4.77) и уравнения для жидкой фазы (5.4.86) и (5.4.87) с краевыми условиями
(5.4.88) и (5.4.89).
Так как правые части дифференциальных уравнений (5.4.72) и (5.4.86), а также
(5.4.75) и (5.4.87) одинаковы, то для них будет справедливо:
<Z(Gy,) d(Lx,) . ,
(5.4.90)
ah ап
dG dL
dh dh
и вместо дифференциальных уравнений для жидкой фазы (5.4.86) и (5.4.87) можно
записать следующие конечные уравнения:
Gy,-G(0)y,(0) = Lx, -L(0)x,(0), i = l,...,n; (5.4.92)
G-G(O) = L-L(O). (5.4.93)
Таким образом получается система уравнений математического описания про-
цесса с дифференциальными уравнениями первого порядка и краевыми условиями,
которая включает в себя следующие уравнения:
356
Глава 5. Физико-химические модели. Построение моделей
• для газовой фазы (уравнение (5.4.73) записывается в явном виде):
/=1 п.
dh GH G dh' ’ ’ ’
gM(G> = _уi = (5.4.94)
у,(,) = К,х„ i =
dG FM M(C)
dh H [ -j
с краевыми условиями (5.4.76) и (5.4.77):
Х(О) = У,(о)> i = l-,n;
G(O) = G(o);
• для жидкой фазы (5.4.92) и (5.4.93):
Gy, -(7(0) у,(0) = Lx, -L(0)x,(0), i = ;
G-G(0) = L-L(O)
с краевыми условиями (5.4.88) и (5.4.89):
x,(H) = х,(0), i = l,...,n; L(H) = L(0).
Следует отметить, что уравнения (5.4.95) заменяют дифференциальные уравне-
ния (5.4.90) и (5.4.91), так как они позволяют при каждом текущем значении у(й) и
GfTi), получаемых при решении дифференциальных уравнений (5.4.94), определять
соответствующие им значения х(й) и L(h). При этом в процессе решения производ-
ная в правой части дифференциальных уравнений (5.4.94) заменяется правой частью
дифференциального уравнения общего баланса массы для газовой фазы (5.4.75).
В окончательном виде система уравнений математического описания этого про-
цесса включает (6л + 4) уравнений и имеет вид:
1 ^l =
(n) dh GHG dh
(i = l,...,n);
2
4
dG = P^_f «<C).
dh н
Gy,- G(0)y,(0) = Lx, - L(0)x,(0) (i = 1,..., n);
G-G(O) = L-L(0);
5W gM(G) = CV-y.) a = i,...,n);
6(„) y^ = K,x, (!=l,...,n)
Vn) x(°) = >'.(0) (!=l,-,n);
2' G(°) = G(o);
(5.4.96)
3(„) x,(H) = x,(0'j (i = l,...,n);
4' L(H) = L(o)
5.4. Математические модели процессов разделения: ректификации и абсорбции 357
Так как дополнительные условия 1^, 2', 3(п)и 4' являются краевыми и заданы
при различных значениях независимой переменной й — й = 0 и й' = Я, то для опреде-
ления частного решения системы (5.4.96), имеющего практическое значение, следует
использовать известный численный алгоритм решения краевой задачи (см. разд. 3.5.1).
Для реализации алгоритма решения краевой задачи для системы дифференци-
альных уравнений (5.4.96) следует выполнить некоторые преобразования [см. (5.4.97)]:
• производные в уравнениях 1<л) и 2 записать в виде конечных разностей;
• правые части указанных дифференциальных уравнений обозначить соответ-
ственно как f и f-
J 1 •'2’
• в уравнениях 3(„> и 4, заменяющих дифференциальные уравнения (5.4.90) и
(5.4.91), вместо текущих значений у, (г=1,..., л) и G следует использовать их
конечные значения у, (Я) («= !,...,«) и G(ff),
• задать начальные приближения для выполнения расчёта %(0) и L(0);
• коррекцию этих начальных приближений проводить по краевым условиям З^и 4'.
Разработка модели процесса в насадочной абсорбционной колонне
Система уравнений, описывающая процесс абсорбции в конечно-разностном виде
(в данном случае Дй = Я — 0 = Я) и аппроксимирующая СОДУ, имеет вид:
iw у,(Я)-у,(0)^ Дй Я а‘ G dh 711
2* G(ff)-G(0)~ Дй
2*] 17 Л/ п П (=1
G(H)y, (Я) - G(0)y, (0) = £(Я)х, (Я) - Ц0)х, (0) (i
4 С(Я)-С(0) = ЦН)-Ц0);
gM(G> = _ у у (j = „J .
6(») у^} = Ktx, (i = l,...,n);
V") М°) = У,(о) (i=l,-,n);
2' G(O) = G(o);
х,(Я) = х,(0) (! = l,...,n);
4' L(H) = L(o}.
= 1,...,п);
(5.4.97)
Результатом решения системы (би + 4) уравнений (5.4.97) являются следующие
(6л + 4) переменные:
• составы паровой и жидкой фаз при й = 0ий = Я, то есть у(0), х(0), у(Н) и
х(Я): 4и переменных, или, строго говоря, изменение этих переменных по вы-
соте слоя насадки, у(й), х(й) при о < h < Я ;
358
Глава 5. Физико-химические модели. Построение моделей
Таблица 5.17. Информационная матрица системы уравнений математического
описания стационарного режима процесса непрерывной абсорбции в насадочной
колонне
л\ G(0) Л W» Vя) ДО) L(H) gM(G) Л»
Диф УР © © © © 6
2* Диф ур © © 7
2*] © 5
3(л) © © © © © © © 9
4 © © ["+] 8
5(") © © 4
6(Л) ["+] 3
Цп) 1
2' 2
Л © 10
4' Кор ур © 11
Рис. 5.44. блок-схема алгоритма поверочно-оценочного расчёта стационарного режима
насадочной колонны абсорбции
5.4. Математические модели процессов разделения: ректификации и абсорбции 359
• локальная скорость массопередачи gM!G> и равно-
весные составы паровой фазы ут для каждого шага
решения дифференциальных уравнений: 2и пере-
менных;
• расходы парового и жидкого потоков при h = 0 и
h = Н, G(0), А(0), G(H) и ЦН): 4п переменных (на
самом деле изменение этих переменных по высоте
слоя насадки, G(h) и £(Л) при о < h < Н )•
Информационная матрица рассматриваемой системы
уравнений (5.4.97) и соответствующий алгоритм её ре-
шения приведены в табл. 5.17 и на рис. 5.44.
В соответствии с рассматриваемым алгоритмом рас-
чёт начинается с задания краевых условий и 2' сис-
темы уравнений МО (5.4.97) и определения у(0) и С(0).
Для решения системы дифференциальных уравнений
и 2 необходимо сначала задать начальное приближение
х(0), соответствующее концентрации жидкости на вы-
ходе из абсорбера (см. рис. 5.43), а затем (после вычис-
ления у(,) и по уравнениям 5(п) и 6(„j) найти но-
Рис. 5.45. Схема циклов
решения краевой задачи
расчёта стационарного
режима процесса абсорб-
ции в насадочной колонне
вые значения у(й) и G(h) приближённой функции решения системы дифференци-
альных уравнений и 2. После этого, задав приближение по расходу потока жид-
кости на выходе из абсорбера Л(0), определяются соответствующие полученным
величинам у(й) и G(h) значения приближённых функций решения х(й) и £(Л) по
уравнениям 3(„) и 4. Цикл решения системы дифференциальных уравнений выпол-
няется в диапазоне 0 < h < Н для независимой переменной h.
Полученные финальные значения функций х(Я) и ЦН) соответствуют точке пода-
чи жидкости в колонну, то есть месту, где должны выполняться краевые условия 3(„) и
4'. Так как результаты решения системы дифференциальных уравнений зависят от
начальных приближений %(0) и L(0), то в этом случае краевые условия 3[„> и 4' превра-
щаются в уравнения коррекции указанных величин вида:
хДЯ){х(О),Е(О)}-х,(о) =0 (г = 1,...,п);
ЦЯ)^(О), L(0)}- L(o) = 0. (5Л98)
Система в общем случае нелинейных уравнений (5.4.98) на каждой итерации ре-
шается относительно х(0) и ЦО), в результате чего получаются новые приближения
для очередного итерационного шага вычислений. Когда будет найдено решение си-
стемы уравнений (5.4.96), то итерационный процесс считается законченным и зна-
чения х(0) и ЦО) одновременно с величинами-функциями x(h), y(h), G(h) и L(h)
являются решениями уравнений МО стационарного режима процесса непрерывной
абсорбции.
Схема циклов решения этой задачи, соответствующая информационной матрице
МО процесса (см. табл. 5.17) представлена на рис. 5.45.
360
Глава 5. Физико-химические модели. Построение моделей
5.5. Идентификация и оптимизация
химико-технологических процессов
Идентификация и оптимизация процессов имеют принципиальное значение при
компьютерном моделировании химических производств. Термин идентификация со-
ответствует латинскому слову отождествление, т.е. обеспечения соответствия моде-
ли и объекта моделирования с помощью данных экспериментальных исследований
и получения адекватной компьютерной модели реального процесса.
Термин оптимизация соответствует латинскому слову наилучший, и в этом случае
ставится задача определения оптимальных (наилучших) условий протекания реального
процесса с применением адекватной компьютерной модели.
Таким образом, решение задачи идентификации должно предшествовать реше-
нию задачи оптимизации технологических процессов, так как только применение
адекватных моделей реальных процессов для определения оптимальных условий их
протекания при решении задачи оптимизации позволяет «переносить» получаемые
расчётные результаты на действующие химические производства.
Особенно важным является решение этих задач при разработке и применении фи-
зико-химических моделей, базирующихся на теоретических предпосылках. Эти моде-
ли должны обеспечивать адекватное предсказание поведения реальных объектов в
широких диапазонах изменения параметров процессов и в связи с этим наиболее
пригодны для определения оптимальных условий протекания процессов, т.е. реше-
ние задачи оптимизации технологических процесс.ов.
5.5.1. Решение задачи идентификации
математического описания
Идентификация представляет собой основной этап построения адекватной мате-
матической модели и сводится к определению конкретного вида функционального
оператора статических моделей Ф (отображают стационарные режимы процессов)
или динамических моделей Ф, (отображают нестационарные режимы процессов) (1.2):
. , (5.5.1)
где t — независимая переменная времени; X — вектор входных воздействий; a —
коэффициенты математической модели.
Задача идентификации заключается в определении структуры системы уравнений
математического описания и значений её коэффициентов, которые обеспечивают
наилучшее совпадение выходных переменных модели и процесса при одинаковых
входных воздействиях (X ). Успешное решение задачи идентификации обеспечива-
ет адекватность (соответствие) модели моделируемому объекту.
Важной особенностью решения задачи идентификации является то обстоятель-
ство, что при этом реальный процесс рассматривается не как самостоятельный объект
исследования, а совместно с контрольно-измерительными приборами (КИП), позво-
ляющими судить о протекании реального процесса по данным наблюдений. При иден-
тификации решающее влияние оказывают экспериментальные ошибки двух типов:
• шум объекта w(t);
• шум приборов v(t).
С учётом этих факторов процедура идентификации схематически может быть
представлена в следующем виде (рис. 5.46), где X =[Х1,..., Х„]т — /«-мерный вектор
5.5. Идентификация и оптимизация ХТП
361
Рис. 5.46. Блок-схема процедуры идентификации динамической математической модели
входных переменных; у = [ур..., уг]т — r-мерный вектор выходных переменных (у —
его рассчитанное по модели значение); у3™" = [у1эксп,..., у„'кс"]т- и-мерный вектор на-
блюдений выходных переменных (и < г) с помощью КИП. (Не все выходные пере-
менные можно и целесообразно измерять.)
Структурная идентификация математической модели предполагает по данным
наблюдения векторов Х(?) и [если возможно, и vv(r), v(r)] определение струк-
туры уравнений математического описания, т.е. вида и размера системы уравнений
МО, а также значений неизвестных коэффициентов a(t).
Как правило, при решении задачи структурной идентификации приходится де-
лать выбор среди конкурирующих моделей с целью определения той из них, которая
наиболее точно отражает экспериментальные данные.
Параметрическая идентификация математической модели проводится после того,
как форма модели ориентировочно выбрана и в распоряжении имеются данные о
переменных на входе X(t) и выходе уэкс"(?) процесса, и заключается в определении
неизвестных коэффициентов a(t) системы уравнений МО.
В случае статической математической модели независимая переменная времени
в уравнениях системы уравнений МО (5.1) отсутствует, и переменные системы не
зависят от времени t (5.5.1).
При решении задачи идентификации для динамических математических моделей
переменные процесса зависят от времени г (5.5.1) и являются решениями дифферен-
циальных уравнений типа (5.2).
Чаще всего динамические математические модели применяются при прямом
компьютерном (цифровом) управлении технологическими процессами. В этом слу-
чае необходимо непрерывно в режиме онлайн в реальном времени с изменением
векторов X(t), w(t) и v(r) выбирать наилучшую модель (структурная идентифика-
ция) и оценивать её коэффициенты (параметрическая идентификация), т.е. решать
задачу адаптивной идентификации, когда модель непрерывно адаптируется к реаль-
ному процессу в смысле совпадения результатов расчётов по ней урасч(0 с данными
наблюдений у’ксп(г).
В главе 1 было показано, что количественный критерий соответствия параметров
модели и данных экспериментов (1.4), по возможности, должен быть квадратичным:
362
Глава 5. Физико-химические модели. Построение моделей
Сг = ^,(уГ-уГ)2 , (5.5.2)
1=1
где w, — весовые коэффициенты, характеризующие степень вклада наблюдаемых значе-
ний выходных переменных в оценку точности модели (в некоторых случаях их значения
принимают равными величинам, обратным оценке дисперсии измерения в z-й точке).
Приведённый критерий соответствия приемлем для решения задач структурной и
параметрической идентификации при использовании математических моделей про-
цессов, не включающих производные (5.1). При этом предполагается, что опытным
путём определены значения некоторых выходных переменных [результатов решения
системы уравнений (5.1)], в частном случае, одной переменной, например т.е.
уГ =ЖГ), 0 = 1, •••>«).
В случае математического описания процессов дифференциальными уравнения-
ми, например, вида (5.2), с различными независимыми переменными — времени t
[как в случае системы уравнений (5.2)] или пространственной координатой, напри-
мер t для объектов с распределёнными параметрами, может использоваться другой
критерий:
,«)
Сг = f X И',(ОЕуГ(0 - У™№ * • (5.5.3)
/о) /-1
Применение обоих критериев идентификации (5.5.2) и (5.5.3) предполагает пред-
варительное решение систем соответственно конечных (5.1) и дифференциальных
(5.2) уравнений для каждой экспериментальной точки i (i = 1,..., n).
Принцип решения задачи идентификации представлен в разд. 1.4 (1.5). В этом
случае во внешнем цикле процедуры решения задачи идентификации задаётся пред-
полагаемое математическое описание процесса, для которого во внутреннем цикле
процедуры решения определяются параметры — коэффициенты** выбранной моде-
ли путём минимизации либо критерия (5.5.2), либо критерия (5.5.3) в зависимости
от того, какая система уравнений решается при реализации математической модели —
соответственно (5.1) или (5.2). После этого во внешнем цикле процедуры решения
задаются другим механизмом протекания процесса — другим видом системы уравне-
ний МО, а во внутреннем цикле с использованием выбранного алгоритма оптимиза-
ции определяются оптимальные значения параметров — коэффициентов модели, обес-
печивающие наименьшее значение одного из критериев (5.5.2) или (5.5.3). Это про-
должается до тех пор, пока не удастся найти такой вид системы уравнений математи-
ческого описания процесса и значения её коэффициентов, которые соответствуют
наименьшей величине либо критерия (5.5.2), либо критерия (5.5.3)***.
Критерии (5.5.2) и (5.5.3) можно рассматривать как количественные показатели
степени адекватности математической модели. Так как они включают в себя данные
опытных измерений, то следует обратить особое внимание на то обстоятельство,
насколько они (конкретная выборка из генеральной совокупности данных —
см. главу 4) являются репрезентативными (представительными). Только применение
* Для объектов с распределёнными параметрами независимая переменная времени t
в критерии (5.5.3) заменяется на пространственную координату t .
** При минимизации критерия (5.5.3) одновременно с коэффициентами, в общем
случае зависящими от независимой переменной дифференциального уравнения, на-
пример t в (5.2), могут определяться и начальные условия, например, Г в (5.2).
*** Величины рассогласования экспериментальных и расчётных значений не долж-
ны быть меньше погрешностей опытных измерений.
5.5. Идентификация и оптимизация ХТП
363
репрезентативных эксперимен-
тальных данных для оценки
адекватности моделей следует
считать правомочным.
Целесообразно рассмотреть
два вида адекватности матема-
тической модели (ММ):
• адекватность состояния;
• адекватность поведения.
Для обеспечения адекватно-
сти состояния обычно прихо-
дится решать задачу идентифи-
кации ММ, в частном случае
задачу коррекции её параметров
(коэффициентов). При этом
параметры модели получают для
какой-либо одной совокупнос-
ти входных переменных. Най-
денное минимальное значение
критерия адекватности (5.5.2) и
(5.5.3) в этом случае служит ко-
личественной оценкой досто-
верности принятой структуры
уравнений МО.
Адекватность поведения оце-
нивается для различных сово-
купностей входных перемен-
ных. Разумеется, для других со-
вокупностей входных перемен-
Рис 5.47. Процедура решения задач структурной и
параметрической идентификации для типового ХТП в
единичном аппарате
ных использование параметров,
найденных при обеспечении адекватности состояния, может привести к существен-
ному отличию критерия адекватности от его минимального значения. В общем слу-
чае, минимальному значению критерия адекватности для другой совокупности вход-
ных переменных соответствует другой набор параметров модели.
Если различие коэффициентов, определяемых при разных совокупностях вход-
ных переменных из области их возможного изменения, невелико, математическую
модель можно использовать для интерполяции свойств объекта моделирования в кон-
кретной области. Если к тому же критерий адекватности незначительно изменяет
свою величину в пределах использованной области изменения входных переменных,
то возможна экстраполяция поведения модели за пределы этой области. Последнее
обстоятельство имеет принципиальное значение при исследовании свойств объекта
моделирования с помощью его математической модели и определения оптимальных
условий протекания химико-технологических процессов, так как на практике экспе-
риментальные данные о функционировании объекта чаще всего получают для огра-
ниченной области изменения переменных и, как правило, приходится прогнозиро-
вать поведение объекта (ХТП) за пределами ограниченной области изменения пере-
менных.
Общая стратегия решения задачи идентификации в единичном аппарате
В соответствии с основными принципами системного анализа (см. разд. 1.1),
используемыми при создании математических моделей ХТП, процедура решения
задачи идентификации для единичного аппарата химической технологии приведена
на рис. 5.47.
364
Глава 5. Физико-химические модели. Построение моделей
С учётом иерархичности химико-технологического процесса, использования прин-
ципа комплексного подхода к исследованию процессов и принципа иерархической
соподчинённости при разработке математических моделей, а также применяемого
при этом структурно-блочного подхода задача идентификации типового ХТП в еди-
ничном аппарате должна последовательно решаться на каждой отдельной ступени
иерархии химического производства. Для этого на каждом иерархическом уровне
ХТП должно планироваться проведение опытных исследований и решение комплек-
са задач структурной и параметрической идентификации в соответствии с процеду-
рой, описанной выше. Полученные результаты должны последовательно использо-
ваться (аккумулироваться) на более высоких ступенях иерархии ХТП, где проводятся
собственные серии опытных исследований и реализуется своя процедура решения
задач идентификации.
Следует отметить, что если результаты решения задач идентификации на отдель-
ных ступенях иерархии ХТП известны заранее из литературных данных или из дан-
ных собственных исследований, они используются для построения адекватных мате-
матических моделей, что позволяет снизить затраты на реализацию приведённой
процедуры идентификации (см. рис. 5.47).
Как следует из рис. 5.47, экспериментальные исследования играют важную роль
на всех этапах решения задачи идентификации.
Экспериментальные исследования могут быть пассивными и активными (см. разд. 4.2).
При пассивном эксперименте ставится большая серия опытов с поочерёдным ва-
рьированием каждой из переменных (пассивный лабораторный эксперимент). Сюда
относится также сбор исходного статистического материала в режиме нормаль-
ной эксплуатации промышленного объекта (пассивный промышленный экспери-
мент).
Активный эксперимент ставится по заранее составленному плану (планирование
эксперимента), при этом предусматривается одновременное изменение всех перемен-
ных процесса в соответствии с теорией активного эксперимента. В результате удаётся
свести к минимуму число необходимых опытов и одновременно выявить наиболее
существенные свойства моделируемого объекта. Обработка и интерпретация результа-
тов активного эксперимента более проста и эффективна, чем пассивного.
В процессе построения адекватной математической модели часто возникает не-
обходимость проведения дополнительных экспериментов. Исходный эксперимен-
тальный материал называется стартовым экспериментом, а дополнительный —
уточняющим экспериментом. Эксперимент, проводимый с целью выбора (дискрими-
нации) конкретного вида уравнений, описывающих процесс из системы конкуриру-
ющих моделей называется дискриминирующим экспериментом.
В последнее время для обеспечения репрезентативности выборки эксперимен-
тальных данных, с использованием которых решается задача идентификации про-
цесса, проводится анализ параметрической чувствительности моделей. Он заключает-
ся в том, что с применением модели оцениваются колебания некоторых, чаще всего,
выходных параметров, связанные с изменением входных переменных и коэффици-
ентов модели (см. рис. 1.10).
С одной стороны, это позволяет выявлять процессы и явления, к точности описа-
ния которых следует предъявлять повышенные требования, а с другой — определить
наиболее чувствительные к колебаниям параметров переменные процесса, и считать
их наиболее информативными для проверки адекватности и коррекции параметров —
коэффициентов. Определение с помощью математических моделей наиболее ин-
формационноёмких точек, т.е. точек на объекте, где следует проводить эксперимен-
тальные измерения, позволяет перевести процедуру, по существу, пассивного экспе-
риментирования при решении задачи идентификации в область активного экспери-
мента с заданием количества и местонахождения приборов для измерения вполне
определённых физических величин.
5.5. Идентификация и оптимизация ХТП
365
Статистический подход к идентификации
При решении задачи идентификации изучаемая система считается стохастической
(вероятностной), так как объект исследования совместно с измерительными прибо-
рами подвержен воздействию большого числа неконтролируемых случайных факто-
ров: объектного и приборного шумов w(z)n v(t) (см. рис. 5.46). В общем случае
входные переменные X(t) и, соответственно, выходные урас,(?) и yxc"(t) являются
реализациями различных случайных процессов. Поэтому единственно правильным
подходом к решению задачи идентификации является статистический подход.
Как было показано в главе 4, в этом случае для обработки результатов экспери-
ментальных исследований — в данном случае для решения задачи идентификации —
используется метод регрессионного анализа.
Регрессионный анализ (см. разд. 4.2) проводится с це-
лью установления конкретного вида уравнений регрес-
сии по результатам экспериментальных исследований и
заключается в вычислении коэффициентов регрессии,
определении их значимости и проверке адекватности
уравнений регрессии.
Таким образом, задача структурной идентификации
сводится к выбору конкретного вида уравнений регрес-
сии, а параметрическая идентификация заключается в
определении значений коэффициентов регрессии.
В результате математические модели (ММ) процес-
сов химической технологии следует рассматривать как
регрессионные соотношения, позволяющие по заданным
значениям входных переменных X определять выход-
ные переменные урасч.
В общем случае, как указывалось в главах 1 и 2, связь
между входными X и выходными у переменными в
модели математически может быть представлена конеч-
ными уравнениями, дифференциальными уравнения-
ми и дифференциальными уравнениями в частных про-
изводных. Решение этих уравнений и их систем отно-
сительно выходных переменных ММ при известных
значениях коэффициентов ММ (в данном случае ко-
эффициентов регрессии) называется решением прямой
задачи.
При решении обратной задачи по результатам изме-
рений значений выходных переменных у”‘сп определя-
ются структура системы уравнений МО и/или её коэф-
фициенты а , т.е. по существу решается задача иденти-
фикации ММ.
Одним из основных достоинств регрессионных мо-
делей (уравнений регрессии) является получение в яв-
ном виде зависимости выходных переменных процесса
от входных. Для этого не требуется реализация сложных
алгоритмов решения систем конечных и дифференци-
альных уравнений (см. разд. 3.2, 3.5), как упоминалось
выше, а необходимо провести серию эксперименталь-
ных исследований — пассивных или активных. Как пра-
Рис. 5.48. Блок-схема
процедуры идентификации
процесса в единичном
аппарате с использованием
регрессионных моделей,
получаемых при обработке
результатов активного
эксперимента
366
Глава 5. Физико-химические модели. Построение моделей
вило, выбирают такие регрессионные модели, которые были бы линейными по па-
раметрам (коэффициентам), что позволило бы в полном объёме реализовать все про-
цедуры регрессионного анализа со статистической оценкой получаемых результатов.
Для построения регрессионной модели в качестве гипотетической эксперимен-
тальной установки может быть использована адекватная физико-химическая модель
ХТП, рассматриваемая в этой главе. Методом статистического моделирования Мон-
те-Карло параметры расчётного модуля адекватной модели процесса «зашумляются»
возмущениями, обеспечивая соответствие случайных ошибок переменных нормаль-
ному закону распределения, в результате чего удаётся моделировать поведение реаль-
ной экспериментальной установки. Путём реализации активного эксперимента I и
П-го порядков с применением гипотетической экспериментальной установки — фи-
зико-химической модели реального процесса с «зашумлёнными» параметрами —
можно получить регрессионные модели, описывающие как области функции откли-
ка вдали от её оптимальных значений, так и модели вблизи оптимума, в так называ-
емой «почти стационарной области» (см. разд. 4.3).
Процедура получения регрессионных моделей такого типа по результатам актив-
ного эксперимента приведена на рис. 5.48.
В главе 4 было показано, что с использованием таких регрессионных моделей
решаются задачи планирования экспериментов и оптимизации процессов, в частно-
сти, экспериментально-статистическим методом Бокса—Вильсона (см. разд. 4.3.3).
В случае обработки результатов пассивных экспериментов (см. разд. 4.2) строят-
ся более сложные регрессионные модели, и в представленной процедуре иденти-
фикации вид уравнений не задается, а выбирается, исходя из экспериментальных
данных, т.е. в представленной на рис. 5.48 блок-схеме первый и второй блок меня-
ются местами. При этом задача оптимизации ХТП решается с использованием из-
вестных алгоритмов оптимизации (см. разд. 3.6), как правило, без постановки до-
полнительных экспериментов для определения оптимального значения целевой
функции.
5.5.2. Решение задачи оптимизации
Оптимизация — это определение оптимальных (наилучших) в смысле некоторого
критерия оптимальности (целевой функции) условий проведения химико-техноло-
гических процессов.
Критерий оптимальности — это некоторый количественный показатель, по кото-
рому оценивается качество функционирования ХТП и/или сравниваются различные
ХТП. Критерии могут носить разный характер: технологический, экономический,
экологический и т.п. Например, в качестве технологического критерия можно рас-
сматривать производительность установки по целевому продукту. Очевидно, что чем
производительность больше, тем лучше ХТП. Решение задачи оптимизации в этом
случае — это определение максимальной производительности. Экологический кри-
терий — например, количество вредных выбросов в окружающую среду. Также оче-
видно, что чем он меньше, тем ХТП лучше. Решение задачи оптимизации в данном
случае — минимизация вредных выбросов.
Однако основными критериями оптимальности являются всё же экономические
критерии. Одним из главных среди них является доход (или прибыль). Подробно эти
критерии будут проанализированы далее. Следует отметить, что какой бы критерий
ни был, он всё равно имеет скрытый экономический смысл. Например, если произ-
водительность по целевому продукту ХТП умножить на рыночную цену этого про-
дукта, то полученное произведение можно рассматривать как экономический крите-
рий оптимальности. Точно так же, если количество выбросов в окружающую среду
умножить на цену штрафов за её загрязнение, то и в этом случае получится крите-
рий, имеющий экономический смысл.
5.5. Идентификация и оптимизация ХТП
367
Как было показано в разд. 1.5 [см. уравнение (1.6)], критерий оптимальности
является скалярной функцией выходных (зависимых) параметров ХТП, которые в свою
очередь зависят (1.7) от собственно входных и оптимизирующих (управляющих) па-
раметров процесса (1.8). В случае более широкой трактовки критерия оптимальнос-
ти при оптимизации процессов с распределёнными по времени параметрами, так называ-
емых нестационарных (динамических) процессов (5.2), и процессов с распределённы-
ми по пространственной координате параметрами (например, протекающих в трубча-
тых аппаратах), его следует рассматривать как некоторый функционал, зависящий
соответственно от функций по времени и от функций по пространственной координате.
На практике часто рассматриваются несколько критериев, достижение которых
может оказаться противоречивым. Например, получить максимум продукции при
минимальных затратах. С математической точки зрения подобная постановка задачи
не корректна — критерий должен быть один. Однако, если эти требования всё же
выдвигаются, то они должны быть удовлетворены, поэтому такой вариант постанов-
ки задачи имеет право на существование и называется многокритериальной задачей
оптимизации.
Процедура решения задачи оптимизации сводится к поиску оптимального — наи-
большего или наименьшего — значения критерия оптимальности (целевой функции
или функционала) с использованием расчётного модуля реального процесса (его адек-
ватной компьютерной модели) — выбранного алгоритма оптимизации при наличии
ограничений I и П-го рода (1.16). В результате задачу оптимизации следует рассматри-
вать как исключительно математическую задачу на экстремум функции или экстре-
маль функционала, результаты которой могут быть получены при реализации на ком-
пьютерах соответствующих алгоритмов математического моделирования и оптимиза-
ции. Правильный выбор критериев оптимальности, адекватность используемых ком-
пьютерных моделей реальных процессов, строгое соблюдение ограничений I и П-го
рода на их параметры в процессе решения задачи и эффективность применяемых
алгоритмов оптимизации позволяют найденные расчётным путём оптимальные значе-
ния параметров технологических процессов переносить на действующие производства.
Формулировки задачи оптимизации при использовании
для её решения математических моделей различных типов
В процессе проектирования новых и при эксплуатации действующих ХТП ста-
вятся и решаются схожие задачи оптимизации.
В случае проектирования новых ХТП задача оптимизации сводится к выбору обо-
рудования, расчёту его конструкционных и технологических параметров и синтезу
схемы обвязки оборудования материальными и тепловыми потоками так, чтобы из
имеющегося сырья произвести заданное количество продуктов требуемого качества
с минимальными затратами и/или с максимальной прибылью.
При реконструкции или диверсификации ХТП задача оптимизации подобна сфор-
мулированной выше с той лишь разницей, что здесь дополнительно требуется, по
возможности, сохранить существующую производственную систему и с минималь-
ными изменениями получить улучшенную, соответствующую решению поставлен-
ных задач, например, приносящую большую прибыль или другой, расширенный ас-
сортимент получаемых продуктов с наименьшими затратами.
В отличие от задач оптимизации, задача оптимального управления действующего
ХТП состоит в выборе режимно-технологических параметров ХТП для максимиза-
ции, например, прибыли. Следует заметить, что прибыль, как будет показано ниже,
выступает в качестве одного из основных экономических показателей, поскольку
включает в себя такие критерии, как выручка, капитальные и эксплуатационные
затраты, налоги, амортизация, кредит и т.п.
В общем случае для задач оптимизации ХТП используются три типа математи-
ческих моделей:
368 Глава 5. Физико-химические модели. Построение моделей
1) физико-химические модели процессов с сосредоточенными параметрами (5.1) и
эмпирические регрессионные модели, получаемые по результатам обработки дан-
ных пассивных экспериментов (4.73), (4.91), которые справедливы в широком
диапазоне изменения параметров процессов;
2) физико-химические модели процессов с распределёнными параметрами (5.2), пере-
менные в которых изменяются с изменением временной координаты (распре-
деление по времени) и/или пространственной координаты (распределение в
пространстве);
3) эмпирические регрессионные модели, получаемые по результатам обработки дан-
ных активных экспериментов, например ПФЭ (4.230) и ОЦКП (4.231), которые
справедливы в узком диапазоне изменения параметров процессов.
Для первого типа моделей (5.1)*, математическое описание которых в неявном
виде с учётом (1.6), (1.7) и (1.8) может быть представлено в виде:
f(x,u,y) = 0 (i = !,...,() (5.5.4)
при решении задачи оптимизации определяются компоненты вектора й'"” — опти-
мальные значения оптимизирующих (управляющих) переменных. В общем случае
при этом следует реализовать алгоритм решения задачи нелинейного программиро-
вания (НЛП) (1.16) с учётом необходимости выполнения уравнений математической
модели (5.5.4):
opt R(u);
йтт<й<йтах-, (5.5.5)
/(?,«, у) = о;
Ф(л, й, у) < 0 .
В результате задача оптимизации для этого типа моделей формулируется следую-
щим образом: определить оптимальные значения оптимизирующих (управляющих)
переменных й из области их допустимых значений [йтт, й™“] (ограничения 1-го
рода) такие, чтобы при выполнении уравнений МО (5.5.4) и ограничений П-го рода
Т(х, й, у) < 0 ,
критерий оптимальности R достигал оптимальной величины (наибольшей или наи-
меньшей) в зависимости от её физического смысла.
Если в число оптимизирующих переменных включены конструкционные парамет-
ры процесса (размеры, типы конструкций и т.п.), то решается задача оптимального
проектирования. Если в число оптимизирующих переменных не включены конструк-
ционные параметры процесса и проводится оптимизация его стационарных режимов,
то решается задача статической оптимизации или оптимального управления стационар-
ными режимами производства. Поэтому оптимизирующие переменные в этом случае
называются управляющими переменными, и поиск их оптимальных значений осуществ-
ляется с целью определения наилучших режимных параметров производств.
Для второго типа моделей (5.2), описывающих процессы с непрерывно-распреде-
лёнными параметрами во времени или пространстве с помощью обыкновенных диф-
ференциальных уравнений первого порядка:
^- = <р,(г, х,й) (<=1,...,^);
dt
Xl(t(0}) = x[Q} (i=l,..., £),
* При решении задач оптимизации вектор х в системах типа (5.1) заменяется на
вектор у — выходные (зависимые) переменные математических моделей (1.9).
I
5.5. Идентификация и оптимизация ХТП
369
где й = (и,, и2,..., иг) — искомый вектор управлений (оптимизирующих переменных),
в соответствии с методом вариационного исчисления функциям-решениям х, = х, (?) *
(i = 1,£) сопоставляется некоторая скалярная величина (критерий оптимальности),
называемая функционалом:
/ч
Y = J <р0(t, х,, х2,..., х„ и„ и2,ur)dt, (5.5.66)
Л
где ф0— заданная функция переменных х, й и независимой переменной t.
Решение задачи оптимизации в этом случае сводится к отысканию вектора уп-
равления й(т), при подстановке которого в выражение функционала (5.5.66) его ве-
личина принимает экстремальное значение. Функции х,(т) (i = 1,..., £) в этом случае
называются экстремалями функционала Y (5.5.6). Причём, в зависимости от того,
придают функции х,(/) (j = l,...,/) функционалу у максимальные или минималь-
ные значения, они называются максималями или минималями.
Эти задачи носят название задач динамической оптимизации, куда относятся задачи
оптимизации пуска (останова) процессов и перевода их с одного режима на другой.
Найденные оптимальные функции x"’’'(f) называются «траекториями» процесса,
для которых должны быть заданы граничные условия. В простейшем случае, когда
начальное и конечное состояния траекторий процесса фиксированы, задание гра-
ничных условий сводится к заданию значений всех неизвестных функций при значе-
ниях независимой переменной № и соответствующих началу и концу траекто-
рий, т.е. задаётся совокупность значений:
Х,(?(о)) = х,(о) а = !,...,£); (5.5.7)
х,(?‘)) = х,(‘) (i = l,..., Г). (5.5.8)
Следует отметить, что в этом случае, так же как и для математических моделей
первого типа, уравнения МО (5.2), включая дифференциальные уравнения, являются
ограничениями при поиске управлений u(t) и экстремалей x(f) функционала у (5.5.66).
Третий тип моделей (4.230) и (4.231), описывающий ограниченные области фазо-
вого пространства вдали и вблизи оптимума, в отличие от двух предыдущих типов
моделей, для решения задачи оптимизации с их использованием требует постановки
дополнительных экспериментов и подробно описан в разд. 4.3.3.
Оптимизация объектов с сосредоточенными параметрами
В общем случае эта задача является задачей нелинейного программирования (1.16),
(5.5.5), и блок-схема процедуры её решения приведена на рис. 2.7. Этапы решения
данной задачи оптимизации приведены на рис. 5.49.
Как следует из рис. 5.49, для решения задачи оптимизации необходимо:
• сформировать (выбрать) критерий оптимальности (целевую функцию) R (1.6);
• найти ресурсы оптимизации — оптимизирующие (управляющие) переменные (1.8);
• определить ограничения I и П-го рода, накладываемые на параметры процесса,
исходя из физико-химических, технологических, конструкционных и других
соображений (1.16);
* t — независимая переменная в СОДУ (5.2), которая может быть временем или
длиной.
370
Глава 5. Физико-химические модели. Построение моделей
Рис 5 49 Этапы решения задачи
оптимизации для объектов с сосредото-
ченными параметрами
• выбрать (разработать) и реализовать два ал-
горитма.
а) алгоритм математической модели (см.
разд. 5.1—5.4),
б) алгоритм оптимизации (см. разд. 3 6),
• реализовать процедуру анализа параметри-
ческой чувствительности используемой адек-
ватной ММ с целью выявления взаимовлия-
ния параметров процесса друг на друга, оп-
ределения чувствительности выбранного кри-
терия оптимальности (целевой функции) к
изменению физико-химических, режимных и
конструкционных параметров ХТП, а также
для выбора оптимальных ресурсов оптимиза-
ции — оптимизирующих (управляющих) пе-
ременных, наиболее сильно влияющих на
критерий оптимальности.
Необходимо заметить, что решение задач
оптимизации для объектов с сосредоточенны-
ми параметрами связано с целым рядом спе-
цифических особенностей. Эти особенности
обусловлены сложностью ХТП, нелинейнос-
тью описывающих их уравнений и ограниче-
ний, накладываемых на физико-химические
параметры ХТП. В конечном счете, все это
сказывается на необходимости формулиров-
ки специальных требований к критериям оп-
тимальности.
В общем случае критерий оптимальности
должен удовлетворять трем основным требо-
ваниям.
Во-первых, он должен быть количественным, т.е. выражаться числом, чтобы мож-
но было количественно сравнивать эффективность различных вариантов проведения
процесса
Рис 5 50 Изменение различных критериев
оптимальности концентрации целевого
продукта х и себестоимости С от расхода
сырья В
Во-вторых, критерий оптимальности
должен быть единственным. Выполнение
этого требования связано с серьезными
затруднениями, так как на практике есте-
ственно желание обеспечить оптимальные
значения нескольких критериев оптималь-
ности.
Например, для получения определен-
ного целевого продукта необходимо стре-
миться к тому, чтобы его концентрация
на выходе была максимальной, а себесто-
имость минимальной. Изменения этих
критериев оптимальности в зависимости
от расхода сырья (оптимизирующая пере-
менная) представлены на рис. 5.50.
Из рисунка следует, что оптимальные
значения ресурса оптимизации будут раз-
личными для отличающихся друг от друга
критериев оптимальности — С и х. По-
5.5. Идентификация и оптимизация ХТП
371
этому, если использовать один критерий, то получается один результат (В°р1 и х™*),
если другой — то иной результат (В°р' и С™"). В результате постановку задачи оптими-
зации с целью определения расхода сырья (В), при котором себестоимость станет
минимальной (Сти), а концентрация целевого продукта максимальной, нельзя при-
знать корректной. Неправильно, например, искать оптимальные условия проведения
процесса, при которых выход продукта будет максимальным, а концентрация примеси
в нем минимальной. Иногда это требования несовместимы.
В настоящее время все большее распространение получает так называемые обоб-
щенные критерии оптимальности, которые являются некоторой функцией рассмот-
ренных частных критериев оптимальности. В этом случае обобщенный критерий
представляется в виде суммы (аддитивный критерий) или в виде произведения (муль-
типликативный критерий) частных критериев. При этом весовые коэффициенты по-
зволяют правильно определить степень вклада всех частных критериев в обобщён-
ный критерий оптимальности. В результате при оптимизации ведётся поиск экстре-
мального значения единственного, но обобщенного критерия оптимальности.
Как уже упоминалось, в случае решения задачи оптимизации к ХТП часто выдви-
гаются несколько требований, которые могут быть формализованы в виде отдельных
критериев. Например, может потребоваться, чтобы ХТП приносил максимальную при-
быль, но при этом был минимален по затратам и по выбросам в окружающую среду,
т.е. оптимален по трём критериям одновременно. В большинстве вариантов такие
задачи не имеют решения.
Тем не менее, всё же существуют способы решения многокритериальных задач.
Применение одного из них возможно, когда различна чувствительность разных кри-
териев к разным управлениям. Пусть имеется к критериев (гр г2,..., гк), а всё множе-
ство управлений U может быть разбито на подмножества U = Ut n U2 n ...n U к, об-
ладающие следующими свойствами:
abs
dr,
ди,
dr,
ди
£*i,£ = l,..., к .
(5-5.9)
Свойство (5.5.9) позволяет осуществить декомпозицию многокритериальной за-
дачи на к корректных (с одним критерием) подзадач оптимизации вида:
max г,(и ), i = l,...,k; иеб
Uj J J J .
Смысл другого способа заключается в том, что многокритериальная задача сво-
дится к однокритериальной. На практике это может быть сделано разными способа-
ми. Самый простой — выделить из всех критериев «самый важный», а остальные
игнорировать. Этот способ является частным случаем компромиссного аддитивного
критерия, который представляет собой взвешенную сумму к критериев:
R(u) = £а,г,(«).
1=1
(5.5.10)
Весовой коэффициент а, оценивает «важность» z-го критерия.
Наконец, можно выделить один «самый важный» критерий гр а «интересы» ос-
тавшихся критериев учесть с помощью ограничений типа неравенств. Например:
max rt(u), г2(и) < с2, г}(и) < с3,..., гк(и) < ск.
372
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.51. Множество неухуд-
шаемых решений и для двух
критериев оптимизации
Рис. 5.52. Возможные ошибки при
«нечувствительности» критерия оптималь-
ности
Если второй критерий по своему смыслу должен быть минимизирован, то мы
ограничиваем его сверху некоторой постоянной с2, если третий критерий должен
быть максимизирован, то мы ограничиваем его снизу некоторой постоянной с3.
Ещё один способ решения многокритериальных задач принципиально отличает-
ся от вышеприведённых. Его принципиальная особенность — отказ от единственно-
сти решения. Предлагается считать, что для многокритериальных задач существует
не единственное решение, а
Рис. 5.53. Чувствительный
(«острый») критерий оптималь-
ности
некоторое так называемое множество равноправных
решений. Это такое множество управлений, внутри
которого изменение любого управления не приво-
дит к ухудшению (уменьшению) всех критериев сра-
зу, а одни критерии уменьшаются, но другие — воз-
растают. Любые управления из этого множества счи-
таются решениями задачи многокритериальной оп-
тимизации. На рис. 5.51 такое множество управле-
ний и выделено жирной линией.
В общем случае множество неухудшаемых реше-
ний представляет собой выпуклую поверхность в про-
странстве критериев оптимизации. Пример поверх-
ности двух критериев приведён на рис. 5.51.
Третье требование к критерию оптимальности —
монотонное изменение его величины в за-
Рис. 5.54. Многоэкстремальный критерий
оптимальности
висимости от оптимизирующих перемен-
ных. При незначительных изменениях
критерия оптимальности в зависимости
от оптимизирующих переменных (рис.
5.52) возникают большие затруднения при
определении их оптимальных значений.
Как видно из рис. 5.52, оптимальные
условия, которые могут быть определены
при таких изменениях, суще-
ственно отличаются от действительных оп-
тимальных условий u°p,,Rmm (велико
Ди = иор‘’ -иор‘). В этом случае критерий
оптимальности нечувствителен к измене-
нию оптимизирующих переменных.
5.5. Идентификация и оптимизация ХТП
373
Когда экстремум критерия оптимальности имеет ярко выраженный характер (рис. 5.53),
также необходимы эффективные методы оптимизации, которые позволяют найти
оптимальные условия — и*, Rmax
В этом случае значительное отклонение от оптимальных условий и°р‘ может при-
вести к существенному изменению показателя качества функционирования ХТП —
критерия /?"“. Поэтому поддержание оптимальных условий в реальном процессе
становится сложной задачей из-за большой чувствительности экстремального значе-
ния критерия оптимальности.
Наличие нескольких экстремумов и точек разрыва функции критерия оптимально-
сти (рис. 5.54) усложняет процедуру оптимизации.
В этом случае необходимо найти либо наибольшее значение функции (точка В),
либо наименьшее значение (точка F), т.е. глобальный экстремум. Если в процессе
оптимизации будет определён локальный экстремум (точка А — локальный максимум
или точка С на отрезке [А, В] — локальный минимум, точка Е — локальный мини-
мум), то это приведёт к неверным координатам оптимальных условий. Определён-
ные сложности могут возникнуть при расчёте глобального максимума (точка В) из-за
разрыва функции критерия оптимальности в этой точке.
Таким образом, необходимым условием успешного решения задачи является ис-
следование характера изменения функции критерия оптимальности. Так как про-
цесс формулировки критерия оптимальности не формализован и в известной степе-
ни носит субъективный характер, необходимо стремиться к тому, чтобы функция
критерия была унимодальной с одним экстремумом и не содержала точек разрыва.
Оптимизация объектов с распределёнными параметрами
Отличительная особенность решения задач оптимизации для таких объектов со-
стоит в том, что в качестве критериев оптимальности в этом случае используются
функционалы Yтипа (5.5.66), и ресурсами оптимизации (оптимизирующими пере-
менными) являются векторы управлений u(t), зависящие от независимой перемен-
ной t (либо время, либо пространственная координата). Определяемый в результате
решения задачи оптимизации оптимальный вектор управлений
йо/,'(0 = [u?“(t), u^'(t), ..., и*(/)] должен не только обеспечивать экстремальное зна-
чение функционалу у, но и удовлетворять математическому описанию химико-тех-
нологического процесса, который для решения на компьютерах (см. разд. 3.5) пред-
ставляется в виде системы дифференциальных уравнений первого порядка (5.2) и
(5.5.6а).
Наиболее наглядно формулировка этой задачи может быть проиллюстрирована
на примере задач о быстродействии. В задачах о быстродействии требуется так выб-
рать управляющие воздействия в каждый момент времени, чтобы перевести процесс
из заданного начального состояния в заданное конечное за минимальное время.
Типичными примерами таких задач служат задачи отыскания оптимальных программ
управления периодическими процессами и близкие им задачи наибыстрейшего пе-
ревода процесса с одного режима эксплуатации на другой.
Кроме того, целый ряд задач в химической технологии, как, например, задачи
выбора оптимальных температурных профилей в трубчатых реакторах, можно также
сформулировать как задачу о быстродействии.
Следует отметить, что задача о быстродействии является частным случаем более
общей задачи с критерием оптимальности, заданным в виде функционала (5.5.66),
если в нём положить:
Фо =1.
(5.5.11)
374
Глава 5. Физико-химические модели. Построение моделей
(»)
(dt = tM -r(0)
(5.5.12)
Тогда
Y =
и, таким образом, функционал (5.5.66) при условии (5.5.11) определяет время пере-
хода процесса из начального состояния х(0) (5.5.7) в конечное x(t) (5.5.8). Далее для
упрощения иногда будем полагать, что И0’ = 0 и, следовательно, задача оптимизации
сводится к минимизации значения (5.5.12), которое в этом случае характеризует
время перехода процесса из начального состояния в конечное.
Для простоты примем, что в рассматриваемой задаче о быстродействии использу-
ется только одно управляющее воздействие u(t), т.е. г = 1 и одна выходная перемен-
ная x(t), т.е. I = 1 (5.5.6а), и тогда система (5.5.6а) преобразуется в одно дифферен-
циальное уравнение вида:
dx
— = <р(г, х, и);
Для более общей формулировки задачи для управления, описывающего ХТП
(5.5.13), откажемся от критерия (5.5.12), характерного для задач о быстродействии, и
запишем функционал в следующем виде:
- ,(*)
T[x(f)]= J[x(z)]2dz. (5.5.14)
о
Предположим, что этот функционал характеризует производительность трубчато-
го реактора, описываемого дифференциальным уравнением (5.5.13) — независимая
переменная t в этом случае является координатой длины трубы реактора. Будем
также считать, что функция и(?) в интервале 0 < t < - профиль изменения темпе-
ратуры по длине реактора, который должен быть выбран таким образом, чтобы фун-
кционал У[х(?)] (5.5.14) был максимальным.
При решении таких задач применяются два подхода — дискретный, реализующий
метод динамического программирования и непрерывный, реализующий принцип макси-
мума Понтрягина.
Методы оптимизации объектов с распределенными параметрами (так называемых рас-
пределенных ХТП) подробно представлены и проанализированы в работах [1,12, 31, 50].
Анализ экономических критериев оптимальности
При оценке эффективности функционирования химических производств поми-
мо технологических критериев существенную роль играют экономические показате-
ли — себестоимость продукции (С), прибыль (77), норма прибыли (Н), приведённые
затраты (3 ), приведённый доход (Дпр) и т.п.
Приведенный доход (руб/год) может использоваться в качестве обобщённого по-
казателя экономической эффективности производства:
Д^=±Ц^-з,-ек,,
7=1
где — отпускная цена на целевой продукт у-го вида, учитывающего его качество,
руб; В — годовой объём выпуска и реализации целевого продукта, например кг/год;
Зэ — суммарные эксплуатационные затраты, например руб/год; Е — нормативный
5.5. Идентификация и оптимизация ХТП
375
коэффициент экономической эффективности капиталовложений: величина, обрат-
ная нормативному сроку окупаемости, год-1; Kt — производственные фонды, руб.
Если известны и не меняются объём выпуска продукции (В = const) и её цена
(Ц = const), то условие Дпр —> max соответствует условию минимума приведённых
затрат (Зпр -э min).
Приведённые затраты определяются в руб/год по формуле:
3 = 3 + ЕК,.
пр э t
При рассмотрении действующих производств неизменными принимаются капи-
тальные затраты (производственные фонды) и требование Дпр —> max совпадает с
условием максимизации дохода (руб/год), который в этом случае определяется сле-
дующим образом:
Д^Д-3.. (5.5.15)
7=1
При этом выражение для вычисления эксплуатационных затрат с п целевыми
продуктами имеет вид:
5,=SCA, (5.5.16)
7-1
где С] — себестоимость (издержки) каждого целевого продукта (например, руб/кг).
Подстановка последнего соотношения (5.5.16) в формулу (5.5.15) приводит к сле-
дующему уравнению для дохода:
7=1
и при условии получения одного продукта (п = 1)
Д=(Ц~ QB.
Как следует из полученных выражений для дохода, в рассматриваемом случае они
полностью совпадают с соотношением для определения прибыли, т.е. для прибыли
(77) будет справедливо:
П=(Ц-С)В. (5.5.17)
Более эффективным экономическим показателем (критерием оптимальности)
является норма прибыли, которая не зависит от объёмов выпуска и реализации про-
дукта и определяется по формуле:
Н = И-_(Ц-^В = Ц^£=Ц^, (5.5.18)
з3 св с с
Одной из задач планирования производства является определение оптимального
выпуска и реализации продукта В (оптимизирующая переменная). При этом в зави-
симости от того, какой выбирается экономический критерий оптимальности (целе-
вая функция), могут получаться различные результаты решения задачи оптимиза-
ции, т.е. отличающиеся друг от друга В°р>.
Сравним возможные результаты решения задачи оптимизации для трёх экономи-
ческих критериев оптимальности:
• себестоимости (Q — первая задача экономической оптимизации;
• прибыли (77) — вторая задача экономической оптимизации;
• нормы прибыли (77) — третья задача экономической оптимизации;
В соответствии с известным экономическим законом для себестоимости продук-
тов будет справедлива следующая зависимость себестоимости от объёма выпуска и
реализации продукта В, которая представлена на рис. 5.55.
В результате решения первой задачи экономической оптимизации получается опти-
мальное значение производительности продукта (объёма выпуска и реализации про-
376
Глава 5. Физико-химические модели. Построение моделей
Рис. 5.55. Зависимость себестоимости
продукта от объёма выпуска и его реализации
дукта) В/р‘, которое обеспечивает мини-
мальную величину его себестоимости С”т.
При этом в соответствии с необходимым
условием экстремума функции С (см. рис.
5.55) будет справедливо утверждение о том,
что В°р‘ соответствует условию равенства
нулю производной dC/dB:
При анализе второй задачи экономичес-
кой оптимизации необходимо определить
оптимальную производительность продукта
В/'/', который соответствует максимуму
прибыли (5.5.17).
В этом случае необходимое условие экстремума функции прибыли и имеет вид:
— =z/-c + sf—-~] = 0
dB [dB dB)
или, после элементарного преобразования:
dC _ Ц-С dL(
dB В dB '
(5.5.20)
(5.5.21)
При этом следует проанализировать два варианта изменения цены с ростом про-
изводительн ости:
I вариант — цена не изменяется с ростом производительности, т.е.
^-0; (5.5.22)
II вариант — цена падает с ростом производительности, т.е.
Рис. 5.56. Зависимость себестои-
мости и прибыли от производи-
тельности, при условии
dH/dB = Q
дЦ п
(5.5.23)
UD
В соответствии с вариантом I будет справедли-
во (5.5.21):
rfC _ ц~с
dB |ву В
и, так как всегда Ц> С, то:
dC
dB
(5.5.24)
(5.5.25)
вГ
Это означает, что В'//' будет соответствовать
правой ветви графика зависимости себестоимости
продукта от производительности (см. рис. 5.55) на
рис. 5.56.
Таким образом, для варианта I второй задачи
экономической оптимизации, когда dn/dB = 0, для
оптимальных В, которые определяются при раз-
5.5. Идентификация и оптимизация ХТП
377
ных критериях оптимальности - прибыли и себестоимости, будет справедливо сле-
дующее неравенство:
В°ПР‘ > В°р1, (5.5.26)
т.е. когда в качестве критерия оптимальности выбирается прибыль В°пр1, должна быть
больше случая, когда в качестве критерия оптимальности используется себестои-
мость В"'" (см. рис. 5.56).
Для варианта II (5.5.23) следует проанализировать три случая:
dH Ц-С d в ; <5-5-27* dn Ц-С 2> я= в ; <5-5-28) dn Ц-С 3> Я" в • <5-5-29)
В случае 1 цена падает медленнее с ростом производительности, чем отношение
Ц-с
В
— >0, (5.5.30)
dB\Bff
и, как и в варианте I, здесь будет справедливо условие (5.5.25) и (5.5.26) — см. рис. 5.56.
В случае 2, когда цена падает с ростом производительности со скоростью, равной
Ц-С
В '
и в соответствии с условием (5.5.19) будет справедливо:
Вор,=Вор‘. (5.5.31)
В случае 3 цена падает с ростом производи-
R ц~с
тельности быстрее, чем отношение —-— и про-
dC
изводная jg становится отрицательной. Это
"/Г
означает, что значению оптимальной производи-
тельности В"р' соответствует левая ветвь графика
зависимости себестоимости продукта от произ-
водительности (см. рис. 5.55) на рис. 5.57.
В результате для случая 3 получается:
<0
dB в^р’
и, соответственно:
Вор' дор'
П < ьс •
Рис. 5.57. Зависимость себестоимос-
ти и прибыли от производительнос-
ти в случае, когда
du dn ц-с
--- и и ---- ------
dB dB В
(5.5.32)
(5.5.33)
378
Глава 5. Физико-химические модели. Построение моделей
dll
Из рассмотрения случая 3 следует, что при условии -<0, в°р> должна быть
dB
меньше В"р‘ как критерия оптимальности.
При рассмотрении третьей задачи экономической оптимизации, когда в качестве
критерия оптимальности выбирается норма прибыли, определяемая по соотноше-
нию (5.5.18), необходимое условие экстремума имеет вид:
с^-ц^
dB dB _q
С2
dH
dB
(5.5.34)
или
dC
dB
По аналогии со второй задачей экономической оптимизации целесообразно про-
анализировать два варианта:
ВТ
С dB
(5.5.35)
D ^ = 0;
’ dB
II) <0.
dB
Для варианта I в соответствии с соотношением (5.5.35) будет справедливо:
dC
dB
(5.5.36)
= 0,
ВТ
т.е.
Bpf = в;р'. (5.5.37)
В случае варианта II в соответствии с соотношением (5.5.35) следует записать:
Рис.
ти и
5.58. Зависимость себестоимос-
нормы прибыли от производи-
<щ <0
дельности в случае, когда —— < и
dB
dC
dB
ВТ
(5.5.38)
т.е. В"р' соответствует левой ветви графика зави-
симости себестоимости продукта от производи-
тельности (см. рис. 5.55 и рис. 5.58) и должна
быть меньше В"'".
Таким образом, для последнего случая будет
справедливо:
В"нр‘ < В°р‘ . (5.5.39)
Приведённый анализ трёх задач экономичес-
кой оптимизации показывает, насколько важно
правильно выбирать критерии оптимальности,
позволяющие оценить экономическую эффектив-
ность химических производств и возможное вли-
яние чувствительности критериев на результаты
решения оптимизационных задач.
6
ПАКЕТЫ
МОДЕЛИРУЮЩИХ ПРОГРАММ
Глава
Системный подход к исследованию химико-технологических процессов (см. главу 1)
предусматривает не только изучение закономерностей протекания процессов в отдель-
ных аппаратах, но анализ производства в целом, с учётом их взаимодействия. Аппараты
(единицы оборудования), соединённые между собой материальными и тепловыми по-
токами, образуют технологическую схему химического производства. В действительно-
сти, задача компьютерного моделирования химико-технологического процесса (ХТП)
состоит в решении задач построения математической модели (ММ), идентификации
(ИДЕНТ) и оптимизации (ОПТ) химического производства, т.е. решения указанного
комплекса задач для технологической схемы всего процесса (см. главы 1 и 2).
Перечисленный комплекс задач решается на третьем уровне иерархии процессов
химического предприятия — на уровне химического производства (см. главу 1), при
этом предусматривается успешное решение аналогичных задач на микро- и макро-
уровне ХТП, т.е. на первом и втором уровнях иерархии предприятия. Решение пос-
ледних детально рассмотрено в предыдущих главах этой книги. Таким образом, для
компьютерного моделирования ХТП (технологических схем химических производств)
необходим мощный инструмент — пакет моделирующих программ (ПМП), который
позволял бы реализовать на компьютерах целый набор приёмов и методов решения
перечисленных задач моделирования на первом, втором и третьем уровне иерархии
химического предприятия.
ПМП представляют собой универсальную программную оболочку, в которой ре-
ализуются три основных режима её работы:
• «изображение процесса» — для графического представления технологической
схемы производства;
• «расчёты» — для выполнения вычислений с применением реализованных в виде
расчётных модулей алгоритмов решения задач компьютерного моделирования;
• «диаграмма процесса» — для представления результатов выполненных расчётов
в виде таблиц, графиков и диаграмм.
Каждый из трёх основных режимов требует реализации специальных модулей, с
использованием которых можно построить технологическую схему любого ХТП и
решать комплекс задач его моделирования на компьютерах. При этом данные, необ-
ходимые для проведения расчётов, как, например, физико-химические свойства ве-
ществ, алгоритмы для вычисления свойств многокомпонентных смесей, различные
алгоритмы для поверочно-оценочных и проектных расчётов аппаратов, включены в
состав ПМП. Это означает, что расчётные модули ПМП используют для вычислений
данные из фактографической базы данных (БД) по физико-химическим свойствам
индивидуальных веществ. Для выбора алгоритмов расчёта свойств многокомпонент-
ных смесей и алгоритмов расчёта аппаратов (единиц оборудования) технологической
схемы в состав ПМП включаются экспертные системы (ЭС), которые с учётом по-
компонентного состава систем, по конкретным данным о диапазонах изменения
температур и давлений производства «предлагают» сделать оптимальный выбор тер-
модинамического метода или вычислительного алгоритма.
380
Глава 6. Пакеты моделирующих программ
В информатике такие ПМП принято относить к классу программных продуктов,
называемых симуляторами, в данном случае — симуляторами химических производств.
Они, как правило, реализуются в виде единого программного комплекса, функцио-
нирующего в операционной среде Windows, и не требуют для работы каких-либо
дополнительных программных продуктов. Симуляторы химических производств яв-
ляются мощным инструментом для химиков-технологов и инженеров-химиков, за-
нимающихся расчётно-технологическим проектированием ХТП и управлением хи-
мическими производствами на действующих предприятиях.
В общем случае с применением современных ПМП — симуляторов химических
производств — решаются следующие задачи:
• анализа, оптимизации и синтеза химико-технологических систем (ХТС) для
проектируемых и действующих производств (см. главу 1);
• исследования динамического поведения ХТС для синтеза систем управления;
• разработки компьютерных систем обучения операторов химических производств,
в частности тренажёрных комплексов.
Поэтому в настоящее время симуляторы химических производств (ПМП) широ-
ко используются в автоматизированных системах прикладной информатики, таких
как САПР, АСУТП, АСНИ и АОС (см. главу 1).
Для современных специалистов в области химической технологии умение пользо-
ваться ПМП является необходимым условием подтверждения своей квалификации
как химика-технолога и инженера-химика.
6.1. История создания пакетов
моделирующих программ
Идея компьютеризации расчётов технологических схем химических производств
возникла в 1960-х годах. Первые разработанные программы использовались в ком-
паниях и фирмах для собственных целей, некоторые из них позднее стали коммер-
ческими. Хорошими примерами первых моделирующих программ являются
FLOWTRAN (фирма Monsanto), CHESS (сокращение от Chemical Engineering
Simulation System) или DESIGN II (фирма ChemShare).
В 1967 году на рынке появилась первая коммерческая программа моделирования
технологических процессов — PROCESS (фирма SimSci). PROCESS тех времён был
создан для работы на больших компьютерах и применён для расчёта нефтегазовых
систем в нефтеперерабатывающей промышленности. В дальнейшем эта программа
была модернизирована и переведена на персональные компьютеры (ПК). В настоя-
щее время этот пакет моделирующих программ известен под названием PRO-П. Ре-
зультатом нефтяного кризиса в 1970-х годах стал проект в Массачусетском Техноло-
гическом Институте (США) по созданию моделирующей программы Advanced System
for Process Engineering (симулятор ASPEN). Одной из целей проекта было совершен-
ствование программ компьютерного моделирования для расчётов технологий аль-
тернативного топлива (производных угля) для защиты стратегических интересов США
в случае продолжения кризиса. Этот программный продукт был коммерциализиро-
ван в 1981 году компанией Aspen Tech под маркой Aspen Plus.
В 1976 году фирма Hyprotech в Канаде реализовала первый интерактивный ком-
пьютерный продукт для моделирования химико-технологических процессов — HYSIM,
став первым продавцом программного обеспечения, обеспечивающего расчёт произ-
водства на ПК. Первыми покупателями этой программы стали предприятия нефте-
газовой промышленности Канады. Преемником ПМП HYSIM в настоящее время
является симулятор HYSYS.
6.2. Принципы функционирования моделирующей программы
381
В 1984 году группа предприимчивых профессоров в Хьюстоне (США) начала раз-
работку программы ChemCad и этот программный продукт стал собственностью из-
дательского дома McGraw Hill. В 1988 году фирма Chemstations (США) стала вла-
дельцем этой программы и полностью изменила её, выпустив программу ChemCad
версии II. Основной целью этой разработки было создание интерактивного продукта
компьютерного моделирования ХТП на базе ПК, с использованием графических
возможностей последнего. Первыми покупателями симулятора ChemCad стали боль-
шие заводы химической промышленности. На сегодняшний день реализован интег-
рированный программный продукт ChemCad версии 5.5.
Из отечественных разработок следует отметить создание фрагментов ПМП — Рек-
тификация (РХТУ им. Д.И. Менделеева, Москва), Технология (фирма «Технософт»,
Москва) и украинский программный продукт ГазКондОйл (Киев).
Основные модули ПМП (симуляторов процессов) были разработаны много лет
назад. Например, база данных индивидуальных веществ; основные термодинамичес-
кие методы расчётов свойств индивидуальных веществ и их смесей; модули расчётов
единиц оборудования (аппаратов) для получения органических веществ, промыш-
ленных газов и вспомогательного оборудования химических производств (воды, пара,
топлива, воздуха, электричества), а также система модулей для формирования отчё-
тов, — всё это входит в программный пакет любой моделирующей программы.
Следует отметить, что для решения таких задач, как, например, подробные расчё-
ты разделения твёрдое/жидкое; теплообменников совместно с моделированием всей
технологической схемы; свойств систем электролитов для неорганических произ-
водств и утилизации отходов с целью обеспечения экологической безопасности; пе-
риодической ректификации и нестационарных режимов работы колонн непрерыв-
ной ректификации; нестационарных режимов работы химических реакторов обычно
оформляют в виде дополнительных программных модулей ПМП, которые интегри-
рованы с основным (базовым) модулем пакета моделирующей программы.
Важными требованиями, предъявляемыми к современным ПМП (симуляторам
химических производств) являются:
• возможность создания пользователем собственного изображения единиц обо-
рудования (аппаратов) технологической схемы;
• наличие возможности включения в программный пакет собственных разрабо-
ток, в частности, алгоритмов расчёта физико-химических свойств многокомпонент-
ных смесей и алгоритмов расчёта единиц оборудования;
• интегрируемость ПМП с другими программными продуктами, прежде всего, с ис-
пользуемыми для монтажно-технологического проектирования, например, с АВТОКАДом.
6.2. Принципы функционирования
моделирующей программы
В ПМП химико-технологический процесс (химико-технологическая система —
ХТС) изображается в виде технологической схемы производства.
Видимая часть этой схемы является набором обозначений аппаратов (единиц обо-
рудования), связанных между собой потоками, и представляет собой определённого
вида принципиальную схему химического производства, которая реализуется в основ-
ном режиме «Изображение процесса» и содержит две категории объектов (рис. 6.1):
• единицы оборудования (аппараты), для расчёта которых используют специаль-
ные вычислительные алгоритмы (иногда для расчёта одного и того же физического
аппарата предлагаются несколько возможных алгоритмов, среди которых нужно выб-
рать наиболее подходящий для конкретного случая);
382
Глава 6. Пакеты моделирующих программ
Рис. 6.1 Принципиальная технологическая схема получения абсолютного спирта
• потоки, связывающие линиями единицы оборудования технологической схемы
(информация о параметрах входных потоков в аппараты включается в число исход-
ных данных для расчёта аппаратов, а в выходных потоках из аппаратов фиксируются
некоторые результаты расчётов единиц оборудования).
Невидимая часть технологической схемы, реализуемая в основном режиме «Расчё-
ты», позволяет при выделении (нажатии на изображение) каждого аппарата и каждого
входного потока всего производства задать параметры для расчёта свойств потоков,
режимные и конструкционные параметры для расчётов аппаратов, а также параметры
сходимости расчётов в используемых при этом вычислительных алгоритмах.
Кроме этих данных, для расчёта аппаратов и потоков необходимы фактографи-
ческие данные о свойствах индивидуальных веществ из соответствующей базы дан-
ных (БД), также следует выбрать адекватный метод расчёта физико-химических свойств
смесей, образуемых этими веществами.
Так, например, при расчёте свойств потоков в зависимости от типа и названия
веществ и их соотношения в многокомпонентной смеси, т.е. состава смеси, а также
задаваемых конкретных значений двух из трёх параметров — давления, температуры
и доли пара в потоке, в соответствии с законом Гиббса определяется величина неза-
данного параметра и энтальпия потока.
По принципиальной технологической схеме симулятор «самостоятельно» иден-
тифицирует рециклический (обратный) поток (см. рис. 6.1), задаёт начальные при-
ближения для его расчёта в выбранной или выбранных автоматически точках её или
их «разрыва».
При отсутствии некоторых физико-химических коэффициентов или констант для
расчётов в базах данных моделирующей программы они могут быть определены из
вводимых в программу экспериментальных данных, например, по фазовому равно-
весию жидкость—пар.
После задания всех параметров для вычислений (рис. 6.2) выполняется расчёт
технологической схемы всего производства (основной режим «Расчёты»), Одним из
наиболее важных результатов расчёта технологической схемы всего производства
является определение для него материального и теплового баланса.
Для определения конструкционных параметров и размеров единиц оборудования могут
быть реализованы алгоритмы расчётов размеров и конструкционных характеристик
различных типов теплообменников, ректификационных колонн, труб и т.д.
6.2. Принципы функционирования моделирующей программы
383
•• Плрзяетры сходимости
йви» расчета:
npccttwurcpaw'
8erere&«a (vZ«£s
С Пмвиамсойств.
Мате.чмсяв от» А>
^ОвнёииЧ
' Рлечег иепаре»--
-ncrpewwstn
f“ Гротраяиййрежся» р«ша
Алгоритм расче
Пстррйярич»
Нясявяймееяылста
рёй»
Стачижэрный
/ЗииамотеиаО сежич
|п>ёлеаое«гел
|ГтСВЮ»«рньай
Г" 3*^cpHa<«a»*mw»a^w*W<>' *••»•«•> рл»<~м
Г" £>х>ю«х»глемеат»в«мя1^ ярсцяи» paoasrc
Г 3&ЮВ!ИОТСЙЖ>М®««ОТ»И!а>^>^^
Г* &«овл»г^6^ж даинв«п9£1«и**йЛте»ра1»<
Рис. 6.2. Параметры сходимости расчетов технологических схем химических производств
Результаты расчётов могут быть представлены в виде отдельных таблиц или гра-
фиков для каждого аппарата или свойств любого потока, либо в виде комплексного
отчёта, генерируемого пользователем, или диаграммы процесса, в соответствующем,
как было показано в начале этой главы, третьем основном режиме работы пакета
моделирующей программы.
В основном режиме «Диаграмма процесса» на изображении принципиальной тех-
нологической схемы производства (рис. 6.3) можно представить некоторые рассчи-
танные результаты свойств всех потоков и всех аппаратов.
Рассматриваемое производство получения абсолютного этилового спирта с со-
держанием целевого продукта 99,99% (мае.) — см. рис. 6.1 и 6.3, состоит из четырёх
аппаратов (единиц оборудования):
• ректификационной колонны с 19 тарелками (7);
• декантатора (г);
• трубопровода (з);
• насоса (7).
Это производство включает два потока питания:
1) поток смеси этанол—вода азеотропного состава (около 5000 кг/час), который
поступает на третью сверху тарелку колонны (7);
2) поток азеотропного агента н-пентана (около 10 кг/час), который поступает на
вторую сверху тарелку колонны (7).
Колонна (7) работает под давлением 3.3 бар, и с её верхней тарелки отбирается
положительный (с минимальной температурой кипения) азеотроп с расслаивающей-
ся жидкой фазой, а в кубовом остатке получается целевой продукт — абсолютный
спирт.
Конденсатор колонны (7) моделируется трубопроводом (з) с газовой фазой, в
котором происходит падение давления, и декантатором (г), где жидкая фаза рассла-
384
Глава 6. Пакеты моделирующих программ
Рис. 6.3. Диаграмма процесса получения абсолютного спирта с рассчитанными данными о
температурах Г (°C), давлениях Р (бар) и величинах расхода потоков W (кг/час)
ивается с образованием незначительного количества отводимой из системы водной
фазы (поток [б]) и органической фазы (поток Щ), поступающей на первую сверху
тарелку колонны (7) (поток [э]) — рециклический поток.
Для расчёта расслаивания системы жидкость—жидкость в декантаторе (г) исполь-
зуется модуль трёхфазного равновесного испарителя (сепаратора) системы жидкость-
жидкость—пар в предположении отсутствия паровой фазы, включённый в моделиру-
ющую программу. При задании доли пара в испарителе близкой к нулю, этот модуль
позволяет моделировать расслаивание жидкой фазы в конденсаторе колонны (7).
6.3. Режимы работы моделирующей программы
Пакеты моделирующих программ позволяют относительно быстро выполнять все
расчёты, необходимые в повседневной деятельности химика-технолога и инженера-
химика.
Математические модели ХТП (см. главу 5) обычно достаточно сложны для вы-
числений. Для компьютерного моделирования простой технологической схемы, на-
пример, из пяти аппаратов и нескольких потоков нужно последовательно рассчиты-
вать все единицы оборудования (аппараты) производства. Одновременно для каждо-
го потока нужно рассчитывать его свойства — температуру, давление, расход, состав,
долю пара и его энтальпию. При наличии в технологической схеме рециклических
потоков необходимо реализовывать итерационные процедуры их расчётов путём пос-
ледовательных приближений к решению. Это очень трудоёмкий процесс, выполне-
ние которого невозможно без применения моделирующих программ.
При разработке новых технологических процессов необходимо проанализировать
множество альтернативных вариантов, и только компьютерное моделирование в среде
ПМП позволяет отбросить неподходящие варианты и за короткое время найти наи-
лучшее решение.
6.3. Режимы работы моделирующей программы
385
Выбор более эффективных систем управ-
ления при решении задач АСУТП требует реа-
лизации динамических моделей аппаратов с
простым регулированием и, возможно, более
сложным, например, каскадным регулирова-
нием. Моделирующие программы позволяют
реализовать динамические модели ХТП совме-
стно с регуляторами и исполнительными уст-
ройствами и выбирать оптимальные условия
для управления производствами.
Возможность реализации динамических
моделей с контурами регулирования в моде-
лирующих программах позволяет строить на их
основе тренажёры для операторов химических
производств.
В условиях действующих производств по-
стоянно приходится искать более эффектив-
ные решения текущих производственных за-
дач. Моделирующая программа поможет про-
анализировать реальную ситуацию, определить
сущность проблемы и пути её наиболее эф-
фективного и недорогого решения.
На рис. 6.4 представлены режимы работы
пакета моделирующих программ.
| Работа с файлами |
+ f
| Изображение процесса |
1 f
| Свойства веществ |
| Свойства смесей |
i t
| Задание данных |
i t
| Расчеты |
4 +
| Вспомогательные расчеты (
+ f
| Конструкционые расчеты |
1 f
| Таблицы результатов |
i f
] Г рафики результатов |
| Результирующий отчет |
| Диаграмма процесса |
Рис. 6.4. Режимы работы ПМП
Режим «Работа с файлами» позволяет со-
здавать новые задания, сохранять их
в памяти компьютера и обеспечивать
стыковку с другими программными
продуктами.
В режиме «Изображение процесса»
выполняется графическое изображе-
ние принципиальной технологической
схемы химического производства со
всеми единицами оборудования (ап-
паратами) и соединяющими их пото-
ками. Для этой цели используется таб-
лица стандартных пиктограмм, соот-
ветствующих типовым аппаратам хи-
мической технологии (рис. 6.5).
Режим «Свойства веществ» служит
для выбора химических компонентов
(веществ), составляющих потоки ХТП.
При этом базой данных (БД) индиви-
дуальных веществ моделирующей про-
граммы представляются все необходи-
мые для расчётов свойства выбранных
компонентов (рис. 6.6).
В режиме «Свойства смесей» рас-
считываются физико-химические и
другие термодинамические свойства
многокомпонентных смесей (фазовые
Рис. 6.5. Стандартные пиктограммы моделиру-
ющей программы для изображения технологи-
ческих схем производств
равновесия, плотности жидкости и
пара и др.) Как правило, для расчёта
одного и того же свойства многоком-
25-4544
386
Глава 6. Пакеты моделирующих программ
компонента
Блада*-»® по коком»
» ВьНмцг кямгюя*^ 1 *«<
9 К-?евма« 1 Hydrogen H2
134 Ethanol 2 Hethane CH4
5Z Siat«n 2 Ethane CZ85
4 Propane csas
5 I-Butane C4HW
$ Z-Kethylpropane C-®10
с Isobutane С4И10
в H-Sutane C4H1D
I-J>entane СШ2
1 2-Hethylhutatie C3H13
1 Isopantana csaiz
6 tf-rentane C'H-IZ
| 6‘wgfntte | Л^енг» | J
Л!мс*с
СК
С<эдкя®й
Рис 6 6 Выбор компонентов многокомпонентной смеси в моделирующей программе
Сагаев
ОК
a??:
г 3C«
r s/i&rt ШЛи .®S4‘
1‘jSav fAacx
' Р®шерн^а,расх: s-gte
OWirt f?ac
j КМШаг» CIJi53&3S6
&tw8 5 4SS1 ?01
i Water CS244SS
Рис 6 7 Задание свойств произвольного потока [Т] в моделирующей программе
6.3 Режимы работы моделирующей программы
387
Моду »w<rp*xw0 < »****ЭД4«*<(и рллкм^ ($Й&) ~'
Т**«
Пейа Т w^gat^j
Дй&®и®»в«
П$£й«ай;да&ле>
’вктютачкя с хиийИйехой ₽сжкие«
Для ъят&ъ
«няя 4рти9 £*ws («$)&$
чяя» сямя $»*а|
Г* $к<Ю*ЬЗ*Ж^^ЮК5^^
t рм <₽*$fc! ДО trtOf^
3<й<ижгиян0сть та}>е>нж:
wepew*
J T^we^Ms^epw^^ &йй^Чйрг<> | QwRO^rppr 1 | OtywKO ^rpor 2 j
Основные параметры медеяиревания
| Йсшмьаэдсмаямдделе» |5^^г«7^й>»ЦЖР
«ОЙС-8
- ?$М1
Mjwcrwwe
:’3
i в^МОДу *> »ХТ рОГОГО Р9£^БТ« И ДО
Заданий теплового и материального баланса
F?X<W $ф'
р) £а=й идчй«я£агй5?«
V •*#-«? J»»#W .?*•:>
" Ч-₽ьп1<до
^«^ииеаиайдаяааеааада Не!
|П на T3pew «
S
£
?
£
Сороса
388
Глава 6. Пакеты моделирующих программ
Моду INS (. 4 J>«f or tt WJ 4t {ЖКТифшбЦрМ И wtfc ЭДбиДО А<аЯЙи№^ЯЙ$ДО i
O^s^waMew| j Csaumsc*^ | Оленка saw1 | 0s«*assw2
Оцеточиы»»M параметра «х^йимости ax ’.
Оснонеы» оценочные зюа<
Г” ~~*~~~~
Оценочные зывчения темпв^ <• < дач
ЫЫ№^ЫЛНЬ**‘ЛЛК>ЯЛ'
Тфэдк |&5Л?-5& С
Twat ffii’in £
?3 J t
тя з | с
Оценочные йиачеыня
для вокоааго продукта
Параметры сходимости: <
1®>к<«арз»ий р" ’ "”
Тт t&V№ |Т (зоеторчаяisartyoui кёхуимякаатимы
<ХрЙКЙТЛСТЬ j
Дн^ч^фРИй^Фвкгев j
Терносифонный кипятильник
Дваягцр» Р” ’ "”
Я(5«ЗВ» 5НПКЦИ1ВЫ
убдардсчма $
ГфиПЦО^Хк * лыиг
Результаты расчета
faaasaaBawsa р::^:.-,,.-- -i::.w
;..... ......с.
T«a®e®»asrp^ws \ , М^г
кадмии» грс-жт---------- , ,Л
Чечней ржтФтагмы 1с№о1&
Шиом^рктатздамы ~-
Фк>т>вг»<1»глй р-т...ы-ит„«*-
Отмена
Рис. 6 8. Задание данных в моделирующей программе для расчета ректификационной
колонны (i) (стр. 387—388)
Р
~ Мид у ЛЬ
1& 2
U&mrwa
PWfctW
нагр^жа
!вйММйММ>ММШ>ШМШШШШМ4С4М>‘
304617 to
|D Пртен&ем&й прсграммай на амояч»«ез
Рис. 6 9 Задание данных в моделирующей программе для расчета декантатора (2) (доля пара
в трёхфазном равновесном испарителе жидкость—жидкость—пар практически равна нулю, и
поэтому остаются две расслаивающиеся жидкие фазы)
6.3. Режимы работы моделирующей программы
389
К ~ проектного л
л!
Зайгжя? вдаьжре® | Свайеп»
Венгели
Фигдагк
*Чжй.
иашшамв
|оПом2<н^'^»«'н»'»л«^ив|::
™*1 Тгтэвсйрег&е* |Йэоти»*г«с1>»й
Число «aswsr» ]
£HTMeTpW&S:
Сортлмодатруб
шеротатосш *„
Перевдй высоту j
|о5Й2
пт
м
«4
m
Дймвтр-^у; еелтне
ищется $ ешд »w«e «»$»р®е^о диаметр
~Т оппвгагредая® » <я<й;жлКзад^о <!<
U
Тамгйфйгзра
ж^аж-средм
В^иивд поЕерочшго росчете седжаг дай оценки цеиеоов^кйносг» Нримаивйй ps
перяОайя джяежя пкаяя. иьетоииен дня нвсколнож feo тре»1 кыймнных зезче
toM0TPwM<WHW#2) й>
j F«W
«ТР!Д
Отмена
8енг«.<!»
Фяпмги
Ж- 3
3
-^В
5
кдАяЭ
«nZseo
n?/sec
С»
Р<
J
Рис 6 10 Задание данных в моделирующей программе для расчета трубопровода (з)
390
Глава 6. Пакеты моделирующих программ
jPJ - Модуль расчета насосе (PUMP) -
Задала параметре®
1 Давпен
О
гйЗЛ)
Опёнка затрат
J
g
Рис 6 11 Задание данных в моделирующей программе для расчета жидкостного насоса (7)
понентной смеси программой предлагается несколько методов, среди которых необ-
ходимо выбрать наиболее подходящий.
Режим «Задание данных» служит для задания исходных данных для расчёта свойств
входных потоков производства и необходимых данных для расчёта всех единиц обору-
дования {аппаратов) технологической схемы процесса.
На рис. 6.7—6.11 показано, как задаются данные для расчёта производственного
потока [Т] и четырёх аппаратов (7), (г), (з), (7) рассматриваемой технологической
схемы получения абсолютного спирта (см. рис. 6.1).
В режиме «Расчеты» выполняются расчеты стационарных и динамических (неста-
ционарных) режимов работы аппаратов технологической схемы непрерывного произ-
водства, а также может быть проведён анализ параметрической чувствительности
химико-технологического процесса, и решена задача его оптимизации. Следует отме-
тить, что расчёты динамических режимов реакторных процессов и абсорбционно-
ректификационных установок, а также периодической ректификации обычно требу-
ют интеграции основного модуля моделирующей программы с соответствующими
дополнительными модулями.
В режиме «Вспомогательные расчеты» определяются, как правило, из экспери-
ментальных данных, параметры процессов, отсутствующие в соответствующих базах
данных программы и необходимые для расчётов. К ним, например, относятся пара-
метры бинарного взаимодействия для расчетов фазового равновесия жидкость—пар
или параметры уравнения Аррениуса для вычисления кинетических констант хими-
ческих реакций
6.3. Режимы работы моделирующей программы
391
Режим «Конструкционные расчеты» используется для определения размеров и конст-
рукционных характеристик аппаратов, например, ректификационных колонн с тарел-
ками и насадками различных типов. Также могут быть найдены типоразмеры (в соот-
ветствии с разными стандартами - США, Германии, Франции и России) теплообмен-
ников различных типов — кожухотрубных, воздушных, пластинчатых и «труба в трубе».
В режиме «Таблицы результатов» результаты всевозможных расчётов, сведённые
в удобные таблицы, предоставляются пользователю в распоряжение для просмотра,
оценки и анализа рассчитанных результатов. При желании можно получить твёрдую
копию (распечатку) этих таблиц (табл. 6.1).
Таблица 6.1. Изменение параметров потоков (температуры, давления, расходов
жидкости и пара) на тарелках ректификационной колонны (i)
CHEMCAD 5.4.2 Стр 1
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:49:03
Тип аппарата: Ректификационная колонна Название аппарата:
Оборудов. # 1
* Чистые потоки *
Темп Давл Жидк Пар Питания Продукт Harp
Тарел С bar kmol/h kmol/h kmol/h kmol/h MJ/h
1 71.2 3.28 421.79 415.10 439.96
2 71.5 3.29 413.43 446.65 0.14
3 72.2 3.30 562.93 438.15 128.19
4 73.3 3.31 568.24 459.47
5 73.8 3.32 570.66 464.77
6 74.1 3.33 571.68 467.19
7 74.3 3.34 572.13 468.21
8 74.4 3.34 572.37 468.67
9 74.5 3.35 572.54 468.91
10 74.6 3.36 572.64 469.07
11 74.7 3.37 572.54 469.18
12 74.8 3.38 570.71 469.07
13 75.1 3.39 551.93 467.25
14 78.4 3.40 462.95 448.47
15 99.0 3.41 449.57 359.49
16 110.7 3.42 463.33 346.11
17 112.7 3.43 466.03 359.87
18 113.0 3.44 466.47 362.57
19 113.1 3.45 363.01 103.46 1.295Е+004
По аналогии, в режиме «Графики результатов» можно получить графическое изоб-
ражение результатов расчётов, например, для фазовых диаграмм жидкость—пар
(рис. 6.12 и 6.13), жидкость—жидкость (рис. 6.14) и профилей изменения концентра-
ций компонентов в ректификационной колонне (i) (Рис. 6.15).
Режим «Результирующий отчет» служит для формирования текстового отчёта (табл. 6.2)
о результатах расчетов, в котором указаны как исходные данные для расчетов, вклю-
чая конфигурацию технологической схемы процесса, так и результаты расчётов с
материальными и тепловым балансами всего производства.
В режиме «Диаграмма процесса» результаты расчётов для потоков и аппаратов
представляются на изображении технологической схемы процесса (см. рис. 6.3).
392
Глава 6 Пакеты моделирующих программ
Массовые проценты, Y Массовая доля Y Температура,
Энатол/вода при 1 01 бар по модели NRTL
Энатол/вода при 1 01 бар по модели NRTL
Массовые проценты, X
Рис 6 12 Графическое
представление результатов
расчета фазового равнове-
сия жидкость—пар по
модели NRTL для бинар-
ной системы этиловый
спирт—вода с положитель-
ным азеотропом
Рис 6 13 Графическое
представление результатов
расчета фазового равнове-
сия жидкость—пар по
модели NRTL для бинар-
ной системы этиловый
спирт—вода с положитель-
ным азеотропом
Рис 6 14 Графическое
представление результатов
расчета фазового
равновесия
жидкость—жидкость
по модели NRTL
для трехкомпонентной
системы
вода—этанол—н-пентан
6 3 Режимы работы моделирующей программы
393
Профиль изменения концентраций, аппарат 1
★ Н-Пентан Этанол Вода
Рис 6 15 Графическое
представление профилей
изменения концентраций
компонентов по высоте
ректификационной
колонны (7)
Таблица б 2 Результирующий отчет по расчету производства абсолютного спирта
(рис 6 1)
CHEMCAD 5.4 2 Стр 1
Имя задания Азеотропная ректификация этилового спирта
Дата. 01/31/2005 Время: 13 50 37
ОТЧЕТ ПО СХЕМЕ
Оборудование Метка Номера потоков
1 Ректификационная колонна 2 Трехфазный испаритель 3 Трубопровод 4 Жидкостной насос 9 1 8 -6 3 -8 4 -9 2 -4 -3 -5 -7
Соединения потоков
Поток Оборудование Поток От к 1 14 2 15 3 13 6 Оборудование От к 2 4 2 2 Поток 7 8 9 Оборудование От к 1 3 2 4 1
Режим расчета * Последов.
Алгоритм испарения Нормал.
Последовательность расчета оборудования
13 2 4
Последовательность оборудования в цикле
13 2 4
394
Глава 6. Пакеты моделирующих программ
Разрываемые потоки рецикла
9
Метод расчета рецикла: Простые итерации
Мах. число итераций 100
Погрешность сходимости рецикла
Расход
Температура
Давление
Энтальпия
Доля пара
1.000Е-004
1.000Е-003
1.000Е-003
1.000Е-003
1.000Е-003
Расчет рецикла сошелся.
КОМПОНЕНТЫ
ID # Наименование
1 8 Н-пентан
2 134 Этанол
3 62 Вода
CHEMCAD 5.4.2 Стр 2
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
ТЕРМОДИНАМИЧЕСКИЕ МЕТОДЫ
Метод расчета Кравн. NRTL
Метод расчета энтальпии Скрытая теплота
Модель плотности жидк. API
NRTL параметры : Tij = Aij + Bij/T + Cij * Ln(T) + Dij * T (T Deg K)
I J Bi j Bji Alpha Aij Aji Cij Cji Dij Dj
1 2 436.69 363.36 0.382 0.00 0.00 0.00 0.00 0.00 0.00*
1 3 877.92 818.00 0.162 0.00 0.00 0.00 0.00 0.00 0.00*
2 3 114.49 520.40 0.482 0.00 0.00 0.00 0.00 0.00 0.00*
CHEMCAD 5.4.2
Стр 3
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
Полный масс. баланс kmol/h kg/h
Вход Выход Вход Выход
Н-пентан 0.136 0.136 9.818 9.815
Этанол 109.778 109.778 5057.382 5057.382
Вода 18.408 18.408 331.614 331.614
Всего 128.322 128.322 5398.815 5398.811
6.3. Режимы работы моделирующей программы
395
CHEMCAD 5.4.2 Стр 4
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
ОТЧЕТ ПО ОБОРУДОВ.
Отчет по строгому расчету ректификации
Оборудование № 1
Название
Число тарелок 19
1 тарелка питания 1
2 тарелка питания 2
3 тарелка питания 3
Режим кипятильника 6
Спецификации кипятильника 1.0000е-005
Компоненты кипятильника, 1 1
Падение давления
в колонне, bar 0.1682
Оценка Т вверху, С 65.5556
Оценка Т низа, С 121.1111
Давление вверху, bar 3.2790
Тепловая нагрузка, MJ/h 12947.5107
Признак счёта 1
Флегма mole, kmol/h 421.7872
Флегма mass, kg/h 28708.6582
Отчет по трехфазному фазовому сепаратору
Оборудование № Название 2
Режим испарителя 2
Парам! 1.0000е-006
Парам2 3.0462
Тепловая нагрузка, MJ/h -11903.3438
Отчет по трубопроводу
Оборудование № Название 3
Метод 1
Диаметр трубы, m 0.2032
Труба по каталогу 40
Длина трубы, m 15.2400
Фактор шероховатости, m 4.5720е-005
Dp/100ft 5.0000
Падение давления, bar 0.0415
Рейнольдс # пар 5.8761е+006
Фактор трения пар 0.0143
Средняя плотность, kg/m3 8.2584
Расчетная скорость, т/sec 30.1496
DP трение, bar 0.0415
Выходное давление, bar 3.2375
Тепловой режим 1
DP/100ft, psi 1.2051
396
Глава 6. Пакеты моделирующих программ
Поток газа, kg/h
Плотность газа, kg/m3
CHEMCAD 5.4.2
28946.9512
8.2584
Стр 5
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
ОТЧЕТ ПО ОБОРУДОВ.
Вязкость газа, N-s/m2 8.5946е-006
Общая длина, m 15.2400
Итерационная массовая
скорость, kg/h 28946.9512
Отчет по насосу
Оборудование № 4
Название
Выходное давление, bar 4.8263
Эффективность 1.0000
Расчетная мощность, MJ/h 8.5853
Расчётн. Pout, bar 4.8263
Высота, m 30.8967
Объённая скорость
потока, m3/h 48.1931
Массовая скорость
потока, kg/h 28314.6367
CHEMCAD 5.4.2 Стр 6
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
СВОЙСТВА ПОТОКА
Поток № 1 2 3 4
Название Питание Н-пентан Питание Этанол Дистиллят Орган.фаза
- - Общие - - Мольн расх, kmol/h 0.1361 128.1861 439.9585 415.1001
Масс расх, kg/h 9.8180 5389.0000 28946.9503 28314.6390
Темп, С 68.0278 43.3334 71.2127 67.7337
Давл, bar 3.4474 3.4473 3.2790 3.0462
Мол доля пара 0.0000 0.0000 1.000 0.0000
Энтал, MJ/h -22.564 -35460. -69993. -74951.
Тс, С 196.5100 248.7667 202.1578 200.1592
Pc, bar 33.6906 68.8947 40.4811 37.0804
Стд отн пл, вода = 1 0.631 0.807 0.647 0.643
Стд отн пл, возд =1 2.491 1.452 2.272 2.355
Градус API 92.6766 43.8384 87.1712 88.4967
Ср мол масса 72.1500 42.0404 65.7947 68.2116
Факт плотн, kg/m3 574.0881 778.0535 8.2584 587.5242
Факт объем, m3/h 0.0171 6.9263 3505.1690 48.1931
Стд жид, m3/h 0.0156 6.6838 44.7745 44.0619
6.3. Режимы работы моделирующей программы
397
Стд пар 0 С, m3/h 3.0500 2873.1182 9861.0746 9303.9070
- - Только пар- - Мольн расх, kmol/h 439.9585
Масс расх, kg/h 28946.9503
Средн мол вес 65.7947
Факт плотн, kg/m3 8.2584
Факт объем, m3/h 3505.1690
Стд жид, m3/h 44.7745
Стд пар 0 С, m3/h 9861.0746
Ср, kJ/kg-K 1.8571
Z фактор 0.9125
Вязкость, N-s/m2 8 .595е-006
Теплопр, W/m-K - - Только жидкость а м 0.0196
Мольн расх, kmol/h 0.1361 128.1861 415.1001
Масс расх, kg/h 9.8180 5389.0000 28314.6390
Средн мол масса 72.1500 42.0404 68.2116
Факт плотн, kg/m3 574.0881 778.0535 587.5242
Факт объем, m3/h 0.0171 6.9263 48.1931
Стд жид, m3/h 0.0156 6.6838 44.0619
Стд пар 0 С, m3/h 3.0500 2873.1182 9303.9070
Ср, kJ/kg-K 2.5769 2.6997 2.6047
Z фактор 0.0168 0.0085 0.0138
Вязкость, N-s/m2 0.0001715 0.0007518 0.0001991
Теплопр, W/m-K 0.0972 0.1732 0.1007
Пов натяж, N/m 0.0109 0.0220 0.0114
CHEMCAD 5.4.2 Стр 7
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
СВОЙСТВА ПОТОКА
Поток № 5 6 7 8
Название Водн.раствор - - Общие - - Сброс Абс.спирт
Мольн расх, kmol/h 24.8580 0.0004 103.4637 439.9585
Масс расх, kg/h 632.2866 0.0285 4766.4952 28946.9503
Темп, С 67.7337 67.7337 113.0800 71.2127
Давл, bar 3.0462 3.0462 3.4472 3.2375
Мол доля пара 0.0000 1.000 0.0000 1.000
Энтал, MJ/h -6941.6 -0.070647 -27483. -69989
Тс, С 308.7827 202.9035 240.7692 202.1578
Pc, bar 108.8754 41.9175 61.4793 40.4811
Стд отн пл,вода = 1 0.888 0.648 0.797 0.647
Стд отн пл,возд = 1 0.878 2.236 1.591 2.272
Градус API 27.8107 87.0249 46.0648 87.1712
Средн мол масса 25.4360 64.7637 46.0692 65.7947
Факт плотн, kg/m3 839.2761 7.5806 679.6995 8.1430
Факт объем, m3/h 0.7534 0.0038 7.0127 3554.8367
Стд жид, m3/h 0.7125 0.0000 5.9868 44.7745
Стд пар 0 С, m3/h 557.1577 0.0099 2318.9993 9861.0746
398
Глава 6. Пакеты моделирующих программ
- - Только пар- -
Мольн расх, kmol/h 0.0004 439.9585
Масс расх, kg/h 0.0285 28946.9503
Средн мол масса 64.7637 65.7947
Факт плотн, kg/m3 7.5806 8.1430
Факт объем, m3/h 0.0038 3554.8367
Стд жид, m3/h 0.0000 44.7745
Стд пар 0 С, m3/h 0.0099 9861.0746
Ср, kJ/kg-K 1.8460 1.8571
Z фактор 0.9183 0.9137
Вязкость, N-s/m2 8. ,520е-006 8.592е-006
Теплопр, W/m-K 0.0192 0.0196
- - Только жидкость — —
Мольн расх, kmol/h 24.8580 103.4637
Масс расх, kg/h 632.2866 4766.4952
Средн мол масса 25.4360 46.0692
Факт плотн, kg/m3 839.2761 679.6995
Факт объем, m3/h 0.7534 7.0127
Стд жид, m3/h 0.7125 5.9868
Стд пар 0 С, m3/h 557.1577 2318.9993
Ср, kJ/kg-K 3.5545 3.5046
Z фактор 0.0041 0.0086
Вязкость, N-s/m2 0.0004442 0.0002696
Теплопр, W/m-K 0.3035 0.1448
Пов натяж, N/m 0.0337 0.014
CHEMCAD 5.4.2
Стр 8
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
СВОЙСТВА ПОТОКА
Поток № 9
Название Рецикл
- - Общие - - Мольн расх, kmol/h 415.1001
Масс расх, kg/h 28314.6373
Темп, С 67.8500
Давл, bar 4.8263
Мол доля пара 0.0000
Энтал, MJ/h -74942.
Тс, С 200.1592
Pc, bar 37.0805
Стд отн пл, вода = 1 0.643
Стд отн пл, возд = 1 2.355
Градус API 88.4968
Средн мол масса 68.2116
Факт плотн, kg/m3 587.8351
Факт объем, m3/h 48.1677
Стд жид, m3/h 44.0619
Стд пар 0 С, m3/h 9303.9061
- - Только жидкость - —
Мольн расх, kmol/h 415.1001
Масс расх, kg/h 28314.6373
6.3. Режимы работы моделирующей программы
399
Средн мол масса
Факт плотн, kg/m3
Факт объем, m3/h
Стд жид, m3/h
Стд пар О С, m3/h
Ср, kJ/kg-K
Z фактор
Вязкость, N-s/m2
Теплопр, W/m-K
Пов натяж, N/m
CHEMCAD 5.4.2
68.2116
587.8351
48.1677
44.0619
9303.9061
2.6056
0.0218
0.0001994
0.1007
0.0114
Стр 9
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
ОТЧЕТ ПО ПОТОКАМ
Поток № 1 2 3 4
Название Питание Н-пентан Питание Этанол Дистиллят Орган.фаза
Темп, С 68.0278 43.3334 71.2127 67.7337
Давл, bar 3.4474 3.4473 3.2790 3.0462
Энтал, MJ/h -22.564 -35460. -69993. -74951.
Мол доля пара 0.00000 0.00000 1.0000 0.00000
Общ, kmol/h Расход, kmol/h 0.1361 128.1861 439.9582 415.1001
N-Pentane 0.1361 0.0000 358.4473 358.3123
Ethanol 0.0000 109.7784 57.6230 51.3073
Water 0.0000 18.4077 23.8882 5.4805
Поток № 5 6 7 8
Название Водн.раствор Сброс Абс.спирт
Темп, С 67.7337 67.7337 113.0800 71.2127
Давл, bar 3.0462 3.0462 3.4472 3.2375
Энтал, MJ/h -6941.6 -0.070647 -27483. -69989,
Мол доля пара 0.00000 1.0000 0.00000 1.0000
Общ, kmol/h Расход, kmol/h 24.8580 0.0004 103.4637 439.9585
N-Pentane 0.1346 0.0004 0.0010 358.4473
Ethanol 6.3157 0.0001 103.4626 57.6230
Water 18.4076 0.0000 0.0001 23.8882
Поток В
Название
Темп, С
Давл, bar
Энтал, MJ/h
Мол доля пара
Общ. kmol/h
Расходы, kmol/h
N-Pentane
Ethanol
Water
9
Рецикл
67.8500
4.8263
-74942.
0.00000
415.1001
358.3123
51.3072
5.4805
400
Глава 6. Пакеты моделирующих программ
CHEMCAD 5.4.2
Стр 10
Имя задания: Азеотропная ректификация этилового спирта
Дата: 01/31/2005 Время: 13:50:37
DISTILLATION PROFILE
Тип аппарата: SCDS
Название аппарата:
Оборудов. # 1
Темп, Давл, * Чистые потоки * Продукт, Harp,
Жидк, Пар, Питания,
Тарел С bar kmol/h kmol/h kmol/h kmol/h MJ/h
1 71.2 3.28 421.79 415.10 439.96
2 71.5 3.29 413.43 446.65 0.14
3 72.2 3.30 562.93 438.15 128.19
4 73.3 3.31 568.24 459.47
5 73.8 3.32 570.66 464.77
6 74.1 3.33 571.68 467.19
7 74.3 3.34 572.13 468.21
8 74.4 3.34 572.37 468.67
9 74.5 3.35 572.54 468.91
10 74.6 3.36 572.64 469.07
11 74.7 3.37 572.54 469.18
12 74.8 3.38 570.71 469.07
13 75.1 3.39 551.93 467.25
14 78.4 3.40 462.95 448.47
15 99.0 3.41 449.57 359.49
16 110.7 3.42 463.33 346.11
17 112.7 3.43 466.03 359.87
18 113.0 3.44 466.47 362.57
19 113.1 3.45 363.01 103.46 1.295Е+004
6.4. Этапы работы моделирующей
программы и основные модули,
обеспечивающие их выполнение
Моделирование химико-технологического процесса с использованием моделиру-
ющей программы включает в себя девять основных этапов, для выполнения которых
используются различные программные модули ПМП:
• создание нового задания;
• выбор единиц измерения;
• построение технологической схемы;
• выбор компонентов;
• выбор термодинамических моделей;
• задание параметров потоков питания;
• задание параметров единиц оборудования;
• запуск программы компьютерного моделирования;
• просмотр и печать результатов.
6.4. Этапы работы и основные модули моделирующей программы
401
Создание нового задания
Задаётся имя папки задания, куда будут помещены все файлы, относящиеся к
данному заданию.
Выбор единиц измерения
Обычно может быть выбран один из четырёх стандартных вариантов системы
измерения физических величин:
. СИ;
• модифицированная СИ;
• метрическая система;
• британская система.
Возможно реализовать любую комбинацию этих систем измерений. Для россий-
ских пользователей наиболее удобной является модифицированная система СИ.
Выбранная система измерения физических величин распространяется на всё зада-
ние. При этом в процессе работы для отдельных единиц оборудования (аппаратов) и
потоков она может быть изменена, а затем восстановлена в первоначальном виде.
Построение технологической схемы
Технологическая схема химического производства обычно изображается с исполь-
зованием стандартных пиктограмм единиц оборудования (аппаратов) и соединяющих
их линий — потоков (см. рис. 6.1, 6.3, 6.5). В моделирующую программу обычно вклю-
чены около пятидесяти пиктограмм аппаратов, и каждой пиктограмме единицы обо-
рудования соогвстствует алгоритм поверочно-оценочного и/или проектного расчёта
аппарата. Все пиктограммы аппаратов имеют имя, соответствующее реализованному
алгоритму расчета, и несколько вариантов изображений, из которых пользователь мо-
жет сделать подходящий выбор. Если предлагаемые пиктограммы аппаратов не устра-
ивают пользователя, он с помощью специального графического драйвера, встроенного
в программу, может создать собственное изображение аппарата или аппаратов.
Модуль, позволяющий создавать изображения технологических схем химических
производств, является одним из трёх основных модулей моделирующей программы.
Выбор компонентов
В моделирующую программу встроена фактографическая база данных (БД) по
свойствам индивидуальных веществ, необходимых для расчёта технологических схем
химических производств. В БД компонентов представлены до 80 свойств-констант и
свойств-зависимостей более чем для 2500 индивидуальных веществ. Для свойств-
зависимостей приводятся вид и коэффициенты уравнений, описывающих эти зави-
симости, как, например, для уравнения Антуана, описывающего зависимость давле-
ния насыщенного пара индивидуального вещества от температуры.
Выбор компонентов выполняется либо по номеру в БД, либо по брутто-формуле
химического соединения, либо по названию вещества. Включение вещества в спи-
сок компонсшов технологической схемы производства означает, что все его свой-
ства могут быть использованы моделирующей программой в процессе выполнения
расчётов. При отсутствии вещества в БД его свойства в программе либо могут быть
рассчитаны по структурным составляющим молекулы (в основном, для органичес-
ких веществ), либо в базу данных могут быть введены пользовательские данные о
свойствах вещества.
Следует отмерить, что для расчётов свойств электролитов и неорганических моле-
кул в БД включены и свойства ионов — анионов и катионов. Компонентами много-
компонентной смеси в случае таких расчётов в соответствии с теорией электролитов
402
Глава 6. Пакеты моделирующих программ
могут быть не только молекулы, но и анионы и катионы слабых и сильных электро-
литов.
В программу также включён модуль определения свойств «псевдокомпонентов»
для непрерывных нефтяных смесей, позволяющий решать задачу моделирования
нефтяных ректификационных колонн по экспериментальным данным о кривой раз-
гонки.
Выбор термодинамических моделей
На этом этапе с использованием специальных модулей рассчитываются следую-
щие свойства многокомпонентной смеси:
• равновесие пар (газ)—жидкость—твёрдое вещество и пар (газ)—жидкость—жид-
кость—твёрдое вещество;
• энтальпия системы, желательно с учётом теплоты смешения жидкости;
• плотность и поверхностное натяжение жидкости;
• вязкость и жидкости и пара;
• теплопроводности жидкости и пара.
Для расчёта каждого из перечисленных свойств многокомпонентной смеси моде-
лирующей программой предлагается множество методов (например, для расчёта рав-
новесия жидкость—пар (газ) — 38 методов). Выбор оптимального метода в каждом
конкретном случае требует глубоких знаний в области химической термодинамики.
Для решения неформализованной задачи выбора метода в моделирующие програм-
мы иногда включаются экспертные системы, которые для смеси с заданным набо-
ром компонентов и определённым составом для фиксированного диапазона темпе-
ратур и давлений осуществляют выбор метода расчёта свойств многокомпонентной
системы.
Задание параметров потоков питания
Для расчёта технологической схемы производства необходимы данные только для
входных потоков всего производства (потоков питания). Параметры выходных пото-
ков из каждого аппарата получаются в результате их расчёта и являются входными
потоками для следующих за ними единиц оборудования, с которыми они непосред-
ственно связаны.
При задании параметров входных потоков (потоков питания) необходимо задать
их общий расход и состав (возможно задание расходов каждого компонента отдель-
но, так как в программе автоматически осуществляется их суммирование и опреде-
ление состава потока). Одновременно в соответствии с правилом Гиббса должны
быть заданы значения двух из трёх параметров — давления, температуры и доли пара
в потоке. По указанным данным в программе автоматически определяется значение
незаданного параметра потока питания и энтальпия потока.
Задание параметров единиц оборудования
Необходимо задать исходные данные для расчёта каждого аппарата. Эти данные
можно разделить на три типа:
• обязательные технологические и конструкционные параметры, количество ко-
торых равно числу степеней свободы решаемой при расчёте системы уравнений;
• технологические параметры, являющиеся начальными приближениями итера-
ционных алгоритмов расчёта (задание их необязательно);
• параметры сходимости расчётов, которые заданы «по умолчанию» (их задание
означает изменение значений приближений, заданных «по умолчанию»).
В табл. 6.3 приведены типовые аппараты, алгоритмы расчёта которых включены
практически во все моделирующие программы. Для расчёта каждого из этих аппара-
6.4. Этапы работы и основные модули моделирующей программы
403
тов необходимо задавать свой собственный набор исходных данных.
Представленные в таблице модули расчёта разделены на модули, предназначен-
ные для расчёта стационарных и нестационарных режимов процессов. В последнем
случае для расчётов всегда необходимо задавать длительность протекания переход-
ного процесса по времени. При расчёте стационарных режимов процессов с рецик-
лическими потоками желательно также задавать начальные приближения для отсут-
ствующих параметров рециклического потока.
Анализ модулей для расчёта стационарных режимов процессов показывает, что
для расчёта химических реакторов используются три алгоритма:
• стехиометрический реактор (приближённый расчёт);
• равновесный реактор;
• кинетический реактор.
Последний позволяет выполнять расчёты как для реакторов с мешалкой (модель
идеального смешения), так и для трубчатых реакторов (модель идеального вытесне-
ния) (см. главы 2, 5). В нём также могут быть реализованы различные тепловые
режимы (изотермический, адиабатический и политропический), а для трубчатого
реактора — ещё и различные режимы движения теплоносителя в рубашке — прямо-
ток или противоток.
Для расчёта ректификации можно использовать пять модулей, хотя периодичес-
кая ректификация не относится к процессам со стационарным режимом. Из остав-
шихся четырёх модулей приближённый расчёт по методике Фенске—Андервуда сле-
дует считать предварительным. Точный расчёт с теоретическими тарелками непри-
емлем для практической реализации для дискретных многокомпонентных смесей,
хотя может применяться для непрерывных нефтяных систем с «псевдокомпонента-
ми». Для последних более предпочтителен специальный модуль для расчёта нефтя-
ных колонн. Модуль точного расчёта ректификации и абсорбции с массопередачей и
химической реакцией следует считать наиболее приемлемым, так как в нём учитыва-
ются конструкции тарелок и типы насадок, а также химические превращения в па-
ровой (газовой) и жидкой фазах.
При рассмотрении модулей для расчёта стационарных режимов процессов следу-
ет обратить внимание на наличие модулей для расчёта аппаратов с твёрдой фазой.
Для расчётов нестационарных режимов реакторов с мешалкой и ректификационных
{абсорбционных) колонн в технологические схемы производств включаются соответ-
ствующие им расчётные модули, а также модули для расчёта динамических регули-
рующих клапанов и ПИД-регуляторов, динамических резервуаров, ёмкостей для сбора
продуктов и модуль запаздывания по времени. Всё это позволяет проводить исследо-
вания системы управления процессом с различными типами регуляторов и регули-
рующих клапанов (исполнительных устройств).
Запуск программы компьютерного моделирования
При запуске моделирующей программы может быть решён следующий комплекс
задач компьютерного моделирования:
• расчёт отдельных единиц оборудования (аппаратов);
• расчёт технологической схемы процесса, в том числе с рециклическими пото-
ками;
• расчёт технологической схемы процесса со статическими контроллерами об-
ратного/прямого действия;
• анализ параметрической чувствительности производства;
• оптимизация химико-технологического процесса;
• расчёт динамических режимов процессов.
Перед запуском программы в меню «Параметры сходимости» устанавливается
допустимая погрешность вычислений при расчёте рециклических потоков и выбира-
ется метод решения системы нелинейных уравнений, необходимый для этих целей
404
Глава 6. Пакеты моделирующих программ
Таблица 6.3. Некоторые расчётные модули моделирующей программы
Для расчёта стационарных процессов
Основные Компрессор
Экспандер
Делитель потока
Сепаратор компонентов
Печь
Теплообменник
Смеситель
Жидкостный насос
Клапан
Двухфазный равновесный испаритель жидкость—пар
Трёхфазный равновесный испаритель жидкость—жидкость—пар
Многоцелевой резервуар
Жидкостный экстрактор
Трубопровод
Статический контроллер обратного/прямого действия
Реакторы Стехиометрический
Равновесный
Кинетический
Ректификация Периодическая
Приближённая
С теоретическими тарелками
Для нефтяных смесей
С массопередачей и химической реакцией
Аппараты с твёрдой фазой Рукавный фильтр
Фильтрующая центрифуга
Дробилка
Кристаллизатор
Отстойная центрифуга
Циклон
Сушильный аппарат
Электрофильтр
Вакуум-фильтр
Гидроциклон
Грохот
Скруббер Вентури
Промывной аппарат
Для расчёта нестационарных режимов процессов
Основные Реактор с мешалкой
Колонна ректификации и абсорбции
ПИД-регулятор
Динамический регулирующий клапан
Динамический резервуар
Ёмкость для сбора продуктов
Модуль запаздывания по времени
6.4. Этапы работы и основные модули моделирующей программы
405
(либо метод простых итераций, либо метод Вегстейна, либо метод главных собствен-
ных значений — см. рис. 6.2). Также устанавливается максимальное число итераций,
режим расчёта стационарного или нестационарного процесса и формат вывода на
монитор компьютера промежуточных результатов итерационных вычислений: при-
знак «отображение окна трассировки» на рис. 6.2.
Расчёт отдельного аппарата может быть выполнен в любое время с известными
для единицы оборудования данными для входных потоков и данными для техноло-
гических и конструкционных параметров аппаратов (см. рис. 6.7—6.11).
Для расчёта технологической схемы без рециклических потоков достаточно задать
данные для всех входных потоков технологической схемы и все технологические
параметры, необходимые для расчёта всех единиц оборудования. При неправильном
задании параметров для расчёта отдельных аппаратов (либо недостаточном числе
параметров, либо большем их числе, чем следует из числа степеней свободы решае-
мой системы уравнений) моделирующая программа самостоятельно «указывает» на
ошибки задания параметров.
При расчёте технологической схемы с рециклическими потоками необходимо выб-
рать один из трёх возможных алгоритмов (см. рис. 6.2) расчёта рециклических пото-
ков и желательно задать начальное приближение для вычисления параметров рецик-
лического потока.
Применение статического контроллера обратного действия при расчёте техноло-
гических схем позволяет обеспечить выполнение требований к производству в целом
(например, получения продукта определённого состава) за счёт изменения выбран-
ного управляющего параметра до тех пор (например, расхода одного из потоков тех-
нологической схемы или его температуры), пока условие, заданное для определён-
ного технологического параметра — требование к производству в целом, не будет
выполнено. По-существу, в этом случае реализуется также итерационный расчёт с
последовательным изменением значения управляющего параметра, которое должно
привести к выполнению предварительно заданных требований к производству.
Анализ параметрической чувствительности производства на компьютере представ-
ляет собой многократный расчёт технологической схемы с оценкой влияния измене-
ния входных переменных и параметров, определяющих состояние процесса, на вы-
ходные результирующие переменные, характеризующие состояние ХТП. Для измене-
ния входных переменных и параметров задают физически обоснованный интервал их
изменения и шаг, с которым в заданном интервале должны изменяться входные пере-
менные. В результате могут быть выявлены управляющие параметры, обеспечиваю-
щие получение продуктов требуемого качества при расчёте технологической схемы со
статическим контроллером обратного действия, и оптимизирующие переменные, наи-
более сильно влияющие на целевые функции при решении задачи оптимизации.
Задача оптимизации химико-технологического процесса может решаться в моде-
лирующей программе для всей технологической схемы с ограничениями первого
рода (задаётся диапазон изменения оптимизирующих переменных) и второго рода
(устанавливаются ограничения на технологические и другие параметры производ-
ства). При этом в программе существует возможность выбора критерия оптимально-
сти (целевой функции) и одного из нескольких включённых в пакет алгоритмов
оптимизации. По-существу, в результате с применением ПМП удается решать раз-
личные задачи нелинейного программирования для технологической схемы хими-
ческого производства (см. главу 5).
Расчёт динамических режимов процессов, как правило, выполняется с использова-
нием дополнительных модулей пакета — модулей для расчёта колонны периодичес-
кой ректификации, динамического реактора с мешалкой, динамической колонны
абсорбции и ректификации. Алгоритмы, включённые в эти модули, представляют
собой реализацию известных численных методов для решения жёстких систем диф-
ференциальных уравнений (см. разд. 3.5.1). В этом случае всегда необходимо зада-
вать продолжительность во времени моделирования нестационарных режимов ис-
406
Глава 6. Пакеты моделирующих программ
следуемых процессов и шаг решения, который обычно специфицирован в програм-
ме «по умолчанию». В технологические схемы для расчёта динамических режимов
процессов обычно включаются ПИД-регуляторы, динамические регулирующие кла-
паны, динамические резервуары и др., которые позволяют проводить исследования
и оптимизацию нестационарных режимов процессов совместно с системами управ-
ления.
Просмотр и печать результатов
Анализ результатов расчётов с использованием пакетов моделирующих программ
— важнейшая задача компьютерного моделирования. Основное требование к полу-
ченным результатам расчетов — их физическая обоснованность, т.е. соответствие
реальным условиям работы химического производства.
Для просмотра результатов расчётов, полученных с использованием ПМП, в про-
грамме предусматривается несколько возможностей:
• некоторые результаты расчётов представляются в экранных меню аппаратов,
куда вводятся исходные данные для расчётов;
• исходные данные для расчётов и полученные результаты вычислений представ-
ляются в виде таблиц (например, см. табл. 6.1);
• результаты расчётов могут быть представлены в виде различных графиков (см.
рис. 6.12—6.15), которые могут создаваться в программе;
• в режиме «Диаграмма процесса» (см. рис. 6.3) результаты расчётов приводятся
непосредственно на изображении технологической схемы процесса рядом с соответ-
ствующими единицами оборудования и потоками (одновременно рядом с изображе-
нием технологической схемы может быть приведена таблица с некоторыми свой-
ствами отдельных или всех потоков);
• полный текстовый отчёт (см. табл. 6.2) обо всех используемых для расчётов
исходных данных и результатах, полученных с применением моделирующих про-
грамм, приводится в режиме «Результирующий отчёт» (структура и размер результи-
рующего отчёта генерируются в программе пользователем).
Все результаты расчётов, изображаемые на дисплеях компьютеров, могут быть
распечатаны и оформлены в виде отчётов о выполненной работе по компьютерному
моделированию химико-технологических процессов.
ЗАКЛЮЧЕНИЕ
Компьютерное моделирование химико-технологических процессов (ХТП) — это
важнейший атрибут исследования, оптимизации, проектирования и управления про-
изводствами в химической и смежных с ней отраслях промышленности. Компью-
терные модели ХТП широко применяются в автоматизированных компьютерных
системах прикладной информатики, таких как:
• автоматизированные информационные системы (АИС), базы и банки данных;
• системы автоматизированного проектирования (САПР);
• автоматизированные системы научных исследований (АСНИ) и автоматизиро-
ванный эксперимент;
• автоматизированные системы управления технологическими процессами
(АСУТП);
• автоматизированные системы обучения (АОС) операторов химических произ-
водств — так называемые тренажерные системы.
В настоящее время химики-технологи и инженеры-химики, работающие в про-
изводственной сфере, исследовательских и проектных организациях, инжиниринго-
вых компаниях, в своей профессиональной деятельности в той или иной степени
сталкиваются как с решением всевозможных задач с использованием компьютерных
моделей реальных процессов, так и с перечисленными выше автоматизированными
системами прикладной информатики. Поэтому современная университетская под-
готовка бакалавров, дипломированных специалистов и магистров по химико-техно-
логическим специальностям должна проводиться с учетом того, что специалисты в
области химической технологии должны:
• знать принципы построения компьютерных моделей ХТП и используемые при
этом вычислительные (численные) методы;
• уметь применять их для решения стоящих перед ними задач;
• понимать, в каких случаях для построения компьютерных моделей ХТП необ-
ходимо выбирать эмпирические модели (основанные на экспериментальных дан-
ных) и в каких случаях — физико-химические модели (основанные на знании теории
процессов).
Основная задача настоящего учебного пособия состоит в том, чтобы дать возмож-
ность студентам овладеть этими знаниями и, в конечном счете, вне зависимости от
их конкретной специальности, соответствовать современным требованиям в области
информационных технологий, предъявляемым в настоящее время к химикам-техно-
логам и инженерам-химикам. Поэтому в пособии подробно освещается теоретичес-
кий материал, связанный с построением компьютерных моделей ХТП и применени-
ем для этой цели численных методов вычислительной математики, с решением задач
идентификации и оптимизации реальных производств.
При компьютерном моделировании ХТП решается задача не только построения ма-
тематической модели реального процесса, но и задачи идентификации (для обеспече-
ния адекватности модели) и оптимизации. Важным этапом компьютерного моделиро-
вания является анализ параметрической чувствительности математической модели. Ре-
шение последней задачи позволяет, с одной стороны, выбирать параметры модели, наи-
более сильно влияющие на ее адекватность, т.е. обоснованно решать задачу идентифи-
кации, а, с другой стороны, анализ чувствительности модели к изменению различных
переменных — параметров — даёт возможность достоверно определять ресурсы оптими-
зации (управляющие или оптимизирующие переменные), т.е. надежно решать задачу
оптимизации.
В учебном пособии широко представлен материал о методике построения двух
основных типов компьютерных моделей химико-технологических процессов — эм-
пирических и физико-химических. В действительности, часто объем знаний для по-
408
Заключение
строения адекватных физико-химических моделей недостаточен и приходится пользо-
ваться эмпирическими моделями, базирующимися на обработке данных экспери-
ментальных исследований. В последнем случае используются статистические методы
корреляционного и регрессионного анализа, а для решения задачи оптимизации —
теория активного экспериментирования.
Задача обеспечения адекватности физико-химических моделей — задача иденти-
фикации — не является тривиальной, и для ее решения также необходимо провести
комплекс экспериментальных исследований с целью определения структуры систе-
мы уравнений, описывающих реальные процессы (структурная идентификация) и ее
параметров-коэффициентов (параметрическая идентификация). Эксперименты мо-
гут проводиться на лабораторных, пилотных, полупромышленных, а иногда и про-
мышленных установках. Очень важно правильно выбрать точки экспериментальных
измерений из генеральной совокупности данных. При этом также желательно при-
менять статистические методы обработки результатов экспериментов.
С позиций построения физико-химических компьютерных моделей ХТП их це-
лесообразно разделить на два типа — модели объектов с сосредоточенными парамет-
рами и модели объектов с распределенными по времени и/или по пространственной
координате параметрами.
В зависимости от типа моделей объектов используются различные подходы для
решения задач их компьютерного моделирования. Так, для построения математичес-
ких моделей стационарных режимов объектов с сосредоточенными параметрами ис-
пользуются системы конечных линейных и нелинейных уравнений, а с распределен-
ными параметрами — системы обыкновенных дифференциальных уравнений и диф-
ференциальных уравнений в частных производных. Нестационарные режимы процес-
сов с сосредоточенными параметрами описываются системами обыкновенных диф-
ференциальных уравнений, а с распределенными параметрами — системами диффе-
ренциальных уравнений в частных производных. При решении задачи идентифика-
ции для количественной оценки адекватности моделей с распределенными парамет-
рами используются интегральные критерии, с сосредоточенными параметрами — сум-
марные. Когда решается задача оптимизации для объектов с сосредоточенными пара-
метрами, как правило, используются методы нелинейного программирования с огра-
ничениями I и II рода, а для объектов с распределенными параметрами — метод дина-
мического программирования и принцип максимума Понтрягина [5,16,21,44].
Для решения задач компьютерного моделирования ХТП используются известные
численные методы вычислительной математики, которые подробно представлены в
настоящем пособии:
• решение систем конечных линейных и нелинейных уравнений;
• интерполяция и аппроксимация;
• численное дифференцирование и интегрирование;
• решение систем обыкновенных дифференциальных уравнений;
• решение систем дифференциальных уравнений в частных производных;
• методы оптимизации.
Решение конкретных задач компьютерного моделирования ХТП — построения ма-
тематической модели, идентификации и оптимизации, предполагает реализацию на
компьютере некоторой комбинации алгоритмов, соответствующих перечисленным
методам вычислительной математики. При этом обычно возникает неформализован-
ные задачи (НФЗ) выбора метода решения и выбора алгоритма (или алгоритмов) рас-
чета. Как правило, такие задачи выбора решаются специалистами на основании их
опыта, знаний и интуиции. В последнее время для выбора методов решения задач
компьютерного моделирования стали применяться экспертные системы (ЭС), вклю-
чающие базы знаний по конкретной предметной области и эвристические процедуры
для оптимального решения задач. В отличие от формализованных задач (ФЗ), для
решения которых применяются алгоритмы вычислительной математики, приводящие
к получению конкретных численных результатов, при реализация эвристических про-
Заключение
409
цедур решения НФЗ в ЭС к получаемым результатам (достоверности выбранного ме-
тода) следует относиться с определенной вероятностью и окончательный выбор вари-
анта решения НФЗ отдать на откуп специалисту.
Важным инструментом для решения задач компьютерного моделирования хими-
ческих производств становятся пакеты моделирующих программ (ПМП), имеющие
единую операционную оболочку, в которую включено большое количество численных
алгоритмов, а некоторых случаях и экспертных систем, для решения задач анализа,
оптимизации и синтеза химических производств. Наличие многочисленных фактогра-
фических баз данных по физико-химическим свойствам индивидуальных веществ и
их смесей, банков данных по расчетным модулям типовых единиц оборудования хи-
мических производств, а также вычислительных алгоритмов для расчета рецикличес-
ких технологических потоков и решения оптимизационных задач позволяют рассмат-
ривать эти ПМП в настоящее время как наиболее эффективный инструмент для ком-
пьютерного моделирования ХТП.
В заключение необходимо отметить, что практически все задачи, решаемые в химичес-
кой технологии и связанные с проектированием, управлением и обучением (тренировкой)
операторов химических производств требуют применения адекватных компьютерных мо-
делей химико-технологических процессов.
ПРИЛОЖЕНИЕ Таблица 1- Стандартное нормальное распределение Схема определения квантиля. Квантил ?
9 1 1® -* о о
Искомый квантиль ООО 0 01 0 02 0 03 004 0 05 0 06 0 07 0 08 0 09
00 0 5000 0 5040 0 5080 0 5120 0 5160 0 5199 0 5239 0 5270 05319 0 5359
0 1 05398 0 5438 0 5478 0 5517 0 5557 0 5596 0 5636 0 5675 0 5714 0 5753
02 05793 0 5832 0 5871 0 5910 0 5948 0 5987 0 6025 0 6064 0 6103 06141
0 3 06179 06217 0 6255 0 6293 06331 0 6368 0 6406 0 6443 0 6480 06517
04 06554 0 6591 0 6628 0 6664 0 6700 0 6736 0 6772 0 6808 0 6844 0 6879
05 0691 5 0 6950 0 6985 0 7019 0 7054 0 7088 0 7123 0 7157 0 7190 0 7224
06 0 7257 0 7291 0 7324 0 7357 0 7389 0 7422 0 7454 0 7486 0 7517 0 7549
07 0 7580 0 7611 0 7642 0 7673 0 7704 0 7734 0 7764 0 7794 0 7823 0 7852
08 0 7881 0 7910 0 7939 0 7967 0 7995 0 8023 0 8051 0 8078 08106 0 8133
09 08159 08186 0 8212 0 8238 0 8264 0 8289 0 8315 0 83 40 0 8365 0 8389
1 0 0 8413 0 8438 0 8461 0 8485 0 8508 0 8531 0 8554 0 8577 0 8599 0 8621
1 1 0 8643 0 8665 0 8686 0 8708 0 8729 0 8748 0 8770 0 8790 0 8810 0 8830
1 2 0 8849 0 8869 0 8888 0 8907 0 8925 0 8944 0 8962 0 8980 0 8997 09015
1 3 0 9032 0 9049 0 9066 0 9082 0 9099 09115 09131 09147 09162 09177
1 4 09192 0 9207 0 9222 0 9236 09251 0 9265 0 9279 0 9292 0 9306 09319
1 5 '0 9332 0 9345 0 9357 0 9370 0 9382 0 9394 0 9406 0 9418 0 9429 0 9441
1 6 0 9452 0 9463 0 9474 0 9484 0 9495 0 9505 09515 0 9525 0 9535 0 9545
1 7 0 9554 0 9564 0 9573 0 9582 0 9591 0 9599 0 9608 09616 0 9625 0 9633
1 8 0 9641 0 9649 0 9656 0 9664 0 9671 0 9678 0 9686 0 9693 0 9699 0 9706
1 9 09713 09719 0 9726 0 9732 0 9738 0 9744 0 9750 0 9756 0 9761 0 9 767
2 0 0 9772 0 9778 0 9783 0 9788 0 9793 0 9798 0 9803 0 9808 09812 09817
2 1 0 9821 0 9826 0 9830 0 9834 0 9838 0 9842 0 9846 0 9850 0 9854 0 9857
2 2 0 9861 0 9864 0 9868 0 9871 0 9875 0 9878 0 9881 0 9884 0 9887 0 9 890
2 3 0 9893 0 9896 0 9898 0 9901 0 9904 0 9906 0 9909 09911 09913 09916
24 0 9918 0 9920 0 9922 0 9925 0 9927 0 9929 0 9931 0 9932 0 9934 0 9936
25 0 9938 0 9940 0 9941 0 9943 0 9945 0 9946 0 9948 0 9949 0 9951 0 9952
2 6 0 9953 0 9955 0 9956 0 9957 0 9959 0 9960 0 9961 0 9962 0 9963 0 9964
2 7 0 9965 0 9966 0 9967 0 9968 0 9969 0 9970 0 9971 0 9972 0 9973 0 9974
2 8 0 9974 0 9975 0 9976 0 9977 0 9977 0 9978 0 9979 0 9979 0 9980 0 9981
2 9 0 9981 0 9982 0 9982 0 9983 0 9984 0 9984 0 9985 0 9985 0 9986 0 9986
3 0 0 9987 0 9987 0 9987 0 9988 0 9988 0 9989 0 9989 0 9989 0 9990 0 9990
3 1 0 9990 0 9991 0 9991 0 9991 0 9992 0 9992 0 9992 0 9992 0 9993 0 9993
3 2 0 9993 0 9993 0 9994 0 9994 0 9994 0 9994 0 9994 0 9995 0 9995 0 9995
3 3 0 9995 0 9995 0 9995 0 9996 0 9996 0 9996 0 9996 0 9996 0 9996 0 9997
3 4 0 9997 0 9997 0 997 0 9997 0 9997 0 9997 0 9997 0 9997 0 9997 0 9998
Приложение
411
Таблица 2 ^-распределение Стьюдента
Схема определения квантиля:
v\l-P 2 0 55 0 60 0 65 0 70 0 75 0 80 0 85 0 90 0 95 0 975 0 99 0 995 0 9995
1 0 158 0 325 0 510 0 727 1 000 1 376 1 936 3 078 6 314 12 706 31 821 63 657 636 619
2 0 142 0 289 0 445 0617 0 816 1 061 1 386 1 886 2 920 4 303 6 965 9 925 31 598
3 0 137 0 277 0 424 0 584 0 765 0 978 1 250 1 638 2 353 3 182 4 541 5 841 12 941
4 0 134 0 271 0 414 0 569 0 741 0 941 1 190 1 533 2 132 2 776 3 757 4 604 8610
5 0 132 0 267 0 408 0 559 0 727 0 920 1 156 1 476 2 015 2 571 3 365 4 032 6 859
6 0 131 0 265 0 404 0 553 0 718 0 906 1 134 1 440 1 943 2 447 3 143 3 707 5 959
7 0 130 0 263 0 402 0 549 0 711 0 896 1 119 1 415 1 895 2 365 2 998 3 499 5 405
8 0 130 0 262 0 399 0 546 0 706 0 889 1 108 1 397 1 860 2 306 2 896 3 355 5 041
9 0 129 9 261 0 398 0 543 0 703 0 883 1 100 1 383 1 833 2 262 2 821 3 250 4 781
10 0 129 0 260 0 397 0 542 0 700 0 879 1 093 1 372 1 812 2 228 2 764 3 169 4 578
11 0 129 0 260 0 396 0 540 0 697 0 876 1 088 1 363 1 796 2 201 2 718 3 106 4 437
12 0 128 0 259 0 395 0 539 0 695 0 873 1 083 1 356 1 782 2 179 2 681 3 055 4 318
13 0 128 0 359 0 394 0 538 0 694 0 870 1 079 1 350 1 771 2 160 2 650 3 012 4 221
14 0 128 0 258 0 393 0 537 0 692 0 868 1 076 1 345 1 761 2 145 2 624 2 977 4 140
15 0 128 0 258 0 393 0 536 0 691 0 866 1 974 1 341 1 753 2 131 2 602 2 947 4 073
16 0 128 0 258 0 392 0 535 0 690 0 865 1 071 1 337 1 746 2 120 2 583 2 291 4 015
17 0 128 0 257 0 392 0 534 0 689 0 863 1 069 1 333 1 740 2 НО 2 567 2 898 3 965
18 0 127 0 257 0 392 0 534 0 688 0 862 1 067 1 330 1 734 2 101 2 552 2 878 3 922
19 0 127 0 257 0 391 0 533 0 688 0 861 1 066 1 328 1 729 2 093 2 539 2 861 2 883
20 0 127 0 257 0 391 0 533 0 687 0 860 0 064 1 325 1 725 2 086 2 528 2 845 3 850
21 0 127 0 257 0 257 0 532 0 686 0 859 1 063 1 323 1 721 2 080 2 518 2 831 3 819
22 0 127 0 256 0 390 0 532 0 686 0 858 1 061 1 321 1 717 2 074 2 508 2 819 3 792
23 0 127 0 256 0 390 0 532 0 685 0 858 1 060 1 319 1 714 2 069 2 500 2 807 3 767
24 0 127 0 256 0 390 0 531 0 685 0 857 1 059 1 318 1 711 2 064 2 492 2 797 3 745
25 0 127 0 256 0 390 0 531 0 684 0 856 1 058 1 316 1 708 2 060 2 485 2 787 3 725
26 0 127 0 256 0 390 0 531 0 684 0 856 1 058 1 315 1 706 2 056 2 479 2 779 3 707
27 0 127 0 256 0 389 0 531 0 684 0 855 1 057 1 314 1 703 2 052 2 473 2 771 3 690
28 0 127 0 256 0 389 0 530 0 683 0 855 1 056 1 313 1 701 2 048 2 467 2 763 3 674
29 0 127 0 256 0 389 0 530 0 683 0 854 1 055 1 311 1 699 2 045 2 462 2 756 3 659
30 0 127 0 256 0 389 0 530 0 683 0 854 1 055 1 310 1 697 2 042 2 456 2 750 3 646
40 0 126 0 255 0 388 0 529 0 681 0 851 1 050 1 303 1 684 2 021 2 423 2 704 3 551
60 0 126 0 254 0 387 0 527 0 679 0 848 1 046 1 296 1 671 2 000 2 390 2 660 3 460
120 0 126 0 254 0 386 0 526 0 677 0 845 1 041 1 289 1 658 1 980 2 358 2 617 3 373
оо 0 126 0 253 0 385 0 524 0 674 0 842 1 036 1 282 1 645 1 960 2 326 2 576 3 219
Таблица 3. F-распеделение Фишера при р = 0.05
V, \V2 1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 оо
1 161 45 199 50 215 71 224 58 230 16 233 99 236 77 238 88 240 54 241 88 243 91 245 95 248 01 249 05 250 09 251 14 252 20 253 25 254 32
2 18 513 19 000 19 164 19 247 19 296 19 330 19 353 19 371 19 385 19 396 19 413 19 429 19 446 19 454 19 462 19 471 19 479 19 487 19 496
3 10 128 9 5521 9 2766 9 1172 9 0135 8 9406 8 8868 8 8452 8 8123 8 7855 8 7446 8 7029 8 6602 8 6385 86166 8 5944 8 5720 8 5494 8 5265
4 7 7086 6 9443 6 5914 6 3883 6 2560 6 1631 6 0942 6 0410 5 9988 5 9644 5 9117 5 8578 5 8025 5 7744 5 7459 5 7170 5 6 878 5 6581 5 6281
5 6 6079 5 7861 5 4095 5 1922 5 0503 4 9503 4 8759 4 8183 4 7725 4 7351 4 6П1 4 6188 4 5581 4 5272 4 4957 4 4638 4 4314 4 3984 4 3650
6 5 9874 5 1433 4 7571 4 5337 4 3 874 4 2839 4 2066 4 1468 4 0990 4 0600 3 9999 3 9381 3 8742 3 8415 3 8082 3 7743 3 7398 3 7047 3 6688
7 5 5914 4 7374 4 3468 4 1203 3 9715 3 8660 3 7870 3 7257 3 6767 3 6365 3 5747 3 5108 3 4445 3 4105 3 3758 3 3404 3 3043 3 2674 3 2298
8 5 3177 4 4590 4 0662 3 8378 3 6875 3 5806 3 5005 3 4381 3 3881 3 3472 3 2840 3 2184 3 1503 3 1152 3 0794 3 0428 3 0053 2 9669 2 9276
9 5 1174 4 2565 3 8626 3 6331 3 4817 3 3738 3 2927 3 2296 3 1789 3 1373 3 0729 3 0061 2 9365 2 9 005 2 8637 2 8259 2 7872 2 7475 2 7067
10 4 9646 4 1028 3 7083 3 4780 3 3258 3 2172 3 1355 3 0717 3 0204 2 9782 2 9130 2 8450 2 7740 2 7372 2 6996 2 6609 2 6211 2 5801 2 5379
11 4 8443 3 9823 3 5 874 3 3567 3 2039 3 0946 3 0123 2 9480 2 8962 2 8536 2 7876 2 7186 2 6464 2 6090 2 5705 2 5309 2 4901 2 4480 2 4045
12 4 7472 3 8853 3 4903 3 2592 3 1059 2 9961 2 9134 2 8486 2 7964 2 7534 2 6866 2 6169 2 5436 2 5055 2 4663 2 4259 2 3842 2 3410 2 2962
13 4 6672 3 8056 3 4105 3 1791 3 0254 2 9153 2 8321 2 7669 2 7144 2 6710 2 6037 2 5331 2 4589 2 4202 2 3803 2 3392 2 2966 2 2524 2 2064
14 4 6001 3 7389 3 3439 3 1122 2 9582 2 8477 2 7642 2 6987 2 6458 2 6021 2 5342 2 4630 2 3879 2 3487 2 3082 2 2664 2 2230 2 1778 2 1307
15 4 5431 3 6823 3 2 874 3 0556 2 9013 2 7905 2 7066 2 6408 2 5876 2 5437 2 4753 2 4035 2 3275 2 2878 2 2468 2 2043 2 1601 2 1141 2 0658
16 4 4940 3 6337 3 2389 3 0069 2 8524 2 7413 2 6572 2 5911 2 5377 2 4935 2 4247 2 3522 2 2756 2 2354 2 1938 2 1507 2 1058 2 0589 2 0096
17 4 4513 3 5915 3 1968 2 9647 2 8100 2 6987 2 6143 2 5480 2 494У 2 4499 2 3807 2 3077 2 2304 2 1898 2 1477 2 1040 2 0584 2 0107 1 9604
18 44139 3 5546 3 1599 2 9277 2 7729 2 6613 2 5767 2 5102 2 4563 2 4117 2 3421 2 2686 2 1906 2 1497 2 1071 2 0629 2 0166 1 9681 1 9168
19 4 3808 3 5219 3 1274 2 8951 2 7401 2 6283 2 5435 2 4768 2 4227 2 3779 2 3080 2 234) 2 1555 2 1141 2 0712 2 0264 1 9796 1 9302 1 8780
20 4 3513 3 4928 3 0984 2 8661 2 7109 2 5990 2 5140 2 4471 2 3928 2 3479 2 2776 2 2033 2 1242 2 0825 2 0391 1 9938 1 9464 1 8963 1 8432
21 4 3248 3 4668 3 0725 2 8401 2 6848 2 5727 2 4 876 2 4205 2 3661 2 3210 2 2504 2 1757 2 0960 2 0540 2 0102 1 9645 1 9165 1 8657 1 8117
22 4 3009 3 4434 3 0491 2 8167 2 6613 2 5491 2 4638 2 3965 2 3419 2 2967 2 2258 2 1508 2 0707 2 0283 1 9842 1 9380 1 8895 1 8380 1 7831
23 4 2793 3 4221 3 0280 2 7955 2 6400 2 5277 2 4422 2 3748 2 3201 2 2 747 2 2036 2 1282 2 0476 2 0050 1 9605 1 9139 1 8649 1 8128 1 7570
24 4 2597 3 4028 3 0088 2 7763 2 6207 2 5082 2 4226 2 3551 2 3002 2 2547 2 1834 2 1077 2 0267 1 9838 1 9390 1 8920 1 8424 1 7897 1 7331
25 4 2417 3 3852 2 9912 2 7587 2 6030 2 4904 2 4047 2 3371 2 282) 2 2365 2 1649 2 0889 2 0075 1 9643 1 9192 1 8718 1 8217 1 7684 1 7110
26^ 4 2252 3 3690 2 9751 2 7426 2 5868 2 4741 2 3883 2 3205 2 2655 2 2197 2 1479 2 0716 1 9898 1 9464 1 9010 1 8533 1 8027 1 7488 1 6906
27 4 2100 3 2541 2 9604 2 7278 2 5719 2 4591 2 3732 2 3053 2 2601 2 2043 2 1323 2 0558 1 9736 1 9299 1 8842 1 8361 1 7851 1 7307 1 6717
28 4 1960 3 3404 2 9467 2 7141 2 5581 2 4453 2 3593 2 2913 2 2360 2 1900 2 1179 2 0411 1 9586 1 9147 1 8687 1 8203 1 7689 1 7138 1 6541
29 4 1830 3 3277 2 9340 2 7014 2 5454 2 4324 2 3463 2 2782 2 2229 2 1768 2 1045 2 0275 1 9446 1 9005 1 8543 1 8055 1 7537 1 6981 1 6377
30 4 1709 3 3158 2 9223 2 6896 2 5336 2 4205 2 3343 2 2662 2 2107 2 1646 2 0921 2 0148 1 9317 1 8874 1 8409 1 7918 1 7396 1 6835 1 6223
40 4 0848 3 2317 2 8387 2 6060 2 4495 2 3359 2 2490 2 1802 2 1240 2 0772 2 0035 1 9245 1 8389 1 7929 1 7444 1 6928 1 6373 1 5766 1 5089
60 4 0012 3 1504 2 7581 2 5252 2 3683 2 2540 2 1665 2 0970 2 0401 1 9926 1 9174 1 8364 1 7480 1 7001 1 6491 1 5943 1 5343 1 4673 1 3893
120 3 9201 3 0718 2 6802 2 4472 2 2900 2 1750 2 0867 2 0164 1 9588 1 9105 1 8337 1 7505 1 6587 1 6084 1 5543 1 4952 1 4290 1 3519 1 2539
8 3 8415 2 9957 2 6 049 2 3719 2 2141 2 0986 2 0096 1 9384 1 8799 1 8307 1 7522 1 6664 1 5705 1 5173 1 4591 1 3940 1 3180 1 2214 1 0000
412 Приложение
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1) Акназарова С.Л., Кафаров В.В. Оптимизация эксперимента в химии и хими-
ческой технологии. М.: Высшая школа, 1978. 319 с.
2) Белман Р. Введение в теорию матриц / Пер. с англ, под ред. В.Б. Лидского.
М.. Наука. Гл. ред. физ.-мат. лит., 1976. 352 с.
3) Бенедек И, Ласло А. Научные основы химической технологии / Пер. с нем
под ред. П.Г. Романкова, М.И. Курочкиной. Л.: Химия, 1970. 376 с.
4) Бобров Д.А., Кафаров В.В., Перов В.Л. Оптимизация химико-технологических
систем: Учебн. пособие. Ч. I. М.: МХТИ им. Д.И. Менделеева, 1979. 48 с.
5) Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии.
Изд. 2-е. М.: Химия, 1975. 576 с.
6) Браунли КА. Статистическая теория и методология в науке и технике / Пер.
с англ. М.С. Никулина; Под ред. Л.Н. Большева. М.: Наука, 1977. 408 с.
7) Бронштейн И.Н., Семендяев КА. Справочник по математике для инженеров и
учащихся втузов. М.: Наука. Гл. ред. физ.-мат. лит., 1986. 544 с.
8) Бусленко Н.П. Моделирование сложных систем. М.: Наука, 1978. 399 с.
9) Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравне-
ния. М.: Высш, шк., 2000. 226 с.
10) Гаврилова ТА., Хорошевский В.Ф. Базы знаний интеллектуальных систем. СПб:
Питер, 2000. 384 с.
11) Гайдышев И. Решение научных и инженерных задач средствами Excel, VBA и
C/C++. СПб. БХВ-Петербург, 2004. 512 с.
12) Гартман Т.Н., Бояринов А.И. Применение ЭВМ в химической технологии:
Учебн пособие. М.: МХТИ им Д.И. Менделеева, 1987. 83 с.
13) Гартман Т.Н., Гулаев В.М. и др. Курс лекций по основам вычислительной
техники: Учебн. пособие. Ч. II. М.: МХТИ им. Д.И. Менделеева, 1977. 48 с.
14) Гартман Т.Н., Епишкин А.П. и др. Курс лекций по основам вычислительной
техники: Учебн. пособие. Ч. I. М.: МХТИ им. Д.И. Менделеева, 1976. 80 с.
15) Гартман Т.Н., Епишкин А.П., Шакина Э.А. Вычислительная математика. М.:
Высш, шк., 1984. 112 с.
16) Гордеев Л.С., Кафаров В.В., Бояринов А.И. Оптимизация процессов химичес-
кой технологии: Учебн. пособие. М.: МХТИ им Д.И. Менделеева, 1972. 275 с.
17) Деккер К., Вервер Я. Устойчивость методов Рунге—Кутты для жестких нелиней-
ных дифференциальных уравнений / Пер. с англ. А.Ю. Захарова, И.А. Куль-
чицкой и С.С. Филиппова; Под ред. А.А. Самарского. М.: Мир, 1988. 334 с.
18) Демиденко Е.З. Оптимизация и регрессия. М.: Наука, 1989. 296 с.
19) Жаров В.Т, Серафимов Л.А. Физико-химические основы дистилляции и рек-
тификации. Л.: Химия, 1975. 239 с.
20) Закгейм А.Ю. Введение в моделирование химико-технологических процессов
М.: Химия, 1982. 288 с.
21) Кафаров В.В. Методы кибернетики в химии и химической технологии: Учеб-
ник для вузов. Изд. 4-е, перераб. и доп. М.: Химия, 1985. 448 с.
22) Кафаров В.В. Принципы создания безотходных химических производств. М.:
Химия, 1982. 288 с.
23) Кафаров В.В., Ветохин В.Н. Основы автоматизированного проектирования
химических производств. М.: Наука, 1986. 624 с.
24) Кафаров В.В., Дорохов И.И. Системный анализ процессов химической техно-
логии. Основы стратегии. М.: Наука, 1976. 500 с.
25) Комиссаров Ю.А., Гордеев Л.С., Вент Д.П. Основы конструирования и проек-
тирования промышленных аппаратов. М.: Химия, 1997. 386 с.
26) Корн Т, Корн Т. Справочник по математике для научных работников и инже-
неров. М.: Наука. Гл. ред. физ.-мат. лит., 1974. 832 с.
414
Рекомендуемая литература
27) Коршунов Ю.М. Математические основы кибернетики. М.: Энергоиздат, 1987.
496 с.
28) Кроу К, ГамилецА., Хоффман Т. и др. Математическое моделирование хими-
ческих производств / Пер. с англ. Э.П. Зиминой, Л.В. Стрельцовой,
В.И. Чуприковой; Под ред. Г.М. Островского. М.: Мир, 1973. 391 с.
29) Кутепов А. М., Бондарева Т.И., Беренгартен М.Г. Общая химическая технология:
Учебник для вузов. Изд. 3-е, перераб. М.: ИКЦ «Академкнига», 2003. 528 с.
30) Левеншпиль О. Инженерное оформление химических процессов / Пер. с англ,
под ред. М.Г. Слинько. М.: Химия, 1967. 414 с.
31) Липунов ЮЛ. Управление процессами. Методы управления предприятием с
использованием информационных технологий. М.: ДМК Пресс; М.: Компа-
ния Ай Ти, 2003. 224 с.
32) Лисицын В.Н. Оптимизация нефтеперерабатывающего завода. СПб.: Химиз-
дат, 2003. 184 с.
33) Лысенко Э.В. Проектирование автоматизированных систем управления тех-
нологическими процессами. М.: Радио и связь, 1987. 272 с.
34) Майзер X., Эйджин И, Тролл Р. и др. Исследование операций: В 2-х томах /
Пер. с англ, под ред. Дж. Моудера, С. Элмаграби. М.: Мир, 1981. Т.1. 712 с.;
Т.2, 677 с.
35) Мак-Кракен Д., У. Дорн У Численные методы и программирование на Фортра-
не / Пер. с англ. Б.Н. Казака под ред. Б.М. Наймарка / М.: Мир. 1977. 584 с.
36) Маринеску И., Мойнягу Ч., Никулеску Р., Ранку Н., Урсяну В. Основы матема-
тической статистики и ее применение / Пер. с рум. Л.С. Кучаева; Под ред. В.
Урсяну. М.: Статистика, 1970. 224 с.
37) Мешалкин В.П. Экспертные системы в химической технологии. Основы тео-
рии, опыт разработки и применения. М.: Химия, 1975. 368 с.
38) Моисеев Н.Н., Иванилов Ю.П., Столяров Е.М. Методы оптимизации. М.: На-
ука. Гл. ред. физ.-мат. лит., 1978. 352 с.
39) Морачевский А.Г., Смирнова Н.А., Пиотровская Е.М. Термодинамика равнове-
сия жидкость-пар. Л.: Химия, 1989. 341 с.
40) Островский Г.М., Волин Ю.М. Методы оптимизации химических реакторов.
М.: Химия, 1967. 248 с.
41) Островский Г.М., Волин Ю.М. Моделирование сложных химических систем.
М.: Химия. 1975. 311 с.
42) Петлюк Ф.Б., Серафимов Л.А. Многокомпонентная ректификация: теория и
расчет. М.: Химия, 1983. 303 с.
43) Рид Р., Праусниц Дж., Шервуд Т. Свойства газов и жидкостей / Пер. с англ,
под ред. Б.И. Соколова. Л.: Химия, 1982. 592 с.
44) Розенброк X., Стори С. Вычислительные методы для инженеров-химиков / Пер.
с англ. Б.М. Авдеева, Ю.В. Ковачича, В.Н. Левицкого. М.: Мир, 1968. 444 с.
45) Салихов З.Г., Арунянц Г.Г., Рутковский А.Л. Системы оптимального управления
сложными технологическими объектами. М.: Теплоэнергетик, 2004. 496 с.
46) Информатика. Базовый курс. Изд. 2-е / Под ред. С.В. Симоновича. СПб.: Питер,
2005. 640 с.
47) Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации: Учебн.
пособие. Изд. 2-е. М.: Физматлит, 2005. 368 с.
48) Тимофеев В. С., Серафимов Л.А. Принципы технологии основного органичес-
кого синтеза: Учебн. пособие для вузов. Изд. 2-е, перераб. М.: Высш, шк.,
2003. 536 с.
49) Трауб Дж. Итерационные методы решения уравнений / Пер. с англ. И.А.
Глинкина; Под ред. А.Г. Сухарева. М.: Мир, 1985. 264 с.
50) Уэйлес С. Фазовые равновесия в химической технологии / Пер. с англ. А.В.
Беспалова, А.П. Жукова и В.В. Паукова; Под ред. В.С. Бескова. М.: Мир,
1989. Ч. 1. 301 с.; Ч. 2. 361 с.
Рекомендуемая литература
415
51) Фрэнкс Р. Математическое моделирование в химической технологии / Пер. с
англ. Д.К. Бейлиной и Э.Ф. Ишмаевой; Под ред. В.С. Тропцова. М.: Химия,
1971. 270 с.
52) Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных
уравнений. Нежесткие задачи / Пер. с англ. И.А. Кульчицкой и С.С. Филип-
пова; Под ред. С.С. Филиппова. М.: Мир. 1990. 512 с.
53) Химмельблау Д. Анализ процессов статистическими методами / Пер. с англ.
В.Д. Скаржинского; Под ред. В.Г. Горского. М.: Мир, 1973. 957 с.
54) Холланд Ч.Д. Многокомпонентная ректификация / Пер. с англ. Б.Ц. Генки-
ной; Под ред. В.М. Платонова. М.: Химия, 1969. 352 с.
Учебное издание
ГАРТМАН Томаш Николаевич
КЛУШИН Дмитрий Витальевич
ОСНОВЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Учебное пособие для вузов
Редактор Д.К. Новикова
Художник И.А. Слюсарев
Дизайнер Н.М. Апрелова
Компьютерный дизайн и верстка С.В. Сухарев
Корректор Е.Н. Евдокимова
ИД №04284 от 15.03.2001
Подписано в печать 8.06.06
Формат 70 х 100/16
Печать офсетная. Усл. печ. л. 33,5
Тираж 2000 экз.
Тип. зак'4544.
Издательско-книготорговый центр «Академкнига»
117997, Москва, Профсоюзная ул., 90
По вопросам поставок обращаться
в отдел реализации ИКЦ «Академкнига»
Тел./факс: (495) 334-73-18
e-mail: bookreal@maik.ru,
web-site: http://www.akademkniga.com
f
Отпечатано с готовых диапозитивов в ОАО «Ивановская областная типография»
153008, г. Иваново, ул. Типографская, 6.
E-mail: 091-018@adminet.ivanovo.ru