И. С. БЕРЕЗИН и Н. П. ЖИДКОВ
МЕТОДЫ
ВЫЧИСЛЕНИЙ
ТОМ ВТОРОЙ
Допущено
Министерством высшего образования СССР
в качестве учебного пособия
для высших учебных заведений
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1959

11-5-2
АННОТАЦИЯ
Во втором томе книги рассмотрены численные методы
решения систем линейных алгебраических уравнений,
уравнений высших степеней и трансцендентных урав-
уравнений, численные методы отыскания собственных зна-
значений, приближенные методы решения обыкновенных
дифференциальных уравнений, уравнений в частных
производных и интегральных уравнений.
Книга предназначена в качестве учебного пособия
для студентов механико-математических и физико-ма-
физико-математических факультетов, специализирующихся по вы-
вычислительной математике, и лиц, интересующихся тео-
теорией и практикой численных методов.
Иван Семенович Березин и Николай Петрович Жидков
МЕТОДЫ ВЫЧИСЛЕНИЙ, т. II
Редакторы Б. М. Будак и А. Д. Горбунов.
Техн. редактор Н. Я. Мурашова. Корректор А. С. Бакулова.
Сдано в набор 16/VII 1959 г. Подписано к печати 3/XI 1959 г. Бумага 60x92J/im
Физ. печ. л. 38,75. Условн. печ. л. 38,75 Уч.-изд. л. 41,96. Тираж 10 000.
Т-11038. Цена книги 14 р. 10 к. Заказ № 604
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15
Типография № 2 им. Евг. Соколовой УПП Ленсовнархоза.
Ленинград, Измайловский пр., 29.

ОГЛАВЛЕНИЕ
Предисловие S
Глава 6. Решение систем линейных алгебраических уравнений
§ 1. Классификация методов 9
§ 2. Метод исключения 10
1. Схема Гаусса с выбором главного элемента A0). 2. Компакт-
Компактная схема Гаусса A3). 3. Обращение матрицы A7). 4. Вычисле-
Вычисление определителей A8). 5. Схема Жордана A9). 6. Схема без
обратного хода B0).
§ 3. Метод квадратного корня 23
§ 4. Метод ортогонализации 25
§ 5. Метод сопряженных градиентов 30
§ 6. Метод разбиения на клетки 41
§ 7. Линейные операторы. Нормы операторов 44
1. Конечномерные линейные нормированные пространства D6).
2. Линейные операторы в конечномерном линейном нормирован-
нормированном пространстве и их связь с матрицами D9). 3. Сходимость
последовательностей матриц и матричных рядов E1).
§ 8. Разновидности методов последовательных приближений ... 54
§ 9. Линейные полношаговые методы первого порядка 56
1. Сходимость линейных полношаговых методов первого порядка.
Простая итерация E6). 2. Метод Ричардсона E9). 3. Обращение
матриц методом последовательных приближений F1).
§ 10. Линейные одношаговые методы первого порядка 61
1. Метод Зейделя F2). . 1. Сходимость метода Зейделя F3).
3. Релаксационный метод F6).
§ 11. Метод скорейшего, спуска , . . ". 67
Упражнения 73
Литература 74
Глава 7. Численные методы решения алгебраических уравнений
высших степеней и трансцендентных уравнений .... 76
§ 1. Введение 76
§ 2. Отделение корней 76
1. Общие замечания G6). 2. Границы расположения корней
алгебраического уравнения G9). 3. Число действительных корней
алгебраического уравнения (83). 4. Отделение действительных
корней алгебраического уравнения (88). 5. Отделение комплекс-
комплексных корней алгебраических уравнений (94).
§ 3. Метод Лобачевского решения алгебраических уравнений . . . 103
1. Метод Лобачевского. Случай различных по абсолютной вели-
величине действительных корней A03). 2. Метод Лобачевского.
Случай комплексных корней A07). 3. Метод Лобачевского, Случай

4 ОГЛАВЛЕНИЕ
близких или равных корней A15). 4. Погрешность метода
Лобачевского A15). 5. Видоизменение Лемера метода Лобачев-
Лобачевского A23).
§ 4. Итерационные методы решения алгебраических и трансцен-
трансцендентных уравнений 128
1. Принцип сжатых отображений и его применение к доказа-
доказательству сходимости итерационных методов A29). 2. Простейшие
итерационные методы: метод секущих и метод Ньютона A35).
3. Метод Чебышева построения итераций высших порядков A40).
4. Построение итераций высших порядков с помощью теоремы
Кёнига A43). А. Теорема Кёнига A43), Б. Построение итераций
высших порядков A45). 5. Метод Эйткена построения итераций
высших порядков A46). 6. Пример A49).
§ 5. Решение систем уравнений 150
1. Метод итераций решения систем специального вида A50).
2. Метод Ньютона A54). 3. Метод скорейшего спуска A61).
§ 6. Отыскание корней алгебраических уравнений методом выделе-
выделения множителей 162
1. Метод Лина выделения множителей A64). 2. Метод Фрид-
Фридмана A67). 3. Метод Хичкока выделения квадратного множи-
множителя A71).
Упражнения 174
Литература 176
Глава 8. Вычисление собственных значений и собственных
векторов матриц 177
§ 1. Введение 177
§ 2. Метод А. Н. Крылова 178
1. Отыскание собственных значений матрицы A78). 2. Отыскание
собственных векторов матрицы A86).
§ 3. Метод Ланцоша 188
1. Отыскание собственных значений A88). 2. Отыскание собствен-
собственных векторов A96).
§ 4. Метод Данилевского 198
1. Видоизменение метода Данилевского B04).
§ 5. Обзор других способов получения характеристического много-
многочлена 208
1. Метод Леверрье B09). 2. Метод окаймления B11). 3. Эскала-
Эскалаторный метод B11). 4. Метод СамуэльсонаB13). 5. Интерполяцион-
Интерполяционный метод BJ4).
§ 6. Определение границ собственных значений 214
1. Случай симметрической матрицы B15). Случай несимметриче-
несимметрической матрицы B25).
§ 7. Итерационные методы отыскания собственных значений и
собственных векторов матриц 228
1. Отыскание наибольшего по модулю действительного собствен-
собственного значения матрицы простой структуры. Случай симметри-
симметрической матрицы B28). 2. Отыскание других собственных значе-
значений и соответствующих им собственных векторов для симметри-
симметрических матриц B31). 3. Отыскание собственных значений и
собственных векторов несимметрических матриц, имеющих простую
структуру B38). 4. Некоторые замечания об отыскании собствен-
собственных значений и собственных векторов матриц общей структуры B42).
§ 8. Ускорение^ сходимости итерационных процессов при решении
задач линейной алгебры 244
1. Ускорение сходимости итерационного метода решения систем
линейных алгебраических уравнений. Общие замечания B45).

ОГЛАВЛЕНИЕ 5
2. Метод М. К. Гавурина B46). 3. Метод Л. А. Люстерника B47).
4. В'-процесс Эйткена B49). 5. Улучшение сходимости итерацион-
итерационных процессов для отыскания собственных значений матриц B51).
§ 9. Неустранимая погрешность при численном решении систем
линейных алгебраических уравнений 251
Упражнения 256
Литература 258
Глава 9. Приближенные методы решения обыкновенных диф-
дифференциальных уравнений 259
§ 1. Введение 259
§ 2. Метод С. А. Чаплыгина 260
1. Теоремы о дифференциальных неравенствах B60). 2. Способ
Чаплыгина построения улучшенных приближений B64). 3. Второй
способ построения улучшенных приближений B69). 4. Метод
Чаплыгина приближенного решения линейных дифференциальных
уравнений второго порядка B73).
§ 3. Метод малого параметра 277
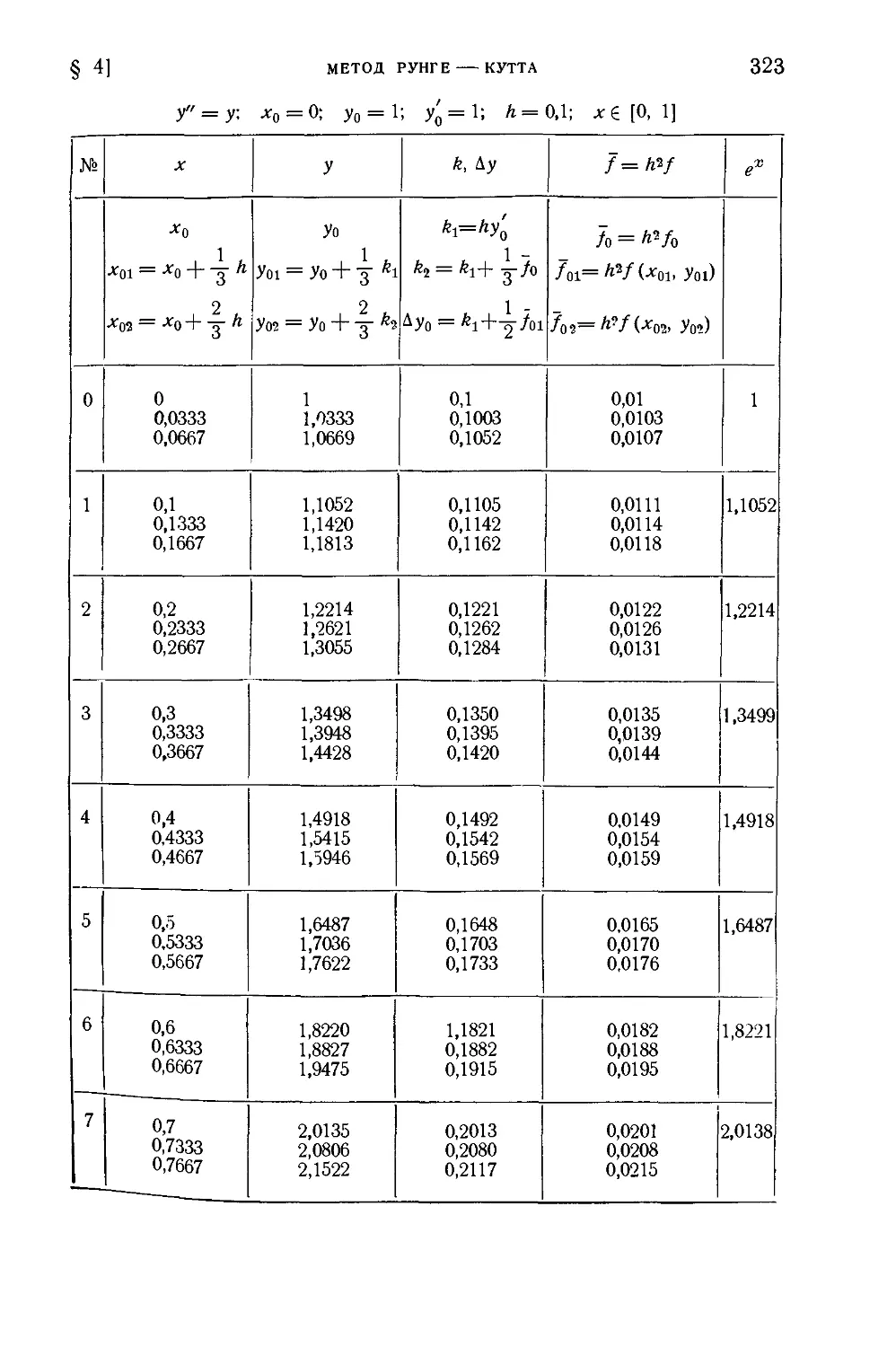
§ 4 Метод Рунге — Кутта 286
1. Метод Рунге — Кутта решения дифференциальных уравнений
первого порядка B86). 2. Метод Рунге — Кутта решения систем
дифференциальных уравнений первого порядка C11). 3. Метод
Рунге — Кутта решения уравнений второго порядка C20).
§ 5. Разностные методы решения обыкновенных дифференциальных
уравнений первого порядка 327
1. Некоторые экстраполяционные формулы для интегрирования
дифференциальных уравнений первого порядка C29). 2. Примеры
интерполяционных формул C32). 3. Метод неопределенных коэф-
коэффициентов вывода разностных формул C36). 4. Метод Крылова
отыскания начальных значений решения C39). 5. Примеры C42).
§ 6. Разностные методы решения обыкновенных дифференциальных
уравнений высших порядков 345
§ 7. Оценка погрешности, сходимость и устойчивость разностных
методов решения обыкновенных дифференциальных уравнений . 354
1. Линейные разностные уравнения C54). 2. Разностное уравнение
для погрешности приближенного решения C56). 3. Оценки погреш-
погрешности решений, получаемых по формулам Адамса C60). 4. Устой-
Устойчивость разностных методов решения дифференциальных уравне-
уравнений C65). 5. Оценка погрешности и сходимость устойчивых раз-
разностных методов решения дифференциальных уравнений C68).
§ 8. Решение краевых задач для обыкновенных дифференциальных
уравнений методом конечных разностей 372
1. Метод конечных разностей решения краевых задач для линей-
линейных дифференциальных уравнений второго порядка C73). 2. Метод
конечных разностей решения краевых задач для нелинейных
дифференциальных уравнений второго порядка C76).
§ 9. Метод прогонки 387
§ 10. Решение краевых задач для обыкновенных дифференциальных
уравнений вариационными методами 391
1. Вариационные методы решения операторных уравнений в гиль-
гильбертовом пространстве C92). 2. Метод Ритца решения вариацион-
вариационных задач C97). 3. Понятие о методе Галеркина D07).
Упражнения 408
Литература 409

6 ОГЛАВЛЕНИЕ
Глава 10. Приближенные методы решения дифференциальных
уравнений в частных производных и интегральных уравнений 410
§ 1. Введение 410
§ 2. Метод сеток решения краевых задач для дифференциальных
уравнений эллиптического типа 412
1. Идея метода сеток D12). 2. Аппроксимация дифференциальных
уравнений разностными D14). 3. Аппроксимация граничных
условий D25). 4. Разрешимость разностных уравнений и способы
их решения D29). 5. Оценка погрешности и сходимость метода
сеток D34).
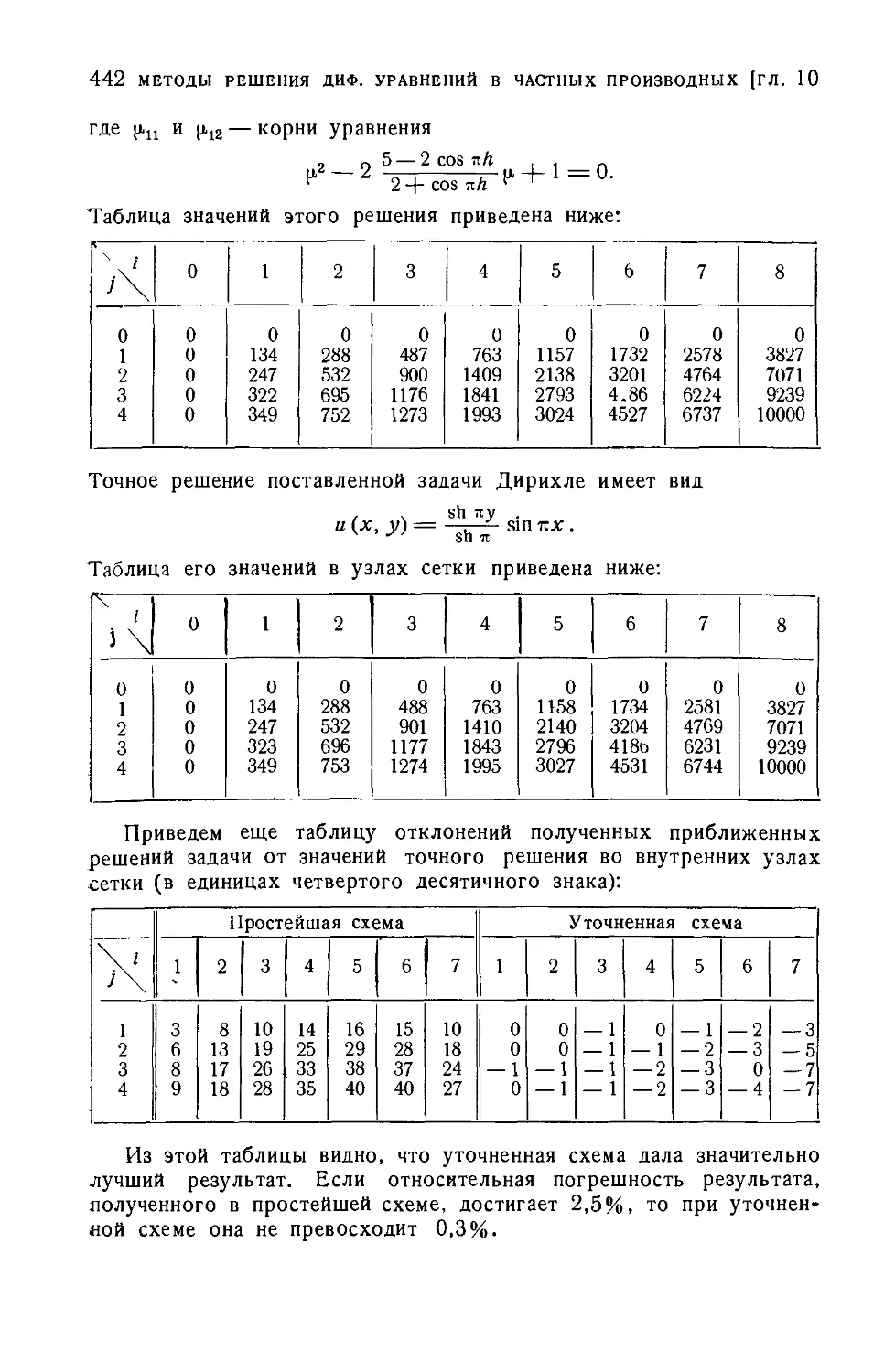
§ 3. Метод сеток решения линейных дифференциальных уравнений
гиперболического типа 443
1. Метод сеток для решения задачи Коши D44). 2. Оценка по-
погрешности и сходимость метода сеток для неоднородного вол-
волнового уравнения D49). 3. Метод сеток решения смешанной
задачи D52). 4. Другие разностные схемы D57).
§ 4. Метод характеристик численного решения гиперболических
систем квазилинейных дифференциальных уравнений в частных
производных 161
1, Уравнения характеристик системы квазилинейных дифферен-
дифференциальных уравнений первого порядка D61). 2. Примеры: уравне-
уравнения характеристик для некоторых систем дифференциальных
уравнений газовой динамики D66). 3. Уравнения характеристик
квазилинейного гиперболического дифференциального уравнения
второго порядка D71). 4. Численное решение квазилинейной гипер-
гиперболической системы двух дифференциальных уравнений первого
порядка методом Массо D74). 5. Численное решение гиперболи-
гиперболической системы трех квазилинейных дифференциальных уравне-
уравнений первого порядка методом Массо D80). 6. Метод Массо
численного решения квазилинейного гиперболического уравнения
второго порядка D84). 7. Основные задачи, встречающиеся при
исследовании плоского безвихревого сверхзвукового установив-
установившегося течения идеального газа D88).
§ 5. Метод сеток решения линейных дифференциальных уравнений
параболического типа 490
1. Метод сеток для решения задачи Коши D90). 2. Метод сеток
для решения смешанных задач. Понятие устойчивости разност-
разностных схем D97).
§ 6. Метод прогонки решения краевых задач для уравнений
в частных произзодных 506
1. Уравнение теплопроводности E06). 2. Уравнение Пуассона E09).
§ 7. Сходимость и устойчивость разностных схем 516
1. Разностная аппроксимация дифференциального уравнения и
граничных условий E16). 2. Понятие корректности и устойчивости
разностной схемы E20). 3. Связь сходимости с корректностью
разностной схемы E26). 4. Некоторые приемы исследования устой-
устойчивости разностных схем E31). 5. Некоторые общие замечания E36).
§ 8. Метод прямых решения граничных задач для дифференциаль-
дифференциальных уравнений в частных производных 537
1. Сущность метода прямых E37). 2. Метод прямых решения
задачи Дирихле для уравнения Пуассона E39). 3. Метод прямых
решения смешанной задачи для уравнения колебаний струны E48).
4. Метод прямых решения смешанной задачи для уравнения
теплопроводности E54).

ОГЛАВЛЕНИЕ 7
§ 9. Вариационные методы решения краевых задач для дифферен-
дифференциальных уравнений математической физики 561
1. Метод Ритца решения операторных уравнений и отыскания
собственных значений операторов в гильбертовом простран-
пространстве E62). 2. Метод Ритца приближенного решения краевых
задач для линейных дифференциальных уравнений в частных
производных второго порядка эллиптического типа E74). 3. Неко-
Некоторые другие вариационные методы E82). 4. Метод Ритца реше-
решения задачи о собственных значениях E85). 5. Метод Галеркина
решения краевых задач E88).
§ 10. Приближенные методы решения интегральных уравнений . . . 590
1. Решение уравнений Фредгольма методом замены интеграла
конечной суммой E90). 2. Решение интегральных уравнений
Фредгольма второго рода методом замены ядра на вырожден-
вырожденное E97). 3. Метод моментов F04). 4. Метод наименьших квадра-
квадратов F08). 5. Метод последовательных приближений F11). 6. При-
Приближенное решение уравнений Вольтерра F13).
Упражнения 618
Литература 620

ПРЕДИСЛОВИЕ
В соответствии со сказанным в предисловии к книге, помещенном
в первом томе, второй том содержит главы 6—10, что соответствует
второй части курса «Методов вычислений», читаемой для студентов
4-го года обучения.
И. С. Березин, Н. П. Жидков

ГЛАВА 6
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 1. Классификация методов
Главой о численных методах решения систем линейных алгебраи-
алгебраических уравнений мы начинаем второй раздел нашей книги, посвя-
посвященный решению алгебраических, трансцендентных, дифференциаль-
дифференциальных и интегральных уравнений. Системы линейных алгебраических,
уравнений наиболее просты и в то же время к ним приводятся
многие задачи численного анализа.
Известное из курса высшей алгебры правило Крамера для решения;
систем линейных алгебраических уравнений практически невыгодно,
так как требует слишком большого количества арифметических опе-
операций и записей. Поэтому было предложено много различных спо-
способов, более пригодных для практики. И в настоящее время значи-
значительная часть литературы по вычислительной математике посвящена
этому вопросу. Однако сейчас еще нельзя указать один или несколько
способов наиболее эффективных в смысле быстроты получения*
решения с нужной точностью и минимального использования запо-
запоминающих устройств. Требуется большая и тщательная теоретическая
и экспериментальная сравнительная оценка многочисленных известных
способов с этой точки зрения. Мы дадим в этой главе лишь не-
несколько уже давно испытанных методов и несколько методов, имею-
имеющих с нашей точки зрения перспективы для практики.
Используемые практически методы решения систем линейных
алгебраических уравнений можно разделить на две большие группы:
так называемые точные методы и методы последовательных при-
приближений. Точные методы характеризуются тем, что с их помощью
принципиально возможно, проделав конечное число операций, полу-
получить точные значения неизвестных. При этом, конечно, предпола-
предполагается, что коэффициенты и правые части системы известны точно,
а все вычисления производятся без округлений. Чаще всего они
осуществляются в два этапа. На первом этапе преобразуют систему"
к тому или иному простому виду. На втором этапе решают упро-
упрощенную систему и получают значения неизвестных.
Методы последовательных приближений характеризуются тем,,
что с самого начала задаются какими-то приближенными значениями

10
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
неизвестных. Из этих приближенных значений тем или иным
способом получают новые «улучшенные» приближенные значения.
С новыми приближенными значениями поступают точно так же и т. д.
При выполнении определенных условий можно придти, вообще
говоря, после бесконечного числа шагов к точному решению.
Под нашу классификацию не подходят способы решения по методу
Монте-Карло. Так названы методы, использующие случайные вели-
•чины, математические ожидания которых дают решение системы.
Пока методы Монте-Карло не могут соревноваться с другими мето-
_аами, названными выше. Поэтому мы не будем ими здесь заниматься.
§ 2. Метод исключения
Мы начнем изучение численных методов решения систем линейных
алгебраических уравнений с точных методов. Простейшим из таких
методов является метод исключения.
С методом исключения мы сталкивались уже в обычном школь-
школьном курсе алгебры. Комбинируя каким-либо образом уравнения
системы, добиваются того, что во всех уравнениях, кроме одного,
будет исключено одно из неизвестных. Затем исключают другое
неизвестное, третье и т. д. В результате получаем систему с тре-
треугольной или диагональной матрицей, решение которой не пред-
представляет труда. Метод исключений не вызывает каких-либо теоре-
теоретических затруднений. Однако точность результата и затрачиваемое
на его получение время будут во многом зависеть от организации
вычислений. Этому вопросу мы и уделим основное внимание.
Рассмотрим ряд схем, осуществляющих метод исключения на
.примере системы четырех уравнений с четырьмя неизвестными:
1.1161 *1 + 0,1254*2 + 0,1397*з+0,1490*4= 1,5471,
0,1582*!+1,1675*2+0,1768*3 + 0,1871 *4= 1,6471,
0,1968 *! + 0,2071 *2 +1,2168*3 + 0,2271 *4= 1,7471,
0,2368 *! + 0,2471 *2 + 0,2568 *3 + 1,2671 *4 = 1,8471.
.Каждой схеме мы припишем то или иное название. Правда, эти
названия не являются общепринятыми.
1. Схема Гаусса с выбором главного элемента. Если вычи-
вычисления производятся не с помощью автоматических вычислительных
машин, то удобно нашу систему записать в следующую схему:
A)
№
п/п.
1
2
3
4
щ
ап
0,11610
0,15820
0,19680
0,23680
0,12540
1,16750
0,20710
0,24710
<*C
0,13970
0,17680
1,21680
0,25680
аи
0.14900
0,18710
0,22710
1,26710
*<
1,54710
1,64710
1,74710
1,84710
Si
3,07730
3,33670
3,59490
3,85490

§ 2]
МЕТОД ИСКЛЮЧЕНИЯ
11
В первом столбце мы записываем номера уравнений. Значение
второго столбца будет ясно дальше. 3-й, 4-й, 5-й и 6-й столбцы
содержат коэффициенты уравнений, а 7-й столбец — свободные
члены. Последний столбец содержит суммы коэффициентов и сво-
свободных членов данной строки.
Выбираем теперь наибольший по модулю элемент а,ц. Будем
называть его главным. В нашем случае это аи — 1,26710. Он в схеме
подчеркнут. Делим все элементы столбца, в котором находится
главный элемент (в нашем случае ai4)> на главный элемент и отно-
отношения с обратным знаком помещаем в столбце яц в той же строке,
где находится делимое:
№
п/п.
1
2
3
4
щ
-0,11759
— 0,14766
— 0,17923
1,11610
0,15820
0,19680
0,23680
0,12540
1,16750
0,20710
0,24710
0,13970
0,17680
1,21680
0,25680
0,14900
0,18710
0,22710
1,26710
bi
1,54710
1,64710
1,74710
1,84710
Ч
3,07730
3,33670
3,59490
3,85490
Будем теперь прибавлять к каждой из строк схемы строку,
содержащую главный элемент, умноженную на соответствующее т-%.
Строку, содержащую главный элемент, в дальнейшем не выписы-
выписываем. Не выписываем также и столбец, в котором содержится глав-
главный элемент, так как он состоит из нулей. В нашем случае получим:
№
п/п.
1
2
3
Щ
— 0,09353
— 0,11862
1,08825
0,12323
0,15436
0,09634
1,13101
0,16281
0,10950
0,13888
1,17077
bi
1,32990
1,37436
1,41604
Si
2,62399
2,76748
2,90398
Мы вписали сюда же значения т^ которые получатся на сле-
следующем шаге. Производим проверку правильности вычислений. Для
этого складываем столбцы а^ и ^ и сравниваем со столбцом s{.
Если расхождения в пределах ошибок округления, то считаем вычи-
вычисления правильными. Если расхождения слишком велики, то повто-
повторяем соответствующие вычисления.
В дальнейшем поступаем с нашей таблицей, как и с предыду-
предыдущей. Выбираем главный элемент (в нашем случае это будет 1,17077)
и делим на него элементы того же столбца. Результаты с обратными
знаками записываются в столбец mt (у нас это уже сделано). Затем
последовательно умножаем строку, из которой взят главный элемент,
на т-% и складываем с соответствующими строками. Производим

12
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
проверку и переходим к следующему шагу. Так продолжаем до тех
пор, пока у нас не останется одна строка. В нашем примере будем
иметь:
№
1
2
1
тг
— 0.07296
<Ч\
1,07381
0,10492
1,06616
0,08111
1,11170
bi
1,19746
1,20639
1,10944
Si
2,35238
2,42301
2,17560
Взяв уравнения, в которых выбирались главные элементы, получим
новую систему, эквивалентную данной:
1,06616*!= 1,10944.
0,10492*!+l,11170*2= 1,20639,
0,15436*1 + 0,16281*2+1,17077*3= 1,41604,
0,23680 *i + 0,24710 *2 + 0,25680 *3 + 1,26710 *4 = 1,84710.
Матрица новой системы треугольная. Решение такой системы не
встретит затруднений. Находим:
1,10944
B)
*, =
*2 =
*о =
*, =
TT066T6-=1'04059'
1,20639 — 0,10492-1,04059
1,09721
1,11-170 1,11170
1,41604—0,15436 • 1,04059—0,16281 • 0,98697
= 0,98697,
1,09473
= 0,93505,
1,17077 1,17077'
1,84710 — 0,23680 • 1,04059 — 0,24710 • 0,98697 — 0,25680 • 0,93505
1,26710
1,11669
1,26710
= 0,88130.
C)
Приведенную нами схему исключения неизвестных назовем схе-
схемой исключения Гаусса с выбором главного элемента. Сам про-
процесс исключения называют прямым ходом, а решение системы
с треугольной матрицей — обратным ходом. При практическом
использовании схемы Гаусса не следует, конечно, разрывать отдельные
этапы, как это сделано нами для облегчения объяснений. Не следует
также выписывать и окончательную систему уравнений.
Контроль обратного хода осуществляется с помощью столбца sb.
Если в окончательной системе заменить bt на s(, то должны полу-
получить вместо хг величины *j+ 1. Проверка полученных результатов
может быть сделана также путем подстановки их в исходную систему
уравнений. В нашем случае получим последовательно в левых частях
равенства: 1,54711; 1,64712; 1,74710; 1,84711. Как мы видим, рас-

¦§ 2] МЕТОД ИСКЛЮЧЕНИЯ 13
хождения между правыми и левыми частями не превосходят двух
¦единиц пятого десятичного знака, что нужно считать удовлетво*
рительным.
Смысл выбора главного элемента состоит в том, чтобы сделать
возможно меньшими т% и тем самым уменьшить вычислительную
погрешность.
Как известно, при работе на цифровых машинах, да и при работе
вручную, наибольшее количество времени затрачивается на произ-
производство действий умножения и деления. Поэтому важно знать, сколько
действий умножения и деления потребуется для решения заданной
системы. Если система имеет порядок п, то после выбора главного
элемента нужно произвести п—1 делений для определения коэф-
коэффициентов тх. Затем нужно умножить строку, содержащую главный
элемент, на каждый из этих множителей. Для этого потребуется
(я+1)(я—1) = п2—1 умножений. Таким образом, первый шаг
работы по схеме Гаусса требует п2-\-п — 2 умножений и делений.
Следующий шаг потребует (п—1J + (я— 1) — 2 таких операций
и т. д. Всего до обратного хода нужно произвести
-2]=*(*+1>B*+1>+*(*+1>-2,t D)
операций умножения и деления. Для обратного хода потребуется
операций умножения и деления, если не производить контроля
с столбцом s^ Столько же операций потребуется при использовании
такого контроля. Итак, всего на решение системы п уравнений
по схеме Гаусса с выбором главного элемента и текущим контролем
потребуется
+ 1._2в + в(в+1)=(в + 6в_1) F)
операций умножения и деления.
2. Компактная схема Гаусса. Придумано много различных видо-
видоизменений схемы Гаусса, дающих те или иные преимущества. При-
Приведем одну такую схему. Рассмотрим сначала систему четырех урав-
уравнений общего вида:
G)

14 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Исходные данные, промежуточные и окончательные результаты будем
записывать в следующую схему:
@) @) @) @) @)
Я@) /г@> /т@) /г@> /г@)
#21 #22 #23 #24 #25
Я@) /г@) /г@) /7@) /т@)
#31 #32 #33 4 #35
J°) „(°) (°) J°) J°)
1 2 3 #44 #45
1 A)
t A)
A(l)
0 ц
c'S
022
032
,ra)
1 eff
,№)
043
Си
^34
Oil
Cl5
<$
cf5(
„A2) (U) A0) (9)
X\ X2 X% Xi
Верхнюю половину схемы мы отводим для коэффициентов и сво-
свободных членов исходной системы, а в нижней половине будут поме-
помещаться промежуточные и окончательные результаты. Верхний индекс
показывает порядок получения промежуточных и окончательных
результатов.
Величины ой просто совпадают с соответствующими величи-
величинами a(Oj> и выписываются здесь лишь для удобства пользования
схемой.
Величины с'2) вычисляем по формулам
сB) = ^. (У =2, 3, 4, 5). (8)
При этом уравнение
_|_ С(|) х^ _)_ СB) х^ _ сB) (9)
эквивалентно первому уравнению исходной системы.
После этого вычисляем величины bfl (i > 1) по формулам
Ь\2 = а\2 — b\{ci2 (j = 2, 3, 4). A0)
Таким образом, о'|^ будут являться коэффициентами при хг во вто-
втором, третьем и четвертом уравнениях системы после исключения
в них неизвестного хх с помощью уравнения (9).
Следующим этапом будет являться получение коэффициентов и
правой части второго уравнения после исключения из него указан-
указанным выше способом неизвестного х^ и последующего деления на

§ 2] МЕТОД ИСКЛЮЧЕНИЯ 15
коэффициент при х2. Очевидно, эти величины с?Ч будут определяться
по формулам: ащ t
Таким образом, после преобразования второе уравнение примет вид
= <& A2)
Далее будем исключать неизвестное х2 из третьего и четвер-
четвертого уравнений. Опять сначала подсчитываем коэффициенты при х3
в третьем и четвертом уравнениях. Они определятся по формулам:
ЬШ = аП - b№ - b\VS (I = 3, 4). A3)
Первые два члена правой части этой формулы дают коэффициенты
при х3 третьего и четвертого уравнений после исключения xlt
а после вычитания последнего члена получим результат исключе-
исключения х2.
Коэффициенты и правая часть третьего уравнения после деления
на коэффициент при х3 примут вид
HJL U = 4, 5), A4)
а само это уравнение запишется в виде
Остается еще исключить х3 из четвертого уравнения. При этом,
коэффициент при xi в нем примет вид
*о=«а - й'сй - *2сй -
а свободный член после исключения х3 и деления на коэффициент
при хА будет
(8)
С45
45 °41С15 °42С35 Й43С35
При этом четвертое уравнение запишется в виде
** = <$. A8)
Нетрудно заметить, что для системы п уравнений при отыска-
отыскании величин b\f~l\ CjiJ) следует поочередно использовать формулы:
ftT^atf-SftS-MP (/ = /. У+1 п), A9)
2. .... я+1). B0)

16
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Если проследить ход вычислений по схеме, то легко обнаружить
закон образования величин bff~l) (|л
Неизвестные хп, хп_и ..., х^
стемы уравнений
и с(|л.
находятся последовательно из си-
си-Ь- 2 с?рхк = cfl+l
k i
(J = я. я — 1 1).
B1)
Будем называть эту схему компактной схемой Гаусса. При реше-
решении системы п уравнений по компактной схеме Гаусса требуется
произвести столько же умножений и делений, как и в схеме глав-
главных элементов. Однако она требует меньше записей. Схема допу-
допускает такой же контроль, как и ранее.
Так как вычисления по компактной схеме Гаусса более систе-
систематизированы, чем по схеме главных элементов, то процесс вычис-
вычислений легче программируется для автоматических машин. С другой
стороны, вычисления по этой схеме могут привести к большой
потере точности. Кроме того, для того чтобы процесс вычислений
был осуществим, нужно требовать отличие от нуля всех b[i~l\
Приведем результаты вычислений при решении приведенной
в начале параграфа системы A) по компактной схеме Гаусса:
1,11610
0,15820
0,19680
0,23680
1Д1610
0,15820
0,19680
0,23680
1,04058
0,12540
1,16750
0,20710
0,24710
0,11236
1,14972
0,18499
0,22049
0,98696
0,13970
0,17680
1,21680
0,25680
0,12517
0,13655
1,16691
0,19705
0,93505
0,14900
0,18710
0,22710
1,26710
0,13350
0,14437
0,14921
1,17425
0,88130
1,54710
1,64710
1,74710
1,84710
1,38617
1,24187
1,06655
0,88130
3,07730
3,33670
3,59490
3,85490
2,75720
2,52279
2,21576
1,88130
Применяя компактную схему Гаусса, мы элементарными пре-
преобразованиями переводим матрицу А системы в верхнюю треуголь-
треугольную матрицу
С = 0 1 с' ' с- ' ... с
\0 0 ' 0 ' V
/Интересно отметить, что если рассмотреть еще матрицу
B2)
0
— I °ц
в =
B3)
Ь(ъ)
Ь
ип,п

§ 2]
МЕТОД ИСКЛЮЧЕНИЯ
17
также получающуюся в процессе наших вычислений, то имеет место
равенство
А = ВС. B4)
Это равенство просто получается, если использовать формулы A9)
и B0). Так как В снова треугольная матрица, то прямой ход при
решении системы уравнений по компактной схеме Гаусса эквива-
эквивалентен умножению системы на треугольную матрицу.
3. Обращение матрицы. Равенство B4) можно использовать
для обращения матриц. Эта задача важна как сама по себе, так и
в тех случаях, когда приходится решать много систем с одной и
той же матрицей, но с различными правыми частями.
Перепишем B4) следующим образом:
А~1В =
.-X
B5)
Матрица С ' будет верхней треугольной, и ее диагональные эле-
элементы равны единице. Поэтому если обозначить элементы ма-
матрицы A~i через йц, то первое из равенств B5) даст п ^~ ' урав-
2
нений для определения dij.
1= 1
tdi^= I
2 3
О О
n,
0,
О ... О,
I.
B6)
Так как матрица В нижняя треугольная, то второе из равенств B5)
п(п— 1)
даст еще ——=—- уравнений для отыскания в?у.
j= 2 3 ... п,
;/$ = 0 0 ... О,
B7)
О ... О,
dn-l, п -\-dnnCn-\, п = 0.

18 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Таким образом, мы получили п2 уравнений для определения неиз-
неизвестных элементов йц обратной матрицы А~х. Решение системы
B6) — B7) не представляет труда. Полагаем в каждом из уравне-
уравнений B6) / = я и находим последовательно dn,n, dn,n-\ dn,u
Затем из уравнений B7) при j = n находим a?n-i, n. dn^iin d\, „.
Потом снова возвращаемся к уравнениям B6) и, полагая в них
i=n—1, находим rfn_i,n_i, ^„_iin_3, ..., rfn-i, ь После этого
из уравнений B7) при j=n—1 находим dn-2,n-i ^i,n-i.
Так, переходя поочередно от системы B6) к B7) и наоборот, мы
в конце концов найдем все йц. Вычислительная схема остается
прежней, только вместо одной строки для неизвестных хг у нас
будет п строк для матрицы А~1.
Если воспользоваться результатами, полученными при решении
примера A) по компактной схеме Гаусса, то без труда найдем, что
матрица, обратная к матрице данной системы, будет такова:
0,93794 —0,06844 —0,07961 —0,08592\
1-0,08852 0,90599 —0,09919 —0,10560 |
—0,11135 —0,11697 0,87842 — 0,12707 Г
V— 0,13546 —0,14018 —0,14381 0,85161/
Интересно заметить, что при этом оказывается
/0,99999 0,00000 0,00000 0,00000\
/
f 0,00000 1,00001 0,00000 —0,00001
A~lA =
I 0,00000 0,00000 0,99999 0,00000
\0,00000 0,00000 0,00000 1,00000
Точность вполне удовлетворительна. Если бы точность нас не
удовлетворила, то для уточнения можно было бы применить какой-
либо метод последовательного приближения, о чем будем говорить
позже.
4. Вычисление определителей. Схемы Гаусса можно применить
для вычисления определителей. При этом никаких новых трудностей
не возникает, поэтому только кратко опишем для примера приме-
применение для этой цели схемы Гаусса с выбором главного элемента.
Анализируя схему Гаусса с выбором главного элемента для
решения системы уравнений, легко убедиться, что при выполнении
прямого хода мы совершаем такие преобразования матрицы коэф-
коэффициентов исходной системы, при которых величина ее определи-
определителя не изменяется. После завершения прямого хода получается

§ 2]
МЕТОД ИСКЛЮЧЕНИЯ
система с такой матрицей, которую путем перестановки строк и
столбцов можно преобразовать в треугольную матрицу, причем на
главной диагонали будут стоять наши главные элементы. Следова-
Следовательно, определитель матрицы исходной системы только знаком
может отличаться от произведения главных элементов. С каким зна-
знаком нужно брать это произведение, легко сообразить, не выполняя
преобразование матрицы к треугольному виду.
Эти рассуждения показывают, что для вычисления определителя
по схеме Гаусса с выбором главного элемента нужно в точности
повторить прямой ход для решения системы по этой схеме (не выпол-
выполняя действий со столбцом свободных членов), а затем взять с соот-
соответствующим знаком произведение главных элементов.
5. Схема Жордана. Ксгда мы решали систему по схеме Гаусса,
то на каждом шаге число уравнений уменьшалось на единицу. Будем
теперь оставлять все уравнения, но при выборе главного элемента
не будем учитывать коэффициенты тех уравнений, из которых уже
выбирался главный элемент. Получим новую схему, которую будем
называть схемой Жордана. Так как здесь нет по существу ничего
нового, то мы лишь проиллюстрируем эту схему на том же самом
примере:
№
п/п.
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
т{
— 0,11759
— 0,14766
— 0,17923
— 0,09353
— 0,11862
— 0,21934
— 0,07296
— 0,14645
— 0,19015
— 0,09841
— 0,13037
-0,17163
аи
1,11610
0,15820
0,19680
0,23680
1,08825
0,12323
0,15436
0,23680
1,07381
0,10492
0,15436
0,20294
1,06616
0,10492
0,13899
0,18299
1,06616
at*
0,12540
1,16750
0,20710
0,24710
0,09634
1,13101
0,16281
0,24710
0,08111
1,11170
0,16281
0,21139
1,11170
1,Ш70
0,13970
0,17680
1,21680
0,25680
0,10950
0,13888
1,17077
0,25680
1,17077
1,17077
1,17077
аи
0,14900
0,18710
0,22710
1,26710
1,26710
1,26710
1,26710
1,26710
bi
1 54710
1,64710
1,74710
1,84710
1,32990
1,37436
1,41604
1,84710
1,19746
1,20639
1,41604
1,53651
1,10944
1,20639
1,23936
1,30711
1,10944
1,09721
1,09472
1,11670
Ч
3,07730
3,33670
3,59490
3,85490
2,62399
2,76748
2,90398
3,85490
2,35238
2,42301
2,90398
3,21794
2,17560
2,42301
2,54912
2,75720
2,17560
2,20891
2,26549
2,38380

20 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Отсюда без труда находим:
л, = 1,04059; x2 = 0,98697; х3 = 0,93504; xi = 0,88130. C0)
При решении по схеме Жордана система приводится к диагональ-
диагональному виду и обратный ход значительно облегчается. Всего для ре-
решения системы п уравнений с текущим контролем по схеме Жордана
требуется произвести
 + 4f-" C1)
операций умножения и деления.
Каждый шаг прямого хода по схеме Жордана эквивалентен умно-
умножению системы уравнений слева на матрицу вида
1
0
0
0
0
0 ...
1 ...
0 ...
0 ...
0 ...
«к
1
а..
0 ...
0 ...
0 ...
1, i 1 •••
0 ...
0
0
0
0
1
C2)
если не выбирать главный элемент, а идти последовательно, исклю-
исключая л:,, х2, . ¦ ¦ с помощью первого, второго, третьего, . .. уравнений.
6. Схема без обратного хода. Приведем еще одну схему исклю-
исключения, при которой вообще не требуется обратного хода. Пусть дана
система уравнений
[ 4 012*2 4
fl21*l 4~ #22*2 4*
= Ьг
! +
4" аппхп — Ьп.
C3)
Рассмотрим матрицу
ап1
—1
0
... аш
... апп
... 0
Ьп
0 /
C4)
Подберем постоянные ух, у2 уп так, чтобы после умножения
первой строки матрицы на ух, второй на у2 я-й на уп и ело-

§ 2] МЕТОД ИСКЛЮЧЕНИЯ 21
жения их с последней строкой в этой последней все элементы, кроме
крайнего правого, обратились бы в нули. Таким образом, уи у2 уп
должны удовлетворять системе уравнений
аххух -Ь а2ху2 +
а22у2-\-
C5)
Умножая обе части последних равенств последовательно на хх, х2, ...
..., хп, где (хх, х2, ..., хп) — решение исходной системы, и скла-
складывая их, получим:
х2-1- ... +аХпхп)-\-
х2-\- ... +а2пхп)-\-
п(апХхх-\-ап2х2-\- ... -\-аппхг) = хх. C6)
Но выражения в скобках равны последовательно Ьх, Ъ2 Ьп. Таким
образом,
= xx, C7)
т. е. правый крайний элемент последней строки будет равен хх.
Совершенно аналогично, если бы мы взяли —1 во втором столбце
последней строки, то крайний правый элемент последней строки
стал бы равен х2. Такие же рассуждения можно провести, беря —1
в любом из первых п столбцов. Рассмотрим теперь клеточную ма-
матрицу
А ¦¦ Ь \
C8)
где А—матрица коэффициентов системы, Ь — столбец свободных
членов, /—единичная матрица и 0 — столбец нулей. Пусть нам уда-
удалось путем прибавления к последним п строкам этой матрицы ли-
линейных комбинаций п первых строк сделать минус единичную матрицу
нулевой. Тогда в силу наших рассуждений нулевой столбец обра-
обратится в столбец неизвестных хх, х2, х3, ..., хп. Схема, которую
мы сейчас проиллюстрируем на том же примере, и будет реализа-
реализацией указанного процесса. За основу будет взята схема Гаусса
с выбором главного элемента. Будем называть данную схему схемой
без обратного хода.

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
№
1
2
3
4
IV
1
2
3
IV
III
1
2
IV
III
II
1
IV
m
и
i
IV
III
II
1
от,
— 0,11759
— 0,14766
— 0,17923
0,78920
— 0,09353
— 0,11862
— 0,17311
0,85414
— 0,07296
— 0,15007
— 0,12509
0,89952
— 0,13545
— 0,11136
— 0,08852
0,93795
«ii
1,11610
0,15820
0,19680
0,23680
1,08825
0,12323
0,15436
0,18688
1,07381
0,10492
0,16016
0,13185
1,06616
0,14441
0,11873
0,09438
j
Л/2
0,12540
1,16750
0,20710
0,24710
0,09634
1,13101
0,16281
0,19501
0,08111
1,11170
0,16683
0,13906
— 1
0,13970
0,17680
1,21680
0,25680
0,10950
0,13888
1,17077
0,20267
— 1
0,14900
0,18710
0,22710
1,26710
— 1
h
1,54710
1,64710
1,74710
1,84710
1,32990
1,37436
1,41604
1,45773
1,19746
1,20639
1,21260
1,20950
1,10944
1,03156
1,05859
1,08517
0,88129
0,93504
0,98696
1,04060
st
3,07730
3,36670
3,59490
3,85490
— 1
2,62399
2.76748
2,90398
2,04229
— 1
2,35238
2,42301
1,53959
1,48041
j
2,17560
1,17597
1,17732
1,17955
— 1
0,88128
0,93505
0,98697
1,04060
Значения неизвестных, содержащиеся в последних четырех стро-
строках, близки к найденным ранее. При решении системы уравнений
по схеме без обратного хода с контрольным столбцом требуется
произвести
^ C9)
операций умножения и деления.
Приведенная схема допускает очевидные обобщения. Так, если
вместо C8) взять
А 5 Ь \
..:.. ...\ D0)
<—С- d J

§ 31
МЕТОД КВАДРАТНОГО КОРНЯ
23
где q произвольная квадратная матрица и d — произвольный столбец,
то действуя по схеме без обратного хода, мы получим на месте
столбца d столбец CA~xb-\-d.
Если же рассмотреть матрицу
А
— С
D1)
Где в — произвольная матрица и 0 — матрица нулей, то нашим про-
процессом мы придем к матрице СА~1В. В частности, если взять матрицу
D2)
то мы придем к матрице А
§ 3. Метод квадратного корня
В том случае, когда матрица А симметрическая, в приведенных
ранее схемах можно сделать ряд упрощений. Мы не будем здесь
останавливаться на этих довольно простых вопросах, а изложим
вместо этого очень удобный для симметрических матриц метод квад-
квадратного корня.
Пусть данная нам система записана в виде
Ах = Ь,
A)
где А — квадратная симметрическая матрица, b—вектор-столбец
из правых частей системы их— вектор-столбец неизвестных. Реше-
Решение системы A) будем осуществлять в два этапа. На первом этапе
представим матрицу А в виде
Л = LL', B)
где L — нижняя треугольная матрица и Z/ — транспонированная по
отношению к L матрица. Такое представление всегда возможно.
Чтобы не осложнять записей, ограничимся рассмотрением систем
четвертого порядка. Будем разыскивать такие а^, что
C)
«U
«21
«31
«41
«К
«22
^32
«43
«13
«23
«33
«43
«14
«24
«34
«44
«11
«21
а31
а41
0
а22
а32
Чг
0
0
азз
а43
0
0
0
а44
а11
0
0
0
ап
а32
0
0
а31
«32
аЗЗ
0
Hi
Чг
а43
а44

24
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Произведя умножение матриц в правой части и приравнивая затем
соответствующие элементы правой и левой частей, получим следую-
следующие уравнения:
D)
an
9
an
«31
= flu,
+ a312 +
au!
«22
2
*21 = a
= «33>
2
12 > «Ua31
51 +«22*32
a3ia41 ¦+
2
= fl13
= ^23
" a32a42
2
, aua41 =
. a21a41 +
+ «ЗЗа43 =
Отсюда последовательно находим:
1 / Й15 Й13 #14
au=|/au, a21— ,— , a31— f— , a41— ,—
У чц У аи У йп
г,
а22
= ' а22 0B1 ¦ 0;32 ^
«42 =
„ _У~„ 2
CCqo V ?*зз Cqi
2
«32.
«43 = '
азз
l/ 2 ^2 2
«44 ^= » 4 «41 «42 «43-
E)
Нетрудно сообразить, как будут выражаться о.ц через а.ц в общем
случае системы га-го порядка.
Нужно заметить, что при действительных а^ могут получиться
чисто мнимые значения ац. Но так как вычисления с чисто мнимыми
величинами нисколько не труднее, чем с действительными, это не
вызовет дополнительных трудностей. Если, кроме того, матрица А
положительно определенная, то мнимых величин вообще не будет.
После того как матрица L найдена, переходят ко второму этапу.
При этом сначала решают систему
Ly=b,
а затем находят х из системы
L'x=y.
F)
G)
Так как обе системы с треугольными матрицами, то они решаются
без труда.
Схема квадратного корня очень удобна, требует небольшого коли-
количества операций умножения и деления и очень небольших записей.
Всего при решении системы п уравнений придется п раз произвести
извлечение корня и проделать
лз 4-
2л
(8)
операций умножения и деления

§ 4]
МЕТОД ОРТОГОНАЛИЗАЦИИ
25
Проиллюстрируем этот метод на примере системы шести урав-
уравнений с симметрической матрицей. Часть коэффициентов мы не выпи-
выписывали, пользуясь симметрией.
6,1818
2,486323
1,040932
0,1818
7,1818
0,073120
2,678891
aik
1,050668
0,3141
0,2141
8,2435
0,126331
0,076473
2,867349
1,026605
0,1415
0,1815
0,1214
9,3141
0,056911
0,066199
0,038066
3,050415
0,474071
0,1516
0,1526
0,2516
0,3145
5,3116
0,060974
0,055300
0,083585
0,099720
2,299543
0,578973
0,2141
0,3114
0,2618
0,6843
0,8998
4,1313
0,086111
0,113892
0,084472
0,219198
0,373697
1,978909
0,367300
7,1818
8,2435
9,3141
5,3116
4,1313
3,1816
2,888522
2,998364
3,041100
1,584361
1,408632
0,726854
Подставляя найденные значения в левые части системы, получим
соответственно
7,181794; 8,243489; 9,314104; 5,311593; 4,131297; 3,181600. (9)
§ 4. Метод ортогонализации
Пусть дана система
Ах=Ь
A)
порядка п. Здесь мы, чтобы избежать в дальнейшем путаницы, над
векторами поставили черточки. Решение системы будем разыскивать
в виде
х =
B)
где
— п векторов, удовлетворяющих условиям
) = 0, при&>/ (k, 1=1,2 п). C)
Здесь рассматривается обычное скалярное произведение векторов
в n-мерном векторном пространстве, т. е. если х = (хх,хг хп) и
— п
У~(Уи У2> ¦••> Уп)> т0 С*. .У) = J?-к».У»- Пусть такие векторы най-
Дены. Как это делается, будет показано ниже. Рассмотрим скалярное
произведение обеих частей системы A) с х®:
(Ах, хЩ = ф, ~хЩ (I = 1, 2, .. ., п). D)

26 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Используя B), получим:
п
(Ах, х(;)) = 2а4(Лх«, *№) = (?, х«) (/=1, 2 га) E)
к = 1
или, в силу выбора векторов х^,
г __
2а*(Ак<*\ х(П) = ф, хО) A=1, 2 га). F)
4 = 1
Итак, для определения коэффициентов ак мы получили систему
с треугольной матрицей. Определитель этой системы равен
(АхЫ, хЫ) (Ах®, х<а>) ... (Ах(пК x~W). G)
Следовательно, если (Ах^К х№) Ф 0 (k=\, 2 га), то ак воз-
возможно найти и находятся они без труда.
Особенно легко определятся ак, если матрица А симметрическая.
В этом случае, очевидно,
(Ах("К х«)) --= (хМ, Ах(П) = (Ах9), x<-V) (8)
и, следовательно,
(AxC\ Щ = 0 при I ф k (I, k = 1, 2 п). (9)
Тогда система для определения ак принимает вид
ак (АхС), х«) = ф, хМ) A0)
Метод можно обобщить. Пусть каким-то образом удалось найти
систему 2га векторов лК1), х&\ ..., х'™); У1', Уа\ ..., У") так, что
= 0 при&>/ (к, /=1,2 га). A2)
Умножая обе части равенства A) на y'jS> и используя представление х
через х^кК как и ранее, получим:
г _ _
2 ), у»1)) = (? Уг>) (г = 1, 2, .... я). A3)
Опять получилась система линейных алгебраических уравнений с тре-
треугольной матрицей для определения ак. Несколько усложнив вычи-
вычисления, можно получить систему диагонального вида. Для этого
построим три системы векторов х^1>, хР>, .... *<"); У1), У2). .... у™);

4] МЕТОД ОРТОГОНАЛИЗАЦИИ 27
j, z& z№>, так что имеют место равенства:
_ _ *~1
J S (* = 2, 3, .... re), A4)
y (k = 2, 3, ...,«)..
>, yr>) = (Л'гда, уг)) = о (а > г). A6)
Тогда
г-1
i=r+l
так как при /< г
2/f
= (Л'гМ, у»)) 4- 2 № (A'~z(r\ У Л) ^0 A8)
и при /> г
ф & >) = Ыг) 4- 2 rffyЛ,
2
r-l
_ _
= (Л*<*>, У»")) 4- 2 ^(r) (^(f). У*) = 0-
Таким образом,
Остановимся подробнее на первом из описанных методов. Рас-
Рассмотрим случай, когда матрица А симметрическая и положительно
определенная. Последнее означает, что для любого вектора х ква-
квадратичная форма его компонент (Ах, х) больше или равна нулю,
причем равенство нулю возможно в том и только том случае, если
вектор х нулевой. Как мы видели ранее, нужно построить систему
векторов *(!), *(а), .... xf-n\ удовлетворяющих условиям
{AxfV, JcW) = O (кфг). B1)
Это построение можно осуществить следующим образом. Исходим
из какой-то системы линейно независимых векторов yW, yP>, .... У"),

28
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
например из системы единичных векторов, направленных по коор-
координатным осям:
= (l, 0, 0 0),
= @, 1, 0 0),
B2)
y«) = @, 0, 0 1).
Далее проводим «ортогонализацию» также, как это делалось в пре-
предыдущей главе. Принимаем л:A)=у1) и ищем х^ в виде
jc'2' ^= ~v@) —I— X'2'jc^4 B3)
Из условия (xV\ Ах^) = 0 находим:
~х C) = уз) _(_ XC)x(i) _(_ \f~xV\
= (х<3\ Ах^) = 0 влекут за собой
B5)
Ищем лг<3' в виде
Условия (х<3\
Далее поступаем так же.
Процесс будет осуществим, так как все (*('>, Ах^) Ф 0. Это же
обеспечит нам разрешимость системы для определения коэффициен-
коэффициентов а.к. Заметим, что в нашем случае это будет процесс настоящей
ортогонализации, как он проводился в предыдущей главе, если
в пространстве векторов ввести новое скалярное произведение при
помощи соотношения
\х, у] = (х, Ау) = (А~х, у).
B7)
Нетрудно проверить, что введенное таким способом скалярное про-
произведение будет удовлетворять всем требованиям, которые к нему
предъявляются.
При решении системы п уравнений по настоящей схеме требуется
произвести
n3 + f" B8)
операций умножения и деления.
Приведем пример на применение этого метода. Возьмем опять
ту же систему, которую мы решали по методу квадратного корня.
Верхняя часть схемы заполнена коэффициентами и правыми частями

§ 41
МЕТОД ОРТОГОНАЛИЗАЦИИ
29
системы. Мы не проверяем здесь положительную определенность
матрицы А, так как это условие не является необходимым для про-
проведения процесса. Вторая сверху часть схемы заполнена компонен-
компонентами векторов лг<*) и коэффициентами X. Они разделены ломаной
линией. Содержание остальных частей не вызывает сомнений. В силу
ошибок округления недиагональные элементы нижней части будут
отличны от нуля. Их можно подсчитывать для контроля. Их можно
также использовать в системе и решать последнюю методом после-
последовательных приближений. В силу значительного преобладания диаго-
диагональных элементов метод будет быстро сходиться.
хB)
Х1Щ
хA)
X®
х(в)
АХ(Ч
Ах®
Ах®
Ax{i>
Ах®
AW
(Ах^\ *<Ч)
(А*гB), *B>)
(А~х®, х{3))
Ш4>, *<*>)
(Ах®, х(ъ))
(Ах*\ х<*>)
А
6,1818
1
— 0,0294
— 0,0500
— 0,0215
— 0,0217
— 0,0268
6,1818
6,1818
0,1818
7,1818
— 0,0294
1
— 0,0286
— 0,0243
— 0,0190
— 0,0368
0,1818
7,1765
7,1765
0,3141
0,2141
8,2435
— 0,0508
— 0,0286
1
— 0,0133
— 0,0288
— 0,0239
0,3141
0,2049
8,2217
8,2217
0,1415
0.1815
0,1214
9,3141
— 0,0229
— 0,0247
— 0,0133
1
— 0,0327
— 0,0666
0,1415
0,1773
0,1091
9,3050
9,3050
0,1516
0,1526
0,2516
0,3145
5,3116
— 0,0245
— 0,0206
— 0,0292
— 0,0327
1
— 0,1625
0,1516
0,1481
0,2397
0,3042
5,2879
5,2879
0,2141
0,3141
0,2618
0,6843
0,8998
4,1313
— 0,0346
— 0,0425
— 0,0295
— 0,0719
— 0,1625
1
0,2141
0,3051
0,2422
0,6686
0,8593
3,9161
3,9161
Ь
7,1818
8,2435
9,3141
5,3116
4,1313
3,1816
h
h
h
h
Сь, *<*>)
7,1818
8,0324
8,7192
4,8330
3,3769
1,4381
«1=1,1618; о, = 1,1193; o3 = 1,0605; o4 = 0,5194; o5 = 0,6386; o6 = 0,3672;
xx = 1,0410; x^ = 1,0507; хъ = 1,0264; х± = 0,4741; хь = 0,5789; х6 = 0,3672.

30 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
В случае несимметрической матрицы процесс ортогонализации
проводится точно так же. Пусть векторы х^\ х@\ ..., х(А> уже
построены. Тогда л:('с+1' ищется в виде
_ к
jt(*+i) = у*+и _|_ ^ й(*+1)^A). B9)
г-1
Коэффициенты ^fc+1) определяются из системы
к _ _ _
2 Г *<Л) (/=1. 2, .. ., k). C0)
Система в случае несимметрической матрицы будет треугольной.
Аналогично строится система «биортогональных» векторов, т. р.
система 2га векторов, удовлетворяющих условию A2). При этом
_уA), у®, ..., Уп)—произвольные п линейно независимых векторов,
а векторы х^\ л:*2), .... *(»> строятся последовательно в виде
к
Коэффициенты 'j'i''*1' находятся из системы
к _ _ _ _
2 ). Уй) = — (^У+1). Ул) С/ = 1. 2 ft). C2)
2
Так же поступаем, отыскивая коэффициенты с^> и d(fc>, при
построении систем векторов A4) и A5), удовлетворяющих усло-
условиям A6). При этом получим две системы:
*-i _ _ _ _ ч
^ c(fc) (Ay (*). У Л) = — (Ду«, У »),
C3)
2 G=1,2 ft — 1),
§ 5. Метод сопряженных градиентов
Пусть А — симметрическая положительно определенная матрица.
Рассмотрим функцию
f(x) = (х, Ах) — 2 E", х). A)
Это—целая рациональная функция второй степени относительно
компонент (xlt хг, ..., хп) вектора х. Поверхности f(x)= const
образуют в и-мерном пространстве /?(п) семейство эллипсоидов
с общим, центром х* = А~ Ь.

§ 5] МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 31
Учитывая симметричность матрицы А, преобразуем разность
f(x) — f(x*). Получим:
f(x) — f(x*) = (х. Ах) — 2 (b, х) — (х*. Ах*) + 2 (b, x*) =
= (х, Ale) — 2 (Ах, х*) + (Ах*, х*) = (х^х*, А (х— х*)). B)
Так как А — положительно определенная матрица, то
/(*)-/(**)> 0, C)
причем знак равенства достигается лишь при х — х*.
Таким образом, задача об отыскании решения уравнения Ах = Ь
эквивалентна задаче об отыскании вектора х, обращающего в мини-
минимум функцию f (х), определенную A). Существует много методов
решения последней задачи. Об одном из таких методов мы здесь и
расскажем.
Берем произвольный начальный вектор х@). Будем смещаться,
начиная с точки, определенной вектором х@), по нормали к эллип-
эллипсоиду /(x)=/(x@)) до тех пор, пока эта нормаль не коснется
какого-то эллипсоида семейства f(x) = const. Получим новую точку.
Вектор, проведенный в эту точку, обозначим через х^К Отыщем
этот вектор. Введем обозначение
Я0' = Ъ— Ах<® D)
и покажем, что вектор г® имеет направление нормали к эллипсоиду
f(x)=f(x@)) при х = х@\ Действительно, нормальное направление
будет совпадать с направлением быстрейшего убывания функции
f(x) — направлением градиента. Таким образом, нам надо найти
такой вектор с, что
E)
принимает наибольшее значение при условии (с, с) = const. Функ-
Функцию, стоящую под знаком производной, можно записать в виде
/С*(°) + ас) = (Зс<°) + ас, Ах® + аЛс) — 2 (Ъ, л:(°) + ас) =
= а2 (с, Ас) — 2а (й°), с) +/(*@)). F)
Таким образом,
^¦/(*<Р) + ос)| = —2(Я°), с). G)
Используя неравенство Буняковского, получим:
), с"J<(г(°>. й°>) (с", с), (8)

32 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
причем при с = /-(°> имеет место знак равенства. Итак, искомое на-
направление будет определяться вектором И0'.
Найдем теперь такое а, при котором /(х^ -\- аИ°>) принимает
наименьшее значение. Используя F) при с = /-@>, найдем, что иско-
искомое а, которое мы обозначим через а0, равно
Итак,
JcW = jc(°) + аой°). A0)
Ha рис. 1 показана геометрическая картина нашего построения при
« = 3.
Можно было бы продолжить наш процесс и получить из х^
вектор х® так же, как мы получили из х1® вектор хAК Мы при-
пришли бы тогда к методу последовательных приближений, носящему
Рис. 1.
название метода скорейшего спуска. Рассмотрим его несколько
позже. В настоящем параграфе будем получать х^ иначе.
Рассмотрим векторное уравнение
-дг(Ц)=О. (И)
Оно определяет гиперплоскость (и— 1)-го измерения. Уравнению A1)
удовлетворяет вектор х = хA\ Ему удовлетворяет и х* = А~1Ь.
Действительно,
(Лг(°), A~lb — j?1)) = G(°), Ъ — А~х^) = G<°\ й1'), A2)
где через И1' обозначен вектор
Как и раньше можно показать, что вектор И1' имеет направление
нормали к эллипсоиду
= /(^A)) A4)

§ 5] МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 33
прИ х = хA). Вектор И0' касается этого эллипсоида в той же точке.
Следовательно, (И0', И1») = 0.
Сечение гиперплоскостью A1) эллипсоидов f(x) = c дает диа-
диаметральные гиперплоскости (я—1)-го измерения, проходящие через
точку, определяемую хA\ Будем теперь проводить наши рассужде-
рассуждения лишь в этой гиперплоскости.
Нормаль к эллипсоиду, получающемуся в сечении f (х) = f (хA))
гиперплоскостью A1), можно получить, проектируя й1' на гипер-
гиперплоскость. Обозначим эту i роекцию через р№ и будем разыскивать
ее в виде
^"A) = й1) + р07(°). A5)
Так как вектор Лй°> ортогонален к гиперплоскости, то и р<-1) дол-
должен быть ортогонален к Ли0'. Это дает
°>)
06)
Будем теперь отыскивать такое а, что / (jeA> -\- арМ) принимает
наименьшее значение. Так как
— 2аGD, &»)+/&% A7)
то искомое значение а, которое мы будем обозначать через л1
равно
A), Pw)
Итак,
x^ = xW-JralpW. A9)
На следующем шаге мы перейдем к гиперплоскости (я—2)-х
измерений, определенной уравнениями A1) и
', л: — л;B)) = 0. B0)
В силу ортогональности pW и
Я2» = Ь — Ах& = 7(D — at ApW B1)
получим, что х* ~ A~lt> принадлежит нашей гиперплоскости [ ним
образом, и эта гиперплоскость будет диаметральной. Отмети... ле
следующие свойства й2'1.
(-B)j 7(о>) = Gd) _ снАрМ, 7(о)) = 0, B2)
= Gd), //I») - at (ApM, pW) = 0. B3)

34 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ' УРАВНЕНИЙ fГЛ. 6
Проекцию нормального к эллипсоиду f(x) = f(xB)) при х = хB)
вектора И2' на гиперплоскость — вектор /?B>— будем разыскивать
в виде
-B) = 7B)_(_р1^A)_ B4)
Нужно потребовать ортогональность р<2) к Аг<0) и ApW. Но
(у2>, лЯ°)) = (Я2» + в1^A), лй°») = (Я2>, АрЩ = ~(г<2\ 7(°) — 7(!)) = о.
B5)
Условие ортогональности //2> и Л//1* записывается так:
Теперь, как и ранее, отыскиваем значение а, для которого
f(x<2) -\-ар&) принимает наименьшее значение. Это значение а, кото-
которое мы обозначим через с^, будет равно
Поэтому вектор х^ будет представляться в виде
B8)
Так же продолжаем и дальше. Получим последовательность
векторов {х(к)}, {№}, {р(к)}, которые определятся рекуррентно сле-
следующим образом:
р(о) = 7(о), B9)
C1)
C2)
( }
C4)
Отметим следующие свойства членов этих последовательностей.
В силу самого построения будем иметь:
= (V*), р(Л) = 0 при (ф J, C5)

^ 5] МЕТОЛ СОПРЯЖЕННЫХ ГРАДИЕНТОВ 35
Далее, при г>/ получим:
G«, pU)) = (й*-1) — a^V'-1'. рЩ =
= &И-Ч, р(Л) — ai_l (^(Л, Л^(*-1)). C6)
Правая часть последнего равенства равна нулю при г=у-|-1 в силу
определения аг_!. При г>/-|-1 она будет равна (г^~1\ р^Ь, т. е.
индекс у /"(i) понизился на единицу. Повторяя рассуждения доста-
достаточное количество раз, мы придем в конце концов к случаю, когда
индекс у г будет на единицу больше индекса у р. Следовательно,
при г>/
7 0. C7)
Наконец, рассмотрим (/•('>, ИЛ) при i Ф j. Пусть, для определен-
определенности i > /. Тогда
= (Я*), ?<л — р,_^и-Ч) = (Я*), р(л> — р^_!G(«, р(»-Ч) = о.
C8)
Так как в п- мерном пространстве не может быть более п взаимно
ортогональных векторов, то на некотором шаге k ^ n мы получим
/-(';)= 0. При этом je(fc)= A~lb. Таким образом, на некотором шаге мы
придем к точному решению системы. Такой способ получения реше-
решения будем называть методом сопряженных градиентов.
Методу сопряженных градиентов можно дать простую алгебраи-
алгебраическую трактовку. Будем таким же способом, как это делалось
ранее, ортогонализировать систему векторов г(°), Лй°) ЛМ°>, ...
Полученные при этом векторы И0), И1' И*), . .. будут обладать
следующими свойствами:
1. Вектор ИЛ) является линейной комбинацией- векторов г(°\
Р
Я*) = С(*)Я"°) + c(*Mr5» + ... + 4*>Л*й~°>. C9)
Это свойство очевидно, если вспомнить ход процесса ортогонализа-
ции, как он определен выше.
2. Вектор И*+1) ортогонален к наименьшему линейному много-
многообразию, содержащему векторы 7<°>, й1) Я*).
Действительно, если /•№+1>=0, то утверждение тривиально.
Если же И**1) =? о, то и каждый из векторов Я°>, й1' /¦(*' не
Равен нулю. Совокупность последних векторов образует базис на-
наименьшего линейного многообразия, содержащего векторы г(°>,
¦ •••, ЛМ°). Вектор /<к+1\ будучи ортогональным ко всем

36 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
векторам базиса, будет ортогональным и ко всему линейному много-
многообразию.
3. Вектор /W= 0 тогда и только тогда, когда И°), Аг^\ .. ., Л'И0'
линейно зависимы.
Если г^ФО, то векторы л'0', И1', ..., И*) как ненулевые взаимно
ортогональные векторы линейно независимы. Это может быть только
в том случае, если порождающие их векторы И0', Аг^°\ .... ЛМ°)
также линейно независимы. Если же /-(fe)=0, то C9) дает линейную
зависимость векторов И0', Л/-(о) ЛМ0).
4. Если № ф 0, то коэффициент с^> в C9) отличен от нуля.
Это свойство есть следствие второго, так как вектор, ортого-
ортогональный к некоторому многообразию, не может принадлежать этому
многообразию.
5. Каждый из векторов Атг<-0) (/и = 0, 1, 2 k) может быть
представлен как линейная комбинация векторов И0', И1) л<*>.
Коэффициенты этой линейной комбинации определяются однозначно,
если ни один из векторов г®, И1' № не равен нулю.
Среди векторов И0', ЛИ0) лМ°> имеется максимальное число
линейно независимых. Таково же число ненулевых векторов среди
Ио), И1' И*). Эти ненулевые векторы образуют базис наи-
наименьшего линейного многообразия, содержащего векторы г^°\
Аг^ Атг(°\ Отсюда и следует утверждение.
Рассмотрим теперь наряду с обычным скалярным произведением
скалярное произведение, определенное равенством B7) предыдущего
параграфа. Последовательность векторов И0', ЛИ0', Л2И°> ЛМ°>,...
можно ортогонализировать в смысле этого скалярного произведения.
Получим новую последовательность векторов р(°) = г(°\ р^ р^с\...
Для этих векторов будут справедливы высказанные нами утвержде-
утверждения 1—5. Кроме того, системы векторов {И4'} и {рЩ будут свя-
связаны некоторыми соотношениями. Векторы //*> при i^.k принад-
принадлежат линейному многообразию, порожденному векторами л'0',
ЛИ0', .... Акг(°\ а вектор /•(fe+1' ортогонален к этому многообразию.
Таким образом, мы будем иметь:
(гМ, pU))=0 при i>J. D0)
Аналогично показывается, что
[р~т, 7Щ = (pd), А7Щ = (V*'), 7Щ = 0 при t>j. D1)
Воспользуемся равенствами D0) и D1) для установления формул,
связывающих векторы р&\ /•(fe>,p(fe+1>, r(*+1), Ар(кК Пусть векторы И0),

с 5] МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 37
7'11, . • •, И*' отличны от нуля. Тогда и векторы р<Р\ р^ р^
отличны от нуля. Вектор л(й+1' по C9) принадлежит линейному мно-
многообразию, порожденному векторами И°\ ЛИ0) Лй+1/-@>. В этом
линейном многообразии можно взять в качестве базиса векторы И0',
й« Я*>, Л*+1Я°). С другой стороны, Лй+1й°)= Л(ЛМ°)),
а вектор ЛМ°> может быть представлен как линейная комбинация
векторов pl°\ р(Ч р(к\ Таким образом, вектор Ак+1г^ может
быть представлен как линейная комбинация векторов Ар(°\ ApW, .. .
.... Ар&\ Векторы Ар(°\ ApW, .. ., Ap{-k~i) принадлежат линейному
многообразию, порожденному векторами г^°\Аг^\ .... ЛМ°> и, следо-
следовательно, могут быть представлены как линейные комбинации век-
векторов г<®, И1' г^к\ Поэтому вектор И*+1) можно записать в виде
7(fe+1) = ^+1O(o) + d(*+i)-(i)+ _ +dJ*+iO(*)_afci^(*). D2)
Помножим обе части равенства D2) скалярно на И*> (/=0, 1, ...
..., k—1). В силу ортогональности векторов И'' и № при I ф j
и равенства D1) получим:
0> D3)
Итак,
7№+1) = 4fc+1O(fc)-aftVfc). D4)
Умножим это равенство скалярно на р(к\ В силу D0) будем иметь:
0 = dj?+1) G(Ч ^fe)) - a, (^(fe), pm). D5)
Коэффициент afe отличен от нуля. Действительно, если 7(fe+1) — 0,
то условие afe==0 означает, что векторы й°), 7О, .... 7<ft> линейно
зависимы, если же /<к+1'> Ф 0, то условие aft^0 означает линейную
зависимость векторов Я°), й1) /-Tfe+1). И то и другое невоз-
невозможно. Скалярное произведение (ApW, рЩ также отлично от нуля.
Поэтому 4*+1) ф 0 и (?(к), р(к)) ф 0. Так как векторы 7к) опреде-
определяются с точностью до постоянного множителя, то мы всегда мо-
можем считать 4*+1)=1. Тогда из D5) получаем:
= 7(*> — ак Ар(к). D7)

B8 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Обозначим через *(*) решение уравнения
b^-Ax = 7W. D8)
Подставляя в D7) вместо /¦<•) их выражения по D8), получим:
>— х^) = акАр(к\ D9)
Итак,
Я E0)
Рассмотрим теперь разность векторов r(-k+i> —p(k+lK Каждый из
этих двух векторов представляется в виде линейной комбинации
векторов И°>, Аг^ Ак+1г(-°\ Так как векторы />(•) определяются
с точностью до постоянного множителя, то мы всегда можем пред-
предполагать, что коэффициенты этих линейных комбинаций при Ак+1г(°)
равны. Тогда разность И*+1)—р(*+ч может быть представлена в виде
линейной комбинации векторов r(°), Arl°\ .... ЛМ°> или векторов
р(о), pW pW:
7(*+i) _p(*+D = po^(o) + p^d) +..._(- pfcp(ft). E1)
Умножим скалярно равенство E1) на Лр(*' (/^0, 1 k—1).
При этом получим:
Po = Pi= ••• =P*_i = 0. E2)
После умножения на АрМ будем иметь:
— G(*+1), Ар(к)) = $к(р(к), АрМ), E3)
или
Gt*+D. ^(^))
Pfc = ~ фо.АЦЩ ¦ E4)
Итак,
p(*+i) = 7(*+« + pfcp(*), E5)
где pfe определяются равенствами E4).
Нетрудно заметить, что коэффициенты ак и f}fc можно также вы-
вычислять по формулам:
G№ 7«)
E6)
(о7)
Мы снова пришли к методу сопряженных градиентов. Рассуждая,
как и прежде, мы придем к выводу, что процесс должен закон-

§ 5] МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 39
читься после k^n шагов. При этом r(fe> = 0 и *(*) = А~1Ь. Может
оказаться, что вследствие ошибок округления Ип) будет отлично от
нуля. Тогда можно проделать еще несколько шагов до тех пор,
пока не получим достаточно малое И*). С другой стороны, может
оказаться, что уже после небольшого числа шагов И*) мало. Тогда
можно и не продолжать процесса.
Метод сопряженных градиентов можно обобщить на случай про-
произвольной неособенной матрицы А, Пусть В — некоторая положи-
положительная определенная симметрическая матрица. Выбираем произволь-
произвольные векторы p$) = q(°) и строим последовательности векторов {р(к)\
и {<7<fe'} ПРИ помощи рекуррентных формул:
4
= ^(*)— акВр(к).
E8)
Эти последовательности будут обладать указанными выше свойст-
свойствами, конечно с заменой матрицы А на матрицу В. В частности,
<7<и)=0. Следовательно,
_ п~1 _
q(°) = 2 акВр(к). E9)
Пусть теперь
р(°) = q(o) = С (Ь — Ах~(°У), F0)
где jc(°)—произвольный начальный вектор и С—произвольная
неособенная матрица. Тогда из E9) следует:
х* = A-1b = jc(°) + 2j Ча C'lBp(li). F1)
Итак, если последовательно, начиная с выбранного jc(°), вычислять
векторы
X ^= X --г— ОСьА С DD . (nz 1
i ft г » Vv /
то получим дгИ^д;*. Для векторов И*) = * — Л^й) из F2) получим:
7(fe+1}=7(fe)-afcC-lB^). F3)
Если вспомнить, что <7@) = Сл(°) и сравнить F3) и соответствующее
равенство E8) для 'д(к+1>, то получим д(к> = С7<.к> при любом k.

40 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Таким образом, E8) можно переписать в виде
х =
;(*)
F4)
Это и будут формулы, соответствующие B9) — C4) для несиммет-
несимметричного случая.
Рассмотрим два частных случая.
1-й случай. Выбираем В = А'А и С = А'. При этом получим*.
р(о) =
. A"pik)) '
F5)
2-й случай. Выбираем В = Л.Д' и С = /. При этом получим:
F6)
Относительно применения этих формул можно сказать то же, что
было сказано выше о применении формул B9)—C4).

§ 6]
МЕТОД РАЗБИЕНИЯ НА КЛЕТКИ
§ 6. Метод разбиения на клетки
41
Обращение матрицы высокого порядка часто удается свести
к обращению матриц низшего порядка, являющихся частью основ-
основной матрицы. Будем называть такие методы обращения матриц жг-
тодами разбиения на клетки.
Пусть нам дана квадратная неособенная матрица А. Разобьем ее
пунктирными линиями на частичные матрицы:
«и я» • a\k «i.ft+i •• а1п
А =
а
"nl
г+1 к
ипк
г + 1, п
п,п
A)
Это можно сокращенно записать так:
А =
"¦21
1-х, к)
-г, п-к)
B)
Здесь Ar,'s сами являются матрицами. Нижние индексы г, s пока-
показывают место частичной матрицы в полной матрице, так же как
индексы элемента аг} показывают его положение в матрице. Верх-
Верхние индексы /, т показывают соответственно число строк и число
столбцов частичной матрицы. Если такое разбиение осуществлено,
то будем говорить, что матрица разбита на клетки или блоки.
Если имеется вторая матрица В с таким же разбиением
(В(г к) В(г п-к)
то
где
В =
А-\-В =
—г, к) в(п-г, п-к)
1 ' В22
i, к)
l
г, п-к)
>Q>m)
Г, 8
Wn-i, к) W»-i, п-к)
^21 ^22
аA, т)
E>r,s •
О; т)
Г, S
Далее, если имеем матрицу
то
\D||J~fc>^ D%~k'n~1)J
». 3)
1
», п-з)
2
AD =
C)
D)
E)
F)
G)

42 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
где
"*' л;
= 4
Г *
Г *• "-
g, —Л
(8).
Обращаем внимание на то, что разбиение на клетки матрицы D
должно быть согласовано с разбиением на клетки матрицы А для
того, чтобы было возможно осуществить умножение клеток. В част-
частности, если взять i=j = k, т. е. если
/Л11
l=L(»-i,i)
\Л21
n-i, n-i)
22
Ып-i, i) Ып-i, n-i) I
0)
то клеточное умножение матриц возможно и произведение будет
разбито на такие же клетки, что и каждый из сомножителей.
Нетрудно сообразить, как будут выглядеть правила действий
с клеточными матрицами, если осуществлять разбиение на большее
число клеток, и в том случае, если мы имеем дело с прямоуголь-
прямоугольными матрицами.
Пусть теперь матрица D в (9) равна А~ . Тогда мы должны
иметь AD = Г
(п, п)
4V
г)
А(г,
i, n-i)
-., n-i) = 0(г, n-i)
-г,
, n-i)
n-i, n-i)
A0)
Здесь через I(}'tr обозначены единичные матрицы соответствующих
порядков, а через 0%™'—матрицы, состоящие из сплошных нулей.
Таким образом, мы сумеем найти Л, если подберем матрицы
?)?'gm) так, чтобы были выполнены равенства A0). Непосредствен-
Непосредственной проверкой убеждаемся, что матрицы D(,?'8m) можно последова-
последовательно находить из равенств:
n(n-i,n-i)_ Г A(n-i,n-i)_ An-i,i)( Ai,i)\-1 Ai.n-in-1
)y
i, n-i)
(ii)

§ 6]
МЕТОД РАЗБИЕНИЯ НА КЛЕТКИ
43
Следовательно, для того чтобы обратить, матрицу А порядка я, нам
придется обратить две матрицы, одна из которых имеет порядок i,
а другая порядок п — i.
Чаще всего берут i равным п—1. Тогда придется обращать
всего лишь одну матрицу порядка п—1. Для ее обращения можно
применять тот же прием. Это в свою очередь потребует обращения
матрицы порядка п — 2. Продолжая этот процесс дальше, мы в конце
концов придем к матрице первого порядка. Таким образом, после-
последовательно обращая матрицы
A2)
мы придем к А" .
Можно дать другой подход к рассмотренному методу. Предста-
Представляем матрицу А в виде
аи ... ах п_х О
апп1
»-i, х •••
а.
-1, П-1
О
ап2 .. . а„,„_1 0)
... О
Дщ
@ 0 ... 0 1). A3)
Изложенный метод показывает, как, зная обратную матрицу для
первого слагаемого правой части, получить обратную матрицу для
суммы всех слагаемых правой части. Идя по такому пути, можно
поставить следующую задачу. Матрица А представлена в виде
А = В -+- uv,
A4)
где В — некоторая квадратная матрица, для которой известна В 1,
и—матрица, состоящая из одного столбца и п строк, и v—мат-
v—матрица, состоящая из одной строки и п столбцов.
Требуется найти Л.
Решение поставленной задачи дает матрица
vB
-1,
A5)

44 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Действительно,
uvB-1
'" 1 vB-Ч ='~~ 1 «B-i + мг>Д"' ~
T'Ib^C =I + vB~lavUV_B'1 ~vB~lu^V_B~1 = I. A6)
Используя формулу A5), можно получать обратные матрицы
в широком классе случаев. Так, например, возьмем
ап О 0 ... О
'0 0 0 ... а„„У
Обратная матрица при этом находится без труда. За матрицы и и v
( 0 1
примем
, г; = A, 0 0).
Тогда формула A5) даст нам обратную матрицу для
• аи 0 0 ... О
A8)
«21
0
0
A9)
. ап1 0 0
Затем таким же образом можно исправить второй столбец, третий
и т. д., пока не придем к матрице А. Формулу A5) можно обоб-
обобщить, взяв вместо и и v матрицы U и V, имеющие соответственно
несколько столбцов и несколько строк.
§ 7. Линейные операторы. Нормы операторов
Прежде чем переходить к изучению методов последовательных
приближений, мы рассмотрим некоторые свойства операторов, кото-
которые нам при этом потребуются.
Пусть А — аддитивный оператор, заданный в линейном норми-
нормированном пространстве х) Н. Этот оператор называется ограничен-
ограниченным, если существует такая постоянная С, что для любого эле-
элемента х?Н выполнено неравенство
|. A)
1) См. § 1, гл. 4.

§ 7] ЛИНЕЙНЫЕ ОПЕРАТОРЫ. НОРМЫ ОПЕРАТОРОВ 45
Ограниченный, аддитивный оператор будем в дальнейшем назы-
называть линейным. Наименьшее из чисел С будем называть нормой,
оператора и обозначать ||Л||. Таким образом, норма оператора
А есть такое число \\A\\, что при любом х?Н выполнено
*11. B)
и с другой стороны, для любого s >• 0 найдется такой элемент
х'?Н, что
Можно дать другое определение нормы оператора, а именно по-
положить
\\А\\= sup \\Ax\\. D)
На!||-1
Нетрудно показать, что оба определения эквивалентны. Дей-
Действительно, неравенства B) и C) можно переписать в виде
11Ау11<И1|, ||л/||>||лц-?, ,5)
где _у = je/||.x|| и У =х'\||х'||—элементы с единичной нормой. По-
Поэтому норма оператора в смысле первого определения будет равна
норме в смысле второго определения. Наоборот, если пользоваться
равенством D) для определения нормы, то будем иметь:
для любого х?Н, т. е. имеем неравенство B). С другой стороны,
в силу определения верхней границы, для любого е>0 найдется
такой элемент х'?Н, ||д;/|| = 1, что
Поэтому норма оператора в смысле второго определения будет равна
норме оператора в смысле первого определения.
Рассмотрим совокупность всевозможных линейных операторов,
определенных на Н. Эти операторы аддитивны, и поэтому для них
определены операции сложения и умножения на число. Покажем,
что эти операции не выводят за пределы множества линейных опе-
операторов. По определению
С = А + В, (8)
если для любого х?Н имеет место
Сх = Ах-\- Вх. (9)
При этом
sup ||C*||< sup ||Ак||+ sup ||?*|| = ||Л||-Н|?||. A0)
И||1 ||||1 ЦЦ1

46 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Итак, С — ограниченный оператор и его норма удовлетворяет не-
неравенству
Далее, пусть
В = сА, A2)
где с — число. Это значит, что для любого х ? Н
Вх = сАх. A3)
При этом
sup ||?*||= sup ||Ci4jc|| = Jc| sup ||Л*||=|с|И|. A4)
IWI-i \\x\\-l \\x\\-l
Итак, оператор В ограничен и его норма удовлетворяет равенству
A5)
Утверждение доказано. Заметим еще, что ||Л||^.О и ||Л|| = 0 тогда
и только тогда, когда А = О, т. е. когда оператор А переводит
любой элемент в нулевой. Первая часть утверждения тривиальна.
Если же || Л ||= 0, то
sup || Л*||= 0, A6)
\\x\\-l
т. е. оператор А переводит каждый элемент х?Н, имеющий еди-
единичную норму, в нулевой элемент. Это же будет верно и для осталь-
остальных элементов Н в силу аддитивности оператора А.
Мы доказали, что для нормы линейных операторов выполнены
все свойства, которые требуются от нормы в линейном нормиро-
нормированном пространстве. Таким образом, совокупность всех линейных
операторов, заданных в линейном нормированном пространстве,
образует в свою очередь линейное нормированное пространство.
Но в множестве линейных операторов определена еще операция
умножения оператора на оператор. По определению
С = АВ, A7)
если для любого х?Н
Сх = АВх. A8)
При этом по первому определению нормы оператора будем иметь:
||с*|ЫИя*||<||л||||я*||<И|||Я|||И|. A9)
Итак, оператор С ограничен и
||С||Н|ЛВ||<И|||В||. B0)
1. Конечномерные линейные нормированные пространства.
В настоящей главе мы будем рассматривать только конечномерные
линейные нормированные пространства. При этом каждый элемент
линейного пространства будет полностью определяться конечной

§ 7] ЛИНЕЙНЫЕ ОПЕРАТОРЫ. НОРМЫ ОПЕРАТОРОВ 47
совокупностью чисел — компонент его по отношению к некоторому
базису. Пусть размерность пространства равна п. Норма элемента
х ? Н будет функцией его компонент
||*||=ср(*1. х2 хп).
При различных определениях нормы функции ср будут различны, но
все они будут обладать рядом общих свойств.
Так как ||сх||= | с \\\х\\, то
<?(сх1у сх2 сд;п) = |с|ср(д;„ х2 хп). B2>
Функция срС^!, х2 хп) непрерывна. Действительно, если х и х' —
два элемента Н с компонентами ixv ха х\ и (л;^, х'2 х'^г
то
\<?{xvx2 *„)-?(*!.*; х'п)\=(\\х\\-\\х'\\Шх-х'\\.B3)
Обозначим
ср @ О, 1, 0 О) = сц. B4)
г —1 раз
Тогда
||jf —jc'IKI*! — x[\al + \x2~^|«2-f- -•• +\х„ — х'п\ап B5)
или
1?(*1. *2 *n) — <P(*J. К Хп)К
<|*i — <!«!+ \хг — х'г\а2-\- ... -+-\хп—х'п\ап. B6)
Отсюда и следует непрерывность ср.
Непрерывная функция ср(дг1( х2 хп) достигает на ограни-
ограниченном замкнутом множестве
•+... +д?=1 B7)-
своего наибольшего значения М < оо и своего наименьшего значе-
значения т > 0. Так как при положительных с
i, сх2 схп) = сер (xv x2 хп), B8)
то
д:„)<^ при л;? + л;22+ ... +4 < 1 .B9)
1, х2 хп)>т при х\ + х\+ ... +4>1- C0)
Отсюда, в частности, следует, что множество элементов, удовле-
удовлетворяющих условию ||.х|| = 1, является замкнутым ограниченным"
множеством пространства R . Это множество не содержит нуле-
нулевого элемента.

48 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Пусть в нашем пространстве введены две нормы ||л:||х и ||*||2.
Рассмотрим множество элементов у?Н, для которых ||_у||1=1.
В силу только что сделанного замечания \\у\\2 на этом множестве
достигает своего наибольшего значения L и своего наименьшего
значения /, I ф 0. Пусть теперь х ф О — произвольный элемент Н.
Тогда
и X
* 2 =
II-«11
II-«II
и так как ||*/||*||i||i = 1, то
'Il*lli<ll*ll2<?||*lli- C2)
Отсюда получаем, что для произвольного ненулевого элемента х?Н
выполнены неравенства
ll 1И<|И<:1И
Они выполнены и для нулевого элемента.
Две нормы ||Arid и ||*||2, для которых выполнено
где х—произвольный элемент Н и т, М, п, N > 0, называются
эквивалентными. Неравенства C3) говорят о том, что имеет место
теорема. В конечномерном линейном нормированном про-
пространстве любые две нормы эквивалентны.
На практике чаще всего используют следующие нормы:
||jc ||i = max | xt |, C5)
Необходимо проверить выполнимость условий, налагаемых на
норму. Условия ||*||^>-0 и ||*|| =?0, если хфО, очевидно, выпол-
выполнены во всех трех случаях. Так же очевидно, что выполнено усло-
условие || с* || = | с | ||*||. Проверим выполнение условия
С 11*11 +
В первом случае будем иметь:
< max | Xi | + max \yt \ = \\x\\j, + Ц^^. C8)
г i
Во втором случае получим:

§ 7]
ЛИНЕЙНЫЕ ОПЕРАТОРЫ, НОРМЫ ОПЕРАТОРОВ
49
Наконец, из неравенства Буняковского следует:
\\х+У\\з
-l/i
+
/$/• =
D0)
Заметим еще следующий факт. Если л;''1'—>х в смысле
какой-то из этих трех норм, то л, —*¦ xf. Так как у нас все
нормы эквивалентны, то последнее заключение будет справедливо,
если х№ —ух по произвольной норме.
2. Линейные операторы в конечномерном линейном нормиро-
нормированном пространстве и их связь с матрицами. Пусть в «-мерном
линейном нормированном пространстве задан аддитивный оператор А.
Пусть этот оператор переводит базисные элементы @, 0, ...
..., 0, 1, 0 0) соответственно в элементы (ан, a2i ani).
Тогда в силу аддитивности он должен переводить элемент
(*!, х2 хп) в элемент (уи у2 уп), где
Уг = =i
Это можно записать в виде матричного равенства
У1 аи
Уч
D1)
Уп)
апп
D2)
Таким образом, каждому аддитивному оператору в п-мерном
линейном нормированном пространстве будет соответствовать
квадратная матрица порядка п. Обратно, каждая квадратная
матрица порядка п определяет при помощи равенства D2) некото-
некоторое отображение «-мерного пространства самого на себя. Нетрудно
проверить, что это будет аддитивный оператор. Поэтому в даль-
дальнейшем мы часто будем отождествлять аддитивные операторы
в «-мерном пространстве с соответствующими им матрицами.
Так как множество элементов х?Н, для которых ||д;|| = 1
образует замкнутое ограниченное множество R№, то непрерывная
функция ||Ах|| компонент (л^, х2 хп) будет на нем ограничена.
Таким образом, имеет место теорема: все аддитивные операторы
на конечномерном линейном нормированном пространстве будут
ограниченными. Поэтому в нашем случае в соответствии с выше-
вышеизложенным мы сможем ввести понятие нормы оператора или

50
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
нормы матрицы. Различным способам введения нормы элемента
будут соответствовать различные определения нормы оператора
или матрицы. Рассмотрим, как будут определяться нормы опера-
операторов или матриц для норм элементов, определенных равенствами
C5) — C7).
Покажем, что если норма элемента определяется равенством C5),
то норма А будет определяться
Действительно,
и если
Ax\\t = max
i
|i=l. TO
2 ai
aikxk
<max
2 \
i ft-1
\aik\-
D3)
D4)
D5)
Пусть max 2 I aa | достигается при I = j. Возьмем в качестве х
fti
элемент с компонентами xk=
ajk = 0. Очевидно, ||x||i=l- При этом
при ujk Ф 0 и хк=1, если
aflcxk
= 2
Следовательно,
S |
k=l
\aik\
D6)
D7)
Утверждение доказано.
Для второй нормы будем иметь:
Пусть ||л;||2=1. Тогда
2= max 2 I «»fe I -
/с г=1
n n
2 2 Ksi
i-l ft=l
D8)
< 2 I xk | max 2 I aik I-
Al A il
A; i=l
D9)

§ 7] ЛИНЕЙНЫЕ ОПЕРАТОРЫ. НОРМЫ ОПЕРАТОРОВ 51
Пусть max 2 \aik\ достигается при k=j. Возьмем элемент х
к г = 1
с компонентами хк = 0 при k Ф J и Xj= 1. Очевидно, ||jc||2=1.
При этом .
n
n
aikxk = 2j | ay | = max Zi I aik I- E0)
i=l k-l i=l к i=l
Для третьей нормы
||Л||з = Ух7. E1)
где Xj—наибольшее собственное значение матрицы А'А. Покажем
это. Пусть ||л;[|з= I. Имеем:
|[Л*||! = (Л*, Ах) = (х, А'Ах). E2)
А1 А является симметрической неотрицательной матрицей. (Это
значит, что для любого х скалярное произведение (Ах, х) ~^> 0.
Известно, что все собственные значения такой матрицы, т. е. такие
значения X, для которых существуют ненулевые х со свойством
Ах = \х, — действительные неотрицательные числах)-) Пусть
\~^\~^- ' • ¦ ~^\i~^- 0 — собственные значения этой матрицы,
а л;(Г), л;'31 л;'™) — соответствующие им ортонормированные
действительные собственные векторы. При этом
х = с^х^ -\- сгх^ -|- ...-+- спл;(п1, E3)
где с3 + с\ -)-...+ с? = 1 и
= >-А + V? + • • • + V^ < ^- E4)
Для х=хМ будем иметь:
|| >1jcA> Ц1 = (jc , A'AxW) = (jcW. Х1д;'11) = Х1. E5)
Таким образом, утверждение доказано.
3. Сходимость последовательностей матриц и матричных
рядов. Перейдем теперь к вопросу о сходимости последователь-
последовательности матриц. Будем говорить, что последовательность матриц
Аи Аг Ат, ... сходится к матрице А, если для всех /, k
имеем а^->ай. Это равносильно условию \\Ап — Л||->¦<). Из этого
определения следует, что если Ат—>-А и Вт—> В, то
Ат-\-Вт^А + В, E6)
АтВт-*АВ. E7)
!) См. И. М. Г е л ь ф а н д, Лекции по линейной алгебре, гл. II.

52
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Далее, если Т— некоторая неособенная постоянная матрица и
Ат^-А, то
Т~гАТ.
E8)
Рассмотрим степенной ряд
Ему можно поставить в соответствие матричный ряд
+ . . . F0)
Этот ряд будет называться сходящимся, если сходится последова-
последовательность его частичных сумм fm(Л) = а0/-f-atA-f-<x2A2-\- ...
. . . -\-amAm. Найдем условия сходимости такого ряда. Имеет место
теорема:
Для того чтобы степенной матричный ряд F0) сходился,
необходимо и достаточно, чтобы все собственные значения Х{
матрицы А лежала внутри круга сходимости степенного
ряда E9).
Доказательство. Приведем матрицу Л к нормальной
форме Жордана при помощи некоторой неособенной матрицы Т:
Т~1АТ = В. Тогда
T-1fm(A)T = fm(T-1AT) = fm(B). F1)
Для того чтобы fm(A) имела предел, необходимо и достаточно,
чтобы fm(B) имело предел. Предел fm(B) будет существовать
тогда и только тогда, когда существуют все lim fm(Bi), где Вг —
m ->oo
«ящики» матрицы В. Пусть Вг соответствует элементарному делителю
(X — Xj)"*. Тогда
F2)
0
0
h
0
h
0
1
0
1
0
0
1
:::
...
... 0
... 0
0
0
h
Он
h 1
0 X,
строк),
0 ... 0
1 ... 0
0 0 0 ... Xj J 0 0 0 ... Хг
2Xj 1 0 ... 0
Л,- ZK; 1 ... У)
F3)
,0 0 0 0 ... X2

§ 7] ЛИНЕЙНЫЕ ОПЕРАТОРЫ. НОРМЫ ОПЕРАТОРОВ
По индукции нетрудно доказать, что при т > и*.
53
Отсюда
fm
1
0
0
(к)
)
0
<
ч
0
fmik)
0
1
2
С
С
S
Л*
0
0
i)
от
• С"
•
1
(ж-
1
(«г-
2
1)
2)
^m-n.+2
и
| m
0
F4)
F5)
Для того чтобы /т(В() была сходящейся последовательностью, не-
необходимо и достаточно, чтобы /т(Хг), /'т0ч) . . . /^-1)(Х^) были
сходящимися последовательностями. Последнее будет выполнено
в том и только в том случае, если Х^ лежат внутри круга сходи-
сходимости ряда /(X).
Возьмем, в частности, ряд
Его радиус сходимости равен 1, и ряд расходится в каждой точке
границы круга сходимости. Следовательно, имеет место теорема.
Для того чтобы сходился матричный ряд
необходимо и достаточно, чтобы собственные значения ма-
матрицы А были по модулю меньше единицы.
Сделаем еще одно небольшое замечание. Пусть X — произвольное
собственное значение матрицы Л. Тогда имеется ненулевой вектор х
такой, что
Следовательно,
Ах = \х.
||Ак||=|Х||И
F8)
F9)
Но ||Лл;|К||Л|| ||.х||. Поэтому получаем ||Л||^.|Х|, т. е. любая
норма матрицы больше или равна модулю произвольного соб-
собственного значения матрицы, т. е.

54 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
§ 8. Разновидности методов последовательных приближений
В методах последовательных приближений решения системы
Ах=Ь исходят из произвольного начального вектора д;0 и получают
векторы xv х2 хк по рекуррентной формуле
Xk+i = Fk(x0, xu .... хк), A)
где Fk — некоторая функция, зависящая, вообще говоря, от матрицы
системы А, правой части Ь, номера приближения k и предыдущих
приближений лг0, х1 хк. Будем говорить, что метод имеет
первый порядок, если Fk зависит только от хк и не зависит от д;0,
xl хк_1. Будем называть метод стационарным, если Fk не
зависит от к.
Простейшим случаем функций Fk будут линейные функции.
Наиболее общий линейный метод последовательных приближений
первого порядка должен иметь вил
B)
где Вк — квадратная матрица и ск — вектор. Естественно требовать
от методов последовательных приближений, что при подстановке
в правую часть A) и B) вместо хк точного решения системы A~lb
мы слева снова получили A~lb. В случае линейного метода первого
порядка это приведет к равенству
А~1Ь = ВкА-1Ь+!к C)
или
'ск = A—Вк)А-1Ь=^Сф. D)
В этом случае мы можем переписать B) в виде
хк+1 = ВкХк + СкЬ, E)
причем Вк и Ск — квадратные матрицы, не зависящие от b и такие,
что
Вк + СкА = 1. F)
Выражение E) можно также записать в виде
= хк — ск (А*к — Ь). G)
Наконец, если существует матрица Ск1, то выражение E) можно
записать в виде _
Ал+1+?;Л = ?. (8)
При этом должно быть
D + EA. (9)

§ 8] РАЗНОВИДНОСТИ МЕТОДОВ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 55
При пользовании формулой (8) мы получим хк+1 в неявной форме.
Поэтому желательно, чтобы матрицу Dk было легко обратить. На
практике обычно берут Dk диагональной или треугольной. В первом
случае метод называют полношаговым, во втором — одношаговым.
Разнообразные схемы, осуществляющие линейные методы после-
последовательных приближений первого порядка, можно считать реализа-
реализацией формул E), G) или (8).
Много линейных и нелинейных методов последовательных при-
приближений можно получить, используя способ наименьших квадра-
квадратов. При этом минимизируется функция
f(x)=\\Ax-~b\\* A0)
или же f(x), сложенная с некоторой постоянной. Разным способам
минимизации и задания нормы будут соответствовать различные
методы решения систем уравнений. Как мы видели в § 5, в случае
симметрической положительно определенной матрицы А можно мини-
минимизировать функцию
/(*) = (*. Ах) — 2(Ь. х). A1)
Один из способов такой минимизации там был рассмотрен. Этот
способ можно обобщить. Выбираем какое-то направление, опреде-
определяемое вектором с. Так же как и в § 5, найдем, что f(x-\~ox) при-
принимает наименьшее значение при а = а*, где
(с, Ас)
Если возьмем вместо а* величину а = Cа*, то будем иметь:
/(*)—/(*+ ас) = Bаа* — а2) (с, А7) = р B — Р) а*2 (с, Ас). A3)
Таким образом, если (с, Ь— Ах) ф 0, то f(x) >/(jc + ac) при любом
Р @ < р < 2).
Идея многих способов минимизации f(x), а следовательно и
решения системы Ах = Ь, заключается в следующем. Задаются началь-
начальным приближением х0. Определяют закон выбора векторов ск (они
могут зависеть от хк). Определяют закон выбора коэффициентов рА
(они могут зависеть от хк). На каждом шаге в качестве последую-
последующего вектора рассматривают
a?cfc, A4)
где а* было определено выше.
Если А не является симметрической положительно определенной
матрицей, то можно вместо системы Ах = Ь рассматривать систему
A'RAx = A'Rb, где R—симметрическая положительно определенная

56 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
матрица. Часто в качестве R берут единичную матрицу /. Это,
конечно, не означает, что во всех случаях придется делать предва-
предварительное преобразование системы. Бывает достаточно использовать
преобразованную систему лишь для построения алгоритма.
§ 9. Линейные полношаговые методы первого порядка
1. Сходимость линейных полношаговых методов первого
порядка. Простая итерация. Линейные полношаговые методы пер-
первого порядка определяются формулами E) и G) предыдущего пара-
параграфа. Исследуем сначала сходимость этих методов. Из формулы E)
следует:
xk+l—A-lb = Bk(xk — A-ib). (О
Применяя формулу A) при fe = 0, 1, ..., т, получим:
xm+l — A-lb=BmBm_l...BlB0(x0 — A-1b). B)
Следовательно,
\\хт+1-А-1Ь\Ш\Вт\\ \\Вт_,\\... ||/у ||Во|| \\хо-А~1Ц. C)
Если ||BTO|j||Bm_1||...||B1||||B0|| стремится к нулю при m-^co.jro
|l*m+i — ^-1^|| стремится к нулю при любом начальном векторе лг0.
Как мы видели в § 7, из этого будет следовать, что все компо-
компоненты хт+1 будут стремиться к соответствующим компонентам А~ Ь.
Для того чтобы произведение норм матриц, стоящее в правой части C),
стремилось к нулю, достаточно потребовать
1|Я*11<Т< 1 (А = 0, 1, 2, ...). D)
В частности, если процесс стационарен, т. е. Вк не зависят от fe,
Вк = В; последнее условие означает, что какая-то из норм В меньше
единицы. ОДнако для стационарного случая можно дать более точ-
точные условия, а именно докажем теорему:
Стационарный линейный процесс
хк+1 = Вхк + СЬ E)
сходится при любом начальном векторе и любой правой части
тогда и только тогда, когда все собственные значения матрицы В
по модулю меньше единицы.
Действительно, легко проверить по индукции, что
^+i = sft+1^o+(sft+sft~1+ ••• +в+1)сЪ. F)
Очевидно, последовательность
{&-\-В*-1+ ...-4- B + l)Cb (fc = 0. 1. 2, ...) G)
будет сходящейся для произвольного вектора b в том и только в том
случае, если сходится матричный ряд

§ 9] ЛИНЕЙНЫЕ ПОЛНОШАГОВЫЕ МЕТОДЫ ПЕРВОГО ПОРЯДКА 57
Но при этом Bft+1->¦(). Следовательно, хк+1 образуют сходящуюся
последовательность при произвольных векторах д;0 и b в том и только
в том случае, когда сходится ряд (8). Как мы видели, ряд (8) схо-
сходится в том и только в том случае, если все собственные значения
матрицы В по модулю меньше единицы. Утверждение доказано.
Полученное нами условие хорошо при теоретических рассужде-
рассуждениях, так как точно отражает положение вещей. Однако оно неудобно
для практических применений, ибо в большинстве случаев собствен-
собственные значения нам неизвестны, а отыскание их представляет задачу
более сложную, чем решение системы линейных алгебраических
уравнений. В главе 8 мы дадим ряд способов оценки максимального
по модулю собственного значения. Пока же будем использовать
нормы матриц, данные в § 7, и неравенство max | \$ | ^||В||. При
этом получим следующие три достаточных условия:
2 |^-|<ц<1 (/=1, 2, ..., п), (9>
2 |*у|<|1.<1 (/=1, 2 д), A0>
2 &у<|*<1. (П)
Пояснений требует только последнее условие. Оно обеспечивает,
что норма ||В||з. равная наибольшему собственному значению Xj,
матрицы В'В, не превышает единицы. Действительно, все собствен-
собственные значения матрицы В'В неотрицательны. Поэтому Х1^Х1 + Х2 + ...
.. . +ХП. Но последняя сумма равна следу матрицы, который и равен
.2 *
Изложенный метод часто называют простой итерацией.
Для применения простой итерации необходимо предварительное
преобразование системы, заданной в виде Лл; = 6, к виду E). Это
можно сделать, например, так. Каждое из уравнений системы
.. -\-а{пхп = Ьг (i= 1. 2 п) A2)
делим на аи и переносим члены с хх, х2 *i-i. xi+l, ...,
в правую часть равенства. При этом /-е уравнение примет вид
Л< Лч * *
пц 1 ан 2
ai, i-i
Для того чтобы этот прием был осуществим, коэффициенты ац
должны быть отличны от Нуля. Кроме того, для обеспечения

58
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
сходимости требуется значительное преобладание диагональных элемен-
элементов над остальными коэффициентами. Так, неравенства (9)—A1)
будут выполнены, если для коэффициентов будут выполнены сле-
следующие неравенства:
2
aU
<1
(/=1, 2 n),
G=1, 2 n),
A4)
A5)
A6)
Приведем пример решения системы методом простой итерации.
Опять будем решать ту же систему, которую мы уже использовали
в § 2 и 3. В верхней части схемы стоят коэффициенты преобразо-
преобразованной системы. Далее идет начальное приближение, в качестве
которого взяты свободные члены преобразованной системы, и идут
последующие приближения:
х"»
~х^
*№
~ХЪ
х<8>
х™
х^
хМ
хг
0
— 0,025314
— 0,038103
— 0,015192
— 0,028541
— 0,051824
1,161765
1,011799
1,049027
1,038527
1,041622
1,040736
1,040994
1,040920
1,040915
1,040940
1,040936
1,040937
1,040936
х2
— 0,029409
0
— 0,025972
— 0,019487
— 0,028730
— 0,075376
1,147832
1,020120
1,058410
1,048077
1,051212
1,050327
1,050587
1,051413
1,050535
1,050534
1,050529
1,050530
1,050530
Ч
— 0,050810
— 0,029811
0
— 0,013034
— 0,047368
— 0,063370
1,129872
0,999199
1,034234
1,024356
1,027253
1,026420
1,026661
1,026592
1,026588
1,026610
1,026606
1,026607
1,026607
— 0,022890
— 0,025272
— 0,014727
0
— 0,059210
— 0,165638
0,570275
0,432689
0,484170
0,470754
0,474964
0,473804
0,474149
0,474051
0,474062
0,474078
0,474073
0,474074
0,474074
— 0,024524
— 0,021248
— 0,030521
— 0,033765
0
— 0,217801
0,777788
0,493906
0,598888
0,572321
0,580689
0,578438
0,579122
0,578931
0,578962
0,578986
0,578974
0,578976
0,578975
Ч
— 0,034634
— 0,043736
— 0,031758
— 0,073469
— 0,169430
0
0,770121
0,287933
0,398231
0,359803
0,369760
0,366660
0,367508
0,367254
0,367257
0,367315
0,367305
0,367309
0,367308

§ 9] ЛИНЕЙНЫЕ ПОЛНОШАГОВЫЕ МЕТОДЫ ПЕРВОГО ПОРЯДЯА 59
Следует отметить, что ошибки, допущенные при вычислении,
будут в дальнейшем исключены последующими приближениями.
Однако при этом могут потребоваться лишние приближения.
Оценим теперь погрешность метода простой итерации. Для этого
воспользуемся равенством
xk+l — A-1b=B(xk — A-lb). A7)
Так как
2 2 A8)
... -\-Вк~1)СЬ-\-Вкх0, A9)
то
~Z A~lf) —(Rle+i~L- Rft+2 _u \Ch _U Rk+i~v O(\\
Л"& + 1 ГЛ U \LJ | LJ —— . . . I U(/ —— LJ Лц. ^iuj
Отсюда
'И1К1|. B1)
2. Метод Ричардсона. Рассмотрим еще один метод последова-
последовательных приближений первого порядка. Возьмем в формуле G)
предыдущего параграфа —Cft = pft/. При этом получим:
**+1=** + Р*(Л** — Ь\ B2)
Проведем подробное исследование этого метода для случая, когда
матрица А симметрическая и положительно определенная. В этом
случае имеется п положительных собственных значений Х1^Х2^-...
...^.Хп матрицы Ann соответствующих им взаимно ортогональных
собственных векторов их, и2, .... ип. Разложим вектор д;0 — A~lb
по этим собственным векторам
_ п
х0— A~lb =2ci«i B3)
i=\
и преобразуем B2) к виду
-А-1Ь). B4)
Тогда
п
- A~lb) = 2 <Ч (
B5)
Хг—А~1Ь = (/+РИ) (*1-^й) = 2 С* A+РЛ) A+РЛ) "г.
г-1
п к

60 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Таким образом,
\ ft -f" I » ft 4-1 ** ^ )
где
Мк= max
0<i<n
1=0
B7)
Зафиксируем k и будем подбирать $j так, чтобы Мк приняло
возможно меньшее значение. При этом мы будем предполагать, что
нам каким-то образом удалось найти такие а и Ь, что
a<li<Cb (!=1, 2 п). B8)
Заменим отрезок [а, Ь] отрезком [—1, +1], введя новое перемен-
переменное
^P± B9)
b—a v '
7с
b—ab—a
При этом многочлен
nP^ C0)
./=0
перейдет в новый многочлен Q*:+i@- Так как Р/;+1@)=1,
то Qfc+i(-^?)= !• Таким образом, перед нами возникает задача
об отыскании многочлена степени fe + 1, равного 1 при t = —^-т-
и обладающего наименьшим максимумом модуля на отрезке [—1,+1]
среди всех многочленов, обладающих такими свойствами. Эту задачу
решает многочлен (см. упражнения к гл. 4)
CD
где Tk+1(t) — многочлен Чебышева, наименее уклоняющийся от нуля.
Корни многочлена Rk+l(t) совпадают с корнями Tk+l(t) и располо-
расположены в точках
Корни же многочлена Pk+i(fy расположены в точках — рг-1. Следова-
Следовательно,
^i=2[(a — b)ti — (a-\-b)\-1. C3)
При этом
W|/?0| [(^^)]~l<1- C4)
Если заранее не ясно, сколько шагов потребуется сделать для
получения нужной точности, то целесообразно использовать й^ в ци-

§ 10] ЛИНЕЙНЫЕ ОДНОШАГОВЫЕ МЕТОДЫ ПЕРВОГО ПОРЯДКА 61
клическом порядке. Задаемся каким-то k, подбираем соответствую-
соответствующие ^ по формуле C3) и производим вычисления по формуле B2),
беря р4 в следующем порядке: ро, pt, ..., pft, po, p2 ръ ...
При k = 0 процесс будет стационарным, при k > 0 процесс будет
нестационарным. Он всегда будет сходящимся в силу неравенств B6)
и C4). Такой способ был впервые предложен Ричардсоном, и поэтому
мы назовем его методом Ричардсона.
3. Обращение матриц методом последовательных приближе-
приближений. Коснемся еще вопроса об обращении матриц методом после-
последовательных приближений. Пусть нам удалось каким-то способом
найти приближенное значение Во для матрицы Л. Предположим,
далее, что некоторая норма матрицы
С0 = 1—АВ0 C5)
меньше единицы, ||С0|| 4^.д <С 1- Образуем тогда последовательности:
, = 1-АВ2;
C6)
к)> °ft+i — ' /iDk+i>
при этом
= Ck-i=Ck-2= • ¦ • =Со • C7)
Таким образом, матрица Ск будет очень быстро стремиться к нуле-
нулевой и, следовательно, матрица Вк к Л. Оценим норму разности
\\Bh — A'l\\. Имеем:
\\Вк - А-1]] = || Л (/- Q - Л|| = НЛ-1^ =
^llBo^-Q-cflUiiBoii • \\(i-co)-l\\. ucof <1|воц T^L.
C8)
§ 10. Линейные одношаговые методы первого порядка
Перейдем теперь к изучению линейных одношаговых методов
первого порядка. Большое количество таких методов можно полу-
получить следующим образом. Представляем матрицу Л в виде суммы
ipex матриц:
A)
Здесь В — диагональная матрица, в матрице С равны нулю эле-
элементы, лежащие на и выше главной диагонали, а в матрице D равны

62
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
нулю элементы, лежащие на и под главной диагональю. Выбираем
какое-то число шф О и осуществляем итерационный процесс по
формуле
(о)-!5 -\-С) х<*+1) + [A — «)-1)] B-\-D\ xW = 6. B)
Если разрешить B) относительно xf+i\ то получим:
П-1 и "]
1ИХТ — *г — (м — О Xi '¦ C)
Особенно часто используется случай и>=1. При этом получается
так называемый метод Зейделя. Рассмотрим подробно этот метод.
1. Метод Зейделя. Метод Зейделя отличается от простой ите-
итерации тем, что, найдя какое-то приближение для компоненты, мы
сразу же используем его для отыскания следующей компоненты.
Вычисления ведутся по формуле
x(*+i)=_y^x(*+i)_ V ^1Х« + Д. D)
По начальному приближению (х(°), х|°) хЩ находим х^1'. Затем
по (xW, xfK ..., х*®\ находим х<Я и т. д. После того как будут
найдены все хС1', таким же образом находим xf\ xf\ ..., пока
не достигнем нужной точности.
Решим ту же систему, которая рассматривалась в предыдущем
параграфе, методом Зейделя. Мы не будем повторять запись коэф-
коэффициентов, а приведет лишь результаты вычислений:
?<р>
]?2)
F»
х^
1,161765
1,011799
1,049027
1,040158
1,040955
1,040950
1,040949
1,040937
1,040936
Хъ
1,147832
1,020123
1,057467
1,049654
1,050021
1,050047
1,050528
1,050530
1,050530
хя
1,129872
0,999199
1,031845
1,026331
0,026593
1,026618
1,026606
1,026607
1,026607
хА
0,970275
0,432689
0,482485
0,474084
0,474057
0,474079
0,474071
0,474074
0,474074
¦*&
0,777788
0,493906
0,591246
0,579940
0,579006
0,578982
0,578970
0,578975
0,578975
*в
0,770121
0,287933
0,361969
0,367221
0,367343
0,367341
0,367341
0,367308
0,367308
Заметим, что здесь, так же как и при простой итерации, можно
было бы сократить вычисления и записи. Прежде всего несколько

§ 10] ЛИНЕЙНЫЕ ОДНОШАГОВЫЕ МЕТОДЫ ПЕРВОГО ПОРЯДКА 63
первых приближений можно было проводить с меньшим количеством
знаков. Наоборот, в последних приближениях, когда старшие разряды
уже установились, нет необходимости выписывать их вновь. После-
Последовательные приближения продолжаются обычно до тех пор, пока
два следующих друг за другом приближения не станут совпадать.
2. Сходимость метода Зейделя. Исследуем теперь сходимость
метода Зейделя. Разрешая B) при со = 1 относительно х(к+1\ полу-
получим:
'Ъ. E)
Это означает, что метод Зейделя эквивалентен простой итерации
с матрицей — (B-\-C)~lD. Таким образом, чтобы метод сходился
необходимо и достаточно, чтобы все собственные значения этой
матрицы были по модулю меньше единицы. Таким образом, должны
быть по модулю меньше единицы все значения X, удовлетворяющие
уравнению
|^| 0. F)
Но корни этого уравнения будут совпадать с корнями уравнения
= 0. G)
Итак мы доказали теорему. Для сходимости метода Зейделя
необходимости достаточно, чтобы все корни уравнения
= 0 (8)
ann*-
были по модулю меньше единицы.
Области сходимости простой итерации и итерации по Зейделю
лишь пересекаются. Это значит, что существуют такие матрицы,
для которых метод Зейделя сходится, а метод простой итерации
нет, и наоборот. Нетрудно показать, что первое и второе достаточ-
достаточные условия (9) и A0) § 9 для сходимости метода простой итера-
итерации будут одновременно достаточными условиями и для сходимости
процесса Зейделя.
Иногда метод Зейделя дает более быструю сходимость, чем про-
простая итерация. Так будет, например, если выполнено условие A4)
предыдущего параграфа. Обозначим

64 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Так как условие A4) выполнено, то р. < 1. Обозначим также
Тогда простой итерации будет соответствовать вычислительная схема
4*+i)= |] CijxW+dt, A1)
5 методу Зейделя схема
4*+1> = 2 сч*(*+Ц + J+i c.^xf) + </,. A2)
По A1) и (9) разность между точным решением х и (Л —|— 1)-м при-
-ближением, пол}гченным простой итерацией, будет иметь оценку
A3)
то же время, если ввести обозначения
i-l п
ll ^- = р.', A4)
то для разности между точным решением х и (/г—1)-м приближе-
приближением, полученным по методу Зейделя, получим оценку
-и
И* —3*+1>|11<>'||* —Jc^Hi. A6)
Но
S |с«1 = Р< + Т<О<1 07)
0 i сюда
I* = max(?i + Ti)>maxr;^1- = |*'. A9)
что и требовалось доказать.
Теорема. Если матрица А симметрическая и положительно
.определенная, а приведение системы Ах = Ь к виду x = Cx-\-d
.осуществляется путем деления уравнений на диагональные эле-
элементы, и последующего перенесения всех членов кроме х,-, где
1 — номер уравнения, направо, то метод Зейдгля сходится.

§ Ю]
ЛИНЕЙНЫЕ ОДНОШАГОВЫЕ МЕТОДЫ ПЕРВОГО ПОРЯДКА
65
Проверим, что при выполнении наших условий все собственные
значения матрицы
— (B-f C)~lD= — (B-f С)'1 С'
B0)
по модулю меньше единицы. Пусть Х$ и Х^— два каких-то собствен-
собственных значения этой матрицы, а г; и z}-— соответствующие им соб-
собственные векторы. Тогда мы можем записать:
(B-f С)
Отсюда
B1)
B2)
Рассмотрим скалярные произведения (Сг$, Zj) и (C'zj, z{). Они бу-
будут представляться в виде
B3)
(C'zh Z,) = — hiBZi, ZJ — XilCZi, Zj), 1
(C'zj, zd = —lf (Bzj, ~zd - I,(Czj, z-). j
Используя свойства скалярного произведения, получим:
Z{) = (Zj, Bzi) = (BZ{, Zj).
Поэтому второе из равенств B3) можно переписать в виде
или
(Gar,, Zj) = — lj (Bzt. Zj) - \j (C'zit zf).
(Cz{. ~Zj) = —
B4)
B5)
B6)
Решая B6) и первое из равенств B3) относительно (Czt, Zj) и
(Czf, Zj), получим:
_ _ I, (Xi— 1) _
(Czt.Zj)= >Ki (Bz
i — w
= i-xx {BZi'Zj)-
B7)

66 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Тогда
B8)
Положив здесь i — j, найдем:
(Asit Ij) = '/jTj^l! (S*i. ~гЦ- B9)
Отсюда
^-- C0)
Так как А положительно определенная, то все ее диагональные
элементы положительны. Поэтому
ii) > 0. C1)
Заметим, что Х=1 не является собственным значением матрицы
— {В-\-С)~1С. Действительно, если бы существовал такой век-
вектор г, что
— (B + C)-iC'z = z, C2)
то мы имели бы
— С'7= (В + Cfz C3)
или
(B + C-f С)г = Аг=0, C4)
а это равенство возможно только при 2 = 0, так как существует
обратная матрица А~1.
Итак, из C0) следует, что
>0, C5)
и утверждение доказано.
Можно доказать также, что если матрица А симметрична и ее
диагональные элементы положительны, то положительная опреде-
определенность матрицы А необходима для сходимости метода Зейделя.
3. Релаксационный метод *). Метод Зейделя является разновид-
разновидностью метода наименьших квадратов. При этом в качестве векто-
векторов ск, о которых говорилось в § 8, берутся в циклическом по-
порядке единичные векторы, направленные по координатным осям.
*) См. обзорную статью М. В. Николаевой «О релаксационном методе
Саусвелла», Труды математического института им. Стеклова,т. XXVIII, 1949 г.

§ 11] МЕТОД СКОРЕЙШЕГО СПУСКА 67
Иногда бывает целесообразно для упрощения вычислений или
для улучшения сходимости изменить порядок уравнений в заданной
системе или же нумерацию неизвестных. Можно пойти и еще дальше,
а именно при каждом цикле процесса последовательных приближе-
приближений брать свой порядок. Так, например, поступают в релаксацион-
релаксационном методе. Выбирают начальное приближение (х®\ х<?\ ..., ^Л
Вычисляют так называемые невязки
\ = «rf+*»*?> + • • • + «iX0) - *,• C6)
Находится jcW, удовлетворяющее равенству
• • + «<»*Г = h, C7)
где I — номер уравнения с максимальной по модулю невязкой. Затем
подсчитываем невязки
Ь. = а^ + aflx$> +...+ а.пх(о) _ b. (j Ф 0 C8)
и подбираем xW, удовлетворяющее равенству
V^) + aH1) + V40)+ • • • 4- v40) = V C9)
где/ — номер уравнения с наибольшей по модулю невязкой. Так
продолжаем и дальше, пока не используем все п уравнений. При
этом будут найдены все х№. Тогда начинаем второй цикл, который
производится так же, как и первый, но вместо (х^\ xf\ .... х*М\
используется (х^\ х\р x»0" Повторение циклов продолжают
до тех пор, пока не достигнут требуемой точности. Иногда при вы-
выборе уравнения, из которого вычисляется «улучшенное» приближе-
приближение, руководствуются не принципом максимальной по модулю не-
невязки, а каким-либо другим. Бо всех случаях стараются брать урав-
уравнения в таком порядке, чтобы в кратчайший срок получить нужное
решение. Этот довольно-таки неопределенный принцип требует от
вычислителя навыка и искусства. Поэтому релаксационный метод
трудно осуществить на машинах.
Релаксационный метод является нестационарным.
§ 11. Метод скорейшего спуска
В качестве примера нелинейных методов рассмотрим в этом па-
параграфе метод скорейшего спуска, о котором уже говорилось в § 4.
В методе скорейшего спуска исходят из некоторого начального при-
приближения x@) = (xW, xf\ ..., хЩ и по нему находят следующее
приближение xW = (xW, xW хМ) по формуле
) = Г(°) -j- а0Я°), A)

68 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
где
?W = (rW, if) rW), B)
п
У г@) 2
Если матрица А не является симметрической и положительно
определенной, как это предполагалось при выводе формул C) и D),
то можно рассмотреть систему А'Ах = А'Ъ, матрица которой сим-
симметрична и положительно определена. В этом случае вместо фор-
формул C) и D) мы получим:
После того как будет найден вектор j^1), по нему находят век-
вектор х@> так же, как х^1' находилось по лс<°>. Процесс продолжают
до тех пор, пока не достигнут требуемой точности.
Мы не будем входить в подробности вычислительных схем для
метода скорейшего спуска, а рассмотрим вопросы сходимости. Огра-
Ограничимся случаем симметрической положительно определенной ма-
матрицы А. Обозначим собственные значения матрицы А через
и соответствующие им ортонормированные собственные векторы
через zu z2 zn. Тогда, если х — произвольный вектор
х = р,^ + p2J2 + .. . + pni"n> (8)
то будем иметь:
(Ах, х) = ^Х1 + ^Х2+ ... +0»^. (9)
Отсюда
Р^) = Хп^- *)<(АХ. Х)<

§ 11] МЕТОД СКОРЕЙШЕГО СПУСКА 69
Следовательно, для нашей матрицы всегда можно найти две такие
постоянные т > О и М > О, что
т (х, х) < (Ах, х)< М (х, х). A1)
Рассмотрим разность /(х^)— f(x^), где f(x) — функция, опре-
определенная формулой A) § 5. Простые вычисления дают
Я°>) = ~^'^ ¦ A2)
Для разности /(х(°>)—/(х*), где х*— точное решение системы, по-
получим:
— /(х*) = (х(°) — х*. А (х(°) — х*)) = (Л~'>), 7@)). A3)
Таким образом,
Разложим вектор г'0' по собственным векторам матрицы А:
7(°) = Т1г, + T2i2 + ... + Тягп. A5)
Тогда
7 ^ ^ Н- • • • + тАл. A6)
Ч A7)
Следовательно,
B0)
Деля каждую из скобок в знаменателе на скобку, стоящую в числи-
числителе, и обозначая
получим:
... + ьпхп) E,х-* + в^-* +... + 5пх-•)'
B2)

70 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
Докажем следующее неравенство: если 0</га<Х^^./ИB=1.
2, ..., я), то для любых действительных чисел 8^ 82, ..., 8n; Sj^.0;
п
2 h = 1 и Xj > 0 имеет место неравенство
il
/5Г <23)
Введем вместо Xj новые числа Xj, определяемые при помоши
равенства
\г = У~тМ)^. B4)
При этом
/S
а левая часть доказываемого неравенства примет такую же форму,
как и ранее:
% ?г 2 ЪК1 = 2 8А: 2 8ДГХ. B6)
t-l г=1 «-1 г=1
Применим к последнему выражению теорему о том, что среднее
геометрическое меньше или равно среднему арифметическому:
Функция
?(XO=X' + i B8)
при X' > 0 убываете интервале @,1), возрастает в интервале A, оо),
имеет наименьшее значение, равное 2, при Х'=1 и принимает наи-
наибольшее значение на отрезке l/ tj > у —\ при У=у ^
и X' = у — , равное
Заменяя в B7) каждое из выражений Xj-|—Т его наибольшим зна-
чением B9), получим:
iWiVTt
что и требовалось доказать.

§ 11] МЕТОД СКОРЕЙШЕГО СПУСКА 7)
Применяя доказанное неравенство к B2), найдем:
причем 0 < q ¦< 1. Отсюда
A - Я) I/ (*@)) — /(**)] = О — ?) С C2)
где через с обозначено выражение [/ (х^) — f(x*)\. Таким образом,
для любого k получаем:
c(l-q)\ C3)
Оценим теперь ||*(*)— х*||3. Имеем:
_ х*||\ = (х~т — х*. х(*> — х*)< ^ (Лх№) — *, х« — х*). C4)
Легко проверить, что
(AxW — I, x<fc)—~х*) = f(x№) — / (х*). C5)
Таким образом,
^^^ки^Т'(зб)
и мы доказали, что метод скорейшего спуска сходится со ско-
скоростью геометрической прогрессии к точному решению.
Можно усовершенствовать метод скорейшего спуска, осуществляя одно-
одновременно несколько шагов. Благодаря этому удается увеличить скорость
сходимости.
Одновременное осуществление р шагов по методу скорейшего спуска
эквивалентно вычислению л^*+1' по формуле
7<*+i) = J<*> + 2Мй)^<*>, C7)
i-o
где, как и ранее, № = Ь — Ах^к\ а коэффициенты а№ подбираются так,
чтобы f(x(-k+t>) приняла наименьшее возможное значение. Это требование
к ау> приводит к системе уравнении
\
141=0 (' = 0,1 р-\) C8)
daf)
*2 «Р> U*7<*\ л^+17<^) = (Л'7<4 7fc)) (г = о, 1, 2 р -1). C9)
3=0

72 решение систем линейных алгебраических уравнений [гл. 6
Исследуем сходимость этого метода. Подберем постоянные е< так, чтобы
многочлен
ч (к) = 1 -2 Hki+i D0)
»=о
имел наименьшее возможное значение максимума модуля на отрезке [т, М].
При к = 0 наш многочлен будет равен 1. Такое построение мы уже осуще-
осуществили в § 8 и видели там, что су (к) просто выражается через многочлены
Чебышева, наименее уклоняющиеся от нуля. При этом sup | у (к) | = Z<4
X?[m, М]
Следовательно, собственные значения матрицы
% D1)
i-0
которые равны 9 (kj) (kj—собственные значения матрицы А) также по
модулю меньше единицы. Поэтому мы можем решать систему
^ D2)
относительно у методом простой итерации:
ук +1) = -(*) + *2 ЧА1 (b - Ajk\ D3)
1=0
Так как простая итерация сходится, то система D2) имеет единственное
решение. Таким решением может быть только xh = A~lb. Обозначим
х\ D4)
В силу D3) имеем:
й(* + 1) = ВЙ«. D5)
Таким образом,
к\ ВпЩ = {АВЧ(к\ п<% D6)
Разложим вектор и^ по собственным ортонормированным векторам мат-
матрицы А: _ _ _
"(&) = 7^+7,7*+ ••• +Т»^». D7)
Тогда
i=l г=1
тглм
г-1 1=1
Итак,
(Аи* +", Ffc +1)) < Z.2 U^fc), «(fc)). D9)
Возьмем теперь в качестве у'&' вектор х^\ полученный по методу ско-
скорейшего спуска. Обозначим
х^> — 3f =u(i) (i = 0, 1, 2,...). E0)

УПРАЖНЕНИЯ
73
Так как
»<* +4 п
, то
E1)
E2)
E3)
Отсюда, как и ранее, получаем:
/ &к)) - f Oh < L2k [f 0F<°>) -/(**))• E4)
Постоянная L определится в силу равенства C4) в § 9 выражением
L==
\М+т f(M+m\*
LAI —/и К \A1-otJ
М+т /"/ Д1+ш\» ,1P-
^ — т + Г \М-т) 'J
E5)
На этом мы пока прервем изучение численных методов решения
систем линейных алгебраических уравнений. Вопросы, связанные
с погрешностями методов и ускорением сходимости удобнее рассма-
рассматривать после того, как будут известны способы отыскания соб-
собственных значений матриц. Поэтому мы вернемся к ним в главе 8.
УПРАЖНЕНИЯ
1. Решить всеми изложенными методами систему линейных алгебраи-
алгебраических уравнений:
2,1546*! -f 0,8431*2 -f 0,3146дг8 -j- 0,1615*4 = 3,1826,
2,8431*!+ 3,1415*2+ 0,6241*з + 0,2131*4 = 4,6123,
0,3146*! -j- 0,6241*2 + 4,8216*з + 0,8245*4 = 5,9681,
0,1615*14-0,2131*2+0,8245*3 4-6,4131*4 = 8,1418.
2. Показать, что если матрица А симметрическая и положительно опре-
определенная, то метод исключения Гаусса эквивалентен последовательной орто-
гонализации единичных координатных векторов в метрике А.
3. Показать, что компактная схема Гаусса применима в том случае,
если все определители
и аи а18
i (ha «23
отличны от нуля.
4. Показать, что если в методе сопряженных градиентов для положи-
положительно определенной матрицы А все векторы И0', г11' /Л"-1'
нуля, то определитель матрицы А равен
отличны
det А =

74
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ [ГЛ. 6
5. Пусть для решения системы Ах = b используется итерационная
формула
где D — некоторая неособенная матрица. Доказать, что метод сходится для
любого начального вектора х@\ если все характеристические корни
матрицы DA расположены внутри круга с центром в точке X = —1 и ра-
радиуса 1.
6. Доказать, что если DA предыдущей задачи есть сА, где с — отри-
отрицательная постоянная, удовлетворяющая одному из условий
или
max
И<
п р
аы | + max V I аЫ — а«с I
» fc=i J
max |
i
то метод последовательных приближений сходится.
7. Доказать, что метод последовательных приближений, приведенный
п упражнении 5, сходится для всех симметрических положительно или от-
отрицательно определенных матриц А, если взять D,= с/, где
\с\< J
max У I
и с<С0 для положительно определенных i ис>0 для отрицательно опре-
определенных А.
8. Пусть для решения системы Ах = b используется итерационная
формула *
]?*+Ч = в-1 [ 1 - А
где В — некоторая неособенная матрица. Доказать, что этот способ схо-
сходится и дает решение исходной системы, если максимальное собственное
значение матрицы С С, где С = АВ меньше, чем минимальное собственное
значение матрицы В'В.
ЛИТЕРАТУРА
Вычислительные методы линейной алгебры, Гос-
Функциональный анализ и прикладная матема-
1. В. Н. Ф ад д ее в а,
техиздат, 1950.
2. Л. В. Канторович,
тика, УМН, т. 3, вып. 6, 1948.
3. Л. Ф о к с, X. Д. X а с к и, Дж. X. Вилкинсон, Заметки о решении
систем совместных линейных уравнений, УМН, т. 5, вып, 3, 1950.
4. М. Ш. Бирман, Некоторые оценки для метода наискорейшего спуска,
УМН, т. 5, вып. 3, 1950.
5. М. Р. Шура-Бура, Оценка ошибок при численном обращении матриц
высокого порядка, УМН, т. 6, вып. 4, 1951.

ЛИТЕРАТУРА 75
6. А. Т ю р и н г, Ошибки округления в матричных процессах, УМН, т. 6,
вып. 1, 1951.
7. М. А. Красносельский, С. Г. Крейн, Замечание о распределении
ошибок при решении систем линейных уравнений при помощи итера-
итерационного процесса, УМН, т. 7, вып. 4, 1952.
8. Л. В. Канторович, Приближенное решение функциональных уравне-
уравнений, УМН, т. 11, вып. 6, 1956.
9. К е р т и с с, Методы «Монте-Карло» для итерации линейных операторов,
УМН, т. 12, вып. 5, 1957.
10. G. F о г s у t h е, Решение линейных алгебраических уравнений может быть
интересным, Bull. amer. Math, Soc., т. 59, № 64, 1953. (Приведена об-
обширная библиография различных методов решения систем линейных
алгебраических уравнений.)
11. Хаусхолдер, Основы численного анализа, ИЛ, 1956.
12. Милн, Численный анализ, ИЛ, 1951.

ГЛАВА 7
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ
И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
§ 1. Введение
В этой главе мы рассмотрим некоторые методы численного
решения уравнений вида
/( = О,
где f (z)— заданная функция действительного или комплексного
аргумента z; в частности, f(z) может быть многочленом степени п от z.
При отыскании приближенных значений корней этого уравнения
приходится решать две .адачи:
1) отделение корней, т. е. отыскание достаточно малых обла-
областей, в каждой из которых заключен один и только.один корень
уравнения;
2) вычисление корней с заданной точностью.
Так как для алгебраических уравнений разработано больше
методов отделения корней и методов их вычисления, то мы в даль-
дальнейшем будем более подробно осинавливаться на алгебраических
уравнениях.
§ 2. Отделение корней
1. Общие замечания. При решении уравнения f(z) — 0 прежде
всего важно предварительно изучить расположение корней в ком-
комплексной плоскости z и заключить каждый корень в достаточно
малую область, внутри которой не было бы других корней. Для
этой цели иногда выгодно применять графические методы.
Если требуется найти только действительные корни уравнения,
то для отыскания грубых значений корней можно построить график
функции y = f(x) и найти абсциссы точек пересечения графика
с осью х (рис. 2).
Иногда удобней представить сначала уравнение в виде

§ 2]
ОТДЕЛЕНИЕ КОРНЕЙ
77
и затем, построив графики функций _у=ср(х) и y = ty(x), найти
абсциссы их точек пересечения, которые и будут приближенными
значениями корней. Например, если нужно найти корни уравнения
х sin х = 1,
то удобно представить его
в виде
1
sin х = —
О
и применить указанный спо-
способ (рис. 3).
Корни уравнения сим-
симметричны относительно х = Рис. 2.
= 0. Поэтому мы можем
рассматривать только положительные корни. Значения xv x2 и,
возможно, еще нескольких корней можно довольно точно опре-
определить графически. Однако на графике не будет хп для больших
значений п. Тем не менее по ходу графиков мы можем сказать, что
значения хп при больших п будут близки к тся. Эти значения можно
Рис. 3.
уточнить. Положим хп — тся -\- е„, где е„ — некоторые небольшие
добавки. Тогда
1
— sin (ял + sj =
ТСЛ-f- S»
В силу малости е„ можно положить sin е„
Это дает
-(— l)"sinsn=O.
1
и мы получили улучшенные значения корней
" ' тел

78 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Если требуется, то можно продолжить уточнение корней, положив
е' .
»
" ' тел ' »
Это дает уравнение для определения е^:
Но
'~™~ 7СЗЛ8 '
1 \П -iq
7СЛ J
Таким образом,
~6~J
6
При желании такой процесс можно продолжить.
Для отыскания комплексных корней уравнения /(z)=0 можно,
положив z— х-\-1у, представить уравнение в виде
где ср (л:, _у) и ф(х, _у) — действительные функции действительных
переменных х и у. Это уравнение эквивалентно системе двух урав-
уравнений:
tp(jc, jO = 0. ф(*. J0 = 0.
Построив кривые tp(x, j)^0 и ф(х, _у) = 0, мы получим действи-
действительные и мнимые части корней уравнения f(z) = 0 как соответ-
соответственно абсциссы и ординаты их точек пересечения.
Имеется много специально разработанных способов графического
решения уравнений, приспособленных для отдельных типов уравне-
уравнений. Большое значение имеют номографические методы решения
уравнений, но мы не будем останавливаться на этих методах.
Для выделения интервалов, в которых находятся действитель-
действительные корни уравнения /(х) —0, если f(x) — непрерывная функция,
можно воспользоваться следующими предложениями:
Если на концах некоторого отрезка непрерывная функция
принимает значения разных знаков, то на этом отрезке урав-
уравнение /(х) = 0 имеет хотя бы один корень.

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 79
Если при этом/(х) имеет первую производную, не меняющую
знака, то корень единственный.
Пусть f(x) есть аналитическая функция переменного х на
отрезке [а, Ь); если на концах отрезка [а, Ь) она принимает
значения разных знаков, то между а и Ь имеется нечетное
число корней уравнения f(x) = 0; если же на концах отрезка [а, Ь\
она принимает значения одинаковых знаков, то между а и Ь
или нет корней этого уравнения, или их имеется четное число
{учитывая и кратность корней).
2. Границы расположения корней алгебраического уравне-
уравнения. Для алгебраического уравнения
n= 0 A)
задача отделения корней решается более просто и точно. Прежде
чем отделять корни уравнения, естественно найти границы области,
в которой расположены все корни уравнения, поэтому мы сначала
приведем ряд способов отыскания этих границ.
Пусть
а = max {| ах|, |а2| |а„|}, а а' = тах{|ао|, |ах| |on-i|}.
Теорема 1. Все корни уравнения A) расположены в кольце
Доказательство. Действительно,
|/(z)|>||aozn| —
но при \z\ > 1 имеем:
__1*Г-1
— и
\г\ — 1 ^ \z\-\ ¦
Следовательно, |/(г:)|>0, как только
K"l JfL^° или KIM-
|Jf-L
j—г
т. е. при |z|^.14-j—г. Таким образом, все корни уравнения
находятся внутри круга радиуса l+
i—г-
Далее, уравнение
•• +««^" = 0 C)
имеет корнями величины, обратные корням исходного уравнения.
По доказанному все корни этого уравнения находятся внутри круга

80 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
радиуса 1-\--, г, т. е. для любого корня zt исходного уравнения
I ап I
имеет место неравенство
Объединяя результаты, получим неравенство B).
Предположим, что все коэффициенты уравнений действительные
числа и а0 > 0. Найдем границы действительных корней уравнения.
Очевидно, достаточно иметь способы определения границ положи-
положительных корней, так как, заменяя х на —х, мы получим уравне-
уравнение, корни которого отличаются от корней исходного уравнения
знаком.
Теорема 2. Обозначим через а максимум абсолютных ве-
вели шн отрицательных коэффициентов уравнения, и пусть пер-
первый отрицательный коэффициент в ряду а0, ах, .... ап есть ат.
т/~а~
Тогда все положительные корни уравнения меньше 1 -+-1/ — .
(Если отрицательных коэффициентов нет, то нет и положительных
корней.)
Доказательство. Заменим положительные коэффициенты
а,, а2 а»п-1 нулями, а все остальные коэффициенты на —а.
Тогда при х > 1 будем иметь:
jc»m+l_l xn-m+l
= аох" — а —-—= > аох" — а -
X— 1
rn—m+\
- О —а}.
Отсюда при х^1-\-Л/ — имеем неравенство /(х)>0, так как
)
-) —а>0,
т /~~сГ
а это и означает, что все положительные корни меньше 1 -)-1/ — .
С помощью теоремы 2 можно найти границы действительных
корней очень грубо. Иногда эти границы можно сузить, применив
следующий простой прием.
Пусть в уравнении коэффициенты а0, а, «m-i неотрица-
неотрицательны, а ат, am+i, ..., ап неположительны и ат<^0. Введем
обозначения:
аохп 4- ахл:"'-!- .. . + am_1xn~m+1 = tp (x).

§ 21 ОТДЕЛЕНИЕ КОРНЕЙ 8.1
Тогда
Первое слагаемое в скобках содержит только положительные сте-
степени х, а второе только отрицательные. Следовательно, при х > О
первое слагаемое возрастает, а второе убывает с возрастанием х,
т. е. при х > 0 функция/(х) возрастает вместе с х. Найдя какое-либо
х=а.^> 0, для которого /(а) > 0, мы можем гарантировать, что все
корни уравнения меньше а.
В общем случае представим /(х) в виде
где F (х) есть многочлен, содержащий все первые старшие по сте-
степени члены многочлена /(х), имеющие положительные коэффициенты
и все члены с отрицательными коэффициентами, а Ф (х) — много-
многочлен, образованный всеми остальными членами исходного много-
многочлена /(х). Тогда, если мы найдем х = а > 0, для которого F (а) > О,
то /(х) > 0 при всех х^-а, так как Ф(х)^0 при х>0 и все
корни уравнения /(х) = 0 будут меньше а.
Хороший способ отыскания верхней границы положительных
корней указал Ньютон. Этот способ основан на утверждении: если
при х = а > 0 имеют место неравенства
/(а) > 0, /' (а) > 0 /W (а) > 0, D)
ото уравнение /(х) = 0 не имеет корней, больших а.
Действительно,
при всех х > а.
Таким образом, способ Ньютона заключается в отыскании зна-
значения а > 0, при котором многочлен /(х) и все его производные
имеют положительное значение. Тогда это значение будет верхней
границей положительных корней.
Замечание. Нижняя граница положительных корней может
быть найдена из уравнения ао-\-а{у-\- ... -\-апуп = Ь такими же
приемами, так как если C есть верхняя граница положительных
корней этого уравнения, то -^ будет нижней границей положитель-
положительных корней исходного уравнения.
Пример. Найти границы действительных корней уравнения
х* — 35х3 -4- 380х2 — 1350х ¦+¦ 1000 = 0.
1-й способ (использование теоремы 2). В данном случае
а =1350, до=1. т=\.

82 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Следовательно, все положительные корни уравнения меньше
1+
Для отыскания нижней границы положительных корней уравнения
рассмотрим уравнение
1 — 35у -j— 380/ — 1350/ + 1000/ = 0.
Так как #о= 1000, а'=1350, т=\, то верхняя граница поло-
положительных корней этого уравнения будет:
1000 _ 2350
"г" 350 ~~ 1350 '
а следовательно, нижняя граница корней исходного уравнения
1350
2350
:0,57.
Итак, все положительные корни уравнения находятся на отрезке
[0,57; 1351].
Для отыскания границ отрицательных корней рассмотрим урав-
уравнение
Zi _|_ 3523 -4- 38022 -)- 13502 ¦+¦ 1000 = 0,
получающееся заменой х на — z. Это уравнение, очевидно, не
имеет положительных корней, а следовательно, исходное уравнение
не имеет отрицательных корней.
2-й способ. Представим
/(х) = х4— 35х3+380х2 — 1350х-(- 1000
в виде
где
F (х) = х* — 35х3 — 1350х, Ф (х) = 380х2 ¦+¦ 1000.
При х = 40 FD0) = 404 — 35- 403 — 1350 • 40 = 266 000 > 0.
Поэтому все корни уравнения меньше 40.
Для отыскания нижней границы снова заменим х на —. Получим:
/t (у) = 1000/ — 1350/ -4- 380/ —35y+l=F1 (у) + Ф1 {у),
где
F1 (у) = 1000/ — 1350/ — 35^, Ф, (у) = 380/ -4- 1.
Fx(l, 5) = 353,75 > 0. Таким образом, положительные корни урав-
уравнения /!(_у) = 0 меньше 1,5, а положительные корни исходного

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 83
уравнения больше у-г-?»0,66. Следовательно, корни уравнения
/(х) = 0 расположены на отрезке [0,66; 40]. Мы получили значи-
значительно лучший результат, чем в первом способе.
Способом Ньютона можно показать, что корни уравнения рас-
расположены на отрезке [0,74; 22], т. е. удается еще улучшить ре-
результат.
3. Число действительных корней алгебраического урав-
уравнения. Оценку числа действительных корней алгебраического урав-
уравнения можно получить с помощью известного правила Декарта.
Это правило мы получим как следствие более общей теоремы, ко-
которую назовем обобщенным правилом Декарта. Эта теорема по-
позволяет находить числа действительных корней обобщенных много-
многочленов. Прежде чем ее формулировать, введем некоторые опреде-
определения.
Пусть дана конечная последовательность действительных чисел
а0, аи а2 ап.
Будем называть индекс т местом перемены знака, если ат_кат < 0
и ат_1 = ат_2= .. . =ат_ки= 0. В этом случае говорят, что
ат-к и ат образуют перемену знака.
Очевидны или легко доказываются следующие утверждения:
1) число перемен знака в последовательности не изменится, если
члены, равные нулю, будут опущены, а оставшиеся члены сохра-
сохранят свое расположение;
2) число перемен знака в последовательности не изменится,
если вставить любое число членов, равных нулю, или рядом с чле-
членом последовательности вставить новый член того же знака;
3) при вычеркивании членов последовательности число перемен
знака не увеличивается;
4) если aj и ak (j < k) не равны нулю, то в последовательности
aj, aj+1 #fc_i, ак будет четное или нечетное число перемен
знака, смотря по тому, будут ли aj и ак иметь одинаковые или
разные знаки;
5) пусть т — место перемены знака в последовательности
а0, ах, .... ат ап.
Тогда число перемен знака в этой последовательности на единицу
больше числа перемен знака в последовательности
— а0, —аи .... — ат_1, ат+1, .... ап.
Пусть cpi(x), ср2 (х) ?п(х)—последовательность функций,
непрерывных вместе со своими производными до порядка п—1

84 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
включительно на отрезке [а, Ь\. Рассмотрим определитель Врон-
Вронского
Имеют место следующие свойства этого определителя:
1) W [/ср,. /ср2 /ср„] = [/ (X)f Г [?1, ср2 ср„]. F)
В самом деле, вторая строка определителя W [/<Pi, /<Рг
имеет вид
Если из нее вычесть первую строку, умноженную на /'//, то она
превратится в
к к к-
Третья строка имеет вид
/ч?+2/'ср; +/"?!, /с?: + 2/'сра'+/"ср2 /с?;;+2/>;+/*?„.
Если из нее вычесть первую, умноженную на /"//, и преобразован-
преобразованную вторую, умноженную на 2/'//, то получим:
М- К К-
Продолжая процесс дальше и вынося затем из каждой строки /,
получим требуемый результат.
2) W4<Pi(/W), «P2
3 н^ (Tl су). ср2 (у) ср„ (jf)]y.ne) (/' (х) ^= о). G)
В самом деле, вторая строка определителя слева имеет вид
а третья строка
Вычтем из нее вторую, умноженную на /"//'. В результате получим:
Аналогично после вычитания из четвертой строки второй, умножен-
умноженной на /'"//', и преобразованной третьей, умноженной на 3/"//',
получим:
т f/З /и ,3 „, f,3

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 85
Продолжая упрощения далее и вынося за знак определителя /',
/'3 /'"~\ получим требуемый результат.
Теорема {Обобщенное правило Декарта). Если на отрезке
[а, Ь\ функции срх (jc), <p2(x) <?п(х) непрерывны вместе с про-
производными до порядка [п—1) включительно и для любой после-
последовательности kt (I ^ kx < k2 < ... <.km^ri)
Пъ-ъ. \J>°-
на [a, b], то число нулей комбинации
(X) + «2?2 (X
с действительными коэффициентами а-г (не равными одновре-
одновременно нулю) на отрезке [а, Ь\ не превышает числа перемен знака
в последовательности аи а2 ап.
Доказательство. При п=\ утверждение тривиально, так
как по условию теоремы все функции ср4 (х) не обращаются на [а, Ь\
в нуль и имеют одинаковый знак. Предположим, что утверждение
справедливо при «<./—1, и докажем, что оно останется спра-
справедливым при переходе к п=1. Пусть
/ г
ф (х) = al(pi (х) + а2ср2 (х) -f • • • + «гТг (*) ( 2 а? Ф
\i l
и р — число нулей функции Ф(х) на [a, b\, a q — число перемен
знака в последовательности аи а2 аь. Если ^ = 0, то, оче-
очевидно, и /7=0, и утверждение верно. Пусть <? > 0 и одна из пе-
перемен происходит на /-м месте. Введем обозначения:
d Ф(х) d чЛх)
и^ = ф*^' 1п-ш = -ч)Ю С/=1.2 /-1),
ТХ^Г)Ъ С/ = /+1 0.
Тогда
Ф (х)
Так как —|—^- на [а, Ь] имеет р нулей, то число нулей р* функ-
функции Ф*(х) по теореме Ролля не может быть меньше р—1, т. е.
р*^-р— 1. С другой стороны, число перемен знака q* в последо-
последовательности
— av — а2, .... — fl{_i, flj+i. .-., аг

86 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
равно G* = <7—1. Так как
wIv ?», ?»/ ?*• %+1 ?»,] =
«Pi
то определители Вронского для системы ср*. <р* ер* f, ср,Р+1. •••
..., ср* обладают тем же свойством, т. е. будут все положительны.
Таким образом, в силу предположения q*^>p*, т. е.
В качестве примера рассмотрим совокупность функций
где Х4—действительные числа и X, < Х2 < ... < Х„. В этом случае
при всех v
1 1 ... 1
X, Хр .. . X.,
ч'ч---'ч
Следовательно, линейная комбинация
ахе\х _|_a2gM; -)-... -\-апе пХ
с не равными одновременно нулю коэффициентами а; не может
иметь нулей больше числа перемен знака в последовательности
а-ъ а2 ап.
Используя свойство B) определителей Вронского и полагая
У = 1пх, получим:
— х w \е , ..., е \у
Таким образом, при х>0
W[xK, Xх», . .., хч]>0.
Следовательно, число положительных корней уравнения
ajXx' -\-a2xl* -\- . . . -\-апх'п =¦ О,

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 87
п
где а-ъ — действительные числа, У^ а] Ф О,ХХ < Х2 < .. . < Хп не прево-
i = l
сходит числа перемен знака в последовательности аи а2 ап.
В частности, правило Декарта имеет место для алгебраических
уравнений
с действительными коэффициентами.
При х —> оо многочлен имеет знак, совпадающий со знаком а0,
а при х = 0—знак, совпадающий со знаком ап. Следовательно,
многочлен имеет четное число положительных корней, если знаки
а0 и ап совпадают, и нечетное число корней, если а0 и ап разных
знаков. Но то же самое можно сказать и о числе перемен знака
в последовательности а0, at an. Таким образом, разность
между числом перемен знака в последовательности а0, а1г . . ., ап
и числом положительных корней есть число четное или
нуль.
Правило Декарта не дает точного числа корней на отрезке [а, Ь],
а лишь устанавливает их верхнюю границу, но зато оно очень
просто, особенно в применении к обычным многочленам. Замена х
на —х позволяет получить также и верхнюю границу числа отри-
отрицательных корней уравнения.
Точное число действительных корней алгебраического уравне-
уравнения, заключенных в данных пределах, может быть определено
с помощью теоремы Штурма.
Теорема Штурма. Пусть дано алгебраическое уравнение
/(х) = 0 степени п, не имеющее кратных корней; найдем произ-
производную f'(x) = f1(x) и обозначим остаток от деления /(х)
на /' (х), взятый с обратным знаком, через /2 (х); остаток от
деления /i(x) на /2(х) с обратным знаком — через Д(х) и т. д.,
до тех пор пока не придем к постоянной. Получим последо-
последовательность функций
/(х), Д(х) /„(*).
Число действительных корней уравнения /(х) = 0, расположен-
расположенных на отрезке [а, Ь\, равно разности между числом перемен
знака нашей последовательности функций при х = а и числом
перемен знака последовательности при х = Ь. (Доказательство
теоремы можно найти, например, в книге А. Г. Куроша «Курс
высшей алгебры».)
К теореме Штурма можно сделать следующие замечания:
1. Функции /(х), fx{x), .... fn{x) можно умножать на положи-
положительные числа.
2. Последовательность функций можно оборвать на такой функ-
функции, которая не обращается в нуль на отрезке [а, Ь).

88 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
3. Если /(х) = 0 имеет кратные корни, то, как и прежде, можЯо
получив последовательность /, fu .... /г, 0; /г не будет постоян-
постоянным. Поделив все функции на /г, получим новую последователь-
последовательность. С помощью этой последовательности можно тем же способом
получить число корней уравнения /(х) = 0 на отрезке [а, Ь\, только
без учета их кратности.
4. Последовательность /, /х, /2 fn, которую мы образо-
образовали, может быть заменена любой другой последовательностью <р0,
'f! срг функций, лишь бы они удовлетворяли следующим усло-
условиям:
а) последняя функция срг на [а, Ь\ не меняет знака;
б) две рядом стоящие функции не могут обращаться в нуль при
сушом и том же значении х;
в) если в последовательности ср0, ср, срг какая-либо функ-
функция, за исключением первой, обращается в нуль при х = а, то две
соседние к ней функции в некоторой окрестности этого значения
имеют различные знаки;
г) отношение сро/^рх при переходе через нуль меняет знак с отри-
отрицательного на положительный.
Такая последовательность функций называется последователь-
последовательностью Штурма.
Теорема Штурма дает хороший в теоретическом отношении спо-
способ определения числа действительных корней, расположенных на
данном отрезке [а, Ь\, но при практическом применении требует
очень большой вычислительной работы. Менее совершенна в теоре-
теоретическом отношении, но более удобна для практики теорема
Бюдана:
Число действительных корней алгебраического уравнения
f(x) = Q степени п, расположенных на отрезке \а, Ь], не пре-
превышает числа потерянных перемен знака в последовательности
/(х), /'(х), .... /<»>(*)
при переходе от х = а к х = Ь, и разность между ними есть
число четное.
4. Отделение действительных корней алгебраического урав-
уравнения. Задача отделения действи1ельных корней уравнения /(х)= 0
заключается в том, чтобы каждый из корней заключить в интервал,
не содержащий других корней уравнения. Обычно для решения
этой задачи сначала находят нижнюю и верхнюю границы всех дей-
действительных корней уравнения, что может быть сделано одним из
тех способов, о которых мы говорили ранее. Затем полученный
отрезок разбивают на более мелкие, обычно равной длины, так,
чтобы в каждом из них не могло содержаться больше одного корня.
Для того чтобы определить длину этих частичных отрезков рас-

§ 2]
ОТДЕЛЕНИЕ КОРНЕЙ
89
смотрим определитель
1 1
... 1
„га—1 jn—\
... X,
.га-1
= Ц(Х{—х^'
(8)
»> 1
где xv x2 хп — корни данного уравнения. Введем обозначение
sk = Xi 4 x<i 4 - - - +4 (9)
и возведем D в квадрат, используя правило умножения определи-
определителей «строка на строку». Получим:
«2
sn—1
г > j
Зная величину D, можно оценить расстояние между корнями. Дей-
Действительно,
D
где штрих означает, что мы в правой части опускаем множитель
ха — JCp. Если М — верхняя граница модулей корней уравнения, то
"
и |ха-
. A1)
BAf)
Для отыскания D найдем D2. Пусть уравнение имеет вид
Тогда
С другой стороны,
Производя деление, получим;
или
... -f-

90 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Приравнивая коэффициенты при одинаковых степенях х, получим:
•?fc+aA-i+a2Sfc-2+ ... -irak_1s1-\-kak = 0 (k=l, 2, ...
(л— 1). «,) = »).
Для отыскания соответствующих выражений при k^-n умножим
наше уравнение на хт и в уравнении
положим последовательно x = xlt x2 хп. Складывая получен-
полученные результаты, найдем:
ransm = 0 (т = 0, 1, . .. ).
Эти формулы нам дают возможность последовательно найти
% sv s2 s>n-2> a тем самым и D2. Например, для кубичного
уравнения х3 -)-аххг -\-а2х -\-а3 = 0 будем иметь:
so=3,
51 + д1 = 0, sl = —a1,
s2 + aiSi + 2a2 = 0, s2 = fli — 2a2,
s3 -j- a^a -+- a2Si + 3a3 = 0, s3 = — a\
- a3S! = 0, s4 = a{ —
а\а
D2 = а\аг — \a\a3 — Aa\ — 27a\ -\- 18a{a2a3.
Обычно этот способ дает очень заниженные значения для inf | хг- — Xj\,
и нужна очень большая вычислительная работа для последующих
подстановок.
Рассмотрим метод Фурье отделения корней, основанный на
теореме Бюдана. Но прежде чем излагать сам способ, докажем не-
несколько вспомогательных утверждений.
1. Если уравнение /(х)=0 имеет на отрезке [a, b] k корней,
а при переходе от а к b в последовательности /(х), /' (х), ...
. . ., /<п'(х) теряется ft-j-2/ перемен знака, то уравнение имеет
еще по крайней мере 21 комплексных корней.
Действительно, пусть между —со и а имеется ki действитель-
действительных корней, а между йи -j-oo k2 действительных корней. По тео-
теореме Бюдана при переходе от —оо к а в последовательности
/(х), /' (х), .... /(">(*) теряется ^-+-2^ перемен знака, а при пере-
переходе от b к -|-оо теряется й2-)-2/2 перемен знака, где 1Х и /2 —
некоторые целые числа. Число перемен знака, теряющихся при пере-
переходе от —оо к -j-oo, равно п. Таким образом, п = kx-\-k2-\-k A-
-\- 214- 2/j -j- 2/2, а число комплексных корней s = n — k1 — k2 — k.
Следовательно,

§ 2]
ОТДЕЛЕНИЕ КОРНЕЙ
91
2. Если функция /(х) на отрезке [а, Ь] имеет две непрерыв-
непрерывные производные и /' (х) на этом отрезке не обращается в нуль,
то функция ср (х) = х ,, является возрастающей в 'тех
точках, где /(х) и f"(x) имеют одинаковый знак, и убывающей
в тех точках, где они имеют разные знаки.
Действительно,
Т W [f'WP ~ I/'WJ9"'
а это означает, что при /(х)/"(х)>0 функция ср(х) возрастает,
а при /(х)/'(х)<0 убывает.
Из второго утверждения можно получить два следствия.
Следствие 1. Если на отрезке [а, Ь\ уравнение f(x) — О
имеет два действительных корня, a f" (x) не обращается в нуль
на этом отрезке, то имеет место неравенство
Действительно, пусть а, р (а < Р)—корни уравнения /(х) = 0 на
отрезке [a, b\; f (х) имеет на отрезке [а, Ь\ только один корень.
Он расположен между х = а и х = р. Кривая y = f(x) на отрезке [а, Ь\
или выпукла или вогнута в зависимости от знака /"(х), поэтому
/(х) и f"(x) на отрезках [а, а] и [р, Ь\ имеют одинаковые знаки
(рис. 4 и 5). Следовательно, функция ср(х) = .
f (х)
на этих
f"{x)<0
Пх)*в
\а р/\
Рис. 4.
Рис. 5.
отрезках возрастает и ср(а) < ср (а), срф) < срF). Но ср(а) = а,
поэтому ср(а)<срф) и, тем более, ср(а)<срF), откуда и следует,
Следствие 2. Если на отрезке [а, Ь] уравнение f (х) = О
имеет один корень хх, а функции /(х), /" (х) не обращаются
в нуль и /(х)/"(х)>0 на [а, Ь] и имеет место неравенство
f(b) /(a)
- ¦ '¦ <^о — а, то его можно нарушить, увеличив а или
уменьшив b на соответствующую величину.
В самом деле, функция ср (х) возрастает при изменении х от а
до xt и при изменении х от хх до Ь, а функция ср(а)—ср(х) будет

92 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
убывать на \xv b\ от -j-co до ср(а)— ср ф), а функция ср(х) — ср ф)
будет возрастать от ср (а) — ср ф) до -\- go на [а, хх\. Если а' ? [а, хх]
и Ь' ? [Xj, 6] и близки к xv то ср(а) — срF')>0 иср(а')- срF)>0
и, таким образом,
Теперь можно изложить способ Фурье отделения действительных
корней алгебраического уравнения /(х) = 0 степени п.
Пусть нам дано уравнение /(х) = 0 степени п. Образуем после-
последовательность /(х), /' (х) /W(x). На отрезке [а, Ь\, на котором
могут быть действительные корни, возьмем ряд возрастающих чисел
a, alt а2, ..., ап, Ь. Если при переходе от а; к ai+1 наша после-
последовательность не теряет ни одной перемены знака, то уравнение не
будет иметь ни одного корня на отрезке [аг, а{+1]. Если теряется
только одна перемена знака, то имеется только один корень и он
уже отделен. При потере двух перемен знака могут быть два слу-
случая: 1) на [сц, оц+1] имеется два корня уравнения и 2) на [ait ai+1]
нет корней. В последнем случае уравнение /(х) = 0 имеет обяза-
обязательно пару комплексных корней. Если потеря перемен знака про-
происходит в первых трех функциях последовательности, то эти два
случая можно различить. В самом деле, /"(х) не имеет корня
в [a;, aju]. Поэтому, если окажется, что
то по следствию второго утверждения /(х) не может иметь двух
корней в [а;, а{+1], т. е. на отрезке нет ни одного корня. Если не-
неравенство не выполняется, то нужно на отрезке [a.t, aj+1] выбрать
точку р и проводить рассуждения с отрезками [а{, C] и [C, ai+1].
В общем случае, когда число потерянных перемен знака при
переходе от а; к ai+1 больше двух или равно двум, но потери
происходят не за счет первых трех функций, вопрос может бьпь
решен следующим образом. Обозначим через Дл число перемен знака
потерянных при переходе от аг- к а{+1 в последовательности
/w(x), f(k+1\x) fn\x).
Общий случай соответствует До>-2. В последовательности До, Д^ ...
найдем первое число, равное 1. Пусть это будет Дт. Тогда Ьт_х
может иметь значение 0 или 2; первый случай невозможен, так как
по условию До^.2, и поэтому можно было бы найти Дг=1 с I < т.
Если при этом Дт+1 ф 0, то всегда можно так уменьшить отре-
отрезок [аг, а{+1], взяваг < а[ < a't+] <\+1, что корень /<т)(х) принад-
принадлежит отрезку fa', a^+1]. a /*m+1)(x) не имеет там корней. Тогда
j(m)(x) не имеет корней на la , a'l и Wl+V at I и, следовательно,

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 93
Дт для них равно нулю. Поэтому первое из Д, равное 1, переме-
перемещается для этих отрезков влево. Для отрезка IV, а'+1] будем иметь
Д„г_2=2, Дт=1, Дт+1 = 0. При этом может оказаться, что Дт не
будет первым из Д, равным единице. Тогда мы так же переместимся
влево и будем повторять наши рассуждения. Таким образом, нам
нужно только рассмотреть случай, когда Дт_1 = 2, Дт= 1, Дт+1 = О
и Дт—первое из Д, равное 1.
В этом случае уравнение f™'^ (х) либо имеет два корня на
W, о^ + 1]> либо не имеет ни одного. Эти случаи можно различить
так, как мы это делали при До = 2, Д1=1, Д2=0. Если имеется
два корня, то мы отделяем их изложенным выше способом, при
этом отрезок [У, а'+1] разобьется на два отрезка ]а'г, Ц и Ш, а'+11
для которых Дт i=l, т. е. первое из Д, равное 1, переместится
влево. Если окажется, что корни комплексные, то можно показать,
что все уравнения
/<™-2> (х) = О, /м (х) = 0 / (х) = О
имеют пару комплексных корней. Тогда мы уменьшим все Д^ при
k <; т—1 на 2 и получим Дт_1 = 0. Таким образом, мы последо-
последовательно подвигаемся влево до тех пор, пока не придем к уже рас-
рассмотренным случаям.
Может случиться, что уравнение /(п-1'(х) имеет два равных
корня в Гаг', аг'+1]. Тогда будет справедлив тот же вывод, если только
само уравнение не имеет кратных корней. Если же двойной корень
принадлежит уравнениям
/<"-2>(х) = 0, /("-3)(х) = 0 /(х) = 0,
то исходное уравнение в данной точке имеет корень кратности п — 1.
Пример. Отделить корни уравнения
х6 - 4х4 -)- 6х3 — Зх2 ¦+¦ 2х ¦+¦ 1 = 0.
Последовательность /(х), /'(х) /С*) будет выглядеть так.:
х3 —Зх2-)-2х+1, ^~^
i?) = 5x*— 16x3+18x2— 6x + 2, f^=5x — 4,
№
= Юх3—24х2+18л:—3, ^-^ = 1.

94 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
По признаку Ньютона находим, что все корни уравнения заклю-
заключены между —1 и -j-1. Составим таблицу знаков последователь-
последовательности в точках —1, 0, -j-1:
х —1 0 -f-1
Г + + +
Г - - +
/'" + + О
На отрезке I—1, 0] имеем До=1, а следовательно, на этом
отрезке имеется один действительный корень. На отрезке [0, 1|
нужно разобраться со знаком • ¦ = 10 (х—1) (х И. По-
Поэтому при значениях х, больших 1, но близких к ней, все произ-
производные будут положительны. Таким образом, последовательность Д
будет иметь вид
4, 4, 3, 2, 1, 0.
Первое из Д, равное 1, будет Д4. Исследуем, может ли уравнение
/"'(х) = 0 иметь действительные корни на [0, 1]:
/"' A) Г" @) _ 0 6__1^ , _п
/№ A) /<*) @) Г (-4) 2 ^ и>
Следовательно, мы должны уменьшить До, Др Д2, Д3 на 2. Полу-
Получим 2,2, 1, 0. Опять нужно исследовать, имеет ли /' (х) = 0 дей-
действительные корни на [0, 1]:
Г A) /' @) _ 3 2__ И_^. , _п
/" A) f" @) ~~ 1 (-3) — 3 -" ' и>
а это означает, что действительных корней нет. Уменьшая еще раз
все Д на 2, получим Д0 = 0. Следовательно, других действительных
корней наше уравнение не имеет, т. е. имеет один действительный
корень на отрезке [—1, 0] и четыре комплексных корня.
5. Отделение комплексных корней алгебраических уравнений.
Мы изложим способ отделения комплексных корней алгебраического
уравнения
/(z) = z»+«i2"-1+ ••• +а„_1* + а„ = 0, A2)
использующий понятие индекса многочлена f(z) относительно неко-
некоторой заданной прямой в плоскости комплексного переменного z.
Пусть на прямой
Rez=a или z = a-\-U (— со < / < -)-со) A3)

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 95
уравнение A2) не имеет корней. Значения многочлена f(z) вдоль
эгой прямой являются функцией t, которую можно записать в таком
виде:
A4)
гдеР(О и Q(f) — действительные функции от t, R (t) = У?1 (t)-\-Q2 (t),
tg cp (/) = р ((' . По условию R{t) не обращается в нуль. R{t) и
<?(t)—непрерывные функции от t при изменении t от—со до-)-со.
Индекс многочлена f(z) относительно прямой A3) определим так:
//,(Rez = a)=^[cp(+co) —ср(—со)|. A5)
Имеет место следующее свойство индекса If\
Если f(z) = f1(z)f2(z), где fx{z) и f2(z) — многочлены относи-
относительно z, то
r A6)
В самом деле, если
f{a + it) = R(t)e^m, fj{a + it) = Rj{t)el:f3(t) (;=1, 2),
то
R {t) = R, (t) ¦ R2 (t), ф (t) = Tl @ + ф2 (t).
Отсюда
Ir (Rez = a.) = — [cp (-1- со) — cp (— со)] =
= ^ {[tPi (+°°) — <Pi (— со)! +[?2 (+ со) — cp2 (— со)]} =
Рассмотрим связь индекса /^(Rez^a) с расположением корней
уравнения A2) относительно прямой Rez=a. Пусть сначала
f(z) = z — z0, где z0 = х0 -\- iy0. В этом случае
Если a—х0 > 0, то при изменении t от —со до -)-со tgcp(^) из-
изменяется от —со до -)-со, а cp (t) от -г- до -^-. (За ср (—со) мы
всегда будем принимать значение угла в пределах (— -^-, -^-j, для
которого тангенс равен lim ^ . ) Следовательно,

96 РЕШЕНИИ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Если а — х0 < 0, то при изменении t от —со до -|-со tgcp(^) из-
изменяется от -j-co до —со, т. е. ср(^) изменяется от -^ до ~ и
Таким образом,
1, если хп < а,
^ A7)
—1, если х0 > а.
Это означает, что для многочлена /(z) = z—z0 индекс относительно
прямой Rez=a будет равен 1, если корень z0 многочлена лежит
слева от прямой Rez=a, и —1, если корень лежит справа от
этой прямой.
Пусть теперь f(z) — произвольный многочлен
z»+-^»-l+ ... -\-а„_1г-\-ан =
= (z — zl)(z — z2) ... (z — zn).
На основании свойства A6)
п
Ir (Re г = a) = 2 7С-^) (Re z = a)-
Но /(-_; \ (Re z = a) равен -)-1, если z^ лежит слева от прямой Re z = a
и —1, если Zj лежит справа от этой прямой. Таким образом,
/r(Rez=a) = &— /, A8)
где k—число корней уравнения f(z) = 0, лежащих слева от пря-
прямой R?z = a, а / — число корней уравнения, лежащих справа от
этой прямой. Так как общее число корней уравнения /(z):= О
равно k-\-l=n, то
_ n+/f(Rez = a) _ n — ff(Rez = a)
к — g • ' — 2 ' ( '
Рассмотрим теперь прямую
Imz=p, или 2 = /-|-/р (—со<^<со), B0)
предполагая, что на ней нет корней уравнения A2). Пусть
f(t+ /р) = Р, (?) + tQ, (t) = Rx (t) e^ W (tf! @ ?= 0),
Определим индекс многочлена относительно этой прямой равенством
1_ф(—оо)]. B2)

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 97
Снова изучим связь индекса /^(Imz —C) с расположением корней
относительно прямой Imz = p, положив вначале, 4to/(z) = z — z0
(zo=xo+tyo):
—Л).
Если р—у0 < 0, то tg ф (^) при возрастании t от —со до х
возрастает от 0 до -)-со, а ф(^) возрастает от 0 до -_-; при воз-
возрастании t от х0 до -j-co Р~-Уо возрастает от —со до 0, а
от ~2 до тт. Таким образом,
/r(Imz=P) = ^ [тг —0]= 1.
Если р—у0 > 0, то tg4*(/) при изменении f от —со до х0
убывает от 0 до —со, а ф(^) убывает от 0 до ^-; при измене-
изменении ^ от л0 до -)-оо tg<]>(/) убывает от -|-оо до 0, т. е. <]>(/) убы-
убывает от ^ до —тт. Следовательно,
/r(Imz=P) = — [— тг— 0] = — 1.
Итак,
Wlm, = » = {+;• 6СЛИ Л>^ B3)
1—1, если jo<P.
т. е. если корень z0 лежит выше прямой Imz=p, то индекс ра-
равен -j-1; если же ниже прямой, то —1.
В общем случае многочлена
= (z — 20 B — z2) ... (z — гп),
используя свойство A6), будем иметь:
п
Р) = 2/,_. Aшг = р)=/> — д, B4)
где р — число корней уравнения f(z) = 0, лежащих выше прямой
Imz^p, a q — число корней, лежащих ниже прямой. Так как
p-\-q = n,
то
/г/гAтг = Р)
Я = —о • B5)

98 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Теперь уже совершенно ясно, как можно выполнить отделение
действительных и комплексных корней уравнения A2).
Для определения числа корней уравнения f(z) = 0, расположен-
расположенных в полосе а0 < Rez< av вычисляем /^(Rez = а0) и If (Rez = ах).
Тогда число корней в этой полосе будет равно
k! — ko = ± \If (Re z^aj — If (Re z = a0)]. B6)
Для определения числа корней в полосе po<Imz<pi вычисляем
If(\mz=$0) и ff(\mz=: pj; тогда число корней в этой полосе будет
P0-p1 = \[If{hnz = $(i)-If{\mz = ^)\. B7)
Зная границы области, в которой расположены все корни урав-
уравнения A2), и применяя этот метод, можно произвести отделение
всех действительных и комплексных корней.
Для вычисления индекса многочлена f (z) относительно прямой
Rez = a необходимо найти приращение ср (t) = arg/ (a -j- it) при воз-
возрастании t от — со до -j- со, так как
If (Re z = а) — — [ср Н- со) — ср (— со)],
где
Функции Q (t) и Р (t) являются многочленами относительно t, причем
если степень п многочлена / (z) четна, то Р (t) имеет степень п,
a Q(t) — не выше п—1; если же степень п нечетна, то P(t) есть
многочлен степени не выше п—1, a Q(t) — в точности степени п.
Так как предполагается, что на прямой Rez = a нет корней урав-
уравнения /(z) = 0, то Р (t) и Q(t) не могут одновременно обращаться
в нуль. Функция ср (t) = arg/ (a -\- it) при изменении t от—со до-)-со
непрерывна, a tg ср (/) = ^ ' терпит бесконечные разрывы в точках t^,
являющихся действительными корнями многочлена P(t). Разрывы -р-тр:
могут иметь один из следующих видов:
Ит ТГт = + °°' 2) . Ит_ож
3) Нт ^=±со; 4) Hrn^=Too. ^
Функция tg <р (/) имеет разрыв в точках <р = л: -j , л: -у, л: -^-,
причем все эти разрывы вида 3).

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 99
Для того чтобы найти приращение ср (t) при переходе по t от — со
до1 -(-со, нужно найти все действительные корни многочлена Р(t):
— со < tt < t2 < ... < tk < -)- со, и рассмотреть последовательность
интервалов: (—со, ^), (/lf t2) (tk_v h)> D> Ч0)- На каждом
из интервалов (/,-, ti+1) tgcp(^) есть непрерывна* функция, а значе-
ния y(t) находятся в интервале I—^—л. —у—те) или ( у—л.
^— тг), где kt — некоторое целое число. При переходе t
через ti+1 в зависимости от типа разрыва р~77\ ПРИ ^ = ^«'-ч значе-
значения ср (t) остаются или в этом же интервале (в случае разрыва вида 1)
или 2)) или выходят из этого интервала, причем в случае разрыва
вида 3) tp (t) уходит из этого интервала возрастая, а в случае раз-
разрыва вида 4) — убывая. Приписывая ср(^) при t = — со значение
/ я я\ Q{t)
угла в пределах I ^-, тг)> Для которого тангенс равен hm ~тг,
\ ? ?} г+-оэи\1)
и следя за изменением ср(^) при переходе через точки tv t2 tk,
мы и найдем приращение ср(^) при возрастании t от —со до -)-со.
В случае четной степени п lim %-f): = 0 и ср (— со) = 0, а ср (-(-со) = /те.
где / — целое число, равное разности числа разрывов ^ вида 3)
и числа разрывов вида 4), т. е. в этом случае индекс равен числу
разрывов вида 3) без числа разрывов вида 4). В случае нечетной
степени п lim
QU)
P(t)
= -j-co. Если lim тг77с=—со,тоср(—co) =
•¦—со
я 21— 1 ,
= — -j , а ср(-|-со)= —^—it, где * равно разности числа разрывов
вида 3) и числа разрывов вида 4) при lim ^ = — со и / равно
разности числа разрывов вида 3) и числа разрывов вида 4) плюс
-|-со
) рр
единица при lim ^ \/. = -|-со. Если lim р, ; =-|-со, то
ср(—оо) = -5-« а ТСЧ0)^—y—л> гДе I — число разрывов вида 3)
без числа разрывов вида 4) при lim Ь^-? = -|-со и / равно раз-
t + +co^ (*)
ности числа разрывов вида 3) без числа разрывов вида 4) минус еди-
единица при lim il-i = — со. Это означает, что если рассматривать
единую бесконечно удаленную точку и положить -|-со=оо — О,
— co=co-j-0 и в этой точке рассматривать типы разрыва так же,
как и в D8), то можно и при четных и при нечетных п сформу-
сформулировать одно и то же правило для вычисления индекса /^(Rez^a),,
Индекс многочлена f (z) относительно прямой Re z = а, на кото-
которой нет корней уравнения /(г) = 0, равен разности числа

100 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
разрывов отношения ji .* вида 3) и числа разрывов вида 4), где P,(f)
и Q (t) — соответственно действительная и мнимая части функ-
функции f(a-\-tt).
Это правило, очевидно, справедливо и для вычисления индекса
/^(Imz^P), если на прямой Imz = p нет корней уравнения f(z) = 0.
Заметим, что для вычисления индекса нет необходимости нахо-
находить корни уравнения P(t) = O, а нужно лишь для каждого из них
найти такой интервал, в котором нет других корней P(t), а также
корней многочлена Q(t).
В заключение рассмотрим два примера.
Пример 1. Отделить корни уравнения
4z3 — 2z2 — 4z — 3 = 0.
Для определения числа действительных корней и их отделения
выписываем ряд Штурма
/0Bг) = 42г3 — 2z2— 4z— 3, Л (z) = 3z2 — z — 1, f2(z)= 26z-\- 29,
/3 BГ) = — 1.
Таблица перемен знака в последовательности Штурма имеет вид:
sign /о (г)
sign Л (г)
sign Л (г)
sign/, (г)
Число перемен знака
— (XI
—
+
—
—
2
0
—
+
—
2
1
—
+
+
—
2
2
+
+
—
1
+
1
+
—
1
Таким образом, действительный корень один и находится в интер-
интервале A, 2).
Для отделения комплексных корней будем вычислять индексы
многочлена относительно прямых Rez = a и Imz=p.
/, — /т ¦* = + !/>.
OJO
имеет
чйен 2t2 — 3 имеет корни м — —у Т ' '2 — тр т ' Р~П\
в этих точках разрывы вида: в /t: ± со, в t2: + °°- Далее,

§ 2] ОТДЕЛЕНИЕ КОРНЕЙ 101
+ оо, a ,im ^ = -оо. т. е. lim Щ±= ± со.
Отсюда
Следовательно, оба комплексных корня лежат слева от прямой
Rez=0, т. е. имеют отрицательную действительную часть.
2) Rez = — I, f{—\-\-it) =
= 4 Ш» — 5 '
Корни уравнения lit2—5 = 0:
/ j~y Q g
Типы разрывов t: oo, tv t2,
q: oo, q: oo, q: oo.
Отсюда //,(Rez = — 1) = — 3, k — l =—3, k-\-l = 3, k = 0. Таким
образом, комплексные корни лежат вправо от прямой Rez = —1,
т. е. в полосе —1 < Re z < 0.
Q(Q З^-У-2
Я (О «з — 2^ — 16^ — 1 *
Корни знаменателя находятся в интервалах
*i€(—2;—1). *2€(— 4;°). 'з€B. з).
Типы разрывов: t^. q: oo, t2- np oo, t3: qr oo, oo: 0, т. е.
/^A1112= 1) = — 3, p — 9 = — 3, p-\-q= 3, p = 0. Следовательно,
выше прямой Imz= 1 корней нет, а это означает, что мнимые части
корней по модулю меньше 1.
Итак, уравнение /(z) = 0 имеет три корня:
zx = cc, Zi,з^
где
Пример 2. Отделить корни уравнения
= 3z* — z3 + 6z2 — 1 \г -+- 3 = 0.
Метод Штурма отделения действительных корней дает такой резуль-
результат: уравнение f(z) = 0 имеет два действительных корня, которые
расположены в интервалах @, 1) и A, 2). Для определения располо-
расположения пары комплексных корей применим изложенный метод.
1. Рассмотрим прямую Rez = 0, т. e. z — it:

102 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Уравнение P(f) = 0 имеет два двукратных корня: *t =— 1 и *2 = 1.
Типы разрывов *,: +oo, *2: —00, 00: 0, т. е. /^.(Rez= 0) = 0,
k —/=0, & + / = 4, & = 2. Следовательно, комплексные корни
лежат влево от прямой Rez = 0, т. е. имеют отрицательную дей-
действительную часть.
2. Рассмотрим прямую Rez =— 2:
/(—2 -\-it) = З*4 — 84*2+ 105 + г [25*3 — 143*],
Q (t) _ 1 25^ — 143*
P (t) ~ 3 t* — 28*2 -)- 35 '
Уравнение t4 — 28*2 + 35^0 имеет корни tx яа—5,2; *2яй —1,1;
*3лй1,1; *4яй5,2. Типы разрывов:
t{. ц: оо, t2: q: 00, *3: + °°. h: + °°. °°: 0-
Отсюда
//(Rez = —2) = —4, k — l = — 4, k-\-l = 4, k = 0,
т. е. левее прямой Rez = — 2 корней нет, и комплексно-сопряжен-
комплексно-сопряженные корни находятся в полосе
— 2<Rez<0.
3. Рассмотрим прямую Imz= 1:
f(t-\-i) = 3ti — t3—12P—8t-\-iA2t3—3t2— 10),
Q(t)_ 12*з —3*г—10
Р (t) ~ W — &— UP — 8t'
Корни уравнения З*4 —*3—12*2 — 8* = 0: *tsa—1,1, *2«—1,.
^з^О, *4яа2,4. Типы разрывов:
tt: q: 00, *2: + оо, *3: + °°> *4- + °°> °°- ®-
Отсюда
//.(Imz=l) = —2, p—q = — 2, p-\-q = A, p=\.
Следовательно, выше прямой Imz=l имеется один корень уравне-
уравнения.
4. Рассмотрим прямую Imz = 4:
f(t-\-Ai) = З*4 — *3 — 282*2+37* + 675 + i D8*3— 12*2—720* + 20),
Q @ _ 48*3 — \2У— 720t + 20
Р (t) ~ 3t* — & — №.& + 37* + 675 •
Корни уравнения З*4 — *3 — 282*2 + 37* + 675 = 0 находятся в интер-
интервалах *!?(—10, — &); *2G(— 2, — 1), *з?A,2), *4^(9, 10). Типы
разрывов:
t{. q: 00, *2: q: 00, *3: q: 00, *4: q: 00, 00: 0,

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 103
т. е. If(lmz = 4) = — 4, p — q = — 4, p-\-q=4, p = 0. Таким
образом, выше прямой Imz = 4 корней нет, а поэтому комплексные
корни расположены по одному в прямоугольниках:
{—2<Rez<0,
{—2<Rez<0, — 4<Imz< —1}.
§ 3. Метод Лобачевского решения алгебраических уравнений
Одним из широко распространенных методов решения алгебраи-
алгебраических уравнений является метод Н. И. Лобачевского, предложенный
им в 1834 г. Впоследствии он был несколько усовершенствован
Греффе, Дандленом, и поэтому в литературе часто его связывают
с их именами. Иногда его также называют методом квадратного корня.
1. Метод Лобачевского. Случай различных по абсолютной
величине действительных корней. Пусть дано уравнение
„=0, A)
о корнях которого известно, что все они действительны и удовле-
удовлетворяют условию
l*l|»|*2|» ... »|*„|- B)
Смысл знака ^> (значительно больше) мы уточним несколько позд-
позднее. Воспользуемся связью между корнями и коэффициентами нашего
уравнения
*„ = -
4-х * =
xlx2x3
а0
X,X2X3... *n = (-l)»f!L.
C)
Вынесем в первом из этих равенств за скобки хх. Получим:
Будем считать, что xt настолько больше остальных корней по абсо-
абсолютной величине, что можно отбросить в скобке все отношения —
и в пределах нашей точности равенство не нарушится. Тогда
во

104 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Аналогично, вынося из второго равенства за скобки хххг, получим:
—+ ••• + ?rj?l=
Предполагая, что отношениями —-, стоящими в скобке, можно
пренебречь по сравнению с единицей, будем иметь:
или
х. яа— ^¦
Продолжая эти рассуждения дальше, найдем:
Х^-^ «=Ь2 »). D)
Таким образом, в нашем случае мы сумеем найти приближенные
значения всех корней уравнения.
Н. И. Лобачевский предложил способ получения из данного урав-
уравнения A) нового уравнения, корни которого равны квадратам корней
исходного уравнения. Если исходное уравнение имело только раз-
различные по абсолютной величине действительные корни, то, применяя
достаточное число раз процесс, предложенный Лобачевским, — квад-
рирование, получим новое уравнение, корни которого удовлетворяют
условию B). Таким образом, мы сможем найти корни последнего
уравнения, а затем и корни исходного уравнения. Изложим процесс
квадрирования. Запишем уравнение A) в виде
а0 (х — xt) (х — х2) ... (х — х„) = 0.
Уравнение, корни которого противоположны по знаку корням урав-
уравнения A), будет иметь вид
Перемножая эти два уравнения, получим:
ао (•*¦ xi) (,•*¦ хч) ¦ • ¦ \х^ хп) ~ ¦
Если теперь положить z = — х2, то получим новое уравнение отно-
относительно z, корни которого равны соответственно
Отсюда, для того чтобы получить нужное нам уравнение, мы должны
перемножить уравнение A) и уравнение, получающееся из него заме-
заменой х на —х, и положить затем —x2 = z. Найдем выражения для
коэффициентов нового уравнения через старые коэффициенты. Нам
нужно перемножить
»-2+ ... +а„_1х + а„=0 E)

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 105
И
flox»-fl1x»-i+ ... +(-1)"-1а„_1х + (-1)«я„ = 0. E')
Произведение будет иметь вид
4х2п - (а\ - 2а0а2) х2" + (<4 - 2a,a3 + 2аоа,) х2" + ...
... +(-l)"fl2[=0. F)
После замены — х2 на z получим:
— 2а1а3-\-2аоа4) z"+ ... +а2 = 0. G)
Коэффициент ftft при zn~k в этом уравнении получается из коэффи-
коэффициентов исходного уравнения следующим образом: из квадрата ак
вычитается удвоенное произведение двух соседних с ним симметрично
расположенных коэффициентов, прибавляется удвоенное произведе-
произведение двух следующих за ними симметрично расположенных коэффи-
коэффициентов и т. д., до тех пор пока не придем к а0 или ап, т. е.
bk = a\ — 2ak_lak+l-\-2ak_2ak+2 — 2ак_3ак+3-\- ... (8)
Возникает вопрос: как узнать, что процесс квадрирования проведен
достаточное число раз? Для того чтобы ответить на него, мы рас-
рассмотрим два уравнения:
получающиеся в процессе квадрирования, причем второе получается
квадрированием первого. Если бы для первого уравнения условие B)
было выполнено, то тем более оно будет выполнено для второго.
Таким образом,
Но так как zt = —у*, то мы получим:
с. ЪЪ;
Ьг-1
(/=1. 2 п)
и, следовательно, в силу того, что с0 = Ь*, будем иметь:
с>~^. (9)
т. е. все коэффициенты ct являются примерно квадратами Ь-%. Мож-
Можно показать, что при этом разделение корней уже имеет место, если
исходное уравнение удовлетворяет нашим требованиям.

106 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
т
0
1
2
3
4
5
6
4
— 2af_1aj+,
4
— 2ai^iai+1
2
аг
— 2йг._1Йг-+1
2«»-2 я»+з
<>
4
— 2aj_jai+i
2«»-2 «i+2
— 2а4_,а<+1
2aj_, ai+2
— 2аг-_1Й,-+1
2aj_2aj+2
1
1
1
1
1
1
1
1
1
1
1
1
1
— 35
1225
— 760
465
216 225
— 103 800
112 425
1 263 938 • 10*
—341 496 • 10*
922 442-10*
850899-10"
— 53 700 • 10"
797 199-10"
635 526 • 103*
— 1438 ¦ 10-44
634 088 • Юз*
402 068-Ю*"
— 1 • 10^4
402 067-1074
380
144 400
— 94 500
2 000
51900
269 361 • 10*
— 98 813.10*
200 • 10*
170 748 -104
291 549 • 10«
— 23 050 -1013
268 499-1013
790 917- 103'
— 1 932 • 1031
718 985 • 1031
516 940-1 Oes
— 2-10в8
516 938-10G8
267 225-1 Oi«
267 225 • 10145
аъ
— 1350
1 822 500
— 760000
1 062 500
112 891-107
— 10 380-10'
102 511-107
105 085 • 101^
— 341-101»
104 744 • 101"
109 713-1043
109 713 - 10*з
120 369-lOei
120 369 -1091
144 887 • lot»?
144 887 - 1018'
a4
Iff»
106
10»
1015
1012
10^4
Ю24
10^8
1048
1096
109Я
10«e
10192

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 107
Рассмотрим в качестве примера решение методом Лобачевского
уравнения (промежуточные вычисления приведены в схеме на стр. 106)
х4 — 35х3 + 380х2 — 1350х + 1000 = 0.
zt = 402067 • 1074; \gZl = 79,6042985;
llg z1= 1.2438172;
x,= 17,5314; /(*,) = —0,02;
22 = ШШ' 10е8 = 664 628. 1062;
]g z2 = 67,8225786; 1 \g z2 = 1.0597278;
x2= 11,4743;
/(x2) = 0,03; *s = ^ngg- 1045=0,542191
Igz3=44,7341523;
l]gzs= 0,6989711; x3 = 5,00001; f(xj = 0,003;
*4 = Ж887' 105 = 0-690193; lg^4 =1,8389706;
l]gz4 =1,9974839; x4 = 0,994223; /(x4) = —0,03.
2. Метод Лобачевского. Случай комплексных корней. Рассмо-
Рассмотрим теперь случай, когда уравнение имеет комплексные корни. Про-
Процесс квадрирования можно будет производить, как и раньше, только
выводы о способе определения корней будут уже недействительны.
Предположим пока, что мы имеем только пару комплексно-сопря-
комплексно-сопряженных корней:
х2 = р (cos <p-f-i sin <p), x3 = p(cos<j>—ism у). A0)
Тогда после т квадрирований получим уравнение, которое будет
иметь пару комплексно-сопряженных корней:
fn (cos 2mcp + i sin 2TOcp),
Пусть, например, остальные корни будут расположены так:
| = lx3|>lx4|> ... >|х„|. A1)

108 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [гЛ. 7
Воспользуемся опять зависимостью между корнями и коэффициен-
коэффициентами уравнения, полученного после т квадрирований:
x\x\ + x\x\ + . .. + x?_jx? = f- (k = 2m),
vk Yk vk \ v-fe v-J:yk _|_ _|_ Yk Yk vk C3
X1X2X3 i xlXiXi I ••• I Xn-2Xn-lXn—7~'
...Xk =
A2)
Если при этом
то
2**Р
Г
*Р*
L
хк хк
A3)
и мы можем найти все действительные корни и модуль пары ком-
комплексно-сопряженных корней. При этом все коэффициенты, кроме
второго, ведут себя, как и раньше, т. е. стремятся к квадратам
коэффициентов предыдущего уравнения, а с2 ведет себя неправильно,
возможно даже меняя свой знак. Последнее и служит признаком
наличия пары комплексно-сопряженных корней. Легко заметить, что
если модуль пары комплексных1 сопряженных корней заключен
между Xj и xi+3, то ведет себя неправильно коэффициент ci+i,
и мы точно так.же можем найти все действительные корни и модуль
пары комплексно-сопряженных корней. Вообще, если уравнение
имеет несколько пар комплексно-сопряженных корней и их модули
различны и отличны от модулей действительных корней, то можно
по тем же признакам определить, где они расположены, и найти
действительные корни и модули всех комплексных корней.
Если мы имеем пару или две пары комплексно-сопряженных
корней, то аргументы этих корней находятся также без труда. Дей-

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 109
ствительно, если имеется только пара комплексно-сопряженных
корней х2, х3, то из исходного уравнения имеем:
4+ ... +х„=-^. A4)
В равенстве A4) нам не известен только cos<p. и он может быть из
Этого равенства найден. Если комплексных корней имеется две пары: х2,
х3 и х4, х5, то в уравнении следует заменить неизвестное на \/у.
Тогда уравнение относительно у примет вид
И будет иметь корнями:
—, — = — (cos<p — isin<p), — = —(coscp + isincp),
xi xi Pi xs Pi
— = — (cos ф — I sin ф), — = — (cos ф + i sin Ф), — —.
Следовательно,
L l l ^ ±« A5)
+ Cos<p + cos| + ^ + ... +
xi Pi Рз xa xn an
что вместе с уравнением
Jte+ ... +х„ = — ^- A6)
определит cos<p и cos4». Для трех пар комплексных корней можно
использовать наряду с исходным уравнением и уравнением, получен-
полученным заменой х на 1/_у еще уравнение, полученное после первого
квадрирования. Для случая трех и более пар комплексных корней,
так же как и для случаев, которые .мы уже. рассмотрели, можно
воспользоваться следующим приемом. Поскольку мы знаем модуль
пары комплексно-сопряженных корней х{ и xi+u то в трехчлене
(х — х^ (х — xi+1) = х2 — 2рх cos <p + р2, соответствующем этой паре,
нам будет неизвестно только p = 2pcos<p. Но его можно найти из
условия, что уравнение делится нацело на х2—рх-|-р2. Проще
йсего это сделать путем деления /(х) на х2 — рх-\-р2. -Получится
остаток вида Р(р) x-\-Q(p), где Р(р)—многочлен степени п—1
относительно р, a Q(p)—многочлен степени п—2. Они должны
обращаться в нуль при одном и том же значении р. Следовательно,
они должны иметь общий делитель, который также можно найги
путем деления.
Другой способ отыскания аргументов комплексных корней пред-
предложил Энке. Всегда можно считать, что уравнение имеет четную

110 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
степень, так как в противном случае его можно умножить на х.
Запишем его в виде
и пусть модуль р пары комплексных корней найден, так что корни
будут:
sincp), xi+1 = p(cos<p — / sin cp). A8)
cp + a2fc = 0, \
-ip sincp = 0. J
После подстановки этих корней в уравнение и приравнивания дей-
действительной и мнимой частей нулю получим уравнение относи-
относительно <р:
p2ft-1cosBk— 1)<р+ ... +a2fc_1pco
B& l) + +-ip sinp
A9)
Умножим первое из уравнений A9) на cos ftp, второе на sin &<р
и сложим их почленно. Затем умножим первое из уравнений A9)
на sin &<р, второе на cos&<p и вычтем первое из второго. В резуль-
результате получим:
B0)
где
' = 7ft-i
B1)
Для того чтобы найти значения, удовлетворяющие обоим уравне-
уравнениям B0), используем выражения для cos«<p и —:—- через cos<p:
cos «<p = B cos cp) — yBcoscp) -\ ^—^-Bcoscp) —
п (п —4)(я —5) _ „-в , я(я —5)(я —6)(я —7) v
31 ^ cos cp; -| щ х
XBcos<p)"-8- ....

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1 1 1
^ + х
X Bcos<p)"-5- С-*><"-5) С-6) B cosт)Я_7 +
+ (я - 5) („ - 6Нн - 7) („ - 8) B cqs y)W_9 _ _
Полагая —2pcos<p=p, получим следующие уравнения для опре-
определения р:
- 2)f -5) м- ] ?ik {k - т ~5)
6) ._, _
Х
B2)
Общий корень р этих двух уравнений также находят простым
делением.
Оба приведенных способа отыскания аргументов комплексных
корней требуют громоздких вычислений.
Рассмотрим пример.
Решить методом Лобачевского уравнение
Схема вычислений и результаты выглядят следующим образом.

112 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
53°
^*
53°
см
го
1
со
о
¦* со
аз ¦* оо
|
со ¦* ¦*
го см
1
1
со см
1
ч* -J.
СМ 53
Г
-
о
о
О CD
О ¦*
аз о оо
см см
ю го
1
1
СО " О
1О ОО СМ
см ^
со см
"-• ГО
1
5Т i
53 1 «
CM 5T
Г
217
1
СО ^f
>-| СО
см 1
СП ОСМ
00 СМ СО
о со
¦* со
1
О ¦* OJ
со аз см
т—1 ^О
см
ю см
см аз
1
+ С
iT +
Q 1 V
СМ 53"
СМ
СМ
Si
^1
263
СО
о
00
00
664
-
со
о о
.1 .1
аз ю
ю t~
со о
¦* о
S оо
СО СО О
00 ^ О
.— соо
о." с
¦з"с
о о о
о оо
аз оо ¦*
аз ю о
00 ~ О
t^ о о
¦* с
> о
со см
аз t^
00 СО
5
•
si
53 Т <»
ч 1
СМ 53
см
-
232
о
1
см
о
о
со
^.
224
со

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 113
а?
см
я
о
со
о о
Я
о
00
с*
о
00
Cl t^
¦*" со"
s?
s
о'
Ю
СЧ
CO
s s
s s
g
о
g
™
СТЭ 00
со у5
2 ю
'. en
о
s
Ю
& в
C^l о
I
g s
i
c5 to
—" o1
о
,-. 1«
4 +
?f

114 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
I
5?
53*
CO
53"
0
53
1
S
2,95/
S g
2 2
8 2 :
t-- CM ¦
t~- CO •
О Ю
¦*" cm"
1
Б
T__l
Ю
en ¦ •
ю"
Г ~
о s>
СП Ю
ю со
го см
I??-
см -
53 1 «•
сз i
(М «3
см
й
S
с?
S
&
25-
ю
LO
'Г
о
СП "
ю"
24-
,43
СП
о"
СМ
ю
ю
со
со
— 00
см" о
с
о
ее"
см
о
СП
(.•О
со
см
о
t
см
СО
со
СП
LI J
т
ье
S
'2 | k
8§S
S
00
о"
f
+1
СП
см
СП
СП
э-
с
о
э-
с
см
сГ
со
см
э-
со
о
S
СП
оо
о"
5
О!
о"

§ 3] МЕТОЛ 1OFA4FBCK0r0 PEUIFHUfl АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 115
3. Метод Лобачевского. Случай близких или равных корней.
Если в уравнении имеется пара близких по абсолютной величине
корней, то наш метод не дает возможности найти каждый из них
в отдельности, так как если, например, х2яе: х3, то в равенстве
два слагаемых будут близки друг к другу. Но тогда мы сумеем
найти из равенства
) + =
произведение х2х3, а дальше будем отыскивать трехчлен х2 —
-+- х2х3, являющийся делителем /(х), что позволит лам найш
р = хг-\~ х3. На этот случай может быть перенесен также метод Энке.
Если имеется несколько пар равных по модулю комплексно-
сопряженных корней или равных по модулю действительных корней,
то может получиться, что процесс квадрирования не приведет к цели.
Так, например, если заданное уравнение будет
то все квадрированные уравнения имеют вид
В этом случае целесообразно сделать замену неизвестного на х—h,
что приведет к разделению корней с равными модулями.
Если корчи уравнения необходимо найти с большой точностью,
то после вычисления их приближенных значений по методу Лоба-
Лобачевского целесообразно произвести их уточнение, используя методы
последовательных приближений, о которых мы будем говорить
позже. Применение этих методов для уточнения требует меньшего
объема вычислений и позволяет избежать трудности работы с очень
большими числами, с которой приходится встречаться в методе
Лобачевского.
4. Погрешность метода Лобачевского. Погрешности в значениях
корней, полученных по методу Лобачевского, могут происходить по
трем причинам:
1) в силу неточности коэффициентов исходного уравнения точные
значения корней не могут быть найдены: это — неустранимая по-
погрешность, не зависящая от способа получения корней, и мы на
ней останавливаться не будем;
2) процесс квадрирования уменьшает величины отношений —^— ,
и чем большее количество раз проведен процесс квадрирования,
тем точнее будут приближенные равенства для определения корней,
но при любом конечном числе квадрирований эти равенства будут

116 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
оставаться приближенными и, следовательно, корни могут быть
найдены только приближенно; погрешность в значениях корней,
происходящая по этой причине, есть погрешность самого метода;
3) в процессе квадрирования получаются числа с очень большим
количеством знаков и их приходится округлять, что вносит допол-
дополнительную погрешность в значения корней, — это погрешность
округления. В дальнейшем мы и рассмотрим погрешность метода
и погрешность округления.
Пусть дано уравнение
x» + al*"-1 + a2*"-2+ ... + fl»_i* + an = 0, B3)
корни которого пока будем предполагать действительными, раз-
различными по абсолютной величине и упорядоченными следующим
образом:
l| |
После s квадрирований мы получим новое уравнение:
х»_|_?lX»-i _|_ *2х»-2 ¦+-...+ V j v ¦+-*„ = 0. B4)
причем, если положить 28 = /я, то
i "^l mm т /пс\
h = Ъ Хгх, . .. х, . B5)
1 <i1<»2< ... <ifc<» 1 "
Для сокращения записей примем обозначение х™ —yt- Тогда
h = 2 УчУи • • • Угк- B6)
l<ij< »2<. <i<n
Рассмотрим отношение
bkbk-ъ
¦ < lk < "
( Oi<2<ifc i
Вынесем -из каждой суммы наибольшее слагаемое
УЛ-'-Уь Н
Ук-х

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 117
=
где выписаны только наибольшие слагаемые. Так как
x m
Ук-
k , то при достаточно большом m ak = "K"SK '' доста-
*fc-i
точно малая величина. Далее, заменяя в числителе все отношения
нулями, а в знаменателе наибольшей величиной —-—, получим не-
неравенство
откуда
(Р«=Ч-'-1). B7)
Если т настолько велико, что 4afcpfc < 1, то из неравенства B7)
следует:
А < 2afcTfc, где ъ = 1- г *>. B8)
Более простой, но несколько более грубой оценкой будет
Ук-i 1
Рассмотрим теперь отношение
¦=Л ^
Заменяя в числителе все слагаемые, кроме первого, нулями, а в зна-
знаменателе наибольшим значением I—-—I , мы уменьшим правую часть,
\ Ук-\ I
у
а заменив все отношения в числителе наибольшим отношением fci-1 ,
Ук
v v 2ot
Напомним, что — <Ч, поэтому —— ^
АОА)
при достаточно больших m невозможно, так как afc -»- 0 при m -»• + со, а pfc не
2afc
зависит от т, и следовательно -х—»- + со при m -»- со.

118 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
а все отношения в знаменателе нулями, мы увеличим правую часть.
Следовательно,
или
откуда
M^rM f Р*уЧ- C0)
Используя неравенство B9), получим:
-1
«XfcPft J
или
Так как ук=х™, то
~ A — 2afcSfc)~"™. C2)
Если x*—приближенное значение хк, полученное после т квадри-
рований, то х\т — -г^~—. Следовательно, C2) можно записать в таком
виде:
- 2aftpfc)"«. C3)
Оценка C3) неудобна тем, что с помощью ее нельзя заранее пред-
предсказать число квадрирований, необходимых для получения нужной
точности. Этот недостаток можно исправить, наложив новые огра-
ограничения на уравнение.
Допустим, что существует такое число 0 <г< 1, что |xi + 1|<>\xx\
(/=1, 2 «—1). Тогда |JCj К/¦¦>-' \Xi\ при j > /. Положив
t = rm, будем иметь yj^t}~гу^ Пусть yhyh .. . yt —некоторое
слагаемое в сумме Ьк— 2 УьУь • • • У^
l<< <i<
Ук
fc(fc+l)
(tl)+(i2)++ltfc) Ь+1,+ .--+гк ^

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 119
а следовательно,
Число слагаемых в сумме, стоящей в правой части неравенства C4),
имеющих одну и ту же степень р, равно числу целочисленных реше-
решений уравнения
удовлетворяющих условию
Так как коэффициенты
Аналогично
откуда
Следовательно,
bk
ix < /2 < • • • < ^ -^ я.
— целые положительные числа, то
01- C5)
¦ ¦ ¦ Уи-\ [1 -\-Qk-i
или
или
-i@1w, C7)
—1- C8)
Таким образом, относительная погрешность зависит только от t, «,
/и и к. Если известно г или хотя бы его нижняя граница, то можно
использовать эту оценку для определения числа квадрирований s
{'2~ = т), необходимых для получения корней с нужной относитель-
относительной погрешностью.
Найдем теперь величину Qk{f). Известно, что число целочислен-
целочисленных решений уравнения
равно коэффициенту при zp в многочлене
Р , (г\ - A ~ гП) A ~ ^"^ • • •

120 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Таким образом,
Вычисление значений Pn,k(t) для всех &=1, 2 п требует
большой вычислительной работы, поэтому целесообразно найти k,
при котором Pn,k(t), где t — фиксированное положительное число,
не равное единице, имеет максимальное значение. Так как
l
~ '
1 jk+1 I I ^ I fi i I jk
где Х^.1, если п—к—1>-&, и Х<1; если п — k—1 < k, то
^ л — 1
2
л—1
Pn,k + i(t)^>Pn,k(t) при &<
Я„, fc+i @ < Рп, к (t) при & >
Это означает, что
max PU}k(t) = P ,n,(t). D0)
*-!¦» » "'LTI
Если в C6) и C7) заменить l-\-Qk(t) и 1 -\-Qk^i(t) через Я г„,((),
то получим оценки, пригодные для всех корней.
В качестве иллюстрации допустим, что нам дано п = 10, /" = 0,9
и произведено четыре квадрирования. Тогда /и = 24=16, / = @,9I6 =
= 0,01853, k = \?] = 5.
Простые вычисления показывают, что
1
1+<?*(/)< 1.01922. a [l-|-Qfc(/)]"< 1.0012.
Отсюда
— 0,0012 < —1— — 1 < 1**1Н**1 < 1.0012—1 = 0.0012.
1,0012
Таким образом, относительная ошибка корней после четырех квад-
рирований не будет превышать 0,0012.
Допустим теперь, что уравнение имеет комплексные корни, но
такие, что соотношение | хк | -^ г | хк_х | сохраняется для корней
с разными модулями, и если хк — действительный корень, а хк+1

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 121
и хк+2 — пара комплексно-сопряженных корней, то
Тогда будут применимы все предыдущие рассуждения лишь с очень
небольшими изменениями. Вместо неравенства C5) будет справедливо
неравенство
D1)
Прч Q/c(O<l левая часть этого неравенства может быть заменена
на ! К | >-1 ух 11 у21 ... | Ук 111 — Qk @1. и следовательно,
\УхIЫ • • • \УнШ -Q*@I < 1**1 < ЫЫ • • • ЫП +Q*@I. D2)
Заменив Qft@ максимальной величиной Р гщ@—1=Q(O> по"
лучим:
1
V)]
-<?<
D3)
Оценим теперь скорость сходимости процесса квадрирования.
Пусть мы провели дополнительное квадрирование. Тогда
2т
<}хк\<
ик-1
1
2т
.-<?!
D4)
где 6/с — коэффициенты нового уравнения. Допустим, что проведено
достаточное число квадрирований, так что t настолько мало, что
можно пренебречь его высшими степенями. При этом
1
¦
т
т
в то время как
t4;3m«i+—,
— сР] ' т
где с коэффициент при t в Q(t). Это показывает, что относительная
погрешность будет убывать в отношении t/2 при выполнении одного
квадрирования.
Все предыдущие рассуждения проводились в предположении, что
при реализации метода Лобачевског'о все вычисления проводились
точно. На практике же приходится ограничиваться лишь конечным
числом разрядов, т. е. проводить округление результатов операций.
Поэтому даже если коэффициенты исходного уравнения были точ-
точными числами, то после некоторого числа квадрирований мы полу-
получим уравнение с приближенными коэффициентами и эта погреш-
погрешность в дальнейшем будет сказываться на коэффициентах, а следова-
следовательно и на корнях уравнений, получающихся при последующих

122 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
квадрированиях. Дать какие-либо точные оценки влияния этих ошибок
округления в коэффициентах квадрированных уравнений очень трудно.
Поэтому мы приведем лишь очень грубые рассуждения, которые
будут указывать на опасность резкой потери точности при применении
метода Лобачевского в том или ином конкретном случае.
Рассмотрим сначала случай уравнения с различными по абсолют-
абсолютной величине действительными корнями. Пусть после s квадрирова-
ний мы получили уравнение
корни которого .У1 = — xf. Предположим, что Ьк имеют т. вер-
верных знаков. Выполняя еще одно квадрирование, получим уравнение
корнями которого будут числа —у\, —у\ —_у*. Так как
то b'it < Ьк. С другой стороны, по самому способу построения квадри-
рованного уравнения
А, hi /П п I уп Л . /п n I
U к ^^^™ v к. ^ If ^ \*^lf А-1 1 ^ If 9&I* j_2 *-^fr— ЧА^-i- 4 | • ¦ «
Можно считать, что % и bk_ibk+i имеют по т верных знаков.
Если bit имеет порядок bk, то это будет означать (при небольших п),
что bit будут также иметь т верных знаков. Но если b/t значительно
меньше, чем bk, что будет в том случае, когда из b\ вычитается
сумма 2 (Pk-ibk+i — Ьк_фк+2-\- .. .), близкая к Ь\, то будем име1ь
резкую потерю верных знаков в Ьк. Если —т~ имеет порядок 10й,
К
то в bit мы теряем примерно h верных знаков. Но
i, <га
У\Уч ¦•• Ук
» J
^j п.г
К г, <и <-.<ik< n У\ У* • • • Ук
так как У. ;—^-^ ~ > 1. Таким образом, по вели-
^ 1 ^*i У\У'1***Ук
чине [l-|-Qft(OJ2 можно судить о потере значащих цифр в b/t.

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 123
Если рассмотреть крайний случай, когда все корни уравнения
равны, т. е. ух=уг= ... =уп = у, то U\ = {Chnyf, a b'k = C^f.
.2
Отсюда —?- = C'j, и так как С* может быть велико, то мы будем
Ьк
иметь большую потерю точности. Например, если га = 10, a & = 5,
ь\
то — =CjO = 252 и, следовательно, можно ожидать потери двух
ьъ
знаков при каждом квадрировании. В случае близких по модулю
корней мы тоже будем иметь большую потерю точности и корни
по методу Лобачевского будут найдены с большой относительной
погрешностью. Точность будет тем лучше, чем лучше разделены
корни.
В случае наличия комплексных корней, но при ограничениях на
модули корней, при которых имеет место неравенство D2), заме-
заменяя Qk(t) через Q(*) = Qrni(O. получим:
ItJ
b'k\ ^ 1-<?<**)
т. е. и здесь по величине отношения ' ' Д '' можно судить о по-
потере точности в результате округлений.
5. Видоизменение Лемера метода Лобачевского. Наряду с ис-
исходным многочленом
P0(*) = ein'*« + e<0)*«-4- ••• +<V+<0' D5)
рассмотрим многочлен
f а'^'л;"-1 -+- ....-+- а^_гх -f а<У] 4-
+ h[ft№*n-i _|_ bpxn-г + ... 4-bW_xx -f- b^\ + ..., D6)
где h — произвольное действительное или комплексное число. В ра-
равенстве D6), как и всюду в дальнейшем, не выписываются явно
члены с А2 и более высокими степенями А. Очевидно,
bT = — (я —/+l)efi A=1. 2 п). D7)
В целях упрощения записи формул мы условимся в дальнейшем
считать все а\ \ b\ \ где / отрицательно или больше и, а также
Ьол> равными нулю. Будем квадрировать многочлен Q0(x). После

124 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
первого квадрирования получим многочлен Qt (х), коэффициенты
которого имеют вид
• • -K4-
х W
2 S(-
J=o
+ 2/t [>*f> + 2 (
Таким образом, Qi(x) примет вид
где
D8)
J-o
J-o
D9)
При последующих квадрированиях мы будем получать многочлены
Q2(x), <2з(*) коэффициенты которых находятся последователь-
последовательным применением формул D9), т. е.
Qk(x) =
где
2
J=o
Зг— 1
J-O
E0)
E1)
Обозначим корни уравнения Р
причем будем предполагать, что
\Xl\>\*2\>--->\*n\-
^0 через xlt x2,

§ 3] МЕТОД ЛОБАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 125
Корнями уравнения Q0(x) = 0 будут: xl-{-h, x2-\-h, •••, xn-\-h.
Если обозначить 2к через т., то корнями уравнения Qk(x) = Q
будут ^(Xl + h)m, —(x2 + h)m — {xn + h)m. He уменьшая
общности, можно предположить, что a(J>)=l, тогда и все а<й)=1.
Так как
+ A)w ...
• • • xf
-m *-т
n~lxn
+ h)m ... (*n
х™ + xf xf~l xf
и А—произвольное число, то
af) = xfx™ ...xf-\- xfxf .. . xf
4-
I — X\ X2 ' ' ' Xi i Xl Х-л Хз ' • • Xi I • • •
+ vm Ym v"* vm—1
An-i+l n-i+2 ' • ' лп-1Лп
Полагая здесь /=1, 2 n, получим:
а(к) _ ^ _(_ д _|_ ^
• • • хп'
bV^xT'xl
4"
m-1 m m . m m—i m
vj лз * * • Хц —y~ X\ лз Л3
>
-1 ^m , ^m ^m-i , jm-\^m _j_ , ^w-l m
E2)
4-
,m „m-l
.-^ .-^ .-W—l
E3)
. J

126 PEIUFHHE АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Предположим сначала, что
l*ll>l*2l> ••• >\Хп\.
Тогда
(A)
гхТ,
> X\ i
t-l «i , m m-1
Л^ -j— Л1 Л2 }
1 _1_ vm
-f- Xi
,m „m-1
H '^^^ "^1 Ли • • • Лу|. t ^Tl '^^^ А] Л3 Л3 • • • Ад ~f~"
1 vm m m m ,
-)- Al Л2 ^з ... Xn -f- . . .
1 ..m „m „m „»n -1
Полагая ct = -yp- ¦ получим:
E4)
или
1,1,
1
х,
, 1 _i 1 _i *
E5)
Если корни действительны, но

§ 3] МЕТОД ЛОВАЧЕВСКОГО РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 127
то из E2) и E3) имеем:
„(M ^ r% v2m
Й2 Sf C,Xi ,
откуда
ГШ-1
in. m-\ , .„»»»-1
r+i -*r+a . . . xn —f- . . .
r + i ... Xn-\Xn ) -+-
—(— ГА] Лг+1 . . . Лп ,
Xr+1
E6)
Следовательно,
+
xn xl
ч~"Ж
> xr-f
cn cn-l
E7)
Рассмотрим теперь случай, когда имеется пара комплексно-
сопряженных корней. Пусть это будут корни хи х2:
Xi = u (cos ср 4-1 sin ср), х2 = p<cos w — i sin ср).
Относительно остальных корней предположим, что они удовлетво-
удовлетворяют условию
I *1 | = I
\Xn .

128 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Тогда из E2) и E3) следует, что
dp = 2Pm cos m<p + х? + .... tip = 2?m~l cos (« — l) ? +
cos i»? + ..., MP = 2P3m-' cos ? +
~lxf cos(m~ 1) <p —)— ....
1jcfcos<p-|-
n — p хъ ... xn, 0n = zp ^з ... xn cos <p
+ j-ra j-m j-ш j-m—1\
A3 A4 ' ' * An-l.An /•
ИЛИ
2m
3m^\ /?\ ?Jml E8)
т. е. мы найдем р и coscp, а следовательно и jclt и л2- Далее,
a?^pimxf, br^Pmxf-1^-2P2m-ixTcos<?, x3^-^-^ E9)
Остальные корни находятся так же, как и в предыдущих случаях,
по формулам E5). Можно рассмотреть аналогично случаи, когда
кратные или комплексные корни имеют промежуточные модули.
Наличие комплексных корней и их место обнаруживаются так же,
как и в методе Лобачевского.
Видоизменение Лемера метода Лобачевского имеет несомненные
преимущества по сравнению с обычным методом Лобачевского, так
как при его применении не приходится извлекать корней высоких
степеней, а также при наличии различных корней с одинаковыми
модулями нет необходимости разъединять эти корни, рассматривая
уравнение Р(х — А) = 0 и применяя к нему повторно метод Лоба-
Лобачевского.
§ 4. Итерационные методы решения алгебраических
и трансцендентных уравнений
Для решения алгебраических и трансцендентных уравнений вида
Дх) = 0 разработано много различных итерационных методов. Сущ-
Сущность этих методов заключается в следующем. Пусть известна доста-
достаточно малая область, в которой содержится единственный корень
х = а уравнения
/ 0. A)

§ 4| ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 129
В этой области выбирается точка х0 — начальное приближение
корня, — достаточно близкая к искомому корню .* = а1 и с помо_цыо
некоторого рекуррентного соотношения
строится последовательность точек хх, х2, ¦ ••, хп, ..., сходящаяся
к х = а. Сходимость последовательности обеспечивается соответ-
соответствующим выбором функции <pft и начального приближения х0. Выби-
Выбирая различными способами функцию <pfc, которая зависит от f(x)
и в общем случае от номера k, можно получить различные итера-
итерационные методы.
Чаще всего по функции f(x) строят функцию <р (*) такую, что
искомый корень х = а уравнения A) является и корнем уравнения
х = ? (*). C)
и затем строят последовательность \хп\ с помощью соотношения
i) (я=1- 2, ...)• D)
исходя из некоторого начального приближения х0. В этом случае
функция <р не зависит от номера k, и методы такого типа мы будем
называть стационарными.
Ниже мы исследуем ряд стационарных и нестационарных методов.
1. Принцип сжатых отображений и его применение к доказа-
доказательству сходимости итерационных методов. Для исследования
сходимости итерационных методов, а также для доказательства суще-
существования корня уравнения широко применяется принцип сжатых
отображений, который мы сформулируем и докажем в общем виде
и в форме, удобной для наших целей.
Пусть R — некоторое метрическое пространство, а Ах — некото-
некоторый оператор, определенный на этом пространстве. Будем говорить,
что этот оператор осуществляет вжатое отображение R в себя,
если существует такое положительное число а, меньшее единицы,
что для любых двух элементов х, y?R имеет место неравенство
р(Ах, Ду)<ар(*. у), E)
т. е. оператор А сближает элементы.
Теорема (Принцип сжатых отображений). Если R — полное
метрическое пространство, а оператор Ах осуществляет сжа-
сжатое отображение R в себя, то существует одна а только одна
неподвижная точка этого отображения, т. е. уравнение
Ах = х F)

130 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
имеет одно и только одно решение. Решение этого уравнения
может быть получено как предел последовательности
xk = Axk_l (k= 1, 2, ...), G>
где хп—произвольный элемент из R.
Доказательство. Пусть х0 — произвольный элемент из R.
Образуем последовательность G) и докажем, что она является
фундаментальной последовательностью. В самом деле, если п ^> т, то
1, Ллг^Хар(*„_!, хт_х),
n_m, x0).
Следовательно,
р(хп, хт)^атр(хп_т, х0).
Но
Р(хп-т. ^
Таким образом,
ат
Р(х„, xm)<jzr
что и доказывает фундаментальность последовательности \хп}, так
как при достаточно большом т и любом га > /и правая часть послед-
последнего неравенства может быть сделана меньше любого заданного
положительного числа.
Из полноты пространства R следует существование элемента
x?R, к которому сходится последовательность [хп\, т. е.
х = lim *n.
Далее, так как
п, х)
и р(^п, х)->0 при и-> оо, то lim Axn = Ax. Но Акп = *я+1-> *.
П->- сю
Следовательно,
х = Ах.
Для доказательства единственности допустим, что существуют
два неподвижных элемента х и у, т. е.
л; = Лл;, у = Ау, р (л;, j) =^= 0.
Но оператор Ах осуществляет сжатое отображение, поэтому
р (Ах, Ау) = р (х, у) < ар (х, у),
что невозможно, так как 0<а< 1.

§ Ц ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 131
Приведем еще одну теорему, которая уточняет доказанный выше
принцип сжатых отображений.
Теорема. Пусть в полном метрическом пространстве R
или на его части, содержащей окрестность S элемента у0:
S=\p(x, _УОХ>}, определен оператор Ах. Пусть для любых
х, y?S
р (Ах, Ау) < ар (х, у) E')
и
Р(АУо. Уо) <A—а)г, E")
где а— некоторое фиксированное положительное число, меньшее
единицы. Тогда в S существует одно и только одно решение
уравнения F), которое может быть получено как предел после-
последовательности G), где х0—произвольный элемент из S.
Эта теорема непосредственно следует из принципа сжатых ото-
отображений, так как если x?S, то
р (Ах, уп) < р (Ах, Ау0) -+- р (Ау0, у0) < ар (х, у0) 4- A — а) /•</•,
т. е. Ax?S. Это означает, что оператор Ах осуществляет отобра-
отображение S в себя. Из E') следует, что это отображение, сжатое.
Совокупность всех элементов S с тем же самым понятием рас-
расстояния р(х, у) можно рассматривать как полное метрическое про-
пространство, так как если \уп\ — любая фундаментальная последова-
последовательность элементов из S, то она сходится в R, т. е. существует
элемент y?R такой, что
у= lim yn.
Но р (уп, Уо) < г, отсюда lim р (уп, _у0) = р ( lim уп, у0) = р (у, уп) < г,
П > оо п ->> оо
т. е. y?S. Теперь уже утверждение теоремы прямо следует
из принципа сжатых отображений.
Рассмотрим применение этого принципа к исследованию схо-
сходимости итерационного метода решения уравнения
х = ср (х) C)
при некоторых ограничениях на функцию <?(х).
Предположим, что уравнение C) имеет корень л = а ив круге
R{\x — а|^г} функция ср(*) удовлетворяет условию Липшица
К|*' — х"\ C)
для любых точек х', x"?R.
Теорема. Каково бы ни было xo?R, последовательность
= \, 2, 3, ...) D)

132 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
сходится к а, если только ср (х) в круге R удовлетворяет усло-
условию Липшица с константой /С< 1, причем скорость сходимости
характеризуется неравенством
|*п—«1<**о —«I- (9)
Доказательство. Совокупность точек круга R, если опре-
определить расстояние между точками х и у соотношением р (х, у) =
— \х—у\, образует полное метрическое пространство. Если x?R,
то у = <?(х) также принадлежит R, ибо
Р СУ. <*) = \У — «I = I <Р (х) — <Р (а) |< К | х — а |< г.
Отображение, определяемое функцией ср (х), есть сжатое отображе-
отображение R в себя, так как для любых х, y?R
(*) —<рСуI<к|*— у\ = Кр(х, у) и к<\.
Поэтому по принципу сжатых отображений в R существует одна и
только одна неподвижная точка, но эта точка х = а. Эту точку
можно получить как предел последовательности
*ft = (p(*ft-i) (*= 1. 2, ...)
при любом хо? R.
Используя условие Липшица (8), имеем:
I хп — а | = | ср (*„_!> — ср (а) |< К\ хп_х — а|,
т. е.
Таким образом, {хп} сходится к а со скоростью геометрической
прогрессии со знаменателем К.
В доказанной теореме мы предполагали существование корня
уравнения C). Принцип сжатых отображений может быть исполь-
использован и для доказательства существования корня.
Теорема. Если функция ср (х) в некотором круге R {| х — х01 ^ г)
удовлетворяет условию Липшица (8) с константой К <С 1 и
в точке х0 имеет место неравенство
\х0— <Р(*о)КA— К)г, A0)
то в R уравнение C) имеет единственный корень х — а, кото-
который может быть найден как предел последовательности
где у0 — любая точка из круга R.
Доказательство. Пусть x?R. Тогда
| ср (*) — Х0 | = | ср (х) — ср (ХО) + ср (*о) — Х0\<
— *оЦ-A—/0

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 133
т. е. функция у(х) осуществляет отображение R в себя. Это — сжа-
сжатое отображение, так как для любых х, y?R
р(<р(*). <?(у)) = \<?(х) — <?Ш<К\У — *\ = Кр(х. У)-
Следовательно, имеет место принцип сжатых отображений, из кото-
которого прямо следует теорема.
Мы требовали от функции у(х) выполнения условия Липшица
с константой /С<1 в некоторой окрестности корня л = а уравне-
уравнения C). Чаще всего функция ср (х) имеет производные, и условие
Липшица с константой К < 1 будет иметь место, если в некоторой
окрестности корня х = а функция ср (х) имеет производную ср' (х),
по модулю меньшую некоторого числа, меньшего единицы, т. е.
|<р'(*)|</С<1. A1)
Если производная ср' (х) непрерывна, то из условия [ ср' (а) [ <[ К < 1
следует выполнение этого неравенства в некоторой окрестности
корня х = а, и для отыскания этого корня можно применить метод
итераций, выбирая начальное приближение х0 из этой окрестности.
Скорость сходимости будет тем больше, чем меньше К.
Введем понятие порядка итерации D) для решения уравне-
уравнения C). Будем говорить, что итерация D) имеет порядок т., если
ср' (а) = ср"(а) = ... = cp(»-i)(а) =0, ср('») (а) ф 0. A2)
Если ср (х) имеет в окрестности корня т. непрерывных произ-
производных, то по формуле Тейлора
у (*) — а = (* — а) у' (а) -+- (х ~ а)" у" (а) + ...
В случае итерации порядка т имеем:
откуда
х
хк-а= К к-1т{ > <р(«> (У. A3)
Обозначая через Мт максимум модуля ср<то) (х) в некоторой фикси-
фиксированной окрестности корня х = а, получим неравенство

134 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
из которого следует:
. +т
к-1
тК-\
Таким образом, если \х0 — а\ < 1 и
хп —
m-1
A5)
ml
— а | = ш < 1, ТО
\хк — а\
m-1
A6)
что дает очень быструю сходимость лй к а.
Для случая, когда ср (х) — действительная функция переменного х
и х = а — действительный корень уравнения C), метод итерации D)
имеет хорошую геометрическую интерпретацию. На рис. 6 и 7
Рис. 6.
изображена геометрическая картина метода итераций D) для слу-
случаев, когда 0 < ср' (*)< К < 1 и — 1 < — К < ср' (*)< 0.
Геометрически видно, что если в окрестности корня х = а имеет
место неравенство 0 < ср' (х) ^.К < 1, то последовательность [хп\
монотонно сходится к корню, причем с той стороны, с которой распо-
расположено начальное приближение х0, а в случае — 1 < — К < ср' (х) < 0
последовательные приближения расположены поочередно с разных
сторон от точки х =а. В последнем случае по двум последова-
последовательным приближениям корня можно судить о достигнутой точности
на каждом шаге, так как отклонение хп от а не больше \хп — хп_1\.
Эти утверждения можно доказать и аналитически, но мы не будем
останавливаться на этом доказательстве.

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 135
2. Простейшие итерационные методы: метод секущих и метод
Ньютона. Если уравнение f(x) = 0 имеет корень х = а, а функ-
функция ty(x) непрерывна в окрестности х = а, то уравнение
A7)
также имеет корень х = я. Функцию ty(x) можно подобрать так,
что итерационный процесс для уравнения A7) будет сходящимся.
Рассмотрим два классических метода, которые можно получить
этим способом.
Пусть f(x)—действительная функция действительного перемен-
переменного х, а х = а — действительный корень уравнения f(x) = 0. Пред-
Предположим, чю в некоторой окрестности точки х = а функция / (х)
вместе с /'(•*) и /" (х) непрерывна, а /' (х) и /" (х) в этой окрест-
окрестности не меняют знака. Это означает, что при переходе через х = а
функция f{x) меняет знак и имеет точку х=а простым кор-
корнем. Пус1Ь х0—точка рассматриваемой окрестности, в которой
f(xo)f"(xo) > 0- В A7) в качестве функции ty(x) возьмем функцию
Тогда уравнение
Y — mlY^—r x — x0 f(Y,_ xof(x)~xf(xQ)
X — ср (X) = х тг-г-т flr\ J \x) 7~Пл ft v \— A °)
/ I*) — / (xo) I (X) — / (x0)
также имеет корнем х = а. За начальное приближение примем любую,
достаточно близкую к а точку xt рассматриваемой окрестности,
в которой /(х{) имеет знак, противоположный знаку f (х0), а после-
последующие приближения будем строить обычным способом:
„ xof{xn-l) — xn-lf (хо) /„ О Q \ /1П\
п — ТТх \ tix \ \п — z> "¦ •••)• (,iy)
Так как, с одной стороны,
, ,„,. _ [ХрГ (а)—/(Хр)] У (я)— f(x0)] —f (a) [xof (a) - af (x0)]
а с другой стороны, по формуле Тейлора
/(*) = f(a)+(x — a) f (а) + (дг~а)* /" (?),
где. $ заключено между а и х, то, полагая х = х0, получим:
Следовательно,
/(*о) -+- (а - х0) /' (а) - (Хо~аJ /" (Е).
-°)г /" F)
2 /(х0)

136 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
При Xq, достаточно близком к х = а, <р' (а) — малое число, и поэтому
существует такая окрестность точки а, в которой будет иметь место
неравенство
|
и если Xi взято из этой окрестности, то последовательность A9)
будет сходиться к х = а.
Так как /(*„) = /(*„) — Да) = /'(?)(*„ — а), то, положив
min
т. =
f (х)\, будем иметь:
B0)
что позволяет на каждом шаге по значениям /(х„) следить за до-
достигнутой точностью.
Геометрически этот метод состоит в том, что значение хп+1
есть абсцисса точки пересечения прямой, проходящей через точки
(*о. /(*о)) и (*»• /(*»))¦ с осью х (рис. 8). Поэтому этот метод
y-ffX)
у JfM<0,f"(X)<0)
Рис. 8.
называют методом секущих или методом линейной интерполяции,
так как на каждом шаге за приближенное значение корня хп+х при-
принимается корень интерполяционного многочлена первой степени,
построенного по значениям f(x) в точках х0 и хп.

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 137
Метод секущих является итерационным методом первого порядка.
Второй классический метод решения уравнения f(x) = О— метод
Ньютона — получим, если положить в A7)
т. е. свести отыскание корня х = а уравнения f(x) = 0 к отысканию
корня уравнения
х = х-$± = 9(х). B1)
Будем предполагать, что на отрезке [а, Ь], содержащем един-
единственный корень х = а, уравнения f(x) = 0, функция f(x) имеет
непрерывные производные /' (х) и /" (х), не обращающиеся в нуль
на этом отрезке. В этом случае
и ср'(а) = О. Это означает, что существует такая окрестность точки
х = а, что если начальное приближение х = х0 взято из этой окрест-
окрестности, то последовательность
*» = *»-1--Й§Ц- («=1. 2. ...) B2)
будет сходиться к .* = а. Начальное приближение х0 целесообразно
выбирать так, чтобы было
О. B3)
Метод Ньютона применим не только для отыскания действительных
корней уравнения f(x) = 0, но и комплексных корней, только нужно
иметь в виду, что при отыскании комплексного корня в случае дей-
действительной функции f(x) начальное приближение х0 нужно брать
комплексным числом, а не действительным.
В случае, если х = а, является действительным корнем уравнения
f(x) = 0, этот метод имеет простую геометрическую интерпретацию.
Значение хп+1 есть абсцисса точки, пересечения касательной к кри-
кривой y = f(x) в точке х = хп с осью х (рис. 9). Поэтому метод
Ньютона часто называют методом касательных.
Как видно из рис. 9 последовательные приближения к дей-
действительному корню в методе Ньютона сходятся к нему монотонно,
приближаясь со стороны х0.
Если за начальное приближение в методе Ньютона взять точку х0,
где f(xo)f"(xo) < 0, то, как видно из рис. 10, мы можем не прийти
к корню х = а, если только начальное приближение не очень
хорошее.
Так как в методе Ньютона ср' (а) = 0, a cp" (а), вообще говоря,
не равна нулю, то метод Ньютона является итерационным методом
второго порядка.

138 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
rff y (f'lx)<0/"(x)>0)
л
у (Лх)>оЛх)<о)
ХрХ,
Рис. 9.
Ряс. 10.
.Хг\Х,Х0

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 139
Скорость сходимости метода Ньютона можно оценить следующим
образом. По формуле Тейлора
О = / (а) = / (хп) + /' (хп) (а - хп) +-1 /" (?) (а - xnY,
где k заключено между а и хп. Отсюда
*» а 2 /' (*)(а *«> •
Следовательно,
] /(S) (а
Если OTt = min | /' (х) |, я /И2 = max |/" (jc)|, где [а, Ь\ — отрезок,
\а. Ь] [а, Ь]
содержащий х0 и а, на котором не меняют знака /' (х) и /" (х), то
ии + 1-а|<^-|^и-а|2- B4)
Это указывает на быструю сходимость метода Ньютона.
Комбинируя метод секущих и метод Ньютона, можно получить
нестационарный метод отыскания действительных корней уравнения
f(x) = 0, преимущество которого заключается в том, что при прежних
предположениях относительно /' (х) и /" (х) последовательные при-
приближения хп и xn+i лежат по разные стороны от корня, и по-
поэтому можно следить в процессе вычислений за достигнутой точ-
точностью, и в то же время он сходится значительно быстрей метода
секущих.
Пусть на отрезке [а, Ь] содержится единственный корень урав-
уравнения f(x) = 0, a /' (х) и f"(x) на эгом отрезке не меняют знаков.
Если /(а)/"(о)>0, то находим х0 и xt по формулам:
а следующие приближения находим по формулам:
Л2п — Л2и-2
ъп-Ъ) J\xin-\) — / \x1n-i)
Если же f{b)f"(b) > 0, то х0 и хх находим по формулам:
Х-Ь-Ш- х _
°~ /'(ftI l~

140 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ ]ГЛ. 7
а следующие приближения—по тем же формулам B6). Как видно
из рис. 11, последовательные приближения х2п и x2n+i всегда рас-
расположены по разные стороны от х = а и первые совпадающие знаки
xin и *2и+1 и будут верными знаками для х = а.
Рис. 11.
3. Метод Чебышева построения итераций высших порядков.
В 1838 г. П. Л. Чебышев предложил метод отыскания действительных
корней уравнения f(x) = 0, частными случаями которого явились
многие, разработанные до него методы. В основе метода Чебышева
лежит представление функции, обратной к функции f(x), по фор-
формуле Тейлора.
Пусть уравнение f(x) = 0 на отрезке [а, Ь] имеет корень х = а.
Относительно функции f(x) предположим, что она непрерывна на
отрезке \а, Ь\ вместе с производными достаточно высокого порядка
и /'(х)Ф0 на \а,Ь\. При этих предположениях функция y = f(x)
имеет обратную функцию x = F(y), определенную на отрезке [с, d],
являющемся областью значений f(x) при х?\а, Ь\. Функция F(у)
имеет столько же непрерывных производных, сколько имеет и f(x).
Так как
x = F\f(x)] (x?\a,b]). y=f\F(y)] (y^lcd]). B7)

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 141
ТО
a=F@). B8)
При у?[с, d] формула Тейлора дает
^^ B9)
где остаточный член может быть записан в виде
Яг+1 = (-1)г+1^т$У+1 C0)
(т) заключено между 0 и j/), или
f^^(x)r\ (si)
Для упрощения записи положим
г
Уравнение
х = <?г(х) C3)
имеет корень х=а, так как cpr(a) = a—V(—1)*—^гр- [/(«)]*= a.
ft-i
Положив
xn+1 = cpr(xn) (« = 0,1 *o€[e.*l). C4)
получим итерационный метод (г —|— 1)-го порядка, так как
<рв)(а) = О (/=1. 2 г).
Если л:0 взято достаточно близко к а, то последовательность \хп\
сходится к а, ибо существует такая окрестность точки а, в которой
|?'(*)|"<*<1.
и для сходимости [хп\ нужно только потребовать, чтобы д:0 при-
принадлежала этой окрестности.
Функцию <fr(x) можно найти в явном виде через /(лг) и ее про-
производные, так как из тождества B7) имеем:
Р" 1/ (*)] /'* (х) + F' [/ (х)} f" (х) = 0,
F" [/ (*)] Г3 (х) + ZF" [/ (х)] /' (х) f" (х) + Г [/ (х)] /'" (х) = 0

142 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
ИЛИ
a1(x)f'(x)=l.
в1 (х) /'" (х) = О,
C5)
т. е-, можно последовательно найти ai(x), a2(x) а следовательно,
и срг (л:). При г = 1
/<*)
/<*П)
C6)
т. е. мы снова получаем метод Ньютона. При г = 2
/'W
/'
2/'8
C7)
Оценка погрешности и скорость сходимости легко получаются
из равенства C1). Полагая в нем х = хп и учитывая C4), получим:
C8)
где I лежит между а и л:га. Если положить L= max |/'(аг)|,
ajglo, Ь]
Mr+1= max |/='('"+1)[/(л:)] | и учесть, что
ж?[а, 6|
то из C8) имеем:
Отсюда следует, что
[а_ Хт
Таким образом, если |л:0—а| < 1 и q\x0— <
|^ш<1, то
D0)

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 143
что указывает на очень быструю сходимость метода. Так, если
ш<0,1 и |л:0—а|<1 то при г=1 (метод Ньютона)
|a — *i|<10 \ (a—л:а[<10 3, fa — лг3|<
при г=2
la — jcKKT15.
1а—XiKKT1, \a — *21<1(Г4,
т. е. количество верных десятичных знаков быстро возрастает.
4. Построение итераций высших порядков с помощью тео-
теоремы Кёнига. А. Теорема Кёнига. Прежде чем излагать указанный
метод построения итераций, докажем теорему Кёнига.
Теорема. Если f{z) и cp(z)— аналитические функции в об-
области |г]<г, содержащей единственный корень z = a уравне-
уравнения f(z)= 0 кратности единица и ср (а) =?^= 0, то
а= lim -?2-, D1)
»> со СП+1
?де сп — коэффициент при zn в разложении yfl no степеням z.
Доказательство. Так как для функции ^ точка z = a
является ближайшей к началу координат особой точкой, то ряд
сходится при всех |г|<а, а ряд
hf>-*" D3>
п=о
сходится при всех z, для которых |г|<г. Отсюда
^cnzn(z-a)=^dnzn
»=о »=о
и
— aco=fifo. cn-i— *сп = <*п («—1,2,...). D4)
Таким образом,
2 k = — ас0 + 2 (<%_i — acft)a* = — cma»+i. D5)
k=0 k=l

144 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Если положить
то из D5) имеем:
D6)
D7)
ст+\
D8)
Если р—некоторое число, удовлетворяющее неравенству |а| <р <г,
то ряд D3) сходится при 2 = р и | dnpn | -» 0. Пусть Л = max| fifrap"|.
Тогда га
D9)
Так как
то при 0 < 8 < В, где S=|S(a)|, существует такое щ, что при
ж>/«о и |l §
a —
А \<х
\т+2
Аа
pm+l В —I
В — Ь \\ р
m+l
E1)
Но
1, поэтому правая часть в E1) стремится к нулю при
т -*¦ оо, т. е.
Hm
Если функция f(z) имеет единственный простой корень 2 = а
в области \z — лг|<г, где х — некоторое число, а f(z) и cp(z) —
аналитические функции в этой области, причем ср(а)=?О, то из тео-
теоремы Кёнига следует, что
Cn{x\
a — x= Hm
где сп (х) — коэффициент при (z — х)п в разложении
по степеням z — х.
Рассмотрим уравнение
х = ср (*) == *
с„(х)
(Р>Щ)
и итерацию
= 0,1,2,...).
E2)
в ряд
E3)
E4;

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 145
Докажем, что последовательность \хп) сходится к а, если л:0 доста-
достаточно близко к а, и итерация E4) имеет порядок не ниже р -4- 2.
В самом деле, если
П=0 n—0
то совершенно аналогично равенству E0) имеет место равенство
где
Sp+l(a, x)= S
ft=0
Отсюда видно, что а—fp(x) имеет множитель (а — x)p+i, поэтому
ср (а) = а и tpW(a)^0 при 1=1, 2, ..., /?-(-1. Это и означает,
что итерация E4) имеет порядок не ниже р -4- 2 и будет сходиться
к а, если д:0 взято из окрестности \z—а|^р, в которой
Б. Построение итераций высших порядков. Функцию срр (х)
можно находить разными путями. Прежде всего, так как ср(х) есть
коэффициент разложения 44—г по степеням z — х, то
E7)
Если известны разложения функций f(z) и ср B) по степеням 2 — л::
/ (г) = 2 ^ (*) (^ - *)*: ср B) = 2 h (х) (z - x)ft, E8)
то
от оо
— X)" = 2 ^ (*) B — X)* • 2
ft-o ft=o

146 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
откуда
bo(x) = ao(x)co(x),
bt (x) = at (x) c0 (x) 4- a0 (x) Cj (a:),
Z>2 (a:) = a2 (a:) c0 (a:) 4- «i (a:) ct (a:) 4- ao (x) c2 (л:),
E9)
bp (x) = ap (at) c0 (a:) 4- ap_! (a:) c1 (x) 4- ... 4- a0 (*) cp (a:),
и Cjc(x) можно найти, используя эти рекуррентные соотношения.
Рассматривая E9) как систему линейных уравнений относительно
со(х), с1(аг), ..., ср(х) и решая ее по правилу Крамера, получим:
до(х) ао(х) 0 0 ... О
*i(jf) М-*) flo(*) 0 ... О
Ьр(х) ар(х) вр_,(дс) ep_s(Jc) ... ei(Jt)
F0)
а0 (х) Ар (х)
х- д>+1(х) .
Заметим, что при ср(,г) = 1 и р = 0 мы снова приходим к методу
Ньютона.
б. Метод Эйткена построения итераций высших порядков.
Эйткен предложил способ получения из данной итерации или из двух
данных итераций одного и того же порядка итерации более высо-
высокого порядка.
Пусть имеются итерации
порядка г, сходящиеся к х=а. С помощью функций <?i(x) и ср2(лг)
построим фунцию Ф (х):
/сеч
Jt - Ti W - % W + Ti [ft W]( '
Тогда итерация
а:„=Ф(а:п_1) (я=1, 2, ...) F4)
имеет порядок выше г, если только выполнено условие
[ср;(а)-1][ср»-1]^0. F5)
Для доказательства этого утверждения заметим, что последова-
последовательность у& = х<?> — р (/ = 1, 2) сходится к а — р и получается
при решении уравнения
(/=1.2) F6)

§ 4] ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ 147
методом итераций, так как
При р = а члены последовательности ¦»]?) = л;?)— а представляют
отклонения х?> от точного значения корня а и получаются приме-
применением метода итераций к уравнению
— a. F7)
Так как ср^ (л:) определяет итерацию порядка г, то имеет место раз-
разложение
Ml) = <*?4" + <*?.Mr+1+ ••• F8)
Далее,
ф / | ач _ а _ A + а) ?1 [?2 A + а)] — Ч\ A + а) St (i + а) _ a __
1 + а — <Pl (I + а) — <РЗ A + а) + ?1 [?2 A + а)]
__ 0] + а) ?t ["а (^) + а1 — И (i) + а1 [<"з A) + а1 а_
а — [<о, (т;) + а] — [<о, (т)) -f a] -f tpx [<o2 (т)) -f a]
а) {"t [ Oi)] + а> — [ (i) + а1 [< (Ti) + а]
) — <о1 (f)) — <o,s (т;) — a + <ot [<o2 (т,)] -f a
i)]—М1 (^)  (ii) + а { [<Q2 (i)]—
+ <ol[«2Ai)]
Подставляя разложения F8) в F9), получим:
| г) ct_^[41)KV+-)r+...l-K
При г >¦ 1 наименьшая степень t] в числителе 2г, а в знаменателе 1,
следовательно, разложение Ф(т) + а) — а по степеням т\ начинается
с ^Зг~1, т. е. Ф(г)(а) = 0 при 1=1, 2 2г — 2, что означает,
что итерация F4) имеет порядок не ниже 2г— 1. При г= 1 наимень-
наименьшая степень т) в числителе не меньше трех, так как члены со вто-
вторыми степенями взаимно уничтожаются, а в знаменателе т\ входит
с коэффициентом
1 - «A) _ а(щ + a(i,aC) = (! _ a(i)) A _ вр,) = [ 1 _ ср; (а)] [ 1 - ср^ (а)].
Если это произведение не равно нулю, то первая степень в разло7
жении знаменателя присутствует и разложение O(a-f-7j) — a no

148 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
степеням т) начинается по крайней мере с if. Следовательно, Ф'(а)=0
и итерация F4) имеет порядок не меньше двух.
В частности, можно положить ср(д-) = срх(jc) ^= ср2(д:); тогда
определяет итерацию не ниже второго порядка, если ср(д-) опреде-
определяет итерацию первого, и не ниже Bг—1)-го порядка, если ср(д-)
определяет итерацию порядка г.
Заметим, что если итерация, определяемая функцией ср(д-), не
сходится, как бы близко к а мы ни выбирали начальное приближе-
приближение л:0 (что, например, будет при | ср' (а) | > 1), итерация, определяе-
определяемая функцией, построенной по формуле G0), будет сходящейся при
выборе начального приближения, достаточно близкого к а, так как
Ф' (а) = 0 и существует окрестность х = а, в которой | Ф' (х) | ^ К < 1,
а это является достаточным условием сходимости итерации, если
только х0 взято из этой окрестности.
При построении итерации
*n=*(*n-i) (»=1. 2. ...),
где Ф(х) определена равенством G0), нет необходимости в явном
виде находить Ф (х), а можно поступать следующим образом. Исходя
из л:0, находим:
() И Jf2=tp(jf1).
Затем определяем х3 с помощью соотношения
где положено
Далее, находим:
и
•^ft ^^ ^ TT~ i ~—
и т. д. Получим нестационарной итерационный процесс:
*М+1 = ?<*«).
+ l). (/=0, 1, 2, . ..).
Точно так же как по ср строилась итерация Ф более высокого
порядка, можно, исходя из Ф, построить итерацию еще более высо-
высокого порядка и т. д.

§4]
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ
149
6. Пример. Проиллюстрируем некоторые из рассмотренных в этом
параграфе итерационные методы на примере отыскания корня урав-
уравнения
/ (л;) = л;3 4- 5л;2 — 15л; — 7 = О,
расположенного между л;=2,4 и х =2,5.
1. Метод секущих.
„ XqJ \Xji~ l) Xji—if \Xq) . л « ..
X n ^= -j- г -7-. г \Jl ^, О, . • . ),
/ (xn-\) —f(x0)
л;0^2,5, f{x0) = 2,375. Начальное приближение л;1 = 2,4,
q) = — 0,376.
п
1
2
3
4
2,4
2,4136677
2,4141927
2,4142128
t(xn)
—0,376
—0,0145312
—0,0005555
—0,0000205
х°Чхп)-хпПхо)
—6,6400
—5,7687888
—5,7350965
—5,7338049
Н*п)-П*о)
—2,751
-2,3895312
—2,3755555
—2,3750205
хоНхп)-хпНхо)
''n+1 1(хп)~Пхо)
2,4136677
2,4141927
2,4142128
2,4142128
т= min I/'(л;) 1 = 28.28, I л:4 — а|< lf{Xi
[2,4; 2,5] т
2. Метод Ньютона.
<8 • К
Г7
хп хп _ j ,,
Г (Xn-l
(я=1. 2, ...), а-0=2,5.
л
0
1
2
3
2,375
0,0843686
0,0019769
0,0000010
28,75
27,3043304
26,6292347
26,6274179
/(-%)
/' <*п)
0,0826089
0,0031035
0,0000742
0,0000000
2,4173931
2,4142878
2,4142136
2,4142136
3. Метод Чебышева третьего порядка.
fix») /*(*п-1)/»(*п
х —r
л
0
1
2
-0,376
0,0019956
0,0000012
/' {хп)
26,28
26,6292520
26,6274179
24,4
24,4857310
24,4852816
/' (JC»)
—0,0143075
0,0000749
0,0000000
2/'»(дс»)
0,0000190
0,0000000
0,0000000
Хп + 1
2,4142885
2,4142136
2,4142136

150 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
4. Метод Эйткена. Используя первые два приближения, полу-
полученные по методу секущих, найдем следующее приближение с по-
помощью равенства:
В этом случае л;1 = 2,4, х2 = 2,4136677, х3 = 2,4141927,
Если использовать первые три приближения, полученных по ме-
методу секущих, то
х -2 4П6677 I (О-0005250J -о 4Н2136
Значение искомого корня с восемью верными знаками
а= 2,4142136.
Таким образом, все восемь верных знаков мы получили по методу
Ньютона после трех шагов, по методу Чебышева третьего порядка—
после двух шагов и после трех шагов по методу секущих и после-
последующего уточнения по методу Эйткена.
§ б. Решение систем уравнений
Решение системы уравнений
*2. .-.. *п) = 0 (/=1.2 я) A)
представляет значительно более сложную задачу, чем решение одного
уравнения. Мы опишем только наиболее распространенные методы
решения систем.
1. Метод итераций решения систем специального вида. Пусть
известно, что система
Xi = cpiC^, x2 хп) A=1. 2 я) B)
в некоторой области пространства хи х2 хп имеет единствен-
единственное решение Xi=^ щ (/=1,2, ...,«), а лг'г0' — числа, соответственно
близкие к О| ((= 1, 2, ...,«). При некоторых ограничениях на
функции cpiC^i' x2, .... хп), исходя из этих приближенных значе-
значений, можно найти приближенные значения сц с наперед заданной
точностью. Это уточнение может быть выполнено с помощью ме-
метода итераций, заключающегося в том, что по дг^, х^\ ..., х^>
находится следующее приближение по формулам:
лга) = cpi(*№, xW jrW) (/=1, 2, .... и).

§ 5] РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ 151
По полученным значениям находятся
xf = срг (*U>, *?), .... *<!') A=1.2 я)
и т. д. Если найдено &-е приближение *<*>, *(*>, .... *М, то (k -f- 1)-е
приближение находится по формулам:
(/=1, 2 и). C)
Если при й->оо л^А)->оц (/=1, 2 я), то говорят, что метод
итераций сходится к искомому решению. Для того чтобы получить
решение с нужной точностью, практически продолжают процесс до тех
пор, пока два последовательных приближения будут совпадать с за-
заданной точностью.
Прежде чем формулировать условия сходимости метода, для
удобства записи соотношений и формулировок введем некоторые
понятия и обозначения.
Будем рассматривать xlt х2, .... хп как компоненты «-мерного
вектора х= (xlt x2, .... хп). Определив норму вектора х равенством
||л:||1= max |*{|, D)
i=i, а, ..., п
можно ввести понятие расстояния между векторами х' и х", положив
р (х', х") = ||*' - х"\\! = max К - х" | E)
Определим оператор
у = Ах, F)
где y=(ylt уг уп), a yi = <?i(x1, x2 хп).
Если положить лгD> = (х[к), *(*', ..., лг^Л, то вместо п равенств C)
можно писать одно векторное равенство:
Будем говорить, что система функций fi(x1, х2, .... хп) (t=\,
2, .... п) удовлетворяет условию Липшица с константой К в неко-
некоторой области О, если лля любых двух векторов *', x"?G имеют
место неравенства
IЬ (*') - Ъ (*") I < К р (х', х") A=1,2,..., п). (8)
Достаточное условие сходимости метода итераций для решения
системы B) дает следующая теорема:
Если на множестве R всех векторов х, для которых р (х, а) ^ г
{а = (а1, а2 ага)], система функций cpi(*i. х2, .... хп) (i=l,
2 п) удовлетворяет условию Липшица с константой К,
меньшей единицы, то при любом начальном векторе х@) ? R по-
последовательность
(/5 = 0. 1. 2, ...) G)

152 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
сходится к а, причем
p(.*W, а)<^р(#, а). (9)
Справедливость этой теоремы легко следует из принципа сжа-
сжатых отображений. В самом деле, оператор Ах осуществляет сжатое
отображение R в себя, так как если x?R и у = Ах, то
р(у, я) = р(Ах, Аз.) — max| ср{(х) — ср{(а) |<Кр(х, а) < г,
i
т. е. y?R. Далее, если х', x"?R, то
р(Ах', Ax") = max\<?i(x')—<?i(x")\^.Kp(x', x").
i
и так как К < 1, то отображение Ах— сжатое отображение R в себя.
Множество векторов R является полным метрическим пространством,
следовательно, по принципу сжатых отображений в R существует
одна и только одна неподвижная точка, т. е. одно и только одно
решение уравнения
х = Ах,
которое будет пределом последовательности G) при любом векторе
л:'0' ? R. Но так как а?/? и а = Ла, то а и есть неподвижная точка,
т. е.
а= lim л**>. A0)
к ->оо
Далее,
Р(аг№), оО^рСАх;'*-1), ЛаХ/СрС*:'*-1), а) A1)
или
р(л**>, аХ/СрС***-1), а)</С2р(л:(*-2), а)< . . . <Ккр(х^, а),
что и доказывает неравенство (9).
Если мы будем понимать под R совокупность векторов х,
для которых р(х> уо)-^г (у0 — фиксированный вектор) и в R си-
система функций <?i(x) (i= I, 2, ...,«) удовлетворяет условию
Липшица с константой /С < 1, а
р[Ау0, уо]<A—К)г, A2)
то из теоремы § 3, уточняющей принцип сжатых отображений, сле-
следует, что система B) имеет в R единственное решение, кото-
которое можно получить методом итераций, исходя из произволь-
произвольного лг(°>?Я.
Предположим теперь, что в некоторой выпуклой области О про-
пространства xv x2, ..., хп функции <?i(x) имеют непрерывные пер-
первые производные у< ' , Ж^-=:тах
oxj J q
и в области О система B)
имеет единственное решение а = @4, а2, .. ., ага). Предположим далее.

§ 5]
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
153
что при некотором начальном приближении лг(°) = Л*@>, х<®
все следующие приближения лК*> = (х^\ xf>, ... <№
(k=\, 2, ...
A3)
не выходят из области О. Тогда
я), A4)
где
~ *>—
некоторая точка отрезка прямой, соединяющей точки
1', .... -к^') и (а1; а2 а?1). Обозначим через Мк
матрицу
дх?
дхп
дх„
A5)
Тогда равенства A4) можно коротко записать в виде одного вектор-
векторного равенства
* -1) — а),
из которого имеем:
A6)
а.= Мк_.1Мк_2 ... УИ^о(лг(°) — а). A7)
Для того чтобы лг'4'->а при k ->oo, достаточно выполнения условия
Л1А._1Л1Й._2 ... M^Mq -*¦ 0 при й -> оо. A8)
Но это условие будет выполнено, если Мк -> 0 при k -*¦ оо, где
... Мп
так как элементы матрицы Mt по абсолютной величине не больше
соответствующих элементов матрицы М, а отсюда уже следует, что
элементы матрицы М:_1Мк_2 .. . МгМ0 по абсолютной величине
не больше соответствующих элементов матрицы Мч. Но для того
чтобы Мк —>¦ 0, необходимо и достаточно, чтобы все собственные
числа матрицы были по модулю меньше единицы, достаточным же

154 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
условием является условие, что какая-нибудь норма матрицы меньше
единицы. Если собственные значения матрицы М по модулю меньше
единицы, то лг'&'->а, а это означает, что если начальное прибли-
приближение выбрано достаточно близким к а, то все х^к) не будут выхо-
выходить из области О, и мы будем иметь теорему:
Если функции cp»C*i. х2, •••> хп) («=1. 2 п) в некото-
некоторой выпуклой области О, содержащей решение а = (ар а2 ага)
системы B), непрерывны и имеют непрерывные первые производ-
производные, то для сходимости метода итераций достаточно, чтобы
у матрицы A9), где УИ^=
дщ
все собственные значения
в
были по модулю меньше единицы, а начальное приближение
д-(°) = (х^\ atW, .... дг№) достаточно близко к решению а = (at>
a2 ara). В частности, это условие будет выполнено, если
какая-нибудь из норм матрицы М меньше единицы.
Из этой теоремы вытекают следующие практически более удоб-
удобные достаточные признаки сходимости метода итераций.
Для сходимости метода итераций решения системы B) до-
достаточно выполнения одного из следующих трех условий:
2Л1у<1 A=1. 2, .... я). B0)
П
2Л1у<1 C/=l. 2 я). B1)
i-l
S М\,<\. B2)
причем в этих случаях за л:'0) можно принимать любой век-
вектор л:@' из окрестности р (х, а)=\\х — а||г<;/- (/=1 или 2,
или 3, в зависимости от того, рассматриваем ли условия B0)
или B1), или B2)), а
II* —«Нз< V X (Xi-*iJ, B3)
¦если только эта окрестность целиком принадлежит О.
Неравенства B0) — B2) соответственно означают, что первая,
вторая или третья нормы матрицы М меньше единицы.
2. Метод Ньютона. Рассмотрим систему п уравнений с п не-
неизвестными
fi(xv х, xJ = 0 Q=l, 2, .... я). B4)

§ 5]
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
155
Относительно функций fi(x) предположим, что в некоторой вы-
выпуклой области О, содержащей решение o. = (o.v а2 ап) си-
системы B4), они имеют непрерывные производные первого порядка
и в некоторой окрестности решения а матрица
df\ dfi dfi
х, дх, '" дх„
/»(*) =
dxt
h
дх„
dfn dfn
дхп
B5)
не вырождена. При этих условиях решение а системы B4) можно
найти следующим образом. Пусть
=c?(x) = x—fxl(x)f(x).
»1 ?»2 • • • gnn
— матрица, обратная к fx (x). Рассмотрим систему уравнений
п
•*4=<Pi(*l. X2 Хп) = Xi — 2 gij (Xl Xn)fj(XvX2 Xj
(/= 1, 2 n), B7)
или коротко в векторной форме
B7')
Решение а = (ар а2 ага) системы B4) является и решением
системы B7), которая имеет специальный вид, рассмотренный в п. 1.
Покажем, что а можно найти методом итераций, описанным в п. 1,
примененным к системе B7), т. е. покажем, что последовательность
(ти=1,'2, ...
B8)
сходится к а, если только начальное приближение л;'0' взято доста-
достаточно близко к а. Для. этого воспользуемся очевидным равенством
— Уд yn + 4Zn—y^\(Z) —
0 j-l
B9)

156 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Введем обозначения:
Гц СУ- z^ = Jwrfi \Уг +'(*i —Уд У
о '
/^и (У. г) Fn(y, г) ... Fln(y, г)\
F(y, z) = ( рк(У' г> ^«(У- г> ••• Р**{У. г)\ C0)
\/?ш(у.г) ^2(У. *) ... Fnn(y,z)J
Очевидно, что при y=z = x
Fifix. х) = Щ&-. F(x. x) = fx(x). C1)
f(z)-f(y) = F(y, г) (г-у). C2)
Так как
хС») = ср (дгС»- Ч), а = ср (а), C3)
то
— а = ср (лг("»-1)) — ср (а) = л*»»-1) — а — /^
= х(те-" — а - /-1 (je(«-4) 1/(л(»-«) — / (а)], C4)
ибо
/(а) = (Л(а1, а2 а„) /„(aP <% ап)) = 0.
Используя C2), можно записать C4) в виде
— а = *(«->) — а — fv\xlm-l)) F (х{т-1}, а) (х*"* — а) =
-!), а)) (х(т~Ч — а), C5)
где / — единичная матрица. Матрица F(_y, z) является непрерывной
функцией своих аргументов, и при x = y = z F(x, x) = fx(x).
Если дК°> достаточно близко к а, то ^(л:'0', л:'0») = fx (x^) ф 0 и
/a'C^W', *«») = /, а матрица Z^1 (л;@>) F (*@). а) достаточно
близка к единичной матрице /, а / — fxl(*P)F(*?> a) близка к ну-
нулевой матрице. Как бы мы ни определили норму вектора х и соот-
соответственно норму матрицы, имеет место неравенство
а [| = || [/ — / (*<«>>) F (*(°>, а)] (х<°) — а) || <
< II / — fx1 (x'°>) F (х<°), а) || • |1 *(°) — аЦ. C6)
Так как нулевая матрица имеет норму, равную нулю, а
l, a)

§ 5] РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ 157
близка к нулевой, то существует такое 8 > 0, что если р (х, а) ^ 8, то
\\I-fZ\x)F{x, а)||</С<1. C7)
Если р (д<°), а) ^ о, то
р(д:A), а)= ЦлК1)—а||</С||дКо)—а||=/Ср(АК°), a)</C8<8.
Следовательно, и
Предположим, что мы уже доказали, что
1», а)<8,
•• «к*- <38)
Тогда
'), а)] (л:'™) — а) ||<
С 8,
т. е. р(л:(то+1», а)<8 и по C7)
||/ f^1 (x^m+v>) F (x^m+v>, а) || < /С.
Таким образом, неравенства C8) справедливы при всех т. После-
Последовательно применяя их, получим неравенство
¦). а)</Стер(л:@), а). C9)
Так как К < 1. то при т -> оо К™ -*¦ 0 и
lim p (л:(те), а) = 0, D0)
что и доказывает сходимость процесса итераций к решению си-
системы B4). На начальное приближение л:@) накладывается условие,
что оно должно принадлежать окрестности р(лг, а)<; 8, в которой
имеет место неравенство C7).
При более жестких ограничениях на функции fi(xv x2 хп)
можно доказать более сильную теорему, доказательство которой
можно найти в статье Л. В. Канторовича «Функциональный анализ
и прикладная математика» (УМН, т. 3, вып. 6, 1948):
Теорема. Если в области О функции fi(xv x2 хп)
имеют вторые производные, не превосходящие по абсолютной
величине числа L, в точке д<°) ? О матрица fx(x) не вырождена
и выполнено условие
h = M2L 8«2 < -1, D1)

158 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
где
|/iD0)- 4" *пО|<8 (/=1. 2 я), |
\ D2)
IIГх (Хо) || ! = max 2 I gfJ (*@>) | < М. I
i J=i )
то система B4) имеет решение х = я, которое находится в об-
области
| х - *(«> || l = max |
и может быть получено как предел последовательности
х(т) = x(m-l) _ /J1 (х(»»-1)) / (дК"»-1)) B8)
и быстрота сходимости оценивается неравенством
B*JW-18. D4)
Векторное равенство B8) эквивалентно системе линейных алге-
алгебраических уравнений
п
W-fi (xim~l)) ^ ~ X^"l>) = ~fi (*М) (' = ! • 2 ")•
У 1 j
D5)
Вычисление последовательных приближений с помощью равенства B8)
или путем решения системы D5) связано с большой вычислительной
работой, так как на каждом шаге нужно решать систему со своей
матрицей или на каждом шаге находить матрицу /^"'(лК™'). В связи
с этим вместо рассмотренного метода решения системы B4), кото-
который носит название метода Ньютона, иногда применяют следую-
следующий более простой метод.
Вместо системы B7) рассматривают систему
Xi = ti (XV Х2 Хп) = Х{ - 2 gij (Xf), Xf> 4°)) X
X/j(*i. x2 xj (/=1, 2 я). D6)
или в векторной записи
х = ф (х) = х - fZ' (*°>) / (*). D6')
где дК°> достаточно близок к решению а системы B4), а следова-
следовательно и D6), которую также решают методом итераций, описан-
описанным в п. 1.

§ 5] РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ 159
От функций fi(xlt х2 хп) будем требовать выполнения тех же
условий, которые накладывались в начале этого пункта. Исполь-
Используя C2), можно записать:
~ (|) (у) = Z—y — fxl (*@)) [/ (z) —f(y)]=Z—y— /
X F (z, у) (г —у) = [/ - /ж V0)) F (z, у)] (г —у). D7)
Если у и z близки к л:'0', то матрица F(z, у) близка к матрице
/ж(дг(°)), а / — fxl(xW)F(z, у) близка к нулевой матрице, т. е.
для некоторого К < 1 можно найти такое г > О, что при р (у, л:'0)) =
= || .У — •*@)Hi-^r и ?(z- x*-°))^.r будет иметь место неравенство
D8)
а из D7)
D9)
т. е. будет иметь место условие Липшица с константой АГ <С 1 - Да-
Далее, из D6')
^ E0)
и выбирая лг<°> достаточно близким к а[р(л;@), а)^г], можно до-
добиться выполнения неравенства
M(x(°)) — x@)\\l<(l—K)r, E1)
а выполнение неравенств D9) и E1), как это было показано в п. 1,
гарантирует, что в окрестности р(лг, лК°))=||л; — хСЦ\1 ^ г суще-
существует единственное решение системы D6'), которое может быть
получено как предел последовательности
)) (от = 2, 3, ... )¦
E2)
где за начальное приближение д:'1' можно взять любую точку ука-
указанной окрестности. Но этим решением и будет лг=а, т. е.
lim л*"»> = а, E3)
m -> со
и сходимость метода доказана.
В цитированной выше статье Л. В. Канторовича показано, что
в условиях теоремы, которую мы приводили выше, быстрота схо-
сходимости последовательности дКто) к а определяется неравенством
—«Hi {q=\-VY^2h <\). E4)
Этот процесс, который можно рассматривать как видоизменение
метода Ньютона, хотя сходится и медленней, чем процесс Ньютона,

160 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
имеет то преимущество, что последовательные приближения по
<52) находятся значительно проще, так как достаточно один раз
найти матрицу fxl(x^).
Хотя мы и обосновали теоретически сходимость метода Ньютона
и его видоизменения, при их фактическом применении неизбежные
в процессе счета ошибки округления все же могут привести к тому,
что решение с заданной наперед точностью не удастся. Вопросы
влияния ошибок округления на точность результата в общем случае
еще не изучены.
Пример. Уточнить по методу Ньютона приближенные значения
решения л;0 = 0,4, _уо = 0,9 системы
— у — 2 = 0,
/2 (х, у) = 2х* + Ъху +у* — 3 = 0.
Для этого будем последовательно решать системы:
где
/i (*o. Уо) = — 0.73, f[x (x0, yo) = 5,0, f[y (x0, y0) =1,6,
/2 (*o. Уо) = — 0.79, /L(Jf0. Уо) = 4.3, Ay (x0. y0) = 3,0;
5.0 Дл:0+1.6Ду0 = 0.73.
4,3 Дл:0 + 3,0 Ьу0 = 0,79;
Дл:0 = 0,114, л:1 = л:04-Дл:о = 0.514)
Ау0 = 0.100, yl=y0+by0 = l .000;
/i(*i. ^i) = 0,084784. /?»(*!. Л) =6,112. ^
Л (*i. ^i) = 0.070392, /^ (*lt jf,) = 5.056. /ty (xlt y^ = 3,542;
6,112 Д*! 4- 2.028 Д^ = —0.084784.
5,056Да:! 4- 3,542ДЛ = — 0,70392;
Ax1 = —0,013826, л:2 = 0.500174,
Ду1 = —0,000138. ^2 =

§ 5] РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ 161
fl(xi.yd = 0.000768, /[ЯТ(*2.Л)=»6.ОО1116. /^(*2.Л) = 2,000072,
/2(*2. л) = 0.000387. /L(x2,y2) = 5,000282. /2!/(х2,у2)~ 3,500246;
6,001116 Д*2 + 2.000072 Ду2 = — 0.000768,
5,000282 Дл:2 + 3,500246 Ду2 = — 0.000387;
Дл:2= — 0.000174. х3 — 0.500000.
Ду2 = 0.000138. ^з=
Таким образом, мы получили точное решение.
3. Метод скорейшего спуска. Кратко остановимся на методе
скорейшего спуска. В этом методе решение системы B4) сводится
к задаче отыскания минимумов функции Ф (хи х2 хп), которую
можно построить различными способами, положив, например,
п
Ф (*i. х2 хп) = 2 Т\ (•»!. х2 хп), E5)
или
п
Ф(*1. ^2 *п)= .2 ау/*(*1. ^2 xn)fj(xlt x2 д:п),
E6)
где aij — элементы некоторой положительно определенной матрицы.
Если а = (ар а2 а„) есть некоторое решение системы B4),
то/<(а) = 0 (/=1, 2 п) и Ф(а)^0. В других точках х
Ф(л:)>0. Таким образом, каждый нулевой минимум функции Ф(л:)
даст решение системы B4) и отыскание решений системы B4) сво-
сводится к отысканию нулевых минимумов вспомогательной функ-
функции Ф (х). Метод скорейшего спуска отыскания последних заклю-
заключается в следующем. Если известно примерное расположение нуле-
нулевого минимума, то выбираем вектор лг<°>=(л:10) *„')> близкий
дФ (*(<>))
к а, вычисляем производные —^ и в направлении вектора
проводим прямую
х = лг<°) — Шх (лг<0)), E8)
проходящую через точку лг<°) в направлении вектора Фя.(х^), орто-
ортогонального к поверхности Ф(л:) = Ф (лг<°)). Определяем Хд и л:*1) =
(°)^Ф'0') из условия минимума функции

162 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
Если Ф(х^>) фО, то продолжаем процесс, исходя из л:'1» и двигаясь
в направлении вектора grad Ф (л:A)) = Фх (*;1))> и снова на прямой
х = х'л—\Фх(х^) отыскиваем точку, в которой
имеет минимальное значение. Если уже найдено &-е приближение
то Xfc находим из условия минимума функции
фл(Х) = Ф (*W— \ФХ(ХМ)) E9)
и полагаем
= х(к) _ \кфх (*(&)). F0)
На каждом шаге придется решать уравнение
с одним неизвестным X, что может быть выполнено одним из опи-
описанных выше методбв.
Реализуя этот метод, мы на каждом шаге движемся в направле-
направлении быстрейшего убывания функции Ф. Если начальное приближе-
приближение выбрано достаточно хорошо и в окрестности искомого решения а
нет других минимумов, то этот процесс быстро даст искомое реше-
решение с заданной точностью. Если в окрестности а имеются другие
минимумы, то при неудачном выборе л:*0) процесс сойдется, но не
приведет к искомому решению.
Применение метода скорейшего спуска на каждом шаге требует
выполнения большой вычислительной работы. Поэтому, вместо того
чтобы двигаться в направлении градиента Ф(л:), можно двигаться
из л:*0) в направлении какого-либо другого вектора, не касательного
к поверхности Ф (х) = Ф (л:'0'). Проще всего брать векторы в на-
направлении координатных осей. Так, в релаксационном методе,
дФ (хф))
имея начальное приближение л:*0', вычисляют производные —^ ,
дФ (х{0))
и если —-5 наибольшая из них, то л:*1) находят из условия
ОХ ^
^^) = 0, F2)
где Ij, — вектор в направлении 1-й координатной оси. Это равно-
равносильно уточнению /-й неизвестной при неизменных остальных.
§ 6. Отыскание корней алгебраических уравнений методом
выделения множителей
Известно, что многочлен
f(x)=txn + alx^-l+ ... +ап_хх + ап A)
с действительными коэффициентами может быть представлен в виде
произведения многочленов степени не выше двух тоже с лействи-

? 61 МЕТОДЫ ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ 163
тельными коэффициентами. Линейные множители в этом разложении
соответствуют действительным корням уравнения
= 0, B)
а квадратичные — парам комплексно-сопряженных корней. Таким
образом, имея способы разложения многочлена на множители, мы
сведем задачу отыскания корней уравнения B) к решению совсем
простых уравнений. В связи с этим разработаны методы выделения
действительных множителей многочлена / (х).
При применении методов выделения множителей приходится вы-
выполнять многократно деление многочлена на многочлен, т. е. нахо-
находить частное и остаток. Если делитель имеет первую степень, то
эго удобно выполнять по схеме Горнера. Пусть требуется найти
частное и остаток от деления многочлена
/(л:) = аол:"-|-а1л:"-1+ ... + а,г..1л:-|-аи C)
на многочлен х — г. Обозначим остаток отделения через R, а част-
частным пусть будет многочлен
Тогда
f(x) = g(x)(x — r)-\-R. E)
Сравнение коэффициентов при одинаковых степенях х в правой и
левой частях тождества E) дает
ao = bo, ak = bk — bk_lr (ft=l, 2 п — 1), an = R — bn_Yr,
F)
откуда
bo = ao, bk = ak-\-bk_xr (ft=l. 2 n — 1), R = an-\-bn_lr.
G)
Вычисления удобно располагать по следующей схеме — схеме Гор-
Горнера:
а0 at а2 а3 ... • ап_1 ап \_r__
V V b2r ... bn_2r bn_Yr
b0 bx b2 b3 ... bn_1 R
где bo = ao, а каждое число нижней строки равно сумме двух чисел,
стоящих над ним.
Так как из E) видно, что R = f(f), то схему Горнера удобно
применять для отыскания значений многочлена f (х) при х = г.
Для отыскания частного
и остатка
R (х) = сох + с,

164 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
от деления многочлена C) на множитель x2-\-px-\-q можно исполь-
использовать следующую схему:
—p
— я
—Pbo
b0 bt
a2 a3 . .
—pb\ —pbi . .
— qb0 — qb1 . .
b<> Ьъ . .
• an-2
. —pbn-3
• —яЬп-ь
• Ьп_2
an-l
— pbn-2
—ЯЬп-ъ
Co
an
— ЯЬп-г
C\
где последняя строка получается как сумма первых трех строк.
Эта схема просто получается из тождества
(х) (8)
сравнением коэффициентов при одинаковых степенях х. Это дает
ao=bo, a1=b1-\-pb0, ak = bk-\-pbk_x-\-qbk_2 (ft = 2, 3,,.., п—2 ,
an-i = со +Pbn-2 + яЬп-з> an = Фп-г + cu
откуда следует:
bo = ao, b1 = a1—pb0, ]
bk = ak—pbk_1 — qbk_2 (ft = 2, 3 n — 2), } (9)
co = av_x— pbn_2— qbn_3, cl~an — qbn_2, I
что и реализовано в схеме.
Нетрудно сообразить, как будет выглядеть схема для определе-
определения коэффициентов частного и остатка при делении многочлена C)
на многочлен хт -\- с1:хт~1 -\- ... -f- dm_lx -\- dm (m < п).
1. Метод Лина выделения множителей. Метод Лина, или метод
предпоследнего остатка, выделения множителя gm(x) степени т из
многочлена
/„(*) = *" + <*,*•»-*+ ... +ап^х + ап A0)
состоит в следующем. За начальное приближение gm(x) берется
некоторый многочлен степени т
gni l (х) = хт + bPxm-1 + ... + bgllX + ft? A1)
и производится деление fn(x) на gm> i(x) до тех пор, пока в остатке
получится многочлен степени т — предпоследний остаток. За сле-
следующее приближение gm,a(x) берется этот остаток, деленный на
коэффициент при хт — приведенный предпоследний остаток, далее
процесс повторяется, т. е. если уже найдено &-е приближение к gm(x)l
gm,k{x) = xm + b?)xm-1+ . .. +&S?-1* + &S?. A2)
то gmt jt+i (x) определяется как приведенный предпоследний остаток
от деления многочлена fn (л:) на gm> fc (x). Процесс продолжают до

Л 6] МЕТОДЫ ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ 165
тех пор, пока коэффициенты двух последовательных приближений
будут совпадать в пределах заданной точности.
Практически приемлемых критериев сходимости этого метода
в общем случае нет. Приведем без доказательства один результат,
практическая ценность которого невелика.
Если av <х2 ат—корни выделяемого множителя gm(x),
a Pn-m(x)=:xn-m-\-c1xn-m-l-ir ... +cn_m_lx-\-cn_m — частное
от деления /„(*) на gm(x), т. е. fn(x) = gm(x)Pn_m(x), то схо-
сходимость метода Лина будет иметь место в случае, когда
=1.2 »)
по модулю меньше единицы и начальное приближение gmj i(x)
выбрано достаточно близко к gm(x). В случае, если наибольшее
из них по модулю есть действительное число, то bf+l) — Ь(Р схо-
сходятся к нулю со скоростью геометрической прогрессии со знамена-
знаменателем, равным модулю этого числа.
При практическом применении метода Лина чаще всего выделяют
линейные и квадратичные множители, так как только эти множители
заранее можно определить достаточно точно и применять процесс
Лина для их уточнения. Но только в случае выделения линейных
множителей, соответствующих действительным корням уравнения
fn(x) = 0, можно дать простые критерии сходимости метода.
Пусть выделяется множитель х — а и х — а ' — его k-t прибли-
приближение, тогда имеет место тождество
где х — <х( +1) есть &+1-е приближение. Из этого тождества имеем:
4*)(*-«№+1)). (И)
го тож
U (a№) = 4*> (aW - а<*+1>); /„ @) = - rfgV
или
откуда
a /„@) -/.(.<*)•
Это равенство можно рассматривать как итерацию для отыскания
корня а уравнения
Так как

166 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
то при выполнении условия | tp' (a) | < 1 найдется некоторая окрест-
окрестность корня л: = <х, в которой будет иметь место неравенство
и итерация A5) будет сходиться, если начальное приближение <хA'
взято из этой окрестности. Условие | tp' (a) j < 1 будет иметь место,
если а — наименьший по модулю корень уравнения /п (х) = О, при
условии, что все корни уравнения действительны и одного знака.
В самом деле, если в этом случае расположить все корни в порядке
возрастания их модулей, т. е.
Ы<|«2|< ••• <К|.
ТО
fn @) = (—!)" aia2 • ¦ • <V. f'n («i) == (а2 — <*i) («з — <*i) ¦ ¦ • (а„ — «i)
^(-i)(l-i)...(.-i). 08)
и так как все отношения — (i = 2, 3 п) положительны и
аг
меньше единицы, то
Пример. Выделить множитель второй степени из многочлена
х* -f- 7л:3 4- 24л:2 + 25л: — 15.
В качестве начального приближения возьмем многочлен
gi, 1 (X) = Л»2.
Не приводя промежуточных вычислений, которые сводятся к деле-
делению многочлена fn (х) = хп -\- аххп~1 -f- ... -\-an_lx-\-an на трех-
член х^-^-щ. x-\-b\ до получения предпоследнего остатка, что можно
выполнить по схеме:
fli «2 а3 ... ап_3 ап_2 an_j an
а(^) и(к) (к) t(k) (ft) »(A') (к) i{k) (к)
— 01 01 С\ 0i C-2 ... 01 СИ—4 01 Cw_3
^) fj(k)c(ft) bik>Cnl5 02*'с(fci 0-(fc)C№)
Ci Ca C3 ... си_з flo «l «a
где последняя строка есть сумма первых трех, при этом хп~2 -\-
'^"-)- ... -\-с(п1зХ — предпоследнее частное, a d^x^^-df ]x -)-
— предпоследний остаток, приведем результаты вычислений
для данного примера.

§6]
МЕТОДЫ ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ
167
k
1
2
3
4
5
6
7
8
9
10
11
12
Приведенный пред-
предпоследний остаток
1
1
1
1
1
1
1
1
1
1
1
1
1,042
1,5597
1,8024
1,9147
1,9639
1,9849
1,9937
1,9974
1,9989
1,9996
1,9998
1,9999
bf
— 0,625
— 0,8145
-0,9186
— 0,9646
- 0,9850
- 0,9937
— 0,9974
— 0,9989
- 0,9996
- 0,9998
- 0,9999
- 0,9999
Приведенное
частное
1
1
1
1
1
1
1
1
1
1
1
1
ЛЬ)
С1
7
5,957
5,4403
5,1976
5,0853
5,0361
5,0151
5,0063
5,0026
5,0011
5,0004
5,0002
Предпоследний остаток
4*»
24
18,4168
16,3293
15,5504
15,2278
15,0946
15,0392
15,0163
15,0067
15,0029
15,0010
15,0005
d[h>
25
27,7238
29,4311
29,7.745
29,9053
29,9606
29,9835
29,9933
29,9971
29,9991
29,9994
29,9997
df>
— 15
-15
- 15
-15
- 15
-15
— 15
— 15
- 15
— 15
lo
- 15
Последнее частное в общем случае имеет вид
уП-2 . (fc) п-3 . _1_/.W г I /)
X -f-Ci X -Ь . . . -\-Сп-ъХ -(-До
и будет являться приближенным представлением второго множителя,
дополняющего искомый множитель gm(x) до fn{x). В нашем при-
примере после 32 шагов имеем:
xi j- 7x3 + 24л:2 + 25л: — 15 ^
яа (х2 + 1,9999л: — 0,9999) (л:2 -+- 5,0002л: -|- 15,0005).
Точное разложение имеет вид
х* + 7л:3 + 24л:2 + 25л: — 15 = (л:2 + 2л: — 1) (л:2 -+- 5л: + 15).
Получили хорошее приближение, хотя начальный множитель л:2 далек
от истинного.
Если использовать полученное разложение для отыскания корней
уравнения
л:4 + 7л:3 + 24л:2— 15 = 0,
то получим для корней следующие значения:
*!=— 2,4141, х2=-0,4142, x%i = — 2,5001 ± 2,958И.
Истинные же значения корней с четырьмя верными десятичными
знаками:
*! = — 2,4142, л:2 = 0,4142, xz, i = — 2,5000 ± 2,9581г.
2. Метод Фридмана. Метод Фридмана выделения множителя gm (x)
многочлена fn(x) не обладает таким единообразием, как метод Лина.
В методе Фридмана, если gm,k{x) есть &-е приближение искомого

168 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
множителя gm(x), для получения (&+1)-го приближения поступают
следующим образом: делят многочлен fn(x) на gm,k(x) так же, как
и в методе Лина, но только до получения последнего остатка; полу-
полученное частное располагают по возрастающим степеням х и делят
на него многочлен fn(x), расположенный также по возрастающим
степеням х, до тех пор, пока в частном получится многочлен сте-
степени т; это частное, деленное на коэффициент при хт, и прини-
принимают за gm,ic+i(x).
Отыскание каждого приближения по методу Фридмана требует
более чем в два раза больше операций, чем в методе Лина, но
в некоторых случаях метод Фридмана имеет значительно лучшую
сходимость, чем метод Лина. Это можно проиллюстрировать на при-
примере выделения линейного множителя, соответствующего наимень-
наименьшему по абсолютной величине корню уравнения /п(л:)=0, если это
уравнение имеет только действительные корни и одного знака.
В самом деле, если искомый линейный множитель имеет вид х — а,
a k-t приближение его есть
guk(x) = x-aw. B0)
то в результате деления fn(x) на g\,ic(x) получим:
B1)
X — о> '
откуда
<к) , I (к)\
и(к) !• ЛИ
t>n-2= lim ——
*-«(*> '
B2)
J
При делении многочлена fn(x), расположенного по возрастающим
степеням, на многочлен qle(x) = б^-i + *п-а* + ... + t>Vxn~2 + хп~1
до получения частного первой степени находим следующее частное:
..._.
"n-l "n-l
которое после деления на коэффициент при х приобретет вид
B3)

§6!
МЕТОДЫ ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ
откуда, принимая во внимание равенства B2), будем иметь:
/«(О) [/«(»<*>)-/« @I «<*>
Эт0 — итерация для решения уравнения
* = <!»(*) ==¦
/«@) [/« <*) - /«@)] - f'n @) /„
169
B4)
B5>
Для того чтобы итерация B4) сходилась к а, достаточно, чтобы
в некоторой окрестности а имело место неравенство
If
B6)
и а было взято из этой окрестности. Но B6) будет иметь место,,
если
|f (a)| =
l_i^
B7>
Если все корни a^ 02, .... an действительны, одного знака и
KKKI (/ = 2, 3, .... л), B8)
то
Т ^ 1/ -3 /ЛЧ
. . . + M(i_ib.Ui_M. . .(i_^L\ B9>
так как
/; («i) = (— 1)" "' («2 - «i) («з — «!)••• («» - ai)-
Методом индукции докажем, что
<30>
Так как при />2 0< — < 1, то при л = 2

170 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
и неравенство C0) справедливо. Пусть оно справедливо при п = т.
Тогда при п = т -\- 1
< 1—¦
1
так как каждая квадратная скобка положительна и меньше единицы.
Таким образом, неравенство C0) справедливо при всех п. Из B9)
и C0) имеем:
Сравнивая A8) и C1), мы видим, что
а это означает, что в рассматриваемом случае метод Фридмана схо-
сходится быстрей метода Лина.
В общем случае области сходимости метода Фридмана и метода
Лина не совпадают.
Проиллюстрируем метод Фридмана на примере, который исполь-
использовался для иллюстрации метода Лина, т. е. выделим квадратный
множитель многочлена
хА -Ь 7л:3 + 24л:2 + 25л: — 15.
За начальное приближение снова возьмем g-iy i (л:) = х2. Результаты
вычислений приведены в таблице:
k
,
2
. 3
4
g% i-iW
1
1
1
1
xl
0
1.83
2.009
1.9993
х°
0
-0,93
-1,004
-0,9997
х^
\
1
1
1
Лервое частное
л:1
7
5.17
4,991
5,0007
X»
24
15.47
14,9771
15,0018
Второе частное
л:*
16,03
14,9396
15,0048
X1
29,44
30,0128
29,9986
х°
-15
-15
-15

§ 6) МЕТОДЫ ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ 171
Таким образом, после трех приближений мы получили результат
почти с такой же точностью, как и после 12 приближений по ме-
методу Лина.
Если по полученному разложению найти корни многочлена, то
получим:
*! = — 2,4135, л?2 = 0,4142, х3,4 = —2,5004 + 2,9580г.
В случае выделения квадратного множителя, если известно k-e
приближение искомого множителя git h (x) = x*-\- b[k)x-{-Ь^, первое
частное хп~2-+-с^)хп~ъ-\- ... + c'fLs* + с(^12 и остаток rWjr-|-r<*>
находятся по схеме, приведенной в начале параграфа, причем оста-
остаток аюжно использовать для оценки точности достигнутого прибли-
приближения. Отыскание второго частного do*}x2 -\~ d^x -f- df\ деля кото-
которое на doft), мы получаем следующее приближение, сводится к вычи-
вычислениям по формулам:
C2)
Щ
СП-2
о ——да—\ап-2 — Сп~чй\ —cn_i
С()
си-2
3, Метод Хичкока выделения квадратного множителя. Произ-
Произведем деление заданного многочлена
„ C3)
на трехчлен
g2(x) = x2->rpx + q C4)
с неопределенными коэффициентами р и q. Обозначив через L {х)
частное от деления, получим тождество
q)L (х) + хР(р, q) + Q(p, q), C5)
где Р(р, q) и Q(p, q)—многочлены от р и q. Для того чтобы при
некоторых значениях р, q трехчлен C4) был делителем /„(дг), необ-
необходимо и достаточно обращения в нуль многочленов Р(р, q) и Q(p, q).
Таким образом, для отыскания коэффициентов квадратичного дели-
делителя C4) многочлена fn(x) нужно найти решение системы
P(p,q) = 0; Q(p,q) = O. C6)
Хичкок предложил для решения этой системы метод, который по
существу является методом Ньютона, но только в методе Хичкока
не используется явный вид многочленов Р и Q, а их значения и
значения производных, нужные в методе Ньютона, находятся путем
двукратного деления fn(x) на приближенное выражение g2(x).

91TJ
Аиэхэиэ
) 4) 9ИН9ЖИ1/9ИAи 99tnfflXff9I/D ИИ1Г0ХЕН ВНОХСИЧН W01T0X9W Э
ииахэхэахооэ a %t)b \4)d)bp '{.D)b \4)d)dp '(«? \4)d)bj(J ^
{Zf) ou и ({v)b \4)d)s '(D)b \v)d)y *((?)* 'D)d)?> '((ч)ь *)
-вы D)b -\- XD)d -j- zx H9i/hX9dx bh иэинэи-эк wHHXBdMXair ox 'bi/эхиж
-они олоионэи аохнэиЛиффбом—D)b и D)d 9ИH9ЖИL•9иdu ъ-ц онхээа
-ей эжА И1/эд 'внохсичн ^охэи ou qxBmgd онжои (9g) Хиэхэиэ
и 'А и rf ou (i 'd)& '(b 'd)j xo aNHiroaeHOdu эннхэвь и
j.9Bi/oasou A-|- xd-\~zx гн (.v)"/ эинэ^этт aonxBdHXaff woeEdo,o
{7b) <
{ •(b'd)n (b'd) * '.(b -d)S— Ф 'd)xd = ф '
Xwoxeou
д ей йотгжвм cmi/Xh oaxDH98Bd хэХтгэь-э (j^) ей ox
*zm Ф lx> -9 -x 'HHdoM 9HHhHL-eed хээии b-\- xd-\-zx H9i/hxgdx
'd)nd-(.b -
:э1Гиа иоявх а чхвэииве онжом (gg)
охь '
0 = (* <rf
IWHhXi/OU 9XBX4I/Xe9d g '(^g) BH9I/hX9dx
{^ 'j^;)!» H9HdoM ей нитго х охээиа wHaEXOffou винвaodиtlH9d9ффи'D¦
.LExqi/Aegd а и b и d ou оахээтгжох ээн1Г91/эои w9XdиtlH9d9ффиlrodIJ
(8E) Ч* 'rf)&+(* '"')(/* +
H- K* 'd) S + (* 'd) yx\ (b + rrf+ zx) + (r) l7 г(А + xd-\- zx) = (r)M/
оахээ'Сжох иэтииве и
+ j2 вн ваонэ '(S?) я Ии*пв1Гоха \х)*] нэ1/ьолони ии1/91Гев^ -5 и
xo 9NHiroaeHodu чхиьХ1/ои ихХи woxe вн онжом мвм 'мэжвмоц
I -i/j] нинзнауал хннхнзтгнзпэнуах и XHroahHVdaaJi/v зинзтза ZL\

§6]
МЕТОДЫ ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ
173
Если начальное приближение/?(°>, ф°) выбрано достаточно хорошо,
то сходимость не вызывает никаких сомнений.
Пример. Снова будем разыскивать квадратичный множитель
многочлена
/< (л:) = х4 4- 7х3 -)- 24л:2 -f 25л: — 15.
Приняв за начальное приближение jo(°)=0, <7@) = 0. двукратным
делением /4(л:) на х2 находим:
Р0 = 25; Qo = —15; Д0 = 7; 50 = 24.
{Для сокращения записи полагаем Рк = Р (/?(*>, qW) и т. д.)
Система D3) примет вид
— 24 Д/?<°) — 7Д?(°> = —25,
— 25Д?(°> = 15.
откуда
рт = Д/?(°> = — 0,625, ?A) = Д^°) = 1,224.
Дальнейшие вычисления понятны без пояснений:
— 1,224
0,625
— 1,224
0,625
1
1
1 D
l «Л
7,0000
— 1,2240
5.7760
— 1,2240
= 4,5520 St
24,0000
— 7,0698
0,6250
17,5552
0.6250
= 18,1802
Pi
25,
-21,
3,
= 7,
0000
4876
6100
1224; Q
— 15.0000
10.9720
, = — 4,0280
12,6086Д//1)-}- 4,5520Д9(х>= 7,1224;
2,8450 Д/?(х> -f-18,1802 Д^1* = — 4,0280;
-1,9075
0,9535
0,6835;
1,9075;
7,0000
1,9075
24,0000
— 9,7139
0,9535
bqW = — 0,3285;
f« = — 0,9535;
25,0000 — 15.0000
—29,0695
4,8557 14,5310
Р2= 0,7862; Q2 = —0,4690

174 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
10.1177 Д/?Сз> _f_ з,1850ДоB)= 0,7862;
3,0369 Др(а> -(-16,1931 До<а> = — 0,4690;
Д/?(а> = 0,0923; До'а> = — 0,0463;
jt?C>= 1,9998; о<3> = — 0,9998.
Отклонение третьего приближения от точных значений р = 2,
о = — 1 равно 0,0002.
УПРАЖНЕНИЯ
1. Показать, что нули многочлена
по модулю не превосходят единственного положительного нуля многочлена
г^-и^г*1- ... -\ап-х\г-\ап\.
2. Показать, что нули многочлена
при ап Ф 0 по модулю не меньше единственного положительного нуля
многочлена
3. Пусть do, rfj dn — положительные числа и
dn>\a\\dn-\+\^i\dn-4+ ••• +\
Показать, что нули многочлена
г"-1+ ... +ап
не превосходят по модулю наибольшего из чисел
4. Показать, что корни уравнения
г»+д1г»-1+ ... +a
не превосходят по модулю наибольшего из чисел
V
п\а1\, Уп | а, |, 1^"л|а3| Vя I а» I •
а также наибольшего из чисел
(ft =1,2 л).
5. Пусть Po~>Pi~>Pi~> ¦¦• ~>Рп^>®- Показать, что в единичном круге
| г К 1 не содержится ни одного нуля многочлена
P0 + P1Z+ ••• +Рп-1*П

УПРАЖНЕНИЯ 175
6. Доказать, что если все коэффициенты р0, рь .... рп многочлена
положительны, то нули его лежат в круговом кольце а ^ | г | -^ C, где
а—наименьшее, а В — наибольшее из чисел — , —, ..., п
Ро' Р\' ' Рп-\
7. Используя теорему Ролля, найти условие действительности корней
уравнения хт 4- рхп -\- q = 0.
8. Для уравнения
раохп -\- atxn-i -\- ... -\-an_lX-\-an = 0
построена последовательность функций
f(x) = a()xn-\-a1xn-'i-\- ... -\-an-iX-\-an,
/i (х) = аох™-1 -f atxn-* -\- ... -\- an-i,
fn (•*) = а0.
Доказать, что число действительных корней уравнения /(х) = 0, превы-
превышающих данное положительное число а, не превышает числа перемен знака
в нашей последовательности при х = а и разность между этими числами
всегда четное число (теорема Лагерра).
9. Найти положительные корни уравнения
x = tgx
с точностью до 10~4.
10. Используя видоизменение Лемера метода Лобачевского, найти все
корни уравнения
Х5 ^_ 0,5x4 — Зх3 -f 27х« -f 13,5* — 81 = 0.
11. Показать, что если внутри некоторого круга с центром в начале
координат уравнение /(х) = 0, где
имеет единственный корень х = а, то
4 **
а0 п1
а\
а0
4
I
ах
а0
0
С1*1 do
an
7
(Воспользоваться теоремой Кёнига с <р (г) = Оо.)
12. Используя метод Ньютона для решения уравнения х2 — N = 0, по-
построить итерацию второго порядка для вычисления YN.
13. Показать, что функция
определяет итерацию

176 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ [ГЛ. 7
т
третьего порядка для отыскания у N (Бейли). (Воспользоваться теоремой
Кёнига с /(х)^х»» — N и <р (х) = 1.)
14. Обобщить метод Хичкока на случай выделения множителей третьей
я четвертой степеней.
15. Методами выделения множителей найти корни уравнения
х* -f 16x8 _|_ 71x3 _|_ 122х -j- 120 = 0
¦с четырьмя верными десятичными знаками.
16. Вычислить с четырьмя знаками два наименьших положительных
корня уравнения
cos х ch x = 1.
17. Вычислить с четырьмя знаками корни следующего уравнения:
Xi _ 0,41x3 -f 1,632x2 _ 9,146х -f 7,260 = 0.
18. Найти с тремя знаками корни уравнения
хъ _ 20,2x4 -f 132,18x3 — 60,592x2 — 72,693х — 14,525 = 0.
19. Найти с пятью десятичными знаками решение системы уравнений
sin х = у -\- 1,32.
cos у = х — 0,85,
20. Найти с пятью десятичными знаками решение системы
Х7_5х2у*+ 1510 = 0,
уь— Зх*у — 105 = 0.
Если известно, что х = 2, у — 3 есть приближенное решение.
ЛИТЕРАТУРА
1. Хаусхолдер, Основы численного анализа, ИЛ, 1956.
2. Милн, Численный анализ, ИЛ, 1951.
3 Л. В. Канторович, Функциональный анализ и прикладная математика
УМН, т. 3, вып. 6, 1948.
4. А. Э й т к е н, О разложении многочленов иа множители итерационными
методами, УМН, т. 8, вып. 6, 1953.
5. Е. Я. Р е м е з, О знакопеременных рядах, которые могут быть связаны
с двумя алгорифмами М. В. Остроградского для приближения иррацио-
иррациональных чисел, УМН, т. 6, вып. 5, 1951.
6. Г. С. С а л е х о в, М. А. М е р т в е ц о в а, О сходимости некоторых ите-
итерационных процессов, Изв. Казанского филиала АН СССР, сер. физ-матем.
и техн. наук, 5, 1954.

ГЛАВА 8
ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ
ВЕКТОРОВ МАТРИЦ
§ 1. Введение
Большое число задач механики и физики требует отыскания
собственных значений и собственных векторов матриц, т. е. оты-
отыскания таких значений X, для которых существуют нетривиальные
решения однородной системы линейных алгебраических уравнений
Ax = ix, A)
и отыскания этих нетривиальных решений. Здесь А—квадратная
матрица порядка п с элементами а^ и х — вектор с компонентами
xv х2, ..., хп. Чтобы найти X, нужно определить корни уравнения
?>(Х) = |Л — Х/| = 0. B)
где /—единичная матрица. На первый взгляд задача кажется очень
простой. Достаточно раскрыть определитель B) и решить получен-
полученное уравнение ге-й степени одним из тех методов, о которых гово-
говорилось в предыдущей главе. Однако при больших значениях п
раскрытие определителя B) обычными методами высшей алгебры
связано с громоздкой и утомительной работой. Основное затруднение
вызвано тем, что X входит в каждый столбец и каждую строку
определителя.
В вычислительной математике выработано много различных прие-
приемов и методов, облегчающих труд по раскрытию определителя B).
Существуют также методы, позволяющие отыскивать собственные
значения и собственные векторы без раскрытия определителя B).
В этой главе мы и займемся этими вопросами. Здесь мы также ко-
коснемся задачи об отыскании значений X, удовлетворяющих уравнению
0, C)
где Ai—квадратные матрицы порядка п.

178 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
§ 2. Метод А. Н. Крылова
1. Отыскание собственных значений матрицы. Академик
А. Н. Крылов одним из первых предложил довольно удобный метод
раскрытия определителя B) § 1.
Суть метода А. Н. Крылова состоит в преобразовании опреде-
определителя ?>(Х) к виду
6ц - X
0)
Ощ — Л *И2 ¦ ¦ • °»1
причем при некоторых условиях уравнения ?>(Х) = 0 и ?>х(Х) = 0
имеют одни и те же корни. Раскрыть определитель Dl(k) значи-
значительно проще, чем D(l), так как X содержится только в первом
столбце. Как мы увидим позже, нам даже не придется вычислять
миноры Dl(k).
Преобразование ?>(Х) к виду A) будем осуществлять следующим
образом. Возьмем первое из уравнений A) § 1:
и умножим его на X. Появившиеся в левой части выражения ХдГ|
заменим на равные им в силу системы A) § 1 выражения:
«ii*i + а»2*2 + • • • + ainxn (i = 1, 2, .... я). C)
Получим новое уравнение:
*2i*i-+-*22*2 + ••• -\-b2nxn = \ixv D)
где
п
Кх = 2 вцви {i=\, 2 я). E)
/,-=1
С уравнением D) поступаем так же, как и с уравнением B). При
этом получим новое уравнение:
*31*1-Г" *32*2 + ••• + ЬЪпХп = Х3*!, F)
где
п
Ьи= 2 bvflkt (i=l. 2 я). G)
fc=i
Этот процесс продолжаем до тех пор, пока не придем к урав-
уравнению
*ni*i + *»2*2 + ... + bnnxn = lnxv (8)
Для единообразия обозначений условимся считать ?14=а14.

§ 21
МЕТОД А. Н. КРЫЛОВА
179
Будем рассматривать вместо системы A) § 1 систему
. . . + ЬшХп = Хх,,
...-+- b2nxn = l2xv
О)
Определитель этой системы как раз и равен ?\(Х). Покажем, что
1 0 ... О
D, (X)
D(X)
... bl
= C = const.
A0)
Действительно, произведение CD (к), если воспользоваться формулой
и условием Ь1к = а1к, может быть записано в виде
Ьп—X Ьп ... Ьщ
[ Л?/21
3"
"ы
A2)
Прибавим к второй строке полученного определителя первую, умно-
умноженную на X. При этом первые две строки нового определителя
будут такими же, как и у D, (X). Затем прибавим к третьей строке
вторую, умноженную на X. Тогда и третья строка станет такой же,
как и у ?>Х(Х). Продолжая этот процесс, мы придем в конце концов
к определителю ?>х (X). Утверждение доказано.
Если С отлично от нуля, то уравнения ?>(Х) = 0 и ?>х(Х) = 0
эквивалентны. Если же С=0, то наше преобразование не приведет
к цели. Посмотрим теперь, как иногда можно обойти этот случай.
Процесс получения коэффициентов Ьц можно интерпретировать
как последовательное получение из вектора
= A, 0, 0
векторов
0)
bin)
при помощи соотношения
где А' — транспонированная
любом /
по отношению к А матрица.
A3)
A4)
A5)
При
A6)

180 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Естественно напрашивается следующее обобщение. Возьмем вместо
того частного вектора Ьо вида A3) произвольный вектор
и получим с помощью его по формулам A6) векторы ?г(/=1, 2, ...,«).
Эю соответствует преобразованию уравнения
в систему
и = *„!*! -+- Ь02х2
и = Ь01Хг
lu=bnxl
-\-blnx
lnxn.
A8)
A9)
таким же процессом, которым преобразовывалось уравнение B).
Определитель системы A9) имеет вид
1 Ьт Ьт ... ЬОп
X Ьп Ьп ... Ь1п
D2(X) =
X" Ьм Ь,
Так же как и ранее, нетрудно убедиться, что
^oi ^оз • • ¦ Ьйп
Ьп Ьп ... Ьш
B0)
D(X)
-i, 2
^Сх^ const.
B1)
Может оказаться, что С = 0, но Сх Ф 0.
Чтобы представить определители ?>Х(Х) или ?>2(Х) в виде много-
многочленов по степеням к, нет необходимости подсчитывать их миноры.
Воспользуемся теоремой Гамильтона — Кэли, утверждающей, что
А'п¦-+- р-^А'4'1 -\- ... -\-рп^\А' -\-pJ=®< B2)
где pv р2. .... рп — коэффициенты характеристического многочлена
?)(Х) = (—^"^"-i-jOjX™-)- ... +pn-.lk-\-pn\. B3)
Умножая равенство B2) на Ьо, получим:
К-\-РФп-х+РгЬп-г + • • ¦ -hPn-А -\-РЛ = 0. B4)
Это векторное равенство дает систему п линейных алгебраических
уравнений для определения п коэффициентов характеристического
уравнения. Определитель этой системы равен Сх. Решать систему
можно любым из приведенных в главе 6 методов. Заметим, что мы

§ 21
МЕТОД А. Н. КРЫЛОВА
181
могли бы с таким же успехом использовать теорему Гамильтона —
Кэли для матрицы А и пришли бы тогда к системе
Го = О. B5)
где с{ = Агс0 и с0 — произвольный начальный вектор.
Рассмотрим пример. Пусть матрица А имеет вид
А =
В качестве вектора с0 возьмем
со = A. О, 0, 0).
Тогда:
B6)
B7)
B8)
и система для определения коэффициентов характеристического мно-
многочлена будет такова:
— Pt — Рз— 26р2—194р1=1973. )
— 2рз—17р2— 174р1= 1651, I
— 3/?3 — 33/?2 — 337/?! = 3260,
— 4/?3 — 21 р2 — 230р! = 2095.
Решая систему B9), найдем:
р1 = —11, р2 = 7, Рз = 72, р4=—9Ъ.
Таким образом, характеристический многочлен примет вид
D (к) = \* — 11X3 -|- 7X2 _)_ 72Х — 93.
с0
1
0
0
0
Ае0
1
2
3
4
26
17
33
21
194
174
337
230
А%
1973
1651
3260
2095
B9)
C0)
C1)
В приведенном примере мы пришли к характеристическому мно-
многочлену. Это оказалось возможным благодаря тому, что Ct Ф 0.
Исследуем теперь подробнее причины, по которым С1 может ока-
оказаться равным нулю. Как уже упоминалось, матрица А (и транспо-
транспонированная матрица А') удовлетворяет своему характеристиче-
характеристическому уравнению D(A) — 0. Но может оказаться, что существуют

182 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
многочлены ср(Х) степени меньше п, для которых также выполнены
равенства
ср(Л) = ср(Л') = О. C2)
Среди таких многочленов имеется единственный многочлен ф(Х) со
старшим коэффициентом 1, имеющий наименьшую степень. Этот
многочлен в линейной алгебре принято называть минимальным мно-
многочленом. Напомним некоторые свойства минимальных многочленов.
Произвольный многочлен ср(Х), для которого ср(Л) = О, делится на
минимальный многочлен. В частности, характеристический много-
многочлен D(X) делится на ф(Х). При этом
D(k) = ^(k)Dn_l(k), C3)
где Dn_l(k) — общий наибольший делитель всех миноров (п—1)-го
порядка матрицы А—X/. Корнями ф(Х) служат все различные корни
D(k). Так, если
D (X) = (-1)" (X - Х0а' (X - Xj)* ... (X - Хлр
ОчФ^, «1 + 02+ •• • +<** = «). C4)
то
ф (X) = (X - X/ (X - X2f ... (X - X/* A < р, < ад. C5)
Возьмем теперь произвольные векторы Ьо и с0. В каждой из по-
последовательностей векторов
Со. Асо Ап70 C6)
и
Ьо. А% А'% C7)
не может быть более п независимых. Более того, для любых век-
векторов ?0 и с0 наверняка имеет место линейная зависимость
<!?(А')Ъ0 = ^(АO0 = 0. C8)
Таким образом, если степень ф(>.) меньше п, то как бы мы ни выби-
выбирали Ьо и с0, системы B4) и B5) будут иметь нулевые опреде-
определители..
Посмотрим теперь, что может дать метод А. Н. Крылова в этом
случае. Все рассуждения будем проводить с матрицей А. Для про-
произвольного вектора с0 найдется многочлен ф_ (X) минимальной сте-
пени со старшим коэффициентом 1 такой, что
<IVo04)c0 = 0. C9)
Назовем его минимальным многочленом вектора с0. Любой другой
многочлен t]j0.), обладающий свойством
<f04)^0 = 0, D0)

§ 2] МЕТОД А. Н. КРЫЛОВА 183
должен делиться на <]>- (X). Следовательно, минимальный много-
многочлен ф(Х) матрицы А, для которого равенство D0) выполнено при
любом векторе с0, должен делиться на минимальный многочлен лю-
любого вектора с0.
Итак, мы приходим к выводу, что если в последовательности C6)
т является наибольшим индексом, для которого векторы
с0, А70, АЧо Ат~% D1)
линейно независимы, а вектор Атс0 линейно зависит от них:
Атс0 = -о^о-а1А'со- ... -ат_Ит""^о. D2)
то многочлен
5
3
1
3
2
3
—2
0
—1
0
4
0
—1
0
1
3
будет являться или минимальным многочленом матрицы А или его
делителем. Этот многочлен мы и получим по методу А. Н. Крылова.
Проиллюстрируем последний случай на следующем примере.
В качестве матрицы А возьмем
D4)
Если снова взять ео = A, 0, 0, 0), то получим:
Лс = E, 3, 1,3),
A2F0 = B7, 24, 6, 24), D5)
Л8с0 = A53, 153, 27, 153).
Вычисления дают
АЧо — 12Л2Со Ч- 45Лс„ — 54~с0 = 0. D6)
Таким образом, многочлен
^— 54 D7)
будет минимальным для вектора с0.
__ На этом примере мы убеждаемся не только в том, что векторы
с0, Ас0, .... Атс0 могут оказаться линейно зависимыми при т < п,
но и в трудностях, которые возникают при обнаружении такой ли-
линейной зависимости. В связи с этим остановимся на методах реше-
решения системы B5).

184 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Рассмотрим матрицу
е1п
где
l
Alc0 = (cfl, ci2 cin). D9)
Задача об отыскании коэффициентов оц в D2) эквивалентна задаче
об отыскании такой линейной комбинации первых т строк мат-
матрицы D8), которая в сумме с (т-(-1)-й строкой обращает первые п
элементов последней в нули. При этом в последнем столбце полу-
получится минимальный многочлен вектора с0. Поэтому целесообразно
для получения нужной линейной комбинации применить метод исклю-
исключения Гаусса. Процесс исключения можно осуществлять и до того,
как будет получена полная матрица D8). Так, получив (си, с12, .... с1п),
мы можем обратить в нуль какой-либо из элементов Сц, прибавив
ко второй строке D8) первую, умноженную на подходящий множи-
множитель тп. При этом в последнем столбце второй строки будет стоять
вместо X выражение X-t-mu. После такого преобразования вторая
строка D8) примет вид
c[v 4 c\ti_v О, c\i+l с\п, 1-\-ти. E0)
Теперь будем умножать на А вектор (с*г .... с* 4_1} 0, с* i с\\.
Получим вместо прежней третьей строки D8) новую строку:
Подберем постоянные т21 и т22 так, чтобы при прибавлении первой
строки D8), умноженной на т21, и строки E0), умноженной на т22.
к строке E1) в последней обратились в нули элементы, стоящие
на /-м и у-м месте, где I 4= j и /<га-|-1. Продолжая этот про-
процесс, мы придем в конце концов к строке, все элементы которой,
кроме крайнего правого, равны нулю. Это показывает нам, что мы
уже получили линейно зависимые векторы. Правый крайний элемент
последней строки и даст нам минимальный многочлен вектора с0.
Преимущество такого метода исключения на каждом шаге состоит
в том, что на А будут умножаться векторы, имеющие все больше
и больше нулевых компонент. Благодаря этому сокращается число
необходимых операций умножения.
Проиллюстрируем это на примере той же матрицы А D4). Возь-
Возьмем прежний вектор с0. Получив Ас0 такое же, как и в D5), исклю-
исключим сп. При этом строка E0) примет вид
0, 3, 1, 3, X —5. E2)

§ 2] МЕТОД А. Н. КРЫЛОВА 185-
После следующего умножения на А получим строку
2, 9, 1, 9, X*—5Х. E3)
Вычтем отсюда первую строку D8), умноженную на 2, и E2), умно-
умноженную на 3. При этом получим:
О, 0, —2, О, X2— 8Х+13. • E4)
Следующее умножение на А даст
2, 0, —8, О, ХЗ — 8X2-ИЗХ. E5>
Вычтем отсюда первую строку D8), умноженную на 2, и E4), умно-
умноженную на 4. Это даст
О, 0, 0, 0, Xs— 12Х2-|-45Х — 54. E6)
Отсюда мы заключаем, что минимальным многочленом вектора с0
является
Хз_12Х2_|_45Х— 54. E7)
Этот же многочлен мы получили и ранее.
Многочлен E7) имеет третью степень. Следовательно, он не сов-
совпадает с характеристическим многочленом, имеющим четвертую сте-
степень. В данном случае мы можем найти недостающий корень харак-
характеристического уравнения. Действительно, след матрицы, т. е. сумма
ее диагональных элементов, должен равняться сумме корней харак-
характеристического многочлена матрицы. В нашем случае он равен 15.
С другой стороны, сумма корней многочлена E7) равна 12. Сле-
Следовательно, недостающее собственное значение равно 3. Нетрудно
видеть, что многочлен E7) можно записать в виде
(X —3J(Х—6). E8)
Таким образом, собственные значения матрицы А равны
Xt = Ха = Х3 = 3; Х4 = 6. E9)
В главе 6 мы уже обращали внимание на важность подсчета
числа операций умножения и деления, необходимых для решения
задачи. Произведем такой подсчет и для метода Крылова в его по-
последнем варианте.
Для образования Ас0 потребуется га2 операций умножения (пред-
(предполагается, что все компоненты с0 отличны от нуля). Исключение
одного из cti потребует га умножений и делений. Последующее
Умножение полученного вектора на А потребует га (га—1) опе-
операций умножения, а исключение двух элементов потребует 2га — 1

186 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
умножений и делений. Продолжая эти подсчеты и дальше, мы
обнаружим, что всего потребуется
га2 + га (га — l)-\-n(n— 2)-f- ... -\-п • 1 + га-|-[га-|-(га — 1)] -|-
—2)]+ ...
+ У' + В F0)
операций умножения и деления.
При этом подсчете мы не учитывали действий с последним столб-
столбцом матрицы D8). Для этих действий потребуется дополнительно
+ ¦.¦+(ra-2))=-3f + 2" F1)
операций умножения.
Таким образом, если все га шагов осуществимы, то метод Кры-
Крылова раскрытия векового определителя потребует
2 F2)
•операций умножения и деления.
2. Отыскание собственных векторов матрицы. Рассмотрим
теперь вопрос об отыскании собственных векторов. Пусть \t является
корнем минимального многочлена, соответствующего вектору с0.
Если степень этого минимального многочлена равна т, то будем
разыскивать собственный вектор xt в виде
** = ТЛ + тИс|> + • • • -г- 1тАт~ %. F3)
Из
Ахг = \гхг F4)
следует:
СоЧ- • • • "f ТтЛ™С0 =
= h (ТЛ + Т2^со-|- ... + 1тАт-%) F5)
или в силу D2)
" 2 •• +Т™-Итс0 —TmX
• • + Тт'4'"" %)• F6)
Итак,
4- aiTm —
-г- «m-iTm - T—i) ^""% = 0. F7)

§ 2] МЕТОД А. Н. КРЫЛОВА 187
Векторы с0, Ас0 Ат~1с0 линейно независимы. Поэтому из F7)
следует:
F8)
Отсюда получаем:
~ Tm-1 =
Tm-2 =
F9)
Мы не выписали повторно первое из равенств F8), так как оно
является следствием остальных и условия
Уч+ат_11Т-1+ ... +0^ + 00 = 0. G0)
Коэффициент ¦[•»» должен быть отличным от нуля, так как в про-
противном случае все остальные коэффициенты ^ были бы равны нулю,
что невозможно, ибо х^ является собственным вектором. Задаваясь
каким-либо значением ~[т Ф 0 (например, 1), мы при помощи ра-
равенств F9) последовательно найдем все остальные ft, а следова-
следовательно, и вектор jcj. Так, для матрицы D4) мы получим, если поло-
положим Xj = 3 и Тз= 1:
Т2 = -9, Ti=l8 G1)
и
х{= \8со — 9Асо-\-А2'со = — 3@, 1, 1, 1). G2)
Нетрудно проверить, что это действительно собственный вектор
матрицы D4), соответствующий собственному значению Х{ = 3.
Если выбрать другое значение ~[т Ф 0, то новый собственный
вектор будет отличаться от предыдущего лишь постоянным множи-
множителем. Таким образом, если степень минимального многочлена век-
вектора с0 равна т и Х^ — произвольный корень этого минимального
многочлена, то в линейном множ«стве, порожденном векторами с0,
Ас0 Ат~1с0, найдется единственный, с точностью до множи-
множителя, собственный вектор xit соответствующий собственному значе-
значению Х{. Для того чтобы найти другие собственные векторы, соот-
соответствующие собственному значению Х{, если такие существуют, и
собственные векторы, соответствующие собственным значениям Х^,
не являющимся корнями минимального многочлена вектора с0, сле-
следует выбрать новый начальный вектор с0, не являющийся линейной
комбинацией векторов с0, Ас0 Ат~1с0, и повторить с ним тот же
процесс, который мы проделали с вектором с0. Иногда придется
повторить это несколько раз.

188 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
§ 3. Метод Ланцоша
1. Отыскание собственных значений. Решение систем B5)
или D2) предыдущего параграфа для определения коэффициентов
характеристического или минимального многочлена можно осуще-
осуществлять методами ортогонализации, изложенными в § 4 главы 6.
Процесс ортогонализации целесообразно проводить после каждого-
умножения на матрицу А. В настоящем параграфе мы и рассмотрим
возникающие при этом алгорифмы.
Выбираем произвольный начальный вектор с0Ф 0 к находим Ас0.
Подберем теперь коэффициент а10 так, чтобы вектор
ci = Лс„ — <х1Осо A)
был ортогонален к вектору с0. Это всегда возможно и условие орто-
ортогональности дает
<?Ц).ш B)
Может оказаться, что ct = 0. В этом случае векторы с0 и Ас^
линейно зависимы и Я1(Х) = Х— <х10 будет делителем минимального
многочлена матрицы А. Тогда дальнейшие действия с вектором с0
прекращаются. Если же с1 Ф 0, то образуем вектор Act и подби-
подбираем коэффициенты <х21 и <х20 так, чтобы вектор
с2 = Асх — a21ct — a2Oco C)
был ортогонален к векторам с0 и cv Это также всегда возможно.
При этом
_ (Ась c"t) . _ (А
a21 ,- —ч ) «20 ,—
(с е) (с
(сь ех) (с0. «о)
Если окажется, что с2^0, то
А (Ас0 — aloco) — а21 (Ас0— а1Осо) — а^ с0 = 0 E)
даст линейную зависимость между векторами с0, и Ас0 и А2с0,
а многочлен
Р2 (X) = (X — а21) (X — аю) — а20 = (\ — а21)Р1 (X) — а20 F)
будет делителем минимального многочлена матрицы А. Если же
с2ф0, то продолжаем процесс ортогонализации.
Пусть нами уже найдены векторы с0, ct ст-ъ удовлетво-
удовлетворяющие условиям:
i,oco
(k=\, 2 m— 1), G)
= 0 при / Ф j, 7кф0 (/, у, fe = 0, 1, 2, ..., m — 1). (8)

§ 3] МЕТОД ЛАНЦОША 189
Тогда подбираем коэффициенты ат, m_b am, m_2 am> 0 так,
чтобы вектор
Ст =
был ортогонален к каждому из векторов с0, cl cm-i- Это воз-
возможно. Коэффициенты ami должны быть определены по формулам
Параллельно с построением системы взаимно ортогональных
векторов с0, ct cm, ... строим последовательность многочленов
Р0(Х)=1; Ят(Х) = (Х —am>m_i)X
ХЯя.-хСХ) — om.m_2Pll,_2(X)— ... — am0P0(X). A1)
Так как в нашем пространстве имеется не более п взаимно ортого-
ортогональных векторов, то на каком-то шаге будем иметь ст =0. При
этом
Аст-\ От, m-iCm-i ат,т-2Ст-2 ... ССт> 0С0 = 0 A2)
даст линейную зависимость векторов с0> Ас0, ..., Атс0 и, следова-
следовательно, многочлен
т-2
Рт W = (X — am, m_0 Pm-i W — S am. *^* W A3)
fc=0
будет делителем минимального многочлена матрицы А. При
т = п Рт(к) будет являться характеристическим многочленом
матрицы А. Если m < п, то выбираем новый начальный вектор с'о,
ортогональный к векторам с0, ct cm_lt и повторяем с ним
тот же процесс. Если этого окажется недостаточно, т. е. общее
количество ортогональных векторов все еще будет меньше п, то
проводим наши рассуждения с новым вектором с'^, ортогональным
ко всем предыдущим, и т. д.
Для симметрической матрицы А равенства G) упрощаются.
Действительно, в этом случае
г — ~^—=— ^= —=—=^*—' ^= ~~=—~r-
(Cf, Cf) (Cf, Cf) (Ci, Ct)
A = 0, 1, 2 ft), A4)
и если /<&—1, то ал+1I = 0. Таким образом, если матрица А
симметрическая, то вместо' G) будем иметь:
?*+i = Аск — a^+i, кск — ал+1, a-xCa-l A5)

190 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Аналогичное упрощение можно получить и для несимметриче-
несимметрической матрицы, заменив процесс ортогонализации процессом биортого-
нализации, подобно тому как это сделано в § 4 главы 6.
Будем исходить из двух начальных векторов с0 и bQ. Найдем
по ним векторы Ас0 и А'Ъй и образуем линейные комбинации
с1 = Ас0 — al0c0; bt = А% — pi0*0. A6)
Коэффициенты а10 и р10 подберем так, чтобы оказалось (Cj, ?0) =
= (#1, со)= 0. Это возможно, если начальные векторы с0 и Ьо не были
ортогональны, так как
_й (ЛСр, ?0) (с~0, А'Ь0) ,7s
аю—Рю— —=—рг ;=—FT"' ^ '
(«о. *о) (с0. *о)
В дальнейшем будем предполагать, что (с0, ?0) Ф 0. Тогда по най-
найденным с1 и ftt строим векторы Ас1 и А'ЪХ и образуем линейные
комбинации
с2 = Асх — Ог^! — а20с0, *2 = Afbl — р2 А — РгА (! 8)
так, чтобы оказалось
(с2, ft!) = (c2. Ь0) = ф2, 70 = фг, с^ = 0. A9)
При этом будем иметь:
„ о (^Ct, fet) (С^ Л^О .
«21 Р21 !=¦—=Т —= =— )
(CV fti) (Ct. ftt)
о (Леь b'o) (ср. Л^т) (cl fei
СС20 ^= Р20 r^ ^— ^= =—z^ = —zz zz
(c0, 60) (co. *o) (co. *o
B0)
и наше построение возможно, если (cv bj Ф 0, (с0, *0) Ф 0. Будем
предполагать, что эти условия выполнены, и продолжим построение
дальше. Пусть у нас уже построены векторы
с0, сх ск, B1)
fto. *i. •••.**. B2)
причем эти две системы биортогональны, т. е.
(bit с,) = 0 при /^у (г, у = 0,1 к). B3)
Тогда строим векторы
Ск — 4 + 1, k-lCk_l— ... —
— — — _
= A'bk-—Pfc+i, kbit — Pit+i, k-ibk-i— •¦• —Pfc+i,0*0

§ 3] МЕТОД ЛАНЦОША 191
так, чтобы
(с*+1. *i) = Фк+v ci) = 0 (/ = 0,1,2 /г). B5)
Условия B5) дают
„ О (Ach, bj) (A'bje, Cj) .. п . , 9R
«A+i, t — Pfr+i, t= .- Гч ——=—=— (* = O, 1 k). {2b)
(Cf, *i) (c4, b4)
При этом, если /<&—1, то
«*+i, » = iWi, » = (^'-1г) = (F*1 ^ =-^' fcl+t) = 0. B7>
(c* *t) (««• *f) (Cj. *»)
Таким образом соотношения B4) примут вид
Наши построения будут возможны до тех пор, пока (ск, Ьк) Ф 0.
Это условие может нарушаться в следующих трех случаях:
а) ск = 0 и Ьк = 0;
б) либо ск = 0, либо Ьк = 0;
в) ск фО, ЪкФ 0, но ск J_ Ък.
B9)
Все эти три случая могут встречаться фактически. Продемонстри-
Продемонстрируем это на примере матрицы D4) § 2.
а) Возьмем сначала
fto=q> = (O. 1.0. 0). C0)
Тогда
Л7О = B, 3, — 2, 0); А% = (Ъ, 3, 0, 0) C1)
и
^>=3. C2)
Следовательно,
q=B, 0, —2, 0); *! = C, 0, 0, 0). C3)
Далее,
Лс1 = A2, 6, —6, 6), Л'^ = A5, 6, —3, —3). C4)
Отсюда
(А~сь Fo) _ Ri (M.lQ fi
(*» co) (ci, bx)
F2 = @, 0, 6, 6); *2 = (—3, 0, —3, —3). C6)

192 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Продолжая процесс, найдем:
Ас2 = (—12, 0, 30, 18), А% = (—27, 0, —9, —9),
(Лез, fei) R
а31 = - - = — о,
(<? *)
73 = @, 0, 0, 0),
б) Возьмем теперь
(Асг, Ьъ)
о — —=г—=— — О,
(с* Ь,)
= @, 0, 0, 0).
При этом
Ь0 = с0 = A,0, 0, 0).
C7)
C8)
Ас0 = E, 3, 1, 3), А'Ь0 = E, 2, —1, —1),
(р. p)
аю= .- Гч =
с1=@, 3, 1, 3),
сх = B, 9, 1, 9),
*1 = @, 2, — 1,— 1),
А% = B, 8, —4, —4),
_ (Acv b0) __ 0
0 =—=^T ¦*.
(«0. *o)
021 == —=—=т\— ==
c2 = @, —3, —3, —3), b2 = @, 0, 0, 0).
в) Наконец, если взять
Cq = A. О, 0, 0), bo = (l. *3Г\ 0.
C9)
то
со = E, 3, 1.3).
, —1,-1),
ёх =A —1^3, 3, 1. 3), \ =@, -J' —!• —
D0)
D1)
D2)
Если минимальный многочлен матрицы А имеет степень т, то
векторы с0, ^4с0, ..., Атс0 и ?0, Л'*о, .... А' Ьо линейно зависимы.
В силу этого наш процесс обязательно закончится не позже чем
через k-^m шагов. При этом в случаях а) и б) мы найдем
линейную зависимость между векторами с0, Ас0 Акс0 или
Sq, A'b0 А'кЬй, а следовательно, и минимальный многочлен мат-
матрицы А или его делитель. Случай в) может встретиться лишь как
исключение при неудачном выборе начальных векторов с0 и Ьо и его
всегда можно избежать, выбрав другие начальные векторы.

§ 31
МЕТОД ЛАНЦОША
193
Предполагая, что мы получили ?^. = 0, или Ьк = 0, последова-
последовательно находим минимальный многочлен А или его делитель по
формулам:
Р0(к)=\,
Р1(к) = (к — а10)Я0(Х),
Р2 (к) = (X - а21) Р1 (к) - а20Р0 (X).
_2 (X) — aft_i, к-зРк-з (X),
-1 (X) — afc> л_2Pfc_,().).
D3)
Р, _, (X) = (X — <**_!, *
Р* (X) = (X — aft, ft_i
В частности, в рассмотренных нами примерах будем иметь: в слу-
случае C0)
D4)
D5)
Я, (X) = X — 3,
Р2 (к) = (X — 6) (X — 3) — 6 = X2 — 9Х + 12,
Я,(Х) = (Х-3) (Х2-9Х + 12)+ b (Х-3) = к'- 12Х2 + 45Х-54,
в случае C8)
Л>(Х)=1, ^
Я1(Х) = Х-5,
Я2(Х) = (Х — 4)(Х— 5) — 2 = Х2 — 9Х+ 18.
Такой способ получения минимального многочлена или его
делителя будем называть методом Ланцоша.
Пусть процесс, осуществляемый по методу Ланцоша, продол-
продолжается до k = n—1. Рассмотрим матрицы
¦ с01 си ... с„_1, д / Ьох Ь1Х ... bn-h
Ice с \ \ Ъ Ъ Ъ
-1, я/
где ctj и ?^ — соответственно компоненты векторов cf и
биортогональности будем иметь:
«о 0 ... 0
D6)
В силу
D7)
0 0 ... 6n_i
где bi = (ci, Ъ{). Следовательно, C~l=D~lB' и B~l=D'1C'.
i
Далее, так как
Acj) =
v A7t) =-- G,. ft4) =
при |/— y|> 1,
D8)

194 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
ТО
B'AC =
Поэтому
-1 «n,n-l6n-l
D9)
E0)
о о
1 «п, п-1
Таким образом, в рассматриваемом случае наш процесс эквива-
эквивалентен приведению матрицы А к тридиагональной форме. Если про-
производить процесс Ланцоша без указанных упрощений, то он будет
эквивалентен приведению матрицы А к верхней треугольной форме.
В симметрическом случае всегда получим тридиагональную форму.
Случай &<га—1 потребует выбора новых начальных векторов,
как это указывалось в начале параграфа. При этом матрица при-
приводится к
А \ 0
E1)
I 0 ! Ак
где клетки Ai имеют вид, указанный выше.
Вернемся еще раз к вопросу о применении метода Ланцоша
в случае симметрической матрицы А. Этот случай особенно выгоден
для этого метода.
Прежде всего отметим, что для симметрической матрицы
ск-х) (ck> Aek-i)
=
к- ек)
> 0, E2)
(Ck-V ek-l) (Ck-V ek-l) (Ck-V Cft-l)
причем знак равенства будет достигаться лишь при ск = 0. Далее,
из условия
^_1_ 1 ^Л/ — ^л ^fc+1, к) *к iA/ * ^Л+1) А* 1 * ft 1 t,^1/ (.^^5/
следует, что никакие два многочлена Pfc (X) и Рк+1 (X) (Л^О, 1, ..., т— 1)
не могут обращаться в нуль при одном и том же значении Х = Х'.
Действительно, если бы Pk+l(k')= Pk (А') = 0, то из E2) и E3) сле-
следовало бы Рк_1(к') = 0. Повторяя эти рассуждения для многочленов
/\(Х) и Pk_i(k), мы пришли бы к выводу, что /\_2(Х') = 0. Про-
Продолжая дальше, мы пришли бы в конце концов к заключению, что
Л)('-') = 0. Но это невозможно, так как Я0(Х)=1.

К 31 МЕТОД ЛАНЦОША 195
Изучим теперь взаимное расположение корней Я4(Х). Много-
Многочлен Pi (X) имеет единственный корень X*/' = <х10. При этом Р2 (Xi") =
_—о2о^)о<0' Следовательно, квадратный многочлен Я2(Х), поло-
положительный для достаточно больших по абсолютной величине значе-
значений X, будет обращаться в нуль в точках Xf и Xi>2), Xf < Х^1' < Х^2).
Для Я3(Х) будем иметь: Ръ(xf) = — а31Я, (Х(,2)) > О, Я8(х?г)) =
= — KgjPj (Хг ) < 0. Так как Я3(Х) отрицателен при достаточно боль-
больших по абсолютной величине, но отрицательных X и положителен
при достаточно больших положительных X, то имеются три корня Я3(Х):
М*. Х!,3', Х33), таких, что Х(,3) < Х(,2) < Х^3) < Х<2> < Х33). Теперь нетрудно
по индукции показать, что рее корни многочленов Рк (X): Х^', X^ft) \$\
действительны, различны и удовлетворяют условиям:
X?» < Х?) < ХB*> < X?-1» < ... < х?>, < ХГ.!) < Х?>. E4)
Пусть это выполнено для &= 1, 2, 3, ..., /. Тогда в силу E3)
Яг+1(Х?)) = -аг+1,г_1Я,-,Dг)) E5)
и, следовательно, в силу E2)
^+.04V*-.0^)<o. E6)
По предположению индукции /эг_1 (X) не имеет кратных корней,
поэтому Pi-i(^P) меняет знак при переходе от / к /-(-!• Следо-
Следовательно, в силу E6) это верно и для Р1+1 (X?'). Так как степени
Р1+1 (X) и Яг_, (X) имеют одинаковую четность, то эти многочлены
должны иметь одинаковые знаки левее и правее множества всех их дей-
действительных корней. Xi' лежит левее всех нулей Pt_i (X), а Ц — правее
всех нулей Р1_1(к). Поэтому Р1+1 (X) должен обратиться в нуль
левее Xi и правее Ц'. Так как он должен обратиться в нуль между
каждыми двумя соседними ~к\ , то утверждение доказано.
Из доказанного следует, что совокупность многочленов /\(Х),
& = 0, 1,2, .... т образует систему Штурма (см. главу 7, § 1).
Поэтому мы можем использовать ее для отделения корней много-
многочлена Рт(к), как это указано в предыдущей главе.
Подсчитаем число операций умножения и деления, необходимых
Для получения характеристического многочлена симметрической
матрицы А порядка п по способу Ланцоша. Пусть процесс, начи-
начинающийся с вектора с0, может быть продолжен вплоть до с„. Конечно,
сп = 0. Вычисление Ас0 потребует п1 умножений. Получение
аш = 04с0, со)/(со, с0) потребует 2п-\- 1 умножений и делений. По-
Поэтому переход от с0 к сх — Ас0 — <х1Осо потребует всего п2 —(- Зга —|— I
опе?аций умножения и деления. На следующем шаге, при переходе
от с, к с2, придется затратить п2 операций умножения для получе-
получения Act, Зи-(-2 операций умножения и деления для получения

196 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ ГГЛ. 8
коэффициентов a2l = (Acl, cl)/(cl, Cj) и аго = (Ас1, со)/(со, с0), 2га опера-
операций умножения для получения с2 = Act — o^Cj — агосо- Таким образом,
всего второй шаг потребует га2-)-5га+2 операций умножения и
деления. Столько же потребует и каждый следующий шаг. Всего
для получения последовательности векторов с0, сх
требуется
сп_1
по-
по1L-(га —2)(га2 + 5га + 2) = га34-4га2 —5га —3 E7)
операций умножения и деления. Нам еще придется подсчитать an>n_i
и an> п_а, для чего нужно Зга-)-2 операций умножения и деления.
Наконец, получение многочлена Я„(Х) требует
... 4-Bга — 3) = (га— IJ E8)
операций умножения. Таким образом, всего для получения характе-
характеристического многочлена матрицы А потребуется
п? + 4га2 — 5га — 3 -+- Зга 4- 2 + (га — IJ = га3 4- 5га2 — 4га E9)
операций умножения и деления.
2. Отыскание собственных векторов. В заключение остано-
остановимся на отыскании собственных векторов, Предположим, что, при-
применяя метод Ланцоша, мы получили ст= 0. Пусть Х{— какой-нибудь
корень минимального многочлена вектора с0. Тогда будем разыски-
разыскивать собственный вектор, соответствующий этому собственному зна-
значению в виде
Условие
То (ci +
Axi = \iXi дает
oco) + Ti (C2 4- O2iС1 4- а20с0) 4- .. .
• 4" Tm-2 (cm-i 4" ат-ь т-2ст-2 4" ат-1, т
"Т" Tm-l (am. m-icm-i 4~ am, m-2cm-2)
-г) 4"
В силу линейной независимости векторов с0, cv ..., ст_1 из F1)
следует:
ТО (Хг aio) — O20Tl = 0'
Tl (Xi — 021) — «3lT2 — TO = 0,
T2P4 — М- О42ТЗ— Tl=0'
i — am-i, m-2) am, т-г\т-\ — Tm-3^
i — Om>m_i)— Tm-2=0.
F2)

§ 3]
МЕТОД ЛАНЦОША
197
Коэффициент 7m-i должен быть отлучен от нуля, так как в про-
противном случае и все остальные коэффициенты ft были бы равны
нулю. Положим, например, Ym-i=l- Тогда остальные коэффи-
коэффициенты ft последовательно находятся из равенств:
Тт-2— (^{ — am, m-i)>
Тт-з = Тт-2 Оч — ат-ь т-г) — ат, т-2-
F3)
To = Tl (*4 — «21) — a31 T2-
Как и для метода Крылова, первое из равенств F2) будет след-
следствием остальных и условия, что Xf является корнем минимального
многочлена вектора с0.
Найдем собственные векторы матрицы D4) § 2. Если за век-
вектор с0 принять C0), то вычисления при Х^=3 дают
Тг= 1 • \
Ti — ^* — аз2 = 0, ^ F4)
ТО = Tl Он — a2l) — «31 = 6 ]
и
*«=@. 6. 0, 0)-h@. 0, 6, 6) = @, 6. 6, 6). F5)
При Х{=6 соответственно получим:
Ti=xi — «32 = 3.
То = Ti (h — <*2i) — «3i = 6
F6)
xi=@, 6. 0, 0)-hF, 0, —6, 0) 4-@, 0, 6, 6) = F, 6, 0, 6). F7)
Можно ввести в рассмотрение многочлены:
<7i M =
Яг О-)z
. — &т, т—ОЯо (X).
^ — ат_ 1, от_2) Qi (X) — ат>,
Ят-l W = (^ —
= 0- — aio) Ят-l Q-) —
F8)
j
Тогда собственный вектор xit соответствующий собственному зна-
значению Xj, можно записать в виде
Многочлен
с0 +¦ 9ОТ_2 (X,) с, -(- ... -(- qx (X{) ~cm_2 ¦+- q0 (X,)
в F8) совпадает с многочленом Рт(к).
F9)

198 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
§ 4. Метод Данилевского
Довольно простой и изящный способ получения характеристи-
характеристического многочлена дал А. М. Данилевский. Суть его метода
состоит в преобразовании уравнения
D(k)=\A — \I\ =
к виду
Pi
—
1
0
X
Pi
— X
1
Ръ
0
— X
... Pn-l
... 0
... 0
Pn
0
0
0 0
1 —X
=0-
A)
B)
При этом определитель B) легко раскрывается, и мы получим:
= ( 1) [X jPjX. —р2^- — . . . —Рп\' C)
Проиллюстрируем ход вычислений по методу Данилевского на
примере матрицы четвертого порядка
А = \
«и ап «ш аи
«31 «ЗД «23 «24
«31 «32 «S3 «34
¦ «41 «42 «43 «44 '
Эта матрица должна быть преобразована к виду
' Pi Р2 Рз Р4'
10 0 0
0 10 0
0 0 10
D)
E)
(нормальная форма Фробениуса) преобразованиями подобия.
Делим все элементы третьего столбца на а43. Если а43 = 0, то
предварительно находим среди элементов аи и а42 отличный от
нуля. Пусть это оказался а42- Тогда меняем местами вторую и
третью строки и второй и третий столбцы. Если а41 = ai2 = aib= О,
то характеристический многочлен матрицы D) примет вид
13
Й12 «
М — X йзд
«32 «34 — X
F)
и наша задача сведется к отысканию характеристического много-
многочлена матрицы третьего порядка.

§ 41 МЕТОД ДАНИЛЕВСКОГО 199
Вычтем теперь из /-го столбца (/=1, 2, 4) полученной матрицы
«11 «12
«21 «М
«43
«93
«43
«14
«31 «32 "Г2- «34
«43
G)
«41 «42 1 «44
третий столбец, умноженный на a4i. При этом матрица примет вид
д.,—
«43
«21 ~
«43
«33«4t
«43
«12 —
«22
«32 —
«13«42 «13
«43
«13«44
«43
«43
«ЗВ«42
«43
О
О
«ЗД
«43
«33.
;43
1
«24 —
«
«34 —
«43
«33«44
«43
О
(8)
Наш процесс эквивалентен умножению матрицы D) справа на
матрицу
(9)
Чтобы получить матрицу, подобную исходной, мы должны умно-
умножить (8) слева на матрицу Bf1, равную
1 О О
О 1 О
1
0
«41
«43
0
0
1
_«42_
«43
0
0
0
1
«43
0
0
0
с
с
1
О
«41 «42 «43 «44
0 0 0 1
A0)
При этом получим:
(
«и —
«21
«44
«23«41
«43
«13«42
«43
«44
о
«18
«43
«23
«43
*33
1
«43
«24 —
«43
Умножение на Bf не изменяет первой, второй и четвертой строк.
Третья же строка получается путем сложения строк (8), умножен-
умноженных соответственно на aiV ai2, «43 и «44-

200 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
На следующем этапе преобразуем третью строку. Это дости-
достигается путем умножения матрицы A0) справа на матрицу
о
J_
о
о
A2)
и последующего умножения слева на матрицу В*
10 0 0
равную
A3)
0 0 10
0 0 0 1
Ход вычислений подобен предыдущему. Матрица А будет приведена
к виду
1
о
Наконец, умножая A4) справа на
1 @Ч&
си
о
1
A4)
0
0
0
Си
О
1
О
Си
О
О
1
A5)
и слева на
мы придем к нормальной форме Фробениуса.
Приведем числовой пример. Возьмем уже
в главе 6 матрицу А:
0,1818
7,1818
0,2141
0,1815
0,1526
0,3114
А =
6,1818
0,1818
0,3141
0,1415
0,1516
0,2141
0,3141
0,2141
8,2435
0,1214
0,2516
0,2613
0,1415
0,1815
0,1214
0,3141
0,3145
0,6343
0,1516
0,1526
0,2516
0,3145
5,3116
0,8998
A6)
использованную
0,2141
0,3141
0,2618
0,6843 ' <17)
0,8998
4,1313
Вычисления сведены в следующую таблицу:

§ 4]
МЕТОД ДАНИЛЕВСКОГО
201
¦^t* со to t^> •— см
00 СМ ОЮ00 О
^^ CM ^ t^ <O LO
оГ оо~ оГ о" о-" со*
— 00 CO 00 CO
* ¦* — ¦sPO —
— — CD CO CT> CO
CM CO CM CD 00 —
со
со
CD S S CO —
CO
I
NNOOD
S CM S ¦* —
Ю O> CD CO О
см CMoqoq ¦*_
co"s s od ю"
см-
OOOOCO О
I I N'T
S CM
я
) CO CM C
8 S
t^ 00
CM ¦*
CD CO
°°. "^
cd" ю"
ст> о
CD CD CD Ю CD 00
^- CM ~- Tf ^- Q?
Ю Ю Ю ^- ^- O)
««CM CO CO 00
oo о о юо
) О^ О^ О^ СО
, ^_ см со с»
Ю « CM
ОЮ00
" " * "
О
о" о" о* о"
I соо-
g"
T 7
т^ 00 СМ^- ^- (
о"сГсГаГо"сГ
ст>
CD t^
о" о
¦* Ю
t^ CM
OS
о о ост>со о
I
— 00 ¦* Ю
о" о" о" со*-
55 со
оо" сп"
— — Ю ¦* CD 00
* *СО
Ю ¦* CD 00
СО — — —
^(NlOO
со см см —,см см
о"о"оо"о*о"о"
CD CT>
см см
^- со
^ о"
СТ> Ю СО (N
ю ^ ст> t^
см ^.^¦^
о'ооо'ео'о О
5^2
00 00 — 00 Ю —
— — см —— со
со то
о* о"
CM CM CMS 00
o*s*o"o*—"о
00 СМ
о" о"
О> тр О> CD
— OCO ¦*
см —-* о
— — — ю
о* s" о" см" о о
00 00 — Ю СО
00 00 — ¦* Ю —
— — со —— см
— ст>
см см
S Ю CMSO
ЮЮ* СО СМ
СО
СОООООО
о о
СО О О О .
S СТ>
см -*
S СО
¦* —
о" о"
-* SS0O
5 со со см
см*
со*о"о —"с о
О 00
— 00
Y
I .„
03
оГ oj
^- Tf 00 СО 00 СО
^- — СО 00 С7> СО
СМ СО СМ СО 00 —
S CT>S CTiCMS
СМ СО Ю Ю -ч^ —
NOcO^1
од од
. . . . Ч.
о" о" —" см" о" см"
см
— см со ¦* ю со
ст> о — см со ¦*
со
Ю CD
s оост> о — см
— — — см см см
I со ее
од од
со -*
СМ СМ

Продолжение
№
25
26
27
28
29
30
31 B7')
32
33
34
35
36
37
38
39C4')
40
41
42
43
44
45
46
(в*-)'
—0,7912
—1,1707
—0,6439
18,9150
—109,8772
196,8627
в,
1,7586
1,7626
27,6943
—275,9574
1161,1832
—1727,3256
Вь
—1,2640
34,1922
—457,0175
2975,2901
—9393,9883
11441,3062
1
5,8220
—0,0429
—9,8071
0
0
0
1,7586
—0,9977
6,1718
—6,8749
0
0
0
0
—1,2640
(—1)—0,7911
—4,8828
1
0
0
0
0
40,3641
2
0,3506
6,8477
—14,7566
0
0
0
1,7626
(—1H,5673
—0,1989
3,8850
1
0
0
0
34,1922
27,0508
166,7532
0
1
0
0
0
—667,7935
3
—0,4036
—0,2244
—12,7307
1
0
0
27,6943
—15,7122
5,1051
—107,8168
0
1
0
0
—457,0175
—361,5645
—2226,3987
0
0
1
0
0
5789,4581
4
7,6438
4,2676
240,7770
0
1
0
—275,9574
156,5627
—47,2471
1076,3620
0
0
1
0
2975,2901
2353,8688
14480,3604
0
0
0
1
0
—27697,1638
5
—44,2717
—24,7128
—1398,2938
0
0
1
1161,1832
—658,7900
186,7001
-4535,9092
0
0
0
1
—9393,9883
—7431,9528
—45681,8262
0
0
0
0
1
69183,1345
6
79,1806
44,2968
2504,7672
0
0
0
—1727,3256
979,9873
—264,4029
6754,9558
0
0
0
0
11441,3062
9051,6663
55600,6712
0
0
0
0
0
—70279,2484
5
47,6205
30,4319
1309,9560
1
1
1
—810,8843
460,0501
—113,8719
3184,6019
1
1
1
1
4598,5187
3638,0686
22334,6771
1
1
1
1
1
—23631,2492
5'
4848,0242
30,6562
1322,6860
—113,6731
3180,7170
22339,5599
N5
О
Ю

с 4] МЕТОД ДАНИЛЕВСКОГО 203
Теперь поясним схему. В первом столбце помещена нумерация
строк. Столбцы, обозначенные цифрами 1—6, предназначены для
элементов исходной матрицы А, матриц В* и В^1, промежуточных
матриц В, . ¦ . Bz^By^ABiBz. . .Bt и окончательной матрицы, полу-
получающихся в процессе вычислений по методу Данилевского. Послед-
Последние два столбца — контрольные.
Первые шесть строк A—6) в столбцах 1—6 использованы для
элементов исходной матрицы А. В столбце S стоят суммы элемен-
элементов А по строкам.
Строки 7 и 8 предназначены для элементов Вх и Bf1. Ввиду
особенностей строения этих матриц, достаточно записать только их
пятые строки. В столбцах 1—6 седьмой строки записаны элементы
пятой строки ?f\ которые просто равны элементам шестой строки
матрицы А. В столбцах 1—6 восьмой строки помещены элементы
пятой строки матрицы В., равные соответственно ЬЪ1 = —,
Элемент аеь, на который производится деление, в схеме подчеркнут.
В столбце S восьмой строки стоит результат деления S, стоящего
в шестой строке, на аГо с обратным знаком. Поэтому он должен
равняться сумме остальных элементов этой строки, если заме-
заменить #55 на —1 (в схеме —1 показана в скобках).
Следующим этапом будет умножение А на Bv Соответствующие
элементы с^ помещены в строках 9—14 и столбцах 1—6. При
этом в столбце 5 будут помещаться результаты деления элементов aib
на а№ или, что то же самое, результаты умножения а1ь на Ььь.
Остальные элементы cik вычисляются по формулам
с« = в{*-Мб*в». A8)
После этого шестая строка примет нужный нам вид. В столбце S,
как и всегда, помещаем суммы элементов строк, а в столбце S' —
результаты вычислений со столбцом строк 1—6 по формулам, ана-
аналогичным A8). Контроль будет заключаться в том, что сумма
столбца S' и столбца 5 должна давать столбец S.
После этого производим умножение на BJ. При этом изме-
изменяется только пятая строка определителя ABlt т. е. строка 13 нашей
схемы. Пятая строка определителя B^ABi равна сумме произведе-
произведений строк АВХ на соответствующие элементы пятой строки Bf \
Для удобства элементы Bf1, на которые умножаются строки ABV
выписаны во втором столбце схемы против соответствующих им
строк. Результат вычислений помещен в строке 15. Эта строка
будет одновременно являться четвертой строкой матрицы В^1.
Дальнейшие вычисления происходят аналогично. Роль ае6 теперь
играет элемент строки 15 и столбца 4. Четвертая строка В2

204 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. &
помещается в строке 16 схемы. Матрица Въ^В^^АВхВг помещается
в строках 17—23 и т. д.
В данном случае искомый характеристический многочлен будет
иметь вид
?)(Х) = Хв — 40,3641Хь + 667,7935Х* — 5789,458 IX3-)-
Ч-27697,1638Х2 —69183,1345Х +70279,2484. A9)
Интересно отметить, что след матрицы А, который должен рав-
равняться коэффициенту при X5 с обратным знаком, в нашем случае
равен 40,3641. Совпадение полное.
Приведенная нами схема не является лучшей. Однако она до-
довольно удобна и проста для объяснений. Она применима для матриц,
любого порядка.
Произведем подсчет числа операций умножения и деления, необ-
необходимых для получения характеристического многочлена матрицы
порядка га по приведенной выше схеме, учитывая применение кон-
контроля.
Получение В1 потребует га -)-1 операций деления. Вычисление
(га—1)-го столбца АВХ потребует га—1 умножений. Получение
остальной части ABt (с включением контрольного столбца) по-
потребует га (га—1) умножений. Наконец, умножение АВ1 на fif1 по-
потребует (га— 1) (га-)- 1) умножений. На следующем шаге, при переходе
от B^ABi и Вг1 ВТ1 ABiB%, нам потребуется соответственно га-|-1
делений, га — 2 умножений, га (га — 2) умножений и (га — 2) (га 4-1)
умножений. Так же производится подсчет и дальше. Таким обра-
образом, всего будет нужно
(га-1)(га+1)-Н(га-1) +
+ (и —2)+ ... +2+1]Bга + 2) = (га2—1)(га + 1) B0>
операций умножения и деления.
1. Видоизменение метода Данилевского. Рассмотрим теперь
одно видоизменение метода Данилевского. Опять для иллюстрации
воспользуемся матрицей четвертого порядка D). Вместо Bt и fif1
возьмем теперь матрицы
0 0 0 аи
B2)

4]
МЕТОД ДАНИЛЕВСКОГО
205
Произведение С, ' А равно
aU a12 «13 °
«21 «22 «23 °
«31 Й32 Й33 °
«42 «43
1
B3)
где
«14
(i, k=l, 2, 3);
j' =-2i* (k= 1, 2, 3, 4).
B4)
Умножение Ci А справа на С, даст
4V
С
$ 0 4V
д()
«24
«32 " 4
„A) 1 „A)
242 ' 4
B5)
где
3
« ^ 1
i= 1, 2, 3, 4;
!=1, 2, 3, 4).
=l, 2),
B6)
Следующим шагом будет являться умножение матрицы B5) на ма-
матрицу CjT1, равную
-aQla^l 1 О О
-a.W/a{1} 0 1 О
-а$/с$ О О 1
l/a\l) OOO
,(П
1
B7)
О
и справа на матрицу
С,=
0 0 0 а\
10 0 4
0 10 4;
i oi4
О {
B8)

206 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Первое умножение даст нам
4Г
о о
0 о
1 О
B9)
где afy' находятся по формулам, аналогичным B4), а второе умно-
умножение приведет к
I2.' О 0 4
4? о о
а?> О 1
C0)
где о^ находятся по формулам, аналогичным B6). Если еще раз
повторить этот процесс и использовать матрицы
000 4?
1 О О а?>
о 1 о 4?
О 0 1 а*2,)
«24 /4
"84 '4
i/432
1 О О
О 1 О
О 0 1
0 0 0
C1)
то мы придем к
-.-1/-.-1/-.-1
ooo
i о о
о l о
о о l
C2)
В общем случае матрицы и-го порядка мы после п—1 шагов при-
придем к матрице
0 О О ... О 4п~"
1 о о ... о 4Z~l)
4Г
О 1 0 ... О а!
ЗП
о о о ... 1 «ЯГ1
C3)

§ 4] МЕТОД ДАНИЛЕВСКОГО
Характеристический многочлен матрицы C3) равен
— X О
1 —X О ...О
О 1 —X ...О
207
О ...0 afn~l)
о
о
i=0
Заметим, что в качестве Cl можно взять произвольную матрицу
вида
0
t
C5)
с t Ф 0. Это вызвало бы лишь добавление одного шага. В то же
время удачным выбором последнего столбца C5) возможно умень-
уменьшить вычислительную погрешность. Можно показать, что выгодна
брать в качестве последнего столбца C5) компоненты вектора,
близкого к собственному вектору А, соответствующему наименьшему
по модулю собственному значению. Описанное нами видоизменение
метода Данилевского соответствует выбору последнего столбца C5)
в виде
Г
C6)
Обозначим через t0 вектор, компоненты которого равны элементам
последнего столбца матрицы C5), и через Sn— матрицу Cfi^ .., Сп.
Тогда если A{n) = C~lC~Ll . . . С^^АС^ ... Сп.хСп, то имеем:
ASn = SnAw. C7)
Так как Л(п) имеет вид C3), то из C7) следует, что каждый стол-
столбец Sn получается из предыдущего путем умножения его на ма-
матрицу А. Первый столбец Sn состоит из компонент вектора t0. Сле-
Следовательно, столбцы матрицы Sn состоят соответственно из компо-
компонент векторов
'о> ^'о* мI • ¦ ¦ • *о- C8)
Этим можно воспользоваться для отыскания собственных векторов
матрицы А, как это было сделано в методе Крылова.
Как в исходном методе Данилевского, так и в данном нами
видоизменении можно увеличить точность, выбирая в качестве эле-
элемента t, на который производится деление, наибольший по модулю

¦208 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
элемент соответствующей строки или столбца. Так, в видоизменен-
видоизмененном методе Данилевского можно взять
1 A
0
0
0
0
t
А
0
0
t
t
1
т
0
h
0
C9)
тде последний столбец Q совпадает с последним столбцом пре-
преобразуемой на данном этапе матрицы, a t — наибольший по модулю
элемент этого столбца, /j и /2 — единичные матрицы. Порядок /2
должен быть больше, чем число столбцов преобразуемой матрицы,
уже приведенных к нормальной форме Фробениуса.
В видоизмененном методе Данилевского, так же как и в исходном,
процесс может привести к матрице вида
тде F — матрица, имеющая нормальную форму Фробениуса. Это
не вызовет никаких дополнительных затруднений, так как харак-
характеристический многочлен F является делителем характеристического
многочлена матрицы А, а остальную часть последнего характери-
характеристического многочлена можно получить, продолжая преобразования
матрицы Av
Возможен следующий контроль метода Данилевского. Вместо А
¦будем преобразовывать матрицу
D1)
где строка b выбрана так, чтобы сумма элементов каждого столбца
матрицы D1) была равна 1. Тогда если выбрать t0 так, что сумма
его компонент также равна 1, то сумма элементов каждого столбца
всех преобразованных матриц будет равна 1.
Видоизмененный способ Данилевского несколько удобнее для
вычисления на автоматических вычислительных машинах.
§ 5. Обзор других способов получения
характеристического многочлена
В настоящее время известно большое число других способов
получения характеристического многочлена. Нет никакой возможно-
возможности изложить их подробно в нашей книге. Поэтому мы в настоящем
параграфе ограничимся лишь кратким обзором некоторых методов,
ле изложенных ранее.

§ 5] ОБЗОР СПОСОБОВ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИЧЕСКОГО МНОГОЧЛЕНА 209
1. Метод Леверрье. Обозначим корни характеристического много-
многочлена через \, Х2, .... Хп. Тогда если
. A)
то
Выражения, стоящие в правой части равенства B), являются сим-
симметрическими функциями корней характеристического уравнения.
Рассмотрим еще следующие симметрические функции корней:
Из курса высшей алгебры известно, что Sk и рк связаны соотно-
соотношениями (формулы Ньютона)
0 (k<n). D)
Отсюда получаем:
E)
J
и мы можем найти все рк, если будут известны Sk. Но Sk равняется
следу матрицы Ак. Поэтому, вычислив Ак (k= 1, 2 и) и найдя
их следы, мы можем найти характеристический многочлен. Процесс
довольно трудоемкий, так как приходится производить большое
количество умножений матриц. Д. К. Фаддеев предложил усовер-
усовершенствование метода Леверрье. Оно состоит в следующем.
Рассмотрим матрицу С(Х), присоединенную для матрицы А — X/.
При этом
F)
где D(X) — характеристический многочлен матрицы А A). Матрицу С (К)
можно записать в виде
где Ci-—квадратные матрицы порядка п, не зависящие от X. Срав-
Сравнивая коэффициенты при одинаковых степенях X в правой и левой

210 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. S
частях F) и учитывая G), получим:
_С0 = (—1)"/,
C2 — ClA = (—l)n-lp2I,
Отсюда получим:
С0=(—1)п~11, (9)
Cl = C0A-\-(— lf-lPlI=(— \)n-l[A+PlI\. A0)
Так как pt определяется следом матрицы А и, следовательно, из-
известно, то мы сможем найти Ct. Умножая равенство A0) на А
и беря след от обеих частей равенства (мы будем обозначать след
матрицы В через Sp(fi)), найдем в силу второго из равенств E):
Sp (С,А) = (—I)" [Sp (Л2) -|_PlSp (A)] =
nll] = (—\)n2p2. A1)
Это нам позволит найти р2. Затем мы находим С2 при помощи
третьего из равенств (8) и умножая С2 на А, найдем:
Sp (С2А) = Sp (СИ2) + (—O-'ftSp (Л) = (-I)" [Sp (ЛЗ) _|_
+ PiSp (Л2) +P2Sp (Л)] = (—I)" [58 +рА -l-ftSil = (—!)" Зр3.
A2)
Продолжая эти рассуждения, мы придем в конце концов к равенству
Sp(Cn_H) = (— Пппрп. A3)
Последнее из уравнений (8) будет служить для контроля правиль-
правильности вычислений.
В процессе вычислений мы найдем определитель матрицы А,
равный (—1)п/?п, присоединенную к А матрицу, равную (—l)nCB_i,
а следовательно и обратную матрицу Л. Если Х$ — корень харак-
характеристического многочлена А и С (к{) Ф 0, то столбцы С(Х^) являются
собственными векторами А, так как
(A — \iI)C(ki) = D(ki)I = 0. A4)

§5] ОБЗОР СПОСОБОВ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИЧЕСКОГО МНОГОЧЛЕНА 211
Это наверняка произойдет, если Х{— простой корень D(X). В слу-
случае, если Х{ — кратный корень D(X), для получения собственных
векторов может потребоваться переход от С(Х) к производным
ее по X.
Метод Фаддеева также требует большого числа операций, но
зато он дает возможность кроме характеристического многочлена
находить еще ряд величин.
2. Метод окаймления. Если записать матрицу А в виде
A5)
где Ап_1 —квадратная матрица, состоящая из элементов первых п— 1
строк и столбцов А, то матрица С(Х), о которой говорилось ранее,
может быть представлена так:
A6)
где многочлен Dn_x (X) является характеристическим для Ап_х и раз-
разбиение A6) на клетки соответствует разбиению A5). В силу ра-
равенства
(An-Un)C(K) = D(\)I A7)
будем иметь:
Таким образом, если известен многочлен Dn_!(X), первое из ра-
равенств A8) даст нам возможность найти gn_i(X), а второе из ра-
равенств даст возможность найти D(X). Этими рассуждениями можно
воспользоваться для отыскания характеристического многочлена D(X),
если, начиная с D2(X), последовательно находить все Dj(X).
3. Эскалаторный метод. Приведем еще один метод, позволяю-
позволяющий использовать собственные значения и собственные векторы
матрицы Ап_и для получения собственных значений и собственных
векторов матрицы A5). Чтобы избежать разбора возможных исклю-
исключительных случаев и не слишком усложнять изложение, предполо-
предположим, что матрица Ап_1 симметрическая и все ее собственные зна-
значения различны. Обозначим собственные значения Ап_1 через Х4:
h < h < h < • • • < K-v
и соответствующие им ортонормированные собственные векторы —
через
*1 = С*н. x2i *„_, i) (/= 1, 2 п— 1).

212 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
При этом
Ап_1Х=ХА, A9)
где
хп-ы xn-i, i ••• Jfn-i, n-i' \0 0 0 ... ^-j.
B0)
Будем предполагать, что в A5) Сп_1 получено транспонирова-
транспонированием Ьп_и Собственный вектор A5) ищем в виде
y = {t)- B1)
где z — некоторый (п—1)-мерный вектор-столбец, a t — число.
Из равенства
Ау = \у B2)
следует:
Первое равенство B3) можно записать в виде
B4)
Так как
XX'=1, B5)
то из равенства B4) следует:
Аг + Х'Ьп_^ = 1г B6)
и
z = (KI — A)~1X'bn_1t. B7)
Собственный вектор А определяется с точностью до постоянного
множителя. Поэтому мы можем выбрать t произвольным числом.
Следовательно, B7) дает возможность найти z, если известно а.
Значение X можно найти, воспользовавшись вторым из равенств B3).
Подставляя туда вместо z его значение по B7), получим:
C^XQJ — A)-1 X'bn_1=k - dn^ B8)
или
? d
Формула B9) показывает, что имеется ровно п собственных значе-
значений А. Эти собственные значения расположены следующим образом:
одно из них меньше Хх, п — 2 расположены между Aj и \+^ и одно

§ 51 ОБЗОР СПОСОБОВ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИЧЕСКОГО МНОГОЧЛЕНА 213
больше чем Хп_1# Так как собственные значения А разделены собст-
собственными значениями Л„_1, то последующее их вычисление по тем
или иным формулам предыдущей главы не вызывает затруднений.
Такой метод получения собственных значений матрицы Л и ее
собственных векторов называют эскалаторным.
4. Метод Самуэльсона. Запишем матрицу А в виде
(а\\ ' ап • ¦ ¦ аы \
"^T^tttswj, ^ C0)
«ni I <*т ... апп I
и пусть характеристические многочлены матриц Л и Ж имеют вид
n[n ] C1)
?»-J. C2)
Между коэффициентами р^ и qi имеют место следующие соотно-
соотношения:
2 = — RS — ql a
= — RMS — <IiRS — q&u 4- ?з.
S - q.RM^'S - ... - qn_2 an
Эти соотношения можно получить, например, следующим образом.
Запишем матрицу С (К), присоединенную к А — Wn1), в виде
(^« r,S)
Условие
даст
i C6)
<Р М Я + ?»-1 (X) (М - X/n_t) = 0.
Отсюда
(M-\In_iyl C7)
ср (X) (аи — X) — ср (X) R (М — X/n_t)"! S = / (X). C8)
Из C8) и следуют C3).
х) /п — единичная матрица порядка п.

214 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ |ГЛ. 8
Применим теперь для отыскания коэффициентов qi метод Кры-
Крылова, взяв за начальный вектор /?'. Получим систему уравнений
iM'n-%R' + .. . + <?„_!#' = 0. C9)
Так как коэффициенты р-г являются линейными комбинациями q^, то
их можно определить (не находя qt) по схеме Гаусса без обратного
хода (см. § 2 главы 6). Это и осуществляет метод Самуэльсона.
5. Интерполяционный метод. Для интерполяционного метода
специальный вид определителя, дающего характеристический мио-
гочлен, не имеет значения. Поэтому мы будем рассматривать произ-
произвольный определитель, элементы которого являются многочленами
от X:
/пО) /аО) ¦•• /тО)
D0)
/mW Ли(М ¦•• fnntt)
Пусть степень многочлена /(X) равна т. Вычислим определитель D0)
при каких-либо т-{-\ различных значениях \t и построим соот-
соответствующий интерполяционный многочлен. Этот интерполяционный
многочлен будет совпадать с /(X). Теоретически метод совершенно
прост. Практически он может потребовать выполнения большого
числа операций. Так как вопросы интерполирования разобраны нами
очень подробно, то в детали входить не будем.
На этом мы и закончим рассмотрение способов приведения ха-
характеристического определителя к многочленному виду.
§ 6. Определение границ собственных значений
Для того чтобы решить полученное тем или иным способом
характеристическое уравнение, желательно иметь представление
о расположении его корней. В предыдущей главе мы уже рассма-
рассматривали подобные вопросы. Однако характеристический многочлен
тесно связан с породившей его матрицей А, и поэтому можно ука-
указать ряд методов, более приспособленных к рассматриваемому слу-
случаю. Кроме того, часто возникает необходимость знать границы
собственных значений и совершенно не требуется характеристиче-
характеристический многочлен. В связи с этим в данном параграфе будут рассмо-
рассмотрены методы определения границ собственных значений матрицы,
не использующие ее характеристического многочлена в явном виде.
Эти методы будут пригодны и для получения границ корней произ-
произвольного многочлена, если записать последний в виде характеристи-
характеристического многочлена некоторой матрицы. Для этого можно исполь-
использовать, например, нормальную форму Фробениусэ.

§ 61
ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ
215
1. Случай симметрической матрицы. Рассмотрим уравнение
Лх = Хх, A)
где А — действительная симметрическая матрица, х— вектор-стол-
вектор-столбец и X — действительное или комплексное число. Известно, что
в этом случае имеется п действительных собственных значений
Xi<X2<...<Xn B)
и п соответствующих им собственных векторов xv х2, ..., хп,
которые можно считать действительными и ортонормированными.
Тогда, если х Ф О— произвольный вектор-столбец:
то
(Ах, x) =
+ XC
Таким образом,
= 11Гх, х)<(Лх, х)
<Xn(x, x) = Xn(
или
Л1 ¦
, X)
(х,х)
C)
D)
E)
F)
Эти неравенства, которые иногда называют принципом Релея, дают
некоторое представление о собственных значениях. Если взять
в неравенстве F) в качестве х собственные векторы, соответствую-
соответствующие собственным значениям \ и Хп, то будут выполнены знаки ра-
равенства. Таким образом, наибольшее собственное значение А равно
Рис. 12.
верхней границе, а наименьшее собственное значение А — нижней
границе отношений, стоящих в F).
Дадим принципу Релея геометрическую интерпретацию. Пусть
отрезок ОВ изображает нормированный вектор х и ОС — вектор Ах.
На прямой ОВ отложим точки Qt так, что 0<34 = Х4 (рис. 12).

216 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Имеем:
(CQi, CQi+i) = CQi ¦ CQi+1 cos a = (X{x — Ax, Xi+1x — Ax) =
= S Q4-h)(h+i-h)ct>0. G)
Отсюда
Таким образом, угол между двумя векторами CQi и CQi+x не может
превышать у. Проведем перпендикуляр CD и заметим, что
(Ах, x)=OD. (9)
Тогда из F) следует, что на отрезках (— оо, D) и (D, оо) также
имеется по крайней мере одно собственное значение. Объединяя (8)
и последнее замечание, мы приходим к выводу, что если провести
С
О
F
D
Рис. 13.
через точку С произвольные прямые СЕ и CF, пересекающие пря-
прямую ОВ соответственно в точках Е и F, и если угол l_ECF'^-^,
то на отрезке EF имеется по крайней мере одно собственное зна-
значение. Это и есть геометрическая интерпретация принципа Релея.
Дадим некоторые приложения этой геометрической интерпрета-
интерпретации. Пусть опять х—произвольный вектор, (х, х)=1. Обозначим
а=(Лх, х), р = (Лх — ах, Ах — ах). A0)
Докажем, что если а < а и
то на отрезке [а, Ь\ имеется по крайней мере одно собственное
значение А. Действительно, a= OD, ф = (CDJ. Пусть ОЕ = а< OD
= ^. Тогда (рис. 13)
Отсюда и следует утверждение.

§ 6] ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ 217
Докажем еще, что если а — произвольное действительное число,
х— произвольный нормированный вектор, а= {Ах, х), f = {А2 х, х),
то на отрезке
[а — (т — 2аа-+-а2)г, a_|_(-f — 2aa-{-a2)J\
найдется по крайней мере одно собственное значение А. Рассмотрим
геометрическую картину (рис. 14).
Отрезок OG берем равным а. Точки Е и F строим так, что
CG = EG = FG.
При этом
i
A5)
Так как угол /_ ECF прямой, то утверждение доказано.
Дадим небольшое обобщение принципа Релея. Возьмем два мно-
многочлена
ср(Х) =
1 J
и рассмотрим
Как известно, собственные значения Х{: Xt <! Ха <^ ...-<; Хп, мат-
матрицы /(Л)^равны /(Х{), i= 1, 2 п. Как и ранее, для произ-
произвольного х Ф 0 будем иметь:
Вследствие этого, построив графики функций у = f(x) и у = _. _ ,
(х, х)
мы сможем судить о собственных значениях А. Так, например, если

218 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
расположение этих графиков имеет вид, показанный на рис. 15, то
мы можем утверждать, что по крайней мере одно собственное зна-
значение находится на отрезке [а, Ь] и по крайней мере одно вне
этого отрезка.
Вычисление матрицы [ф(/4)|~\ входящей в определение f(A),
связано с большими затруднениями. Можно несколько видоизменять A8)
с целью упрощения вычислений. Предположим сначала, что все
yf(x)
* у-
Рис. 15.
собственные значения ф (А) положительны. Тогда существует мат-
матрица, обозначаемая [ф(Л)]а, такая, что
Обозначим
При этом
{1с,ПА) х) ^ (I, [ф (А)Г\ (А)
(х, х) (х, х)
±L—k
__ (У.Т(Л)У)
(у. ФИ) у)
(х.х)
A9)
B0)
B1)
и мы можем вместо A8) рассматривать правую часть B1) при про-
произвольном ненулевом векторе у. Если условие о положительности
собственных значений ф(Л) не выполнено, то можно взять
Тогда правая часть B1) перейдет в
(ф (А) у, у (Л) у)
B2)
B3)

§ 6]
ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ
219
Рассмотрим теперь некоторые частные случаи /(X). Пусть
/Г(Х) = 1 , где а — произвольное действительное число. В этом
случае можно утверждать, что в последовательности
1
1
имеются
меньшие
числа
B4)
большие и
(*, (А- а/) X)
-*1)х, (А—*1)х)
B5)
У
А,
.
0
а а кп
(рис. 16).
Возьмем
Рис. 16.
t
теперь / (X) = (X — аJ. В этом случае
{(А-а!) х, (A-af)x)
B6)
(х, х) (х, х)
и найдутся две точки пересечения y = f(x) и у — \ (рис. 17).
Если обозначить абсциссы точек пересечения через а и Ь, то можно
утверждать, что имеется по край-
крайней мере одно собственное зна-
значение на отрезке [а, Ь] и по
Рис. la
крайней мере одно вне его. Вычисления приводят к отрезку A3).
Пусть, далее, /(X) = ~ -)- -?¦, а > 0. Тогда
_ Г271
(х, х) а (у, Ау) •
Снова получим две точки пересечения графиков y = f(x) и у=%
(рис. 18). Если все собственные значения А положительны, то на
отрезке [а, Ь] имеется по крайней мере одно собственное значение.

220 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. &
В данном случае а и Ь определяются при помощи равенств:
Возьмем еще один случай. Пусть /(>¦) = ( г~у) •
g = ___ \ _ .
а' (х, х) + (Ах, Ах)
Опять будет две точки пересечения графиков _у =
B8)
этом
B9)
и _у =
Рис. 19.
Абсциссы этих точек определяются следующим образом:
По крайней мере одно собственное значение А лежит на отрезке [а, Ь\
(рис. 19).
Наконец, возьмем /(Х) = ( (- у\ . При этом
х]
C1)
a* (Ax, Ax)
По крайней мере одно собственное значение А удовлетворяет нера
венствам
а
где
а= 1 -1-8 —/^ 4-28,
(рис. 20).
1 4-й4-VхS2 + 28.
C2)
C3)

§ 6] ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ 221
На этом мы закончим рассмотрение различных случаев исполь-
использования обобщенного принципа Релея.
Покажем на примере, как можно использовать полученные
формулы. Возьмем снова матрицу Л § 4 (см. A7) § 4). Будем
выбирать различные векторы х и применять наши формулы. Сна-
Сначала выберем ~х — A, 0, 0, 0, 0, 0). При этом а —(Ах, лг) = 6,1818
и у = (А*:, Ах:) =38,4352, и если взять а = а = 6,1818, то фор-
формула A3) даст нам, что на отрезке [5,7121; 6,6515] имеется
по крайней мере одно собственное значение матрицы А. Возьмем,
далее, лГ= @, 1, 0, 0, 0, 0). При этом <x = (AJc, jc) =7,1818 и
•]•= (Ах, Ах) — 51,8120. Снова выбрав а = а = 7,1818, по фор-
формуле A3) получим, что на отрезке [6,6982; 7,6654] находится по
крайней мере одно собствен-
собственное значение матрицы А.
Теперь выберем jc = (O, 0,
1, 0, 0, 0). Это даст
а = (Ах, х)= 8,2435, т =
= (Ах, Ах) = 68,2464, и
если взять а = а = 8,2435,
то по формуле A3) найдем
отрезок [7,7039; 8,7831].
При лГ=(О. 0, 0, 1, 0, 0)
а = (Ах, *)=9,3141, у — (Ах, ЛлГ) = 87,3873. Возьмем здесь а= 10.
Тогда формула A3) даст отрезок [8,9486; 11,0514]. Наконец, возь-
возьмем * = @,0,0, 0,-1,2). -~. Это даст а —(Ах, *) = 3,6475.
На основании принципа Релея заключаем, что имеется собствен-
собственное значение меньшее найденного а. Нетрудно проверить, что все
собственные значения матрицы А положительны. Полученная далее
формула D3) показывает, что все собственные значения матрицы А
больше 2. Таким образом, нам удалось найти пять непересекаю-
непересекающихся отрезков: |2; 3,6475]; [5,7121; 6,6515]; [6,6982; 7,6654];
17,7039; 8,7831]; [8,9486; 11,0514], в каждом из которых содер-
содержится по крайней мере одно собственное значение А. Корнями много-
многочлена A9) § 4, получившегося путем раскрытия векового опреде-
определителя матрицы А по способу Данилевского, являются числа:
3,5922564; 5,62574641; 6,05652110; 7,28694071; 8,24088053;
9,56175808.
Как мы видим, нам удалось довольно простыми средствами от-
отделить пять из шести корней многочлена. Не все полученные фор-
формулы имеют практическое значение. Однако примеры дают воз-
возможность уяснить пути использования принципа Релея для отде-

222 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8-
ления собственных значений. Сформулируем теперь некоторое
уточнение принципа Релея.
Рассмотрим наряду с симметрической действительной матрицей А
еще положительно определенную действительную матрицу В. Будем
обозначать собственные значения матрицы В через \х^.
0<|Ч02< ••• On- C4)
Собственные значения v,-, f=l, 2, ..., п, матрицы В~ХА также
действительны и их можно определить при помощи соотношения
vj = min max _' _ . C5)
(Bx)
5
Здесь ищется минимум при всевозможных значениях с^к максимумов
записанного отношения для всевозможных ненулевых векторов
х = (xlt х2, .... хп), компоненты которых связаны I—1 соотно-
соотношениями:
(/=1, 2 /—1). C6)
Мы не будем приводить доказательства высказанного утверждения,
так как оно довольно громоздко. Желающих ознакомиться с ними
мы отсылаем к специальной литературе по теории матриц (см., на-
например, Гантмахер Ф. Р., Теория матриц, Гостехиздат, 1953,
глава X, § 7).
Из равенства C5), в частности, следует:
IV«>*f>IV«- C7)
Неравенствами C7) можно воспользоваться, если известны собствен-
собственные значения В и В~1А. Рассмотрим, например, такой случай.
Матрица С получается из матрицы А путем деления строк А после-
последовательно на положительные числа ръ ръ ..., рп. Этот процесс
можно записать как умножение А справа на В, где
/Pi 0 ... (К
А ... О . C8)
0 ... Рп1
Поэтому, если v{ — собственные значения С, то
C9)
к
Дадим теперь ряд оценок максимальных и минимальных соб-
собственных значений действительной положительно определенной ма-
матрицы А. Обозначим через d определитель А и через S—след
матрицы А. Рассмотрим
__ __

§ 6] ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ 223
И
Так как среднее арифметическое положительных чисел не меньше
чем их среднее геометрическое, то будем иметь:
{;<№)"•
Неравенство можно усилить, если заменить в левой части неравен-
неравенства Х{ на Хх, а в правой части Х< на нуль. Тогда получим:
П-1
D3)
Неравенство D3) дает оценку минимального собственного значения А
снизу. Воспользуемся теперь D2) для того, чтобы получить оценку
наибольшего собственного значения сверху.
Преобразовывая D2), получим:
п-1 /——
D4)
Если подставить в правую часть вместо Х4 любое число [а, превы-
превышающее собственные значения А, то получим оценку сверху для
собственных чисел А:
П'ЛГ\ D5)
В качестве [а можно взять, например, S. Эту оценку можно уточ-
уточнить, воспользовавшись рекуррентной формулой
. D6)
Получим убывающую последовательность чисел
D7)
для которой
lira н=?о>1п- D8)
к ->оо
Можно показать, что {io=jcj*-1, где х0 является наибольшим поло-
положительным корнем уравнения
П-1
хп— Sx-+-(n— I) yd = 0. D9)
Неравенство D3) также можно уточнить. При х^.у^.0 имеем:
E0)

224 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Положим здесь S—x, y = S— Xt и применим D2). При этом по-
получим:
K>S — VS" — nd(n-1)". E1)
Эта оценка лучше, чем D3).
Последние неравенства можно использовать не только для поло-
положительно определенных матриц. Пусть А произвольная действи-
действительная неособая матрица. Матрица А'А будет симметрической и
положительно определенной. Обозначим собственные значения А'А
через {i4:
О < H-i < Н-2 < ••• <1V E2)
При этом, если Х4—собственное значение А и х±— соответствующий
собственный вектор, то из
Ala == \i~Xi E3)
следует
(Ахг, Ахг) = l^ (xt, хг) E4)
или _ _
{XA'A*) E5)
В силу принципа Релея будем иметь:
Hi<Uil2<(V E6)
Таким образом,
рп< V S — V 5» — red
max
где d — определитель А и S—след АА', т. е. S=
Полученные нами для симметрических матриц результаты пере-
переносятся и на эрмитовы матрицы. Матрица А называется эрмито-
эрмитовой, если Л = Л' (здесь черта над А означает комплексную сопря-
сопряженность). Все собственные значения эрмитовой матрицы—действи-
матрицы—действительные числа. Она имеет п взаимно ортогональных собственных
векторов. Принцип Релея применим к эрмитовым матрицам, только
вместо (х, х) и (х. Ах) нужно брать (у, х) и (у. Ах), где у—век-
у—вектор, компоненты которого комплексно-сопряженные по отношению
к компонентам х числа. Следовательно, все оценки, основанные на
принципе Релея, сохранятся с соответствующими видоизменениями.
Так же можно перенести и остальные оценки.

§ 6]
ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ
225
2. Случай несимметрической матрицы. В главе б мы доказали,
что любая норма матрицы больше модулей ее собственных значе-
значений. Этим можно воспользоваться для оценки модулей собственных
значений сверху. В частности, мы получим:
(/=1. 2, ..., я).
п
max 2|fliftl>lxjl
к i—1
E8)
Если использовать третью норму матрицы, то получим уже извест-
известное неравенство E6). Неравенства E8) можно также записать в виде
~ " E9)
и 1
| lj |<; min { max 2j I ««|. max 2 I °»fc I } •
1 '- - к i=l )
Рассмотрим наряду с матрицей А еще матрицы
±
F0)
Это — эрмитовы матрицы. Пусть Xj = (XjU Xj2 Xjn) — норми-
нормированный собственный вектор А, соответствующий собственному
значению Xj:^
. Тогда
n
Отсюда
2
Г, 8=1
П
Г, 8-=1
F1)
Г, 8-=
П
' — 2U crsxjsxjr>
r, s=l
F2)
где bra и crg—соответственно элементы В и С. Из F2) получаем:
Г, 8=1
Г, 8=-1
И
Таким образом,
г=1
| = max 2u I brS •
Г 8 = 1
F3)
F4)

226 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Аналогично найдем:
п п
lS|| S|l- F5)
|r,| S|r.l
S Г=1 г 8=1
Мы получили оценки действительной и мнимой частей собственных
значений.
Уточним несколько последний результат. Если обозначить соб-
собственные значения эрмитовой матрицы В через [^ -^ [а2 -^ ... <[ jxn,
а собственные значения эрмитовой матрицы С — через vt -^ v2 ^. ...
... О„, то в силу принципа Релея из F2) следует:
1
J
Vi<P,<vn. J F6)
Это—более точные оценки, чем F4) и F5), хотя их использование
связано с получением собственных значений матриц В я С.
Пусть матрица А действительная. Тогда матрица В будет сим-
симметрической и для получения {ix и [ап можно использовать приве-
приведенные ранее оценки. Матрица D = iC = y(A— А') будет действи-
действительной кососимметрической. Такая матрица может иметь только
чисто мнимые или нулевые собственные значения. Действительно,
если X — ненулевое собственное значение D н х ФО — соответствую-
соответствующий собственный вектор, то будем иметь:
X (х, х) = (Dx, x) = (х, D'x) = (D'x, x) = — X (х, х) F7)
или
X = — X. F8)
Так как элементы D — действительные числа, то собственные зна-
значения будут попарно сопряжены. -Обозначим ненулевые собствен-
собственные значения D через
± *>i. ± *>2 ± /ft. Bг < га). F9)
Собственные значения С будут отличаться от собственных значе-
значений D только лишь делителем /. Поэтому 1 Pj I -^ max j jx& [. Оце-
к
ним max | р.к |. Сумма попарных произведений собственных значений D
к
будет равна
G0)
и в то же время она равна коэффициенту при Х"~2 в разложении
одределителя |Х/^—D\ по степеням X. Последяий коэффициент ра-
равен сумме всех главных миноров второго порядка матрицы D. (Глав-

§ 61
ОПРЕДЕЛЕНИЕ ГРАНИЦ СОБСТВЕННЫХ ЗНАЧЕНИЙ
227
ными минорами порядка к матрицы D с элементами d^ называются
миноры вида
G1)
где 1 <[ ti < i2 < ... < ik -^ re.) В нашем случае будем иметь:
— dra О
r<t
Г<8
Обозначим max | drs | = max
следует:
Отсюда
r<s
G2)
через g. При этом из G2)
-'—" G3)
G4)
Эта оценка менее точна, но осуществляется проще.
В заключение этого параграфа покажем, что если обозначить
п п
G5)
то каждое собственное значение X матрицы А лежит по крайней
мере в одном из кругов
\z — arr\*CPr G6)
и по крайней мере в одном из кругов
\z — aSs\^-Qs- G7)
Пусть I — собственное значение Лих= (xv хг хп) — соот-
соответствующий собственный вектор. Тогда
л).
G8)
Пусть max | jcj | = ] jer |. При этом из
lxr — arrxr=; 2 «г
S-1

228 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
следует:
|Х —вгг||*г|<*М*г|. (80)
и так как | xr \ ф 0, то получаем G6). Если провести эти же рас-
рассуждения для транспонированной матрицы, имеющей те же самые
собственные значения, то получим G7). Утверждение доказано.
Из G6) и G7) снова следует E9). Кроме того, если
d = min(|arr| — Pr)>0, (81)
г
ТО
§ 7. Итерационные методы отыскания собственных
значений и собственных векторов матриц
1. Отыскание наибольшего по модулю действительного соб-
собственного значения матрицы простой структуры. Случай сим-
симметрической матрицы. Будем предполагать сначала, что матрица А
имеет простую структуру. Это значит, что если порядок матрицы А
равен п, то имеется п линейно независимых собственных векторов А.
Обозначим собственные значения матрицы А через Л{: | X,) ^ | У^ | ^ • • •
. ..^|ХП|, и соответствующие им линейно независимые собствен-
собственные векторы — через хи х2, .. •, хп.
Произвольный вектор v может быть записан в виде
A)
Образуем последовательность векторов:
Av = a^Xi
A2V = a.\kiXi -)- О2Л2Л2 -)-... -|-а„лид;и, ^\
Вынося в последнем выражении Xt за скобки, получим:
Akv = \1 [ад + «2(?) ^+...+а„(^) хп]. C)
При этом если о^ =? 0 и | Xt | > | Х<| для i^-2, то
Г,—
Таким образом, для достаточно больших к вектор A v будет бли-
близок к собственному вектору матрицы А, соответствующему наиболь-
наибольшему по модулю собственному значению. Может случайно оказаться,
что 8^ = 0, т. е. компонента v по направлению вектора х\ равна

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 229
нулю. Однако это не изменит принципиально наших выводов. В про-
процессе вычислений в связи с ошибками округления мы неизбежно
введем соответствующую компоненту. Введенная компонента в конце
концов забьет все остальные. Может оказаться лишь, что потре-
потребуется значительное число итераций.
Далее, будем обозначать t-ю компоненту некоторого вектора и
по отношению к произвольным координатным векторам ev e2, ..., еп
через (m)j. Тогда из B) следует:
\к+1
)
Таким образом, при достаточно больших k величина
Xt = к % F)
будет близка к наибольшему по модулю собственному значению.
При практических вычислениях показателем того, что мы достаточно
хорошо приблизились к хх и к Xj, будет постоянство отношений
(с требуемой точностью) соответствующих компонент A +1г» и Ли.
Пусть, в частности, матрица А симметрическая. Тогда векторы \х^
можно считать ортонормированными и за приближенное значение
собственного вектора Xi будем брать
7.
ь А 91
(Здесь везде берется третья норма главы 6.) Так как хг ортонор-
мированы, то для Xt можно получить более точное приближение.
Обозначим (Akv, Akv) = ck. В силу D) будем иметь cft = a?Xifc-{-
—|- сьа^-а* -+- ••• Ч-Яп^» и, следовательно, cft+1/cft = Xi-|-О (-Л) .
Покажем еще, как можно уточнить значение \, если А есть сим-
симметрическая матрица. Положим
xl^x^s. Xi = Xi-|- 8. (8)
Тогда, так как
Ахх— \хх~ О,
—* *—* —
Ах\ — Х
(9)
где тг), вообще говоря, отличен от нуля, то
Аё— ХХГ— 8^ — 37 = т^. A0)

230 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Считая 8 и s малыми, отбросим последний член левой части как
малую величину более высокого порядка. При этом равенство A0)
перейдет в
Ае~— Х,7— Ьхг = т). (П)
Умножим скалярно обе части равенства A1) на jq. Получим:
(Al, Jx) — Xt (sT xt) — 8 (xv xj = (i xj. A2)
Ho
(M, xj = (Г, Axt) = Xt (в, *x) A3)
и (лг1( jc1)=1. Следовательно, равенство A2) даст
Полученное 8 можно использовать для уточнения найденного при-
приближенного значения Хь если заменить в правой части хх на Х\.
Умножим теперь обе части равенства A1) на д;{(/ = 2, 3, .... п).
Получим:
{As, хг) — Xt (s", xt) = (i хг). A5)
Ho
= X<(s, xt) A6)
и, следовательно,
Он— ^i)(s. xi) — С*). Xi)< A7)
G, xt) = J1' x\ A = 2, 3, ... n). A8)
Найдем еще (s, xj. Так как
то
1=(х1-(-е. ¦*i + s)= 1+2(jelf s)-(-(s, e) B0)
и
(Xlt 8) = — 1(8". Г). B1)
Выражения A8) и B1) позволяют оценить норму вектора е. Дей-
Действительно,
, п п
||8"||2 = (8. 7) =
i-l i-2

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 231
Таким образом,
Перепишем A8) в виде
,,- - ч | I Си. Xj) | _ !(¦>), *f)| 1_
|(s. *1Л— и, —A.I — ix. I
Так как
то
1—bt
f = 2. 3 га). B4)
B5)
= 2, 3 га). B6)
В силу B3) будем иметь:
п _
1
B7)
]
и так как L^r (i = 3, 4 п) меньше чем ]~-, то
I AiI IЛ11
B8)
Это выражение может служить оценкой для ||s||, если использовать
вместо Xj и Х2 какие-то их приближенные значения.
2. Отыскание других собственных значений и соответствую-
соответствующих им собственных векторов для симметрических матриц.
Используем теперь векторы Akv для отыскания других собственных
значений. Обозначим 1-ю компоненту вектора Akv через vki. Если
единичные векторы е,-, направленные по осям координат, предста-
представить в виде
ei = euXl-\~ei2x2-\~ ... -\-е{пхп, B9)
то будем иметь:
_ / п _ п \ п
vm = (A v> «D = B OLfX^xj, 2 euXj ) = 2 ^;aj-«« C0)
или
J-1
где обозначено
C2)

232 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Составим определитель
C3)
1, Г Щ + l, S
Воспользовавшись равенствами C1), получим:
Р# = Фг*Ьа1 — Ьафгд Х?+1Ха* Н- фг1Ьл — Ьа1Ьгг) ^Х+1 +
-h (br3bsl - *rl*83) Xf+1X3* + Фг1Ь83 - *8l*r3) ^*+1 + • • •, C4)
где многоточием обозначены остальные члены, содержащие к3, Х4, ...
Таким образом,
Xt - х2) 4-
55
••• • C5)
Аналогично найдем:
¦4- ... • C6)
Отсюда
— bsibrl) (Xj—Х?) 4- (bnbal—brXbm)
h • • •
— ^2) 4"
».*
¦4- ...
C7)
Пусть Xt и
превышают по модулю остальные значения |Х$| и
Ф 0. Тогда
C8)
_
Аналогично можно получить произведение трех и большего числа
собственных значений. Так, если Х1§ Х2 и Х3 превышают по модулю
остальные собственные значения, то
C9)

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 233-
где
Vkr
v
, r vk+l, s vk+l, t
vk+-i,t
D0)
Нужно отметить, что при больших к строки написанных выше опре-
определителей почти пропорциональны. Следовательно, сами определи-
определители будут близки к нулю. Это приведет к большой вычислитель-
вычислительной ошибке. Если же ограничиваться небольшими значениями к,
то получим большую ошибку метода. Вследствие этих причин Х2, Х8
и т. д. можно найти с небольшой точностью.
В связи с этим рассмотрим еще один метод отыскания проме-
промежуточных собственных значений в случае, когда А есть симметри-
симметрическая матрица. После того как \ и х1 найдены, возьмем вместо А
новую матрицу:
i = А — Xj
D1)
где под a:ia;i понимается произведение вектора-столбца с компонен-
компонентами Хх и вектора-строки с теми же компонентами по правилу умно-
умножения матриц. Ах — также симметрическая матрица. При этом
\*Х* ¦¦ '" /\Х- ¦¦ '" Д<л<ж*X.. ¦¦ '" /\jC.. "¦" AiX* '—
так как
D2)
D3)
В то же время
= 2, 3, 4 п), D4)
так как векторы Х{ и Xj ортогональны при t Ф j. Таким образом,
матрица Ах будет иметь те же собственные значения и собственные
векторы, что и А, за исключением \. Вместо Xt матрица Ах будет
иметь собственное значение 0, и ему соответствует собственный век-
вектор хх После того как будут найдены Х2 и х2, можно дальше
повторить этот процесс, и мы найдем, в конце концов, все X; и х-г.
При этом можно каждый раз понижать порядок матрицы. Пусть
д;1 = (л;11> х21, .... хп1). Обозначим
¦*31
D5)
хп\

234 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ (ГЛ. 8
л рассмотрим матрицу
D6)
где (j, — некоторая постоянная.
Произведение ВВ' будет равно
Но
Хц<х — о
<ш'4-/и-1 —:
хпа' — а' 4- [ш'аа' == [*u — 1 + [a (l —
D8)
]«'. D9)
„ -, г, то все элементы первой
A + -*и)
строки D7) обратятся в нуль, кроме левого крайнего, который
будет равен единице. В силу симметрии матрицы ВВ' все элементы
лервого столбца D7), кроме верхнего, будут нулями. Далее, при
V- = /1 I „ ч имеем:
Таким образом, если взять [а = -
аа' - 2jxaa' 4-
W = ^=± аа' 4-
- *!i) аа' = 0.
E0)
Итак, ВВ' = I. Следовательно, В'АВ имеет такие же собственные
значения, что и А. Возьмем матрицу
1
0
О
E1)
Произведение В'АВ$ равно Ххр. Действительно, В$ = xv Ax1 = \1x1
и Х1В'х1^=Х1^. Таким образом, р является собственным вектором
матрицы В'АВ, соответствующим собственному значению Хх. Это
может быть только в том случае, если В'АВ имеет вид
E2)
/А, 0\
'АВ = (о а)-
Дальнейшие вычисления можно производить с симметрической мат-
матрицей Аи имеющей собственные значения Х2, Х3 Хп. Если .yt —
собственный вектор Av соответствующий собственному значению Х|,
то из
AJi = hyi E3)

$ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 235
следует:
U/ \о AjXyJ U yJ Ы
I) E5)
У{ I \ I
/о \
Таким образом, В _ ] будет собственным вектором А, соответ-
\Л /
ствующим собственному значению Х4. В дальнейшем мы можем по-
поступить с At так же, как мы поступили с А.
Рассмотрим еще один способ получения Х2, Х3 Х„. Пусть \
и хх уже найдены. Рассмотрим произвольный вектор х и образуем
у = х — (х, xt) ху. E6)
Этот вектор ортогонален xv Действительно,
(xv ~у) = (х, ~хг) — (х, ~xt) (xv ~ху) = 0, E7)
так как (хи xt) = \\xl\\2=l. Поэтому разложение у по векторам xt
имеет вид
у = а2х2-\-а3х3-\- ... -МЛ E8)
и
А*у~ = а2Х^2 4- asXsJcs 4- ... + вяХ!Е*п. E9)
Таким образом, если |Х2|>|Х{| при />3, то
L^X2. F0)
Найдя Х2 и х2, можно искать следующее собственное значение и
следующий собственный вектор, взяв за начальный вектор:
z = x — (х, xt)xt — (х, х2)х2 F1)
и т. д. Нужно только помнить, что при этом в связи с ошибками
округления при итерациях будут появляться компоненты собствен-
собственных векторов, соответствующих наибольшим по модулю собствен-
собственным значениям матрицы А. Поэтому время от времени необходимо
исключать такие компоненты по формулам E6), F1) или им подобным.
Промежуточные собственные значения можно также определить,
если рассмотреть вместо матрицы А матрицу А — jj,/ или jj./ — А,
где (j, — соответствующим образом подобранное число. В частности,
если (j, > Xj и А — положительно определенная матрица, то итера-
итерация с матрицей jj,/ — А даст наименьшее собственное значение. Можно
использовать и многочлены более высокой степени относительно
матрицы А.

236 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ 1ГЛ. 8-
Пример. Проиллюстрируем теперь наши рассуждения простым
примером. Пусть матрица А имеет вид
2—100
А =
—1
2 —1
0 -1
2 —1
0 —1
F2)
За начальный вектор примем х = A, —1, 1, —1). Итерации дадут:
№
0
1
2
3
4
5
6
7
8
1
2
—1
0
0
1
3
10
35
125
450
1625
5 875
21250
2
—1
2
—1
0
—1
—4
—15
—55
—200
—725
—2 625
—9500
—34375
3
0
—1
2
—1
1
4
15
55
200
725
2 625
9500
34375
4
0
0
—1
2
—1
—3
—10
—35
—125
—450
—1625
—5 875
—21 250
Отношения соответствующих компонент восьмой и седьмой ите-
итераций последовательно равны
3,61702; 3,61842; 3,61842; 3,61702.
Они уже достаточно близки. Более точное приближение для собствен-
собственного значения мы получим, если поделим скалярный квадрат вектора,
полученного при восьмой итерации, на скалярное произведение век-
векторов, полученных при седьмой и восьмой итерациях. В результате
получим:
\\ = 3,61804. F3)
Соответствующий нормированный собственный вектор будет иметь
вид
? = @,37182; —0,60147;0,60147; —0,37182). F4)
При этом оказывается, что
л? — Xijcl = (—0,000147; —0,000098; 0,000098; 0,000147), F5)

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 237
и поправка 8 по формуле A4) настоящего параграфа примет вид
8 = — (if, **) = —0,000008. F6)
Составим теперь определители C3) для нашего случая. Получим:
1625 —2625
;") =
8")
Pia
5875
21250
—9500
—34375
= -78 125; ОД =
5875 —9500
= —15 625.
F7)
Остальные определители ничего нового не добавят. Отношение
в данном случае равно
= о и
Х2= 1,38196.
F8)
Определители у^ в данном случае все равны нулю. Поэтому для
отыскания следующих собственных значений применим преобразование
матрицы А с помощью матрицы В D6). Вычисления дают:
0,37182 0,60147 —0,60147 0,37182
—0,60147 0,73628 0,26372 —0,16302
0,60147 0,26372 0,73628 0,16302
—0,37182 —0,16302 —0,16302 0,89922
В =
В'АВ =
3,61815 0,00007 0,00008 0,00012
0,00007 0,81194 —0,25039 —0,46329
0,00008 —0,25039 1,68884 —0,80775
0,00012 —0,46329 -0,80775 1,88119]
Расхождения с теоретическими результатами получились за счет оши-
ошибок округления.
Теперь мы должны отыскивать собственные значения матрицы
третьего порядка:
/ 0,81194 —0,25039 —0,46329*
Л1={—0,25039 1,68884 —0,80775 J. F9)
\—0,46329 —0,80775 1,88119/
Получим их итерационным способом, начиная с вектора л: = @, 0, 1).
Итерированные векторы будут иметь следующие компоненты:
0
1
2
3
4
5
6
7
0
—0,46329
—1,04545
—2,87618
—5,57137
—11,05492
—23,75378
—54,90002
0
—0,80775
—0,05552
—3,39092
—12,12902
—35,77135
—99,02542
—266,1301
1
1,88119
4,40597
8,81766
20,65291
51,23042
130,3901
333,2812

238 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Отношения соответствующих компонент последних двух векторов
равны последовательно 2,311; 2,687; 2,556. Приближенное значение Х^
будем находить, используя скалярные произведения так же, как и
в предыдущем случае. При этом получим:
Х.а = 2,6003. G0)
Обращаем внимание на то, что у нас получилось другое значение X*,
чем в первом случае. В данном случае это произошло благодаря
тому, что начальный вектор при итерации с помощью матрицы А
оказался ортогональным к собственному вектору хг. Таким образом,
фактически F8) дает не Ха, а Х3. Точные значения собственных зна-
значений матрицы А с шестью десятичными знаками таковы:
Х1 = 3,618034, Х2 = 2,618034, Х3= 1,381966, Х4 = 0,381966.
3. Отыскание собственных значений и собственных векторов
несимметрических матриц, имеющих простую структуру. Обобщим
теперь полученные для симметрических матриц результаты на более
общий случай. Предварительно напомним некоторые факты из ли-
линейной алгебры. Пусть А — произвольная матрица с действительными
или комплексными элементами aik. Матрица А*, элементы которой а*к
удовлетворяют условиям а*к = aki (транспонирование и комплексная
сопряженность), называется сопряженной по отношению к А. Если
Л = Л*, то матрица А называется эрмитовой. Эрмитова матрица
имеет простую структуру и все ее собственные значения действи-
действительны. Систему собственных векторов эрмитовой матрицы можно
считать ортонормированной в соответствующем комплексном вектор-
векторном «-мерном пространстве R. Вследствие этого на эрмитовы матрицы
можно перенести с необходимыми видоизменениями результаты, по-
полученные для симметрических матриц.
Рассмотрим связь между инвариантными многообразиями матрицы А
и сопряженной матрицы А*. Пусть некоторое линейное многообра-
многообразие М инвариантно относительно А, т. е. из х ? М следует Ах ? М.
Рассмотрим совокупность N векторов y?R, ортогональных к каж-
каждому вектору х?М. Если размерность М меньше п, то множе-
множество N не пусто. Очевидно, N в свою очередь является линейным
многообразием. Покажем, что это многообразие инвариантно отно-
относительно А". Действительно, если х — произвольный вектор из М,
то для любого вектора y?N имеет место (Ах, у) = 0. Но (Ах, у) =
= (х, А*у) и, следовательно, A*y?N, что и требовалось доказать.
Пусть матрица А имеет простую структуру и xv х2, • • .. хп — ее
линейно независимые собственные векторы, соответствующие соб-
собственным значениям Xt, Х2, . .., Х„. Линейное многообразие, построен-
построенное на векторах хи хг, .... xk_v xk + l, ..., хп, будет иметь раз-

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 239
мерность п — 1. Следовательно, в R имеется вектор ун, ортогональный,
этому многообразию. Как явствует из предыдущего, ук будет являться
собственным вектором А*. При этом ук не может быть ортогональ-
ортогональным хк. Следовательно, умножив его на подходящий множитель,
можно достигнуть того, что (atjj, ук) = 1. Проведя эти рассуждения
для всех k= 1, 2, ..., п, мы придем к выводу, что А* имеет про-
простую структуру и собственные векторы А и А* можно выбрать так,
что они будут образовывать биортонормированную систему, т. е.
(Xi, yj) = hj-
Отметим еще, что если А и А* имеют общий собственный век-
вектор х Ф О, то собственные значения, которым соответствует этот
собственный вектор, будут комплексно сопряжены. Действительно,
если Ах = \х и А*х = рх, то
1(х, х) = (Ах, х)=(х, А*х)=~?(х, х), G1)
откуда и следует утверждение.
Матрицу А называют нормальной, если она перестановочна с своей
сопряженной АА* = А*А. Перестановочные матрицы А а В всегда
имеют общий собственный вектор. Действительно, если А*: = Хл:,
х ф О, то АВкх = \Вкх. Начиная с некоторого р, линейное много-
многообразие М, построенное на векторах х, Вх Вр~1х, будет инва-
инвариантно относительно В. Следовательно, в этом многообразии будет
существовать собственный вектор В: By = ру. Но любой вектор этого
многообразия является собственным для А. Тем самым утверждение
доказано. В частности, если А — нормальная матрица, то для А я А*
будет иметься общий собственный вектор. Как следует из предыду-
предыдущего, собственные значения, которым соответствует этот общий
собственный вектор, будут комплексно сопряжены. Обозначим най-
найденный таким образом общий собственный вектор А и А* через хх
и пусть Алг1 = Х1л:1. Тогда Л*л:1 = Х1л:1. Рассмотрим линейное многооб-
многообразие М векторов, ортогональных к xv Как следует из предыдуще-
предыдущего, это линейное многообразие будет инвариантно как относительно
А, так и относительно А*. Такими же рассуждениями, как и ранее,
придем к выводу, что в М будет существовать общий собственный
вектор х2 для А и А". При этом, если Ах2 = )-2Х2> т0 А*хг^=^-2Х2.
Очевидно, (хи х2) = 0. Затем можно провести такие же рассуждения
в линейном многообразии векторов, ортогональных к^,и х2, и т. д.
В конце концов, мы придем к заключению, что нормальная матрица
имеет полную ортонормированную систему собственных векто-
векторов. Эти векторы являются также собственными векторами А*, при-
причем соответствующие собственные значения комплексно сопряжены.

240 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Можно показать, что наличие полной ортонормированной системы
собственных векторов является необходимым и достаточным условием
нормальности матрицы. Нормальная матрица будет являться эрмито-
эрмитовой тогда и только тогда, когда все ее собственные значения дей-
действительны.
Из изложенного видно, что и для нормальных матриц можно
провести рассуждения, аналогичные тем, которые были проведены
для симметрических матриц. При отыскании модулей собственных
значений матрицы простой структуры, не являющейся нормальной,
может оказаться целесообразным наряду с векторами Акх образовы-
образовывать векторы А*ку и рассматривать их скалярное произведение. При
этом если
х = а1х1 4 02*2 4 ... + аЛ. I 72
где {хк} и [ук] образуют биортогональную систему векторов, то
(А*х, A*kJ) = «1р11 Xt \и -f «2р21 X, Г 4- • • ¦ 4- а АIК Г- G3)
Если матрица А имеет несколько равных или близких корней,
то это не вызывает никаких принципиальных затруднений. Так, если
для матрицы А простой структуры Xt ^= Х2, то разложение B) примет
вид
k k k kX+ +а& G4)
Таким образом, при |^|> |Х$| (/=3, 4 п) снова будем иметь:
75
При этом один из собственных векторов, соответствующих собствен-
собственному значению Хи будет приближенно равен Akv при достаточно
большом к. Второй собственный вектор, соответствующий собствен-
собственному значению Xlt можно получить, если взять другой начальный
вектор. Однако неизбежные ошибки округления будут изменять ком-
компоненты Akv по направлению векторов xt и х2 и тем самым замед-
замедлять сходимость. Медленная сходимость будет наблюдаться также
и при наличии близких корней. Если матрица имеет два равных по
модулю, но различных корня, превышающих по абсолютной величине
все остальные корни, то сходимости вообще наблюдаться не будет.
Во всех трех случаях мы сможем при больших k написать при-
приближенные равенства:
Akv яй otiXiXi 4 а^Х
G6)

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 241
Таким образом, между тремя векторами Akv, Ak+1v и Ak+rv будет
иметь место приближенная линейная зависимость. Нетрудно прове-
проверить, что эта линейная зависимость может быть записана в виде
Ak+2v —
k+1
= 0.
G7)
Следовательно, если в процессе вычислений мы обнаружим, что век-
векторы Akv, Ak+1v и Ak+2v связаны некоторым линейным соотноше-
соотношением вида
lv + qAkv = 0,
G8)
то \ и \ будут удовлетворять квадратному уравнению
G9)
Фактически квадратное уравнение можно получить, если рассмотреть
определители
= 0 (г, s = 1, 2 п; г Ф s, vki = i
vk+l,r vh+l,s
Vk+2,r Vk+i,S
(80)
Рассмотрим пример на применение этого метода. Ниже приведены
матрица четвертого порядка, для которой ищутся собственные значе-
значения и собственные векторы, и результаты итерации с ее помощью
вектора (—1, 1, 0, 0):
№
0
1
2
3
4
5
6
7
8
9
1
—2
—7
0
—1
—1
3
—4
—28
304
—1872
8 896
—33 728
91904
—60 672
2
1
—5
—1
0
1
2
—33
203
—919
3181
—6 081
—9857
216 433
—1 538 083
3
1
—2
—3
—1
0
—1
—1
40
—333
1942
—9065
34136
—92 889
63 050
4
1
—4
—2
0
0
1
—2
5
—12
29
—70
169
—408
985
Как видно из этой таблицы, отношения соответствующих компо-
компонент последовательных итераций ведут себя довольно беспорядочно,

242 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ I ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
имеют место перемены знаков.; Это указывает на наличие комплекс-
комплексных корней. Уравнение для определения Хх и Xj будет иметь вид
1 —33 728 —9857
z 91904 216 433
z% —60 672 —1538 083
Отсюда
= 0. (81)
,02*+ 20,05 = 0 (82)
и
z= — 4,01 ± 1,99г. (83>
Точные значения корней в данном случае будут
z= — 4 ± 2/. (84)
У нас получились довольно грубые значения. Это объясняется тем,
что мы провели недостаточное число итераций и, вообще говоря,
корни определять было еще рано.
После того как будет решено уравнение G9), можно найти и
собственные векторы. Из равенств G6) получаем:
Ak+1v— \1Alcv = а2х? (Х2 — Xi) лгь
Ak+1v— X2Akv = a1lUh— h)xt >
Эти результаты можно обобщить на случай, когда имеется более
двух равных по модулю или близких по модулю собственных зна-
значений.
4. Некоторые замечания об отыскании собственных значений
и собственных векторов матриц общей структуры. Рассмотрим
теперь кратко случай, когда матрица не является матрицей простой
структуры. Если элементарные делители А — X/ имеют вид
(X - X/', (X - Х/> (X - \т)кт (86)
(некоторые Х{ могут совпадать), то найдутся такие векторы:
УРГеФ ~%\ (/=1.2 и). (87)
что
Aef = U??; A'ef = X^° +3°; • • ¦; М\ = h~ePt + п._!. (88)
Общее количество векторов ер равно порядку матрицы п, и их можно
принять за базис и-мерного векторного пространства.
Запишем произвольный вектор v в виде
(89)

§ 7] ИТЕРАЦИОННЫЕ МЕТОДЫ ОТЫСКАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 243
Здесь i>i принадлежат инвариантному для матрицы А линейному
многообразию, построенному на векторах е[г\ е%] е$ ¦
В силу равенств (88) при р > kt и ^^-у> 1 будем иметь:
^ ^ Х?-^+14Л. (90)
При j= 1 получим:
Ap^i) = ^i\ (91)
Таким образом,
и.ви —з/~г" • • • ~|—^» * ^р ^i • (92)
За норму вектора v примем величину
2 214гI3- (93)
Тогда из (92) следует:
lim AVi~h 1 _Ср V1 ¦ = 0_ (94)
Таким образом, с увеличением р вектор Apvt будет все больше и
больше приближаться по направлению к вектору e*\\ если только
я *( =? 0. Аналогичная картина будет наблюдаться и с остальными ком-
компонентами Vj вектора v.
Из только что полученного результата можно сделать следую-
следующие заключения. При возрастании р вектор Apv будет неограниченно
приближаться к инвариантному многообразию, порожденному векто-
векторами (87), соответствующими наибольшим по модулю собственным
значениям. Если \ — единственное наибольшее по модулю собствен-
собственное значение кратности единица, то будут справедливы те же выводы,
которые мы делали для матриц простой структуры. Если Х1 — един-
единственное наибольшее по модулю собственное значение и кратность
его больше единицы, то поведение вектора Apv будет определяться
элементарными делителями матрицы А — XI, соответствующими соб-
собственному значению \. Если все они простые, то исследование про-
проводится так же, как и для матрицы простой структуры. Если имеется

244 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
элементарный делитель (к — Х^ с наибольшим k, то при больших р
вектор Apv будет находиться в инвариантном многообразии, поро-
порожденном некоторыми векторами eis), e^ е$ системы (87), соот-
соответствующими \v Все векторы и этого многообразия будут обладать
свойством {А — \1)к а = О или
(-1)к\ка = 0. (95)
Поэтому при достаточно больших р векторы Apv, Ap+1v Ap+kv
будут связаны линейной зависимостью вида (95). При этом \ нахо-
находится из уравнения
X* - фД* Ц-еда-2 - ... + (-1)* 1к = (к - \)к = 0. (96)
Если имеется несколько элементарных делителей наивысшей степени,
то в характере поведения векторов Apv изменения не произойдет,
но вместо уравнения (96) получим уравнение (к — Х1)ы = 0, где
I — число соответствующих элементарных делителей.
Аналогично исследуется случай, когда имеется несколько раз-
различных максимальных по модулю собственных значений. В каждом
таком случае при достаточно большом р векторы Apv, Ap+1v, . . .
..., Ap+rv будут связаны некоторой линейной зависимостью вида
0. (97)
При этом максимальные по модулю значения Xf находятся из урав-
уравнения
Так как подробный разбор всех возможных случаев потребовал бы
длинных рассуждений и так как матрицы, не имеющие простой
структуры, встречаются сравнительно редко в вычислительной прак-
практике, мы этим заниматься не будем. Желающих изучить эти вопросы
подробнее отсылаем к специальной литературе (см., например,
К. А. Семендяев, О нахождении собственных значений и инва-
инвариантных многообразий матриц посредством итераций, ПММ,
т. 7, 3, 1943, стр. 193—222).
§ 8. Ускорение сходимости итерационных процессов
при решении задач линейной алгебры
В шестой главе были рассмотрены итерационные методы реше-
решения систем линейных алгебраических уравнений и в предыдущем
параграфе рассмотрены итерационные методы отыскания собственных
значений матриц. На практике часто случается, что при применении
этих методов нужно произвести очень много итераций для получения

§ 8] УСКОРЕНИЕ СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ 245
результата с требуемой точностью. В связи с этим возникает необ-
необходимость применять те или иные методы ускорения сходимости.
В этом параграфе мы и рассмотрим некоторые из методов ускорения
сходимости для указанных выше задач.
1. Ускорение сходимости итерационного метода решения си-
систем линейных алгебраических уравнений. Общие замечания.
Стационарный итерационный метод решения системы линейных алге-
алгебраических уравнений
Ах = Ъ A)
можно записать в виде
хь+1= Вхъ + СЬ, B)
где В и С — такие матрицы, что
В-\-СА = 1 C)
(см. главу 6). Из B) следует
хк+1 — х = В(хк — х) D>
или
х = Вк+1(х0 — х). E)
Обозначим максимум модуля собственных значений матрицы В
через \. Пусть р — наивысшая степень элементарного делителя,
соответствующего наибольшему по модулю собственному значению.
Тогда из формулы (94) предыдущего параграфа следует, что при
больших значениях k будет иметь место асимптотическое равенство
В связи с этим будем численно характеризовать скорость сходи-
сходимости итерационного процесса B) величиной
/?(?)=—1оц.\ G)
При этом скорость сходимости будет примерно обратно пропорцио-
пропорциональна числу итераций, необходимых для получения решения с за-
заданной точностью.
Систему A) можно бесчисленным множестром способов привести
к виду B). В силу изложенного это нужно делать так, чтобы макси-
максимум модуля собственных значений матрицы В был возможно меньшим.
Рассмотрим случай, когда B = f(A) и С = #(Л), где /и g—неко-
g—некоторые многочлены. Условие C) в данном случае примет вид
fiA)+g{A)A = I. (8)
Если обозначить собственные значения матрицы А через Xi
(е'=1, 2 п), то для сходимости итерационного процесса B)
нужно потребовать

246 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Предположим теперь, что все собственные значения матрицы А
действительны и расположены на отрезке [т, М\, где т > 0.
Постараемся использовать эту информацию для наилучшего выбора
многочлена /(X). Прежде всего в силу (8) для /(X) должно быть
выполнено условие
= 1. A0)
Многочлен /(X) должен иметь наименьший максимум модуля на
отрезке [т, М] среди всех многочленов данной степени s, удовле-
удовлетворяющих условию A0). Мы уже решили такую задачу в главе 6.
Искомый многочлен будет равен
м-
где Ts(x) — многочлены Чебышева, наименее уклоняющиеся от нуля.
При этом
maxJ/(X)| = 71±U-^<1 A2)
X g [то. М]
М — т)
и сходимость обязательно будет иметь место. В простейшем случае
можно взять в качестве /(X) многочлен первой степени. Он должен
иметь вид
/(Х)=1-СХ. A3)
При этом
2. Метод М. К. Гавурина. Можно подойти к вопросу об уско-
ускорении сходимости и несколько иначе. Пусть итерационная формула B)
уже построена. Начиная с некоторого л;0, построим по формуле B)
векторы xv x2 -^s+i- Поставим следующую задачу: подобрать
коэффициенты оц так, чтобы линейная комбинация
.. -|_as(^s4i — ^s) A5)
возможно лучше приближала точное решение системы A). Будем
предполагать, что матрица В имеет простую структуру и что все
ее собственные значения действительны. Обозначим собственные
векторы В через zv z2 zn и запишем разложение х1—х0 по
векторам z^ в виде
х1 — х0= cxzx + c2z2 + .. . +¦ cnzn. A6)
При этом
**+i - ** = cj&i -f- cjJ&i -f- ... г cBXjJ№. A7)

§ 8] УСКОРЕНИЕ СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ 247
Точное решение х может быть "записано в виде
со
X = Х0 Н- ^ (Хк + 1—Хк) = Х0 + 2 foXfo -+- C212Z2 + . . . + Cn)%Zn) =
A8)
Таким образом, разность между точным решением A8) и прибли-
приближенным A5) представится так:
X —У = ^ ci [ZTb — Р
где через P(ty обозначен многочлен
Р (к) = а0 + «Л + ¦ • ¦ + ^. B0)
Очевидно, наша задача сводится к тому, чтобы сделать величины,
стоящие в квадратных скобках A9), возможно меньшими. Пусть нам
известна верхняя граница М < 1 модулей собственных значений В.
Тогда надо выбрать многочлен Р(к) так, чтобы он на отрезке [—М, М]
наилучшим образом аппроксимировал функцию ^ г. Решение этой
задачи также сводится к многочленам Чебышева, наименее уклоняю-
уклоняющимся от нуля. Можно показать (см. упражнения к главе 4), что
где
Применяя этот метод, предложенный М. К. Гавуриным, мы можем
производить несколько итераций по формуле B) и затем улучшать
полученные результаты, используя многочлен РХ
3. Метод Л. А. Люстерника. Пусть теперь нам известно (при-
(приближенно) наибольшее по модулю собственное значение X* матрицы В.
Будем сначала предполагать, что оно действительно, единственно и
что матрица В имеет простую структуру. Разложим хг — х0 по
собственным векторам матрицы В:
! о & r22\ + zn. B3)
Тогда
x
m+1 — xm=Bm(^ — x0) = rf^fгх + d2l?z2 + . . . -h</„Сг„ B4)

248 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
и
оо
х хт == ^j (xm+k+l хт+к) ==
Ч" - ЧР - 1п ~
При достаточно большом т будем иметь приближенные равенства
B6)
B7)
Таким образом, можно ожидать, что вектор
•*¦ — хт-\~- 7*(хт+1—хт) B8)
I — A.J
будет ближе к точному решению х, чем л;т и хт+1. Оценим порядок
ошибки х — х', предполагая, что Х1=Х1-|-е, где е^0( ^ 1,
a Xj — следующее за Хг по величине модуля собственное значение В.
Если ввести матрицу
Ч
то, с одной стороны, В1(х — хт)=х — х', а с другой стороны,
используя B5), имеем:
В1(х—хт) =
откуда получим:
Поэтому
х-х' = 0A?). C1)
Так как по B7) порядок л;—хт равен О(Х7!), то улучшение сходи-
сходимости будет тем больше, чем меньше отношение
. Если

§ 8] УСКОРЕНИЕ СХОДИМОСТИ ИТЕРАЦИОННЫХ ПРОЦЕССОВ 249*
\г близко к 1, то целесообразно вместо формулы B8) использовать
X = Хт-\ ^(хт+р— хт) C2)
1 \
Вывод этой формулы аналогичен выводу формулы B8). Метод при-
применим и в том случае, когда \ — кратное собственное значение.
Пусть теперь Х1 — комплексное число. Если матрица В действи-
действительна, то существует и комплексно-сопряженное собственное зна-
значение \. Обозначим соответствующие этим собственным значениям
комплексно-сопряженные собственные векторы через zx и z2. Тогда
при больших значениях т будем иметь приближенное равенство
Далее, из
C3)
™ d2z2, )
находим:
(Xl + Xl) (Xm + 1 — Xm) — (Xm+2 — Xm bl) ^5 XThd^ -\-lf\d2Z2- C5)
Таким образом, можно взять
х = Хт+ l(h+\i+^ • C6>
Величины Хх—j- Xj и Х^ можно, например, найти как коэффициенты
квадратного уравнения, о котором говорилось в предыдущем пара-
параграфе. Можно использовать и два наибольших по модулю соб-
собственных значения. При этом будет применима формула, аналогич-
аналогичная C6). Приведенный метод был предложен Л. А. Люстерником.
4. §2-процесс Эйткена. Можно использовать равенство B6) и
иначе. Запишем его для компонент Xi — х[т) вектора ошибки л; — хт
в виде
Xi - *(Г> = aiXf + «2Xf Н- • ¦ • + «Л. C7)
Опять предположим, что Хг преобладает по модулю над остальными
собственными значениями. Тогда при большом т можно приближенно
считать:
..(т) 1 т )
<т+1) jffl+1
; — XI = OtjAi ,
_ im+2
C8>

'250 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Исключим из этих трех равенств величины cq и Xt. Обозначая
Т+1)-хТ] = ЬхТ\ \
получим:
Следовательно,
„(m) <я»+2) _
%
x(m+2) _
) л.
C9)
D0)
D1)
D2)
Получили Ь2-процесс Эйткена, о котором говорилось в предыдущей
главе. Указанный способ можно обобщить на случай, когда пре-
преобладающими считаются два или больше собственных значения.
Так, пусть
D3)
D4)
Тогда
Д4т) = а^Г A - К) + «2*? A - h),
Д24т) - - atf A - ^iJ - a2Xf A - Х2)а,
Д3*И = aix» A _ Irf + a2Xf A - Х2K,
^xf) = _ aixf A - X/ - a2Xf A - X2L.
Используя выражения D3) и D4), нетрудно показать, что
г
Таким образом,
= 0.
D5)
х(т)
д2*|
i
да4"" ^
дз^ш) &
Д2*
Зх(т)
4 Ат)
т)
X
D6)

5 9j ПОГРЕШНОСТЬ ПРИ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 251
Аналогичные формулы мы получим, если будем считать преобладаю-
преобладающим 3, 4 и т. д. собственные значения.
Формулы D2) и D6) находят применение для улучшения сходи-
сходимости самых различных процессов.
5. Улучшение сходимости итерационных процессов для оты-
отыскания собственных значений матриц. Кратко коснемся вопроса
06 улучшении сходимости итерационных процессов для отыскания
собственных значений матриц. И в этом случае мы находим неко-
некоторую последовательность чисел вида
Хъ ^— ОС 1^*1 —)— 0^2 3 —т— ... —1— &*1"п (™ —— ^» 1» J, у ...). D/)
Преобладающее по модулю собственное значение, определяемое
с помощью этого равенства, будет найдено тем точнее, чем меньше
отношение \l2/^i\- Поэтому если нам известны приближенно Хх
и Ха, то можно вместо последовательности D7) рассматривать
последовательность
р п р п
Ур = 2 сьхк = S^i JB CftXf = ^ <*ьРр Он)' D8)
где
1 / ¦* \
D9)
Если известно грубо положение всех собственных значений
Xi, Х3 Хп, то для уточнения собственного значения X; можно
использовать итерацию с матрицей Pt(A), где
Pt (A) = (A- Xl/) (А - ill) .. . (Л-Х*_!/) (Л-Х*+1/) .. . (Л-Х;/). E0)
§ 9. Неустранимая погрешность при численном решении
систем линейных алгебраических уравнений
Пусть требуется решить систему линейных алгебраических ура-
уравнений
Ах = Ъ. A)
На практике часто бывает так, что мы не знаем точно ни матрицы А,
ни вектора Ъ. Предположим, что вместо матрицы А нам дана матрица А*
и вместо вектора b дан вектор Ь*. Тогда вместо вектора х мы
сумеем найти только вектор х*, удовлетворяющий системе уравнений

252 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. &
При этом возникает задача об оценке отклонения вектора л;* от век-
вектора х, т. е. об оценке Цл:— х*\\, где норма понимается в том или
ином смысле.
Аналогичная задача может возникнуть и в том случае, когда
матрица А и вектор В известны точно, но в процессе решения
системы A) были допущены те или иные погрешности. Тогда
вместо точного вектора решения х мы получим некоторый при-
приближенный вектор л;*. Вычисляя Ах*, мы получим не Ь, а Ь*. Опять
возникает необходимость оценить Цл: — л:*|| по известной раз-
разности b — b*. Так как вторая задача есть частный случай первой,
то мы ограничимся первым случаем.
Пусть
А* = А — в; Ъ*=Ъ—1. C)
Тогда
(А* + е) (х — х*) = (А* + е) х — А*х* — вх* = Ь — вх* D)
или
+ е)(х— **)||<||5|| + ||е|| ||*1. E)
Определяя различным образом нормы векторов, мы получим раз-
различные оценки. Воспользуемся сначала третьей нормой векторов,
введенной в шестой главе:
f\\3 = ^(r. г). F)
Тогда согласованная с ней норма матрицы А будет равна
где через Х^'^ обозначено наибольшее собственное значение симме-
симметрической матрицы А'А. Из равенства B) получаем
H'*ls=ll*ls. (8>
Но
||А*?Ч|з = (А*х*, А*~х*) = (?•. А*'А*х*). (9)
Обозначим собственные значения матрицы А* А* через \f*'A*. Так как
мы предположили, что матрица А* невырожденная, а матрица А*'А*
является симметрической, то все Xj положительны. Им соот-
соответствует ортонормированная система собственных векторов
Mt, u2 ип, образующая базис нашего пространства. Пусть
х* = с1и1-\-с2и2-\- ... +сппп. (Ю)
Тогда из (9) и A0) получаем:
|| л*7*112 — ЛА*'А*-L. ЛА*'А* Л- Л-гНА*'А*

§ 9] ПОГРЕШНОСТЬ ПРИ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 253
Обозначим минимальное из \f*А* через Хт1ил*. Из A1) следует:
м л*—"ж II3 ^ \А*'А*( 2.2, , 2\ ЛА*'А* м —»ц2 ,.оч
\\Ах lU^-^mta (C1 + C2+ • • • -{-Сп) = ктЫ \\Х \\3. A2)
Таким образом.
Из (8) и A3) находим:
тЛЛ.*'Л* ||ТГ*|| S И А* II
' '-nun II* Из <> 11° Из
ИЛИ
||>ц ^ И^ Us
II х || <
Поэтому второе слагаемое правой части неравенства E) может быть
оценено следующим образом:
Очевидно,
Уменьшаемое в правой части неравенства A7) оценивается так же,
как мы оценивали (8). При этом получим:
Р||з. A8)
Вычитаемое в правой части A7) может быть оценено так:
||_/11 ~г*\\\ г* 11 = 11 И~*- ~ЙЧ1 ~\/~\ее II*- ^-*ll nqi
I!8*.* •* )||з-^- ||8Нз 11* — * Из— ' Лтах II* * Из* (iy)
Таким образом,
Р(/^/Э||Л — *'||,. B0)
Если (>-т*иЛ*)а—(>-mL)a > 0, то E) и B0) дают
и $ и jS ' "u ' \ шал i Ш11Х / " " » ,л ^
(Xmin J—(XmLK
Это и есть искомая оценка.
Приведем пример на применение полученной формулы. Пусть
дана система:
26,7*i — 5,1*2 + 1,3*з — 0,3*4 = 43,888,
— 5, l*i — 28,6*2 + 6,2*з + 1,2*4 = — 58,203,
1,3*i + 6,2*2 + 29,1*з — 4,3*, = 88,390,
— 0,3*i + 1,2*2 — 4,3*з + 27,1*4 = 98,664.

254 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. &
Будем предполагать, что коэффициенты и правые части системы
заданы точно, но в процессе решения системы вследствие ошибок,
округления мы получили не точное решение, а приближенное:
л-1 = B; 2,5; 3; 4).
В этом случае вектор 8 будет выглядеть так:
8"= @,538; —0,03; 0,190; 0,764).
Итак, ||8||3:=0,95. Матрица е в нашем случае нулевая. Поэтому
ц- ;>[[ ^ НГП»
^min )
Так как матрица А симметрическая, то (iS^1*)^ = I ^AI ¦ • Для
\к Imin нетрудно получить грубую оценку |Х |mia> 16,1. Такии
образом,
Возьмем теперь в качестве нормы вектора r — (rlt r2 гп>
величину
S B2)
1 = 1
Тогда согласованная с ней норма матрицы А с элементами ai}
будет равна
|e<jl- B3)
i » = i
Перепишем равенство D) в виде
\ ^ А*~Ч — А*~\~х* — А*-\\, B4)
где \ = х — х*. Отсюда следует:
Р||2<1И-18||2 + 11^-41211*12+ IM^ell, ||T||2. B5)
Будем предполагать, что погрешности Sjfc настолько малы, что.
\\А*-Ч\\2±\\А*-Ч\\2\\х*\\2
1—11А Ы\\2
< IU* II2II412+ И^'^И
1-|Ц*-Ч|2

§ 9] ПОГРЕШНОСТЬ ПРИ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 255"
Последнее справедливо в том случае, если ||-<4*~ ||2||е||2< 1. Далее,,
заметим, что
, п п п
fc="i "" ¦¦' з »=1 *-1 lk kj ^ *=1 к-1
B7)
где через Е обозначено
Е = max | eik \ B8)
I, к
и через bik обозначены элементы матрицы А
Здесь Ль — алгебраическое дополнение элемента ah матрицы А*
и Д* — определитель матрицы А*. Таким образом, оценка для р||2
/ п п \
при ? < 1 /( 2 2 I *й I ) примет вид
' \ 1 к J
i=i
п п
S.
2 ^"
12-
1—4
C0>
Такая же оценка справедлива и для каждой компоненты вектора I.
Однако для компонент можно получить и более точную оценку.
По B4) имеем:
(|. C1)
Отсюда
п _ п п
i i = l i — 1 i«-l
Подставляя сюда вместо ||?||2 выражение C0) и используя B9), по-
получим:
SI4.I -
I fc I jS" Ъ = 1 || 0 || 2 "Г ^ II % || 2
1 •/ ' ^ ДМ П П \ОО)'
, ^vv
Неудобство этой оценки состоит в том, что приходится вычислять-
определители высокого порядка.

¦256 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
Приведенные рассуждения показывают, что в некоторых случаях
влияние неточности коэффициентов и правых частей на решение
может оказаться значительным. Так, например, если величина
Ч = \
C4)
велика, так что qE будет близко к единице, то правая часть C0)
или C3) будет велика. В связи с этим вводилось ряд характеристик,
аналогичных C4), так называемой «обусловленности» систем. При
этом система считалась хорошо обусловленной, если небольшие
изменения в коэффициентах и правой части мало изменяют решение
системы, и плохо обусловленной, если небольшие изменения в коэф-
коэффициентах и правой части вызывают большие изменения в решении
системы. Пока эти вопросы еще не исследованы до конца.
В этом параграфе мы рассматривали только неустранимые по-
погрешности. В процессе решения системы будут возникать также и
ошибки округления. Однако, для того чтобы изучить влияние оши-
ошибок округления, нужно детальнее учесть алгоритм и вычислитель-
вычислительные средства. Пока такие исследования проведены лишь для отдель-
отдельных алгоритмов. Рассуждения, которые при этом приводятся, очень
¦громоздки. Поэтому мы здесь этих вопросов касаться не будем.
УПРАЖНЕНИЯ
1. Найти все собственные значения матрицы
4,1313 1,1617 2,1426 1,1718
0,1041 0,8144 3,1518 2,1413
1,1617 0,9864 0,8114 1,4656
3,1415 4,1617 2,3114 1,1681
2. Показать, что в методе Ланцоша можно подбирать векторы с& и Т^,
«сходя из условий:
а)_с& — линейная комбинация с0. Ас0 Ак~1сй; bjc — линейная комби-
комбинация Ьо, А'Ь0 А'к~1Ь0;
б) скалярное произведение (с^, Ьк) минимально.
3. Показать, что если с0 в методе Ланцоша ортогонален к одному из
собственных векторов-строк матрицы А, скажем vit то множитель X — X* вы-
выпадает из_ tym (к); аналогично, если Ьо ортогонален к одному из векторов-
столбцов щ. с
4. Рассмотрим произвольную одноколонную матрицу ха =
и мат-
состоящую из одной строки
i = (rfi, d-i, ..., dn). Обозначим

УПРАЖНЕНИЯ
257
Доказать, что
Рп
Pn-i
А
сп
СП+ 1
'с
сп сп+1
где /?i — коэффициенты характеристического многочлена матрицы А:
О (X) = (—1) (X —р^к —р$К — ... —/?yj_jX — Рп)г
5. Доказать, что если матрица А имеет вид
аи аш 0 0 ... О О
#*>! #22 #%J ^ • • • О О
О dig, <% аи ... О О
О О О
ап, n-i
причем все "hth_1ahtk+1 >° (А = 1. 2 л —1), то все собственные значе-
значения А действительны.
6. Используя результаты последней задачи, доказать, тто все корни
многочленов Лежандра действительны.
7. Показать, что все корни матрицы D § 6 удовлетворяют неравенству
It*» I < g ctg — , где g определено там же.
8. Показать, что уравнение
при | Ло I =^= 0 эквивалентно уравнению
О •"! "f" X/n Лп
/
' «1
0
= 0.
о -4 м»
9. Пусть собственные значения А удовлетворяют условию
Xi>A2>... > X^j—1 > Xn > О
и мы приближенно знаем Xlt Xj, Xn_lt Х„. Доказать, что тогда для уточне-
уточнения Xj итерационным способом лучше всего взять матрицу А—pi где
/>=—(Xj+X»), а для уточнения Х„ — матрицу A~ql, где 9 = 7r(Xi+ ^п-г>-
10. Показать, что собственные значения матрицы и-го порядка вида
2—1 0 0 ... О 0]
—1 2—1 0 ... О О
0—1 2—1 ... О О
равны
О 0 ... —1 2
(*=¦!, 2 п).

258 ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ВЕКТОРОВ МАТРИЦ [ГЛ. 8
11. Исследовать, при каких условиях итерация
будет давать лучшую сходимость, чем итерация
b.
12. Получить следующую оценку для нормы разности || х — х" || 3 между
точным х и приближенным х* решениями системы Ах = Ь:
П,( S
где S = Ла: — Ах*, \ А\ — определитель А.
13. Используя обозначения § 9, получить следующую оценку:
b1
1
(S, V
+ (
f n
2
n
2
i
N
4
l
) (?,
l
1
Vi~ ft~i ""/ \i='l ft^l
14. Провести геометрический анализ влияния изменения коэффициентов
системы на ее решение.
ЛИТЕРАТУРА
1. В. Н. Ф а д д е е в а, Вычислительные методы линейной алгебры, Гостех-
издат, 1951.
2. В е й л а н д, Представление векового уравнения в виде многочлена, УМН,
т. 2, вып. 4, 1947.
3. Хаусхолдер, Основы численного анализа, ИЛ, 1956.
4. М. Л. Бродский, Вероятностные оценки погрешностей при определении
собственных значений и собственных векторов варьирующейся матрицы,
УМН, т. 7, вып. 5, 1952.
5. И. М. С т е с и н, Вычисление собственных значений при помощи непре-
непрерывных дробей, УМН, т. 9, вып. 2, 1954.
6. М. А. Красносельский, О некоторых приемах приближенного вы-
вычисления собственных значений и собственных векторов положительно
определенной матрицы, УМН, т. 11, вып. 3, 1956.
7. О. F о г s у t h е, Решение линейных алгебраических уравнений может быть
интересным, Bull. Amer. Math. Soc, т. 59, № 64 A953).
8. К. А. С е м е н д я е в, О нахождении собственных значений и инвариант-
инвариантных многообразий матриц посредством итераций, ПММ, 7, 1943.

ГЛАВА 9
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
§ 1. Введение
Обыкновенные дифференциальные уравнения встречаются довольно
часто в различных прикладных вопросах. При этом во многих слу-
случаях имеют дело с уравнениями, общее решение которых не выра-
выражается в квадратурах. Поэтому возникает необходимость применять
те или иные методы, дающие приближенное решение задачи. С не-
некоторыми из таких методов встречаются уже при изучении общей
теории обыкновенных дифференциальных уравнений. Так, например,
в общей теории обыкновенных дифференциальных уравнений изучается
вопрос о возможности представления решения уравнения в виде ряда
у(х) = ао-\-а1(х — хо)-\-аг(х — лгоJ+... -\-ап(х —хо)п-\-... A)
или же более общего ряда
... -\-ап(х-х0)п+ ...], B)
где о — некоторое число, не обязательно целое и положительное.
Если решение можне представить в виде A) или B) и если удается
фактически найти достаточно большое количество коэффициентов
а0, av .... ап так, что абсолютная величина суммы остальных чле-
членов, т. е.
+ СО
2 ак(х — хо)к
или соответственно
I*—*оГ S
к=п+1
меньше, чем заданная нам допустимая погрешность, то соответ-
соответствующий отрезок ряда может служить приближенным представле-
представлением искомого решения. Таким же образом можно использовать
тригонометрические ряды или ряды по другим ортогональным функ-
функциям.

260 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
При доказательстве существования решения дифференциального
уравнения у=/(х>у) D)
с начальным условием у(ха)=у0 (или же системы таких уравнений)
часто используют метод последовательных приближений Пикара. При
этом точное решение получается как предел последовательности
где Уа(*)> у1 (х) уп(х), .... E)
х
f (я=1. 2. ...). F)
Процесс последовательных приближений Пикара сходится при вы-
выполнении таких условий:
1. Функция f(x, у) непрерывна в области R={\x—лго|<;а,
\У-Уо\<Ь}-
2. Функция f(x, у) удовлетворяет в R условию Липшица по у;
1/(*. у)—f(*. у)\<Цу-у1
Здесь L — постоянная, не зависящая от х, у и у, а точки (дг, у) и
(л;, ~у) — произвольные точки области R.
При выполнении этих условий уп(х) равномерно сходится к функ-
функции^ (л;) на !лг0 — Л, xa-\-h], где Л = пнп(а, -^j и M = sup \f(x, y)\,
и функция у(х) удовлетворяет дифференциальному уравнению D) и
начальному условию.
Если метод последовательных приближений сходится и может
быть фактически осуществлен для достаточно больших п, так что
\уп(х)—у(х)\ не превышает заданной нам допустимой погрешности,
то мы можем принять уп (х) за приближенное решение задачи.
Мы не будем здесь подробно останавливаться на этих методах,
достаточно хорошо изложенных в общих курсах.
Методы, которые мы будем изучать, можно разделить на две
большие группы. Одни из них дают приближенное решение в виде
аналитического выражения, другие — в виде таблицы. Будем назы-
называть первую группу методов аналитическими, вторую — числен,'
ними.
Мы начнем изложение с аналитического метода, предложенного
академиком Сергеем Алексеевичем Чаплыгиным.
§ 2. Метод С. А. Чаплыгина
1. Теоремы о дифференциальных неравенствах. Метод Чаплы-
Чаплыгина основан на его теореме, которую он назвал теоремой о диф-
дифференциальных неравенствах. Приведем доказательство этой тео-
теоремы в формулировке, несколько более уточненной по сравнению
с данной самим С. А. Чаплыгиным.

§ 21 МЕТОД С. А. ЧАПЛЫГИНА 261
Теорема 1. Пусть функции f(x, у) и F(x, у) непрерывны
$ области
(а>0, *>0) A)
и удовлетворяют условию
/(*, y)*CF(x. у). B)
Пусть, далее, у = у(х) и y = U(x)—решения дифференциаль-
дифференциальных уравнений
У = /(х, у), U' = F(x. U), C)
проходящие через точку (л:0, у0), определенные при х0 ^ х ^ х0 -)- а
и лежащие между у0 — Ь и уо-\-д. Тогда если f(x, у) удовлетво-
удовлетворяет в нашей области условию Липшица, то при х0 ^ х ^ х0 -)- с
имеет место неравенство U(x)^.y(x). Более того, если в не-
некоторой точке х1>х0 имеет место неравенство U (xj > у (х^,
то U(x)>y(x) при всех х?[хг, хо-{-а].
Для доказательства рассмотрим
W —У = F(x, U) —f(x. у) D)
и обозначим U — y = z. Тогда для z получим следующее диффе-
дифференциальное уравнение:
z' = F(x, U) — f(x, U — z). E)
Рассматривая здесь U как известную функцию х и обозначая
F(x, U) — f(x, U — z) = g(x, z), F)
получим, что z удовлетворяет дифференциальному уравнению
z' = g{x, z) G)
и начальному условию z(xo) = 0. Запишем уравнение G) в виде
z' — g(x, 0) = g(x, z) — g(x, 0). (8)
На основании B) имеем:
g(x. 0) = />(*. U)—f(x, ?/)>0. (9)
Так как f(x, у) удовлетворяет условию Липшица, то
\g(x, z) — g(x, 0)| = 1/4*. U)—f(x. U — z) — F(x, U) +
+/(*. U)[ = \f(x. U)—f(x, U — z)[4?L[z\. A0)
Таким образом,
— L\z\^z' — g(x, 0)<A|z|. A1)
Предположим, что вопреки утверждению теоремы в некоторой
точке *! отрезка \х0, хо + а] U^Xy^xJ. Так как U(xo)=y(xo),
то на отрезке [х0, xt] найдутся точки, где U(х) =у(х). Не уменьшая

262 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
общности, мы можем предположить, что эта точка единствен-
единственная и что она совпадает с х0. Тогда U(xo) — y(xo) и U (х) < у (х)
для всех точек (л:0, xt]. На отрезке [х0, х^\ неравенство A1) можно
записать в виде
Lz<z' — g(x, 0)< — Lz. A2)
Отсюда
z' — Lz = <?(x)>g(x, 0)>0 A3)
и для всех точек [х0, х±\
X X
z= f eL (*-*)<? (t)dt^. ^ eL^x-t)g{t, 0)fltf>0, A4)
ха
что противоречит нашему предположению. Итак, мы доказали, что
на всем отрезке [л;0, хо-\-а] U (х) >. у (л;) или z^.0.
Может оказаться, что z= 0 при х ? [л;0, хо-\-а]. Тогда U (л;) =у(х),
g(x, 0)^0 и F(х, U)=f(x, U). Это может быть даже тогда,
когда f(x, у) совпадает с F(x, у) не всюду в области R. Так, если
F(x,y) = \, f(x, y)=\ — {y — xf, A5)
то
F(x, y)>f(x, у) A6)
всюду, за исключением точек, лежащих на прямой у = х. Но диф-
дифференциальные уравнения
U' = F(x, U), y' — f(x, у) A7)
имеют совпадающее решение у = U = х, удовлетворяющее началь-
начальному условию у@) = ?/@) = 0.
Предположим теперь, что имеется такая точка хг?\ха, хо-\-а\,
в которой U(Xj) ~>y\xx). Покажем тогда, что на всем отрезке
[х1, хо-\-а] будет иметь место неравенство U(х) >у(х). Если бы
это было не так, то нашлась бы такая точка х2?\х1, хо-^-а], что
U (лг2) = у (х2) и U(x)>y(x) на (xv x2). Обозначим через х'о бли-
ближайшую к хх точку отрезка [л;0, хг\, в которой U(х'Л = у(х'Х На
интервале (л:^, хЛ неравенство A1) может быть записано в виде
— Lz<z' — g(x, 0)<Az. A8)
Отсюда
2' + Z.z = <p(.t)>g-(x, 0)>0 A9)
или
х х
J J 0. B0)

с 21 МЕТОД С. А. ЧАПЛЫГИНА 263
В силу нашего предположения, что z (хг) = О, будем иметь:
С e-L{x-t)g(fi 0) dt = о BП
x'o
или g(x, 0) = 0 при х? [х'о, x2], так как *-¦& (»-'>> о. Но тогда
правая часть неравенства A8) даст
z'— Lz = ty(x)^g(x, 0)=0, *6[<-*J, B2)
или
а; а;
z= JVfe'-'ty (*)<#< jeL(x-t)g{t, O)dt = O, B3)
а это противоречит нашему предположению, что ,г(л:1)>0. Теорема
доказана полностью.
Сделаем несколько замечаний к доказанной теореме.
1. Если вместо B) предположить, что
У) B4)
в рассматриваемой области (что делал С. А. Чаплыгин), то при всех
х > х0 будет U > у. Действительно, в силу неравенства B4) будем
иметь U' (лг0) > у' (х0). Отсюда U (х) > у (х) при всех х > х0 и
достаточно близких к х0. В силу теоремы 1 это будет справедливо
и при всех х?(х0, хо-\-а].
2. Если бы вместо F (х, у) взять непрерывную функцию у(х, у)
такую, что
/(*. .У)>?(*. У) B5)
в рассматриваемой области, то, повторяя рассуждения доказатель-
доказательства теоремы 1, мы доказали бы, что решения уравнений
в/ = <р(*. и), У=/(х,у), B6)
удовлетворяющие начальным условиям и (х0) = у (х0) = у0 при
х?\х0, хо-\-а], удовлетворяют неравенству
и(хL,У(х), B7)
причем, если в какой-то точке хг?\х0, хо-\-а], и(х)<Су(х),
то и(х)<.у{х) при всех х? \хг, хо-\-а].
Теорема о дифференциальных неравенствах Чаплыгина позволяет
в некоторых случаях отыскать границы U(х) и и(х), в которых
заключено точное решение у(х).
На практике чаще всего для отыскания U и и подбирают функ-
функции F(x, у) и у(х, у) так, чтобы имели место неравенства

264 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
F(x, y)^f(x, .у)><р(*. У)> а уравнения
U' = F (х, U), и' = <? (л:, а) B8)
легко интегрировались бы в квадратурах.
Рассмотрим такой пример. Пусть дано уравнение
и нам требуется найти решение его при О^л;^ 1, удовлетворяющее
начальному условию у @) = 0. В качестве функций F (х, у) и tp (л;, у)
можно взять
F(x, y)= *
В результате получим следующие функции U и и:
хъ
U = tgx; и = -д-.
Иногда удается подобрать так функции U и и, что и (л;0) =
^U(xo) = yo и
-g—/(*. t/)>0. -g—/(*.«) <0. B9)
Тогда, очевидно, будем иметь U^-y^.u. Такими функциями, напри-
например, будут:
X
C0)
Действительно,
U) = \f(x, yo)\+-LY-f(x, yo+Y) =
= \f(x,yo)\—f(x,yo) + LY-\f(x,yo+Y)-f(x, y0)}. C1)
В силу условия Липшица, фигурная скобка по модулю не больше LY.
Таким образом,
U' — f(x.U)>0. C2)
Аналогично доказывается, что
u'—f(x. и)<0. C3)
2. Способ Чаплыгина построения улучшенных приближений.
Не всегда удается такими способами получить сразу достаточно
тесные границы для у(х). Поэтому возникает задача об улучшении
этих границ. С. А. Чаплыгин предложил способ по найденным U
и и получать улучшенные приближения ?/, и и,. При этом прихо-
приходится накладывать довольно сильные ограничения на функцию f(x, у).

§ 21
МЕТОД С. А. ЧАПЛЫГИНА
265
д2/
а именно предполагать, что -—¦ сохраняет свой знак в области, огра-
ограниченной кривыми y=(J(x) и _у=и(л:) и прямыми х=х0 и
х = хо-\-а. Геометрически это означает, что сечения поверхности
Рис. 21.
z = f(x, у) плоскостями х = const будут либо все время выпуклы,,
либо все время вогнуты (рис. 21).
Рассмотрим некоторое сечение поверхности z = f(x, у) плоскостью-
х = const (рис. 22). Через и, у, U на рис. 21 обозначены соответ-
соответственно точки пересечения кривых у=и(х), y = y(x),y=U(xy
У
плоскостью сечения, а через А и В — проекции и и U на сечение-
поверхности z = f(x, у).
Проведем секущую АВ и касательную AT, если -^ > 0, и ВТ,
если -g-j- < 0. Произведя такие построения при каждом х рассмат-
рассматриваемой области, получим две поверхности, одна из которых обра-
образована секущими, другая — касательными. Одна из поверхно-
поверхностей, будем обозначать ее z = F (л;, у), будет расположена над.

266 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
поверхностью z = /(;t, _у)> другая z = tp(;t, _у) будет расположена
дод поверхностью z = f(x, у). Таким образом,
F(*.y)>f(x.y)>4Kx.y)- C4)
Заметим, что функции F (х, у) и у(х, у) линейны относительно у.
Следовательно, уравнения
C5)
интегрируются в квадратурах. Пусть U^ и и^ соответственно реше-
решения этих уравнений, удовлетворяющие тем же начальным условиям,
что и прежде. Покажем, что эти функции удовлетворяют поставлен-
поставленным условиям. В самом деле, вдоль кривой y=U(x) имеем:
-g. —/(*,?/)> 0 C6)
и, кроме того, f(x, U)= F(x, U). Таким образом, -j— — F(x, ?/)>>0
и U^>Ult а из неравенства f(x, y)<^.F(x, у) следует U^y.
Аналогично проводится доказательство и для и.
Приведем аналитическое изложение этого метода. Будем пред-
лолагать, что -т-^ > 0. Имеем:
da
C7>
Обозначим у—u = z. Вычитая из верхнего равенства нижнее и
применяя к разности f(x, у)—f(x, и) формулу Тейлора, получим:
Т = гГ ^И(*) C8)
где и^^^З'- Решение этого уравнения при начальных данных
z(xo) = O дает поправку, которую нужно прибавить к и(х), чтобы
получить у(х). Отбросим член с z2. Тогда функция Z(x), удовлетво-
удовлетворяющая уравнению
4§ ^ C9)
и начальным условиям Z(xo) = 0, будет удовлетворять неравенству
Z<^.z. С другой стороны, если положить ф(л:)^О, то решением
уравнения C9) с нулевым начальным значением будет тождествен-
тождественный нуль (по теореме единственности). Таким образом,

Л 2] МЕТОД С. А. ЧАПЛЫГИНА 267
и если принять ux=u-\-Z, то будем иметь и^^^у, что нам
и требовалось:
dx
Для улучшения оценки сверху рассмотрим уравнения
-^=/ (*. U) + в (*) (б (х) > о), J
|
Положим ?/ — З7^^ и вычтем из верхнего равенства нижнее. Полу-
Получим:
Ц (*)• D1)
Введем обозначение
/(,.^)=-/(,,M)=/?Wj D2)
Тогда
f(x,U)-f(x,y) = tF(x) + $(x), D3)
где
=/(jc. ^ -/(*. y)-{U-y) /{X' "iZfuX' U) =°
^")]. D4)
Обозначим через tpW функцию
у() : (<(/)-
Производная этой функции равна
x, U)-f(x, x)
L ЙТ ^
= ^Щ^- (^<«Л<^ D6)
Так как по предположению д 2' ^- 0» т0 ^'(^^О. Поэтому
<р (т) — неубывающая функция и <р(у) > tp (и). Отсюда {J (л:) ^ 0. Таким
образом, решение уравнения
g , D7)

268 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
обращающееся в нуль при х = х0, будет при х > х0 удовлетворять
неравенству T^.t. Так же как и для Z, мы получим Г^-0. Поэтому,
если принять Ut = U — Г, то получим улучшенную верхнюю функцию
= f(x, U) + (U, -U) /(*>*g-/(*>"> = F (x>
При -5-^ < 0 порядок действий будет обратным.
В приведенном выше примере имеем-^-j=2>0. Следовательно,
мы можем применить наши рассуждения. Уравнение для определения Z
будет
dZ _ 2*3 лгв
~37—л~Г~г~ 9 •
Его решение, обращающееся в нуль при д: = 0, имеет вид
- Г -х- хь
Z = e6 J е в JL-dx.
о
Таким образом,
Уравнение для Т примет вид
dT
«L г
COS X
I (I—
dx.
J
(l-^)cos^
Процесс уточнения границ можно повторять неограниченно, если
только квадратуры выполнимы. Как было показано акад. Н. Н. Лузи-
Лузиным, последовательность у — ип, если -д-у^- 0, или Un — у, если
-г^-^О, будет стремиться к нулю как —— в предположении, что
начальное приближение взято достаточно близким к у. Это очень
быстрая сходимость, такая же, как и у метода Ньютона для реше-
решения алгебраических и трансцендентных уравнений. Общность между

§ 2) МЕТОД С. А. ЧАПЛЫГИНА 269
методом Ньютона и методом Чаплыгина не заканчивается на этом.
Можно показать, что метод Чаплыгина является обобщением метода
Ньютона на нелинейные функциональные уравнения.
К сожалению, обычно метод Чаплыгина приводит к очень слож-
лым квадратурам, не выражающимся в элементарных функциях.
3. Второй способ построения улучшенных приближений. Улуч-
Улучшенные приближения и, и U^ можно находить по способу Чаплы-
гина только в том случае, когда -~ сохраняет свой знак в рассмат-
рассматриваемой области. Дадим еще один способ получения улучшенных
приближений, свободный от этого недостатка.
Теорема 2. Пусть функции f(x, у), F(x,y), y(x) и U (х)
определены как и в теореме 1. Тогда если положить
И (х) = U'(x)—f(x.U (х)), D8)
то функция
х
(/, (х) = U (х) — f e-L(°°-4 (t) dt, D9)
x0
где L — константа Липшица для функции f(x, у), является
верхней функцией на отрезке [х0, хо-\-а] и на этом отрезке
имеет место неравенство
E0)
Очевидно, U^ (x) <C U (х). Далее,
X
U\(x)—f(x. Ul{x))=U\x)—h^x)+L J
= /(*. Ut(x))—f(x. U^x)) + L\U(x) — t/1(x)l>0. E1)
Следовательно, у{х) ^.U1{x), что и требовалось доказать.
Совершенно аналогично доказывается, что если и (х) является
нижней функцией и мы образуем
Aj (*) = и' (х) — f (х, и (х)). E2)
то
их {х) = и (х) — f e~L <*-% (f) dt E3)
x0
также будет нижней функцией и будет удовлетворять неравенствам
и (х) < их {х) < у {х).
И в этом случае мы можем, по крайней мере теоретически,
неограниченно продолжать процесс получения последовательных при-
приближений. В связи с этим докажем следующую теорему:

270 ПРИВЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Теорема 3. Пусть f(x, у), F(x,y), у(х), U{х) определены
как и в теореме 1. Положим
h0 (х) = U' (x) —f(x, V (х)) E4)
и образуем последовательности
X
Un(x) = Un_1(x)— {e~L(a!-t)hn_1(t)dt («=1,2,...), E5>
hn(x)=Un(x)~f[x, Un(x)] («=1,2,...). E6)
Тогда последовательность {Un(x)) равномерно на [х0, хо-\-а\
сходится к у(х).
Прежде всего отметим, что все функции Un(x) определены
в каждой точке отрезка [л;0, хо-\-а], так как они заключены
между U(x) и у(х) и не могут выйти за пределы рассматриваемой,
области до пересечения с прямой х = хо-\~а.
Далее, рассмотрим ряд
Uo (х) + [U, (х) - Uo (х)} + •.. + Wn (х) — ?/„_! (*I + • • • E7)
Если подставить сюда вместо разностей Un(x) — Un_x(x) их выра-
выражения из E5), то получим:
?/„(*)— /*-b*8-Q[Ao(O + Ai(O+ ••¦]#. E8)
X
Отсюда следует, что ряд E7) равномерно сходится, если равно-
равномерно сходится ряд
*o(*)+*i(*)+ •••+*„(*)+••• E9)
Дифференцируя E5), получим:
U'n(x) = u'n-l(x) — An_i(je)+L J е-6«"-«hn_x(t)dt. F0)
X,
Отсюда находим, подставляя вместо hn_1(x) перед интегралом его
выражение через Un_l и /:
X
Urn(x)=f(x. f/n_i) + L f e-tfr-Vhn-iMdt. F1)
Таким образом,
X
f е-ьь-Ч^ММ. F2>
CCq

§ 21 МЕТОД С. А. ЧАПЛЫГИНА 271
В силу условия Липшица получим:
х
hn (х) < 2А f e-L(*-^hn_i (f) dt. F3)
xa
Определим теперь последовательность \Hn{x)\ при помощи рекур-
рекуррентного соотношения
х
Нп{х) = 2L f e~L(*-Wn_^@ dt, F4>
х0
причем в качестве Н0(х) возьмем ho(x). Очевидно, что hn(x)^.Hn(x).
Произведем оценку Нп(х). Для этого выразим все Нп(х) через Н0(х).
Подставляя в Н2(х) выражение Ht(x) через Н0(х) и меняя порядок
интегрирования, получим:
=2L Гe-L(°°-QH1(t)dt=BLJ Г«-¦«»-«I
J J ] |
Хо Xq \Хо J
XX X
= {2Lf f dxf e-^x-^H0(x)dt^--BLJ f (x—x)e-L^-^H0(x)dx. F5i
Xa t Xo
Аналогично для Н3(х) будем иметь:
x
H3(x) = 2L Je-L&-
xa
Xlt
•) I J
х„ \x0
X X
== BLf j dx j\t — x) e-Lv>-*H0(x) dt =
xn
X
= BLK j {x 2TJ e~L (*-W0 (x) dx. F6)
х„
Покажем по индукции, что
х
Н Гл — fOfV I ^ ' n — Llm — tMJ (f\/ff (R7\
ха

272 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Действительно,
х
(х) = BL) f e~L <f»-*>Hn @ dt =
= BL)
n+1
X I t I
f «-*«»-«> | f V-**'1 e-*V-*)H0(x)dx \dt =
x x
Х„ X
X
if ill
что и требовалось доказать.
Обозначим через Мо верхнюю границу ho(x) на [х0, хо-\-а\.
Тогда
X
^r Mof(x- О*'1 *-? *»-
Отсюда следует абсолютная и равномерная сходимость ряда 2^Л»(*)«
оо
Поэтому ряд ^ hn(x) также абсолютно и равномерно сходится и,
п=о
следовательно, [Un(x)\ стремится равномерно к некоторой непре-
непрерывной функции Y(x). Покажем, что Y(х) будет являться решением
дифференциального уравнения
К'(*)=/(*• 10- G0)
Для этот рассмотрим
X X
t. UJ-f(t, Y)]dt + fhn(f)dt = rn(x). G1)
х0 х„
Так как Un(x) равномерно стремится к К (л;), a hn(x) к нулю,
то гп(х) равномерно стремится к нулю. Интегрируя E6) и исполь-
используя равенства Un(x0)~y0, можно G1) записать в виде
<f. Y)dt+rn{x). G2)

§ 2] МЕТОД С. А. ЧАПЛЫГИНА 273
Отсюда
х
f G3)
что и требовалось доказать.
Так как при любом п Un(x0) = y0, то и У(хо)=уо. Тем самым
теорема доказана полностью. В силу теоремы единственности реше-
решения дифференциального уравнения Y(х) =у(х).
4. Метод Чаплыгина приближенного решения линейных диф-
дифференциальных уравнений второго порядка. На этом мы закончим
рассмотрение метода Чаплыгина для уравнений первого порядка.
Рассмотрим теперь некоторые факты, связанные с применением
метода Чаплыгина к линейным уравнениям второго порядка. Будем
рассматривать частное решение уравнения
У(х)-\-р(х)У(х)-\-д{х)у(х) = г(х), G4)
удовлетворяющее начальным условиям у(хо)=уо, у'(хо)~у'о.
Относительно коэффициентов уравнения будем предполагать, что
р(х), д(х) и г(х) — непрерывные функции на некотором от-
отрезке [а, Ь\, содержащем точку х0, а р(х) непрерывно дифферен-
дифференцируема на этом отрезке. Рассмотрим, кроме того, дважды непре-
непрерывно дифференцируемую на [а, Ь\ функцию v(x), удовлетворяющую
при х ^ х0 неравенству
v" (х) +р (х) v' (х) +q(x)v (х) > г (х) G5)
и начальным условиям v{xQ)=y0, v'(xo)=y'Q. Применяя теорему
Тейлора, будем иметь:
— хо) /о + (*~2*0J У" (*°) + ° К* — *оJ1 - G6)
— хо) /о + {*~2*оУ% v" (х0) + о \{х — хо)% G7)
Так как v" (х0) > у" (х0), то при достаточно малом | х — хо\ и
х — х0 > 0 имеет место неравенство v (x) > у (х). Но в отличие
от того, что мы имели раньше для уравнения первого порядка, мы
уже не можем утверждать, что v (x) > у (х) на всем отрезке, где
выполнено условие G5). Так, рассмотрим уравнение
Частное решение его, удовлетворяющее начальным данным _у@) =
=У@) = 0, будет, очевидно, у(х) = 0. Если же взять уравнение
= tp (л;),

274 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
то решение его, удовлетворяющее условиям v @) = v' @) — 0,
будет
X
v — Г tp (t) sin (л: — t) dt,
о
что легко проверяется простыми вычислениями. Функция v может
принимать отрицательные значения при х > х0, даже если ф (л;)
всюду положительна. Возьмем, например, у(х) = е~ах, где а — не-
некоторое положительное число. Тогда
v(x)= / e-a'sin(x—t)dt= aS "'
х — cos x
о
Возьмем x = tz-\-e, где е>0 — фиксированное, как угодно малое
число. При этом
cose — a sin в , ?-а<7Г+!>
При достаточно большом а 1)(х-\-г) будет отрицательным, так как
1 отрицательный член
a sin в
* будет преобладать над осталь-
JT+fN. ными. Геометрически дело
здесь заключается в следую-
Рис. 23. щем. Синус, стоящий под зна-
знаком интеграла, меняет знак,
причем положительный множитель при нем имеет относительно
большие значения там, где синус отрицателен (рис. 23).
Исследуем теперь общий случай. Введем функцию z (x) —
= v(x)—у(х). Она будет удовлетворять неравенству
z"+p(x)zr+q(x)z>0 G8)
и начальным условиям z (л:0) = z' (х0) = 0. Наряду с этим неравен-
неравенством рассмотрим уравнение
t" — р (х) Г — p'(x)t-Jrq(x)t = 0 G9)
и пусть t (х) — некоторое его решение, положительное на некотором
отрезке [л:0, xt\ ? \а, Ь\. Умножим неравенство G8) на t(x), а урав-
уравнение G9) на z (х) и вычтем из первого второе. Получим:
{z"t — t"z) +/? (z't + zt') +p' (tz) > 0. (80)
Ho
z"t — t"z = (z't — t'z)',, (81)
a
(82)

§ 2] МЕТОД С. А. ЧАПЛЫГИНА 275
Поэтому неравенство (80) можно записать в виде
(z't — zt')'-lr(pzty>0. (83)
Интегрируя в пределах (л;0, х), получим:
(z't-t'z)\xXo+pzt\xXn>V (84)
или
z'(x)t(x)— t'(x)z(x)+p(x)z(x)t(x)>0. (85)
Поделив на t(x), получим:
[^Щ ]0. (86)
а отсюда на основании теоремы Чаплыгина о дифференциальных
неравенствах для уравнений первого порядка следует, что z (х) > 0.
Таким образом, если нам удастся найти некоторое положительное
решение t(x) уравнения G9), то на соответствующем отрезке
v(x)>y(x).
Пусть Т (х)—решение уравнения G9), удовлетворяющее началь-
начальным условиям Т (х0) = 0, 7" (л:0) = 1. Может оказаться, что оно
не пересечет нигде ось х на [л:0, Ь\. В этом случае v (x) >у (х) на
всем отрезке [л:0, Ь\. Пусть теперь найдется такая точка xl^[x0, Ь\,
где Т (х) пересекает ось х. Покажем, что при этом найдется
такая функция z (x), что для нее будет выполнено неравенство G8)
и соответствующие начальные условия, но она становится отри-
отрицательной в некоторых точках отрезка [хи xl-\-e], где е>0 про-
произвольно.
Для доказательства рассмотрим решение 7\(л;) уравнения G9),
удовлетворяющее начальным данным Т1(х1-\-г) = 0, 7\(л;1-|-е) = —1.
В силу теоремы о разделе-
разделении нулей решений линей-
линейного дифференциального
уравнения второго порядка
на [л:0, ATj] найдется такая
точка х = а, что 7\ (а) = 0.
¦ГЛ
Без уменьшения общности
можно считать, что других Рис- 24.
нулей Tt(x) между а и
Х2~xl-\-e нет, так как иначе мы могли бы взять за а ближайший
слева от х2 нуль 7\(x) и за х0 ближайший слева от а нуль Т(х).
Графики Т(х) и Tt(x) показаны на рис. 24.
Обозначим через h (x) функцию
z" (х) +р (х) г' (х) +q(x)z (x) = h (x). (87)
В силу наших предположений й(л:)>0. Для ^(л:) будем иметь:
Т'[ (х) —р (х) Т[ (х) —р' (х) Т, (х) + q (х) Т, (х) = 0. (88)

276 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Как и ранее, умножим (87) на Tt(x), a (88) на z (х) и произведем
вычитание. Получим:
= hTl. (89)
Интегрируя в пределах (л:0> х2), получим:
(z'T, - zT[) Q + (pzTJ IJ = fh (x) 7\ (x) dx (90)
или
x,
z(x2^ = J h{x)Tl(x)dx. (91)
x0
Подбирая в качестве h (x) функцию с такими же свойствами, что и
в приведенном выше примере, мы сумеем достичь того, что
х,
j h (x) 7\ (x) dx < 0. (92)
х„
Таким образом, мы получили, что какова бы ни была функция v(x),
удовлетворяющая неравенству G5) и начальным условиям v(xo)=yo,
v' (хо)= У'о' на интеРвале (хо> xi) всегда v (x) > у (х). С другой
стороны, какое бы е > 0 мы ни взяли, найдется такая функция v(x),
для которой выполнены неравенство G5) и начальные условия
v(xo)=yo; v'(xo) = y'o, но (
Точка х1 называется порогом применимости теоремы Чаплы-
Чаплыгина. Порог применимости можно находить и иначе. Для этого
в уравнении G9) произведем замену
или
t =at. (94)
Такая замена законна и а непрерывна, если t Ф 0. При этом
r = f(a'4-a2). (95)
и уравнение G9) перейдет в
а'+ а2— ро— /?'4-<7 = 0. (9о)
Если использовать для отыскания порога применимости теоремы
Чаплыгина уравнение (96) вместо G9), то мы должны найти наи-
наибольший отрезок [xQ, xt], на котором существует непрерывное
решение (96).
Так как уравнение Риккати, вообще говоря, в квадратурах не
интегрируется, то применение метода Чаплыгина к линейным урав-

§ 3]
МЕТОД МАЛОГО ПАРАМЕТРА
277
нениям второго порядка встречает большие затруднения. Еще боль-
большие трудности возникают при использовании метода Чаплыгина для
линейных уравнений высших порядков, для нелинейных уравнений
высших порядков и систем уравнений. Поэтому этих вопросов мы
здесь касаться не будем.
§ 3. Метод малого параметра
В ряде механических и физических задач приходится сталки-
сталкиваться с дифференциальными уравнениями, содержащими некоторые
параметры. При этом иногда удается найти частное решение диффе-
дифференциального уравнения для некоторых фиксированных значений
этих параметров, удовлетворяющее начальным условиям. Тогда
пытаются разыскивать решение дифференциального уравнения в виде
ряда по степеням Xt— \f\ Х3 — Х|о) \к — \f\ где ки \2 Хк —
входящие в уравнение параметры и \f\ Xg \у — их частные
значения, при которых найдено частное решение. Возможность
такого разложения при некоторых предположениях о дифферен-
дифференциальных уравнениях была впервые изучена Пуанкаре в его книге
«Новые методы небесной механики» в 1892 г. Сейчас мы приведем
его теорему. Для сокращения записей ограничимся случаем системы
двух уравнений и одного параметра.
Пусть нам дана система
-g
=/%(*, Y,Z,l)
и требуется найти ее решение, удовлетворяющее условиям: при
х = х0, Y = Ко, Z = Zo, Предположим, что при X —Х„ мы умеем
находить такое частное решение и оно будет
К=ср(х); Z = «K*). B)
Введем новые переменные и параметр следующим образом:
y=,Y — <p(x); z = Z~ <]»(*); р = Х — Хо- C)
После подстановки в систему получим:
или
dz
d<\>
dx -
D)
E)

278 приближенные Методы решения обыкновенных уравнений [гл. 9
Обозначим правые части E) соответственно через /t (x, у, z, |а) и
/2(лг, у, z, (а). Теперь нам нужно найти решение системы
dz
Их
= U(x, у, z, (а),
F)
обращающееся в нуль при х = х0. При (а = 0 таким решением
будет .у==0, z=0. Следовательно, f^x, О, О, 0)==0, /2(лг, 0, 0, 0) = 0.
Будем предполагать, что fl и /2 являются аналитическими функ-
функциями у, z и (а:
2
i, j, fe=o
f2(x, y, z, |*)=
i
G)
J
где а,-д и йуд. — непрерывные функции л: в некотором отрезке [а, C],
содержащем точку л:0, и ряды сходятся при |_у|<1 р, \z \ ^ р, |(а| <; р
и любом х, принадлежащем [а, C]. Так как /t (х, 0, 0, 0) = 0 и
/2(лг, 0, 0, 0) = 0, то а0, о, о=0, *о, о.о^О. Будем разыскивать
решение системы F), обращающееся в нуль при х = х0, в виде
(8)
Сначала определяем функции уп(х) и zn(x) так, чтобы ряды (8)
формально удовлетворяли системе. Подставляя (8) в F), получим:
= У а-
^-^= S
П-1
Приравнивая коэффициенты при (а в левой и правой частях, на-
находим:
dz.
A0)
Отыскиваем решение этой системы линейных дифференциальных
уравнений, удовлетворяющее условиям ух (хй) = zx {xQ) = 0. Затем

§ 3] МЕТОД МАЛОГО ПАРАМЕТРА 279
приравниваем коэффициенты при (i2 левой и правой частей:
dx
«оса
= *ioo^a 4- *
При этом последние слагаемые
«» (*) = аш 4- а2ОоЛ! ¦+" awz
4"
4- «ioi^i 4- «oii^i,
4" ЬШУ\ 4" V*i-
смЛ,
\
A1)
являются уже известными функциями х. Таким образом, нам нужно
найти решение системы
-J*- = «100 У2 4" «010*2 4" U2 (X),
dz ^13)
пХ J
удовлетворяющее начальным условиям y2(x0) = Q, z2(xo) = 0. Эта
система отличается от предыдущей только свободными членами.
Вообще для определения функций уп(х) и zn(x) нам придется
отыскивать решение системы
т = «10о.Уп 4- «oio^n 4- ип
dzn
dx
= ЬтУп 4- *oio*n 4- vn (x),
A4)
удовлетворяющее начальным условиям уп(хо) = 0, zn(xo) = 0, где
ип и vn являются многочленами от уи уъ .... уп_1 и zv z2 zn_l
с коэффициентами ащ и Ьцк. Если нам известна фундаментальная
система решений соответствующей однородной системы, то все
уп и zn могут быть найдены с помощью квадратур.
Установим теперь сходимость полученных таким образом рядов.
Обозначим через М верхнюю границу модулей функций fl и /2
при я?[а, р], |^|<р. |*Кр. I^Kp- Найдем оценку для моду-
модулей коэффициентов пщ и Ьук. Произведем эту оценку хотя бы
для ащ. Обозначим _у = /-1в*Р, г = г2е1*, p = rseu. Здесь 0^.rv
Г2> гь < р. При этом
fl(X, у, Z, (i) =
/Дх, у, z, |*) =
k, I, m=0
oo
V
Zi (
k, I, n»«0
A5)
A6)

280 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Перемножим A5) и A6) и проинтегрируем произведение по tp, <j/ и 9
в пределах от 0 до 2т:, Получим:
2it 2it
о о о
оо 2тс
к, I, т, к',1', т'=о О
/Г
ХаХ (I — I') Ф //ill I oi (ifl — W') 6 //fi / 1 7\
J
0 0
Ho
2tc
Аналогичные результаты получатся и для остальных интегралов.
Таким образом,
2ж 271 2тс со
ооо 4, г, т=о
Заменяя |/р на М2, будем иметь:
Отсюда следует, что
I2 ги'гшг2т
или
^- B2)
Здесь л{ могут принимать любые значения от 0 до р. Для доказа-
доказательства сходимости мы используем мажорантные ряды. Ряд
Ы B3)
к,1, т=о
будет называться мажорантным по отношению к ряду
оо
2 аытУк^т. B4)
ft,!, т=о
если при любых k, I, m
АЫт>\ак1т\. B5)

§ 31 МЕТОД МАЛОГО ПАРАМЕТРА 28 Г
Рассмотрим функцию
p 1 —
р
Коэффициент при y^z1^ в разложении этой функции по степеням у,
z, (х будет положителен и больше чем
м
В силу полученной нами оценки для коэффициентов аЫт, ЬЫт этот
ряд будет мажорировать ряды для fl и /2. Тем более, будет
мажорировать их ряд для функции
B8>
p 1 —
Рассмотрим тогда вспомогательную систему уравнений
B9>
-J
dx dx г
J
и найдем ее решение, обращающееся в нуль при л: = л:0. Для этого
применим к ней тот же метод, что и для исходной. Функции Kt
и Zt должны удовлетворять системе уравнений
XLBxmyi+ZC+Z i <30)
ctx )
и начальным данным Kt (л;0) = Zl (х0) = 0. Применяя метод по-
последовательных приближений к системам A0) и C0), нетрудно
убедиться, что
^1>Ы; ?!>!*![. C1)
Те же рассуждения дадут
Уп>\Уп\1 Zn>\zn\
при любом п. Итак, если мы докажем сходимость рядов
n=l n=l
то докажем и сходимость рядов (8). Для того чтобы убедиться
в сходимости рядов C3), достаточно доказать, что решение

282 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
системы B9), обращающееся в нуль при л;=л;0, может быть пред-
представлено в виде рядов по степеням jx.
Положим У -\- Z -\- (х = рФ. Тогда система B9) перейдет в
d<b _ 2Mb A + Ф)
rfj — р A _ Ф) •
Функция Ф при л: = л:0 равна —. Решим уравнение C4) разде-
разделением переменных. Получим:
A — Ф) С1Ф 2MdX
фA + ф) —~Г~
или
Отсюда
1пФ —21пA+Ф) = ^-(д;~д;0) + 1пС C7)
или
air
C8)
Подберем С так, чтобы было выполнено начальное условие. По-
Получим:
ш
C9)
A + Ф)»
Итак,
Обозначим
алг
а + Ф)»- ot+p)»e -а> D1)
Тогда
ф2 + ^2—1)ф-|-1=о. D2)
или
ф_ 1 _i__L + у '~
' ^ 2а ~ 2а
Если а мало, то
D4,
Взяв здесь знак минус (чтобы Ф удовлетворяла начальным условиям)
леред второй дробью, получим:
+... D5)

§ 3] МЕТОД МАЛОГО ПАРАМЕТРА 283
Таким образом, Ф, а следовательно, и Y и Z представимы в виде
ряда по степеням а, если только |а| <[ -j, т. е. если
2M (х-х0)
т. D6)
а этого всегда можно достигнуть выбором достаточно малого jx.
В свою очередь а может быть представлено в виде ряда по сте-
степеням (х. Тем самым доказана сходимость рядов C3), а следовательно
и рядов (8). Уравнения B9) показывают, что будут сходиться ряды
и для производных. Этим мы и закончим доказательство теоремы
Пуанкаре.
Изложенный метод применим и к уравнениям высших порядков,
содержащим параметр.
Иногда, если само уравнение не содержит параметра, его можно
ввести искусственно. При этом обычно параметр вставляют так,
чтобы при нулевом значении его решение получалось без труда. Тогда
находят решение в виде ряда по степеням параметра и затем дают
параметру такое значение, при котором получается исходное урав тние.
В качестве примера рассмотрим уравнение
%j D7)
Вместо уравнения D7) возьмем
. D8)
Очевидно, уравнение D7) получится из уравнения D8) при е= 1.
Будем искать решение уравнения D8) в виде
•• D9)
Подстановка D9) в D8) даст
У'о + ?Х' + е2Х + • • • + т2Уо 4- тЧУ1 + тЧ*у2 + .. .
...=е/(*)[Л + еу1 + е2Л+ .••]• E0)
Для определения у0 получим уравнение
Х + »2Л = 0. E1)
Его общее решение имеет вид
уо = A cos mx-\- В sin mx. E2)
Уравнением для определения уп будет
г 1. E3)

284 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Таким образом, мы можем последовательно находить все уп при
помощи квадратур. Так, если начальные данные будут заданы
при д; = 0, то функции уп могут быть последовательно определены
по формулам
X
^/п_1 @ sin m (х — t) dt. E4)
Получив решение Y в виде ряда D9), мы затем полагаем е=1.
Конечно, мы должны предварительно убедиться в том, что ряд
D9) сходится при е= 1.
Фактически используют не полные ряды, а лишь их отрезки.
Поэтому нужна дополнительная оценка величины отброшенных
членов.
Метод малого параметра часто используется в теории'нелинейных
колебаний. Не останавливаясь здесь на теоретических вопросах,
связанных с существованием периодического решения и возможностью
его представления в виде ряда по степеням параметра, рассмотрим
один пример. Пусть дано уравнение
х + си: + р*2 = F cos mt. E5)
Будем разыскивать периодическое решение этого уравнения, имею-
имеющее ту же частоту, что и Fcosutf. Произведем замену перемен-
переменных 9 = со/. При этом уравнение E5) перейдет в
|5 . E6)
Потребуем, чтобы функция л; (9) удовлетворяла следующим условиям:
л: (9 + 2гс) = х (9), -I
х @) = А, | E7)
Здесь штрихом отмечена производная по 9.
В качестве параметра выберем р и будем разыскивать х (9) и о>
в виде рядов по степеням р:
:(9)=xo(9L-?*i(9L-P2 _,.-.,
E8)
От функций хг @) потребуем
*, (9 4- 2тг) = *, (9),
E9)

-§ 3] МЕТОД МАЛОГО ПАРАМЕТРА 285
Для упрощения полагаем также, что амплитуда F мала:
F = pF0. F0)
Подставляя E8) и F0) в E6), получим:
•••) — p/7ocos9 = 0. F1)
Приравнивая нулю члены, не содержащие р, находим:
<о»*; + «*о = 0. F2)
Общее решение этого уравнения имеет вид
in^-9. F3)
Из условий E9) получаем:
иH = /а; Л = ^; 50 = °- F4)
Итак,
a;0 = ,4cos9; u>0 =)/<*• F5)
Приравняем теперь нулю члены, содержащие р в первой степени.
Получим:
ту; -\-axl= — 2womlX^ — х20 + Fo cos 9, F6)
или после подстановки вместо л;0 его значения
о»Х + о*, = (гшошИ — i Л2 + Fo) cos 9 — 1Л^ cos 29. F7)
Так как л^ должна быть периодической функцией, то член с cos 9
в правой части должен обратиться в нуль. Поэтому
0 = 0 F8)
или
Таким образом, общее решение уравнения F7) примет вид
Условия E9) дадут
Итак,
*i = 7?- (— cos 6 -+- cos 29). G2)

286 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 91
Продолжая процесс, найдем:
х = A cos 9 -+- ~- (— cos 9 + cos 29) -f- .. . , I
\ G3)
§ 4. Метод Рунге — Кутта
Методы, рассмотренные в предыдущих параграфах, давали при-
приближенное представление решения в аналитической форме. Как
мы видели, их применение связано с выполнением большого числа
интегрирований, а это не всегда может быть осуществлено практи-
практически. Перейдем теперь к изучению численных методов, позво-
позволяющих получить таблицу значений решения. Мы начнем с метода,
предложенного Рунге и усовершенствованного Кутта и другими
математиками.
1. Метод Рунге—Кутта решения дифференциальных уравнений
первого порядка. Пусть нам требуется найти решение дифферен-
дифференциального уравнения
/=/(*. У). A>
удовлетворяющее начальному условию у = у0 при л: = л:0. Будем
предполагать, что в рассматриваемой области f(x, у) имеет не-
непрерывные частные производные до некоторого порядка п. Тогда
искомое решение будет иметь непрерывные производные до по-
порядка л. —|— 1, и мы можем записать:
АУо = У(х)-уо = (х- х0) у'о + {х у; + ...
••• + V+iiT -УГ ц + ° A * - *о Г1)- B)
Обозначим х — xo = h. При достаточно малом h мы можем отбро-
отбросить в B) член о (\х — -*ч)|П+1) и приближенно считать
У ЬУ +
Может оказаться, что для получения Д_у0 с нужной нам точностью
не требуется использовать все члены C).
Производные, входящие в правую часть C), могут быть факти-
фактически найдены. Так,
Уо = /(хО.Уо)=и D)
Далее,

§ 4] МЕТОД РУНГЕ — КУТТА 287
Чтобы запись последующих производных была менее громоздкой,
введем операторы
то
Л.(«) = (дх + fd-y) U=LCmf дхт-*ду*' F)
ft = O }
Для этих операторов будут справедливы следующие равенства:
А т (и 4-1>) ^ ^m (й) -I- ^m (f). \
т\ -г ; tov >-r tov ;.
^j (йг;) ^ Аг (и) v -\- uA1 (v). J
Заметим, далее, что
Л Ито (и)] = Ат+1 (и) 4- «^ (/) Лто-1 (^) • (8)
Действительно,
[ТО -1 ТО
ft=0 J ft=0
Ho
TO
-*дУ* J •
дхду
К — 1 ft ^= 1
TO-1
ft—0
и
TO
*A
TO
= V rft f* Г
ftTo L
ft=0 "" °У ft_0 "Л "*
ТО+ 1
(Сто + ^то)/* г ^Лтоь1(й), A1)
ft—0 "

288 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
что и требовалось доказать. Применение оператора А1 к функции
и (х, у) эквивалентно дифференцированию этой функции по х в пред-
предположении, что у является решением дифференциального урав-
уравнения A). Таким образом, последовательно дифференцируя A), мы
получим:
/" = А1[А1 (/)] = А2 (/) + А, (/)
A2)
С увеличением порядка выражения для производных становится
все более и более громоздкими, даже при операторной записи.
Рассмотрим еще операторы
т
Лй(«) = (^ + /о|р= ? С*/,* дхГ-акд* (/о = const). A3)
дхд
ft-0 "
Для них также выполнены равенства G), а (8) переходит в
А\Ат(и)]=Ат+1(и). A4)
Таким образом,
Ат=\А1\т. A5)
Производные Уо*> мы получим, если в A2) заменим / на /0,
a Aj на Ау
Мы убедились, что производные у^\ входящие в C), могут
быть фактически вычислены. Но в связи с тем, что формулы A2)
очень громоздки, их непосредственное использование в C) для
вычисления Д_у0 вряд ли может оказаться полезным на практике.

§ 4]
МЕТОД РУНГЕ КУТТА
Рунге предложил вместо этого составлять линейную
нацию
/VA (Л) +А**2 (Л) + . . . +/VA (Л)
с постоянными коэффициентами pri некоторых функций
М*) = Л/6. Ъ) (/=1. 2 г),
где
289
комби-
A6)
A7)
Л-i (А)
A8)
и oq, Ру — постоянные, <xt = 0. Таким образом,
&! (Л) = hf (х0, уо),
k2 (h) = hf (x0 + a2h, y0 + p2l&t).
k3(,h) = hf(x0-\-a3h, Л + Рз1*1 + Рз2*2). О9)
h (h\ h f (v* I ft h \t I H ?> I Q h I I Q h \
rCf \**/) 'vj \"^0 \ {Apflrf Vn \ vT\ 1 Г rf2 2 Г * " • Г гТ ? — \ ? 1/"
Зная <х{, Ру и выбрав шаг h, мы можем последовательно вычислить
все kt \h).
Выбор постоянных pri, a{, Ру производится так, чтобы раз-
разложение C) и разложение A6) по степеням Л совпадали до возможно
более высоких степеней h при произвольной функции f (х, у) и про-
произвольном шаге h. При этом функция
будет обладать свойствами
tpr @) = <f'r @) = <?"r @) = ... = tp<rs> @) = 0, tp^1) @) ф 0, B1)
и мы должны подобрать pri, <х{, Ру так, чтобы s было возможно
большим для произвольных h и f (х, у).
Разность между точным значением Ду0 при продвижении на
один шаг длиной h и приближенным значением его, вычисленным
по формуле
B2)
т. е. погрешность метода на одном шаге, будет равна
где

290 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Условие tpr(O) = O в нашем случае будет выполнено всегда.
. Условие tpW @) = 0 означает
У,? =Pnki] @) +рл№ @) + ... +prrkf @). B4)
Производная, стоящая в левой части равенства, может быть всегда
вычислена указанным ранее способом. Займемся сейчас вычислением
производных №@).
Для &! (А) будем иметь:
k'1(h)=f(x0,y0), kf(k) = O при />2. B5)
Для &j(A) при /> 1 получим:
*; (А) =/(?!.
. %>• B6)
Чтобы сделать выражения менее громоздкими, снова введем опе-
операторную запись. Обозначим
= [о,
т
~къ'к д
Г27>
Операторы Вто' обладают следующими свойствами:
B8)
Применение оператора By к некоторой функции от 5{ и t)j экви-
эквивалентно дифференцированию этой функции по h. Заметим, что
i. 41I + К BW_t [a-^I] • B9)

§ 4] МЕТОД РУНГЕ—КУТТА 291
Применяя к B6) правила B8) и B9), последовательно получим:
ft'(А)=/ft. чО + *М" I/ ft, -m)], C0)
ki (h) = 2В? [/ ft, т,,)] + ЛВ^1) [/ ft, %)] + At,," ^^-. C1)
&Г (Л) = ЪВ*?> I/ ft. Ч,)] H- 3V; ^^^ + AB?> [/ft. 7,,)] -+-
+ 3M;'^)[^f^]+K''^1. C2)
*?v.(A) = 4B?' |/ft, ,01 [^%^]
+ (<У ^ + ЧГ |f^- • C3)
= 5в1^ [/ ft. n [^|^1]
H- ABl111/ ft. Hi)] + lOAtf
+ 15A «
C4)
И в этом случае наряду с операторами Вт введем операторы
т
Ж> [Т (х, у)\ = 2 qj,«r-* hi (°I* жЙй- C5)
Для операторов В^ будут справедливы соотношения B8), а равен-
равенство B9) заменится на
W [Ж [?(*. Л]} = ВЙ+1 [?(*. ^)]. C6)
Таким образом,
&2Ш* C7)

292 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Итак, при Л = 0 мы получим:
k1@)=2B[i}lf0].
@) =
< @) B(/> [§?] + U" @) ^,
30< @) В(а" [f^] W
Рассмотрим теперь некоторые частные случаи.
1-й случай: г= 1. При этом
<Pi (Л) = ^ (л;0 + Л) — .у (л;0)—puhf (л:0. j/0),
?[ № = У (л;0 + h) —Puf (х0, у0).
При Л = 0 получим:
C8)
C9)
D0)
D1>
и '<р^@) = 0 для произвольной / тогда и только тогда, когда ри=\.
Далее,
^'(О) = _уц D2)
и, вообще говоря, в нуль не обращается. Таким образом, прибли-
приближенная формула
(*о. Уо) D3)
D4)
имеет ошибку метода на одном шаге, равную
x-i
Говорят, что в этом случае погрешность метода на одном шаге
имеет порядок Л2. Интегрирование дифференциального уравнения
по формуле D3) называют иногда способом Эйлера.
2-й случай: г=2. При этом
<р2 (^) = У (х0 + Щ — у0 — [p^ki (h) + p22k2 (Л)], D5)
/ 'Ul D6)

§ 4] МЕТОД РУНГЕ — КУТТА 293
Таким образом, ср^ @) = 0 для произвольной / в том и только в том
случае, если
/>21+/>22=1- D7)
Далее,
< @) = X - №1 (°) +РпК @I = Л (/о) — РхёЖ (/о)- D8)
Необходимым и достаточным условием обращения ср^' @) в нуль
будет _
Л = 2paW. D9)
т. е.
1 = 2/>22«2, 1 = 2/>22р21. E0)
Третья производная tp'" @) будет равна
Г @) = А, (/0) + А, (/0) ^ - 3/>22Bf (/0) E1)
и, вообще говоря, в нуль не обращается. Таким образом, беря
Рг\> Рж> а2> Рг1> удовлетворяющие условиям
/>22а2 ^ -^ '
Р22Р21 = "о" '
E2)
мы получим формулы, имеющие порядок ошибки Л3. Из E2) сле-
следует, что р22 Ф 0, а.2Ф 0, $2i Ф 0 и a2 = p2f Равенства E21 являются
системой трех уравнений относительно четырех неизвестных. Эта
система имеет бесчисленное множество решений. Каждое решение даст
формулу, имеющую порядок ошибки Л3. На практике следует выби-
выбирать такие решения E2), которые дают удобные для вычислений фор-
формулы. Можно, например, взять <х2 = р21=1. Тогда р22 =Ри = у >
и получаем приближенную формулу
д4 E3)
Возьмем еще вариант: a2 = P2i = -o' • Тогда р22^1, р21 = 0, и по-
получим формулу
Л.Уо^&2; k1 = hf(x0, у0); &2 = Л/(д;0 +|, Л + |)- E4)
Можно также подбирать р21, р22, Ог, р21 так, чтобы в E1) сокра-
сократилась часть членов. Так, например, если потребовать, чтобы
E5)

294 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
о
то, используя A5), C6) и D9), найдем 4/^2 = Зр22 или/722 = -т.
2 1
При этом О2 = Р21= -г и /?21 = -т« Получаем формулу
E6)
Остаточный член при выбранных р21, />22, <*2- P21. удовлетворяющих
системе E2), оценивается по общей формуле B3), причем в нашем
случае
<РГ (h) = У'" (*о + А) — [paftf
X ^(Х° + ^ (Х° + h)) ~ At C^> I/fe. ^l+A^'l/fe. 4J]}. E7)
3-й случай: г^З. В этом случае
<Рз(°) =Уо — IAi*l@) +Рз2&а@) +р33&з @)] =
= у'о — [Psi + />32 + Рзз1 /о- E8)
Отсюда
/>31+/>32+А»з=1. E9)
Далее,
= А (/0) - [2p32Bf' (/0) ¦+¦ 2рззб13) (/0)]. F0)
Чтобы срд @) обращалась в нуль при произвольной /, необходимо
я достаточно, чтобы
Л = 2p^Bf + 2p33Sf' F1)
или
Рз2). I ( }
Равенство нулю третьей производной даст
= Л (/о) +\ if о) f- - [ЗР32В2 (/0) + 3pei? @)
' (/о) + Зр^ @) ^J = 0. F3)

§ 4] МЕТОД РУНГЕ — КУТТА 295
Но ife(A)=jfo + pafti(A) и <(А) = 0. Далее, %(А)=
^) и^ следовательно,
< @) = М* (°> = 2Рз2Йа) (/о)- F4)
Поэтому равенство F3) можно записать в виде
(/о) + ЗрззШ" (/о) + 6РззРз2Да' (/о) fj-. F5)
Оно может выполняться для произвольных / только в том случае,
когда
Л = 6/>зЗр32б1а). F6)
F7)
Из равенства F6) следует, что операторы Л, и В^ могут отличаться
только постоянным множителем. Поэтому
F8)
и равенство F6) переходит в
F9)
Равенства F8) и F1) показывают, что операторы А1 и Bf1 также
отличаются лишь постоянным множителем. Это возможно лишь при
условии
<*3 = Р31+Р32- G0)
При этом
W G1)
В силу G1), F8), C7) и A5) мы получим из F7):
А> = C/>з2<*з + 3/>зз<*з) Л G2)
или
з G3)
Приравняв четвертую производную нулю и использовав F8) и G1),
мы получим равенство
Л (Л) + за (/о) a[ fg) +
(Л) + за (/о) a[ fg) + а2 (/0) дА + л; (/о)
(/о) + MPv&vtoAi (/о) «зЛ
Н- 1^3зРз2а^2(/о)^. G4)

296 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Его, вообще говоря, удовлетворить не удастся, так как в левой
части содержится член ^(/оЦ-^М , а в правой такого члена нет.
Итак, если подобрать величины р31, р&, Рзз> az< аз. Р21» Рз1> Рзг
удовлетворяющими системе
аЗ =
2 1
1
G5)
РззРз2<*2 = "g" •
то получим формулу Рунге — Кутта, с порядком погрешности на
одном шаге Л4.
Последние три равенства G5) при выбранных <х2 и <х3 можно
рассматривать как систему линейных алгебраических уравнений
относительно р32 и р33. Для совместности этой системы необходимо
и достаточно обращение в нуль определителя
1
Отсюда
или
0 РзЗа2 -q
G6)
1
6"
4 4
— Р32<*2
1
а2 ~2
a 1
аа з
= 0,
а2<*з («з — а2) — Рз2«2 B — За2) = 0.
G7)
G8)
Последнее из уравнений G5) показывает, что р33 Ф 0, а2 Ф 0, рз2 Ф 0.
Поэтому мы можем поделить G8) на <х2. Это даст
«з («з — «2) — Рз2<*2 B — За2) = 0.
Итак, мы сначала должны подобрать <х2, <х3, р21, $31,
они удовлетворяли системе
«2 = в>1>
а3 (а3 — аг) — рз2а2 B — За2) = 0,
G9)
так, чтобы
(80)

§ 4] МЕТОД РУНГЕ — КУТТА 297
и затем найти р33, р32, p3i последовательным исключением из си-
системы
'
1
(81)
Рассмотрим некоторые варианты.
а) Возьмем a2 = P2i = -o. <*з=1- Тогда третье из уравнений (80>
даст р32 = 2- Второе уравнение (80) дает p3i = — 1- Затем последо-
последовательно находим />зз = -?-. Рз2 = -з. Рз1 = ~ъ' Получаем прибли-
приближенную формулу
где
1 = hf(x0, у0); k2 = hf(x0+^, Уо + 12 1)' 1 (83)
5"# При этом р32 = -о"> Р
(84)
12 2
б) Возьмем О2=р21 = -з. аз = ~5"# При этом р32 = -о"> Рз1^
Рзз=-^, Рз2 = С Рз1=-4". Получаем вторую формулу
где
/1 l
«j ^ nf(x0, y0), k2 = я/l x0 -\- тгh, .УоЧ-тг
(85)
1 q О
в) Возьмем O2 = p2i = -.т. аз^т« При этом р32 = -т. Рз1^0.
4 1 2 „
Рзз = -Q-, /?32 = "о" • Рз1 = "о" • итсюда
У
где
(87)
В последнем случае левая часть G4) будет отличаться от правоИ
лишь на член Ax (/$№)*.

298 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Остаточный член выражается по общей формуле
5 (88)
Мы не будем здесь выписывать выражения для ср^1 v>(Л) ввиду его
громоздкости.
4-й случай: г = 4. Имеем:
tf (°) = Уо — \Рц + Р*2 + P,s +PJ U (89)
Отсюда tp^(O) = O тогда и только тогда, когда
/>41+/>42-Г-/>43-Г-/>44= 1. (90)
Далее
?1 @)=Уо - \РшК @) +pi3K @) +рХ щ =
= Ах (/о) - 2 [р&ЪТ (/0) Н-рвВР' (/0) +PiiBf (/о)]- (91)
¦Отсюда
1fi f'
f
(92)
Приравняв нулю третью производную, получим:
Л (/о) 4- А (Л) ^ = 3Р42б^ (/о) + ЗР48В!?' (/о) +
+ 6/>4зМ2' (/о) ^ f 3P44^4) (/о) +
+ 6р44р42ВA2) (/о) ^ +¦ 6Р44Р43В13' (/о) ^ • (93)
Отсюда
А, = ЗрмВ?' -Ь Зр4Д3) + Ър±М\ (94)
7t = 6/>43p32fif' + 6р44р4-Д3) + 6р44р4зВA3). (95)
Наконец, приравнивание нулю четвертой -производной даст
Л (/о) Н- з J, (Л) А (^-) 4- Л (Л) ^-+А (/о) (^)
= 4/>42Вза) (/о) + 4Р4зВз3) (/о) + 4р44В(/' (Л) +¦
24^43 fii3) (/о) Bf> (§5-) + 1 ?P«P-SP (/о) ^ -Н
12Р44М-/' (/о) §? + 12Р44р43^3)(/о) ^ +¦
J. (96)

§ 4] МЕТОД РУНГЕ — КУТТА 299
В (96) (тгЧ входи
и справа. Поэтому
В (96) (тгЧ входит множителем только в последние члены слева
43МA2). (97)
Равенство (97) показывает, что Аг и В\' отличаются лишь постоян-
лым множителем. Это возможно лишь в том случае, когда
«2 = Р21- (98)
Тогда _ _
Мч = аА. (99)
а (97) переходит в
Из (99) и (95) следует, что А1 и Bf также отличаются лишь по-
постоянным множителем. При этом должно быть
A02)
Поэтому (95) переходит в
Р4зРз2«2 + А4М2 + Puh&s = j- (ЮЗ)
Аналогично из (92) получим:
<*4 = Р41+Р42 + Р43. A04)
В^аД A05)
и
P42«2 + Pi3^3 + РаЧ = 2" • ( Х 06)
Равенство (94) даст
Р42«2 + />4з<хз -+ Расц = "з . A07)
Сравнивая члены с производными третьего порядка в (96), получим:
^ (Ю8)
Из равенства (96) мы получаем еще следующие два соотношения:
"s • A09)
Обращение в нуль пятой производной мы обеспечить в нашем слу-
случае не можем.

300 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Собирая все соотношения, связывающие величины /?4i, оц, ру,
мы получим следующую систему уравнений:
аз = Рз1
3 , 3 , 3 1
/>42<Х2 + />43<ХЗ +^44014 = "J .
ЛзРзгОгОз +/744р42а2а4
(HI)
j_
:24'
Из последнего уравнения системы следует, что ри Ф 0, р43 ф О,
р32 =?0, а2Ф 0. Поэтому, если нам каким-то образом удалось найти
величины оц и р^, то /?4j могут быть найдены последовательным
исключением из следующей системы:
J_
4*
1
A12)
1
Найдем4 теперь соотношения, связывающие оц и Ру. Возьмем вось-
восьмое, десятое и одиннадцатое уравнения системы A11) и будем рас-
рассматривать их как систему линейных алгебраических уравнений
относительно pi3 и ри. Для совместности этой системы требуется:
1
1-
= 0.
(ИЗ)

§ 4]
Отсюда
или
МЕТОД РУНГЕ КУТТА
1
a, a
0
<x3 4
.а о
= 0
301
A14)
A15)
Соотношение A15) позволит нам выразить C32 через а2 и а3, если
1 1
Oj^ty, и даст равенство а2=а3, если а2 = у.
Умножая восьмое уравнение на а4 и вычтя из него девятое, по-
получим:
6" а4 — -g = ЛзРз2«2 (а4 — а3) • A16)
Проделаем тоже самое с пятым и шестым уравнениями, а затем
с шестым и седьмым. Это даст два равенства:
4 — аз).
11
у а4 — ^-
A18)
у а4 — ^- = />12а2 (а* — а2) + />4за3 (а4 — а3).
Умножим A17) на 02 и вычтем из A18). Будем иметь:
( а4 "" т) ~~ а2( 2"а4"" 3") =^«а3 (а3 — <h) (a4 — а3). A19)
Подставим сюда вместо/>43(а4 — а3) его выражение из A16); полу-
получим:
jai — 4) "" a2 (у a4"" т)] = (т К4 ~ "8") аз((Хз""
A20)
или
+ Заз — За2а3 = [ 12^32о?2 —
|—4а2а3] а*. A21)
Прибавим теперь к левой части A21) утроенную левую часть A15),
а к скобке в правой части учетверенную левую часть A15). При
этом равенство A21) перейдет в
Так как р32 фО, а2ф 0, то
а4=1.
A22)
A23)

302 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Потребуем теперь совместности пятого, шестого, седьмого и один-
одиннадцатого уравнений системы A11) относительно />42, /?43, ри с уче-
учетом A23). Это возможно только, если
Отсюда
«2
4
4
0
1
а,
¦1
0
4
4
о [
1
«3
4
0
1
1
1
*48р32а
1
1
1
1
~2
1
3
1
4
1
2 24
12
8
6
„ 1
= 0.
A24)
= 0.
A25)
Раскрывая определитель и производя некоторые сокращения, найдем
еще одно соотношение, связывающее сц и ру:
зМ2112а2<*з — 8а2 — 8а3 + 6] = A ^ а2) A — а3).
A26)
Наконец, последнее соотношение мы получим, если потребуем сов-
совместности восьмого, девятого и одиннадцатого уравнений A21) от-
относительно />4з и ри. Это даст
Отсюда
аз
0
J_
J_
24
j_
j_
8
24
= 0.
A27)
= 0
A28)
и окончательно
— «з) =
р43а3 (а3 — 1).
A29)

§ 41
МЕТОД РУНГЕ — КУТТА
303
Итак, для удовлетворения системе A11) мы сначала подбираем а(
и ру, удовлетворяющие условиям:
— а^ = 0,
— 8а2 — 8а3 + 6] = A — а2) A — а3),
р42а2A — ад) = Р4зРз2а2C—4а3) + Р43аз(а3 — 1).
A30)
а затем находим piit решая систему A12). Рассмотрим некоторые
частные варианты формул Рунге — Кутта, имеющих порядок
погрешности на одном шаге hb.
а)<*2=2-, аз = ". Рзг—у. При этом р21 — у, p3i = 0.a4=L
Р«=1. Р42=0, Р« = 0, Р44 = у, />43 = -з. Р«="з. /?4i = -6"-
Получаем формулу
где
= ft/ (*0 + А,
Это одна из наиболее распространенных формул Рунге—Кутта.
12 1
б) Полагаем а2 = -^, а3 = -~-. Тогда 321 =  • а4 = 1 • Рзг = 1 >-
В = — 1 В =1 В =—1 В —1 =- =- ——
i==-g-. Получаем следующую формулу:
A33>
где
A34>

304 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
в) Полагаем О2 = Р21 = -т. аз = -а~- Тогда Рзг —"о". Рзг = 0>
pix = -г-. При этом получаем:
Дуо«5-р- \kx +4Й3+ k4], A35)
где
x = hf(x0, yoy.
A36)
При желании набор формул можно увеличить. Погрешность
каждой из этих формул равна
'V4W- 120
тде
A37)
<р4 ф) = у (ХО + И) — у (Х0) — [pixkx (Jl) +/>42*2 Ф) +
A38)
Вычисления показывают, что при г =5 мы не достигаем увели-
увеличения порядка точности. Поэтому эти формулы применения не на-
находят.
Можно получить формулы, имеющие порядок ошибки Л6, но
при этом придется брать г^.6. Получаются очень громоздкие фор-
формулы, неудобные для практики. Поэтому о них мы говорить не
будем.
Применяя ту или иную формулу Рунге — Кутта, мы найдем при-
приближенное значение Ду0, а следовательно и ух — у (х0 + К). Затем
можно взять за начальную точку хх = хо-\-h и за начальное значе-
значение yx = y(x0-\~h) и продвинуться еще на один шаг такой же или
другой длины. Повторяя этот процесс, мы получим таблицу значе-
значений искомого решения в некоторых точках.
Приведем примеры на применение формул Рунге — Кутта. Будем
искать решение уравнения у=у, удовлетворяющее начальному
условию j@)—1 на отрезке [0, 1J. Шаг вбзьмем равным 0,1.

§ 4|
МЕТОД РУНГЕ КУТТА
305
Точным решением будет у~ех и его значения будут даны позже.
Ход вычислений будет виден из таблицы. Применяется формула
= А/(.** +-|> >» + -§-); h = hf(Xi+h,yi-\-2ki-k{).
X
xt
xi + ~2
xt+h
0.0
0,00
0.05
0,10
0,1
0,10
0.15
0,20
0,2
0,20
0.25
0,30
0.3
0,30
0,35
0,40
0,4
У
yi+2ki-k1
1,0000
1.0000
1,0500
1,1100
1,1052
1.1052
1,1605
1.2267
1,2214
1,2214
1,2825
1.3557
1,3498
1,3498
1,4173
1.4982
1,4917
fix, у)
/(¦*», Уд
/(«+4-.»+*)
f(xi+htyi+2ki-kl)
1.0000
1,0500
1.1100
1,1052
1.1605
1,2267
1,2214
1,2825
1,3557
1,3498
1,4173
1,4982
ft/
h
0,1000
0.1050
0.1110
0,1105
0,1160
0,1227
0,1221
0,1282
0,1356
0,1350
0,1417
0,1498
h
ks
0,1000
0,4200
0,1110
0.6310
0,1105
0,4640
0,1227
0,6972
0,1221
0,5128
0,1356
0,7705
0,1350
0,5668
0,1498
0,8516
2k,
2^-ki
0,2100
0,1100
0,1052
0,2320
0,1215
0,1162
0,2564
0,1343
0,1284
0,2834
0,1484
0,1419

306 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Продолжение
X
0,40
0,45
0,50
0,5
0,50
0,55
0,60
0,6
0,60
0,65
0,70
0,7
0,70
0,75
0,80
0,8
0,80
0,85
0,90
0,9
0,90
0,95
1,00
1,0
У
1,4917
1,5663
1,6567
1,6486
1,6486
1,7310
1,8299
1,8220
1,8220
1,9131
2,0224
2,0136
2,0136
2,1143
2,2350
2,2254
2,2254
2,3366
2,4703
2,4595
2,4595
2,5825
2,7299
2,7181
/С*. У)
1,4917
1,5663
1,6567
1,6486
1,7310
1,8299
1,8220
1,9131
2,0224
2,0136
2,1143
2,2350
2,2254
2,3366
2,4703
2,4595
2,5825
2,7299
А/
0,1492
0,1566
0,1657
0,1649
0,1731
0,1830
0,1822
0,1913
0,2022
0,2014
0,2114
0,2235
0,2225
0,2337
0,2470
0,2460
0,2582
0,2730
0,1492
0,6264
0,1657
0,9413
0,1649
0,6924
0,1830
1,0403
0,1822
0,7652
0,2022
1.14Э6
0,2014
0,8456
0,2235
1,2705
0,2225
0,9348
0,2470
1,4043
0,2460
1,0328
0,2730
1,5518
0,3132
0,1640
0.1569
0,3462
0,1813
0,1734
0,3826
0,2004
0,1916
0,4228
0,2214
0,2118
0,4674
0,2449
0,2341
0,5164
0,2704
0,2586

§ 41
МЕТОД РУНГЕ КУТТА
307
X;
h
2A
0,0
0,0
0,0333
0,0667
0,1
0,1000
0,1333
0,1667
0,2
0,2000
0,2333
0,2667-
0,3
pop
0,4
у»
Уг
, 2fts
1,0000
1,0000
1,0333
1,0689
1,1052
1,1052
1,1420
1,1814
1,2214
1,2214
1,2621
1,3055
1,3498
1,3498
1,3948
1,4428
1,4918
f(Xi, Уд
f(xt. Уд
/(¦Ч + y.yi+Tf)
/ 2h i?M
1,0000
1,0333
1,0689
1,1052
1,1420
1,1814
1,2214
1,2621
1,3055
1,3498
1,3948
1,4428
hfi = kt
A/, = k%
0,1000
0,1033
0,1069
0,1105
0,1142
0,1181
0,1221
0,1262
0,1305
0,1350
0,1395
0,1443
3*.
0,1000
0,3207
0,4207
0,1105
0,3543
0,4648
0,1221
0,3917
0,5138
0,1350
0,4329
0,5679
A*
0,1052
0,1162
0,1284
0,1420

308 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Продолжение
ч
0,4000
0,4333
0,4667
0,5
0,500
0,5333
0,5667
0,6
0,6000
0,6333
0,6667
0,7
0,7000
0,7333
0,7667
0,8
0,8000
0,8333
0,8667
0,9
0,9000
0,9333
0,9667
1,0
У<
1,4918
1,5415
1,5946
1,6487
1,6487
1,7037
1,7623
1,8221
1,8221
1,8828
1,9476
2,0137
2,0137
2,0808
2,1524
2,2254
2,2254
2,2996
2,3787
2,4594
2,4594
2,5414
2,6288
2,7180
/(¦*«. Уд
1,4918
1,5415
1,5946
1,6487
1,7037
1,7623
1,8221
1,8828
1,9476
2,0137
2,0808
2,1524
2,2254
2,2996
2,3787
2,4594
2,5414
2,6288
0,1492
0,1541
0,1595
0,1649
0,1704
0,1762
0,1822
0,1883
0,1948
0,2014
0,2081
0,2152
0,2225
0,2300
0,2379
0,2459
0,2541
0,2629
0,1492
0,4784
0,6276
0,1649
0,5286
0,6935
0,1822
0,5843
0,7665
0,2014
0,6456
0,8470
0,2225
0,7136
0,9361
0,2459
0,7887
1,0346
0,1569
0,1734
0,1918
0,2117
0,2340
0,2586

§4]
МЕТОД РУНГЕ КУТТА
1 ,
309
хг
xf
, h
xi + ~2
0,0
0,00
0,05
0,05
0,10
0,1
0,10
0,15
0,15
0,20
0,2
0,20
0,25
0,25
0,30
0,3
0,30
0,35
0,35
0,40
0,4
yt
У1
У. + 2" h
yi + ^h
Уг + ks
1,000000
1,000000
1,050000
1,052500
1,105250
1,10517
1,105170
1,160429
1,163191
1,221489
1,22140
1,221400
1,282470
1,285524
1,349952
1,34986
1,349860
1,417353
1,420727
1,491933
1,49183
/(¦*/. Уд
/(¦*<. Л)
/(*|+4"*+т)
f(Xi+^,yi + ^)
f(x{ + h,yt + ku
1,000000
1,050000
1,052500
1,105250
1,105170
1,160429
1,163191
1,221489
1,221400
1,282470
1,285524
1,349952
1,349860
1,417353
1,420727
1,491933
h
hfi = h
hh = h
0,100000
0,105000
0,105250
0,110525
0,105517
0,116043
0,116319
0,122149
0,122140
0,128247
0,128552
0,134995
0,134986
0,141735
0,142073
0,149193
Щ
2*3
6Ду<
0,100000
0,210000
0,210500
0,110525
0,631025
0,110517
0,232086
0,232638
0,122149
0,697390
0,122140
0,256494
0,257104
0,134995
0,770733
0,134986
0,283470
0,284146
0,149193
0,851795
АЛ
0,105174
0,116231
0,128456
0,141966

310 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННО" '. УРАВНЕНИЙ [ГЛ. 9
Продолжение
0,40
0,45
0,45
0,50
0,5
0,50
0,55
0,55
0,60
0,6
0,60
0,65
0,65
0,7^
0,7
0,70
0,75
0,75
0,80
0,8
0,80
0,85
0,85
0,90
0,9
0,90
0,95
0,95
1,00
1,0
1,491830
1,566421
1,570151
1,648845
1,64873
1,648730
1,731166
1,735288
1,822259
1,82213
1,822130
1,913236
1,917792
2,013909
2,01377
2,013770
2,114458
2,119493
2,225719
2,22556
2,225560
2,336838
2,342402
2,459800
2,45962
2,459620
2,582601
2,588750
2,718495
2,71830
/(*!. Л)
1,491830
1,566421
1,570151
1,648845
1,648730
1,731166
1,735288
1,822259
1,822130
1,913236
1,917792
2,013909
2,013770
2,114458
2,119493
2,225719
2,225560
2,336838
2,342402
2,459800
2,459620
2,582601
2,588750
2,718495
?<
0,149183
0,156612
0,157015
0,164884
0164873
0,173117
0,173529
0,182226
0,182213
0,191324
0,191779
0,201391
0,201377
0,211446
0,211949
0,222572
0,222556
0,233684
0,234240
0,245980
0,245962
0,258260
0,258875
0,271850
0,149183
0,313284
0,314030
0,164884
0,941381
0,164873
0,346234
0,347058
0,182226
1,040391
0,182213
0,382648
0,383558
0,201391
1,149810
0,201377
0,422892
0,423898
0,222572
1,270739
0,222556
0,467368
0,468480
0,245980
1,404384
0,245962
0,516520
0,517750
0,271850
1,552082
|
0,156897
0,173398
0,191635
0,211790
0,234064
0,258680

4|
МЕТОД РУНГЕ КУТТА
311
Приведем таблицу значений ех с пятью верными десятичными
знаками:
X
ех
0,1
1,10517
0,2
1,22140
0,3
1,34986
0,4
1,49182
0,5
1,64872
0,6
1,82212
X
ех
0,7
2,01375
0,8
2,22554
0,9
2,45960
1,0
2,71828
Как мы видим, результаты получились довольно хорошие.
2. Метод Рунге — Кутта решения систем дифференциальных
уравнений первого порядка. Метод Рунге — Кутта без труда пере-
переносится на системы обыкновенных дифференциальных уравнений.
Для сокращения записей ограничимся системой двух уравнений:
~Г7=/(х. у, z); ?L = g{x, у, z),
dx
A39)
и будем разыскивать ее решение, удовлетворяющее начальным
условиям у(хо)=уо, z(xo) = zo. Как и ранее, образуем функции
где
А (Л) =
A40)
= Уо + Рг^х + Ma + • • • + Pi, i- ik{_ x;
A41)

312 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Задача опять будет заключаться в подборе постоянных ai( p^, ~{ц,
ai> Py> 1ij< Pri> Ян так> чтобы разложения функций
АИ> — IPrA Ф) +pr2h (h)+ ... +Р„К (A)]. A42)
A*o — folk (A) + ЯтА (A) + • • ¦ + ЯггК (A)] A43)
по степеням h начинались с возможно более высоких степеней h.
Введем операторы
m\ f4 t dmu
J g
r\s\t\
r+s+t=m
dxr dys
VI _m! f,4
— Zi rlsltl-'oZo
дта
r+s+t=m
Как и ранее, получим:
Используя A46) и формулы, аналогичные G), получим:
(ft) At (*|
4 А
+ As (go) -aS- + Л (/о) -^ -а7 + Л Ы -^- -jz-,
, A46)
A47)
A48)

4] МЕТОД РУНГЕ КУТТА 31$
(g0) + ЗЛХ(/о) Ах (**) + ЗЛ (go) A, ( «*
Далее, вводим операторы
= 1
A49)
A50)
~л'
Очевидно,
г Г 1 Г) i A51)
Заметим также, что
-1 [^д> У-J, A52)
Ж с?> [/ (Tif ^, сд = с^»+1 [/ (Ti, ч*. Q] 4-
(A) CUL, [^(ТУ' ^ ] + mg (*) Cg-г [а/(\* ^-]. A53)
Операторы Вт' и С^' зависят от параметра Л. Их значение при
А = 0 будем отмечать чертой сверху.

314 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Используя свойства операторов В„ и С^1, находим (при / > 1):
k- (A) = 2Bii) М*'
o
(A) M*
-т.
< 154>
i/ а,, ч,. o
C (А) в!4
со
Члены в фигурных скобках для нас сейчас значения иметь не будут.
Таким образом,
kA0)=2B[l)(f0),
кГ ф) = зй" (Л) + з< @)
@)
12С-
С @)Ж
A55)
Аналогично получим:
+ зч; @) ^+зТТ @) М,
A56)

4]
МЕТОД РУНГЕ КУТТА
315
При /=1 будем иметь:
Л\ (Л) = /„; k[}) (Л) = 0 U > 1); l[ (Л) = g0; № (Л) = 0 (J > 1).
Будем получать формулы Рунге — Кутта, имеющие порядок погреш-
погрешности на одном шаге Л5. Для этого необходимо, чтобы функции
<Р (h) = У (*о + Щ — У Оо) — 1/>4 А (
ф (Л) = z (x0 + h) — z (х0) — [q^ (Л) +
(Л) +
обладали свойством
ср @) = ср' @) = ср" @) = ср'" @) = cpdv) @) = 0;
ф @) = ф' @) = ф" @) = ф'" @) = ф^1у) @) = 0.
Равенство нулю первых производных даст
Ра +/>42 +А»з ~\-Ри = 1>
+ А»3+/>44= 1- |
+ ^43+544= 1- I
Из ср" @) = ф" @) = 0 следует:
Ах =
Лх = 2qi2C?) + 2feCi3) + 2-744C14'.
Приравнивая нулю третьи производные, получим:
Наконец, равенство нулю четвертых производных даст
A57)
A58)
A59)
A60)
A61)
Д2) (ft) ^f (И) + **PulJ? (So) В?(f) +

316 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
4 24WJ? (ft) В? (|>) + 12р^В? (/о) |> +
4-12/удз™ (/„) $ +1 ^«5» (/„) f +
+ 24/УУ 3Д*> (/0) (f J + 24pjjf» (/о) ^i3> ( $) +
+ 24, jyj?) (/o) S» (?) + 24PJi3B? (/o) S« (f ) -h
^ (ft) f ^ + 12p43T33Cf (ft) f- -h
(ft) -f 412pttT41c?> (ft) (f) 4
4 UPuiJJ? (/o) ^ # 4 24pttT41T.C« (ft) -^ ^. A62)
9 (ft) -4- ЗА (/0) Ax (M) + зA, (^ ^ (^L) 4- Л (/о) ^- 4
4 Л Ы (^J = *qJS» (ft) + 4^43cf (ft) + 4^' (ft) 4
l? (/o) C? (^) + 24^4Д2) (/0) C?' (^) 4
^ (А) С« (^) 4 24ад32С?> (ft) Cf (^) +
2) (ft) C<" ( *f) 4 24^43Cf (^ C» (^) 4
4 Р
4 24,JJa^f (/o) f "
fif (ft) ^o + 12^TeC?> (ft) ^ 4
ft)
4 24,tt7up.B« (/„) ^ ^ 4 24^7e7.C» (ft) (?f • A63)
Из полученных равенств теми же рассуждениями, которые при-
применялись для одного уравнения, покажем, что наши постоянные
удовлетворяют следующей системе уравнений:

§ 4] метод рунге — кутта 317
1. <Х2 = Р21 = Т21' а2 = Р>21 = 721.
2. а3 = Рз1 + Рзг = 7з1 + 7з2. аз=?м+]*з2 = 7з1 + 7зг.
3. «4 = P141+P'42+F'43= «« = P~« + Ptf + Us =
= 741+742 + 743- =741 + 742 + 743.
4- />41+/>42+/>43+/>44= Ь Я
J _ _ .
5. />42«2+/'43a3+/'44a4=-2"> ~ ~ ' ~ " ' ~ "
7.
_ 1
8 • ~Г V44 1431Л4 ^ >
= -П
11. />44Р4зРз2а2 = 4" •
44^3=12
— — 1 _ 1
/>4474з7зг«2 = 24 . ^Р^зРзгОг = -^ •
J_
= 24'
_ J_
4'
A64)

318 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ {ГЛ. 9
Проанализируем теперь систему A64). Возьмем 11, 15, 16 и
17-е уравнения системы в левом столбце. Легко видеть, что эти
уравнения эквивалентны системе уравнений
/'44043032«2 = 4" •
в ? - я ъ \ A65>
Р4Я ?<П аЧ Ря? Рч? I
Четыре соответствующих уравнения правого столбца будут эквива-
эквивалентны системе
Р*43
._
1
( I
¦п } A66>
Таким образом, вместо восьми исходных уравнений можно взять
шесть следующих:
/L4043032='2 = ^44Т43Т32О2 = "9Д . (]67>
A68)
24
Ря? _P_41 Тя? . а» Рэд
Т4Я Pas Т4Я Тте а<> Тз4 Тзд
Используя равенства A68), мы получим из 8-х и 9-х уравне-
уравнений A64):
р42О2 + 04заз = Т42О2Ч-Т4заз. ) ...^
t A69)
j
Тринадцатые уравнения A64) будут являться следствиями 9-х урав-
уравнений и "A69). Исключая рц и Цц из 10, 11 и 14-го уравнений и
используя A69), найдем:
043а2аЗ («2 аз) Т43(Х2аЗ (а2 аз) = 2 (Щ. <Х2) 04303202. )
048«2а8 («2 — а8) — ( ) 2 ( )
Уравнения A70) не являются независимыми, так как по A68)
р- = М. A71)
Рза Тз2

§ 4] МЕТОД РУНГЕ — КУТТА
и, следовательно, опять по A68)
T43 T43
РзЗ "i<& . Р4З Т4Я
Кроме того,
319
A72)
A73)
Таким образом, достаточно взять одно из уравнений A70), напри-
например первое. Оказывается и оно является следствием предыдущ! х.
Действительно, если рассматривать первые 11 уравнений A64) как
систему для определения оц, f^, pri, то должно быть выполнено
четвертое из соотношений A30). Точно так же, если рассматривать-
эти уравнения как систему для определения щ, fy, qri, то должно
быть выполнено соответствующее соотношение
о3 (а3 — <h) =
^«
A74)
Последовательно упрощая первое из уравнений A70) и используя
при этом A68) и указанные соотношения, мы придем в конце кон-
концов к тождеству
02 02 = 02 — <Х2. A75)
Итак, искомые постоянные должны удовлетворять 1 —11 урав-
уравнениям A64) и, кроме того, A68) и A69). Проще всего решать по-
полученную систему следующим образом. Находим а{, Ру, pri так,
как это указывалось ранее. Таким же образом находим aj, fy> qri.
Затем последовательно получаем fy и р^, используя первые три
строки A64), A68) и A69). Это даст
721 О2,
732 =-~,
7з1 = а, — t,
Р21 = «2.
аЗ
Т« = 1 — 742 — Т43.
A76)

320 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Проще всего просто положить <х{ = а.{, Ру = Ру, 7# = 7у> Рн — Ян-
Легко видеть, что это не противоречит нашей системе. Так, напри-
например, можно пользоваться формулами:
A77)
где
A78)
Последний вывод можно применись для произвольных систем обык-
ловенных дифференциальных уравнений первого порядка.
3. Метод Рунге—Кутта решения уравнений второго порядка.
Уравнения высших порядков могут быть сведены к системе уравне-
уравнений первого порядка и, следовательно, к ним также будет применим
метод Рунге — Кутта. Но так как в этом случае правые части будут
иметь очень простой вид, то можно получить более простые схемы
для их решения.
Рассмотрим уравнение второго порядка
У' = /(х, у. У) A79)
и будем отыскивать его решение, удовлетворяющее начальным дан-
данным: у(хо)=уо, У(хо)=Уо. Это уравнение может быть сведено
к системе
, .. ч } A80)
z'=f(x, у, z). ) к
Чтобы сократить записи, будем подробно разбирать только фор-
формулы, имеющие порядок погрешности на одном шаге А*. При этом

§ 4]
уравнения для определения оц,
вид:
МЕТОД РУНГЕ— КУТТА
321
pri, qri примут
Р21
2. а3 =
3.
4.
5.
i Т31 Г Т32"
= 1,
j_
: 2 '
J_
3 '
<?ззаз = 2" •
з з *
= Т31 + Т32.
.= 1.
1
6- />ЗзРз2а2 = " .
Q ~й
_^2_^ Р32 _РЗЗ
аЪ Тз2 Ы
Для системы A80) получим:
/3 (А) = А/[х0
A81)
A82)
Наиболее простые формулы получатся, если
Psibi +/>зз7з1 = °- A83)
В этом случае в силу второго и четвертого уравнений A81)
= —. Такому условию удовлетворяет, если положить aj^af;

322 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Py = Py =-^ = Y^, вариант б) формул, имеющих порядок ошиб-
ошибки й4, рассмотренной нами ранее. При этом
- - - 1 \
Я2 = 0-2 ^= Р21 ^= Р21 ^= 721 ^= 721 "Г >
2
аз = аз — Рзг = Рзг = 7з2 == 7з2 = "з"
3
Раз =933^x1 /?32 = 9'з2=
A84)
Проиллюстрируем применение этой формулы на примере урав-
уравнения
У"=у. A86>
Найдем два его частные решения. Одно из них должно удовлетво-
удовлетворять начальным условиям _у@)=1, _у'@)=1, другое _у@)= I,
У@) =—1. Точными решениями в этом случае будут ех и е~х.
Правый столбец отведем для значений точного решения. Вычисления
в нашем случае упростятся благодаря тому, что в правой частя
отсутствует у'. Ход вычислений будет виден из первой таблицы.
(См. стр. 323).
Как мы видим, результаты пол}'чились неплохие.
Аналогичные схемы можно получить и для других вариантов
значений оц, C^, pri. Приведем три готовые схемы, не входя в под-
подробности их получения (см. стр. 326).
Мы уже говорили о том, как можно производить оценку погреш-
погрешности формул Рунге — Кутта для одного уравнения первого порядка.
Аналогичные рассуждения годятся и для систем уравнений и урав-
уравнений высших порядков. Но оценки эти буд}гт очень грубыми, так
как они получатся в результате сложения большого числа отдельно
оцениваемых выражений. Не будем здесь проводить всех выкладок,
так как они очень громоздки, а практически ценность результата
незначительна.
Для варианта а) формул Рунге — Кутта, имеющих порядок
погрешности на одном шаге й6, Бибербахом была получена следую-
следующая оценка:
\y(x,)—yi\< 1 v_i | • A87>

§ 4] МЕТОД РУНГЕ КУТТА
у" = у, *0 = 0; уо = 1; У;=1; Л =0,1;
323
[0,
№
0
1
2
3
4
5
6
7
X
*0
х<л = хо + "з л
-*02 = -*0+-д-Л
0
0,0333
0,0667
0,1
0,1333
0,1667
0,2
0,2333
0,2667
0,3
0,3333
0,3667
0,4
0,4333
0,4667
0,5
0,5333
0,5667
0,6
0,6333
0,6667
0,7
0,7333
0,7667
У
Уо
Уо1 = Уо + "з ki
У02 = Уо + у kt
1
1,0333
1,0669
1,1052
1,1420
1,1813
1,2214
1,2621
1,3055
1,3498
1,3948
1,4428
1,4918
1,5415
1,5946
1,6487
1,7036
1,7622
1,8220
1,8827
1,9475
2,0135
2,0806
2,1522
k, Ду
кг = h+ g-7o
ДУо = *i+-2"/oi
0,1
0,1003
0,1052
0,1105
0,1142
0,1162
0,1221
0,1262
0,1284
0,1350
0,1395
0,1420
0,1492
0,1542
0,1569
0,1648
0,1703
0,1733
1,1821
0,1882
0,1915
0,2013
0,2080
0,2117
7о = Л'/о
/oi= Л2/ (-«oi, УоО
/05=Л?/(.*02, Уо?)
0,01
0,0103
0,0107
0,0111
0,0114
0,0118
0,0122
0,0126
0,0131
0,0135
0,0139
0,0144
0,0149
0,0154
0,0159
0,0165
0,0170
0,0176
0,0182
0,0188
0,0195
0,0201
0,0208
0,0215
1
1,1052
1,2214
1,3499
1,4918
1,6487
— |
1,8221
2,0138

324 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Продолжение
№
8
9
10
X
0,8
0,8333
0,8667
0,9
0,9333
0,9667
1.0
У
2,2252
2,2994
2,3785
2.4592
2,5412
2,6286
2,7178
к, Ду
0,2225
0,2299
0,2340
0,2459
0,2541
0,2586
F=-№t
0,0223
0,0230
0,0238
0,0246
0,0254
0,0263
ех
2,2255
2,4596
2,7183
№
0
1
2
3
4
5
y" = y; -
X
0
0,0333
0,0667
0,1
0,1333
0,1667
0,2
0,2333
0,2667
0,3
0,3333
,0,3667
0,4
0,4333
0,4667
0,5
0,5333
0,5667
<о = о, уо = 1;
у
1
0,9667
0,9355
0,9048
0,8747
0,8465
0,8188
0,7915
0,7671
0,7410
0,7163
0,6933
0,6706
0,6483
0,6059
0,6068
0,5865
0,5676
k, Ду
-0,1
— 0,0967
- 0,0952
— 0,0904
— 0,0874
— 0,0860
— 0,0818
— 0,0791
— 0,0778
— 0,0740
— 0,0715
— 0,0704
— 0,0670
— 0,0648
— 0,0638
— 0,0608
- 0,0588
— 0,0578
0,1; л? [0,1]
/ = Л2/
0,01
0,0097
0,0094
0,0090
0,0087
0,0085
0,0082
0,0079
0,0077
0,0074
0,0072
0,0069
0,0067
0,0065
0,0061
0,0061
0,0059
0,0057
е~х
1
0,9048
0,8187
0,7408
0,6703
0,6065

§ 41
МЕТОД РУНГЕ КУГТА
325
Продолжение
№
6
7
8
9
10
X
0,6
0,6333
0,6667
0,7
0,7333
0,7667
0,8
0,8333
0,8667
0,9
0,9333
0,9667
1,0
У
0,5490
0,5307
0,5135
0,4966
0,4800
0,4645
0,4492
0,4342
0,4201
0,4063
0,3927
0,3800
0,3675
k, Ду
— 0,0550
— 0,0532
— 0,0524
— 0,0498
— 0,0481
— 0,0474
— 0,0451
— 0,0436
— 0,0429
— 0,0408
— 0,0394
— 0,0388
/=А«/
0,0055
0,0053
0,0051
0,0050
0,0048
0,0046
0,0045
0,0043
0,0042
0,0041
0,0039
0,0038
е~я
0,5488
0,4966
0,4493
0,4066
0,3679
у" = f (x, у), порядок ошибки Л4
№
0
1
X
*0
1
x<" = x°+ih
xx = x0 + h
У
Уо
1 r
У02 = Уо + 4- k->
У1 = Уо + лУо
дУо
k'
к1
k; Ду
/
"F" (/о ~г ^JOl)
= дУо +
/01
/о,
7
/о = л*/с
= W(x0b
У01)
Уо?)
yi)

326 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
к
3
о
о.
о
с
К
авк
Доб
ч*
II
•о;
•о;
11
й
Ч
*
С
&
ч°
о
СО
•вй
1
чГ
тИ
•ft*
СО
1
•вй
41
чГ
_|_
S
й
ч?"
+
о
й
г- |<М
+
О
*|«
о
ч
ю
•Ч
см
•о;
<м
t
II
II
ii
«
ч?*
_1_
о
й
чГ
+
о
й1
-|см
+
о
••
1
2
Й^
и:
о
&
1
о
о
*
+
о .
II
II
•о;
+ •
_|_
О
||
II
||
II %
ч
-1 :'
S
о
о
а
о.
о
с
S
о
.оба
ч
^~
-ч
^»
ч"
СО
1
•о;
II
-^
см
11
ч
+
СО
г
_ 1С
Г
Й
S
й
о
О
1 J
-f-
CD ^
a
•4
CO ]<M
1
1
•u;
CO \*z?
о
i
о
•ft*
00
о
й"
+
о
jsIcm
~j~
o
4
- 4*
„ см
* +
- чГ
ч??
ч,
CO
1
1
•ft:
CO
I
1
О
тИ
00
1
-
s
Й
CM
о
CM
о
4
r>
4S*
+
4*
CO
+
1
•ft*
CO
1
|
1
_|_
о
eo
•ft*
1
s
Й
1
e
о
4
•
•
о
й1 .
1 •
^ft*
Й
CM
о ,
Й
II
•o;
4-
+ •
s •
l" *
о
11
о
4
II "
II
4
-1 :

•§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 327
Здесь у (xt) — точное решение в точке хи a _yt — соответствующее
приближенное значение. Предполагается, что в области \х— хо| <а,
\у—yQ\ < b f(x, у) и ее производные до четвертого порядка вклю-
включительно удовлетворяют условиям:
\f(x,y)\<M.
di+kf
дх1 дук
N
X Хп
Беря вместо A88) условия
\f(x, у)\<М,
Лоткин получил другую оценку:
i , , i ^ 73
di+kf Li+k
дх1ду"
A88)
A89)
A90)
A91)
которая иногда выгоднее A87). И та и другая оценки очень грубы
и практически малопригодны.
На практике пользуются приемом Рунге, производя вычисления
дважды: один раз с шагом h, а втором —с шагом 2й, или -^-. Об этом
мы уже говорили в главе 3, когда обсуждали вопрос о практической
пригодности формул остаточных членов при численном интегриро-
интегрировании.
§ 5. Разностные методы решения обыкновенных
дифференциальных уравнений первого порядка
Большим недостатком метода Руиге—Кутта является то, что для
получения одного нового значения решения дифференциального урав-
уравнения приходится подсчитывать правую часть уравнения в нескольких
точках. Если правая часть сложна, это связано с большой вычисли-
вычислительной работой. Сейчас мы перейдем к разностным методам реше-
решения обыкновенных дифференциальных уравнений, применение которых
требует только однократного вычисления правой части на каждом
шаге. Ограничимся пока случаем одного уравнения первого порядка.
Пусть требуется найти решение уравнения
y'=f(x, у),
A)
удовлетворяющее начальному условию у(хо)=уо. Предположим, чго
нам удалось каким-то образом найти приближенные значения у(х)
в точках хт, хт_, хт_и (xrn_i = xm — lh, h — шаг). Обозна-
чим
=yi и
f{xit ^)=/j. По f
fm~h МОЖНО

328 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
построить то или иное приближенное представление }\х, у(х)] в виде
функции, которая легко интегрируется. Пусть это будет ср(х). Тогда
можно приближенно считать
Таким образом, мы продвинем таблицу значений у(х) на один шаг.
Затем можно снова применить такой же прием и продвинуться еще
на один шаг и т. д.
Для того чтобы было возможно начать этот процесс, нам необ-
необходимо знать, кроме начального значения _у0, значения у(х) в точ-
точках xlt х2, ..., хк. Их можно отыскивать либо методом Рунге —
Кутта, либо одним из тех аналитических методов, о которых гово-
говорилось выше. Сами разностные методы дают итерационные способы
для отыскания _ур _у2 ук- Как это делается, мы укажем несколько
позже.
Наиболее простой способ приближенного представления f[x, y(x)]
дает интерполяция алгебраическими многочленами. Только его мы и
будем рассматривать. Обозначим через Lm,^(х) алгебраический интер-
интерполяционный многочлен, принимающий в точках хт, хт_х, .... хт„к
соответственно значения fm, /m_i, .... fm-k- При этом
к
?т.*<*) = 2 /«-Л<*). C)
где Pi(x) не зависят от fj. Введем новое временное t, положив
х — xm = th. Тогда Р{(х) перейдут в многочлены Qi(t) степени k,
не зависящие ни от шага й, ни от т. Таким образом,
т+
J
lfm-Ь D)
где
l
л
E)
— постоянные, не зависящие ни от /, ни от т, ни от h.
Беря различные значения j и различные формы интерполяцион-
интерполяционного многочлена, получим различные разностные формулы числен-
численного интегрирования дифференциальных уравнений. Эти формулы
носят название жстраполяционных в связи с тем, что они полу-

§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 329
чены путем интегрирования интерполяционного многочлена, проэкстра-
полированного на отрезок [хт, хт+1].
При построении интерполяционного многочлена можно исполь-
использовать, кроме fm, /m_1 fm-k' eu*e неизвестное нам значение fm+1.
Повторяя предыдущие рассуждения, мы придем к формуле
при этом и в правую и в левую части входит неизвестное значе-
значение ут 1# Поэтому для отыскания ут нужно решить алгебраиче-
алгебраическое или трансцендентное уравнение. Чаще всего это уравнение
решают методом последовательных приближений. Для сходимости
его придется потребовать выполнения условия h | f_11 М{ <С 1, где
= sup
ду
в рассматриваемой области. Формулы типа F) назы-
ва.ются интерполяционными. Из второй главы известно, что точ-
точность экстраполирования обычно бывает меньше точности интерпо-
интерполирования. Поэтому следует ожидать, что формулы типа F) будут
давать лучшую точность, чем формулы типа D). В справедливости
этого утверждения мы убедимся при исследовании остаточных членов.
1. Некоторые экстраполяциэнные формулы для интегрирования
дифференциальных уравнений первого порядка. Рассмотрим неко-
некоторые частные случаи разностных формул. Возьмем у = 0 и запи-
запишем Lm<k(x) в виде интерполяционного многочлена Ньютона для
интерполирования назад:
2.
Тогда
h f Lm,k(xm-\-th)dt =

330 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Здесь
12'
J
о
i
24
,. 251
dt ~TX)'
l
+
2) (< + 3) (f + 4)
120
j>5
:288€
(9)
Дальнейшие значения для коэффициентов сц будут
19087
5275
1 070 017
аа =;
1 082 753
6 ~ 60 480' 7 ~ 17 280' 8 ~ 3 628 800' "9 — 7 257 600'
Таким образом, формула (8) примет вид
(Ю)
251
95
Целесообразно ввести в рассмотрение величины <?»
Тогда формулу A1) можно переписать в виде
Эта формула носит название экстраполяционной формулы Адамса.
Схема для вычислений Ду и
Адамса будет выглядеть так:
Схема для вычислений Ду и у по экстраполяционной формуле

§ 5| РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 331
X
Хт-Ъ
Xm—1
xm-l
xm
у
Ут-з
Ут-i
Ут-l
Ут
^y
Ду»-з
А*.-,
q = hf
Qfti—B
Чт-i
Чт-l
Чт
*
т- а
Чт--
*
Чт-»
2
. . .
9т-1
• • •
Предполагая, что третьи разности почти постоянны, можно огра-
ограничиться первыми четырьмя членами формулы A2). По известным
значениям у о, у . у , у находим а , а , а , а
¦?т-з' ¦'т-1 Jm-l ¦>т "т-з "т-2 "m-i' "m-
Затем по формуле Адамса находим значение Ly и, прибавляя его
к ут, находим ут+1. Это позволит нам продвинуться в таблице зна-
значений q и ее разностей на один шаг вниз и получить по формуле
Адамса еще одно значение Ду и т. д.
Иногда бывает целесообразно выражать значения Ду непосред-
непосредственно через y'i = fi. Для этого выразим разности, входящие в фор-
формулу A2), через значения у'. Получим:
зл
A3)
Если ограничиться одним членом правой части, то придем снова
к формуле Эйлера
Ут+1 = Ут + ^'т- A4)
Два члена правой части дадут
У+
Три члена правой части дадут формулу
Четыре члена правой части приведут к
= Ут + й
06)
07)
Возьмем теперь у— 1 ив качестве Lm.jc(x) снова интерполяционный
многочлен Ньютона для интерполирования назад G). При этом

332 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
получим:
m 1-1 -"m
-- / [
m-l
.
Здесь
' ft
A8)
а0 =
+ i
= J* <# = 2,
/•
-1
_
fl3 —
t_
3 •
«.
=j
1 <(<+!)(< +2) (^+3)^
-l
28 _
= 90' °e~
1 036 064
628800'
24
18 229
29
—
90"
a, = :
35 424
7 120 960'
2 025 472
7 257 600'
A9)
Если ограничиться разностями до четвертого порядка и взять в ка-
, , „ 29 30 1
честве коэффициента при четвертой разности вместо ^ число ^7. = -^-.
т. е. изменить этот коэффициент всего лишь на щ, то получим
особенно простую для вычислений формулу:
2. Примеры интерполяционных формул. Рассмотрим теперь
примеры интерполяционных формул. Возьмем в качестве интерпо-
интерполяционного многочлена опять формулу Ньютона для интерполиро-

§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 333
вания назад,
i-m, к = fm+ 1 ¦
вания назад, но за начальную точку примем не хт, а хт+1:
i ^ V т 1) f% |
21
t(t+\)...(t + k-
¦/*.. к. B1)
При у = 0 интегрирование по^ придется проводить по отрезку [ —1,0].
Получим:
Д., =у _у =
... (t+k-\)
kl
/к... к dt =
к •
B2)
В этом случае
flo= fdt= 1.
_
в,—
-l
24
720'
863
0480" а'
33 953
a, = —
3 628 8U0'
275
24 195'
57 281
' 7 257 600'
B3)

334 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Мы получили интерполяционную формулу Адамса:
Ут Ут+1 2 У ,_i_ T2 ^т 24*? 1
т+2 т-g
720^-i 160 \»
2
Эта формула может быть использована для контроля вычислений,
произведенных по экстраполяционной формуле. Ее можно исполь-
использовать и для уточнения приближенных значений для Дуда, получен-
полученных другими способами. При этом можно пользоваться той же
схемой, что и для экстраполяционной формулы Адамса. По при-
приближенному значению Ут+1 находим qm+l, q1 \> Фт' Чъ \ • Затем
171+гг '№>~"п
2 &
используем интерполяционную формулу Адамса и уточняем зна-
значение Дуда. Исправляем q , q1 t, q1 , q3 t. Снова по интер-
a a
поляционной формуле Адамса уточняем Ду и затем q t> Ч1 i»
Ч\п' Чъ !• Это продолжаем до тех пор, пока исправляемые величины
т--
не будут изменяться при той точности, с которой производятся
вычисления. Первое приближение для Ду можно получить также
путем экстраполяции высшей разности q3 l на один шаг и по-
последующего вычисления разностей низшего порядка. Можно также
предварительно представить Ду в виде линейной комбинации yi
и у'., а уж затем производить последовательные приближения. При
этом если ограничиться первым членом формулы, то получим:
Если взять два члена, то будем иметь:
—
2
у =у 4-—(/ ,4-у'). B6)
При трех членах получим:
У+
при четырех
_а). B8)
¦*т ' 24
при пяти
тB51у'гп+г + 6^у'т-шу'т-^106Ут--1Ьт
B9)

§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 335
Рассмотрим еще один случай. Пусть j = 1, а в качестве Lmt k
возьмем интерполяционную формулу Стирлинга:
В результате интегрирования получим:
Ущ+l Ущ-1
хт+\
-*
-1
При этом
г
-1
_ V t-i _ i
Г t(t"— 1)
а^ J ~^Г-
а*= J -Ж1-
90'
Таким образом, наша формула примет вид
C0)
C2)
Если выразить здесь разности через _у?, то получим, принимая
во внимание разности первого, второго и третьего порядка:
C4>

336 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Последняя формула содержит у'т+г и вряд ли будет полезна на
практике.
При желании набор формул можно было бы значительно увели-
увеличить. Можно получать новые формулы беря линейные комбинации
формул, полученных для различных j н различных Lm, к(х). Все
эти формулы можно записать в виде
где у\= f (хг, _уг), а( и ^ — постоянные, не зависящие ни от у (х),
ни от А, ак Ф 0. Характерным для полученных ранее формул было
то, что они давали точное значение для у(х), если у(х) является
.алгебраическим многочленом степени не выше некоторого р.
3. Метод неопределенных коэффициентов вывода разностных
формул. Можно и не прибегать к помощи интерполирования для
получения формул C7), а воспользоваться методом неопределенных
коэффициентов. Разложим ут+ч н у'т+ч по формуле Тейлора до
членов с производными порядка р-\-\. Получим:
= у -4-vAy' -4-
-4-
C8)
Потребуем, чтобы после подстановки C8) и C9) в C7) коэф-
коэффициенты при /z°, А1, А2, ..., hp в правой и левой частях получен-
полученного равенства были бы равны для произвольной функции у(х).
Зто даст нам следующие равенства:
к
S«v = 0, D0)
[«,* —ф*-'] = 0 E=2 />);
— SP,= O. D1)
0
Всего имеем /?+1 однородных линейных алгебраических уравнений
•относительно 2/г + 2 неизвестных аг и р4. Таким образом, мак-
максимальное значение р равно 2k. Ошибка метода на одном шаге
или локальная ошибка метода будет определяться разностью между
левой и правой частями. Член с наименьшей степенью А в этой

§ 51 РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 337
разности будет равен
= C
P+i
D2)
V1
Можно было бы ожидать, что чем больше будет р, тем точнее
будет формула C7). Однако это не всегда так в связи с возникающими
при вычислениях по этой формуле погрешностями округления.
Выведенные нами ранее формулы будут являться частными
случаями формулы C7). Приведем таблицу значений р и Cp+1hp+1
для этих формул:
№
1
2
3
4
5
6
7
8
9
10
И
12
13
Ут+l
Ут+2
Ут+3
Ут+i
Ут+2
Ут+3
Ут-и
Ут+1
Ут+1
Ут+2
Ут+3
Ут+i
Ут+2
Ут
Ут+1
Ут+2
Ут+3
Ут =
Ут+1
Ут+2
Ут
Ут =
Ут+1
Ут+2
Ут+3
— V =
1т
Формулы
*/-
= \hWm+l-y'm\
= ^Л[23/т+а-16^+1 + 5.
= 4Л[55)'т+з-59>'1+2 +
+ 37^+1-9>
= 1Н7Ут + 2-2У'т + 1 + у'т]
= -3A[8W-5/m+2 +
-4- 4v . < — v
I sm+l '
hy'm + l
^[Ут+1 + Ут]
H Г- F . f f л
= -j2 [5Ут+2 + &Ут+1-Ут\
_5v' ,, _U у
°Jm+l i У
= 720ЛИ)';+4 + 64б/т+з-
-264^+а+106У;+1-19у
3" /1[Ут+2+^У/т+1 + Ут]
С]
т]
']
т\
'1
ml
т\
k
1
2
3
4
2
3
4
1
1
2
з
4
2
/>
1
2
3
4
2
3
4
1
2
3
4
5
4
>
>
29 Л*
~зо Л
-и"
19 Л5
~20 Л
180 Л
—La»
90 Я

338 ПРИБЛИЖЁННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ' УРАВНЕНИЙ [ГЛ. 9
Уже этот обзор формул дает основания ожидать, что интер-
интерполяционные формулы дают лучшую точность, чем экстраполяци-
онные.
Найдем теперь несколько формул типа C7) методом неопреде-
неопределенных коэффициентов. Условимся называть формулу C7) разност-
разностным уравнением или уравнением в конечных разностях. Число k
назовем порядком этого уравнения, а число р—степенью. Попро-
Попробуем найти формулу второго порядка, экстраполяционного типа,
имеющую степень 3. Тогда р2 = 0. Коэффициент а2 без уменьшения
общности можно считать равным единице. При этом уравнения D0)
и D1) примут вид
2-A + ^ = 0; } D3)
«i+:
«;+в*1 ^=1!:} D4>
Уравнения системы D4) дадут ^ = 4, ctt = 4. Далее, получим
fH=2, Oq:= — 5. Таким образом, искомая формула примет вид
Ут+г + 4ут+1 — Ъут = h [4/m^ + Ь'т\ D5)
Найдем теперь при k = 2 формулу интерполяционного типа, имею-
имеющую /? = 4. Уравнения D0) и DJ) примут вид (опять полагаем а2 = 1)
04+1=0,
в1+16 —
D6)
1 4
В этом случае последние три уравнения дадут В2=-о-, 3i=-r
о о
и al=0. Из остальных уравнений получаем [30 = -^, ао=: — 1. Мы
снова пришли к формуле C5).
Можно рассматривать и более сложные разностные уравнения:
к к к
2 <MWv + h 2 Bvjf' , +п2 2 ?У' = 0. D7)
К формулам такого типа мы придем, например, если в качестве
Lm,k (х) будем брать интерполяционный многочлен Эрмита. При-

§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 339
менять формулы типа D7) удобно лишь в тех случачх, когда про-
производные от f(x, у) легко находятся и легко вычисляются. Можно
еще усложнить D7), включив туда производные более высоких
порядков.
4. Метод Крылова отыскания начальных значений решения.
Коснемся теперь немного способов вычисления начальных зна-
значений yv y2, .... ук, основанных на разностных формулах. При-
Приведем один такой способ, предложенный академиком А. Н. Крыловым.
Рис. 25.
Ограничимся случаем k = 3. Возьмем кусок диаграммы Фрезера
и запишем три интерполяционные формулы, пути для которых
указаны пунктиром, тире и тире с пунктиром. Эти формулы имеют
вид
2
,
\ D8)

340 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Интегрируя их в пределах от 0 до 1, получим:
= <fe + у Я1 , - ¦& я1+1 + i <73 з •
*+i
*+?
D9)
Положив в первом из равенств D9) /г=0, во втором k = 1 и
* третьем k =¦ 2, будем иметь:
, 1 „
-& Я2, - i Я\
Д^2=92 + 1г q\ +-пг Я\
E0)
Выражения в правых и Левых частях зависят от j0, yv y2, y3, и мы
имеем систему уравнений для определения уи у2, у3- Ход вычисле-
вычислений по этим формулам лучше всего показать на примере. Рассмот-
Рассмотрим уравнение у'=у и будем отыскивать его решение, удовлетво-
удовлетворяющее начальному условию .у@)= 1. При этом если шаг равен 0,1,
то <7о=О>1- Принимаем приближенно &yo=qo. Отсюда находим
первое приближение для yv которое мы будем обозначать через уп.
В нашем случае _уи=1,01. Теперь мы имеем возможность найти
первое приближение для q\ = ql — q0. В нашем случае <?i = 0,101

и <7\ =0,001. Вычисляем второе приближение для у1—у12 и находим
т9\ = 1'1005-
E1)
Поэтому исправленное значение для ql будет <7i=O.HOO5 и для q\
Т
будет q\ =0,0100. Найдем теперь первое приближение для у2—у21
по формуле
4- Я\ = 1.1005 + 0,1100 + 0,0050= 1,2155. E2)

§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 341
Теперь мы можем найти д2, д\ и д*:
; 9з =0-1216 —0,1100 = 0,0116; 9? = 0,0016. E3)
?
Тогда
,0050+0,0007 = 1,3425 E4)
9з=0,1342; д\ =0,1342 — 0,1216 = 0,0126;
А = 0,0010; д\ = — 0,0006.
E5)
Пересчитывая по формулам E0) значения уи у2, уъ, находим:
Т Ч\ —ТУ ^i ~г~ "од" i\ = 1.Ю49,
^д1-^.д^ = 1,2685,
+ j Я\ + 4" Ч\
= 1.4482.
E6)
Вычисляем заново значения разностей
^ =0,11049; 92=0,1268; 9з=0,1448,
Я\ = ft —9о = 0.0105.
% = 0.0059,
= 9з — 3ft + 3ft — д0 = — 0,0042.
E7)
После нового пересчета у1у у2, уъ находим:
_у1+ = 1,1049, ^2з=1,2233, ^зз = 1,3562. E8)
Так как расхождения с предыдущими приближениями еще очень
велики, то проделываем вычисления еще раз. Получим:
9! =0,11049, q2 =0,12233, д3 =0,13562, \
^ =0,0105, ^=0,0013, 93з =0,0001,
у16= 1,1051, ^24 = 1,2213, ^34= 1,3493.
E9)

342 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Новый пересчет даст
9i =0,11051,
^=0,0105,
q2 ^= 0,12213, q3 =0,13493,
q\ =0,0011, g* =0,0001,
F0)
yie= 1,1051, _у2в= 1,2213, _y35= 1,3499.
В дальнейшем изменений происходить не будет.
Как мы видели ранее, для сходимости процесса последовательных
приближений достаточно, чтобы собственные значения некоторой
матрицы, составленной из частных производных правых частей, были
по модулю меньше 1. В нашем случае решается методом последо-
последовательных приближений систем'а
1. Л)—
. .Уз)].
Уз=Уг + 2Ц —
Соответствующее вековое уравнение примет вид
19Л1.А
24
. Л)].
24
1 +
24
19Af,A
24
lOlvk-yfl .
~24
1 + -
24
24
Мф
24
~24~
- —X
= 0.
F2)
Раскрывая определитель, получим:
361
_(
-—
1Н2 + ±М^ = О. F3)
При достаточно малом h все корни этого уравнения по модулю
меньше единицы.
б. Примеры. Проиллюстрируем теперь ход вычислений по раз-
разностным формулам при решении дифференциального уравнения пер-
первого порядка У—у с начальным условием _у@)=1 и шагом 0,1.
Начальные приближения находились с помощью рядов с пятью вер-
верными десятичными знаками. Все разностные формулы брались не
более чем до третьих разностей. Для интерполяционных способов
при отыскании Ду методом последовательных приближений за началь-
начальные приближения брались результаты, полученные по экстраполя-
ционным способам. Промежуточные результаты вычислялись с шестью
десятичными знаками. Окончательные результаты округлялись до пяти
десятичных знаков.

§ 5] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ 1-ГО ПОРЯДКА 343
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
д
¦'т
У
1,00000
1,10517
1,22140
1,34986
1,49182
1,64871
1,82210
2,01373
2,22551
2,45956
2,71822
. 1 1
4т-г 2 q™~
Ду
0,14196
0,15689
0,17339
0,19163
0,21178
0,23405
0,25866
1 5 а
/,-Г2 qm-
q
0,100000
0,110517
0,122140
0,134986
0,149182
0,164871
0,182210
0,201373
0,222551
0,245956
, 3 з
i-г 8 qm-
ql
10 517
11623
12 846
14196
15 689
17 339
19163
21178
23 405
-V.
q*
1106
1223
1350
1493
1650
1824
2015
2227
q3
117
127
143
157
174
191
212
_L
12
Is
24 Чт-Ч,
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
У
1,00000
1,10517
1,22140
1,34986
1,49183
1,64873
1,82213
2,01376
2,22555
2,45961
2,71829
0,14197
0,15690
0,17340
0,19163
0,21179
0,23406
0,25868
q
0,100000
0,110517
0,122140
0,134986
0,149183
0,164873
0,182213
0,201376
0,222555
0,245961
0,271829
q1
10 517
11623
12 846
14197
15 690
17 340
19163
21179
23 406
25 868
q*
1106
1223
1351
1493
1650
1823
2016
2227
2462
q*
117
128
142
157
173
193
211
235

344 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Ут+1 Ут-l = ^ + Я Л
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
У
1,00000
1,10517
1,22140
1,34986
1,49182
1,64872
1,82211
2,01374
2,22552
2,45958
2,71825
Я
0,100000
0,110517
0,122140
0,134986
0,149182
0,164872
0,182211
0,201374
0,222552
0,245958
Я1
10 517
11623
12 846
14196
15 690
17 339
19163
21 178
23 406
Я"
1106
1223
1350
1494
1649
1824
2015
2228
Я3
117
127
144
155
175
191
213
'т+1
-1 ~ ^г
,+±A
X
0,0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
У
1,00000
1,10517
1,22140
1,34986
1,49182
1,64872
1,82211
2,01375
2,22553
2,45960
2,71827
Я
0,100000
0,110517
0,122140
0,134986
0,149182
0,164872
0,182211
0,201375
0,222553
0,245960
0,271827
Я1
10 517
11623
12 846
14196
15 690
17 339
19164
21178
23 407
25 867
Я*
1106
1223
1350
1494
1649
1825
2014
2229
2460

§ 6] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ 345
Сравнение полученных результатов со значениями ех дает следую-
следующую таблицу ошибок (в единицах пятого десятичного знака):
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1.0
1-й способ
0
0
0
0
0
1
— 2
— 2
— 3
— 4
— 6
2-й способ
0
0
0
0
+ 1
+ 1
+ 1
+ 1
+ 1
+ 1
+ 1
3-й способ
0
0
0
0
+ 1
0
— 1
— 1
— 2
— 2
— 3
4-й способ
0
0
0
0
+ 1
0
— 1
0
— 1
0
— 1
Как видно из этой таблицы, интерполяционные способы имеют за-
заметное преимущество в точности по сравнению с экстраполяционными.
Формулы, при помощи которых мы решали уравнение в 3-м и 4-м
случае, связывают значения _уА+1 не с ук, а с ук^и и поэтому может
случиться, что значения ук с четными индексами и нечетными инде-
индексами будут слабо связаны друг с другом. Так это и произошло
в четвертом случае. Тогда прибегают к сглаживанию или самих зна-
значений функции или их разностей.
Полученные нами способы без каких-либо дополнительных рас-
рассуждений переносятся на системы обыкновенных дифференциальных
уравнений первого порядка. При этом, конечно, придется парал-
параллельно решать все уравнения системы.
§ 6. Разностные методы решения обыкновенных
дифференциальных уравнений высших порядков
Уравнения высших порядков могут быть сведены к системе
уравнений первого порядка. Поэтому на них переносятся все те
методы, о которых говорилось в предыдущем параграфе. Однако
при этом получаются системы очень специфичного вида, для которых
возможны упрощения общих методов. К этому вопросу мы сейчас
и перейдем.
Пусть задано дифференциальное уравнение
' = А*. у. У)
A)
и требуется найти его решение, удовлетворяющее начальным усло-
условиям: уСх^=у0, У(хо)=Уо' Воспользуемся тем же способом,

346 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
который мы применяли для уравнений первого порядка. Предпо-
Предполагаем, что нам известны значения у и у' в точках хт, хт_х хт_к.
Находим тогда значения fm, fm_t fm-ч и строим интерполя-
интерполяционный многочлен Ньютона для интерполирования назад:
f4
Интегрируя его по t в пределах {0, ?], получим:
При $ = 1 будем иметь:
Х = У +
тде а{—коэффициенты экстраполяционной формулы Адамса. По D)
мы можем вычислить у'т+1. Интегрируя C) по k в пределах [0, 1],
лолучим:
f1 ~t~ • • • ~t~a /ft !• E)
где
l ?
"'-U"~'tl<f + t-l)dt. F)
Вычислив коэффициенты а{, мы сможем найти у и тем самым
продвинуться на один шаг.
На практике приходится сталкиваться с уравнениями, в которых
J(x, у, у') не зависит от у'. Тогда нет необходимости на каждом
шаге вычислять у'. Поэтому целесообразно совершенно исключить у'
из E). Для этого проинтегрируем C) по % в пределах [—1,0].

§ б] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ 347
Получим:
-1 О
fh ]dt_ , А,
где
Вычитая (8) из E), найдем:
Д2у ^у —2 у —I— v =
При этом
о о
l i.
—\)dt. A0)
В частности,
it
о -e
О -?
1 +
1 A1)
о -5
19
240 '
_ 19 . _
— 240' a5 —P5 —
120
_ 863
—Рб—12^008 * J

348 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Таким
образом,
= h2fm Ч
мы
1
получим:
-г,-,,
9 р
10 ' "
19
1-у, ~т~
fm-t
863
1008
Эта формула носит имя Штёрмера. Процесс вычислений по фор-
формуле Штёрмера идет так же, как и для уравнений первого порядка,
только вместо q = hf(x, у) берут r = h2f(x, у).
В качестве примера рассмотрим уравнение
у"=у
A3)
и будем отыскивать его решение, удовлетворяющее начальным дан-
данным: _у@) = 1, у @) = 1. Будем использовать формулу A2) до
третьих разностей. Начальные четыре значения возьмем из таблицы,
полученной по формуле Рунге — Кутта.
Получим таблицу:
X
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
У
1
1,1052
1,2214
1,3499
1,4919
1,6488
1,8222
2,0138
2,2256
2,4597
2,7184
^y
1285
1420
1569
1734
1916
2118
2341
135
149
165
182
202
223
246
r = h*f
0,010000
0,011052
0,012214
0,013499
0,014919
0,016488
0,018222
0,020138
0,022256
0,024597
г»
1052
1162
1285
1420
1569
1734
1916
2118
2341
ПО
123
135
149
165
182
202
223
г»
13
12
14
16
17
20
21
Как мы видим, вычисления оказались очень несложными — про-
производятся в уме. Записей очень мало. Результаты довольно точ-
точные.
Рассмотрим еще пример интерполяционной разностной формулы
для решения дифференциальных уравнений второго порядка. На

§ 6] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ 349
этот раз применим интерполяционную формулу Стирлинга:
J m> 24 ^ «г
A4)
Как и ранее, получим:
•••]
<«¦
В частности, при ?=1 будем иметь:
где
— С*
<x2i+2 — J —
О
1
—!)... (^3 — Р)
dt,
BГП))
A7)
Интегрируем еще раз A5) по $ в пределах [О, 1]. Будем иметь:
1 S
о о
24

350 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ.
где
— См С
= j d\ J
о о
1 i
R2i+1
о о
Интегрирование A5) по % в пределах [—1, 0] даст
о %
A9)
-1 О
где
-1 О
о е
¦dt.
¦]. B0)
B1)
Вычитая B0) из A8), получим:
Vi+--.]. B2>
где
так как под знаком внутреннего интеграла стоит нечетная функ-
функция t, a
/ /
О -?

§ 6) РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ 351
В частности,
о -6
1
о -6
24
31
60 480
289
3628800 '
B5)
Подберем теперь такую функцию срот, для которой бы
столбец fk являлся столбцом вторых разностей. Это можно сделать
бесчисленным множеством способов. Можно, например, произволь-
произвольным образом задать <pLy и последовательным сложением с /0, fv
/2, ... заполнить столбец первых разностей искомой функции,
а затем произвольным образом задать <р_^ и последовательным сло-
сложением с cpj_v, ер* , срЗ., ... получить таблицу значений <pt. Будем
обозначать <pJ+Vi через f~*,h, а срг — через /Г2.
Левая часть B2) является второй разностью для значений yiy
взятой в точке т. Правая часть B2) является второй разностью от
-a
¦]¦
B6)
взятой также в точке т. Поэтому первые разности этих двух таб-
табличных функций могут отличаться только на постоянную. Таким
образом,
B7)
Эта постоянная С будет равна нулю, если при /и = 0 она нуль,
т. е. если
л-^6=/р [»Л4+««A+V?/,+8Л+88/7/.+ • • •]• B8)
Последнее равенство будет выполнено, если подходящим образом
выбрать /I,1,. Будем предполагать, что это сделано и С в B7) равно
нулю. Тогда, еще раз применяя такие же рассуждения, получим:
VS
B9)

352 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Опять если выбрать /г_1 так, что будет выполнено равенство
то B9) перейдет в
^=A18oC+Vm+V3m+Vffl+Vl+ • • •] CD
или, если использовать B5),
/--2_i__L/ L_ fi I 31 fi
m > \2 J m 240 •/™~r 60480 •/™
+---1- C2>
При этом f_\, и f_\ нужно выбрать так, чтобы были выполнены ра-
венства:
,, ,, Ь2 Г f -1 I _1_ fl L_ fS I 31 fa
Ji Уо \J,/t -Г 12 •'¦/• 240 •/l/a^^ 60 480у'/а
__289_,7
3 628 800/Vj
C3)
60 480 J о "
289
~~ 3 628 800 J о"
Равенство C2) называют формулой суммирования Гаусса.
В качестве примера на применение формулы суммирования
Гаусса рассмотрим задачу о колебании математического маятника.
Дифференциальное уравнение этих колебаний
¦ ¦а ^ т- sin ср (.он^
путем замены независимой переменной
x = ty/j- C5)
приводим к виду
J° - = — sin ср. C6)
Пусть начальные условия будут: ср @) = 60° = ^ = 1,04720, со' @) = 0.
о
Шаг h возьмем равным 0,2. Вычисления будем производить по
формуле
где rm = h2fm = — 0,04 sin cpOT.

§ 6] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ 353
Предварительно вычислим значения ср для х = ± 0,2 и х =
= + 0,4, пользуясь формулами:
;, cp_(n+1)=cp_n-0,2cp'_n+0,02cp':n, ]
?n == — S'n fn-
Вычисления дадут
ш, = cp_2 = 0,9782,
C8)
> C9)
= ?-!= 1.0299. | ^
Теперь уточним эти значения по формуле C7). Для этого вы-
:ляем г1 = г_1 и г2 = г_2 и разности г*, которые можно найти
для пяти известных значений гт. Далее, воспользовавшись тем, что
А
240
числяем Г1 = г_1 и г2 = г_2 и разности Г* которые можно найти
я пяти известных значений гт. Далее, в
г°
~г в этих строках не достигает 0,5 единицы последнего разряда,
находим x_2 = x2 и s_1 = s1 по формуле хп = -гк-гп. Находим г-1;
г-1 = (^ — ср0) — -jj rj/t = — 0,01732 D0)
и r-a:
г-2 = ср0 —хо= 1,05009. D1)
Заполняем таблицу г^,. и гга и исправляем ср^ и ср2 по формуле C7).
Получим:
ср1 = г1-а + х1 = 1,02991.
cp2=rja-|-x2 = 0,97840.
Исправленные значения вставляем в таблицу. При этом значение rt
и г2 не изменяются.
Теперь можно продвигаться дальше. Проще всего это можно
осуществить путем экстраполяции значений х„. Для этого соста-
составляем таблицу разностей хя, экстраполируем вторую разность на
один шаг и находим т3 = — 259. Отсюда ср3 = г~а + х3 = 0,8938.
Это дает г3 = —0,03118 и т3 = —260. Исправление не влияет на
полученные значения ср3 и гв. Поэтому после исправления разностей
можно продвигаться на следующий шаг. Результаты вычислений
приведены в данной ниже таблице.

354 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. Э
хп
—0,4
—0,2
0,0
0,2
0,4
0,6
0,8
1.0
1.2
1.4
1.6
1.8
2,0
2,2
0,9784
1,0299
1,0472
1,0299
0,9784
0,8938
0,7781
0,6344
0,4671
0,2819
0,0856
—0,1140
—0,3092
—0,4922
0,98116
1,03277
1,05009
1,03277
0,98116
0,98637
0,78040
0,63635
0,46859
0,28281
0,0591
—0,11441
—0,31018
у
—0,49378
5 161
1732
—1732
—5 161
—8479
—И 597
—14 405
—16776
—18 578
—19 690
—20 032
—19577
—18 360
—3 318
—3 429
—3464
—3 429
—3 318
—3 118
—2 808
—2 371
—1802
—1112
—342
+456
+1217
+1890
г\
—Ш
—35
+35
+Ш
200
310
437
569
690
770
797
762
673
rl
+76
70
76
89
110
127
132
121
80
27
-35
—89
rl
—6
+6
13
21
17
5
—И
—41
—53
—62
—54
+12
7
8
—4
—12
—16
—30
—12
—9
+8
—276
—286
—289
—286
—276
—260
—234
—198
—150
—93
-29
+38
+101
+ 157
<
— 10
—3
+3
10
16
26
36
48
57
64
67
63
56
<
7
6
7
6
10
10
12
9
7
3
Л
—7
Интерполируя, легко находим, что ср = О при х =1,6857. Точ-
Точное значение х с четырьмя десятичными знаками равно 1,6858.
Можно было бы получить еще ряд формул. Но мы этим огра-
ограничимся, так как уверены, что читатель или сам сумеет получить
удобные в данных конкретных условиях формулы, или найдет их
в многочисленных руководствах, посвященных этому вопросу. За-
Заметим только, что и в этом случае могут найти применение фор-
формулы типа D7) предыдущего параграфа.
§ 7. Оценка погрешности, сходимость и устойчивость разностных
методов решения обыкновенных дифференциальных уравнений
1. Линейные разностные уравнения. Прежде чем переходить
к вопросам, указанным в заголовке данного параграфа, рассмотрим
некоторые вопросы теории линейных разностных уравнений. Эта
теория близка к теории линейных обыкновенных дифференциаль-
дифференциальных уравнений. Поэтому доказательства здесь приводиться не будут.
Линейным разностным уравнением k-ro порядка называют выра-
выражение вида
= д(п), A)

§ 7]
ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ
355
где щ (я), b (я) — заданные функции целочисленного аргумента п,
ак(п)ф0, ао(п)фО. Если Ь(п)==О, т. е. A) принимает вид
то уравнение называется однородным. В противном случае уравне-
уравнение называется неоднородным. Решением уравнения A) или B)
называется всякая функция целочисленного аргумента п, после под-
подстановки которой в уравнение последнее обращается в тождество
по п. Ясно, что если задать у0, yv .... ук_1 (начальные значения), то
мы можем по A) или B) последовательно вычислить все уп.
Имеют место следующие утверждения:
1. Если yW, у&\ .... у№ являются частными решениями одно-
однородного линейного разностного уравнения B), то и любая их ли-
линейная комбинация
с постоянными коэффициентами
нения B).
2. Если, кроме того, определитель
будет являться решением урав-
уравD)
отличен от нуля, то любое частное решение B) может быть пред-
представлено в виде C), т. е. C) дает общее решение уравнения B).
Частные решения yQ\ у&\ ..., у№ в этом случае называют линейно
независимыми.
3. Общее решение уравнения (V) можно представить как сумму
какого-то частного его решения и общего решения однородного
уравнения B).
4. Если у№, уФ\ .... уФ> являются частными решениями B),
для которых определитель D) отличен от нуля, то функция
zn =
n-l
)
и
5*-
y?U
yfU
yfU
yfU-г
v®
yfU •
... >fi
: If'1
"S
E)

356 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
является частным решением неоднородного уравнения A) (аналог
метода вариации постоянных).
Если коэффициенты а,-(я) уравнения A) или B) не зависят от п
(тогда мы их будем обозначать просто аг), то будем говорить, что
A) или B) являются уравнениями с постоянными коэффициентами.
Начиная с этого момента, мы будем предполагать, что а* (я) не
зависят от п.
Будем тогда разыскивать решение уравнения B) в виде
Уп = гп. F)
При этом для определения неизвестных значений z получим алгеб-
алгебраическое уравнение
akzk + flfc.xa* + • •. + alZ + а0 = 0. G)
Это уравнение называется характеристическим для B). Если все
корни zlt z2, .... zk характеристического уравнения простые, то
«?. «• г» (8)
образуют линейно независимую систему решений B). Часть кор-
корней Zi или все корни могут оказаться комплексными. Мы ограни-
ограничимся случаем, когда все коэффициенты ai действительны. Поэтому
комплексные корни будут попарно сопряжены. Пусть, например,
zk = р (cos ср -f-1 sin cp); ,z^ = p(coscp— /sincp). (9)
Тогда этой паре комплексно-сопряженных корней будут соответство-
соответствовать два действительных частных решения уравнения B):
pncosrtcp, pnsin«cp. A0)
Если произвести такую замену для каждой'пары комплексно-сопря-
комплексно-сопряженных корней, то полученные решения совместно с решениями,
соответствующими действительным корням, снова образуют k ли-
линейно независимых решения B).
Если Zi является корнем G) кратности г, то частными реше-
решениями B) будут:
2%, IIZ1}, n2Zf, .... rtr-1Zf. A1)
И в этом случае комплексные корни можно заменить действитель-
действительными. Во всех случаях мы сможем получить k линейно независи-
независимых действительных решения уравнения B).
2. Разностное уравнение для погрешности приближенного
решения. Перейдем теперь к вопросу об оценке погрешности раз-
разностных способов решения обыкновенных дифференциальных урав-
уравнений. Ограничимся случаем одного уравнения первого порядка
?L
A2)

§ 7J ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 357
Будем предполагать, что f(x, у) обладает непрерывными производ-
производными до некоторого порядка р~^-\ в области Gх):
\У — У(.*)\<г (*о<*<*о + 0. A3)
где у(х)— решение A2), удовлетворяющее начальному условию
у(хо) = уо, а г таково, что приближенное решение, выходящее за
пределы области G, становится неинтересным. При этом у(х) будет
обладать в G непрерывными производными до порядка р+1.
Численное решение A2) будем отыскивать по формуле
SPi/.+i = O. A4)
i=0 i=0
предполагая, что начальные значения у0, yv . . ., ук_1 нам заданы.
Прежде чем переходить к основным вопросам этого параграфа,
наложим некоторые ограничения на коэффициенты формулы A4).
При этом будет удобно ввести в рассмотрение многочлены
Pi* + Po I ( }
и оператор Е, определенный при помощи равенства
Еуп = Уп+1 или Ey(x)=y(x + h). A6)
Тогда A4) можно записать в виде
P(E)yn-ho(E)fn = 0. A7)
Естественно считать, что все коэффициенты сц и ф{ действительны
и что акф0. Предположим, далее, что p(z) и o(z) не имеют
общих множителей. Это связано со следующими соображениями.
Если бы нашелся такой многочлен ср(г), что
И 0B) = срBH1B), A8)
где рх(гг) и o1(z)—многочлены, то A7) можно было бы записать
в виде
= 0. A9)
!) По поводу сходимости и оценки погрешности разностного метода
в случае разрывной правой части см. Б. М. Б у д а к и А. Д. Горбунов,
О разностном методе решения задачи Коши для уравнения у' =f{x, у)
и для системы уравнений х'г = Xf (t, Xi хп), t = 1,..., л с разрывными
правыми частями, Вестник МГУ, сер. матем. № 5, 1958, стр. 7—11, или
А. Д. Горбунов и Б. М. Будак, О разностном методе решения задачи Коши
Для системы уравнений х\ = X{(t, хг хп) (/ = 1 л) с разрывными
правыми частями, Научные доклады Высшей школы, физ.-мат. науки, № 6,
1958, стр. 25—29.

358 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ-[ГЛ. 9
Если обозначить
= <!»„ B0)
то A9) перейдет в
ср(?)ф„=О. B1)
Начальных условий у0, yt, .. ., yk_t будет достаточно для того, чтобы
найти сначала решение B1), а затем B0). Так как разностное урав-
уравнение B1) линейно и имеет постоянные коэффициенты, то фп на-
находятся без труда. Но тогда уп будут находиться из уравнения B0),
имеющего порядок ниже, чем уравнение A7).
Нас будут интересовать только такие формулы A4), которые
обеспечивают равномерную сходимость приближенного решения
к точному при А-»-0. (Предполагается, конечно, что начальные
значения задаются точно и все вычисления производятся точно.)
Поэтому потребуем, чтобы для любого е > 0 существовало такое
8 > 0, что как только h < 8, то
— е<Л»-м—.У(*)<е (' = 0, 1, 2. .... к). B2)
Здесь nh = x—л:0. Вследствие B2) имеем:
к
г=0
к
(*) = 2 «i (Ук+i ¦+¦
1=0
6- Таким образом, по A4)
\У(Х)\
к
2<
1=0
к
к
Так как, вообще говоря, у(х)ф0, то 2ai^0 ИЛИ
1=0
B3)
0. B4)
Это третье ограничение на A4).
Положим
Р(г) = (г-1)Р1(г). B5)
При этом A4) перейдет в
Р1(?)(Л+1—Л) —*о(?)/« = 0. B6)
Суммируя равенства B6) по I от 0 до я, получим:
i — Л) = ° (?) 2 А/,. B7)
1-0
Переходя в B7) к пределу при п -»• оэ, получим:
о;
Pi (О [> (*) — Л1 = о О) / / К. > @1 Л. B8)

§ 7] ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 359
Так как у{х) должно удовлетворять уравнению» A2), а оA)=?0
в силу второго предположения, то
Pi(l) = p'0) = o(l). B9)
Это четвертое ограничение на A4). Равенства B4) и B9) необхо-
необходимы для равномерной сходимости точного решения разностного
уравнения к точному решению дифференциального.
Будем теперь под уп понимать значение точного решения у(х)
дифференциального уравнения A2), удовлетворяющего начальному
условию у(хо)=уо, в точке хп = xo-\-nh и под /п—значение
f (хп, уп). Эти величины не будут удовлетворять уравнению A4),
но будут удовлетворять некоторому другому разностному уравнению
P(E)yn-ho (?)/.+•'. = 0. C0)
где 1п можно выразить по формуле D2) § 5 и в некоторых случаях
можно оценить.
Обозначим через уп численное решение, фактически полученное
по формуле A4), и через еп—разность
Уп—Уп = *п- C1)
Так как формула A4) применима лишь в том случае, если заданы
первые k значений Уг'-Уо, У\, ••., Ук+v то будем предполагать,
что известны оценки для первых k значений е4. Задача заключается
в том, чтобы получить оценки для всех et.
При численном решении мы получим уп, удовлетворяющие не
уравнению A4), а некоторому другому уравнению:
р(?)Я,= Ло(?)/я+л|п. C2)
Здесь /„ = /(*„, уп) и т)п — некоторая величина, появление кото-
которой вызывается следующими причинами:
1. Как правило, мы можем находить не точные значения /п,
а лишь приближенные fn.
2. Вычисления по формуле A4) ведутся с округлениями.
3. Если A4) — интерполяционная формула, то уравнение для опре-
определения yn+jc может быть решено только приближенно.
Таким образом, т)п определяется ошибками, возникающими на
данном шаге при вычислении уп+к по формуле A4) без учета оши-
ошибок начальных значений и ошибки метода. Величину % иногда также
Удается оценить.
Вычитая C0) из C2), получим:

360 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Применив формулу Лагранжа
Jn — /n=/ (хп< Уп) — / (*п. Уп) = On — Уп) /у (хп< С„)
(С„€E„. Уп)) C4)
и обозначив /у (хп, ?„) = тп, мы можем переписать C3) в виде
P(E)Bn=ho(E)mnen-\-yln-j-ln. C5)
Отсюда мы можем получить последовательно оценки для всех е$,
если известны оценки для е0, et ?ft-i. 'n> ^n- mn-
3. Оценки погрешности решений, получаемых по формулам
Адамса. Чтобы проиллюстрировать предыдущие рассуждения и по-
показать, как их можно применять в практических случаях, рассмот-
рассмотрим подробнее экстраполяционную и интерполяционную формулы
Адамса. При этом мы будем считать, что т]п=0.
Экстраполяционная формула Адамса может быть записана в виде
г
Л+1 =Ук + h 2 <xjk_ lt C6)
где
г
^/C8)
о
При этом
хкл-1
/ . C9)
Последнее выражение можно записать в виде
2 / D0)
г=0
Здесь через 1к обозначено следующее выражение:
""ft+i
I— J /[?. y&)\d%. D1)
i-o хк
Величину 1к нетрудно оценить. Для этого заменим подынтегральное
выражение в . D1) интерполяционным многочленом Ньютона для

§ 7] ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 361
интерполирования назад с остаточным членом
н-
t(t+\)..,(t+r) rfr+1/[&, У E)]
. D2>
Проинтегрировав интерполяционный многочлен, мы получим первую
сумму в левой части D1). Таким образом,
1
1) ...(* +г) dr+1/[t у(?)
(Г +1)'
Используя теорему о среднем, получим:
dt. D3>
/* = —i
и, обозначая через Mr+i максимум модуля ,, в рассмат-
риваемой области, найдем:
|/4|</ = й'+1аг+Д+1. D5>
Переходя к абсолютным величинам и обозначая через L постоянную-
Липшица для функции f(x, у), будем иметь:
_ D6>
г-=0
Это неравенство можно получить прямо из формулы C5) при •/)„ = (),
используя оценки для 1п и тп.
Покажем теперь, как можно перейти от этой рекуррентной,
оценки к оценке |еп| через данные в начале счета величины. Рас-
Рассмотрим разностное уравнение
г
~ D7>
Если в качестве начальных значений для Ек выбрать положительные
величины, большие чем модули соответствующих вк, то при любом fe
будем иметь Ек^\ек\.
Характеристическое уравнение для D7) будет иметь вид
г
ср {z) = zr+* — zr — /zZ-2 | ец | zr~* = 0. D8)
i=0

362 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Если обозначить его корни через zv z2, ..., zr+1 и частное реше-
решение уравнения D7) через D, то общее решение D7) может быть
записано в виде
D9)
Так как срA) <0 и
4{\-\-hLA) = {\+hLA)rhLA — Aisled A -}-hLA)r~* > 0, E0)
где
Л=2|о,|. E1)
то уравнение D8) имеет корень zv заключенный в пределах
1 < гх < 1 -\-hLA, E2)
Поэтому, полагая С2 = С3= ... =Сг+1 = 0 в D9), мы получим
такое решение E-k = Cxz*-\-D уравнения D7), которое при доста-
достаточно большом положительном Сх будет удовлетворять неравенству
Ек^\ек\ при всех k = 0, 1, ..., г—1, а следовательно и при всех
к^>0. Выбором Сх займемся после определения константы D, пред-
представляющей собой частное решение уравнения D7). Подставляя
в D7) D вместо Ек, получим:
/ + AZ-2 \at\D=0, E3)
откуда
1L E4)
i-0
Поэтому
Подберем теперь постоянную Cv Пусть начальные г значений sq,
€1( .... ег_1 нам известны и все они не превышают по абсолютной
величине е > 0. Тогда, для того чтобы все ЕкAг = 0, 1, .... г— 1)
были не меньше е, достаточно взять
С + <56>
Таким образом, мы находим:
^**-1). E7)

§ 7] ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 363
Если воспользоваться правой частью неравенства E1), то E7) можно
заменить более грубым неравенством:
^-ЛКвО + АМ^ + ^Ю+АМ)*-!]. E8)
Воспользуемся теперь неравенством
<<?а E9)
и заменим Л на Хк~х° . Тогда
k
I Л -Л К *eAL {Хк~Хо) + uh leAt (Xk~Xo) ~ !]•
Если подставить сюда выражение для I и положить е = 0, то уви-
увидим, что при А—»• 0 правая часть стремится к нулю при фиксиро-
фиксированном положении хк. Таким образом, приближенное решение,
полученное по методу Адамса, сходится к точному решению,
если начальные значения задавать точно и все вычисления произ-
производить точно.
Для интерполяционного метода Адамса рассуждения будут ана-
аналогичны. Формулу записываем в виде
г
где
P« = (-O'SC^ F2)
И
bi= f <« + »...«+t-l)dL m
-1
Как и ранее, находим:
2 r+a!^+il^+i. F4)
i=0
Мажорирующее уравнение примет вид
г
?*+! = ?* + ?* 2 IP«|?* + l-i + *~ ' = *Г+Я 1 *г + 2 | А1г+1. F5)
г=о
Его частное решение равно
О", D _^j
г=0

364 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Характеристическое уравнение в данном случае имеет вид
г
zr = zr-i 4- Lh 2 | Pi | zr-K F7)
Оно имеет единственный корень, заключенный между 1 и +°°. если
только Z-A|po| < 1. Обозначим его через z0- Тогда получаем следую-
следующую оценку:
го— 1), F8)
где через е, как и раньше, обозначено наибольшее из значений
При этом мы считали, что уравнение относительно Уь+i на ка-
каждом шаге может быть решено точно.
Для сравнения двух формул Адамса в смысле точности приведем
уравнения для определения z0 и коэффициенты при hr+ Mr+1/L в том
и другом случае.
Экетрапо л яци онна я формула Адамса
Уравнение z0 Коэффи-
Коэффициент
z = 1 + Lh 0,5
1 + |Lhf + ~ 0,2083
I 4 / I
1 < z0 < 1 + Lh ~ 0,1023
\<zo<\ + ^Lh 0,0523
Интерполяционная формула Адамса
Уравнение г0 Коэффи-
Коэффициент
¦ = l + Lhz r-lj- 0,5
4т- 0,0833
i 0,0357
Lh
24 v.~ , ^--t-5*+1) 0,0186
19) 0,0105

§ 7] ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 365
Как мы видим из этой таблицы, оценки для интерполяционной
формулы Адамса получились лучшими, чем для экстраполяционной.
Это подтверждает, до некоторой степени, факт, обнаруженный нами
лри практических вычислениях.
Совершенно аналогично можно получить оценки и для других
формул, которые нами введены.
4. Устойчивость разностных методов решения дифферен-
дифференциальных уравнений. Вернемся снова к общей формуле A4). Нам
будет полезно иметь выражение вп+к через все предыдущие щ.
Введем обозначения:
X = %<Xfc1; uv=yv— X/v; u,=y, — X/,. F9)
При этом C3) можно записать в виде
р (?)(«« — un)=qn, G0)
где
fc-i
Яп = 2 (% - Х«,) Е> (/„ _ /„) + ijn + 1п. G1)
.7=0
Обращаем внимание на тот факт, что в правой части суммирование
происходит до ./' = &—1, а не до J = k. В этом и смысл указан-
указанного преобразования.
Будем разыскивать решение уравнения G0) в виде
G2)
где zn является решением неоднородного уравнения G0) и удовлет-
удовлетворяет нулевым начальным условиям, а 9П удовлетворяет уравне-
уравнению G0) при дп = 0 и тем же начальным условиям, что и ип — ип.
Таким образом,
1 = z = = Zv =0# G3)
•и, (v = 0, 1, 2 А;—1). G4)
Для отыскания zn введем величины gn (аналог функции Грина),
удовлетворяющие следующим условиям:
0 при i < k,
¦ и G5)
при i = k.
при п^С
при п > 0.
При этом
п+к п+к к
A р ,
0 при »>0 (?6)
gn+k-,4, = 2 gn+k-fi № 2, = 2
0 0
gn+k,4, 2 gn+kfi № , 2 gn+k-v 2 i,+i
*—0 v-=0 v=0 i=0
к п + к
= 2 <*i 2 gn+fc-»2v+i. G7)
{-0 v-0

366 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Введем вместо v новый индекс суммирования, положив v-|-i=:/.
Тогда
п+к к п+к+г
2 gn+k-, Ч-, = 2 <Ч 2 gn+k-j+iZy G8)
Так как Zj = O при _/< k, то нижний индекс во внутренней сумме G8)
можно считать нулем. Верхний предел суммирования по j можно
положить равным n-\-k в силу начальных условий для gn. Поэтому
п+к к п+к п+к к
-чЯч = 2j ai 2ll en+k-j+izj= Zi zj^J aign+k-j+i =
i=0 j*0 j=0 i-0
v=o
Отсюда, в силу
или по G5)
Следовательно,
G6),
"п+к-
получим:
п-'к
-«»+* =
п+к
2jQgr
п
v = 0
п
2g-n
v=0
п+к
t+fc-v9v
+Jfc-v#v +^n+
-*. G9)
(80)
(82)
Отметим тот факт, что для отыскания gn и 6П нам придется
находить решения одного и того же уравнения
p(E)vn = 0. (83)
Поведение решений этого уравнения при возрастании п будет опре-
определяться расположением корней характеристического уравнения
р(*) = 0. (84)
Если, все корни уравнения (84) расположены внутри или на гра-
границе единичного круга, причем корни, лежащие на границе, не
являются кратными, то при любых начальных значениях vn будут
оставаться ограниченными. Если же уравнение (84) имеет корни,
расположенные вне единичной окружности или же кратные на этой
окружности, то имеется бесчисленное множество решений уравне-
уравнения (83), неограниченно возрастающих по абсолютной величине по
показательному или степенному закону при п-+оо. Эти выводы
основываются на представлении общего решения линейного одно-
однородного разностного уравнения с постоянными коэффициентами,
данном в начале параграфа.

§7]
ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ
367
Таким образом, при наличии кратных корней уравнения (84) на
единичной окружности или при наличии корней, расположенных вне
единичной окружности, мы столкнемся, вообще говоря, с неограни-
неограниченным возрастанием |бп| и \gn\. Это вызовет по (82) неограничен-
неограниченное возрастание \ип+к —ип+ч\> а тем самым и \уп+к—Уп+ч\- Такое
явление чрезвычайно невыгодно для вычислительной практики, так
как связано с быстрым накоплением ошибок.
Проиллюстрируем это примером. Будем искать решение диффе-
дифференциального уравнения у=у, удовлетворяющее начальному усло-
условию j/ @) = 1. Решение будет разыскиваться на отрезке [0, 1}
с шагом А ^ 0,1 по разностной формуле
Уп+2 + 4уп+1 - Ьуп = h [4/n+1 + 2/„]. (85)
полученной в § 5. Это — экстраполяционная формула второго по-
порядка, имеющая наивысший относительно h порядок ошибки на
шаге, равный 4. В нашем случае (85) перейдет в
Уп+2 + 3,6уп+1 — 5,2у„=0; уо= 1. (86>
Точное решение уравнения (86) имеет вид
, (87)
где ;?!« 1,105168 и z2zzi — 4,705168 являются корнями квадратного
уравнения
z2 + 3,62 — 5,2 = 0 (88)
и С — постоянная, зависящая от выбора yv Точным решением диф-
дифференциального уравнения будет ех. Возьмем в качестве ух значе-
значение е0'1 с шестью верными десятичными знаками: ух= 1,105171, и
будем последовательно находить уп по (85) также с шестью деся-
десятичными знаками. Результаты вычислений приведены в таблице:
п
0
1
2
3
4
5
6
7
8
9
10
Уп
1,000000
1,105171
1,221384
1,349907
1,491532
1,650001
1,815963
2,042538
2,089871
3,097662
— 0,284254
(Уп-Уп) -Ю»
0
0
19
— 48
293
— 1280
6156
— 28785
135 670
— 638 059
3 002 536
Как мы видим, ошибки чрезвычайно быстро растут. Хотя было
сделано мало шагов, последние значения совершенно не удовлетво-

368 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ 9
рительны. Взяв любую экстраполяционную формулу второго порядка
с худшей ошибкой метода, например формулу Адамса, мы полу-
получили бы значительно лучшие результаты. В данном случае ?\ дает
неплохое представление е°<1п на отрезке [0, 1]. Так при я=К)
разность ей<ы — z^ достигает лишь 77 единиц шестого десятичного
знака. Поэтому казалось бы, что, взяв более грубое значение уи
при котором С в формуле (87) обратится в нуль, мы можем суще-
существенно улучшить результаты. Однако, в силу ошибок округления,
второе слагаемое в (87) рано или поздно начнет сказываться и
исказит результаты. Вычисления по (85) при ух= 1,105168 дают:
п
0
1
2
3
4
5
6
7
8
9
10
Уп
1,000000
1,105168
1,221395
1,349852
1,491787
1,648797
1,821623
2,015192
2,215192
2,507999
2,490202
(eo-ln-yn)>W
0
3
8
7
38
— 76
496
— 2149
10349
— 48396
228 080
Сначала погрешности умеренны, но затем они все быстрее и
быстрее растут. Если бы продолжить наши вычисления дальше, то
погрешности превысили бы значения уп.
В связи с отмеченным явлением будем называть формулу чис-
численного интегрирования A4) устойчивой, если все корни уравне-
уравнения (84) лежат или внутри или на границе единичного круга, при-
причем последние не являются кратными. В противном случае назовем
формулу A4) неустойчивой. Вообще говоря, неустойчивые формулы
дают неудовлетворительные численные результаты и должны при-
применяться с большой осторожностью.
б. Оценка погрешности и сходимость устойчивых разностных
методов решения дифференциальных уравнений. Дальнейшую
оценку будем производить для того случая, когда формула числен-
численного интегрирования A4) устойчива.
Нам необходимо принять некоторые меры предосторожности для
того, чтобы исследуемые функции не выходили из области G, в ко-
которой проводятся все рассуждения. Это потребует некоторых до-
лолнительных предположений. Прежде всего предположим, что А

§ 7] ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 369
настолько мало, что для постоянной Липшица L функции f(x, у)
выполнено неравенство
^ L< 1. (89)
На основании принципа сжатых отображений можно утверждать,
что если
у) (90)
и и(х) — заданная непрерывная функция, удовлетворяющая нера-
неравенству
\Z(x)-u(x)\<r(l-\\\L), (91)
где г было определено ранее (см. начало п. 2), то уравнение
и(х)=у(х) — \/(х, у) (92)
имеет в G одно и только одно решение у (х). При этом
\y—y\<\tt — tt\ + \\\\f(x.y) — f(x. У)\<\и-и\+Щу—у\
(93)
или
\У —У К A — Ix I L)~l | и — и | = Z-! | и — и |. E4)
Необходимо также наложить некоторые ограничения на погреш-
погрешности т]п, 90, 0J, .... 6fc_lf ln. Будем предполагать, что
2 К | + max | % | < е (95)
^ h
и что для любой р-\-\ раз дифференцируемой функции у{х)
(96)
где Мр+1= sup \у(Р+1Цх)\ на [д:0, хо-{-а] и С — постоянная, не
зависящая от у(х).
Обозначим max \uj — и^-| = 0. Так как формула A4) предпо-
лагается устойчивой, то можно найти такую постоянную g, что при
любых п
Ш<& \К\<&. (97)
Сначала получим искомую оценку, не исследуя вопрос о том,
находятся ли ип и уп в области G или нет. Затем мы наложим еще
одно ограничение на е и А, которое обеспечит нам невыхождение
и„ и уп из G.

37Э ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ* ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Начнем с оценки \qn\. По-<71) и (94) имеем:
kv к h 21 h - р*«г Ч- \ & I и - и I +1 vr+\ц<
fc-1
max !«„ —
или если обозначить
то
J9v|<AZ-2 max J «^ - e
Поэтому формула (82) даст
D (Ai2 max |и _
v=0 I |J.<v+fc-l
Bo no (95)
и о (96)
5l
v=0
Следовательно,
max l^-
v=0
p+1
08)
(99)
A00)
. A01).
(Ю2)
A03)
C'ahp). A04)
Наряду с величинами | un—un\ рассмотрим последовательность:
величин wn> определенную рекуррентным соотношением^
п+к-1
( C'p) ). A05)
Возьмем
При этом, очевидно,
-i = g- (s
max \% —
A06)
<107)

§ ?| ОЦЕНКА ПОГРЕШНОСТИ, СХОДИМОСТЬ И УСТОЙЧИВОСТЬ 371
Взяв в A05) п =; 0, получим:
wk = hLigw^! + g (e + Mp+1C'ahp) =±=
= g(e + Mp+1C'ahp)(l +hL2g)>wk_1 A08)
и кроме того, wk >• max | и — и |. Нетрудно доказать по индукции,
что при любых га^О имеет место
u—u\. A09)
Заменим в A05) п -+- k на n-\-k—1. Получим:
7t+ft-2
wn,k_1 = hL2g 2 Wv + ^(e + AIJ,+1C'aA3'). A10)
Вычитая из A05) выражение (ПО), найдем:
w«+* = ««+*-! (l+ALjg). (Ill)
Решение разностного уравнения A11) с начальным условием A06)
имеет вид
+
Итак,
I 2„+* - «n+ft | < g (e + Mp^C'aA3') /х"\ A13)
Искомая оценка получена. Необходимо только обеспечить, чтобы
мы не вышли за пределы области G. Обеспечим для этого выпол-
выполнение условия (91). Это потребует еще одного ограничения. Будем
предполагать, что
ge^a (в + Mp^C'ahp) < г A -1 X | L). A14)
При этом
I», —«,|<«в<вв<'-A—|X|L) (v<ft—1). A15)
Предполагая, что неравенство
] A16)
выполнено при v = A—1, k, .... k-\-n—1, получаем по A13) и
(П4):
\un+k-un+k\<r(l-\l\L). A17)
Таким образом, пока Arv^a, неравенство A16) будет иметь место.
Неравенство (ИЗ) полностью обосновано.
Теперь, использовав неравенство (94), будем иметь:
\Уп+к~ Уп+к\ < g{* + Mp+1C'ahp) eeL*a {I -[ЦЦ-1. A18)
Это и есть окончательная оценка.

372 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Полученная нами оценка является очень грубой. Но и более
точные оценки будут иметь очень ограниченное применение, так как
обычно бывает трудно ограничить входящие в оценку величины.
До сих пор хороших эффективных оценок не имеется.
Отметим одно следствие из полученной оценки. Если в A18)
устремить h к нулю, зафиксировав х и считая п = х . х°, то в пре-
пределе получим:
\Уп—У(*)\<с*- A19>
Это неравенство характерно для устойчивых формул.
Неравенство A18) можно было бы обобщить на случай систем
уравнений, если ввести в рассмотрение вместо абсолютных величин
•соответствующие нормы.
§ 8. Решение краевых задач для обыкновенных
дифференциальных уравнений методом конечных разностей
Замена дифференциального оператора разностным может быть
использована не только при решении задачи Коши для обыкновен-
обыкновенных дифференциальных уравнений, но и при решении краевых задач.
Пусть дано дифференциальное уравнение
у=/(х.у.У), A)
и нам требуется найти его решение, удовлетворяющее одному из
условий следующего вида:
у(а) = а. у(Ь)=$ B)
или
У(а) = а, /0)=р. C)
или
У(а) — ку(а) = а; / 0) + ft^ (*) = р. D)
Будем предполагать, что выполнены все условия, обеспечивающие
существование такого решения.
Разобьем отрезок [а, Ь\ на п равных частей точками
= a-\-ih (/ = 0, 1, 2 п; h = ^^-\. E)
Эти точки хк будем называть узлами. В каждом из узлов заменим
производные через комбинацию значений функции в некоторых узлах
по формулам численного дифференцирования. Получим систему п — 1
уравнений относительно у(х$=у^ Присоединяем к ним уравнения,
получающиеся из краевых условий. Будем иметь п-\-\ уравнений
относительно у0, ух уп. Решаем эту систему и находим при-
приближенные значения искомого решения в узлах ЛГ{.

§ 8] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 373
Применение такого метода требует решения следующих вопросов:
1. Нужно выбрать формулы численного дифференцирования,
достаточно хорошо аппроксимирующие производные и не выводящие
нас за пределы промежутка.
2. Проверить разрешимость системы и указать метод ее решения.
3. Дать оценку точности полученных результатов.
Первый вопрос несложен. В главе 3 мы дали много формул
численного дифференцирования. Нужно только заметить, что при-
применение более точных формул может усложнить систему, а приме-
применение менее точных формул потребует введения большого числа
узлов и тем самым увеличения числа уравнений системы.
1. Метод конечных разностей решения краевых задач для
линейных дифференциальных уравнений второго порядка. Рас-
Рассмотрим, как решаются второй и третий вопросы для уравнения 1)
У" — q(x)y = r (х) (q(x)> 0). F)
Заменим вторую производную в узле х-% выражением
7
При этом получим систему линейных алгебраических уравнений
Уг+1-'2У1+У<-1_д.у.:=г. (/==ii2 я-1). (8)
Если наши краевые условия имеют вид B), то к уравнениям (8)
еще добавятся
Jo-а; уп=$. (9)
Если наши краевые условия имеют вид D), то добавляем к (8) еще
два уравнения:
Полученная система линейных алгебраических уравнений будет раз-
разрешима при любых а, р и /-j, если соответствующая однородная
система имеет только тривиальное решение. Обозначим
(И)
Пусть дана произвольная система п-\- 1 чисел: у0, yv ..., уп;
докажем, что если при любых i 1(уд^Ь, то наибольшим поло-
положительным числом среди у-х может быть только у0 или уп.
1) Здесь q (x) и г (х) предполагаются дважды непрерывно дифферен-
дифференцируемыми. О разностных схемах решения краевых задач для уравнения
(k (х) у')' — q (х) у = г (х) с разрывными k (x), q (х) иг (х) см. Л. Н. Тихо-
Тихонов н А, А. Самарский, ДАН СССР, т. 122, 562—566, 19оо.

374 ПРИБЛИЖЁННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ 1гЛ. 9
Действительно, пусть ук = М — наибольшее положительное число
из Уо> Ук • • • • Уп< такое, что по крайней мере одно из чисел ук+1
или ук_1 меньше М. Если бы наше утверждение было неверно, то
такое ук обязательно нашлось. По предположению
Если заменить здесь ук+1 и yk_t на М, то мы увеличим левую
часть. Таким образом,
М-™+М-ЧкМ = -дкМ>0. A3)
Но это невозможно, ибо qk~^Q и М > 0.
Точно так же доказывается, что если мы имеем систему
чисел у0, у1г .... уп, для которой l(yt)^.O, то наименьшим
отрицательным числом среди них может быть только у0 или уп.
Теперь мы в состоянии доказать, что система (8) при краевых
условиях (9) имеет только тривиальное решение, если а = [3 = г% = 0.
Действительно, если бы она имела нетривиальное решение, то среди
чисел yv ..., уп нашлось бы или наименьшее отрицательное или
наибольшее положительное, а это противоречит только что дока-
доказанным утверждениям. Докажем теперь то же самое для системы (8)
с граничными условиями A0) при а=[3 = /-, = 0.
В граничных условиях A0) будем предполагать, что k^.0 и
kx^>0 и по крайней мере одно из этих чисел отлично от нуля.
Исключая у2 из уравнений
~ 2ft ~ — kyo = O A5)
находим
l + kh
Совершенно так же найдем:
Уп_1= l + k^h yn. U7)
Пусть теперь имеется какая-то система чисел у0, у1 уп> удо-
удовлетворяющая нашей однородной системе, такая, что не все у^
равны нулю. Опять приходим к выводу, что наибольшее положи-
положительное из них или наименьшее отрицательное могут быть только
на концах. Пусть у0 будет наибольшим положительным значением»
Будем предполагать, что h настолько мало, что -к-дг1Аг<1. Из

§ 81 РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ УРАВНЕНИЙ 375
равенства A6) следует, что yi^~y0. Так как в силу нашего пред-
предположения не может быть^у, >^у0, то yi = y0- Но тогда из дока-
доказанных нами утверждений следует, что все ух равны друг другу.
При атом из (8) и A0) при <х = C = /-,^0 следует, что.у,= 0.
Таким же образом доказывался, что среди чисел ух нет наимень-
наименьшего отрицательного.
Решение системы (8) не встречает затруднений, поэтому мы
этого касаться здесь не будем
Перейдем к оценке погрешности. Будем рассматривать только
граничные условия вида (9).
Докажем сначала еще одно утверждение. Если в узловых точ-
точках даны две системы значений у0, уи ..., уп и Ко, Уъ .. ., Yn
такие, что
НУхХ — \ЧУг)\ ('=1.2 Я— 1), A8)
а на границе
Уо>\Уо\. Уп>\Уп\<
то при всех i будет
Уг>\Уг\-
Действительно, из A8) следует:
ЦУх — УгХО: ЦУг+УгХО, B1)
а из A9)
Уо+Уо>О, K+j>0 J
Поэтому, в силу доказанных на стр. 373 —374 утверждений,
имеем B0).
Будем, как обычно, обозначать через ух точное значение реше-
решения дифференциального уравнения F) и через ух — приближенное
решение, полученное путем решения системы (8). Через е, обозна-
обозначаем разность „
*г = Уг~Уг-
Величины s, удовлетворяют системе
где Rx есть погрешность, вызванная заменой второй производной
формулой численного дифференцирования G), и может быть оценена
как
1#,1<-&Ж4, Ж4= max |У*Ч*)|. B5)
Рассмотрим систему чисел т),, удовлетворяющую условиям:
Ъ**-1-9>Ъ = -&М< {i=U2 „-I),}
0 )

376 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
В силу только что доказанного утверждения будем иметь
Мы еще увеличим наши величины, если будем рассматривать значе-
значения, удовлетворяющие системе
%< + Р<-1 = —g-M4 (/=1,2 я-1); ро = Ри=О.B7)
Итак, Р{>-Ге4|. Решение системы B7) находится без труда. Дей-
Действительно, уравнение B7) говорит о том, что вторая разность
величин р{ постоянна. Таким образом, величины р,- можно рассмат-
рассматривать как значения некоторого многочлена второй степени в точках Х{.
Этот многочлен имеет вид
?Mi(x-aHb-x)t B8)
Максимальное значение многочлена B8) на отрезке [а, Ь] дости-
гаегся в точке л: — —\-—, и оно равно
(b - g)«
96 *
Таким образом,
\4\<^{b-af. C0)
Если решение у(х) имеет ограниченную четвертую производную, то
из C0) следует, что е4->0 при А->0.
Недостатком этой оценки, как и всех аналогичных оценок,
является то, что в нее входит четвертая производная от искомого ре-
решения, которую обычно бывает трудно оценить.
2. Метод конечных разностей решения краевых задач для
нелинейных дифференциальных уравнений второго порядка. Перей-
Перейдем теперь к нелинейным уравнениям второго порядка. Этот случай
потребует более громоздких рассуждений.
Будем рассматривать дифференциальное уравнение
У = /(х,у.У) C1)
и граничные условия
аоу (а) — аУ (а) = а; ^ ф) + ру (Ь) = р. C2)
При этом будем предполагать, что f(x, у, z) — непрерывная функ-
функция в некоторой области G пространства х, у, z, выпуклой отно-
относительно у и z, и что а0, alt [30, ^ — неотрицательные числа. В даль-
дальнейшем мы наложим на функцию f(x, у, z), область G и постоянные
Oq, alt po, px некоторые дополнительные ограничения.
Как и ранее, разбиваем отрезок [а, Ь] на п. равных частей
точками:
Ь~а
а = х0 < xt < х2 < ... < Arn_! < хп = Ь\ х( — лг{_! = А =
C3)

§ 8| РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 377
Снова аппроксимируем дифференциальное уравнение в точке дг^.
соотношением
Ук + l—2Ук + Ук-1 fl У& + 1 — Ук-1\ (Ь i 9 „ \\
-ЛХ1 ^1 = J\xk< Ук< 2h / ' — — )'
C4)
а граничные условия — соотношениями:
C5)
Мы получили систему л —J— 1 уравнений относительно (я 4" 1)-го не-
неизвестного Ук. Отличие от предыдущего состоит в том, что теперь-
система, вообще говоря, нелинейна.
Дадим прежде всего итерационный способ решения такой системы.
Итерации будем проводить по схеме
\ C6>
J
Здесь, как и обычно, индекс вверху означает номер приближения.
На каждом шагу нам придется решать несложную систему линейных
алгебраических уравнений. На основании предыдущего следует, что
эта система всегда имеет единственное решение. Получим это реше-
решение в явном виде. Обозначим для краткости
На каждом шаге — это известная величина.
Будем разыскивать укг+1) в виде суммы
Лг+1) = **+<*• C8>
где zk удовлетворяет системе
zk+l - 2zk -f- zk_, - /.*/?) (ft = 1, 2 n - 1),
a tk удовлетворяет системе
( >
Ясно, что если нам удастся найти такие zk и <ft, то ук, полученное
по формуле C8), будет удовлетворять C6).

378 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ {ГЛ. 9
Отыскание tk не встречает затруднений. Действительно, первое
из равенств D0) означает, что вторая разность функции tk равна
«улю. Таким образом, tk должна иметь вид
, D1)
где Сх и С2 — постоянные, которые следует подобрать так, чтобы
<5ыли выполнены граничные условия. Это накладывает следующие
«граничения на С, и С2:
U — U
= о<А — а, -? = а,
(У»
D2)
Получили систему двух линейных уравнений для определения Сх
v С2. Чтобы эта система имела определенное решение, необходимо
и достаточно требовать отличия от нуля определителя
Д==
11 h
Ро Рол + -?
D3>
Это требование мы будем считать выполнен11ым. Тогда, решая си-
систему D2), найдем:
С — 1
ui — т
ч
h
1
I
Pi
h
Ро
а
Р
1
D5)
Для отыскания zft, удовлетворяющих C9), подберем сначала
величины giu(i. k = Q. I, 2, ..., я), для которых выполнены-сле-
выполнены-следующие соотношения:
0 AФ k)
я:
(/=
ft =
0.
1,
1.
2,
2, .
, п.
, я;
—
1).
D6)
D7)
Величины
будем искать в виде
(с/ +d) (eft-4-/) (/<!ft).
(сft -Н d) (в/ + /) (/ > ft).
D8)
D9)

8] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ' ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 379
где с, d, e, f— постоянные, подлежащие определению. Ясно, что
при t Ф k для построенных таким образом величин g^ будут вы-
выполнены верхние из условий D6), ибо g^k являются тогда много-
многочленами первой степени по k. При i=k будем иметь:
gk, k+i — 2«ю + &*_! = (eft + d) (eft +/ + e) — <2{ck + d) (eft +/L-
+ (cA + rf — C)(ek+f) = e(ck + d) — c(ek-\-f) = ed — cf. E0)
Итак, нижнее условие D6) даст
ed — cf=\. E1)
Условие D7) повлечет за собой
)() = Q. E2)
Вторая скобка (ei-\-f) не может быть тождественно равна нулю,
так как тогда было бы gik~Q. Поэтому из E2) следует:
Совершенно аналогично из D8) получим:
р0 (ci + d) (ел + /) + р! (C'+rf)g = [р0(en
или
Из E3) и E5) следует:
= 0.
E4)
E5)
E6)
Будем рассматривать E1) и E6) как систему линейных алгебраи-
алгебраических уравнений относительно ed и с/. Определитель этой системы
равен
J ^о ^ E7)
«o \Po« + -^j -Д-
и по нашему предположению отличен от нуля. Таким образом,
1 —1
1
0
h
— а) +
ЛД
E8)
E9)

380 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Уравнениям E3), E5), E8), E9) удовлетворяет бесчисленное мно-
множество решений. Чтобы закрепить какое-то из них, положим с = а0.
Тогда из E3) следует d = ir, a E8) и E9) дают е^~,
, Ро (* — «)
. Таким образом,
т) (Р°* - Р°й - %¦
F0)
Нетрудно видеть, что ?й является симметрической функцией своих
индексов, т. е. что gik=^ gk%- Таким образом, соотношения D6),
D7) и D8) будут справедливы при замене i на k, и наоборот.
Рассмотрим
Очевидно,
zk+i-2zk
n-l
F1)
itk_l)fV = h2fkr). F2)
т. е. zk, определенные F1), удовлетворяют первому из равенств C9).
Далее,
/Г» = 0,
П-1
F3)
Я«(г) = А2 2 [Poftn + Pi ^"f'"]/Г» = 0.
П-1
т. е. и второе условие C9) выполнено.
Окончательно находим:
4
F4)
Мы можем раз и навсегда вычислить g{k и единообразным процес-
процессом находить последовательные приближения.
Перейдем теперь к исследованию сходимости этого процесса.
п-1
Прежде всего произведем некоторые оценки. Оценим А2 Д] gikf(\
Имеем:
П-1
п-1
п-1
F5)

§ 8] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 381
П-1
Чтобы закончить оценку, нужно вычислить 2lSifcl- Для этого за"
метим, что все gik имеют отрицательный знак. Поэтому
п-1 п-1
п-1
Таким образом, 2 | g» I есть решение уравнения
1. F7)
F8)
). F9)
где и и v—некоторые постоянные. Потребуем выполнения усло-
условий F8). Условие Ro (z) = 0 даст
1
удовлетворяющее граничным условиям
Л0(г) = Л„(г)
Но из F7) следует, что
а условие Rn(z)^0:
G0)
= o. G1)
Итак, а к v удовлетворяют системе уравнений
!И = —РАМ —
Определитель этой системы равен
а0Л — а,
Решая систему G2), найдем:
G2)
и = - ~ [«АД + (ft - 1) (otop! -
G3)
G4)
G5)

382 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Квадратный, трехчлен (Ле2 —|— иЛе —|— х») примет наибольшее зна*
чение при k = —*к-, и это значение равно
 (и2 — Щ.
Подставляя сюда вместо и и v их значения, найдем:
i- (и2 - 4») = ^ [Л2га*Д2 + 2 (оД - а^о) Л» (» — 1) А -4-
+ I» — IJ («ор, - а^ — 4а1р0« (п + 1) АД — Ь^
""
8Л'Д5
8Л'Д
8Л2Д?
a)
где Aj определено в D3). Таким образом,
те-1
А 2 *«/<,"
—с)«Х« max )
где
1 , 1
G6)
G8)
G9)
Нам потребуется еще оценка h ^ Si'k x Slt k 1/('">. Имеем:
1=1
ре,
1
* + i
gu
— ?
2
k + l
"*.*-! fir)
1
— gi. S-l
2
1
2
1ах|/И
те-1
г =1
1 = 1
ft+1
g<,
S + l
те-1
t =1
— ?¦*, S-i
2
ft.» i
Ha
те-1
(80)
(81)
(82)
те-1
i-l
(83)

§ 8] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 383
Таким образом,
г те—1
2 L-i
Отсюда
max V
Si, k+i Si, k—i
2
*
1
2
^ ) 1
If1*-'-1!—*да+*
n — \
n *• u\ ("'oPi aiPo)
(84>
= ~ I (« - 2) Ai - (» - 1) («0P1 - «iPo) К
Окончательно получаем:
\,k+i— Si,k-i f{r)
где
1
¦ aiPo)b (85)
(86)
(87>
Заметим, что в оценках G8) и (86) величины /W не обязательно
должны быть определены функцией f(x, у, z), а могут быть произ-
произвольными заданными числами.
Пусть f(x, у, z) в рассматриваемой области G удовлетворяет
условию Липшица по у и z:
\f(x. у, г) —fix. у, г)\<Ц\у-у\+12\г-г\. (88)
Рассмотрим множество R всевозможных совокупностей п -f- I
чисел у0, ух у„. Будем обозначать такие совокупности {ук\.
Множество R можно сделать метрическим пространством, если опре-
определить расстояние между двумя совокупностями {ук\ и \zk\, как
(89)
+L2 max
1h
2Л
Нетрудно проверить, что все аксиомы метрического пространства
при этом будут выполнены^ В дальнейшем будем рассматривать
только такие совокупности {ук\, для которых
Ук-
Ук+i — Ук-
2Л
G (А = 1, 2 л —1).
(90)

384 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Для каждой такой совокупности формула
= Т 1«Ро 0 — а
-apol +
(91)
определит отображение
элемента [ук), принадлежащего R, в элемент \zk), принадлежащий R.
Если даны две такие совокупности \ук) и [ук]. то в силу G8) по-
получим:
2Л
2Л
)J
2Л
il
— аJX, (Z.t max \y{— yi\-\-
max
0< i <
2Л
Аналогично, используя (86), найдем:
2Л
Таким образом.
2Л
2Л
(94)
Обозначим
Если f < 1, то (95) показывает, что отображение А сжатое. В даль-
дальнейшем мы будем предполагать, что это условие выполнено.
Для применения принципа сжатых отображений требуется еще
выбрать начальное приближение 1уШ и область G такими, чтобы
все последующие приближения не выходили из области G. Для этого
достаточно потребовать, чтобы для {уШ было выполнено условие (90)
и чтобы к области G принадлежали все точки (хк, ук, zk), для ко-
которых
(97)
-г* —
2Л
<(*—в)
1-1
(98)

§ 8] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 385
Действительно, в этом случае неравенства (93) и (94) обеспечивают
принадлежность всех последующих приближений к G.
Итак, при всех вышеуказанных предположениях будет применим
принцип сжатых отображений, и следовательно, уравнения C4) и C5)
имеют решения, удовлетворяющие неравенствам (97) и (98), и эти
решения могут быть получены методом последовательных прибли-
приближений C6) при подходящем выборе начальных приближений [yf>\.
Нам остается исследовать вопрос о сходимости конечноразност-
ного решения к точному решению краевой задачи и об оценке откло-
отклонения этих решений. Сделаем еще два предположения относительно
функции f(x, у, z):
1. Функция f(x, у, z) непрерывна в области G вместе со всеми
своими производными до второго порядка.
2. Краевая задача имеет решение у(х), лежащее в G. Исполь-
Используемое разностное уравнение также имеет решение, принадлежа-
принадлежащее G.
Условимся о некоторых обозначениях. Точное решение краевой
задачи C1) и C2) будем обозначать через <р(л:) и его значение
в узле хк через <ps. Пусть f[x, <р(лг), ср' (х)] = F (х) и F(xk) = Fk.
Через Мк обозначим тах|<р(*) (д:)| при х?[а, Ь]. Приближенное
решение краевой задачи, полученное приведенным выше способом,
будем обозначать через ук (& = 0, 1, 2 «). Наконец, обозна-
обозначим f[xk, yk, у*-"~У*-*) = /&; гк = ук-ук.
Рассмотрим выражение
ЗЪ + Ъ-!-*2?* <ft=1- 2 "-1)-
Разлагая <рй+1 и cpfe_1 по формуле Тейлора относительно точки хк
до членов, содержащих производные четвертого порядка, получим:
s (ft=l. 2 п— 1), A00)
где
Ы<^^4. A01)
Аналогично найдем:
1 Фп t )
д =a — alhp0,
>
A02)
где
j |y. (ЮЗ)
Так как jft удовлетворяет уравнению
=L 2 п-1) A04)

386 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
и граничным условиям C5), то, вычитая, получим.
=l, 2 »—1).
л
A05)
Повторяя рассуждения, при помощи которых мы нашли у%+1> (фор-
(формула F4)), получим:
= Yt lai?iP« — »iPo(* — а) Ро — ai
п-1
]. (Ю6>
Отсюда сразу же следует сходимость. Стремление к нулю при /г->-0
первых двух членов правой части видно непосредственно. Стремле-
Стремление к нулю последнего члена следует из неравенства G8).
Рассмотрим теперь
A07>
Это выражение можно записать в виде
Та 2Л ^ 2Л
Снова применяя разложение по формуле Тейлора, получим:
^-yk + l7hn~X = h2^+4+l7hk~X (*=!• 2 »-
где
Используя A06), найдем:
tk'1
), (Ю9>
(ПО)
*]. (HI)
Если вспомнить неравенство (85), то из A09) и A11) видно, что
?*+'~~У*-1 стремится к <р? при Л ->• 0 (й=1, 2 п—1).

§ 9] метод прогонки 387
Равенство A06) можно использовать и для оценки \ек\. Обозна-
Обозначая через N верхнюю границу функции \f(x, у, z)\ в G из A06),
получим:
IЧ К щ М2 [2а1р1 + ар (Ь - а)\ +
(а
^ф-а?ЦМг A12)
Мы не стремились дать здесь наилучшую оценку. Как и все оценки
такого типа, она мало эффективна, а ее получение требовало бы
громоздких рассуждений.
Конечноразностные методы могут быть использованы и для ре-
решения краевых задач для обыкновенных дифференциальных уравне-
уравнений более высокого порядка. Они могут быть использованы и для
решения краевых задач с другими не рассмотренными здесь типами
граничных условий. При этом обычно не возникает никаких прин-
принципиальных затруднений при составлении конечноразностного ана-
аналога заданной задачи. Но, естественно, возникают трудности при
доказательстве сходимости и оценке погрешности.
§ 9. Метод прогонки 1)
Этот метод разработан в Математическом институте им. В. А. Стек-
лова АН СССР. Проиллюстрируем его на примере линейного диф-
дифференциального уравнения второго порядка:
y"=p(x)y + q(x), A)
где р (х) и q(x)—непрерывные функции, р (х) > 0. Пусть гранич-
граничные условия имеют вид
у'(а)=ск)у(а)+а1, B)
/(*)=Po.y(*)-Hi. C)
Задачу A), B), C) можно, как мы видели, решать конечноразност-
ными методами. Можно было бы применить и следующий прием.
Задаемся произвольными начальными данными
у (а) = а; у' (а) = о^а -\- av D)
лишь бы было выполнено граничное условие B). Находим решение
задачи A), D). При этом, возможно, придется применить один из
численных методов, приспособленных для решения задачи Коши.
!) При написании данного параграфа использована рукопись неопубли-
неопубликованной статьи И. М. Гельфаида и Локуциевского, любезно предоставлен-
предоставленная авторами в наше распоряжение.

388 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Обозначим полученное решение через yl(x). Тогда общее решение
уравнения A) можно записать в виде
у (х) = СЛ (х) 4- C2z2 (х) 4-у, (х), E)
где zx(x) и z2(x) — линейно независимые решения уравнения
z"(x)=p(x)z(x). F)
Так как для искомого решения у(х) должно быть выполнено гра-
граничное условие B), то должно иметь место
Cxz\ (а) + <V? (а) +у[ (а) = Cla0/sl (а) + СяаЛ (а) + аоу1 (а) + «Р G)
или
Cxz\ (а) 4- С^'% (а) = а0 [СЛ (а) 4- <V2 (с)]. (8)
Таким образом, нам надо разыскивать все решения F), удовлетво-
удовлетворяющее условию
z'(a) = aoz(a). (9)
Совокупность таких решений образует однопараметрическое семей-
семейство. Чтобы получить его, достаточно задать каким-либо образом
г(а)=-(Ф0 и найти решение z{x) уравнения F), удовлетворяющее
условиям:
г(с) = Т; ?(с) = аоТ. (Ю)
При этом
A1)
где С подбирается так, что для у(х) выполнено C). Это дает
12
Если, как мы предполагаем, задача A), B), C) имеет единственное
решение, то С должно определиться однозначно.
Теоретически изложенный метод идеален по своей простоте.
Однако он может привести к большим вычислительным погрешно-
погрешностям. Для того чтобы показать это, исследуем поведение решения
z(x) yp-авнения F). Дифференцируя zz', получим:
^| ^4-?2>0. A3)
Отсюда
X
= f |/>«I2(&L-^'2 (?)} Л+г(о)? (а), A4)
(т)) 4-У1 (т))} dij -j- 2г (а) ? (а) (jc-c) 4- ^2 (а).
A5)

§ 9] метод прогонки 389
В нашем случае z(a)z'(a) = a0z2(a). Как и ранее, будем предпола-
предполагать, что Оо>0. При этом формула A5) показывает, что z(x) будет
расти по абсолютной величине вместе с возрастанием х. Следова-
Следовательно, z(x) может быть очень велика при х = Ь, особенно если
нижняя граница р(х) большая. Вследствие этого для получения у(х)
по формуле A1) с достаточной точностью нужно будет сохранять
в уг(х) и z(x) большое количество разрядов.
Метод прогонки и придуман для того, чтобы избежать этих труд-
трудностей. Суть метода состоит в следующем. Формула A1) показы-
показывает, что совокупность решений дифференциального уравнения A),
удовлетворяющих граничному условию B), есть семейство, завися-
зависящее от одного параметра. Будем разыскивать линейное дифферен-
дифференциальное уравнение первого порядка вида
у'(х) = ск)(х)у(х) + а1(х) A6)
такое, что каждое решение A1) принадлежит к числу решений A6).
Естественно, при х = а мы должны получить условие B), и поэтому
а0 (а) = «о, at (a) = at. A7)
Так как A1) должна удовлетворять A6), то
y[-\-Cz' =ck)(x)yl-\-Cck)Cx)z + al(x). A8)
Это тождество, выполняющееся при любом значении С. Поэтому
г' = «о«г; У1 = а0^х)у1-\-а^х). A9)
Дифференцируя первое из этих равенств и используя F), получим:
z" = p(x)z = a'o (х) z + a0 (x) ? = [а'о (х) -+- а* (х)] z. B0)
или
а'о(х) + о?о(х)=:р(х). B1)
Точно так же, дифференцируя второе из равенств A9) и используя
A), получим:
у"х = Р (х) у1 + q (х) = а'о (х) у1 + а0 (дг) у[ + а[ (х) =
= [а; (х) + а^ (х)] yt + а0 (*) at (*) + а[ (х), B2)
или
B3)
Таким образом, наша задача свелась к отысканию функций
и а^д:), удовлетворяющих системе дифференциальных уравнений
первого порядка
j = />(*), 1
j B4)

390 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
и начальным данным A7). Сначала мы интегрируем первое из урав-
уравнений B4), а затем второе. Найдя о^(х) и ^(х), мы можем полу-
получить
^b). B5)
Этим самым мы совершили прямую прогонку, перегнав граничное
условие B) с левого конца на правый. Равенства B5) и C) рассмат-
рассматриваем как систему уравнений для определения уф) и у' ф). Урав-
Уравнения B5) и C) могут совпадать, и тогда краевая задача имеет бес-
бесчисленное множество решений, представляемых формулой A1). Они
могут быть несовместны и тогда краевая задача не имеет решения.
Если же система B5), C) имеет единственное решение, то на пра-
правом конце мы получим данные Коши для уравнения A). Но лучше
использовать не уравнение A), а уравнение A6), находя его реше-
решение на отрезке fa, b\, принимающее при х=Ь полученное нами
значение у(Ь). Этот процесс называют обратной прогонкой.
Исследуем теперь поведение решений уравнений B1) и B3) при
прямой прогонке и уравнения A6) при обратной прогонке. Заме-
Заметим, что уравнение B1) получается из уравнения F), если произ-
произвести замену переменных
X
Г a (X) dx
z=* еа . B6)
Действительно,
z' = ck)(x)z; г" = о? (*)«-+-«;(*)« B7)
и подстановка этих выражений в F) даст B1). Начальные условия
для z, дающие нужное нам решение ао(д:), будут: z(a)= I, z'(а) =а0.
При этом, ао(л:) = — будет представляться в виде отношения выра-
выражений A4) и A5), которые положительны. Если z быстро растет,
то ао(л:) будет быстро убывать. Уравнение B3) для определения at(jc)
линейно и коэффициент при at(x) положителен. Следовательно, его
решение, имеющее вид
х х i
- f а, (а>) dx - (' щ, (х) их я f о„ (tj) йт)
a1(*)=a1e " -М а f ea q{t)(K. B8)
— j ои d (x) dx
благодаря наличию множителя е а не будет быстро расти.
При обратной прогонке мы решаем уравнение A6) при заданном
значении у на правом конце. Это также не даст быстрого роста.

§ 10] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 391
§ 10. Решение краевых задач для обыкновенных
дифференциальных уравнений вариационными методами
В настоящем параграфе мы рассмотрим вариационные методы
решения краевых задач для обыкновенных дифференциальных урав-
уравнений, позволяющие получить приближенное решение краевой задачи
в аналитической форме. Свое название эти методы получили потому.,
что их первое применение было связано с заменой краевой задачи
для дифференциального уравнения некоторой вариационной задачей.
Так, решение краевой задачи
^ f(x), A)
у(а) = а, уф) = $ B)
заменяется задачей об отыскании функции у(х), удовлетворяющей
условиям B) и обращающей в минимум функционал
b
J= f[p (х) У2 -\-q(x)y* + 2f(x)y]dx. C)
a
Если р(х)>0 и непрерывно дифференцируема, a q (x) и f(x)
непрерывны и q(x)^>0, то решение краевой задачи A) и B) суще-
существует и единственно в классе всех непрерывно дифференцируемых
функций, удовлетворяющих B), и обращает J в минимум.
Более общая краевая задача A) и
aoy(a)~i-aly'(,a) = a,
при Gtj ф 0, pj Ф 0 может быть заменена задачей об отыскании мини-
минимума функционала
ь
=f [Р
\- «оУ2 (а) + 2ay (c)J +
E)
в классе всех непрерывно дифференцируемых функций (выполнения
граничных условий можно не требовать).
И в том и в другом случае дифференциальное уравнение является
уравнением Эйлера для вариационной задачи. Идя по этому пути,
можно найти и другие функционалы, для которых минимум дости-
достигается после подстановки в них решения краевой задачи. При этом,
если функционал имеет вид
ь
J=fF(x, у, у' y<»))dx. F)

392 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
то дифференциальное уравнение соответствующей краевой задачи
будет представляться в виде
КЛ+^ +Aг?/> = 0. G)
Однако вариационное исчисление не является единственным путем
для получения функционалов, принимающих минимальное значение
при подстановке в них решения краевых задач. Можно, например,
решая краевую задачу для дифференциального уравнения
= /, (8)
рассматривать функционал
ь
J= Г [L(y) — f\2dx (9)
а
в классе всех функций, удовлетворяющих граничным условиям и
обладающих достаточным количеством непрерывных производных.
Можно заменить функционал (9) более общим функционалом
ь
=f
A0)
где Р(х) — некоторая положительная весовая функция. Ясно, что
функционалы (9) и A0) принимают наименьшее значение, равное нулю,
при подстановке в них решения краевой задачи. Такой способ полу-
получения функционалов, минимизирующихся решением краевой задачи,
иногда называют методом наименьших квадратов.
1. Вариационные методы решения операторных уравнений
в гильбертовом пространстве. Рассмотрим теперь указанные спо-
способы с более общей точки зрения. Пусть Н — некоторое гильбер-
гильбертово пространство и А — аддитивный оператор, определенный на
каком-то всюду плотном в Н множестве На. Назовем оператор А
положительным, если для любого элемента у ? Нд имеет место
(АУ. У)>0. A1)
причем равенство нулю возможно только при у=0. Оператор
называется симметричным, если для любых двух элементов у, z,
принадлежащих Нд, имеет место
(Ay, z) = (y, Az). A2)
Заметим, что для симметричности оператора А в комплексном
гильбертовом пространстве необходимо и достаточно, чтобы

§ 101 РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 39&
скалярное произведение (Ау, у) было действительным числом
для любого у?НА.
Действительно, если оператор А симметричен, то
{Ау, у) = (у, Ау) = (Ау, у), A3>
т. е. (Ау, у) — действительное число. Для доказательства достаточ-
достаточности рассмотрим тождество
4(Ау, z) = (A(y + z), y+z) — (А(у — г), у— z) +
+ i[(A(y + iz), y + iz)—(A(y — iz), y — iz)\. A4>
Поменяв здесь местами у и z, получим:
4(Аг, y) = {A(y + z), y + z) — (A(z— у), z— у) +
iy), z — ly)\. A5)
Если заменить все входящие в A5) величины на комплексно-сопря-
комплексно-сопряженные и воспользоваться свойствами скалярного произведения и
предположенной действительностью (Ау, у), то найдем:
= (A(y+z), yJf-z) — (A{y—z). у —
+ / [(А (у + iz) y + iz) — (А (у — iz), у — te)J. A6)
Из A4) и A6) получаем:
(Ау, z) = (y, Az), A7)
т. е. оператор А симметричен.
В силу только что доказанного положительный оператор
в комплексном гильбертовом пространстве симметричен.
В дальнейшем мы будем предполагать, что наш оператор А
положителен, а если гильбертово пространство Н действительно, то-
дополнительно предположим, что он симметричен.
Рассмотрим уравнение
Ay = f. A8)
где /?Я — заданный элемент и у?НА—искомый элемент. Это
уравнение не может иметь более одного решения. Если бы имелось
два решения ух и у2 (у^фУг)* т0 мы имели бы
—Л) = О A9)
и
(А(у1—у^, у1— л)=*0. B0)
что невозможно, так как А положительный оператор и ух — у2ф0.
Далее, если уравнение A8) имеет некоторое решение ylt то
оно дает функционалу
•/СУ) = (Ау, у) — (y,f) — (/, у) B1)

394 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
минимальное значение. Действительно J(y) принимает только
действительные значения. Возьмем произвольный элемент г?НЛ.
Положим z = ух -\-1. Тогда
J(z)=(Az, z)-(z, /)-(/. z)=(A (Л+О, л+9-(Л-К /)-(/. Л+0 =
= J(y1)+(Al, Л) + Ил. Q + ИЛ t) — (t. /)—(/, t) =
= АЛ) + if, Ay,-f) + (Ay, - f, t) + (At. t), B2)
и так как Ay,—/=0 и (At, t)>0, то
J(z) = J(yJ + (At, t) > J(yJ. B3)
Утверждение доказано.
Обратно, если найдется такой элемент yi?HA, который
дает функционалу J(y) наименьшее значение, то у, будет реше-
решением уравнения A8).
Для доказательства возьмем произвольный элемент г?НЛ и про-
произвольное действительное число X. Тогда yi~\-te?HA и
J(yl-\-lz)^.J(yi). B4)
Но
= (А (у, -1-Х*), у, +lz) —
—l(f, z) —l(z, f) =
,z)+lHAz,z). B5)
•Отсюда
2X Re [(АУ1 — f, z)\ + X2 (Az, z) > 0, B6)
•или
— f,Z)]+-Wz, 2)>0 при I > 0, )
0, )
0. j
2Re КЛу! — /, 2I + X (Аг, 2) < 0 при X <
•Соотношения B7) будут справедливы для любых действительных
X только в том случае, если
Re [(Ay.—f, 2I = 0. B8)
Заменив г на (г и проведя те же рассуждения, получим:
Im[(Ay,—/, 2I = 0. B9)
"Таким образом,
ИЛ — /.*) = 0. C0)
В случае действительного пространства мы вместо B8) сразу полу-
-чим C0). Так как НА всюду плотно в Н, то из C0) следует:
AVi-/=0. C1)
что и требовалось доказать.

§ 10] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 395
Функционалы C) и E) можно было бы получить как раз таким
образом. Так, если
ау
то уравнение A) можно записать в виде
Ay = -f.
Будем сначала рассматривать однородные краевые условия D), т. е.
положим там а. = C = 0. Пусть у и z — две какие-то функции,
удовлетворяющие однородным условиям {4). Тогда
ъ ъ
(Ay, z) = f \i-A~
а
Ь
-+- j qyz dx = —py'z + j py'z' dx -+- j qyz dx =
a a
b
= (—py'z-\-pz'y)
ydx-
Но, в силу D) (при а =C = 0), имеем:
(-py'z+pz'y)\ba = 0.
Таким образом,
ь
(Ay, z) = У* [^ A (pz') + qz] ydx = (y, Az)
a
и оператор А симметричен.
В данном случае функционал B1) примет вид
ь ь
J(y) = (Ay, у) + 2 (у, /) = f [- ±. {ру') _|_ qy] ydx+ 2 Jyf dx =
a a
b r
a + J [p/2+w2+2/vldx =
ь
=—py'y
= J [/»/' +«У2+ 2/ylrf*
Это совпадает с E) при a =C = 0.
Отбросим теперь предположение, что a =C = 0. Обозначим
через z произвольную, но фиксированную, достаточное число раз
Дифференцируемую функцию, удовлетворяющую неоднородным крае-
краевым условиям D), и будем разыскивать у в виде

396 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Тогда ух будет удовлетворять однородным краевым условиям D) и
дифференциальному уравнению
Я
= ? (рУ) -яу~[ж М - Н =/-
Таким образом, ух должна обращать в минимум функционал
/' + q? +b[f-4l № + Н } dx +
¦ РоР (*)?(*) aop (a) ? (a)
н й ^ •
Ho
ь ь
2 / [— Ж (pz/) -sr4z]ydx = — 2pz'y [ + 2 / Ipz'y'
a a
ь
~P (а)у (a) + 2 У [^y + qzy] dx.
a
Поэтому J(y) можно записать в виде
J(y)= J \pG' + z')* + qCy + z
a
ft
- / \pz'% + qz2 + 2fz] dx + ^p (b) [у ф) + г ф)? -
a
— -^ P («) IJ (e) + * (a)P + -^ J
Так как z(x) — фиксированная функция, то отсюда следует, чта
искомое решение задачи A), D) будет минимизировать функционал
ь
•/00 = j [pyli + Qf + yy\dx-\-
f {a) —

§ 101 РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 397
Аналогично можно было бы получить и функционал C). Функцио-
Функционалы (9) и A0) можно рассматривать как частные случаи
/112. C2)
Перейдем теперь к вопросам, связанным с приближенным оты-
отысканием функций, реализующих минимум функционала. Теоретико-
функциональная сущность этих методов состоит в следующем. Нахо-
Находят какую-то последовательность подпространств НА:
Н^сНТс ... сНТа ... сНл, C3)
такую, что задача о минимуме функционала B1) при у^Нд*
решается элементарными средствами (хотя бы принципиально). Такое
решение уп и принимается за приближенное решение задачи. Чаще
всего каждое из подпространств Н^ бывает конечномерным. Если,
например, в Нд имеется счетный базис gv g2, .... gn, ..., то
в качестве Н{д можно взять подпространство, порожденное
gv ft. •••. gn-
При этом приходится сталкиваться со следующими вопросами.
Последовательность приближенных минимизирующих функций ylt
Уг, .... уп, ... такова, что
¦/(Л) S ЛУг) > • • • > ЛУп) > ..•>«. C4)
где через т. обозначено минимальное значение функционала B1) при
У^Нд. Следовательно, существует
lim J(yn) = M^.m. C5)
Нужно подбирать Яд' так, чтобы было М = т. Но даже и при
этом условии нельзя делать вывода, что lim yn существует и
lim yn=y, C6)
где через у обозначена функция, реализующая минимум B1) при
у?НА. Поэтому Hj* нужно выбирать так, чтобы и условие C6)
было выполнено. Наконец, на практике мы всегда ограничиваемся
каким-то решением уп, и следовательно, нам необходимо уметь
оценивать разность между точным решением задачи у и прибли-
приближенным уп.
2. Метод Ритца решения вариационных задач. Посмотрим,
как решаются эти задачи в случае функционала
ЛУ)= / f{x. y,y')dx C7)

398 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
при некоторых краевых условиях. Функцию / будем предполагать
непрерывной. Возьмем какую-нибудь систему функций
У(х\ аи а2 ап), C8)
зависящих от п параметров а1% а2, ..., ап, число которых можно
неограниченно увеличивать и таких, что при всех значениях пара-
параметров в некоторой области они удовлетворяют краевым условиям
(последнее требование не обязательно, если краевые условия есте-
естественны). Зафиксируем п и будем использовать в качестве допусти-
допустимых функций в C7) только функции C8). Подставляя C8) в C7),
получим некоторую функцию п переменных
J=<S>(a1, а2 ап), C9)
и наша задача свелась к отысканию минимума такой функции. Этот
минимум находится обычным образом. Приравнивая нулю частные
производные
.g- = 0 0=1.2 в). D0)
получаем систему уравнений для определения av a2 ап. Пусть
ах, а2, ..., ап будет решением этой системы (условия существова-
существования и единственности решения предполагаются выполненными). Тогда
Уп = У(х; аи а2 ап). D1)
Как мы видели, lim J(yn) существует. Наложим некоторые
та» со
ничения на семейства у{х; аи аг ап), обеспечивающие выпол-
выполнение условия lim J(yn) = т. Для этого достаточно потребовать
«->¦ со
следующее: для каждого г > 0 и для каждой допустимой функции
краевой задачи можно подобрать такое п и такие значения пара-
параметров а\, а*, .. ., а*, что если
/п = у(х;а\, а; <), D2)
то на отрезке [а, Ь]
Действительно, тогда и для функции у(х), дающей точное решение
минимальной задачи C7), можно подобрать такую функцию у*п, что
будут выполнены условия D3). При этом
ь
J{fn)- J(y)= /[/(*• Уп- /»)-/(*• У- У'?х

§ 10} РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 399»
может быть сделано как угодно малым в силу непрерывности /.
Таким образом,
Ъ D5>
где т\ как угодно мало. Тем более
j7i. D6>
(Здесь уп — минимизирующая функция в семействе C8) .) Неравен-
Неравенство D6) и показывает, что J(yn)-> J(y).
Сейчас мы перейдем к одному эффективному способу построе-
построения функций у(х\ at, a2 ап). Нам придется наложить некото-
некоторые дополнительные ограничения на функцию f(x, у, у'). Ограни-
Ограничимся краевыми условиями вида
у{а) = а; у{Ъ) = $. D7>
Как и всегда, будем предполагать, что вариационная задача имеет
единственное решение у(х) в классе гладких функций, удовлетво-
удовлетворяющих краевым условиям D7). Относительно функции f(x, у, у'}
будем предполагать следующее:
1. Для каждого числа М должно существовать такое число R,
что любая функция, удовлетворяющая краевым условиям D7) и
неравенству
6
f f(x, у, y')dx<CM, D8)
а
должна также удовлетворять неравенству
\y\<R; *€[*. ь\. D9)
2. Для каждого числа R можно подобрать такие постоянные
с > 0, d, /»> U что при всех х и у, принадлежащих области G:
а О <&, — #<.у<#, E0)
и произвольном z, —oq <C z <С оо, имеет место неравенство
/С*. У, z)^>>c\z\p+d. E!)
Возьмем произвольную систему непрерывно дифференцируемых
на [а, Ь\ функций <ро(*)- TiM ?«(•*) Для которых выпол-
выполнены следующие условия:
= «Pfc(ft) = O (k=l, 2, ...). E2)
2. При любом п функции <?[(х), <?д{х), .,., <?'п(.х) линейно
независимы.

400 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
3. Для любой непрерывной на [а, Ь] функции F(x) и для
любого е > 0 можно найти обобщенный многочлен
Fn W = fli<P'i (*) + а2< (*) + • • • + ап?'п (х)
такой, что
\F(x)-Fn(x)\<e х?[а. Ь\.
В качестве функции <роС*) можно, например, взять
<Ро (х) = а + jE^(x — а)<
а в качестве функций <?к(х) (fe^l, 2, ...)
<?к(х) = (х — а)"(х — Ь),
или
х — а
E3)
E4)
E5)
E6)
E7)
За функции у(х; av a2, ..., ап), о которых говорилось выше,
будем брать многочлены
yn(x) = yQ(x)-\-a1yl(x)-1[- ... -\-апуп(х). E8)
Очевидно, при любых п и at многочлены E8) удовлетворяют крае-
краевым условиям D7). Подставляя E8) в C7), получим:
2 ап).
E9)
Докажем, что эта функция достигает своего наименьшего значения
при некоторых конечных значениях at. Для этого возьмем какую-
нибудь систему значений а{: а*, а* а* и обозначим
Ф (а*, а* flQ — М. F0)
Ясно, что нам достаточно рассматривать только такие значения а^
для которых функция Ф имеет значения меньшие или равные М.
Тогда, в силу первого условия, наложенного на f(x, у, z), найдется
такое R, что будет выполнено неравенство D9). Но при этом мы
можем ограничиться областью О определенной E0), где выполнено
неравенство E1). В силу этого неравенства будем иметь:
Отсюда
v
/
-\-d\dx. F1)
F2)

§ 10] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 401
ИЛИ
/
/с=1
\ I7
dx J- .
F3)
Применяя неравенство Минковского х), найдем:
Обозначим
Тогда неравенство F4) можно записать в виде
(Ь п
F4)
F5)
1
М2.
F6)
Второй множитель левой части последнего неравенства как непре-
рывная функция Х4 на единичной сфере ( ибо 2 ^* = 1 ) достигает
\ *-i /
там своего наименьшего значения о. Это 8 не может быть нулем,
так как функции у'к линейно независимы. Таким образом, из нера-
неравенства F6) следует:
F7)
Итак, мы получили, что множество тех значений ait для которых
функция Ф не превышает М, образует замкнутое ограниченное мно-
множество пространства Rn. Следовательно, найдется такая система
значений сг-, для которых эта функция принимает свое наименьшее
значение.
Заметим, что для многочленов E8) выполнены условия пол-
полноты D3). Действительно, в силу третьего предположения о функ-
функциях <?/е(х) Для любого е>0 и любой непрерывно дифференцируе-
1) См., например, Л. А. Л ю с т е р н и к, В. И. Соболев, Элементы
функционального анализа, ГТТИ, 1951, стр. 347.

402 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
мой допустимой функции у{х) найдутся такое п и такие ait что
У
- ?; (*) - 2 ак9'к (х)
/с=1
min
in (e, -^).
F8)
Отсюда
— <р0 (*) —
/с=1
a L /c = l J
< е. F9)
Поэтому мы можем утверждать, что litn J(yn) = m-
П •> оо
При наших предположениях о функции f(x, у, z) мы можем
доказать и большее. Покажем, что из последовательности функ-
функций уп (х), минимизирующих функционал C7), можно выделить схо-
сходящуюся подпоследовательность. Прежде всего заметим, что мы
можем предполагать неравенство F2) выполненным для всех п.
Таким образом,
ь
dx < Mv G0)
Поэтому неравенство Гельдера даст нам
\Уп(х1)—уп(хг)\ =
X,
а?,
X,
J |
а?,
где
, Ъ\, ^-\-у=\.
G1)
G2)
Это означает, что последовательность функций уп (х) равностепенно
непрерывна. Она является и равномерно ограниченной, так как R,
определяющее область G, можно считать одним и тем же для всех
функций последовательности. Тогда на основании теоремы Арцеля
мы можем утверждать, что найдется подпоследовательность из функ-
функций уп(х), сходящаяся к некоторой предельной функции у{х):
litn уП{(х)=у(х).

§ 10] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 403
Нот= lim J(yn\ = J( lim .У». 1=./(у). Таким образом, j/(*) =
nf > со х 1/ | nf > со * J х-" г ¦* \ I
Дальнейшие рассмотрения будем проводить для краевой задачи A)
и B) при тех предположениях о р(х), q(x) и f(x), которые были
сделаны ранее. Прежде всего покажем, что в этом случае выпол-
выполнены требования 1 и 2 на функцию f(x, у, z). В этом случае
f(x, у, /)=pW/ + ?Wy + 2/W^. G3)
Пусть J(y) < М. Тогда
ь ь
fp(x)y'2dx^M + 2 f\f(x)\\y\dx. G4)
а а
Обозначим
min p(x) = r; max \y(x)\ = Y. G5)
a>?[b] (i[ Ь]
0,6]
Из G4) следует:
ь ь
/ у'2 dx <^ (- ¦— / | f(x) | dx. G6)
а а
Кроме того, очевидно,
х
у (х) = а + Г / (*) йл:. G7)
а
Поэтому
Ь
К<|«1+/|/(*I<**. G8)
а
Применяя неравенство Буняковского, получим:
1х. G9)
а
Из G9) и G6) следует:
— ay 2-+-L J \f(X)\dx. (80)
а
Преобразовывая это неравенство, найдем, что Y должна удовлетво-
удовлетворять условию
ь \
I — J \f(x)\dx\Y-\-\a\» у——*-<0. (81)

404 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Последнее неравенство будет выполнено только при Y, заключен-
заключенных между следующими двумя числами:
ь
-а)\ f\f(x)\dx\ +2r\a\f\f(x)\dx.
La J a
(82)
Таким образом если обозначить "грез R значение величины (82),
где выбран знак «-)-» перед корнем, то 0< Y ^ R.
Проверка того, что выполнено второе условие, тривиальна.
Достаточно взять следующие значения:
р = 2; c = r; d = — 2R max I/(*)[. (83)
а? 6 [а, Ь]
Таким образом, все предыдущие рассуждения применимы к нашему
случаю.
Но здесь мы можем пойти и дальше. Рассмотрим J(y^) — J(y\
Обозначим
Уп — У = Ч(х). (84)
Тогда
ь
п)-ЯУ) = f[P
Ь
2 ([р(х)у'щ' + q{х)ущ +f(x)ij\dx. (85)
Произведем интегрирование по частям в первом члене второго
интеграла, учтя, что »] (с) = т) ф) = 0. Получим:
ц' dx = [р(х)у'щ]ьа- f [p(x)y'Y -ndx =
'ndx. (86)

§ 10] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОВЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 405
Таким образом,
ь
J(Уп) — J(y)= J[p(x) Щ'2 + Я (х) Щ2} dx —
а
Ь
— 2 Г {[/?(¦*)./]' — я(х)у — f{x)\t\dx, (87)
а
и так как у удовлетворяет дифференциальному уравнению A), то
ь
J(Уп) — J(y)= (\р(х) (Уп — УJ + Я(х)(уп— УJ] dx. . (88)
а
Следовательно,
ь _
/ (Уп—.v'J dx -^ (89)
а
о
\Уп—у\< / \у„~.
Так как У(.уп) — J(y)->-0 при /i-xxi, то мы приходим к заклю-
заключению, что вся последовательность {уп} стремится к у. При этом
неравенство (90) даст оценку погрешности.
В нашем случае функция Ф, минимум которой приходится оты-
отыскивать, имеет вид
где
= Л + 2 2 Акак + 2 2 А&цак, (91)
/С-1 1 = 1 /С = 1
= / [Р (х) ф;2 4- ? W <й + 2/ (л) <р0] d*. (92)
=1.2 я).
(93)
U д) (94)
а
известные постоянные числа.

406 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
Таким образом, для отыскания коэффициентов ак получим си-
систему линейных алгебраических уравнений
= 0 (А=1. 2 я). (95)
Чтобы эта система имела решение и притом единственное, необхо-
необходимо и достаточно, чтобы соответствующая однородная система
имела только тривиальное решение. Но это так и будет в нашем
случае. Действительно, если бы имелась нетривиальная система зна-
значений alt a2, . . ., ап, удовлетворяющая системе
= 0 (А=1, 2 п), (96)
то, обозначая
Фп = «1?1 + «2?2 + • • ¦ + ЗДп (97>
и используя значения Лй, мы получили бы
ь
f[P^)?n9k+^M^n9k}dx = 0 (? = 1,2 я). (98)
а
Умножая каждое из этих равенств на соответствующее ак и скла-
складывая полученные равенства, мы нашли бы
ь
j[pWn+4{x)tn]dx = Q. (99)
а
Равенство (99) противоречит нашему предположению о том, что
функции ср^, <pg, ..., <р/ линейно независимы.
Изложенный нами метод решения вариационных задач был впер-
впервые- предложен Ритцем и поэтому носит название метода Ритца.
Методом Ритца можно решать и краевую задачу D) с нулевыми а
и р. При этом принимаем
?*(*)=(* — а)к(х — Ъ? (А = 2, 3, ...), A00)
а функции ср0 и <рх подбираем так, чтобы при любых с0 и с1 были
выполнены условия
= 0, I
% [<о<Ро Ф) + схЪ. Ф)\ + Рх [с0 ?; (*) + с, <р[ Щ = 0. / (Ш1)
Это возможно осуществить, если взять
=(JC - ^ Iх -ь - 2h+l7*-*>]' A02)

§ 10] РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФ. УРАВНЕНИЙ 407
Случай ненулевых а и C можно свести к случаю нулевых заме-
заменой искомой функции
у(х)=г(х) + Ъ{х), A04)
где б (х) — некоторая функция, удовлетворяющая краевым усло-
условиям D).
3. Понятие о методе Галеркина. Рассмотрим теперь кратко
метод академика Б. Г. Галеркина. Хотя он и не связан по своей
идее с предыдущим, но часто приводит к тем же вычислениям.
Пусть нам требуется решить дифференциальное уравнение
L(y)=f A05)
при некоторых однородных краевых условиях. Опять выбираем
полную систему независимых функций {срл (л:)}, удовлетворяющих
краевым условиям. За уп(х) принимаем
.Уп) 2
и требуем выполнения следующих условий:
б
0 (*=1, 2 я). A07)
Если бы нам удалось так подобрать у{х), удовлетворяющую крае-
краевым условиям, что было бы выполнено
ь
f[L(y)—f\<fk(x)dx = O (* = 1, 2, ...). (Ю8)
то в силу полноты системы функций {cpj(Jc)} отсюда следовало бы,
что у(х) удовлетворяет уравнению A05). В нашем же случае можно
ожидать, что уп(х), удовлетворяющее A07), будет близко к точ-
точному решению у(х) при достаточно больших п. Теория метода Га-
Галеркина более сложна, и мы ее здесь излагать не будем. Заметим,
что если L(y) — линейный дифференциальный оператор, то для
определения коэффициентов получается система линейных алгебраи-
алгебраических уравнений. Эта система совпадает с системой (95) для слу-
случая задачи A), B), если функции ук(х) выбирать как и в предыду-
предыдущем случае. Преимущество метода Галеркина состоит в том, что
не приходится разыскивать вариационную задачу, эквивалентную
краевой задаче.

408 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ УРАВНЕНИЙ [ГЛ. 9
УПРАЖНЕНИЯ
1. Найти решение уравнения
в виде ряда
Jf+1+ ... + апх°+к + •••
2. Методом последовательных приближений найти решение уравнения
/ = У.
удовлетворяющее начальному условию у @) = 1.
3. Пусть для дифференциального уравнения у' =/(*, у) найдены функ-
функции Uo (х) и и0 (х) такие, что:
а) Uo (•*) и и0 (х) определены на отрезке х0 < х < х0 + а;
б) Uo (х0) = и0 (х0) = у0;
B)t/JW-/fet/0W)>0, «о (•«)-/(•«. «(>(•*))< 0 при^0<-«<
¦<лго+й. Тогда, если /(л:, у) — непрерывная функция в области, опреде-
определенной неравенствами
•*о< •*<*<)+я; «о (•*)< У < #о (•*).
и является там монотонно возрастающей функцией у при всяком фиксиро-
фиксированном х, то последовательность, образованная из Uo (x) при помощи ре-
рекуррентной формулы
со
Un = Уо+ jfix, Un-i)dx,
монотонно убывает и сходится к решению уравнения y'=f(x, у), удовле-
удовлетворяющему начальному условию у (хо) = Уо- Аналогично последовательность,
построенная из м0 при помощи рекуррентного соотношения
ип = Уо + //(•*• un-i)
монотонно возрастает и сходится к такому же решению. Доказать.
4. Заменить условие монотонного возрастания функции f(x, у) по у
в предыдущем упражнении на монотонное убывание и исследовать поведе-
поведение введенных там последовательностей функций Un (x) и ип (х).
5. Считая р. малой величиной, найти периодическое решение уравнения
g + «33, = Ма - W g + X sin *
(со, а > 0, f. (а > 0 — постоянные).
6. Исследовать остаточный член формулы Рунге—Кутта при г=2 в пред-
предположении, что выполнены неравенства A38) § 4.
7. Различными численными методами найти решение уравнения

УПРАЖНЕНИЯ
409
удовлетворяющее начальному условию у @) = 1. Решение разыскивать на
отрезке [0, 1] с четырьмя верными значащими цифрами.
8. Различными численными методами найти решение уравнения
rf»y __ 0,0003 Л*у\»
их** ~f~^^V\d~x)
на отрезке [0; 0,75], если начальные условия имеют вид у @) = 1,у'@)=0.
9. Различными численными и вариационными методами найти решения
краевой задачи:
/'-¦
у@) = 1; уA)=е-1.
ЛИТЕРАТУРА
1. Л. В. К а н т о р о в и ч, В. И. Крылов, Приближенные методы высшего'
анализа, Гостехиздат, 1952.
2. Л. В. Канторович, Функциональный анализ и прикладная матема-
математика, УМН, т. 3, вып. 6, 1948.
3. Л. К о л л а т ц, Численные методы решения дифференциальных уравне-
уравнений, ИЛ, 1953.
4. А. Н. Крыло в, Лекции о приближенных вычислениях, Гостехиздат, 1951.
5. Ш. Е. М и к е л а д з е, Новые методы интегрирования дифференциальных
уравнений, Гостехиздат, 1951.
6. В. Э. М и л н, Численное решение дифференциальных уравнений, ИЛ, 1955.
7. С. Г. М и х л и н, Прямые методы в математической физике, Гостехиз-
Гостехиздат, 1950.
8. М. Р. Ш у р а - Б у р а, Оценки ошибок численного интегрирования обык-
обыкновенных дифференциальных уравнений, ПММ, т. 16, вып. 5, 1952.
9. Н. С. Бахвалов, К оценке ошибки при численном интегрировании
дифференциальных уравнений экстраполяционным методом Адамса,
ДАН СССР, 1955, т. 104, № 5, 683—686.
10. А. Д. Г о р б у н о в и Б. М. Б у д а к, О сходимости некоторых конечно-
разностных процессов для уравнений у' =/(лг, у) и у' (х) = /(х, у (х),
у(х — г(х))), ДАН СССР, 119, № 4, стр. 644—647, 1958, или
Б. М. Будак и А. Д. Горбунов, О сходимости некоторых конечно-
разностных процессов для уравнений у' =/(лг, у) и у' (х) =/(*, у (*)>.
у (х — г (х))), Вестник МГУ, № 5, 1958, стр. 23—32.

ГЛАВА 10
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ И ИНТЕГРАЛЬНЫХ
УРАВНЕНИЙ
§ 1. Введение
С дифференциальными уравнениями в частных производных
и интегральными уравнениями приходится встречаться в самых разно-
разнообразных областях естествознания, причем получить их решение
в явном виде, в виде конечной формулы, удается только в самых про-
простейших случаях.
В связи с этим особое значение приобретают приближенные ме-
методы решения различных задач для дифференциальных уравнений
в частных производных, систем дифференциальных уравнений в част-
частных производных и интегральных уравнений или, как часто гово-
говорят, задач математической физики.
В настоящей главе мы и рассмотрим некоторые, наиболее рас-
распространенные методы решения задач математической физики. При
этом мы ограничимся в основном методами решения задач для ли-
линейных дифференциальных уравнений в частных производных вто-
второго порядка с двумя независимыми переменными и линейными
интегральными уравнениями, в которых искомая функция зависит
только от одного независимого переменного. Изложение методов
для случая произвольного числа переменных было бы связано
с очень громоздкими записями, в то время как основные идеи мето-
методов, а также возникающие при их реализации трудности хорошо
усматриваются в простейших случаях.
Что касается нелинейных уравнений, то хотя отдельные задачи
для нелинейных уравнений и были разрешены, однако общая теория
приближенных методов для нелинейных уравнений все еще отсут-
отсутствует. В последнее время численным методам решения задач для
нелинейных уравнений уделяется много внимания, но их разработка
еще не достигла такого состояния, при котором их можно было бы
включить в учебное пособие.
Как и в случае обыкновенных дифференциальных урав-
уравнений, приближенные методы решения различных задач для

& 2] ВВЕДЕНИЕ 411
дифференциальных уравнений в частных производных можно раз-
разбить на две группы:
1) методы, в которых приближенное решение получается в ана-
аналитической форме, например в виде отрезка некоторого ряда, и
2) методы, с помощью которых можно получить таблицу при-
приближенных значений искомого решения в некоторых точках рас-
рассматриваемой области, —численные методы.
К первой группе относится прежде всего метод Фурье решения
краевых задач для дифференциальных уравнений в частных произ-
производных, при применении которого точное решение получается в виде
некоторого ряда, а за приближенное решение может быть принята
сумма некоторого ч юла первых его членов. Метод Фурье решения
классических задач математической физики подробно излагается
в курсе математической физики, и мы на нем совсем не будем оста-
останавливаться. Из методов первой группы мы рассмотрим лишь
вариационные методы решения краевых задач для уравнений в част-
частных производных и близкий к ним метод Галеркина.
Наиболее широко распространенным методом численного реше-
решения задач для дифференциальных уравнений в частных производных
является метод сеток, или метод конечных разностей, а также метод
характеристик решения уравнений и систем уравнений гипербо-
гиперболического типа, который в сущности также является конечнораз-
ностным методом, только в этом методе дифференциальное уравне-
уравнение в частных производных или система таких уравнений предва-
предварительно сводится к эквивалентной ей системе обыкновенных
дифференциальных уравнений, которая и решается разностным ме-
методом. Описанию метода сеток для решения некоторых задач мате-
математической физики в основном и посвящена эта глава.
Особое место занимает метод прямых, который в зависимости
от способа его реализации может быть отнесен как к той, так
и к другой группе методов. В этом методе ищется приближенно
решение дифференциального уравнения в частных производных
вдоль некоторого семейства прямых. При этом вместо дифферен-
дифференциального уравнения в частных производных получается система
обыкновенных дифференциальных уравнений. Если эта система ре-
решается в конечном виде, то мы получаем приближенное решение
дифференциального уравнения в частных производных в виде си-
системы функций, приближенно представляющих искомое решение
вдоль рассматриваемых прямых. Если же система обыкновенных
дифференциальных уравнений решается численными методами, то
и приближенное решение уравнения в частных производных полу-
получается в виде таблицы, и в этом случае этот метод можно отнести
к группе численных методов.
В последнем параграфе главы изложены методы приближенного
решения линейных интегральных уравнений типа Фредгольма и Воль-
терра.

412 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
В силу значительных трудностей, возникающих при приближен-
приближенном решении дифференциальных уравнений в частных производных,
мы ограничимся при изложении из педагогических соображений
только простейшими уравнениями и простейшими задачами для них,
причем во многих случаях не приводятся доказательства сходимости,
а также оценки погрешностей, если даже они существуют. Эт&
отнюдь не означает, что описанные методы неприменимы для реше-
решения других более сложных задач.
§ 2. Метод сеток решения краевых задач для
дифференциальных уравнений эллиптического типа
Метод сеток является одним из самых распространенных мето-
методов численного решения краевых задач для дифференциальных
уравнений эллиптического типа1). При изложении этого метода мы
ограничимся краевыми задачами для линейных дифференциальных
уравнений с двумя независимыми переменными.
1. Идея метода сеток. Идею метода сеток изложим на примере
решения задачи Дирихле для уравнения
д^и , ди , , ди
+ СЛа
где а, Ь, с, d, g, f—функции независимых переменных х и у, опре-
определенные в конечной области G с границей Г. Относительно этих
функций предположим, что они непрерывны в О+Г, а и J поло-
положительны в G+Г, a g неположительна в ней.
Пусть необходимо найти решение уравнения A), непрерывное
вплоть до границы Г, принимающее в точках границы заданные зна-
значения ср, т. е.
«|г=?. B)
где ср — непрерывная функция на Г.
Для отыскания приближенного численного решения этой задачи
проведем два семейства параллельных прямых:
x = xo-\-ih A = 0, ± 1, + 2, ...),
(k = 0, ± 1. ±2. ...).
Точки пересечения этих прямых назовем узлами. Два узла назовем
соседними, если они удалены друг от друга в направлении оси х
или у на расстояние шага сетки в направлении этой оси. Будем
рассматривать только те узлы, которые принадлежат G-j-Г. Те
!) По поводу применений метода конечных разностей в теории уравне-
уравнений эллиптического типа см. обзорную статью О. А. Ладыженской, УМН,
т. XII, вып. 5 G7), 1957, стр. 123—148.

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 413
из них, у которых все четыре соседних узла принадлежат этому
множеству, назовем внутренними. Множество внутренних узлов
назовем сеточной областью и обозначим через G*. Те узлы, у ко-
которых хотя бы один соседний узел не принадлежит к рассматри-
рассматриваемому множеству, назовем граничными, а совокупность их назо-
назовем границей сеточной области и обозначим через Г*. Для каждого
внутреннего узла (i, k) составим разностное уравнение, заменив
в точке (х0 -\- ih, у0 -(- kt) производные, входящие в уравнение A),
разностными отношениями, положив, например,
— U
ОН.)
дх J
1-1, ft.
:*, к)
2h
dyj(i, к)'
21
P
C)
где принято обозначение uik=u(x0-\-ih, yo-\-kl). Обозначая значе-
значения коэффициентов уравнения A) в узле (I, k) через aik, bik, cik,
dik> gik> fik> получим для узла (i, k)
разностное уравнение
luih — ailc
Us г,,,—I
7"
D)
Рис. 26.
Такие уравнения можно записать
для каждого внутреннего узла. Если jj
узел (i, k) является граничным узлом,
то и-гк в этом узле положим равным
значению функции <р в точке Г, бли-
ближайшей к этому узлу, т. е. просто снесем в граничные узлы значе-
значения функции <р из ближайших к ним точек границы Г. Таким обра-
образом, для отыскания значений uiH решения во внутренних узлах мы
получим систему линейных алгебраических уравнений, в которой
число уравнений равно числу неизвестных. Если эта система разре-
разрешима, то, решив ее, получим приближенные значения искомого
решения на конечном множестве точек, являющихся внутренними
узлами.

414 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Сразу же возникает ряд вопросов:
1. Разрешима ли полученная система разностных уравнений к
если разрешима, то какими способами она может быть ре-
решена?
2. Насколько будут близки полученные при этом значения к зна-
значениям точного решения задачи Дирихле в соответствующих точ-
точках?
Можно сразу сказать, что погрешность, получаемая при этом
методе, складывается из трех погрешностей, имеющих разную
природу:
а) погрешность, возникающая в результате замены диф-
дифференциального уравнения разностным уравнением, зависящая от
точности аппроксимации дифференциального уравнения разност-
разностным;
б) погрешность, возникающая за счет сноса граничных условий
с Г на границу сеточной области Г*;
в) погрешность, возникающая в результате того, что решение
разностной системы уравнений, вообще говоря, может быть найдено
только приближенно.
Совокупность погрешностей а) и б) дает нам погреш-
погрешность метода, а погрешность в) есть вычислительная погреш-
погрешность.
3. Можно ли, неограниченно сгущая сетку, получить ре-
решение, сколь угодно близкое к точному решению краевой задачи
для уравнения A), т. е, возникает вопрос о сходимости метода
сеток.
В этом параграфе мы постараемся дать ответы на поставленные
вопросы для некоторых конкретных краевых задач.
2. Аппроксимация дифференциальных уравнений разностными.
Применяя метод сеток для решения краевых задач, мы прежде всего
сталкиваемся с задачей замены дифференциальных уравнений раз-
разностными уравнениями. Эта замена может быть выполнена разными
способами.
Один из способов аппроксимации дифференциального уравнения
разностным заключается в том, что производные, входящие в диф-
дифференциальное уравнение, заменяются линейными комбинациями зна-
значений функции а в узлах сетки по тем или иным формулам числен-
численного дифференцирования. Такой прием был применен при построении
разностного уравнения D) в п. 1. В зависимости от того, какими
формулами численного дифференцирования будем пользоваться, по-
получим различную точность аппроксимации дифференциального урав-
уравнения разностным. Рассмотрим, например, погрешность, получаемую
в результате замены дифференциального уравнения A) разностным
уравнением D). Предполагая, что решение краевой задачи для
уравнения A) имеет непрерывные производные до четвертого

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 415-
порядка включительно, имеем следующие равенства:
и (xj + h, ук) — u(xj— h, ук) _
2h
и (•**. Уй + 0 — « (•**, У и — 0 _
21
| «?(**. У)
h, yy) — 2и (xj, yk) + u(Xj — h, yk)
— 2м (Xj, yk) + и (Xj, yk — l)
/2
(б)
которые легко получить, разлагая левые части по формуле Тейлора
в окрестности точки (xit yk). Используя эти соотношения, имеемi
lUiU = (пгк а"а? + bik «J. + Cik < + dik U'y + SiHU\ <«<, »*) +
«. F)
где
Если ввести обозначения
TO
Таким образом,
- fik ={L(u) — /}(i> fc) -f- Rik = Rikt

416 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
т. е., заменяя дифференциальное уравнение A) разностным уравне-
уравнением D), мы совершаем ошибку, равную R^, которая имеет по-
порядок № относительно шага h (полагая а = — = const).
Если мы возьмем уравнение Пуассона
и квадратную сетку h = l, то при описанном способе замены произ-
производных получим следующее разностное уравнение:
, ft
»-!, ft
f
— l
ik-
,1m
При этом для погрешности аппроксимации Ri k будем иметь оценку
6
A1)
(М.к)
В разностной схеме A0) для узла (/, k)
участвуют четыре соседних узла, располо-
расположенных по «кресту».
Другой способ получения разностных
уравнений состоит в следующем. Для полу-
получения разностного уравнения, аппроксими-
аппроксимирующего дифференциальное уравнение в
узле {I, k), рассмотрим N узлов, располо-
расположенных определенным образом около точки
(/, k). Для простоты записи узел {I, k) будем
остальные рассматриваемые узлы перенумеруем
, N. Составим линейную комбинацию
Рис. 27.
•обозначать 0, а
•числами 1, 2,
<с неопределенными коэффициентами Ср где Uj — значение и в узле j.
Предполагая у функции и наличие п-\-1 производных, разложим Uj
ло формуле Тейлора в окрестности узла 0. Подставим эти разло-
разложения Вчлинейную комбинацию и сгруппируем члены с одинаковыми
-производными от функции и. Получим
N
член*
Заметим, что -[ik линейно выражаются через Су Остаточный член
Qhn+1KMn+1, где |9|^1, К — некоторое число,
•будет иметь вид
«е зависящее от h,
дп+1и
дхпду ' '*
— наименьшая по абсолютной величине разность координат узла 0

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 417
и узлов j (У = 0, 1, 2, .... N). Далее, подбираем коэффициенты с}
таким образом, чтобы правая часть в равенстве отличалась бы
возможно меньше от дифференциального выражения /,(«) в точке 0.
Для этого потребуем, чтобы коэффициенты при производных в урав-
уравнении совпадали бы с коэффициентами при соответствующих произ-
производных в правой части A2):
flo = T2O; *o = To2; 0 = Tll; co=Tlo; do=Toi". ?o=Too.
и, кроме того, коэффициенты при старших производных в A2) до
порядка г B<;/¦<;/г) обращались бы в нуль, т. е.
уг/с = 0 при 2 < i -\- k < г.
Если при этом система уравнений относительно с,- имеет решение,
то мы найдем такие с,-, при которых
Л'
2 = [L («)]0 -f Whr+1
з-о
'AL
A3)
Используя достаточно большое число узлов N, можно получить доста-
достаточно хорошую аппроксимацию дифференциального уравнения в узле 0,
заменяя дифференциальное уравнение раз-
разностным уравнением
N
Рис. 28.
з-о
Этот способ имеет то преимущество, что
можно рассматривать не только прямо-
прямоугольную сетку, но и другие сетки
(треугольную сетку, сетку параллело-
параллелограммов и др.).
Для внутренних узлов, достаточно
удаленных от границы, расположение
узлов, участвующих в линейной комбина-
комбинации для составления разностного уравнения в них, можно и целесо-
целесообразно сохранять. Для узлов, близких к границе, это не всегда
удается. Но этот способ для этих узлов при другой конфигурации
узлов, участвующих в линейной комбинации, часто позволяет полу-
получать разностные уравнения гой же точности. В частности, этот
способ позволяет и граничные условия аппроксимировать достаточно
точно.
Если имеется произвол в выборе решения системы для с3, то
выбирают наиболее простое решение с тем, чтобы получить наибо-
наиболее простые разностные уравнения.
Рассмотрим этот метод на примерах аппроксимации уравнений
Пуассона для разных сеток и некоторых других примерах.
Сначала рассмотрим разностную аппроксимацию уравнения Пуас-
Пуассона, если сетка квадратная с шагом Лив разностном уравнении
Для узла 0 участвуют узлы, помеченные номерами 1, 2, 3, 4 на

418 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
рис. 28. Учитывая равноправие в уравнении х и у и симметричное
расположение узлов, очевидно, имеет смысл искать разностную
аппроксимацию вида
1и0 = соио + с, (и, + и2 4- и3 + и4).
Предполагая у функции а наличие достаточного числа производных
и разлагая щ по формуле Тейлора в окрестности узла 0, будем иметь:
д
u(x0-\-h, y0
, А*
A30
Для того чтобы 1и0 аппроксимировало оператор Лапласа
необходимо потребовать выполнения условий
т. е.
Окончательно получаем:
1и° = 2А« l"i 4- «2 4- «з 4- «4 — 4и0] =
, Аз

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 419
Если в разложении A3) ограничиться разложением по формуле Тей-
Тейлора с остаточным членом в производных четвертого порядка и
положить
дх*ду
то для R будем иметь следующую оценку:
ду<
Заменяя (ДаH через /0 и отбрасывая R, получим разностное урав-
уравнение
аппроксимирующее уравнение Пуас-
Пуассона 0-f-*? = /• причем погреш-
погрешность аппроксимации не превосхо-
ДИТ -g-^4-
Рассмотрим теперь разностную
аппроксимацию уравнения Пуассона,
в которой используются узлы, изо- Рис 29.
браженные на рис. 29. Из тех же
соображений, что и в предыдущем примере, будем искать разностную
аппроксимацию вида
1а0 = соио
4- «2 4- «з 4- «4) 4- сг (а6 4- «6 + ui 4- us)-
Разлагая щ по формуле Тейлора и приводя подобные члены, будем
иметь:
о 1,2
о 1,2
«14- «2 4- «з 4- «4 = 4мо + -2Г «, 4- а^H
+ Ж ИЗ + 28в^. 4- 70«?>, + 28^, +
+ • • ••

420 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
т. е.
Ч = (со + 4с. + *сл) во+ А»(с, 4- 2с,) (и® 4- и$)о +
4(«4 2
(С + 2« К' + «S?) +^("^ + вО-)о +¦
Для того чтобы 1и0 аппроксимировало оператор Лапласа, положим
h2 (с, + 2с2) = 1.
Подберем с2 из того условия, чтобы члены с производными четвер-
четвертого порядка могли быть получены путем дифференцирования опе-
оператора Лапласа. Для этого нужно положить с2 = ^р. Тогда для с0, сх
получим следующие значения:
10_, __2_
Ж [(S + ^)' (^ + «й 4- 2 ^ «¦ + <^
где /? зависит. от производных восьмого порядка и имеет поря-
порядок Л6.
Так как
d% . д"и ,. .
то
6! \дх* ^ дх*ду* ^ ду* )о +
и разностное уравнение
4 {их 4 "а 4 цз 4 ч) 4 ( 4 "в + "? 4 "в) — ^Oцo =
- gH (.5)
дает аппроксимацию уравнения Пуассона с точностью до Л6.
Если при выводе разностной аппроксимации воспользоваться раз-
разложением по формуле Тейлора с остаточным членом, содержащим

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 42?
производные восьмого порядка, то, введя обозначение
дх7ду
ду>>
для остаточного члена, дающего погрешность аппроксимации, будем
иметь оценку
, „ . , 520л6 ..
Пользоваться полученной разностной аппроксимацией уравнения
Пуассона можно только в случае, если функция / задана аналити-
аналитически. Если же она известна только в узлах сетки или имеет слож-
сложное аналитическое выражение, то дифференцирование ее будет за-
затруднительно. Поэтому в этом случае аппроксимацию упрощают,
отбрасывая член с Л6 и заменяя (Д/)о через
В самом деле,
где
max
о
\
дх*
дх*ду
ду*
Рис. 30.
1
Подставляя вместо (Д/)о комбинацию -^ (f1 —)— /2 —(— /3 Ч- /4 — 4/0),
мы отбрасываем члены шестого порядка относительно h и полу-
получаем разностную аппроксимацию
и2 + и3 + и4) + («5 + «е +  + «8) — 2Оио =
? A6)
аппроксимирующую уравнение Пуассона с точностью до Л4.
Рассмотрим теперь разностную аппроксимацию уравнения Пуас-
Пуассона для сетки из правильных треугольников со стороной h (рис. 30).
При составлении разностного уравнения для узла 0 возьмем шесть
ближайших окружающих его узлов 1, 2, 3, 4, 5, 6 и составим ли-
линейную комбинацию
1и0 = 2 ^щ.
Разлагая и^ по формуле Тейлора в окрестности узла 0, будем иметь,
учитывая, что координаты точек 1, 2, ..., 6 соответственно будут
(см. стр. 422).

Iw
V
<M
<M
<M
4-
л
„
>\
¦«!
-|-
H,
i
^
1
H
<N
ч
о
~r
a
•C j
+
^a
a
ii
Ii
О
+
4S
I"»
\
+
a
-j-
-
<N
X
«5
+
a
^|§
-
CM
+
a
IN
Ц
ii
II
a
О
;
a
i™
CM
^-^
V
a
Ц
CM
« I —
+
a
«
(N
-f-
a
-\-
„
+
о
II
II
О
*
I
1
"Is
t „
^a
«|s
1
va
« c.
v H
a
a°
и
II
a'
о
•
a
"^
Iй i
^. Iе4
1
|
a
Its
1
1
+
a
'С I"
|
a
CM
1
— |(N
1
•c
"+"
a3
||
II
о
I
a
' --
101§
is
CN
*
a
ep
|C"
a
a
4-
ii
II

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 423
Учитывая симметрию оператора Лапласа и симметричное располо-
расположение рассматриваемых узлов, можно положить с1 = с2= ... = св,
Тогда
в
lll0 = C0U0 -f С, 2 ui = (С0 + 6С,) Uo 4"
-Н «11 f «> + «й» 4- тпт («S 4- 2«
4- w
Для того чтобы 1и0 аппроксимировало оператор Лапласа, нужно по-
положить
2 ч —*•
откуда
с — — — • с = 2
Итак,
/и0 = -д^- [«! 4- и2 4- "з 4- «4 4- аь 4- "в — 6и0] =
= К' 4- <0о + "пг ("й- 4- ^) «* + «Я 4- /?.
Если разлагать и$ по формуле Тейлора с остаточным членом в про-
производных шестого порядка, то
Уравнение Лапласа Ди = 0 аппроксимируется разностным уравне-
уравнением
"i 4-"а 4-"з 4- 4" «5 4-"е — 6ио = О A7)
с точностью до Л4, а уравнение Пуассона Ди=/ аппроксимируется
разностным уравнением
3 +  4-4-"e — 6«о = -2-/о-т--^-(д/)о A8)
с точностью Л4, а разностным уравнением
-2-/0 A9)
с точностью до h2.

424 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
В заключение приведем пример разностной аппроксимации урав-
уравнения
для случая квадратной сетки с шагом h при выборе узлов, отме-
отмеченных на рис. 31. В силу сим-
симметрии расположения узлов и сим-
симметрии уравнения относительно х
и у можно искать разностную
аппроксимацию в виде
10
12
I ь ЛаЛ I I О лМШ %
г=5 t=9
Рис. 31.
При наличии производных шестого
порядка у функции и разложение по формуле Тейлора дает
2 ¦
4 ¦ 2Ш6/гв
б!
откуда
где
Л*
6!
/г.
Чтобы разностный оператор 1и0 аппроксимировал диффгренциаль-
ный оператор -g^4+2 ^" dy» +1^*"' "уЖН0 ПОТРебовать выполне-

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 425
ния условий
откуда
Таким образом,
- А (их -4- и2 + и4) 4- ^ («6 + «6 + и, -4- «в) 4-
+ i («
где
Ж I 8#A) + 2^C) + ^;з) I <
Следовательно, разностное уравнение
20и0—
+ («в + в10 + «п + 2) = Л4/о B1)
аппроксимирует уравнение B0) с точностью до /г2.
Этих примеров достаточно для уяснения способов построения
разностных аппроксимаций дифференциальных уравнений, и, следуя
им, читатель может построить разностные аппроксимации для дру-
других конкретных уравнений, имеющие необходимую точность. Необ-
Необходимо только помнить, что, строя разностную аппроксимацию той
или другой точности, нужно предполагать, что решение уравнения
имеет необходимое число производных, а это накладывает опреде-
определенные требования на коэффициенты уравнения, на область и на
функции, входящие в краевые условия. Если они таковы, что решение
может иметь производные только до какого-то определенного по-
порядка, то не имеет никакого смысла при решении задачи методом
(¦>ток использовать аппроксимации более высокого порядка, так
ь Ь! нх использование усложнит работу, но отнюдь не улучшит ре-
результата.
3. Аппроксимация граничных условий. Решая методом сеток
краевую задачу для дифференциального уравнения в частных произ-
производных, мы заменяем заданную область О с границей Г, на кото-
которой заданы граничные условия, сеточной областью О* с границей Г*,

426 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
состоящей из граничных узлов. Как правило, граничные узлы не
будут находиться на Г. Поэтому возникает задача замены граничных
условий для дифференциального уравнения граничными условиями
для разностного уравнения, составляемого только для внутрен-
внутренних узлов, даже в случае задачи Дирихле. При других типах кра-
краевых задач условия на границе будут содержать производные иско-
искомого решения, которые при переходе к разностным уравнениям
должны быть заменены разностными отношениями. Таким обра-
образом, почти всегда приходится решать задачу аппроксимации гранич-
граничных условий.
Остановимся сначала на задаче Дирихле, которую мы уже рас-
рассматривали в п. 1. Там был рассмотрен способ аппроксимации гра-
граничных условий, заключающийся в том, что значения искомого ре-
решения в граничных узлах мы задавали равными значениям заданной
функции ср в точках Г, ближайших к этим узлам. Иногда этот снос
выполняют из точки Г, ближайшей к данному граничному узлу,
в направлении одной из осей координат. И в том и в другом слу-
случае мы вносим погрешность, величина которой зависит от близости
границ Г и Г*. Очевидно, что снесенное в граничный узел значение
решения будет отличаться от значения истинного решения краевой
задачи в этом узле на величину порядка расстояния этого узла от
точки Г, из которой происходит снос.
Только в том случае, когда все граничные узлы попадут на Г,
перенос граничных условий делать не нужно, и мы не вносим ни-
никакой дополнительной погрешности. Поэтому сетку целесообразно
выбирать так, чтобы граница Г* сеточной области О* была бы воз-
возможно более близка к границе Г. Для этого иногда целесообразно
отказаться от квадратной сетки, а рассматривать прямоугольную
сетку или треугольную сетку, или какую-либо другую. Если сетка
уже выбрана, выполнен снос граничных условий и методом сеток
найдено приближенное решение во всех внутренних узлах, то по-
погрешность, полученная за счет сноса граничного условия, может
быть уменьшена. Простейший способ уменьшения этой погрешности
заключается в следующем.
По найденным значениям решения во внутренних узлах экстра-
экстраполируем решение в точки границы Г, из которых сносились гра-
граничные значения в граничные узлы. Находятся разности экстраполи-
экстраполированных и заданных значений и в соответствии с ними вносятся
поправки значений в граничных узлах. По этим поправкам нахо-
находятся поправки решения во внутренних узлах путем решения соот-
соответствующих однородных разностных уравнений. Это требует по-
повторных пересчетов.
На рис. 32 изображена геометрическая картина описанного про-
процесса уточнения решения. На этом рисунке изображено сечение
плоскостью параллельной оси и (в пространстве х, у, и), пересе-
пересекающейся с плоскостью хОу по узловой линии, на которой

мм м, мг л
Рис. 32.
м4
$ 21 МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 427
находится граничный узел М. Предположим, что в узел Ж сносится
значение граничной функции tp из точки М, где М — точка пересече-
пересечения узловой линии с границей Г. Пусть во внутренних узлах Ми
Мг расположенных на узловой линии, найденные значения ре-
решения изображаются ординатами MtN°. Экстраполируя по этим
значениям в точку М, получим
новое значение а, изображен-
изображенное отрезком MN0. График
интерполяционного многочлена
изображен пунктирной линией.
Разность экстраполированного
значения и значения ср(/И) изо-
изображается отрезком N№. Так
как полученное экстраполя-
экстраполяцией значение в М больше
<р(Ж), то значение в гранич- _| LJ—L 1 L 1 ± :•—*-х
ном узле М изменяем в сто-
сторону уменьшения, т. е. вносим
поправку N'NU. Находим по-
поправки в каждом внутреннем узле путем решения однородных раз-
разностных уравнений с граничными условиями, равными соответ-
соответствующим поправкам, внесенным в значения в граничных узлах,
и, прибавляя эти поправки к ранее найденным значениям в соот-
соответствующих узлах, найдем новое приближение к искомому реше-
f нию (отрезки NtNt). Снова выпол-
S няем экстраполяцию и т. д.
Этого пересчета можно избежать,
заранее составляя для значений
функции в граничных узлах особые
уравнения, отличные от уравнений
во внутренних узлах. Достаточно
удобный для практики способ со-
ш ставления этих уравнений предло-
-j- жил Коллатц. Каждому граничному
узлу А (рис. 33) соответствует
Рис. 33. точка В, лежащая на пересечении
границы Г с прямой, принадлежа-
принадлежащей сети (узловая прямая), удаленная от А на расстояние 8^ < А,
а также ближайший к А внутренний узел сетки С, лежащий на продол-
продолжении отрезка ВА (предполагается, что сетка достаточно мелкая).
Тогда для узла А можно написать уравнение
-Л»
B2)

428 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Это уравнение означает, что значение иА получается линейной интер-
интерполяцией значений и0 и срв. Получаемая при этом погрешность бу-
будет порядка /г2.
Используя при составлении уравнения для значения и в гранич-
граничном узле большее количество узлов, можно получить более точную
аппроксимацию. Например, Микеладзе при решении задачи Дирихле
/
г}
А
-и*
/
1
/
1
?
t
/
t
/
/
(з
0
1
-л*
/
4
\
h
\
Рис. 34.
Рис. 35.
для уравнения Пуассона предлагает следующие уравнения для опре-
определения значения и0 в граничном узле 0:
h Acf3 -f" ^И4 J ^ Ч\~\- Щ '
л+8 л+;
2 (Л + 8)
(см. рис. 34)
e-f-
A-f-
2(s+
B3)
B4)
(см. рис. 35)
Порядок погрешности будет в этом случае /г3.
Такого типа формулы могут быть получены с помощью второго
способа аппроксимации дифференциального уравнения разностным,
описанного в п. 2.
Рассмотрим теперь аппроксимацию других граничных условий,
встречающихся при решении краевых задач для эллиптического диф-
дифференциального уравнения второго порядка. Наиболее общий вид
линейных граничных условий следующий:
где а, р и ср — заданные функции точки границы Г, -s производ-
производная по нормали определенного направления (например, по внутрен-
внутренней нормали), причем предполагается, что а2-(-р2>0. При а = 0,
[3=1 получим задачу Дирихле, при а=1, р = 0 получим задачу
Неймана. В зависимости от а и р на различных кусках границы Г
условия могут быть разные (на одних кусках заданы значения ре-
решения, на других кусках — значения нормальной производной,
на третьих кусках—их линейная комбинация с переменными

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 429
коэффициентами). В этом случае переход от заданных граничных
условий на Г к условиям на границе Г* сеточной области сильно услож-
усложняется из-за наличия в граничных условиях нормальной производ-
производной. При этом переходе нормальная производная должна быть за-
заменена через разности значений в узлах сетки. Ограничимся слу-
случаем квадратной сетки и укажем простейший способ построения
уравнений для граничных узлов. Пусть 0 — один из граничных узлов.
Перенесем в этот узел нормаль из точки границы Г ближайший к 0.
Всегда можно найти два таких п
внутренних или граничных узла,
что направления проведенные из
узла 0 в них будут образовывать
прямой угол. Тогда, обозначая угол
направления Zt с направлением нор- N
мали через ср0 (рис. 36), будем
иметь:
да
дп
да
да .
-^Sincft,
т
Производную по направлению 1^
приближенно заменим отношением
их — и0
Рис. 36.
—"О
B6)
, а производную по направлению U—отношением . ,
где Ц—расстояние /-го узла от узла 0 (./=!. 2). Тогда будем
иметь приближенное равенство
да ах — а0
и для граничного узла 0 вместо заданного граничного условия
на Г будем иметь уравнение
= ?о. B7)
где Oq, $о, ср0 — значения соответствующих функций в точке гра-
границы Г, ближайшей к узлу 0. При этом мы совершаем погрешность,
заменяя нормальную производную линейной комбинацией значений
функции в узлах, а также перенося нормаль и функции а, р, ср
с Г в узел 0.
Такие уравнения записываем для каждого граничного узла. При-
Присоединяя их к уравнениям для внутренних узлов, получим систему
линейных алгебраических уравнений, в которой число уравнений
равно числу неизвестных и равно числу внутренних и граничных
узлов.
4. Разрешимость разностных уравнений и способы их реше-
решения. Применяя метод сеток для решения краевой задачи для линей-
линейного дифференциального уравнения с линейными граничными

430 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
условиями, мы получаем систему линейных алгебраических уравне-
ний.число которых равно числу неизвестных. Естественно возникает
вопрос о разрешимости этой системы и способах ее решения. Рас-
Рассмотрим эти вопросы для системы D), которая получается при ре-
решении задачи Дирихле для уравнения A) методом сеток при раз-
разностной аппроксимации, изложенной в п. 1 настоящего параграфа.
Эта система имеет вид
, ui + lk — 2игк +u U 2u + u
i + l,k гк +i-l,k _, h
й = aik — -\- bik
_, „ ai+i,ft —a<-i, к , , ui,k+i — ui,k-i ,-„ _ f
-+- Cik 2Л ' ik 27 r-gikaik — Jik'
где число неизвестных u^ равно числу уравнений, т. е. числу вну-
внутренних узлов. Перепишем эту систему в другом виде, сгруппиро-
сгруппировав члены, содержащие одни и те же неизвестные. Получим систему
lUik = Aikui+l, k-\-BikUi-.iik-\-CikUi, k+i-\-DikUiy ft_i — EikUik=fik,
где
л — ^л-^L r —^i*._^ r —
*гк — "I- > °ik — ' ~ik ~~
21
2/ ' №~"""'ft2 ~Г~ /2 Sift-
Drt=i^_"«
Так как мы предполагаем, что а, Ь, с, d, g непрерывны в области
G + Г, причем а > 0, b > 0, g<!0 в G + Г, то при достаточно
малых h, l коэффициенты Aik, Bik, Cik, Dik, Eik будут положительны
во всех узлах сеточной области. Будем предполагать, что это усло-
условие выполнено. В этом случае имеет место теорема (принцип
максимума):
Если Vik — какая-либо система значений в узлах сетка и
для каждого внутреннего узла lvik^-0, то vik во внутренних
узлах О* не могут иметь положительного максимума, а если
во всех внутренних узлах lvik^.O, то vik во внутренних узлах
не могут иметь отрицательного минимума. Исключением
является случай vik = const.
В самом деле, пусть vik? const и во всех внутренних узлах
меет место неравенство lvik^>0. Предположим, что v^k достигает
положительного максимума М в некотором внутреннем узле. Тогда
можно найти такой внутренний узел (i0> k0), в котором Viatko=M
и хотя бы в одном соседнем с ним узле значение vlyk меньше М.
В выражении lvioko заменим vik на М, тогда будем иметь строгое
неравенство
М [А{ kii + BilK +Cik 4- Diiko - EiakJ > 0.
Ho
A + B + Cioko

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 43Г
Таким образом, g.. ~> О, что невозможно. Следовательно, наше
допущение было неверно и первая часть утверждения доказана.
Вторая часть доказывается совершенно аналогично.
Теперь легко показать, что система D) имеет решение и притом
единственное. Для этого достаточно доказать, что соответствующая
однородная система (/^ и все значения в граничных узлах равны
нулю) имеет только тривиальное решение, а это сразу следует
из принципа максимума. Так как если бы решение однородной
системы было отлично от нуля хотя бы в одной точке, то оно-
должно достигать на Г* либо наибольшего положительного значе-
значения, либо наименьшего отрицательного значения, что невозможно,
так как на Г* по условию uik = 0. Следовательно, однородная"
система имеет лишь тривиальное решение, а неоднородная система D)
имеет одно и только одно решение.
Совершенно аналогично можно доказать разрешимость систем
уравнений, которые получаются при решении задачи Дирихле для1
уравнения Пуассона методом сеток при всех разностных аппрок-
аппроксимациях, которые мы рассмотрели в п. 2, а также системы урав-
уравнений, в которой для граничных узлов записываются уравнения по-
способу Коллатца, так как во всех этих случаях для разностных
операторов имеет место принцип максимума1).
Для решения получаемых систем могут быть использованы
методы, изложенные в главе 6. Часто применяют метод простой
итерации или метод Зейделя. Докажем сходимость этих методов
применительно к системе D), дополненной уравнениями Коллатца
для определения значений в граничных узлах. Для применения метода
простой итерации удобней систему переписать в таком виде:
ua=^ai+uk+^.ui_1,k+^ul,k+1+^kui,^-^, B8>
UA =
В этом случае, когда коэффициент g в уравнении A) строго-
отрицателен, а сетка выбрана настолько мелкой, что Aik, Ва, Cik,
?>й> Eik положительны, сходимость процесса простой итерации
и процесса Зейделя доказывается очень просто, так как тогда-
в системе B8) все коэффициенты положительны и сумма коэффициен-
коэффициентов в правой части каждого уравнения строго меньше единицы,.
в силу неравенства 8^ < h, a
Aik + Ва + Cik + Dik — gik = Е№,
т. е.
') Соответствующие рассуждения аналогичны приведенным на стр. 373.

432 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Этого достаточно для сходимости обоих процессов итерации, при-
причем скорость сходимости будет определяться величиной
J«c"
q = max
Л, г, к
(см гл. 6).
Это доказательство не пройдет, если g может обращаться в нуль,
так как в этом случае в некоторых уравнениях сумма коэффициен-
коэффициентов будет равна единице. Поэтому мы приведем отдельно доказа-
доказательство сходимости итерационных методов решения системы B8)
для случая g<! 0.
Начнем с простой итерации. В этом случае последовательные
приближения находятся из соотношений
Aik in)
Bik
Cik
„(»).
.(») }хк
г, А-1 Е™
B9)
а(п+\) _ .
Введем обозначе' ил:
bA+h
г, к
~Чк
Eik
max | а;/ , аА
Cik
Ы:Ь =
; ъ= max
n)\
= M(n\
Назовем граничные узлы узлами первого разряда. Внутренние узлы,
у которых среди соседних имеется хотя бы один граничный узел,
назовем узлами второго разряда. Внутренние узлы (не принадлежащие
предыдущим разрядам), у которых среди соседних имеется хотя
бы один узел второго разряда, назовем узлами третьего разряда
и т. д. Таким образом, все граничные и внутренние узлы мы разо-
разобьем на конечное число разрядов, причем каждый узел будет при-
принадлежать к одному и только одному разряду. Пусть число раз-
разрядов равно т. Тогда из неравенств
«г-1, к Н
а:
in)
I , Dik
(n)
для узлов первого разряда будем иметь неравенство

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 433
для узлов второго разряда — неравенство
. (п+1) I -
|<*ift I <.
< \Aik + В№ + Cft + Dik _m.n i А* Д« С* 5
I ?« I 4ft 4k c-ik Zi
<[1 — 7A— S)
для узлов третьего разряда — неравенство
I 4ft I 4ft 4ft 4ft ^ift
наконец, для узлов т-то разряда — неравенство
откуда будем иметь неравенство
где
0<р = тах{8, 1—ТA—8)
или
и так как р* -> 0 при & -^ + оо, то М{кт)-+0 при k -> + оо и М(п) -> О
при « -> оо, а это означает, что процесс простой итерации сходится.
Рассмотрим теперь сходимость процесса Зейделя в случае, если
g=0. Для исследования сходимости этого метода перенумеруем все
внутренние и все граничные узлы, которые не находятся на Г и для
которых записываются особые соотношения по Коллатцу следую-
следующим образом. За первый узел примем один из граничных узлов,
не принадлежащих Г, или если таковых нет, то один из внутренних
узлов, у которого среди соседних есть граничный узел; за второй
узел примем один из узлов, среди соседних у которого будет пер-
первый узел; за третий примем узел, у которого соседним будет вто-
второй узел, и т. д. Перепишем систему уравнений B8) в порядке
новой нумерации узлов (т. е. искомых неизвестных) и для ее реше-
решения будем применять метод Зейделя. Если мы возьмем фиксирован-
фиксированный узел k и в правой части уравнения для этого узла исключим
последовательными подстановками значения (га-|-1)-го приближения
в узлах предыдущих по номеру, то значение («-)-1)-го приближе-
приближения решения в этом узле можно представить в следующем виде:
«1п+1) = 2 сРиф + 2 bi% - 2 dfh (k = 1, 2 N) C0)
1=1 ;-l г = 1

434 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
(N—число узлов, не лежащих на Г, М — число узлов на Г). Коэф-
Коэффициенты Ck\ bk\ d^u1 не зависят от номера п. Все коэффициенты с$
и Ь$ неотрицательны, так как они получаются сложением и умно-
умножением неотрицательных чисел. Далее, при любом k имеет место
равенство
2^+S^=i- C1)
Это равенство следует из таких соображений. Коэффициенты скг)
и b\i не зависят от граничных значений и правых частей. Поэтому
если положить ср=1, /=0 и за нулевое приближение и^ принять
значения, равные единице, во всех узлах, то при всех k и п будем
иметь и(™)=1, а отсюда и будет следовать равенство C1). Так как
при любом k хотя бы один из коэффициентов Ь^ Ф 0, то 2С^< 1.
N
Пусть [j, = max 2cftJ < !• Если ик решение системы B8), то
к г~1
Вычитая его из равенства C0), получим:
откуда
Отсюда, если ввести обозначение M{n) = sup\ u^—и*|, будем иметь
к
неравенство
а следовательно,
+1)<^(п), или
Так как [i<l, то [i,n+1—>0 при я->сю и M^n+V> —> 0 при я—>оо.
Таким образом, сходимость метода Зейделя для нашей системы
доказана.
5. Оценка погрешности и сходимость метода сеток. Оценим
погрешность, которая получается при решении задачи Дирихле для

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 435
уравнения A) п. 1 методом сеток. При этом будем предполагать,
что решение и (х, у) уравнения
д2и . да , , да , ,
W + C^ + d'dy + ga = f' A>
удовлетворяющее на границе Г области О условию
«|г = ср, B)
имеет в области О ограниченные и непрерывные вплоть до гра-
границы Г производные до четвертого порядка включительно. Для
этого коэффициенты уравнения а, Ь, с, d, g, функции / и ср должны
иметь производные до определенного порядка, а граница Г должна
быть достаточно гладкой. Кроме того, будем предполагать, что
а, Ь, с, d, g удовлетворяют требованиям п. 1 и в каждой точке
области О выполнено неравенство
где р и q — полуоси эллипса с осями, параллельными координат-
координатным осям с центром в некоторой точке (Xj, y0), целиком содержа-
содержащего внутри себя область О.
Пусть эта задача решается методом сеток с прямоугольной
сеткой с шагами It и I по оси х и у соответственно, при этом
во внутренних узлах используется разностное уравнение D), а зна-
значения решения в граничных узлах полагаются равными значениям
граничной функции ср в соответствующих ближайших к ним точках.
Таким образом, обозначая значения приближенного решения задачи
через U{j, будем иметь для них систему уравнений
?A, ft_i—EikUik = fik
для внутренних узлов,
*/* = ?« D)
для граничных узлов, где
л aik i Cik . о агк Сгк . г ** i Чк . }
Aik-JT + - ^" -W W Ь* — -^^ J-
о _** d*. E -2п* . 2b*-gik.
Будем предполагать Ли/ настолько малыми, что А{к, В{к, С^к, Dik, E^k
положительны во всех узлах (/, k). Мы видели (п. 2), что если
функция и(х, у) имеет в О непрерывные и ограниченные производ-
производные до четвертого порядка включительно, то
F)

436 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ {ГЛ. 10
где
| cik\+a*\dik\) Мг),
дЧ
/ !<7>
Если (/0, k0) — граничный узел, а В — ближайшая к нему точка
границы Г, из которой сносится значение ср, то, используя формулу
конечных приращений, получим:
U- ъ «а =
дх
Ъу
или
, Г); Жх = max{|-^
Если ввести обозначение stt для погрешности, т. е.
то для граничных узлов будет иметь место неравенство
Вычитая из уравнения F) соответствующее уравнение D), для
погрешности sik во внутренних узлах получим разностное уравнение
fsrt — Kik \u)- y°z)
Решение системы C2) будем
искать в виде
ik — ik —i— ч ik * \ )
в
где
=0 для внутренних узлов,
= sik для граничных узлов
рис 37. #« = #«00 Для внутренних узлов,
?tt = 0 для граничных узлов.
На основании свойства максимума | т)й | достигает наибольшего зна-
значения на границе сеточной области; таким образом,
Для оценки %ik докажем следующее утверждение:
Если на сетке заданы две системы значений г»у и Уц такие,
что во всех внутренних узлах имеет место неравенство

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 437
а в граничных узлах Vy ~^> \ v^ \, то всюду в сеточной области О*
имеет место неравенство
Vi} >\vi}\.
В самом деле, неравенство IV\j ^ — | /г»у | эквивалентно двум
неравенствам:
I (Уц - f«) < 0; / <ytJ -+- vit) < 0,
а неравенство V^ >-1 vtj | на Г* эквивалентно неравенствам
Vij — %>0; Ку + г»у>0 на Г.
Но в силу принципа максимума и минимума (см. п. 4) Vi} — v{j
и Vtj-\-Vij в этом случае не могут достигать во внутренних узлах
отрицательного минимума, а на Г* они неотрицательны. Следова-
Следовательно, Vij—Vij^-0 и V^-\-Vij ^.0 во всех внутренних узлах, т. е.
j \j\
всюду в О*-)-Г*.
Рассмотрим теперь вспомогательную функцую
с неопределенным пока коэффициентом X > 0. На основании равен-
равенства F)
lWik = [L (W)](i> k) + Rik (W) = (Z. (W) )(t> ky
так как Rik(W) = 0.
Отсюда
0) Г aik ¦ &a
— — 2X | _-|-_
^ ^2 JJ<
« 1 *
*«
Выберем X так, чтобы во всех внутренних узлах имело место нера-
неравенство
P" q* p q
Для этого достаточно положить
max {(a + a»*) M4 + 2 (| с | + a« | rf |) Me}
Й"
minl - I - I -1 ld
в

438 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Тогда на основании доказанного утверждения имеет место нера-
неравенство
в каждом внутреннем узле, так как ?у = 0 в граничных узлах,
a W{j > 0. Таким образом,
max {(а + а?*) -<И4-|-2 (I с |+а2 | d |) Л13}
—X
24
a Lp2 #2 р ?
(Уй — УоJ \ /
?2 /^
max {(a + a'*) M4 + 2 (| с | + a2 | d \) Af8}
24
„,!„[¦-?+*._ i?i_ ill]
G Lp2^?2 P «- J
C4)
В случае уравнения Пуассона и квадратной сетки оценка запи-
записывается значительно проще, так как a = b=\, c = d = 0
C5)
и если вместо эллипса взять круг радиуса R, то
h. C6)
Если для граничных узлов составляются уравнения по Коллатцу
и сетка квадратная, то имеет место оценка
min —4--—ии-_.
X
— УоJ
¦)•
1 я I I/ 14.
Mo = max < 3-5- .
G
C7)
(см. Коллатц, гд, IV, стр. 281).
Из этих оценок следует, что если мы будем неограниченно из-
измельчать сетку, то последовательность решений, получаемых ме-
методом сеток, будет сходиться равномерно к точному решению
задачи Дирихле.
Приведенные оценки имеют тот недостаток, что они содержат
максимумы модулей производных от искомого решения. Они должны
быть определены из дополнительных соображений или получены
приближенно по найденным значениям решения в узлах заменой
производных разностными отношениями.

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 439
На практике для оценки погрешности решения, полученного
методом сеток, часто используют принцип Рунге, заключающийся
в следующем.
Пусть известно, что порядок погрешности решения при исполь-
использовании квадратной сетки с шагом h есть п, т. е. в точке (х, у)
погрешность гд(х, у) может быть приближенно представлена в виде
sh(x,y)^k(x, у) /г",
где k(x, у) от h не зависит. Пусть Uh(x, у) и U2h(x, у) — решения
краевой задачи, полученные методом сеток при шаге h и 2/г со-
соответственно. Тогда, если и(х, у) есть точное решение, то
и (х, у) = Uh (х, у) -|- sft(х, у); и (х, у) = U2h (x, у) -f- s2ft (x, у)
или
Uh — U2h = S2ft — Sft-
Далее, по условию
eft =» к (х, у) hn; e2ft яа к (х, j>) 2"й" яа 2% (х, j>).
Следовательно, ?/д — U2h «к [2П — 1] sft (x, .у), откуда
f)«^=^». C8)
При решении задачи Дирихле для уравнения A) методом сеток,
когда в граничных узлах решение определяется из уравнений
Коллатца, погрешность имеет относительно h порядок га = 2.
Следовательно,
Пример. Найдем методом сеток решение задачи Дирихле для
уравнения Лапласа j-5-Ь -r-j = 0 в квадрате со стороной, равной
единице, при следующих граничных условиях:
и@, _у) = 0; a(l,_y) = sinity; и(х,0) = 0; и(х, 1) = 0.
Возьмем квадратную сетку с шагом h = 0,125.
Используя простейшую разностную схему, получим следующую
систему уравнений для отыскания значений и в узлах сетки:
я,+1, j-M»-i, j + и», j+i + ai, j-i — 4иу = 0 (/, у =1,2 7),
uoj = uio = u% a = 0; Щ = sin ¦KJh (i, J = 0, 1,2 8).
Решение этой системы в общем случае h = — , где га — целое > 0,
найдем с помощью аналога метода Фурье. Будем искать частные
решения этой системы вида
a<ft = cpW sin r ¦Kjh U,J=Q, 1,2 га; г=1, 2 га-1; «=-)•

440 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Это решение удовлетворяет граничным условиям
«&=«$?• = о.
но не удовлетворяет граничным условиям при / = 0 и t = п.
Функцию ср(г) целочисленного аргумента / найдем из условия, чтобы
были удовлетворены уравнения для внутренних узлов. Подстановка
дает
(cpWj+cp^j) sin лг/А+срС'") [sin лг (/+1) A+sin лг (/— 1) Л—4 sin лг/Л]=
= [cpW х -1- cp^j — 2 B — cos лгЛ) cpf] sin лг/Л = О
или
ср^ _|_ ^ _ 2 B — cos лгЛ) ср<Я = 0 (/ = 0,1,2 п).
Общее решение этого однородного разностного уравнения
имеет вид
где Хг>1 и V, 2 — корни характеристического уравнения
X2 —2B —cosritA)X+l =0.
а Лг и Вг — произвольные постоянные.
Таким образом,
4} = (ЛГХ*, 1 + BrK, 2) sin лс/й.
Решение системы разностных уравнений, удовлетворяющее всем
граничным условиям, будем искать в виде
uij = 2 (Лхг 14- ВГК, 2) sin лтуА,
где постоянные Лг, Вг(г =1, 2 п—1) подберем так, чтобы
были удовлетворены граничные условия при / = 0, i = n. В нашем
случае из граничных условий имеем:
2 (Л- 4- 5Л sin лг/Л = 0; 2 (V?, i + 5rX" 2) sin rnJk = sin *№•
r-l r=l
Функции sin лг/Л образуют на множестве {0, 1,2 л} полную
и
ортогональную систему функций, т. е. 2 sin лгу A sin /и/А = 0
при г Ф I. В нашем случае это дает
Аг-\-Вг = 0 (г=1,2 л—1).
Л1Х?>1-|-В1Х?>11=1,
Х?>2 = 0 (г =2, 3, .... п— 1),

§ 2] МЕТОД СЕТОК РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 441
откуда
Л1
(л = 2, 3 и—1)
, - X
12
— Л12
sin те/А
(/, у = 0, 1,2 и).
В нашем случае и =8. Ниже приведена таблица значений Иу для
/ = 0,1,2 8 и j = 0, 1, 2, 3, 4. Значения му при у = 5, 6, 7, 8
не приводятся, так как «у и точное решение и(х, у) симметричны
относительно прямой _у = 0,5 = 4Л. (Значения иц даны в единицах
четвертого десятичного знака.)
\ 1
у\
0
1
2
3
4
0
0
0
0
0
0
1
0
137
253
331
358
2
0
295
545
713
771
3
0
498
920
1203
1302
4
0
777
1435
1876
2030
5
0
1174
2169
2834
3067
6
0
1749
3232
4223
4571
7
0
2591
4787
6255
6771
8
0
3827
7071
9239
10000
Если при той же сетке применить более точную разностную-
аппроксимацию оператора Лапласа
>\j-
6/1*
4- at_i, J
то получим следующую систему уравнений для и^-:
4 («1+1, J+«i-l, i+«l, j+i+'«i, j-l) +
+ («i + l, j+i + «l-i, j+l + «»-l, y-l + «i+l, ,j-l) — 20ay = О'
(Л У =1.2 7),
a<y=«io=aiR = O, ugj=smi:jh (/, y = 0, 1,2 8).
Точно так же, как и раньше, можно показать, что решение это*,
системы имеет вид
fill
/,y = 0, 1.2 8),

442 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где \хи и [х12 — корни уравнения
5 — 2 cos nh
+10
2+cos „ft ^+1=0-
Таблица значений этого решения приведена ниже:
ч
0
1
2
3
4
0
0
0
0
0
0
1
0
134
247
322
349
2
0
288
532
695
752
3
0
487
900
1176
1273
4
0
763
1409
1841
1993
5
0
1157
2138
2793
3024
6
0
1732
3201
4.86
4527
7
0
2578
4764
6224
6737
8
0
3827
7071
9239
10000
Точное решение поставленной задачи Дирихле имеет вид
. . sh гсу .
Таблица его значений в узлах сетки приведена ниже:
\
»\
0
1
2
3
4
0
0
0
0
0
0
1
0
134
247
323
349
2
0
288
532
696
753
3
0
488
901
1177
1274
4
0
763
1410
1843
1995
5
0
1158
2140
2796
3027
6
0
1734
3204
4180
4531
7
0
2581
4769
6231
6744
8
0
3827
7071
9239
10000
Приведем еще таблицу отклонений полученных приближенных
решений задачи от значений точного решения во внутренних узлах
сетки (в единицах четвертого десятичного знака):
;\
1
2
3
4
Простейшая схема
1
3
6
8
9
2
8
13
17
18
3
10
19
26
28
4
14
25
33
35
5
16
29
38
40
6
15
28
37
40
7
10
18
24
27
Уточненная схема
1
0
0
— 1
0
2
0
0
— 1
— 1
3
— 1
— 1
— 1
— 1
4
0
— 1
— 2
— 2
5
— 1
— 2
— 3
— 3
6
— 2
— 3
0
— 4
7
— 3
— 5
— 7
-7
Из этой таблицы видно, что уточненная схема дала значительно
лучший результат. Если относительная погрешность результата,
полученного в простейшей схеме, достигает 2,5%, то при уточнен-
уточненной схеме она не превосходит 0,3%.

§ 3] МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 443
§ 3. Метод сеток решения линейных дифференциальных
уравнений гиперболического типа
В этом параграфе мы изложим метод сеток решения основных
задач для дифференциальных уравнений вида *)
, дЪ ,дЪ , ди , .да
L ab^c + d
где a, b, с, d, g, /— заданные функции переменных х и у и ab > О
в рассматриваемой области плоскости х, у. Для определенности
будем считать а и b положительными.
Мы рассмотрим решение двух основных задач:
1. Решение задачи Коми, заключающейся в отыскании решения
и{х, у) уравнения A) в области О{_у^0}, удовлетворяющего
начальным условиям:
Я.,
= ф(лг) (— оо < х < + оо), B)
у=о
где ср и ф—заданные функции переменного х.
2. Решение смешанной задачи, заключающейся в отыскании
решения и (х, у) уравнения A) в области ОЦЗ^л:^")-. .У^-Oj,
удовлетворяющего начальным условиям:
и\у=о=<?(х); ¦?- =ф(х) (РО<7) B0
и некоторым условиям на прямых х = ф и х = f. Мы ограничимся
тремя типами условий на этих прямых:
краевое условие первого рода
), C)
краевое условие второго рода
ди
0. D)
краевое условие третьего рода
(У) (У>0), E)
где Ф, W, F, 8 — заданные функции переменного у.
!) О применении метода сеток к более общим уравнениям гиперболического
типа см. цитированную на стр. 411 обзорную статью О. А. Ладыженской,
а также статью С. К. Годунова «Разностный метод численного расчета раз-
разрывных решений уравнений гидродинамики». Матем. сб., т. 47 (89): 3, 1959,
271—306.

444 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Если на обеих прямых х=$ и х = -]¦ заданы краевые усло-
условия первого рода, то мы будем говорить, что имеем первую крае-
вую задачу; если на обеих прямых заданы краевые условия второго
рода, то будем говорить, что имеем вторую краевую задачу, и,
наконец, если на обеих прямых мы имеем краевые условия
третьего рода, то будем говорить о третьей краевой задаче. Часто
встречаются и такие задачи,
j'5
J-3-
J'O
0
(UL
1--4 F-3l*-2i*-11=0 М /Ч? ЬЗ 1=4
Рис. за
когда на прямых х=$
и х = -)¦ задаются условия
разных типов.
1. Метод сеток для
решения задачи Коши.
Проведем два семейства
параллельных прямых:
х = Ш (/=0,±1, ±2, ...);
У = П (У=0, 1,2),
т. е. покроем полуплоскость
у^-0 сеткой прямоуголь-
прямоугольников со сторонами Ли/
по осям хну соответственно. Вершины прямоугольников назовем
узлами сетки. Узлы, расположенные на прямой у=0, несущей
начальные данные, назовем граничными узлами. Для каждого
внутреннего узла (/, J) составим разностное уравнение, аппроксими-
аппроксимирующее дифференциальное уравнение A) в этом узле, замени»
входящие в него производные разностными отношениями:
ди и•, ч ¦ — и• ди и- •_,. — и^
дх ~ ^~2Л ~' ду~ ~ 21
гг, 1-1
где иу=и(/й, у7). Получим разностное уравнение
lUxi ^= пхл • '¦ гт; ' Ьи —'
ы»+1,1~а1-1,,
2/г
_¦_ j
Г "ij
i. j+l — ui, j-l
или
где
ijui+hJ + Dijui_hj + Ециц =
Ь,,
hi
2/
21 ' ^ ~~ Л* ^ 2Л
2а,, 2b,
j G)
* G'>
• (8)

3]
МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ
445
Из этого уравнения видно, что если сетка настолько мала, что
во всех узлах Ац Ф 0 (Лу < 0), то, зная значения решения в узлах
(у—1)-го и у-го горизонтальных рядов, можно найти решение во
всех узлах (у —f- 1)-го горизонтального ряда.
Для того чтобы найти приближенное решение задачи Коши,
необходимо знать значения решения на двух начальных рядах у = 0
и У = 1. Их можно найти из начальных условий одним из двух
следующих способов.
Первый способ. В начальных условиях B) заменим про-
разностным отношением «*i ~ «<о t Тогда для
!/ = 0
изводную
ду~
/
определения значений в узлах первых двух горизонтальных рядов
будем иметь:
= ср (/Л) =
(9)
или
Второй способ. Привлечем еще один горизонтальный ряд
ди
J = —1 и производную ^—
заменим разностным отношением
L —«г,-1
21
из начальных условий B) будем иметь:
¦¦1 — «*, -1 _.,,.
«10 = 9t-
21
Значения и{, _1 нам не нужны. Исключим их, используя разностное
уравнение для узла (I, 0), считая, что уравнение A) удовлетворяется
и на начальной прямой:
Получим:
или
«1,1
о) «1. 1 = /
, о
-i, о + ?!о«ю =
го
Таким образом, значения решения на первых двух рядах будут
¦определяться следующим образом:
«ю =
[/
ю
A0)
Второй способ в некоторых случаях предпочтительнее, так как
в этом случае мы имеем лучшую аппроксимацию начальных условий.

446 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Особенно простые соотношения получаются для дифференциаль-
дифференциального уравнения
дЪ _дЪ _ f ,
дх* д^ —J u '
в случае квадратной сетки /г = /. В этом случае разностное урав-
уравнение имеет вид
"i.j+i — «f.y-i — «f+i.j + Щ-uj = — h2fij< 01)
а для вычисления значений на первых двух рядах будем иметь:
при первом способе
при втором способе
Погрешность аппроксимации. В результате замены
дифференциального уравнения A) разностным уравнением G) и на-
начальных условий B) условиями (9) или A0) мы вносим погреш-
погрешность, которую назовем погрешностью аппроксимации (или ио-
грешностью метода). Предполагая у решения и (х, у) задачи Коши
существование ограниченных производных до четвертого порядка
включительно и используя разложение решения по формуле Тейлора
в окрестности узла (/, у), точно так же, как и в случае эллипти-
эллиптических уравнений (см. § 2), получим:
-П)\ = \Lu —/\{1,л
где'
*Ч = ? 1аЛ'] ~ *« ,*'«?° + КС + 2Л* uV>' A5>
а и I, и I обозначают k-t производные от и(х, у) в некоторой
точке, отличной от узла (/, у), а а. = -г. Если ввести обозначение
Что касается погрешности аппроксимации начальных условий,
то в первом способе аппроксимации начальных условий по фор-
формулам (9) первое начальное условие не вносит никакой погрешности,
а второе начальное условие вносит следующую погрешность:
«i,i-"io _(ди\ ,/>_,!. i А~»_,,, , ,

§3] МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 447
(и",— значение второй производной в некоторой точке). Таким
зом,
«го = Т.: «*! = ?» + ' Oh + ri) • (^)
г{ = ^ и |г,|<-^-Л18. A7)
При втором способе аппроксимации начальных условий имеем:
образом,
где
где
Далее,
<С;
где /?й имеет вид A5) с у=1. Исключая и»,_ь как прежде,,
получим:
" 1
где
или
~
(ТО)
A8>
A9)
Для уравнения A') при a=l эта оценка будет иметь вид
Выбор сетки. Если мы хотим получить методом сеток реше-
решение, сколь угодно близкое к точному решению задачи Коши для
гиперболического уравнения, то нельзя произвольно выбирать со-
соотношения шагов сетки по осям хну. Для иллюстрации рассмо-
рассмотрим решение задачи Коши для простейшего дифференциального-
уравнения гиперболического типа
с начальными условиями
= ?(*);
ди
ду
(.— оо < х < оо)

448 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
методом сеток. Будем использовать прямоугольную сетку с шагом h
по х и I по у. Пусть / = а/г. В этом случае будем иметь разност-
разностное уравнение
luu = -
tizh^ = Q
ИЛИ
«1-
Зная значения решения в узлах первых двух горизонтальных рядов,
можно последовательно вычислить значения решения на втором,
третьем и т. д. рядах. При этом значения решения в узле S(i, j)
¦будут определяться начальными данными на отрезке оси х, вы-
высекаемом прямыми, выходящими из этого узла и образующими
с осью х углы, тангенсы которых равны ± а. Треугольник, обра-
образованный этими прямыми, назовем треугольником определенности
разностной схемы. Если через тот же узел провести две выходя-
выходящие из него характеристики до пересечения с прямой у = 0, то
лолучим еще один треугольник — треугольник определенности
дифференциального уравне-
уравнения. Известно, что решение
и(х, у) задачи Коши для диф-
дифференциального уравнения в
узле S(l, J) будет полностью
определяться начальными дан-
данными на основании последнего
треугольника. Пусть шаг / по
9
\
\
Рис. 39.
оси у больше h, т. е. а > 1.
Тогда треугольник определен-
определенности разностной схемы це-
целиком содержится внутри
треугольника определенности
дифференциального уравнения
(рис. 39). Покажем, что в
этом случае при постоянном а
¦и при /г, стремящемся к нулю таким образом, чтобы точка S была
все время узлом сетки, значения решения в узле S, получаемые
методом сеток, могут не сходиться к значению истинного решения
задачи Ко_ши в этой точке. Это просто показать следующим образом.
При указанном способе стремления к нулю h треугольник опре-
определенности разностной схемы все время остается неизменным и при-
приближенное решение в этой точке при любом h будет целиком опре-
определяться начальными данными на отрезке CD, Если мы будем
изменять начальные данные на отрезках АС и DB, то на решения
разностных уравнений в точке 5 это изменение совершенно влиять
не будет, а значения решения задачи Коши для дифференциального
уравнения будет существенно зависеть от этих изменений. Следова-

§ 3] МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 449
тельно, в этом случае мы не можем говорить о сходимости реше-
решений, получаемых методом сеток, к решению задачи Коши для диф-
дифференциального уравнения. Отсюда вывод, что для сходимости
последовательности приближенных решений, получаемых мето-
методом сеток при постоянстве отношения а = -г, при h ->• 0 необ-
необходимо выполнение условия а^1, т. е. треугольник определен-
определенности дифференциального уравнения должен совпадать или содержаться
внутри треугольника определенности разностной схемы, имеющего
ту же вершину.
В общем случае треугольник определенности дифференциального
уравнения становится криволинейным, но и в этом случае для схо-
сходимости необходимо выполнение условия, чтобы треугольник опре-
определенности дифференциального уравнения содержался бы внутри
треугольника определенности разностной схемы. Это требование
налагает определенные требования на соотношение шагов, т. е. на
выбор сетки. При некоторых требованиях гладкости коэффициентов
и начальных функций указанное выше условие является и доста-
достаточным для сходимости последовательности решений, получаемых
методом сеток, к точному решению задачи Коши для дифферен-
дифференциального уравнения A).
К вопросу выбора сетки мы еще вернемся в дальнейшем уже
в связи с исследованием устойчивости разностных схем (см. § 6).
2. Оценка погрешности и сходимость метода сеток для не-
неоднородного волнового уравнения. Оставляя в стороне общий
случай, рассмотрим оценку погрешности решения задачи Коши для
неоднородного волнового дифференциаль-
дифференциального уравнения, получаемого методом
сеток:
дх% ду*
с начальными условиями
A0
\
\
\
\
\
(-оо<*<оо)
\
\
\
для случая квадратной сетки l = h. Разностное уравнение в этом
случае имеет вид A1). Мы его перепишем в более удобной форме:
В левой и правой частях уравнения A Г) входят разности значе-
значений и в узлах, соединенных на рис. 40 пунктирной линией. Значе-
Значения решения на первых двух горизонтальных рядах определим

450 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
с помощью равенств A3):
1
2
Используя AГ). будем иметь следующие равенства:
— h2 Jj /i-v, j-v-1.
0
j-s
Суммируя их почленно, получим:
1-2
}-2 j-i-a
2l о
а_0 v = 0
где
= si~s2 — s3,
l-l 1-2
2 о
^ " ¦ ~ 1 1 • .V, 7 .
B0)
j-2 5-2-a
^1 ^1
Сумма Sl содержит лишь значения решения и в узлах первого гори-
горизонтального ряда, отмеченных
на рис. 41 жирными точками,
г S2 — значения решения и в
узлах нулевого горизонталь-
горизонтального ряда, тоже отмеченных
жирными точками. Сумма S3
содержит значения правой
части / в узлах сетки, отме-
отмеченных крестиками. Обозначим
через Vij значения точного
решения задачи Коши в узлах
сетки, т. е. Vij = u{ih, jh),
а под иц будем понимать зна-
значения решения, полученные
методом сеток. Через гц обо-
обозначим разность «у — v^, т.е.
погрешность приближенного решения. Докажем, что вц по абсо-
абсолютной величине не превосходит некоторой постоянной
0
У
s
Рис. 41.

§ 3] МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 451
умноженной на А2. Будем предполагать, что задача Коши имеет реше-
решение с непрерывными и ограниченными производными до четвертого
порядка включительно. Мы видели, что для точного решения 1)ц
имеют место равенства
*«« = /у + Яу. A4')
где | Яц | .^ -g- M4 или
hi „
j
где
|г*|<^-Ж4 + -^Ж3. A9')
Вычитая из (И) и A3) почленно соответствующие равенства A4')
и A0'), получим для погрешности si3- систему уравнений
ыц = — RfJ = — ^-еуж4, ]
. = — ri-
B1)
Воспользовавшись явным представлением решения разностной си-
системы B0), будем иметь:
1-2
а ^-а j-ъ-а
j j <x*=0 v=0
B2)
Все слагаемые второй суммы нули; первая сумма содержит j сла-
слагаемых, каждое из которых не превосходит -г^-7И4--)--—Ж3; третья
сумма состоит из —- слагаемых, каждое из которых по абсо-
абсолютной величине не превосходит единицу. Таким образом,
Если узел (/, J) имеет координаты (д:0, у0), то jh = y0. Отсюда
Л2 Л2
14} I < lo- (М4А + 2Ж3) у0 + -тк- У20М .
При фиксированных х0, у0 и А —»¦ 0 погрешность гц в этой точке
стремится к нулю как А2. Это означает, что последовательность
решений задачи Коши, получаемая методом сеток, сходится к точ-
точному решению задачи.

452 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
3. Метод сеток решения смешанной задачи. Метод сеток
решения задачи Коши для уравнения A) с небольшими изменениями
может быть применен и для решения смешанной задачи. Рассмотрим
сначала первую краевую задачу:
Найти решение уравнения A) в области О {C ^ х.
удовлетворяющее начальным условиям
ди
0
К},
и 1„„<>=
ду
и граничным условиям
(о < у <
B')
C)
Отрезок [р\ у! можно с помощью линейного преобразования пере-
переменного х свести к отрезку [0, 1], поэтому в дальнейшем мы будем
полагать C = 0, т=1.
Проведем две системы параллельных прямых:
x = ih (i = 0, 1, 2
., п; п = —
y = jl (j = 0, 1, 2 т; ml <; К <
и точки пересечения их назовем узлами сетки. Узлы, лежащие на
прямых х = 0, л: = 1, у = 0, назовем граничными, а лежащие
внутри области О — внутренними узлами.
Для каждого внутреннего узла, так же
как и в случае задачи Коши, напишем
разностное уравнение G), аппроксими-
аппроксимирующее дифференциальное уравнение A)
в этом узле. Значения искомого решения
в узлах нулевого горизонтального ряда
и во внутренних узлах первого ряда
найдем с помощью начальных условий
по формулам (9) или A0), значения же
решения в граничных узлах, лежащих
на прямых х = 0 и л: = 1, определим из
граничных условий, положив
Цу = ф1 UI) = %\ uni = *2 (У/) = %¦
Тогда, используя уравнение G), мы можем найти последовательно
приближенные значения решения во внутренних узлах второго ряда,
затем в узлах третьего горизонтального ряда и т. д., т. е. сможем
вычислить значения решения во всех узлах сетки.
Если граничные условия заданы на прямых х = 0 и х = 1 на
отрезках разной длины, то решение может быть найдено в узлах
сетки, отмеченных на рис. 43 жирными точками. Заметим, что
в первой краевой задаче, если предполагать, что значения граничных
функций Ф1 и Ф2 в граничных узлах вычисляются точно, то граничные
./
А.
1
У
-*•
h
i
Рис. 42.

§ 3]
МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ
453
условия не внесут дополнительной погрешности по сравнению
со случаем задачи Коши.
Рассмотрим теперь вторую и третью краевые задачи. Для того
чтобы не повторять рассуждений, будем рассматривать случай, когда
при х = О и х =з 1 заданы условия
ffe Ы =Рг{У) [0<Jf<n. D')
i
т. е. третью краевую задачу, так как, полагая bt (у) = 82 (у) = О,
получим как частный случай и вторую краевую задачу. Если для
решения задачи используется такая же сетка, как и в случае первой
краевой задачи, то в этом случае значения
в граничных узлах, расположенных на пря-
прямых х = О и х = 1, не могут быть непо-
непосредственно определены из граничных усло-
условий. Для этих граничных узлов нужно
записать разностные уравнения, аппрокси-
аппроксимирующие дифференциальные соотношения
на границе.
Аппроксимация граничных условий может
быть выполнена следующим образом. Про-
Производные
ди
дх
ди
дх
х-1
в граничных
узлах @, у), (га, J) заменим соответственно
конечными разностями
Z
хч
ч-Х
цц-'
un,—un-l.j
Рис. 43.
h h
Тогда для граничных узлов (О, Д (га, j), используя условия D'),
можно записать следующие разностные уравнения:
4- \juoj =
h
B3)
Легко видеть, что погрешность аппроксимации граничных условий
в этом случае будет первого порядка относительно А. Поэтому
начальные условия также достаточно аппроксимировать с этой точ-
точностью, т. е. для отыскания значений решения в узлах первых
двух горизонтальных рядов можно воспользоваться равенствами (9').
Итак, для определения приближенных значений решения в гранич-
граничных и внутренних узлах сетки имеем систему уравнений
¦Aijui, Я-1 + ?i?"i,j-l + CijUi + 1, i + DijUi_Uj -4- EijUij=fij
A</<га—1; 1<У<т). G')
uij + Uqj (8VA — 1) = fiFtf, itnj\\-\- bvh\ — м„_ i,; = hF4
d<y<m). B3')
«»=<№ «ii = ?i + % (/ = 0, 1, 2, .... ra). (9'>

454 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
С помощью уравнений (9') мы найдем значения решения во всех
узлах первого и нулевого горизонтальных рядов, включая и узлы
@, 1), (га, 1); из уравнений G') найдутся значения решения во всех
внутренних узлах второго горизонтального ряда, а с помощью урав-
уравнений B3') найдем значения решения в граничных узлах второго
горизонтального ряда. Далее переходим к третьему горизонтальному
ряду и т. д.
Более точную аппроксимацию граничных условий можно полу-
получить, заменив входящие в них производные центральными разностями.
Это можно сделать двумя способами *)•
Первый способ. Кроме рассматриваемых узлов, привлечем
еще узлы —1 к п-\~1 вертикальных рядов (см. рис. 44) и будем
аппроксимировать граничные условия в узлах @, у) и (га, у) соот-
соответственно разностными уравнениями
UU UUunj = F2j. B4)
Для исключения значений m_i,_,- и un+Uj используем разностные
уравнения, аппроксимирующие дифференциальное уравнение в узлах
@, J) и (га, Д т. е.
щ j = fnj.
Подставляя в них m_i,_,- и un+lij из уравнений B4), получим:
AOjun, i+1 + BOjuOl j-.i + (COj + DOj) uij + (Eoj + 2hbijDnj) uOj = |
= /oi + 2ADoiFw. !
-\- Dnj) un_ltj + (Enj- 2kZ2)Cnj)X
X unj = fnj — 2hCnjF2j. J
Так как аппроксимация граничных условий в этом случае имеет
порядок А2 (в предположении, что уравнение A) имеет место и
на границах х = 0 и х=1, а также предполагая, что решение
можно гладко продолжить за эти прямые), то естественно и началь-
начальные условия аппроксимировать с точностью до А2, т. е. использо-
использовать формулы A0) для uiQ, uu A</<га). Для определения зна-
значений решения в узлах @, 1) и (га, 1) поступим следующим
образом.
!) Кроме этих способов, можно для улучшения аппроксимации граничных
условий воспользоваться идеей, описанной в разностном методе решения
краевой задачи для обыкновенного дифференциального уравнения на стр. 373.

¦§ 3]
МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ
455
Запишем уравнения B5) для узлов @, 0) и (га, 0), т. е. просто
положим в них у'=0:
Ax)"oi + воо«о, -1 + (соо
ю
«оо =
(Сп0 + Dno) «п-1, 0
и, используя аппроксимацию второго начального условия, с по-
помощью центральных разностей
1 — цо. -1 ,
21 —
un0 = fn0- 2hCn0F20,
ого
21 ™
исключим mOi _j и мП; _j. Получим:
(Аоо + ^оо) «01 = /оо + 2/Воо'Ь +
+ 2AD0DF10 - (С,,, + Doo) 9i — (?
«»i = /„о + 2гЗД« - 2ACn0F20 -
— (cno + On0) <Pn-i — (?no —
CnO) cpn.
Окончательно получим следующую систему уравнений для отыска-
отыскания значений решения во всех внутренних и граничных узлах:
AjUi, j+i + Bi}uit j_i
«0, j+l
+ (E
oj
.Д. J + l + BnjUn, }-l
И„_ь _; +
ni) Mni = fnj - 2hCniF2j,
{Aoo + Boo) «oi =
+ 2AD00F10 -
(An0 + BnQ) unl = fnQ
— (cno
Doo) cp0.
_! — {Ем — 2hb20Cn0) cpn,
«ii= /it-0 -f Б
Используя ее, можно последовательно находить значения решения
в узлах первого ряда, затем второго ряда и т. д.
Второй способ. Будем рассматривать сетку, сдвинутую
на у в направлении оси х (см. рис. 45). При таком выборе сетки
граничные узлы @, j) и (га, j) уже не будут лежать на прямых

456 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
x = Q и х=1. Граничные условия D') будем аппроксимировать
разностными уравнениями
a\i — uoi
I
ul3 + uoj =
I
"!' $ _1_ » nj ~Г П li j _
Г °2j § — 2i'
B7)
Очевидно, мы снова имеем аппроксимацию второго порядка относи-
относительно А, поэтому и начальные условия нужно аппроксимировать
с такой же точностью, т. е. для вычисления значений мй, utl исполь-
использовать равенства A0). Таким образом, окончательно получим сле-
следующую систему разностных уравнений:
B8)
(AiQ +
Нужные нам для счета значения сро> ?»• Фо> Фп можно получить
с помощью экстраполяции или вообще с помощью продолжения
B + Ъ1}[) ulf - B -
A <*<«— 1; l<7<m).
-h
-t
У
0
t
3
ni
n
n+1
1=0
х=о
Рис. 44.
'П-1
Рис. 45.
функций ср и ф за пределы их области определения, сохраняя нуж-
нужную гладкость. Значения приближенного решения на истинных гра-
границах л: = 0 и х=\ могут быть после решения системы B8)
найдены с помощью интерполяции. Система B8), как и во всех

§ 31
МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ
457
предыдущих случаях, решается последовательно, т. е. находятся
значения сначала в узлах первого горизонтального ряда, затем
в узлах второго горизонтального ряда и т. д.
4. Другие разностные схемы. Мы рассматривали простейшие
разностные схемы. Методами, изложенными в § 2, можно построить
множество других разностных схем, которые будут с различной
точностью аппроксимировать дифференциальное уравнение A), на-
начальные условия B) и в случае смешанной задачи граничные усло-
условия. Все схемы можно разбить на два типа: явные схемы и неявные
схемы. Явными схемами называют такие схемы, что при любом у
в каждое из уравнений, связывающих значения искомого решения
на горизонтальных рядах у", у—1 у — т, входит лишь одна
точка ряда у", так что значение решения в каждом узле у'-го гори-
горизонтального ряда можьо вычислить независимо от его значений
в других узлах этого ряда (исключая граничные узлы). Неявными
схемами называют такие схемы, когда для определения значений
решения в узлах у'-го ряда при известных значениях решения во всех
предыдущих рядах нужно решать систему уравнений, связывающих
значения решения в узлах у'-го ряда. Все рассмотренные выше схемы
являются явными схемами. Приведем пример простой неявной раз-
разностной схемы для простейшего гиперболического уравнения
Lu = ir^ — S = °. B9>
причем будем для простоты рассматривать квадратную сетку
с шагом h.
Будем строить разностную аппроксимацию дифференциального
оператора Lu в узле (/, у), используя значения функции и в семи
Hj
ii(h
а.
-nit,
Hit
j)
jib
+tj+>)
Рис. 46.
узлах, изображенных на рис. 46. Предполагая у функции и(х, _у>
существование непрерывных производных до четвертого порядка
включительно, разложим функцию по формуле Тейлора с остаточ-

458 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
ным членом в производных четвертого порядка. Будем иметь:
д . д \ . № ( д . д
д \2
+)" + 4+)
, ди . h? diu №> д*и
Составим линейную комбинацию
с неопределенными коэффициентами с0, cv ..., с6 и подберем
их так, чтобы после подстановки разложений в правой части
. ди ди д^и
исчезли функция и и производные -^—, -^—, -^—^—, а члены со
вторыми производными давали бы оператор Lu. Для этого нужно
лотребовать, чтобы с0, ct c6 удовлетворяли системе уравнений
& 6 = О,
— c3 — с4 • =0,
+ С3 — С4 + С5 — С6 = 0,
— сэ + с4 =0,
= -р ,
-+- С4 4- СЪ + С6 = — — .
Добавим pine одно уравнение

§ 3]
МЕТОД СЕТОК РЕШЕНИЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ
459
Тогда, решая систему, получим для с0, cv c2 св следующие
значения:
_ 2 _ _ _ __1_. _ 2_
При этих значениях коэффициентов после подстановки в 1щ^ раз-
разложений по формуле Тейлора и приведения подобных членов
получим:
4- ^ [^i + R2 + R, + Я4 - 4 (Я5 + л,)].
Отбрасывая члены с R{ для уравнения -г-^
разностную аппроксимацию
-^0, получим
< -1,
i_1)=0, C0)
погрешность которой будет порядка А2.
Используя указанный способ и привлекая большее количество
узлов, можно построить разностные аппроксимации как для диф-
дифференциального уравнения B9), так и для общего уравнения B),
имеющие больший порядок точности, причем в зависимости от вы-
выбора системы узлов получим явные или неявные схемы. Например,
набор узлов, изображенный на рис. 47, даст явную схему, а набор
узлов, изображенный на рис. 48, даст неявную схему.
(и
(и
Jfi,
(U
+1)
J)H
-1)
-г)
2J)
H
(H
JlH
H
M
(I.
a.
m,
{Ф
/>//
M
>V-2)
Рис. 47.
Рис. 48.
Нужно заметить, что разностные аппроксимации высокой точ-
точности для дифференциального уравнения можно применять только
в том случае, если заранее известно, что решение имеет производ-
производные нужных порядков. Кроме того, чтобы не потерять выигрыш
в точности решения, который мы хотим получить, применяя раз-
разностную аппроксимацию высокого порядка точности для дифферен-

460 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
циального уравнения, нужно использовать аппроксимации начальных
и граничных условий такой же точности.
Помимо этого нужно всегда помнить, что не всякая разностная
схема может быть использована для практического счета, если
даже при выборе этой схемы имеет место сходимость последова-
последовательности решений, полученных с помощью ее, при неограниченном
измельчении сетки к точному решению задачи, так как схема может
оказаться непригодной из-за резкого накопления погрешности при
счете. Здесь мы приходим к понятию устойчивости разностных
схем, которое будет подробно изложено в § 6.
Пример. Найдем методом сеток решение задачи
и(х, 0) = ср(л:) = 0,2л: A—.
sin
ди
= 0,
2/=0
Для решения применим квадратную сетку с шагом А = 0,05. Зна-
Значения искомого решения uiQ и utl (j = 0, 1, 2 20) находим
по формулам:
"io — <Pi = ?(»*).
Для отыскания приближенных значений на последующих горизон-
горизонтальных рядах пользуемся уравнением
Результаты приведены в таблице (в единицах четвертого десятичного
разряда):
\. х,
У г \^
0
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
и (хи 0,5)
i
0
0
0
0
0
0
0
0
0
0
0
0
0
0,05
15
28
50
66
74
76
70
58
42
21
— 1
0
0,10
56
65
94
124
142
144
134
112
79
42
— 1
0
0,15
116
122
139
170
194
200
186
155
112
57
0
0
0,20
186
190
198
209
228
236
221
186
133
70
— 2
0
0,25
265
264
260
256
251
249
236
199
144
74
0
0
0,30
340
335
322
302
277
251
227
194
140
74
— 2
0
0,35
405
398
377
343
302
255
209
168
124
64
— 1
0
0,40
457
447
419
377
321
260
196
139
92
49
— 2
0
0,45
489
478
447
397
335
262
190
120
64
26
— 2
0
0,50
500
489
456
405
338
265
186
115
54
13
— 2
0

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 461
Значение решения при л:>0,5 не приведены, так как решение
симметрично относительно прямой х = 0,5. В последней строке
приведены значения точного решения задачи при _у = 0,5. Сравнение
последней и предпоследней строк показывает, что метод сеток дает
очень хорошее совпадение с точным решением.
§ 4. Метод характеристик численного решения гиперболических
систем квазилинейных дифференциальных уравнений
в частных производных
При изложении метода характеристик мы ограничимся случаем
гиперболических систем двух и трех квазилинейных уравнений пер-
первого порядка и одним квазилинейным гиперболическим дифферен-
дифференциальным уравнением второго порядка с двумя независимыми пере-
переменными х).
1. Уравнения характеристик системы квазилинейных диф-
дифференциальных уравнений первого порядка. Рассмотрим си-
систему п дифференциальных уравнений в частных производных пер-
первого порядка
7-1
где a-ij, bij, С;— заданные функции переменных х, у, и1, и2 «я —
непрерывные и непрерывно дифференцируемые в некоторой области
изменения своих аргументов. Такие системы называют квазили-
квазилинейными.
Пусть иг(х, у), и2(х, у) ип(х, у) — некоторое непре-
непрерывно дифференцируемое в области О плоскости х, у решение
системы A), а С—некоторая гладкая кривая без кратных точек,
расположенная в области G. Поставим такой вопрос: можно ли по
значениям решения иу(х, у), иг{х, у) ип(х, у) на кривой С,
используя систему A), найти на кривой С значения частных произ-
ВОДНЫХ Pi =-faT' <li = -fy-t
Значения частных производных pit qi (/=1, 2, ..., п) на кри-
кривой С связаны п соотношениями
п
2 (aifPj + biflj) = ct (/=1.2 я), B)
3=1
!) По поводу применения метода характеристик к решению уравнений
гиперболического типа см. также статью И. М. Г е л ь ф а н д а, Некоторые
задачи теории квазилинейных уравнений, УМН, т. XIV, вып. 2 (86), 1959,
87—15&

462 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
получающимися из системы A), и я дифференциальными соотноше-
соотношениями
pidx + qidy = dui A=1. 2 п), C)
где дифференциалы берутся вдоль кривой С. Таким образом, для
определения pit qi (/=1, 2 п) получаем систему 2я линейных
уравнений первого порядка.
Предполагая, что в рассматриваемой точке кривой С dx ф О,
систему C) можно переписать в таком виде:
Pi = -4i-%+% ('=1.2 п), D)
а затем из системы B) исключить неизвестные р^. Для отыскания q^
получим следующую систему уравнений:
п п
^ 2fli»^u» (* = 1. 2 п). E)
Если из этой системы можно найти qv q2, ..., qn, то с помощью
системы D) найдутся и plt p2 рп (мы предполагали, что
в рассматриваемой точке кривой С dx Ф 0. Если это не так, то
dy ф 0 и систему C) можно переписать в виде
4i = -Pi%+% d=1.2 п) D')
и из системы B) исключить qt. После исключения получим систему
п п
2 (Щз аУ — ЬЧ dx)Pj = c%dy—^i bi) duj (/ = 1,2 n), E')
определитель которой отличается, может быть, только знаком от
определителя системы E). Обозначим определитель матрицы коэф-
коэффициентов системы E) через Д, т. е.
г — Й12 dy ... bln dx — % dy
... b2ndx — ашdy E)
bnldx — anldy bn%dx — a^dy ... bnndx — anndy.
Рассмотрим два случая:
1) определитель Д не обращается в нуль ни в одной точке
кривой С;
2) определитель Д на кривой С тождественно равен нулю.
В первом случае система E) имеет относительно q-t единственное
решение, а следовательно, в каждой точке кривой С по значениям
иг(х, у), и2(х, у) ип(х, у) на С и системе A) можно одно-
однозначно найти частные производные этих функций.
Во втором случае, так как мы исходим из существующего ре-
решения системы A), система E) должна быть совместной, но так

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 463
как определитель ее равен нулю, то система E) имеет бесконечно
много решений. Таким образом, во втором случае по значениям
иг(х, у), и2(х, у), ..., ип(х, у) на С и системе A) нельзя одно-
однозначно определить частные производные решения на кривой С.
В этом случае кривую С называют характеристикой системы A),
соответствующей данному решению системы. Кривую С вместе
со значениями решения вдоль нее, т. е. кривую в я + 2- мерном
пространстве х, у, иг, и2 ип, будем называть характеристи-
характеристической кривой. Характеристика С будет ее проекцией на пло-
плоскость х, у.
Тангенс угла наклона касательной к характеристике С с осью х
А = -~- удовлетворяет уравнению
И 82 • • • 2П 2» ^= О. G)
Ьп1 — \ап1 Ьп2 — Хап2 ¦.. Ьпп — \апп
В фиксированной точке (х, у, и1, и2> • • • • "и) эт0 будет уравнение
степени я относительно А. Если оно имеет я действительных раз-
различных корней, то говорят, что в этой точке система A) является
гиперболической системой. Если это свойство имеет место в каждой
точке некоторой области пространства х, у, иг, и2 ип, то
говорят, что система A) суть гиперболическая система в этой
области. Только такие системы мы и будем рассматривать.
При заданном решении ut(x, у), и2(х, у), ..., ип(х, у) гипер-
гиперболической системы A) в каждой точке области G, где это реше-
решение определено, уравнение G) имеет п действительных различных
корней, определяющих п направлений касательных к характеристи-
характеристикам, соответствующих данному решению. Обозначая через Xit А2 Ам
корни уравнения G), являющиеся (при заданном решении иу(х, у),
и2(х, у) ип{х, у)) функциями х и у, мы получим п дифферен-
дифференциальных уравнений
dy = \i(x, y)dx (/=1,2 я). (8)
Каждое уравнение определяет однопараметрическое семейство кри-
кривых— интегральных кривых этого уравнения, покрывающее область G.
Через каждую точку пройдет одна и только одна кривая семейства.
Рассматривая все уравнения или, что то же самое, рассматривая
уравнение G) как дифференциальное уравнение первого порядка я-й
степени, мы получим при заданном решении аг (х, у), и2(х, у), ...
.... ип(х, у) системы A) я налагающихся однопараметрических
семейств кривых, или я семейств характеристик. Через каждую
точку области О будет проходить одна и только одна характери-
характеристика каждого семейства.

464 МЕТОДЫ РЕШЕЧИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Если система A) существенно квазилинейна, то ее характери-
характеристики существенно зависят от выбора решения системы и могут
быть определены только, если известно решение. В случае линейной
системы коэффициенты а^, Ьц в A) не зависят от щ, и2 ип
и из уравнения G) характеристики могут быть найдены независимо
от выбранного решения.
Предположим, что кривая С плоскости х, у есть характеристика
системы A), соответствующая заданному решению иг(х, у),
и2(х, у) ип(х, у). На кривой С определитель Д обращается
в нуль, но так как система E) совместна, то и все определители,
получающиеся заменой в Д &-го столбца столбцом правых частей
системы E), должны также обращаться в нуль. Обозначим опреде-
определитель, получающийся заменой в Д 1-го столбца столбцом свобод-
свободных членов системы E), через Д,. Тогда на кривой С функции иг(х, у),
и2(х, у) ип{х, у) будут связаны п-\-\ соотношениями
Д = Д]==Д2 = ... =Д„ = 0. (9)
Не все эти условия являются независимыми между собой. Так как
система A) по условию гиперболическая, то матрица
Ьп— Хап Ьк— Хаи ... bw— \aln
¦¦¦ bw—
Ьп1 — Хат Ьп« — Хага2 ... Ъпп — \ап
имеет в точках кривой С ранг, равный п— 1. В этом случае хотя бы
одна из матриц, получающихся из последней заменой одного из
столбцов столбцом свободных членов системы E), будет иметь
также ранг п—1. Пусть это будет матрица, полученная заменой k
столбца. Тогда из условий
Д = 0 и Д* = 0 A0)
будут следовать все остальные условия в (9). Таким образом, на
характеристике С решение ut(x, у), и2(х, у), .... ип(х, у) связано
двумя условиями A0), называемыми уравнениями характеристик.
Первое из них называют уравнением направления характеристики,
а второе — дифференциальным соотношением на характеристике.
При данном в области G решении системы A) мы имеем п семейств
характеристик и на каждом из этих семейств имеем свое дифферен-
дифференциальное соотношение.
Заметим еще, что если мы будем рассматривать не характе-
характеристику, а характеристическую кривую, то она может принадлежать
нескольким решениям системы A), и если снять требование непре-
непрерывной дифференцируемости решения, то при непрерывности реше-
решения разрыва первых производных могут быть только на характе-
характеристике. Такие решения можно получить следующим образом.
Возьмем два решения uW(x, у) и uf>(x, y)(i= lt 2, .... п), имею-

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 465
щие непрерывные производные в области О, содержащей общую
характеристику С, являющуюся проекцией на плоскость (х, у)
характеристической кривой, принадлежащей обоим решениям, и рас-
рассмотрим решение
Щ (х, у) = <
«W(x, у) с одной стороны С,
uf)(x, у) с другой стороны С
=1, 2 я).
Это решение будет непрерывно в области О, но на С будет иметь
разрыв первых производных.
В заключение этого пункта выпишем уравнения характеристик
для случаев я=1; п = 2; п = 3.
п=1. Если уравнение имеет вид
ди . , ди
а з \- о з—= с,
дх ' ду
то уравнение направления характеристик будет
bdx — ady = 0, A1)
а дифференциальное соотношение на них
с dx — a du = 0. A2)
я = 2. Уравнения направлений характеристик
rfy — Xjrfx^O (/=1.2). A3)
где Х4 — корни уравнения
!!-C
•
= 0.
Дифференциальные соотношения на характеристиках
Ci dx — пц dni — «12 dlh, *ia—Mw
Cdx-andtn-oadu, *M-XiaM
= 0
или
(\.А -\-B)du1-\-Cdu2-\-Mdx-\-Ndy = 0,
где
Л =
; в =
i f- —
йц Cj
*W at2
•
A4)
A5)
A6)
A7)
:3. Уравнения направлений характеристик
dy — \dx = Q (/=1.2.3).
U8)

466 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где Xj—корни уравнения
bu — Хдп btf — i
— Хй
13
= 0.
Дифференциальные соотношения на характеристиках
et dx — аи dux — ап йщ — я13 du3 bn — Х4аи Ьш —
c3dx —
— Х*я32 bm —
или
где
i du2
a31 *32 —
a13 *!?—
*33 —
3
&23
*83
A9)
= 0 B0)
B1)
B2)
bm —
Может случиться, что условие B0) будет удовлетворяться на
какой-либо характеристике тождественно. В этом случае вместо
условия B0) нужно на этой характеристике взять другое условие,
которое может быть получено заменой в определителе A9) другого
столбца столбцом свободных членов системы E).
2. Примеры: уравнения характеристик для некоторых систем диф-
дифференциальных уравнений газовой динамики. В качестве примеров при-
приведем дифференциальные уравнения характеристик для некоторых систем
дифференциальных уравнений газовой динамики, где метод характеристик
находит широкое применение.
1. Плоское и осесимметричное сверхзвуковое установившееся течение
идеального газа. Случай безвихревого движения. Система дифференциаль-
дифференциальных уравнений в этом случае имеет вид
где
_
dy dx
tf=i —
k— 1
k—
a:= —
k —
/? = — A — W—
U и V— составляющие безразмерной скорости по направлениям х и у, вы-
выражающиеся через составляющие действительной скорости и, v по фор-
формулам U = ¦==- , V = -=— , Wm = l/ -j- г- йп, где k — постоянная
Wm wm r k—\

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 467
газового потока, Oq — скорость звука в покоящемся газе. Для плоского движе-
движения а = 0, для осесимметричного а = 1 (в этом случае х — ось симметрии).
Уравнения характеристик для этой системы будут следующие: уравне-
уравнения направления характеристик
dy — \{dx = 0 (/=1, 2),
где Х4 — корни уравнения
—ХЯ L — XK
1 X
или
= 0,
—Yk^ — lh _
jj . А, -
При сверхзвуковых скоростях Xj, X2 действительны и различны. Вычисляя
определители A7), получим:
' А = — Я; В = 0; С = — Ц М = 0; ЛГ = — а/?.
Отсюда, используя A6), получим следующие дифференциальные соотноше-
соотношения на характеристиках:
Х*Я d(J + L d V + a/? dy = 0.
Учитывая, что XjX2 = -jt , и заменяя dy из уравнений направлений характе-
характеристик, получим следующие дифференциальные уравнения характеристик
рассматриваемой системы:
1-е семейство 2-е семейство
dy = Xj dx, dy =
dU + \,dV-\- ^dx = 0.
Иногда уравнения характеристик записывают в другой форме, принимая
за искомые функции W и 9, где
W = W2+ К2; ?/ = IF cos 9; V=W sin 9
(W имеет смысл абсолютной величины безразмерной скорости в данной
точке, а 9 — угол наклона направления скорости с осью х). Если, кроме
того, ввести угол ц (угол Маха) с помощью соотношений
sin р. = |/ 2w; созц=|/ — _
то, выполнив замену искомых функций в уравнениях характеристик, при-
придем к следующему результату:
1-е семейство 2-е семейство
где где
_ sin ц sin Hg ц _ sin ц sin 9 tg ц
С08(|»+в) ' П COS(9-(X)

468 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Из этих уравнений следует, что если в точке (х, у) известно направле-
направление скорости 6 и мы отложим по ту и другую сторону от него углы, рав-
равные (л, то получим направления характеристик, проходящих через эту точку.
Эти направления называют направлениями Маха, а линии, имеющие в ка-
каждой точке направление Маха, называют линиями Маха. Таким образом,
характеристики совпадают с линиями Маха. Физический смысл их состоит
в том, что если в некоторой точке сверхзвукового потока поместить источ-
источник малых возмущений, то оии будут сказываться только в области, огра-
ограниченной линиями Маха, выходящими из этой точки (в осесимметричном
пространственном случае это будет конус Маха).
2. Плоское и осесимметричное сверхзвуковое установившееся движе-
движение идеального газа. Случай вихревого движения. Система уравнений
в этом случае имеет вид
дх
ду
где U, V, Н, К., L, R имеют прежний смысл, Q = ^— A — IP — К2),
гср
S — энтропия, Ср — постоянная величина (удельная теплоемкость газа при
постоянном давлении).
Для того чтобы выписать дифференциальные уравнения характеристик,
найдем корни уравнения A9) и определители Mi, Nit P^ Q A2). Будем иметь:
—Ш L—XK 0
V XV XQ
U
W
= — Q {V— W) (XV/— 2КХ + L) = 0.
JJ
или
Далее,
Подставляя их в соотношение B0), получим следующие дифференциальные
соотношения на характеристиках:
= \iHQ(V—\iU); Ni^
Q [(V — XiU) (XiHdU+L dV — vRXtdx) + Q (L — XfK) dS\ = 0.
При / = 1 имеем:
Q2 (L — XtK) dS = 0, или dS = 0.

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 469
Окончательно имеем следующие дифференциальные уравнения для характе-
характеристик:
1-е семейство
U dy — V dx = О,
2-семейство
dy — X, dx = О,
(V— A,?/) (HdU + \3HdV—<jR dx) + Q (Я— /<) AS = О.
3-е семейство
dy — X3 dx = 0,
(V — \SU) (HdU + XzHdV — aR dx) + Q (H— K)dS = 0.
Первое семейство характерно тем, что направление характеристики
в каждой точке совпадает с направлением скорости потока в этой точке,
т. е. характеристики первого семейства являются линиями тока; энтропия
вдоль них сохраняет постоянное значение. Две другие характеристики, вы-
выходящие из данной точки, будут совпадать с линиями Маха.
3. Одномерное неустановившееся течение в трубах. Безвихревое
течение. Система дифференциальных уравнений движения идеального газа
в этом случае имеет вид
ди . ди . 2 да _ „
ди . 2 / да . да\ _ aln/
где х — координата вдоль оси трубы, и — скорость в сечении х трубы
в момент времени t, а — местная скорость звука, / = / (х) — площадь по-
поперечного сечения трубы.
Уравнения направлений характеристик имеют вид
= 0 (/ = 1, 2),
где \{ — корни уравнения
. 2а
Х
k—\
= 0,
(и-Х)
или
\ 2 = И ±
Здесь мы видим, что система будет гиперболической всегда, в то время как
в случае установившихся течений она будет гиперболической лишь в сверх-
сверхзвуковой области.
Определители А, В, С, М, N будут иметь следующие значения:
Следовательно, дифференциальные соотношения на характеристиках будут:
— и) du + 2 ada-\- a?u ^?Z at = 0
к ^^ 1 CLX

470 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
или, подставляя Xj и сокращая на а, будем иметь:
2
" dx
Итак, дифференциальные уравнения характеристик таковы:
1-е семейство
dx — (и + a) dt = 0;
аи
2-е семейство
dx — (и — a) dt = 0; т т a da — du-\-au , dt = 0.
4. Одномерное неустановившееся течение в трубах. Вихревое течение.
В этом случае уравнения движения имеют вид
ди ди 2 да at dS _ п
udx~l'dt~l'k—\adx k(k—\)evdx~"'
ди , 2 / да . <
ds
где и, а имеют прежний смысл, 5 — энтропия, с„ — постоянная (удельная
теплоемкость газа при постоянном объеме).
Уравнения направлений характеристик
где \{ — корни уравнения
и —X
2а
k—\
0 0
(/=1, 2, 3),
k(k—\)cv
0
и —X
= 0,
или
X] = и; Хз = и -|- а; Х3 = и — а.
Дифференциальные соотношения на характеристиках получим из урав-
уравнения B0):
du
а —
— \)cv
audt
ds
da u —
0
0
и —

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 471
При / = 1 это условие превращается в тождество. Поэтому условие на ха-
характеристиках первого семейства получим, используя другое соотношение:
и — Х4 a du
., аГ In / . 2 .
а и — \„ audt -— + -^—j da
= dS[(u— X4J— a2]=0,
0 0 dS
откуда следует, что на характеристиках первого семейства
Окончательно будем иметь следующие уравнения характеристик:
1-е семейство
dx — и dt = 0,
2-е семейство
dx — (и + a) dt = 0,
A-da-t hlh 1Ч dS-au^
k — \ ' k(k— \)cv dx
3-е семейство
dx — (u — a) dt = 0,
3. Уравнения характеристик квазилинейного гиперболического
дифференциального уравнения второго порядка. Рассмотрим теперь
квазилинейное дифференциальное уравнение второго порядка
дх^ ' дх ду ' dy^ J K '
/¦ ди ди
где о, о, с, / — заданные функции х, у, и, ^-, ^-, непрерывные
и непрерывно дифференцируемые в некоторой области изменения
своих аргументов.
Предположим, что в плоскости х, у задана некоторая гладкая
кривая С: {х = х(-ц); у = у(т]); х'г{т\)-\-у'\т\)> 0}. Пусть вдоль
кривой С задана функция и (х, у), являющаяся дважды непрерывно
дифференцируемым в области G, содержащей кривую С, решением
уравнения B3), а также заданы и ее производные первого порядка
,-, ди ди г* ~,
вдоль L:p^-^~, q^~. Снова поставим вопрос: можно ли на С
„ д"*и д2и
найти частные производные второго порядка r = -r-^, s— , —,
/ = Л~5* используя уравнение B3)?

472 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ (ГЛ. 10
Для отыскания г, s и t вдоль кривой С имеем три соотношения:
ar-\-2bs-\-ct=f, )
rdx + sdy = dp, I B4)
sdx-\-tdy = dq, j
где все дифференциалы берутся вдоль кривой С.
Рассмотрим B4) как систему трех линейных алгебраических
уравнений для неизвестных г, s и t с определителем
Д =
а
dx
0
10
dy
dx
с
0
dy
= ady2— 2b dxdy-\-c dx2.
Нас будут интересовать два случая:
1) определитель Д отличен от нуля на кривой С;
2) определитель Д тождественно равен нулю на кривой С.
В первом случае вторые производные г, s и t функции и (х, у)
определяются вдоль кривой С единственным образом.
Во втором случае, так как мы исходим из существующего ре-
решения и(х, у), система B4) будет совместна, и мы получим бес-
бесконечное множество значений г, s и t в каждой точке кривой С.
В этом случае кривую С называют характеристикой уравнения B3),
соответствующей заданному решению и (х, у), а кривую С вместе
с заданными на ней значениями и, р, q—характеристической
кривой.
Если кривая С является характеристикой при заданном реше-
решении и(х, у), то вдоль нее имеет место соотношение
ady2 — 2bdxdy-\-cdx2 = 0, B5)
или
ат%-2Ь^ + с = 0. B6)
\dx) dx '
Разрешая это уравнение относительно -р , получим:
dy =
dx
Если Ь2 — ас > 0, то получим два обыкновенных дифференциальных
уравнения первого порядка, которые определят два однопараметри-
ческих семейства интегральных кривых, покрывающих область О,
где определено решение и (х, у). Эти два семейства называют пер-
первым и вторым семействами характеристик, соответствующими дан-
данному решению и(х, у) уравнения B3). Через каждую точку области С?
проходит одна и только одна характеристика каждого семейства.
Если в некоторой области изменения х, у, и, р и q уравнение B6)
dy
имеет два действительных различных корня для -j-, то говорят.

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 473
что в этой области уравнение принадлежит к гиперболическому типу.
Только такие уравнения мы и будем рассматривать.
Если уравнение B3) линейно, т. е. a, b и с не зависят от иу
-5^, -?¦, то характеристики не зависят от выбора решения и оба
семейства характеристик можно найти, интегрируя уравнения B7).
Если кривая С для данного решения и(х, у) является характе-
характеристикой, то из совместности системы B4) следует, что все опре-
определители третьего порядка матрицы
а 1Ъ с f
dx dy О dp
О dx dy dq
на кривой С должны обращаться в нуль, т. е.
26 с f
Д,=
dy О dp
Д2 =
Д3 =
dx
а
dx
0
а
dx
dy
с
0
dy
1b
dy
dq
f
dp
dq
f
dp
0 dx dq
= с (dp dx — dq dy) — 2b dp dy +fdy2 = 0,
= — cdqdx— adpdy-\-fdxdy =
= a (dq dy — dp dx) — 2b dq dx +fdx2 = 0.
B8)
Используя условие, что С есть характеристика и исключая из со-
соотношений B8) dy с помощью соотношения B7), во всех трех
случаях получим:
(a dp — fdx) (b±Yb2 — ас) -\-acdq= 0. B9)
Знаки в B9) соответствуют знакам в B7). Таким образом, имеют
место соотношения:
a dy — (b ± Y&2 — ас) dх = 0,
(adp — f dx) (b + Yb2 — ас) + ас dq = 0,
du=pdx-\-q dy,
C0)
называемые уравнениями характеристик. Первое из них называют
уравнением направления характеристик, а последние два — диф-
дифференциальными соотношениями вдоль характеристик.
Если ввести обозначения
— v ь* — ас
C1)

474 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ (ГЛ. 10
то уравнения характеристик можно переписать следующим образом:
для первого семейства
dy—lidx^0; a(dp-\-\2dq)—fdx = Q; du—pdx-\-qdy, C2)
для второго семейства
dy — l^dx — O; a{dp-\-\dq)—fdx — O\ du=p dx-\-qdy. C3)
Относительно характеристических кривых уравнения B3) можно
сделать такое же замечание, как и о характеристических кривых
системы уравнений первого порядка, т. е. она может принадлежать
нескольким поверхностям и = и(х, у), которые будут касаться вдоль
нее. Можно построить решения уравнения B3), которые на ха-
характеристике С будут непрерывны вместе с первыми производными,
а вторые производные будут терпеть разрыв. Разрывы такого рода
называют слабыми разрывами.
4. Численное решение квазилинейной гиперболической системы
двух дифференциальных уравнений первого порядка методом
Массо1). Для численного решения различных задач для гиперболи-
гиперболических систем квазилинейных дифференциальных уравнений первого
порядка может быть применен метод Массо, в основе которого
лежит замена дифференциальных уравнений характеристик, выведен-
выведенных в п. 1, соответствующими конечноразностными уравнениями.
Мы подробно изложим этот метод применительно к системе двух
квазилинейных уравнений.
Идея метода следующая. В плоскости х, у рассмотрим две
близкие точки 1 и 2 (рис. 49). Обозначим координаты этих точек
через (xv yt) и (х2, Уг)- Пусть в этих точ-
точках известны значения искомых функций и
и v, удовлетворяющих квазилинейной гипер-
гиперболической системе уравнений
ди , ди dv . , dv
g^ + *„ ^, + 012 gj + *,2 ^ = С„
ди . . ди . dv . . dv
дх "Г" °2i Щ"+" °22 дх + °22 dj — с*'
C4)
•" «Z1 Их значения в точках 1 и 2 обозначим соот-
соответственно их, t/j и и2, v2. Через точку 1
Рис. 49. проведем прямую в направлении характе-
характеристики первого семейства характеристик,
выходящей из точки 1, а через точку 2 — прямую в направлении
характеристики второго семейства, выходящей из точки 2. Эти пря-
1) Метод Массо улучшался и применялся для решения ряда задач раз-
различными авторами, в частности Христиановичем.

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 475
мые пересекутся в некоторой точке 3. Координаты х?К у^> этой
точки являются решением системы
тде ХЭД — угловой коэффициент касательной к характеристике первого
семейства в точке 1, УЩ—угловой коэффициент касательной к ха-
характеристике второго семейства в точке 2, являющиеся соответ-
соответствующими корнями уравнения A4) в точках 1 и 2.
Уравнения C5) получаются из уравнения направления характе-
характеристики первого семейства в точке 1 и уравнения направления ха-
характеристики второго семейства в точке 2 заменой входящих в них
дифференциалов конечными разностями.
Далее, заменяя дифференциалы, входящие в дифференциальные
соотношения на соответствующих характеристиках, конечными раз-
разностями, получим систему уравнений для определения значений и
и v в точке 3, которые мы обозначим через Ц1' и v?K Эта система
имеет вид
где Ж1), В'1), CW, MM, NW (i=l, 2) суть значения определителей
A7) в точке /. Решая эту систему относительно и^\ v?>, найдем
первое приближение функций и и г/ в точке 3. Это приближение
может оказаться недостаточно точным, так как мы заменили харак-
характеристики, выходящие из точек 1 и 2, отрезками прямых, в то
время как точка 3 на самом деле должна быть точкой пересечения,
вообще говоря, криволинейных характеристик, и, кроме того, диф-
дифференциалы всюду мы заменяем конечными приращениями. Поэтому
может возникнуть необходимость в уточнении координат точки 3
и значений и и г/ в этой точке. Это уточнение можно выполнять
двумя способами.
Первый способ. Вычисляют угловые коэффициенты X*1) и X'1)
характеристик первого и второго семейства в точке 3, найденной
в первом приближении, и вводят средние арифметические
C7)

476 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Точно так же находят средние арифметические
2 ч
Ма) = -2-,
C8)
где Аз1', В'з", С'з\ М^\ Nal)— значения А, В, С, М, N в найденном
первом приближении точки (х(а\ у*?\ ui^, vi^). Искомые величины
второго приближения точки 3: xf\ yf\ uf\ vf\ находят, решая
последовательно следующие системы линейных алгебраических урав-
уравнений:
C6')
-л) = о.
Получим уточненные значения координат точки 3: xf>, yf\ и уточ-
уточненные значения искомых функций в этой точке и^>, v^>. Если их
еще раз нужно уточнять, поступаем аналогично, принимая в качестве
точки 3 вновь полученное приближение. Процесс продолжают до
тех пор, пока значения величин х3, у3, и3, v3 для точки 3, полу-
полученные при двух последовательных приближениях, будут совпадать
с заданной точностью').
Второй способ. Используя найденные значения х?\- уМ, и^К
iAl\ находим:
о
и за X® принимаем первый корень уравнения A4), в котором а^,
Ьц взяты для точки (дс<у, У^), и^, да<у), а за Х^> принимаем второй
корень уравнения A4), в котором ву, Ьц взяты в точке
(¦*аз' -Уаз' "аз1 дааз)' далее вычисляем значения определителей А, В,
1) Если расстояние между точками / и 2 невелико, то достаточно сде-
сделать два уточнения, так как в дальнейшем точность возрастать не будет.

(хд^й+вВД («?>-«,)+cffl («Р> - «,)+Aiffi Da) - х,
§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 477
/-> >« it / A) A) A) A)\ «C) г>B) ^2) ялB) »гB)
С, /И, Л/ в точке \х\{, y\i, u\i, v\i): А\?, ВЦ, СЛз» /W13, л/и
и в точке Dз\ У(ё, и$. ей): 41'. Bg. eg. Alg, Мз' и находим
xf2), 3/P', и^2), г;^2), последовательно решая системы
— х \ \
C5")
C6")
Для дальнейшего уточнения процесс продолжаем аналогично, исполь-
используя вновь найденные значения величин в точке 3 ').
Точность, с которой можно получить значения х3, у3, и3, v3
в точке 3, естественно зависит также и от близости точек 1 и 2.
Умея решать описанную выше элементарную задачу отыскания
точки (х3, у3, и3, v3) по двум известным точкам (хх, ух, uv vj
и (х2, Уъ и2, v2), можно числен-
численно решать различные задачи для
системы C4). Рассмотрим неко-
некоторые из них.
А. Задача Коши. Задача Коши
заключается в отыскании реше-
решения системы C4), если функции
и и v заданы на некоторой дуге
тладкой кривой С, не имеющей
характеристических направлений
ни в одной точке. Численное ре-
решение этой задачи по методу
Массо заключается в следующем.
На дуге кривой выбираем ряд до- ~ц
статочно близких точек (рис. 50).
На этом рисунке выбранные точки
Рис. 50.
занумерованы числами 1, 2, 3 7. По точкам 1 и 2, выше указан-
указанным методом, находим точку 8 (т. е. ее координаты и значения и
и г/ в ней). Это сделать можно, так как для точек 1 и 2 все
нужные величины известны из начальных условий. Затем по точкам
2 и 3 находим точку 9 по точкам 6 и 7 — точку 13. Теперь
ряд точек 8, 9, ..., 13 рассматриваем как исходный и продолжаем
См. сноску на стр. 476.

478 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
построение. Процесс можно продолжать до тех пор, пока не будет
заполнен «треугольник» acb, в котором сторона ас есть ломаная
линия, являющаяся некоторым приближением к характеристике пер-
первого семейства, выходящей из точки а, а ломаная be есть прибли-
приближение к характеристике второго семейства, выходящей из точки Ь.
Указанное построение можно выполнить и с другой стороны кривой С.
При этом получим «треугольник» adb, стороны аи и bd которого
являются соответственно приближениями к характеристике 2-го
семейства, проходящей через точку о, и к характеристике 1-го се-
семейства, проходящей через точку Ь. При этом в явном виде нахо-
находится область, в которой можно найти решения системы при на-
начальных условиях, заданных на участке ab кривой С. Для точного
решения эта область образуется
четырьмя характеристиками, выхо-
выходящими из концевых точек и соот-
соответствующими решению, опреде-
определяемому начальными условиями.
Если система нелинейна, то эти
характеристики заранее неизвестны,
и мы попутно получаем их прибли-
приближения с помощью ломаных линий.
В случае линейной системы сеть
характеристик может быть заранее
построена, и нужно только в точках
их пересечения находить значения и
х и v, используя дифференциальные
соотношения на характеристиках.
Б. Задача Гурса. В задаче
Гурса требуется найти решение и, v
системы C4), если на двух характеристиках ab и ас, выходящих
из одной точки а, заданы значения и и v, причем значения соответ-
соответствующих функций, заданных на характеристиках, совпадают в общей
точке а. (Само собой разумеется, что заданные функции и и г/ на
каждой характеристике таковы, что дифференциальные уравнения
характеристик удовлетворяются.)
ЧислЪнное решение этой задачи методом Массо состоит в сле-
следующем. На дугах характеристик ab и ас берется ряд близких
точек (рис. 52) 1, 2 9 в нашем случае. В этих точках зна-
значения и и v известны. С помощью нашего элементарного построе-
построения по точкам 4 и 5 находим точку 10, по точкам 3 и 10 —
точку 11; по 2 и 11—точку 12; по 1 и 12 — точку 13. Далее,
принимая ряд точек 5, 10, 11, 12, 13 за новый ряд, продолжаем
то же построение. При этом мы заполним элементарными четырех-
четырехугольниками «четырехугольник», аппроксимирующий криволинейный
четырехугольник, две стороны которого суть заданные дуги ха-
характеристик ab и ас, а две другие есть дуги характеристик вторых
Рис. 51.

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 479
семейств, выходящие из концов b и с. Таким образом, снова опре-
определяется область, в которой можно построить решение по заданным
значениям.
В. Первая смешанная задача. Эта задача заключается в построе-
построении решения и и v системы C4), если на дуге ab, являю-
являющейся характеристикой, и
У
25
Рис. 52.
на дуге ас, которая ни в
одной точке не имеет харак-
характеристического направления,
заданы значения и и г/. При
этом предполагается, что
в общей точке а значения
соответствующих функций
согласованы и характери-
характеристика второго семейства,
выходящая из точки о, лежит
внутри угла Ьас (рис. 53).
Решение первой смешан-
смешанной задачи сводится к после-
последовательному решению за-
задачи Коши и задачи Гурса изложенным выше методом, нужно только
начинать с решения задачи Коши с начальными данными на дуге ас.
При этом мы сможем построить решение в «треугольнике», аппрокси-
аппроксимирующем треугольник acd, ограниченный дугой ас и дугами двух
характеристик разных семейств, выходящих из концов а и с. При
этом приближенно определится
вторая характеристика ad,
выходящая из точки а, кото-
которая вначале была неизвестна,
а также определятся значения
и и г; в узлах этой характе-
характеристики. Далее, решение за-
задачи в области. dab сводится
к решению задачи Гурса, так
как и и г/ будут известны на
обеих характеристиках, выхо-
выходящих из точки а
Г. Вторая смешанная за-
*-т дача. Эта задача заключается
в отыскании решения систе-
системы C4), если известны значе-
значения и и г; на характеристике ab
и известна линейная комбинация a.u-\-$v = f на кривой ас, не
имеющей характеристических направлений, где а, [3 и/—заданные
функции точки дуги ас. При этом предполагается, что вторая
характеристика, выходящая из точки а, лежит вне угла Ьас, и,
Рис. 53.

480 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
кроме того, значения и и г; в точке а кривой ab удовлетворяют
соотношению аи-|-{3'У = / в этой точке.
Для решения этой задачи поступают следующим образом. На дуге
характеристики ab берем ряд точек 1,2,3,... (рис. 54). Из точки 1
проводим в направлении характеристики второго семейства прямую
до пересечения с кривой ас. Пусть это будет точка 5. Из диффе-
дифференциального условия на характеристике второгосемейства и граничного
условия находим киев этой точке. По найденной точке 5 и точке 2
обычным путем найдем точку 6,
по точкам 6 н 3 —точку 7 и т. д.
Ряд точек 5,6, 7, ... принимаем
за исходный ряд и процесс по-
повторяем. Таким образом, мы
можем заполнить сетку в области,
ограниченной кривыми ab, ас
и характеристикой второго се-
семейства, проведенной из точки b
до пересечения с кривой ас.
5. Численное решение гипер-
болической системы трех квази-
0 " линейных дифференциальных
РИС 54. уравнений первого порядка ме-
методом Массо. Метод Массо, изло-
изложенный в предыдущем пункте, может быть применен и для числен-
численного решения гиперболической системы трех квазилинейных уравне-
уравнений первого порядка:
dv , dw , . dw
а
du
11 dx
du
du
dx
du_
dy
du
dy
du
dv
dv
dv
dv
dv
dw
~dx~
dw
dw
dy
dw
~dj
= C2.
C9')
Элементарная задача в этом случае решается следующим образом.
Пусть 1 и 2 — две близкие точки, в которых известны все вели-
величины Х{, yt> щ, vt, wt (i = 1, 2). Будем обозначать через Х1{, Х^, X3i
корни уравнения A9) в порядке их возрастания, вычисленные для
точки /. Обозначим через О середину отрезка, соединяющего точки 1
и 2. Координаты этой точки суть
^ (^ + ^); Л О
Положим, что в этой точке

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 481
Из точки 1 проведем прямую в направлении характеристики, соот-
соответствующей Хп, т. е.
У — У1=\Лх — хх),
а из точки 2 проведем прямую в направлении характеристики, соот-
соответствующей Х32, т. е.
У — У2 = *-за (х — х2).
Точку их пересечения обозначим номером 3. Координаты этой точки
найдутся из решения системы
Из уравнений
найдем новые координаты точки О1(х^У
m xo Xi Уг Уо
D2)
D0)
D1)
Вводя обозначение
3
линейной интерполяцией определяем значе-
значения и, v, w в точке Ot:
D3)
Рис. 55.
1 + -A) J
Далее, принимая отрезки 13, 23 и 0хЗ за характеристики и исполь-
используя дифференциальные соотношения B1) вдоль характеристик, пишем
систему уравнений для определения первых приближений и, v, w
в точке 3:
0-^) +
-^^) + ^'(x^-xW) =
D4)
где Ж1,4, N'tl\ Р'г1\ С1,4 — значения М, N, Р, С в точке i (/==0,, 1, 2).
Найдя точку 3: (х^\ у^\ и^\ v^\ ta'^Y производим ее уточнение
одним из следующих способов.

482 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Первый способ. Вычисляем значения ХA3\ Х|3, Х33, используя
первое приближение точки 3, а также М^, N^\ Р{з\ Сз4- Находим
величины
1
Pf = i- (р« + Pi,1'); С<2) = 1 (С*1» + СП </ = 0, 1, 2).
Находим координаты уточненных точек 0 и 3 по формулам:
= У1—U (Х — х
0
D1')
") J
и значения v<2\ aj2), v^\ w'^> — по формулам:
x{2) — x a, 4- -Яа,
vB) ^ _2 L u{2) __ ~ 1. С42'ч
..B) • 0 ii. B1 > *¦ /
Dа)- «О + M2> K>-Wl)+cf»D2) - ^0 = о,
Используя эти формулы, вычисляем Хао, Жо11, Л/о1', Яо4. Со1', а затем
Жоа), Л^о2), Р(о\ С03' и находим значения и3"\ о3а), tw32). решая систему
уравнений
D4')
Таким образом, мы находим второе приближение точки 3 и про-
продолжаем уточнение до совпадения с заданной точностью двух
последовательных приближений 1).
Второй способ. Этот способ аналогичен первому, но только
берутся не средние арифметические величины по формулам D5)
в точках / и 3, а значения этих величин вычисляются в средних
точках отрезков 13, 23, 03. В остальном процесс уточнения остается
такой же.
См. сноску на стр. 476.

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 483
С помощью этого элементарного построения задача Коши и задача
Гурса решаются точно так же, как было описано в предыдущем
пункте. При решении задачи Коши с начальными данными на дуге ab
(рис. 56), не имеющей характеристических направлений, решение
У
0\
— X
у by t-хараш
Рис. 56. Задача Коши.
Рис. 57. Задача Гурса.
можно найти в криволинейном четырехугольнике, ограниченном
крайними характеристиками, выходящими из точек а и Ь, а в задаче
Гурса в криволинейном четырехугольнике, ограниченном двумя
заданными характеристиками и двумя другими характеристиками
экстремальных направлений, выходящими из концов заданных харак-
характеристик (рис. 57—59). Первая смешанная задача решается путем
sxapam
Рис. 58. Задача Гурса.
Рис. 59. Задача Гурса.
последовательного решения задачи Коши, а затем задачи Гурса;
только при постановке задачи нужно требовать, чтобы кривая ab,
не являющаяся характеристикой, лежала бы вне угла, образованного
крайними характеристиками, выходящими из точки а, а заданная
характеристика ab не должна быть ближайшей к кривой ab (рис. 60
и 61). На остальных задачах в этом случае мы не будем останавли-
останавливаться ввиду многообразия их постановок.

484 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
6. Метод Массо численного решения квазилинейного гипер-
гиперболического уравнения второго порядка. Рассмотрим теперь квази-
квазилинейное дифференциальное уравнение второго порядка гиперболи-
гиперболического типа 1)
D6)
Для этого уравнения мы получили следующие уравнения характе-
характеристик:
1-е семейство 2-е семейство
dy — Xt dx = 0, dy — \2dx = 0,
a (dp -f- X2 dq) — / dx = 0, a (dp + Xt dq) — / dx = 0,
du=pdx-Srqdy. du = pdx 4-qdy.
Снова предположим, что в двух близких точках 1 и 2 плоскости х, у
известны значения а, р, q, т. е. известны точки (хх, ух, ult pu qx)
У
tsxapan/n.
с 2- харак/п.
¦*-J7
Рис. 60. Первая смешанная задача. Рис. 61. Первая смешанная задача.
и (х2, уг, и2, рг, q2). Проведем через точку 1 прямую в направле-
направлении характеристики 1-го семейства, выходящей из этой точки,
а через .точку 2 — прямую в направлении характеристики 2-го се-
семейства, выходящей из точки 2. Координаты х^\ у^ точки их пере-
пересечения удовлетворяют уравнениям:
где Х^. — значения \{, вычисленные в точке j.
г) См. Ф. И. Франк ль, С. А. X о и с т и а н ов и ч, Р. Н- Але-
Алексеева, Основы газовой динамики, ЦАГИ, 1938.

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 485
Далее, заменяя в дифференциальных соотношениях входящие
в них дифференциалы конечными разностями, будем иметь систему
уравнений для отыскания р{*\ д^\ и^:
(.47)
К, (#' - ь)\ - /2 К' - *¦) = о.
ai' fi — значения а и / в точке / (/= 1, 2). (Последнее соотношение
мы получили, заменив в дифференциальных соотношениях для обеих
характеристик дифференциалы конечными разностями, а затем взяв
их полусумму.)
Таким образом, решая последовательно системы D6) и D7), мы
найдем первое приближение точки 3: (х<?\ у^\ р<?\ д^\ и?А. Уточ-
Уточнение полученных значений может быть выполнено способами,
совершенно аналогичными тем, которые были описаны в п. 3, где
было рассмотрено решение системы двух квазилинейных уравнений
первого порядка. Решение задач Коши, Гурса и смешанных задач
также не будет по существу отличаться от решения соответствующих
задач, описанных там, поэтому мы не будем на них останавливаться.
Заметим лишь, что при постановке задачи Коши и первой смешан*
ной задачи на кривой, не являющейся характеристикой, мы должны
задать функцию и и производную от нее по направлению, не каса-
касательному к кривой, несущей начальные значения, так как по этим
данным в точках этой кривой могут быть вычислены обе частные
производные- Во второй смешанной задаче не на характеристике
можно задать функцию и или линейную комбинацию ее частных
производных.
Пример. Найти методом характеристик несколько значений
решения системы уравнений
du dv
ду дх '
удовлетворяющего начальным условиям
и@. У) = cos у, v@, у) = sin у

486 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Дифференциальные уравнения характеристик этой системы имеют вид:
1-е семейство 2-е семейство
dy = 0;
vdu-\-e'Zx dy = 0. v dv + и du + е~гх dx = 0.
Для численного решения задачи возьмем на отрезке, несущем на-
начальные данные, шесть равноотстоящих точек. Координаты этих
точек и значения и и о в них приведены в таблице:
= !Tdx>
м
щ
Щ
1
0
1,0
0,5403
0,8415
2
0
1,1
0,4536
0,8912
3
0
1,2
0,3624
0,9320
4
0
1,3
0,2675
0,9636
5
0
1,4
0,1700
0,9854
6
0
1,5
0,0707
0,9975
Для отыскания координат точки j, лежащий .на пересечении
характеристик двух разных семейств, выходящих из точек / и /+1,
и значений и и о в этой точке имеем систему уравнений
(?)..
> .
где
\{п) ц
= 2. 3,...).
Отсюда получаем следующие расчетные формулы:
У) —Уг+Ъ XJ —-7м)\У} —yi)-\-xi> uj —ui
_v
(»=1. 2, ...)¦

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 487
Итерации проводим до тех пор, пока ху, уу, иу, vy будут с за-
заданной точностью равны соответственно xf+v>, yy+l\ uy+l\
13
/5
Рнс. 62.
Для точки 7 (рис. 62) итерации величин
себя следующим образом:
_уМ,
>M ведут
п
1
2
3
4
5
х(п)
0,0642
0,0565
0,0573
0,0572
0,0572
у<»>
1,1
1,1
1,1
1Д
1Д
0,4215
0,4354
0,4342
0,4344
0,4344
0,8356
0,8429
0,8421
0,8423
0,8423
Ниже приведены окончательные результаты для двух слоев
точек, округленные до третьего десятичного знака. В скобках ука-
указаны погрешности приближенных значений ai и vit т. е. разности
значений а^ и v^ и значений точного решения и, v в точках xit yit
в единицах третьего десятичного разряда.
Xi
У1
щ
Щ
7
0,057
1,1
0 434 F)
0,842 @)
8
0,044
1,2
0,351 D)
0,892 @)
9
0,033
1,3
0,262 C)
0,933 @)
10
0,021
1,4
0,168B)
0,965 @)
11
0,010
1,5
0,071 A)
0,988 @)

488 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Продолжение
1
хг
щ
Щ
12
0,102
1,2
0,333 E)
0,842 @)
13
0,077
1,3
0,252 D)
0,892 @)
14
0,054
1,4
0,164C)
0,933 @)
15
0,032
1,5
0,070B)
0,966 @)
На рис. 62 изображено примерное расположение точек (х{, у^)
(масштаб по оси х в два раза больше, чем оси у).
7. Основные задачи, встречающиеся при исследовании пло-
плоского безвихревого сверхзвукового установившегося течения
идеального газа. Любые случаи плоского установившегося движения
идеального газа при сверхзвуковых скоростях при отсутствии силь-
сильных разрывов (разрывов U и V) можно получить, если известны
методы решения следующих задач.
Задача 1. Поле скоростей (т. е. U и V) задано в плоскости х, у
на дуге а'о некоторой линии С, не являющейся характеристикой.
Требуется найти поле скоростей в области, ограниченной дугой а'о
и двумя характеристиками разных семейств, выходящими из то-
точек а и 'о.
-*-х
Рис. 63.
Рис. 64.
Задача 2. Поле скоростей известно на дугах а'о и ас двух
характеристик разных семейств, выходящих из точки а. Требуется
найти поле скоростей в области, ограниченной этими дугами и ду-
дугами характеристик, выходящими из точек 'о и с.
Задача 3. Поле скоростей задано на дуге а'о характеристики
того или другого семейства, выходящей из точки а, лежащей на
твердой стенке ас, заданной уравнением. Предполагается, что

§ 4] МЕТОД ХАРАКТЕРИСТИК ЧИСЛЕННОГО РЕШЕНИЯ ГИПЕРБОЛИЧ. СИСТЕМ 489
граница стенки лежит между характеристиками, выходящими из точ-
точки а. Требуется определить поле скоростей в области, ограниченной
дугой а'о, стенкой ас и характеристи-
характеристикой второго семейства, выходящей из
точки 'о.
Задача 4. Поле скоростей задано
на дуге а'о характеристики, где а
лежит на свободной границе ас, урав-
уравнение которой неизвестно (под свобод-
свободной границей мы понимаем кривую,
вдоль которой абсолютная величина О
скорости постоянна, а направление ее Рис. 65.
совпадает с касательным направлением
к этой кривой в данной точке). Требуется найти уравнение свобод-
свободной границы и поле скоростей в области, ограниченной дугой а'о,
свободной границей ас и характеристикой второго семейства, выхо-
выходящей из точки 'о. Очевидно, что свободная граница расположена
между характеристиками, выходящими из точки а.
Для численного решения этих задач можно применить метод
Массо. Подробно на этом методе останавливаться нет необходимости,
так как задача 1 есть задача Коши, задача 2 — задача Гурса, задача
3 —задача, которую мы раньше назвали второй смешанной задачей.
В задаче 3 нужно только иметь в виду, что на твердой стенке усло-
условием на U и V будет требование, что направление скорости совпа-
совпадает с направлением, касательным к стенке. Решение этих задач
-*-х
Рис. 66.
Рис. 67.
было подробно рассмотрено раньше. Остановимся на решении за-
задачи 4, так как раньше мы не рассматривали аналогичную задачу.
Для численного решения задачи 4 возьмем на дуге достаточно
густую сетку точек (точки /, 2, 3, 4 на рис. 67). Так как в точке а
известны U и V, то в этой точке можно вычислить абсолютную
величину скорости и найти ее направление, т. е. направление сво-
свободной границы в этой точке. В направлении ее проводим луч до

490 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
пересечения с лучом, выходящим из точки 1 в направлении харак-
характеристики второго семейства, проходящей через эту точку (точка 5
на рис. 67). Значения U и V в точке 5 можно найти, используя
дифференциальное соотношение вдоль характеристики второго се-
семейства, выходящей из точки 1, если в нем дифференциалы заменим
конечными разностями и постоянство абсолютной величины скорости
вдоль свободной границы. Таким образом, мы найдем U и V в этой
точке, а следовательно и направление свободной границы в этоП
точке. По точкам 5 и 2 обычным приемом найдем точку 6, по 6
и 3 — точку 7, по 7 и 4 — точку 8. Таким образом, мы найдем
новый ряд точек, расположенных на новой характеристике первого
семейства. Далее, повторяем изложенный процесс, считая этот ряд
исходным. Уточнение можно выполнить каждый раз с помощью
приемов, описанных ранее. Таким образом, после конечного числа
шагов мы найдем приближенно свободную границу и поле скоростей
в рассматриваемой в задаче области.
Умея находить поле скоростей в каждой из четырех задач, можно
решать более сложные задачи, комбинируя эти четыре, а также
находить другие величины, характеризующие движение газовой среды
(например, давление р и плотность р), используя соотношения, свя-
связывающие их со скоростями.
§ 5. Метод сеток решения линейных дифференциальных
уравнений параболического типа
Рассмотрим решение задачи Коши и смешанных задач для линей-
линейного дифференциального уравнения параболического типа') вида
, ди д*и , ди , ...
где а, Ь, с, d — заданные функции переменных х и t и а > 0.
1. Метод сеток для решения задачи Коши. Пусть необходимо
найти решение и(х, t) уравнения A) в полуплоскости t > 0, удовле-
удовлетворяющее начальному условию
и Ос 0) = ср (х) (—оо<х<оо), B)
где срСх) — заданная функция.
Для отыскания приближенного решения этой задачи методом
сеток рассмотрим прямоугольную сетку узлов, образуемую точками
') По поводу применения метода сеток в теории уравнений параболи-
параболического типа см.: И. Г. Петровский, Лекции об уравнениях с частными
производными, ГТТИ, 1953; О. А. О л ей ни к, Разрывные решения нелиней-
нелинейных дифференциальных уравнений, УМН, т. XII, вып. 3 G5) 1957 (§ 7 и
библиография в конце, статьи); О. А. Ладыженская, обзорная статья,
цит. на стр. 412 (и библиография в конце статьи).

§ 51
МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ
491
пересечения двух семейств параллельных прямых:
x = th(t = o, ±i, ±2,...); t=Ji C/ = o. 1, 2,...)
Для каждого узла (i,j)U^> 1) запишем разностное уравнение, аппро-
аппроксимирующее с некоторой точностью уравнение A). Для этого
ди д^и .. .
заменим производные -^—, -^—^ в узле (г, у) соответственно разност-
разностными отношениями
2А
Производную --5Т- в узле (г, J)
будем заменять одним из трех ^.
разностных отношений: ^.
ui.j+i — uij ui.j—ui,j-\ О-
Т
-з -г -i о 12
Рис. 68.
21
В соответствии с этими способами аппроксимации производных мы
получим три типа разностной аппроксимации дифференциального
уравнения A):
-bti 2Л
-*i*i=f»
-Ьи^±
«1-1,.,
D)
«1+1, ,—
2h
E)
Разностное уравнение (З) содержит значения решения в четырех
узлах, изображенных на рис. 69, и аппроксимирует уравнение A)
с точностью до ОA-\-№)\ разностное уравнение D) содержит

492 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
значения решения в четырех узлах, изображенных на рис. 70, и аппро-
аппроксимирует уравнение A) также с точностью до О{1-\-№)\ в раз-
разностное уравнение E) входят значения решения в пяти узлах
(рис. 71), и аппроксимация уравнения A) в этом случае будет
(Н
(Ц
Jltt
*'J)
(н,
па.*
-я
Рис. 69.
Рис. 70.
0 (J2-\- h2). Для узлов нулевого горизонтального ряда 7 = 0 из на-
начального условия B) имеем:
%>=<р(/А) = (р{ (/ = 0, ±1, ±2,...). F)
Первая и третья разностные схемы являются явными схемами,
а вторая — неявная.
Особенно простой вид разностные уравнения C)—E) приоб-
приобретают для уравнения
, ди д^и п ....
dt дх% *¦ '
Если ввести обозначение а— -г^,
то будем иметь:
i-i,,-). C')
(н.
(U
Ш
+/;
]Ш*
-/;
и)
A -f 2а) ац — а (и4+1>
Рис. 71.
Естественно возникает вопрос: какую из трех схем целесооб-
целесообразнее использовать и какое соотношение между Ли/ брать?
С точки зрения простоты расчетных формул целесообразно выби-
выбирать а так, чтобы разностное уравнение было наиболее просто.
Из этих соображений в уравнениях C') — E') целесообразно поло-
положить а=-»-. Тогда будем иметь очень простые разностные урав-
уравнения: иг+1,1 + и1-1,1 ,о"ч
ui.i+l = о » <.° >
= 2u
tii_u
D")
E")

§ 5]
МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ
493
Для вычислений проще всего первая схема, так как из начальных
условий известны значения решения в узлах начального ряда, по ним
легко находятся значения решения в узлах первого ряда, затем
второго ряда и т. д. При использовании второй схемы приходится
решать систему уравнений. При решении задачи с помощью третьей
разностной схемы нужно каким-то образом вычислить значения
решения в узлах первого ряда, после чего счет идет так же легко,
как и по первой схеме. С точки зрения точности аппроксимации
дифференциального уравнения A) третья разностная схема лучше
других. Но эту схему при практических расчетах использовать
нельзя по другой причине. При счете по этой схеме вычислительная
погрешность, избежать которой невозможно ввиду округлений резуль-
результатов, возникнув на каком-либо шаге, быстро растет в дальнейшем
и через небольшое количество шагов полностью исказит решение.
Это просто проследить с помощью так называемой е-схемы.
Пусть счет ведется по схеме E") и до А-го горизонтального
ряда вычисления велись точно, а при вычислении uik была допу-
допущена погрешность величины е. Предполагая, что все дальнейшие
вычисления ведутся снова точно, эта погрешность будет распро-
распространяться при дальнейших вычислениях следующим образом:
k-
l
k-
k-
k-
k-\
k-
k-\
-2
-3
-4
-5
-6
k + 2
k+3
k + 4
k + b
k + 6
/ — 6
<¦> ooooooo
/ — 5
0
0
0
0
0
0
s
— 12s
0
0
s
— 4s
17s
273s"
— 1096s
1 — 4
0
0
0
0
0
— 10s
71e
1 + 2
0
0
0
s
— 6s
31s
— 144s
641s
/ — 3
0
0
0
0
s
— 8e
49s
— 260s
/ + 3
0
0
0
0
s
— 8s
49s
— 260s
1 — 2
0
0
0
E
— 6s
31s
— 144e
641s
1 + 4
0
0
0
0
0
— 10s
71s
/— 1
0
0
s
— 4s
17s
— 68s
273s
— 1096s
0
0
0
0
0
0
s
— 12s
0
s
— 2s
7e
— 24s
89e
— 338s
1311s
t + 6
0
0
0
0
0
0
0
e
Из этой таблицы видно, что малая погрешность, допущенная
при вычислении uih, быстро растет при переходе к следующим слоям.
Это, конечно, очен!» упрощенная схема, так как на самом деле при

494 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
счете погрешности возникают на каждом шаге и будут каким-то
образом взаимодействовать. Во всяком случае, этот пример пока-
показывает, что пользоваться третьей разностной схемой по меньшей
мере опасно.
Если мы будем использовать для решения уравнения A') раз-
разностное уравнение C"), то распространение s-погрешности будет
иметь вид:
У\
k — \
k
k + \
k + 2
k + 3
k+4
1—5
0
0
0
0
0
0
1 — 4
0
0
0
0
0
0,0625e
/ — 3
0
0
0
0
0,125e
0
1 — 2
0
0
0
0,25e
0
0,25e
l—\
0
0
0,5e
0
0,375e
0
l
0
?
0
0,5e
0
0,375e
'+1
0
0
0,5e
0
0,375e
0
i + 2
0
0
0
0,25e
0
0,25s
/ + 3
0
0
0
0
0,125e
0
1 + 4
0
0
0
0
0
0,0625e
0
0
0
0
0
0
Из таблицы видно, что в этом случае погрешность не только
не возрастает, а даже уменьшается.
Мы пришли к понятию устойчивости разностной схемы. Раз-
Разностную схему называют устойчивой, если вычислительная погреш-
погрешность при переходе от одного слоя к другому не возрастает; если же
вычислительная погрешность быстро растет, то схема называется
неустойчивой. Рассуждения, приведенные выше, хотя они н не
являются достаточно строгими, показывают, что разностная схема C")
для решения задачи Коши для уравнения теплопроводности устой-
устойчива, а схема E") неустойчива. К этому вопросу мы еще вернемся
в этом параграфе и подробно его рассмотрим в § 7.
В заключение этого пункта приведем доказательство сходимости
последовательности решений задачи Коши для уравнения (Г) с на-
начальными условиями B), получаемых методом сеток с использо-
использованием разностной схемы C") при стремлении h к нулю.
Пусть (х0, t0) — некоторая фиксированная точка верхней полу-
полуплоскости. Построим сетку, удовлетворяющую условиям
где га—целое число, причем так, чтобы (х0, t0) была узлом сетки.
Для удобства применим следующую нумерацию узлов. Через (г, /)
будем обозначать узел, находящийся на пересечении прямых
x = xo-+ih; t = jl. При этой нумерации точка (х0, t0) будет
узлом <0, 2га). Решение задачи, получаемое методом сеток при
выбранном шаге h (а следовательно, и /), будем обозначать через и'?1).

§ 5] МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ 495
Таким образом, uf) есть решение системы
Uf).+ i = ^kl+^k^ (/ = 0, ±1, ±2, ...; у = 0, 1, 2, ...)
«fo) = ?i ('=0. ±1. ±2, .-.)•
Легко видеть, что
atl = 4"
„(A) __ 1 у (-¦
«0, 'in <w» __J an
г=<—n
Так как to = nh2, то «Wan можно еще записать и таким образом;
(h)
«о, 2„ =
! l rn+l
= -n
где ср2» = ? (*o + 2/A). Рассмотрим выражение
_ Y~n {2ri)\
Все входящие в него факториалы заменим по формуле Стирлинга
е*™ @<бга<1),
где е — основание натуральных логарифмов. Тогда gn i будет
выглядеть так:
6?n "n+i "n-i
1 П
Обозначим jc0 4- 2г/г через т). Будем уменьшать /г так, чтобы пря-
прямая х = т) = const была все время узловой линией. Тогда
. _ -д — хр. „____. J_ _ ______ h
2А ' Л2 ' и ~~ 2^о

496 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Отсюда gni есть функция т), h. Обозначим ее через ghiy\). Рассмо-
Рассмотрим предел gh(rj) при /г->-0 указанным выше способом. Очевидно,
при /г->-0 п, I будут стремиться к бесконечности, а — к нулю.
Будем иметь:
еэд еп+г 6п-г
j n g2in 12(п+г) 12 (n-i)
gftGl) = 77= ''"'"
— /2
= —~= Hm —.. ' — lim
Уя ft>o
1
Далее,
n
г--п
2*o
0 ft"
Таким образом,
(t]—x )a
Но известно, что
есть точное решение уравнения A) с начальными условиями B).
Следовательно,
lim и&?2» = и(*о. ^о)-
Хотя здесь и не все рассуждения проведены с достаточной стро-
строгостью (не обоснованы предельные переходы), но мы не только
показали сходимость последовательности «W к точному решению,
но еще получили интегральную форму точного решгния.

§ 5] МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ 4Э7
2. Метод сеток для решения смешанных задач. Понятие
устойчивости разностных схем. Рассмотрим смешанные задачи для
уравнения теплопроводности
!«— — — —— О П">
Эти задачи ставятся следующим образом. Требуется найти решение
уравнения A') в прямоугольнике R = {a^.x^.b; 0 ^.t ^.Т], удо-
удовлетворяющее начальному условию
и(х, О) = ср(*) (a<x<6) B')
и граничным условиям
[>!? 1 -42(О @<г<Г), B")
где 3,, р2> Тр Тг> фр'1*2— заданные функции переменного t. Выбор
функций р,, р2> Ti> Тг позволяет получать различные задачи. Напри-
мгр, если р,^р2^0; -c1^j2^l. T0 будем иметь первую краевую
задачу, при ^^^==1; ~A = -B==0—вторую краевую задачу.
При решении смешанных задач методом сеток, кроме аппро-
аппроксимации дифференциального уравнения и начальных условий, необ-
необходимо аппроксимировать также и граничные условия. Простейшие
разностные схемы для решения смешанных задач следующие. Рас-
Рассматриваем сетку точек (а-\- ih, jl), где i = 0, 1, 2, .... п; j = 0, 1,
2 m\ h— ~ . Будем считать a = 0: b =\ и h = — . Узлы,
n n
лежащие на прямых х = 0; х=1; ? = 0, будем считать граничными
узлами, все другие—внутренними. Для внутренних узлов выписы-
выписываем разностные уравнения того или другого типа, аппроксими-
аппроксимирующие дифференциальное уравнение (Г), например уравнения C')
или D'), или E'). Для узлов, лежащих на начальной прямой t = 0,
из начальных условий имеем:
«й = ?< (/ = 0. 1, 2 п).
Для граничных узлов, лежащих на прямых х = 0, х=\, запишем
соотношения

498 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
аппроксимирующие с точностью до h граничные условия B"). Таким
образом, мы можем получить три следующие разностные схемы:
G)
(*=1, 2 и— 1; ; = 0. 1, 2, .... т~ 1),
«п—
(/=1. 2
(/=1. 2 /и),
f (i = 0. 1. 2 и);
у = 1, 2
(и— 1);
> = h \j (h
G=1, 2
= 0, 1, 2, .... д);
(i=l, 2 в— 1; y==0. 1, 2, ..., m—1).
G = 1, 2 «),
> (i = 0, 1. 2 л).
(9)
Иногда для лучшей аппроксимации граничных условий привлекают
еще два вертикальных ряда узлов (—ft, j[), ((n-\-l)h, j'l) или рас-
рассматривают сетку, сдвинутую на у в направлении оси х. В этом
случае можно получить для граничных условий аппроксимацию
второго порядка относительно h. Построение этой аппроксимации
ничем не отличается от аппроксимации граничных условий для сме-
смешанных задач уравнений гиперболического типа, которые мы рас-
рассматривали в предыдущем параграфе, поэтому здесь мы на эгом
останавливаться не будем. Так или иначе при любом способе аппро-
аппроксимации мы получаем для отыскания значений решения смешанной
задачи во внутренних и граничных узлах столько уравнений, сколько
имеется неизвестных. Решая эту систему линейных алгебраических
уравнений, мы найдем приближенные значения решения поставленной
задачи во всех узлах сетки. Для явных схем разрешимость полу-
полученной системы не вызывает сомнений, для неявных схем ее нужно
исследовать в каждом отдельном случае. Для схемы (8) это нетрудно
сделать.
Значительно сложней решается вопрос о том, насколько близки
полученные методом сеток значения решения в узлах к значениям
точного решения смешанной задачи для дифференциального урав-
уравнения и можно ли вообще путем измельчения сетки получить методом

§ 5] МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ 499
сеток приближенное решение, сколь угодно близкое к точному
решению. Естественно, что интерес могут представлять только такие
разностные схемы, с помощью которых можно получить прибли-
приближенное решение, достаточно близкое к точному, так называемые
сходящиеся разностные схемы. Разностная схема называется схо-
сходящейся при заданном способе стремления h и / к нулю, если
решения системы разностлых уравнений стремятся при этом к точ-
точному решению задачи для дифференциального уравнения. В этом
определении предполагается, что мы умеем точно решать системы
разностных уравнений, но практически мы можем найти лишь при-
приближенное решение этой системы. Поэтому из сходящихся раз-
разностных схем практический интерес могут представлять только те
разностные схемы, для которых малые погрешности, допущенные
в процессе решения разностных уравнений, не могут привести
к большим отклонениям от точного решения системы. Такие схемы
мы назвали устойчивыми. Пока мы оставим в стороне вопрос
об исследовании сходимости разностных схем, а остановимся на
исследовании устойчивости разностных схем G)—(9) для случая
первой краевой задачи, т. е. в предположении, что |51 = р2 = Ог
-^ = -(¦2=1. В дальнейшем мы докажем некоторые общие теоремы
о сходимости и устойчивости разностных схем, из которых можно
будет сделать заключения о сходимости рассматриваемых нами раз-
разностных схем для первой краевой задачи для уравнения теплопро-
теплопроводности.
Сначала уточним понятие устойчивости разностной схемы, о ко-
котором пойдет речь. Мы будем предполагать, что значения граничных
функций в граничных узлах вычислены точно. Далее, будем пред-
предполагать, что при отыскании решения разностных уравнений погреш-
погрешность допущена на р-м слое, а дальше счет ведется точно. За счет
погрешности на р-м слое мы получим добавок 1)ц к точному решению
разностной схемы. Без ограничения общности можно считать, что
погрешность допущена на начальном слое. Тогда добавки 1)ц будут
являться решением той же самой системы уравнений, но только
значения их в граничных узлах, лежащих на прямых х = 0, x=U
равны нулю, а значения в граничных узлах начального слоя равны
допущенным погрешностям. Разностную схему будем называть-
устойчивой, если для всякого е > 0 найдется такое 8 ]> 0, что
как только
будет иметь место неравенство
п-1

500 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
для любого У, лишь бы /1^.Т, причем 8 не зависит от h и /.
Фактически это понятие непрерывной зависимости решения разностной
схемы от начальных значений. Поэтому этот тип устойчивости назы-
называют еще устойчивостью по начальным значениям.
Перейдем теперь к исследованию на устойчивость схем G) — (9).
Мы докажем, что схема G) устойчива при а^-»- и неустойчива
при а > -х; схема (8) устойчива при всех а; схема (9) неустой-
неустойчива при всех а. Здесь везде а = -р-.
Для доказательства этого утверждения рассмотрим функцию
wf)=sin— A = 0, 1, 2, .... га; й=1,2 га—1).
Легко проверить, что
I ° (кФ т)>
Будем искать частные решения разностных уравнений G) — (9) вида
где 1к — некоторое число, которое нужно определить. Рассмотрим
сначала разностную схему G). Подстановка в G) дает
Xi+ sm = A
или
Xfc = 1 — 4a sin2 ъ—.
in
При каждом фиксированном k V&) удовлетворяет граничным
условиям v^) = v&) = 0. В силу линейности и однородности раз-
разностного уравнения линейная комбинация частных решений будет
также решением разностного уравнения, удовлетворяющим граничным
условиям:
п-1
-\J • km _
Постоянные aft подберем так, чтобы были удовлетворены и началь-
начальные условия в узлах (/,0) (/= 1, 2 га— 1), т. е.
п-1

§ 5] МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ 501
Для того чтобы найти ак, умножим обе части равенства на sin
и просуммируем по / от 1 до л — 1. Получим:
п-1
Далее, возводя то же самое равенство в квадрат и суммируя по
от 1 до л—1, получим:
п-1
В точности таким же приемом для J, отличного от нуля, по-
получим:
п-1
п-1
Отсюда очевидно, что если при всех k
имеет место неравенство |XS|^1, то
п-1 п-1
и, полагая о = г, докажем устойчивость ./fjX
разностной схемы. Так как в нашем
kit
случае \к = 1 — 4а sin2-^- , то | \к \ ^ 1
при
Рис. 72.
у. Таким образом, разностная схема G) устойчива при
Покажем теперь кеустойчивость этой схемы при а > -^. В этом
случае для каждого достаточно большого л можно найти такое
целое число k0 < л, что | \ко | > 1 -j- p., где ц > 0 и не зависит от л.
Это можно видеть из построенного на рис. 72 графика. Рассмот-
Рассмотрим теперь следующее частное решение разностного уравнения:
Для этого решения
п-1
V
= Р
,^г\<) =р"т5-
п-1

602 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Следовательно, если сумма квадратов погрешностей в узлах началь-
п-1
ного ряда 2 ^io"'8 не равна нулю, то при очень малом шаге h,
г = 1
когда для отыскания решения в прямоугольнике R нужно сделать
п-1
большое число шагов в направлении оси t, сумма 2j v\f для боль-
г = 1
ших J будет весьма велика, а это и означает, что разностная схема
неустойчива.
Рассмотрим теперь разностную схему (8). Следуя нашему ме-
методу, ищем частные решения вида
(k) sj ¦ knl
v\y = Xi sin —.
Подстановка в разностное уравнение (8) дает
/1 i о ч 1 ¦, ¦ kill , , Г . Ы (I + 1) . . kv. (I — 1) 1 •>, , . Ы1
< 1 + 2а) li sin — - ак>к [sin ^ + sin \ >\ = Xj-' sin -^
или
Так как
(^ j0 (k =1,2 n—\),
то при всех а имеет место неравенство
^ 1 — 2a (cOS ~ — Л
из которого следует, что при всех а разностная схема (8) устойчива.
Для разностной схемы (9) подстановка ¦y^^X^sin • в раз-
разностное уравнение дает
1 sin = 2aXj. I sin — ~ ; 2sin \-
n «\ n n '
¦sin' - ¦ ¦ •—- Ш
или
—1=0.
Обозначая 4a sin2 -=— через у4, получим:
4 + 2-^-1=0
или

§ 5] МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ 503
Таким образом, при всех а имеет место неравенство
|»*.а|> 1.
Используя частное решение вида
fy — t^fc.asin —
и рассуждая точно так же, как и при доказательстве неустойчивости
схемы G) при а>-~-, мы убеждаемся, что схема (9) неустойчива
при всех а.
Мы рассмотрели простейшие разностные схемы для уравнения
теплопроводности. Можно построить другие разностные схемы,
например, используя способы построения разностных схем, опи-
описанные в § 2, причем можно получить схемы, дающие значительно
лучшую аппроксимацию, чем мы имели для рассматриваемых схем,
но каждый раз необходимо исследовать их на устойчивость, так
как только устойчивые схемы представляют практический интерес.
Все разностные схемы разбиваются на два класса: явные схемы
и неявные схемы. Явные схемы позволяют очень просто вычислить
значения искомого решения в узлах от-го горизонтального ряда,
если известны значения решения на предыдущих рядах. Но они
имеют существенный недостаток: для того чтобы они были устой-
устойчивы, необходимо налагать сильные ограничения на сетку. Так,
в схеме G) для устойчивости должно быть выполнено ограничение
/ . 1
а = Тз^>'о что требует очень мелкого шага по t, т. е. если нужно
иайти решение на конечном отрезке изменения t, то количество го-
горизонтальных рядов узлов должно быть очень большим. Кроме
того, если в ходе решгния нужно уменьшить шаг по л:, то нельзя
этого сделать, не уменьшая шага по t.
Неявные схемы, например схема (8), свободны от этого недо-
недостатка, но использование их связано с другой трудностью: для оты-
отыскания значений решения в узлах т-то горизонтального ряда при
известных значениях в узлах предыдущих рядов приходится решать
систему алгебраических уравнений с большим числом неизвестных.
Если для решения этих систем применять метод итераций, то
увеличение шага по времени, допустимое в этом случае, приводит
к увеличению числа итераций, необходимых для отыскания решения
системы с заданной точностью. Если за начальные приближения
принимать соответствующие значения в узлах предыдущего ряда,
что вполне естественно, то с увеличением шага по t число необхо-
необходимых итераций растет, хотя и не пропорционально увеличению
шага, а медленней, все же эффект выигрыша времени за счет уве-
увеличения шага по t в значительной мере пропадает. В связи с этим
возникает необходимость в более эффективных методах решения
систем алгебраических уравнений, получающихся при использовании

504 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
неявных разностных схем. В следующем параграфе мы изложим
метод прогонки, разработанный в Математическом институте
им. Стеклова АН СССР.
Пример. Методом сеток найти решение уравнения
ди д^и
удовлетворяющее условиям
и(лг, О)=яптглг @<д:<1); и @, f) = и A, f) = 0.
Воспользуемся простейшей устойчивой явной разностной схемой
выбрав шаг по оси х Л ^= 0,1 и шаг I по оси t: / = -^- = 0,005.
Ниже приведена таблица значений решения в узлах сетки (в едини-
единицах четвертого десятичного знака). Так как решение симметрично
п
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
it \^
0
0,005
0,010
0,015
0,020
0,025
0,030
0,035
0,040
0,045
0,050
0,055
0,060
0,065
0,070
0,075
0,080
0,085
0.09D
0,095
0,100
0,025
0,050
0,075
0,100
0,025
0,050
0,075
0,100
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,1
3090
2939
2795
2658
2528
2404
2287
2174
2068
1967
1871
1779
1692
1609
1530
1456
1384
1316
1252
1190
1135
2414
1886
1474
1152
10
15
18
17
0,2
5878
5590
5316
5056
4808
4574
4349
4137
3934
3742
3558
3384
3218
3061
2911
2768
2633
2504
2381
2270
2154
4593
3588
2804
2191
19
30
36
37
0,3
8090
7694
7318
6959
6619
6294
5987
5693
5416
5150
4898
4658
4430
4213
4007
3810
3624
3446
3288
3117
2975
6321
4939
3859
3015
27
41
49
40
0,4
9511
9045
8602
8182
7780
7400
7037
6694
6365
6055
5758
5476
5208
4953
4710
4480
4260
4072
3853
3680
3485
7431
5806
4537
3545
31
48
57
60
0,5
10000
9511
9045
8602
8182
7780
7400
7037
6694
6365
6055
5758
5476
5208
4953
4710
4480
4260
4072
3853
3680
7813
6105
4770
3727
33
50
60
47

§ 5]
МЕТОД СЕТОК РЕШЕНИЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ
505
относительно прямой х = 0,5, то в таблице даны лишь значения
решения для
х = 0; 0,1; 0,2; 0,3; 0,4; 0,5.
В строках 21—24 таблицы приведены значения точного решения
задачи в указанных там узлах таблицы, а в строках 25—28—по-
25—28—погрешности приближенного решения в соответствующих узлах. Отно-
Относительная погрешность не превосходит 2%. При сравнительно боль-
большом шаге Л ^= 0,1 результат совсем неплохой. Используем теперь
неустойчивую явную разностную схему
Для того чтобы не ухудшать аппроксимации дифференциального
уравнения разностным уравнением, шаг h no оси х возьмем рав-
равным 0,05, а шаг по оси t : 1= 2Л2 = 0,005, т. е. оставим его преж-
прежним. Ниже приведена таблица полученных значений решения
(строки 0—7) снова в единицах четвертого десятичного разряда.
В строке 7 приведены значения точного решения задачи для t =
= 0,030, а в строке 8 указаны погрешности приближенных значе-
значений, полученных по указанной схеме, при /=0,030. Как видно из
таблицы, после шести шагов по оси t погрешности настолько ве-
велики, что по абсолютной величине в некоторых узлах даже превос-
превосходят значения точного решения. Это вполне естественно, так как
схема неустойчива, поэтому небольшие погрешности в начальных
значениях решения очень быстро возросли.
В строке 9 приведены значения решения при / = 0,030, полу-
полученные по неявной схеме
U} — 2atj -f- ut-i,j)
при той же сетке (Л = 0,05; /=0,005), а в строке 10 — погреш-
погрешности этих значений. Как видим^ неявная схема дает хороший ре-
результат, так как после шести шагов относительные погрешности не
превосходят 1%.
п
0
1
2
3
4
5
6
7
8
9
10
v\
0
0,005
0,010
0,015
0,020
0,025
0,030
0,030
0,030
0
0
0
0
0
0
0
0
0
0
0
0
0,05
1564
1488
1412
1352
1244
1392
164
1163
999
1172
с
0,10
3090
2938
2794
2650
2562
2170
3738
2298
—1440
2316
—18
0,15
4540
4316
4104
3904
3684
3732
1808
3376
1568
3402
—26
0,20
5878
5588
5314
5048
4830
4332
6282
4372
—1910
4405
—33
0,25
7071
6723
6391
6083
5727
5907
2007
5259
3252
5299
—40
0,30
8090
7692
7314
6940
6714
5532
11284
6017
—5267
6063
—46
0,35
8910
8472
8050
7684
7110
8032
—758
6626
7384
6678
—52
0,40
9511
9041
8603
8141
7967
6137
15283
7074
—8209
7128
—54
0,45
9877
9391
8925
8511
7909
8815
—723
7346
8069
7402
—56
0,50
10000
9508
9040
8580
8304
6724
15088
7437
—7651
7495
—58

506 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
§ 6. Метод прогонки решения краевых задач
для уравнений в частных производных1)
Метод прогонки мы изложим на примере решения краевых
задач для уравнения теплопроводности и для уравнения Пуассона.
1. Уравнение теплопроводности. Пусть требуется найти реше-
решение уравнения
ди 2 /• +\ д"*и /1 \
удовлетворяющее условиям:
и(х, О) = ср(-*0 (а^.х*СЬ), B)
ди
— a.0(t)u\ =олA),
C)
.Для решения этой задачи применим следующую разностную схему.
Возьмем сетку узлов: х{= a -{-it -{- -^\ h; tj=Jlii = —1, 0, 1, .... /V;
j=0, 1, 2, ...; h= ~7,п\ и для внутреннего узла (i, j) запишем
разностное уравнение
,или
(/ = 0, 1, 2 Л/—1; у=1, 2, 3, ...). E)
аппроксимирующее уравнение A) в узле (/, j) с точностью до
0 G-4-Л2). В граничных узлах запишем следующие соотношения:
я,,о=<р4 = ?(*«) (/ = —1. 0, 1, 2 ЛО, F)
(У=1, 2, ...; ao^=
/ = 1, 2. . . .; %j = р0 (^); р^ = pt (*,) ). G2)
!) При написании данного параграфа использована рукопись неопубли-
неопубликованной статьи И. М. Гельфанда и Локуциевского, любезно предоставлен-
предоставленная нам авторами.

-§ 6] МЕТОД ПРОГОНКИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 507
Из методических соображений рассмотрим сначала предельный слу-
случай Л=0 (так называемый метод прямых, о котором подробнее
см. § 8). Полагая и(х, tj) = Vj(x); y.(x, tj) = ^(х), в этом случае
будем иметь:
^? «>-i (*) (У = 1 • 2, .. .)• (8)
Таким образом, для отыскания i^(jc) (при известной Vj_l(x)) имеем
краевую задачу (8), A0). Для ее решения применим метод про-
прогонки, описанный в § 9 главы 9. В соответствии с этим методом
для отыскания Vj(x) находим функции cty(x) и а^(х) (а <^.х 4^.Ь),
Згдовлетворяющие уравнениям:
) «« (*) ГГТ7 i-i (>
и начальным условиям:
aof ali(a) = alJ, A2')
т. е. совершаем прямую прогонку. Далее, из системы
определяем Vj(b) и, интегрируя уравнение v'(x)=aOj(x)Vj(x)-+-
-4-atj(x) с начальным условием Vj(b) на правом конце, находим
функцию Vj(x), т. е. выполняем обратную прогонку.
Так как vo(x)= <?(x), то, используя этот метод, найдем после-
последовательно vt(x), v2(x) т. е. приближенные выражения для
решения и(х, f) на прямых tj=jl. Если ао(/)^>О, то при числен-
численном решении системы A1) и уравнения (8) м.ы не будем иметь рез-
резкой потери точности при отыскании значений Vj(x).
Теперь видоизменим этот метод применительно к методу сеток,
т. е. рассмотрим случай h Ф 0. В этом случае метод прогонки мы
будем применять не к дифференцируемому уравнению, а к гранич-
граничной задаче для разностного уравнения второго порядка F) с гра-
граничными условиями Gй), (Jz) (J считаем фиксированным, а «t,^_i —
известными).

508 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Уравнения E) и G) при j = т можно записать в таком виде:
A4)
где
Aim = Cim=\; Bim=l-\-—T-; Din = — -—-ui,m^; A6)
2l^ k
2 - ha.om . Qm= 2halm .
2 + Apom' m~ 2 + Apo»"
A7)
В соответствии с идеей метода прогонок будем перегонять левое
граничное условие A5,) в правый граничный узел, т. е. будем на-
находить такие Pim и Qim, чтобы при всех / = 0, 1, 2 N
A8)
Подставляя Ui-i.m из A8) в A4), будем иметь:
или, разрешая относительно
где
j+1, то — 7ГБ 7^—p—== л -г i + l, m.
Теперь решение находится просто. Зная Aim, Bim, Cim, Dim, POrn
и Qq^, находим с помощью рекуррентных соотношений A9), B0)
Р%т< Qim и Далее с помощью A8) находим последовательно mjv-з, т>
UN-3, m> «... Uo, m, М_1, т-
Погрешности, допущенные при вычислении a^j, a^, $oj, $xj, при
этом методе не могут сильно сказаться tfa результате, если o^j > 0.
В самом деле, если \Pim\ < 1, то из A9) следует, что и |P( + i, т \ < 1 •
так как Aim = Cim = '\, a Bim>\. Но при оо, m > 0 \Рйт\<\,
поэтому |-P{OT|<C 1 при всех /. Погрешности в Oqj и а^- вызовут
погрешности в Рот и Q^^ и будут сказываться на значениях Pim,
Qim. Покажем, что они не возрастают. Если bPim погрешность
в Pim,' т0 с точностью до членов первого порядка относительно bPim

§ 6]
МЕТОД ПРОГОНКИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
509
В нашем случае Aim = Cim= 1 и множитель при bPim в правой
части равен Р*. , т. е.
и^ i + l, т — *i + l, mu^im-
Но |Я{+1( т|<1. Следовательно, с возрастанием I погрешность
будет убывать. Из равенства B0) видно, что при вычислении Qi+l m
значение Qim умножается на Р{+1>т< т. е. на величину, по модулю
меньшую единицы, а это означает, что погрешность значения Qim
при переходе к Qi+itm тоже не будет возрастать. При обратной
прогонке погрешность при вычислении и-хт не может возрастать,
так как каждое предыдущее значение умножается на Р,-. t m,
a |Pi,J<l.
Если [х(х, t) = const; a,-(/) = const; Pj(/)^const (/ = 0, 1),
то Pim не зависят от от и их следует вычислить только один раз.
Это уменьшает объем вычислительной работы.
Отметим, что мы специально записали уравнение A4) в общем
виде, хотя в нашем случае Aim = Cim= 1 и все соотношения имели
бы более простой вид. Мы это сделали, желая показать, как можно
применять метод прогонок для решения граничных задач для ли-
линейных разностных уравнений второго порядка, с которыми при-
приходится встречаться во многих вопросах.
2. Уравнение Пуассона. Пусть в прямоугольнике R {а
Cd\ требуется найти
Г Ь;
решение
сона
уравнения Пуас-
Пуасудовлетворяющее гранич-
граничному условию „
ди
-5 \- &и = р на границе
прямоугольника (я — внеш-
внешняя нормаль). B2)
¦+-Х
Рис. 73.
Для решения задачи применим метод сеток, выбрав в качестве
узлов точки с координатами
= с
= —1,0.1,2 п;
= -1.0,1.2....,/»; А=
п
т

510 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10'
Для внутренних узлов (i, j) запишем разностные уравнения
ul+lJ—2ulj + ui_lij uiij+1 — 2ui} + uiij_l
"г /2 —Jij
А2
A = 0. 1,2 n— 1; У = 0, 1, 2 от — 1), B3>
аппроксимирующие уравнение B1) с точностью О (№-\-Р), а гра-
граничные условия B2) аппроксимируем с той же точностью соотно-
соотношениями:
1 —"
1, О
"i, та-1
7
i
г 
7 = 0, 1,2 от— 1),
B4t)
' B42>
= 0,1.2 n— 1).
Таким образом, мы получим систему тп -\-2(т-\-п) уравнений
с таким же количеством неизвестных Му.
Используя граничные условия B43)—B44), выразим щ, _ь
через uin, Uiim-U Будем иметь:
2-/«„..
2 —
2+ /ai
aim ~ im U ™"
где
kin =
lai
Используя эти соотношения, исключим в системе B3) неизвестные
ui, -i> uim- Если ввести обозначение 7=-^, то получим систему
i, о — B-h2T — ftioT) ai0 + ти{1
j + TMi, j -1 — 2 A + т) «у +-
i_i, о =
где
(У=1, 2 от —2),
= Fim_l A = 0, 1, 2 п— 1),
Ui = h2f» l/=l. 2 от-2);
B7)

§ б] МЕТОД ПРОГОНКИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 511
Эту систему коротко можно записать в виде
^ =Ti (* = 0, 1. 2 я_1), B9>-
где
Vi = (tii0, U{1 Щ,т-\У, Fi = (Fto< Fi\ Fi,m-l),
2A + 7)+*йТ f 0 ...О О
t _2A + T) Y ...0 °
0 f —2A + 7) ---0 °
О О О ...-г _2
C0>
Граничные условия B4,) и B42) можно переписать в виде
2 — haoi 2h$oj
" + =4" + ^ (У = 0, 1.2 m-1),
C1.)
ni.i 2=K^nj 2=н^пРщщ C/ = 0. 1. 2 m-1),
C1,)
где
2-haoj
+y j 2 —AanJ5 Z*i ~ 2-ha.nf
C2).
Положив
Уо =^ \ZW)' ^bi- ¦••> zo, m-i)> r ^ (гп0> гп1- •••> Zn,m-V<
k00 О О ...О о \ /*no 0 0...0 0
Ь ( fr10"-0 ?
(
0 0 O...O\B.,/ \0 0 0... О
можно записать системы C1,) и C12) в таком виде:
C4).
•»rt_i = /?t»n + r. J
Окончательно имеем следующую систему уравнений:
C5,)
vin=Aivi-\-vi_1-\-Fi (/ = 0,1,2 rt—1). C52)
^„_, = Л«Л-|-г. C5s).

512 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Эту систему будем решать методом прогонки. Прямую прогонку
мы совершим, если найдем такие матрицы Х{ и векторы yit чтобы
при всех i имело место равенство
vi_l = Xivi-\-yl A = 0, 1, 2 я). C6)
Для отыскания Х{ и у{ подставим v{_x из C6) в C52). Получим:
vl+l-\~(Al-\~Xi)vi-\~yt = F~i (i = 0, 1, 2 n—1)
или
Таким образом,
Xi^ = -(Ai^rXi)~\ C7)
Уг+1 = 04* + **)"' (fi - Уд = Х{+1 Gi ~ Fd. C8)
Так как Хо и у0 известны, то с помощью C71 и C8) мы сможем
найти Xt и yi при всех i=l, 2, 3 п. Из C53) и C6)
при i = n получим:
(R~Xn)vn = yn-7 C9)
и, следовательно, сможем найти vn. Далее, используя C6), после-
последовательно находим i»n_i, vn-2 ^о> v-i* T- е-> выполнив об-
обратную прогонку с помощью C6), найдем все нужные значения иу
A = 0, 1, 2 п; У = 0, 1, 2, ..., т).
При этом способе вместо решения системы из тп-\~2(т-\-п)
уравнений необходимо обратить п -\- 1 матриц порядка т, что зна-
значительно экономичнее с точки зрения объема вычислительной
работы. Естественно оси целесообразно ориентировать так, чтобы
было т < п.
Покажем, что погрешности в граничных значениях а0^, a,j, %j, fiij,
не приведут к значительным погрешностям в значениях и.ц, полу-
получаемым этим методом, если только Ooj>0. Ограничимся случаем
ki0= kim—0 A = 0, 1, 2 т—1), что равносильно тому, что
на отрезках у=с, y = d (a^.x^.b) заданы граничные условия
первого рода: u\y=c = u\^d = 0.
Для того чтобы доказать это утверждение, покажем сначала, что
||*i||j<l. Если kio = kim = O (t = 0. 1 т— 1). то
— 2A-И) f 0 0...00 0
Y — 2A-И) Y 0...00 0
' = А = | 0 f — 2 A + i) f ... 0 0 0
0 0 0 0...0 1 — 2A-f
D0)

§ 6] МЕТОД ПРОГОНКИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 513
Матрица А симметрична, поэтому она имеет полную ортонормиро-
ванную систему собственных векторов zv z2, ..., zm, соответ-
соответствующих собственным значениям Хг, Х2, ..., \т. Любой /и-мерный
вектор z можно представить в виде
z = alzl-\-a2z2-\- ... -\-amzm,
a
т _
Az = 2 аА zi
i=l
И
m m
2 ^ min | >ч |2 2 «! =
1, a, ..., m i=l
|Х,Н|г||"
»-l, a, ...,m d
Таким образом,
||Лг||з>т!п|Хг|||г||3. D1)
i
Покажем, что min|Xj|>2, а для этого просто вычислим харак-
х
теристический определитель матрицы А, т. е.
Dm(k) =
— 2 A + у) — X f 0 0...0 0 О
f —2 A + Т) — X Y 0...00 О
О f — 2A-И) — X f ... О О О
О 0 0 0... О f — 2A+ тг)— X
D2)
Раскрывая его по элементам первой строки, имеем:
?>m(X) = -[2(l+T)+XlDm-l(X)-T2Om_2(X). D3)
Это соотношение можно рассматривать как линейное разностное
уравнение второго порядка относительно Dm (X). Его общее реше-
решение имеет вид
Dra(X)=Cl(.f+C#f, D4)
где [Аг и [а2 — корни уравнения
т. е.
1*2 = —
D5)

514 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Для сокращения записи положим 1-t-f~b~o" = P- Тогда
D6)
Для отыскания С,, С2 заметим, что
D,(X) = —2A+Т) —Х = —2р;
поэтому
- 2P = c, (- p 4- VT^f)
4p* - T2 = Cx (- p + VT^^fJ + C2 (- p - У?2 - 72J
откуда
Dn (X) = ^J=^. {[- p + Ур^?Г - [- P - УР^
D7)
Легко проверить, что DOT(X)^0 при рк ^i-cos—~Г\ • 1<^^т- или
Xft = — 2 — 2T(l— cosj^-j) (ft=l. 2 m). D8)
Отсюда следует, что min |Xi|>2 и из D1)
t
1И^11з>2|п||8. D9)
Докажем теперь, что если ||^||,^1, то l|^i+i||3 <! 1.
В самом деле, пусть w — произвольный вектор, а
z = — (AA-Xi)~'lw = Xi^w.
Так как w = — {A-\~X{)z, то
1й!!з=||(л^^)г||з>|И?||з-цх^||з.
Но |И?||з> 2||^||,. а ||^г||з<||^||з1|г||з<||г||8. Отсюда
а это означает, что
Так как ||^о||я— шах l^ojl*^' (ПРИ aoj > 0), то при
1—0, 1,а, .... m-i
всех i

§ 6] МЕТОД ПРОГОНКИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 515
Погрешности в значениях граничных функций вызовут погреш-
погрешности в XQ, F{, R, г, которые будут распространяться при прямой
и обратной прогонках и скажутся на значениях и.ц. Вместо точных
значений всех величин мы получим приближенные значения
с погрешностями bXt, byit §Fj, §г>г. Предполагая, что вычислитель-
вычислительных погрешностей мы не допускаем, будем иметь:
Xt+l = - {A + *d~ll *Ux +^i+i = - (^ \
откуда
Xi+l (А + Х{) = - /; (Хш 4- ЬХ^) (А,
ЬХШ(Лг 4-Х< +-ЬХ{) +-XUlbXi = 0
или
ЬХШ = - Х1+1 ЬХг (А{ +Xl + bXiyx = XUl ЬХ{ (Xi+l 4- ЬХШ).
Таким образом, для линейной части погрешности имеем равенство
S-Xi+i =Xi+l bXiXi+l.
Но так как ||^Vi+1||3-< 1, то
т. е. погрешность bXt не возрастает с возрастанием I.
Далее.
т. е. для линейной части погрешности имеет место равенство
Ь>ш = Xi+i (&Л - &д 4 bXUl (y( - F0.
из которого видно, что в силу ||^; + ilU^l быстрого роста по-
погрешности byi + l не будет.
Так как обратную прогонку мы выполняем с помощью рекур-
рекуррентного соотношения C6), то
Vi _, = хгщ 4 л-; vi - г + ^ _, = (х{ 4 wf<) («i 4 8»
и для линейной части погрешности §г^_г имеем:
bvi _ х = Хг bvi 4- ЬХ^{ 4 Ъуь
т. е. и при обратной прогонке нет резкого возрастания погрешности.

516 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
§ 7. Сходимость и устойчивость разностных схем
В §§ 2, 3, 5 мы изложили метод сеток решения некоторых
задач для простейших дифференциальных уравнений в частных произ-
производных. Сходимость метода доказывалась в каждом отдельном слу-
случае своим приемом. В § 5 было введено понятие устойчивости раз-
разностной схемы, играющее важную роль в решении задач методом
сеток. В настоящем параграфе мы изложим метод сеток в более
общем виде, рассмотрим связь сходимости и устойчивости и изло-
изложим некоторые методы исследования устойчивости. Эти вопросы
обстоятельно освещены в монографии В. С. Рябенького и А. Ф. Фи-
Филиппова «Об устойчивости разностных уравнений», которая и была
использована при написании данного параграфа.
1. Разностная аппроксимация дифференциального уравнения
и граничных условий. Рассмотрим в re-мерном пространстве
область G с границей Г, состоящей из нескольких кусков Г{
(t= 1, 2 т), которые могут иметь общие части или даже сов-
совпадать между собой.
Пусть в области G нужно найти решение дифференциального
уравнения
L(u) — f = 0 A)
с граничными условиями
Ш = <?{ A=1, 2 т), B)
где /—заданная в G функция, срг — функции заданные на Гг, a L
и 1{ — некоторые дифференциальные операторы.
В замкнутой области G-\~T для каждого /г@</г</го) опреде-
определим некоторое множество точек, которое назовем сеткой и обо-
обозначим через Gh. Дифференциальному оператору L поставим
в соответствие некоторый разностный оператор Rh, преобразующий
функцию uh, определенную на Gh, в функцию Rhuh, определенную
на некотором множестве G°h cz Gh. При этом будем предполагать,
что какова бы ни была точка Р области G, при достаточно малом h
в любой ее окрестности найдутся точки, принадлежащие Gh и G%.
Дифференциальному уравнению A) поставим в соответствие раз-
разностное уравнение
/». C)
где fh определена на 0° и в точках G°h совпадает с /. Каждому
граничному условию /<(и) = ср; на Гг поставим в соответствие неко-
некоторое разностное граничное условие
где оператор rih определен на некотором множестве Tih из Gh
и переводит функцию uh, определенную на Tih, в функцию rih (ult).

§ 7] сходимость и устойчивость разностных схем 517
определенную на множестве Г?А с Tlh, a <plh — функции, определен-
определенные на Г?А, некоторым образом соответствующие функциям срг. Спо-
Способ этого соответствия зависит от способа переноса граничных
условий с Гг на Tih.
Будем предполагать, что между функциями cpift выполнены усло-
условия согласования, под которыми мы будем понимать такие условия,
связывающие <?ih в отдельных точках, которые являются необходи-
необходимыми и достаточными для существования хотя бы одной функции uh,
удовлетворяющей условиям D).
Пусть U и F — классы функций, определенных на G, а
Фг(г=1, 2 т)—классы функций, определенных на Г{, такие,
что при и??/ определены L(u) и Ц(и), при этом L(u)? F, /i(a)€ ®»-
Будем предполагать, что в каждом из этих классов определена
норма, вообще говоря, своя в каждом классе, обладающая обычными
свойствами нормы. Эти нормы обозначим соответственно через || и|| р.,
II f\\ Иг,
Пусть для функций uh, определенных на Gh, определена норма
||ий||р.; для функций Д, определенных на G?, —норма ЦДЦ^ и
для функций yih, определенных на Г?й, —норма ||<Рй||ф • Функции
u?U, fczF, определенные на G, имеют смысл и на Gh, следова-
следовательно, для них имеют смысл нормы ||и||р- , \\f\\F , оператор Rhu
и т. д. Будем предполагать, что нормы || ||р-,.|| \\F • \\ IU,
определены так, чтобы для любых функций u?U, f?F и сргс Фг
имеют место предельные соотношения:
E)
при h—>0. В этом случае мы будем говорить, что соответствую-
соответствующие нормы согласованы.
Говорят, что разностное уравнение C) и граничные условия D)
аппроксимируют дифференциальное уравнение A) и граничные
условия B) на классе функций U, если для любой функции u?U
при h —>¦ 0 имеют место соотношения:
Rhu\\Fh^Q, F)
)iA^0 (*=1, 2 т), G)
где через [k(u)]ih обозначен оператор переноса граничных условий
с Г, на Yih.
Далее, говорят, что порядок разностной аппроксимации равен k,
если для любой функции u?U и 0</г<Ло имеют место

518 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
неравенства
|| L (u)-Rhu || Fh<HkM, (8)
<кк М{ (i=\, 2 т), (9)
где М и М{ не зависят от h.
Пример. Рассмотрим уравнение
в области G={0<x<l; 0 < t < 7"} с граничными условиями:
10(и)=и (х, О) = сро(х) на Г0={0<х<1; * = ()},
/х (и) = «;(*, О) = срг(х) на Гг={0<х<1; t = 0],
/2(и)=и@, 0 = ?г@ на Г2={х = 0; 0<^<7),
на Г3={*=1; 0<^<7}.
Под сеткой Gft будем понимать совокупность точек (xj = ih, tj=j'l)
(j = 0, 1,2 M; j = 0, 1, 2 Л/), где /г = 1; / = а/г (а = const)
/JV ^ 7" < / (Л/ -|- 1). Определим операторы:
_ gft (х, ^ + 0 -2uh {х, t) + uh (x,t-
RhUh = ^
uh (x +h,t)- 2uh (x, t) + uh(x- h, t) о
^ Ha Uft>
= tiii(x, 0) на Гой,
. ч uh (x, I) — uh (x, 0) _
/¦2ft(«ft) = M°. 0 на Г2Й,
Гъп («ft) — «й (• • 0 на ГЗЙ.
Здесь Oa—совокупность точек (ih, jl) (i= 1, 2 Л1— 1;
7=1, 2, ..., Л/—1),
Гол—совокупность точек (ih, 0) (i = 0, 1, 2 M),
Tlh— совокупность точек (ih, 0), (ih, 1) A = 0, 1, 2 Л1),
F2ft— совокупность точек @, jl) (j=0, 1,2, ..., Л/),
T3h — совокупность точек A,/Q (У^=0, 1, 2 Л/),
- -pO __ г. p» __ p . r0 p . pO p

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 519
Положим, далее,
fhixit tj) = f{ih, jl); <Рой(*г) = <Ро(^); <ргй(*«) = <рг(г/г)
(г = 0, 1, 2 Ж);
?2й (tj) = ср2 (Л); Тзй (fj) = ср3 (Л) (/ = 0.1.2 N).
Условиями согласования здесь будут условия:
той @) = to @); той @) + *Pm @) = ъ* @:
Той О) = Тзй (О)! Toft @ -M?i»(l) = Тзй @.
которые получаются из следующих соображений. Точка @, 0) при-
принадлежит Г№, Г1Й и T2h, а точка @, /) принадлежит Tlh и Г2Й. Сле-
Следовательно, значения uh в этих точках можно вычислять различ-
различными способами:
Ч @, 0) = %„ @); uh @, 0) = ср2я @);
uh (О, I) = cpoft @) 4- /cplft @); «ft @, 0 = ср2;, @.
откуда
Той @) — <p2ft @); Той @) + ifiK @) = ?2ft (О-
Аналогично получим и два других условия согласования.
За класс 'U примем совокупность функций с непрерывными
производными второго порядка в замкнутой области G, за F—со-
F—совокупность всех непрерывных в G функций, а за Ф{—совокупность
всех непрерывных функций на 1\. Нормы в этих классах функций
введем следующим образом:
||и||?Г = тах|и|; \\f\\F= max |/|; ||<р{|| = max | ср41.
о о г»
Для сеточных функций нормы введем так:
\Ы\ин = таах\иь\'' ll/ftlljrA= таох1/л1: ll?iftlU(ft = max|cpift|.
h °h r»A
Так определенные нормы будут согласованы, так как при /г->0
II«II^-*H«II^
Далее, при h -> 0
IIL W ~ «ft" II ph ^0; || [It (u)\ih - rih («) || Ф(й ^ 0 0 = 0.1.2. 3).
Если вместо класса U дважды непрерывно дифференцируемых
в Q функций взять класс Ul всех функций, имеющих непрерывные

520 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
производные четвертого порядка, то
moax
IIМ«)]<» —»¦<»(«)Нфй = 0
: = 0, 2, 3)
— г1й(иI1ф11,<-9-тах
lft * G
Таким образом, разностная схема
Rfluh = fh; /"{и(и) = <Pift 0 = 0, 1, 2, 3)
аппроксимирует в классе U дифференциальное уравнение с гранич-
граничными условиями, а в классе 0х будем иметь аппроксимацию пер-
первого порядка.
2. Понятие корректности и устойчивости разностной схемы.
Совокупность разностного уравнения C) и разностных граничных
условий D) назовем разностной схемой решения задачи A) — B).
Введем следующие определения.
Будем говорить, что разностная схема C) — D) корректна, если
при достаточно малом шаге h ее решение существует при любых Д
и cpift (i=\, 2 т), для которых выполнены условия согласо-
согласования, и для любого е > 0 существует такое 8 = 8 (е) > 0, что для
данного решения uh разностной схемы C)—D) и любого uh, где
A=1.2
т),
будет иметь место неравенство
II«»-и» II vh<*
сразу для всех h @ < h < /z0), как только
A0)
<п)
О2)
Это означает, что решение uh непрерывно зависит от правой части
уравнения и правых частей граничных условий, причем зависимость
равномерная по h.
Если уравнение C) и граничные условия D) линейны, то данное
выше определение корректности равносильно следующему: разност-
разностная схема C) — D) корректна, если решение uh существует при
любых Д и cpiA, причем

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 521
Разностную схему C) — D) называют устойчивой по правой
части, если ее решение существует и \\uh — ий||р- <е для любых
uh, удовлетворяющих A0), при ||/ — /Ц^ < 8 и cpift = cpift (/=1,2,
3 т).
Разностную схему называют устойчивой пор граничным условиям
rih(Uh) = 9ih (/=1.2 p<m).
если неравенство A1) имеет место при / = / и 4ih = 4ih (г'=/7~Ь
-j- 1 т) и
h<* (t=l. 2 Р).
Если разностная схема такова, что условия, входящие в послед-
последнее определение, являются аналогичными начальным условиям для
дифференциальных уравнений гиперболического или параболического
типа, то их называют начальными условиями для разностного
уравнения и говорят об устойчивости разностной схемы по на-
начальным условиям. Так как это понятие в дальнейшем встречается
достаточно часто, то уточним его.
Пусть t, xu х2 хп — координаты точек рассматриваемого
пространства и сетка Oh лежит в полупространстве t ^> t0 и состоит
из слоев 50, Sp S2, ... Под слоем Sj мы понимаем множество
точек сетки, лежащих в плоскости t = to(l)-\-jl, где to(l)-+to при
/—>0. Пусть первые р граничных условий D) (р^т) однозначно
определяют значения uh в узлах слоев 50, St Sq-v Эти р
условий мы и назовем начальными условиями разностного уравне-
уравнения C), если для любого j (j = q, q -f- 1, . ..) по значениям uh
в узлах слоев Sj_v Sj_2 Sj-q< используя только те уравнения
из C) — D), которые связывают значения uh в узлах слоев Sj_q<
Sj_q+l Sj, можно однозначно определить значения uh во всех
узлах слоя Sj. При этих условиях решение uh уравнения C), удо-
удовлетворяющее граничным условиям D), существует и единственно.
В примере, приведенном в п. 1. условия rOh (ий) = ср0 и rlh (ий) = cplft
являются начальными условиями в этом смысле и р = д = 2,
a to(l) = to = O.
Если разностная схема удовлетворяет требованиям, входящим
в определение начальных условий, то начальные условия можно
задавать на любых q последовательных слоях 5^_д+1, Sj_q+2, .. •
..., Sj, при этом решение будет однозначно определено на всех
последующих слоях 5^+1, 5^+2, ... Для таких начальных условий
введем обозначение
'«*.*(«*) = ?»,* (/=1.2 р). A3)
ПУСТЬ \\rih,j(uh)hih— норма функции rihij(uh). аналогичная
норме \\rih(uh)\\^,h (l= 1, 2 р). Помимо нормы ||aft||Pft.

522 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
характеризующей поведение uh на всей сетке Oh, введем нормы,
характеризующие поведение uh на каждом слое Sj, т. е. введем
норму ||ий||5 , зависящую только от значений uh в узлах слоя Sj.
При всех j эти нормы должны определяться совершенно одинаково.
Потребуем, чтобы норма ||«ft||s. была согласована с нормой ||ий||р.
в том смысле, что существует такая константа С, не зависящая
от h и uh, что для любой функции uhcUh имеет место нера-
неравенство
П j J
Назовем разностную схему C) — D) равномерно устойчивой
по начальным условиям в области Oh, если найдутся такие по-
постоянные К, §о и ^о> что ПРИ любых j~^>q—1, 8 < \ и h < h0
для любых uh и uh, заданных на слоях Sj_q+l, Sj_q+2, ... из соот-
соотношений
\\rihj(uh)-rih^(uh)\\^h<b (/=1, 2 р),
= rih («л) О' =Р + 1 т).
при любом N^j — q-\-l и Sjv с: Oh следует неравенство
Это означает, что при изменении меньше чем на 8 начальных усло-
условий, задаваемых на любых q последовательных слоях, и сохранении
без изменений разностного уравнения и остальных граничных усло-
условий решение разностной схемы на любом из последующих слоев
изменится не больше чем на Kb.
Устойчивость по начальным условиям всегда следует из равно-
равномерной устойчивости по начальным условиям.
В случае линейной разностной схемы равномерная устойчивость
по начальным условиям означает, что из соотношений
ft<8 (/=1,2 p);
следует неравенство
при всех Л/>>/—9+1 и Sjv с Oh.
Пусть область О лежит в полосе to^t ^.Т. Пусть при лю-
любом j^-q—1 для любой функции, заданной на q последователь-
последовательных слоях сетки 5}_д+1 Sj, определена норма || ||и), где
нижний индекс q указывает количество последовательных слоев, от
значений функции uh на которых зависит норма, а верхний индекс /
указывает номер самого верхнего слоя из них.

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 523
Теорема. Если при любом у >- q — 1 для любых функций uh
и uh, заданных на слоях Sj_q+l, Sj_q+2, ..., Sj+l и удовлетво-
удовлетворяющих уравнениям
Rhuh = /: #ft«ft = /; rih (uh) = cpift; rih (uh) = cpift (/ = p -\- 1 m),
A5)
имеет место неравенство
1)и*||^. 06)
где постоянная К не зависит от h, j, uh, uh (I — шаг сетки по
переменной t), то разностная схема C) — D) равномерно устой-
устойчива по начальным условиям при любых нормах || ||ф. и \\ \\s ,
удовлетворяющих неравенствам
p
lk».j(«ft) — rih,j(uh)\\<
A7)
в которых L и No не зависят от h, uh, uh.
Доказательство. Пусть uh и uh определены в узлах слоев
Sj_q+V Sj_q+2< ••• и удовлетворяют уравнениям A5). Тогда по
неравенству A6) при всех N^-j имеем:
Так как (N — j)l^.T — t0<io{\-\-Kl)N~J^.eKi-T'to). Отсюда и из
неравенств A7) следует, что
- uh || Sn< Щ,е* <Г-У g|| rih, j (Ий) - rtht
а это и означает, что разностная схема равномерно устойчива по
начальным значениям.
Эту теорему, дающую признак равномерной устойчивости раз-
разностной схемы по начальным условиям, грубо можно сформулиро-
сформулировать следующим образом:
Для равномерной устойчивости по начальным условиям, до-
достаточно, чтобы ошибка допущенная при вычислении решения
при переходе от одного слоя к другому возрастала бы не более
чем в A —(— Л7) раз, где I — шаг сетки по t.
Рассмотрим теперь связь равномерной устойчивости по началь-
начальным условиям с устойчивостью по правой части.
Будем рассматривать разностную схему C) — D), предполагая,
что первые р граничных условий в ней являются начальными усло-
условиями в ранее определенном смысле. Разностное уравнение C)

524 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
и граничные условия D) есть система уравнений, в которой не-
неизвестными являются значения uh в узлах сетки Oh. Все уравнения
этой системы разобьем на группы, включив в k-ю группу все те
уравнения, в которые входят значения ик на k-м слое, но не входят
значения в узлах вышележащих слоев Sk+l, Sk+2, •.. Совокупность
этих уравнений обозначим так:
т) A8)
Если uh известна на слоях 50, Sl 5fc_1, то система A8) одно-
однозначно разрешима относительно значений uh на Sk. Обозначим
через ||/||(fc) норму, зависящую только от значений /, входящих
в систему A8), согласованную с ||/||^, в том смысле, что для
h
h
произвольной функции /, определенной на Оп> выполняется не-
неравенство
max ||/||№)<т Ц/11,.
к п
где f — постоянная, не зависящая от h и /.
Теорема. Если разностная схема C) — D) равномерно
устойчива по начальным значениям для всех таких /, что
II/—/II f "^^о. область Oh лежит в полосе to^t^.T, суще-
h
ствуют такие постоянные С, 80> й0, что при k^-q, Ь < 80,
h < h0 и любых uh и uh, совпадающих на слоях Sk_lt Sk_2, ¦ . ¦
и удовлетворяющих соотношениям
функции uh и uh на Sk удовлетворяют неравенству
и для любых uh и uh, совпадающих на слоях Sk_v Sk_2, ....
выполнено неравенство
B1)
где D — постоянная, ар — порядок дифференциального уравне-
уравнения по t, то разностная схема C) — D) устойчива по правой
части.
Доказательство. Пусть uh и ^удовлетворяют уравнениям

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 525
где ]|/ — f\\F ^ 8, и одним и тем же граничным условиям
h
rxh («л) = rlh (й„) = cpift (/=1,2 m).
Обозначим через ukh функцию, удовлетворяющую граничным усло-
условиям rlh(ukh) = ylh, совпадающую с uh на слоях 50, St Sk
(т. е. удовлетворяющую уравнению /?y*fcft=/), а на слоях Sk+l,
Sk+2, • ¦ . удовлетворяющую уравнению Rhukh = f. Здесь q — 1 <^
^&<;Л/. Функции uk+ith и ukh совпадают на слоях 50, Sl Sk,
а на Sk+l удовлетворяют уравнениям
'
Из неравенства ||/—f\\F ^8 и условия согласования норм
ft
и \\j\\p следует неравенство
h
т. е. для икь, и ик+ин выполнены условия, аналогичные условиям A9)
теоремы. Поэтому
||и**—
а в силу неравенства B0)
B2)
На слоях 5fc+2, 5fc+3, ... функции икп и %+i,ft удовлетворяют одним
и тем же уравнениям, а их начальные условия по неравенству B2)
мало отличаются друг от друга. Следовательно, в силу равномер-
равномерной устойчивости по начальным значениям из B2) следует, что
при к ^ Л/
B3)
Так как на 50, Sl 5g_t имеем иа_1,й = uh = ий, а на Sq,
Sq+l. ... функции и9_1,й и йй определяются из одинаковых урав-
уравнений, то и9_1,h=uh. С другой стороны, на Sn имеем uN = uh. По-
Поэтому, написав неравенства B3) для k = q, q-\-\, . . ., N и сложив
их почленно, получим:
Так как область лежит в полосе to^t <! 7\ то N1 ^ Г — f0. По-
Поэтому в последнем неравенстве правая часть меньше некоторой
постоянной, умноженной на 3. В силу условия coi ласования

526 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
норм ||ий||р и ||aft||s следует, что
всех h < /Zq имеет место неравенство
норм ||ий||р и ||aft||s следует, что при достаточно малом 3 для
II «ft— %llp <е-
п
а это и означает устойчивость по правой части.
Корректность разностной схемы равносильна устойчивости раз-
разностной схемы по правой части и всем граничным условиям. Из
последней теоремы следует, что для некоторых разностных схем
нет необходимости проверять устойчивость схемы по правой части,
а достаточно проверить устойчивость по начальным значениям, что
сильно упрощает проверку корректности разностной схемы.
3. Связь сходимости с корректностью разностной схемы.
Из корректности разностной схемы C) — D), аппроксимирующей
дифференциальное уравнение A) с граничными условиями B), сле-
следует сходимость последовательности решений разностной схемы
к точному решению граничной задачи для дифференциального урав-
уравнения. Поэтому вместо доказательства сходимости достаточно уста-
установить корректность разностной схемы. Это следует из теоремы:
Если решение дифференциального уравнения A) с граничными
условиями B) существует и принадлежит U, а разностная
схема C) — D) аппроксимирует уравнение A) с граничными усло-
условиями B) на классе U и корректна, то при h -»¦ 0 решения uh
разностной схемы сходятся по норме к решению и граничной
задачи для дифференциального уравнения, т. е.
Если уравнения A) и C) и граничные условия B) и D)
линейны и порядок аппроксимации равен k, то имеет место
следующая оценка скорости сходимости:
II« - «л II v <h" \MN + 2 MiNi) • <24>
причем
Доказательство. Если u?U: L(u)=f; /,-(и) = ср;> то,
обозначая Rhu через /, rih(u) — через ср;ь, из условия аппроксима-
аппроксимации при достаточно малых h имеем:
II/-/II* <5; 11<р«*-й*11ф <*.
П 1П

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 527
а тогда из условия корректности следует, что при достаточно малом 8
имеет место неравенство
В линейном случае, так как
Rh4 =/=?(«): rih (uh) = cpift = [<p,]tt
TO
L (и) — #ft« = Rhuh — Rhu = Rh (uh — u) = Rhvh,
\U (u)]ih — rih (и) = гш (uh) — rih (и) = rih (vh),
где vh = uh—и. Тогда из условия, что мы имеем аппроксимацию
порядка k, следует
\\Rhvh\\F <A*M; \\rik(vh)\L<-^Mt.
п *л
В силу корректности разностной схемы для любой функции uh имеет
место неравенство
т
||„ +2 ^||г«(«Л)|| B6)
откуда и получаем требуемую оценку скорости сходимости, полагая
uh = vh и используя оценки для vh.
Для доказательства неравенства B5) по свойству норм имеем:
Ци|| вг < II" — uh\\v +\\uh\\v •
п п п
Но ||и — ий||р. ->0 при й->0, а для ||«й||р имеет место нера-
венство B6). Отсюда, переходя к пределу, и получим неравен-
неравенство B5).
Заметим следующее:
Если некоторые из граничных условий B) аппроксимируются
точно, т. е. при некоторых / Г^сГ» и для u?U rih(u) = li(u),
<Pifc = [(Pi]<ft = (Pi на Г?л. то требование устойчивости по соответ-
соответствующим граничным условиям в доказанной теореме можно
отбросить и требовать лишь устойчивость по правым частям
и всем остальным граничным условиям.
Представляет интерес следующая теорема, используя которую
можно обосновать метод Рунге приближенной оценки погрешности
метода сеток:
Теорема. Если уравнение (Z) и граничные условия D)
линейны и выполнены условия предыдущей теоремы, а аппрок-
аппроксимация такова, что существуют пределы
lim A"* {Lu - Rhu) = ф; lim A"* ([lt (u)]lh - rih (и)) = ф„ B7)
ft-X) ft>0

528 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где и— решение задачи A) — B), т. е. существуют такие функ-
функции ф и ф|, что
lim \\h-\L(u)-Rhu)-^\\F = 0,
ft->0 h
a w есть решение граничной задачи
ф; li(w) = h (/ = 1,2 т), B9)
принадлежащее к некоторому классу W, на котором Rh и rih
аппроксимируют L и Ц, то
lim \\h~k(uh—и) — w\\ =0. C0)
ft--> 0 u h
Доказательство. Пусть и — решение граничной задачи
A) — B), a uh—решение разностной схемы C) — D). Пусть Rhu=],
/•ift (и) = cpift. По условию теоремы
k ft; h'k (cpift - ?{й) = [if(\
где IKH, ->0 и ||aift|| -»¦ 0 при А-»-0. т. е.
n ift
«ft) - rift (и)) = Щй + aift. )
Если w есть решение задачи B9), то по определению аппроксимации
где HPftllj и ||р1й||ф ->0 при Л->0. Так как Rh и rift линейны,
то из последнего равенства и равенств C1) имеем:
Rh (h'k («ft -«)-«) = ай -Рй,
/¦ift(A"fc («ft — «) — да) = aift — pift.
Так как при й->0 правые части по соответствующим нормам
стремятся к нулю, то в силу корректности разностной схемы C)—V4)
lim \\h~k(uh — и) — w\\v =0.
ft ft
\
ft->0
v
ft
Эта теорема позволяет оценить погрешность в решении, которую
мы получаем, заменяя дифференциальное уравнение разностным.
Пусть uh и и^—решения разностной схемы при h — hx и h=h%,
где hl = ch2(c > 1) и сетка О^ есть часть сетки Од,. Если выполнены

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 529
условия последней теоремы, то
ик = а + h> + ° (Л?)-- ик = и + h> 4- о (hi).
Исключая из этих равенств w, получим:
откуда
и — и, яй —т.—г (X — и, \
Этой формулой иногда пользуются для получения более точного
решения, чем и^ •
Пример. Пусть в области О с границей Г требуется найти
решение уравнения
y)u'y + e(x, у)и =
где а, Ь, с, d, e, f—заданные функции, непрерывные в О 4-Г,
удовлетворяющие следующим условиям:
а>0; 6>0; а-|-?>9>0; | с |< Ma; \d\^Mb; e<0
(М и q—положительные постоянные), а ср — заданная функция, не-
непрерывная на Г. Будем предполагать, что область О лежит в круге
х2 4- у2 < №¦ Рассмотрим сетку Gh, состоящую из точек x = lh,
y^jh, лежащих в О-(-Г. Назовем граничными узлами сетки Oh
те ее точки, для которых хотя бы одна из четырех ее соседних
точек (х ± й, у), (х, у + h) лежит вне О-)-Г.
Рассмотрим следующую разностную схему:
— 2uv 4- e,-i, j) 4- -даг(и«.j+i — 2и.; 4- uij.O 4-
«*lr. =<Pilr .•
где и,ц = ап{111, jh), a ay, 6y, Cy, dy, ey, /у — значения соответ-
соответствующих функций в точке x = ih, y—jh, а cpt — функция, полу-
полученная из ср непрерывным продолжением на всю область О.
Докажем корректность этой схемы. Пусть
v (х, у) = е
= еА

530 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ, 10
Так как
_ еА [(x-hy+у) _ 2Ah (x + 6tA) е
(—l<fll<l).
62A) б
+ eA [(<*-»>'+»"] = Ah2 {[ 1 + 2A (x + 93AJ] X
_ц 2A (x + 94AJ] e41(^+W'+2/a]}
; —1<в4<0).
1 + 2Л (y 4- 95AJ] X
(j; 4- 96AJ] e-4 [<*>+(»+Wl}
@<в6<1; —1 <96<0),
то
< л A 4- 2Л«2) (ay 4- bti) 4-1 cy \AR -f | rfy | ЛЯ <
< Л A 4- 2ЛЯ2) (су 4- Ьф 4- МЛ# (ву 4- Ьф = С (ciij 4- by)
Отсюда
Яйх» = Rhe* (Д2+') — RheA ("¦+»¦) < — С (су 4- *у) < — Сд.
а
г» = еАЛЗ (еА — е-4 <а!'+»а -Д2)) > еА — ел if+tf-R') > еА — 1.
Если ий есть решение разностной схемы при |/|<С^8 и |cpj<
<(еА— 1)8, то
^й (мй — г»5) > 0 в Oft и ий — vb < 0 на Гй.
Следовательно, uh — vb не может иметь положительного максимума
в Gh-\-Th (см. § 2) и uh — х»8<0. Аналогично получим неравенство
ий4-г»8> 0, т. е.
\uh\<vb
и
||вЛ||р. = max \uh |< Ьел^№+1\
'' °ь
а это означает, что однородная задача Rhuh = 0; uh |r ^0 имеет
h
только тривиальное решение. Следовательно, рассматривая раз-
разностную схему как систему линейных алгебраических уравнений
с неизвестными значениями uh в узлах сетки, можно заключить, что
ее определитель отличен от нуля, а поэтому разностная схема имеет
решение при всех / и ср. Так как оценка uh не зависит от h, то

§ 7[ СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 531
разностная схема корректна, если за || \\р , \\ \\„ взять макси-
h h
мумы абсолютных величин соответствующих сеточных функций на
соответствующих множествах.
Из теоремы сходимости корректной разностной схемы будет
следовать, что если граничная задача для нашего дифференциального
уравнения имеет дважды непрерывно дифференцируемое решение,
то uh равномерно сходится к этому решению при h -»¦ 0.
4. Некоторые приемы исследования устойчивости разностных
схем. Исследование устойчивости с помощью принципа макси-
максимума. Если для разностной схемы C)—D) имеет место в какой-
либо форме принцип максимума, то часто удается, используя его,
доказать устойчивость по правой части и устойчивость по гранич-
граничным условиям этой разностной схемы. Такой прием был исполь-
использован в примере п. 3, где использовался принцип максимума
в форме: если Rhuh^-0 и rih(uh) = 0, то uh не может иметь поло-
положительного максимума ни внутри, ни на границе области.
Исследование устойчивости с помощью индекса разностной
схемы. Если разностная схема линейна и р граничных условий
являются начальными условиями в том смысле, в котором они были
определены в п. 2, то при любом k^>q—1 значения uh на любом
слое Sjc+l можно выразить в виде линейной комбинации значе-
значений uh в точках слоев Sk, Sk_v ... и члена, зависящего только
от правых частей fh и ср,й разностной схемы C) — D). Максимум
суммы абсолютных величин коэффициентов этой линейной ком-
комбинации по всем узлам сетки называют индексом I разностной
схемы C) — D). Если область О конечна, a h и I — соответ-
соответственно шаги сетки по пространственным координатам xv
хг, ..., хп и времени t, то если существует постоянная С > 0,
не зависящая от h и I, такая, что /< 1 -\-Ы, а нормы опре-
определены следующими равенствами:
KIls =max|«J; \\rih(uh) ||ф = max
sk lh so> Sl
то разностная аппроксимация C) — D) равномерно устойчива
по начальным условиям.
Это утверждение непосредственно следует из теоремы о равно-
равномерной устойчивости по начальным условиям, так как неравен-
неравенства A6) и A7), фигурирующие в условии этой теоремы, будут
иметь место, если положить
|Ы|«= max \uh\.
Sk-q+l Sk
Приведем пример применения этого способа исследования устой-
устойчивости.

532 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Рассмотрим дифференциальное уравнение
ди д^и „
в области G={0^,t^T; 0<;jc^1J с граничными условиями
и(х, 0) = ср(х); и@, 0 = «A, 0 = 0.
где ср@) = срA) = 0.
Эта задача аппроксимируется с помощью разностной схемы
где utj = uh(ih, jl), а сетка состоит из точек x = ih, t=jl
^ = rh2 (r = const <y); 'l = 1'2 N< Nh=\;
j = 0, 1, 2, .... M; уИГ<
Так как
ui>j+l = rui-.Uj-\-<,\ —2r)
то /=1, и поэтому разностная схема устойчива.
Для того же уравнения и при той же области О рассмотрим
граничные условия
и(*. 0) = <р(*); (^г+аи) =0; (-g?- + *«) =0.
\ох /х=0 \ох 1х-\
Разностное уравнение оставим прежним, а граничные условия для
разностного уравнения запишем в виде
Тогда
— 2г)
1
Таким образом,
f It 1 1 \
/^max <1, -л г, -5—.¦ , , >
_,- ( l — л^л 1 + bjh )
и рааностная схема будет устойчива, если'только имеют место не-
неравенства а^О; Ь^>0.
Исследование устойчивости путем изучения роста единич-
единичной ошибки. Пусть снова разностная схема C) — D) линейна

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 533
и первые р граничных условий являются начальными. Если при
вычислении решения разностного уравнения допущена ошибка, рав-
равная е, только в одном узле слоя Sk, а во всех других узлах мы не
делаем новых ошибок, то она вызовет ошибки в некоторых узлах
слоев Sk+l, Sk+2. Если эти ошибки быстро растут с возрастанием
номера слоя, то можно ожидать, что схема не будет устойчивой, а
если же они не растут, то можно надеяться на устойчивость.
Эго — метод исследования устойчивости с помощью г-схемы, о
котором мы говорили в § 5. Эги соображения лежат в основе прин-
принципа устойчивости, применимого к исследованию многих явных
разностных схем.
Пусть область О конечна, а l—шаг сетки по t, hv h2, ¦ ¦ ¦, hn —
шаги сетки по xv x2 хп. Если разностная схема лин°йна
и первые р граничных условий являются начальными условиями
для разностного уравнения, имеющего вид
где a = a(t, xv x2, ..., хп)^а0 > 0, а через 2 обозначена сумма
членов, содержащих значения uh. в узлах слоев Sk_v Sk_2, ...
..., Sk_q, и vh есть решение однородного уравнения Rhuh = 0,
rih(uh) = 0 (/=/?-|-1, р -\~2, .. ., т), равное нулю во всех узлах
слоев Sk_q+l, Sfc_g+2 Sk, кроме какого-либо одного узла
слоя Sk, где vh = 1 и любое такое решение на любом слое
Sk (К ~^> k) удовлетворяет неравенству
^v^^CiK—kf-1, C2)
где С не зависит от k, К, I, hv h2, ..., hn и от выбора точки,
в которой vh=l, то разностная схема C)—D) устойчива по
правой части в норме
Для доказательства представляем / в виде суммы функций, каж-
каждая из которых отлична от нуля лишь в одном узле сетки. Тогда uh
будет суммой решений, аналогичных vh и оцениваемых по нера-
неравенству C2).
Исследование устойчивости методом разделения переменных.
Этот метод исследования устойчивости мы уже применяли в § 5.
Здесь мы проиллюстрируем его еще на одном примере.
Рассмотрим разностный метод решения задачи о колебании гиб-
гибкой струны, закрепленной на концах х = 0; х=\, рассмотренный
в примере п. 1 данного параграфа. Разностная схема и сетка те же,
что и в указанном примере. Для исследования устойчивости рас-
рассмотрим однородное разностное уравнение с однородными граничными.

534 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
условиями, кроме начальных, т. е будем рассматривать схему
uh (х, t + l)- 2uh (x, t) + uh (x, t - /)
Khuh — -p
uh(x+h,t)-2uh(*,f)
-
-
roh (ttft) = uh (ih, 0) = cp0 Щ, rlh («0 = М/*.0
rih («*) = «ft @, П) = 0. r3ft («0 = uh №. Л) = 0
и применим к ее решению метод разделения переменных, положив
Так как коэффициенты уравнений не зависят от t, можно взять
w(j) = \3, где X — пока неизвестная величина. Подставляя иЛ =
в разностное уравнение, получим:
или
Мы имеем линейное разностное уравнение с постоянными коэффи-
коэффициентами. Для v(k) в силу граничных условий имеем:
Будем искать решение этого уравнения в виде v(k) = ak, где а —
искомая величина. Подстановка в уравнение после сокращения
на ак-2 дает
или
откуда
а, =-
Общее решение уравнения имеет вид
где Cj, C2—произвольные постоянные. Из граничных условий имеем:
^O, т. е. 02 = — ^,
JV _
= C1(a*-o^=0. т.е. -Ji.= /l=

§ 7] СХОДИМОСТЬ И УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ 535
или, так как a.i = —-, ол = — = е ? . Отсюда
Система функций vm(k) (/и = 1, 2 N—1) ортогональна и
полна, т. е.
N-1
S. Tikm . Tikrn-, . .
sin „ sin = 0 (m Ф nti),
и любая функция cp(ft), определенная на множестве точек 0, 1, 2, ...
. . ., Л/, для которой ср @) = ср (Л/) = 0 представляется в виде линей-
линейной комбинации этих функций.
Для р получим следующее равенство:
р = at + Оа — 2 = 2 cos -^ 2 = — 4 sin2
откуда
Следовательно,
Для устойчивости разностной схемы нужно потребовать, чтобы
все Xf были по модулю меньше или равны единице и среди них
не должно быть кратных (рассуждения те же, что и в § 5, так как
любое решение uh представляется в виде линейной комбинации
решений вида (C0-\-CJ-\~ ... -\~Cp_Jp~l)\3v{k), которое соответ-
соответствует корню характеристического уравнения X кратности р). Так
как Х^а = 1 и при всех т = 1, 2 Л/ — 1 \ Ф Х2, то это воз-
возможно лишь в том случае, если
т. е. при /-sin2-^ < 1 или г < (т = 1, 2 Л/— 1).
W
Итак, устойчивость будет иметь место, если при всех т= 1, 2, ...
.... Л/—1 будет выполнено неравенство
1_ \_
h "^ m
sin —
или при -г-< 1.

536 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Из теоремы сходимости устойчивой разностной схемы будет
следовать, что в нашем случае при -г ^ 1 и h—>0 последователь-
последовательность иь будет сходиться к точному решению граничной задачи для
дифференциального уравнения.
Изложенные выше приемы исследования устойчивости разностных
схем применимы в основном для разностных схем, аппроксимирующих
дифференциальные уравнения с постоянными коэффициентами.
Исследование устойчивости разностных схем для уравнений с пере-
переменными коэффициентами, как правило,—очень сложная задача.
Если уравнение с непрерывными коэффициентами*) рассматривается
в конечной области, то на практике применяют следующий принцип:
Заменяем в уравнении все переменные коэффициенты постоян-
постоянными, полагая их равными значениям переменных коэффициен-
коэффициентов в какой-либо точке Р области. Если при любом выборе
точки Р полученная разностная схема с постоянными коэффи-
коэффициентами будет устойчива, то устойчива и разностная схема
с переменными коэффициентами.
В случае нелинейного дифференциального уравнения задача иссле-
исследования устойчивости разностной схемы еще больше усложняется.
В этом случае Исследуют устойчивость в окрестности искомого ре-
решения для линеаризованного уравнения.
5. Некоторые общие замечания. При численном решении
краевых задач для дифференциальных уравнений в частных произ-
производных методом сеток могут быть использованы только сходящиеся
разностные схемы, так как только в этом случае можно рассчиты-
рассчитывать на получение приближенного решения, достаточно близкого
к точному решению задачи. Но и сходящиеся разностные схемы
не всегда могут быть использованы при практическом решении за-
задачи, так как при применении метода сеток при вычислении значе-
значений граничных функций и правой части неизбежно возникают по-
погрешности, и чтобы эти погрешности не исказили истинного решения
разностной схемы, последняя должна быть устойчивой по граничным
условиям и по правой части. При использовании неустойчивой раз-
разностной схемы искажение истинного решения тем сильней, чем
мельче сетка, при использовании же крупной сетки мы не можем
рассчитывать, что решение разностной схемы будет близко к точ-
точному решению краевой задачи для дифференциального уравнения
в силу плохой разностной аппроксимации уравнения.
Далее, при решении разностной задачи в процессе счета нам
неизбежно придется округлять значения решения в узлах сетки.
!) О разностных схемах для уравнений с коэффициентами, допускаю-
допускающими разрывы см. сноску на стр. 373, а также доклад А. А. Самарского
в Трудах конференции по дифференциальным уравнениям в Ереване,
ноябрь, 1958 г.

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 537
Наличие этих ошибок может также сильно исказить картину реше-
решения, поэтому необходимо требование устойчивости разностной схемы
относительно ошибок, возникающих в результате округлений значе-
значений решения в узлах сетки. Так как ошибки округления значений
решения в узлах сетки, по крайней мере, в простейших случаях
можно компенсировать изменением правой части разностного уравне-
уравнения, то особенно существенно требование устойчивости по правой
части. Наконец, нужно иметь в виду, что мы всюду рассматривали
устойчивость как свойство, связанное лишь с разностным уравне-
уравнением и граничными условиями для него, совершенно не принимая
во внимание алгоритм, используемый для решения разностной схемы.
Однако даже в том случае, когда разностная схема устойчива по
граничным условиям и по правой части, при неудачном выборе
алгоритма для счета решения этой разностной схемы может произойти
сильное накопление вычислительной погрешности, в этом случае
уже неустойчивым будет сам процесс счета. Неустойчивые алгоритмы
счета практически непригодны в случае мелкой сетки. На это явле-
явление мы уже указывали при изложении метода прогонки решения
краевых задач. В книге В. С. Рябенького и А. Ф. Филиппова
«Об устойчивости разностных уравнений» приведены пример раз-
разностной схемы и алгоритмы получения решения схемы, из которых
одни являются устойчивыми, а другие неустойчивыми.
Вопросы устойчивости разностных схем и вычислительных алго-
алгоритмов приобретают особое значение при использовании современ-
современных быстродействующих вычислительных машин, и исследованию
этих вопросов уже сейчас посвящено большое количество работ.
§ 8. Метод прямых решения граничных задач
для дифференциальных уравнений в частных производных
1. Сущность метода прямых. Пусть в прямоугольной области
0{а<л;<р; у0 <[ у < у0 -J-1} (рис. 74) необходимо найти решение
эллиптического дифференциального уравнения
g ^=f{x, у),
A)
(a, fr>0 в G-4-Г).
удовлетворяющее граничным условиям:
и{х, л4-0 = «Pi(«) («<*<?), )
и (а, у) = ф„О0; и (р, у) = ^ (.у) (уо<У<Уо-\~ 0. J
где <pi(x), <\>i(y) (/ = 0, 1) — заданные функции.
Метод прямых приближенного решения этой задачи, предложен-
предложенный М. Г. Слободянским, заключается в следующем. На отрезке

538 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
[у0, уо-\-1] возьмем точки yk = y0-\-kh (k = 0, 1,2 п), h = -~~r
и проведем прямые у = ук. Предполагая существование достаточно
гладкого решения и(х, у) задачи A) — B), положим в уравнении A)
У=Уо
¦Г
?-J
Рис. 74.
У — Ук (ft = 1, 2 п) и заменим производные по у разностными
отношениями, например, воспользовавшись равенствами
ди_ 1
ду
у=ук
(Л2),
C)
где и^(л:)^и(л:, _у^). Получим следующую систему п обыкновенных
линейных дифференциальных уравнений второго порядка:
= /* W
(Л2)
(Л=1. 2 я).
Пренебрегая в них членами О (Л2) и обозначая через Uh(x) прибли-
приближенные значения решения и(х, у) на прямой у = ук для их опреде-
определения, получим систему уравнений
= l. 2 я).

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 539
Используя граничные условия на Г, имеем:
E)
и (а) = % (ук); Uk ф) = ^ (ук) (Л = 1. 2 я).
Система D) обыкновенных дифференциальных уравнений с гранич-
граничными условиями E) аппроксимирует с точностью до й2 дифферен-
дифференциальное уравнение A) с граничным условием B) и называется си-
системой уравнений метода прямых.
Общее решение системы D) будет линейно зависеть от 2я про-
произвольных постоянных. Используя граничные условия E) для
отыскания этих постоянных, получим систему 2я линейных алгеб-
алгебраических уравнений, решив которую мы и найдем функции Uk(x)
(&=1, 2 я), аппроксимирующие решение задачи A) — B) на
прямых у = ук (&=1, 2 п).
В зависимости от способа замены производных по у разностными
отношениями мы будем иметь разные системы метода прямых,
с различной точностью аппроксимирующие дифференциальное урав-
уравнение A).
Этот метод удобнее всего применять в том случае, когда коэффи-
коэффициенты в уравнении A) не зависят от х. В этом случае система D)
будет системой обыкновенных линейных дифференциальных уравне-
уравнений с постоянными коэффициентами1).
Метод прямых можно рассматривать как предельный случай
метода сеток, если, используя прямоугольную сетку, шаг сетки
по оси х устремить к нулю.
2. Метод прямых решения задачи Дирихле для уравнения
Пуассона. Пусть в области G, указанной в п. 1, требуется найти
решение уравнения
с граничными условиями
yo-irl) = <?1(x) (a<X?), )
и(х, yo-irl) = <?1(x) (a<X?), )
J
«(«. у) = <!¦<>(*): «(Р. У) = 1>iСу) (Уо<у<Л+О- J
!) По поводу областей применения метода прямых и построения раз-
различных схем метода прямых см. доклад акад. А. А. Дородницына в книге:
Конференция «Пути развития советского математического машиностроения
и приборостроения», пленарные заседания, Москва, 12—17 марта 1956 г.,
особенно стр. 47—50.

540 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Применяя для решения задачи F) — G) метод прямых и заменяя
производную
разностным отношением
получим следующую систему уравнений метода прямых:
uUx) + -fclUk+1(x) — 2Uk(x) + Uk_1(x)]=fk(
(ft=l. 2 я),
с граничными условиями
= 1. 2 я).
(9)
аппроксимирующую уравнение F) с точностью до й2.
Рассмотрим более точную аппроксимацию уравнения F), предпо-
предполагая большую гладкость решения задачи F) — G). Для этого за-
заметим, что из разложения функции и(х, у) как функции перемен-
переменного у в окрестности точки ук по формуле Тейлора следует:
«С*. Ук+д — 2и(х, У
Совершенно аналогично
ду~*
дуг
_ ,2
— П
¦
(х, Ук)
ду1*
(х, ук)
ду*
r
д*и(х, у Л
Исключая из этих двух равенств а * • будем иметь:
Учитывая, что из дифференциального уравнения F)
д^и(х, у.) д?и(х, у.)
{/k)=f(xy)yiA = f{x)
и заменяя в A0) все производные -з-j , получим:
KW2

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 541
Отбрасывая член с О (Л4), получим следующую систему уравнений
метода прямых:
(*=1. 2 я), A1)
Un+i(x)=<fi(x)
с граничными условиями
= 4»i СУ*) (* = 1. 2 я), A2)
аппроксимирующую задачу F) — G) с точностью я4.
Так как системы уравнений (8) и A1) линейны, то общее реше-
решение каждой из них равно сумме некоторого частного решения и
общего решения соответствующей однородной системы, последнее
не зависит от /, от граничных функций, а также и от размеров
области G, если задано я, поэтому его можно найти раз и навсегда,
что мы и сделаем сейчас.
Рассмотрим однородную систему уравнений, соответствующую
системе (8):
U lU(x) 2U(x) + U(x)] = 0 (ft = l. 2 я),
U0(x) = Un+1(x)=i0. (8')
Будем искать частные решения этой системы вида
Uk(x) = T(k)v(x). A3)
Подстановка в (8') дает
(ft=l. 2 я),
Т(О)=Т(«-И) = О A4)
или
Для отыскания ^(&) получим однородное разностное уравнение
т (ft + 1) — [2 — кЧЦ т (ft) + т (ft —¦ 1) = 0 A6)
с граничными условиями
т@) = т(я+1) = 0. A7)
Общее решение разностного уравнения A6) имеет вид
itf. A8)

542 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где С: и С2 — произвольные постоянные, а 1( и Хз— корни харак-
характеристического уравнения
X2 — [2 — Л282]Х+1=0.
Из граничных условий A7) имеем:
т (я + 1) = CxX?+1 + СХ+1 = Сх (Х?+1 - Х2И+1) = 0.
Отсюда
D1) =1 или 41= yi=e»+1 (s = 0. 1. 2 я).
27Д8
Но так как X^^l, то Xi=em+1 и
7IJS
Зная Xj и Х2, можно найти и неизвестную постоянную 8, ибо по
свойству корней квадратного уравнения
tcig rfs
2 — Л282 = \ + Х2 = e»+i + ^~^+i = 2 cos^
Х2 =
откуда
os_ Д2 sin 2(re+1) — Л2 sin 2/ (s —и, 1 п), (.!»>
а
Ts(*)=C1\eM+1 — e M+1J^Csin^-pr = Csin—^——. A9)
Нетривиальные решения будут только при s= 1, 2, .... п. Из урав-
уравнения A5) имеем:
«"(*) —&2«(*) = 0
или
г;8(х) = Л8Ла:+В8еЛ B0)
Итак, мы имеем п частных решений линейной однородной системы (8')'-
Uk,. (х) = [Аае'»' + В.е-^] sin "S (У* ~ Уо) (s=l, 2 я). B1)
которые между собой линейно независимы, а следовательно, общее
решение этой системы имеет йид
п
Uk (х) = ^ sin Jji (Л-^ (^eV + В,*"V). B2>
8 = 1
где 4 и В, — произвольные постоянные.

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 543
Совершенно аналогичными рассуждениями можно показать, что
общее решение однородной системы, соответствующей системе A1),
имеет вид
ик (х) = 2sln т"(л - Уо) И*е **х—B«e~ va <23>
8=1
где
24 sin" д (У^7 Уо)
(s=l. 2 я), B4)
созЛОУ-Уо))
а Д' к В8 — произвольные постоянные.
Имея общее решение однородных систем, соответствующих
системам (8) и A1), в каждом конкретном случае можно найти
частное решение этих систем, например, методом вариации постоян-
постоянных, а следовательно найти общее решение неоднородных систем,
а затем, используя граничные условия для функций Uk(x), полу-
получить систему линейных алгебраических уравнений для отыскания 2я
¦произвольных постоянных As и Bs (или As и Bg), решив которую
мы и найдем функции Uk(x), являющиеся приближенными значе-
значениями решения и(х, у) задачи F) — G) на прямых у = ук.
В случае прямоугольной области сходимость решения задачи
(8), (9) к решению задачи F), G) в предположении достаточной
гладкости последнего и оценка погрешности метода могут быть
получены с помощью принципа максимума для решения системы
(8), (9); для доказательства сходимости решения задачи A1), A2)
к решению задачи F), G) и вывода оценки погрешности метода
этот подход уже неприменим *).
__ !) Укажем один подход, не опирающийся на принцип максимума, приггд-
ный как в случае системы (8), (9), так и в случае системы A1), A2).
Пусть требуется решить задачу Дирихле:
ДМ = О, 0<х<а, 0<у<Ь; и\х=0 = <р (у), и \х=а = и \у=0 = и \у_ь = 0,
где ср (у) — нечетная периодическая с периодом 2/ функция, имеющая
при — оо<у<+оо непрерывные производные до (р— 1)-го порядка и
кусочно-непрерывную производную р-то порядка; р>1. Вычитая из точного
решения этой задачи
+ ОО
Sh \m {a — х) ¦кт
т=1
полученного методом разделения переменных, точное решение задачи (8), (9),
представленное в виде
+со
:h ат (а — х) о . 2 Kmh
?1 а Sm\my, <om = -у sin -|-,
т=0

544 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Если область G имеет вид криволинейной трапеции (рис. 75),
ограниченной прямыми у—у0, у = уо-\-1 и кривыми х = а.(у),
•* —РО0 (Уо ^ У ^ Уо ~+~ 0. то описанная схема применения метода
прямых не является вполне корректной. Оказывается, что суще-
существуют очень простые области 6, для которых краевая задача для
системы обыкновенных дифференциальных уравнений метода прямых
при некоторых п будет неразрешима. В связи с этим может быть
предложена1) другая схема метода прямых, свободная от указанного
недостатка. Опишем эту схему на примере решения задачи Дирихле
и|г = ср(х, _у)|г для уравнения Лапласа, если область имеет вид,
изображенный на рис. 75,
Строится контур Г5, составленный из линий у = уо-^-Ъ;
у = у0 -\-1 — 8; х =. а (у) -\- 8; х = р (у) — 8, где 8 > 0 — достаточно
получим:
V
Sh \т (а — х) Sh vm (a — х)
Sh \ma
4I = 1 т=т0'
При любом niQ в силу свойств <р (у) будет
+ СО
Sh
sin
т=т0
| —- ]
\< )
причем константа, входящая в 01 —- | , без труда выписывается явно.
1
Если т0 уже выбрано, то, исследуя разности Хот — <от и шт — 1т при
1 ^ т ^ Щ, нетрудно получить:
Таким образом, для погрешности метода получаем оценку
Аналогично в случае применения системы A1), A2) получаем:
Ьк (х)=\и (х, ук) - ик (х) | = О
Таким же способом получается оценка погрешности метода при применении
систем (8), (9) и A1), A2) к решению задачи Дирихле для уравнения Пуас-
Пуассона. (Прим. ред.)
!) Е. X. Костюкович, О сходимости метода прямых ..., ДАН СССР,
118, № 3, 1958.

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 545
малое число. Рассмотрим систему прямых у = ук = у0 -(- 8 4- kh
(h= ~ ). Абсциссы точек, а также и сами точки пересече-
пересечения прямой у = ук с контуром Г5 обозначим через хк>1, хк,2.
Решаем k-t уравнение системы (8), в которой положено/ft(x) = О,
только на общей части [ак, j3ft] отрезков [хк_и1; хк_и2\, [хк1; хк2\,
1хк+ы- хк+и г1. считая, что h настолько мало, что общая часть
Рис. 75.
этих отрезков есть отрезок. Краевые условия для Uk(x) зададим
следующим образом:
Uk(x) = <f(a(yk), yk) при
). Ук)
B5)
где ср(х, у) — заданная в задаче Дирихле граничная функция. Реше-
Решение рассматриваемой таким образом системы (8) с граничными
условиями B5) ищем методом последовательных приближений,
принимая за первое приближение, для Uk (х) на отрезке ак ^ х ^. j3ft:
а следующие приближения при т. = 2, 3, 4,
уравнений
=l, 2
я),
находим из системы
= о
-*- 9 = <
B6)
(ft = l я).
Л) = cp0 (x); t/Si — cp (x,
Обозначая через Uf] {x) значения Uk (x) при данном h, можно по-
показать, что при наличии у решения и(х, у) непрерывных производных

546 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
по у до третьего порядка включительно в области G и при
соответствующем выборе /г = /г(8)( lim /г(8) = 0) имеет место
0<8>0
сходимость приближенного решения к точному решению за-
задачи и(х, у):
lim max max | и (х, ук) — Uf] (х) \ — 0.
г, dus (х, у) _
Если предположить, что , 8 равномерно непрерывна в G,
то этот процесс можно проводить не строя вспомогательного кон-
контура Г6.
Эта схема обобщается на общие линейные эллиптические урав-
уравнения с переменными коэффициентами и на области более общего
вида, чем изображенные на рис. 75.
Пример. Найти решение уравнения
в квадрате —0,5 ^х, у 4^0,5, если граничные условия нулевые:
и \х=± 0>5 = и \у_±й>ъ = 0.
Для решения задачи применим метод прямых с тремя проме-
промежуточными прямыми _у=0, у=±0,25. Значения Uk(x) решения
на этих прямых будем находить используя систему уравнений ме-
метода прямых вида (8) с я = 3. Будем иметь систему
U" (х) + 16 [U2 (х) — 21/, (х)] = — 1.
if г (х) + 16 [U3 (x) — 2U2 (x) + U, (x)] = — 1; 1/„ (х) = 1/4 (х) = 0,
U» (x)-\-l&[U2(x) — 2Us(x)]=— I
с краевыми условиями
Ui(— 0.5) = ^(+0,5) = 0 (/ = 1, 2, 3).
Частное решение неоднородной системы ищем в виде Ut = А{ = const.
Подстановка в систему дает
А1-2А2 + А3 = -±,
I
откуда

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ УРАВНЕНИЙ 547
Используя выражение B2) для общего решения соответствующей
однородной системы, общее решение системы можно записать
в виде
x (х) = sin 0,25тг (Сге^х -\-Dxe-b>x) + sin 0,5тс (С2е'¦#>
+ sin 0.75ТГ (С3е^ + D3e-^) + А =
U2 (х) = «in 0,5тг (С^
D2e-*<*) + Х^- (С3е^ + D3e ~^) + А,
-Н sin тг (С2е5^ + D2e-5^) + sin 1,5тс (С3е5^ + D3e-«*») 4- -g- =
3 (x) = sin 0,75ir (Cxe+b'x + D^-^) + sin 1,5тс (C2e'^x + D2-4^) 4-
4- sin 2,25tu (C3e ^ ^
*») 4--^ (C3e5sa; + ^3^"^) 4-"^.
где по A8)
8? = 4- 16 sin2^ = 9,3726, 8, = 3,0611,
82 = 4- 16 sin2-^-=32, 82 = 5,6568,
8g = 4- 16 sin2-^=54,6274, 8з = 7,3910.
о
Удовлетворяя граничным условиям и учитывая симметрию, т. е.
считая Ci=^Di, получим:
|/2 Сх Ch 0,58j 4-2C2Ch 0,582 4-/2 Q Ch 0,583 = — А,
2С, Ch 0.58J — 2C3Ch 0,583 = — -^-.
1/2 Ci Ch 0,58! — 2С2Ch 0,582 4-/2 С3Ch 0,583 = — А-.
Отсюда
С, = — 0,0266, С2 = 0, С3 = —0,00009.
Таким образом,
Ul (х) = U3 (х) = 0,0938 — 0,0376 Ch 3,0611л; — 0,00013 Ch 7,3910л,
U2 (х) = 0,1250 — 0,0532 Ch 3,061 \х 4-0,00018 Ch 7,3910x.

548 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Приближенное значение решения в центре квадрата будет U2 @) =
= 0,0720, а точное же значение решения в этой точке «@, 0) =
^0,0736.
3. Метод прямых решения смешанной задачи для уравнения
колебаний струны. Рассмотрим сначала метод прямых приближен-
приближенного решения простейшего уравнения колебаний струны
в области 0^.х 4^1; 0 ^ / < оо, при следующих начальных
и граничных условиях
«lt=o = cPiW; ~Ж _ =сРгМ @<.*</);
«@, 9 = ф,(9; a(l.t) = ^(f) @<г<оо). B8)
Проведем систему параллельных прямых
= 0, I, 2 ге+1; я = тГТ
и обозначим через ик(х) значения точного решения и(х, у) за-
задачи B7) — B8) на прямой х = хк, т. е. ик {х) = и (хк, /). Если
заменить разностным отношением
-тъ{и(хк+1, t)—2u(xk, t)-\-u(xk_lt t)\,
B9)
то получим следующую систему уравнений метода прямых:
ul(t) — ±[Uk+l(t)-2Uk(t)-\-Uk_1(t)]=fk(t)
(ft = 1. 2 я),
с начальными условиями
= 1, 2 re), |
(ft = 1, 2 re), | C0)
аппроксимирующую уравнение B7) с точностью до я2.
Чтобы получить систему уравнений метода прямых, более точно
аппроксимирующую уравнение B7), воспользуемся равенством, ана-
аналогичным равенству A0):
u(xk+i> t) — 2u(xk, t)-\-u(xk_v t) =
^w>]0<*., ас

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 549
Из дифференциального уравнения B7)
K k ' — v k ' f (x A — и (?\ f (t\
Тогда соотношение A0) после подстановки да» да
д*и(хк v
¦ у
у*
дает
Отбрасывая член О (Л4) и заменяя при этом «й(<) на Uk(t), получим
следующую систему уравнений метода прямых:
J I/* @ -И wl1/* + *@ + Ut-1(t)] —
12
=1. 2
C1)
с начальными условиями
Uk @) = ?, (хк) = cplft; Uk @) = ср2 (хк) = cp2i k (ft = 1, 2 я). C2)
Эта система уже дает аппроксимацию порядка А4.
Здесь, как и в п. 2, легко построить общие решения однород-
однородных систем, соответствующих системам дифференциальных уравне-
уравнений метода прямых B9) и C1).
Построим для примера общее решение системы
6" и* @ + ТТ[Uk+dt) + l/*-i @l —
6""*W-!--j2"
1 = 0 (ft = l. 2
C3)
соответствующей системе C1). Частные решения этой системы будем
искать в виде
Подставляя в систему C3), получим:
T <*-
-l)} = 0 (ft = l. 2
"@ [!" Т (A)+ -jj T (* +0 + -J3

550 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
или
т<* + 1)-ат<*)+т<*1)g2 = const. C4)
Для отыскания i (k) получаем разностное уравнение
[ ^] (А —0 = 0 C5)
с граничными условиями
Т@) = т(»+1) = 0. C6)
Его общее решение имеет вид
где Хх и Х^ — корни уравнения
Из граничных условий имеем:
Т(О) = С1+С2 = О; Са = —Сх;
Т (я + 1) = dX?+1 + CX+1 = Сх (ХГ+1 - X?+1) = 0.
Таким образом,
1 = /l=^+i
= /l=^+ (S = O, I, 2 «),
Л2
или так как ХХХ2 = 1, то
Далее,
2 [12 — 58W] ^s
откуда
24 sin^ „ , д5 ¦¦ 24 sin2." "
2/
(s = 1, 2 я), C7)
rfsft ttisft
(s = 1. 2 я) C8)
(при s = 0 получаем тривиальное решение Yo(^) —0).

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 551
Из уравнения C4)
!» @ = 0.
или
vs (t) = As cos 8/ -\- Bs sin 8S/.
Таким образом,
Uk, s (t) = sin —JL (As cos bst + Bs sin 8,0.
Общее решение однородной системы C3), следовательно, имеет вид
Vk (t) = 2dsin ~г~(Лз cos *st+Bs sin ^ C9)
где Aa, Bs — произвольные постоянные. Найдя методом вариации
постоянных частное решение неоднородной системы C1), получим
общее решение ее как сумму частного решения и построенного
общего решения C9) однородной системы. Постоянные As и Bs
(s = 1, 2, .... п) найдутся из условий C2).
Однородная система, соответствующая системе B9), имеет общее
решение
п
Uk @ = ^ sin -^-*. (С„ cos b'j + Ds sin bj) (? = 1,2 и), D0)
s=-l
где
D1)
Сходимость решений, полученных методом прямых, к обобщен-
обобщенному решению задачи B7) — B8) имеет местох) в любом прямо-
прямоугольнике О^л:^/; 0^/^7\ если начальные и граничные ус-
условия нулевые, а для функции f(x, t) имеют место неравенства
/У fpdxdt<C: \jPdx\ <C;
0 0 Lo -It—0
//A®
dxdt < С
с некоторой положительной константой С. Общий случай начальных п
граничных условий сводится к этому случаю при выполнении
!) В. И. Лебедев, Уравнения и сходимость дифференциально-раз-
дифференциально-разностного метода, Вестник МГУ, № 10, 1955, стр. 45—47.

552 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
некоторых требований на гладкость функций <pi. <рг. <l>i> Фг и условий
сопряжения.
Остановимся теперь на решении методом прямых задачи о коле-
колебаниях неоднородной струны
Prain>0, °(*)>3mta>0. 0<ж</, 0<t<T, D2)
а@. /)=ф1(/), u(l,t)=\{t), 0<t<T, D3)
«(ж, О) = ср1(л:)> «,(дг, 0)=<p2(jc). 0<л:</. D4)
Приближенные значения решения этой задачи на прямых х = хк = kh,
k = Q, 1, .... re4-1; (ге+1)я = /, можно получить, как решение
системы обыкновенных дифференциальных уравнений с постоянными
коэффициентами
D5)
= q(xk), fk(t)= f(xk, t),
Может быть предложен следующий способ доказательства схо-
сходимости и оценки погрешности метода х).
Положим 7й@ = иС*й> 0 — ий@- Для TftW получаем, применяя
разложения по формуле Тейлора, систему
То(Ч=Т„+1(О=О, Tft@) = T;@) = 0 (ft=0. 1, 2, .... re+l), D7)
где
| Rk @ | < M = M3.MM;r + Ma.М„жа; +1 MaMMu;a;a;, D8)
причем M.Q, М„', УИ,", Mu , Mu , Mu —максимумы модулей
Си XX ХЗСХ
величин, обозначенных в индексе, при О^х^/, 0<;/^7\ Положим
ft-0
') Б. М. Б у д а к, О методе прямых для некоторых краевых задач,
Веси.ик МГУ, № 1, 1956, стр. 3—11.

8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 553
В силу D6), D7). D8) и неравенства Коши — Буняковского, диф-
дифференцируя D9), получаем:
dt jU Ift^ftlft I ЧкЬк) I ~ ^J "ft /j2
_ 9 V
k
в
г" 2л 4khRk =
(Tft+i — Tit) — gV-iTft (fft — Tft-i)
ft*
= -^ {«„T^+i [Tn+i — Т„] - aoT^ [Ti - To]}
Ь 1 * Ъ 1
ft^2<
ft=l ' ft=l
Так как /@)^0, то, следовательно,
7@ <
Далее, вследствие To (t) = 7n+iW^0 будет
<r n+1
Следовательно, в силу неравенства Коши — Буняковского

554 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
откуда
m+1
h
amin
Сопоставляя E0) и E1), получим оценку
, О —
Pmin S
¦h.
E1)
E2)
Здесь константа М выражается через константы М^, .... Ми
В цитированной на стр. 551 заметке дается также выражение
М через коэффициенты уравнения, свободный член /(х, t) и на-
начальные и граничные функции cplt cp2, фх, ф2.
4, Метод прямых решения смешанной задачи для уравнения
теплопроводности. Рассмотрим сначала метод прямых решений сме-
смешанной задачи для простейшего уравнения теплопроводности
ди_
dt
_
«@, 0 = <W
E3)
E4)
заменяя разностным отношением производную по х. При наборе
прямых
= 0. 1. 2 я
используя приближенное равенство
или равенство A0') с заменой в нем производных
из диффе-
дифференциального уравнения получим две системы уравнений метода
прямых:
= h @
(ft=l, 2 я),
E5)

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 555
1 и'к (о + -^ [u'k+'i @ 4- tfi-i (<)] -
= 1, 2 я),
E6)
J
из которых первая дает аппроксимацию уравнения с точностью я2,
а вторая с точностью я4.
Из начального условия для и(х, t) получаем начальные условия
для Uk(t), одинаковые в обоих случаях:
= 1. 2 я).
E7)
Построение общих решений однородных систем уравнений, соот-
соответствующих системам E5) и E6), проводится точно так же, как
и в случае уравнения колебания струны, так как, отыскивая частные
решения однородных систем вида
мы получим для ¦(¦ (к) в точности те же самые разностные уравнения,
что и в п. 3, с граничными условиями 7 @).= f (я-)- 1) = 0, а для
отыскания v(t) получим уравнение
т. е.
^s if) =
E9)
Следовательно, общее решение однородной системы, соответствующей
системе E5), будет иметь вид
Uk(O = S Сs sin
s=l
=l. 2 я), F0)
где
2/
= l, 2 я),
F1)
а общее решение однородной системы, соответствующей системе E6),
имеет вид
= ^] Ds sin ^^- e~°s * (k = l, 2, .... я), F2)
s=-l

556 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где
24 sin^ ~ "
Гб + cos
21 (s = l, 2 re). F3>
Далее, при заданных /, ф^ ф2 находятся, например, методом вариации
постоянных общие решения систем E5) и E6), а неизвестные
постоянные CS(DS) находятся из начальных условий E7).
В книге А. Н. Тихонова и А. А. Самарского «Уравнения мате-
математической физики» 1953 г. сходимость решения задачи E5), E7)
к решению задачи E3), E4) и оценка погрешности при соответ-
соответствующей гладкости свободного члена /(х, t), начальной и гра-
граничных функций доказывается с помощью принципа максимума для
решения системы E5), E7).
В цитированной на стр. 550 заметке сходимость решений
задач E5), E7) и E6), E7) к решению задачи E3), E4) в любом
прямоугольнике О^х^/; 0<;/^Г доказана на основе приме-
применения теорем вложения при условии, что начальные и граничные
условия нулевые, а правая часть /(х, t) удовлетворяет условиям
т i
ffr*xat<c.
0 0
)
_0 —(=0
т i
где С — некоторая положительная константа.
Рассмотрим теперь применение метода прямых с заменой про-
производных по х разностными отношениями к уравнению теплопро-
теплопроводности с переменными коэффициентами.
Приближенные значения решения краевой задачи
F4)
P>Pmin>0, a>am.n>0 @<*</. 0</<T). J
й@, t) = tyl(t), u{l, t)=4}2(t) (O^Ct^CT), F5)
и(х, О) = ср(х) @<х</) F6)
на прямых х = хй = &я, (п-\- 1)я = 1 (k = 0, 1 п -4- 1) можно
получить, решая систему обыкновенных дифференциальных урав-
уравнений с постоянными коэффициентами:
F7)
ак = а(хк)> Qk = cl(xk)' fh @ = / (хк< 0 F°)
ик@) = cp(xft), wo(O=4iWi M»+i W ^4г@- F9)

§ 8) МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 557
В цитированной на стр. 551 статье предложен следующий способ
доказательства сходимости и оценки погрешности метода. Поло-
Положим ik(t) = u(xk' t) — ик @. где и(хк, t) — значение точного
решения задачи F4) — F6) на прямой х = xk = kh. Для величин
(/ получаем систему
0 (ft = 0, 1. 2, .... я + l), G1)
Rk\<M = M,.MUx + Л4.. Mu^ + 4 ЛМ« w G2)
где константы М„ Ми определяются как в предыдущем
XXX
параграфе. Рассмотрим величину
Дифференцируя G3), мы, в силу G0), G1), G2) и неравенства Коши —
Буняковского, аналогично тому, как это сделано в соотношений E0),
получим:
dt "
k=\
В силу неравенства Коши — Буняковского и G3') имеем:
Следовательно,
Для величины -jk имеет место неравенство
xh (I — хл
fk<h : , л«). (si*)
°min '
получающееся аналогично неравенству E1). Из E1*) и G4) выте-
вытекает оценка
^ ь. . ' *' ft' iu ni ».ii.n^/
1 V P
minamin
). G5)

558 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Все это делается совершенно аналогично тому, как в предыдущем
параграфе при оценке I(t) и fk(t). Заметим, что константа М, как
и ранее, может быть выражена через известные функции.
В случае замены производной по t разностным отношением,
т. е. при выборе семейства прямых t=tk = kh (k=0, I, 2, . . .),
можно также построить системы уравнений метода прямых, аппро-
аппроксимирующие с разной точностью дифференциальное уравнение E3)').
Приведем две системы2).
ц(лг,
Заменим зт-
ot
разностным отношением
2ft
Тогда получим систему уравнений для отыскания приближенных
значений Uk(x) решения и(х, t) на прямых t=tk вида
Uk(x)-^-[Uk+1(x)~-Uk_l(x)]=fk(x),
G6)
с граничными условиями
tf*(O)=<l>i0*)=<W.*; t/*@ = **('») = **,* (*=1. 2, 3, ...)• G7)
Эта система аппроксимирует уравнение E3) с точностью Л2.
Систему уравнений, аппроксимирующую уравнение E3) более
точно, можно получить следующим образом. Предполагая, что реше-
решение и(х, t) задачи E3), E4) достаточно гладко, запишем следующие
разложения по формуле Тейлора:
= u(x. tk)+hu't
u(x,tk — h) = u
— hu't
t=th
t-t,.
t't,.
t-u
ft*
T
+ О (h3),
t-t,.
1) Метод прямых с сохранением производных по х широко применялся
также к квазилинейным уравнениям параболического типа; см., например,
Rot he, Zweidimensionale parabolische Randwertaufgaben als Orenzfall eindi-
mensionaler Rondwerfaufgaben, Math. Annalen, т. 102, Heft 4/5, 1929;
A. H. Колмогоров, И. Г. Петровский, Н. С. Пискунов, Иссле-
Исследование уравнения диффузии..., Бюлл. МГУ, вып. 6, 1937; О. А. О л е й н и к,
А. С. Калашников, ЧжоуЮй-линь, Задача Коши и краевые задачи
для уравнений типа нестационарной фильтрации, И АН СССР, т. 22, № 5,
1958; Чжоу Юй-линь, Краевые задачи для нелинейных параболических
уравнений, Матем сб., т. 47 (89), № 4, 1959.
2) Простейшую схему такого варианта метода прямых, ее сходимость
и оценку погрешности см. в книге В. И. Смирнова, Курс высшей матема-
математики, т. 4, Гостехиздат, 1951, стр. 737—739.

§ 8] МЕТОД ПРЯМЫХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФ. УРАВНЕНИЙ 559
h h
Умножая третье равенство на —-~-> четвертое на у и складывая
их с первым и вторым равенствами, получим:
и(х, tk-Jrh) + u(x, tk — h) —
— \ Wt (*. h + h) — u't (x, tk — A)] = 2« (x, tk) + О (h*)
или
у A) — «; (*• <ft — A)] 4- О (Л4). G8)
Заменяя в G8) производные по t из уравнения E3) и отбрасывая О (Л4),
получим для определения приближенных значений Uk(x) решения
и(х, t) на прямых t=tk систему
U'k+l (х) - U"k^ (х) - j [Uk+i (х) — 2Uk (x) -I- !/»_! (х)] =
= l, 2. ...).
G9)
с граничными условиями
Uk(Q)=^.k; ик{1) = Ьл (ft=l. 2, ...)• (80)
Системы G6) и G9) можно решать как рекуррентные системы, если
каким-либо способом найти Ul(x).
Пример. Построить методом прямых приближенное решение
задачи
¦3r=dsr + 1: "Lo="Uo=«Ux=°-
Для этого отрезок [0, и] разделим на четыре части и проведем
через точки деления прямые. Если Uk(t) (Д> = 0., 1, 2, 3, 4) при-
приближенные значения решения на прямых х = -^— (& = 0, 1, 2, 3, 4),
то для отыскания Uk(t) имеем систему линейных дифференциальных
уравнений
с начальными условиями

560 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Частное решение неоднородной системы можно искать в виде
Ui = Ai = const.
Подстановка в систему дает
А — А — Зя2 • А — ^
*i — ^з — ~32Г' Л2 — -g- •
Общее решение однородной системы получаем из F2). Таким образом,
общее решение неоднородной системы имеет вид
Ul (t) = С1 sin - е l
sine a +Csme 3
= Ct sin ^ Г"?' + С2 sin «"* + С3 sin ^ *"* + х
!/,(/) = С, sin -^ Г* + С2 sin Ц- Г* 4 С3 sin ^ Г* 4 ^- =
-4* I n -°1
2 +С
где
16 • 24 sin* -?- 16-24 sin^ ^-
^
о1
„2/5+ cos -^-J
= 0,9984, аа=-^ ^- = 38,9073.
16 • 24 sin" ^-
= 2,2458.
я21 5 + cos —I
Для определения С^ С2, С3 из начальных условий получаем систему
ч — сз——х-
откуда
Ct=:—1.2700; Са = 0; С3 = — 0.0374.

§ 9]
ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
561
Итак, окончательно
?/j (() = U3(t) = 0,9253 — 0,8980е-°>998« — 0,
U2(t)= 1,2337 — 1,
Для точного решения на прямой х = -j- имеем:
ии ; в я ^ B*
fc-o
B*4-
Для наглядности приведем следующие данные:
t
Точное решение
Приближенное решение
0,5
0,4620
0,4750
1,0
0,7663
0,7698
По поводу других применений метода прямых к решению краевых
задач для уравнений в частных производных см. цитированные выше
статьи Б. М. Будака и В. И. Лебедева, а также Я. И. Алиха-
шкин, Решение задачи о несовершенной скважине методом прямых,
Вычислит, математ., № 1, 1957; Б. М. Будак, А. Д. Горбу-
Горбунов, Метод прямых для решения одной нелинейной краевой
задачи в области с криволинейной границей, ДАН, т. 118, № 5,
1958, стр. 858—862 или А. Д. Горбунов, Б. М. Будак,
Метод прямых для решения одной нелинейной краевой задачи
в области с криволинейной границей, Вестник МГУ, № 3, 1958,
стр. 3—11; О. М. Белоцерковский, Расчет обтекания круго-
кругового цилиндра с отошедшей ударной волной, Вычислительная мате-
математика, сб. 3, 1958; Е. А. Григорьева, Метод прямых в сме-
смешанных задачах для параболических систем, ДАН, т. 119, № 4,
стр. 649—651, 1958; Л. И. Камынин, О применении метода конеч-
конечных разностей к решению уравнения теплопроводности, ИАН СССР,
Серия математическая, 17 A953), стр. 163—180 и стр. 249—268;
П. И. Пушкин, Обтекание эллипсов и эллипсоидов дозвуковым
потоком газа, Вычислит, математ., № 2, 1957.
§ 9. Вариационные методы решения краевых задач
для дифференциальных уравнений математической физики
Среди приближенных методов решения уравнений в частных про-
производных значительное место занимают вариационные методы. В неко-
некоторых областях механики эти методы являются самыми распространен-
распространенными. В § 10 главы 9 мы уже рассматривали вариационные методы
решения краевых задач для обыкновенных дифференциальных уравне-
уравнений. Здесь мы рассмотрим применение этих методов к решению краевых
задач для линейных дифференциальных уравнений в частных произ-

562 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
водных второго порядка эллиптического типа. Как уже говорилось,
в основе вариационных методов лежит замена краевой задачи для
дифференциального уравнения эквивалентной ей вариационной зада-
задачей. Приближенное решение краевой задачи сводится к построению
приближенного решения соответствующей ей вариационной задачи.
Более подробно мы остановимся на методе Ритца приближенного
решения вариационных задач, соответствующих тем или иным крае-
краевым задачам, поэтому, чтобы не обосновывать сходимость этого
метода в каждом конкретном случае, мы изложим этот метод в об-
общем виде, а в конкретных случаях будем лишь проверять выпол-
выполнение условий, при которых этот метод применим.
1. Метод Ритца решения операторных уравнений и отыска-
отыскания собственных значений операторов в гильбертовом простран-
пространстве. Пусть на линейном множестве НА, всюду плотном в гильбер-
гильбертовом пространстве Н, определен аддитивный оператор Ли/ —
некоторый элемент из Н. В НА требуется найти элемент, являющийся
решением уравнения
Ay=f. A)
В § 10 главы 9 было показано, что если оператор А положителен,
то уравнение A) имеет не более одного решения, и если решение
уравнения A) существует, то функционал
J(y) = (Ay, у) - (/, у) - (у, /), B)
определенный на НА, достигает на этом элементе наименьшего зна-
значения, т. е. если обозначить через z решение уравнения A), то
= inf УО0 = |*. C)
и наоборот, элемент, реализующий минимум функционала J(y) на Нл,
является решением уравнения A).
В дальнейшем мы всегда будем предполагать существование
решения уравнения A) и будем лишь рассматривать способы при-
приближенного построения этого решения.
Для построения приближенного решения уравнения A) в пред-
предположении, что А — положительный оператор, строят последователь-
последовательность {zn} (zn?Hj), обладающую тем свойством, что
lim У(гп) = inf УСУ) = |*. D)
п + со Н
Последовательности, для которых имеет место условие D), называют
минимизирующими. Если минимизирующая последовательность ока-
окажется сходящейся к элементу z?HA, то этот элемент будет являться
решением задачи о минимуме функционала J(y) в НА, а следова-
следовательно и решением уравнения A). За приближенное решение урав-
уравнения A) принимают некоторый член zn этой последовательности.

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 563
Как уже отмечалось ранее, не каждая минимизирующая последо-
последовательность является сходящейся. Для того чтобы каждая миними-
минимизирующая последовательность сходилась к решению z уравнения A),
нужно наложить на оператор А дополнительные ограничения. Таким
требованием будет положительная определенность оператора А.
Оператор А называют положительно определенным, если суще-
существует такая положительная постоянная К2, что для любого эле-
элемента у ? На имеет место неравенство
(Лу, у)>К*\\у\\*. E)
Заметим, что положительно определенный оператор является и по-
положительным оператором.
Теорема. Если А положительно определенный оператор,
то любая минимизирующая последовательность \zn) (zn ? НА)
функционала B) сходится к решению z вариационной задачи, т. е.
lim \\zn — z\\ =0. F)
В самом деле, если z—решение вариационной задачи, то Az=f и
J(z)=(Az, г) —(г. /) — (/. z) =
= (Az, z) — (z, Az) — (Az, z) = — (z, Az) = p.
Далее,
J(zn) — p = (Azn, zn) — (zn, /) — (/, zn) + (z, Az) =
= (Azn, zn) — (zn, Az) — (Az, zn)-\-(z, Az) =
= (A (zn — z), zn) — (zn — z, Az) = (A (zn — z), zn) — (A (zn — z), z) =
= (A(zn-z), Zn-
Так как j(zn)->\>., то \\zn — z\\2->0, что и доказывает наше утвер-
утверждение,
Таким образом, если А — положительно определенный оператор,
то за приближенное решение уравнения A) можно принять элемент zn
любой минимизирующей последовательности при достаточно большом п.
Один из способов построения минимизирующей последователь-
последовательности предложил Ритц. Метод Ритца заключается в следующем.
В На выбирается последовательность элементов хъ х2, .... хп, ...,
обладающая следующими свойствами:
1) любое конечное число членов этой последовательности линейно
независимо;
2) для любого s > 0 и любого элемента у ? На найдется такое т
и такие числа а1у а2, ..., ат, что имеет место неравенство

564 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
При фиксированном целом п строится линейная комбинация
п
ап = 2 Чхк (8)
с произвольными численными коэффициентами aft (будем предпола-
предполагать, что Н — действительное гильбертово пространство и ак — дей-
действительные числа). Функционал J (ип) будет функцией alt a2, ...,an:
•/(««)= 2 *j<xk(Axj, x*)-2 2a,(/, xj). (9)
j,k-=l j=l
Постоянные alt a2, .... an выбираются так, чтобы J(un) принимал
наименьшее значение на совокупности всевозможных линейных ком-
комбинаций (8). Для этих значений
^ = 0 (у=1, 2. ....«), (Ю)
т. е.
2 а*(Лх*. х-) = {f, Xj) (У = 1, 2 /г). A1)
Йв 1
Таким образом, для отыскания а.к получается симметричная
система линейных алгебраических уравнений. Определитель этой
системы отличен от нуля, так как если на НА ввести скалярное
произведение
[х, у] = (Ах, у), A2)
что возможно, так как А — симметричный и положительно опреде-
определенный оператор, то определитель системы есть определитель Грама
системы линейно независимых элементов х^, х2 хп. Поэтому
система A1) имеет единственное решение. Обозначим через zn ли-
линейную комбинацию вида (8), где в качестве коэффициентов взято
решение системы A1). Последовательность {zn} будет являться,
минимизирующей последовательностью. В самом деле, пусть задано
s > 0. Так как \>.= Inf J(y), то найдется элемент v?HA, для
*В
которого
В силу свойства 2) последовательности xv х2 хп, ... найдутся
такое целое число т и такие числа ах,а2, .... ат, ч го при заданном т) > 0
т
и vm= 2 aixi имеет место неравенство (A(v — vm), v — vm) < т). Но
il
J(v) — J(vm) = (Av, v) — (Avm, vm) — 2(f.v) + 2 (/, vm) =
= {Av, v) — (Avm, vm) 4.2 (Az. vm—v) =
= — lvn — v, vm — v] + 2 [г; — vm, v},-\- 2 \z, vm ~ v].

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 565
(Здесь [ ] означает скалярное произведение, определенное равен-
равенством A2).) Применяя неравенство Буняковского, будем иметь:
№ — vm, v] | < y\v — vm,v — vm] [v, v] =
= V(A (v — vm), v — vm) Y(Av, v) < VvV(Av, v),
| [z, vm — v) I < Y\z, z] [vm — v,vm — v] < Y~4 Y{Az, z).
Отсюда
i J(v) - J(vm) | < | (A (vm — v), vm - v) | + 2 | [v - vm, v] 14-
\[z, -om — v) I < ij + 2Yi [V(Av, v) + Y(Az. z)].
Так как (Av, v), (Az, z) — фиксированные числа, то t\ можно вы-
выбрать так, что будет иметь место неравенство
\J(v) — J(vm)\<^. A4)
Из A3) и A4) следует, что |i<^W<e-|-ii, но тогда заведомо
[j.<; J(zm)< fJ-4"s и ПРИ всех ч^-т имеем [j.^ 7(zn) < ?4"^. а это
и означает, что
lim J(zn) ==[J.,
П->-со
т. е. \zn) — минимизирующая последовательность.
Заметим, что если вместо системы элементов xv x2, . •., хп,
которые мы будем называть координатными, взять новую после-
последовательность координатных элементов _Ук Уь •••> Уп> •••> свя*
занную с xlt х2, ..., хп, ... соотношениями
к
то минимизирующие последовательности, построенные по методу
Ритца, использующие {хп} и {уп}, дадут один и тот же результат.
Процессом ортогонализации можно построить такую последователь-
последовательность \уп}, что ук будет выражаться через xlt x2, .... хк с помощью
равенств A5), а
0 {1гф I),
, „ ' A6)
1 (й /)
В этом случае система, аналогичная системе A1), примет вид
«j = (/. ^) G=1. 2 ft) A7)
|ед 2 ^^ A8)
.?'— 1

566 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Заметим также, что вместо свойства 2) системы координатных функ-
функций {xi} достаточно требовать полноту системы {Ахг} в Н, т. е.
потребовать от {jqj, чтобы при любом у?Н и е > 0 существовали
такие ге и а,, «2, ..., ап, что
ly —2«,^*J<e, A9)
так как из этого свойства следует свойство 2). В самом деле,
пусть у^На и е>0 — заданное число, a v = Ay. Тогда по свой-
свойству {Axj\ можно найти такое п и такие aj, что
!п II —
V — 2 <^ Л* J< УТ/С.
Далее, используя неравенство E), имеем:
(A(y-vn), y-vn)^.\\A(y-vn)\\ \\y — «w||<:
I и I
Отсюда, сокращая на V(A(y — vn), у — vn) и возводя обе части
в квадрат, получим:
(A(y—vn), y — vn)<e,
т. е. получим неравенство G).
Если имеется способ отыскания чисел 8, меньших [i., но сколь
угодно близких к р., то можно получить оценку точности прибли-
приближения zn к решению z уравнения A). Для этого воспользуемся уже
ранее использованным неравенством
из которого следует, что
\ \b, B0)
что и позволяет оценить точность приближения zn через J(zn).
Рассмотрим теперь задачу отыскания собственных значений
оператора А, т. е. таких значений X, для которых уравнение
Ау—Ху^О B1)
имеет нетривиальные решения. Последние называются собственными
элементами оператора А, соответствующими собственному значе-
значению X.
На оператор А наложим следующие ограничения. Будем пред-
предполагать, что оператор А симметричен и ограничен снизу.

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 567
Оператор А называют ограниченным снизу, если существует
такое число N, что для любого у ? Ид имеет место неравенство
(Ay, y)^N\\y\\\ B2)
Теорема. Для симметричного оператора А все собствен-
собственные значения действительны, а собственные элементы, соответ-
соответствующие различным собственным значениям, ортогональны.
Действительно, если Хд— собственное значение оператора А,
а у0 — соответствующий ему собственный элемент, то
АУо — VVo = O- B3)
Умножая обе части скалярно справа на у0, получим:
(Лу0, Уо) — \)(Уо, Уо) = О.
откуда
(Л Уо) С24Ч
B4)
Х°~ (Уо-Уо) *
а так как числитель и знаменатель—действительные числа, то Хд—
действительное число. Пусть теперь X! и Xj-—различные собственные
значения оператора А, а гх и z2— соответствующие им собственные
элементы. Тогда
Агх— X1z1 = 0; Az2 — Xa^a^O.
Умножим первое из них скалярно справа на z2, а второе скалярно
слева на гх и вычтем почленно. Получим:
(Azv z2) — (zu Az2) — (X1 — XfiiZi, z2) — 0.
В силу симметричности оператора А имеем (Azt, Z2) = (zlt Az2), т. е.
(kt—XaHzj, z2) — 0,
и так как \Ф\2, то (zlt Z2) = 0-
Задача отыскания собственных значений оператора может быть
сведена к вариационной задаче.
Теорема. Если А — ограниченный снизу симметричный опе-
оператор, а \ — нижняя грань значений функционала
a zx — элемент, для которого J(z1) = \1, то \ есть наименьшее
собственное значение оператора A, a zx — соответствующий ему
собственный элемент.
В самом деле, пусть т; — произвольный элемент из НА, at —
произвольное действительное число. Обозначим через ср(?) функцию
)} + (Аг1г г{)
гх + t-ц) — Р (г), г]) + 2t Re

568 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
По условию она достигает минимума при ? = 0, но
ь 11)} fa. г,) - 2 Re {fa, g)} (Azh Zl)
Отсюда
(zu ^ReftA^, т))}— Re{(zv п)} (Azv zJ = 0.
а так как J(z1) = \1, то (A?!, z1) = X1(z1, Zj) и
Re{(Aslf ij)}—Х^е{(г„ ij)} = Re {(Az, — Хл, ij)}=0.
Заменяя -r\ на /т), нолучим:
Im [(Az1 — 'k1zv tj)} = 0.
т. e.
—X^!, 7)) = 0.
Ho 7j — произвольный элемент из Нл, а Я^ всюду плотно в Н, т. е.
Azx — \гх = 0,
и утверждение будет доказано, если мы покажем, что X! — наимень-
наименьшее собственное значение. Пусть X' — любое другое собственное
значение оператора А, аг' — его собственный элемент. Тогда
Az' — XV = 0 и (Аг', z') — l'(z', z') = 0.
Отсюда
(г', г') -" ^ен^ (у, у) »
Это заканчивает доказательство утверждения.
Отыскание следующих по величине собственных значений опе-
оператора А тоже может быть сведено к вариационной задаче. Это
следует из теоремы:
Если \^ <] Х2 <^ ... -<! Хп — первые п собственных значений сим-
симметричного ограниченного снизу оператора A, a zu z2 zn —
соответствующие им ортонормированные собственные элементы,
и zn+i — элемент, реализующий минимум функционала B5) «а
множестве элементов у ?Нд, удовлетворяющих дополнительным
условиям
(у, Zi) = 0 A=1, 2 и), B6)
то zn+1 — собственный элемент оператора А, соответствующий
собственному значению Х„+1, где
п+1' п+1

§ 9) ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 569
Для доказательства возьмем произвольный элемент ? ? НА и по-
п
ложим т\ = \ — 2 (?• «й)«й- Тогда (т), <г*) = 0 (у = 1, 2 ге)„
так как
(т), zt)=a, zj) - .2 а. «*) («*. ^)=а, г$ — a, z-)=о,
f о (ЛФТ)
ибо (zk, zj) = { . Этим свойством обладает и элемент tt\,
[ 1 (к = 7)
где ? — любое действительное число, а также и ?п+1 -f-^т). Функция
достигает минимума при ^^0. Но это означает, что i)/@) = 0. Из
этого условия, так же как и раньше, доказывается, что
(Azn+i — Xn+1zw+1. ij) = 0.
Докажем, что и (Агп+1—Хп+1г:п+1, 1) = 0. Действительно,
(Azn+1 Xn+i zn+1, к) ^
и
4- 2 fe. 5) (Агп+1 —
ft-i
Но
— Xn+1(zn+1, «ft) = (Xft —Xn+1)(«n+i. «ft) = 0
в силу симметричности оператора А и ортогональности zn+1 ко всем
zk(k=l, 2, ..., re). Таким образом, для любого i?HA имеем
(Агп+1 — Xn+1zn+1, ?) = 0, а поэтому
Если X' — любое собственное значение, следующее по величине
за Хи, a z' — его собственный элемент, то z' ортогонален всем zk
(ft=l. 2 re) и
у _ (Az', z') . ,
что полностью доказывает утверждение.
Вариационная задача, соответствующая задаче отыскания ге-го
собственного значения оператора А, может быть сформулирована
и следующим образом:
Среди всех элементов у?НА, удовлетворяющих условиям
(У, У)=\\У\\2=1, (У, «ft) = 0 (?=1,2 ге-1), B8)

570 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где zk — собственные элементы, соответствующие собственным
значениям Xlt Х2 ^n-i> найти минимум функционала Ji(y)=:
= (Ау, у). Минимум этого функционала и будет Хп, а элемент,
его реализующий, будет собственным элементом, соответствую-
соответствующим Хп.
Метод Ритца приближенного решения этих задач (предполагая
существование их решений) заключается в следующем.
Рассматривается последовательность координатных элемен-
элементов {хп}, обладающая такими свойствами:
1) любое конечное число их: xlt x2, .... хп, линейно независимо;
2) для каждого элемента у ? На и любого е > 0 существуют
такие целые числа т и п и совокупности действительных чисел
alt а2 ат и Ьи Ьг Ьп, что
»т Л
у —JSe**« <s> B9)
s. C0)
(Предполагается, что Н— действительное гильбертово пространство
и скалярное произведение элементов—действительное число.) По-
Положим
и
2 C1)
и выберем ак так, чтобы ип обеспечивало минимум функционала
и
Л(кп)= 2 akai (Axk, xj) C2)
при условии, что
и
(ип, ип) = 2 akai (Хк. хг)=1. C3)
Решение этой задачи выполняем по правилу неопределенных мно-
множителей Лагранжа, т. е. составляем вспомогательную функцию
Ф («!, «2 «„) = (Ли„, и„) — X (ип, ип) =
и и
и ищем безусловный минимум этой функции. Отсюда
= 0 (* = 1, 2 я)
, *,) — X ^ «г (**. *

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 571
ИЛИ
и
2а,[(Л*к, хг) — Х(хк, xt]=0 (й=1, 2 я). C4)
Определитель этой системы Dn (к) обязан быть равным нулю,
так как все сц не могут быть равны нулю одновременно. Таким
образом, для отыскания X имеем уравнение степени п:
(Axh xj—k (хъ X]) (Ах2, xj—k (хь xi) ... (Ахп, xj—k (xn, xj
(Axlt x2)—k(xb X2) (Ax?, x2)—к(хъ x2) ... (Axn, x2)—k(xn, x2)
(Axb x^—kixi, xn) (Ax2, xn)—k(x2, xn)... (Axn, xn)—k(xn,xn)
= 0.
C5)
Если Xon — корень этого уравнения, то Dn (Xon) = 0 и система C4)
имеет нетривиальное решение при Х = Хоп. Пусть оно <х°, <х°, ..., а°.
При любом действительном \>. Ф 0 система чисел [i.a°, [jux°, ..., ра°
будет также решением системы C4). Выберем jj, так, чтобы выпол-
выполнялось условие (ип, ип) = 1 и через с^, о^, ..., ап обозначим
[j.a'J, {10^, ..., jia^ при данном значении р.. Тогда будем иметь
тождества
и и
2 «* (Ахк, хг) = Хо„ 2 Ч (**. *i) (/=1,2 re), C6)
2 «л (**.*i) = 1. C7)
л,г=1
Умножим C6) на аг и просуммируем по / от 1 до п. Получим:
и и
2 «Л (Ахк, хг) = Хо„ 2 «Л (**. -^г) = \)п-
к, 1=1 к,1 = 1
Но
2 ЧЧ (А*к> хг) = ( А [ 2 «Л ). 2 аг*г) = (Аип, ип).
Таким образом,
коп = (Аип, ип). C8)
Это показывает, что все корни уравнения C5) действительны и один
и
ИЗ них дает минимум функционалу Jt (у) на множестве ип =
(ип, ип)= 1. Этот минимум, очевидно, равен наименьшему по вели-
величине корню уравнения C5), который мы обозначим через Х,п.

572 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
С возрастанием ге Хш не возрастает и в то же время остается не
меньше \. Таким образом,
lim \n^\.
П ->СО
Докажем, что
lim Xln = Xlt
Рассмотрим сначала случай \ > 0. В этом случае оператор А
положительно определенный, так как для любого у?НА имеем
(Ау, у)^-\(у, у). По определению нижней грани Xt для любого
s > 0 найдется такой элемент и ? НА, что Xt ^ (Аи, и) < X, -f- е.
Из свойства 2) последовательности [хп\ следует, что найдется такой
и
элемент vn = 2 bkxk, что
[и —vn, и — vn] = (Л (и — гд, и — vn)< s.
Отсюда, обозначая
Н.у11о = /ПуГуЬ C9)
имеем:
или
(Avn, Vn) = \\vX
Но (Л(и—г>п), и—vn)^-\(u—vn, и—vn). Отсюда (a—vn, и—г»л)^у-
или ||u-vn||
ким образом,
где 8-* 0 вместе с е. Так как \ш =
(Av v
< , Vn' VnJ < )-, -f- 8. При т > re имеем Xm < Xln и, следовательно,
1%. vn)
lim Хш = Хг.
Если Xj <; 0, то введем вспомогательный оператор
D0)
Это положительно определенный оператор, так как
- У).

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 573
Далее,
Inf <^f} = l. D1)
Я (У. У)
и
Если ип = 2 Ч*к и («„. «„) = 1. то
Ы(ЛЛ, иJ = inf[(Лип, un)-\-(l—\)(un, un)]=l
Отсюда по ранее доказанному
lim infGVn> un)= lim (Xln + A — \))= 1,
П->со П-> со
т. е.
lim Xln=X1.
П->-со
Для отыскания следующего по величине собственного значения
ищем минимум функционала Jl(un) = (Aun, un) при условиях
и
К, ип) = 1; (ип> zn) = 2 аЛрг (^, хг) = 0, D2)
л, г=1
п
где 2n^2Pft-"-ft — приближенное значение первой нормированной
собственной функции. Для этого составляем вспомогательную
функцию
ф(<*1. Ч ап) = (Аип, ип) — 1(ип, ип)—р(ип, zn)
и приравниваем нулю ее частные производные по ак. Это приводит
к системе
и
2 К Кл**> *i) — х (**• *i)l — И-Р* (**. хг)} = 0. D3)
Если обе части равенства D3) умножить на (Зг и просуммировать
по I от 1 до п, то получим:
2 Ч^КЛхк, хг) — \(хк, *,)]—!* 2 P*Pi(**. *i) = 0,
л,г=1 л, г=1
или
Pi №**• хг) - Чхк, *,)] } -1*(zn, zj = 0.
Но из системы C6)
п п
*i) = ^1« S Pi (**. *i).
г1

574 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
откуда
п \п \
2 Ч \ 2 h l(Axk, хг) — X (хк, хг)] \ — {1 (*„, zn) =
k = l [1=1 )
п п
= 2 Ч 2 (\п — х) h (Хк, хг) — p (zn, zn) ==
= (xm — Xi) («». ^n) — t1- (*n- 2"n) = 0.
Так как (ип, гп)^0 и (гп, zn)= 1, то [j.^0 и система D3) совпа-
совпадает с системой C6). Отсюда, как и прежде, заключаем, что искомый
минимум равен второму по величине корню уравнения Dn(X) = 0.
Аналогично ищутся и следующие собственные значения опера-
оператора А. Они приближенно равны следующим по величине корням
уравнения C5). Нужно только отметить, что точность приближения
следующих собственных значений меньше.
2. Метод Ритца приближенного решения краевых задач для
линейных дифференциальных уравнений з частных производных
второго порядка эллиптического типа. В конечной области G,
ограниченной кусочно-гладким контуром Г, задано уравнение
где/?—положительная непрерывно дифференцируемая в области O-j-T
функция, a q и /—непрерывные в G-4-T функции, при этом д^-0.
Рассмотрим следующие краевые задачи:
Найти решение уравнения D4), удовлетворяющее на границе Г
одному из следующих трех краевых условий:
«|Р = 0, D5)
-° D6)
(о — непрерывная неотрицательная функция, не равная тождественно
нулю, are — внешняя нормаль);
du
Чп
= 0. D7)
г
Мы рассматриваем нулевые краевые условия, так как общий
случай может быть сведен к рассматриваемому, если в О-)-Г можно
найти какую-нибудь достаточно гладкую функцию ир удовлетво-
удовлетворяющую ненулевым заданным условиям и вместо функции и искать
функцию v = u—и1# Такая замена приведет нас к краевой задаче
для уравнения, отличающегося от уравнения D4) только правой
частью, но уже с нулевыми начальными условиями.

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 575
Рассмотрим гильбертово пространство L2(G) действительных
функций, интегрируемых с квадратом в области G, в котором ска-
скалярное произведение определено равенством
fffl D8)
о
В этом пространстве выделим три множества функций М, Ж„ и Мо,
элементами которых являются дважды непрерывно дифференцируе-
дифференцируемые функции в О-)-Г, удовлетворяющие соответственно краевым
условиям D5), D6) или D7).
Покажем, что оператор Lu положителен на множествах М и М„,
а также и на множестве Мо, если в последнем случае q (х, у) ф 0.
В самом деле,
(Lu, и) — I I uLudxdy =
H- J f qiPdxdy =
Если и?М, то и|г=0 и
- E0)
Если (Lu, и) = 0, то -^ = -^ = 0 ии = С = const, но и |г = 0, т. е.
С = 0 и и^О, а это и показывает, что (Lu, и)^>0 при всех и ? М
и (Lu, и) = 0 только при и = 0, что и означает положительность
оператора Lu на М.
Если и ? Ж„, то из D9) и D6) имеем:
(Lu, *)=f f{p[(?)%^%f] + 1»}dxdy+fpo*d8. E1)
в г
Так как р > 0, 9>-°> °>0 и о^О, то (Z-и, в)>0 и равенство
нулю возможно лишь при -^ = -^ = 0, т. е. при и = С = const.
Но если (Z-и, и) = 0, то и Г pou2ds = C2 С pads = 0, а это озна-

576 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
чает, что С=0 и и = 0, а следовательно, Lu—положительный
оператор на М„.
Если и ? Мо и q фО, то
Равенство нулю возможно лишь при / / /?|(-s-) +(з~) \dx dy и
G
f Г qu2dxdy = 0. Из первого следует, что и = С = const, а из вто-
о
рого, так как д^О, следует, что и = 0, т. е. и на Мо оператор Lu
положителен, если q ф 0.
Если q(x, y)==0, то Lu не будет положительным оператором
на Жо, так как для любой функции и, тождественно рапной в G 4- Г
любой постоянной С, имеем (Lu, и) —0, а и^О. Но в этом случае
решение краевой задачи D4), D7) существует не при всех /. Рас-
смотрим условия, при которых задача имеет решение. Пусть функ-
функция и удовлетворяет уравнению D4) с^ = 0и краевому условию D7).
Проинтегрируем по области О тождество
д I ди\ , д
Будем иметь:
Но
в
ди
так как -т-
условию
^0. Таким образом, функция / должна удовлетворять
J jfdxdy=0. E4)
Выделим из ^г(О) функции, удовлетворяющие этому условию. Их
совокупность образует в L2(G) линейное множество L2(G). Для Z2(G)
сохраним то же скалярное произведение, что и в L2 (G). Полученное
гильбертово пространство примем за основное. В нем выделим
множество Мо дважды непрерывно дифференцируемых в G-\~ Г функ-
функций, удовлетворяющих на Г условию D7). На этом множестве Lu
будет уже положительным оператором. Действительно, при и ? Мо

§ 9) ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 577
из E2) имеем:
Если (La, и) = 0, то ^ = ^ = 0ив = С = const. Но так как и ? Мй,
то
f Judxdy = C JJdxdy = 0,
о о
откуда С = 0 и и (х, у) = 0, что и доказывает положительность
оператора Lu на Мо.
Заметим, что в Мо уравнение D4) имеет единственное решение,
чего нет в Мо, так как в Мо при <7 = 0 решение определяется
с точностью до постоянного слагаемого.
На основании общей теории п. 1, если краевые задачи D4) — D5),
D4)—D6), D4) — D7) имеют решения, что мы всегда будем пред-
предполагать, то они будут также и решениями следующих вариацион-
вариационных задач:
Решение задачи D4)—D5) является решением задачи о мини-
минимуме функционала
на множестве М,
решение задачи D4)—D6) является решением задачи о минимуме
функционала
J(u)=f f {p [^y + №y]+qu*-2fu}dxdy+fpcu>ds E6)
с г
на линейном множестве Ма\
решение задачи D4) — D7) является решением задачи о минимуме
функционала E5) на линейном множестве Мо, если q (x, у) ф 0, и
решением задачи о минимуме функционала
на линейном множестве Мо функций, удовлетворяющих условию D7)
и условию
J fudxdy = 0, E7)
G
при этом функция / должна удовлетворять условию E4).

578 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Для того чтобы к решению вариационных задач можно было
применить метод Ритца, нужно показать, что оператор Lu на соот-
соответствующих линейных множествах является также и положительно
определенным оператором. Тогда на основании общей теории будет
иметь место сходимость в среднем минимизирующих последователь-
последовательностей, полученных по методу Ритца, к точным решениям соответ-
соответствующих краевых задач.
Положительную определенность оператора Lu нетрудно доказать
при некоторых дополнительных ограничениях, воспользовавшись
следующими утверждениями, которые мы приведем без доказательства.
(Доказательства можно найти в книге Михлина С. Г. «Прямые
методы в математической физике» или в книге Куранта и Гильберта
«Методы математической физики», т. 2, гл. 7.)
Если функция и(х, у) дважды непрерывно дифференцируема
в области G-f-Г и на кусочно-гладкой границе Г области G обра-
обращается в нуль, то существует такая положительная постоянная А,
не зависящая от и, что имеет место неравенство
называемое неравенством Фридрихса.
Если функция и дважды непрерывно дифференцируема в об-
области G-f-Г, то существует такая постоянная В > 0, не зависящая
от и, что справедливо неравенство
ff { / / [(?) (%)} у 1\ E9,
G ' G J
которое также называют неравенством Фридрихса, а также нера-
неравенство
F0)
где D и Е — положительные постоянные, не зависящие от и, кото-
которое называется неравенством Пуанкаре.
Пусть теперь и ? М. Тогда по E3) имеем:

§ 9) ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 579
Положим ро = Inf р(х, у). По условию ро>0. Используя
(а>, У)€.О+Т
первое неравенство Фридрихса E8), имеем:
Так как р0А = /С2 > 0, то это и означает положительную опреде-
определенность оператора Lu на М.
Пусть теперь и ? Mz. В этом случае оператор Lu будет поло-
положительно определенным, если
inf q(x, y) = qo>0, F1)
(X, У)?О+Т
или
inf о(х, у) = ао> 0. F2)
Пусть <7о > 0. Если и?М„, то по E1)
что и доказывает положительную определенность Lu на Ма. Если
о0 > 0, то
Обозначим через 8 наименьшее из чисел р0 и pQcsQ, и положим
К2 = ЪВ, где S — постоянная в неравенстве Фридрихса E9) Имеем:
= K2\\u\\2,
т. е. Lu — положительно определенный оператор на Ж„.
Для вариационной задачи, соответствующей краевой задаче
D4) — D7), также рассмотрим два случая.

580 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Если q(x, _У)><7о> 0. то Lu— положительно определенный
оператор на Мй, так как по E2) в этом случае
/
а
>qa[ [
V
V
откуда и следует утверждение.
Если q(x, у) = 0, то Lu— положительно определенный опера-
тора на Мо. В этом случае
О G
и так как / / udxdy = 0, то из неравенства Пуанкаре следует:
о
(Lu, U)^j>
где К2 = Щ- > 0, что и показывает положительную определенность
Lu на Мо.
Итак, сходимость метода Ритца будет иметь место при тех
ограничениях, при которых мы показали положительную опреде-
определенность оператора Lu.
Для построения минимизирующей последовательности по методу
Ритца выбираем последовательность координатных функций
<Pi(*. У)> Ъ(х> У) <Рп(*> У) F3)
удовлетворяющих следующим условиям:
1) <?г(х' У) дважды непрерывно дифференцируемы в О + Г;
2) <?i(x> У) удовлетворяют заданным краевым условиям;
3) любое конечное число этих функций линейно независимо;
4) для любого s > 0 и любой функции и, принадлежащей
к множеству допустимых функций рассматриваемой вариационной
задачи, найдутся такое целое число п и такие числа av а2, . . ., ап,
чю
( \
Для выполнения последнего условия достаточно потребовать,
чтобы для и ? L2 (О) и любого е > 0 нашлись такие bv Ьъ . .., 6т, что
г т -12
G L i-l J

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 581
В случае краевой задачи D4) — D7) от координатных функций <р*
можно не требовать выполнения краевых условий.
Члены минимизирующей последовательности имеют вид
и„(х, .У) = 2 <*{?«(*. У), F5)
где числовые коэффициенты а-х суть решение системы
п
2 ?i (i—\. 2 п). F6)
a Aik и Bi выражаются через коэффициенты уравнения D4) и коор-
координатные функции следующим образом:
1
F7)
dxdy.
Все утверждения этого пункта распространяются и на случай
любого числа независимых переменных, т. е. на краевые задачи
для уравнения
га га
?42 ?/• D4°
где рц — непрерывно дифференцируемые функции переменных
ху> х2, .... хт в конечной области О с гладкой границей Г, удо-
удовлетворяющие условию, что в любой точке О-|-Г квадратичная
форма
положительно определенна, q и / — непрерывные функции в О-)-Г,
причем 9^-0, с граничными условиями одного из следующих видов;
и |г = 0, D57
Ж cos С1*^ + ом = 0>
=
Jr
где о — неотрицательная непрерывная на Г функция и

Б82 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
3. Некоторые другие вариационные методы. Кроме метода
Рита существует ряд других приближенных методов решения
вариационных задач, соответствующих краевым задачам. Не оста-
останавливаясь на них подробно, кратко изложим сущность некоторых
из них на примере задачи Дирихле для уравнения D4).
Метод Л. В. Канторовича. Для простоты предположим,
чго область G, в которой ищется решение уравнения D4) с крае-
краевыми условиями D5), ограничена прямыми х = а, х = Ь и двумя
кривыми у = у1(х), у = у2(х) (а<х< Ъ\ у2(х)> yt(x)). Как
алы видели, решение задачи сводится к решению задачи о минимуме
функционала
\
u)-2(u, f) = f
в
на множестве М дважды непрерывно дифференцируемых функций,
обращающихся в нуль на границе. В методе Канторовича прибли-
приближенное решение ип (х, у) ищется в виде
п
«»(х. y)=H>fk (•*) % (х, у), F8)
где ср& (х, у) — заданные дважды непрерывно дифференцируемые
функции, обращающиеся в нуль на границе Г, за исключением,
быть может, прямых х = а\ x = b, a fk(x) — неизвестные функции.
Подставляя ип (х, у) в J(u) и выполняя интегрирование по пере-
переменному у, получим:
ь
j(an) = j Ф \х, f, (х), /2 (х) /„ (х); /; (х), f2 (х), ...,/; (х)] dx,
F9)
где Ф — известная функция своих аргументов. Для отыскания/&(х)
имеем вариационную задачу о минимуме однократного интеграла.
Выписывая систему уравнений Эйлера
и присоединяя краевые условия
/&(а)=Л(?) = 0 (fc=l, 2 п), G1)
получим краевую задачу для системы линейных дифференциаль-
дифференциальных уравнений второго порядка, решая которую, найдем /&(х)
(&=1, 2 л), а следовательно и мя(х, у).
Можно показать, что в нашем случае система имеет вид
!/а(Ж)
J L(un)<?kdy = 0 (ft=l, 2 л). G0')
0i (a;)

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 583
В качестве функций ср& можно брать, например, функции
% (*. У) = СУ — Ух (*)) (Л (*) — У) Ук~1> G2)
или
При некоторых ограничениях на гладкость решения можно по-
показать, что последовательность {мп}, в которой срА имеют вид G2)
или G3), равномерно сходится к решению краевой задачи
(см. Л. В.Канторовичи В. И. Крылов, Приближенные методы
высшего анализа, гл. 4, ГИТТЛ, 1952).
Метод Куранта. Если в уравнении D4) правая часть имеет
непрерывные производные до некоторого порядка т. Курант пред-
предложил вместо функционала J(u) рассматривать функционал
,74,
Очевидно Л (м)>- /(#), а для функции и, реализующей минимум
функционала J(u) на множестве М, имеет место равенство JY (и) =J(u),
так как Lu=f. Таким образом, решение краевой задачи D4) — D5)
реализует минимум и функционала G4). Если мы построим мини-
минимизирующую последовательность {ип(х, у)} функционала ^(м), то,
очевидно, при п -> оо
Это позволяет получить дополнительные заключения о характере
сходимости ип к и. Например, если решается задача Дирихле для
уравнения Пуассона (р = 1; q ^ 0) и т = 0, то
(IJ -
- G4/)
Построим минимизирующую последовательность {ип)\ будем иметь:
dy^.O. G5'>
f f(bun
По формуле Грина
) ff?(x. У.

584 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ |ГЛ. 10
Отсюда по неравенству Буняковского
Un(x, у)—и(х, .у)|<
///- G6)
Первый множитель в правой части ограничен некоторой постоянной С,
а это означает при учете G5'), что {ип(х, у)} равномерно схо-
сходится к и (х, у).
МетодТреффтца. В методе Ритца приближенное решение
ищется в классе функций, удовлетворяющих краевым условиям, но
не удовлетворяющих дифференциальному уравнению. В противопо-
противоположность этому в методе Треффтца приближенное решение ищется
в классе функций, удовлетворяющих уравнению, но не удовлетво-
удовлетворяющих краевому условию.
Пусть снова рассматривается краевая задача D4) — D5). Обозна-
Обозначим через vo(x, у) решение уравнения D4) и пусть vt(x, у),
"V2(x, у), ..., vn(x, у) — линейно независимые решения соответ-
соответствующего однородного уравнения, т. е.
Lvo=f; Lvk = 0 (ft=l. 2 и). G7)
Тогда линейная комбинация
п
"п (*• У) = ""о + 2 аЛ G8)
будет снова решением уравнения D4): Lun = f. Требуется так по-
подобрать коэффициенты <х&, чтобы функция ип(х, у) в каком-то
смысле наиболее точно удовлетворяла граничным условиям D5).
Например, можно подобрать а^ о^, .... ап так, чтобы интеграл
G9)
принимал бы наименьшее значение.. В этом случае для отыскания
ох. <х2, ...-, ап мы получили бы систему линейных алгебраических
уравнений
^ = 2 Cunvkds = 0 (ft = l. 2 л). (80)
В методе Треффтца от ип требуется, чтобы разность ип и точ-
точного решения задачи и обращала в минимум функционал

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 585
т. е. ах, аз а.п подбирают так, чтобы обращалась в минимум
функция
Ф («!. а2 ап) =
Т(^)"]} <82>
Следовательно, ах, а2 ап должны являться решением системы
№ _ 9 /* Л Г^(Ц« — и) <Ь& | д(ы№ —ы) ди&1 ,
А«*~ JJ\Pl дх ~дх~^ 5^ dyJ"
^xdy = Q (83)
(Л=1, 2 л).
Интеграл в (83) можно преобразовать так, чтобы неизвестное нам
решение и не входило. В самом деле, используя формулу Остро-
Остроградского, интеграл в левой части (83) можно преобразовать так:
=f J
G
G
J M" ~~ U) dX dy + / [Р ^
G Г
Так как Lvk=Q, а м|г^0, то систему (83) можно переписать
в виде
^unds = O (ft=l, 2, ...,«). (83')
г
В эту систему и(лг, у) уже не входит. Решая ее, находим
ар а2 ап, а следовательно и мп(х, у).
Отметим, что если ип(х, у) — приближенное решение краевой
задачи, полученное по методу Треффтца, а и (х, у) — точное реше-
решение, то имеет место неравенство
Ла„)<У(а) = 11. (84)
т. е. метод Треффтца дает приближение к (а снизу.
4. Метод Ритца решения задачи о собственных значениях.
При решении ряда задач математической физики, в частности при
решении уравнений в частных производных методом Фурье, при-
приходится решать задачу о собственных значениях дифференциаль-
дифференциальных операторов.

586 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Рассмотрим несколько простейших задач о собственных значениях.
Пусть требуется найти значения X, для которых уравнение
\u=0. (85)
где р (х) — положительная непрерывно дифференцируемая функция,
a q(x) — непрерывная на отрезке [а, Ь] функция, имеет нетриви-
нетривиальное решение, удовлетворяющее краевым условиям
W' (а) + рх и (а) = 0; а2и' (Ь) + р2м (Ь) = 0 (а» + ^ > 0; /=1,2).
(86)
Рассмотрим гильбертово пространство L2(a, b) и линейное мно-
множество М функций дважды непрерывно дифференцируемых на [а, Ь\у
удовлетворяющих краевым условиям (86). На этом множестве опе-
операторов Lu симметричен и ограничен снизу. Действительно,
если и, v? M, то
(Lu, v) = -fv?(p?)
= ~ Г Тх\а+ J P Tx Jxdx+ J quvdx =
а а
Ь Ь Ь
а~ f и -от [р S)dx + / 1UVdx =(и- Lv)'(87>
а а
ибо в силу краевых условий (86) внеинтегральный член обра-
обращается в нуль, и
(Lu, u)= f[p{^ + qu2]dx^m\nq(x)juzdx = N\\u\\2t (88)
где N = min q(x).
На основании общей теории п. 1 для отыскания собственных
значений X оператора Lu с краевыми условиями (86) можно при-
применить вариационные методы, в частности метод Ритца.
Выбрав в М систему координатных функций (^(д;)), обладаю-
обладающих свойствами, указанными в п. 1, ищем приближенное выражение
для собственных функций в виде
п
(89)

§ 9 ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
Для отыскания значений ак имеем систему уравнений
п
2iO.j(Afj — X/?v) = 0 (/=1, 2 я),
587
(90)
где
= / ЯУгУ}dx — J ^ (р 2?) У} dx; Вц = j у{ (x) yj (x) dx,
а а а
(91)
в которой X должно быть корнем уравнения
D(k) =
Аи-~ХВ
¦1 Xd^
А12—
-2 —
-П
\ — ^Bni Ano —
Ann —
= 0.
(92)
По доказанному ранее корни этого уравнения дают приближенные
значения первых п собственных значений, а функции (89), в кото-
которых <х& есть решения системы (90) при X, равном соответствую-
соответствующему корню уравнения (92), будут приближенными выражениями
для соответствующих собственных функций.
Рассмотрим теперь задачу о собственных значениях для оператора
<93>
где р (х, у) — положительная непрерывно дифференцируемая в О + Г
функция, a q—непрерывная в О + Г функция. Для примера рас-
рассмотрим краевые условия
и|г = 0. (94)
Мы уже видели, что этот оператор симметричен на множестве М
дважды непрерывно дифференцируемых функций, обращающихся
в нуль на Г, принадлежащих к гильбертову пространству L2(G).
Так как
u2dxdy, (95)
то он ограничен снизу, т. е. и в этом случае применима общая
теория п. 1. В соответствии с этой теорией приближенные выра-
выражения для собственных функций ищем в виде
ип(х, y)='?aioi(x, у).
4-1
(96)

588 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где {v{(x, у))—последовательность координатных функций, обла-
обладающая свойствами, указанными в п. 1. Для отыскания <х{ имеем
систему уравнений вида (90), где теперь
(97)
BH
=J J vdx- y)vj(x- y)dxdy.
а приближенные значения собственных значений находятся как корни
уравнения (92), где Лу, Вц определяются равенствами (97).
Для отыскания коэффициентов а{, входящих в приближенное вы-
выражение собственных функций (86), в системе (90) нужно положить X
равным одному из этих корней.
Совершенно аналогично можно было бы рассмотреть и другие
виды граничных условий, но на этом мы останавливаться не будем.
б. Метод Галеркина решения краевых задач. Метод Галеркина
не является вариационным методом. Он не требует предварительного
сведения краевой задачи для дифференциального уравнения в част-
частных производных к вариационной задаче и поэтому он в некотором
смысле более универсален, чем метод Ритца. Основная идея этого
метода была изложена в § 9 главы 9. Мы рассмотрим кратко его
применение к решению краевых задач для уравнений в частных
производных, ограничиваясь уравнениями вида
д ( ди\ д ( ди\ , ди . ди , с /по.
и граничными условиями вида D5), D6) или D7). При этом бу-
будем предполагать, что p,r,s,q, f — непрерывные функции в рас-
рассматриваемой области О, включая границу Г, р непрерывно диф-
дифференцируема и р (х, у) > 0 в G + Г.
В методе Галеркина приближенное решение краевой задачи для
уравнения (98) с граничными условиями вида D5), D6) или D7)
ищется в виде
п
«п(*. У)= 2 <W(*. У).
i
где vu v2 vn — первые п функций последовательности
{vk(x, у)}, обладающие следующими свойствами:
1) функции Vi(x, у) дважды- непрерывно дифференцируемы
О + Г

§ 9] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 589
2) любое конечное число их линейно независимо;
3) для любой дважды непрерывно дифференцируемой функции v,
удовлетворяющей граничным условиям, и любого е > 0 найдется
га
такая линейная комбинация этих функций 2 aivi(x' У)> что
г-1
dx dy=
3 р га \|)
^ (i dxdy<e-
\
A00)
Коэффициенты а.-х (t = 1, 2 п) определяются как решение системы
L(un)vk(x, y)dxdy =
= I f fi>k(x. y)dx dy (k = 1, 2 n) A01)
или
n
2Vj = s* (*=1. 2 n). A02)
где
v v v v
В случае, если r = s = 0 и q^>0, то при одной и той же
системе координатных функций [vh(x, у)) метод Ритца и метод,
Галеркина дают одну и ту же последовательность {ип(х, у)}, а это
доказывает, что она, как и в методе Ритца, в среднем сходится
к точному решению краевой задачи.
Для уравнения (98) с краевыми условиями одного из видов D5),
D6) или D7) при условиях на коэффициенты, которые сформулиро-
сформулированы выше, и при выборе последовательности координатных функ-
функций, удовлетворяющей условиям 1) — 3), последовательности {ип},
полученные по методу Галеркина, сходятся в среднем вместе с произ-
производными первого порядка к точному решению краевой задачи и
соответствующим производным этого решения, если только гра-
граница Г кусочно-гладкая и в случае краевых условий D7) q(x, у)фО,

590 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
а в случае краевых условий D6) о — достаточно гладкая на Г
функция.
Метод Галеркина применим и к задаче о собственных значениях
для дифференциального оператора Lu при тех же типах краевых
условий, но мало надежен для отыскания приближенных выражений
для собственных функций.
Обоснование сходимости метода Галеркина мы не приводим, так
как это заняло бы много места. Интересующихся отсылаем к книге
Михлина С. Г. «Прямые методы в математической физике», где эти
вопросы рассмотрены достаточно подробно.
§ 10. Приближенные методы решения интегральных
уравнений
В этом параграфе мы рассмотрим некоторые методы приближен-
приближенного решения интегральных уравнений, ограничиваясь в основном
линейными интегральными уравнениями Фредгольма первого рода
ь
lfK(x,s)y(s)ds=f(x), A)
а
интегральными уравнениями Фредгольма второго рода
ь
y(x) — \ff<(x.s)y(s)ds=f(x) B)
а
и интегральными уравнениями Вольтерра первого и второго рода,
имеющими соответственно вид
х
, s)y(s)ds = f(x). C)
ее
, s)y(s)ds=f(x), D)
где f(x) и К(х, s)—заданные функции, а у(х) — искомая функция.
1. Решение уравнений Фредгольма методом замены интеграла
конечной суммой. При решении интегральных уравнений Фредгольма
приходится встречаться с решением двух задач: 1) отыскание реше-
решения неоднородного интегрального уравнения при заданном значении
параметра X и заданной правой части/(х); 2) отыскание собственных
значений и собственных функций ядра К (х, s), т. е. отыскание
таких значений параметра X, при которых однородное уравнение
ь
k 0 B')

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 591
имеет нетривиальное решение у (х). Эти значения X и соответствую-
соответствующие им нетривиальные решения и называются, соответственно, соб-
собственными значениями и собственными функциями ядра К(х, s).
Будем сначала предполагать, что ядро К(х, s) и правая часть/(х)
непрерывны и, даже больше, имеют непрерывные производные до
некоторого порядка. Тогда и решение уравнения имеет производные до
того же порядка.
Для решения интегральных уравнений можно применять метод
замены интеграла, входящего в уравнение, конечной суммой, исполь-
используя для этого те или иные квадратурные формулы.
Пусть за основу принята некоторая квадратурная формула
jF (xj) + R (F), E)
где абсциссы xv x2 xn, принадлежащие отрезку [a, b], и
коэффициенты Alt A2 An не зависят от выбора функции F (х),
a R(F) — остаточный член квадратурной формулы. Положим в инте-
интегральном уравнении B) х = хг (i=l, 2, ..., п). Тогда
s)y(s)ds=f(xt) (/ = 1, 2 л). F)
Заменим в F) интеграл с помощью квадратурной формулы E).
Будем иметь:
У(хг)-Ъ %iAJK(xi.Xj)y(Xj)=f(xd+Wii Ri = R[K(xl.s)y(s)]. G)
Отбрасывая в системе G) Х(/^), получим для отыскания приближен-
приближенных значений Y{ решения у(х) в узлах xlt x2 хп линейную
систему алгебраических уравнений
Yi-\ 2 AjKiiYJ = fl (/=1,2 «), (8)
где введены обозначения К^—К(х^ х}), /(Xj)=/j. Решив эту
систему, мы найдем значения Ylt Y2 Yn, по которым процес-
процессом интерполяции можно получить и приближенное решение инте-
интегрального уравнения B) на всем отрезке [а, Ь\. За аналитическое
выражение приближенного решения уравнения B) можно принять
функцию
Y (х) = f (х) + X 2 AjK (x, Xj) Yj, (9)
принимающую в узлах xlt x2, .... хп значения Ylt Y2 Yn.

592 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
В случае уравнений Фредгольма первого рода A) вместо системы (8)
будем иметь систему
X 2 AjKijYj = fi (i = 1, 2 «). (8')
Если в качестве квадратурной формулы берется обобщенная
формула прямоугольников, то
х1 = а; хг = а-\-к; ...; xn = a-\-(n—\)h;
1 " n
если берется обобщенная формула трапеций, то
л—1 /'
Л
если же берется обобщенная формула Симпсона, то п = 2щ-\-\:
f, a
2fn
Л_ . . 4Л.
И Т. Д.
Этот метод может быть применен и для решения нелинейных
интегральных уравнений вида
ь
JK{x, s, y(x), y(s))ds=f(x), A0)
а
но в этом случае вместо системы (8) получим систему
^AjK^Xi, xf, Yi. Y})=fi (/=1. 2 «), A1)
которая уже будет нелинейной.
Вернемся к интегральному уравнению B). Если это уравнение
однородно, то и система (8) будет однородной системой. Она будет
иметь нетривиальное решение в том и только в том случае, когда
определитель системы (8) равен нулю. Приравнивая нулю этот опре-
определитель, получим алгебраическое уравнение, вообще говоря, сте-
степени п относительно X. Решая это уравнение, найдем, вообще
говоря, п корней \lt к2 Хи, которые будут приближенными зна-
значениями первых п собственных значений ядра К(х, s). Подставляя

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 593
в однородную систему, соответствующую системе (8), одно из най-
найденных значений Xj и находя линейно независимые решения этой
системы, получим приближения к линейно независимым собственным
функциям ядра К(х, s), соответствующим данному собственному
значению.
Если X не равно ни одному из этих корней, то однородная
система имеет только тривиальное решение, а система (8)—един-
(8)—единственное решение.
При выборе квадратурной формулы в этом методе нужно иметь
в виду, что чем более точную формулу мы применяем, тем большую
гладкость ядра и решения, а следовательно и /(х), нужно требовать.
Попытка применения более точных квадратурных формул для полу-
получения более точного приближения при несоблюдении этого условия
может привести совсем к обратному результату.
В случае, если правая часть или ядро К(х, s) (или их произ-
производные) имеет особенности, целесообразно предварительно выполнить
некоторые преобразования с тем, чтобы получить более хорошее
интегральное уравнение, с помощью которого можно будет полу-
получить более точное приближенное решение исходного уравнения. Для
этого могут быть полезны следующие приемы.
Если ядро гладкое, а правая часть /(х) имеет особенности, то
можно вместо у(х) ввести новую неизвестную функцию;
z(x) = y(x)—f(x).
Подстановка ее в уравнение дает
ь ь
. s)z(s)ds = lf K(x, s)f(s)ds,
т. е. мы получим уравнение в точности того же вида, но в котором
правая часть будет уже более гладкой, а следовательно, и реше-
решение z(x) будет более гладким. Найдя z(x), затем найдем и искомое
решение у(х).
Очень часто встречаются уравнения, в которых ядро К(х, s)
или его производная по s имеет разрывы на диагонали x = s. В этом
случае уравнение предварительно выгодно переписать в виде
Г
1— xj
La
Г 1
у(х) 1— xj>(x, s)ds\ — lJK(x, s)[y(s) — y(x)]ds=f(x).
J
Подынтегральная функция во втором интеграле будет правильной,
так как на диагонали х = s разность у (s) — у (х) обращается в нуль,
ь
а [ К(х, s)ds уже не будет содержать неизвестной функции и его

594 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
часто можно вычислить в явном виде. Применение метода к этому
последнему интегральному уравнению даст лучший результат.
Часто встречаются интегральные уравнения с ядрами вида
К{х, s)=H{x>s\ @<а<1),
где Н(х, s) — гладкая функция. От уравнений с такими ядрами
целесообразно перейти к уравнениям с итерированными ядрами, кото-
которые уже не будут иметь особенности при х = s. (Об итерации ядер
см., например, И. Г. Петровский, Лекции по теории интегральных
уравнений.)
Рассмотрим теперь вопрос об оценке погрешности решения, полу-
получаемого по этому методу, предполагая в уравнении B) наличие
у ядра К{х, s) и правой части f(x) непрерывных производных до
порядка q. Тогда и решение будет иметь непрерывные производные
до порядка д.
Если обозначить определитель системы (8) через ?)(Х), а алге-
алгебраические дополнения его элементов через D^ (X), то решение
системы (8) можно будет записать в виде
Из системы G) будем иметь:
п
W
Обозначим через тц погрешность приближенного решения в точке
т. е.
а через -ц(х) обозначим разность у(х) — Y(х), где Y(x) опре-
определяется формулой (9). Тогда из A2) и A2') имеем:
п
Если ввести обозначения
? им
'"лам > Р= тах I # |: R = R[K(x, s)y(s)].
TO
A3)

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 595
Для -ц(х) получим следующее равенство:
т) (х) = у (х) — Y (х) =
п п
= X 2 AjK (х, xj) у (xj) -+- \R — X 2 А3К(х, xj) Yj.
Отсюда получается следующая оценка:
или
n
2 \Aj\\ Mo= max \K{x. s)\. A3')
а< <b
В оценках A3) и A3') все константы могут быть вычислены, кроме
константы р. Константа р есть максимум абсолютной величины оста-
остаточного члена квадратурной формулы для F = K(x, s)y(s) при всех
х?[а, Ь]. Для формул трапеций, Симпсона, Гаусса и многих других
остаточный член имеет вид
где kn — некоторая постоянная, зависящая от п, а ? — некоторая
точка отрезка [а, Ь]. Таким образом,
||<n||
[а, Ь)
В нашем случае F(s) = K(x, s)y(s)(x — параметр). Таким образом,
ft—0
га
|()|<2 CkmMkNm_k,
[а, Ъ] &=0
где введены обозначения:
= шах
= max
|
a<s<b
A4)
Постоянные Nk нам неизвестны, так как неизвестно решение. Но их
можно оценить. Для этого продифференцируем интегральное уравне-
уравнение B) k раз. Будем иметь:
ь
^ (&) (х),

596 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
откуда
\\ k; Рк = max
ИЛИ
Пк*?\ЦМк(Ь-а)Ы
Таким образом,
га га
max | F{m) (s) |< | X | No ф ~ а) 2 СктМкМт_к + 2
2, A5)
где
га га
C1 = |X|(ft-eJC*AlsAlm_it; С2=2С1ЖЛ.4 A6)
— постоянные величины, которые можно найти, так как ядро К (х, s)
и f(x) известны. Обозначим через Qo максимум абсолютной величины
приближенного решения Y(x). Из оценки A3') будем иметь:
или
га
i-i "
Если
то
7-1 J
Следовательно, погрешности т^ и tj (jc) можно оценить через извест-
известные величины.
Напомним, что: для обобщенной формулы трапеции с п ордина-
ординатами kn = j а' ъ , т = 2; для обобщенной формулы Симпсона
с п = 2р + 1 ординатами kn = qq /2pyt ¦ m = 4; для формулы Гаусса
с п ординатами ^п= [Bb)i]s Bв+1) ' т==2""

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 597
Пример. Найти приближенное решение уравнения
1
y(x)-\-J x (е*8 — 1) у (s) ds = ех — х.
о
Воспользуемся квадратурной формулой Симпсона:
/
о
Тогда для отыскания приближенного решения в точках х = 0; 0,5; 1
получим систему
Yx =1,
J_ (ео,а5 _ 0 у2 +1 (е0'5 - 1) К3 = ew - 0,5,
3"
или
1,0947 К2 4-0,0541 Kg = 1,1487,
0,4325 К2 4-1.2864 Kg = 1,7183.
Решая ее, получим:
Yl = \, K2 = 0,9999, К3 = 0,9996.
Точное решение интегрального уравнения у(х)=-1. Как видим,
результат достаточно хороший.
2. Решение интегральных уравнений Фредгольма второго рода
методом замены ядра на вырожденное. Если в уравнении B) ядро
К(х, s) вырожденное, то решение этого уравнения может быть най-
найдено в конечном виде. В самом деле, пусть
п
К(х, s) = 2 Ai{x)Bi{s).
Можно считать, что А1{х), А2(х), .... Ап(х) и В1(х), В2(х), ...
.... Вп(х) суть системы линейно независимых на отрезке [а, Ь]
функций. Так как интегральное уравнение будет иметь вид
J A8)
г=1
то решение его можно искать в виде

598 МЕТОДЫ РЕШЕНИЯ ДИф. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
где Q — некоторые постоянные. Подставляя у(х) в уравнение A8)
и сокращая на X, получим:
СИ* (*) — ^ ^ (х) J] CJ f Aj (s) Bt (s) ds —
i1
Вводя обозначения
f
»=1 a
ь
= f Aj (*) 5i
и принимая во внимание линейную независимость функций А1(х\
А2(х) Ап(х) для отыскания C,-(i=l, 2, .... л), получим
систему линейных алгебраических уравнений
С, —X
=1. 2, .... л).
A9)
Если определитель системы A9) О (X) отличен от нуля, то система
имеет единственное решение для Ciy C2 Сп и решение инте-
интегрального уравнения у(х) будет найдено в явном виде. Если же
при данном значении X определитель О(Х) равен нулю, то X будет
собственным значением ядра К(х, s). В этом случае, находя все
линейно независимые решения соответствующей однородной системы,
мы в явном виде найдем все линейно независимые между собой соб-
собственные функции ядра К(х, s), соответствующие данному собствен-
собственному значению X.
Метод приближенного решения интегральных уравнений Фред-
гольма с помощью замены ядра близким к нему вырожденным ядром
основан на следующей теореме:
Теорема. Если
, s)y(s)ds =
, s)z{s)ds = fl
B0)
B1)
— два интегральных уравнения, R(x, s, X) — резольвента второго
из этих уравнений и существуют такие константы 8, в, М,

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 599
что имеют место неравенства
ь
s)\ds<:b, B2)
e. B3)
ь
J | R (х, s, X) | ds < М B4)
а
и выполнено условие
B5}
то уравнение B0) имеет единственное решение у(х) и
U(*)-«(*)l< Г^Г^'+'т^ +«A+1НЛЦ. B6)
где N = max | / (х) \.
<<6
Доказательство. Предполагая существование ограниченного
решения B0), обозначим через Со верхнюю границу его абсолютной
величины на отрезке [а, Ь] и рассмотрим интегральное уравнение
ь
y(x) — \f H(x, s) у (s) ds = F (х),
а
где
ь
F(x)=f(x) — \f(H(x, s)—K(x, s))y(s)ds.
Тогда
ь
y{x) = F(x)-\-\f R(x, s, \)F(s)ds.
a
Далее, так как
ь
\F(x)\<\fW\ + \b\f\K(x. s)-H(x. s)\\y(s)\ds^N-\-\l\bC0,
a
TO
Ь
\ + \\\f\R(x, s, \)\\F(s)\ds<
a
X | 8C0 +1 X | (ЛГ +1 X18Q M,
или
Со<|
откуда
l-\l\o(l+\X\M) ¦

600 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Таким образом, при выполнении условия B5) все решения уравне-
уравнения B0) ограничены одной и той же постоянной, как бы мы ни
выбирали f(x), а это означает, что X не является собственным значе-
значением и интегральное уравнение B0) имеет только единственное реше-
решение, ибо если бы X было собственным значением ядра, то, прибавляя
к какому-либо решению неоднородного уравнения B0) собственную
функцию ядра К(х, s), мы снова получили бы решение уравне-
уравнения B0). Но собственная функция может быть взята такой, что
максимум ее абсолютной величины будет больше любого наперед
заданного числа, а это означает, что и для уравнения B0) можно было
бы найти решение сколь угодно большое по абсолютной величине.
Докажем теперь оценку B6). Мы имеем:
ь
H(х, s)(у(s) — г(s))ds = F(x) — h(*) = ф(•*)
Ь
у (х) — z(х) = Ф(х) + 1 f R (х, s, l)<5(s)ds.
а
ь
\у(х) — .г(х)|<|Ф(х)| + |Х|/|Д(х, s, \)\\3>(s)\ds.
ИЛИ
Но
\Ф(х)\ =
X J (Я (х, s)-К (х, s) )y(s)ds+f (х)-Л (х)
Следовательно,
\У(х) —
| М)
Из доказанной теоремы следует, что если можно построить
достаточно близкое к ядру К(х, s) вырожденное ядро Н (х, s), то,
решив уравнение с вырожденным ядром Н(х, s), мы получим реше-
решение, близкое к решению уравнения с ядром К(х, s) при той же
правой части. Более того, если мы построим последовательность
вырожденных ядер Нп(х, s), равномерно сходящуюся к ядру К(х, s),
то последовательность решений zn(x) уравнений с ядрами Нп(х, s)
будет равномерно сходиться к решению у (х) уравнения с ядром К (х, s).
Способы построения вырожденных ядер, близких к данному
ядру К(х, s), могут быть самыми различными. Например, ядро К(х, s)
можно приближать частичными суммами степенного или двойного

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 601
тригонометрического ряда, если ядро К(х, s) разлагается в равно-
равномерно сходящийся в прямоугольнике а 4^ х, s ^ b степенной или
тригонометрический ряд, или приближать его алгебраическими или
тригонометрическими интерполяционными многочленами.
Бэтмен предложил определять вырожденное ядро Кп(х, s),
аппроксимирующее ядро К(х, s), с помощью равенства
Кп(х, s) K(x,st) K(x,s2) ...K(x,sn)
К(хь s) К(хь st) К(хь s2) ... К(хь sn)
К(хп, s) K(xn, st) K(xn, s2) ... К(хп, sn)
= 0,
B7)
где xt, x2, .... хп\ st, s2 sn — некоторые точки отрезка [а, Ь].
Представляя элементы первого столбца в виде
К„(х, s)-\-0;
, s); 0+K(x2, s); ...; 0+К(хп, s)
и разлагая определитель B7) на сумму двух определителей, после
несложных преобразований получим явный вид ядра:
0
К(хь
К(хп,
К(хь
К(х2,
К(хп,
s)
S)
Sl)
Sl)
Si)
К(х,
К(хь
К(хп,
k\Z
К(хп,
si)
Sl)
s2)
So)
K(x, i
K(xn,
s2) ...
So) . ..
K(x,
K(xb
K(xn
K(xv
K(xn
sn)
sn)
Sn)
Sn)
Sn)
Sn)
B8)
откуда видно сразу, что это ядро вырожденное. Это ядро можно
также переписать в виде
0 K(x,st) K(x,s2) ...K(x,sn)
K{xt,s) /C^.st) K(xt,s2) ...K(xltsH)
Kn (x, s) = K (x, s) —
K(xn, s) К (xn, s,) К (хп, s2) ... К (хп, sn)
K(xlt
K(xlt s2) ...
sn)
K(x, s)
st) К(,x2, s2) ... К(х2, sn)
K(xn, st) K(xn, s2) ... K(xn, sn)
K(xb sx) K(xv s2) ... K(xb sn)
K(Xo,
K(xn,
K(xb
K(x2,
Sl)
Sl)
Sl)
Sl)
K(x2,
K(xn,
K(xt,
K(x2,
s2)
So)
s2)
s2)
... K(x2,
... K(xn,
... K(xh
... K(x2,
Sn)
Sn)
Sn)
Sn)
К (xn, st) К (хп, s2) ... К (хп, sn)

602 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
= К(х. s) —
K(x,
К(хп
К(хь
К(хп,
S)
S)
s)
to to
Si)
К(х,
К(хь
К(хп,
К(хх,
К(Хо,
К(хп,
Sl)
Sl)
Sl)
s,)
s2)
s->)
... K(x,
... K(xn,
... K(x2,
... K(xn,
Sn)
Sn)
Sn)
Sn)
Sn)
Sn)
Из этого представления видно, что Кп(х, s) совпадает с К(х, s)
на 2га прямых х = хг; s = Si (/=1, 2 га).
Бэтмен предложил также способ построения резольвенты, а следо-
следовательно и явного решения интегрального уравнения, если ядро К(х, s)
интегрального уравнения представимо в виде суммы ядра Н(х, s),
для которого известна резольвента, и вырожденного ядра Ht (x, s).
Если ядро
п
К (х, s) = Н (х, s) — 2 Л (х) gl (s), B9)
г-1
a r(x, s, X) есть резольвента ядра Н(х, s), то резольвента R(x, s, X)
ядра К (х, s) имеет вид
R(x, s, X)=-
г (х, s, X)
(•*)
Чп (х)
Хх»,
ХП2
... 1
-f- Ххц Хх12
Xx2l 1 4" XX22
Хх
18
Хх1п
Хх2п
Xxn9 Xxra8
C0)
где
«К(«) = gi
Ь
r(x, s, \)ft(s)ds.
r<(x, s, X)gl (х)dx,
ds-
C1)
Используя этот результат, иногда целесообразно приближать ядро
не вырожденным- ядром, • а суммой вырожденного ядра и ядра
с известной резольвентой.

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 603
Для ядра Кп(х, s), построенного по способу Бэтмена, резоль-
резольвента определяется из уравнения
Rn(x, s, I) K(x, s^ K(x, s2) ... К(х, sn)
К(хь s) Ац А12 ... А1п
К (хп, s) Ап\ АП2 ... Апп
где
ь
= 0, C2)
Sk) — ^\ K(x3> t)K{t, sk)dt. C3)
а
Тогда приближенное решение уравнения B) может быть записано
в виде
ь
x)-\-\ f Rn(x, s, \)f(s)ds.
Результаты Бэтмена мы приводим без доказательства, которое
можно найти в книге Л. В. Канторовича и В. И. Крылова «При-
«Приближенные методы высшего анализа».
Пример. Найти решение интегрального уравнения
1
у (х) -\- С х (exs — 1) у (s) ds = ех — х.
о
Ядро уравнения К(х, s) = x(exs—1) аппроксимируем суммой пер-
первых трех членов разложения К(х, s) в ряд Тейлора, т. е. положим
у-3<;2 v-4?3
Н(х. s) = x2s^ g-H g-,
и вместо исходного уравнения рассмотрим интегральное уравнение
1
2 (*) + Г И (х, s) z (s) ds = е* — х.
о
Решение последнего ищем в виде
г (х) = е* — х + Ctx2 ¦+- С2х3 + c*x*.
Для определения постоянных Cv C2, С3 получим систему
L h С h С

604 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Решая ее, получим следующий результат:
С1== —0,5010. С2 = —0,1671, С3 = — 0,0422.
т. е.
z(x)=e* — x — 0,5010л:2 — 0,1671*3 — 0,0422л:4.
Точное решение интегрального уравнения: _y(je)=l. Из найденного -
приближенного решения при л: = 0; 0,5; 1,0 имеем:
2@) = 1,0000, z@,5) =1,0000, 2A)= 1,0080.
т. е. расхождение с точным решением всего 0,008.
3. Метод моментов. В методе моментов [приближенное решение
интегрального уравнения ищется в виде суммы f(x) и линейной комби-
комбинации заранее выбранных линейно независимых между собой функций
<Pi(*). <fr(x) ?„(*), т.' е.
М*) = /(*) +2 О<Р«(*) C4)
г-1
с неопределенными коэффициентами Cv С2 Сп. Коэффициенты
С,, С2, ¦.., Сп отыскиваются следующим образом. Рассмотрим опе-
оператор
ь
Lu = a(x) — \ J К{х, s)u(s)ds — f(x). C5)
а
Подставив вместо и(х) функцию Yn(x), получим:
п ( Ь \ Ь
LYn = ^iCiUi(x)-\ f K(x, s)<?i(s)dsi — \ f K(x, s)f(s)ds =
i=l to ) a
= Ф(*; Cp C2 Cn).
Потребуем ортогональность функции Ф(х; С, Сп) ко всем
функциям срг(л:), срг(л:), .._., <?п(х) на отрезке [а, Ь], т. е. потребуем
выполнения условий
ь
JLYn- ^(*)dx = 0 (/=1.2 я). C6)
а
Получим систему п линейных алгебраических уравнений для отыска-
отыскания d, C2, .... Сп. Система будет иметь вид
п
2 Cj \ati — Щ\ = XTi (/ = 1.2 и). C7)
3-1

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 605
где
ь ь ь
аУ = / ?' № <?j (х) dx; py = J dx J /С (х, s)(fi (x) у} (s) ds;
о о о
ц = f dx f K(x. s)<?i{x)f(s)ds. C8)
а а
Решая эту систему, мы и найдем Ct, C2 Сп, а следовательно
и приближенное решение Yn(x) интегрального уравнения B).
В основе этого метода лежит следующая идея. Пусть cpi(je),
<fi(x), .... уп(х)—первые п функций полной ортонормированной
системы {tps(jc)}. Для того чтобы функция Y(x) была точным реше-
решением интегрального уравнения B), необходимо и достаточно орто-
ортогональности LY (х) ко всем функциям системы {cpfc (д:)}, так как
в этом случае будем имгть LY(x) = 0. При отыскании приближенного
решения функция Yn(x) содержит лишь п параметров Сх, С2 Сп,
с помощью которых, вообще говоря, можно удовлетворить лишь п
условиям ортогональности, что мы и сделали, потребовав ортого-
ортогональность LYn к ?i(x), (р2(-*0> ••., tp»C*O. Требование ортонормиро-
ванности системы {ср& (дг)} в проведенных рассуждениях излишне.
Достаточно требовать лишь полноту системы \<ук(х)\ и линейную
независимость любого конечного числа функций этой системы, так
как процессом ортогонализации можно из нее получить полную
ортонормированную систему {<1>*(л:)} такую, что любая функция %(*)
будет линейной комбинацией конечного числа функций системы [tyk (x)).
Этот метод есть не что иное, как метод Галеркина решения инте-
интегральных уравнений.
Применение метода моментов равносильно замене ядра К(х, s)
вырожденным ядром Кп(х, s), строящимся следующим образом.
Предполагая ортонормированность системы {%(.*:)}, разложим
ядро К(х, s) как функцию х в ряд Фурье по этой ортонормирован-
ортонормированной системе функций и за Кп(х, s) примем га-ю частичную сумму
этого ряда. Получим:
п
KJx, s) = 2 ««(«)?<(*).
J-1
где
ь
Ui(s) = jK(x, s)<
а
Если теперь к уравнению
) — \JKn(x, s)y{s\ds ~f(x) =

606 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
применить метод моментов, то получим точно такое же решение,
как и для уравнения B), ибо система, аналогичная системе C7),
может отличаться от нее только коэффициентами ру. Обозначим их
через $$. Будем иметь, учитывая ортонормированность системы
функций {<fjt(x)}:
ь ь
Кп(х, s)tpi(^)tpj(s)ds =
Ь Ь п
uk (s) tps (x) <fi (x) <pj (s) ds =
a a fc=l
n b Ь Ь
= 2 / «ft (s) tpj (s) ds J (pft (x) tp,- (x) dx= J u{ (s) <?j (s) ds.
k—la a a
С другой стороны,
ь ь
$ij = fdxfK (х, s) 9i (x) ъ (s) ds =
a a
bib \ Ь
= J \Ъ (*) / * (*• s) 9i (*) d* I ds = / ^ (*) ui («) ds-
о l о Jo
Таким образом,
Следовательно, приближенные решения обоих интегральных уравне-
уравнений совпадают. Но решение Yn(x) уравнения с вырожденным
ядром Кп(х, s), полученное методом моментов, будет его точным
решением. Это и показывает равносильность метода моментов методу
замены ядра вырожденным ядром, строящимся специальным спо-
способом.
Это замечание позволяет использовать оценку, полученную в тео-
теореме п. 2, для оценки точности решения, полученного по методу
моментов.
Метод моментов можно применять и для решения нелинейных
интегральных уравнений, но в этом случае вместо системы C7)
получим нелинейную систему.
Пример. Найти два первых собственных значения и соответ-
соответствующие им собственные функции однородного интегрального урав-
уравнения
1
Lu = и (х) — X Г К (х, s) и (s) ds = 0,
о
где
(x(l—s) (i
1\(Х, ъ)— | 5A_д;) ((

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 60?
Для решения задачи применим метод моментов. Приближенное
решение будем искать в виде
— х)-\-Сх(\ —х){\ —2х).
Для отыскания коэффициентов А, В, С в соответствии с методом
моментов имеем три уравнения:
1
f<?i(x)Lu3(x)dx = 0 (/=1, 2, ЗУ,
о
где
?1(*)=1; %(*) = *(!—*): <р„(*)зз*A—*)A—2*).
Подстановка и3(х) в Lu дает следующий результат:
x(l — *)A — 2л:) —
-.
""*" 60
Далее,
i
1
J
о
В
зо
Приравнивая нулю определитель полученной системы, после неслож-
несложных вычислений получим:
(X2 — 180Х + 1680) (X — 40) = 0.
Корнями этого уравнения будут:
Х1 = 9,8751, Та = 40, Х3= 170,1249.
Подставляя в систему найденные значения Xt и 1% и решая ее отно-
относительно А, В, С, получим:
для X = \
А = — 0,01176В, С = 0,

608 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
1
или, определяя В из условия нормировки Г у2 (х) dx = 1 для соб-
о _
ственной функции, соответствующей значению \, получим выра-
выражение
yl(x) = — 0,0684 + 5,817x(l — х);
= Х2
А = В = 0; С—-произвольное число.
Нормируя, получим собственную функцию, соответствующую вто-
второму собственному значению:
У2(х)= 14,49л: A — х){\ — 2х).
Точные величины собственных значений этого уравнения:
Xt = л2 = 9,8696 .... Ха = 4л2 = 39,4784 ....
а соответствующие им собственные функции:
у1 (х) = У 2 sin tzx, у2 О) = Y 2 sin
Погрешность первого собственного значения около 0,06%, а вто-
второго собственного значения примерно 1,3%. Что касается собствен-
собственных функций, то приближенное значение первой собственной функ-
функции близко к точному, в то время как приближение ко второй
функции значительно хуже.
4. Метод наименьших квадратов. Для уравнения B) будем
искать приближенное решение Yn(x) вида
М*) = 2с4<р<(*). C9)
Где снова cpt(л:), ср2(л:), •¦¦> ТиМ — некоторые заданные линейно
независимые функции. Подстановка Yn(x) в оператор Lu, где
ь
Lu=zu(x) — \ jK(x, s)a(s)ds—f(x), D0)
а
дает
п Ь п
LY*=S см{х)—х / к {х-s) Sс^(s) ds -f(x)=
= Ф{х;С1,Сг Cn). D1)

§ 101 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 609
Постоянные Cv C2 Сп будем находить из условия минимума
интеграла
ь
j=f ФЦХ; Cv C2 Cn)dx, D2)
а
т. е, из условий, что
Используя явное выражение для функции Ф:
=0 (/=1, 2 л). D3)
)
>-f(x),
J
{ D4)
г—1 I J
для отыскания С,, С2, ..., Сп получим систему линейных алгеб-
алгебраических уравнений
п
'^iaijCj = bi (i = l, 2 л), D5)
7-1
где
X
X
i <p< (*) — X J К (x, s) «pi (s) ds
h= ff(x)\<?i(x) — lfK(x, s)9i(s)ds \dx. D6)
a L a
Изложенный метод пригоден и для отыскания приближенных
значений первых собственных значений ядра К(х, s). Для этого
полагаем f(x) = 0 и приравниваем нулю определитель системы D5).
Получим уравнение га-й степени относительно X, решая которое и
найдем приближенные величины первых собственных значений
ядра К(х, s).
Пример. Найти решение интегрального уравнения первого рода
1
Г К (х, s) u(s)ds = x — 2x9 -|- х4,
где
'*(! — .
— х)

610 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
К аналогичному уравнению приводит задача об отыскании стати-
статической нагрузки, под действием которой струна единичной длины,
закрепленная на концах х = 0 и х=\, примет форму, описывае-
описываемую правой частью уравнения.
Первое приближение к решению будем искать в виде
Тогда
i
Lut =х — 2ха + х*— f K(x, s)(Cl-\-C2s)ds =
о
г
д- V v3 J_ i^4 I 1
й метод наименьших квадратов дает для отыскания Ct и С2 сле-
следующую систему уравнений:
о
f La dLUidx- l Г 17 I Ci I 4C2 1-Q
о
или
Решение этой системы
C1 = 2,4286, C2 = 0,
т. е.
ux (x) = 2,4286.
Второе приближение будем искать в виде
и2 (х) = Ct + С2Х 4- С9х2.
Тогда
1
—1 К(х, s) (
о
12

§ 10] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 611
и метод наименьших квадратов дает для отыскания Cv C2, С3
систему
17 , Сл С, 5С
3-4-5-7
17
~~ 5-7-8
13
4-5-9
3-4-5
5-8
5Ct
4-6-7
4-5-6 ^ 4-6-6-7
11С8
-Нт
5-7-9 ' 3-5-8-12
ПС, , 9С3
" Т- 5 • 6 • 8 Г1М2~
= 0,
= 0
или
84Ct + 42C2 + 25C3 = 204,
252CX + 128C2 + 77C3= 612,
450C,+ 231C2 + 140C3=1092.
Решение этой системы будет:
С1 = 0. С2=12, С3 = —12.
Таким образом,
—х).
Это — точное решение уравнения, что легко проверить прямой под-
подстановкой в уравнение.
б. Метод последовательных приближений. Для приближен-
приближенного решения уравнения B) может быть применен метод последо-
последовательных приближений, заключающийся в следующем.
Решение у(х) уравнения B) ищем в виде ряда по степеням X:
у (х) = ср0 (х) -\- Xtpt (х) -\- ... -)- X tpn (х) -\- ... D7)
Подставляя его в уравнение и приравнивая коэффициенты при
одинаковых степенях X, получим:
ь
<Pi (х) = JK(x, s) ер0(s)ds,
= J К (х, s) tpt (s) ds,
, s (pn_t (s)ds.
D8)
J

612 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Если ядро К{х, s) ограничено по модулю постоянной М, то ряд
сходится равномерно при ) X j < м , _ и у (х) есть решение инте-
интегрального уравнения B). За приближенное решение можно принять
га-ю частичную сумму ряда.
Если ]/(.*) |< N, то
1 ь(х)
Отсюда
МИ F — а);
\y(x)-Yn(x)\ =
— аJ; ...;
— а)п, ...
— a))n =
\ — \l \ M (b — a)
Это и дает оценку погрешности приближенного -решения
D9)
г=0
если все квадратуры вычисляются точно. Если же квадратуры нельзя
выполнить, то для вычисления интегралов можно применить те или
иные квадратурные формулы. В этом случае удобно пользоваться
следующей вычислительной схемой.
Пусть Kij = K(xiy Xj), где xlt x2, ¦¦., хп — абсциссы квадра-
квадратурной формулы; ср„(Xi) = <pni; у(хг) = уг; f(Xj)=fi. Приближен-
Приближенное значение для <?п(хг) будем обозначать через cpnj, а для у(хг) —
через Yt. Если А{ — коэффициенты квадратурной формулы, то
9т+1. г =
Исходя из этого соотношения, вычисления можно вести по следую-
следующей схеме:
X?
1
2
п
^AnKnn
?02
fu
Ym
Ym\
Ym?
Y

§ Ю] ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 613
Сначала в столбцах 1, 2, .... п выписывается указанная в схеме
матрица, а в следующем столбце выписываются значения сро(л:)=/(л:)
в узлах xv x2 хп. Для заполнения следующего столбца умно-
умножаем элементы первого столбца на соответствующие элементы
столбца свободных членов. Сумма попарных произведений их даст
первый элемент нового столбца. Для получения второго элемента
этого столбца берем сумму попарных произведений элементов вто-
второго столбца на соответствующие элементы столбца свободных
членов и т. д. После заполнения столбца ср^ для заполнения сле-
следующего столбца поступаем совершенно аналогично, только вместо
столбца свободных членов берем последний полученный столбец.
Процесс продолжают до тех пор, пока с точностью, с которой
ведутся вычисления, следующий столбец становится нулевым. Зна-
Значения приближенного решения в узлах получим, суммируя соответ-
соответствующие элементы вычисленных столбцов по строкам.
6. Приближенное решение уравнений Вольтерра. Из теории
интегральных уравнений известно, что если ядро К(х, s) есть
непрерывная функция в области R {a-^ s-^ x-^ b}, a f(x) — непре-
непрерывная функция на отрезке [а, Ь], то интегральное уравнение Воль-
Вольтерра второго рода
х
у (х) — X J K(x. s)y (s) ds = f (x) D)
а
имеет единственное непрерывное решение у (х) при любом зна-
значении X. Это решение можно искать в виде
со
\к(х). E0)
Подставляя этот ряд в уравнение D) и сравнивая коэффициенты
при одинаковых степенях X, получим:
J, s)<t>k(s)ds. E1)
a
Если
jV= max \f(x)\, a M = max| K(x, s)\,
a<x*cb В
TO
Отсюда, если мы примем за приближенное решение уравнения D)
га-ю частичную сумму ряда E0):
п
М*)=2Лр*(*). E3)
г=0

614 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
то погрешность его может быть оценена следующим образом:
\y(x)-Yn(x)\ =
k-n+i
E4)
k=n+l
Более грубая, но вместе с тем более простая оценка погрешности
следующая: обозначим через L произведение \\\М(Ь — а) и в оценке
Ln+1N
E4) вынесем общий множитель -.— ; получим:
Ряд, стоящий в фигурной скобке, мажорируем рядом
Тогда получим следующую оценку:
л + 2
При этом предполагается, что п настолько велико, что L<ra-|-2.
Если в E1) квадратуры не берутся, то для их вычисления
можно использовать квадратурные формулы, лучше всего с равно-
равноотстоящими абсциссами. Будем, например, использовать обобщенную
формулу трапеций. Если отрезок [а, Ь\ разбить на S равных частей
и ввести обозначения Л = —=—; хк = а-\-kh\ K{x^, Xj)—Kip
Чп (хк) = <?пк> а приближенные значения для tp^ обозначить через cpnft,
то будем иметь:
хк
<?п+1, к = j К (хк, s) <pn (s) ds s»
к-lfn, k-l) +^ftft tPnfcb
a
h
или
<Pn+i, к =
+ W«*1 (* = °. !• 2 S). E6)
Вычислив (p№+i, *, мы получим приближенные значения решения инте-
интегрального уравнения D) в узлах хк по формулам
п _
Уп,к = ^1Гь,к (А = 0. 1, 2 S). E7)

§ 101 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 615
При использовании обобщенной формулы Симпсон^ разбиваем
отрезок [а, Ь] на 25 равных частей точками xk = a-\-kh; h= ~д.
Тогда, применяя формулу Симпсона для вычисления интеграла
:= I К(х2к, s)<?n(s)ds,
J
а
будем
tPn + l, 2ft
иметь:
А A, — |
• • • -Ь K2k,2k_ifn,
G1 = 0, 1,
4
2ft
2;
(К 2ft. 1?»!
-0 4-2 0
, ...; k
~h ^2ft, 3<Р»3 Ч~ ¦
" 2ft, гТп, 2 ~i~ ".2fe,
к, 26-2?», 2ft-2) ~Ь
= 1, 2, 3. ...
4?», 4
,^2ft,
, 5).
и, 2ft}
E8)
Значения tpra+1, ^ для нечетных k придется находить интерполяцией.
Для приближенного решения уравнения D) можно применять
также метод прямой замены интеграла, входящего в уравнение,
конечной суммой по какой-либо квадратурной формуле. Например,
при использовании обобщенной формулы трапеции, разбивая отрезок
[а, Ь] на п частей точками х0 = а; хх = а -)- h; ...; хп = а -|- nh = b,
будем иметь:
Ук—^j К(хк, s)y(s)dsmyk — ~
а
• • • -\~кк, к-
ИЛИ
АХ
откуда
( /с-1
E9)
Таким образом, шаг за шагом найдем все значения Yk.
Что касается интегральных уравнений Вольтерра первого рода
, s)y(s)ds=f (x), C')
то при дополнительном предположении, что ядро К(х, s) и f(x) —
непрерывно дифференцируемые функции, К{х, х) > а > 0, его можно

616 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
свести к интегральному уравнению Вольтерра второго рода. В самом
деле, дифференцируя уравнение C), будем иметь:
X
\К{х, х)у{х) + \ j К'х{х, s)y(s)ds=f'(x),
а
пу(х) будет решением интегрального уравнения Вольтерра второго
рода
Пример. Найти решение интегрального уравнения
X
/р — х J-. р — Ьх
e-*-°y{s)ds= у—
/
о
Первый способ. Ищем решение в виде
у (х) яй К4 (*) == % (*) + <р! (*) + <Р2 (*) + Ъ (х) + ?4 (*)•
где
X
, s)<fk.1(s)ds.
В результате интегрирования получим:
(х) (-х + е-^)
X
?iW = / е-*-в<р„(«)<
0
X
cp2(x) ^ / e-x-syx (s)d
0
X
J
0
—
is = 1[3.
rs = ^- [E
f7e-a:
¦¦ 20ea;
~Ьх — 30е-7а;4- 5e"9a; 4 е

§ 101 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 617
откуда
4 (х) =
Точное решение этого уравнения
Для сравнения приведем значения точного решения и приближен-
приближенного решения при х = 0 и х=\. Имеем:
.у @) = 1.00000, у{\) = 0,36788,
/4@)= 1,00000, К4A) = 0,36783.
Второй способ. Будем вычислять значения решения в точках
х = 0; 0,2; 0,4; 0,6; 0,8; 1,
используя для замены интеграла в уравнении обобщенную формулу
трапеций с шагом h = 0,2. Таблица значений Кц и fk имеет вид:
Xi
0
1
2
3
4
5
1,00000
0,81873
0,67032
0,54881
0,44933
0,36788
Кн
0,81873
0,67032
0,54881
0,44933
0,36788
0,30119
Км
0,67032
0,54881
0,44933
0,36788
0,30119
0,24660
К»
0,54881
0,44933
0,36788
0,30119
0,24660
0,20190
Кц
0,44933
0,36788
0.30U9
0,24660
0,20190
0,16530
Ки
0,36788
0,30119
0,24660
0,20190
0,16530
0,13534
А
1,00000
0,68377
0,48576
0,35706
0,27002
0,20883
Вычисления дают следующий результат:
/„ =/о= 1.0000.
Y, = \ [А 4- 4 KWYO] = 0,8206,
1 — у
~ К20 Yo + hK2l Kt] = 0,6731
2
^з = \ Г/з 4- 4 ^зо^о +- h (Ku Y, 4- К32 Y2)] = 0,5518,
1--2-К33 J
К4 = \ Г/4 + A Ki0Y0 +- h {KilY1-^Ki2Yi-^Ki3
1 - 4- К* l
Myj]= 0,3705.

618 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
Ниже приведена таблица значений точного решения и погреш-
погрешность полученного приближенного решения:
ук
У(хь)
Yk-y(*k)
0
1,0000
1,0000
0,0000
0,2
0,8206
0,8187
0,0019
0,4
0,6731
0,6703
0,0028
0,6
0,5518
0,5488
0,0030
0,8
0,4522
0,4493
0,0029
1
0,3705
0,3679
0,0026
УПРАЖНЕНИЯ
1. Построить разностную аппроксимацию оператора Лапласа, если сетка
состоит из вершин правильных шестиугольников со стороной h.
2. Построить разностную аппроксимацию бигармонического оператора
Lu =
дх*
+ 2-
дх*ду*
д*и
ду* '
в которой участвуют узлы: (/, Д (/, j ± 2), (/, j ± 1), (/ ± 1, Д (/ ± 2, Д
(/ ± 1, У ± 1), где через (/, J) обозначен узел с координатами xt = ih, yj = Jl,
а Л и /—соответственно шаг сетки по осям х и у. Рассмотреть случай
3. Показать, что для уравнения
ди ди ,. ..
-дТ~ -дх-=/{Х^)
с начальными условиями
разностная схема
и (х, 0) = <р (д:)
— Y ("i+i, j + «i-i,j)] 2F ("i+i, i — "i-i, j) = f(lh, jl).
где сетка состоит из точек с координатами х$ = Ih, tj = Jl, аппроксимирует
уравнение только при / ;> Ch (С = const) и корректна при / <; Л.
4. В области 0-<лг, t^n дано дифференциальное уравнение
с начальными условиями и (х, 0) ^= ср (х) и граничными условиями и @, t) =
= и (тс, t) = 0. Пусть сетка состоит из точек с координатами Х{ = Ih;
tj = jh u,j=0, 1,2, ..,, п; h= — J. Показать, что разностная схема
IT ("i+i, j — 2«у + Щ-х, j — "i+i, j-i + 24 j-i — "i-i, j-i> +
+ -j ("i, j — "i, j-i) = Uv
"io = <P (lflY> uoj = О'. unj = 0
аппроксимирует краевую задачу, равномерно устойчива по начальным зна-
значениям и неустойчива по правой части.

УПРАЖНЕНИЯ 619
5. Пусть в области O^.t^.T; 0^Lx^.a задано дифференциальное
уравнение
ди д?и
с начальными условиями и (х, 0) = tp (x) и граничными условиями
ди
дх
аз-о
ди_
дх
= 0.
х—а
Пусть выбрана сетка точек xi = lh; tj = jlil = 0, 1, 2, ..., n; h =—-;
y = 0, 1, 2, ..., m; т1^.т\. Показать, что разностное уравнение
J- (Щ, j + 1 — иф = р- (Ui + 1, j — 2йу + Щ-Ь j)
с граничными условиями
им = f (lh); u1j — uoj = O; unj — un-bj = 0 (*)
устойчиво при о = Tj, <!¦„-. а если заменить условия (*) на следующие:
и«о = ?('Л); Зиу — 4иу + «оу = 0; Зи„у —4^-!, у+"п-2, ^ = 0,
то становится неустойчивым.
Указание. Для доказательства последнего утверждения за начальные
данные принять ий = -^, где е — сколь угодно малое число, и найти общее
решение разностной схемы.
6. Используя метод прогонки, найти решение уравнения Пуассона
dtu д*и _
di ~
в квадрате 0^.х, у<!1 с граничными условиям
взяв квадратную сетку с шагом h = 0,1 и простейшую разностную аппро-
аппроксимацию оператора Лапласа.
7. Методом Ритца найти первые два собственных значения оператора
Лапласа, если область G квадрат со стороной 1, а функция на границе
обращается в нуль.
8. Различными методами найти решение интегрального уравнения
f_L
sin* @<лг<тс),

620 МЕТОДЫ РЕШЕНИЯ ДИФ. УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 10
ЛИТЕРАТУРА
1. Л. В. К а н т о р о в и ч, В. И. Крылов, Приближенные методы выс-
высшего анализа, Гостехиздат, 1952.
2. Л. В. К ан торов и ч, Функциональный анализ и прикладная матема-
математика, УМН, т. 3, вып. 6, 1948.
3. Л. В. К а н т о р о в и ч, Приближенное решение функциональных урав-
уравнений, УМН, т. 11, вып. 6, 1956.
4. Л. Коллатц, Численные методы решения дифференциальных уравне-
уравнений, ИД 1953.
5. О.А. Ладыженская, Метод конечных разностей в теории урав-
уравнений в частных производных, УМН, т. 12, вып. 5, 1957.
6. Л. А. Л ю ст ер ник, О разностных аппроксимациях оператора Лап-
Лапласа, УМН, т. 9, вып. 2, 1954.
7. В. Э. Мил н, Численное решение дифференциальных уравнений, ИЛ,
1955.
8. С. Г. М и х л и н, Прямые методы в математической физике, Гостех-
Гостехиздат, 1950.
9. Д. Ю. Панов, Справочник по численному решению уравнений в част-
частных производных, Гостехиздат, 1951.
10. Д. Ю. Панов, Численное решение квазилинейных гиперболических
уравнений в частных производных, Гостехиздат, 1957.
11. B.C. Рябенький, А.Ф.Филиппов, Об устойчивости разностных
уравнений, Гостехиздат, 1956.
12. Richtmayer, Difference methods for initial value problems, NY, 1957.