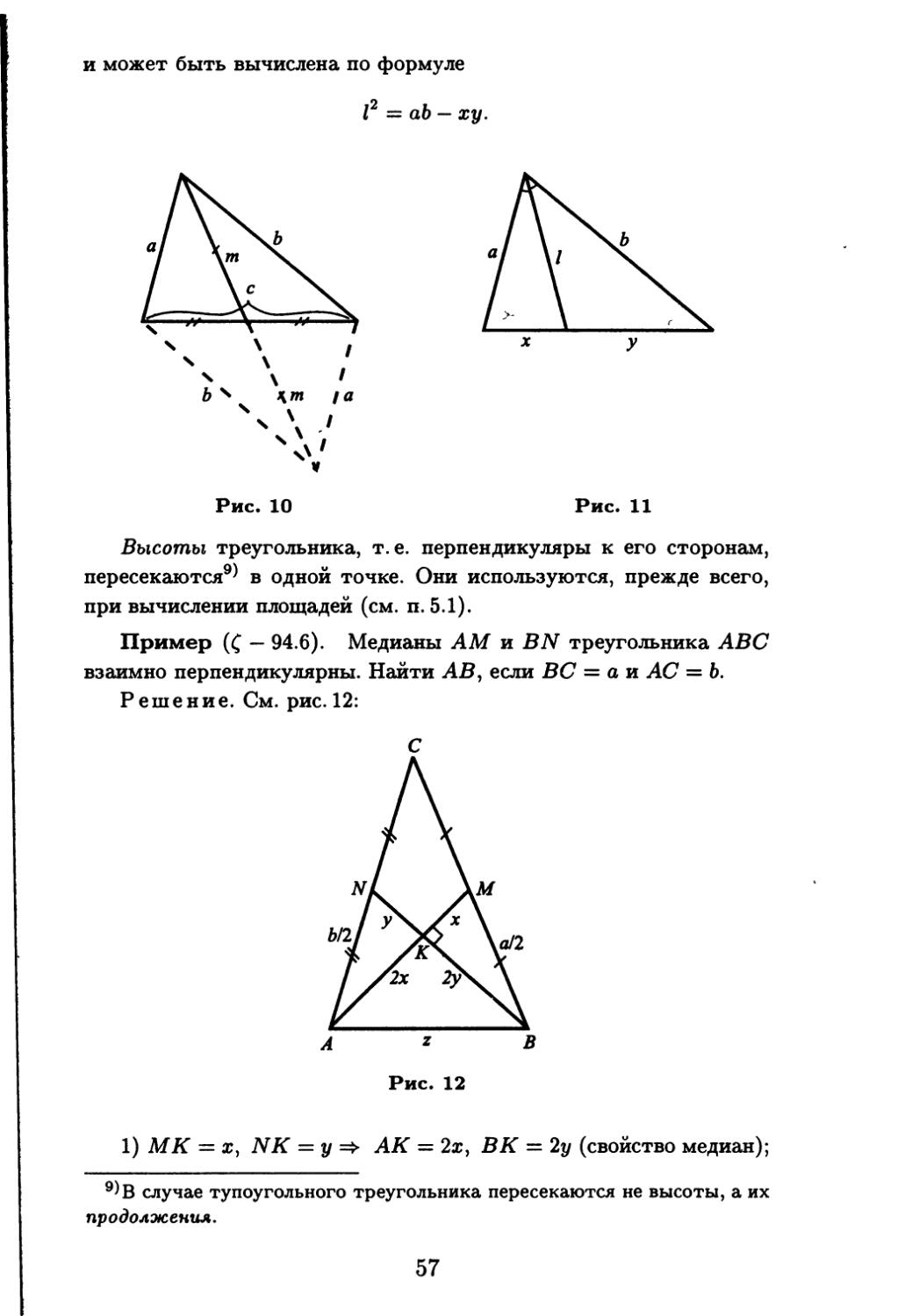
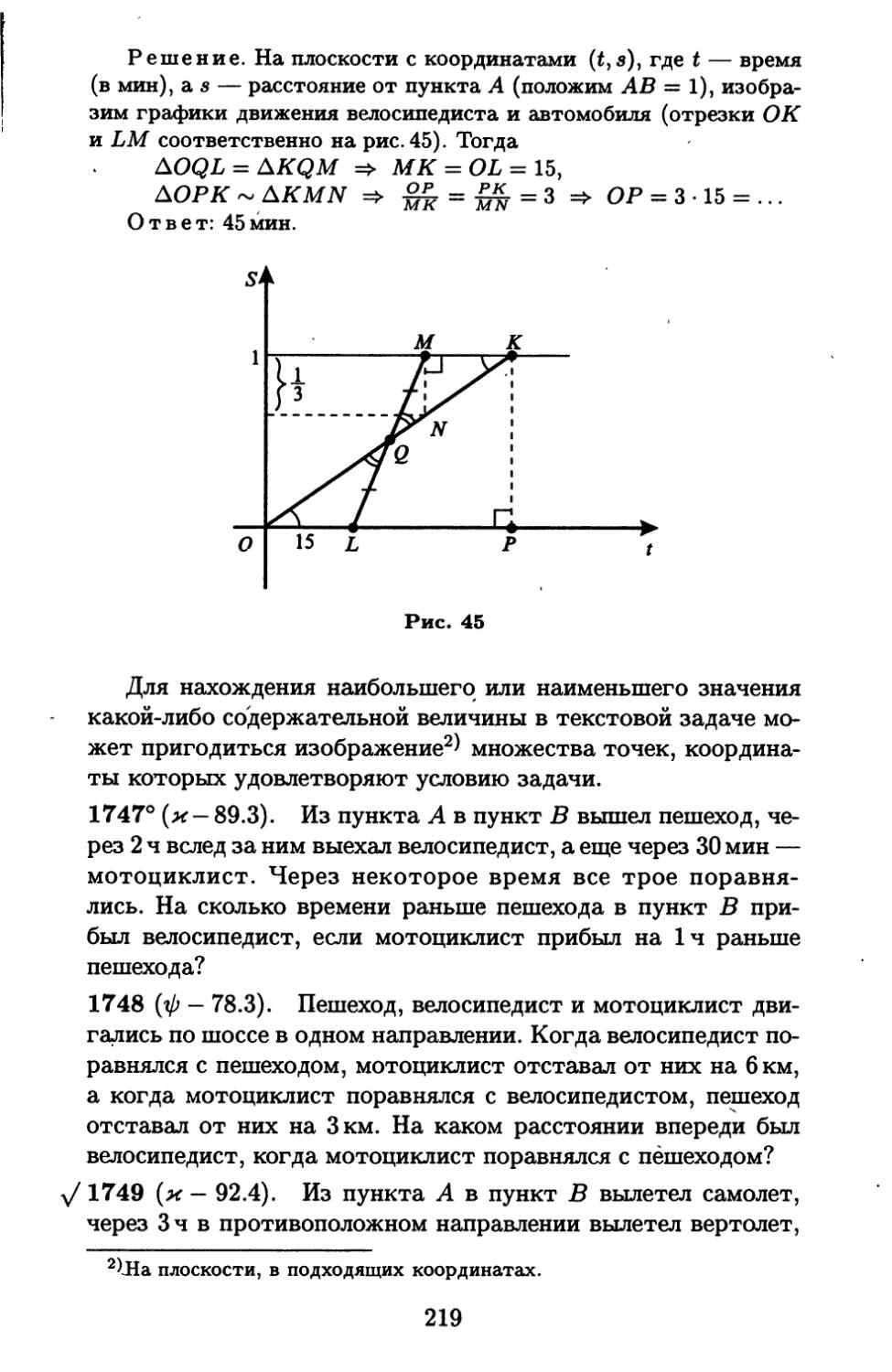
Текст
1Л»
И’
И. Н. Сергеев
шУ/Д
МАТЕМАТИКА
О
задачи с ответами
и решениями
••£•••£ ’iS’’ '» f ,Д * 4.' i~i? •”"* * ’ * -•
••• : • i • • •’ • t . '
начала -анализа тригонометрия^
J ’Й3 ’’
абитуриенту % f':
'г- F
ЧЗГИ“;
I?;.
И.Н. Сергеев
МАТЕМАТИКА
задачи с ответами и решениями
Учебное пособие
2-е издание, дополненное
УНИВЕРСИТЕТ
КНИЖНЫЙ дож
Москва Гином
2004 Лаборатория знаний
УДК 51(075)
ББК 22.1
С 32
Работа выполнена при поддержке Российского гуманитарного научного фонда (проект № 02-06-00057а)
Сергеев И. Н.
С32 МАТЕМАТИКА. Задачи с ответами и решениями: Пособие для поступающих в вузы. — М: КДУ, 2004. — 2-е изд., доп.— 360 с., ил.
ISBN 5-98227-031-8
Пособие представляет собой сборник задач по школьному курсу математики (включая алгебру, геометрию и начала анализа) и предназначено для подготовки к вступительному экзамену по математике в любой вуз. Специальный порядок задач, разработанный опытным преподавателем, обеспечивает максимальный обучающий эффект. При последовательном изучении материала знания абитуриента развиваются по спирали: пройдя очередной ее виток, он оказывается подготовленным по всем разделам математики на существенно более высоком уровне, чем раньше.
Содержатся варианты письменных вступительных экзаменов по математике в МГУ им. М. В. Ломоносова, проводившихся в 2002-2003 гг., а также программа по математике для поступающих в МГУ.
Для старшеклассников и учителей, абитуриентов и репетиторов.
УДК 51(075)
ББК 22.1
ISBN 5-98227-031-8
© Издательство «КДУ», 2004
Оглавление
Введение......................................... 11
1. Уникальность настоящего сборника....... 11
2. Структура книги........................ 12
3. Несколько слов о фундаментальных задачах... 13
4. Краткое описание генеральных методов...... 14
5. Условные обозначения................... 15
6. Как пользоваться задачником............ 17
Часть I. Фундаментальные задачи
Глава 1. Первичные понятия, факты и приемы
1. Элементарные сведения....................... 18
1.1. Задачи на вычисление значений.......... 18
1.2. Модуль и знак числа, допустимые значения... 19
1.3. Отбрасывание оснований степени......... 21
1.4. Понятие логарифма...................... 21
2. Тригонометрия............................... 22
2.1. Вычисление тригонометрических выражений ... 23
2.2. Простейшие уравнения................... 24
2.3. Формулы двойного и половинного угла. 25
2.4. Формулы тригонометрии.................. 25
2.5. Отбрасывание тригонометрических функций ... 27
2.6. Введение вспомогательного угла......... 27
3. Логарифмы..................... J........... 28
3.1. Вычисление логарифмов.................. 29
3.2. Отбрасывание логарифмов................ 29
3.3. Особенности применения формул.......... 30
3.4. Случаи переменного основания........... 31
4. Системы и текстовые задачи.................. 32
4.1. Системы................................ 32
4.2. Прогрессии............................. 34
4.3. Пропорции, доли, проценты и концентрации.. 36
4.4. Движение и работа...................... 39
5. Геометрия................................... 42
5.1. Простейшие задачи...................... 42
5.2. Применение тригонометрии............... 46
3
5.3. Касательные, секущие и хорды........... 49
5.4. Дуги окружности и углы................. 52
5.5. Медианы, высоты и биссектрисы.......... 56
5.6. Стереометрия........................... 59
5.7. Координаты и векторы................... 63
Глава 2. Квадратные уравнения и неравенства
6. Квадратный трехчлен......................... 66
6.1. Дискриминант и формула корней.......... 66
6.2. Разложение на линейные множители....... 67
6.3. Теорема Виета и обратная к ней......... 68
7. Уравнения и неравенства, квадратные
относительно различных выражений............ 69
7.1. Биквадратные уравнения и неравенства..... 70
7.2. Уравнения и неравенства, квадратные
относительно ах........................ 70
7.3. Уравнения и неравенства, квадратные
относительно ioga#..................... 71
7.4. Уравнения, квадратные относительно sin х
или cos х.............................. 72
8. Дополнительные соображения.................. 73
8.1. Учет области допустимых значений....... 73
8.2. Комбинации различных функций........... 75
8.3. Оптимальный выбор новой переменной....... 76
8.4. Роль грубых оценок..................... 77
8.5. Учет области значений выражения........ 78
9. Простейшие приложения....................... 79
9.1. Системы, сводящиеся к квадратным
уравнениям............................ 79
9.2. Квадратные уравнения и неравенства
в текстовых задачах.................... 81
9.3. Использование квадратных уравнений
в геометрии............................ 84
Часть II. Генеральные методы решения задач
Глава 3. Метод перебора
10. Расщепление уравнений и неравенств..........87
10.1. Расщепление уравнений................. 87
10.2. Метод интервалов...................... 88
* 10.3. Расщепление неравенств............... 90
10.4. Разные задачи, связанные с расщеплением. 91
4
11. Перебор случаев............................. 93
11.1. Раскрытие модулей и метод интервалов... 93
11.2. Исследование основания логарифма или степени.................................. 96
11.3. Зависимость от параметра.............. 97
11.4. Перебор вариантов в текстовых задачах.. 98
11.5. Целочисленный перебор.................101
12. Развитие метода интервалов.................104
12.1. Обобщенный метод интервалов...........104
12.2. Метод областей........................106
13. Разложение на множители....................109
13.1. Разложение с помощью формул тригонометрии... 109
13.2. Дублирование корней в ответе..........110
13.3. Использование однородности.............111 •
13.4. Разные методы разложения на множители..112
13.5. Уравнения третьей и четвертой степени..113
14. Возведение уравнений и неравенств в квадрат.115
14.1. Иррациональные уравнения..............115
14.2. Иррациональные неравенства............116
14.3. Разные задачи на возведение в степень..117
15. Тригонометрические уравнения, неравенства и системы..........................120
15.1. Выбор корней из данного промежутка.....120
15.2. Учет тригонометрических неравенств.....122
15.3. Трудности при отборе корней...........124
16. Перебор случаев в геометрии.................126
16.1. Обоснование геометрической конфигурации ... 126
16.2. Перебор вариантов расположения........129
16.3. Неоднозначность в ответе..............132
Глава 4. Метод равносильных преобразований
17. Сравнение чисел и выражений.................135
17.1. Задачи на сравнение...................135
17.2. Сравнение чисел в процессе решения.....136
17.3. Оценки в геометрии....................138
17.4. Цепочки неравенств....................140
18. Некоторые особенности преобразований........142
18.1. Изменение области допустимых значений.142
18.2. Случаи неодинаковых оснований.........144
18.3. Специальные действия с радикалами.....145
19. Различные системы и совокупности...........146
5
19.1. Метод подстановки......................147
19.2. Метод сложения.........................148
19.3. Системы в текстовых задачах............149
19.4. Необычные равносильные преобразования...151
19.5. Разные способы избавления от модулей...152
20. Область значений и экстремумы функций.......154
20.1. Исследование функций без производной...154
20.2. Условные экстремумы....................156
20.3. Исследование области значений в процессе решения.....................................157
20.4. Экстремальные ситуации в уравнениях и неравенствах...............................159
20.5. Исследование величин в текстовых задачах.... 162
21. Геометрические вопросы......................165
21.1. Сравнение площадей и объемов......... 165
21.2. Исследование геометрических величин и параметров............................... 170
21.3. Геометрические преобразования..........173
Глава 5. Метод обозначении
22. Замена переменных...........................177
22.1. Избавление от радикалов с помощью обозначений.................................177
22.2. Выявление устойчивых выражений.........178
22.3. Тригонометрические замены и подстановки... 181
22.4. Учет делимости посредством подстановки.182
22.5. Обозначения и переобозначения в текстовых задачах.........................183
23. Переменные, параметры, функции..............186
23.1. Привлечение функций....................186
23.2. Изменение роли букв, входящих в условие.187
23.3. Введение дополнительных переменных.....189
24. Переменные в геометрии......................191
24.1. Обозначения для длин и углов...........191
24.2. Метод координат........................193
24.3. Задачи с возможным участием векторов....195
25. Графические иллюстрации.....................197
25.1. Числовая прямая........................197
25.2. Исследование графиков..................199
* 25.3. Упрощение выкладок с помощью свойств параболы..............................201
6
25.4. Числовая окружность...................203
26. Зависимость графиков от параметра..........205
26.1. Сечения графиков......................205
26.2. Взаимное расположение графиков........208
26.3. Использование параметра в качестве одной из координат..........................209
26.4. Задачи на расположение парабол........211
27. Привлечение геометрии......................215
27.1. Геометрический смысл модуля...........215
27.2. Эффект от геометрической интерпретации ... 216
27.3. Применение геометрии в текстовых задачах... 218
28. Дополнительные построения в геометрии......220
28.1. Стандартные построения................220
28.2. Сравнение площадей и объемов частей фигуры......................................223
28.3. Разные задачи, использующие дополнительные построения...................226
Глава 6. Метод следствий 29. Основные типы следствий......................230
29.1 . Следствие, заложенное в постановке задачи... 230
29.2 . Метод проверки.......................232
29.3 . Метод подбора........................234
30. Получение и применение оценок..............236
30.1. Выводы на области допустимых значений..236
30.2. Разные задачи, использующие оценки.....237
30.3. Оценки в текстовых задачах............240
31. Специфика геометрии........................241
31.1. Получение различных следствий.........241
31.2. Угадывание особенностей конфигурации...246
31.3. Метод подбора в геометрии.............250
32. Элементы логики............................253
32.1. Приведение к противоречию.............253
32.2. Переход от общего к частному..........255
32.3. Следствия, связанные с количеством решений ... 257
32.4. Различные логические связи между утверждениями...............................260
33. Задачи с целыми числами....................261
33.1. Оценки целочисленных переменных.......261
33.2. Использование делимости...............264
33.3. Экстремальные-целочисленные задачи.....266
7
34. Проекции и сечения........................267
34.1. Проектирование на прямую.............268
34.2. Проектирование на плоскость..........269
34.3. Сечение фигур плоскостями............273
Приложение А. Программа по математике
I. Основные понятия......................279
II. Содержание теоретической части устного экзамена....................................280
III. Требования к поступающему.............282
Приложение Б. Дополнительные разделы
Б.1. Элементы комбинаторики................284
Б.2. Задачи, использующие предел...........284
Б.З. Производная.......'...................284
Б.4. Исследование функций с помощью производной.................................285
Б.5. Касательная...........................287
Б.6. Интеграл............................. 288
Б.7. Нахождение площадей с помощью интеграла.. 288
Б.8. Разные задачи на применение производной и интеграла.................................289
Приложение В. Варианты заданий 2002 г.
В.1. Механико-математический факультет, март ... 292
В.2. Механико-математический факультет, май.... 292
В.З. Механико-математический факультет, июль ... 293
В.4. Факультет вычислительной математики и кибернетики, апрель.......................294
В.5. Факультет вычислительной математики и кибернетики, июль.........................294
В.6. Факультет вычислительной математики и кибернетики (отделения бакалавров), июль... 295
В.7. Физический факультет, март............295
В.8. Физический факультет, май.............296
В.9. Физический факультет, июль............296
В.10. Химический факультет, май............297
В. 11. Факультет наук о материалах и Факультет биоинженерии и биоинформатики, апрель.......297
В. 12. Химический факультет и Факультет наук о материалах, июль..........................298
8
В. 13. Биологический факультет и Факультет биоинженерии и биоинформатики, май...........298
В. 14. Биологический факультет, Факультет фундаментальной медицины и Факультет биоинженерии и биоинформатики, июль.....299
В. 15. Факультет почвоведения, май..........299
В.16. Факультет почвоведения, июль..........299
В. 17. Геологический факультет, май.........300
В. 18. Геологический факультет, июль........301
В.19. Географический факультет, май.........301
В.20. Географический факультет, июль........302
В.21. Филологический факультет (отделение лингвокриминалистики), апрель ... 303
В.22. Филологический факультет (специальность «прикладная лингвистика»), июль..............303
В.23. Экономический факультет (отделение экономики), июль..................304
В.24. Экономический факультет (отделение менеджмента), июль...............305
В.25. Экономический факультет (вечернее отделение), июль..................305
В.26. Факультет психологии, июль............305
В.27. Институт стран Азии и Африки (социально-экономическое отделение), июль ... 306
В:28. Социологический факультет, июль.......306
В. 29. Факультет государственного управления (специальность «антикризисное управление»), июль........................................307
Приложение Г. Варианты заданий 2003 г.
Г.1. Механико-математический факультет, март ... 308
Г.2. Механико-математический факультет, май.... 308
Г.З. Механико-математический факультет, июль ... 309
Г.4. Факультет вычислительной математики и кибернетики, апрель..................... 309
Г.5. Факультет вычислительной математики и кибернетики, июль.................310
Г.6. Факультет вычислительной математики
и кибернетики (отделения бакалавров), июль... 311
Г.7. Физический факультет, март..............311
Г.8. Физический факультет, май...............311
9
Г.9. Физический факультет, июль...............312
Г.10. Химический факультет, май...............312
Г.11. Химический факультет и Факультет наук о материалах, июль....................313
Г.12. Факультет наук о материалах, апрель....313
Г. 13. Биологический факультет, апрель.......314
Г. 14. Биологический факультет, Факультет фундаментальной медицины и Факультет биоинженерии и биоинформатики, июль.....314
Г. 15. Факультет биоинженерии и биоинформатики и Географический факультет, май..........315
Г.16. Факультет фундаментальной медицины, май.., 315
Г.17. Факультет почвоведения, май............316
Г. 18. Факультет почвоведения, июль..........316
Г.19. Геологический факультет, апрель........317
Г.20. Геологический факультет, июль..........317
Г.21. Географический факультет, июль.........318
Г.22. Филологический факультет (отделение лингвокриминалистики), март.......318
Г.23. Филологический факультет (отделение теоретической и прикладной лингвистики и отделение лингвокриминалистики), июль .... 319
Г.24. Экономический факультет (отделение менеджмента), апрель..............319
Г.25. Экономический факультет (отделение экономики), июль..................320
Г.26. Экономический факультет (отделение менеджмента), июль................320
Г.27. Экономический факультет (вечернее отделение), июль...................321
Г.28. Факультет психологии, июль.............321
Г.29. Институт стран Азии и Африки (социально-экономическое отделение), июль ... 321
Г.30. Социологический факультет, июль.......322
Г.31. Факультет государственного управления (специальность «антикризисное управление»), июль....................................322
Г.32. Высшая школа бизнеса, апрель..........323
Г.ЗЗ. Высшая школа бизнеса, июль............324
Ответы............................................325
10
Введение
Перед Вами оригинальный сборник задач, предназначенный для подготовки к письменному вступительному экзамену по математике в любой вуз.
Этот задачник принципиально отличается от всех пособий данного типа. Он позволяет абитуриенту полностью, причем самостоятельно или с помощью консультанта подготовиться к экзамену за сравнительно небольшой срок: от двух-трех недель до одного года. Книгу может использовать и учитель математики, черпая в ней материал для проведения уроков или контрольных работ.
1. Уникальность настоящего сборника
Во-первых, задания расположены именно в таком порядке, в каком их следует выполнять абитуриенту для достижения максимального эффекта при повторении уже знакомых разделов математики и изучении еще не пройденных.
Основная идея, на которой базируется расположение материала, состоит в том, что подготовка к экзамену должна происходить как бы по спирали. Пройдя очередной виток такой спирали, абитуриент оказывается на более высоком уровне подготовки. При этом после прохождения каждого, в том числе и начального, витка он в той или иной степени уже готов к экзамену, причем по всем разделам программы: это особенно важно в случае проведения досрочных вступительных испытаний.
В стандартных пособиях для поступающих в вузы разные разделы математики проходятся последовательно в более или менее общепринятом порядке, в результате чего абитуриент, основательно изучив и отработав одни темы, не успевает порой даже познакомиться с другими, не менее важными, но стоящими в конце списка (обычно такая роль отводится геометрии, до которой, как правило, так дело и не доходит). Этого недостатка прежде всего лишен предлагаемый сборник.
Во-вторых, настоящая книга позволяет осуществить полный курс подготовки по математике. Работая с этой книгой,
И
читатель познакомится со всеми типами заданий, со всеми идеями и методами их решений, которые реально встречаются на письменных вступительных экзаменах. Здесь нет искусственных задач, никогда не предлагавшихся абитуриентам и придуманных исключительно для демонстрации каких-либо специальных трюков.
В основу сборника легли задачи вступительных экзаменов, проводившихся начиная с 1977 г. на различных факультетах МГУ им. М. В. Ломоносова. Они представляют собой результат коллективного труда математиков механико-математического факультета, факультета вычислительной математики и кибернетики, а также физического факультета МГУ.
В сборник вошли практически все наиболее ценные, содержательные и поучительные, по мнению автора, задачи, проверяющие не только подготовку абитуриента, но и его умение мыслить в нестандартной математической ситуации. Тексты многих задач сознательно изменены как для унификации их формулировок, так и для усиления их методического воздействия.
В-третьих, предлагаемый задачник выделяется из огромной массы подобных изданий относительной краткостью, что в сочетании с полнотой делает его особенно удобным для абитуриентов, имеющих не очень большой запас времени для подготовки.
Многие считают, что для подготовки к вступительному экзамену необходимо набить руку на решении большого числа однотипных задач, доведя до автоматизма применение стандартных приемов. Такая точка зрения хороша только тем, что не создает дополнительных проблем преподавателю.
Куда полезнее, по-видимому, предложить поступающему не слишком изнурительную подборку разнообразных задач, в которой каждая следующая задача развивает предыдущую и заставляет вспомнить кое-что из ранее пройденного материала. Именно эту цель и преследовал автор настоящего сборника.
2. Структура книги
Книга состоит из двух основных частей, разбитых на главы и параграфы, каждый из которых разделен на несколько
12
пунктов. В начале каждого пункта (параграфа) даны необходимые предварительные пояснения и решены один-два демонстрационных примера.
Основу сборника составляют задачи для самостоятельного решения, которых насчитывается более двух тысяч. Однако лишь ровно тысяча из них (см. п. 5 ниже) имеет обязательный характер: для полной подготовки к экзамену достаточно решить именно эту тысячу — остальные задачи могут пригодиться для закрепления навыков.
В качестве приложений в книге содержатся: программа по математике для поступающих в МГУ им. М. В. Ломоносова, дополнительные задачи из разделов, не входящих в эту программу (но включенных когда-либо в школьную программу), а также задания вступительных экзаменов и олимпиад по математике, проводившихся на разных факультетах Московского университета в 2002 г.
Все задачи пронумерованны подряд, а ответы к ним помещены в конце книги.
3. Несколько слов о фундаментальных задачах
В первую часть сборника, состоящую из двух глав, включены простейшие задачи, элементарные составляющие, из которых впоследствии, как из кирпичиков, складываются более сложные задачи. Наряду с алгеброй, сюда входит и геометрия, которая, в отличие от традиционного ее местоположения, пронизывает весь предлагаемый курс и органично вплетается в другие его разделы.
Задачи первой главы требуют лишь самых примитивных знаний и навыков, незатейливых рассуждений и выкладок, однако умение их решать совершенно необходимо в дальнейшем.
Вторая глава посвящена квадратным уравнениям и неравенствам: в ней закрепляются и развиваются первичные понятия, факты и приемы, с которыми читатель знакомился на протяжении первой главы.
Таким образом, вся первая часть книги — это базовый уровень, нулевой (не первый!) виток спирали, о которой говорилось выше.
Особого разговора заслуживают логарифмы и сопутствующий им материал, который, согласно обычной школьной программе, проходится лишь в 11-м классе. Если подождать, по
13
ка эта тема будет пройдена в школе, то, вероятнее всего, она просто не будет усвоена поступающим в требуемой степени.
Имеет смысл досрочно (быть может, даже самостоятельно) изучить логарифмы по школьному учебнику или по другой литературе. Предполагается, что именно так и поступит читатель при работе уже с первой частью задачника.
4. Краткое описание генеральных методов
Вторая часть сборника разбита на четыре главы (витка спирали), которые соответствуют, по классификации автора, четырем уровням подготовки к экзамену, четырем глобальным методам решения математических задач. Строго говоря, это даже не методы, а наиболее общие способы, или типы, рассуждений. Да и деление задач на классы по этому признаку носит весьма и весьма условный характер. 5
Метод перебора соответствует первому уровню подготовки — разветвленному. Идея перебора случаев стара, как мир, и применима к широкому классу задач.
Довольно часто приходится рассуждать по-разному в зависимости от каких-либо обстоятельств: от знака величины, стоящей под модулем, от знаков левой и правой части уравнения или неравенства при возведении в квадрат, от того, равен или не равен нулю коэффициент при неизвестной, и т. п. Отдельное исследование каждого из возникающих случаев как раз и составляет суть метода перебора.
Метод равносильных преобразований подробно изучается на следующем, продвинутом уровне. Он, конечно же, применялся и в предыдущих разделах пособия, но в этой главе, поскольку задачи становятся более сложными, он раскрывается в полном объеме, рассматривается с разных позиций, а его приложения оказываются более серьезными.
В основе метода равносильных преобразований лежит переход от начальной задачи к некоторой новой, в определенном смысле более простой и, что самое главное, равносильной исходной. К этой преобразованной задаче впоследствии и адресуется изначально поставленный вопрос. Без такого подхода бывает особенно трудно обойтись при решении задач с параметрами.
Метод обозначений позволит абитуриенту подняться на еще более высокий, творческий уровень. Название этого
14
метода ассоциируется, прежде всего, с введением новой переменной, что составляет лишь вершину айсберга.
Автор понимает метод обозначений в широком смысле, а именно, как метод обогащения задачи, например, добавлением новых переменных или функций, привлечением графических иллюстраций, дополнительными построениями в геометрии и другими проявлениями математической изобретательности. Иными словами, задача наделяется более богатой и содержательной структурой и с ее помощью исследуется более просто, а полученные в итоге выводы затем истолковываются в исходных терминах.
Метод следствий относится к заключительному, утонченному уровню подготовки абитуриента. Необходимость в его применении возникает всякий раз, когда рассуждать равносильно нет воможности или надобности.
Если, для начала, попытаться вывести из условия хоть какие-нибудь следствия, подметив или угадав хоть что-нибудь полезное, то затем, при удачном исходе, можно довести решение и до логического конца. Разумеется, для этого требуется повышенная наблюдательность или изощренность в рассуждениях, но, как показывает опыт, на проявление именно этих качеств абитуриента иногда и рассчитывают экзаменаторы.
5. Условные обозначения
Непосредственно после номера каждой задачи в скобках указано, на каком факультете, в каком году она предлагалась и какой по порядку шла в варианте. При этом год обозначен лишь двумя последними цифрами, а факультет — греческой буквой в соответствии со следующим перечнем (названия факультетов, их отделений и специальностей даны по состоянию на 2004 г.):
ц — механико-математический факультет;
х — факультет вычислительной математики и кибернетики;
£ — физический факультет;
X — химический факультет;
у — факультет наук о материалах;
/3 — биологический факультет и факультет фундаментальной медицины;
7г — факультет почвоведения;
15
A — геологический факультет;
7 — географический факультет;
ip — филологический факультет (специальность «прикладная лингвистика»);
е — экономический факультет;
— факультет психологии;
а — институт стран Азии и Африки (социально-экономическое отделение);
о — социологический факультет;
р — факультет государственного управления (специальность «антикризисное управление»).
Номера наиболее важных, обязательных задач, о которых говорилось выше в п. 2, помечены галочкой.
Условная трудность задачи (по сравнению с другими задачами того же пункта) отмечена следующими значками около ее номера:
° — задача полегче;
* — задача потруднее;
* — переусложненная или слишком муторная задача (разумеется, по мнению автора книги).
Например, задача, помещенная под номером 27, начинается записью «^/ 27* (/1 — 86.2)...». Это означает, что она была второй по счету в варианте механико-математического факультета в 1986 г., а так как ее номер имеет галочку и звездочку, она является обязательной и относительно трудна (правда, задачи без звездочек из других параграфов могут оказаться куда более трудными).
В формулировках задач, как правило, опущены стандартные фразы тина: «решить уравнение», «решить неравенство», «решить систему», «вычислить», «сравнить» и т. д.
В решениях демонстрационных примеров начальные и конечные уравнения, неравенства, системы, совокупности или выражения, во избежание повторов, в большинстве своем заменены многоточием.
В тексте приняты следующие математические обозначения:
N,Z,Q, R — множества натуральных, целых, рациональных действительных чисел соответственно;
(а;Ь), [а; 6], [а;Ь), (а;Ь]—числовые промежутки;
(а, Ь), (а, Ь,с) — наборы чисел, координат;
V, Л — любой из знаков =, >, <, /.
16
6. Как пользоваться задачником
В заключение, дадим несколько советов читателю, собравшемуся самостоятельно готовиться к вступительному экзамену по настоящему задачнику:
1) если у Вас достаточно времени на подготовку, изучайте все пункты подряд — ведь каждый следующий пункт предполагает знание предыдущих;
2) прежде чем браться за задачи очередного пункта, прочитайте его преамбулу и, решив демонстрационную задачу по-своему, сравните получившееся решение с предложенным: если Ваше решение оказалось нерациональным или, хуже того, ошибочным, сделайте соответствующие выводы на будущее;
3) решайте сначала обязательные задачи, и если в какой-нибудь из них Ваш ответ хотя бы отчасти не сошелся с правильным, непременно найдите ошибку и усовершенствуйте метод решения, а для его закрепления порешайте близкие задачи из числа необязательных;
4) если у Вас не получается задача, отмеченная кружочком, прочитайте более внимательно предварительные пояснения или дополнительную литературу, посоветуйтесь с товарищем или наставником — так или иначе узнайте, как решается задача (в противном случае Вы рискуете неправильно усвоить весь соответствующий раздел);
5) если у Вас не получается задача со звездочкой, не отчаивайтесь: гораздо важнее, чтобы получились остальные обязательные задачи;
6) хорошо, если Ваш ответ оказался правильным, но еще лучше, если метод решения согласуется с названием пункта (параграфа) и комментарием к нему;
7) если Вы получили правильный ответ, проанализируйте текст решения: он должен обосновывать правильность ответа, и лучше, если такой текст получается автоматически или после незначительного редактирования, а не как результат переписывания начисто.
Желаю успеха!
И. Сергеев
Часть I
ФУНДАМЕНТАЛЬНЫЕ ЗАДАЧИ
Глава 1. ПЕРВИЧНЫЕ ПОНЯТИЯ, ФАКТЫ И ПРИЕМЫ
Лиха беда начало.
§ 1. Элементарные сведения
Предполагается, что читатель умеет оперировать с многочленами и дробями^ а также знает следующие формулы сокращенного умножения1^: (х ± у)2 = х2 ± 2ху 4- у2, (х ± у)3 = х3 ± Зх2у 4- Зху2 ± у3,
х2 - у2 = (х 4- у)(х - у), х3 ±у3 = (х± у)(х2 qp ху 4- у2)
и следующие основные формулы действий со степенями и радикалами2^:
ах+* = axav, (ab)x = ахЬх, Vab= Va\/b,
ax~v = ax/av, (a/b)x = ax/bx, y/a/b — \/a/y/b, y/a = a1/<n,
1.1. Задачи на вычисление значений
Процедуру вычисления лучше оформлять не по действиям, а в виде цепочки равенств, начинающейся исходным выражением и кончающейся ответом.
Пример (г/) — 84.1). Вычислить3^
/ 3(^-0,125:1 iMeoV1 . /679.10-3 . п
каждой формуле, содержащей несколько знаков типа ± или берутся либо только верхние знаки, либо только нижние.
2)В последней формуле, в отличие от предыдущих, никаких ограничений на а не накладывается.
3)Именно в этом, по умолчанию, и состоят все задания настоящего пункта.
18
Решение.4^
— ( А . <679 . 21 \ 90 480-7(5-2).3 __ 480 3 _
“ I 480(7-1-I I )-3 I * \ 70 70 / ~ 3-(17-i0)-8-9-10 ~ 8 — • • •
Ответ: 180.
у/1 (^-84.1).
у/ 2 (тг — 96.1).
уз (А-98.1)5)
4 (Л - 93.1).
5 (А - 94.1).
У 6 (тг —98.1).
У 7* (а-99.3).
/928 10-2 _ Л fiV ( (42-3^4-3,3:0,03):Д \ \ 0,8 ’ / • I (з|:0,625-0,84:0,8):0,03 J
((^3 - ^27)2 + 7) ((^3 4- W)2 - 7) .
/9а2 —1652 a2b-3ab2\2 . ( 8a3-b3\
\ За+46 ab ) ’ 2а-Ь ) *
/8ay/a-j-by/b (4^/^+2\/б\
V 4^+276 Va0J V 4а-5 ) ’
7у/Зу/а—7у/5у/Ь , ____За—55_____
6у/Зу/а+6у/5у/Ь ’ 9а+155+6\/15а5 ’
(у/а+ y/ab+b+by/b) 2 (1 —by/b} 2 (6+Ь-1 _2)(1+ь+х/ь)2
- b(b+y/a)2tfi-
1.2. Модуль и знак числа, допустимые значения
Решение следующих задач рекомендуется оформлять в виде логической цепочки равносильных объектов (уравнений, неравенств, систем, совокупностей), начинающейся условием и кончающейся ответом. После любого перехода, в случае необходимости, можно делать пояснения, обосновывающие его правильность. Особенно тщательно нужно следить за изменением ОД36\ добавляя условия, переставшие действовать, в систему с остальными.
Система обозначается знаком {, а совокупность — знаком [. Частными проявлениями системы и совокупности следует признать двойное неравенство и, соответственно, знак плюс-минус.
Пример 1 (С — 83.2). Решить уравнение |ж2 — 121 = 4.
4) Здесь и ниже исходное и конечное выражение, уравнение, неравенство и т. п. в решении не повторяются, они заменены многоточием (эту манеру не следует перенимать!).
5) Выражение, содержащее буквы, рассматривается только при тех значениях букв, при которых оно определено, однако выяснять, когда именно это имеет место, без специального на то указания, не требуется.
6)ОДЗ — область допустимых значений (обычно для неизвестной величины).
19
Решение.
... & х2 - 12 = ±4 о х2 = 12 ± 4 о И = У16, у/б <=>...
Ответ: х = ±4, ±2\/2-
Пример 2 (х — 93.2). Решить неравенство7^ > 1. Решение.
... (*-3)-(*+2) <0 <=> -Ц < 0 О х - 3 < о -^ ...
г—О Х—&
Ответ: х < 3.
8° (С-83.2). |2 — 5ж2| = 3.
9° (А - 79.1). \2х - 3| = 3 - 2а:.
V 10 (р- 01.2). |а:2 - 13а: + 35| = |35 - а:2|.
у 11 (С-96.3). -1 < |а:2 - 7| < 29.
12° (V» - 86.2). У8 - За:2 = 1.
У 13° (л- - 01.2). у/х2 — 4 = у/х — 2.
14° (л- - 95.2). vW - 3 > 1.
у/15° (тг - 87.2). у/2х + 3^2.
16° Ь - 96.1). х/9 4- бх > \/2 — х.
У 17 (А-97.1). у/|® + 1| - 1 > у/|а: + 1| - 97.
18° (е-85.1). 4ж —1 \ 4 Зж+1 3’
19° (С-86.2). Х 1 3-х’
у/ 20° (А-87.3). —з < 1
21° (С-87.1). 1 > 1 ®+2 х—2*
У 22° (ст-97.1). 1+1.
23 (х -93.1). 9 -1 (x+l)2 L
24 (А-01.1). 1»~3|+2 <0 |2®-3|-5 и’
у/ 25 (7-97.1). |»-1|+10 9 4|®-1|+3
у/26* (х -01.1). |ж—11 |ж-Ц| |х-2| “ |®+2|-
у/ 27* (д - 86.2). Решить неравенство
/(Л®)) > (Л*))2, где Ля) = 2а:2 - 1.
7) Всюду ниже предполагается, что если в задании фигурирует одно лишь уравнение (неравенство или система), то это уравнение (неравенство или систему) требуется решить.
20
1.3. Отбрасывание оснований степени
Отбрасывание оснований степени в уравнении или неравенстве удобно осуществлять с помощью следующего утверждения: пусть основание а больше 1, тогда8)
V а9 О f V д,
если же 0 < а < 1, то после отбрасывания оснований знак V меняется на обратный^ Л.
Пример 1 (б - 83.1). 2х+2 • 5х+2 23х • 53х.
Решение.
... <=> 10х+2 103х о х + 2 Зх <£>...
Ответ: х 1.
Пример 2 (С - 82.4). 2(5Х“1 - 3х"2) = 5х - Зх+1.
Решение.
... 3*-2(3з _ 2) = 5т-1(5 _ 2) 3х"3 = 5Х“3
о (3/5)х-3 = (3/5)° о х - 3 = О ...
Ответ: х = 3.
28° (е - 86.1). 5х+1 = (1/5)®-2.
У 29 (С-95.1). 2х-1 -3х = 0,5 • 64-х.
У 30° (Л - 97.4). (2/3)2х2 > (2,25)х2~10.
У 31 (тг- 99.3). (8/7)1/ж2 = (7/8)-1/|2-ж21 .
32° (а-92.1). 2х+8 + 27 • 2х"1 - 10 0.
1/ЗЗ0 (С-99.2). 22х-5 _ 41-2 _ 322х/5 _ gg
У 34 (С-82.4). 2х+2 - 5х-1 < 7 • 2х-3 - 3 • 5х-2.
35 (А - 82.3). СЛ н 1 ю н 1 II н 1 ьо 1 СЛ н 1 со ю
,/36* (С-98.3). 2x4-7 1 Л,_ _ 2x4-1 ' 2~^~ - 32х-1 > 9х - 2~^~.
1.4. Понятие логарифма
Показатель степени, в которую нужно возвести а, чтобы получить Ь, называется логарифмом числа b по основанию а и. обозначается символом loga b. По определению, этот символ имеет смысл
8) Здесь и ниже под знаком V или Л подразумевается, любой (фиксированный в данном контексте) из знаков =,>,<, >, , ф.
9)Не противоположный! Например, знак > меняется на <, а знак =
не меняется вовсе.
21
д/37 (а — 94.2).
у/ 38° (тг — 90.1).
39 (тг —94.2).
у/ 40* (б —82.3).
J 41* (А -85.1).
тогда и только тогда, когда выполнены ограничения
1 # а > О, b > О, при которых, таким образом, справедливо представление Ь = alog“ ь.
Пример (е - 81.2). 6 • 5* - 5х+1 + 6 • 5х-1 = 22. Решение.
5х-1(6 • 5 - 52 + 6) = 22 5х-1 = 2 (= 5log= 2)
<=> х — 1 = log5 2 <=> ...
Ответ: ® = 1+ log52.
2® log2 7 . ух2+х _ j
2-3х-2 > з*-1.
3х -21-х = 5-2х -31-х.
33+1/2__. 22®~1_____33+5/2
Сравнить 210Ss 5 — 0,1 и 510ёз2.
§ 2. Тригонометрия
Тригонометрические функции числа1 2) определяются с помощью тригонометрического круга-, данное число изображается точкой, но не на прямой, а на единичной окружности2). Абсцисса и ордината этой точки — это косинус и синус данного числа соответственно. Геометрически можно определить также и тангенс (котангенс).
Желательно помнить или уметь быстро восстанавливать в памяти следующие формулы:
1) основное тригонометрическое тождество и другие формулы, связывающие функции одного угла'.
sin2 х + cos2 х = 1,
1 + tg2® = i + ctg2® = ^;
2) формулы двойного и половинного угла (в частности, формулы понижения степени и универсальной подстановки):
sin 2х = 2 sin х cos х,
cos 2х — cos2 х — sin2 х = 2 cos2 х — 1 = 1 — 2 sin2 х,
2 sin2 | = 1— cos ж, 2 cos2 | = 1 + cos х,
tg® = тттг, sin®=-j^, cosa: = i=£, rflet = tgf,
x 2 X 1—COS X ftr — s*n X 1—cos X .
ъо 2 14-cosr’ 0 2 14-cosr sin x ’
1)Или, что то же, обобщенного угла в радианах.
2) Числовая ось по-просту «намотана» на круг, как нитка на катушку.
22
3) формулы приведения, общий вид которых таков: . х f ? f(x), если п — четно,
f (%п ±х) = < ' ; !
J '2 7 [ ? g(x), если n — нечетно,
где f — любая тригонометрическая функция, g — соответствующая ей кофункция, а на месте вопросительного знака стоит плюс или минус в зависимости от того, какой знак принимает исходное выражение для острого угла ж;
4) формулы сложения:
sin(s ± у) = sin х cos у ± cos х sin у,
cos(s ± у) = cos х cos у sin х sin у,
5) преобразование произведения в сумму:
2 sin х cos у = sin(s + у) 4- sin(s — у),
2 cos х cos у = cos(s 4- у) + cos(s — у),
2 sin х sin у = cos(s — у) — cos(x 4- у);
6) преобразование суммы в произведение:
sin х ± sin у = 2 sin cos ,
cos х 4- cos у = 2 cos cos
cos x — cos у = — 2 sin ^y^ sin
2.1. Вычисление тригонометрических выражений
Формулы тригонометрии позволяют выразить значение тригонометрической функции от какого-либо числа через значения других тригонометрических функций или от других чисел.
Пример (х—80.1). Найти cos2a и |ctga|, если sina = 1/3.
Решение, sina = 1/3
=> cos2а = 1 - 2sin2 а = 1 - 2 (1/3)2 = 7/9
=> |cosa| = у/1 — sin2 а = — (1/3)2 = х/8/3
=>|ctga| = ® = ^ = V8.
Ответ: 7/9, \/8.
У 42° (А-00.2).
43 (^-86.1). у/ 44 (х —94.2). у/ 45 (тг — 96.1).
Найти tg2a, если tgy = |.
Найти tg22a, если cosa = — х/7/6.
Найти cos2(a — 7г/4), если tga = — 1/х/7.
Найти cos (а 4- тг/З), если sina =—3/5 и tga>0.
23
у/ 46 (х — 95.2). Найти sin 2а, если
| sina| = 3/х/1б и 7г/2 < a < 7г.
у/ 47* (тг — 00.3). Найти tg 2a, если
sin a = 4/5 и sin 4a > 0.
у/ 48* (£ — 87.3). Найти cosa и tg^, если sin a = —x/5/3 и 0 < a < Зтг/2.
у/ 49* (х — 99.1). Сравнить
arccos (—3cosa — 1) если tg a = \/3.
и 197Г/24,
2.2. Простейшие уравнения
Простейшие тригонометрические уравнения решаются по формулам
sins = а о х = (—l)n arcsina 4- тгп,
cos х = а о х = ± arccos а 4- 2тгп,
tg х = а о х = arctg а 4- тгп,
ctg х = а <=> х = arcctg а 4- тгп, где п G Z, или непосредственно на тригонометрическом круге.
Пример (£ — 77.1). sin2 х = 3/4. Р ешение.
... О sins = ±\/3/2 ...
Ответ: х = ±7г/3 4- тгп, где п 6 Z.
50° (7 - 95.1). 2 cos(7r(s - 1)) = у/3. у/ 51° (С -77.1). ctg2 я = 3.
24
у/ 52° (0-92.1).
53° (х - 80.2). ^/54° (7-84.1). у/55 (е —81.2). У 56 (^-80.1).
4 cos2 (5х — тг/3) = 3. у/2 sin2 5х = sin 5х.
2 sin | cos За: = cos За;.
3 sin2 х = cos2 х + 1.
/о‘82а: _ Зу/З
V О — 3tg 2х •
2.3. Формулы двойного и половинного угла
Применяются формулы 1) и 2) из преамбулы настоящего параграфа.
Пример (7 — 92.1). cos 2s 4- sin ж = 1.
Решение.
... о (1 — cos 2s) — sin ж = 0 о 2 sin2 х — sin ж = 0
О sin я (sin ж — 1/2) = 0 О sins = 0, 1/2 <=>...
Ответ: х = 7гп, (—1)*тг/6 4- тгА:, где п,к G Z.
57° (7-94.1). sin 2х = cos х.
58° (х —80.2). sin 2s = УЗ sin х.
у/ 59° (д - 80.2). sin 2х 4- У5 cos х = 0.
у/ 60° (0-96.1). Vasins 4- sin2s = 0.
61° (С - 78.1). 2 sin ж 4- 3 sin 2s = 0.
62 (х —93.3). coss = 14- cos 2s.
у/ 63 (с-79.1). sin f 4-1 = coss.
У 64 (^-88.1). 1 4- cos | 4- cos s = 0.
65 (тг — 01.1). 2 4- cos 2s = 4 cos2 s.
,/66 (тг —84.2). 2 cos2 s = 1 4- \/2 — cos 2s.
67 (тг - 95.1). 6 sin2 s 4- cos 2s — 3 = 0.
у/ 68 (^ -86.2). cos2 s — cos 2s = sin s.
у/ 69* (7-90.1). cos2 6s 4- sin2 3s — 1 = 0.
у/ 70* (7-85.1). л/б sin s 4- cos 2s 1.
у/ 71* (А - 94.6). 4 cos s — sin 2s < 0.
2.4. Формулы тригонометрии
Применяются разные формулы 1) — 6), приведенные в преамбуле настоящего параграфа.
25
Пример (Л — 91.1). sin 7s cos я = sin 6s. Решение.
... <=> sin 7s cos s = sin 7s cos s — cos 7s sin s
о cos 7s sin s = О о
7 s = 7t/2 4- 7гп, где n G Z, s = 7rfc, где к G Z,
Ответ: s = тг/14 4* тгп/7, лк, где п, к G Z.
72° (тг - 86.1). 73 (е —80.4). у/ 74 (тг - 83.2). У 75 (/5-81.2). 76 (<р - 79.2). sin х = 2 sin (х — k/S). sin (тг/З — x) 4- cos (тг/6 — x) = л/3. cos (x 4- 7r/3) 4- sin (s 4- тг/6) — cos 2x = 1. sin (3s 4- 7тг/2) = cos (Зтг/2 — 6s). sin (2s 4- 5тг/2) — 3 sin(s — Зтг) = 1 4- 2 sin s.
77 (А-97.3). sin (s — 7тг/6) — cos (s — 7тг/3) = cos (2s — тг/2).
78 ((-81.1). sin (s — 7r/3) 4- 2 cos (s 4- тг/6) '= 0.
у/ 79 (0 - 80.1). 1 4- 2 cos 3s cos s — cos 2s < 0.
у/ 80 (С - 94.1). sins sin3s = 1/2.
81 (х - 00.2). cos 3s 4- sin s sin 2s = 0.
82 (С-98.1). sin 3s — sin 2s cos s = 0.
у/ 83 (С - 99.1). sins — sin (3s/2) cos (s/2) = 0.
84 (С - 83.1). sin 3s 4- sin 5s = sin 4s.
85 (р-01.1). sin s 4- sin 3s = y/2 sin 2s.
86 (7 - 78.2). cos s — 2 cos 3s 4- cos 5s = 0.
87 (А-94.4). cos s 4- cos 3s 4- cos 5s = 0.
88 (С — 89.1). sin 5s — sin s = \/8 cos 3s.
89 (С - 95.1). sin 7s — sin s = cos 4s.
У 90 (С-97.1). cos 9s — cos 7s = sin s.
у/ 91 (С-99.1). sin 14s = cos 4s — sin 6s.
92 (тг - 87.1). 5 sin 2s = sin 9s — sin 5s.
У 93 ((-99.1). cos 7s 4- cos 3s 4- 2 sin2 s = 1.
94 (( - 96.1). cos 3s — sin (7s — тг/2) = cos 5s.
у/ 95* (7 - 79.2). sin (s — 7r/3) — sin (s 4- 5тг/6) = cos (s 4- 7t/4) .
У 96* (х —97.3). tg (s 4- 7t/4) 4- tg (s - 7t/4) = tg s.
у/ 97* (0-86.1). Найти наименьший неотрицательный корень
уравнения 2 sin (ж 4- 7г/3) = 2 cos (ж 4- тг/6) — \/3.
26
2.5. Отбрасывание тригонометрических функций
Уравнения вида
sin f = sin д или cos f = cos g
решаются переносом обеих частей в одну сторону с последующим
разложением на множители3 4^ или с помощью утверждений
sin f = sin д О
f = д + 2тгп
f = тг — д 4- 2тгп
О f = (~1)пд 4- 7гп,
cos f = cos д о f = ±д 4- 2тгп, где n Е 1
Пример (Л — 86.1). sin (х 4- тг/6) = sin ж. Решение.
х 4- 7г/6 4- х = тг 4- 2тгп, где n Е Z,
х 4- тг/6 = х 4- 2тгА:, где к G Z, (решений нет)
2х = 5тг/6 4- 2тгп <=>...
Ответ: х = 5тг/12 4- тгп, где n Е Z.
Если уравнение имеет вид
sin / = cos д, то его можно свести к одному из перечисленных выше, преобразовав какую-либо из тригонометрических функций в соответствующую ей кофункцию с помощью дополнительного^ угла по формуле sin / = cos (тг/2 — /) или cos д = sin (тг/2 — д).
у/ 98° (А-94.4). у/ 99° (С-93.2).
1оо (с-00.1). у 101 (б —88.3). у/ 102* (тг — 92.1). у/ 103* (/3 — 91.2). у/ 104* (А-01.2).
sin 7х = sin 7.
cos5x = cos(5 4- х).
sin 5х 4- sin 2х = sin 7х.
sin (х 4- 7г/4) cos (4я — тг/4) = cos х cos 2х.
2(sin 6х — sin 4х sin 2х) = cos &х 4- cos 2х.
sin 2х 4- sin Зх 4- cos 5я = 1.
Найти все отрицательные корни уравнения 1 4- sin 7х = (cos ~ 4- sih ^)2 .
2.6. Введение вспомогательного угла
Основная идея рассматриваемого метода состоит в следующем: если выражение a sin х 4- bcos х поделить5^ на у/а2 4- Ь2, то его
3)По формулам 6) из преамбулы настоящего параграфа.
4>До тг/2.
5) Случай, когда нормирующий делитель \/а2 + Ь2 равен нулю, интереса не представляет.
27
можно свернуть6 *^ в синус или косинус суммы или разности исходного аргумента со специально подобранным числом ср, которое и называется вспомогательным углом.
Пример (Л — 85.4). 3 sin х + 5 cos х = \/17.
Решение.
-®?sinx + ^-cosx=
о cos (а? — у?) = где ip — arccos ^=,
О х — ip = ±7г/4 + 2тгп, где п 6 Z, я = (^±7г/4 + 2тгп <=>...
Ответ: х = arccos(5/\/34) ± тг/4 4- 2тгп, где п 6 Z.
У 105 (х-82.1).
106 «-96.1).
у/ 107 (£ - 79.1).
У 108 « - 94.2).
109 (С-01.1). v/110* (б-88.2). у/ 111* (^-91.4). У 112 (Л-79.3).
sin2x 4- \/3cos2a; = х/2.
1 — х/3 sin Зя = cos Зя.
cos5x — 1 — sin5x.
5 cos я 4- 2 sin х = 3.
cos Зя = | sin x 4- cos x.
2cosx(l 4- cosx) = 1 — \/3sin2x.
В sin я 4- cos 197Г = cos я. 7Г
Найти все а, при которых уравнение
4 sin я 4- 5 cos я = а
имеет хотя бы один корень.
§3. Логарифмы
При естественных ограничениях, связанных с существованием логарифмов1^, справедливы следующие основные формулы:
0) aloga b = b — основное логарифмическое тождество;
1) loga be = loga b 4- loga c — логарифм произведения;
2) loga | = loga b — loga c — логарифм частного;
3) loga bp = p loga b — логарифм степени;
4) loga b = — переход к новому основанию
и следующие полезные дополнительные формулы:
3') loga9bp = flogab;
4') 10баЬ= Т^'
6)По формулам сложения 4) из преамбулы настоящего параграфа.
!>См. определение в п. 1.4.
28
3.1. Вычисление логарифмов
Ключевым преобразованием логарифма может оказаться переход к новому, удачно подобранному, основанию.
Пример (х — 84.1). Найти loga/6a2 3b, если loga Ь = 7.
Решение. loga6 = 7
=► loe а3Ъ - log° а3ь = = 2±1 = -12 =
1оКа/Ь ° ° — lOga а/Ь loga a—loge Ь 1-7 6
Ответ: —5/3.
у/ 113° (А — 89.1). Сравнить 21og25 и Slog^
у/ 114* (тг — 99.1). Сравнить
arccos (-|) log81 и. sin tg3 (-^) ctg
у/ 115 (</? — 88.1). Вычислить •
V кт" / logi50 5 log6 5
116 (е - 89.2). Вычислить
V 7 log280 2 1ОК35 2
у/ 117 (0-98.1). Найти logs^. если logab = v/5.
118 (£ — 82.3). Найти log^j если k>gba = y/3.
у/ 119° (тг — 93.1). Найти log2|sina|, если cos2a = 3/4.
У 120*(б-92.1). Найти log14/25 |cosa|-Mog14/25 |cos3a|, если
sin (a 4- тг/4) 4- cos (a 4- тг/4) = —^4/5.
3.2. Отбрасывание логарифмов
f vg f,g>o,
Отбрасывать логарифмы удобнее всего с помощью следующего утверждения: пусть основание а больше 1, тогда2
loga/Vloga£ о
если же 0 < a < 1, то после отбрасывания логарифмов знак V меняется на обратный Л.
Из двух условий 3) / >Ои0>Ов последней системе, как правило, достаточно оставить только одно — при правильном его выборе другое условие будет выполнено автоматически. Для представления данного выражения в виде логарифма может пригодиться формула
Ь = loga аь.
2)См. сноски ®>, 9> в п. 1.3.
3) Связанных с изменением ОДЗ.
29
Пример (Л — 00.1). log^ (5ж — 4) 8.
Решение.
...<=> log^ (5х - 4) log^ л/2 8 <=> 0 < 5я - 4 16 <=>...
Ответ: 4/5 < х ^4.
у/ 121° (тг - 86.2). 122° (</? - 80.2). log5(l —a;) < log5(a; 4-7). Найти область определения функции /(а:) = vzlog3 (ж2 - 3).
у/ 123° (х —97.2). yiogtgfc(®~2) > 1.
у/ 124* (а - 99.1). у/ 125° (тг - 84.3). у/ 126 (е - 80.1). 127 (С - 95.5). у/ 128 (А - 99.5). у/ 129 (V> - 96.2). ,/130 (£-96.3). 131 (С - 97.5). 132° (е — 80.1). 133 (С - 98.5). у/ 134 (£ — 88.2). у/ 135* (С - 01.5). у/ 136 (С - 81.4). У 137* (д - 86.3). | log2(3x - 2)4 = lg(fg~3x) 7210g7 Л log2 |1 + 9/ж2| < 1. 1°ё2 |ж-1|-1 — 1-|log3(x + 2)| > 2. 2 < |21og1/2(3a; + 1) — 4| 3. . -3 < log1/2(a: + 5)2 < 2. 1 + log1/4log3(4 -х) > 0. log^log1/3(2: + 2) ^2. log1/5 (26 —3х)+ 2 <0. log3log1/8 ((3/2)” - 1/2) < -1. 21og^3 + log^(3’2-3 - 1/9) < log^26. log2 log3 < log1/8 log1/9 51о8з 7T5 < 1. gi log| a: 1 д.11°g3 ®
3.3. Особенности применения формул
При использовании формул, содержащих логарифмы, обычно меняется ОДЗ уравнения или неравенства4^. В связи с этим нужно вовремя отмечать для себя расширение ОДЗ и добавлять в систему необходимые ограничения.
Пример (х - 94.1). log5 (ж + 1) + log5 (х + 5) = 1.
4) Например, из-за того, что положительность произведения — более слабое условие, чем положительность каждого из сомножителей.
30
Решение.
Г logs((® + l)(® + 5)) = logs 5 (®+l)(z + 5) = 5
|x + 1>0 |x + 1>0
( x(x 4- 6) = 0
x > — 1 (=> x 4- 6 > 0)
Ответ: x = 0.
138° (С - 95.5). 139° (С - 92.3). 140° (С - 85.3). 141 (С - 83.3). 142 (С - 96.5). 143 (тг —99.4). 144 (V> - 87.2). 145 (% - 00.1). 146 (^ - 80.4). 4iog2 х + х2 < 8 31og3x5 = 6 + log3x. logi/9 х + logs 9а: < 3. | log4 | log2 x > 1. log2 x2 - 21og8(—x5) = 3. 5 l°g3 x2 > |log3(-x3). log2 (x2 - 2x - 1) - log2 (x - 1/2) = 1. logs + logs = !• log1/2 (x - 1/2) + log1/2 (x - 1) 1.-
147 (e-82.3). log3 ((x + 2)(x + 4)) +log1/3 (x + 2) < | log^ 7.
148 (тг-85.2). Ig(9-x) = -21g45.
149(^-91.1). lg(x + 4)>-21g5l?.
ч/150 (ст - 89.2). logj/3 (x - 5) > 2 log!/3 (ч/я + 1 - 2).
3.4. Случаи переменного основания
Если основание логарифма зависит от неизвестной величины или от параметра, то можно:
— либо сразу перейти к конкретному числовому основанию;
— либо действовать как обычно, а при отбрасывании логарифмов вспомнить об ограничениях, накладываемых на основание (см. пп. 1.4 и 3.2).
Пример (7 - 86.2). log,2 ч/б + log,. = у-Решение.
•••** 4^ log* 3 — 3 log, 5 = Т (|-3)1°gI5= т.
» -2 log,. 5 = 1-» log, 5-2 = log, х » х = 5-2 •» ...
Ответ: х — 1/25.
У 151° (7-80.2). log.t_13 = 2.
31
у/ 152° (д - 82.1). logx+1 (х2 - За: + 1) = 1.
У 153 (тг-95.3). i^-log21^2.
у/ 154 « - 81.4). log_j_ 0,4 > 0.
155° (х - 90.1). logl2+1 10 < 1.
у/ 156 (тг - 93.3). log9a.2+1 37 > 1.
у/ 157* (е - 99.1). log1+|7l+17| (|3х + 8| + |7а: + 17|) 1.
§ 4. Системы и текстовые задачи
Логика решения систем и текстовых задач существенно различна: при решении систем нужно следить за равносильностью переходов, а в текстовой задаче требуется из условия вывести определенное следствие, и если в результате получится однозначный ответ, то его проверка не нужна.
4.1. Системы
Существует два стандартных способа решения систем: подстановка и сложение.
При сложении уравнений их предварительно умножают на заранее выбранные числа. Однако на практике при этом лучше запи
сывать не результаты умножения, а только сами множители возле соответствующих уравнений. Так, в приведенном ниже примере
эти числа образуют два столбца, и так как коэффициенты в них не пропорциональны1^, полученная система равносильна исходной.
тт ( qa 1 \ f 4х + = 5
Пример (а — 86.1). <
[2ж 4- Зу = —6.
Решение.
4х + 7у = 5
2х 4- Зу = —6
-3
7
1
-2
2х = -15 - 42 о <
1 ?/ = 5 4-12
Ответ: х = —57/2, у = 17.
У 158 (/1 — 79.3).
159 (б-86.2).
' 2 , 3 _ 1
2х—у ' х—2у 2
2________1 _ _1_
2х—у х—2у 18 *
Зя 4- 4sin?/ = —11
—2х 4- 5 sin I/ = 7/2.
чем свидетельствует неравенство (—3) • (—2) #7-1.
32
160 (А-79.3). ] у/2у + л/12 ctg х = 4 у/8у — у/П ctgx = 1.
161 (е - 86.2). <] 6 cos х + 7 logy 3 = -10 —5 cos x + 2 logy 3 = 0,5.
162 (тг - 85.1). « 7 • 2® + 6y = 2 3 • 2x+1 - 5y = 93.
163 (С-99.4). < 164 (С-79.3). < г-4 О CM Ю 11 II t 4 CM 1 II II + t & £ 4 ; 1 1сч ю 00 Sb
165* (V> - 89.3). 21ogx 8 + 3y = 24 -2 log3 0,5 + у = 8.
166 (V> - 80.2). 4 b- CM II II + 1 £
167* (С-94.5). < 168 (<р - 00.4). < |®-l| + |y-5| = l у = 5- |x- 1|. x + у = тг/4 tgz + tgy = 1.
169* - 77.2). ftgztgy = 5 -2\/6 [ж + у = тг/4.
170 (£ — 77.2). Найти все а, при которых любое решение си-
стемы 1
x + y = a
2x — у = 3
удовлетворяет неравенству х > у.
171* (£ — 81.2). Найти все а, при которых система
• J ax 4- у = 1
X 4z — 2y = a
имеет бесконечно много решений.
2 И. Н. Сергеев — Математика
33
4.2. Прогрессии
В арифметической прогрессии ai,a2,... каждый следующий член отличается от предыдущего некоторым постоянным слагаемым d, называемым разностью, а в геометрической прогрессии2 З^ 61,62,- • — постоянным множителем д, называемым знаменателем прогрессии. Общий член и сумма п первых членов арифметической прогресии вычисляются по формулам
ап = ai + d(n - 1), Sn = 21 у— п, а геометрической — по формулам
bn=bign"1) 5„ = (Ь1^’ 9/1
[6i n, q = 1.
Пример (£—96.2). Сумма первых трех членов арифметической прогрессии равна 15, а сумма третьего и пятого членов равна 22. Найти первый член и разность прогрессии.
Р ешение.
f S3 = 15 |^з + as = 22
{ai + d = 5
ai +3d= 11 Ответ: 2 и 3.
Q14-(ai+2d) . 3 = J5
(а 1 Ч- 2d) + (ai Ч- 4d) = 22
-1 1
1 О
3) |2d = 6
1 ai = 5 — d
172° (£ — 92.5). Девятый член арифметической прогрессии в 2 раза больше десятого, а сумма шестого и двенадцатого членов равна 8. Найти первый член и разность прогрессии.
у/ 173° (£—79.2). Седьмой член арифметической прогрессии равен 21, а сумма первых семи членов равна 105. Найти первый член и разность прогрессии.
174 (А —92.1). Шестой член арифметической прогрессии равен 33, а сумма девятого и одиннадцатого членов равна 98. Найти сумму первых четырнадцати членов прогрессии.
175 (б — 98.2). Второй член арифметической прогрессии равен 2, а сумма пятого и шестого членов равна 9. Найти сумму первых двадцати членов прогрессии.
2> Согласно определению, в геометрической прогрессии нет нулевых членов!
З)3десь и далее по поводу чисел, написанных возле системы, см. п.4.1.
34
у/ 176 — 87.1). Сумма первых пяти членов геометрической
прогрессии на 3/2 больше, чем сумма первых трех членов, а пятый член равен учетверенному третьему. Найти четвертый член прогрессии, если ее знаменатель положителен.
177 (а—93.2). Сумма третьего и пятого членов арифметической прогрессии равна 8. Найти сумму первых семи ее членов.
178 (/? — 91.3). Лыжник проходил каждый следующий виток круговой трассы на одно и то же время дольше, чем предыдущий. На второй и четвертый витки он затратил в сумме 3 мин. 20 с. За какое время лыжник прошел первые пять витков?
у/ 179 (х — 88.1). Найти сумму первых двадцати членов арифметической прогрессии, если сумма третьего, седьмого, четырнадцатого и восемнадцатого ее членов равна 10.
у/ 180 (х — 89.2). Произведение первого, третьего и одинна-• дцатого членов геометрической прогрессии равно 8. Найти произведение второго и восьмого ее членов.
У 181* (х — 90.2). Среди первых двадцати пяти членов арифметической прогрессии сумма членов с нечетными номерами на 19 больше, чем с четными. Найти двенадцатый член прогрессии, если ее двадцатый член равен утроенному девятому.
у/ 182 (х —95.1). Разность арифметической прогрессии отлична от нуля, а сумма членов с четвертого по четырнадцатый равна 77. Найти номер того ее члена, который равен 7.
у/ 183* (тг — 95.1). Четвертый член арифметической прогрессии равен половине второго, который на 36 больше, чем третий член некоторой геометрической прогрессии. Найти первый член арифметической прогрессии, если он вдвое больше первого члена геометрической прогрессии и впятеро больше второго члена геометрической прогрессии.
184 (б—87.2). В магазине продано 12 т орехов трех сортов по цене 6, 4 и 2руб/кг на общую сумму 42 тыс. руб. Количества проданных орехов первого, второго и третьего сорта образуют арифметическую прогрессию4). Найти эти количества.
у/ 185*(х—94.5). Найти /(... (/(/(6)))...), где f(x) - х-1+4.
186*,(тг — 01.5). Найти 7 + 77 + 777 + • • • + 7.. .7.
п
4)По определению, именно в том порядке, в котором они перечислены.
35
2*
4.3. Пропорции, доли, проценты и концентрации
Проще всего текстовые задачи решаются по действиям, т. е. путем последовательного нахождения из данных задачи тех или иных числовых значении, вплоть до значения искомой величины. Другой способ — перевод условия задачи на язык уравнений и неравенств с неизвестными величинами.
Пример 1 (тг — 83.1). Поле разделено на три участка. За день были вспаханы половина первого участка и три четверти второго, а третий участок, который составляет четверть всего поля, был вспахан полностью. Какая часть поля вспахана за день, если она вдвое больше второго участка?
Решение. Площадь всего поля примем за единицу, а площадь второго участка —за х, тогда
| (1 — х — |) + + | = 2х => 4-4х-1+6х + 2 = 16х
=> 14 я = 5 => 2х = ...
Ответ: 5/7.
Одной из важнейших характеристик раствора, сплава и т. п. является концентрация (обычно процентная) — величина, показывающая, какое количество данного вещества содержится в единице смеси.
Пример 2 (Л — 97.5). В траве вода составляет 70% от общей массы, а в сене 40%. Сколько нужно скосить травы, чтобы получить 5 т сена?
Решение. В искомом количестве хт травы и в 5т сена содержится одно и то же количество тонн сухого вещества, равное
(1-0,7) х = (1-0,4)-5 => ...
Ответ: Ют.
187° (тг — 93.1). Число 128 представлено в виде суммы четырех слагаемых, относящихся друг к другу, как 2 : 3 : 5 : 6 соответственно. Найти эти слагаемые.
у/ 188 (а —98.3). Зимой 9% коренного населения города занято народным промыслом. Летом 28% коренного населения уезжает из города, но доля занятых промыслом среди оставшейся части остается неизменной, а общая численность населения составляет 80% от прежней за счет приезжающих туристов. Сколько процентов населения летом занято промыслом?
189 (а — 01.3). За последний год численность населения города уменьшилась на 4%, а число безработных увеличилось на
36
5%. Сколько процентов от общего числа жителей составляют безработные, если год назад их было 8%?
у/ 190* (</? — 01.4). Писатели западник и славянофил опубликовали по одной книге, причем второй — тиражом, на 5% большим, чем первый. Количество страниц в книге у западника на 10% меньше, а в среднем на страницу текста буква «ф» у него встречается на 75% чаще, чем у славянофила. В чьем тираже больше букв «ф» и на сколько процентов?
у/ 191 (А — 98.4). Из цистерны в бассейн сначала перелили 50% имевшейся в ней воды, затем еще 100 л и, наконец, еще 5% остатка. В итоге количество воды в бассейне возросло на 31%. Сколько воды было в цистерне вначале, если в бассейне вначале было 2000 л воды? '
у/ 192* (/3—95.4). Саша и Коля дважды обменивались марками, причем каждый раз седьмая часть Сашиных марок обменивалась на половину Колиных. Сколько марок было вначале у Саши и сколько — у Коли, если у Саши после первого обмена стало 945 марок, а у Коли после второго — 220?
193° (а — 94.1). Если запланированный биржей объем торгов на август увеличить втрое, то суммарный объем торгов в июле и августе возрастет вдвое. Во сколько раз надо увеличить план на июль, оставив неизменным план на август, чтобы суммарный объем торгов возрос втрое?
194° (тг — 94.1). С двух полей, первое из которых по площади вдвое меньше второго, собрали урожай свеклы. Средняя урожайность составила 150ц/га, в то время как на первом поле собрали по 156ц/га. Какова урожайность на втором поле?
у/ 195 (р — 01.3). Покупатель приобрел костюм со скидкой 20% и плащ со скидкой 40%, заплатив в сумме за обе покупки 9180 руб, что на 32% меньше их суммарной первоначальной стоимости. Найти первоначальную цену костюма и плаща.
196 (е — 01.2). Брокерская фирма приобрела два пакета акций, а затем продала их на общую сумму 7 680 тыс. руб, получив при этом 28% прибыли. За какую сумму фирма приобрела каждый из пакетов акций, если при продаже первого пакета прибыль составила 40%, а при продаже второго — 20%?
у/ 197 (А—96.6). Вкладчик в начале года часть имевшихся у него денег положил в один банк под 60% годовых, а остальные деньги — в другой банк под 40% годовых. Через два года
37
суммарное количество денег на обоих счетах удвоилось. Какую часть денег вкладчик положил в первый банк?
198* (е — 95.4). В банк помещен вклад в размере 3900 руб под 50% годовых. В конце каждого из первых четырех лет после начисления процентов на счет дополнительно вносилась одна и та же сумма. К концу пятого года после начисления процентов размер вклада увеличился по сравнению с первоначальным на 725%. Какая сумма добавлялась ежегодно?
199° (А — 94.7). На первом этапе производства дискет содержание кремния в них увеличивается по отношению к предыдущему на 25%, на втором — на 20%, на третьем — на 10%, а на четвертом — на 8%. На сколько процентов в итоге увеличивается сддержание кремния?
у/ 200° (£ — 78.2). Руда содержит 40% примесей, а выплавляемый из нее металл — 4%. Сколько металла будет выплавлено из 24 т руды?
201 (тг — 97.4). Из сосуда с 10%-м раствором спирта отлили треть содержимого, долив водой до 5/6 первоначального объема. Каким стало процентное содержание спирта в сосуде?
202 (А—01.6). К водному раствору кислоты добавили 1 кг воды, отчего его концентрация уменьшилась в 5/3 раза. Во сколько раз уменьшится концентрация полученного раствора, если добавить к нему 2 кг воды?
у/ 203 (х—00.2). В результате испарения из раствора 2 кг воды концентрация соли в нем возросла на 0,2, а после добавления к получившемуся раствору 10 кг воды — стала вдвое меньше первоначальной. Найти первоначальную концентрацию соли.
у/ 204° (б—80.4). Имелось два слитка массой 150 и 250кг, состоявших из цинка, меди и олова. Первый слиток содержал 40% олова, второй — 26% меди, а процентное содержание цинка в обоих слитках было одинаково. Сплавив эти слитки, получили новый слиток, в котором оказалось 30% цинка. Сколько килограммов олова содержится в новом слитке?
205 (А—95.6). Имелось два слитка, содержавших медь. Масса первого слитка была на Зкг больше, чем второго. В первом слитке содержалось 40% меди, а во втором — 10%. Сплавив эти слитки, получили новый слиток, в котором оказалось 30% меди. Определить массу полученного слитка.
38
206 (тг—99.5). Сколько литров 3%-го раствора спирта нужно добавить к 1 л 6%-го, чтобы получить 5%-й раствор?
207 — 00.1). Сколько литров 0,5%-го и 2%-го растворов
уксусной кислоты нужно смешать, чтобы получить 30 л 1,5%-го раствора?
у/ 208 (7 - 81.3). Смешав 40%-й и 60%-й водные растворы кислоты и добавив 5 кг воды, получили 20%-й раствор. Если бы вместо воды добавили 5 кг 80%-го раствора, то получился бы 70%-й раствор. Сколько смешали 40%-го и 60%-го растворов?
у/ 209* (А—89.5). Из сосуда, содержавшего 9кг водного раствора соли, отлили часть раствора и добавили столько же (по массе) воды, а затем опять отлили столько же раствора. В итоге количество соли в сосуде уменьшилось в 9/4 раза. Найти массу добавленной воды.
4.4. Движение и работа
В задачах на движение полезную роль играет величина, называемая скоростью и показывающая, какое расстояние объект проходит за единицу времени.
Пример 1 (Л —00.3). Путь от одного причала до другого лодка прошла с постоянной скоростью за 4 ч, а катер с остановками — за 2 ч, хотя его скорость впятеро больше скорости лодки. Сколько времени потратил катер на остановки?
Решение. Без остановок катер прошел бы весь путь в 5 раз быстрее лодки, значит, на остановки он потратил 2—| -4 = 1|ч.
Ответ: 1| ч.
При решении задач, связанных с работой, роль скорости выполняет производительность, показывающая, какое количество работы субъект производит за единицу времени.
Пример 2 (тг — 86.3). Два насоса, работая вместе, наполняли бассейн за 8 ч. После ремонта насосов производительность первого из них увеличилась в 1,2 раза, а второго — в 1,6 раза. В результате они стали наполнять бассейн за 6 ч. За сколько часов наполнит бассейн один лишь первый насос после ремонта?
Решение. Пусть производительности насосов равны соответственно х и у (бассейнов в час), тогда
х + у =1/8 8 1 J_ =
1,2 х +1,6 у = 1/6 -5 6 1,2а: "
Ответ: 10.
39
у/ 210° (тг—95.4). Из пункта А в пункт В двигалась колонна машин. В середине пути у одной из машин произошла поломка, на устранение которой ушла 1/12 часть времени, за которое колонна проходит весь путь. Во сколько раз нужно увеличить скорость отставшей машине, чтобы приехать в пункт В одновременно с колонной?
211° (/? — 87.2). Из пункта А по реке отправляется плот. Одновременно навстречу ему из пункта В отправляется катер. Встретив плот, катер сразу поворачивает и идет по течению. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если собственная скорость катера вчетверо больше скорости течения реки?
у/ 212 (7—95.2). Теплоход затратил на путь по течению реки от пункта А до пункта В 5 ч, а на обратный путь — 8 ч. 20 мин. Найти собственную скорость теплохода, если АВ = 100 км.
у/ 213 (ст—89.3). Ахиллес догонял черепаху, и когда расстояние между ними сократилось в 19 раз и составило 6 м, черепаха остановилась. Какой путь с момента начала погони проделала черепаха, если ее скорость в 37 раз меньше скорости Ахиллеса?
у/ 214 ((£—99.1). Автомобиль проехал часть пути по ровной дороге со скоростью 80 км/ч, а другую — по бездорожью со скоростью 20 км/ч. Какую часть пути составляла ровная дорога, если средняя скорость автомобиля оказалась равной 40 км/ч? 215 (тг — 89.2). Автобус проехал первую часть пути из пункта А в пункт В со скоростью 80 км/ч, а вторую — по бездорожью со скоростью 40 км/ч. На обратном пути скорость по бездорожью составляла ЗОкм/ч, а на остальной части — 90км/ч. Найти время движения автобуса из А в В, если на обратный путь он потратил на 25 мин меньше и АВ = 370 км.
216 (А — 79.4). Расстояние между двумя городами скорый поезд проходит на 4 ч быстрее товарного и на 1 ч быстрее пассажирского. Скорость товарного поезда составляет 5/8 скорости пассажирского и на 50 км/ч меньше скорости скорого. Найти скорость товарного поезда.
^/217* (V> — 82.5). Из пункта А в пункт В вышел пешеход и одновременно из В в А — мотоциклист. Встретив пешехода, мотоциклист развернулся, довез пешехода до пункта В, а затем добрался до пункта А, Во сколько раз в результате непредусмотренных разъездов мотоциклист проиграл во времени, если пешеход, наоборот, выиграл во времени в 4 раза?
40
у/ 218* (/1 — 97.3). Из пункта А в пункт В со скоростью 80 км/ч выехал автомобиль. Через некоторое время из А в В выехал второй автомобиль, который доехал до пункта В и после 20-минутной остановки отправился назад. На расстоянии 48 км от В он встретил первого, а в момент прибытия первого в В был на расстоянии 120 км от него. На каком расстоянии от А второй автомобиль обогнал первого, если АВ = 480 км?
219° (тг — 84.1). Производительности трех насосов относятся как 5 : 4 : 2. За 5 ч первый насос перекачал на 6 м5 воды больше, чем третий. Найти производительность второго насоса.
У 220* (А—97.6). Пять одинаковых труб начали заполнять один бассейн. Когда он был заполнен на треть своего объема, две трубы переключили для заполнения второго бассейна. Когда первый бассейн был заполнен наполовину, еще одну трубу переключили на второй бассейн, и оба бассейна наполнились одновременно. Найти отношение их объемов.
221 (тг — 81.1). Три бригады укладывают рельсовый путь. Первая и третья бригады вместе укладывают в месяц 15 км пути, а все три бригады вместе укладывают в месяц вдвое больший путь, чем первая и вторая бригады вместе. Сколько километров пути в месяц укладывает третья бригада, если вторая и третья бригады вместе укладывают определенный участок пути вчетверо быстрее, чем одна вторая бригада?
у/ 222 (тг — 90.2). Трактористы А и В вспахали поле. В первый день они вспахали треть поля, причем А работал 2 ч, а В — 3 ч. Оставшуюся часть поля они вспахали на другой день, причем А работал 5 ч, а В — 4,5 ч. За какое время тракторист В мог бы вспахать поле один?
223 (тг — 91.2). Три сенокосилки вместе скашивают поле за 5 ч, первая и вторая — за 10 ч, а вторая и третья — за 8 ч. За сколько часов скашивает поле каждая из них в отдельности?
у/ 224 ((^ — 81.4). Двое рабочих должны были изготовить по 36 деталей. Первый из них приступил к работе на 4 мин позже второго, но треть задания они выполнили одновременно. Полностью выполнив свое задание, первый рабочий после двухминутного перерыва снова приступил к работе и к моменту выполнения задания вторым рабочим изготовил еще 2 детали. Сколько деталей в час изготавливал каждый рабочий?
41
225* (A — 79.4). Экскаваторщик выкопал две траншеи в разных местах: сначала он вырыл траншею длиной 5 м, потом переехал на другое место и вырыл траншею длиной Зм. На рытье первой траншеи он затратил времени на 1 ч 12 мин меньше, чем на переезд и рытье второй траншеи. Если бы производительность экскаватора была вчетверо меньше, то время рытья первой траншеи равнялось бы времени переезда. Сколько метров траншеи в час выкапывал экскаватор?
У 226* (тг — 92.2). На перевозку разных строительных материалов грузовик по-разному расходует горючее. В первый день половину рабочего времени он возил щебень, а половину — песок; во второй день 1/7 времени он возил щебень, 4/7 — песок и 2/7 — кирпич; в третий день 1/4 времени он возил щебень, 3/8 — песок и столько же — кирпич. На сколько процентов израсходует грузовик дневной норматив горючего, возя целый день щебень, если в первый день он израсходовал его на 95%, а во второй и в третий — перерасходовал на 10/7% и 5/4% соответственно?
§5. Геометрия
Отличительной особенностью любой истинно геометрической задачи является то, что для ее понимания необходим чертеж
х5.1. Простейшие задачи
Следующие формулы геометрии желательно помнить:
1) площадь треугольника (рис. 2) с полупериметром р и радиусами вписанной г и описанной R окружностей1^ равна
с 1 1. •
S = -an = -be sin а = рг =
7^ = \/р(р-а)(р-Ь)(р-с),
а площади трапеции и параллелограмма равны
S = -y-h и S = ah,
где а и b — основания, a h — высота;
2) в прямоугольном треугольнике (рис. 3) с медианой т и высотой h, опущенными на гипотенузу с, имеют место следующие
Остальные обозначения показаны на рис. 2.
42
равенства:
Рис. 2
Рис. 3
3) площадь четырехугольника с диагоналями di,d2 и углом между ними равна
S = |did2sin</?;
4) площадь описанного многоугольника равна
S = pr, где р — полупериметр многоугольника, г — радиус вписанной в него окружности;
5) длина окружности и площадь круга радиуса г соответственно равны
С = 2тгг и S = 7гг2.
Пример 1 (у? — 98.2). Радиус О А = 10 окружности с центром О делит хорду ВС = 12 пополам. Найти АВ.
Решение. См. рис.4: ОА ± ВС
=> х = \/102 — 62 = 8 => г/ = 10 — x = 2=>z = д/г/2 4- б2 = ...
Ответ: 2^Т0.
Некоторые полезные геометрические утверждения не называются теоремами, а разбираются в школьном курсе в виде задач.
Пример 2 (/3 — 93.5). В выпуклом четырехугольнике ABCD отрезок, соединяющий середины диагоналей, равен отрезку, соединяющему середины сторон AD и ВС. Найти угол между прямыми АВ и CD.
Решение. См. рис. 5:
1) KLMN — параллелограмм, т. к. К, L,M,N — середины отрезков и KL || MN || АВ, KN || LM || CD (средние линии в соответствующих треугольниках);
43
2) KM = LN => KLMN — прямоугольник;
3) KL ± MN => AB ± CD.
Ответ: 90°.
227° (A — 87.1). Найти площадь правильного треугольника, сторона которого равна стороне ромба с диагоналями 10 и 12.
228° (А — 80.2). Найти периметр правильного треугольника, если центр описанной около него окружности удален от хорды, равной 2, на расстояние 3.
229° (7 — 77.2). В треугольнике АВС основание D высоты CD = \/3 лежит на стороне АВ. Найти АС, если АВ = 3 и AD = ВС.
у/ 230° (х—80.3). Найти площадь прямоугольного треугольника, один из катетов которого равен 13, а высота, опущенная на гипотенузу, равна 12.
У 231 ((/? — 90.3). В прямоугольном треугольнике АВС с гипотенузой АВ проведены медиана СМ и высота СН, причем точка Н лежит между А и М. Найти АН : AM, если СМ : СН = 5 : 4.
232* (х — 77.2). Один из углов треугольника равен разности двух других, наименьшая сторона треугольника равна 1, а сумма площадей квадратов, построенных на двух других сторонах, вдвое больше площади описанного около треугольника круга. Найти наибольшую сторону треугольника.
233 — 80.3). Окружность радиуса х/3, вписанная в прямо-
угольный треугольник АВС, касается катета АС в точке К. Найти ВК, если ZA = 30°.
44
у/ 234 (J3 — 81.3). Окружность радиуса 3, центр О которой лежит на гипотенузе АВ прямоугольного треугольника, касается катетов. Найти площадь треугольника, если О А = 5.
235 (а — 94.3). Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС в точках Е и D соответственно. Найти ZB, если АЕ = 1 и BD = 3.,
у/ 236 (А — 89.4). В треугольнике АВС проведена биссектриса CD прямого угла. Из точки D опущен перпендикуляр DM = = х/З на сторону АС, Найти ВС, если AD = 2v/3.
237° (тг—90.3). На стороне АВ = 4 треугольника АВС с углами Z.A = 30° и ZB = 130° как на диаметре построена окружность. Найти площадь части круга, лежащей внутри треугольника.
у/ 238 (тг —80.3). Две равных хорды окружности образуют вписанный угол величиной 30°. Найти отношение площади части круга, лежащей внутри угла, к площади всего круга.
239* (ср — 79.1). Точка пересечения двух общих касательных к двум непересекающимся окружностям, меньшая из которых имеет радиус г, лежит на линии их центров на расстоянии 6г от центра большей окружности и делит отрезок касательной между точками касания в отношении 1 : 3. Найти площадь фигуры, состоящей из двух частей, ограниченных касательными и ббльшими дугами окружностей.,
у/ 240 (х — 77.4). Найти площадь выпуклого четырехугольника с диагоналями 3 и 4, если отрезки, соединяющие середины противоположных сторон, равны.
241° (£ — 97.4). Прямая, параллельная стороне АВ треугольника АВС, пересекает стороны АС и ВС в точках М и N соответственно. Найти AM : СМ, если площадь треугольника MCN вдвое больше площади трапеции AMNB.
у/ 242* (<р — 00.2). Прямая, параллельная стороне АВ = 5 треугольника АВС и проходящая через центр вписанной в него окружности, пересекает стороны ВС и АС в точках М и N соответственно. Найти периметр четырехугольника ABMN, если МN = 3.
у/ 243* (б — 87.5). В треугольнике АВС на сторонах АВ и АС взяты точки М nN соответственно так, что AM : МВ = 3:2
45
и AN : NC = 4 : 5. В каком отношении прямая, проходящая через точку М параллельно ВС, делит отрезок BN1
у/ 244* (тг — 93.4). Через точку пересечения диагоналей трапеции проведена прямая, параллельная основаниям и пересекающая боковые стороны в точках Е и F, причем EF = 8. Найти основания трапеции, если их отношение равно 4.
5.2. Применение тригонометрии
Тригонометрия в геометрических задачах применяется в основном по трем направлениям:
0) соотношения в прямоугольном треугольнике (см. рис. 3)
a b а b
-=sina, - = cosa, T=tga, -=ctga:
c c b a
1) теорема синусов для треугольника (см. рис. 2)
а Ъ
= 2Я’ sin a sin р
2) теорема косинусов для треугольника (см. рис. 2)
а2 = Ь2 + с2 — 2bc cos а.
Одним из важных приложений теоремы косинусов можно считать равенство параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Пример 1 (С — 95.4). В треугольнике даны два угла а, /3 и радиус R описанной окружности. Найти высоту, опущенную из вершины третьего угла.
46
Решение. См. рис.6: а = 2Bsina (теорема синусов)
=> h = asin/3 = ... (из прямоугольного треугольника).
Ответ: 2Bsinasin/3.
Пример 2 (А — 84.4). Найти площадь треугольника АВС, если АВ = х/20, ВС = АС 4- 2 и cos ZA = 1/\/5.
Решение. См. рис.7:
1) (х 4- 2)2 = х2 4- 20 — 2хх/20 • (теорема косинусов)
=> х = 2;
2) sin ZA = у/1 - 1/5 = 2/у/5
=> Sabc = |s\/20sin ZA = | • 2 • \/20 • = ...
Ответ: 4.
245° (^—88.2). Найти высоту, опущенную на гипотенузу прямоугольного треугольника с острым углом а и радиусом описанной окружности R.
у/ 246° (А — 00.4). Найти отношение высот треугольника АВС, опущенных из вершин А и В соответственно, если cos ZA = = 1/5 и sin ZB = 1/2.
247° (/? — 77.2). В четырехугольнике ABCD углы А и В — прямые, tg ZD = 2/3 и ВС = AD/2 = АВ 4- 2. Найти АС.
у/ 248° (х — 94.4). В четырехугольнике ABCD углы А и С — прямые, АВ = ВС = 3 и BD = 5. На сторонах AD и CD взяты точки Е и F соответственно так, что АЕ = 1 и CF = 2. Найти площадь пятиугольника ABCFE.
249 (тг — 82.4). Одно из оснований равнобедренной трапеции равно 4. Найти расстояние между точками касания с ее боковыми сторонами вписанной в нее окружности радиуса 4.
у/ 250* (^ — 82.4). В параллелограмме ABCD биссектриса угла А пересекает биссектрисы углов В и В в точках К и L соответственно, а биссектриса угла С пересекает те же биссектрисы в точках NnM соответственно. Найти отношение площади четырехугольника KLMN к площади параллелограмма ABCD, если АВ = 2 и AD = 5.
251 (А—77.4). Найти острые углы прямоугольного треугольника, если центр вписанной в него окружности делит биссектрису прямого угла в отношении \/3 : \/2, считая от вершины.
у/ 252* (7—94.5). Найти высоту, биссектрису и медиану, проведенные из вершины одного угла треугольника, если они делят
47
этот угол на четыре равные части, а радиус описанной около треугольника окружности равен R.
253° (£ — 92.4). Найти площадь треугольника, в котором даны сторона а, противолежащий угол а и прилежащий угол /3. 254° (£—95.4). Найти биссектрису прямого угла прямоугольного треугольника с гипотенузой с и острым углом а.
255 (£ — 93.4). В окружность радиусом R вписан равнобедренный треугольник с углом а при основании. Найти радиус вписанной в треугольник окружности.
У 256 (£ — 97.4). В окружность диаметром 25 вписан равнобедренный треугольник с боковой стороной 20. Найти радиус вписанной в треугольник окружности.
257 — 78.2). Около треугольника АВС описана окруж-
ность с диаметром AD = 2. Найти ВС, если АВ = 1 и Z.BAD : Z.CAD = 4:3.
у/ 258 (А — 88.4). Окружность радиуса 5 с центром О, лежат щим на стороне АВ треугольника АВС, касается сторон АС и ВС. Найти радиус окружности, описанной около треугольника АВС, если АО = 13 и ВО = 7.
у/ 259* (х —01.2). На основании АС равнобедренного треугольника АВС взята такая точка D, что CD = 2 и биссектриса CL треугольника перпендикулярна прямой DL. Найти AL.
260 (</? — 86.4). Прямая, параллельная стороне АВ треугольника АВС, пересекает стороны АС и ВС в точках D и Е соответственно. Найти ВС, если АВ = 8, Z.C = 60°, DE = 3 и ВС = DC.
261 (ip — 84.4). На сторонах АВ = 4 и ВС = 5 треугольника АВС с острым углом В взяты точки D и Е соответственно, причем D — середина АВ. Найти DE, если BE = 3, а площадь треугольника АВС больше площади треугольника DBE на 7Л5/4.
у/ 262 (ip — 92.3). На стороне АВ ромба ABCD взята точка N так, что AN : BN = 2:1. Найти tg Z.DNC, если А.А = тг/З.
263 (б — 77.4). В выпуклом четырехугольнике ABCD точки K,L, М и N — середины сторон АВ, ВС, CD и AD соответственно, а О — точка пересечения отрезков КМ и LN. Найти АС и BD, если КМ = a,LN = bn ЛЬОМ = тг/З.
48
у/ 264 (тг — 95.6). Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, относятся как 1 : 3 й пересекаются под углом 60°. Найти меньшую диагональ этого четырехугольника, если бблыпая равна д/13.
у/ 265* (£ — 90.4). На стороне АВ треугольника АВС с углами Z.A = a, ZB = 3 и высотой АН взята такая точка К, что АК : ВК = 1:2. Через точку К проведена окружность, касающаяся стороны ВС = а в точке Н. Найти радиус этой окружности.
266* (а — 97.2). На стороне АС треугольника АВС взята точка М так, что Z.ABM = 45° и Z.CBM = 30°. Найти АС и AM : МС, если АВ = 4 и ВС = 5.
У 267* (тг — 97.5). Биссектриса угла ZC = 60° треугольника ' АВС равна 5\/3. Найти tg ZA и ВС, если АС : ВС = 5:2.
268* (£ — 88.4). Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке М так, что ВМ : МС = 2:1. Найти Z.BAD, если Z.CAM = а.
5.3. Касательные, секущие и хорды
Справедливы следующие важные теоремы об окружностях, касательных, секущих и хордах.
1. Свойство касательных: касательные2), проведенные из од-ной точки к окружности, равны.
2. Свойство описанного четырехугольника: суммы противоположных сторон описанного четырехугольника равны3).
3. Теорема о касательной и секущей: если из одной точки к окружности проведены касательная и секущая, то квадрат касательной равен произведению секущей на ее внешнюю часть4).
4. Теорема о секущих: если из одной точки к окружности проведены несколько секущих, то произведение каждой секущей на ее внешнюю часть есть величина постоянная.
5. Теорема о пересекающихся хордах: произведения отрезков каждой из двух пересекающихся хорд равны.
2)Под касательной здесь понимается ее отрезок от данной точки до точки касания.
3) Верно и обратное: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
4) Секущая здесь — это ее отрезок от данной точки до наиболее удаленной точки сечения, а внешняя часть — до ближайшей.
49
Пример (е — 96.5). На продолжении хорды АВ = 5 взята такая точка С, что ВС = 3. Найти радиус окружности, если ее центр удален от точки С на расстояние 7.
Решение. См. рис. 8:
(7 + г) • (7 — г) = (5 + 3) • 3 (теорема о секущих)
=> г2 = 72 - 8 • 3 = 25 => г = 5.
I
Ответ: 5.
у/ 269° (тг — 87.4). Две окружности радиусов 2 и 8 касаются друг друга внешним образом в точке А. Общая касательная к ним, проведенная через точку А, пересекает другую общую касательную в точке В. Найти АВ.
270 (а — 99.6). Окружности радиусов 2 и 3 касаются друг друга внешним образом в точке А. Общая касательная к ним в точке А пересекает в точке В другую общую касательную, касающуюся в точке С меньшей окружности с центром О. Найти радиус окружности, вписанной в четырехугольник О АВС.
271 (А — 82.5). Вписанная в треугольник АВС окружность касается сторон АВ, ВС и АС в точках K,L и М соответственно. Найти KL, если AM = 2, МС = 3 и ZC = тг/З.
у/ 272 (7 — 93.4). Вписанная в треугольник АВС окружность касается сторон АВ = 4 и АС = 3 в точках М и N соответственно. Найти площадь треугольника AMN, если ВС = 2.
273 (д — 83.3). Вписанная в треугольник АВС окружность с центром О касается стороны ВС в точке К. Найти площадь треугольника ВОК, если АС = a, Z.ABC = а, а периметр треугольника АВС равен 2р.
50
yj 274* (x — 88.4). Вписанная в треугольник АВС окружность касается стороны АВ в точке D. Найти АС, если АС = CD, ВС = 11 и cos Z.A = 1/6.
у/ 275 (тг — 01.6). Найти расстояние между центрами вписанной и описанной окружностей прямоугольного треугольника с катетами 3 и 4.
276 (£—94.4). Найти острые углы прямоугольного треугольника, в котором радиусы вписанной и описанной окружностей относятся как 2:5.
у/ 277° (а — 91.2). Найти площадь четырехугольника ABCD со сторонами АВ = CD = 9, в который можно вписать окружность радиуса 4.
278 (£ — 98.4). Площадь равнобедренной трапеции, описанной около окружности, равна 10. Найти боковую сторону трапеции, если один из углов при ее основании равен 45°.
у/ 279° (/1 — 77.2). В трапецию с боковыми сторонами 3 и 5 можно вписать окружность. Найти основания трапеции, если средняя линия делит ее площадь в отношении 5:11.
280 (£ — 99.3). Найти боковую сторону АВ описанной около окружности равнобедренной трапеции ABCD площадью \/3, если ВС : AD = 1:3.
281* (ст — 00.5). Найти площадь четырехугольника ABCD, описанного около окружности радиуса 2, если АВ = 5, ВС = 6 и ZA = 90°.
282* (/? — 94.4). Диагонали трапеции ABCD пересекаются в точке Е. Найти радиус окружности, вписанной в треугольник ВСЕ, если ВС = 1, а углы при основании AD = 4 равны* arctg 2 и arctg 3.
283 (/1 — 85.3). Окружность касается в точках М и N продолжений сторон АВ = 13 и ВС треугольника АВС за точки А и С. Найти площадь треугольника, если АС =1, а через точки А,С,М и N можно провести окружность.
у/ 284* (£ — 01.4). Найти площадь треугольника АВС с углом ZA = 120°, если его вершины В, С и середины сторон АВ, АС лежат на одной окружности радиуса 7.
285 (б — 89.5). Окружность, проходящая через вершины А и С треугольника АВС, пересекает стороны АВ и ВС в точках D и Е соответственно. Найти ZACB, если СЕ = 1, BE = = CD — 4 и AD : BD = 4 : 1.
51
у/ 286 (А — 01.5). Окружность, проходящая через вершину А треугольника АВС, касается стороны ВС в точке М и пересекает стороны АВ и АС в точках К и L соответственно. Найти АС : АВ, если КВ : LC = 1 : 2 и СМ : ВМ = 3 : 2.
287* ((/? — 88.4). Окружность, касающаяся сторон AD и CD параллелограмма ABCD, проходит через точку В и пересекает стороны АВ = 8 и ВС в точках Е и F соответственно. Найти AD, если АЕ : BE = 4 : 5 и BF : CF = 8 : 1.
у/ 288* (/1 — 01.3). Окружность, проходящая через вершины А, В и С параллелограмма ABCD со сторонами АВ = 3 и ВС = 5, пересекает прямую BD в точке Е. Найти BD, если BE = 9.
289* — 96.6). Хорда АВ окружности радиуса R, перпендикулярная ее диаметру CD, пересекает хорду СЕ = а в точке F. Найти CF, если AF : BF = 1:3.
5.4. Дуги окружности и углы
Справедливы следующие теоремы об измерении углов дугами окружности.
1. Параллельные прямые высекают на окружности равные дуги.
2. Вписанный угол измеряется половиной дуги, на которую опирается.
3. Вписанные углы, опирающиеся на равные дуги, равны5).
4. Вписанный угол, опирающийся на диаметр, — прямой6).
5. Свойство вписанного четырехугольника: суммы противоположных углов вписанного четырехугольника равны (по 180°)7\
6. Угол между касательной и хордой, выходящей из точки касания, измеряется половиной дуги, содержащейся внутри угла.
7. Каждый из двух вертикальных углов между пересекающимися хордами измеряется полусуммой двух дуг, на которые они опираются.
8. Угол между секущими измеряется полуразностью двух дуг, на которые он опирается.
5) Верно и обратное: если данный отрезок виден под равными углами из двух точек, лежащих по одну сторону от него, то эти точки лежат на одной окружности с концами отрезка.
6)й наоборот.
7) Верно и обратное: если суммы противоположных углов четырехугольника равны, то его можно вписать в окружность.
52
Пример (Л — 98.6). Диагонали вписанного четырехугольника ABCD пересекаются под прямым углом в точке Е. Найти площадь четырехугольника, если AD = 13, ВС = 26 и BE = 10.
Решение. См. рис.9:
1)'AADE ~ АВСЕ (£С —АВ/2 = Z.D — вписанные углы);
2) х = 10 • 13/26 = 5 => у = \/132 - 52 = 12 => z = 24;
3) Sabcd = |(х + z)(10 + у) = |(5 + 24)(10 + 12) = ...
Ответ: 319.
у/ 290° (£ — 96.4). Прямая, касающаяся окружности в точке К, параллельна хорде АВ = 6. Найти радиус окружности, если АК = 5.
291 (/1 — 82.2). Диагонали вписанной в окружность трапеции взаимно перпендикулярны. Найти площадь трапеции, если ее периметр равен 18, а основания относятся, как 1 : 7.
292 (£ — 95.8). Трапеция ABCD с основаниями ВС = а и AD = b вписана в окружность. Найти радиус окружности, если Z.CAD = а.
293* (А — 00.6). Во вписанную трапецию с основаниями 3 и 5 вписана окружность. Найти площадь пятиугольника, образованного меньшим основанием трапеции, ее боковыми сторонами и перпендикулярными им радиусами окружности.
у/ 294* (/1 — 00.3). Окружность, проходящая через вершины С и D параллелограмма ABCD, касается прямой AD и пересекает прямую АВ в точках В и Е. Найти АЕ, если AD = 4 и СЕ = 5.
53
295° (7 — 83.3). На катете АС — а прямоугольного треугольника с углом Z.B = Р как на диаметре построена окружность, пересекающая гипотенузу АВ в точке К. Найти площадь треугольника СКВ.
296 (тг —88.2). Через точку К диаметра АВ окружности проведена хорда MN. Найти АВ, если Z.ABM = 30°, ZBMK = = 15° и МК = 3.
297* (£ — 98.6). Сторона АВ четырехугольника ABCD служит диаметром описанной около него окружности радиуса R, а диагонали пересекаются в точке Е. На стороне АВ взята точка F так, что окружность с диаметром BF касается прямой АС в точке Е. Найти площадь четырехугольника ABCD, если ZBAC = а.
298° (а — 00.2). Найти радиус окружности, если вписанный в нее угол, сторонами которого служат хорды длины 1 и 2, опирается на дугу в 120°.
у/ 299° (А — 95.7). Диаметр AD окружности, описанной около треугольника АВС, делит угол А пополам. Найти АС : BD, если sinZC = 1/4.
300* (тг — 96.5). Диагональ BD вписанного в окружность че-тыреугольника ABCD является биссектрисой угла В = 60°. Найти BD, если АВ — 3 и АС — Зл/7.
301 (тг — 85.4). Хорда AD окружности, описанной около равнобедренного треугольника АВС, пересекает его основание ВС в точке Е. Найти АВ, если АЕ = DE = 3.
у/ 302* (тг — 00.6). Биссектрисы внутренних углов треугольника, равных 30°, 60° и 90° соответственно, продолжены до пересечения с описанной около него окружностью. Найти площадь треугольника с вершинами в полученных точках пересечения, если площадь исходного треугольника равна 2.
303 — 78.5). Найти площадь пятиугольника ABCDE, вписанного в окружность единичного радиуса, если АВ = \/2, ВС = CD, ZABE = тг/4 и Z.DBE = тг/6.
у/ 304 (ст — 98.4). Четырехугольник ABCD вписан в окружность. Найти АВ, если ВС = 7, CD = 4, cos ZC = 1/2 и sin Z. ABD = 1/3.
305 (д — 89.3). Боковая сторона АВ и основание ВС трапеции ABCD касаются окружности, описанной около треуголь
54
ника ACD. Найти площадь этого треугольника, если AD = 3 и Z.B = 120°.
306* (/1 — 94.4). Диагонали трапеции ABCD пересекаются в точке Е. Прямая, касающаяся в точке Е описанной около треугольника ВСЕ окружности, пересекает в точке F продолжение основания AD = а трапеции за точку D. Найти EF, если DF = b.
307* (/1—01.3). В трапеции ABCD с боковой стороной CD = = 30 диагонали пересекаются в точке В, а углы AED и BCD равны. Окружность радиуса 17, проходящая через точки С, D и В, пересекает основание AD в точке F и касается прямой BF. Найти высоту трапеции и ее основания.
у/ 308* (/1 — 97.4). Хорды АС и BD окружности пересекаются в точке Е, а касательная, проходящая через точку В, параллельна АС. Найти площадь треугольника ВСЕ, если АЕ : AD = = 3 : 4, а площадь треугольника BCD равна 16.
у/ 309* (£—93.6). Окружность касается сторон угла с вершиной С в точках А и В. На этой окружности внутри треугольника АВС взята точка Л/, находящаяся на расстоянии а и b от прямых АС и ВС соответственно. Найти расстояние от точки М до прямой АВ.
у/ 310* {ф — 92.3). Диагонали BD и СЕ вписанного в окружность радиусом 2\/2 пятиугольника ABCDE пересекаются в точке М. Найти площадь треугольника АВС, если ВС || AD, АС || DE, CD || BE и Z.BMC = 45°.
у/ 311 (£ — 96.8). Найти угол В остроугольного треугольника АВС с высотой ВН = h, если расстояние между проекциями точки Н на стороны АВ и ВС равно а.
у/ 312 (Д — 95.5). Окружность с центром О, проходящая через вершины В, С и D четырехугольника ABCD, пересекает стороны АВ и AD в точках EnF соответственно. Найти Z.ABO, если EF = BE, ВС = CD = DF и ZA = 90°.
у/ 313* (/1 — 91.4). Окружность с центром в точке Н, служащей основанием высоты ВН треугольника АВС, проходит через вершину В и пересекает стороны АВ = а и ВС в точках М и N соответственно. Найти ВС, если МВ — т и NB = п.
314* (А — 93.5). На стороне АВ треугольника АВС как на диаметре построена окружность, пересекающая стороны АС
55
и ВС в точках D и Е соответственно. Прямая DE делит площадь треугольника пополам и образует с прямой АВ угол в 15°. Найти углы треугольника АВС.
У 315 (£ — 95.8). Диаметр АВ окружности параллелен хорде CD. Прямая, касающаяся окружности в точке А, пересекает прямые ВС и BD в точках М и N. Найти АВ, если AM = т и AN = п.
316* (х — 97.4). На стороне ВС треугольника АВС взята такая точка D, что Z.CAD = 3Z.BAD. Отрезок AD пересекается с биссектрисой угла С в точке Е, причем точки С, D и Е принадлежат окружности с центром на стороне АС. Найти cos Z.ACB, если АС : АВ = 3:2.
у/ 317* (С — 99.6). Две окружности пересекаются в точках А и В. Хорда АС = а первой окружности касается второй окружности, а хорда AD = b второй окружности касается первой. Найти ВС, если BD = с.
318* (/1 — 99.4). Две окружности пересекаются в точках А и В. Прямая, проходящая через точку В, пересекает окружности в точках С и D по разные стороны от прямой АВ. Касательные к этим окружностям в точках С и D пересекаются в точке Е. Найти АЕ, если АВ = 10, АС = 16 и AD = 15.
5.5. Медианы, высоты и биссектрисы
Медианы треугольника, делящие, по определению, его стороны пополам, пересекаются в одной точке, и каждая из них делится этой точкой в отношении 2:1, считая от вершины. Медиана, проведенная к данной стороне, вычисляется из равенства параллелограмма (см. п. 5.2), построенного на этой стороне и удвоенной медиане8^ как на диагоналях (рис. 10):
с 4- (2m)2 = 2а2 + 2Ь2.
Биссектрисы треугольника, делящие, по определению, его углы пополам, пересекаются в одной точке — центре вписанной окружности. Биссектриса угла треугольника делит противолежащую сторону в отношении прилежащих сторон (рис. 11)
х : у = а : Ъ
8) Медиана продлевается на свою длину за середину стороны.
56
и может быть вычислена по формуле
I2 = ab — ху.
Рис. 10
Рис. 11
Высоты треугольника, т. е. перпендикуляры к его сторонам, пересекаются9^ в одной точке. Они используются, прежде всего, при вычислении площадей (см. п. 5.1).
Пример (£ — 94.6). Медианы AM и BN треугольника АВС взаимно перпендикулярны. Найти АВ, если ВС = а и АС = Ь.
Решение. См. рис. 12:
Рис. 12
1) МК — ж, NK = у => АК = 2ж, В К = 2у (свойство медиан);
9)В случае тупоугольного треугольника пересекаются не высоты, а их продолжения.
57
\* + (2у? = (а/2)2
2) у2 + (2г)2 = (Ь/2)2
(теорема Пифагора) =>
z2 = (2х)2 + (2j/)2
(5(х2+у2) = ^ V2 = 4(®2 + у2)
2 — а2+Ь2
5
Ответ: ^°2j'l>2.
у/ 319 (х — 95.3). Медианы AM и CN треугольника АВС взаимно перпендикулярны. Найти площадь треугольника АВМ, если ВС = а и АС = Ь.
320 (£ — 98.4). Медианы ВМ и CN треугольника АВС пересекаются в точке К. Найти расстояние от точки К до прямой ВС, если ВС = a, Z.B = (3 и ZC = 7.
у/ 321 (£ — 00.3). Найти угол С треугольника АВС со сторонами АС = а, ВС = b и медианой СМ = т.
322 (</? — 80.4). В треугольнике АВС проведены высота ВН и медиана ВМ. Найти cos Z.MBH, если АВ = 1,ВС = 2 и AM = ВМ.
у/ 323 (А — 99.4). Найти углы треугольника АВС, если его медиана ВМ равна половине стороны АС, а один из углов, образованных биссектрисой BL и стороной АС, равен 55°.
324 (£ — 94.4). В равнобедренном треугольнике высоты, опущенные на основание и на боковую сторону, равны тип соответственно. Найти стороны треугольника.
325 (£ — 01.4). В треугольнике АВС с острыми углами ZA = = a, Z.B = /3 и стороной АВ = с продолжения высот АН и В К пересекаются в точке D. Найти расстояние от точки D до прямой АВ.
у/ 326 (/1 — 78.3). В остроугольном треугольнике АВС проведены высоты АН и СК. Найти радиус описанной около треугольника АВС окружности, если НК = 2\/2, а площади треугольников АВС и ВНК равны 18 и 2 соответственно.
327 (^ — 93.4). В остроугольном треугольнике АВС проведены высоты АН и СК. Найти площадь круга, описанного около треугольника КВН, если АС = 1 и Z.KCH = а.
у/ 328 (£ — 96.7). В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AL. Найти AL, если BL = b и CL = с.
58
329 (a — 92.4). В треугольнике АВС проведена биссектриса AD. Найти cos Z.ADC, если АВ = 4 и АС = ВС = 12.
330 (тг — 83.4). В треугольнике АВС проведена биссектриса BD — Зл/2/2. Найти площадь треугольника, если ВС = 2 и DC = 1.
у] 331 (7 — 92.4). Найти стороны треугольника АВС, если его биссектриса BL = 4 и медиана AM = 4 перпендикулярны ДРУГ ДРУгу.
332 — 95.4). В треугольнике АВС периметром 28 биссек-
трисы AD и BE пересекаются в точке М. Найти АВ, если АВ = ВЕиВМ = 2МЕ.
у/ 333 (а — 95.4). Продолжение биссектрисы CD треугольника АВС пересекает описанную около него окружность в точке Е. Найти АС, если АВ = 3, ВС = 2 АС и DE = 1.
334 (тг — 99.6). На высоте СН = у/Ъ/З треугольника АВС со стороной АВ = УЗ/2 лежит центр окружности, вписанной в угол В. Найти радиус окружности, если АН : ВН = 2:1.
у/ 335 (7—00.4). На сторонах АВ = 6 и ВС треугольника АВС взяты точки М и N соответственно так, что ВМ = BN. Перпендикуляры к прямым АВ и ВС, опущенные из точек N и М соответственно, пересекаются в точке К, а прямая В К пересекает сторону АС в точке L. Найти BL, если AL = 4 и CL = 5.
336* (/1 — 99.4). В трапеции ABCD с боковыми сторонами АВ = 9 и CD = 5 биссектриса угла D пересекает биссектрисы углов А и С в точках М и N соответственно, а биссектриса угла В пересекает те же две биссектрисы в точках L и К, причем точка К лежит на основании AD. В каком отношении прямая LN делит сторону АВ, а прямая МК — сторону ВС1 Найти MN : KL, если LM : KN = 3 : 7.
5.6. Стереометрия
Следующие формулы стереометрии желательно помнить:
1) объем цилиндра и призмы равен
V = So н,
а объем конуса и пирамиды равен
V=\soH, о
где So — площадь основания, & Н — высота;
59
2) площадь боковой поверхности цилиндра и прямой призмы равна
5б = Ро Я, а площадь боковой поверхности конуса и. правильной пирамиды равна
s6 = ipoz,
где Ро — периметр основания, а I — образующая конуса или апофема пирамиды;
г 3) объем описанного многогранника равен
v = l5ar'
где Sn — площадь полной поверхности многогранника, аг — радиус вписанного в него шара;
4) площадь сферы и объем шара радиуса г равны
S = 4тгг2 и V = ^ят3.
Пример (£ — 91.2). В конус вписана сфера, площадь которой равна площади основания конуса. Найти угол между образующей конуса и плоскостью его основания.
Р ешение. См. рис. 13, где изображено сечение, проходящее через ось конуса и центр сферы:
Рис. 13
4тгг2 = тгЯ2 => Я = 2г => tgа = | => 2а=...
Ответ: 2arctg |.
337° (7 — 80.3). В правильную шестиугольную пирамиду с высотой Я вписан один конус, а около нее описан другой ко
60
нус с радиусом основания R. Найти разность объемов этих конусов.
338° (х — 00.3). Конус вписан в правильную четырехугольную пирамиду. Их общая высота равна 9/4, а радиус вписанной в конус сферы равен 1. Найти разность объемов пирамиды и конуса.
у/ 339 (/3 — 96.4). Через вершину S конуса проходит плоское сечение SAB площадью 42. Точки А и В делят длину окружности основания конуса в отношении 1:5. Найти объем конуса, если Z.SAB = arccos (3/>/58).
у/ 340 (£ — 96.6). Найти объем прямоугольного параллелепипеда, диагональ которого равна d и образует с двумя смежными гранями углы а и /3 соответственно.
у/ 341 (ip — 81.5). Найти сторону основания правильной треугольной призмы объемом V, если угол между диагоналями двух ее боковых граней, проведенными из одной вершины, равен а. 342° (£ — 97.4). Найти сторону основания правильной треугольной пирамиды объемом 36, если ее высота вдвое больше радиуса окружности, описанной около основания.
у/ 343 (А — 77.5). Найти радиус сферы, описанной около правильной треугольной пирамиды со стороной основания, равной а, и углом р между боковыми ребрами.
344 (£ — 95.6). Найти двугранный угол при ребре основания правильной треугольной пирамиды, если угол между ее боковыми ребрами равен р.
у/ 345 (7—98.5). В правильной пирамиде SABC проведены биссектриса AL боковой грани SAB и медиана ВМ основания АВС. Найти LM, если АВ = 1 и AS = 2.
346 (х — 98.4). На высоте правильной треугольной пирамиды взята точка, удаленная от бокового ребра пирамиды на расстояние 4/\/13 и делящая высоту в отношении 1:2, считая от вершины. Найти объем пирамиды, если ее боковые грани наклонены к основанию под углом тг/6.
347 (£—97.6). Найти высоту пирамиды, основанием которой служит треугольник со сторонами 7, 8 и 9, если ее боковые ребра наклонены к основанию под углом 60°.
у/ 348 (а — 99.4). Найти объем пирамиды, если ее основанием служит прямоугольный треугольник с гипотенузой 3 и углом 30°, а боковые ребра наклонены к основанию под углом 60°.
61
у/ 349 (/3 — 98.4). Основанием пирамиды SABC с высотой SH служит прямоугольный треугольник АВС с гипотенузой АВ, а двугранные углы при ребрах основания равны по arcsin (5/13). Найти площадь боковой поверхности пирамиды, если АН = 1 аВН = 3\/2.
350° (С — 00.6). Найти радиус сферы, описанной около правильной треугольной пирамиды объемом 9\/3 и высотой 3.
351° (С — 96.7). Найти объем правильной четырехугольной пирамиды, если радиус описанной около нее сферы равен 2, а боковое ребро в \/2 раз больше ребра основания.
352° (С — 89.4). Боковое ребро правильной четырехугольной пирамиды вдвое больше ее высоты. Найти отношение радиуса вписанной в пирамиду сферы к апофеме пирамиды.
у/ 353 (С — 94.8). В правильной пирамиде SABC с высотой SH и ребром основания АВ = а угол между боковым ребром и плоскостью основания равен ip. Найти площадь сечения пирамиды плоскостью, проходящей через точку Н параллельно ребрам SA и ВС.
354 (£ — 78.5). Плоскость, параллельная ребру AS — а\/2 и ребру ВС = а основания АВС правильной пирамиды SABC, проходит на расстоянии d от ребра AS. Найти площадь сечения пирамиды этой плоскостью.
у/ 355 (С—95.6). Найти объем правильной четырехугольной пирамиды с высотой Н и двугранным углом а при боковом ребре.
356* — 96.6). В правильной пирамиде SABCD с вершиной S боковое ребро равно а, а двугранный угол при этом ребре равен <р. Найти площадь сечения пирамиды плоскостью, проходящей через точки В, D и середину ребра SC.
357* (А — 99.6). Все ребра правильной пирамиды SABCD с вершиной S равны по 2. Плоскость, параллельная прямым АС и SB, пересекает ребра АВ и ВС в точках М и N. Найти периметр сечения пирамиды этой плоскостью, если MN = \/2. у/ 358* (тг — 82.5). В правильной пирамиде SABCD с высотой 4 сторона основания ABCD равна 6. Точки М и N — середины ребер ВС и CD. Найти радиус сферы, вписанной в пирамиду SMNC.
у/ 359* (А — 00.8). Какими должны быть радиусы четырех одинаковых шаров, чтобы их можно было разместить внутри дан
62
ной сферы радиуса R и при этом каждый шар касался сферы и трех других шаров?
у/ 360 (7—00.3). На воздушном шаре, двигавшемся относительно Земли вдоль заданной параллели на постоянной высоте, было совершено кругосветное путешествие. На какой широте совершалось путешествие, если разность расстояний, пройденных верхней и нижней точками шара, оказалась равной удвоенному диаметру шара?
5.7. Координаты и векторы
В координатном пространстве расстояние между точками Ai = (xi,yi,zi) и Аг = (s2,SZ2,Z2) вычисляется по формуле
А1А2 = х/(xi - х2)2 4- (yi - У2)2 4- (zi - z2)2,
длина вектора а = (x,y,z) — по формуле
|а| = х/я2 4- у2 4- z2;
скалярное произведение векторов ai = (si,yi,zi) и а2 = (x2ly2,z2) равно
ai -а2 = Х1Х2 4-2/12/2 4-21*2 = |ai| • |а2| cosy?,
где у? — угол между этими векторами.
Уравнение плоскости с нормалью10^ п = (а,Ь, с) и уравнение сферы с центром (а,/3,7) и радиусом R имеют соответственно вид
ах 4- by 4- cz = d и (х — а)2 4- (у — /З)2 4- (z — 7)2 = R2.
На координатной плоскости действуют аналогичные формулы и аналогичные уравнения прямой и окружности11^, но с участием только двух из трех координат: х и у.
Пример (е — 81.3). Найти площадь фигуры, заданной12^ системой
(у С 6 - 2|х|
[у > 3 - |х|/2.
10) Вектором, перпендикулярным этой плоскости.
п)Вместо плоскости и сферы соответственно.
12)На координатной плоскости (эта фраза здесь и всюду в подобных задачах опущена).
63
Решение. См. рис. 14:
1) Л1,2: 6 —2|®| =3 - |®|/2 о |®| = 2 & х = ±2.
2) S = 2(| (6-3) -2) = 6.
Ответ: 6.
у/ 361° (а — 96.2). Найти площадь фигуры, заданной системой р > -И -1 [t/ — 2|я| 4- 3.
у/ 362 (i/ — 00.2). Найти площадь фигуры, заданной системой
{х2 4- у2 9
2/4-1 0
3t/4-6 > 2|ж|.
у/ 363* (д — 91.3). Найти площадь фигуры, заданной системой х2 4- у2 4х — 4у — 6
х 1.
у/ 364° (А — 90.2). Прямая у = — 2x4-2 пересекается с прямой у = х и с осью абсцисс в точках А и В соответственно. Найти площадь треугольника АВО, где О — начало координат.
У 365* (х — 99.2). Прямая у = 4 — (2 — у/3)х пересекает в точках А и В окружность с центром в начале координат и радиусом 4. Найти сумму длин хорды и меньшей дуги АВ.
64
366* (б — 01.3). Найти площадь пятиугольника ABCDE, где А = (0; 2), В = (1; 7), С = (10; 7), D = (7;1), а Е — точка пересечения прямых АС и BD.
у/ 367* (р — 01.4). Найти площадь пятиугольника ABCDE, где А = (9; 1), В = (2;0), D = (1; 5), Е = (9; 7), а С — точка пересечения прямых BE и AD.
у/ 368* (7 — 00.5). Эпицентр циклона, движущийся прямолинейно, во время первого измерения находился от метеостанции в 24 км к северу и 5 км к западу, а во время второго — в 20 км к северу и 10/3 км к западу. На каком наименьшем расстоянии от метеостанции пройдет эпицентр?
у/ 369 (£ — 80.2). Найти координаты точки в пространстве, лежащей на оси абсцисс и равноудаленной от точек А = (1; 2; 3) и В = (2;3;4). *
у/ 370 (С—78.3). Найти уравнение плоскости, проходящей через точку А = (1; 2; 3) перпендикулярно прямой АВ, где В = = (4;6;9).
у/ 371 (£ — 79.2). Найти угол между векторами а — (6; —2; —3) и 5=(5;0;0).
3 И. Н. Сергеев — Математика
Глава 2. КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Чем дальше в лес, тем больше дров.
§ 6. Квадратный трехчлен
Функция вида
/(х) = ах2 + Ьх + с
с ненулевым старшим коэффициентом а называется квадратным трехчленом.
Если дискриминант D = Ь2 — 4ас квадратного трехчлена неотрицателен, то квадратный трехчлен раскладывается на линейные множители, т. е. приводится к виду
f(x) = а(х - xi)(x - ж2),
\ в котором числа si.2, образующие пару корней квадратного трехчлена, определяются по формуле
—b ± \/b2 — 4ас Ж1’2 =----Га-----•
Если же дискриминант отрицателен, то квадратный трехчлен на линейные множители не раскладывается, но зато принимает значения только одного знака — того же, что и старший коэффициент.
Квадратные неравенства решаются с помощью следующего утверждения: пусть а > 0, a si,2 — пара корней квадратного трехчлена, тогда
f(x) <0 — между корнями, f(x) >0 — за корнями.
6.1. Дискриминант и формула корней
Количество корней квадратного уравнения полностью определяется знаком его дискриминанта: если D > 0, то корня два, если D = 0, то корень один1), а если D < 0 — ни одного корня.
^Этот корень называется кратным, поскольку является результатом слияния двух корней квадратного трехчлена, — но при подсчете количества корней уравнения на вступительном экзамене такой корень следует считать только один раз.
66
Пример - 92.1). 8х - 1 < 4х2.
Решение.
. . . <=> (х — Х1)(х - Х2) > о, где Х1.2 = 4±V^2~4,1. = <=>...
Ответ: х < 2-г/З 2+^/3 2 > Х 2 ’
372° (х-95.1). 2ж I а?+3
373° (7 - 86.1). х-1 \ 1 х24-6:е—4 6 *
374 (% —95.1).
375 (тг - 01.2). |2®-3| = х2.
376 (А - 01.3). (5/7)®-2 • (7/5)1/(®-1) = 125/343.
377 (А-97.1). Сколько корней имеет уравнение
\/б(а:2 + 2) + 2ж\/5 = #35(х2 - 2) + 2а:х/7?
378 (7-8O.I). Найти все а, при которых уравнение
х2 — 2ах 4- 2а — 1 = О
имеет ровно два различных корня.
у/ 379* (а — 01.5). Найти все а, при которых уравнение ах2 4- (2а 4- 2)х 4- (а 4- 3) = 0
имеет два корня и расстояние между ними больше 1.
6.2. Разложение на линейные множители
Одним из важнейших преобразований квадратного трехчлена следует признать его разложение на линейные множители. Ни в каких пояснениях это преобразование не нуждается: ведь оно проверяется элементарным раскрытием скобок и приведением подобных членов. К тому же в большинстве случаев указанное разложение можно получить в уме.
Пример (х — 83.1). Найти область определения функции
\/16 — х2 log2 (ж2 — 5х 4- 6)
Г16-®2^0 (ж2 — 5® + 6 > 0 Ответ:— 4 ж < 2, 3<х Г М (рус. 16) [(х-2)(х-3) >0 ^4.
67
3*
[ ' )---(—н----►
-4 2 3 4 х
Рис. 15
380° (тг — 97.1). Найти все решения неравенства (х + З)2 < 5х + 11
на отрезке [—3; 0].
у/ 381° (е - 84.1).
у/ 382 (е - 89.1).
Iqct Ц > Л 1ио8 2я^+3
Найти область определения функции
t, ч vZ25^
Л®) = >л . О'
383 (7 - 88.1).
у/ 384 (7-97.1).
Найти область определения функции f(x) = log_a. (12 —х2 -х).
Найти область определения функции
/(а:) = л/х2 - 2а: - 3 + log3+a. (9 - а:2).
4—
385 « - 86.1). (1/4)“5“ < 8®.
У 386 (е - 80.2). 54®2-з*+1/2 < (1/5)
—40г2
6.3. Теорема Виета и обратная к ней
Теорема Виета гласит: если числа xi,2 представляют собой пару корней квадратного2^ трехчлена х2 4- рх 4- д, то они удовлетворяют системе
{Х1 4- Х2 = —р
Xi • Х2 = q.
Верна и обратная теорема: если числа xi,2 удовлетворяют последней системе, то они представляют собой пару корней упомянутого квадратного трехчлена.
Обратная теорема, утверждающая, в частности, что пара чисел восстанавливается по их сумме и произведению однозначно3^, позволяет решать системы определенного вида практически без выкладок.
2) Приведенного!
3^С точностью до перестановки чисел в паре.
68
Пример (Л - 87.4). 12х 4- Зу = 16 1 log2 х 4- log2 у = 3.
Решение. 2х 4- Зу = 16 «=> log2(xy) = log28 х > 0 2х 4- Зу = 16 о (2х) • (Зу) = 48 2х 4- Зу = 16 о < ху = 8 х > 0 (=4 + 12) 1) (= 4 • 12) <=> 2х = 4 2) 12 . О
х > 0 Ответ: х = 2, у = 4; > Зу = 12 х = 6, у = 4/3. 4
у/ 387 (А — 99.2). Найти ал 4- Зал #2 4- %2, где xlt2 — корни квадратного трехчлена
/(ж) = 2х2 + (1 - Зх/2)а; - \/3 + 2^2.
У 388 (С - 80.2).
У 389 (х- 85.1).
390 (Л - 80.3).
У 391 (С-96.5).
у/ 392 (х —01.1).
У 393* (^-91.3).
*+у -
- -2
1 х+у
Г 6х - 2 • 3» = 2
[6х • 3» = 12.
< log2 (ж2 + у2) = 5 2 log4 х + log2 у = 4.
log2(2a:2 — у2) = 2 61ogg(—a:) + log2 у2 = 4.
2 • 51-w = log3 ж-2
5У 4- log3 х = 4.
< log3 x - 2* 4- у = 3 у 2У 4- 2У log3 х = 4.
§ 7. Уравнения и неравенства, квадратные относительно различных выражений
В настоящем параграфе рассматриваются уравнения и неравенства, преобразующиеся к виду1)
а(и(х))2 4- Ъи(х) 4- с V 0,
х)Как и прежде (см. п. 1.3), под знаком V подразумевается любой из знаков =,>,<, > ,
69
где а / 0, а и(х) — одна из функций ж2, a®, loga ж, sin ж, cos х. &ля разложения на множители левой части, представляющей собой квадратный трехчлен относительно переменной и = и(ж), совершенно не обязательно явно заводить эту новую переменную2^.
7.1. Биквадратные уравнения и неравенства
Слово «биквадратное» означает «квадратное относительно квадрата неизвестной».
Пример (тг — 96.2). Зя4 — 4 < Их2.
Решение.
... Зя4 - Их2 - 4 < О (х2 - 4) (х2 + 1/3) < О
О х2 < 4 (т. к. х2 + 1/3 >0) <=> |ж| < 2 ...
Ответ: — 2 < х < 2.
у/ 394° (тг - 82.3). х4 - 13я2 - 48 = 0.
V 395 (С - 95.3). (1/4)2®4 • 327а:2+1 > 16"1.
у/ 396* (£ — 93.7). Про числа а < 0 и Ь известно, что уравнение ах2 + Ьх + 2 = 0
имеет одним из своих корней число х = 7. Решить неравенство ах4 + Ьх2 + 2 > 0.
7.2. Уравнения и неравенства, квадратные
относительно ах
См. комментарий к п. 1.3 и 1.4.
Пример (7 - 77.3). 4х - 2®+1 = 3.
Решение.
... О р2 - 2р - 3 = 0, где р = 2®, О (р - 3)(р + 1) = 0 2х = 3 (т. к. р + 1 > 0) <=>...
Ответ: ж = log23.
397° (х - 98.1). 4х + 2х - 2 = 0.
398° (А - 84.1). 4х - 8 • 2х - 128 = 0.
399° (х - 90.1). 4х + 3 • 2Ж+2 = 160.
400° (тг - 95.2). 52ж = 115 • 5х"1 + 50.
2)Ну, разве лишь для сокращения записи!
70
401° « - 95.2). 402 (C - 96.5). 403 (тг - 91.1). 404 (% - 96.1). 405 (^ - 85.2). 406 (a - 96.1). 407 (C - 97.2). 408 (тг - 99.1). 409 (7 - 87.1). 410 (0 - 86.2). 411 (( - 96.3). 412 « - 81.3). 413 (7-96.2). 414 (yr-91.2). 415* (C - 85.4). 9®+1 + 3я+2 _ is = 0. 4®-°’5 + 2®+1 - 16 < 0. 25® + 24 • 5®"1 < 1. 4® + 5 > 4 • 2®. 3 • 9® < 8 • 3® + 3. 3 • 4® - 7 • 2®+1 - 5 > 0. 25® - 24 • 5®-1 + 2 > 5l08s 3 4. 3® - 88/3® = 42. 7® — 14 • 7_® > 3logs2 + 3. 2® - 1 < 6 • 2~®. 5®/2 - 52-3®/2 = 24 • 5-®/2. 32®/100® = 2 (0,3)® + 3. 9 (1/81)® - 17 (1/27)® - 2 (1/9)® > 0. log2 (3 - 5 • 2®) = 2x + 1. При каждом a решить уравнение
4® - 2а(а 4-1) 2®"1 + а3 = 0.
7.3. Уравнения и неравенства, квадратные относительно log0x
См. комментарий к задачам из § 3.
Пример (А — 94.5). (1 — 2 log2 х) log2 х + 3 = 0. Решение.
... 4Ф 212-1-3 = 0, где Z = log2;r, 4» {I + 1) (I - 3/2) = 0
log2 х = -log2 х = 3/2
Ответ: х = 1/2, 23^2.
416 (/? - 80.2). ч/ 417 (х-93.2).
418 03-95.1).
419° (тг - 78.2).
420 « - 84.2). ^/421 (С-95.2). у/ 422 (тг - 81.2).
2 log2 х - 31og2 I - 11 = 0.
logi/з x = log3 %.
4 log^ x + log2 16z5 = 0.
log2 x — 4 log2 x + 3 > 0.
41og25 5z > 5 - logs x.
(| log3 x - 6) logg x > 4(2 - logg a:).
2 lg2 x + (1 - ч/2) 1g x2 = 2 yfL
71
у/ 423 (х - 98.2). log4 X 4- 2 log* 4 = 3.
У 424 (а - 86.4).
7.4. Уравнения, квадратные относительно sin я ИЛИ COS X
См. комментарий к задачам из § 2.
Пример (у? — 82.1). 2 cos 2х = —5 sin х.
Решение.
2 4- (1 — 2s2) = —5s, где s = sin ж,
<=> 2s2 — 5s — 3 = О (s — 3) (s 4-1/2) = 0 <=> sin я = -1/2 Ответ: x = (—l)n+1 4-тгп, где n € Z.
425° (ст-86.3). 2 sin2 ж — 5cosx = 4.
426° (V>- 85.1). 3sinx — 2cos2 x 4- 3 = 0.
427° (A - 87.2). 2 cos2 ж 4- 7sinx = 8.
428 (7 - 93.2). sin x = cos2 x — | logy^ sin |.
429 (7-91.1). 2cos2 x — 7cosz = 2sin2 x.
430 (e - 85.2). 2 sins = 3ctgx.
431 (A - 78.1). x/2sinx 4- ctgfc = 0.
432° (тг —99.2). sin x = cos 2x.
433° - 01.1). 3cos2x 4- 4 sin x = 1.
434° (0 - 00.2). 3cos2x 4-44- llsinx = 0.
435° (x - 96.2). 5 4- cos 2x = 6 cos x.
436° (0-93.1). cos 2x 4- 2 cosx — 3 = 0.
437° (0 - 90.1). 3 cos 2x = 4 — 11 cosx.
438° (C - 92.2). 8cos2x — 3cosx = 5.
439 (0 - 87.1). 7 sin(2x - 5тг/2) 4- 9 cos x 4-1 = 0.
440 (a - 92.2). 3cos2 x 4- llcos2x - 10 cos x 4-12 = 0.
441 (e - 87.1). cos2# 4- 3x/2sins — 3 = 0.
442 (e - 98.3). cos 2x — x/Scosx — 2 = 0.
443 (тг - 80.2). 2 — cos 2x 4- 2>/2 cos(x 4- тг/2) = 0.
444 « - 85.1). 2 cos2 | — 1 = cos 2x.
445 (<p - 84.2). cos cos f 4- cosx = j.
72
у/ 446 (х — 83.1). cos(2x 4- тг/4) 4- cos(2x — тг/4) 4- 4 sin х = * = 2 4- \/2(1 — sin ж).
447 (/? — 84.2). cos2x 4- 2 cos я 4- 7 = 2sin(^ 4- х) 4- 4sin2 j. у/ 448 (х — 81.2). 2 cos 2х 4- cos2 f — 10 cos ( — x) 4-1 = | cos х.
у/ 449 (J3 — 88.1). Найти наименьший положительный корень уравнения
6 sin ~ sin f 4- 2 cos Д^ cos | + 1 = 0.
у/ 450 (л — 95.5). Найти все а, при которых уравнение
2cos2х — 4аcosx 4- а2 4- 2 = 0
не имеет корней.
§ 8. Дополнительные соображения
Задачи настоящего параграфа позволят читателю основательно закрепить материал, содержащийся в § 1-3, и одновременно повысить свое мастерство в решении квадратных уравнений и неравенств.
8.1. Учет области допустимых значений
Преобразования уравнений и неравенств часто сопровождаются изменениями ОДЗ, которые порождают дополнительные трудности.
Пример (Л — 83.3). log3 (5х2 4- 6х 4-1) 0.
Решение.
... <=»0<5.-+6я + Ю « Г(» + «(» + */5)>0
(х(х 4-6/5) 0
Ответ: —6/5 х < —1, —1/5 < х 0.
4—Н-------—Н--------►
f 1 4 0 х
Рис. 16
^/451° (А-94.5) у/ 452 (тг - 79.2).
453 (е - 85.1).
>/4х — 3 — а:2 0 0.
(ч/2^)2.
'sin а: = v 1 — 2 sin2 х.
х—з >
73
7454 (л--82.2). 455 (х - 80.1). 456 (тг - 98.2). 457 (тг - 97.2). 7458 (С-87.4). \/1 — 4 sin х = л/1 — 4 cos 2х. log7 = log7 ^6- log2(x2 - 5) = | log^l - х). logi/7 (*2 + Зх) < log1/7 (5х - 1). Найти область определения функции = yiogj/2 (Зх2 - 2х).
У 459 (А-83.3). 460 (х - 97.2). 461 (7 - 99.1). 7462 (92 — 87.2). log8in 5 (х2 - Зх + 2) > 2. log. (Зх - 2) = 2. log4l-8(a;2 - 2а: - 3) = 1. log5_Х2 (2а:2 - 8х - 2) = 1 + logg.^ 2.
463 (е — 78.1). logi_2Х2 я — J 1ов2(1-2хг)4 •
464 (е —78.3). a + ^-log.^-^).-465° (х - 95.2). log3 х + log3(x + 2) = 1.
466° (А - 79.2). log2 (х -1) + log2 х = 1.
467° (х-86.1). 468 (у> - 79.3). 469 (С - 95.2). 470 (£-89.1). 7471 (л--94.3). 472 (С - 89.3). 473 (£ - 81.1). 474 (С - 94.2). ^475 (7-91.2). 7476 (А-00.3). 7 477 (л--77.2). 7 478 (£ — 92.2). 7479 (А-97.2). 480 (С - 95.5). 7481 (х-77.3). 482 (J3 - 93.2). log3 (а; - 8) = 2 - log3 х. 1 + Нх/г (4 - х) > -logi/2 (х - 1). 2 + 61og8 х = log2 (6а: + 18). log49 (2а:2 + х - 5) + log^ (1 + х) = 0. log4 (х - 2) + log1/2 (4 - х) 0. log2 (х + 4) + 2 log2 7® = 5. 3 log8 (x - 2) = log2 72a: - 1. 1 log2 (x — 2) — | = log1/8 73a: - 5. 1 log2 (a: - 2) - 1 logx/4 ^Jx - 5. log4 ((x - 5) (a: + 6)) + log1/4 ((a: - 5) (a>3)) 1. 21g (x + 1/2) - 1g (x - 1) = 1g (x + 5/2) + 1g 2. log5 jzf + log5 (x2 - 17x + 60) = 1 + log5 2. 2 — log3x = log3 (||x| + 2). 510g1/3(®2+2x) J/5. log1/75(6l+1-36»)>-2. log2 (9х + 2 • 3® — 5) = 1 + 2 log4 (3l+1 - 4).
483 (7 - 97.3). log|sin v| (9* - 3®+3 + 30) = log,8in ¥| (3х + 3).
74
484 (a — 01.2). logsin х (3 sin х — cos2x) = 0.
у/ 485* (7 — 00.2). Найти все а, при которых уравнение 1оёа-6,5(*2 + 1) = 10go-6,5((a - 5>)
имеет ровно два различных корня.
у/ 486* (£ — 90.5). При каждом а решить уравнение
\/2х + а = 2.
8.2. Комбинации различных функций
Уравнения и неравенства могут оказаться квадратными относительно довольно сложных выражений, таких как1) и(у(х)), где u, v — какие-либо функции из числа рассмотренных в § 7, а также, возможно, линейные, квадратичные, степенные и т. д.
Пример (Л - 96.2). cos 7х + 2cos ~ = |.
Решение.
... о 2с2 — 1 4- 2с = |, где с = cos <=> (с — |) (с4-1) = 0
о cos^ = | <=> +27гп, где п е Z, <=>...
Ответ: х = 4- где п G Z.
487 (7 - 88.2). 488 (С-01.3). 23«-V2 4. .jZI > 1 + 2-3г. ^Зж2+я: _ g = 2.8®2+а:/3
у/ 489 (% —85.2). 490 (тг - 79.1). у/ 491 (С-94.3). у/ 492 (С-98.3). ,/493 (7-79.1). 494 (у> —81.2). у/ 495 (0 — 78.4). ,/496 (7-8I.I). 497° (7 - 99.1). у/ 498 (А-97.2). 52г-х2/3 < 52-2® (^/й)®2 + 24. = 1. 5^ _ 53-ч/г < 20. 272/1 + 27 • З3/®"1 - 36 = 0. 41oge х _ g . 21og9 х + 21о8з 27 = 0. Iog2 (2 - х) - 8 log1/4 (2 - х) 5. log| (х — х2 + 3) 4- Slogj/з (х - х2 + 3) + 2 0. log3(2a: + 1) = 2 log2l+13 + 1. 2cos4x — sin2x = —1. 3 cos 8x = 14(sin 2x — cos 2x)2 — 3.
499 (А—92.4). sin х sin 3x4-74-2 sin2 х = 14 cos х cos 3x4-7 cos2 х. ^Или еще более сложных.
75
501 (0 - 78.1).
502 (7 - 89.1).
У 503 (А - 98.3).
504 (^-77.1).
^/505 (Л-00.4).
У 506 (С-01.2).
V 507 (С - 80.3).
508 (7-78.4).
509 (С - 01.5).
у/ 510 (С-97.3).
У 511* (^ - 82.3).
у/ 512* (С — 01.7).. При каждом а решить неравенство 3(2х — а) + 5ау/2х — а — 2а2 > 0.
9 cos Зх cos 5х + 7 = 9 cos Зх cos х + 12 cos 4х. cos 2 (х + тг/З) + 4sin(x + тг/З) = 5/2.
sin (х — тг/З) = cos (2х — 2тг/3).
5+й4з7 = 7с‘83а:-
3 tg2 х — 8 cos2 х + 1 = 0.
4 cos2 х + tg2 х 3.
(l/S)1-’ • 3^ > 1/9.
3 \/log3 x + log3 3x = 11.
^/log9 (3x2 — 4x + 2) + 1 > log3 (3x2 — 4x + 2). y21og9(5x2 -4) > log3 \/5x2 - 4.
^/log4(x-5) > log{/4
v^8cosx — 1 = (\/2 — v^^/cosx.
8.3. Оптимальный выбор новой переменной
Новые переменные в следующих задачах рекомендуем постараться выбрать так, чтобы полученные при этом квадратные уравнения и неравенства оказались по возможности более простыми.
Пример (А — 95.2). х2 — 6 |ж|.
Решение.
... <=> т2 — т — 6 0, где т — |ж|, <=> (ттг — 3) (т + 2) 0
<=> |ж| 3 (так как т 4* 2 > 0) <=> ...
Ответ: х —3, х 3.
513° (7-87.2).
514° {Р- 96.2).
д/515 (х —94.1).
у/ 516 (А-93.2).
У 517 (С-00.3).
у/ 518 (г —83.3).
У 519 (С-94.5).
х2 + 2|х| < 8.
(х - 7)2 - |х - 7| = 30.
(4|х - 1| + 1/2)2 = 11(х - I)2 + 5/4.
х/1 — cos2 х + 6 cos 2х = 0.
2х2 + л/2х3 < х:
log3 (х2 - 2) < log3 (||х| - 1).
log2/2 4х 4- log2 = 8.
76
520 (А - 95.2). 521 (А - 80.1). 522 (А - 84.1). 523 (С - 94.3). 524 (V» - 83.1). 525 (С-81.3). 526 (х - 82.3). 25~® - 5-х+1 > 50. 7~® - 3 • 71+® > 4. 3.9®+i _ б • 3х - 1 = 0. б*-1 + 5 (О.г)*-2 = 26. (1/4)*"2 = 25-® + 9. 9 _ 10+4,/2 2^=7 — 4 Решить неравенство
где f(x) = 2х + 2, д(х) = 2Х + 10.
527 (0 - 90.2). 528 (х —77.1). 529 (7 - 83.1). 530 (х - 90.2). 531 (А - 78.1). 532 (е - 77.2). д2г+0,5 _ 10.272*/3 > Ц/3 22®+1 _ 21 (1/2)2х+3 + 2 > 0. cos2 2х — 5 sin2 х + 1 = 0. 2 sin2 х + sin2 2х = 5/4 — 2 cos 2х. —5 cos 4х = 2 cos2 х + 1. 8 sin4 x + 13 cos 2x = 7.
8.4. Роль грубых оценок
Для исследования иррациональных корней квадратного трехчлена часто бывает достаточно лишь выяснить, между какими целыми числами лежит значение квадратного корня из данного числа2 .
Пример (£ — 88.1). cos 2х 4- 8 sinх = 3.
Решение.
... <=> 1 — 2s2 + 8s = 3, где s = sin х, О s2 — 4s 4-1 = 0
О s = 2 ± \/3 <=> sins = 2 — \/3 (так как 1 < \/3 < 2) ...
О т в е т: х = (—l)n arcsin(2 — л/3) 4- тгп, где п € Z.
533° (£ — 96.1). 4sinх 4- cos 2х 4- 3 = 0.
^534 (С -84.1). tgs + ^_ = 0.
535° (x - 97-3). 536° (тг —01.1). 537° (тг - 88.1). 538° (V> - 97.1). 539° (x- 94.1). 8 cos 2x 4-16 cos x 4- 7 = 0. ‘ sins = 2ctgs. 3 cos x 4- 2 tg x = 0. 3 cos2 x + 4 sin x = 9. 12 sin 5s = cos 10s 4- 7.
2) Обычно из дискриминанта.
77
540° (р - 01.2). у/ 541 « - 82.1). 542 (<р - 87.1). 543° (/3 - 99.1). 544° (7 - 81.2). V 545 (а-99.2). х/ 546’ (ф - 90.1). 3 cos 2х — 6 sin х — 2 = 0. cos х 4- \/17 cos f = 0. 2 cos 2x 4- 4 cos x = sin2 x. 8 cos 6s — 12 sin 3x = 3. 2 cos x 4- 3 cos 2x = 3. 4 sin 4s cos 2s 4- 5 cos 3s = 5 cos 5s. 4 sin2 (2(s 4- тг/2)) — - 2(v/5 - x/3) cos(2s - тг) 4- >/15 - 4 = 0.
х/ 547 (ц - 96.1). х/ 548 (С - 01.2). х/549’(^ - 77.3). нения 5 5>/5 4» 6 = о sin2 X sin X 2 sin 2x cos 5®2 — sin(5®2 4- 2x) = 0. Найти наименьший положительный корень урав- cos(ttx2) = cos(tt(x2 4- 2х 4-1)).
550 (<р - 83.1). 551° (Р - 97.1). х/ 552 (<р - 89.3). х/553 «-99.3). 554 (е - 84.1). 555 (С-91.3). х/ 556 (я- - 94.3). х/557* (тг — 98.3). х/558 (С-00.3). 559 (<р - 84.1). х/560’ (V>-99.2). log5 -1) = log5 rh-tog3®4-log3 (t + l) = 1. tog2x4.i (2x 12x 4" 3) = 2. 21og4(® 4-1) - | log1/v^(® - 5) < 3. log2 (x 4- 2) = 7 - log2 (5т 4- 6). tog49 (« + 3) - log7 (x 4- 2) < 0. lg(x4-5)>-21g3l7. togo.s log4 1 4- log4 log2(16x2) = 0. 2x/3* 4- (УЗ)’ - УЗ • 3х 4- у/З = 0. 27* 4- 9® = 3l+1. a;log7 4 + 5.21овт1 - 4 = 0.
8.5. Учет области значений выражения
При отборе корней квадратного трехчлена относительно какого-либо выражения иной раз полезно вовремя задаться вопросом о том, какие значения может принимать само это выражение.
Пример (А - 96.4). 2 • 2~2х2 - 7 2~х2 4- 3 > 0.
Решение.
... ^ (2~х2 - 3)(2~х2 - 1/2) > 0, причем 0 < 2~х2 2° = 1,
2~*2 < 1/2 -х2 < -1 <=>х2>1 •»...
Ответ: х < —1, х > 1.
561 (С - 90.1). х2 - 4|®| -1 = 0.
78
у562 (д-89.1).
У 563 « - 93.3).
564 « - 00.2).
565 (я- - 99.3).
У 566 (/3 - 78.4).
567’ (а - 98.2).
5/568’ (А-91.4).
569’ (е - 98.4).
570 (С - 87.2).
у/ 571’ (х- 90.3).
572’ (х- 85.3).
У 573’ (р - 01.6). у/ 574’ (е - 98.5).
3 — 4| cos®| = 4 sin2 х.
\/log2 ® = 2 log2 yfx - 1.
375-i _ 1Q. 3—Z?-i _ j
2-2*2+1 _ 12.2-*2 +5 = о.
32 log| х 1 = 4.3lo8s*.
32(т+1)2+1 _ g7.3х2+2х 4-18 = о.
^sin х । 2^—2 sin® jg
з . 642Sin2(»+V4) _ 392 . ззтг® + 16 _ о
4 — cos(2tt(13® + 9)2) = 5sm(7r(13x + 9)2).
arccos (| + cos(тг *£+“)) - = 0.
Найти все а, при которых область значении функции f(x\ = а2+2а2-4 * \ / ®2 —2®+3
содержится в интервале (—3; 2).
§ 9. Простейшие приложения
Для успешного решения задач настоящего параграфа читатель должен не только уметь решать квадратные уравнения и неравенства, но и свободно владеть материалом из § 4 и § 5.
Если при решении текстовой или геометрической задачи один из корней квадратного уравнения отбрасывается как не подходящий по смыслу задачи, то второй корень в этой ситуации обязательно подойдет и его можно не проверять1^.
9.1. Системы, сводящиеся к квадратным уравнениям
См. комментарий к п. 4.1.
{х 4- = 3
4х + 4» = 32.
Решение.
(х = 3-2-2» Гж = 3-2-2»
1 4(3 - 2 • 2») +4» = 32 ** [(2» - 10)(2» + 2) = 0
^Ведь искомая величина в условии задачи должна была принимать какое-то значение!
79
12” = 10 ...
(х = 3-2 10
О т в е т: х = —17, у = log2 10.
575° (0 - 94.1). х + 2у = 6 Зх2 — ху + 4у2 = 48. к Зх 4- у - z = 4
У 576 (i/-00.1). < х — 2у 4- 3z = 0 х2 + 2у+ z2 = 6х.
577° (V> - 82.2). (х + 2у = у2 -х2 + 3 |23«+» = 512.
578° (тг - 94.2). 3-2х+у = 13 22х+1 + Зу = 35.
579° (д - 94.2). 2® + 2у = 1 Зу — бу2 = 2®-1.
7 580° (<р - 83.2). < ьо *£ Н № ± II + + + Оо II р
7 581° (д - 80.4). < х3 - у/у = 1 5г6 -8х3у/у + у = 1.
7582 « -99.5). { 2»/*+з®/» = 16 7? -72г = '(75 + х/2)-1.
7583 (Л-00.5). < х + у + у/х + у = ЗЪ х2 + у2 = 325.
584 (С-98.5). 31og2(2®-v) _ 1 4®+» _ 2Х+» = 12. (31og52: + log^y = 3
7 585* (С - 00.5). log5(y - х - 2) + I + 1о6125(У - я + 2)3 = log5 12- ' 5 (logy х + log,, у) = 26
586 (% - 96.3). < xy = 64 у < X.
80
J 587* (тг- 98.4). { 3j/
[21og3y+ logy3 = 3s.
У 588 (£ — 81.2). Найти все а, при которых система f х2 4- у2 = 1 [ж-by = а
имеет единственное решение.
У 589* (V> — 94.2). Известно, что х = 1, у = — 1 — одно из решений системы
Зах + Ъу = х/3 tg(l 111тг/6) ах2 + Ъу2 = 2.
Найти остальные решения системы.
9.2. Квадратные уравнения и неравенства
в текстовых задачах
См. комментарий к п. 4.2-4.4.
Пример (/3 — 88.3). Два экскаватора, работая вместе, вырывают котлован за 2 ч. 24 мин. За сколько часов вырывает котлован один первый экскаватор, если он делает это на 2 ч дольше, чем один второй?
Решение. Если первый экскаватор вырывает котлован за х ч, то 111 5
х + Г^2 = 2Й =* ^~2)+х = -х(х-2)
.=> 5х2 — 34ж + 24 = О => (ж — 6) (х — 4/5) = 0 => х = 6, так как х > 2.
Ответ: 6.
590° — 85.). В первый день столяр сделал два шкафа и
одну полку, во второй — один шкаф и две полки, а в третий — один шкаф. Количества времени, затраченные им в первый, второй и третий день, образуют геометрическую прогрессию2^. За сколько часов столяр делает шкаф, если полку он делает за 5 ч?
у/ 591 (д — 95.1). Найти первый член геометрической прогрессии, если третий ее член равен —10, а седьмой член в сумме с квадратом третьего дает утроенный пятый член.
2)См. сноску 4) в п. 4.2.
81
у 592 (х — 01.1). Суммы первых трех и первых пяти членов арифметической прогрессии равны 27 и 80 соответственно. Сумма какого числа первых членов равна 486?
593 (А —80.4). В первый рабочий день месяца в магазине было продано 105 телевизоров, а в каждый следующий — на 10 телевизоров больше, чем в предыдущий. После досрочного выполнения месячного плана, составлявшего 4000 телевизоров, ежедневно продавалось одинаковое количество телевизоров, на 13 меньшее, чем в последний день выполнения плана. На сколько процентов был перевыполнен план, если в месяце было 26 рабочих дней?
У 594 — 97.3). Сумма первого и последнего членов конечной
возрастающей геометрической прогрессии равна 164, а произведение второго и предпоследнего ее членов равно 324. Найти последний член прогрессии.
у/ 595° — 84.5). Первый член геометрической прогрессии с
целочисленным знаменателем равен 5, а утроенный второй член превышает половину третьего больше, чем на 20. Найти знаменатель прогрессии.
596 (</? — 78.1). Две бригады общей численностью 15 человек дежурили на объекте в течение 69 ч. Первые 48 ч дежурили по очереди члены первой бригады, распределив время поровну, а остальное время — члены второй бригады, распределив остаток дежурства также поровну. Сумма времени дежурства одного члена первой бригады и одного члена второй бригады оказалась меньше 9 ч. Сколько человек в первой бригаде?
у/ 597 (£—83.4). После деления двузначного числа на сумму его цифр в частном получилось 7, а в остатке 6. После деления того же числа на произведение его цифр в частном получилось 3, а в остатке 11. Найти это число.
у/ 598* (а — 00.2). В течение двух лет в городе наблюдался рост числа жителей. Найти процент прироста числа жителей за первый год, если он на 1 меньше, чем за второй год, и не 5,2 меньше, чем за два года.
у/ 599 (х — 96.2). Имелось два раствора кислоты в воде: 60%-й и 20%-й. Первую смесь получили из некоторого количества первого раствора и 15 л второго, а вторую смесь — из того же количества первого раствора и 5л второго. Сколько литров первого раствора использовано для приготовления ка
82
ждой смеси, если концентрация кислоты в первой смеси вдвое меньше концентрации воды во второй?
у/ 600° (А — 93.3). Два экскаватора вырыли котлован: сначала первый работал Зч, а затем второй — 2 ч. За сколько часов вырыли бы котлован оба экскаватора, работая вместе, если один первый экскаватор выполнил бы эту работу на 4 ч быстрее, чем один второй?
601 (х — 81.1). Три сенокосилки за 4ч скосили траву с поля: сначала с площади 11га — первая и вторая сенокосилки вместе, а затем с площади 14 га — первая и третья. Первая сенокосилка скашивает в час Зга, вторая — на ага меньше, а третья — на 2а га больше (первой). Найти а, если 0 < а < 1. 602 (ф — 84.2). Два насоса за 4 ч подают 96 м3 воды. Если бы второй насос подавал на 6м3/ч воды больше, то на накачивание 1 м3 воды второй насос тратил бы на 3 мин больше, чем первый. Сколько воды в час подает первый насос?
603° (тг — 87.3). Один турист проходит 20км на 2,5 ч быстрее другого. Если бы первый турист уменьшил свою скорость на 2 км/ч, а второй увеличил в полтора раза, то их скорости стали бы одинаковыми. Найти скорость второго туриста.
604 (</?—92.4). Из пункта А в пункт В выехала машина, а через 20 мин — мотоциклист, скорость которого равна 90 км/ч. Мотоциклист догнал машину в пункте С и повернул обратно. Когда машина прибыла в В, мотоциклист проехал половину пути от С к А. Найти АС, если АВ = 80 км.
д/605 (Д — 90.3). Из пункта А в пункт В, расстояние между которыми равно 300 км, выехал легковой автомобиль, а из В в А одновременно с ним — грузовой. После встречи, которая произошла через 4 ч, легковой автомобиль увеличил скорость на 15 км/ч, а грузовой — на 30 км/ч. Найти первоначальную скорость легкового автомобиля, если он прибыл в пункт В на 1 час раньше, чем грузовой в А.
у/ 606* (А — 77.2). Два бегуна стартовали друг за другом с интервалом в 2 мин. Второй бегун догнал первого на расстоянии 1 км от точки старта, пробежал еще 4 км и повернул обратно, встретившись с первым бегуном через 20 мин после старта первого бегуна. Найти скорость второго бегуна.
607 (7 — 89.2). Из пункта А по дороге, идущей в гору, одновременно отправились пешеход со скоростью 6 км/ч и ав
83
тобус. Доехав менее чем за 1 ч до пункта В, находящегося на расстоянии 12 км от А, автобус поехал обратно и через 12 мин встретил пешехода. Найти скорость автобуса на подъеме, если она вдвое меньше его скорости на спуске.
608° (х— 97.1). Пункты А, В и С расположены последовательно вдоль реки, вниз по ее течению. В 12.00 из В в А отплыла лодка. Достигнув пункта А, она повернула назад и в 14.00 прибыла в С. Найти собственную скорость лодки, если АВ = 4 км, ВС = 14 км, а скорость течения реки равна 5 км/ч.
у/ 609* (ft — 78.2). Пароход идет от пристани А на притоке вниз по его течению 80 км до реки, а затем вверх против течения реки до пристани В, затратив на весь путь 18 ч. Обратный его путь занимает 15 ч. Найти длину пути от А до В и скорость притока, если собственная скорость парохода равна 18 км/ч, а скорость течения реки— Зкм/ч.
у/ 610 (7—85.3). Две реки с прямолинейными руслами и одинаковой скоростью течения впадают в одном и том же месте в озеро, образуя между собой угол 60°. От двух причалов А и В, расположенных на разных реках, одновременно вышли байдарка и лодка, собственные скорости которых равны, соответственно, 10 и Зкм/ч. Байдарка достигла озера через 2ч, а лодка — через 4. Найти скорость течения рек, если АВ = 28 км.
9.3. Использование квадратных уравнении
в геометрии
См. комментарий к пп. 5.1-5.6.
Пример (е — 88.5). На стороне АС треугольника АВС взята точка D так, что AD = 15, cos ZBDC = —|| и ZABC4-ZADB = 7r. Найти периметр треугольника АВС, если ВС = 10.
Решение. См. рис. 17:
1) ДАВС - ABDC (ZABC = тг - ZADB = ZBDC)
=> 1^ = =>х2 + 15х-100 = 0=> (х-5)(х4-20) = 0 => ж = 5;
2) 202 = у2 4- Ю2 4- 2 • у • 10 • || (теорема косинусов для ДАВС) => у2 4- 13г/ - 300 = 0 => (у4- 25) (у - 12) = 0 => у = 12;
3) Равс = Ю 4- 20 4-12 = ...
Ответ: 42.
61Г (а—86.2). Найти площадь ромба ABCD с углом tg ZB = = \/8 и диагональю BD = 3.
84
у/ 612 (б — 80.2). В прямоугольный треугольник периметром 36 вписана окружность. Найти стороны треугольника, если гипотенуза делится точкой касания в отношении 2 : 3.
613° (7 — 78.3). Сторона KN прямоугольника KLMN лежит на гипотенузе АС прямоугольного треугольника АВС, а вершины L и М — на катетах АВ = 3 и ВС = 4 соответственно. Найти стороны прямоугольника, если его площадь равна 5/3, а периметр — меньше 9.
у/ 614* (/3—85.4). На стороне AD треугольника AMD взяты такие точки В и С, что Z.AMC = Z.BMD = тг/2 и /ВМС = Найти площадь треугольника ВМС, если площади треугольников АМС и BMD равны р и q.
615 (б—99.3). Найти площадь параллелограмма ABCD с диагоналями АС = \/2а, BD = \/За и углом /ВАС = 60°.
у/ 616 (/3—80.4). Найти стороны параллелограмма ABCD периметром 26, если /В = 120°, а радиус вписанной в треугольник ABD окружности равен \/3-
у/ 617 (х — 78.4). Биссектриса угла А трапеции ABCD пересекает основание ВС в точке Е. Вписанная в треугольник АВЕ окружность касается сторон АВ = 2 и BE в точках М и N соответственно. Найти /BAD, если MN = 1.
у/ 618 (х—94.4). Найти периметр треугольника АВС с биссектрисой BD = 8\/7, если АВ = 21 и CD = 8.
у/ 619 (б—81.5). Диагональ АС вписанного в окружность четы-реугольника ABCD является биссектрисой угла А и пересекается с диагональю BD в точке К. Найти КС, если АК = 6 и ВС = 4.
620* (тг — 94.5). Диагонали вписанного в окружность четы-реугольника ABCD перпендикулярны и пересекаются в точ
85
ке К. Расстояние от точки С до середины отрезка AD равно 5/4, а от точки К до прямой ВС — 1/2. Найти AD, если АК = 1.
621* (б — 90.3). Окружность касается катетов АВ и ВС прямоугольного треугольника АВС в точках KhL соответственно, а ее центр О лежит на гипотенузе АС. Найти АК, если LC = 23/16 и АК : КМ = 5 : 23, где М — точка пересечения окружности с гипотенузой, лежащая между О и С.
у/ 622 (ср — 89.4). Хорда АВ круга с центром О пересекает радиус ОС = 2 в точке D. Найти радиус окружности, касающейся отрезков AD, DC и дуги АС, если OD = \/3 и Z.ADC = 2тг/3. 623* (/1 — 95.4). Диагонали вписанного в окружность четы-реугольника ABCD пересекаются в точке К. Расстояние от точки В до прямой AD равно 3, а площадь треугольника ADK равна 25/2. Найти AD и ВС, а также радиус окружности, если АВ = CD = 5 и AD > ВС.
624* (£ — 77.4). Найти углы описанной трапеции, если около нее можно описать окружность, радиус которой в д/3/2 раза больше 'высоты трапеции.
625° (х—81.4). Два шара радиуса г касаются друг другаи боковой поверности конуса, а также его основания — в точках, симметричных относительно центра. Найти объем конуса, если его высота в 4/3 раза больше радиуса основания.
у/ 626* (£ — 81.5). Площадь сечения правильной четырехугольной пирамиды плоскостью, проходящей через вершину ее основания перпендикулярно противоположному боковому ребру, вдвое меньше площади основания пирамиды. Найти отношение высоты пирамиды к боковому ребру.
Часть II
ГЕНЕРАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
Глава 3. МЕТОД ПЕРЕБОРА
Бабушка надвое сказала: либо будет, либо нет, либо дождик, либо снег.
§ 10. Расщепление уравнений и неравенств
Под расщеплением мы понимаем решение уравнения или неравенства вида
</>1(х)«... -<рп(х) V О
путем изучения знаков1^ каждого из сомножителей <fi(x).
При этом, естественно, возникает перебор случаев, который оформляется обычно одним из двух способов: либо каждый случай рассматривается отдельно — и тогда их в тексте решения желательно пронумеровать, либо все они рассматриваются вместе, в виде единой совокупности уравнений, неравенств, систем и т. п.
10.1. Расщепление уравнений
Для того чтобы произведение равнялось нулю, мало обнулить хотя бы один сомножитель — необходимо побеспокоиться о том, чтобы остальные сомножители при этом имели смысл.
Пример (д — 80.1). (х2 4- х — 6) у/х 4-1 = 0.
Решение. Рассмотрим два случая:
. (х2 4-х — 6 = 0 f (х 4-3)(х — 2) = 0 _
1) < о < о х = 2;
' [х + 1 > 0 [х -1
Понятие знака в данном контексте охватывает не две, а три возможности: положительность, отрицательность и нулевизна.
87
2) х 4-1 = 0 о х = —1.
Ответ: х = —1, 2.
627° (е — 86.3). v/Зх + 4 (9х2 + 21х + 10) = 0.
7 628° (А-83.1). (х 4-1) \/х2 — Зх — 6 = 2х 4- 2.
у/ 629° — 81.1). < x — у 4- \/x2 — 4j/2 = 2 x5 y/x2 — 4?/2 = 0.
630° (А-95.3). < x3 y/x - у =0 2y2 + у = 21 + 2xy.
631° (0 - 85.1). ...1.-$ 4-1 = —L- 5х-х2-6 2-х'
у/ 632 (А-79.1). При каждом а решить уравнение =
у 633 (тг — 00.1). X 1- l7-i _ i-a18 -X^ a:13 —1 ’
634° (А-00.1). 2 2-^ = 0..
635 (С - 97.2). 7 4^ = 1 + 3(|)\
у 636 (тг —92.3). £ L^±3+2*/2 + l = 0.
У 637 (А-88.3). (2х2 - 5х + 2) (log2x(18x) + 1) = 0.
638 (<р - 98.3). log3(7-6») _ 2 log3(2—a)
639 (А - 01.3). log8(-s) 1
loggC-5®-4) log3(a2—4a) _ log2 5
У 640 (е —00.3).
logs I®24-2®-2) log2(®24-2®-2)'
641 (С - 00.1). 3cos3x 4- = 3cosx.
у/ 642* (С-00.1). ^+6sin2x + l = 0.
У 643 (А-90.3). 1 — (2cosx4- \/3)ctgx = 2sinx.
у/ 644 (д-81.2). 4 x/sinx cos у = 0 2 sin2 x — cos 2y — 2 = 0.
10.2. Метод интервалов
Неравенство F(x) V 0, левая часть которого представляет собой стандартную функцию
F(x) = (х - zi)*1 (х - Х2)к2 •... • (х - хп)кп, ki е Z, решается так называемым методом интервалов, который сводится к организованному исследованию знаков функции F. Это иссле
88
дование производится путем последовательного прохождения интервалов, на которые разбивается числовая ось точками х»: лучше, конечно, двигаться справа налево, так как на самом правом интервале стандартная функция всегда положительна, а при переходе через очередную точку Xi она либо меняет знак, если соответствующая степень ki нечетна, либо не меняет, если эта степень четна.
Пример (х - 97.1). —i > 1.
Решение.
1--4<о <о (₽£48)...
Ответ:1<®<2.
Рис. 18
В разобранном примере можно было обойтись и без рисунка, поскольку знак дроби ^4 практически всегда2' совпадает со знаком произведения (® — 2)(х — 1), а это уже квадратный трехчлен (см. §6).
у/ 645 (тг —98.2).
646° (ст - 89.1).
647° (тг - 00.1).
648° (А - 96.1).
У 649° (х — 89.1).
650° (ст - 98.1).
651° (х - 94.1).
652° (0 - 00.1).
653° (А - 89.2).
654° (тг - 95.3).
655 (<р - 86.1).
656 (д - 77.1). v/657 (/3-84.1).
658 (V» - 89.1).
659 (х - 80.3).
(х2 — 4х)2 16.
»2.Т-5.£±4 > 0.
о—Ж
1 < 1
3—2® 1-
1 < X
х—96 ж—96*
ж+1 ж—3 1
Зж 2*
2ж-1 3*
2-Зж s г
°-
4х + 7 < |.
х + 3 + < 0.
2>3а исключением ситуации, когда дробь не имеет смысла, а произведение равно нулю.
89
660 (7 - 00.1). 661 (% —81.1). 662 (С - 96.2). 663 (С - 95.3). 664 (С - 97.2). У 665 (^-82.1). у/ 666 (у - 01.1). ,/667 (ст-00.3). У 668 (Л-95.1). У 669 (^-99.2). У 670 (% —99.1). Х х+5 ’ > 25(я + 2)- 2 ж—7 9 х—3 5—х’ х х—2 х — 1 х ' 2х < 1 х2—4 х+1 ’ 2ж—3 3—2» х 2х2— 4х ’ 3 । О з х—2 ж+4* + -J- > -1- »+6 ’ х—2 ж—3 ’ 7 । 9 I 1 П ж2-5»+6 »-3 1 U- 1 > 1 ж2+8®-9 3«2-5«+2- 1 9 l+1/х
У 671 (Л-01.1).
У 672* (^-90.3). У 673 (7 - 93.3). (_£ + 5 15_\2 > I \ 2^ 8 88—32»/ Найти область определения функции _z ч /4х — х2 — 4 /(ar) = V х^ + х-2-
10.3. Расщепление неравенств
Правила расщепления строгий неравенств восходят к известной поговорке: минус на минус дает плюс. Нестрогие неравенства расщепляются по тем же правилам с заменой в них всех строгих неравенств нестрогими. На практике, однако, довольно часто случается, что какой-то из сомножителей имеет вполне определенный или почти определенный знак. Это обстоятельство, конечно же, облегчает работу по расщеплению неравенства, но только при очень внимательном отношении к делу.
Пример (Л - 88.2). (х2 + 8х + 15) \/х + 4 > 0.
Решение. Рассмотрим два случая:
1) х + 4 = 0 х = —4;
. f х + 4 > 0 f х > —4 (=> х + 5 > 0)
2) S 9 О < / к, х 0x^-3.
'[х2 + 8х + 15>0 |(х + 3)(х + 5) >0
Ответ: х = —4, х —3. 3
3)Строгими считаются неравенства со знаками < и >, а нестрогими — со знаками и > .
90
674° (А - 94.6). 675 (<р - 98.1). |®| (а;4 - 2a;2 - 3) > 0. ж244а:43 а |х+1|
676 (А-98.1). х2+5х—6 А |«+4| <»•
677° (х —78.1). 678 (е - 86.3). 679* (а - 95.5). 680 (С - 96.2). (х — 1) \/х2 — х — 2 > 0. х/—25ж2 + 15а; - 2 (8а;2 - 6а; + 1) 0. — х2 — 3 (V2cosx — х/1 4“ cos2z) > 0. ж—2 А жаДО+Зж—х$
681 (/? — 01.1). Ух2+5х—84 >> а х—7 и‘
682 (а —01.1). х/2ж2-5ж-3 < а б+Зх/Зж-2х2 ’
683 (м-81.1). у/х—5 п logy2 ‘
684 95.2). •уЛс2 —16 а 1—log3(7—а:) > °-
685 (7 - 98.1). а/4ж2- 13ж+3 +1 а l0gx/4 3
686 (х —84.1). 687 (А-99.1). “Ч(2;ж) > о. хл—о — Найти область определения функции / т 4- 2 = V т 4. ъ + !)• V х । о
10.4. Разные задачи, связанные с расщеплением
В следующих задачах читатель столкнется не только с войро-сами расщепления неравенств, но и с некоторыми другими, в частности, с выбором новой переменной.
Пример (А - 98.5). log1/3(х - 2) logl + 1-
Решение. ... _ 2Z2^3i-2 \ <=> , г 0, где 1 = log1/3(x - 2), 0 >0
(рус. 19) 1о81/з(а' 2) 2 0 < я 2 1/9
-1/2 log1/3(x -2)<0 1<х-2^\/3
Ответ: 2 < х 19/9, 3 < х 2 4- \/3.
688° (С - 80.4). 2®"1 > (1/16)1Д.
689° (С - 97.5). З*"3 <
91
Рис. 19
690° (С - 98.3). 4^ < ^83*~7.
У 691 (V> - 90.2). (I)27*’1 + i (|)1/ж < |.
692 (x -95.3). 2^ <2^ + 1.
л/ 693 (C- 99.2). |2-^j|<3.
у/ 694 (£ — 01.3). log3(x3 + x2 - 2x) — 2 log9(x2 - x) log3 5.
695 (X-82.2). log1/4 f=| >-1.
л/ 696 - 01.2). log2 log1/2 |f±| 0.
у/ 697° (£ - 82.2). Найти все а, при которых уравнение 5х — 17а = 21 — 5ах
имеет корень, больший 3.
у/ 698° (х - 96.1). уД2х + I)4 - (2х + I)2 + (2® + I)2 0.
у 699 (А-77.1). И-З*-1—31 > е 4-9а'-11-3*-1-5 и‘
у/ 700* (х- 91.3). 491о8« 5 _ 7!og. 5 _ 2 > о.
701 (д-95.2). ^ТГ>-3
log2 X
702 (0 - 87.3).
703 (V» — 86.3). Ш>4
704 (<р - 00.3). 1 । 1 < 2 log2 X ' 2-log2 х
705 (0 - 85.3). 1 1 logsC3-2®) 4—log5 (3—2ж) ’
у/ 706 (А-96.4). 1 < 1 log9(-27х) " log3 (-®) •
у/ 707 (х —98.1). 1 4 > k>g2 f - 1. 10б2 J 8
708 (А-90.4). logi/б аг15 ~ 2 < 7 log125 х12 log,
709 (7 - 92.3). (log, 2 - 1) log2 2x > 3/2.
у/ 710 (0 - 01.3). 1О£>2 x —3 << О 61og. 2-1 -4-
92
711 (х- 87.3).
У712 (д-00.1).
713 (х- 94.3).
1ое(г+1)2 8 + 31og4 (х + 1) > 37/4.
log4a.2 х2 log8l4 х4 1.
Найти все отрицательные решения неравенства
1 , > 1
1°ёз cos х 8 log3
714 (тг - 98.3).
У 715 (ст - 99.5).
716° (А - 97.3). у/ 717° (А-91.3).
718° (тг - 96.3).
,/719 (7-90.3).
|®+1|-1 |х+1| —2'
22+v/®rT - 24
2i+7®=T
у/ 720* (х - 99.2). (2х + 10/ж) |loga_3/2(x2 - 4х + 4)| 9|loga._3/2(a:2 -4х + 4)|.
у/ 721* (д—99.5). Найти все а, при которых множество решений неравенства
а + 2 —2Ж-2 5а + 5
а + 3 2(2» + За + 3)
содержит какой-либо луч на числовой прямой.
§11. Перебор случаев
Логическая природа задач настоящего параграфа такова, что при их решении идея перебора случаев оказывается как нельзя кстати.
11.1. Раскрытие модулей и метод интервалов
Если раскрывать модуль по определению
1°1 =
а,
—а,
а > О, а < О,
то приходится разбирать по меньшей мере два случая1^. Условие, которое при раскрытии модуля накладывается на стоящее под ним
^Атои три: иногда нулевое значение лучше как раз не подключать к положительным или отрицательным, а рассматривать отдельно.
93
выражение, желательно не оставлять без внимания, а включать
в систему с результатом раскрытия этого модуля.
Пример (д — 84.1). х2 + Зх 4- |х 4- 3| = 0.
Решение. Рассмотрим три случая: .
1x4-3 >0 1x4-3 > 0
2) S z . ч О S <=> х = -1;
^х(х 4- 3) 4- (х 4- 3) = 0 ^х 4-1 = 0
оЧ Гх4-3 < 0 Гх4-3 < 0
3) < ч ч о < — решении нет.
7|х(х4 3)-(х43) = 0 [х - 1 = 0
Ответ: х = —3, —1.
При раскрытии нескольких модулей сразу можно сэкономить на числе рассматриваемых случаев с помощью метода интервалов (см. п. 10.2): для этого достаточно отметить на числовой оси точки,
в которых обнуляются или теряют смысл выражения под модулем, и определить знаки выражений на каждом из полученных интервалов.
722° (х - 00.1). |®| = 2 — х.
723° (А - 90.1).
724 (а - 98.3). 3|ж| —11 3x414 х—3 " 6-х *
725 (а - 01.1). 1 . 1 \ о х41 + |®| .
У 726 (е-85.2). ®log1/2(l/3 - х) > |®|.
727° (е - 81.1). х2 — 6х + 8 + |® — 4| = 0.
728 (е - 00.1). 3|® + 2| + х2 + 6® + 2 = 0.
У 729 (х —98.1). 9«» \ 5x43 ' |х42|‘
730 (0 - 99.2). ^>2x4-5.
731 (7 - 00.2). |2® + 8| — |® — 5| = 12.
732 (J3 - 95.2). |® — 1| + |2® — 3| = 2.
733 (s-84.3). 2|® - 4| + |3® + 5| 16.
У 734 (7 - 96.1). |5® — 3| — |7® — 4| = 2® — 1.
735 (^ - 91.3). 1*+1|+1»-2| < I х4199
у/ 736 (А-85.3). k~2l I
737 (а-92.3). 4-2|а:+4|
738 (£-87.3). с4 V/ Н ’"t Н м 1 । еч н
94
У 739 »-79.3). и^-гЯх + 21.
У 740 („-88.2). pl-21 +’I»+ 4 = 4.
I 2х — у = 3.
У 741 (а - 97.2). 4|х + 1| - 1 = 3|2х + 5| - 2|х + 5|.
У 742 (0 - 98.1). |х2 + х - 2| + |х + 4| х2 + 2х + 6.
У 743 (д - 98.1). 3 з/|х + 1| -3 > у/х2 - 2х - 3.
744 (д - 98.1). 22х - 2х+2 + |2Х - 1/2| = -7/2.
у/ 745 (7 — 01.2). | cosx| — x/3sin(97r/2 + х) = 1.
у/ 746 (s - 00.1). Ъу/х2 + 2х + 1 = 7 + х + (х/-х2 - 5х - 4 )2 .
у/ 747 (С - 00.5). 2^1og2(x - 2) = 3 - log2(2x + 1). .
yj 748 (д - 98.3). 3 • 2COS1+3 у/'-™2* + 11 • 22cosх - 34 = 0.
У 749* (£ — 92.7). Нечетная функция /, определенная на всей числовой прямой, задается формулой
2 f(x) = 1----7= при X > 0.
у/Х
Какой формулой задается эта функция при х < 0? Решить уравнение f(x) = 0.
у/ 750* (тг — 00.6). Функция /, определенная на всей числовой прямой и периодическая с периодом 8, задается формулой f(x) = 8х — х2 при х 6 [0; 8].
Решить уравнение
f(2x + 16) + 23 = 5f(x).
У 751* (б — 97.5). Нечетная функция /, определенная на всей числовой прямой и периодическая с периодом 4, задается формулой
/(ж) = 1 — |х — 1| при 0 х 2.
Решить уравнение
2/(я)/(я - 8) + 5/(х + 12)4-2 = 0.
752* (б — 97.5). Нечетная функция /, определенная на всей числовой прямой й периодическая с периодом 4, задается формулой
f(x) = 2х(х 4- 2) при — 2 х < 0.
95
Решить уравнение
2/(—3 - а;) - 3
753* (х - 01.6)2). [а; + 1/2] = х6/2 - [аг].
11.2. Исследование основания логарифма или степени
Если основания степени или логарифма зависят от неизвестной величины, то при их отбрасывании (см. п. 1.3 и 3.2) приходится рассматривать случаи, когда эти основания больше или меньше единицы3). Условия, накладываемые на основания, естественнее всего включать в систему с результатом отбрасывания.
Пример (7 - 85.2). log^ (3 - х) > 1.
Решение. Рассмотрим два случая:
I т 1
1) I & 1 < X < 3/2;
[3-я;>х>0
{О < х < 1 _ /Л .
=> 3/2 < х < 1 — решении нет.
О < 3 — х < х
Ответ: 1 < х < 3/2.
754’ (7 - 94.3). У 755 (<р —92.2). 756 (<р - 90.2). 757 (е —93.1). 758 (а-91.5). 759 (тг - 96.2). /760 (х —96.2). /761 (х —81.2). log,. (2 - х - а;2) > 0. log^ (20а: + За:2 — х3) 3. 1°ёх-2 (Зх - а:2) < 2. Iog8»-i9 < 2. l°giogl/2llog1/7a:>0. I°g4»-X2 х = log12_3x X. ioS2X+3(x ~ 2)2 = logl/e+i/2 (® - 2)2. = (3a: - 5)logvas (2+5»-»a). (Xv+4x = 2/5(^”®/3)
762* (е - 77.3). < x3 = у-1 1 x > 0.
2) Через [ж] обозначается целая часть числа х, т. е. наибольшее целое число, не превосходящее х. Например: [тг] = 3, [—тг] = —4.
3) Случай равенства единице также бывает содержательным.
96
11.3. Зависимость от параметра
Действия или рассуждения, применяемые при решении задач с параметрами, могут зависеть от того, какие именно значения принимают эти параметры, — тогда возникает перебор случаев.
Пример (£ — 97.7). Найти все а, при которых неравенство 10go(®2 + 4) > 1 выполняется для всех х.
Решение. Рассмотрим два случая:
1) а > 1: х2 4- 4 > а — верно при любом х а < 4;
2) 0 < а < 1: 0 < х2 4-4 < а — не верно, например, при х = 0.
Ответ: 1 < а < 4.
763 (С - 96.7). При каждом а решить неравенство 2 - logo х < loga(x - 1).
764 (С - 98.7). При каждом а решить неравенство loga(3a® - 5) < х 4-1.
765 (С-99.8). При каждом а решить неравенство log2o log3 х2 > 1.
766 (д - 92.3). По данным числам а = log^ х и b = log2 х
найти logvxyz (yz/x3)2.
767 (х —82.5). При каждом а решить уравнение |я 4- 3| — а^х — 1| = 4.
768 (А-91.6). При каждом а решить уравнение |я 4- 2| 4- а\х - 4’| = 6.
769* (С-84.4). Найти все а, при которых уравнение 2|я — а| 4- а — 4 4- х = 0
имеет хотя бы один корень, причем все его корни принадлежат отрезку [0; 4].
770* (/1 — 98.6). Найти все а, при которых уравнение (х2 — (а + 1)я 4- 3(а — 2)) \oga_x(2a - х — 1) = 0 имеет хотя бы один корень на отрезке [—1; 2], а вне этого отрезка корней не имеет.
4 И. Н. Сергеев — Математика
97
у/ 771° (б — 78.3). Найти все а, при которых система
ах 4- 2у = а 4- 2
1 2ах 4- (а 4-1)1/ = 2а 4- 4
имеет хотя бы одно решение.
у/ 772 (/1 — 95.3). Найти все а, при которых любое решение системы
X-a2 log3 у = 1
х + За log3 у = 1
удовлетворяет неравенству у > 1 — х.
У 773* (/1 — 86.5). Найти все а, при каждом из которых для любого b система
{х — by 4- az2 = О
2Ьх 4- (Ь — 6)1/ — Sz = 8
имеет хотя бы одно решение.
у/ 774 (7 — 92.2). Найти все тройки (а, 5, с), при которых уравнение
ах2 4- Ьх 4- с = О
имеет единственный корень х = — 1, причем
а 4“ Ь 4“ с = 1.
775 (7—96.5). Найти все пары (а, 5), при которых ненулевые векторы
и = (а(2 — 6), 2а — 3, а(Ь — 2)) и v = (2 — b, а — 2, b — 2) . коллинеарны, но не равны. Найти все а = 5, при которых эти векторы перпендикулярны.
у/ ТТЪ* (тг — 01.4). Существует ли арифметическая прогрессия, у которой сумма любого числа первых членов равна утроенному квадрату этого числа?
у/ 777* (а—98.5). Найти все натуральные п, при которых арифметическая прогрессия не восстанавливается однозначно по ее семнадцатому члену и сумме п первых членов.
11.4. Перебор вариантов в текстовых задачах
Для отбрасывания посторонних значений искомой величины в текстовых задачах иногда требуются дополнительные соображения.
98
Пример (7 — 78.1). Пароход спустился вниз по реке на 60 км до устья впадающего в реку притока и поднялся вверх по притоку на 20 км, потратив на весь путь 7 ч. Найти собственную скорость парохода, если скорости течения реки и притока равны по 1 км/ч.
Решение. Если х км/ч — скорость парохода, то
= 7 => 6°(® - 1) + 20(® + 1) = 7(x2 - 1)
=> 7х2 - 80х 4- 33 = 0 => (х - 11)(® - 3/7) = 0 => х — 11, так как х > 1.
Ответ: 11 км/ч.
Неожиданные трудности возникают, когда альтернатива содержится непосредственно в условии задачи, отчего оно трактуется неоднозначно и уже этим порождает перебор вариантов.
778° (х — 94.3). Найти первый член геометрической прогрессии, если произведение второго и четвертого ее членов равно 25, а сумма третьего и пятого равна —15.
779 (ст — 99.2). Найти разность арифметической прогрессии и первый ее член, если его квадрат равен сумме первых пяти членов прогрессии с нечетными номерами и на 1 больше суммы первых пяти членов с четными.
у/ 780* (/2 — 99.2). Сумма членов конечной геометрической прогрессии, первый член которой равен 1, а знаменатель положителен, равна 40/27. Сумма тех же членов с чередующимися знаками (первый член с плюсом, второй — с минусом и т. д.) равна 20/27. Найти знаменатель прогрессии.
у/ 781 (А — 86.4). Студенческий стройотряд за 820руб оборудовал прямоугольную спортплощадку площадью 0,1га, установив с противоположных, более длинных, сторон трибуны, а с двух других — проволочную сетку. Стоимость установки одного погонного метра трибун и сетки равна соответственно 7 руб и 3 руб. Найти длины сторон площадки.
у/ 782* (б — 81.5). В двух сосудах емкостью по 15 л каждый находилось всего 15 л спирта. Первый сосуд долили доверху водой, после чего второй сосуд долили доверху смесью из первого. Затем из второго сосуда отлили в первый 6 л смеси, после чего во втором сосуде оказалось спирта на 1л меньше, чем в первом. Сколько литров спирта было первоначально во втором сосуде?
783° (А — 85.3). Первый рабочий изготовил 60 деталей на 3 ч быстрее второго. За сколько часов второй рабочий изготовит
99
4*
90 деталей, если, работая вместе, они изготавливают 30 деталей в час?
у/ 784 (ср—79.4). Производительность трех линий, работающих вместе, в полтора раза выше, чем производительность первой й второй линий вместе. Задание для первой линии вторая линия выполняет на 2 ч быстрее, а вторая и третья вместе — еще на 2 ч 48 мин быстрее. За сколько часов выполняет это задание первая линия?
785 (х — 78.2). Из пункта А в пункт В выехал грузовой автомобиль. Через час вслед за ним выехал легковой автомобиль, который прибыл в В одновременно с грузовиком. Если бы они выехали одновременно из пунктов А и В навстречу друг другу, то встретились бы через 1ч 12 мин после выезда. Сколько часов провел в пути грузовик?
786 (тг — 82.1). Легковой и грузовой автомобили двигались по шоссе навстречу друг другу. За полчаса до встречи расстояние между ними равнялось 75 км. Найти скорость легкового автомобиля, если он проезжает 90 км на 20 мин дольше, чем грузовой — 40 км.
у/ 787 — 88.4). Из пунктов А и В навстречу друг другу од-
новременно выехали легковой и грузовой автомобили. Встретившись через 4 ч, они продолжили свой путь, и легковой автомобиль прибыл в пункт В на 6 ч раньше, чем грузовой — в пункт А. Сколько часов провел в пути грузовик?
788 (/? — 86.3). Два лыжника вышли со старта одновременно по одному и тому же маршруту, причем скорость первого лыжника составила 7/6 скорости второго. Через 20 мин вслед за ними со скоростью 18 км/ч отправился третий лыжник, который догнал второго на 30 мин раньше, чем первого. Найти скорость первого лыжника.
у/ 789 (е — 85.5). Два пешехода вышли из пункта А в одном направлении с интервалом в 40 мин и прибыли в пункт В с интервалом в 10 мин. Если бы они вышли одновременно, то прибыли бы в пункт В с интервалом менее, чем в 50 мин. Сколько времени был в пути каждый пешеход, если скорость одного из них вдвое больше скорости другого?
У 790* (/1 — 87.4). Два поезда выехали одновременно в одном направлении из городов А и В, расстояние между которыми равно 60 км, и одновременно прибыли на станцию С, располо
100
женную на прямой АВ. Обратный путь каждый из них проделал ровно на 2 ч быстрее, поскольку один из них увеличил скорость на 25 км/ч, а другой — на 20. Найти первоначальные скорости поездов.
791* (х — 01.3). Из пункта А в пункт В, расстояние между которыми равно 180 км, выехал велосипедист и одновременно с такой же скоростью из В в А — другой. Когда расстояние между ними было меньше 70 км, первый велосипедист увеличил скорость на 10 км/ч, затратив в итоге на весь путь 15 ч. Если бы он сразу ехал с увеличенной скоростью, то встретил бы второго на Зч раньше. Найти первоначальную скорость велосипедистов.
792* (V> — 00.3). Первый трактор вспахивает поле втрое быстрее второго и на 2 ч быстрее третьего, а все вместе они вспахивают поле за 7 ч 12 мин. Найти наименьшее время , за которое они могут вспахать два таких поля, если для переезда с одного поля на другое любому трактору требуется 40 мин.
11.5. Целочисленный перебор
Если неизвестная величина принимает только целочисленные значения, то в принципе для решения задачи достаточно, ограничив эти значения с двух сторон, свести задачу к конечному перебору. Однако использование уравнений или неравенств позволяет порой существенно сократить перебор и тем самым значительно облегчить решение.
Пример (а—91.4). Ученик перемножил два данных натуральных числа и допустил ошибку, увеличив цифру сотен на 1. Поделив для проверки полученный результат на меньшее из данных чисел, ученик получил в частном 32 и в остатке 4. Н&йти данные числа, если их разность равна 10.
Решение. Если х — меньшее из чисел, то
х(х 4-10) 4-100 = 32ж 4-4 => х2 — 22х 4- 96 = 0
=> (х — 6)(ж — 16) = 0 => х = 16,
т.к. если х = 6, то в произведении
х(х 4-10) = 6 -16 = 96
нет цифры сотен.
Ответ: 16 и 26.
793° (<£—91.1). Разложить число 1991 на простые множители.
101
794° (</? — 82.2). Найти все решения неравенства log1/3 \/5х + 26 log1/3 (ж + 4), для которых число х 4-1 /2 — целое.
795 (б — 83.4). Сколько точек с целочисленными координатами находится строго внутри фигуры, ограниченной,линиями х = 3/2, х = 129, у = log2 х и осью абсцисс?
у/ 796 (ст — 86.5). Найти все целочисленные решения системы
2х2 4- 2у2 4- 24я - 28?/ 4-167 < О х 4- 2у < 15/2.
797° — 84.6). Найти все трехзначные числа, у которых
вторая цифра вдвое меньше третьей, а сумма самого числа с числом, получающимся из него перестановкой первой и третьей цифр, делится на 10.
У 798 (/1 — 01.4). Найти все трехзначные натуральные числа, которые больше суммы квадратов своих цифр ровно на 517.
у/ 799 (</? — 00.6). Расшифровать ребус
* 4- * = Л
— X :
* 4- * — О
в котором буквы и зведочки обозначают цифры, причем разные буквы — разные цифры.
800 (ср — 98.4). А, И, Б сидели на трубе в указанном порядке. К ним стали подсаживаться другие буквы так, что порядковый номер очередной буквы в русском алфавите равнялся сумме цифр порядковых номеров двух предыдущих букв. С некоторого момента буквы стали циклически повторяться. Какая буква в цикле встречалась наиболее часто? Может ли цикл при каких-либо других начальных буквах состоять из одной буквы? Если да, то из какой?
у/ 801° (х—01.2). Сумма первых четырех членов целочисленной арифметической прогрессии равна 56, а ее двенадцатый член больше 67, но меньше 74. Найти двадцатый член прогрессии.
802 (/3 — 01.4). Два спутника с одинаковыми скоростями летали по круговым орбитам, причем каждый делал один оборот за целое число часов. Раньше чем через 50 ч, но позже чем
102
через 42 ч после начала наблюдения первый спутник сделал 4 оборота, а второй — 5, причем разрыв между этими событиями составил более часа. Найти отношение радиусов орбит.
у/ 803 (б — 00.2). Интервалы движения городских автобусов по трем маршрутам, проходящим через общую остановку, составляют 15, 20 и 24 мин соответственно. Сколько раз в день с 7.55 до it.05 на этой остановке одновременно встречаются автобусы всех трех маршрутов, если одна из таких встреч происходит в 12.35?
804* (/1 — 00.3). По дороге длиной 2 км, соединяющей пункты А и В, курсируют без остановок два автобуса. Достигнув пункта А или В, каждый из автобусов немедленно разворачивается и следует к другому пункту. Автобусы стартуют одновременно из пунктов А и В и движутся со скоростями 51 км/ч и 42 км/ч соответственно. Сколько раз за 8 ч движения автобусы поравняются друг с другом:
1) в пункте В;
2) строго между пунктами А и В?
у/ 805 (б — 86.3). Воздушную линию обслуживают самолеты трех типов. Каждый самолет первого, второго и третьего типа может принять на борт соответственно 230, 110 и 40 пассажиров, а также 27, 12 и 5 контейнеров. Все самолеты линии могут принять на борт одновременно 760 пассажиров и 88 контейнеров. Найти число действующих на линии самолетов каждого типа, если их общее число не превосходит 8.
у/ 806 (б — 83.5). На факультет подано от школьников на 600 заявлений больше, чем от производственников. Девушек среди школьников больше, чем среди производственников в 5 раз, а юношей среди школьников больше, чем среди производственников, в п раз, где п — целое число и 6 п 13. Найти общее количество заявлений, если среди производственников юношей на 20 больше, чем девушек.
807 (б — 86.5). За несколько дней работы один рабочий изготовил больше другого на п деталей, где 127 п 132. Если бы второй рабочий увеличил свою производительность вдвое, то он за то же время изготовил бы на 77 деталей больше, чем первый. Найти производительности рабочих, если каждая из них выражается целым числом деталей в день.
у/ 808 (/1 — 00.2). Игорь и Петя ходили за грибами: Игорь нашел 35 грибов, среди которых было несколько подосинови
103
ков, а Петя грибов не нашел. Игорь взял себе белые грибы, а остальные отдал Пете. Петя, обнаружив среди них червивый подберезовик, выкинул его. Сколько было найдено подосиновиков, если их доля в грибах, принесенных домой Петей, оказалась равной доле белых в грибах, найденных Игорем?
у/ 809* (а — 98.6). Ученик перемножил два данных натуральных числа и допустил ошибку, увеличив произведение на 372. Поделив для проверки полученный результат на меньшее из данных чисел, ученик получил в частном 90 и в остатке 29. Найти данные числа.
810 (х—82.4). Имеется два проекта застройки микрорайона: по первому предполагается построить несколько одинаковых домов, содержащих в общей сложности 12 096 квартир, по второму — на 8 домов больше, также одинаковых, но с ббльшим числом квартир в каждом и содержащих в общей сложности 23625 квартир. Сколько домов предполагается построить по первому проекту?
у/ 811 (а — 00.6). Найти сумму всех натуральных чисел п, для которых числа 5600 и 3024 делятся соответственно на п и п+5.
812 (е — 90.4). Найти натуральные числа а, Ь, с, образующие возрастающую геометрическую прогрессию с целочисленным знаменателем и максимальной суммой, при условии, что Ь и с — делители чисел 2240 и 4312 соответственно.
813* (х — 78.4). Множество содержит более семи различных, попарно не взаимно простых натуральных чисел. Найти эти числа, если их наименьшее общее кратное равно 210, а произведение делится на 1920 и не является квадратом целого числа.
§ 12. Развитие метода интервалов
Метод интервалов, обсуждавшийся ранее в п. 10.2 и 11.1, допускает ряд обобщений. Предлагаем некоторые из них (см. также п. 14.3).
12.1. Обобщенный метод интервалов
Пусть левая часть неравенства F(x) V 0 — не стандартная функция (см. п. 10.2), но произведение
104
элементарных функций, не обязательно вида <pi = (x — Xi)ki. Тогда можно применить так называемый обобщенный метод интервалов: отметить на числовой оси все точки, в которых сомножители обнуляются или теряют смысл, и на каждом из образовавшихся интервалов определить знак1) функции F.
Существует и более продвинутый метод решения таких неравенств2), а именно, метод замены множителя: любой неудобный сомножитель <pi заменяется более удобным, имеющим тот же знак (но, возможно, другой модуль), а если в результате такой замены расширяется ОДЗ, то в систему с полученным неравенством включаются и пропавшие ограничения на неизвестную величину.
Пример « - 94.1). 0.
Решение.
... (т к- энак log2 и совпадает ( 0^
(а: + 2 > 0 со знаком и — 1 при и > 0) (а: > —2
Ответ: — 2 < х < —1, х 1/2.
Советуем читателю тщательно продумывать3^ те правила, по которым он будет заменять множители в следующих задачах.
814° « - 93.1).
815° (С-01.1). у/ 816° (А-95.4). У 817° (д-83.1). х/818° (тг —80.4). х/819 (д-88.2), х/820 (д-89.2).
х/ 821 (е-00.3).
822 (тг —01.3).
823 (д - 91.2).
824 (е - 98.1).
825 (д-98.2).
2»-1 <- 0
2«-1 и-
2^18
3*—2 < п
а/6+s—ж2 у/б+ж—ж2
2ж+5 ж+4
(4а:2 — 16а: + 7) log2 (а: — 3) > 0.
^5г_412 4"г > 0.
log., (1—2ж—ж2) > р
>ов8_^(«+1+^)
1о$8(**-в*+5) < ...
logat*3) log2(i2-3) ’
logx-2 X 10gx_2 4.
loga (l-3»/2) > .
log9 (2«) ' '
log3_2a!(14a: - 2a:2) 0.
log 2»+2 (10a:2 4- x — 2) 0.
1)Его постоянство на таких интервалах обеспечивается непрерывностью функции F (вытекающей из элементарности функций ^t ).
2) Позволяющий свести обобщенный метод интервалов к стандартному и потому лишенный тех неприятностей, которые могут возникнуть при определении знака функции.
3)И непременно формулировать в тексте решения в виде пояснений!
105
826 (тг - 89.3). 827 (д-97.2). У 828 (/? - 79.4). у/ 829 (х —98.2). у/830 (д-97.2). У 831 (тг-00.4). У 832 (х —97.2). logx+i (2х2 -Зх + 1) ^2. iog.+1 <1- (х2 + х — 6)2 4. log2 (5 - х) logx+11 -6. (1 - f) 1°613-3-2* 4 < 1. logj 2 < log6_a 2. log^ 2 ss log2a.21
833 (( - 99.3). У 834 (<д - 01.2). 835* (д-94.3). 2 < 1 log3(x+l) log9(x+5)’ 1 > 1 t 1 logi/ia(2®2-l) " logi/4* logi/з*’ 1°б2-5а;3+ log2 (2-5x) "« loge (6z2-6z+l) ’
836° (( - 93.5). l*+3|+* > 1 ®+2 >
у/ 837° (д-97.1). ,/838 (е-99.1). 21—2* —2g~a —13—2a | 1 5-|3-2* | logk|_2 - 3|0.
У839* (д-98.2). i+logy'S %/s+4+logi/2(13—a) - |x2+2«-3|-|2x2- 10aH-8|
У 840* (а-00.4). У 841* (%—99.6). (4 - a;)®2-9 - sin2 10° < (4 - ®)10^ю» . При каждом a G [—1; 0] решить неравенство lo&z+ate2 - (a + 1)® + a) > 1.
842* (х — 01.6). Функция f определена на всей числовой прямой, возрастает и принимает только отрицательные значения. Решить неравенство
2/(ж2—2ж—112)+|У(ж2—2ж—112)—3/(—2ж\/32—2ж)| (зУ(-2«х/32-2а:-112)-2У(-2я:х/32-2я:))7
12.2. Метод областей
Дальнейшее развитие метода интервалов, обобщенного однажды в п. 12.1, состоит в переходе от координатной прямой к координатной плоскости (см. п. 5.7), в результате чего этот метод преобразуется в метод областей.
В новой ситуации исследуемые выражения зависят не от одной, как прежде, а от двух переменных: точки, в которых эти выражения обнуляются или теряют смысл, теперь собираются в кривые4\
4)В частности, прямые.
106
а интервалы, на которые ранее точки разбивали числовую прямую, теперь превращаются в области, на которые кривые разбивают плоскость5^.
В следующем примере исследование фигуры, заданной на координатной плоскости неравенством, сильно упрощается вследствие того, что при любом раскрытии модулей это неравенство становится линейным, а значит, граница фигуры есть ломаная.
Пример (Л — 81.4). Найти площадь фигуры, заданной неравенством
|y-l| + |j/-a:|
Решение. Рассмотрим два случая:
1)у = 1: — ж| 4 о |ж — 1|^4 1 —4^х^1 + 4;
2) у = х : — 1|^4 О |х — 1|^4 о 1—4^х^1+4.
Данная фигура — четырехугольник ABCD (рис. 20), диагонали которого делятся точкой пересечения О пополам. Следовательно, это параллелограмм и
Sabcd = АВ • BD = 4 • (4 4- 4) = ...
Ответ: 32.
Рис. 20
у/ 843 (А — 99.3). Найти площадь фигуры, заданной системой
< У (я - У - л/З) > о х2 + у2 3.
5)Если исследуемые выражения задаются элементарными функциями, то каждое из них в каждой из полученных областей будет иметь постоянный знак.
107
844 (е — 91.5). Найти площадь фигуры, заданной неравенством (х2 + у2 - 1) (х2 + у2 - X - у) 0.
у/ 845* (тг — 96.6). Найти площадь фигуры, заданной неравенством
lOgg2±y2 (х -у) > 1. 2~
846 (х — 83.3). Найти площадь фигуры, заданной неравенством
2|ш — 1| + |2/ + 2ж — 1| ^5.
у/ 847 (б—94.4). Найти уравнение наименьшей окружности, которая ограничивает фигуру, заданную неравенством
|2t/ 4- Зя - 2| 4- |3я 4- 6| < 6.
848* (е — 96.6). Найти все а, при которых площадь фигуры, заданной неравенством
|2я4-т/| 4- |я -т/4-3|
равна 24.
У 849 (А — 95.8). Найти площадь фигуры, заданной неравенством
х2 4- у2 4- 6(я - \у\) 0.
^/850 (б — 88.4). । Найти площадь фигуры, заданной неравенством
|</ - я2/2| 4- |t/ 4- я2/2| 2 4- х.
д/851* (7 — 00.6). Найти наименьшее а > 0, при котором система
ffl + |t/| = 2 [я2 4- у2 = а2
имеет ровно четыре различных решения. При этом а найти площадь фигуры, заданной неравенством
2|х| + |у|-2
х2 4- у2 _ а2
852* (тг — 00.4). Решить систему
< \х — у\ — х = 2 |3ж - у| + х = 2
и изобразить множество решений на координатной плоскости.
108
853* (б — 82.5). Изобразить на координатной плоскости множество решений уравнения
22/+ |2/-3/ж| = 4 ~ |3/ж - 1|
и найти все точки этого множества, имеющие наибольшую ординату.
у/ 854* (/2—01.6). Найти все а, при каждом из которых графики функций
разбивают координатную плоскость ровно на пять частей.
§13. Разложение на множители
Надеемся, что читатель уже давно оценил по достоинства силу операции разложения на множители. В настоящем параграфе эта операция будет находиться в центре внимания.
13.1. Разложение с помощью формул тригонометрии
Формулы тригонометрии (см. §2) позволяют расщеплять самые разные уравнения.
Пример (х — 78.). sin х 4- sin Зх = 3 cos2 х.
Решение.
... 4Ф 2 sin 2х cos х = 3 cos2 х О 4 sin ж cos2 х = 3 cos2 х
о / . . л cos X — 0
<=> cos2 x(4smx — 3) = 0 <=>...
v ' [ sin ж = 3/4
Ответ: х = ^ + im, (—l)fc arcsin | 4- тгА:, где п, к € Z.
855° (тг—94.1). 856° (£-83.1). 857° (V» - 84.3). 858 (А-00.2). 859 (С-98.1). 860 (£ — 89.3). sin3 х — sin2 х = sin2 2х. 4 cos3 х 4- 3\/2 sin 2х = 8 cos х. 2 sin х(5 4- cos 2х) = 5\/2 sin 2х. 2 sinх = 3cosхsin j. 4 cos x cos 2x sin 3x = sin 2x. sin x(3 sin 2x sin3 x 4-12 sin 2x sin x — 16 cos x) 4- 4- 2sin4x = 0.
861 (£-97.2). 862 (х —88.2). 863 (х - 85.1). sin 2x — sin 4x = (cos 2x 4-1) cos 3x. cos 7x 4- cos x = 2 cos 3x(sin 2x — 1). 4(sin6x 4- sin4x) = cosx(4sin2 5x — 5).
109
864 (у> - 78.3).
У 865 (х - 79.1). у/ 866 (тг - 89.2). у/ 867 (>3 — 01.2).
У 868 (а-98.1).
У 869 (а-91.3).
870 (А - 77.3).
871* (7 - 80.4). у/ 872* (7 - 80.4). у/ 873* (£-77.4).
5 sin х + 6 sin 2х + 5 sin Зх + sin 4a: = 0.
sin 2x — cos 2x = 1 + y/2 cos x.
a/3cos2 x — 2 sin 2a: cos 2a: — x/3sin2 x = 0.
cos(2a: — тг/З) — sin x = 1/2.
sin2 x + sin2 6x = 1.
cos2 (тг/4 + x) = cos2 (тг/4 — x) + t/Scosx.
sin2 (2 + 3x) + cos2 (тг/4 + 2a:) =
= cos2 (2 — 5a:) + sin2 (тг/4 — 6a:).
sin6 x + cos6 x = Ц cos 2a: — |.
sin8 x — cos8 x = | cos2 2x — | cos 2x.
x/2cos(x/5 — тг/12) — \/6sin(a:/5 — тг/12) = = 2 sin (я/5 4- 2тг/3) — 2 sin (Зя/5 4- 7r/6).
13.2. Дублирование корней в ответе
При решении следующих тригонометрических уравнении читателю, с целью тренировки, рекомендуется устранять в окончательном ответе дублирование одних серий корней другими1 \ Это можно делать, анализируя получаемые формулы корней, но лучше, конечно, заранее анализировать сами уравнения.
Пример (тг — 78.1). cos х = cos Зх 4* 2 sin 2х.
Решение.
... <=> 2 sin 2ж sin ж—2sin2s = 0 <=> sin2s(sins—1) = 0 <=> sin2s = 0 (т.к.: sins = l => coss = 0 => sin2x = 2sinxcosx = 0)
<=> 2x = 7гп, где n G Z, <=>...
Ответ: x = тгп/2, где n G Z.
874° (/3-82.2).
У 875 (7-82.2).
876 (x — 96.1).
877 (C - 90.3).
у/ 878 ((p-81.1).
879 (x-00.2).
sin2 х 4- COS2 Зя = 1.
sin х sin Зя 4- cos 4я = 0.
sin 5я — sin я cos 4я = 0.
sin я sin 5я = cos 4я.
зт(2я — 7тг/2) 4- sin(37r/2 — 8я) 4- совбя = 1.
соз0,2я — соз0,8я 4- соз0,6я = 1.
принципе, дублирование не является ошибкой, но отражает некоторую недоработку ответа. Оно превращается в явную ошибку, если, например, при подсчете количества корней на каком-либо участке учитывать повторяющиеся корни по нескольку раз.
110
880* (A - 77.3). sin2(l,5a:) + sin2 (тг/4 - 2,5a:) = = sin2 (5,5a:) + sin2 (тг/4 — 6,5a:).
13.3. Использование однородности
Однородным многочленом (второй2) степени) относительно переменных и и v называется выражение вида аи2 + buv 4- си2. Если разделить3^ его на v2 , то относительно переменной t = и/v получится трехчлен at2 4-bt 4-с, который можно пытаться раскладывать на линейные множители. Впрочем, иногда это лучше делать сразу, без деления.
Пример (Л — 85.4). 4 sin2 х 4- 4 sin х cos х 4- 6 cos2 х = 3. Решение.
... 4 sin2 х 4- 4 sin х cos х + б cos2 х = 3(sin2 х 4- cos2 х)
<=> sin2 х 4- 4 sin х cos х 4- 3 cos2 х = 0 (=> cos х / 0: иначе sinx = 0 = cos ж, что невозможно, т.к. sin2 х 4- cos2 х = 1)
<=> tg2 х 4-4tgx 4-3 = О <=> (tgx 4-l)(tgx 4-3) = 0 <=>...
Ответ: х = —тг/4 4- тгп, — arctg 3 4- тгА:, где п, к G Z.
881° (х- 94.2). 882° (е - 84.1). 883 (С - 97.1). 884 (а - 97.3). 885 (С - 98.1). 886 (С-91.1). sin 2х 4- cos2 х = 0. sin2x = 2x/3cos2x. sin x 4- sin 3x = 4 cos3 x. 5 sin2 x 4- 3 sin x cos x — 4 = 0. cos 4x — sin 3x cos x 4- cos 2x = 0. 8 — 7 sin 2x = 12 sin2 x.
887 (тг - 79.3). 888 (тг - 88.3). 889 (С - 96.3). 890 (А-98.2). 891 (7 - 94.2). 892 (е - 82.3). 893 (тг —01.5). sin 2x = (x/3 — 1) cos2 x 4-1. 5 • 4® — 11 • 6® + 2 • 9® = 0. 32® = ((0,6® + 2) 25®. log9(4® - 2 • 18®) 2a:. 9® > 4® - 6®. 5 • 251/® + 3 • 101/® < 2 • 41/®. Найти все целочисленные решения уравнения Зя2 4- Ъху 4- 2у2 = 7.
2) Понятие однородности распространяется и на многочлены других степеней.
3) Случай, когда деление невозможно, рассматривается отдельно.
111
894* (i/> — 85.6). Найти все а, при каждом из которых существует единственная целочисленная пара (ж, у), удовлетворяющая системе
'Зя2 + Ihq/+ 10t/2 = 7
< х + у > О
4а2 я - Зау < 0.
у/ 895 (А — 99.4). Найти двузначное число, произведение цифр которого, увеличенное на 1, впятеро меньше суммы квадрата цифры десятков с ушестеренным квадратом цифры единиц.
у/ 896 (а — 96.5). Окружность, проходящая через вершины А и С треугольника АВС, пересекает стороны АВ и ВС в точках D и Е соответственно. Найти Z.BCD, если BD : ЕС = 2 : 11, BE : АР = 1 : 7 и ZB = 60°.
13.4. Разные методы разложения на множители
Универсальным методом разложения выражений на множители был и остается метод группировки. В сочетании с формулами тригонометрии он дает особенно сильный эффект.
Пример (х — 87.1). (14-2 sin х) sin х = sin 2х 4- cos х. Решение.
(1 4- 2 sin х) sin х — (cos х 4- 2 sin х cos х) = 0
(1 4- 2 sin х) (sin х — cos х) = 0 <=>
2 sin х = —1 sin х = cos х
sin ж = —1/2
tg x = 1 (т. к. cos я # 0, иначе sin х = 0 = cos х) Ответ: х = (—1)п+1тг/6 4- тгп, тг/4 4-тгА:, где n,ке%.
897° (тг —93.2).
898 (С-97.1).
у/ 899 (тг —97.2).
900 (% —95.3).
у/ 901* (^-91.2).
902* (тг - 79.3).
903° (х —87.1).
sin3 х — cos3 х 4- sin х — cos х = 0.
cos &х 4- 4 cos 2х = 0.
2 sin 2х 4- 2 sin х — 3 = 6 cos х.
cos 2х = 2(cos х 4- sin x).
(cos# — l)(sinx — | cos 2# — 1) = sin2 x.
tg 2x — 4 sin x cos x 4-1. = 4 sin2 x.
y/x 4- 3t/ = 9
x — 1 = (^4 !)</•
904° « - 84.3). 2x+3 4- 2z3 16 4- 2xz3.
у/ 905 (/I - 99.1). 3(x+3)2 4-1/9 3х2"2 4- 272x+3.
112
906 (С - 01.3). 18х - 9x+1 - 2х+2 + 36 = 0.
907* (х - 00.2). 12х + 6х - 2 • 4х - 2 • 3х - 2х+1 +4 = 0.
908 (С — 86.4). х log2 х2 + 1 = 2х + 2 log4 х.
у/ 909 (а—95.2). log2 (х2 — 4х + 3)-log2 (х — l)log2 (х — 3) = 1.
у 910 („-00.2). = 2
I 8х — у = 1.
У 911' (^ - 83.2). (х - 4)2 log4 (х - 1) - 2 lOg4 (х - I)2 =
= (х- 4)2 log(a._|) 4-2 log^,!) 16.
у/ 912 (л- -78.5). v/7(9v/x5T3-3'/xT::5) =
_ 32х/®2-з+1 _ 3^2-з+1 + _ 18
913* (Л - 00.7). 2(2 - х2 - х) = vT^T2 (За:2 - 6х + 4).
914 (£ — 99.7). При каждом а решить уравнение
logo (х2 - За) = loga (ах2 - За:).
у 915 (£ — 00.7). При каждом а > 1 решить неравенство
ах(а - 1)х - 2ax+1 - (a - 1)х + 2a 0.
у/ 916* (А — 97.5). Найти все а, при которых система
а(х - 4) - 3(1/ 4- 2)
2/4- \/х = 0
имеет ровно два различных решения.
у/ 917* (/2 — 87.5). Найти все пары (а%5), при которых система х2 - у2 4- а(х + у) = х-у + а
х2 4- у2 4- Ьху — 1 = 0
имеет не менее пяти различных решений.
13.5. Уравнения третьей и четвертой степени
При разложении многочленов на множители могут оказаться полезными следующие утверждения.
1. Если многочлен
f(x) — аохп 4- aix®""1 4-k an-ix 4- ап
с целыми коэффициентами at имеет рациональный корень, представимый в виде несократимой дроби p/q, то свободный член ап и старший коэффициент ао делятся на р и на q соответственно
113
(в частности, если ао = 1, то любой рациональный корень является целым).
2. Если многочлен имеет корень хо, то он делится на двучлен х — Xq.
Пример (С-78.3).
Решение.
х. 2х2 1 << Л 2г3 — 2х2 — ®4-3 Л (х4-1)(2х2 — 4®4-3) р
(считаем 2®2 — 4х 4- 3 > 0, т.к. D < 0) .
Ответ: х —1, 1 < х < 3.
Рис. 21
В приведенном примере рациональные корни кубического многочлена 2ж3 — 2х2 — х 4- 3, согласно первому из перечисленных выше утверждений, искались среди дробей р/g, где р = ±1,±3 и q = 1, 2, а после нахождения первого же корня хо = —1 многочлен был разложен на множители. В чистовом же решении от всех этих операций осталось только само разложение.
918° (ip - 88.2). 84(х3+8) = 167(®2+2®).
2_®w4 - 2и2 + 2® < 0
У919 (х-95.5). < У Л У
у va ' |8х_/ + 2®-1 = 0.
У 920* (/3 - 99.3). log8_7a. (х3 - За;2 - 37х/8 + 55/8) 4-
' 4- 2 log(8_7i)2 (х 4- 3) = 1.
921* (0 - 00.4). lOg4 (16(х - 2)2) log3/16 -
- | log64(x3 - 6х2 4- 12х - 8)2 < ^.
922 (7 — 91.5). Найти все а, при которых система
&п/ — 25 = 0
< х2 = у 4- 2х х2 4- у2 а2 имеет хотя бы одно решение.
у/ 923* (а — 98.7). Найти все а, при которых система
ж4 — (а — 1)\/а 4- 3 у 4- а4 4- 2а3 — 9а2 — 2а 4- 8 = 0
у = у/а 4- 3 х2
имеет ровно три различных решения.
114
у/ 924* (х — 01.6). Найти все а, при которых система
х3 — (а 4- З)#2 4- (За 4- 2)х — 2а 0
х3 — (а 4- З)#2 4- За# < 0
имеет единственное решение.
925* — 01.5). При каждом а решить неравенство
ах4 4- х3 4- (2а 4- За3)#2 4- 2# 4- 6а3 > 0.
у/ 926* (/1 — 96.6). Найти все а, при которых уравнение (#2 - х 4- а2 4- 2)2 = 4а2(2#2 - х 4- 2)
имеет ровно три различных корня.
у/ 927 (б — 79.3). Из сосуда, первоначально наполненного спиртом, отлили 2 л и долили 2 л воды. Когда эту операцию проделали еще два раза, спирта в сосуде стало на Зл меньше, чем воды. Сколько спирта осталось в сосуде?
§ 14. Возведение уравнений и неравенств в квадрат
При возведении обеих частей уравнения или неравенства в квадрат решения могут как теряться, так и приобретаться. Этих неприятностей можно избежать, если, во-первых, возводить в квадрат только в одном случае — когда обе части уравнения или неравенства неотрицательны1 \ во-вторых, внимательно следить за изменением ОДЗ.
14.1. Иррациональные уравнения
Пример (7 — 93.1). У13 — 2х = 5 — х. Решение.
{5 — х 0 J х 5
13 — 2х = (5 — х)2 |(х-6)(х-2) =0
Ответ: х = 2.
В разобранном примере случай, когда условие2^ 5—х 0 не выполнено, явно невозможен, а неравенство 13 — 2х 0, пропавшее в результате исчезновения знака квадратного корня, стало следствием нового уравнения, полученного после возведения в квадрат.
Другие случаи рассматриваются отдельно, причем зачастую они даже не выписываются по причине их очевидной несостоятельности.
Необходимое для возведения уравнения в квадрат.
115
928° (л- - 97.1). х = у/8х 4- 9.
929° (А - 96.1). у/Зх — 5 = х — 11.
930° (а - 97.1). 73(ж + 2) - 79 + 2х = 0.
931 (7-00.1). у/Зх 4- 2 = 2х — 4.
932 (0 - 77.1). х/6 — 4х — х2 = х 4- 4.
933 (С-88.3). \/4 — &х — х2 = х 4- 4.
934 (7 - 82.1). х + 72Ж2 - 14a: + 13 = 5.
У 935 (^-96.1). 72a:2 - 21a: + 4 = 2 - Ila:.
936 (7 - 99.2). 72a:2 — 8a: + 5 = x - 2.
937 (С - 98.2). 73a: - x2 - 2 = 2x - 3.
У 938 (С-85.2). y/x4 — 2x — 5 = 1 — x.
у/ 939* {у - 01.3). 1/2 - x2 = 71/2 - x.
7940 (С-99.2). y/x+ 2 y/2x + 1 = x + 4.
941 (а-91.1). \/3x — 5 — y/4 — x = 1.
7942 (тг — 98.1). \/x 4-1 — \/4x — 3 = 1.
943 (^ - 01.1). y/x 4" 2 4* 78 — x = \/15.
7944 (е-82.2). y/x + 1 — 72a: — 5 = y/x - 2.
7 945 (С-00.2). 77+2 + y/x + 2 = 73a: + 1.
14.2. Иррациональные неравенства
Как видно из следующих двух примеров, случай, когда возведение неравенства в квадрат запрещено, может оказаться3) как совершенно «бесплодным», так и вполне содержательным.
Пример 1 (А — 84.2). yj2x2 — 18s 4-16 < х — 4.
Решение.
х > 4
{х — 4 > О
О 2х2 - 18ж 4-16 < (х - 4)2
(х-1)(х-8) ^0
Ответ: 8 х < 10.
х(х — 10) < 0
Пример 2 (е — 88.2). ^х2 4- я — 6 > —х — 1. Решение. Рассмотрим два случая:
1)
—х - 1 > 0
х2 4-ж -6 > (-х - I)2
х — 1
х < -7
о х < —7;
3)В зависимости от знака решаемого неравенства.
116
. X V I •«- -X
(х2 + х —6^0 Цх — 2)(х4-3)^0 Ответ: х < —7, х > 2.
946° (С - 79.4).
7947 (А-84.2).
948 (А-92.2).
7949 (0-80.3).
950 (А - 01.2).
951 (е - 83.3).
7952 (р-89.2).
953 (А - 94.3).
954 (е - 95.1).
955 (^ - 88.3).
956 (р - 87.3).
7957 (е—98.1).
7958* (V>-93.2).
7 959* (А-99.7).
7 а:2 + х — 2 < х.
у/х2 — Зх + 2 Зх — 3.
710а: — 1 + 1 5х.
у/—х2 + 6х — 5 > 8 — 2а:.
у/х2 — 8а: + 12 > х — 5.
4(х - 1) < 73а:2 + 19х + 20.
72а:2 + х > 1 + 2а:.
724 — 10а: + х2 > х — 4.
2а: — 5 < у/х2 — х — 6.
2а: - 17 < 781-а:2.
72а:2 + 15х - 17 > х + 3.
у/х2 + Зх + 2 — у/х2 — х + 1 < 1.
у/Т^х -yji> 1/73.
74х — а:2 — 3 > у/х2 — 7а: + 12 — у/х2 — 5х + 6.
14.3. Разные задачи на возведение в степень
Трудно не согласиться с тем, что возводить в квадрат уравнение логически несколько проще, чем неравенство. Поэтому в чуть более серьезных задачах, содержащих иррациональные неравенства, может прийти на помощь обобщенный метод интервалов (см. п. 12.1), благодаря которому достаточно временно заменить все решаемые неравенства уравнениями, а затем, отметив на числовой оси корни полученных уравнений и выделив ОДЗ, выбрать те интервалы, на которых выполнены нужные неравенства.
Пример (Д — 82.1). log1/5(i/x2 — 3 — х 4- 2) 0.
Р ешение.
... о 0 < \/х2 — 3 — х + 2^1 о х — 2 < \/х2 — 3 х — 1.
Применим обобщенный метод интервалов (рис. 22)4^:
{х — 1 > и
х2 - 3 = (х - I)2
4)На рисунке заштрихована часть числовой оси, которая не входит в ОДЗ последнего двойного неравенства, а его решение выделено жирным.
117
лч л ~ ] х — 2 О
2)^-2-V^3«|(i_2)! = i!_3 «
3) х2 - 3 > О Ответ: \/3 <=> |х| у'З. (///////4 1 ► ->/3 V5 2 х Рис. 22
960° (7 - 96.3). 961° (е - 79.1). 962° ftp-90.1). у/ 963 (д —99.1). х/2 — х2 = |ж| — 1. у/37 — 48 ctg х = 8 ctg х - 5. x/lOcosx — x/4cosx — cos2z = 0. yKl: + ytg(9’ 2x)_o.
У 964 (7 - 00.6). 965 (м - 96.2). у/ 966 (м - 00.1). 967° (х - 78.3). У 968 (V» — 99.1). У 969 (С-01.2). у/cos 2x 4- 2 sin2 z 4- sin z 4-1 — < / = 1. у sin ж-f-l ^/17• 9» -4» >3® -3-2x. 2y/b • 6® - 2 • 9х - 3 • 4х + 3® < 2x+1. y/2(5x + 24) - y/5* - 7 /5х + 7. 5x—3 < j У7ж—4 Д > _J_. УЗ—x x—2
970 (а-93.1). 971 (^-83.2). у/ 972 (е-88.3). 973* (гр - 98.3). 974* (х - 82.3). Уж2—5x4-8 \ -| 3-x У51—2x—x2 -i 1—x л/x^-j-x—6 4~3x-f~13 i s+5 ' le У4a:4-7 —3a:+5 л 16-3«2+22x U’ Зх + 2. У5ж2 —1
У975 (м-90.3). 976 (С - 00.2) . 977 (С-97.3). у/ 978* (а-99.5). Vl^-l < l+x X- y/x2 + |x — 4| — 18 > x - 4. y/x2 + x + 4 2x + |3x - 2|. Уж^—3—3 -I |x+2|-5 X-
У979 (м-96.2). 980 (^ - 85.3). ДЗ'?3+-4ТЖ) ^V^-3. log1/3 (x + y/x - 1) > -1.
118
у 981 (а - 96.4). 982 (а - 98.5). i°gi/2 + 2 - х + 4) -1 + log1/2 3. 1оё2х-3 (д/х + 2 + X - 3) 1.
У 983* (д-89.2). х/2 — х2 4- 2х 4- х — 2 log3 (5/2 - х) + log3 2 "
у/ 984 (а-01.4). (1 + log3 х) \/log3a. </х/3 2.
985° (д - 80.4). л/х2 + 4ху - Зу2 = х + 1 х -у = 1.
986° (х - 77.2). 987° (А - 99.2). у/х + у — 1 = 1 у/х - у + 2 = 2у — 2. (4х 4- 5у = \/16я2 — 251/2 |^2 4- 6х — 7 = 0.
У 988 (7 - 94.3). < log2 (10 - 3j/) + log1/2 (2у - 5х) = 0 у/х + 2у + 1 - у/11 — Зу = у/2х + 4у - 12.
у/ 989 (а-97.5). Найти площадь фигуры, заданной системой \/4 — х2 —у У^ ~ к 4“ 1| 4- 3.
990 (тг - 97.6). При каждом а решить неравенство \/а2 — х2 > а 4-1.
У 991 (^-89.5). При каждом а решить неравенство х 4- 2а — у/Зах 4- 4а2 > 0.
у/ 992 (л--99.7). При каждом а 0 решить неравенство х/я2 — 4 а. X
993 (С - 97.7). При каждом а решить неравенство а — 2 < (а — 1)х/я 4-1.
994* (А - 86.5). При каждых а, b > 0 решить неравенство 1—-— 1-1 V х2 а2 > х b
119
у/ 995 (А — 95.7). При каждом а решить неравенство
р(Л*)) < О,
где f(x) = у/х — а, д(х) = у/х2 — 4z + 4 — 3.
у/ 996 (/3 — 78.3). На прямой, касающейся в точке А данной окружности с центром О и радиусом 2, взята такая точка В, что Z.ABO = 7г/3. Найти радиус окружности, касающейся отрезков АВ, ВО и данной окружности (внешним образом).
997* (А — 99.8). Две окружности радиусов х/19 и у/76, касающиеся друг друга внешним образом, касаются также некоторой полуокружности и ее диаметра. Найти радиус полуокружности.
§ 15. Тригонометрические уравнения, неравенства и сйстемы
Существенную помощь в работе с корнями тригонометрических уравнений способен оказать тригонометрический круг (см. §2), который представляет собой единую графическую модель, наиболее полно отражающую свойства всех тригонометрических функций и их аргументов.
15.1. Выбор корней из данного промежутка
Отбирать корни тригонометрического уравнения, удовлетворяющие заданному условию, можно путем анализа получаемых формул1) корней, но лучше стараться это делать на более раннем этапе.
Пример ((3 — 85.2). Найти все корни уравнения
3 cos 2х — 5 sin (х — тг/2) = 1
на отрезке [тг; 5тг/2].
Решение.
...<=> 3(2 cos2 х — 1) + 5 cos х = 1 о (cos х — 1/2) (cos х 4- 4/3) = О о cos я = 1/2.
Учитывая, что тг х 5тг/2 (рис. 23), получаем: х = 2тг ± тг/З.
Ответ: х = 5тг/3, 7тг/3.
998° (7 — 94.1). Найти наибольший отрицательный корень уравнения
\/3 cos Г 4- 2х ) — 2 cos2 х = 0.
\ a J
Содержащие целочисленные параметры.
120
у/ 999 (е — 91.1). sin(37r 2х) = соз(тг 2®) — зт(тг 2х).
1000 (С - 86.3).
у/ 1001 (А - 96.7).
1002 - 00.1).
У 1003 (х- 00.1).
1004 (д - 86.1). у/1005* (е —01.5).
у/ 1006 (е - 94.3).
1007 (0 — 95.3).
= х
<
2 sin х + sin 2а: = 2 cos2 |.
sin 5|ат| = sin(—3).
4а: sin За: = За: + |а:|.
sina: sin |а:| 1/2.
2 cos (у/х + тг/2) — у/З = 0.
x/3cos (тг-yir ^/6/а: — а: — 4^ +
+ 3 sin (тгх у/Ъ/х2 — Ь/х — 1) = У12. log3 ((а: + 10) cos а:) = log3 Найти все корни уравнения
sin 2х = sin (тг/2 — х) на отрезке [0; Зтг/2].
1008 (а — 01.2). Найти все корни уравнения
5 sin2 2х 4- 8 cos3 х = 8 cos х, удовлетворяющие условию Зтг/2 х < 2тг.
у/ 1009 (ip — 88.3). Найти все корни уравнения 2 sin2 х 4- cos4x = О, удовлетворяющие условию |х| < 3/2.
1010° (£ — 80.1). Найти все корни уравнения sin х cos f 4- cos x sin ~ |
на отрезке [—Зтг/2; тг].
121
1011 (/3 — 94.3). Найти все корни уравнения 3tg2 (тгх — тг/8) = 1
на интервале (3/2; 3).
1012 (е — 83.2). х/4 — х2 (sin 2тга: — 3 cos тга:) = 0.
у/ 1013 (Л — 95.5). (2v/3sin(7ra: + Зтг) — tg(?ra: — тг/2)) х х log2(4 - х2) = 0.
(y/3cos + sin х
1014*(0-88.5). < Х (л/11 “У2 -4а: -2у - б) = О
| + 2sin yf cos =
k = 2cos уу sin + sin2
4 12 О о
у/1015 (д- 87.1). cos^ = ^.
1016 (А —99.1). cos(6sinx) = —1.
у/ 1017 (б — 82.4). sin (|тг sin х) = |.
1018 (б — 89.4). Найти все корни уравнения
tg(3sinx) = —1
на интервале (тг/2; Зтг/2).
у/1019 (х- 91.2). tg(^4-^sins) = l.
1020 (б — 99.4). х = | arctg(tg6x 4- cos7x).
у/ 1021* (б - 99.5). х 4- | arccos(cos 15я 4- 2 cos4я sin 2я) = ~.
1022* (/1 — 98.4). Найти все а, при которых хотя бы одна общая точка графиков функций
у = —2/3 — arcsinx и у = —2/3 — 2 arctgax
имеет положительную ординату.
15.2. Учет тригонометрических неравенств
Если в задаче явно или неявно участвуют тригонометрические неравенства, то стоит попытаться как-то учесть их не решая.
Пример (д - 79.1). Найти все корни уравнения
1 4- 5 sin х 4- 2 cos2 х = О, удовлетворяющие неравенству cos х 0.
Решение.
...<=> 1 4- 5 sin х 4- 2(1 - sin2 х) = 0 <=> (sin х 4-1/2) (sin х — 3) = О sin х = —1/2.
122
Учитывая неравенство cos® 0 (рис. 24), получаем ... О т в е т: х = —тг/6 + 2тгп, где п g Z.
1023° (д - 80.2). у/ 1024 (д - 94.1). у/ 1025 (д - 89.1). у/ 1026 (А - 80.2).
1027 (А - 96.3).
ж = 1+^*-
4 sin ж—2 cos 2а: — 1 = q cos 2з:+а/3 cos х—2
(365ж tg х)х 6#2 tg х = 677ГЖ tg х.
2—3 sin a:—cos 2а: л 6 а:5—тга:—тг2 *
Найти все корнй уравнения
cos 10а: — cos 8х _ cos 6х — cos 4а: 2а:2 4- тгх — тг2 2х2 + тга: — тг2 на интервале (0; тг).
1028 (тг — 85.3). Найти все корни уравнения (1 + tg2 х) sin х — tg2 х + 1 = 0, удовлетворяющие неравенству tg х < 0.
у/1029 (д - 97.1).
у/ 1030 (7 - 96.3).
1031 (х - 89.3).
1032 (тг - 77.3).
у 1033 (е - 77.1).
1034 (тг - 91.3).
1035 (А - 89.3).
(2 sin2 х — 3 sin х + l)^tgx = 0. log_ sin x (cos2 x + | sin 2a: + 1) = 0. log2 (3 cos x — sin x) + log2 sin x = 0. |tgx| = tgx-^.
COS Ж — I pQQ I (2ж+3,14)2 “ I cosa;|-
x/2cos(x 4- 7Г/4) — sin# = | cosx|.
Найти все корни уравнения
Icosxl J-----L = cos 2x — 1
cos#
на отрезке [—Зтг; — 2тг].
123
1036 (/I - 88.1). у/ 1037 (/3 — 98.1).
1038 (^-95.3).
1039 (А-95.3). у/ 1040 (б-98.2).
1041 (б-96.4).
1042 (х —88.2). у/ 1043 (д - 82.3). у/ 1044 (д —91.1). у/ Ю45 (х-92.2). У1046 (тг—01.5). у/ 1047 (х —98.3).
х/1 — cos 2х = sin 2х.
х/1 — cos 2х = x/2sinx(cos3: — 2/3).
x/2sinx — x/2^Hcosx = 0.
x/sinx = — cos х.
tg ж 4- x/2 sin ж = 0.
\/12 sin x = x/sin 2x.
x/2 cos x = \/—Зг/Ззтя — 4.
y/5 cos x — cos 2x 4- 2 sin x = 0.
y/4 cos 2ж — 2 sin 2x = 2 cos x.
x/sin я > y/— cos x.
2 log^ sin x • log^ sin 2x — log2 sin 2x < log2 sin x. (4 4- x/3) sin x 4- 2\/3 4-1 < cos2x 5 cos# — 3.
15.3. Трудности при отборе корней
При решении задач, сводящихся к исследованию тригонометрических систем, часто возникают трудности, которые связаны прежде всего с несоответствием друг другу тригонометрических функций или их аргументов, содержащихся в разных уравнениях и неравенствах.
тт / оо 14*2sm2x - 3x/2sinx 4*sin2x
Пример (х- 83.2). -----—--------—-------= 1.
2 sin х cos x — 1
Решение. 2 sin2 x — 3\/2 sin x 4-2 _
sin 2х — 1
(sin х — >/2/2)(sins —>/2) 2 sin ж cos г — 1
Г sin ж = у/2/2
\2у/2/2 • COS X / 1
Ответ: х = Зтг/4 4- 2тгп, где п 6 Z.
= 0
{sin я = х/2/2 (рис. 25) COS Ж / \/2/2
1048° (<p —92.1). (\/3 coss+sin x)2 _ у/з ^+2 sin 2a: 2
У1049 (x —97.2). 6 sin x—2 cos 2a:—4 cos2 x—3 = q \/7sin x—3 cos x
У1050 (e - 93.2). 1051 (e - 95.2). 1052* (s-82.4). 1053 (тг —96.5). sin 3x _ i cos(a:—7r/6) sin 3x л 2cos2a:+l ~ u’ sin 4a: -i sin 6a: ’ (1 — cos 8x) tg x = 6 sin2 4x ctg x.
124
1054 (тг — 98.4). ctgx 4-ctg2x = — tg3x.
у/ 1055* (V> — 98.4). Найти все корни уравнения
tg Sx — tg 6х = -г--:-"
sm 4х
на отрезке [—тг/4; Зтг/4].
1056 (б —87.1).
1057 (б— 96.3).
1058 (/1 — 95.3).
у/ 1059 (х —98.3).
1060* (% —77.5).
(2 sin ж — l)^/cos(x 4- Зтг/4) = 0.
(tg - tg х) ^/б cos cos | — cos я - 3 = 0.
x/sin Зх tg(2x — тг/6) = 0.
tg #\/sin х — 2 cos я — 1 = 0.
Найти все корни уравнения
2 — х/З cos 2х 4- sin 2х = 4 cos2 Зх, удовлетворяющие неравенству cos(2x — тг/4) > 0. у/ 1061* (/1 — 98.2). Найти все корни уравнения
2 cos 4- 2 (Vb — 1) sin = 2 — >/5, удовлетворяющие неравенству cos < 0. у/ 1062 (£ — 95.7). Найти все х, при которых числа
sin х, | sin 2х, sin Зя образуют возрастающую арифметическую прогрессию.
1063* (б — 00.5). Найти все ж, при которых числа
2СО8(5ж—Зтг/4) (i/2)c°s(3x—тг/4) 5/--^ 5со8(ж+тг/4)
образуют убывающую геометрическую прогрессию.
125
1064 (тг - 97.3). у/ 1065 (тг - 99.2). 2 sin2 х -1^1 = 0. COS X | cosx — 1/2| = sin# — 1/2.
1066* (х —99.3). у/ 1067* (А - 98.3). yi+sin(2»-,/3) =_gina;cosa. Найти все корни уравнения \/1 — sin 2х — \/2 cos Зх = 0
на отрезке [—Зтг/2; —тг].
1068 - 87.4). Уз/4-cosx = v'3/4 “ cos3a:-
1069* (тг — 96.4). Найти все корни уравнения
\Jx 4- sin ж = \/х — sin 2я
на интервале (—2тг; 2тг).
1070 (д - 82.3). у/1071* (7 - 77.5). у/ 1072* (д - 83.2). \/2 cos х sin 2х = у/5 sin х 4- 4 sin 2х. 2 sin(3x 4- тг/4) = \/1 4- 8 sin 2х cos2 2х. log2 (cos2z 4- cos f) = log2(sinx 4- cos f).
1073° (е - 79.1). 4 sin у — 6\/2 cos x = 54-4 cos2 у cos 2x = 0.
у/ 1074 (х - 99.3). Найти все решения системы
< 2 sin Зх 4- 2 cos 4х = 1 4- \/2 2 sin 7х — 2 sin х = у/2
на отрезке [0; тг].
у/1075* (V» - 99.3). Г sin2 х 4- cos2 у = 3/4 < cos х sin у = \/б/4 I cos х 0.
§ 16. Перебор случаев в геометрии
Необходимость в геометрическом переборе возникает тогда, когда трудно или невозможно одинаково рассуждать сразу во всех случаях, которые могут представиться для заданной конфигурации.
16.1. Обоснование геометрической конфигурации
Если фигура, рассматриваемая в геометрической задаче, описана в условии не совсем однозначно, то для полного выяснения
126
вопроса о взаимном расположении тех или иных элементов этой фигуры требуются дополнительные усилия.
Пример (7 — 84.2). На стороне правильного треугольника, равной 24, взята точка на расстоянии 11 от ближайшей вершины. Найти расстояние от этой точки до центра треугольника.
Решение. См. рис. 26.
Пусть данная точка М лежит на стороне АВ. Тогда CM ^h = 24sin60° = 12>/3 > 11
и без ограничения общности считаем, что AM = 11,
=> х2 = (12—ll)2+(/i/3)2 = 1+(4х/5)2 = 49 (теорема Пифагора). Ответ: 7.
1076° (а — 93.3). На боковой стороне ВС равнобедренного треугольника АВС и с углом Z.B = 120° как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найти расстояние от вершины А до центра окружности, если AD = у/3.
1077° (х — 81.3). Найти стороны треугольника АВС с высотой СН = >/3 и углом ZA = 7г/3, если радиус описанной около него окружности равен 5.
1078° (б — 97.3). Найти сторону ВС треугольника АВС со стороной АВ = л/5, медианой ВМ = 2^2 и высотой ВН = 2, если Z.B 4- ZC < 90°.
у/ 1079° (А—94.7). В треугольнике площадью Зх/15/4 две стороны равны 2 и 3 соответственно, а медиана, проведенная к третьей стороне, меньше ее половины. Найти радиус описанной около треугольника окружности.
1080° (е — 78.2). Найти сторону квадрата ABCD площадью, большей 225, если некоторая точка М расположена на плос-
127
кости так, что МВ = MD = 13 и МС = 5х/2. Где лежит точка М: вне квадрата или внутри него?
у/ 1081 (/1 — 89.3). На стороне CD трапеции ABCD с основаниями AD = 4 и ВС = 3 взята такая точка Е, что отрезок АЕ делит среднюю линию трапеции в отношении 2:5. Найти отношение высоты ЕН треугольника AED к высоте трапеции.
1082 (ср — 82.4). Диагонали параллелограмма ABCD относятся, как 1 : х/3, АВ = BD = 1. Найти площадь той части круга, описанного около треугольника BCD, которая не принадлежит кругу, описанному около треугольника ACD.
1083 (х — 83.4). Угол при основании равнобедренного треугольника равен 30°, а медиана, проведенная к боковой стороне, равна \/7. Найти отношение площади треугольника к площади той его части, которая лежит в круге радиусом 2/д/З с центром в вершине, противолежащей основанию.
у/ 1084* (^—97.5). Две окружности касаются друг друга внешним образом в точке А. Через точку В их общей касательной АВ = 6 проведены две прямые: одна пересекает первую окружность в точках К и L, а другая — вторую окружность в точках М и N. Прямые KN и LM пересекаются в точке Р. Найти отношение площадей треугольников KLP и MNP, если BL = 9 и ВМ = 5.
1085* (тг—95.4). Две окружности, радиусы которых относятся как 1 : (9—4\/3), касаются друг друга внутренним образом. Найти угол между двумя равными хордами большей окружности, касающимися меньшей окружности, если одна из этих хорд перпендикулярна линии центров окружностей.
1086* — 01.4). Пятиугольник с вершинами A,B,C,D и Е
вписан в окружность. Найти АЕ и площадь пятиугольника, если BD = BE = 10, a ABCD —: трапеция с основаниями AD = 13 и ВС = 3.
1087* (Д—89.4). В окружность радиуса 2 вписан правильный шестиугольник. На продолжении его стороны АВ за точку А взята точка С так, что АС = х/1Т — 1. Из точки С к окружности проведена секущая CD с внешней частью СЕ = 2. Найти Z.BCD, если угол DBE — тупой.
у/ 1088 (7 — 99.6). Ребра треугольной пирамиды равны 15, 12, 12, 9, 9 и 3. Найти объем пирамиды и радиус описанной около нее сферы.
128
16.2. Перебор вариантов расположения
В решении следующих геометрических задач требуется разобрать разные варианты расположения и либо убедиться в том, что все они приводят к одному и тому же ответу1), либо отбросить2) невозможные варианты, оставив единственно возможный.
Пример (д-86.2). Окружности радиусов 2 и 4 касаются друг друга в точке А. Прямая, проходящая через точку А, пересекает меньшую окружность в точке В, а бблыпую — в точке С. Найти АС, если ВС = 3\/2.
Решение. См. рис. 27. а, б:
ДАС1В ~ ДАОгС (равнобедренные треугольники с равными углами при основаниях), следовательно, АВ : АС = 2 : 4 = 1 : 2.
Рассмотрим два случая:
а) окружности касаются внешним образом,
=> AC = 2BC/3 = 2i/2;
б) окружности касаются внутренним образом
=> АС = 2ВС = 6\/2>8 (— диаметр большей окружности), следовательно, этот случай невозможен.
. Ответ: 2\/2.
(а) №
Рис. 27
1089° (£—89.2). Найти высоту треугольника площади S, опущенную на сторону, прилежащую к углам а и /3.
1090° (£ — 95.4). Найти высоту АН и угол при вершине В треугольника АВС, если АС = 5, АВ = с и ZA = а.
Х)С этой целью полезно попытаться провести несколько более тонкое рассуждение, чтобы получаемые выводы не зависели от деталей расположения.
2) Обоснованно!
5 И. Н. Сергеев — Математика
129
1091 (С — 96.4). Длины окружностей с центрами О и Q относятся, как у/2 : 1, а АВ •— общая хорда этих окружностей. Найти AAQB, если А АО В = 60°.
у/ 1092 (7 — 97.2). Две касающиеся друг друга окружности радиусов Г1 < Г2 касаются внутренним образом третьей окружности. Центры окружностей служат вершинами равнобедренного треугольника, угол при основании которого больше 70°. Найти периметр этого треугольника.
у/ 1093 (д — 79.2). Лучи АС и ВС пересекают полуокружность с диаметром АВ в точках D и Е соответственно. Найти АВ, если CD = СЕ = 1 и ZABC = 60°.
у/ 1094 (/1 — 96.3). Точка О — центр окружности, описанной около треугольника АВС, а М — середина стороны АВ. Найти площадь этого треугольника, если описанная около треугольника АМО окружность пересекает прямую АС в точке N, причем MN = 8, AN = 7 и AM О А — 45°.
у/ 1095 (д — 87.3). Радиус окружности, вписанной в равнобедренный треугольник АВС с основанием АВ, равен 4. На прямой АВ взята точка D, удаленная от прямых АС и ВС на расстояния 3 и 11 соответственно. Найти cos ACBD.
1096* (/1 — 98.4). Окружность, вписанная в равнобедренный треугольник АВС, касается его основания АС в точке D и боковой стороны АВ в точке Е. Продолжение хорды DF окружности пересекает сторону АВ в ее середине М. Касательная к окружности, проходящая через точку F, пересекает сторону АВ в точке G. Найти АА, если MG : EG = 2:3.
1097* (х — 99.4). Из точки М окружности с центром О и радиусом 4 на диаметры АВ и CD опущены перпендикуляры МН и МК. Найти площадь треугольника МНК, если ААОС = 7г/9 и АМН К = 2тг/9.
у/ 1098* (д — 93.4). Две окружности с центрами А и В и радиусами 2 и 1 касаются друг друга. Точка С их общей касательной удалена от середины отрезка АВ на расстояние (3/2)3/2. Найти площадь треугольника АВС, если она больше 2.
1099* (х— 82.6). Расстояние от центра описанной около треугольника АВС окружности до стороны АВ на 2 больше, чем до стороны АС. Касательная к окружности в точке С пересекает прямую АВ в точке D. Найти радиус окружности, если \ABAC - ААСВ\ = AADC и \АВ - АС\ = 8/х/З.
130
1100* (тг — 84.4). Окружность, проходящая через вершины В и С треугольника АВС со стороной ВС = а и углом ZB = 75°, пересекает стороны АВ и АС в точках МnN соответственно. Найти ВМ, если BN = b и Z.ABN = 30°.
1101* (х — 99.4). На стороне ВС треугольника АВС взята точка D так, что Z.CAD = 2Z.BAD, Окружности радиуса 8 и 4, вписанные в треугольники ACD и ABD соответственно, касаются прямой ВС в точках, удаленных друг от друга на расстояние х/129. Найти AD.
у/ 1102* (/1 — 95.5). Три параллельные прямые касаются в точках А, В и С сферы с центром О и радиусом 4. Найти Z.ABC, если площадь треугольника АОС равна 4, а площадь треугольника АВС больше 16.
у/1103* (А - 85.6). На ребре ВС = 4 куба АВСРА'В'С'Р' взята середина М, а на ребре A'D' — точка N такая, что A'N = 1. Найти длину кратчайшего пути из точки М в точку N по поверхности куба.
1104* — 79.4). Вне правильного тетраэдра ABCD взята
точка М такая, что МА = МВ = МС = д/97, MD = у/2. Найти объем тетраэдра.
1105* (д—86.6). Стороны АВ = 6 и CD основания ABCD пирамиды SABCD параллельны, AD = 4, AS = 2 %/14 и /J3AD = = 120°. Найти объем пирамиды, если через каждую из прямых АВ и CD можно провести по плоскости, которые не содержат основание пирамиды и пересекают ее по равным четырехугольникам.
1106* (/1—84.5). Основание ABCD пирамиды SABCD имеет своей осью симметрии диагональ АС = 9, которая пересекается с диагональю BD в точке Е так, что АЕ < ЕС, Через середину бокового ребра пирамиды проведена плоскость, параллельная основанию. Некоторое сечение образовавшейся усеченной пирамиды пересекает ее ребра BBZ, DDf и представляет собой правильный шестиугольник со стороной 2. Найти площадь треугольника ABD.
1107* (х — 84.6). Многогранник ABCDА'В'CD' с гранями ABCD, A'B'C'D', АА'В'В, ВВ'С'С, CC'D'D и AA'D'D вписан в сферу радиуса у34- Расстояние между параллельными гранями ABCD и A,B,CfDf равно 2. Объем многогранника
131
5*
равен 98/15, площадь грани А'В'С'Р' равна 5. Найти АА', если АВ : CD = А'В' : CD' ф 1.
1108* (х—91.6). Две грани восьмигранника (основания) расположены в плоскостях а и /3, а среди остальных шести граней (боковых) одна часть — равные между собой трапеции, другая часть — равные между собой равнобедренные треугольники. Каждая боковая сторона треугольника совпадает с боковой стороной трапеции, а каждая боковая сторона трапеции совпадает либо с боковой стороной другой трапеции, либо с боковой стороной треугольника. Основания всех трапеций, равные х/13, лежат в плоскости а и образуют многоугольник площади 12, а все другие основания трапеций и все основания треугольников лежат в плоскости /3. Сфера касается всех граней восьмигранника, а площадь ее поверхности относится к суммарной площади боковых граней, как тг : 5. Найти радиус сферы, если он больше 3, но меньше 4.
16.3. Неоднозначность в ответе
Если в условии задачи не удается устранить неопределенность конфигурации, то в результате и ответ может оказаться неединственным. В такой ситуации необходимо по-настоящему убедиться3^ в том, что каждое из полученных значений искомой величины реализуется геометрически.
Пример (е — 95.5). Найти сторону АС треугольника АВС, если радиус описанной около него окружности равен 5, АВ = 6 и ZA = 30°.
Решение. См. рис. 28. а, б:
3>А лучше бы убедить еще и экзаменатора!
132
1) ВС = 2 • 5 sin30° = 5 (теорема синусов);
2) 52 = 62 4- х2 — 2 • 6 х cos 30° (теорема косинусов)
=> х2 — 6^3 х 4-11 = 0 => ж = 3х/3±4;
3) оба значения х реализуются, так как в треугольниках со сторонами б, ж и углом в 30° между ними третья сторона, по теореме косинусов из п. 2), равна 5.
Ответ: 3\/3 ± 4.
у/ 1109° (б—91.3). Окружность диаметром \/10 проходит через вершины А и В прямоугольника ABCD, а касательная к ней, проведенная из точки С, равна 3. Найти ВС, если АВ = 1.
у/ 1110 (А — 01.4). Прямая, проходящая через вершину основания равнобедренного треугольника, делит его площадь пополам, а периметр — на части 5 и 7. Найти площадь треугольника. Где лежит центр описанной окружности: вне треугольника или внутри него?
у/ 1111* (^ — 91.4). Точки К, L и М делят соответственно сторону АВ, ВС и CD выпуклого четырехугольника ABCD в отношении АК : КВ = CL : LB = СМ : MD = 1:2. Найти площадь четырехугольника, если КL = 4, LM = 3, а диаметр описанной около треугольника KLM окружности равен 5.
у/ 1112* (/? — 97.5). Через середины сторон АВ, ВС и вершину С треугольника АВС проведена окружность радиусом \/2, касающаяся стороны АВ, Найти Z.C, если АС = 2.
1113* (% — 98.5). Хорды АВ и CD окружности пересекаются в точке К, хорды CD и EF — в точке L, а хорды АВ и EF — в точке М. Найти радиус окружности, если ВК = AM, СК = DL, FL = 5,LM = 4 и Z.LKM = тг/4.
1114* (б — 97.3). Касательная к описанной около треугольника АВС окружности радиуса 2, проведенная через вершину С, пересекает в точке D продолжение стороны АВ за точку В. Найти секущую AD, если АС = \/12 и Z.CDA 4- Z.ACB = = 2Z.BAC,
у/ 1115* (х—86.4). Через точку А окружности радиуса х/б проведена касательная, пересекающая в точке В продолжение диаметра CD окружности под углом 60°. Найти медиану ВМ треугольника АВС.
1116* (х — 01.4). Диагонали параллелограмма ABCD пересекаются в точке Е. Расстояние между центрами окружностей, описанных около треугольников AED и CED, равно 16,
133
а радиус окружности, описанной около треугольника АЕВ, равен 5. Найти площадь параллелограмма, если BD = 12.
1117* (£ — 88.6). Боковые грани пирамиды SABC одинаково наклонены к основанию АВС, АС = 3, ВС = 4, SC = >/38, Z.ACB = 90°. В пирамиду вписан цилиндр: нижнее его основание лежит в плоскости АВС, а верхнее имеет по одной общей точке с каждой боковой гранью. Найти радиус основания цилиндра, если площадь его боковой поверхности равна 8тг/3.
1118* (х — 00.4). Основанием прямой призмы служит ромб ABCD с углом ZA = 120°. На боковых ребрах АА', ВВ' и СС' взяты такие точки К, L и М соответственно, что угол между прямыми KL и АВ равен 45°, а между прямыми LM и ВС — 30°. Найти угол между плоскостями KLM и АВС.
1119*(х — 00.6). Основанием пирамиды SABC служит треугольник АВС со сторонами АВ = 15 л/2, ВС = 20 и радиусом описанной окружности, равным 5\/5- На сторонах основания как на диаметрах пострены три сферы, пересекающиеся в центре О четвертой сферы, которая в точке S касается некоторой плоскости, параллельной плоскости АВС. Площадь части четвертой сферы, заключенной внутри трехгранного угла, образованного лучами О А, ОВ и ОС, равна 8тг. Найти объем пирамиды SABC.
Глава 4. МЕТОД РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ
Семь раз отмерь, один раз отрежь.
§17. Сравнение чисел и выражений
Задание, состоящее в сравнении двух данных величин а и Ь, понимается так: выяснить, какой из знаков >, < или = следует поставить вместо знака V в соотношении а V Ь, чтобы оно стало верным? Наиболее распространенная форма вопроса1) для такого задания — «Что больше: а или Ы*.
17.1. Задачи на сравнение
Сравнение двух чисел а и Ь, удобно производить путем равносильных преобразований неравенства2) а V b с временно неизвестным знаком V, который в результате преобразований должен стать очевидным.
Пример (х—82.1). Сравнить3 *^ у/18 V 4log23+log< А. Решение.
... Зч/2 V 22 log2 3 • 41084 А (=9-£) <=> 11ч/2 V 3-5
<=> 121 • 2 V 9 • 25 <=> 242 V 225 — верно, когда знак V есть > . Ответ: >.
1120° (х- 92.1). {/ff v {/iff:
1121° (А-94.1). &47 V У13.
1122° (е-82.1). {/2 + 3tgf V {/—2cos?r.
ч/1123 (0 - 94.2). ч/П V 951о8з (H-|)+lioge2
1124 (А-85.1). 3log25 + 1(Йlg2 V 510g23+ ^lo.
ч/1125 (е-88.1). $ + а/2УЗ.
Предполагающая и соответствующую форму ответа.
2) Возможно, равенства.
з>В дальнейшем мы, по возможности, будем опускать само задание,
когда это не будет вызывать неясностей.
135
у/ 1126 (тг — 98.2). Найти cos у, если tga = | и тг < а < 2тг. Сравнить
lcosfl v "тг-
У1127* (7 —01.4). arcsinj V
^/1128 (х — 79.1). Разность конечной арифметической прогрессии ai,..., Пб равна 6, а знаменатель конечной геометрической прогрессии bi,..., &8 равен \/2, причем а± = bi = 3. Сумма членов какой прогрессии больше: арифметической или геометрической?
у/ 1129 (А — 94.8). Из пункта А в пункт В можно доехать тремя маршрутами: через пункт С, через пункт D или напрямую. Пункт А связан с пунктами В, С и D грунтовыми дорогами, а пункт В с пунктами С и D — шоссейными, причем АВ = 80 км, АС = 40 км, AD = 30 км, СВ = 60 км, DB = 100 км. Скорость по грунтовой дороге больше 15 км/ч, но меньше 30 км/ч, а по шоссе — на 40 км/ч больше. По какому маршруту можно быстрее добраться из А в В?
17.2. Сравнение чисел в процессе решения
Часто бывает, что сравнение чисел не входит явно в постановку задачи, но является одним из элементов ее решения, например, служит пояснением к очередному преобразованию или даже представляет собой самостоятельный, серьезный этап решения.
Пример (у? — 85.1). Найти все корни уравнения \/2 cos2 х = cos х на интервале (—5,5; —4).
Решение.
. . . COS s(cos X — l/x/2) = 0 X = ...,
т.к. —7тг/4 > —5,5 <=> тг < 22/7 (= 3,142 ...) — верно.
Ответ: х = —7тг/4, —Зтг/2.
у/ 1130° (х—87.2). Сколько различных корней имеет уравнение у/бх2 +2ху/3 + 3 = -2х?
у/ 1131° (А — 96.2). Какие из чисел х = ±1, ±4 являются решениями неравенства
|2/3 - Ig5|x < 2/3 - 1g 5?
у/ 1132° (А - 88.1). (х - 2) (|х| + у/3 - 1 - l/v'S) = 0.
136
1133 (ст-97.5).
1134 (д-84.4).
1135 (А-93.4). у 1136 (д-87.2).
1137 (7-01.1).
У1138 (7 - 89.3).
1139 (<д - 99.4).
Ж!>21+3 J\/2x —1| = у/2х-1.
। 2V“2 = 3,2y+3x 1/Зх2 + 1 + xy = y/x + 1.
I log 2 cos *gx2> log2cos a? v'Sx + 4. log 75-4/2 (7x ~ 2x2 ~ 6) > 2-logv/зТ— •s/2l(a'2 — 9) 0. logio-^ (16x/5-x2) < 1. l°gi -2 cos x (cos 2x + sin x + 2) = 0.
1140 (д - 85.1). 6cosx - 1/3 = x/32cosx - 17/9.
У1141 (Vi - 79.1) 4 cos x - ^/3 = i/з + 4^/6 - (16x/3 - 8x/2) cos x. у/ 1142 (x - 99.2) . (sin x + cosx - y/2) /-111 - x2 - 30 = 0. 1143* (д — 82.4). л/4х4 — 3 — x8 (1 — cos(2?r(5x — 9x2))) / 0.
У1144 (тг - 00.5). sin (тг>/8 - x2) = 1/2.
1145° (v - 99.1). 49sin2 x - 7 (4л/3 + 5\/2) sinx + 20\/6 = 0.
1146° (/1 — 78.2). Найти все корни уравнения
^cos 2х । ^cos2 х __ д
на отрезке [3/4; 4/5].
у/ 1147° (х — 95.3). Найти все корни уравнения
2COS X | 2.2 ~ cos х
= 2у/б
на интервале (тг/З;
137
1148* (/1 - 00.3). Найти все корнй уравнения
. х 9. . х х . х 1 х 9
cos х sin - 4- — sm z 4- 2 sin - cos - 4- sin - — - cos - = —, 4 10 4 2 4 2 4 20
принадлежащие отрезку [—9тг/2; —Зтг/2].
у/ 1149* (/1—97.3). Найти ближайший к 13тг/4 корень уравнения
10 . п 3 30
sm х cos 2х 4- sm х 4- — sm2o; = -cos#4- —•
11 4 44
1150* (/1—85.4). При каких значениях а = 0,24тг, 0,26тг, 0,6тг уравнение
(О — 5ж , За\ z_ . / ч /Т7Г\ л --------F log3 — ) (6sm(a — х) - vl8) = 0 7Г------7Г J
имеет хотя бы один корень на интервале (0; тг/З)?
yj 1151 (£—91.5). Найти все а, при которых все корни уравнения
Зах2 4- (За3 — 12а2 — 1)я — а(а — 4) = 0 удовлетворяют неравенству |х| < 1.
17.3. Оценки в геометрии
Решение некоторых геометрических задач также предусматривает сравнение чисел, как-то: длин, углов, площадей и т. д.
Пример (А — 83.2). В прямоугольном треугольнике АВС с гипотенузой АВ = 3 и катетом ВС = 1 на стороне АС взята точка К так, что АК : КС = 1:7. Что больше: АС или ВКЧ
Решение. См. рис.30:
Рис. 30
138
AC = \/32 - l2 (теорема Пифагора) => СК = || AC = => В К = ^72/8 + 1 = \/57/8 (теорема Пифагора).
Сравним: AC V ВК \/8 V ^/57/8 <=> 64 V 57 — верно, когда знак V есть >.
Ответ: АС.
1152° (х — 89.1). Можно ли разместить правильный треугольник со стороной 3 внутри круга радиусом У1б?
у/ 1153 (х — 85.2). Основание ВС трапеции ABCD равно 10, BD = 17,5 и Z.ADB = 30°. Что больше: ВС или CD1
1154 (/1 — 90.1). Найти площадь треугольника АВС, со сторонами АС = 6, ВС = 5, углом Z.A = 30° и высотой ВН < 1/у/2.
1155 (тг — 97.5)._Найти высоту СН треугольника АВС, если
она меньше ^/3/2, АС = 2, ВС = 3, а расстояние от центра описанной около треугольника АВС окружности до стороны АВ равно половине радиуса этой окружности.
1156° (А — 97.6). В ромб, одна из диагоналей которого равна 10, вписан круг радиуса 3. Найти площадь части ромба, лежащей вне круга, и сравнить ее с 9.
1157 (/1—94.3). В круге радиуса 1 проведены хорды АВ = \/2 и ВС = 10/7. Найти площадь части круга, лежащей внутри угла АВС, если угол ВАС — острый.
1158 (а — 98.4). В треугольнике АВС со сторонами АС = = ВС = 12 и АВ = 6 AD — биссектриса. Найти радиус описанной около треугольника ACD окружности и сравнить его с 6,5.
у/ 1159 (а—01.5). В треугольник АВС со сторонами АВ = \/2, ВС = х/5 и АС = 3 вписана окружность с центром О. Что больше: Z.BOC или 112,5°?
д/1160 (д — 84.3). На луче, выходящем из середины D гипотенузы АВ прямоугольного треугольника АВС под прямым углом к ней и пересекающем один из катетов этого треугольника, отложен отрезок DE, равный половине АВ. Отрезок СЕ = 1 равен одному из катетов. Найти площадь треугольника АВС и вычислить ее приближенное значение с точностью до 0,01.
у/ 1161* (</? — 83.4). Найти площадь общей части треугольника AMD и прямоугольной трапеции ABCD с основанием AD = = 14/3, если Z.C = 150°, AD = CD, AM = DM, а точка
139
М находится на расстоянии 7/5 от прямой AD в той же полуплоскости от нее, что и точка В.
t
17.4. Цепочки неравенств
Если данные числа сравнивать друг с другом неудобно, то можно попытаться вставить между ними такое число, с которым каждое из данных чисел в отдельности сравнивать более удобно. В результате получается цепочка неравенств4 *^.
Пример (д - 93.1). . -
log»+i11 10gl23 11
Решение.
f v'lSlogu^ +1) logu 123 • logu(x + 1)
Vogu(* + 1) #0
f(^5-log 123)logll(x + l)>0 logn(ic + 1)<0
)logn(x + l)/0
ilog1/7^ + 2 V tg^.
log logi log5 X > 0.
It 3
Имеет ли область значений функции
Для сравнения же геометрических величин возможно создание цепочек непосредственно из геометрических объектов, например, из отрезков.
У1162 (^ -98.2).
1163 (7-95.2).
у/ 1164 (б —90.1).
общие точки с промежутком [log3 15; оо)?
1165 (/1 — 95.2). Сколько различных корней имеет уравнение log2(40 — 5я2 4- 2х х2) = х 4- 3?
У 1166 (/1 — 99.2).
2»+2 = 49a:2/4 + 4
2«+2 _ 4 2xx2(14 - 2X+2).
✓ 1167’(7 - 96.4) (3»-^eeos(-l/2)) CI-1<,^(277))\0 v x — 8sm(2417r/12)
4^B цепочке могут встречаться и равенства, важно лишь, чтобы все
неравенства были одноименными.
140
1168 (a — 92.5). log1/7(10 - x2) • log1/Z2 |sinx| > 0.
у 1169 (A - 99.8). logs/2+5 sinx > log^.^+g sinx.
1170 (7 — 97.2). Найти наибольший отрицательный корень уравнения
sin(7r(x2 4- х)) = cos(tt(x 4-1)).
1171 (7 — 79.5). Найти все решения неравенства cos (3/2) — 4х — х2 >0
на интервале (—33/8; 0).
1172 (/3 - 81.4). (2Ж 4- 3 • 2-®)21o82®-Io82(®+6) > 1.
1173 (А - 86.3). 2r6*~4*~ 3 = 3.
v ' 6х - 9х - 1
у/' 1174° (А — 83.2). В прямоугольном треугольнике АВС с гипотенузой АВ = 2, катетом АС = 1 и биссектрисой AL М — точка пересечения медиан. Что больше: AL или AM?
1175 (б — 79.2). В треугольнике АВС проведены высоты BD = 11,2 и АЕ = 12. Найти АС, если BE : ЕС = 5:9.
у/ 1176 (б — 79.2). На плоскости расположены точка М и прямоугольник ABCD с диагональю 10 и площадью 48. Найти расстояние от точки М до наиболее удаленной от нее вершины прямоугольника, если МВ = MD = 13.
1177 (и — 99.4). В круг с центром О вписан четырехугольник ABCD со стороной АВ = 10 и перпендикулярными диагоналями, причем Z.COD = 3Z.AOB, Найти площадь круга и сравнить ее с 510.
1178* (/? — 86.4). На стороне АС = 3\/3 треугольника АВС взята точка М так, что AM : МС = 1:2. Через точку М проведена прямая, параллельная АВ и пересекающая сторону ВС = У13 в точке N. Биссектриса угла А пересекает отрезок МN в точке L, а радиус описанной около треугольника AML окружности равен Уб + 3 Д. Найти АВ.
у/ 1179* (V> — 94.3). На стороне АВ = 14 тупоугольного треугольника АВС взята точка L, равноудаленная от прямых АС и ВС, а на отрезке AL — точка М, равноудаленная от вершин А и В. Найти sin ZC, если ML = 1 и ZA = 45°.
1180* (7 — 87.3). Окружность радиуса 2>/5, проходящая через вершины А и В треугольника АВС, касается прямой АС
141
в точке А и высекает на прямой ВС отрезок длины 4\/5. Через точку В проведен перпендикуляр к прямой ВС, пересекающий прямую АС в точке D. Найти площадь треугольника АВС, если BD = 2.
§ 18. Некоторые особенности преобразований
При использовании равносильных преобразований можно столкнуться с весьма специфическими трудностями, преодоление которых требует дополнительного мастерства.
18.1. Изменение области допустимых значений
Изменение области допустимых значений в результате некоторых преобразований наблюдалось и ранее: например, в п. 1.2, 3.2, 3.3, 3.4, 8.1. В настоящем пункте собраны задачи, в которых либо это изменение не сразу бросается в глаза, либо имеется соблазн незаметно сузить ОДЗ.
Пример (/3 - 91.1). 4'/г+^-13-27^1+20 = 0.
Решение.
Г2 • 4^+1 - 13 • 2^+1 + 20 = 0
|(2^«-|)(2'/г+‘-4)=0 e/f+1=, .
|^+1И2 v 522
у/х = log2 | - 1 (= log2 5 - 2 > 0) ...
О т в е т: х = (log2 5 — 2)2.
у 1181 (д-85.2). ^1т + 1^>1^т.
1182° (С-95.1). tgf = l- cosx.
у/ 1183 (е — 84.3). sin2х + 2cos4a: = 3 + 1+t^8х
1184* (х-78.2)1). (1 + tg2 |) (sin4а:cos5х-sin | cos = = sec2 | (sin cos | — sin 5x cos 4x).
у/1185° (e - 83.2). tg3a: = tg5a:.
1186 (C - 01.1). tg(a: + 1) ctg(2a: + 3) = 1.
1187* (x - 01.3). tga: + tg 2x + tg x tg 2a: tg3x = tg3a: + tg4a:.
1^По определению, sec sc =
142
У 1188* (д-84.2).
^/1189 (А-99.5).
У1190° (7-83.2).
^/1191° (А -79.2).
1192 (А-95.2).
Найти ближайший к корень уравнения sin 2тгх _
1 + tg (тгх/2)
|- cos2 2х + Зу/— cos 2х + 1/4| =
= |cos2 2х + Зу/— cos2а: — 1/4|.
log2 (\/х2 - 4х + 3) >
> logl/2 7xs-4®+v'®+i+i + 1ф 14- lg (1 + х2 - 2а:) — lg (1 + х2) = 21g (1 -х). log2(ll -х) + log2(x + 1) =
= log2((x + 1)(х2 + 5х — 5)).
1193 (х - 92.3). log5 (х + 2) + log5 (1 - ®) С
logs (U “ аг)(а;2 - 8х 8)).
log2^r+31og8^f <1.
4 log2 х + log2 О - log2 (х - 1) - log! х.
log9 qr + 1о8з(® + 5) = 1.
log3(x - 2) - log9(x2 - Юх + 25) = log3 2.
2 log7 (x — 2) = log7 (x — 10)2 — 2.
log4 (3 - 3x)2 log2(x2 - 1).
log9 (x2 - 5x + 6)2 = | log^ 2fi+log3 |x - 3|.
< logj, у + logy x = 5/2
4y/x-3y/y = 1.
logs-t-^a:3 + 10x2 + 20x) • log3(x + 4) —
= log3(3x2 + 8x).
log3-z(2a: + 1) • tog2«+ix2
+ !) • log3a+i(x + 2).
^21+4»-»^ (7-X) 1
1о8х+з(21 + 4x - x2) 4’
log^3-logh > 0
Iog2®3-a:log2x3
(x2 4- 4) lg sin2 3x + x2 lg cos2 2x =
= 4 lg(cos 2x sin3 3x).
31/2+log3 cos x । gl/2 = gl/2+log9 sin x
У 1194 (С-00.3).
1195 (х-87.2).
1196 (С-97.3).
1197 (С-98.1).
1198 (% - 88.1).
1199 (е —96.1).
У 1200 (^т—78.4).
1201 (д —89.4).
1202° (д - 96.1).
у/1203 (% —99.3).
^/1204 (д - 01.2).
у/1205 (тг - 97.4).
У1206 (д-99.1).
у/1207 (д - 77.3).
143
у/ 1208 (а — 95.1). Найти все х, при которых числа
—1, х2 4- 2х, sin (arcsin х3) образуют геометрическую прогрессию.
у/ 1209 (А — 79.6). Найти все а, при которых уравнение
о 6х 9л/3 Л
х2 4- /== 4- —— 4- 36 = О vsina cos а
имеет единственный корень.
1210 (£ — 89.5). При каждом а определить знаки корней уравнения
(2х)2 - 4ху/а& + Зо+1 + а - 3 = 0.
1211* (V> — 83.5). При каждом а решить систему
{2cosx 4- asint/ = 1
logz sin у = logz a • loga (2-3 cos x)
logo z + loge (l/2a - 1) = 0.
18.2. Случаи неодинаковых оснований
Один из способов оперировать с логарифмами, имеющими разные основания, — перейти к новому основанию, а степени с разными основаниями можно, к примеру, прологарифмировать.
Пример (е - 97.1). З1 *’1 = 5i2+3x.
Решение.
...<=> |я • log5 3 = х2 4- Зх <=> х(х 4- 3 - sgn х • log5 3) = 0
_ 2) ® = 0
х = — 3 +• sgn® • log5 3 (< 0 => sgn® = —1)
Ответ: ® = 0, —3—log53.
У1212 (^-78.1).
У1213 (е - 79.5).
1214 (е —85.3).
Ьёз | • log2 х - log3 = 1 4- log2 v/ж.
log5 (ж2—6ж—6)2—log,! (ж2—6ж—6)3 Q
44-ж-зА
При каждом а решить уравнение
log2 х 4- loga х 4- log4 х = 1.
2)По определению, sgn а? =
кает равенство |х| = х • sgn я.
1, х > 0,
0, х = 0, откуда, в частности, выте-
-1, х < 0,
144
у/1215 (д- 01.1). а ; > log2(101 • 10х - 102+2х) - - log5(101 • 2х - 52+х • 22+2х).
у/ 1216* (А-97.5). 1217 (д — 86.3). : У1218 (х- 88.4). * у/ 1219 (л - 00.3). 2 jyl°gl/17 1°8з х > ^°81/3 1°б17 х ' }х2+2 + 3х2 2 • 5х3+1. }х >6-9lx-1l. !х2 • 3х < 6. ( д2(1—х) §х2—5x44
1220 (7-97.5). ) logl/5 Ух+З , V 1о81/б(:с+1)
у/ 1221* (е-97.2). | 1222 (С - 95.7). I [1/2)^(х2-2х-15)3 7(«+з)2(х-5) L Три каждом а решить неравенство дх/х+Т > 20-1.
у/1223 (х- 01.2). 2 у/ 1224 (тг - 96.3). а >lg(»2-l) (a; + l)lg2 ;2’og4® = S/X2.
1225 (е-77.3). < yi-i'oe.v = 1 + logj. (1 - 3y/x) = logj. 4.
18.3. Специальные действия с радикалами
Полезно замечать сопряженные радикалы \/а 4- \/b и у/а — памятуя о том, что в произведении они дают рациональное выражение а — Ь.
Пример (х ~ 97.2). (2 4- х/З)* 4- 2 < 3(2 - у/3)х.
Решение.
... <=> р 4-2 < Зр""1, где р = (2 4- х/3)ж (=> (2 - у/3)х = р"1),
о p2 4- 2p — 3 < Ответ: x < 0. : 0 <=> (p 4- 3)(p - 1) < 0 <=> (2 + \/3)x <!«...
Иногда удается извлечь корень из выражения вида а ± Ъу/с, преобразовав его в полный квадрат (выражения того же вида)3).
1226° (А - 94.2). Вычислить 3 • у/8-2у/7 V3-a/7
У1227 (д - 78.1). Вычислить ^40/2-57| - ^40у/2 + 57. 3 *
3) Или воспользовавшись формулой сложных радикалов
\/а ± by/c = J± угде d = у/а2 — Ъ2с.
145
1228° (х — 82.3). (v^+1)tft (v^-l)-*.
у/ 1229 (д - 01.1). 26х + 27 9(6 - Л0)х + 3(6 + х/1б)ж-
1230* (х — 00.6). (26 + 15V3)1 -5(7 + 473)® +
+6 (2 + у/3)х + (2 - у/3)х = 5.
у/ 1231 (х - 93.1). log^-^+i VS (4х - х2 - 2) > 0.
1232 (х - 01.3). log^+ys+v's * + Ь&(л^ + л/3 - Л) = = 3/2 + loga 2у/б.
1233” (д- 95.2).
V 1234 95.1). » 0.
1235 (а - 93.4). log,. (За; - 2) - 2 =______________________
= \/log2 (За: - 2) + 41oga
у/ 1236 (х — 93.2). Найти все корни уравнения х/Зсозж — sin# = v 1 4- 2 cos2 я — \/3sin2x на отрезке [0; тг].
1237* (х - 96.3). 02 sin а; - | cos 2а; + =
= | 4- 4sinx 4-1 cos2 х.
1238* (А - 85.5). х/Зя2 - 7х 4- 3 - х/ж^2 =
= х/Зя2 — 5х — 1 — у/х2 — Зх 4- 4.
у/ 1239* (х — 98.6). Найти все а, при которых уравнение
(х/х2 — Зах 4- 8 4- х/я2 - Зах 4-6)* 4-
4- (х/я2 — Зах 4- 8 — у/х2 — Зах 4-6)* = 2(х/5)* имеет единственное решение.
у/ 1240 (/1 — 96.3). Треугольник АВС вписан в окружность радиуса 2х/3, причем АВ = 4 и ZA = 60°. Найти среднюю линию МN этого треугольника, параллельную АС, и расстояния от точек М и N до ближайших к ним точек, в которых прямая МN пересекает окружность.
§ 19. Различные системы и совокупности
В настоящем параграфе развиваются изложенные в п. 4.1 методы решения систем и их приложения к текстовым и логическим задачам, а также к уравнениям и неравенствам с модулями.
146
19.1. Метод подстановки
Подстановка применяется не только для исключения неизвестных. Не менее продуктивной может оказаться и частичная подстановка^ а именно, замена одного выражения другим, равным ему в силу какого-либо уравнения, содержащегося в системе.
{х___1/ - 6
3 3 10к
х — у = 126.
Решение.
{х — у = 6 J х — у = 6
(х - у) (х2 + ху + у2) = 126 [6 • ((ж - у)2 4- Зху) = 126
I х - у = 6 I х + (-у) = 6 [62 + Зху = 21 (х • (—у) = 5 Ответ: х = 1, у = —5; х — 5, у = —1.
1)
X = 1
-у= 5
2)
5 4Ф-...
1
1241° - 80.3).
1242° (е-96.2).
У 1243 (i/ - 99.2).
у/1244 (А - 01.5).
У1245 (х —95.1).
'у-х = 5
< zx = (z — 4)у + 30 2zx = (2z - 4)j/.
х + 3» = 2
* х3 + 27» = 26.
f(1/4)-W2 + log32/ = 504
}4® 2х-1 log^ у + log2 у = 84.
'«3t , -5---- _ 5
( 2 ~ 2x+y-xy °
2x + y+j% = 4 + xy.
Найти все целочисленные решения системы
2ху 4- Зх = 14
ху 11.
у/ 1246* (а — 01.6). Найти все а, при которых система
а{х 4- 2) 4- у = За а 4- 2я3 = у3 4- (а 4- 2)я3
имеет не более двух решений.
^См. теорему Виета в п. 6.3.
147
19.2. Метод сложения
Уравнения складываются как для исключения неизвестных, так и для понижения степени, разложения на множители или какого-то другого упрощения. Вариант оформления решения методом сложения предложен в п. 4.1.
тт i пл\ Г 2®2 4- j/2 - 4® + 2у = 1
Пример (е — 79.4). < о о
' [З®2 - 2у2 - 6® - 4У = 5.
Решение.
( 2®2 + у2 - 4® 4- 2у = 1 2 3 Г 7®2 - 14® - 7 = О (З®2 - 2у2 - 6® - 4у = 5 1 -2 ** yiyi _ 14^ + 7 = 0
Ответ: х = 1 ± \/2, у = —1.
При сложении уравнения можно умножать не только на числа, но и на буквенные выражения, зависящие от неизвестной величины или от параметра. При этом равносильность обеспечивается, как и обычно, простой непропорциональностью множителей.
1247° (е - 79.4). Зя2 4- 2у2 — Зя + 5у = 3 4,5я2 4- Зу2 - Зя + 8у = 7.
' 1248° (е — 80.3). * Зя2 4- 2ху — 9я — 4у 4- 6 = 0 5я2 4- 2ху — 12я — 4у 4- 4 = 0.
у/ 1249 - 82.3). < я2 — 4яу 4- у2 = 3 у2 - Зху = 2. к
у/ 1250 (А - 00.5). < 2я44-у2 = 10 я2 4- 2у4 = 10.
1251 (х- 77.3). [sin2(—2я) - (3 - л/2) tg 5у = [tg2 5у + (3 - д/2) sin(—2я) = М|~-.
1252* (х —97.4). 41 + 5 • 2х - 2 • 3» = 2 ' 2 • 9» + 2х + 2 • 3» = 1.
1253* (7 — 95.1). • (у/х(х 4- Зу) = 36 (х/у(3я4-у) = 28.
1254 - 77.4). < я + log2 у = у log2 3 + log2 я я log2 72 + log2 я = 2у 4- log2 у.
148
1255 (тг — 94.4). Найти все решения системы
sinxcos?/ = 1/4 cos х sin у — —1/4,
удовлетворяющие условиям —тг/2 < х < тг/2, —тг/2 < у < тг/2.
У 1256 (б —81.4).
1257 (/3—80.5).
sin х cos у = —1/2 tgxctgy = 1.
3 sin3 х — 3 cos2 x 4- 7 sin x — cos 2x 4-1 = 0 cos2 x 4- 3 cos x sin 2x — 8 sin x = 0.
У 1258* (0 — 92.4). Найти все пары (а, 5), при которых система
х3 — 5я2 4- 7х — а, х3 — 8х 4- b = 0
имеет не менее двух различных решений.
у/ 1259* ((/? — 00.5). Найти все а, при которых уравнения (2а — 1)я2 4- бах 4-1 = 0 и ах2 — х 4-1 = 0 имеют хотя бы один общий корень.
у/ 1260* (А — 97.8). Найти все а, при которых система ((2х — 1)а2 — (х2 — х 4- 1)а — (х3 — 4я2 4- 3) = 0 |^(5 — Зх)а2 4- (5я2 — 5х — 2)а — (2я3 — 8я2 4- 6) = 0 не имеет решений.
1261* (£ — 88.5). Найти все а, при которых система
аху 4- я — 2/ 4- 3/2 = 0
х 4- 2у 4- ху 4-1 = 0
имеет единственное решение.
19.3. Системы в текстовых задачах
При решении некоторых текстовых задач нужны именно равносильные преобразования.
Пример (7—90.1). Произведение первого и пятого членов геометрической прогрессии равно 12, а второй член равен утроенному четвертому. Найти второй член прогрессии.
149
Решение. Условие задачи записывается в виде
(bibs = 12 (b2b4 = 12 Jb2/3 = 12 fb2 = ±6
(Ь2 = ЗЬ4 ** |б4 = Ьг/З ** (62д2 = Ь2/3 ** [д2 = 1/3.
Ответ: ±6.
Если для решения задачи достаточно лишь вывести следствие, то круг возможных преобразовании системы расширяется: например, уравнения можно умножать или делить друг на друга.
у/ 1262 (тг — 00.2). Первый, второй и четвертый члены арифметической прогрессии равны соответственно первому, второму и третьему членам некоторой геометрической прогрессии. Найти ее знаменатель.
1263 (V>—00.2). Первый член геометрической прогрессии равен 10, а сумма второго и третьего равна целому числу, кратному 4 и не превосходящему 1000. Найти знаменатель прогрессии, если он больше 1.
У 1264 (7 — 98.2). Найти знаменатель геометрической прогрессии, если сумма первых трех ее членов равна —7, а пятый член меньше второго на 14, но больше шестого.
1265 (б—87.2). В магазине продано 10,5 т орехов трех сортов по цене 6, 4 и 2 руб/кг на общую сумму 33 тыс. руб. Количества проданных орехов первого, второго и третьего сорта образуют геометрическую прогрессию. Найти эти количества.
у/ 1266 (а — 01.3). Из пункта А в пункт В, расстояние между которыми равно 10 км, отправился пешеход, через 50 мин после него — велосипедист, а еще через 25 мин — бегун. Велосипедист догнал пешехода в середине маршрута, а бегун — в конце. Скорости пешехода, бегуна и велосипедиста образуют арифметическую прогрессию. Найти эти скорости.
у/ 1267* (/? — 79.2). Из двух пунктов, расстояние между которыми равно 2400 км, выехали одновременно навстречу друг другу пассажирский и скорый поезда, которые через некоторое время встретились. Если бы оба поезда шли со скоростью скорого поезда, то их встреча произошла бы на 3 ч раньше, а если бы со скоростью пассажирского, то на 5 ч позже фактического момента встречи. Найти скорости поездов.
1268* (х — 79.3). От пристани А вниз по реке отправились одновременно пароход и плот. Пароход, дойдя до пристани В, расположенной в 324 км от А, простоял там 18 ч и отправился назад. В тот момент, когда он находился в 180 км от А,
150
второй пароход, отправившийся из А на 40 ч позже первого и имеющий ту же собственную скорость, нагнал плот, успевший к этому времени проплыть 144 км. Найти собственную скорость пароходов и скорость течения реки.
1269 (б — 77.1). Для разгрузки парохода выделено две бригады грузчиков. Если ко времени, за которое разгружает пароход одна бригада, прибавить время, за которое разгружает пароход другая, то получится 12 ч. Определить эти времена, если их разность составляет 45% времени, за которое бригады разгружают пароход вместе.
У 1270 (А — 77.1). Бак наполняется через одну из двух труб, причем через первую трубу на 1ч быстрее, чем через вторую. За время наполнения бака через вторую трубу первая труба может пропустить 3 м3 воды. Если бы емкость бака была на 2м3 больше, а пропускная способность второй трубы на 4/Зм3/ч больше, то за время наполнения бака через вторую трубу первая труба могла бы пропустить 2 м3 воды. Найти емкость бака.
19.4. Необычные равносильные преобразования
Рассуждая тоньше, чем обычно, при работе со сложными системами, совокупностями или какими-либо другими высказываниями (содержащими неизвестные) можно добиться значительного их упрощения, сэкономив на арифметике за счет более рациональной логики.
Пример (тг — 90.5). Найти все ж, при которых наименьшее из. чисел 2x4-3 и х 4- 5 больше —1.
Решение.2^
. /Л о . (2x4-3 > -1 (х > -2
min (2х 4-3, х 4- 5) > — 1 <=> < 4^...
I х 4- 5 > —1 I х > —б
Ответ: х > —2.
1271 (А — 84.3). Найти sin а, если
cos 4а < —7/8 и cos2a^—1/4.
у/ 1272 (/1 — 94.4). Найти все х, при которых наибольшее из чисел За: — 4 и log2 (5 • 22х~4 - 2х"1 + 1)
положительно.
2) Наименьшее из чисел а и b принято обозначать через min (а, Ь).
151
у/ 1273 (/2—95.4). Найти все х е [0; тг], при которых выражения 1 л л tg х и -------------------------2 cos 2х
cos 2х
имеют разные знаки.
у/ 1274 (б — 77.5). Найти все а, при которых неравенство 25t/2 4- 1/100 > х — аху + у — 25я2 выполняется для всех таких пар (хуу), что |я| = |у|.
у/ 1275* (/1 — 99.3). Найти все х, при которых хотя бы одно из двух выражений
|ж — 3|(|я — 5| — |ж — 3|) - &х и |ж|(|ж| — |ж — 8|) 4- 24 неположительно, а его модуль не меньше модуля другого. у/ 1276 (7—97.6). Изобразить на координатной плоскости множество точек (ж,у), для которых существует остроугольный треугольник со сторонами 1, |я| и y/^у. Найти уравнения кривых, ограничивающих это множество.
у/ 1277* (/1 — 01.2). Найти все ж, при которых чйсла log2(2x2 4- 4я), log2(8 — х2 — 19я) и log2(z2 — 15х 4- 7|) являются длинами сторон некоторого равнобедренного треугольника.
1278* (7 — 96.6). Найти все а, при которых многочлен f(x) = х3 — (4 4- а)х2 4- Ьах — а2
имеет тройку корней, являющихся квадратами сторон некоторого неостроугольного треугольника.
19.5. Разные способы избавления от модулей
Решая уравнение или неравенство, содержащее выражение под модулем, можно обойтись без исследования знака этого выражения, если отойти от стандартного пути3) и при переходе к новой системе или совокупности проявить изобретательность.
Пример (£ — 95.3). 2|х 4-1| = 2 — Зх.
Решение.
/2(® 4-1) = ±(2 — 3®) Г®=^(=0,4)
(2-30 0 (0 2/3
Ответ: х = 0.
3)Который состоят в раскрытии модуля по определению (см. п. 11.1).
152
1279° (х-79.2). 1280° (е - 86.1). У1281 (А-91.2). | 1282 (<т — 00.3). | 5|4г-6| _ 253®-4. J|x+l| _ ^у/2)~2х+3. х2 — 2х — 1| — х + 1 = 0. х2 — Зх| = 2х — 4.
1283 (х- 97.3). |х2 — 4у + 3| + у = 1 2х + 2у = 1.
1284 (С - 98.5). < х + |а: + у — 11 = 0 у — 3 + у/х — у + 6 = 0.
1285 (А-98.2). | У1286 (е - 89.3). |: 1287 (V> - 98.1). 1288 (х - 96.3). |4 — х2| — х2| = 1. г + 1 + | — х — 3| | — 6 = х. 4х - |х - 2| + 3| = 16. х + |1 - х|| > 3.
1289 (С - 97.5). < у + |х + 1| = 1 |у-х| = 5.
1290° (7 - 77.1). у/ 1291 (С -98.2). |: У1292 (х-00.1). | 1293 (д - 93.1). ( У1294 (х-01.3). I 3|х —1| >х + 3. с2 + 2х — 7| < 2х. \х2 — 8х + 2| — х21 > 2х + 2. ' З/?)35® < 1 . у|4х2- 12х —1| 1ри каждом а решить неравенство |2х + а| < х + 2.
1295 (е- 82.2). * 1296 (а - 00.1). | у/ 1297 (0 - 83.3). 8 1298° (х — 91.2). у/1299 (е-01.1). |а у/ 1300 (х- 01.1). т у/ 1301 (д- 00.1). } у/ 1302 (0 - 82.2). 1 у/ 1303* (х — 98.3). У1304 (д — 92.1). 6 х—5 -I —11 % * 2х-1| > ► + 6|3 — \/х 4- 5| > х. с2 — 8х 4-15| 115 — я2|. ж-1| |аН-1|’ я: —41 — |ж—11 |ж—3|4-|а:—2| х— 3| — |ж— 2| |ж—4| .4- 2 sinX | cosx| = 0. | sin3 я| 4-13 cos3 х — cos x = 0. • sin(# 4- тг/З) 4- | sin(x — тг/6) | = 1.
153
1305* (х - 97.3). 3 4- | sin x — 3coss| = 3sins 4- coss.
1306* (x - 81.5). Найти все решения уравнения
| sin(2s — 1)| = cos x,
удовлетворяющие условию |s| < 2тг.
1307* (д - 01.4). у/ 1308 (А-96.3).
1309 (А-92.3).
1310* (^>-77.2).
| cos2ssin6s| 4-1 cos6ssin2s| = sin log .^1 (x - 1) = 2.
|2x-3|
I logs з • log3 x4 - 5 log,, x* 21 = 2 logx 25.
/(l + 21og|xyl 2) logl+j, |а:У| = 1 x - у = 2\/5.
§ 20. Область значений и экстремумы функций
Исследование функций на экстремум представляет собой мощный аппарат для решения сравнительно трудных задач определенного типа (см. п. 20.4).
20.1. Исследование функций без производной
Чтобы доказать, что наибольшее (наименьшее) значение функции равно числу М, необходимо и достаточно установить два факта: во-первых, что значений, бблыпих (соответственно, меньших) числа ЛГ, функция не принимает, и во-вторых, что значение М она принимает хотя бы в одной точке.
При исследовании функции на максимум или минимум без производной могут пригодиться теоремы о средних1 \ оценка для суммы двух взаимно обратных чисел2), а также умение выделять полный квадрат в квадратном трехчлене, сворачивать тригонометрическое выражение с помощью вспомогательного угла (см. п. 2.6), выделять целую часть в дробном выражении (см. п. 25.2) и т. д.
Пример (х— 82.2). Найти все х, при которых функция f(x) = 3 — 2 sin2 2х — 2 cos 2х
принимает наименьшее значение. х
Решение.
f(x) = 3 - 2(1 — cos2 2х) — 2 cos 2s = 2 (cos 2s — 1/2)2 4-1/2 1/2,
*) Например, о средних арифметическом А = «1±^±£а. и геометрическом G = ^si....хп неотрицательных чисел si,...,sn, для кото-
рых справедливо неравенство А > G, причем А = G <=> si = • • • = sn.
2)Если а > 0, то а 4- 1/а > 2, причем а 4- 1/а = 2 <=> а = 1.
154
причём последнее неравенство обращается в равенство, тогда и только тогда, когда
cos 2х = 1/2 о 2х = ±7г/3 + 2тгп, где п 6 Z, о ...
Ответ: х = ±тг/6 4- тгп, где п 6 Z.
1311° (б — 94.2). Найти область значений функции
/(ж) = — Зх2 + 12х — 3.
1312° (£ — 78.2). Найти все точки экстремума функции
f(x) = \j2x2 - ж 4- 2.
У 1313 (7 — 00.4). Найти наибольшее значение функции у (а:) = tg ( | iog1/3 (2 - \Д + Зх-х2) ) при условии arctg > -.
у/ 1314 ((/? — 78.4). Найти наибольшее и наименьшее значения функции
/(ж) = sin2 х 4- cosх — 1/2.
1315* (б — 81.6). Принимает ли функция /(ж) = sin2 х — 12 sin х cos х 4- 3 cos2 х — 2 \/66 хотя бы в одной точке положительное значение?
1316 (тг — 90.4). Найти наименьшее значение функции /(ж) = 1 4- 4 sin ж — 2х
на отрезке [0; тг].
у/ 1317 (7 — 81.2). Найти наибольшее значение функции f(x) = |я| — х/2 4- sin2 х
на отрезке [—тг/2; тг/2].
1318 (V> — 78.4). Найти наибольшее значение функции ас/ ч Ю
f (х) = —--------— 4- cos х.
х2 4- 4тгя 4- 40
у/ 1319 (V> — 78.4). Найти наименьшее значение функции f{x) — 4я 4- 9тг2/я: 4- sinх
при х > 0.
155
у/ 1320 (х — 91.1). Найти наибольшее и наименьшее значения функции
f(x) - ___+ 1_____
Л (Зя 4-1)2 4-1’
у/ 1321 (б —97.6). Найти все а, при которых периметр фигуры, заданной неравенством
а2 + х2 - ST > °-принимает наименьшее значение.
у/ 1322 — 80.5). Доказать неравенство
2(2® - 1)* + 1 + (1 - 2(2® - I)4) sin 2у 0 и найти все пары обращающие его в равенство. 1323* (А — 98.7). Найти наибольшее и наименьшее значения функции
f(x) = cosx 4- 4cos 4- 7cos 4- 6cos
2 4 8
20.2. Условные экстремумы
Максимум или минимум выражения, подчиненного данному условию, называется условным. Если исследуемое выражение содержит несколько переменных, то всякое равенство, связывающее эти переменные, позволяет по существу уменьшить их количество.
Пример (х — 86.2). Найти координаты точки, лежащей на прямой — 4х — Зу = 25 и наименее удаленной от начала координат.
Решение. При данном в задаче условии квадрат расстояния между точками (ж, у) и (0,0) равен
„2.2 J|/-4i-25\2 25„2 । 200^ । 625
х +у =х 4- (—з—) = -дХ 4- — х+т, 200/9 а а его минимум достигается в точке х = — = —4, в которой
у==2^4 =3
Ответ: х = —4, у = —3.
у/ 1324° (а — 92.6). Найти все при которых сумма квадратов корней квадратного трехчлена
f(x) = х2 — 2ах 4- 2а2 — ба 4- 8
принимает наименьшее значение.
1325 (/1 — 89.4). Найти все а, при которых выражение
(zi 4-2x2)(x2 4-2x1),
156
где xi э2 — корни квадратного трехчлена f(x) = х2 4- ах 4- а 4-1/5,
принимает наименьшее значение.
у/ 1326 (7 — 01.3). Найти наименьшее значение выражения 2х2 — 4у2 — z2 4- 6х 4- 4yz
при условии, что числа ж, у, z образуют арифметическую прогрессию, а числа х — z, z — у, 2х — геометрическую.
у/ 1327* (х — 97.6). Найти наибольшее и наименьшее значения выражения х2 4- 2у2 при условии
х2 — ху 4- 2у2 = 1.
1328* (б — 98.6). Среди точек (х,у) с целочисленными координатами, удовлетворяющими неравенству
/2aAlogft (М+М-14) \3у/ <3,
найти наименее удаленные от точки (2, —2).
1329* (х — 93.5). Найти все пары (а, 5), при которых точка с координатами, удовлетворяющими системе
а2х — у = 2а2 — 2Ь < х — by = 2 — 2а2 у = 2 -х,
наименее удалена от точки (3, —1).
20.3. Исследование области значений в процессе решения
Информация об области значений функции и о точках, в которых она принимает свои экстремальные значения, может оказаться полезной даже тогда, когда вопрос об этом специально не задается.
Пример « - 77.3). log7 х - log^ | > 2. Решение.
log7 х + > 2 0 < log7 X / 1 (т.к. а+|^2<=>а>0
и а+| = 2<=>а=1) <=>...
Ответ:1<ж<7, х >7.
1330° (а - 97.4). log1/3 |® - 2| - 1о§2_г 3^2.
157
1331° (е - 92.2). 1^—0.
у/ 1332 (£ — 00.7). Найти все а, при которых уравнение 25® - (2а + 5) • 5х"1/® + 10а • 5“2/® = 0
имеет ровно два корня.
1333 (а — 00.5). Найти все а, при которых неравенство |я2 — 2х 4- а| > 5
не имеет решений на отрезке [—1; 2].
у/ 1334 (А — 95.8). Найти все а, при которых неравенство 9® < 20 • 3® 4- а
не имеет ни одного целочисленного решения.
у/ 1335 (ц — 95.3). Найти все а, при которых функция f(x) = а(2 sin х 4- cos2 х 4-1)
не принимает значений, ббльших 3.
1336 (7 — 95.6). Найти все а, при которых функция f{x) = log25_a2(cosx 4- x/Ssinx - а) определена для всех х.
у/ 1337 (а — 96.6). Найти все а, при которых неравенство Iog2q-15 > 0
выполняется для всех х.
1338 (тг — 88.5). Найти все а, при которых система х2 4- 2ах 4- 4a2 — 5a 4- 3 < 4 sin у — 3 cos у 0 у < 2тг
имеет единственное решение.
1339 (V> — 96.3). Найти область определения функции /(я) ±= (—6 sin2 2х — 2 sin 2х cos 2х 4- 8 — х/3)~^2.
у/ 1340 (б — 88.6). Найти все а, при которых неравенство |3sin2 х 4- 2a sin# cos# 4- cos2 x 4- a| < 3 выполняется для всех x.'
у/ 1341* (тг — 98.6). Найти все а, при которых уравнение 5 cos z 4- sin х 4- cos(x — </?)= a
158
имеет корень
1) хотя бы при одном
2) при любом
у/ 1342 (/2 — 96.4). Найти все а, при которых уравнение
2 cos2 22х~х2 = а 4- \/3sin 22х~х2+1
имеет хотя бы один корень.
1343 (А — 99.3). Найти наибольшее значение а, при котором уравнение
arctg |9® + 4*+ау/2 6Х| =5 О имеет хотя бы один корень.
1344* (б — 78.5). Найти все а, при которых неравенство
а(4 — sin х)4 — 3 4- cos2 х 4- а > О выполняется для всех х.
у/ 1345* (А — 89.6). Найти все а, при которых уравнение (а2 4- 8а 4-16)(2 — 2 cosх — sin2 х) 4-
4- (32 4- 2а2 4- 16a)(cosx — 1) 4- За 4-10 = О не имеет корней.
1346* (/1 — 01.5). Найти все ж, которые не являются корнями уравнения
4\/2я4 4- х3 = а \/4 —а2 (х 4- 4х2 — 8)
ни при каком а.
у/ 1347* (тг — 00.7). Найти все а, при которых для любого Ь уравнение
|я — 2| 4- Ь|2я 4-1| = a имеет хотя бы один корень.
20.4. Экстремальные ситуации в уравнениях и неравенствах
Уравнение или неравенство кардинально упрощается, если для его выполнения необходимо и достаточно, чтобы одно или несколько выражений сразу принимали свои экстремальные значения. Задачи, основанные на этой весьма популярной идее, как правило, не бывают слишком простыми.
159
„ ™ I cos4x 4- sin2w = -2
Пример (Л — 83.4). <
I х — у = 2тг.
Решение.
у = х — 2тг
... cos4x = —1 (т. к. cos4x —1
sin2(x — 2тг) = —1 и sin2y —1)
{sin 2х = — 1 (=> cos 4х = 1 — 2 sin2 2х = — 1) <=>...
у = х — 2тг
Ответ: х — ~ 4- тгп, у = — 4- тгп, где п 6 Z.
1348° (х - 98.3) ат2 4-?/2 4-2(ж — ?/) 4-2 = 0.
1349* (А — 90.5) Найти все пары (а, 6), при которых уравнение (Зх2 — 2а2 4- ab)2 4- (За2 — ab 4- 2Ь2 — 12я)2 4- 4 = 4х — х2 имеет хотя бы один корень.
у/ 1350° (х - 99.1) X2 4- 1 4- |ж - 1| = 2|ж|.
1351° (£ — 96.8) При каждом а решить уравнение (log2 3) '/®+e+2 = (log9 4) Vx4+a5-6a-5
у/ 1352 (a — 94.6) Найти все а, при которых уравнение а2х2 4- 2а(\[2 — 1)я 4- \Jx — 2 = 2\[2 — 3 имеет хотя бы один корень.
у/ 1353* (х- 01.4)
1354° (Л - 83.4)
1355* (д-93.3)
1356° (тг - 01.3)
1357° (а - 93.5) у/ 1358° (х - 93.5) у/1359 (С - 01.7)
%/4а: — х2 + \/4а: — а:2 — 3 = 3 + \/2х — х2.
{3 sin За: + cosy = —4 х + у = Зтг/2.
(cosy + sin а: — 1)х
< x(tg2(a:-тг/З)+ tg2(y+ тг/6)) = 0 (sin# — cos?/)(2 — sin2j/ 4- sin?/) = 0. x2 — cos 2x2 4-1 = 0.
sin2 x 4- 3z2 cos x 4- 3x2 = 0.
2(1 4- sin2(x — 1)) = 22x~x\
При каждом а найти все корни уравнения
cos 2х 4- 2 sin2 (х 4- а) 4- 2 = sin а, принадлежащие отрезку [тг; 2тг].
у/ 1360 (х — 92.2) х/1 + cos бх sin = 2\/2 cos
160
1361 (/1—93.4) Найти все а 6 (—тг/2; 0), при которых уравнение
\/2cos(x 4- а) — 1 = sin 6х — 1
имеет хотя бы один корень.
1362 (7 — 98.4) sin я 4- л/Зсозя = 2 4- 3cos2 (2х 4- тг/6).
у/ 1363 (V> — 93.3) Найти все корни уравнения .
1 . 9 / 7Г \ . л л г-
sin я 4- — 4- sin Зх = cos Зх — v 2 у/2 V 12/
на отрезке [—2тг;2тг].
1364* (V>-92.1) 3 sin 2тгя > \/2 sin 4тгя 4- 3 cos 2тгат 4- \/32.
1365* (X -91.4) cos4 х = | cos 2х 4- | cos2 х cos Sx.
1366* (е - 82.6) 8 cos х cos у соз(я — у) 4-1 = 0.
1367* (Х-01.6) При каждом а решить уравнение
• 2 . • 2 sm х 4- sin 2х 4- sin2 Зх — 2a(sin х 4- sin 2х 4- sin Зх) 4- 4- cos я - cos Зя 4- 2а2 = 0.
У1368 (/1—99.2) |log2(2x4-7)| = log2(l + |z+3|)+log2(l-|a>+3|).
у/ 1369* (х — 81.4) При каждом а решить уравнение
(l+(a+2)2) log3 (2а: - a:2)+(l+(3a-l)2) logn (1 - а:2/2) = = log3 (2а: - а:2) + logu (1 - а:2/2).
1370* (х — 89.5) Найти все а, при которых уравнение
Incr а2+4тг2+4 _
ol/tf 4ж—ж2—2(а—2тг)|а:—2|+4тга
= у/(х — 5а + Ютг — 34) (|тг — я| — а 4- тг 4- 2) имеет хотя бы один целочисленный корень.
у/ 1371* (А — 95.9) При каждом а решить систему
х 1
< log2(|q|a;2—Зж-4-4) _ к —|ж| (ж+1)2 k log2( —Зж+4) “ °
1372 (А — 98.8) Найти все а, при которых уравнение
х2 — 4ах 4- 4а2 4-1 х — 2а
4- я2 - 2х - 1 = 0
имеет хотя бы один корень.
1373 (7 - 94.4) logj/2 (tgitx + ctg же) = 8(2a:2 + За: + 1). (|a: + 1| — 1 x
1374 (д - 97.5) J (2« + 2*-2 + 22-*) cos 2^+ 1 + cos же + 3 + 22®-3 = 0.
6 И. Н. Сергеев — Математика
161
1375* (тг—83.5) Найти все а 6 (2; 5), при которых уравнение log2 (3 — | sinax|) = cos(7rz — 7г/6)
имеет хотя бы один корень на отрезке [2; 3].
у/ 1376* (7Г - 89.5) (ж - х2 - |) х
х log^/з (2 4- 2 cos2 х — cos 2х 4- 3 cos2 тгя) > —2.
1377* (тг - 81.5) 3+2со»(а!-У) =
= sin2(*-y) + ч/з + гж-^соз2 V-
{у4 — 4у3 - 16у2 — 8ху — 4х2 + 32у + 64 = О зтбтпг + sin(7r(2y2 - х)) -
—у/х(х — 6) + 13 cos (тг(г/2 + 2а: + 1/2)) = 0. у/ 1379* (х — 83.6) arcsin2 х + arccos2 х — 5тг2 /4 =
= ч/2 — |j/| (5 sin2 х — 6sina:cosa: — 9cos2 x + 3^33).
7 1380* - 98.5) ^13 + З31-”" < ч/бе"2*2 - 1.
у 1381* (x - 00.5) г2""2 * + = 21+
20.5. Исследование величин в текстовых задачах
Условие текстовой задачи иногда не определяет изучаемую величину однозначно, а задает для нее целый диапазон. Тогда ответом, в зависимости от вопроса задачи, служит либо множество всех значений этой величины, либо ее экстремальное значение.
Пример (х — 00.3). Первая бригада рабочих одинаковой производительности мостила один участок дороги, а вторая, имевшая на б рабочих больше, — другой, втрое больший участок. Какое наименьшее число рабочих могло быть в первой бригаде, если свою работу она выполнила быстрее?
Решение. Для числа п рабочих в первой бригаде имеем ~ < п+6 4* 6 < Зп 4Ф’ 71 > 3 71>шах — ♦ • •
Ответ: 4.
у/ 1382° (А — 95.5). Поезд был на 16мин задержан в пути на расстоянии 80 км от пункта назначения, в который он прибыл, тем не менее, раньше времени, так как увеличил скорость на 10 км/ч. Какой могла быть его первоначальная скорость?
1383° (7 — 97.4). Танкер наполняется через две трубы не менее чем за 6 ч. За какое время он наполняется через одну первую трубу, если через одну вторую трубу это происходит на 5 ч быстрее?
162
1384° (A — 96.5). Сколько воды нужно долить к 1л 96%-го раствора кислоты, чтобы концентрация полученного раствора не превышала 40%?
у/ 1385 (/2 — 81.3). В двух сосудах содержались растворы соли: в первом 5 кг, а во втором — 20 кг. В результате испарения воды процентное содержание соли в первом сосуде увеличилось в х раз, а во втором — в у раз, причем ху = 9. Какое максимальное количество воды могло при этом испариться?
1386 (i/ — 00.4). Три сплава содержат металлы А и В: первый сплав — 20% и 30% соответственно, второй — 50% и 20%, а третий — 30% и 40%. Сколько килограммов каждого сплава нужно взять, чтобы получить 10 кг нового сплава, содержащего ровно 25% металла А и минимальное, при этом условии, количество металла В?
у/ 1387* — 88.5). За время t первый рабочий сделал йа 3 де-
тали больше второго, который увеличил производительность труда на 0,2 детали в минуту и через некоторое целое число минут обогнал первого (в общей сложности) на 2 детали. Найти наибольшее возможное значение t при данных условиях.
у/ 1388 (а — 99.4). Кандидат в депутаты имеет право на одно бесплатное выступление в газете, увеличивающее число его сторонников на 1000 человек, а также на выступления по радио и по телевидению, увеличивающие число сторонников на 40% и 80% соответственно и стоящие 32 и 47 тыс. руб соответственно. В каком порядке и количестве нужно выступать кандидату в этих средствах массой информации, чтобы, израсходовав не более 112 тыс. руб, приобрести наибольшее число сторонников?
у/ 1389 (б — 96.3). В контейнер упакованы изделия двух типов общим весом 321кг. Стоимость и вес одного изделия первого типа составляют 40 тыс. руб и 12 кг, а второго — 60 тыс. руб и 15 кг. Какова наибольшая и наименьшая возможная стоимость находящихся в контейнере изделий?
1390 (А — 97.7). Стоимость изготовления п банок пропорциональна величине п2 4- 4п 4- 24. При каком п стоимость изготовления одной банки минимальна?
у/ 1391 (А—99.6). Третий и восьмой члены арифметической прог-ресии равны 13 и —7 соответственно. При каком количестве членов этой прогрессии их сумма максимальна, и чему она равна?
163
6*
1392* (х— 95.5). Требуется построить несколько одинаковых домов суммарной жилой площадью ровно 2500 м2. Стоимость одного дома площадью х м2 складывается из стоимости материалов — bix3/2 тыс. руб, строительных работ — Ь2я тыс. руб и отделочных работ — Ьз#1/2 тыс. руб, где чйсла b2, Ь3 образуют Геометрическую прогрессию: их сумма равна 21, а произведение — 64. Если бы было построено 63 дома требуемой суммарной площадью, то затраты на материалы были бы меньше, чем на строительные и отделочные работы. Сколько следует построить домов, чтобы общие затраты были минимальными?
у/ 1393 (б — 94.5). При производстве п телевизоров в месяц завод расходует на изготовление каждого телевизора не менее, чем 4- 270 — |90— тыс. руб, а после продажи получает за каждый телевизор не более, чем 540 — тыс. руб.
При каком п может быть получена наибольшая ежемесячная прибыль при данных условиях?
1394 (а — 95.3). Вкладчик в начале первого квартала кладет на счет в банке некоторую сумму. В конце квартала на нее начисляется х%, после чего он снимает половину исходной суммы. На оставшуюся часть счета в конце второго квартала начисляется у%, где х + у = 150. При каком х счет вкладчика в конце второго квартала будет максимальным?
у/ 1395 (б — 97.4). Банк планирует вложить на один год 40% имеющихся у него средств клиентов в проект А, а остальные 60% — в проект В. Проект А может принести прибыль в размере от 19% до 24%, а В — от 29% до 34%. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наибольший и наименьший уровень этой ставки, при которых чистая прибыль банка будет обязательно заключена в пределах от 10% до 15% от имеющихся у него средств.
1396* (б—97.4). Имеется три пакета акций. Суммарное количество акций первых двух пакетов и суммарная их стоимость равны соответственно количеству акций третьего пакета и их стоимости. Первый пакет вчетверо дешевле второго, а одна акция первого дешевле одной акции второго на величину от 16 до 20 тыс. руб. Цена же одной акции третьего пакета заключена в пределах от 42 до 60 тыс. руб. Какой наибольший и наименьший процент от общего количества акций может содержаться в первом пакете при данных условиях?
164
у/ 1397* (7 — 00.5). Из пункта А вниз по реке отправляется катер с собственной скоростью v. В пункте В, где в реку впадает приток, катер поворачивает к пункту С, расположенному на притоке так, что АВ = ВС. Изобразить на координатной плоскости все точки (ж, у), для которых время движения катера из А в С при скоростях течения реки и притока, равных х и у соответственно, меньше, чем в стоячей воде.
у/ 1398 (А — 01.6). Пункты А и В расположены на двух разных взаимно перпендикулярных дорогах, пересекающихся в пункте С, причем АС — ВС = 275 км. Два мотоциклиста одновременно начинают движение из пунктов А и В в сторону пункта С со скоростью 44 км/ч и 33 км/ч соответственно. Через какое время после начала движения расстояние между мотоциклистами будет наименьшим и каким именно?
1399* (х — 80.5). Две точки движутся по концентрическим окружностям в противоположных направлениях. В начальный момент они лежали на одной прямой с центром на расстоянии 16. Через 11с после старта расстояние между ними равнялось л/207. Кроме того, с интервалом в 11 с были зафиксированы два момента, когда расстояние между точками равнялось х/158. Каково наименьшее расстояние между точками?
§21. Геометрические вопросы
Метод равносильных преобразовании в известном смысле затрагивает и непосредственно геометрию. Так, сравнение площадей или объемов сходных фигур порой равносильно сравнению только их высот или оснований или каких-то других элементов (п. 21.1). Возможны преобразования самого чертежа, сохраняющие определенные его свойства, и в этом смысле равносильные (п. 21.3). Наконец, исследование выражений на максимум или минимум также практикуется в геометрических задачах (п. 21.2).
21.1. Сравнение площадей и объемов
Площади треугольников удобно сравнивать друг с другом с помощью следующих трех основных правил:
— если треугольники имеют общую высоту, то их площади относятся, как соответствующие основания;
— если треугольники имеют общее основание, то их площади относятся, как соответствующие высоты;
165
— если треугольники имеют общий угол, то их площади относятся, как произведения сторон, образующих этот угол.
Аналогичные правила можно сформулировать и для сравнения объемов тетраэдров, пирамид или призм.
Пример (х — 93.3). На сторонах АВ и АС треугольника АВС взяты точки D и Е соответственно так, что AD = BD и АЕ = 2 СЕ. Найти отношение площадей треугольников АВС и. CDE.
Решение. См. рис.31:
Sadc = -^Sabc (пары треугольников с общими высота-
Scde = -^Sadc ми из вершин С и D соответственно)
=> ScDE = I • ^Sabc = ^SaBC-
Ответ: 6:1.
1400° (х — 94.4). На стороне АС треугольника АВС площадью 4 взята точка D так, что АС = 4 PC. Найти BD, если АВ = 2\/3 и Z.ABD = 60°.
Рйс. 31
1401° (/? — 00.3). На сторонах АВ = 6 и АС — 4 треугольника АВС взяты точки D и Е соответственно. Найти площадь треугольника ADE, если ВС = 8, AD = 2 и АЕ = 3.
1402° (<р — 85.4). На стороне АВ треугольника АВС со стороной ВС = 15 и высотой ВН = 5 взята точка D так, что AD = 5,8 и BD = 7,2. Найти площадь треугольника BCD, если она больше 3.
1403° (тг — 01.4). В равнобедренном треугольнике АВС с углом Z А = 30° при основании АС = 2 проведены биссектриса AL и медиана AM. Найти площадь треугольника AML.
1404° (<р — 99.3). Медианы AM и BN треугольника АВС пересекаются в точке К. Найти площадь треугольника АВС, если площадь четырехугольника CMKN равна 5.
166
у/ 1405 (А—97.4). На гипотенузе АС прямоугольного треугольника АВС с катетами АВ = 5 и ВС = 4 взята точка D, М — точка пересечения медиан треугольника ABDb a N — точка пересечения медиан треугольника BCD. Найти площадь треугольника BMN.
1406* (тг — 99.5). На медианах AM, BN и СК треугольника АВС площадью 2 взяты точки Р, Q и R соответственно так, что АР: PM = 1 : 1, BQ : QN = 1 : 2 и CR : RK = 5 : 4. Найти площадь треугольника PQR.
1407° (£ — 99.4). На основании АС и боковой стороне ВС ранобедренного треугольника АВС с углом Z.A = 45° взяты такие точки М и N соответственно, что AM = 2 СМ и Z.CMN = 60°. Найти отношение площадей треугольника CMN и четырехугольника ABNM.
1408° (х — 95.4). На катетах АС и ВС прямоугольного треугольника АВС взяты точки D и Е соответственно так, что CD = СЕ = 1. Отрезки АЕ и BD = \/1б пересекаются в точке О, а площадь треугольника ADO на 1/2 больше площади треугольника ВЕО. Найти АВ.
у/ 1409 (А — 78.4). На сторонах АВ и ВС треугольника АВС взяты точки D и Е соответственно так, что AD : BD =1:2 и СЕ : BE = 2:1. Отрезки АЕ и CD пересекаются в точке О. Найти площадь треугольника АВС, если площадь треугольника ВС О равна 1.
1410 (£ — 00.4). На стороне АВ треугольника АВС взята точка D, а на продолжении стороны ВС за точку В — точка Е так, что длина отрезка BD составляет 85% длины АВ, а длина отрезка СЕ — 120% длины ВС. Какой процент от площади треугольника АВС составляет площадь теугольни-ка CDE1 »
1411 (7 — 90.4). На сторонах АВ,ВС и AD параллелограмма ABCD взяты точки K,L и М соответственно так, что АК : КВ = 2 : 1, BL : LC = 1 : 1 и AM : MD = 1 : 3. Найти отношение площадей треугольников LBM и КВМ.
1412 (7 — 91.4). На стороне AD и диагонали АС параллелограмма ABCD взяты точки Е и F соответственно так, что АС = 3 AF и AD = 4 АЕ. Прямая EF пересекает сторону ВС ‘ в точке G. Найти площадь параллелограмма, если площадь че-
тырехугольника ABGF равна 8.
167
у/ 1413 (tp—81.3). Биссектриса угла А параллелограмма ABCD со стороной АВ — 6 пересекает сторону ВС и диагональ BD в точках М и N соответственно так, что МС = 4. Найти площадь треугольника BMN, если высота параллелограмма, опущенная на основание AD, равна 3.
1414* (/1 — 98.4). На продолжении стороны ВС параллелограмма ABCD за точку С взята точка Е, а отрезок АЕ пересекает диагональ BD и сторону CD в точках F и G соответственно. Какую часть площади параллелограмма составляет площадь треугольника AFD, если AF = FG 4- 1 и EG = 3?
1415 (тг — 79.4). Диагонали трапеции ABCD с основаниями AD = 30, ВС = 24, стороной АВ = 3 и углом Z.A = тг/З пересекаются в точке О. Найти площадь треугольника CDO.
1416 (А — 96.7). В трапеции ABCD боковая сторона AD = 9 перпендикулярна основаниям, диагонали пересекаются в точке О, АО = 6 и CD = 12. Найти площадь треугольника ВСО.
у/ 1417 (7 — 98.3). Диагонали трапеции ABCD с основаниями AD > ВС пересекаются в точке О. Площадь трапеции равна 48, а площадь треугольника АОВ — 9. Найти AD : ВС. 1418 « — 95.6). Диагонали трапеции ABCD с основаниями AD = а и ВС = b пересекаются в точке О. Найти отношение площади треугольника АВО к площади трапеции.
1419 (х — 96.4). На сторонах АС и ВС треугольника АВС взяты такие точки D и Е соответственно, что AD = 2 DC, а площади треугольников ABD и AED равны 3 и 1 соответственно. Отрезки АЕ и BD пересекаются в точке О. Найти площади треугольников АВО и DEO.
1420* (/1 — 01.3). Биссектриса угла OAQ пересекает две окружности с центрами О, Q и общей хордой АВ в точках С, D, а отрезок OQ — в точке Е соответственно. Найти ВС : BD и площадь четырехугольника OAQD, если площади треугольников ОАЕ и QAE равны 18 и 42 соответственно.
у/ 1421 (V» — 87.5). Диагонали четырехугольника ABCD пересекаются в точке О. Площади треугольников ВОС, COD и AOD равны 20, 40 и 60 соответственно. Найти Z.BAO, если АВ = 15, АО = 8 и Z.AOB > 31°.
1422° (V> — 84.4). На окружностях радиусов 4 и 5 с общей хордой АВ взяты точки С и D, раположенные на линии цен
168
тров на расстоянии 15 друг от друга. Найти площадь четырехугольника ACBD.
у/ 1423 (ф — 83.4). Найти стороны вписанного в окружность радиуса 7 четырехугольника ABCD, если АВ = ВС, Z.D = = 120°, а площади треугольников ABD и BCD относятся как 2:1.
1424* (а — 01.4). Диагональ АС выпуклого четырехугольника ABCD является диаметром описанной около него окружности и пересекается с диагональю BD в точке Е. Найти отношение площадей треугольников АВС и ACD, если АЕ : ЕС = = 2 : 1 и Z.BAC = 30°.
1425* (х — 00.4). Найти длину окружности, вписанной в пятиугольник ABCDE) если ВС = СЕ, ЗАС 4- 2BD = 5у/5, а площади треугольников ADE и АВС равны соответственно площадям треугольников CDE и BCD.
1426 (ф — 88.5). На сторонах АВ и ВС треугольника АВС взяты точки К и L так, что КВ : АВ = 1 : 2 и LB : СВ = 1:4. Через точки K,L и В проведена окружность, а через точку К — прямая, пересекающая окружность в точке М, а отрезок BL — в точке N. Найти площадь треугольника KLM, если BL = 6, BN = 2, MN = 3, а площадь треугольника АВС равна 32.
1427* (7 — 97.5). В угол с вершиной О вписаны две непересе-кающиеся окружности: большая касается сторон угла в точках А и В, а меньшая — соответственно в точках С и D. Прямая AD пересекает ббльшую окружность в точке Е, а меньшую — в точке F. Найти отношение площадей треугольников AOD и COD, если СО = 2, EF = 1, а АЕ — среднее арифметическое между OD и EF.
1428° (£ — 98.6). Площадь сечения, проходящего через боковое ребро и высоту правильной треугольной пирамиды, вдвое больше площади ее основания. Найти площадь боковой грани, если боковое ребро равно у/13.
у/ 1429° (£ — 95.8). На ребре AS правильной пирамиды SABC объемом V взята точка D так, что SD : DA = тп :п. Расстояние от центра основания АВС до плоскости BCD равно d. Найти площадь треугольника BCD.
1430 (б — 77.5). На сторонах АВ, ВС и АС основания АВС пирамиды SABC объемом V взяты точки К,ЬиМ соответствен
169
но так, что АК : КВ = BL : LC = СМ : МА = 1 : 2. Через середину ребра SA параллельно основанию пирамиды проведена плоскость, пересекающая отрезки SK, SL и SM в точках Р, Q и R. Найти объем призмы, одно из оснований которой совпадает с треугольником PQR, а другое лежит в плоскости АВС.
у/ 1431 (х — 83.3). На боковых ребрах АА' и ВВ' треугольной призмы АВС А'В'С объемом V взяты точки D и Е соответственно так, что AD = DA' и BE : В'Е = 1:2. Найти объем части призмы, заключенной между плоскостями АВС и DEC. 1432* (/2—99.6). Основанием пирамиды SABCD служит трапеция ABCD с основаниями AD : ВС = 5:2. Диагонали трапеции пересекаются в точке Е, а центр О вписанной в пирамиду сферы лежит на отрезке SE. Найти площадь полной поверхности пирамиды, если SO : ЕО = 7 : 2, а площадь грани SBC равна 8.
21.2. Исследование геометрических величин и параметров
В следующих задачах изучаются значения параметров, определяющих геометрическую конфигурацию, в частности, их наибольшие и наименьшие значения. Возникают здесь и экстремальные геометрические ситуации, подобные тем, что встречались в п. 20.4.
Пример (х~96.4). Найти радиус окружности, описанной около треугольника АВС площадью, не меньшей 6, если АС 3 и ВС 4.
Решение. См. рис.32:
6 Sabc = | • х • у • sin ZC | • 3 • 4 • 1 = 6
=> ZC = 90° => АВ = \/32 4- 42 = 5 — диаметр окружности. Ответ: 5/2.
у/ 1433 (б — 85.6). Диагонали четырехугольника ABCD площадью не более 4 пересекаются в точке Е, а площади треугольников АВЕ и CDE равны по 1. Найти ВС, если AD = 3.
у/ 1434 (б — 96.5). В треугольнике АВС со стороной АС = 8 и биссектрисой BL отношение площадей треугольников ABL и CBL равно 3:1. Найти длину BL, при которой высота ВН — наибольшая.
у/ 1435 (А — 98.5). Найти угол С того треугольника АВС со стороной АВ = 16, высотой СН = 3,9 и описанной окружностью радиуса 10, у которого медиана СМ — наименьшая.
170
1436* (х — 91.4). Три окружности с суммой радиусов 12\/2 и центрами А, В, С касаются друг друга внешним образом. Найти наибольшее значение длины окружности, проходящей через все точки касания, если ЛАВС = 2arcsin(l/3).
1437 (ip — 83.3). При каждом целом п найти все возможные значения АВ : АС, при которых существуют такие треугольники АВС и А'В'С', что АВ = А'В', АС = А'С', ЛА = 60°, ЛА' = 120° и В'С" : ВС = у/п.
1438* (х — 95.5). Две окружности с центрами О и Q и радиусами г и R соответственно касаются друг друга внешним образом в точке К, Через точку А окружности радиуса R проведена касательная, пересекающая другую окружность в точках В и С так, что ВС : АВ = р и отрезок АС пересекает отрезок ОК. Найти:
1) условия на г, R и р, при которых возможна такая геометрическая конфигурация;
2) ВС.
у/ 1439 (х — 99.5). Найти площадь поверхности параллелепипеда объемом 8, вписанного в сферу радиуса л/З.
у/ 1440* (/3 — 84.4). Основанием пирамиды с высотой SH = а служит ромб ABCD со стороной 4а/9, диагональю АС = 2а/3 и центром симметрии Н. Через точку А и середину ребра SC проведена плоскость, образующая с плоскостью основания пирамиды угол в 45°. Найти площадь сечения пирамиды этой плоскостью. Сколько таких плоскостей существует?
у/ 1441* (х—94.6). В тетраэдре ABCD ребра AD и BD взаимноперпендикулярны, а на ребре АВ взята такая точка М, что
171.
квадрат суммы расстояний от вершин А, В и С до прямой DM равен удвоенной сумме квадратов расстояний от тех же вершин до точки D. Найти СМ, если CD = 20 и /DAB = = arctg х/Т/З-
1442* (/1—97.6). Около пирамиды SABC описана сфера. Вторая сфера радиуса 1 касается первой внутренним образом в точке S, а также — плоскости АВС. Найти объем пирамиды, если AS = 3, cos /LBAC = 4/5 и /BAS = /CAS = 45°.
1443* (£ — 78.5). На каком расстоянии от ребра AS правильной пирамиды SABC с вершиной S, должна проходить плоскость, параллельная ребрам ВС = а и AS = Ь, чтобы площадь сечения пирамиды этой плоскостью была максимальной?
1444* (/1 — 94.5). Найти наибольшее значение объема тетраэдра ABCD, если AD 4, BD 7, CD 9, АВ = 5, ВС < 6 и АС < 8.
1445* (А — 83.6). В тетраэдре ABCD ребро AD перпендикулярно плоскости АВС, АВ = АС = у/b и /ВАС = 2/BDC. В пирамиду помещен цилиндр с образующей, параллельной AD, и наибольшей площадью боковой поверхности. Центр ближайшего к ребру ВС основания цилиндра удален от этого ребра на расстояние, равное 11/16 медианы AM треугольника АВС. Найти объем пирамиды.
1446* (х — 78.5). Найти радиус наибольшего шара, помещающегося в пирамиде SABCD объемом 1/6, если АВ = 1, ВС = CD и AS+DS = \/2, а диагональ BD основания ABCD делит его площадь пополам.
1447* (е — 82.6). Меньшее основание равнобедренной трапеции вдвое больше суммы ее боковых сторон. В какое наибольшее целое число раз площадь полной поверхности фигуры, полученной вращением трапеции вокруг меньшего основания, может быть больше площади трапеции?
1448* (£—85.5). Сфера с центром S проходит через вершины основания ABCD правильной пирамиды SABCD. Отношение площади полной поверхности пирамиды к площади сферы равно а. Найти /ASB и все а, при которых возможна данная конфигурация.
1449* (А—00.8). В прямоугольном параллелепипеде размером а х а х b расположены 9 шаров. Восемь из них — одинакового радиуса, причем каждый касается трех граней параллелепипеда
172
и двух соседних шаров, а девятый шар внешним образом каг сается всех восьми шаров. Найти радиус девятого шара, если он не превосходит а/4. При каких значениях величины Ь/а задача имеет решение?
1450* (б — 86.6). Площадь боковой грани АА'В'В наклонной треугольной призмы АВСА'В'С равна 64, а косинусы двугранных углов при боковых ребрах А А' и В В1 равны х/10/4 и 1/4. В эту призму вписана вторая треугольная призма так, что вершины одного ее основания лежат на сторонах треугольника АВС, а вершины другого — на соответствующих сторонах треугольника A'Bf С. Какую наименьшую площадь боковой поверхности может иметь вписанная призма?
1451* (£ — 90.6). В правильной пирамиде SABC AD — высота основания АВС. Конус с вершиной А и образующей AD касается своей боковой поверхностью основания пирамиды и боковых граней AS В и ASC. Считая AD : SD = а, найти:
1) отношение площади боковой поверхности конуса к площади основания пирамиды;
2) границы изменения этого отношения при изменении а;
3) все а, при которых конус не имеет точек вне пирамиды.
1452* (х — 97.6). Через точки М, N и К, взятые на ребрах AD, АВ и соответственно в грани АВС пирамиды ABCD объемом V, проведена плоскость, пересекающая прямую CD в точке L. Прямые АК и ВК пересекаются с ребрами ВС и АС в точках Е и F соответственно. Найти объем пирамиды ACLN, если AN = NC, AM = MS, АК = ЗКЕ и В К = = 2KF.
21.3. Геометрические преобразования
В условиях некоторых задач настоящего пункта в явном виде присутствуют преобразования плоскости или пространства. Другие задачи решаются с помощью преобразований элементов чертежа: сдвигов, поворотов, симметрий, гомотетий и т. п.
Пример (7 — 95.4). Вокруг четырехугольника ABCD со стороной АВ = 2 и взаимно перпендикулярными диагоналями описана окружность радиуса 3. Найти CD.
Решение. См. рис. 33. а:
АВ + CD= 2Z.AEB = 2-90° = 180° (угол между хордами1^).
1^См. п.5.4.
173
- o f
Повернем дугу CD по окружности до совпадения точки О' с точкой ' В (рис. 33. d), тогда
Z.ABD' = (360°- АВ - С'Ьэ/г = 90° => AD' — диаметр
=> х2 = 62 — 22 = 32 (теорема Пифагора) => х = ...
Ответ: 4\/2.
Одним из любопытных преобразовании, сохраняющих площадь фигуры, является ее перекраивание, т. е. отрезание каких-либо частей фигуры и пристраивание их в другое место.
Рис. 33
1453° (^ — 81.2). Катеты прямоугольного треугольника равны по а каждый. Поворотом этого треугольника на угол 45° вокруг вершины его прямого угла получен другой треугольник. Найти площадь общей их части. ,
1454 (б — 00.4). На стороне АВ треугольника АВС взята точка О так, что АВ : ОВ = 3:2. При повороте этого треугольника вокруг точки О, переводящем вершину С в вершину В, вершина А переходит в точку D, лежащую на стороне АС. Найти отношение площадей треугольников COD и АВС.
у/ 1455 (х — 00.4). В угол вписаны четыре окружности: первая имеет радиус 1, а каждая следующая касается предыдущей и имеет больший радиус. Найти сумму длин второй и третьей окружности, если площадь круга, ограниченного четвертой окружностью, равна 64тг.
1456* (б — 98.5). Две окружности радиусов 4 и 3 касаются друг друга. Прямые АВ и CD касаются меньшей окружности в точках В и С, а большей — в точках А и D. Найти радиус окружности, касающейся отрезков АВ, CD и AD.
1457* (£ — 98.7). Вписанная в треугольник АВС окружность касается сторон АВ и ВС в точках М и N, а биссектриса
174
угла А пересекает прямую МN в точке L. Найти расстояние от точки L до прямой АС, если ZA = а и АС = Ь.
у/ 1458 (£ — 99.6). Прямые АВ и АС касаются окружности с центром О. Найти АО, если АО < ВО = СО = а, АВ = Ь, АС = си b / с.
1459° (£ — 94.6). Найти диаметр окружности, описанной около четырехугольника ABCD со сторонами АВ = a, CD = b и перпендикулярными диагоналями.
у/ 1460 (/1 — 96.3). Через вершины А и В треугольника АВС проведена окружность, пересекающая стороны ВС и АС в точках D и Е соответственно. Площадь треугольника CDE всемеро меньше площади четырехугольника ABDE. Найти DE и радиус окружности, если АВ = 4 и ZC = 45°.
1461° (£ — 90.2). Найти площадь равнобедренной трапеции, если ее диагональ d образует с основанием угол а.
7 и перпендикулярными диагоналями.
1462° (х — 95.4). Найти площадь равнобедренной трапеции с основаниями 3,
у/ 1463° (тг — 01.6). Найти площадь равнобедренной трапеции со средней линией т и перпендикулярными диагоналями.
у/ 1464 (£ — 96.4). Найти площадь трапеции ABCD с боковой стороной АВ = а, если расстояние от середины отрезка CD до прямой АВ равно Ь.
у/ 1465 (£ — 94.8). Основаниями призмы ABCDА'В'CD' служат трапеции ABCD и А'В'С'Р', сумма площадей двух параллельных боковых граней равна S, а расстояние между ними равно d. Найти объем многогранника BDA'B'C'D'.
у/ 1466 (Д — 90.4). Найти радиус окружности, описанной около четырехугольника ABCD, если АВ = 2, АС = 5, AD = 4 и ABAC = ADAC.
1467 (/1 — 97.4). Найти площадь вписанного в окружность четырехугольника ABCD, если его диагонали пересекаются в точке Е, BD = 6, AADB = тг/8 и AD • СЕ = DC • АЕ.
у/ 1468 (/1 — 98.3). Диагонали BE и СЕ выпуклого пятиугольника ABCDE являются биссектрисами углов при вершинах В и С соответственно. Найти площадь пятиугольника ABCDE, если А А = 35°, AD = 145°, а площадь треугольника ВСЕ равна 11.
175
1469* (s — 84.5). Найти сторону CD ъъшуююгъ четырехугольника ABCD площадью (АВ • CD 4- ВС • АР)/2, если ВС = 4, ZA = тг/2 и ZP = 7г/3.
у/ 1470 (/? — 99.4). На основаниях AD и ВС трапеции ABCD во внешнюю сторону построены квадраты ADEF и BCGH. Найти AD, если ВС = 2, FG = 18 и GO = 7, где О — точка пересечения диагоналей трапеции.
1471* (£ — 01.8). На прямой последовательно расположены точки А, В и С. Три полуокружности построены как на диаметрах: на отрезках АВ и ВС — в одну полуплоскость, а на отрезке АС — в другую. Найти отношение площади фигуры, ограниченной полуокружностями, к площади треугольника с вершинами в их серединах.
1472* (7 — 01.4). На сторонах ромба ABCD как на гипотенузах в общую с ромбом полуплоскость построены равнобедренные прямоугольные треугольники АКБ, BLC, CMD « DNA. Сумма площадей ромба и четырехугольника KLMN равна 12. Найти АВ.
1473* (х — 01.5). Трапеция с высотой \/3 4- д/2 и основанием \/8 вписана в окружность радиуса \/Ь. Каждый из четырех отсекаемых сторонами трапеции сегментов отражен внутрь трапеции относительно отсекающей его стороны. Найти площадь фигуры, состоящей из тех точек трапеции, которые не принадлежат ни одному из отраженных сегментов.
1474* (А — 80.5). Найти площадь фигуры, заданной системой
||®-у|-|у-1|| = ®-2у+1
* (х _ 1)2 + (г/ _ 1)2 L
1475* (б — 97.6). Множество задано неравенством
, 10?/-24-у2 Л
10g а»2+ 1039 -ОКЛ--- 0’
1147 850
Найти площадь фигуры, равной объединению всех множеств, получающихся из данного поворотами против часовой стрелки на углы tp Е [0, тг].
1476* (А — 85.6). Конус с образующей 5 и высотой 4 вращается вокруг оси, проходящей через его вершину перпендикулярно высоте. Найти площадь сечения полученной фигуры вращения плоскостью, проходящей через ось вращения.
176
Глава 5. МЕТОД ОБОЗНАЧЕНИИ
Голь на выдумки хитра.
§ 22. Замена переменных
В отличие от вводившихся ранее (например, в § 7) обозначений с целью сокращения записи, теперь им придается иной смысл: записанная в новых переменных задача оказывается по существу проще, а первоначальная информация о задаче восстанавливается после возвращения к исходным переменным.
22.1. Избавление от радикалов с помощью обозначений
Если обозначить корень из какого-либо выражения новой буквой, то возведение его в квадрат произойдет на более позднем этапе решения, когда станет понятно, какие значения он принимает.
Пример (тг — 77.1). 2у/х + 5 = х + 2.
Решение. •••<=> 2у/х 4- 5 = (х + 5) — 3.
Обозначим у/х 4- 5 = г:
2г = г2 — 3 о (г — 3)(г 4-1) = О о г = 3 (т.к. г 0).
Вернемся к х:
у/х 4- 5 = 3 о х 4- 5 = 9 <=> ...
Ответ: х = 4.
1477° (х - 93.1). у/х 4- 4 = х 4- 2.
1478° (х - 98.1). 7 — х = 3\/5 — х.
1479° (<т - 99.1). у/х — 1 = 6 — я.
1480° (х - 79.2). у/х + 3 > X + 1.
1481° (^ — 97.2). у/х 4- 3 > 5 — 2х.
у/ 1482° (тг - 81.3). V4Z-8 х - 5.
у/ 1483 (А - 83.1). (х + 1)д/16а: + 17 = (х + 1)(8ж - 23).
1484 (д - 94.2).' 3x/F+4 = 5 - 2|® + 2|.
у/ 1485 (х - 94.2). Ух^З < 3 - - 6|.
1486 (е -93.3). Зх/аГ+2 6 - |z -2|.
177
1487 (7 - 01.2).
1488° (е - 83.1).
1489° (A - 94.3).
у/ 1490 (x- 89.2).
1491 (С - 99.5).
1492 (Д - 93.3).
У1493 (х - 99.2).
1494 (у - 00.3).
1495 (х —84.4).
1496 (х- 94.3).
у/ 1497* (е-99.2).
1498* (х —83.5).
|а: — 6| + х/За: + 1 5.
а:2 + Vx2 + 11 = 31.
х2 + 2^х2 + Зх — 4 = 4 — Зх.
8V12 + 16х - 16а:2 + 4а: = 33 + 4а:2.
\/7 - log2 х2 + log2 х4 > 4.
+ 21"® > 7 - (1/2)®-2.
При каждом а решить уравнение
(х - 3)(х +1) + 3(х - 3)АЛ-Ц = (а _ 1)(а + 2). V х — о
22.2. Выявление устойчивых выражении
Задание, в котором неоднократно встречаются одни и те же выражения, можно заметно упростить, если обозначить эти выражения новыми буквами.
Пример (V> — 89.2).' | cos2 | — j| = 3coss + 1.
Решение.
...<=> |1 + coss — 2/3| = 2(3coss + 1)
4Ф |3coss + 1| = 6(3coss + 1) <=> 3coss + l=0
(т.к. |а| = ба о а = 0, где а = 3 cos s + 1)
о coss = —1/3 о ...
Ответ: s = ±arccos(—1/3) 4- 2тгп, где п G Z.
Многочлены, зависящие от s и у симметрично1^, всегда выражаются через две новые переменные р = s+y и q = ху, связанные друг с другом неравенством р2 4q.
1499° (х - 95.2). | log2l = 1 - log2x(x2 - 5х + 6).
*)Т. е. не меняющиеся при перестановке этих букв местами.
178
71500° (х-99.3).
У1501 (х- 93.3).
1502 (х - 96.5).
у/1503° (е-01.4).
1504 (е - 79.5).
1505 (е - 87.4).
1506 (х- 93.4).
у/ 1507 (ip - 79.2).
у/ 1508 (е - 91.4).
|1о8х+1 >ДХ ~ 2)4 + 2| >
>-3 + log_^ у/(х - 2)6.
|3* _ 4| + |х2 _ 4Д. + 3| Зх + 4а. _ х2 _ 7
|1 + сов(тгу/х) | + |а:2 — 15а: + 44| =
= 15а: — х2 — cos(ttx/x) — 45. log2 (2х - 3) • log^(4х+2 -12 • 2®+3 +144) > 32. l°g3x+7 (4а:2 + 12а: + 9) +
+ 1оё2х+з (6а;2 + 23а: + 21) = 4-
| log,..! (х2 - 8а: +16) +
+ log4_ir (5а: — х2 — 4) > 3.
6а:2 + 17ху + 7у2 = 16
\l°g2l+!,(3z + 7у) = 3.
^iag^^-xy - 2х + у + 2) +
< + log2+jz(a:2 - 2а: + 1) = 6
Jogi-zG/ + 5) - log2+jz(a: + 4) = 1.
Найти наименьшее значение функции
/(а:) = (х — 2) (4+ (х — 1)(а: - 4))(а: - 3).
у/ 1509 (тг — 99.6). Найти все а, при которых уравнение (х2 + х)(х2 + 5а: + 6) = а имеет ровно три различных корня.
1510 (7 - 99.3). v'l®2 + 14а: + 47| - 1 = |а: + 7| - 1.
у/ 1511 (а — 95.6). Найти все а, при которых неравенство х2 + 4а: + 6а|а: + 2| + 9а2 0 имеет не более одного решения.
1512° (е-96.1).
|-®|-^ТЗ = 1
1513 (х- 91.3).
1514 (А-98.7).
\/2х-1 + х/уТЗ = 3 2ху — у + 6а: = 7.
а:(1 + у) = у + 7 х2у — ху2 = 6.
179
{х 4- Зху 4- у = 3 4-10\/2 X2 + у2 = 11.
1516 (А - 97.7). |® + у - Зху + 13| + |®2!/ + ху2 - 30| = 0.
у/ 1517 (С—95.7). Найти наименьшее значение ху при условии
{х + у = За — 1 х2 + у2 = 4а2 — 2а + 2.
1518* (/3 — 86.5). Найти все а, при которых система
У1519 (7-01.1).
2х2 — 2ху + 10?/2 = а4 — 6а3 + 9а2 — 19 + \/85 х2 + 2ху — Зу2 = 4
имеет хотя бы одно решение.
9 • 2х • 5" - 5 • Зх+у = 3х • 5"
2^-2 . з»-®+1.51-» _ 1
{2х+у . 3» . 6х+» • 9® = 144
log.+А(27х • 9У + 4х+у) log5 (j + X) = 2. . V «4-2 5g —10
у/ 1521* (ip - 93.1). 33=^ -7 = 2 •3‘Я=^.
1522 (ip - 81.4). I log3 (5® — 6)3 - log3 (5® - 6)3 • log3 x6 = = -61od|-
\2x + y| + log3 (|y| - 2® + 5) - 20 = 0
у/ 1523 (x-85.5). (2® + y)2 - 7(2® + y) log3 (|y| -2® + 5)-
- 81og^ (|y| - 2® + 5) = 0.
1524* (x —00.5). При каждом а решить систему
{у2 - Зу log2(4®2 + (14а — 10)® + 8а — 8) +
+ 2 log4(4®2 + (6 — 2а)® + 4а2 — 8а + 4)2 = 0 5у2 — 8у log4 (4®2 + (6 — 2а)® + 4а2 — 8а + 4)2 +
+ 31og2(4®2 + (14а — 10)® + 8а — 8) = 0.
1525* (х—94.5). Числа ai,... ,аэ удовлетворяют равенствам log2 ап log2 (an_ian+i) = log2 an_x • log2 an+i • log2 (4a2),
где n = 2,3,4 и ai = 2, a5 = 21/25. Найти log2 (a2 + 2аз — a^). 1526* (A — 86.6). При каждом a < 9 найти все корни уравнения
Зх/З tg sin х - sin sin2 х 4- ) 4-
4- cos2 — 7 cos 2x) = 6 tg2 (~ sin x 4- y1) - a на отрезке [0; 2тг].
180
1527* (х — 01.5). При каждом а решить неравенство
За — 1 — (8а — 5) • 3~2 V" iog8i(*2+6x+9)
3(а + 2) • |ж + 3|2 v/10gi’+3i s.
22.3. Тригонометрические замены и подстановки
Формулы тригонометрии (см. §2), связывающие друг с другом самые разнообразные выражения, позволяют осуществлять замены, сводящие тригонометрические уравнения к алгебраическим. При этом, правда, ОДЗ уравнения может сужаться.
Пример (б — 84.2). cos 2х = \/3sin 2х — 1.
Решение. Рассмотрим два случая:
I tgx — не определен
£ 4- тгп, где п G Z,
т.к. cos2 (f + тгп) = \/3sin2 (£ + тгп) — 1;
2) tg х — определен, обозначим tg х = t:
= ^Т+е7 - 1 1 - <2 = 2\/3t - (1 +12) 2 = 2\/3t,
вернемся к х: > tg х = 1/\/3 4Ф х = тг/6 4- тгк, где к е Z.
Ответ: х = тг/2 4- тгп, тг/6 4- тгк, где п,к € Z.
Замена, преследующая противоположную цель — свести алгебраическое уравнение к тригонометрическому, производится обычно в форме подстановки х = /(£), где f — какая-либо из тригонометрических функций2^.
у/ 1528 (А — 78.1). tg2x 4- sin2x = | ctgx.
1529° (р - 89.1). 2 cos (2х - тг/З) 4-1 = cos (я 4- тг/З). у/ 1530 (а - 00.3). 3sin2z - 1/2 = 4 cos (ж - тг/4).
1531 (д-98.1). yjsm 2® + (л/З + 1) cos (х + тг/4) + х/З/2 + 3+
4- 2 sin (х 4- тг/4) = 0.
у/ 1532 (х — 94.3). х/sin 2х = \/1 — cos я 4- sin х,
1533* (х -99.5). tgl4x4-3ctgl4x4-sin6x —
-2V2sin(3x + J) = 7^T.
у/ 1534 (7 - 00.3). 3(sinх — 1) 4- 4 cosх 4- cos(2x 4- 4 arctg |) = 0. у/ 1535* (ф — 01.3). 3sin2x — 3 cosх — 6 sinх 4- 2 sin 2х 4- 3 = 0.
2)Стбит побеспокоиться, чтобы область значений функции f охваты-
вала все исследуемые значения х.
181
У 1536* (А-81.6).
1537* (е - 81.6).
У1538* (0-85.5).
имеет уравнение
+7/2 + 2®2 = 1.
|® + УГ^| = х/2(2а:2 - 1).
Сколько различных корней на отрезке [0; 1]
8®(1 - 2®2)(8®4 - 8а:2 + 1) = 1?
22.4. Учет делимости посредством подстановки
Чтобы зафиксировать факт делимости (нацело3^) переменной а € Z на ненулевое число d € Z, достаточно перейти к новой переменной q 6 Z, сделав подстановку а = dq.
Пример (е—94.1). Найти все целочисленные решения системы 7875а:2 = 567t/3 |х| 25.
Решение.
f З2 • 53 • 7х2 = З4 • 7у3
(|®| < 25
53а:2 = З2у3
|®| 25
(=> a:i : 3, у\ : 5).
Обозначим х = 3a?i, у = 5j/i, где yi 6 Z:
Г 53(3iCi)2 = 32(5j/i)3 ^{х1—У1 (J3«i| < 25 4*'[|a:i| 25/3
2) 3)
±1 ±8
1 4.
Вернемся к x и у: ...
Ответ: ж = 2/ = 0; х = ±3, у = 5; х = ±24, у = 20.
у/ 1539 (V>—79.5). Найти все целочисленные решения уравнения 3(® - З)2 + 6j/2 + 2z2 + 3y2z2 = 33.
у/ 1540 (7—98.6). Найти все целочисленные решения уравнения
Зх = Зу2 ± 4у — 1
и доказать, что для любого из них число х3 ± у3 — нечетно.
1541*(^-99.5).
cos3 (ж + 4у + тг/4) + ,1п(2я+12у_т/4) = о cos(3® + тг/4) + gin3(4!C_12s,_j/4) = 0.
у/ 1542 (у—01.4). Найти наименьшее нечетное натуральное число, кратное 9 и дающее остаток 7 при делении на 13.
1543 (V> — 94.5). Абитуриенты сдавали экзамены в два потока в нескольких аудиториях, число которых было равно числу
3)Этот факт обозначается в виде соотношения а : d.
182
абитуриентов, экзаменовавшихся в каждой аудитории. Если бы экзамены проводились в другом корпусе, то их пришлось бы провести в три потока в нескольких аудиториях, в каждой из которых абитуриентов удалось бы рассадить по рядам так, что количество рядов и количество людей в ряду были бы равны количеству аудиторий. Какое наименьшее число абитуриентов могло быть проэкзаменовано при этих условиях?
1544 (^—77.3). Первая бригада изготовила деталей на 15% больше, чем вторая. Все детали уложили в 2 ящика: в первый ящик — менее 1000 деталей, а во второй — более 1000. Сколько деталей положили в первый ящик, если в нем оказалось 2/3 деталей, изготовленных первой бригадой, и 1/7 — второй?
у/ 1545 (х — 98.4). Найти число студентов, сдававших экзамен, если шестая их часть получила оценку «удовлетворительно», 56% — «хорошо», а 14 человек — «отлично», причем отличники составили более 4%, но менее 9% от общего числа экзаменовавшихся студентов.
1546* (/? — 97.4). В двух коробках лежали карандаши: в первой — красные, во второй — синие, причем красных — больше. Сначала 40% карандашей из первой коробки переложили во вторую. Затем 20% карандашей, оказавшихся во второй коробке, переложили в первую, причем половину из переложенных карандашей составляли синие. В итоге красных карандашей в первой коробке оказалось на 10 больше, чем во второй. Найти общее количество карандашей.
22.5. Обозначения и переобозначения в текстовых задачах
Правильный выбор неизвестных и единиц измерения в текстовой задаче облегчает, возможно, не только арифметическую, но и логическую часть ее решения.
Пример (Л — 98.4). Одна бригада выполняет работу на 2 ч быстрее другой, но на 7 ч дольше, чем обе вместе. Выполнят ли они вместе эту работу быстрее, чем за 7 ч. 57 мин?
Решение. Если обе бригады вместе выполняют работу за хч, то первая — за (х Н- 7) ч, а вторая — за (х + 9) ч, поэтому
“То + тг? — 7 х2 + 7х + х2 + 9х = х2 + (7 + 9)х + 7 • 9
Г~рУ Ж-р/ X v '
=>х2=63<(8-£)2 = 64-2-£ + 5^ х < 7g.
Ответ: да.
183
1547° (7 —91.3). Числа ах, а2, аз образуют арифметическую прогрессию, а числа ах, аз — геометрическую. Найти ai, если ai 4- а2 + = 21.
1548 (</? —85.2). Числа аг, а?, аз, образуют арифметическую прогрессию, а числа ai, a2, a<, 4- 12 — геометриче-
скую. Найти а2.
у/ 1549 (7 — 99.2). Сумма первых пяти членов возрастающей арифметической прогрессии равна 15, а их произведение равно 1155. Найти шестидесятый член прогрессии.
у/ 1550* (/? — 93.4). Первые члены двух геометрических прогрессий равны по 1, сумма вторых членов этих прогрессий равна 3, а сумма пятых — равна 161. Найти сумму шестых членов данных прогрессий.
у/ 1551 (б —79.3). В начале года 5/6 некоторой суммы денег положили в первый банк, а оставшуюся часть — во второй. Через год в результате начисления процентов сумма этих вкладов стала равной 670 руб, а еще через год — 749 руб. Если бы первоначально 5/6 исходной суммы положили во второй банк, а оставшуюся часть — в первый, то через год сумма вкладов стала бы равной 710 руб. Какова была бы величина вклада через два года, если бы первоначально всю исходную сумму положили во второй банк?
1552 (/? — 77.3). Две бригады приступили к работе в 8.00. Сделав вместе 72 детали, они разделились, и к 15.00 за время раздельной работы первая бригада сделала на 8 деталей больше, чем вторая. Если бы первая бригада делала в час на одну деталь больше, а вторая — на одну деталь меньше, то за время раздельной работы первая бригада сделала бы на 8 деталей больше, чем вторая, уже к 13.00. Сколько деталей в час делала каждая бригада?
1553 (х — 86.2). Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле, другой площади. Вся работа заняла 12 ч. Если бы три комбайна выполнили половину всей работы, а затем оставшуюся часть сделал один из них, то работа заняла бы 20 ч. За сколько часов два комбайна могут убрать первое поле?
1554 (7 — 86.3). Три одинаковых цистерны начали одновременно заполняться водой, причем вначале первая цистерна была пуста, а вторая содержала воды вдвое больше, чем третья.
184
Все три цистерны были заполнены одновременно. Сколько литров воды в минуту поступало в третью цистерну, если в первую поступало 120л/мин, а во вторую — 40л/мин?
у/ 1555 (х — 90.4). Два насоса, работая вместе, наполняют бассейн водой за 10 ч, причем первый из них наполняет бассейн на 15 ч быстрее второго. Первый насос включили в 6.00, второй — в 8.00, а в 12.00 в бассейне оказалось 400 м3 воды. Какова емкость бассейна?
1556° (х — 84.2). Один экскаватор вырыл котлован, затем другой экскаватор вырыл такой же котлован. Работая вместе, они вырыли бы эти два котлована в 49/24 раза быстрее. Найти производительности экскаваторов, если их сумма равна 70 м3/ч.
1557° (х — 77.1). Из пункта А в пункт В выехал с почтой мотоциклист и, проехав 2/3 пути, передал почту велосипедисту, который доставил ее в пункт В. В итоге средняя скорость движения почты на пути из А в В оказалась равной 40 км/ч. Найти скорость мотоциклиста, если она больше скорости велосипедиста, а сумма этих скоростей равна 100 км/ч.
у/ 1558 (7 — 01.3). Из пункта А в пункт В одновременно выехали велосипедист со скоростью 25 км/ч и мотоциклист. Доехав до пункта В, мотоциклист развернулся и сразу же отправился назад, встретив велосипедиста на некотором расстоянии от пункта В. Если бы скорость мотоциклиста была на 37,5% меньше, то это расстояние оказалось бы втрое меньше. Найти скорость мотоциклиста.
1559 (тг—78.3). Имеются два слитка: процентное содержание золота в первом слитке в 5/2 раза больше, чем во втором. Если сплавить равные по массе их части, получится слиток, содержащий 35% золота, а если сплавить оба слитка целиком, то получится слиток, содержащий 40% золота. Во сколько раз первый слиток массивнее второго?
у/ 1560 (V> — 86.4). Имеются три килограммовых слитка: количества золота в первом, втором и третьем слитках образуют геометрическую прогрессию. Если сплавить 500 г первого слитка и 200 г второго, то в получившимся слитке будет содержаться столько же золота, сколько его содержится в 300 г третьего слитка. В скольких граммах второго слитка содержится столько же золота?
185
1561* (х — 92.4). Имеются три сплава: первый содержит 60% алюминия и 40% хрома, второй — 10% хрома и 90% титана, третий — 20% алюминия, 50% хрома и 30% титана. Из них нужно приготовить новый сплав, содержащий 45% титана. Какие значения может принимать процентное содержание хрома в этом сплаве?
у/ 1562* (б — 78.4). Имеются три сплава: первый содержит 70% олова и 30% свинца, второй — 80% олова и 20% цинка, третий — 50% олова, 10% свинца и 40% цинка. Из них нужно приготовить новый сплав, содержащий 15% свинца. Какое наибольшее и наименьшее процентное содержание олова может быть в этом сплаве?
§23. Переменные, параметры, функции
Разделение величин на переменные и константы, неизвестные и параметры, аргументы и функции — весьма условно и неоднозначно. Оно сильно зависит от воли и фантазии того, кто работает над задачей, и может существенно повлиять на ход ее решения.
23.1. Привлечение функций
С исследованием области значений функции в связи с решением конкретной задачи мы уже сталкивались ранее (п. 20.3,20.4). В настоящем пункте этот функциональный подход развивается и усложняется, а именно: вводятся абстрактные функции и изучаются различные их свойства1 \ наличие которых может подсказать оригинальный способ решения задачи.
Пример (р — 93.2). Найти все а, при которых уравнение
4* + (а2 + 5)2* + 9 - а2 = 0
не имеет корней.
Решение. Уравнение
... /Ю = о,
где t = 2х > 0, a f(t) = t2 + (а2 4- 5)t + 9 — а2 — возрастающая функция, не имеет корней тогда и только тогда, когда
0 £ (/(0); оо) о /(0) 0 о 9 - а2 > 0 О |а| 3 <=>...
Ответ: — 3 а 3.
Такие как монотонность, ограниченность, четность, периодичность и т. д.
186
у/ 1563 (<ф — 97.4). Найти все а, при которых уравнение 4х + 2х+2 + 7 = а _ 4-х _ 2.21-*
имеет хотя бы один корень.
У 1564 (jj, - 01.1). Зх - 2|ж - 2| = Зу/Зх 4-18 - 2 |^3ж 4-18 - 2|.
1565* (// — 83.4). Найти все а, при которых система
' 112- б| - (12^/с^ - 7|+________________
{ + |24д/со8 + 1з| = 11 - ySin
2(х2 + (у- а)2) - 1 = 2yjx2 + (у-а)2 —3/4 имеет хотя бы одно решение.
У 1566* (х - 89.5). (2а; + 1) (1 + у/{2х + I)2 + ?) +
+ х (1 + vzJ2T7) = 0.
1567* (х — 97.6). Найти все а, при которых уравнение
\/ж2^24^2Т118жТ7 = 5у/7х — х2 + Va2-lla + 18
имеет единственный корень.
1568* — 91.5). При каждом а ± решить уравнение
2х 4- а _ 2х — а
COS 2х2 4- 2ах 4- 5а2/2 C°S 2х2 — 2ах 4- 5а2/2 ’
1569* (/1 — 01.6). Основание ABCD прямоугольного параллелепипеда ABCD А'В* CD' повернули в своей плоскости на 30° вокруг точки пересечения диагоналей АС и BD (вершина А повернулась в направлении D), а боковые грани заменили гранями АА'В, А'В'В, ВВ'С, В'С'С, CC'D, C'D'D, DD'A и D'A'A. Найти все значения, которые может принимать периметр и площадь сечения полученного многогранника плоскостью, параллельной плоскости прямоугольника ABCD, имеющего периметр 26 и площадь 42.
Ч •
23.2. Изменение роли букв, входящих в условие
Задача может измениться до неузнаваемости, если параметр принять2^ за неизвестную величину или, наоборот, неизвестную — за параметр. Такое толкование бывает полезным, в частности, уже при разложении на множители.
2)Хотя бы временно.
187
Пример (V> — 77.5). При каждом а решить неравенство 9х+1 4- 8 • 3ха - а2 < 0.
Р ешение.
... о а2 - 8 • 3х • а - 9 • 9х > 0 о (а - 9 • 3х) (а + 3х) > 0
Г а > Зх+2 Гх<—2 + log3a а < -3х х < log3(-a).
Ответ: х < —2 + logs а при а > 0; х < log3(—а) при а < 0; при а = 0 решений нет.
у/ 1570° (/? — 94.5). Найти все я, при которых неравенство (4 - 2а)х2 4- (13а - 27)я 4- (33 - 13а) > 0 выполняется для всех а 6 (1; 3).
у/ 1571* (тг — 93.5). Найти все а, при которых неравенство . 7а24-а —2 1
х 4---------— 7а — 1
х 4- а 4-1
не имеет неотрицательных решений.
у/ 1572* (тг — 92.5). Найти все а, при которых неравенство 2ах 4- 2у/2х 4- 3 — 2х 4- За — 5 < 0 выполняется для всех х е [—1; 3].
у/ 1573 ((/? — 80.5). Найти все а < —4, при которых уравнение х2 4- ах — Зх — 2а = 2
имеет наименьший корень.
1574 (тг — 88.5). Найти наибольший корень уравнения х2 4- (ЗаЬ 4- За — 2)я 4- ЗаЬ 4- 5а = 17
при а > 1, 5 > 0.
у/ 1575 (/1 — 89.6). Найти наименьшее я, при котором существуют ?/, z, удовлетворяющие уравнению
х2 4- 2у2 4- z2 4- ху — xz — yz = 1.
у/ 1576 (у — 98.4). sinx(cos 2х 4- cos6i) 4- cos2 x = 2.
1577* (A - 92.6). (cos2ttz 4- costh/)2 4- 028 - 2y2 - 2yz = = (yz — 82) (4 4- x2 4- 4x sin ttz).
1578* (x - 85.5) У|ж2 - 2y2 + 2z2 + Юг + 6y + - 17 +
+ xl 3x2 — 2\/3(cos Tty + cos 7rz)a: + 4 = 0.
188
1579* (& — 01 7} 3 cos ж+2s*n x = cos2a; I cos ж4-sin x
\ • /' COS X COS'2 X ' COS X
x a/3 4- 2я - 2т/ + 2xy — x2 — y2.
1580* (x — 84.5). Найти все решения системы
{х3 4- х2(13 — у — z) 4- х(2у 4- 2z — 2yz — 26) 4-
4- 5yz — 7y — 7z = —30
x3 4- я2(17 - у — z) - x(2t/ 4- 2z 4- 2yz — 26) 4-
4- у 4- z — 3yz = 2,
для которых 4 x < 7.
23.3. Введение дополнительных переменных
Появление в задаче новых переменных, действующих наряду с исходными, раскрывает неожиданные внутренние связи, не осуществимые в принципе в отсутствие этих новых переменных. В качестве одной из таких переменных иной раз может выступать даже бывшая константа.
Пример (Л - 94.1). 2 >/17 V 8,(24)?
Решение. Обозначим 0,(24) = х, тогда
100т = 24 4-х => х = || = Д.
Сравним:
2\/17 V 8^ <=> уД7 V 4-1| <=> 17 • ЗЗ2 V 42 • 342
О ЗЗ2 V 32-34 (= ЗЗ2 — I2) — верно, когда знак V есть >. Ответ: >.
1581° (ф — 94.1). Верно ли неравенство
3log2 5 < y91og25 4-28?
у/ 1582° (7 — 87.4). Найти все решения системы
sin(2x 4- у) = 0 cos(x 4- у) = 1,
удовлетворяющие условиям —7Г х < 7Г, —2тг < у < —7Г.
1583* (ст—00.6). Найти все а, при которых квадратный трехчлен
/(х) = (а2 + 1)х2 + 4х+ — а 4-1 имеет два различных ненулевых корня, а их отношение является целым числом.
189
1584° ((/? — 89.5). Найти все а, при которых система < x + y + z = x2 + 4у2
х + 2у + 3z = а
имеет единственное решение.
1585* (х — 83.5). Найти все целочисленные а, при которых система
6х2 4- 24t/(x 4- у) 4- 2(3а — 2)х 4- 4(3а — 2)t/ 4-3 = 0 4(х2 4- у2) 4- (4а 4- 2)у 4- 2а2 = 8xt/ 4- (4а 4- 2)х 4- 5/2
имеет хотя бы одно решение.
у/ 1586* (7 — 85.5). Найти все а е (—1; 1), при каждом из которых выражение
1 — 2\/4х2 4- 4аху 4- J/2 4- 8т/ 4-18
принимает наибольшее значение лишь для одной пары (x,t/). у/ 1587* (7 - 95.5). tfx - 3/2 4- ^10 - х = 3.
1588* (х—90.4). х/9х2 - 48х - 214-х/9х2 - 51х - 15 |3х-6|.
1589* (/3 - 79.5).
(х/3 4-1)(1 4-cos(xj/)sin(xt/)) =
= (х/З 4-1) sin2(xt/) 4- cos(2xj/) х2у2 - у2 4-1 = 0 1/х2 4- у2 6.
у/ 1590 (х~ 00.6). При каждом о е [-1; 0] решить неравенство
\Jx 4- 2а > х 4- \/2а.
1591* (тг — 84.5). Найти все а, при которых уравнение
у 5а 4- у/5а — х — х2/4 4- х 4- х2/4 = 0 имеет хотя бы один корень.
1592* (/1 — 94.6). При каждом а решить уравнение 2х2 4- 2ах — а2 = \/4х 4- 2а 4- За2.
у/ 1593* (б — 83.6). При каждом а > 0 решить неравенство
а3х4 4- 6а2х2 — х 4- 9а 4- 3 > 0.
у/ 1594 (б — 85.4). Найти наименьшее значение функции ,, ч 2х2 4-х 4-1
“ За:2 - х + 2‘
190
1595* (V>—99.4). Найти все а, при которых область значений функции
содержит промежуток (—1; 3]. При каждом таком а найти область значений этой функции. *
у/ 1596 — 86.6). Найти наименьшее значение суммы х 4- Ьу
при условии
х2 — &ху 4- у2 4- 21 < О х,у > 0.
1597* (х — 00.5). Найти наибольшее значение выражения 14я2 4- 40я 4- у — 324,5
при условиях 4я2 4- 20# 4- у 162 и 20я2 — 80я 4- у < 8.
§ 24. Переменные в геометрии
Геометрическую задачу фактически можно свести к алгебраической, выбрав какие-либо параметры, связанные с конфигурацией задачи, и составив для них уравнения и неравенства. Естественными параметрами, в частности, служат координаты ключевых точек изучаемой фигуры или даже их наборы1 \
24.1. Обозначения для длин и углов
Усилия, затрачиваемые на решение задач настоящего пункта, напрямую зависят от того, какие именно геометрические величины выбраны в качестве неизвестных.
Пример (£ — 99.6). Высоты ВН и В К ромба ABCD пересекают его диагональ АС в точках М и N (точка М лежит между А и N). Найти НК, если AM = а и MN = Ъ.
Решение. Обозначим НК = х, ВО = у, DL = ку (рис. 34):
। = 2^ = 2 _ к Ц±ВНК ~ &BMN и DO = ВО = у)
\^+ь = ^=к (&DHK ~ &DAC nCN = АМ = а) + гДь ~ 2 => х = = ...
Ответ:
Пары или тройки координат, отождествляемые с векторами (см. § 5.7).
191
D
Рис. 34
1598 (*0 — 90.4). Диагонали трапеции ABCD пересекаются в точке О. Найти площадь трапеции, если отношение площади треугольника AOD к площади треугольника ВОС равно 4, AD =; 16, АС 4- BD = 36 и Z.CAD = 60°.
у/ 1599 (тг — 91.4). На диагональ BD трапеции ABCD опущены перпендикуляры AM и CN, причем точка М расположена между В и N. Найти CN, если АВ = CD, ВМ : DN = 2:3, AD = 4 и ВС = 3.
у/ 1600* (Д — 92.3). Окружность радиуса 6 касается катета АС и гипотенузы АВ прямоугольного треугольника АВС с периметром 54, а ее центр лежит на катете ВС. Найти площадь треугольника АВС, если АС > 10.
1601* (£ — 80.5). На стороне АС треугольника АВС взята точка D так, что CD = 3 AD. Окружность, проходящая через точки С и D, касается луча АВ. Найти радиус этой окружности, если Z.A = a, Z.B = /3 и АВ = с.
1602* (тг—92.4). Две окружности с центрами М nN, лежащими на стороне АВ треугольника АВС, и радиусами 2 и 5 соответственно касаются друг друга внешним образом. Первая из них проходит через точку А и пересекает сторону АС в точке К, а вторая проходит через точку В и пересекает сторону ВС в точке L. Найти радиус описанной около треугольника АВС окружности, если АК : BL = 2\/2 + ч/3 : 5>/3, а отношение площади треугольника ALN к площади треугольника ВКМ равно 15\/3 : 8.
у/ 1603 (Д — 88.4). Окружность радиуса \/3 касается стороны АС и продолжений сторон АВ и ВС треугольника АВС площадью — 3. Найти Z.ACB, если Z.BAC = 60°.
192
1604* (<ф — 86.5). В трапецию ABCD с основанием AD = 20 и углом ZB = ср вписана окружность. Найти ее радиус, если периметр треугольника ВСЕ, где Е — точка пересечения лучей АВ и DC, равен 60.
1605* (гр — 96.4). Окружность с центром О касается лучей АВ, АС и отрезка ВС, который пересекается с отрезком АО в точке D. Найти радиус окружности, вписанной в треугольник АВС, если AD : OD = 2:3, ВС = 7 и /А = 60°.
1606* (£—79.5).- В ромб ABCD со стороной а вписана окружность, касательная к которой пересекает стороны АВ и AD в точках М и N соответственно. Найти МВ и ND, если MN = Ьи/А = <р.
1607* (х—81.6). Площадь грани ASB пирамиды SABC равна Перпендикуляры ко всем граням пирамиды, восстановленные из центров вписанных в них окружностей, пересекаются в одной точке. Найти объем пирамиды, если Z.BCS = = arctg AS = SB и SC • AC = 20.
24.2. Метод координат
В большинстве задач настоящего пункта присутствуют взаимноперпендикулярные оси, которые при желании можно объявить координатными.
Пример (х — 92.3). На стороне АВ угла /ВАС = 30° взяты точки М и N на расстоянии 2 и 6 от вершины А. Найти радиус окружности, проходящей через точки М, N и касающейся стороны АС.
Решение. Пусть А — начало координат, ось абсцисс направлена вдоль луча АВ, а ось ординат — в ту полуплоскость, которая содержит точку С (рис. 35). Тогда если О = (х, у) — центр окружности, & К — точка касания со стороной АС, то:
1) АК = \/2 • 6 = 2\/3 (теорема о касательной и секущей).
=> К = (2x/3cos30°, 2x/3sin30°) = (3, ч/З); .
2) х = = 4 (точка О лежит на серединном перпендикуляре
к отрезку MNY,
3) ОМ = ОК => (4 - 2)2 + у2 = (4 - З)2 4- (у - ч/З)2 => 2 ч/Зг/ = 14-3 — 4 = 0 => у = 0.
Ответ: 2.
1608° (б — 78.2). Внутри прямоугольника ABCD взята точка М так, что AM = \/2, ВМ = 4ч/2 и DM = 2. Найти cos /ВАМ и площадь прямоугольника, если АВ = 3 ВС.
7 И. Н. Сергеев — Математика
193
у/ 1609° (£ — 87.5). Внутри прямоугольного треугольника АВС с гипотенузой АС взята точка М так, что площади треугольников АВМ и ВСМ составляют треть и четверть площади треугольника АВС соответственно. Найти ВМ, если AM = а и СМ = с.
у/ 1610 (7 — 94.4). На катетах АС = 1 и ВС = 4 прямоугольного треугольника АВС во внешнюю сторону построены квадраты ACEF и BCGH. Продолжение медианы СМ треугольника АВС пересекает отрезок EG в точке N. Найти CN.
1611* (х — 79.3). Диагонали вписанного в окружность четырехугольника ABCD пересекаются в точке Е под прямым углом. Продолжение высоты ЕН треугольника АВЕ пересекает сторону CD в точке М. Найти ЕМесли АВ = 4, AD = 8 и Z.BDC = а.
у/ 1612 (б — 86.4). Внутри прямоугольника ABCD со сторонами АВ = 6 и AD = 3 4- 3\/2/2 расположены две окружности: первая, с центром Е и радиусом 2, касается сторон АВ и AD, а вторая, с центром F и радиусом 1, касается первой окружности и стороны CD. Найти площадь треугольника CFGb где G — проекция точки В на прямую EF.
1613* (х — 00.6). Через концы диагонали АС = 26 параллелограмма ABCD проведена окружность, а через концы диагонали BD = 6 — вторая, пересекающая первую в точках М и N. Найти расстояние от точки пересечения диагоналей до прямой MN, если расстояние между центрами окружностей равно 10.
у/ 1614 (V> — 77.4). В окружность радиуса 17 вписан четырехугольник, диагонали которого взаимно перпендикулярны и
194
находятся на расстоянии 8 и 9 от центра окружности. Найти стороны четырехугольника.
у/ 1615* (А — 80.5). Хорды АА', ВВ' = 18 и СС' сферы радиуса И взаимно перпендикулярны и пересекаются в точке М, находящейся на расстоянии >/59 от центра окружности. Найти АА', если СМ : МС' = (8 + х/2) : (8 - х/2).
1616* (/1 — 97.6). Две сферы касаются друг друга внешним образом в точке, лежащей внутри куба ABCD А'В'С'D' с ребром 1. Одна из сфер, радиуса 1/3, касается плоскости АВС в точке В, а другая касается плоскости А*В'С в точке В', лежащей на отрезке С"D'. Найти расстояние от точки касания сфер до точки С, если С'Е' : D'E' =1:2.
1617* (/1 — 00.6). Основанием пирамиды SABCD служит параллелограмм ABCD, Найти площадь грани ASD, если площади граней ASB, BSC и CSD равны соответственно 5, 6 и 7, а плоскости ASC и BSD перпендикулярны.
24.3. Задачи с возможным участием векторов
Использование векторных обозначений делает выкладки более компактными и позволяет применить серьезный аналитический аппарат, опирающийся на скалярное произведение (см. § 5.7).
Пример (е — 78.2). Диагонали четырехугольника ABCD пересекаются в точке Е. Найти косинус угла между векторами АВ и DC, если АЕ = СЕ — 2, BE = 1, DE = 4 и /.ВЕС = тг/З.
Решение. Обозначим АВ = х, DC — у, ЕВ = й, Ед = v (рис. 36):
195
7*
x = tt4-v, y = 4tt + v, |u| = 1, |v| = 2, и • v = 1 • 2 • cos f = 1
COSZ(x, й) = = 4u2+5u.vW_________ =
\ “/ |x|-|ld ^/й2 +2й-v+v2• у 16u2 +8й v+v2
Ответ: 13/14.
- wutvA+Ui--
у/ 1618 (б — 79.2). На боковой стороне АВ = 8 равнобедренного треугольника АВС с основанием АС = 12 взята точка D так, что AD : BD = 1:3. Найти угол между векторами cAaCD.
у/ 1619 (х — 93.4). На стороне ВС равнобедренного треугольника АВС с основанием АС взята точка D так, что BD : CD = = 2:1. Точка Е — середина стороны АВ, а точка F — середина отрезка DE. Найти радиус описанной около треугольника АВС окружности, если CF = DE = \/23/2.
у/ 1620 (д —88.4). Угол между скрещивающимися прямыми АВ и CD равен arccos (>/35/10). Точки Е и F — середины отрезков АВ и CD, а прямая EF перпендикулярна прямым АВ и CD. Найти ZACB, если АВ = 2х/5, CD = 2л/7 и EF = У13.
1621* (7—83.5). На ребрах АВ, ВС и CD правильного тетраэдра ABCD с ребром 1 взяты точки К, Ln М соответственно так, что АК = 1/2 и BL = СМ = 1/3. Плоскость KLM пересекает прямую AD в точке N. Найти угол между прямыми NK и NL.
1622* (V> — 79.4). Точка М равноудалена от вершин А и D правильного тетраэдра ABCD, а от каждой из вершин В п С находится на расстоянии \/3/2. Прямая МС перпендикулярна высоте DH треугольника ACD. Найти объем тетраэдра.
1623* (/1—82.5). Грани SAB и SAC пирамиды SABC — прямоугольные треугольники, ребро AS перпендикулярно медиане AM основания АВС и AS = AM. Сечение пирамиды плоскостью, не проходящей через середины ребер AS и ВС, — равнобедренная трапеция DEFG с основаниями DE и FG, причем D — середина ребра BS, а точка F лежит на ребре АС и AF = 3 CF. Найти отношение площадей трапеции DEFG и грани SBC.
1624* (£ — 80.6). Два одинаковых прямых круговых конуса с углом а между высотой и образующей имеют общую вершину и расположены по одну сторону от данной плоскости,
196
касаясь ее своей боковой поверхностью. Угол между высотами конусов равен /3, причем а 4- /3 < тг/2. Найти угол между образующей одного конуса, лежащей в данной плоскости, и плоскостью основания другого.
1625* (х—99.6). Радиус сферы, описанной около прямоугольного параллелепипеда ABCDA'B'C'D' объемом V, равен Я, а MiNi, M2N2, M3N3 — общие перпендикуляры к парам скрещивающихся прямых А'С' и АВ', ВС' и AC, DC' и AD' соответственно. Найти сумму объемов тетраэдров AA'MiNi, ABM2N2 и ADM3N3, если АА' 4- АВ 4- AD = а.
§ 25. Графические иллюстрации
Вспомогательным элементом, привнесенным в условие алгебраической задачи, может служить не только новая переменная, но и геометрический образ уже имеющейся переменной, интерпретируемой как координата точки на прямой, окружности или плоскости.
25.1. Числовая прямая
Самой простой графической иллюстрацией следует признать числовую ось (которая уже применялась прежде при использовании метода интервалов, см. п. 10.2,11.1). Так, в следующем примере по расположению точек а и b на оси можно узнать, верно ли, например, что для всех х > а выполнено неравенство х Ь.
Пример (а — 93.6). Найти все а, при которых неравенство х2 4- 2|ж — а| а2
выполняется для всех х.
Решение. Рассмотрим три случая:
1) х = а: а2 + 2\а — а\ а2
— верно при любом а;
2) х > а: (х — а)(х 4- а 4- 2) 0 х^—а — 2
— верно для всех х > а о а — а — 2 а —1;
3) х < а: (ж — а)(х 4- а — 2) 0 О
— верно для всех х < а о а —а 4- 2
х — а 4- 2
4Ф а < 1.
Ответ: —1 а 1.
у/ 1626° (£ — 00.7). Найти все а, при которых неравенство (ж2 — (а 4- 2)х — 2а2 4- 4а) \/1 — х 0
имеет ровно одно решение.
197
1627 (ip — 91.6). Найти все а, при которых неравенство logz-a Я2 < 2
имеет хотя бы одно решение, для которого |я| < 0,01.
у/ 1628* (б — 84.6). Найти все а, при которых ровно одно решение неравенства
\/а3 4- а2 — а — 1 • х3 — \/а3 + а2 • х2 4- \/а4 - а2 • х — а2 < 0 удовлетворяет условию а < х < 2а 4-1.
у/ 1629 (7 — 93.5). При каких а уравнение
х4 4- {а — 5)я2 4- (а 4- 2)2 = 0
имеет четыре различных корня, образующих арифметическую прогрессию?
1630 (х — 82.5). Найти все а, при которых уравнение
((х — а — I)2 — 2) (х — а — I)2 = а2 — 1
имеет различных положительных корней больше, чем отрицательных.
у/ 1631 (7 — 78.5). Найти все а, при которых система
(\х2 - 5я 4- 4| — 9я2 — 5я 4- 4 4- 10я|я| = 0
х2 — 2(а — 1)а; 4- а(а — 2) = 0
имеет единственное решение.
1632* (А — 01.8). Найти все а 1, при которых уравнение sin tgx = 0
имеет на отрезке [2атг; (а24-1)тг] ровно шесть различных корней.
у/ 1633* (ст -* 97.6). Найти все а, при которых уравнение sin 2а sin2 ах 4-1 = (1 4- sin 2а) sin ах
имеет ровно четыре различных корня на отрезке [—тг; тг].
1634* (V> — 98.6). Найти все а и Ь, при которых уравнение
arcsin ^а2~х2 - а 2sin7rax - larcsin + а • 2sin,r,,a: I = 2аЬ имеет не менее десяти различных корней.
1635 (х — 81.3). Из пункта А в пункт В выехал автомобиль и одновременно с ним из пункта С, расположенного между А и В, в пункт А выехал второй автомобиль. Прибыв одновременно в пункты назначения, они сразу же выехали навстречу
198
друг другу и, повстречавшись в пункте D, одновременно прибыли: первый в А, второй в В. Автомобили ехали с постоянными скоростями, но сделали по одной остановке одинаковой продолжительности: первый на пути от В к D, второй — от С к А. Найти CD, если АС = 270 км и СВ = 180 км.
у/ 1636 (7 — 99.3). Пункты А и В расположены на реке: из А в В вышел катер, а из В в А одновременно с ним — моторная лодка. Пройдя 3/4 пути от А к В, катер встретился с лодкой, а достигнув В, повернул обратно и прибыл в А одновременно с ней. Найти отношение собственных скоростей катера и лодки. 1637 (е — 85.5). Два пешехода вышли из пункта А в одном направлении с интервалом не более, чем в 40 мин, и прибыли в пункт В с интервалом не менее часа. Если бы они вышли одновременно, то прибыли бы в пункт В с интервалом не более, чем в 20 мин. Сколько времени был в пути каждый пешеход, если скорость одного из них в полтора раза больше скорости другого?
у/ 1638* (б — 80.5). Пункты А, В, С и D расположены последовательно на прямой дороге так, что АВ : АС : AD = 1:2:4. По этой дороге через равные промежутки времени в одном направлении с одинаковой скоростью едут автобусы. Из пункта А в разное время с одной и той же скоростью отправились три пешехода: первый — в В, второй — в С, третий — в D. Первого пешехода обогнали 3 автобуса, второго — 4, причем в моменты выхода из Л их не обгоняли очередные автобусы. Сколько автобусов обогнали третьего пешехода с учетом того, что в момент выхода из А и в момент прихода в D его обогнали очередные автобусы?
25.2. Исследование графиков
Привлечение к решению задачи графиков сопутствующих функций привносит в ее условие совершенно новое, геометрическое видение, которое на языке формул дается с гораздо бблыпим трудом.
Пример (д — 79.4).
Решение. Обозначим
№)= 2^7=3-^, д(х) = 1 4- log2 (х + 2)
(см. графики на рис. 37) и рассмотрим пять случаев:
1) —2 < х < -1/2 : ... 4Ф f(x) < д(х)
— неверно, т.к. f(x) > 3 > 2 = р(0) > д(х)\
199
2) —1/2 < х < 0 : ... О f(x) < д(х)
— верно, т.к. f(x) < /(0) = 0 < 1 = д(-1) < д(х)\
3) 0 < х 1 : ... <=> f(x) > д(х)
— неверно, т.к. f(x) /(1) = 2 < д(х)\
4) 1 < х 2 : ...<=> f(x) > д(х)
— неверно, т.к. f(x) ^/(2) = 12/5 < 1+3/2 < 1 + log2 3 = д(1) < д(х) (так как 3/2 < log2 3 <=> 23 < З2, что верно);
5) х > 2 : ... <=> f(x) > д(х)
— неверно, т.к. f(x) < 3 = д(2) < д(х).
Ответ: —1/2 < х < 0.
1639° (б — 84.2). Найти наименьшее значение функции f(x) = 2|ж — 3| + |3ж — 2|.
1640° — 85.4). Найти наибольшее и наименьшее значения
функции
/(ж) = |я2 + я| + |я2 + 5х + 6|
на отрезке [—2,5; —0,5].
у/ 1641 (х — 93.5). Сколько корней имеет уравнение 2х+1 + г1"® = 1 — 4ж — ж2?
1642* (v? - 87.5). > l±12Stk±61
1643 (7 — 88.5). Доказать, что при всех х > 0 справедливо неравенство
X2 + 7ГЯ + 4тг cos х > 0.
200
у/ 1644* (А — 83.5). Автобус проходит путь АЕ, состоящий из участков АВ = 10 км, ВС = CD = 5 км и DE = 6 км. Согласно расписанию, выезжая из пункта А в 9.00, он проходит пункт В в 9.00, пункт С в 9.20, пункт D в 9.40. Может ли автобус двигаться без остановок с такой постоянной скоростью, чтобы время его полного движения от А до Е в сумме модулями отклонений от расписания в моменты прохождения пунктов В, С и D не превосходило 53 мин?
1645* (б — 92.3). Фабрика получила заказ на покраску 6000м ткани в один цвет и 2000 м — в другой. Каждый рабочий фабрики затрачивает на покраску 5 м ткани в первый цвет одинаковое время, такое же, как на покраску Зм ткани во второй цвет. Как разделить 214 рабочих фабрики на две бригады, чтобы выполнить заказ за наименьшее время, если все рабочие приступят к работе одновременно и каждая бригада будет красить ткань только в один цвет?
у/ 1646* (х — 91.5). Принимает ли функция
/(ж) = | ((ж+0,003)0’45 + (1-ж)б’4й) + | (®+0,003)ti«45 ~ (1-ж)б’4й |
хотя бы в одной точке х е (0; 1) значение, меньшее 3,17?
1647* — 82.5). Найти все а, при которых неравенство
а3|т/| у/2(а2 -х2)
имеет наименьшее количество целочисленных решений.
у/ 1648* (i/ — 00.6). х2 = arcsin(sinx) 4- Юж.
1649* (б —96.6). Найти все а, при которых фигура, заданная неравенством7
bl < |ж|)2 4- arcsin(sin(a — |ж|)),
представляет собой 14-угольник.
25.3. Упрощение выкладок с помощью свойств параболы
Представив наглядно параболу, участвующую в условии задачи, можно сравнительно легко, без трудоемких вычислений, получить ответы на некоторые существенные вопросы.
Пример (А — 78.3). log3 log9/16 (ж2 — 4ж 4- 3) 0.
Решение.
... 0 < log9/16 (я2 - 4ж 4- 3) 1 <=> 9/16 < х2 - 4ж 4- 3 < 1
201
Г (® — 3/4)(® — 13/4) О
1 (ж — xi)(x — хг) < 0, где #1,2 = 2 ± \/2 (расположение корней видно из рис. 38).
Ответ: 2 — \/2 < х 3/4, 13/4 х < 2 4- у/2.
1650° (х - 86.1). log5/4 (я2 4- Зя - 7/4) 1.
yieSl"(T-79-2).
у/ 1652° (х — 80.4). Найти все а, при которых уравнение (За - 1)я2 4- 2ах 4- За — 2 — О
имеет два различных корня.
1653 (А - 80.3). : 1654 (Л - 77.2). с2 + 4|а: - 3| - 1х + 11 = 0. с2 — |5а: — 3| — х < 2.
1655 (е - 78.1). < |а:2 + х — 1| = 2а: — 1 X < тД/3.
1656 (х-97.1). ’ 1657 (/3 - 97.3). 1658 (у - 84.3). функции /8а:2 - 45а: + 62 = 7 - За:. У|1 - 8а:| - 2 х + 1. Найти наибольшее и наименьшее значения /(а:) = х2 — 5|а: + 1| — 2
на отрезке [—3; 3].
1659* (/? — 82.4). Найти наибольшее и наименьшее значения функции
/(я) = я4 \/(я2 4- 6я 4- 9)(я2 4- 2я 4-1)
на отрезке [—4; —5/4].
202
25.4. Числовая окружность
О роли тригонометрического круга в отборе корней тригонометрического уравнения читатель хорошо знает по задачам из § 15. Исследование указанной модели вызывает затруднения, и прежде всего из-за зацикливания числовой окружности. Это явление можно, хотя бы визуально, устранить, представляя окружность в виде спирали, т. е. изображая ее витки не слитно, а раздельно.
Пример — 81.3). Найти все корни уравнения
cos7x — \/3sin7x = — \/2
на интервале (2тг/5; бтг/7).
Решение. ...<=> cos (7х 4- тг/З) = — \/2/2.
С учетом неравенств
Д? < х < ЗАтг < 7х + % < б|тг О г 10 О О
получаем (рис. 39)
7х 4-f = Зтг 4-5тг ± j О ...
Ответ: х = 5тг/12, 2тг/3±тг/28.
1660 (7-95.3).
(cos 2х 4- 3 sin х — 2) tg х а/187тг2 + Збтггс - 36а:2
у/ 1661 (а — 96.3). Найти область определения функции
х/36 - х2 log3 (а:2 + 2а: - 8) J (®) =---------;----------------•
' 2 sm х — 1
1662 (х — 95.4). logcosa. cos2 х
> logCO8a._1/2 (cos2 х - cos а: - 14a: - x2 - 51/4) .
у/ 1663 (С—96.8). Для каждого а найти количество различных корней уравнения atga: + cos 2а: = 1 на отрезке [0; 2тг].
203
1664 (£ — 99.7). Найти все а, при которых уравнение cos2я + 2 cosx - 2а2 - 2а 4-1 = О
имеет ровно один корень на промежутке [0; 2тг).
1665 (/1 — 94.6). Найти все а Е [—тг/2; тг/2], при которых уравнение
sin 2х 4- sin х 4- sin(x — а) = sin а 4- sin(x 4- а) имеет ровно пять различных корней на отрезке [—7тг/4; 5тг/4]. 1666 (А — 01.4). Найти все корни уравнения
cos х — cos 2х — sin 2х = 1
на отрезке [—Зтг/2; —тг/6].
у/ 1667* {я — 00.3). Найти все решения неравенства х/б — 10cos# — sinх < sinх — cosх, принадлежащие отрезку [—тг; тг].
1668* (а — 00.4). л/11 — 8cos4x — 4sinxcosx = 3sinх 4-cosх. У1669 (/1 — 99.3). Найти все а, при которых положительные корни уравнения
/х \ f3x \ . х
cos I — 4- а ) — cos I — 4- а 1 — sin — ' 4 / \ Z J а
образуют арифметическую прогрессию.
1670 (7—99.4). Найти все а, при которых среди корней уравнения
sin 2х 4- 6а cos х — sin х — За = 0
найдутся два, удаленные друг от друга на расстояние Зтг/2. у/ 1671 (/2 — 01.2). Имеет ли уравнение
12 cos (Зтг/2 4- х) = |4 — 5cosx|
хотя бы одну пару корней, расстояние между которыми не превосходит тг/2?
1672* (/1 — 99.5). Найти все а Е [—2; 1], при которых расстояние между любыми различными корнями уравнения
sin2x 4- |2а 4-1| sin# 4- |а| = 2|а| cos я 4- sin х 4- |2а2 4- а| не меньше, чем тг/2.
204
1673* (/z — 00.5). Найти все а, при которых уравнение (|а( — 1) cos 2х 4- (1 — |а — 2|) sin 2х 4-
4- (1 — |2 — а|) cos х 4- (1 — |а|) sin х = 0 имеет на интервале (—7г; тг) нечетное число различных корней.
у/ 1674* (7 — 97.3). Найти сумму различных корней уравнения | cos я| — cos Зя = sin 2х, принадлежащих отрезку [—8тг; 7тг].
1675* (/2—96.4). Найти все а, при которых сумма различных корней уравнения
cos х — sin 2х 4- sin 4х = a(ctg х 4- 2 cos Зя), принадлежащих отрезку [Зтг/4, 22тг/3], максимальна. 1676* (тг — 97.6). Найти наибольшее и наименьшее значения выражения_______
(-Зук-с°£2х + 72- т/ЗсОЗЯ - 1) X
X + УП - v^COSy + 1) .
1677* (/1 — 95.6). Пусть Xi — наибольший отрицательный корень уравнения
\/3sinx — Зсоэя = 2а — 1,
Х2 — наименьший положительный корень уравнения
2 cos2 х — 2 sin2 х = а.
Найти все а, при которых |#i| #2-
§ 26. Зависимость графиков от параметра
Привлекая к решению задачи графики функций или множества, зависящие от параметра, можно определить, к&к они должны располагаться, чтобы выполнялось требование задачи, и на основании этого сделать вывод об искомых значениях параметра.
26.1. Сечения графиков t
Сечения использовались ранее при построении фигур на координатной плоскости в п. 12.2. В настоящем пункте изучаются сечения графиков функций прямыми линиями (или полуплоскостями).
205
Пример (у? — 77.4). При каждом а определить число корней уравнения _______
-\/2|х| — х2 = а.
Решение. Пересекая прямыми вида у = а график функции
j---2 IУ2 = 21®1 - х2 /у2 + (I®I - I)2 = 1
у = у/2\х\—х2 11 ’ п
[«/ 0 (у О
(состоящий из двух полуокружностей, рис.40), получаем...
Ответ: 0 при а < 0, а > Г, 3 при а = 0; 4 при 0 < а < 1;
2 при а = 1.
1678° (А — 01.7). Найти все а, при которых уравнение
|2я 4- 6| 4- |2я — 8| = ах 4-12
имеет единственный корень.
у/ 1679 (7 — 92.5). Найти все а, при которых уравнение
|я2 — 1| 4- |я2 — х — 2| = х2 4- Зх 4- а имеет ровно три различных корня.
1680 (х — 92.5). Найти все а, при которых уравнение 5|ж — За| 4- |я — а2| 4- 4я = а
1) имеет бесконечно много корней;
2) не имеет корней.
1681* (/1 — 96.6). Найти все а, при каждом из которых хотя бы для одного b уравнение
|я2 — 1| 4- ах = |я2 — 8х 4-151 4- b
1) имеет более пяти корней;
2) имеет ровно пять различных корней.
206
у/ 1682 (б — 83.6). Найти все а, при которых уравнение
х — а = 2|2|я| — а2|
имеет ровно три различных корня, и найти эти корни.
1683* (х — 84.5). Найти все а, при которых неравенство
1. । . . (, . п2 4п 4- 3 \ ,
-|а + 2| • |х + а + 4| - Qa + 2|-|о + 2|" ) ,1а; + 21 +
4- -|а4- 2| • |х -а| < 2 имеет ровно два различных решения.
1684* (/? — 95.6). Найти все а, при которых уравнение
(х2 — 6|я| — а)2 4- 12(я2 — 6|я| — а) 4- 37 = cos имеет ровно два различных корня.
у/ 1685 ((/? — 01.5). Найти все а, при которых фигура, заданная системой
{2у - х 1 у 4- 2х 2 у 4- ах —1 содержится в некотором круге.
у/ 1686* (тг — 95.5). Найти все а, при которых система
4х = а 4- 3 - у2 4- 2у х2 + у2 = 2у
имеет ровно два различных решения.
1687* (тг — 98.6). Найти все а, при которых система
у/—у2 — 2х = ах
у > a 4- 5/2 имеет хотя бы одно решение.
у/ 1688 (тг — 96.6). Найти все а, при которых решения неравенства
у/х 4- а х
образуют на числовой прямой отрезок длины 2|а|.
1689* (х — 97.5). Найти все х, для каждого из которых неравенство ___________
\/х2 4- 2я 4- a > ах2 4- (1 — а)(2х — 1) — 2 выполняется при всех а е [—2; 0].
207
26.2. Взаимное расположение графиков
Ответ в каждой из следующих задач получается как результат исследования взаимного расположения на координатной плоскости графиков удачно выбранных функций.
Пример (а — 91.6). Найти все а, при которых система f х2 4- у2 = 1 [у - |х| = а имеет ровно два различных решения.
Решение. Пересекая единичную окружность ж2 4-у2 = 1 графиками вида у. = |х| 4- а (рис. 41. а) и замечая, что касание имеет место при
О А = \/2 => а = -\/2
(см. равнобедренный треугольник О АВ на рис. 41. б), получаем... Ответ: а = — \/2, —1 < а < 1.
yj 1690 (б — 77.5). Найти все а, при которых неравенство 3 — \х — а\> х2
имеет хотя бы одно отрицательное решение.
1691* (х — 95.4). Для каждого а решить неравенство |я 4- 2а| 1/х.
у/ 1692* (Д — 78.5). Найти все а, при которых уравнение х\х 4- 2а| 4-1 — а = О имеет единственный корень.
208
1693* {tp — 83.5). Найти все а, при которых уравнение
|1 — ая| = 1 4- (1 — 2а)х 4- ах2
имеет единственный корень.
1694* (7 — 95.5). При каждом а найти количество корней уравнения
х2 4- а = 35 cos х при — тг х < тг, где b — наименьшее значение суммы квадратов корней квадратного трехчлена
/(«) = t2 - \Z5-3c2 • t + (3/2 - с2) .
у/ 1695* (7 — 94.5). Найти все а, при которых уравнение
а 4- д/бя — ж2 — 8 = 3 4- х/1 4- 2ах — а2 — ж2
имеет единственный корень.
1696* (х — 90.6). Найти все а, при которых для любого Ь неравенство
|log6 + хоа+знзхд.г _ 9Ь2 _ 9Ь _ Х|
10g6 4- 100+36+4x^.2 _ (6Ь + 2)х 4- 9Ь2 4-156 4- 3
имеет хотя бы одно решение.
26.3. Использование параметра в качестве одной из координат ч
Ниже читателю предлагается интерпретировать условия всех задач как соотношения, задающие множества точек на плоскости с координатами х и а.
Пример (^ — 97.7). Найти все а, при которых неравенство
выполняется для всех х 6 [1; 3].
Решение. Множество пар (а, ж), удовлетворяющих неравенству, изображено на рис. 42 (пунктирная линия в нем не содержится). Сечение этого множества прямой вида а = const содержит отрезок [1; 3] тогда и только тогда, когда
а < ai | ai + 4 = 1 J <21 = —3
гДе { \
[а>а2, [2-За2 = 1 [а2 = 1/3.
Ответ: а —3, а > 1/3.
209
у/1697° (х — 87.5). Найти все а, при которых ни одно решение неравенства
(а — х2)(а 4- х - 2) < О
не удовлетворяет условию х2 < 1.
1698 (А — 00.7). Найти все а, при которых любое решение неравенства
х2 — а < 0
удовлетворяет неравенству
(х 4- 2а)\/3 — х < 0
у/ 1699 (А — 78.5). Найти все а, при которых система
’ х2 4- (5а 4- 2)х 4- 4а2 4- 2а < 0
х2 4- а2 = 4
имеет хотя бы одно решение.
у/ 1700* (е — 92.6). Найти все а, при которых неравенство
х2 — Зх 4- 3|я 4- а| 4- а 0
имеет наибольшее количество целочисленных решений.
1701* (/1 — 97.6). Найти все а, при каждом из которых среди решений неравенства
у(а — ж2)(ж2 4- а) 4- а > х
есть ровно два различных целочисленных решения.
210
1702* (x— 79.5). Найти все а, при которых уравнение
( 9 ПтгаЛ /-------------
a — х — cos —-— v 8 — ах = О
\ 4 J
имеет на отрезке [—2; 3] нечетное число корней.
1703* (ст — 99.6). Найти все а, при которых неравенство
10&ая:2+2а2а;+1
arcsin 4(я + 3а)>
> logOx2+2O2®+i ^/16 arcsin-4(a: + За)
не имеет решений на отрезке [—5; 6].
26.4. Задачи на расположение парабол
При решении задач настоящего пункта читатель может научиться делать выводы о расположении на числовой прямой корней квадратного трехчлена1)
f(x) = ах2 4- Ьх 4- с, а О,
не пользуясь формулой корней, а применяя лишь теорему Виета2\ а также умело оперируя знаком старшего коэффициента а и дискриминанта D = Ъ2 — 4ас, абсциссой хо = — Ъ/(2а) вершины параболы и значениями функции f в отдельных точках, в частности, значением /(0) = с.
Пример (б — 77.4). Найти все а, при которых уравнение logs (9* + 9a3) = х
имеет два различных корня.
Решение. Уравнение
• • - о 9® 4- 9a3 = 3х о /(3х) = 0, где f(t) = t2 -t + 9a3, tQ = 1/2, имеет два различных корня тогда и только тогда, когда (рис. 43)
f D > 0 f 1 > 36a3
< , ч о < о о ...
(/(0) > 0 (9a3 >0
Ответ: 0 < a < 1/\/36.
1704° (£ — 94.7). Найти все а, при которых система
( х2 — 12# 4- а < О
( х 2
имеет хотя бы одно решение.
^Или о взаимном расположении двух парабол на плоскости.
2)См. п.6.3
211
у/ 1705° (С — 94.7). Найти все а, при которых уравнение 2а(я 4-1)2 - |я 4-1| 4-1 = О имеет четыре различных корня.
1706 (ф — 77.5). Найти все а, при которых система Гх2 4- (у 4- З)2 < 4 1 у = 2ах2
имеет хотя бы одно решение.
1707* (7 — 90.5). Найти все а, при которых уравнение (а 4- 1)я2 4- (|а 4- 2| — |а 4- Ю|)я 4- а = 5 имеет два различных положительных корня.
у/ 1708* (^ — 93.5). Пусть я1>2 — корни квадратного трехчлена f(x) = (а — 1)я2 — (2а 4- 1)я 4- 5а 4- 2.
Найти:
1) все а, при которых xi,x2 > 1;
2) все Ь, при которых выражение (#i—6)(я2—5) принимает постоянное значение для всех а, для которых оно определено. 1709* (х — 88.5). Найти все а, при которых уравнение
((2ж 4- а)\/22а —4а2 — 24 — 2(х2 4- х) 1g а) lg -в^9-"2- = О имеет не менее двух различных корней, один из которых неотрицателен, а другой не превосходит —1.
у/ 1710 (ц — 92.6). Найти все ж, при которых неравенство (а 4- 2)ж3 — (1 4- 2а)х2 — &х 4- (а2 4- 4а — 5) >0 выполняется хотя бы для одного а е [—2; 1].
212
1711* (/3 — 99.5). Найти все х > 1/2, при которых неравенство
4я3?/2 - 6ат32/ — Юж2?/2 — 16ж3 4- Пят2?/ + 8ху2 +
4- 50я2 — 4ху — 2у2 — 52ж — у 4-18 < О выполняется для всех у е (1; 2ж).
-/1712° (£ — 98.7). Найти все а, при которых неравенство l°gi/2(z2 4- ах 4-1) < 1
выполняется для любого х < 0.
1713° (£ — 98.8). Найти все а, при которых система
< log3(y - 3) - 21og9a: = 0 (х 4- а)2 — 2у — 5а = 0
имеет хотя бы одно решение.
1714* (J3 — 87.5). Найти все а, при которых система
9ж2 - бху + у2 + бх — 13?/ 4-3 = 0
< 13ж2 4- бху 4-10?/2 4- 16ж 4- 2у — 4ах — бау 4-
4- а2 — 2а 4-1 = 0
имеет хотя бы одно решение.
yj 1715 (б — 95.6). Найти все а, при которых уравнение
х — 2 = у/2 — 2(а 4- 2)ж
имеет единственный корень.
1716* (х — 81.5). Найти все а, при которых неравенство
(а3 + (1 - \/2)а2 - (3 + у^)а + Зу^я2 + 2(а2 - 2)х + а > —\/2 выполняется для любого х > 0.
1717 —81.5). Найти все а, при которых наименьшее зна-
чение функции
/(ж) = 4ж2 — 4ах 4- (а2 — 2а 4- 2)
на отрезке [0; 2] равно 3.
у/ 1718 (р —91.5). Найти все пары (р, д), при которых неравенство
|ж2 + рх 4- д| > 2
не имеет решений на отрезке [1; 5].
213
у/ 1719 (б — 78.5). Найти все а, при которых неравенство
а2 4- 2а — sin2 х — 2а cos х > 2
выполняется для любого х.
1720* (х — 86.6). Найти все пары (а, 5), при которых наибольшее значение функции
„ ч 9 5ж+5-ж-2 z 5Ж — 1 о г f(x) = - - ----------- 4- (а — Ь)- • --- 4- 2а 4- Ъ
Jy 7 4 5Ж 4-5“ж 4-2 k '2 5Ж 4-1
на отрезке [—1; 1] —минимально.
1721* (х — 96.3). При каждом а решить уравнение
25х - (а - 1)5Ж 4- 2а 4- 3 = 0.
1722* (7 — 84.5). Найти все а, при которых система
{у(ах — 1) = 2|я 4-11 4- 2ху
ух + 1 = х - у
имеет хотя бы одно решение.
1723* (б — 80.5). При каждом целочисленном а решить уравнение
. , о 9 X
5 — 4 sm х — 8 cos - = За.
а
1724* (А —88.6). Найти все а, при которых область значений функции
ч sins 4-2(1 - а)
/(я) = п \„ а — cos2 х
содержит отрезок [1; 2].
1725* (б — 91.6). Найти все а, при которых уравнение
sin2 х 4- (а — 2)2 sinх 4- а(а — 2)(а — 3) = 0
имеет на отрезке [0; 2тг] ровно три различных корня.
1726* (/? — 83.5). Найти все а, при которых система
2а cos2{х — у) 4- 8а2 cos(x — у) 4- 8а2(а 4-1) 4- 5а < 0
х2 4- у2 4-1 > 2ах 4- 2у 4- а - а2
выполняется для любых х и у.
1727* (х — 98.5). Найти все а, при которых система3)
3) Через max (х, у) обозначается наибольшее из чисел х и у.
214
'max (2 — 3t/, у 4- 2) 5
< ^a2 4-arccosvT — x2 — 16 — arcsin x — arcsin2x > y2 4- 2ay 4- 7
имеет хотя бы одно решение.
у/ 1728* (А — 77.5). Найти все а, при которых система
{х2 4- 2ах За2 — 8а 4- 4
х2 4- 4ах > 2 4- 5а — За2
имеет хотя бы одно решение.
х/ 1729* (/? — 77.5). Найти все а, при которых корни уравнений
9 ЗД/ _ л 9 12х
х2 4----h 2а = 0 и ж2 4-------а = О
а а
перемежаются (т. е. каждое из уравнений имеет два корня и между ними лежит корень другого уравнения).
1730* (/1 — 99.5). Найти все а, при которых сумма длин интервалов, составляющих множество решений неравенства
х2 4- (2а2 4- 6)я - а2 4- 2а — 3
х2 4- (а2 4- 7а — 7)х — а2 4- 2а — 3 <
не меньше 1.
1731* (/1 — 98.6). Сколько интервалов образует на прямой у = 2 — х ортогональная проекция на эту прямую фигуры, заданной системой
(у2 - х2)2 4- 6(т/2 - х2) - (у 4- я)2 4- Ъу 4- 7х 4-1 < О
у > 1 - х7
§ 27. Привлечение геометрии
Удачная геометрическая модель для условия казалось бы сугубо алгебраической задачи может свести эту задачу к геометрической.
27.1. Геометрический смысл модуля
При работе с модулями полезную роль играет геометрическая интерпретация выражения вида |х — а| как расстояния от точки х до точки а на числовой прямой.
Пример (V> - 95.1). |2х - 15| = 22 - |2х 4- 7|.
215
Решение. См. рис.44:
... о \у - 15| 4- \у - (-7)1 = 22, где у = 2х, -7 у < 15 о ...,
т.к. если точка у лежит на числовой оси между точками 15 и —7, то сумма расстояний от нее до этих точек равна 15 — (—7) = 22, если она лежит правее точки 15, то — (—7)| > 22, а если левее точки —7, то \у — 15| > 22.
Ответ: —7/2 х 15/2.
|у-(-7)| lv-151
Рис. 44
1732° (А-78.2).
у/ 1733° (С-00.5).
1734 (б—97.1).
|5ж - 13| - |6 - 5ж| = 7.
3 3х-1 - 9| + |9®/2 - 3| 24.
sin’M| + |l-sin^^| = 0 4 11 4
< 11 ’
ку4_|а;|_|у + 2| = г/4-|а;|-|у + 2|.
у/ 1735 (7 — 94.6). Найти все а, при которых уравнение
у х 4- 3 — 4\/z — 1 4- у х 4- 8 — б\/х — 1 = а
имеет хотя бы один корень, причем все его корни принадлежат отрезку [2; 17].
1736* (7—97.6). Найти все а, при которых фигура, заданная уравнением
|я — 2а| 4- |я 4- 2а| 4- |t/ — 2а| 4- \у 4- 2а14- |z - а| 4- \z 4- а| = а2 4^ 9,
содержит шар радиуса тг/2.
27.2. Эффект от геометрической интерпретации
Придав разумный геометрический смысл всем соотношениям и выражениям, фигурирующим в условии задачи, можно сильно продвинуться в ее решении.
Пример (а—89.5). Найти все пары (а, 6), при которых система
(8х 4- (а2 + ab + Ь2)у = 4 ца — Ь)х 4- 26у = 2
имеет бесконечно много решений.
216
Решение. На плоскости с координатами (ж, у) прямые Зх 4- (а2 4- ab + Ь2)у = 4 и (а — Ь)х 4- 26т/ = 2
имеют бесконечно много общих точек, когда они совпадают, т. е. ко-
гда соответствующие их коэффициенты пропорциональны:
8 : (a2+ab+b2) : 4 = (а-b) : 26 : 2
{а — 6 = 4 Га4-(—6) = 4
42+ЗаЬ = 52 а (-Ь) = -12
Ответ: а = б, b = 2; а = —2, b = —6.
1737 (б—95.6). Найти все пары (а, Ь), при которых уравнение ||ж — 4| — 2| — ах 4- 4х - b = О
имеет ровно три различных корня, а выражение а2 4- (b — I)2 принимает наименьшее значение.
у/ 1738 (7 — 86.5). При каждом а е (0; 1) найти наименьшее значение выражения
(а:2 + у2)- 2а(х - у)
при условии зт(тг:п/) = 0.
1739 (х — 01.3). Найти все решения системы
Зх 4- у — 3
х2 4- у2 4- 4х 4- 2у11,
при которых выражение
х2 4- у2 — 6х — 8у 4- 25
принимает наименьшее значение.
1740 (7 — 01.6). Найти все целые а, при которых система
х2 4- у2 — 2х 4- 4у а2 4- 10а 4- 20
5я2 4- 51/2 — 2ах 4- 4ау 5 — а2 к
не имеет решений.
у/ 1741* (^>—97.6). Найти все пары (а, Ь), при которых система
х2 + у2 + 5 = Ь2 + 2х — 4у
' х2 + (12 - 2а)х + у2 = 2ау + 12а - 2а2 - 27
имеет два различных решения (хх,ух) и (а^Уг), удовлетворяющих равенству
Х1 -х2 _ Ух + у2
У2-У1 Хх + Х2 ’
217
у/ 1742 (7 — 99.5). Найти все а, при которых система (у2 — (2а 4- 1)у 4- а2 4- а — 2 = О
( (ж - а)2 + у2 4- у/(х - а)2 4- (у - З)2 = 3
имеет ровно одно решение.
х2 4- у2 — 14# — 10?/ 4- 58 = 0
1743* (х—96.5). ^х2 + у2_ 16а. _ 12у + юо +
4- у/х2 + у2 + 4х- 20у 4-104 = 2\/29.
1744 (/? — 89.5). Какое наибольшее значение принимает выражение 2х 4- у — z при условии х2 4- Зу2 4- z2 = 2?
у/ 1745* (б — 85.5). Найти все решения (ж, у, z, t) системы
{х2 4- у2 = 4 z2 4-12 = 9 xt 4- yz 6, для которых сумма х 4- z принимает наибольшее значение. 1746* (/? — 92.5). Найти наименьшее значение выражения
1 [ За b \
с у \/1 — я2 \/1 — у2 J при условии
fay + Ьх < с а2 4- 2Ьсх > Ь2 4- с2 624- с2 < 2Ьсх
>а,Ь,с,х,у > 0.
27.3. Применение геометрии в текстовых задачах
Задачи на движение допускают толкование условия в виде графиков зависимости пройденного пути1) от времени, в результате чего вступают в силу геометрические законы.
Пример (Л — 78.2). Из пункта А в пункт В выехал велосипедист, а через 15 мин вслед за ним выехал автомобиль. Автомобиль догнал велосипедиста на середине пути от А до В, а прибыл в пункт В, когда велосипедисту оставалось проехать еще треть пути. За какое время велосипедист проехал путь от А до В?
Возможно, с учетом направления.
218
Решение. На плоскости с координатами (t, s), где t — время (в мин), аз — расстояние от пункта А (положим АВ = 1), изобразим графики движения велосипедиста и автомобиля (отрезки ОК и LM соответственно на рис. 45). Тогда
AOQL = AKQM => МК = OL = 15,
АОРК - AKMN => = 3 => ОР = 3 • 15 = ...
Ответ: 45мин.
Для нахождения наибольшего или наименьшего значения какой-либо содержательной величины в текстовой задаче может пригодиться изображение2) множества точек, координаты которых удовлетворяют условию задачи.
1747° (х — 89.3). Из пункта А в пункт В вышел пешеход, через 2 ч вслед за ним выехал велосипедист, а еще через 30 мин — мотоциклист. Через некоторое время все трое поравнялись. На сколько времени раньше пешехода в пункт В прибыл велосипедист, если мотоциклист прибыл на 1ч раньше пешехода?
1748 (V> — 78.3). Пешеход, велосипедист и мотоциклист двигались по шоссе в одном направлении. Когда велосипедист поравнялся с пешеходом, мотоциклист отставал от них на 6 км, а когда мотоциклист поравнялся с велосипедистом, пешеход отставал от них на Зкм. На каком расстоянии впереди был велосипедист, когда мотоциклист поравнялся с пешеходом?
у/ 1749 (х — 92.4). Из пункта А в пункт В вылетел самолет, через Зч в противоположном направлении вылетел вертолет,
21На плоскости, в подходящих координатах.
219
а еще через 3 ч они поравнялись. Самолет прибыл в В в 13.30, а вертолет в А — в 20.30. Найти время вылета самолета из А. у/ 1750 (б — 99.3). Первая и вторая бригады, работая вместе, выполняют задание не более, чем за 9 дней, вторая и третья — не менее, чем за 18 дней, а первая и третья — ровно за 12 дней, причем третья бригада имеет максимально возможную при указанных условиях производительность. За сколько дней выполняет это задание одна вторая бригада?
у/ 1751* (е — 83.5). В магазине продаются карандаши: красные по 10 коп и синие по 7 коп. На покупку карандашей можно потратить не более 10 руб, причем количества карандашей разного цвета не должны различаться более, чем на 5. Сколько красных и сколько синих карандашей нужно купить, чтобы суммарное их количество было максимальным и при этом денег было потрачено как можно меньше?
§ 28. Дополнительные построения в геометрии
Идея дополнительных построений в геометрии напоминает, в некотором смысле, идею, введения новых переменных в алгебре: оба указанных действия приводят к обогащению задачи и к выявлению скрытых ранее связей между различными элементами ее условия.
28.1. Стандартные построения
Дополнительные построения регулярно используются при решении геометрических задач определенного типа. К таким построениям можно отнести: проведение радиусов или хорд в окружности, достраивание трапеции до параллелограмма или треугольника, построение пропорциональных отрезков при параллельных прямых, построение углов с соответственно параллельными сторонами на плоскости (в пространстве) и многое другое.
Пример (7 — 79.3). На стороне АВ = 6 треугольника АВС как на диаметре построена окружность, пересекающая сторону ВС в точке D. Найти АС, если BD = 4 и CD = 2.
Решение. См. рис.46:
Z.ADB = 90° (угол, опирающийся на диаметр) => => х2 = б2 - 42 = 20 => у2 — х2 + 22 = 24 => ?/ = ... Ответ: 2\/б.
1752° (7 — 81.4). На стороне АС = 2 треугольника АВС как на диаметре построена окружность, пересекающая сторону
220
AB = 3 в точке D и сторону ВС в точке Е. Найти АЕ, если AD : BD = 2 : 3.
у/ 1753* (х — 91.5). Две окружности касаются друг друга внешним образом в точке А. Из конца В диаметра АВ первой окружности проведены две прямые, касающиеся второй окружности в точках М и N. Продолжение хорды AM пересекает первую окружность в точке К. Найти площадь фигуры, ограниченной отрезками касательных и большей дугой второй окружности, если МК = у/2 4- л/3 и Z.AMB = 15°.
у/ 1754 (х — 01.5). В выпуклом шестиугольнике ABCbEF со сторонами АВ = 3, ВС = 4, CD = 5 и EF = 1 все углы равны. Найти DE и AF.
1755° (б — 95.3). Найти диагональ BD трапеции ABCD с основанием ВС = 10, если АВ = 36, CD = 34 и cos Z.B = —1/3. у/ 1756 (д — 80.3). Средняя линия трапеции равна 4, а отрезок, соединяющий середины оснований, равен 1, Найти основания трапеции, если углы при однрм из них равны 40° и 50°.
1757 (тг — 77.4). Найти площадь трапеции ABCD с боковой стороной АВ = а и диагональю BD = Ь, если ВС = CD = = AD/2.
у/ 1758 (е — 99.4). Найти площадь трапеции ABCD с основанием AD и диагоналями АС = 5а, BD = 7а, если Z.CAD = = 2ZADB.
1759 (е — 85.3). На стороне АС треугольника АВС взяты точки D и Е так, что прямые BD и BE делят медиану AM на три равные части и АЕ = AD 4- 3. Найти АС. *
221
у/ 1760 (тг—96.4). На сторонах АВ и ВС параллелограмма ABCD взяты точки Е и F соответственно так, что АЕ : BE = 2:1 и BF : CF = 3 : 1. В каком отношении прямая DE делит отрезок AF?
1761 (тг — 86.5). На стороне АС треугольника АВС взята точка N так, что АС = 4 AN. Медиана AM = 5 пересекается с отрезком BN = 10 в точке О. Найти MN, если Z.AOB = = 135°.
у/ 1762 (7 — 82.3). На стороне АВ треугольника АВС взята точка N так, что BN = 3. Площадь треугольника равна 2л/3, ВС = 1 и ZC = 7г/6. В каком отношении прямая CN делит медиану ВМ треугольника?
1763° (б — 80.3). Две окружности радиусов 7 и 12 касаются общей прямой с одной стороны от нее. Найти расстояние между точками касания, если оно в в 2\/5/5 раз меньше расстояния между центрами.
у/ 1764° (£ — 98.4). Две окружности радиусов 2 и 3 касаются внешним образом друг друга в точке А, а общая касательная к ним, проходящая через точку А, пересекает две другие общие касательные в точках В и С. Найти ВС.
1765* (х—90.5). В треугольник АВС площадью 3i/15 вписана окружность радиуса х/15/3. Этой окружности и лучей С А и СВ касается другая окружность, радиуса ^125/27. Найти tg ZАВС, если АС — наибольшая сторона треугольника.
1766* (£ — 87.6). В правильную пирамиду SABCD вписана сфера радиуса 2. Этой сферы, граней BSC, CSD и основания ABCD пирамиды касается другая сфера радиуса 1. Найти объем пирамиды и двугранный угол при боковом ребре.
у/ 1767° (тг — 78.4). Прямоугольный треугольник с катетами 3 и 4 лежит в некоторой плоскости, а его гипотенуза — еще в одной плоскости, образующей с первой угол а. Найти угол между меньшим катетом треугольника и второй плоскостью. 1768° (б — 92.4). Двугранный угол при ребре АВ тетраэдра ABCD равен тг/4. Найти Z.DAC, если Z.DAB = тг/2 и ZBAC = = Зтг/4.
у/ 1769* (/1 — 77.5). Высотой пирамиды SABC служит ребро SC = 2, а основанием — правильный треугольник АВС со стороной 4а/2. Найти угол и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S
222
и середину ребра ВС, а другая — через точку С и середину ребра АВ.
1770* (£ — 98.8). Найти ребро основания А,ВС правильной призмы АВСА'В'С с боковым ребром АА' = 2, если угол между скрещивающимися прямыми АС и А'В равен а < 60°. 1771* (А — 87.6). Боковое ребро и сторона основания ABCD правильной пирамиды SABCD равны \/4Т и 8 соответственно. На продолжении ребра SA за точку А взята точка М на расстоянии 12 от плоскости CD. Найти AM.
у/ 1772* (б—98.4). Из вершин равнобедренной трапеции ABCD с основаниями AD = 10 и ВС = 2 в одну сторону от плоскости ABCD восставлены к ней перпендикуляры А А' = 1, В В1 = = СС' = 2 и DD' = 4. На отрезках А'С и B'Df взяты точки М и N соответственно так, что ArM : СМ = DfN : B'N = 2:1. Найти MN.
28.2. Сравнение площадей и объемов частей фигуры
Отличие задач настоящего пункта от задач п. 21.1 состоит в том, что сравнение площадей (объемов) теперь сопровождается дополнительными построениями.
Пример (е — 79.2). На продолжении основания ВС трапеции ABCD взята такая точка В, чтапрямая АЕ отсекает от трапеции треугольник, площадь которого составляет 2/5 площади трапеции. Найти СЕ, если AD = 6 и ВС = 3.
Решение. Обозначим Sabcd = s = 31 4- зг 4- зз (рис.47): si : (зг 4- Зз) = 3 : 6 = 1 : 2 (пары треугольников S2 : Зз = а : b с равными высотами)
. 2 2 2 4
=> 32 + S3 = 38 => 32 = 38 — 58 = 15 3
223
=> х : 6 = a :b = : |s = 2 : 3 (из подобия треугольников)
=> x = 6 • 2/3 = ...
Ответ: 4.
1773° (а — 97.6). На сторонах АВ и AD прямоугольника ABCD площадью 36 взяТы точки Е и F соответственно так, что АЕ : BE = 3 : 1 и AF : DF = 1:2. Отрезки DE и CF пересекаются в точке О. Найти площадь треугольника FOD. 1774° (тг — 00.5). На основании ВС = 3 трапеции ABCD с высотой 5 взята точка Е, F — середина стороны CD, &G — точка пересечения отрезков АЕ и BF. Найти площадь четырехугольника AGFD, если AD = 5 и BE = 2.
1775 (J3 — 91.4). На стороне CD трапеции ABCD с высотой 7 и основаниями AD = 8, ВС = 6 взята точка Е так, что прямая BE делит диагональ АС в точке О в отношении АО : СО = 3:2. Найти площадь треугольника СОЕ.
у/ 1776 (/? — 87.4). Точка Е на боковой стороне CD трапеции ABCD площадью 30 взята так, что 2CD =3ED, a F — середина стороны АВ. Отрезки АЕ и DF пересекаются в точке О. Найти площадь треугольника АОЕ, если AD = 2 ВС.
1777 (99 — 01.3). На сторонах АВ и CD трапеции ABCD с основаниями AD = 2 ВС выбраны соответственно точки М и N так, что AM : МВ = 2:1, CN : ND = 3:4. Найти отношение площадей четырехугольников AM ND и BMNC.
1778 (£ — 00.4). На сторонах АВ и CD трапеции ABCD с основаниями AD = ЗВС взяты точки М и N соответственно так, что AM : МВ = 3 : 5 и CN : ND = 2:7. Найти отношение площадей четырехугольников BMNC и AM ND.
у/ 1779 (/1 — 95.4). На стороне АВ трапеции ABCD с основаниями AD = 2 ВС взята точка М так, что AM : ВМ = 2:3. На противоположной стороне взята точка N так, что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найти CN : DN.
1780* (/1—00.4). Через середину М боковой стороны АВ трапеции ABCD проведен перпендикуляр, пересекающий сторону CD в точке N. Площадь четырехугольника AMND впятеро больше площади четырехугольника BMNC, CN = 3, DN = 15 и МС = 4. Найти MD.
у/ 1781 (х ~ 86.4). На стороне АВ = 5 и основании АС = 6 равнобедренного треугольника АВС взяты точки D и Е со-
224
ответственно так, что АЕ = BD = 2. Прямые BE и CD пересекаются в точке О. Найти площадь треугольника ВОС.
1782* (/? — 82.5). На стороне ВС треугольника АВС взяты точки D и Е так, что BD : DE : ЕС = 2 : 3 : 3. На продолжении стороны АВ за точку В взята точка F так, что АВ : BF = 1:2. Прямые АЕ и AD пересекают отрезок CF в точках G и Н соответственно. Найти отношение площадей четырехугольника DEGH и треугольника АВС.
1783* (/? — 01.5). В треугольник АВС со сторонами АВ = 6, ВС = 5, АС = 7 и высотой ВН вписан квадрат, две вершины которого лежат на стороне АС, одна на стороне АВ и одна на стороне ВС. Через центр квадрата и середину М стороны АС проведена прямая, пересекающая отрезок ВН в точке К. Найти площадь треугольника МКС.
у/ 1784 (х — 80.4). Окружность, вписанная в равнобедренный треугольник АВС площадью S, касается стороны АВ в точке К. Перпендикуляр КН, опущенный на основание АС треугольника АВС, отсекает от него четырехугольник КВСН площадью s. Найти Z.A.
1785 (А — 79.5). Основанием пирамиды SABC служит правильный треугольник АВС со стороной \/3, а площадь боковой грани SAB равна д/5/6. Вершина S проектируется в точку Н, лежащую внутри треугольника АВС на расстоянии 1 от стороны АС, причем sin Z. АВН : si.nZ.CBH = 2:1. Найти объем пирамиды.
1786 (£ — 86.5). На ребре BD тетраэдра ABCD взята точка Е так, что DE : BE = 3:5. Найти отношение, в котором плоскость, проходящая через точки А и D параллельно медиане ВМ треугольника АВС, делит объем тетраэдра.
у/ 1787 — 77.5). На ребрах AD и BD тетраэдра ABCD взяты
точки Е и F соответственно так, что DE : АЕ = SF : BF = = 1:2. Найти отношение, в котором плоскость, проходящая через точки Е и F параллельно ребру CD, делит объем тетраэдра.
1788* (х — 87.6). На ребрах AD,DC,BC и АВ тетраэдра ABCD взяты точки K,L,M и N соответственно так, что отрезки КМ и LN пересекаются в точке О, причем 40М = = ЗОК, 25ON = 24OL и DK • AN - АК • BN = АК • AN. В каком отношении плоскость KLM делит объем тетраэдра?
8 И. Н. Сергеев — Математика
225
1789* (/1 — 78.5). Через середины ребер AD и ВС тетраэдра ABCD объемом 5 проведена плоскость, пересекающая ребро CD в точке М так, что DM : СМ = 2:3. Найти площадь сечения тетраэдра указанной плоскостью, если расстояние от нее до вершины равно 1.
1790* (£—91.6). Основанием пирамиды SABCD служит трапеция ABCD с основаниями ВС : AD = 1:2. Плоскость, проходящая через вершину S параллельно ВС, пересекает отрезок АВ в точке М так, что AM : ВМ = 2:1. Площадь сечения пирамиды этой плоскостью'равна з, а расстояние от нее до прямой ВС равно d. Найти:
1) отношение, в котором указанная плоскость делит объем пирамиды;
2) объем пирамиды.
28.3. Разные задачи, использующие дополнительные построения
Одним из ключевых моментов в решении следующих задач является дополнительное построение.
Пример (д — 95.3). На сторонах АВ, ВС и АС треугольника АВС взяты точки D,E и F соответственно. Отрезки DE и BF проходят через центр вписанной в треугольник окружнбсти, а прямые DE и АС — параллельны. Найти CF и периметр треугольника АВС, если АС = 15, AD = 4 и СЕ = 6.
Решение. См. рис.48:
а = AD = 4 (так как Z.DAO = Z.FAO ='£AOD) b = СЕ = 6 (аналогично)
226
=> х: у = a: b = 2: 3 => x = 6, у = 9 (так как х 4- у = 15) => и : (и 4- 4) = v : (v 4- 6) = 2 : 3 (так как ADBE ~ &АВС) => и — 8, v = 12 => Равс = 15 4- (4 4- 8) 4- (6*4-12) = ... Ответ: 9; 45.
1791° (/1 — 88.3). Биссектриса угла ZA = 80° параллелограмма ABCD пересекает сторону ВС в точке Е. Найти радиус окружности, касающейся лучей АЕ, DC и отрезка АВ = 7.
у/ 1792 (£—83.5). Прямая, параллельная гипотенузе АВ прямоугольного треугольника АВС, пересекает катеты АС и ВС в точках D и Е соответственно, а на гипотенузе взята точка F. Найти площадь треугольника АВС, если DE = 2, BE = = BF = 1 и Z.BCF = а.
у/ 1793 (х—88.3). Гипотенуза АВ прямоугольного треугольника АВС является хондой окружности радиуса 10, а диаметр этой окружности, параллельный гипотенузе, содержит вершину С. Найти площадь треугольника АВС, если Z.A = 75°.
1794* (х — 96.4). Через центр О вписанной в треугольник АВС окружности, радиус которой втрое меньше отрезка АО, проведена прямая, параллельная стороне ВС = $2 и пересекающая стороны АВ и АС в точках М и N соответственно. Найти площадь треугольника АВС, если периметр треугольника AMN равен 3^2.
у/ 1795* (/? — 79.3). В трапецию вписана окружность радиуса г, а хорда, соединяющая точки касания окружности с боковыми сторонами, параллельна основаниям трапеции и равна а. Найти площадь трапеции.
1796* (А — 79.5). Окружность с центром О касается сторон ВС = 121|, CD = б| и AD выпуклого четырехугольника ABCD с тупым углом D. Найти ОС, если АВ = ZA = = arcsin | и Z.B = arccos ( —1|).
О X DD /
1797* (х — 98.5). Диаметр АВ = 10 пересекает хорду CD в ее середине Е. Касательные к окружности в точках В и С пересекаются в точке F, а отрезки AF и СЕ — в точке G. Найти площадь треугольника CFG, если АЕ = 1.
1798* (V> — 85.5). Хорда длины R\/2 окружности радиуса R пересекает хорду АВ той же длины и диаметр АС в точках D и Е соответственно. Найти площадь треугольника ADE, если Z.CED = а.
227
8*
1799* (A — 77.4). Радиус АО окружности с центром О пересекает в точке D сторону ВС вписанного в окружность треугольника АВС с высотой АН = \/2х/3, а продолжение биссектрисы AL этого треугольника пересекает окружность в точке Е. Найти отношение площадей треугольника ОАЕ и четырехугольника ODLE, если АЕ = 4>/2 и AADH = тг/З.
1800* (£ — 86.6). Биссектриса AL треугольника АВС с высотой АН = h и медианой AM = т делит отрезок МН пополам. Найти расстояние от вершины А до точки пересечения высот треугольника АВС,
1801* (х—97.5). В треугольнике АВС взята точка О так, что радиусы описанных около треугольников АОВ и АОС окружностей равны 4 и 5 соответственно, а расстояние между их центрами равно 6. Найти ОС, если АВ = 6 и АС = 7.
1802* (£ — 82.6). Прямая, проходящая через центры вписанной и описанной окружностей треугольника, перпендикулярна одной из его биссектрис, а отношение расстояния между этими центрами к радиусу описанной окружности равно а. Найти углы треугольника.
у/ 1803* (а — 00.4). В тетраэдре ABCD двугранный угол при ребре АС равен тг/4. Найти BD, если АВ = 2, AD = у/2, ABAC = тг/6 и ACAD = тг/2.
у/ 1804* (£ — 00.6). Найти радиус сферы, описанной около тетраэдра ABCD, если АВ = ВС = 2, АС = 1, а ребро CD = 4 перпендикулярно ребрам АВ и АС.
1805* (V> — 00.5). Ребро SA пирамиды SABC перпендикулярно плоскости ее основания АВС со стороноами АВ = АС = 5 и ВС = 6. Найти радиус сферы, описанной около пирамиды, если радиус вписанной в нее сферы равен 2SA/7.
у/ 1806* (А — 01.8). Найти радиус сферы, описанной около правильного тетраэдра, две вершины которого лежат на диагонали куба с ребром 2, а две другие вершины — на диагонали его грани.
1807* (А — 99.7). Найти объем куба ABCDA'B'C'D', если сфера радиуса \/41 проходит через точки А, В, С и середину ребра A'D'.
1808* (£ — 99.8). Через вершины В' и D прямоугольного параллелепипеда ABCDA'B'C'D' с ’ребрами АВ = ВС = 2а и
228
АА1 = а проведена плоскость, параллельная прямой АС. Найти радиус шара, касающегося этой плоскости и трех граней параллелепипеда с общей вершиной В.
1809* (£ — 82.5). На боковом ребре SA правильной пирамиды SABC взята точка £>, через которую проведено сечение пирамиды, пересекающее апофемы граней SAC и SAB в точках М и N. Прямые DM и DN образуют углы /3 с плоскостью основания АВС. Найти Z1MDN, если Z.DMS = Z.DNS — а.
1810* (х—80.6). Для каждой вершины пирамиды SABC сумма выходящих из нее ребер одинакова. Косинус угла между ребрами SB и АС равен 1/3, радиус вписанной в пирамиду сферы равен ^/3/13 и SA2 4- SC2 = 12. Найти объем пирамиды, если он не превосходит 5/3.
1811* (£ — 79.6). Треугольник АВС со сторонами АС = 2а и АВ = ВС = Ь лежит в плоскости, которая касается в точке В шара радиуса г. Через точки А и С проходят две скрещивающиеся прямые, касающиеся шара и образующие с плоскостью угол а каждая. Найти расстояние между этими прямыми.
Глава 6. МЕТОД СЛЕДСТВИИ
С паршивой овцы хоть шерсти клок.
§ 29. Основные типы следствий
Предлагаемый в настоящем параграфе материал демонстрирует принципиальное отличие метода следствий от метода равносильных преобразований.
29.1. Следствие, заложенное в постановке задачи
При решении задачи, в которой нужно найти лишь необходимое условие (следствие) заданного вида, имеет смысл не делать то, что не требуется, и в частности, не искать то, что не спрашивается1 \
Пример ((^—78.2). Значение а подобрано так, что уравнение \J х — х/З 4- а2х2 4- 2ах ^х/б — х/з) = 6\/2 — 9
имеет хотя бы один корень. Решить это уравнение.
Решение.
... => у/ х — х/З 4- а2х2 4- 2ах (х/б — х/З) 4- (х/б — х/З) = О => у/х — х/З 4- (ах 4- х/б — х/З} =0 => ...
Ответ: х = х/З.
1812 (/1 — 96.2). Найти log2/3/x 4- log^/5C2/, если
\°%х/ух =1°&х/Ух'
у/ 1813 (/1 — 99.3). Для некоторых чисел х / у и z выражения
, 1 у/яУ
И 1®&х2у5г %
принимают одно и то же значение. Найти это значение.
у/ 1814 (тг — 00.2). Найти tg и cos(a—Д), если
cos а 4- cos Р = 0,3 и sin а 4- sin Д = —1,1.
.^Особенно,- если оно и не ищется.
230
1815 (д - 00.4). Найти
sin(ai + 7) sin(/? + 7) sin(a + 7) sin(/3 + 7) _ 4
cos 7 cos(a + /? + 7) ’ cos a cos /3 9'
У1816 (тг — 99.4). Сумма десяти чисел равна нулю. Сумма всех их попарных произведений также равна нулю. Найти сумму кубов этих чисел.
у/ 1817 (х — 96.1). Числа a, b, с, d образуют геометрическую прогрессию. Найти Ь3 4- с3, если а 4- d = 10 и ad = 7.
1818 (/1 — 93.2). Сумма первых пяти членов геометрической прогрессии впятеро больше первого.члена, а сумма первых пятнадцати членов равна 100. Найти сумму первого, шестого и одиннадцатого членов этой прогрессии.
у/ 1819 (/1 — 97.2). Сумма первых членов данных арифметической и геометрической прогрессий равна —3, сумма третьих членов равна 1, а сумма пятых членов равна 5. Найти разность арифметической прогрессии.
1820 (7 — 94.2). Сумма первых двадцати пяти членов одной арифметической прогрессии впятеро больше суммы первых двадцати членов другой арифметической прогрессии, имеющей ненулевую разность. Найти отношение разностей этих прогрессий, если девятнадцатый член первой прогрессии вчетверо больше двенадцатого члена второй.
1821* (А — 94.9). В течение трех лет четыре бригады поочередно разрабатывали месторождение горючих сланцев. Время работы каждой бригады и суммарное количество выработанной ими продукции по годам соответственно равны: в первый год — 1,2,5,4 месяца и 10 млн. т, во второй год — 2,1,4,5 месяцев и 14 млн. т, в первые 8 месяцев третьего года — 3,2,1,2 месяца и 7 млн. т. Сколько тонн сланцев выработали эти бригады в оставшиеся 4 месяца, работая с прежней производительностью по одному месяцу каждая?
у/ 1822 ((/? — 90.4). От двух сплавов массой 7 и Зкг с разным процентным содержанием магния отрезали по куску одинаковой массы. Затем кусок первого сплава сплавили с остатком второго, а кусок второго — с остатком первого, причем процентное содержание магния в новых сплавах оказалось одинаковым. Найти массы отрезанных кусков.
1823 (тг—97.3). Из порта А в порт В, расстояние между которыми равно 108 км, в 9.00 по озеру отправляется лодка. Одно
231
временно из порта В навстречу ему отправляются яхта и катер. Лодка встречается с яхтой в 12.00, а с катером — в 13.00. На сколько километров отстанет катер от яхты в 14.00?
1824 (7 — 88.3). Из пункта А в пункт С, расстояние между которыми равно 80 км, выехал мотоциклист. Одновременно навстречу ему из пункта В, находящегося между А и С на расстоянии 5 км от С, выехал велосипедист, а из пункта С — автомобиль. Через сколько часов встретились мотоциклист и велосипедист, если за 20 мин до этого автомобиль догнал велосипедиста, что, в свою очередь, произошло вдвое раньше (с момента выезда), чем встреча автомобиля с мотоциклом?
у/ 1825 (7 — 77.4). Грузовой и легковой автомобили выехали одновременно из пункта А в пункт С: первый — по прямой дороге длиной 360 км, а второй — по окружной дороге, проехав сначала путь АВ = 120 км со скоростью, вдвое большей скорости грузовика, затем путь ВС = 1000 км со скоростью, увеличенной еще на 40 км/ч, и прибыв в пункт С на 1 ч 15 мин позже грузовика. Если бы легковой автомобиль проехал с увеличенной скоростью весь свой путь, то прибыл бы в пункт С на 1 ч позже грузовика. Найти скорость грузовика.
1826 (7—96.2). Функция / —периодическая с периодом \/2. Найти /(—\/8), если
3/2(0) + 7/(ч/72) + 4 = 0 и /2(х/2) + 3/('/18) +20/9 = 0.
у/ 1827* (ф — 78.5). Функция
f(x) = ах2 + Ьх + с
удовлетворяет неравенствам
Л-1)<1, /(1)>-1 И ЛЗ)<-4.
Определить знак коэффициента а.
29.2. Метод проверки
Метод равносильных преобразований замечателен тем, что совмещает вывод следствий и их проверку в одном действии. Иногда же проще совершать указанные операции последовательно: например, сначала из условия задачи вывести, что ему могут удовлетворять только какие-то конкретные значения неизвестной, а затем проверить, какие из них действительно подходят. В этом и состоит метод проверки.
232
„ ,, fV®s + 2z-3-|3j/-l| = 0,
Пример (£ — 99.5). < ----------- У '_________
[4 х/Эу2 - бу 4-1 + х/®2 - 4® 4- 3 = 0.
Решение. Решим второе уравнение системы
f9j/2-б!/ 4-1 = 0 f(3j/-l)2=0 Г у = 1/3
^х2—4х 4-3 = 0 Цх —1)(х —3) = 0 ^х = 1, 3.
Проверим, какая из двух найденных пар (х, у) удовлетворяет первому уравнению системы:
1) х = 1, у = 1/3 — удовлетворяет, т.к. I2 4- 2 • 1 — 3 = 0;
2) х = 3, у = 1/3 — не удовлетворяет, т.к. З2 4- 2 • 3 — 3 0.
Ответ: х = 1, у = 1/3.
1828° (А — 84.3). Найти sina, если sin2a > 3/5 и tga 1/3.
1829 (х- 01.2). < 3 sin х 4- cos у = 0 6cosx — 2 sin 3/ = 7.
1830° (д - 90.2). 2|sins _ y^c|smx|
1831 (С - 01.5). < fl sin 1/1 sin 2/- Jcosx — 1|2 4-1 sin?/|2 = 4.
1832° (е - 82.2). yjx + 3 - х/2х - 1 = х/3® - 2.
1833* (ст - 01.6). з/ 24ж з/ 243s 1 x у X
1834° (А-96.5). x2 — xy = 201/ 5xy — by2 = 4x.
1835* (тг - 79.5). 10x2 4- 5t/2 — 2xy — 38x — 6y 4- 41 = 0 3x2 — 2y2 4- 5xt/ — 17x — 6y 4- 20 = 0.
1836 (е - 97.2). < Г '|8т1М| + (я-у-2)2^0 J2® + 3| s£2. cos 10® - 2sin5x > 3 • 4» - 3 • 2y+2 4- 27/2
1837* (0-98.5). i ((2 - x/3)4" + (2 + л/З)4" + 2)1/2 + 4- 141og2 cos 10® 4- 6 cos5® (2y 4-1)3/2.
1838* (%-94.5). При каждом а решить систему
(х2 4- ах 4- 3 = 0
1 sin2 air 4- cos2 + 2y2 = sin
у/ 1839* (£ — 01.7). При каждом целом а решить уравнение bgx2+e2/4 (За:)°2+1 = а2 + 1.
233
29.3. Метод подбора
Метод проверки из предыдущего пункта логически противоположен методу подбора, согласно которому сначала, наоборот, как-то подбирается2^ подходящее значение неизвестной, а затем доказывается^ что другие ее значения не годятся.
Пример (Л — 95.1). \/5х — 6 4-х = 4.
Решение. Обозначим f(x) = \/5х -6 4-х:
1) /(2) =4 => х = 2 — корень уравнения;
2) если х 2, то /(ж) /(2) = 4, т.к. функция f возрастает.
Ответ: х = 2.
1840° (х — 91.1). у/х + 4 + х-2 = 0.
1841° (е - 95.1). у/х + 3 = 9 - х.
1842° (х - 96.2). у/х + 5 > 7 - х.
1843 (д — 97.1). V25 — 24cosa: = 4cosa: — 3.
1844 (х - 92.1). х + log2 (2х - 31) = 5.
1845 (С - 78.4). log3(3x - 8) = 2 - х.
1846 (тг - 90.6). log2(2 - За:) > 4х + 1.
1847 (а - 94.5). |® - 41+'/зГ®| 5х/3 - 4 • 4^*
1848 (х-94.5). ( f ,+?2Siny2t1=3° л л ( 8j/|а:|(а:2 + j/2) + тг3 + 4тг = 0.
' у3 - 9а:2 + 27а: - 27 = 0
1849* (д - 77.4). z3 - 9у2 + 27у - 27 = 0
k а:3 - 9z2 + 27z -27 + 0.
1850* (V- - 82.6). log(х2 + 2х — 2) =
= log2+v^(a;2 +2®-3). 1851* (х - 98.6). log2(4х 4-1) log5(4x 4- 4) 4-
4- log3(4x 4- 2) log4(4z 4- 3) = 21og3(4z 4- 2) log5(4z 4- 4). у/ 1852* (/1 — 01.4). Существуют ли А, В, р и для которых функция
/(ж) = (sin(x - 7г/3) 4- 2)2 4- Acos(x 4- 4- Bsin(2x 4- V0
есть константа? Найти все возможные значения этой константы. 1853* (/1 — 80.5). Найти все а, при которых неравенство log1/a (х/ж2 4-ая4-5 4-1) log5 (х2 4- ах 4- 6) 4- loga 3 > 0 имеет единственное решение.
2)Как именно подбирали, объяснять не нужно, например, угадали.
234
1854* (х — 99.5). Найти все а, при которых уравнение
^ж2+2ая:+4а—3
-2 =
а —2 х + а
имеет на отрезке [—4; 0] ровно два различных корня.
у/ 1855° (б —95.4). Годовая добыча руды на месторождении, составив вначале 100 т, ежегодно увеличивалась на 25%, а затем на протяжении 3 лет не менялась. Сколько лет разрабатывалось месторождение, если общий объем добычи руды на нем составил 850 т?
1856° (А — 80.4). Из пункта А в гору выехал автомобиль, который в первую секунду проехал 30 м, а в каждую следующую — на 2 м меньше, чём в предыдущую. Через 9 с из пункта В навстречу ему выехал автобус, который в первую секунду проехал 2 м, а в каждую следующую — на 1 м больше, чем в предыдущую. Какое расстояние проехал автобус до встречи с автомобилем, если АВ = 258 м?
у/ 1857 (/1 — 00.2). Найти седьмой член убывающей арифметической прогресии, если сумма пятых степеней первых семи членов этой прогрессии равна нулю, а сумма их же четвертых степеней равна 51.
1858° (х —99.1). Пункты А, В, С и D расположены последовательно на прямой дороге, а расстояния АВ, ВС, CD образуют геометрическую прогрессию. Из пункта А со скоростью 5 км/ч вышел пешеход, который за 3 ч добрался до D и, повернув обратно, через 2 ч прибыл в В. Найти ВС.
1859 (б — 77.2). Из пункта А в пункт В выехал велосипедист. Когда он проехал четверть пути, из пункта В навстречу ему выехал мотоциклист, который, добравшись до А, поехал с увеличенной скоростью обратно и прибыл в В одновременно с велосипедистом, потратив на обратный путь столько же времени, сколько до встречи с велосипедистом. Во сколько раз мотоциклист увеличил скорость на обратном пути?
I860* (i/ — 99.3). Из пункта А в пункт В отправились бегун и пешеход, а из В в А одновременно с ними — второй пешеход. Скорость бегуна равнялась 12 км/ч, а скорости пешеходов вначале были одинаковы. Бегун и второй пешеход встретились и, побеседовав, отправились в В, причем пешеход уменьшил свою скорость в полтора раза. Пешеходы прибыли
235
в В одновременно, но позже бегуна на время, вдвое превышающее время беседы. Найти скорость первого пешехода.
§ 30. Получение и применение оценок
Для Того чтобы, не нарушая равносильности перехода, воспользоваться следствием, выводимым из данной системы1 \ достаточно просто вписать это следствие в систему.
30.1. Выводы на области допустимых значений
Совершенно нелепо было бы рекомендовать читателю всегда начинать решение уравнения или неравенства с выписывания его ОДЗ (см. п. 1.2). Тем не менее, в некоторых, сравнительно редких, случаях отдельные оценки для области допустимых значений приносят реальную пользу или даже представляют чуть ли не единственно возможный путь решения.
Пример (а - 97.3). V3 - Зх = х — 1.
Решение.
J уз(Г^) + (1 - х) = о ... О < 1 — X = U ...
^1 — х О
Ответ: х = 1.
1861 (0 - 84.3). Л + 21og2 (1 - f^) =
= 1°g2tSl + 21og2^.
1862 (о - 94.4). 2sinx — 1 л/бзш2# — 6sinx — 12.
1863 (х - 83.2). (у/х2 — 4х + 3 + 1) k>g5 | +
+ | (л/8® - 2х2 - 6 + 1) 0.
1864 (А - 78.3). 108. ^>0.
1865 (е - 95.3). log 3.-1 (х — |) > 1.
1866 (7 - 82.4). , log?-» (4 - У) < 0
(3 - х) < 0.
1867 (х- 98.2). |ч/х-4-3| > |х/9- х - 2| + 1.
1868* (Л - 85.5). у/(х + 2)(2х - 1) - Зу/х + 6 =
= 4 - у/(х + 6)(2х - 1) + Зу/х + 2.
частности, из одного уравнения или неравенства.
236
1869 (х- 00.3).
1870 (^-00.4).
у/1871 (е - 95.2).
1872 (е - 91.2). у/1873* (е — 96.2).
1874* (д - 98.3).
1875* (х —85.4).
1876* (х —89.4).
log5_4a._l2(5 - 9а: - 2а:2) log^Jl - 2а:).
2-Hog^a„2g_3 > bg;c2_2x_3(a:2-2a:-2)2.
2|Sin»| + logti, (-^Ц1) = 0.
1оЯ„,1оЯз"~а1/Г'^п-
log7(19—16ж|ж|)—log49(l—4ж)2 п
3-4х-|4ж-3| и*
log2 + ¥ + \х +х) 1°бз(-2х - я2) >
> 1оёз (|И + 1) l°g2(-2z - ^2)«
21ogr_3j«। (42x2-14|z|+1)
—— ^L
1 | COS x| V^2x-’3 I co“ • I -dco«2e .
1877* — 96.4). arccos3z 4- arcsin(x 4-1) 7тг/6.
у/ 1878* (A—93.6). Найти все а, при которых ровно одна точка графика функции
у = 2х 4- 1g а • у/соз(2атгх) 4- 2cos(a7rx) — 3 4-1
лежит в области (2х — 7)2 4- 4(1/ — З)2 25.
30.2. Разные задачи^ использующие оценки
Об эффективности оценок можно судить уже по экстремальным ситуациям в уравнениях и неравенствах (см. п. 20.4). Впрочем, некоторые другие задачи также решаются проще с помощью оценок, выводимых из условия с целью сокращения перебора случаев или для получения впоследствии еще более сильных выводов.
{х2и2 — 2х 4- V2 = 0
7 2 4 J-4J- 3 п
2х — 4х + 3 4- у = 0.
Решение.
{(ху — 1/у)2 = 1/у2 — у2 (т.к. у 0, иначе — 2х = 0 и 2(х — I)2 = —1 — у3 3 = 0, что неверно)
_ /1Л/2-У2 >0 _ Гм 1 _ _ ,
Подставим у — — 1 в систему: f(-s4-l)2 =0 (2(ж-1)2 = 0
Ответ: х = 1, у = —1.
1879° (х - 94.2). 2х > |ж| 4-1.
237
1880* (е - 90.2). а/25 + I16*2 - 25| = 4 + 4|® + 1|.
У1881 (е - 98.3).
1882 (х —87.4).
2а:+ 3
4v/lTx- 5’
(2 + 3 cos 2®) х
х (\/2 cos 2® + 3 sin ® + 3 — 2 sin х + 1) = 0.
log2 sin® — log2 2у +
< + I log2 cos х - log2 2y| = -2
1884 (A—98.6). +x - ^|-3®+^ < -14 + x - v^|.
1885* (/i — 97.5). При каждом а решить уравнение
k1 + + = . +1 _i| + ш
1883* (д - 96.4).
У 1886 (e — 93.4). Найти периметр фигуры, заданной системой 2|® + 2| arcsin((y — I)2) тг(ж + 2) \2|у- 1|-х > 0.
1887* (х-01.4). г ircsin |2-4 = 2тг — 7ГЯ. ZX — 1
у/ 1888* (7 — 01.5). 4arcsin(2x — 7) — arccos(5® — 124) = 6тг/я.
1889 (7-83.4). < 2|x2-2a;-3|-log2 3 _ 3-3/-4 4|1/| - \у - 1| + (у + З)2 8.
у/ 1890* (а -99.7). < [ж2 - 2у2 65 - ®4 - 3*+3 |®2 + Зх+2 > у2 - 2у + 25.
1891 (^-84.7). < 'д2х+у-1 + 4.32Х-1 2
4® + у 2 — log3 4.
у/ 1892* (х - 96.5). < у/х + 2 + \/®2 + 5® + 5 > 2
®2 + 6® + 5 0.
'У + 2 = (3-®)3
1893*.(/? - 93.6). < (2z - у)(у + 2) = 9 + 4у х2 + z2 = 4®
0.
у/1894* (х — 01.5). I ® — 1| + |® + 1| + |® - 2| + |® + 2| + ...
... + I® - 100| + |т + 100| = 200®.
238
у/ 1895* (х — 86.5). 2x/3sin5o; — x/3sinx =
= cos 24# cos x 4- 2 cos 5x — 6.
1896* (e — 90.5). Найти все корни уравнения
— Ctg2(27rx) cos(ttx) 4- sin(7rx) = л/2
на отрезке [—3; 1].
1897* (ip — 85.5). Для каждого а решить уравнение
3 cos х sin а — sin х cos а — 4 cos а = 3\/3.
1898* (гр — 88.6). Найти наибольшее а, при котором неравенство
Vat(8x - х2 - 16) + - —> ~^а\ созтгх| ох — xz — 1о 3
имеет хотя бы одно решение.
у/ 1899* (тг —94.4). Найти все пары (а, 5), при которых система а 4- sin Ьх < 1
х2 4- ах 4-1 О имеет единственное решение.
1900* (fi — 78.4). Найти все а, при которых система
( х2 + 2ху - 7у2 iqpf Зх2 + Юху — 5у2 —2
имеет хотя бы одно решение.
1901* (д — 95.6) Найти все a G [0; 2тг], при которых система
{х2 + у2 + 2z(x + у + z) — sin а = 0
(х + 1) sin2 | + у2 у/х + a2 y/z + sin = О имеет хотя бы одно решение.
' |у + 1/х | + |х — у + 13/6| = х + 1/х + 13/6
1902* (7-80.5).
1903* (%—79.5).
1904* (£—90.5).
< х2 + у2 = 97/36 х < 0. •
!/sinx = log2|^^|
< (бу2 + 2y)(4si”2 х + 4cos2 х) = 25у2 + бу + 1
>1 < 1-
' 1 + tg(uz) sin2(xy) + cos(2xy) (cos х + sin(vy)) |sin (2xy) | 2 + 2-ytg(u2)cos(u(x + y))+
k + cos(2u(x + y)) = 0.
239
1905* (Д-97.6).
1906* (/i - 88.6).
Найти все а, при которых система sin a; sin у = 1/z2 cos х cos у = —
< sin(a;-2/) = g2±^
0 у ir/2
z > О
имеет единственное решение.
30.3. Оценки в текстовых задачах
Роль неравенств особенно велика в тех текстовых задачах, в которых ощущается недостаток уравнений или избыток логически возможных вариантов.
Пример (тг—88.4). Два вида корма для животных отличаются содержанием белков, жиров и углеводов: в первом корме белков в 8 раз больше, чем жиров, и в три раза больше, чем углеводов, а во втором — белков и углеводов в 2,5 раза больше, чем жиров. Можно ли за счет смешивания этих кормов приготовить корм, в котором углеводов в 3 раза больше, чем жиров?
Решение. В первом виде корма углеводов в 8/3 раза больше, чем жиров, а во втором — в 2,5 раза. Поэтому в обоих видах корма углеводов больше, чем жиров, но менее чем в 3 раза, каковое свойство сохраняется при смешивании.
Ответ: нет.
у/ 1907 (А — 87.5). В 7.00 от причала А отправились две лодки, которые прошли сначала 8 км по озеру, а затем 5 км по течению реки до причала В. Первая лодка прибыла в В не позднее 9.50, а вторая — не ранее 10.40. Какова собственная скорость первой лодки, если она в 4/3 раза больше скорости второй, а скорость течения реки равна 2 км/ч?
1908* (б — 85.4). В 6.00 из пункта А в пункт В по течению реки отправились лодка и катер. Лодка прибыла в В в 16.00, а катер, дойдя до В, сразу же повернул назад и, встретив лодку не позднее 14.00, прибыл в А не ранее 22.00. Найти время
240
прибытия катера в В, если его собственная скорость вдвое больше собственной скорости лодки.
у/ 1909* (/2—86.4). Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. В 9.00 из села в город выехал мотоциклист, а из города в село — велосипедист. Мотоциклист двигался по шоссе быстрее, чем по грунтовой дороге в 3/2 раза, а велосипедист — в 5/3 раза. Мотоциклист приехал в город в 14.20, велосипедист в село — в 16.00, причем встретились они в 12.00. Успел ли бы мотоциклист приехать в город до 14.40, если бы весь путь ехал с первоначальной скоростью? 1910* (/1—93.5). Из пункта А в пункт В выехали два мотоциклиста и одновременно из В в А со скоростью 60 км/ч — третий. Через 45 мин расстояние между первым и вторым мотоциклистами было вдвое больше, чем между первым и третьим. Через 1 ч после старта расстояние между первым и вторым было равно расстоянию между первым и третьим, а расстояние, которое осталось проехать третьему до А было равно расстоянию между первым и вторым через 1ч 30 мин после старта, а также было равно 2/5 расстояния между первым и третьим через 1ч 30 мин после старта. Найти АВ.
1911* (х — 77.4). Города А, В, С и D соединены прямыми непересекающимися дорогами АВ = 6 км, ВС = 14 км, CD = = 5 км и AD = АС = 15 км. Из одного города одновременно вышли три туриста по разным маршрутам, проходящим через все города и состоящим из трех дорог каждый. Первый и второй туристы перед прохождением третьих дорог встретились в городе, а третий закончил маршрут на 1 ч раньше последнего. Найти скорости туристов, если они заключены в интервале от 5 до 8 км/ч, а скорость третьего туриста больше скорости второго и на 1/2 км/ч меньше скорости первого.
§31. Специфика геометрии
Задачи по геометрии практически всегда решаются путем выведения следствий из условия.
31.1. Получение различных следствий
В настоящем пункте собраны задачи, из условия которых требуется вывести вполне определенное следствие, причем в некото
241
рых задачах геометрическая конфигурация, хотя и недоопределена, задает искомую величину однозначно.
Пример (Л —86.2). Стороны АВ, ВС, АС треугольника АВС образуют арифметическую прогрессию. Найти отношение высоты АН треугольника к радиусу вписанной в него окружности.
Решение. См. рис.49: Равс = 4-аг 4-аз = Заг
=> агЛ = 2Sabc = Равс • г — Загг => h : г = Заг : аг = . • • Ответ: 3 : 1.
1912° (А — 78.4). Радиус описанной около треугольника АВС окружности равен 2, АС = 3 и ZA = тг/6. Доказать, что площадь треугольника меньше 3.
1913° (А — 9L5). Продолжения сторон АВ и CD вписанного в окружность четырехугольника ABCD за точки В и С соответственно пересекаются в точке Е, причем Z.AED = 60° и Z.ABD = 3 Z.BAC. Доказать, что AD — диаметр окружности. 1914° (7 — 85.4). Углы А, В, С треугольника АВС образуют арифметическую прогрессию с разностью 2тг/9. Точки А', В' и C't лежат на равном расстоянии от центра О вписанной в треугольник окружности на отрезках ОА, ОВ и ОС соответственно. Доказать, что углы треугольника А'В'С также образуют арифметическую прогрессию, и найти ее разность. у/ 1915 (х — 79.4). Из точки К, лежащей внутри остроугольного треугольника АВС, опущены перпендикуляры KL = I, КМ = ти KN = п на стороны ВС = а, АС = b и АВ = с соответственно. Найти отношение площади треугольника АВС к площади треугольника LMN.
1916* (е — 93.6). Найти площадь остроугольного треугольника, если отрезки, соединяющие основания его высот, равны 5,12 и 13.
242
1917* (7 — 95.4). В треугольнике АВС со сторонами АВ = 3, АС — 5 и ВС = 7 проведена биссектриса AD. Найти произведение радиусов двух окружностей: описанной около треугольника ABD и вписанной в треугольник ACD.
у/ 1918 (ф — 89.4). В четырехугольнике ABCD расположены две окружности: первая касается сторон АВ, ВС и AD, а вторая — ВС, CD и AD. На сторонах ВС и AD взяты точки Е и F соответственно так, что отрезок EF касается обеих окружностей, а периметр четырехугольника ABEF на 2р больше периметра четырехугольника ECDF. Найти АВ, если CD = a.
у/ 1919 (тг — 89.4). Диагонали прямоугольника ABCD со сторонами АВ = 12 и AD = 5 пересекаются в точке Е. Найти отношение расстояний от точки Е до центров окружностей, вписанных в треугольники ADE и АВЕ соответственно.
у/ 1920 (А — 94.8). Доказать, что если около описанного четырехугольника можно описать окружность, диаметр которой совпадает с одной из диагоналей этого четырехугольника, то разности его противоположных сторон равны.
1921* (ф — 99.5). Найти площадь вписанного в окружность четырехугольника ABCD, если АВ = 9, CD = 4, АС = 7 и BD = 8.
1922 (£ — 00.6). Точка О — центр окружности, описанной около треугольника АВС со сторонами АС = а и ВС = Ь. На стороне ВС взята точка D так, что прямые AD и СО перпендикулярны. Найти BD.
у/ 1923* (£—92.6). Серединные перпендикуляры к сторонам АВ и ВС треугольника АВС пересекают его высоту ВН в точках М и N. Найти ВМ, если BN == а, а радиус описанной около треугольника АВС окружности равен R.
у/ 1924 (£ — 00.8). Полуокружность, построенная на стороне ВС разностороннего остроугольного треугольника АВС как на диаметре, пересекает высоту АН = а в точке F, причем FH = Ь. Найти расстояние от точки А до точки пересечения высот треугольника АВС.
1925* (£—01.8). Прямая, параллельная стороне АС треугольника АВС с углом Z.A = тг/4, пересекает стороны АВ и ВС в точках М и N соответственно. На отрезках AN и СМ как на диаметрах построены окружности, общая хорда которых
243
пересекает отрезок MN в такой точке В, что MD : DN = = х/З : 1. Найти ЛАСВ.
у/ 1926* (тг — 98.5). Диагонали четырехугольника ABCD пересекаются в точке Е. Найти ЛАЕВ, если АВ = ВС = CD, АЕ = DE и ЛСВО ф ЛАСВ.
1927* (б — 84.4). Центр окружности, проходящей через середины сторон АВ — 2\/19, ВС = 4 и АС треугольника АВС, х&жяп на биссектрисе угла С. Найти АС.
1928 (/1 — 81.4). Трапеция ABCD с основанием AD вписана в окружность, на дуге CD которой взята точка Е. Найти отношение периметра треугольника АВЕ к радиусу вписанной в него окружности, если Z.CED = 120° и ЛАВЕ — ЛВАЕ = а.
1929* (б — 94.6). На стороне AD выпуклого четырехугольника ABCD взята точка Е, а отрезки СЕ и BD пересекаются в точке F. Найти отношение АВ : АС, если CF : EF = 2:1, CD : FD = 5 : 3 и Z.ABD 4- ЛАСО = 180°.
1930* (х—98.6). Биссектриса AL = \/3 4- х/2 — 1 остроугольного треугольника АВС со стороной АС = 2, точкой. Я пересечения высот и центром О описанной окружности делит отрезок ОН пополам. Найти радиус окружности.
1931* (£ — 85.6). Найти сторону ВС остроугольного треугольника АВС с углом ЛА — а, высотами ВН, СК и центром О описанной окружности, если площадь четырехугольника АНОК равна S.
1932* (тг — 94.5). Через точку С проведены две прямые, касающиеся данной окружности в точках А и В. На большей из дуг АВ взята точка D. Найти расстояние от точки D до хорды АВ, если CD = 2 и sin ЛАСО • sin ЛВСD = 1/3.
1933* (£—01.8). Окружность пересекает одну сторону острого угла АОВ в точках А, С (ОС < О А) и касается другой стороны в точке В. На дуге АВ (не содержащей С) взята точка D, удаленная от прямых АС, ОВ, АВ на расстояния а, Ь, с соответственно. Найти расстояние от нее до прямой ВС.
у/ 1934* (х — 99.4). Две окружности радиусов 2 и 3 с хордами АС и ВС соответственно касаются прямой АВ. Найти АВ, если ЛАСВ = тг/6.
1935* (£ — 89.6). Две окружности радиусов г и 2? пересекаются в точках А и В и касаются прямой в точках С и D.
244
Прямые АВ и CD пересекаются в точке Е так, что точка В лежит между А и Е. Найти:
1) радиус описанной около треугольника ACD окружности;
2) отношение высот треугольников ЕАС и EAD, опущенных из вершины Е.
1936* (х — 92.5). Две окружности пересекаются в точках А и В. На одной окружности взята точка С, а на другой — D так, что прямая AD касается первой окружности, а прямая АС — второй. Найти площадь треугольника CAD, если ВС = 3, BD = 6 и tg Z.CAD = -1/2.
1937* (£ — 78.6). Одна окружность с центром О пересекается с другой окружностью в точках А и В, а с ее диаметром ОС — в точке D. Луч с вершиной С пересекает дуги АО и AD в точках Е и F. Найти EF, если АЕ = а и BE = b.
у/ 1938* (£—00.8). Через точку А проведены три прямые: две из них касаются данной окружности в точках К и L, а третья пересекает окружность в точках В и (7, а также хорду KL в точке М. Найти AM : МС, если АВ : ВС = 2:3.
у/ 1939 (£—98.8). Через конец L биссектрисы CL треугольника АВС проведена перпендикулярная ей прямая, пересекающая сторону АС = а в точке D. Найти CD, если ВС = Ь.
1940* (V> — 98.5). Через центр окружности, вписанной в треугольник АВС с биссектрисой AL = а, проведена прямая, пересекающая стороны АВ и ВС в точках М и N. Окружность, вписанная в треугольник ABL, касается стороны АВ в точке К. Найти отношение площадей треугольников ABL и MBN, если ВК = Ь и ВМ 4- BN = с.
1941* (б — 92.5). Продолжения сторон АВ и CD выпуклого четырехугольника ABCD пересекаются в точке Е, а продолжения сторон ВС и AD — в точке F. Прямая EF перпендикулярна биссектрисе угла AED. Найти АВ, если АЕ = 12, DE = 8, а площади четырехугольника ABCD и треугольника ВЕС равны.
у/ 1942* (б — 84.6). Основанием пирамиды SABCD с высотой SH служит прямоугольник ABCD, диагонали которого пересекаются в точке Н. Плоскость пересекает ребра SA, SB, SC и SD в точках К, L, М и N соответственно так, что SL — 7, SN = 7/6, SK 4- SM = 25/6 и SK > SM. Найти SK и SM.
1943* (/1 — 98.5). Сфера касается боковых ребер и плоскости основания ABCD пирамиды SABCD, все ребра которой рав
245
ны по 2 4- л/2. Через точки L и N касания с ребрами SB и SD проведена плоскость, пересекающая ребра SA и SC в точках К и М. Найти SK, если площадь проекции четырехугольника KLMN на плоскость основания пирамиды равна 4/3.
у/ 1944 (£ — 97.8). Основанием пирамиды SABCD служит прямоугольник ABCD, Найти SA, если SB = 2, SC = 3 и SD = 4.
у/ 1945* (х — 00.5). На боковых ребрах SA, SB и SC пирамиды SABC с равновеликими боковыми гранями взяты точки А', В' и С" соответственно так, что SA': SA = 2 : 5 и SB' : SB = = 5:6. Найти отношение объемов пирамид SA'B'C' и SABC, если площади их боковых поверхностей относятся как 47 : 90.
1946* (/1 - 97.5). Три равные хорды АА', В В1 и СС' шара радиуса 7 проходят через точку S так, что AS = 8, A'S = 3, BS > B'S и CS > C'S. Найти радиус сферы, описанной около пирамиды SABC.
31.2. Угадывание особенностей конфигурации
Иногда интуиция подсказывает, что описанная в задаче геометрическая фигура обладает специальным свойством1 \ Однако пользоваться им по праву можно только после доказательства.
Пример (у? — 87.4). Медианы AM = BN — 3 треугольника АВС пересекаются в точке К, причем точки К, М, N и С лежат на одной окружности. Найти АВ.
Решение. См. рис.50:
АК = % AM = |BN = В К (свойство медиан)
Которое может носить как общий характер, так и частный, основанный на числовых данных или каких-то мелких деталях.
246
=>а = £ => кВ AM = kABN => ЛАВС = ЛВАС => АС = ВС => МС = NC => кКМС = kKNC => у = гр = 90° (так как 4- гр = 180°)
=> AM — медиана и высота => АВ = АС = 3/ sin 60° = ... Ответ: 2\/3.
у/ 1947° (х~ 97.5). Две окружности касаются друг друга внешним образом в точке А. Общая касательная к ним касается первой окружности в точке В, а второй — в точке С. Прямая АВ пересекает вторую окружность в точке D. Найти СР, если АВ = 5 и AD = 4.
1948 (б—86.4). В окружность радиуса 2\/7 вписана трапеция ABCD. Ее снование AD является диаметром окружности и пересекает хорду СЕ в точке F. Найти площадь треугольника BEF, если AF : DF = 1 : 3 и Z.BAD = 60°.
1949 (А — 92.5). Основание AD = 8 вписанной в окружность трапеции ABCD пересекает хорду СЕ в точке F. Найти расстояние от центра окружности до прямой АЕ, если ВС = 2, AF — Зи Z.BAD = 45°.
1950 (х — 78.3). Окружность радиуса 1, вписанная в угол С равнобедренного треугольника АВС, касается стороны ВС в точке К и пересекает основание АВ в точкахЬиМ так, что точка L лежит между А и М. Найти площадь треугольника BLK, если КВ = 15/8 и tg Z.B = 8/15.
1951* (7 — 86.4). Найти сторону АВ выпуклого четырехугольника ABCD, если ВС = \/3, BD = 1, Z.CBD = 120° и Z.BAC = Z.CAD = 30°.
у/ 1952* (/2 — 99.4).- Диагональ АС выпуклого четырехугольника ABCD является биссектрисой угла А и пересекается с другой диагональю в точке Е. Найти Z.ABD, если ВС = CD, Z.BCD = 160° и Z.CED = 130°.
у/ 1953* (х — 94.4). На высотах АН и В К треугольника АВС взяты соответственно такие точки М и N, что Z.ANC — = Z.BMC = 90°, Z.MCN = 30° и MN = 4 4- 2\/3. Найти биссектрису CL треугольника MCN.
у/ 1954 (тг — 81.4). Четырехугольник ABCD вписан в окружность с центром О. Найти площадь треугольника АО В, если Z.AOB = Z.COD = 90°, AD = 2 ВС, а высота ВН треугольника ABD равна 9.
247
у/ 1955 (7 — 96.4). Сумма квадратов косинусов трех углов треугольника равна 1. Найти площадь треугольника, если радиусы вписанной и описанной окружностей равны УЗ и 3\/2.
1956* (х — 98.6). Диагонали описанного около окружности четырехугольника ABCD пересекаются в точке Е. Найти CD, если АВ > ВС > СЕ, BE = 4 4- У2, а площадь и периметр треугольника ВСЕ равны 14 и 7 соответственно.
1957* (б — 98.6). Найти радиус описанной около треугольника АВС окружности, если
АС—АВ _ АВ—ВС ВС+АВ “ ЛВ+АС ’
АВ = с, а расстояние от центра окружности до точки пересечения медиан треугольника равно d.
1958* (jlz — 97.4). Хорда KL описанной около треугольника АВС окружности пересекает стороны АС и ВС в точках М и N соответственно. Найти высоту СН треугольника CKL и его площадь, если АВ = 3, MN = 1, А АС В = arcsinj, ZB = Z.CMN, а площадь четырехугольника ABNM равна 2.
1959* (/1 — 00.4). Две окружности касаются друг друга внешним образом в точке А. Прямая, проходящая через точку А, пересекает первую окружность в точке В, а вторую — в точке С, причем АВ = 5 и АС = 4. Касательная к первой окружности, проходящая через точку В, пересекает вторую окружность в точках D и Е (BD < BE). Найти СЕ и расстояние от точки А до центра окружности, касающейся отрезка AD и продолжений отрезков ED и ЕА за точки Du А.
I960* (х— 99.6). Найти радиус окружности, описанной около остроугольного треугольника АВС с углом А.А = 75°, высотой АН = 1 и периметром 4 4- Уб — х/2.
1961* (х — 00.4). На стороне АВ треугольника АВС с углом ZC = 120° взята такая точка D, что sin Z.ACD : sin Z.BCD = = 4:3. Через середину отрезка CD = У13 проведена прямая, пересекающая стороны АС и ВС в точках М и N соответственно, причем точка М отстоит от прямой АВ вдвое дальше, чем N. Найти площадь треугольника АВС, если площадь треугольника MCN равна ЗУЗ.
У1962° (7 — 84.4). Угол между соседними боковыми ребрами правильной четырехугольной пирамиды равен 60°. Через середину высоты пирамиды проведена прямая, пересекающая
248
боковое ребро под прямым углом. Пирамида высекает на этой прямой отрезок, равный 6. Найти боковое ребро пирамиды.
1963* (х~87.4). Основанием пирамиды SABCD служит квадрат ABCD. Точка Е лежит на ребре AS, а ее проекция F на основание пирамиды — на отрезке АС. Найти разность объемов пирамид SABCD и EABD, если Z.ADS = Z.AEC = 90°, АВ = а и AF : CF = Ь.
1964 (/3 — 82.3). В правильную пирамиду SABCD, все ребра которой равны а, вписана пирамида S' А'В'CD' с равными ребрами, вершиной S' на основании ABCD пирамиды SABCD и точками Af, Br, С и Df на ее апофемах. Найти объем вписанной пирамиды.
у/ 1965 (х — 84.4). В правильную пирамиду SABCD с боковым ребром \/3 и ребром основания 2 вписана четырехугольная пирамида с равными ребрами, вершиной, лежащей на основании ABCD, и основанием, вершины которого лежат на апофемах пирамиды SABCD. Найти объем вписанной пирамиды.
у/ 1966 (/1 — 95.5). Основанием пирамиды с высотой 5 служит треугольник со сторонами 7, 8 и 9. Сфера касается плоскости каждой боковой грани в точке, лежащей на стороне основания пирамиды. Найти радиус сферы.
1967* (/2—98.6). Сфера радиуса 3 касается плоскости каждой боковой грани треугольной пирамиды в точке, лежащей на стороне основания пирамиды. Найти объем пирамиды, если плоские углы при ее вершине равны 90°, 105° и 75°.
1968 (£ — 01.6). Основанием пирамиды служит треугольник со сторонами 7, 8 и 9. Высоты боковых граней, проведенные из вершины пирамиды, касаются вписанной в пирамиду сферы радиуса \/5/2. Найти объем пирамиды.
1969 (х — 85.4). Основанием пирамиды с высотой 2 служит ромб с острым углом 30° и площадью 8. Шар касается плоскости каждой боковой грани в точке, лежащей на стороне основания пирамиды. Найти объем шара.
1970* (£ — 98.6). Высота SH правильной треугольной пирамиды SABC касается сферы, проходящей через точки А, В и S. Найти радиус сферы, если АВ = 2 и SA = 4.
1971* (/1—79.5). Основанием пирамиды SABC с равными боковыми ребрами служит треугольник АВС, в котором ZA =
249
= тг/2, Z.C = тг/6 и ВС = 2\/2. Сфера радиуса 1 касается плоскости АВС, ребер AS, BS и продолжения ребра CS. Найти длину касательной, проведенной к сфере из точки А.
1972* (х- 89.6). Основание Н высоты SH пирамиды SABC лежит на медиане СМ треугольника АВС. Середина G отрезка SH равноудалена от вершины S и точек Е, F, лежащих на ребрах SA, SB соответственно. Расстояние между серединами ребер АВ и SC равно 4\/l3, SH = 8, АВ = 16>/2, EF = 8у/2/5 и Z.SMC < 30°. Найти радиус вписанной в пирамиду сферы.
1973* (б - 86.6). Ребро CD = х/93/6 тетраэдра ABCD перпендикулярно его грани АВС с тупым углом В, сторонами ВС = 3, АС = 4 и радиусом 8/\/15 описанной окружности. Найти площадь сечения тетраэдра плоскостью, проходящей через вершину D, точку пересечения медиан треугольника АВС и центр вписанной в него окружности.
1974* (/1 — 01.5). Основанием пирамиды SABC служит треугольник со сторонами АВ = ВС = 15 и АС = 18. Двугранные углы при ребрах АВ и ВС равны по arctg |, а при ребре АС — Сфера, центр которой лежит с плоскости АВС, касается боковых граней в точках K,L и М. Найти радиус сферы, описанной около пирамиды SKLM.
1975* (х — 99.5). Многогранник ABCDE, у которого вершины А и Е симметричны относительно плоскости BCD, а вершины В и D — относительно плоскости АСЕ, вписан в шар радиуса 3. Найти отношение объема многогранника к объему шара, если АС = ВС = 3\/2.
1976* (х — 01.6). Сфера касается всех боковых ребер правильной пирамиды SABCDEF, причем ребер SA и SB — в точках К и L соответственно. Точки К, L и S лежат по одну сторону от плоскости, которая касается сферы в точке М, принадлежащей грани SAB, и пересекает ребра SA и SB в точках G и Н соответственно. Прямые КМ и LM делят апофему грани S АВ на три равных отрезка. Найти объем пирамиды и радиус сферы, если АВ = 9 и GH = 3\/11-
31.3. Метод подбора в геометрии
Угадывание особенностей геометрической конфигурации может происходить в форме самого настоящего подбора, напомина
250
ющего, с точки зрения логики, соответствующий алгебраический метод, который рассмотрен в п. 29.3.
Пример (Л — 84.4). Найти площадь треугольника АВС, если АС = 5, АВ + ВС = 7 и cos ZА = 4/5.
Решение. Проведем высоту СН (рис. 51), тогда
АН = AC cos А = 4, НС = AC sinA = 3:
1) если В = Н, то
АВ + ВС = АН 4- НС = 7 и Sabc = | • 3 • 4 = 6;
2) если же В В, то (см. рис. 51):
либо АВ > АН (В = В' на рис. 51) => АВ 4- ВС > АН 4- НС = 7, либо АВ < АН (В = В" на рис. 51) => АВ+ВС < АН+НС = 7, что противоречит условию задачи.
Ответ: 6.
Методом подбора, в частности, можно доказать геометрические факты, обратные к утверждению 2 из п. 5.3 и утверждениям 3,5 из п. 5.4 (см. соответствующие сноски в тексте).
Рис. 51
1977° (х — 84.3). Окружность, проходящая через вершины А, В и С трапеции ABCD с основанием AD = 16 и боковой стороной CD = 8\/3, пересекает прямую AD в точке К. Найти ВК, если Z.AKB = 60°.
у/ 1978 (х — 97.5). Середины высот треугольника лежат на одной прямой, а наибольшая его сторона равна 10. Какое наибольшее значение может принимать его площадь?
у/ 1979° (/3—83.4). Продолжения боковых сторон АВ и CD трапеции ABCD площадью 6 пересекаются в точке Е. Прямая, проходящая через точку Е и точку пересечения диагоналей трапеции, пересекает основания ВС и AD в точках F и G
251
соответственно, а на отрезке ЕС взята точка Н. Найти площадь треугольника EFH, если EF : EG = ЕН : СН = 1:3.
у/ 1980* (7 — 99.5). Диагонали описанного около окружности четырехугольника ABCD пересекаются в точке В, лежащей на отрезке MN, соединяющем середины сторон AD и ВС соответственно. Найти радиус окружности, если АВ = 3, АС = = V^nME:NE = 3:l.
у/ 1981 (х—89.4). Диагонали прямоугольника ABCD пересекаются в точке Е, симметричной точке F относительно прямой АВ. Найти ВС, если ААЕВ = 2 ACFD, а площадь пятиугольника AFBCD равна 5\/3.
1982 (£ — 91.4). Перпендикуляр, проведенный из вершины А выпуклого четырехугольника ABCD к стороне ВС, пересекает диагональ BD в точке Е. Найти АВ, если BE = a, DE = b и ABAC = АВ DC = 90°.
у/ 1983* (ст —99.3). В выпуклом четырехугольнике ABCD углы ВАС и BDC равны, а площадь круга, описанного около треугольника BCD, равна 25тг/4. Найти:
1) радиус описанной около треугольника АВС окружности;
2) площадь четырехугольника ABCD, если АС = 4, ВС = = 3 и ABAD = 90°.
1984* (7 — 99.4). Биссектрисы AD и BE треугольника АВС пересекаются в точке F, AAFE = 60°.
1) Найти АС.
2) Найти площадь треугольника АВС, если АВ = 2 и . ACED = 45°.
1985* (7 — 89.5). В выпуклом четырехугольнике ABCD со стороной AD = 2 расстояние между центрами вписанных окружностей в треугольники ABD и ACD равно \/2. Найти ВС, еслп AABD = AACD = 90°.
у/ 1986* (х — 96.6). Две окружности пересекаются в точках А и В. Хорда CD одной окружности пересекается с хордой EF другой окружности в точке G. Найти AG, если BG = 2, АВ — = 3CG = 9 EG и FG = 3PG = 6CG.
1987* (£ — 81.6). Биссектрисы углов АиВ вписанного четырехугольника ABCD, в котором CD : ВС = а, пересекаются в точке Е, лежащей на стороне CD. Найти отношение:
1) расстояний от точки Е до прямых AD и ВС;
2) площадей треугольника ADE и ВСЕ.
252
1988* (£ — 84.6). Две окружности радиусов г < Я, касающиеся внешним образом друг друга, касаются третьей окружности в точках А и В, а также некоторой прямой в точках С и D. Прямые АВ и CD пересекаются в точке Е. Найти длину касательной, проведенной из точки Е к третьей окружности.
у/ 1989° (7 — 88.4). Плоскость, параллельная ребрам AD и ВС тетраэдра ABCD, пересекает ребра АВ, АС и BD в точках Е, F и G соответственно. Найти отношение АЕ : BE, если AD : ВС = 1 : 3 и EF : EG = 3 : 1.
у/ 1990* (д — 87.6). Сфера касается ребер AD, BD, ВС и АС тетраэдра ABCD в точках К, L, М и N соответственно. Найти KL, если MN = 7,NK = 5, LN = 2у/29 иКЬ = LM.
1991* (д — 01.5). Основанием прямой призмы АВСА'В'С с высотой 4/7 служит треугольник АВС со сторонами АВ = = ВС = 1 и АС — 3/7. Через точку пересечения диагоналей грани АСС'А' на расстоянии 4/13 от точки А проводится плоскость, делящая объем призмы пополам. Какова наибольшая площадь сечения призмы такой плоскостью?
1992* (д — 91.6). Сторона основания АВС правильной призмы АВС А'В'С равна д/З. Сфера радиуса 7/2 касается плоскости АВС и продолжений ребер ABf, BCf и CAf за точки А, В и С. Найти боковое ребро призмы.
§ 32. Элементы логики
В настоящем параграфе разбираются такие логические приемы, как доказательство от противного, метод исключения, вывод частного следствия из общего утверждения, а также вопросы, связанные с существованием и единственностью решений, равносильностью высказываний или односторонними следствиями между ними, включениями множеств или их равенством и т. п.
32.1. Приведение к противоречию
Наиболее естественный способ опровергнуть какое-либо утверждение состоит в рассуждении от противного, а именно: предположив, что опровергаемое утверждение справедливо, требуется прийти к противоречию.
Пример (7 - 96.3). cos 3^+1)z cos = 1.
253
Решение.
...<=> cos(3?r + 1)х 4- cos 2х = 2 <=> cos(3?r 4- 1)я = cos 2х = 1
((Зтг 4- 1)ж = 2тГП
1 2х = 2тгА:, где п, к G Z
__ 27ГП
~ Зтг+1
= 2тгк О х = О,
т.к. если к 0, то
2тгп = 2тгА;(37г 4-1) => тг = —6^2fe G Q, что неверно.
О т в е т: х = 0.
Ответ на вопрос, какой из нескольких логически возможных случаев1^ реализуется в условии задачи, можно получить методом исключения: т. е. обоснованно отбросив все случаи, кроме одного, сделать вывод, что только этот единственно оставшийся случай и имеет место в действительности.
1993 — 96.5). Пусть #i}2 — корни квадратного трехчлена
f(x) — х2 — (5а — 2)2х — За2 — 7а 4-1.
Найти все а, при которых для любого b функция g(t) — cos(b7rt) cos((xi 4- ^2)7Г^) является периодической.
у/ 1994 (</? — 98.6). Найти все а, при которых уравнение
sin2 (х 4- 6) — (а — 1) sin(x 4- 6) sin7rx 4- (а — 1) sin2 тгх = 0 имеет единственное решение.
у/ 1995* (х — 95.5). Найти все целочисленные решения уравнения х2 4- 19531ООЖ2/ - 1995100г/2 = 0.
у/ 1996 — 86.5). В ящике находятся 13 черных шаров и 17 бе-
лых. Разрешается:
а) увеличить на 2 число черных шаров, уменьшив на 1 число, белых;
б) увеличить на 1 число черных шаров, увеличив на 2 число белых;
в) уменьшить на 2 число черных шаров, увеличив на 1 число белых;
г) уменьшить на 1 число черных шаров, уменьшив на 2 число белых.
Можно ли, совершая в каком-либо порядке и количестве описанные действия, добиться, чтобы в ящике оказалось 37 черных шаров и 43 белых? ---------------------- ।
^Составляющих в совокупности полное событие.
254
1997* (A — 83.5). Катер проходит по реке путь AD, состоящий из участков АВ = 11 км и ВС = CD = 2 км, а скорость течения равна 5 км/ч. По расписанию, выходя из пункта А в 8.00, он прибывает в пункты В, С и D в 8.00, в 8.00 и в 9.00 соответственно. Если бы катер двигался без остановок с постоянной собственной скоростью, то сумма модулей его отклонений от расписания в моменты прибытия в пункты В, С и D не превышала бы уменьшенного на полчаса времени, необходимого катеру для прохождения 5 км в стоячей воде. Какой из пунктов находится выше по течению: А или £>?
у/ 1998 (тг — 01.6). Можно ли на прямоугольном участке размером 1мх4м посадить три дерева на расстоянии не менее 2,5 м друг от друга так, чтобы одно из деревьев располагалось в углу участка?
1999° (/1 — 92.2). Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке Е, ААВЕ = 60° и AC BE = 70°. Точка М на прямой АС взята так, что ADME = = 80°. Где лежит точка М: на диагонали АС или на ее продолжении?
у/ 2000 (/1—93.3). Диагональ равнобедренной трапеции равна 8 и является биссектрисой одного из углов. Может ли одно основание этой трапеции быть меньше 4, а другое равняться 5?
2001* (А — 90.6). На сторонах АВ и ВС треугольника АВС выбраны точки D и Е соответственно так, что ABED = = ABAC. Площадь круга, описанного около треугольника ADC, впятеро больше площади круга, описанного около треугольника BED, а площадь треугольника BED в 16/9 раза больше площади четырехугольника ACED. Может ли при этих условиях выполняться равенство ADAE = 45° ?
32.2. Переход от общего к частному
Если какое-либо утверждение в условии задачи справедливо при всех значениях переменной2), то для продвижения в решении задачи бывает достаточно лишь удачно подобрать конкретные значения этой переменной, чтобы получить наиболее содержательные следствия.
2)йли наборов переменных.
255
Пример — 78.4). Найти все пары (а, 6), при которых равенство
a(coss — 1) 4- b2 = cos(as 4- Ъ2) — 1
выполняется для всех х.
Решение.
1. Положим х = 0:
Ь2 = cos b2 — 1 => < & $ => Ъ = 0.
j^cosb = 1
2. Положим х = 2тг:
0 = cos(2?ra) — 1 => 2тга = 2тгп, где п 6 Z, => a 6 Z.
3. Положим х — тг:
—2а = cos(?ra) — 16 [—2; 0] => а е [0; 1] => а = 0, 1.
4. Проверим а = Ъ = 0: 0 = cos 0 — 1 — верно.
5. Проверим a = 1, Ъ = 0: cosx — 1 = cos ж — 1 — верно. Ответ: a = 0,1; Ъ = 0.
2002 (д — 93.6). Найти все а, при которых неравенство logs (a cos 2я — (1 4- a2 — cos2 x) sin x 4- 4 — a) < 1 выполняется для всех x.
у/ 2003 (A — 96.8). Найти все а, при которых для любого Ъ уравнение
cos(5 4- ab 4- Ьх) 4- 2 cos(62x) = За2 имеет хотя бы один корень.
2004* (А—98.8). Найти все а, при которых для любого Ъ^2 неравенство
(6 - 1)а; + 20 - (b- I)-2 < -6+Л 1
— 1 J X выполняется при всех х < 0.
2005* (/1 — 89.6). Найти все а, при которых для любого Ъ система
' 2(1 + \у\)а + (Ъ2 —2Ъ + 2)х = 3 ху(х 4- Ъ — 1) = 2a2 — За 4-1 имеет хотя бы одно решение.
2006* (х — 01.7). Первый член последовательности ai,a2, • • • равен 1, а каждый последующий член равен удвоенной сумме всех предыдущих. Найти aia2 • • • • • a2ooi-
у/ 2007* (х — 99.7). Последовательность ai, а2,... удовлетворяет при* каждом натуральном п условию
256
I an 4- 2, если n — нечетно, an+l — S Q
I 2an, если n — четно.
Найти ai999, если ax =0.
у/ 2008* (х — 01.7). Функция / удовлетворяет при каждом х равенству
f(x + 1) = f(x) 4- 2х 4-1.
Найти /(2001), если /(0) = 0.
2009* (х — 99.7). Функция / удовлетворяет при любых х, у равенству
/ х + 2у\ = Да;) + 2/(у)
7 \ 3 / 3
Найти /(1999), если /(1) = 1 и /(4) = 7.
у/ 2010* (б — 00.7). Функция / определена на отрезке [2/5; 5/2] и удовлетворяет на нем системе
(cos(2/(a:)) - 6 cos2 f (|) = \о /(а;) тг/2.
Решить уравнение /(ж) = 5тг/12.
32.3. Следствия, связанные с количеством решений
Исходя из различных свойств3^ выражений, входящих в уравнение, неравенство или систему, можно получать какие-либо необходимые условия для того, чтобы число решений было заданным, а затем проверять, какие из них являются к тому же и достаточными.
Пример (б — 77.3). Найти все а, при которых система
(х2 4- у2 = 2(1 4- а)
|(х 4- у)2 = 14
имеет ровно два различных решения.
Решение.
{х2 4- у2 = 2(1 4- a) f 2ху = 12 — 2а
х2 4- 2ху 4- у2 — 14 ((я — у)2 = 4а — 10.
3)Таких как четность или нечетность, инвариантность относительно перестановок или других преобразований переменных, ограниченность, монотонность и т. д.
9 И. Н. Сергеев — Математика
257
1. Если пара (х, у) — решение системы, то пары (—ж, —у), (у, х) и (—3/, —х) — также решения, а в случае х 3/, все четыре пары различны. Поэтому если система имеет ровно два решения, то
х = у => а = 5/2.
2. Пусть а = 5/2:
{2жз/ = 7 f—у—
z ч9 о х = у = ±v?/2 —ровно два решения. (® - уу = о
Ответ: а = 5/2.
у/ 2011° (jj, — 90.4). Найти все а, при которых уравнение х2 — 2а sin cos х 4- а2 = 0
имеет единственный корень.
2012 — 95.5). Найти все а, при которых неравенство
cosa: - 2у/х2 + 9 < - а
имеет единственное решение.
2013 (х — 98.5). Найти все а, при которых уравнение
2 1+«2 — a cos 4- а2 = |
имеет единственный корень.
у/ 2014 (х — 99.6). Найти все а, при которых уравнение
+ 2а| = а2 + 1
имеет нечетное число корней.
2015 (б — 90.6). Найти все а, при которых система
{(3 - 2у/2)у 4- (3 4- 2у/2)У - За = х2 4- &х 4- 5
у2 — (а2 — 5а 4- 6)я2 = О
—6 х < О
имеет единственное решение.
2016 (б — 87.6). Найти все а, при которых система
(3 • 2^1 4- 5|ж| 4- 4 = Зз/ 4- 5я2 4- За
[х2 4-з/2 = 1
имеет единственное решение.
у/ 2017 — 84.5). Найти все а, при которых система
2/ > (ж - а)2
ж > (з/ - а)2
имеет единственное решение.
258
2018 {ip — 92.5). Найти все а, при которых система ах2 4- 4ая — у + 7а 4-1 = 0 ау2 —х — 2ау 4- 4а — 2 = 0 имеет единственное решение.
2019 (7 — 97.4). Найти все а, при которых система ах2 — 2ах — 2у 4- 4а — 2 О
ау2 4- 4а?/ — 2х 4- 7а 4- 4 О
имеет единственное решение.
2020* (/? — 91.5). Найти все а, при которых система z cos(x — у) 4- (2 4- ху) sin(x 4- у) — z = О ж2 4- (у - I)2 4- z2 = а 4- 2х, (х + у + a sin2 z) ((1 — a) In (1 — ху) 4-1) = О имеет единственное решение.
у/ 2021* (х — 86.5). Найти все а, при которых система л/|2/ + 3| = 1 - \/5|я| 16а — 9 — бу = 25я2 4- у2 имеет ровно четыре различных решения.
у/ 2022 (/2 — 01.6). Найти все а, при которых система (а — 1)я2 4- 2ах 4- а 4- 4 О ах2 4- 2(а 4- 1)я 4- а 4-1 > О имеет единственное решение.
у/ 2023* (0 — 01.6). Найти все а, при которых система sin х = cos(x\/6 — 2а2) cos х = (а — 2/3) sin(#x/6 — 2а2) имеет на отрезке [0; 2тг] единственное решение.
2024* (/2 — 98.5). Найти все а, при которых система cos2 (тле?/) — 2 sin2 (тле) — 3sin2(7r?/) — 2 4- tg(?ra) = О cos(fl\n/) — | sin2 (тле) — 2 sin2 (iry) — | 4-| tg(?ra) = О log2 (1 + 4sin2 (22 - JL) - - y2j 1
имеет ровно четыре различных решения.
• 2025* (б — 99.7). Найти все а, при которых система asin |2z| 4- log5(x \/2 — бх8) 4- a2 = О < ((?/2 — 1) cos2 z — у sin 2z 4-1) х
х (1 4- у/к 4- 2z 4- х/тг — 2z) — О
259
9*
имеет не более двух различных решений, но не менее одного. Найти эти решения.
32.4. Различные логические связи между утверждениями
В задачах настоящего пункта изучаются высказывания, состоящие по существу в том, что одно из двух данных утверждений влечет другое или, более того, равносильно ему.
Пример (д — 94.1). Число х удовлетворяет условиям tg2s = —3/4 и cos2x<0.
Обязательно ли при этом определено выражение logtg » tg х и чему оно равно?
Решение.
' sin 2х z
----------Т" < ° . Л Л cos х О ...=>< cos 2х => sin 2х = sin х cos х > 0 => <
cos2x<0 |/ = tga:>0.
Поэтому
• = => 8t = -3 + 3t2 => (t-3)(t-i) = 0 => t = 3,
а искомое выражение имеет смысл и равно
logtg. t = log1/v^3 = -2.
Ответ: да; —2.
2026 (б — 88.5). Найти все а, при которых уравнение а(2а — 1) sin3 х 4- 3 cos3 х — 2а2 sin х = О равносильно уравнению
logi/2 (3tgx - 1) - log2 (3 tg ж + 1) - log1/V2 (5 - tga:) = 1.
у/ 2027 (x — 88.5). Найти все а, при которых система
{ах 4- Зу = 6a — 4 х 4- у = 2a равносильна системе
я2 - 2у4 - &х 4- 8 = О
х2 4- у2 — (2a 4- 4)я 4- 2(а2 4- а 4- 2) = 0.
2028 (х—80.5). Найти все а, при которых число корней уравнения
3(я2 4- a2) = 1 — (9а2 — 2)х не превосходит числа корней уравнения
х 4- (За - 2)2Зж = (8а - 4) log3 (За - 1/2) - Зя3.
260
</2029* (7 — 87.5). Найти все натуральные а, при которых выражение (я 4- у 4- З)-1 имеет смысл для всех пар чисел х, у < 0, для которых имеет смысл выражение 1g (ху — а), 2030* (х- 93.6). Найти все а, при которых область определения функции f (т} — _________________________-_______
J ' 3cosx—2 cos3 x — \/2a
совпадает с областью определения функции
л(х] =________е
' sin3 ж+cos3 х— а 3 cos х — 2 cos3 х — у/2а ’
2031* (ф — 87.6). Доказать, что из неравенства
у/х^1 + \Лг2 - 1 > 2 вытекает неравенство
х + + у/х* — 2х2 + 1 >1 + 2 у/х2 - 1.
2032* (А — 79.6). Найти все х 0, при которых из системы abx > 4а 4- 76 4- я а, b О
вытекает неравенство аб > 5.
/2033* (а — 98.6). Доказать, что четыре точки пересечения кривых, заданных уравнениями
у = х2 — 2х и (я/3)2 4- у2 = 1, лежат на одной окружности, и найти ее радиус.
§ 33. Задачи с целыми числами
Идеи из §§ 29, 30 развиваются с учетом специфики целых чисел.
33.1. Оценки целочисленных переменных
В предлагаемых здесь задачах особую роль играют оценки области значений выражений, содержащих целочисленные переменные, или области допустимых значений этих переменных.
Пример (х — 97.6). Найти все целочисленные решения уравнения
(х2 4- у2)(х 4- у - 3) = 2ху.
Решение. Неравенство
я2 4-1/2 2\/х2у2 = 2|хз/|
261
обращается в равенство тогда и только тогда, когда |х| = |у|. Поскольку (х + у — 3) 6 Z, то уравнение выполняется в следующих пяти случаях:
1) х = у = 0; [ х = 0 2) < |^х 4- у — 3 = 0 О CQ II II $
3) И° ^х 4- у — 3 = 0 ф II II 50 0
4) W [ж + у-3 = 1 <=> X = у = 2;
5) = ~У [х 4- у - 3 = -1 Ответ: х = у = 0; — решений нет. х = у = 2; х = 0, у = 3; х = 3, у = 0.
у/ 2034° (д — 96.1). Найти все целочисленные решения неравенства \/х3 — 5х — 3 6 — х.
2035 (/3 — 96.5). Найти все пары натуральных чисел х,у, удовлетворяющие системе
{2х 4- 47 < 22у - 2у2
7х 4-14 4у.
2036 (J3 — 92.4). Найти все целочисленные решения системы
х2 4- у2 < 16х - 22у - 171
ЗОх — у2 > 252 4- х2 4- 14г/.
У 2037 (7—01.5). Найти все целые а, при которых графики функций
V = - 2а) и у = log2(x - 2а3 - За2)
пересекаются в точке с целочисленными координатами.
у/ 2038* (/1 — 90.5). Найти все целочисленные решения уравнения log2 (2х 4- 3?/ - 6z 4- 3) 4- log2 (За: — 5у 4- 2z — 2) 4-
4- log2 (2у 4- 4г — 5ж 4- 2) > z1 — 9г 4-17. 2039* (/1 — 00.5). Найти все а, при которых уравнение
((!) + (1Г’ -»(»)“ -I) -
X («)2-2 + (|)2“'2"’3 - 4 (|)2“-5 + 2) = 0 имеет хотя бы один корень и все его корни — целочисленные. 2040 (А—88.5). Первые 80 км пути из одного пункта в другой автобус едет по шоссе, а оставшиеся 120 км — по грунтовой
262
дороге, на 2 ч дольше. Совершив более четырех рейсов по маршруту туда и обратно, он затратил менее 168 ч, включая стоянки в конечных пунктах. Найти скорости движения автобуса по шоссе и по грунтовой дороге, если за время, которое автобус провел в движении, он со скоростью, равной среднему арифметическому этих двух скоростей, проехал бы 2100 км.
у/ 2041 (ср — 77.1). В двух ящиках содержится в общей сложности более 29 деталей. Число деталей первого ящика, уменьшенное на 2, более чем втрое превышает число деталей второго, а утроенное число деталей первого ящика превышает удвоенное число деталей второго менее чем на 60. Сколько деталей содержится в каждом ящике?
2042 (х— 86.3). Число двухкомнатных квартир в доме вчетверо больше числа однокомнатных, а число трехкомнатных квартир также кратно числу однокомнатных. Если увеличить впятеро число трехкомнатных квартир, то их станет на 22 больше, чем двухкомнатных. Сколько всего квартир в доме, если их не меньше 100?
2043 (б — 78.4). Когда груз разложили в вагоны по 80 т, один вагон оказался недогружен. Когда груз переложили в вагоны по 60 т, понадобилось на 8 вагонов больше и один вагон опять оказался недогружен. Когда же груз переложили в вагоны по 50 т, понадобилось еще на 5 вагонов больше и все вагоны оказались полными. Найти вес груза.
у/ 2044* (А — 84.5). Три мальчика хотели вместе купить две одинаковые игрушки. Сложив все свои деньги, они не смогли купить даже одну игрушку. Если бы у первого мальчика было вдвое больше денег, то им на покупку двух игрушек не хватило бы 34 руб. Когда количество денег третьего мальчика утроили, у них после покупки игрушек осталось еще 6 руб. Сколько стоила одна игрушка, если первоначально у второго мальчика было на 9 руб. больше, чем у первого?
2045* (А — 84.5). В саду было подготовлено четное число ям для посадки деревьев. После посадки яблонь, груш и слив, оказалось, что использовано менее трети ям, груш посажено на 6 больше, чем яблонь, а свободных ям осталось втрое больше, чем посажено слив. Если бы яблонь посадили втрое больше, то свободных осталось бы 59 ям. Сколько ям для посадки было подготовлено?
263
33.2. Использование делимости
Решая следующие задачи, полезно, помимо оценок неизвестных, вовремя подмечать и использовать их делимость на какие-либо числа.
Пример (д — 92.4). Мастер делает в час целое число деталей, большее 5, а ученик — на 2 детали меньше. Один мастер выполняет заказ за целое число часов, а два ученика вместе — на 1 ч быстрее. Из скольких деталей состоит заказ?
Решение. Пусть мастер делает х > 5 деталей в час и выполняет заказ за у ч, тогда число деталей в заказе равно
ху = 2(х — 2)(у — 1) => ху — 4у = 2х — 4 ^=2 + х — 4
1)
-4=2
У = 4
х = 6
4
----- е N => 4 : (х — 4) > 1
х — 4
2) 4
3
8
х
=> ху = 6- 4 = 83 =
Ответ: 24.
у/ 2046 (а—97.7). Найти все целочисленные решения уравнения Зху 4-14# 4- 17у 4- 71 = 0.
2047* (б—89.6). Найти все целочисленные решения уравнения 9я2?/2 4- &х2у 4- $ху2 4- х2 4- 18ги/ 4- 2у2 4- Зх 4- 7у 4- 6 = 0.
у/ 2048* (х — 96.5). Найти все целочисленные решения уравнения 14ж4 - 5у4 - Зх2у2 - 123х2 4- 82t/2 4-51 = 0.
2049 (/1 — 97.3). Найти все целочисленные решения системы 4ж2+2я:3/+1 __ ?|з/|-l(z 4. 2)
. 37TZ sm —— = 1.
2
2050* (х — 79.4). Найти все целочисленные корни уравнения (Зх - Д2 + 160гс + 800)) = 1.
2051* (гр — 99.6). Найти все а, при которых система
J 12я2 — 4х — 2ху 4- Зу — 9 = 0 аху 4- ayz 4- axz > xyz имеет ровно пять различных решений в натуральных числах. 2052* (х — 01.4). cos((x 4- 7у/х)я) sin((4x 4- у/х)я/2) = 1.
cos
264
у/ 2053 — 79.5). Пусть — несократимая дробь, где т
и п — натуральные числа. На какие натуральные числа можно сократить дробь ln+2m, если известно, что она сократима?
у/ 2054 (б — 93.5). За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5% в месяц, затем 111, 7| и, наконец, 12% в месяц. Под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на 180%. Определить срок хранения вклада.
2055 (ст — 97.4). В детском саду был проведен опрос. На вопрос, что вкуснее: каша или компот, — большая часть детей выбрала кашу, меньшая — компот, а один затруднился ответить. Среди любителей компота 30% предпочли абрикосовый, а 70% — грушевый. Среди любителей каши 56,25% предпочли манную, 37,5% — рисовую, а один затруднился ответить, какую именно кашу он любит. Сколько детей было опрошено? 2056* (б — 98.7). Три фермера привели для продажи на ярмарку баранов: первый — 10, второй — 16, третий — 26. В первый день они установили одинаковую цену, и каждый продал не менее одного барана, но не всех. Во второй день они продали остальных баранов, опять же по одинаковой, но более низкой цене. По какой цене продавались бараны в первый и во второй день, если каждый из фермеров выручил от продажи по 3 500 руб?
2057 (тг — 77.5). Рота солдат, прибывшая на парад прямоугольным строем по 24 человека в ряд, была перестроена в виде квадрата. После того как часть солдат выбыла, оставшийся состав перестроили так, что число рядов уменьшилось на 2, а число солдат в каждом ряду стало на 26 больше числа новых рядов. Сколько солдат было в роте?
у/ 2058 (А—00.6). Любая из трех барж разной грузоподъемности за несколько рейсов (при полной загрузке каждого рейса) может перевезти некоторый груз, причем баржа с наименьшей грузоподъемностью — за 15 рейсов, а две другие баржи — за 3 совместных рейса (также при полной загрузке). За сколько рейсов баржа с наибольшей грузоподъемностью перевозит этот груз?
2059* (б — 84.4). Две бригады землекопов одинаковой производительности каждый вырыли по одинаковому котловану.
265
Вторая бригада работала на полчаса больше первой. Если бы в первой бригаде было на 5 человек больше, то она закончила бы работу на 2 ч раньше. Найти число землекопов в каждой бригаде.
У 2060* (/3 — 99.6). Два велосипедиста стартовали одновременно в противоположных направлениях из точек А и В круговой велотрассы. Найти отношение их скоростей, если из первых 15 встреч велосипедистов после старта только третья и пятнадцатая произошли в точке А, а к моменту их пятой встречи каждый из них проехал не менее одного круга.
2061* (/2 — 88.5). Два мотоциклиста стартовали раздельно в одной точке стадиона в гонке на 30 кругов, причем второй начал движение, когда первый прошел полкруга. Один из зрителей вышел со стадиона, когда мотоциклисты были рядом. Когда через 4 мин он вернулся, мотоциклисты снова были рядом. Если бы первый мотоциклист после 14 кругов увеличил скорость вчетверо, а второй мотоциклист после 12 кругов — вдвое, то они финишировали бы одновременно. С какой разницей во времени финишировали мотоциклисты, если пришедший первым проезжал более 5 кругов в минуту?
33.3. Экстремальные целочисленные задачи
При нахождении наименьших или наибольших значений целочисленных величин могут пригодиться самые разные приобретенные ранее навыки: например; по подбору значений, удовлетворяющих заданным свойствам.
Пример (д — 95.1). Найти наибольшее целочисленное решение неравенства
4-32х+1 +3Х < 1.
Решение. Функция f(x) = 4-32х+1+Зх, где ж G Z, возрастает, причем
/(—2) = 4 • З"3 + З"2 < 1 < Д-1) = 4 • З’1 + З"1 => Жшах = .. • Ответ: х = —2.
Немалую роль может сыграть и умение выводить точные оценки и доказывать их достижимость, а также анализировать данные задачи с точки зрения их оптимальности.
у/ 2062 (/2—96.5). Какое наибольшее число членов может содержать конечная арифметическая прогрессия с разностью 4 при условии, что квадрат ее первого члена в сумме с остальными членами не превосходит 100?
266
2063* (б — 01.7). Найти наибольшее целое а, при котором хотя бы для одного целого b уравнение
364я2а — 556 = -20020s4
имеет ровно четыре различных корня, два из которых относятся как 3 : 5.
у/ 2064 (х — 97.4). Из сосуда, первоначально содержавшего чистый спирт, отлили треть и добавили столько же воды. Эту операцию проделали в общей сложности п раз. При каком наименьшем п содержание спирта стало меньше 10%?
у/ 2065 (7 — 79.4). В школьной газете сообщается, что процент учеников некоторого класса, повысивших во втором полугодии успеваемость, заключен в пределах от 2,9% до 3,1%. Каково наименьшее число учеников в таком классе?
у/ 2066 (б — 84.5). Из строительных деталей двух видов можно собирать дома трех типов: 12-, 16- и 21-квартирных. Для сборки 12-квартирного дома необходимо 70 деталей первого вида и 100 второго, для сборки 16-квартирного — ПО и 150 деталей, а для сборки 21-квартирного — 150 и 200 деталей соответственно. Всего имеется 900 деталей первого вида и 1300 второго. Сколько и каких домов нужно собрать, чтобы общее количество квартир в них было наибольшим?
2067* (х — 87.5). С завода на стройку на автомашине грузоподъемностью 10 т нужно перевезти 24 больших бетонных блока массой по 3,6 т и 510 маленьких — по 0,2 т. Автомашина вмещает 44 маленьких блока, а большой блок занимает место 14 маленьких. Найти наименьшее число рейсов, достаточное для перевозки всех блоков.
2068* (б — 96.4). В контейнер упакованы изделия трех типов общим весом 326 кг. Стоимость и вес одного изделия первого типа составляют 4 руб. и 12 кг, второго — 5 руб. и 16 кг, а третьего — 6 руб. и 15 кг соответственно. Найти наименьшую и наибольшую возможную суммарную стоимость находящихся в контейнере изделий.
§ 34. Проекции и сечения
Переход от данной геометрической фигуры к ее проекции или сечению можно рассматривать, по большому счету, как аналог перехода от данного алгебраического соотношения к следствию из него.
267
34.1. Проектирование на прямую
Ключевым моментом в решении задач настоящего пункта может оказаться проектирование всего чертежа или каких-либо его элементов на прямую или на несколько разных прямых.
Пример (Л — 95.6). Высота прямоугольного треугольника, опущенная на гипотенузу, делит биссектрису одного из острых углов в отношении (1 4- \/2) : 1, считая от вершины. Найти острые углы треугольника.
Решение. См. рис. 52:
ОЛ. _ АН _ АО COSO _ АО _ (1+у/2)х _ 1 _
cos la - - ль cosa - лг - x+(1+v/2)x - 7^ => 2а - ...
Ответ: 45°.
У 2069 (б — 87.5). На сторонах АВ и АС треугольника АВС взяты точки MhN соответственно так, что AM : ВМ = 2:3 и AN : CN = 4 : 5. В каком отношении прямая СМ делит отрезок BN?
Рис. 52
2070 (£ — 99.4). На сторонах АВ и АС треугольника АВС взяты точки М и N соответственно, а отрезки BN и СМ пересекаются в точке К, Найти ВК : NK, если AN : CN = = 2 : 3 и СК : МК = 5 : 2.
2071 (£ — 97.6). На сторонах АВ и АС угла ВАС взяты точки N и L соответственно так, что NB = LC и ВО : LO = = т : п, где О — точка пересечения отрезков CN и BL. Найти AN : АС.
у/ 2072 (А — 96.6). Катеты прямоугольного треугольника равны 36 и 48. Найти расстояние от центра вписанной в треугольник окружности до высоты, проведенной к гипотенузе.
268
у/ 2073 (х — 93.4). В квадрат площадью 18 вписан прямоугольник так, что на каждой стороне квадрата лежит по одной вершине прямоугольника. Найти площадь прямоугольника, если его стороны относятся, как 1 : 2.
2074* (£ — 97.6). На сторонах острого угла с вершиной О взяты точки А и В. На луче О А взята точка М на расстоянии 3 О В от прямой ОВ, а на луче О В — точка N на расстоянии 3 О А от прямой О А. Найти MN, если радиус описанной около треугольника АОВ окружности равен 3.
2075* (7 — 01.6). На одной стороне угла с вершиной Q взяты точки А, В и С, а на другой — D, Е и F так, что AE1DF, DB1AC, BF1.DE и ЕС1АВ. Отношение AD к расстоянию от точки Q до центра описанной вокруг четырехугольника ADFC окружности равно 6 : 17. Найти Z.Q.
у/ 2076* (£ — 01.4). В трапеции ABCD с боковыми сторонами АВ = a, CD = с и основанием ВС — b угол Z.B — прямой. Окружность, проходящая через точки С и Р, касается стороны АВ в точке Е. Найти площадь треугольника ECD.
2077* (</? — 91.5). Боковая сторона АВ трапеции ABCD перпендикулярна основанию ВС. Окружность, проходящая через точки С и Р, касается прямой АВ в точке Е. Найти расстояние от точки Е до прямой СР, если AD = 4 и ВС = 3.
2078* (/1—00.6). Вершины квадрата ABCD со стороной 25/4 лежат на сфере. Параллельные друг другу прямые проходят через точки A, B,C,D и повторно пересекают сферу в точках А', В', С', Df соответственно. Найти РР', если AAf = 2, ВВГ = = 10 и СС' = 6.
2079* (/1 — 00.6). Параллельные плоскости q и о ррлят тетраэдр ABCD на три части так, что объем средней части меньше объемов каждой из крайних. Расстояния от точек А и С до плоскости q равны 10 и 8 соответственно, расстояния от точек А и В до плоскости а равны 15 и 10 соответственно, а расстояние от точки Р до этой плоскости меньше 12. Найти отношение площадей сечений тетраэдра плоскостями q и а, если одно из этих сечений — трапеция.
34.2. Проектирование на плоскость
Проектирование пространственной фигуры на плоскость позволяет иной раз увидеть ее в совершенно неожиданном ракурсе.
269
Пример (д — 93.5). На , диагонали АС параллелепипеда ABCDA' В'С D' взята точка М, а на прямой В1 С — точка N так, что отрезки MN и BD параллельны. Найти их отношение.
Решение. Проекция параллелепипеда (рис. 53, а) на плоскость, перпендикулярную прямой В'С, представляет собой два равных параллелограмма АВВ'А' и DCC'D' с общей стороной А1 В1 = DC на рис. 53, б (обозначения сохранены прежними), где MN || BD:
(MN = DK ДАКА' = ЛС'МС)
4 v ' => BD = 3MN.
[BK = 2MN (ДСВК ~ &CNM)
Ответ: 1 : 3.
Уместно напомнить, что при проектировании плоской фигуры на какую-либо новую плоскость, расположенную к исходной под углом у?, площадь фигуры уменьшается в secy? = 1/cosy? раз.
(б)
Рис. 53
у/ 2080° (у?—90.5). Основанием пирамиды SABCD служит квадрат ABCD со стороной 15, а радиус вписанного в пирамиду шара равен 3. Найти высоту пирамиды, если она совпадает с ребром SA.
2081° (х — 82.4). Площадь основания и площадь боковой поверхности правильной шестиугольной пирамиды равны, & и S соответственно. Найти наибольшее расстояние, на которое удалены точки основания пирамиды от ее боковой грани.
у/ 2082 (/1—95.6). Двугранные углы при ребрах АВ, ВС и АС пирамиды SABC равны 90°, 30° и 90° соответственно. Плоскость пересекает ребра SB, SC, АС и АВ в точках К, L, М и N соответственно, причем четырехугольник KLMN — трапеция, основание KL которой втрое меньше основания MN, а высота равна 13. Найти площадь этой трапеции, если AS = ВС = 13.
270
у/ 2083* (х — 99.4). Основание высоты SH пирамиды SABCD лежит внутри грани ABCD, а высоты боковых граней, опущенные из вершины S, равны по \/2. Найти SH, если АВ = 2, ВС = 6, Z.ABC = тг/З и Z.ADC = 2тг/3.
у/ 2084* (А — 94.10). Найти площадь сечения единичного куба ABCDA'B'C'D' плоскостью, проходящей через середину диагонали BD' перпендикулярно ей.
2085* « - 77.5). На ребрах АА' и ВС куба ABCDA'B'C'D' с ребром 1 взяты точки Е и F соответственно так, что АЕ = = 1/3 и BF = 1/4. Через эти точки и центр куба проведена плоскость. Найти расстояние от нее до вершины В'.
2086* (/1 — 96.5). На ребрах АА', АВ, В'С' и ВС единичного куба ABCD А' В'С'D' взяты точки К, L, М и N соответственно так, что AL = 2/3, В'М = 1/4 и CN = 3/10. Какое из ребер АВ или AD пересекается с плоскостью, параллельной отрезку LM и содержащей отрезок KN? В каком отношении это ребро может делиться плоскостью?
у/ 2087 (/2 — 92.5). На прямой I в пространстве последовательно взяты такие точки А, В и С, что АВ = 10 и ВС = 22, а расстояния от этих точек до прямой т равны 12, 13 и 20 соответственно. Найти расстояние между прямыми I и т.
2088* (V> — 92.5). На ребрах АВ, AC, CD и BD тетраэдра ABCD взяты точки К, L, М и N соответственно, а точки Е и F — середины ребер AD и ВС. Прямые КМ, LN и EF пересекаются в одной точке, а угол между скрещивающимися прямыми AD и ВС равен 45°. Найти площадь четырехугольника KLMN, если AD = 9, ВС = 8 и АК : КВ = 5 : 1.
2089* (/1—83.5). На ребрах SA и SB пирамиды SABC с высотой SH = h взяты точки D и Е соответственно. Через точки D, Ей точку пересечения медиан треугольника АВС проведена плоскость, пересекающая ребро ВС в точке F. Через точку F проведена плоскость, параллельная грани AS В и пересекающая ребра АС и SC в точках М и N соответственно. Найти отношение площади основания пирамиды к площади ее полной поверхности, если SE : BE =1:2, CF : BF = = (AD : SD)2, а радиус вписанной в пирамиду CFMN сферы равен г.
у/ 2090* (х— 94.6). Все высоты тетраэдра ABCQ, равны между собой. Найти BD, если АВ = 9, ВС = 13 и Z.ADC = 60°.
271
2091* (х — 77.5). Серединный перпендикуляр к ребру BS пирамиды SАВС пересекает ребро АС под прямым углом. Грань BSC по площади равна грани ASB, а грань ASC — вдвое больше. Сумма расстояний от некоторой точки М, лежащей внутри пирамиды, до всех граней пирамиды равна МВ 4- MS. Найти МВ, если АС = \/б и BS = 1.
2092* (А — 84.6). Найти отношение площадей поверхности вписанного и описанного шаров для пирамиды SABC с высотой SH = 2, если АВ = АС = CH = 1, ВС = \/35 а прямая АН перпендикулярна ребру АВ.
2093* (А — 83.6). Ребро SA пирамиды SABC перпендикулярно ребрам АВ и АС, АВ = АС = 1, cos /ВАС = 4/5 и /.ВАС = 2/BSC. Какую наибольшую площадь боковой поверхности может иметь находящийся в пирамиде прямой круговой цилиндр, образующая которого параллельна ребру ВС? 2094* (/1—96.5). Сфера радиуса л/З касается плоскости основания АВС правильной треугольной пирамиды SABC в точке, лежащей на луче АС, а также касается луча AS и плоскости SBC. Найти наибольшее значение АС, если tg /SAC = = 2/v/3.
у/ 2095* (£ — 93.8). Два шара радиуса г касаются друг друга и данной плоскости с одной стороны рт нее. Цилиндр радиуса R > г касается боковой поверхностью шаров и плоскости (с Фой же стороны). Найти радиус шара, большего, чем данные, и касающегося обоих данных шаров, цилиндра и плоскости. 2096* (х — 88.6). Внутри сферы, пересеченной плоскостью, расположены три шара, два из которых одного радиуса, а третий — меньшего. Каждый из шаров касается двух других, сферы и плоскости. Синус угла между данной плоскостью и плоскостью, проходящей через центры шаров, равен 1/х/5, а косинус угла между радиусами меньшего и большего шаров, проведенными в точки их касания со сферой, равен 4/5. Найти расстояние от центра сферы до данной плоскости, если оно больше 14, а расстояние между центрами сферы и меньшего из шаров равно 15.
2097* (/1 — 90.6). Основанием правильной пирамиды SABC с боковым ребром олужмъ треугольник АВС со стороной 2\/3. В трехгранный угол при вершине А вписана сфера. Другая сфера, втрое большего радиуса, касается первой сферы,
272
плоскостей SAC и АВС, а на прямой SB высекает отрезок, равный 6/У7. Найти радиус второй сферы.
у/ 2098* (/1 — 99.6). Три шара радиусов 1, 2 и 5 расположены так, что каждый из них касается двух других и двух данных плоскостей. Найти расстояние между точками касания меньшего из этих шаров с плоскостями.
2099* (£ — 00.8). Дан прямой конус высотой 6 и радиусом основания 3. Точка А находится на расстоянии 3 от оси конуса и на расстоянии 4 от плоскости его основания. В плоскости основания взята такая точка В, что прямая АВ имеет с конусом единственную общую точку С, расположенную на расстоянии 2 от плоскости основания. Найти расстояние от точки В до вершины конуса.
34.3. Сечение фигур плоскостями
Даже если сечения в явном виде не участвуют в условии задачи, можно попробовать провести одно или несколько сечений пространственной фигуры, с помощью чего обнаружить какие-либо важные или скрытые от глаза свойства этой фигуры.
Пример (^—94.4). Через вершины А, В и С четырехугольной пирамиды SABCD проведена сфера, пересекающая боковые ребра SB и SC в точках М и N соответственно так, что ВМ : SM = = 1:3. Через точки А, С, D и N проведена другая сфера. В каком отношении она делит ребро SA, если SA : SB = \/П: у/7?
Решение. См. рис.54:
Рис. 54
1) SA SK = SB SM (теорема о секущих для сечения первой сферы плоскостью SAB) => SK = SMy/7/ll
=>SK :SA = SMy/l/ll : SBy/11/7 = (3®-7) : (4x11) = 21 : 44;
273
2) сечения обеих сфер плоскостью SAC совпадают, так как проходят через точки А, С и поэтому вторая сфера проходит через точку К и
SK : КВ = 21 : (44 - 21) = ...
Ответ: 21 : 23.
2100° (£ — 01.6). В правильную треугольную пирамиду с высотой 4 и стороной основания 2 вписан шар. Найти расстояние между точками его касания с двумя боковыми гранями.
у/ 2101 (£ — 01.6). В правильной треугольной пирамиде SABC, все ребра которой равны по 10 а, на ребре SC взята такая точка К, что SK : КС = 1:4. Найти периметр сечения этой пирамиды плоскостью, параллельной ребру SB и медиане СМ треугольника АВС.
у/ 2102 (/? — 81.5). Два скрещивающихся ребра тераэдра равны 12 и 4, а остальные ребра — по 7. Найти расстояние от центра вписанной в тетраэдр сферы до наибольшего ребра.
у/ 2103 (£ — 84.5). В правильную треугольную пирамиду, высота которой в а раз меньше стороны основания, вписан куб так, что одна его грань лежит в основании пирамиды, одно ребро — в боковой грани и по одной вершине — в двух других боковых гранях. Найти отношение объемов пирамиды и куба. 2104* (£—97.8). В правильную треугольную пирамиду с двугранным углом а при боковом ребре вписана сфера радиусом г. Найти объем пирамиды, вершинами которой служат центр сферы и точки ее касания с боковыми гранями.
у/ 2105 (б—99.6). Боковое ребро d правильной треугольной пирамиды служит диаметром сферы, пересекающей два других боковых ребра в их серединах. Найти объем пирамиды.
2106* (/1 — 93.5). Сфера радиуса R делит каждое из ребер АВ, ВС, CD и AD тетраэдра ABCD на три равные части и проходит через середины ребер АС и BD. Найти высоту тетраэдра, опущенную из вершины Н.
у/ 2107* (А — 01.7). Сфера диаметром AD = \/3 касается плоскости треугольника АВС в точке А. Отрезки BD и CD пересекают сферу в точках М и N соответственно. Найти MN, если АВ = 3, АС = 3\/5 и Z.BDC = тг/З.
2108* (7 — 99.6). Все плоские углы трехгранного угла с вершиной S равны по 90°. Сфера пересекает одно из ребер этого трехгранного угла в точках Ai и Л2, второе — в точках
274
и В2, а третье — в точках С± и С2. Найти площадь треугольника А2В2С2, если площади треугольников SA^B^, SA^Ci, SB1C1 и SA2B2 равны 15/2, 10, 6 и 40 соответственно.
2109* (х—96.6). Сфера проходит через вершины А, В и С тетраэдра ABCD и пересекает ребра АР, BD и CD в точках К, L и М соответственно. Проекции центра сферы на плоскости ABD, BCD и ACD лежат на ребрах АВ, ВС и АС соответственно. Найти периметр треугольника KLM, если AD = 10>, ВС : BD = 3:2, АВ : CD = 4\/3 : 11, а расстояние между серединами ребер АВ и CD равно 13.
2110* (£ — 99.8). Высота SH правильной четырехугольной пирамиды SABCD служит диаметром некоторой сферы. Найти длину линии пересечения этой сферы с поверхностью пирамиды, если AS = а, а боковые грани наклонены к плоскости основания под углом <р.
2111* (б — 00.6). Центр шара радиуса 1 совпадает с центром основания правильной треугольной пирамиды с высотой 2\/2 и стороной основания 2\/3. Найти площадь той части боковой поверхности пирамиды, которая лежит внутри шара.
у/ 2112* (/1 — 98.5). Четырехугольная пирамида SABCD с высотой SH вписана в сферу, центр которой лежит в плоскости основания ABCD. Найти CS и CD, если СН = 4, AS = 15/4, AD = 3, АВ = BS, а диагонали четырехугольника ABCD пересекаются в точке Н.
у/ 2113* (/1 — 96.6). Основанием вписанной в сферу четырехугольной пирамиды SABCD служит параллелограмм ABCD. Найти BD, если SA = 4, SB = 8, SD = 7 и Z.SAC = Z.SBC = = Z.SDC.
2114* (А — 84.6). Основанием вписанной в сферу четырехугольной пирамиды SABCD служит трапеция ABCD с основаниями ВС = 1, AD = 14- у/2 и углом Зтг/8. Основание Н высоты пирамиды лежит вне трапеции, причем прямые ВН и AD перпендикулярны. Найти радиус сферы, если АН = 1 и SH = \/2 + 2лЛ.
у/ 2115* (7 — 89.4). Сфера касается ребер АВ = 1 и AD тетраэдра ABCD в точке А, а ребер ВС и CD — в точке С. Найти площадь сферы, если BD = 2 и Z.ABC = Z.BAD = 90°.
2116* — 89.5). Основанием пирамиды SABC, вписанной
в сферу, служит правильный треугольник АВС со стороной
275
4л/3. Найти радиус сферы, если SA = SB = 8, а косинус двугранного угла при ребре АВ равен 2/\/ТЗ.
2117* (ц — 99.6). Основание высоты SH = ^/5/21 треугольной пирамиды SABC лежит внутри грани АВС. Найти радиус описанной около пирамиды сферы, если SA = 1, SB = 2, Z.ASB = 120° и Z.ACB = 60°.
2118* (/1 — 89.5). Прямая EF параллельна плоскости, в которой лежит прямоугольник ABCD, все стороны которого, а также отрезки АЕ, BE, CF, DF и EF касаются шара. Найти объем этого шара, если АВ = 1 и EF = 3.
2119* (/1 — 81.5). Тетраэдры ABCD и BCDE расположены по разные стороны от плоскости BCD. Прямая DE параллельна плоскости АВС и удалена от нее на расстояние в а раз большее, чем от центра вписанного в тетраэдр BCDE шара. Найти суммарную площадь сечения этих тетраэдров плоскостью, проходящей через середину ребра AD параллельно плоскости АВС, если площадь грани АВС равна s, а площадь поверхности тетраэдра BCDE с высотой ВН равна S, причем tgZHPE:tgZBPE = 5.
2120* (х — 90.5). Основанием пирамиды SABCD с высотой SH = 3\/3/2 служит прямоугольник ABCD, диагонали которого пересекаются в точке Н. На ребрах АВ = 6 и AD = 9 взяты точки М и N так, что AM = 4 и AN = 6. Найти площадь сечения пирамиды плоскостью, проходящей через точки М и N параллельно ребру AS.
2121* (£ — 99.7). Найти плоский угол при вершине S правильной треугольной пирамиды SABC, если ее боковое ребро вдвое больше радиуса сферы, проходящей через точку А и касающейся плоскости SBC в точке В.
2122* (7 — 82.5). На ребрах AD, ВС и диагонали B'D' грани единичного куба ABCDA'B'C'D' взяты точки M,L и N так, что МА = 2,tgZ.BLM = 4 и B'N : D'N = 9 : 16. Найти площадь сечения куба плоскостью MLN.
2123* (/1—94.5). Найти радиус сферы, касающейся ребер AD, DD', CD единичного куба ABCDA'B'C'D' и прямой ВС.
2124* (х — 95.6). На ребре СС куба ABCDA'B'C'D' с ребром 4 взята точка М так, что МС = 3. Найти радиус наибольшей сферы, касающейся плоскости BDD' и проходящей через точку М и середины ребер ВС и DC.
276
2125* (i/ — ОО.Ь). Через вершину А, середину М ребра В1 С' и точку К ребра DD' единичного куба ABCDA'B'C'D' проведена плоскость, делящая площадь грани А*В*CD' в отношении 1 : 19. Найти АК.
у/ 2126* (тг - 98.5). На ребрах АА' и СС' куба АВСРА'В'С'Р' взяты точки М и N ссоответственно так, что AM = 2А'М и CN = 2 CfNr В каком отношении делит объем куба плоскость, проходящая через точки М, N и В?
2127* (х — 95.6). На трех ребрах, выходящих из вершины А куба ABCDA'B'C'D' с ребром 5, взяты точки М, N и К соответственно так, что Z.NMA = arcsin(l/x/5), биссектриса AL треугольника AKN равна 2\/2/3, площадь треугольника АКМ равна 2, а объем тетраэдра AMNK меньше 1. Найти радиус сферы, касающейся плоскости MNK и трехгранного угла куба при вершине С".
2128* (i/—01.6). Основанием призмы АВСА'В'С", описанной около сферы, служит треугольник АВС со стороной АВ = 1 и углом Z.B = 90°. Боковая грань АВ В1 А1 — прямоугольник, tgZA'AC = х/З, а угол между плоскостями ВСС и АСС равен 60°. Найти боковое ребро призмы.
2129* (х — 98.6). Точка А лежит на ребре двугранного угла величиной 7г/3. Точки В и С лежат внутри этого угла, причем В± и Ci — их проекции соответственно на одну его грань, а В2 и С2 — на другую. Найти ВС4 если АВ = 3 \/25 — 4\/3, АС = У19 - 4\/5, АВг = 9\/2, АВ2 = 6\/3, АСг > АС2 и Z.B1AC1 = ЛВ2АС2 = тг/12.
2130* (х — 85.6). На ребрах АВ, АС и AD правильного тетраэдра ABCD, описанного около сферы радиуса 5^6/2, взяты точки К, L и М соответственно так, что КВ = 15, MD = 10 и объем пирамиды AKLM равен 375\/2. Найти сумму радиусов двух шаг ров: вписанного в пирамиду AKLM и описанного около нее.
у/ 2131 (/3 — 00.5). Внутри правильной треугольной призмы со стороной основания равной а расположены три одинаковых шара, каждый из которых касается двух других шаров, двух боковых граней и обоих оснований призмы. Найти радиус четвертого шара, касающегося трех указанных шаров и одного из оснований призмы.
2132* (е — 01.6). Центры двенадцати шаров равных радиусов совпадают с серединами ребер правильной шестиуголь
277
ной пирамиды/ Найти двугранный угол при ребре основания пирамиды, если известно, что шар, вписанный в пирамиду, касается всех двенадцати данных шаров.
2133* (£ — 83.6). В трехгранный угол с вершиной S, плоские углы которого равны по а, а двугранные углы при ребрах — по /3, вписаны два шара. Они касаются с разных сторон плоскости, пересекающей ребра трехгранного угла в точках А, В и С так, что AS = BS > CS. Найти:
1) угол между прямой, проходящей через центры шаров, и плоскостью SAB\
2) отношение радиусов шаров.
2134* (С — 92.8). Три шара радиуса г касаются друг друга и боковой поверхности прямого конуса (снаружи). Найти расстояние от вершины конуса до плоскости, проходящей через центры шаров, если эта плоскость перпендикулярна высоте конуса, а его образующая составляет с высотой угол а.
2135* (/1 — 85.5). Коническая поверхность с вершиной S, лежащей на сфере с центром О и радиусом Я, пересекает сферу по окружности с центром О\ и радиусом гх. Плоскость, проходящая через точку О перпендикулярно прямой SO, пересекает коническую поверхность по окружности с центром О2 и радиусом г2. Найти расстояние от этой плоскости до точки Oi, если SO2 = а.
Приложение А.
Программа по математике
Настоящая программа состоит из трех разделов.
В первом разделе перечислены основные математические понятия, которыми должен владеть поступающий как на письменном, так и на устном экзамене.
Второй раздел представляет собой перечень вопросов теоретической части устного экзамена. При подготовке к письменному экзамену целесообразно познакомиться с формулировками утверждений этого раздела.
В третьем разделе указано, какие навыки и умения требуются от поступающего на письменном и устном экзаменах.
Объем знаний и степень владения материалом, описанным в программе, соответствуют курсу математики средней школы. Поступающий может пользоваться всем арсеналом срёдств из этого курса, включая и начала анализа. Однако для решения экзаменационных задач достаточно уверенного владения лишь теми понятиями и их свойствами, которые перечислены в настоящей программе. Объекты и факты, не изучаемые в общеобразовательной школе, также могут использоваться поступающими, но при условии, что он способен их пояснять и доказывать.
В связи с обилием учебников и регулярным их переизданием отдельные утверждения второго раздела могут в некоторых учебниках называться иначе, чем в программе, или формулироваться в виде задач, или вовсе отсутствовать. Такие случаи не освобождают поступающего от необходимости знать все эти утверждения.
I. Основные понятия
1. Натуральные числа. Делимость. Простые и составные числа. Наибольший общий делитель и наименьшее общее кратное.
2. Целые, рациональные и действительные числа. Проценты. Модуль числа, степень, корень, арифметический корень, логарифм. Синус, косинус, тангенс, котангенс числа (угла). Арксинус, арккосинус, арктангенс, арккотангенс числа.
3. Числовые и буквенные выражения. Равенства и тождества.
4. Функция, ее область определения и область значений. Возрастание, убывание, периодичность, четность, нечетность. Наибольшее и наименьшее значения функции. График функции.
279
5. Линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрические функции.
6. Уравнение, неравенство, система. Решения (корни) уравнения, неравенства, системы. Равносильность.
7. Арифметическая и геометрическая прогрессии.
8. Прямая на плоскости. Луч, отрезок, ломаная, угол.
9. Треугольник. Медиана, биссектриса, высота.
10. Выпуклый многоугольник. Квадрат, прямоугольник, параллелограмм, ромб, трапеция. Правильный многоугольник. Диагональ.
11. Окружность и круг. Радиус, хорда, диаметр, касательная, секущая. Дуга окружности и круговой сектор. Центральный и вписанный углы.
12. Прямая и плоскость в пространстве. Двугранный угол.
13. Многогранник. Куб, параллелепипед, призма, пирамида.
14. Цилиндр, конус, шар, сфера.
15. Равенство и подобие фигур. Симметрия.
16. Параллельность и перпендикулярность прямых, плоскостей. Скрещивающиеся прямые. Угол между прямыми, плоскостями, прямой и плоскостью.
17. Касание. Вписанные и описанные фигуры на плоскости и в пространстве. Сечение фигуры плоскостью.
18. Величина угла. Длина отрезка, окружности и дуги окружности. Площадь многоугольника, круга и кругового сектора. Площадь поверхности и объем многогранника, цилиндра, конуса, шара.
19. Координатная прямая. Числовые промежутки. Декартовы координаты на плоскости и в пространстве. Векторы.
II. Содержание теоретической части устного экзамена
Алгебра
1. Признаки делимости на 2, 3, 5, 9, 10.
2. Свойства числовых неравенств.
3. Формулы сокращенного умножения.
4. Свойства линейной функции и ее график.
5. Формула корней квадратного уравнения. Теорема о разложении квадратного трехчлена на линейные множители. Теорема Виета.
6. Свойства квадратичной функции и ее график.
7. Неравенство, связывающее среднее арифметическое и среднее геометрическое двух чисел. Неравенство для суммы двух взаимно обратных чисел.
280
8. Формулы общего члена и суммы п первых членов арифметической прогрессии.
9. Формулы общего члена и суммы п первых членов геометрической прогрессии.
10. Свойства степеней с натуральными и целыми показателями. Свойства арифметических корней n-й степени. Свойства степеней с рациональными показателями.
11. Свойства степенной функции с целым'показателем и ее график.
12. Свойства показательной функции и ее график.
13. Основное логарифмическое тождество. Логарифм произведения, степени, частного. Формула перехода к новому основанию.
14. Свойства логарифмической функции и ее график.
15. Основное тригонометрическое тождество. Соотношения между тригонометрическими функциями одного и того же аргумента. Формулы приведения, сложения, двойного и половинного аргумента, суммы и разности тригонометрических функций. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование произведения синусов и косинусов в сумму. Преобразование выражения a sin х 4- b cos х с помощью вспомогательного аргумента.
16. Формулы решений простейших тригонометрических уравнений.
17. Свойства тригонометрических функций и их графики.
Геометрия
1. Теоремы о параллельных прямых на плоскости.
2. Свойства вертикальных и смежных углов.
3. Свойства равнобедренного треугольника.
4. Признаки равенства треугольников.
5. Теорема о сумме внутренних углов треугольника. Теорема о внешнем угле треугольника. Свойства средней линии треугольника.
6. Теорема Фалеса. Признаки подобия треугольников.
7. Признаки равенства и подобия прямоугольных треугольников. Пропорциональность отрезков в прямоугольном треугольнике. Теорема Пифагора.
8. Свойство серединного перпендикуляра к отрезку. Свойство биссектрисы угла.
9. Теоремы о пересечении медиан, пересечении биссектрис и пересечении высот треугольника.
281
10. Свойство отрезков, на которые биссектриса треугольника делит противоположную сторону.
11. Свойство касательной к окружности. Равенство касательных, проведенных из одной точки к окружности. Теоремы о вписанных углах. Теорема об угле, образованном касательной и хордой. Теоремы об угле между двумя пересекающимися хордами и об угле между двумя секущими, выходящими из одной точки. Равенство произведений отрезков двух пересекающихся хорд. Равенство квадрата касательной произведению секущей на ее внешнюю часть.
12. Свойство четырехугольника, вписанного в окружность. Свойство четырехугольника, описанного около окружности.
13. Теорема об окружности, вписанной в треугольник. Теорема об окружности, описанной около треугольника.
14. Теоремы синусов и косинусов для треугольника.
15. Теорема о сумме внутренних углов выпуклого многоугольника.
16. Признаки параллелограмма. Свойства параллелограмма.
17. Свойства средней линии трапеции.
18. Формула для вычисления расстояния между двумя точками на координатной плоскости. Уравнение окружности.
19. Теоремы о параллельности прямых в пространстве. Признак параллельности прямой и плоскости. Признак параллельности плоскостей.
20. Признак перпендикулярности прямой и плоскости. Теорема об общем перпендикуляре к двум скрещивающимся прямым. Признак перпендикулярности плоскостей. Теорема о трех перпендикулярах.
III. Требования к поступающему
На экзамене по математике поступающий должен уметь:
1) выполнять (без калькулятора) действия над числами и числовыми выражениями; преобразовывать буквенные выражения; производить операций над векторами (сложение, умножение на число, скалярное произведение); переводить одни единицы измерения величин в другие;
2) сравнивать числа и находить их приближенные значения (без калькулятора), доказывать тождества и неравенства для буквенных выражений;
3) решать уравнения, неравенства, системы (в том числе с параметрами) и исследовать их решения;
4) исследовать функции; строить графики функций и множества точек на координатной плоскости, заданные уравнениями и неравенствами;
282
5) изображать геометрические фигуры на чертеже; делать дополнительные построения; строить сечения; исследовать взаимное расположение фигур; применять признаки равенства, подобия фигур и их принадлежности к тому или иному виду;
6) пользоваться свойствами чисел, векторов, функции и их графиков, свойствами арифметической и геометрической прогрессий;
7) пользоваться свойствами геометрических фигур, их характерных точек, линий и частей, свойствами равенства, подобия и взаимного расположения фигур;
8) пользоваться соотношениями и формулами, содержащими модули, степени, корни, логарифмические и тригонометрические выражения, величины углов, длины, площади, объемы;
9) составлять уравнения, неравенства и находить значения величин, исходя из условия задачи;
10) излагать и оформлять решение логически правильно, полно и последовательно, с необходимыми пояснениями.
На устном экзамене поступающий должен дополнительно уметь:
11) давать определения, формулировать и доказывать утверждения (формулы, соотношения, теоремы, признаки, свойства и т.п.), указанные во втором разделе настоящей программы;
12) анализировать формулировки утверждений и их доказательства;
13) решать задачи на построение циркулем, линейкой; находить геометрические места точек.
Приложение Б.
Дополнительные разделы
Б.1. Элементы комбинаторики
2136 (Л —78ч2) Сколькими способами можно разбить на две команды группу из 7 мальчиков и 8 девочек так, чтобы в первой команде было 4 мальчика и 3 девочки?
2137 (<£ — 78.2) Автобусный билет считается счастливым, если первые три цифры его шестизначного номера нечетны и различны, а вторые — четны, причем цифры 7 и 8 не стоят рядом. Сколько существует различных номеров счастливых билетов?
2138 (С — 77.3) Найти все отрицательные члены последовательности ai,аг,..., удовлетворяющей при любом натуральном п равенству
А4п+4 143
" Рп+2 4РП’
где и Рт — числа размещений и перестановок соответственно.
Б.2. Задачи, использующие предел
2139 (х~97.4) Бассейн наполняется п насосами: первый насос, работая один, наполняет бассейн за 2ч, второй — за 4ч,..., п-й — за 2П ч. При каком наименьшем п все насосы, работая одновременно, наполнят бассейн быстрее, чем за 1 ч 1 мин? Можно ли наполнить бассейн за 1 ч?
2140 (i/ — 99.5) Знаменатель бесконечно убывающей геометрической прогрессии отрицателен. Найти все целые п, при которых сумма членов с нечетными номерами больше суммы членов с четными номерами на величину, равную второму члену, умноженному на число п2 + Юп + 20.
2141 (б — 95.5) Найти все х 6 [—3; 1], при которых неравенство х (тг(х + 1) — 4arctg(3a2 + 12а 4- 11)) > 0 выполняется для любых целых а.
Б.З. Производная
2142 (7 — 82.2). Найти все х, при которых производная функции f(x) = 5 — 8 cos (За: 4- тг/11)
равна 12.
284
2143 (тг —80.2). Найти все х, при которых производная функции /(ж) = 4х — sin 2х 4- 4\/2 cos х равна нулю.
2144 (х — 86.3). Найти все х е (тг/2; тг), при которых производная функции
/(ж) = (cos (тг/2 — х) 4- cos х) cos х cos (тг/2 — х) равна нулю.
2145 (/3—83.2). Найти все ж, при которых производная функции /(ж) = Зя2 In х — 36# In х — 7х3 4- 108#
равна нулю.
Б.4. Исследование функций с помощью производной
2146 (/? — 80.2). Найти наибольшее и наименьшее значения функции
f(x) = 2я3 — Зх2 — 36я 4-10
на отрезке [—5; 4].
2147 (тг — 77.2). Найти все точки экстремума функции /(ж) = хе~3х.
2148 (7 — 84.3). Найти наименьшее значение функции f(x) = 6х4-е~6ж.
2149 (7—77.3). Найти промежутки монотонности и все точки экстремума функции
f(x) = я/ln х,
2150 (А — 78.3). Найти наименьшее значение функции f(x) = х In х — х In 5
на отрезке [1; 5].
2151 (тг — 79.2). Найти наименьшее значение функции f(x) = х 4- 4/(х - 2)2
на отрезке [0; 5].
2152 (б — 80.4). Найти наибольшее значение функции /(ж) = 5 cos х — cos5x
на отрезке [—тг/4; тг/4].
2153 (х — 78.2). Найти все точки минимума функции
-/ ч /х х . х х - 3
/(*) = V3cos - 4- sm ---2~• '
285
2154 (ip — 83.3). Найти наибольшее и наименьшее значения функции
f(x) = 24я — cos 12я — 3 sin 8х
на отрезке [—тг/6; тг/6].
2155 (х — 84.3). Найти все точки минимума функции f(x) = х2 (18 sin Зя — 45 cos Зя) +
4- я(12 cos Зя 4- 30 sin Зя) 4- 68 sin Зя — 170 cos Зя.
2156 (/1 — 79.3). Найти все точки минимума и наибольшее значение функции
/(я) = я3 — 2я|я — 2|
на отрезке [0; 3].
2157 (б — 79.4). Найти наибольшее и наименьшее значения функции
/(я) = |я2 4- 2я - 3| 4- - In я
на отрезке [1/2; 4].
2158 (тг — 82.3). Найти наименьшее значение функции /(я) = —|2я3 4- 15я2 4- 36я - 30|
на отрезке [—3; 2].
2159 (/3 — 89.2). Найти наименьшее значение функции
' = 2а:3 - 9а;2 + 12а: + 1
на отрезке [0; 3].
2160 (тг—91.5). При каждом а < 0 найти наименьшее значение функции
/(я) = (я - а)3/3 - (я - а)г/2
на отрезке [0; 1].
2161 (б — 78.5). Найти все а, при которых функция /(я) = sin 2я — 8(а 4-1) sin я 4- (4а2 4- 8а — 14)я возрастает и не имеет критических точек.
2162 (х—77.5). Найти все а е [0; тг/2], при которых наименьшее значение функции
/(я) = Зя4 4- 4я3(соз а — sin а) — Зя2 sin 2а на отрезке [—sin а; sin а] минимально.
2163 (/1 — 77.3). Доказать, что наименьшее значение функции /(я) = cos я sin 2я на отрезке [—тг; тг] больше —7/9.
286
Б.5. Касательная
2164 (/3 — 79.1). Найти все х, при которых касательные к графикам функций
f(x) = Зсов5я и д(х) = 5 cos Зя 4- 2 в точках с абсциссой х параллельны.
2165 ((/? — 80.3). Найти абсциссу точки пересечения с осью абсцисс касательной к графику функции
/(я) = 4я — я2 в точке с абсциссой 3.
2166 (£ — 79.4). Найти абсциссы точек пересечения с осью абсцисс тех касательных к графику функции
/г \
/(а:) = ГЗз;
которые образуют с положительной полуосью абсцисс угол Зтг/4, отложенный в положительном направлении.
2167 (V> — 77.2). Найти все я, при которых касательная к графику функции
/(я) = я3 — Зя2 — 7я 4- 6 в точке с абсциссой я отсекает от положительной полуоси абсцисс вдвое меньший отрезок, чем от отрицательной полуоси ординат.
2168 (V> —80.4). Найти площадь треугольника, образованного осями координат и касательной к графику функции
/(*) = 2-^-7
в точке с абсциссой 1.
2169 (х~90.3). При каждом а > 0 найти площадь и периметр треугольника, образованного осями координат и касательной к графику функции у = азшя в точке с абсциссой —4тг/3.
2170 (</? —82.3). Найти площадь треугольника, образованного осью ординат и двумя касательными к графику функции
f(x) = 6я 4- я2 : '
в точке минимума и в точке с абсциссой —2.
2171 (V> — 82.2). Найти точку пересечения двух касательных к графику функции
/(я) = sin Зя в точках с абсциссами тг/18 и 5тг/18.
287
2172 (тг —86.4). Найти площадь треугольника, образованного осью абсцисс и двумя касательными к графику функции
f(x) = х2/2 — х 4- 5, проведенными из точки (0, 3).
2173 (х—78.3). Найти уравнения всех касательных к графику функции
/(х) = —х2/2 + 2, проходящих через точку (1/2, 2) и пересекающих в двух различных точках график функции
д(х) = \/4 — я2.
2174 (/3—82.4). Найти уравнения всех касательных к графику функции _____
f(x) = \/1 — 2х2, образующих с осями координат треугольник площади 1/\/2.
Б.6. Интеграл
2175 (/1 — 77.1). Найти все решения неравенства
[ (2 — 4t + 3t2)dt х,
Jo
удовлетворяющие условию х > 0.
2176 (/1 — 78.2). Найти все корни уравнения
/ cos(£ 4- х2) dt = sin х
Jo
на отрезке [2; 3].
2177 (/? — 78.2). Найти все а и 6, при которых функция
f(x) = asin(7rx) 4- b
удовлетворяет условиям
/'(1) = 2 и [ f(x)dx = 4.
Jo ‘
Б.7. Нахождение площадей с помощью интеграла
2178 (7 — 80.1). Найти площадь фигуры, ограниченной осью абсцисс и линией
у = 2(х — I)2 — 8.
2179 (тг — 81.3). Найти площадь фигуры, ограниченной линиями у = х2 4- 2 и у = 4 — х.
288
2180 (£ — 80.4). Найти площадь фигуры, ограниченной линиями у = |а:2 - 4|, х = -1
и отрезком [—1; 2] оси абсцисс.
2181 (х — 77.2). Найти площадь фигуры, ограниченной линиями у = х2 — 2х 4- 2, у = х2 4- 4х 4- 5 и у = 1.
2182 ((/? — 77.2). Найти площадь фигуры, ограниченной линиями у = sinx, 2/ = cosx, х = 0 и х = тг/2.
2183 (/? — 77.3). Найти площадь фигуры, ограниченной графиком функции
f(x) = х2 — 4х 4- 5
и двумя касательными к нему в точках с абсциссами 1 и 4.
2184 (/? — 81.4). Найти площадь фигуры, ограниченной графиком функции
/(ж) = 4х — х2
и двумя касательными к нему, проведенными из точки (5/2, 6). 2185 (^ — 79.2). Найти все а > 0, при которых площадь фигуры, ограниченной линиями
1 2 2
2/ = 1 — х и у = ах, равна Ь. При каких b задача имеет решение?
2186 (б — 79.4). При каком а > 1 площадь фигуры, лежащей в полуплоскости х 0 и ограниченной линиями
у = ах2, у = ах2/2, у = 1 и у = 2, максимальна?
Б.8. Разные задачи на применение производной и интеграла
2187 (х — 88.3) Среди точек, лежащих на линии у = 1 — 2х2, найти ближайшую к точке (1; 3/4).
2188 (е — 77.3) Найти наименьшее расстояние от точки (0, —2) до точек, лежащих на линии
2189 (тг — 87.5) При каком х е [—1; 2] точка с абсциссой х, лежащая на линии
у = у/4 — 2х — х2/2 4- ж3/3, наименее удалена от начала координат?
10 И. Н. Сергеев — Математика
289
2190 (х — 83.4) Среди точек, лежащих на линии у = 1 4- cos х при 0 х 7Г, найти ближайшую к прямой
л/Зя 4- 2у 4- 4 = 0.
2191 (х~85.3) При каком а е [—3/5; 3/2] площадь треугольника, одна вершина которого совпадает с началом координат, а две другие имеют абсциссу а и лежат соответственно на линиях \
у = Зх2 — 10# 4-2 и у = — 2х2 4- 5х — 10, максимальна?
2192 (/1—80.4) При каком а е [1/2; 1] площадь треугольника, образованного осью абсцисс, прямой х = 2 и касательной к графику функции f(x) = \[х? в точке с абсциссой а, минимальна?
2193 (А — 77.3) При каком а > 0 площадь фигуры, ограниченной линиями
х2 4- 2ах 4- За2 а2 — ах
у = ~г^— и У =
. максимальна?
2194 (у - 01.5). | logx+2(х3 4- 5,5я2 4-10,2х 4- 6,385) 1.
2195 (А — 96.8) Найти все а, при которых неравенство ах2 4-1 > 4я — За
выполняется для всех х 6 (—1; 0).
2196 (V> — 90.5) Найти все а > 0, при которых любой положительный корень уравнения
2я3 4-х2— х — а — 1=0
удовлетворяет неравенству
12я3 — 7х > 6а 4-1.
2197 (х — 92.6) Найти все а, при которых неравенство тг 4- 6(я2 4- ах)/5 4- cos(x2 4- ах) 4- sin (2х2 4- 2ах 4- тг/З) < 0 выполняется для всех х е [тг/2; Зтг/2].
2198 (/1 — 00.5), Найти все а, при которых уравнение (2а 4- 4)я2 4- (5а 4- 10)я 4- а 4-10 = 0
имеет два различных корня и строго между этими корнями расположен ровно один корень уравнения
(а — 1)я4 — (а — 1)я3 — (а — 7)я2 4- (10а 4- 5)х — а 4-12 = 0.
290
2199 (A — 78.5) Пункт А находится в поле на расстоянии 8 км от прямолинейной дороги, на которой стоит пункт В. Скорость автомобиля по дороге вдвое больше, чем по полю. Если ехать на автомобиле из пункта А по полю до любой точки С, находящейся на дороге, а затем по дороге до В, то на это уйдет времени не меньше, чем если ехать из А в В напрямик по полю. Найти АВ.
2200 (б — 77.4) Трапеция вписана в окружность радиуса R. Центр окружности лежит внутри трапеции, а одно из оснований равно R\/3. При какой боковой стороне площадь такой трапеции максимальна?
2201 (х — 78.3) Найти наибольший объем прямоугольного параллелепипеда, основанием которого служит квадрат, а периметр боковой грани равен 6.
2202 (<р — 86.3) Найти высоту цилиндра, вписанного в сферу радиуса 6 и имеющего наибольший объем.
2203 (7 — 96.5) Найти наименьший объем прямого конуса, описанного около сферы радиуса г, и высоту конуса при этом объеме.
2204 (</>--81.5) Найти высоту и радиус основания прямого конуса, вписанного в сферу радиуса R и имеющего наибольший объем.
2205 (х — 81.4) Два шара единичного радиуса касаются друг друга и боковой поверхности прямого конуса, а также его основания — в точках, симметричных относительно центра. Найти угол между образующей конуса и плоскостью его основания, при котором объем конуса минимален.
ю*
Приложение В.
Варианты заданий 2002 г.
В.1. Механико-математический факультет, март
2206. log^G — х — s2) 4- log2(s2 — 2s 4-1) > 2 log4(s2 — 4s 4- 3)2.
2207. На диагонали AC выпуклого четырехугольника ABCD взята точка О, равноудаленная от прямых АВ, ВС и AD. Найти углы четырехугольника, если Z.AOB = 110°, Z.COD = 90° и ОС = OD.
2208. Найти восемнадцатый член арифметической прогрессии, если первый и одиннадцатый ее члены — натуральные числа, а сумма первых четырнадцати членов равна 77.
2209. Ребро SA пирамиды перпендикулярно ее основанию, которым служит правильный шестиугольник ABCDEF. Вершины В и С удалены от прямой SD на расстояния ^/23/14 и ^/15/14. Найти площадь треугольника ASD и ее отношение к наименьшей из площадей треугольных сечений пирамиды, проходящих через SD.
!у/х — 9ху = 2 z/y — 9yz = б Зх/z — 3zx = 2.
2211. Найти все а, при которых все корни уравнения
б sin (2s — Цтга) 4- sin (Цтга) 4- За3 — 7а2 + За 4-1 = = 2(3а2 — 4а — 1) cos (s — Цтга) 4- б(а — 1) sin s образуют на тригонометрическом круге ровно четыре точки, служащие вершинами трапеции.
В.2. Механико-математический факультет, май
2212. Найти дроби
tg a tg fl tg 7 sin a sin fl sin 7
tga 4-tg/3 4-tg7 sin(a 4-/? 4-7)
если они положительны и одна втрое больше другой.
2213. ^s-s^-l 4- у/х 4- ^1 - 2s 0.
292
2214. Найти расстояние от точки М на боковой стороне CD трапеции ABCD до вершины А, если Z.D = Z.CAD = /ВАМ = = arccos | и АВ = 9.
2215. Найти все а, при которых уравнение
loga+1х + logx(19 - 8а) = 2
имеет хотя бы два корня, а произведение всех его корней не меньше 0,01.
2216. Сфера высекает на ребрах АВ, ВС, CD и DA тетраэдра ABCD равные отрезки КК\ LL', ММ1 и NNf (точки K^L^M и N лежат ближе к прямой АС, чем K^L^M и N). Найти отношение объемов тетраэдра ABCD и пирамиды М'KKrLfесли и /KLM = 90°.
2217. Найти все ж, при которых и 1^7 — целые числа.
В. З. Механико-математический факультет, июль
2218. log2/3^+log1/2^tl >2.
2219. Через центры А и В двух сфер единичного радиуса, касающихся друг друга и третьей сферы радиуса \/б, проведена плоскость, удаленная от центра О третьей сферы на расстояние 1. Найти угол между проекциями на эту плоскость прямых ОА, О В и сравнить его с arccos |.
2220. Велосипедист преодолел расстояние АВ = 75км^причем за 2 км до промежуточного пункта С он заподозрил, что едет медленно, и в пункте С увеличил скорость. Время его движения с каждой из двух скоростей оказалось пропорциональным самим скоростям, а время, потраченное на первые 18 км, — в полтора раза бблыним, чем на последние. Найти АС.
2221. На стороне AD вписанного четырехугольника ABCD взята такая точка М, что AM = 3/2, DM = б, ВМ || CD и СМ || АВ. Найти ВС.
2222. Найти все а, при которых сумма арктангенсов корней уравнения
х2 -I- (1 — 2а)х + а — 4 = 0
больше тг/4.
2223. Найти наименьшее значение выражения (х + у — z)2 при условии
'1 «5 (* + у)2 4/3
< 8 < (у + z)2 9
10 (z + x)2 11.
293
В. 4. Факультет вычислительной математики и кибернетики, апрель
2224. Найти площадь фигуры, заданной системой
Зу — х б < у/Зх 6 — х
2225. |3 - log2(9x2 - ЗОх 4- 25)| log5_3l & > -4.
2226. Одна окружность вписана в треугольник АВС с углом ZB = = arccosj, а другая касается первой окружности, стороны АС ta продолжений сторон АВ и ВС. Найти периметр треугольника, если произведение радиусов окружностей равно 20.
2227. Найти tg |х|, если
(б sin х 4-15 cos х 4- ч/б) (\/б — 2 д/sin |ж|) = 0.
2228. Найти все а, при которых система
(cos(37r\/a2 — х2) = 1
I 2|а®|-Н । 23” 1аж। < 17
имеет наибольшее количество решений.
2229. Найти радиус наибольшего шара, который можно вписать хотя бы- в один параллелепипед, у которого четыре ребра равны по 3, а остальные — по 2.
В.5. Факультет вычислительной математики и кибернетики, июль
2230. Найти все а, при которых уравнение
а4х 4- а2 4- (2 4- \/2)л 4- 2\/2 = п2(п 4- \/2) 4- 4sc
имеет беконечно много корней.
2231. 2 cos(arcsin х) — sin (jarccoss) 0.
2232. Найти угол между прямой АС' и прямой, проходящей через середины ребер АА' = 2 и BfCf = 6 прямоугольного параллелепипеда ABCDA'В'СD' с ребром АВ = 3.
2233. Из пункта А в пункт В в 8.00 отправился пешеход, а в 10.00 — велосипедист и мотоциклист. Скорость мотоциклиста втрое больше скорости велосипедиста. Мотоциклист обогнал пешехода не позднее чем в 10.15, а велосипедист — не позднее чем через 45 мин после
294
этого. В котором часу прибыл в В мотоциклист, если пешеход пришел в В в 14.00?
2234 J /13 cos я 4- 98 sin у — /13 cos х 4- 2,8 sin у = 4
2 /13 cos ж 4- 28 sin у — /70 sin 3/4-8 = 2.
2235. В треугольнике АВС площадью 90/3 AL — биссектриса, а окружность с центром на стороне ВС и радиусом 35 проходит через точки А и L. Найти радиус описанной около треугольника АВС окружности, если АВ2 — АС2 = 216.
В.6. Факультет вычислительной математики и кибернетики (отделения бакалавров), июль
2236. sin 2х 4- 3 cos х = 0.
2237. См. задачу 2230.
2238. 5 • 2х - 3х Зж+1 - 2х+2.
2239. См. задачу 2231.
2240. См. задачу 2232.
2241. См. задачу .2233.
2242. См. задачу 2235.
В.7. Физический факультет, март
2243. 2 sin2 4s tgsins 4- cos 8s = 1.
2244. 2Iog®+1 ((х'Ь1)(9х2+6х'Ь1))_22I°82 3+i°g«+i(3a:+i) । 4 _ q
2245. 0»+4*-*2 < 1.
O — X
2246. Точка С делит хорду АВ окружности радиуса 6 на части АС = 4 и ВС = 5. Найти расстояние от точки С до ближайшей точки окружности.
2247. 15/2ж2 ~ у4 = 4х “ Зу
]^4/2s2 — у4 = Зх — 2у.
2248. Конус с углом а между осью и образующей вписан в двугранный угол 4а: каждая грань содержит ровно по одной образующей. Найти угол между осью конуса и ребром двугранного угла.
2249. При каждом а решить систему
4 log2 х 4- 9 logg у < 4(а2 4- а) logl ху 8(а2 + а).
295
2250. Внутри треугольника АВС с прямым углом С и высотой СН взята такая точка О, что О А = ОВ = а, а середина D отрезка ОС удалена от точки Н на расстояние Ъ. Найти CD.
В.8. Физический факультет, май
99к 1 tog2(4s~3) _ 2
log3r - log3 2 ’
2252. cos8sctgs 4-2sin2 4s = ctgs.
2253. 44/Ж = |s 4-5|.
2254. Биссектрисы BL и СК треугольника ABC co сторонами AB = 14, BC = 6 и AC = 10 пересекаются в точке О. Найти OL.
f2l+1log9y-22l=2
2255. < о
(9 • 2 log27 у - log^ у = 9.
2256. Окружность, проходящая через вершину В треугольника АВС, касается стороны АС в ее середине L и пересекает стороны АВ и ВС, отношение которых равно 3 : 2, в точках М и N соответственно. Найти отношение площадей треугольников ALM vlCLN.
2257. При каждом а решить неравенство
(s2 4- 2х — а2 — 4а — 3)(sin х 4- 2х) > 0.
2258. Ребро SC = 4\/5/5 пирамиды SABC перпендикулярно ее основанию АВС — прямоугольному треугольнику со сторонами АС = 1 и ВС = 2. Сфера касается плоскостей SAC, SBC и АВС, причем последней — в точке отрезка АВ. Найти:
а) радиус сферы;
б) радиус окружности, по которой сфера пересекает грань SAB.
В.9. Физический факультет, июль
2259. cos 5s - cos 15s = ctg 5s.
2260. ®<1.
2261. 15^>1 + (|)1.
2262. Площадь равнобедренной трапеции равна 48. Найти расстояние между точками касания с ее боковыми сторонами вписанной в нее окружности радиуса 3.
2263. Числа ai, аг, аз образуют арифметическую прогрессию, а числа ai — 1, аг 4-1, аз 4-15 — геометрическую. Найти ai, если ai 4- аг 4- аз = 24.
296
2264. На ребре АВ правильного тетраэдра ABCD взята точка Е так, что АЕ : BE = 1:2. Найти радиус сферы, описанной около пирамиды ACDE.
2265. При каждом а > 1 решить неравенство
logi/9(x2 - 6х - а2 - 5а 4- 12) < —1
и найти все а, при которых множество значений ж, не являющихся решениями неравенства, представляет собой промежуток длины, меньшей 2\/3.
2266. Во сколько раз площадь треугольника АВС больше площади треугольника, вершинами которого служат точки касания со сторонами треугольника АВС вписанной в него окружности, если ее радиус втрое меньше радиуса окружности, описанной около треугольника АВС.
В. 10. Химический факультет, май
2267. 2 sin ~ cos f = sin х.
оойй Гз tg ж Ч-40 log3 г/2 = 163
ZZOo. < _ sin(s4-7r/4)
logy 9 cos х
2269. |43х - 24х+2 • 3x+1 4- 20 • 12х • Зх| 8 • 6Х(8Х”1 4- 6х).
2270. Найти радиус окружности, описанной около треугольника АВС, если биссектрисы его углов А и В пересекаются в точке £>, а радиус окружности с центром О, описанной около треугольника ABD, равен 6 и Z.ABO = 30°.
2271. Найти объем усеченной пирамиды ABCDEA'В'С D'Ег, основаниями которой служат правильные пятиугольники со сторонами АВ = 4 и А1 В1 = 2, если объем пирамиды AA'B'C'D'E' равен v.
2272. При каждом а решить уравнение
у/—х3 4- (а — 1)ж2 4- (а — 1)ж 4- а = 2ж2 4- Зх 4- 2 — а.
В.11. Факультет наук о материалах и Факультет биоинженерии и биоинформатики, апрель
2273. Найти все ж, для которых точки графика функции у = —-j-лежат не выше соответствующих точек графика функции у = 2х. 2274. log3(® - 5)2 - 4 = log^z - 1).
2275. у/х2 - Зху + j/2 + 1 + |2®2 + 5ху - 3j/2| = 0.
297
2276. \/3 sin(3x — тг/5) 4-2 sin(8x — тг/З) =
= 2sin(2s 4- Итг/15) 4- 3cos(3s — тг/5).
2277. Диаметр BD = 12\/7 окружности, описанной около остроугольного треугольника АВС с углом В, синус которого равен 2/\/7, пересекает прямую АС в такой точке В, что АЕ : ЕС = 5:7. Из точки Е опущены перпендикуляры ЕМ и EN на стороны АВ и ВС. Найти MN.
2278. Найти все а, при которых неравенство
4х + 4"х + 8 |2Х 4- 2“х - а| 4- На < 26 4- 2а(2х 4- 2"х)
имеет хотя бы одно решение.
В. 12. Химический факультет и Факультет наук о материалах, июль
2279. 41/а! - 5 • 22+1/а= + 64 = 0.
2280. +
(IX - 2| + |у - 1| < 1.
2281. log17_l2 (56 - х2 + 10х) < | (log3+v^(8 + 3/7) + log3+vZ7 2) . 2282. (63 cos2 f — sin2 |) cos2 x = tg2 2x 4- sin2 x.
2283. Из точки К окружности, касающейся в точках А и В сторон угла ZC = 120°, опущены перпендикуляры KL = 4, КМ и KN = 2 на стороны АВ, ВС и АС соответственно. Найти площадь треугольника KLM.
2284. Найти все а, при которых уравнение
2 х • 4 4- sin — + cos — - 2 = а3 - За + а 4- V2 4 4
имеет единственный корень.
В. 13. Биологический факультет и Факультет биоинженерии и биоинформатики, май
2285. 2\/2 sin2(х — к/Ь) — 5 sin х 4- 5 cos х 4- 2 х/2 = 0.
2286. (2|2x"1( - 1)(х/4-2-12х-11 - 3-1) > 0.
2287. Найти радиус окружности, проходящей через вершины А и В треугольника АВС, с углами ZA = a, Z.B = Д и площадью S, и касающейся прямой АС в точке А.
2288. log2 (у/2х2 - 1 4- |х|) log|x+3)(2х2 - 1) log2 |х 4- 3|.
2289. На ребрах AD и ВС куба ABCD А' В'С' D' взяты точки М и N соответственно так, что AM : МD = 2 : 1 и BN : NC = 1:3.
298
В каком отношении делит объем куба плоскость, проходящей через точки М, N и центр грани
В. 14. Биологический факультет, Факультет фундаментальной медицины и Факультет биоинженерии и биоинформатики, июль
2290. |х - 2| > 2х + 1.
2291. sin2 2х 4- sin2 Зх = 1.
2292. Найти площадь треугольника, вершинами которого служат точки касания окружности, вписанной в треугольник со сторонами 4, 6 и 8.
2293. log2 |2х| — 5 log2 |2х| 4- 2|х| log2 |2х| — 4|х| 4-6^0.
2294. Найти все а, при которых уравнение
(х2 + 2(а — 2)х 4- а2 — 4а)2 4-
4- (а 4- 5) (х2 4- 2(а — 2)х 4- а2 — 4а) — а2 4- 8а 4- 2 = 0 имеет:
а) единственный корень;
6) ровно два различных корня.
В. 15. Факультет почвоведения, май
2295. Найти угол между часовой и минутной стрелками в 13.10.
2296. Найти tg За, если sin а = 2 cos а.
2297. 4
2298. Найти все х 6 (0; 2тг), при которых наибольшее из чисел sinx и cos(x4-7t) равно 1/2.
2299. 6 *^^10^.
2300. Найти площадь фигуры, заданной неравенством
х2 + у2 < 2|®| + 4|у|.
2301. Найти радиус сферы, касающейся всех ребер пирамиды с высотой Н и правильным треугольником со стороной а в основании.
В. 16. Факультет почвоведения, июль
2302. |5 - 7х| < 2.
2303. Вычислить cos^1.
2304. Доказать, что если а = \/20 4- >/50, то число а3 — 30а — целое, и найти его.
299
2305. log3 log4 x log9 log2 8x.
2306. Найти все корни уравнения
1 /-л------
у = — V—2 cos ж, V—2 sins
принадлежащие интервалу (—тг; тг).
2307. Найти радиус двух равных окружностей, помещенных в прямоугольный треугольник с гипотенузой с и острым углом а так, что каждая из них касается одного из катетов, гипотенузы и другой окружности.
2308. Найти все а, при которых уравнение
(X3 - 1)(х2 - 16) lg(15a - х) - lg(® - a)
имеет единственный корень.
В. 17. Геологический факультет, май
2309. < 0.
2310, х/6х - я2 - 8 - у/7-2® > - ж2 - 15.
2311. - 5)2 - 8 + 41og5_I(6® - х2 - 5) = 0.
{2 sin(2s + у) sin у = cos 2х
sin 2х — sin 2у = v 2.
2313. В треугольнике АВС с высотой СН = 2 отношение биссектрисы CL прямого угла к медиане СМ равно \/6 : 1. Найти площади треугольников CHL и АВС.
2314. На полевых работах геолог собирает образцы двух типов: образец первого типа весит 3 кг и требует проведения 5 анализов, а второго — 4 кг и 7 анализов соответственно. Какое наименьшее и наибольшее количество образцов суммарным весом не более 149 кг можно собрать, чтобы с ними требовалось провести в общей сложности не менее 249 анализов?
2315. Найти все a > 0, при которых неравенство
а 4- 2х > 5 ах — 4 х
выполнено для всех х > 10.
2316. В правильной пирамиде SABC расстояние между боковым ребром SA и ребром ВС = \/3 основания АВС равно 3\/3/4. Найти отношение площади боковой поверхности пирамиды к площади сферы, проходяшей через вершины S, А и середины ребер АВ, ВС.
300
2318.
В. 18. Геологический факультет, июль
2317. 2£1+L + 1 >
log.-, = 2 х 4- у = ху 4-1.
2319. 32“х 4- 6(ч/3)2-2х > (1/3)^х2+ж-2-3.
2320. Пункт А делит путь между пунктами В и С в отношении АВ : АС = 1 : 2. Из пунктов А и В одновременно навстречу друг другу вышли два поезда. Время движения первого поезда из А в В не менее чем в 6 раз меньше времени движения второго из В в С. Третий поезд, скорость которого равна разности скоростей первых двух, затратил на путь от В до С не менее чем в 9 раз больше временй, чем первый до встречи со вторым. Найти отношение скоростей первого и второго поездов.
2321. Найти все корни уравнения
| sin 2ж| 4- cosх = О,
принадлежащие отрезку [—\/3; 8/3].
2322. На продолжении основания АС = 3 равнобедренного треугольника АВС с биссектрисой CD взята такая точка В, что СЕ = = 4 и Z.CDE = 90°. Найти площадь треугольника АВС.
2323. Найти все а, при которых площадь фигуры, заданной системой
у л/1 -®2 ф| |®|, больше 4 + 2>/2 + тг/2.
2324. На ребрах АА' и АВ единичного куба ABCD А' В'С' D' взя-ты точки М и N соответственно так, что AM = 1/3 и AN = Ъ/А Найти площадь сечения куба плоскостью, проходящей через точки М и N параллельно прямой АС.
В.19. Географический факультет, май
2325. 1/х < 2.
23 26. 22х+1 - 15 • 2х 4-10 = 612х"1 - 1|.
2327. На отрезке, соединящем середины MnN сторон АВ и ВС треугольника АВС соответственно, взята точка К так, что КМ : AM = = 1 : 2 и KN = ВМ. Найти:
а) отношение площадей тругольников АВ К и АСК\
б) ZBCA, если Z.AKC = 90°.
301
2328. Из пунктов А и В одновременно навстречу друг другу выехали грузовик и мотоцикл соответственно. Доехав до преграды С, они вернулись в исходные пункты и одновременно добрались до пунктов назначения по окружной, вдвое более длинной дороге. Если бы они, также одновременно, выехали из пунктов назначения, в точности повторив маршруты друг друга, то оказались бы одновременно в пункте В. Найти:
а) отношение скоростей грузовика и мотоцикла;
б) время их движения до встречи, если мотоцикл добрался до С на 35 мин позже грузовика.
2329. Найти радиус сферы, описанной около тетраэдра ABCD с ребрами АВ = 3, AD = 8, CD = 3, ВС > 9 и углами Z.BAD = = Z.ADC = 90°, если прямые АВ и CD образуют угол в 60°.
2330. Найти все а, при которых уравнение
(а - 1) cos2 х - (а2 4- а — 2) cos х 4- 2а2 - 4а 4- 2 = 0
имеет на отрезке [0; 4тг/3] более одного корня.
В.20. Географический факультет, июль
2331.
2332.
2333.
1Х 21 — г-2-
4 sin х — 3 _
4 sin2 х 4- sin х — 3
Найти два различных корня х 1,2 уравнения
х2 — брх 4- q = 0,
если р, xi, Х2, q — геометрическая прогрессия.
2334. Правые колеса тележки, диаметрами 30 и 40 соответственно, испачкавшись об окрашенную точку А на дороге, оставляют на ней следы, о которые в дальнейшем колеса уже не пачкаются. Найти на отрезке АВ = 10 000:
а) наименьшее расстояние между следами;
б) общее количество следов.
2335. На стороне АС треугольника АВС взята такая точка К, что АК = 8, КС = 1 и ЛВКС = Z.ABC. Найти:
а) ВС;
б) ZC, если радиус описанной около треугольника АВК окружности равен Зч/З.
|х3 = 5x4'1/
2336. <„
I У = 5у 4-х.
302
В.21.
2337.
2338.
Филологический факультет
(отделение лингвокриминалистики), апрель
2x4-1 < 4
х 4- 4 х 4-1 *
Конец диаметра d, стягивающего полуокружность, соеди
нен хордами с двумя точками, делящими эту полуокружность на три равные части. Найти площадь фигуры, ограниченной этими хордами и заключенной между ними дугой.
2339. При каждом прочтении рукописи автор увеличивает ее объем на 10 страниц, а редактор уменьшает на 20%. Найти первоначальный объем рукописи в следующих случаях:
а) после прочтения рукописи автором, а потом дважды — редактором, в ней стало 800 страниц;
б) после последовательного прочтения рукописи автором и редактором, а затем еще раз автором и редактором ее объем остался прежним.
2340. Решить систему
х/3 sin х 2 sin у — cos х
у — х = 7г/б.
Указать те ее решения, которые удовлетворяют уравнению x/sinx (1 — sin 2у) = 0.
2341. Найти сумму корней уравнения
х 4-1 = 2 log2(2x 4- 3) — 2 log4(2002 - 2"х).
2342. При каждом а решить уравнение
х/И+1 - х/Й = а-
В.22. Филологический факультет
(специальность «прикладная лингвистика»), июль
OQ/1Q log»6 ir-arcsin f п
2343’ "7fe(^72) > °-
2344. Найти площадь треугольника АВС с углами 60° и 45°, если радиус окружности, проходящей через середины его сторон, равен 3.
2345. ^/1 4- tg2 х 4- x/2sin(7r/4 — 2х) 4- \/3(cosx — sinx) = 1/ctgx.
2346. Значение а подобрано так, что наименьший корень уравнения
х х3 4- 2х = 4х2 — 4
303
удовлетворяет неравенству
д5г — 4 > а~®2+4г — 4
Решить это неравенство.
2347. В правильную четырехугольню пирамиду, боковая грань которой составляет с высотой угол в 45°, вписан шар радиуса 6. Найти:
а) площадь основания пирамиды;
б) сумму объемов бесконечной серии вписанных шаров, начинающейся с данного, в которой каждый следующий шар касается предыдущего и всех боковых граней пирамиды.
2348. Людоед из племени «Мумбо-Юмбо», словарь которого поначалу составлял 300 слов, на целый год отбился от племени, и его словарный запас каждые полгода (оставаясь целочисленным) уменьшался на одно и то же число процентов. Эллочка Щукина, свободно обходившаяся тридцатью словами, поступила в вечернюю школу и стала узнавать новые слова: ежемесячно — по 20% от того количества, которые одичавший людоед помнил к концу первого полугодия. Какое наименьшее количество месяцев нужно про-, учиться Эллочке, чтобы при данных условиях через год ее словарь наверняка стал богаче словаря людоеда?
В.23. Экономический факультет (отделение экономики), июль
2349. Помещается ли треугольник со сторонами 2, 3 и 2 в круге диаметром \/10?
2350. (1 - 2®/5)7+111-612 > 1.
у — ху — X = 11 ху2 — х2у — —30.
2352. Бригада выполняет задание за 42 дня. Если бы рабочих в бригаде было на 4 больше и работали бы они на 1 ч в день дольше, то задание было бы выполнено не позднее, чем за 30 дней, а если еще на 6 человек больше и еще на 1 ч дольше — то не ранее, чем за 21 день. Найти наименьшую, при данных условиях, численность бригады, а при этой численности — продолжительность рабочего дня.
2353. log2 cos3(tt/6 — х) • log2 cos2s 4- log2(sin5s 4- sins) = 0.
2354. Найти все а, при которых неравенство
V^s2 — 6as 4- 10a2 + ^3 4- 6as — s2 — 10a2
> tfy/За + 24 - 3/v/2 + |y - y/2a2\ + |j/ - V3a\ имеет единственное решение.
2351.
304
2355. Найти объем общей части двух единичных кубов, имеющих общую вершину и расположенных так, что ребро одного куба лежит на диагонали другого и наоборот.
В.24. Экономический факультет (отделение менеджмента), июль
2356. Найти площадь треугольника АВС со сторонами АС = 3, ВС = 6/х/З и углом ZB = 60°.
2357. (1 - 2®/5)7+111-6а:2 = 1.
2358. См. задачу 2351.
2359. Бригада выполняет задание за 42 дня. Бели бы рабочих в бригаде было на 4 больше и работали бы они на 1 ч в день дольше, то задание было бы выполнено за 30 дней, а если еще на б человек больше и еще на 1 ч дольше — то за 21 день. Найти численность бригады и продолжительность рабочего дня.
2360. logy^sinx logy^ ctg х 4-log2(l + cos2x) = 0.
2361. См. задачу 2354.
В.25. Экономический факультет (вечернее отделение), июль
2362. См. задачу 2356.
2363. См. задачу 2350.
2364. См. задачу 2351.
2365. См. задачу 2359.
2366. См. задачу 2360.
2367. См. задачу 2354.
2368. Найти объем общей части двух единичных кубов, имеющих общую вершину и расположенных так, что ребро одного куба лежит на диагонали грани другого и наоборот, а среди плоскостей граней кубов нет совпадающих.
В.26. Факультет психологии, июль
2369. у<г + 1 > х - 2.
2370. logl+1(x2 + Зх - 10) > 2.
2371. 22'+ (1/2)2'-1 = 3.
2372. На катете АС прямоугольного треугольника АВС как на диаметре построена окружность, пересекающая сторону АВ в точке Е.
305
На стороне ВС взята такая точка F, что BF = 2CF, а отрезок AF пересекает окружность в такой точке G, что прямые EG и АС параллельны. Найти FG.
2373. cos 6s — 3 cos 5s + cos 4s — 4 cosх 4- 5 = 0.
2374. |s3 4- 7s2 - Ils - 6| 4- |s3 - 12s2 - 5s 4- 3| = 18s2 - 2s - 13.
B.27. Институт стран Азии и Африки (социально-экономическое отделение), июль
2375. ^^^0.
2376. sin 8s 4- 2 sin 5s cos s = 0.
2377. s \/2 - x s2 - s - 2 - \/2 — s.
2378. |loga.+1 2 + log2 | + |*°ё2(4® + 4) + logl+1 2| < %.
2379. Найти медиану AM треугольника ABC co сторонами AB = 8, BC = 6 и биссектрисой BL = 6.
2380. Решить систему ,
{arcsin 3s 4- arccos 2y = тг/4 arccos 3s arcsin 2y = 5tt2/64
и для каждого решения сравнить: 3s — 2у V 1/2 — $2.
2381. Найти все а, при которых система
(х2 4- у2 - 6|s| - 6|j/| 4-17 0
(s2 4- у2 — 2у = а2 — 1
имеет хотя бы одно решение.
В.28. Социологический факультет, июль
2382. x/3s 4-10 = х 4- 2.
2383< 1о*Ц^з+^+х-14 1оЧ t-®2 + 5® - 6) < 0.
2384. Найти угол А треугольника АВС со сторонами АВ = 2, АС = 4 и медианой AM = \/7.
2385. Куплен товар двух сортов: первого на 1200 руб, а второго на 1500 руб, причем второго — на 10 кг больше и на 20 руб/кг дешевле, чем первого. Сколько куплено товара первого сорта?
2386. Основанием пирамиды, вписанной в шар радиуса Я, служит квадрат. Одно из боковых ребер пирамиды перпендикулярно плоскости основания, а наибольшее ребро образует с ней угол а. Найти
306
боковую поверхность пирамиды и вычислить ее при R = >/17 и а = arcsin ^/8/17.
2387. Найти все а, при которых уравнение
(1 + л)ж2 -Ь (1 — л)ж + (а + 3) = О
имеет хотя бы один корень и все его корни — целочисленные.
В.29. Факультет государственного управления (специальность «антикризисное управление»), июль
2388. Первую половину пути из деревни в город турист преодолел пешком со скоростью 5 км/ч, а вторую — на автобусе со скоростью 45 км/ч. Найти среднюю скорость туриста.
2389. 9® — 2 • 3®+1/2 -9 = 0.
239°. - -g--1— < 3 - х.
9 —"Г
2391. На окружности диаметром 10, описанной около правильного треугольника, взята точка, удаленная от одной из его вершин на расстояние 9. Найти сумму расстояний от этой точки до двух других вершин треугольника.
2392. За сколько часов два экскаватора вместе выкапывают котлован, если в одиночку они делают это на 4 ч и, соответственно, на 9 ч дольше?
2393. Найти все а, при которых система
Г (ЗУФ1 + 11/1 - 3)(|х| + 3|j/| - 9) = о,
((а: - а)2 + у2 = 25
имеет ровно три различных решения.
2394. Пятеро пиратов делят между собой 10 монет: сначала свой вариант дележа предлагает самый старший из них, и если с ним не согласно большинство пиратов, то его вариант отвергается, затем свой вариант дележа предлагает самый старший из оставшихся пиратов, и если больше половины из них с этим вариантом не согласны, то он также отвергается, и т. д. Как в итоге распределятся монеты между пиратами, если каждый из них руководствуется только желанием получить как можно больше монет?
Приложение Г.
Варианты заданий 2003 г.
Г.1. Механико-математический факультет, март
2395. Найти первый член целочисленной арифметической прогрессии, сумма первых шести членов которой отличается от суммы следующих шести членов менее чем на 450, а сумма первых пяти членов которой превышает более чем на 5 сумму любого другого набора различных членов.
2396. yggoZ.O3.
2397. На продолжении биссектрисы AL треугольника АВС за точку А взята такая точка В, что AD = 10 и Z.BDC = Z.BAL = = 60°. Найти площадь треугольника АВС. Какова наименьшая площадь треугольника BDC при данных условиях?
2398. Найти площадь фигуры, заданной системой
Г+ 3 - 2®-1| + |у + log2 ®| = |21-1 - 3 + log2®|
(I® - 1| + |х - 3| + |у| = 2 - у.
2399. Точка О расположена в сечении АА'С'С прямоугольного параллелепипеда ABCDА'В'CD' размером 2x6x9 так, что Z.OAB 4- Z.OAD 4- Z.OAA' = 180°. Сфера с центром О касается плоскостей А'В'С', АА1 В и не имеет общих точек с плоскостью AA’D. Найти расстояние от точки О до этой плоскости.
2400. Найти все а, при которых расстояние между любыми двумя соседними корнями уравнения
cos a cos Зх — sin За sin х 4- 2 sin 2а cos 2х = 3 sin а
не превосходит тг/З.
Г.2. Механико-математический факультет, май
2401 • |7-log3 Зх| + |4 —logg 9x21 |logg^81x|*
2402. cos f yj5 cos(2s — тг) 4- 8 sin (x 4- f) — 5 4- sin | x/2 cos x = 0.
2403. На высоте BH треугольника ABC с углом ZB = 50° и стороной ВС = 3 взята такая точка В, что Z.ADC = 130° и AD = = х/З. Найти угол между прямыми AD и ВС, а также Z.CBH.
308
2404. Уравнение 21+х+p + g21_a: = О имеет ровно два различных корня, а их сумма равна 4. Найти произведение всех различных корней уравнения (х2 — 5х — 300)(ж2 — рх — q) = 0.
2405. Найти объем пирамиды SABCD с боковыми ребрами AS = = BS = CS = 2 и ребрами основания АВ = ВС = 8/5, вписанной в сферу радиуса 5/3, касающуюся линии пересечения плоскостей ASD и BSC.
2406. Найти все а, при которых неравенство
1обх + 1обх-1 > 0
имеет хотя бы три целочисленных решения.
Г.З. Механико-математический факультет, июль
24°7-
2408. |5logl 122 - xlog5 х 4- 614| = 636 - 5log’ 122 - xlog« х.
2409. Найти целочисленный знаменатель конечной геометриче-ской прогрессии, первый член которой меньше последнего, но не более чем на 17, а сумма членов которой со второго по последний не меньше 26.
2410. Через вершины АиВ треугольника АВС проведена окружность, касающаяся прямой ВС, а через вершины В и С — окружность, касающаяся прямой АВ. Продолжение их общей хорды BD пересекает отрезок АС в точке В, а продолжение хорды AD одной окружности пересекает другую окружность в точке F. Найти АЕ : ЕС, если АВ = 5 и ВС — 9. Сравнить площади треугольников АВС и ABF.
2411. Найти все а, при которых уравнение
sin arccos(5s) = а + arcsin sin(7s — 3)
имеет единственное решение.
2412. Высота АН тетраэдра ABCD пересекает его высоту BE, но не лежит в одной плоскости ни одной из других его высот. На отрезке НЕ = 4 взята точка О, равноудаленная от граней тетраэдра, образующих двугранный угол 30° при ребре CD = 5. Найти площадь сечения тетраэдра, проходящего через точку О и являющегося прямоугольником.
Г.4. Факультет вычислительной математики и кибернетики, апрель
2413. Найти знаменатель геометрической прогресси, сумма первых тридцати членов которой равна увдвоенной сумме первых десяти членов.
309
2414. Найти углы при основании АС равнобедренного треугольника АВС, если отношение расстояний от центра вписанной в него окружности до вершин А и В равно к. При каких к задача имеет решение?
{x/sinrr х/cos3 х + sin2 х
тг/4 < |ж — 7г/2| 2тг.
2416. Найти диагонали сечения прямоугольного параллелепипеда ABCDА'В'СD' с ребрами АВ = a, AD = b и АА' = с, проходящего через точки А, С', пересекающего ребро В В1 и имеющего при этом наименьшую площадь..
2417. Найти все а, при которых система
{^2®2+3i/2 — 4r-|-8i/+16 । g!/24-8x — 5 • 5х2+2®+4i/-|-4
x2 4- у2 4- 12s — Sy = a
имеет хотя бы одно решение, причем все они удовлетворяют условию 2х 4? Зу 0.
2418. arcsinsins 4- 2arccoscoss х — 5.
Г.5. Факультет вычислительной математики и кибернетики, июль
2419. logs-» > -1.
2420. x/sins sin3s = cos я.
2421. Найти область значений функции
/(s) = у/х2 - Зх 4- 2 - х.
2422. Через ближайшую к вершине S правильной пирамиды SABCD точку вписанной в нее сферы радиуса 2х/б и через точку касания сферы с боковой гранью SAB проведено сечение пирамиды, параллельное ребру АВ = 12х/2 ее основания. Найти площадь этого сечения.
2423. Найти все а, при которых система
{£х__2х+у <С le^a-iei
5.2Х+* - 9 • 4* > 54 имеет хотя бы одно решение.
2424. На стороне AD = у/3 4-1 параллелограмма ABCD с углом ZA = 60° взята точка М, а на стороне АВ = 3 — такая точка ЛГ, что AN : NB = 2:1. На прямой, проходящей через точку N параллельно AZ), внутри параллелограмма взята такая точка L, что AM = LN. Прямые ВМ и CL пересекаются в точке К. Найти Z.BNK.
310
Г.6. Факультет вычислительной математики и кибернетики (отделения бакалавров), июль
2425. 3|х 4-2| --4|х 4-1| 2.
2426. См. задачу 2419.
2427. См. задачу 2420.
2428. При каждом а решить уравнение 4х 4- 25х а = 3 • 10х.
2429. См. задачу 2421;
2430. См. задачу 2422.
2431. См. задачу 2424.
Г.7. Физический факультет, март
2432. cos Зх — 2 sin 2х — cos х — sin х — 1 = 0.
2433. 7log3(2 4- х)8 < 8 log2(—х 4-1)7 log3 2.
2434. (4* - 2 • 2* - 3) log2 а: - 3 > 4^ -4*.
2435. В равнобедренный треугольник АВС с основанием АС = = 4\/3 вписана окружность радиуса 3. На высоте ВН взята такая точка Z), что DH = 2, а продолжение отрезка AD пересекает окружность в точке Е. Найти DE.
{17 । 12 _ о
2хй4-3у ' Зх2 —2у
6 I 34 о
Зхй-2у 2х2+3у ~ °"
2437. Найти наименьшую сторону треугольника площадью 6\/6 и периметром 18, если расстояние от центра вписанной в него окружности до одной из его вершин равно 2\/42/3.
2438. При каждом а решить уравнение у/х 4- у/у/а — ху = а.
2439. Найти площадь сечения АВС' правильной призмы АВСА'В'С' объемом 4 с основанием АВС, а также радиус описанной около нее сферы, если в пирамиду С'АА'В'В можно вписать шар.
Г.8. Физический факультет, май
2440. 2 sin(6 cos х cos 2х — 3 cos Зх) = 1.
2441. 7l’=27
1 [5s •4l+1 = 32.
2442. logj 1 (x2 ~ 5a: + 6) < log20 5.
311
2443. Биссектрисы AL и В К треугольника АВС со сторонами АВ = с, ВС = а и АС = Ъ пересекаются в точке N. Отрезки KL и CN пересекаются в точке М. Найти LM : МК.
2444. х/12х2 4- 42х 4-1 4- |2х2 4- 7х| > 9.
2445. Окружность касается боковых сторон АВ и ВС равнобедренного треугольника АВС в точах М и 2V, а также описанной около него окружности. Найти MN : АС, если ZB = а.
2446. При каждом а решить неравенство л/7 - loga х2 >(1-2 log|x| a) loga x.
2447. Найти радиус сферы, касающейся плоскости оснрвания АВС правильной пирамиды SABC с ребром АВ = а в точке С, а бокового ребра SA — в такой точке М, что SM : МА =1:2.
Г.9. Физический факультет, июль
2448. tg2 х — б cos 2х = 6.
2449. |х2 4- Зх| 4- х2 - 2 > 0.
2450. log25(5x - 1) log5(5x+2 - 25) < 4. •
2451. Биссектриса угла В трапеции ABCD со средней линией MN = \/5 пересекает боковую сторону CD в точке N. Найти BN, если AN = 4.
9449 I = 9 - I® + 2у|
4- 4у — 2) 4- 2/(4?/ 4- 2) = 41.
2453. Точка О — центр окружности, вписанной в треугольник АВС с углом ZA = а. Луч АО пересекает описанную около треугольника окружность радиуса R в точке D. Найти OD.
2454. При каждом a > 1 решить неравенство
212а-11.ж2-2ж-Ц П г2 — (а — 2)® — 2а
2455. Сфера радиуса 5/(4\/14) касается плоскости основания АВС пирамиды SABC и всех ее боковых ребер, деля их в равных отношениях, считая от вершины S. Найти объем пирамиды, если АВ = 5, ВС = 9 и АС = 10.
Г. 10. Химический факультет, май
2456. Найти все а, при которых уравнение
ах2 4 (а4 1)я 4-1 = 0 имеет единственный корень.
2457. х log3 х 4-1 log3 х log2 3 4- х log3 2.
312
2459. Найти объем тетраэдра ABCD с ребрами AD = 3, CD = 5, прямыми углами /ABD, /.CBD, /ВАС и двугранным углом тг/12 при ребре АС.
2460. Найти все целочисленные решения системы
{ж3 — Зу2 — 4х + 18у — 26 > О
х3 4- у2 — 4х — Зу 4-14 < 0.
2461. Окружность, вписанная в пятиугольник ABCDE с целочисленными сторонами, касается стороны ВС в точке К. Найти ВК, если АВ = 1 и CD = 3.
Г.11. Химический факультет и Факультет наук о материалах, июль
2462. Найти все а, при которых х = 1 — одно из решений неравенства -2— > 0.
х—а
2463. cos2 8х 4- sin2 х = 2 sin2x cos2 8х.
2464. log^+v^(2 - |х - 1|) > log^jo(2® - х2).
2465. (1 + (1 + + х/Г+7) = 8
2466. Расстояние от центра окружности, описанной около четырехугольника ABCD с перпендикулярными диагоналями, до стороны АВ равно 2. Найти CD.
2467. Найти все а, при которых уравнение
'(х + \/2г)2 + (у + x/2t)2 = 25 + 2ау/25 - а2
< х2 + у2 — а2
г2 +12 — (25 — а2)/2 имеет хотя бы одно решение.
Г.12. Факультет наук о материалах, апрель
2468. Т • 5^ = 100.
2469. log1/3 (1 + (х2 - Зх + 2)2) = х/х2 - 6х + 8.
2470. ^т^З.
2471. На ребрах В В' = DD' = 3 куба ABCDA'B'C'D' взяты такие точки М и N соответственно, что ВМ : МВ' = DN : ND' = = 2:1. Найти все диагонали сечения куба плоскостью AMN.
2472. Найти количество членов арифметической прогрессии ai,...,a8i с первым членом тг/4 и разностью Зтг/10, для которых система
313
x sin an + у cos an = 1
xtgan - yctgan = 1
не имеет решений.
2473. Автомобиль треть пути в одну сторону шел со скоростью ж, а остальные две трети — со скоростью у. На обратном пути он половину времени шел со скоростью ж, а вторую половину — со скоростью у. Каким при этом могло быть отношение а > 1 его средней скорости движения туда к средней скорости движения обратно?
Г. 13. Биологический факультет, апрель
2474. log2(l 4- 2х) = 14- log2 х.
2475. 1 - «/£=£ < х.
у 7—4 2!
2476. В работе симпозиума в первый день участвовали биологи и математики. Во второй день математиков прибавилось, отчего их доля изменилась на 1/20. В третий день прибавилось биологов, отчего доля математиков изменилась на 7/100, став на 1/25 меньше первоначальной доли биологов. Найти долю биологов в первый день.
2477. 4 • з2х+г/2х - 8 . зх+У*х 4- 2 = |4 • 3®+1/4х - 1|.
2478. На сторонах АВ и ВС квадрата ABCD взяты точки М nN соответственно так, что отрезки AN = 3 и DM = 4 пересекаются в точке О, причем cos Z.DOA = q. Найти площадь квадрата.
2479. Найти все а, при которых система
- |ж - 1* 2| - |ж - 22| - ... - |ж - 20321 = 0
< у2 4- (а - 5 • 106 * *)у 4- 25 • Ю10 = 0
z2 4- 5 • 103 * *z 4- а = 0
хотя бы одно решение.
Биологический факультет, Факультет фундаментальной медицины и Факультет биоинженерии и биоинформатики, июль
2 cos2 (х 4- тг/4) 4- 3 cos(2s 4- тг/2) = —3.
у/х2-2 > -
4—2г
0og„ у/2х log4 х = -1.
Два мотоциклиста стартовали одновременно по общей трас-
се, а третий задержался на старте и выехал позже, со скоростью
в 8/5 раза большей скорости того мотоциклиста, который пришел
имеет
Г.14.
2480.
2481.
2482.
2483.
314
к финишу первым. Третий финишировал через 4 ч после момента общего старта, но на 2 ч раньше второго, которого он догнал за 1 ч своего движения. Во сколько раз скорость первого мотоциклиста превышает скорость второго?
2484. Через вершины А, В и С ромба ABCD проведена окружность с центром О, а через вершины А, В и D — еще одна, с центром Q. Найти /DAQ, если OQ : AQ = 4.
2485. (3 -х)log2(l + ^/7)*2+3*+2 > log3(8 + 2</7)(1+1)'/гтт.
Г. 15. Факультет биоинженерии и биоинформатики и Географический факультет, май
2486. ctg(117r/2 - 4х) 4- tg х = у/3 (1 - .
2487. В треугольнике ABC AL и AM — биссектриса и медиана соответственно. Найти LM, если /.ВАМ = 45°, /САМ = 30° и BL = 6.
2488. < х 4- 3(л/2 + 1) - |* + 3(v^4-1)|.
2489. Два трактора начали одновременно пахать каждый свое поле. Когда первый трактор, производительностью 0,93га/день, вспахал свое поле, второму осталось вспахать еще хга. Если бы они с самого начала поменялись полями, то когда бы первый закончил работу, второму осталось бы вспахать еще у га. Разность площадей полей, на которых работали первый и второй тракторы, соответственно, на 25% меньше (у — х) га. Найти производительность второго трактора.
2490. Плоскость, параллельная оси цилиндра, делит границу его нижнего основания в отношении 2:1. Сфера касается этой плоскости, боковой поверхности и обоих оснований цилиндра в точках, лежащих в одной плоскости с его осью. Найти отношение объемов цилиндра и сферы, если оно больше 5\/23.
2491. Найти все а, при которых числа
Т—-—5, х/16 - a2 cos 36, 15- a21-|c|
1О61/343 3
определены, но ни при каких b и с не образуют арифметическую прогрессию.
Г. 16. Факультет фундаментальной медицины, май
2492. log_1_x(4x 4-25) = 2.
2493. Найти все ж, при которых sin ж, tgs, 1/cos ж — геометрическая прогрессия.
2494. \/2 — х — \/4 4- х \/х 4- 3.
315
2495. Окружность с центром О касается сторон угла А в точках В vl С. Отрезок АО пересекается с окружностью и с хордой ВС в точках D и F соответственно, а прямая BD с отрезком АС — в точке Е. Найти Z.BCO, если площадь четырехугольника CEDF равна площади треугольника ABD.
2496. Найти область значений функции
2497. Найти все а, при которых хотя бы для одной пары чисел Ь,с функция
f{x) = сж4 + a(ab — 1)ж3 — 2Ъ — 2
не удовлетворяет хотя бы одному из условий /(—1) —2Ъ или
/(1) < -2-
2498. Количество сотрудников фирмы ежегодно возрастало в одно и то же число раз и за б лет увеличилось» на 20 615 человек. Найти первоначальную численность сотрудников фирмы.
Г. 17. Факультет почвоведения, май
2499. log^* - 1) - log^* - 1) = 2.
2500. \/3sin2s 4- 2 sin2 x = 1.
2501. Найти двузначное число, если после его деления на сумму его цифр получилось в частном бив остатке 8, а после деления числа, записанного теми же цифрами, но в обратном порядке, на разность его цифр получилось в частном 15 и в остатке 2.
2502. Найти все целочисленные решения уравнения х2 4- 5у2 4- 34z2 4- 2ху — 10sz — 22yz — 0.
2503. 10g_4x24-12x-8 14® — 5| > 0.
2504. Найти периметр и площадь сечения куба ABGDA'В'С'D' с ребром а, проходящего через точки А и В' параллельно диагонали А'С.
Г. 18. Факультет почвоведения, июль
2505. cos2 4х — 2 cos 4ж — 3 = 0.
2506. + = 1
[71’' 4-log/® -у) = 1
2507. |®2 - |®| 0.
2508. Найти наименьшее значение функции f(x) = УЗт2 4- 5 — л/3:г2
на отрезке [0; 3].
316
2509. Треугольник АВС вписан в окружность с диаметром АВ = = 4, а в его угол В вписана вторая окружность радиуса 3/4, касающаяся первой внутренним образом. Найти ZB.
2510. Найти все а, при которых отрезок [0; 3] содержится в множестве решений неравенства
<°-а— лх
Г. 19. Геологический факультет, апрель
2511. sin(s — тг/6) + 2 cos2 х = 1.
2512. log_2_x(-3 - 2х) > log_2_x(-3s/2).
2513. Найти сумму членов целочисленной геометрической прогрессии, 51, Ьг, Ьз с целым знаменателем, если она не является возрастающей, но Ьз на 39 больше, чем
2517.
2515. Окружность, проходящая через вершины В и С треугольника АВС, пересекает стороны АВ и АС в точках М и N соответственно. Найти ZA, если ZC = тг/З, Z.BNC = тг/4 и ВМ = 2MN.
2516. Найти все а, при которых уравнение
2тг2 (х — I)2 + 4а cos 2тпг — 9а3 = О имеет единственный корень.
22~х = 4?/5/2
у/х2 Ч- у2 + 1 - 2я Ч- у/х2 Ч- г/2 — бгг — 2?/ Ч- 10 = \/5 -
2518. Основанием пирамиды SABC служит правильный треугольник АВС со стороной \/3, а боковое ребро SA = \/3/3 перпендикулярно плоскости основания. Найти расстояние между прямыми АВ и SC.
Г.2О. Геологический факультет, июль
2519. -g.TL2. 4. 2z+5 < 0 |х42| х+2 и’
2520. 4;е+1/2 _ уг —1/2 = 7г41/2 _ 22®+1.
2521. Из пункта А в пункт В вышел пешеход и одновременно из В в А — другой, причем через 50 мин они встретились, а прибыли в пункты назначения с интервалом в 4 ч. Сколько часов был в пути каждый из них?
2522. fix2 - у2 + 3 = 0 1 6j/3-18j/-13®3 -Зх = 0.
317
2523. Прямоугольный треугольник АВС с катетами АС = 2 и ВС = у/2 вписан в окружность, хорда CD которой пересекает отрезок АВ в такой точке В, что АЕ : АВ = 1:4. Найти площадь треугольника ABD.
2524. x/cos Зх log4 tg(x 4- \/3/2) = 0.
2525. Найти все а, при которых уравнение
3*х2 _ За + з4-«х2 = 9бх + 34-а
имеет хотя бы один нечетный (целый) корень.
2526. Высота SH правильной пирамиды SABCD в \/5 раз больше ребра ее основания. Через ребро SA проведена такая плоскость, пересекающая ребро ВС, что площадь сечения ею пирамиды минимальна. В каком отношении эта плоскость делит объем пирамиды?
Г.21. Географический факультет, июль
2527. Найти отношение десятого члена знакочередующейся геометрической прогрессии к пятому, если разность ее девятого и третьего членов равна шестому члену, умноженному на 24/5.
2528. ^>7 + ®.
2529. Какое наименьшее количество элементов может содержать множество натуральных чисел, в котором доля четных чисел меньше 2/3, а нечетных — не больше 36%?
2530. Найти площадь выпуклого четырехугольника ABCD и сравнить ее с 2\/15, если отрезки, соединяющие середины его противоположных сторон, перпендикулярны, причем АС = 4 и Z.CAB = = Z.DBA = 75°.
2531. Найти все а, при которых уравнение (sin х — log4 a) (sin я — 2 4- 2а) = 0
имеет на отрезке [тг/2; 5тг/2] ровно два корня.
Г.22. Филологический факультет (отделение лингвокриминалистики), март
2532. (2х 4- 5)"1 < (2х+3 - 2)”1.
2533. .Сколько различных корней на отрезке [—2; 0] имеет уравнение sin 5тгх 4- cos 2тгх = 0?
2534. Найти разность арифметической прогрессии ai, аг,..., удовлетворяющей для некоторой геометрической прогрессии 61,6г,••• равенствам
ai = bi, a4 = Ьз, агаз — = 8.
318
2538.
2535. Зная углы Z.DAC = a, Z.ABD = /3 и сторону CD = с вписанного четырехугольника ABCD, найти площадь треугольника ACD.
2536. Вовочка написал домашнее сочинение, допустив ряд орфографических и пунктуационных ошибок. Его сестра исправила часть ошибок, от чего количество пунктуационных ошибок оказалось в пределах от 15,5% до 18% прежнего их числа, а количество орфографических — уменьшилось втрое, составив 25% от прежнего числа пунктуационных.
а) Могло ли в новом тексте содержаться ровно 6 ошибок?
б) Какое наименьшее число ошибок содержалось в первоначальном тексте?
Г.23. Филологический факультет (отделение теоретической и прикладной лингвистики и отделение лингвокриминалистики), июль
2537. cos 4ж = cos4 х — sin4 х.
З®3+8 cosy = 27х2+2х |cosу\
2 sin у = log2 х.
2539. В равнобедренном треугольнике АВС с основанием АС = 1 медианы AM и CN пересекаются в точке D под прямым углом. Найти ZA и площадь четырехугольника BMDN.
2540. В двух студенческих группах одинаковой численности каждый студент изучает хотя бы один из языков: английский или французский. Количество изучающих английский язык в первой группе вчетверо больше, а французский — втрое меньше, чем во второй, причем не менее чем по 5 студентов в каждой группе изучают оба языка. Каково минимальное число студентов в группе при этих условиях?
2541. Найти все а, при которых для любого b неравенство (х - 2а - Ь)2 + (у - а - 36)2 < 1/2
имеет хотя бы одно целочисленное решение.
Г.24. Экономический факультет (отделение менеджмента), апрель
2542. 2 • 4х — 31 • 2х — 16 = 0.
2543. Три раза с интервалом в неделю фермер скашивал одно и то же количество травы на лугу, еженедельный прирост травы на котором составлял 10%. Какой процент составила масса всей скошенной травы от ее количества перед первым покосом, если в итоге она уменьшилась на 78,3%?
319
2544. В правильном треугольнике АВС со стороной 1 АН — высота, а углы прямоугольного тругольника AHD образуют арифметическую прогрессию. Какова наименьшая площадь общей части этих треугольников при данных условиях?
2545. 6х ч/1 - 9ж2 + 18х2 - Зу/2х -1-0.
2546. Найти все а, при которых уравнение
a2 sin _ х) + sin2 (- а\/4х2 4- 8 - 8х = \ 2 / a-f-1 у
= 3 4- arcsin |1 — ж|
имеет единственный корень.
Г.25. Экономический факультет (отделение экономики), июль
2547. х/5 - 4х - х2 -2х - 1.
2548. Найти если х 4- у = —12 и ху = 2.
{4 • 49х — 4 • 7х+у log7 3 4- 9У = 9
49” 4-12 • 3® logs 7+у - 4 9V = 9.
2550. На первом складе сахара было больше чем соли на 16 т, а на втором — на 4. С первого склада вывезли 1/п часть сахара и 1/3 часть соли, а со второго — 1/п и 1/5 соответственно, причем с первого склада сахара вывезли на 2 т больше чем соли, а со второго — на 3. При каких целых п это возможно? Сколько соли при этих п было вначале на каждом складе?
2551. Найти площадь четырехугольника ABCD, если АВ = ВС = = 3 A AD = DC = У13, а вписанная в угол Z.ABC = 60° окружность проходит через вершину D.
2552. Найти все а, при которых уравнение
3 А+2 - 16а2 ^32я 4- 32 = ^х2 4- Зх 4- 2
имеет единственный корень.
2553. Какого наибольшего объема многогранник, имеющий ровно пять вершин, можно поместить в шар радиуса 2 А?
Г.26. Экономический факультет (отделение менеджмента), июль
2554. х/5 - 4х - х2 = -2х - 1.
2555. Найти А + А, если х 4- у = 12 и ху = 6. х у
Г 3 • 4* + 2®+1 • Зу - 9У = 0
2556. <
| 2 • 4* - 5 • 2* • Зу + 9У = -8.
320
2557. На складе сахара было на Ют больше чем соли. С него вывезли 1/п часть сахара и 1/3 часть соли, причем сахара вывезли на 2 т больше чем соли. При каких целых п это возможно? Сколько соли при этих п было вначале на каждом складе?
2558. Найти площадь четырехугольника ABCD, если АВ = ВС = = 8, AD = DC = 6, а описанная около треугольника АВС окружность радиуса 5 не проходит через вершину D.
2559. См. задачу 2552.
Г.27. Экономический факультет (вечернее отделение), июль
2560. 2561. 2562. 2563. 2564. 2565. 2566. См. задачу 2547. См. задачу 2548. См. задачу 2556. См. задачу 2557. См. задачу 2551. См. задачу 2552. См. задачу 2553.
Г.28. Факультет психологии, июль \
2567. 1063x4-3 5 = 2.
2568. sin Зя sin ж = —1/8.
2569. |3х + 1| + у/Зх + 4 < 3.
2570. Найти диагональ и площадь трапеции с меньшим основанием 4, вписанной в окружность радиуса у/7, если параллельная основаниям хорда длиной 5 проходит через точку окружности, касательная в которой параллельна одной из боковых сторон трапеции. 2571. При каких а уравнение 2|ж—9а| — 2а2+35+х = 0 не имеет корней? При каких (остальных) а все решения этого уравнения принадлежат отрезку [—30; 63]?
Г.29. Институт стран Азии и Африки (социально-экономическое отделение), июль
2572. Найти область значений выражения 4ж~2»“1 — 4у 4. 4х — 4
при 3^х^4и1^у^2.
2573. (|х| — 5)2 - |5 - х| = 30.
11 И. Н. Сергеев — Математика
321
2574. В правильный треугольник АВС со стороной а вписана окружность, которая в точках касания с его сторонами касается внешним образом трех окружностей того же радиуса с центрами D,E vlF. Найти площадь общей части треугольников АВС и DEF. 2575. Найти корни уравнения tg(s + тг/4) 4-1 = 2 (\/2 4-1) ctg х, принадлежащие отрезку [тг/4; 7тг/4].
2576. ^(l/2)x/log4«2 (2®2) log8as4(4®4)—1 - 1^ х
х у/(х2 4- 8я 4- 15)(256х2 - 24х - 1) 0.
2577. Какой промежуток наименьшей длины и при каких а и Ъ представляет собой область значений функции f(x) = |^(х)| на отрезке —1 х С 1 при условии, что |а — 6| 1 и функция
д(х) = х2 4- 2(а — Ъ)х 4- За — b удовлетворяет условиям д(1) • д(—1) 0?
Г.30. Социологический факультет, июль
2578. \/2х 4“ 3 4- \/х — 2 — \/Зх 4- 7.
2579. | log0, j (6 + х) < log0> Iх-
2580. Найти сторону АВ четырехугольника ABCD со стороной CD = 3 и взаимно перпендикулярными диагоналями, вписанного в окружность радиуса 2.
2581. В начале предвыборной гонки предпочтения избирателей распределялись по трем кандидатам на должность мэра, как 1:2:1, а в конце — как 5:5:6, из-за отказа от голосования 40% избирателей (остальные избиратели своего мнения не меняли). Сколько процентов сторонников каждого кандидата отказалось от голосования?
2582. Двое рабочих изготовили в общей сложности 316 деталей, причем первый работал на 3 дня дольше, но изготовил на 4 детали меньше второго, так как делал в день на 2 детали меньше. Сколько деталей он делал в день?
2583. Найти все а, при которых уравнение
(1 4- а)х2 4- (1 — а)х 4- (а 4- 3) = 0
имеет три различных корня, образующих геометрическую прогрессию. Найти эти корни.
Г.31. Факультет государственного управления (специальность «антикризисное управление»), июль
2584. На одну автозаправочную станцию со склада ежедневно нужно поставлять 8 т бензина, а на вторую, расположенную на
322
расстоянии Зкм первой, — 4 т. Где выгоднее всего разместить бензосклад?
2585. |2х 4- 8| > 8 - |1 - х|.
2586. Три предприятия на равных началах прокладывают 16 км дороги. Первое проложило 10 км дороги, второе — 6, а третье внесло свою долю деньгами, уплатив 16 млн. руб. Как разделить эти деньги между первым и вторым предприятиями?
2587. На гипотенузе АВ прямоугольного треугольника АВС взята такая точка Z), что AD, CD, BD — геометрическая прогрессия с первым членом 1 и знаменателем \/2. Найти Z.BCD.
2588. Для каждой пары чисел а и Ъ решить неравенство
Ьх2 4- а 0.
2589.
х 4- у 4- z = 2 2ху — z2 = 4.
2590. Может ли семья из четырех человек пройти по мосту быстрее, чем за 32 мин при следующих условиях: идти можно только с фонариком, который в наличии только один; мост выдерживает не более двух человек, причем если идут двое — то со скоростью более медленного; Василий проходит мост за 2 мин, Анна — за 4, Игорек — за 10, а Марья Ивановна — за 16?
Г.32. Высшая школа бизнеса, апрель
2591. 22ж2 4- Юж = х/1276т3 4-364ж2.
2592. После того, как 1500 новых вкладчиков открыли в банке счета на общую сумму 7 млн. 800 тыс. руб, средний размер вклада, составлявший 6 тыс. руб, уменьшился на 10%. Определить число старых вкладчиков банка.
2593. |<х + 4 - 2| > •
2594. Найти координаты центра и радиус окружности, описанной около треугольника с вершинами (—5; —1), (—2; 0) и (2; —2).
2595. Найти область определения функции
/(®) = ^/log4/l, I - log2 2® • log8/l 1.
2596. Биссектриса угла А трапеции ABCD пересекает боковую сторону CD в точке Е. Найти АЕ, если BE = 8, ВС 4- AD = 17, а площади треугольников АСЕ и ADE равны.
2597. (х — l)6(sin4x 4- sin4)1/<6 4- (х 4- l)6(sin2 — sin2s)1/<6 = 0.
2598. Найти все а, при которых система
323
11*
j (l«l + |yI - a) (l«l + Is/1 + к + id - 2a) = 0 (®2 + y2 = 1/a2
имеет ровно четыре различных решении.
Г.33. Высшая школа бизнеса, июль
2599. о.
2600. Сумма кредитов, выданных банком населению, составляет 25% от суммы кредитов, выданных предприятиям. Какой процент от общего объема кредитования в этом банке приходится на долю предприятий?
2601. 2ctgs |sins| + 1 = 0.
2602. J51og32^ + ^ + 1о81/г(3У - 8) = 0 [ж2 + 2х + у2 + у = 12.
2603. Найти стороны параллелограмма ABCD с вершинами А = = (—3; —6), С = (5; 12) и серединой (1; 9) стороны ВС.
2604. Найти все целочисленные решения уравнения
2х2 = 2у2 4- Зху 4- 7.
2605. Внутри равнобедренного треугольника АВС с основанием АС и углом ZB = 80° взята такая точка М, что /МАС = 30° и /МСА = 10°. Найти /ВМС.
2606. Найти все а, при которых уравнение
25х5 4- 25(а - 1)х3 - 4(а - 7)х = О
имеет ровно пять различных корней, образующих арифметическую прогрессию.
I
Ответы
Во всех ответах к тригонометрическим уравнениям, неравенствам и т. п. молчаливо предполагается, что параметры п, А:, тп,... пробегают множество Z целых чисел, а явно указаны лишь необходимые дополнительные ограничения на них. Образцы правильного оформления ответов см. в примерах из § 2.
1. 271.
2. 47.
3. -1.
4. 2.
5. 7/2.
6. 8.
7. 0.
8. я = ±1.
9. х 3/2.
10. х = 0, 70/13, 13/2.
11. -6 < х < 6.
12. х = ±7^3.
13. х = 2.
14. х < -2/3, х > 2/3.
15. -3/2 х 1/2.
16. -1 < х 2.
17. х —98, х 96.
18. х < -1/3.
19. х > 3.
20. х < -72, х > 72.
21. —2 < х < 2.
22. х < 0, 0 < х < 1.
23. —4 х < -1, -1 < х 2.
24. — 1 < х < 4.
25. 3/7 <х< 11/7.
26. х = 0, ±72.
27. х —1, х — 0, х 1.
28. ж = 1/2.
29. х = 2.
30. —75 < х < 75.
31. х = ±1.
32. х -5.
33. х = 3.
34. х > 4.
35. х = 5/2.
36. х < 3/2.
37. х = 0, -2.
38. х < 2 — log3 2.
39. х= |log3/2
40. х = 1/2 ± log4/3 10.
41. <.
42. 120/119.
43. 203/121.
44. -77/4.
45. (ЗТЗ-4)/10.
46. -3/5.
47. 24/7.
48. -2/3; -75.
49. <.
50. х= 1 ±1/6±2п.
51. X = ±7г/6 ± 7ГП.
52. х = тг/15 ± 7г/30 ± 7гп/5.
53. х = 7гп/5, (—l)fc7г/20 ± 7г/с/5.
54. х = тг/6 ± 7гп/3, (- 1)л27г/3 ± ±4тг/с.
55. х — тг/4 ± 7гп/2.
56. х = 7г/8 ± 7гп/2.
57. X = 7г/2 ± 7ГП, ( —l)fe7r/6 ± ±7г/с.
58. X = 7ГП, ±7г/6 ± 2тг/с.
59. х = 7г/2 ± 7ГП.
60. х = 7гп, ±Зтг/4 ± 2тгАс.
61. х = 7гп, ±arccos(—1/3) ± 2тгА:.
62. х = тг/2 ± 7гп, ±7г/3 ± 2тгк.
63. х = 27гп, (-О^+Ч/З ± 2тгА;.
64. х = тг ± 2тгп, ±4тг/3 ± 4тг/с.
65. х — тг/4 ± 7гп/2.
66. X — ±7г/8 ± 7ГП.
67. х — я/Ь ± 7гп/2.
68. х = 7гп, тг/2 ± 2тгк.
69. х =
70. —7Г ± 27ГП X 2тгп.
71. тг/2 ± 2тгп < х < Зтг/2 ± 2тгп.
72. х = тг/2 ± 7гп.
73. х = 2тгп.
74. х = тг/2 ± 7гп, ±7г/3 ± 2тгк.
75. X = 7Г/6 ± 7ГП/3, ( —l)fc7F/18 + 4-тгАс/З.
325
V
сч
V
A\
I
V/ н V° cn V
I H
CO CN .
V/
О H H co Л V V II H о о H
гЧвчеО^ЮОЬаОО cococococococococo
О
CM
00
168. х — 7ГП, у = 7г/4 — тгп;
х = 7г/4 + 7Г&, у — — тгк. 169. X = 7г/8 ± 7г/12 + 7ГП, у = 7г/8 qp тг/12 — 7ГП.
170. а < 6.
171. а = -2.
172. 20 и -2.
173. 9 и 2.
174. 546.
175. 1130/7.
176. 1/2.
177. 28.
178. 8 мин 20 с.
179. 50.
180. 4.
181. 17.
182. 9.
183. 50.
184. 2,5, 4 и 5,5 т.
185. 5 + (1/5)п.
186. |(^(10"-1)-п).
187. 16, 24, 40, 48.
188. 8,1%.
189. 8,75%.
190. Западник; 50%.
191. 1000л.
192. 1085 и 30.
193. 5.
194. 147ц/га.
195. 5400 и 8100 руб.
196. 2400 и 3600 тыс. руб.
197. 1/15.
198. 210 руб.
199. 78,2.
200. 15 т.
201. 8%.
202. 1,8.
203. 0,6.
204. 170.
205. 9 кг.
206. 0,5.
207. 10 и 20.
208. 1 и 2 кг.
209. Зкг.
210. 6/5.
211. 2/5.
212. 16 км/ч.
213. Зм.
214. 2/3.
215. 4 ч 45 мин.
216. 50 км/ч.
217. 11/4.
218. 160 км.
219. 1,6м3/ч.
220. 36 : 31.
221. 9.
222. 18.
223. 40/3, 40, 10.
224. 20 и 18.
225. 15.
226. 90.
227. 61УЗ/4.
228. Зх/5б.
229. у/7.
230. 202,8.
231. 2 : 5.___
232. У2/(4-7г).
233. \/15 + 6^/3.
234. 147/8.
235. тг/6.
236. УЗ + 1.
237. х/3 4-2тг/3.
238. (3 + 7г)/(б7г).
239. 10г2(х^+27г/3).
240. 6.
241. \/2) : х/2.
242. 11.
243. 18 : 7.
244. 5 и 20.
245. R sin 2а.
246. 5 : 4л/6.
247. 2\/ТЗ.
248. 228/25.
249. 32/5.
250. 9 : 20.
251. тг/12, 5тг/12.
252- 27^87- R-
253. a2 sin/?sin(a +/?)/(2sina).
254. csin2a/(2sin(a 4-тг/4)).
255. Ksin2atg(a/2).
256. 6.
257. (х/2 4- х/б)/2.
258. 91/(6 4- х/б).
259. 1.
260. 24/7.
261. х/10.
262. 9х/3/11.
263. х/а2 4-Ь2 ±аЬ.
264. х/7.
a sin(ct-h9)(14-3sin2 3)
°* 12 sin a sin$ ‘
327
266. ^41 - 1072(75-1), 4л/2 : 5.
267. 75/4, 7.
268. 2 arctg(5 tg а).
269. 4.
270. 6 - 276.
271. 5^3/7.
272. 25715/64.
273. (p — a)2 tg(a/2)/2.
274. 9.
275. 75/2.
276. arcsin(4/5), arccos(4/5).
277. 72.
278. 72 716.
279. 1 и 7.
280. 72.
281. 300/17.
282. 18/(25 + 27130 + 7445).
283. 1573/4.
284.
285. arccos(—715/20).
286. 9:8.
287. 10.
288. 34/9.
289. 4aR2/(16R2 - За2).
290. 25/8.
291. 16.______________
oqo 7(ь~д)2+(<,+д)2 tg2~6 4 sin а
293. 3715/2.
294. 16/5.
295. (a2 cos2 /3 ctg 0)12.
296. 276.
297. R2cosa(l + sina).
298. 1.
299. 1 : 715.
300. 473.
301. 372.
302. 1 + 73.
303. 1 + 375/4.
304. 757(276 - 1)/(з73).
305. зТЗ/4.
306. 7(а + 6)6.
307. 450/17, 255/8, 960/17.
308. 9.
309. Tab.
310. 4.
311. arcsin(a//i).
312. Зтг/7.
313. am/n.
314. 45°, 60° и 75°.
315. y/mn.
316. 2/v/7.
317. c(a/b)2.
318. 24.
319. ^/(4b2 — a2)(a2 — 62)/4.
320. a sin /3 sin 7/(3 sin(£ 4- 7)).
4m2 —a2—b2 2ab
.321. arccos 322. 4/5.
323. 90°, 10°, 80°.
324. -y 2nf , (две), -,-^n „ 4m2 —n2 ^4m2—n2
325. cos a cos /?/(sin(a + /?)).
326. 9/2.
327. 7rtg2a/4.
328. Cy/2 + c/b.
329. -721/9.
330. 1577/16.
331. 715, 2713, 375.
332. 8.
333. 75.
334. 76/12.
335. 5.
336. 1 : 1, 5 : 9; 5 : 21.
337. ttHR2/12.
338. 27(1 - тг/4).
339. 48Я-Т1Т. . ________
340. d3 sin a sin /?7CO®2 a ~ sin2 0-
341. ^8Vsin f/73(2 cos a - fj.
342. 6
343. a/ (4sinfyi-|sin2^).
344. arccos (tg £ / 75).
345. T5T/6.
346. 216.
347. 21715/10.
348. 27/16.
349. 91/25.
350. 7/2.
351. 6.
352. 76(5 - T15)/10.
353. 2a2/(9T5cosip).
354. 4ad/T5 - 8T2d2/5.
355. 2H3(tg2(a/2) - l)/3.
356. a2 71 - ctg2(^/2)/2.
357. 2+75+75.
358. 12/(13 + 741).
359. T2R/(T2 + T5).
360. (1——arccos—) °.
361. 16.
362. 9(тг + l)/24
363. 1 + Зтг/2.
328
364. 1/3.
365. 472- Т3 4-2тг/3.
366. 36.
367. 33.
368. 60/13 км.
369. (15/2,0,0).
370. Зя + 4у + 6z = 29.
371. arccos(6/7).
372. х е R.
373. -3 - 713 < х < -3 4- 713.
374. х - —4, -1.
375. х = -3, 1.
376. х = 3 ± Л-
377. 1.
378. а / 1.
379. —2 - 272 < а < 0, 0 < а < —2 + 272.
380. —2 < х < 0.
381. -2 0^3.
382. —5 х < —4, — 2 < х 5.
383. —4 < х < -1, -1 < х < 0.
384. -3 < х < -2, -2 < х < -1.
385. -1 < х < 4.
386. х < -1/6, х > 1/12.
387. —2.
388. х = 1, у = -3/2;
х — —2, у = 3.
389. х = 1, у = log3 2.
390. х = у = 4.
391. х = -2, у = ±2.
392. х = 1/3, у = 1.
393. х = 81, у = 0.
394. х = ±4.
395. -3 х < 3.
396. -77 < х < 77.
397. х = 0.
398. х = 4.
399. х = 3.
400. х = 2.
401. я = 0.
402. х < 2.
403. х < -1.
404. х е Ж.
405. х < 1.
406. х log2 5.
407. х 1.
408. х = log3 44.
409. х > 1.
410. х < log2 3.
411. х = 2.
412. х = log0>3 3.
413. х log1/32.
414. х = -1.
415. х — log2 а2 при а < 0;
х — log 2 Д2 > 1°ё2 а ПРИ а > о» при а = 0 корней нет.
416. х = 1/2, 25/2.
417. х = 3, 1/27.
418. х = 1/2, 1/16.
419. О < х < 2, я > 8.
420. 0<я< 1/125, х > 5.
421. О < х < 9”2, х > 94.
422. я = 1/10, юА
423. х = 16, 4.
424. О < х < 1, х > 9.
425. х = ±2тг/3 + 2тгп.
426. х = — тг/2 4- 2тгп, (—l)fc+17r/6 + тгк.
427. Корней нет.
428. х = тг/2 4- 27гп.
429. х — ±arccos(—1/4) 4- 2тгп.
430. х = ±тг/3 4- 2тгп.
431. х — ±Зтг/4 4- 2тгп.
432. х = тг/6 4- 2тгп/3.
433. х — тг/2 4- 2тгп,
(—1)* arcsin(—1/3) 4- тгАс.
434. х — (—1)п+1тг/6 4- тгп.
435. х — 2тгп.
436. х — 2тгп.
437. х = ±7г/3 4- 2тгп.
438. х = 2тгп, ±arccos(l/3) 4- 2?rfc.
439. х = ±2тг/3 4- 2тгп.
440. х = ±arccos(l/5) 4- 2тгп.
441. х = (—1)п7г/4 4- тгп.
442. х = ±5тг/6 4- 2тгп.
443. х = (—1)п7г/4 4- тгп.
444. х = 2тгп/3.
445. х = ±7г/3 4- 2тгп.
446. х = (-1)п7г/6 4- тгп.
447. х = тг 4- 2тгп.
448. х = (—1)п7г/6 4- тгп.
449. 2тг/3.
450. а < -2, а > 2.
451. 1 < х < 3.
452. х > 3.
453. х = (—1)птг/6 4- тгп.
454. х = —тг/2 4- 2тгп.
455. х = 4.
456. х = -3.
457. 1/5 < х < 1, х > 1.
458. -1/3 х < 0, 2/3 < х 1.
459. 1/2 х < 1, 2 < х 5/2.
12 И. Н. Сергеев — Математика
329
460. х = 2.
461. х = 5.
462. х — -1.
463. х = 1/2.
464. х = УТГ/4.
465. х — 1.
466. х = 2.
467. х = 9.
468. 1 < z < 2, 3 < х < 4.
469. х = 3.
470. х = 3.
471. 3 х < 4.
472. х = 4.
473. х = 5.
474. х = 3.
475. 5 < х 6.
476. х < —6, х 6.
477. х = 3/2.
478. х = 14.
479. х = 9/5.
480. -3 х < -2, 0 < х 1.
481. х 0, log6 5 х < 1.
482. х - 1.
483. х = 3.
484. х = (—1)п7г/6 4- тгп.
485. 7 < а / 7,5._
486. х = 3 — + 5 при — 4 < а /
/ —1; при остальных а корней нет.
487. х > 1/6.
488. х = -1, 2/3.
489. х < 3 - х/З, х > 3 4- х/3.
490. х = 1.
491. О х < 4.
492. х = 3.
493. х = 9, 81.
494. х < 0, 63/32 х < 2.
495. О х 1.
496. х - -1/3, 4.
497. х = (—1)птг/12 4- тгп/2.
498. х = тг/8 4- тгп/2.
499. х = arccos | 4- тгп.
500. х = arccos | 4- f п.
501. х = (—1)Лтг/6 - тг/3 4- тгп.
502. х = тг/2 4- 2тгп/3.
503. х = тг/12 4- тгп/3, arcctg 6/3 4- тг/с/3.
504. х = тг/4 4- тгп/2.
505. х = тг/4 4- тгп/2.
506. -(3 4- х/5)/2 < х 0.
507. х = 81.
508. -1 < х 1/3, 1 х < 7/3.
509. -У17 < х < -1, 1 < х < х/17.
510. 6 О < 5 4-27+'/П.
511. х =; ±тг/4 4- 2тгп.
512. х > 2а2 4- а/2 при а < 0;
х > а2/18 4- а/2 при а 0.
513. —2 < х < 2.
514. х = 1, 13.
515. х = 6/5, 4/5.
516. х = ±arcsin(3/4) 4- тгп.
517. О < х < (3 -х/5)/4.
518. —2 < х < -х/5; х/2 < х < 2:
519. х = 2, 1/128.
520. х — log5 10.
521. х < -1.
522. х = -1.
523. х = 1, 3.
524. х = 2 — log2 9.
525. х = 3.
526. х > 1.
527. х > | log3 Ц-.
528. х | log2 3 — 1.
529. х — ±7г/6 4- тгп.
530. х = ±7г/3 4- тгп.
531. х = ±7г/6 4- тгп, ± arccos(—3/5)/2 4- тг/с.
532. х — ±7г/6 4- тгп.
533. х — (—1)п arcsin(l — х/3) 4- тгп.
534. х = (—1)п arcsin 4- тгп.
535. х = ± arccos 4- 2тгп.
536. х = ± arccos - 4- 2тгп.
537. х = (—1)п arcsin 4- тгп.
538. х = (—1)п arcsin 4- тгп.
539. х = (-1)п arcsin 4- f п.
540. х = (—1)п arcsin ^|~3- 4- тгп.
541. х = ±2 arccos 4- 4тгп.
542. х = ± arccos 4- 2тгп.
543. х = -zp— arcsin ^|~3- 4- fn.
544. х = ± arccos 4- 2тгп.
545. х — ^п,
(—l)fc arcsin
546. х = ±5тг/12 4- тгп.
547. х = (—1)п arcsin(x/5/3) 4- тгп.
548. х = (1 ± х/1 4- 5тгп)/5, где п 0.
549. т = (х/3-1)/2.
330
550. х = (1 + ч/5)/2.
551. х = (%/13- 1)/2.
552. х = \Zi7-4.
553. 5 < х < 2 + л/Т7.
554. х = (2\/1бТ - 8)/5.
555. х > (чЛ-3)/2.
556. (7 - ^33)/2 х < 3.
557. х = 24~4^.
558. z = 21og3^+VZ.
559. х = log3
560. х = 7log2 —Г-.
561. х = ±(2 + ч/б).
562. Корней йет.
563. х = 2<3+^/2.
564. х = logj 5.
565. 2 — log| 3 < х 2.
566. -0 < х -0, 0 х < 0.________________
567. х = ±^/-1оё2^^.
568. х - 5±^1°8з(2+'/3).
569. х = -1 ± 0.
570. х = (—1)п7г/6 4- 7гп.
571. х = (—l)n arcsin(l/3)/2 4-тгп/2.
572. х = (-9 ± 0/2 + 2п)/13, где п 0.
573. х = -3, -2, 1.
574. 3 - 20 < а < 00 - 2.
575. х = 4, у = 1; х = —2/3, у = 10/3.
576. х = 1, у = 2, z = 1; х = 44/25, у = -28/5, z = -108/25.
577. х = 2, у = 3; х = 33/8, у = -27/8.
578. х = 2, у = 1; х = —1, у = 23/2.
579. х — 1 — log2 3, у = 1/6.
580. х = 0, у = —3.
581. х = &3,у = 4.
582. х = 1, у = 3.
583. х — 10, у = 15; х = 15, у = 10.
584. х = у — 1.
585. х — 1, у = 5.
586. х = 32, у = 2.
587. х = -1, у = 1/0;
х — 3/2, у — 9.
588. а = ±0.
589. х = -1/4, т/ = 5/4.
590. 20.
591. —2.
592. 12.
593. 42,3%.
594. 162.
595. 3.
596. 9.
597. 83.
598. 4.
599. 5.
600. 8/3.
601. а = 1/2.
602. 20 м3.
603. 4 км/ч.
604. 60 км.
605. 45 км/ч.
606. 20 км/ч.
607. 15 км/ч.
608. 10 км/ч.
609. 290 км, 2 км/ч.
610. 4 км/ч.
611. 90/4.
612. 9, 12 и 15.
613. 2 и 5/6.____________
614 р+д ~ ^р2 +q2 +2рд cos 2<р
615. а2(3 4-0)/4.
616. 8, 5.
617. 2тг/3.
618. 60.
619. 2.
620. (04 - 2)/4.
621. 6/23.
622. 201-9.
623. 10, 2; 50/2.
624. тг/4, Зтг/4.
625. 127гг3.
626. (1 4- 03) : 8.
627. х = -4/3, -2/3.
628. х = —2, 5.
629. х = 4, у = 2;
х = 4/3, у = -2/3.
630. х = 0, у = -7/2;
х = 21,1/ = 21.
631. х = 1.
632. х — 5а/3 при а / 0;
при а = 0 корней нет.
633. х = -1, 0.
634. х = -2, 3.
635. х = log4/5 4.
331
12*
636. х = 1.
637. х = 1/6, 2.
638. х = -3.
639. х = -4.
640. х = 5.
641. х = iarcsin ^/2/3/2 4- тгп/2.
642. х = - arcsin ~ 4- fn.
643. х = 5тг/6 4- 2тгп.
644. х = (—1)птг/4 4- тгп, у = тг/2 4-4-тгАс.
645. х 2 — \/8, х = 2, х 24-х/8.
646. х < 1, 4 < х < 5.
647. х 1, х > 3/2.
648. х 1, х > 96.
649. -1 < х < 1.
650. -6 х < 0.
651. -1 < х < 1/2.
652. х < -2, х -1.
653. х —2, —1 < х 1.
654. х —2, 0 < х 1/4.
655. х < —1, — 1 < х < 1.
656. х < 1, х = 2.
657. 1 < х < 3 - х/З, х > 3 4- х/З.
658. х < -2 - х/2, - 1 < х < —2 4- х/2.
659. х < -1, 2 < х < 5.
660. х < —5, 1 х 2.
661. х -7/5, 2 < х 13/5.
662. х < 2, 2 < х < 3, х > 5.
663. х < 0, 2/3 х < 1.
664. х < —2, -1 < х < 2.
665. х < 0, х = 3/2, х > 2.
666. —4 < х < -1, -1 < х < 2.
667. -6 < х < 0, 2 < х < 3, х > 6.
668. -5 < х 1, 2 < х < 3.
669. х < -9, 2/3 < х < 1, х 11/2.
670. х —2, -1 < х < 0, х > 0.
671. 1 < х 2, 7 < х < 8.
672. х -1, 2 х < 11/4, 11/4 < х 3, х 4.
673. —2 < х < 1, х = 2.
674. х —х/З, х — 0, х х/З.
675. -3 х < -1.
676. —6 < х < —4, — 4 < х < 1.
677. х - -1, х 2.
678. 1/5 х 1/4, х = 2/5.
679. 1 х тг/2, х = 3.
680. —2 < х < 0, 2 < х < 5.
681. х = -12, х > 7.
682. х < -х/3/2, х = -1/2, 3, х > 2х/3.
683. х = 5, х > 4 4- х/2.
684. х = —4, 4 < х < 7.
685. О < х 1/4, 3 < х < 4.
686. х < — \/5, х = 1.
687. -3 < х -2, х = 0.
688. х > 0.
689. х < О, 1 < х < 3.
690. О < х < 1/3, х > 4.
691. О < х < log3 2.
692. х < 0, х > 1/2.
693. х < 3, х > 21/5.
694. —2 < х < О, 1 < х < 3.
695. х —9, х > 3.
696. х -8, х > 12.
697. а < -3, а > -1.
698. х —1, х = —1/2, х 0.
699. i^log3 log3 | O<log3 f •
700. 1 < х < 5*°82 7.
701. О < х < 1, 1 < х < 4, х > 64.
702. 1/4 < х 1/2, 0 2.
703. х < -101/3, -1 < х < О, О < х < 1, х > 101/3.
704. О < х < 1, х = 2, х > 4.
705. -311 < х < -11, 1 < х < 3/2.
706. -27<х < -1, -1/27<х < 0.
707. О < х < 4, х = 8.
708. О < х 5-V4, 1 < х < 52/7.
709. О < х 1/4, 1 < О \/2.
710. 1/8^1 <1, 1<О16, х>64.
711. О < х 2*/б - 1, х > 63.
712. x^-2-3/f-2~3/4<x<-l/2, 1/2 < х < 2~3/4, х > 2-3/7.
713. х = —27гп, где n Е N.
714. -3 < х < -2, х = -1,
О < х < 1.
715. х < —2, х — 0, х > 2.
716. О х < 900, х > 3600.
717. х = 0, х > 16.
718. х = —3, х > 1.
719. 1 х < 5, х > 10.
720. 2 < х < 5/2, х = 3..
721. а < —3, а = —1, а 3.
722. х = 1.
723. х = -2.
724. —2 < х < 2, 2 < х < 3, х > 6.
725. -1 < х < О, 0 < х 1/J2.
726. х -5/3, 0 х < 1/3.
727. 1 = 3, 4.
332
728. х — —4, -1.
729. -(9 + v/57)/4 < х < -2, — 2 < х < -1, х > 3/2.
730. х —2, | х < 1,
1 < х < У^з-з
731. х = -25, 3 4
732. х = 2/3, 2.
733. х -13/5, х > 3.
734. х 4/7.
735. х < -199, -66 < х < 200.
736. х < 0, х > 2.
737. х < -8, -6 < х < -2, х > -2.
738. х < 2, х = 3, х > 4.
739. -5 х < -4, - 2 < х $ -2 + \/3.
740. х = 3/2, у = 0;
х = 3/4, у = -3/2.
741. х -5, х = -5/4.
742. —6 х —1, х 0.
743. 3 х (11 + V61)/2.
744. х = О, 1.
745. ±arccos(—1/(\/3 + 1)) + 2тгп.
746. х = -3.
747. х = 17/6, (3 + V89)/4. .
748. х = ±тг/3 + 2тгп.
749. f(x) = 2/>/=х -1; х = ±4, 0.
750. х = l+8n, 7+8А:, где п,к G Z.
751. х = -3/2 + 4п, —1/2 + 4к, где п,к е Z.
752. х = —1/2 + 8п, где п € Z.
753. х = 0, \/2.
754. (\/5 - 1)/2 < х < 1.
755. 1 < х 4.
756. 2 < х (7 + х/17)/4.
757. О < х < 1/3, х > 2/3.
758. О < х < 1/7, 1/2 < х < 1.
759. х = 1, 3.
760. х = 1, -15/11.
761. х = 2, (5 + \/ТЗ)/2.
762. х = 1, у - 1; х = 2, у- 1/8.
763. 1 < х < (1 + VI + 4а2)/2 при 0<а<1;х>(1 + VI + 4а2)/2 при а > 1; при остальных а решений нет.
764. х < loga при 0 < а < 1; loge I < * < log. 3=7 ПРИ 1 < < а < 3; х > log0 | при а 3; при остальных а решений нет.
765. -За < х < -1, 1 < х < За при О < а < 1/2; х<—За, х>За при а > 1/2; при остальных а корней нет.
766. 6 при а # 0;
6 при а = 0.
767. х = 1 при |а| > 1; — 3 х 1
при а = — 1; х — 1, ----
а — 1
при |а| < 1; х 1 при а = 1. 768. х = 4 при |а| > 1;
х 4 при а = —1;
х = 4, (4а—8)(а+1) при |а| < 1; —2 х 4 при а = 1.
769. 4/3 < а 2.
770. 1 а 3, а = 4.
771. а / 0.
772. а / -3.
773. -1/2 а 2/3.
774. а = с= 1/4, 6=1/2;
а = 0, 6 = с = 1/2.
775. а = 3, b е R; а # 1, 3/2, 2, 6 = 2. а = 6 = (1 ± \/7)/2.
776. Да.
777. п = 33.
778. -5/2.
779. -1/5; 1, 4.
780. 1/3.
781. 50, 20 м.
782. 5 л.
783. 9.
784. 8.
785. 3.
786. 90 км/ч.
787. 12.
788. 14 км/ч.
789. 30 мин, 1 ч.
790. 50 и 40 км/ч.
791. 10 км/ч.
792.29/2ч.
793. 11 • 181.
794. х = -3|,-2|,±1|,±|.
795. 642.
796. х = —7, у = 7; х = —6, у = 6.
797. 248, 436, 624, 812.
798. 618, 659, 698.
7 + 1 = 8
— X
799. 1 + з = 4.
II II II 6:3 = 2
800. И. Да, Р.
801. 119.
333
802. 4 : 3.
803. 5.
804. 1) 6; 2) 192.
805. По 2 самолета каждого типа.
806. 832.
807. 19 и 31 деталей в день.
808. 8.
809. 49 и 83.
810. 27.
8J1. 30.
812. 8, 56, 392.
813. 6, 10, 14, 30, 42, 70, 105, 210.
814. О < х < 1/2.
815. 2 < х 3.
816. х log3 2, 1 < х < 5.
817. -2^х^-1, х = 3.
818. 3 < х < 7/2, х > 4.
819. О < х < 1/4, 1 < х < 5/4.
820. -2 О < -х/2,
О х < -1 4- 72.
821. —2 < х < -\/3, 5 < х < 6.
822. 3 <
823. 2/9
824. О <
х 4.
х < 1/2.
х (7 - т/47)/2,
1 < х < 3/2.
825. х < -1, 2/5 < х 1/2, х > 1.
826. -1 < х < 0, 0 < х < 1/2,
1 < х < 5.
827. —1 < х < 0, 0 < х < 1, х 5.
828. О < х 1.
829. -1 < х < О, 1 х < 5.
830. log2 | ^х<2, 2<x<log2
831. О < х < 1, 3 < х < 5.
832. —1/х/2 < х -1/73, 1/х/З х < 1/72.
833. -1 < х < 0.
834. х > 1.
835. —1/3 х < О, 1/5 < х < (3 - 73)/6.
836. -5 < х < -2, х > -1.
837. х > 3.
838.
839.
-3 < х < —2, —4 < х < 1, 1 5/3 < х < 11.
3 < х 4. < х < 5/3,
840. -3 < х < 3, 3 < х < 4.
841. х > 2 при а — —1; 1 < х а+2, х > 1— а при — 1 < а < < -1/2; 1 < х < 3/2, х > 3/2 при а = —1/2; 1 < х < 1 — а,
х а + 2 при —1/2 < а < 0;
х 2 при а = О-
842. -13 - 757 < х < 8.
843. 3(7Г + 2)/4.
844. 1 4- тг/2.
845. 2х/3 4-тг/3.
846. 25.
847. (х + 2)2 +(г/-4)2 = 13.
848. 6.
849. 27тг + 18.
850. 15/2.
851. 2/л/5, 4 — 4тг/5.
852. х = 0, у = —2; —2 х 2,
у = 2 4- 2х; рис. 55.
853. См. рис. 56; 9/5 х 3,
у = 5/3.
854. О а 1.'
855. х = 7гп, тг/2 4- 2тгА:.
856. х = тг/2 4- тгп, (—1)*7г/4 4- тг/с .
857. х — лп, ±7г/4 4- 2тгЛ:.
Рис. 56
Mho
858. х = 2тгп, ± 2arccos
859. х = тг/2 4- тгп, 7г/с/5.
334
860. х = irn/2, ±arcsin ^/2/3 + irk.
861. x = | + %n, о о '
(—l)fc arcsin + irk.
862. x = £ + In, о о
(~2~ arcsin f fc-
863. x = тг/2 4- тгп, (-^ь+Ч/ЗО 4- ?r/5fc.
864. x = тгп/2, ±2тг/3 4- 2тг/с.
865. x = тг/2 4- тгп,
тг/4 4- (—1)*тг/6 4- тг/с.
866. х = тг/4 4- тгп/2, (—l)fcтг/6 4- тг/с/2.
867. х = тгп, ±7г/3 — тг/6 4- 2тгк.
868. х = тг/IO 4~ тгп/5, тг/14 4- тг/с/7.
869. х = тг/2 4- тгп.
870. х = 7г/164-тгп/8, тг/4 — 24-тг/с, тг/12 4- 2/3 4- тгтп/З.
871. х — ±тг/6 4- тгп.
872. х = тг/4 4- тгп/2, тг/2 4- тгк.
873. х = 5тг/4 4- 5тгп,
± 57Г/8 - 257Г/24 4- 5я±.
874. х = тгп/4.
875. х = тг/6 4- тгп/3.
876. х = тгп/4.
877. х = тг/10 4- тгп/5.
878. х = тг/8 4- тгп/4, тгАс/З.
879. х = 5тг/4 4- 5тгп/2, Ютг/с/3.
880. х = тгп/4, 7г/32 4- тгк/8.
881. х = тг/2 4- тгп,
— arctg(l/2) 4- тгА:.
882. х = тг/2 4- тгп, тг/З 4- тг/с.
883. х = тг/2 4- тгп, тг/4 4- тгк.
884. х = тг/4 4-тгп, — arctg 4 4-тг&.
885. х = тг/2 4- тгп,
(arctg 2)/3 4- тгк/3.
886. -arctg44-тгп, arctg(l/2)±7rfc.
887. х — тг/4 4- тгп, тг/З 4- тг/с.
888. х = log2/3 2, log2/3 |.
889. х - log3/5 2.
890. log2/9(l + •Д) х < log2/92.
891. х > log3/2
892. -1 < х < 0.
893. х = ±5, у = 4=4;
х — ±13, у — qp20.
894. -5/11 < а -1/3.
895. 74. ______ ,
896. arcsin ^/3/199.
897. х = тг/4 ± тгп.
898. х — тг/4 ± тгп/2.
899. х = ±2тг/3 ± 2тгп.
900. х = — тг/4 + тгп.
901. х = 2тгп, —тг/4 + тгк.
902. х = тг/8 ± тгп/2, ±7г/6 ± тгк.
903. х = 9, у = 2.
904. х < 1, ж > 2.
905. х -11/6, х = 0.
906. х = log32, 21og23.
907. х = 0, log3 2.
908. х = 1/2, 2.
909. х = 5.
910. х = 5/8, у = 4.
911. х = 5/4, 5, 6.
912. х = 2, 9.
913. х = 0, 1, ±2v/2/3.
914. х = — а — 3 при 0 < а < 1, 1 < а 3; х = а, —а — 3 при а > 3; при остальных а корней нет.
915. х loga-x х 0 при
1 < а < 2; х 0 при а = 2; О х loga_x 2а при а > 2.
916. -3/2 а < -3/4, - 3/4 < а < 0.
917. а = ±1, b = —2; а е R, b = 2.
918. х = —2, 4/3, 3.
919. х — 0, у = ±1.
920. х = -1.
921. -6 < х < 3/2, 3/2 < х < 2, 2 < х < 5/2, 5/2 < х < 10.
922. а —5\/5/4, а 5\/5/4.
923. а = 2.
924. а > 3.
925. При а решений нет;
при — < а < 0; х > О
при а = 0; Х<
д> ->+^ПЕприО<а_5
Х € ® при а> Т2-926. а = ±v^, ±(х/15+ 1)/4 . 927. 1/2 л.
928. х = 9.
929. х = 18.
930. х = -1/3.
931. х = (19 + х/137)/8.
932. х = -1.
335
- st
V/A
H л co cm >
V/ H V I cm |
о • H И A co, . * н V/
1 . i<cm" H cm
V . м > V/ <n v V у/ 10 H H V н H >„ V
v/^° | v a v/ v > a CO V/V/ V V/r-ч CM I V
f H H H CO* r-1 I co 1-1 CM
<3
s Ct к
о л R
lOCDboOcidr-icMco ЬЬЬЬЬоОоОаОаО 0)0)00)0)0)0)0)0)
CM 0)
С0
со
0)
со
с0^ЮС0Ьа00)ОгЧСЯС0^<ЮС0Ьа00)О»нСЯе0^,10С0Ь оОООгЧСМсО^ЮСО ь ао О О н см со
ююсососососососо со со со ь ь ьь ь
0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0)0) 00)0)0)0)0) О) О) О) ооооо оо о
1002. х = 0, —тг/2 4- 2тгп/3, (—1)*тг/18 —тг&/3, гдеп,& G N.
1003. х тг/4, —тг/4 + тгп х тг/4 ± тгп, где n G N.
1004. х = (-тг/2 ± 7г/6 + 2тгп)2, где n G N.
1005. х = (>/89 — 6)/3, (х/41- 6)/3.
1006. х = 2тгп, тг ± 2тг&, где п —1, к —3.
1007. х = тг/6, тг/2, 5тг/6, Зтг/2.
1008. х = Зтг/2, 2тг, 2тг—агссоз(2/5}
1009. х = ±тг/6, ±тг/4.
1010. х = тг/24, ±тг - 7тг/24.
1011. я = 2|±|, 3|-|. о о 1 о о
1012. х = ±2, ±3/2, ±1/2.
1013. х = ±1/6, ±11/6, ±\/3.
1014. х = -2, у = -1.
1015. (—1)* arcsin(±7r/4±27rn)-1 ± 4-тг/с, где п 0.
1016. х — ±агс8ш(тг/6) 4- тгп.
1017. х = (—l)n arcsin(l/8) 4- тгп, (—1)к arcsin(5/8) 4- тг/с, (—l)m+1 arcsin(7/8) 4- тгтп.
1018. х = тг 4- агсзт(тг/12), тг — агсэт(тг/4).
1019. х = (-1)п+1тг/4 4- тгп.
1020. х = ±тг/14.
1021. х = —тг/26, тг/34.
1022e 2cos2(l/3) < а Е
1023. х = 2тгп, —тг/2 4- 2тг&.
1024. х — 5тг/6 4- 2тгп.
1025. х = тг/5, тгп.
1026. х = (—1)птг/6 4- тгп, тг/2 4- 2тгАс, где к ф 0.
1027. х = тг/2 4- тгп/7, где п = ±1, ±2, ±3.
1028. х = — 7г/6 4- 2тгп.
1029. х = тгп, тг/6 4- 2тг&.
1030. х = —тг/4 4- 2тгп.
1031. х = тг/4 4- 2тгп, arctg (1/2) 4- 2тг&.
1032. х = 5тг/6 4- 2тгп.
1033. х = —1,07, тг/2 4- тгп.
1034. х = 2тгп, —Зтг/4 4- 2тг&.
1035. х = -11тг/4.
1036. х = тгп, тг/4 4- тг/с.
1037. х = тгп, — агссоз(—1/3)4-2тгА:.
1038. х = тг/2 4- 2тгп, 2тг/3 4- 2тг£.
1039. х = тг — arcsin 4- 2тгп.
1040. х = тгп, тг — arcsin 4- 2тг&.
1041. х = тгп, тг/6 4- 2тг/с.
1042. х = —тг/3 4- 2тгп.
1043. х — —тг/3 4- 2тгп.
1044. х — 2тгп, —тг/4 +*2тгА:.
1045. тг/2 4- 2тгп х < Зтг/4 4- 2тгп.
1046. 2тгп < х < тг/2 4- 2тгп.
1047. —тг/3 4- 2тгп.
1048. х — тг/3 4- тгп.
1049. х = тг — arcsin(3/4) 4- 2тгп.
1050. х = тг/6 4- тгп.
1051. х = тгп.
1052. х = ±тг/104-тгп, ±Зтг/104-тг&.
1053. х = тг/4 4- тгп/2, ±тг/3 4- тгк.
1054. х = тг/4 4- тгп/2, ±тг/3 4- тгк.
1055. х = тг/84-тгп/4, тг/44-тгАс/10, где п = 0, ±1,2, fc = ±l,±2,±3,±4.
1056. х = 5тг/6 ± 2тгп, —тг/4 ± тгк.
1057. х = тг/3 ± 4тгп.
1058. х — тг/12 ± 2тгп, 2тг/3 ± тг/, тгтп, — 5тг/12 4- 2тг/с.
1059. х — тг ± 2тгп, агссоз(1/\/5) — — arcsin(l/\/5) ± тг(2& ± 1).
1060. х = 5тг/48±тгп, 17тг/48±тг&, 7тг/24 ± тгтп.
1061. х = —тг ± 24тгп, 7тг 4- 24тг&.
1062. х= —тг/24-2тгп, —тг/3±2тгА;.
1063. х — 7тг/12 ± 2тгп, Птг/12 ± 2тгк.
1064. х = тгп, ±тг/4 ± 2тгЛ:.
1065. х — тг/4 4- 2тгп, тг/2 4- 2тгк.
1066. х = 23тг/36±тгп, 35тг/36±тг/с.
1067. х - -Птг/8, -21тг/16.
1068. х = тг/2 4- тгп, тг 4- 2тг&.
1069. х = 0, 2тг/3, тг, 4тг/3.
1070. х = тгп, 2тг/3 ± 2тгк.
1071. х = тг/12±2тгп, 17тг/12±2тгЛ:.
1072. х = тг/6 ± 4тгп, 5тг/6 ± 2тг&.
1073. х = ±Зтг/4 ± 2тгп, у = (—1)*тг/6 ± тгк.
1074. х = тг/12, Птг/12.
1075. х = ±тг/6 ± 2тгп, у = (—1)лтг/4 4- тг/с;
х = ±тг/4 ± 2тгп, у = (—l)fcTr/3 ± тгк.
1076. х/7.
1077. 6\/2 + 1, 5\/3, 2.
1078. \Лз.
1079. 8/\/15.
337
1080. 17; внутри.
1081. 2 : 3.
1082. (Зх/З - тг)/18.
1083. (2тгТЗ + 9) : 27.
1084. 625 : 121.
1085. 30°.
1086. 3; 4098/61.
1087. arcsin Ь^э/ZZ.
1088. 9Т55Т/4; 15/2._______
1089. ^/2Ssinasin/3/sin(a + /3).
1090. 6с sin a/762 + c2 — 26c cos a,
arccos ( ./~bco8a------Y
\ у/b2 +c2—2bc cos a J
1091. 90°.
1092. 4ri 4- 2f2.
1093. 2.
1094. 5672.
1095. 3/4.
1096. arccos(3/4).
1097. 4v/3sin(7r/9)sin(2%/9).
1098. 1572/8.
1099. 2^7/3.
1100. (1 + 73)6/2 - (V2)a/2.
1101. (31 + T129)/2.
1102. 5tt/12.
1103. ТбТ.
1104. 12576/4.
1105. 2873.
1106. 4.
1107. ,/8.____________
1108. 3 ^/(17 + T20T)/22.
1109. 3(75±l)/2.
1110. 16/3, вне; 875/3, внутри.
1111. 27; 189/25.
1112. 30°, 150°.
1113. 753, 713.
1114. 3/sinl5°, 3/sin75°.
1115. ^5(2 ± 73)/2.
1116. 192/17, 1728/25.
1117. 1/3,2/3.
1118. arccos(9/7150 ±2473).
1119. 50(572 ±4).
1120. >.
1121. >.
1122. <.
1123. <.
1124. >.
1125. >.
1126. -1/710; <•
1127. <.
1128. Геометрической.
1129. ACB.
1130. 2.
1131. x = -4.
1132. x = 2.
1133. x > 7/9.
1134. x = 0, у = log2 x=|log22^8, У = 2 + log2(3 - 75).
1135. -1 < x < 0, 0 < x < 4.
1136. 3/2 < x < 2.
1137. -710<x<-3, 3< z^TIO.
1138. 0 < x < 3, 25/8 < x < 710.
1139. x = тг — arcsin + 2irn.
1140. x = ± arccos 4.2im,
± arccos + 2irk.
1141. x = ±%/4 + 2irn.
1142. x = -5, -6, —7тг/4.
1143. 1 < x < 73,
x / (5 + 725 + 36nW18, где n = 5,. ..,9; —y3<x < —1, x / (5 - 725 + 36fc)/18, где k = 15,... ,22.
1144. x = ±У8-((-1)п/6 + п)2, где n — 0,1,2.
1145. x = (—l)n arcsin 4- тгп.
1146. x — тг/4.
1147. x = 2тг ± arccos log2(\/6 — 1).
1148. x = -237Г/6, -197Г/6, — 117г/6, —4 arccos (—9/10).
1149. x = 37Г 4- arccos(10/ll).
1150. a = 0,26тг, 0,6тг.
1151. a = 0, 24-V^<a<24-\/5.
1152. Да.
1153. CD.
1154. 3(3\/3- 4)/2.
1155. 3 y/3/19.
1156. 75/2 -97Г > 9.
1157. 1/2 4-10^/6/49 4-
4- Зтг/4 — arcsin(5/7).
1158. 8^2/3 > 6,5.
1159. Одинаково.
1160. (V2 + l)/2 « 1,21.
1161. 49(3^3—5)/3.
1162. <.
1163. 1 < x < -?/5.
1164. Да.
338
1165. 3.
1166. х = 0.
1167. 4тг/9 О < 8sin(Tr/12), х = log3 28.
1168. — х/10<ж <— тг, — тг<х< — 3, 3 < х < тг, тг < х < х/10.
1169. 8 х < 4 + 2х?6, х = тг/2, 5тг/2.
1170. х = х/2/2 - 1.
1171. —2 - х/4 4- cos(3/2) х < 0.
1172. х > 3.
1173. х = log3/2 ^|±1.
1174. AL.
1175. 15.___
1176. 7у/29/5.
1177. 50тг(2 + /2) > 510.
1178. 7.
1179. (4 - /2)/6.
1180. 5/5/3.
1181. х -3, -1 < х < 1, х > 1.
1182. х = 2тгп, тг/2 + 2irk.
1183. Корней нет.
1184. х — 2тгп, ±7г/3 4- тгк, 7г/12 4- 7Г771/6.
1185. х = тгп.
1186. х = — 2 4- тгп.
1187. X — тгп.
1188. х = 4.
1189. х — тг/4 4- тгп/2, ±тг/3 4- тгк.
1190. -1 < х 0.
1191. х = -3.
1192. х = 2.
1193. —2 < х < -1.
1194. 1 - х/2 < х < 2/3, 1 < х < 1 4- х/2.
1195. 1 < х 2.
1196. х = -3, -2, 1.
1197. х = 4, 8.
1198. х = 3.
1199. -4 х < -1, 1 < х 2.
1200. х = 5/3.
1201. х = 1/9, у = 1/81.
1202. Корней нет.
1203. -1/3 < х < 0, 0 < х < 2,
2 < х < 3.
1204. -3 < х < 2 - 2\/б,
2 - 2\/б < х < -2, - 2 < х < 2, 2 < х < 2 4- 2\/б, 2 4- 2\/б < х < 7.
1205. -1 < х < 0, 0 < х < 2.
1206. х = \/2, тг/2 4- 27гп.
1207. х — 5тг/12 4- 2тгп.
1208. х = -1.
1209. а = 57г/6 4- 2тгп, тг/18 4- 2тгА:, 13тг/18 4- 2тгтп.
1210. х = 0 при а = 0; х > О при а 3; при остальных а корней нет.
1211. х = ±arccos + 27ГП>
у = (-1)* arcsin^ 2^з^) + тг/с, z ~ Т=^а при 0 < а ^/3, а 1/4; при остальных а корней нет.
1212. х = х/3/8, 1.
1213. х < -1, -1 < х < 1 - х/15, х 7.
log2 а
1214. X = 4 3 |о82! в4-2 ПрИ д > О, а / 1, 2"2/3; при остальных а корней нет.
1215. х < —2, 0 х < 1g 101 - 2.
1216. Решений нет.
1217. х = 0, х log5 3.
1218. log72 54 х 1°89/в(3/2).
1219. - log2 6 < х < 1.
1220. ж = 4- 21og59.
1221. х -3, х = 5.
1222. х — 1 при а < 1;
х>(а—I)2 log2 2—1 при 1.
1223. х 2.
1224. х = 2, 1/8.
1225. х = 16, у = 4.
1226. 1.
1227. -10.
1228. -1 < х < 2, ж > 3.
1229. х < log6+v/I59,
х loS6-v^53’
1230. х = ±1.
1231. 2-у/2<х^1, 3 ^х <2 +у/2.
1232. х = (у/2 + -v/З + \/5)2, (У2+Л+ч/б)"1/2.
1233. х = -s/5.
1234. -15/4 О - 3/2, - 3/2 < х 5/2.
1235. 2/3 < х < 1, 1 < х 2.
1236. 0 х тг/З.
1237. х = (- 1)птг/6 + тгп.
1238. Х — 2.
1239. -2/6/3 < а < 2/6/3.
339
1240. /6 + 1; /16 - /6, /10 - 1.
1241. x = 10, у = 15, z = 6.
1242. x = -1, у = 1.
1243. x = 3, у = 1/9.
1244. x = 1, у = 5; х = 5/2, у = 2.
1245. х = -14, у = -2.
1246. а = ±1, -1/2 а < О, О < а 1/2.
1247. х = 2, у = -1;
х = 12/7, у = -1/7.
1248. х = -1/2, у = 9/4;
х = 2, у е R.
1249. х = +1//2, у = Tl/V^.
1250. х = /2, у = ±/2;
х = —/2, У = +/2.
1251. х = (-l)n+1 тг/8 + тгп/2, у = — arctg(/2/2)/5 + rrfc/5.
1252. х = log2(v6 - 2), 2/ = log3((/6-2)/2).
1253. x = 9, у = 1.
1254. x = 1/(2 log2 3-1), у = 2/(2 log2 3 - 1).
1255. x = тг/12, у = -тг/12;
х = 5тг/12, у = —5тг/12.
1256. х = —тг/4 + тгп + irk/2, у = —тг/4 + тгп — тгк/2.
1257. х = (—1)" arcsin(l/3) + тгп.
1258. а = 2, Ь = 3.
1259. а = -3/4, 0, 2/9.
1260. а = О, 1, -3/4.
1261. а/1, -1/2, (—7±4/2)/2.
1262. 1, 2.
1263. (-1 + /1 + 8п/5)/2, где п = 6,7,... ,250.
1264. 2.
1265. 1,5, 3 и 6т.
1266. 4, 8 и 12 км/ч.
1267. 60 и 100 км/ч.
1268. 15 и Зкм/ч.
1269. 20/3 и 16/3 ч.
1270. 2м3.
1271. ±/5/8.
1272. х > log2(8/5).
1273. тгп/4 < х < тг/8 + тгп/4, где п = 0,1,2,3.
1274. 50.
1275. 3 / х 5.
1276. См. рис. 57; у = —а:2 — 1, у = ±(х2 - 1) .
1277. х = -8.
1278. 6-2/5 < а 2\/5-2, а = 4.
1279. х = 7/5.
1280. х = 1/4.
1281. х = 2, 3.
1282. х = 4, (1 + /17)/2.
1283. х = (/7-3)/2, у = (4- /7)/2; х = (/19-5)/2, У = (6 - /19)/2.
1284. х = -1, у = 1.
1285. х = ±/3/2, ±/5/5.
1286. х = -4, 2.
1287. х = -17/5, 11/3.
1288. х > 2.
1289. х = 5/2, у = -5/2.
1290. х < 0, х > 3.
1291. —2 + /II < х < 2/7.
1292. х О, 1 х 2, х 5.
1293. х < -1/12, 0 < х < 1/12, X > 6.
1294. —(а + 2)/3 х 2 — а при а 4; при а > 4 решений нет.
1295. х < 1, 1 < х $ 4.
1296. х < 2, х > (5 + /17)/4.
1297. -5 < х < 20.
1298. х < -3, х > -1/3.
1299. О О 15/4, х > 4.
1300. О < х < 1, х > 1.
1301. 3 < х < 4, 4 < х < 7.
1302. х = (—1)п+1тг/4 + тгп.
1303. х = тг ± arctg 2 + 2тгп.
1304. х = — тг/3 + 7ГП.
1305. х = arctg 3 ±
± arccos + 27ГП-
1306. х = 1 + тг/2 4- тгп, 1/3 4- тг/6 4- 7гЛ:/3, где п = ±1, k = -6, —2,-1,0,4,5.
1307. х = ±Зтг/88 4- 7г/4п.
340
1308. х = 5/4.
1309. х = -У5, 25, 5<5+v/3T)/4.
1310. x = (3 + 2<Д)/2, У = (3 - 2УЗ)/2.
1311. [-3, 0].
1312. imin = 1/4.
1313. tg(llog1/3 (2-Л)).
1314. 3/4, —3/2.
1315. Да.
1316. 1 - 2тг.
1317. 1 4- Зтг/4.
1318. 10/(40 — 4тг2) 4-1-
1319. 12тг - 1.
1320. 1/2, -1/2.
1321. а = 4:75.
1322. х — 1/2, у = —я/^ 4- тгп.
1323. 18, -9.
1324. а = 2.
1325. а = -1/4.
1326.
1327.
1328.
-9.
2у/2 2у/2
2>/2-1 ’ 2^+1 ’ X = —6, у = —9; X •=
-5,
у = —10; х = 10, у = 5. 1329. а = b = 0; а е R, Ь = -а2 -1.
1330. х < 1, х = 5/3.
1331. -1 ^х<2, х = 3.
1332. 0 < а < 1/50, а > 25/2.
1333. -4 а 2.
1334. а -99.
1335. -3 а < 1.
1336. -5 < а < -724, - 754 < а < -3.
1337. 15/2 < а < 8, а > 12.
1338. а = -1/2, 2.
1339. X е R.
1340. -12/5 а 0.
1341. 1) —75б - 1 < а у/26 4- 1;
2) -726 4-1 < 726-1.
1342.
1343.
1344.
1345.
1346.
1347.
1348.
1349.
-1 < а < 2.
а = —75.
а > 3/82.
а < -10/3, -3 < а < —2.
а < -8/7, -1/2 < а < О, а > 3/9.
а = 5/2.
х — —1, у = 1.
а — 4:2, b = 4-2; а — 275,
Ь = 72; а = -272, Ъ - -75.
1350. х = 1.
1351. х = (-5 ± 73)/2 при а = (1 4: ТЗ)/2; при остальных а корней нет.
1352. а = (1 - 75)/2.
1353. х = 2.
1354. х — тг/2 4- 2тгп, у = тг — 2тгп.
1355. х = тг/6 4- 2тгп, у = —тг/З 4- 2тгЛ:;
X = ТГ/З 4" ТГ7П, у = —тг/6 4- тг(тп 4- 21).
1356. х = 0.
1357. х = 0, тг 4- 2тгп.
1358. х= 1.
1359. х = Зтг/2 при а = тг/2 4- 2тгп; при остальных а решений нет.
1360. х = —тг/З 4- 4тгп/3.
1361. а = —5тг/12, -тг/12.
1362. х = тг/6 4- 2тгп.
1363. х = -тг/12, 2тг - тг/12.
1364. х = 3/8 4- п.
1365. х = тг/4 4- тгп/2.
1366. х = ±тг/3 4- тгп, у = 4=тг/3 4- ir(k - п).
1367. х — тгп, 2тг/3& при а = 0; при а =/ 0 корней нет.
1368. х = -3.
1369. х = 1 при а = 1/3; при остальных а корней нет.
1370. а = 2тг — 8, 2тг — 1, 2тг.
1371. х = 0, —1 при а = 0; х — О при а 0.
1372. а = 0, 1.
1373. х = -3/4.
1374. х = 2.
1375. а = 9тг/13, 15тг/13.
1376. х = 1/2.
1377. х = 1, у = 1 4- тг/2 4- тгп.
1378. х = 4 -у2/2, ye R; х = п/4 -3 4: 7(104-п)/2, У = 1 =F 7(10 4- п)/2, где п —10.
1379. х = -1, у = 4:2.
1380. х = 0.
1381. х = 4:тг/6 4- тгп.
1382. Менее 50 км/ч.
1383. Более 15 ч.
1384. Не менее 1,4 л.
1385. 55/3 кг.
1386. 25/3, 5/3 и 0.
1387. 6 ч 30 мин.
341
1388. Сначала в газете, а затем в любом порядке 2 раза по радио и 1 раз по телевидению.
1389. 1260 и 1100 руб.
1390. 5.
1391. 6; 66.
1392. 156.
1393. 300; 600.
1394. 100.
1395. 15%.
1396. 15%; 12,5%.
1397. См. рис. 58.
1398. 7 ч, 55 км.
1399. 12.
1400. 2.
1401. Зх/15/4.
1402. 36(572 + 6)/13.
1403. (2л/3 - 3)/6.
1404. 15.
1405. 20/9.
1406. 1/6.
1407. (7-ЗТЗ) : 11.
1408. 5.
1409. 7/4.
1410. 102.
1411. 6.
1412. 24.
1413. 27/8.
1414. 1/6.
1415. 1075.
1416. 108/5.
1417. 3:1.
1418. аЬ/(а + Ь)2.
1419. 9/4, 1/4.
1420. 3 : 7; 200.
1421. 30°.
1422. 7577/4.
1423. 775, 775, 2721, 721.
1424. 7 : 8.
1425. тг75.
1426. 17/3.
1427. 1 + 75/2.
1428. 775/4.
1429. -5- Х-.
771-f-71 а
1430. V/8.
1431. 5V/18.
1432. 126.
1433. 3.
1434. 3\/2.
1435. тг — arcsin(4/5).
1436. 67Г.
1437. (3 ± \/5)/2 при п = 2; 1 при п = 3; при остальных п треугольников нет.
1438. 1) 2(1Др) < у <
г, R,p> 0;_________
р74Яг(14-р)-Я^р2
> 1+p
1439. 24.
1440. 714а2/27; одна.
1441. 22.
1442. 18/5.
1443. а73Ь2 - а2/(46).
1444. 876.
1445. 4713/5.
1446. (3 - 75)/4.
1447. 8.
1448. тг/4 + агсзт((2тга — 1)/72) при 0 < а < 1/тг.
1449. yl|а2 — аб + 62/2 — а/4 при 1 О/a (1 + Т2)/2.
1450. 72. ____ ________
1451. 1) тг : 75+а;
2) 0 < а < тг 73/5;
3) 0 < а 1.
1452. От 0 до 3V/2.
1453. а2(Т5- 1)/2.
1454. 1 : 6.
1455. 12тг.
1456. 24/7.
1457. (bsina)/2.
1458. 7а2 - 6с.
1459. 7о2 +62.
1460. 72; 75.
1461. (d2sin2a)/2.
1462. 25.
1463. ш2.
1464. ab.
342
1465. Sd/3.
1466. 5>/17/8.
1467. Э-/2.
1468. 22.
1469. 4>/3-
1470. 22/7.
1471. 1 : тг.
1472. 2\/3.
1473. 8 + 4>/б - 10 arcsin(2v/6/5).
1474. тг/8.
1475. 112% - 12\/3.
1476. 50arccos(4/5).
1477. х = 0.
1478. х = 1, 4.
1479. х = (13 - s/21)/2.
1480. -3 х < 1.
1481. х > (21 - >/89)/8.
1482. 2^1^11.
1483. х = -1, 4.
1484. х = -15/4, -3, -7/4.
1485. х = 3, 4 < х 7.
1486. -2 5% х -1, х = 2.
1487. 5 х (25 - л/145)/2.
1488. х = ±5.
1489. х = -4, 1.
1490. х = 1/2.
1491. х = л/5.
1492. -1/3 <х< -1/8.
1493. О < х < 1/5, 1/5 < х < 1, 1 < х 2.
1494. х < —2, х > 0.
1495. —27/2 О < —23/8, 23/8 <ж$27/2.
1496. х 0.
1497. 0 < х 3.
1498. х = 1 - \/а2 -2д + 5,
1 4- Уа2 4- 4 а 4- 8 при а < —2; х — 1 — у/л2 — 2а 4- 5, 1 — \/а2 4- 4а 4- 8 при —2
а < -1/2, -1/2 < а 1; х = —3/2 при а = —1/2;
х ~ \/а^ — 2а + 5,
1 — \/а2 4- 4а 4- 8 при а > 1.
1499. 0 < х < 1/2, 1 х < 2, 3 < х 6.
1500. -1 < х (1 - >/5)/2, 0 < х (1 + х/5)/2, х >(1 + У13)/2.
1501. log3 4 х 3.
1502. х = 9.
1503. log2 3 < х < log2 49 — 4, х > log2 7.
1504. х = —1/4.
1505. 2 < х < 5/2, 5/2 < х < 3.
1506. х = 6/11, у = 10/11.
1507. х = -2, у = 1.
1508. -7/16.
1509. а = 9/16.
1510. х = -9, -8, -6, -5.
1511. а 2/3.
1512. х = у = —2.
1513. х = у = 1; х = 5/2, у = -2. 1514. х = 3, у = 2;
х — -2, у = —3;
х = 3 ± >/10, у = -(3 т х/10)-1515. х = 3, у = \/2;
х = \/2, у = 3.
1516. х = 2, у = 3; х = 3, у = 2; х = -9 4:^/248/3, у = -9 4: У248/3.
1517. -9/10.
1518. а < -1, а > 4.
1519. х = 2, у = 1.
1520. х = 4 log3 2 — 2 log2 3, у = 31og2 3 - 41og3 2.
1521. х = 2.
1522. х = 3/2, 36/25.
1523. х = -20, у = 36;
х = 3, у = 10.
1524. ж = (а —3)/4, у = log2(15a2 - 26а 4- 7) - 2 при а < 1/3, а > 7/5;
х = —(а 4-1)/2, у = 14- log2(4a — За2 — 1) при 1/3 <а<1; х = 1 — а, У = log2(12a—5а2 4-7)—2 при 1<а<7/5; х< — 1, х>0, у = = log2(4x2 4- (14а — 10)я 4-4-8а —8) при а = 1; при а = = 1/3, 7/5 решений нет.
1525. 1, 10/9.
1526. х = Зтг/2 при а = 9;
при а < 9 корней нет.
1527. -3 - l/ч/З х < -3, -3 < х -3 4-1/\/3 при а —1/4;
- 4 < х -3 - <р(а), -З-1/л/З -3,
- 3 < х —3 4- 1/х/З,
— 3 4- <р(а) х < — 2 при —1/4 < а < 1/10;
343
- 4 < х < -3, -3 < х — 2 при а = 1/10;
— 4 < х —3 — 1/\/3,
— 3 — <р(а) х < —3, — 3 < х — 3 4- <р(а),
— 3 4-1/\/3 х < —2 при 1/10 < а < 1/3;
- 4 < х -3 - l/v/3,
- 3 4-1/х/З <х< -2 при а 1/3,
1528. х = тг/2 4- тгп,
± arctg(\/2/2) 4- тгк.
1529. х = — 7r/3±arccos(3/4)4-27rn, 2тг/3 4- 2тгЛ:.
1530. х = тг/4 ± 2тг/3 4- 2тгп.
1531. х = ±117Г/12 4- 2тгп.
1532. х = —тг/4 ± тг/4 4- 2тгп, тг/4 4- лк.
1533. х = 2тг/3 4- 2тгп, тг/6 4- 2тгк.
1534. х = (—l)nf —arctg (I) 4-тгп.
1535. х = 2тгп, тг/2 4- 2тгЛ:,
2 arccos(l/\/5) 4- 2тгт, 2arccos(l/\/5) — тг/2 4- 2тг/.
1536. х = -у/2/2, sin(7r/12).
1537. х = -</2/2, sin(57r/12).
1538. 4.
1539. х = 6, у = ±1, z = 0;
х = 0, у = ±1, z — 0.
1540. х — 15п2 — 6п, у = Зп — 1, где n G Z.
1541. х = -7г/12 4-тгп/3, у = —тг/24 4- тгп/6 4- тгк.
1542. 189.
1543. 648.
1544. 764.
1545. 300.
1546. 38.
1547. 7, 7 ± 7\/2.
1548. 6.
1549. 231.
1550. 573.
1551. 864 руб.
1552. 13, 11.
1553. 9.
1554. 80.
1555. 750 м3.
1556. 30 и 40м3/ч.
1557. 80 км/ч.
1558. 50 км/ч.
1559. 2.
1560. 500.
1561. От 25 до 40%.
1562. 75 и 55%.
1563. а 17.
1564. х = 6.
1565. а = 6п, 6к 4- 2, 6m 4- 3, 614- 5.
1566. х = -1/3.
1567. (11 - \/77)/2 а < 2, 9 < а (11 4- \/77)/2.
1568. х = 0, ±а\/5/2.
1569. 26; [42; (253 4- 84\/3)/8].
1570. 3 - \/б О 2, х < 3 4- х/б.
1571. -1 —1/5.
1572. а < 1/2.
1573. а = -4.
1574. х0 = 3.
1575. х = -y/ljb.
1576. х — —тг/2 4- 2тгп.
1577. х = ±2, у = 4=128, z = ±127,5.
1578. х = —2\/3/3, у = z = 1; х = -2х/3/3, у - 7, z = -9.
1579. х = тгп, у = тгп — 1.
1580. х = 7, у = z = 6.
1581. Да.
1582. х = 0, у = —2тг;
X = ±7Г, у = —тг.
1583. а = (t ± Vt2 + 4t — 4)/2, где t = 16/(2 + n + 1/п),п = = ±2, ±3, ±4, ±5, 6,..., 17.
1584. а = -17/48.
1585. а = -1.
1586. -1/3 5$ а 1/3.
1587. х = (23 ± 12л/5)/4.
1588. о 8^85,
17+\/349 < _ < 27+4\/66
6 Х 9_‘
1589. х = у = TV'lr2+1?; у/^ + 161 * 4
х - ±1Г и = 15^+2
1590. 0 < х < 1 - 2v^a при 0 < а 1/8;
1 — 2\/2а < х < О
при 1/8 < а 1/2;
—2a х < 0 при а > 1/2; при остальных а решений нет.
1591. -1/20 а 0.
344
1592. х = О, 1 при а = 0;
х = (1 - а + VI +За2)/2 при ? < lal < 2/7з;
х = (1 - а + VI + За2)/2, (-1 - а - V3a2 -3)/2 при |а| 2/73.
1593. х 7 3 при а = 0;
х 7 (1 - VI - 12а)/(2а), х (1 + 0 - 12а)/(2а) при 0 < а < 1/12;
х е R при а i.
1594. 7/23.
1595. а = 9; [-1; 3].
1596. 773.
1597. 30.
1598. 9073.
1599. 713/2.
1600. 121,5.
1601 c(5~4cosq) sin/3 8 sin а sin (а+/3)
1602. 7у/2.
1603. 30°.
1604. 30 sin ср/(4 4- cos (р).
1605. 7\/27.
1606. c°s у)
I 4-2аЬ(а — cos </?)—и2 sin2 <р ± 2
1607. 787/4.
1608. 7/ТбЗ; 78/5.
1609. 7(3а2 + 8с2)/35.
1610. 4/717.
1611. 2-/4 tg2 а + 3. .
1612. 3(472 —5)/4.
1613. 8._________
1614. 7848±16у5р8, 7308± 167208-
1615. 20.____
1616. 713/19.
1617. 738.
1618. arccos(377/8).
1619. 12/5.
1620. arccos(5/8).
1621. arccos(46/V^64T).
1622. 2V5/3.
1623. 5710/32.
1624. f — arccos fcos (p — .
2 у r COS p у
1625. iV- |V3K2 x o 3
X ((°2~24Д2)2 ~2°V) •
1626. 1/2 7 a 7 1.
1627. а < -0,99, -0,02 < а < 0, О < а < 0,01.
1628. а = -1, 72.
1629. а = -5, -5/13.
1630. О 0.
1631. а = -1, 1 < а < 3, 4 < а 7 6.
1632. а - 3, 710 7 а < 711.
1633. а = Зтг/4, 7/2 7 а < 9/2.
1634. а = 4,5,..., Ь = —2; а = 3,4,..., Ь=-1.
1635. 20км.
1636. 9 : 7.
1637. 40 мин и 1 ч.
1638. М.
1639. 14/3.
1640. 4; 3/2.
1641. 0.
1642. -2/3 < х < 0.
1644. Нет.
1645. 137 и 77 человек.
1646. Да.
1647. 72/2 < а < 1, 72 < а <2.
1648. х = 0, (9 + 781 + 12тг)/2.
1649. Зтг/2 < а 7 7тг/2.
1650. -(3 + 273)/2 7 х < -7/2, 1/2 < х 7 (-3 + 2ТЗ)/2.
1651. х < -1, (7 - 75)/2 < х < 3, 4 < х < (7 + 73)/2, х > 8.
1652. (9 - 717)/16 < х < 1/3, 1/3 < х < (9 + 717)/16.
1653. X = (11 - Т29)/2, (3 + Т13)/2.
1654. —5 < х < 3 + 78.
1655. JC = (-3+717)/2.
1656. х = -(3 + Тб1)/2.
1657. -5 + 723 7x7 -1/8, 3/8 7 х 7 3 - 75, X > 3 + 75.
1658. -1; —53/4.
1659. -тЗ/4; -3.
1660. X = тт, (—1)*тг/6 + тгк, где n,k = 0,±1, 2.
1661. -6 7 х < —Птг/6, — 11тг/6 < х < —4, 2 < х < 5тг/6, 5тг/6 < х 7 6.
1662. -13 7 х < —4тг, — 4тг < х < —11тг/3, — 7тг/3 < х < —2тг, — 2тг < х < —5тг/3, — тг/3 < х 7 1-
345
1663. 3 при |а| > 1, а = 0; 5 при
а = ±1; 7 при 0 < |а| < 1.
1664. а = -2, 1.
1665. —тг/2 < а < -7г/3, —7г/3 <
< а < — тг/4, а = тг/З, тг/2.
1666. х = —Зтг/2, —5тг/4, — тг/2 — arcsin(l/2x/2).
1667. arccos 6010^ х < ^. 1668. х = тг/12 + 2тгп, 5тг/12 + 2%fc. 1669. а = —тг/2 + 2%п.
1670. а = ±1/6, ±1/2/6.
1671. нет.
1672. -1 - /2/2 а -1;
а = -2, 0, 1, /2/2.
1673. О а < 1, 1 < а < 2, а = 3. 1674. —70тг/3.
1675. а = -/3/2.
1676. 10 - /3; -(1 + /11 - /З)2. 1677. 1/2 - •/) а < -1, а = 2. 1678. а —4, а = -2/3, а = 1/2, а 4.
1679. а = 2, 10/3.
1680. 1) таких а нет;
2) а < —8, а > 0. 1681. 1) а = -8;
2) -8 < а < -4ч/3.
1682. х - -2, |, при а = -2; х = —0, | при а = —
1683. а = -2 ± з/З.
1684. а = -3, 9.
1685. -1/2 < а < 2.
1686. -8 < а < 0.
1687. а -2, -1/2 а 0. 1688. а = 2, (1 - х/2)/2.
1689. х -1 - ч/З,
- 1 + ч/З х < (7 + х/22)/3. 1690. -13/4 < а < 3.
1691. О < х -а 4- \/а2 + 1 при а —1;
О < х —а — \/а2 — 1,________
—а 4- \/а2 — 1 ж -о + \/а2 4- 1 при а < — 1. 1692. а < (ч/б - 1)/2, а > 1. 1693. а = 1, 0.
1694. 2 при — 1 — тг2 а < 1;
1 при а = 1; 0 при осталь
ных а.
2 а < 3, 3 < а < 4.
1695.
1696. а -7/2.
1697. а О, 0 3.
1698. -9 а -1/4, О 0.
1699. -\/2 < а < -16/17, О < а < ч/2.
1700. а = -4, -5/2 а -9/4.
1701. -15 а < -5, а = 1.
1702. а -4, а = 1, 8/3 а < 4, а > 4.
1703. а 1, а = О, а > 2.
1704. а 20.
1705. О < а < 1/8.
1706. а < (-3 - ч/б)/16.
1707. 5 < а < 7.
1708. 1) 1 < а (2 4- vT3)/4;
2) b = 7/3.
1709. а = 3/2, 5/3; 2 а < 4.
1710. х < —1, — 1 < х < 0, х > 2.
1711. 5/6 х < 1, 1 < х 3/2.
1712. а < ч/2.
1713. -7/3 а < 6.
1714. -4/3 а 11/4.
1715. а -3/2.
1716. -\/2 а < 1; ч/2.
1717. а = 1 - у/2, 5 4- ч/ТО.
1718. р = -6, q - 7.
1719. а < —2 — ч/б, а > \/2.
1720. а = Ь = -1/6. ________
1721. х = log5 a~x+>/a^-10a-1-l при а < —|;
X = 10g5 a-l±/a^-10a-JU при а > 11;
х — 1 при —| а < 11;
при остальных а корней нет.
1722. а -5 - 4ч/2, а > 0.
1723. х — к/2 4- тгп, 2тгЛ: при а — —1; х — ±2тг/3 4- 2тгп при 4 = 0;
х — ± arccos ( - 4- 2тгп
при а — 1; при остальных а корней нет.
1724. 1/3 О < 3/4, 3/4 < а 33/32.
1725. а = 0, 2, (3 4-ч/5)/2.
1726. а < -1 - V^/4, - 1/2 < a < 0.
1727. а -У13, а 11/3.
1728. а < 2/3, а > 2.
1729. -3 а < 0.
1730. а 3, a > 4.
1731. Два.
346
1732. х 6/5.
1733. 1 х 3.
1734. х = -1, у = —3;
х = 1, у = — 1.
1735. 1 а 3.
1736. а = ±9.
1737. а = ±2/5, Ъ = 4/5.
1738. —а2 при 0 < а 2 — \/2;
2 — 4а при 2 — у/2 < а < 1.
1739. х = -9/5, у = 12/5.
1740. а = -11,-10,...,-3.
1741.а = 4, —3 —\/35<Ь<3 — \/35, - 3 + ч/Зб < 6 < 3 + л/45.
1742. —2 а < 1, 1 < а 4.
1743. х = 217~5/^, _ 180+2У4Т5
У ~___ 29
1744. /32/3.
1745. х = 4//13, у = t = 6//13, z = 9//13.
1746. 4.
1747. 48 мин1.
1748. 2 км.
1749. 5.30.
1750. 24.
1751. 57, 61.
1752. 24/^'145.
1753. 4г/3±10тг.
1754. 6, 8.
1755. 36, 8\/19 .
1756. 3, 5.
1757. ЗаЪ/4 .
1758. 42\?51а2/25.
1759. 10.
1760. 4 : 5.____
1761. х/13 ± 6\/2.
1762. 3 : 5.
1763. 10.
1764. 2х/б.
1765. -х/15.
1766. 1024/9, 2arctg(x/34/4).
1767. arcsin (| sin а).
1768. тг/З.
1769. тг/4, 2/л/З.
1770 а /8(1г5°?^Г
'и- V 1+2 cos а ’
1771. ЗхДТ/2.
1772. у/$.
1773. 4.
1774. 49/4.
1775. 48/5.
1776. 10/3.
1777. 44 : 19.
1778. 9 : 23.
1779. 3 : 29.
1780. 20.
1781. 4.
1782. 5 : 8.
1783. 3\/б/2. __________
1784. arccos у/2(1 — s/S).
1785. л/3/4.
1786. 9 : 95.
1787. 7 : 20.
1788. 213 : 67.
1789. 3.
1790. 1) 7 : 20; 2) 9ds/4.
I 7Q1 ______Z_____
ctg 20°4-ctg 50° •
1792. tg2a(l +2cos2a)2/2.
1793. 40.
1794. 1.
1795. 8r3/a.
1796. /6^/2.
1797. 27/4.
1798. R2.
4 sin a Sin2(4£ + #J
1799. 4/3.
1800. (m2 - fe2)/(2h).
1801. (21 - /357)/4.
1802. 2 arcsin ^7°2 , • у/1 —а2 arccos a — arcsin —,
тг — arccos а — arcsin ^'1^°2.
1803. 2.
1804. 2/19715.
1805. V?69/8.
1806. 1//2.
1807. 512.
1808. -7=--— =
>/2+ctg( j arctg V)
= i^a.
1809. 2 arcsin (| sin a+ + & у/ cos2 a — sin2 /3).
1810. 2/6/3.________________
jgjj 2at%ay/2rbsin sin2 a
cos2 а
1812. 5/9.
1813. 1/18.
1814. -11/3, -0,35.
1815. 4/5.
1816. 0.
347
1817. 70.
1818. 20.
1819. 2.
1820. 1.
1821. 3 млн.
1822. 2,1кг.
1823. 45.
1824. 5/8.
1825. 60 км/ч.
1826. -4/3.
1827. а < 0.
1828. ±1/У10.
1829. х = arccos(27/28) + 2тгА:, у = тг 4- arcsin( 17/28) 4- 2я4; х = — arccos(27/28) 4- 2тгт, у = — arcsin( 17/28) 4- 2тгп.
1830. х = 4/3, тгп.
1831. х = ±arccos(l - \/3) 4- 2тгп, у =. — тг/2 4- 2тг2А:.'
1832. х = 1.
1833. Корней нет.
1834. х = у = 0; х — 5, у = 1; х - -10/3, у = 2/3.
1835. х = 2, у = 1.
1836. х = —2, у = —4;
х = —1, у — —3.
1837. х = — 7г/30 4- 2тгп/5, у = 1.
1838. х = 1, у = 0 при а = —4; х = —3, у = 0 при а = 4; при остальных а решений нет.
1839. х = 3 при а = 0;
х — ±3 ± 2у/2/2 при а = ±1;
х = 3 ± х/5/2 при а = ±2; х = ±3/2 при а = ±3.
1840. х = 0.
1841. х = 6.
1842. х > 4.
1843. х — 2тгп.
1844. х = 5.
1845. х = 2.
1846. х < 0.
1847. х = 3.
1848. х = 1, у = —тг/2.
1849. х = у = z =J3.____
I860, х = -1 ± ч/11 + 4\/3.
1851. х — 1/4.
1852. Да; С = 9/2.
1853. а = 2.
1854. 1 < а < 2, 2 < а 3.
1855. 6.
1856. 20 м.
1857. -3 4/51/196.
1858. 5 км.
1859. 2.
1860. 6 км/ч.
1861. х = 3/2.
1862. х = —тг/2 + 2тгп.
1863. х - 1.
1864. О < х < 23/35.
1865. 1/3 < х 2/3.
1866. 2 < х < 3, 3 < у < 4.
1867. 4 О < 13/2.
1868. х = 7.
1869. -5 < х < -2 - 2>/2, — 4 I < 0, 0<х<1/2.
1870. 3 < х < 1 + ч/5, х > 10/3.
1871. х = —5тг/6 + 2тгп.
1872. -1/6 х < 1/2.
1873. 3/4 < х < 1.
1874. -2 < х < -3/2, х = -1.
1875. -1/3 < х < (-7 - 77)/42, (-15 - \/197)/84 х < 0, 0 < х < (13- ч/141)/84, (13 + \/ПГ)/84 х < 1/3.
1876. х = 3/2, — тг/З + тгп х < —тг/4 + тгп,
тг/4 + 7ГП < X тг/3 + 1ГП.
1877. (-5 - 2>/3)/26 0^0.
1878. 1 < а < 2, 2 < а < 3.
1879. х > 1.
1880. х -5/4, х = -1/4.
1881. 9/16 < х < 15.
1882. х = (-l)n arcsin(5/6) + тгп.
1883. х = arctg (|),
У /2 -2 (arctg (|) - |)2.
1884. х < -1 - ^4>/2/3+ 1, х > -1 + У4л/2/3+1.
1885. х = ±^/(2 - а)/6, ±/^а/2 при —1 а 0;
х = ±^/ (2 — а)/6
при 0 < а < 1/2;
х = 0, ±У(2-а)/6 при 1/2 а 2;
х = 0 при а > 2; при а < —1 решений нет.
1886. 10 ± 2\/5.
1887. х = 3/2.
1888. х = 3.
1889. х = -1, 3, ; у = -3.
348
1890. х = 1, у = 3.
1891. х = 1/2 — log3 2, у — 2 log3 2.
1892. х = -1.
1893. х = 4, у = —3, z = 0;
х = 2, у = —1, z = 2.
1894. х 100.
1895. х = тг/З 4- 2тгп.
1896. х = -7/4, 1/4.
1897. х — я/6 4- 2тгп
при а = 5тг/6 4- 2тгЛ:;
х — 5тг/6 4- 2тгп
при а = —5тг/6 4- 2тгЯ:. 1898. а = 1/9.
1899. а = 2, b = тг/2 4- 2тгп;
а = -2, b е R.
1900. а < -1.
1901. а = 0, тг, 2тг.
1902. х = -3/2, у = 2/3;
х = -2/3, у = 3/2.
1903. х = тг/2 4- 27гп, у = —1. 1904. х = 2тгп, у —
z = (arctg 2 4- тгтп) х
v 16?rn24-2fc4-l
Х 2тгп(8/±3) ’
„ _ 8Z±3
и — 27ГП 1б7ГП2+2*;+1 ’
v = 47rnI+5fc, гДе n # 1905. 117Г/24 х < тг/2. 1906. —2тг а < 0, 2тг < а 4тг. 1907. 4 км/ч. 1908. 12.00.
1909. Нет.
1910. 90 км.
1911. 7, б|, б| км/ч.
1914. тг/18.
1915. abc : (атп + Ып + dm).
1916. 195.
1917. 35/32.
1918. а + р.
1919. 10 : 3.
1921. 1820х/21/341.
1922. (Ь2 - а2)/Ъ.
1923. R2/а.
1924. (а2 — Ь2)/а.
1925. тг/З.
1926. 120°.
1927. 10.
1928. 2х/3(1 + 1/(сов f - |)).
1929. 5 : 9.
1930. (Тб - 72 + 2)/\/2 + 72.
1931. 27^tga.
1932. 2-73/3.
1933. ab/c.
1934. Тб.
1935. 1) VrR-, 2) y/r-.y/R.
1936. 9(3v/10- 8)/10.
1937. y/ab.
1938. 4 : 3.
1939. 2аЬ/(а + Ь).
1940. (а + 25) : с.
1941. 4.
1942. 5/2, 5/3.
1943. 2, 2/3.
1944. х/ГТ.
1945. 1 : 3.
1946. 8.
1947. 6.
1948. Зу/З.
1949. 19/726.
1950. 375/272.
1951. у/30/5.
1952. 40°.
1953. 7 + 4у/3.
1954. 45/2.
1955. 6\/б + 3.
1956. 6.^_____
1957. y/d2 + с2/3.
1958. 1/2; 3/4.
1959. 6, 2.
1960. у/6 - у/2.
1961. 27х/3/2.
1962. 8.
1963. v'2‘L3<bt2),.
6\/Ь(Ь+1)
1964. .
3>/2(>/2+1)
1965. 1/12.
1966. >/6.
1967. 48.
1968. 80/3.
1969. 5ч/5тг/6.
1970. 8V?.
1971. 75-1.
1972. 8(275- 1)/7.
1973. 73.
1974. 97221/266.
1975. 1 : 2тг.
1976. 72976, (27 - 3\ЛТ)/(472).
1977. 8.
1978. 25.
1979. 3/32.
1980. 3/2.
1981. 2.______
1982. у/а(а + Ь).
349
1983. 1) 5/2; 2) 234/25.
1984. 1) 60°; 2) 2/у/З.
1985. л/3.
1986. 1; 4.
1987. 1) 1; 2) а - 1.
1988. 2rR/(R — r).
1989. 1.
1990. 9.
1991. 169'/187/5292.
1992. 1.
1993. а = 2/5.
1994. 1 < a < 5.
1995. х — у — 0.
1996. Нет.
1997. А.
1998. Нельзя.
1999. На диагонали.
2000. Нет.
2001. Нет.
2002. О а < 1.
2003. а = -1.
2004. а 0.
2005. а = 1/2, 1.
2006. 2^000 • 3^99000 '
2007. 21001 - 4.
2008. 4 004 001.
2009. 3997.
2010. х = 1+2/х/З.
2011. а = 0, 2sinl.
2012. а = 2.
2013. а = -3/2.
2014. а = ±1.
2015. а = -1, 2.
2016. а = 4/3.
2017. а- -1/4.
2018. а = 0, ±1/(2v/З)-
2019. а = 1/3.
2020. а = 1.
2021. а= 1/16, 1/128.
2022. а = -3/4, 4/3.
2023. а = -1/3, -5/3, ±1, ±х/3.
2024. а = 9/4 + 4п.
2025. x = l/&5,y-z = Q при а = —1//8; х = 1//5, у — 1, z — тг/4, х = 1/ v5, у = —1, z = —тг/4 при а = —1/2 4- /3/8.
2026. а = 1.
2027. а = 2, 3.
2028. а = 2/3.
2029. а = 3, 4,... .
2030. а < —1, а > 1.
2032. О < х /35.
2033. /161/9.
2034. х = -1, 3.
2035. х — 1, у = 6; х = 1, У = 7; х = 2, у = 7.
2036. х = 11, у = -9.
2037. а = -2, 0.
2038. х = 5, у = z — 4.
2039. а = 1, 5/2.
2040. 40 и 30 км/ч.
2041. 24 и 7.
2042. 132.
2043. 1750 т.
2044. 35 руб..
2045. 94.
2046. х — —4, у — —3; х = —6, у = —13; х = —14,7/ = —5.
2047. х = —2, у = 0; х = О, у = —2; х = —3, у = 0;
х = -1,2/ = 2.
2048. х = 2, у = ±3; х = -2, У = ±3.
2049. х — ±1, у — 4=1, z — —1.
2050. х = -31, —7.
2051. 5/11 < а 6/13.
2052. х = (4п — З)2, где п > 0.
2053. 11.
2054. 1 год.
2055. 27.
2056. 375 и 125 руб.
2057. 144.
2058. 4.
2059. 25 и 6.
2060. 5 : 7.
2061. 0,9 мин.
2062. 8.
2063. а = -187.
2064. 6.
2065. 33.
2066. Один 16- и одиннадцать 12-квартирных.
2067. 20.
2068. 105 и 126 руб.
2069. 27 : 10.
2070. 5 : 2.
2071. п : т.
2072. 12/5.
2073. 8.
2074. 18.
2075. arcsin(l/3).
350
2076. b-Jac/2.
2077. 2УЗ.
2078. 2.
2079. 134 : 129.
2080. 8._______________
2081. J2s(l-(s/S)2)//3.
2082. 52._____
2083. 2/3/2- 4.
2084. 3/3/4.
2085. 11//170.
2086. АВ; в любом отношении от 0 до 1 : 56, считая от А.
2087. 12.
2088. 5/2.
2089. (17 - /17)г : 8Л.
2090. /133.
2091. /16/6.
2092. 6:(УТ9+2У7+-У3+2У15)2.
2093. Зтг ____У i9+eyio--3—
10 /10+бУй5+/19+бУк1-з
2094. (11/3 + 3/7)/4.
г2(2Я+/ЗЯг+г2)2 4(Я-г)2
2095.
2096. (42 + 12/11)/5.
2097. 1/-/3, 19/(25/3).
2098. /31/20.
2099. /53.
2100. 6/7.
2101. (17 + 2уЗ)а.
2102. 3/13/(/13 + /5).
2103. (a/3 + s/8 + 2)3 : 36а.
2104. cos2 |V1 — 2cosa.
2105. /12d3/12.
2106. 4Л/2//7.
2107. 3/4.
2108. 50/2.
2109. 41(2/105 + 11-УЗ + 15)/110.
2110 3q s‘n2/arct$ cos у) /1+cos2 ip
2111. 4тг/3.
2112. 5, 16/3.
2113. 9.
2114. (2 + x/2)/2.
2115. 6?r.
2116. 2/85/3.
2117. УН/2.
2118. 36?r/(ll/IT).
2119. s/4 + S/2 — 2Ь/(4а).
2120. 3/183/2.
2121. arccos vZ4~1
4
2122. 21/20.
2123. /8-/5.
2124. (36 + 31/2)/4.
2125. /16/3.
2126. 25 : 47.
2127. (36 —9-/6)/5.
2128. (2/3 — 2)/3.
2129. У148 - 34УЗ.
2130. 15^
2131. а(\/3 — 1)/12.
2132. arccos(6 — \/33).
2133. 1) arcsin tg y) ;
2) (^ctg2 a _ 1 - tg f) : : (y3ctg2f -1 + ctg f).
2134. -^-(-^cosa-l).
_2_2 i_2 2 9p2 2
2135. 1+7д3Г 2-
2136. 1960. 2
2137. 7200.
2138. -63/4, -23/8.
2139. 6; нет.
2140. n = -6, -5, -4.
2141. -3 О < ~2, x = 1.
2142.x = (-l)n£-£ + fn.
2143. x = (-l)n| + тгп.
2144. arcsin 5 + 5,
1 • 2
7Г — - arcsm |.
2145. x = 2, e2.
2146. 54; -135.
2147. Xmax = 1/3.
2148. 1.
2149. (0; 1),(1; e] — промежутки убывания, [e; 00) —
промежуток возрастания, ^min — в.
2150. -5/e.
2151. 1.
2152. 3/3.
2153. +4тгп.
2154. ±(4tt + 3/31/2 - 1.
2155. —I arcsin -X. + n.
2156. 2/3; 21.
2157. 21 +3 In 2; 0.
2158. -118.
2159. 1/10.
2160. -a3/3 - a2/2.
351
2161. a < —2 - x/5t a > \/5.
2162. a = a, — a, где a = arctg .
2164. x = тг/8 4- тгп/4, Tvk.
2165. 9/2.
2166. 0, 8.
2167. x = 3.
2168. 2.
2169. о(4тг/3 — УЗ)2/4; (^-73)(l + | + y1 + ^).
2170. 25/4.
2171. (тг/6; тгУЗ/6 + 1/2).
2172. 6.
2173. у = -x + 5/2.
2174. у = ±У2х + у/2.
2175. х = 1.
2176. х = у/2я, .
2177. а = -тг/2, Ь = 2.
2178. 64/3.
2179. 9/2.
2180. 9.
2181. 9/4.
2182. 2у/2 — 2.
2183. 9/4.
2184. 9/4.
2185. а = ЭЬ2/6 - 1 при 0 < b < 4/3.
2186. а - 1.
2187. (1/2; 1/2).
2188. 4/У5.
2189. х = 1.
2190. (0; 2).
2191. а = 3/5.
2192. а = 4/5.
2193. а = УЗ.
2194. -1,9 х -1,7, х > -1.
2195. а > -1/3.
2196. О < а < 1/54.
2197. а < -Зтг/2 - 5/9.
2198. а < -3, а > 6.
2199. О АВ < 1бУз.
2200. 2Rsin^..
2201. 4.
2202. 4\/3.
2203. 8тгг3/3; 4г.
2204. 4R/3; 2y/2R/3.
2205. 2 arctg 3+/I?.
2206. < х < 1;
1<3;<^1±У?з
2207. 50°, 90°, 110°, 110°.
2208. -5..
2209. 8/УЗЗ, у/15/14.
2210. х = | tga, у = | tg2a, z — tg4a, гдеа = ±|,±^,±^.
2211.a = l/3, 4/3, ±6/11, 18/11.
2212. 2, 2/3.
2213. x = 0, | х 1,
2215. а < 0, 2 < а <
2216. 32 : 5.
2217. х = -1/3, -1/2, -3/4, 1.
2218. О < х << 2.
2219. arcsin < arccos |.
2220. 300/13 км.
2221. 3.
2222. а > 2.
2223. (3 + У8 - УГ1)2/4.
2224. 15/2.
2225. -1 х 1, 4/3 < х < 5/3.
2226. 10У5.
2227. —2, 11/2.
2228. -УЗ < а < -4/3, 4/3 < а УЗ.
2229. 1/2.
2230. а = —У2.
2231. -1 х < -7/8, х = 1.
2232. arccos
2233. 10.00.
2234. х = ± arccos | + 2тгп, у = (—1)к arcsin | ± irk.
2235. 7УЗ.
2236. х = 4- тгп.
2238. 0 2.
2243. х = jn, (—l)k arcsin 4; тг/с.
2244. x = 1.
2245. 2 - x/13 x < 0, 3 < x 2 4- vT3.
2246. 2.
2247. x = у = 0; x — 2\/7, у — \/l.
2248. arcsin .
2 cos a
2249. x = у = 2±V'2<a2+a)
при a < —1, a > 0;
x = у = 1 при a — —1, 0; при остальных а решений нет.
2250. У о2/2 -&2.
352
2251. х = 3.
2252. х — ±7г/4 4- тгп, тг/2 4- тгк.
2253. х = -9, (-1 4- \/33)/2.
2254. у/7.
2255. х = 1, у = 27.
2256. 4/9.
2257. а 4-1 < х < 0, х > -а - 3 при а —3;
а + 1 < х < — а — 3, х > О при — 3 < а < —2;
х > 0 при а = —2;
—а — 3 < т < а 4-1, х > О при — 2 < а < —1;
—а — 3 < х < 0, т > а 4- 1 при а —1.
2258. а) 2/3; б) 4^/5/15.
2259. х — 7г/10 4- 7гп/5, (—l)fc7r/15 4- тгА:/5.
2260. х < 1, 3/2 < х 2.
2261. О < х < log3/4
2262. 9/2.
2263. 4, 28.
2264. Зх/6/4.
2265. х < 3 - \/а2 4- 5а 4- 6, х > 3 — х/а2 4- 5а 4- 6
при а —3, а —2;
ж G R при остальных а. -(5 4-\/13)/2 <а^ -3, - 2 а < -(5 4- >/13)/2.
2266. 6.
2267. х = тгп/2.
2268. х = тг/4 4- тгп, у = 9.
2269. х О,
log4/3 4^X5$ log4/3 7, * > log4/3 12.
2270. 6.
2271. 7v.
2272. х = — 1 ± у/a при а 0;
при а < 0 корней нет.
2273. (1 - 77)/2 х < 1,
® > (1 + Л)/2.
2274. х = 7/5.
2275. х = 1, у = 2; х = -1, ' у = -2.
2276.x=|f + fn, _£±f + ^fc.
2277. 20.
2278. -8 < а < 4, а > 7.
2279. х = 1/4, 1/2.
2280. х = у = 1.
2281. —4 < х -3,9,
4 < х < х/17.
2282. х = 2тгп/7, 2тгЛ:/9, где n / 7m, к ф 9Z.
2283. 8.
2284. а = О, (3 ± х/5)/2.
2285. х — тг/4 4- (—1)п тг/6 4- тгп.
2286. х = 1/2.
/ Ssin(a4"3)
V 2sin^ShT3-2288. х < -4, —4 < х < -3, — 3 < х — 1 х/3.
2289. 133 : 803.
2290. х < 1/3.
2291. х — 7г/10 4- тгп/Ъ.
2292. 15\/15/32.
2293. х -2, -1 х < О, О < х 1, х 2.
2294. а) а = 2 4- х/2; б) а < 2 - х/2 а - 1, а > 24- /2.
2295. 25°.
2296. 2/11.
2297. х < О, 0 < х < 1, х = 2.
2298. х = тг/6, 4тг/3.
2299. Л = 0, х 1g15 6.
2300. Юл- 4-16.
2301. а(У№ + £ - |)/(Н^З).
2302. 3/7 < I < 1.
2303. -\/2-ч/2/2.
2304. 70.
2305. 1 < х 64.
2306. х = -Итг/12, -7зг/12.
2307 ________с s*1} 5* cos а_
* (sina+cos«)(l+sina+cos а) *
2308. 1/15 < а < 1/8, 1/8 < а < 4/15, а = 1/2, 1 5$ а < 4.
2309. х -1, 7/2 х < 5.
2310. х = 3, 7/2.
2311. х = (1 + >/17)/2.
2312. х = + тгп, 3/ = -f + irk-,
х = | + irm, у = + irl.
2313. 72, 12.
2314. 36, 49.
2315. 2/5 a 11/2.
2316. 6br/(9v/39).
2317. x < 1/3, x > 2.
2318. x = 1, у = 1/2.
2319. x —2, x > 2.
2320. 2.
2321. x = ±7г/2, 57t/6.
2322. 9x/15/4.
2323. a < 1.
353
2324. 31УШ/288.
2325. х < 0, х > 1/2.
2326. х = 3, log2(3 — х/7).
2327. а) 1 : 3; б) arcsin(l/x/8)-
2328. а) 2 : 3; б) 2 ч 48 мин.
2329. 5.
2330. -1/3 < а 3/10, а = 1.
2331. х = 3.
2332. х = (-1)п+1зг/6 + тгп.
2333. xi = —3, Х2 = 9;
Xi = 2, Х2 = 4.
2334. а) Ютг; б) 160.
2335. а) 3; б) тг/З ± arccos(5/6).
2336. х = у = 0; х = — у = 2;
х = у = х/б; х = ±Qi, у = = qza2; X = ±02, у - =FQi, где ai,2 = У(5 ± \/5Т)/2.
2337. —4 < х -5/2, -1 < х 3.
2338. 7rd2/24.
2339. а) 1240; б) 40.
2340. ж G R, у = ж + f •
х = тгп, у = 4- тгп;
х = + 27г/с, у = J + 27г/с.
2341. log2 11.
2342. х = ±(1 - а2)2/(2а)2
при 0 < а 1; при остальных а корней нет.
2343. О < х < 1, тг/2 < х 2.
2344. 9(3 + \/3).
2345. х = тг/4 + згп, —5зг/6 + 2згА:.
2346. -1 < х < 0.
2347. а) 144(3 + 2^5);
б) 144зг(1 + 35х/2/49).
2348. 5 месяцев.
2349. Да.
2350. -1/2 < я: < О, 7/2 О < 5/2.
2351. х = -2, у = 3; х = -3, у = 2; х = —1, у = 5; х = —5, у = 1.
2352. 20 человек, 6 ч.
2353. х = (- 1)п тг/6 + згп, (—1)*тг/18 + тгк.
2354. а = х/5/2.
2355. 2(2 - хЛ)/3.
2356. Зх/З/2.
2357. -1/2 0 0, 7/2 sC х < 5/2.
2359. 20 человек, 6 ч.
2360. х = тг/4 + 2згп, arcctg(l/x/2) + 2vk.
2368. 2(7х/2 - 9)/3.
2369. -1 < х < (5 + х/13)/2.
2370. х > 11.
2371. z = 0.
2372. 1.
2373. х = 2тгп.
2374. х = 2.
2375. х < 1, х 2.
2376. х = 7гп/6.
2377. -1, х = 2.
2378. -15/16 < х < 1 \/2 - 1, \/2 - 1 < х < 15.
2379. </190/2.
2380. х = — | sin | sin
2381. \/13 - 1 а 6.
2382. х = 2.
2383. 2 < х < 5/2, 5/2 < х < 3.
2384. 60°.
2385. 15 кг.
2386. (2 sin о + \/2 + 2 sin2 о) х х \/2Я2 cos о = 54.
2387. а = -1, —5/7, -3.
2388. 9 км/ч.
2389. х = 3/2.
2390. х < -\/17, —4 х < -3, —3 < х < 3, \/17 < х 5.
2391. 9.
2392. 6.
2393. а = ±4, 6.
2394. 8, О, 1, О, 1.
2395. 54. ___
2396. х = 0, ^5/2 х ^/2.
2397. 25-/3, 75/3.
2398. 2.
2399. 3.
2400. а = тгп.
2401. О < х < З-4, З-4 < х 1.
2402. х = %/2 + тгп, — arccos х/2/5 + 2агк.
2403. 90°, 20°.
2404. 4800.
2405. 96х/3/125.
2406. -1 < а < 1/5.
2407. х = -3.
2408. х = 1/25.
2409. 2.
2410. 25 : 81, одинаковы.
2411. зг — 3 — 7/5 а < зг — 3 + + 7/5, а = зг - 3 + y/Tl/Ь.
2412. 10(2 - х/З).
354
2413. -1, ± 7^-.
2414. 2 arcsin 5/fc.2.^8~A При k > 0.
2415. х = —Зтг/2, 5тг/2, 0 х < < тг/4, 2тг х 7тг/4 4-4- arccos(l/\/2 — 1).
2416. у/а2 4- Ь2 4- с7,
2417. 66 - 2УГТ7 < а < 66 + 2/117.
2418. тг + 5/2 х Зтг - 5/2, х г? (11тг + 5)/4.
2419. -1 < х < 1, 2 х < 3.
2420. х = ±тг/4 + 2тгп.
2421. [—2;—3/2) U [—1;оо).
2422. 27/3.
2423. а > 3/2.
2424. 7тг/12.
2425. х = 1.
2428. а > 3/2.
2432. х = —тг/2 + 2тгп, (-1)*+1 тг/12 + тгк/2.
2433. х < —2, —2 < х < -1/2.
2434. 0 < х 1/2, х log2 3.
2435. (1 + /33)/2.
2436. х = ±2, у = 3.
2437. 5.
2438. х = (°±/2v^~<>2) при о _ = 0, 1 а / 22/3; при остальных а корней нет.
2439. 5/3/3, 2/6/3.
2440. х = ± arccos 4- 2тгп, ± arccos 4- 2тг/с.
2441. х = 3/2, у = 0.
2442. х < -2, < х < 2,
3 < х < х > 7.
2443. (а 4- с)/(Ь 4- с).
2444. х —4, х 1/2.
2445. 1/(1 4-sin(a/2)).
2446. а3 < х < 1, х > 1 при 0 < < а < 1; 0 < х < 1, 1 < < х < а3 при а > 1; при остальных а корней нет.
2447. 2а</3/23.
2448. х — ±тг/3 4- тгп.
2449. х -2/3, х > 1/2.
2450. log5 626 — 4 < х < log5 26.
2451. 2.
2452. х = 5, у - 1;
х = 1/3, у = -11/3.
2453. 2flsin(a/2).
2454. х < —2, 1/2 < х < 1, х > 1 при а = 1/2; а? < а, х > — 2 при а —2; х < —2, х > а при — 2 < а ф 1/2.
2455. 1125/224.
2456. а = 0, 1.
2457. О < х log2 3, х 2.
2458. х = 1,
2459. 3/2.
2460. х = 0, ±2, у = 3.
2461. 1/2.
2462. О < а < 1.
2463. х = тг/2 4- тгп.
2464. О < х < 2.
2465. х = 0.
2466. 4.
2467. -5 а 5.
2468. х = 2, log2 5.
2469. х = 2.
2470. 3/7 О < 1, х > 3.
2471. 3\/2, 7/2 (две), 9/2 (две).
2472. 8.
2473. 1 < а 18 4-12\/2.
2474. х = (1 4- \/3)/2.
2475. 3/4 0 0, х > 7/4.
2476. 51/100.
где а = log3
2478. ----—=.
25-24^/1-<72
2479. 2 101 608 О < 4000000, 6000000 О О 250 000.
2480. х — тг/4 4- тгп.
2481. х -у/2, v/2 О < 2, О (8 4-\Л0)/3.
2482. х =
2483. 15/8.
2484. arcsin .
2485. -1 < х 2.
2486. х = тг/15 4- 7гп/5.
2487. 3(V^-1).
2488. 3 О < “З/V^, -3/\/2 <
<х < 0, 0 < z О-
2489. 0,31 га/день.
2490. 24 : 1.
2491. -4 О < 1
355
2492. х = -4.
2493. х = тг/4 4- тгп.
2494. -(1 4- 2v/29)/5 х 2.
2495. 30°.
2496. (—оо; 0) U [1/2; оо).
2497. а = -1.
2498. 1984.
2499. х = 1.
2500. х = 7г/12 4- тгп/2.
2501. 74.
2502. х = 7п, у = Зп, z = 2п, где п G Z.
2503. 1 < х < 5/4, 5/4 < х < 3/2.
2504. а(х/2 4- 75), а27б/4.
2505. х = тг/4 4- тгп/2.
2506. х = 0, у — —1; х = 1, у = 0.
2507. х -2/3, х = 0, х 2/3.
2508. 4у/2 - 375.
2509. 2arctg(l/4).
2510. а < -6, а > -1/3.
2511. х — тг/З 4- 2тгп, х = —тг/9 4- 2тг/с/3.
2512. х -6, -3 < х < -2.
2513. 39.
2514. х —2, х - -1, 7 < х 8.
2515. тг/4 - arctg(x/3/5).
2516. а - -2/3, 0.
2517. х = 3/2, у = 1/4.
2518. 3/7зГ-
2519. -7 О < -2, -2 < х -1.
2520. х = 1/2.
2521. 1, 5.
2522. х = 0, у = ±73;
х = Уз7119, у = 11^/3/119;
х = -уз/Ш, у = -П^/З/Ш.
2523. 972/19.
2524. х = ±тг/6 4- тгп, тг/4 - ТЗ/2 4- 2тг&.
2525. а = log3(18 ± 9ТЗ), log3(10 ± 719).
2526. 1 : 41.
2527. -б"5/3.
2528. х 6, -1 х < О, О < х (х/73-7)/2.
2529. 14.
2530. 2\/2(х/3 4-1)} <•
2531. 1/4 < а < 1/2, а = 1, 3/4 < а 4.
2532. —2 < х < 0.
2533. 9.
2534. ±2.
2535 с2 sinffsin(o!4-ff)
2536. а) нет;Пб) 21.
2537. х = тгп/3.
2538. х = 4а, у = атг/2 4- 2тгп, где а = О, ±1.
2539. arctg3,. 1/4.
2540. 28.
2541. а п/5, где п Е Z.
2542. х = 4.
2543. 90.
2544. л/3/16.
2545. х = ±72/6, (х/2 ± Тб)/12.
2546. а = 3.
2547. -2 х 1.
2548. -207.
2549. х = log7 3, у = 2;
х = log7(5/3), у = -1.
2550. 24 и 80 т при п = 4.
2551. ЗТЗ.
2552. а -72/4, -1/4 а 1/4, а 72/4.
2553. 36.
2554. х = -2.
2555. 7.
2556. х = -1/2, у = log3(372).
2557. 6 т при п = 4.
2558. 336/25.
2567. х = л/5/3 - 1.
2568. х = ±| arccos —+ тгп.
2569. х = -4/3, -1 < х 0.
2570. 5, 975^/196.
2571. < а < 7;
о = 7.
2572. [1/16; 12].
2573. х = 11, -(11 + >/1бТ)/2.
2574. \/Зо2/6.
2575. х = тг/2, тг + arctg(l/v/2), Зтг/2.
2576. х -5, -3 0^ -1/ ^4.
х = -1/32, 1/8, 1/^/4.
2577. [0; 2] при а = —1, 5 = 0 или а = 1/3, Ъ = 2/3.
2578. 1 = 3.
2579. О < х 3.
2580. у/7.
2581. 25%, 62,5%, 10%.
2582. 10.
2583. а = 7 : х = 2, 4, 8.
2584. На первой станции.
356
2585. х -5, х -1.
2586. 14 и 2 млн. руб.
2587. arccos(l/v/3).
2588. х
а > 0 > Ь;
£ при а О < 5; х — любое при а, Ь $$ 0; решений нет при а > О, b 0.
2589. х = у - 2, z = -2.
2590. Да.
2591. т = 0, 2.
2592. 500.
2593. 4 х < 5, х > 21.
2594. (-2; -5), 5.
2595. х = 2, 4 < х < 8.
2596. 15.
2597. х = -1, тг/2 — 1 4- тгп.
2598. 2-V4 < а 1, а = 21/4.
2599. х < —5, х = 3.
2600. 80.
2601. х = 27г/3 4- тгп.
2602. х — -2, у = 3.
2603. 12, 10.
2604. х = 3,'у = 1;
х = — 3, у = —1.
2605. 70°.
2606. а = -2.
I
1
УНИВЕРСИТЕТ книжный дом
Вышли в свет
А. И. Черноуцан
ФИЗИКА.
Задачи с ответами и решениями
3-е издание.
119234, г. Москва,а/я 587, Тел ./факс: (095) 939-40-36 939-40-51 E-mail: kdu@kdu.ru Http://kdu@kdu.ru
Учебное пособие содержит более полутора тысяч задач по элементарной физике, из них почти 400 задач с решениями, остальные — с указаниями и ответами. Задачи охватывают все темы программы вступительных экзаменов в вузы. Особенностью данного пособия является весьма широкий спектр трудности задач, как решенных, так и предлагаемых для самостоятельного решения: от самых простых, обучающих писать элементарные уравнения и иллюстрирующих основные законы физики, до весьма нетривиальных, соответствующих по уровню предлагаемым на приемных экзаменах в самые сильные вузы физического профиля. Пособие содержит справочное приложение «Основные формулы и законы физики».
Учебное пособие предназначено как для самостоятельной работы школьников и абитуриентов, так и для использования преподавателями на уроках в школах и техникумах и на подготовительных отделениях и курсах.
Автор пособия А. И. Черноуцан — профессор Российского государственного университета нефти и газа им. И. М. Губкина, автор многих популярных книг для школьников и студентов, заместитель главного редактора журнала «Квант».
УНИВЕРСИТЕТ книжный дом
Вышли в свет
119234, г. Москва,а/я 587, Тел ./факс: (095) 939-40-36 939-40-51 E-mail: kdu@kdu.ru Http://kdu@kdu.ru
С. Д. Комаровская
Современная английская грамматика. Практический курс (Вслед за «Мёрфи»)
Учебник по грамматике английского языка для слушателей подготовительных отделений вузов, учащихся старших классов специальных школ, лицеев и гимназий, студентов первых курсов вузов, а также для лиц, изучающих английский язык самостоятельно.
Предлагаемая книга ставит цели активной отработки и овладения навыками употребления основных грамматических структур, необходимых как для перевода, так и для правильного оформления речи при коммуникативном общении. Практикум построен на принципах единой методологии подачи грамматических явлений, содержит свыше 6000 предложений, подлежащих переводу на английский язык, обеспечивает высокую рекуррентность всех видов речевой деятельности.
Впервые в учебной практике осуществлена концепция подбора материала для юнитов-упражнений по многим грамматическим структурам по тематическому принципу основных англоязычных стран — Англии, Шотландии, Уэльса, Канады, США, Австралии, Новой Зеландии с использованием богатства общеупотребительной лексики живого русского языка. Примеры для тем, взятые из многих отраслей науки и техники, истории и литературы, культуры и философии, экономики, юриспруденции и других областей, обыгрываются и подаются в виде законченных миниатюр, микро диалогов и фактологических подборок.
Все это интенсифицирует овладение грамматикой языка и позволяет сделать учебный процесс увлекательным и мотивированным.
Учебник рассчитан на 130-170 часов аудиторной работы и, соответственно, 65—80 часов самостоятельной работы.
Учебное издание
Игорь Николаевич Сергеев
МАТЕМАТИКА
Задачи с ответами и решениями
Учебное пособие
Компьютерная верстка Кулешов С. А., Карпов Б. В. Художественное оформление обложки Макух Т. А.
Подп. в печать 12.02.04.
Формат 60x84/16. Бумага газетная.
Печать офсетная. Объем 22,5 печ. л.
Тираж 5000 экз. Заказ № 958.
ООО «Издательство «КДУ», 119234, г. Москва, а/я 587.
ТелУфакс: (095) 939-40-36, 939-40-51.
E-mail: kdu@kdu.ru Http://www.kdu.ru
ООО «БИНОМ. Лаборатория знаний», 119071, Москва, Ленинский проспект, 15, а/я 32. Телефакс: (095) 955-03-98. E-mail: lbz@aha.ru.
Отпечатано в полном соответствии с качеством предоставленных диапозитивов в ОАО «Дом печати — ВЯТКА».
610033, г. Киров, ул. Московская, 122.
Данное пособие представляет собой сборник задач по всему школьному курсу математики ....и предназначено для подготовки к вступительному экзамену по математике в любой вуз.
Для удобства абитуриента . в пособии содержатся варианты письменных вступительных экзаменов по математике в МГУ им. М.В. Ломоносова, агтакже программа по Математике для поступающих в МГУ.