Lothar Collatz, Julius Albrecht
Aufgaben aus der
Angewandten Mathematik I
Gleichungen in einer und mehreren Variablen
Approximation en
Herausgegeben von b. Collate und J. Albrechf
Bearbeitet von E. Bredendick, L. Eisner, H. Feldmann, I. Kupka,
R, Nicolovius, G. Opfer und W. Wetter ling
Unter Mitarbeit von J. Feldmann, K. P. Hadeler, W. Krabs,
L. Krause, O. Kuhl, H. Mierendorff, F, Natterer, J. SpieS, H. Spre-
nger und J. Werner
Berater: J. Dzewas
AKADEMFE-VERI,AG • BERLIN
1972

Л.КОЛЛАТЦ,
Ю.АЛЬБРЕХТ
ЗАДАЧИ
ПО ПРИКЛАДНОЙ
МАТЕМАТИКЕ
Перевод с немецкого
С. Н. Киро
Под редакцией
X. Д. Икрамова
БИБЛИОТЕКА
КАЗАНСКОГО
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА УХ'^

УДК 518.5
Имя первого из авторов хорошо известно советским читателям по перево-
переводам его книг: «Численные методы решения дифференциальных уравнений»
(ИЛ, 1953), «Задачи на собственные значения» («Наука», 1968), «Функцио-
«Функциональный анализ и вычислительная математика» («Мир», 1969), «Теория при-
приближений» (совместно с В. Крабсом) («Наука», 1977).
По численным методам издан целый ряд учебников, но практически не
имеется задачников. Предлагаемая книга в какой-то степени заполняет этот
пробел. Изложение охватывает следующие разделы: вычисления, связанные с
многочленами, итерационные методы решения уравнений с одним и с многими
неизвестными, задачи на собственные значения, интерполяция, численное ин-
интегрирование, теория приближений.
Книга представляет интерес для студентов-вычислителей, а также для спе-
специалистов различных областей, применяющих численные методы в своей ра-
работе. .
Редакция литературы по математическим наукам
20204—023
К ——-23—78 © Перевод на русский язык, «Мир», 1978
041@1) —78

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В настоящее время курс численного анализа входит в програм-
программу всех математических факультетов и факультетов прикладной
математики, а также многих технических вузов. За последние годы
у нас вышел ряд учебных руководств как по его отдельным разде-
разделам, так и по всему курсу в целом; отметим, в частности, замеча-
замечательную книгу Н. С. Бахвалова «Численные методы».
Если с учебниками дело обстоит относительно благополучно, то
совсем иная ситуация с задачниками. До сих пор имелась только
одна книга подобного рода: Н. В. Копченова, И. А. Марон, «Вычис-
«Вычислительная математика в примерах и задачах», «Наука», 1972 (из-
(изданная большим тиражом, но тем не менее давно разошедшаяся).
Предлагаемый перевод на русский язык «Задач по прикладной
математике» должен в какой-то степени восполнить указанный де-
дефицит. Книга охватывает следующие разделы: решение линейных
и нелинейных уравнений с одним и многими неизвестными, вы-
вычисления с многочленами, интерполяция, численное интегрирова-
интегрирование, теория приближений и гармонический анализ. Задачник со-
составлен коллективом авторов из ФРГ под общим руководством
Л. Коллатца и Ю. Альбрехта. (Имя профессора Коллатца хорошо
известно у нас по переводам его книг «Численные методы решения
дифференциальных уравнений», «Функциональный анализ и
вычислительная математика», «Задачи на собственные значения».)
Помимо студентов-вычислителей есть еще одна категория чита-
читателей, которых может заинтересовать эта книга. Знакомство в той
или иной мере с численными методами становится сейчас необходи-
необходимым для специалистов во многих областях, далеких от математи-
математики, — химиков, биологов, социологов и др. Для них существую-
существующие учебники численного анализа слишком солидны. Книга же
Коллатца и Альбрехта вполне элементарна и может быть исполь-
использована для самообразования.
X. Икрамов

ПРЕДИСЛОВИЕ
Эта книга задумана как первоначальное введение в некоторые
разделы прикладной и вычислительной математики. Она рассчи-
рассчитана на широкий круг читателей.
В каждом разделе мы начинаем с конкретных частных задач,
непосредственно или косвенно связанных с такими областями при-
применения, как физика, техника, математическая экономика или вы-
вычислительные машины, или же с элементарной математикой, а за-
затем постепенно подводим читателя к более общим задачам и общим
методам их решения. Кроме того, приводятся задачи, на которых
читатель мог бы поупражняться в применении отдельных специаль-
специальных методов. .
В книге рассмотрены следующие темы: уравнения с одним и
многими неизвестными, номография, интерполяция и аппроксима-
аппроксимация. При этом обсуждаются некоторые основополагающие теоремы
и методы, например теорема о неподвижной точке для сжимающих
отображений и метод Ньютона.
Поскольку это задачник, а не учебник, не очень страшно, что
разные главы писались разными авторами и что ввиду этого, воз-
возможно, не выдержан единый стиль изложения.
Л. Коллатц, Ю. Альбрехт

1. УРАВНЕНИЯ G ОДНИМ НЕИЗВЕСТНЫМ
Р. Николовиус ,
при участии JI. Коллатца и Ю. Фельдманна
1.1. Введение
В соответствии с общим замыслом этого сборника задач в дан-
данной главе мы старались представить рассматриваемый предмет
возможно более многосторонне. Ограниченность объема книги не
позволила нам, однако, достичь хоть какой-нибудь полноты и вы-
вынудила быть краткими. Так, например, мы с сожалением отказа-
отказались от того, чтобы давать более длинные серии задач, аналогия
ных друг другу по методу решения и сложности, как это принято
при школьном обучении. К счастью, особенно в случае этой главы,
легко можно построить задачи, подобные предлагаемым ниже, в
большем количестве.
Другим средством для достижения краткости был последова-
последовательный отказ от задач с «конкретным физическим» содержанием.
Это оправдано лишь тем, что предмет данной главы, допускающий
многочисленные применения, служит основой последующих глав,
которые уже и содержат больше «конкретных» задач и мотивов для
составления таковых.
Цель § 1.2— на материале элементарных задач ввести читате-
читателя в две основные идеи численной математики. Это, во-первых,
представление, что определенное высказывание о числе в большин-
большинстве случаев требует указания границ, между которыми оно за-
заключено, и, во-вторых, поиск возможностей улучшить при помощи
итераций указанные границы так, чтобы удовлетворить заданным
требованиям к точности. Параграф 1.3, в котором идет речь о тех-
технике вычислений, является основополагающим для дальнейшего.
В § 1.4 описаны некоторые более или менее простые преобразова-
преобразования многочленов, используемые как вспомогательное средство при
получении грубых приближений к корням многочленов; задачи,
относящиеся к методам Греффе1 и Бернулли, можно здесь пропус-
пропустить. Напротив, § 1.5 и первая часть § 1.6, где излагаются итера-
итерационные методы, весьма важны. В то же время вторая часть § 1.6
и § 1.7, посвященный различным дополнениям, снова задуманы
как необязательные.
1 Ниже мы будем называть его методом квадрирования. Основную идею
метода предложили независимо Данделен A826), Лобачевский A834) и Греф-
Греффе A837).—Прим. перев.

/. Уравнения с одним неизвестным
1.2. Элементарные методы
В этом параграфе на ряде простых примеров показывается, как
можно приближенно решать уравнения или находить границы для
их корней элементарными средствами и в отдельных случаях даже
без привлечения вычислительных устройств.
Задача 1. Найти последовательно улучшаемые границы для по-
положительного корня х = ]/l3 уравнения х2 — 13 = 0.
Решение. Пусть натуральные числа п я k таковы, что
в силу возрастания функции х2 — 13 при х> 0,
п2<13£2<(я+1J. B)
При меньших k число п находится проще, а большие k дают луч-
лучшие оценки корня. Так, при k = 2 находим п = 7; полагая теперь
а = 2х — 7, видим из A), что 0 < а < 1 и, следовательно,
101<1, C)
а потому
3,571 < — < х < — < 3,608.
28 28
Отсюда легко получаем улучшенные границы для а, именно
2 3
— < а < — , и далее
IOK
так что
D)
3,6055 < -J5Z5L < х < -^ < 3,6065.
5488 5488
На следующем шаге получим
3,605 525 < х < 3,605 553 E)
и т. д.
Можно поступить несколько иначе — еще раз возвести C) в
квадрат (снова полагая х2 = 13):
0 < а* = — 5656х + 20393 < 1; F)
таким образом,
^fgi ,6056.
5656 5656

1.2. Элементарные методы
Улучшение приближений можно продолжать либо при помощи
итераций, как выше, либо используя дальнейшие возведения в
квадрат.
Задача 2. В задаче 1 применить значение k — 5.
Ответ, п = 18, 0< а = 5х — 18 < 1; по аналогии с задачей 1
3,605551 2<Ж - -1ЙГ!1_- <х<Ж<3,6055556. G,
Задача 3. Применить в задаче 1 другие значения k, а также про-
провести метод последовательного возведения в квадрат.
Задача 4. Аналогичным образом найти границы для -\f2 и -\f\\.
Задача 5. Как перейти от A) к B) в случае корня из дроби?
Рассмотреть примеры 1/ —, 1/ —.
Задача 6. Найти границы для положительного корня уравнения
х2 — 2х — 2 = 0 по методу задачи 1.
Решение. При переходе к соотношению C) следует заменить
х1 выражением вида px-\-q. Легко видеть, что —< х <. ;
приО<а = 2л: — 5<1 имеем
= 4*2 — 20л:+ 25 = — 12* + 33<1; (8)
таким образом,
2,66 < — < х < — = 2,75
и далее
2,7291 < -g- < х < -|- < 2,7408,
2J306 < -^- <х< -^ <2,7325.
2187 6912
Другая возможность — возвести (8) в квадрат еще раз; тогда
получиц
0<а4 = — 504*+1377<1, (9)
откуда
И т. Д.
2,730 15 < -^- < х < -^- < 2,73215,
о04 504

10 /. Уравнения с одним неизвестным
о ш
Задача 7. Найти границы для вещественного корня х = у 2
уравнения х3— 2 = 0 по аналогии с задачей 1.
Решение. В силу возрастания функции Xs — 2 и того, что
<2< , можно исходить из соотношения —<.х<.— ;
64 27 4 3
имеем 0 •< а = 12л: — 15 < 1, так что
0<а2= 144л:2 — 360л: + 225 <1, A0)
0<а3 = — 6480л:2 + 8100* + 81< 1;
следовательно,
0<а3 + 45а2 = — 8100л: + 10206<46.
Отсюда получаем
^<*< 1J6,
405 50
7 3
и теперь с помощью соотношения -г^н < а < -^=- можно дальше
улучшать оценки A0) и A1). Может также идти речь об использо-
использовании более высоких степеней а и исключении из соотношений для
двух последующих степеней члена с л:2; например, используя соот-
соотношения
0<а3 = 81 (—
A2)
0 < а4 = 81 B400л:2 — 1744л: — 1935) < 1,
получаем оценку
0 < а4 + 30а3 = 81 A512л:— 1905) < 31,
откуда
'•25992< ■£■<*< £г + Tik-<1'26018-
Задача 8. Для корня х уравнения х3 — 2л: — 2 = 0, заключен-
заключенного между 1 и 2, найти более узкие границы.
Решение. Для а = 2 — х выполняется соотношение 0<а<1;
это дает
0<а2 = л:2 — 4х + 4<1,
0<а3 = 6л;2 — 14л; + 6< I,
4 = 26л:2 — 46л:<1, A3)
а5 = 98л;г — 144л: — 52<1;

1.2. Элементарные методы
отсюда
— 6<а3— 6а2 = 10* —18<1, так что
1 9 — 12 <-- г <Г 19 — 1 Q
1,2- ]о <*< ]о -1,У,
— 13<3а4 — 13а3 = 44* — 78<3, так что
^4Ll,85, A4)
44 44
— 49 < 13а5 — 49а4 = 382* — 676 < 13, так что
полученные значения можно улучшить с помощью итераций, как
в задаче 1., Учитывая, что в выражении для а4 отсутствует свобод-
свободный член, имеем
0<26* — 4б<— ; A5)
х
23 ^ 1 13
отсюда < *, или — < , и тем самым
1о х 23
1>7б9 <Jg-<x<-^L< 1,791. A6)
\о 598
Далее, <а<.— назначит,
59
,00161;
133-23
окончательно,
1,769 271 <— + 0'00106 <д^<-^- + "'""'"' < 1,769293.
Вычисления с десятичными дробями можно, конечно, выпол-
выполнять с большей точностью при помощи настольной счетной машины.
Задача. 9. Для вещественного корня многочлена х3 + * — 3,
как и в предыдущей задаче, выполняются неравенства 1 < х < 2.
Улучшить эту оценку.
Ответ. Полагая а — х— \ и используя оценку
+ 17 <3, . A8)

12 /. Уравнения с одним неизвестным
получаем на первых трех шагах
1<*'<-^-<1,2143, 0<а<—,
14 14
<x<<l,2143, <a<,
14 14е 14 14е 14
1,213 400 <х< 1,213412. A9)
Задача 10. Оценить cos 20°.
Указание. Справедливо соотношение 4 cos3 20° — 3 cos 20° =
= cos C • 20°) = -j .
Задача 11. Указать границы для координат двух точек пере-
пересечения гипербол у = и х2 — У2=1.
х—\
Указание. Здесь целесообразнее исключить х, а не у, так как
при этом получается простое уравнение yi — Чу — 1 = 0. Для по-
положительного корня следует использовать более высокие степени
а, а для отрицательного можно обойтись степенями до а4.
Задача 12. Найти границы для положительного корня х урав-
уравнения f (х) = ех — х — — = 0.
Решение. Легко получаем, что / (—) ~Ve <К2,89—
=—0,05<;0; ввиду неравенства
4
+ + ++> + + >
4 2! 3! 4! 4 2! 3!
B0)
/ О \ i О Л
выполняется также неравенство И— > 1 1 =
Р Ч 3 4 9 81
7 12
= —— > 0; тем самым показано, что — < х <. —. Далее, мы
можем оценить f(x) сверху, оценив сверху соответствующий ос-
остаток ряда:
«! (л + I) ! п! I (л + 1) (я + 1) (п + 2)
B1)
я+ I U+ W / «! ft+ \-x
Если теперь положить х — = а, то будем иметь 0<а< —
2 6

1.2. Элементарные методы 13
' 4 ^ 36 '
B2)
о 3 , . 3 1^-1
= хл х*1 А х <
2 4 8 216
и т. д. Но в соответствии с B0) и B1) при я = 3 имеем
/ 4 4 6 \
/ поскольку < ~— = — 1
1 '- *-т ь)
1 , л-2 , ха _,.,., п _ 1 , х2 , д:3 .
5 5 3
следовательно, х2 <С.х3 < Зх2, откуда с учетом
второго неравенства B2) получаем два неравенства
•xH+' + 4*>+* + <
- <23>
в которых члены с квадратами можно исключить, используя пер-
первое неравенство B2). Окончательно получаем
917 О
0,618 < -fif- < х < 4 < 0,667;
о51 3
таким образом, 0,118<а, 0,0139 < а2, 0,00164 < а3 и х<0,65.
Для получения дальнейших улучшений нужно привлечь больше
членов ряда B0).
При вычислении корней весьма полезным может оказаться так-
также биномиальный ряд
A+х)* = 2(Йх* (ix|<i).
Задача 13. Вычислить с помощью биноминального ряда
г 25 24 5 / 1 \'^
Решение. Имеем Кб = |/ — • — = -у ^1 - -J ,
следовательно,
j/бГ^А у/
2 к\
1
\\
7
1 25/
21
5
2
1
22- 5
33
24
1
53 :
429
1
25 . 55
28 -5е 29 • 59 211 • 511 212 ■ 513 21в • 515

14 1. Уравнения с одним неизвестным
Так как наши биномиальные коэффициенты убывают по абсо-
абсолютной величине, можно при оценке остатка ряда взять в качестве
мажоранты сумму геометрической прогрессии и, следовательно,
для получения нижней границы умножить последний член на ^-.
Вычисления легко выполняются без вспомогательных вычисли-
вычислительных средств и дают
— 2,449489742783181 |<5 . 10'15.
Задача 14. Вычислить аналогично
Ответ.
7
« {/~ • — = ~ (' + —
V 64 125 4 V Т 125 У
= 1,25992104990038... .
Задача 15. Вычислить аналогично у 5.
Ответ. , ..
V 16 81 2 V 81
Задача 16. Использовать такое же разложение в ряд для вы-
вычисления V 5.
Задача 17. Вычислить / 2~ = — 1/1 , /3~ =
7 J/ 50
Задача 18. Используя метод, аналогичный методу Адамса
A878) для вычисления логарифмов, и беря в качестве исходных
величины
d='/ 126
125
вычислить корни
VT= — ad, /To = За.

1.3. Техника вычислений с многочленами 15
1.3. Техника вычислений с многочленами
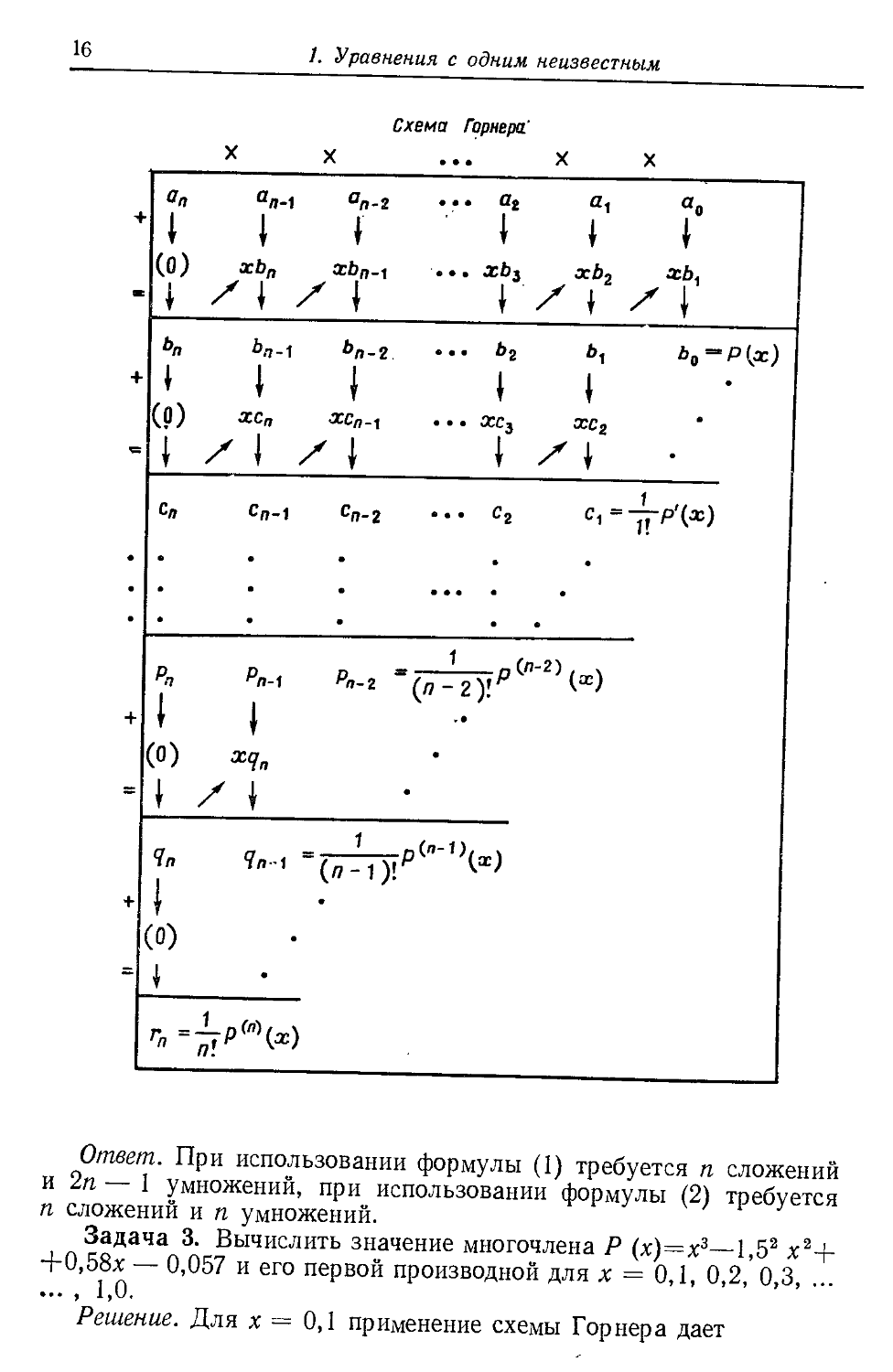
Здесь прежде всего нужно отметить схему Горнера как стан-
стандартное вспомогательное средство для вычисления значений много-
многочленов и их производных. Пусть дан многочлен
Р (х) = 2 akxk = а0 + aiX + • • • + а^Х"- + апх\ A)
Используя скобки, этот многочлен можно, очевидно, предста-
представить также в виде
Р (х) = а0 + х (at + х (а2 -\ \-х (an_t + xan)...)). B)
на чем и основана схема Горнера. В первой строке (см. схему) вы-
выписываем заданные коэффициенты аи начиная со старшего, и за-
затем для заданного значения х прежде всего вычисляем, как это
указывают стрелки и знаки действий, величины
К = а„, +-Х<0
Ь„_1 = an_t + xbn = а„_1 + хап,
Ьп-2 = ап-2 + xbn_i = а„_2 + х (an_j + хап), C)
Ьо = а0 + xbt = а0 + х (at -\ \-х (an_t + хап)...),
непосредственно приходя к виду B). Если нас интересует значение
первой производной, проводим вычисления таким же способом еще
раз, исходя теперь из bt, причем Ьо пропускаем (а0 выпадает вслед-
вследствие дифференцирования). Последовательно получаем значения
сп = Ьп
хс„ = an.j + 2апх,
= ап_2 + 2an_tx + За,,*2, D)
ct = bl + хс2 = at + 2а2х + ••• + папхп~х = Р' (х).
Вот несколько задач на схему Горнера.
"' Задача 1. Показать, что в дальнейших строках схемы Горнера
появляются производные высших порядков с соответствующими
множителями.
Указание. Коэффициенты при щ в выражениях для b0, ct,
dz, ... , Рп-2> Яп-и г-п образуют часть треугольника Паскаля.
Задача 2. Сколько сложений и умножений нужно для вычис-
вычисления значения Р(х) согласно A) (где сначала должны быть вы-
вычислены степени х) и согласно B)?

16
Л Уравнения с одним неизвестным
Схема Горнера'
X ... л
On
1
@)
(p)
1
ся
l"
(о)
\
Чп
)
@)
1
n, -
1
xbn
/ \ /
\
xcn
/ \ У
ш
P
\
X4n
/ \
4n~\
•
•
-±P<"\x)
f
Xbn-i ...
bn-2 •••
1
XCn-i
' \
Cn-2
•
•
' (n-J)
Cj l?1 O(g
l l l
xb$ xbo яЬ*
\ / \ s \
b2 Ьл Ь0=Р(х)
\ \
I S \
•
(x)
Ответ. При использовании формулы A) требуется и сложений
и 2п — 1 умножений, при использовании формулы B) требуется
п сложений и п умножений.
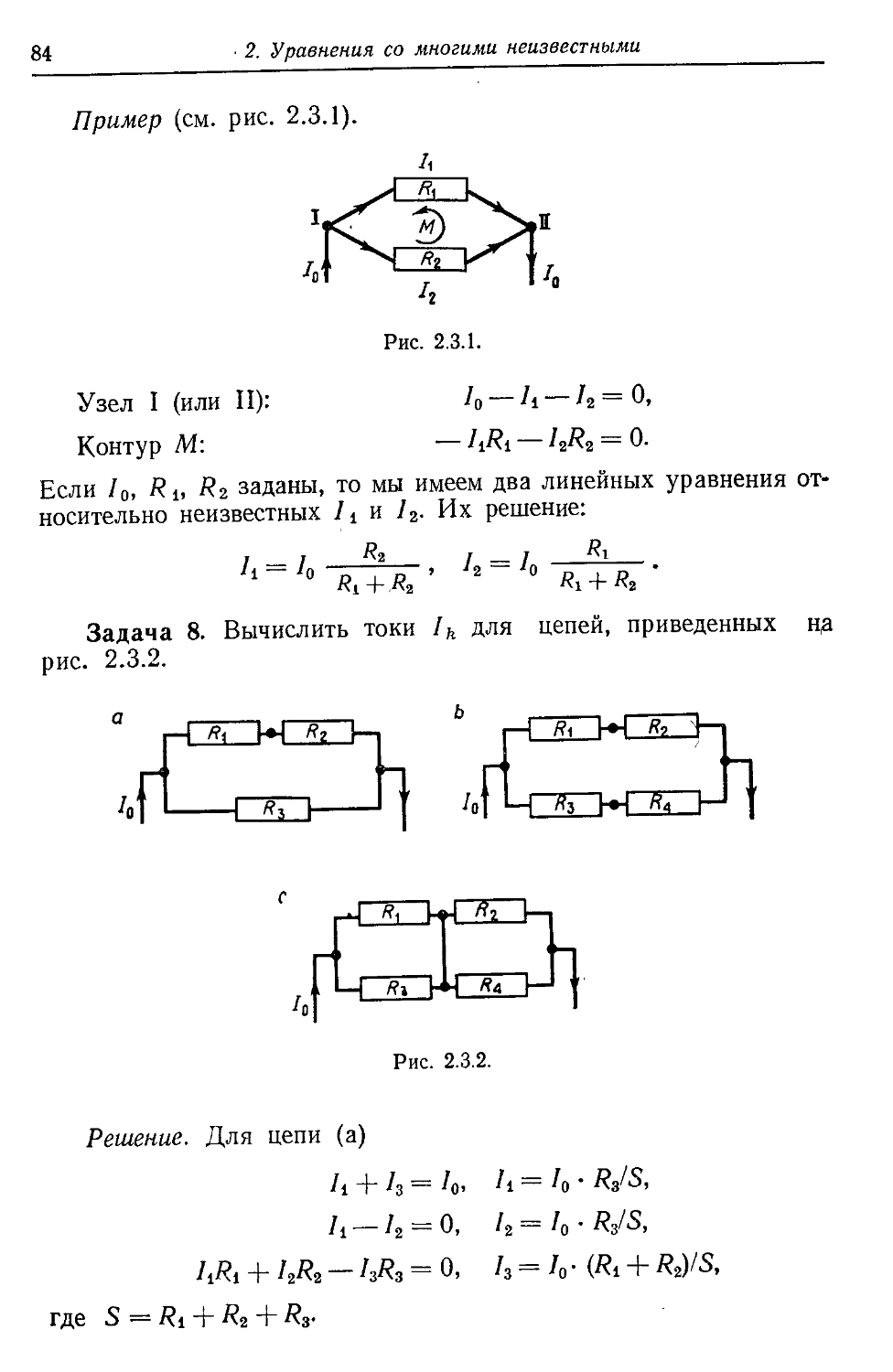
Задача 3. Вычислить значение многочлена Р (х)=х3—1,52 х2+
+0,58х — 0,057 и его первой производной для х = 0,1, 0,2, 0,3, ...
... , 1,0.
Решение. Для х = 0,1 применение схемы Горнера дает

1.3. Техника вычислений с многочленами
17
1 —1,5 0,58 —0057
0,1 —0,14 0.044
1 —1,4 0,44 —0,013 = Я @,1)
0,1 -0,13
1 —1,3 —0,31 = Р'@,1)
Для последующих значений х соответственно получаем
х=
р
Р'=
0
+0
+0
,2
,007
,10
0
+о
—0
,3
,009
,05
0
—0
—0
,4
,001
,14
0
—0
—0
,5
,017
,17
0
—0
—0
,6
,033
,14
0
—0
—0
,7
,043
,05
0
—0
+•0
,8
,041
,10
0
—0
—0
,9
,021
,31
1
+ 0
+0
,0
,023
,58
Впрочем, при равноотстоящих друг от друга значениях х нет не-
необходимости вычислять все значения многочлена с помощью схемы
Горнера. Именно, если вычислены п + 1 (в нашем случае 4) значе-
значений многочлена, то можно составить таблицу разностей (см. гл. 3)
и, поскольку разности и-го порядка постоянны, дальше вычислять
значения многочлена путем продолжения таблицы с использова-
использованием лишь п сложений для вычисления каждого значения:
X
0,1
0,2
0,3
0,4
Р
-0,013
+ 0,007
+ 0,009
-0,001
0,5 -0,017
0,6 - 0,033
0,7 -0,043
+ 0,020
+ 0,002
-0,010
-0,016
-0,016
-0,010
-0,018
-0,012
-0,006
о
+ 0,006
+ 0,006
+ 0,006
+ 0,006
+ 0,006
+ 0.006
Построение
таблицы разностей
Ее продолтепие
Задача 4. Вычислить Р (х) = xi — 4х3 + 5,5х2 — Зх + 0,5
для всех х = 0,In при п = 0, 1, 2, ... , 20.
Задача 5. Упростит ли вычисления в задаче 4 подстановка
х = у+1?
Ответ. Да, если вычисления проводятся по схеме Горнера;
нет—при использовании таблицы разностей.
Задача 6. Вычислить Р (х) = хв — 2\х5 + 175л:4 — 735*3 +
4- 1624*2 — 1764х + 720 для х = 1, 2, 3, ... , 10 и для х = 0,5,
1,5, 2,5, ... 9,5.
Задача 7. Найти многочлен Q (у), в который переходит много-
многочлен Р (х) = хь 4- 15х4 4-ЭОх3 4- 270х2 4- 405* + 243 в результате
сдвига всех корней на +2, т. е. в результате подстановки х = у—2.
Решение. Проводя вычисления по полной схеме Горнера, полу-

18 Л Уравнения с одним неизвестным
чаем величины -д- />(А)(—2), которые, согласно теореме Тейлора, и
будут коэффициентами преобразованного многочлена:
1 15 90 270 405 243
_2 —26 —128 —284 —242
1
1
1
1
13
—2
11
—2
9
—2
7
— 2
64
—22
42
—18
24
—14
10
142
—84
58
—48
10
121
—116
5
1
1
1
Таким образом, Р (у — 2) = Q (у) = у5 + Ьу* + Юг/3 + Юг/2 +
+ 5^+1.
Задача 8. Решить задачу 7 при х = £ — 3. Каковы корни мно-
многочлена Р (х)?
Задача 9. Многочлен Р (х) — х* — 2*3 + Зх2 — Ах +2 имеет
двойной корень х = 1. Разделить Z3 (х) дважды на л;— 1.
Решение. Величины bk+1 и cft+2 для х = 1 являются коэффициен-
коэффициентами при хк в выражениях Р (х)/(х — 1) и Р (х)/(х — IJ;
1
1
2
1
1
1
3
—1
2
0
4
2
2
2
2
2
1 о
Следовательно,
_—_х —х + х— ,
■ = х2 + 2.
(л- - I)»
Задача 10. Модифицировав надлежащим образом схему Горне-
ра, разделить последовательно многочлен Р (х) — х* — 5*3 + Ъх2-\-
+ 5л; — 6 на х — 3, х — 2, х + 1. Каков четвертый корень?

1.3. Техника вычислений с многочленами
19
Перед дальнейшими задачами следует описать метод деления
пополам (или «взятия в вилку») для нахождения нуля непрерывной
функции/ (х). Если/ (х) на концах интервала la, b\ {b> а) имеет
разные знаки (скажем, / (а) < 0, / ф)> 0; з противном случае
можно рассмотреть —/ (х),), то по теореме Больцано / (х) имеет в
этом интервале по крайней мере один нуль. Положим теперь ао=а,
bQ=b, do=bo—а0 и образуем последовательность интервалов [ап,
Ьп] (п = I, 2, 3, ...) согласно формуле
[ап.и а"-1 + &"-1] в случае / ( «-» + 6-»)>0,
"-' + *-», Щ в случае /( a»Jl+ *"-*) <0.
E)
Если окажется, что / ( "-' ——) = 0, то корень найден и
процесс заканчивается. В противном случае / (ап) << 0 и
п) > 0. и мы полагаем dn = Ь„ — ап = -у dn_j..
Задача 11. Заключить в вилку положительный нуль функции
f (Х) = xz + х2 — 2х — 2.
Решение. Имеем f A) = —2, f B) = +6; пользуясь схемой
Горнера, вычисляем:
n
0
1
2
3
1
1
1
1
an
,25
,375
b
2
1
1
1
n
,5
,5
,5
/
\
+o,
—o',
-o,
ап + Ьп \
2 )
625
984 375
259 765 625
Для того чтобы по возможности предотвратить дальнейшее уве-
увеличение числа разрядов, стоит провести новую оценку; легко
устанавливаем, что /A,38) < 0, /A,46)> 0, и начинаем счет за-
заново:
n
0
1
2
3
1
1
1
1
an
,38
,38
,40
,41
bn
1,46
1,42
1,42
1,42
1С
\
+o
—0
—0
in + bn \
2 )
,039688
,096 000
,028 679

20 1. Уравнения с одним неизвестным
Таким образом, получаем оценку
| я —1,415 | < 0,005; F)
исходя из нового оценочного интервала [1,410, 1,418], можно про-
продолжить счет и заключить наш корень х = у^2 в более узкие гра-
границы.
Задача 12. Заключить таким же образом в вилку корни много-
многочлена из задачи 3.
Рассмотренные задачи показывают, что в общем случае для оп-
определения значения многочлена степени п с предписанной точ-
точностью необходимо принимать во внимание в п раз больше деся-
десятичных знаков, чем у заданного значения аргумента; это особенно
неудобно при больших п, а также тогда, когда, например, ищется
приближенное значение корня, который непредставйм в виде ко-
конечной десятичной дроби. С другой стороны, если округлять по
обычным правилам, то оценки погрешности легко могут» конечно,
оказаться неверными.
Выход из этого затруднения предлагает интервальная арифме-
арифметика, или арифметика границ, которая в настоящее время приоб-
приобретает во все возрастающей степени и теоретический интерес.
(В этой арифметике алгебраические аксиомы поля должны быть
надлежащим образом видоизменены.) Используются два вида пред-
представления для интервалов: вместо числа а рассматривают интервал
А = Га, а! или А = Га — а, а + а], G)
при этом подразумевается, что
а < а < а, соответственно а — а < а < а + а. (8)
При втором виде представления можно по-разному определять
а; можно, например, использовать среднюю точку рассматриваемо-
рассматриваемого интервала (тогда будет а = а = а, и можно применять обще-
общеизвестный способ записи а + а) или взять в качестве а значение,
получающееся при каком-либо приближенном вычислении с обыч-
обычным округлением. В любом случае вычисления с интервалами G)
проводим по правилам вычислений с соответствующими неравен-
неравенствами (8), причем, если нужно округлять, то всегда округляем
только во внешнюю сторону. Деление на интервалы, содержащие
число 0, считается невозможным.
Проведение вычислений по схеме Горнера теперь модифициру-
модифицируется: все числа заменяются интервалами. Это должна пояснить
следующая задача.
Задача 13. Вычисляя с четырьмя десятичными знаками, опре-
определить интервал для значения многочлена

1.3. Техника вычислений с многочленами
21
у = р (х) = х3 + [— 1.52, — 1,49] х2 + [0,577, 0,581 ] х +
+ [—0,0575, —0,0568],
при условии что х лежит в интервале [0,445, 0,450] (ср. с задачей
3); коэффициенты многочлена заданы, скажем, как результаты не-
неких измерений.
Решение. Схему Горнера можно записать, например, следую-
следующим образом:
[1, 1] [—1,5200, —1,4900] [+0,5770, +0,5810] [—0,0575, —0,05-58]
[+0,4450, +0,4500] [—0,4838, —0,4628] [+0,0414, +0,0532]
[1, 1] [—1,0750, —1,0400] [+0,0932, +0,1182] [—0,0161, —0,0036]
(Знаки, которые в силу округления (во внешнюю сторону!) до че-
тырех»цифр приводят к увеличению интервала, напечатаны жирно.)
При более объемистых схемах Горнера предпочитают писать гра-
границы интервалов одну под другой.
Задача 14. Провести вычисления в той же задаче, используя
второе из представлений G, 8) и взяв в качестве «средних точек»
интервалов числа задачи 3 и х = 0,448, а далее беря значения,
получаемые обычным округлением-
Указание. Записать приближенно все числа как тройки
= (а, + а, — _а)
(9)
так что, например, Ао = (—0,0570, +2-10, —5-10~4).
Задача 15. Определить для корней многочлена из задачи 13
границы с 4 десятичными знаками.
Решение. Вычисляем, взяв х = х =х, и стараемся так опреде-
определять интервалы для у, чтобы верхняя, соответственно нижняя, гра-
граница как можно ближе подходила к 0. При вычислениях с четырь-
четырьмя знаками получаем следующие значения:
X
0,1485
0,1486
0,1606
0,1607
0,3581
0,3582
0,4100
0,4101
0,9316
0,9317
1,0010
1,0011
У_
—0,0021
—0,0021
0
+0,0001
+0,0001
0
—0,0076
—0,0076
—0,0307
—0,0307
0
+0,0001
У
—0,0001
—0
+0,0023
+0,0023
+0,0062
+0,0061
0
—0,0001
—0,0001
0
+0,0351
+0,0351

22
/. Уравнения с одним неизвестным
Соответствующие крайние значения х и будут искомыми грани-
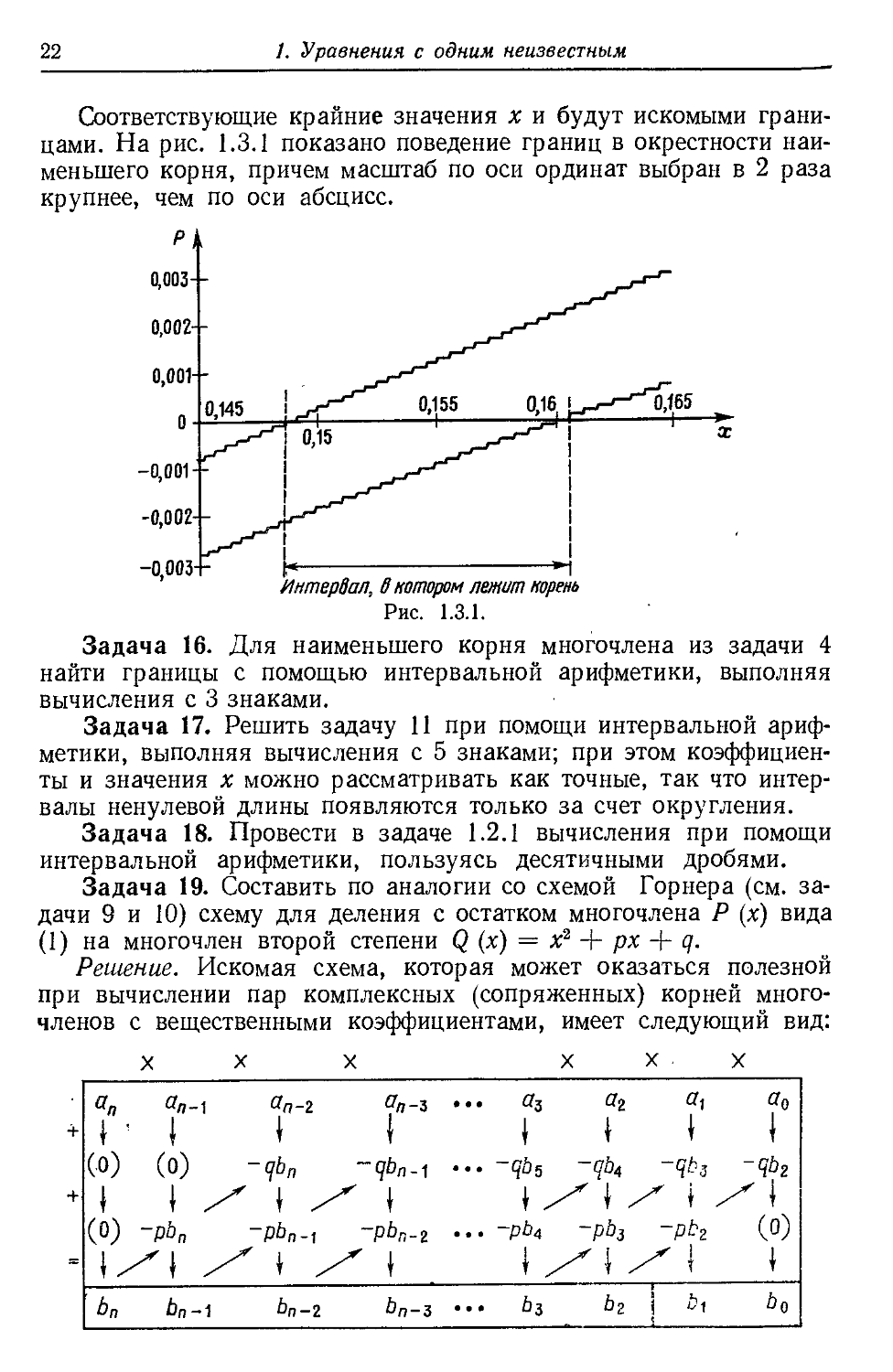
границами. На рис. 1.3.1 показано поведение границ в окрестности наи-
наименьшего корня, причем масштаб по оси ординат выбран в 2 раза
крупнее, чем по оси абсцисс.
-0,002- -
-0,003-F
Интервал, 6 котором летит корень
Рис. 1.3.1.
Задача 16. Для наименьшего корня многочлена из задачи 4
найти границы с помощью интервальной арифметики, выполняя
вычисления с 3 знаками.
Задача 17. Решить задачу 11 при помощи интервальной ариф-
арифметики, выполняя вычисления с 5 знаками; при этом коэффициен-
коэффициенты и значения х можно рассматривать как точные, так что интер-
интервалы ненулевой длины появляются только за счет округления.
Задача 18. Провести в задаче 1.2.1 вычисления при помощи
интервальной арифметики, пользуясь десятичными дробями.
Задача 19. Составить по аналогии со схемой Горнера (см. за-
задачи 9 и 10) схему для деления с остатком многочлена Р (х) вида
A) на многочлен второй степени Q (х) = х2 + рх + q.
Решение. Искомая схема, которая может оказаться полезной
при вычислении пар комплексных (сопряженных) корней много-
многочленов с вещественными коэффициентами, имеет следующий вид:
+
+
=
ап
\ '
(о)
1
@)
\у
Ьп
X X
а„ ,
\
(о) -
\ /
-pbn
' \ S
Ьп-1
ап 2
\
qbn
\ /
Pbn-1
} х
Ьп-2
X
I
-рЬп-г
Ъп-г
X
1
... ~pb4 -/
• • • Ьз
а2
1
1 .
X
!
а,
♦
\
X
I
-цЬг
У 1
(о)

1.4. Преобразование многочленов 23
Результат записывается в виде
л—2
= Q (х) R (х) + Ь& + b0, где R (x) = ^ Ьк+гхК A0)
Задача 20. Та же, что и задача 19, только для деления на мно-
многочлен более высокой степени.
1.4. Преобразование многочленов
В этом параграфе будут описаны некоторые преобразования
многочленов, которые могут облегчить нахождение приближенных
значений корней. При этом в рассмотрение включаются также
комплексные корни. Однако все, что относится к комплексным
корням, можно опустить, помимо самого указания на возмож-
возможность существования таких корней.
В задаче 1.3.7 уже был описан сдвиг корней, который часто ис-
используется для того, чтобы обратить в нуль второй по старшинству
коэффициент ап_х многочлена Р (х) вида A.3.1) и тем самым сгруп-
сгруппировать корни вокруг нуля (в силу теоремы Виета). Далее, с по-
помощью подстановки х = с-у можно добиться, например, того, что-
чтобы а0 = ±ап, что приводит к соответствующей группировке кор-
корней внутри и вне единичного круга. Наконец, преобразование х —
— \1у переводит внутренность единичного круга в его внешность
и наоборот, так что если требуется находить приближения для кор-
корней путем пробной выборки, то ясно, что поиски можно вести для
х и у, изменяющихся в единичных кругах, а в случае вещественных
корней — соответственно в интервалах [—1, +1].
Задача 1. Применив три указанных выше преобразования к
многочлену Р (х) = х3 — 6х? —2х + 12, найти приближения для
его корней.
Решение. Подстановка х = у + 2 приводит (при помощи схемы
Горнера) к многочлену
а подстановка у — 2z дает затем
4- Р(х) = R(z) = г3 -3,52-1.
Этот многочлен, как показывает вычисление совсем небольшого
числа его значений или же эскизный график, имеет в интервале
[—1, +1] лишь один корень, равный примерно —0,3. Таким обра-
образом, получаем xt = 2zi + 2 л; 1,4; точным значением является
■\f'l. Далее, подстановка z = lit дает
-Lr(z) = S(t) = 1 —3,5t2 — t\

24
/. Уравнения с одним неизвестным
что приводит к значению t2 — 0,5 (точному) и тем самым к хг =
= 2//2 + 2 = 6 и значению ts » —0,6, которому соответствует
х3 ж —1,33 (точное значение равно —У^2).
Задача 2. Применяя вышеуказанные преобразования, найти
приближенные значения для (если угодно, только вещественных)
корней уравнения
Р(х) = х5 — 5х4 — 4х3 + 20х2 — Ъх + 25 = 0.
Решение. Подстановка х = у + 1 приводит к
Р (х) = Q (У) = У5 — 14^3 — 12г/а + 8^ + 32,
а подстановка у = 2г (х = 2г + 1) дает
-1 р (х) = R (г) = г5 — 3,5г3 — 1,5г2 + 0,5г + 1.
2
Наконец, запишем еще (z — \lt)
= tb + 0,5** — 1,5t3 — 3,5*2 + 1.
а:
Рис. 1.4.1.
Рис. 1.4.2.
A)
B)
C)
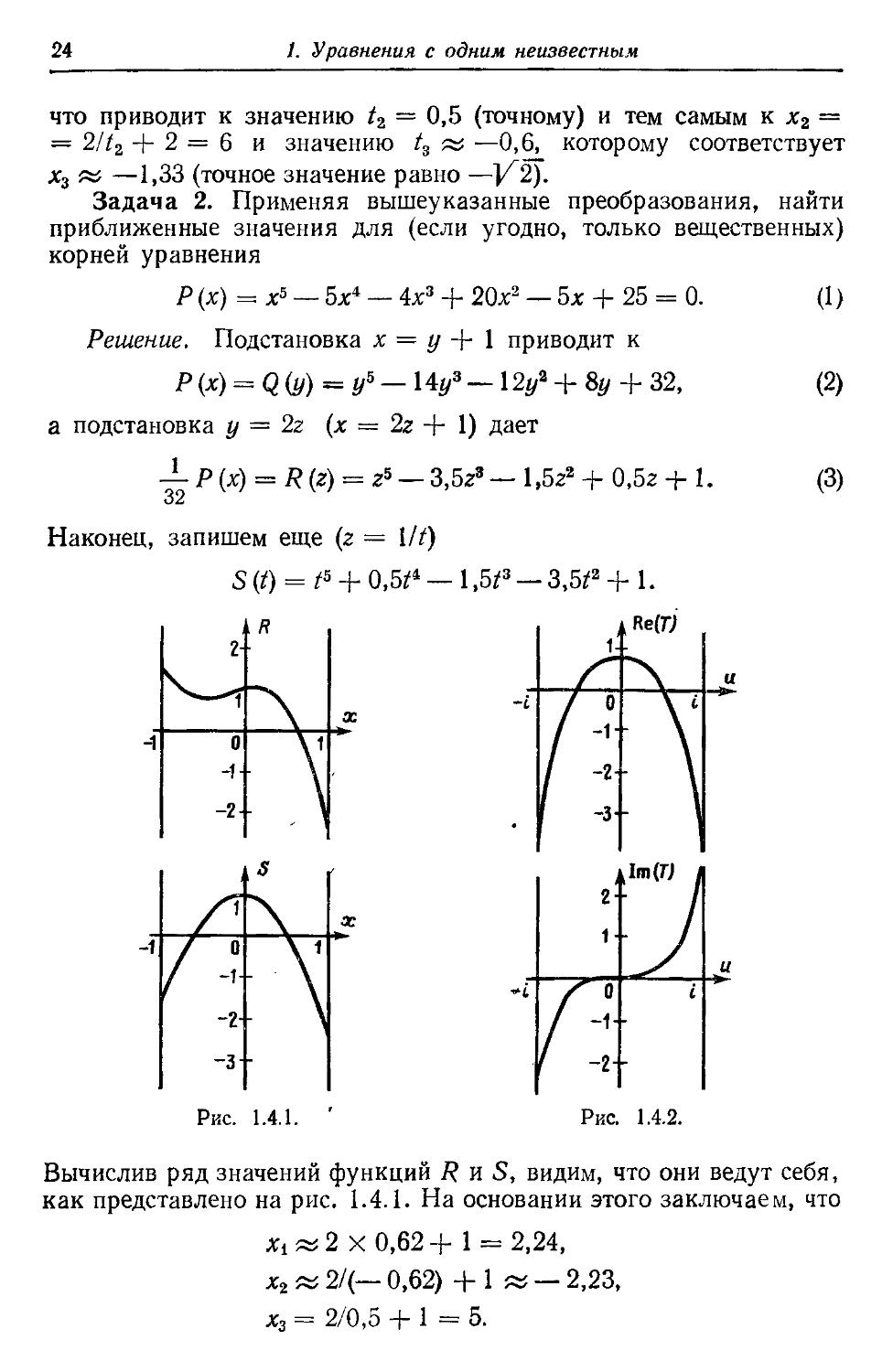
Вычислив ряд значений функций R и S, видим, что они ведут себя,
как представлено на рис. 1.4.1. На основании этого заключаем, что
*!«2 Х0.62+ 1 = 2,24,
*2«2/(— 0,62)+1 « — 2,23,
х3 = 2/0,5 + 1=5.

(точными решениями служат ±y^5, +5, ±0-
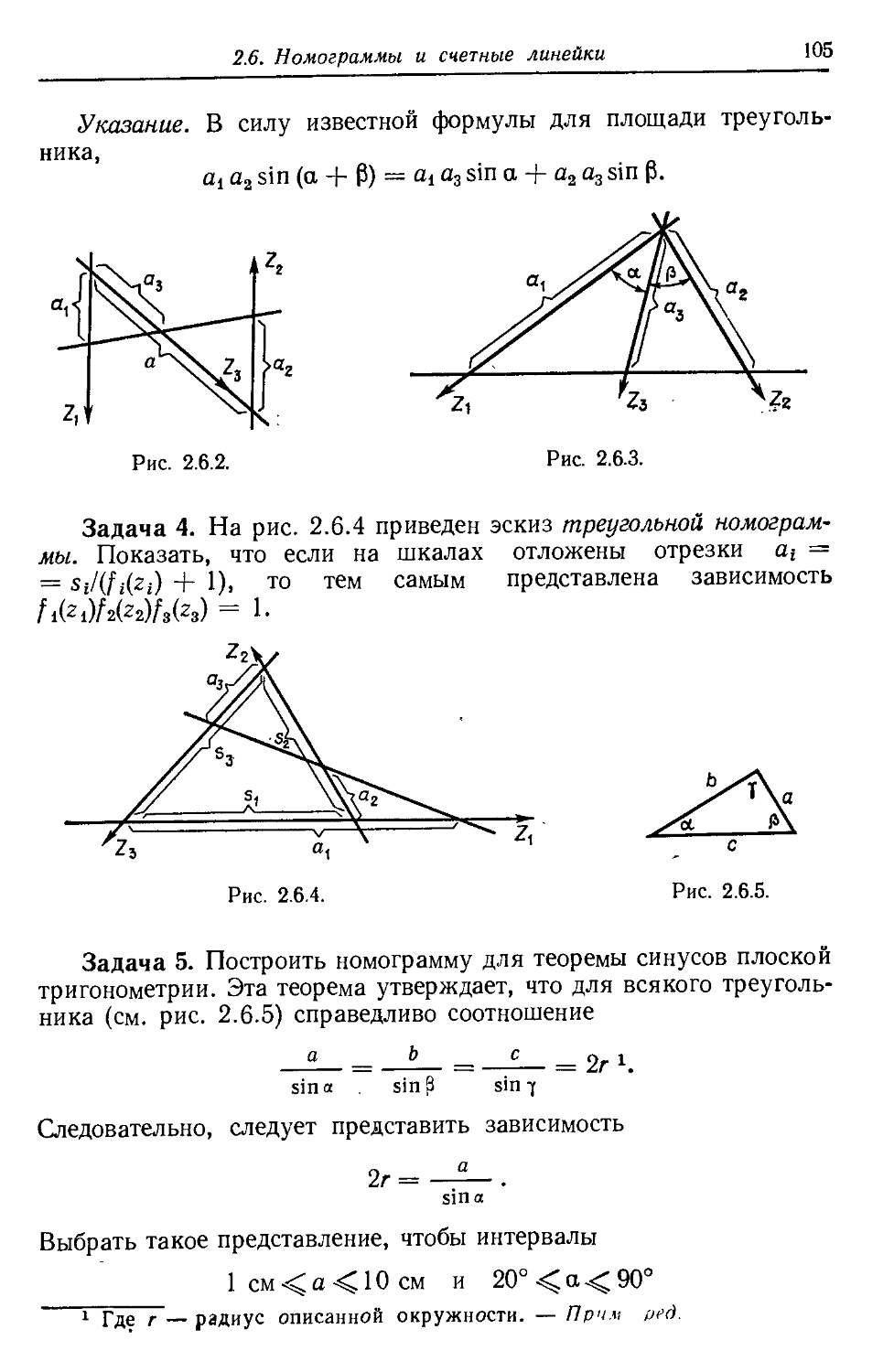
Задача 3. Найти приближения для корней уравнений
1.4. Преобразование многочленов 25
Минимум функции R (г) при г « —0,45 указывает на то (в связи
с этим следует продумать соответствующую более простую ситуа-
ситуацию для многочлена у — х2 + 0,25), что вещественную часть двух
оставшихся комплексно сопряженных корней нужно искать вбли-
вблизи именно этого значения. Произведя еще раз сдвиг корней, теперь
посредством подстановки г = и—0,45, приближенно получим
Т {и) = ы8 — 2,25н4 — 1,475и3 + 2,3138н2 — 0,071 Зн + 0,7718; D)
изменение вещественной и мнимой частей Т(и) при чисто мнимых
значениях и показано на рис. 1.4.2; соответственно в качестве гру-
грубого приближения можно принять, что
х45 « 2 (— 0,45 ± 0,40 + 1 = 0,1 ± 0,8(-
ия
ай
Pj (х) = х* + бх3 — 28х2 — 62* — 13 = 0,
р2 (х) = х3 — 6х2 + 8х — 1 = 0,
Ра(х) = х5 -{-Их4 + Ю1лг2 + 1 \х + 10 = 0.
Указание. Разумеется, вовсе не обязательно последовательно
применять все три преобразования; для упрощения вычислений
можно также выполнять преобразования приближенно. В случае
многочлена Р3(х) мы получим сумму корней, равную единице, если
положим х = у — 2.
Задача 4. Показать, что общее дробно-линейное преобразова-
преобразование
* = -2К±*- E)
У + с
можно свести к последовательному применению преобразований
трех вышеназванных типов.
С дальнейшими простыми преобразованиями читатель встре-
встретится в последующих задачах.
Задача 5. Пусть коэффициенты многочлена Р (х) вида A.3.1)
удовлетворяют соотношениям at — an_t (i = 0, 1, ..., п). Свести
решение уравнения Р(х) — 0 к решению уравнения степени не
выше л/2 и некоторых квадратных уравнений. Численный пример:
Р(х) = х6 + х5 — 9х* + 2Х3 — 9х2 +х + 1 = 0.
Решение. Так как многочлен Р(х) в результате подстановки
х—1/у (с последующим умножением на у") переходит сам в се-
себя, то наряду с каждым корнем xh имеется также корень llxk.
При нечетном п одним из корней является — 1 = 1/(—1) и мож-
можно выполнить деление на х + 1. Следовательно, можно считать,

26 1. Уравнения с одним неизвестным
что п четное. Делим на х"'2 и производим подстановку х +
Н = z, с учетом вытекающих из нее соотношений х2 +
X
+ 4 = г2-2' x* + -L = z»-3z, x* + -L = z*-4z2 + 2
л-2 х3 х*
После нахождения и/2 корней zk получаемого при этом многочлена
остается решить квадратные уравнениях2 — zhx + 1 = 0 (k =1,...,
/г/2). Численный пример:
= 0, г2 = + 3, г3 = — 4,
Задача 6. Аналогичным образом рассмотреть случай аг =
= —an_i (i = 0,1, ... , п).
Указание. При нечетном п разделить на х — 1, при четном п —
на х2 — 1.
Задача 7. Подобным же образом рассмотреть случаи
at = (_i)«-i an_t иа, = -(-1)»-* ая.г.
Указание. Использовать подстановку х — z.
х
Задача 8. Решить уравнение хв—2х5 — 68х4— 16*3 — 272х2—
—32* + 64 = 0.
Остальную часть параграфа можно пропустить.
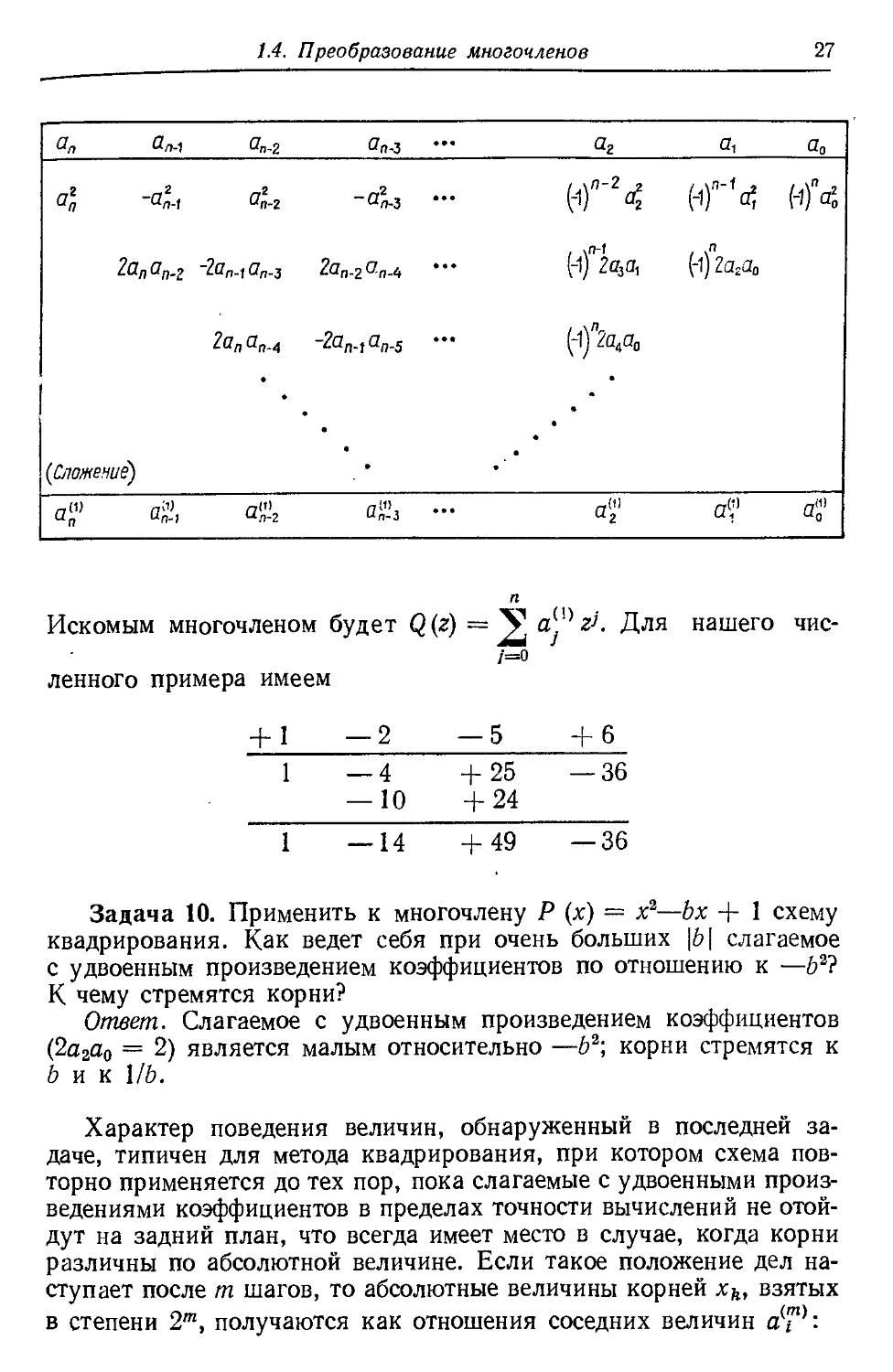
Задача 9. Для заданного многочлена Р (х) найти многочлен
Q (г), корнями которого служат квадраты zh = xh2 корней xk урав-
уравнения Р (х) = 0. Численный пример: Р (х) = х3 — 2х2 — Ъх + 6.
Решение. Представляя многочлен в виде произведения
Р (х) = 2 ajXi = ап • П (* - xh), F)
/=о k=\
видим, что нужно лишь помножить Р (х) на
aHf\(x + xJ G)
/=0 А=1
и затем положить х2 = г. Умножение можно выполнять по схеме
квадрирования:

1.4. Преобразование многочленов 27
ап апЛ
2апап.г
(Сложение)
ап-г
-2а„,ап.3
2а„а„.4
а»г
ап-з "•
2^7_ л С * • • •
-2an-tan-5 '"
•
аЯ!з -
аг
(-1) 2£?3а,
s
*
а»'
(-1)П2ага0
Искомым многочленом будет Q(z) = Уа'"г', Для нашего чис-
ленного примера имеем
+1 —2 —5 +6
1 —4 +25 —36
— 10 +24
I —14 +49^ —36
Задача 10. Применить к многочлену Р (х) — х2—Ъх + 1 схему
квадрирования. Как ведет себя при очень больших \Ь\ слагаемое
с удвоенным произведением коэффициентов по отношению к —Ь2?
К чему стремятся корни?
Ответ. Слагаемое с удвоенным произведением коэффициентов
Ba2a0 = 2) является малым относительно —Ь2; корни стремятся к
Ъ и к 1/6.
Характер поведения величин, обнаруженный в последней за-
задаче, типичен для метода квадрирования, при котором схема пов-
повторно применяется до тех пор, пока слагаемые с удвоенными произ-
произведениями коэффициентов в пределах точности вычислений не отой-
отойдут на задний план, что всегда имеет место в случае, когда корни
различны по абсолютной величине. Если такое положение дел на-
наступает после т шагов, то абсолютные величины корней xh, взятых
в степени 2т, получаются как отношения соседних величин а^'

28
/. Уравнения с одним неизвестным
Лт)
следовательно, | xh
2т г
С")
(8)
Это можно теоретически обосновать при помощи теоремы Виета о
корнях многочлена. При вещественных xh знак корня определяется
подстановкой в многочлен.
Задача П. Для численного примера из задачи 9 выполнить
дальнейшие шаги квадрирования и по ходу их выполнения полу-
получить приближения для \xh\ согласно (8). В заключение указать
сами корни.
Решение. (Корни степени 2т целесообразно вычислять при помо-
помощи логарифмов.)
ak—l
— 14
+49
—36
—196
+98
+2401
—1008
-1296
0,85714
1.87С83
3,74166
+ 1393
-1296
—9604
+2786
+ 1940449
—254016
-1679616
0,98212
1,94169
3,14635
—6818
+ 1686433
—1679616
—4,6485-10'
+ 0,3373-10'
+2,8441-1012
—0,0229-1012
—2,821 МО12
0,99949
1,99143
3,01444
—4,3112-10' +2,8212-Ю12 —2,8211-Ю12
—1,8586-1015
+0,0056-1015
+7,9592-1024
—0,0002-Ю24
—7,9586-Ю24
1,00000
1,99981
3,00028
—1,8530-1015 +7,9590-1024 —7,9586-Ю24
—3,4336-Ю30
—0,0000-Ю3"
+6,3346-10«
+0,0000-10»
—6,3339-1049
1,00000
2,00000
3.00000
—3,4336-1030 +6,3346-Ю49 —6,3339-Ю49
1,00000
2,00000
3,00000
Подстановкой в первоначальное уравнение определяем знаки кор-
корней и получаем xt = 1, х2 = —2, х3 = 3.
Задача 12. Решить методом квадрирования уравнение Р(х) =
= х* — 9х3 + 20х2 — 9х + 1 =0.

1.4. Преобразование многочленов 29
Ответ. хиг = у C ± Уъ), х3>4 = 3 ± 2 V2 .
Задача 13. Вычислить квадрированием корни уравнения
хь + Xi _ 4хз — 6х2 + 2х + 5 = 0.
Задача 14. Определить приближенно наименьший положитель-
положительный нуль функции cos х, применяя процесс квадрирования к неко-
некоторому отрезку ряда
1 z . г2 г3 . , 2.,
1 \- • •• (г = X2).
2! 4! 6!
В случае когда имеется несколько корней одинаковой абсолют-
абсолютной величины (в частности, когда имеются пары комплексно со-
сопряженных корней), в некоторых столбцах слагаемыми с удвоен-
удвоенными произведениями коэффициентов нельзя пренебречь. Та-
Такие столбцы при составлении отношений нужно пропускать, при-
причем в случае s пропущенных смежных столбцов мы получаем в ре-
результате [\xh\2tn)s+1.
С помощью метода Бернулли, несколько похожего на метод
квадрирования, можно вычислять суммы степеней
Н - 4 + 4 + ■'' + Хп (9)
корней многочлена вида
Р (х) = хп — pix"-1 - р2хп-2 рп, A0)
используя рекуррентную формулу
Н = PilV-i + P2H-2 +■•■+ РпН-п (* = 1, 2, 3,...); A1)
при этом предполагается, что
1*_ (я_1, = 1*_ (в_2) = • • • = р.* = t*_i = 0, !*0 = k. A2)
Задача 15. Для я=3 при всех & > 1 доказать, что значения,
вычисленные при помощи указанной выше рекуррентной форму-
формулы, удовлетворяют равенству [лй = х\ + х-к2 + **•
Решение. Прежде всего, по теореме Виета имеем
U-i = Pi • 1 = Xi + х2 + х3,
^2 = Pi • (Ч + Pi • 2 = (Xi + x2 + х3J — 2 (XiX2 + XiX3 + x2x3) =
= x\ + xl + xl, A3)
Ъ = Pi • V-2 + Рг • f^i + Рз ' 3 = (xi + х2 + х3) ( х\ + х\ + х\) —
— (XiX2 + XiX3 + X2X3) ■ (Xi + X2 + X3)

30
/. Уравнения с одним неизвестным
теперь для k > 4 можно провести доказательство по индукции,
также путем непосредственных вычислений.
В методе Бернулли также проявляется эффект «разделения»
корней различной абсолютной величины, хотя и слабее, чем в ме-
методе квадрирования. Зато он позволяет получить больше информа-
информации.
Задача 16. Определить по методу Бернулли наибольшие по
абсолютной величине корни уравнений
a) х3 = Зх2 — 4,
b) х3 = — х2 + 4х + 4,
c) х3 = — 2х2 + 4х + 8.
Решение. Выписав коэффициенты pi на полоске бумаги и сдви-
сдвигая ее вдоль столбца величин ц й, вычисляем следующие числа:
k
—2
— 1
0
1
2
3
4
5
6
7
8
9
10
2/
21 + 1
а
0
0
k
3
9
15
33
63
129
255
513
1023
2049
2?l+1 + 1
22Й-2 J
b
0
0
k
—1
9
—1
33
—1
129
-1
513
-1
2049
22i+i + 1
—1
с
0
0
k
—2
12
-8
48
—32
192
-128
768
—512
3072
3- 22/
—1 - 2?'+i
Для уравнения (а) последовательность цм!цъ сходится, и по-
поэтому следует ожидать, что ее предел 2 является корнем. Впрочем,
ничто не говорит о том, какова будет его кратность, фактически
Xj = х2 = 2 является двойным корнем уравнения (а).
Для уравнения (Ь) последовательность jj,2Z+2/[i2z сходится к 4,
а нечетные jj, 2Ы сохраняют свое значение постоянным. Это типично
при двух корнях различных знаков и одинаковой абсолютной ве-
величины, имеющих одинаковую кратность; ср. с (9). Здесь корни
хх = 2 и х2 = —2 простые.

1.5. Теорема о неподвижной точке 31
Для уравнения (с) последовательности M.2/+2/|% и Цаг+з^зм схо-
сходятся к 4, a jLLa/+i/2jLL2/ = — V3. Это означает, что кратности по-
положительного (р) и отрицательного (q) корня различны и, в силу
(9), удовлетворяют соотношению р = ; таким образом,
q = 2р. Находим: xi = 2, х2 = х3 = — 2.
Задача 17. По методу Бернулли определить наибольший по
абсолютной величине корень уравнения хг = 2х2 + Ъх — 6 из за-
задач 9 и 11.
Решение. Имеем последовательность
k |Xfe
1
2
3
4
5
6
7
8
9
10
2
14
20
98
212
794
2060
6818
19172
60074
Обнаруживаем, что р, k+1l^ h -> +3, и устанавливаем, что xi = 3
является точным решением.
Задача 18. Вычислить по методу Бернулли наибольший корень
уравнения из задачи 12.
Задача 19. Решить задачу 13 при помощи метода Бернулли.
1.5. Теорема о неподвижной точке и итерации
Задача 1. Пусть многочлен из задачи 1.4.10 имеет конкретный
вид Р (х) = х2 — 100* + 1. Вычислить приближенно путем ите-
итераций корни уравнения Р (х) = 0.
Решение. Согласно указанной задаче, имеем Х{\) ta0,01, x^m
« 100. Если записать рассматриваемое уравнение в виде
* = 1^(*г+1) =/(*), A)
то видно, что правая часть при малых х лишь мало меняется с изме-
изменением х, поскольку f'(x) = я/50. Поэтому мы ожидаем, что итера-
итерационный процесс
/(*«)=-755" (*2 + 0 B)
будет сходящимся, если начать с не слишком большого значения
х0. Таким образом, например, при х0 = ±10 имеем

32 /. У равнения с одним неизвестным
*j= 1,01,
х, = 0,020201,
х3 = 0,01000408080401
и т. д,, тогда как при х0 = 0
х, = 0,01,
*8 = 0,010001,
*3 = 0,01000100020001,
х4 = 0,010001000200050...
и т. д., причем у х3 и х4 совпадают уже 13 десятичных знаков.
Для вычисления хB) представление B) не подходит, так как
вблизи этого корня /' (х) » 2; при а > 0 имеем / A00 + а) =
= 100,01 + 2а+а2/100> 100 -f а. Между тем если записать
*й+, = £(*„)= 100 L, C)
то производная g'(x) = лг2 будет малой при х я; 100; есди провести
итерации, начиная с х0 = 100, то получим
je, = 99,99,
х2 = 99,989998999899989...,
х3 = 99,989998999799959...,
х4 = 99,989998999799949...
и т. д., с примерно таким же улучшением точности.
Задача 2. Дать оценки погрешностей в задаче 1.
Решение. После того как мы убедились в существовании решения
х в интервале 0 < х < 0,0101, можно записать разложение по
формуле Тэйлора
х - xn+i = f{x)-f (xn) = -jy- /' О) (* - хя), D)
где I лежит где-то между х и хп. Так как все хп@ < п < 4) нахо-
находятся в указанном интервале, то |/'(|)| <: 0,000202 = /С и имеют
место оценки
I* — xn+i |</С| х — хп| = /С|х — хп+1 + х„+) — хя|<
</С{|х —xn+i| + |xn+1 —xj), E)
откуда
| х xn+i | -^ ^ | хл+1 хя |. F)

10ДОВОЩРТОРГА|
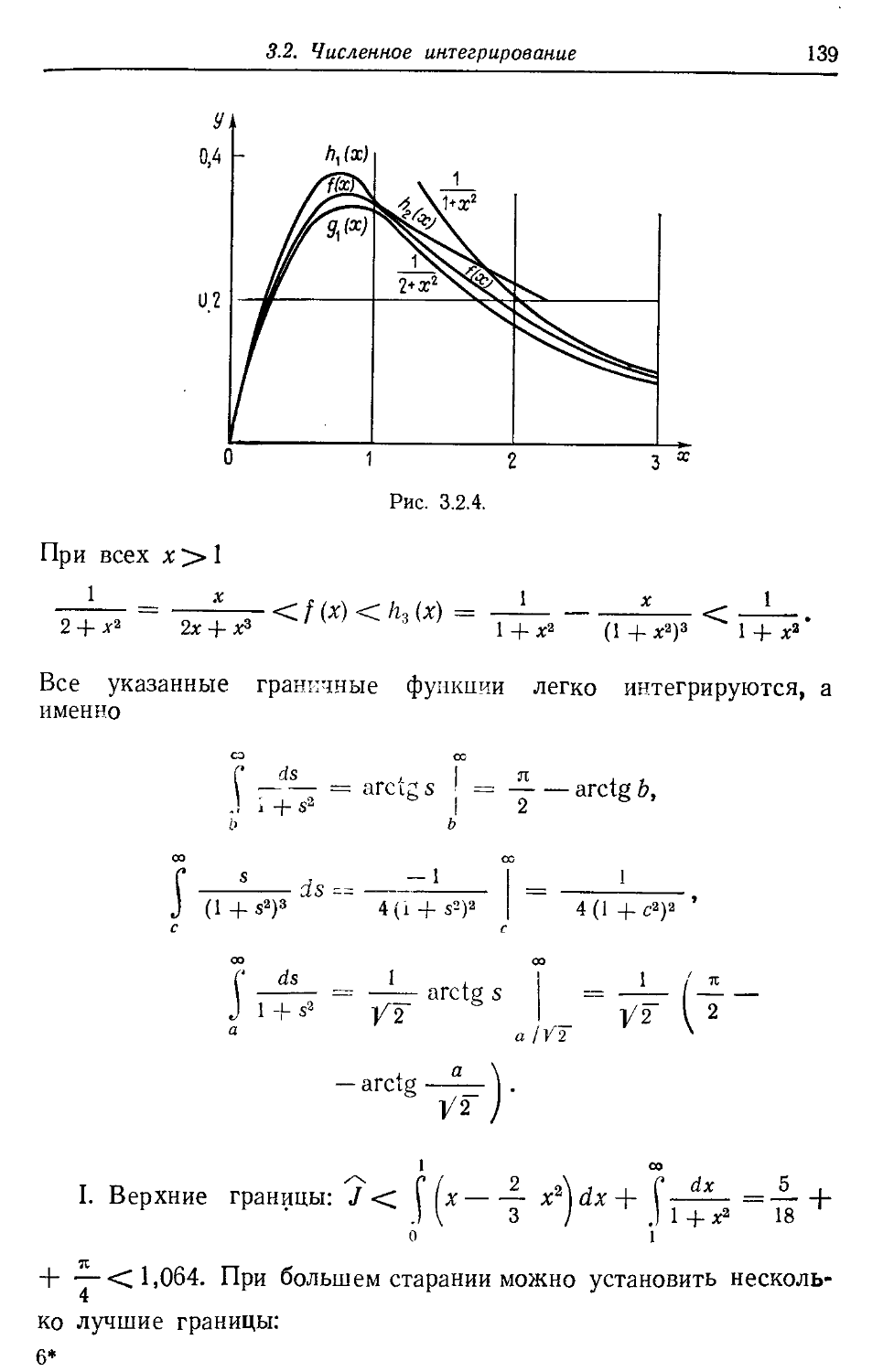
Теорема о неподвижной точке 33
Скажем, для п = 3
, _ | ^ 0,000202 g JQ-14^1 1 1Л-17 /7\
4 0,999798
Аналогично поступаем и в случае второго решения.
Существование решения было использовано здесь в качестве
предпосылки для оценки погрешности, однако именно метод итера-
итераций, в виде соответствующих теорем о неподвижной точке, предос-
предоставляет возможность весьма общих доказательств существования
и единственности решения.
Теорема о неподвижной точке понадобится нам ниже для трех
случаев: а) для случая банахова пространства, Ь) для случая п-
мерного вещественного векторного пространства, с) для случая
(одномерного) пространства вещественных или комплексных чисел.
Случай (с) найдет применение в этом параграфе, а случай (Ь) — в
гл. 2. На этих двух случаях мы делаем ударение, тогда как случай
(а), охватывающий оба случая (Ь) и (с), служит здесь для абстракт-
абстрактного разъяснения математической сути вещей и может послужить
для вывода соответствующих теорем в других специальных слу-
случаях.
Банахово пространство R — это прежде всего линейное про-
пространство, т. е.
Г для его элементов и, v, w, ... определена операция, называе-
называемая сложением, относительно которой jR образует абелеву группу
(нулевой элемент записывается как 0 (или как 0), обратный к v
элемент как —v и сумма и + (—v) как и — v);
2° элементы пространства можно умножать на множители а,
Ь, с, ... из некоторого поля (в наших рассмотрениях это будут толь-
только вещественные или комплексные числа), так что при и, v 6 jR
также аи + bv 6 jR, причем 1-й = и и выполняются законы ас-
ассоциативности и дистрибутивности a(bu) — (ab)u, a(u + v) = au-\-
+аи, (а + Ь)и = аи + Ьи.
Очевидно, что re-мерное вещественное векторное пространство
Rn обладает этими свойствами, равно как и пространство R ве-
вещественных (R = jRj) или комплексных чисел1. В качестве множи-
множителей выступают для пространства Rn вещественные числа, а для
пространства комплексных чисел — комплексные же числа.
Далее, в банаховом пространстве
3° каждому элементу u£R соотнесена его норма (или длина)
\\u\\ — вещественное число >0, такое, что ||ы|| = 0 только при
« = 0, ||а«|| = |а|-||ы|| и справедливо неравенство треугольника
Ни + о|| <
1 Обычно символ £R используется как (стандартное) обозначение одного
лишь поля вещественных чисел. — Прим, ред. i ,„ — >
2^206 I БИБЛИОТЕКА |

34 /. Уравнения с одним неизвестным
В Rn можно ввести различные нормы; мы выбираем здесь эв-
клидову норму ||u|| = l/ V ц5 (где и} обозначают компоненты
вектора и = (ut, ... , ип)).
В R по определению полагается || и \\ = \ и \ .
Свойства нормы в обоих случаях выполняются.
Наконец, банахово пространство
4° является полным; это означает, что для каждой последова-
последовательности Коши ип (п = 0, 1, 2, ... , ип 6 R), т. е. последователь-
последовательности, для которой справедливо соотношение lim \\ит — ип\\ = О,
т, п-*ао
существует предельный элемент и, такой, что lim \\и — ип\\ = О,
Л->оо
также являющийся элементом пространства R. Это свойство вы-
выполняется в наших пространствах Rn и R, но оно, например, нару-
нарушилось бы, если бы мы вместо К взяли пространство рациональных
чисел с рациональными множителями, так как не все предельные
элементы рациональных последовательностей представляют собой
рациональные числа.
Далее, рассматриваются операторы Т (называемые также пре-
преобразованиями, отображениями; в случае (с) это — функции f (x)),
которые отображают область своего определения Dcz R снова в R,
v — Ти; при этом ставится вопрос о неподвижных точках, т. е.
об элементах, которые отображаются сами в себя, иначе говоря,
о решениях уравнения и = Ти. Имеет место следующая
Теорема. Пусть в случае (а) при приведенных выше предположе-
предположениях Г — 4° (а в случаях (Ь) и (с) при определении нормы согласно
3°) можно из области определения Dcz R оператора Т так выбрать
полное подмножество Fez D, что для некоторого числа К из интер-
интервала 0 < /С< 1 выполняется условие Липшица: при любых и, v из F
\\u — v\\. (8)
Пусть, далее, дан такой элемент и0 6 F, что все итерации
un+i = Tun (n = 0,1,2,...) (9)
определены и являются элементами F. (Так будет, например, если
можно доказать, что «шар», состоящий из всех элементов v, таких,
что
и»—«нк-гЦг ""* —"oil» (Ю)
весь содержится в F.) Тогда уравнение и — Ти имеет в F точно одно
решение и, к которому сходится последовательность ип и которое

1.5. Теорема о неподвижной точке 35
лежит в шаре A0), т. е. удовлетворяет неравенству
II" —«ilK—T И «1 —«oil- (И)
1 — л
Замечания. В случаях (Ь) и (с) для обеспечения полноты нужно
в качестве F брать замкнутое множество; обычно используют (ги-
пер)шары или параллелепипеды, соответственно интервалы ве-
вещественной прямой или круги комплексной плоскости, включая
границу.
При помощи неравенства A1) можно оценить точность получен-
полученного приближения, для чего нужно два последних приближения
отождествить соответственно с и0 и ut.
Наряду с A1) имеет силу также оценка
Ни — «оИ<—Цг "  — "о И- (На)
1 — л
Для доказательства теоремы нужно прежде всего показать,
что lim || ит — ип\\ = 0. Пусть, скажем, т~>п; тогда, посколь-
т, л->оо
ку все uk 6 F, имеем в силу (8)
II и« — и» II < II ит — um_i || -f || un_i — um_21| + ... + || un+1 — un ||<
2 || Ui_Uo || + _ + Kn Ц Ui_Uf) Ц <
||«1-«о|| = -^-(|ы1-Ыо||, A2)
1 — л
что при п -*■ oo стремится к нулю. В общем случае, когда не обяза-
обязательно т> п, соответственно используем минимальное из значе-
значений тип. Тем самым ввиду полноты F установлено существование
предельного элемента и 6 F, для которого, как легко доказать,
действительно и — Ти. Если бы в F имелись два решения и = Ти
и v = Tv Ф и, то в силу (8) мы имели бы
II и — v \\ = || Ти — Tv || < К I! и — v ||< \\ и — v || A-3)
и тем самым пришли бы к противоречию. Наконец, доказательство
соотношения A1) можно провести аналогично переходу от E) к
F). _
Задача 3. Определить с помощью итераций х — j/^13.
Решение. Если итерационный процесс представить в виде
дсл+1 = /(дся) = дся + |хD-13) (« = 0,1,2,...), A4)
то желательно иметь значение f'(x) = 1 + 2цх малым по абсолют-
абсолютной величине; это достигается при и « —1/2х. Согласно задаче
1.2.1, при^ = —1/7
2*

36 1. Уравнения с одним неизвестным
f = 0,1,2,...), A5)
Я. A6)
и при 7/2 <; х ^4 получаем границу
Для х0 — 3,5, соответственно округляя, находим
Xi = 3,607,
х2 = 3,6055,
х3 = 3,60555282 + —• Ю'8.
Значение х3 не округлено, так что можем утверждать, что
||*3 — х2\\= \х3 — х2\ < 5,3-10; поэтому, согласно A1),
1
1—у
. Ю, A7)
откуда следует, что выполняется A0). Возможно, впрочем, и еще
уменьшить /С.
Задача 4. Согласно задаче 1.2.7, для вещественного значения
у^2 справедлива оценка 1,25 < x<Z 1,26. Используя A1), найти
более узкие границы.
Задача 5. При помощи итераций получить приближение для
cos 20° (ср. с задачей 1.2.10).
Задача 6. Решить задачу 1.3.11 при помощи итераций, приме-
применяя при этом интервальную арифметику (см. формулу A.3.7)).
Задача 7. Решить при помощи итераций уравнение sin x —
= 2х— 1/2.
Решение. В качестве итерационного процесса предлагается
xn+i = 0,25 + 0,5 sin хп; при этом К = 0,5. Отправляясь от х0 =
= 0,5 (=2х0 — 1/2) и используя четырехзначные таблицы, полу-
получаем
хх = 0,4897, х2 = 0,4852, х3 = 0,4832, хк = 0,4823, хъ = 0,4819,
*6 = 0,48175, х7 = 0,48165, хъ = 0,4816 = х9= *10= ....
Задача 8. Вычислить наименьшее положительное решение урав-
уравнения х-sin х + 1 = 0.
Ответ, х та 3,4368, решением является также —3,4368.
Задача 9. Решить задачу 1.2.12 методом этого параграфа.
Задача 10. Вычислить при помощи итераций лежащий между

1.5. Теорема о неподвижной точке
37
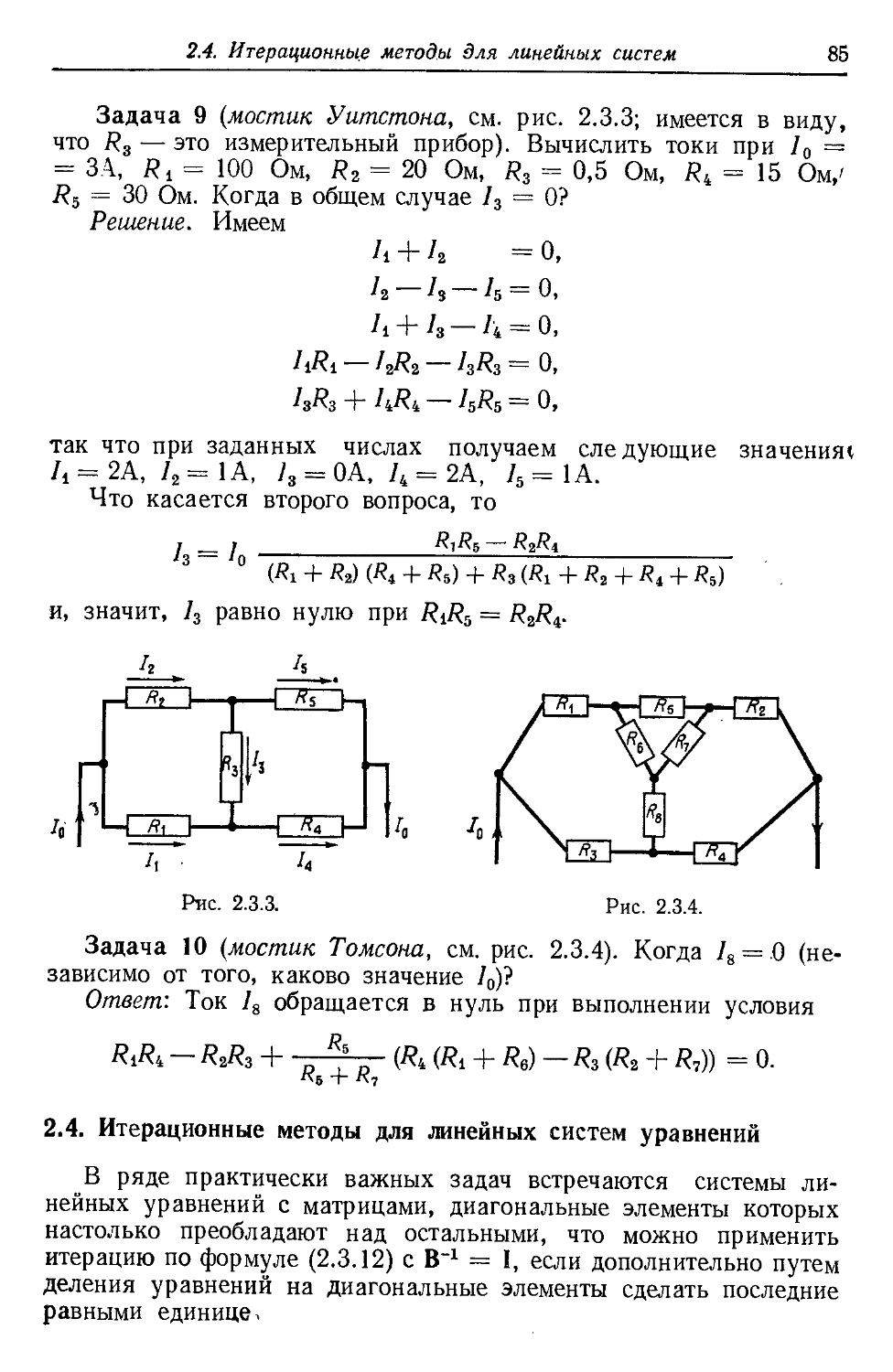
1 и 2 вещественный корень уравнения Р(х) = хв — Зх5 — 5х* +
-!- 18л;3 + Зх2 — 21х + 9 =0.
Указание. Так как Р'(х) в интервале [1,2] меняет знак, прием,
аналогичный приему A4), не срабатывает. Поскольку, далее, Р(х)
на концах интервала имеет одинаковый знак, нужно принять во
внимание такие случаи: а) два вещественных корня, Ь) один ве-
вещественный двойной корень, с) ни одного вещественного корня.
Так как при уменьшении интервала положение не улучшается,
стоит сначала определить корень производной.
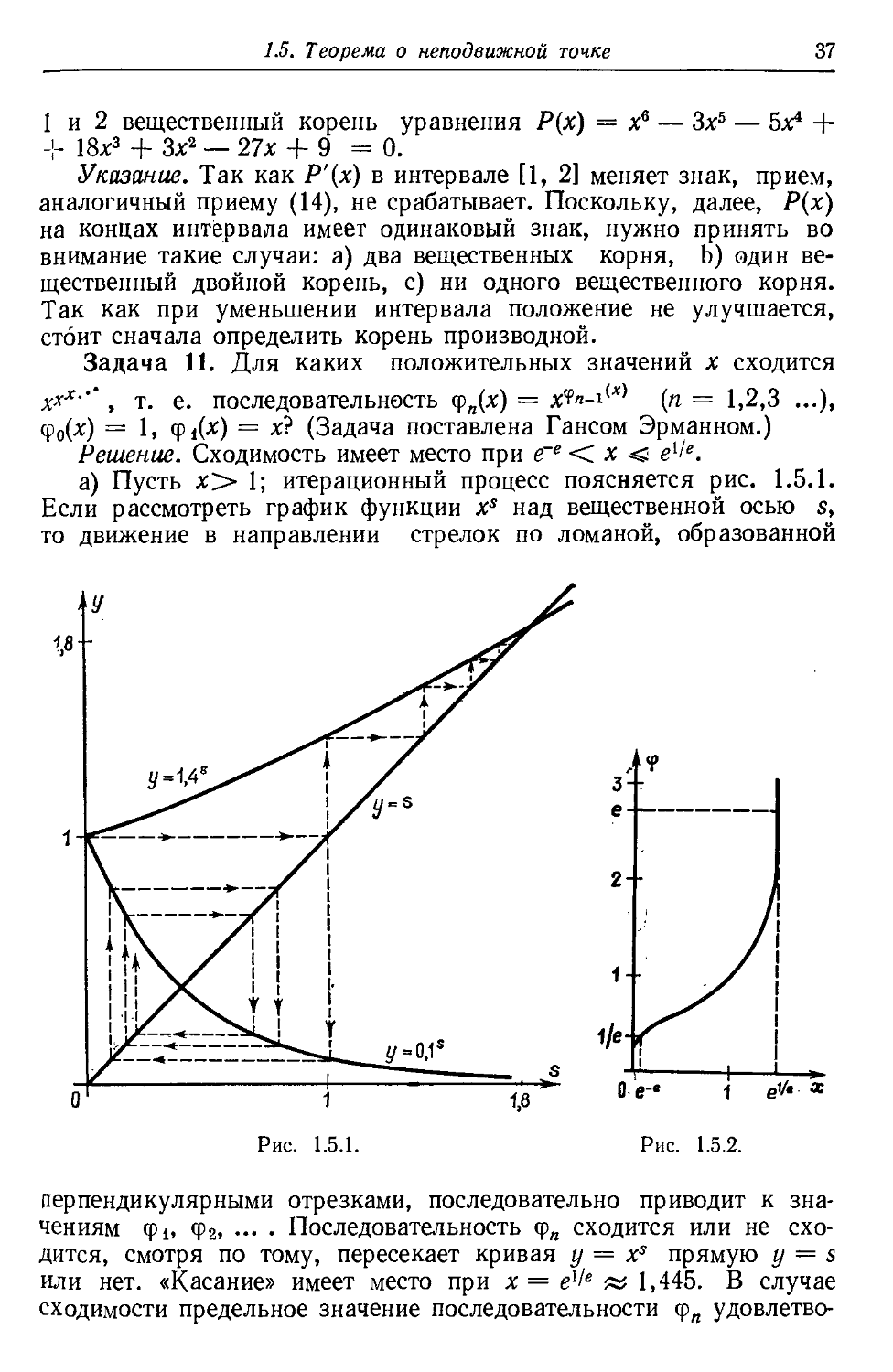
Задача П. Для каких положительных значений х сходится
х**'"', т. е. последовательность (рп{х) = tftn-\{x) (п = 1,2,3 ...),
(fo(x) = 1, (pt(x) = x? (Задача поставлена Гансом Эрманном.)
Решение. Сходимость имеет место при е~е < х <g e{le.
а) Пусть х> 1; итерационный процесс поясняется рис. 1.5.1.
Если рассмотреть график функции Xs над вещественной осью s,
то движение в направлении стрелок по ломаной, образованной
Рис. 1.5.1.
перпендикулярными отрезками, последовательно приводит к зна-
значениям ф1, ф2, ... . Последовательность ф„ сходится или не схо-
сходится, смотря по тому, пересекает кривая у = Xs прямую у = s
или нет. «Касание» имеет место при х = elle « 1,445. В случае
сходимости предельное значение последовательности фп удовлетво-

38
1. Уравнения с одним неизвестным
ряет уравнению ф =*?; график для этого уравнения представлен
на рис. 1.5.2.
Ь) Аналогично рассматриваем случай лс< 1; если наша после-
последовательность сходится, то сходимость является теперь не монотон-
монотонной, а «осциллирующей». Предельное значение z тех х, для которых
сходимость еще имеет место, соответствует ситуации, когда кривая
у'— zs пересекает прямую у = s под прямым углом.
1.6. Метод Ньютона и метод ложного положения
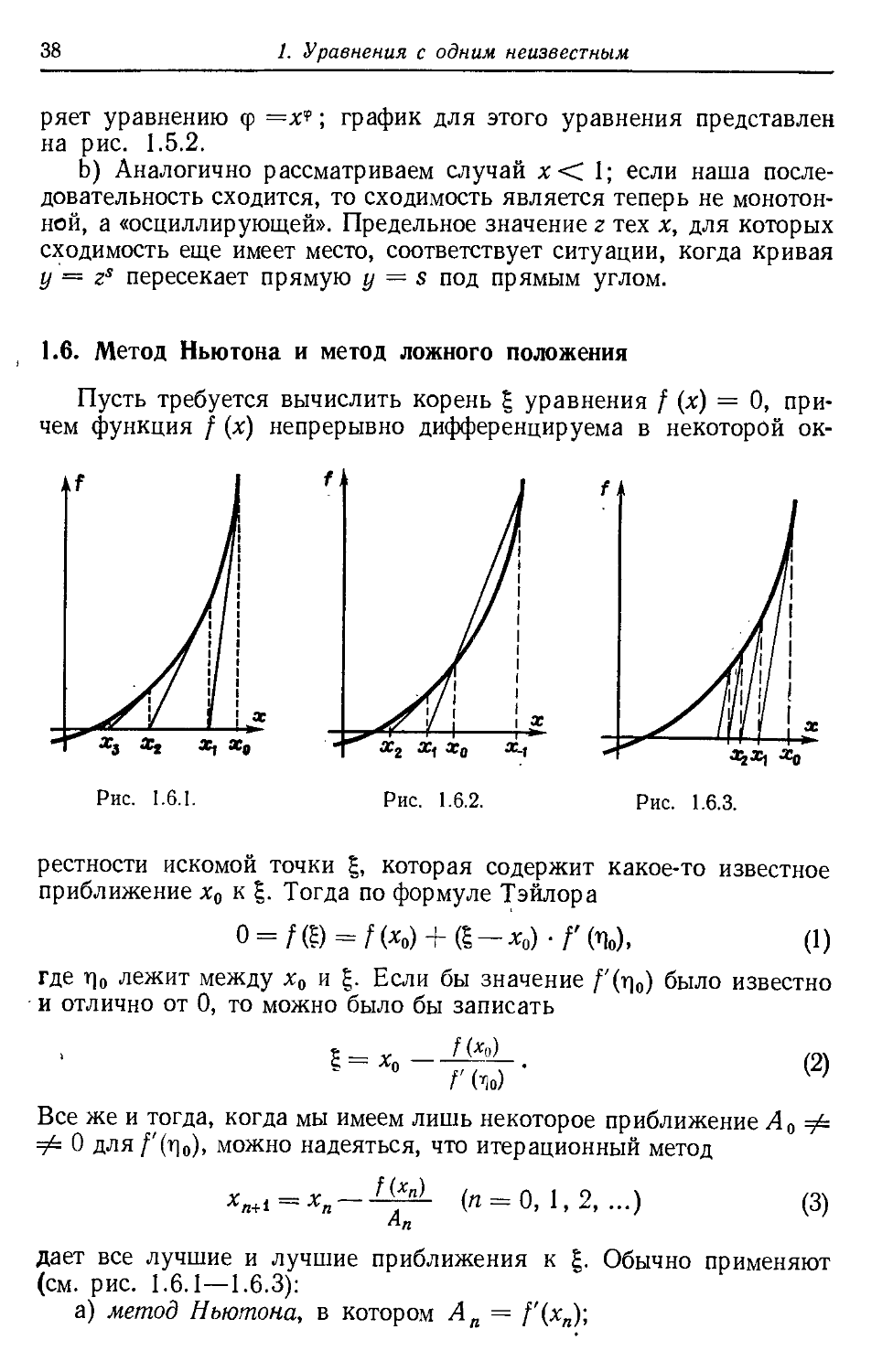
Пусть требуется вычислить корень | уравнения / (х) = 0, при-
причем функция / (х) непрерывно дифференцируема в некоторой ок-
X, а* X, Х0
Рис. 1.6.1.
рестности искомой точки £, которая содержит какое-то известное
приближение х0 к £. Тогда по формуле Тэйлора
О = f (g) _ f (хЛ -)- № х) • f (ц), (I)
где т]0 лежит между х0 и |. Если бы значение /'(гH) было известно
и отлично от 0, то можно было бы записать
;= хп —
f(*o)
Г Ы
B)
Все же и тогда, когда мы имеем лишь некоторое приближение Ао
Ф 0 для /'(Ло). можно надеяться, что итерационный метод
Хп+1 — Хп
fi*n)
(« = 0,1,2,...)
C)
дает все лучшие и лучшие приближения к \. Обычно применяют
(см. рис. 1.6.1—1.6.3):
а) метод Ньютона, в котором Ап = /'(*„);

1.6. Метод Ньютона и метод ложного положения 39
b) метод ложного положения, в котором Ап = (/ (хп) —
— f{xn-i))l(xn — xn-i)' причем для начала нужны две абсциссы x.t>
х0 и две ординаты f(x_t), f(x0);
c) упрощенный метод Ньютона, в котором Ао = Ai = Аг =
... = f (х0); (аналогично и в методе (Ь) можно положить Ао =
= At ==... = (/ (х0)— f (x.^/iXo— x.t)).
Для оценки погрешности можно, вообще говоря, последний
шаг C) толковать как первый шаг упрощенного метода Ньютона и
применять теорему предыдущего параграфа. Однако возможны и
независимые оценки.
Задача 1. Вычислить ^13 по методу Ньютона и по методу лож-
ложного положения с x_t = 4, х0 = 3, провести сравнение 6 задачей
1.5.3 и дать оценки погрешности.
Решение. Полагая / (х) = х2 — 13, получаем
по методу Ньютона по методу ложного положения
х{ ж 3,6666, хг ж 3,5714,
х2 ж 3,606060, х% ж 3,608695,
х3 ж 3,6055513, х3 ж 3,605536323,
х4жЗ,60555127546398938... xk ж 3,605551269...
Описанный в задаче 1.5.3 способ действий — это как раз упро-
упрощенный метод Ньютона, представленный специальным образом.
Согласно этой задаче, при правильном округлении имеем
и для интервала, содержащего х3 и х4,
3,60555127 < х < 3,60555131, 3,605535 <: х < 3,605553,
К =0,9 -Ю-8, Я = 4,6- Ю-4,
|*-*t|<2,5.10-«, |*-*4|<7,5-Ю-».
Задача 2. Вывести специальную одностороннюю оценку по-
погрешности для метода Ньютона, примененного для нахождения
х = У а, попробовать ее на числах задачи 1.
Решение. Полагая
xn+i = -г(хп + —) (я =• 0, 1, 2,...), D)
имеем

40 /. Уравнения с одним неизвестным
следовательно, xn+i > х = У~а, если х0 было взято положитель-
положительным (тогда и все хп положительны). Далее,
xn+i ~х = -\^ B**л+1 - 2х2) = -1- [х*п+1 -х'- (xn+i - xf] <
где m = min (хп, alxn). Итак,
J G)
8m
и для примерз с 1^13
хк — 0,9 ■ 106<х <: xk = 3,60555127546398938.
Эти две задачи показывают, что в методе Ньютона число
правильных знаков обычно примерно удваивается1: \xn+i —1|«
жС ■ \хп — 11" с т = 2. При этом говорят о квадратичной сходи-
сходимости; в общем случае т называют порядком метода. Метод лож-
ложного положения, как можно доказать, имеет порядок т = —A +
+ У~Ъ) ж 1,618, а простой метод итераций (§ 1.5) — по большей
части порядок т = 1.
Задача 3. Используя G), оценить V~2 и \Пл.
Ответ. Для 1^2 при х0 = 1 имеем ^ = 3/2, £2 = 17/12, *3 =
= 577/408, т = 2/*2 = 24/17 и окончательно
1,41421354 < VI < 1,41421569.
Если для 1^14 мы уже располагаем хорошим приближением х0 =
= 3,74165, то а/хо = 3,7416647735624 ±103, т = х0 и
VT4 = 3,741657386777 ± 4 • 102.
Задача 4. Вычислить V133 и проверить, насколько хорошим
приближением для s = tt2/4 является г =14 —
г ж 2,4674374, s« 2,4674011.
Задача 5. Дать условие того, что последовательность прибли-
приближений по методу Ньютона стремится к корню \ уравнения / (£) = 0
сверху (соотв. снизу).
1 За одну итерацию. — Прим. ред.

1.6. Метод Ньютона и метод ложного положения 41
Ответ. f"(x)> О (соотв. f"(x) < 0) в некоторой окрестности £.
Задача 6. Улучшить значения корней в задачах 6 и 8 из § 1.2
и вещественных корней в задачах 2, 3, 12 и 13 из § 1.4 при помощи
метода Ньютона и метода ложного положения.
Задача 7. Решить рассмотренными здесь методами трансцен-
трансцендентные уравнения из задач 1.2.12, 1.5.7 и 1.5.8.
Задача 8. Резервуар для нефти имеет форму лежащего ци-
цилиндра с радиусом 1 м. Какова высота уровня нефти, если резер-
Рис. 1.6.4.
вуар заполнен на q = 1/4 своей емкости (вариант для аудиторных
занятий: рассчитать шкалу для соответствующего измерительного
стержня, т. е., например, определить высоты всех уровней, отве-
отвечающих наполнениям 2, 4, 6, ... ,50%).
Решение. При длине резервуара / зависимость объема нефти от
угла а (см. рис. 1.6.4, где изображено поперечное сечение резер-
резервуара) дается формулой (мы используем радианную меру угла,
но сообразно с имеющимися в наличии вычислительными средства-
средствами можно, естественно, использовать и градусную)
у = гЧ . — (а — sin а). (8)
Далее, для высоты уровня получаем
а
h = г 1 — cos — . (9)
Разрешение этой формулы относительно а и подстановка в (8) при-
приводят к неудобной формуле; на практике предпочтительнее опре-
определить сначала а из (8) и затем вычислить h по формуле (9). Для
этого нужно найти решение (которое существует и единственно)
уравнения
V = rH-nq, A0)
а следовательно, уравнения
а — sin а — 2nq = 0.

42
/. Уравнения с одним неизвестным
Это можно сделать по методу Ньютона:
ап — sin an — 2л<?
1 — COS an
(И)
Если в качестве начального значения взять а0 = 2,4, то имеем
(для q = 1/4)
(
0
1
2
3
2,4
2,31
2,30988
2,3098837
sin at
0,68
0,7390
0,7390899
0,7390875
1С
ОС; — Sin Я; —
0,15
0,0002
—0,0000062
—0,0000001
1 — cos at
1,74
1,6737
1,6636
Видно, что точность можно повышать последовательно; поэтому в
начале таблицы можно обойтись без интерполирования. Исходя
из последнего значения а, вычисляем по формуле (9), соответствен-
соответственно округляя, h = 59,6 см.
Остальную часть этого параграфа и весь следующий можно про-
пропустить.
\ Задача 9. Какие особенности возникают при решении уравне-
уравнения х2 = 0 по методу Ньютона? Применим ли здесь метод ложного
положения?
Ответ. По методу Ньютона будем иметь х^ — -%■ хп, и для соот-
ветствующей последовательности уже не имеет места сходимость
порядка 2 (см. выше). Дело здесь в том, что корень \ = 0 двойной
и, следовательно, /'(|) = 0. Для построения последовательности
итераций в случае двойных корней рекомендуется метод
У - V О / (*л)
лп+1 — хп L f, , .
I \лп)
а в случае р-кратных корней — метод
f(xn)
(га=0, 1,2,...),
xn+i = xn — р-
Г
(«=0, 1,2,...).
A2)
A3)
Формулы эти следует применять разумно. Так, если нет кратных
корней, однако имеется несколько изолированных, но очень близ-
близких, то соотношение \xn+i — хп\ ж ^—^\хп — xn_i\, выполняющееся
для метода Ньютона, подсказывает, что на большом расстоянии
от корней целесообразно использовать вместо метода Ньютона
формулу A3). В то же время вблизи каждого из этих корней нужно
снова полагать р = 1.

1.6. Метод Ньютона и метод ложного положения 43
При методе ложного положения, используя последовательность
чисел Фибоначчи
<Ро=1. ?1 = 1. ?г = 2, ?2 = 3, ?4 = 5, 95 = 8. — » A4)
определяемую формулой
Т* = Т*-1 + Тм Для £=2,3,4
получаем, что формально справедливо соотношение
^.(я =1,2,...). A5)
Если х0 и х_4 имеют одинаковые знаки или ровно одно из значе-
значений х0 или x_i равно 0, то итерации сходятся; равным образом
сходятся они, когда это имеет место для хп и xn_i при каком-ни-
каком-нибудь п. Метод наверняка дает осечку в случае, если для какого-
нибудь п справедливо соотношение х0 — — (9n/?n-i) x-i- Наконец,
если хо~ (l + У§)х-1, то, как легко показать, для после-
последовательности Ф*=9а 0 + Vr5)9ft-i(^=l» 2,...) также спра-
справедливы соотношения фА = фА_4 + Фа-2 и
* A
Y A6)
так что знаменатели в A5) постоянно убывают по абсолютной ве-
величине и, следовательно, итерации альтернирующе расходятся.
Задача 10. Решить задачу 1.5.10 при помощи метода Ньютона.
Решение. Отправляясь от х0 = 2, имеем
Xi= 1,857,
*2= 1,79421,
«3=1,76318.
Поскольку |лс3—х2\ « 0,494 \х2 — xt\, пробуем применить фор-
формулу A2). Пусть снова х0 = 2. Тогда
дс1 = 1,71429,
*2= 1,73209,
д;3= 1,732050808.
Задача 11. Рассмотреть ту же задачу для уравнения Р(х) =
= 10л:в—29л;5+21л^—40л^+116л;—84=0, применяя метод Ньютона,
соответственно формулу A3), и отправляясь от х0 = 2.

44
/. Уравнения с одним неизвестным
Ответ. Корнями являются Ху — 1,5, хъ = 1/^2, х3 = 1,4, хк =
= — V2, x5 = iV /
Задача 12. Построить пример вещественной функции /(#), для
которой метод Ньютона при определенном х0 сходится к числу s,
не являющемуся корнем / (х).
Ответ-образец. Функция f(x)= sin Bя —) + 1 (см.
рис. 1.6.5) обладает этим свойством при х0 = 1 (и при всех х0 =
= 2* с целыми k также будет s = 0).
0,25 0,5
Рис. 1.6.5.
Рис. 1.6.6.
~~" Задача 13. Выяснить, к какому из корней 0, ±1 уравнения
хг — х = 0 сходится метод Ньютона, если начинать с произволь-
произвольного х0.
Решение. См. рис. 1.6.6^ исходить из значений х0 — ±—У~3,
в которых достигаются экстремумы, нельзя, ввиду равенства
f (х0) = 0; далее, из рисунка видно, что при хо<. Уз име-
О
ет место сходимость к —1 и при х0 > -| У~3 — сходимость к
+ 1. При х0 = ± — \ГЪ имеем х^ = — х0, х2 = — Xi = х0, хъ =
5
= —х0 и т. д., так что сходимости нет; при |#0|<— Кб по-
О
следовательность хп стремится к нулю. Для начальных точек из

1.6. Метод Ньютона и метод ложного положения 45
оставшейся области — ]/5 < | х0 \ < — |/3 некоторое приближе-
5 3
ние хп становится либо <^ |/3 , либо > — |/3, и можно,
3 3
используя приведенное на рис. 1.6.6 построение, указать подоб-
подобласти, приводящие к аппроксимации ± 1, и точки, приводящие
к /' (хп) = 0.
Задача 14. Указать метод порядка >3 для извлечения квад-
квадратных корней и опробовать его для VT3 при х0 = 3, как в за-
задаче 1.
Решение. Если положить х = У а и хп = х A + е) (пусть | е | <
< 1), то имеем
*„ = х(Ц-е),
*2=*2A+2е + е2), A7)
*4 = xi (i 4- 4e 4- 6s2 + 4s3 + e*)
и т. д.,
откуда получаем
•^л+1 == = X • =
A8)
8 + 16в
8+ 16г+
A9)
и дальнейшие формулы с соответствующими биномиальными ко-
коэффициентами. Формула A9) означает двукратное_применение ите-
итерационного шага D) и, следовательно, дает для У^13 каждое второе
значение из последовательности задачи 1. Для A8) имеем
xi = 3,6
х2 = 3,605551272...
х3 = 3,605551275463989293119221267... (= — . —., 2186871699 \
3 V 5 1297 2186871697 )
18
5
18
5
18
5
\
)'
1299
1297
1299
1297
\
Г
2186871699
2186871697

46
/. Уравнения с одним неизвестным
Таким образом, здесь возникает возрастающая последовательность,
которую вместе с A9), или D), или A8) при х0 = 4 можно исполь-
использовать для заключения корня в вилку. При этом настольная счет-
счетная машина требуется лишь на последнем шаге.
Для уравнения / (х)=0 можно различными способами улучшить
метод Ньютона до более высокого порядка сходимости. Вводя
сокращенную запись / (хп) = fn, /' (хп) = fn' и т. д., в предположе-
предположении соответствующей дифференцируемости имеем
Хп+1 ~ Хп — fn - fn
f'n
fn
2j in >n
= хя —
fnfn
in 2 '" 'п
f'n fn
If f
oi 'n >n
(порядок 3), B0)
f'n fn О
fn
f'n
2!
1 „„ _J_
3! " 2!
In In о 'n In
= Х„ —
Ля+1 — лп
f'3—f f' f" -L— ^r*
'o I n In Ы i g /n 'c
2/;
(порядок 4), B1)
(порядок З), B2)
*л+1 — xn ,
<23)
Задача 15. Какие две из этих формул приводят к A8) и A9)?
Задача 16. Опробовать приведенные формулы на нескольких
примерах этой главы.
1 В 1838 г. в работе, удостоенной медали Московского университета,
П. Л. Чебышёв предложил способ построения приближений любого порядка
и особо рассмотрел приближения по методам B2) и B3). Эта работа была
опубликована лишь в 1951 г. Такой же способ независимо и исходя из дру-
других соображений предложил в 1870 г. Э. Шредер. В случае когда / (х) — мно-
многочлен, способу Чебышёва — Шредера можно придать такой внд, чтобы
итерации осуществлялись при помощи многочленов же (без деления). —
Прим перев.

1.7. Дополнения 47
Задача 17. Какой порядок получается при применении этих
формул к уравнению хг = 0 (задача 9)?
Задача 18. Пусть для некоторого корня уравнения f (х) — О
известны приближения xn_i и хп. Указать улучшенную формулу, в
которой используются fn_i, fn и /„'.
Ответ. Берем параболу х = а + bf + ср и получаем
x^i = xn-p + q(p-q(xa-xn^1)), B4)
где
p*=-!jh и ?= — ■
'я ^я /я_1
Задача 19. Определить порядок формулы B4) в случае извле-
извлечения квадратного корня.
Ответ. Полагая xn_i = х A + ея_4) и хя = х{\ + еп), имеем
Ед х е^ D + Еп-1 + 2е„)
следовательно, порядок равен 3.
Задача 20. Опробовать формулу B4) на нескольких примерах
этой главы.
Ответ-образец. Пусть x=Y^x-i — 4, х0 = 3, как в задаче 1.
Имеем
^«3,6122,
х2« 3,605550,
х3 « 3,6055512754639897.
Задача 21. Вывести из разложения Тэйлора до члена с f" фор-
формулу, пригодную в случае двойных корней и в других подобных
случаях, и опробовать ее на задаче 1.5.10.
Указание. Формула такова:
fn fn
Пока квадратный корень мал по сравнению с fn', можно работать
с формулой хп+1 = хп — fn'lfn" (выводимой также из метода Нью-
Ньютона при помощи правила Лопиталя); когда это уже не так, полу-
получаем два значения, из которых для дальнейших итераций нужно
выбрать одно.
1.7. Дополнения
Метод Берстоу, который мы прежде всего хотим описать, служит
для того, чтобы вычислять с помощью итераций квадратный дели-
делитель

48
/. Уравнения с одним неизвестным
многочлена Р (х), заданного формулой A.3.1), в предположении,
что для этого квадратного делителя известно приближение
Qn(x) = xi + pnx + qn. B)
Сначала мы делим Р (х) на Qn{x) по схеме задачи 1.3.19: Р {х) =
= Qn(x)-R(x) + btx + b0; затем то же делаем с R (х):
я—4
R (х) = Qn (х) -S(x) + c3x + с2, где 5 (х) = ^ cft+4 x\
так что указанная схема становится двухстрочечной. Наконец,
решаем систему уравнений
ап + с3тп= Ьи
C)
относительно ап и хя и получаем коэффициенты
Ря+1 = Рп + °п > Qn+i = Я„ + -*„> D)
вообще говоря, лучшего приближения Qn+i{x) для Q (х). К этому
приближению применяется тот же процесс.
Задача 1. Показать, что этот метод является методом Ньютона
для уравнений b^p, q) = bo(p, q) = 0 (см. гл. 2).
Указание. Дифференцируем Р (х) = Q (x, p, q)-R(x, p, q) +
+ bi(p, q)x + bo(p, q) частным образом по р и q и затем сравниваем
с остатками от деления R(x, p, q) и Q (x, p, q) и x-i?(x, p, q) на
Q (ж. Р, Я)-
Задача 2. Разложить многочлен Р (х) = х* — Зх2 — 6х + 6
на квадратные множители и определить его корни. Принять Q0{x)=
= х2 + 2х + 5.
Решение. Проводим вычисления по схеме
1
1
1
0
-2
-2
-2
-4
Ы
3
-5
+ 4
+ 2
-5
-3
-6
+ 10
-4
0
F.)
6
-10
-4
(Ьо)
и получаем систему уравнений

1.7. Дополнения 49
5о0 — 4то=0,
20<Х0 — Зто= —4,
откуда 0О= —16/65 да — 0,25, то= —20/65« —0,31; следовательно,
Qi(x) = х2 + 1,75л:+ 4,69.
Следующий шаг можно выполнить с помощью счетной линейки.
Получаем
Q2 = л:2 + l,735x+ 4,735.
Для дальнейших шагов стоит использовать настольную счетную
машину. Мы найдем, что
Q3 == л:2 + 1, 73205л: + 4,73205.
В заключение проводим проверку путем вычисления значений верх-
верхней половины схемы и получаем из ее левой части частное
#4 = *» ~ 1 ,73205л: + 1,26795.
Точным разложением является Р {х) — [л:2 + VH • х + C + ]/3)] •
• \хг — j/ • х + C — |/~) ] ; искомые корни равны
V3 ± —
о 2,
х12 = — — V3 ± — /9 + 4|^3 « — 0,8660254 ± 1,9955077i,
2
Л = + — /3 ± — |/д — 4 УЗ » + 0,8660254±0,7196869/.
хЗЛ +
Задача 3. Выделить из многочлена задачи 1.4.2 квадратичный
множитель, корни которого аппроксимируются данными там приб-
приближениями л:4,5 = 0,1 ± 0,8 i.
Задача 4. В задаче 1.5.10 нужно было рассмотреть предположе-
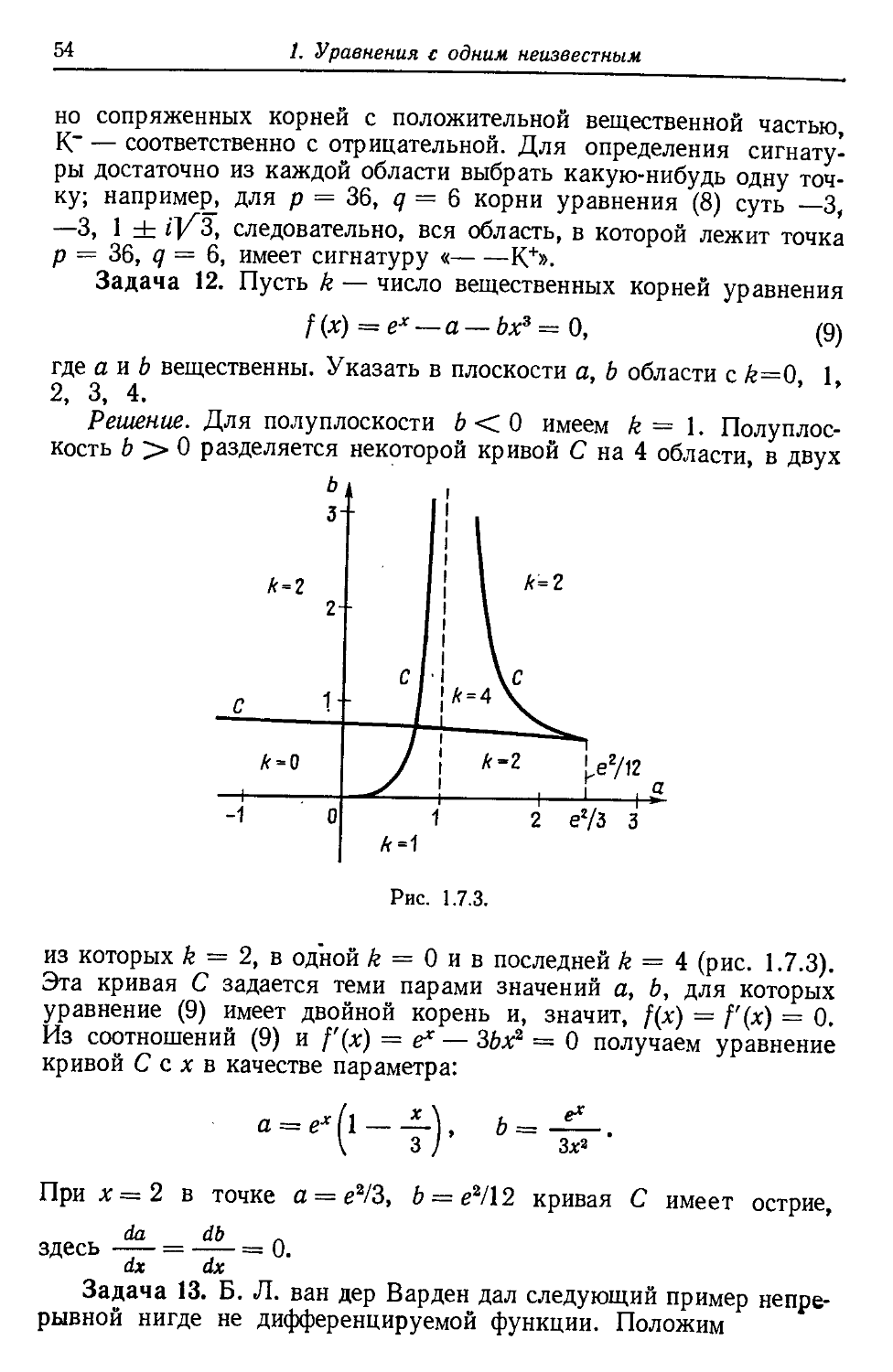
предположение, что имеется двойной корень. Выделить квадратичный множи-
множитель, отправляясь от Qo = (х— 1,6J.
Замечание. Это — еще один выход из положения в случае пло-
плохой сходимости метода Ньютона при двойных корнях.
Задача 5. Уточнить делитель Q0(x) = {х— 1,5J для многочле-
многочлена из задачи 1.6.11.
Ответ. Qi(x) = х2 — 2,95867л: + 2,18838 с корнями х1 « 1,487,
х2 « 1,472. При решении уравнения обнаруживается численная
неустойчивость, и при дальнейших вычислениях также получаем
плохую сходимость, так как здесь имеются три близких корня;
см. ниже.
Задача 6. Разработав соответствующий метод для случая ку-
кубичных делителей, уточнить делитель Qo = (л:— 1,4K в той же за-
задаче.

50 /. Уравнения с одним неизвестным
Ответ. Пусть после двух делений по схеме на Qn (х) = х3 -\-
+ рп х2 + qnx + гп получены остатки b2 х2 -+- btx + b0 и сь л:2 -\-
+ ckx + с3. Тогда, если положить pn+i = рп + ря, ^«+1 = Яп. + V
rn+i = гп -(- т-я, системой уравнений, соответствующей системе C),
будет
(с3 —с4ря —с69л + с5р2)ря +(с4 —
(— с4 дп — съ гп + съ Рп Яп) Ря + (сз — сь Яп) °п + с4 тя = Ьь E)
(— C4^ + CbPn Гп) Рп — сЬгп ап + С3ТЯ = &0.
Таким образом, находим
Q» (х) = х3 — 4,2994л:2 + 6,3436л: — 3,6268
и т. д. Разумеется, чтобы получить приемлемые приближения для
корней, делитель следует определить достаточно точно. Это лежит
в самой природе данной задачи; метод определения делителя чис-
численно вполне устойчив.
Задача 7. Указать упрощенные варианты метода A) — D) и
метода задачи 6, соответствующие упрощенному методу Ньютона.
Решение. Обращая соответствующую матрицу, решаем систему
уравнений C) (соотв. E)) только на первом шаге и приходим к фор-
формулам ап = aibt 4- aobo и т. д. При дальнейших шагах ограни-
ограничиваемся верхней частью схемы и подстановкой bt в эти формулы.
Задача 8. Что соответствует правилу ложного положения для
метода A) — D)?
Решение. Для трех различных точек плоскости р, q находим
значения 64 и Ьо и через эти точки проводим плоскости
6,»В|^а|Р + М + У| A = 0,1).
Теперь, решая систему уравнений Во = 0, 54 = 0, определяем
новую точку, а первую точку предыдущего шага отбрасываем.
Задача 9. Найти чисто мнимый корень уравнения z sin z 4- 1 =
= 0 (ср. с задачей 1.5.8).
Решение. Проще всего, конечно, положить z = iy и решить
уравнение —ysh у -\- 1 = 0 методом Ньютона; при этом получаем
приближенно г/0 = 1, г/j = 0,93555, у2 = 0,93203, у3 = 0,93202.
Но можно также попытаться выделить множитель 1 — ог2, для чего
повторно применяем схему Горнера, обрывая каждый раз ряд
о г4 г6
1 +2 oj- 4- rj-- • • в соответствующем месте, а именно тогда,
когда коэффициент ряда становится существенно меньше проме-
промежуточного результата (а0 = —1):

1.7. Дополнения
51
1
1
1
1
1
1
1
-1
0
-1
-1
1
7
6
1
"б
7
6
8
6
1
Ь-
0
I -£
1
1
1
1
6
7
+ 36
4
об
+ 12
1
120
1
|
1 7
а, =-1--=-£■*-1,
1 j 1
120 1 5040
7 1
216 j
13
~540
7 13*" 1969
а*= б' 855= 1710
-1,1515
Далее будет а3 = —1,1511955, так что окончательно получаем
г1>2 « ±0,932021.
5 заключение параграфа мы хотим привести еще три задачи,
которые показывают, что при определенных обстоятельствах в
специальных ситуациях специальные методы приводят к цг/.и быст-
быстрее, чем описанные выше стандартные методы.
Задача 10. Как перемещаются в комплексной плоскости г =
— и + iv корни многочлена Р (г) = г4 + 423 + г2 + р, когда р
пробегает вещественные числа от —оодо +оо?
Решение. Разлагая Р(г) на два квадратичных сомножителя,
получаем
Р(г) = [г* + (а + 2) г + J- (а + 2) (а2 - 3I1> - (а - 2) 2 +
= —!_(аа —3J(а2 —4),
4а2
F)
—(a

52
/. Уравнения с одним неизвестным
Корни и значения р, отвечающие различным (положительным) а,
изображены на рис. 1.7.1. Из условия dP(z)/dz = 4г3 + 12z2 +
+ 2г = 0 находим точки разветвления:
а = 2,
' = 0,
'= — C7 ±14 VI) =
18,51
— 0,010,
2,823,
0,177.
G)
Рис. 1.7.1.
Задача 11. В каких областях вещественной плоскости р, q
уравнение
P(z) = z* + 4z3 + z2 + <7z + p = 0 (8)
имеет соответственно только вещественные корни, пару или 2 пары
комплексных корней и каковы знаки вещественных частей корней?
(Последний вопрос допускает «физическое» истолкование: каковы
должны быть значения вещественных параметров р, q, для того
чтобы все решения дифференциального уравнения yIV + 4г/'" +
+ У" + ЯУ' + РУ — 0 оставались ограниченными при х -> + оо?)
Решение. Граничные кривые в плоскости р, д, при переходе че-
через которые комплексные корни меняют знак вещественной части,
задаются теми значениями р, q, при которых имеется корень вида
z = гсо (с вещественным со). Подстановка z = /со в (8) с учетом
того, что со* — со2 + р = 4со2 — q = 0, дает параболу Л: 16р =

1.7. Дополнения
53
= 4<7 — q2; другую разделительную линию дает корень 2 = 0;
это — прямая В: р = 0. Тем самым плоскость р, q делится на 4 об-
области с корнями, имеющими k = 1, 2, 3, 4 отрицательных вещест-
вещественных частей. Исследуя поведение вещественных частей, мы вы-
выделяем в плоскости р, q еще кривую С, характеризуемую тем, что
для принадлежащих ей точек (р, q) можно выделить из многочлена
Р (г) множитель (г + аJ с двойным корнем г = —а. Эта кривая в
параметрической форме задается уравнениями р = а2A—8а+3а2),
К"
—1 1 1
-10 -1 -0,1 -0,01
у
yf -
^г *
+
К"
50-
го-
10-
2-
А
0,5-
0.2-
/ 0,02-
0,01-
0,005-
0
-0,01-
-0,1-
-1-
-ю-
9
к+
к" / к'
т/
(
0,01 0,1 1
+
К"
10
р
к;
к
Рис. 1.7.2.
q = 2аA—6а+2а2) и при р = 9/4, q = —6 имеет двойную точку.
Чтобы стало возможным изобразить указанные кривые в окрест-
окрестности нулевой точки, на рис. 1.7.2 произведена изменяющая мас-
масштаб замена координат
ТЛ + Ю6г/2]-
Плоскость р, q делится нашими кривыми на 9 областей. Каждой
области приписана некая «сигнатура», при этом «+» означает по-
положительный корень, «—» — отрицательный, К+ — пару комплекс-

54
1. Уравнения с одним неизвестным
но сопряженных корней с положительной вещественной частью,
К" — соответственно с отрицательной. Для определения сигнату-
сигнатуры достаточно из каждой области выбрать какую-нибудь одну точ-
точку; например, для р = 36, q = 6 корни уравнения (8) суть —3,
—3, 1 ± г'Т^З, следовательно, вся область, в которой лежит точка
р = 36, q = 6, имеет сигнатуру « К+».
Задача 12. Пусть k — число вещественных корней уравнения
f(x) = ex — a — bx3 = 0, (9)
где а и b вещественны. Указать в плоскости a, b области с £=0, 1,
2, 3, 4.
Решение. Для полуплоскости b < 0 имеем k = 1. Полуплос-
Полуплоскость b > 0 разделяется некоторой кривой С на 4 области, в двух
b
3-
2-
1-
-1
2 ег/3 3
Рис. 1.7.3.
из которых k = 2, в одной £ = 0 и в последней k = 4 (рис. 1.7.3).
Эта кривая С задается теми парами значений а, £, для которых
уравнение (9) имеет двойной корень и, значит, f(x) = f'(x) = 0.
Из соотношений (9) и f'(x) = е* — ЗЬх2 = 0 получаем уравнение
кривой С с х в качестве параметра:
3*2
При х —2 в точке а = е2/3, 6 = е2/12 кривая С имеет острие,
da db n
здесь = = 0.
dx dx
Задача 13. Б. Л. ван дер Варден дал следующий пример непре-
непрерывной нигде не дифференцируемой функции. Положим

1.7. Дополнения 55
R(x)
D(x)
= л: —цел (л:),
__ j R(x),
1 \-R(x),
если
если
R(x)<
R(x)>,
VI Pi)
AUJ
:i/2,
► 1/2,
где цел(лг) обозначает ближайшее к л: не превосходящее его целое
число. Ясно, что при х, меняющемся от 0 до 1/2, D(x) линейно воз-
возрастает с угловым коэффициентом 1, а затем до х = 1 убывает с
угловым коэффициентом —1 и что D(x) является периодической
функцией с периодом 1. Функция, которую мы хотим рассмотреть,
задается формулой
ft=0
т. е. это сумма всех таких пилообразных функций с наклоном зуб-
зубца 45° и шириной зубца 1, 1/10, 1/100 и т. д. Решить уравнения
f(x) = 1/3 и f(x) = 0,3.
Решение. Очевидно, можно ограничиться значениями 0 < х<
< 1/2.
Алгоритм вычисления f(x) состоит в том, что, начиная слева,
последовательно отбрасывают по одной цифре в десятичной за-
записи числа х, причем если на каком-то этапе первая цифра >5,
то переходят к десятичному дополнению, и в заключение все сум-
суммируется; например, для х — 0,148375 имеем
0,148375
48375
1625
375
25
5
f (x) = 0,198780
Таким образом, из конечных десятичных дробей х получаем снова
конечные десятичные дроби / (х) самое большее с таким же числом
знаков и из рациональных х снова рациональные f(x). Определим
частичные суммы для f{x) формулой
оч
Легко выводится последовательность полезных оценок

56
/. Уравнения с одним неизвестным
0<f(x)<-f,
A3)
Sn (x) < / (x) < Sn (x) + -jL • 10"** (л = 0, 1, 2,...).
Решение уравнения / (х) = 1/3 можно поэтому провести так. При
0 <: х <: у имеем D (х) = х, следовательно, л: ^ 1/3 <г х + 5/90,
откуда 0,27 < х <: 0,34. Теперь можно при помощи приведенного
выше неравенства для п = 1 исключить интервал 0,27 < х <s 0,3
и тем самым еще сузить границы. Так последовательно получаем
ч=0: 0,27
1: 0,313
2: 0,3142
3: 0,31431
4: 0,314325
5: 0,3143256
6: 0,31432575
7: 0,314325763
8: 0,3143257642
9: 0,31432576431
10: 0,314325764325
<лг<0,34,
<дг<0,317,
<дг<0,3145,
<лг<0,31434,
<лг<0,314327,
<лг<0,3143259,
<х<0,31432578,
<х<0,314325767,
<х<0,3143257645,
<лг<0,31432576434,
<лг<0,314325764327,
S0=x,
i=ZX—U,О,
S2=3x—0,61,
S3= Ax—0,924,
Sk=5x—1,2383,
S5= Ax—0,92397,
S6=3x—0,609644,
S7=2at—0,2953182,
Ss=3x—0,60964396,
S9=4x—0,923969724,
Su=5x—1,2382954883.
Усматривая периодичность промежуточных оценок, делаем пред-
предположение
698501
2222220
и, действительно, легко проверяем, что f(x) = 1/3. Далее, из на-
нашего метода явствует однозначность решения в интервале 0 <: х <:
< 1/2.
Вторая часть задачи, заключающаяся в решении уравнения
/ (х) = 0,3, призвана продемонстрировать, что эта однозначность
имеет место никоим образом не всегда. Мы получаем, что решения-
решениями служат
х = 0,3, 0,29, 0,28, 0,27, 0,26, 0,25,
0,2499, 0,2498, 0,2497, 0,2496, 0,2495,
0,249499, 0,249498
а также и предел этой последовательности х =■ 247/990.

1.7. Дополнения 57
СПИСОК ЛИТЕРАТУРЫ1
Д ю р а н Э. (Е. Durand), Solutions numeriques des equations algebriques,
т. 1, Paris, Masson et Oe, 1960.
Загускин В. Л., Справочник по численным методам решения уравне-
уравнений, Физматгиз, М., 1960.
К о л л а т ц Л. (L. Kollatz), Функциональный анализ и вычислительная
математика, «Мир», М., 1969. (К разделам об итерационных методах.)
О б р е ш к о в Н. (N. Obreschkoff), Verteilung und Berechnung der Null-
stellen reeller Polynome, Berlin, Dtsch. Verlag. d. Wiss., 1963.
*O p т е г а Дж. и В. Р е й н б о л д т (J, M. Ortega, W. С. Rheinboldt),
Итерационные методы решения нелинейных систем уравнений со многими
неизвестными, «Мир», М., 1975.
х Здесь и в списках литературы к остальным главам звездочкой поме-
помечены работы, добавленные при переводе. — Прим. ред.

2. УРАВНЕНИЯ СО МНОГИМИ НЕИЗВЕСТНЫМИ
И. Купка при участии Л. Коллатца, X. Мирендорфа,
Р. Николовиуса, X. Шпренгера и В. Веттерлинга
2.1. Задачи на собственные значения для матриц
Помимо своего теоретического значения, в частности для оценки
погрешности при решении систем линейных уравнений, задачи,
которые мы здесь рассмотрим, имеют и непосредственные практиче-
практические применения, прежде всего к линейным колебательным систе-
системам. Наша первая задача наряду с пояснением этого положения
вещей служит и для предварительного рассмотрения ряда проблем,
касающихся рациональных решений.
Задача 1. Пусть три единичные массы подвешены на пружинах
с коэффициентами упругости (противодействующая удлинению си-
сила на единицу удлинения) cit c2, с3 соответственно, как показано
на рис. 2.1.1. Вычислить основные частоты и формы колебаний для
случая Ci = 8, с2 = 3, с = 11 и указать другие тройки коэффи-
коэффициентов упругости, приводящие к рациональным решениям.
Решение. Если обозначить силы, действующие на массы, через
КI, а отклонения от положения равновесия через yt (i = 1, 2, 3),
то имеем уравнения (точка означает дифференцирование по вре-
времени)
— yi = Ki — K2 = cxyx — с2 (у2 — z/i),
— уг = /С2 — /Са = с2 (г/2 — уг) —- с3 (г/3 — г/а)> A)
Полагая (ниже векторы обозначаются малыми жирными буквами,
матрицы — большими жирными буквами) у = x-sinco/, приходим
к задаче на собственные значения
О
и % = ш2. B)
Пусть 1 обозначает единичную матрицу. Необходимым условием
существования ненулевого решения является обращение в нуль
определителя

2.1. Задачи на собственные значения
59
det(C —М) =
-f- С% Л. ~~
С2 + С3
— С,
о
— с3
О — с3 с3 — %
Г0 3 /л j Ор \ О/ч \ \ 2 1 /л л 1 О/"> /^ |
+ Зс2 с3) % — схс2 с3] = 0. C)
Определитель раскрыт по обычному правилу для оп-
определителей третьего порядка. Для нашего численного
примера имеем
Xs — 36Я2 + 299Я — 264 = 0, D)
откуда собственные значения равны %х= 1, Х2 = 11,
Х3 = 24; их можно вычислить при помощи методов гл. 1.
Из B) получаем соответствующие собственные векто-
векторы (отношения амплитуд колебаний масс) с точностью
до произвольного амплитудного множителя:
Xi=|10j, х2=| О), х3 = ( —13 | - E)
И/ V- 3/ V И
Чтобы отыскать другие рациональные случаи, положим теперь
сз = ci ~Ь С2 и С2 = {plq)cu где р и q — целые числа. Мы найдем,
что
2,3
± V9P2 + 8pq + Аф] ; F)
под корнем стоят квадраты целых чисел при (р, q) = G, 4), B4, 7),
C, 8) [рассмотренный выше случай], (9, 10), (8, 11), A5, 14), B4,
17), A1, 18), E, 26), A3, 28) и других значениях. Коэффициент
ct выбирается произвольно, так что мы можем получать целочис-
целочисленные значения (при с4 = 2q) или десятичные периодические
дроби
Еще одна возможность — взять с4 = 2с3, с, — — с2. Тогда
Чз = -f
pq
q2] .
G)
Имеем (р, q) = C, 5), E, 16), G, 8), G, 33), A1, 24), A3, 35), A6, 39),
C2, 45) и т. д.; кроме того, р и q можно поменять местами.
Задача 2. Протяженная изотропная среда подвержена дефор-
деформации, при которой единичный куб с ребрами

60 2. Уравнения со многими неизвестными
(
е2 = 1 |, е3 =
0
переходит в параллелепипед с ребрами
/3/2\ _ /1/2
ei=( 1/2 ], е2= 1
\1/2/ V 0
Каковы главные оси деформации, т. е. направления, которые со-
сохраняются при деформации?
Решение. Деформация описывается симметричной матрицей
'3/2 1/2 1/21
1/2 1 0 ], (8)
1/2 0 1
для которой Аег = ег, I = 1, 2, 3. Искомые направления являются
собственными векторами xt матрицы А. Ее характеристический
многочлен
det(A — М) = — К3 + ^-к2 — -^+1 (9)
имеет корни Xj = -*-, Х2 = 1, Х3 = 2. Отвечающими этим собствен-
собственным значениям собственными векторами (определяемыми с точ-
точностью до скалярного множителя) служат
A0)
Отметим попарную ортогональность различных собственных век-
векторов: если х/ обозначает вектор-строку, полученную путем транс-
транспонирования вектор-столбца хг, то
х(' xk = 0 для i Ф k.
В этом сборнике мы не будем рассматривать общую задачу на
собственные значения Ах = %Вх, а будем заниматься лишь специ-
специальной задачей на собственные значения
\х = Хх A1)
с квадратной матрицей порядка п

2.1. Задачи на собственные значения
61
А =
ait al2
A2)
Как известно, определитель матрицы А — XI, который является
многочленом степени п относительно X (называемым характеристи-
характеристическим многочленом матрицы А), обращается в нуль в точности
при X, равных собственным значениям:
det (А — М) = 0.
A3)
Чтобы можно было использовать методы решения уравнений, опи-
описанные в гл. 1, необходимы методы определения коэффициентов
характеристического многочлена по элементам матрицы. Имеется
целый ряд таких методов, и в большинстве из них прежде всего
пытаются, используя преобразование подобия
= ТВТ-Х (так что В^
A4)
получить более простую матрицу В, которая имеет те же собствен-
собственные значения, что и матрица А, ибо det(B—XI) = det [T(A—
—МУГ1] = detT-det(A—X^-detT = det(A—XI)], но у которой ко-
коэффициенты характеристического многочлена вычисляются проще.
В качестве примера таких методов рассмотрим метод Хессен-
берга, в котором соотношение A4) используется в форме
AT + ТС = 0,
A5)
которую оно принимает при В = —С, причем предполагается, что
Т и С имеют вид
1
0
т =
о
'22
о
о
о *„, t,
33
0
0
0
tn3

62
2. Уравнения со многими неизвестными
Сц Ci2
—1 с22
О -1
С1, п-\
С3, л-1
A6)
О 0 ... -1 сй
Схему, по которой проводится вычисление матриц Т и С и опреде-
определяется1 характеристический многочлен, поясняет следующая це-
целочисленная
Задача 3. Решить задачу A1) на собственные значения для мат-
матрицы
— 6 —80 290 80
— 1 —60 119 26
— 1 —100 180 37
2 312 —529 —104
А =
Решение. В схеме
Суммы
1
7Я
8 21
-7
0
28
33
—*■
0
0
0
0
1
-6
-6
-1
-1
2
0
0
0
1
-to»
72
-80
-60
-100
312
0
0
1
-727
3531
А
60
290
119
180
-529
0
1
-123.
326
-5030
39
80
26
37
-104
1
6 го
8 22
-4 25
24 29
1
1
0
0
0
6,
-1
0
0
т
05
0
-и
-и
2,
50„
-7т
-1
0
-4«
0
0
1в
-5.
1f0,,
-««
-6,3
-1
0
0
0
,4
8016
6,7
11,в
-з,.
индексы при числах указывают порядок, в каком они вы-
вычисляются. Согласно A5), все скалярные произведения строк двой-
двойной длины матрицы (А Т) на столбцы матрицы ( J ) дают нуль.
При этом нули распределены так, что при последовательном умно-
умножении строк матрицы (AT) на столбцы матрицы ( J, ) использу-
используется каждый раз ровно один неизвестный элемент, который тем са-
1 Необходимо отметить, что не всякую матрицу А можно привести к фор-
форме A6). Возможность такого приведения означает, например, что минималь-
минимальный многочлен матрицы А совпадает с ее характеристическим многочленом.
В общем случае матрица С может иметь на побочной диагонали помимо —1
еще н нули. См. также замечание к задаче 3.—Прим. ред.

2.1. Задачи на собственные значения
63
мым и определяется. После получения каждого очередного столбца
матрицы Т находим сумму элементов столбца и осуществляем про-
проверку путем вычисления скалярного произведения строки-суммы
на предыдущий столбец матрицы (IV После того как матрица С
построена, можно теперь рекурсивно, рассматривая главные ми-
миноры матрицы С + XI (см. в связи с этим, например, Р. Цурмюль
[1964], стр. 3251), вычислить матрицу
F =
0
0
0
0
0
0
... о
... о
... 1
0
1
fu
1
/lO
/20
1
'а, п—1
fni fni In
A7)
в последней строке которой стоят коэффициенты характеристиче-
характеристического многочлена. Вычисление проводится по такой схеме: для оп-
определения fih нужно составить сумму произведений стоящих выше
в том же столбце элементов матрицы F на элементы г-го столбца
матрицы С, стоящие в одноименных строках (т. е. взять скалярное
произведение соответствующих частичных столбцов), и при k> О
прибавить еще /(_,, h_t. Слева для проверки вычисляются суммы
элементов строк.
Для п = 4 имеем формулы
/lO = cll>
/20 = Cl2 '
/2! =
/30 = Cl3 "
/31 =
/32 =
/40 = C14 -
/41 =
/42 =
/43 —
С22
с23
С24
/lO
+ /iO.
+ сзз ■
+ с33 •
С38 *
+ С34 •
С34
/го>
/21 I /20>
1 +/«,
/го ~Ь С44 '
/21 + С44
1 + СН ■
С44-
/зо>
/31 ~
A8)
/зо»
/
1 +/
32-
Таким образом, характеристический многочлен матрицы A4) равен
X4 — 10Х3 + 35Х2 — 50Х + 24; его корнями являются 1, 2, 3, 4.
Для собственных векторов хг матрицы А и уг матрицы В спра-
1 Или: Д. К. Фаддеев и В. Н. Фаддеева [1963]. — Прим. ред.

64
2. Уравнения со многими неизвестными
ведливы соотношения
= 0, x, =
0=1,2, ...,
A9)
130
21
23
-51
90
15
16
—34
70
11
11
—21
64
9
8
—12
Векторы уг определяются совсем просто: прибавляем ht к каждому
диагональному элементу матрицы С, полагаем последнюю компо-
компоненту вектора yt равной 1 и последовательно вычисляем остальные
его компоненты в обратном порядке, беря скалярное произведение
на последнюю, предпоследнюю и т. д. строки матрицы С + М-
Проверкой правильности вычислений служит обращение в нуль
скалярного произведения на первую строку. Окончательно полу-
получаем следующую матрицу X со столбцами х^:
B0)
Замечание. Если какой-нибудь диагональный элемент матри-
матрицы Т обращается в нуль, можно использовать любой другой
не обращающийся в нуль элемент того же столбца, что равносильно
просто перестановке строк матрицы Т. Может также случиться,
что какой-то столбец матрицы Т весь состоит из нулей, так что схе-
схему нельзя продолжать. В этом случае на место диагонального эле-
элемента ставим неопределенную величину е (в повторном случае
ставим е2 и т. д.), а после проведения вычислений полагаем е = 0,
в результате чего матрица С распадается на блоки (ср. с указанным
местом в книге Р. Цурмюля [1964] и со следующей задачей).
Задача 4. Решить задачу на собственные значения A1) для
матрицы, указанной в приведенной ниже схеме.
Решение.
a+ 3
a
1
1
1
a+3
1
a
1
1
a+ 3
1
1
a
1
a+3
1
1
1
a
1
1
0
0
0
-a
-1
0
0
3
0
1
1
1
-3
-a-2
-1
0
I
I
£
0
0
6
0
-e
-8
e2
0
0
0
■ 62
-e2
-£2
0
1
-1 i
-a + 1
Контрольные суммы могут совпадать лишь с точ-
точностью до высших степеней е. Полагая е = 0, видим указанное
распадение матрицы С на блоки; для собственных значений полу-
получаем уравнения

2.1. Задачи на собственные значения
65
det (— а + 1 + к) = — а + 1 + к = 0,' дающее
det (— а + 1 + К) = — а + 1 + Я, = О, дающее
—1
— а — 2 +
2(а+1)Ъ+(а
— 3)= О, дающее
,1 = а — 1,
Яз = а — 1,
Я,3 = а — 1,
Я,4 = а + 3.
Таким образом, вычислять матрицу F (см. A7)) нет необходимости.
Собственные векторы также лучше определить непосредственно
(ср. с A9)):
1
1
0
0
1
0
—1
0
1
0
0
—1
1
1
1
1
Вместо первых 3 векторов можно взять любые их линейно неза-
независимые комбинации, поскольку они отвечают одному и тому же
собственному значению.
Задача 5. Применить метод Хессенберга к матрицам
a)
Ответ. Собственные значения:
1 1
1 1
1 1
1 1
1
1
4
1
1 N
1
1
4 >
V /
И
/ \
' 4
3
2
. 1
3
6
4
2
2
4
6
3
1
2
3
4
а)
О
1
3
6
Ь)
А C-/5)
1,38
1,91
3,62
13,09
\
с)
-14,062
— 0,004167
-17,066
соответствующие им собственные векторы (столбцы):
12 0 1
— 12 0 1
0—1 12
0—1—12
3-206
а)

66
2. Уравнения со многими неизвестными
2 2 2 2
_1 _ /5 1 — /5 —1 + J/5 1 + /5
j 1 + /5 1 — j/5 I — /5 1 + /5
—2 2—2 2
/ 0,5593 0,6090 0,5625 \
с)| — 0,7753 0,1440 0,6149 .
\ 0,2934 —0,7800 0,5527/
Задача 6. В задаче 3 матрица А заменяется транспонирован-
транспонированной матрицей А'.
Решение. Если к матрице А уже применялся метод Хессенберга,
то целесообразно использовать полученные при этом результаты.
Напомним в этой связи правила вычислений с транспонированными
величинами: для любых матриц В, С справедливы соотношения
(В')' = В, det В'= det В, (ВС)' = С'В';
B1)
в случае когда у матрицы В существует обратная матрица В,
существует также (В') и
(В') = (В)'.
При помощи этих правил прежде всего получаем
det (А — XI) = det (А' — XI),
B2)
B3)
т. е. собственные значения матриц А и А' одни и те же. Из соотно-
соотношения AT + ТС = 0 вытекает, что
A' r-i + Т' С = 0,
B4)
и мы, как и выше, определяем собственные векторы zt матрицы
С и собственные векторы ut матрицы А' с помощью соотношений
(С + Яг1)гг = 0, Tut = zt, B5)
аналогичных соотношениям A9). Специальный вид матрицы Т'
позволяет непосредственно решать уравнение T'u* = z, без на-
нахождения Т'.
Ответ. Z = (z,, гъ z3, z4), U = (щ, и2, щ, щ),
Z =
1
7
8
j
1
8
10
— 18
1
9
14
-31 ■
1
10
20
-40

2.1. Задачи на собственные значения 67
г,-
Собственные векторы хг матрицы А и собственные векторы uh транс-
транспонированной матрицы А' всегда связаны между собой соотноше-
соотношениями
u'k\i = 0 при I ф k.
Удостоверимся в этом:
1
-36
43
7
1
—72
100
8
1
-116
169
31
1
-150
220
40
Задача 7. Выразить симметричную матрицу А из задачи 2 че-
через ее собственные векторы х4 и собственные значения Kt. Какие
симметричные матрицы А имеют те же собственные векторы и про-
произвольные наперед заданные собственные значения Aг?
Решение. Образованная из двух векторов-столбцов a, b по фор-
формулам mlk — atbk, i, k = 1,2, ... , n, матрица М = ab' называет-
называется диадическим произведением а иЬ1. Для любого вектор-столбца
с произведение ab'c всегда является вектором, имеющим направле-
направление вектора а, или же нулевым вектором, если b и с взаимно орто-
ортогональны. Используя диадические произведения, наши матрицы А
можно представить в виде
А = <
Действительно,
., „ Av /IV /v'v\ / ■ 10 4 /9Т\
V*t t —™ ^^™J '~~' vlAl I Л ,Л £ If t 1, £/^ «J» I £* I f
Отсюда
B9)
1 Заметим, что это — тензорное (кронекерово) произведение а'(
Прим. ред

68
2. Уравнения со многими неизвестными
При |j, t = %it i = 1, 2, 3, получаем матрицу, которая встретилась
в задаче 2.
Задача 8. При фиксированных значениях а, В, у, б применить
метод Хессенберга к матрицам
а)
Ь)
а
т
а
3
а
т
«31
«41
+
«12
«32
«42
2
тт
Т
3
3
«13
«33
«43
а
3~
а
3
а
3
«34 Г
1
т
3
±,
2 Н
^ _т_
6
^ _L
6
а
3~
Т
а
т
t
+ ~з
Р , т
+ — + —
2 6 j
где
16T + 64S,
ai2 = a2l = —42а—126 —12т + 128S,
а13 = а31 = — 49а + 306 — 28^ — 246,
*14
= а41= 133а —66 —20т+ 88,
а22 = 36а + 46 + 9у + 2568,
«23 = «32 = 42а— 106 + 217 — 488,
«24 = «42 = —И4а+26+ 15у+ 168,
а33 = 49а + 256 + 49у + 98,
а34 = а43 = — 133а — 56 + 35у — 33,
а44= 361а + 6 + 257 + 5.
Ответ. Собственные значения: а) а, 6, у; Ь) 495а, 666, 99у,
3308 Собственные векторы (столбцы):
а) /—
Ь) /-
7
6
7
19
6
2
5
—1
—4
3
7
5
8
16
—3
1

2.2. Итерации в задачах на собственные значения
69
2.2. Итерации в задачах на собственные значения
Задача 1 (итерационный метод фон Мизеса). По
/9—2 — 4\ /О
А= —2 14 —4 и zo= О
V—4 —4 18/ \1
A)
построить несколько векторов zh = Azft_,(& = 1, 2, 3, ...) и просле-
проследить за отношениями одноименных компонент zhH (I — 1, 2, 3) со-
соседних векторов Zk и за последовательностью кратных векторам
zk векторов yk длины 1. Провести сравнение с точными решениями
х задачи на собственные значения Ах = Хх.
Решение. Получаем такую примерную схему (с контрольными
столбцовыми суммами 2):
г
ч.
ч
А
9 -2 -4
-2 14 -4
-4 -4 18
3 8 10
7,.
*о
0
0
1
1
0
п
1
Zi
-4
-4
18
10
-0,2120
-0,2120
0,9540
—
—
18
z2
-100
-120
356
136
-0,2572
-0,3087
0,9157
25
30
19,78
2з
-2084
-2904
7288
2300
-0,2567
-0,3578
0,6978
20,84
24,20
20,47
z<
-42100
-65640
151136
43396
-0,2475
-0,3860
0,8887
20,201
22,603
20,738
.. •
...
• • ■
•
2»
— OO
-oo
+ oo
+ 0O
-0,2182
Л Л7СЛ
0,8729
21
21
21
Собственными значениями являются "кх = 6, X2 = 14, X3 = 21,
рассматриваемые отношения стремятся к наибольшему собствен-
собственному значению hg, а последовательность у^ стремится к соответст-
соответствующему собственному вектору х3 из тройки нормированных соб-
собственных векторов
2//6Л /_2//14\ /-1//21Ч
= 1 1//6 ], х2 = [ 3//П|, Хз=[-2/|/2Т|> B)
1//6 /
у
если только исходный вектор не ортогонален к вектору х3. Кроме
того, по локализационной теореме Л. Коллатца для симметричной
матрицы А частные гкл1г^г<1 ограничивают с обеих сторон собствен-
собственное значение. Например, для к = 4 имеем
20,201 <Я,3(= 21) < 22,603.
C)

70
2. Уравнения со многими неизвестными
Задача 2. Видоизменить итерации в предыдущей задаче так,
чтобы после каждого шага результирующий вектор был ортогона-
ортогонален а) вектору х3, Ь) векторам х3 и х2; в качестве исходных векто-
векторов взять соответственно а) (—1, 1, 0) и Ь) A, 1, 1).
Решение. Требование ортогональности означает в случае (а),
что мы должны спроектировать вектор zk = Azh_, на перпендику-
перпендикулярную к х3 плоскость согласно формуле (полагаем zk = zft — ах3
и умножаем скалярно на х3)
Ч = Ч — ( zh, x3) х3, D)
а в случае (Ь), — что мы должны воспользоваться формулой
zh= zh у zh, x3jx3 у zh, х2 J х2.
Теоретически достаточно было бы провести ортогонализацию лишь
на первом шаге, однако из-за ошибок округления или неточностей
определения xt это нужно делать чаще. В верхней части схемы по-
получаем
а)
А
9 —2 4
-2 14 —4
—4 —4 18
1
1
0
Zl
-12
14
4
Ч
-152
+204
+64
Ч
-2032
+2904
+ 944
Ч
-'ПШ
+40944.
+ 13504
Ь)
9
-2
-4
А
—2
14
—4
—4
-4
18
Zo
1
1
1
h
8
4
4
Ч
48
24
24
В то время как в случае (а) мы приближаемся к ^2 и х2, в случае
(Ь) итерации дают (в два шага) 1,их,, если провести вычисления,
как в задаче 1. Для получения оценки при помощи локализацион-
ной теоремы можно без округления умножить еще раз на мат-
матрицу А. Окончательно имеем
а) 13,71 <Я2(= 14) < 14,31, Ь) ^ = 6. E)
Задача 3 (частные Рэлея). По последним приближениям из за-
задач 1 и 2 вычислить в качестве улучшенных приближений для соб-
собственных значений частные Рэлея

2.2. Итерации в задачах на собственные значения
71
р /7 ч _ (zft,
(z
F)
Решение. Формула #(z) = (z, Az)/(z, z) для частного Рэлея
(экстремальные значения которого при некоторых условиях диф-
ференцируемости суть собственные значения, а точки, в которых
экстремум достигается, — соответствующие собственные векторы)
означает некое усреднение использовавшихся выше покомпонентных
частных. Получаем
/? (z3) = 20,941 для задачи 1,
R(z3) = 13,99538 для задачи 2 (а), G)
R (z,) = 6 для задачи 2 (Ь).
Два первых приближения для собственных значений существенно
лучше, чем приближения для собственных векторов, так как част-
частное Рэлея в окрестности собственного вектора изменяется пропор-
пропорционально квадрату длины вектора-приращения.
Задача 4. Сначала провести итерации по фон Мизесу для
/—5,7 -61,1 -32,9\ /1\
А= 0,8 11,9 7,1 и zo= 1 , (8)
V—1,1 —11,8 —1,2/ \1 /
затем заменить А на А + 51 (где I — единичная матрица).
Решение. Сначала получаем следующую схему:
"и
А
-5,7 -61,1 -32,9
0,8 11,9 7,1
-1,1 -11,8 -7,2
-6 -61 -33
гк
N/(Z/(,H*)
Zo
1
1
1
3
0,577
0,577
Z,
-99,7
19,8
-20,1
-100
-0,9622
-0,1940
-99,7
19,8
-20,1
Ч
19,8
13,15
20,75
53,7
-0,6275
0,6576
-0,1986
0,6641
-1,032
Нз
-1599
319,65
-326,35
-1605,7
-0,9615
П HQ99
-0,1962
-80,76
24,31
-15,73
320,6
207,55
336,75
864,9
0,6296
0,4076
0,6614
-0,2005
0,6493
-1,032
Никакой сходимости не обнаруживается. Так бывает всегда (если
не считать некоторых специальных начальных векторов), когда
существует несколько собственных значений с максимальным мо-
модулем. В таких случаях рекомендуется произвести сдвиг собствен-
собственных значений, который достигается заменой А на А + d\ с подхо-

72
2. Уравнения со многими неизвестными
дящим числом d. В рассматриваемом случае при d = 5 получаем
схему
А
-0,7 -61,1 -32,9
0,6 16,9 7,1
-1,1 -11,8 -2,2
-1 -56 -28
zo
1
1
1
3
0,577
0,577
0,577
z,
-94,7
24,8
-15,1
-85
-0,9561
0,2504
-0,1524
-94,7
24,6
-15,1
Ч
-952.Z
236,15
-155,25
-871,3
-0,9587
0,2373
-0,1563
10,05
9,522
10,28
z3
-8654,5
2126,9
-1397,6
-7925,2
-0,9594
0,2358
-0,1549
9,089
9,007
9,00Z
г.
-77914,4
19098,05
-12502,75
-71319,1
-0,9596
0,2352
-0,1540
9,003
8,979
8,946
Ч
-701010,3
171656
-112145,1
-641499,4
-0,9598
0,2350
-0,1535
8,997
8,988
8,969
х2
Нормированные итерированные векторы стремятся к собственному
вектору
/—94\ /—0,95988... \
х, = —- I 23 = ( 0,23496 ... ) (9)
/9590 \_15у1 V-0.15317.../'
отвечающему собственному значению А,( = 9. Другие собственные
значения суть %2 = 4, Х3 = 1, отвечающие им нормированные соб-
собственные векторы суть
—0,95988 ..Л
0,15317...
— 0,23486.../
0,56568../
— 0,42426...
0,70710...,
Первоначальная матрица А имеет собственные значения %1 = А,
К2 = —1, %3 = —4 и те же самые собственные векторы.
Следующим итерационным методом, который мы рассмотрим,
будет метод Якоби. Он применим лишь к симметричным матрицам
и состоит в том, что мы пытаемся преобразовать матрицу А к диаго-
диагональному виду
A0)
D = Т'АТ с ортогональной матрицей Т' = Т
(И)
путем расщепления преобразования Т на последовательность дву-
двумерных преобразований ТгТ2-Т3' ... (=Т), каждое из которых име-
имеет вид

2.2. Итерации в задачах на собственные значения
73
С S
1
П
, где с2 + s2 = 1
A2)
(все внедиагональные элементы, кроме двух указанных элементов
s, равны нулю); с и s можно трактовать как соответственно cos ф
и sin ф, где ф —• угол, на который производится вращение (с после-
последующим зеркальным отражением) в плоскости xt, xk. Если задаться
целью обратить в нуль элемент (Цъ. Ф 0 матрицы А, то с и s нужно
выбрать по формулам
с =
A3)
где
£ =
sign alh
sign^~
"Ik
Тогда мы получим матрицу В = Т
k-м столбцами1:
в случае аи = akh,
в противном случае.
п с измененными £-м и
с%аа
ьи
bih = Ьы = О,
— 2csaik,
ajh,
A4)
6;i = afl в остальных случаях.
1 И одноименными строками. — Прим. ред.

74
2. Уравнения со многими неизвестными
Отметим, что выполняется соотношение bH2 + bkk2 = %2 + akk2 +
-(-- 2щ2 и, значит, сумма квадратов диагональных элементов увели-
увеличивается. Соответственно на ту же величину уменьшается сумма
квадратов внедиагональных элементов, откуда следует сходимость
к диагональной матрице. Разумеется, элементы, которые однажды
обратились в нуль, при последующих шагах могут снова стать не-
ненулевыми.
Метод Якоби требует довольно значительного объема вычисле-
вычислений. С другой стороны, он численно устойчив и применим даже в
исключительных случаях, как, например, при кратных собствен-
собственных значениях. Поэтому он стал стандартным методом для электрон-
электронных вычислительных машин. При этом можно обрабатывать вне-
диагональные элементы просто поочередно, в то время как при руч-
ручном счете предпочитают выбирать на каждом шаге наибольший по
абсолютной величине элемент.
Задача 5. Применить метод Якоби к матрице
Решение. Получаем такую схему (числа округлены):
i-.k
c,s
Тг...-Tn
Am
1
0
0
2
-1.
0
0
1
0
-1
2
-1
0
0
1
0
-1
2
1
0,7071
0,7071
-0,7071
0
3
0
0,7071
2
-0,7071
-0,7071
-0,7071
0
0
1
0,7071
0
0
1
0,7071
0,7071
2
1
0,6881
0,6280
-0,6280
0,4597
3,3660
0,3251
0
-0,7071
-0,7071
0
0,3251
1
-0,6280
3
0,4597
0,3251
-0,3251
-0,8881
0
-0,6280
1,6340
0,6280
-0.6280
0,4597
3,3660
0,2768
0,1704
2
0,8517
-0,4318
-0,77?6
-0,4654
0,2768
0,6136
0
3
0,5241
-0,6474
-0,0938
0,7563
0,1704
0
2,0204
1
0,9951
0,5821
-0,7014
0,4113
3,3936
0
0,1695
2
0,0991
0,4919
0,7065
0,5087
0
0,5860
0,0169
-0,6474
-0,0938
0,7563
0,1695
0,0169
2,0204
1
0,9927
0,4997
-0,7076
0,4996
3,4142
0,0020
0
0,4919
0,7065
0,5087
0,0020
0,5860
-0,0168
3
0,1207
0,7130
0,0084
-0,7011
0
'0,0168
1,9998

2.3. Метод исключения для линейных систем уравнений
75
0,1997
-0,1016
0,4996
3,4142
0,0020
0,0000
2
0,9999
0,5004
0,1066
0,5004
0,0020
0,5858
0
3
0,0119
-0,1071
0,0000
0,1071
0,0000
0
2,0000
1
■ 1,0000
0,5000
-0.1011
0,5000
3,4142
0
0,0000
2
0,0007
-0,5000
-0,1071
-0,5000
0
0,5858
0,0000
-0,7071
0,0000
0,1011
0,0000
0,0000
2,0000
Таким образом, по мере того как Ат при т-> оо превращается в
диагональную матрицу, на диагонали которой стоят собственные
значения в некоторой последовательности, зависящей от выбран-
выбранных в начале пар /, k, в столбцах матрицы Т4- ... -Тт появляются
стоящие в соответствующей последовательности нормированные
собственные векторы.
Задача 6. Решить методом Якоби некоторые из приведенных в
задаче 2.1.1 задач на собственные значения.
2.3. Метод исключения для линейных систем уравнений
Самым известным методом решения линейной системы уравне-
нии
или
a2ix,
0)
an2x2
\- аппх„= Ь„,
с не обращающимся в нуль определителем det (А) можно считать
гауссов алгоритм исключения, который состоит в том, что сначала
составляется эквивалентная система с треугольной матрицей и
затем ее уравнения решаются одно за другим. Начинаем с того,
что вычитаем первое уравнение, помноженное на с21 = a2i/afl,
C3i — flsi/fln. ••■. сш = flni/flii (можно считать, что atl ^=0;
в противном случае меняем уравнения местами), соответственно
из 2-го, ... , п-го уравнений, благодаря чему в этих урав-
уравнениях исключаются члены с хх и, таким образом, получается си-
система из п— 1 уравнений относительно неизвестных х2, ..., х„.
К этой системе применяем тот же способ и т. д., пока, наконец, не
останется одно уравнение относительно х„. После этого, идя в об-

76
2. Уравнения со многими неизвестными
ратном порядке, последовательно вычисляем хп, xn_it ... , xlt ис-
используя в каждой промежуточной системе первое уравнение.
Задача 1. Решить методом Гаусса систему уравнений
4*,
хх + 6х2
j -f 4х2
2х2 + Зх3
4 = 3,
4 = 6,
х4 = 4,
4 = 7,
контролируя вычисления при помощи строчных сумм.
Решение. Записывая сГ) справа вслед за суммами st элементов
по строкам (включающими и правые части наших уравнений), по-
получаем схему
«и
4
3
г
1
0
3
6
4
2
2
4
6
3
3,75 2,50
2,50 5,00
„ 1, 25 2,50
1
3,3333
1, 6667
-1
1
2
3
4
1,25
2,50
3,75
1,6667
3,3333
2,50
2
3
6
4
7
3,75
2,50
6,25
0
5
5
Si
K
21
19
17
11,25
12,50
13,75
5
10
7,5
0,75
0,50
0,25
0,6667
0,3333
0,5
В заключение можно для проверки подставить найденные xt в не-
некоторые из заданных уравнений, а также вычислить определитель
исходной системы как произведение левых верхних элементов мат-
матриц в левой части схемы:
det (А) = 2,5 • 3,3333 • 3,75 - 4= 125.
B)
Задача 2. Видоизменить схему в предыдущей задаче так, чтобы
появлялись только целые числа.
Решение. На первом шаге умножаем уравнения с 2-го по га-е на
ап, прежде чем вычесть из них первое уравнение, умноженное на
at j, и аналогично поступаем на дальнейших шагах, причем можно,
естественно, при случае производить сокращения:

2.3. Метод исключения для линейных систем уравнений
77
4
3
2
1
а*
0
3
6
4
2
15
10
5
1
2
4
6
3
10
-20
10
40
20
-1
1
2
3
4
5
10
15
20
40
60
2
be
3
6
4
7
15
10
25
0
60
120
Si
13
21
19
17
45
50
55
60
120
160
Множитель
4
4
4
3
3
2
При работе с настольной счетной машиной вычислительную
схему удобно привести к более компактной форме Банахевича,
так как здесь имеется возможность «накапливать» скалярные про-
произведения, не записывая промежуточные результаты. Именно,
имеем
bubi2...bin
А = С • В, В =
1
С =
О
*>п, п—1
•1
C)
где ctj те же, что и выше, a btj — коэффициенты первых уравнений
каждой нашей промежуточной системы (первые строки матриц в
левой части схемы при прежнем способе записи). Таким образом,
мы вычисляем по формулам
. = a,k —
D)
cth = iflih — ciXbik сг. h-\bk~\. k)
попеременно строку матрицы В и столбец матрицы С (отметим, что
здесь фигурируют —cih, а не cih) и аналогично прежнему обраба-
обрабатываем правые части.
Задача 3. Решить задачу 1 по схеме Банахевича.
Решение. Обычно матрицу —С записывают (без диагональных
элементов) в левом нижнем углу матрицы В:

78
2. Уравнения со многими неизвестными
в
с
4 3.
3 6
2 4
1 2
4 3
-0,75 | 3,75
-0,50 -0,6667
-0,25 -0,3333
0 1
2
4
6
3
2
2.50
3,3333
-0,5
-1
1
2
3
4
1
1,25
1,6667
2,50
2
bi
3
6
4
7
3
3,15
0
5
Si
13
21
19
17
13
11,25
5
7,50
При матрицах больших размеров рекомендуется для дополнитель-
дополнительного контроля использовать столбцовые суммы (см., например,
Р. Цурмюль [1964], стр. 63).
Задача 4. Решить при помощи алгоритма Гаусса систему
Xi + 2х2 -Ь хь = 1,
Х2 ■+■ х3= 2.
Решение. Так как на втором шаге процесса исключения веду-
ведущий элемент обращается в нуль, для исключения берем второе
уравнение (на что указывает стрелка на схеме):
Ш
-1
0
—
XL
-2,33..
г
-г
1
0
Ш
. 1,33
1
2
1
3
1
Ш
0,66....
bi
1
1
2
2
2
2
Si
5
0
4
5
4
5
Су
1
0
0
Один из вариантов алгоритма Гаусса состоит в том, чтобы перед
каждым шагом выбирать в столбце, используемом для исключения,
наибольший по абсолютной величине элемент (поиск ведущего эле-
элемента); это во многих случаях улучшает численную устойчивость
алгоритма, так как потеря верных знаков ввиду вычитания почти
одинаковых чисел отодвигается на конец вычислений. Случай по-
появления нулей обходится при этом сам собой.

2.3. Метод исключения для линейных систем уравнений
79
Задача 5. Решить систему
12*,— 2х2 + 9х3 = 9,
Зх, + 9х2 + 4х3 = — 49,
применяя указанный способ поиска ведущего элемента.
Решение. Округляя после каждого умножения и деления до
трех знаков после запятой, имеем:
1
|12|
3
-6272,597
12
-z
9
112,166 |
9,500
-1484,333
3
9
4
2,253
1,750
L^o.oioJ
8034,500
bi
28
9
-49
37,253
-5f,Z50
-30,345
Si
54
28
-33
51,676
-40,000
-80,359
-0,083
-0,250
- 0,781
Проверка путем подстановки дает так называемый вектор-невязку
(или просто невязкуI
г = b — Ах = |
25.093
-0,002
-5,712
E)
Большая величина невязки в рассматриваемом случае показывает,
что решение проведено неудовлетворительно; это объясняется
прежде всего потерей знаков при исключении на втором шаге.
Понятно, что полученные значения х также являются достаточно
плохими приближениями. См. далее задачи 6 и 7.
Для того чтобы рассмотреть возникающую здесь проблему, как
можно оценить погрешность приближенного решения при помощи
невязки, нужно привлечь теорему о неподвижной точке из § 1.5.
Прежде всего укажем три наиболее употребительные нормы для
векторов и:
= 2
(норма суммы модулей), Fа)
1 Ниже г — от Residuum (остаток). — Прим. ред.

80 2. Уравнения со многими неизвестными
u , =
(эвклидова норма), Fb)
|| u ||oo = Hm 1/ ^ \ut \p= max I ut I (норма максимума
"-"-00 i=i l<i<n модуля). Fс)
Для всякой нормы векторов (ниже индекс при норме опускается)
можно ввести соответствующую норму матриц:
|| А || — sup -—— = sup || Аи || , G)
и+0 || и || || и И =1
которая, с одной стороны, согласована с нормой векторов в том
смысле, что
II Аи || < || А || • II и || (для всех А и и), (8)
и, с другой стороны, является наименьшей согласованной нормой
в том смысле, что число || А || в неравенстве (8) нельзя уменьшить1.
Далее, очевидно, что выполняются соотношения
II АВ || < || А|| • || В || , II I || = 1, (9)
а также третья аксиома нормы из § 1.5. \
Можно показать, что для трех приведенных выше случаев нор-
норма матрицы А задается формулами
л
II А || ±= max У \aik\ , A0а)
|| A|| 2=max о„ A0Ь)
|| А И» = max У |alk|. A0c)
Здесь а t являются сингулярными числами матрицы А; это положи-
положительные значения квадратных корней |/[i t из собственных значений
[л* матрицы АТА (которая при невырожденной матрице А положи-
положительно определена, а в противном случае положительно полуопре-
полуопределена и потому имеет только вещественные собственные значения
>0). Для вещественных симметричных матриц сингулярные числа
равны абсолютным величинам (вещественных) собственных значе-
значений: CTj = \%t\.
1 В принятой в нашей литературе терминологии подобные нормы назы-
называются подчиненными или операторными. При этом указанная ниже нор-
норма || А || 2 называется спектральной (ввиду ее связи с собственными значения-
значениями матрицы АТА). —Прим. ред.

2.3. Метод исключения для линейных систем уравнений 81
Пусть теперь х — решение уравнения Ах — b = 0 (где матри-
матрица А невырождена) и х0 — некоторое приближение с невязкой
г0 = b — Ах0. Полагая s0 = х — х0, легко получаем, что As0 =
= г0, откуда s0 = A!^ и, значит, в силу (8),
II Sg || < II А || • ||го||. A1)
Матрица А большей частью точно не известна, так что вычис-
вычисление или хотя бы оценка нормы ||А~Ч| согласно формулам A0)
затруднительны. В случае эвклидовой нормы, если мы располагаем
какой-нибудь нижней границей для наименьшего uit обратная к
ней величина служит верхней границей для ] |A-1112-
Если есть какое-нибудь приближение В для А (знать саму
матрицу В нет необходимости), то, полагая b •— Ахг = гг, S; =
= х — хг (/ = 0, 1, 2, ...), можно организовать итерационный
процесс
Х1+1 = X; + В'1 (Ь — AXJ = X; + В!"; (i = 0, 1 , 2, ... )' A2)
при этом в формуле A.5.8) мы полагаем К= II I — B~XA || . В слу-
случае /С<1 согласно формуле A.5.11) имеем
^11хг1 —хг|| =
х —xi+1|| < уз^11хг+1 —хг|| =
I — А
Г, If (i=0, 1, 2, ...).
Совершенно аналогичным образом можно доказать несколько более,
простую формулу
Цх-хг|! <—Ц;1|хг+1-хг|| = —!— II В!", || <!
I — А 1 — А
< —— || В || • || гг || (i = 0, 1, 2,...) A4)
1 — А
(ср. с A.5.11а)).
Задача 6. Используя формулу A1) с || ||2 и формулы A3) и
A4) с || Hi и || П.», дать оценки погрешности в задаче 5.
Решение. Согласно задаче 2.1.5, имеем ai(A)> 0,0041667>
> 1/240, следовательно, ЦА! |2 < 240 и, в силу A1) и E),
|| х —хо||2< 240- 25,8 < 6300, A5)
так что можно гарантировать лишь знак последней компоненты.
Если при таком же правиле округления, как и в задаче 5, вычис-
вычислить матрицу В путем решения уравнений, правыми частями ко-
которых служат единичные векторы, то получим

82 2. Уравнения со многими неизвестными
/—60,972 —14,364
B-i= —14,381 — 3,433 +18,519
+ 78,100 +18,500 —100,000;
/—6272,4754
х /-1484,806 , A6)
\+8034,500/
т. е. лишь незначительно измененное решение. Далее имеем
0,079 0,153 —0,156
= ( 0,020 0,035 —0,036
v—0,100 —0,200 0,200
'A7)
/— 1976,083 \ / —8248,558>
в-1Го= -466,660), Xl= -1951,466
\+ 2350,909 J \+ 10565,409 у
В норме суммы модулей имеем К\ = 0,392, || Вг0||1 = 4973,652,
|| В'1 Hi = 196,606, || г0 IU = 32,380 и
согласно A3): || х — х4||, < 3209 («: 4107),
согласно A4): || х — х01|4 (< 8182) « 10473.
Эти оценки, будучи верны для суммы модулей, и подавно, конечно,
имеют силу для отдельных компонент вектора х — х4, соответст-
соответственно х — х0. В случае A3) значение В!-,, уже вычислено при оп-
определении X! и потому легко можно найти первую границу, так
что взятая в скобки оценка через | |В-11 [ 4- J |r0111 нецелесообразна.
Обратная ситуация имеет место при использовании формулы A4);
здесь если уж прилагать усилия для вычисления В^Гд, то тогда
легко определить и х4 и лучше будет обратиться к формуле A3).
В норме максимума модуля соответственно имеем
согласно A3): || х — х4 \\„ <. 2531 (< 4846),
согласно A4): || х —х0||со(< 5062) ^9692.
Задача 7. Продолжить решение предыдущей задачи, сделав
несколько итерационных шагов согласно A2), и затем, проследив
за поведением отношений одноименных компонент соседних векто-
векторов В!-;, провести экстраполяцию путем добавления соответст-
соответствующего кратного последнего вектора В!-;.

2.3. Метод исключения для линейных систем уравнений 83
Решение. Вычисляем на первом шаге «продолженных итераций»
/ 7,923 \ /—622,3314 /— 8870,8894
г = 0,083 ? в-if, = -146,9681 х2 = - 2098,434 (i 8)
\—1,768/ \+ 797,122/ \—11362,531/
и получаем вектор частных
/(—622,331)/(— 1976,083L /0,314932\
q = ( (—146,968)/( —466,660) )~( 0,314936 1
\(+ 797,122)/(+ 2530,909) / \0,314955/
со средним значением компонент1 0,314941 = qm. Если допустить,
что это значение лишь весьма мало меняется при дальнейших ите
рациях, что с точки зрения теории собственных значений является-
вполне оправданным предположением (ср. с методом итераций
по фон Мизесу из § 2.2), то можно ожидать, что формула
x2-x2-t- \qm-tqm-f- qm-t -)в П - x2 -f- x_q^ » ri U^
даст существенно уточненное приближение для решения. И в самом
деле, мы получаем
/—9156,9754 /+0,0114
х2 = х2 +0.4597-В-1г1 = I —2165,995], г2 = -0,002 , B0)
\+ 11728,968/ \+0,008/
так что, согласно A4),
II х —~х2 || оо<: 4,326.
Точное решение: х = (—9157, —2166, +11729).
В электрической цепи без источников, состоящей из сопротив-
сопротивлений Rh (k = 1, 2, ... , п), токи Ik (k = 1, 2 и) в ее ветвях
вычисляются при помощи двух правил (законов) Кнрхгоффа:
1° «Правило узла». Для каждого узла цепи выполняется соот-
соотношение 2/fe = 0, где k пробегает множество индексов всех про-
протекающих через узел токов. Притекающие токи считаются положи-
положительными, утекающие — отрицательными.
2° «Правило петли». Для каждого замкнутого контура (петли)
выполняется соотношение 2i/fe = 2/fe^fe = 0, где k пробегает
множество индексов всех сопротивлений, из которых состоит кон-
контур. Если контур обходится в некотором фиксированном направ-
направлении, то токи того же направления считаются положительными,
а токи противоположного направления — отрицательными.
1 Ниже индекс m—от Mittelwert (среднее значение).— Прим. ред

84
2. Уравнения со многими неизвестными
Пример (см. рис. 2.3.1).
Узел I (или II):
Контур М:
/о —/i —/. = 0,
— liRi — '2^2 = О-
Если /0, Rit R2 заданы, то мы имеем два линейных уравнения от-
относительно неизвестных It и /2. Их решение:
i i °2 / ;
М — 'О "^—~^~ » У2 ~ 'О
°1 "Ь °2
Задача 8. Вычислить токи /ft для цепей, приведенных на
рис. 2.3.2.
Рис. 2.3.2.
Решение. Для цепи (а)
/± — /» = 0, I2 = I0-R3/S,
hRi + I2R2 - /3Я3 = 0, /3 = /о • («i +
где S =

2.4. Итерационные методы для линейных систем
85
Задача 9 (мостик Уитстона, см. рис. 2.3.3; имеется в виду,
что R3 — это измерительный прибор). Вычислить токи при /0 ==
= ЗА, Ri= 100 Ом, R2 = 20 Ом, R3 = 0,5 Ом, Я4 = 15 Ом/
R5 = 30 Ом. Когда в общем случае /3 = 0?
Решение. Имеем
h + h = 0,
/l+/8 —/4 = 0,
— I2R2 — hR3 = 0,
так что при заданных числах получаем следующие значения»
/i = 2A, /2=1A, /, = 0A, /t = 2A, /5=1А.
Что касается второго вопроса, то
/з=/о
А1А5
R2)
и, значит, I3 равно нулю при RtR5 = R2Rt.
X
Рис. 2.3.3.
Рис. 2.3.4.
.0 (не-
Задача 10 (мостик Томсона, см. рис. 2.3.4). Когда /
зависимо от того, каково значение /0)?
Ответ: Ток /8 обращается в нуль при выполнении условия
— R2R3 ~Ь
+ Re) -
+ /?7)) = 0.
2.4. Итерационные методы для линейных систем уравнений
В ряде практически важных задач встречаются системы ли-
линейных уравнений с матрицами, диагональные элементы которых
настолько преобладают над остальными, что можно применить
итерацию по формуле B.3.12) с В = I, если дополнительно путем
деления уравнений на диагональные элементы сделать последние
равными единице ^

86
2. Уравнения со многими неизвестными
Задача 1. Решить методом итераций систему уравнений
2—1 ON / 1/3N
1 2 -1 х= 1
0-1 2/ \—1/3 j
A)
и указать границы погрешности.
Решение. Легко приводим систему к виду
1
6
1
2
1
6
о
= - + — О
- — о
о
J_
2
о
х,
= 0,1,2,...), B)
удобному для итерации, и, отправляясь от нулевого начального
вектора, получаем такие числа:
0
0
0
0
0
0
-0
1
,1667
,5000
,1667
0
0
0
2
,4167
,5000
,0833
0
0
0
3
,4167
,7500
,0833
0
0
0
4
,5417
,7500
,2083
0
0
0
5
,5417
,8750
,2083
0
0
0
6
,6042
,8750
,2708
0,
0,
0,
7
6042
9375
2708
0
0
0
8
,6355
,9375
,3021
...
...
. ■ •
0
0
0
22
,6665
,9996
,3331
0
0
0
23
,6665
,9998
,3331
0
0
0
24
,6666
,9998
,3332
0
0
0
25
,6666
,9999
,3332
Из трех норм для матриц B.3.10) для оценки подходит только вто-
вторая (спектральная), так как для других норм получается/С=1. Для
спектральной нормы /(= ||/—Л||2 = 1^2/2, и с учетом округления
имеем
X —X
■25 112
< 2,415-
—х
24|
<3,2- IO-
IOЗадача 2. Видоизменить метод предыдущей задачи так, чтобы
последовательно использовать уже вычисленные компоненты но-
нового вектора вместо компонент старого.
Решение. Этот видоизмененный метод называется методом Га-
Гаусса — Зейделя или отдельношаговым1, в отличие от предыдущего
1 В оригинале Einzelschrittverfahren. — Прим. ред.

2.4. Итерационные методы для линейных систем
87
общешагового1 метода, или метода Якоби. В рассматриваемом слу-
случае метод Гаусса — Зейделя приводит к следующим значениям:
ч .
х; —
0
0
0
0
0
0
0
1
,1667
,5843
,1255
0,
0,
0,
2
4589
7922
2294
...
0,
0,
0,
И
6663
9996
3331
0,
0,
0,
12
6665
9998
3332
0
0
0
13
,6666
,9999
,3333
Вместо B) мы имеем теперь
1 О О'
— 1/2 10
О —1/2 1
>\ / l/6\ /I
iу v-i/6; v
0 1/2 0
0 0 1/2 |x (l- = O,l,2,...),
0 0
D)
или же, если умножить на матрицу, обратную к стоящей слева
матрице (это нужно не для итерации, а лишь для оценки),
/1/6 \ /0 1/2 0
хг+1= 7/12 + 0 1/4 1/2
\l/8 / \0 1/8 l/4/
Здесь применимы все 3 нормы из § 2.3, и мы получаем
х — х1з||, < 1,79- 10,
х —-Xia Ни, < 4,5 • 10.
E)
F)
Вторая оценка точнее, но зато труднее вычисляется.
Задача 3. Если на краях тонкой и всюду, кроме краев, теплоизо-
теплоизолированной пластины поддерживать постоянное во времени распре-
распределение температуры, то внутри нее в конечном счете также уста-
устанавливается не изменяющееся со временем распределение темпе-
температуры, удовлетворяющее некоторому дифференциальному урав-
уравнению в частных производных, а именно уравнению Лапласа.
Для прямоугольной пластины, изображенной на рис. 2.4.1, при
указанных там граничных условиях решением будет
Т =
y (l-i/)
COS X.
2
G)
Если на рассматриваемую область наложить какую-нибудь квад-
квадратную сетку, то уравнение Лапласа можно приближенно заме-
1 В оригинале Gesamtschrittverfahren. — Прим. ред.

2. Уравнения со многими неизвестными
нить требованием, чтобы значение температуры в каждом узле было
равно среднему арифметическому ее значений в четырех соседних
узлах. Решить при помощи итераций 6 уравнений, составленных
для показанной на рис. 2.4.1 сетки, и сравнить решение с точными
значениями.
(8)
Рис. 2.4.1.
Решение. В обозначениях рис. 2.4.1 имеем
а = 0,25 + 0,256 + 0,5с,
b = 0,25а + 0,5d,
с = 0,2165 + 0,25а + 0,25d + 0,25е,
d= 0,256 + 0,25c + 0,25/,
е = 0.125 + 0,25с + 0,25/,
/ = 0,25d + 0,25е.
Этот вид уравнений уже годится для итераций. Для нормы B.3.10с)
К= ||1 —А ||«, = 0,75, (9)
так что сходимость обеспечена. Вычисляя по методу Гаусса — Зей-
деля, получаем (исходные, значения взяты на основании грубой
оценки):
я =
ап=
Ьп=
Сп =
dn =
еп=
fn —
0
0,6
0,3
0,5
0,2
0,3
0,1
1
0,5750
0,2438
0,4853
0,2073
0,2713
0,1197
2
0,5536
0,2421
0,4746
0,2091
0,2736
0,1207
3
0,5478
0,2415
0,4741
0,2091
0,2737
0,1207
4
0,5474
0,2414
0,4741
0,2091
0,2737
0,1207
5*
0,547400
0,241400
0,474050
0,209050
0,273700
0,120700
Точные
значения
0,54290
0,23806
0,47016
0,20617
0,27145
0,11903
На помеченном звездочкой шаге 5 вычисления проведены по методу
Якоби, так что, согласно формуле B.3.13), справедлива оценка
(а, Ь, с, d,e,f) — (а5, Ь5, с5, d5, е5,
,5
A0)

2.4. Итерационные методы для линейных систем
89
В последнем столбце даны для сравнения точные значения реше-
решения первоначальной задачи, а не точные значения решения систе-
системы (8).
Задача 4. По аналогии с задачей 2.3.7 провести экстраполя-
экстраполяцию для задачи 1.
Решение. Ввиду своеобразия ситуации, заключающегося в том,
что на каждом шаге попеременно то средняя, то крайние компонен-
компоненты остаются постоянными, стоит использовать лишь каждый второй
шаг. Для векторов х4, хв, х8 имеем следующие значения частных
|хг = (х8 — х6)г/(х6 — х4); (i = 1, 2, 3):
14 = 0,5008, fi2 = 0,5000, fi3 = 0,5008.
Если взять просто jj, = 0,5, то
0,6668 \
-хв)= 1.0000
\ 0,3334/
(И)
A2)
будет существенно улучшенным приближением; после следующего
итерационного шага можно провести оценку погрешности.
Задача 5 (верхняя релаксация). Провести итерации для задачи
2 так, чтобы последовательные изменения отдельных компонент1
брались с множителем 1,2.
Решение. Здесь достигается еще большее ускорение сходимости:
.11
щ =
0
0
0
0
г
0,
0,
о,
1
2000
7200
2320
0
0
0
2
,5920
,9504
,3238
0
0
0
3
,6518
,9953
,3324
0
1
0
4
,6668
,0005
,3338
Оценку погрешности можно провести по аналогии с задачей 2.
Задача 6. После надлежащего преобразования решить при по-
помощи итераций систему уравнений
Xi + 3*2 + 9х3 + лг4 = 10,
#1 + Х2+ Х3 + 5*4 = 6,
2^ + 7*2 + 3*3 + 2*4= 15,
A3)
4*j + 2*2
*4 = 9,
По методу Гаусса — Зейделя. — Прим. ред.

90
2. Уравнения со многими неизвестными
отправляясь от начальных векторов
х° = I 0 I'll
,0 / \1
A4)
и применяя как метод Гаусса — Зейделя, так и метод Якоби.
Решение. Удобной для итераций является такая запись системы:
*1 = ( 9
x2 = (i5 —:
3 4/ '
A5)
— Хг—Хъ
Для всех трех начальных векторов метод Гаусса — Зейделя схо-
сходится очень быстро: после 6—8 шагов получаются 4 верных знака.
Метод Якоби сходится медленно: после примерно 25 шагов — лишь
2 верных знака. Для первого и третьего начальных векторов этот
последний метод приводит к осциллирующей сходимости для ком-
компонент итерируемых векторов, например для третьего начального
вектора имеем
1
1
0
0
1,7500
1,8571
0,6667
0,8000
х2
0,95476
1,12857
0,20873
0,34524
1,23538
1,38135
0,39692
0,53870
Хн
1,32542
1,46587
0,45354
0,59727
Х12
1,25436
1,39914
0,40885
0,55103
Ххз
1,31046
1,45181
0,44413
0,58752
Верные
знаки ре-
решения X
1,28571
1,42857
0,42857
0,57143
Причиной такого поведения является свойство монотонности ите-
итерационной матрицы Т, используемой в соотношении х = Тх + г:
так как все элементы Т отрицательны, то для х > у будет Тх <:
< Ту (неравенства здесь следует понимать покомпонентно). Отсю-
Отсюда следует, что если х0 < х2 < хь то
Вектор-решение х заключен между двумя подпоследовательностя-
подпоследовательностями итераций — с четными и нечетными индексами, вследствие чего
на каждом шаге итераций мы получаем двустороннюю оценку для
отдельных компонент, которая, однако, в вышеприведенном слу-
случае является еще очень грубой.
Метод Гаусса — Зейделя часто приводит к более быстрой схо-
сходимости, чем метод Якоби. Этот эффект проявляется тем слабее,

2.4. Итерационные методы для линейных систем
91
чем меньше по абсолютной величине «новые» компоненты по срав-
сравнению со «старыми». Это иллюстрирует
Задача 7. Отправляясь от нулевого вектора, решить методом
Гаусса — Зейделя систему уравнений
*i= 0,39 . + 0,24*2 — 0,48*з + 0,23*4,
*2 = 0.72 — 0,05*, + 0,44*3 + 0,31 *4,
*3 = 0,56 — 0,10*i + 0,03*2 — 0,55*4,
xk= 0,47 + 0,12*1—0,07*2 +
A7,
При этом сначала проводить отдельные шаги итерации «сверху
вниз», начиная с вычисления первой компоненты, а потом повто-
повторить процесс «снизу вверх», начиная с четвертой компоненты.
Решение. Если начинать с первой компоненты, то получим:
Хо
0
0
0
0
Xl
0,39000
0,70050
0,54202
0,52738
0,41925
1,10101
0,26104
0,47195
Ч
0,63749
0,94929
0,26515
0,50922
0,60767
0,96414
0,24809
0,50272
х5
0,61794
0,95411
0,25033
0,50490
При вычислениях в обратном порядке достигается существенное
ускорение сходимости:
«о
0
0
0
0
0,59299
0,99836
0,30150
0,47000
Xj
0,61443
0,95814
0,25321
0,50444
х3
0,61547
0,95560
0,24982
0,50452
х4
0,61549
0,95546
0,24968
0,50444
0,61549
0,95546
0,24967
0,50444
Задача 8. Пусть дан итерационный процесс
ХП+1 ■*•/!+ Уп>
Уп+i = xn — yn + 3,
л = 0. 1. 2
A8)
Как зависит сходимость от выбора начальной точки? Что будет,
например, при х0 = 0,9, у0 = 1,85?
Решение: Единственной неподвижной точкой является х — 1,
у = 2. Складывая уравнения A8), получаем xn+l + yn+i = 3; это
означает, что независимо от того, какова исходная точка, все ите-
итерации лежат на одной прямой. Если, скажем, *„ = 1 + е, уп =

92
2..У равнения со многими неизвестными
= 2 — е, то xn+i = 1—2е, yn+i = 2+2е, т. е. при е =£ 0 расстоя-
расстояние до точки A,2) на каждом шаге удваивается. Итерационный
процесс сходится (за один шаг!) для тех и только тех точек (х0,
г/0), для которых у0 = 1 + х0. В заданном числовом примере улуч-
улучшение на первом шаге никоим образом не указывает на сходимость:
п =
*п=
Уп=
0
1
0
,9
,85
0
2
1
,95
,05
2
1,1
1,9
3
0,8
2,2
1
1
4
,4
,6
5
0,2
2,8
6
2,6
0,4
7
—2
5
,2
,2
8
7
—4
,4
,4
Задача 9. Соответственно исследовать слегка видоизмененный
по сравнению с A8) итерационный процесс
Xn+i — Хп + Ую
п=0, 1,2 A9)
г/«+1 = *л — 2^„ + 3,
Решение. Неподвижной точкой здесь является точка х = 0,6
у ==1,2. Полагая хп = 0,6 + sn, уп = 1,2 + tn, имеем
л = 0, 1, 2,... . B0)
^л+1 = sn — 2^л,
Непосредственно проверяется, что квадратичная форма
Фп = — sl + sntn + tl (n = 0,1,2,...) B1)
сохраняет свое значение при итерациях, так что при Фо ф 0 все
у.
\
\
ф=ф0
t
\
\@,6;1,2) s
Рис. 2.4.2.

2.5. Нелинейные системы уравнений
93
итерации лежат на гиперболе
— s2 + st +1* = Фо B2)
и, следовательно, сходимости нет (см. рис. 2.4.2). На прямых
2 2
имеем Фо = 0, и легко показать, что на первой прямой имеет место
сходимость, а на второй, за исключением самой неподвижной точ-
точки, — расходимость.
2.5. Нелинейные системы уравнений
Как и при вычислении корней многочленов и решении линейных
систем уравнений, итерационные методы также играют здесь осо-
особую роль. При этом вопрос о существовании решения и проблема
нахождения подходящих начальных приближений имеют такое же
значение, как и для нелинейных уравнений с одним неизвестным.
Помимо использования общего описываемого ниже метода Нью-
Ньютона, можно приводить заданные уравнения к виду, удобному для
итераций, и различными другими способами.
Задача 1. Построить итерации для системы уравнений:
у(х-\) = \, х* = у* + 1. A)
Решение. Из рис. 2.5.1 видно, что существуют ровно два ве-
\ч
S/
Рис. 2.5.1.
щественных решения. Для определения решения, находящегося
в первой четверти, подходит итерационный процесс
, , 1
Уп
л=0, 1, 2,...
B)
Уя*1
= + Y дг„2+1 — 1 ,

94
2. Уравнения со многими неизвестными
который можно провести на манер метода Гаусс а — Зейделя. Име-
Имеем:
п=
хп=
Уп=
0
2,0000
1,7321
1
1
1
5773
2198
1
2
1,8198
!,5204
5
1,7164
1,3950
3
1,6577
1,3221
16
1,7168
1,3955
4
1,7564
1,4439
5
1
1
17
1,7166
1,3952
,6926
,3656
...
...
18
1,7167
1,3954
Поочередно применяя вытекающие из теоремы о среднем соот-
соотношения
— xn-- — (yn-yn.ih
C)
Уп+i — Уп =
{где
что
промежуточные точки), находим в предположении,
1
xn+i — xn | < 0,744 | хп — xn_i | ,
Уп*1 — Уп I < °'744 I Уп — Уп-l I •
D)
Отсюда при помощи теоремы о неподвижной точке из § 1.5 (после
проверки условия о принадлежности шару) получаем оценки
— xib
<8- Ю-4.
I у — г/18
Для другого решения итерационный процесс
E)
F)
Уп+i —

2.5. Нелинейные системы уравнений
95
дает значения
п=
хп=
Уп=
0
1
-0,5
— 1
—0
1
,1180
,4721
2
—1,1058
—0,4749
—1
—0
3
,1070
,4746
10-*.
G)
с оценками
I х — х3
I У —Уз
Задача 2. Решить при помощи итераций систему уравнений
Ъх — 6# + 201g*+16 = 0,
2х+ y — lO\gy— 4 = 0
и указать оценки для решения.
Решение. Для применения итераций преобразуем данные урав-
уравнения к виду
13
х = ц>(х, у) = 10
, Т 1
у = ijj (х, у) = 10
Итерации будем проводить по формулам
%и == Ф (xh, У к) =
Уи+i
h, yh) =
= - J- ■ xh + — yk,
Отправляясь от х0 = y0 — 1 и используя четырехзначные таблицы
логарифмов, получим (по методу Якоби) следующие значения:
k
0
1
2
3
4
5
6
0
0,1585
0,1905
0,1964
0,1978
0,1980
0,19805<
<*е<
<0,19810
У»
0
0,3981
0,4693
0,4842
0,4872
0,4879
0,48795<
<Уе<
<0,48800
uk
0,2000
0,2798
0,2932
0,2962
0,2967
0,29687
0,6000
0,6715
0,6850
0,6877
0,6883
0,68839

96 2. Уравнения со многими неизвестными
Для оценки погрешности по теореме о неподвижной точке вы-
выбираем область 0,19<#<0,20, 0,48<г/<0,49. В этой области
<: @,25 + 0,3) • 1п 10 .10*W^SW<0.2533.
дх ду
< @,2 + 0,1) -In 10- 10°-6+«-2-«-2-H>--.*>-' < 0,3376.
дх
ду
В качестве постоянной Липшица получаем К = 0,3376. При ис-
использовании нормы |] (х, у) у = max { | х | , | у | } имеем
К II (х« — хь, у6 — уь) ||< 0,51 • 10"*.
Учитывая указанные в таблице интервалы для хв, у6, получаем
0,19805 — 0,000051 < д;<: 0,19810 + 0,000051,
0,48795 — 0,000051 < у < 0,48800 + 0,000051,
т. е.
0,197999<*< 0,198151,
0,487896 < у < 0,488051.
Удостоверяемся, что эта область, в которой должно находиться
решение, лежит внутри выбранной нами области. Точное решение
после округления до десятого десятичного знака имеет вид
х= 0,1980960243,
у = 0,4879992188.
Задача 3. Решить по методу задачи 2 системы уравнений:
a) 2х— у — 6 lg х — 3 = 0,
15*— Юу — 60\gy— 6 = 0,
b) х — у — 6\gx— I =0,
х—Зу — 61gj/— 2=0,
c) 6х — Ьу — 301gA: —12 = 0,
Зх — Зу + 30 lg у + 10 = 0,
d) 15*— 20у — 601gx— 6 = 0,
Ах— by — 2Q\gy— 5 = 0,
используя каждый раз в качестве начальных значений х0 = у0 —0.
Ответ. Решения, округленные до десяти десятичных знаков:
а; х = 0,3029129998, у = 0,7179185283.
Ь) х = 0,7927457928, у = 0,3979421176,

2.5. Нелинейные системы уравнений
97
c) х = 0,3991790830, у = 0,4720082425,
d) х = 0,8085489367, у = 0,5832927715.
Задача 4. Исследовать сходимость последовательности комп-
комплексных чисел ап, задаваемой соотношением_а2п+1 = ап (п = 0,
1, 2, ...); пусть при этом ао=^=Ои для ап+1 = Уап рассматриваются
различные возможные случаи однозначного определения корня:
случай (а):- 1. < arg an+i < -у ,
i> ,i ч 1С ^ 3jT
случаи (b): — <argan+1 < — ,
случай (с): -j <argan+1< -j ,
случай (d): -^ <argan+1< — n.
Ответ. Во всех случаях | а„ | сходится к 1.
Случай (а). Здесь всегда даже lim с„= 1.
Случай (Ь). Последовательность ап сама по себе расходится
для всех а0 Ф 0, но подпоследовательности, получающиеся из нее
взятием членов через один, сходятся к (— 1 ± ]/3 )/2.
Случай (с). Последовательность ап снова расходится для
а0 Ф 0, но каждая из последовательностей а3п, a3n+i и a3n+2 (" =
= 0,1, 2,...), взятая сама по себе, сходится; их пределами слу-
служат точки единичной окружности еа, е", е", где a = 2tW7 (см.
рис. 2.5.2).
Iman
Полуплоскость
для
1та„
Rean
Рис. 2.5.2.
Рис. 2.5.3.
Случай (d). Здесь для £ = 0,1,2,3,4 сходятся последова-
последовательности a5n+h(n = 0, I, 2,...), пределами которых являются
числа еф с |3 = 2та/31 и q = 5,9, 10, 18, 20 (см. рис. 2.5.3).
Во многих случаях, особенно для больших систем, построение
подходящих итерационных процессов представляет значительные
4—206

2. Уравнения со многими неизвестными
трудности, которые часто можно преодолеть при помощи метода
Ньютона; этот метод мы теперь и рассмотрим.
Пусть вектор х = (хи ... , хп) есть решение системы уравнений
с п неизвестными
/,(х) = 0 (»= 1 п), (8)
где функции ft дважды непрерывно дифференцируемы, и пусть из-
известно некоторое достаточно хорошее приближение х„ для х. Тогда
по формуле Тэйлора
@=) U (х)=/г(х0) + J /,, к(*о) (хк -\ k) + rt{l=l,..., п) (9)
(х0 k — компоненты вектора х0, Д. k = df/дхЛ. Обозначим еще
через f0 вектор, составленный из компонент /; (х0), через Fo —
матрицу, составленную из Д. k(x0), и т. д. Тогда, опуская члены
высшего порядка малости г, и предполагая, что матрица Fo
имеет обратную, приходим к формуле
Fo (xj — х0) = — f0, или х4 = х0 — FT%. A0)
Здесь уже вместо х мы пишем х1; так как, ввиду отбрасывания ос-
остаточных членов, при вычислении по этой формуле можно надеять-
надеяться лишь на некоторое лучшее приближение. Продолжая этот про-
процесс далее, получаем метод Ньютона
xft+1 = xfc-F*-1fb (ft =0,1,2,...), (П)
а также упрощенный метод Ньютона
хш = хк — ^\ (£=0,1,2,...), A2)
в котором матрица обращается только один раз. Для оценки по-
погрешности, если ее нельзя провести непосредственно, можно при-
привлечь теорему о неподвижной точке из § 1.5, причем в обоих слу-
случаях последний шаг считается начальным шагом упрощенного ме-
метода Ньютона.
Задача 5. Решить задачу 1 при помощи а) упрощенного и
Ь) обычного методов Ньютона и оценить погрешность. Пусть в обо-
обоих случаях х0 = B, 1), соответственно (—1, —0,5).
Решение. Если записать систему A) в виде (Xj = х, х2 = у)
A3)
то имеем
F 1
Л
У
2х
= у{х —
х—\\
-2у)'
1)
—1
г1
= 0,
/
=
X
— X
2—1
2(л:2
= 0,
Л--1
+ У2 - х)
— у
— х 2 (х2 + у2 — х)

2.5. Нелинейные системы уравнений
99
'1/3 l/6\
■о V2/3 —1/6/'
соответственно
1/2 — 2 \ _4 /—2/9 —4/9
,— 2 1 )■ Fo = 1 — 4/9 1/9 У
Поэтому итерационное предписание выглядит так1:
а)
j
i h h 6
соответственно
— xft
b)
— xh
A4)
A5)
Мы получим
а)
ы
xk=
*k=
*к=
у =
Хк =
Ук=
0
2
1
-1
-0,5
2
1
—1
-0,5
следующие числа:
1
1,6667
1,3333
-1,1111
—0,4722
1,6667
1,3333
-1,1111
—0,4722
2
1,7037
1,4074
— 1,1067
—0,4749
1,7197
1,3974
—1,1069
—0,4746
3
1,7199
1,4008
-1,1069
—0,4746
1,7167
1,3953
4
1,7178
1,3945
5
1,7164
1,3949
6
1,7166
1,3954
Ниже
— это компоненты вектора

100 2. Уравнения со многими неизвестными
Обозначим правую часть в A5) через Txfe. Для получения оценки
погрешности по теореме о неподвижной точке нужно прежде всего
определить постоянную Липшица. В случае положительного реше-
решения имеем для любых векторов u, = (ut, vt) (i = 1, 2)
ij — Tu2 =
— J_щ — -j u2 — -у v^iui — и2)
«о V< («i — U,)
6 2 з /v 2!
1 1 ,1 .1
т__и2 + _,1+_,2)(О1_
A6)
В предположении, что 1,70 <: ut < 1,72, 1,39 < vt <: 1,41, для
нормы максимума модуля (по строкам, см. § 2.3) будет
|| Тщ -- Ти21| < 0,444 • II  — и2 II . A7)
В соответствии с этим для верхней двухстрочной графы таблицы
получаем
|| u —u61| <0,8 • || и5—щ || <5 • Ю-4. A8)
Аналогично можно провести оценки и в других случаях.
Задача 6. Применить метод Ньютона к решению системы урав-
уравнений из задачи 2.
Решение. Пусть функции ф (х, у) и ар (х, у) те же, что в задаче 2,
и пусть, далее,
/ (х, у) = х — <р (х, у), g(x,y) = y — ty (х, у).
Отправляясь от х0, у0, проводим итерации по формулам (ср. с (9))
/ (xk, yk) = fx (**. У к) (xk+i — xk) + fy (xk, yk) (уы — yk) = 0,
8 (**- У к) = 8х (**• У к) (xk+i — xk) + gy (xh, yk) (yk+i — yk) = 0,
Л= 0,1,2,....
При этом частные производные используются в виде
fx(x,y) = i +Yxinl0> fy(x>y) = —^-xiuio,
gx(x,y) = -у In 10, gy(x,y)= 1 — — г/In 10.
Если начинать с x0 = y0 = 0, то точность в четыре знака достига-
достигается уже за четыре шага.

2.5. Нелинейные системы уравнений
101
Задача 7. Решить методом Ньютона системы уравнений из за-
задачи 3.
Задача 8 (релаксация). Найти решение нелинейной системы
уравнений
I {yCt y) = ZX —\- у — 1 = u,
g (x, y) = xs + 6x2y — 1=0.
Решение. Если x0, y0 — некоторое приближение к решению, то,
пренебрегая нелинейными поправочными членами, находим:
/ (х0 + s, уо + &) = f (х0, г/0) + 4х0г + 2г/08,
1х*+12хоУо)е-
8 (х0 + е, у0 + 8) = g (х0, у0)
Теперь попытаемся улучшить приближение, выбрав е и б так, что-
чтобы обе правые части обратились в нуль, и взяв затем xi = х0 +е,
У \ = Уо + б- Таким же образом поступаем с приближением хь у^
и т. д., до тех пор пока не будет достигнута желаемая точность.
Следовательно, на каждом шаге требуется решать систему из двух
линейных уравнений с двумя неизвестными. Начальное приближе-
приближение можно получить графически. При х0 = 2/3 и у0 = 1/3 имеем
(промежуточные результаты даны округленно):
k
0
1
2
3
0
0
0
2/3
,694
,6868
,6866
0
0
0
Ун
1/3
,222
,2385
,2391
f
0
0
8
(*ft. Ук)
0
,0126
,0003
.Oie-5
g(*h> Vh)
bill
— 0,0242
— 0,0010
-2,5!0-5
e
1/36
— 0,0072
— 0,0002
— 5,610—5
0
0
1
5
-1/9
,0165
,0006
,510—5
Точное решение (округленное до 10 знаков):
х = 0,6865944219, у = 0,2391154525.
Ход вычислений соответствует здесь методу Ньютона. Другой
способ действий иллюстрирует
Задача 9. Найти решение нелинейной системы уравнений
f(x, у, г) = З*2 + -^-у2 + 22-5 = 0,
g (х, у, г) = 6xyz — x + 5y + 3z =0,
h (х, у, z) = bxz — yz — 1 = 0.
Существование решения предполагается.
Решение. В качестве пригодного для начала вычислений приб-
приближения можно взять х0 = 5/4, у0 = 0, г0 = 1/4. Отправляясь от

102
2. Уравнения со многими неизвестными.
этих начальных значений, будем поочередно придавать каждой из
трех переменных малое изменение, которое по возможности умень-
уменьшает абсолютные величины наших «невязок» / (xh, ук, zh), g (xh,
У hi zk)> h (Xk> Uh> 2fe). На последнем шаге все три поправки опреде-
определяются одновременно так, чтобы линейные части вызванных ими
изменений наших трех функций привели бы значения этих функ-
функций к нулю (ср. с предыдущей задачей 8).
В приведенной ниже таблице использованы обозначения fh =
= / (Xh, Уh, Zfe) И Т. Д.
к
0
1
2
3
4
5
Xh
1,25
1,25
1,25
(+ 0,03)
1,28
1,28
(+0,00447)
1,28447
Vh
0
(+0,1)
0,1
0,1
0,1
(+ 0,03)
0,13
(—0,00026)
0,12974
0,25
0,25
(-0,1)
0,15
0,15
0,15
(+ 0,00895)
0,15895
-0,25
—0,2350
—0,2750
—0,0473
—0,03695
0,00009
gk
-0,5
0,1875
—0,1875
—0,2148
-0,03024
0,00001
hh
—0,5625
0,5375
—0,0775
—0,0550
-0,05950
0,00021
Точное решение (округленное до 10 знаков после запятой):
х= 1,2844570503,
у = 0,1297565120,
2 = 0,1589186226.
2.6. Номограммы и счетные линейки
Зависимость между несколькими, скажем п, переменными в оп-
определенных случаях допускает такое графическое представление,
что по значениям п — k переменных значения остальных k пере-
переменных можно определить путем простой процедуры считывания;
обычно k = 1. Такие графические счетные устройства называют
номограммами. Методами их составления занимается номография.
Наиболее распространенными являются номограммы из вырав-
выравненных точек, сетчатые и транспарантные.

2.6. Номограммы и счетные линейки
103
Подробное изложение этого круга вопросов можно найти в кни-
книгах П. Лакки [1954], В. Майер цур Капеллена [1953], Р. Шредера
[1965] и Ф. А. Виллерса [1957]1.
Функциональную зависимость между тремя переменными мож-
можно представить на плоскости при помощи трех (функциональны»)
шкал. Номограмма из выравненных точек строится так, чтобы любые
три связанные друг с другом рассматриваемой зависимостью
Рис. 2.6.1.
точки получались как точки пересечения этих трех шкал с некото-
некоторой прямой.
Пусть zt (i = 1, 2, 3) —три переменные. Тогда уравнениями
x=fi(zt), y^
(/ = 1,2,3)
задаются три кривые. Для того чтобы три точки, принадлежащие
этим кривым, лежали на одной прямой, площадь треугольника с
вершинами в этих точках должна равняться нулю, т. е. должно
выполнятьс я условие
М2з) £зB3) 1
= 0.
Это уравнение и описывает функциональную зависимость, пред-
представляемую тремя нашими кривыми. Оно называется основным
уравнением номограммы. Во многих случаях его можно получить
из простых геометрических соображений.
Задача 1. На рис. 2.6.1 приведена номограмма из выравненных
точек с тремя параллельными шкалами. Пусть на шкалах отложены
отрезки аь = /;/; B;) (где U — масштабные множители), причем
выполнены два условия
k h 1з ' d2 k
! А на русском языке — в книгах Н. А. Глаголева [1961], М. В. Пент-
ковского [1959] и Г. С. Хованского [1976]. — Прим. перев.

304 2. Уравнения со многими неизвестными
Доказать, что на номограмме представлена зависимость
h (Zi) + /2 fe) = /з (zs).
Доказательство. По известной теореме элементарной геомет-
геометрии имеем
т. е.
^3 /3 — ^1 ^1 ^2 /2 'Я ' 3
d, ~ d2
Использование второго из предположенных условий дает
h h /з — 'i k fi = U h /2 — h '3 /з I
следовательно,
Но в силу первого условия ltl2 = laih + ^2). откуда и следует на-
наше утверждение.
Задача 2. На рис. 2.6.2 мы видим эскиз N-образной номограммы.
Доказать, что если на шкалах отложены отрезки at = lift(Zi), при-
причем выполнены условия
h — а>
/з (з; f , .
'2 + i\ Гз (гз)
то тем самым представлена зависимость
Mzi) = Mzg)/з (Za).
Указание. Использовать тот факт, что
а2 а — а,,
Задача 3. На рис. 2.6.3 изображена звездчатая номограмма.
Доказать, что если на шкалах отложены отрезки аг = /г/
причем выполнены соотношения
/ _ / sing , / sin (а +
'2 — '1—Т~Г > 3 = М Т~1
n^ р
3 Т
sin
то номограммой представлена зависимость
h() ЫЫ f(j

2.6. Номограммы и счетные линейки
105
Указание. В силу известной формулы для площади треуголь-
треугольника,
Oia2sin (а + Р) = aiазsin o. + a2a3sin p.
Рис. 2.6.2.
Задача 4. На рис. 2.6.4 приведен эскиз треугольной номограм-
номограммы. Показать, что если на шкалах отложены отрезки а-г =
= Si/(fi(Zi) + 1), то тем самым представлена зависимость
/lBl)/2B2)/,B.) = 1.
Рис. 2.6.4.
Рис. 2.6.5.
Задача 5. Построить номограмму для теоремы синусов плоской
тригонометрии. Эта теорема утверждает, что для всякого треуголь-
треугольника (см. рис. 2.6.5) справедливо соотношение
а = b = с = 2л 1.
sin о
sin
sin
Следовательно, следует представить зависимость
sin a
Выбрать такое представление, чтобы интервалы
1см<а<10см и 20°<а<90°
1 Где т — радиус описанной окружности. — Прим ред.

106 2. Уравнения со многими неизвестными
составляли существенную часть шкал для а и а соответственно.
a) Вычертить номограмму с тремя параллельными шкалами.
b) Вычертить N-образную номограмму.
Указание, а) Нашу функциональную зависимость можно выра-
выразить в виде
log Bл) = — log sin a + log a.
Взять /i == 20 см, /2 = 10 см, dj = 8 см, /3 Bз) = log Bz3), /ifo) =
= —log sin 2Ь /2B2) = log z2. Остальные нужные для построения
номограммы величины вычисляются согласно задаче 1.
Ь) Зависимость, которую нам нужно представить, можно за-
записать так:
а = sin a • 2г.
Взять lt = 1 см, /2 = 10 см, а = 13 = 13 см, ft (z4) = zit f2 (z2) =
= sinz2, /3B3) = 2z3.
Задача 6. Построить номограмму с тремя параллельными шка-
шкалами или N-образную номограмму для закона Ома
Обратить внимание на то, чтобы были хорошо представлены интер-
интервалы 50 В <: U <: 250 В, 20 Ом <s Я «: 200 Ом. Шкалы градуиро-
градуировать в вольтах (В), амперах (А) и омах (Ом).
Задача 7. Начертить номограмму с тремя параллельными шка-
шкалами или N-образную номограмму для вычисления силы, действую-
действующей на тело массы m A0 кг <: m <: 1000 кг) на высоте h E0 км <:
<g h <g 250 км) над поверхностью Земли.
Указание. Согласно закону всемирного тяготения, эта сила К.
выражается формулой
К у тМ
Л2
Ради простоты принять, что Земля имеет форму шара. Масса Земли
М = 5,95-1024 кг. Радиус Земли г0 — 6,36-103 км. Постоянная
всемирного тяготения у = 6,66-10~8 Н-м2/кг2.
Задача 8. Начертить звездчатую номограмму для фокусного
расстояния g составной тонкой линзы. Пусть линза составлена из
двух линз с фокусными расстояниями gly g2, которые изменяются
в интервале 100 см <: g'v g2 < 400 см.
Указание. Для фокусного расстояния составной линзы справед-
справедливо соотношение

2.6. Номограммы и счетные линейки 107
Задача 9. Начертить треугольную номограмму для полного
увеличения v микроскопа, построенного из двух линз с фокусными
расстояниями gt, g2, находящихся друг от друга на расстоянии
t = 16 см. Пусть представляет интерес область 2 ем «S git g2 <
<: 10 см. Величина «четкого» поля зрения s0 = 25 см.
Указание. Выполняется соотношение v-g1-g2 = t-s0.
Задача 10. Построить номограмму с тремя параллельными
шкалами для атмосферного давления р на высоте h @ км <: h <
< 10 км) в зависимости от давления р0 на уровне моря
G40 мм рт. ст. <: р0 <: 780 мм рт. ст.).
Указание. Давление меняется с высотой по формуле
которую в данном случае удобно использовать в виде
7,99 км
Наряду с номограммами для вычислений с небольшими требо-
требованиями к точности во многих случаях используются специаль-
специальные счетные линейки. Если исходить из трех шкал, а именно двух
шкал X = fi(x), Y = f2(y) для исходных величин и одной шка-
Рис. 2.6.6.
лы Z = /3(z) для результата (см. рис. 2.6.6, на котором представлен
принцип действия счетной линейки), то имеем основное уравне-
уравнение вида
в частности, при /х(/) = /3(/) можно обойтись двумя шкалами.
В случае более сложных функциональных зависимостей обычно
можно выйти из положения, применяя подходящее «расщепление»
зависимости и соответственно большее число считываний.
Задача 11. Изготовить специальную счетную линейку для вы-
вычислений по формуле
_L + —- —

108
2. Уравнения со многими неизвестными
определяющей фокусное расстояние составной линзы (а также ре-
результирующее сопротивление при параллельном соединении).
Решение. Здесь fr(t) = fz(t) = Ш) = 1/£ Для t >■ \ получаем
линейку, изображенную на рис. 2.6.7.
a. 20 10 7 б 5 к 3
15
от 2010 76 5
1.5
Рис. 2.6.7.
Задача 12. Изготовить специальную счетную линейку для вы-
вычисления коэффициента роста капитала при сложных процентах.
Решение. В силу соотношения К = Ко-хп (х = 1 +щ) имеем
If
lglg—= lglg* + Ign;
поэтому в соответствии с A) полагаем fi(t) = /3(/) = lg lg /, fz(t) =
= lg /. Если желательно охватить большую область значений вре-
времени1, то область значений на шкале для Д и /3 можно поделить
(!„„ ,,„
2
ibfilihlili!
МЧИ1
1.01
1.1
1 П fTTirf
I'l'i'i'i'i'iiiiiiimi
3 4
|||||||||
I'l'l
1 Ч И
ll!|ll
Ь
3 4
III lllllll
I'l Hill
«2
'[ 1 i i 1 i i I
1.2
5
llll|ll|llll
J11J If I
1.03
6 7
illllll'ii'll
il||lll|li"li
tOA
IIJIJ IJIIltJfJI LJJi'iiJ I ii
1.3
| !II|MI|! III|IHI|I
6 8 10
20
W 1.5
8 9
flllf
1.05
Illlj
L6
ipii'iiiBiii'f«"|i|iir
50 100
III j
lllllll
1.06
lllllllfllll
1.8 2
'ITiHIill
Illllllllllll'
1.08 1.1
I'l'l'l'l"
|ф|™и|
1000 10000 .
Рис. 2.6.8.
на несколько частей. На рис. 2.6.8 показан случай деления на три
части.
Задача 13. Пусть канат длины 1L подвешен в точках (—а, 0) и
(а, 0) горизонтальной оси. Изготовить специальную счетную ли-
линейку для определения наибольшего провисания каната г.
Решение. Справедливы соотношения
так что с помощью таблицы гиперболических функций можно лег-
легко изготовить счетную линейку со вспомогательной шкалой для |.
1 Без увеличения длины линейки. — Прим. ред.

2.6. Номограммы и счетные линейки 109
Ценою значительной предварительной работы можно исключить g
и таким образом сократить число считываний с двух до одного
(рис. 2.6.9). Для этого при различных значениях z решается урав-
уравнение
ch \ — г\ — 1 = 0
и по полученным значениям \ строится шкала Z = log (A/|) sh |).
Далее берутся две обычные шкалы для log t, что позволяет при по-
помощи одного считывания найти zla и произвести последующее ум-
умножение на а.
Г1
1 I r 1,1,1,1,1,1,1
: r i1
\1
[ ll'l'l'l'l'l'l'l'l'l'l'
10 ' 1
z
Illllllll
'I'll
3 A
ilil|liMibllll|1l||l]l|l|!lll
I'l'l'l'l'l'lwlpllf
2 3
|1111|1111|11к|1111|11Ц|
2 3 4'
5 6 7 8 9 10 "I
|||||У|1п|||||||1ш1||||| t
lliP[llll|llipi]l|iliijiiii|iiiiiii|]| i
4 5 6 7 8 9 10 J
lll|llll|llll|llll|llll|lll| 1
5 6 7 8 9 10 J
Рис. 2.6.9.
Задача 14. Изготовить специальную счетную линейку для оп-
определения дальности бросания w для случая свободного бросания
над плоскостью в зависимости от начальной скорости v и угла бро-'
сания ф, отсчитываемого от горизонтали.
Указание. Имеет место соотношение
logw =2 log v — log g + log sin 2<p.
Задача 15. Изготовить счетную линейку для решения квадрат-
квадратного уравнения х2 + ах + b = 0.
Указание. Если ввести в качестве параметра величину q = b/a2,
то имеем
.2 = а( Г* V4"
Шкалы строятся независимо для случаев вещественных и комплекс-
комплексных корней.
Задача 16. Изготовить специальные счетные линейки для опре-
определения объема консервной банки, конуса, шарового сегмента.
СПИСОК ЛИТЕРАТУРЫ
К о л л а т ц Л. (L. Kollatz), Задачи на собственные значения, «Наука»,
М., 1968.
— , Функциональный анализ и вычислительная математика, «Мир», М.,
1969.
*Ортега Дж. и В. Ре и н 6о лд т (J. M. Ortega, W. С. Rheinboldt),
Итерационные методы решения нелинейных систем уравнений со многими
неизвестными, «Мир», М., 1975.

ПО 2. Уравнения со многими неизвестными
•Фаддеев Д. К. и В. Н. Ф а д д е е в а, Вычислительные методы ли-
линейной алгебры, 2-е изд., М.—Л., 1963.
Цурмюль P. (R. Zurmuhl), Matrizen und ihre technischen Anwendungen,
4-е изд., Berlin, Gottingen, Heidelberg, 1964.
— , Praktische Mathematik fur Ingenieure und Physiker, 5-е изд., Berlin,
Heidelberg, New York, 1965.
Шварц X.-P., X. Рутисхаузер, Э. Штифель (H. R. Schwarz,
H. Rutishauser, E. Stiefel), Numerik symmetrischer Matrizen, Stuttgart,
1968.
По номографии
В и л л е р с Ф. (F. A. Willers), Methoden der praktischen Analysis, Berlin,
1957.
•Глаголев Н. А., Курс номографии, 2-е изд., «Высшая школа», М.,
1961.
Л а к к и; П. (P. Luckey), Praktische Anleitung zum Entwerfen von graphi-
schen Rechentafeln, 1954.
Майер цур Капеллеи В. (W. Meyer zur Capellen), Leitfaden der
Nomographie, Berlin, Qottingen, Heidelberg, 1953.
*П е н т к о в с к и й М. В., Считающие чертежи. Номограммы, 2-е изд.,
Физматгиз, 1959.
*Х ованский Г. С, Основы номографии, «Наука», М., 1976.
Шредер P. (R. Schroeder), Praktische Einfuhrung in die Nomographie,
Munchen, 1965.

3. АППРОКСИМАЦИИ
Э. Бредендик при участии Л. Коллатца, Г. Опфера,
Й. Шписса и Й. Вернера
3.1. Интерполяция
Постановка задачи. Среди вещественных функций одной пере-
переменной легче всего проводить вычисления с многочленами. Поэто-
Поэтому часто пытаются представить данную функцию f (x) многочленом
/п-й степени Рт(х), т. е. принимают Рт(х) в качестве приближения
для / (х).
Для того чтобы получить такой аппроксимирующий многочлен,
можно, например, задать п + 1 значений xt(i = О, 1, ... , п):
хо<х,<...<хп, A)
при которых многочлен Рт(х) совпадает с f (x). Таким образом,
если положить yt = f(xt) (i = О, 1, ... , п), то это правило интер-
интерполяции запишется так:
у% = Рт (xi) (i = 0, 1, 2, ..., п). B)
При этом ищется многочлен наименьшей степени, для которого
выполняются соотношения B).
В случае п — 1 получаем хорошо известную линейную интер-
интерполяцию.
Задача 1. Показать, что имеется не более одного многочлена
п-й степени, для которого выполняется B).
Решение. Пусть Рп{х) и Qn(x) удовлетворяют соотноше-
соотношениям B). Тогда многочлен п-й степени Rn(x) = Рп(х)—Qn(x) имеет
п + 1 корней A); поэтому по основной теореме алгебры Rn(x) = 0,
Задача 2. Коэффициенты ak интерполяционного многочлена
п
Рп(х) — 2 а*х* можно определить из системы линейных уравне-
уравнений
Показать, что если выполнено условие A), то эта система разре-
разрешима.
Указание. Применить соответствующие теоремы о системах ли-
линейных уравнений, убедившись в том, что однородная система

112 3. Аппроксимации
уравнений
PjxJ = а0 + at Xi + а2х* + ... + а„х? = О (I = О, 1 л)
имеет только тривиальное решение а0 = а( = ... = ап = 0.
Определитель нашей системы, будучи определителем Вандермон-
да, отличен от нуля, поскольку xt Ф х} при i Ф \.
Задача 3. Построить п + 1 многочленов я-й степени (pt(x),
таких, что
0 при 1ф]
Тогда многочлен
будет решением нашей задачи интерполяции (интерполяционная
формула Лагранжа).
Ответ.
,х\ _ (X — Xj) ... (X — Х,_\) (X — Хих) ...(Х — Хп)
(Xi— *l) ... (Xl — XU1) (Xt — Xi+i) ... (X{ — Xn)
Задача 4. Получить формулу, аналогичную формуле Лагран-
Лагранжа, для решения следующей задачи. Заданы п + 1 троек чисел
(*;> Уь У/) (i = 0, 1 п), причем
Найти многочлен наименьшей степени Qm(x), такой, что
У1 = Qm (Xi),
(t = 0, 1 л), B)
Указание. Положить
п
Qm (х) = V [yt -f (x — xt) (at yt + Р( y't] <f2. (x)
i=Q
(<Pi(x) те же, что и в задаче 3).
Ответ: fS,- = 1, at = — 2<р/(х,).
Задача 5. При помощи кубической интерполяции (многочлена-
(многочленами третьей степени) определить приближенное значение дляе0-15:

3.1. Интерполяция 113
Г по методу задачи 3, отправляясь от четырех значений
*о — и, у о — е — i,
х, = 0,1, г/, = е0'1 =» 1,10517,
*2 = 0,2, г/2 = е0>2 = 1,22140,
х3 = 0,3, у3 = е0'3 = 1,34986;
2° по методу задачи 4, отправляясь от четырех значений
х, = 0,2, yt = у\ = е0-2.
(Сравнить с верными знаками: 1,16183.)
Определение 1. Пусть дана функция г/ (х), и пусть Рп(х) — ин-
интерполяционный многочлен n-й степени, для которого справедли-
справедливы соотношения
У(хд = yi = Pn(xt), i = 0, 1, ...,«; хгфхк при i=£k.
Тогда
Rn+t(x) = y(x)-Pn(x)
называется остаточным членом.
Задача 6. Превести оценку остаточного члена для функции
у (х), п + 1 раз непрерывно дифференцируемой в интервале 1.
Решение. Пусть х Ф xt (i = 0, 1, ... , п) — какая-нибудь фик-
фиксированная точка из /. Рассмотрим функцию f (t), определенную
равенством
f{t) = y(t)-Pn(t)-c(t-x0)(t-Xl)...(t-xn)
с
с _ у(х)-Рп(х)
(х — хо)(х — х1)...(х — хп)
Ясно, что/ (хг) = 0 для i = 0, 1, ... , п и/ (х) = 0. Таким образом,
функция / (t) имеет по крайней мере п + 2 различных нулей в /.
После повторного применения теоремы Ролля получаем тогда,
что ее (п + 1)-я производная имеет по крайней мере один корень |,
причем Ъ, лежит в наименьшем интервале, содержащем все точки
х, х0, х„ ... , хп. Следовательно, Цп+Ч1) = У{п+1)A) — с (п+ 1)! =
= 0, так что, согласно определению с,
У (х) — Рп (х) = гу("+1) © (х — х0) (х — х^ ... (х — х„).
(«+ 1)!
Задача 7. ЕслиУИ — верхняя граница для \y(n+i)(x)\ в интерва-
интервале /, то для остаточного члена справедлива оценка

114 3. Аппроксимации
М
|(х—хо)(х—х,)... (х-хп) 1 при всеххб/.
(п+ 1)!
a) Как велика наибольшая возможная погрешность при линей-
линейной интерполяции?
b) Имеются ли функции у (х) и точки х, х0, ... , хп, для кото-
которых в оценке достигается знак равенства?
Решение, а) |/ (х) — /\(х)| < (х, — хо)г М/8.
Ъ) Из общей оценки остаточного члена следует, что такой функ-
функцией является",' например, у (х) — х"+1 + апхп4- ... + а0, посколь-
поскольку г/<л+1>(х) = (и +1)!.
Задача 8. Пусть нам даны пятизначные таблицы десятичных
логарифмов у (х) = lg х для х € [1, 10] с расстоянием между опор-
опорными точками h = 10~3. Будет ли погрешность интерполирования
при линейной интерполяции меньше чем 5-Ю?
Решение. В силу того что у"{х) = —lg е\хг, lg е = 0,4343 ... ,
имеем
|Яя(х)|<-~- lge<6- Ю-8 для всех х6[1, 10].
8
Значит, погрешность интерполирования в интервале [1,10] всюду
меньше чем 5-10~5.
Задача 9. Интерполяционный многочлен легко определяется,
если искать его в виде
Р„(х) = сй + ск(х — х0) -\-Съ(х — хо){х — хд-\-... Н-
Ч- сп(х — хо)...(х — хп_х).
Составить соответствующую возможно более простую вычислитель-
вычислительную схему.
Решение. Для коэффициентов сг получается следующая система
уравнений треугольного вида:
Уа = со>
г/i = с0 + с, (Xi — х0),
у2 = с0 + Ci (х2 ~ х0) + с2 (хг — х0) (х2 — Xi),
уп = с0 + с, (хп ~ х0) -Ь ■• • + си (хп — х0)... (хп — хп^).
Отсюда находим
Уг — У» _ t/i — Уо
„ „ r Vt —Уо „ *г — Ч Xi — х0
со — Уо< ci — ■ > сг = ; И т- Д-

3.1. Интерполяция
115
Поэтому первые строки искомой простой вычислительной схемы
могли бы выглядеть так:
*о У о (= со)
Уг
У\ —Уо
Уг — Уо
Уг — Уо У1 — Уо
х2 —
Задача 10. Используя метод, описанный в задаче 9, найти ин-
интерполяционный многочлен 3-й степени, проходящий через точки
11 2 1/1Г
@, 0), (y.-g-). (-j, *2~), A, 1)- Использовать какую-нибудь грубую
таблицу значений функции sin я*.
Определение 2. Пусть заданы п + 1 пар чисел (хи yt), причем
при i Ф /. Выражение
t, xk] =
У1—УЬ.
называется разделенной разностью первого порядка. Здесь, само
собой разумеется, i Ф k и i k 6 {0, 1, ... , п). ^Выражение
,..., xt+i, xt] —
называется разделенной разностью порядка р.
Замечание. Повторным применением теоремы Ролля можно (по
индукции) показать, что для всякой п раз непрерывно дифферен-
дифференцируемой функции у (х) справедливо соотношение
[хп, xn_i х0] —
У(п) F)
где | — некоторая промежуточная точка, х0 < | < хп х (см., на-
например, Цурмюль [1957]2).
Задача 11. Показать, что значение разделенной разности не
зависит от порядка следования ее аргументов.
Решение. Покажем по индукции, что разделенная разность по-
порядка р допускает представление в виде
1 При условии, что *о — наименьшее, а хп — наибольшее из значений
j. — Прим. ред.
* Или Н. С. Бахвэлов 11975]. — Прим. перев.

116 3. Аппроксимации
\х х- x x-1 =
I У1+1 I
(xi+p ~~ xi) (xi+p ~~ xi+l) ••• (Xi+P — xi+
Для p = 1 имеем
IV v 1 У>+' — У1 _ У1 I i/i+i
*!+i — *i *i — xi+i xi+p — xi
Пусть наше утверждение доказано для разделенных разностей по-
порядка р — 1. Тогда
p< xi+p-li ••• • xi+u [xi+p-u ••• > *j+i> *iJ __
> ••• • Xi+1> Xi\ =
Л1+Р
i+l xi+i) ■■• (xi+l — xi+p)
i Уг+р
xi+p) (xi+p — xi+l) ••• (xi+p — xi+p-l
_[" m I Уш i
L (*i — *£+.) ••• (xi — xi+p-l) (xUl — Xt) ... (Xi+1 — XUp_t)
(xi+p-l xi) ••■ (xi+p-l xi+p-'.
Слагаемые, имеющие в качестве множителя yt и yi+p, входят в сум-
сумму уже в нужном виде. Для всех /, отличных от I и / + р, мы име-
имеем по два члена, и суммой этих двух членов будет как раз
Ю
(х, - xt) (х/ - хш) ... (дс/ - */_!> (х,- — х/+1)... (дс/ - xi+p) •
Из этого представления разделенной разности и следует наше ут-
утверждение.
Задача 12. Показать, что многочлен
рп (х) = Уо + lxi> хо\ (х — хо) + [*2> xi> хо\ (х — хо) (х — xi) + — +
служит решением задачи интерполирования (это — интерполя-
интерполяционный многочлен Ньютона).

3.1. Интерполяция 117
Решение. Если учесть симметрию разделенных разностей отно-
относительно их аргументов, то мы обнаружим, что величины, появ-
появляющиеся в вычислительной схеме из задачи 9, как раз и будут
указанными разделенными разностями.
Интерполяционный многочлен Ньютона имеет по сравнению с
интерполяционным многочленом Лагранжа то преимущество, что
при добавлении новых узлов интерполирования не нужно повто-
повторять заново все вычисления.
Задача 13. Провести для интерполяционного многочлена Нью-
Ньютона оценку остаточного члена.
Решение. Пусть х Ф Xi (i — 0, 1, ... , п) — произвольная фик-
фиксированная точка. Тогда в силу равенств
X, Xo, Xi, ... , Xn\—
имеем
X—Xq
fv v v 1 — J*' *o] ~ [*0. *l1
[A, Aq, AJJ " ,
Л£ — X^
X> Хц, ... , Xn_i\ [-^Q) % t ... , Xfi\
У(х) = Уо + [х, xo](x — xo),
[x, x0] = [x0, xt] +(x — Xt) [x, x0,
[X, Xo, ... , Xn_t] = [Xo, Xi, ... , Xn] + (X —Xn)[X, Xo, Xt, ... , Xn].
Если в правые части вместо разделенных разностей подставим их
значения из последующих строк, то с учетом симметрии разделен-
разделенных разностей получим
у(х) = Уо+1х1,хо](х—хо) + ... +[х„,хп_1 хо](х— хо)...(х—xn.t)+
■\-[х, хп, xn_i, .... хо](х — хо)...(х — хп) =
= Рп(х)+[х, хп, xn_t, .... хо\(х — хо)...(х — хп).
Но х— произвольная точка, и, значит, для всех х Ф Xi справед-
справедливо соотношение
Rn+i (X) = [X, Хп, Хп.„ ... , Хо) (X — Хо) ...(X— Х„).
В случае когда функция у {х) является п + 1 раз непрерывно диф-
дифференцируемой, из C) следует, что

118 3. Аппроксимации
где % лежит в наименьшем интервале, содержащем точки х, х0,
X|, ... , Хп.
Задача 14. Построить интерполяционные многочлены для функ-
функции
f(X)=lgX—^-
по следующим опорным точкам:
a) х= 1, 2, 4, 8, 10,
b) х = 2, 4, 8, 10,
c) х = 4, 8, 10,
d) х = 2, 4, 8.
Для всех этих случаев вычислить приближенное значение lg 5,25
и сравнить его с табличным значением. Дать оценку погрешности
остаточного члена и сравнить между собой полученные для рас-
рассматриваемых четырех случаев результаты.
Решение. Составляем схему для разделенных разностей и опре-
определяем по ней коэффициенты интерполяционных многочленов.
В качестве этих многочленов получаем
a) Р4 (х) = О.ООПдг4 — 0,0264л:3 + 0,2221 х2 — 0,6965* + 0,4997,
b) Р3(х)= —0,006л:3 + 0,0109л:2 — 0,0238л: — 0,1905,
c) Р2(х)= —0,0013л-2 + 0,0601 х — 0,3668,
d) Р2 (х) = 0,0031 л-2 + 0,0071 х — 0,2255.
Табличным значением lg 5,25 является 0,7202. Абсолютные вели-
величины разности между табличным значением и значениями, полу-
полученными интерполированием, равны
a) 0,0695,
b) 0,0123,
c) 0,0022,
d) 0,0135.
Задача 15. На отрезке [—1, +1] провести интерполяцию мно-
многочлена (п + 1)-й степени Q (х) со старшим коэффициентом 1 мно-
многочленом п-й степени Рп{х) так, чтобы наибольшая возможная по-
погрешность \Q (х) — Рп(х)\ была минимальной. Как следует выбрать
узлы интерполяции?
Решение. Из общей формулы для остаточного члена следует,
что
Q (х) — Рп (х) = (л- — х0) (х — л-,)... (л- — хп).

3.1. Интерполяция 119
Интерполяционные узлы х0, х^, ... , хп нужно выбрать так, чтобы
минимизировать
max \(x — xQ)(x — xi)...(x — xn)\.
xel-u i]
Согласно результатам теории аппроксимации (см. § 3.3) минимум
достигается в случае, когда
(х — х0) (x — xt)...(x — хп) = ~- Tn+i (х),
где Тп+[(х) = cos ((я + 1) arc cos x) — многочлен Чебышёва (я+1)-й
степени. Таким образом, узлы х0, xt, ... , хп являются корнями
многочлена Tn+i(x), т. е.
Задача 16. Пусть х0 = 0, х, = 1, х2 — 2, х3 = 3 и известно,
что в интервале —1 < х <. 4 производная четвертого порядка не-
некоторой функции допускает оценку
3<г/D)(х)<4.
Указать две функции р (х) и а{х) (нарисовать их графики), такие,
что в интервале —1 <х<4
Какой отсюда следует результат относительно экстраполяции, т. е.
относительно оценки остаточного члена вне интервала х0 = 0 «з
<: х < 3 = х3?
Решение. Остаточный член имеет вид
Rt(x)= У^® х(х-1)(х-2)(х-3), где 5€[-1,4].
Поэтому в качестве искомых функций можно взять
4!
Вот некоторые значения этих функций (границы для погрешности):
х р(х) а (х)
—13 4
—0,5 0,820 1,095
0,5 -0,157 —0,117
1,5 0,070 0,094

120 3. Аппроксимации
Отсюда видно, что при экстраполировании, по сравнению с интер-
интерполированием, погрешности получаются большие.
Задача 17. Вычислить остаточный член для примеров из задач
10 и 5.1 и нарисовать на графике границы для остаточного члена.
Задача 18. Пусть требуется составить четырехзначную табли-
3/
цу функции у(х) = у х в интервале 1 <: х <: 1000. Какой ве-
величины должен быть шаг таблицы h, чтобы
a) при линейной,
b) при квадратичной
интерполяции полностью использовалась точность таблицы, т. е.
чтобы погрешность (абсолютная величина остаточного члена) была
меньше чем 5-10~4? Провести вычисление для двух вариантов:
Г во всем интервале 1 <: х <: 1000 берется один и тот же шаг Л;
2° в интервале 1 <: х <: 100 берется шаг hiy а в интервале
100 <: х <: 1000 — шаг Л2.
Ответ, а) Г h <: l/*180-10~2; например, можно взять h = 10
2° hi <. 1/180• 10~2, Л22<: 180/т^Щ hz < 6,227.
Конечные разности. Часто используются выражения вида
f (х + К) — / (х), где h — фиксированное вещественное число. Опе-
Операцию образования разности записывают короче так:
Эта операция линейна: Д (af (x) -f- bg (x)) = аД/ (х) + bAg (x). Ите-
Итерации этой операции определяются формулой
Д'+1/ = Л(Л'/) (t=l, 2, ...),
причем полагают А1/(*) = Л/(*) и А0/ (х) = f(x). Например,
Д2/(х) = Д (/(* + /*)-/(*)) =
= (f(x + 2h)-f(x+h)) _(/(* +ft)_/(*))=*
Задача 19. Показать, что если функция у (х) является k раз
непрерывно дифференцируемой в интервале х0 <: х <: х0 + kh, то
справедливо соотношение
Указание. Применить теорему о среднем значении и индукцию.
Задача 20. Показать, что если у (х) — многочлен п-й степени,
то
А(п+1) у (х) = 0.

3.1. Интерполяция
121
Решение. Согласно задаче 19, имеем Ara+1 у(х) = /гга+У'1+1>(£)—О,
так как (п + 1)-я производная многочлена n-й степени равна нулю.
Задача 21. Показать, что при равноотстоящих друг от друга
узлах xt — х0 + ih и при обозначениях Д*г/г = Д*г/(х;), £ =
= (х — xo)/h интерполяционный многочлен Ньютона принимает
вид
Рп (*) = Уо + ( f ) АУо
Схела вычисления интерполяционного многочлена для случая
равноотстоящих узлов (см. предыдущую задачу). Значения функ-
функции г/, записываем слева одно под другим:
X
*0
X\
Хз
ч
У(х)
Уо
У\
Уг
Уз
Ау
Д(/о = 1/] — Уо
У\ == У2 — У\
д - -
vy
Д2 Уо = Д</1 — Д?/о
Д2 l/j = Д1/2 — Д?/г
Д3«/
Д3 у0 = Д2 i/x — Д2 %
и наш интерполяционный многочлен считываем непосредственно
с верхней (наклонной) строки.
Пример. Кубическая интерполяция для т/х в интервале
8<х< 11 (h = 1):
8
9
10
11
12
у
2,0
2,08008
2,15443
2,22398
2,28943
А»
0,08008
0,07435
0,06955
0,06545
— 0
— 0
-0
\2у
,00573
,00480
,00410
0
0
Vy
,00093
,00070
А*»
— 0,00023
Следовательно,
Р3 (*) =* 2
0,08008 — fх —J
0,00573 -f
• 0,00093.

122 3. Аппроксимации
В качестве приближения для производной четвертого порядка
можно использовать значение Д4г/; при этом получаем
Имеем
(х) » — (х — 8) • 0,00023.
х_
4! " ' 0.5625 _ ^
при 9<х< 10,
так что в интервале 9 < х < 10 достигнута табличная точность.
Вычисление самой четвертой производной г/<4> (х) дает даже оценку
при
з /—
так что многочлен Ps(x) приближает функцию ухе табличной
точностью во всем промежутке 8 <С х <^ П.
После многочленов наиболее удобными для вычислений явля-
являются рациональные функции; поэтому представляет также интерес
интерполирование при помощи рациональных функций.
Пусть Rmtn — класс всех рациональных функций <р (х) одной
вещественной переменной х вида
9(х) =
2
v=0
причем предполагается, что выполнено некое условие нормиров-
нормировки, скажем Ьп — 1. Если требуется функцию/ (х) интерполировать
с помощью функции ф (х) из этого класса так, чтобы соотношение
9{Xj) = f{Xj), / = 1,2 т + п+\,
выполнялось в т + п + 1 точках xJt то мы получаем
^ v x) -f{Xi) ^ bw x) =0, I - 1, 2, ..., т + п + 1,
v=0 v—0
т. е. (неоднородную, поскольку Ъп — 1) линейную систему уравне-
уравнений относительно /л + п + 1 неизвестных коэффициентов а,, 6,.
Задача 22. Проинтерполировать функцию / (х) = 2х функцией
Ф (х) = (х2 + ах + &)/(сх + of) класса /?2>i, причем совпадение
значений / (х) и ф (х) требуется при х = 0, 1, 2, 3 Будет ли «еле-

3.1. Интерполяция
123
дующее» значение ф D) хорошим приближением для / D)?
Решение. Система уравнений
1 + а + b = 2 (с + d),
4 + 2а + b = 4 Bс + d),
9 + За + b = 8 (Зс + d),
имеет решение а = 3, 6 = 6, с = —1, d = 6. Интерполирующая
функция
принимает при х = 4 значение фD) = 17, тогда как /D) = 16.
Задача 23. Сравнить рациональное приближение из преды-
предыдущей задачи с полиномиальным приближением для f (x) посредст-
посредством многочлена третьей степени р (х), который совпадает с f (x)
при х = 0, 1, 2, 3, и начертить графики погрешностей et(x) =
= Ф (х) — f (х) и е2(х) = р(х) — f (x).
Решение, р (х) = F + 5х + х3I(з. Графики погрешностей при-
приведены на рис. 3.1.1.
Рис. 3.1.1.
Задача 24. Для функций
а) /(*,*/)= '
2 + х + у + 2х2 +
b) f(x,y) =
1
2 + х + у + х*
определить по образцу задачи 22 рациональную функцию ф (х,у)
вида (а + bx + cy)l(d + ex + fy), совпадающую с / (х, у) в точках
@,0), A,0), (-1,0), @, 1), @,-1).
Решение. В случае (а) получаем
. . 1 — 2лг — Зу
2 — 7х + Ну

124 3. Аппроксимации
а в случае (Ь) формальные выкладки дают
I — х
<Р (х,У) = ■
но эту функцию нельзя рассматривать как настоящее решение, так
как при х = 1, у = 0 она принимает неопределенное значение вида
0/0 вместо значения 1/4.
3.2. Численное интегрирование
Пусть / (х) — вещественная функция, определенная на интер-
интервале [а, Ь] вещественной оси, для которой существует интеграл
» ь
Римана [f(x)dx. Под численным интегрированием понимают на-
а
хождение приближенного значения этого интеграла. Во многих
случаях к приближенным методам прибегают ввиду того, что под-
подлежащий вычислению определенный интеграл не выражается через
элементарные функции; примером может служить (V*2dx.
•о
Прежде всего рассмотрим случай, когда [а, Ь] — конечный ин-
интервал и / — ограниченная на нем функция. В этом случае наиболее
часто применяемый численный метод интегрирования состоит в том,
что интеграл от / заменяется некоторой линейной комбинацией зна-
значений f(xh) в п + 1 точках xk£[a, b\:
^Akf{xk). A)
a k=0
Формула A) называется квадратурной формулой, коэффициенты Ak—
квадратурными коэффициентами (или весами), абсциссы xh — узла-
узлами квадратурной формулы.
Опишем некоторые типы квадратурных формул и приведем их
вывод.
3.2.1. Квадратурные формулы, порожденные интерполяционны-
интерполяционными формулами. Пусть х0, хи ..., хп — различные точки интервала
[а, Ь], служащие узлами интерполяции для некоторой интерполи-
интерполирующей функцию f(x) функции 1(х). Имеем
где R(x) — остаточный член. Предположим, что/(л;) = V/
причем все интегралы

3.2. Численное интегрирование
125
можно вычислить точно. Тогда мы получаем такую квадратурную
формулу:
Задача 1. Пусть п = 1, х0 = а п xt = b. Функция f(x) интер-
интерполируется по формуле Лагранжа. Какая получится квадратурная
формула?
Решение. В рассматриваемом случае интерполяционным много-
многочленом Лагранжа для / будет линейная функция
{f(a)(b-x) + f(b)(x-a)}.
b — a
Поэтому во введенных выше обозначениях имеем
= \{Ъ-а),
1 * 1
= - \{x — a)dx = —.{b —
b —a J 2
и мы получаем следующую квадратурную формулу:
B)
Она называется формулой трапеций.
Задача 2. Объяснить это название.
Решение. Величина -^(Ь — a)(J(d) -f f(b)) есть площадь трапе-
трапеции с вершинами a, b, f{b) и f{a) (рис. 3.2.1).
Задача 3. Пусть / — непрерывно дифференцируемая п + 1 раз
НЬ)
Щ
а Ь
Рис. 3.2.1.

126 3. Аппроксимации
на la, b] функция, такая, что
\Pn+i) (t)\<Mn+1 для 16[а,Ь].
Дать простую оценку погрешности для квадратурной формулы,
которая порождается интерполированием по Лагранжу по п + 1
различным точкам хк 6 [а, Ь].
Решение. Остаточный член интерполяционной формулы Лагран-
жа имеет вид
^§ х - х0) (х - х.)... (х - хп).
Поэтому для погрешности F квадратурной формулы имеем
\F\=
\Rn+i(x)dx <f \Rati(x)\dx,
откуда
Задача 4. На примере формулы трапеций показать, что, приме-
применяя интегральную теорему о среднем значении, можно прийти к
лучшим оценкам, чем C).
Решение. В рассматриваемом случае
J 2!
Произведение (х — а)(х — Ь) сохраняет знак в интервале [а, Ь\;
следовательно,
где
Задача 5. Пусть функция f(x) квадратично интерполируется по
Лагранжу, п = 2, х0 = a, Xi = (а + ЬI2, х2 = Ь. Какова соот-
соответствующая квадратурная формула?

3.2. Численное интегрирование
127
Решение. Наш интерполяционный многочлен таков:
(х-а)(х-Ь)
/(*) =
а+Ь\
х - —Z— \(х-Ь)
а+ Ь .
а-—т—\(а-Ь)
■f(a)
a+b \ (a + b
— а\ —-— — b
■*■
(x — a) Ix —
г
2
a+b
X
F-a) 6-
a + 6
■/(&)■
Интегрированием получаем искомую квадратурную формулу:
4/(-2±А)+ /(&)}. E)
Она называется формулой Симпсона (или формулой парабол).
При заданном интервале интегрирования [а, 6] квадратурные
формулы B) и E) обычно применяются таким образом: сначала
интервал разбивается на п подынтервалов длины h = (b — a)ln
и затем к каждому такому подынтервалу применяется соответствую-
соответствующая формула. Пусть ft = f(a + ih) (t = 0, 1, ..., n).
Для формулы трапеций получаем:
I dX :
b—a
2л
F)
для формулы Симпсона (здесь нужно предпол ожить, что п является
четным):
J / (х)
dx
±- (/0 + 4/, -V 2/2 + 4/3 + ... + 2fn_2 + 4U + /„).
Задача 6. Разделив интервал [0, я/2] на четыре подынтервала
тс/2
длины я/8, вычислить ("sinxdx по формуле трапеций и по формуле
о
Симпсона. В качестве значений подынтегральной функции взять
следующие:
0
0
я/8
0,382683
я/4
0,707107
Зя/8
0,923880
я/2
1,00000
sinx
Решение. При применении формулы трапеций получается
0,987116; применение формулы Симпсона дает 1,000135.

128
3. Аппроксимации
Задача 7. При помощи формулы D) ответить на вопрос, когда
формула трапеций дает нижнюю и когда верхнюю границу для
искомого значения интеграла.
Решение. Погрешность для формулы трапеций имеет вид
F = F ~ а) Г (*])> гДе 116 [а, Ь].
Поскольку
J f(x)dx =
отсюда следует, что если /" <С 0 в [а, Ь] (т. е. функция / вогнута),
b b
то Т < U(x)dx, а если /" > 0 в [а, Ь] (т. е. / выпукла), то U{x)dx
а .а
3.2.2. Метод Ромберга. Пусть промежуток интегрирования раз-
разбит на 2* равных частей и для этого разбиения по формуле трапе-
трапеций получено значение Г**'. Значения Г(о' совпадают со значением
вычисляемого интеграла, если интегрируемая функция f(x) линей-
линейна, т. е. является многочленом первой степени. По формуле
Т(к) =
m—\ ~ ' т—1
: —1
называемой формулой Ромберга, построим следующую Т-схему:
@)
тC)
1 о
@)
т@)
1 3
2 ' 4
1 3
2
Можно показать, что для интегрируемых по Риману функций все
столбцы и все наклонные строки Т-схемы сходятся к искомому
значению интеграла.
Задача 8. Выписать явные формулы для следующего фрагмента
Т-схемы:

3.2. Численное интегрирование 129
Г(О)
,A)
O
Решение. Пусть ^ = а + i (b — а)/4 (i = 0,..., 4). Тогда
ПГ У Со) + 2 (/ С») + / О + / Са))
&-а ^^ + 4^^ + /(х4)] (формула Симпеона),
2/ (^2) + 4/ (*3
+ 32/ (*,) + 12/ (х2) + 32/ (дд + 7/ (*4)] (форму-
ла Ньютона — Котеса)
3.2.3. Квадратурные формулы Гаусса. Во всех приведенных до
сих пор квадратурных формулах, таких, как формула трапеций и
формула Симпеона, и во всех формулах, получаемых по методу
Ромберга, используются равноотстоящие узлы. В случае квадра-
квадратурных формул Гаусса это уже не так. Грубо говоря, смысл квадра-
квадратурных формул Гаусса состоит в том, чтобы при наименьшем воз-
возможном числе узлов точно интегрировать многочлены наивысшей
возможной степени. Можно показать, что при п гауссовых узлах
по полученной исходя из них с помощью интерполирования квадра-
квадратурной формуле можно точно интегрировать все многочлены сте-
степени ^ 2п — 1.
Задача 9. Составить квадратурную формулу с двумя узлами,
по которой точно интегрируются многочлены до третьей степени
включительно.
Решение. Искомая формула имеет такой вид:
ь
dx = ctf (xt) + c,f (x2) +#(/).
J / (х)
Если R(f) для f(x) = a0 + a^x -f- a2x2 -f a3x3 обращается в нуль
для любых ai, то
Va 5-206

130 3. Аппроксимации
= с, (a0 + aiXi + агх\ + а3х]) + с2 (а0
Отсюда, приравнивая коэффициенты при а,- (/ = 0, 1, 2, 3) справа
и слева, получаем систему уравнений
ct + с2 = Ъ — а,
c2x2 = -^Ф* — а2),
Ее решение:
6— а
Ci = с2 = —
_ a+ & Т^З 6 —а
2 3 2
▼ 2 3 2
Следовательно, искомая квадратурная формула такова:
f£
2 3 2
V3~ Ь—а
Задача 10. Разделив интервал [0, л/2] на четыре подынтервала
длины я/8, вычислить Гsinxdx по вышеприведенной формуле Гаусса.
о
Решение. Нам нужны следующие 8 узлов и соответствующие
им значения синуса:

3.2. Численное интегрирование
131
Узлы
0,082987
0,309712
0,475686
0,702411
0,868385
1,095110
1,261084
1,487809
Значения
подынтегральной
функции
0,082919
0,304784
0,457949
0,646060
0,763287
0,888979
0,952421
0,996559
5,092958
ф
Таким образом, Г sindx» — • 5,092958= 1,000000.
$ 16
16
(х, у) : f- г/а = 1 I (а > 0)
а2 J
выражается формулой
ф
V
U = 4 f V 1— A— aa)sina/
Этот интеграл при а ^= 1 не вычисляется в элементарных функциях.
Вычислить его приближенно для а = 1,2, выполнив четыре первых
шага по Ромбергу.
Решение. Нужными значениями функции / (t) =
= V)
t
fit)
-A
0
l
l
— as
я/16
,0083
)sin2^ являются:
I я/8
1 1,0317
Зя/16
1,0657
1
я/4
,1045
5я/16
1,1420
1,1728
7я/16
1,1930
я/2
1,200
Имеем
т)) = TA + ll2)" '-7279'

132 3. Аппроксимации
i^ 1J326,
52= EizlH «1,7314,
О
S3= 4Г4ГГз = 1,7314,
15
S= 1,7314,
15
4 63
Таким образом, U = 4-1,7314 = 6,9256.
Задача 12. Как хорошо известно,
1 dx — к.
.) 1 + х2
о
Определить приближенно тс, проведя для указанного интеграла
4 итерации по Ромбергу. (Следует записывать промежуточные ре-
результаты каждой итерации.)
Задача 18. Сколько нужно найти значений функции f(x), если
ь
мы хотим вычислить \f(x)dx при помощи 2, 3, или 4 итераций по
а
Ромбергу? Сколько значений функции потребуется, если надо
провести п итераций по Ромбергу (п = 1, 2, 3, ...) ?
Задача 14. При пересчете натуральных логарифмов \пх в де-
десятичные lgx используется формула
Minx— lgx для всех х>0,
где М — некоторая постоянная. При подстановке сюда х == 10
для М получается выражение
ю
M=iiii = _i_, откуда JL-miO-f -£-•
In 10 In 10 3 М J х
I
Определить приближенно ИМ, вычислив значение интеграла при
помощи четырех итераций по Ромбергу (с записью всех промежуточ-
промежуточных результатов). Сравнить полученное значение с точным значе-
значением ММ = 2,3026... .

3.2. Численное интегрирование
133
Задача 15. Вероятность того, что наблюденное значение нор-
нормально распределенной случайной величины будет меньше заданно-
заданного числа х, дается формулой
w =
1 Г -t*/2
if!"
dt.
Определить приближенно w для а) х = 1/2, Ь) х = 1, с) х = 5,
вычислив интеграл при помощи трех шагов по Ромбергу (с записью
всех промежуточных результатов). При этом воспользоваться тем,
что
-L- L-"/2dt = ±+-±=
V2it J 2 /2л
dt
и 1/У2л = 0,3989... , а также следующими значениями подынте-
подынтегральной функции:
t
—t3/2
е
0
1
1/8
0,9922
1/4
0,9692
~3/8
0,9321
1/2
0,8825
3/4
0,7548
1
0,6065
5/4
0,4578
5/2
0,0439
15/4
0,0009
5
0,0000
(Точные до четвертого знака после запятой значения w таковы:
а) 0,6915, Ь) 0,8413, с) 1,0000.)
Задача 16. Как и в задаче 11, определить приближенно длины
эллипсов
а) ^- + «/2=1, Ь) -|- + /=1,
выполнив три шага по Ромбергу. Нужные значения подынтеграль-
подынтегральных функций:
/ > +
/1 4-
3 sin2 t
24 sin^:
0
1
1
1,1997
2,1248
1
3
ir/4
,5811
,6056
Зя/8
1,8870
4,6352
л/2
2
5

134
3. Аппроксимации
(Точные до четвертого знака после запятой значения таковы:
а) V = 9,6884, Ь) V = 21,0100.)
Задача 17. Математический маятник (рис. 3.2.2) длины / при
размахе а имеет период колебания Т = 4]fTFg К, где# — ускоре-
ускорение силы тяжести и
тс/2
J Л Г а
о у 1 — sin2 -у sin2<p
При малых углах а интеграл К, приближенно равен я/2, так что в
этом случае приближенно Т = 2nVl/g. Маятник, для которого
я V l/g = 1, называется секундным маятником, так как для та-
Рис. 3.2.2.
кого маятника при малых а половина периода колебания как раз
равняется 1с. Половина периода колебания секундного маятника
при любом размахе а дается формулой Т/2 = B/ц)К- Вычислить
приближенно интеграл для К,
a) для а = 5°, выполнив 2 шага по Ромбергу,
b) для а = 10°, выполнив 2 шага по Ромбергу,
c) для а = 45°, выполнив 3 шага по Ромбергу.
Используя результат пункта (а), определить приближенно 2/я.
Используя результаты пунктов (а)—(с), подсчитать, на сколько
секунд в день врут часы с секундным маятником при размахе коле-
колебаний 5°, 10° и 45°? Спешат часы или отстают? Нужные значения
подынтегральной функции
F (а, Ф) = 1
V
1 — sin2 -„- sin2 <p
приведены в следующей таблице:
5°
10е
45°
0
1
1
1
■к/8
1,0109
«/4
1,0005
1,0019
1,0388
Зя/8
1,0690
п/2
1,0010
1,0038
1,0824

3.2. Численное интегрирование
135
Задача 18. Кривая, по которой сопрягаются два прямолиней-
прямолинейных участка дороги, часто строится так: для первой половины кри-
кривой кривизна /С пропорциональна длине кривой, а вторая полови-
половина симметрична первой. Таким образом, если s — длина, отсчиты-
отсчитываемая от начала кривой, и К — кривизна, то
K = cs,
где с — некоторая постоянная. Отсюда, как можно показать, вы-
вытекает, что в прямоугольных координатах наша кривая задается
так (при а — Ynlc):
s/a s/a
х = а Г cos — fdt, у = а Г sin — t2dt.
о 6
Такие кривые называются клотоидами или спиралями Корню, а
указанные выше интегралы — интегралами Френеля. Положив
с = я (так что а = 1), вычислить для s = 0,5, 0,75, 1, 1,3, 1,5 при
помощи численного интегрирования по Ромбергу соответствующие
точки клотоиды. Достаточно трех шагов. Нужные значения подын-
подынтегральных функций приведены в таблице ниже:
COS
sin
t
n
2
7Г
2
0
1
0
0
0
0
,125
,9970
,0245
0
0
0
,1875
,9985
,0552
0
0
0
,25
,9952
,0980
0,
0,
0,
32b
9863
1652
0
0
0
,375
,9757
,2191
0,5
0,9239
0,382?
0
0
0
,5625
,8790
,4768
0
0
0,
,65
,7877
6160
0,
0
0
75
,6344
,7730
0,
0
0
975
,7748
,9970
1
0
1
-о,
о,
125
4052
9142
1,3
—0,8838
0,4679
1
—0
—0
,5
,9239
,3827
Задача 19. В предыдущей задаче при а = 1 найти ту точку
спирали Корню, в которой угол наклона касательной составляет
45°. Значения соответствующих интегралов вычислить, выполнив
два шага по Ромбергу.
Ответ, s = У2/2 = 0,7071, х = 0,6647, у = 0,1771.
3.2.4. Границы для интегралов. При численном интегрировании
наряду с приближенными формулами представляет также интерес
нахождение нижних и верхних границ для интегралбв, Следующие
задачи показывают, как можно получать такие границы.

136
3. Аппроксимации
Задача 20. Найти границы для интеграла J = f/ (x)dx в слу-
а
чае, когда дважды непрерывно дифференцируемая функция / (х)
является выпуклой, соответственно вогнутой в интервале М =
— [а, Ь], т. е. когда вторая производная f (х) не меняет знака в М,
а именно /" > 0, соответственно /" < 0 в М.
Решение. Значение интеграла заключено между (см. рис. 3.2.3)
площадью Т трапеции, одной из сторон которой служит хорда,
а а*Ь Ь «
2
Рис. 3.2.3.
соединяющая концевые точки графика, и площадью S трапеции,
у которой одной из сторон служит касательная к графику в средней
точке х = (а + Ь)/2 отрезка М. Имеем Т = ф — a) {f (а) -\- /(й))/2
и S = (Ь — а) /((а + ЬI2). Эти границы можно уточнить путем
разбиения отрезка интегрирования, например многократного деле-
деления его пополам.
Задача 21. Другой, очень простой и часто применяемый прин-
принцип основан на «монотонности» интеграла; при этом способе подын-
подынтегральную функцию приближают снизу и сверху интегрируемыми
в замкнутом виде функциями g (x), h (x). Что это дает?
Решение. В обозначениях задачи 20 пусть
для всех
Ь].
Тогда
Задача 22. Используя принципы, описанные в задачах 20 и 21,
определить границы для эллиптического интеграла
1
= f
dx

3.2. Численное интегрирование 137
Этот интеграл сингулярен (интегрируемая функция имеет особен-
особенность при х = 0).
Решение. Положим N = х + хъ и / (х) = N~lf2.
I. Совсем грубая оценка. Следуя методу задачи 21, оценим по-
подынтегральную функцию при помощи интегрируемых в замкну-
замкнутом виде функций:
<f(x) =
Ух + х3 Ух
Интегрирование (с подстановкой s = и2 для случая функции g (x))
дает
2arctg VI = 2 Г* -^- = \g (s) ds<\f (s) ds <
X
< f h (s) ds = 2 1/7.
о
Таким образом, беря * = 1, получаем грубые границы: я/2 < У<2.
II. Несколько лучшая оценка. Делим отрезок 10, 1] пополам
и используем только что выведенную оценку, беря х = 1/2; как
следует из соотношения
4Л/5/2/" = 3A + 6х2 + 9х4) — 12(л;2 + л;4)>0 при 0<х<1,
в отрезке [1/2, 1] подынтегральная функция выпукла и, следова-
следовательно, применим метод задачи 20. В результате находим:
y>2arctg j/1 + l /Т1ТУуз = 1'23096 +
+ — V3 ±10-5== 1,23096 +0,46188± 2- 10~5> 1,6928
1 О
+ — A,97202) ± 2 • 10'5 < 1,9073.
4

138 3. Аппроксимации
То, что границы получились все еще довольно грубые, объясняется
главным образом сингулярностью части интеграла, отвечающей
интегрированию по отрезку 10, 1/2].
Задача 23. По-методу задачи 21 определить границы для ин-
интеграла
xdx
Решение. Положим / (х) = хШ, N = х3 + х + 1. При 0 < х
< 1 имеем (см. рис. 3.2.4)
х- х* + -£ = gi(x)<f (x)<hdx) = х— ~х\
О О
так как
Таким образом,
-j = §
или
0,25 <./< 0,278.
Задача 24. В обозначениях задачи 23, оценить несобственный
интеграл
Решение. Оценим подынтегральную функцию снизу и сверху.
В интервале 1 < х < 2 имеем (см. рис. 3.2.4)
так как здесь
К (х) -f(x)= A ~~f [D -х2) + 2х]> 0.

3.2. Численное интегрирование
139
При всех х > 1
1 х
■<f(x)<h3(x) =
1
X2 A + X2K 1 + X*
Все указанные граничные функции легко интегрируются, а
именно
1 : I g2
A+S2
to
4(i + s2J
= —=r arctg s
4A+ c2J '
ajVI
1/2
- arctg —— .
j/2
I. Верхние границы: У < И* л;2)^л-+ \ —
■IV з / ,) 1
■ х2 18
Н ■< 1,064. При большем старании можно установить несколь-
4
ко лучшие границы:
6*

140 3. Аппроксимации
1 2 оо
Т < Г hi (х) dx + f h2 (x) dx +[hs(x)dx = — + — —
J ,f »' У z
0 1 2
1
_arctg2--i^< 1,0092.
1 се
II. Нижние границы: J > \ gi(x) dx + ( —^ = \-
0 0
— -arctg ~L.\ > 0,926.
2 & V2~ )
Задача 25. Посмотреть, насколько трудоемко вычисление ин-
интеграла задачи 23 «в замкнутом виде».
Решение. Применяются обозначения из задачи 23. Уравнение
N (х) = 0 имеет ровно один вещественный корень, и притом отри-
отрицательный; пусть, скажем, х = —а. Тогда N (x) допускает разло-
разложение
N (х) = 1 + х + х3 = (х + а) (х2 — ах + — V
а
и x/N можно разложить на простейшие дроби:
х а2 1 1 аЧ+ 1 .
~~N ~ Т х+а Т." М(х) '
здесь и в дальнейшем используются для краткости обозначения
А = 3 — 2а, b = (l + —Y'2 M() x2 a+
Теперь вычисляем неопределенный интеграл:
С
J
Ах , а2
dx
, а2 ,
dx = — In
2
2
9 .1
x2 — ах -\
air,
— а2\п \ х-{-а
3 — а , 2х — а .
arctg — \- с.
о
Нarctg
о о
Первые два члена можно объединить в один
2
Поскольку In I = 0, это выражение стремится к нулю при х-*- с».
Таким образом,

3.2. Численное интегрирование 141
3 — а
Г , 2 —а . , а ~\\
^ = _1_ Г^1па+ 3-^ ГЛ
N A { 2 b [ 2
Задача 26. Найти численные значения результатов задачи 25.
Решение. Корень х — —а находим по одному из способов гл. 1;
при этом получается а = 0,68232780 ±10"8. В дальнейших вычис-
вычислениях используем шестизначные таблицы функций и потому про-
проводим их только с шестью знаками. Скорее всего, оба указываемых
ниже вычисленных значения интегралов имеют 5 верных десятич-
десятичных знаков; совершенно же грубая оценка погрешности гаран-
гарантирует 4 знака:
1 се
Г Л dx = 0,260069 ± 10, Г — dx = 0,957144 ± 10.
J N J N
о о
Задача 27. По образцу предыдущих задач и в тех же обозначе-
обозначениях рассмотреть случай подынтегральной функции 1/jV.
Решение. Разложение на простейшие дроби здесь таково:
-ах+ — A -а)
1 а 1 а
N (дг) А х + а ( 1
А \х2 — ах + —
V а
отсюда следует, что
dx.
NW
хг — ах + —
1
I

142 3. Аппроксимации
Прикидочный расчет с использованием логарифмической линейки
дает такие численные значения:
1 се
Г — = 0,63±2- 10, Г — = 0,915 ± Ю.
J N J N
о о
Задача 28. Рассмотрим интеграл J =\f{x)dx, где функция
а
f (х) при х = а имеет особенность вида / (х) = g(x)/]/ x — а (в по-
последующем всюду имеется в виду неотрицательное значение кор-
корня), причем функция g (x) в интервале la, b] трижды дифференци-
дифференцируема и для ее третьей производной известна оценка: |g"'(x)| < М3
при х 6 [а, Ь]. Указать для J приближенное выражение N и оце-
оценить погрешность г = N — J; проверить формулу на примере
J Vx + х*
Решение. Пусть a = 0, Ъ = 2/г, А> 0. Если заменить g(x) квад-
квадратичной функцией Р (х), которая совпадает с g (х) в точках х = 0,
/г, 2/г, то значение нашего интеграла можно вычислить в конечном
виде:
2ft
JV = f £-&- dx = 2 *2h Fg @) + 8g(h) + g B/г)).
J yfx 15
о r
Согласно задаче 3, остаточный член R(x) = g(x)—Р (х) можно
записать в виде #(*)= *(Х ~Н)(*~Щ g'" (I), где 0<|<2/г.
о!
Поэтому
2ft 2ft
I I HI J I , i \ К (X) , - /W9 f ,/— , 9 o, r.,9, .
| s |=| iV—7 | ^ \ -—-^r~ dx <J —- \ у x (x2 — 3hx + 2/г2) dx =
о ' *
h3
М3
315
Для указанного тестового примера имеем
±=. £() ^(+)
/1 + ж 8
x | £'" | = М3 = 4" •
1] 8
L ^W'-76521;
15 I /1,5 /2

3.3. Теория приближений 143
|8| = | N — Jt\<C— • — - = — да0,0060.
^ 8 315 8 168
В действительности У4 = In C + У 8) да 1,76275, так что факти-
фактическая погрешность составляет только 0,00246.
Задача 29. Вычислить приближенное значение N интеграла
J(x) =
1 -f- s2
6
используя несколько первых членов разложения cos x в степенной
ряд. Оценить погрешность, в частности при х= 1.
Х^ X* Xе
Решение. Для g (х) = 1 4 при 0 <[ х <![ 1 имеем
s ' " 2! 4! 6! v ^ \
| g(x) — cosx| <-^-; для
8!
х
JL
5
справедлива такая же оценка: \J (х) — Af (x)\ <1 1/8! < 1/40000.
В результате мы получаем следующую таблицу значений, с по-
погрешностью меньшей A/4)-10~4:
N(x)= Г M$-ds = —L_ fllllarctgx — 391x + — x3
w J l + s? 720 V 3
о
J(x)
0,4
0,3708
0,7
0,5671
0,68295
3.3. Теория приближений в нормированных функциональных
пространствах. Чебышёвские приближения
Общая задача приближения функций состоит в следующем;
Пусть дана функция f одной вещественной переменной, областью
определения / которой является либо интервал, либо дискретное
множество точек. Далее, пусть задана норма (см. § 1.5) в прост-
пространстве функций, которую будем обозначать через || ||. Пусть,
наконец, задан класс приближающих функций g (x, ai7 ... , ап),
зависящих от п вещественных параметров ait ... , ап, например
класс многочленов ^ciiX1 или соответствующий класс рациональ-
рационально
ных функций, и т. д. Требуется найти такие п параметров by, ... ,
bn, что
II f(x) — g (х, Ьх,..., Ьп) ||< || / (х) — g (х, аи .:., ая) ||
для всех аи ..., ап.

144 3. Аппроксимации
Так определенная функция g (x, bit ... , bn) называется наилуч-
наилучшим приближением для функции f {х). Наилучшее приближение
не всегда существует, а если и существует, не всегда определяется
однозначно. Те точки множества /, в которых приближающая функ-
функция g максимально отклоняется от функции /, называются экстре-
экстремальными точками функции-отклонения е (х) = / (х) — g {x).
Если используется норма
|| / || = max | / (х) | или II / || = max \w(x)f (x) \ ,
где w (х) > 0 — весовая функция, то говорят о приближении в смыс-
смысле Чебышёва, или, короче, о Т'-приближении1. Если же применяется
норма
/ \1/2
дискретном случае || f(x) || =
(IH1
то мы имеем приближение в смысле Гаусса, называемое также приб-
приближением по методу наименьших квадратов или же среднеквадра-
среднеквадратичным. И в этом случае тоже можно вводить весовые функции.
При разных нормах соответствующие наилучшие приближения,
вообще говоря, значительно отличаются одно от другого.
Чебышёвские приближения, которыми мы в первую очередь
будем заниматься в этом параграфе, играют большую роль в при-
приложениях, например при задании функций в вычислительных ма-
машинах. В самом деле, вводить функцию в машину в виде таблицы
невыгодно, так как, с одной стороны, таблицы требуют много места
в памяти и, с другой стороны, поиск нужного значения функции
также отнимает много времени. Обычно подлежащую вычислению
функцию/ (х) заменяют некоторой другой функцией g (x), которая
вычисляется проще; при этом функцию g (x) часто определяют так,
чтобы она на рассматриваемом отрезке отклонялась от функции
/ (х) не больше чем на заданную величину е, т. е. g (x) определяют
как наилучшее Т-приближение функции / (х). Правда, найти наи-
наилучшее Т-приближение, вообще говоря, намного труднее, чем, ска-
скажем, наилучшее среднеквадратичное приближение, которое полу-
получают из так называемых нормальных уравнений. Кроме тех совсем
немногих случаев, когда наилучшее приближение можно указать
в явном виде, оно определяется лишь при помощи специальных
алгоритмов путем итераций.
1 Т — от Tschebyscheff, немецкой [ранскрипнии фамилии П. Л. Чебы-
Чебышёва. — Прим. ред.

3.3. Теория приближений 145
Задача 1. а) На плоскости даны две точки Pt = {xt, yt), i = 1,
2. Провести прямую вида g {x) = а0 так, чтобы расстояние
max \yt — ао[ между этими двумя точками и прямой было минималь-
минимальным возможным.
Ь) Даны три точки Pt = {xt, yt), i = 1, 2, 3. Провести прямую
g (х) = а0 -\- aiX так, чтобы расстояние max \yt— а0— aiXt\ меж-
между этими тремя точками и прямой было минимальным возможным.
Таким образом, в обоих случаях нужно определить наилучшее
Т-приближение относительно точек Р {, Р2, соответственно Р4,
Ръ Р3. Пробуя различные положения прямых на рисунке, убе-
убедиться, что наилучшее приближение достигается тогда, когда оба,
соответственно все три, отклонения равны по абсолютной величине,
а знаки их чередуются.
Задача 2. Даны точки Р4 = (—4, 1) и Р2 = E, 4). Найти наи-
наилучшее Т-приближение вида g (x) = а^х.
Решение, g (x) = х/3. Отклонения равны и имеют один и тот же
знак.
Задача 3. Даны точки Р1 = @, 2) и Рг = F, 4). Найти наи-
наилучшее Т-приближение вида g {х) = atx.
Решение. Любая прямая g (х) = а^х с 1/3 <^ а4 <^ 1 будет наи-
наилучшим Т-приближением.
Задача 4. Найти наилучшее Т-приближение вида ах2 + Ъх -\- 1
для 0 (нулевой функции) на отрезке [—1, 1].
Решение. Нам нужно подобрать коэффициенты а, Ь так, чтобы
минимизировать
max | ах2 -)- Ъх -\- 1 | .
При х = 0 имеем ах2 + Ъх -\- 1 = 1 для всех а, Ь. Поэтому добить-
добиться Т-отклонения, меньшего единицы, невозможно. С другой сто-
стороны, при а — Ъ = 0 Т-отклонение как раз равно 1. Более общим
образом, всякий многочлен вида —ах2 + 1 с 0^а^2 отклоня-
отклоняется на рассматриваемом отрезке от нуля не больше чем на 1.
Задача 5. Найти наилучшее Т-приближение вида ах2 + х + 6
для функции 0 на отрезке [—1, 1].
Решение. При х = ±1 имеем ах2 + х + b = а ± 1 + Ь. Раз-
Разность этих значений функции независимо от значений а и Ь равна 2.
Следовательно, наилучшее Т-приближение не может иметь Т-от-
Т-отклонения от функции 0, меньшего чем 1. Для того чтобы Т-отклоне-
Т-отклонение, равное 1, достигалось, необходимо, чтобы а + Ь = 0. Если
а = Ъ = 0, то мы имеем многочлен ах'1 + х + Ь = х с наибольшим
отклонением от нуля на отрезке [—1, 1], равным 1. Более общим
образом, всякий многочлен вида ох2 + х — а с \а\ <; 1/2 имеет
Т-отклонение от функции 0 на отрезке I—1, 1], равное 1.
Задача 6. Найти наилучшее Т-приближение вида х2 + ах + Ъ
для 0 на отрезке [—-I, 1].

146 3. Аппроксимации
Решение. Так как х2 + ах + Ь при х = ±1 принимает значения
1 ± а + Ь, а при х = О значение 6, то Т-отклонение не меньше
max (|1 + а\12, |1—а\12). Поэтому берем а = 0. Сравнив значения
многочлена х2 -\- b при л; = 1 и х = 0, мы найдем, что
|| х2 + Ъ || = max | х2 + Ъ | > max ( | 1 + Ъ \ , | Ъ \ ).
—\<х<\
Правая часть минимальна при Ь = —1/2. Итак, мы нашли, что
х2 — A/2) дает наилучшее Т-приближение для 0 на отрезке [—1, 1].
Это решение единственно.
Задача 7. Непрерывную функцию / (х) на отрезке la, b\ мы
хотим приблизить в смысле Т-нормы многочленом Р (х) =^
степени <^я. Показать, что если для некоторого такого многочлена
Р0{х) функция-отклонение / (х) — Р0{х) в п + 2 последовательных
точках а <: х{ < х2 < ... <хп+2 <; Ъ принимает значения положи-
положительного и отрицательного знака поочередно, то для Т-отклонения
справедлива
min |
Р(Л =
оценка
/(*;)-
Ро
min
,(*;) 1
max
<р(Л-
1/
(х) — Р{х) |
max | f{x) —
a<x<b
Ро
(X)
(теорема Балле-Пуссена).
Решение. Так как Р0{х) является возможным кандидатом в наи-
наилучшие приближения, то по определению Т-отклонения правая
часть неравенства выполняется. Допустим, что не выполняется
левая часть, т. е. что
mini/&)-/>„&) |>Р(/).
Пусть Q (х) — наилучшее Т-приближение для / (х) на [а, Ь]. Тогда
многочлен Р0(х) — Q (х) в точках xt (i = 1, ...,« + 2) принимает
значения положительного и отрицательного знака поочередно и
имеет, следовательно, п + 1 нулей. Но это противоречит основной
теореме алгебры.
Задача 8. Используя теорему Валле-Пуссена, доказать такой
факт. Пусть для непрерывной функции / (х) на [а, Ь] требуется
найти наилучшее по Чебышёву приближение в виде многочлена
степени <д. Если у функции-отклонения / (х)—Р(х) имеются п+2
последовательно идущих экстремальных точек xt (i = 1, ... , я+2),
в которых она принимает свое наибольшее по абсолютной величине
значение попеременно с положительным и отрицательным знаками,
т. е. если
f(x)-P(x) || , где 1= ±1,

3.3. Теория приближений 147
то Р (х) является наилучшим Т-приближением для / (х) на [а, Ь].
Решение. По теореме Валле-Пуссена
min | f(Xi)-P(Xi) |<p(/) < max | f(x)-P(x) \ .
I a<x<b
Поскольку | / (Xi) — Р (xt) | = max \ f (x) — P (x) \ , отсюда cpa
a<x<b
зу следует наше утверждение.
Определение 1. Эги п + 2 экстремальные точки функции-от-
функции-отклонения, в которых она последовательно меняет знак, называют-
называются точками альтернанса.
Усилением только что доказанного факта служит следующая
важная
Теорема об альтернансе. Пусть непрерывную в отрезке la, b]
функцию f (x) требуется приблизить в смысле Т-нормы многочле-
многочленом степени <^я. Многочлен Р(х) является наилучшим приближе-
приближением для функции f (x) тогда и только тогда, когда имеется л+2
точек альтернанса.
Мы уже показали, что условие альтернанса достаточно для того,
чтобы приближение было наилучшим. Доказательство необходи-
необходимости этого условия см., например, у Раиса [ 196431.
Используя характеризацию наилучшего приближения, давае-
даваемую теоремой об альтернансе, можно в простейших случаях нахо-
находить многочлен наилучшего приближения. Отметим, что теорема
об альтернансе верна не только для приближения многочленами,
а и для приближения функциями, удовлетворяющими так называе-
называемому условию Хаара (см., например, Мейнардус П964Р).
Задача 9. Для непрерывной на отрезке [а, Ь] функции / (х) с
минимальным значением т и максимальным значением М найти
наилучшее Т-приближение вида g (х) = а0.
Ответ, g (х) = (т + М)/2.
Задача 10. Для дважды непрерывно дифференцируемой на от-
отрезке [а, Ы функции / (х), удовлетворяющей всюду на этом отрезке
условию f"(x)> 0, найти наилучшее Т-приближение вида g (х) =
= а0 + ахх.
Решение. Согласно теореме об альтернансе многочлен g (x) =
= а0 + ахх тогда и только тогда является наилучшим приближе-
приближением, когда имеются 3 точки альтернанса хи х%, х3. Точка х2 за-
заведомо должна лежать внутри отрезка [а, Ь], и потому должно вы-
выполняться соотношение
fW-/W = 0, т. e. f'(x,) = ai.
Так как f"(x)> 0, то f'(x) монотонно возрастает и, следовательно,
1 Или у Бахвалова [ 19751. Теорема об альтернансе обычно называется
теоремой Чебышёва. — Прим. перев.
2 Или Березин и Жидков [1966]. — Прим.. перев.

148
3. Аппроксимации
может принимать значение ai только один раз. Значит,
и х3 = Ъ. Согласно теореме об альтернансе имеем
f(a)-g (а) = / (Ь) - g ф) = - (/ (х2) - g (x2)).
Из этих уравнений следует, что
= f(b)-f(a)
1 Ь-а
Задача И. Построить графически наилучшее приближение вида
g (х) = а0 + aix для дважды непрерывно дифференцируемой функ-
функции / (х) на [a, b\ cf"(x)>0.
Решение. Равенство а4 = (/ (Ь) —/ (а))/{Ь—а) из задачи 10 оз-
означает, что (см. рис. 3.3.1) прямая g (х) = atx + а0 должна быть
N
М
Рис. 3.3.1.
параллельна хорде MN, соединяющей точки (a, f (а)) и (b, f (b)).
Если записать уравнение для наилучшего приближения в виде
аМ-Ш±Ш = а.(х-2±
то становится ясно, что искомая прямая должна проходить через
середину D хорды MQ, соединяющей точки (a, f (а)) и (с, / (с)).
Таким образом, искомое наилучшее приближение дается изобра-
изображенной на рисунке прямой g.
Задача 12. Найти наилучшее Т-приближение в виде многочлена
первой степени g (х) = а0 + atx для функций
a) V
b)
с) f{x) = arctg*

3.3. Теория приближений 149
на отрезке [0, 1]. (В случае (а) определить наилучшее приближение
и графически.) Как велика погрешность?
Ответ.
a) g(x) = x + -1 ,
b) g(x) =х+~^
c) g (х) = 0,7854л: + 0,0355.
Задача 13. Применяя формулу sin Зх = 3sin х — 4siiA:, мы
можем вычислять любые значения синуса, если только знаем его
значения на отрезке [0, я/6]. Найти для sin x наилучшее чебышёв-
ское приближение на отрезке [0, я/6] при помощи линейной функ-
функции (воспользовавшись результатами задачи 11) и вывести элемен-
элементарное правило для вычисления sin x.
Решение. Прямая gt, проходящая через точки @, 0) и (я/6, 1/2),
имеет уравнение
о
у = —хта 0,955 х.
те
Параллельная этой прямой касательная g2 к синусоиде касается
ее в точке (arc cos C/я), sin (arc cos C/я))); уравнением этой каса-
касательной будет
у = — х + — (V*2 — 9 — 3 arc cos —) « 0,955 х + 0,010.
Уравнение прямой, параллельной этим секущей и касательной и
равноудаленной от них, таково:
у = — х + — (|/^Г9—3 arc cos —) « 0,955л; + 0,005.
Следовательно, элементарное правило для вычисления значений
синуса гласит:
sin х «0,995л; + 0,005;
при этом справедлива оценка
| sin х — 0,995л- — 0,0051 < 0,005.
Если бы мы вычисляли по известному правилу sin x « х, то при
л; = я/6 получили бы погрешность (я/6)—A/2) «0,0236, т. е. бо-
более чем четырехкратную.
Модификация. Если желательно ограничить относительную по-
погрешность, то можно аналогичным образом построить приближение
для sin xlx.

150 3. Аппроксимации
Задача 14. Рассматривается функция / (х) — Их на отрезке
[1, 2]. Определить для нее наилучшее Т-приближение и наилучшее
среднеквадратичное приближение вида
a) g(x) = a0,
b) g (х) = а0 + atx.
Указать погрешность приближения. Определить с помощью теоре-
теоремы Валле-Пуссена границы для Т-отклонения; при этом в качестве
«функции сравнения» Р0(х) использовать наилучшее приближение,
полученное по методу наименьших квадратов. Нарисовать графики
заданной функции, приближающих функций и функций-отклоне-
функций-отклонений.
Решение. Для наилучшего среднеквадратичного приближения
должно быть минимальным выражение
\1/2
~g(x)fdx\ ,
а тем самым и
Приравнивая к нулю частные производные последнего выражения
по at, получаем нормальные уравнения, из которых можно опреде-
определить коэффициенты аю наилучшего приближения в смысле Гаусса.
a) aOG = ln2, погрешность s2=0,0195,
aQT = 0,75, погрешность е = 0,25.
b) a0Q = — 0,4767, аю = 1,4081, погрешность е2=0,0007,
1_ _ 3 _1
аот~- 2 ' arr-— +yf~
= 1,4571, погрешность е =0,0429.
Задача 15. Пусть среди всех многочленов я-й степени g (x)
является наилучшим Т-приближением для функции / (х) на отрезке
[а, Ь], и пусть h (х) — какой-нибудь другой многочлен n-й степени.
Что будет тогда наилучшим Т-приближением для / (х)—h (x)?
Ответ, g (х)—/г (х).
Задача 16. Пусть функция / (х) непрерывна на отрезке [a, b\ и
g (x) — наилучшее ее Т-приближение в классе многочленов степени
не выше п. Доказать единственность этого наилучшего приближе-
приближения.

3.3. Теория приближений 151
Решение. Пусть многочлены g (x) и h(x) — наилучшие Т-прибли-
жения для / (х). Тогда многочлен (g (x) + h (x))/2 тоже будет мно-
многочленом наилучшего Т-приближения, так как
1 1 I
2 ^2 2
< —Р(Л + — Р(/)=р(/) для всех x6[a, b\.
По теореме об альтернансе в отрезке [а, Ь\ существуют точки xt <
< х2 < ... <хп+г, такие, что
i
/ (xi) (S (xi) + h (xt)) — (— 1)' s E для i — 1 /if2,
2
где
l
s =
(£(*) +А (*))
6 = ±1.
Таким образом, выполняется соотношение
-у I/ (*i) -8 (**)] + —-U (xt) - h (xt)] - (- 1)«8 6,
откуда
/ (*i) — g (*i) = / (xt) — h (xt) = (— 1)' e I
и, значит, многочлен g (x)—h (x) имеет п -f- 1 нулей. Но отсюда
по основной теореме алгебры следует, что g (x) = h (x).
Задача 17. Почему эта теорема единственности не противоре-
противоречит результатам, полученным в задачах 4 и 5?
Задача 18. Найти многочлен вида g (х) = а0 + а2я2, дающий
наилучшее Т-приближение для функции f (х) = \1{хг + 1) на от-
отрезке [0, 1].
Указание. Произвести замену хг = |. Тогда рассматриваемая
задача сведется к нахождению многочлена вида g (Е) = а0 + а2|,
дающего наилучшее Т-приближение для функции f (|) = 1/(| + 1)
на отрезке [0, 1].
Задача 19. Для функции 4л;3 — Зх на отрезке I—1, 1] найти
наилучшее Т-приближение вида g (х) = а0 4- atx и указать точки
альтернанса.
Ответ, g (х) = 0. Существующие по теореме об альтернансе
три- точки альтернанса определяются неоднозначно.
Задача 20. Показать, что если функция f (x), для которой ищет-
ищется наилучшее Т-приближение в виде многочлена степени не выше
п, имеет (п + 1)-ю производную, не обращающуюся в нуль внут-
внутри отрезка [а, Ь], то существует ровно и + 2 экстремальных точек.
Концевые точки отрезка принадлежат к числу точек альтернанса.

152
3. Аппроксимации
Решение. Пусть многочлен п-й степени g (х) служит наилучшим
Т-приближением для функции / (х). Тогда по теореме об альтернан-
се существуют п + 2 точек хь хг, ... , хп+2, таких, что
£.(*i) = (—!)'£ И Для »=1,2,...,л + 2,
где|=±1, e(x) = f(x)—g(x).
Если бы функция-отклонение е (х) имела экстремальных точек
больше, чем указанные п + 2, т. е. если бы ее график был бы при-
примерно такого вида, как на рис. 3.3.2, то существовало бы такое
П'1
е(х)
е(х)
_ у
Рис. 3.3.2.
число с с \с\^ ||е||, что функция е (х)—с обращалась бы в нуль по
крайней мере в п -\- 2 точках. Но тогда по теореме Ролля (п + 1)-я
производная функции е (х)—с, которая в силу соотношения
«=0
), обращалась бы в нуль по крайней мере в одной точ-
точке, вопреки сделанному предположению.
При помощи соответствующего построения (см. рис. 3.3.3) и
рассуждения показывается, что концевые точки отрезка являются
точками альтернанса.
Задача 21. Доказать, что при приближении непрерывной чет-
четной (соотв. нечетной) функции / (х) на симметричном относительно
нулевой точки отрезке, скажем на отрезке [—1, 1], многочленами
степени не выше п наилучшее приближение также будет четной
(соотв. нечетной) функцией.
Решение. Пусть / (х) — нечетная функция, т. е. / (х) = —f(—x)
для всех х 6 [—1, И, и g (x) — ее наилучшее Т-приближение.
Тогда
р(/)= max \f(x) — g(x)\= max \f(—x)—g(—x)\ =
= max | —f(—x) + g(—x)| = max \f(x) + g(—x)\.

3.3. Теория приближений 153
Из единственности наилучшего приближения1 следует, что g (х) —
= —g (—х) для всех х 6 [—1. И, т. е. что функция g (x) нечетна.
Доказательство для случая, когда / (х) — четная функция, про-
проводится совершенно аналогично.
Задача 22. Пусть на отрезке [—1, 1] определены четная функ-
функция / (х) и нечетная функция g (x). Показать, что для Т-отклонения
при Т-приближении многочленами п-й степени выполняется соот-
соотношение
Р(/ + £)> max (p(/), pig)).
Решение. Пусть многочлен h (х) является наилучшим Т-приб-
Т-приближением для функции f (x) + g (x). Тогда
\f(x)+g(x)-h(x)\^p(f+g) для всех *£[—1,1]
и
|/(— x) + g(—x) — h(— х) |< р (f + g) для всех *6[— 1,1]
Складывая эти два неравенства и учитывая, что f (х) = f (—х) и
g (х) = —g (—х), получаем
/(д)_-1(й(д) + й(—*)) <p(/ + g) для всех *6[—1,1].
Поскольку (h (х) + h (—х))/2 также является многочленом степени
<фг, отсюда следует, что р (/) ^ р (/+<§■)• Аналогично показываем,
что р (£)< р (/ + g)-
Задача 23. Среди всех многочленов (п — 1)-й степени отыскать
наилучшее Т-приближение для функции / (х) = хп на отрезке
[-1, П.
Решение. По теореме об альтернансе для наилучшего приближе-
приближения g (х) должны найтись п + 1 точек xi < х2 < ... < xn+i, та-
таких, что
е(*,) = Д? —£(*,) = (—1)'£||е|| (»=1,2, ..., л + 1),
где
£=±1, б(х)
Во всех внутренних точках хи значит по крайней мере в п — 1
точках, которые мы обозначим через xt , г = 1, ... , п — 1, должно
быть e'(xi ) = 0. Так как е (х) — многочлен п-й степени, то е'(х)—
многочлен (п—1)-й степени и, следовательно, все корни х{ явля-
являются простыми. Пусть h (х) = в(хJ—р2, где р= ||е||. Все внут-
внутренние экстремальные точки для е(х) являются двойными корнями
для h (х), потому что для них, в силу равенства s'(x(- ) = 0,
h' (*.r) = 2s (xir) ■ г' (xir) = 0.
1 См. задачу 16. — Прим. ред.

154 3. Аппроксимации
Так как, далее, |е (±1I = р1, то должно выполняться соотношение
е2 (х) — р2 = М A — х2) s'2 (х) для всех х 6 [— 1, 1].
Приравнивая старшие коэффициенты, получаем, что М = 1/л2.
Таким образом,
Кр2 — в2 (х) = ± — VI—х2 е' (х).
/г
При переходе через каждую точку альтернанса производная е'(х)
меняет знак. Если в промежутке (а, Р) она положительна, то в
этом промежутке
е' (АС) П
У р2 — е2 (дг) у 1 — л;2
Интегрирование дает
arc cos _1Ш_ = п arc Cos д: -f- С,
Р
откуда
б (х) = р cos (n arccos x + С),
или
е (х) = р [cos С cos (n arccos х) — sm С sin (n arccos x)\
Поскольку е (х) — многочлен, то должно быть sin С = 0 и, следо-
следовательно, cos С = ±1. Но согласно2 задаче 25 старший коэффи-
коэффициент в выражении cos (n arccos х) равен 2". Значит, cos С = 1
и р = 1/2". Таким образом, е (х) = (l/2")cos (/г arccos x) есть
многочлен со старшим коэффициентом 1, дающий в интервале (а,
Р) наилучшее приближение для нулевой функции. Но если два
многочлена совпадают в сколь угодно малом интервале, то они
совпадают всюду. Следовательно, многочлен g (x) =
= (l/2"-1)cos (n arccos x) есть многочлен со старшим коэффициен-
коэффициентом 1, служащий на отрезке [—1, 1] наилучшим приближением
для нулевой функции. Ясно, что его Т-отклонение от нуля равно
1/2".
Определение 2. Многочлены Тп(х) = cos (n arccos x) называются
многочленами Чебышёва (или Т'-многочленами) п-й степени.
Задача 24. Доказать, что для всех п справедлива формула
п—\
cos/iS = 2" cos" б + У Х{п) cos* б,
/=0
где Я((,п> , X\n) , .... Я^, —некоторые постоянные.
1 См. задачу 20. — Прим. ред.
2 Нижеследующей. — Прим. ред.
2

3.3. Теория приближений 155
Решение. Проведем доказательство по индукции. Для п = 1
наше утверждение очевидно, так как cos 9 = cos 9 + 0. Пусть
оно верно для всех т <; п. Покажем, что оно верно для п + 1.
Поскольку
, о r> a — Р Я + 8
cos a + cos р = 2 cos — cos ——— ,
имеем
cos(n+ 1)9 +cos (n—1)9 = 2cos9cos«9. (=•)
Отсюда по предположению индукции следует, что
Г л—1 1 п—\
cos (п + 1) 9 = 2 cos 9 2" cos" 9 + ^ Я,)п) cos* 9 — ^ ^ cos* 6
и, значит,
л
cos (п + 1) 9 = 2" cosn+19 + V v; cos' 6.
«=0
Задача 25. При помощи выведенного в задаче 24 соотношения
показать, что многочлен Чебышёва Тп(х) = cos (n arccos x) дейст-
действительно является многочленом п-й степени.
Указание. Положить 9 = arccos х для —1 <^ х ^ 1.
Задача 26. Указать точки альтернанса при Т-приближении
функции хп на отрезке [—1, 1] многочленом (п—1)-й степени.
Ответ. xt = cos {inIn), i = 0, 1, 2, ... , п.
Задача 27. Вывести из формулы (*) задачи 24 рекуррентную
формулу
Тп (х) = 2х Tn_i (х) — Тп_2 (х) для всех п
и с ее помощью вычислить первые 5 многочленов Чебышёва. Нари-
Нарисовать их графики.
Ответ. То = 1, Tt = х, Тг = 2х2— 1, Т3 = \хъ—Ъх, Г4 = 8х4—
82
Задача 28. Для функции / (х) = anxn+an_ixn~1+ ... + ^0
на отрезке [а, Ь] найти наилучшее Т-приближение среди многочле-
многочленов степени <; п —1 и показать, что Т-отклонение равно
Ь— а
Указание. Свести эту задачу к задаче о наилучшем Т-приближе-
Т-приближении функции х" на отрезке [—1, 1] многочленом (п—1)-й степени,
положив

156
3. Аппроксимации
а. ft].
Задача 29. Каковы первые 5 многочленов Чебышёва для
резка [0, 1]?
Ответ: Г0(х) = 1,
от-
отГ2(х) = 8х2 —
Т\ (х) = 32д;3 — А8х2 + 18х — 1,
Г4 (х) = 128х4 — 256д;3 + 160x2
Задача 30. Найти многочлен степени -^4, который дает наи-
наилучшее Г-приближение для функции / (х) = хъ на отрезке [0, 3].
Задача 31. Отыскать для функции / (х) = х3 на отрезке [0, 1]
наилучшее Т-приближение среди многочленов второй степени.
Задача 32. Аппроксимировать функцию / (х) = х3 на отрезке
[0, 1] линейной функцией, найдя многочлен первой степени, даю-
дающий наилучшее Т-приближение для многочлена, служащего отве-
ответом к задаче 31.
Задача 33. Найти многочлен первой степени, который дает
наилучшее Т-приближение для функции / (х) = х3 на отрезке [0, 1],
и сравнить его с результатом задачи 32.
Задача 34. Указать многочлен второй степени, который на от-
отрезке [0, 1] отклоняется от функции х* меньше чем на 1/10.
Решение. Для многочлена
Г; (х) = 128х4 — 256Х3 + 160ха — 32х + 1
1
п ри 0 <^ х <^ 1 справедлива оценка
i 2х3 _i_ JL. х2 —
4 4 ' ' 128
Аналогичным образом для многочлена
Т* (у\ . 49 у3
* 3 \ /
. Отсюда следует, что
i
^ 128 *
получаем
\2х3
х
16
<—•
16
1 Многочлены Т*п называются смещенными многочленами Чебышёва.—
Прим. перев.

3.3. Теория приближений
157
Следовательно,
х4 7 х2
4
4- 7 v
^ 8
7
128
1
"" 128
1
16
9
128
„ 1
- 10 "
Определение 3. Две функции f (х) и g (x) называются взаимно
ортогональными на отрезке [а, Ь\ с весом р (х), если
\p(x)f{x)g{x)dx=0.
а
Задача 35. Показать, что два многочлена Чебышёва Тп(х) и
Тт(х) взаимно ортогональны на отрезке [—1, 1] с весом р (х) =
1—х2. Точнее,
0 при тфп,
к при т = п = 0,
— при т = л>0.
Указание. Сделать подстановку х = cos 9.
Задача 36. Пусть возможно разложение функции / (х) в ряд по
многочленам Чебышёва:
jTj{x). (**)
Tn(x)Tm{x)
Показать, что коэффициенты разложения вычисляются по форму-
формулам
2 »• / (х) 7) (х)
ci = — -==: dx
Л Д ]/ 1 — *2
} = 0, 1, 2
Указание. Умножить разложение (**) на Tj(x) и воспользовать-
воспользоваться результатом задачи 35.
Задача 37. Разложить функцию / (х) = \х\ на отрезке [—1, 1]
в ряд по многочленам Чебышёва. Оборвав этот ряд на втором чле-
члене, сравнить полученное приближение h (x) с наилучшим Т-приб-
лижением g (х) вида а2х2 + atx + а0.
Ответ. |*| = А + ±
■К ж
in1 —
(х),

158 3. Аппроксимации
3.4. Гармонический анализ
Наложение друг на друга двух синусоидальных колебаний од-
одной и той же частоты, но с различными фазами и амплитудами снова
дает синусоидальное колебание той же частоты, но, вообще говоря,
с новыми фазой и амплитудой. Далее, наложение гармонических
колебаний различных частот, кратных некоторой одной частоте,
скажем колебаний A 4sin (со^ + ф!), A2sin B&t + <p2), ...
...,Ansm(n<ut + Tn)> Дает некоторое периодическое колебание,
имеющее частоту самого медленного колебания. Колебание
Аг sin (<ot + ф4) называют при этом основным колебанием, его пе-
период Т —• основным периодом и его частоту / = оз/2я — основной
частотой. Прочие колебания называются обертонами. В зависи-
зависимости от величины амплитуд составляющих колебаний и их фаз в
результате наложения могут получаться колебания самых разно-
разнообразных форм, но все имеющие период Т.
Теперь ставится вопрос, можно ли разложить периодическое
колебание наперед заданных формы и периода в бесконечный ряд
гармонических частичных колебаний. Выяснением этого вопроса
и занимается гармонический анализ, где исследуют, допускает ли
заданная на некотором отрезке функция приближение в виде три-
тригонометрического многочлена п-й степени или, более общо, разло-
разложение в бесконечный ряд по тригонометрическим многочленам.
Формально каждой функции / (х), интегрируемой на отрезке
I—тг, тг], можно сопоставить ряд вида
1 °°
— ао + ^ (а" C0S ПХ + Ь" sin "**
с коэффициентами, зависящими только от /. Этот ряд называется
рядом Фурье, соответствующим функции / (х) (или рядом Фурье
для / (х)). Возникает вопрос, сходится ли ряд Фурье для данной
функции f (х) при всех или лишь при некоторых определенных зна-
значениях х, и если при всех, то сходится ли он к / (х). Ни на один из
этих вопросов на сегодня нет полного ответа. Все же имеется сле-
следующий часто используемый результат.
Пусть кусочно гладкая функция / (х) определена в отрезке
[—-тг, тг] и вне этого отрезка периодически продолжена с периодом
2тг. Ряд Фурье, соответствующий этой функции, во всех точках х,
в которых / (х) непрерывна, сходится к / (х), а во всех точках х,
в которых имеются разрывы, сходится к среднему арифметическо-
арифметическому односторонних предельных значений слева и справа, т. е. к
(/ (х—0) + / (*+0))/2.
(Функция / (х), определенная на некотором отрезке, называется
кусочно гладкой, если она сама кусочно непрерывна, т. е. непрерывна
на всем отрезке, за исключением конечного числа точек, где она

3.4. Гармонический анализ 159
имеет разрыв первого рода1, и если кусочно непрерывна также ее
первая производная j' (x). Доказательство см., например, у Смир-
Смирнова [1974].)
Определение 1. Всякая система функций /х(х), f2(x), ... , опре-
определенных на отрезке [а, Ь], для которой
ь
[ ft (х) fi (x) dx = 0 при i ф},
а
называется ортогональной системой.
Задача 1. Показать, что на отрезке [—я, я] косинусы cos nx
(п = 0, 1, 2, ...) и синусы sin nx (n = 1, 2, ...), взятые как порознь,
так и в совокупности, образуют ортогональную систему функций.
Задача 2. Пусть на отрезке [—я, я! задана функция / (х). Сре-
Среди тригонометрических многочленов степени не выше п подыскать
наилучшее приближение для / (х) по методу наименьших квадра-
квадратов.
Решение. Коэффициенты тригонометрического многочлена
V = l
надо определить так, чтобы минимизировать величину
п
— h — У. (К
cos v* + Кsin
v=l
Раскрывая квадрат под знаком интеграла и пользуясь соотноше-
соотношениями ортогональности
■к (
f sin nx sin mxdx=\
—X (
II
Г sin nx cos mx dx — 0,
0 при тфп,
к при т = п,
0 при тфп,
Г cos nx cos mxdx= I 2ir при m = n = 0,
ir при т~пфО,
1 Такие разрывы характеризуются существованием односторонних пре-
предельных значений слева и справа. — Прим. ред.

160 3. Аппроксимации
получаем
Ж 1С П 1С
$ = Г f» (х) dx + j k\dx + 2 k\ j cos2 vjc At +
v=l
n
— 2^0 j f(x)dx — 2^ k^ J
l
/ (X) cos vx dx —
V=l — 1С
— 2 У l Г / (x) sin vx dx.
V=l —1С
Введя величины
1 г 1 г
а =— / (х) cos vx dx и 6 =— /(x)sinvxdx,
Я J 1С J
—тс —к
перепишем последнее соотношение в виде
я
V=l
и далее в виде
— 2У k а т:-2У I b к
[-2
V=l
v=l
Величина R будет наименьшей при k0 = ao/2, ftv = av, /v = 6v для
v= 1, ..., п. Таким образом, наилучшим приближением в смысле
Гаусса для f(x) является
1
g (х) = — а0 + ^ (flv cos VJC + 6vsin
v=l
Замечание. Если в качестве приближающих функций брать ли-
линейные комбинации элементов любой другой ортогональной си-
системы, то наилучшее приближение по методу наименьших квадра-
квадратов можно определить совершенно таким же образом.

3.4. Гармонический анализ
161
Определение 2. Ряд
cos
sin
с коэффициентами
1
а„ = — \ f(x) cos nx dx.
(л = 0, 1, 2,...)
= — \ f (x) sin nx dx
1С
называется рядом Фурье, соответствующим функции f (x).
Задача 3. Какой вид имеет ряд Фурье четной, соответственно
нечетной, функции?
Ответ. Ряд Фурье четной функции содержит только члены с
косинусами, нечетной — только члены с синусами.
Задача 4. а) Найти ряд Фурье для функции / (х) = \х\ при
х 6 I—л, я! и представить графически приближение этой функции
с помощью тригонометрического многочлена четвертой степени.
Ь) Найти сумму ряда
т 1
А Bп -
]
Решение, а) Так как периодическое продолжение функции
/ (х) — \х\ является непрерывным и кусочно гладким, то ее ряд
Фурье на отрезке [—я, я! сходится к ней, а вне этого отрезка —
к ее периодическому продолжению. Имеем
ао= — \ \x\dx — — I хйх — к,
ТС J
следовательно,
4
7

162 3. Аппроксимации
b) Подставив в соотношение (*) х = О, получаем
Bл-1)"
Задача 5. а) Найти ряд Фурье для функции / (х) = х в про-
промежутке [—я, я].
Ь) Найти сумму ряда
2л —1
Решение, а) Функция / (х) = л: нечетна, и ее периодическое
продолжение есть кусочно гладкая функция с разрывами в точках
х = Bk + 1)я, k = О, ±1, ±2, .... Согласно приведенной выше
теореме, ряд Фурье сходится в промежутке —я < х<.п кхив
точках разрыва к 0. При —я <. х<Сл имеем
х=2\ (-Un-iJlRJE.
n=l
b) Подставив в полученное разложение х — тс/2, находим:
2я — 1 4
Задача 6. Найти ряд Фурье для функции / (х) = х2: а) в про-
промежутке @, 2я); Ь) в промежутке (—я, я). Что можно утверждать
о сходимости ряда Фурье в самом промежутке и в концевых точках?
Ответ.
со
\ 4и2 ,, V4 / cos nx it sin nx
a/ —;; r
Л2
Ряд сходится в промежутке @, 2я) к / (х) = х2, а в концевых
точках — к 2я2.
со
U\ л 'V' / 1 \п cos nx
1 -^ п~2 '
Ряд сходится во всем замкнутом промежутке [—я, я] к / (х) —х2.
Задача 7. Найти выражения для коэффициентов ряда Фурье
кусочно гладкой функции / (х), определенной на произвольном
интервале [а, а + /].
Решение. Положим

3.4. Гармонический анализ
163
Когда точка х пробегает интервал [а, а + /], точка £ пробегает
интервал [—я, к]. Ряд Фурье для функции g(Q в интервале
[—к, к] имеет вид
' OS
8 (I) = " + У, « cos ng + bn sin лЕ) ,
где
(n=0, 1. 2, ...)
= -L J /(^-g + ^+aj
„ ^ 2u 2ti
Полагая | = x — к а, получаем
n=\
i— x + basinn — x\,
где
a+l
an= — j f(x) cosn^-xdx,
bn= ( /Wsin n——
(n = 0, 1,2, ...).
Задача 8. Найти ряды Фурье для указанных на рисунке функ-
функций (форм колебаний). Ниже со = 2tJT.
Г Прямоугольные функции.
= -^-jsincox -\ sin3ox +
si
5
f (x) = COS (OJC COS 3@X +
TZ |_ 3
J
Н cos5coa: + ... 1.
5 J 1

164
3. Аппроксимации
2° Односторонняя прямоугольная функция.
) = — + — [sincox + —sin Зш: +
2 тс I 3
siпбш:
3° Пилообразные функции.
f (х) = — sin ш -| sin 2ш: +
2
—sin3(ox
1
...
1
.I
94 Г 1
f(x)= — sin cox !-sin2(uJC
n [ 2
1 1
-\ sin3(ox—...
3 J
4° Треугольные функции.
/ (x) = sin cox sin Зшл; -(-
' w яг I 9
+ -^-sin5<ax—...I
/ (jc) = cos ax -\ cos Зш: +
u 9
_!_ cos 5ax + ...
25 J
5° Односторонняя треугольная функция.
/ (х) = — + -^- [coscox + — cos Зш: +
1 1 2/4 Г
Н cos 5(ujc + ... + —- cos 2ых +
25 J к |
25
|_
1 1 1
Н cos бсохН cos IOcojc + ... .
У 25 J
6° Трапециевидная функция.
I in г
и 2ic
о = а— =асо,

3.4. Гармонический анализ 165
АЛ Г
/ (х) = — sin b sin (их +
— sin36 sin3cojc + ... . _yo \ /г
7° Модуль синусоиды.
2
2Л Г, 2
= 1
11 |_ 1 •
coscox —
О
о 2 "I
cos 2ш: cos Зш: —... .
3-5 5-7 J
8° Положительная часть синусоиды.
2 2 1
:—г cos 2а>х — -—- cos 4ых — ... ,
1-3 3-5
Задача 9. Разложить функцию f (х) = х2 — х при 0< х
(продолжив ее соответствующим образом): а) в ряд, содержащий
только синусы; Ь) в ряд, содержащий только косинусы.
Указание. Ряд, содержащий только синусы (соотв. косинусы),
получим, продолжая функцию f (х) = х2 — х на промежуток
(—я, 0) как нечетную (соотв. четную) функцию.
Задача 10. Пусть на промежутке @, я) задана функция / (х)=
= х2(п—х). Беря различные ее периодические продолжения, полу-
получить различные разложения в ряд Фурье. Продолжить ее, в част-
частности, так, чтобы результирующая периодическая функция / (х)
a) была четной с периодом 2я (т. е. / (х) = / (—х) и / (х + 2я)=
b) была нечетной с периодом 2я (т. е. / (х) = —/ (—х) и
f(x + 2П) = f (х));
c) имела период % (т. е. / (х + я) = / (х));
d) имела период 2тс (т. е. / (х + я) = / (х)) и, кроме того, удов-
удовлетворяла условию / (х + я) = —/ (х).
Нарисовать эти продолжения. Какие особенности отличают
каждый из соответствующих рядов Фурье?
Ответ. Ряд Фурье содержит
a) лишь косинусы;
b) лишь синусы;
c) как синусы, так и косинусы, но и те и другие лишь для чет-
четных п;
d) как синусы, так и косинусы, но лишь для нечетных п.
Во многих случаях функция, ряд Фурье которой желательно

166
3. Аппроксимации
найти, задана только в табличном виде. Тогда коэффициенты Фурье
надо находить численно. Примером может служить
Задача 11. Пусть в некотором колебательном процессе значе-
значения независимой переменной х (времени) и зависимой переменной
у = / (х) задаются таблицей:
X
У
0
—2
тс/6
—0,62
тс/3
0,62
it/2
1
2я/3
0,88
я/6
1,12
7я/6
2,85
2,61
Зя/2
5я/3
Пя/6
— 1,12—2,35—!
Приблизить наше колебание тригонометрическим многочленом
третьей степени, оборвав разложение в ряд Фурье на третьем чле-
члене. Изобразить это приближение графически.
Указание. Функция / (х) определена не на всем отрезке [0, 2я],
а лишь в дискретном множестве равноотстоящих точек Xj = xo-\-jh,
где х0 = 0, h = u/6, / = 0, ... , 12. Для вычисления интегралов,
которыми выражаются коэффициенты Фурье, разбиваем интервал
[0, 2я] на п = 12 подынтервалов и к каждому из них применяем
формулу трапеций C.2.6). Тогда коэффициенты Фурье принимают
вид
2 ^
=Ot 1,2, ...).
2 "-1
— У
0
/=0
Замечание. К тому же самому результату мы придем, если рас-
рассмотрим нашу задачу как задачу дискретной аппроксимации и
потребуем минимальности величины
/ИГ m
2 /(^^)- 2
V /=о L *=
Q
Подробнее об этом см. у Цурмюля [1957].
TV/2
J /
СПИСОК ЛИТЕРАТУРЫ
К § 3.1
БерезинИ. С. и Н. П. Жидков, Методы вычислений, т. 1, 3-е изд.,
«Наука», М., 1966.
Островский A. (A. Ostrowski), Vorlesungen iiber Differential- und In-
tegralrechnung, т. 2, Basel, Stuttgart, Birkhauser, 1961.
Ц у р м ю л ь Р. (R. Zurmuhl), Praktische Mathematik, Berlin, Gottingen,
Heidelberg, Springer Verlag, 1957.
Штрубеккер К. (К. Strubecker), Einfiihrung in die hohere Mathema-
Mathematik, Miinchen, Oldenbourg, 1956.

3.4. Гармонический анализ 167
К § 3.2
Березин И. С. и Н. П. Жидков, Методы вычислений, т. 1, 3-е изд.,
«Наука», М., 1966.
Крылов В. И., Приближенное вычисление интегралов, 2-е изд., «Нау-
«Наука», М., 1967.
Цурмюль P. (R. Zurmiihl), Praktische Mathematik, Berlin, Gottingen,
Heidelberg, Springer Verlag, 1957.
Штифель Э. (Ё. Stiefel), Einfiihrung in die Numerische Mathematik,
Stuttgart, Teubner, 1965.
К § 3.3
Ахиезер Н. И., Лекции по теории аппроксимации, 2-е изд., «Наука»,
М., 1965.
'Березин И. С. и Н. П. Ж и д к о в, Методы вычислений, т. 1, 3-е изд.,
«Наука», М., 1966.
Демидович Б. П., И. А. Марон и Э. 3. Шувалова, Чис-
Численные методы анализа, 3-е изд., «Наука», М., 1967.
Мейнардус Г. (G. Meinardus), Approximation von Funktionen und
ihre numerische Behandlung, Berlin, Gottingen, Heidelberg, New York,
Springer Verlag, 1964.
Натансон И. П.. Конструктивная теория функций, Гостехиздат,
М—Л., 1949.
Райе Дж. (J. R. Rice), The approximation of functions, т. 1, Linear theory,
Addison-Wesley Publishing Company, 1964.
К § 3.4
'Бахвалов Н. С, Численные методы, 2-е изд. «Наука»," М., 1975.
•Березин И. С. и H.S П. Жидков, Методы вычислений, т. 1,
3-е изд., «Наука», М., 1966.
Островский A. (A. Ostrowsky), Vorlesungen iiber Differential- und
Integralrechnung, т. 3, Basel, Stuttgart, Birkhauser, 1954.
"Смирнов В. И., Курс высшей математики, т. 2, 21-е изд., «Наука»,
М., 1974.
Цурмюль P. (R. Zurmiihl), Praktische Mathematik, Berlin, Gottingen,
Heidelberg, Springer Verlag, 1957.
Штифель Э. (E. Stiefel), Einfiihrung in die numerische Mathematik,
Stuttgart, Teubner, 1965.
Штрубеккер К. (К. Strubecker), Einfiihrung in die hohere Mathema-
I;
tik, Miinchen, Oldenbourg, 1956.

ОГЛАВЛЕНИЕ
Предисловие редактора перевода , 5
Предисловие , , , 6
1. Уравнения с одним неизвестным < . 7
1.1. Введение . . < , 7
1.2. Элементарные методы , 8
1.3. Техника вычислений с многочленами , 15
1.4. Преобразование многочленов , 23
1.5. Теорема о неподвижной точке и итерации , 31
1.6. Метод Ньютона и метод ложного положения 38
1.7. Дополнения 47
Список литературы . . , < 56
2. Уравнения со многими неизвестными 58
2.1. Задачи на собственные значения для матриц , 58
2.2. Итерации в задачах на собственные значения . 69
2.3. Метод исключения для линейных систем уравнений ..... 75
2.4. Итерационные методы для линейных систем уравнений .... 85
2.5. Нелинейные системы уравнений 93
2.6. Номограммы н счетные линейки , . . , 102
Список литературы , 109
3. Аппроксимации ....,,,.,,.....,. ,111
3.1. Интерполяция , .111
3.2. Численное интегрирование 124
3.3. Теория приближений в нормированных функциональных простран-
пространствах. Чебышёвские приближения 143
3.4. Гармонически й анализ 158
Список литературы 166
ИБ № 474
Л. Коллатц, Ю. Альбрехт
ЗАДАЧИ
ПО ПРИКЛАДНОЙ МАТЕМАТИКЕ
Редактор В. И. Авербух. Художник А. В. Шипов. Художественный редактор В. И. Шапо-
Шаповалов. Технический редактор Г. Б. Алюлина. Корректор А. Я. Шехтер.
Сдано в набор 18/II 1977 г. Подписано к печати 28/VII 1977 г. Бумага тип. № 2
60X9071A=5.25 бум. л. 10,50 печ. л. Уч.-нзд. л. 8,57. Изд. № 1/8814. Цена 65 коп. Зак. 206.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2.
Ярославский полиграфкомбинат Союзполиграфпрома при Государственном комитете Совета
Министров СССР по делам издательств, полиграфии и книжной торговли.
150014, Ярославль, ул. Свободы, 97.