Г. ПАРКУС
Неустановившиеся
температурные
напряжения

Г. ПАРКУС
НЕУСТАНОВИВШИЕСЯ
ТЕМПЕРАТУРНЫЕ
НАПРЯЖЕНИЯ
Перевод с немецкого
В. И. РОЗЕНБЛЮМА
Под редакцией
Г. С. ШАПИРО
Ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1963

531
П 18
УДК 539.377
instationare
wArmespannungen
VON
HEINZ PARKUS
o. Professor an der technlschen
Hochschule in WIen
WIEN
SPRINGER-VERLAQ
1959
Л Tlaptcyc. Неустановившиеся температурные напряжения.
M., Физматгиз, 1963 г., 252 стр. с илл.
Редактор Н. И. Розалъская.
Гехн. редактор Я. Я- Мурашова. Корректор И. А Володяева.
Сдано в набор 4/1V 1963 г. Подписано к печати 2/VIII 19'63 г. Бумага 84xl08V32.
Физ.-печ. л. 7,875. Условй. печ. л. 12,92. Уч.-изд. л. 13,47.
Тираж 6000 экз. Цена книги 82 к. Заказ № 1311.
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой УЦБ и ПП Ленсовнархоза.
Ленинград, Измайловский пр., 29*

ОГЛАВЛЕНИЕ
Предисловие редактора русского перевода б
Из предисловия автора 8
Глава I. Некоторые общие законы термоупругости ... 9
§ 1. Основные уравнения 9
§ 2. Энергия деформации и принцип Даламбера .... 12
§ 3. Принцип Гамильтона. Минимум потенциальной
энергии 14
§ 4. Дополнительная энергия 16
§ 5. Однозначность решения 19
§ 6. Изменение объема 19
§ 7. Термоупругий потенциал перемещений 21
§ 8. Функция Грина 23
§ 9. Квазистатический анализ неустановившихся 1ермо-
упругих напряжений 26
Глава II. Процессы нагрева и охлаждения 30
§ 1. Мгновенный источник в неограниченной среде ... 30
§ 2. Мгновенный диполь в неограниченной среде .... 33
§ 3. Мгновенный источник на поверхности
полупространства; поверхность теплоизолирована 34
§ 4. Мгновенный диполь на поверхности
полупространства; температура поверхности постоянна 37
§ 5. Мгновенный местный нагрев поверхности
полупространства 41
§ 6. Сферическая полость в неограниченной среде ... 49
§ 7. Сплошной и полый цилиндры кругового поперечного
сечения; первое решение 54
§ 8. Сплошной и полый цилиндры кругового поперечного
сечения; второе решение 64
§ 9. Мгновенный нагрев цилиндра 67
§ 10. Длинный цилиндр, нагреваемый на участке
поверхности 74
§ 11. Длинный полый цилиндр, нагреваемый по всей
поверхности 79
§ 12. Длинный цилиндр, неравномерно нагретый в
окружном направлении , . . . . 87
§ 13. Температурные напряжения в сфере 94
§ 14. Точечный нагрев диска 99

4
ОГЛАВЛЕНИЕ
Глава III. Периодические изменения температуры . . . . 104
§ 1. Общие замечания 104
§ 2. Полупространство с периодически изменяющейся
температурой поверхности 105
§ 3. Периодический тепловой источник в
неограниченной среде 106
§ 4. Периодические линейные и поверхностные источники 108
Глава IV. Движущиеся источники тепла 111
§ 1. Общие замечания 111
§ 2. Движущийся точечный источник на поверхности
полупространства 113
§ 3. Движущийся точечный источник на поверхности
тонкой пластины 116
§ 4. Вращающееся температурное поле 120
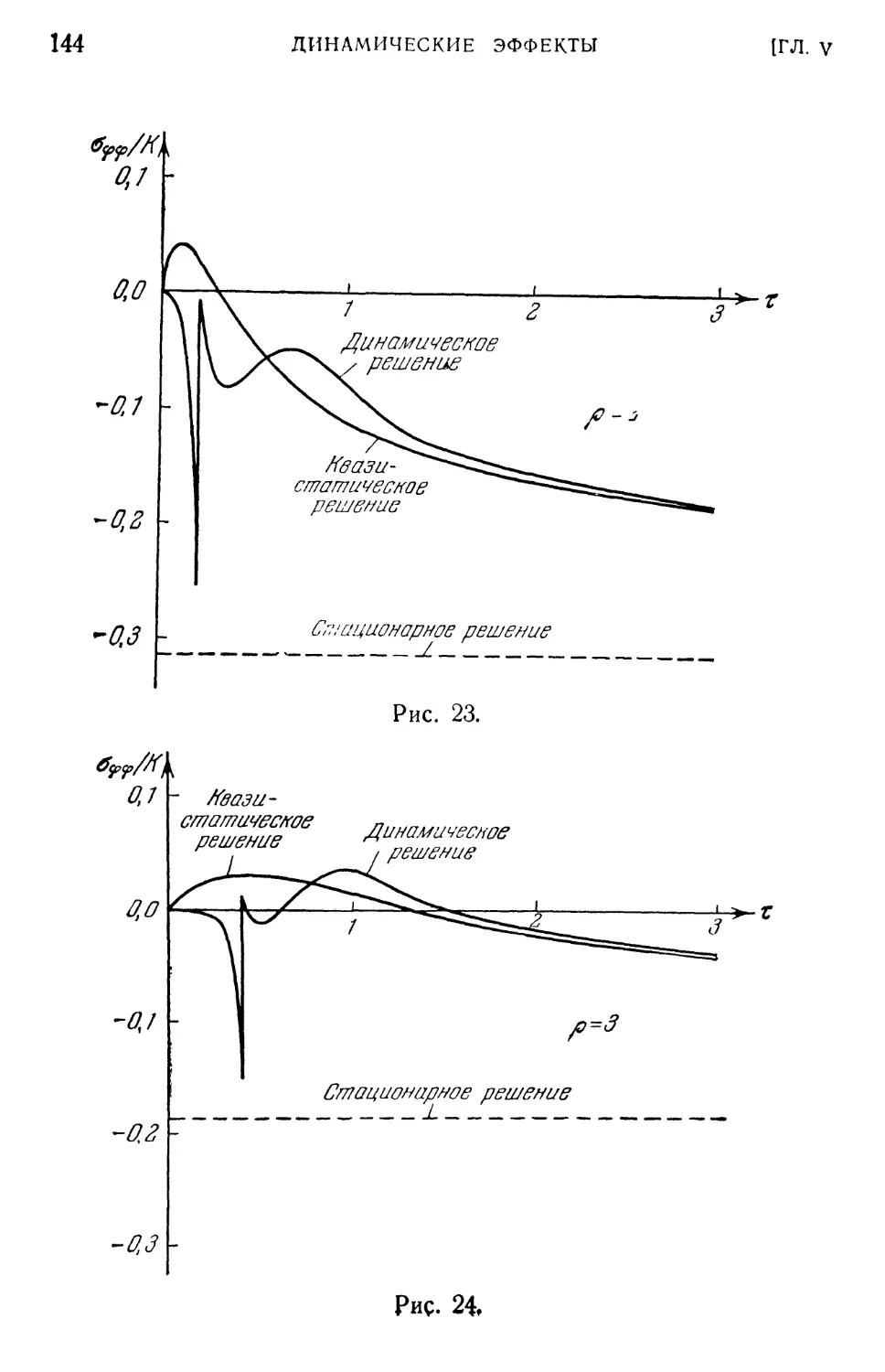
Глава V. Динамические эффекты 126
§ 1. Общие замечания 126
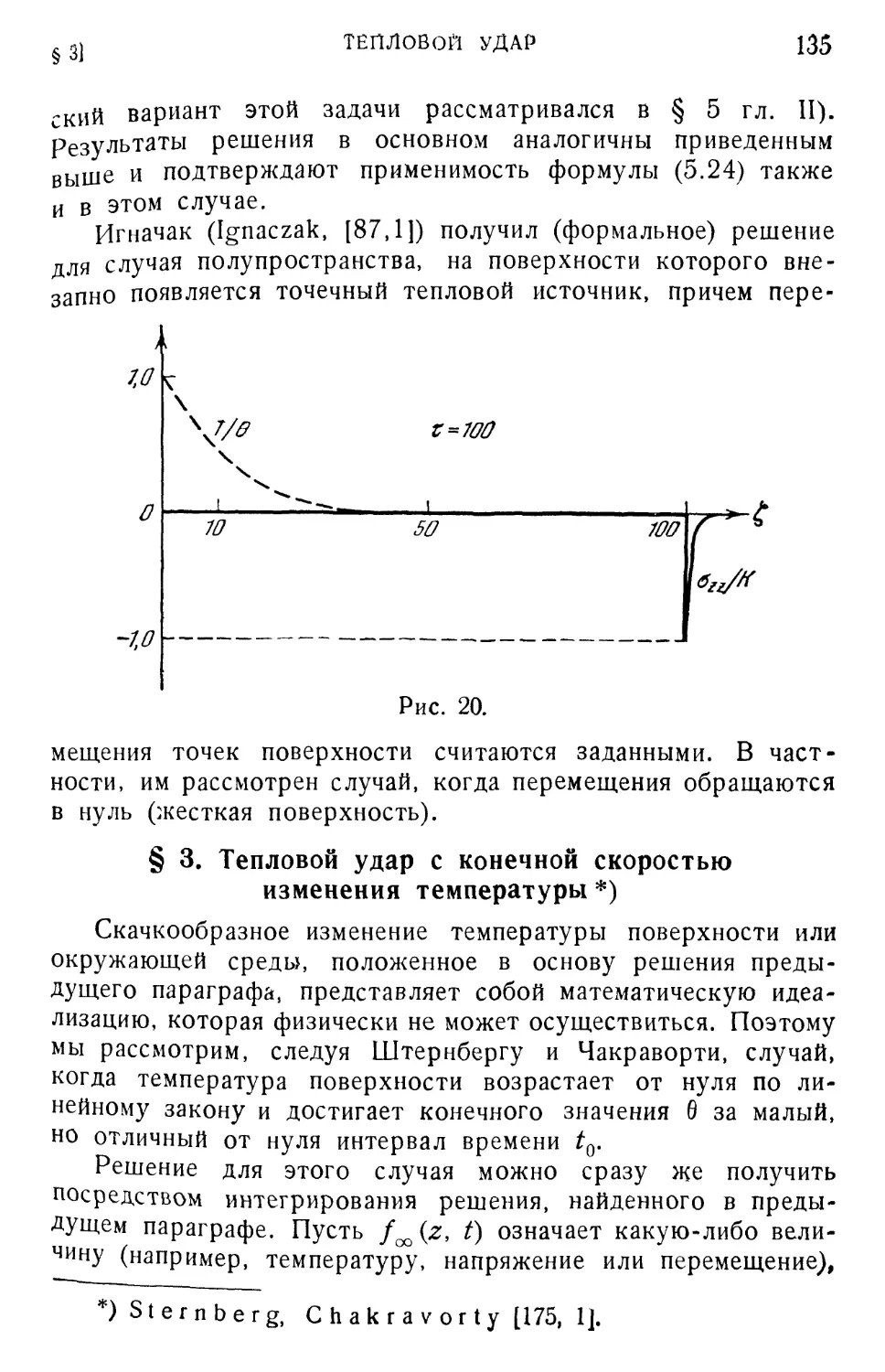
§ 2. Тепловой удар на поверхности полупространства . . 129
§ 3. Тепловой удар с конечной скоростью изменения
температуры 135
§ 4. Мгновенный источник в неограниченной среде . . . 138
§ 5. Сферическая полость в неограниченной среде . . . 140
§ 6. Периодические изменения температуры 145
§ 7. Периодический тепловой источник в
неограниченной среде 146
§ 8. Точечный нагрев диска 148
§ 9. Тепловой удар на поверхности длинного сплошного
цилиндра 151
§ 10. Термическое возбуждение колебаний пластинок . . 154
§ 11. Тепловой удар на поверхности пластинки 156
Глава VI. Температурные напряжения при вязкоупругом
поведении материала 162
§ 1. Введение 162
§ 2. Зависимости между напряжениями и деформациями 163
§ 3. Упруго-вязкоупругая аналогия 168
§ 4. Термовязкоупругий потенциал перемещений , . . . 171
§ 5. Стационарные и квазистационарные температурные
поля 172
§ 6. Полупространство с периодически изменяющейся
температурой поверхности 174
§ 7. Сферическая полость в неограниченной среде . . . 175
Глава VII. Температурные напряжения при
упруго-пластическом поведении материала 180
§ 1. Условие текучести и закон течения 180
§ 2. Упруго-пластическая сфера 186
§ 3. Толстостенная труба 193

ОГЛАВЛЕНИЕ
5
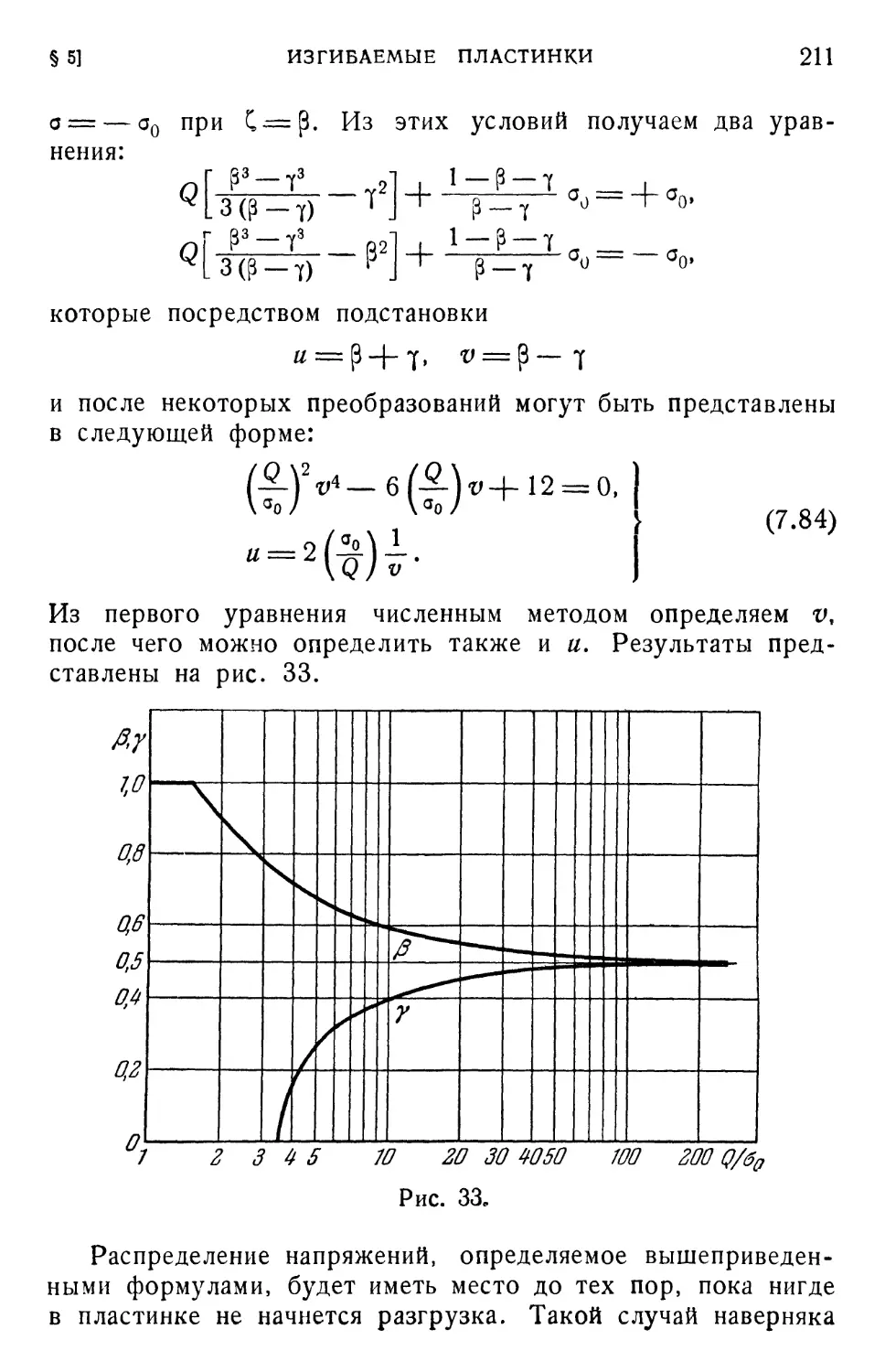
§ 4. Точечный нагрев диска 199
§ 5. Изгибаемые пластинки 206
Литература 215
При ложение
Г. П а р к у с. О поле температуры при случайном
распределении температуры на поверхности 230
Г. П а р к у с. Тепловые напряжения при случайно меняющейся
температуре поверхности 233
Предметный указатель 252

ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
Интерес к исследованию нестационарных температурных
напряжений возник в начале нашего века. Например, еще
Рэлей ]) рассматривал поле напряжений в неограниченной
плите, имевшей первоначально равномерную температуру и
охлажденной так, что по ее поверхностям поддерживается
постоянная температура. Влияние периодических изменений
температуры для тонкостенных сосудов, имеющих одну или
несколько осей симметрии, изучал Г. Эйхельберг2). В
дальнейшем Г. Гринберг3) исследовал напряжения, возникающие
при охлаждении сферы. Для толстых плит, цилиндров и сфер
ряд результатов с приложениями, существенными для
бетонного строительства, получил Г. Н. Маслов4).
Стремительные темпы развития техники самолето- и
ракетостроения, энергетических установок и ядерных
реакторов привели к бурному росту исследований по
нестационарным температурным напряжениям. Помимо работ, основанных
на квазистационарном рассмотрении проблемы, был решен
ряд новых задач, учитывающих влияние инерционных членов.
Кроме того, были исследованы тела, наделенные не только
упругими, но также вязкими и пластическими свойствами.
Книга Г. Паркуса, предлагаемая читателю в русском
переводе ставит целью подвести итог недавним исследованиям,
l) Rayleigh, On the Stresses in solid Bodies due to unequale
heating and on the double refraction resulting therefrom. Phil. Mag. I,
ser. 6 A901), 169.
2)Eichelberg G., Temperatur ferlauf und Warmespannungen
in Verbrennungsmotoren. Forschungsarbeiten VDI, вып. 263 A923).
3) Grinberg G., Uber durch ungleichformige Erwarmung
erregten Spannungszustand. Z. f. Phys. A926), 548—555.
4) Маслов Г. Н., Задача теории упругости о термоупругом
равновесии. Известия научно-исследовательского института
гидротехники, 23 A939), 130—219,

ПРЕДИСЛОВИЕ РЕДАКТОРА
7
выполненным в этой области до 1959 г. Книга
представляет собой продолжение и завершение монографии
Э. Мелана и Г. Паркуса «Термоупругие напряжения,
вызываемые стационарными температурными полями», перевод
которой был у нас опубликован в 1958 г.
К данному изданию в качестве приложения добавлен
перевод двух последних работ Г. Паркуса, посвященных
определению полей температуры и напряжений в случае, когда
температура на поверхности тела задана как стационарная
случайная функция. Решение доводится до числовых
результатов для упругого и вязкоупругого полупространства,
а также для упругого круглого цилиндра. В случае упругого
полупространства проводится не только квазистатическое,
но и динамическое исследования.
Перевод основного текста книги выполнен В. И. Розен-
блюмом, а перевод приложений — Н. А. Форсман.
Хочу выразить признательность Г. Паркусу, любезно
приславшему перечень опечаток, обнаруженных в оригинале.
Г. С. Шапиро

ИЗ ПРЕДИСЛОВИЯ АВТОРА
Настоящая монография представляет собой продолжение
и частичное завершение систематического изложения теории
температурных напряжений, начатого в книге Э. Мелана и
Г. Паркуса «Температурные напряжения, вызываемые
стационарными температурными полями». Названная книга была
посвящена стационарным температурным полям и идеально
упругим материалам. В предлагаемой книге будут рассмотрены
неустановившиеся процессы как в идеально упругих, так и
в вязкоупругих и упруго-пластических телах. Отдельные
ссылки на первую книгу (которую при цитировании мы
будем кратко называть «Мелан— Паркус») оказались
неизбежными, однако я надеюсь, что новая книга может быть понята
без обращения к предшествующей монографии. Интерес
к проблеме температурных напряжений в последние годы
значительно повысился, о чем свидетельствует, в частности,
непрерывно возрастающее количество публикуемых работ.
Я полностью включил в библиографический указатель все
известные мне публикации. При этом, однако, литературные
источники, цитированные в первой книге, заново не
указываются, исключение сделано лишь для тех работ, которые
имеют непосредственное отношение к излагаемым вопросам.
Я сердечно благодарю за поддержку всех коллег,
приславших мне свои работы.
Проф. Эрнст Мелан, по инициативе которого были
написаны обе книги, к сожалению, не смог участвовать в
подготовке этой монографии вследствие загруженности другими
работами. Я хочу поблагодарить его за многочисленные
советы. Его идеи в особенности повлияли на содержание главы IV.
Вена, декабрь 1958.
Г. Паркус

ГЛАВА I
НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ
§ 1. Основные уравнения
Для рассмотрения вопросов, которым посвящена настоящая
монография, необходимо внести некоторые дополнения в
уравнения, выведенные в гл. II книги Мелана — Паркуса[6]. При
этом мы вначале ограничимся случаем однородного и
изотропного материала, подчиняющегося закону Гука, причем будем
считать, что модуль сдвига G и коэффициент Пуассона [х не
зависят от температуры.
Нестационарное температурное поле Т(х, уу z, f)
вызывает напряженное состояние, которое изменяется с течением
времени *). Таким образом, в сущности, рассматривается не
задача статики, а задача динамики. Однако, за некоторыми
исключениями, изменения температуры обычно происходят
достаточно медленно, так что, вообще говоря, можно
пренебречь влиянием ускорений и рассматривать движение как
некоторую последовательность состояний равновесия**).
Такой подход можно назвать «квазистатическим». Имея в виду,
однако, задачи, рассмотренные в гл. V, мы здесь остановимся
на выводе уравнений с учетом ускорений.
*) Мы предполагаем, что температурное поле не зависит от
вызываемых им деформаций. Строго говоря, это не совсем верно,
поскольку при деформировании выделяется или поглощается теплота,
которая влияет на распределение температуры. Это влияние, вообще
говоря, весьма мало (Duhamel [44], Lessen [106,4], Weiner
[194,2], Park us [147,1]), однако может иметь значение, если
изменение температуры вызывается не внешними источниками тепла,
а исключительно самими деформациями, как, например, в задаче
термоупругого демпфирования при расширении вала (С h a d w i с k
и. Sneddon [32], Lockett [109]).
**) Эта гипотеза предложена Дюамелем.

Ю НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. I
Уравнения равновесия {B.1), Мелан — Паркус [6]} в этом
случае заменяются уравнениями движения
*) Seth [166] рассмотрел две задачи для случая конечных
перемещений.
ал)
где р — масса единицы объема.
Мы ограничимся (как это было принято в Мелан —
Паркус [6]) рассмотрением случая, когда перемещения и
производные перемещений малы *). Тогда применимы геометрические
соотношения {B.2), B.3), Мелан — Паркус [6]}
а также условия совместности {B.4), Мелан — Паркус [6]}.
Уравнения закона Гука {B.7), B.9), B.10), Мелан — Паркус
[6]} также остаются без изменений:
Необходимо, однако, внести дополнения в систему уравнений
термоупругости в перемещениях. Подставим соотношения
закона Гука в уравнения движения A.1) и после
преобразований, аналогичных тем, которые применялись при выводе
соотношений {B.11), Мелан — Паркус [6]}, получим три
уравнения:
A.2)
где е — объемное расширение.
Наряду с прямоугольными декартовыми координатами
х, у, z часто используются цилиндрические координаты г, ср, z
и сферические координаты г, ср, Ф. Приводим сводку
соответствующих формул.
Цилиндрические координаты. Предполагается, что имеет
место симметрия вращения относительно оси z. Тогда
компоненты перемещения в окружном направлении и напряжения ог
и о обращаются в нуль, а компоненты перемещения в
радиальном и осевом направлениях и, w не будут зависеть от ср.

*tl
ОСНОВНЫЕ УРАВНЕНИЯ
И
Основные уравнения принимают вид (ср. Мелан — Паркус [6],
гл. VIII):
A.3)
A.4)
A.5)
Оператор Лапласа в этом случае имеет форму
дг2 * г dr^dz2 г дг \ дг)^ dz2 "
Сферические координаты. Предполагаем, что имеет
место симметрия относительно начала координат. Тогда
отличной от нуля будет только компонента перемещения
в радиальном направлении и (г, t). Напряжения ог , а «, а#г
обращаются в нуль, а все остальные величины не зависят
от углов ср и Ь. Уравнения движения имеют вид (см. курсы
теории упругости)
A.6)
Зависимости между перемещением и относительными
удлинениями и условие совместности получим в форме
A.7)

12 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТЙ [ГЛ. I
Исключение напряжений и деформаций из уравнений A.6), A.7)
при помощи закона Гука приводит к уравнению для
перемещения и
A.8)
где
§ 2. Энергия деформации и принцип Даламбера
Пусть в момент времени t тело находится в
деформированном состоянии, характеризуемом перемещениями
ui(x, у, z, t). Сообщим телу (при неизменных значениях
времени и температуры) виртуальные перемещения but,
выводящие его из этого мгновенного состояния, таким образом,
чтобы новое состояние было геометрически возможным, т. е.
совместным со сплошностью тела и с условиями закрепления.
Умножим каждое из трех уравнений A.1) соответственно
на Ьих, Ьиу, buz, сложим и проинтегрируем по всему объему
тела; в результате получим:
A.9)
Применяя формулу Гаусса, преобразуем объемный интеграл
в поверхностный, распространенный по всей поверхности тела:
Здесь через nk обозначены компоненты вектора нормали,
который считается положительным, если он направлен наружу.
Воспользуемся известным соотношением теорий упругости *)
A.10)
*) См., например, Sokolnikoff, Theory ol Elasticity, 2-е изд.,
N. Y., 1956, стр. 39.

§ 2] ЭНЕРГИЯ ДЕФОРМАЦИИ И ПРИНЦИП ДАЛАМБЕРА 13
где рх, pyi pz—компоненты вектора поверхностной нагрузки,
и определим «упругий потенциал» единицы объема тела W
и полную «упругую потенциальную энергию» («энергию
деформаций») U при помощи соотношений
A.11)
Легко проверить, используя закон Гука, что а^ = д\^/де^.
При этом на основании правил вариационного исчисления
получаем
При помощи зависимостей
последнее соотношение можно представить также в виде
Выражение
A.12)
представляет собой виртуальную работу, совершаемую
внешними поверхностными нагрузками на виртуальных
перемещениях; поэтому соотношению A.9) можно придать следующую
форму:
A.13)
Мы получили, таким образом, «принцип Даламбера»: при
виртуальном перемещении тела из некоторого мгновенного
состояния работа, совершаемая внешними силами и силами

14 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. I
инерции, равна изменению энергии деформации. Заметим, что
при виртуальных перемещениях распределение температуры
остается неизменным, поэтому варьирование осуществляется
изотермически.
Вообще говоря, внешние силы реакции не совершают
работы на виртуальных перемещениях («идеальные связи») и
поэтому не входят в уравнение A.13).
Принцип Даламбера в статическом (и квазистатическом)
случае переходит в принцип виртуальных перемещений
ЬА = Ьи A.14)
и является, таким образом, его обобщением. Следует также
подчеркнуть, что функция состояния /У, определенная
выражением A.11)*), отнюдь не всегда идентична работе
деформации, накопленной телом в действительности. Последняя
не является функцией состояния и зависит от
последовательности приложения нагрузок и изменений температуры.
§ 3. Принцип Гамильтона. Минимум потенциальной
энергии
Принцип Гамильтона можно вывести непосредственно из
уравнения A.13). Вместо отдельного мгновенного состояния
тела будем теперь рассматривать непрерывную
последовательность таких состояний между двумя фиксированными
моментами ? = 0 и t. При помощи вариаций but образуем из этих
состояний последовательность близких состояний, причем
потребуем, чтобы в начальный и конечный моменты
рассматриваемого интервала времени варьированное состояние совпадало
с действительным: but\ — 0. Интегрируя по интервалу [0, t]
о
соотношение A.13), справедливое для каждого момента этого
интервала времени, получим:
*) Эта функция, с точностью до аддитивного температурного
члена, представляет собой «свободную энергию» тела.
A.15)

§ 3] ПРИНЦИП ГАМИЛЬТОНА 15
Кинетическая энергия тела определяется выражением
(Lie)
Вычислим вариацию:
При интегрировании последнего соотношения по интер-
валу [0, t], с учетом условия §#. | = 0, получим:
о
При этом уравнение A.15) принимает форму
A.17)
Здесь символ варьирования в левой части равенства вынесен
за знак интеграла, поскольку U и К являются функциями
состояния, которые определяются только мгновенным
состоянием тела и не зависят от того, каким образом это состояние
было достигнуто.
Если внешние силы консервативны (например, постоянны),
то они имеют потенциал V\ при этом
A.18)
Объединим потенциал U внутренних сил и потенциал
внешних сил в суммарный потенциал
n = l/-f U. A.19)

16 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. 1
При этом уравнение A.17) можно представить в следующей
форме:
t
bj(TL — K)dt = Ot A.20)
о
являющейся обычной формулировкой принципа Гамильтона.
В статическом и квазистатическом случаях уравнение A.13)
переходит в уравнение A.14); соответственно принцип
Гамильтона перейдет в принцип минимума потенциальной
энергии (принцип Дирихле)
8П = 0, A.21)
согласно которому из всех геометрически возможных
(устойчивых) положений в действительности реализуется то,
которому отвечает минимум потенциальной энергии. Наличие
в этом случае минимума следует из рассмотрения второй
вариации, которая оказывается положительной *).
§ 4. Дополнительная энергия
В статическом и квазистатическом случаях, наряду с
принципом минимума потенциальной энергии, имеет место другой
минимальный принцип, называемый принципом минимума
дополнительной энергии или принципом Кастильяно.
Для его вывода воспользуемся принципом виртуальных
перемещений A.14):
f1ilL°ik^dV = f%pMdO. A.22)
V i k O i
Напомним, что согласно определению but эти вариации
должны обращаться в нуль на тех частях поверхности тела,
где заданы перемещения. Вследствие этого поверхностный
интеграл, вообще говоря, следовало бы распространять только
по той части О' поверхности, где заданы усилия. Однако
можно, конечно, снять это ограничение и рассматривать
вариации более общего вида, принимая, что тело полностью
или частично «освобождено» путем устранения всех или
некоторых закреплений. При этом виртуальная работа реакций
уже не будет обращаться в нуль.
*) См., например, Т р е ф ф ц Е., Математическая теория
упругости, перев. с нем., ОНТИ, 1934.

§ 4]
ДОПОЛНИТЕЛЬНАЯ ЭНЕРГИЯ
17
Можно, таким образом, учитывая введенное в начале этой
главы предположение о малости деформаций, выбрать, в
частности, в качестве виртуальных действительные изменения
конфигурации тела, поскольку при этом условия совместности
и закрепления, очевидно, будут выполнены. Тогда вместо
уравнения A.22) получим:
A.23)
Примем теперь, что напряженное состояние аш и внешние
силы pt также подвергаются варьированию, и рассмотрим
близкое состояние напряжений и нагрузок cik-\rbaik, Pi-\-bpt.
Варьирование можно осуществлять таким образом, чтобы
близкое состояние также являлось статически возможным
(т. е. не нарушало условий равновесия). Тогда для этого
состояния также будет справедлив принцип виртуальных
перемещений, который на основании A.23) можно представить
в виде
Вычитая отсюда уравнение A.23), получим принцип
виртуальных сил
A.24)
Введем функцию состояния U*, определяемую соотношениями
A.25)
Вычисляя Ы/* и используя закон Гука, обнаруживаем, что
левую часть уравнения A.24) можно рассматривать как
вариацию функции ?/*; одновременно получаем зависимости
ец = д№*/дсц. Если Г==0, то U* можно получить
преобразованием функции U, выражая eik через aik при помощи закона
Гука. Если ТфО, то такое преобразование невозможно.

18 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. I
Теперь уравнение A.24) можно представить в виде
A.26)
Величину if*— У UtPtdO будем называть «дополнительной
о i
энергией». Уравнение A.26) представляет собой принцип
Кастилъяно, согласно которому «среди всех статически
возможных напряженных состояний в действительности
реализуется то, которому соответствует минимум дополнительной
энергии». Наличие минимума следует из рассмотрения второй
вариации, которая будет положительной.
В отличие от принципа минимума потенциальной энергии,
основанного на варьировании деформированного состояния
тела, принцип Кастильяно вытекает из сравнения близких
напряженных состояний.
Если к поверхности тела вместо распределенных нагрузок
приложены сосредоточенные силы Рг Рт, то интеграл
в левой части уравнения A.26) следует заменить суммой
2 япРп> где чеРез ап обозначен «активный путь» силы Рп,
п
т. е. проекция перемещения, которое получает точка
приложения силы Рп при деформировании тела, на направление
этой силы. Пусть if* выражена через нагрузки Рп, т. е.
[J*— U*(Pv ..., Рт); тогда из уравнения A.26) находим:
Отсюда, вследствие произвольности вариаций ЬРп, следует:
A.27)
Мы получили теорему Кастильяно: производная от U*
по внешней сосредоточенной силе равна активному пути
этой силы.
Отметим, что Е. Reissner *) установил более общий
принцип, заключающий в себе как частные случаи вариационные
принципы A.21) и A.26) и применимый также при конечных
деформациях.
*) R e i s s n е г Е., On a variational theorem for finite elastic
deformations, Journ. of Math, and Physics, 37, 129 A953).

§6]
ИЗМЕНЕНИЕ ОБЪЕМА
19
§ б. Однозначность решения
При введенном ранее предположении о малости
перемещений и производных от перемещений уравнения теории
упругости будут линейными, поэтому имеет место принцип
суперпозиции. Чтобы рассмотреть вопрос об однозначности решения
этих уравнений с соответствующими краевыми условиями,
предположим, что одному температурному полю отвечают
два различных решения: ufK oW и uf\ of). Тогда, согласно
принципу суперпозиции, разность этих решений должна быть
решением тех же уравнений при 7" = 0, т. е. уравнений не-
нагруженного тела при исходной температуре. Но по теореме
единственности Кирхгофа *) это решение тождественно равно
нулю, следовательно,
иф = uf,
0A) _ аB)
и и
Необходимо, однако, подчеркнуть, что теорема Кирхгофа
справедлива при условии, что напряжения и перемещения
непрерывны и однозначны**). Поэтому, например, если при
нагреве возникают области течения, то после охлаждения
напряжения полностью не исчезнут и возникнет некоторое
остаточное напряженное состояние (см. гл. VII).
Единственность также может не иметь места при больших
перемещениях, которым соответствуют нелинейные уравнения
теории упругости. Например, на границе устойчивости
решение разветвляется и может существовать несколько состояний
равновесия.
§ 6. Изменение объема
Покажем, что статические или квазистатические
температурные напряжения не вызывают изменения объема свободно
деформируемого тела ***).
*) См., например, Трефц Е., Математическая теория
упругости.
**) См. Reissner H. [156].
***) Н i e k e [74, 3].

20 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. 1
Согласно уравнению {B.9), Мелан — Паркус [6]}
объемное расширение определяется соотношением
Первый член в правой части выражает долю локального
изменения объема, вызываемую действием напряжений.
Интегрируя по всему объему тела, найдем полное приращение
объема
Заметим, что
поскольку в выражении
второе слагаемое правой части обращается в нуль в силу
уравнений равновесия
а первое слагаемое равно 2и°и* так как ~д~=== W ^риме-
i
няя формулу Гаусса, получим:
Мы рассматриваем случай свободной деформации тела, когда
напряжения на поверхности отсутствуют. При этом, согласно
уравнению A.10),
и, следовательно,
A.28;

§ 7] ТЕРМОУПРУГИЙ ПОТЕНЦИАЛ ПЕРЕМЕЩЕНИЙ 21
Итак, изменение объема, вызванное действием напряжений,
равно нулю, поэтому приращение объема будет определяться
только прямым воздействием температуры:
A.29)
§ 7. Термоупругий потенциал перемещений
Термоупругий потенциал перемещений, введенный ранее
при построении частного решения статических
уравнений {B.11), Мелан — Паркус [6]}, можно использовать также
и в динамическом случае. Воспользуемся снова
подстановкой {B.12), Мелан —Паркус [6]}
тогда уравнения A.2) примут вид
Интегрируя по / и приравнивая нулю произвольную
функцию, получающуюся при интегрировании, придем к
следующему обобщению уравнения {B.13), Мелан — Паркус [6]}:
A.30)
По уравнениям закона Гука находим напряжения,
соответствующие потенциалу Ф:
Исключая здесь A 4-а)аТ, при помощи A.30) получим:
A.31)
В цилиндрических координатах при условии симметрии
д п
относительно оси z, т. е. при -т-=0, имеют место анало-

22 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЁРМОУПРУГОСТИ [ГЛ. I
гичные формулы (см. также формулы A.3) — A.5)):
}A.32)
Наконец, в сферических координатах в случае симметрии
относительно начала будем иметь (см. также формулы
A.6)-A.8)):
A.33)
В этом случае, однако, введение потенциала перемещений
едва ли дает какие-либо преимущества, поскольку задача
состоит в определении лишь одной функции — радиального
перемещения и, — удовлетворяющей уравнению A.8).
Соотношения A.30), A.31) и A.32) применимы также в
случае плоского деформированного состояния (см. Мелан —
Паркус [6], гл. V, § 1), если всюду положить -^-==0.
В случае плоского напряженного состояния введем
вместо Ф потенциал перемещений ч7 (см. Мелан —
Паркус [6], гл. V, § 2):
Вследствие условия azz = Q вместо уравнений A.2) будем
иметь два уравнения, из которых одно имеет вид
A.34)
а второе получается отсюда заменой х на у и и — на г;.
Вводя функцию ч? и интегрируя, приходим к обобщению
уравнения {E.14), Мелан — Паркус [6]} для динамического случая
A.35)

§8]
ФУНКЦИЯ ГРИНА
23
При помощи ранее выведенных формул {E.12), Мелан —
Паркус [6]} находим соответствующие напряжения
2G
Аналогично в полярных координатах:
A.36)
A.37)
§ 8. Функция Грина
Методы, основанные на введении функции Грина,
наиболее широко применяются в теории потенциала *). Их, однако,
можно распространить также на нестационарные задачи
теории теплопроводности **). Рассмотрим два случая:
а) В момент t = 0 тело имеет начальную
температуру F(x, у, z). При ^>0 поверхности тела О сообщается
распределение температуры б (х, у, z, t).
Функция Грина T(Q, P, t — т) определяется в этом случае
как температура в точке Q(?, т], С) в момент t, создаваемая
«мгновенным источником» ***) интенсивности Ж = 1, который
действует в точке Р(х, у, z) в момент т, причем на
поверхности тела О поддерживается температура 7=0.
Таким образом, Т является решением уравнения
теплопроводности
*) См., например, Kellogg О. D., Foundations of Potential
Theory, Berlin, 1929, стр. 236.
**)Carslaw — Jaeger [1], стр. 291.
***) Будем говорить, что имеет место действие мгновенного
источника интенсивности М, если в соответствующей точке
мгновенно выделяется количество теплоты КМ/а.

24 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. I
при краевом условии
Т=0 на О, A.39)
и в точке Q = P при t->x имеет место особенность вида
A.40)
причем R = [(x — ?J + (у — т]J + (г — СJ]2.
б) Тело имеет в момент ^ = 0 начальную
температуру F(x, у, z). При ^>0 происходит теплообмен со
средой, имеющей температуру 0 (х, у, z, t). Функция Грина
здесь определяется так же, как в предыдущем случае, с той
разницей, что краевое условие A.39) заменяется условием
теплообмена со средой, имеющей нулевую температуру:
^fc=hf на О. A.41)
Можно показать *), что как в случае а) так и в
случае б) распределение температуры в теле выражается
формулой
A.42)
где йУд = й%йг\Л — элемент объема, cLOq — элемент
поверхности тела, S, у], С—переменные интегрирования.
Символ d/driQ означает дифференцирование по переменным ?, г], С,
соответствующее направлению внешней положительной
нормали к поверхности. Функция Грина обладает свойством
симметрии: T(Q, P, t — т)=71(Р, Q, t — т). В случае плоского
распределения температуры Т(х, у, t) сохраняются
приведенные формулы, необходимо только интеграл по объему
заменить интегралом по некоторой плоской области, а вместо
интеграла по поверхности ввести криволинейный интеграл
*) Carslaw — Jaeger [l].

§8]
ФУНКЦИЯ ГРИНА
23
по контуру этой области. Выражение A.40) в этом случае
заменяется особенностью вида
где R = [(x — if + (у — U>2]T-
Пользуясь приведенными результатами, можно построить
функцию Грина для поля напряжений. Заметим для этого,
что уравнение A.42) допускает очень простое физическое
истолкование. Поскольку dT/dnQ представляет собой
температуру в точке Р, создаваемую тепловым диполем единичной
интенсивности в точке Q, из уравнения A.42) следует, что
температурное поле в теле можно рассматривать как
результат действия мгновенных тепловых источников,
распределенных внутри тела, и мгновенных диполей, распределенных по
поверхности. Принимая, что краевые условия являются
однородными *), найдем распределение напряжений о'
соответствующее мгновенному тепловому источнику единичной
интенсивности, действующему в момент / = 0 в точке Q внутри
тела, и распределение напряжений а" соответствующее
диполю интенсивности а, действующему в момент х в точке Q
на поверхности тела, причем ось диполя совпадает с
нормалью к поверхности. При этом, согласно A.42),
напряженное состояние тела определяется формулой
аи(Р, t) = f f fo'tJ(P, Q, t)F(Q)dVQ —
v
t
— f dx f f в".. (P, Q, t — т) 6 (Q, x) dOQ. A.44)
о ' of
Температурное поле, соответствующее напряжениям а?.,
можно легко найти из уравнения A.42) посредством диф-
дТ'
ференцирования: Т"=а-^—.
*) То есть в каждой точке поверхности тела либо напряжение,
либо перемещение обращается в нуль. Если краевые условия не
являются однородными, то соответствующие им напряжения
вычисляются отдельно, после чего окончательное напряженное
состояние можно найти посредством суперпозиции.

26 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. I
§ 9. Квазистатический анализ неустановившихся
термоупругих напряжений
Как уже было отмечено в § 1, хотя определение
неустановившихся температурных напряжений является по существу
динамической задачей, однако вследствие того, чао
изменения температуры обычно происходят медленно, инерционные
эффекты часто можно не принимать во внимание (гипотеза
Дюамеля). Исключения составляют лишь такие случаи, когда
внешние воздействия вызывают резкие изменения
температуры на поверхности тела. Более подробно эти вопросы
рассматриваются в гл. V. В первых главах мы ограничимся
рассмотрением исключительно «квазистатических» задач и
поэтому не будем удерживать в уравнениях динамические
члены, имеющие множитель р.
При этих условиях единственное различие между
проблемами установившихся и неустановившихся температурных
напряжений заключается в уравнении теплопроводности,
которое в неустановившемся случае (при отсутствии непрерывно
распределенных тепловых источников) имеет вид
4? = аДГ. A.45)
Термоупругий потенц тал для квазистатического случая
определяется уравнением
АФ-=|±^аГ, A.46)
решение которого легко найти.
Дифференцируя A.46) по t и учитывая A.45), получаем:
дФ 1-f f* А~
А -зг- = 1 аа А Г.
Ot 1 —(х
Интегрирование этого уравнения *) приводит к зависимости
t
Ф=±±?*а/ ГЛ+Фо-ИФ^ A.47)
6
*) G о о d i е г 163,2].

§91
КВАЗИСТАТИЧЕСКИЙ АНАЛИЗ
27
г де Фг — произвольная гармоническая функция (ДФа = 0),
Ф0=Ф(/ = 0) — потенциал перемещений, соответствующий
начальной температуре Т0(х, у, z), т. е. АФ0 = ~_** аГ0.
Подстановка в уравнение A.46) показывает, что
выражение A.47) действительно является решением. Если начальная
температура тела равна нулю, следует положить Ф0 = 0.
Чтобы удовлетворить краевым условиям задачи, следует, как
обычно (см. Мелан — Паркус [6]), сложить решение,
определяемое потенциалом Ф, с решением однородных уравнений
теории упругости.
При квазистатическом рассмотрении неустановившихся
температурных напряжений время t является параметром,
поэтому можно непосредственно использовать решения
соответствующих стационарных задач при условии, конечно, что
при получении этих решений не было использовано
уравнение теплопроводности.
Очевидно, что высказанные соображения будут
справедливы также в частных случаях плоской деформации и
плоского напряженного состояния. В последнем случае, в
частности, решая уравнение A.35) при р = 0, получим потенциал
перемещений ч? в следующем виде:
t
W=(l+p)aafTdt-)-WQ-!rtWv A.48)
о
причем, так же как в предыдущем случае, следует
положить ч70 == 0, если начальная температура равна нулю.
Случай диска при наличии теплообмена на боковых
поверхностях следует, однако, рассмотреть заново, поскольку
уравнение теплопроводности {E.19), Мелан — Паркус [6]}
в этом случае будет иметь следующий вид:
д7— т2Т = — . 4?, гп2=~. A.49)
a dt \h v ;
Здесь принято 6 = 0, т. е. предполагается, что температура
среды не зависит от времени и пространственных координат;
это предположение во многих важных случаях реализуется
на практике. В уравнении A.49) обозначено: k — коэффициент
теплопередачи между диском и средой, X—коэффициент
теплопроводности, h — толщина диска.

28 НЕКОТОРЫЕ ОБЩИЕ ЗАКОНЫ ТЕРМОУПРУГОСТИ [ГЛ. I
Применяя к уравнению A.49) преобразование Лапласа *)
оо
Г(х, у, z, s) = j 7(х, у, z, t)e-*'dt9
о
получим:
\ а) а
где Т0(х, у) — начальная температура диска.
Аналогичное преобразование уравнения A.35) (при р = 0)
дает:
Ач7*==A+!1)аГ*.
Подставляя сюда Т* из предыдущего уравнения, приходим
к зависимости
а
Пусть ЧГ0 — частное решение уравнения
ДЧГ0 = A+|*)а7,о. A-50)
тогда
или, после обратного преобразования,
A.51)
Очевидно, что ч?0 = ЧГ (? = 0) представляет собой (с
точностью до постоянной интегрирования) потенциал
перемещений, соответствующий начальной температуре Г0. Легко
убедиться, составляя выражение Ач7 при помощи соотноше-
*) Введение в теорию преобразования Лапласа излагается,
например, в книгах Q. D о е t s с h [2,3].

§9]
КВАЗИСТАТИЧЕСКИЙ АНАЛИЗ
29
ний A.49), A.50) и применяя интегрирование по частям,
что A.51) действительно является решением уравнения A.35)
при р = 0. Если существует предел ИтГ = Гоо, то из
t->QO
уравнения A.51) находим:
t->oo т
что соответствует решению для установившего состояния
(см. также {E.22), Мелан — Паркус [6]}).

ГЛАВА II
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ
§ 1. Мгновенный источник в неограниченной среде*)
Пусть в точке Л(?, т], С) идеально упругого
неограниченного тела в момент t = О мгновенно выделяется количество
теплоты Q — pcM**). При этом температура в точке А
скачкообразно возрастает до бесконечности, после чего
начинает убывать, и в конечном счете во всем теле
восстанавливается первоначальная температура, которую будем
принимать равной нулю. Очевидно, что наличие внезапного
подъема температуры противоречит предположению о возможности
квазистатического подхода; кроме того, в окрестности
точечного источника возникает пластическая область. Здесь,
однако, мы не будем принимать во внимание эти обстоятельства.
Решение уравнения A.45), соответствующее принятому
начальному состоянию, имеет вид ***)
Т = —*L—e-M*at, B.1)
Dnat) 8/2
где R=[(x — ?J-f-(y — ^-{-(z — Q2]- Подставляя это
температурное поле в соотношение A.47), найдем потенциал
перемещений
t
<* = ?«/" (а(Г°<> e-Rviat dt + Ф0 + *Ф,.
40 у тс •'
*) Nowacki [136,4]. Мы рассмотрим здесь также задачу
о мгновенном источнике в полупространстве с неподвижной
поверхностью.
**) с — удельная теплоемкость на единицу массы, р — плотность.
***) Cars law — Jaeger [1].

§ 1] МГНОВЕННЫЙ ИСТОЧНИК В НЕОГРАНИЧЕННОЙ СРЕДЕ 31
Здесь для краткости обозначено
Вводя новую переменную u==R/B Yat),dt——(R2l2auz)dat
получим:
оо
2G R V* J
Интеграл в правой части можно выразить через интеграл
ошибок Гаусса
и
учитывая, что
найдем:
При достаточно больших значениях времени (т. е. при t—>oo)
перемещения и напряжения должны возвращаться к нулевым
значениям. Это условие будет выполнено, если положить
Фл = — -^ — Ф, = 0
0 2G R ' 1
В результате окончательно получим:
Ф—1?И^У- <2-з>
Внося это значение Ф в соотношения A.31) (без учета
динамических членов) и учитывая зависимости
д r w Ч1 2 и2 6R х — %
— [zx\(u)\=-f=e-u , — =__ и т. д.,
ди у к дх R

32 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. 11
найдем напряжения
R2 \\ R* ) IR \2}СЦ) Vnat J
Ч т^—it К* — ^J — RHe-W™] B.4)
(и две аналогичные формулы для оуу и згг), а также
B.5)
(и две аналогичные формулы для cyz и агх).
Чтобы решение было однозначным, должны выполняться
следующие условия:
а) перемещения и напряжения обращаются в нуль на
бесконечности;
б) значение Ф при /?->0 конечно; при этом перемещения
стремятся к бесконечности не быстрее, чем -^-, напряжения —
не быстрее, чем -^ .
Легко видеть, что условие а) выполнено. Вычисляя
радиальное перемещение и при /? = 0, получим:
Следовательно, условие б) также выполнено. Таким
образом, решение B.4), B.5) удовлетворяет всем условиям
задачи; наложение второго решения при этом является излишним.
Распределение температуры B.1) (при Ж=1) представляет
собой функцию Грина для бесконечного тела. Поэтому
распределение напряжений в этом теле при произвольной
заданной начальной температуре F(x, у, z) можно вычислить

§ 21 МГНОВЕННЫЙ ДИПОЛЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 33
по следующей формуле, вытекающей из зависимости A.44):
оу(х,у. *. О = ///*'/,(*. У. ^ 6, ч, С, О/7E. Ч. С)Л^Л.
v B.6)
Здесь через о'. обозначены напряжения, вычисляемые по
формулам B.4), B.5) при Ж=1.
Поскольку напряженное состояние характеризуется
центральной симметрией, можно также воспользоваться
формулами A.33), подставив в них R вместо г. В результате
получим:
B.7;
§ 2. Мгновенный диполь в неограниченной среде*)
Пусть мгновенный диполь действует в момент t = О
в точке А (?, т], С) идеально упругого неограниченного тела
с нулевой начальной температурой. Такой диполь можно
рассматривать как предельное положение двух тепловых
источников интенсивности -f- М и — М, когда эти источники
беспредельно сближаются вдоль прямой (оси диполя) таким
образом, что произведение Ml остается конечным, когда
расстояние / стремится к нулю **). Обозначим через Т
температурное поле B.1), создаваемое мгновенным тепловым
источником, тогда для случая диполя получим:
где через д/дп обозначено дифференцирование по
направлению оси диполя в координатах ?, т], С. Пусть, например,
ось диполя совпадает с осью z\ тогда
B.8)
*) Now ас k i [137,7].
**) Carslaw — Jaeger [1].

34 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
Соответствующий термоупругий потенциал перемещений
можно сразу же получить, дифференцируя выражение B.3):
B.9)
Соответствующее поле напряжений определяется по
формулам B.4).
§ 3. Мгновенный источник на поверхности
полупространства; поверхность теплоизолирована*)
Пусть в начале координат О упругого полупространства
z ^ О в момент t — 0 мгновенно выделяется количество
теплоты Q = pcM. Если поверхность z — О полностью
теплоизолирована, то на этой поверхности дТ/dz = 0; нетрудно
проверить, положив R2 = х2 -f- у2-\- z2, что распределение
температуры в этом случае по-прежнему будет иметь
вид B.1). Поэтому можно также непосредственно
воспользоваться термоупругим потенциалом B.3). Переходя к
цилиндрическим координатам г, ср, z и применяя соотношения A.32)
(при р = 0), получим:
\ B.10)
*) Nowacki [137, 7].

§3]
МГНОВЕННЫЙ ИСТОЧНИК
35
Это напряженное состояние не удовлетворяет, однако,
всем краевым условиям на поверхности z = 0 поскольку
на этой поверхности (включая точку R = 0) обращается
в нуль только касательное напряжение сгг. Чтобы выполнить
краевое условие azz = 0, необходимо наложить на
полученное распределение напряжений другое подходящее решение.
Как отмечалось ранее*), такое решение в осесимметричном
случае можно получить при помощи функции напряжений
Лява. Учитывая, что функции J0(kr)e~lzy zJ0(kr)e"lz являются
бигармоническими, положим **):
B.11)
Вычислим при помощи соотношений {(8.10), Мелан — Пар-
кус [6]} напряжения о/:/., соответствующие функции Ц если
при этом положить or2|2=()=0, то получим А = 2рВ, и
выражения для напряжений примут вид:
B.12)
*) Мелан — Паркус [6], гл. VIII.
**) Введенную здесь переменную А не следуе! смешивать
с коэффициентом теплопроводности.

36 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ {ГЛ. И
Оставшуюся неопределенной величину В(к, t) найдем из
условия ^г + ^гг^^ ПРИ Z — ^* Чтобы ВЫПОЛНИТЬ ЭТО уСЛОВИе,
нужно представить напряжение агг, определяемое
формулой B.10), в виде интеграла Фурье — Бесселя. Это проще
всего сделать, представляя термоупругий потенциал
перемещений B.3)*) в форме интеграла Фурье — Бесселя
ф(г, 0, Q = _-*L.Ierf(—$=) =
V J 2G г \2V at)
со
^ — -^jfjo (И erf с (X Vat) dl.
о
Поскольку azz определяется дифференцированием Ф по г,
здесь принято Z — 0. Через erfc (я) обозначена
дополнительная функция Гаусса: ^
2 г
erfc(и) = у^ / e~xl dk=\— erf (и).
и
Составляя указанное выше краевое условие и сравнивая
оба подынтегральных выражения, получим:
В (X, t) = A~^)/Cl erfc (X Vat). B.13)
Таким образом, поля напряжений и перемещений определены
полностью. Равномерная сходимость интеграла при t > 0
легко доказывается.
Путем интегрирования по t можно найти распределение
температуры и напряжений для случая непрерывно
действующего теплового источника. Пусть S{t) (кал/сек) —
производительность этого источника, тогда, положив dQ =
=zocdM = Sdt, получим:
B.14)
*) E r d ё 1 у i и др. [4], т. 2, стр. 92; интеграл легко вычислить,
если продифференцировать его по Vat = а, найти получающийся
интеграл Вебера и результат снова проинтегрировать по а. См.
также далее, § 4 гл. II.

§ 4] МГНОВЕННЫЙ ДИПОЛЬ 37
где f и Qjj — температура и напряжение, соответствующие
мгновенному источнику тепла Q=l. Если, в частности,
S = const, то, используя уравнение B.1), найдем:
B.15)
Из уравнений B.3), B.13) получим соответственно:
B.16)
B.17)
§ 4. Мгновенный диполь на поверхности
полупространства; температура поверхности постоянна*)
В начале координат О упругого полупространства z^>0
в момент t = 0 действует мгновенный тепловой диполь.
Поверхность z — 0, r>0 поддерживается при постоянной
температуре, равной нулю.
Легко видеть, что и в рассматриваемом случае имеет
место распределение температуры, выражаемое формулой
B.8) при Е = 7} = С —0. При этом термоупругий потенциал
перемещений Ф выражается формулой B.9), при помощи
*) Nowacki [137, 7].

38 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
которой по формулам A.32) находим соответствующие
значения напряжений в цилиндрических координатах:
Здесь обозначено:
Чтобы удовлетворить краевым условиям
B.18)
B.19)
на поверхности z = 0, необходимо наложить на приведенное
решение второе напряженное состояние, которое можно
получить при помощи функций напряжений Лява. При этом
мы можем непосредственно использовать выражение B.11),
положив в нем А = — A—2ц) В, чтобы удовлетворить уело-

§4]
МГНОВЕННЫЙ ДИПОЛЬ
39
вию ozz = 0. В результате получим следующие значения
напряжений:
B.20)
Для определения величины В(\, f) служит условие orz-}-Grz=0
при z = 0. При этом необходимо представить orz\z^0
интегралом Фурье — Бесселя. Вначале при помощи уравнения
B.9) получим:
. B.21)
В правильности этого интегрального представления легко
убедиться прямой проверкой. Воспользуемся для этого

40 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
интегральной формулой Вебера *)
B.22)
Дифференцируя это соотношение по параметру at, а второй
интеграл уравнения B.21) — по параметру У at—а., придем
к зависимости
Таким образом,
Составляя краевое условие и используя значение
получим следующее выражение для величины В (к, t):
B.23)
Решение рассмотренной задачи одновременно определяет
функцию Грина для полупространства с нулевой начальной
температурой и с произвольным заданным распределением
*) В а т с о н [7].

§51
МГНОВЕННЫЙ МЕСТНЫЙ НАГРЕВ
41
температуры поверхности 6, поскольку распределение
напряжений в этом случае можно определить по уравнению A.44)
при подходящем распределении диполей на поверхности
§ б. Мгновенный местный нагрев поверхности
полупространства *)
Упругое тело, заполняющее полупространство 2^>0, имеет
температуру 7 = 0. В момент / = 0 круговая область радиуса
r — b на поверхности z = 0 мгновенно нагревается до
постоянной температуры Г = Г0 и затем поддерживается при
этой температуре. Остальная часть поверхности сохраняет
температуру Г = 0.
Эта задача может иметь определенное практическое
значение, поскольку быстрые местные нагревы поверхности тела
встречаются достаточно часто.
Решение этой задачи можно получить при помощи метода
функции Грина, рассмотренного в § 4 этой главы. Мы,
однако, приведем прямое решение, основанное на
использовании свойств симметрии задачи.
Найдем вначале температурное поле. Применяя к
уравнению A.45) преобразование Лапласа
и учитывая начальное условие Г (г, z, 0) = 0, получим:
B.24)
Решение этого уравнения легко получается методом
разделения переменных и имеет следующий вид:
B.25)
*) Bailey [11].

42 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
*) В а т с о н [7].
**) См., например, Erdeiyi и др. [4] 1; см. также
соотношение B.34в).
Здесь в показателе экспоненты выбран отрицательный знак,
поскольку температура на бесконечности должна оставаться
ограниченной. Произвольная функция Л ($, X) определяется
из краевого условия при 2 = 0, которое после
преобразования принимает вид / _ ,
* f / /о ппм г ^ п
Используя разрывный интеграл *)
B.26)
непосредственно получим:
Таким образом, изображение решения имеет вид
B.27)
Используя таблицу преобразования**), сразу же получаем
оригинал решения в следующей форме:
B.28)
Полученное решение имеет формальный характер,
поскольку пока мы не доказали, что несобственные интегралы
сходятся и что при подстановке решения в краевые условия
и в дифференциальное уравнение можно делать необходимые
перемены порядка интегрирования и предельного перехода.
Эти вопросы рассмотрены в оригинальной работе Бейли.
Перейдем теперь к определению напряженного состояния.
Мгновенное изменение температуры поверхности вызывает
волны напряжений, которые будут рассмотрены в § 2 гл. V.

»5]
МГНОВЕННЫЙ МЕСТНЫЙ НАГРЕВ
43
Здесь мы рассмотрим квазистатическую составляющую
решения, которая практически определяет состояние после
прохождения волны.
Как и прежде, будем пользоваться потенциалом переме-
щений Ф. Применяя преобразование Лапласа к уравнению
A.47) при Ф0 = 0, получим:
ф* = _}_+? аа — + -% . B.29)
Если подставить сюда значение Г* из уравнения B.27) и
вычислить соответствующие напряжения, то обнаружится,
что интегралы на поверхности z — 0 расходятся. Эту
особенность можно устранить путем подходящего выбора
функции Фр При этом можно воспользоваться тем условием, что
при t—>co должно иметь место стационарное решение.
Согласно известной теореме теории преобразования Лапласа
lims/*(s) = lim/@.
если предел lim/(f) существует. Применим эту теорему
t->oo
к функции Ф* и поставим условие, что предел lim $Ф*
существует; при этом получим *): ,s~>0
Таким образом получаем следующий результат (который
можно применять не только в рассматриваемом случае):
^ = Т^^-^Г-ТЮ). B.30)
Здесь Гоо^ lim sT* представляет собой стационарную тем-
s-»0
пературу, которая устанавливается при достаточно больших
значениях времени. Условие АФ2 = 0 при этом будет
выполнено, поскольку Гоо, очевидно, удовлетворяет стационарному
уравнению теплопроводности.
Используя значение Т* из уравнения B.27), в
рассматриваемом случае получим:
оо
Ф*(л *. S) = ^f Jx{U)J,{\r) e'"Z~e~XZ dk, B.31)
о
*) G о о d i e г [63, 2].

44 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. It
где
Теперь изображения напряжений о/у, соответствующие
потенциалу Ф*, можно вычислить при помощи уравнений
A.32) (при р = 0), заменив в них о/;. на с/у и Ф на Ф*. При
этом получим:
} B.32)
Можно показать, что интегралы равномерно сходятся и
что напряжения о* (а следовательно, и напряжения с) являются
непрерывными функциями г и z при 2^-0. Ha поверхности
z = О напряжение с*2 в соответствии с краевыми условиями
обращается в нуль, однако касательное напряжение остается, и
для устранения его необходимо ввести дополнительное решение.
Как неоднократно отмечалось ранее, такое второе
решение можно получить при помощи функции напряжений Лява.
Имея в виду краевое условие, которому необходимо
удовлетворить, положим
Легко убедиться, что при этом дифференциальное уравнение
ДД/,* = 0 будет выполнено. Вычисляя по формулам {(8.10),

§5]
МГНОВЕННЫЙ МЕСТНЫЙ НАГРЕВ
45
Мелан — Паркус} напряжения огг и arz, соответствующие L*t
и используя краевые условия
c*2 —0, а*г = — агг при 2 = 0,
получим для множителей Л и В следующие значения:
При этом функция L* и соответствующие ей
напряжения о*., вычисляемые по формулам {(8.10), Мелан — Пар-
кус [6]), будут определены полностью. Вычисляя эти
напряжения и складывая их с напряжениями а* отвечающими
потенциалу перемещений Ф*. получим изображения
суммарных напряжений ъц = a* -f- а* в следующем виде:
B.33)

46
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
Остается по изображениям этих напряжений найти их
оригиналы. Для этого потребуются следующие формулы
обратного преобразования:
B.34)
Эти формулы можно получить при помощи цитированных
выше таблиц Erdelyi с учетом теорем смещения и
свертывания. Формула е) выведена посредством дифференцирования
формулы д) по z.
Применяя эти формулы к соотношениям B.33) и изменяя
порядок интегрирования и обратного преобразования Лапласа,
получим окончательные значения напряжений. Аналогично
можно найти перемещения и и v, соответствующие
потенциалу Ф и функции напряжений L.
Нетрудно доказать, что пол>ченное формальное решение
является равномерно сходящимся.

§5]
МГНОВЕННЫЙ МЕСТНЫЙ НАГРЕВ
47
На поверхности z = 0 напряжения ozz и arz обращаются
в нуль, а напряжения агг и о имеют следующие значения:
B.35)
Используя формулы B.26) и учитывая значение Cv найдем
значения напряжений сразу же после повышения температуры
(т. е. при t->Q-\-):
B.36)
Эти значения согласуются с величинами начальных
напряжений, возникающих при мгновенном нагреве цилиндра (гл. И,
§ 9) или сферы*) (гл. II, § 13).
При достаточно больших значениях времени (т. е. при t—>co)
будут иметь место установившиеся поля температур и
напряжений. Соответствующие решения можно получить
непосредственно из уравнений B.27) и B.33) при помощи предельного
перехода. Учитывая, в частности, что lim a./=limsa*
*) Sadowsky [158] рассмотрел сходную задачу для случая,
когда температура круговой области бесконечна, а температура
остальной части поверхности и полупространства остается равной
нулю.

48
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
получим следующие значения стационарных напряжений *)
B.37)
Приведем также изображения компонент перемещения я и -до
в радиальном и осевом направлениях:
B.38)
Оригиналы и и ?е> легко получить отсюда при помощи
формул преобразования B.34); в частности, стационарные
перемещения будут иметь вид
B.39)
Очень простые выражения получаются для стационарных
напряжений на поверхности 2 = 0, где интегралы выражаются
*) Стационарный случай рассматривался многими авторами;
Sternberg [174] и М с D о w е 11 [118] получили замкнутые
решения, выраженные через эллиптические функции.

§ 6] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 49
через элементарные функции *). Соответствующие формулы
имеют вид
B.40)
§ 6. Сферическая полость в неограниченной среде**)
Рассмотрим бесконечную упругую среду с температурой
Т = 0, содержащую сферическую полость радиуса /?. В
момент t = 0 поверхность этой полости мгновенно нагревается
до температуры Г0 и далее поддерживается при этой
температуре. Учитывая, что в рассматриваемом случае централь-
ной симметрии: Д = ^~2 Ч 'ТТ-* получим решение
преобразованного уравнения теплопроводности B.24) в
следующем виде:
Г* (г, s) = — \A(s)e-rVJ^ + B(s)e+rV1^\.
Из условия, что Т* -> 0 при г -> сю, получаем Л E) = 0.
Определив далее функцию A (s) из краевого условия
при r = R,
получим изображение решения в следующем виде:
B.41)
*) См., например, Magnus — Oberhettingeг, Formein
und Satze fur die speziellen Funktionen der mathenatischenPhysik, 2
Aufl., Berlin, 1948, стр. 50.
**) Sternberg [174, 1].

50 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
Применение обратного преобразования*) дает**):
Г (л 0=^о— erfc^J-. B.42)
Переходим к определению полей напряжений и
перемещений. В рассматриваемом случае отлична от нуля только
радиальная компонента перемещения и (г, t)> через которую
компоненты напряжения можно выразить по следующим
формулам, вытекающим из уравнений A.7):
B.43)
Вследствие этого задача сводится к решению одного
дифференциального уравнения A.8)
дг2~^ г ' дг г2 — 1 — р. а дг в
Общее решение этого уравнения имеет вид
г
Перемещение и напряжения должны обращаться в нуль на
бесконечности, поэтому Сг = 0. Примем, что поверхность
полости свободна от напряжений
огг = 0 при r = R.
Используя первое уравнение B.43), получаем, что в этом
случае С2 = 0. Таким образом, окончательно
B.44)
Полученное решение обладает любопытной особенностью,
заключающейся в том, что и (R, t) = О при всех значениях ?,
т. е. независимо от вида температурного поля радиус по-
*) См. уравнение B.34, в).
**) Carslaw — Jaeger [l].

§ 6] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 51
лости при нагреве остается неизменным *). Таким образом,
выражение B.44) одновременно дает решение для случая,
когда поверхность полости закреплена.
Подставив значение B.44) в уравнение B.43), получим:
} B.45)
Используем теперь найденное для рассматриваемого
случая распределение температуры B.42). Вводя безразмерный
радиус р и безразмерное время т,
получим:
где
B.46)
B.47)
Этот интеграл можно вычислить в замкнутой форме. Вводя
новую переменную С = р""~_ , представим его в виде
и после интегрирования по частям получим окончательно:
B.48)
*) Это будет справедливо только для квазистатического
решения, см. также § 7, гл. VI.

52 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЙ [ГЛ. II

§ 6J СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 53

54 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ (ГЛ. И
Учитывая, что при достаточно больших значениях
времени (т. е. при х->эо)
найдем установившееся состояние:
1 + fx aRT0 ( 1\ ЕаТ0 р*-1 )
1 ** z v p y I р. , 1 f2
а ~а - ?аГ° р2+1 Г- Г° I
На поверхности р = 1 имеем о = о^ = — ЕаТ0/(\ — ;
Как можно видеть из уравнения B.45), эти значения окруж
ных напряжений имеют место не только при ^->оо, но и
в продолжение всего процесса нагрева.
На рис. 1—4 показаны температура, перемещения и
напряжения в различные моменты времени т в зависимости от
безразмерного радиуса р. Безразмерные переменные,
введенные на фигурах, определяются следующим образом:
f —JL и — 1~** и 7— 1~~*х „
Т0 ' и —  -f (а " «RT0 ' "~ ?аГ0 °-
Рассматривая зависимость решения от времени (т. е. считая,
что р фиксировано), замечаем, что 7\ и и —агг являются
монотонно возрастающими функциями т; о возрастает,
достигает положительного максимума и далее стремится к
отрицательным стационарным значениям.
§ 7. Сплошной и полый цилиндры кругового поперечного
сечения; первое решение
Рассмотрим цилиндр длины /, имеющий вначале
температуру Г —0. Начиная с момента ^=0, температура среды
около внутренней и наружной цилиндрических поверхностей
произвольно изменяется с течением времени, оставаясь осе-
симметричной. Примем вначале, что на торцевых
поверхностях происходит теплообмен со средой, температура которой

§ 7] СПЛОШНОЙ И ПОЛЫЙ ЦИЛИНДРЫ; ПЕРВОЕ РЕШЕНИЕ 55
равна нулю *). Это условие включает в себя предельные
случаи как полностью теплоизолированного торца, так и торца
с постоянной температурой, равной нулю.
Для определения температурного поля следует решить
уравнение A.45) с начальным условием Г = 0 и с краевыми
условиями
= 0, B.50)
B.51)
где г и z — радиальная и осевая координаты, Rt и Ra —
внутренний и внешний радиусы цилиндра. Постоянные ап, ...
.... dl2 в каждом частном случае легко определяются по
формулам {A.7), Мелан—Паркус [6]). Применяя
преобразование Лапласа к уравнению A.45), получим уравнение B.24),
решение которого можно выбрать аналогичным тому
решению, которое было использовано в § 5:
где
B.52)
Это решение можно получить из выражения B.25), если
заменить в нем f на щ и X на ik. Через /0 и К0 здесь
обозначены модифицированные функции Бесселя.
Подставив Т\ в краевые условия B.50), получим два
-однородных линейных уравнения относительно постоянных Сх
и С2; эти уравнения будут иметь нетривиальное решение
в том случае, если определитель обращается в нуль. Из
*) Эту задачу рассматривал Trostel [186, 1], который,
однако, не применял преобразования Лапласа. Частный случай
рассмотрел Воск [20]. Стационарную задачу изучал В ц с к е n s [29, 1J.

56 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. 11
этого условия находим:
tg t = a"b"-*»b" . B.53)
Бесконечное (счетное) множество корней этого уравнения
определяет собственные значения тл (л=1, 2, 3...) нашей
задачи, которые при заданных ап, а12, blv bl2 можно
считать известными.
Собственные функции, соответствующие собственным
значениям Т/1» легко определяются. Поскольку определитель
равен нулю, оба уравнения, определяющие Сх и С2, будут
идентичными, и поэтому можно, например, выразить С2
через Cv причем последняя постоянная останется произвольной.
Выбирая соответствующим образом эту постоянную, получим
собственную функцию в следующем виде:
Z (Тяг) = Сх cos 4nz + C2 sin inz, B.54)
где
С\ = lna12 C0S Ти' + «11 S{tl 7/А
С2 = Тя«12 Sin Тя* — «И COS Тя/.
Заметим, что собственные функции Z(fnz) образуют полную
ортогональную систему, поскольку они являются решением
краевой задачи Штурма — Лиувилля.
При помощи суммирования по п получим следующее
общее решение:
Т* = S I Vo (V) + ВпК0 (X.r)] Z (Т„*). B.55)
Л-»1
Здесь значения Х„, соответствующие ^п, вычисляются по
формуле B.52).
Две последовательности постоянных Ап и Вп определяются
из двух краевых условий B.51). Для того чтобы получить
изображение этих условий, нужно вместо Т подставить Т*%
а функции сра и cpf. заменить их изображениями y*a(z, s) и
<?i(z, s). Если подставить теперь Т* из уравнения B.55) и

§ 7] СПЛОШНОЙ И ПОЛЫЙ ЦИЛИНДРЫ; ПЕРВОЕ РЕШЕНИЕ 57
представить функции <р* и ср* рядами по собственным
функциям
со оо
<? (*. s) = 2 с« (s) Z(V), ср* (г, s) = 2 с'й (s) Z hnz), B.56)
то из сравнения рядов получим:
Здесь и далее символ ' означает дифференцирование по
аргументу, т. е., например, /0(я) = —-3-. Два приведенных
уравнения позволяют вычислить искомые постоянные Лп и Вп\
температура Т* при этом будет полностью определена.
Поскольку функции Z(fnz) образуют ортогональную
систему, коэффициенты разложений сап и сьп будут иметь
следующий вид:
B.57)
B.58)
где
Сходимость рядов B.56) для встречающихся в приложениях
функций ср*, ср* устанавливается при помощи известных
критериев.

58 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. I!
Используя для вычисления «нормы» N„ выражение
функции Z(-\nz) в форме B.54), получим:
— — § f"
+ [(T>?2-4)C0ST^ +2тявпвИ81птвП^- B-59)
Чтобы окончательно определить температурное поле,
необходимо произвести обратное преобразование решения Г*.
Такое преобразование целесообразно выполнять в каждом
частном случае отдельно, используя при этом наряду с
таблицами изображений также общую формулу обращения.
Считая, что Т* найдено, обратимся к задаче определения
напряжений; вначале найдем потенциал перемещений Ф.
Поступая так же, как в § 5, поставим условие, что предел НтзФ*
существует. Тогда, как и прежде, будет справедлива
зависимость B.30), подставив в которую значение Г* из
уравнения B.55) сможем найти изображения напряжений о*, по
формулам A.32). Мы не приводим здесь соответствующие
окончательные выражения, поскольку их легко получить в
частных задачах.
Построенное решение дает отличные от нуля радиальные
и касательные напряжения на внешней и внутренней
цилиндрических поверхностях г = Ra и г = Rt. Чтобы устранить
эти напряжения, наложим на полученное решение
дополнительное «бестемпературное» (т. е. относящееся к случаю
Г = 0) напряженное состояние а* которое можно найти при
помощи функции напряжений Лява. Соответствующие
уравнения приведены в гл. VIII, § 1 книги Мелана — Паркуса [6],
в них следует лишь заменить L на L*, поскольку здесь мы
рассматриваем изображения.
Возьмем функцию напряжений в виде
сю
^ = ^2Д'о<Т.') + ?*о(Т.г> +
+ Enrlx (Тяг) + «„г/С, (Т„г)] Z' (T„z), B.60)
где согласно уравнению A.54)
z'(T/i*) = — CiSinTrt2-f C2cos-[rt2. .B.61)

§ 7] СПЛОШНОЙ И ПОЛЫЙ ЦИЛИНДРЫ; ПЕРВОЕ РЕШЕНИЕ 59
Легко проверить, используя приведенные далее значения
производных, что введенная функция удовлетворяет бигар-
моническому уравнению AAL* = 0 при произвольных
значениях постоянных Dn, .... Нп.
Дополнительные напряжения о*;. следует подчинить
краевым условиям
? = -?• ? = -? "Р" r = Ra, r = Rr B.62)
из которых определятся последовательности постоянных
D„ Нп.
Приведем вначале сводку производных функции L*,
которые потребуются для вычисления напряжений (для
упрощения записи мы опускаем здесь символ суммирования,
поэтому формулы относятся к п-му члену Ln);
Очевидно, что LLn — гармоническая функция, поэтому
уравнение kLLn = Q действительно выполняется.

60 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ II
Внося приведенные выражения в уравнения {(8.10),
Мелан —Паркус [6]}, получим компоненты напряжений в
следующем виде;
B.63)
Далее следует подставить эти значения напряжений в
краевые условия B.62). Мы, однако, не будем здесь заниматься
определением постоянных Dn, ..., Нп и обратным
преобразованием изображений суммарных напряжений о*, = о* + <з!.,
IJ IJ IJ
поскольку эти вычисления целесообразно проводить для
отдельных частных случаев.
Полученное решение дает свободные от напряжений
внешнюю и внутреннюю цилиндрические поверхности, но на
торцах цилиндра, вообще говоря, остаются нормальные
напряжения czz и касательные напряжения orz. Однако эти на-

§ 7J СПЛОШНОЙ И ПОЛЫЙ ЦИЛИНДРЫ; ПЕРВОЕ РЕШЕНИЕ 61
пряжения не дают результирующей силы и пары сил и,
следовательно, образуют самоуравновешенную систему,
Самоуравновешенность касательных напряжений и отсутствие
момента нормальных напряжений непосредственно следуют
из осевой симметрии задачи. Далее, поскольку обе
цилиндрические поверхности свободны от напряжений, результирующая
осевая сила (если она возникает) должна иметь одно и то же
значение во всех поперечных сечениях цилиндра. Но условие
отсутствия напряжений на цилиндрической поверхности
выполняется для каждого /1-го члена решения в отдельности,
поэтому для постоянства осевой силы необходимо, чтобы по
крайней мере одна функция Z(fnz) обращалась в отличную
от нуля постоянную. Однако в действительности этот случай
не имеет места.
Таким образом, согласно принципу Сен-Венана, можно
считать, что заметное влияние напряжений, действующих на
торцевых поверхностях, будет обнаруживаться только
поблизости от этих поверхностей. Если, однако, необходимо, чтобы
напряжения на торцах полностью отсутствовали, то следует
ввести дополнительные функции Лява. Соответствующие
формальные указания можно найти в работе Тростеля.
Отметим в заключение, что уравнения этого параграфа
легко распространить на случай, когда цилиндр простирается
от z — 0 до z — оэ. Для этого необходимо лишь заменить
ряды Фурье соответствующими интегралами Фурье; например,
вместо соотношения B.55) следует принять
Г = f [Л/0 (Xr) + BK0 (Xr)] Z (Tz) dV B.64)
о
Зависимость между X и 7 по-прежнему имеет вид B.52).
Функции Z(~[Z) теперь должны удовлетворять только
краевому условию B.50) при z = 0, поэтому они будут иметь
вид
Z (fz) = bn sin *\z — Ъу?\ cos fz. B.65)
Для определения коэффициентов Л G) и В (*f) заданные
краевые функции <р*(г> s) и ср*B, s) представляются в форме

62 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ 1ГЛ. 11
интегралов
B.66)
При этом, естественно, предполагается, что такое предста-
оо
вление возможно, т. е., в частности, что интегралы / |f*|^
о
оо
и I |<p*|fite существуют. «Спектральные функции» са и с1
о
в этом случае определяются соотношениями *)
B.67)
где Ь(к—^) — дельта-функция Дирака, определяемая
зависимостью
B.68)
Функция Дирака симметрична: 8(—х) = Ь(х). Соотношения
B.66) и B.67) являются обобщением на случай бесконечного
интервала зависимостей B.56), B.58), выведенных для
интервала длины /.
Для вычисления нормы N следует выражение B.65) для
функции Z подставить в третье уравнение B.67). Поскольку
*) См., например, Morse P. M., Feshbach H., Methods
of Mathematical Physics, New York, 1953, стр. 764.

§ 7] СПЛОШНОЙ И ПОЛЫЙ ЦИЛИНДРЫ; ПЕРВОЕ РЕШЕНИЕ 63
в левую часть этого уравнения входит В-функция, интеграл
в правой части будет расходящимся. Чтобы уравнение имело
смысл, умножим его*) на непрерывную функцию Ф(Х) и
проинтегрируем по X от 0 до оо. При этом функцию Ф (X)
следует выбрать так, чтобы двойной интеграл в правой части
после изменения порядка интегрирования сходился. Полагая
ф(К) = е~х и учитывая соотношение B.68), получим:
оо
Гe-KN(K s)b{\ — 7)<Л = е-Ш(т, s) =
о
оо оо
= J Z (tz) dz j e~xZ (кг) dk.
о о
Подстановка сюда Z дает
со
Ne~i = I [bn sin fz — ?127 cos fz] X
о
y[ b4* I bl* 2^I2 ] d„
Воспользуемся табличными интегралами **)
где через El обозначена интегральная показательная функция
*) См. например, Friedman В., Principles and Techniques
of Applied Mathematics, New York, 1956, стр. 136.
**) О г б b n e r W., H о f r e i t e r N., Integraltafel, 2 A950), 127,
со
„ JC2v+1
Wien, стр. 91; следует иметь в виду, 4TOsh;c=: V 9 , - -.
лтА (ZV + 1I
v-0

64 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. I!
При помощи дифференцирования по f и по а находим из
этих соотношений другие необходимые интегралы и в
результате получаем:
A/ = ~(fc'ii+7%). B.69)
Теперь можно составить уравнения для определения
коэффициентов Л и В. Эти уравнения совпадают с уравнениями
B.57), если в последних отбросить индекс п.
Все последующие вычисления, в том числе построение
термоупругого потенциала и функции Лява, производятся
так же, как в случае цилиндра конечной длины. При этом
сохраняются все выведенные уравнения, в которых
необходимо лишь заменить суммирование по т\п интегрированием по f.
Очевидно, что при t->oo полученные решения будут
соответствовать случаю установившегося распределения
температуры. При этом (так же, как и в предыдущих
параграфах) выполнение обратного преобразования оказывается
излишним, поскольку, если предел lim T и, следовательно,
предел lim oif существуют, то
lim r = limsr*, lim a.. = lim 5a* .
*->oo 5->0 /->ao lJ s->0 *
Треммель рассмотрел родственную задачу о цилиндре
с распределенными в объеме тепловыми источниками,
производительность которых убывает с течением времени по
экспоненциальному закону *). Поля температур и напряжений такого
типа возникают при схватывании бетона.
§ 8. Сплошной и полый цилиндры кругового поперечного
сечения, второе решение
В предыдущем параграфе предполагалось, что на
торцевых поверхностях цилиндра происходит теплообмен со средой,
температура которой равна нулю. Если температура среды
отлична от нуля (например, равна температуре среды около
цилиндрических поверхностей), то следует найти второе
решение, к рассмотрению которого мы теперь переходим.
*) Tremmel [185, 3J.

§ 8] СПЛОШНОЙ И ПОЛЫЙ ЦИЛИНДРЫ; ВТОРОЕ РЕШЕНИЕ 65
Для упрощения вычислений будем предполагать, что длина
цилиндра велика по сравнению с его диаметром. Тогда
влияние температуры торцов, вообще говоря, будет быстро осла -
бевать при удалении от торца, поэтому для приближенного
вычисления напряжений вблизи какого-либо из торцов можно
принять, что цилиндр является «полубесконечным».
Мы рассмотрим здесь только концевое сечение z — 0.
Очевидно, что метод применим также длл рассмотрения
другого концевого сечения z = l. Вместо краевых условий B.50)
и B.51) теперь примем
B.70)
= 0. B.71)
Поскольку температура и напряжения при z -> со должны
оставаться ограниченными, мы, поступая так же, как в § 7,
получим температуру Т* в следующей форме:
B.72)
/2=1
где
B.73)
Здесь У0 и iV0 — функции Бесселя первого и второго рода
нулевого порядка. Поскольку 7V0 при г->0 неограниченно
возрастает, для сплошного цилиндра следует положить В = О
и А=\.
Подставляя решение вначале в однородные краевые
условия B.71), получим два уравнения для определения Л и В:
Определитель этой системы уравнений должен равняться нулю.
Корни ^ = ХЛ (д= 1, 2, 3, . . .) соответствующего
трансцендентного уравнения определяют собственные значения рас-
B.74)

66 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
сматриваемой задачи. Соответствующие собственные функции
U (кпг) имеют вид B.73), где следует считать, что В
выражено через Л при помощи любого из уравнений B.74).
Собственные функции образуют в интервале [/?., Ra]
полную ортогональную систему с весовой функцией г:
f rU (\nr) U (kinr) dr = 0 (тф п).
Остается удовлетворить краевому условию B.70). Для этого
представим краевую функцию фо(г» О» ИЛИ соответственно ее
изображение ф* (г, s), в виде ряда по собственным функциям
B.75)
Коэффициенты этого разложения имеют вид
B.76)
Мы не будем здесь приводить явное выршжение нормы Мп,
поскольку ее можно легко вычислить в каждом отдельном
случае при помощи следующих неопределенных интегралов:
Используя краевое условие B.70), получим:
B.77;
Дальнейшие вычисления совершенно очевидны. Вначале из
уравнения B.30) находим потенциал перемещений Ф*. Функ-

§9]
МГНОВЕННЫЙ НАГРЕВ ЦИЛИНДРА
67
цию напряжений Лява в рассматриваемом случае возьмем
в форме, указанной в {(8.41), Мелан — Паркус [6]}:
со
^=S[^o(V)+^,(V) +
+ W(v)+W(v)]«~v+
оо
+ 2 [p^(V)+<4(V)+«(V)+C^(V)] *~v-
B.78)
Соответствующие напряжения о*. можно получить
непосредственно из уравнения {(8.42), Мелан — Паркус [6]}. Для
сплошного цилиндра, очевидно, следует положить s'n=s"n=0,
t' = f = 0.
п п
Коэффициенты выражения B.78), как и прежде,
определяются из условия отсутствия напряжений на внешней и
внутренней цилиндрических поверхностях:
?+?=0, ?+^ = ° при r = Rt, r = Ra.
Таким образом, задача построения изображения решения
формально решена. Так же как в первом решении, можно
установить, что напряжения, остающиеся на торцевых
поверхностях, образуют самоуравновешенную систему, поэтому
возникающие погрешности будут иметь значение только
поблизости от торцов.
Обратное преобразование, однако, в этом случае
представляет гораздо большие трудности, чем в первом решении,
и приводит к необходимости использования численных
методов. Для этой цели в особенности подходит метод Папу-
лиса *).
§ 9. Мгновенный нагрев цилиндра
Сплошной круговой цилиндр радиуса R и длины / имеет
вначале температуру, равную нулю. В момент t = 0
температура поверхности повышается до значения Т= Т0 и далее
остается неизменной; температура торцевых поверхностей
остается равной нулю.
*) Papoulis A., A new method of inversion of the Laplace
Transform Quart. Appl. Math., 14, 405 A957).

68 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
Эта задача является частным случаем задачи,
рассмотренной в § 7 гл. II и соответствует значениям ап = Ьп = си= 1,
ап — ?12 = с12 = 0, сра=Г0 в краевых условиях B.50) и
в первом краевом условии B.51). Второе краевое условие
B.51) заменяется требованием ограниченности температуры
и напряжений на оси цилиндра г = 0. При этом
постоянная Вп в выражении B.55) будет равна нулю, а
уравнение B.53) принимает вид tgf/ = 0, которому соответствуют
собственные значения -[д = ятг// (#=1, 2, 3 ...). При этом
из выражения B.54) получаем собственные функции
z (In*) = — cos In1 sin In* = (— 0Л+1 sin In*-
Используя уравнения B.58) и учитывая, что ср* = TJs и
Nn = -~t находим коэффициенты разложения с^ = сп
сп (s) = (- 1)я+1 1J± A - cos Тя0 =
( 1^а ПРИ я=1. 3- 5
( 0 при п = 2, 4, 6, ...
Далее из первого уравнения B.57) находим:
Лл = слE)//0(Х„Д).
Таким образом, окончательно получим изображение
температуры в следующем виде:
r(r.z.s)=*Z- J -А^йп^. B.79)
л=1, 3,5
где X =1/ 7^4 * ^ля вычисления напряжений не
требуется знать оригинал T(r, z, t), поэтому обратное
преобразование можно выполнить после того, как будут найдены
изображения напряжений. При достаточно больших
значениях времени будет иметь место установившееся конечное
распределение температуры 7^:
л-1, 3,5

§ gj МГНОВЕННЫЙ НАГРЕВ ЦИЛИНДРА 69
Определив потенциал Ф* из уравнения B.30) и вводя
сокращенные обозначения:
получим из уравнений A.32) соответствующие напряжения:
(здесь суммирование производится по значениям п—\, 3,
5, .. .)• Пользуясь асимптотическим представлением
справедливым для больших положительных значений х,
можно доказать, что ряды в последних формулах равномерно
сходятся по г для 0 ^ г <J R. Это непосредственно следует
из признака равномерной сходимости Абеля, поскольку,
например, ряд V — sin "^2 сходится, а коэффициенты при
^™ Т/1
п
-~sin^nz образуют при фиксированном г ограниченную и
Т/г
монотонную последовательность.
Функция напряжений Лява B.60) в данном случае будет
иметь вид

70 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ (ГЛ. II
где снова следует полагать л=1, 3, 5, ... Пользуясь
выражениями B.63), находим из краевых условий B.62) при
r — R два уравнения для определения коэффициентов Dn и Еп\
Решение этих уравнений имеет вид
где через Рп и Qn обозначены следующие, не зависящие от 5
выражения:
B.80)
При этом получаем следующие формулы для напряжений а

§91
МГНОВЕННЫЙ НАГРЕВ ЦИЛИНДРА
71
Здесь обозначено:
B.81)
Решение завершается проведением обратного
преобразования полученных выражений. Мы приведем соответствующие
вычисления для компоненты напряжения а*г = <з*гг ~ha*r-
Как можно видеть из соответствующих уравнений, задача
заключается в выполнении обратного преобразования
выражений — fn(r,s) и —gn(r,s). Мы воспользуемся здесь
общей формулой обращения *)
где с следует выбирать так, чтобы Ф* (s) была
аналитической функцией комплексной переменной 5 во всей
полуплоскости Re О) > с. В случае, когда Ф*= —fn(r, s), получаем:
Подынтегральное выражение имеет полюс второго порядка
5 = 0 и простые полюсы в точках, где XnR = ± 1фт, т. е.
в точках s — — a (-бг+ТяЬ через Рю здесь обозначены
*) См., например, Д ё ч, Руководство [2].

72
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
корни*) функции Бесселя У0 : У0 фт) = 0. Таким образом,
можно положить с = 0. Для вычисления интеграла
воспользуемся теоремой вычетов и образуем замкнутый путь
интегрирования из мнимой оси и полуокружности в левой
полуплоскости. Интеграл по этой полуокружности обращается
В нуль, когда ее радиус р стремится к бесконечности,
поскольку
->0
при Re (s) <; 0. Таким образом, получаем:
Далее, используя зависимость
находим:
B.82)
легко
B.83)
*) Численные значения приведены в книге Янке — Эмде [5].

МГНОВЕННЫЙ НАГРЕВ ЦИЛИНДРА
73
В результате получаем следующую формулу для радиального
напряжения:
0гг=С ^ [Рп ('• *)-~гГ°п С. t) + nnSn (r) Gn (/?, t)] sin Лпг.
п
B.84)
Аналогично выполняется обратное преобразование остальных
компонент напряжения, приводящее к формулам
B.85)
Здесь функции Кп(г, t) и Hn(r, t) имеют следующие
значения:
/ q2
Л MR)
B.86)
Легко доказать, используя соотношения Fn(R, t) = 0,
$п (R) = 1/(ятгул/?), Vn (R) = — l/(mz), что краевые условия
при г = /? будут формально выполнены. Исследование рядов
и их производных с учетом равномерной сходимости
показывает, что полученное решение является не только формаль-

74 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. 11
ным, но и в действительности удовлетворяет как краевым
условиям, так и дифференциальным уравнениям задачи.
При ?—>оо получаем стационарное распределение
напряжений.
§ 10. Длинный цилиндр, нагреваемый на участке
поверхности
Рассмотрим сплошной круговой цилиндр радиуса R,
простирающийся от z = — сю до z = -\-oo\ начальная
температура цилиндра равна нулю. В момент ^ = 0 температура
участка поверхности между сечениями z — — / и z = -\-l
повышается до значения Т0 и далее остается постоянной;
при этом температура остальной части поверхности
по-прежнему остается равной нулю.
Из соображений симметрии следует, что этот случай
идентичен задаче о полубесконечном цилиндре, простирающемся
от z — 0 до z = oo, участок поверхности которого между
сечениями z = 0 и z = l поддерживается при температуре Г0,
а торцевая поверхность 2 = 0 полностью теплоизолирована.
Таким образом, здесь можно применить решение B.64),
положив в нем В = 0 (поскольку функция К0 при г—>0 не
является ограниченной);
Здесь принято, что в выражении B.65) для функции Z (fz)
коэффициенты имеют значения Ьп = 0, — у?12 = 1,
соответствующие краевому условию dTjdz — О при z = 0. В
краевом условии B.51) на поверхности г = Ra = R следует
положить си=\> с12 = 0 и взять заданную краевую функцию
<рл(?, t) в следующем виде:
Принимая во внимание зависимость B.69), из уравнения B.67)
получим:

§ 10] ЦИЛИНДР, НАГРЕВАЕМЫЙ НА УЧАСТКЕ ПОВЕРХНОСТИ 75
Подстановка Т* в первое краевое условие B.51):
оо
T*(R, z, <0 = ср*= Г cacos-tzdf
о
дает А = га//0 (^/?). Учитывая этот результат, получим
окончательно:
B.87)
ГДе \ = у 72Ч—• Интеграл в последнем соотношении
равномерно сходится по г и по 2 при г < R.
Последующие вычисления выполняются в точности так же,
как в предыдущем параграфе. Прежде всего находим
потенциал перемещений из уравнения B.30):
Обозначив
получим соответствующие напряжения из уравнения A.32):

76 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. И
Здесь функции f(r,s), g(r,s) и h (r, s) идентичны
функциям fn (л s), gn (r, s), hn (r, s) предыдущего параграфа,
в которых чп заменено на ^, а \п — на X.
Дальнейшие формулы, в частности функцию напряжений
Лява L* и соответствующие напряжения о*., можно также
получить почти без вычислений из соответствующих
выражений предыдущего параграфа. Приняв
можем непосредственно использовать для вычисления
напряжений о* уравнения B.63); необходимо только отбросить
индекс п, заменить суммы интегралами и положить Z(^z) =
= — sin fl cos 72. Из краевых условий а*г =—o*f, o*rz =
= —a*rz при r = R при этом получаем:
где
B.88)
При атом получим следующие формулы для напряжений о* :

§ 10] ЦИЛИНДР, НАГРЕВАЕМЫЙ НА УЧАСТКЕ ПОВЕРХНОСТИ 77
со
72 = С -J- J *[V (г) g (R> s) sin T/ sin ~[z d^
0
oo
С 4- / tVF (г) g- (Я, s) sin f Z cos 72 d-p
o.. =
Здесь введены обозначения:
B.89)
Обратное преобразование решения производится так же, как
в предыдущем параграфе. В результате получаются
следующие формулы:
B.90)

78 ПРОЦЕССЫ НАГАЕВА И ОХЛАЖДЕНИЙ [ГЛ. И
где
B.91)
Так же как в предыдущем примере, можно убедиться в
справедливости полученного формального решения.
Стационарное распределение напряжений можно найти
при помощи предельного перехода при t->oo.

§ ц] ЦИЛИНДР, НАГРЕВАЕМЫЙ ПО ВСЕЙ ПОВЕРХНОСТИ 79
§ 11. Длинный полый цилиндр, нагреваемый
по всей поверхности
Полый цилиндр внутреннего радиуса /?/ и наружного
радиуса Ra имеет температуру Т (г, t)> которая не
изменяется в окружном и осевом направлениях, но является
произвольной функцией радиуса г и времени t. Концевые сечения
цилиндра закреплены неподвижно *).
При принятых предположениях имеют место уравнения
для случая плоского деформированного состояния. Найдем
вначале общее выражение для напряжений **). Для этого
заметим, что, поскольку наша задача является осесимме-
тричной и поскольку ezz = О, все напряжения будут
выражаться через радиальное перемещение и по формулам A.4):
B.92)
перемещение и удовлетворяет уравнению A.5), которое
в данном случае принимает вид
д2и 1 да и __ 1+f* дТ^ 2 94
Общее решение этого уравнения имеет форму
г
u==Clr+^+\p^j f xT(x. t)dx. B.95)
*/
где Сх и С2 — произвольные постоянные. Поскольку на
внешней и внутренней цилиндрических поверхностях отсутствуют
нагрузки, на этих поверхностях должно выполняться
условие агг = О или
*)
*) См. по этому поводу замечание в конце этого параграфа.
*)Timoshenko — Goodie r, Theory of Elasticity, N. V\,
1951, стр. 408.

80 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ II
где г принимает значения г = /?^, r = Ra. Отсюда получаем:
С, = -[±?A-2^.74*,,, *). С2 = ТА_С1, B.96)
где через
B.97)
обозначена средняя температура цилиндра с внешним
радиусом г. Уравнения B.92) в этом случае дают:
B.98)
Мы применим полученные формулы к следующей частной
задаче *): цилиндр имеет нулевую начальную температуру,
в момент t=0 на внешней и внутренней цилиндрических
поверхностях начинается теплообмен со средами, имеющими
соответственно постоянные температуры bt и Ьа. В этом
случае имеют место краевые условия B.51), которые мы
представим в следующем виде:
где через h{ и ha обозначены относительные коэффициенты
теплопередачи. Мы воспользуемся известным в литературе **)
решением этой задачи теплопроводности и приведем здесь
лишь окончательный результат, который имеет следующий вид:
B.99)
B.100)
Я»1
*) Jaeger [91].
**) Cars law — Jaeger [1].

§ Ц] ЦИЛИНДР, НАГРЕВАЕМЫЙ ПО ВСЕЙ ПОВЕРХНОСТИ 81
где
B.101)
B.102)
B.103)
Здесь через $п (п=\, 2, . . .) обозначены расположенные
в порядке возрастания неотрицательные корни (которые всегда
будут простыми) уравнения
andn-b„cn = 0. B.104)
Подставив теперь выражения B.100) в уравнения B.98),
после некоторых преобразований получим:
B.105)
B.106)

82
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ
[ГЛ. II
Для сплошного цилиндра (Ra~ Rt ha = h, ва = 9) имеют
место аналогичные результаты:
B.100а)
B.104а)
B.105а)
Рассмотрим три примера. Другие задачи изучались Гей-
слером (Heisler [70]).
а) Сплошной цилиндр. Начальная температура равна
нулю. Температура поверхности 6 постоянна. Полагая h->cot
получаем из приведенных выше уравнений следующие
формулы для напряжений:
где теперь
B.1056)
B.1046}
В таблицах 1 и 2 приведены значения радиального и
окружного напряжений в зависимости от безразмерного
радиуса р=-^- и безразмерного времени i — atjR2.

4 til- ЦИЛИНДР, НАГРЕВАЕМЫЙ ПО ВСЕЙ ПОВЕРХНОСТИ §3
0,95
-
0,9
0,75 0,8 0,85
1 1
лше A -
0,7
напряже
0,6
2 ^
•=5
СО |
1. Радр
0,4
лица
0,3
Таб
0,2
°~
о

84 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [Т.П. П

§ И] ЦИЛИНДР, НАГРЕВАЕМЫЙ ПО ВСЕЙ ПОВЕРХНОСТИ 85
0,1
0,4
0,3
-0.2
z
Рис. 5.
Рис. 6.

86 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
О ОМ 0,00 0,73 0,16 0,20
Z
О 0,02 0,04 0,06 0,08 0J
Рис. 8.

§ 121 ДЛИННЫЙ ЦИЛИНДР, НЕРАВНОМЕРНО НАГРЕТЫЙ 87
б) Сплошной цилиндр. Начальная температура равна
нулю; имеет место теплообмен (согласно второму
уравнению B.99)) со средой с температурой 0.
В этом случае будут применимы уравнения B.100а)—
B.105а), содержащие безразмерный параметр hR. На рис. 5 и б
приведены радиальные и окружные напряжения в зависимости
от р и х для случая hR — 5. На рис. 7 показана зависимость
окружного напряжения от параметра hR на поверхности
цилиндра р=1 для различных моментов времени т.
в) Полый цилиндр, Начальная температура равна нулю;
внутренняя поверхность r==R( теплоизолирована, внешняя
поверхность r = Ra имеет постоянную температуру 6.
Этот случай описывается уравнениями B.100) — B.106)
при ht = 0, ha = oc, Ьа = д. На рис. 8 приведено окружное
напряжение на внешней поверхности г — Ra в зависимости
от безразмерного времени т для различных значений
отношения радиусов R(/Ra.
Приведенные формулы относятся к случаю цилиндра с
неподвижными торцами. Если торцы цилиндра свободны, то мы
можем наложить на торцевые сечения постоянные осевые
напряжения таким образом, чтобы результирующая осевая сила
обращалась в нуль. При этом радиальные и окружные
напряжения останутся без изменений, однако для осевого
напряжения вместо уравнения B.93) следует теперь принимать
<згг = агг-^~а . На основании принципа Сен-Венана
полученное решение применимо на достаточном удалении (по
меньшей мере равном Ra) от концов цилиндра.
§ 12. Длинный цилиндр, неравномерно нагретый
в окружном направлении
Рассмотрим бесконечно длинный круговой цилиндр
радиуса R, начальная температура которого равна нулю. В
момент ? = 0 поверхности цилиндра мгновенно сообщается
температура Т=Т0е1п<?, где через ср обозначен полярный угол.
Применяя преобразование Лапласа к уравнению
теплопроводности, записанному в полярных координатах A.45), получим:

8В ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
При этом краевое условие будет иметь вид
Решение этой краевой задачи, ограниченное при г-^0, имеет
форму
г{г''-8)=т«1^Ш)е1т- Bло7)
Обратное преобразование выражения B.107) производится
при помощи теоремы вычетов точно таким же образом, как
Рис. 9.
аналогичное преобразование в § 9 гл. II. В результате
получается соотношение
B.108)
где через fym обозначены положительные корни уравнения
JM = 0- B-109)

§ 12] ДЛИННЫЙ ЦИЛИНДР, НЕРАВНОМЕРНО НАГРЕТЫЙ 89
Значения*) функции F(r, t) для /г== 1,2,3 приведены на
рис. 9—11, на которых обозначено z = at/R2.
Поскольку рассматривается случай плоской деформации,
можно воспользоваться уравнением A.47), положив в нем
ф0 = 0, так как начальная температура равна нулю. Далее,
поскольку предел lim T существует, функция Ф должна
*-»оо
стремиться к не зависящему от времени предельному значе-
1. дФ * т*
нию, следовательно, lim — — 0. Из этого условия получим:
*->оо 0t
Окончательное выражение для Ф будет при этом иметь
следующий вид:
где обозначено р = /*//?. Соответствующие напряжения
вычисляются по формулам **):
B.110)
*) Horvay (82, 2].
**) Goodier [63, 2].

90
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЙ
(ГЛ. U
к
a,

§ 12] ДЛИННЫЙ ЦИЛИНДР, НЕРАВНОМЕРНО НАГРЕТЫЙ 91
Чтобы устранить напряжения на поверхности цилиндра,
необходимо найти дополнительное напряженное состояние,
которое (см. Мелан — Паркус [6], гл. V, § 1) можно построить
при помощи функции напряжений Эри F. В рассматриваемом
случае положим *):
F(rt <?) = R2(Anpn + Bnpn+2)einv.
Соответствующие напряжения имеют вид
B.111)
г9
Из краевых условий
о„-И„ = 0, о^Ч-% = 0 при р=1
находим:
B.112)
Результирующие напряжения находим при помощи
суперпозиции aij = oij-\-aij. Здесь можно просуммировать ряды,
которые входят в часть решения, не зависящую от
времени t. Представляя функцию рл в виде разложения Фурье —
*) Goodiei [63,2J.

92 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. И
Бесселя по функциям Jn фтр) и используя формулы
при k Ф in,
при k — m,
получим
B.113)
Умножая обе части этого уравнения на рл+1 и интегрируя
почленно по р от 0 до р, получим вторую формулу
(р<1). B.114)
Наконец, умножая обе части последнего равенства на р п
и интегрируя от р до 1, получим третью формулу
B.115)
При помощи этих формул можно представить выражения
для напряжений в следующем виде:
2п(п — \)
B.116)

ДЛИННЫЙ ЦИЛИНДР, НЕРАВНОМЕРНО НАГРЕТЫЙ 93
Здесь
B.117)
Заметим, что стационарные (т. е. не зависящие от t) члены
в выражениях для напряжений сгг, оГ(р и о исчезли. Таким
образом, эти напряжения при ?->оо обращаются в нуль, и
остается лишь осевое напряжение ozz — — ЕаТ. Этот
результат согласуется с теоремами о плоских температурных полях,
не вызывающих напряжений (Мелан — Паркус [6], гл. III, § 2).
Таким образом, задача в принципе решена. Остается
доказать, что полученное решение не является чисто
формальным. Для этого вначале нужно доказать, что полученные
ряды и соответствующие производные равномерно сходятся
по г и по t для всех г < R и, следовательно, представляют
непрерывные функции. При этом дифференциальное
уравнение внутри области будет выполнено. Равномерная сходимость
будет иметь место также при г = R, если / ^ т > 0. Таким
образом, краевые условия также удовлетворяются. При^ = 0,
однако, сходимость уже не будет равномерной вследствие
разрывного характера заданного изменения температуры,
которая при /* = /? скачкообразно изменяется от нуля до
значения TQeinv. Это, на основании уравнения B.116), вызывает,
однако, разрыв только в окружном напряжении о , для ко-
торого вследствие зависимостей lim5o= -г-,—г—гт , limorr = 0
t+0 3 4(п + 1) ^0 гг
получим:
(P=l).
(P<i).

94 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ (ГЛ. II
Таким образом, окружное напряженке на поверхности г==/?
скачкообразно изменяется от нуля до значения —ЕаТ/(\ —\i).
Аналогичное заключение на основании четвертого уравнения
B.116) будет иметь место также для осевого напряжения azz
(см. также гл. II, §§ 5 и 13 и гл. V, § 9).
При помощи полученных результатов можно, используя
разложение Фурье по переменной ср, получить решение для
случаев, когда температура поверхности произвольно
изменяется в окружном направлении.
На полученное решение можно наложить равномерное
распределение осевых напряжений, выбрав' их так, чтобы
результирующая осевая сила обращалась в нуль. При этом
напряжения огг, о и о не изменятся, а для напряжения azz
вместо последнего соотношения B.116) получим azz = orr-\-o ;
при этом изменятся также радиальное и осевое
перемещения и и w.
§ 13. Температурные напряжения в сфере
Рассмотрим сплошную сферу радиуса R в случае
произвольного температурного поля Т (г, t), обладающего
центральной симметрией. Найдем возникающие при этом напряжения,
считая, что сфера свободно деформируется.
Эта задача, в особенности случай мгновенного нагрева,
неоднократно рассматривалась в литературе *). Изучался также
более общий случай, когда температурное поле не обладает
центральной симметрией, но является осесимметричным **).
Уравнение A.46) для потенциала перемещений в
рассматриваемом случае центральной симметрии принимает
следующий простой вид:
дг { дг ) l—i*. Г ' '
Отсюда после двукратного интегрирования находим:
г
ф=1+^ * [хТ{х, t)dx.
1 — и- з ./
о
*) Hopkinson [811, Grunberg [66], Me Ian [121, 7J.
•*) Trostel [186, 2J.

§ 13]
ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В СФЕРЕ 95
Через
Г (г, t)=^~ f хЧ{х, t)dx B.118)
о
здесь обозначена средняя температура сферы радиуса г. При
этом из уравнения A.33) получаем
\ B.119;
В этих выражениях добавлено равномерное напряженное
состояние
2 Еа ~
°гг = <\,<р = °ы> = ^ т=7 г (/?' ^'
что позволяет удовлетворить условию отсутствия напряжений
на поверхности сферы r = R.
Мы используем полученные формулы для определения
напряженного состояния в сфере, которая вначале имеет
постоянную температуру Г0 и нулевые напряжения, и
поверхность которой мгновенно охлаждается до нулевой
температуры и далее поддерживается при этой температуре
посредством погружения сферы в жидкость.
Найдем вначале температурное поле, Уравнение A.45) и
этом случае принимает вид
а_ д2(гТ) __ дТ
г дг2 ~ dt '
Разыскивая решение в форме произведения и учитывая
начальные краевые условия, получим *):
оо
Т(г, 0 = ^ ? *=УР- sin ^ е-"««*. B.120)
Бесконечный ряд сходится при t > 0 равномерно по г и по t
и, таким образом, представляет непрерывную функцию,
которая при ?->-(-0, в силу соотношения
*) Carslaw — Jaeger [1], стр. 200.

Рис. 12.
0,75 0,20
Рис. 13.

§ 13] ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В СФЕРЕ 97
действительно удовлетворяет начальному условию. Выполняя
интегрирование согласно формуле B.118), находим среднюю
температуру:
оо
Л = 1
B.121)
Безразмерные переменные Т/Т0 и Т/Т0 приведены на рис. 12
и 13 в зависимости от безразмерного времени at/R2 при
различных значениях параметра rjR.
О 0,2 0,4 0,6 0,6
Рис. 14.
При известных значениях Г и Г напряжения вычисляются
по формулам B.119). Они приведены на рис. 14 и 15 в
зависимости от r/R для различных значений параметра о = atiz2IR2.
Постоянная К при этом имеет значение К — EaTQ/(\—jx).
Наибольшим по абсолютной величине будет окружное
напряжение о = АГ, возникающее на поверхности сферы
в момент ? = 0. Радиальные напряжения всегда являются
сжимающими, они имеют абсолютный максимум огг — — 0,386/С
в центре сферы г = 0 в момент t = 0,575/?2/а7г2.

98 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
Если разность температур 70 между сферой и жидкостью
достаточно велика, то в материале сферы возникает
пластическое течение. При этом при полном охлаждении сферы
к
-0,4\
-о,з
-0,2
-0.1
0,0
0,1
0,2
0,3
0,4
0,5
ДО
«F6
-
-
-
-
!
7
025_
0,1
i
0.2
^\\
-^7 \\
I 1
ОА 0,6
Рис. 15.
i
0.8
¦ > г
1,0 *
напряжения полностью не исчезают. Этот случай рассмотрен
в § 2 гл. VII.
Некоторое представление о величинах напряжений,
возникающих даже при относительно небольших разностях тем-

§ 14]
ТОЧЕЧНЫЙ НАГРЕВ ДИСКА
99
ператур, дает следующий численный пример. Пусть при
охлаждении сферы из стали с модулем упругости ?"==2,1 • 106 кг/см2,
коэффициентом Пуассона |л = 0,3 и коэффициентом линейного
расширения а= 1,25-10" возникает разность температур
7" = 200° С. Наибольшим напряжением при этом будет
окружное напряжение а на поверхности r = R в момент / = 0,
равное
в = ^L = K = 7500 кг/см2.
Для наибольшего по абсолютной величине радиального
напряжения получим следующее значение:
огг = — 0,38б/С = — 2895 кг/см2.
Если принять, что коэффициент температуропроводности
а = 460 см2/час, а радиус сферы составляет 20 см, то этот
максимум возникнет в момент ^ = 0,013 час = 45 сек.
§ 14. Точечный нагрев диска
Рассмотрим бесконечный диск толщины h, в котором в
момент / = 0 в начале координат начинает действовать
источник тепла постоянной производительности *) S. В момент
t=r-$ источник тепла удаляется**). Этот процесс
приблизительно соответствует случаю точечной сварки.
Пусть диск достаточно тонок, так что напряженное
состояние можно считать плоским. Вследствие осевой
симметрии все величины будут зависеть только от расстояния г от
источника тепла и от времени /. Будем считать, что тепловые
и упругие свойства материала не зависят от времени. Можно
получить простые формулы, если не учитывать теплообмен
между поверхностью диска и окружающей средой, то есть
если считать, что поверхность диска теплоизолирована ***).
Распределение температуры в процессе нагрева 0 < t < Ь
выражается уравнением G.516) § 4 гл. VII при р = 0:
*) 5 означает количество тепла, выделяемое в единицу
времени.
**) Par k us [147, 3].
***) Это предложение будет снято в § 4 гл. VII. Там будет
рассмотрен также случай течения материала,

100 ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ [ГЛ. II
Здесь ^х=5/2тсХ/г, где X — коэффициент теплопроводности.
Далее из уравнений G.57) и G.58) находим радиальное
перемещение:
Выполняя здесь интегрирование и учитывая, что функция A (t)
должна равняться t, чтобы было выполнено условие и = О
при г = 0, получим:
B.123)
При этом напряжения можно определить по формулам
2G \ ди { и /1|ч тм пп u(r,t) )
^ = ^[~ + \"%-^ + ^^]==:-orr-EaT. J
B.124)
Уравнения B.123) и B.124) применимы только для периода
нагрева 0 < t < ft. В момент t — ft источник тепла удаляется.
Возникающие при этом поля температуры и напряжений
можно получить, приняв, что в момент t = b начинает
действовать источник тепла производительности — S. Отмечая
штрихом температуры, перемещения и напряжения для
интервала времени t > ft, получим:
(t > »).
B.125)
Мелан *) рассмотрел случай, когда вместо источника тепла
конечной производительности «S ккал\сек в момент t = 0
внезапно выделяется количество тепла Q ккал (мгновенный
источник). Формулы для этого случая можно получить из
приведенных выше, полагая, что ft стремится к нулю,
a «S одновременно неограниченно возрастает таким образом,
•) Mel an [121,6].

Рис. 16.
Рис. 17.

102
ПРОЦЕССЫ НАГРЕВА И ОХЛАЖДЕНИЯ
[ГЛ. II
что lim %S = Q. Из уравнения B.125), обозначая в = Q/2vlh
и используя разложение Тейлора
Рис. 18.
получим (заменив обозначение Т на Г):
B.126)
Аналогично можно найти радиальное перемещение а из
уравнения B.123), выполняя дифференцирование по t и под-

§ 14]
ТОЧЕЧНЫЙ НАГРЕВ ДИСКА
103
ставляя е вместо ?:
а (г, 0 = 0+l*)a-7-U— е"^). B.127)
Уравнения B.124) остаются без изменений, необходимо лишь
подставлять в них значение и согласно уравнению B.127).
На рис. 16—18 приведены значения температуры,
радиальных и окружных напряжений в зависимости от радиуса г при
различных значениях параметра at для случая действия
мгновенного теплового источника; на этих рисунках обозначено
уц = #?. Все переменные г2, l/at, M/T, EolM/g имеют
размерность квадрата длины и должны поэтому измеряться
в одинаковых (произвольных) единицах.
Легко видеть, что в первый момент напряжения имеют
значения
Еааг
Если Х = 0, т. е. если рассматривается идеальный тепловой
изолятор, то это напряженное состояние вследствие условия
а = 0 остается неизменным, причем as = Q/2nch (здесь через с
обозначено количество тепла, необходимое для повышения
температуры единицы объема на 1 градус).
Если а > 0, то окружное напряжение off в области г < R
будет отрицательным (/? = 2,242 у at ); наибольшее
растягивающее окружное напряжение действует при г = 3,585 У at
и имеет значение aff — 0,054EaM/at. Радиальное напряжение отт
всюду является сжимающим.

ГЛАВА HI
ПЕРИОДИЧЕСКИЕ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
§ 1. Общие замечания
В этой главе будут рассматриваться напряжения в упругих
телах, подвергающихся воздействию температурных полей,
которые периодически изменяются с течением времени.
Предполагается, что продолжительность периода достаточно велика,
так что можно применять квазистатический подход.
Мы не будем рассматривать начальную стадию процесса
и ограничимся изучением установившегося чисто
периодического состояния. При этом напряженное состояние также
будет периодическим, и поэтому в выражении потенциала
перемещений A.47) можно отбросить непериодическую часть,
полагая Фг = 0.
Температуру, напряжения и перемещения можно
представить рядами Фурье в зависимости от времени t. Вследствие
линейности уравнений можно ограничиться изучением
произвольного члена этих разложений.
Таким образом, положим:
Т = Тл cos mt -|~ T0 sin iut, )
\ C 1)
Ф = Фх cos at + Ф2 sin at, J J
гле Tt и Ф? являются функциями только координат.
Дифференцируя уравнение A.47) по t и сравнивая коэффициенты,
получим:
Ф1==-1±^^Г2, ф2 = +*±!^7\. C.2)
Как следует из уравнения A.46), к функциям Ф{ и Ф2 можно
добавить произвольные гармонические функции.

§2]
ПОЛУПРОСТРАНСТВО
105
& 2. Полупространство с периодически изменяющейся
температурой поверхности
Пусть упругая среда заполняет полупространство z^>0.
Заданная температура поверхности имеет вид
T=TQcos(»t при z = 0. C.3)
Когда переходный процесс затухнет, решение уравнения
теплопроводности A.45) дает следующее распределение
температуры в полупространстве *):
Т= ТЬехр (-«}/"¦?¦ )сов (г ]/"¦?-«/). C.4)
При этом из уравнения C.2) получим:
* ~Т±? ~ То «Р (- ' VJa) Si« [«< ~ * /"?) • <3"б>
Предположим, что поверхность z — О не нагружена. Тогда
на этой поверхности будут иметь место условия azz — arz = 0,
которые, используя уравнения A.32) и применяя
цилиндрические координаты, можно представить в следующем виде:
Легко видеть, что эти условия выполнены и напряжения oZ2
и агг обращаются в нуль всюду в теле. Для остальных
компонент напряжения из уравнений A.32) получаем следующие
выражения:
о„ = о„ = -20дф = -^1. О-в)
Чтобы выяснить, является ли это решение окончательным
или требуется наложить другое (бестемпературное)
напряженное состояние, необходимо рассмотреть краевые условия на
«несобственных» краях г = оо и z = oo. Вообще говоря,
необходимо потребовать, чтобы все напряжения при z-^oo
обращались в нуль. Легко видеть, что полученное решение
*) Cars law — Jaeger [1J, стр. 46.

106 ПЕРИОДИЧЕСКИЕ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ [ГЛ. III
удовлетворяет этому условию. Однако, поскольку
напряжения не зависят от г, они не будут исчезать при г-»аз; в то
дФ
же время радиальное перемещение и = -г- всюду равно нулю.
Таким образом, решение применимо для случая кругового
цилиндра произвольного радиуса, простирающегося от z== О
до ? = oo, и закрепленного так, что радиальные перемещения
на цилиндрической поверхности всюду обращаются в нуль.
Поскольку напряжения убывают по экспоненциальному закону
при возрастании zt решение можно применять в качестве
приближенного также для случая конечного длинного цилиндра
длины /, если /1/ ~ достаточно велико (для
практических целей примерно ^ 5).
§ 3. Периодический тепловой источник
в неограниченной среде *)
Точечный источник с периодически изменяющейся
производительностью 5 (t) = S0 cos Ы действует в точке
бесконечного упругого пространства. Воспользуемся сферической
системой координат R, ср, 9-, начало которой совпадает с
источником. По соображениям симметрии, температура и
напряжение не должны зависеть от координат <р и &. Кроме
того, температурное поле должно иметь особенность вида 1/R
в точке R = 0. Ввиду этого примем согласно уравнению C.1)
Подставляя это выражение в уравнение A.45), учитывая, что
А —-ж ~Тп \R2~7w)' и пРинимая во внимание, что Г должно
убывать при возрастании Rt получим:
C.7)
*) Nowacki [137,5].

ПЕРИОДИЧЕСКИЙ ТЕПЛОВОЙ ИСТОЧНИК 107
При этом
Т (%f f) — * e-*R [Л cos (со/ — *R) + В sin (at — %R)].
Для определения постоянных А к В рассмотрим поток тепла
в единицу времени через сферическую поверхность радиуса /?,
центр которой совпадает с источником. При /?->0 этот
поток тепла будет равен производительности S теплового
источника. Таким образом,
откуда
Таким образом, температурное поле будет окончательно
характеризоваться следующей формулой:
Т (/?, t) = -J^- • -— e-xR cos (ю/ — x#). C.8)
При помощи уравнений C.1) и C.2) получаем
соответствующее значение термоупругого потенциала:
здесь Ф1 и Ф2 — произвольные гармонические функции; кроме
того,
Принимая во внимание центральную симметрию задачи,
положим Ф1 = бу/?, Ф2 = C2jR\ при этом радиальное
перемещение и будет иметь вид
а ~~df>=^2G ~R6~XR \[ (* + "o")sin7^— kcosx/? [cosatf —
-[(^ + ^)cosx/? + ^inx/?]sin^}-ClCOS^ + C2Sin^.
Теперь необходимо учесть, что перемещения при R—>0
возрастают не быстрее, чем 1/R (см. § 1 гл. II). Из этого
условия находим, что Сх = 0, С2 = ~-^ и' слеД°вательно,
ф = ш' ~я [e'xR sin (ы ~х/?) — sin ^i- ^3-10)

IOS Периодические изменения температуры [ГЛ. m
Соответствующие напряжения вычисляем при помощи
уравнений A.33):
C.11)
Как напряжения, так и перемещения обращаются в нуль при
§ 4. Периодические линейные и поверхностные
источники *)
Используя результаты предыдущих разделов, можно при
помощи интегрирования получить решения для случаев
линейных или поверхностных источников.
Рассмотрим вначале совпадающий с осью z бесконечно
длинный линейный источник, имеющий производительность
5 (t) = s0 cos Ы на единицу длины. В полярных
координатах г, <р, z все переменные будут независимы от координат z
и ср, и мы приходим, таким образом, к плоской осесимме-
тричной задаче. Полагая R2 = r2-\-z2, s0 — dS0/dz, получим
при помощи уравнения C.8) следующее температурное поле
для случая линейного источника:
оо
T(r, t) = ^ f -~ е-** cos (о>* — %R) dz.
о
Учитывая соотношение RdR = zdz и вводя обозначения
р = %г, р = Rjr, получим отсюда:
*) Nowacki [137,5].

4] ПЕРИОДИЧЕСКИЕ ЛИНЕЙНЫЕ И ПОВЕРХНОСТ. ИСТОЧНИКИ 109
Заметим, что интеграл
оо
представляет собой модифицированную функцию Бесселя
/С0 (z) *). Положив z = (l—Qp = "J/r—2/ р, получим:
Таким образом, распределение температуры можно выразить
следующей формулой:
Г (г, O = ^[^o(xr)cosa)^ + 1/O(xr)sina)^]f C.12)
где ?/0 и VQ — табулированные функции **). Точно таким же
способом можно найти термоупругий потенциал перемещений.
Обозначив
1 — jA а) 2тсЛ ч '
и интегрируя соотношение C.10), получим ***):
*) E г d ё 1 у i и др., Higher transcendental functions, 2 A953),
стр. 82, формула A9), New York.
**) См., например, Янке — Эмде, Таблицы функций [5];
в этих таблицах табулирована, однако, не функция /С0, а функция //@Ч
Эти функции связаны соотношением KQ (х V—'i) = -^- Н§] {х VI).
***) Очевидно, что можно воспользоваться также
уравнением C.2).

НО ПЕРИОДИЧЕСКИЕ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ [ГЛ. Ill
Заметим, что здесь интегрированием получена только та часть
функции Ф, которая непосредственно зависит от Г, а
пространственная гармоническая функция \/R заменена плоской
гармонической функцией lnxr. Используя соотношение
lim К0(р У— 2/) = — In p -f- с + ..., можно легко доказать,
р->о
что дФ/дг обращается в нуль при г->0. В результате
получим:
©=-g-{[t/0(xr) + ln(xr)]sina)/ —V0(xr)cosa>/}. C.14)
Соответствующие напряжения можно вычислить при помощи
формул A.32). При этом целесообразно дифференцировать
не функции U0 и V0 порознь, а непосредственно функцию К0.
В качестве второго примера рассмотрим плоский
источник тепла, занимающий всю плоскость z = Q и имеющий
производительность s (t) = s0cos at на единицу площади.
Соответствующие температуры и потенциал перемещений можно
получить из уравнений предыдущего параграфа, выполняя
интегрирование по площади и принимая для элемента
площади выражение dA = 2,xrdr. При этом найдем:
со
7 (*' V = Ж f It е"/Я cos (о)/ — х/?) dn
О
Интегрирование здесь легко выполняется при помощи
соотношения г dr = RdR и приводит к следующему результату:
T(z, t) = ^e-*z[cos(ut — ia) + sin(ut — '*.z)]. C.15)
Аналогично можно найти потенциал перемещений. Поскольку,
однако, в этом случае напряжения зависят только от
координаты zy можно найти напряженное состояние
непосредственно по уравнению A.31)
Все остальные напряжения равны нулю.

ГЛАВА IV
ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА
§ 1. Общие замечания
Распределение температуры в однородном изотропном
теле, отнесенном к неподвижной, связанной с телом системе
координат *), подчиняется дифференциальному
уравнению A.45)
аЬТ = ?. D.1)
Рассмотрим теперь, как изменится это уравнение, если
система координат испытывает трансляционное перемещение по
отношению к телу.
В этом случае изменение температуры -тг at за интервал
времени dt, наблюдаемое в точке этой подвижной системы,
будет складываться из двух составляющих. Первая
составляющая определяется тем, что в неподвижной точке
пространства температура изменится с течением времени (если
поле нестационарно); вторая составляющая возникает
вследствие того, что наблюдатель, связанный с подвижной
системой, за время dt переместится на расстояние d$ = x>dt и
в результате попадет в точку с другим значением
температуры. Эта вторая составляющая будет иметь значение
d§ • vr= b • VTdt, где Ь — вектор скорости подвижной
координатной системы по отношению к телу и
VT—локальный температурный градиент. Вывод уравнения
теплопроводности основан на составлении теплового баланса элемента
тела, который определяется только первой составляющей,
*) В духе линеаризированной теории упругости мы не
учитываем изменение формы, вызываемое температурой и напряжениями

112
ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА
[ГЛ. IV
поэтому нужно вычесть вторую составляющую из
наблюдаемого изменения температуры. При этом в системе
координат, совершающей трансляционное перемещение со
скоростью Ь, уравнение теплопроводности D.1) принимает
следующую форму:
abT=^ — \>V7\ D.2)
Это уравнение остается справедливым также в том случае,
когда система координат совершает не только
трансляционное, но и вращательное перемещение, характеризующееся
вектором угловой скорости to. При этом Ъ будет означать
скорость рассматриваемой точки системы, которая по
известной формуле кинематики будет равна
D = »o + »Xt. D.3)
Здесь iH — мгновенная скорость начала координат и г —
радиус-вектор точки в подвижной системе.
Будем называть стационарным распределение
температуры, для которого в неподвижной, связанной с телом
системе координат dT/dt = 0 и которое, следовательно, не
зависит от времени. Соответственно будем говорить, что
распределение температуры является квазистационарным
по отношению к движущейся системе, если в движущейся
системе координат температура не будет зависеть от
времени *). При этом в уравнении D.2) исчезает член dT/dt и
скорость (рассматриваемая в подвижной системе координат)
также не зависит от времени.
Поскольку при квазистатическом рассмотрении проблемы
температурных напряжений динамические эффекты не
принимаются во внимание, соответствующие уравнения теории
упругости не будут зависеть от движения системы отсчета,
и поэтому их можно использовать без изменений также
в случае введенной здесь системы координат, движущейся
по отношению к телу.
*) R о s e n t h a 1 D., The theory of moving sources of heat and
Its application to metal treatments, Trans. A. S. M. E, 68 A946), 849.
В этой работе выведена частная форма уравнения D.2).

§2] ДВИЖУЩИЙСЯ ИСТОЧНИК ПОЛУПРОСТРАНСТВА ИЗ
§ 2. Движущийся точечный источник
на поверхности полупространства
На поверхности z — О упругого полупространства z^>0
движется равномерно и прямолинейно точечный источник
постоянной производительности S. Поверхность полностью
теплоизолирована.
Эту задачу можно рассматривать как упрощенную схему,
соответствующую выполнению шва при сварке. Очевидно,
что остаточные напряжения, возникающие при полном
остывании, при этом подходе вычислить нельзя.
Примем, что начало координат нашей подвижной системы
находится в точечном источнике, а ось х совпадает с
траекторией. Если предположить, что процесс продолжался
достаточно долго, т. е. что точечный источник движется из
положения х — — оо, то для наблюдателя, находящегося
в движущейся системе координат, поля температуры и
напряжений будут являться стационарными и, следовательно,
рассматриваемый процесс можно считать квазистационарным.
Обозначим через v постоянную скорость источника. Тогда
уравнение теплопроводности D.2) примет вид
Решение этого уравнения имеет следующую форму *):
D.4)
D.5)
где R = }fx2-\-y2-\-z2. Это решение соответствует
рассматриваемому случаю точечного источника, а также
удовлетворяет заданному краевому условию, что можно видеть
из выражения
D.6)
*) Carslaw — Jaeger [1]; часто приводит к цели
подстановка Т = е~шхи (х, у, z)\ при этом функция U удовлетворяет
дифференциальному уравнению MJ — u2Lf = 0.

114
ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА
[ГЛ. IV
которое при z — 0 обращается в нуль всюду, за исключением
начала координат. Термоупругий потенциал перемещений
определяется уравнением A.46)
D.7)
Дифференцируя это уравнение по х и подставляя значение
дТ/дх из уравнения D.4), получим:
1+(Х
Интегрирование этого уравнения дает:
D.8)
где Ф0—произвольная гармоническая функция. В
правильности этого решения можно убедиться посредством
подстановки в уравнение D.7). Внося в формулу D.8) значение Т
из уравнения D.5), получим при соответствующем выборе Ф0
следующее соотношение:
где
D.9)
D.10)
По формулам A.31) вычисляем соответствующие напряжения:
D.11)

§ 2]
движущийся источник полупространства
115
Заданные краевые условия на свободной поверхности имеют вид
°zz = °> a^ = °> <*гу = ° ПРИ Z = °-
решение D.11) удовлетворяет только второму и третьему
из этих условий. Таким образом, необходимо на полученное
решение наложить второе напряженное состояние ai,,
соответствующее нагружению поверхности полупространства
нормальным напряжением
D.12)
для случая, когда температура Г —0. Решение этой
классической задачи теории упругости может быть получено
различными способами *). Проще всего использовать решение
Буссинеска для сосредоточенной единичной силы,
приложенной в точке ?, т], 0 поверхности полупространства. Умножая
это решение на рй\йч\ и интегрируя по всей поверхности О,
т. е. по переменным \ и г\ от — сю до -)- оо, получим:
D.13)
) См., например, Т р е ф ц Е., Математическая теория упругости.

Пб ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА [ГЛ. IV
Здесь обозначено:
Значения напряжений D.13) на поверхности z = 0 следует
определять путем предельного перехода при ^->0-f~. Вообще
говоря, вычисление этих интегралов весьма затруднительно,
поскольку они не выражаются в замкнутой форме.
Новацкий *) рассмотрел задачу о движении точечного
источника по поверхности упругого полупространства, когда
эта поверхность поддерживается при температуре Г = 0.
Поступая так же, как в § 4 гл. II, можно заменить здесь
точечный источник диполем; при этом вместо температурного
ноля D.5) следует ввести температурное поле D.6) с
обратным знаком, то есть
г = 1ST "^ О+»Я) *-•<*+*>. DЛ5)
Соответствующий потенциал перемещений можно найти,
дифференцируя уравнение D.9) по —z. На поверхности
z = О при этом остаются касательные напряжения, которые,
так же как и в предыдущем случае, можно устранить при
помощи соответствующего решения Буссинеска **).
При помощи интегрирования по у можно найти плоское
деформированное состояние, возникающее при движении
линейного источника.
§ 3. Движущийся точечный источник на поверхности
тонкой пластины***)
Точечный источник****) постоянной производительности 5
движется равномерно и прямолинейно со скоростью v в
бесконечной пластине параллельно ее поверхностям; эта схема
в первом приближении описывает процесс выполнения
сварного шва.
*) Nowacki [137,6].
**) Nowacki [137, 6] вместо этого использовал
представление решения двойными интегралами Фурье.
***) Mel an [120, 1].
****) Точнее говоря, рассматривается линейный источник
длины h, где h — толщина пластины.
D.14)

ъ] ДВИЖУЩИЙСЯ ИСТОЧНИК НА ПОВЕРХНОСТИ ПЛАСТИНЫ Ц7
Введем декартову систему координат, оси х, у которой
лежат в срединной плоскости пластины, и примем, что все
переменные не зависят от z, а также что огг = тхг =
===т =0*); таким образом, мы приходим к задаче
о плоском напряженном состоянии. Пусть начало координат
совпадает с источником тепла, а ось х направлена по
направлению движения. Если мы, кроме того, предположим, что
процесс продолжался достаточно долго, т. е. что уже
выполненный сварной шов простирается до х = — оо, то можно
рассматривать процесс как квазистационарный и использовать
уравнение теплопроводности в формуле D.4), где к=д2/дх2-{-
-f- д2/ду2. Мы при этом пренебрегаем потерей тепла на
поверхностях пластины. Если эту потерю учесть, то в
соответствии с соотношением A.49) вместо уравнения D.4)
следует принять
Д7 — тЧ -f- 2о> ~ = 0. D.16)
Применяя подстановку Т == e-^U (r), получим решение
этого уравнения в следующем виде **):
r = We~***o(PO. D-17)
где
В случае плоского напряженного состояния термоупругий
потенциал перемещений определяется уравнением A.35)
(при р = 0)
Д? = A+|А)а7\ D.18)
Дифференцируя это уравнение по х и подставляя значение
дТ/дх из уравнения D.16), получим:
А <№ 1+Р- / 9Т АТч
*) Можно также считать, что рассматриваются осредненные по
толщине значения.
**) Carslaw — Jaeger [1J.

118
ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА [ГЛ. IV
или, учитывая уравнение D.18),
Интегрирование этого уравнения дает:
, D.19)
где W0 — произвольная гармоническая функция и, кроме того,
D.20)
В правильности этого решения можно убедиться посредством
подстановки его в уравнение D.18) и интегрирования по
частям с учетом зависимости D.16).
По формулам A.36) находим напряжения
D.21)
Эти выражения существенно упрощаются, если пренебречь
теплообменом на поверхностях пластины, то есть если
положить т = 0 и соответственно f = 0. В этом случае,
подставляя в формулы D.21) значение Т из уравнения D.17j
при р = со и обозначив
"-¦го- <4-22>
получим следующие значения напряжений:
D.23)

3] ДВИЖУЩИЙСЯ ИСТОЧНИК НА ПОВЕРХНОСТИ ПЛАСТИНЫ 119
Таблица 3
_
х>0<
\х = 0
\х<0
у/х
< 0,0000
0,3287
0,7500
1,3333
2,2913
4,8990
: —4,8990
—2,2913
—1,3333
—0,7500
—0,3287
0,0000
шГ
ох =
а2 =
а, =
а2 =
о2 =
°1 =
а2 =
а2 =
°1 =
а2 =
а1==
с2 =
а2 =
а, =
а2 =
а1==
с1==
а2 =
°1 =
а2 =
а2==
0,1
4,275
—7,071
4,297
—7,107
4,362
—7,214
4,451
—7,363
4,540
—7,509
4,631
—7,660
4,725
—7,815
4,820
—7,973
4,918
—8,134
5,012
—8,298
5,119
—8,466
5,196
—8,594
5,222
—8,637
0,5
0,2826
—0,9965
0,2898
—1,0220
0,3124
—1,1010
0,3452
—1,2171
0,3815
—1,3451
0,4216
—1,4866
0,4660
—1,6430
0,5150
—1,8158
0,5692
—2,0068
0,6291
—2,2179
0,6952
—2,4510
0,7493
—2,6419
0,7698
—2,7088
1,0
0,0424
—0,2396
0,0446
—0,2518
0,0518
—0,2926
0,0632
—0,3574
0,0772
—0,4365
0,0943
—0,5331
i 0,1152
—0,6521
0,1407
—0,7954
0,1719
—0,9715
0,2099
—1,1866
0,2564
—1,4492
0,2979
—1,6838
0,3131
—1,7702
1
1,5
0,0090
—0,0698
0,0112
—0,0862
0,0122
—0,0942
0,0165
—0,1271
0,0222
—0,1716
0,0300
—0,2316
0,0405
—0,3127
0,0547
—0,4221
0,0738
—0,5698
0,0996
—0,7691
0,1345
—1,0382
0,1483
—1,1452
0,1815
—1,4016
2,0
0,0022
—0,0219
0,0025
—0,0242
0,0033
—0,0326
0,0050
—0,0487
0,0074
—0,0726
0,0111
;—0,1083
0,0165
—0,1616
0,0247
—0,2410
0,0368
—0,3595
0,0549
—0,5363
0,0819
—0,8002
0,1105
—1,0801
0,1221
—1,1937
Здесь принято ?0 = 0, поскольку при этом условие
отсутствия напряжений в пластине на бесконечности будет
выполнено. Это следует из ассимптотических представлений
Для главных напряжений ог и с2 получим следующие

120
ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА
[ГЛ. IV
выражения:
с10=~[<з -1-0 ±VTc —о У 4- 4а2 1 =
1.2 2 L лс-лг ' уу г V лл уу/ ' лгу J
Направления главных напряжений определяются соотношением
* о 2а-*У У
tg 2v = i— = -=- .
алл ауу х
Некоторые численные значения для Af=l приводятся в
таблице 3.
§ 4. Вращающееся температурное поле *)
Диск газовой турбины подвергается воздействию горячих
газов. Вследствие этого температура диска, если не
учитывать изменения ее по толщине, вообще говоря, будет
зависеть от радиальной и окружной координат г и ср и от
времени t. Если предположить, что турбина работает уже
достаточно долго в неизменных условиях эксплуатации, то
возникнет состояние, при котором температура в
определенной точке диска будет периодически изменяться, то есть
после каждого полного оборота будет возвращаться к одному
и тому же значению. Если мы введем теперь неподвижную
в пространстве и, следовательно, вращающуюся по
отношению к диску систему координат, то по отношению к этой
системе температурное состояние будет являться
квазистационарным.
Пусть со — постоянная угловая скорость вращения диска;
тогда саг будет скоростью произвольной точки в окружном
направлении. Учитывая, что —-г— будет представлять
градиент температуры в этом направлении, получим уравнение
теплопроводности D.2) для случая теплоизолированных
торцевых поверхностей диска в следующем виде:
дГ+--4^(). D.24)
*) Melan [120,3].

- 4] ВРАЩАЮЩЕЕСЯ ТЕМПЕРАТУРНОЕ ПОЛЕ 121
]У1ы попытаемся удовлетворить этому уравнению, задавая
распределение температуры в форме произведения
Г (г, <р) = /?(г)Ф(<р),
где Ф(ф) должна быть периодической функцией. Допустим,
что она представлена рядом Фурье и рассмотрим общий член
этого разложения
Г (г, ср) = Rx (г) cos щ -+- /?? (г) sin дер.
После подстановки в уравнение D.24) и разделения членов
с cos/icp и sin мер получим следующие два уравнения *):
Отсюда следует, что Rx и R2 являются цилиндрическими
функциями от комплексного аргумента г у -^- . Поскольку
решение при г = 0 должно оставаться ограниченным, следует
воспользоваться функциями Jn или 1п. Выбрав функцию Jn,
после отделения вещественной и мнимой частей получим:
/?i (г) = Jn (И = Ря (кг) + lQn (кг), |
где
Поскольку коэффициенты дифференциального уравнения
вещественны, как вещественная, так и мнимая части D.25)
должны являться решениями. Умножая их на пока
неопределенные постоянные, получим:
Т(г, 9)== С, \Рп (kr) cos щ — Q„(Xr) sin/i<p] +
+ C2 \Qn (kr) cos щ + Pn (kr) sin щ\. D.27)
В уравнении теплопроводности D.24) теплообмен на тор-
чевых поверхностях диска не учитывается, поэтому
температура диска определяется исключительно температурой на
*) Штрих означает дифференцирование по г.

122 ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА 1ГЛ. IV
границе r = b, на которой укреплен обдуваемый газами
лопаточный венец. Положим
T=T0cosny при r = ft.
Внося это значение в уравнения D.27), получим:
D.28)
D.29)
При этом решение принимает следующую окончательную
форму:
Т(г, ср) = А («, ср) Рп (Хг) + В («, ср) Qn (кг), D.30)
где
D.31)
Заметим, что
Будем предполагать, что напряженное состояние турбинного
диска с достаточной точностью можно рассматривать как
плоское. При этом, поступая так же, как в предыдущем
параграфе, найдем следующее значение термоупругого
потенциала перемещений:
чг=_A+!х)^у,г^+ч?-о.
Подставив сюда значение Т из уравнения D.30) и
отбросив ч70, получим:
W = 0 + & "^ [В (п> & Рп (И - Л <"• ?) Qn (HI- D.32)
По формулам A.37) вычисляем соответствующие напряжения:
\ D.33;

ВРАЩАЮЩЕЕСЯ ТЕМПЕРАТУРНОЕ ПОЛЕ 123
где
D.34)
Поскольку здесь мы рассматриваем напряжения *),
вызванные температурным полем, в качестве краевых условий
следует принять
D.35)
Напряженное состояние D.33) не удовлетворяет этим
условиям, поэтому необходимо найти второе напряженное
состояние, которое мы, как обычно, получим при помощи функции
напряжений Эри. Используя бигармонические функции вида
rn cosny, rn+2cos шр, /-"sin/гср, гл+2 sin /гер, возьмем функцию
Эри в следующей форме: '
^ N\ А ( b2rn , гп+2\ , В /. Ь2гп . . гп+2\1
Постоянные сг, ..., d2 пока являются произвольными.
Соответствующие напряжения имеют вид **):
D.36)
Внося в краевые условия D.35) напряжения о^ = otj-\- o/y и
группируя коэффициенты при функциях А(п, ср), В (п, ср),
*) Очевидно, что на температурные напряжения будут
накладываться напряжения, вызванные вращением диска, действием
Центробежных сил лопаток и т. д.
**) Мелан — Паркус [6].

124
ДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛА [ГЛ. IV
получим следующие четыре уравнения для определения
четырех постоянных сг d2:
b2
Решение этих уравнений имеет вид
D.37)
Таким образом, поставленная задача решена. При численных
расчетах следует иметь в виду, что аргумент |Xr| в области
вблизи края r — b при практически встречающихся
соотношениях (большие числа оборотов) будет очень велик. При
этом представление функции Jn (Кг) степенным рядом будет
неприменимо и при вычислениях следует использовать
следующую асимптотическую формулу:
Здесь обозначено

§41
ВРАЩАЮЩЕЕСЯ ТЕМПЕРАТУРНОЕ ПОЛЕ
125
Производные функций Рп (кг) и Qn (кг) получаем
посредством дифференцирования уравнения D.25), например:
Сравнивая здесь вещественные и мнимые части, получим:
Аналогично находим вторые производные:
Заметим, что расчетам температурных напряжений в дисках
газовых турбин посвящена обширная литература *).
Приведенное решение является математически строгим,
но основано на значительных физических упрощениях; оно
может быть обобщено на случаи дисков переменной толщины,
произвольного распределения температуры, учета зависимости
постоянных материала от температуры, пластичности,
ползучести и т. д. К сожалению, при этих обобщениях почти
всегда необходимо обращаться к численным методам решения.
*) См., например, работы Holms и Faldetta [80], Horvay [82],
Костюка [102], Leopold \\Щ, Малинина {113], Manson [\Щ, МШеп-
son и Manson [124], Norbury [135], Singh [170], Strub [117], Suhara
[178], Thompson [183], Wahl [191].

ГЛАВА V
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
§ 1. Общие замечания
В главе первой отмечалось, что определение
температурных напряжений в случае изменяющихся с течением времени
температурных полей является, в сущности, не статической,
а динамической задачей, которую, однако, часто можно
рассматривать как квазистатическую, пренебрегая влиянием
ускорений. Такой подход мы применяли во всех
предшествующих разделах и даже в случаях внезапных изменений
температуры, т. е. при так называемых тепловых ударах. Теперь
мы исправим возникающие при этом погрешности.
Если принимать во внимание ускорения, то вместо }фав-
нений равновесия, использовавшихся в гл. II—IV, следует
применять уравнения движения A.1). Соответствующие
изменения в остальных уравнениях теории температурных
напряжений были указаны в гл. II. Мы обратимся теперь к решению
этих уравнений. Так же как в статическом случае, мы будем
при этом, вообще говоря, пользоваться термоупругим
потенциалом перемещений, который теперь удовлетворяет уравне-
""ю1,'30,: »-^-?{^
Сравнение с формулами эластокинетики показывает, что
постоянная с является не чем иным, как скоростью, с которой
распространяются волны расширения в упругой среде*).
*) См., например, Пфейффер П., Колебания упругих тел,
ГТТИ, 1934.

§ п
ОБЩИЕ ЗАМЕЧАНИЯ
127
Уравнение E.1) часто встречается в механике и физике
под названием волнового уравнения. Имеются различные
способы его решения, из которых мы кратко рассмотрим
два: преобразование Лапласа и метод запаздывающего
потенциала.
Применим к уравнению E.1) преобразование Лапласа,
считая, что в момент t = О тело находится в «естественном»
состоянии, то есть что как смещения, так и скорости *)
равны нулю**); при этом будем иметь начальные значения
ф = 0, дФ/с^ = 0, и уравнение E.1) примет вид
ДФ* — 4" Ф* = 1^ ъТ*. E.3)
С2 1 — [X v '
Часто применяемый метод решения этого уравнения основан
на использовании разложений по собственным функциям ***).
Для этого необходимо подчинить функцию Ф* одному
краевому условию, например условию обращения в нуль
нормального или касательного напряжения на свободной
поверхности. Собственные значения \t и собственные функции Ut
определяются из решений уравнения
Ш = \Ю, E.4)
где U удовлетворяет краевым условиям, наложенным на
функцию Ф*. Будем считать, что как неизвестная функция Ф*,
так и заданная функция Г* представлены в виде рядов по
собственным функциям:
i i
Подстановка в уравнение E.3) с учетом соотношения E.4)
приводит к следующему выражению для коэффициентов at:
ci
ai — ~тг •
I c2
*) По отношению к инерциальной системе отсчета.
**) Если имеются начальные смещения и напряжения, то
вызванное ими движение изучается отдельно и накладывается на
общее решение.
***) Курант Р., Гильберт Д., Методы математической
Физики, т. 1, Гостехиздат, 1951.

128
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ V
Часто можно избежать применения этого весьма трудоемкого
способа, если не стремиться подчинить функцию Ф*
определенному краевому условию. Последнее всегда можно сделать,
поскольку функция Ф* является лишь некоторым частным
решением уравнений упругости. Поэтому можно ограничиться
нахождением какого-либо частного решения уравнения E.3),
что сделать гораздо проще, чем получить решение,
удовлетворяющее определенным краевым условиям. Полагая,
например,
ф* == AT*
и учитывая, что в случае нулевой начальной температуры Г*
удовлетворяет уравнению B.24), после подстановки в
уравнение E.3) получим:
Таким образом, искомое решение имеет вид
E.5)
где Ф*—любое решение однородного уравнения E.3).
Остается лишь выполнить обратное преобразование
функции E.5).
Запаздывающим {объемным) потенциалом V (х> у, z, t)
называют функцию
где R = У (х — %J -f- (у — у]J -\-(z — СJ. Интегрирование
распространяется на область тела, заключенную внутри сферы
радиуса R — ct с центром в точке х, у, z.
Можно показать *), что эта функция удовлетворяет
дифференциальному уравнению
*) К у р а н т Р., Гильберт Д;, Методы математической
физики, т. 2, Гостехиздат, 1951.

g 2] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ПОЛУПРОСТРАНСТВА 129
и начальным условиям V = Q, dV/dt~0 при t = 0. Она
построена в точности так же, как ньютоновский потенциал
пространственного распределения масс, однако распределение
масс берется для момента времени, предшествующего
данному на R/c единиц времени.
Применительно к уравнению E.1) это означает, что
функция
»(».у.».о=--???Я/га*У~*''''**'«
*<г* E.6)
представляет собой термоупругий потенциал перемещений
для тела, которое в момент t = 0 находится в покое и
свободно от напряжений *). Определенным краевым условиям при
этом удовлетворить нельзя, что, однако, как отмечалось
выше, не является существенным.
Так же как в статическом случае, напряжения и
перемещения, соответствующие потенциалу Ф, вообще говоря,
не будут удовлетворять всем краевым условиям задачи,
поэтому необходимо найти дополнительное решение
однородных («безтемпературных») уравнений A.2)
которое следует выбрать таким образом, чтобы оба решения
в сумме удовлетворяли заданным условиям на поверхности.
Получение этого второго решения даже в статическом случае
представляет собой достаточно трудную задачу. В
динамическом случае такие решения получены лишь для немногих
наиболее простых задач, к рассмотрению которых мы теперь
обратимся.
§ 2. Тепловой удар на поверхности полупространства **)
Упругое полупространство z ^> 0, а также среда,
заполняющая область z < 0, вначале находятся при темпера-
*) Если Ф=*0 при ?=^0, то, очевидно, все пространственные
производные любого порядка обращаются в нуль; кроме того,
^s0 при t~Q—.
**) Эта задача впервые была решена Даниловской [40,1],
[40,2]. Позже ее вновь рассматривал Мига [131,3], [131,4], по-ви-
Димому, не знавший о русских работах.

130
Динамические эффекты
[ГЛ. V
туре Г = 0. В момент / = 0 температура среды повышается
до значения б и далее остается постоянной.
Такое скачкообразное изменение температуры поверхности
или граничащей с ней среды называют «тепловым ударом».
Следует ожидать, что в этих условиях ускорения имеют
существенное значение и поэтому квазистатический подход
будет неприменим.
Найдем вначале температурное поле. Для этого следует
решить уравнение A.45) с краевым условием
|1 = А(Г —9) при 2 = 0, E.8)
где через h обозначен относительный коэффициент
теплоотдачи. Значение h = Q соответствует случаю полностью
теплоизолированной поверхности, в случае /г—>со
температура поверхности мгновенно принимает значение 0. Применяя
преобразование Лапласа к уравнениям A.45), E.8) и полагая
k = d2/dz2, получим:
Н2Т* я rfT* h
JLL- — ±F = 0, ~ АГ = —-6 при z = 0. E.9)
dz2 a dz s r ч
Поскольку 7\ а значит, и Т* должны оставаться ограниченными
при z->oo, решение краевой задачи E.9) будет иметь вид
Г*=- — p-zVm % E.10)
Выполняя обратное преобразование, получим *):
r/9==erfc(^r)-e"+"erfc(w+/zV^)- EЛ1)
В частном случае h—>oo это решение принимает следующую
форму:
r=6erfc(w)- EЛ2)
Будем рассматривать случай одномерного движения, при
котором и = v = 0, w = w(z, t). Тогда
a &w 1 Г 1 —2р. | /1 I ч т!
е^ = ?уу = 0' ezz=ir = T7qrL-2G~"°« + ^1 + »l'>arJ'
E.13)
*) Е г d ё 1 у i [4], т. I, стр. 246.

§ 2] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ПОЛУПРОСТРАНСТВА 131
Из третьего уравнения движения A.1) получим:
дг ~~~v dt2
Дифференцируя это соотношение по z и подставляя
значение dwjdz из E.13), придем к следующему уравнению:
d2azz 1 дЧ'гг __ 1 + fx д2Т t-
Здесь, согласно зависимости E.2), через с обозначена
скорость распространения продольных волн.
Для того чтобы найти решение уравнения E.15) с
краевым условием
о^ = 0 при 2 = 0, E.16)
соответствующим случаю отсутствия напряжений на
поверхности, вновь воспользуемся преобразованием Лапласа, при
помощи которого получим *):
Ф-^<,=\~Р^Т\ 4 = 0 при z = 0. E.17)
Будем искать решение в виде
c*zz = Ae-zslc + BT*.
Подставив это выражение в дифференциальное
уравнение E.17) и приняв во внимание соотношение E.9), найдем:
о 1 +{* 5
В=Т=^Ч* 1-aslc*-
Краевое условие E.17) приводит к зависимости
А = — ВТ*\ п = — В ——AV-_4 .
В результате получаем следующее изображение решения;
— К h^a (P'Szic_p-zVm\
' / С2 \ г г- г-ч ^ '*
(s-^yVs+hVa)
ЕаЬ
°гг
К-
1 —2р.
E.18)
*) В данном случае проще рассматривать непосредственно
уравнение E.15), минуя введение термоупругого потенциала
перемещений.

132
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ V
Чтобы выполнить обратное преобразование, воспользуемся
разложением на простые дроби
Применяя теорему смещения и используя таблицы
изображений *), получим:
Здесь функции /^ и F2 имеют следующие значения:
при t < z/c,
H ' E.19)
при t > z/c.
0Л2« (rf-*)/C
E.20)
В частном случае /г—>оо эти выражения принимают
следующий вид:
E.21)
*) E r d ё 1 у i [4].

§ 2] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ПОЛУПРОСТРАНСТВА 133
Вычисление остальных компонент тензора напряжений не
вызывает затруднений: все касательные напряжения
оказываются равными нулю, а для нормальных напряжений охх и
а из закона Гука и соотношений E.13) вытекают
следующие значения:
р- ЕаТ /к 00
ахх = ауу — Г=7 а« ~~ Т^]Г ' v*'2**
Отбрасывая инерционные члены, т. е. полагая в
уравнении E.14) р = 0, и учитывая при этом краевое условие
а =0 при z = 0, легко получим квазистатическое решение
«„ = 0. охх = оуу = --^. E.23)
Весьма поучительно сравнить оба полученных решения.
Отметим прежде всего, что на поверхности z = 0 оба
решения дают одинаковый результат, заключающийся в том,
что на этой поверхности по всем направлениям действуют
равные между собой сжимающие напряжения
°=-Т-У- <5-24>
Аналогичное сравнение динамических и соответствующих им
квазистатических решений для цилиндра, сферы, бесконечной
среды с полостью, и локально нагреваемого
полупространства показывает, что формула E.24) будет справедлива также
и в этих случаях, но только для момента tf—>0-(-. т. е.
непосредственно после воздействия теплового удара. В
последующие моменты времени напряжение на поверхности
в динамическом случае может даже превзойти
соответствующее квазистатическое значение (как показано, например, на
рис. 22).
Иным будет положение внутри области, занятой телом.
Как можно видеть из соотношения E.19), составляющая
напряжения, выражаемая функцией F2, представляет собой
продольную упругую волну, фронт которой движется со
скоростью с от поверхности внутрь тела. Рассмотрим
произвольную точку внутри полупространства. Вначале в ней
возникает только составляющая напряжения, соответствующая
функции Fv В момент t = z/c к этой точке приходит волна,
соответствующая функции F2, напряжение скачкообразно

134
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
возрастает и затем быстро уменьшается, приближаясь к
квазистатическому значению. На рис. 19 и 20 приведены
полученные Мура (Т. Мига, [131,4]) для случая /г->оо
зависимости напряжения (azJK) и температуры (Т/6) от безразмерной
координаты С == czja для двух различных значений времени
x — cHja. Фронт волны находится при этом в точке С = т,
скачок напряжения имеет величину К- Максимальное значение
10
Ot5
О
^0,5
4,0
Рис. К
напряжения агг также равно /С, оно достигается, как можно
видеть из рис. 20, на фронте волны на достаточном
удалении от поверхности. В действительности это максимальное
значение не будет достигнуто вследствие демпфирования,
которое в решении не учитывалось.
Кривые на рис. 20 отчетливо показывают, что вскоре
после прохождения фронта волны напряжение ozz
практически становится равным квазистатическому значению ozz = 0.
Аналогичные результаты имеют место и при h < оо,
однако в этом случае при прохождении волны напряжение
изменяется непрерывно.
Решение динамической задачи о местном внезапном
нагреве поверхности полупространства было получено Бейли
(Bailey [111) для малых значений времени / (квазистатиче»
\
\Г/Э
\
г = /

§3)
ТЕПЛОВОЙ УДАР
135
ский вариант этой задачи рассматривался в § 5 гл. II).
Результаты решения в основном аналогичны приведенным
выше и подтверждают применимость формулы E.24) также
й в этом случае.
Игначак (Ignaczak, [87,1]) получил (формальное) решение
для случая полупространства, на поверхности которого
внезапно появляется точечный тепловой источник, причем пере-
7,0
4,0
ч
Z = 10U
Рис. 20.
мещения точек поверхности считаются заданными. В
частности, им рассмотрен случай, когда перемещения обращаются
в нуль (жесткая поверхность).
§ 3. Тепловой удар с конечной скоростью
изменения температуры *)
Скачкообразное изменение температуры поверхности или
окружающей среды, положенное в основу решения
предыдущего параграфа, представляет собой математическую
идеализацию, которая физически не может осуществиться. Поэтому
мы рассмотрим, следуя Штернбергу и Чакраворти, случай,
когда температура поверхности возрастает от нуля по
линейному закону и достигает конечного значения 8 за малый,
но отличный от нуля интервал времени tQ.
Решение для этого случая можно сразу же получить
посредством интегрирования решения, найденного в
предыдущем параграфе. Пусть /^ («г, t) означает какую-либо
величину (например, температуру, напряжение или перемещение),
*) Sternberg, Chakravorty [175, 1].

136
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ V
найденную при краевом условии, соответствующем
скачкообразному изменению температуры поверхности; обозначив
через /(?, t) значение той же величины при произвольно
изменяющейся с течением времени температуре
поверхности Г @, t), получим, что бесконечно малое изменение
температуры поверхности dT, происходящее в момент t = А,
вызовет в момент t приращение dfy равное
<*/ = /«,(*. t-X)dT@, А).
Отсюда посредством интегрирования находим:
E.25)
Примем в качестве краевого условия линейное изменение
температуры
E.26)
и подставим в уравнение E.25) вместо функции /от
выражение E.12) для температуры и затем выражения E.19),
E.21) и E.22) для напряжений. В результате после
вычисления интегралов получим:
E.27)
E.28)
E.29)

§ 3]
ТЕПЛОВОЙ УДАР
137
В этих соотношениях использованы безразмерные
переменные Сити постоянная /С, введенные в § 2 гл. V. Через
#(т) обозначена единичная функция Хевисайда
«W_P "'¦ '<<>• E.30,
{ 1 при т > 0.
В рассматриваемом случае напряжения изменяются
непрерывно, однако их производные по времени и по
пространственной координате имеют разрывы, которые
распространяются со скоростью с.
Квазистатическое решение по-прежнему имеет вид E.23).
1 / 4
АЪазистатическое
решение
*-г
Рис. 21.
На рис. 21 показаны графики зависимости
безразмерного напряжения агг/К от безразмерного времени т*в точке
С=1 при различных значениях т0= c2tQ/a. Как можно
видеть из графиков, максимум напряжений быстро уменьшается
с увеличением т0. При т0=3 этот максимум составляет лишь
около 14% от его значения при т0=0 (мгновенный нагрев).
Например, для углеродистой стали (\i = 0,3, О —- 8 • 105 кг/см2,
Р = 7,85 г/см3, а = 0,13 см2/сек) из формулы E.2)
получаем скорость волны расширения с = 6 • 105 см/сек, а
зависимость между временем t и безразмерной переменной т
будет иметь вид / = 3,7 • 10-13т сек. При этом значение
хо=3 будет соответствовать времени нагрева ^0=10~ сек.

138
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
Таким образом, даже при столь малой продолжительности
нагрева максимум динамических напряжений снижается на 86%.
Эти результаты показывают, что при встречающихся в
действительности соотношениях повышение напряжений
вследствие динамических эффектов, вообще говоря, не имеет
практического значения.
§ 4. Мгновенный источник в неограниченной среде*)
В § 1 гл. II была рассмотрена в квазистатической
постановке задача о неограниченном упругом теле, в котором
в момент t = О действует мгновенный источник. Теперь мы
рассмотрим эту задачу с учетом инерционных членов в
основных уравнениях.
Распределение температуры по-прежнему выражается
формулой B.1). Соответствующее изображение имеет вид
T* = ^Re~RVW- С5-31)
Подставив это значение в уравнение E.5), получим:
^ 2G (с2 \ п -г-^о.
где Кх по-прежнему имеет значение B.2). Функция Ф0
удовлетворяет уравнению
и поэтому имеет вид
Фо =
Функция Ф, а следовательно, и функция Ф* при /?->оо
должны обратиться в нуль, поэтому необходимо положить
Далее функция Ф стремится к нулю при t->oot поэтому
lim $Ф* = 0.
*) Nowacki [137, 10].

4] МГНОВЕННЫЙ ИСТОЧНИК В НЕОГРАНИЧЕННОЙ СРЕДЕ 139
Определив из этого условия постоянную Л, получим
E.32)
Обратное преобразование не вызывает затруднений *) и
приводит к следующему соотношению:
E.33)
где
E.34)
Нетрудно видеть, что здесь мы приходим по существу к
такому же положению, как в § 2 гл. V. Здесь также
возникает волна, определяемая функцией F2, которая
распространяется от источника со скоростью с. Вследствие условия
F2(R, R/c) = 0 эта волна вызывает не скачкообразные, а лишь
непрерывные изменения напряжений. После того как
сферическая волна пройдет некоторую фиксированную точку,
напряжения в этой точке быстро приближаются к
квазистатическому значению. Действительно, поскольку при R<^ct
то функция Ф принимает значение, данное формулой B.3).
Напряжения, соответствующие потенциалу E.33),
вычисляются при помощи зависимостей A.33), в которых г
следует изменить на R. Соответствующие формулы мы здесь
не приводим.
При помощи интегрирования по t можно получить
температуры и напряжения для случая непрерывно
действующего теплового источника, который появляется
в момент ? = 0 (см. также § 3 гл. II). В рассматриваемом
*) Е г d ё 1 у i [4J, т. I, стр. 229 и 246.

140
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ V
случае целесообразно произвести это интегрирование в
пространстве изображений, где оно сводится просто к делению
на s. Приняв, что производительность S постоянна, после
обратного преобразования получим для Т выражение B.15)*),
а значение Ф будет следующим **):
при t <C Rjc
при t ;> Rjc
где
E.35)
\ E.36)
В этом случае тоже возникает сферическая волна,
распространяющаяся от теплового источника, который является ее
центром.
§ 5. Сферическая полость в неограниченной среде***)
Рассмотрим влияние ускорений в задаче, которая в
квазистатической постановке была рассмотрена в § б гл. II.
Распределение температуры B.42) остается без изменений,
однако дифференциальное уравнение, определяющее радиаль-
*) Величину с, которая ранее означала удельную темплоем-
кость на единицу массы, не следует смешивать со скоростью с
Поэтому первую величину мы будем здесь обозначать через сж
**) Nowacki [137, 11].
***) Sternberg, Chakravorty [175, 2].

§ 5] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 141
ное перемещение и (г, t) теперь следует взять в форме A.8)
где с имеет значение E.2). Применяя к этому уравнению
преобразование Лапласа с учетом зависимости B.41) и
начальных условий
дг
получим:
E.37)
Легко получить решение этого уравнения, остающееся
ограниченным при г->схэ; это решение имеет вид
иЧг. s) = ±(± + ±r)c1(s)e-'*"-\-
1 1 — fx u s2 r2(as — c2)
где Сг является произвольной функцией s.
Краевые условия здесь те же, что и в квазистатическом
случае. Поскольку зависимости B.43) также остаются в силе,
то, используя условие, что поверхность полости г = R
свободна от напряжений, получаем:
.E.38)
Обратное преобразование (подробности которого приведены
в Цитированной работе Штернберга и Чакраворти A75, 2))

142
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
приводит к следующим соотношениям:
, E.39)
где использованы безразмерные переменные р, х, С,
введенные в § 6 гл. II и принято обозначение ^=-^~.
Остальные обозначения имеют следующие значения:
Через Н по-прежнему обозначена единичная функция,
определенная соотношением E.30); для |/"/г следует брать
главные значения. Символ Re перед комплексной функцией
означает, что берется ее действительная часть.
При помощи соотношений B.43) можно теперь получить
выражения для напряжений. Эти весьма сложные выражения
здесь не приводятся; их можно найти в цитированной выше
оригинальной работе.

5] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 143
Единичная функция #(<о) входит в выражения как
перемещений, так и напряжений; это означает, что в
рассматриваемом случае будет возникать сферическая волна,
распространяющаяся от поверхности полости р=1 со скоростью с.
Остальные члены в приведенных выражениях дают некоторый
рассеянный эффект, возникающий одновременно во всей среде.
На фронте волны, которому соответствует условие со = О,
напряжения скачкообразно изменяются на величины
В отличие от случая, рассмотренного в § 2 гл. V, величина
скачка напряжений убывает по мере удаления от начала.
Динамическое
решение
7
Хвази-
стаглическое
решение
1 з
Стационарное
решение
*-г
/> = 1
Рис. 22.
При достаточно больших значениях времени (т->со)
динамическое решение при р < со переходит в статическое
решение B.49). На рис. 22—24 показана зависимость окружного
напряжения <з //С от времени в трех различных точках
Р= I, 2, 3. Вычисления производились для значений ц = 0,25
и 7 = 0,20. Хотя значение у было принято необычно

144
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
0,1
0,0
-0,1
-0,2
\
' \ » i
\
I
-
{ \ 1 2
\ \^-^ Динамическое
\ д\/ решение
статическое "-
решение
/?-*
\ ^
.?>
-Я«?
Стационарное решение
Рис. 23.
-Яг?
-4J
Стационарное решение
Рис. 24,

ПЕРИОДИЧЕСКИЕ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ 145
большим *), оно позволяет отчетливо выявить особенности
динамических эффектов.
Графики на рис. 22 показывают, что окружное
напряжение на поверхности полости вначале испытывает
непродолжительные колебания и затем быстро приближается **) к
квазистатическому постоянному значению —1. Отмеченные
колебания приводят к повышению динамических напряжений на
поверхности по сравнению с их квазистатическими значениями.
На рис. 23 и 24 можно видеть ранее отмеченное
скачкообразное изменение напряжений при прохождении фронта волны.
В последующем динамическое решение быстро приближается
к квазистатическому.
§ 6. Периодические изменения температуры
Мы обратимся теперь к кругу вопросов, рассмотренных
в квазистатической постановке в гл. III, и проведем
исследование с учетом инерционных членов. Если принять, так же
как в гл. III, что переходный процесс затух, то можно
будет ограничиться рассмотрением чисто периодического
решения, для которого можно воспользоваться представлениями
температуры Т и термоупругого потенциала перемещений Ф
в форме C.1). Подставив эти выражения в уравнения E.1),
получим:
ДФг + ^Ф/ = -ЬЬ%;Г/ (/=1.2). E.40)
Найдем вначале частное решение, которое можно искать
в форме
Ф^Л^ + Л/, E.41)
Заметим, что согласно уравнению A.45) функции 7\ и Т2
удовлетворяют зависимостям
ДГ, = -!-Г2. ДГ2 = —?-7\. E.42)
*) Для стали при диаметре отверстия 2R = 5 см f имеет
величину порядка 10~7.
**) Вычисление для стали при y = 7 • 10 (что соответствует
Диаметру полости около 60 см) показывает, что различие между
этими двумя решениями за время порядка 10~12 сек уменьшается
До значения около 5%.

146
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. v
подставив которые в уравнение E.40) получим:
(? Аа - ± АВ) Тх + ? Аа + ? Аа) Т2 = \±± аГ,
Полагая вначале /=1, а затем /=2 и сравнивая в обоих
случаях коэффициенты при 7\ и Г2, получим по два
уравнения для определения четырех коэффициентов Aik\ решение
этих уравнений дает:
с2
E.43)
К частному решению E.41), вообще говоря, можно добавить
любое решение Ф^ однородного уравнения E.40).
§ 7. Периодический тепловой источник
в неограниченной среде*)
Формулы, выведенные в предыдущем параграфе, применим
к задаче, рассмотренной в § 3 гл. III. Распределение
температуры C.8) остается без изменений, следовательно,
2
Учитывая значение E.43) и вводя обозначение
E.44)
E.45)
из уравнений E.41) получим следующие выражения:
Здесь добавлены обе функции Ф^ и Ф^, которые вследствие
центральной симметрии рассматриваемой задачи являются
решениями однородного уравнения
*) Nowacki [137, 11].

§7]
ПЕРИОДИЧЕСКИЙ ТЕПЛОВОЙ ИСТОЧНИК
147
и имеет поэтому следующую форму:
Ф,=—r-cos f--rf sin .
1 R с ' R с
Напряжения и перемещения должны обращаться в нуль при
/^__>сю. Потребуем также, чтобы функция Ф при R~~>0
оставалась ограниченной *). Из этих условий получаем:
0l~~ 2G ' 2~~ 2G ш '
коэффициенты Dx и D2 пока остались неопределенными.
Причина этого заключается в фундаментальном различии
свойств решений уравнения Пуассона A.46) (или
гармонического уравнения), которому в квазистатическом случае должна
удовлетворять функция Ф, и, с другой стороны, волнового
уравнения E1), которое определяет функцию Ф в
динамическом случае. Если решение гармонического уравнения для
бесконечной области однозначно определяется двумя
условиями, сформулированными в § 1 гл. II, то по отношению
к волновому уравнению положение будет иным. Здесь лля
обеспечения однозначности решения необходимо ввести
дополнительное условие, которое можно сформулировать
следующим образом: из двух математически равноценных
распространяющихся сферических волн, а именно расходящейся
волны вида -р cos со (t — R/c) и сходящейся волны вида
-п cos to (t-\- R/c), только первое решение является физически
А
возможным. Это решение соответствует волне, движущейся
от источника в бесконечность, тогда как второе решение
дает волну, которая движется из бесконечности к «стоку» и
физически не может быть реализована **).
Итак, нужно определить постоянные Dx и D2 таким
образом, чтобы не возникала сходящаяся волна, то есть чтобы
функция Ф' имела вид
Ф' = ф^ cos Ы + Ф'2 sin со/ = -?- cos со (t — R/c) +
+ -^ sin со (t — R/c). E.46)
*) См. § 1 гл. И.
**) См., например, Франк, Мизес, Дифференциальные и
интегральные уравнения, т. 2, или Kupradse, Randwertaufgaben
der Schwingungstheorie und Integralgleichungen, Berlin, 1956.

148
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
Для этого мы располагаем двумя константами, определив
которые получим
C = Cl = D2t D = C2^=— Dv
Таким образом, окончательно решение имеет следующий вид:
0 = ^-^{«-^[cosM-x/?)+-^.sIn((D^-x/?)] —
— cos со (t — R[c) — -^- sin со (t — R/c) 1. E.47)
Соответствующие напряжения определяются при помощи
соотношений A.33).
Используя ряды Фурье, можно при помощи выведенных
формул получить решение для случая произвольного
периодического источника.
§ 8. Точечный нагрев диска *)
В § 14 гл. II и в § 4 гл. VII рассмотрена в
квазистатической постановке задача о тонком бесконечном диске,
в котором в момент ? = 0 начинает действовать точечный
источник постоянной производительности. Здесь мы
рассмотрим возникающие динамические эффекты, считая, что
материал является идеально упругим.
Будем основываться на первом уравнении движения A.3).
в котором вследствие осевой симметрии задачи следует
положить crz = 0. Выражая напряжения через радиальное
перемещение и при помощи формул G.53) и G.54), получим
следующее дифференциальное уравнение:
д2и , 1 да и 1 д2и ,А . ч дТ /гг ,0ч
дг г дг г с\ дг дг
где
Полученное уравнение также является волновым; применяя
к нему преобразование Лапласа и учитывая, что при ? = 0
*) Park us [147, 2].

§8]
ТОЧЕЧНЫЙ НАГРЕВ ДИСКА
149
О, получим следующее уравнение:
Если учитывается теплообмен между поверхностями диска и
окружающей средой, то изображение температуры будет
выражаться формулой G.49). Внося это значение в
приведенное выше уравнение, придем к следующему общему решению:
и* = О + V) «Т \а*х (s ~) + BIX (s {-) -
.(, + Р-А/Ф \У «У J
Поскольку напряжение, а следовательно, и #*/г при г—>оо
должны оставаться ограниченными, следует положить В = 0.
Учитывая далее, что \imu* = 0 и принимая во внимание
г->0
соотношение
*i (*) = 4+(in J+с)/!(*)-•?+ ....
получим для постоянной Л следующее значение:
c2(s + $)~as2 '
Таким образом, изображение радиального перемещения будет
иметь следующий вид:
Как показывают решения, рассмотренные в §§ 2—5 этой
главы, влияние динамических членов оказывается
существенным лишь в течение короткого промежутка времени после
прохождения волны напряжений. Мы ограничимся здесь
рассмотрением не слишком большой области, окружающей
точечный источник, которую волна, движущаяся со скоро-

150
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
стью cv будет проходить достаточно быстро *); при этих
условиях достаточно найти решение и для малых значений
времени t. Учитывая это, заменим выражение для и* его
асимптотическим представлением, справедливым при больших
значениях s:
E.51)
Теперь обратное преобразование легко выполняется **) и
приводит к следующему соотношению:
E.52)
где функции Ux и U2 имеют следующие значения:
E.53)
Мы видим, что в этом случае также возникают волны
перемещений и напряжений, определяемые функцией U2-
Заметим, что
E.54)
поэтому для разности напряжений
*) Для стали С] — 800 м/сек.
**) Е г d е 1 у i [4J, т. 2, стр. 277, 283.

§ g] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ЦИЛИНДРА 151
получим следующее выражение:
E.55)
Легко убедиться, что всегда а > агг; действительно,
допустим, что функция
имеет положительные корни. Так как функция Ei (—х)
отрицательна при всех положительных х, то эти корни должны
лежать справа от точки х=\\ далее, поскольку
функция f (х) непрерывна и обращается в нуль при х—>со, то
по теореме Ролля производная
должна была бы по крайней мере один раз обратиться в нуль
в интервале 1 < х < со, что, однако, не имеет места в
действительности.
§ 9. Тепловой удар на поверхности длинного
сплошного цилиндра*)
В § 12 гл. II была рассмотрена в квазистатической
постановке задача о бесконечно длинном круговом цилиндре,
который вначале имеет температуру, равную нулю и
поверхности которого в момент t = 0 внезапно сообщается
некоторая произвольно распределенная по окружности
температура. Рассмотрим теперь эту задачу в динамической
постановке, причем для простоты будем считать, что температура
поверхности постоянна. Температурное поле для этого случая
получим из выражения B.108), положив # = 0:
E.56)
*) Мига [131,1], [131,4].

152
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ. V
Для определения радиального перемещения и воспользуемся
первым уравнением A.5), которое вследствие условия dw/dz = О
будет иметь вид*)
дг2 ~+" г дг г2 с2 dt2 ~ 1— (х аГ» E'57)
где ? имеет значение E.2). Применяя к уравнению E.57)
преобразование Лапласа, получим:
где для Т*, согласно уравнению B.107), следует принять
следующее значение:
Г=Т± /ofrlgg) E.59)
Частное решение уравнения E.58) будем искать в виде
Учитывая, что
ле1ко получаем:
E.60)
Однородное уравнение E.58) имеет решения 1г (sr/c) и Кг (sr/c)*
второе из которых не остается ограниченным при г->0
и поэтому должно быть отброшено. Таким образом, приходим
к решению
E.61)
Для определения постоянной В служит краевое условие
arr — Q при r~R или
*) Мы предполагаем, что концевые сечения цилиндра не
смещаются.

§ 9] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ЦИЛИНДРА 153
которое можно представить также в форме
[ A - V-) ^г /о (sRIc) - A - 2р) /, (sR/c) ] В =
= (l+rt^4- + d-2|*)^- 7/^S! • E-62)
Обратное преобразование здесь оказывается весьма трудоем-
к iM и приводит к сложным и трудно обозримым выражениям *).
В отличие от примеров, рассмотренных в §§ 2—5, здесь
волны, возникающие на поверхности, не уходят в
бесконечность, а отражаются и приводят к возникновению колебаний,
которые, однако, для практически встречающихся условий
оказываются несущественными. Мы ограничимся здесь
вычислением и и о на поверхности r = R при малых значениях t,
т. е. непосредственно после воздействия теплового удара.
Используя асимптотические представления, справедливые для
больших значений z,
получим из уравнений E.60)—E.62) при больших |s| и при
Таким образом, при малых значениях t
при r = R. E.63)
Окружное напряжение а при г — R определяется из
соотношения
О — Р) о„— Г°гг = 20 lew - A + fx) a Г]-
которое вследствие условия огг = 0 принимает вид
0w = T^rK-A+ti)a7'o] при г = /?- E4)
Учитывая, что и—>0 при t—>0, замечаем, что здесь снова
динамические напряжения на поверхности, по крайней мере
*) Мига [131,4].

154
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
trvr. v
сразу же после воздействия теплового удара, совпадают
с квазистатическим значением, найденным в § 12 гл. II; при
этом формула E.24) также оказывается справедливой.
§ 10. Термическое возбуждение колебаний пластинок
Для изучения динамического поведения тонких пластинок
при действии быстро изменяющихся температур,
воспользуемся уравнением изгиба пластинки {G.9), Мелан — Паркус [6]},
которое при наличии внешней нагрузки р на единицу
срединной поверхности имеет вид
A bw = -? — а A -f-ji) Дт.
Добавив к нагрузке/? даламберову силу инерции—pbd2w/dt2
(8— толщина пластинки), получим:
NAkw + ?ь^г *= Р — 0 + V) Na Ат- E-65)
Здесь, в соответствии с уравнением {G.1), Мелан — Паркус [6]},
через т обозначен коэффициент при z в линейной
аппроксимации температуры T(x,y,z, t), причем х, у являются
координатами в срединной плоскости пластинки. Умножив
уравнение G.1) на z и проинтегрировав по толщине пластинки 5 = 2/г,
получим
А
t(jc, у, 0 = -рг f zT(x> У. Z> t)dz- E.-66)
-h
Для решения уравнения E.65) представим прогиб w в виде
суммы квазистатической составляющей ws и динамической
составляющей wd:
w=^ws-^wdy E.67)
где ws удовлетворяет уравнению
АГД kws = р — A + V) Nt. At. E.68)
Составляющую ws подчиним тем же краевым условиям,
которые накладываются на полный прогиб w. Эти условия, оче-

§ 10] ТЕРМИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ ПЛАСТИНОК 155
видно, зависят от способа закрепления пластинки. Подставив
выражение E.67) в уравнение E.65) и учитывая соотношение
E.68), получим для определения wd следующее
дифференциальное уравнение:
E.69)
Поскольку ws уже удовлетворяет краевым условиям,
наложенным на прогиб w, составляющую wd следует подчинить
однородным краевым условиям, соответствующим принятому
способу закрепления. Постоянная х имеет следующее значение:
E.70)
Уравнение E.69) представляет собою известное
дифференциальное уравнение колебаний пластинки, вызванных
фиктивной нагрузкой р = — v2Nd2wJdt2, причем, в отличие от
уравнения E.65), отсутствует воздействие на краях пластинки.
Эта задача хорошо изучена в литературе*). Аналитические
трудности могут, однако, быть значительными, поскольку
функции, применяемые в качестве собственных функций,
могут оказаться недостаточно изученными.
Отметим, что метод, основанный на представлении
прогиба в форме E.67), можно применить также для изучения
термически возбуждаемых изгибных колебаний балок**).
Если принять, что поперечное сечение балки постоянно, то
вместо уравнения E.65) будем иметь следующее исходное
уравнение:
„. d4w . _ d2w „ д*Ъ /с _1ч
Здесь F и J означают площадь и момент инерции
поперечного сечения, а величина б имеет следующее значение:
0 (х, t) = fzT (х, z, t) (IF. E.72)
F
Дальнейшее исследование производится так же, как в случае
пластинки.
*) См. учебники по теории колебаний.
**)Во1еу [22,2], Boley and Barber [23].

156
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
[ГЛ V
§ 11. Тепловой удар на поверхности пластинки*)
Рассмотрим свободно опертую по всем сторонам
прямоугольную пластинку |л;|<;#, |у|<^с, к поверхности z =
= -\-bj2 = -\-h которой, начиная с момента ? = 0,
подводится тепло, причем количество тепла, подводимое за
единицу времени к единице поверхности, равно постоянной
величине q. Нижняя поверхность пластинки z — — 8/2 = — h и
края х=±Ь, у=±с считаются полностью
теплоизолированными. Распределение температуры при этом зависит только
от координаты 2 и от времени t и, следовательно,
определяется уравнением
E.73)
при краевых и начальных условиях
E.74)
Решение этой задачи легко может быть найдено при помощи
преобразования Лапласа и имеет следующий вид**):
E.75)
Вычисляя при помощи соотношения E.66) величину т,
получаем:
'(в-4Л-5 2 >--*> («.те
\ /2 = 1,3,5 /
Поскольку т зависит только от t, то Дт = 0.
*)Boley and Barber [23].
**) Carslaw — Jaeger [1J, стр. 104.

§ 11] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ПЛАСТИНКИ 157
Теперь необходимо решить уравнение E.65), которое
вследствие отсутствия внешней нагрузки р будет иметь форму
E.77)
На краях пластинки должны обращаться в нуль прогибы и
изгибающие моменты:
при х — ±ЬУ
при у = ±с.
Эти условия при помощи соотношений {E.6), Мелан — Пар-
кус [6]} можно представить в следующем виде*):
E.78)
Найдем вначале квазистатический прогиб ws, для
определения которого получим, полагая р = 0, следующее
уравнение:
ДДда, = 0. E.79)
Краевые условия для ws имеют вид E.78). Положим
ws = C (**+ У2) + wsl + wsV E.80)
где wsl и ws2 являются бигармоническими функциями,
которые мы подчиним следующим краевым условиям:
где
E.81)
E.82)
E.83)
*) Вывод этих уравнений основан на использовании закона
Гука, поэтому они остаются в силе также и в динамическом случае.

158
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
1ГЛ V
Легко проверить, что при этом краевые условия E.78) будут
выполнены. Положим далее *):
где
[ E.84)
E.85)
Функция wsl удовлетворяет при произвольных Ап и Вп двум
первым краевым условиям E.81), а функция ws2
удовлетворяет при произвольных Сп и Dn третьему и четвертому
краевым условиям E.82). Чтобы удовлетворить остальным
краевым условиям, воспользуемся рядами Фурье
где
v5.86)
При этом из условий E.81) и E.82) получим:
*) Q I г k m a n n К., Flachentragwerke, Wien, 1956, стр. 209.

§ 11) ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ПЛАСТИНКИ l'g9
и два аналогичных уравнения относительно Сп и Dn.
Решение этих уравнений имеет вид
E.87)
Таким образом, квазистатический прогиб найден. Ряды E.84)
и их производные любого порядка равномерно сходятся
внутри прямоугольной области, занятой пластинкой.
Для определения динамической составляющей прогиба wd
воспользуемся обычным представлением *)
wd= 2 2 ?««(') cos a„* cos p,ny. E.88)
/2 = 1,3, 5 /72 = 1, 3, 5
При этом удовлетворяются однородные краевые условия,
налагаемые на функцию wd:
<a^ = 0, Aie^ = 0 при x=±b, y=±c.
После подстановки в уравнение E.69) получим:
E.89)
Теперь необходимо правую часть этого соотношения также
представить в виде двойного ряда, который проще всего
получить, подставив выражение
^5= 2 2 /f^cosa^cosp^y E.90)
в уравнение E.68), которое после интегрирования при р = 0
будет иметь вид
*) Тимошенко С. П., Колебания в инженерном деле, М.,
Физматгиз, 1959 (начало координат в этой книге выбрано в углу
пластинки).

160
динамические эффекты
[ГЛ. V
Используя ряд
получим:
E.91)
Возвращаясь к соотношению E-89), получим следующее
дифференциальное уравнение относительно qnn:
q -f-oJ п =—k т, со т = (ос2+32Ух. E.92)
чпт i птгг^пт ntfl rim \ п » гот;/ v /
Применение к этому уравнению преобразования Лапласа
с учетом условий
дает
Выполнив обратное преобразование, получим:
Подставив сюда значение т из уравнения E.76), придем
к следующему выражению:
E.93)
Таким образом, рассматриваемую проблему можно считать
решенной (по крайней мере формально). Однако если квази-

§ 11] ТЕПЛОВОЙ УДАР НА ПОВЕРХНОСТИ ПЛАСТИНКИ 161
статический прогиб ws выражается в форме простого ряда
и не вызывает трудностей при численных расчетах, то
динамическая составляющая wd имеет вид тройного ряда,
вычисления при помощи которого будут чрезвычайно сложными.
Бодей и Бербер (Boley, Barber [23]) вычислили отношение
2,0
19
18
17
16
15
13
12
V
Ю
О 0,5 10 15 3,0 2,5 3.0 3,5 4,03
Рис. 25.
максимального прогиба ^тах в центре пластинки к
наибольшему квазистатическому прогибу wsmSL1L при различных
значениях параметра В = bfBb ]/ах), принимая, что Ъ < с.
Результаты представлены на рис. 25, откуда следует, что при
уменьшении толщины пластинки влияние инерционных членов
возрастает. Очевидно, что здесь остаются в силе
соображения, приведенные в § 3 гл. V.

ГЛАВА VI
ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
ПРИ ВЯЗКОУПРУГОМ ПОВЕДЕНИИ МАТЕРИАЛА
§ 1. Введение
В основу решений предыдущих разделов было положено
представление о «линейно упругом» материале, т. е. о таком
материале, который всегда подчиняется закону Гука. Кроме
того, предполагалось, что материал однороден и изотропен,
а также что модуль упругости, коэффициент поперечного
сжатия и коэффициент линейного расширения являются не
зависящими от температуры постоянными. Эти
предположения вполне приемлемы для большинства технически важных
материалов, по крайней мере до тех пор, пока
рассматриваемые разности температуры не слишком велики, а
температура не превышает некоторого предельного значения,
зависящего от материала, и пока напряжения не достигают
границы текучести.
При более высоких температурах положение, однако,
будет иным. При повышении температуры не только заметно
снижается предел текучести (в результате чего пластические
деформации возникают при существенно меньших
напряжениях), но почти у всех материалов обнаруживается более или
менее отчетливо выраженное явление вязкого течения. При
этом продолжающееся деформирование имеет место даже при
постоянных значениях температуры и нагрузки и если и
прекращается, то лишь тогда, когда уровень напряжений
окажется достаточно низким. Наконец, при высоких
температурах характеристики материала уже не остаются более
постоянными, но изменяются в зависимости от температуры *).
*) См., например, Freudent ha l [52,1], Н off [79,7].

§ 2] ЗАВИСИМОСТИ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ 163
Совокупность этих явлений, вообще говоря, существенно
более сильно влияет на системы температурных напряжений
(являющихся собственными напряжениями), чем на
напряженные состояния, возникающие под действием нагрузок.
Поэтому учет реологических эффектов имеет большое значение
при проектировании элементов конструкций, подвергающихся
воздействию высоких температур.
В настоящей главе мы рассмотрим явление вязкого
течения, а в следующей главе обратимся к изучению
упруго-пластических задач. Предположим поэтому, что напряжения не
достигают границы текучести, соответствующей заданной
температуре. Предположим далее, что деформации являются
малыми, а также что материал однороден и изотропен и что
физические постоянные, входящие в решение, не зависят от
температуры. Следует отметить, что постоянные,
характеризующие вязкость материала, существенно зависят от
температуры и, во всяком случае, влияние температуры на
значение этих постоянных будет гораздо большим, чем изменение
в зависимости от температуры модуля упругости или
коэффициента теплового расширения. Учет этой зависимости
в принципе возможен, однако приводит к тому, что даже
в простейших задачах возникает необходимость проведения
большой вычислительной работы, при этом часто получаемые
решения не обладают достаточной общностью. Поэтому лишь
в единичных случаях можно ставить вопрос о
соответствующем уточнении результатов. С другой стороны, проведенные
до настоящего времени исследования влияния переменной вяз*
кости позволяют считать, что расчеты на основе
предположения о постоянстве вязкости дают удовлетворительные
значения напряжений *).
§ 2. Зависимости между напряжениями и деформациями
Для формулировки реологических законов, связывающих
напряжения и деформации, целесообразно, наряду с
напряжениями Оц и деформациями е^, рассматривать девиатор
напряжений stj и девиатор деформаций etj. Эти тензоры
*)Freudenthal [52,1], [52,2], Hilton [75,3], Н i 11 о n — Н а з-
san — Russell [76].

164
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ. VI
определяются соотношениями
sij = °ц — °8//' *ц = *ij — е8*7» F •1)
где 8^ — символ Кронекера, а через а и е обозначены
среднее нормальное напряжение и среднее удлинение:
F.2)
При помощи этих девиаторов закон Гука может быть
выражен в форме следующих соотношений:
F.3)
F.4)
Уравнения F.3) и F.4) описывают поведение линейно
упругой среды или среды Гука. Моделью этой среды может
служить пружина (рис. 26, а).
Простейшую возможную зависимость между напряжениями
и деформациями для вязкоупругого тела можно получить,
добавляя к соотношениям
закона Гука член,
выражающий ньютонов закон
вязкости, согласно которому
напряжения
пропорциональны скоростям изменения
деформации.
Соответствующие модели можно получить
при помощи введения
вязкого сопротивления
(демпфера). Последовательное
или параллельное соединение
пружины и вязкого
сопротивления будет
соответственно приводить к среде
Максвелла (рис. 26, б) и
к среде Кельвина (или Фой-
хта) рис. 26, в.
Соответствующие зависимости между напряжениями и деформациями
имеют вид
Среда
Гука
а)
Среда
Максвелла
б)
Рис. 26.
Среда
Кельвина
в)
F.5)

§ 2] ЗАВИСИМОСТИ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ 165
для среды Максвелла и
F.6)
для среды Кельвина; при этом соотношение F.4) остается
без изменений. Последнее означает, что при
гидростатическом сжатии или растяжении тело ведет себя как вполне
упругое. Постоянную & в случае среды Максвелла называют
«временем релаксации», а в случае среды Кельвина —
«временем запаздывания». Эта постоянная имеет значение & = 7?/C,
где т] — коэффициент вязкости материала.
Различие в поведении обоих тел отчетливо
обнаруживается, если рассмотреть, например, свободный от
напряжений стержень с закрепленными концами, температура
которого в момент t = О мгновенно понижается до значения —- Т0
и далее остается постоянной. Поскольку при этом
вхх 2 ~ 1 — 2[Д. ахх ~
0 — "у » sxx — "g" ахх> ехх — и> ? — ? • ~з °'
уравнение F.5) примет вид
F.7)
а из уравнения F.6) получим:
~Jf + A-2A)» °*х = A-2^)9 ?аГо- F>8)
В случае среды Гука решение будет следующим:
°хх = ЕаТ0. F.9)
Учитывая, что решение для среды Максвелла при ft—>oq
должно переходить в соответствующее решение для среды
Гука, из уравнения F.7) получим:
ахх = ЕаТ0 ехр (- | A + I») т) ' $¦ * °>
Решение для среды Кельвина получим из уравнения F.8);
поскольку вследствие скачкообразного изменения температуры
в начальный момент ахх Ф О при t->0-\~, то
соответствующее общее решение будет иметь вид
°хх = ?аГо [ 1 + С ехр (уЕ|г 1)] • F-11)

166
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ. VI
При & —>0 это решение переходит в соответствующее
решение для среды Гука. Графики изменения напряжений в
рассмотренных трех случаях приведены на рис. 27. Для среды
Гука и для среды Иаксвелла напряжения при мгновенном
охлаждении скачкообразно изменяются на величину ЕаТ0.
В идеально упругом материале эти напряжения остаются
неизменными, в среде Максвелла начинается вязкое течение,
вследствие которого напряжение непрерывно убывает,
асимптотически приближаясь к нулевому значению. В среде
Кельвина, напротив, скачок напряжения при мгновенном
охлаждении прегышает соответствующее упругое значение, к которому
это напряжение в последующем асимптотически приближается.
* >
7ХХ
\
Среда
Гуна
а)
*sxl
t
Среда
Максвелла
б)
Рис. 27.
4*г'
t
\
Среда
Хельвина
в)
Таким образом, в среде Максвелла тело реагирует на быстрое
охлаждение как вполне упругое и затем разгружается с
течением времени, тогда как в случае среды Кельвина имеет
место явление запаздывания по сравнению с упругим случаем,
вызванное внутренним сопротивлением.
Поведение материалов, применяемых на практике, вообще
говоря, гораздо сложнее, чем поведение рассмотренных
моделей. Поэтому для достижения большей точности следует
использовать более или менее сложные комбинации трех
основных случаев (например, параллельное соединение сред
Гука и Максвелла). Кроме того, необходимо принимать во
внимание возможные нелинейности в поведении материала.
Если, однако, основываться на применении простейших
моделей то, по крайней мере для металлов при высоких темпе-
рат\ pax, можно использовать схему Максвелла. Схема
Кельвина применима, как показывает рис. 26, в прежде всего для
изучения затухающих колебаний в материалах с внутренним
трением,

§ 2} ЗАВИСИМОСТИ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ 167
Наиболее общие линейные *) зависимости между
напряжениями и деформациями для вязкоупругих, механически и
термически изотропных тел могут быть представлены в
следующей форме:
F.12)
Здесь через P(D), ..., H(D) обозначены полиномы
относительно оператора D =~ d/dt
F.13)
Коэффициенты рп, ..., hn содержат постоянные материала,
в наиболее общем случае они могут быть функциями
координат и времени. Например,
(Среда Гука),
(Среда Максвелла),
(Среда Кельвина)
F.14)
«Нормальным телом» назван упомянутый выше случай
параллельного соединения среды Гука и среды Максвелла. Он
*) Нелинейные случаи в этой книге не рассматриваются.

168
ВЯЗКОУПРУГИС МАТЕРИАЛЫ
[ГЛ. Vt
включает в себя, в частности, три предыдущих случая для
несжимаемого тела F (D) = 0.
Поскольку соотношения между напряжениями и
деформациями для вязкоупругих материалов содержат время, то даже
при постоянных значениях температуры и нагрузок
соответствующие задачи будут нестационарными и, следовательно,
динамическими. Однако и здесь, за очень немногими
исключениями, возможен квазистатический подход, который мы
будем применять всюду в последующем.
§ 3. Упруго-вязкоупругая аналогия
Алфрей *) впервые заметил, что анализ поведения вязко-
упругих тел может быть сведен к рассмотрению некоторых
эквивалентных упругих задач. Однако установленная им
аналогия относится лишь к случаю несжимаемого материала.
Воспользовавшись преобразованием Лапласа, Ли **)
распространил эту аналогию на случай, когда материал сжимаем.
На случай температурных напряжений аналогия Алфрея была
Обобщена (при некоторых ограничениях) Хилтоном ***),
а аналогия Ли — Штернбергом ****).
Полная система уравнений линейной вязкоупругой
квазистатической задачи состоит из уравнений равновесия,
геометрических соотношений (см. § 1 гл. I) и зависимостей
между напряжениями и деформациями F.12). К ним следует
присоединить условия на поверхности и начальные условия.
Краевые условия на той части поверхности, где заданы
напряжения, имеют вид
3j°ijnf = Pi- F.15)
Здесь через tij обозначены компоненты вектора внешней
нормали. При формулировке начальных условий будем
предполагать, что в начальный момент напряжения и температура
равны нулю. Будем считать, что равны нулю также все про-
*) А 1 f г е у Т., Non-homogeneous stresses in visco-elastic
media, Quart. Appl. Math. 2 A944), 1.13.
**) Lee E. H., Stress analysis in visco-elastic bodies, Quart.
Appl. Math. 13 A955), 183.
***) Hilton [75, 2].
****) Sternberg [174, 2].

§3]
УПРУГО-ВЯЗКОУПРУГАЯ АНАЛОГИЯ
169
изводные по времени до достаточно высокого порядка.
Наконец, примем, что все коэффициенты полиномов F.13)
являются постоянными. Применяя к этой системе уравнений
преобразование Лапласа и учитывая упомянутые начальные
условия, получим в пространстве изображений следующие
уравнения:
- / = О,
i
* 1 / dui ди* \
геометрические соотношения о* — Р^ е*
У bij~ P(S) *IV
зависимости между напряже- И. .
* /7 (S) , # аТ"*^
ниями и деформациями f (s) K h
F.16)
Краевые условия примут вид
Ui=uh 2j°ijnj = ph F.17)
j
причем первое условие имеет место на той части
поверхности, где заданы перемещения Ut, а второе — на той части
поверхности, где заданы напряжения pt.
Уравнения F.16) и F.17) совпадают с уравнениями
линейно упругого тела той же формы, если для модуля сдвига
и коэффициента Пуассона принять значения
/-/ч 1 0E) /ч /<—2G „,ч Я E) ,ft1ftN
Таким образом, исходная вязкоупругая задача о
температурных напряжениях оказалась сведенной к эквивалентной чисто
упругой задаче. Решив эту задачу в пространстве
изображений и выполнив обратное преобразование, получим решение
(по крайней мере формальное) исходной задачи.
Если вязкоупругое тело несжимаемо, то F (s) e== 0; при
этом для эквивалентного упругого тела р- (s) = г/2. Заметим,
что хотя эквивалентное упругое тело имеет ту же форму и
такой же объем, как заданное тело, однако, вообще говоря,
распределение температуры в нем ц заданных нагрузок и

170
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ. VI
перемещений на поверхности будет совершенно иным.
Действительно, преобразованная по Лапласу функция ср*(х, у, z, s)
определяет некоторое пространственное поле, которое,
вообще говоря, будет совершенно отличным от поля,
соответствующего исходной функции ср(лг, у, z, t). Исключением
является случай, когда как температура, так и поверхностная
нагрузка имеют вид произведения функции координат на
одну и ту же функцию времени. Такое положение будет
всегда иметь место, например, в случае стационарных
температурных полей, где функция, зависящая от времени,
обращается в постоянную. При этом в эквивалентном
упругом решении переменные разделяются, т. е. это решение
будет иметь форму произведения функции от координат на
некоторую функцию, зависящую от 5. Таким образом,
пространственные поля, определяемые этим решением, будут
такими же, как и в вязкоупругом решении, отличие будет
заключаться лишь в множителе, зависящем от времени.
Заметим, что часто даже в общем случае, когда переменные
не разделяются, можно представить решение в виде ряда по
функциям, в которых переменные разделены. При этом
вследствие линейности задачи каждый из членов разложения
можно рассматривать отдельно *). Ли **) заметил, что для
получения решения на базе упруго-вязкоупругой аналогии
иногда целесообразно не применять эту аналогию в той
форме, в которой она приведена выше, а вначале решить
заданную вязкоупругую задачу, считая, что она является
вполне упругой, затем, преобразовав это решение по
Лапласу, получить эквивалентное упругое решение и лишь
тогда ввести зависимости F.18) и выполнить обратное
преобразование. Этот метод в особенности удобен, если
соответствующее упругое решение уже известно.
В i ачестве примера выведем уравнения среды Максвелла
посредством преобразования упругих уравнений равновесия
в перемещениях {B, 11), Мелан — Паркус [6]}. Применяя
преобразование Лапласа, получим:
*) Hilton [75, 2].
*) См. сноску на стр. 168.

§ 4] ТЕРМОВЯЗКОУПРУГИЙ ПОТЕНЦИАЛ ПЕРЕМЕЩЕНИЙ 171
Коэффициент [х заменим его значением F.18), тогда
3Q (s) F (s) Д«; + [Q (s) F (s) + 2Н (s) P(s)]^ =
= 6H(s)P(s)ol^-. F.19)
Для среды Максвелла, согласно уравнениям F.14),
Учитывая эти соотношения и выполняя обратное
преобразование, получим искомые уравнения:
F.20)
§ 4. Термовязкоупругий потенциал перемещений
Понятие термоупругого потенциала перемещений в том
смысле, в каком он используется в соотношениях ui = дФ/di
(см. § 7 гл. I), можно легко распространить на случай вязко-
упругого тела.
Квазистатический упругий потенциал удовлетворяет
уравнению A.46), которое посредством преобразования Лапласа
можно представить в следующем виде:
A—|х)АФ* = A +р)аГ\
Заменив [х его значением F.18), получим дифференциальное
уравнение, определяющее изображение термовязкоупругого
потенциала перемещений
[2Q (s) F (s) + H(s) P (s)] ДФ* = ЗЯE) Р (s) aT*. F.21)
Для выполнения обратного преобразования нужно задать
конкретную форму полиномов Q{s) и т. д. В частности,
будем иметь:
среда Максвелла:

172
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ. VI
среда Кельвина:
нормальное тело:
2QF+^P^^f)-f-[2A1.7f)^ + d']S' HP=l+^v
При этом, например для среды Максвелла, получим:
\dt ^ 3A—fx) $J^ 1 —[х \^ ^ »/ ^ ^
Аналогичное преобразование соотношений A.31) (прир = 0)
дает:
В частности, для среды Максвелла получим отсюда:
Обратное преобразование этого соотношения с
использованием теоремы о свертывании дает:
§ 5. Стационарные и квазистационарные
температурные поля
F.24)
На основании аналогии, сформулированной в § 3 гл. VI,
можно считать (оставляя пока в стороне математические
трудности), что каждая решенная квазистатическая упругая
задача сразу же дает соответствующее вязкоупругое решение.
Далее мы приведем вычисления для некоторых простейших
случаев и начнем с рассмотрения стационарных и
квазистационарных температурных полей.
Поскольку упругие напряжения при этом не зависят от
времени, мы приходим к рассмотренному в § 3 гл. VI слу-

§ б] СТАЦИОНАРНЫЕ ТЕМПЕРАТУРНЫЕ ПОЛЯ 173
чаю разделяющихся переменных. Однако множитель,
зависящий от времени, на который нужно умножить упругие
напряжения, чтобы получить вязкоупругое решение для разных
слагаемых, вообще говоря, может быть различным. Примером
такого положения является задача о толстостенной трубе.
Упругое решение для этого случая приведено в § 1 гл. VI
Мелан — Паркус [6]. Заметим, что все члены в выражениях
для радиальных и окружных напряжений {F.12), Мелан —
Паркус [6]} имеют одинаковый, зависящий от упругих
постоянных множитель GK\ в то же время в выражении для
осевого напряжения агг два слагаемых содержат, кроме того,
множитель [х. Поэтому вязкоупругие радиальные и окружные
напряжения будут распределяться в пространстве так же, как
в упругом случае, отличаясь от него лишь множителем,
зависящим от времени, распределение же осевого напряжения
в пространстве будет иным, поскольку здесь отдельные
слагаемые будут иметь различные коэффициенты, зависящие от
времени.
Приведем вычисление множителей, зависящих от времени,
для частного случая среды Максвелла. Из уравнений F.18)
и F.14) получим:
\ F.25)
Согласно упруго-вязкоупругой аналогии необходимо вначале
найти изображение упругих напряжений. Поскольку эти
напряжения не зависят от времени, то
(°*/)упр — 7 fyW
Далее необходимо заменить упругие постоянные
соответствующими выражениями F.25), т. е.

174
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ. VI
Выполняя теперь обратное преобразование, получим:
Таким образом, осевое напряжение слагается из двух
компонент, убывающих с различными скоростями. Все
напряжения в конечном счете стремятся к нулю, однако предельные
значения перемещений будут отличны от нуля.
Необходимо подчеркнуть, что приведенные формулы
являются приближенными, поскольку относятся к случаю
материала с достаточно большим временем релаксации fr.
Действительно, при выводе этих формул подразумевалось,
что стационарное температурное состояние будет достигнуто
раньше, чем разовьется заметное вязкое течение.
§ 6, Полупространство с периодически изменяющейся
температурой поверхности
В § 2 гл. III была рассмотрена задача об идеально
упругом полупространстве, температура на поверхности которого
периодически изменяется по закону Г= T0coswt. Рассмотрим
теперь случай, когда пространство является вязкоупругим.
Поскольку температура C.4) выражается в виде
произведения функции, зависящей от времени, и функции, зависящей
от координат, мы имеем случай, когда переменные
разделяются. При этом сразу же получим:
о2г = о,г = 0. F.27)
Рассмотрим, в частности, среду Максвелла, для которой
согласно соотношению F.25)
1 — fJL (S) Ч ' \— (Л S-fl/u
Учитывая эти соотношения, из C.6) получим изображения
F.26)

§ 7] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 175
обратное преобразование которых дает:
Подставив сюда значение Т из соотношения C.4), получим
окончательно:
F.28)
Здесь опущен член, содержащий множитель e~t/b', поскольку
он соответствует переходному процессу, который считается
уже затухшим.
§ 7. Сферическая полость в неограниченной среде*)
Возвратимся к задаче, рассмотренной в § 6 гл. Н, считая
теперь, что среда является вязкоупругой. На основании уже
применявшейся упруго-вязкоупругой аналогии изображение
искомого радиального перемещения и* {г, t) получим из
уравнения B.44) в следующем виде:
Здесь через /* обозначено изображение функции
F.29)
F.30)
Соответственно из уравнения B.45) получим изображения
напряжений
F.31)
*) Sternberg [174.2J.

176
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ VI
Подставив сюда выражение F.18), соответствующее данному
материалу, можно выполнить обратное преобразование. При
этом предполагается, конечно, что функции и {г, t) и o(r,t)
являются I-функциями, т. е. что преобразование Лапласа
для них существует. По физическим соображениям можно
ожидать, что это будет иметь место в действительности.
Мы ограничимся здесь рассмотрением двух частных
случаев вязкоупругих тел — среды Максвелла и среды Кельвина.
а) Среда Максвелла. Необходимые выражения даются
соотношениями F.25); подстановка их в уравнения F.29)
и F.31) и преобразование при помощи формулы обращения
L \s+W s )— ft +ll ft )e —
^-j-J—[3A-,0+2A-2,*)«-«»'],
rllsf(r, S)] = ±f(r, t), f{r, 0)^0,
и с учетом теоремы о свертывании приводит к решению
F.32)
F.33)
Здесь
Согласно соотношению (б.30)
F.34)
F.35)
При помощи правила Лопиталя легко показать, что
\img(rt t) = 0 и lim/z(r, ^) = 0. Таким образом, напряжения

§ 7] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 177
в теле в стационарном состоянии обращаются в нуль, что
для среды Максвелла не является неожиданным.
б) Среда Кельвина. При помощи соотношений F.14)
из уравнений F.18) получим:
F.36)
F.37)
F.38)
Функции g и h определяются здесь так же, как и прежде,
необходимо только значение О' в формуле F.34) брать не
из соотношения F.25), а из соотношения F.36).
В отличие от случая среды Максвелла и в соответствии
со свойствами среды Кельвина, описанными в § 2 гл. VI,
перемещение и напряжения в этом случае при /->оо
стремятся к упругим значениям B.44) и B.45).
Полученные формулы справедливы для любого
температурного поля, которое должно удовлетворять лишь
начальному условию 7 (г, 0) = 0. Если остановиться на случае
распределения температуры B.42), то из уравнения B.47)
получим:
/(г, t) = R%F(9i х), F.39)
причем здесь функция F (р, х) определяется соотношением
B.48), а безразмерные переменные р и т имеют значения B.46).
Далее, из второго уравнения F.34) получаем:
F.40)

178
ВЯЗКОУПРУГИЕ МАТЕРИАЛЫ
[ГЛ. VI
Учитывая это значение, из уравнения F.35) найдем:
g(r, 0 = -*^{<h(p. т)-Р1/^ф2(Р. x)-erfcC-
— e~«*[l 1/"ш erf (/ V^)+ l]+ l}. F.41)
Здесь через фг и ^2 обозначены вещественная и мнимая части
функции
*(^) = t1 + /j'2 = erfc(C)expB:2-C2). ?=7^Т> F-42)
а безразмерная постоянная аз имеет значение
F.43)
F.44)
F.45)
в случае среды Кельвина. В правильности формул F.40) и
F.41) проще всего убедиться посредством дифференцирования.
Численные расчеты по этим формулам, проведенные
Штернбергом (Sternberg [174,2]), показали, что полезно
использовать следующие асимптотические представления, справедливые
для достаточно малых значений со:
Таким
образом,
в случае среды
М
со =
со =
аксвелла
СО = -:
1 +
3A-
и
3A-
R2
•V-
J^L
Я2
aft
.j?!

§ 7] СФЕРИЧЕСКАЯ ПОЛОСТЬ В НЕОГРАНИЧЕННОЙ СРЕДЕ 179
Некоторые результаты вычислений представлены на рис. 28,
где построена зависимость окружного безразмерного
напряжения о от безразмерного времени х на поверхности
Рис. 28.
полости р = 1. Определение безразмерного напряжения о дано
в § 6 гл. II. Здесь снова можно видеть характерные
особенности обоих вязкоупругих материалов, представленные ранее
на графиках рис. 27, б, в.

ГЛАВА VII
ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
ПРИ УПРУГО-ПЛАСТИЧЕСКОМ ПОВЕДЕНИИ
МАТЕРИАЛА
§ 1. Условие текучести и закон течения
Если значения напряжений в твердом теле достигают
некоторой определенной границы, то возникает течение
материала. В стадии течения напряженное и деформированное
состояния являются упруго-пластическими, поэтому при
полном снятии напряжений деформации не возвращаются к
нулевым значениям *). С другой стороны, устранение нагрузок
или температурных градиентов, вообще говоря, не приводит
к полному исчезновению напряжений, так как при этом
появляются остаточные (или собственные) напряжения,
которые образуют самоуравновешенную систему и при новом
нагружении тела накладываются на вновь возникающие
напряжения. Примером остаточных напряжений могут служить,
в частности, напряжения, возникающие вследствие быстрого
охлаждения при закалке.
Для того чтобы установить, когда напряженное состояние
достигает границы текучести, необходимо сформулировать
условие текучести. Предлагались разнообразные условия
текучести, из которых в настоящее время чаще всего
применяется условие Губера — Мизеса**). Обозначим через olf
о2, а3 главные нормальные напряжения в теле, через о0 —
*) Теория пластичности прекрасно изложена в книгах: X и л л Р.,
Математическая теория пластичности, Гостехкздат, 1956, и Пра-
гер В., Ход ж Ф., Теория идеально пластических тел, М., ИЛ,
1956.
**) Важное значение имеют также результаты Генки и Эйхин-
гера.

§ 1] УСЛОВИЕ ТЕКУЧЕСТИ И ЗАКОН ТЕЧЕНИЯ 181
предел текучести при одноосном растяжении и введем
«эквивалентное» напряжение о при помощи соотношения
с2 = 1 [(ах - о2J + (о2 - о3J + (о3 - огП G.1)
При этом условие текучести Губера — Мизеса будет иметь
вид _
c = oQ. G.2)
Пользуясь определением девиатора напряжений F.1), это
условие можно представить также в форме
з22Ы2=Ч G.з)
1 J
из которой вытекает, в частности, что величина о2/3
идентична второму инварианту девиатора напряжений и,
следовательно, пропорциональна так называемой энергии
формоизменения (т. е. той части полной энергии деформации,
которая зависит от изменения формы тела, происходящего при
неизменном объеме). Отсюда следует предложенная Генки
интерпретация условия Мизеса, согласно которой
пластическое течение возникает тогда, когда накопленная в единице
объема энергия формоизменения достигает некоторого
критического значения. Всестороннее (гидростатическое) сжатие
или растяжение любой величины, отвечающее напряженному
состоянию вида а1 = а2 = а3, вызывает только изменение
объема и поэтому, согласно условию G.1), не может
привести к возникновению пластического течения. Этот
результат согласуется с экспериментальными данными.
Другую интерпретацию условия текучести Мизеса
положил Надаи, заметивший, что выражение -~- о представляет
собой касательное напряжение на гранях октаэдра, оси
которого совпадают с главными осями напряжений.
Условие текучести соответствует границе между упругим
и пластическим состояниями. Для так называемого «идеально
пластического» материала, то есть для такого материала,
который не обладает упрочнением, условие текучести
выполняется всюду в пластической области, причем предел
текучести а0 является константой или зависит от температуры.
Для упрочняющихся материалов о0 в пластической области

182
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ tlVI. yil
зависит от пластического деформирования. Далее мы будем
рассматривать только идеально пластический материал.
Для того чтобы найти напряжения в пластической области,
вообще говоря, помимо условия текучести, должны быть
даны зависимости между напряжениями и деформациями *).
Предлагались различные формы таких зависимостей, при
этом среди более простых в математическом отношении
вариантов наилучшее согласование с экспериментальными
результатами дают уравнения Прандтля — Рейсса. Согласно
этим уравнениям приращение девиатора деформаций
пропорционально девиатору напряжений и его приращению:
G.4)
Здесь девиатор деформации etj определяется соотношением
G.1). Изменение объема является чисто упругим также и
при наличии пластических деформаций, т. е.
где — = а). В отличие от закона деформирования среды
Максвелла F.5), с которым уравнение G.6) внешне схоже,
*) Пример задачи, в которой для определения напряженного
состояния достаточно иметь только условие текучести, рассмотрен
в § 2 гл. VII.
G.5)
Приращения деформаций и напряжений, фигурирующие в
уравнениях G.4) и G.5), относятся не к фиксированной точке
пространства, а к определенной материальной частице,
поэтому
Если, однако, перемещения и их производные малы, то
нелинейный член -д- dx можно отбросить, и уравнения G.4) и
G.5) примут следующий вид:
G.6)
G.7)

§ 1] УСЛОВИЕ ТЕКУЧЕСТИ И ЗАКОН ТЕЧЕНИЯ 183
коэффициент пропорциональности d\ (или а)) не является
константой материала, а представляет собой новую
неизвестную функцию координат и времени. Соответственно мы имеем
дополнительное (отсутствующее в упругом случае) уравнение,
выражающее условие текучести.
Отбрасывая в уравнениях G.4—7.7) упругие члены (т. е.
принимая, что модуль упругости бесконечно велик), получим
уравнения Леей— Мизеса, которые соответствуют случаю,
когда можно пренебречь упругой составляющей полного
формоизменения. Таким образом, эти уравнения строго
применимы только для случая так называемого
жестко-пластического тела, которое вообще не испытывает никаких
упругих деформаций и, следовательно, до достижения
границы текучести ведет себя, как абсолютно жесткое тело.
Если изменения напряжений таковы, что все напряжения
возрастают пропорционально, то их можно представить
в виде o.. — C(t)G0., где С — монотонно возрастающий
параметр, о0. — некоторое, не зависящее от времени
напряженное состояние. При этом из уравнений G.6) после
интегрирования получим:
G.8)
Здесь через Ф = -^- шСdt обозначен коэффициент пропор-
о
циональности, для определения которого следует, как и
прежде, использовать условие текучести. Уравнения G.8)
были предложены Генки. Согласно этим уравнениям
мгновенное деформированное состояние полностью определяется
мгновенным напряженным состоянием и не зависит от истории
нагружения. При использовании общих уравнений Прандтля —
Рейсса такое однозначное соответствие уже не будет иметь
места.
Хотя, таким образом, уравнения Генки справедливы лишь
при существенных ограничениях, тем не менее благодаря их
простоте они весьма часто используются, в особенности
русскими авторами *).
*) См., например, Соколовский В. В., Теория
пластичности, М., Гостехиздат, 1950.

184
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
Уравнения Прандтля — Рейсса (а также их частные
случаи— уравнения Леви — Мизеса и Генки) будут справедливы
всюду в пластической области тела, до тел пор, пока там
не наступает разгрузка, т. е. пока выполняется условие
do ^ О (или do = 0, если материал является идеально
пластическим). Если напряженное состояние в данной точке
изменяется таким образом, что do < 0, то соответствующий
элемент испытывает разгрузку и его поведение определяется
законом Гука, взятым в форме уравнений G.6) и G.7) при
o) = Q. При новом нагружении пластическое течение
возобновится лишь тогда, когда снова будет выполнено условие
текучести. В результате в случае температурных полей,
зависящих от координат и от времени, возникают чрезвычайно
сложные положения *).
Некоторые теоретические результаты, а также
экспериментальные данные, указывают на то, что существует связь
между законом напряжение — деформация и условием
текучести и что, следовательно, эти важные составные части
теории пластичности нельзя выбирать независимо. Указанная
связь формулируется при помощи введенного Мизесом
представления о «пластическом потенциале» ^*(о/)**).
Приращения пластических деформаций de? представляются в виде
deP=4l-d^ G-9)
где d\ — коэффициент пропорциональности. Поскольку
пластическое изменение объема отсутствует, то deP—aePj*
2l также
да и'
т. е. g не должно зависеть от гидростатического давления.
*) Чтобы преодолеть эти затруднения, Мура (Мига [131, 6]) и
другие японские авторы предложили методы, опирающиеся на
весьма упрощенные предположения, сводящиеся к тому, что: а) при
температурах, не превосходящих некоторое значение Г0, материал
ведет себя, как идеально упругий, и не течет ни при каких
значениях напряжений, б) при температурах, превышающих значение Т0,
материал становится идеально пластическим, причем а0 = 0. Эти
предположения могут быть использованы лишь для немногих
материалов.
**) X и л л Р., Математическая теория пластичности, М., Гое-
техиздат, 1956; П par ер В., Проблемы теории пластичности, Физ-
матгиз, М., 1958.

§ и условие текучести и закон течения 185
В частности, если имеют место зависимости Прандтля —
Рейсса, то согласно уравнениям G.4) dg/do^^^s^ и,
следовательно,
1 i j
= -§- K°i - *2J + (°2 - *зJ 4- (e3 - *№ 4- с
Приняв для постоянной интегрирования с значение с = — о^/З,
находим, что уравнение g(piJ) = Q совпадает с условием
текучести Мизеса.
Вообще будем говорить, что закон течения (закон
деформирования) G.9) ассоциирован с условием текучести / @^=0,
если g==f. В этом смысле уравнения Прандтля — Рейсса
ассоциированы с условием текучести Мизеса.
В некоторых случаях вместо условия текучести Мизеса
проще использовать условие текучести, предложенное Треска.
Согласно этому условию пластическое течение начинается
тогда, когда локальное максимальное касательное напряжение
будет равно заданной величине:
2^„,ах = а1 — а3 = а0 (а1 > °2 > °з)> GЛ °)
где сг и о3—соответственно наибольшее и наименьшее
главные нормальные напряжения. Таким образом, граница
текучести теперь определяется не одной, а шестью функциями
/l = °1 — °3—°0» /2 = 02 —°1 —а0» /з —°3—°2—°0> \
/4 = а3—а1 — а0' /5 = а1 — °2 — а0' /б = а2—а3 — а0' /
На границе текучести по крайней мере одна из этих
функций (зависящая от того, какая пара главных
напряжений является определяющей) будет равна нулю.
Соответствующее обобщение пластического потенциала
и закона течения G.9) было предложено Койтером,
принявшим
^¦=-^^+---+-^^- <7-12>
Здесь /л, .,., fm — те функции текучести G.11), которые
в данном напряженном состоянии обращаются в нуль.
Как показывают решения, полученные в гл. И,
напряжения, возникающие при внезапном нагреве или охлаждении

186
Упруго-пластические материалы [гл. vii
тела, обычно имеют максимальные (квазистатические) значения
на поверхности тела. Поэтому пластическое течение, вообще
говоря, также начинается на поверхности.
§ 2. Упруго-пластическая сфера*)
Сфера радиуса R находится под воздействием зависящего
от времени температурного поля Т (г, t), обладающего
центральной симметрией (см. также § 13 гл. II).
Применяя сферические координаты и используя условие
симметрии, получим, что два из трех главных напряжений
равны между собой, о = о$а, поэтому условие текучести
Мизеса примет вид
K-°w\=°0' G-13)
Будем считать, что а0 не зависит от температуры. Если
предположить, что материал является идеально пластическим,
то уравнение G.13) будет иметь место всюду в пластической
области. Подставив G.13) в условие равновесия
г дагг
2 дг
и интегрируя, получим:
G.14)
G.15)
где сх (t) — постоянная интегрирования. Таким образом,
напряжения в пластической области вычисляются независимо от
соотношений между напряжениями и деформациями и,
следовательно, рассматриваемое напряженное состояние является
статически определимым.
Распределение напряжений в упругой области было
найдено ранее в § 13 гл. II. Обозначая две постоянные
интегрирования через c2(t) и cs(t), будем иметь:
G.16)
*) Фрейденталь (Freudenthal [52, 2]) рассмотрел случай
вязкоупруго-пластической сферы.

§2]
УПРУГО-ПЛАСТИЧЕСКАЯ СФЕРА
187
Здесь, как и прежде, Г (г, t) — средняя температура сферы
радиуса г (см. уравнение B.18)). Если поверхность сферы,
имевшей начальную температуру Г0, внезапно охлаждается
до температуры 7=0, то при достаточно большой разности
температур Т0 на поверхности начинается пластическое
течение. Пластическая область будет распространяться от
поверхности сферы внутрь, причем одновременно возникает область
разгрузки, которая также распространяется от поверхности
внутрь. Таким образом, следует различать три области:
внутреннее чисто упругое ядро, затем пластическая зона и,
наконец, внешняя область, которая первоначально была
пластической, но в которой вследствие имевшей место
разгрузки изменение напряжений снова происходит по упругому
закону. Ввиду этого определение остаточных напряжений,
имеющих место в сфере после полного охлаждения, будет
весьма трудоемким. В частных задачах можно вычислять
малые изменения напряжений за достаточно малые интервалы
времени АЛ принимая при этом, что функции
интегрирования ct (f) в каждом интервале времени можно считать
постоянными.
Можно достичь существенного упрощения, если принять,
что материал несжимаем *). Подставляя в уравнение G.7) де-
, и ди 1
формации е _ —, ггг = -т- и полагая jx == -к-, получим:
Зе = ^Ч-2^ = За(Г-70).
Интегрирование этого уравнения с учетом условия #@, t) = 0
дает:
и (г. t) = ar[f(r, t) — T0]. G.17)
Радиальное перемещение а (г, t), таким образом, не зависит
от напряженного состояния и, следовательно, от
возникновения пластических зон. Найденное деформированное
состояние можно в свою очередь использовать для определения
напряжений. Учитывая соотношение G.17) и принимая во
внимание, что дТ/дг = 3(Т— Т)/г, из уравнения G.1) полу-
*) Ломакин [НО], Park us [147, 4J. Эту задачу ранее
рассматривал Л. М. Качанов; см. Прикл. Мат. и Мех. (Прим. ред.)

188
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
чим следующие соотношения, определяющие эквивалентное
напряжение о:
G.18)
Выбор знака при с основан на том, что в рассматриваемом
случае охлаждения сферы всегда Т — Т^О. Графики без-
f j
размерной величины —^— приведены на рис. 29. Соотно-
шения G.18) справедливы до тех пор, пока в
рассматриваемой точке эквивалентное напряжение а возрастает или по
крайней мере не убывает, т. е. пока -^ (Г — 7)^0. При
-дг(Т — Т) < 0 наступает разгрузка и изменение
напряжения следует закону Гука.
Обозначим теперь через р (t) координату той точки г = р,
в которой в момент t начинается пластическое течение, а
через т(г) — тот момент времени, в который в точке с
координатой г начинается разгрузка. Согласно уравнениям G.18)
р(^) и т(г) определяются соотношениями
G.19)
и
G.20)
На рис. 30 приведены графики р//? и azjR2 в зависимости
от безразмерного радиуса rjR и безразмерного времени atlR2,
при этом через 2R обозначен диаметр сферы; р зависит
от предела текучести при растяжении, а0 = ъК, причем
/t = 6Gar0.
Кривые построены для значений х = 0,1; 0,2; 0,3; 0,5; 0,7<

§2]
УПРУГО-ПЛАСТИЧЕСКАЯ СФЕРА
189
Графики на рис. 30 показывают, что при охлаждении
сферы вначале будут существовать три области: упругая
область /, пластическая область //, в которой разность Т — Т
т-т
Рис. 29.
еще продолжает возрастать, и, наконец, область ///, в
которой происходит разгрузка после имевшего место
пластического течения. Дополняя уравнения G.18), справедливые
только для ?<!т(/-), законом разгрузки, будем иметь для

190
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
любого t:
a = 60a[f(r, t) — T(r, f)\ в области /,
a = a0 в области //,
o = aQ — 6Ga [f (г, т)—Г (г, х) — Т (г, 0 + Г (г, 0]
в области ///.
G.21)
При дальнейшем охлаждении всюду в пластической области,
а следовательно, и в упругой области наступает разгрузка.
При этом область // исчезает, а граница между
областями / и /// определяется соотношением г = р0=р(т).
Вычисление напряжений теперь не вызывает затруднений.
Интегрируя уравнение равновесия G.14)
дагг 2 , ч 2 -
и учитывая краевое условие огг = 0 при г = /?, получим:
R _
0„ = _2 [Щ^-dx, G.22)
где о определяется соотношениями G.21). В частности,
остаточные напряжения, отвечающие состоянию Г = 0 при /->оо,
будут определяться следующими формулами:
G.23)
Пользуясь соотношением з = arr-f~ °> находим окружное
остаточное напряжение
G.24)

УПРУГО-ПЛАСТИЧЕСКАЯ СФЕРА
191
Таким образом, ядро сферы г<^р0 после остывания будет
находиться в состоянии всестороннего равномерного
растяжения.
Формулы G.21—7.24) справедливы при условии, что при
охлаждении не будет снова достигнута (в обратном
направлении) граница текучести. Разность Т—Г имеет наибольшее
0,05
Рис. 30
J^l? M°L°>
W 0,5 0,6 0,7 0,8 0,9 W
Рис. 31.
значение, равное Т0, на поверхности г == R в момент ? = 0.
При этом согласно уравнению G.21)
— \ х
Ммакс= |а0— 6ОаГ0| =A — х)/С = —— а0-
Эта величина не должна превосходить значение предела
текучести при сжатии о0. Поскольку предел текучести при
повышении температуры убывает, то, вообще говоря, о0>о0.
Если, в частности, ао = а0, то для того, чтобы не возникало

192 УПРУГО-ПЛЛСТИЧЕСКИН МАТЕРИАЛЫ (ГЛ VI!
повторное пластическое течение, должно выполняться
условие -1^х<1. При х>1 вся сфера остается упругой и
остаточные напряжения не возникают.
/г
0,2
0,0
-0,2
-0А
-0,6
-0,8 (
Рис. 32.
V
1
1 0,5
(-
[-
.
0.6
i
0,7
,'N^^, ^ /•
\
\
\
\
\
\
\
\
Для численных расчетов представим решение в виде
где функция F(r) определяется следующим образом:
Графики функций (—j—) и F(r) построены на рис. 31.
С их помощью легко вычислить остаточные напряжения для
произвольного значения х. На рис. 32 построены кривые
для х = 0,3.

§3]
ТОЛСТОСТЕННАЯ ТРУБА
193
§ 3. Толстостенная труба*)
Труба внутреннего радиуса **) а и наружного радиуса Ь
подвергается воздействию внутреннего давления р и
стационарного поля температуры Т{г), не изменяющейся в осевом
и окружном направлениях. Предполагается, что напряжения
так велики, что имеет место пластическое течение.
Воспользуемся цилиндрическими координатами ryz. Если
предположить, что труба достаточно длинна, то можно
считать, что напряжения и деформации не зависят от z.
Поскольку поперечные сечения остаются плоскими, то ezz =
= const. По соображениям симметрии, напряжения огп афср, а,,
являются главными.
Как в упругой, так и в пластической областях трубы
имеет место условие равновесия
г-^п. + а а =0 G.25;
fly ' ГГ <рср v '
и геометрические соотношения
егг = -г—, 6 = —, G.26)
где и — радиальное перемещение. Будем считать, что
деформации являются малыми.
Рассмотрение этой задачи на базе условия текучести
Мизеса и уравнений Прандтля — Рейсса приводит к большим
математическим трудностям. Напротив, если использовать
условие текучести Треска, то решение (справедливое, конечно,
при определенных ограничениях) оказывается сравнительно
простым. Предположим прежде всего, что
< > <>„ > °rr G-27>
При этом условие Треска G.11) принимает вид
/ = "-,-0гг-во = 0. G.28)
*) Bland [19]; эту задачу рассматривал также Мура (М и-
га [131,5]), который использовал закон Генки и рассмотрел
некоторые вопросы устойчивости.
**) Далее не будет возможности смешивать это обозначение
с коэффициентом температуропроводности а.

194
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VH
Примем также, что как предел текучести о0, так и упругие
и тепловые константы материала можно считать постоянными
в рассматриваемом интервале температур.
В соответствии с уравнениями G.12) закон течения,
ассоциированный с условием текучести G.28), дает
de?=-de?, de? = 0. G.29)
Таким образом, осевая деформация ezz является вполне
упругой и, следовательно,
е„ = \ 1°« - *ia" + °w>l + аТ- G-30)
Если труба находится в плоском деформированном состоянии,
то eZ2 = 0, вообще же ezz зависит от результирующей осевой
силы
Подставляя сюда значение azz из уравнения G.30) и
выражая 0<рФ через агг при помощи уравнения G.25), после
интегрирования получим:
G.31)
При выводе этого соотношения учтены краевые условия
orr~Q при r = b, огг== — р при г = а. Таким образом,
деформацию ezz можно считать известной. Для открытой
трубы осевая сила Я = 0, для трубы с закрытыми
концами Р = ка2р.
Изменение объма Зе = е,,.-+-е^-f-е^ является вполне
упругим. Подставив в выражение G.26) соотношение G.7),
получим:
Подстановка сюда значений ozz из уравнения G.30) и о(
из уравнения G.25) приводит к уравнению

§ 3J ТОЛСТОСТЕННАЯ ТРУБА L95
которое можно представить также в форме
Выполнив интегрирование, найдем радиальное перемещение
G.32)
где через С обозначена постоянная интегрирования. Это
соотношение справедливо как в упругой, так и в
пластической областях.
Распределение температуры в стационарном случае имеет
вид (см. Мелан — Паркус [6])
T=M+2N\nr, M=. llln}b , N = cyn~7Tl ..G.33)
In^ — \па 2(\nb—\na) v '
Температура на внутреннем и внешнем контурах трубы
имеет значения Т=Тг при г = а, 7 = 0 при r = b. Легко
получить, что
G.34)
Переходим к вычислению напряжений. В упругой области
имеет место закон Гука
G.35)
G.36)
Исключая из этих соотношений а и используя значение огг
из уравнения G.30) и значение а из уравнения G.25),
получим дифференциальное уравнение относительно агг;

196
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
Двукратное интегрирование этого уравнения дает для случая
температурного поля G.33) следующее значение радиального
напряжения в упругой области:
«гг^+^-^Шг. G.37)
Граница г —р упругой области определяется условием G.28),
которое при помощи соотношения G.25) сводится к виду
Подставляя сюда значение огг из формулы G.37), найдем
одну постоянную интегрирования:
Таким образом, в упругой области
Внутри упругой области должно быть г гг < а0, поэтому
величина г тт при углублении в упругую область должна
убывать от ее значения а0 на границе г = р. Это будет
иметь место при возрастании г, если
G.38)
Таким образом, упругая зона является внешней областью (г > р)
трубы.
Если a0-j- j-?— =0, то всюду в упругой области г -—- =
= acpcp—arr== — f^r"=ao- B этом случае при достижении
границы текучести в некоторой точке возникает мгновенное

§ 3]
ТОЛСТОСТЕННАЯ ТРУБА
197
течение всюду в поперечном сечении трубы. Этот случай
называют «неустойчивым течением» *).
Условие G.38), наверное, выполняется, если N > 0; в этом
случае Тх < 0 и внутренняя поверхность трубы холоднее,
чем наружная. Если Тг > 0, т. е. если труба изнутри имеет
более высокую температуру, то согласно соотношениям G.33)
условие G.38) будет тем не менее выполнено, если разность
температур внутренней и внешней поверхностей не больше чем
Tl<2(l-v.)-^\n±. G.39)
Будем предполагать, что это условие выполняется **).
Из краевого условия аГГ = 0 при r — b получим вторую
постоянную интегрирования
С2=~\П1)-С1Т;.
Теперь уравнение G.37) (справедливое в области р <^ г <С Ь)
будет иметь следующий вид:
EaN . Ь 1 / EaN\ 2/ 1 1 \ ,- ,т
Зная огг можно найти из уравнений G.25) и G.30)
напряжения о и azz в упругой области. Соответствующие
выражения имеют следующий вид:
v-?*K-')+i(*+?M^)- <7-41'
e« = ?e„ + j^B|*In6 —21пг —ц).+
+ *(*о+^)?-ЕаМ- G-42)
*) См. Мига [131,5]
**) Для углеродистой стали (<х = 12.10~б /°С, ?=2,1.106 кГ\см%,
ft = 0,3, а0 = 2500 к Г /см2) получим Тх < 139 In — °С.

198
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ ГГЛ VII
Приравнивая значения — из уравнений G.32) и G.36),
найдем постоянную интегрирования С:
G.43)
В пластической области имеет место соотношение
из которого с учетом условия о0 = const после
интегрирования получим:
где К — постоянная интегрирования. Для определения этой
постоянной используем условие непрерывности огг на упруго-
пластической границе. В результате получим:
G.44)
Остается удовлетворить краевому условию агг = — р на
внутренней поверхности г = а:
G.45)
Из этого уравнения определяется р.
Напряжения о и aZ2 в пластической области
определяются из соотношений G.25), G.30) и G.31) с учетом
уравнения G.44).
Пусть на трубу вначале воздействуют температурные
градиенты, а затем — медленно возрастающее внутреннее
давление; при этом пластическое течение, начинающееся на
внутренней поверхности трубы, возникнет в момент, когда
р = а. Соответствующее внутреннее давление будем назы-

§ 4]
ТОЧЕЧНЫЙ НЛГРЕВ ДИСКА
19$
вать критическим р — рс. Оно определяется из
соотношения G.45) при р = д:
1 / . EaN \ Л а2\ EaN . b t- Aa.
Если рс отрицательно, то это означает, что труба будет
находиться в пластическом состоянии в результате действия
только температурных напряжений. В оригинальной работе
Бланда (Bland) изучено влияние упрочнения материала,
исследованы различные неравенства и другие вопросы,
а также приведены численные примеры. При практических
расчетах целесообразно для заданного распределения
температуры (которое, конечно, должно удовлетворить
неравенствам G.38) и G.39)) решить вначале уравнение G.45),
задаваясь различными значениями — и определяя
соответствующее давление р. Получив зависимость р от —, можно
для заданного р легко найти радиус границы р. При р = b
труба будет полностью пластической. Зная р, можно
вычислить напряжения и перемещения в упругой и пластической
областях. После этого необходимо проверить
неравенство G.27), поскольку выведенные формулы справедливы
лишь в том случае, когда это неравенство выполняется.
При разгрузке трубы, т. е. при устранении
температурной разности и внутреннего давления, происходит чисто
упругое формоизменение (если, конечно, возникающие
остаточные напряжения не достигнут снова границы текучести).
Соответствующие чисто упругие напряжения о^., о' , <з'гг
определяются по формулам, приведенным в книге Мелана —
Паркуса (§ 1 гл. VI), в которых знаки перед температурой
и внутренним давлением следует изменить на обратные.
Суперпозиция первоначальных напряжений, вызванных
нагрузками, и напряжений разгрузки о' дает остаточные (или
собственные) напряжения.
§ 4. Точечный нагрев диска*)
В бесконечном диске в момент t = 0 начинает
действовать точечный тепловой источник постоянной
производительности 5. В момент t = b действие источника прекращается.
*) Par k us [147,3].

200
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ VII
Такой процесс может иметь место, например, при точечной
сварке *).
Для упрощения будем определять поля температур и
напряжений в диске при следующих существенных
ограничениях. Диск является достаточно тонким, так что все
величины можно заменить их средними значениями по толщине,
и следовательно, напряженное состояние является плоским;
изменение толщины, вызванное температурой и напряжениями,
можно не учитывать; все механические и тепловые константы
материала не зависят от температуры. Вблизи источника, где
температура теоретически бесконечно велика, эти
ограничения можно рассматривать лишь как весьма грубое
предположение.
Вследствие осевой симметрии задачи все величины
зависят только от расстояния г до точечного источника и от
времени t.
Найдем вначале температурное поле. При наличии
теплообмена между диском, имеющим температуру Г (г, t),
и окружающей средой с температурой Т—0 уравнение
теплопроводности будет иметь вид A.41)
дТ (д2Т . 1 дТ\ QT .- ._ч
где а — коэффициент температуропроводности материала,
Р = 2k/cph, k — коэффициент теплоотдачи между диском
и средой, с — удельная теплоемкость на единицу массы,
р — плотность материала диска, h — толщина диска.
Применяя к уравнению G.47) преобразование Лапласа
и учитывая начальные условия Т(г, 0) = 0, получим:
Л?- + 1Л1—1±±.Г = 0. G.48)
dr2 ' r dr a x '
Двумя решениями этого уравнения являются
модифицированные функции Бесселя /0 и К0. Поскольку температура Т
при г->со должна оставаться ограниченной, следует
использовать только решение /С0, т. е.
Г^СК0(гЬГ^-)- G.49)
*) См. также § 14, гл. II, где получено решение для идеально
упругого материала без учета теплообмена между пластиной и
окружающей средой.

М
ТОЧЕЧНЫЙ НАГРЕВ ДИСКА
201
Тепловой поток в единицу времени, протекающий через
малый цилиндр, окружающий тепловой источник, должен
равняться производительности источника. Поэтому
Подставляя сюда значение Т* из уравнения G.49) и
учитывая, что К'0=—Kv Vim rKl(mr) = —, получим следующее
значение постоянной интегрирования С:
Принимая во внимание, что
и используя теорему свертывания, получим оригинал
решения в следующем виде:
t
Г(г. 0 = |/ехр(-рх-^)^. G.51а)
О
Это выражение можно преобразовать при помощи
интегрирования по частям; в результате получим:
G.516)
здесь через Ei обозначена интегральная показательная
функция *).
Обратимся теперь к вычислению напряжений. Поскольку
в окрестности теплового источника температура
теоретически неограниченно высока, там сразу же возникает
пластическая область. Пусть r = R(t) — граница этой области.
Пренебрегая динамическими эффектами, будем иметь
следующие соотношения **).
*) См. стр. 63.
**) Об учете динамических эффектов см. § 8 гл. V.

202 УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ VII
Всюду в диске'.
условие равновесия
дагг
дг '
геометрические соотношения
G.52)
G.53)
{и — радиальное перемещение).
В упругой области r^R:
закон Гука
В пластической области 0<><^/?:
условие текучести Мизеса
а2 — а в -I- а2 = а2
ГГ ГГ <fcp ' срср О»
уравнения Прандтля — Рейсса
G.54)
G.55)
G.56)
Из соотношений G.52) — G.54) можно вывести уравнение
для перемещения и:
Решение этого уравнения имеет вид
где А п В— произвольные функции. Поскольку напряжения
при г->оо должны обратиться в нуль, следует положить

§4]
ТОЧЕЧНЫЙ НАГРЕВ ДИСКА
203
В = 0. Используя выражение G.51а) для температуры Г,
получим окончательно:
где
G.57)
G.58)
Подстановка выражения G.57) в уравнение G.54) дает
следующие значения напряжений:
о„ = 20*™~А<Ь , о„ = -о„-ЕаТ. G.59)
Соотношения G.57) — G.59) справедливы в упругой области.
В пластической области напряженное состояние является
статически определимым; используя оба уравнения G.52)
и G.55) и учитывая, что напряжения при г = 0 должны
оставаться ограниченными, получим:
Crr = <Vp = — °0- G'6°)
Здесь знак минус означает, что имеет место
напряженное состояние сжатия. Подставив полученные значения в
уравнения Прандтля — Рейсса G.56) и исключая ш, получим:
Общее решение этого уравнения, удовлетворяющее условию
и @, t) = 0, имеет вид
и (г, t) = r[C(t)+D(r)]t G.61)
где С и D — неопределенные функции. При переходе через
окружность r = R (t), разделяющую пластическую и
упругую области, агг и и должны изменяться непрерывно. Из
первого условия получаем:
Д@ = -5д-Я2+Ф(Я. *). G.62)
Поскольку, согласно соотношению G.58),

204
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
замечаем, что напряжение сгг всюду в диске является
сжимающим.
Как следует из условия текучести, окружное
напряжение с при r = R может либо изменяться непрерывно, либо
испытывать скачок от значения—а0 в пластической области
до значения, равного нулю, в упругой области. Приняв
первую возможность и учитывая соотношения G.60), из второго
условия G.59) получим:
T[R(t),t] = ^. G.63)
Это уравнение определяет радиус границы R(t). Можно
видеть, что хотя радиус R изменяется, температура на этой
границе остается постоянной. Окружное напряжение,
которое в центральной части диска является сжимающим,
возрастает при удалении от центра и переходит в растягивающее
напряжение. Далее, из соотношения G.54) следует, что на
границе — = -^ = — A — ^ _JL -j_ qlT. Поскольку, однако, R
произволен, из уравнений G.61) и G.63) получаем:
С @ -f D (г) = const = -§ . G.64)
Таким образом, все неизвестные величины найдены.
Полученное решение справедливо до тех пор, пока нигде
в пластической области диска не наступит разгрузка, т. е.
пока -37" ^0- Заметим, что согласно уравнению G.55)
-ей ч д , , ч 3d, ч
0 Ж = {сгг + °w) Ж (сгг + V ~~2Ж ^гг\Р)-
Напряжения в момент начала разгрузки имеют значения G.60),
а их изменения определяются законом Гука G.59). Таким
образом,
- да о д / с тч I 3 д , с ~. 1 с дТ
°?=-2оо? (~ЕаТ) + -а0Ж(-ЕаТ) = т Еаа0 w .
Из уравнения G.51а) следует, что dT/dt>0, пока в точке
г = 0 действует тепловой источник, т. е. пока продолжается
период нагрева диска. В продолжение этого времени
полученные решения справедливы. Далее согласно уравнению G.51а)

§4]
ТОЧЕЧНЫЙ НАГРЕВ ДИСКЛ
205
дТ/дг < 0, поэтому из уравнения G.63) вытекает соотношение
rf/? dT/dt п
Л ~~ dT/dR '
Таким образом, радиус границы возрастает.
В момент t = b действие теплового источника
прекращается. Результирующее температурное поле Тх (г, t) можно
получить посредством наложения второго температурного
поля, соответствующего тепловому источнику
производительности — S, который начинает действовать в точке г = 0
в момент t — b. Таким образом,
7\(/\ t) = T(r, t) — T(r, t — ft) (f>8). G.65)
Полагая dTl[dt = 0, получим уравнение
определяющее момент г > 8-, до которого (в фиксированной
точке г) температура продолжает возрастать. Далее она
начинает убывать и в конечном счете принимает начальное
значение, равное нулю.
Итак, при прекращении действия теплового источника
температура сразу начинает убывать в начале координат и
в его окрестности (т. е. при малых г), но она будет
некоторое время продолжать возрастать на больших расстояниях
от начала. Поэтому, в то время как пластическая область
продолжает расширяться, внутри ее появляется зона упругой
разгрузки; в результате возникает весьма сложное
распределение напряжений, которое мы не будем здесь рассматривать.
Если, однако, предположить, что продолжительность
действия теплового источника 8 достаточно велика для того,
чтобы практически установилось стационарное тепловое
состояние, то напряженное состояние можно легко исследовать;
в частности, нетрудно найти остаточные напряжения,
возникающие при полном охлаждении диска. Учитывая, что
lim Т(г, /) = lim sT* (r, s) = ^К0 (г лГ$- ) = Г (г), * 7.67)
получим:
7\(r, t) = T(r) — T(rt t — Ъ), G.68)

206
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
и следовательно,
^<°
для всех значений г и ^>$. Таким образом, охлаждение
начинается одновременно во всем диске, поэтому остаточные
напряжения можно сразу же получить путем суперпозиции
двух систем напряжений. Первая система определяется
приведенными выше уравнениями G.57) — G.64), в которых Т
следует заменить, в соответствии с уравнением G.67),
функцией Т'. Вторую систему получаем из тех же уравнений,
подставив вместо Т температуру Т" = — Т' и заменив предел
текучести а0 на — 2а0. Действительно, при остывании вновь
будет достигнута граница текучести; если при этом
возникающая пластическая зона будет не больше первоначальной,
то эквивалентное напряжение должно вначале уменьшиться
до нуля, а затем, изменяясь в противоположном направлении,
вновь достигнуть значения о0.
Радиусы границы, соответствующие температурам Т' и Тп',
на основании соотношения G.63) определяются уравнениями
Г (#') = -^ , Г (R") = —T (Я") = — 4J- • G.69)
Эти уравнения показывают, что R" < R'. Следовательно,
принятые предположения действительно имеют место.
§ б. Изгибаемые пластинки *)
К свободной от нагрузок пластинке с начальной
температурой, равной нулю, на верхней поверхности подводится
переменное количество теплоты q(f) (в единицу времени на
единицу поверхности), причем q@) = 0. Нижняя поверхность
и кромки пластинки теплоизолированы. Обозначим толщину
пластинки через 2h и предположим, что пластинка может
свободно деформироваться **). Как и прежде, предполагаем,
что свойства материала не зависят от температуры.
*) Wei пег [194,1].
**) Такая схема может иметь место, например, при
аэродинамическом нагревании пластинки (несущей плоскости), движущейся
из состояния покоя.

§5]
ИЗГИБАЕМЫЕ ПЛАСТИНКИ
207
Найдем вначале температурное поле. Введем систему
координат х, у, z в пластинке таким образом, чтобы
плоскость х, у совпадала со срединной плоскостью пластинки.
Тогда при принятых предположениях температура будет
зависеть только от координаты z, изменяющейся в направлении
толщины пластинки, и от времени t:T = T(z, t). Строгое
решение этой задачи теплопроводности можно получить
только в форме бесконечных рядов. Такое решение слишком
сложно и не позволяет получить обозримое решение задачи
определения напряжений. Поэтому мы будем основываться
на приближенном решении температурной задачи, которое
получим, применяя разложение по степеням z и отбрасывая
члены, следующие за квадратичными *):
T(z, 0 = Г0@ + *т@ + *МО + ...
На верхней поверхности пластинки z = -\-h краевое
условие имеет вид ^-з— = Я @> на нижней поверхности
2 = — h задано -^—= 0. Из этих условий получаем:
T(z, t) = T,(t) + ^(z + ^K). G.70)
Оставшаяся неопределенной температура Г0 (t) срединной
плоскости пластины не входит в формулы для напряжений
и поэтому в дальнейшем не будет учитываться.
До тех пор, пока нигде в пластинке не достигается
граница текучести, напряжения могут быть определены при
помощи следующих формул, вытекающих из обычных
предположений теории тонких пластинок **)
Е г (d2w , d2w\ n . ч "I )
Е [ , (д2т . d2w\ п . ч -,1 !
Ьу = т^[еуу + ^-*(-д^+Р "g^rJ-O + rt^J-
___ Е ( _ d2w \
°хУ — i + lx [exy z дхду)' j
G.71)
*) Другой вывод предложен в работе W e i n ё г [194,1].
**) См. Мелан — Парк.ус [6].

208
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
Здесь ехк, г , гху— удлинения и сдвиг в срединной
поверхности, w — прогиб. Вычисляя результирующие усилия
и результирующие моменты
и подставляя найденные выражения в уравнения G.71),
получим:
G.72)
где
G.73)
Поскольку в рассматриваемом случае температура не зависит
от х, у, и поскольку пластинка может свободно
деформироваться, все внутренние усилия и моменты обращаются
в нуль. Далее, согласно уравнениям G.70),
при этом
G.74)
а все остальные компоненты напряжения обращаются в нуль.
Воспользуемся условием пластичности Мизеса G.2), которое
в этом случае принимает вид
G.75)

§9]
ИЗГИБАЕМЫЕ ПЛАСТИНКИ
209
Вводя безразмерную переменную С = -^- и обозначая для
краткости
T=fw=Q®- G-76)
представим уравнение G.74) в следующем виде:
a = Q(|--C2). G.77)
Наибольшее по абсолютной величине напряжение действует
на поверхностях пластинки С= ±1. Предположим, что имеет
место подвод тепла к пластинке (q (t) ^ 0), и что q
монотонно возрастает от начального значения ^@) = 0 до
определенного максимального значения qm. При этом пластическое
течение начинается на поверхностях пластинки, когда Q(t)
достигнет значения *)
Q@ = |o0. G.78)
При дальнейшем возрастании Q у нижней и верхней
поверхностей пластинки образуются две пластические зоны,
симметричные относительно срединной плоскости. Обозначим
через С — ± Р границы между упругой и пластической
областями. Распределение напряжений в пластической области
будет следующим:
а = — о0 при 1>|С|>р. G.79)
В упругой области 0^jC|<;^ напряжения по-прежнему
следуют отвечающему температурному полю параболическому
закону G.77), в котором, однако, толщину пластинки 2h
следует теперь заменить толщиной 2C/г упругой области.
Кроме того, необходимо наложить равномерное
растягивающее напряжение, так как результирующее усилие должно
обратиться в нуль. Вследствие симметрии результирующие
моменты при этом не возникают. Таким образом,
a==Q(x-!;2) + 1Tia0' °<1Ч<Р- G-80)
*) Чисто упругий случай при различных условиях
теплообмена на поверхности г = -f- /г, подробно рассмотрел Г е й с л е р
(Heisler).

210
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ VH
Поскольку условие текучести имеет место также на границе
упругой области, то при переходе из упругой в пластическую
область напряжение о должно изменяться непрерывно.
Подставив в уравнение G.80) значения С = р и а=— а0>
получим:
Р=Л|\ G.81)
Распределение напряжений, определяемое формулами G.79)
и G.80), будет справедливо до тех пор, пока максимальное
растягивающее напряжение в упругой области (при С = 0)
не достигнет границы текучести. Из условия
(<0С=о = ^у + —jr- ao = °о
и соотношения G.81) получаем, что это произойдет при
3
Р = -д-, т. е. тогда, когда Q достигнет значения
G.82)
Если Q превышает значение G.82), то возникнет третья
пластическая область, распространяющаяся в обе стороны от
срединной плоскости. Обозначив границы этой области
через ± 7&, получим следующее распределение
напряжений:
G.83)
Распределение напряжений в упругой области, как и прежде,
найдем из тех условий, что, во-первых, это распределение
(поскольку оно определяется непосредственным воздействием
температурного поля) должно быть параболическим с равной
нулю равнодействующей и, во-вторых, что напряжения в
пластической области должны быть уравновешены посредством
наложения некоторого постоянного напряжения.
Величины р и 7 определяются из условий непрерывности
напряжений, которые имеют вид а = -г~ао ПРЙ ^=7 и

§5]
ИЗГИБАЕМЫЕ ПЛАСТИНКИ
211
о = — а0 при С —р. Из этих условий получаем два
уравнения:
которые посредством подстановки
и после некоторых преобразований могут быть представлены
в следующей форме:
G.84)
Из первого уравнения численным методом определяем v%
после чего можно определить также и и. Результаты
представлены на рис. 33.
0,8
0,6
0,5
Ofi
0,2
°1 2 3 4 5 70 20 30 4050 /00 200 Q/60
Рис. 33,
Распределение напряжений, определяемое
вышеприведенными формулами, будет иметь место до тех пор, пока нигде
в пластинке не начнется разгрузка. Такой случай наверняка

212
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ Ц\П. VII
будет иметь место до тех пор, пока пластические области
увеличиваются или, по крайней мере, не убывают, т. е.
пока р не возрастает, а у не уменьшается. На рис. 33 можно
видеть, что такое положение реализуется, когда функция Q(t)
не убывает (т. е. когда Q(t)^>0).
Пусть теперь Q(t) начинает монотонно убывать после
того, как было достигнуто максимальное значение Q/n. Если
при этом возникает разгрузка, то нужно наложить
добавочные напряжения, изменения которых определяются
законом Гука G.77). Возникающее при этом положение
Рис. 34.
показано на рис. 34. Сплошной линией показано
распределение напряжений, соответствующее значению Q = Qi/}i
пунктирной линией показаны напряжения разгрузки, отвечающие
значению Qm — Q. Вычитая эти напряжения из первого
распределения, получим результирующее поле напряжений,
показанное штриховкой. Такое наложение напряжений будет
законно, если при этом напряжения в пластической области
убывают. Легко видеть, что это имеет место при условии
pm ^> —==¦, что в соответствии с уравнением G.84) отвечает
значению Qm^\3a0. Большие значения Qm мы здесь
рассматривать не будем.
При вычислении остаточных напряжений, возникающих
при полном охлаждении пластинки, следует рассмотреть
различные случаи, поскольку при разгрузке может быть вновь
достигнута (в обратном направлении) граница текучести.
В этом случае значение предела текучести следует
заменить на 2о0.

§5]
ИЗГИБАЕМЫЕ ПЛАСТИНКИ
213
Случай /. О < Qm <;-о-<з0. Согласно уравнению G.78)
в этом случае в момент максимального подвода тепла
распределение напряжений является чисто упругим, поэтому
при полном охлаждении напряжения в пластинке будут
равны нулю.
Случай II. ^-о0 < Qm <; Зо0. Из уравнения G.78) (в
котором а0 теперь должно быть заменено на 2о0), получим,
что напряжения разгрузки, которые надо наложить на
решение, будут чисто упругими, пока Qm не превзойдет
значения За0. Распределение напряжений, соответствующее Q,n,
определяется уравнениями G.79) и G.80). Напряжения
разгрузки вычисляются по уравнению G.77), в котором Q
следует заменить на Qm. Вычитая, получаем остаточные
напряжения, возникающие при охлаждении:
G.85)
при
при
Здесь $т определяется из уравнения G.81) при Q = Qm.
32
Случай III. За0 < Qm ^ -^- а0. В этом случае при
разгрузке достигается (в противоположном направлении) граница
текучести. При этом напряжения разгрузки ое определяются
уже не уравнением G.77), а уравнениями G.79) и G.80),
в которых Q следует заменить на Qm, а а0 — на 2а0:
G.86)
при
при
Величина 8 определяется из соотношения, аналогичного G.81):
G.87)
Чтобы получить остаточные напряжения, нужно вычесть
напряжения G.86) из напряжений от, определяемых
уравнениями G.79) и G.80), в которых нужно снова заменить Q
на Qm и различать три области: |C|<[im, ?m<|C|^&,
&<|С|<1.

214
УПРУГО-ПЛАСТИЧЕСКИЕ МАТЕРИАЛЫ [ГЛ. VII
Случай IV. -Q- o0 < Qtn •< -Q- o0. Распределение
напряжений при Q = Qm теперь определяется из уравнения G.83).
Напряжения разгрузки вычисляются снова по уравнению G.86).
При вычислении необходимо теперь учитывать, что
существуют четыре области: |С|<чт, 1m<W<Pm' Рт<1Ч<Л
64
8<;|С|<;1. Когда Qm достигает значения -д~а0, остаточное
напряжение ст — ае в срединной плоскости ? = 0 достигнет
границы текучести.
64
Случай V. -g- a0 < Q/n <^ 1 За0. Теперь разгрузка
приводит к повторному пластическому течению также в средней
области пластинки, поэтому напряжения разгрузки будут
определяться уравнениями G.83), в которых о0 должно быть
заменено на 2а0:
G.88)
Величины 8 и 7) определяются из уравнения G.84) или могут
быть найдены при помощи графика, рис. 33. При этом Q/a0
следует заменить на Q„,/2a0. Легко видеть, что имеет место
условие
0<7)<Тш<рт<8<1.
Вычитая соотношение G.88) из G.83), снова получаем
распределение остаточных напряжений, возникающих при полном
охлаждении пластинки.
В последующей работе Ландау и Вейнера (Landau, Wei-
ner [103]) был рассмотрен случай, когда вместо подвода
тепла задано распределение температуры в пластинке, причем
снова предполагается, что температура не зависит от х и
от у. В качестве примера рассмотрено охлаждение
пластинки.

ЛИТЕРАТУРА
А, Монографии, часто цитируемые в тексте
1. Car si aw H. S. and Jaeger J. C, Conduction of heat in
solids, Oxford, 1947, цитируется как «Carslaw—Jaeger»
(готовится русский перевод).
2. Doetsch G., Anleitung zum praktischen Gebrauch der Laplace-
Transformation, Munchen, 1956 (имеется русский перевод:
Д ё ч Г., Руководство к практическому применению
преобразования Лапласа, Физматгиз, Москва, 1958); цитируется как
Дёг, Руководство.
3 Doetsch G., Einfuhrung in Theorie und Anwendung der
Laplace-Transformation, Basel, 1958; цитируется как «Doetsch,
Einfuhrung».
4. Erdelyi — Magnus — Oberhettinger — Tricomi,
Tables of integral transforms, 2 тома. New York, 1954,
Цитируется как «Erdelyi».
5 Jahnke E., E m d e F., Funktionentafeln mit Formeln und Kur-
ven, Leipzig (имеется русский перевод: Янке Е, Эмде Ф.,
Таблицы функций с формулами и кривыми, Физматгиз, 1959);
цитируется как «Янке—Эмде».
6. М е 1 а п Е., Р а г k u s H., Warmespannungen infolge stationarer
Temperaturfelder, Wien, 1953 (имеется русский перевод: М е-
лан Э., Паркус Г., Термоупругие напряжения, вызываемые
стационарными температурными полями, Физматгиз, 1958);
цитируется как «Мелан — Паркус».
7. Watson G., N., Theory of Bessel functions, Cambridge, 1944
(имеется русский перевод: Ватсон Г. Н., Теория бесселевых
функций, Москва, 1949); цитируется как «Ватсон».
Б. Температурные напряжения
8. А г gy r is J. H., Kelsey S., A) Energy theorems and
structural analysis. Part II. Aircraft Engng 26, 410 A954);
— B) The matrix force method of structural analysis and some
new applications, Aero. Res. Counc. London, Rep Mem. 3034
A957).
9 В a d e r W., Zur numerischen Bestimmung der
Warmespannungen, Z. angew. Math. Mech. 36 A956), 331.

216
ЛИТЕРАТУРА
10. В a eh r H. D., Nichtstationare Warmespannungen in ausge-
mauerten Behaltern und die Berechnung der Ausmauerung an
Hand eines Temperatur-Schaubildes, Ing/-Arch. 25 A957), 330.
11. Bailey J. L., A thermoelastic problem in the half-space.
Диссертация, Michigan State University, 1958.
12. Barber A. D., Weiner J. H and Boley B. A., An analysis
of the effect of thermal contact resistance in a sheet-stringer
structure. J. Aeronaut. Sci. 24 A957), 232.
13. Behlendorff E., Uber die Bestimmung der
Warmespannungen in einer Kugel, Math. Nachr. 8 A952), 59.
14 Белов А. В., О температурном режиме окружающей среды,
обеспечивающем заданные напряжения на поверхности
бетонной плиты. Гидротехническое строительство, 1953, № 2.
15. Белов А. В., Васильев П. И., Практический способ
определения температурных напряжений в бетонной плите при
гармонических колебаниях температуры наружного воздуха,
Гидротехническое строительство, 1952, № 9.
16 В i j 1 а а г d P. P., Differential equations for cylindrical shells with
arbitrary temperature distributions J. Aero/Space Sci 25 A958), 594.
17. Biot M. A., A) Thermoelasticity and irreversible
thermodynamics, J. Appl. Phys. 27 A956), 240 (имеется русский перевод:
Б и о М., Термоупругость и термодинамика необратимых
процессов, Сб. «Механика», № 3);
— B) Influence of thermal stresses on the aeroelastic stability of
supersonic wings. J. Aeronaut. Sci. 24 A957), 418.
18. Bisplinghoff R. L., A) The finite twisting and bending of
heated elastic lifting surfaces, Mitt. Inst. Elugzeugstatik and
Leichtbau E. Т. Н. Zurich. 1957, 4.
— B) Further remarks on the torsional rigidity of thermally
stressed wings, J. Aero/Space Sci. 25 A958), 657.
19. Bland D. R., Elastoplastic thick-walled tubes of workhardening
material subject to internal and external pressures and to
temperature gradient, J. Mech. Phys. Solids 4 A956), 209 (имеется
русский перевод в сборнике «Механика»).
20. Bock Ph., Die Warmespannungen eines endlichen Zylinders un-
ter dem EinfluB einer periodisch veranderlichen Temperaturver-
teilung, Mitt. Hauptver. Deutsch. Ing. in der Tschechoslowak.
Republik 27 A938), 94, 114.
21. Bogdanoff J. L., Note on thermal stresses, J. Appl. Mech.
21 A954), 88.
22. Boley B. A., A) The determination of temperature, stresses,
and deflections in two-dimensional thermoelastic problems, J.
Aeronaut. Sci. 23 A956), 67;
— B) Thermally induced vibrations of beams, J. Aeronaut Sci 23
A956), 179;
— C) The calculation of thermoelastic beam deflections by the
principle of virtual work, J. Aeronaut. Sci. 24 A957), 139.
23. Boley B. A. and Barber A. D., Dynamic response of beams
and plates to rapid Heating, J. Appl. Mech. 24 A957), 413.
24. Boley B. A. and Barrekette E. S., Theimal stress in
curved beams, J. Aero/Space Sci. 25 A958), 627.

ЛИТЕРАТУРА
217
25. В о И е n r a t h F., Some remarks upon the problem of
temperature shock in aircraft, AGARD, Rep. 90 A956).
26. Borchardt C. W., Untersuchungen fiber die Elasticitat fester
isotroper Korper unter Berikksichtigung der Warme, Mber. Akad.
d Wiss., Berlin 9 A873).
27. Born J. S. and Horvay G., Thermal stresses in rectangular
strips, II. J. Appl. Mech 22 A955), 401
28. Brooks W. A. Jr, Griffith G. E. and S trass H. K., Two
factores influencing temperature distributions and thermal stresses
in structures, NACA Techn Note, 4052 A957).
29. Buckens F., A) Determination des tensions thermo-elastiques
dans un tube cylindrique, Mem. Acad. Roy. Belg. 27 A952), 1628;
— B) Theorie limite du flambage d'une plaque circulaire chauffee
en son centre, Ann. Soc. Sci., Bruxelles, 68 A954), 63;
— C) Theorie limite du flambage d'une plaque circulaire chauffee
en son centre, Deformees caracteristiques, Ann. Soc. Sci.,
Bruxelles, 68 A954), 157.
30. Buckland F. F., Gatzemeyer J. В., Transient
temperature and thermal stress in locomotive gas turbine buckets,
A. S. M. E. Ann. Meet, Chicago, 1955, Pap. 55-A-179.
31. Budiansky В., Mayers J., Influence of aerodynamic
heating on the effective torsional stiffness of thin wings, J.
Aeronaut Sci. 23 A956), 1081.
32. Chad wick P., Sneddon 1. N., Plane waves in an elastic
solid conducting heat, J. Mech. Phys. Solids 6 A958), 223.
33. Chang С. С, С h u W. H., Stresses in a metal tube under both
high radial temperature variation and internal pressure, J Appl.
Mech. 21 A954), 101.
34. Chen S. Y., Transient temperature and thermal stresses in skin
of hypersonic vehicle with variable boundary conditions, ASME
Ann. Meet., New York, 1957, Pap. 57-A-9.
35. С h m e 1 к a F., Warmespannungen in einem Prantl-Reussschen
Korper, Ostrerr. Ing.-Arch. 10 A956), 133
36. С h w a 11 a E., S t e i n e r H., Uber das Einbeulen von Druck-
schachtpanzerungen, Osterr Bauzeitschr. 12 A757), 57.
37 Cof f i n L. E., A) A study of the effects of cyclic thermal
stresses on a ductile metal, Trans. ASME 76 A954), 931;
— B) Design aspects of high-temperature fatigue with particular
reference to thermal stresses, Trans. ASME 78 A956),
527.
38. С о p e 1 a n d R. E., Shrinkage and temperature stresses in
masonry, J. Amer. Concrete Inst. 28 A957), 769.
39. D a h 1 O. G. C, Temperature and stress distribution in hollow
cylinders, Trans. ASME 46, A924), 161.
40. Даниловская В. И. A) Температурные напряжения в
упругом полупространстве, возникающие вследствие внезапного
нагрева его границы, ПММ 14 A950), № 3;
— B) Об одной динамической задаче термоупругости, ПММ 16,
A952), № 3.
41. De resie wicz H., Plane waves in a thermoelastic solid, J.
Acoust. Soc. Amer. 29 A957), 204.

218
ЛИТЕРАТУРА
42. Derski W., A) The state of stress in a thin circular ring, due
to a non-steady temperature field, Arch. Mech. Stos 10 A958), 255;
— B) Der Spannungszustand in einer dunnen Kreisplatte zufolge
eines nichtstationaren Temperaturfeldes (на польском яз.),
Rozpr. Inzyn. 6 A958), 253.
43. D u b e r g J. E., Aircraft structures research at elevated
temperatures, AGARD Rep. 3, 1955.
44. D u h a m e 1 M. C, Second memoire sur les phenomenes thermo-
mecaniques, J. de l'Ecole Polytechn. 15 A837), 1.
45. D u r e 11 i A. J., T s а о С. H., Determination of thermal stresses
in three-ply laminates, J. Appl. Mech. 22 A955), 190
46. E n d r e s W., Warmespannungen in Rohrleitungen, Forschung 23
A957), 33
47. Erin gen A. C, Thermal stresses in a multiple layer beam,
Proc. First Midwest. Conf. Solid Mech., Engng Exp. Sta Univ.
of 111., 69, 1953.
48 Fazekas G. A. G., Temperature gradients and heat stresses in
brake drums, S. A. E. Trans. 61 A953), 279.
49 F о г г а у M. J., Thermal stresses in plates, J. Aeronaut. Sci. 25
A958), 716.
50. Forray M. J., Z a i d M., Thermal stresses in a circular
bulkhead subjected to a radial temperature distribution J. Aeronaut.
Sci. 25 A958), 63.
51 F о u s t A. S., Conditions in heat transfer problems which
create high thermal stress. Heat-Transfer Symposium. Univ of Mich.
Press 1 A953).
52. F r eu d e n t h a 1 A. M., A) On inelastic thermal stresses in
flight structures, J. Aeronaut. Sci. 21 A954), 772;
— B) Effect of rheological behavior on thermal stresses, J. Appi.
Phys. 25 A954), 1110;
— C) Problems of structural design for elevated temperatures,
Trans. New York Acad. Sci. II, 19 A957), 4.
53 Fritz R. J., Evaluation of transient temperature and stresses,
Trans. A. S. M. E. 76 A954), 913.
54 Gate wood B. E., A) Thermal loads on joints, J. Aeronaut.
Sci. 21 A954), 645;
— B) Effect of thermal resistance of joints upon thermal
stresses, J. Aeronaut. Sci. 24 A957), 152;
— C) Thermal stresses, McGraw-Hill, New York, 1957 (имеется
русский перевод: Гейтвуд Б. Е., Температурные
напряжения, ИЛ, 1959).
55. Gate wood В. Е., Inelastic combined thermal and applied
stresses in skin-stringer aircraft structure, J. Aeronaut. Sci. 25
A958), 212.
56 Geckler R D, Thermal stresses in solid propellant grains,
Jet Prop. 26 A956), 93.
57 G e e r t s m a J., A remark on the analogy between thermoelasti-
city and the elasticity of saturated porous media, J. Mech. Phys.
Solids 6 A957), 13.
58. G e г а г d G., Life expectancy of aircraft under thermal flight
conditions, J. Aeronaut. Sci. 21 A954), 675.

ЛИТЕРАТУРА
219
59 Gerard G. and Gilbert A. C, Photo-thermoelasticity: an
exploratory study, New York Univ. Res. Div., TN Rep. SM
56—11, 1956.
60 Goldberg J. E., Axisymmetric flexural temperature stresses
in circular plates, J. Appl. Mech. 20 A953), 257.
61 Goldberg M. A. Investigation of the temperature distribution
and thermal stresses in a hypersonic wing structure, J Aeronaut.
Sci. 23 A956), 981.
62 Г о л о в а н о в С. Г., Расчет остаточной напряженности от
процессов охлаждения в стали и чугуне, Вестник машиностроения,
1953, № 7.
63 Goodier J N, A) Thermal strees in long cylindrical sheljs
due to temperature variation round the circumference and through
the wall, Canad. J of Res. 15 A937), 49;
— B) On the integration of the thermo-elastic equations, Philos.
Mag. VII, 23 A937), 1017;
— C) Thermal stress and deformation, J. Appl. Mech. 24 A957),
467.
64. Green A. E., Radok J. R. M., Rivlin R. S., Thermo-elastic
similarity laws, Quart. Appl. Math. 15 A958), 381.
65 Griffith G. E., M i 11 e n b e r g e r G. H., Some effects of joint
conductivity on the temperatures and thermal stresses in aerody-
namically heated skin-stiffener combinations, NACA Techn. Note
3699 A956).
66 Griinberg G., Uber die in einer isotropen Kugel durch un-
gleichformige Erwarmung erregten Spannungszustande, Z Phys.
35 A925), 548.
67 Гутман С. Г., Определение тепловых напряжений при
гармонических колебаниях температуры, Изв. ВНИИ гидротехники
им. Веденеева 47 A952), 72; 51 A954), 23.
68 Н a m m i 11 F. G., Axial-temperature gradient bending stresses
in tubes, J. Appl. Mech. 25 A958), 109.
69 Heaps N. S., Transient thermal stress in a flat plate due to
non-uniform heat transfer across one surface, Aeron. Res. Counc.
London, 1956, Curr. Pap. 299.
70 H e i s 1 e r M. P., Transient thermal stresses in slabs and
circular pressure vessels, J. Appl. Mech. 20 A953), 261
71 Heldenfels R. R., Vosteen L. F., Approximate analysis of
effects of large deflections and initial twist on torsional stiffness
of a cantilever plate subjected to thermal stresses, NACA, Techn.
Note, 4067 A957).
72 Hemp W. S., A) Fundamental principles and methods of ther-
moelasticity, Aircraft Engng 26 A954), 126;
— B) Thermo-elastic formulae for the analysis of beams. Aircraft
Engng 28 A956), 374.
73 Herrmann G, On a complementary energy principle in linear
thermoelasticity, J. Aero/Space Sci. 25 A958), 660.
74 Hi eke M., A) Uber ein ebenes unstetiges Temperaturspann-
ungsproblem, Z. angew. Math Mech. 34 A954), 121;
— B) Uber ein ebenes Distorsionsproblem, Z. angew. Math. Mech.
35 A955), 54;

220
ЛИТЕРАТУРА
— C) Eine indirekte Bestimmung der Airyschen Flache bei un-
stetigen Warmespannungen, Z. sngew. Math. Mech. 35
A955), 285.
75. Hilton H. H., A) Thermal stresses in bodies exhibiting
temperature-dependent elastic properties. J. Appl. Mech. 19 A952),
350;
— B) An extension of Alfreys elastic-viscoelastic analogy to vis-
coelastic thermal stress problems. Rep. No. TSVE-TR-2 on
contract No. AF 33F16) —291, Dept. Aeron. Engng, Univ.
of Illinois, 1953;
— C) Thermal stresses in thick-walled cylinders exhibiting
temperature-dependent viscoelastic properties of the Kelvin
tvpe, Proc. Second. U. S. Nat. Congr. Appl. Mech. стр. 547,
1954.
76. H i 11 о n H. H., Hassan H. A., Russell H. G., Analytical
studies of thermal stresses in media possessing
temperature-dependent viscoelastic properties, Wright Air Development Center Rep.
53—322 A953).
77. H i r s с h f e 1 d K-, Kreisformiger Stollen unter Temperaturbean-
spruchung. Ing.-Arch. 23, 270 A955).
78 Hlinka J. H., Landau H. G., Paschkis V., Charts on
elastic thermal stresses in heating and cooling of slabs and
cylinders, ASME Ann. Meet., New York, 1957, Pap. 57-A-238.
79. Hoff N. J., A) Structural problems of future aircraft, Proc.
Third, Anglo-American Aer. Conf., 1951, стр. 103;
— B) The thermal barrier. Structures, ASME Ann Meet, New
York, 1954, Pap. 54-A-207;
— C) High temperature effects in aircraft structures, AMR. 8
A955), 453;
— D) Approximate analysis of the reduction in torsional regidity
and of the torsional buckling of solid wings under thermal
stresses, J. Aeronaut Sci. 23 A956), 603;
— E) Thermal buckling of supersonic wing panels, J. Aeronaut.
Sci. 23 A956), 1019;
— F) Buckling at high temperature, J. Roy. Aer. Soc. 61 A957),
756;
— G) (редактор): High temperature effects in aircraft
structures, London, 1958.
80. Holms A. G., F a 1 d e 11 a R. D., Effects of temperature
distribution and elastic properties of materials on gas-turbine-disk
stresses, NACA Rep. 864, 1947.
81 H о p k i n s о n J., On the stresses caused in an elastic solid by
inequalities of temperature, Messenger of Math 8 A879),
168
82 Horvay G., A) Thermal stresses in perforated plates, Proc.
First U. S. Nat. Congr. Appl. Mech. 1952, стр. 247.
— B) Transient thermal stresses in circular disks and cylinders,
Trans. ASME 76 A954), 127;
— C) Thermal stresses in rectangular strips-I, II., Proc. Second.
U. S. Nat. Congr. Appl. Mech. 1954, стр. 313, J. Appl.
Mech. 22 A955), 401;

ЛИТЕРАТУРА
221
— D) Stress relief obtainable in sectioned heat-generating
cylinders, Proc. Second Midwestern Conf. Solid Median.
Purdue Univ., 1955, стр. 45.
83. H о r v а у G., Clausen I. M., Stresses and deformations of
flanged shells. ASME Ann. Meet. New York, Dec. 1953. Pap.
53-A-43.
84. H о u b о 11 J. C, A study of several aerothermoelastic problems
of aircraft structures in high-speed flight, Mitt. Inst. Flugzeug-
statik und Leichtbau E. Т. Н. Zurich, 5, 1957.
85. H о у 1 e R. D., Transient temperature stresses in axially
symmetrical systems with special application to a solid rotor of a steam
turbine, Proc. Inst. Mech. Engng 3—8 A955).
86. H u t h J. H., Thermal stresses in conical shells, J. Aeronaut. Sci.
20 A953), 613.
87. Ignaczak J., A) Thermal displacements in an elastic semi-
space due to sudden heating of the boundary plane, Arch. Mech.
Stos. 9 A957), 395.
88. Ignaczak J. B) Thermal stresses in a long cylinder heated
in a discontinuous manner over the lateral surface, Arch. Mech.
Stos. 10 A958), 25;
— C) Thermal displacement in a non-homogeneous elastic semi-
infinite space caused by sudden heating of the boundary,
Arch. Mech. Stos. 10 A958), 147;
— D) Thermal stresses due to a nucleus of thermo-elastic strain
in an elastic semispace, containing a hemispherical pit at
a free surface, Bull Acad. Pol. Sci., s. techn. 6 A958), 151.
89. Ignaczak J., Nowacki W., Two cases of discontinuous
temperature field in an elastic space and semi-space, Bull. Acad.
Pol. Sci. s. techn. 6 A958), 309.
90. I s а к s о n G., A simple model study of transient temperature
and thermal stress distribution due to aerodynamic heating, J.
Aeronaut. Sci. 24 A957), 611.
91. Jaeger J. C, On thermal stresses in circular cylinders, Philos.
Mag. 36 A945), 418.
92. Jager K., Warmespannungen in Stahlbetonstabwerken, Osterr.
Ing. Z. 1, 184 A958), 219.
93. Jasper N. H., Temperature-induced stresses in beams and ships,
David W. Taylor Mod. Basin Rep. 937, 1955.
94. Johns D. J., Approximate formulas for thermal-stress analysis,
J. Aero/Space Sci. 25 A958), 524.
95. Jung H., A) Zur Berechnung von Warmeaustauschern, Osterr.
Ing.-Arch 10 A956), 382;
— B) Ober die Bestimmung der Warmespannungen in ungleich-
formig erwamten Kontaktofen, Osterr. Ing.-Arch. 11 A957),
96 Karush W., Martin A. V., Thermal contraction of a split
hollow cylinder, J. Appl. Phys. 24 A953), 1427.
97 Kent С. Н., Thermal stresses in spheres and cylinders, Trans.
ASME 54 A932), 185.
98. К i h a r a H., M a s u b u с h i K-, Theoretical studies on the
residual welding stress, Rep. Transport. Tech. Res. Inst. 6 A953).

222
ЛИТЕРАТУРА
99 К 1 о р р е 1 К-, S с h б n b а с h W., Warmespannungen in rech-
teckig berandeten Schieben, Stahlbau 27 A958), 122.
100 Klosner J. M., Forray M. J., Buckling of simply supported
plates under arbitrary symmetrical temperature distributions, Л.
Aeronaut. Sci. 25 A958), 181.
101 Kochanski S. L., Argyris J. H., Some effects of kinetic
heating on the stiffness of thin wings, Aircr. Engng 29, 310
A957); 30 A958), 32.
102. Костю к А. Г., К определению температурного поля и
температурных напряжений в турбинных дисках, Теплоэнергетика,
№ 3 A956).
103. Landau H. G., Wei пег J. H., Transient and residual
stresses in heat-treated plates, J. Appl. Mech. 25 A958), 449.
104. L a n g h a a r H. L., S t i p p e s M., Three-dimensional stress
functions, J. Franklin Inst. 258 A954), 371.
105 Leopold W. R., Centrifugal and thermal stresses in rotating
disks, J. Appl. Mech. 15 A948), 322.
106. Lessen M., A) On similarity of thermal stresses in elastic
bodies, J. Aeronaut. Sci. 20 A953), 716;
— B) Thermoelasticity and thermal shock. J. Mechan. Phys.
Solids 5 A956), 57;
— C) On the motion of a thermo-viscoelastic solid, Proc Third.
Midwestern Conf. Solid. Mech. 20, 1957;
— D) The motion of a thermoelastic solid, Quart. Appl Math.
15 A957), 105;
— E) Thermoelastic damping at the boundary between dissimilar
solids, J Appl. Phys. 28 A957), 364.
107 Lessen M., Duke С. Е., On the motion of an elastic
thermally conducting solid, Proc. First Midwestern Conf. Solid. Mech.,
Engng Exp. Sta. Univ. of 111. 14, 1953.
108 Levy S., A) Determination of loads in the presence of thermal
stresses, J. Aeronaut. Sci. 21 A954), 659;
— B) Thermal stresses and deformations in beams, Aeronaut.
Engng Rev. 15 A956), 62.
109 Lockett F. J., Effect of thermal properties of a solid on the
velocity of Rayleigh waves, J. Mech. Phys. Solids 7 A958), 71.
110. Ломакин В. А., Упруго-пластическое равновесие шара в
нестационарном температурном поле, ПММ 19, 1955, № 2.
111. Loveless E., Boswell А. С, The problem of thermal
stresses in aircraft structures, Aircraft Engng 26 A954), 122.
112. Madejski J., Ahnlichkeitstheorie fur thermoelastisch-plastische
Erscheinungen (на польск яз.), Rozpr. Inzyn. 5 A957), 481
113. Ma л и нин Н. Н., Расчет вращающегося неравномерно
нагретого диска переменной толщины, Инженерный сб. АН СССР,
IX, 1953.
114. Man son S. S., (A Determination of elastic stresses in gas-
turbine disks, NACA. Rep., 871, 1947;
— B) Direct method of design and stress analysis of rotating
disks with temperature gradient, NACA. Rep 952, 1950;
— C) Stress investigations in gas turbine disks and blades, SAE
Quarterly Trans. 3 A949), 229;

ЛИТЕРАТУРА
223
— D) Analysis of rotating disks of arbitrary contour and radial
temperature distribution in the region of plastic
deformation, Proc. First U. S. Nat. Cong. Appl. Mech., 1952,
стр. 569;
— E) Temperature, thermal stress, and shock in heat-generating
plates of constant conductivity and of conductivity that
varies linealy with temperature, NACA Techn. Note 2988
A953);
—F) Behavior of materials under conditions of thermal stress,
NACA Rep., 1170 A954).
115. M a r J. W., S с h m i t L. A., Some structural penalties associated
with thermal flight, Trans. ASME 79 A957), 990.
116. Matz W., Berechnung der Ausmauerung stahlerner Gefafie,
Berlin— Gottingen— Heidelberg, Springer-Verlag, 1953.
117. Mazet R., Sur un modele admissible pour l'etude des vibrations
thermoelastiques d'une eprouvette en cours de fluage, 9, Int.
Kongr. angew. Mech, В Kissel 8 A957), 293.
118. McDowell E. L., Thermal stresses in an infinite plate of
arbitrary thickness, Proc. Third Midwestern Conf. Solid Mech., 72, 1957.
119 McDowell E. L., Sternberg E., Asymmetric thermal
stresses in a spherical shell of arbitrary thickness, J. Appl. Mec-
han. 24 A957), 376.
120. M e 1 a n E., A) Warmespannungen in einer Scheibe infolge einer
wandernden Warmequelle, Ing.-Arch. 20 A952), 46.
— B) Warmespannungen in Platten mit Warmeverlust an den
Oberflachen, Osterr. Bauzeitschrift 8 A953), 89;
— C) Warmespannungen infolge eines rotierenden Temperatur-
feldes, Osterr. Ing.-Arch. 8 A954), 165:
— D) Warmespannungen in einem kreisrunden Behalter infolge
warmen Fullgutes, Osterr. Bauzeitschrift 9 A954), 81;
— E) Warmespannungen infolge einer quasi-stationaren Tempe-
raturverteilung. Anz. Osterr. Akad. Wiss., Math.-Naturw.
Kl. 12 A954), 183.
121. Mel an E., F) Spannungen infolge nicht stationarer Tempera-
turfelder, Osterr. Ing.-Arch. 9 A955), 171;
— G) Warmespannungen bei der Abkuhlung einer Kugel, Acta
Phys. Austr. 10 A956), 81.
122. Merckx K. R., A) The time and temperature dependence of
thermal stresses in cylindrical reactor fuel elements, Trans.
ASME 80 A958), 505;
— B) The dependence of thermal stresses in cylindrical reactor
fuel elements upon the method of cooling. Trans. ASME
80 A958), 985.
123. Meyer J. H., Thermoelastic distortion and wing structural
design. Aeronaut. Engng Rev. 18 A957), 46.
124. Mi 11 en son M В., Manson S. S., Determination of stresses
in gas-turbine disks subjected to plastic flow and creep,
NACA Rep 906, 1948
125. Miller D. R., Cooper W E., Structural problems of a
sodium— cooled nuclear reactor, ASME Semi-Ann. Meet.,
Pittsburgh, 1954, Pap. 54-SA-75.

224
ЛИТЕРАТУРА
126. Miller К. A. G, The design of tube plates in heat exchangers.
Inst. Mechan. Engng Proc. (B) IB, 215 A952).
127. M i n d 1 i n R D., Force at a point in the interior of semi-infinite
solid, Physics 7 A956), 195.
128. Morgan A. J. A., A proof of Duhamels analogy for thermal
stresses, J. Aeronaut. Sci. 25 A958), 466.
129. Mossakowska Z. and N о w а с к i W., Thermal stresses in
transversally isotropic bodies, Arch. Mech. Stos. 10 A958), 569
130 Mossakowski J., The state of stress and displacement in a
thin anisotropic plate due to a concentrated source of heat, Arch
Mech. Stos. 9 A957), 565.
131. Mura Т., A) Thermal strains and stresses in transient state,
Proc. Second Japan Nat. Congr. Appl. Mech., 1952, стр. 9;
— B) Extremum principles of thermal elasto-plastic problems,
Res. Rep. Fac. of Engng, Meiji Univ. 6 A955);
— C) Buckling type deformation of thin plates due to welding,
Res. Rep. Fac. of Engng, Meiji Univ. 7 A956);
— D) Dynamical thermal stresses due to thermal shocks, Res.
Rep. Fac. of Engng, MSiji Univ. 8 A956);
— E) Unstable plastic yield o; a hollow cylinder under internal
pressure and thermal stresses, Res. Rep. Fac. of Engng,
Meiji Univ. 9 A957);
— F) Residual stresses due to thermal treatments, Res. Rep.
Fac. of Engng, Meiji Univ. 10 A957).
132. Mura Т., К i n о s h i t a N., Expression of initial stresses based
on Greens functions, First Meeting Japan. Soc. Appl. Math.
Mech., 1956.
133. Neubauer R., Temperatur- und Spannungsverteilung in aus-
gemauerten zylindrischen ReaktionsgefaBen, Berlin—Gottingen—
Heidelberg, Springer-Verlag, 1958.
134. Nishimura G. and Suzuki M., Horizontal deformation of
a Japanese two-storied frame house, Bull. Earthq. Res. Inst.
Tokyo Univ. 32 A954), part. I, 113.
135. Norbury J. F., Thermal stresses in disks of constant thickness,
Aircraft Engng 29 A957), 132.
136. Nowacki W., A) Warmespannungen in anisotropen Korpern,
I: (на польск. яз.), Arch. Mech. Stos. 6 A954), 481;
— B) Warmespannungen in Zylinderschalen (на польск. яз.),
Arch. Mech. Stos. 8 A956), 69
— C) The state of stress in a thin plate due to the action of
sources of heat, Publ. Int. Assoc. Bridge Struct. Engng
16 A956), 373;
— D) State of stress in an infinite and semi-infinite elastic
space due to an instantaneous source of heat, Bull.'Acad.
Pol, Sci., CI. IV 5 A957), 77.
137 Nowacki W., E) The state of stress in an elastic space due
to a source of heat varying harmonically in function of time,
Bull. Acad. Pol. Sci., CI. IV 5 A957), 145;
— F) A quasi-stationary thermo-elastic problem in three
dimensions, Bull. Acad. Pol. Sci., CI. IV 5 A957), 155;

ЛИТЕРАТУРА
225
— G) The state of stress in an elastic semi-space due to an
instantaneous source of heat, Bull. Acad. Pol. Sci., CI. IV, 5
A957), 165;
— (8) The state of stress in a thick circular plate due to a
temperature field, Bull. Acad. Pol. Sci., Gl. IV, 5 A957), 227;
— (9) The stresses in a thin plate due to a nucleus of thermo-
elastic strain. Arch. Mech. Stos. 9 A957), 89;
— A0) A three-dimensional thermoelastic problem with
discontinuous boundary conditions, Arch. Mech Stos. 9 A957),319;
— A1) A dynamical problem of thermoelasticity, Arch. Mech.
Stos. 9 A957), 325;
— A2) A plane distortion problem, Arch. Mech. Stos. 9 A957),
417;
— A3) Two steady-state thermoelastic problems, Arch. Mech.
Stos. 9 A957), 579;
— A4) The state of stress in an elastic slab due to a steady heat
source, Bull. Acad. Pol. Sci., s. techn. 6 A958), 301;
— A5) Non-steady state thermal stresses in an infinite cylinder
of rectangular or circular cross-section, Bull. Acad PoL
Sci., s. tech. 6 A958), 321.
138 Nowinski J., A) Warmespannungen in einem dickwandigen
Kugelbehalter aus transversal isotropem Werkstoff (на польск,
яз.), Arch. Mech. Stos. 7 A955), 363;
— B) The principle of stationary free energy in the
thermoelastic analysis of thinwalled tubes, Arch. Mech. Stos 9
A957), 357.
139. Nowinski J., Olszak W., Warmespannungen in
dickwandigen anisotropen Zylindern (на польск. яз.), Arch. Mech. Stos. 5
A953), 221.
140. Nowinski J., Olszak W., U r b a n о w s k i W., On the
thermoelastic problem in the case of bodies of any type of
curvilinear orthotropy, Bull. Acad. Pol. Sci, CI. IV 4 A956), 97.
141. Osgood W. R., Residual stresses in rnetals and metal
construction, New York, Reinhold Publ. Corp., 1954.
142. О г и б а л о в П. М., Деформация трубы под действием
внутреннего давления при переменной температуре, Инж. сб, т. 20,
1954.
143. Pa hi G., Zulassige Last- und Temperaturanderungen bei Dampf-
turbinen, Brennstoff-Warme-Kraft 9 A957), 541.
144 Панасюк В. В., Подстригая Я. С, Ярема С. Я.,
Температурю нарушения в цилиндричнш оболонщ, ДАН УРСР,
1955, № 3.
145. Р а г i a G., Stresses in an infinite strip due to a nucleus of ther-
mo-elastic strain inside it, Bull. Calcutta Math. Soc. 45 A953).
83.
146. Parkes E. W., A) The alleviation of thermal stress, Aircraft
Engng 25 A953), 51;
— B) Transient thermal stresses in wings, Aircraft Engng 25
A953), 373;
— C) Wings under repeated thermal stress, Aircraft Engng 26
A954), 402;

226
ЛИТЕРАТУРА
— D) Panels under thermal stress, Aircraft Engng 28 A956),
180;
— E) The stresses in a plate due to a local hot spot, Aircraft
Engng 29 A957), 67.
147. Parkus H., A) Ober eine Erweiterung des Hamiltonschen Prin-
zipes auf thermoelastische Vorgange, Federhofer—Girkmann—
Festschrift, стр. 295, Wien, 1950;
— B) Das Prinzip von Castigliano bei warmebeanspruchten K6r-
pern, Osterr. Bauzeitschrift 6 A951), 89;
— C) Stress in a centrally heated disk, Proc Second U. S. Nat.
Congr Appl. Meeh, 307, 1954;
— D) Spannungen beim Abkuhlen einer Kugel, Lng.-Arch. 28
A959), 251—254.
148. Peck С F., Jr., В о n e 11 i F M., Mavis F. Т., Temperature
stresses in iron work rolls Iron Steel Eng 31 A954), 45
149. Pell W. H., Thermal deflections of anisotropic thin plates,
Quart. Appl. Math. 4 A946), 27.
150. PI an tern a F. J., Konstruktive Probleme im Zusammenhang mit
dem Aufheizen Dberschall-Flugzeugen (на голландск. яз.). De
Ingenieur, 66 A954), 31.
151. Pohle F. V., Oliver H., Temperature distribution and thermal
stresses in a model of a supersonic wing, J. Aeronaut. Sci. 21
A954), 8.
152. Poritsky H., Fend F. A., Relief of thermal stresses through
creep, J. Appl. Mech., 25 A958), 589
153. Prager W., Thermal stresses in viscoelastic structures, Z. angew.
Math. Phys. 7 A956), 230 (имеется русский перевод: П р а-
гер В., Температурные напряжения в упруго-вязких
конструкциях, сб. «Механика» № 1 D1), A957), 75—81).
154. Pride R. A., Hall J. В., Jr., Transient heating effects on the
bending strength of integral aluminum-alloy box beams, NACA
Techn. Note 4205 A958).
155. Przemieniecki J. S., Transient temperature distributions and
therma] stresses in fuselage shells with bulkheads or frames,
J. Royal Aeronaut. Soc. 60 A956), 799.
156. Reissner H, Eigenspannungen und Eigenspannungsquellen, Z.
angew. Math. Mech. 11 A931), 1.
157. Roy S. K-, On the biharmonic analysis of thermal stresses
around openings in structures, Proc. First Congr. Theor. and
Appl. Mech., 125, 1955, Kharagpur, Indian Inst of Technology
158. Sadowsky M. A., Thermal shock on a circular surface of
exposure of an elastic half space, J. Appl. Mech 22 A955),
177.
159. S a 1 v a d о r i M. G.. Live load and temperature moments in shells
of rotation built into cylinders, J. Amer. Concr. Inst. 27 A955),
149.
160 Sanders W. В., Jr and Trabant E. A., An analytical
method of evaluating thermal stresses in gas-turbine blades,
Aeronaut. Engng Rev. 16 A957), 52.
161. Santini P., Thermoelastodynamik von SchalenfJugeln (на итал,
яз.), Aerotecnica 37 A957), 201.

ЛИТЕРАТУРА
227
162. Schneider P. J., Variation of maximum thermal stress in
free plates, J. Aeronaut. Sci. 22 A955), 872.
163 Schuh H., A) On the calculation of temperature distribution
and thermal stresses in parts of aircraft structures at supersonic
speeds, J. Aeronaut. Sci. 21 A954), 575;
—B) Transient temperature distributions and thermal stresses
in a skin-shear web configuration at high-speed flight for
a wide range of parameters, J. Aeronaut. Sci. 22 A955),
829.
164. Schulze H., Zur Frage der Temperaturbeanspruchung in mas-
siven Brucken, Dtsch. Eisenbahntech. 5 A957), 443, 575.
165. S e s t i n i G , Calcolo termo-meccanico delle turbazioni a vertici
compensatori di dilatazione, Termotecnica 9 A953), 399.
166. Seth B. R., Finite thermal strain in spheres and circular
cylinders, Arch. Mech., Stos. 9 A957), 633.
167. Sharma В., A) Stresses in an infinite slab due to a nucleus of
thermoelastic strain in it, Z. angew. Math. Mech. 36 A956), 75;
— B) Thermal stresses in infinite elastic disks, J. Appl. Mech.
23 A956), 527;
— C) Stresses due to a nucleus of thermoelastic strain A) in an
infinite elastic solid with spherical cavity and B) in a
solid elastic sphere, Z. angew. Math. Phys. 8 A957),
142;
— D) Thermal stresses in transversely isotropic semi-infinite
elastic solids, J. Appl. Mech. 25 A958), 87.
168. Singer J., A) The effect of amplitude on the torsional vibra*
tions of solid wings subjected to aerodynamic heating»
J. Aeronaut. Sci. 24 A957), 620;
— B) Thermal buckling of solid wings of arbitrary aspect
ratio, J. Aero Space Sci. 25 A958), 573.
169. Singer J., Hoff N. J., Effect of the change in thermal
stresses due to large deflections on the torsional rigidity of wings,
J. Aeronaut. Sci. 24 A957), 310.
170. S i n g h К Р., Centrifugal and thermal stresses in rotating discs,
Proc. First Congr. Theor. and Appl Mech., 169, 1955, Kharagpur,
Indian Inst of Technology.
171. Sobey A. J., Thermo-elastic similarity, Aircraft Engng 26
A954), 298
172. Sokolowski M., Axially-symmetrical problems of thermo-ela-
sticity for a cylinder of unlimited length. Bull. Acad. Pol. Sci.,
s techn. 6 A958), 207.
173. Stern M., Analysis of thermal stresses in conical shells, J.
Aeronaut. Sci. 22 A955), 506.
174. Sternberg E., A) Transient thermal stresses in an infinite
medium with a spherical cavity, Proc. Kon. Ned. Akad. Wetensch,
B60 A957), 396;
— B) On transient thermal stress in linear viscoelasticity, Proc.
Ill V. S. Nat. Congr. Appl. Mech., N. Y., 1958, 673—683.
175. Sternberg E, Chakravorty J G, A) On inertia effects
in a transient thermoelastic problem, Trans, ASME E26, No. 4
A959), 503—509;

228
ЛИТЕРАТУРА
— B) Thermal shock in an elastic body with a spherical
cavity, Quart. Appl. Math. 17 A959), № 2, 205—218.
176. Sternberg E., McDowell E. L., On the steady-state ther-
moelastic problem for the half-space, Quart. Appl. Math. 14
A957), 381.
177. St rub R. A, A) Distribution of mechanical and thermal stresses
in multilayer cylinders. Trans ASME 75 A953), 73;
— B) Methode generate de calcul des tensiones mecaniques et
thermiques dans les disques de profil quelconque, Bull,
techn. Suisse Rom. 80 A954), 97.
178. Suhara S., Uber die Spannungen in einer Kreisscheibe veran-
derlicher Dicke, deren Elastizitats- und Warmeausdehnungskoeffi-
zienten Funcktionen der Temperatur sind (на японск. яз.), Ргос.
Fac. Eng. Keiogijuku Univ., 1, 43 A948).
179. Sullivan W. J., Jr., Theory of aircraft structural models
subject to aerodynamic heating and external loads, NACA Techn
Note, 4115 A957).
180. Symposium on thermal fracture (Ed. by W. D. Kingery), J. Amer.
ceramic Soc. 38 A955), 1.
181. Teodorescu P. P., Uber das ebene Problem der Thermoelasti-
zitat (на рум. яз.), Bull. Sci. Acad. Rep. Pop. Romine, Sect
Mat. Fiz. IX, 471 A957).
182. Thompson A. C, Thermal stresses around a heated hole in
a large glass plate, J. Amer. ceramic. Soc. 40 A957), 244.
183. Thompson A. S., A) Stresses in rotating disks at high
temperature, J. Appl. Mech. 13 A946), 45;
— B) Thermal stress in power-producing elements, J. Aeronaut.
Sci. 19 A952), 476.
184. Thrun Z., Thermische Verformungen und Spannungen in dun-
nen Platten mit veranderlicher Dicke (на польск. яз.), Rozpr.
Inzyn. 4 A956), 523.
185. Tremmel E., A) Beitrag zum Problem der Warmespannungen
in Scheiben, Ing.-Arch. 23 A955), 159;
—B) Uber die Anwendung der Plattentheorie zur Bestimmung
von Warmespannungsfeldern, Osterr. Ing.-Arch. 11 A957),
165;
— C) Warmespannungen beim Abbinden von Massenbeton,
Osterr. Ing.-Arch. 13 A959), No. 2, 58—81.
186. T г о s t e 1 R., A) Instationare Warmespannungen in Hohlzylin-
dern mit Kreisringquerschnitt, Ing.-Arch. 24 A956), 1.
187. Trostel R, B) Instationare Warmespannungen in einer Hohl-
kugel, Ing.-Arch. 24 A956), 373;
— C) Warmespannungen in Hohlzylindern mit temperaturabhan-
gigen Stoffwerten, Ing.-Arch. 26 A958), 134.
188. Van der Linden С. А. М., Thermal stresses in a plate
containing two circular holes of equal radius, the boundaries of
which are kept at different temperatures, Appl. Sci. Res (A)
6 A956), 117.
189. Винокуров С. Г., Температурные напряжения в пластинках
и оболочках, Изв. Казанского филиала АН СССР, Сер. физ.-
мат. и технич. н., 3 A953), № 18*

ЛИТЕРАТУРА
229
190. V о s t e e n L. F., Fuller К. Е , Behavior of a cantilever plate
under rapid heating conditions, NACA Res. Mem., RML 55 E 20
C, 1955.
191. Wahl A. M, Stress distribution in totating disks subjected
to creep, including effects of variable thickness and temperature,
A. S. M. E. Ann. Meet. New York, 1956, Pap. 56A—162.
192. Wang A. J., Prager W., Thermal and creep effects in work —
hardening elastic-plastic solids, J. Aeronaut. Sci. 21 A954), 343.
(имеется русский перевод в сборнике «Механика», ИЛ).
193. We g ner U., Zwei Probleme der Elastizitatstheorie, Z. angew.
Math. Mech. 33 A953), 300.
194. Weiner J. H., A) An elastoplastic thermal-strees analysis of
a free plate, J. Appl. Mech. 23 A956), 395;
— B) A uniqueness theorem for the coupled thermoelastic
problem, Quart. Appl. Math. 15 A957), 102.
195. W i 11 a m s M. L., Large deflection analysis for a plate strip
subjected to normal pressure and heating J. Appl. Mech. 22 A955),
458.
196. Z e n d e r G. W., Pride R. A., The combirrations of thermal and
load stresses for the onset of permanent buckling in plates,
NACA Techn. Note, 4053 A957).
197. Z о 11 e r K., Warmespannungen beim Anheizen von Kesseltrom-
meln, Ing-Arch. 23 A955), 51.
198. Zorski H., A) On a certain property of thermoelastic media,
Bull. Acad. Pol. Sci., s. techn. 6 A958), 327;
— B) Singular solutions for thermoelastic media, Bull. Acad. Pol.
Sci., s. techn. 6 A958), 331.
199. Z u k W., Thermal buckling of clamped cylindrical shells, J.
Aeronaut. Sci. 24 A957), 389.
200. Z w i с k S. A., Thermal stresses in an infinite, hollow
case-bonded cylinder, Jet Propulsion 27 A957), 872.

ПРИЛОЖЕНИЕ
Г. Паркус
О поле температуры при случайном распределении
температуры на поверхности ])
При решении задач теплопроводности источники тепла,
которые могут располагаться внутри тела или на его
поверхности, обычно считаются детерминированными функциями
места и времени. Это предположение применимо не всегда.
Если, например, тело движется в турбулентном потоке
воздуха, то течение в известных пределах носит случайный
характер. Переносимое на тело количество теплоты, которое
возникает вследствие сжимаемости и вязкости воздуха, будет
при этом также случайной функцией.
Цель настоящей работы состоит в выводе некоторых
зависимостей для поля температуры2). Для определенности
введем некоторые ограничения. Прежде всего мы будем
иметь дело с однородным, изотропным телом, тепловые
свойства которого не зависят от температуры. Далее
предположим, что тепло подводится только к поверхности тела
и, наконец, примем, что этот подвод тепла представляет
собой стационарный, случайный процесс.
Пусть тело в момент времени t0 всюду имеет
температуру* 7" = 0, а на его поверхности при t > t0 происходит
теплообмен со средой, имеющей температуру 6. Тогда для
любой точки тела Р(х, у, z) температуру Т в момент
времени t можно представить с помощью соответствующей
1) Parkus H., Temperaturfelder bei zufallsabhangiger Ober-
flachentemperatur. Anz. Oesterr. Akademie <i Wissenschaften 98
A961), 153.
2) Математическая основа применяемого здесь метода изложена
в работе Моэла ['J. Приложения освещены в работе Богданова и
Гольдберга [2\.

СЛУЧАЙНОЕ РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НА ПОВЕРХНОСТИ 231
функции Грина Т (Q, Р, t — т) в форме
t
A)
Здесь О обозначает поверхность тела, Q(?, т), С) — точку на
д
этой поверхности, а -^ производную в направлении
внешней положительной нормали к поверхности. Функция Грина
определяется как температура в точке Q в момент времени t,
вызванная действием мгновенного источника интенсивности 1,
находящегося в момент времени т в точке Р. Пусть Т будет
решением уравнения теплопроводности
B)
вида
регулярная функция, C)
где
удовлетворяет условию на границе
D)
При очень больших значениях коэффициента теплообмена,
h—>оо, температура поверхности стремится к температуре 0
окружающей среды.
Пусть теперь температура 0 представляет собой
стационарную или, по крайней мере, слабо стационарную
случайную функцию 1). Вследствие линейности задачи среднее
значение (математическое ожидание) этой функции можно, не
нарушая общности, приравнять нулю. Тогда согласно A)
будет равна нулю и величина математического ожидания
температуры тела в каждой его точке
М [Т (Р, 01 = 0. E)
1) Существование интеграла A) зависит от корреляционной
функции от 0 (см. [2] или [3]).

232
ПРИЛОЖЕНИЕ
Далее примем, что 6 можно представить в виде
произведения (или суммы произведений) типа
F)
При этом F и G могут быть в общем случае случайными
функциями. В дальнейшем мы будем, однако, считать F (Q)
детерминированной функцией. Тогда для корреляционной
функции имеем
G)
где /?0(т) является корреляционной функцией G (t). Тогда
с помощью уравнения A) для корреляционной функции
температуры внутри тела получим
(8)
причем
(9)
Двумя практически важными видами корреляционных
функций являются
(Ю)
(И)
где 8(лг) обозначает дельта-функцию Дирака.
Корреляционная функция вида A0) носит название белого шума. Он
соответствует полностью случайному процессу, при котором
не существует корреляции между значениями функции,
относящимися к двум различным моментам времени. Функция
вида A1) очень удобна для вычислений и может, например,
служить хорошим приближением для описания атмосферной
турбулентности. Подставляя A0) и A1) в (9), получим
A2)

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 233
или
?/0). A3)
При известных средней величине и корреляционной функции
распределение температуры в смысле корреляционной теории
рассматривается как известное.
При /0 > — со следует воспользоваться преобразованием
Лапласа. Разумеется, в этом случае надо прибегнуть уже
не к обычному, а к так называемому двойному или
двумерному преобразованию [5].
Проблеме определения поля напряжений, связанных с
полученным температурным полем, посвящается отдельная
работа.
ЛИТЕРАТУРА
1. Mohal J. Е., Stochastic Processes and Statistical Physics, Jotirn.
Roy. Statist. Soc, Ser. B, XI 2 A949), 150.
2. Bogdanoff J. L., G о i d d e г g J. E., On the Bernoulli — Euler
Beam Theory with Random Excitation, Journ. Aero/Space Sc. 27,
371 A960).
3. Carslaw H. S., Jaeger J. C, Conduction of Heat in Solids,
2 изд., Oxford, § 14, 1 A959).
4. Я г л о м А. М., Введение в теорию стационарных случайных
функций. Успехи матем. наук, A952).
5. Voelker D., Doetsch G., Die zweidimensionale-Transforma-
tion, Basel, 1950.
Г. Паркус
Тепловые напряжения при случайно меняющейся
температуре поверхности 1)
В предыдущей работе I1) были получены основные
зависимости для полей температур в твердом теле в случае,
когда температура на поверхности тела представляет собой
некоторую случайную функцию. При этом отмечалось, что
l) Park us H., Ternperaturspannungen bei. Zufallabhongiger
Oberflachentemperatur. ZAMM, 1962, № 6.

234
ПРИЛОЖЕНИЕ
для исследования таких полей и для определения
соответствующих им напряжений оказывается особенно удобным метод
преобразования Лапласа. В этом случае приходится иметь
дело с так называемым двойным преобразованием.
В данной статье этот вопрос трактуется более подробно.
I. Основные уравнения
На упругое тело, начальная температура Т которого
всюду равна нулю, начиная с момента t — О, действует
поверхностная температура О (Q, t), где через Q обозначена
любая точка поверхности О. Пусть внутри тела нет
источников тепла, а деформация на поверхности тела не стеснена
никакими условиями. Внешние силы могут не существовать.
Для температуры Т(Р, t) в любой точке тела имеем
A21. § 14. A))
* _
Т(Р, l) = —afd*§HQ, x) dT(Q'^f~x) dO, (l)
U
где Т—функция Грина, п — внешняя положительная нормаль
к поверхности и а — коэффициент теплопроводности.
Применив к A) преобразование Лапласа и обозначив через F* (s)
преобразованную функцию F (t), согласно теореме
свертывания получим
Г (Р, s) = — a§ G* (Q, s) ^^'/'^ dO. B)
Для термоупругого поля напряжений al (P, t) с
преобразованием с* (Р, s) получается аналогичное выражение [3]
о;. (Р, s) = -1 е* (q, s) Р;у (p. q. s) do. C)
где Pij(P, Q, t) означает напряжение в точке Я, которое
в момент ? = 0 создается находящимся в точке Q
мгновенным диполем с интенсивностью а. Ось диполя предполагается
совпадающей с нормалью к поверхности.
Пусть температура поверхности представляет собой
случайную функцию, которая может быть представлена в виде
D)

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 235
При этом как F, так и О могут быть случайными функциями.
В дальнейшем, однако, будем считать F (Q)
детерминированной заданной функцией. Предполагаем далее, что
математическое ожидание G (t) равно нулю:
E)
Тогда согласно B) и C) математическое ожидание
температуры и напряжения также равно нулю в каждой точке.
В самом деле, для любой случайной функции x(t) имеем
F)
Существование преобразования по Лапласу х*($) зависит
от корреляционной функции x(t).
Выведем теперь соотношение между корреляционной
функцией Rx(tv t2) случайного процесса x(t) и
корреляционной функцией Rx* (Sh S2) его преобразования по Лапласу x*(s).
Имеем
G)
где
(8)
(9)
Двойной интеграл в (8) представляет собой так называемое
двумерное или двойное преобразование по Лапласу
функции Rx{tv t2). Обозначив это преобразование двумя
звездочками, получим следующее важное соотношение:
A0)

236
ПРИЛОЖЕНИЕ
В частности, если x*(t)— стационарная или, по меньшей
мере, слабо стационарная случайная функция (причем x(t)==-0
при t < 0), то при (tv t2) > 0 имеем
Rx(tvt2) = R(*z). x = \t2 — tx\. (И)
Если обозначить через R* (s) преобразованную по Лапласу
функцию R(t), то немедленно получаем (см., например, [4])
A2)
Существование R* (s) достаточно для существования х* (s)
(СМ. [^6]).
Подставим теперь в формулу C) выражение D) для
температуры поверхности и построим корреляционную функцию
или, используя G) и обозначив через RG(tv t2)
корреляционную функцию для G (t):
A3)
Аналогичное выражение для поля температуры получается
из равенства B).
Во многих практически важных случаях можно
рассматривать случайную функцию G (t) как стационарную. Две часто
применяемые корреляционные функции будут тогда
ЯС0 = 8(*) (Н)
и
R(x) = e~x\ т>0, A5)
где §(т) означает дельта-функцию Дирака. Корреляционная
функция типа A4) называется белым шумом.
Соответствующая вариация /?@), разумеется, неограниченна, что
следует учитывать при физической интерпретации результатов.

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 237
Если A4) подставить в (8), обозначив т = |?2 — tx\, то
получим
Гаким образом,
Учитывая, что /?*($)=—г—, из A5) и A2) имеем
A4a)
A5a)
Формула A3) переходит в зависимость
A4Ь)
для белого шума и в соотношение
A5b)
для экспоненциальной корреляционной функции A5). Обрат-
ное преобразование (см. [4], формулы (А2-76) и (А4-42))
для A4Ь) дает окончательно
A4с)
и для A5Ь)
(^2>/1). A5с)
На основании упруго-вязкоупругой аналогии (см. [3],
раздел VI, п. 3) выведенные соотношения имеют силу и для

238
ПРИЛОЖЕНИЕ
вязкоупругих материалов, если их свойства не зависят от
температуры. Нужно лишь заменить в выражениях(A3) для р*.
упругие константы на соответствующие функции, зависящие
от s. Обратимся теперь к некоторым примерам применения
полученных результатов.
И. Вязкоупругое полупространство
Пусть температура б (t) поверхности z = 0
полупространства z^O не зависит от положения. Тогда для
преобразованных по Лапласу упругих компонент напряжения
имеем (см. [3], уравнение (III,6))
«*h=ей*=-2 т^GaT* <*¦ *>¦ (а,=°- <16)
Действительные напряжения определяются теперь на основе
упруго-вязкоупругой аналогии. В случае линейного, так
называемого «нормального материала», у которого зависимость
между напряжениями [3] и деформациями имеет вид ([3],
уравнение C,6))
A7)
где stj и etj — компоненты вектора напряжений и
деформации, а а и е — соответственно среднее нормальное
напряжение и среднее удлинение, согласно аналогии получим
A8)
Для поля температур имеем
ТЦг, s) = Q*{s)e r a. A9)

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 239
Пусть температура поверхности 8 (t) стационарна при / > О
и имеет корреляционную функцию A5), так что
#е(х) = Се-*1Ч B0)
Тогда внутри тела
r7(z, si. s2) = M[T*(z, s})T*(z, s2)) =
==ехр[-^(|/"^+уЛ^-)]/?ГEь s$.
Учитывая равенство A5а), получим
R*T\z, slt s2) = c(l +_^_)d*(*, Sl)D*(z. s2), B1)
где
B2)
Согласно уравнению A8) отсюда для преобразованной по
Лапласу корреляционной функции поля напряжений находим
ЯГ(*. su s2) = k(\ +-j^~)B4z, sJBUz, s2), B3)
где
B4)
В*(z, s)—il+yi)(l+ M) + 2A -2fx) (*2 + V) D*{Z' S)' I
Обратное преобразование выражения B2) дает (см. [7],
стр. 246)
Здесь
B5)
B6)
a Re означает действительную часть. Для обратного
преобразования В* (z, s) необходимо сперва воспользоваться
разложением на отдельные дроби
. B7)

240
ПРИЛОЖЕНИЕ
где обозначено
B8)
Отсюда немедленно следует
B(-z' () = A + ц)», + 2 A - (i) »3 'X=T-YX
X [(&,— ^3)е"-х'КеФB:, х, 0 — (&2 — х&з)*~" Яеф (*> >•> 01-
B9)
Согласно уравнению A5с) этим определяются
корреляционные функции поля температуры и напряжений.
Входящий в уравнение A5с) интеграл нельзя представить
в замкнутой форме. Однако в некоторых частных случаях
для R0 (я, tv t2) можно дать приближенные выражения. Для
этого целесообразно использовать следующее соотношение:
о
= L-l<G\s)e"st7 j H{t)esidt\, t2^tv C0)
где H(t) и G (t) — две любые /,-функции. Соотношение C0)
получается при двойном /,-преобразовании {[4], формула
(А4-42)}, если просто произвести обратное преобразование.
Рассмотрим теперь случай, когда момент времени tx близок
к нулю, тогда как момент t2 очень велик. Пусть
так что
о

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 241
Тогда получим
После подстановки в уравнение C0) и обратного
преобразования с учетом, что
согласно уравнению A5с), окончательно получим
C1)
Для чисто упругого (гуковского) тела Ьх = &3 = 0, &2= 1,
для максвелловского тела Ьх — Ьъ — Ь, ft2 = 0 и кельей-
новского тела frj —0, d2=l, ft3 = fr. Постоянный
множитель в уравнении C1) имеет вид
Гук,
Максвелл, C2)
Кельвин,

242
Приложение
При tl = t2 = t для вариации поля напряжений, согласно
уравнению A5с), имеем
C3)
где B(z, t) определяется при помощи равенства B9).
Числовые результаты. Выражение C3) для мощности
было определено численно для материала, подчиняющегося
закону Гука. Результаты с точностью до множителя
пропорциональности справедливы также для поля температуры.
Рис. 35.
Если в уравнении B9) положить 9^1 = ^3 == ^> &2 — 1» т0
оно перейдет в зависимость
В безразмерных переменных
C4)

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 243
уравнение принимает вид
C5)
причем
/ (х) = e-x2 Re [е2и'У erfc (у + ix)] = е~У2и (х, у). C6)
Функции и(х, у) табулированы ([2], стр. 486).
Рис. 36.
На рис. 35 изображен график функции хр(х) для
различных значений х. Подсчитанное на основании этой
функции изменение рассеивания yRa(z, t, t) по глубине
полупространства для различных моментов времени представлено
на рис. 36.
III. Упругий круглый цилиндр
Бесконечно длинный цилиндр радиуса R при t < 0 имеет
всюду нулевую температуру. При t > О температура на
поверхности г =z R дается в виде
6(Q, t) = TQ(f)ei№* (л=1. 2, 3 ...). C7)

244
ПРИЛОЖЕНИЕ
где ср—полярный угол, a T0(t) — случайная функция. Тогда
L — преобразование температуры внутри тела будет (см. [3],
уравнение (II, 107))
C8)
Если корреляционная функция для T0(t) вновь задается
уравнением B0), то, как и прежде, будет
где
C9)
D0)
Обратное преобразование этого выражения получается при
помощи комплексного обратного интеграла и использовании
теоремы о вычетах. После длительных промежуточных
выкладок получим
/и = 1
где
D1)
D2)
а рт — положительные корни уравнения
D3)
Воспользовавшись равенствами A5Ь) и A5с), теперь можно
получить корреляционную функцию. Появляющийся при этом

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 245
интеграл может быть вычислен путем замены
интегрирования суммированием и окончательно для tx = t, /2 = ^-|-&
получается
RT(r, cp, t, t + b) = Ce2i^lg2(r)e-^-+-
оо
+ 2т*@ J ка(г)(е-т*+е-")[^ +
т = \ т
оо оо
W m«l 1 = 1
Xf_^_ + (l *)e-<*»+W]\. D4)
L <% + <** V *m + *l/ JJ
При 0 = 0 отсюда получается мощность температурного
поля.
Расчет соответствующих величин для поля напряжений
существенно сложнее. Ниже он намечается лишь в общих
чертах. В качестве отправного пункта удобно выбрать
термоупругий потенциал. Для него можно положить (см. [3],
стр. 10 и 14)
t
Ф = |=Ь^аа f Tdt.
о
^-преобразование и подстановка значения Г* из C8) дает
D5)
Вычисленные отсюда с помощью известных формул (см. [3],
стр. 66) компоненты напряжения не удовлетворяют, однако,
граничным условиям на цилиндрической поверхности. На
цилиндрической поверхности получаются следующие радиальные

246
ПРИЛОЖЕНИЕ
нормальные и касательные напряжения:
D6)
где
D7)
Поэтому на решение необходимо наложить второе,
«свободное от температуры» напряженное состояние, которое
уничтожит напряжения D6) на поверхности. Его можно получить
из функции напряжений Эри, которая задается в виде (см. [3],
стр. 61)
D8)
где р = r/R. На поверхности р -— 1 соответствующие радиаль
ные и касательные напряжения равны
D9)
Приравняв эти выражения соответствующим выражениям D6),
получим два уравнения для определения А*п и В*п. Таким
образом, определяется напряженное состояние в
пространстве изображений, а отсюда и корреляционная функция
R?)(r, ?, sv s2) = M[o*u(r, cp, sj-a'ulr, cp, s2)l E0)
соответствующая каждой компоненте напряжения. При
обратном преобразовании возникают значительные трудности, и

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 247
оно приводит к чрезвычайно сложным выражениям. Поэтому
приходится прибегнуть к числовым методам, аналогичным
методам, применяемым при одинарном преобразовании
Лапласа *).
Числовые результаты. Для поля температуры с
круговой симметрией определена мощность на оси цилиндра г = 0.
Сначала из уравнения D2) находим
Если теперь положить ^ = т:, то единственным параметром,
входящим в уравнения, будет f. Примем, что ^ = 0,1.
2 3 4 5
Рис. 37.
На рис. 37 показана зависимость функции DQ@, t) от
времени согласно уравнению D1) и мощность RT @, t, t)
согласно ^уравнению D4). Можно видеть, что практически
в интервале времени т = 8 наступит стационарное состояние.
*)Papoulis A, A new method of inversion of the Laplace
transform, Quart, Appl. Math. 14, 405 A957).

248
ПРИЛОЖЕНИЕ
IV. Упругое полупространство.
Динамическое исследование
До сих пор рассматривались квазистатические процессы,
то-есть предполагалось, что в уравнениях движения можно
пренебрегать инерционными членами. В дальнейшем
откажемся от этого допущения.
Пусть, как и в разделе II, температура на поверхности
при t > О задана в виде 0 (t). Тогда, поскольку не
принимается во внимание взаимное влияние полей температуры и
напряжений, для распределения температуры внутри
полупространства можно воспользоваться уравнением A9). Однако
для компоненты напряжения огг вместо уравнения A6)
получится
где
— скорость волн расширения в упругой среде и
Р = ^^27пт"- E2>
а
Для двух других составляющих напряжения имеем
Из граничного условия o^ = 0 на поверхности z = 0
полупространства определяется постоянная k и отсюда
E4)
Теперь можно определить корреляционную функцию для о.
в пространстве изображений. Из уравнения G\ находим
E5)

ТЕПЛОВЫЕ НАПРЯЖЕНИЯ ПРИ МЕНЯЮЩЕЙСЯ ТЕМПЕРАТУРЕ 249
Если вновь предположить, что /?9 имеет частный вид B0),
то уравнение E5) переходит в зависимость
2х
где
E7)
Оригинал функции B*(z, s) имеет вид (см. [7], стр. 246
и 242).
E8)
При этом
E9)
Функция Ф определяется из равенства B6), тогда как для ф
имеем
Уравнение A5с) дает корреляционную функцию
F0)
F1)
Вычисление интегралов в каждом конкретном случае следует
производить числовым методом.

250
ПРИЛОЖЕНИЕ
Для корреляционной функции составляющей напряжения ахх
из уравнения E3) находим
Rx (*- *v *2> = A_\J № (*> *v *д — #4* №zt (z. *v t2) +
+ Rtz(*' *v t2)]+{E*?RT{z. tv t2)). F2)
Здесь Rz дается формулой F1), a RT согласно равенствам
B1) и B5) имеет вид
t2>tv F3)
Для RzT получаем
R7r(z, sv s2)=VcR[\ +-^y#*0z, sx).&(z. s2).
причем D* находится согласно равенству B2). После
обратного преобразования имеем
F4)
где В определяется из уравнения E8), a D — из равенства B5).
Для взаимно корреляционной функции составляющих
напряжений а и а окончательно находим
F5)
В этом случае, как в разделе И, можно в некоторых
частных случаях получить приближенные зависимости для
выражений F1), F3), F4). Ход выкладок остается тем же.

ЛИТЕРАТУРА
251
ЛИТЕРАТУРА
1. Parkus H., Temperaturfelder bei zufallsabhangiger Oberflachen-
temperatur, Anz. Oesterr. Akademie d. Wissenschaften, 98 A961),
153.
2. С a r s 1 a w H. S., Jaeger J. C, Conduction of Heat in Solids,
2 Aufl, Oxford, 1959.
3. Parkus H., Instationare Warmespannungen, Wien, 1959.
4. Voelker D., Doetsch G. Die zweidimensionale Laplacetransfor-
mation, Basel, 1950.
5. Яглом А. M., Введение в теорию стационарных случайных
функций. Успехи матем. наук.
6. М о h а 1 J. E., Stochastic Processes and Statistical Physics, J. Roy.
Statist. Soc, Ser. B, 2 A949), S. 161 ff.
7. E r d ё 1 у i et al., Integral transforms, I, New York, 1954.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аналогия Алфрея 168
— вязкоупругая 168, 237
Балка, ее изгибные колебания 155
Время запаздывания 165
— релаксации 165
Вязкость 164, 165
Гипотеза Дюамеля 9,26
Девиатор деформаций 163
— напряжений 163
Дельта-функция 39
Диполь тепловой 33, 37
Диск 27, 99, 120, 148, 199
Закон вязкости Ньютона 164
— Гука 10, 164
Законы реологические 163
Источник тепловой 36, 96, 106, 108,
НО, 113, 116, 139, 146, 148
мгновенный 23, 31, 33, 34, 100,
138
Координаты сферические 11, 22
— цилиндрические 10, 21
Материалы вязкоуиругие 162
— идеально пластические 181
— упруго-пластические 180
Напряжения остаточные
(собственные) 180, 190, 199, 205, 212
Пластинка 154, 206, 214
Поле температурное вращающееся
120
квазистационарное 172
стационарное 172
Полость сферическая 49, 140, 175
Полупространство 34, 37, 41, 105, 113,
115, 129, 135, 174, 238, 248
Потенциал запаздывающий 128
— перемещений термовязкоупругий 171
термоупругий 21
— пластический 184
— упругий 13
Преобразование Лапласа 28, 43, 46,
233, 235
Принцип виртуальных перемещений
14
сил 17
—Гамильтона 14, 16
Принцип Даламбера 13. 14
— Дирихле 16
— Кастильяно 16, 18
— минимума дополнительной энергии
16
потенциальной энергии 16
Распределение температуры на
поверхности тела случайное 230, 233
Состояние деформационное плоское
22, 27
— напряженное плоское 22, 27
Среда Гука 164, 167
— Кельвина 164, 165, 167, 177
— линейно упругая 164
— Максвелла 164, 165, 167, 176
— Фойхта 164
Тело жесткое 183
— идеально пластическое 181
— нормальное 167
Теорема единственности Кирхгофа 19
— Кастильяно 18
Теплопередача, ее уравнение 26, 27,
112
Течение вязкое 162
Труба толстостенная 173, 193
Удар тепловой 126, 129, 130, 135, 151, 156
Уравнение волновое 127
— Генки 183, 184
— Леви — Мизеса 183, 184
— Прандтля — Рейса 182, 184
Условие Губера — Мизеса 180
— текучести 180, 185
Функция Гаусса дополнительная 31,
36
— Грина 23, 32
— напряжений Лява 35, 38—44, 58,
67
— Хевисайда единичная 137
Цилиндр круглый 54, 64, 67, 74, 79,
82, 87, 243
Шар 94, 186
Шум белый 236
Энергия деформации 1.'
— дополнительная 18
— потенциальная 13
— тела свободная 14