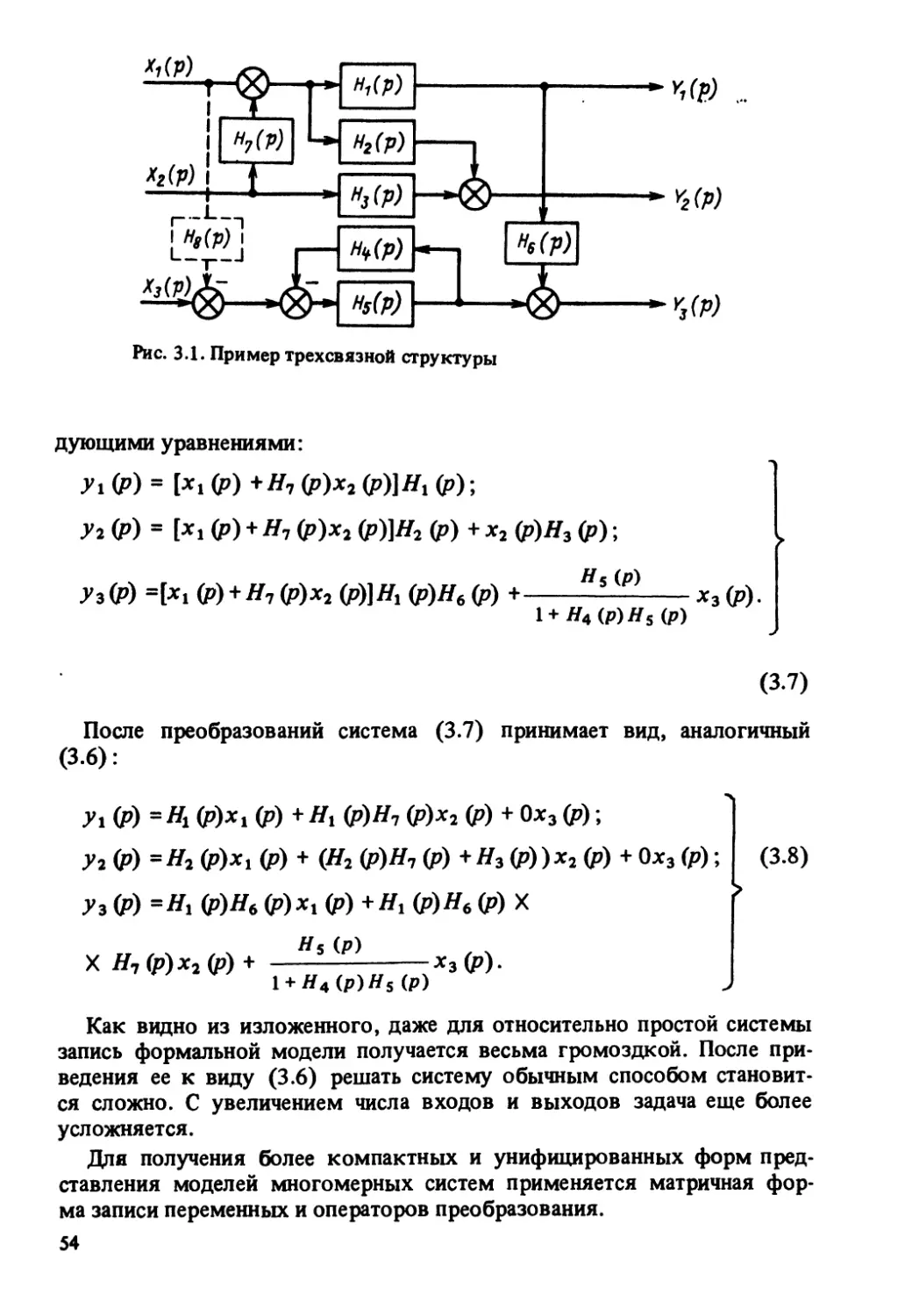
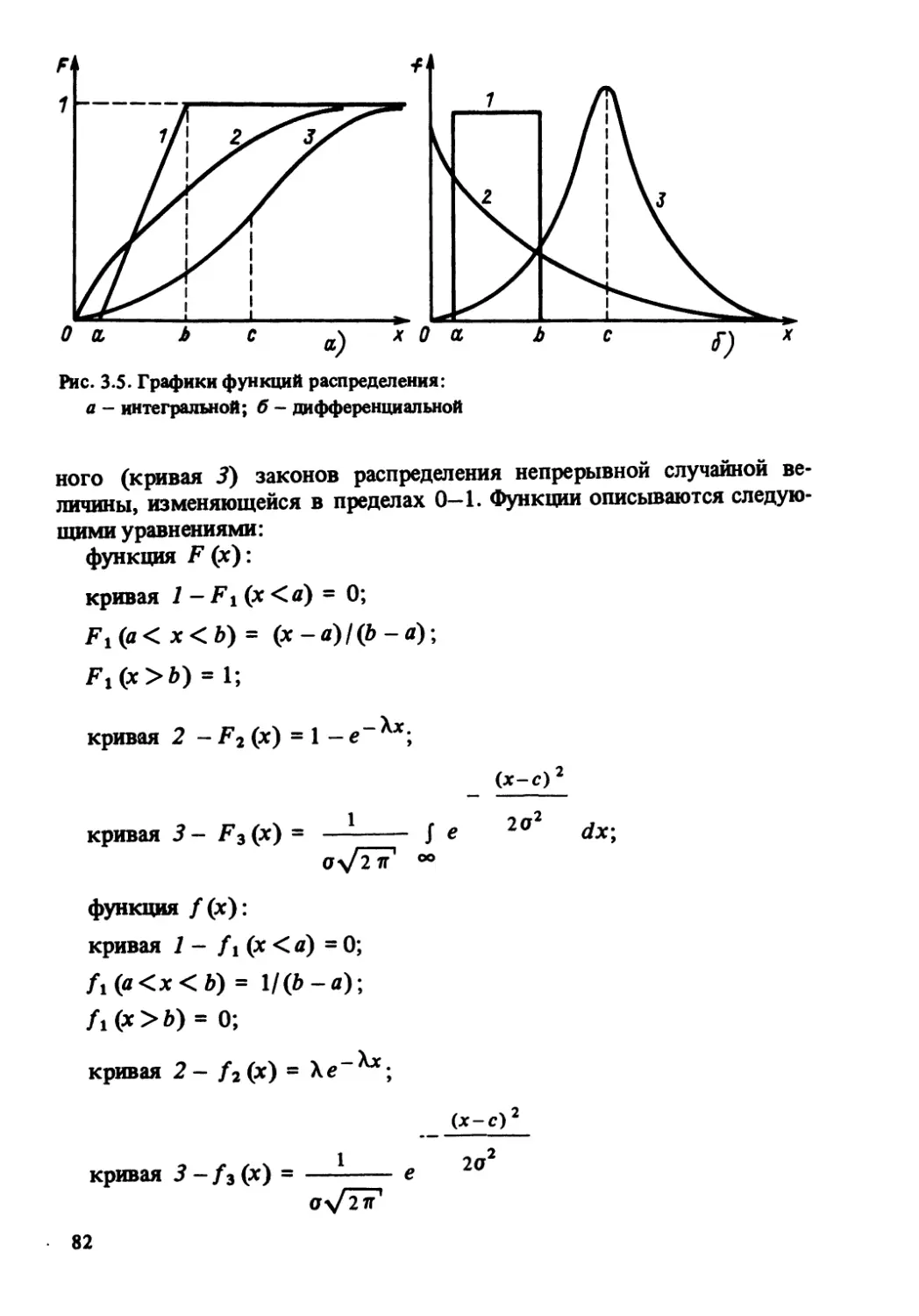
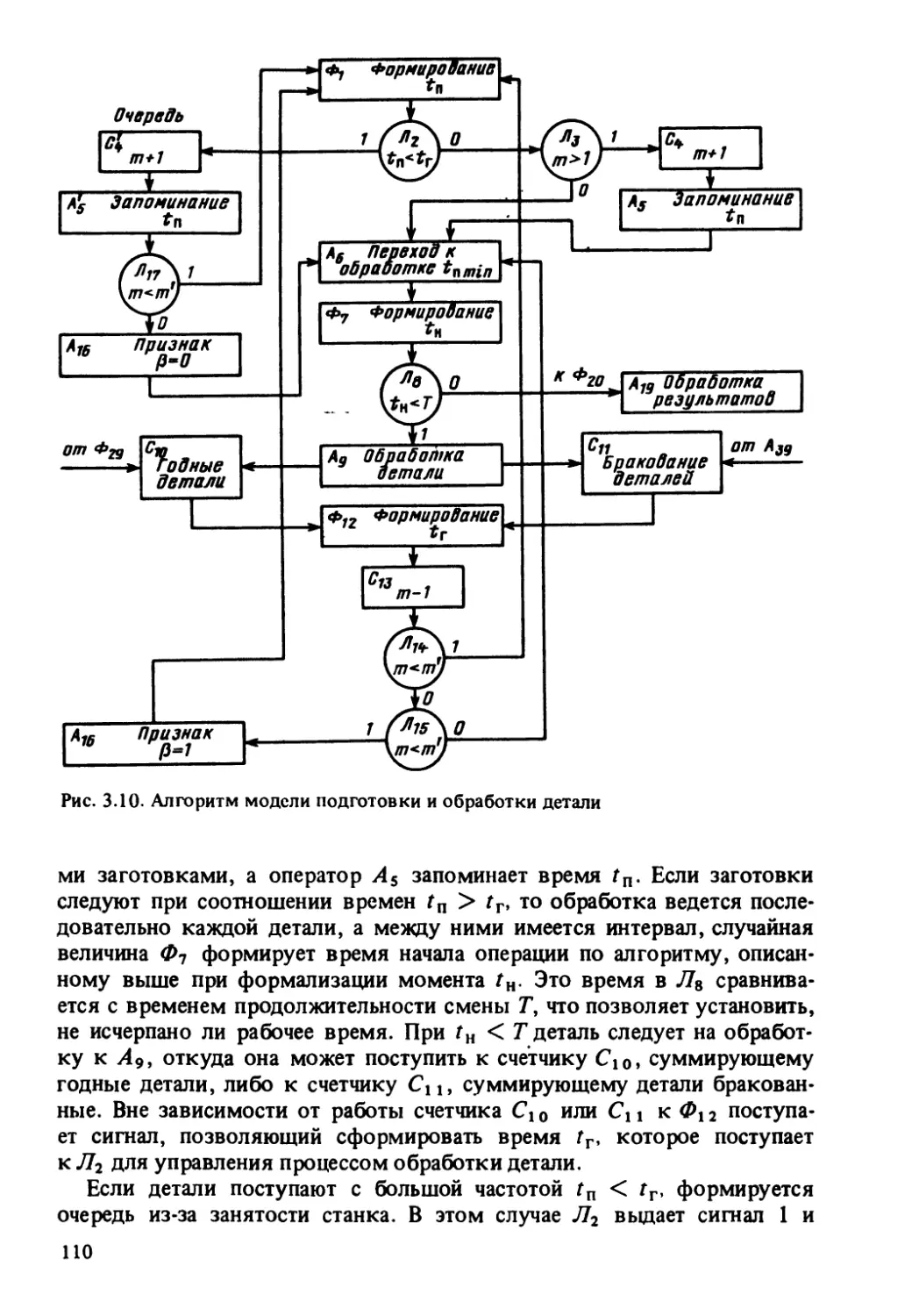
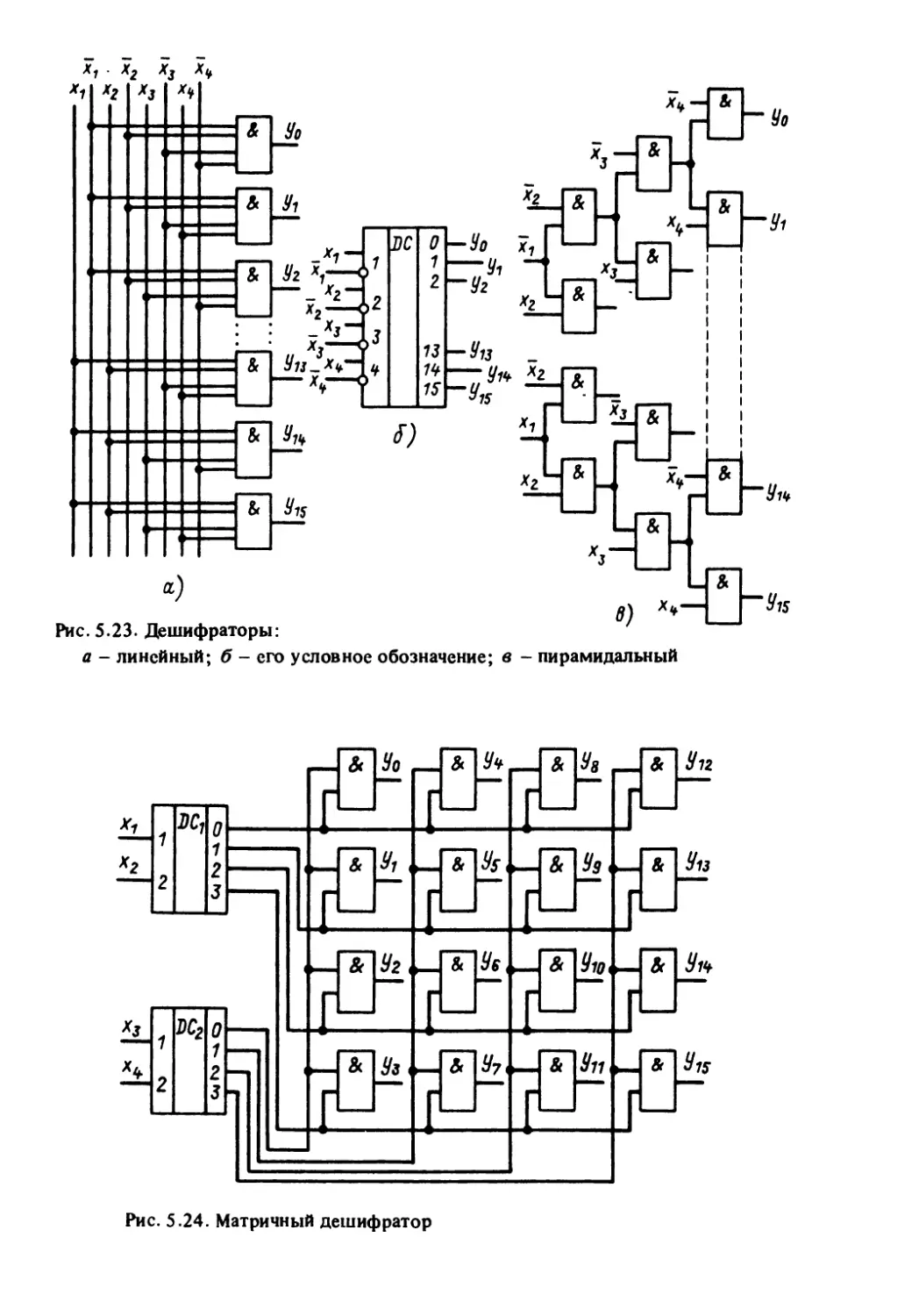
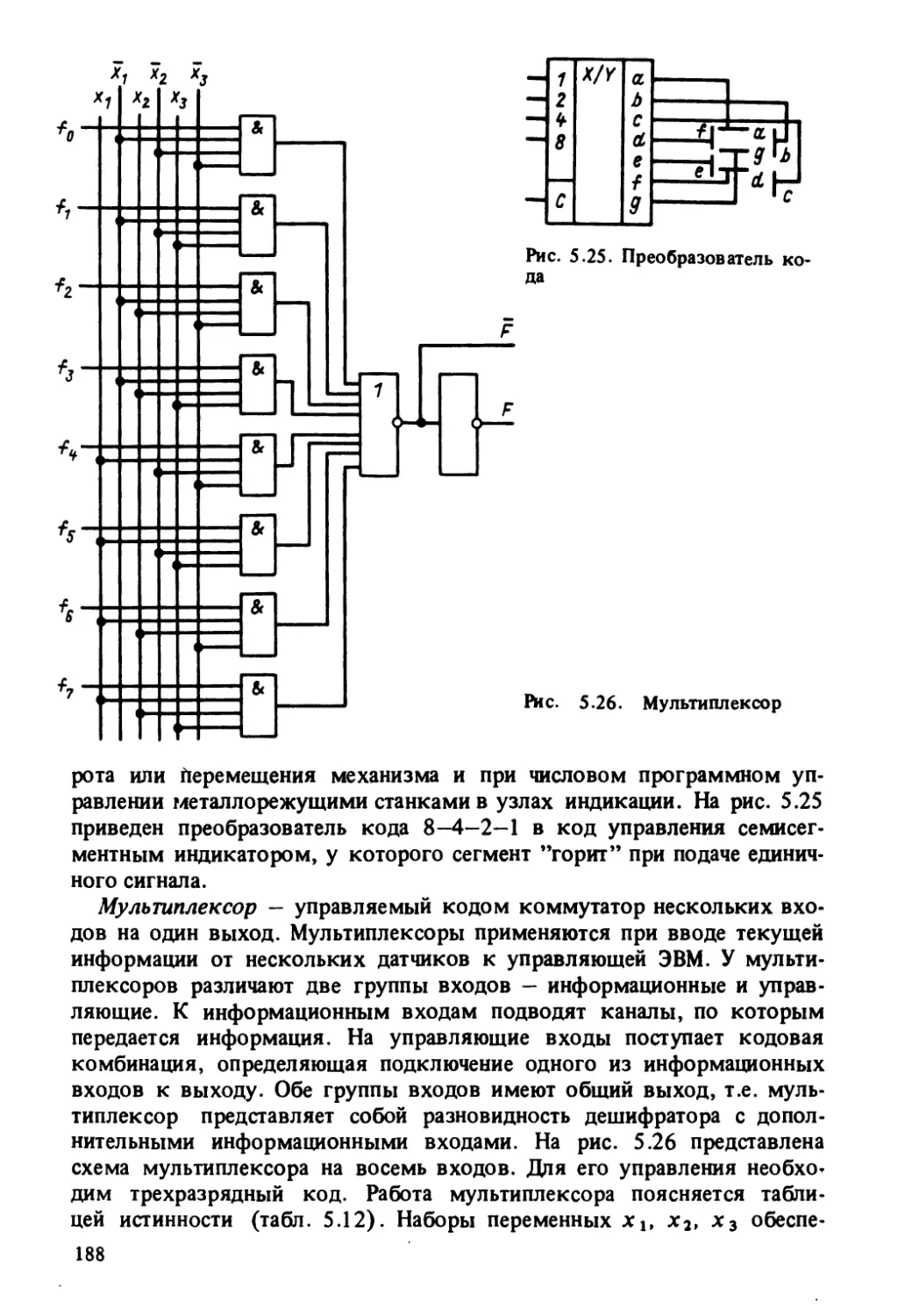
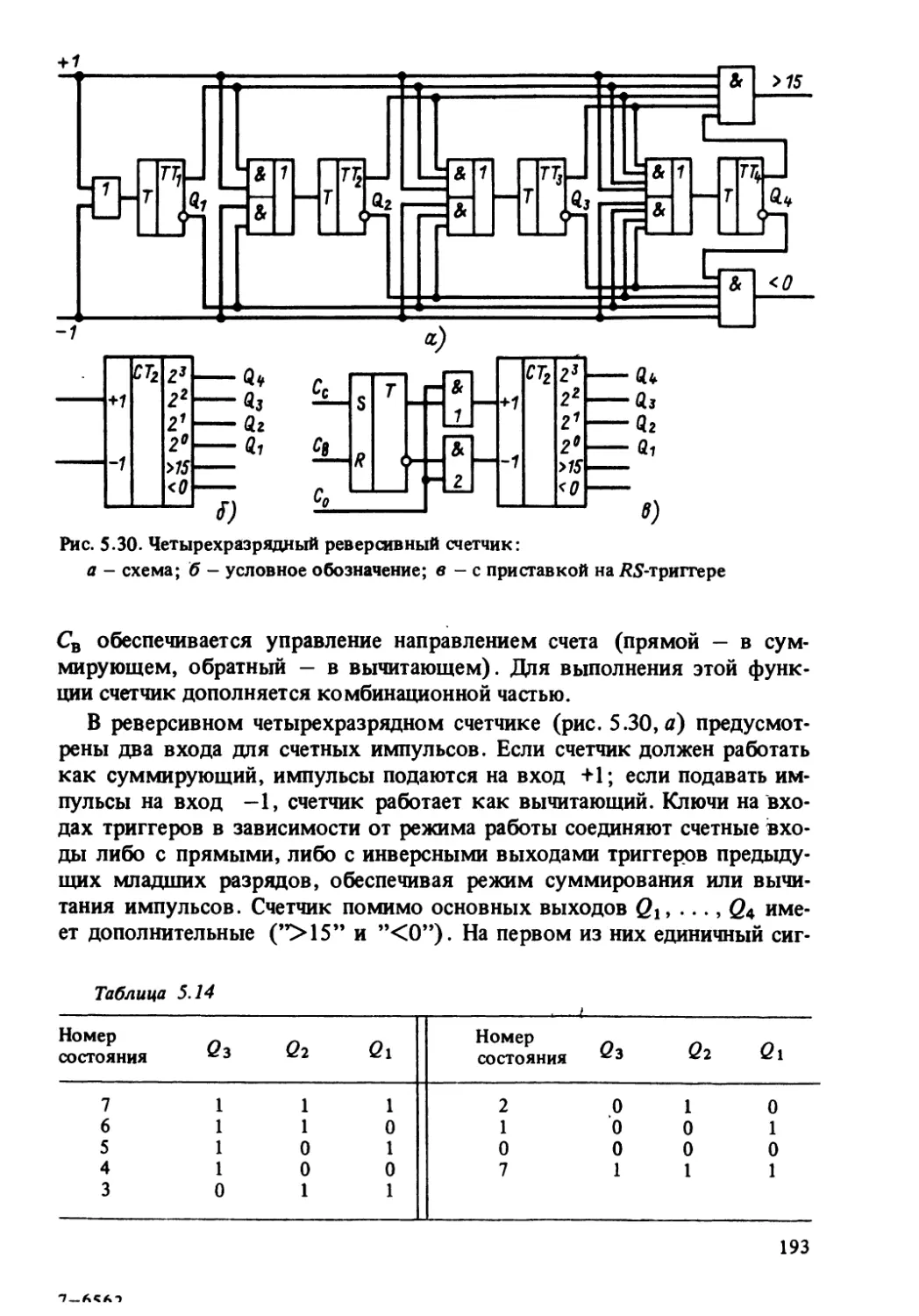
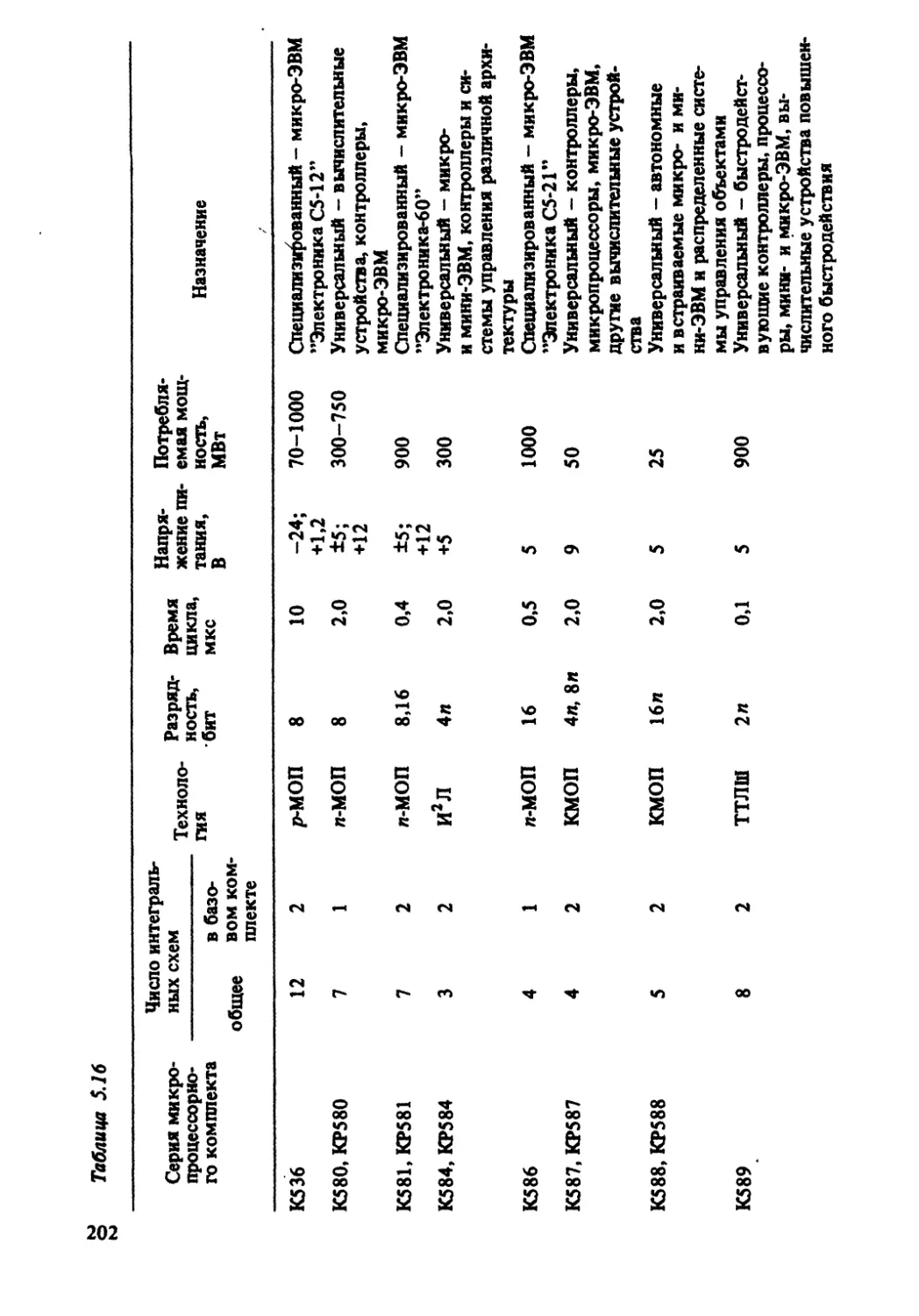
Автор: Корытин А.М.
Теги: автоматика системы автоматического управления и регулирования интеллектуальная техника технология управления оборудование систем управления техническая кибернетика электроэнергетика электротехника технологические процессы сбор и преобразования технической информации
ISBN: 5-283-00506-2
Год: 1988
АВТОМАТИЗАЦИЯ
ТИПОВЫХ
ТЕХНОЛОГИЧЕСКИХ
ПРОЦЕССОВ
И УСТАНОВОК
Для студентов вузов
ББК 31.291
А22
УДК 681.51(075.8)
Рецензенты: кафедра автоматизированного электропривода Мос-
ковского энергетического ин-та (зав. кафедрой проф. Н.Ф. Ильинский),
проф. В.Г. Созонов
Автоматизация типовых технологических процессов и уста-
А22 новок: Учебник для вузов/А.М. Корытин, Н.К. Петров, С.Н. Ра-
димов, Н.К. Шапарев. -2-е изд., перераб. и доп. - М.: Энерго-
атомиздат, 1988.—432 с.: ил.
ISBN 5-283-00506-2
Рассмотрены принципы построения автоматизированных систем уп-
равления технологическими процессами (АСУ ТП). Показаны место и
роль электропривода в АСУ ТП, отражены вопросы сбора и преобразо-
вания технологической инф'ТЧАЦнн Первое издание вышло в 1980 г.
в издательстве ”Вища школа”. Настоящее издание переработано в соот-
ветствии с новой программой.
Для студентов вузов специальности ’’Электропривод и автоматиза-
ция промышленных установок и технологических комплексов”, может
быть полезен студентам и других специальностей.
А 2302050000497 ББК 31.291
А----------------193-88
051(01) -88
Учебник
[Корытин Александр Михайлович,! Петров Николай Константинович,
Радимов Сергей Николаевич, Шапарев Николай Константинович
АВТОМАТИЗАЦИЯ ТИПОВЫХ ТЕХНОЛОГИЧЕСКИХ
ПРОЦЕССОВ И УСТАНОВОК
Редактор В.А. Елисеев. Редактор издательства Л.А. Решмина
Художественные редакторы В.А. Гозак-Хозак, Г. И. Панфилова
Технические редакторы Н.М. Брудная, Г.Н. Лядухина. Корректор СВ. Малышева
ИБ № 1859
Набор выполнен в издательстве. Подписано в печать с оригинала-макета 09.11.88.
Т-17895. Формат 60x88 1/16. Бумага офсетная N® 1. Печать офсетная. Усл.печ.л. 26,46.
Усл.кр.-отт. 26,46. Уч.-издл. 28,51.Тираж 17000экз. Заказ 6562. Цена 1р. 30 к.
Энергоатомиздат, 113114, Москва, М-114, Шлюзовая наб., 10.
Отпечатано в ордена Октябрьской Революции и ордена Трудового Красного Зна-
мени МПО ’’Первая Образцовая типография имени А.А. Жданова” Союзполиграф-
прома при Госкомиздате СССР. 113054, Москва, М-54, Валовая, 28.
© Издательское объединение ”Вища школа”, 1980
ISBN 5-283-00506-2 © Энергоатомиздат, 1988
ПРЕДИСЛОВИЕ
В современном промышленном производстве особое значение приобре-
тает развитие автоматизированных систем управления технологичес-
ми процессами (АСУ ТП). Внедрение автоматизированных систем
управления в различные сферы хозяйственной деятельности, и в пер*
вую очередь в проектирование, управление оборудованием и техноло-
гическими процессами, способствует ускорению научно-технического
прогресса. Для решения этих задач необходимо осуществить подготовку
квалифицированных специалистов, способных создавать и обслужи-
вать современное промышленное производство, базирующееся на вычис-
лительной технике, гибких автоматизированных системах и робототех-
нических комплексах.
Специалист в области электропривода и автоматизации промышлен-
ных установок, занимающийся разработкой, монтажом и наладкой
современных систем управления промышленным оборудованием, по ха-
рактеру своей деятельности сталкивается как с теоретическими, так и с
практическими задачами автоматизации. Решить эти задачи рациональ-
ного использования автоматизированных электроприводов различного
назначения без глубокого знания теории и практики автоматического
управления, микроэлектроники, теории электропривода,технологйчес-
"кихпроцессов, вычислительной , техники, экономики невозможно.
ТИгим обстоятельством следует объяснить введение в учебные планы
50-х годов курса ’’Комплексная автоматизация промышленных устано-
вок”, который к началу 70-х годов был существенно преобразован и рас-
ширен и получил название ’’Автоматизация типовых технологических
процессов и промышленных установок”.
Для решения задач проектирования и эксплуатации АСУ ТП инжене-
ру требуются знания принципов построения математических моделей
технологических процессов и оборудования, элементов теории сбора и
переработки ДеЗоюлогйческой информации, формирования сигналов
управления. д^ля передачи их исполнительным органам приводам
различных типов, обеспечивающим функционирование систем в соот-
ветствии с поставленными задачами, а также практические знания функ-
циональных и структурных принципов построения АСУ ТП. Инженеру
необхОДяйьГ Также знания в области вычислительной и микропроцес-
сорной техники. Все это нашло отражение в программе курса ’’Авто-
3
матизация типовых технологических процессов и установок”, которая
является результатом коллективного опыта и труда ряда учебных и науч-
ных школ электроприводчиков Советского Союза.
Настоящий учебник написан в соответствии с одноименной програм-
мой на базе учебного пособия ’’Автоматизация типовых технологичес-
ких процессов и промышленных установок”, вышедшего в 1980 г. в
издательстве ”Вища школа”. В процессе работы над учебником многие
главы были написаны заново, а другие переработаны в соответствии с
замечаниями и пожеланиями, полученными авторами в рецензиях и
отзывах на учебное пособие. Для удобства использования учебного
материала он сопровождается примерами, которые облегчают усвое-
ние некоторых сложных вопросов.
В соответствии с программой учебник состоит из двух частей. В пер-
вой части рассмотрены теоретические вопросы сбора и переработки
технологической информации, принципы построения типовых АСУ
ТП, применение вычислительной техники как основы управления систе-
мами. Вторая часть посвящена изучению АСУ ТП металлообработки с
применением систем числового программного управления, которыми
оснащается станочный парк — основа машиностроения. Металлорежущие
станки распространены во всех отраслях народного хозяйства, поэтому
сведения об АСУ ТП металлообработки могут быть использованы подав-
ляющим большинством молодых специалистов. Вместе с тем этот ма-
териал является основой для изучения автоматизированных систем уп-
равления другими технологическими процессами и технологическим
оборудованием. Учебник может быть использован как при изучении
курса, так и при выполнении курсовых и дипломных проектов.
Авторы искренне признательны коллективу кафедры автоматизи-
рованного электропривода Московского энергетического института
(зав. кафедрой проф. Н.Ф.Ильинский) и проф. В.Г. Созонову за боль-
шой труд по рецензированию рукописи, а также проф. В.А. Елисееву
за тщательное научное редактирование рукописи. Их труд позволил
существенно улучшить отдельные главы книги и принят авторами с
глубокой благодарностью.
Все замечания и пожелания по содержанию учебника просьба на-
правлять по адресу: 113114, Москва, М-114. Шлюзовая наб., 10, Энерго-
атомиздат.
Авторы
ЧАСТЬ /.ПРИНЦИПЫ ПОСТРОЕНИЯ АСУ ТП
Глава первая
СОВРЕМЕННОЕ ПРОМЫШЛЕННОЕ ПРОИЗВОДСТВО
И АСУ ТП
1.1. ОБЩИЕ ПОЛОЖЕНИЯ
^Развитие современного производства идет по пути создания высоко-
эффективных промышленных установок, обеспечивающих интенсифика-
> цию технологических процессов, и систем управления ими. При этом
постепенно был осуществлен переход от ручного управления техноло-
гическими процессами к автоматизированным и далее - к полностью
автоматическим. Все это привело к выделению r Hqvjff д^упрамАммм
самостоятельного раздела, перед которым ставятся задачи разработки
методов и систем автоматизации технологических процессов. К 1974 г.
эти системы получили название ’’Автоматизированные системы управле-
ния технологическими процессами (АСУ ТП)”, и появились первые
ГОСТ, регламентирующие терминологию, основные положениям в даль-
нейшем - весь процесс создания, введения в эксплуатацию и собственно
эксплуатацию таких систем.
. Введение ГОСТ не только определило содержание работ по созданию
АСУ, но и позволило более строго сформулировать цели и задачи учеб-
ных курсов для подготовки инженеров-специалистов в области разработ-
ки и эксплуатации этих систем. Такая роль государственных докумен-
тов по стандартизации требует их изучения в процессе подготовки спе-
циалистов для того, чтобы они в дальнейшей инженерной деятельности
строго придерживались требований ГОСТ и выполняли все их предпи-
сания.
Автоматизированной системой управления (АСУ) называется чело-
веко-машинная система, обеспечивающая автоматизированный сбор
и переработку информации, необходимой для оптимизации управле-
ния в различных сферах человеческой дятельности. АСУ технологичес-
кого процесса (АСУ ТП) - это автоматизированная система управле-
' ния для выработки и реализации управляющих воздействий на техноло-
гический объект управления в соответствии с принятым критерием
качества управления. Определенный таким образом термин ”АСУ ТП”
является основополагающим при формулировании всех последующих
задач автоматизации технологических процессов. ГОСТ устанавливает
также определение технологического объекта управления как сово-
купности технологического оборудования и реализованного на нем по
соответствующим инструкциям или регламентам технологического
процесса производства.
5
1.2. КЛАССИФИКАЦИЯ И СТРУКТУРА СОВРЕМЕННЫХ
ТЕХНОЛОГИЧЕСКИХ ОБЪЕКТОВ УПРАВЛЕНИЯ
Множество разнообразных технологических объектов управления,
отличающихся физической природой, видом перерабатываемого сырья и
энергии, технологическим оборудованием, затрудняет рассмотрение всех
видов технологии. Однако в системе промышленного производства
можно выделить два существенно отличных класса технологических
процессов: добычу исходного сырья и переработку сырья или полу-
фабриката в готовый продукт. В последнем случае готовым продуктом
может быть и полуфабрикат, служащий исходным материалом для
дальнейшей переработки. В свою очередь каждый из этих классов тех-
нологических процессов имеет специфические стороны. Так, первый
может быть разделен на добычу твердых, жидких или газообразных
продуктов. Во втором — переработка сырья или полуфабриката — вы-
деляются отрасли с технологией изменения агрегатного состояния или
химического состава вещества и процессы, технология которых на-
правлена на изменение формы исходной заготовки или исходного ма-
териала.
Транспортировка сырья, полуфабрикатов и готовой продукции
может* рассматриваться в качестве самостоятельного класса. Здесь
можно выделить технологические и межпроизводственные или меж-
отраслевые транспортные средства.
На рис. 1.1 показана классификация промышленного производ-
ства по указанному выше признаку. Каждый класс имеет два четко
выраженных подкласса. В подклассе добычи твердого сырья выделе-
ны три самостоятельные отраслевые технологии: подземных и откры-
тых разработок и воднотранспортная (драги, земснаряды и др.); под-
класс добычи жидкого или газообразного сырья представлен техноло-
гиями бурения и откачки. |
Подкласс получения продукции, связанной с процессами измене-
ния агрегатного или физико-химического состояния материала, при-
сущ таким отраслям, как энергетика, химическая промышленность,
металлургия (доменное, сталеплавильное производство, электрохи-
мическая металлургия и др.). В этих процессах используются различные
виды энергии (тепловая, электрическая, химическая, атомная). Энерго-
носитель поступает к технологическому агрегату в виде пара, газа,
компонентов исходных материалов (например, кокс в доменном и
агломерационном производстве). Управляемыми параметрами здесь
являются поток материала и его состав, а такя^поток эне^гонос^ и
его состав.
В данном случае технологическими объектами управления являют-
ся транспортные, дозирующие и массоизмерительные устройства, под-
готавливающие технологический процесс изменения агрегатного и
физико-химического состояний исходных продуктов и собственно
6
| Промышленное производство |
£
Добыча сырья
Твердого Жидкого, газо- образного
Переработка сырья в товарный продукт
С измене- С измене-
нием нием
химсостава формы
Откры- " тая Бурение
Подзем- " ная Откачка
Подводная(драги,
земснаряды)
Энергети- ческая - Резание•
Металлург " гическаяХ - Прокатка
Химиче- ская Штам- повка
Транспортировка сырья и готового продукта
Технологи- j ческая Межцеховая, межзавод- ская
1 |
Манипу- ляторы Железно- " дорожная
Транс- ' партеры А в тома- | бальная
- Краны Авиа- ционная
додная"]
Рис. 1.1. Классификация промышленного производства
процессы этих преобразований. Непрерывность протекания физико-хи-
мических процессов определяет их взаимную связь с транспортировкой
и дозированием, что позволяет рассматривать весь технологический
комплекс как единый технологический объект управления.
Подкласс производства продукции, связанный с изменением формы
исходного сырья или полуфабриката, включает любые процессы поточ-
ного или индивидуального производства. К ним могут относиться про-
катка, штамповка, волочение, формовка, обработка резанием и т.д.
Здесь используется только один вид энергии - механическая, источни-
ком которой R ПППЯВПЯЮТПРМ большинстве случаев СЛУЖАТ автомати-
зированный электропривод. Управляемым параметром является поток
энергии.
Объединение ряда производственных механизмов в общий техно-
логический комплекс осуществляется с помощью транспортных средств
и механизмов изменения ориентации изделия. Наиболее характерной
машиной в таком производстве становится управляемый манипулятор —
промышленный робот.
Подкласс изменения формы значительно шире, чем показано на
рис. 1.1. Выбирая наиболее широкую область технологии - металло-
обработку - как пример массовых, наиболее характерных и распро-
страненных технологических процессов, приходится отказываться
от рассмотрения других специфических производственных процессов.
Технологическая транспортировка объединяет устройства пере-
мещения сырья, полуфабрикатов и готовой продукции в соответст-
вии с расположением технологического оборудования и требования-
ми технологического процесса.
Приведенйая классификация свидетельствует о том, что техноло-
гическими объектами управления, относящимися непосредственно к
7
I
компетенции инженеров-электроприводчиков, являются производ-
ство товарной продукции путем изменения формы и технологичес-
кая транспортировка при обслуживании этого производства. Для этих
технологических объектов дарактерно применение автомати^ирппям.
ного электропривода, с помдщью которого осуществляется целенап-
равленное изменение параметров и режимов технологического процесса,
'обеспёЧёИие требуемой производительности и качества продукции. ‘
При организации современного технологического процесса выде-
ляются ^цри подсистемы преобразования: вещества, энергии, инфор-
мации. Среди перечисленных подсистем невозможно выделить глав-
ную и второстепенные. Они в своем функционировании равноправ-
ны, так к$к образуют автоматизированный технологический комп-
лекс (АТК)у представляющий собой совокупность совместно функ-
ционирующих АСУ ТП и технологического объекта управления.
При рассмотрении вопросов совершенствования технологических
процессов обращает на себя внимание роль человека в сфере мате-
риального производства. Создание новых технологических процес-
сов, разработка новых производительных механизмов, появление новых
управляемых источников энергии приводит к тому, что роль человека
практически сводится к переработке информации и выдаче управляю-
щих воздействий. Этот процесс складывается из следующих этапов: а)
накопления и хранения априорной информации (процесс обучения и
знакомства с конкретным технологическим объектом); б) приема
исходной информации, содержащей конкретное оперативное задание по
управлению объектом, получаемое непосредственно перед работой; в)
сбора текущей информации о соответствии хода технологического
процесса~установленному заданию и перегрузках оборудования; г)
преобразования трех видов информации (априорной, исходной и теку-
щей)” в целях принятия решения на управление объектом; д) воздей-
ствия на органы управления объектом эффекторами (рукой, ногой,
голосом и т.п.) для реализации принятых решений.
С развитием материального производства низкая информацион-
ная производительность человека-оператора становится тормозом тех-
нического прогресса. Человек не успевает воспринимать через органы
чувств возросшее количество показаний индикационных приборов,
необходимых для принятия соответствующего правильного решения. Он
не в состоянии запомнить все правила управления технологическим
оборудованием и рекомендации по ведению процесса. В ряде случаев,
даже приняв правильное решение, оператор не успевает передать команду
управляемому объекту. Попытка решить задачу путем увеличения числа
операторов выдвигает проблему согласованности их действий.
Речь, естественно, идет не об ограниченности интеллектуальных и
творческих возможностей человека, а о том, что нерационально и неэф-
фективно использовать человека для переработки большого объема
информации при ее шаблонной повторяемости в каждом цикле техно-
8
логической операции и что управление человеком-оператором быстро-
протекающими процессами невозможно. , оЛх
Таким образом, только механизация переработки информации с
помощью АСУ ТП снимает это препятствие на пути технического про-
гресса в области материального производства.
1.3. МЕСТО И РОЛЬ ЭЛЕКТРОПРИВОДА В АСУ ТП
В технологических процессах формообразования электропривод
является ас.нстм-ы-м управляемым источникоммеханической энергии.
Применение гидропривода характерно для сравнительно ограниченной
области технологических процессов. Этот вид управляемого источника
механической энергии применяется обычно в металлорежущих станках,
некоторых типах землеройных машин, подъемных кранах и некоторых
других механизмах. Его характерной чертой является электрическая
система у прав ле ни я/аналогичная применяемым в АСУ ТП. Обычно лю-
ТЗоитГзменение хода технологического процесса, переход от одной опера-
ции к другой сопровождаются изменением технологических скорос-
тей или усилий, т.е. изменением потока подводимой энергии. Таким об-
разом, механическая энергия в этих процессах выступает как основ-
ной управляемый технологический параметр.
Интенсификация технологических процессов, повышение точности,
совершенствование технологии, стремление к ведению процессов с мини-
мальными потерями энергии обусловили тенденции современного эта-
па развития автоматизированного электропривода, началом которого
можно считать появление быстродействующих полупроводниковых
источников питания электродвигателей. Характерным для этого эта-
^й^автоматйзации электропрИвбдов^Гвляется не только интейсивное
и повсеместное применение полупроводниковой техники, но и широ-
кое внедрение унифицированных управляющих устройств, предназна- _
ченных исключительно для преобразования информации.
Такие устройства-резко повышают быстродействие процессов уп-
равления и расширяют возможности реализации сложных алгоритмов
управления. Получает развитие аналоговая и цифровая управляющая
техника. Подобного типа управляющие устройства становятся все более
сходными с элементами электронных вычислительных машин, а струк-
тура автоматизированного электропривода полностью приобретает
явные черты типовой структуры АСУ. Современный электропривод
функционирует вместе с автоматизированной системой управления,
которая вырабатывает управляющее воздействие в соответствии с кри-
териями минимальной длительности переходных процессов, минималь-
ных потерь энергии, ограничения рывков и др. По аналогии с АСУ ТП
следует применять термин ’’автоматизированная система управления
электроприводом (АСУ ЭП)” - более строгий, чем термин ’’автомати-
зированный электропривод”. Термин АСУ ЭП будет применяться при
дальнейшем изложении.
9
Аналогия целей управления, унификация внутренней структуры,
определяемой основными этапами информационного процесса, при-
менение для автоматизации электропривода~Тех Жё Элементов управ-
ляющих устройств, что и для различных рангов АСУ ТП, - все это позво-
ляет при определении места и роли электропривода в АСУ ТП сделать
следующие выводы.
1. АСУ ЭП предназначена для непрерывного или дозированного изме-
нения потока механической энергии, необходимой для технологичес-
кого процесса формообразования.
2. В АСУ ЭП в качестве объекта управления выделяются элементы
энергетического канала: преобразующее, электродвигательное и пере-
даточное устройства. Они осуществляют преобразование и передачу
рабочему органу потока энергии. Управление потоком энергии может
осуществляться путем воздействия на любой из этих трех элементов
одновременно или порознь.
Преобразование информации происходит в управляющих каналах,
выполненных в виде различных блочных устройств — как аналоговых,
так и цифровых. Выделение энергетического и информационного кана-
лов обусловлено различием решаемых ими задач и критериев качества
функционирования. Так, для энергетического канала важнейшими пока-
зателями являются пропускная способность, диапазон изменения пото-
ка энергии и потери, определяющие энергетический КПД. Для информа-
ционного канала главными являются его быстродействие при выпол-
нении различных математических операций, возможность с высокой
точностью реализовать сложные законы управления. Энергетический
КПД таких элементов равен нулю.
3. Типовыми функциональными блоками внутренней структуры
современных АСУ ЭП являются: а) блоки памяти — от уставок реле
и напряжений сравнения до устройств хранения программ, записан-
ных на магнитной или перфорированной ленте; б) блоки текущей
информации, включающие в себя датчики и специальные устройства
преобразования и кодирования первичного сигнала обратной связи;
в) блоки управления, формирующие сигналы управления на основе
преобразования исходной и текущей информации; г) блоки связи
с объектом — устройства преобразования и усиления сигналов, выра-
ботанных информационным каналом, до вида и уровня, необходимых
для воздействия на управляемый источник питания двигателя или сам
двигатель.
4. АСУ ЭП в АСУ ТП выполняет роль конечногот исполнитепь^ого
звена. Она реализует законь^хуправления, формируемые вышестоящи-
ми уровнями технологических АСУ. Эти уровни, обеспечивая контроль
за состоянием технологических параметров, задают уставки для уст-
ройств управления АСУ ЭП, которая представляет собой самый нижний
уровень в иерархической структуре АСУ. '
10
5. АСУ ЭП обеспечивает автоматическую отработку выдаваемых.
человеком-оператором или АСУ ТП заданий, контролируя их выполнен
ние с помощью обратных связей по напряжению, току, скорости, Конт-
-рилв за Тёкнологическими характеристиками Данного механизма осу-
ществляет АСУ ТП, выдающая задание управляющему устройству АСУ
ЭП, которая является подчиненным элементом АСУ ТП.
Унификация элементов управляющей техники, применяемой в АСУ
ЭП и АСУ ТП, обусловила тенденцию прямого цифрового управления,
при котором функции управления АСУ ЭП принимают на себя вычис-
лительные устройства АСУ ТП. В этом случае происходит слияние^всех
функций управления как технологией, так и электроприводом в об-
ШбМ устройстве.
1.4. НАЗНАЧЕНИЕ, ХАРАКТЕРИСТИКА И СТРУКТУРА
СОВРЕМЕННЫХ АСУ ТП
Основное назначение АСУ ТП состоит в автоматической оптимиза-
ции технологического процесса. В таких системах обеспечивается реали-
зация совершенных законов управления и как следствие - наиболее
эффективное ведение технологического процесса и высокое качество
продукции, т.е. выпускается максимально возможное количество гото-
вой продукции при обеспечении необходимого ее качества и допусти-
мой загрузки технологического оборудования. При этом в идеальном
случае затраты должны быть минимальными. Это означает, что техноло-
нический комплекс и саму технологию необходимо спроектировать
таким образом, чтобы оборудование имело наименьшие габаритные
размеры и массу. Конструкция оборудования должна гарантировать
минимум потерь в узлах трения, а технология - максимальное исполь-
зование исходного продукта и энергии. Наконец, ведение технологи-
ческого процесса должно обеспечить выпуск готовой продукции с наи-
меньшим полем допусков и минимум брака.
Единственный критерий, способный объединить перечисленные пока-
затели, - экономический. Если стоимостные эквиваленты не установ-
лены, повышение эффективности достигается путем оптимизации одного
или двух наиболее существенных параметров. При двух параметрах при-
ходится отыскивать компромиссное решение. Еще более сложны поис-
ки компромисса между минимумами расхода трех основных компонен-
тов: материала, энергии и информации.
В целевой классификации АСУ ТП по типовым задачам управления,
определяющей их назначение, можно выделить следующие группы:
АСУ ТП. обеспечивающие стабилизацию (поддержание) заданного
рационального или оптимального технологического режима, т.е. таких
технологических параметров, на которые действующие возмущения
оказывают существенное влияние. Например, к ним можно отнести
системы стабилизации скорости резания при торцовой обработке дета-
11
лей больших диаметров на металлорежущих станках, системы стабили-
зации скорости шлифования при уменьшении диаметра шлифовального
круга и др.;
АСУ ТП, отрабатывающие с установленной точностью заданное или
непрерывно задаваемое рациональное (оптимальное) изменение техно-
логического процесса. Такие системы программного или следящего уп-
равления применяются в роботах-манипуляторах, станках с ЧПУ, лиф-
товых подъемниках и пр.;
АСУ ТП, самостоятельно (автоматически) выбирающие наилучший
по какому-либо признаку технологический режим и обеспечивающие
его поддержание либо автоматически выбирающие наилучшую траекто-
рию перемещения рабочего органа и обеспечивающие ее отработку с
установленной точностью. К таким системам оптимального управле-
) ния относятся АСУ ТП агрегатов оптимального раскроя материала,
I системы дистационной перестройки, рассчитывающие и реализующие
v оптимальную программу обжатий металла в отдельных клетях стана
непрерывноиПрсгкатки, и т.д.
Характерной особенностью современных АСУ ТП является высокая
производительность переработки информации при практически неогра-
ниченном объеме памяти. Эта особенность базируется на применяемых
в системах быстродействующих средствах вычислительной техники:
программируемых контроллерах, микропроцессорах, управляющих
вычислительных машинах (УВМ). Высокая информационная произво-
дительность УВМ обеспечивает реализацию указанного назначения
АСУ ТП.
Применение быстродействующей вычислительной техники обеспечи-
вает вторую характерную особенность АСУ ТП — их высокую гибкость,
что позволяет существенно повысить гибкость технологического объек-
та управления при переходе на новую технологию. Перестройка сво-
дится к ’’очистке” памяти управляющей машины и вводу с програм-
моносителя новых данных. Даже для весьма сложных технологичес-
ких комплексов время перенастройки не выходит за пределы несколь-
ких десятков секунд.
Дополняя, а в дальнейшем заменяя человека, АСУ в известной мере
копирует его функциональную структуру.
На рис. 1.2 схематически показаны основные функциональные связи,
устанавливаемые в системе человек - технологический объект управ-
ленца. Для выполнения заданных операций управления человек должен
получить ряд сведений, которые принято называть внешней инФоома-
цией. Эта неизменная информация хранится в памяти оператора и вклке
чает основные^ характеристики технологического процесса и порядок
^выполнения операций управления в нормальных и аварийных оежи-
^махТ^Очевидно, отбор этой информации должен быть весьма тщатель-
ным, так как перегрузка памяти большим количеством цифр и ситуа-
ционных событий неизбежно приводит к частичной потере некоторых
12
Рис. 1.2. Структура управления технологическим объектом человеком-операто-
ром или АСУ ТП
данных и нарушению порядка операций управления. За изменением
технологических характеристик, представляющих собой совокупность
управляющих параметров и возмущающих воздействий, человек сле-
дит с помощью органов-рецепторов, из которых наибольшую нагрузку
несет зрение. Человеку приходится наблюдать за показаниями комплек-
са приборов, некоторые предельные параметры могут фиксироваться
с помощью звуковых сигналов. Восприятие текущей информации так-
же может нарушаться, что вынуждает ограничивать количество индика-
торов. Сопоставление исходной и текущей информации и принятие
решения осуществляются центральной нервной системой. После вы-
работки управляющей информации в результате принятия решения в
периферийную нервную систему поступают сигналы. Их следствием яв-
ляется реализация команд управления с помощью эффекторов - рук,
ног, голоса.
По аналогичному принципу строится функциональная структура лю-
бой АСУ, в том числе и АСУ ТП. На рис. 1.2 указаны рецепторы, память,
мышление, эффекторы, присущие человеку-оператору, и их аналоги
в АСУ ТП. Сохраняя в качестве самостоятельных блоки внешней и те-
кущей информации, процессор и устройство связи с объектом, АСУ ТП
выполняет две функции: информационную и управляющую. Информа-
ционную функцию АСУ ТП ГОСТ 19194-73 определяет как функцию,
целью которой является сбор, преобразование, хранение информации
о состоянии технологического объекта управления, передача ее для
последующей обработки.
Управляющая функция АСУ ТП имеет своей целью выработку реше-
ний и осуществление управляющих воздействий на технологический
объект управления. Как видно, в исполнении задач информационной и
управляющей функций принимает участие процессор, совмещающий
13
переработку, хранение и выработку управляющей информации, пере-
даваемой в виде управляющего воздействия технологическому объек-
ту управления по каналам устройства связи.
Рассмотрим функциональные блоки, показанные на рис. 1.2. В блок
внешней информации управляющего устройства, содержащий внешнее
и оперативное запоминающие устройства, для длительного хранения
вводятся априорная информация об объекте и технологические инструк-
ции. В эти же запоминающие устройства от общего пульта управления
вводится также исходная оперативная информация о текущем задании.
Текущая информация о технологическом процессе с помощью датчи-
ков технологических параметров вводится в блок текущей информа-
ции управляющего устройства.
Основными узлами управляющего устройства являются процессо-
ры - логические и арифметические блоки, в которых априорная, исход-
ная и текущая информация преобразуется в управляющие команды.'
Сложность этих устройств зависит от сложности задач, решаемых АСУ.
На выходе системы установлены устройства связи с объектом, предназ-
наченные для преобразования управляющих команд в управляющие
воздействия достаточной мощности.
Уровень совершенства АСУ зависит от совершенства элементов ее
структуры и характеризуется степенью ’’самостоятельности” в выработ-
ке и реализации управляющих воздействий при ведении технологичес-
кого процесса. Сложность элементов внутренней структуры АСУ нахо-
дится в тесной связи с характером технологического процесса. Если
этот процесс допустимо рассматривать детерминированным, то его мо-
дель будет проще.
В тех случаях, когда ход технологического процесса не удается свес-
ти к детерминированному, т.е. возможны некоторые отклонения слу-
чайного характера (изменение качества материала, его физических
свойств, характеристик рабочего органа и т.п.); внутренняя структу-
ра АСУ существенно усложняется. В таких системах априорная инфор-
мация содержит формулировку цели управления и математическую
модель процесса, которая позволяет определить наилучший путь дости-
жения этой цели. Чем большее число случайных факторов подлежит
учету, тем сложнее математическая модель процесса и элементы внут-
ренней структуры АСУ. Все это приводит к удорожанию системы, ус-
ложнению эксплуатации и существенному снижению надежности. По-
этому рациональный путь создания работоспособных АСУ ТП повьппен-
ной надежности состоит в совершенствовании не только отпельньр^эле-
ментов системы, но и технологического процесса, совершенствование
которого должно быть направлено на повышение детерминированности
последнего, в результате чего исключается или сводится до минимума
влияние случайных факторов. Только одновременное совершенствова-
ние системы управления и технологического процесса может привести
14
к созданию надежно функционирующих автоматизированных управляе-
мых комплексов.
Во внешней структуре АСУ ТП могут быть выделены системы раз-
личных уровней или подсистемы АСУ ТП, выделяемые по функциональ-
ному или структурному признаку, отвечающему конкретным целям
И задачам. Если функции системы ограничены одним механизмом, то
она называется локальной. Примером тому может служить система
безотходного пореза металла, управляющая подвижным упором нож-
ниц обжимного прокатного стана. Эта локальная АСУ ТП обеспечивает
при раскрое минимум отхода металла с учетом срочности выполнения
заказов. Она располагает информацией о длинах раската, стандартных
длинах слябов, объемах и сроках выполнения заказов и вырабатывает
задание на перемещение упора для АСУ ЭП.
Если механизмы, управляемые локальными системами, тесно связа-
ны между собой технологическим процессом, то для их взаимной ко-
ординации создается узловая АСУ ТП.~Объединение локальных АСУ ТП
в узловые может быть осуществлено по территориальному или функ-
циональному признаку. В этом случае устанавливается общая ситуа-
ционная связь расположенных на одном агрегате рабочих органов или
механизмов. Узловыми АСУ ТП являются, например, системы управ-
ления печами, клетями и механизмами склада продукции обжимного
прокатного стана.
Локальные АСУ ТП, объединенные в узловые системы по функцдо^
нальному признаку, совместно участвуют в управлении общим для всего ,
узла “технологическим парЖет^^ примером
’такой узловой АСУ ТП являются системы регулирования скорости,
толщины, натяжения полосы в листовых прокатных станах. Каждый из
параметров формируется всеми клетями стана. К узловым АСУ ТП
можно отнести различные типы копировальных агрегатов (станки^
раскроечные автоматы).
В этих гигтрмях комплекс технологических объектов подчинен об-
щим технологическим закономерностям, в связи с чем здесь не мо^
гут применяться локальные АСУ Т11 различной производительности.
Построение такЬго узла исходит из единой для всех объектов заданной
произ води тел ьности.
Следующий уровень систем управления — комплексные АСУ ТП —
обусловлен необходимостью взаимной связи узловых АСУ ТП в целях
управления технологическими линиями и комплексами. Это, напри-
мер, автоматизированные станочные линии, роботизированные комплек-
сы станков, комплекс агрегатов и механизмов обжимного прокатного
стана, тонколистового стана горячей прокатки, роторный землерой-
ный комплекс.
Организованные в единую систему комплексные АСУ ТП, дополнен-
ные информационными узлами и автоматизированными системами пере-
работки информации отделов и служб предприятия, образуют автомати-
15
__£_
АСУ ОП
i—
АСУ П
Комплексные,
цеховые
АСУ ТПК
АСУ ТПУ1
асу тпуг
АСУ ТПУЗ
Узловые
АСУ ТПЛ1\^\АСУ ТПЛгГ^\АСУ тплз
ZEEzfzEEZ
ТОУ Z ТОУ 3
АСУ ТПЛЬ
АСУ ТПЛ5\^\АСУ ТПЛб
zee
ТОУ 5
Локальные
ZEE
ТОУ 1
ГОУ 4
ZEE
ГОУ б
Технологические
объекты
управления
f
h i
V
т
1
Рис. 1.3. Иерархия построения автоматизированного комплекса на базе локаль-
ных и узловых АСУ ТП. Стрелками показаны: управляющие воздействия (обра-
щены к нижнему уровню), потоки информации (обращены к верхнему уровню),
взаимные информационные связи между локальными и узловыми АСУ ТП
зированную систему управления предприятием — АСУ П. Несколько
объединенных АСУ П образуют систему управления отраслью промыш-
ленности - АСУ ОП. Такой принцип построения внешней структуры
(рис. 1.3) получил название подчиненного, или иерархического. Иерар-
хия АСУ ТП определяет порядок подчинения взаимосвязанных подси-
стем общей системы, которая в пределах отрасли промышленности осно-
вывается на выработке определенной стратегии, реализуемой по опти-
мальным законам с учетом возможностей конкретных промышленных
предприятий, цехов, технологических комплексов, механизмов. Сущ-
ность иерархического принципа состоит в том, что каждый из уровней
вырабатывает задание-уставку, обязательную для подчиненного ему
уровня.
В последние годы при разработке АСУ ТП технологических линий
и комплексов ранги иерархии сокращаются в связи с применением пря-
мого цифрового управления, которое осуществляется централизован-
но с помощью общего вычислительного управляющего комплекса.
Происходит замена структурной иерархии алгоритмической. Здесь
иерархическую структуру приобретает алгоритм работы управляющей
вычислительной машины (УВМ).
С повышением ранга уровня усложняются решаемые задачи. Это
требует более совершенной техники, однако характер задач (стабили-
зация, программное, оптимальное управление) и функции отдельных
составляющих систем управления остаются неизменными.
16
Таким образом, АСУ ТП представляет собой комплекс технических
Средств технического, информационного, математического и програм-
лшого обеспечения для управления технологическими объектами, ко-
торый обеспечивает оптимальный Цри данной структуре и технических
^средствах уровень автоматизации сбора и переработки Информации для
формирования управляющих сигналов и передачи их без потерь и иска^~
жения на исполнительные механизмы в целях достижения наиболее эф-
фективной работы технологического объекта управления в целом. “
Глава вторая
ПЕРЕРАБОТКА ТЕХНОЛОГИЧЕСКОЙ ИНФОРМАЦИИ
Z1. ОБЩИЕ ПОЛОЖЕНИЯ
Функционирование АСУ ТП неразрывно связано с переработкой пото-
ка технологической информации. АСУ ТП формообразования строят
на основе автоматизированного электропривода, поэтому специалист
по автоматизированному электроприводу должен знать общие положе-
ния по информационному обеспечению процесса управления, общие
принципы получения и преобразования технологической информации,
"включая переход от аналоговой к цифровой форме представления
информации, способы кодирования сигналов, передачи информации и
ЗАщиты 66 dt помех. Он должен уметь на основе известной структуры
АСУ ТП (локальной или узловой), требований по точности измерения
и поддержания выходных параметров системы определять объем каж-
дого из типов информации (априорная, дехнологиуская), рассчиты-
вать разрядность устройств измерения, преобразованияи передачи ин-
формации* выбирать наиболее целесообразный код по условиям точ-
ности, помехозащищенности, оценивать пропускную способность кана-
лов связи, в том числе с учетом действия помеху
При изучении материалов данной главы следует усвоить обйще поло-
жения по количественной оценке информации, принципам получения,
способам преобразования и передачи технологической информации,
ее кодирования и защиты от помех. В связи с этим совсем не обяза-
тельно запоминание сложных формул и зависимостей; необходимо
четкое понимание, в каких случаях они используются и какими должны
быть результаты расчетов.
Навыки применения расчетных соотношений можно приобрести в
процессе выполнения курсового и дипломного проектов, если темати-
ка их определяет существенный объем информационного обеспечения.
При изучении главы достаточно уметь применить теоретический мате-
риал для расчетов. Поэтому можно рекомендовать проработать предла-
гаемые примеры, варьируя параметрами, либо составить аналогичные
примеры на основе материалов технологической практики.
17
2.2. ПОСТАНОВКА ЗАДАЧИ.
УПРАВЛЯЕМОСТЬ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
Для реализации целенаправленно и результативно протекающего
технологического процесса он должен быть управляемым. Применитель-
но к ^технологическим объектам это означает, что в процессе их функ-
ционирования необходимо осуществлять непрерывные возпайствия
на исполнительные органы, чтобы при внешних возмущениях обеспе-
чить получение единственного необходимого результата. Чем совер-
шеннее управление, тем точнее, однозначнее будет совпадение фак-
тического результата технологического процесса с требуемым. Такая
наиболее общая и весьма упрощенная постановка задачи управления
может быть существенно конкретизирована и даже формализована.
Так, протекание управляемого технологического процесса может
быть представлено как последовательность сменяющихся режимов или
состояний. Менее совершенное управление обеспечивает только под-
держание некоторого рационального заданного режима, или отработку
требуемой траектории, или последовательность перехода из одного ре-
жима в другой; более совершенное обеспечивает получение требуемого
конечного результата, выбор наилучшего (оптимального) режима рабо-
ты и траектории перехода при минимальных затратах средств, материа-
лов и энергии.
Нарушения управления делают технологический процесс неупорядо-
ченным: снижается вероятность получения заданных результатов и по-
вышается вероятность появления нежелательных результатов (появ-
ляются бракованные детали из-за выхода их размеров из поля допуска,
ошибочно выбирается направление движения транспортирующего ме-
ханизма и т.п.). В упрошенной интерпретации идеально управляемым
технологическим процессом называется такой, в котором из многих
равновероятных результатов благодаря управлению^ обеспечивается
пЬлучение одного, единственно необходимого Практически^гакое управ-
ление является либо неоправданно дорогостоящим, либо нереализу-
емым вообще.
Более реалистичным является следующее определение: допустимым
уровнем качества управления технологическим процессом является та-
кой, при котором с требуемой вероятностью обеспечивается ограничен-
ное число допустимых результатов (уровней качества). Это может оз-
начать, например, необходимость обеспечения с вероятностью 0,99 тол-
щины полосы прокатываемого металла с точностью ± 0,03 мм на 99%
длины полосы и ±0,01 мм на 100% ширины полосы.
Учитывая, что качество продукции определяется обычно нескольки-
ми показателями (иногда неравнозначными), можно связать совершен-
ство управления с числом допустимых результатов (исходов) техно-
логического процесса, которое можно трактовать как общее число
вариантов завершения технологического цикла, включающее выпуск
18
кондиционной продукции или брака, аварийные ситуации, остановки
и т.д. ________________
Для количественной оценки степендХ1еупорядоченнострГ)технологи-
ческого объекта вводится понятие (Энтропии некоторой функ-
ции числа возможных результатов п (исходов). При условии, что ис-
ходы равновероятны, такая функция должна принимать значения:
а) Н = 00 при бесконечно большом числе возможных исходов
п = 00;
б) Н = 0 при одном единственно возможном исходе п = 1;
в) Н = ЕЯ/ = Пп^ т.е. неупорядоченность системы определяется
суммой неупорядоченностей ее составляющих.
Перечисленным условиям удовлетворяет логарифмическая функ-
ция
Я = logtfn. (2.1)
Основание логарифма а обычно принимается равным основанию си-
стемы счисления, при которой определяется и. Тогда при п =а энтропия
равна единице, а при п = а = 2 — двоичной единице, при п = а = 10 —
десятичной. Если все п результатов равновероятны и какой-либо из
них обязательно должен иметь место, то вероятность появления каждо-
го из них равна Р = 1/и, откуда Рп = 1. Энтропия объекта может быть
выражена через вероятность получения этого результата
Н = log, --=-log,P. (2.2)
р
Тогда при м = °° Р = 0 и Н = при п-\ Р = 1 и Я = 0.
В реальных условиях возможны неравновероятные исходы, поэтому
энтропия объекта по выбранным признакам определится усредненным
ее значением по отдельным результатам (значениям признаков) с уче-
том вероятности их появления. В теории вероятности такая величина
называется математическим ожиданием и равна сумме произведений
случайной величины (в нашем случае энтропии отдельного результа-
та Я,) на вероятность ее появления т.е.
п п п
Н = S PiHi= S P.log,-- =- S Р№аРг (2.3)
i =1 1=1 Pi i = 1
Выражение (2.3) известно как формула Шеннона. Ниже рассмотрен
один из достаточно простых вариантов ее приближенного анализа.
Будем считать, что работа технологического агрегата может завер-
шиться одним из п независимых друг от друга результатов, вероятности
которых Pz- могут меняться в широких пределах:
Pi = , (2.4)
19
где at — коэффициент, который всегда положителен и не может пре-
п
вышать п, так как Р( < 1, т.е. О < az<n. Так как S Р;=1,то
П ' = 1
’S а, --= 1 и
/ = 1 п
S af=n. (2.5)
/= 1
Подставив Р. из (2.4) в (2.3), после преобразований получим
Н = logan - s «flog^a,-. (2.6)
и ; = !
Рассмотрим два крайних случая:
1. Возможные исходы практически равновероятны:
Л = Рг =... = Рп = —; Д1 = а2 =... = а„ = 1;
п
Н = 10gaH. (2.7)
2. Возможные исходы предельно неравновероятны, т.е. вероятность
одного практически равна единице, а остальных — нулю:
Р\- 1, Рг =Рз = • • • = Рп = О и ai = «’> а2 = «з = • • • ап = О'»
Н = loge« —-nloge«---------- S 01oge0. (2.8)
” n » = 1
4
После раскрытия неопределенности 0-<» получим Н = 0. Как видно,
повышение упорядоченности процесса функционирования объекта уп-
равления, т.е. увеличение различий вероятностных характеристик ко-
нечных результатов, соответствует уменьшению энтропии объекта от
Нщах = до Hmin = 0*
Пример 2.1. Для снижения металлоемкости полосового проката
проведена реконструкция АСУ ТП тонколистового стана, в результа-
те которой резко уменьшился выход некондиционного (бракованного)
металла и повысился выход полосы с минусовым допуском по толщи-
не. Изменение эффективности процесса прокатки представлено в
табл. 2.1.
Определить энтропию процесса прокатки по признаку стабильнос-
ти толщины полосы до и после реконструкции.
20
Таблица 2.1
Допуск Годовой объем, выпускаемого металла, млн. т до реконструк- после реконст- ции рукции Gj/
Положительный Отрицательный Нулевой Брак Всего 0,6 0,08 0,8 1,6 0,2 0,3 ' 0,4 0,02 2 2
Полагая, что структура качества продукции в табл. 2.1 отражает ве-
роятности появления конкретных статистически независимых результа-
тов, и учитывая, что годовой объем всей продукции G = 2 млн. т, опре-
деляем вероятность отдельных результатов как
Л
и по (2.3) находим энтропию.
До реконструкции
4 Gi 'Gi
, Hi =- S —log io---=0,56 десятичной единицы (дес. ед.).
i = 1 с G
После реконструкции
4
Н2 =- £ — log 10 — = 0,27 дес.ед.
i= 1 G G
Как и следовало ожидать, реконструкция повысила стабильность
толщины проката и обеспечила снижение энтропии по этому признаку.
Обычно не бывает равновероятных результатов, к тому же чаще все-
го они бывают статистически зависимыми.
В общем случае события, заключающиеся в появлении признаков
А и В, считаются статистически зависимыми, если наступление одно-
го из них меняет вероятность наступления другого, т.е. в этом случае
речь идет о сложных событиях, заключающихся в совместном появле-
нии нескольких взаимозависимых признаков. Вероятность такого слож-
ного события Р (АВ) определяется произведением вероятности появле-
ния одного из них Р(А) на вероятность появления другого после того,
как произошло первое Р(В/А), т.е.
Р(АВ) = Р(А)Р(В/А)\ )
Р(АВ) = Р(В)Р(А!В). j (2.9)
21
Пример 2.2. Типичным примером статистически зависимых событий
является подача на сборку деталей разного размера из общего накопи-
теля. После подачи каждой детали вероятность появления детали опре-
деленного размера меняется, так как меняется общее число деталей в
накопителе.
Так, если в накопителе было пх = 15 деталей первого размера и п2 =
= 5 деталей второго размера, то при подаче первой детали, допустим,
первого размера, вероятность ее появления была
Р\а = «1 / («1 + п2) = 15/(15 + 5) = 0,75.
Если на сборку поступило восемь деталей первого размера и четыре
детали второго размера, то вероятность появления детали первого раз-
мера
р =О-8)---------------- = 15^8 = !_ =0>87
[(Л1+л2)-(8 + 4)] 20-8-4 8
Если бы в накопителе было очень много деталей, то в начале потреб-
ления вероятность менялась бы очень мало, т.е. статистическая связь
была бы очень слабой, а именно при пх = 1500 и п2 = 500 мы имели бы
P'le = + и2) = 1500/2000 = 0,75.
После подачи на сборку восьми деталей первого размера и четырех
деталей второго размера получим
P'i'e = (1500 — 8)/(2000 — 8 — 4) = 0,752.
В этом случае вероятность сложного события, заключающегося в
двукратном появлении детали первого размера при первой и тринад-
цатой подачах, будет:
при наличии в накопителе 20 деталей
=ХЛ = 0,75 0,87= 0,65,
при наличии в накопителе 2000 деталей
Р1в = = 0,75 0,752 = 0,565.
1 о 1 о 1 о 7 7 7
Если события статистически независимы, то вероятность их со-
вместного появления равна произведению безусловных вероятностей.
Возможен случай, когда сложное событие с признаком А может про-
изойти лишь после обязательного наступления одного из несовмест-
ных событий с признаком В. Тогда полная вероятность
п
Р(А) = S Р(^)Р(Л/5Г). (2.10)
i = l
22
Учет статистических связей влияет на вероятность сложных событий,
заключающихся в совместном наступлении ряда простых. Естественно,
это отражается на энтропии объекта. Соответствующие выражения для
определения энтропии могут быть получены подстановкой в (2.4)
выражений для безусловной и условной вероятностей.
Рассмотрим пример: технология обеспечивает выпуск продукции,
качество которой определяется двумя статистически связанными призна-
ками: А (три уровня А2, Л2, А3) и В (два уровня В19 В2). Это мо-
жет быть, например, чистота поверхности и твердость заготовки при ме-
таллообработке.
Абсолютные (безусловные) вероятности появления каждого уровня
каждого признака: P(Ai), Р(Л2), Р(А3) и P(Bi), Р(В2). Условные
вероятности появления, например, признаков А после появления В и
признаков В после появления А равны соответственно Р(А/В) и
Р(В/А). Тогда энтропия данного технологического объекта по призна-
ку качества в соответствии с (2.3)
Н(А, В) =- S (2.11)
ik
Учитывая статистическую связь признаков В с А
Р^Вк) = (2.12)
получаем
Н(А, В} =- S P(^.)P(Mf) Oog W + logP(B*/4z)), (2.13)
ik
ИЛИ
H(AB) =- S PtA^gPtAi) S PiBjjAi) -
i к
- P(Ai)Z P^/A^PiBJAi). .. (2.14)
к
Полагая S P(BkIAj) = 1 как сумму условных вероятностей событий,
к
образующих полную группу, получаем:
абсолютную энтропию события с признаком А
Н(А) =- X P(4z)logP(4z);
i
условную частную энтропию события с признаком В по одному из
признаков
Я(В/Л/) =- S P(B*/4z)log (B*MZ);
к
23
общую условную энтропию события с признаком В по всем призна-
кам А
Н(В/А) =-S P(Ai')H(B/Ai).
i
Изложенное позволяет сделать следующие выводы.
1. Наибольшая энтропия характерна для объекта с равновероятны-
ми и статистическими независимыми исходами. Она равна
Н =-logP.
2. При выявлении различий в вероятностях исходов энтропия будет
меньше, чем в первом случае,
Н «-SPflogPp
приближаясь к -logP/ при выравнивании вероятностей.
3. Установление статистических взаимосвязей приводит к дальней-
шему уменьшению энтропии за счет использования условной энтропии
н =- 2 Р(А^Р(Вк/А^ (Bk/Ai).
ik
Это означает, что более глубокое изучение объекта, подлежащего автома-
тизации, снижает в нашем представлении уровень его начальной неупо-
рядоченности или энтропии.
Отсюда следует, что управление объектом должно быть тем более
совершенным, чем больше мы хотим снизить начальную неупорядочен-
ность его функционирования по выбранным признакам. Таким образом,
количественной характеристике степени снижения неупорядоченности
объекта (уменьшению энтропии) можно поставить в соответствие ве-
личину, характеризующую необходимый для этого объем управления.
Для количественной оценки необходимого объема управления вве-
дена величина, численно равная изменению энтропии и называемая
информацией:
7 = ДЯ = Янач ~ Якон > 0. (2.15)
Если имеет место не уменьшение энтропии, а ее увеличение, то прира-
щение называется дезинформацией.
Если в результате управления число возможных вариантов функцио-
нирования объекта уменьшилось с инач до лкон, то*
/= log «нач - log "кон = log . (2.16)
лкон
а при равновероятных исходах
г . Леон
7 = log---. (2.17)
Р нач
При повышении вероятности конечного исхода до Ркон = 1
7 =-10gPHa4- (2.18)
Наиболее часто употребимой единицей информации является двоич-
ная единица (дв. ед.), которая называется бит. Она определяет объем
информации, необходимый для исключения одного из двух равнове-
роятных иахо лов,
Для управляющего звена энтропия объекта - это энтропия датчиков,
характеризующих его функционирование? а необходимая для ее при-
нижения .информация определяется системой команд, выдаваемых ис-
полнительным звеньям или промежуточным преобразователям. Таким
образом, управление осуществляется как бы не самим объектом, а его
моделью, представляемой различными датчиками. В связи с этим мож-
но считать, что энтропия определяется множеством состояний всех
датчиков и вероятностными характеристиками этих состояний.
2.3. ПОЛУЧЕНИЕ ИНФОРМАЦИИ О ТЕХНОЛОГИЧЕСКОМ
ОБЪЕКТЕ УПРАВЛЕНИЯ
Как было показано в гл. 1, в процессе управления оператор переда-
ет управляющему устройству априорную и исходную информацию, а
объект управления - текущую. Управляющее устройство информирует
оператора ^“принятых решениях и передает объекту управляющую
информацию. Рассмотрим основные каналы связей АСУ ТП (см. гл. 1).
Связи управляющего устройства с оператором. Связь управляющего
устройства с оператором может быть прямая (оператор — управляю-
щее устройство) и обратная (управляющее устройство - оператор).
Прямая связь. Оператор вводит в управляющее устройство априор-
ную и исходную информацию, содержащую в себе сведения о цели и
программефункционированиятехнологического агрегата, характеристи-
ки его предельных возможностей и допустимых отклонений от требуе-
мых значений параметров готового продукта. К ним относятся различ-
ные константы (числа), определяющие, например, твердость, чистоту
обработки и геометрические размеры детали, предельные токи, угло-
вые скорости и температуры двигателей; регламентированные цикли-
ческие последовательности команд и условия, разрешающие их пода-
чу; функциональные зависимости (целевые функции), связывающие
обобщенный критерий качества процесса с характеристиками режи-
мов отдельных механизмов. Содержание сведений определяется кон-
кретной технологической задачей, а форма представления должна быть
пригодна для ввода их в управляющее устройство.
>^г^^орнаяП1Пфе-рмащ1я включи г универсальные сведения, не изме>
Ч£яемые_при переходе от одновх-^ншораз1Уюра^цродукции к другому
Она может содержать численно-буквенные характеристики приоритет
тов тех или иных ситуаций, которые используются при решении задач
25
перехода, например, от эксплуатационных алгоритмов к аварийным
и т.п.
Исходная информация содержит сведения, касающиеся данного типо-
размера продукции. Это прежде всего геометрия детали или химичес-
кий состав партии отливок, типы инструментов, последовательность
их смены и параметры отдельных технологических операций (глубина
резания, скорость подачи резца на станке, последовательность смены
калибров и обжатия на прокатном стане и т.п.).
Априорная и исходная информация физически может быть представ-
лена только на каком-либо материальном носителе: в виде графическо-
го изображения на чертежах, лерфокарт. перфолент магнитных лент,
магнитных дисков, т.е. материальных тел, на которые было призведено
физическое (с затратой энергии) воздействие. Обычно в современных
АСУ ТП это сигнал в виде импульса тока или напряжения, передавае-
мый по проводам из точки передачи в точку приема и несущий необхо-
димый запас энергии для возмущения приемника. Информация с одного
носителя на другой переносится с помощью считывания и записи. Считы-
вание не меняет количества информации на носителе. Сам процесс пере-
носа в пространстве и времени называется передачей информации по ка-
налам связи. Возможно искажение информации в результате воздействия
помех (амортизации чертежа, внешних наводок в линии связи и т.п.).
Рассмотрим ряд примеров априорной информации. Необходимо осу-
ществить раскрой полосы случайной длины L на стандартные заготов-
ки длиной /{* при минимальном остатке с учетом срока выполнения за-
каза. В управляющее устройство вносится в качестве априорной инфор-
мации т численных значений стандартных длин Zz-, объемов и сро-
ков ti выполнения каждого заказа. При каждом раскрое должна быть
известна длина исходной заготовки L. Тогда в простейшем случае пу-
тем перебора с учетом коэффициента приоритета, учитывающего объем
и срочность заказа (ai = wz-/rz.), можно подобрать такую комбинацию
стандартных длин Zz- в количестве nz- каждая, чтобы получить мак-
4 т
симум выражения S соблюдая при этом условие
т Z = 1
S nz-Zz- < L.
i=l
Значительно сложнее происходит подготовка априорной информации
при управлении механизмами со сложной траекторией перемещения
рабочего органа, например газорезательными автоматами, роботами-
манипуляторами, копировально-фрезерными станками и др. Основным
первичным источником информации в этом случае является чертеж,
определяющий траекторию или комбинацию траекторий движения.
В применявшихся ранее системах управления чертеж или другой точ-
ный макет траектории устанавливался под контактным или бесконтакт-
26
ным щупом, который, следя за чертежом, обеспечивал перемещение
рабочего органа. В силу специфических недостатков таких методов в
настоящее время применяются системы, в которых вся априорная ин-
формация преобразуется в рационально выбранные кодовые комби-
нации цифровых или буквенных символов, наносимых на программо-
носитель (чаще всего перфоленту), и вводится в память управляющего
устройства.
Для сокращения времени подготовки исходных данных широко ис-
пользуются ЭВМ. С примером подготовки в ЭВМ исходных данных
для программирования сложной траектории можно познакомиться
в гл. 12.
Обратная связь. Такая связь служит для информирования оператора
о ходе технологического процесса и о принятых управляющим устрой-
ством решениях путем постоянного или периодического (по запросу)
вывода необходимой информации в форме, легко воспринимаемой ор-
ганами чувств оператора — обычно зрением и слухом — как обладающи-
ми наиболее высокой информационной пропускной способностью. Это
могут быть стрелочные или цифровые приборы, подключаемые к входу
или выходу управляющего устройства либо к датчикам, а также комп-
лекс индицирующих и регистрирующих приборов в виде цифропечатаю-
щих устройств и электронных индикаторов (дисплеев).
Комплекс вопросов, связанных с приемом информации оператором
от управляющего устройства, изучается специальной наукой — инже-
нерной психологией, которая, рассматривая оператора как звено в
замкнутой системе управления, решает ряд специфических вопросов.
При разработке АСУ ТП наиболее сложной задачей является увязка
доли участия оператора в управлении игхлдя ич его способности к прие-
му и переработке информации, скорости моторных реакций и др.
Большое значение имеет форма представления информации, т.е., спо-
соб ее кодирования. Большинство патчиков и управляющих устройств
оперируют сигналя*™ прАпстаппяющими импульсы тока или потен-
циальные уровни. Стрелочные приборы преобразуют их в положение
стрелки на Шкале, цифровые - в комбинацию цифр. Для информации,
не требующей оперативной реакции, но необходимой для дальнейшего
анализа, лучше всего подходят самописцы, графопостроители, различ-
ного типа запоминающие накопители информации.
Выдача оператору той или иной информации в сложных АСУ ТП
организуется специальным программным обеспечением УВМ. Это оз-
начает, что УВМ осуществляет периодический опрос датчиков и по-
стоянную перезапись полученных значений в память, периодическую
выдачу информации на тот или иной индикатор или регистратор. Циф-
ропечатающие устройства могут получать от УВМ и фиксировать ин-
формацию о производственно-технологических и экономических по-
казателях объекта.
27
Структура и форма представления информационного потока от уп-
равляющего устройства к оператору зависят от ’’уровня” оператора и
режима работы управляющего устройства. Информация операторов
’’нижнего уровня”, наиболее приближенных к технологическому объек-
ту управления, требует, как правило, оперативной реакции; форма ее
представления должна обеспечивать легкое, быстрое восприятие (циф*
ровые табло, стрелочные приборы). Информация для операторов ’’верх-
него уровня” (технологов-программистов) должна быть всесторонней и
исчерпывающей, обеспечивающей дальнейший ее анализ; форма пред-
ставления - распечатка на бумаге в виде цифр, графиков и т.п.
Если управляющее устройство управляет технологическим объектом,
а оператор только осуществляет контроль, то его обязанности сводят-
ся к наблюдению за ходом процесса. Здесь достаточно непрерывной
индикации лишь наиболее важных показателей, характеризующих ка-
чество процесса (толщина прокатываемой полосы, усилие в канатах
экскаватора,положение подъемника и т.п.). Если оператор управляет
технологическим объектом, а управляющее устройство работает в ре-
жиме советчика, т.е. только вырабатывает управляющую информацию,
то оператор должен получить от управляющего устройства рекоменда-
ции на управление и реализовать их. Возможен так называемый инфор-
мационный режим, когда управление технологическим объектом осу-
ществляют операторы нижних уровней, а ЭВМ лишь собирает информа-
цию, обрабатывает ее и передает операторам высших уровней (техно-
логические и производственные службы предприятия).
Связи управляющего устройства с технологическим объектом уп-
равления. Эта связь может быть прямая (управляющее устройство —
технологический объект управления) и обратная (технологическое
устройство - управляющее устройство).
Прямая связь. По этому каналу исполнительным элементам техно-
логического объекта передаются воздействия от управляющего устрой-
ства. Основные задачи этого канала — преобразование управляющего
сигнала В управляющее воздействие, пригодное по своей природе и
Еиду для подачи его на управляющий вход исполнительного органа
технологического объекта управления.
Иногда управляющее устрайство должно включать и отключать раз-
личные клапаны, электромагниты, электроприводы. В этом случае
возникает задача усиления мощности сигнала релейного типа. При уп-
равлении от УВМ технологической линией необходимо согласовывать
выходы управляющего устройства и многочисленные входы исполни-
тельных органов; кроме того, необходимо сформировать сигнал уп-
равления для каждого исполнительного устройства и подать его на тех-
нологический объект управления после логического анализа техноло-
гической ситуации в целях определения условий, при которых эта опера-
ция может быть выполнена.
28
Специфической задачей разработки канала прямой связи является
согласование его пропускной способности с быстродействием УВМ,
обусловленным динамическими показателями технологического
объекта управления.
Обратная связь. Получение информации о текущем состоянии техно-
логического объекта необходимо для выработки управляющей инфор-
мации. Источниками текущей информации являются различные обрат-
ные связи, контролирующие значения выходных параметров и возму-
щений. Канал обратной связи включает в себя первичные преобразова-
тели контролируемого параметра в сигнал (датчики) и вторичные пре-
образователи сигнала датчика в сигнал, форма которого позволяет
ввести его в управляющее устройство. При этом используются преоб-
разования непрерывных (аналоговых) сигналов в непрерывные и не-
прерывных в цифровые, когда непрерывно изменяющийся технологи-
ческий параметр преобразуется в дискретную комбинацию выходных
сигналов, представляющую собой цифровой код. Такое аналого-циф-
ровое преобразование выполняется непосредственно первичным им-
пульсным или кодовым датчиком либо первичный датчик дает на выхо-
де разность потенциалов, которая вторичным преобразователем пре-
образуется в код.
При преобразованиях сигналов часто возникает необходимость фильт-
рации первичного сигнала и отделения полезного сигнала от сигналов
помех. В ряде случаев приходится контролировать параметры, кото-
рые не поддаются непосредственному измерению (например, средне-
квадратичный ток, КПД, производительность, диаметр рулона, запас
кинетической энергии, планово-экономические показатели технологи-
ческой линии и дрО. Подобные задачи решаются применением датчи-
ков, контролирующих параметры, по которым вычисляется значение
искомой величины.
Текущая информация используется также для сигнализации и кос-
венной диагностики предаварийных и аварийных ситуаций. С ее по-
мощью может также фиксироваться занятость того или иного меха-
низма технологического объекта управления, что позволяет осущест-
вить в управляющем устройстве логический анализ ситуации и решить
задачу выбора целесообразного продолжения технологической опера-
ции.
2.4. ПРЕОБРАЗОВАНИЕ ТЕХНОЛОГИЧЕСКОЙ ИНФОРМАЦИИ
Материальным носителем информации является сигнал, который
помимо информации несет также некоторую энергию, полученную от
источника информации. Эта энергия воздействует на приемник. Сигна-
лы носителей внешней (априорной и исходной) информации должны
передавать сведения о задачах и целях: управления. Сигналы текущей
информации, вырабатываемые датчиками, должны обеспечивать не-
29
обходимую простоту и высокую достоверность преобразования техно-
логического параметра в сигнал. Может оказаться, что природа или па-
раметры полученного сигнала непригодны для того, чтобы передавать
его по каналам информации. В этом случае необходимо осуществить
преобразование сигнала. При всех преобразованиях сигналов смысл
сообщения, полученного при считывании с датчиков и поступающего
к управляющему устройству, не должен претерпевать изменений.
В преобразовании сигналов можно выделить два аспекта:
преобразование природы, формы и параметров сигнала (модуля-
ция, квантование и пр.);
установление однозначного соответствия между отдельными вида-
ми сигналов и состояниями управляемого и контролируемого пара-
метров (кодирование: состояние— сигнал; перекодирование: сигнал-
сигнал; декодирование: сигнал-состояние).
2.4.1. Виды и форма сигналов
Для управления АСУ ТП наиболее часто используются электрические
сигналы, £еже — механические, гидравлические, пневматические. Клас-
сификация представления сигналов в АСУ ТП приведена на рис. 2.1, в
соответствии с ней сигналы делятся на две группы:
аналоговые или непрерывные, способные в определенном диапазо-
не находиться в бесконечно большом количестве состояний;
дискретные, способные в определенном интервале находиться в ко-
нечном числе состояний (ток в цепи, коммутируемой реле; выходной
сигнал логического элемента или узла цифровой схемы и т.д.).
Аналоговые сигналы могут быть потенциальными с линейным и не-
линейным преобразованиями первичного состояния и частотными или
гармоническими, отрабатывающими изменение первичного состояния
Рис. 2.1. Классификация представления сигналов
30
Рис. 2.2. Квантование сигналов по уровню (а) и времени (б)
соответствующим изменением амплитуды, частоты или фазы сигнала.
Получение первых осуществляется более простыми устройствами;
вторые являются более гибкими, устойчивыми к помехам, позволяют
осуществлять гальваническую развязку цепей.
Дискретные сигналы бывают квантованными по уровню и време-
ни. Они являются лишь определенным приближением к аналогу пара*
метра, измеряемого датчиками или полученного в преобразованном
виде.
Для источников аналоговых сигналов характерна большая, чем у
дискретных, чувствительность к помехам и инструментальным погреш-
ностям преобразователей (дрейф нуля, температурные колебания коэф-
фициентов усиления и т.п.). Источники дискрехньньсигналов лишены
этих недостатков, так как образующие их элементы работают не в
усилительном, а в релейном режиме.
Квантовани'е сигналов по уровню сводится к замене текущих значе-
ний непрерывного сигнала конечным числом его уровней. На рис. 2.2, а
показан непрерывный сигнал y(t), который в результате квантования
заменяется ступенчатой функцией ф(у). Разность уровней Ду (Г) назы-
вается разрешающей способностью сигнала или шагом квантования по
уровню. Пока сигнал не изменится на Ду (О, преобразователь фикси-
рует предыдущее значение его уровня. Только после достижения сиг-
налом нового уровня квантования преобразователь фиксирует этот
уровень. Если в интервале изменения времени от tj до ti + t приращение
сигнала не выходит за пределы шага квантования в одну или другую
сторону, то прибор фиксирует постоянное значение у/. Шаг квантова-
ния определяется требуемой точностью измерения переменной и обес-
печивается разрешающей способностью квантующего преобразователя.
Чем выше разрешающая способность преобразователя, тем меньше шаг
квантования. Он зависит от допустимой относительной погрешности
измерения 6:
MX5W) -ymin(t)), (2.19)
31
где ymax(t}> Утт(^ ~ соответственно максимальный и минималь-
ный уровни сигнала.
Число уровней квантованного сигнала с учетом нулевого вычисля-
ется по формуле
Ущах^ Ут1п^ . ,
л =------------ + I.
(2.20)
Количество информации (в битах), содержащееся в таком сигнале,
составит
I = log п. (2.21)
С учетом (2.19) и (2.20) получим объем информации в зависимости
от допустимой погрешности:
/ = log (1/6 + 1).
(2.22)
Квантование непрерывного сигнала по уровню позволяет ограничить
конечным числом бесконечное множество измерений. В этом случае
система в большей степени защищена от помех, амплитуда которых
должна быть меньше шага квантования по уровню, чем при использова-
нии аналогового сигнала.
Квантование непрерывного сигнала y(t) по времени (рис. 2.2, 6}
сводится к замене большого числа значений непрерывного сигнала
конечным числом мгновенных значений, фиксируемых через опреде-
ленный промежуток времени Т = Д/\ Последний называется шагом
или периодом квантования по времени и может быть постоянным или
переменным.
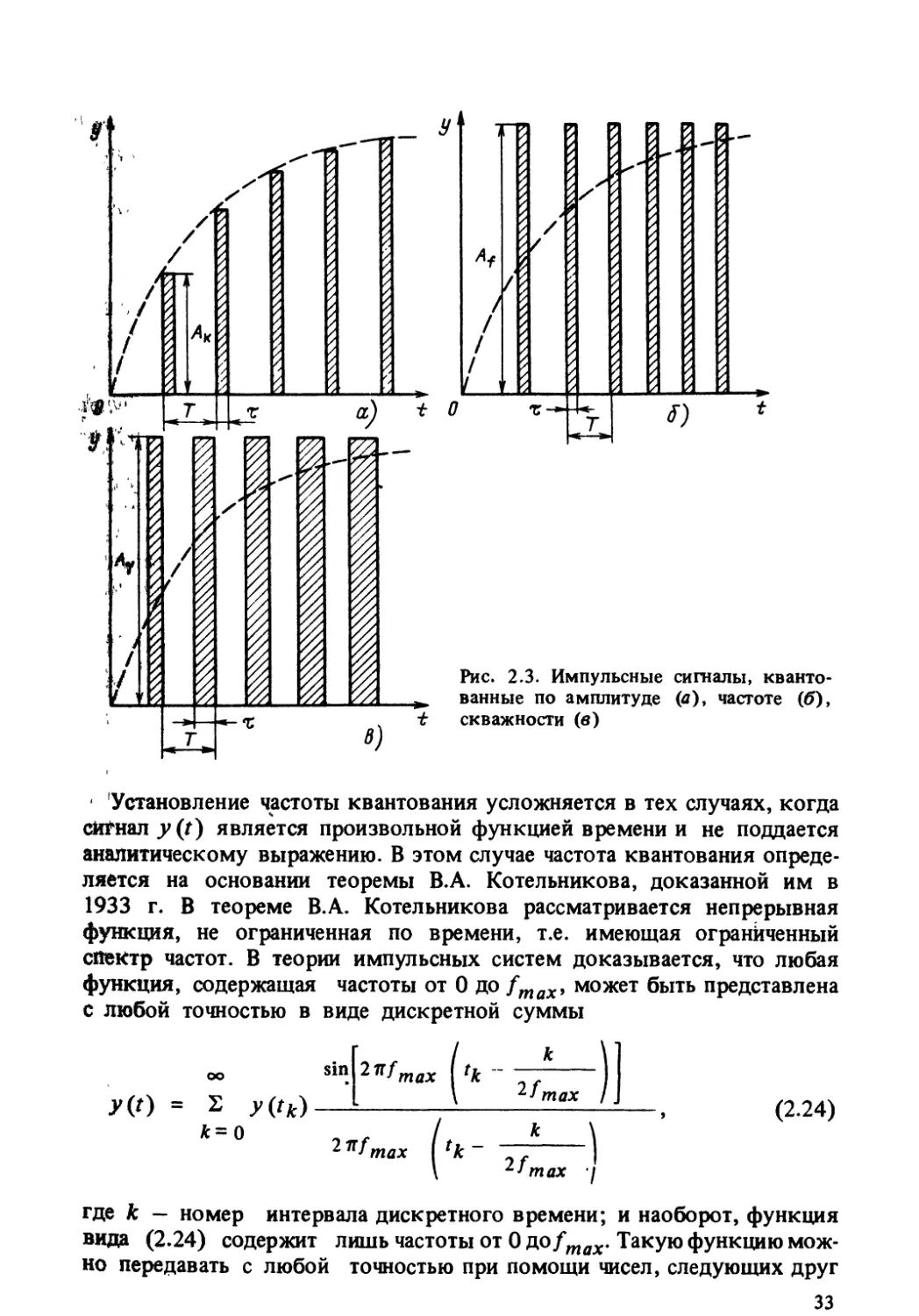
Дискретные сигналы могут быть представлены в виде импульсов,
модулированных по амплитуде Л, частоте f = 1/Т и скважности у =
= т/Т, как показано на рис. 2.3, a-в. Время существования сигнала
на входе измерительного устройства обозначено т. При амплитудной
модуляции в моменты времени (к = 0, 1, 2, ..., ш) фиксированное
значение амплитуды импульса А к равно значению непрерывного сигна-
ла в данный момент времени. При модулировании по частоте частота им-
пульсов пропорциональна аналоговому сигналу; при модуляции по
скважности скважность пропорциональна измеряемому сигналу.
Внутри шага кватования Т между соседними фиксированными значе-
ниями исходный сигнал может быть воспроизведен с точностью, кото-
рая определяется частотой квантования f = 1/Т. Если известно аналити-
ческое представление сигнала, шаг квантования выбирается таким,
чтобы максимальное изменение первичного сигнала за время Т не пре-
вышало шага квантования по уровню by:
dt
Т < by.
max
(2.23)
32
Установление частоты квантования усложняется в тех случаях, когда
сигнал j(r) является произвольной функцией времени и не поддается
аналитическому выражению. В этом случае частота квантования опреде-
ляется на основании теоремы В.А. Котельникова, доказанной им в
1933 г. В теореме В.А. Котельникова рассматривается непрерывная
функция, не ограниченная по времени, т.е. имеющая ограниченный
спектр частот. В теории импульсных систем доказывается, что любая
функция, содержащая частоты от 0 до fmax, может быть представлена
с любой точностью в виде дискретной суммы
[/ Л \
2 яfmax I fk ~ ~ I
-------i------maX '*-—, (2.24)
\ I'max i
где к — номер интервала дискретного времени; и наоборот, функция
вида (2.24) содержит лишь частоты от 0 до fmax* Такую функцию мож-
но передавать с любой точностью при помощи чисел, следующих друг
33
за другом через интервалы времени
= ^Мтах-
(2.25)
С учетом этого (2.24) можно представить следующим образом:
оо
y(t)= S y(kbt)
к = О
/ 7Г , А
sin —-— (tj, - к Дг)
\ Дг К
(2.26)
Бесконечная сумма (2.26) в каждый момент времени k&t будет
содержать лишь одно слагаемое, равное истинному значению функ-
ции в этот момент. Все остальные слагаемые обращаются в нуль. Это
можно пояснить следующим: так как в (2.26) = k&t только у сла-
гаемого с порядковым номером к, то для этого слагаемого после под-
становки получим неопределенность типа 0/0. После раскрытия этой
неопределенности получим 1. Числитель остальных слагаемых равен 0,
так как аргумент получается кра!ным я, а знаменатель этих слагаемых
всегда отличен от 0.
Рисунок 2.4 иллюстрирует теорему В.А. Котельникова. Функция
y(t) заменяется множеством функций, каждая из которых превраща-
ется в нуль в моменты времени k&t и имеет истинное значение у (/#)
для собственного момента времени. Внутри интервала Дг функция
определяется суммой составляющих
приближенно. Следовательно, при
частоте квантования f = 2fmax функ-
ция, содержащая ограниченный
спектр частот, воспроизводится абсо-
лютно точно, если шаг квантова-
ния определяется по (2.25).
Пример^ 2.3. Для замкнутой сис-
темы следящего электропривода,
которая имеет частоту пропускания
/пр = Ю Гц, в целях повышения
помехоустойчивости и точности при-
менен цифровой датчик угловой
координаты. Точность измерения рас-
согласования составляет 1/8 мак-
Рис. 2.4. Иллюстрация теоремы В.А. Ко-
тельникова
34
симального отклонения, т.е. возможны 17 уровней рассогласования.
По этим данным необходимо определить частоту квантования сигна-
ла рассогласования и количество информации, передаваемой в блок
текущей информации.
Сигналы должны передаваться с частотой
fk = 2/пр = 2 - 10 = 20 Гц.
Считая уровни рассогласования равновероятными, определяем коли-
чество информации на одно измерение в соответствии с (2.16) при
лкон = 0-*
/(1) = log 17 = 4,1 бит.
В практике АСУ ТП более вероятны случаи передачи сигнала, огра-
ниченного во времени. Такой сигнал может быть представлен неогра-
ниченным спектром частот (fmax -►<»). Здесь необходимо ограничить
максимальную частоту квантования значением 2fmax- В этом случае
следует ожидать погрешности при определении функции по ее дискрет-
ным значениям. Погрешность будет зависеть от принятой частоты кван-
t
тования. Так, для экспоненциальной функции y(t) = Ае т эта связь
имеет вид
?К « —-_tg -^(1-52)
ЯТ 2
(2.27)
В табл. 2.2 приведены результаты расчетов экспоненты для т = 1 с.
Таблица 2.2
Погрешность воспро- изведения, % 10 5 1 0,5 0,2 0,1
Частота квантования исходной функции, 20 81 2022 8078 50 080 195 405
Гц Частота квантования после интерполяции функции, Гц 1,12 1,59 3,55 5 8 11,2
Как видно, при допустимой погрешности 0,1 % частота квантова-
< ния должна превышать 195 кГц. Такая высокая частота требует су-
щественного усложнения преобразователя информации.
Значительное уменьшение частоты квантования при той же погреш-
ности может быть достигнуто путем аппроксимации воспроизводимой
функции. Аппроксимация осуществляется линейным интерполирова-
35
нием, среднестепенным или равномерным приближением. Даже при
линейной интерполяции, когда в интервале времени Аг функция ме-
няется по линейному закону, частота квантования значительно умень-
шается. В табл. 2.2 приведены данные также для аппроксимированной
функции с т = 1 с. Как видно, при погрешности 6 = 0,1 % частота кванто-
вания уменьшилась более чем в 17000 раз, что существенно уменьша-
ет сложность преобразования информации.
2.4.2. Кодирование сигналов
Кодирование сигналов служит для обмена информацией между от-
дельными составляющими АСУ ТП, ее обработки и хранения с требуе-
мой точностью и надежностью. Кодирование состоит в использовании
кода - универсального способа отображения информации при ее пере-
даче, обработке и хранении. Код представляет собой систему соответ-
ствий между элементами сообщений и сигналами, при помощи кото-
рых эти элементы можно зафиксировать.
Различные виды сигналов одной физической природы называются
символами. Конечная совокупность символов, выбранная для передачи
конкретного сообщения, называется словом. Полная совокупность
символов, обеспечивающих передачу необходимой номенклатуры сооб-
щений — слов, образует алфавит. В свою очередь совокупность слов и
правил их последовательного представления образует язык и его син-
таксис.
Язык символов определяет принцип действия тех устройств, кото-
рые будут воспринимать и воспроизводить эти символы. От морфоло-
гии языка будет зависеть длина слов. В АСУ ТП применяются два спосо-
ба передачи сообщений: параллельным кодом — все символы одного
слова передаются одновременно по каналам, число которых соответ-
ствует длине слова; последовательным кодом - символы одного сло-
ва передаются друг за другом по одному каналу. Таким образом, язык
и его морфология определяют число элементов, необходимых для пере-
дачи слов, а также число считывающих каналов при параллельной (од-
новременной) передаче сообщений по каналам либо время при последо-
вательной передаче сообщений по одному каналу.
Выбор кодов определяется спецификой восприятия и преобразова-
ния информации, характерной для данного уровня АСУ ТП и ее состав-
ляющих. Основными требованиями, которые выдвигаются при выборе
способа кодирования, являются: экономичность отображения информа-
ции, простота технической реализации устройств кодирования, удоб-
ство выполнения вычислительных операций и надежность передачи
сообщений.
Для выполнения этих требований, особенно связанных с удобством
выполнения вычислительных операций, наиболее пригоден цифровой
алфавит, число символов в котором зависит от основания системы
36
счисления и обычно не превышает 10. Он позволяет осуществлять коди-
рование не только чисел, но и понятий.
При помощи такого алфавита с основанием п любое число можно
представить в виде
о
М = 2 г= aN_\ nN~l + . .. + ахп + дои°. (2.28)
/=2V-1
Если опустить л^, то получим более компактную запись TV-разряд-
ного (от N— 1 до 0) числа М:
М = • • • а i^o- (2.29)
Из (2.28), (2.29) следует, что одно и то же число М в зависимости
от основания п при кодировании формируется из разного количества
символов в одном разряде и количества разрядов. Например, цифро-
вой трехразрядный десятичный вольтметр, представляющий информа-
цию в коде с основанием 10, имеет в каждом разряде 10 различных
цифр (символов) и может с точностью до единицы младщего разряда
выдать 1000 (0, 1, 2, ... 999) различных значений измеряемого напря-
жения. Для осуществления той же операции в двоичном коде (коде с
основанием 2) потребуется 10 разрядов с двумя значащими цифрами
В каждом из них (210 = 1024). 30 значащих цифр (знаков) в первом
случае несут ту же информационную нагрузку, что и 20 знаков во вто-
ром случае.
Экономичность кодирования будет тем выше, чем меньше знаков
следует затратить на передачу одного и того же сообщения. При переда-
че сообщений по каналу связи количество знаков определяет также и
необходимое для этого время. Таким образом, выбор кода (основа-
ния системы) влияет на поток передаваемой информации и время пере-
дачи.
. Найдем основание кода, при котором потребуется минимальное чис-
ло элементарных знаков для передачи сообщений. Пусть п - число сим-
волов в разряде (основание кода), &N — число разрядов. Тогда возмож-
ное количество различных сообщений составляет
М = nN. (2.30)
Наиболее экономичному коду соответствует минимум произведения
числа символов п на число разрядов N, т.е. nN -> min. Определяя N
из (2.30) и умножая на л, получаем
nN = nX—. (2.31)
In п
Минимум левой части (2.31) определится, если найти оптимальное
значение п. Берем производную правой части (2.31) по л и, приравни-
37
вая ее 0, получаем уравнение для определения п: 1пи — 1 = 0, откуда
оптимальное значение основания кода nopt = е « 2,72.
Хотя минимум аппаратуры и дает кодирование с основанием е, одна*
ко его невозможно реализовать. Близки к оптимальному коды с основа-
ниями 3 и 2. По соображениям простоты технической реализации явное
преимущество на стороне кода с п = 2, при котором для хранения, пере-
дачи и обработки информации необходимы дискретные элементы с дву-
мя устойчивыми состояниями (”да” - ’’нет”, ’’включено” - ’’отклю-
чено”). Поэтому двоичный код получил широкое распространение в
цифровых устройствах контроля и управления.
При вводе двоично-кодированной информации в УВМ для компакт-
ности записи часто используют коды, основания которых являются це-
лой степенью чисел 2 - 23 =8 (восьмеричный) и 24 = 16 (шестнадцате-
ричный) .
При представлении числа в двоичной системе п = 2, аяу равно 0 или 1.
Например, число 12ю в двоичной системе записывается 1100. В восьме-
ричной системе (п = 8) используют восемь цифр: 0, 1,2, 3, 4, 5, 6 и 7,
поэтому ai принимает значения от 0 до 7. Например, восьмеричное чис-
ло 241 равно десятичному числу 161:
2418 = 2 • 82 + 4 • 81 + 1 • 8° = 16110-
В шестнадцатеричной системе для изображения чисел применяются
цифры от 0 до 15 (всего 16 цифр); обозначения первых десяти цифр
от 0 до 9 совпадают с десятичным, а остальные шесть цифр (от 10 до 15)
обозначаются латинскими буквами Л, В, С, D,E и F.
Так, шестнадцатеричное число
Л1Г1б = 10 -162 + 1 • 161 + 15 • 16° =25911О-
Изображения десятичных чисел от 0 до 20 в двоичной, восьмерич-
ной и шестнадцатеричной системах представлены в табл. 2.3.
В связи с использованием различных систем счисления необходимо
знание правил перевода чисел из одной системы в другую. Проще всего
выполняется перевод восьмеричных и шестнадцатеричных чисел в двоич-
ные и обратный, так как основания этих систем есть целые степени чис-
ла два (8 = 23, 16 = 24). Для перехода от восьмеричного числа к двоич-
ному (переход 8 -► 2) следует заменить каждую его цифру соответствую-
щим трехразрядным двоичным числом. Например, для числа 241 переход
осуществляется так:
2 4 1
010 100 001 = 10100001;
при этом 0 в старшем разряде отбрасывается.
Для перехода от шестнадцатеричного числа к двоичному (16 -*2)
каждую его цифру заменяют соответствующим четырехразрядным
38
Таблица 2.3
Система счисления Система счисления
Десятич- ная Двоич- Восьме- Шестнадца- теричная Десятич- Двоич- Восьме- ричная Шестнад- цатерич- ная
ная ричная ная ная
0 0 0 0 11 1011 13 В
1 1 1 1 12 1100 14 С
2 10 2 2 13 1101 15 D
3 11 3 3 14 1110 16 Е
4 100 4 4 15 1111 17 F
5 101 5 5 16 10000 20 10
6 110 6 6 17 10001 21 11
7 111 7 7 18 10010 22 12
8 1000 10 8 19 10011 23 13
9 1001 И 9 20 10100 24 14
10 1010 12 А
двоичным числом. Для числа Л lFt 6 переход выглядит так:
А 1 F
1010 0001 1111 = 1010000111112.
Для перехода от двоичной к восьмеричной (2 -* 8) или шестнадцате-
ричной (2 16) системе необходимо, начиная с младшего разряда, раз-
бить двоичное число на группы по три (для перехода 2 ->8) или по четы-
ре (для 2 -► 16) разряда, дополняя при необходимости нулями группу
в старших разрядах. Например, для исходного двоичного числа
11010111102
Переход 2 -► 8 будет
. 001 101 011 НО
1 5 3 6 = 15368,
В переход 2 -► 16 для этого же числа будет
ООН 0101 1110
3 5 Е = 35Е16.
Переходы от десятичной к рассмотренным системам (10 -*2, 10 -*8,
10 16) удобнее всего производить по методу деления. По этому мето-
ду исходное число в десятичной системе последовательно делится на ос-
нование числа искомой системы. Остатки от деления образуют резуль-
тат перевода, причем старший разряд соответствует последнему остат-
ку, а младший — первому. Ниже даны примеры преобразований деся-
39
тичного числа 1479 в двоичную, восьмеричную и шестнадцатеричную
системы.
Преобразование 10 -* 2:
1479/2 = 739 (остаток 1) - младший разряд
739/2 = 369 (остаток 1)
369/2 = 184 (остаток 1)
184/2 = 92 (остаток 0)
92/2 = 46 (остаток 0)
46/2 =23 (остаток 0)
23/2 = 11 (остаток 1)
11/2 =5 (остаток 1)
\5/2 = 2 (остаток 1)
2/2 = 1 (остаток 0)
1/2 = 0 (остаток 1) - старший разряд
N2 =10111000111.
Преобразование 10 -* 8:
1479/8 = 184 184/8 = 23 23/8 = 2 2/8 = 0 (остаток 7) - младший разряд (остаток 0) (остаток 7) (остаток 2) - старший разряд N* = 2707.
Преобразование 10 -+ 16:
1479/16 = 92 (остаток 7) - младший разряд
92/16 = 5 (остаток 12)
5/16 = 0 (остаток 5) - старший разряд
JV16 = 5С7.
Кодовые слова могут иметь одинаковую или различную длину, h со-
ответствии с этим код называется равномерным или неравномерным.
Равномерные коды получили наибольшее распространение в системах
обработки и передачи информации. Неравномерные коды применяются
в системах, учитывающих статистические свойства сообщений и связы-
вающих длину сообщений с частотой их передачи. Чем чаще передается
сообщение, тем короче должен быть его код. Такой метод используется
в коде Шеннона—Фано. По этому же принципу, набирая номер телефо-
на справочной службы или вызывая скорую помощь, мы пользуемся
кодовой комбинацией из двух цифр, а не из 6—7, обычно необходи-
мых для связи с другими абонентами.
Представление числовой информации в УВМ выполняется при помо-
щи двоичного позиционного кода (2.28), (2.29) с естественным распре-
делением весов разрядов 2N~1, ..., 2, 2° (где N — число разрядов).
В соответствии с требованием простоты алгоритмов выполнения ариф-
метических операций с учетом знака и ограниченности разрядной сет-
ки УВМ для представления относительных чисел применяют специаль-
40
ные коды: прямой, обратный и дополнительный. Во всех этих кодах
введен специальный знаковый разряд.
В прямом коде знак кодируется значением 0 для положительных
и 1 — для отрицательных чисел, а абсолютная величина числа представ-
ляется двоичным позиционным кодом. Например, двоичное число
1100 (+12) в прямом коде записывается 0.1100. Прямой код удобен
при выполнении операций умножения, так как знак произведения полу-
чается автоматически. Однако он не обеспечивает замену вычитания
чисел сложением их кодов, что затрудняет его использование при выпол-
нении операции вычитания. Этот недостаток устраняется при примене-
нии обратного и дополнительного кодов, отличающихся от прямого
способом представления отрицательных чисел.
Обратный код отрицательного числа образуется путем инвертирова-
ния всех значащих разрядов. Например, двоичное число —1100 (—12)
в обратном коде записывается 1.0011. Дополнительный код отрицатель-
ного числа отличается от обратного тем, что после инвертирования
разрядов в младший разряд добавляется 1. Например, двоичное число
—1100 в дополнительном коде записывается 1.0100.
Суммирование чисел в обратном и дополнительном кодах выпол-
няется поразрядно, включая и знаковые разряды, причем в дополни-
тельном коде отпадает необходимость в циклическом переносе и опера-
ция сложения реализуется проще, чем в обратном коде.
В ряде устройств АСУ ТП (связь с оператором, вывод информации
для индикации и числового программного управления) нашли приме-
нение двоично-десятичные коды. В этих кодах каждая десятичная циф-
ра представляется четырьмя двоичными (тетрадой). Так как четыре
двоичных символа дают шестнадцать комбинаций, а используется толь-
ко десять из них, то возможно множество вариантов кодирования деся-
тичных цифр - их число составляет 2,9 Ю9.
Применение нашли несколько систем кодирования десятичных цифр
двоичными тетрадами (табл. 2.4). Код 8 42 1 дает естественное пред-
ставление десятичных цифр в двоичной системе, так как соответствует
весам двоичных разрвдов в позиционном двоичном коде. Этот код, а
Таблица 2.4
Код Десятичные числа
0 1 2 3 4 5 6 7 8 9
84 2 1 0000 0001 0010 ООП 0100 0101 оно 0111 1000 1001
5 12 1 0000 0001 0101 оно 0111 1000 1001 1010 1011 1111
2 из 5 11000 00011 00101 00110 01001010100110010001 10010 10100
Грея 0000 0001 ООН 0010 ОНО 0111 0101 0100 1100 1101
Позицион- ный 0000 0001 0010 ООН 0100 0101 оно 0111 1000 1001
41
также код 5 12 1 используются в системах ЧПУ металлорежущих
станков.
Применяют также двоично-десятичные коды, в которых каждая де-
сятичная цифра кодируется пятью и более двоичными. Избыточность
таких кодов можно использовать для контроля и коррекции переда-
чи и обработки данных. К ним относится код 2 из 5, в котором каждая
кодовая комбинация содержит две единицы и три нуля.
Кроме позиционных систем представления информации существуют
также непозиционные системы. Из них наибольшее распространение
получил код Грея, в котором комбинации, представляющие соседние
по значению числа, отличаются лишь в одном разряде.
В табл. 2.4 показаны числа от 0 до 9 в коде Грея и для сравнения —
в позиционном двоичном коде. Использование кода Грея повышает
надежность аналого-цифрового преобразования, устраняя неоднознач-
ность считывания в кодовых датчиках перемещения и сводя к мини-
муму возможные погрешности преобразования. Недостатком кода
Грея является сложность выполнения в нем арифметических операций,
поэтому при вводе в УВМ он обычно преобразуется в позиционный код.
2.5. ПЕРЕДАЧА И ЗАЩИТА ИНФОРМАЦИИ ОТ ПОМЕХ
2.5.1. Пропускная способность канала связи без помех
Передача информации от управляющего устройства к технологичес-
кому объекту и в обратном направлении, обмен информацией с выше-
стоящими и смежными уровнями АСУ ТП осуществляются при помощи
каналов связи. Для нормального протекания процесса управления ка-
налы связи должны обладать соответствующей пропускной способно-
стью или емкостью.
Предельная скорость передачи информации по каналу определяет
его емкость
С . lim -!*» ,
Т -► ОО Т
где q — количество различных символов, передаваемых за время Т.
Для повторяющихся циклических процессов отрезок времени Т ра-
вен времени цикла. Если передавать сигналы со скоростью S = 1/т им-
пульсов в секунду, где т — время передачи одного импульса, то за вре-
мя Т можно передать п импульсов:
п = Т/т = ST.
Бинарный (двоичный) канал, пропускающий только элементарные
сигналы 0 и 1, позволяет за время Т передать количество комбинаций
элементарных сигналов не более
q = 2Л = 2ST = 2Г/Т.
42
Емкость такого канала связи обратно пропорциональна длитель-
ности импульса т = 1/S:
C^L-S.
т
Пусть за время одного импульса т может быть передано одно из m
различных элементарных сообщений (т — число различных символов
в алфавите). Тогда q = mST и емкость канала
ST
С = logm— = 5 iOg w. (2.32)
т
Например, m = 32, т = 0,01 с. Тогда
С = logw/r = log 32/0,01 = 500дв.ед/с.
Емкость или пропускная способность канала связи может быть вы-
ражена в двоичных единицах на символ. Для бинарного канала
С = 1 дв.ед/символ, а для рассмотренного примера С = logw =
» 5 дв.ед/символ.
Допустим, что источник информации передает непрерывную последо-
вательность из двух сообщений А и В, имеющих одинаковую вероят-
ность Р(А) = Р(В) = 0,5, и на передачу каждого из них требуется вре-
мя г = 1 с. В этом случае энтропия источника на одно сообщение со-
ставляет
Н =- (0,5 log 0,5 + 0,5 log 0,5) = 1 бит/сообщение.
При т = 1 с пропускная способность канала С = 1 бит/с, а средняя
скорость передачи сообщений по каналу
С/Н = 1 сообщение/с.
. Если изменится вероятность сообщений А и В, например Р(А) =
= 0,1, Р(В) = 0,9, то уменьшается энтропия источника:
Н =— (0,1 log 0,1 + 0,9 log 0,9) « 0,5 бит/сообщение.
При такой энтропии источника для наилучшего использования про-
пускной способности канала (С = 1 бит/с) необходимо увеличить ско-
рость передачи сообщений до значения, равного
С/Н = 2 сообщения/с.
Она будет достигнута, если по каналу будет передаваться информа-
ция от двух таких источников. Таким образом, если к входу канала
подключен источник сообщений с энтропией на символ (сообщение),
равной емкости канала связи, то источник согласован с каналом. Ес-
43
ли же энтропия источника меньше емкости канала, то емкость кана-
ла используется не полностью, т.е. канал будет недогружен и в ста-
тистическом смысле не согласован с источником (ОН).
Такое согласование осуществляется с помощью статистического
кодирования, которое позволяет повысить энтропию передаваемых
сообщений и сократить их избыточность. Для дискретных сообщений
избыточность И показывает, какая доля исходного числа элементов
сообщения может быть устранена с помощью статистического коди-
рования
И = 1 - (2.33)
При энтропии источника, превышающей емкость канала, передача
информации без искажений невозможна.
2.5.2. Пропускная способность канала связи с помехами
и принципы построения помехозащищенных кодов
Помехи искажают часть передаваемых сообщений, и на приемной
стороне (рис. 2.5) при наличии помех (шумов) нет полной уверен-
ности в том, что принято именно то сообщение (или элемент сообще-
ния), которое было передано.
Искажение, производимое помехой, состоит в том, что передаваемый
сигнал будет не опознан или принят за другой. Например, пусть пере-
дается сигнал 1010, и помеха исказила нули так, что они превратились
в 1, т.е. неверно приняты 50% передаваемых символов. Теперь на при-
емной стороне будут приняты только 1, причем невозможно отличить
истинные 1 от ложных. Таким образом, чтобы исказилась вся переда-
ча, достаточно в данном случае принять неверно только половину сим-
волов.
Для того чтобы передавать информацию с возможно меньшими ис-
кажениями по каналу связи с помехами, следует использовать помехо-
защищенные или корректирующие коды. Первые из них позволяют
обнаружить ошибки, а вторые — не только обнаружить, но и испра-
вить их.
Принципы обнаружения и исправления ошибок поясняются при по-
мощи геометрических моделей кодов. Любой и-элементный двоич-
ный код можно представить в виде и-мерного куба, в котором каждая
вершина отображает кодовую комбинацию, а длина ребра равна едини-
це. В таком кубе расстояние между вершинами, измеряемое минималь-
Рис. 2.5. Схема передачи сообщений
44
Рис. 2.6. Геометрическая модель двоич-
ного кода при п = 3
ным количеством ребер, называется
кодовым расстоянием d. Кодовое
расстояние - минимальное число
элементов, в которых одна кодовая
комбинация отличается от другой.
На рис. 2.6 показан куб при п = 3, на вершинах куба размещается
восемь кодовых комбинаций. Если использовать (разрешить) для пе-
редачи информации все восемь комбинаций (d = 1), то образуется не-
помехоустойчивый двоичный код. При использовании четырех из вось-
ми комбинаций появляется возможность обнаружения одиночных
ошибок, а кодовые комбинации отстоят друг от друга на расстоянии
d -=2. Например, выбраны комбинации ООО, 110, 011 и 101. Прием ком-
бинации 100, отстоящей от выбранных 000, ПО и 101 на расстоянии
d = 1, свидетельствует о том, что при передаче произошла одиночная
ошибка. Таким образом, недоиспользование возможных комбинаций,
приводящее к избыточности кода, дает возможность обнаруживать
ошибки.
Для того чтобы код не тойько обнаруживал ошибку, но и обладал
возможностью исправить ее, следует повысить его избыточность. Для
этого выберем в трехмерном кубе вершины, находящиеся друг от дру-
га на расстоянии d = 3. Возможны четыре пары разрешенных комбина-
ций: 000 и 111, 001 и 110, 100 и 011,010 и 101. Код, состоящий из двух
комбинаций любой пары, позволяет исправить одиночную ошибку
Или обнаружить две ошибки без возможности их исправления.
В общем случае корректирующая способность кода однозначно опре-
деляется кодовым расстоянием
d = г + $+ 1,
(2-34)
где г — число обнаруживаемых ошибок; s - число исправляемых оши-
бок; обязательное условие г > $. При г = s код позволяет обнаружить
2х или исправить х ошибок.
Для кода, позволяющего только обнаруживать ошибки,
d = г + I. (2.35)
Для кода, предназначенного только для исправления ошибок
d = 2s+l. (2.36)
Указанные принципы используются для построения различных много-
45
разрядных помехоустойчивых кодов, классификация которых представ-
лена на рис. 2.7. С методиками формирования и реализацией конкрет-
ных кодов можно познакомиться, например, в [19, 37].
Глава третья
ИДЕНТИФИКАЦИЯ ТЕХНОЛОГИЧЕСКИХ ОБЪЕКТОВ
УПРАВЛЕНИЯ
Целью данной главы является краткий, но систематизированный
обзор принципов и основанных на них методов получения формаль-
ных моделей объектов и процессов, состоящих из последовательнос-
тей различных операций.
В современной литературе под идентификацией понимаются обыч-
но экспериментальные методы получения динамических моделей. В на-
стоящем учебнике понятие идентификации применено в самом широ-
ком смысле, т.е. охватывает все вопросы, связанные с представлением
в виде формул, таблиц, графов и т.п. как различных элементов техно-
логического оборудования, так и технологических операций и процес-
сов. Это позволяет вести рассмотрение весьма обширного и разнород-
ного материала с единых методических позиций.
При отборе материала авторы стремились включать наиболее совре-
менные методы: с одной стороны, наиболее целесообразные в практи-
ке АСУ ЭП и АСУ ТП формообразования, а с другой, достаточно до-
ступные всему составу студентов.
Глава является наиболее объемной, а материал — в значительной сте-
пени новым для изучения. Это объясняется стремлением охватить и
систематизировать многообразие методов идентификации технологи-
ческих объектов. При изложении материала широко использованы при-
46
меры. Некоторые из них поясняют теоретический материал, другие,
например 3.6, 3.10, доводят решение задачи до получения количествен-
ного результата.
Следует обратить внимание на заключительный материал п. 3.4.5.
В нем изложен пример построения алгоритма модели технологическо-
го процесса с позиций оценки его результатов в условиях действия
случайных возмущений.
При изучении материала необходимо стремиться к анализу методов
и приемов построения модели технологического процесса и сопостав-
лять их с уже изученными в предыдущих курсах. Особенно полезно
самим студентам на базе изученного материала других курсов и инфор-
мации о технологических объектах, полученной в процессе производ-
ственной практики, формировать примеры — аналоги практических
задач.
3.1. ЗАДАЧИ ИДЕНТИФИКАЦИИ
Объективные закономерности, присущие процессам переработки
информации, обусловливают аналогию функциональных структур че-
ловека-оператора и управляющего устройства любого типа. Эта анало-
гия распространяется не только на перечень этапов переработки инфор-
мации, но и на их содержание. Чтобы управлять технологическим объек-
том, управляющее устройство должно располагать информацией о его
свойствах и состоянии в данный момент времени. Эти данные обеспе-
чиваются введением в управляющее устройство априорной и текущей
информации, объем которой зависит от сложности объекта и задач,
им выполняемых. Любой объект рассматривается как система с входа-
ми и выходами. В том числе технологический объект можно предста-
вить как систему, входными исполнительными устройствами которой
являются различного рода исполнительные приводы с передаточными
устройствами, а выходными - параметры технологического процесса.
В этом случае управляющее устройство должно вырабатывать воздей-
ствия на входы технологического объекта, так чтобы выходные тех-
нологические параметры для обеспечения требуемого качества выпус-
каемой продукции принимали заданное или оптимальное значение и не
превышали допустимых значений. Это значит, что управляющие воз-
действия и их последовательность должны формироваться управляю-
щим устройством с учетом особенностей технологического объекта,
его состояния и тем самым обеспечивать необходимое целенаправлен-
нее протекание технологического процесса. Следовательно, для высо-__
^качественного управления технологическим объектом необходимо
знать связи (закономерности), существующие между его входными и
выходными управляемыми величинами. Такие связи между выходами
и входами объекта, представленные формализованно, носят название
модели или алгоритма функционирования объекта. Без такой формаль-
47
ной модели объекта невозможна разработка целенаправленного управ-
ления им. Чем универсальнее, точнее модель технологического объек-
та, тем эффективнее и результативнее можно осуществить управление.
Принципы и методы получения и-представления формальных моде-
лей объекта, а также сам процесс получения таких моделей называются
индентифи кацией.
Из курсов ’’Теория электропривода”, ’’Системы автоматического
управления электроприводами” и других известны примеры аналити-
ческих моделей элементов автоматизированного электропривода: пе-
реходные и частотные характеристики систем электропривода и двига-
телей, зависимости выходного напряжения тиристорных преобразова-
телей от угла управления тиристорами и т.п.
Обычно это одномерные объекты, имеющие один вход и один выход,
чаще всего линейные, детерминированные, т.е. обладающие неизмен-
ным во времени характером и параметрами преобразования входной
величины в выходную. Одному объекту может соответствовать несколь-
ко моделей, отражающих разные стороны функционирования, но мо-
жет существовать универсальная модель, описывающая различные
объекты одним аналитическим выражением. Например, формула меха-
нической характеристики электропривода отражает связь между ско-
ростью и моментом в статике, а дифференциальное уравнение или пере-
даточная функция представляет собой модель объекта в динамике.
Однако современные технологические объекты - это объекты, имею-
щие несколько входов и выходов, взаимовлияющих друг на друга,
связанных нелинейными зависимостями со случайными возмущения-
ми. Возможно сочетание непрерывно меняющихся входных и выход-
ных величин и дискретных операций. Такие объекты требуют не толь-
ко непрерывного изменения самих технологических операций, но и
соблюдения определенной заданной последовательности, смены этих
операций, а также учета аварийной ситуации объекта.
Для объектов, требующих оптимального управления, используется
специфический тип модели — целевая функция, представляющая зави-
симость критерия качества функционирования объекта от его вход-
ных воздействий. Многообразие объектов обусловило появление различ-
ных методов получения моделей, а также форм их представления. При-
меняются аналитические^^^эксдщгиментальные методы получения моде-
лей, которые МОгут^быть представлены в виде аналитических выраже-
ний, таблиц, графов, циклограмм и др. Для сложных объектов, под-
верженных случайным возмущениям различного характера в непрог-
нозируемых сочетаниях и последовательности, разрабатываются сто-
хастические модели, в которых исходные величины, интервалы време-
ни и параметры преобразования заданы законами распределения и ста-
тистическими характеристиками.
Применительно к технодогическим объектам возникают специфи-
ческие проблемы определения границ идентифицируемого объекта и
48
оценки качества модели. Границы идентифицируемого объекта опре-
‘дёЛЯЮТСЯ, во-первых, детальмо сфо^р^дированной _целыо, т.е. перечнем
всех технологических параметров, поведение которых влияет на качест-
во продукции, и, во-вторых, перечнем внешних Факторов, в той или
иной степени влияющих на основные технологические параметры.
Обычно при идентификации для удобства построения моделей идут
по пути расчленения модели объекта на математически однородные
элементы или типовые звенья. После такой декомпозиции синтез моде-
ли исследуемого объекта сводится к синтезу структуры и параметров
оператора Фм, преобразующего многомерные векторы входных уп-
равляющих Хм и возмущающих ZM воздействий в вектор управляе-
мых выходных координат Ум с требуемым уровнем адекватности
Гм = Фм { *М } •
Если возможен перенос возмущений к выходу модели, то указанное
соотношение записывается в виде
?м = Фм { + ZM. (3.1)
' При идентификации по управляющим входам полагают возмущаю-
щие воздействия равными 0, т.е. получают модель в виде первого чле-
на правой части (3.1). Оценка качества модели может производиться
путем анализа ее адекватности объекту, в частности путем вычисле-
ния суммы квадратов отклонений данных расчета на модели Ym и ре-
зультатов эксперимента на объекте у 0:
п
1= 2 Оо-Км)2-
1 = 1
При синтезе модели стремятся достигнуть соотношений I = /т|Л
или I = /доп- Если эти условия не удовлетворяются, то модель чрезмер-
но упрощена и необходимо выбрать другой ее тип. Если /доп не зада-
но, то применяются специальные методы оценки адекватности модели
объекту.
Кроме требований точности формальные модели (алгоритмы функ-
ционирования) должны, как правило, удовлетворять следующим тре-
бованиям: *
определенности - модель должна исключать различные варианты ее
толкования;
массовости — модель должна быть пригодной для широкого диапазо-
на численных значений исходных данных;
результативности - она должна позволять выполнять расчет с исполь-
зованием известного математического аппарата;
надежности - модель должна обеспечивать с течением времени тре-
49
буемую точность совпадения данных, полученных с использованием
модели и эксперимента.
Многообразие технологических процессов не позволяет дать кон-
кретные рекомендации по выбору методов разработки моделей различ-
ных технологических объектов. Ниже рассмотрены лишь основные,
наиболее часто используемые приемы разработки моделей объектов.
3.2. АНАЛИТИЧЕСКИЕ МЕТОДЫ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ ТЕХНОЛОГИЧЕСКИХ ОБЪЕКТОВ
3.2.1. Модели элементов
Аналитические методы традиционны при рассмотрении формальных
моделей элементов электропривода и в связи с этим наиболее знакомы
студентам. Они базируются на знании фундаментальных закономернос-
тей электромеханического преобразования энергии. Аналогичный под-
ход возможен и при использовании гидравлических и пневматических
приводов, он может быть распространен на элементы рабочего техно-
логического оборудования.
Любая сложная силовая структура, состоящая из нескольких конту-
ров, в которых происходит преобразование энергии из одного вида
в другой, может быть разбита на отдельные элементы. Каждый из них
осуществляет получение энергии, ее накопление, передачу другому
элементу, расходование на полезную работу или рассеивание некото-
рой части энергии в виде потерь.
Знание природы элементов позволяет математически описать про-
цессы преобразования энергии. Обобщив различные методики и форма-
лизовав связи одного элемента с другим, можно получить уравнения,
описывающие процессы в сколь угодно сложных и разнородных сило-
вых структурах технологических процессов. Рассмотрение только тех-
нологических процессов формообразования позволяет остановиться
на системах с сосредоточенными параметрами и элементами.
Для получения обобщенных моделей элементов с сосредоточенны-
ми параметрами введем понятие разности потенциальных уровней U.
Будем понимать под этим расход энергии на единицу преобразован-
ного продукта. Введем также переменную количества Q — численную
меру объема преобразуемого продукта. Произведение этих величин
даст работу, необходимую для изменения на U потенциальных уров-
ней количества продукта Q:
UQ = А.
Мощность, расходуемая на изменение потенциального уровня со ско-
ростью dQ/dt, определяется соотношением
р = и^-.
dt
50
Для иллюстрации приведены уравнения электрической и механи-
ческой цепей:
электрическая цепь:
И = + lq,
dt2 dt с
или
и = L —+ Ri+ --Ji dt,
dt С
1;де q - заряд; R, L, С - активное сопротивление резистора, индуктив-
ность катушки и емкость конденсатора, включенных в цепь;
1 механическая цепь:
М = J — + р— + кв,-
dt2 dt
или
dt <*>о
' Иде J — момент инерции; 0, со — угол и угловая скорость двигателя;
' 0 « Мп/а)0— жесткость механической характеристики двигателя; к =
‘ = Л^а — жесткость кинематического звена. Второе слагаемое второго
уравнения момента характеризует суммарный момент сопротивле-
ния AfcJ
< Элементы, связанные соединениями, в которых не происходит на-
копления и преобразования вещества или энергии, образуют структу-
ру системы, отражающую технологический процесс преобразования
'&их видов продуктов. Для анализа такой структуры используются
ЙЬа закона:
’ f сумма расходов продукта в любом разветвлении равна 0:
П dQf
Е —= 0; * (3.2)
4»1 dt
сумма разностей уровней потенциалов в любом контуре равна 0:
s Uj = 0. (3.3)
i=l
Решение уравнений типа (3.2) и (3.3) может дать принципиально
разные результаты.
51
Если многоконтурная система имеет один вход и один выход, то
система дифференциальных уравнений первого порядка, описывающих
процессы в элементах, даст дифференциальное уравнение, порядок ко-
торого определяется числом накопителей энергии в системе. Такие од-
ноканальные (одномерные, односвязные) системы изучались в кур-
сах ’’Теория электропривода”, ’’Системы управления” и др.
Технологические объекты управления, как правило, являются мно-
госвязными системами, имеющими несколько входов и выходов. Для
них характерна зависимость каждого выхода от всех входов системы.
Математическая модель такой системы представляет собой систему
дифференцицальных уравнений различного порядка, в левой части
каждого из этих уравнений фигурирует одна из выходных перемен-
ных, а в правой — все входные. Для анализа подобных систем их мате-
матические модели обычно представляют в матричной форме.
3.2.2. Модели многосвязных систем
Для современных АСУ ТП характерно объединение в единую систе-
му отдельных приводов и механизмов и даже объединение сложных
технологических агрегатов в комплексно-автоматизированные тех-
нологические линии, гибкие автоматизированные производства. При-
мерами первых могут служить станки с ЧПУ, отрабатывающие при об-
работке детали сложные траектории и обеспечивающие оптимальный
режим резания; примерами вторых — технологические линии прокат-
ного производства. Основной особенностью таких систем является
невозможность рассмотрения их как механической совокупности от-
дельных механизмов. Это обусловлено взаимосвязью и взаимовлия-
нием друг на друга управляемых технологических параметров.
Для обеспечения требуемого качества продукции необходимо одно-
временно управлять многими взаимосвязанными переменными (тех-
нологическими параметрами) путем напрерывного воздействия на
различные исполнительные механизмы. В подобных системах измене-
ние одного управляющего или возмущающего воздействия вызыва-
ет изменение нескольких управляемых переменных й наоборот - каж-
дая управляемая переменная зависит от нескольких управляющих воз-
действий. Многосвязными являются большинство систем, у которых
есть несколько возможностей управлять одним объектом, подвержен-
ным обычно нескольким внешним воздействиям. Подобные системы
называют также многоканальными или многомерными.
В многоканальных системах в отличие от одноканальных входные
воздействия и выходы объекта в каждый момент времени описыва-
ются как многомерные векторы, а сам объект — оператором А, пре-
образующим вектор входных воздействий X в вектор выходных пере-
менных У:
У = АХ. (3.4)
52
В этом случае можно говорить об аналогии между оператором А и
передаточной функцией в одноканальных системах. В многоканаль-
ных системах решаются те же задачи, что и в одноканальных, т.е, стаби-
лизация, программное и следяющее управление, оптимизация. Здесь
также решается вопрос об устойчивости системы, качестве ее дина-
мики. Представляя систему многомерной, необходимо уметь путем
структурных преобразований упрощать внутреннюю структуру слож-
ной системы, соединять ее с другими системами и т.д. Самостоятель-
ной задачей является получение и представление формализованных
моделей таких систем.
Основным физическим принципом, положенным в основу аналити-
ческих методов получения моделей многомерных объектов, являет-
ся метод универсальных уравнений.
Записав уравнения по типу (3.2), получим, например, для устано-
вившегося режима трехсвязной линейной системы уравнения вида
#1 1У1 + 01272 ^а1зУз ~ £>1 1*1 + £>12*2 + £>13*3*,
02 171 + 02 272 + 02 з7з ” £>2 1*1 + £>2 2 х2 + &2 3х 3*, >
(3.5)
03171 +03272 +03з7з - £>31*1 + £>32*2 +£>33*3,
где jq, х2, х3 - входные, а у19 у2, Уз — выходные переменные; ац9
by — коэффициенты - вещественные числа, которые могут принимать
таюке и нулевые значения.
При записи уравнений динамики структура системы уравнений бу-
дет аналогичной (3.5), но вместо yf- и х- будут фигурировать времен-
ные функции Xj(t) и 7/(0 или их операторные изображения xi(p)
*yt(P)> а вместо коэффициентов Ьц - операторные полиномы.
После решения системы уравнений (3.5) или ее динамического ана-
лога она принимает вид
71 = Сц*1 + 012*2 + 01з*з;
72 = 02 1*1 + 022*2 + 023*3; f
Уз = 031*1 + 032*2 + 033*3,
(3.6)
где С/ - вещественный коэффициент для уравнений статики или пере-
даточная функция для уравнений динамики.
Модель системы в виде уравнений (3.5) или (3.6) может быть оп-
ределена любой внутренней структурой, т.е. связи между каналами
могут быть обусловлены непосредственным взаимодействием пере-
менных, прямыми связями входа с различными выходами и обратны-
ми связями от выходов к входам. На рис. 3.1 приведена система, об-
ладающая указанными свойствами. Эту систему можно описать сле-
53
Рис. 3.1. Пример трехсвязной структуры
дующими уравнениями:
У1 (Р) = Ф) + Я7 (р)х2 (р)]Я1 ф);
У2 (Р) = [*i (Р) + Hi (р)х2 (р)]Н2 (р) + х2 (р)Я3 (р);
Уз(Р) =[*1 Ф) + Я7 (р)х2 (p)]Hi (р)Н6 (р) +--—--------х3 (р).
1 + Я4(Р)Я5(р)
(3-7)
После преобразований система (3.7) принимает вид, аналогичный
(3.6):
У1 (р) =Н2 (p)xt (р) + (р)Н2 (р)х2 (р) + 0х3 ф);
У2 Ф) = Н2 (р)х, (р) + (Н2 (р)Н2 (р) + Н3 (р) ) х2 (р) + 0х3 (р); (3.8)
Уз (р) =Я, (р)Н6 (p)Xi (р) +Я! (р)Я6 (р) X f
я 5 (Р)
X Я7 (р)х2 (р) + -------------Х3 (р).
1 + Я4(Р)Яз(Р)
Как видно из изложенного, даже для относительно простой системы
запись формальной модели получается весьма громоздкой. После при-
ведения ее к виду (3.6) решать систему обычным способом становит-
ся сложно. С увеличением числа входов и выходов задача еще более
усложняется.
Для получения более компактных и унифицированных форм пред-
ставления моделей многомерных систем применяется матричная фор-
ма записи переменных и операторов преобразования.
54
Например, система (3.5) в матричной форме может быть представле
на в виде
AY = ВХ,
(3.9)
где X, Y - матрицы входных и выходных переменных; А, В - матрицы
преобразований.
Система (3.6) принимает вид
Y = СХ.
(3.10)
Под матрицами в данном случае понимается упорядоченная, т.е.
выполненная по определенному правилу, табличная форма записи цифр,
буквенных коэффициентов или передаточных функций и полиномов.
Так, в (3.10) матрицы имеют вид
У1 1 С1 2 3
Y = У2 ; х = ; с = С21 С22 С2з
Уз Хз С31 С32 СзЗ
Главное преимущество матричной формы записи заключается в том,
что, составляя матрицы по определенным правилам, можно трансфор-
мировать в матричную форму не только запись переменных, но и опе-
рации над ними.
При наличии некоторых навыков операции над матрицами также лег-
че воспринимаются, чем операции с множеством переменных. Матема-
тическое обеспечение современных ЭВМ располагает программами,
ориентированными на унифицированное матричное представление
задач анализа и синтеза многомерных систем, что позволяет широко
применять для этих целей современную вычислительную технику.
Использование матричного представления объекта весьма эффек-
тивно при анализе и синтезе системы по динамическим показателям.
Одним из наиболее современных методов анализа динамики много-
мерных систем является метод пространства состояний. Под перемен-
ными состояния и образуемым ими пространством состояний понима-
ется совокупность величин, позволяющих по известным входным сигна-
лам для t t0 определить выходные сигналы для t>t0-
В качестве переменных состояния могут приниматься как выходные
переменные, так и их производные. Так, для одномерной системы, опи-
сываемой дифференциальным уравнением и-го порядка, переменными
состояния будут значения у и (п— 1) производных в момент t = 0,
позволяющие в дальнейшем при решении дифференциального уравне-
ния классическим методом определить постоянные интегрирования^
Для многомерной системы понятие переменных состояния рассмот-
рим на примере электропривода с системой управления преобразова-
55
тель-двигатель при действии на преобразователь двух управляющих
воздействий Ui и и2- Динамическая модель такой системы имеет вид
J dbi г-1с= — —; с dt
еп = ссо + //? я + I — ; dt ^еп Тп + еП = ^П1 + ^П2М2- dr > > (3.11)
Выберем в качестве переменных состояния интересующие нас ве
личины, приняв их, выходами системы, и обозначим их
еп=7з-
Запишем выражения для динамической модели объекта в виде систе-
мы дифференциальных уравнений в канонической форме:
dy1.
—— = «11У1 + а12у2.+ ...+ alnyn+ fi(x);
dt
dy2
—— = а21У1+а22у2 + ...+ а2пуп + f2(x)-,
dt
dyn
— = ап1У1 +«п2У2+---+аппУП + ^(х).
at
Применительно к примеру система будет иметь вид
di с 1
— =------i - - w+ — en + 0wi + 0u2 +0/с;
dt L LLn
= — i + Ocj + 0en + Ot/i + 0и2 —- Ic;
dt J J
. 0/ +0w- -L еп + -^И1 + *21Uj+0/ci
dt TB Ta rn
(3.12)
(3.13)
или в матричной форме
dY(r)/dr = AY(r) + BF(r),
или, если раскрыть матрицы,
56
Здесь Y(r) - столбец неизвестных выходных функций времени или
переменных состояния; F (г) - столбец задающих (входных) функ-
ций времени; А, В — квадратные матрицы постоянных коэффициен-
та.
Сравнивая (3.14) с записью дифференциального уравнения первого
дорядка
Г dt
Й располагая формулой его решения
‘ t
У (О = Jo ePt + / еР (t ~т) f (х>т)
Ijje т — переменная интегрирования, можно доказать, что и для матрич-
ного выражения системы дифференциальных уравнений можно напи-
др аналогичное выражение для ее решения:
t
Y(0 = Y(0)eAf + J ek (t~T} BF (f)dr.
Го
Здесь матричная экспоненциальная функция е А г может быть пред-
ставлена рядом
A t2 f3
ekt = 1 + Ar + А2 — + A3-----+ ...
2! 3*
57
Требуемые для получения временных функций суммирование и ум-
ножение матриц выполняются на ЭВМ по типовым программам.
Как и одномерные системы, многомерные решают задачи стабили-
зации совокупности параметров, программно-следящего их изменения
или оптимизации.
Специфичным для многомерных систем является возможность нера-
венства числа входов и выходов, обычно пу < пх, а также взаимовлия-
ние каналов друг на друга. Формально это взаимовлияние представля-
ется в виде перекрестных связей с передаточными функциями Н2 (р),
Н$(р)9 Hi (р) на рис. 3.1. Если они являются объективным проявле-
нием природы управляемого объекта, они называются естественными.
Если введены специально, например для нейтрализации взаимовли-
яния, — искусственными или корректирующими.
Например (рис. 3.1), для компенсации влияния уt нау3, представ-
ленного в виде естественной связи с передаточной функцией Я6 (р),
необходимо на вход х6 подать с входа Xi корректирующую связь с пе-
редаточной функцией
1 +Я4 (р)Я5 (р)
я8ф)=--------4 Я!(Р)Я6(Р).
Я5 (р)
Тогда выражение для у3 (р) в (3.8) примет вид
Уз(р)=Н1(р)Н6(р)х1(р)^Н1(р)Н6(р)Н1(р) X
Hs (р) /
х х2 (р) +------------ х3(р)~
1 + Я4(р)Я5(р)
1+Я4(р)Я5(р) \ * 1
Н2(р)Н6(р)х2(р) \ ,
Я5(р)
ИЛИ
Н5 (р)
Уз (р) = Я, (р)Яб (р)Я7 (р)х2 (р) +---------------х3 (р).
1 + Я4 (р)Я5(р)
Здесь у3 становится независимым от х i.
Рассматривая систему
матрицы
Y(p) = Н(р)Х(р),
где
(3.8), можно ввести понятие передаточной
Н(р) =
Я1 (р) Я1 (р)Я7 (р)
н2(р) Я2(Р)Я7 (р) + я3 (р)
я, (Р)Я6(Р) Я, (р)Н6 (р)Н2 (р)
О
О
Я5(Р)
58
1+ Я4(р)Я5(р)
Диагональные элементы матрицы
Ми (р) = Я1 (р); М22 (р) = н2 (р)Н2 (р) + Н3 (р);
к z \
Мзз(р)= -------------
1 + Я4(р)Я5 (р)
является собствен ними передаточными функциями. Они отражают
зависимость выхода от ’’своего” входа; остальные (обозначим их £)
являются несобственными. Тогда
Мг1(р) L 1 2 (р) *13 (р)
Н(р) = ^2 1 (Р) М22(р) Ъ2з (р)
*31 (р) L32 (р) Мзз(р)
Очевидно, чтобы каналы стали автономными, передаточная матрица
должна стать диагональной.
При частотных методах исследования если на один из входов подать
гармонический сигнал частоты то на всех выходах появятся гармо-
нические сигналы той же частоты, но с разными амплитудами и фазами,
т.е. может быть введено понятие собственной и несобственной ампли-
тудно-фазовых характеристик.
Аналогично можно рассматривать переходную матрицу, отражаю-
щую временную реакцию выходов на единичные скачки на входах.
При построении сложных систем из многомерных звеньев, как и
при использовании одномерных звеньев, очень удобны и наглядны
структурные схемы из звеньев и связей между ними, которые изобража-
ются двойными линиями.
Хотя наиболее универсальным подходом при анализе и преобразова-
нии такой системы является совместное решение систем уравнений в
матричной форме, возможны и привычные структурные преобразова-
ния. Правила преобразования и методы их обоснования в многомер-
ных системах хорошо ассоциируются с одномерными, хотя и имеют
свою специфику.
Для простоты рассмотрим преобразования с матричными звеньями
одинакового размера, когда число входов равно числу выходов. Тогда
при последовательном соединении матричных звеньев с передаточны-
ми функциями Hi (р) и Н2 ф) эквивалентное звено описывабтся мат-
рицей
Н(р) = Н, (р)Н2 (р),
при параллельном - матрицей
Нф) = Нх (р)+Н2(р),
59
при антипараллельном - матрицей
H(p) = (E-H1(p)Hi(p))-1H1(p),
где Е — единичная матрица.
Схожи и правила переноса точек ответвления и суммирования.
Самостоятельной проблемой многомерных звеньев и систем явля-
ется выбор исходной модели, определяющей в дальнейшем число вхо-
дов и выходов. По существу до выполнения анализа модели неизвест-
на значимость отдельных выходов для функционирования системы
при решении поставленной перед ней задачи. До анализа модели трудно
также оценить, все ли входы (исполнительные элементы технологичес-
кого агрегата) существенно влияют на выбранные выходы (технологи-
ческие параметры).
В этом плане выделяют полностью управляемые системы, когда
все выходы зависят от всех входов, и полностью наблюдаемые, когда
нет переменных состояния, не связанных с выходами.
3.3. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ПОЛУЧЕНИЯ МОДЕЛЕЙ
ТЕХНОЛОГИЧЕСКИХ ОБЪЕКТОВ УПРАВЛЕНИЯ
3.3.1. Поставновка задачи
Если для получения модели аналитические методы идентификации
неприемлемы в связи с недостаточным знанием алгоритмов функцио-
нирования технологических объектов управления либо по причине
сложности и экономической нецелесообразности разработки моделей
на их основе, то применяются экспериментальные методы получения
моделей технологических объектов управления. Модели, полученные
на основе эксперимента, не столь универсальны, как аналитические,
но более просты по своей структуре и позволяют применять однотип-
ный математический аппарат.
Экспериментальные методы идентификации базируются на пассив-
ном либо активном эксперименте. В первом случае исследуются режи-
мы естественной эксплуатации технологических объектов управления,
во втором задаются такие, которые наилучшим образом выявляют его
свойства. Во время эксперимента измеряются значения интересующих
нас технологических параметров (управляемых выходных перемен-
ных) и факторов, на них влияющих (управляющих входных перемен-
ных и возмущений). Эти данные позволяют выбрать математическое
выражение и определить входящие в него коэффициенты, исходя из
обеспечения адекватности модели объекту. Полученная таким об-
разом модель должна с заданной степенью точности соответствовать
реальному объекту, т.е. расчетные и экспериментальные значения выход-
ных переменных при заданных управляющих воздействиях и возму-
щениях должны совпадать в динамических и статических режимах.
60
Проведение эксперимента и последующая обработка его результа-
тов для создания модели усложняются в связи с тем, что технологичес-
кие объекты управления, как правило, многомерные и недетерминиро-
ванные. Поэтому при проведении серии повторяющихся эксперимен-
тов при подаче одинаковых входных переменных на выходе можно
получать различные значения одной и той же технологической пере-
менной. Такое различие объясняется действием случайных сочетаний
неучтенных факторов. Если разбросы незначительные, то задача сводит-
ся к оценке степени приближения модели к результатам эксперимен-
та. При значительных отклонениях под сомнение ставится правиль-
ность выбора типа модели. В ряде случаев возникает даже необходи-
мость сначала установить сам факт наличия закономерности между вход-
ными и выходными величинами. В этом случае решающее значение при-
обретает задача определения объема эксперимента. Под объемом экс-
перимента понимают количество учитываемых факторов, частоту по-
вторения однотипных экспериментов и их количество. Чем больше
число повторений опыта, тем достовернее модель, т.е. тем больше ве-
роятность нахождения истинного значения переменной в более узком
интервале эксперимента.
Исходя из изложенного, можно установить следующие основные эта-
пы получения модели технологического объекта управления по экс-
периментальным данным:
планирование объема эксперимента: количества контролируемых
параметров, числа измерений и кратности их повторения;
выбор типа математической модели (уравнения регрессии);
выполнение эксперимента и обработка данных;
определение количественных характеристик (коэффициентов) при-
нятого типа модели;
проверка значимости полученных коэффициентов по влиянию на
них разброса результатов экспериментов;
проверка адекватности модели объекту.
Если две последние проверки дают отрицательный результат, то про-
водится уточнение объема эксперимента, эксперимент повторяется,
уточняется модель объекта.
Далее излагаются принципы идентификации как одномерных детер-
минированых объектов в статике и динамике, так и многомерных
Недетерминированных объектов в статике. В более широком объеме
этот материал можно проработать в [3].
3.3.2. Идентификация одномерных детерминированных объектов
Задача состоит в представлении в аналитическом виде существую-
щей связи между входом и выходом одномерного объекта. Полагаем,
что при эксперименте случайные помехи отсутствуют и в эксперимен-
тально снятых значениях нет разбросу Для таких объектов модель
61
наиболее часто описывается полиномом вида
у = д0 + + а2х2 + ... + апхп.
Степень полинома ориентировочно можно определить по разностям
экспериментально снятых ординат функции при постоянных прираще-
ниях аргумента. Она принимается равной такому порядку разностей,
при котором они становятся примерно постоянными во всем диапазо-
не изменения входной величины. Например, при неизменных разностях
между ординатами модель описывается полиномом первой степени,
при неизменных разностях между разностями второго порядка - по-
линомом второй степени и ьд./
Оптимальной может считаться модель, у которой при определен-
ных расчетом коэффициентах сумма квадратов отклонений расчет-
ных Ур и экспериментальных уэ значений будет минимальной, т.е. мини-
мизируется функционал
п
F(af) = min S(y3-^p)2, (3.15)
1
где п — число опытов.
Для определения коэффициентов модели составляют систему урав-
нений типа
bF{ai)lbai = 0. (3.16)
Совместное решение полученных уравнений относительно д, дает
такие их значения, при которых удовлетворяется условие (3.15).
Для упрощения (3.16) целесообразно начало отсчета абсциссы xt
помещать в середину интервала экспериментально снятых значений и
пользоваться симметричными значениями xi (одинаковыми, но раз-
личными по знакам). В этом случае все суммы нечетных степеней х
будут обращаться в нуль, что существенно упростит систему урав-
нений.
Например, если в качестве модели выбран полином второй степени
Ур = ао + (3.17)
то функционал (3.15) имеет вид
F(at) = min S [j3- (a0 + a1x + a2x2)]2.
1
Коэффициенты являются неизвестными переменными. В соответствии
с (3.16) составляем систему уравнений:
62
J—=—2 S (уэ/ - a0 - «J*, - a2x/ ) = 0;
“flo /= 1
AF "
=—2 S (y3f — e0 — atXj — o2Xf )Xj = 0;
l=l
$
V n
=-2 S (y3i -a0- a Si - a2xf)x] = 0.
1=1
^Приравнивая суммы нечетных степеней xi нулю, получаем
п п
Чя + в2 2 Xi?= 2 УэГ
i = 1 i = 1
n n
E xz - E y3jXj9
i=i f=i
n n n
E x2+a2 E x* = E /Э1-Хр
f=l i = l i=l
Решение относительно коэффициентов:
n n n n
2 уэ1- S xj- E y3iX] S xf?
f=l i=l i = l /=1
n i n \ 2
n Ex)*- / E xf-2 j
i = l \ i=l /
n n " n
E xi n E y3i xi - . E y3i e Xi
Рассчитав коэффициенты и подставив их в (3.16), получим уравнение
регрессии.
Пример 3.1. Получить аналитическую зависимость скорости холос-
того хода двигателя сих х от тока возбуждения питающего генератора,
<али эксперимент дал значения, приведенные в табл. 3.1.
63
Таблица 3.1
^в,э» 10 А 50 100 150 200 250 300 350 400 450
"х,х,э. рад/с 38 65 90 115 133 150 162 172 178
wx,x,p- р«/с 36,6 65,5 91,2 113,7 133 149,1 163 171,7 178,2
Двигатель и генератор - типа П-21, РНом = 0,037 кВт, (7НОМ = 220 В,
4i,ном ~ А, А»,иом = ^ном = 152 рад/с.
Для облегчения расчетов примем х = /в/50 и у = сд /100 и пере-
несем ось .у в точку в абсциссой х = +5. Тогда исходные данные при-
мут вид табл. 3.2. Расчеты сумм для (3.18) приведены в табл. 3.3.
Рассчитываем коэффициенты:
_ 11,03 • 708 - 68,6 -60 .
«о 2 1,33,
9 • 708 — 602
fl, = 10,6/60 = 0,177;
9 • 68,6 - 11,03 • 60 ЛЛ,_
а2 = ------------------- =-0,016,
9 • 708 - 602
получаем уравнение модели (3.17):
у = 1,33 +.0,1 Tlx - 0,016х2.
Таблица 3.2.
ХЭ -4 -3 -2 -1 0 1 2 3 4
Уз 0,38 0,65 0,9 1,15 • 1,33 1,5 1,62 1,72 1,78
Таблица 3.3
2 4 2
Уз *э ХЭ Х3 Узхз Узхз
0,38 —4 16 256 -1,52 6,08
0,65 -3 9 81 -1,95 5,85
0,9 -2 4 . 16 -1,80 3,6
1,15 -1 1 * 1 -115 1,15
1,33 0 0 0 0 0
1,5 1 1 1 1,50 1,5
1,62 2 4 16 3,24 6,48
1,72 3 9 81 5,16 1,55
1,78 4 16 256 7,12 2,85
2уэ= 11,03 = 0 Sx* = 60 =
= 708 = 10,6 = 68,6
64
3-2. Универсальная характеристика
‘й№£ятеля постоянного тока последова-
«доьного возбуждения и результаты ее
вдйггификации
^родставив истинные значения параметров и вернув ось у в исход-
положение, имеем
Й I 1 \ I г \2
= 1,зз + 0,177 I — - 5 - 0,016 —- 5 ,
100 \ 50 / \ 50 /
экспе-
окончательном виде
Шфх X = 4>5 + 0,674 7В - 0,64 • 10" 3 /в.
й^равнение расчетных данных по полученному выражению с
фронтальным дано в табл. 3.1.
видно, модель дает высокую точность совпадения с эксперимент
так как она строилась для конкретного диапазона изменения
величины, то при дальнейшем увеличении ZB могут появить-
^Йклонения.
^|Ьзможны Другие уравнения для моделирования одномерных детер-
-“^ррванных объектов.
рис. 3.2 представлены результаты идентификации универсаль-
естественной характеристики двигателя постоянного тока последо-
ьного возбуждения. Ее модель имеет вид
а0 + а1х + а2х~1,
S после расчета коэффициентов и замены переменных
Ж = 0,84 - 0,0784/* + 0,25 ЬТ*1,
О
€□ /соном; М* = М/Мном ~ относительные значения скорости
Момента двигателя.
^Обобщенная модель в виде полинома имеет вид
т
Л»
i = 1
(3-19)
^де п I - целое или дробное число любого знака.
65
Возможны другие виды моделей. Так, если при равных прираще-
ниях х3 величина у3 растет примерно в геометрической прогрессии,
следует применять модели вида
у = abx или у = аеЬх. (3.20)
О целесообразности выбора такого типа модели свидетельствует
также линейный характер зависимости между хэ и lgj>3 так как из
(3.20)
1g Уэ = 1g * + *3lg£-
Во всех случаях для определения коэффициентов применяется ме-
тод минимума суммы квадратов отклонений.
3.3.3. Идентификация многомерных объектов
Получение модели многомерных объектов по результатам экспери-
мента осложняется прежде всего тем, что на исследуемый параметр
влияет много факторов, которые сложно разделить на существенные
и несущественные, поэтому трудно определить число входов объекта,
подлежащих учету.
В отличие от одномерных объектов затруднена геометрическая ин-
терпретация модели. Так, для двух входных параметров, влияющих на
третий выходной, приходится обращаться к двухмерной области. Увели-
чение входов требует рассмотрения многомерной гиперповерхности,
описываемой уравнением с несколькими аргументами и не поддающей-
ся геометрической интерпретации.
Вместе с тем модель, отражающая зависимость исследуемого парамет-
ра или критерия от многих переменных, должна быть достаточно инфор-
мативной, достоверной и удобной в пользовании.
При значительном числе входов модель может быть нелинейной
и иметь сложный рельеф с вершинами, впадинами, гребнями. Поиск
экстремальных точек (вершин и впадин) на этой поверхности путем
изменения входных величин составляет содержание оптимального уп-
равления. Обычно такая модель называется целевой функцией или по-
верхностью отклика, а оптимальное управление обеспечивает работу
технологического объекта управления в области экстремального зна-
чения критерия качества.
Получить по данным эксперимента модель объекта управления, точ-
но воспроизводящую поверхность отклика, весьма сложно. Поэтому на
практике часто ограничиваются ее линейным или квадратичным при-
ближением, выбирая диапазон изменения переменных в ограниченной
области. Это возможно, если функция непрерывная и выпуклая. Гра-
ницы области обычно выбирают так, чтобы в нее попал экстремум или
предельно допустимые значения^ и х7«.
66
Такой подход может дать в большей степени качественное, нежели
количественное решение. Оно сводится к оценке влияния различных
факторов на исследуемую переменную у и дает возможность прене-
бречь некоторыми из них.
Метод, позволяющий получить многомерную модель объекта управ-
ления на основе эксперимента, получил название факторного анализа,
^ередко он называется методом планирования эксперимента, фактор-
ным экспериментом и т.п. Применительно к детерминированному
объекту метод заключается в следующем:
для объекта выбирают факторы х., оказывающие существенное влия-
ние на выхода; определяют области изменения
составляют программу (план) эксперимента;
принудительно изменяя в избранных пределах и сочетаниях, оп-
ределяемых программой эксперимента, фиксируют значения^;
рассчитывают коэффициенты уравнений модели. \
Основными условиями проведения эксперимента являются:
выбор независимых друг от друга входных величин х;
возможность и наблюдаемость изменения у;
возможность задания xz- с точностью, превышающей точность изме-
рения^.
При постановке задачи выбирается центр области варьирования с
координатами у0, х10, х20 -- и устанавливаются границы области
варьирования. По возможности область выбирается меньшей, что повы-
шает точность модели. Выбор границ осуществляется с учетом влия-
ния помех, так чтобы последние были намного меньшими, чем плани-
руемое отклонение входной величины ximax или xt min от начального
значения х/0.
Природа объекта управления такова, что могут иметь различные
физическую природу и размерность. Поэтому желательно пользоваться
относительными величинами входных переменных. В качестве базовых
удобно выбирать предельные отклонения Axf. В этом случае
f xi max * “ max ~ xiо) !&xi ~
xi т in * т in xi о) !^xi - 1>
(3.21)
' Х/0‘ = (хю =
При таком подходе ось у помещается в центр идентифицируемой
области, для которой
Xi0 ~ (xi max + xi min)
План проведения эксперимента и методика расчета коэффициентов
зависят от выбранного типа модели. В наиболее часто встречающем-
ся виде многомерная модель представляется степенным полиномом,
содержащим также члены, учитывающие совместное действие факто-
67
ров. Модель, порядок которой не превосходит второго, имеет вид
У = ^0*0 + «1*1 +«2*2 +«11*1 + «22*2 +«12*1*3, (3.22)
где’х0 — фиктивная переменная, вводимая для унификации членов
модели и всегда равная 1.
После выбора типа модели определяется объем эксперимента. Необ-
ходимо установить, сколько раз, в какой последовательности и в ка-
ких различных сочетаниях надо изменять xf, чтобы при минимальном
объеме эксперимента получить достаточно достоверный результат.
При идентификации методом планирования -эксперимента прини-
мается следующая последовательность операций:
все члены уравнения модели, содержащие переменные X/, их квад-
раты и произведения записывают в виде линейных уравнений aixi
и нумеруют последовательно при составлении полинома
У] = «0*0 +«1*1/ +«2*2/ + «3*3/ + «4*4/ +«5*5/
или в общем виде
п
2 «,.xf/, (3.23)
f = 0
где п - число членов уравнения регрессии; / = 14W — номер экспери-
мента;
для определения коэффициентов уравнения я,- в соответствии с ме-
тодом минимума суммы квадратов отклонений записывают функцио-
нал
N / П v 2
F = min S ( y3j - S «/*// j ,
i= 1 \ f=l I
где N- число экспериментов (опытов), берут частные производные это-
го функционала по коэффициентам и, приравнивая их нулю, получают
систему уравнений ЪР/Ъ^ = 0, из которой определяют
Более просто получить результат, если считать, что минимум откло-
нений имеет место при совпадении результатов расчетной модели и экс-
перимента в точках проведения опытов, т.е. полагать
п
y3j = S «/*,/•
1 = о
В этом случае коэффициенты должны удовлетворять системе линейных
уравнений вида (3.23). В матричной форме эта система имеет вид
Y = ХА, (3.24)
68
где Y — матрица-стобец экспериментальных значений у с числом элемен-
тов М равных числу опытов; А - матрица-столбец коэффициентов
tf с числом элементов, равным числу членов полинома п\ X — матрица
входных воздействий размером ЛГх и.
Чтобы матрицу X сделать квадратной и далее диагональной, умно-
жим обе части (3.24) на транспонированную матрицу Хг. Обозначим
JC* X = С и получим
X'Y = СА,
откуда
A = C-1X'Y. \ (3.25)
5 Если выбрать определенную последовательность изменения входов
jfp то квадратная матрица С и обратная ей матрица С"1 будут диаго-
нальными. Тогда система (3.25) разбивается на п независимых урав-
нений, каждое из которых будет включать лишь один неизвестный ко-
эффициент
I N \ I
Ъ = 2 / N, (3.26)
\/=1 //
где ] ~ номер опыта.
Диагональность матрицы С"1 определяется таким варьированием х,
которое подчиняется условиям:
, ’симметричности - сумма xi одного столбца должна быть равна нулю;
”нормированное™ - сумма х? одного столбца должна быть равна
числу опытов с разными сочетаниями х,.;
ортогональности - сумма xf_ t xf должна быть равна нулю.
Удовлетворяя этим условиям, составляем таблицу планирования
эксперимента (табл. 3.4) для двух факторов согласно (3.22) так, что-
бы получить четыре разные комбинации значений переменных хх их2.
Из таблицы видно, что число комбинаций значений переменных равно
М = 22 = 4,
Таблица 3.4
& *0 *1 Х2 Х3=Х1Х2 *4 =*} -и — V.2 Х5 Xj
0 1 2 3 4 5
+ — — + + +
+ + — — + +
+ — + — + +
+ + + + + +
69
причем сумма xz в колонках 1, 2 равна нулю; сумма х] в колонках
4, 5 равна 4; сумма в колонке 3 равна нулю.
Колонки 4 и 5 имеют значения, аналогичные колонке 0, т.е. не дают
дополнительной информации, поэтому следует ограничиться четырьмя
колонками х0, xl9 х2 и jqx2 (участок табл. 3.4, очерченный двойны-
ми линиями). Получим модель вида
У = 0о*о + аххх + а2х2 +а3х1х2.
Минимизируя функционал
4
F = min 2 (уэ-ур2 = О,
i = 1
путем приравнивания нулю частных производных по получаем систе-
му уравнений
4 4 4
Ла0+п1 Sxv. + n2 2*2/=
1 1 1
4 4 4 4
ао 2 2 x^i + а2 2 x\jx2j ® »
111 1
4 4 4 4
Л0 ^Х^^а\ 2 xijX2f^a2 ^X2j = ^Х2]У]*
11 11
Если эксперимент спланирован с выполнением условий симметрич-
ности, нормированное™ и ортогональности, то рассмотренные выраже-
ния окажутся проще, так как
4 4
X xXj = 2 x2j = 0;
11
Sx2/ = Sx2/=4;
1 1
X\jX2j ~ 0*
1
С учетом этого выражения для расчета коэффициентов получим в
соответствии с (3.26)
70
Эксперимент, при котором перебираются все возможные сочетания
Хр называют полнофакторным или ПФЭ2Л. Он дает возможность опреде-
лить только коэффициент при входных воздействиях первого порядка
и их сочетаниях. Такой ПФЭ называют планом первого порядка.
Кроме ПФЭ2Л применяется дробный факторный эксперимент (ДФЭ),
который позволяет уменьшить объем эксперимента. По числу коэффи-
циентов выполняются эксперименты для реализации (3.23). Так, если
требуется определить четыре коэффициента - л0, а2, а*, то доста-
точно провести четыре эксперимента, удовлетворяющих требованиям
ПФЭ. Это соответствует двухфакторному эксперименту, где колонка
х^х2 заменена колонкой х3. Для модели типа
У = aQ ^а1х1 + а2х2 ^а3х3
вместо N = 23 =8 достаточно провести четыре опыта. В таблице плани-
рования эксперимента (табл. 3.4) колонка 0 заполняется плюсами,
1 — чередованием плюса и минуса через одну строку, 2 — через две
строки, а 3 формируется путем умножения построчно колонок 1 и 2.
Модель в абсолютных единицах после определения коэффициентов
записывается в виде
= aQ +fli
*1 “ *10 *2 - *20 *1 - *10
--------+ а2----------+ а з-------
Дх! Дх 2 Дх j
*2 - *20
Дх2
Пример 3.2. Получить линейное уравнение регрессии поверхности
отклика, отражающей зависимость объемной производительности то-
карного станка J от глубины резания Гр и подачи на оборот s при по-
стоянной скорости резания. Поверхность отклика в виде графиков
/р = /(s) ПРИ фиксированных J приведена на рис. 3.3. Полагая, что гра-
фики построены по данным эксперимента с высокой повторяемостью,
задаемся уравнением регрессии вида
J = яо*о + а\ *р + a2s + a3tps.
1. Принимаем в качестве
с координатами Гр = 4 мм, 5 =
= 0,7 мм/об; J = 400 см3/мин.
2. Выбираем интервалы варь-
рования Дгр = 1 мм; Ду =
= 0,1 мм/об, определяющие гра-
ницы области abcd.tp min =3 мм;
smin = 0,6 мм/об; tpmax = $ мм;
8тах ~ 0,8 мм/об.
центра индентифицируемой области точку
Рис. 3.3. Поверхность отклика
71
3. Составляем таблицу ПФЭ2” (табл. 3.5).
Таблица 3.5
*0 *1 = Гр X2=S XiX2=tpS y=J
+ — + 285
+ + + - + + 435 + ' - 350 + + 530
4. Задаваясь четырьмя сочетаниями принятых значений tpmaXi
tpmin и smax* smin и фиксируя соответствующие этим сочетаниям зна-
чения J, из графиков рис. 3.3 в соответствии с (3.26) и табл. 3.5 опреде-
ляем коэффициенты:
4
S xoyf
1 285 + 435 + 350 + 530
а =---------- =--------------------- =400;
4 4
1 -285 + 435 - 350 + 530
а =-----------=------------------------= 82.
4 4
2 *2/ У]
1 -285 - 453 + 350 + 530
2хЗ/>/
J+285 - 435 - 350 + 530
5. Записываем уравнение модели в натуральных единицах:
J = 400 + 82 *р ~ 4- + 40 1 ~ 0,7 + 8 ~ 0,7 ,
1,0 0,1 1,0 0,1
или после приведения
J= 16 + 26гр + 80s +
Из полученного уравнения видно, что поверхность отклика не явля-
ется плоскостью, так как коэффициент при tps не равен нулю. Так как s
на порядок меньше tp, то является наиболее значительным фактором.
72
Адекватность модели можно проверить, задавшись, например, значе-
ниями tp = 4 мм и s = 0,7 мм/об. Полученное из уравнения значение
J = 392 и есть значение критерия в центре области, которое соответст-
вует исходной реальной поверхности с погрешностью 2 %.
3.3.4. Динамическая идентификация
Многие технологические объекты управления, функционирование
которых в динамике еще недостаточно изучено, не могут быть описаны
аналитически. Для получения их динамических моделей также приме-
няются экспериментальные методы. Целью последних является нахож-
дение аналитических выражений, описывающих динамику объекта уп-
равления с требуемой степенью точности. В отличие от статических мо-
делей динамические связывают выходную величину с входным воздей-
ствием в процессе их изменения во времени.
В практике предшествующих дисциплин для записи динамических
моделей линейных систем использовался аппарат дифференциальных
уравнений. Как правило, технологические объекты управления явля-
ются системами, элементы которых имеют нелинейные характеристи-
ки и описываются уравнениями высоких порядков.
ь В передаточных устройствах электропривода имеются люфты, воз-
можно наличие сухого трения, приходится учитывать упругости их
элементов и т.д.
Применение методов математического моделирования избавляет
исследователя от решения дифференциальных уравнений, но при этом
необходимо иметь аналитические модели всех звеньев.
Экспериментальные методы позволяют получить формальную мо-
дель практически любого объекта по результатам обработки экспери-
ментальных данных. Существуют активные и пассивные эксперименты.
Активный эксперимент основан на задании объекту специально
сформированных управляющих или возмущающих воздействий. По
реакции объекта на эти воздействия устанавливаются и оцениваются
его динамические свойства. Обычно изучается реакция на скачкооб-
разные, гармонические или импульсные воздействия. Полученные пере-
ходные или частотные характеристики позволяют определить, на-
пример, для линейной системы передаточные коэффициенты, по-
стоянные времени отдельных звеньев и динамические свойства объек-
та в целом.
Не для всех систем может быть поставлен активный эксперимент.
Иногда он может быть неприемлем из-за дороговизны специального до-
полнительного оборудования, высокой стоимости его монтажа, неред-
ко его реализация невозможна по условиям техники безопасности.
В этих случаях применяется пассивный эксперимент. Сущность его
заключается в фиксации значений входных и выходных переменных
в нормальных эксплуатационных динамических режимах.
73
Одним из сравнительно несложных современных методов дина-
мической идентификации, основанных на результатах пассивного экс-
перимента, является метод Калмана. Сущность его заключается в сле-
дующем:
в процессе эксплуатации через строго фиксированные интервалы
времени записывают значения входных и выходных параметров;
выбирают наиболее простой вид аналитической модели, записан-
ной в виде разностного уравнения того или иного порядка;
по результатам эксперимента и принятого типа модели методом
минимума суммы квадратов отклонений определяют коэффициенты
разностного уравнения;
решают разностное уравнение и сравнивают полученные динами-
ческие характеристики с экспериментом;
при больших отклонениях задаются разностным уравнением более
высокого порядка и повторяют расчет.
Сопоставление изложенной выше методики динамической идентифи-
кации с порядком выполнения статической идентификации свидетель-
ствует об их аналогии. Отличие состоит лишь в моделях: модель в ста-
тике описывается алгебраическим уравнением, динамическая модель —
разностным.
Для дифференциального линейного уравнения А>го порядка аналогом
будет разностное уравнение вида
Уп = АоУп-1 + Л1Уп-2 + - • • * Ак-1Уп-к +
+ BQXn_ i + В\ХП-2 + . . . + Вк-\Хп_к,
где п — номер точки эксперимента; А, В — коэффициенты разностно-
го уравнения. Оно может быть принято в качестве исходной модели
при динамической идентификации.
Поскольку порядок идентифицируемого объекта обычно неизвес-
тен, следует начинать с наиболее простой модели, а именно — разност-
ного уравнения первого порядка вида
Уп = ^о.Уи-1 + ВЛ-v
Если модель окажется недостаточно адекватной, следует взять в ка-
честве модели разностное уравнение второго порядка
Уп ~ АфУп-1 + А^Уп-г + Ввхп-1 + Bixn—2-
Далее, используя методику минимизации суммы квадратов откло-
нений, т.е. функционала вида
п
F=min Е (y3i -ypi)2,
i = 1
74
-цолучаем систему уравнений
”. .0; ’-£-.0; 1^=0.
ал0 Ьл, дв0 дв,
из которых можно определить коэффициенты Ло, А ц Во, Вг, удовлет-
воряющие критерию оптимальности.
А Пример 3.3. Для анализа температурного режима мощного редукто-
ра фиксировалось нарастание температуры масла в картере при прило-
жении номинальной нагрузки. Результаты измерений приведены в
<абл. 3.6. Требуется определить постоянную нагрева редуктора.
>> Таблица 3.6
$ ’
' *.4 0 1 2 3 4 5 6 7 8 9
Q °с 12 38,7 54,9 64,8 70,7 74,3 76,6 77,9 78,7 80
г- ^модели, С - - 54,916 - 70,709 - - - 78,66 -
Л Из данных эксперимента видно, что температура изменилась от ®нач =
F 12 °C до 0уст = 80 °C. Для идентификации используем разностное
уравнение первого порядка
вя = Ло®л_1 + Bq® у ст-
Для упрощения расчетов примем интервал времени измерений заме-
>ЬДг = 2ч.
Для минимизации суммы квадратов отклонений запишем функцио-
нал
т т
F~ min 2 (0ЭЛ—= т*п ~^о®уст)2-
1 1
Приравняем нулю частные производные от функционала:
т
я?. — = 2(®л—Л0®л-1 — ^о®уст)®и—1 “ 0;
я Эл° 1
" Эр т
\ = (®/1 —Aq ®п _ ! - Bq ®у ст) ®уст = 0
' 6Bq J
lu-
ll с учетом того, что
•М m
V 2®уст
— J71 ®уст И ^уст 0,
75
получим систему канонических уравнений:
Ао S 1 + Bow0ycT = Z ®л;
1 1
Ло 2 +#о®уст ®и-1 =
1 1 1
откуда
т т т
т Z0w0w_j- 0Я
т I т \2
m S - I Z ®и-1 1
1 \ 1 I
mm mm
2вл 20л-1
11 1 1
(m i m \ 2
mS0ti- 2 0,^
1 \ 1 '
где m— число экспериментальных точек.
Так как интервал времени принят равным 2 ч, то из полученных
экспериментально данных при т = 4 выбираем точки:
t, ч 0 2 4 6 8
ф 3 о О — 54,9 70,7 76,6 78,7
О о 1 ф* 12 54,9 70,7 76,6 -
Тогда
4 4 4
S ©я = 282; S ©„_! =215; S = 14,139;
4
2 ®пвп-1 s 16 110.
1
Подставляя полученные значения в выражения для Л0 и50, полу-
чаем Л о = 0,368; Во = 0,632, и разностное уравнение при 0уст = 80 °C
76
Принимает вид
©и = 0,368 ел_!+ 50,5. 1
Для проверки адекватности модели по полученному выражению
рдочитаны значения 6 при тех же интервалах времени (табл. 3.6).
Сравнивая расчетные данные с данными эксперимента, убеждаемся
в Хорошей адекватности модели объекту. Это позволяет сделать вы-
вод о возможности описания объекта дифференциальным уравнением
первого порядка вида
• ?
<7 ^-+©=©уст,
at
решением которого является
X® = ©уст (1 - e~t/T) + ©нам е~'/Г,
rte, полагая 0 = 0Л, 0нач = i и Г = лДг, при п = 1 получаем
- Л0 = е"Д'/г,
откуда
Т =-&t/lnAQ =—2//и 0,368 = 2/0,9997 = 2 ч.
Постоянная нагрева равна 2 ч, и дифференциальное уравнение имеет
ВВД
, 2—+ 0 = 80.
dt
3.3.5. Экспериментальные модели недетерминированных
объектов
• Выше рассматривались простейшие случаи получения эксперименталь-
ным путем гладких, устойчиво, без разбросов повторяющихся анали-
тических моделей. Пригодность такой модели оценивалась по допусти-
мому максимальному отклонению от эксперимента. На практике на
эксперимент оказывает влияние действие многих малозначащих факто-
ров в различных непрогнозируемых сочетаниях. Поэтому при повто-
рении опытов с одними и теми же значениями входов получают непов-
торяющиеся значения выходов. Разброс выходных величин, его причи-
ны и характер могут быть различными. Они могут вызываться систе-
матическими погрешностями, являющимися функцией времени (из-
менение сопротивления резистора при изменении температуры, дрейф
Нуля усилителя и т.п.). Разброс может быть вызван пороговым дейст-
вием какого-либо неучтенного фактора и при эксперименте давать
77
повторяющуюся зависимость, имеющую характер ломаной линии. Весь-
ма часто на разброс влияют отклонения случайного характера.
Для устранения систематических погрешностей применяют много-
кратное повторение необходимой номенклатуры опытов при различ-
ных сочетаниях значений входов в случайной последовательности (ран-
домизация). Так, при двухфакторном эксперименте с 7V, равным
4 опытам, с приведенными ранее сочетаниями и х2 (см. табл. 3.4)
при первом эксперименте проводят опыты в последовательности 1,
2, 3, 4, затем меняют последовательность - 3, 1, 2, 4 и т.д. Случайные
последовательности номеров опытов получают, пользуясь таблицами
случайных чисел (отбрасывая повторяющиеся числа и значения, боль-
шие Д’). Квазислучайные последовательности получают, используя
различные алгоритмы, например алгоритм Неймана. По этому алго-
ритму для получения случайных чисел в пределах 0 ... 1 выбирают
произвольное число, меньшее единицы, возводят его в квадрат, бе-
рут из середины результата необходимое число разрядов, вновь воз-
водят в квадрат и т.д.
Когда действует порогово-дискретный фактор, применяют сглажи-
вание. Наиболее простой метод сглаживания — по способу скользя-
щей средней. Состоит он в вычислении средней ординаты для фикси-
рованных значений абсцисс:
для Xj у1г = (Уо +У1 +У2)/3-,
для х2 у2г = О'! + у2 + У3)/3,
для хп упг = О'л-1+ Уп + Уп+i)/!,
где упг - п-я ордината на гладкой (сглаженной) кривой.
Когда разброс вызван действием случайных факторов, задача услож-
няется тем, что значения переменных и параметров, полученные при
проведении эксперимента, являются лишь приближенными оценками
неизвестных истинных значений, т.е. эти значения получены со случай-
ными погрешностями, а следовательно,' и сами оценки являются слу-
чайными величинами.
Для приближенного выбора вида модели результаты эксперимента
фиксируют в виде точек в системе прямоугольных координат. При
слабом действии случайных помех просматривается обобщенный ха-
рактер зависимости: линейная или нелинейная, возрастающая или спа-
дающая. Задавшись видом уравнения регрессии, можно получить ко-
эффициенты методом наименьших квадратов и далее оценить адекват-
ность уравнения регрессии и истинной модели объекта.
Если разброс столь значителен, что визуально невозможно оценить
характер закономерности и предварительно выбрать модель, то при-
ходится увеличивать серии повторяющихся опытов. При этом чаще
78
повторяются наиболее характерные и вероятные значения, определяю*
щие физическую сущность объекта, что позволяет задаться тем или иным
типом модели.
В общем и весьма упрощенном виде подход к идентификации неде-
терминированных объектов можно рассматривать следующим образом.
Полученная по результатам эксперимента модель является лишь при-
ближенной оценкой истинных параметров и определяет интервал, в ко-
тором находятся истинные значения, с той или иной достоверностью.
Чем меньший разброс наблюдается во время эксперимента, тем выше
достоверность нахождения истинного значения в данном интервале.
В соответствии с теорией вероятности при стремлении числа опытов
к бесконечности интервал стремится к нулю, а достоверность - к еди-
нице.
Следовательно, планирование эксперимента* для идентификации не-
детерминированных объектов должно определять такие его объем и
число повторений, при которых будет обеспечена заданная достовер-
ность модели. Эти задачи решаются с использованием аппарата мате-
матической статистики, корреляционного и регрессионного анализов.
При решении этих задач пользуются положениями теории случайных
событий и процессов. Событие - это любой факт, фиксируемый во
время эксперимента. Численной мерой объективной возможности на-
ступления события является вероятность. Вероятность простого собы-
тия определяется расчетным путем только для опытов, сводящихся
к схеме случая: события независимы, равновероятны, какое-либо од-
но обязательно должно произойти. Эта вероятность Р* определяет-
ся как отношение возможного числа событий с интересующим нас
исходом п* к общему числу возможных событий т*:
Р* = п*!т*.
Большинство реальных опытов нельзя свести к схеме случая. По-
этому экспериментально определяется статистическая вероятность Р
как отношение числа опытов и, в которых наблюдался интересующий
нас исход, к общему числу проведенных опытов т:
Р = п/т.
Согласно теореме Бернулли при разность Р* — Р стремит-
ся к нулю.
События бывают: достоверные (Р * = 1), невозможные (Р* = 0),
случайные (0 < Р* < 1); совместные (одновременные) и несовмест-
ные; зависимые (появление одного меняет вероятность появления
другого) и независимые. Под потоком событий понимают следующие
друг за другом события в случайные моменты времени.
Вероятность совместного наступления нескольких простых незави-
симых событий равна произведению вероятностей наступления каж-
дого из них. Вероятность наступления одного из нескольких несов-
79
местных событий равна сумме вероятностей наступления каждого
из них.
Случайные события определяются также численными характерис-
тиками - случайными величинами. Они могут быть непрерывнымй,
например время г*, в течение которого произошло к событий, и ди-
скретными, например число событий к в интервале времени
Связь случайной величины с вероятностью его появления математи-
чески описывается законами распределения случайных величин. Эти
законы определяются по результатам статистической обработки данных
эксперимента.
Законы распределения чаще всего представляются в виде интеграль-
ной F (х) или дифференциальной / (х) функции распределения. Первая
применяется для дискретных величин и определяет вероятность того,
что случайная величина не превышает некоторого фиксированного ее
значения хк, т.е. вероятность ее нахождения в интервале
F(x) = Р (—°° <Х<Хк).
Пример 3.4. Высоконадежная система аварийной сигнализации со-
стоит из трех дублирующих друг друга блоков. Вероятность безотказ-
ной работы каждого блока Р = 0,9. Построить график интегральной
функции распределения числа отказов системы.
Определим вероятность безотказной работы для несколькких слу-
чаев:
число отказавших блоков не превышает одного (л < 1 или п = 0),
т.е. одновременно работают три блока. Тогда вероятность такого слож-
ного события
Р(0) = Р(п < 1) = ЛР2Р3 = 0,93 = 0,729;
число отказавших блоков меньше двух (п < 2), т.е. п = 0 или п = 1.
Определим вероятность того, что исправны все блоки либо любые два,
т.е. имеют место четыре несовместных события. Так как вероятности
безотказоной работы одинаковы, то
Р(1) = Р(и<2) =ЛР2Рз н-ЗР^а -Р3) =
= 0,93 + 3 • 0,92 (1 - 0,9) = 0,972;
число отказавших блоков меньше трех (п < 3), т.е. п = 0, или п = 1,
или п = 2, следовательно,
Р(2) = Р(п < 3) = Р- + 3PiP2 (1 -Р3) +
+ ЗЛ(1 - Р2) (1 -Р3) = 0,999;
число отказавших блоков меньше четырех (и < 4), т.е. п = 0, п = 1,
п = 2, п = 3, следовательно,
80
Рис. 3.4. График интегральной функ-
ции отказов
Р(3) = Р(п<4) = Р- +
+ ЗЛР2(1-Р3) +
+ ЗР,(1-Р2)(1-Р3) +
+ 3(1-Р1)3 = 1.
График функции изображен на рис. 3.4. Он позволяет по прираще-
нию функции определить вероятность попадания случайной величины
интервал значений. Так', вероятность Р2,з того, что число отказов
Судет 2 или 3, т.е. 1 < п < 4, равна Р2 з = Р(3) - Р(0) = 1 - 0,729 =
М^0,271.
Непрерывная случайная величина имеет непрерывную функцию
распределения. Ею могут быть время наступления одного или несколь-
jpix отказов, время обработки детали, ее размер, процентное содержа-
ние компонентов и др. Для непрерывных случайных величин вводится
дифференциальная функция распределения
' /(х) = dF(x)/dx.
f Эта функция представляет собой скорость или плотность измене-
ния вероятности при изменении х. Интегрируя f (х) и подставляя в нее
конкретное значение хк = Ь, получаем вероятность того, что х не пре-
высит Ь:
ь
? P(-oo<x<Z?)= ] f(x)dx.
Фиксируя нижнний предел, найдем вероятность нахождения случай-
ной величины в интервале а-b:
ь
P(a<x<b) = J f(x)dx.
а
Следовательно, вероятность нахождения случайной величины в ин-
тервале Дх определяется площадью под графиком f (х), ограниченной
этим интервалом.
На рис. 3.5, а представлены графики интегральной функции распре-
деления F(x), а на рис. 3.5, б - дифференциальной функции/(х) для
равномерного (кривая 7), экспоненциального (кривая 2) и нормаль-
81
Рис. 3.5. Графики функций распределения:
а - интегральной; б - дифференциальной
ного (кривая 3) законов распределения непрерывной случайной ве-
личины, изменяющейся в пределах 0—1. Функции описываются следую-
щими уравнениями:
функция F (х):
кривая 1 - F1 (х <а) = 0;
Fi (а < х < Ь) = (х - а)/(Ь - а);
Fi(x>b) = 1;
кривая 2 - F2 (х) = 1 - е~ ^х;
(х-с)2
кривая 3 — F3(x) = —1 J е 2 °2 dx;
О^2п' °°
функция /(х):
кривая 1 - fi (х < а) =0;
fi(a<x<b) = Ц(Ь-а)-,
fi(x>b)= 0;
кривая 2- f2(x) =
(х-с)2
кривая 5-/з(х) = —------е 20
82
Статистические исследования показали, что экспоненциальному за-
кону хорошо подчиняются случайные отказы элементов АСУ в период
Анормальной эксплуатации, а нормальному — в период старения.
J Количественные показатели законов распределения определяются
^Следующими численными характеристиками случайных величин:
I; математическим ожиданием - величиной, вокруг которой группи-
руется большинство случайных значений, это — усредненные по вероят-
ности значения случайных величин:
> для дискретных случайных величин
п
М (х) = S Xj Pj Cx) ;
i = 1
для непрерывных случайных величин
М(х) = J xf(x)dx.
— 00
Пределы интегрирования ограничиваются исходя из допустимых
Значений параметра;
модой — Мо (х) — наиболее вероятным значением случайной вели-
Н<Йы; при х = Mo f (х) достигает максимума;
медианой - Me (х) — величиной, для которой справедливо равен-
ство
* Р(х< Me) = Р(х> Me),
то соответствует значению х, делящему площадь f (х) пополам.
г , Разброс случайных величин относительно среднего значения — ма-
тематического ожидания — характеризуется тремя величинами:
отклонением или центрированной величиной
«(х) = х, -М(х); (3.27)
дисперсией
S(x) = М (х,- - М (х))2; (3.28)
среднеквадратичным отклонением
а(х) = y/Sjx)1. (3.29)
Обобщающими характеристиками случайных величин являются
моменты:
начальный
= М (х«)
83
и центральный
= М(х-М(х))«.
Для q = 1 начальный момент равен математическому ожиданию,
для q =2 центральный момент есть дисперсия случайной величины.
Центральный момент третьего порядка (q = 3) характеризует асим-
метрию законов распределения. Коэффициент асимметрии
К = Д3/о3.
Центральный момент четвертого порядка (q = 4) — эксцесс, харак-
теризует островершинность распределения. Коэффициент эксцесса
Е = М4/о4.
Аналогичные понятия относятся и к случайным величинам, подчи-
няющимся многомерным законам распределения.
Рассмотрев эти определения, перейдем к сущности корреляционного
анализа.
Корреляционный анализ позволяет установить статистическую связь
между случайными переменными и оценить количественно меру ее
тесноты: от отсутствия связи (переменные независимые) до наличия
жесткой функциональной связи между переменными.
Одним из самых распространенных параметров оценки тесноты
статистической связи между переменными является корреляционный
коэффициент
п
S (xf - M(x))(yz- М (у))
г = —------------------------ , (3.30)
ло(х)а(у)
где
/ — !
/ П
. а(х) = / S (Xi -М(х))2/< (х); (3.31),
V * = 1
здесь (х) = nxi/n.
Аналогичные выражения можно записать и для у.
При наличии между случайными переменными величинами линей-
ной связи вида у = а0 + а jX коэффициент корреляции равен г = +1,
при обратном знаке перед вторым членом г =—1. Чем меньше статис-
тическая связь между х и у, тем меньше г. Он принимает значение, рав-
ное нулю, при их полной независимости друг от друга.
Действительно, при у =а0 ±а>х справедливо равенство
у,- — М(у) =±Я! (xz —М(х)),
84
тогда
п
± д 1 2 (х - М (х))2
7п / п
Z (х-М(х))2 ± /д2 S (х-М(х))2
i=l V /= 1
Если статистическая связь между переменными отсутствует, то при
^вменении х величина у остается неизменной или принимает симметрич-
ные значения относительно среднего М(у). Тогда числитель (3.30)
равен нулю, так как в выражении
п
2 (X,--М(х))О, -М0'))
/= 1
каждому значению одного сомножителя соответствуют два равных по
величине, но противоположных по знаку значения второго сомножителя.
Так как экспериментальные данные являются случайными величи-
нами, то и рассчитанный по ним коэффициент г также будет величиной
случайной. Следовательно, его отличие от нуля является лишь предполо-
жением (гипотезой) и требует подтверждения. Значимость г проверяет-
ся путем сравнения величины
Я= гх/л^Т
сч
С данными табл. 3.7, где приведены критические значения значимости
Якр для различного числа опытов п и вероятности Р.
?’ При Н > Якр предположение о наличии статистической связи между
у их можно принять с вероятностью Р,указанной в таблице.
Пример 3.5. Необходимо установить наличие и характер влияния
стажа работы наладчиков автоматической линии на качество продук-
ции по данным табл. 3.8, где зафиксированы у - число бракованных
Таблица 3.7
л Вероятность Р п Вероятность Р
0,9 0,95 0,99 0,999 0,9 0,95 0,99 0,999
10 1,65 1,9 2,29 2,62 16 1,65 1,93 2,41 2,87
11 1,65 1,9 2,32 2,68 17 1,65 1,93 2,42 2,9
12 1,65 1,91 2,35 2,73 18 1,65 1,93 2,43 • 2,92
13 1,65 1,92 2,37 2,77 19 1,65 1,93 2,44 2,94
14 1,65 1,92 2,39 2,81 20 1,65 1,94 2,45 2,96
15 1,65 1,92 2,40 2,85
85
Таблица 3.8
У 14 14 10 12 10 8 4 10 6 2
X 2 4 4 6 6 7 8 9 9 10
yi -J'cp 5 5 1 2 1 -1 -5 1 -3 -7
- хср -4,5 -2,5 -2,5 -0,5 -0,5 0,5 1,5 2,5 2,5 3,5
деталей на 100 шт. выпушенных и стаж наладчиков в месяцах х. Там же
приведены разности между jz,xf- и их средними значениями.
1. Определим оценку математического ожидания переменных у
их как среднее арифметическое:
ю ю
Уср = 2 ^/Ю = 9; *ср= 2 xf/10 = 6,5. к
1 1
2. Найдем коэффициент корреляции по (3.30) :
1 о
S (У/ - 9)(xz - 6,5)
г= ‘,-... .....i—/--------------- =-0,85.
/10’ /10 1
/ 2 (у,- -9)2 /2 (х,- - 6,5)2
V 1 V 1
Судя по коэффициенту корреляции, связь между у и х достаточно
сильная и отрицательная,, т.е. как и следовало ожидать, после наладки
линии более опытными наладчиками снижается брак продукции.
3. Проверим значимость коэффициента корреляции г:
Н= Г5/л- 1'= 0.85 <10- 1'= 2,55.
Критическое значение Якр из табл. 3.7 при п = 10 и вероятностиР = .
= 0,99 равно Якр = 2,29. Следовательно, так как Н > Якр, то с Р = 0,99
можно принять гипотезу о наличии линейной статистической связи
между у их.
Способы выявления нелинейной корреляции и решение подобных
задач для многомерных объектов отражены в [3].
Если установлены коррелирование двух переменных, их теснота и
достоверность статистической связи, то необходимо далее получить
модель объекта в виде уравнения регрессии требуемой достоверности,
полученного в результате регрессионного анализа.
Под уравнением регрессии у на х понимается зависимость средних
значений у при заданном значении х от этой переменной. Так, если за-
даться интервалом х^ =±Дх и по экспериментальным точкам, попав-
шим в этот интервал, вычислить ^/ср = Ъу-/п^ то точка с координата-
86
ми Л'/Ср» xi будет принадлежать линии регрессии у на х. Если задаться
интервалом = ± &у и выполнить указанные выше вычисления, то по-
лучим точки линии регрессии х на у.
Для получения достоверного уравнения регрессии объекта по дан-
ным активного эксперимента необходимо:
убедиться, что разброс значений у и х допустим для использования
их средних значений при вычислении коэффициентов уравнения регрес-
сии; если разброс недопустим, то следует либо повысить точность из-
мерений, либо увеличить объем эксперимента, либо перейти на другой
тип модели;
определить коэффициенты уравнения регрессии и численные значе-
ния разброса их значений, обусловленные случайным характером изме-
ренных .у их;
оценить значимость каждого коэффициента, сравнив найденное его
значение и разброс; если значение коэффициента намного меньше раз-
броса, то мы вправе полагать, что отличие коэффициента от нуля слу-
чайно. Это позволяет отбросить незначащие коэффициенты и получить
уравнение регрессии в окончательном виде;
оценить адекватность полученной модели по отклонению средних
значений у. полученных расчетным путем по уравнению модели, от дан-
ных эксперимента на реальном объекте;
записать уравнение регрессии в абсолютных единицах.
Ниже приводится пример, который позволяет компенсировать крат-
кое изложение принципа получения модели недетерминированного
объекта.
Пример 3.6. Вал механизма передает момент М и испытывает кон-
сольную нагрузку F. Для оценки влияния их значений на выходной
сигнал датчика момента U на работающем механизме был проведен
ПФЭ2Л с 10-кратным повторением каждого опыта. Данные приведены
в табл. 3.9, в которой приняты обозначения: М = х,, F = х2, U=у. Слу-
чайный разброс U вызван случайными нагрузками, обусловленными
сильной низкочастотной вибрацией механизма. В табл. 3.9 приведены
также значения U, полученные при статическом нагружении вала, для
сравнения с усредненными экспериментальными значениями.
Решение 1. Выбираем область идентификации, ограниченную
реальными эксплуатационными режимами
Мтах = х1тах = ±20кНм; | | = 20 кН • м; х1ср =0;
min min
Fmax = х2 max =±50 кН; | Дх21 = 50 кН; х2ср=0.
т in т in
Напряжение датчика может меняться в пределах
Umax “ Утах = ± 100 мВ.
min min
87
Таблица 3.9
N *0 *1 *2 *1*2 У1 У2 Уз
1 + + + 75 76 68
2 + + — • — -29 -30 -28
3 + — + — -30 -21 -21
4 + — - + -17 -27 -19
У4 У$ Уб У7 У8 У9 Ую Уст
86 73 75 80 70 69 79 75
-20 -27 -27 -19 -26 -19 -23 -25
-31 -26 -25 -24 -32 -27 -25 -23
-19 -17 -16 -18 -18 -26 -18 -21
2. Анализ погрешности измерений показал, что у подчиняется нор-
мальному распределению, которое характеризуется математическим
ожиданием и дисперсией. В качестве уравнения регрессии из соображе-
ний. изложенных в п. 3.3.3, принимаем
У = а0 +atXi + а2х2 + a3*i*2-
3. Оценим, достаточен ли объем эксперимента при имеющем место
уровне помех для получения достоверного уравнения регрессии. Для
этого проверим однородность дисперсии опыта в различных точках
поверхности отклика, т.е. одинаков ли примерно разбросу во всех че-
тырех опытах.
Определим среднеарифметические значения ^ср как лучшую оцен-
ку математического ожидания:
к
Jcp = 2 У,/^
i = 1
где к = 10 — число повторов каждого опыта.
Найдем выборочные дисперсии в каждом опыте:
к
S(y)= s (yz-Jcp)2/A
i = 1
где f = к-1 — число степеней свободы или разность между числом по-
второв каждого опыта и числом независимых констант Z, определен-
ных по данным опыта. В данном случае для определения S (у) исполь-
зуется одна константа ^ср.
Проверка однородности дисперсии по критерию Фишера:
^расч = (у) 1^2 О') *,
88
Таблица 3.10. Значения F - критерия Фишера
Л /1
2 3 4 5 6 9 12
7 4,7 4,4 4,1 4,0 3,9 3,7 3,6 3,2
8 4,5 4,1 3,8 3,7 3,6 3,5 3,3 2,9
i 9 4,3 3,9 3,6 3,5 3,4 3,2 3,1 2,7
> ю 4,1 3,7 3,5 3,3 3,2 3,0 2,9 2,5
; 11 4,0 3,6 3,4 3,2 3,1 2,9 2,8 2,4
30 3,3 2,9 2,7 2,5 2,4 2,2 2,1 1,6
*40 3,2 2,9 2,6 2,5 2,3 2,1 2,0 1,5
- —
здесь (у) и S2 (у) — большая и меньшая дисперсии, при расчетах ко-
ЮрыхЛ =/2 = 9.
i ^расч сравнивается с данными табл. 3.10, в которой FTagn представ-
ляет собой значения критерия Фишера.
^табл находят на пересечении столбца и строки /2 • В нашем слу-
чае это 9 и 9; при этих значениях FTa6n = 3,2. Если Fpac4 < Гтабл,
^0 в 95 случаях из 100 можно гарантировать однородность дисперсий,
i следовательно, можно пользоваться уср для расчета коэффициентов
регрессии.
При определении Fpac4 для сокращения расчетов достаточно ис-
пользовать Smax (у) и Smin (у), так как в этом случае получим наиболь-
шее значение Грасч.
Проверка однородности по критерию Кохрена (табл. 3.11) дает бо-
дрее надежные результаты, особенно при большом числе опытов. В этом
случае определяется
/*
Срасч “ $тах(У) / ^-(у),
где Smax(y} — максимальная дисперсия; 5/(у) — дисперсия каждого
оЛыта при данном сочетании и х2, в том числе и Smax (у); N = 4 -
число опытов в примере.
По табл. 3.11 при f = 9 и W= 4 <7табл = 0,5. Если <7расч < СтабЛ, то с
достоверностью, при которой рассчитана таблица, дисперсию можно
считать однородной.
В табл. 3.12 приведены результаты расчетов уср и S(y) для каждой
из серии опытов.
По полученным значениям S(y) выполнен расчет
51(7)
30,8
^расч =-------------------------------- --------------------------- 0,39.
Si (у) + S2 (У) + 53 (у) + $4 (У) 30,8 + 17,7 + 14,9 + 14,5
89
Таблица 3.11. Значения G - критерия Кохрена
А/ f
2 4 9 10
2 0,98 0,91 0,8 0,79 0,5
3 0,87 0.75 0,62 0,6 0,33
4 0,77 0,63 0,5 0,49 0,25
5 0,68 0,54 0,42 0,41 0,2
Так как Срасч < ^табл» то дисперсии однородны и средние значе-
ния х и у можно использовать для определения коэффициентов а,-.
На этом основании можно сделать вывод о достаточном объеме экспе-
римента и правильном выборе типа модели.
4. Определяем коэффициенты уравнения регрессии по выражению
N
S х ij
/=1
получаем:
(+1) -75,1 + (+1 )• (-24,8) + (+1 )•(-26,2) + (+1)(-19,5)
д0----------------------------—
(+1)75,1 + (+1) • (-24,8) + (-1) • (-26,2) + (-1) - (19,5)
Д1 = ----------------------------------------------------
(+1) 75,1+ (-1) • (-24,8) + (+1) • (-26,2) + (-1) • (-19,5)
а2 = ---------------------------------------------------------
_ (+1) 75,1+ (-1) - (-24,8) + (-1) • (-26,2) + (+1 )•(-19,5)
а3- --------------------------------------------------------= 26,6.
4
Для сравнения: коэффициенты, рассчитанные по уст (см. табл. 3.9)
имеют значения, равные соответственно 1,24,24, 26.
Таблица 3.12
N -У ср «О')
1 75,1 30,8
2 -24,8 17,7
3 -26,7 14,9
4 -19,5 14,5
5. Оценим значимость коэффициен-
тов уравнения регрессии. При пол-
нофакторном эксперименте диспер-
сия коэффициентов определяется по
выражению
5(e) = SB(y)/N,
где SB(y) - дисперсия воспроизво-
димости опыта, которая рассчиты-
90
Таблица 3.13. Значения t - критерия Стыодента
/ст 3 6 9 12 15 18 2i . 24 29 «>
t 3,18 2,45 2,26 2,18 2,13 2,1 2,08 2,06 2,04 1,96
IT
вается по формуле
2 5. Си)
, „ , . i=i $10')+$20')+$з0')+54 0')
$в00 = ----------- = --------------------------=
N N
30,8+17,7+14,9+14,5 1П сс
= ----------------------= 19,55.
4
Тогда
'у 8(a) = 19,55/4 = 4,9.
ж'<1о этому значению можно найти доверительный интервал, в кото-
находятся истинные значения коэффициентов уравнения регресии
достоверностью Р
Да) < аист < (аэ + Ад).
||йтервал определяется по выражению
Да = t\JS (а),
Где t — табличное значение критерия Стьюдента (табл. 3.13).
Значение t вычисляется по числу степеней свободы
/ст= (k-l)N = (10-1)4 =36,
тргда t = 1,96, а
Да = 1,96 х/491 = 4,33.
> Коэффициент считается значимым, если |а| > |Да |. Тогда в рассмат-
риваемом примере коэффициент а0 считается незначимым (а0 < Да),
Тл. принимается а0 = 0, и с учетом этого модель (с достоверностью
Fs0,95) имеет вид
У = 24*! + 23,3 х2 + 2696х1х2.
6. Оценим адекватность модели объекту (датчику). Для этого по
предыдущему выражению определим урасч в каждом из четырех фак-
торных экспериментов (см. табл. 3.9) :
У1 расч = 24(+1) + 23,3 (+1) + 26,6 (+1) = 73,9;
91
Уг расч = 24 (+1) + 23,3 (-1) + 26,6 (-1) =-25,9;
Узрасч = 24 (-1) + 23,3 (+1) + 26,6 (-1) =-27,3;
У4расч = 24 (-1) + 23,3 (-1) + 26,6 (+1) '=-20,7.
Дисперсия адекватности, т.е. отклонение расчетных и эксперимен-
тальных значений, рассчитывается по выражению
N
*$ад О') = S О'эксп ~ Д'расч)2//ад»
i= 1
где /ад = 1а, здесь 1а — число коэффициентов уравнения регрессии
/а = 3; /ад = 4 - 3 = 1; уЭксп = УСр (см. табл. 3.12), тогда
^ад О') = Ю((75,1 - 73,9)2 + (-24,8 + 25,9)2 + (-26,2 + 27,3)2 +
+ (—19,5 + 20,7)*) = 53,1.
Модель может оказаться неадекватной объекту из-за ошибок при
определении коэффициентов, неверно выбранного типа модели и из-за
неверной оценки значимости коэффициентов. Чтобы исключить вли-
яние на оценку адекватности случайного разброса у, т.е. оценить аде-
кватность только по типу модели, следует сравнить по критерию Фи-
шера З'адО'), отражающую суммарный эффект, и (у), отражающую
влияние помех:
^ад.расч = Яад (У)/$в О') = 53,1/19,55 = 2,7.
По табл. 3.10 для = /ад = 1 и /2 = /ст = 36
^табл = 3,5 > ^ад, расч = 2,7.
Следовательно, принятая модель с достоверностью 95% адекватна дат-
чику момента.
7. Уравнение модели в абсолютных единицах
Х1 “ х 1 ср . х2 “ х2ср
У = ----7---" + *2 —-----~
А*! Ах 2
х хз —хзср
+ а3~----
Ах3
Таккакх1сп =х9гп =0, A*i = 20, Ах2 =50, то
д vp х vp ' * w 9
24 23,3 26,6
У= ----+ -------Х2 +-------*1*2-
20 50 1000
Согласно принятым обозначениям у = С/, Xi =М,х2 = F, получим
U = 1,2М + 0,46F + 0,0266MF.
92
3.4. ФОРМАЛИЗАЦИЯ ДИСКРЕТНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ОПЕРАЦИЙ (ТЕХНОЛОГИЧЕСКИХ ЦИКЛОВ)
3.4.1. Структура формирования технологического цикла
Полный технологический цикл изготовления готовой штучной про-
дукции всегда представляет собой совокупность отдельных техноло-
гических операций, сменяющих друг друга в определенной последо-
вательности. Причинами смены операций могут быть команды челове-
ка-оператора или автоматического устройства, выдающего их после
получения сигналов от датчиков об окончании предыдущей операции
в соответствии с заложенной в него программой. В то же время очень
редко можно обеспечить нормальную работу агрегата, ориентируясь
на ’’жесткую” программу, не способную адаптироваться к неожидан-
ным ситуациям, возникающим в технологическом цикле. Так, если на
какой-либо операции становится очевидным появление брака, то опе-
ратор или автоматическое устройство следующей командой должны
предусмотреть не продолжение обработки, а останов агрегата и уборку
бракованной детали. Аналогичная ситуация возникает при поломке
оборудования, превышении допустимых значений параметров процес-
са, несоответствии параметров исходной заготовки техническим ус-
ловиям.
При управлении технологическим циклом необходимо формиро-
вать дискретную последовательность (программу) команд исполнитель-
ным элементам технологического объекта управления (электро- и
гидроприводам). Формирование команд осуществляется управляющим
устройством, называемым дискретным автоматом (рис. 3.6), на осно-
ве логического анализа ситуации, о которой сообщают различные дат-
чики положения детали, завершения или качества протекания очеред-
ной технологической операции, по командным и оповестительным
входам. Только зная, как и при каких условиях должна формировать-
ся нужная последовательность состояния объекта управления, можно
сформулировать задание на синтез управляющего устройства.
Таким образом, хотя общая функциональная структура АСУ ТП I
остается такой, как представлена на рис. 1.2, методы построения мо- т
дели технологического цикла принципиально отличны от рассмотрен-
ных выше методов получения моделей объекта, отражающих непрерыв-
ное его функционирование в процессе выполнения технологической
операции ~——
Существуют различные формы ^представления моделей дискретных
последовательное!ей операций, т.е. моделей технологического цикла.
Они могут представляться”в виде таблиц, циклограмм, графов, фор-
мул и тд. Предполагая, что все технологические последовательности в
конечном счете представляют собой повторяющиеся циклы, следует
выделить два существенно отличных вида моделей: ^со^да^ционные^
и последовательна^ первом случае дальнейшее функционирова-
93
Воздействия оператора
(командные входы
дискретного автомата)
Технологические
возмущения
Оповеститель -
ныв входы
дискретного
автомата
Рис. 3.6. Структура управления технологическим циклом при помощи дискрет-
ного автоматического устройства
Выходы
технологических
объектов
(датчики)
ние объекта определяется только состоянием объекта при выполне-
нии предшествующей операции; во втором — последовательностью
смены предшествующих операций.
Для удобства деления цикла на отдельные элементы вводится поня-
тие технологического такта или состояния, (т\е. конечного интервала
^ременй, КбГДа aipeiar рабиыст т'ПеизмеДной комбинацией включен-
ных (отключенных) командных (кнопки, ключи), оповестительных
. (датчики) и исполнительных (электро-, гидроприводы, электромагни-
ть^муфты) элементов._______________________ - — __ —
ибщазГпоследовательность формализации технологического цикла
состоит из следующих этапов:
1) составления содержательного описания, в котором в произволь-
ной повествовательной форме описывается технологический цикл при
нормальном его ходе и аварийных ситуациях;
2) разбиения цикла на такты, характеризуемые неизменным состоя-
нием исполнительных приводов и контролируемых параметров;
3) анализ переходов от одного такта к другому при нормальных
и аварийных ситуациях для выявления поичин переходов, т.е. выявле-
ния изменения состояния командных и исполнительных органов вызы-
вающих переход;
4) установления причинно-следственных и логических ситуацион-
ных связей между входами и выходами объекта управления, обуслов-
ленных требованиями технологии;
5) составления формализованного графического представления алго-
ритма функционирования в ваде таблицы, циклограммы, графика
и т.п.
3.4.2. Комбинационные детерминированные модели.
Таблицы истинности
В качестве комбинационных (как наиболее простого вида) моде-
лей, в которых дальнейший ход цикла определяется состоянием вхо-
дов и выходов объекта управления только в данном такте, часто ис-
пользуются таблицы истинности, отражающие однозначное соответствие
дискретных состояний входов и выходов объекта управления.
Активное (включенное) или пассивное (отключенное) состояние
исполнительного элемента (входа) или уровень контролируемого выхо-
да (высокий, низкий) может обозначаться любыми символами. Обычно
для этих целей используются дискретные величины 1 и 0.
. При числе входов п возможны N = 2п сочетаний комбинаций их еди-
ничного и нулевого уровней. Поскольку последовательность смены ком-
бинаций в данном случае роли не играет, в таблице истинности их удоб-
но располагать в виде кодов натурального ряда двоичных чисел, т.е.
чередуя 0 и 1 для первого входа через одно состояние, для второго —
через два, для третьего - через четыре и тд. Особо следует отметить.
что не все комбинации состояний входов (исполнительных приводов)
и датчиков реально Moiyr иметь место.
'^Пример 3.7. Произвести сортировку’деталей на три группы по разме-
ру, равному b. 2Ь и больше ЗЬ, открыв заслонки бункеров-накопите-
лей, предназначенных для отбора деталей каждого типа. Контроль разме-
ров деталей можно осуществить тремя датчиками dx — d3, установлен-
ными (рис. 3.7) поперек роликового транспортера. Обозначив бунке-
ры2>1 ,Б2 и53, выделим следующие ситуации (табл. 3.14):
1) идет деталь размера b — перекрыт один из датчиков (Jt или d2,
или d3), открыт бункер(такты 4,2,1);
2) идет деталь 2Ь - перекрыты два датчика (d19 d2 или d2i J3),
открыт бункер Б2 (такты 6,3);
3) идет деталь размером более ЗЬ - перекрыты все три датчика,
открыт бункер Б 3 (такт 7).
Таблица истинности составляется для всех возможных комбина-
ций командных датчиков. Число таких комбинаций равно N = 2п = 8,
где п = 3 — число командных входов (число датчиков). Состояния дат-
чиков обозначаются двоичным кодом натурального ряда чисел, что
позволяет упростить заполнение таблицы. Выходные сигналы 0 или 1
соответственно означают, закрыт или открыт бункер.
Рйс. 3.7. Установка датчиков
для контроля размеров дета-
ли
95
Таблица 3.14
Номера ком- бинаций (тактов) Состояние
входов выходов
<*1 Bi Е2 Б3
0 0 0 0 0 0 0
1 0 0 1 1 0 0
2 0 1 0 1 0 0
3 0 1 1 0 1 0
4 1 0 0 1 0 0
5 1 0 1 0 0 0
6 1 1 0 0 1 0
7 1 1 1 0 0 1
Незаполненные клетки состояний выходов (такт 5) соответствуют
нереальной ситуации, когда деталь перекроет датчики dx и d3 и не пе-
рекроет d2; она может возникнуть лишь в результате неисправности
датчика J2- Эти клетки заполняются нулями для предотвращения ава^
рийной ситуации (все бункеры закрыты, звучит сигнал).
3.4.3. Последовательностные детерминированные модели
В отличие от !<ЬмбИНИ1Щбннь1^ составлении последо-
вательностных моделей необходимо отражать однозначное соответ-
ствие состояний выходов комбинациям состояний входов как в дан-
ном такте, так и в предыдущих. Следовательно, одна и та же комбина-
ция входов в данном такте может вызвать переход в разные новые сп-
стояиия в зависимости от того, каким было предшествующее состояние
Поэтому в модели должны быть отражены не только данный такт, но и
предыстория.
В зависимости от сложности объекта используются различные виды
моделей. В простейшем случае применяются циклограммы, в которых
состояния отражают условным изображением включенного или от-
ключенного исполнительного элемента в виде наличия или отсутст-
вия линии. При большом числе состояний применяются таблицы со-
стояний л графы. Более конкретно методика составления мопетёй'
изложена на примерах.
Циклограмма. Она представляет собой ряд горизонтальных строк,
равных числу командных и исполнительных элементов. Строки услов-
но разбиты на отрезки, число которых равно числу элементарных техно-
логических тактов. Включенное состояние элемента на строке обозна-
чается сплошной линией, отключенное — отсутствием ее. Вертикальны-
96
Рис. 3.8. Циклограмма работы грузо-
вого подъемника
ми линиями на циклограммах по-
казана ’’передача управления” -
причинно-следственные связи меж-
ду командными и исполнительны-
ми элементами.
Элемент Обозна- чение элемента Номер такта
l\2 3 * 5 6 7 8 9
Команд- ный SB SQ1 SQ3 SQ2 SB SQ3 SQ1
SQZ saz Г”
Исполни- тельный КМ1 KMZ f KM1'
Когда элемент включен, совокупность тактов называется периодом
включения, а когда отключен — периодом отключения. Такт, предшест-
вующий периоду включения, называется включающим, а периоду от-
ключения — отключающим.
Пример 3.8. Рассмотрим циклограмму работы грузового подъемни-
ка (рис. 3.8). Грузовой подъемник с тележкой от подачи кратковре-
менной команды кнопкой SB (пуск) идет вверх [кнопка SB включа-
ет контактор ’’Вперед” КМ1 (SB -> КМ1), после чего отключается
(такт 1)]. В начале движения отключается нижний конечный выклю-
чатель SQ2 (такт 2). После достижения крайнего верхнего положе-
ния кабина воздействует на верхний конечный выключатель SQ1, кото-
рый дает команду на отключение КМ1 (такт 3, SQ1 -> КМ1). Контак-
тор КМ 1 отключается (такт 4). После выката тележки отключается ко-
нечный выключатель SQ3 (такт 5) и включается контактор ’’Назад”
КМ2, подъемник идет вниз (такт 6, SQ3 КМ2), отключается SQ1
(такт 7). После воздействия внизу на нижний конечный выключатель
SQ2 отключается КМ2 (такт 8, SQ2 КМ2), кабина останавливается
(такт 9).
Таблица состояний. Число строк таблицы соответствует числу состоя-
ний, число столбцов — числу возможных комбинаций переменных;
крайний левый столбец фиксирует номера исходных состояний. Над
таблицей приводится мнемограмма. В клетках проставляются номе-
ра состояний, обусловленных исходным состоянием и возникшей ком-
бинацией управляющих переменных.
Пример 3.9. Подъемник перемещается с одного уровня на другой
реверсивным приводом, включаемым исполнительными элементами
контакторами КМ1 и КМ2. Пуск подъемника осуществляется по коман-
де от этажных кнопок SB1, SB2, SB3, SB4. Аварийные ситуации предот-
вращаются реле перегрузки, конечными выключателями SQ1 и SQ2
и контролем закрытия дверей шахты SQ3, SQ4. Все командные пере-
менные сведены к четырем: пуск вверх ПВ — нажаты кнопки ’’Вверх”
SB1, SB3 на первом или втором этаже; пуск вниз ПН - нажаты кноп-
ки ’’Вниз” SB2, SB4 на первом или втором этаже; есть разрешение дви-
97
Таблица 3.15
PH
РВ
ПН ПН
ПВ ПВ
ПВ ПВ
Номера тактов
Состоя н ис-----------------------------------------------------------
1 2 3 4 5 6 7 8 9 10 И 12 13 14 15 16
Движение вверх 3 3-.-3 3 1111111 1 3 3 3 3
(состояние 1)
Движение вниз 3333 3333222 2 2 2 2 2
(состояние 2)
Кабина неподвижна 3333 3313313 2 2 3 3 3
(состояние 3)
гаться вверх РВ — закрыты все двери, не нажат конечный выключа-
тель SQ1, нет перегрузки; есть разрешение двигаться вниз PH — закры-
ты все двери, не нажат конечный выключатель S02, нет перегрузки.
Число возможных состояний три: 1 — движение вверх, 2 - движе-
ние вниз, 3 — кабина неподвижна.
Таблица состояний (табл. 3.15) содержит три строки и 24 - 16 столб-
цов. Число столбцов равно числу комбинаций командных переменных.
В первой строке исходным является состояние 1 (движение вверх),
поэтому во всех клетках, соответствующих действию РВ, проставля-
ется 1. При отсутствии разрешения на движение вверх (отсутствует РВ)
кабина не движется, в этих клетках ставится 3. Аналогично заполняет-
ся вторая строка, т.е. где есть PH — ставится 2, а в остальных — 3.
В третьей строке указывается исходное состояние кабины 3, поэто-
му 3 проставляется: в клетках 1-4, так как нет РВ и РН\ в клетках
8, 9, 16, так как нет вызова (отсутствуют ПВ и ПН); в клетках 5 и 15,
так как здесь разрешение противоречит вызову (есть ПВ, нет РВ и на-
оборот). В клетках 7,10 ставится 1, а в клетках 12, 13 - 2, так как
разрешение соответствует вызову. Состояние командных органов для
клеток 6, 11, 14 нереально при нормальной эксплуатации (есть одно-
временно два вызова: вверх и вниз). В такой ситуации кабина может
оставаться неподвижной, т.е. ставится 3.
Граф-схема. При представлении цикла в виде графа в вершинах
(кружках) проставляются номера (коды) состояний. Вершины соеди-
няются стрелками, отражающими переходы из одного состояния в дру-
98
РИС. 3.9- Граф-схема алгоритма функцио-
нирования подъемника
гое. Над стрелками записываются
комбинации переменных, обуслов-
ливающих этот переход.
На рис. 3.9 представлен граф, опи-
сывающий работу подъемника из
примера 3.8. Граф имеет три вершины (состояния 1, 2, 3) (см.
табл. 3.15). Пуск из состояния 3 (подъемник неподвижен) в состоя-
ние 1 или 2 (движение вверх или вниз) обусловлен наличием требуе-
моц команды (ПВ или ПН), отсутствием противоположной (ПН или
ПВ) и наличием разрешений (РВ или PH). Обратный переход обуслов-
лен только отсутствием разрешения (РВ или PH), т.е. снятие ПВ или ПН
останова не вызывает. Сохранение состояния 1 или 2 обусловлено толь-
ко наличием РВ или PH а состояние 3—их отсутствием. В скобках над
или под стрелками указаны номера комбинаций переменных (такты),
соответствующие данному переходу.
Представление тем или иным образом алгоритма функционирования
зависит от степени их освоения и приобретенных навыков.
3.4.4. Стохастические модели
При создании моделей технологических операций и процессов прихо-
дится сталкиваться с такими случаями, когда моделируемое явление
не удается описать в виде детерминированных функциональных свя-
зей. Причиной этому могут быть как сильное влияние различных слу-
чайных возмущений, так и принципиально случайный характер самого
явления, т.е. интересующее нас явление не искажено помехами, а вы-
звано совместным действием различных случайных факторов.
Наиболее типичным случайным явлением являются отказы оборудо-
вания и элементов автоматики в период их нормальной эксплуатации.
С одной стороны, опыт показывает, что рано или поздно, с большей
или меньшей интенсивностью отказывают большинство деталей или
электронных узлов, а с другой - совершенно невозможно предска-
зать точно момент времени, когда произойдет отказ.
Очевидно, можно говорить лишь о вероятности наступления одного
или нескольких отказов в определенном интервале времени либо о
том, что время безотказной работы (число отказов равно нулю) не
превысит определенного значения.
Аналогичная постановка вопроса справедлива применительно к по-
грешностям измерения параметра. В силу целого ряда случайных фак-
торов невозможно предсказать, какова будет погрешность при кон-
кретном измерении, хотя ясно, что она не бывает больше какого-то
99
значения и что существует понятие средней погрешности по конеч-
ной совокупности измерений. Случайным можно также представить
отклонение параметров заготовок и даже готовых деталей от норма-
тивных. При этом для годных изделий эти отклонения находятся в пре-
делах допусков, для бракованных превышают допуск.
В рассмотренных случаях, особенно при взаимодействиии и взаимо-
влиянии различных случайных факторов, поведение интересующего
нас параметра и его значение не могут быть представлены как функ-
ция взаимодействия средних значений определяющих его факторов.
Конечный результат должен быть получен в виде случайной величины
как результат взаимодействия случайных факторов в повторяющих-
ся реализациях процесса. Только после статистической обработки по-
лученных результатов можно говорить об оценке среднего значения
и разброса. Такая модель процесса в отличие от детерминированной
называется стохастической (случайной).
Стохастические модели также отражают объективные закономер-
ности, присущие данному процессу, однако представление их в виде
детерминированных функций либо невозможно, либо нецелесообраз-
но на данном этапе. Для их представления используется аппарат слу-
чайных функций, когда случайные явления и процессы характеризу-
ются случайными величинами, подчиняющимися вероятностным зако-
нам, кратко описанным в п. 3.3.5.
Статистически устойчивые (достоверные) результаты моделирова-
ния случайных явлений и процессов могут быть получены лишь по
достаточно большому числу реализаций (опытов), причем чем боль-
ше разброс значений случайной величины, тем большее число реализа-
ций требуется. Реально такое моделирование возможно лишь с исполь-
зованием быстродействующих ЭВМ.
Для этой цели ЭВМ должна иметь возможность:
генерировать последовательность случайных чисел с заданными зако-
ном распределения и параметрами (математическое ожидание, диспер-
сия и т.п.);
вычислять вероятность наступления случайного события, подчиняю-
щегося определенному закону, в заданном интервале времени;
воспроизводить факт наступления случайного события и тд.
Во всех указанных случаях необходимо знать закон распределения
случайной величины или события и его параметры. Необходимые для
этого данные получают, проводя натурный эксперимент по реализации
подобного явления. Статистическая обработка такого эксперимента
позволяет не только выявить статистические закономерности случай-
ного явления, но и оценить достоверность результатов в зависимости
от объема эксперимента (числа реализаций).
Начальным этапом обработки экспериментальных данных является
построение вариационного ряда и гистограммы. Для этого фиксирует-
ся ряд значений дискретной случайной величины х (например, число
100
бракованных деталей за одну смену) в течение п смен. Совокупность
значений называется выборкой или статистическим рядом.
- Располагая разные измеренные значения в порядке возрастания,
получаем вариационный ряд. Далее составляем таблицу частот, в кото-
рой каждому значению из вариационного ряда xi ставится в соответ-
ствие экспериментальная частота наблюдавшегося явления:
’ Д/д = л/д/«д’
где Л/д ~ число смен, когда было х, бракованных деталей; ид - общее
число смен, когда проводились наблюдения.
Ерли случайная величина непрерывна (погрешность измерения),
то ее экспериментальные значения представляются в виде интерваль-
ной таблицы частот, в которой указаны интервалы значений
случайной величины, а также, как и для дискретной величины, часто-
ты попадания ее в этот интервал
= w/h/wh>
где — число значений случайной величины, не выходящих за преде-
лы /-го интервала; тп — общее число зафиксированных значений слу-
чайной величины.
‘ ho данным интервальной таблицы строят гистограмму, представляю-
щую! собой ряд сопряженно расположенных на горизонтальной оси
прямоугольников, основание которых равно интервалу с,—с/+1 значе-
ний случайной величины, а площадь равна Др
' Построив графики по данным таблицы частот или гистограммы,
Можно по их виду предложить гипотезу о соответствии данных опы-
та тому или иному закону. После этого проводится проверка степени
соответствия экспериментальных данных предполагаемому закону.
Проверка производится с использованием различных критериев согла-
сия; Наиболее распространенным является критерий х (хи-квадрат)
Пирсона. Использование указанного критерия иллюстрируется при-
мером.
Пример 3.10. По данным проверки, выполненной технологическим
контролем, для п = 60 плат с микроэлектронными компонентами коли-
чество плат ту с числом некондиционных паек на 1 плату Xj составило:
X; о 1 2 3 4 5 6 7
8 17 16 10 6 2 0 1
•а Определим математическое ожидание как среднее число бракован-
ных паек на одну плату:
MW = Хср = z — = 2,13
г = 1 п
101
и выборочную дисперсию:
S(x) = S (х,-х )2 -L = 2,1.
/=1 п
Из полученных результатов можно сделать вывод, что данная случай-
ная величина подчиняется закону Пуассона, для которого основным
признаком является равенство математического ожидания и дисперсии:
М(х) = S(x).
Закон Пуассона дает вероятность Р (х) наступления ху редких собы-
тий в каждом ряду независимых испытаний, которая имеет вид
Л (х) = ~~ е~а, (3.32)
где а - интенсивность появления событий. Оценкой а может служить
среднее число событий на одно испытание.
Подставляя в (3.32) значения xz и а = хср, получаем теоретические
значения вероятности Р (х) наступления xz событий в одном испыта-
нии. Сравнение его с экспериментальными частотами mjn позволяет
сделать предварительный вывод о достоверности принятого предположе-
ния о соответствии эксперимента закону Пуассона.
Результаты расчетов сведены в табл. 3.16.
Таблица 3.16
0 1 2 3 4 5 6 7
mf/n 0,133 0,283 0,266 0,167 0,1 0,033 0 0,017
Р(х) 0,135 0,271 0,271 0,18 0,09 0,036 0,012 0,0034
Для количественной оценки достоверности вычисляется критерий
Пирсона (хи-квадрат):
/
х2 = s
(т^/п - ?(х))2 л 2
Р(х)
где I = % — число интервалов.
Полученное значение х2 сравнивается с критическим табличным
значением ХкР Для разных значений достоверности Р или значимос-
ти а = 1 —Р, приведенным в [26, табл. 7]. Найдем число степеней сво-
боды
/ = 1 = 8-1- 1= 6,
102
Hie / » 1 — число параметров, вычисленных предварительно для опреде-
ления закона Пуассона. Таким параметром в нашем случае является
математическое ожидание.
Для достоверности Р = 0,95 или значимости а = 1 - 0,96 = 0,05 при
числе степений свободы f = 6 по табл. 7, приведенной в [26], имеем
х’р = 1,63 >0,2.
Следовательно, гипотезу о соответствии числа бракованных паек зако-
ну Пуассона можно принять достоверной на 95 %.
Получив подтверждение о подчинении случайных событий конкрет-
ному закону распределения, нужно иметь возможность осуществить
моделирование потока таких событий, например генерированием их
численных характеристик.
При этом может оказаться необходимым генерировать случайные
числа, равные числу событий в заданном интервале времени (целые
величины), либо значения погрешностей измерения (дробные напрерыв-
ные величины).
Существуют различные пути решения этой задачи.
Первый способ — хранение таблиц случайных величин в памяти ма-
шины. Обычно в них помещены числа с равномерным законом распреде-
ления. Так, если нужны случайные числа в интервале 0-0,9 (прираще-
ние вероятности 0,1), то выбирают одно число, если в интервале
0—0,9 — выбирают пары чисел (приращение вероятности 0,01). Такой
способ требует большого объема оперативной памяти машины (106 -
107 ячеек). Он характеризуется малым быстродействием. Быстродей-
ствие -снижается в связи с тем, что для получения чисел с неравномер-
ным распределением выбираемые из памяти числа в пределах 0-1 ис-
пользуются как значения вероятности, по которым далее вычисляет-
ся случайная величина с интересующим нас законом распределения.
Так, для экспоненциального закона
P(Y\ = а~^ХЭКСП
реализуется алгоритм
*эксп =—— 1пР(х) =— -~-1пХравн’
Л Л
где хРавн “ случайная величина при равномерном законе распреде-
ления.
Второй способ, основанный на подсчете в единицу времени числа
частиц при радиоактивном излучении или превышений определенно-
го значения шумовых помех электронной машины или операционного
усилителя, заключается в применении генераторов случайных чисел.
Если число частиц или переходов помехи через пороговое значение
четно, генерируется значение 1, если нет - 0.
103
При параллельной работе т генераторов в ячейках появляются т
разных двоичных чисел, хорошо подчиняющихся равномерному за-
кону распределения. Недостаток метода - невозможность повторно-
го воспроизведения данной реализации.
Третий способ, получивший широкое распространение, заключает-
ся в генерировании псевдослучайных последовательностей чисел на
интервале 0—1 с использованием специальных алгоритмов.
Так, алгоритм
где£0 =0; + 1 =£/+ 1-IO’8; z0 =0,011; F — символ целой части,
дает примерно 108 неповторяющихся чисел в интервале 0—1, распре-
деленных по равномерному закону.
Для нормального закона генерируют сначала случайные числа
с равномерным распределением, а затем числа с нормальным зако-
ном распределения по алгоритму:
= [sign (2 - 1)] /- Л-1П (4$f (1 - $,)),
где
sign =
1 при х > 0,
< 0 при х = 0,
—1 при х < 0.
Существуют также многофакторные стохастические модели для мо-
делирования зависимых событий и тд. При необходимости с этими
вопросами можно познакомиться в специальной литературе по мате-
матической статистике и теории вероятности [26, 32].
3.4.5. Моделирование сложных недетерминированных объектов
Примерами недетерминированных объектов могут служить много-
операционные станочные линии, многоклетьевые прокатные станы
и т.п. Используя рассмотренные выше методы, можно получить формаль-
ные модели отдельных операций, механизмов, технологических цик-
лов.
Желательно до принятия окончательного варианта решений на стадии
разработки объекта изучить различные варианты как структуры ком-
плекса в целом, так и частных решений по производительности от-
дельных позиций, объему промежуточных накопителей полуфабри-
катов, принципов подачи заготовок, надежности и т.п.
104
Для этой цели можно построить ’’жесткую” модель, задавшись един-
ственно правильным результатом обработки, точным размером дета-
ли, неизменными технологическими скоростями и временами обра-
ботки, пауз и т.д. Можно создать более совершенную ’’гибкую” модель,
учитывающую реально возможный случайный разброс указанных пара-
метров и исход отдельных операций.
Наконец, возможен такой подход, когда в модели объединяются де-
терминированные элементы, в которых можно пренебречь реально воз-
можными случайными колебаниями, и элементы, подверженные случай-
ным колебаниям, для которых описание возможно только с помощью
законов распределения случайных величин и событий. Такая модель
при всей ее сложности и трудности разработки может оказаться доста-
точно достоверной для того, чтобы, изучая за небольшое время с по-
мощью ЭВМ ее многочисленные реализации, сделать вывод о перспек-
тивности и эффективности различных вариантов. В этом случае резуль-
таты ’’эксплуатации” модели в течение года могут быть получены за
несколько часов. При моделировании учитываются многочисленные
случайные факторы, действующие на реальном объекте (параметры за-
готовок, времена их обработки, количество и характер отказов, не-
синхронность работы отдельных узлов, переполнение накопителей
и т.п.). По среднестатистическим результатам судят о производитель-
ности и надежности технологии при данном варианте ее организации.
Для таких исследований применяется специальный математический
аппарат теории массового обслуживания, особенно эффективный при
описании поточного производства штучной продукции (формообра-
зования). В этом случае моменты появления заготовок в начале линии,
продолжительность обработки на промежуточных операциях, началь-
ные и конечные размеры в допустимых пределах являются случайны-
ми величинами.
Для экономии машинного времени моделирование сводится к фик-
сации моментов наступления случайных событий, а интервалы време-
ни, когда не происходит изменения характеристик и параметров, при-
нимаются равными нулю.
В терминологии теории массового обслуживания поступающие на ли-
нию заготовки называются заявками, а их обработка - обслуживанием.
Последовательное поступление заготовок образует поток заявок. Сте-
пень детерминированности потока заявок может быть самой различ-
ной. Например, наступление отказов в системе характеризуется зна-
чительно большей степенью случайности, чем выпуск изделий хорошо
отлаженного конвейера. Потоки задаются в виде законов распределе-
ния, параметры которых определяются заранее различными методами.
Если допустить, что поток заявок обладает свойствами стационар-
ности, ординарности и отсутствия последействия, то такой поток назы-
вается простейшим и описывается распределением Пуассона, соглас-
но которому вероятность поступления к заявок за интервал опреде-
105
ляется по выражению
Распределение временных интервалов между поступлениями за-
явок получается при к = 0, а именно:
Р(0, tk) = е"Х'\
где X — параметр потока.
Представление технологических линий в виде систем массового
обслуживания предполагает объединение в этом понятии технологии,
оборудования, персонала и организации обслуживания.
Элементы систем называются приборами или каналами, а время
нахождения детали на обработке — временем занятости канала. Систе-
ма массового обслуживания может быть одноканальной и многока-
нальной.
По способу организации поточной технологии системы массового
обслуживания делятся на системы:
с отказами, когда появление заявки в момент занятости всех кана-
лов приводит к уходу ее из системы без обслуживания;
с ожиданием, когда поступившая заявка ожидает неограниченно
долго освобождения какого-либо канала;
с ограничением, когда ограничены могут быть либо время ожида-
ния, либо размеры накопителя, на котором происходит ожидание. При
превышении ограничения заготовка уходит необслуженной.
Отнесение системы массового обслуживания к тому или иному клас-
су обусловливает подход к понятию эффективности ее функционирова-
ния. Так, для системы с отказами критерием эффективности будет ве-
роятность отказа, а для системы с ожиданием — среднее время ожида-
ния или длина очереди заявок (размеры накопителя). Система с ограни-
чением является наиболее общим случаем. Она характеризуется как
вероятностью отказа, так и параметрами очереди. Для определения ве-
роятности отказов могут быть предложены весьма сложные выраже-
ния, что подтверждает целесообразность замены аналитических иссле-
дований подобных объектов их статистическим моделированием.
Весьма существенна при моделировании системы массового обслу-
живания дисциплина очереди заявок. По этому принципу выделяют:
обслуживание в порядке поступления заявок, когда освободивший-
ся канал занимает наиболее давняя заявка;
случайное обслуживание, когда не учитывается время ожидания;
обслуживание с приоритетом (самое распространенное), когда заяв-
кам разного типа предоставляется различного рода приоритет. Осво-
бодившийся канал занимает заявка с наивысшим приоритетом.
106
Различные формы соблюдения дисциплины очереди дают различную
эффективность функционирования технологической линии.
Решение подобных задач резко усложняется при рассмотрении много-
канальных систем. При необходимости учета многомерности заявок
и многопозиционного обслуживания только статистическое модели-
рование дает единственную возможность анализа технологических
систем массового обслуживания на стадии проектирования.
Ниже рассмотрен один из возможных подходов к построению обоб-
щенного машинного алгоритма — модели поточного процесса произ-
водства штучной продукции.
Основными видами операций в таких процессах являются операции
обработки или сборки изделия (преобразование вещества), операции
преобразования энергии и операции управления (преобразование ин-
формации). В качестве примера выбрана модель процесса обработки.
Чтобы модель была достаточно универсальной, для ее описания целе-
сообразно использовать обобщенные характеристики и параметры,
к числу которых относятся:
1) случайные дискретные интервалы времени, на границах кото-
рых происходит смена состояний процесса. К ним относятся: интер-
валы, через которые происходит подача заготовок, длительность под-
готовительных операций, время обработки, время наступления или
устранения отказов. Случайный характер этих величин обусловлен
тем, что они зависят от сочетания многих нерегламентированных фак-
торов;
2) случайный характер режима занятости технологического агрега-
та, который определяет характер подачи заготовок с очередями или
паузами;
3) параметры процесса амортизации рабочего инструмента либо
разладки систем управления, обусловливающих изменение времени
обработки, появление брака и т.п.;
4) параметры потока отказов и восстановлений оборудования (ин-
тенсивность отказов, время их устранения и т.п.), а также интенсив-
ность и причины появления брака.
Как показывает опыт, учет этих факторов при моделировании позво-
ляет достаточно полно и достоверно проанализировать технико-эконо-
мическую эффективность того или иного варианта технологического
процесса. С этой целью необходимо в процессе моделирования форми-
ровать в виде случайных величин с заданным законом распределения
моменты начала и конца обработки каждой детали, исходные и конеч-
ные (после обработки) размеры деталей, а также признаки, опреде-
ляющие нормальный и ненормальный ход операции.
Рассмотрим конкретные примеры формализации таких отдельных
элементов модели, как исходная заготовка, очередность подачи и др.
Исходная заготовка. Ее модель характеризуется количественными
параметрами (масса, размеры, температура, твердость) и качественны-
107
ми признаками (годная, бракованная, прошла или нет обработку). Яв-
ляясь случайными величинами, эти параметры задаются путем генери-
рования случайных чисел с требуемым законом распределения и соот-
ветствующими параметрами этого закона. Ряд параметров, колебания
которых несущественны, задаются фиксированными.
Момент начала операции может быть принят совпадающим с мо-
ментом поступления новой детали, если сумма времен обработки
/-й детали и время подготовки к приему новой r}.+ 1 меньше г' + |,
т.е. = tl*1 если 1 < r'n+ 1. В противном случае начало обработ-
ки совпадает с окончанием подготовки, т.е.
ГН = + 4+1’ еСЛИ + ГГ/+1 > ГП+1‘
п К 1 1\ 1 II
При этом время формируется как случайная величина.
Очередность подачи. Рассмотренная выше формализация будет аде-
кватна реальному процессу лишь при идеальной синхронизации всех
агрегатов автоматической линии. Если линия состоит из станков, то
возможны случаи, когда станок работает вхолостую, ожидая деталь,
либо заготовки образуют очередь, ожидая, когда освободится станок.
Наибольшее количество деталей в очереди определяется емкостью
накопителя (бункера, транспортера).
Формализация очереди осуществляется путем счета числа загото-
вок п в очереди. Если Nmin п < Nmax, предыдущая часть линии счи-
тается работающей; если п > Ntnax. линия останавливается, подача
заготовок прекращается (формируется команда ’’Останов”).
Ожидание станком детали формализуется отсутствием износа ин-
струмента или станка (станок отключен) либо его уменьшением (ста-
нок работает на холостом ходу).
Износ инструмента и разладка станка. Износ инструмента и разлад-
ка станка вызывают снижение производительности либо ухудшают ка-
чество изделий, увеличивают число бракованных деталей. Во всех слу-
чаях последствия износа выражаются как функция интервала време-
ни г- гнал, прошедшего с момента пуска линии после очередной на-
ладки.
Например, вероятность появления бракованной детали
^бр = + “ ^нал)$> (3.33)
где Ро - начальное значение вероятности^рака непосредственно после
наладки; v и $ - эмпирические коэффициенту.
В зависимость от t— Тнал можно поставить разброс размера детали
(дисперсия о), длительность обработки гк и т.д.
Необходимость в очередной подналадке определяется превышением
Рбр» о или tK допустимых значений либо истечением нормативного сро-
ка наладки Тн.
108
Время наладки считается случайной величиной с нормальным зако-
ном распределения, параметры которого существенно зависят от ква-
лификации персонала.
Длительность операции. Длительность операции гоп - важнейший
технико-экономический показатель. Может быть фиксированной вели-
чиной, если можно пренебречь колебаниями, и случайной с разбросом,
зависящим от параметров заготовки и состояния станка.
Надежность. Интенсивность наступления отказов оборудования влия-
ет на производительность и появление бракованных деталей. Более под-
робно материал излагается в гл. 7.
Момент наступления отказа определяется путем сравнения вероят-
ности наступления отказа Рот, получаемой по расчетной формуле соот-
ветствующего закона, с вероятностью равномерного распределения
Рравн» генерируемой как случайная величина.
Отказ считается наступившим, если в момент Г/ Рот >Рравн Отка-
зы учитываются двух типов: Р10Т, Got и ^2от> г2от- Первый соответ-
ствует кратковременной остановке станка, второй сопровождается пол-
ным ремонтом и переналадкой, после которых вероятности Р2от и г2от
отсчитываются от нового нулевого значения.
Появление брака задается вероятностью его появления как функции
времени, параметров станка и инструмента.
Формализация элементов технологического цикла позволяет рас-
смотреть построение операторной схемы алгоритмов моделирования
обработки. Целью алгоритмов моделирования является оценка произ-
водительности технологического процесса в условиях действия случай-
ных возмущений. Рассмотрим две составляющие алгоритма моделиро-
вания. Первая составляющая представляет модель подготовки детали
(ее выдачу, формирование очереди, ограничение подачи деталей при
заполнении накопителя) и, собственно, ее обработку в целом
(рис. 3.10). Вторая составляющая осуществляет моделирование само-
го процесса обработки, учет случайных отказов, разладки станка, слу-
чайного брака (рис. 3.11).
На рис. 3.10, 3.11 введены следующие обозначения: A. — арифмети-
ческие операторы запоминания и вычисления различных величин; Фу -
формирователи реализаций случайных процессов: Q - счетчики дета-
лей или событий; Л[ - логические операторы, проверяющие наличие
или отсутствие формального признака.
Формирование момента поступления заготовки tnj и суммирова-
ние их случайных интервалов гп осуществляется оператором Фх. По-
лученный момент времени поступления заготовки сравнивается с вре-
менем готовности станка к приему заготовки ГгвЛ2. При гп > tr опе-
ратор Л2 формирует сигнал 0, к оператору Л3 поступает разрешаю-
щий сигнал и количество деталей сравнивается с 1, при т < 1 к опера-
тору Аб поступает сигнал на обработку этой первой детали. Если на
выходе Л3 формируется 1, то счетчик суммирует ее с уже прошедши-
109
Рис. 3.10. Алгоритм модели подготовки и обработки детали
ми заготовками, а оператор As запоминает время Гп. Если заготовки
следуют при соотношении времен tn > гг, то обработка ведется после-
довательно каждой детали, а между ними имеется интервал, случайная
величина Ф7 формирует время начала операции по алгоритму, описан-
ному выше при формализации момента /н- Это время в Л8 сравнива-
ется с временем продолжительности смены Г, что позволяет установить,
не исчерпано ли рабочее время. При tH <Т деталь следует на обработ-
ку к А9, откуда она может поступить к счетчику Сю, суммирующему
годные детали, либо к счетчику С1Ь суммирующему детали бракован-
ные. Вне зависимости от работы счетчика Сх 0 или С\ i к 2 поступа-
ет сигнал, позволяющий сформировать время Гг, которое поступает
к Л2 для управления процессом обработки детали.
Если детали поступают с большой частотой Гп < гг, формируется
очередь из-за занятости станка. В этом случае Л2 выдает сигнал 1 и
110
| От Л9
ЬпреВсление
*о и
"~У
Формирование
*отк о j
"22
О
Определение
о од счет Etg
Ztn<7
_______0J__________
Ф33 Определение
*0ТК2»*р2
Ф>ф Формирование
Ч и tK
А 35 Вычисление
35 t^min^T^t^
А37 Определение
twsfnin(Tj
Формирование
' /пг ~
АЛ Определение
Определение
^и,и *н,к
Az? Определение
^бр
О
Выбор cL,r
К GlO
л2е
1
£<Рбп
A J7 Определение
*отк
i
Ф39 Формирование
_________*р»бр
*
Ада Определение
____________ *г_
♦ * С„
Рис. 3.11. Алгоритм мо-
дели обработки результа-
тов технологического
процесса
л30 \ 7
у
о
счетчик С4' добавляет к своему содержимому — количеству поступив-
ших деталей т — единицу. Арифметический оператор Л5 запоминает
/ц — время ожидания в очереди — и передает управление Лх 7. В Лх 7
* количество поступивших деталей т сравнивается с максимальной ем-
костью бункера т*. При выдаче сигнала 1 к поступает сигнал на вы-
дачу очередной детали в очередь. Здесь время хранения детали в бун-
кере неограниченное, и формирование времени ожидания в очереди
ИС требуется. Если бункер переполнен (т Ут'), сигнал к Фх не по-
ступает, т.е. следующая деталь в очередь не поступает. По сигналу О
оператора Л17 арифметический оператор Л16 передает признак 0 = 0
оператору Л6, который принимает очередную деталь, имеющую вре-
мя tn mini т.е. раньше других деталей, поступивших в бункер.
Дальнейшее функционирование модели аналогично описанному
при подаче деталей на обработку без очереди: от А6 сигнал поступа-
ет к Ф7, далее к Л8, А9 и через С10 или Сц - на Ф12 . От оператора
111
Ф12 сигнал передается к С13. Здесь из т вычитается единица - учет
обработанной детали. Логический блок Л14 проверяет возможность
подачи детали - не перегружен ли накопитель т < т' — и передает
команду Фх на выдачу без поступления детали (С4 и С4 на эту ко-
манду не реагируют, но А5' или Л5 время tnj суммируют). Если нера-
венство не удовлетворяется, то на выходе J714 формируется сигнал О
и команда поступает к Лх 5; здесь проверяется возможность подачи де-
талей в накопитель. Такая возможность появляется, когда число дета-
лей в накопителе станет меньше т"\ это количество несколько мень-
ше максимальной емкости т . Разница определяется конструкцией
накопителя. Если на выходе Л15 появляется сигнал 0, то команда пере-
дается А6, который моделирует прием детали из накопителя (очереди).
При формировании 1 на выходе Лх 5 можно пополнять очередь, коман-
да поступает к Л16, где сформирован признак а = 1. По сигналу Л16
Фх выдает очередную деталь и время гп/-. Далее схема работает, как бы-
ло описано выше.
Алгоритм обработки результатов технологического процесса
(рис. 3.11) начинает работать по сигналу об окончании смены от Л3.
На рис. 3.10 весь алгоритм представлен оператором Л19. Структура
оператора обработки детали А9 представлена на рис. 3.11. Оператор
Ф2о формирует длительность операции tQ и момент ее окончания tK =
= гн + г3, если не было отказа, или tK = rH + tQ + ty + гд, где t3 - вре-
мя занятости станка, если при обработке детали был отказ. При этом
с операторов, формирующих время ремонта гр и доработки детали
поступают сведения в оператор, который выдает tK в виде суммы
четырех составляющих. Ф2 i формирует момент готк и признак отка-
за 7. Если отказ первого рода, т.е. кратковременный, то не надо пере-
считывать вероятность и 7 = 1. Если отказ второго рода, то 7 = 0. Л22
проверяет, произошел ли отказ при свободном станке. Если в Л22
сформирована 1, управление передается оператору А 2 3, где подсчиты-
вается суммарное время работы станка на обработке деталей 2г0.
Оператор Л24, сравнивая это время с Тн, определяет необходимость
подналадки. Если подналадка не нужна (на выходе Л24 сигнал 1), то
оператор Ф2 5 формирует случайную величину интервала времени подго-
товки гпг, а оператор Л26 определяет момент готовности станка к при-
ему очередной детали tr = tK + гпг. Деталь обрабатывается в Л27, где
определяется вероятность брака Р$р, аЛ28 проверяет ее качество. Если
некоторая величина е > Pgp, то деталь ’’обработана” с заданным ка-
чеством и Ф29 ’’выдает” параметры а и признаки г после обработки,
а счетчик Сх 0 учитывает годную деталь.
В процессе обработки возможны отказы, которые моделируются
отдельными группами операторов. Отказ при станке, занятом обработ-
кой детали на выходе Л22 0, передает управление Лзо, который при
7 = 1 передает управление Ф31, а при 7 = 0 - Ф3 3. В первом случае фор-
мируется новое начало времени отказа r0TK i и время ремонта грЬ
112
во втором случае формируются те же величины, но соответствующие
отказу второго типа готк2 и ^р2- В каждом из этих случаев в А32 опре-
деляется время очередного отказа после устранения предыдущего.
ф34 формирует время доработки детали гд и новое время окончания
операции tK.
Если требуется наладка станка Sr0 > Тн, то Л24 передает команду
оператору Л35, который вычисляет времена ТХТ2 и тип очередного
отказа после переналадки. Ф36 определяет время начала наладки Гн>н
и конца наладки rH,K, после чего команда передается оператору Л27.
Появление бракованной детали определяет Л28, сигнал 1 которого
соответствует е < Рбр, управление передается Л37, где по аналогии с
Л35 определяется готк. Оператор Ф38 формирует время продолжи-
тельности ремонта при возникновении брака гр бр» а Л39 определяет
время готовности станка tr после ремонта. По сигналу этого оператора
счетчик Ci 1 учитывает бракованную деталь.
В процессе моделирования выводятся на печать время обработки
дета ей, число годных и бракованных деталей, времена устранения
отказов по различным причинам и другие показатели. На основе этих
данных можно дать статистические оценки эффективности процесса,
целесообразной частоты наладки, уровня надежности и т.д.
Гпава четвертая
АЛГОРИТМЫ УПРАВЛЕНИЯ
Целью главы является развитие и дополнение знаний студентов,
Получаемых в курсах ’’Теория автоматического управления”, ’’Си-
стемы управления электроприводами” и др., в области принципов фор-
мирования и реализации различных законов управления АСУ ТП с уче-
том специфики технологических объектов управления. Эта специфи-
ка заключается в необходимости решать традиционные задачи стабили-
зации, программного или оптимального управления применительно
К многомерным объектам, в формировании дискретной последова-
тельности технологических операций с учетом логического анализа
технологического объекта и т.п.
Излагаемые ниже вопросы автономизации каналов многомерных
систем, идеи инвариантного управления, элементы теории дискрет-
ных автоматов являются весьма актуальными в практике разработ-
ки АСУ ТП и обычно практически не включаются в традиционные для
специальности 21.05 дисциплины.
Сжатость изложения материала может быть восполнена с помощью
многочисленной справочной и монографической литературы.
В рамках одной главы невозможно осуществить исчерпывающее
рассмотрение принципов и практических решений в указанной облас-
ти* В связи с этим рассматриваются выборочно лишь некоторые спе-
113
цифические вопросы, которые либо характерны для АСУ ТП, либо не
всегда находят отражение в основных профилирующих дисциплинах.
При изучении курса следует в уже освоенных дисциплинах, особен-
но в теории электропривода, системы управления электроприводами
и др., отыскивать аналоги приведенных примеров и самостоятельно
ставить задачи и разрешать их, пользуясь приведенными ниже мате-
риалами.
Все положения иллюстрируются примерами, которые следует рас-
сматривать наравне с теоретическим материалом.
4.1. ЗАДАЧИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ОБЪЕКТАМИ
Целенаправленное и результативное функционирование объекта
управления обеспечивается подачей на его входы сигналов от управ-
ляющего устройства по определенным правилам — алгоритмам.
Под алгоритмом управления понимают совокупность правил при-
ложения управляющих воздействий к исполнительным элементам
объекта управления, обеспечивающих его функционирование с целью
решения поставленной перед объектом задачи. Вырабатывает указан-
ные воздействия управляющее устройство на основе уставок и ограни-
чений, введенных оператором (априорная информация), и сигналов
датчиков, вводимых обратными связями (текущая информация).
В этом смысле алгоритм управления определяет закон функциони-
рования управляющего устройства, обобщенная функциональная струк-
тура которого изображена на рис. 1.2.
Алгоритм управления, его структура и параметры зависят не толь-
ко от задачи управления, но и от того объекта, которым предстоит
управлять. Многообразие объектов управления, не поддающихся ти-
пизации, отсутствие единой четкой классификации задач управления
затрудняют классификацию алгоритмов управления.
Для упрощенного представления можно выделить среди алгорит-
мов управления две наиболее обобщенные и укрупненные группы:
алгоритмы управления состоянием и сменой состояний. К первым
могут быть отнесены алгоритмы поддержания заданного рациональ-
ного либо предварительно рассчитанного оптимального значения тех-
нологического параметра. Они получили название алгоритмов стаби-
лизации или регулирования. Среди них выделяют регулирование по
отклонению координаты и регулирование по возмущению. К этой груп-
пе могут быть отнесены также алгоритмы статической оптимизации,
когда управляющее устройство автоматически осуществляет поиск та-
кого сочетания значений технологических параметров, при котором
достигается наилучшее (оптимальное) значение некоторого крите-
рия качества функционирования объекта управления.
Если для достижения оптимального критерия качества необходимо
задавать недопустимые значения параметров объекта управления, то
114
формируются предельно допустимые алгоритмы, обеспечивающие
наибольшее приближение к оптимуму.
К алгоритмам второй группы следует отнести алгоритмы отработ-
ки заданной рациональной или заданной оптимальной траектории -
алгоритмы программно-следящего управления. К ним также могут
быть отнесены алгоритмы отработки заданной рациональной или опти-
мальной дискретной последовательности смены технологических опе-
раций, образующей технологический цикл.
В отличие от перечисленных алгоритмы динамической оптимиза-
ции обеспечивают автоматический выбор оптимальной траектории
или ее формирование, коррекцию в процессе отработки в зависимос-
ти от меняющихся условий таким образом, чтобы сохранить наилуч-
шее значение критерия качества функционирования.
Наиболее современным и перспективным является оптимальное уп-
равление, которое хотя и является обычно наиболее трудно реализуе-
мым, но зато дает наибольший технико-экономический эффект. Реше-
ние задач оптимального управления по существу стало реальным в свя-
зи с применением в системах автоматизации микропроцессоров и ми-
ни-ЭВМ.
4.2. АЛГОРИТМЫ СТАБИЛИЗАЦИИ ЗАДАННОГО ПАРАМЕТРА
4.2.1. Инвариантность по управлениям в многомерных системах
Для автоматизированных технологических агрегатов, а тем более
линий или комплексов, характерно представление их в виде многомер-
ных систем. В них наблюдается зависимость управляемых координат
как от своего управляющего или возмущающего воздействия, так
и от других.
Формальные модели таких объектов, как показано в п. 3.3.3, пред-
ставляют собой системы взаимосвязанных алгебраических или диффе-
ренциальных уравнений. Это делает весьма специфичными методы ана-
лиза и синтеза устройств управления подобными системами, существен-
но отличающимися от традиционных, используемых для аналогичных
целей в одноканальных устройствах управления.
Существенное облегчение анализа и синтеза рассматриваемых си-
стем обеспечивает вычислительная техника. Весьма важно понимание
принципов и методов преобразований таких систем, что позволяет
упростить решение задач управления.
Специфична постановка задачи о качестве управления многомерны-
ми системами в статике и динамике. Множество входных воздейст-
вий и управляемых координат обусловливает большое число струк-
турных и параметрических вариантов по обеспечению стабильности,
устойчивости и т.п. Весьма важной задачей является синтез устройств,
делающих автономными каналы управления отдельными координа-
115
тами. При этом сигналы управления другими координатами являются
для данного канала возмущающими воздействиями.
Самостоятельная задача - компенсация действия возмущений дан-
ного канала и отработка с требуемым качеством управляющего воз-
действия.
Среди многомерных систем более вероятно появление не полно-
стью управляемых или не полностью наблюдаемых систем. К ним отно-
сятся системы, у которых имеется часть, переменные состояния кото-
рой (внутренние, не являющиеся входными или выходными) не зави-
сят соответственно от управляющих воздействий или выходных коор-
динат. Устойчивость таких частей обычно не связана с устойчивостью
основной (управляемой, наблюдаемой) части системы. С выявлением
таких частей недостаточно четко справляется аппарат передаточных
матриц, оперирующий входными и выходными воздействиями. Зна-
чительно эффективней в этом случае метод пространства состояний.
Причинами появления таких областей является применение различных
перекрестных связей для автономизации каналов либо для инвариант-
ной компенсации возмущений.
В общем случае задача синтеза управления в многомерной системе
сводится к тому, чтобы для заданного многомерного объекта и опре-
деленных требований к качеству регулирования при известной систе-
ме возмущений и ограничений на управляемые координаты опреде-
лить структуру и параметры такого многомерного регулятора, кото-
рый обеспечит необходимое качество регулирования. Такая задача ре-
шается как вариационная, когда качество регулирования (например,
точность поддержания заданных значений) представляется в виде
функционала от управляющих воздействий. Достижение экстремаль-
ного значения функционала является решением задачи многомерной
оптимизации.
Многоканальные (многомерные) системы могут быть астатически-
ми и статическими. Особую группу составляют инвариантные много-
канальные системы, в которых ставится задача высокой степени ком-
пенсации (вплоть до полной) действия возмущений.
Впервые идеи инвариантности были высказаны в 40-х годах совет-
ским ученым В.Г. Щипановым и детально разработаны академиком
Н.Н. Лузиным. Дальнейшее развитие принцип инвариантности полу-
чил в работах академиков В.С. Кулебякина и Б.Н. Петрова. Б.Н. Петров
предложил фундаментальный принцип двухканальности, определяю-
щий принципиальную возможность создания инвариантной системы.
Сущность принципа заключается в том, что для компенсации действия
возмущения по одному каналу должен существовать второй канал,
по которому проходит инвертированное компенсирующее действие
возмущения в виде усиленного сигнала, пропорционального возмуще-
нию. Необходимость измерения возмущений при таком решении часто
очень усложняет задачу.
116
В многоканальной системе можно выделить перекрестные связи
для автономизации каналов, компенсирующие их естественное взаимо-
действие, перекрестные связи, компенсирующие действия контроли-
руемых возмущений соседних каналов, и, наконец, собственные обрат-
ные связи по отклонению, частично устраняющие действие различных
неконтролируемых возмущений.
В качестве примера применения принципа инвариантности рассмот-
рим задачу автономизации каналов многоканальной системы. При
этом формируется структура, в которой за счет введения перекрест-
ных связей управляемые координаты инвариантны к ’’чужим” управ-
ляющим или возмущающим воздействиям и зависят только от
’’своих”.
. Частный случай автономности предусматривает инвариантность по
отношению к задающим воздействиям. Здесь возможны два случая:
перекрестная компенсирующая связь, подаваемая на вход данного
канала, контролирует задающее воздействие другого канала;
аналогичная связь контролирует выход другого канала, т.е. дру-
гую управляемую координату.
Наиболее общий случай записи матричного уравнения, например
для трехмерной системы, до автономизации имеет вид
*1 ^11 ^12 ^13 /1
X х2 + e/2i d22 d23 X л
*з ^3i d32 d33 /з
или
AY = ВХ+ Df,
гдеУ, X, f— матрицы-столбцы управляемых координат, задающих и
возмущающих воздействий.
Приняв для упрощения f = 0, получим два вида записи уравнения:
у Y = А”1 ВХ и B-1AY = X.
Первая запись соответствует формальному представлению системы,
У которой каждая из выходных координат зависит от всех управляю-
Щих воздействий; вторая - представлению, когда каждое управляю-
щее воздействие влияет на все выходы. Соответственно первая фор-
ма может быть использована для анализа системы, вторая - для
синтеза.
117
Полагая в первом случае А“1 В = С, получим
У\ Сц С12 С\ 3
У2 = с2 1 С22 с2 3 X
Уз С31 Сз2 с 33
*1
х2
Чтобы система получилась автономной, необходимо, чтобы матрица
была диагональной. Тогда система будет описываться тремя незави-
симыми уравнениями
У1 = enxt;
У2 =£22*2 :
Уз = с33х3.
Однако недиагональные коэффициенты отражают естественное взаи-
мовлияние каналов в системе друг на друга и для данной физической
природы элементов системы изменены быть не могут. Задача может
быть решена введением компенсирующих перекрестных связей. До-
пустим, необходимо компенсировать действия первого и третьего ка-
налов на второй. Введем на вход второго канала компенсирующие
связи по заданию от первого канала с передаточными коэффициен-
тами и от третьего к3. Тогда система уравнений в матричной фор-
ме примет вид
У1
У2
Уз
Cj 1 С12
(С21 — £22^1) С22
С31 С32
С1 3
(С23~~ С22к3)
*1
Х2
х3
Из полученного видно, что условия полной инвариантности второго
канала по заданию первого и третьего имеют вид
<?2 1 - С22&1 =0 И с23 -с22к3 =0,
откуда
ki~c2i/c22\ к3-с23/с22.
• Пример 4.1. Стенд, предназначенный для испытаний объемных гидро-
приводов, оборудован нагрузочным устройством Н в виде машины по-
стоянного тока, связанной через генератор НГ и синхронный двига-
тель СД с сетью переменного тока для рекуперации энергии нагруже-
ния (рис. 4.1,а).
Нагрузочное устройство должно обеспечивать возможность задания
нагрузок гидроприводу в широком диапазоне и поддержания их задан-
ных значений. Изменение скорости гидро двигателя (гидромотора)
ГМ осуществляется изменением производительности питающего гидро-
118
Рис. 4.1. Стенд для испытания гидроприводов:
а - схема силового контура; б - эквивалентная структурная схема системы
управления
насоса ГН. Требуется синтезировать систему управления нагрузкой,
инвариантную по угловой скорости.
Исходя из баланса расхода жидкости в контуре ГН -* ГМ, уравнений
электрического равновесия цепи НГ Н и механического равновесия,
можно записать уравнение системы в операторной форме*:
Мгд^у (ГГпР + О + *7д =
Мн —(Гяр+ 1) +ссо= &н,г^в,н,г‘»
с
Мгд - мн =
где Мгд, Мн — операторные изображения моментов, развиваемых гидро-
двигателем и нагружателем; со - изображение угловой скорости; Ггп,
Тя — постоянная времени гидропривода, обусловленная сжимаемостью
жидкости, и электромагнитная постоянная якорной цепи; су — коэф-
фнциент, определяющий утечку рабочей жидкости; qa - коэффициент
пропорциональности между угловой скоростью и расходом жидкости
гидродвигателя; - коэффициент передачи гидронасоса, связываю-
щий его производительность с углом наклона блока поршней у (вход-
ное управляющее воздействие); &н,г - коэффициент передачи нагру-
зочного генератора; с — коэффициент двигателя нагружателя;
AMj — суммарный момент инерции и момент потерь на трение в сило-
вом контуре стенда; £/в,н,г — изображение напряжения возбужде-
ния НГ
Получена система уравнений трехсвязной системы с двумя управ-
ляющими входными воздействиями у и t/B,H,r, одним возмущающим
*Для упрощения записи в написании операторных величин символ р опущен,
например
М(р) М, <jO(p) со, £/в,н,г (Р) — ^в,н,г-
119
ДМ2 и тремя управляемыми Мгд, Мн и w координатами. В ней мож-
но обеспечить однозначное управление лишь двумя выходными пере-
менными, в качестве которых принимаем Мн и со, а Мгд определяем
как зависящую от них. Исключив Мгд и приняв ДМ^ = 0, получим си-
стему уравнений, описывающих стенд как двухканальную систему:
су (ТгпР + 1)^н + (Т’гпР + ОР +
— (ТяР + 1)МН + С(л> = ^н,г ^в,н,г»
с
или, введя сокращенные обозначения коэффициентов,
auMH + ai2co = Ь^у;
а2 1 + а22 Ы " ^2 ^В,Н,Г-
Разрешив уравнения относительно со и Мн, получим
°21 b 1 у - а 11 Z>2 ^в,н,г л л Л Гт
со -------------------------=—с 117 + с 12 ^в ,н ,г;
О 11^22 - 0220 12
/*22^17- Я12^2^В,Н,Г -г
Мн =--------------------------С2 1 7 “ с22 ^В,Н,Г’
О 11 022 “ *21 О 12
или в матричной форме
(4-1)
со
^11 С12
С*2 1 С*2 2
где — передаточные функции для со и Мн по управляющим воз-
действиям.
Как видно из (4.1), как угловая скорость, так и момент нагрузки
зависят от двух управляющих воздействий (рис. 4.1, б). Зависимость со
от 7 отражает действие на угловую скорость изменения угла наклона
блока поршней гидронасоса, а зависимость от С/в н г — действия на со
момента нагрузки на валу гидромотора.
Во втором уравнении зависимость момента Мн от своего задания
^в,н,г необходима, а зависимость его от 7 либо вообще должна быть
устранена, либо должна формироваться как функция со по соответ-
ствующему закону. Так как при испытаниях гидропривода нужна ими-
тация нагрузки, не зависящей от скорости, то следует автономизиро-
вать канал управления нагрузкой. В управляющее воздействие этого
канала введем сигнал, компенсирующий составляющую c2i 7
(рис. 4.1,5, штриховые линии), т.е.
С2 1 7 - С22 (^В.Н.Г + С2 1 О,С 7) =. Л/н »
120
Где с2ю,с ~ передаточная функция обратной связи, компенсирующей
естественное действие у наЛГн. Тогда
= (С2 1 ~~ с22 с2 1 О,с) 7 + с22 ^3 В,Н,Г-
Чтобы исключить влияние у, полагаем коэффициент при этой коор-
динате равным нулю, откуда
^210,С = C2i/c22.
, Раскрывая значение с21 ис22, получаем
; о22 Ъх ckQy
•< С210,С ~~ ---- = ' * Г"
«12*2 *н,г (ггпР+1)Р+<7М1
И, обозначая
' ; ” 'VO,C> *О,С»
*Н,Г?Д
Окончательно имеем
НГ: к
_ *о,с
^2 10, С------------" •
ТУпЛьсР +Зго,сР+1
Следовательно, для автономизации канала управления нагрузкой,
т.е. независимости нагрузки от задания по скорости, надо на его. вход
подать сигнал задания у через звено второго порядка с параметрами
^о,с» Ггп» Го, с-
4.2.2. Стабилизация по отклонению
от неконтролируемых возмущений
4 В п. 4.2.1 рассматривался случай обеспечения автономности кана-
ЛОв- путем введения перекрестных связей по задающим (входным)
воздействиям. При этом предполагалось, что имеется возможность
контроля этих воздействий с помощью первичных датчиков, преобразо-
вания их в электрический сигнал и передачи по каналу перекрестной
связи.
Аналогичные рассуждения применимы и к независимым внешним
/ Воздействиям типа возмущений, действующих в каждом канале либо
Ф&цих для всех каналов. В то же время иногда технически довольно
Вяожно, а порой и невозможно осуществить контроль входных воз-
Вействий. Кроме того, ряд причин (возмущений), вызывающих откло-
йения управляемых координат, может либо быть вообще неизвестен,
Шбо представлять собой случайную совокупность трудно прогнози-
руемых факторов.
121
Решение задачи автономизации каналов управления, т.е. достиже-
ния инвариантности по отношению к другим каналам, в этих случаях
имеет свою специфику. Если нельзя получить информацию об изме-
нении входного (задающего) воздействия, контролируя его непосред-
ственно, т.е. первопричину изменения выходной координаты, то сле-
дует использовать возможность получения необходимой информации
путем измерения соответствующей выходной координаты.
При этом предполагается наличие возможности контроля выход-
ной координаты первичным датчиком. Это более реально, так как без
такой возможности нельзя вообще контролировать качество процесса.
Рассмотрим конкретные решения. Система уравнений, описывающих
трехканальный объект управления в статике или динамике и разрешен-
ных относительно входных задающих воздействий, имеет вид
ацУ1 + + а13.Уз = *1*1 + <ЛЛ;
в21^1 + ^11Уг + Л2зУз = *2*2 + <^2/2!
а31У1 + A32J2 + вззУз = *3*3 + ^з/з-
При желании сделать координату у2 зависящей только от х2 и мало
зависящей от f2 необходимо на вход х2 подать сигналы перекрестных
связей по У! и ,у3, а также для ослабления действия f2 применить отри-
цательную обратную связь по у2. Тогда второе уравнение системы при-
мет вид
ацУ1 + a2iy2 + а23Уз = Ь2(х2^к1ух -к2у2 +
+ ЛхУз) + d2f2,
или
(а21 - Ь2к2)у2 + (а22 + Ь2к2)у2 +
+ (а23 - b2k3)y3 = b2x2 + d2f2.
Приняв условия инвариантности д21 -Ь2кх = 0 и а23 - Ь2к3 = 0 и
определив
Ад = ^21/Ь и к3 = а23/Ь2,
получим для второго канала
&2х2 d2f2
у2 = --------- + ------------ .
а22 + Ъ2к2 а22 + Ь2к2
Явление взаимовлияния каналов устранено введением перекрестных
положительных (компаундирующих) связей, действие собственного
возмущения f2 ослаблено введением обычной отрицательной обрат-
ной связи по^2.
122
4.3. АЛГОРИТМЫ ПРОГРАММНОГО УПРАВЛЕНИЯ
ЗАДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ ОПЕРАЦИЙ
Системы программного управления технологическими процессами
решают задачи перевода технологического агрегата из одного состоя-
ния в другое по заданной или оптимальной траектории. Такая общая
постановка может быть конкретизирована рядом частных задач:
программным перемещением рабочего органа (резца, лифта, прокат-
ных валков, сверла) в точки с заданными координатами;
последовательным перемещением рабочего органа в процессе обра-
ботки деталей по траекториям, определяющим конфигурацию гото-
вой детали;
отработкой циклически повторяющейся последовательности техно-
логических операций, сопровождающейся сменой инструмента, техно-
логических скоростей и т.п.
В зависимости от решаемых задач различными будут и алгоритмы
программного управления, и • технические средства, их реализующие.
Алгоритмами могут быть аналитические или табличные функции вре-
мени, обусловливающие такое изменение управляющего воздействия,
при котором ход технологического процесса приближается к требуе-
мому. Это возможно при относительно детерминированном характе-
ре возмущающих воздействий. Например, такие условия имеют мес-
то при позиционировании прокатного валка при отсутствии в клети
прокатываемого металла, перемещении сверла для сверления но-
вого отверстия и т.д.
Значительно сложнее решается задача контурного копирования,
т.е. перемещения по заданной траектории с требуемыми статической и
динамической погрешностями. Характерной особенностью систем про-
граммного управления является также необходимость логического
анализа текущей ситуации, связанная с выбором возможности продол-
жения технологического цикла или аварийного останова. В более слож-
ных случаях возможна необходимость выбора различных вариантов
продолжения цикла либо повторения отдельных его элементов. В лю-
бом случае функционирование управляющего устройства обусловле-
но конкретным алгоритмом управления.
Структурно системы программного управления могут выполнять-
ся как разомкнутыми (невысокая точность, незначительное влияние
возмущений), так и замкнутыми, отличающимися повышенной точ-
ностью при значительных возмущениях. В первом случае задача отно-
сительно проста и достаточно надежно решается применением дискрет-
ного (шагового) привода, во втором — применением сложных следя-
щих электроприводов аналогового или цифрового типа.
Возможно применение систем комбинированного типа, когда осу-
ществляется дискретное позиционирование рабочего инструмента в опор-
ные точки с последующим непрерывным отслеживанием отдельных
участков траектории, определяющей конфигурацию детали.
123
Далее рассматриваются вопросы, связанные с методами анализа и
синтеза по заданному алгоритму дискретных управляющих автомати-
зированных устройств, составляющих основу современных управля-
ющих устройств программного управления.
4.3.1. Элементы теории дискретных автоматизированных устройств
Под дискретным автоматизированным устройством понимают уп-
равляющее устройство, осуществляющее переработку априорной и
текущей информации в управляющую, причем носителями всех пере-
численных составляющих информации являются дискретные по уров-
ню и во времени сигналы. Это означает, что состояние сигнала каж-
дого входа (выхода) автоматизированного устройства характеризует-
ся двумя уровнями: минимальным, условно обозначаемым 0, и макси-
мальным, обозначаемым 1. При наличии нескольких входов (выходов)
комбинацию минимальных и максимальных (нулевых и единичных)
уровней можно воспринимать двояко:
как наличие или отсутствие на каждом входе (выходе) задающего
или командного сигнала, поступающего на какой-либо исполнитель-
ный элемент;
как кодовую комбинацию, обозначающую, например, двоичное
число, количество разрядов п которого равно количеству входов (вы-
ходов). Следовательно, можно говорить о многоуровневом выходном
сигнале с числом уровней N = 2п.
В первом случае дискретное логическое автоматизированное уст-
ройство решает задачи логического анализа ситуации, определяемой
рядом действующих или отсутствующих факторов, во втором — ариф-
метическое устройство, осуществляет преобразование информации пу-
тем выполнения арифметических операций над числами.
Как логические, так и арифметические устройства реализуются при-
менением ограниченного числа типовых элементарных операций над
дискретными сигналами и сходных методов синтеза и анализа.
Дискретизация по времени означает, что в течение конечного ин-
тервала времени ti9 именуемого тактом, состояние сигнала либо их
комбинация остаются неизменными. Пронумерованная последователь-
ность таких тактов образует автоматное время.
Дискретные управляющие устройства в соответствии с требования-
ми технологического цикла (см. § 2.3) бывают комбинационными
и последовательностными. Первые характерны тем, что комбинация
состояний выходных сигналов Ук/- в данном такте ti однозначно оп-
ределяется комбинацией входных сигналов Xj в этом же такте време-
ни, т.е.
YKi = Х№).
где X - оператор (алгоритм) преобразования.
124
. Комбинационные автоматы называют также автоматами с нулевой
памятью. /
У последовательностных автоматов комбинация состояний выхо-
дов в такте tj зависит не только от комбинации состояний входов в
данном такте, но и от того, какими были комбинации состояний вхо-
дов в п предыдущих тактах, т.е.
Уп/ = X(XZ; xi_l,... . x(i_n))-
Их называют также автоматами с ненулевой памятью, так как для вы-
работки своих выходных (управляющих) сигналов они должны не
только ’’знать”, что сейчас (в данном такте) происходит на входе, но и
’’помнить”, что было раньше.
По характеру реакции на входное воздействие различают асинхрон-
ные автоматы, у которых изменение состояния выходов происходит
Сразу после изменения входных, и синхронные, у которых изменение
выходов происходит лишь в том случае, если после изменения вход-
ных сигналов поступит синхронизирующий сигнал, разрешающий пре-
образование.
Для создания самого сложного дискретного автомата любого типа
достаточно иметь элементы, реализующие операцию ИЛИ—НЕ (инвер-
сия дизъюнкциии или операция Пирса) либо операцию И—НЕ (инвер-
сия конъюнкции или операция Шеффера), т.е. так называемый функ-
ционально полный набор.
^Доследовательносгные автоматы отличаются от комбинационных
также наличием обратных связей, по которым на в хо!дьТа^~о мата ТТОда-
ются сигналы, соответствующие состоянию выходов в предыдущем
такте.
Ниже рассмотрены достаточно обобщенные методы анализа и синте-
за дискретных автоматов с использованием элементов минимальной
_ ц средней степеней интеграции.
Основные этапы синтеза дискретного автомата следующие:
1) составление задания на разработку в виде содержательного опи-
сания, где формулируются требования управляемого объекта к авто-
мату, т.е. описания, на какой исполнительный элемент объекта и в
каком такте должен быть подан минимальный (0) или максималь-
ный (1) уровень сигнала данного выхода автомата, чтобы с учетом
состояния задающих входов и выходов, воспринимающих сигналы
обратных связей, обеспечить требуемое функционирование управ-
ляемого объекта;
2) получение формальной модели автомата на основе содержатель-
ного описания в виде таблиц, графов, матриц и т.п. (см. § 3.4);
3) получение на основе модели объекта исходной или минималь-
ной формы аналитического представления оператора преобразования,
реализуемого автоматом и обеспечивающего требуемый закон функцио-
нирования управляемого объекта. Эта часть синтеза является основ-
125
ной и базируется на аксиомах и постулатах Булевой (двоичной) ал-
гебры;
4) разработка принципиальной схемы автомата на основе получен-
ной в п. 3 его формальной модели и используемой конкретной элемент-
ной базы;
5) разработка и согласование узлов связи автомата с оператором
и управляемым объектом, защита от помех и т.п.
Далее приводятся основные положения двоичной алгебры. Отноше-
ния между двумя элементами здесь определяются отношением экви-
валентности, обозначаемым знаком равенства, и тремя операциями:
сложения (дизъюнкции), обозначаемой знаками <+> или<V>,ум-
ножения (конъюнкции) - < • > или «С Л > и отрицания (инверсии) —
«->.
При выполнении всех трех операций отношения эквивалентности
определяются следующими выражениями:
0 + 0 = 0; 0 0 = 0; б = 1;
1 + 0 = 1; 1 0 = 0; 1=0.
0 + 1 = 1; 0 1=0;
1 + 1 = К 1 • 1 = 1;
Эти постулаты позволяют обосновать законы двоичной алгебры.
Законы одинарных элементов:
универсального множества:
х + 1 = 1;
х- 1 = х;
нулевого множества:
х + 0 = х;
х • 0 = 0.
Законы отрицания (теорема Моргана):
двойного отрицания:
х = х;
дополнительности:
х + х = 1;
х • х = 0;
двойственности:
Xi + х2 = Xj -х2;
Xj -х2 = хх + х2.
126
комбинационные:
щйггологии:
+ X = х; х х = х;
|(W
^амймутативные или переместительные:
fe"+*3 = х2 +х,;
^ЗЙоциативные или согласовательные:
^+х2) +х3 =х,+ (х2 + х3);
$|^*2)Хз = -*1 (Х2 *з);
да^рибутивные или распределительные:
Й|4^ + хз) = Xi х2 +XjX3;
^*‘ЧХ2 хз) = (Х1 +*2)(Х1 +Х3);
абоВрбции или поглощения:
+ -«г,
"1 ’.у1
склеивания:
*»Ла +XjX2
^дар^цая алгебра дуальна относительно сложения и умножения,
закона двойственности (Моргана) было обобщено Шен-
следующей теореме: инверсия произвольной комбинации
переменных, связанных знаками < + > и <•>, эквивалент-
на &йэде в ней значений переменных их инверсиям при одновремен-
+ хз -х4 = (Xi +х2)(х3 +х4).
•111
Переключательной функцией (ПФ) называют переменную, значе-
Ш.^Р°й зависят от значений других двоичных переменных—аргу-
Переключательная функция задается в виде соответствия ее
каждому набору (комбинации) значений ее аргументов. Пе-
^КЛЮЧательные функции считаются разными, если отличаются значе-
бы для одного набора.
аргументах число наборов N = 2Л, а число переключательных
2# = 21Л
127
Запись наборов и ПФ легко выполняется в виде натурального ряда
двоичных чисел. Наборы нумеруются по значениям двоичных чисел
от 0 до 2я - 1.
Суперпозиция ПФ состоит в том, что аргументы сами могут являть-
ся ПФ, т.е. если .у = f(z z2) и z х = /\ (х1э х2), z2 = (х3, *4 ), то у =
= /(х1,х2,х3,х4).
Используя это свойство, можно наращивать число аргументов и на-
ращивать ПФ от самой простой до сколь угодно сложной. Минималь-
ный набор таких элементарных функций, который с помощью супер-
позиции может создать любую ПФ, называется функционально полным
или базисом. Это И-НЕ Xj х2 - штрих Шеффера, ИЛИ-HE Xi +х2
стрелка Пирса. Эти наборы составляют основу микроэлектроники.
Используя законы двоичной алгебры, можно осуществлять однознач-
ный переход из одного базиса в другой.
Набор И, ИЛИ, НЕ называют основным функционально полным.
Применительно к нему разработаны современные методы синтеза.
4.3.2. Синтез комбинационных автоматов
Операторы, реализуемые комбинационными автоматами, устанавли-
вают однозначную связь комбинаций входных и выходных перемен-
ных для каждого значения автоматного времени Г/:
Уц = М (*tf У * * * * X2i Xni)\
У mi “ (*1/ x2i xni ).
Для создания сложных комбинационных автоматов используют
элементарные комбинационные автоматы (логические элементы),
которыми реализуется функционально полный набор двоичных функ-
ций. Элементарным комбинационным автоматом будем называть ав-
томат, реализующий ПФ двух переменных.
Синтез комбинационных автоматов производится для статической
части такта, т.е. инерционность логических элементов не учитывает-
ся. Синтез комбинационных автоматов начинается с содержательного
описания функционирования объекта и составления таблицы истин-
ности (см. п. 3.4.2).
Для получения аналитического выражения, определяющего необхо-
димую структуру автомата, записываются исходные формы переклю-
чательной функции в виде совершенной дизъюнктивной (СДНФ) или
конъюнктивной (СКНФ) нормальной формы.
Дизъюнктивная нормальная форма представляет собой дизъюнк-
цию (сумму) минтермов, а СКНФ - конъюнкцию (произведение)
макстермов.
Минтермом или конституэнтой единицы называется логическая
128
фуйкция, принимающая значение 1 только на одном наборе перемен-
ных. Образуется как конъюнкция всех входных переменных с отрица-
нием тех, которые в данном наборе равны нулю. Число минтермов рав-
но ЧИслу наборов.
Макстермом или конституантой нуля называется логическая функ-
ций, ’ принимающая значение 0 только на одном наборе переменных.
Образуется как дизъюнкция входных переменных, где переменные
данного набора, равные 1, взяты с отрицанием. Число макстермов рав-
но числу наборов.
, Две эти формы эквивалентны. При минимизации удобно пользо-
иинжСДНФ-
^Рассмотрим4/методы синтеза автоматов с минимальным количест-
вом элементов, которые называются минимальными или оптималь-
ным#.
njlferod Квайна. Этот метод состоит из следующих этапов.
По табл. 4.1 истинности записывается СДНФ. Число слагаемых
равно числу наборов, где синтезируемая функция равна 1, а число со-
Множителей в каждом слагаемом - числу аргументов. Над аргумента-
миИфИНИмающими в данном наборе значение 0, ставится знак отри-
МНМ:
+ Х\Х2.
Таблица 4,1
Xi 0 1 0 1
х2 0 0 1 1
у 0 110
В полученной СДНФ отыскиваются смежные минтермы (отли-
чаются знаком только одного аргумента). Склеиваясь по этому аргу-
менту, смежные минтермы образуют импликанты - конъюнкции с
числом сомножителей, меньшим на один. Импликанты в свою очередь
мо!гут склеиваться между собой. Несклеивающиеся импликанты на-
Зываются простыми. Смежные минтермы и импликанты приведены
нцже:
Смежные минтер- Смежные им- Простая импли-
пликанты канта
*iX2x3x4, __
> XjX2x3,
^дХэХ3х4 J __
- - ? *2*3 -
<Х|Х2Х3Х4, П _ _
1 - г х^гХз,
Х| х2 х3х4, J
129
3. Полученная сокращенная СДНФ приводится к тупиковой форме
путем:
а) устранения избыточных импликант (избыточной называется им-
пл и канта, ’’покрывающая” минтермы, уже покрытые другими импли-
кантами);
б) применения закона поглощения для простых импликант и остав-
шихся минтермов
хгх2 + х1х2х3хл = XiX2;
в) проведения испытания отдельных членов. Для этого отбрасыва-
ется одно из слагаемых, а в оставшиеся выражения подставляются зна-
чения аргументов, обращающие испытываемый член в 1. Если остав-
шаяся часть при этом тождественно равна 1, то испытываемый член лиш-
ний, и наоборот. Метод Квайна применим до числа аргументов не бо-
лее 5, 6. При^большем числе применяют машинный метод Мак-Класки.
Метод Вейча-Карно. Наибольшее распространение сегодня получил
’ ^летод карт Карно. Суть его заключается в табличном представлении
минтермов СДНЪ и графической интерпретации их склеивания. Карта
Карно — это таблица с числом ячеек, равным числу наборов аргумен-
тов. В каждую ячейку можно вписать один набор (минтерм), причем
смежные минтермы должны бы быть в соседних клетках. Это обеспе-
чивается специальным подбором минтермов для каждой ячейки. Что-
бы упростить эту задачу, применяют различные способы маркировки
сторон карт Карно. Ниже описаны два наиболее распространенных спо-
соба (рис. 4.2).
На каждой из сторон карты половина клеток соответствует единич-
ному значению одного аргумента, а половина - нулевому. На проти-
воположных гранях аналогичная маркировка для другого аргумента
делается со сдвигом на одну клетку. В клетках тех наборов, где функ-
ция принимает единичное значение, пишется 1, где нулевое - 0.
При втором способе аргументы разбиваются на две группы с рав-
ным или неравным числом аргументов. Для одной группы хгх2 (пер-
вые номера) отводятся столбцы, для другой х3х4 (последние номера) -
строки.Прямое или инверсное значение аргумента определяется двоич-
ной цифровой маркировкой столбцов.
Охватывая единичные клетки контурами, проводим склеивание
смежных минтермов. Контуру из двух клеток соответствует одно-
ступенчатое склеивание, из четырех - двухступенчатое и т.д. Число
клеток в контуре может быть только четное. В образующихся импли-
кантах (простых) остаются переменные, которые в контуре не меняли
знак. Их число равно п-k, где п - число аргументов.
Чтобы функция была минимальной, необходимо накрыть все едини-
цы минимальным числом контуров максимальной площади. Контуры
могут пересекаться. В тупиковой алгебраической форме, полученной
из карты Карно, это означает:
130
о о
0 1
11
1 о
г,**
1 о
Xj Хг Xj х2 х1 х2 х1 х2
СО X, *2 Х3 Хх> С* Xi хг i3 х* C1Z Xi X2 Xj X<t Xy XZ Xj x4
Cl Xj XZ Х3 X» с5 _ Xi XZ Xj X<t ^13 Xi X2 Xj Xx, &9 Xi x2 Xj Xx>
Х1 х2 Xj Х4 c7 Xi x2 Xj X¥ C15 Xi X2 X3 Xxt On Xf xz Xj Xx>
Сг Xi Хг х3 х„ Xi XZ Xj Xx, CjXf. X1 xz Xj X^ _ Ojq X1 x2 Xj XV
Рис. 4.2. Составление карты Карно
число контуров равно числу слагаемых;
площадь контура определяет число сомножителей в слагаемом;
пересечение контуров означает тавтологию минтерма:
х,х2 + ххх2 = ххх2.
Минимизация частично определенных функций. Частично определен-
ная функция — это такая функция, значение которой задано не для всех
наборов аргументов. Это означает, что некоторые наборы аргументов
невозможны или недопустимы в реальных условиях. В таблице истин-
ности и карте Карно такие наборы обозначают знаками неопределен-
ности X или Если эти наборы нереальны, значит, ПФ можно опреде-
лить из соображений ее наилучшей минимизации, т.е. проставить в клет-
ках 0 или 1 вместо знака неопределенности.
Минимизация в монофункциональных базисах. Основой для получе-
ния минимальной формы в монофункциональном базисе (Шеффера или
П^рса) служит тупиковая форма СДНФ. Целью перехода к монофунк-
циональному базису является исключение из этой формы одной из опе-
раций <+> или <•>. Делается это так: для перехода в базис Шеффе-
ра (И—НЕ) необходимо взять двойное отрицание всего выражения, а
для перехода в базис Пирса (ИЛИ—НЕ) - двойное отрицание каждого
слагаемого и общего выражения и применить закон Моргана-Шеннона.
Пусть у = XjX2 + XjX2x3 + х3х4, тогда
Ущ - Xtx2 + XjX2X3 + Х3х4 = XjX2 • Х!Х2Х3 х3х4;
У» = Xj Х2 + Xj Х2 Х3 + Х3 Х4 = Xj +х2 +Xj +х2 +х3 +х3 +х4.
Пример 4.2. Разработать автомат, реагирующий не менее чем на два
сигнала из трех (мажоритарный автомат).
131
Таблица 4.2
*1 0 1 0 1 0 1 0 1
*2 0 0 1 1 0 0 1 1
*3 0 0 0 0 1 1 1 1
У 0 0 0 1 0 1 1 1
Рис. 4.3. Мажоритарный автомат:
а - карта Карно; б - логическая схема
1. Составим таблицы истинности (табл. 4.2).
2. Запишем СДНФ:
У = Х1Х2Х3 + *1*2*3 + *1*2*3 + *1*2*3-
Чтобы получить склеивание в СДНФ, надо утроить *i*2*3, тогда
каждый из этих членов склеится с первым, вторым и третьим слагае-
мыми. Для наглядности рассмотрим карту Карно (рис. 4.3, а).
3. Карта Карно подтвердила возможность склеивания четырех мин-
термов и получение трех неизбыточных импликант:
У = *!*2 +*1*з + *2*3-
4. Двукратное инвертирование дает минимальную форму в базисе
Шеффера
У = *1*2 +*1*з + *2*з = *1*2 *1*3 ’*2*3-
5. Логическая схема автомата имеет вид рис. 4.3, б.
43.3. Синтез последовательностных автоматов. ,
Конечные автоматы
Как отмечалось выше, последовательностные автоматы осуществля-
ют преобразование двоичных входных переменных не только с учетом
текущей комбинации на входе в данном такте автоматного времени,
но и с учетом того, что было в предыдущих тактах.
Создание последовательностного автомата, способного запоминать
предшествующие данному такту комбинации сигналов на входе,обеспечи-
вается наличием в комбинационном автомате не только внешних (ра-
бочих) входов X и выходов У, но и вспомогательных (внутренних)
переменных Z, которые должны иметь возможность давать различ-
ные комбинации для каждого такта, подлежащего запоминанию, и реа-
лизуемых в виде обратных связей. Эти внутренние переменные, по-
даваемые на вход комбинационной схемы, как бы корректируют ре-
зультат от воздействия внешних входов, учитывая предыдущие си-
туации.
Таким образом, задача внешних входов - задать текущую комби-
нацию, а внутренних — сохранить и задать на входе комбинацию, од-
нозначно соответствующую сформировавшейся на выходе в предыду-
щем такте (кодирующую ее). В этом случае выходная комбинация
формируется с учетом предыдущего такта. В следующем такте внут-
ренний переменные внесут очередную коррективу (если их комбина-
ция будет отлична от предыдущей) и, следовательно, новые значения
выходов уже несут в себе следы двух предыдущих тактов и т.д. Ко-
личество таких состояний М внутренних переменных Z называется
весом последовательностного автомата.
Число внутренних переменных mz, обеспечивающих возможность
кодирования всех М состояний, называется объемом памяти автома-
та и равно
даг = [log2THj.
Внешними входными переменными автомата определяется коли-
чество его возможных входных комбинаций, а внутренними - через
сколько комбинаций внешних начинает повторяться коррекция внут-
ренними. Так, если тх = 3 и mz - 2, то автомат будет иметь восемь
состояний с повторяющейся коррекцией через четыре такта.
Следствием этого является характерная особенность последова-
тельностных автоматов: у них вследствие коррекции Z возможны
разные комбинации выходов при одинаковых комбинациях на внеш-
них входах. Технических вариантов реализации даже простых после-
довательности ых автоматов может быть очень много. Достаточно на-
гляднслГ является схема последовательностных автоматов, приведен-
ная на рис. 4.4 и представляющая собой наиболее общий случай.
Входы У логикой комбинационной схемы формируют выходы
™ в данном такте. В формировании Y1 при этом участвуют внутрен-
133
Рис. 4.4. Схема последовательностного
автомата
ние переменные Zf ~ 1, комбина-
ция которых сформировалась в
предыдущем такте t - 1. Перемен-
ные Zr “ 1 сформировались узлом
управления в цепи обратной связи,
который может включать: ком-
бинационную логику, временные
задержки и синхронизующий вход.
Как видно из схемы, именно
узел ОС обеспечивает ’’запомина-
ние” путем приема на вход выходной комибанции автомата в данном
такте и передачу ее с временной задержкой на входы автомата в сле-
дующем такте.
Разрыв цепи ОС превращает последовательностные автоматы в комби-
национные. Важную роль играет характер задержки: если блок ОС »
имеет синхронизирующий вход, ’’отпирающий” и ’’запирающий” цепь
обратной связи в каждом такте, - это синхронный автомат. У него
равенство Zr-1 = Zr наступает только после ’’отпирания” синхроим-
пульсом цепи обратной связи.
Благодаря обратной связи последовательностные автоматы обла-
дают специфическим свойством, отличающим их от комбинационных
и характерным для замкнутых систем управления — они могут быть
устойчивыми и неустойчивыми. Устойчивым будем называть состоя-
ние, когда комбинация выходов меняется лишь вследствие измене-
ния входа. Неустойчивые автоматы могут после установления комби-
нации входов несколько раз менять комбинацию на выходе, проходя
ряд неустойчивых состояний. Такой процесс может завершиться пе-
реходом в устойчивое состояние (затухание колебаний) либо продол-
жаться неограниченное время (автоколебания).
Комбинационные автоматы (разомкнутые) всегда устойчивы, как и
разомкнутые аналоговые звенья. Формальным признаком устойчи-
вого состояния является равенство
Z'-1 = zf,
а неустойчивого — неравенство
Z'”1 Ф Z*.
Период автоколебаний равен двойному времени задержки сигнала в ОС.
Для последовательностных автоматов, как и для комбинационных,
134
применяются также алгебраические и табличные формы задания опера-
тора преобразования Хп. В отличие от КА, где оператор Хк задается в
виде связи рабочих входов X* и выходов Y*, для задания оператора
последовательностного автомата нужно определить связь не только
между рабочими (внешними) входами и выходами, но и между вспо-
могательными (внутренними).
При алгебраической форме задания записываются уравнения выхо-
дов, связывающие в общем случае рабочие выходы Y1 с рабочими
X? и вспомогательными Z* ~1 входами,
У1 = fly (х 1 ’ х2 »• • • » хр » z 1 1» z2 1» • • •» zm 1) »
4 = fsy (*'i. • • • > xp-< zi *. 4 1.. 4 *)
и уравнения переходов, связывающие выходы внутренних переменных
Zf ”1 с рабочими X* и вспомогательными входами,
х',..., х£; z'"1, z'"‘......z^-*);
. 4 “X2............xp\ z\ z2 *.........4 *)>
где p9 s — число входов и выходов внешних переменных; т, q — число
входов и выходов внутренних переменных.
При табличной форме задания составляются таблицы выходов и пе-
реходов, при объединении которых получается таблица состояний.
В реальных последовательностных автоматах комбинационные и пос-
ледовательностные части не разделяются, а с целью упрощения и сокра-
щения числа элементов объединяются в одно целое. Это повышает ис-
пользование элементов.
Для построения сложных последовательностных автоматов, како-
выми являются большинство цифровых устройств, широко применя-
ются элементарные последовательностные автоматы-триггеры, основ-
ные типы которых рассмотрены в п. 5.4.2.
Ниже на конкретных примерах рассмотрены несколько методов
синтеза последовательностных автоматов.
Пример 4.3. Насос Н должен автоматически включаться при достиже-
нии рабочей жидкостью нижнего уровня, контролируемого поплавко-
вым датчиком JH, и выключаться при достижении верхнего уровня,
контролируемого датчиком dB.
В цикле работы питателя выделяем четыре такта:
1 — уровень ниже dn (питатель работает, резервуар наполняется);
2 — уровень выше dn, но ниже d3 (питатель работает, резервуар
наполняется);
135
Таблица 4.3
Элементы системы Такты преды- дущего цикла - I п Такты после- - дующего цикла
1 2 3 4
0 0 1 0
UH 0 1 1 1
мв н 1 1 о 0
3 — уровень достиг dB (питатель отключился, жидкость расходует-
ся, уровень понижается);
4 - уровень ниже dB, но выше dH (питатель отключен, уровень пони-
жается) .
Указанная последовательность отражена в табл. 4.3.
Предполагается, что происходит непрерывное повторение одинако-
вых циклов (наполнение - расход). Для синтеза рассмотрен один из
циклов.
Выходная переменная Н принимает разные значения при одинако-
вых значениях входных переменных (такты 2 и 4), но при разных
их значениях в предшествующих тактах 1 и 3. Это является харак-
терным для последовательностного автомата. Для отработки требуе-
мой последовательности необходимо ’’запомнить” предыдущий такт.
Введем внутреннюю обратную связь
У = с(х,)(с(Х/)+хв), (4.2)
где с(Xf) - конъюнкция входных переменных, не изменяющихся в со-
седних тактах: c(Xj) - конъюнкция переменных, изменяющихся в
соседних тактах; хъ — внутренняя переменная.
В соответствии с (4.2) запишем:
для тактов 1,2
я, = £(<Гн + Яв');
для тактов 3,4
где Яв - внутренняя переменная в виде обратной связи по выходу.
Преобразуя последнее выражение, получаем
ЯП =
Контактные и бесконтактные схемы представлены на рис. 4.5.
Схемы работоспособны в нормальных условиях, однако при аварий-
ном залипании нижнего датчика (dH = 0, dB = 1) вариант I не допустит
включения, а вариант II допустит включение насоса, что вызовет пере-
лив.
136
Рис. 4.5. Контактные и бесконтактные схемы управления насосом:
а, б - по варианту I; в, г - по варианту II
Рассмотрим этапы более общего синтеза последовательностного
автомата, у которого переход из одного состояния в другое зависит
не только от прихода очередного тактового импульса, но и от усло-
вий, сформированных ’’внешней” логикой — различными датчиками
и внешними управляющими командами.
Этт 1. Составим описание цикла функционирования механизма или
агрегата, для автоматизации которого разрабатывается автомат. Уста-
новим количество состояний (тактов), когда не меняются состояние
ни одного дискретного исполнитльного элемента, составляющее цикл
работы механизма, и причины перехода из одного состояния в другое.
В зависимости от причин может меняться последовательность смены
состояний, но не их номенклатура. Под причинами понимается сраба-
тывание какого-либо датчика или командного органа либо изменение
какого-либо сочетания их состояний. Например, в описании цикла уста-
новлено, что цикл состоит из пяти тактов (состояний а! . . . а5), перехо-
ды которых обусловлены различными сочетаниями команд оператора
*1 —и сигналов датчиков zY — z4 (рис. 4.6).
Этап 2. Составим формальный портрет, отражающий все реально воз-
можные переходы из одного состояния в другое и условия этих пере-
ходов. Он может быть составлен в виде тактовой таблицы, структурной
схемы алгоритма или в виде графа, вершинами которого являются со-
стояния, а ребра отражают причины перехода из одного состояния в дру-
гое. Над ребрами записаны логические условия перехода.
На рис. 4.6, б показан возможный вариант такого графа.
Этап 3. Произведем кодирование состояний. Чтобы автомат ’’знал”,
какое в данном такте состояние, он должен иметь узел, на выходах кото-
рого появляется 1 в зависимости от состояния, а именно: на первом -
ПРИ «1» на втором — при а2 и т.д. Таким узлом может быть дешифратор
(см. гл. 5) с тремя триггерами на входе (см. рис. 4.6, в). При кодирова-
137
Рис. 4.6. Последовательностный автомат к примеру:
а - схема воздействия; б - граф-схема; в - электрическая схема
нии состояний каждому состоянию ставится в соответствие комбина-
ция состоянии выходов триггеров.
Чтобы закодировать пять состояний, нужны три триггера с выхода-
ми Co>2i><?2:
Состояние Д1 ........... О 0 1
Состояние а 2 ........... О 1 О
Состояние а3 ............О 1 1
Состояние а 4 ........... 1 О О
Состояние а5 ........... 1 0 1
При такой кодировке не используются три комбинации состояний
138
ЮЙВД0® триггеров:
О
О
1
;0С
О
1
1
,4'г,
4 Составим таблицу переходов (табл. 4.4), в которой на осно*
ваЕЙ Графа отразим переход каждого выхода каждого триггера при
^^Х,Возможнь1Х переходах автомата из одного состояния в другое,
же таблице укажем логические условия каждого перехода и
состояние входов JK каждого триггера при известном переходе его
характерные только для выбранного J/C-триггера и рассмот-
©ею^ев п. 5.4.2.
. л-ЭЙ&Г 5- По таблице перехода запишем логические уравнения, связы-
входы триггеров с командными входами х сигналами датчиков z
триггеров Q через дешифратор состояний. Запись уравне-
ни>|нроизводится следующим образом: для каждого входа каждого
Триггера для переходов, где данный вход равен 1, записывается про-
;1ф&йение исходного состояния на логическое условие его перехода
д ПФЙадующее. Уравнения имеют вид
e2(Zi +2^2) + a4z3x3 = a2z2 + a4z3x3;
aiX^zi +a3z2x3;
fiJ’‘atx1x2zl + a^iX2Z2-,
«jz, + a3z2x3,
VjMUKW 4.4
Код ис- ходного состоя- Новое со- стояние Условия ния Перехода Состояние входов триг- геров
ния Ji Ki J1 Ki Jo Ко
•'< ',-!? ' 001 02 оз 010 X; *2 Z j 011 *1*2*2 0 0 /"*w 1 1 /V/ 1 0
010 01 Оз 011 £1 _ 011 *1*2 0 0 1 0 1 1
on 04 100 *2*3 1 1 1
100 05 101 *3*3 — 0 0 1
'-'Л* ,zt 101 01 001 7 2 22*3 1 0 — 0
Ирк м еч ан и е. Знак означает, что состояние входа безразлично.
139
J2 = 03^2*3 >
/l2 = ^5 Z1Z2Z3-
Полученный автомат (рис. 4.6, в) может обеспечить пятитактовый
цикл управления какими-либо исполнительными элементами. Их не мо-
жет быть менее трех (чтобы получилось пять разных состояний), но
больше может быть (10, 20 и т.п.), т.е. каждое состояние будет отли-
чаться комбинацией включенных и отключенных элементов (станков,
механизмов).
4.4. АЛГОРИТМЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
4.4.1. Постановка задачи оптимального управления в АСУ ТП
Оптимальным управлением в АСУ ТП считается такое, которое обес-
печивает наиболее вы годный, компромисс при минимизации трех ком-
понентов технологического комплекса: материала, энергии, инфор-
мации.
Определение оптимальности процесса зависит от конкретных усло-
вий, в которых он реализуется. Критериями оптимальности могут быть:
максимум производительности, минимум себестоимости, требуемое
качество продукции, минимум затрат энергии и ряд других. Эти опти-
мумы, как правило, не совпадают, поэтому в каждом случае приходит-
ся выбирать в качестве основного тот или иной критерий либо сово-
купность их с учетом весовых коэффициентов.
Помимо локального оптимума технологического механизма сущест-
вует глобальный оптимум технологического агрегата или линии, опре-
деляющий иерархическую подчиненность оптимального ведения про-
цесса в интересах оптимальности функционирования участка, цеха,
предприятия и даже отрасли. В каждом отдельном случае выбор кри-
териев оптимальности осуществляется в результате тщательного тех-
нико-экономического обоснования.
Задача оптимизации решается на стадии системного проектирова-
ния комплекса ’’технология — оборудование — электропривод — си-
стема управления”. При решении этой задачи предполагается существо-
вание связи между характеристиками технологического процесса и кри-
терием его эффективности. Такая связь называется целевой функцией.
Она связывает ^правл^п^^оздействия через управляемые коор-
динат£Г1^_с критерием эффективности хода процесса /^т.е.
F уп; *!,...,х„).
Если имеется аналитическая модель вида у/ = f (xl9 . .. , хп), то це-
левая функция представляется в виде F = /(хь .. ., хп). Ее по-
лучение является главной и наиболее сложной задачей при синтезе алго-
ритмов оптимального управления.
140
Целевая функция должна удовлетворять требованиям:
/^нозначностиуОдна целевая функгщядолжна отражать изменение
тппм£О одного критерия; при наличии нескольких критериев соответ-
доукшще частные целевые функции F, образуют с весовыми коэффи-
циентами линейную комбинацию - общую целевую функцию F =
(соответствия. Характер целевой функции и количественные харак-
теристики объекта управления нужно выбрать так, чтобы обеспечить
наиболее успешную оптимизацию процесса;
{^управляемости. В качестве аргументов должны фигурировать толь-
ко технологические параметры, поддающиеся управлению посредством
регулируемых приводов;
^ориентированности на конкретный критерий, определяющий эконо-
ь^ческую эффективность;
^экстремальности (выпуклости) ^Должна быть выбрана целевая функ-
ция, ИМёющая четко выраженную экстремальную область.
Целевая функция не должна иметь разрывов и несколько экстре-
мальных областей. При невозможности реализовать это условие по-
иск сужается ограниченной локальной областью, имеющей больший
экстремум и удовлетворяющей всем остальным условиям существо-
вания целевой функции.
Совокупность ограничений определяет технологическую область
существования целевой функции. Если целевая функция в этой об-
ласти имеет экстремальный характер, то задача управления заключа-
ется в том, чтобы вести процесс в районе, близком к наибольшему
экстремуму. Такое управление называют оптимальным или экстре-
мальным. Если экстремум находится за пределами технологически
допустимой области, то задача автоматического управления состоит в
том, чтобы ввести процесс в режим, которому соответствует макси-
мальное значение критерия эффективности, соответствующее грани-
це этой области. Такое управление называют предельным.
Управление, при котором достигается и поддерживается максималь-
ное значение F, независимо от возмущений называется статической оп-
тимизацией. Целевая функция в этом случае не зависит от времени.
Управление, когда система выбирает наивыгоднейшую траекторию пе-
рехода из одного состояния в другое, называется динамической опти-
мизацией.
Степень определенности управляемого процесса является одной из
особенностей разработки алгоритма оптимизации. Существуют методы
оптимизации, которые позволяют осуществить ее даже при отсутствии
полной модели процесса. Реализация подобных алгоритмов даже ста-
тической оптимизации возможна лишь при применении УВМ с вы-
соким быстродействием.
141
4.4.2. Оптимизация многомерных линейных объектов в статике
Методика формирования алгоритма управления, излагаемая ниже,
предполагает, что модель объекта и целевая функция достаточно хо-
рошо определены, т.е. известны структура и параметры формальных
моделей. Функции непрерывны, детерминированны и имеют производ-
ные в любой точке. Учитывая, что объект определен хорошо, а реализа-
ция обратных связей в данном случае может представлять определен-
ные трудности, предполагаем разомкнутую систему управления.
Методика получения алгоритма состоит из следующих этапов:
записывается уравнение или система уравнений модели управляе-
мого объекта. Это могут быть уравнения линейной регрессии вида
п
- S Ajixi »
i = 1
после выбора критерия эффективности записывается выражение
для целевой функции. Например, при оптимизации по качеству целе-
вая функция представляется как сумма квадратов отклонений управ-
ляемых технологических параметров от заданных значений:
т
F = 2 О'/-/,)2.
/ = 1
где jy — заданное значение управляемой координаты; т — число уп-
равляемых координат;
из выражения целевой функции иисключаются подстановкой в
него модели объекта. Тогда
т 1 п i л
/ 1 2
(7 - S Фу ( j/y — S Ац xi I ,
/=1 \ /=1 /
где Фу - весовой коэффициент. В общем случае число управляемых
координат не равно числу управляющих воздействий т ¥= л;
приравниваются нулю частные производные вида 9(7/ Ъх- и решается
система уравнений относительно xf«. В результате получаются алгорит-
мы оптимального управления вида
т
xiopt ~
/=1
Определяемые из этих уравнений управляющие воздействия являют-
ся оптимальными, так как они определены по заданным значениям у/
и минимизируют отклонение от них реального процесса.
142
4.7. Структура управления про
доедем, оптимизированным по мини
отклонений от задания
Проверка характера экстрему*
ма осуществляется по знаку вто-
рой производной cPG/dx?. При
положительном ее значении имеет
место максимум, при отрицатель-
ном^ минимум. Проверка может
быть выполнена и по знаку прира-
щении ДО при подстановке уп-
равляемых координат Xi с прира-
щением tte. Если Д(7 < 0, то име-
ет место максимум, при обрат-
ном знаке — минимум целевой
функции. Структура управления
процессом показана на рис. 4.7.
Широкий круг задач статической оптимизации может быть сведен
к линейным целевым функциям и линейным ограничениям. Например,
п
необходимо определить экстремум функции G = S Л х. при нали-
УЛ '
^«ограничений двух типов: по управляющей координате Rmin <xz <
< по линейной комбинации (модели объекта) Qmjn^ ^Bjxj
< QmaX' Для решения таких задач применяется метод линейного про-
граммирования и его модификации — симплекс-метод, позволяющий
использовать ЭВМ.
уяснения метода линейного программирования рассмотрим
его графическую интерпретацию на примере для двух переменных.
Пример 4.4. Месячная программа прокатки на сортовом стане по
двуй маркам стали не может превысить Xi < 8000 т, х2 < 6000 т. Огра-
ничения диктуются возможностями поставки исходных заготовок це-
хами-смежниками. Затраты времени по каждому сортаменту: =
® 0,04 чт"1, t2 =0,08 ч-т"1. Месячный фонд технологического времени
колеблется в пределах 400 ч < Т < 600 ч. Расход энергии при прокат-
ке: = 8 кВт ч/т, W2 = 12 кВт ч/т.
Необходимо определить номенклатуру и объем сортаментов, обес-
печивающих минимум расхода электроэнергии Gmin. Целевая функ-
143
Рис. 4.8. Графическая интер-
претация оптимизации двух-
мерного объекта методом ли-
нейного программирования
ция имеет вид Gmax = max(8xj + 12х2); Gmjn = min(8Xi + 12х2) при
ограничениях по объему 0 < < 8000 т; 0 <х2 < 6000 т и ограниче-
ниях по фонду времени 400 ч < 0,04хг + 0,08х2 < 600 ч.
Графически указанные зависимости представляются в виде контура,
ограниченного прямыми, которые описываются уравнениями ограни-
чений. Так, для прямых, показанных на рис. 4.8, уравнения имеют вид:
Прямая линия Уравнение
АВ х2 = 6000
CD Xi =8000
ВС 0,04Xi + 0,08 х2 = 600
DE 0,04Xi +0,08х2 =400
В свою очередь функционал G описывает семейство параллельных
прямых, положение каждой из которых определяется значением функ-
ционала. Очевидно, для определения значения функционала можно
использовать величины xt и х2 только внутри или на границе области
ABCDE, Если учесть, что увеличение значения функционала соответ-
ствует удалению описываемой им прямой от начала координат, то ми-
нимум может быть при касании контура в точках Е или D, а максимум -
при ’’выходе” из контура, т.е. при касании в точках В или С.
При заданных параметрах экстремальными точками оказались Е и
С. Точка Е соответствует минимуму функционала Gmjn = 60 000 кВт ч,
т.е. уравнение NN' имеет вид 8Xj + 12х2 = 60 000. Соответственно точ-
ка С определяет Стах = 106 000 кВт ч, а уравнение КК' имеет вид
8Xi + 12х2 = 106 000.
1 Так как КК1 почти параллельна ВС, то перераспределение сортамен-
тов мало скажется на расходе электроэнергии. Так, при Xi = 3000 т и
х2 = 6000 т (точка В) расход электроэнергии составит (линия LL')
G = 8-3000+ 12-6000 = 96 000 кВт-ч. Можно выбрать удовлетворитель-
144
\ную программу, варьируя линией, обеспечивающей минимальный рас-
' ход электроэнергии.
Г Использовать графическую интерпретацию и графический метод ре-
шения задачи линейного программирования при числе переменных
большем двух и особенно трех крайне затруднительно, а для АСУ ТП
характерны многокоординатные объекты, где число управляемых па-
раметров может измеряться десятками. В этих случаях для решения
задач линейного программирования вводится понятие и-мерного про-
странства, каждая точка которого определяется и-координатами х1?
х2, ...» хп. Тогда связь вида F = AQ + + А2х2 + ... + Апхп опи-
сывает гиперплоскость в и-мерном пространстве. Полагая в этом вы-
ражении все координаты постоянными (кроме одной), получаем урав-
нения прямых на гиперплоскости.
Система из т линейных уравнений, в которые превращаются нера-
венства ограничений, на границах области существования технологи-
ческого процесса имеет вид
А 1 1 х 1 + Л12*2 + • • • + 1ПХП = 1 0 ’>
АцХ1 + А22Х2 + • • • + ^2ПХП = ^20 >
Ат 1 *1 + Ат 2 х2 + • • • + Атпхп ~Ато>
и при условии неотрицательности переменных они образуют систему
гиперплоскостей, выделяющих в п-мерном пространстве выпуклый
многогранник, ограничивающий область сущестования процесса.
Благодаря неотрицательности ограничений все вершины многогран-
ника будут лежать на положительных координатных полуплоскостях.
Это значит, что в его вершинах часть переменных равна нулю, а часть —
больше нуля.* В этом случае для решения задачи линейного программи-
рования используется аналитический симплексный метод. Его геомет-
рическая сущность заключается в отыскании такой вершины много-
гранника, координаты которой обусловливают максимум (или мини-
мум) функционала, имеющего вид G = Ф^ + Ф2х2 + ... + ^пхп-
В поиске выделяют два этапа: выбор начального плана или определе-
ние координат какой-либо вершины и отыскание экстремальной верши-
ны (улучшение начального плана) путем замены нулевого значения од-
ной из координат на ненулевое. Соответственно другая координата,
значение которой не было равно нулю, должна принять нулевое зна-
чение. Присваивать ненулевое значение рекомендуется той координа-
те» которая сильнее влияет на величину G.
Такой подход обеспечит минимальное время поиска экстремальной
вершины. Поиск выполняется в следующей последовательности:
в функционале исключают переменные, определяющие полуплос-
кость, на которой лежит проверяемая вершина; такое исключение осу-
145
Рис. 4.9. Схема прокатки полосы в трех клетях непрерывного стана
ществляется путем выражения этих переменных через другие из систе-
мы неравенств ограничений;
оставшиеся переменные полагают равными нулю, это позволяет по-
лучить значения основных переменных и функционала;
по коэффициентам при неосновных переменных в выражении для
функционала и их знакам определяют степень влияния переменных
на изменение функционала в необходимую сторону.
Пример 4.5. Конечная группа сортового прокатного стана состоит
из трех клетей (рис. 4.9). При прокатке заготовка последовательно
проходит через все клети. Каждая из них имеет свой привод и общий
источник питания. Необходимо получить алгоритм расчета и опреде-
лить значения уставок нажимных устройств клетей, обеспечивающих
деформацию исходной заготовки от Ло Д° и не вызывающих пере-
грузку источника питания. Перегрузочная способность двигателей не
является ограничением.
. Программа обжатий должна быть оптимизирована по минимуму
потерь времени на прохождение металла между клетями, последней
клетью и агрегатом резки. В упрощенном виде формальная постанов-
ка задачи выглядит следующим образом:
1) суммарная деформация металла складывается из деформаций,
выполняемых всеми клетями:
Ло ~ = Д/ц + ДЛ2 + ДЛ3.
Для получения высокого качества поверхности проката в последней
клети должно быть возможно меньшее обжатие (деформация Дй3 не
должна превышать 10 мм);
2) токовая нагрузка электропривода линейно зависит от деформа-
ции металла и не зависит от скорости прокатки (магнитные потоки
двигателей номинальные):
А* = Л,х i + ai »
где/х>х i - ток холостого хода.привода клети; а/ - коэффициент про-
порциональности ;
146
дотери времени линейно зависят от деформации:
—— + —— + —- = (Lifti + £2й2 + £3й3),
vi v2 »3 «'г
"ЛЙгг— неизвестная ширина заготовки; wc — объем металла, проходя-
между валками за 1 с; 14 -г3 - скорости прокатки в клетях.
!0 - Д&!; й2 = й0 - АЛ] - Дй2 и
i0 - Дй, - Дй2 - Дй3,
й = — [Ло(^1 +Ьг+Ь3) -A^(£,+L2+L3) -
< "с
(Ь2 + L з) ~ £ з],
*о - (*i + Л2ДЛ2 + к3 ДЛ3).
|К|р^видно, потери времени будут уменьшаться с увеличением сум-
^ЙШШ^рмаций, поэтому предпочтительно увеличение обжатия в на*
(коэффициенты при АЛ
Коэффициенты равны
*1
аг
аз
*з
Коэффициенты
= 50 мм;
= 10 мм;
= 4200 А;
= 1200 А;
= 100;
= 60;
= 50;
= 2.
уменьшаются с ростом номера
й0 = 270;
й» = 4;
й2 = 3;
уравнения ограничений
fat + ДЛ3 = 30;
ЖЖ + 60Дй? + 50Дй3 < 4200 - 1200
Л’1 .ш 3
ЖяЙЩкой функции
= min [270 - (4ДЙ, + 3 Дй2 + 2Дй3)]
max (4АЛ! +ЗАЛ2 +2ДЛ3).
^^Й?^ешения задачи симплекс-методом необходимо превратить не-
ограничений по перегрузке и по ДЛ3 в равенства.
) 147
Рис. 4.10. Графическое по-
строение для оптимизации
процесса прокатки симплекс-
методом
Для этого введем фиктивные переменные ДЛ4 и ДЛ5. Физический
их смысл: ДЛ4 не вызывает деформации и увеличения времени, но
влияет на перегрузку (дрессировочные валки после третьей клети), а
ДЛ5 незначительно влияет на деформацию, но не влияет на нагрузку
и время. Окончательно имеем
ДЛ3 + ДЛ5 = 10;
ДЛ1 + ДЛ3 + ДЛ3 =40;
5ДЛ1 +34Л2 + ДЛз + ДЛ4 = 150;
Gmin =.min [270 - (4ДЛ! + 3 ДЛ2 + 2ДЛ3)].
Для геометрической иллюстрации решения задачи на рис. 4.10, б
изображен многогранник аг ...а8> выделенный в трехмерном (при
ДЛ4 = ДЛ5 = 0) пространстве состояний плоскостями, описываемы-
ми уравнениями ограничений.
Таблица 4,5
ai Ар мм А2, ММ А3, мм G, кВт- ч/т
*1 25 0 10 —
а2 17 13 10 139
аз 0 30 10 160
*4 0 0 10 —
*5 30 0 0 —
*6 15 25 0 135
а1 0 40 0 150
«8 0 9 0 -
148
Вершины многогранника, кроме а2, <1^ лежат на координатных
полуплоскостях. Необходимо определить координаты вершины, об-
условливающие неотрицательный минимум функционала G. При реше-
нии задачи были определены координаты всех вершин (табл. 4.5).
Из анализа результатов расчета видно, что варианты ait а 4, а5 не
удовлетворяют условию, так как его выполнению мешает ограниче-
ниепо перегрузке.
Из остальных вариантов оптимальным является а6, где Gmin =
я 135 кВт-ч/т. Но так как здесь = 0 и ДЛ2 > то качество про-
ката будет низким. Вот почему следует предпочесть вариант а2, где
Gmin 4 №9 кВт-ч/т, т.е. немного больше, чем в я6, но зато в а2 имеет
место постепенное снижение обжатия при переходе от первой клети
к третьей.
4.4.3. Оптимизация нелинейных объектов
Наиболее часто модели технологического комплекса представляют
собой сложную нелинейную зависимость со многими переменными.
Нелинейными являются уравнения ограничений и целевая функция.
Может оказаться, что получение надежных уравнений модели либо
невозможно, либо технически и экономически нецелесообразно. В ря-
де случаев не ставятся жесткие требования к абсолютной оптимиза-
ции процесса в связи с тем, что более оправданным является достиже-
ние частичного оптимума при малых затратах, чем абсолютного при
больших. В этих случаях применяются градиентные методы, получив-
шие широкое развитие. J
Сущность методов заключается в том, чтобы представить целевую
функцио в виде гиперповерхности и-го порядка в (и+ 1)-мерном про-
странстве. ’’Рельеф” такой поверхности, называемой поверхностью
отклика, сложен и нестабилен. В процессе приложения возмущений к
объекту и с течением времени меняются абсолютная высота ’’вершин”
и глубина ’’впадин” - точек максимума и минимума целевой функции.
Меняются также расположение экстремумов и их количество, крутиз-
на ’’склонов”. Ограничения обозначают на этом ’’рельефе” границы
запретных областей.
Управляющее устройство в результате пошагового изменения управ-
ляющих переменных должно обеспечить поиск и достижение экстре-
мума целевой функции. Такое управление наиболее удобно осущест-
влять с помощью ЭВМ.
Эффективность поиска экстремума характеризуется:
скоростью достижения экстремума поверхности отклика; при мно-
гошаговой процедуре поиска и быстройротекающих процессах может
°казаться, что система практически все время находится в поиске, а
в экстремальной точке работает мало;
149
универсальностью, т.е. способностью отыскивать экстремум для
’’трудных” поверхностей;
точностью определения истинного оптимума; система должна про-
должать поиск при достижении временных оптимумов, обусловлен-
ных случайными изменениями неконтролируемых переменных;
простотой применяемых алгоритмов и вычислительных устройств.
Эти показатели зависят от методики выбора коррекции после каж-
дого шага и ее направления. При этом необходимо, чтобы после каждо-
го шага происходило уменьшение (при минимизации) или увеличе-
ние (при максимизации) целевой функции, т.е.
F(x)z >F(x)j + l или F(x)i < F(x)i+V
rpfiF(x){ - значение целевой функции для выбранных на i-м шаге
переменных.
Чтобы достигнуть этого, применяются рекуррентные соотношения,
связывающие значения переменной на предыдущем и последующем
шагах:
xi+l = xi+ х/ dp
гдех- их> + j — значения переменных до и после выполнения шага;
X. - скалярная величина, определяющая шаг; dz- — градиент-вектор,
определяющий направление шага.
На рис. 4.11 изображена двухмерная поверхность отклика с тремя
экстремумами. Эффективность шага для достижения экстремума оп-
ределяется не столько величиной шага, сколько направлением с мак-
симальным градиентом.
Под градиентом функции в точке х [обозначается gradF(x),
TF(x); VF(x)] понимается вектор, координаты которого в и-мер-
ном пространстве определяются частными производными функции
F (х) в точке х по всем переменным. Градиент определяет направле-
Рис. 4.11. Двухмерная поверхность отклика
но
ина, но которому крутизна поверхности имеет максимальное значе-
ние» В этом смысле стратегия градиентных методов напоминает симп-
пексчметод.
"доставляющие градиента в Z-й точке определяются соотношениями
' я dFi ; dFi i dFi
V'fFCO = —V'2F(x) = —L ; v'„F(x) = —L .
dxi dx2 dxn
Его модуль
2
В Целом вектор d задается соотношением
. dF/dxi
d « V F(x) = —— .
/и ’
/ S (dF/dx^2
Рабочая процедура поиска экстремума при градиентном методе
состоит из следующих этапов:
с учетом ограничений, определяющих допустимые значения пере-
менных состояний, находят их начальные условия;
для определения количества и характера экстремумов ориентиро-
вочно анализируют область существования целевой функции;
в процессе управления на каждом шаге определяют градиент и шаг,
после чего оценивают эффективность сделанного шага по отношению
к предыдущему и производят проверку достижения экстремума.
\ В зависимости от способа выбора шага и оценки градиента (направ-
ления поиска) различают ряд модификаций градиентных методов.
Глава пятая
ТЕХНИЧЕСКИЕ СРЕДСТВА, ПРИМЕНЯЕМЫЕ В АСУТП
Изучение материала главы представляет собой известные трудности.
Они состоят прежде всего в том, что технические средства, применяе-
мые в АСУ ТП, в последние годы претерпели существенные изменения.
Изменилась аппаратная база: схемы различного назначения, собранные
из отдельных элементов, заменены интегральными, что не могло не
сказаться на технических решениях и технологии выполнения каналов
переработки информации АСУ ТП. Широкое применение микропроцес-
^Ров И микро-ЭВМ позволило перейти от схемных к алгоритмичес-
151
ким решениям информационной части систем, поэтому наиболее важ-
ным является изучение принципов действия отдельных элементов
АСУ ТП, основу которых составляют современные интегральные схе-
мы и широко применяемые в промышленности микромодули.
Особым классом технических средств являются датчики технологи-
ческих величин как основа информационного обеспечения АСУ ТП.
По принципу действия они для всех технологических процессов при-
званы выявлять механические (угловая скорость, скорость линейного
перемещения, путь, перемещение, толщина, усилие, момент, мощность,
угол поворота и др.), теплотехнические (температура, давление, рас-
ход газа, жидкости, объем, уровень и др.), химические (pH, концентра-
ция агентов, их соотношение и др.), радиационные и другие величины.
Наиболее часто в схему выявления и преобразования технологических
величин могут входить комбинации средств и устройств измерения
технологических параметров. Однако практическая реализация датчи-
ков и преобразователей зависит от технологического процесса, мощ-
ности установки, особенностей эксплуатации.
Студенты в § 5.3 должны освоить только общие принципы работы
технических средств, применяемых в АСУ ТП, и рассчитывать на само-
стоятельность технических решений для каждой отрасли промышлен-
ности. В связи с этим они обязаны при решении конкретных задач
ориентироваться на следующие этапы работы:
изучение технологического процесса и использование известного
в отрасли информационного обеспечения для непосредственного из-
мерения технологических параметров ;
при невозможности непосредственного измерения технологических
параметров — рассмотрение в тесном контакте со специалистом-тех-
нологом возможности косвенного выявления технологических пара-
метров при помощи электромеханических величин, определяющих
работу технологического оборудования и АСУЭП;
в любом случае — осуществление поиска прототипов, сходных с
объектами автоматизации, и изучение датчиков технологических па-
раметров для использования лучшего технического решения как по
точности измерений, так и по конструктивным особенностям и надеж-
ности их работы в условиях конкретной технологии;
при отсутствии стандартных решений, дающих возможность полу-
чить заданную точность измерения технологических параметров, при
наличии сил, средств и времени на опытно-конструкторские разработ-
ки — принятие на себя труда по созданию датчиков в соответствии с
государственной системой приборов.
5.1. СВЕДЕНИЯ О СТРУКТУРЕ ТЕХНИЧЕСКИХ СРЕДСТВ АСУ ТП
5.1.1. Виды обеспечения АСУ ТП
АСУ ТП должна включать: техническое, программное, информацион-
ное обеспечение как основу системы и организационное обеспечение в
виде инструкций, регламентаций и описания структур системы.
Техническое обеспечение или комплекс технических средств (КТС)
включает устройства получения информации о параметрах технологи-
ческого процесса и состоянии технологического оборудования, форми-
рований и передачи управляющей информации, представлений инфор-
мации оперативному персоналу, передачи информации на исполнитель-
ные устройства - АСУ ЭП, а также в смежные АСУ и АСУ более высо-
кого уровня иерархии.
Программное обеспечение АСУ ТП включает общее программное
обеспечение (поставляется в комплекте со средствами вычислитель-
ной техники) и специальное программное обеспечение - совокупность
программ, реализующих функции конкретной системы и обеспечиваю-
щих ее функционирование.
Информационное обеспечение определяет единую систему кодирова-
ния технологической, технической и экономической информации, а так-
же априорную и оперативную информацию.
Организационное обеспечение включает описание функциональной,
технической и организационной структур системы, инструкции и дру-
гие регламентирующие документы для оперативного персонала, участ-
вующего в управлении АСУ ТП. Оперативный персонал состоит из опе-
раторов автоматизированного технологического комплекса, управляю-
щих технологическим объектом, и эксплуатационного персонала, обес-
печивающего заданное функционирование системы в целом. Основ-
ная работа оперативного персонала происходит вне контура управле-
ния. Оперативный персонал вводит в систему необходимые алгорит-
мы управления, осуществляет контроль за работой АСУ ТП и при отка-
зе технических средств и в аварийных ситуациях принимает на себя
управление технологическим объектом. В этом режиме оперативный
персонал, используя рекомендации по рациональному управлению,
выработанные комплексом технических средств, выполняет частично
или полностью функции управления. Оперативному персоналу, налад-
чикам и проектантам приходится сталкиваться с одними и теми же
задачами анализа поведения системы в нормальных и аномальных режи-
мах. Следовательно, каждому из них необходимо располагать мини-
мумом сведений о принципе действия и возможностях технического
обеспечения АСУ ТП для выполнения функций, предписанных долж-
ностными инструкциями. В состав технических средств АСУ ТП входит
вычислительная техника — управляющее вычислительное устройство
на базе УВМ того или иного ранга. В АСУ ТП обычно применяются все
структурные элементы УВМ с конструктивным выделением функцио-
153
нально специализированных блоков, дополненные системой датчиков
информации технологических параметров. Это обстоятельство позво-
ляет считать, что изучение технических средств АСУ ТП следует совмес-
тить с изучением узлов УВМ как наиболее общих устройств и допол-
нить изучение рассмотрением характеристик датчиков технологической
информации и устройств связи с объектом управления. Это тем более
целесообразно, так как управление идет в реальном времени в любых
УВМ — аналоговых, комбинированных и цифровых. Последние в по-
давляющем числе АСУ ТП являются основными техническими средст-
вами вычислительной техники, поэтому ниже рассматривается АСУ ТП,
построенная на базе цифровой УВМ.
5.1.2. Общая характеристика и классификация
основных узлов УВМ
На рис. 5.1 показана структурная схема АСУ ТП, базирующаяся на
УВМ с исполнительными устройствами в виде АСУ ЭП и датчиками,
установленными на технологическом оборудовании.
УВМ включает в себя следующие элементы (блоки): блок,запоминаю-
щий сведения об объекте и текущие задания, поступающие во внеш-
нюю память с пульта управления; блок сбора и преобразования инфор-
мации о текущем состоянии объекта и действующих возмущениях;
блок центральный — процессор, выполняющий заданные алгоритмом
преобразования информации для выработки управляющего воздей-
ствия, организующий взаимодействие всех элементов УВМ, и состоя-
щий из арифметического, логического, управляющего и оперативного
запоминающего устройств (ОЗУ); блок прямых связей с объектом
управления, передающих управляющие воздействия.
УВМ имеют ряд вспомогательных элементов, необходимых для
организации процесса управления. К ним относятся средства связи
человека с машиной, предназначенные для получения оперативным пер-
соналом информации о ходе технологического процесса, коррекции
алгоритма управления и принятия необходимых мер в аварийных си-
туациях и средства ввода—вывода информации, включающие различ-
ные регистрирующие, индицирующие и запоминающие устройства (пер-
фоленточные, перфокарточные и строкопечатающие, записи на кас-
сеты и гибкие диски), экранные пульты - дисплеи, пишущие машин-
ки, графопостроители.
‘ На вход УВМ от датчиков поступает текущая информация, в основ-
ном аналогового вида (напряжение, ток, частота, угол поворота и т.п.).
Так как УВМ оперирует с дискретными величинами, то аналоговые
сигналы датчиков необходимо преобразовывать в дискретную фор-
му при помощи аналого-цифровых преобразователей. Однако для уп-
равления исполнительными механизмами (управляющими органами)
в большинстве случаев необходимы непрерывные сигналы, а УВМ выра-
154
Связь с АСУ другого уровня
Рис. 5.Г. Структура автоматизированного технологического комплекса
батывает управляющие сигналы в дискретной форме, поэтому необ-
ходимо осуществлять их цифро-аналоговое преобразование.
' Для уменьшения объема оборудования и стоимости аналого-цифро-
вые £(АЦП) и цифро-аналоговые (ЦАП) преобразователи производятся
Одйоканальными, а для поочереДного подключения сигналов от каждо-
го датчика к общему АЦП цсполызуются коммутаторы.
5.1.3. Принципы организации связи УВМ
с технологическим объектом управления
v В составе АСУ ТП возможны различные принципы построения свя-
зи УВМ с объектом управления: синхронный, асинхронный и комбини-
рованный. *
При синхронном принципе связи процесс управления разбивается
циклы равной длительности при помощи тактовых импульсов, вы-
даваемых таймерами. В каждом цикле, начинающемся с приходом так-
тового импульса на устройство управления, происходят последователь-
г ный опрос и преобразование сигналов датчиков в цифровую форму.
Эти операции и запоминание преобразованных величин в УВМ должны
происходить за интервал времени, в течение которого контролируемые
параметры технологического .процесса могут измениться лишь в до-
пустимых пределах.
После поступления очередной партии текущей информации к УВМ
и ее запоминания происходит расчет новых значений управляющих
воздействий и после их преобразования — передача к исполнительным
органам. Закончив расчет управляющих воздействий, УВМ прерывает
вычисления до прихода тактового импульса.
Для того чтобы АСУ ТП имела возможность реагировать на события,
вызванные отклонением хода технологического процесса от заданного,
155
или аварийные ситуации, используется асинхронный принцип связи УВМ
с объектом управления. Такая возможность обеспечивается введением
функции прерывания. УВМ реагирует на импульсы прерывания с уче-
том приоритетного уровня одних сигналов прерывания перед другими.
Необходимость ранжирования уровней приоритета вызвана тем, что
одни события могут быть более важными, чем другие. Задаче с более
высоким приоритетом разрешается останавливать обработку задачи,
имеющей приоритет низшего ранга. После завершения обслуживания
высокоприоритетного прерывания система возвращается к выполне-
нию прерванной программы.
Возможно применение комбинированного принципа связи УВМ с
объектом, при котором наряду с тактовыми импульсами таймера ис-
пользуются сигналы прерывания от датчиков, фиксирующих аварий-
ную ситуацию на объекте. Они переводят УВМ на работу по программе
для аварийного режима.
5.1.4. Основные режимы работы УВМ в составе АСУ ТП
Функции АСУ ТП, а следовательно, и УВМ подразделяются на инфор-
мационные и управляющие. Для выполнения информационных функ-
ций УВМ работает в режимах сбора данных и советчика. Информацион-
ные функции АСУ ТП заключаются в централизованном контроле за со-
стоянием объекта управления и вычислительных и логических опера
циях информационного характера, выполняемых УВМ в режиме сбо-
ра данных.
К функциям централизованного контроля относятся:
непрерывное, периодическое или по вызову измерение, оператив-
ное отображение и регистрация значений технологических параметров
и показателей состояния технологического оборудования;
обнаружение, регистрация и сигнализация отклонения технологи-
ческих параметров и показателей состояния оборудования от установ-
ленных пределов, в том числе и сигнализация о срабатывании блокиро-
вок и защит;
оперативное отображение и регистрация результатов математичес-
ких и логических операций, выполняемых УВМ и в общем случае -
комплексом технических средств.
Режим работы УВМ по сбору данных является наиболее простым.
Технологический процесс в этом режиме управляется оперативным
персоналом, который изучает процесс при различных условиях рабо-
ты для построения его математической модели. Такой режим может
быть вспомогательным при эксплуатации АСУ ТП, обеспечивая уточне-
ние (коррекцию) математической модели объекта и алгоритма уп-
равления.
Функциональная схема УВМ в режиме сбора данных отличается от
приведенной на рис. 5.1 тем, что из нее исключено устройство прямой
156
связи с объектом, а на выходе процессора установлены средства фик-
сации результатов. В этом месте между процессором и технологическим
объектом управления действует оперативный персонал.
Режим работы УВМ в АСУ ТП.в качестве советчика является более
сложным по сравнению с описанным выше. Он возможен на началь-
ной стадии внедрения АСУ ТП и позволяет проверить достоверность
принятой модели процесса и алгоритма управления. Опытный опера-
тор, управляя процессом и следя за рекомендациями УВМ, может об-
наружить неправильную комбинацию рекомендуемых для вспомога-
тельных органов уставок, вызванных неточностью модели процесса
или алгоритма управления, и устранить ее.
Число контролируемых параметров процесса в режиме работы УВМ
в качестве советчика оперативного персонала измеряется десятками
и даже сотнями. Так как оператору самому приходится изменять ус-
тавки; число управляемых параметров, для которых производятся
вычисления, сравнительно невелико. Поскольку возможности челове-
ка ограничены количеством изменяемых уставок в единицу времени,
а также в связи с увеличением вероятности ошибки при работе в высо-
ком темпе участие человека в процессе управления является весьма
серьезным недостатком режима работы УВМ в качестве советчика.
В режиме советчика к функциям вычислительных и логических
операций, помимо операций, присущих централизованному контролю,
относятся:
диагностика протекания и прогнозирования хода технологического
процесса и состояния оборудования;
подготовка информации для оперативного персонала и выполнение
процедур обмена информацией со смежными и вышестоящими АСУ ТП.
Управляющие функции УВМ в АСУ ТП сводятся к определению
рационального режима ведения технологического процесса; формиро-
ванию и передаче на входы исполнительных устройств управляющих
воздействий, обеспечивающих реализацию выбранного режима. Эти
функции позволяют реализовать следующий по сложности режим ком-
бинированного (супервизорного) управления, при котором УВМ ис-
пользуется в замкнутом контуре (рис. 5.1) и уставки регуляторам
управляющих органов задаются непосредственно машиной. Основное
преимущество этого режима по сравнению с режимом советчцка со-
стоит в возможности обеспечения оптимального протекания техно-
логического процесса путем оперативного воздействия на него. В дан-
ном режиме рассчитанные значения уставок передаются от процессо-
ра регуляторам управляющих органов посредством устройств связи
с объектом. В этом режиме оперативный персонал работает вне кон-
тура управления и роль его состоит во вводе в систему алгоритма ра-
боты, контроле за работой АСУ ТП; в аварийных ситуациях, при отка-
36 УВМ оператор принимает на себя управление технологическим
объектом.
157
При изменениях вида или формы исходных материалов либо конеч-
ного продукта могут потребоваться новые уравнения или новые значе-
ния коэффициентов уравнений, входящих в алгоритм управления;
эти расчеты производятся УВМ следующего, более высокого уровня
иерархии либо УВМ данного уровня, если остается достаточное коли-
чество машинного времени от реализации алгоритма управления. В по-
следнем случае УВМ работает в режиме разделения времени между ре-
шением задач управления и вычислениями по оптимизации процесса
управления.
Возможна разновидность использования УВМ в замкнутом контуре
управления, при котором сигналы к исполнительным органам посту-
пают непосредственно от процессора через устройство связи. Такой ре-
жим называется режимом непосредственного (прямого) цифрового
управления.
При непосредственном цифровом управлении УВМ рассчитывает
не уставки регуляторов, как при комбинированном управлении, а
реальные воздействия и передает их непосредственно исполнительным
органам.
Одним из главных преимуществ режима непосредственного цифро-
вого управления является его гибкость, заключающаяся в возмож-
ности перехода к другим алгоритмам управления для отдельных кон-
туров путем внесения изменений в программу УВМ.
5.2. ЭЛЕМЕНТНАЯ БАЗА ТЕХНИЧЕСКИХ СРЕДСТВ
Развитие электроники, начиная с 60-х годов, связано с появлением
и быстрым совершенствованием интегральной элементной базы, ис-
пользуемой при разработке аппаратуры для вычислений и управления
и обеспечивающей приемлемые для практики габариты, массу и на-
дежность вычислительных и управляющих устройств.
В развитии технологии и схемотехники цифровых интегральных
схем условно можно выделить три этапа. Первый этап — разработка
базовых серий интегральных схем, выполняющих простые логические
функции (И—НЕ, ИЛИ—НЕ, И-ИЛИ-НЕ). Эти интегральные схемы
имели от 10 до 50 элементов в одном корпусе. Второй этап — разра-
ботка более сложных функционально законченных узлов (счетчиков,
регистров, дешифраторов, полусумматоров) с числом элементов в кор-
пусе от 50 до 500. Третий этап — разработка'сложных функциональных
устройств с уровнем интеграции от 500 до 10 000 элементов на одном
кристалле. Дальнейшее развитие интегральных схем продолжается в
направлении роста степени интеграции, быстродействия, помехоустой-
чивости, снижения потребляемой мощности.
В соответствии с ГОСТ 17021-75 показателем сложности интеграль-
ной схемы является степень интеграции, характеризуемая числом со-
держащихся в ней элементов и компонентов и определяемая по фор-
158
КУ входов
Резисторы
муле
к = lgA\
где£— коэффициент, определяющий степень интеграции (округляет-
ся до ближайшего большего целого числа); N — число элементов и ком-
понентов интегральной схемы.
Условные обозначения интегральных схем отражают их принадлеж-
ность к классам, группам и сериям. Серия объединяет схемы по их
технологическому и конструктивному признакам и является более
или менее законченным набором, необходимым для построения опре-
деленного класса устройств. Условное обозначение интегральных схем
состоит из следующих элементов (ОСТ 11073.915-80):
первый элемент — цифра, обозначающая группу (1,5,7 — полупро-
водниковые; 2, 4, 6, 8 - гибридные; 3 - пленочные, керамические) ;
второй элемент — три цифры, обозначающие порядковый номер раз-
работки серии микросхемы (от ООО до 999);
третий элемент - две буквы, обозначающие подгруппу и вид инте-
гральной схемы в соответствии с ее функциональным назначением;
четвертый элемент — условный номер разработки микросхемы по
функциональному признаку в данной серии.
Для интегральных микросхем, используемых в устройствах ши-
рокого применения, вначале проставляется буква К. Первые два эле-
мента образуют обозначение серии микросхем. Например, К155 ЛА1 —
это полупроводниковая микросхема широкого применения с поряд-
ковым номером разработки 55, функциональным назначением ЛА (ло-
гический элемент И—НЕ) и условным номером разработки по функ-
циональному признаку 1.
По типам базовых логических элементов выпускаемые электронной
промышленностью серии цифровых интегральных схем реализуются в
виде: резистивно-транзисторной логики (РТЛ), диодно-транзисторной
логики (ДТЛ), транзисторно-транзисторной логики (ТТЛ), эмиттер-
но-связанной логики (ЭСЛ), логики с инжекционным питанием (И2Л),
элементов на МОП-транзисторах, в том числе с дополняющими типа-
ми проводимости (КМОП).
Элементы РТЛ реализуют функцию ИЛИ-HE (рис. 5.2). Если на
всех т входах (^ .. . хт) сигналы равны 0, то транзистор VT закрыт
и выходной сигнал соответствует единице. При подаче единичного сиг-
нала хотя бы на один вход транзистор открывается и на выходе N сиг-
нал становится равным 0. Резисторы в цепи базы Rq выполняют функ-
цию ИЛИ на входе транзистора. Однако они не обеспечивают развяз-
, поэтому входы оказывают взаимное влияние друг на друга.
и Ясм обеспечивают требуемый ток коллектора от источ-
ника питания с напряжением п и напряжение смещения на базе.
Дементы РТЛ (особенно с непосредственными связями) обладают
сравнительно высоким быстродействием.
159
Рис. 5.2. Схема элемента РТЛ
Рис. 5.3. Схема элемента ДТП
Элементы ДТЛ реализуют функцию И—НЕ. Если подать нулевой
сигнал хотя бы на один из ап входов (рис. 5.3), то транзистор УТзакры-
вается, так как его вход оказывается зашунтированным открытым
входным диодом VDXj. Только тогда, когда на все т входов поступает
единичный сигнал и входные диоды VD1X -VDim закрыты, ток про-
текает от источника питания через резистор Rx, диод VD2 (или резис-
тор R2) к базе транзистора УТ, вызывая переход транзистора в режим
насыщения, при котором выходной сигнал равен 0. В цепи связи ис-
пользуется резистор R2 (в дискретном исполнении) или диод VD2
(в интегральном исполнении).
Элементы ТТЛ являются одними из наиболее распространенных.
На рис. 5.4 представлена схема базового элемента ТТЛ, в которой мож-
но выделить три основных каскада: входной на транзисторе УТХ, реа-
лизующий функцию И, фазоразделительный на транзисторе VT2 с воз-
можностью реализации на нем функции ИЛИ и выходной усилитель
на транзисторах VT3 и КГ4 (’’сложный” инвертор).
Если на входы транзистора УТХ поступает единичный сигнал, то
входные p-и переходы смещены в обратном направлении и ток проте-
кает через резистор R^ и коллекторный переход, вызывая работу тран-
зистора в активном инверсном режиме. Если же хотя бы на одном
из входов (*! или х2) потенциал нулевой, то входной р-п переход шун-
тирует выходной р-п переход, обусловливая работу транзистора в режи-
ме насыщения, и сигнал на выходе входного каскада равен нулю.
Фазоразделительный каскад предназначен для разделения сигна-
ла и управления выходным каскадом. Сигнал на коллекторе УТ2 (в
точке К) противоположен по фазе сигналу, поступающему от входно-
го каскада, а сигнал на эмиттере УТ2 (в точке Э) совпадает по фазе с
сигналом на входе.
Назначение выходного каскада — реализация операции ’’инверсия”,
усиление сигнала и обеспечение быстрого переключения последующих
элементов. Если на все входы транзистора УТХ поданы единичные сиг-
налы, транзисторы УТ2 и УТ4 открыты и выходное напряжение близко
160
ЙГ-Г^
Bic. 5.4. Схема базового элемен-
та ТТЛ
6
Рис. 5.5. Схема ключевого тран-
зистора с диодами Шоттки
к нулю. Если хотя бы на одном из входов нулевой сигнал, то транзис-
торы КГ2 и РТ4 закрыты и выходное напряжение соответствует еди-
ничному.
В элементах ТТЛ для повышения быстродействия используют диоды
Шоттки VD, которые включают в обратном направлении параллельно
переходу коллектор—база FDj и в прямом направлении в цепь базы
FDa ключевого транзистора VT (рис. 5.5). Из-за отсутствия у диодов
Шоттки диффузионной емкости удается время переключения у элемен-
тов ТТЛШ снизить до единиц наносекунд.
Логические элементы, построенные на токовых ключах (эмиттер-
но-связанная логика ЭСЛ) являются наиболее быстродействующими.
Они работают по принципу переключения токов при малых изменениях
входных сигналов. Схема элемента (рис. 5.6) состоит из переключа-
теля тока, входная половина которого образована транзисторами
VT\ — VT3 с общими эмиттерами и коллекторами, а входные сигна-
лы поступают к их базам; другая половина включает в себя транзис-
тор КТ4. Выходные сигналы снимаются б эмиттерных повторителей
на транзисторах КТ5 и VT6. На выходе реализуются функции ИЛИ—НЕ
(выход Zj) и ИЛИ (выход z2). Резистор через который протекает
ток /г, обусловленный напряжением смещения [7СМ, играет роль ис-
точника (генератора) тока. UCM снимается с выхода делителя, одним
плечом которого является транзистор КТ7 включенный по схеме эмит-
терного повторителя, а другим - резистор Ясм. Постоянное напряже-
ние на базу транзистора поступает с делителя, состоящего из резисто-
Р°в /?3 и диодов VDX и ИЛ2. Так как выходное сопротивление
схемы мало, а входное велико, паразитные емкости и емкость нагруз-
ки мало сказываются на работе схемы.
На рис. 5.7, а приведена схема инвертора на МОП транзисторе VT
P-типа. Исток И транзистора подключен к нулевому потенциалу. К за-
161
Рис. 5.6. Схема элемента ЭСЛ
Рис. 5.7. Схема инвертора:
а - на МОП транзисторе; б - с
дополняющими типами проводимос-
ти (КМОП)
+^и,л
твору 3 (вход схемы) прикладывается управляющее напряжение;
выходом схемы является сток С. При изменении напряжения на за-
творе изменяется сопротивление между истоком и стоком (от сотен
ом до сотен мегаом), что приводит к изменению тока, протекающего
через транзистор, и изменению выходного напряжения. Если на затвор
поступает напряжение высокого уровня (сигнал 1), сопротивление
между истоком и стоком падает и на выходе устанавливается низкий
уровень напряжения (сигнал 0). Если же на вход поступает напряже-
ние низкого уровня, сопротивление транзистора становится очень боль-
шим и на выходе устанавливается высокий уровень напряжения.
Наряду с транзисторами p-типа используют МОП транзисторы «-ти-
па, для которых питание и управление производят положительными
напряжениями.
В основе всех логических схем на МОП транзисторах с дополняющи-
ми типами проводимости (КМОП) лежит КМОП инвертор (рис. 5.7, б),
у которого — транзистор л-типа, a VT2 — транзистор p-типа. Затво-
ры обоих транзисторов объединены, на них поступает напряжение. При
подаче на вход напряжения высокого уровня (сигнал 1) транзистор
VTi открывается, a VT2 закрывается, и наоборот, при подаче на вход
напряжения низкого уровня (сигнал 0) открывается транзистор VT2,
a V7\ закрывается. Схемы с КМОП транзисторами отличаются малой
потребляемой мощностью и более высоким быстродействием, чем
схемы с МОП транзисторами.
Они обладают высокой помехоустойчивостью и малой чувствитель-
ностью к изменениям напряжения питания, поэтому схемы с КМОП
транзисторами наиболее перспективны для устройств АСУ ТП. В тех
случаях, когда необходимо максимальное быстродействие цифровых
управляющих устройств, следует применять ЭСЛ.
162
5.3. ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ АСУ ТП
5.3.1' Государственная система приборов
Управление технологическим процессом возможно на основании
получаемой информации о его состоянии и ходе. Разнообразие тех-
нологических процессов различных отраслей промышленного производ-
ства обусловило необходимость получения информации о большом чис-
ле технологических параметров. Проведенные в начале 70-х годов
Институтом проблем управления исследования по оценке размеров
области такой информации позволили создать кадастр величин, под-
лежащих измерению. Кадастр содержит свыше 2000 измеряемых вели-
чин, охватывающих отрасли разработки сырьевых ресурсов, энергети-
ку, производство промышленной, сельскохозяйственной и других
видов продукции и товаров.
На рис. 5.8 представлена структура кадастра. Кадастр — системати-
зированный свод сведений, составляемый периодически или путем
непрерывных наблюдений над соответствующими объектами. Он объеди-
няет физические величины, которые определяют состояние технологи-
ческих объектов управления различных отраслей. К ним относятся
величины пространства и времени, механические, электрические и маг-
нитные, акустические, световые, а также относительные.
Кадастр определяет перспективы развития номенклатуры средств
измерений — датчиков технологических процессов. При таком много-
образии измеряемых технологических параметров трудно рассчиты-
вать на успешную разработку датчиков в различных организациях
СССР без их систематизации и унификации.
Рациональное сокращение номенклатуры технических средств авто-
матизации и их конструктивных элементов и узлов достигается на ос-
нове последовательного применения агрегатных способов построения
снизу доверху, начиная от конструирования простейших функциональ-
ных блоков и кончая проектированием сложных автоматизированных
систем управления.
Научные основы конструирования системы приборов, базирующие-
ся на агрегатном принципе построения, впервые были определены акад.
В.А. Трапезниковым в начале 50-х годов. В конце 50-х годов была сфор-
мулирована проблема создания единой для всей страны Государствен-
ной системы промышленных приборов и средств автоматизации (ГСП),
представляющей рационально организованную совокупность приборов
и устройств, удовлетворяющих принципам агрегатирования и предназ-
наченных для построения автоматизированных систем измерения, кон-
троля, регулирования и управления технологическими процессами в
различных отраслях промышленности.
В 60-е годы были разработаны научные основы построения ГСП,
структуры, принципы совместимости приборов и устройств. В это же
время были обоснованы и определены значения унифицированных
163
Величины
простран-
ства
и времени
Линейные
Площадь
Объем
Время
Скорость
Акустиче-
ские
величины
Звуковое
давление
Механиче- ские величины
Масса Величины в области излучения
Плотность
Удельный
объем
Язлучение
Сила Облучен-
ность
Давление
Ускорение
Частота
Плоский
угол
Энергия
Мощность
Вязкость
{объемный)
Расход
{массовый)
Рис. 5.8. Структура кадастра измеряемых величин
Электрические
и магнитные
величины
Относи-
тельные
величины
Ток Активная мощность
Количество электриче- ства Коэффициент мощности
Электриче- ское напряжение Частота
Магнитный потенциал
Плотность тока
Магнитная проницае- мость
Напряжен- ность электриче- ского поля
Потери
Емкость Электро- магнитная энергия
Диэлектри- ческая про- ницаемость
Мощность реактивная
Электриче- ское сопро- тивленае Иглы шаго- вых сдвигов
Тврмо-ЗДС
Магнитный поток
tgd
Магнитная
индукция
Индуктив- ность—
Магнитное поле
Термическое
сопротивле-
ние
Тепловые величины Коэффициент трения Световые величины
КПД
1 а |
Температур Состав про- мышленных продуктов Освещен- ность
Количество теплоты Яркость
Содержание продуктов
Тепло- емкость Оптическая плотность
Концентра- ция J¥o
Удельная тепло- емкость
pH Отражение и рефракция
Коэтти- Кислот- ность
циент теп- Рассеяние света
лоотиачи ( Г— Соленость
Тепловой поток
Теплопро- водность цветность
Влажность
Коэффици- ент тепло- проводности
Контроль качества (неразрушаю- щий)
Температур ный коэффи
цивнт
пневматических и электрических аналоговых сигналов связи; позднее
был разработан комплекс стандартов ГСП, в том числе ГОСТ 12997-84
’’ГСП. Общие технические требования”, закрепивший законодатель-
но структуру и основные принципы построения ГСП.
В основу построения и развития ГСП положены следующие системо-
технические принципы:
возможность сведения многообразия функций автоматического
контроля, регулирования и управления к ограниченному числу типо-
вых функций;
минимизация номенклатуры технических средств с учетом макси-
мального удовлетворения потребности народного хозяйства на основе
создания агрегатных комплексов технических устройств и параметри-
ческих рядов приборов;
построение технических средств (приборов и устройств) на осно-
ве типовых унифицированных блоков и модулей;
агрегатное построение сложных систем управления на основе типо-
вых унифицированных приборов и устройств;
совместимость приборов и устройств ГСП при работе за счет уни-
фикации сигналов связи, используемых для обмена между изделиями
ГСП (информационная совместимость), унификации конструкций и
присоединительных размеров (конструктивная совместимость), уни-
фикации метрологических характеристик средств измерения и обеспе-
чения на этой основе рационального построения измерительных цепей
в системах (метрологическая совместимость).
Для более подробного ознакомления с ГСП можно рекомендовать
(2].
5.3*2. Принципы построения первичных измерительных
преобразователей (датчиков технологических параметров)
Получение информации о состоянии объекта управления обеспечи-
вается в ГСП с помощью разнообразных устройств, которые предназна-
чены для выработки сигнала, несущего измерительную информацию
как в форме, доступной для непосредственного восприятия операто-
ром, так и в форме, пригодной для использования в АСУ ТП. Соответ-
ственно измерительные устройства по виду вырабатываемой ими инфор-
мации делятся на измерительные приборы и измерительные преобразо-
ватели (датчики) (рис. 5.9).
К измерительным приборам относятся устройства, предназначенные
Для выработки измерительной информации в форме, доступной для не-
п°средственного восприятия оператором. Измерительные преобразова-
тели (ИП) — это устройства, предназначенные для выработки измери-
тельной информации в форме, удобной для передачи, преобразования,
° работки и хранения сигнала, но не поддающейся непосредственно-
му восприятию наблюдателя.
165
Рис. 5.9. Структура измерительных устройств ГСП
Различают ИП с естественными и унифицированными выходными
сигналами. Измерительные преобразователи с естественными выход-
ными сигналами — устройства, в которых осуществляется первичное
(обычно однократное) преобразование измеряемой физической вели-
чины. Несмотря на большое разнообразие измеряемых величин виды
естественных выходных сигналов в ГСП удается ограничить десятью.
К ИП с естественным представлением информации относится большая
группа устройств — термоэлектрические преобразователи, термометры
сопротивления, тензорезисторы, дифференциально-трансформаторные
датчики. Такие ИП применяются в локальных устройствах контроля
и автоматизации либо при централизованном контроле сравнительно
простых объектов. Измерительные преобразователи с унифицирован-
ными выходными сигналами имеют на выходе сигналы, предусмот-
ренные соответствующими стандартами; в большинстве случаев приме-
няются унифицированные сигналы, приведенные на рис. 5.9. Для пре-
образования естественных сигналов в унифицированные в ГСП пред-
усмотрены нормирующие преобразователи.
Структуры ИП несмотря на разнообразие измеряемых величин в
АСУ ТП могут быть сведены к четырем видам (табл. 5.1). Структура
166
Прямое (однократ-
ное) преобразова-
ние
Последовательное
прямое преобразо-
вание
Дифференциаль-
ная
С обратной связью
(компенсационная )
*вых = *1*ВХ
п
*вых = П Мвх
i = 1
*ВЫХ = ” ^2)*ВХ
*1
*ВЫХ ----——*вх
1+ ktk2
5CS^1
п
Sc = 2 S/
Z=1
8cs8i
-------- + 5 J -------
ki + k2 ki + k2
Примечание. В таблице приняты следующие обозначения: хвх - измеряемая величина; хвых - выходная величина;
- погрешность i-го элемента ИП; Ос - общая погрешность ИП; kj - коэффициент усиления f-го элемента.
однократного прямого преобразования реализуется в ИП с естествен-
ными выходными сигналами, например в термоэлектрических преоб-
разователях, датчиках давления и перепада давления.
Если первичное преобразование измеряемой величины не дает удоб-
ного для использования сигнала, применяют структуры с нескольки-
ми последовательными ИП.
Дифференциальная структура в ИП применяется тогда, когда изме-
рение основывается на сопоставлении результатов преобразования
измерительной информации, полученной в реальных и в некоторых
эталонных условиях. Преимущество этой структуры по сравнению с
предыдущими состоит в значительном уменьшении погрешности, об-
условленной изменением параметров источника питания и окружаю-
щей среды.
Наиболее совершенной является структура с отрицательной обрат-
ной связью, получившая название компенсационной схемы. Достоин-
ство схемы — компенсация изменений параметров измерительного
тракта вследствие того, что выходной сигнал непрерывно сравнивает-
ся с измеряемой величиной. Отрицательная обратная связь существен-
но снижает влияние погрешности звеньев прямого канала на резуль-
тат преобразования. При к^к2 > 20-г30 общая погрешность преобразо-
вания 6С определяется практически только погрешностью канала об-
ратной связи 52, и в связи в этим требования к точности прямого ка-
нала могут быть понижены.
Наряду с ИП в АСУ ТП применяются промежуточные преобразова-
тели, например АЦП и ЦАП, преобразующие аналоговые сигналы ИП
в цифровые, необходимые для ввода в ЭВМ, и цифровые в аналого-
вые — для связи ЭВМ с исполнительными органами в системах комби-
нированного управления.
5.4. УСТРОЙСТВА ХРАНЕНИЯ И ПЕРЕРАБОТКИ ИНФОРМАЦИИ
5.4.1. Запоминающие устройства
Запоминающие устройства (ЗУ) предназначены для записи, хране-
ния и выдачи информации, содержанием которой являются сведения
о возможностях технологического агрегата, технологические инструк-
ции и программа, по которой должно выполняться конкретное задание.
Основными операциями с ЗУ, называемыми обращением к памяти,
в общем случае являются занесение информации в память (запись) и
выборка информации из памяти (считывание). В зависимости от реа-
лизуемых с памятью операций обращения различают память с произ-
вольным обращением, в которой возможны как считывание, так и за-
пись данных (оперативная память), и память только для считыва-
ния информации (постоянная память ПЗУ). Запись информации в
ПЗУ производится в процессе изготовления или настройки микро-
схемы.
168
Память микро-ЭВМ представляет собой иерархическую структуру,
состоящую из ЗУ (характеризуемых быстродействием и емкостью),
и содержит следующие ее основные типы:
регистровую память, встраиваемую в состав интегральных схем цен-
трального процессорного элемента и состоящую из 8-24 регистров;
сверхоперативную память емкостью примерно 64 слова и временем
выборки порядка нескольких десятков наносекунд;
оперативную память емкостью 4—16К слов с возможностью нара-
щивания до 64-128К слов;
постоянную память емкостью 8—64К слов;
внешнюю память на гибких мини-дисках или малогабаритных кас-
сетных накопителях.
По принципу действия устройства памяти можно разделить на маг-
нитные, магнитомеханические и электронные (полупроводниковые).
Как правило, ЗУ содержит множество одинаковых запоминающих
элементов, образующих запоминающий массив, отдельные ячейки кото-
рого предназначены для хранения двоичного кода. Количество разря-
дов кода определяет ширину выборки памяти.
Способ организации памяти зависит от методов размещения и по-
иска информации в запоминающем массиве. По этому признаку раз-
личают адресную, ассоциативную и стековую памяти.
Рассмотрим принцип действия элементов магнитной оперативной
памяти. В качестве элементов оперативной памяти мини-ЭВМ широко
используются ферритовые сердечники. На рис. 5.10, а изображен сер-
дечник 1 с двумя одновитковыми обмотками - входной 2 и выход-
ной 5. Характеристика намагничивания (рис. 5.10, б) имеет близкую
к прямоугольной форму. Запоминание двоичной информации сердечника-
ми с прямоугольной петлей гистерезиса основано на существовании двух
устойчивых состояний остаточного намагничивания противополож-
ного знака. Состоянию с остаточной индукцией +ВГ можно поставить
в соответствие единичное значение, а состоянию —Вг - нулевое зна-
чение. Установка сердечника в единичное состояние (запись 1) произ-
водится подачей в обмотку 2 (входную) импульса тока, создающего
поле напряженностью +Нт. При этом сердечник переводится в еди-
ничное состояние независимо от исходного состояния и после снятия
входного импульса переходит в состояние +Z?r.
Для установки сердечника в нулевое состояние (запись 0) во вход-
ную обмотку подается импульс тока, создающий напряженность
’“flm, после снятия которого сердечник переходит в состояние —Вг.
Записанная информация может храниться неограниченное время и не
разрушается при исчезновении напряжения. Для считывания в обмот-
ку 2 подается импульс тока, как при записи 0. Если до подачи этого
импульса сердечник находился в состоянии 1, то при считывании ин-
дукция в сердечнике изменяется от +2?г до -Вг и в обмотке 3 (вы-
ходной) возникает сигнал считывания 1 с ЭДС ех (рис. 5.10, в). При
169
a - сердечник с обмотками; б - характеристика намагничивания; в - сигналы
считывания с ЭДС
нулевом исходном состоянии при считывании индукция в сердечни-
ке меняется незначительно и наводится сигнал считывания 0 с ЭДС
е0, близкой к 0. Таким образом, сигналу соответствует считыва-
ние 1, сигналу е0 — считывание 0.
Так как при считывании информация, записанная в сердечнике, сти-
рается, то после этого выполняется регенерация, восстанавливающая
информацию в сердечнике.
Рост требований к быстродействию ферритовых ОЗУ обусловил
уменьшение размеров сердечников от 2 мм в диаметре (время пере-
ключения 1,5 мкс) до 0,4-0,6 мм (время переключения 0,2-4),25 мкс).
Для выбора нужных сердечников в запоминающем массиве и уп-
равления их состояниями применяется метод совпадения токов, осно-
ванный на использовании прямоугольности петли гистерезиса феррито-
вых сердечников. Рассмотрим в качестве примера принцип действия
ОЗУ с двухкоординатной системой выборки адресов. Ферритовые сер-
дечники, предназначенные для хранения одного двоичного разряда, про-
шиты проводниками, образующими обмотки различного назначения.
Сердечники, число которых равно числу подлежащих запоминанию
слов, объединяются в матрицы. Одна матрица хранит по одному раз-
ряду всех записанных в память слов, а набор матриц, равный числу
разрядов в слове, образует куб памяти.
На рис. 5.11 представлена матрица, предназначенная для хранения од-
ного разряда каждого из 16 слов. Матрица выполнена в виде сетки го-
ризонтальных Хх — Х4 и вертикальных Kj — У4 шин, в местах пересе-
170
Рис. 5.11. Матрица оперативного ЗУ на
ферритах
чения которых расположены сер-
дечники 1-16. Шины служат для вы-
бора по заданному адресу опреде-
ленного сердечника с целью записи
и считывания информации. Кроме
шин сердечники ’’прошиты” про-
водниками, образующими обмотки
записи (ОЗ) и считывания (ОС).
бос
Работа ОЗУ протекает в последовательности считывание— запись. Для
считывания из какой-либо ячейки необходимо пропустить по адрес-
ным шинам импульсы отрицательной полярности. Амплитуда импуль-
сов выбирается такой, чтобы она не вызывала перемагничивания сер-
дечников всех ячеек, кроме той, где адресные шины пересекаются
(избранная ячейка), и чтобы создаваемая импульсами этих обмоток
суммарная напряженность в сердечнике была достаточна для его пере-
магничивания. Например, для считывания из 10-й ячейки следует про-
пустить импульсы тока по шинам Х3 и У2- Пренебрегая помехами, мож-
но полагать, что считыванию 1 соответствует появление импульса в ОС,
а считыванию 0 — его отсутствие. Зигзагообразная последовательность
”прошивки” сердечников обмоткой считывания обеспечивает взаимо-
компенсацию сигналов помех. При построении куба памяти из матриц
одноименные шины всех матриц последовательно соединяются между
собой.
В микро-ЭВМ на всех уровнях иерархии ЗУ (кроме внешних) выпол-
няются в виде полупродниковых интегральных схем. Полупроводнико-
вые ЗУ обладают рядом достоинств, которые обусловили их широкое
применение:
более широкий диапазон быстродействия и функционального назна-
чения, чем у магнитных ЗУ, что позволяет использовать их в качестве
регистров, ЗУ сверхоперативных (СОЗУ), оперативных (ОЗУ), по-
стоянных (ПЗУ) и перепрограммируемых постоянных (ППЗУ);
конструктивная, электрическая и технологическая совместимость
с быстродействующими интегральными микросхемами микропроцес-
соров;
высокие надежность и емкость.
Недостатком полупроводниковых ЗУ с произвольным обращением
является их энергозависимость: они потребляют энергию в режиме хра-
нения информации и теряют информацию при отключении питания.
По режиму занесения информации полупроводниковые ЗУ также де-
лятся на оперативные и постоянные, по принципу выборки информа-
ции — на устройства с произвольной и последовательной выборкой.
171
Таблица 5.2
Тип элемента, значение
Показатель ----------------------------------------------------------------
эсл ТТЛ ТТЛШ И2Л л-МОП КМОП
Емкость, 256-1024 256-1024 1024-4096 4096 4096 4096
бит Время выбор- 10-45 50-100 50-60 150 55-200 200-300
ки считыва- ния, нс Потребляв- 0,5-2,5 0,5-1,5 0,3-0,5 0,1 0,05-0,24 0,02
мая мощ-
ность,
мВт/бит
В качестве элементов полупроводниковых ОЗУ используют бипо-
лярные транзисторы, биполярные транзисторы с диодами Шоттки, поле-
вые МОП транзисторы и- ир-типов, а также получившие название комп-
лементарных МОП транзисторы (КМОП), полевые транзисторы со
структурой металл—диэлектрик—нитрид кремния (МНОП), приборы
с зарядовой связью (ПЗС), транзисторные структуры с инжекционным
питанием (И2Л).
Качество ЗУ характеризуется следующими показателями: емкостью
одного кристалла, т.е. объемом информации, которая может хранить-
ся в одной микросхеме, временем выборок при считывании информа-
ции и удельной потребляемой мощностью. Повышение качества связа-
но с ростом емкости и уменьшением времени выборок и удельной
потребляемой мощности. Характеристики статических ЗУ произволь-
ной выборки, построенных из различных типов базовых логических
элементов, приведены в табл. 5.2.
Интегральная схема полупроводникового ЗУ обычно выполняется
в виде заключенного в корпус кремниевого кристалла, в котором об-
разованы массив запоминающих элементов для хранения одноразряд-
ных слов, а также схемы адресной дешифрации, формирователи запи-
си, усилитель считывания, схемы управления и межэлементные соеди-
нения.
В качестве статического запоминающего элемента (ЗЭ) использует-
ся триггер на двух многоэмиттерных транзисторах с непосредственны-
ми связями; разрядные (информационные) эмиттеры 1.1 и 2.1
(рис. 5.12, а) служат для записи в ЗЭ или считывания из него бита, а
остальные (адресные) эмиттеры — для выборки ЗЭ. Информационные
эмиттеры присоединены к общим для всех ЗЭ одного разряда слов раз-
рядным шинам 0 и 1, а сигналы записи и считывания 0 и 1 имеют один
и тот же уровень потенциала. К каждой из разрядных шин Зп/Сч под-
ключены разрядные усилители записи УЗ и считывания УС
172
Рис. 5.12. Запоминающее устройство:
а - статическое; б - динамическое
Запоминающий элемент может находиться в следующих режимах:
хранение информации, выбранное состояние, запись. Принимаем, что
ЗЭ находится в состоянии 0, если транзистор VTX открыт. В режиме
хранения (ЗЭ не выбран) эмиттерный ток открытого транзистора замы-
кается на землю через адресный эмиттер и адресную шину, находящие-
ся под потенциалом логического 0. Информационные эмиттеры в этом
режиме заперты, для чего на них подается потенциал, превышающий
максимальный уровень логического 0, но не достигающий минималь-
ного уровня логической 1.
При выборке данного ЗЭ на его адресные эмиттеры с выходов деши-
фраторов адреса подается потенциал логической 1, который выше потен-
циала информационных эмиттеров. В этом режиме адресные эмиттеры
запираются, а коллекторный ток открытого транзистора протекает
через его информационный эмиттер, что обеспечивает возможность
считывания из ЗЭ или записи в него информации. Состояния 0 и 1 запо-
минающего элемента определяются по наличию тока соответственно
в разрядной шине 0 (открыт транзистор VTt) или в разрядной шине 1
(открыт транзистор КТ2).
Считывание производится без разрушения информации; при считы-
вании на входы обоих усилителей записи подается нулевой сигнал, на
их выходах будет сигнал логической 1, предотвращающий ответвле-
ние в них тока считывания (тока информационного эмиттера). При счи-
тывании ток протекает от информационного эмиттера открытого тран-
зистора к базовой цепи усилителя считывания, вызывая отпирание
его выходного транзистора.
Для записи 0 или 1 в запоминающий элемент с соответствующего
усилителя записи на подключенный к нему информационный эмиттер
подается нулевой сигнал. Пусть производится запись 1 в триггер, нахо-
дящийся в единичном состоянии (открыт транзистор КТ2). Подача
нулевого сигнала на эмиттер 2.1 не изменяет состояния триггера. Если
173
же триггер находился в нулевом состоянии, то подача нулевого сигна-
ла на эмиттер 2.1 открывает транзистор VT2, транзистор VTX при этом
закрывается и триггер переходит в единичное состояние.
Динамические полупроводниковые ЗУ с произвольной выборкой
имеют высокую степень интеграции и быстродействие, низкую стои-
мость и поэтому находят самое широкое применение в микро-ЭВМ.
Запоминающим элементом динамических ЗУ служит ’’запоминающая
емкость”, в качестве которой используются паразитные емкости неко-
торых цепей. Будем полагать, что отсутствие заряда на запоминающей
емкости соответствует нулевому, а наличие — единичному состоянию.
При этом считывание информации сводится к определению состояния
запоминающей емкости. Так как запоминающая емкость из-за утеч-
ки заряда может сохранять единичное состояние ограниченное время,
в динамических ЗУ необходимо периодически осуществлять восстанов-
ление хранимой информации.
Схема запоминающего элемента динамического ЗУ на МОП транзис-
торах приведена на рис. 5.12, б. Паразитная емкость С (затвора тран-
зистора VT2) является запоминающей емкостью. Шина Y использует-
ся для ввода в ЗЭ (вывода из ЗЭ) бига информации при записи (при
считывании).
При считывании подается сигнал R, открывающий транзистор КГ4,
и паразитная емкость Су шины Y получает заряд от источника +£.
Затем на шину X подается средний уровень сигнала синхронизации
записи (считывания) CWR, открывающий транзистор VT3, но недоста-
точный для открытия транзистора VT\. При этом если ЗЭ хранит 1,
то паразитная емкость С заряжена и открыт транзистор VT2i создаю-
щий вместе с открытым транзистором VT3 цепь разряда емкости Су.
Низкий уровень сигнала D на шине Y свидетельствует о том, что ЗЭ
хранил 1, т.е. инверсную величину. Если же емкость С разряжена (ЗЭ
хранит 0), транзистор VT2 закрыт, сигнал CWR не вызывает разряда
емкости Су и высокий уровень сигнала D соответствует хранению 0 в
ЗЭ. Таким образом, к усилителю считывания от шины Y поступает
инверсное значение хранимого в ЗЭ двоичного знака.
Таблица 5.3
Тип элемента (вид
Показатель ЭСЛ (ПЗУ, ППЗУ) ТТЛ (ПЗУ, ППЗУ) ТТЛШ (ПЗУ, ППЗУ)
Емкость, бит 256-1024 1024-4096 1024-4096
Время выборки считы- вания, нс 20 50-100 50-60
Потребляемая мощность, мВт/бит 0,8-1,0 0,1-0,5 0,1-0,2
174
При записи на шину Y подается сигнал D, который соответствует
запоминаемому двоичному знаку. Затем на шину X подается высокий
уровень сигнала CWR, открывающий транзистор VTl9 который подклю-
чает к шине Y емкость С. Эта емкость независимо от своего предыду-
щего состояния заряжается при записи 1 либо разряжается при запи-
си 0.
В динамических ЗУ периодически производится регенерация ин-
формации, при которой в ЗЭ записывается инверсное значение храни-
мого кода. После каждой четной регенерации в ЗЭ оказывается исход-
ный код, а после нечетной — его инверсия. В ЗУ есть схема, которая
указывает, какой код (прямой или инверсный) хранит ЗЭ в данный
момент.
Постоянные запоминающие устройства (ПЗУ) в управляющих вы-
числительных системах служат для хранения программ и другой неиз-
меняемой информации. Важным преимуществом ПЗУ по сравнению
с полупроводниковыми ОЗУ является сохраняемость информации
при выключении питания. Классификация полупроводниковых ПЗУ
представлена на рис. 5.13, а основные показатели ПЗУ и ППЗУ приве-
дены в табл. 5.3.
Наиболее простыми и широко применяемыми являются масочные
ПЗУ. Они строятся на основе диодов, биполярных и МОП транзисторов.
Запоминающие устройства на основе МОП транзисторов подобно
биполярным ЗУ строятся в виде полностью заполненных матриц, в
которых сигнал 1 записывается присоединением затвора к входной
шине, а при записи 0 затвор остается неподключенным.
Основной недостаток масочных ПЗУ — отсутствие возможности
оперативно изменять информацию без изготовления новой микросхе-
мы, что особенно неудобно на этапе отработки программ в системе.
Значительно более удобны электрически программируемые ПЗУ,
однако записывать информацию в них необходимо до установки в
системе.
Наиболее универсальны перепрограммируемые ЗУ-ППЗУ, которые
незаменимы при макетировании и отладке микропроцессорных си-
запоминающего устройства)
р-МОП (ПЗУ) л-МОП (ПЗУ) КМОП (ППЗУ) МНОП (ППЗУ) ЛИПЗ-МОП (ППЗУ)
4096-8192 500 8192 - 65 535 300 4096 250-300 4096 2000 16 384 500
0,01 0,01 0,01 0,01 0,01
175
ПЗУ
стем и при использовании в аппаратуре, периодически требующей из-
менения содержимого ПЗУ.’ Перепрограммируемые запоминающие уст-
ройства изготовляются на основе технологии лавинно-инжекционных
МОП транзисторов с плавающими затворами (ЛИПЗ-МОП), МНОП
структур. На основе МНОП транзисторов строят ЗУ, сохраняющие ин-
формацию при отключенном питании. Они отличаются от обычных
МОП структур тем, что имеют дополнительный слой нитрида кремния,
расположенный между пленкой двуокиси кремния и металлическим
электродом затвора. Благодаря дополнительному слою заряды полу-
чили возможность накапливаться в области поверхности раздела нитрид
кремния - двуокись кремния и сохраняться при отключении пита-
ния в течение нескольких лет.
Перепрограммируемые запоминающие устройства на основе МНОП
структур позволяют электрически изменять содержимое, в том числе
избирательно. Их недостаток — медленное считывание - пока являет-
ся основным ограничением для применения в качестве ПЗУ программ.
Они чаще всего используются в качестве медленного ОЗУ в тех слу-
чаях, когда необходимо сохранить информацию при отключении пи-
тания.
5.4.2. Триггеры
Подавляющее большинство цифровых устройств содержит в качест-
ве основных элементов различные типы триггеров. Триггер — это эле-
мент, обладающий двумя устойчивыми состояниями. По ГОСТ 2.743-82
триггеры классифицируются по ряду признаков:
по способу записи информации — на асинхронные и синхронные;
по способу синхронизации — на синхронные со статическим управле-
176
нием записью, синхронные двухступенчатые, синхронные с динами-
ческим управлением;
по способу организации логических связей:
триггеры с раздельной установкой 0 и 1 (Л5-триггеры);
триггеры со счетным входом (Т-триггеры);
универсальные триггеры с раздельной установкой 0 и 1 (JK-триг-
геры) ;
триггеры задержки (D-триггеры);
триггеры задержки с управляемым приемом информации по одному
входу (DK-триггеры);
комбинированные триггеры (RST-, JKRS-, DRS-триггеры и др.);
триггеры со сложной входной логикой.
Входы триггеров и сигналы, подаваемые на них, делятся на инфор-
мационные, управляющие состоянием триггера, и вспомогательные,
служащие для предварительной установки триггера в заданное состоя-
ние и его синхронизации.
Асинхронные триггеры реагируют на информационные сигналы в
момент их появления на входах; синхронные триггеры реагируют на
эти же сигналы, но при наличии разрешающего сигнала на специально
предусматриваемом входе С. Триггеры со статическим управлением
реагируют на информационные сигналы при подаче на вход уровня 1
(прямой С-вход) или 0 (инверсный С-вход). Реакция триггеров с ди-
намическим управлением на информационные сигналы происходит
в момент изменения сигнала на С-входе от 0 к 1 (прямой динамичес-
кий С-вход) или от 1 к 0 (инверсный динамический С-вход).
Состояние триггера определяется сигналом Q на его прямом выхо-
де или сигналом Q на инверсном выходе.
Рассмотрим функционирование основных видов триггеров.
Асинхронные /W-триггеры имеют два информационных входа: S
для установки 1 и R для установки 0. Они обычно строятся на двух ло-
гических элементах И—НЕ либо ИЛИ—НЕ, охваченных перекрестными
обратными связями. Функционирование триггера, построенного на
Таблица 5.4
S(n) RW 2 (Л) 2(л+1) Режим
0 0 0 0 Хранение
0 0 1 1
0 1 0 0 Установка 0
0 1 1 0 То же
1 0 0 1 Установка 1
1 0 1 1 То же
1 1 0 Запрещенная
1 1 1 j комбинация
177
Рис. 5.14. Асинхронный ЯЗ-триггер:
а - схема; б - условное обозна-
чение
Рис. 5.15. Синхронный ЯД-тригтер:
а - схема; б - условное обозначе-
ние
элементах ИЛИ—НЕ DI, D2 (рис. 5.14, а), описывается при помощи
табл. 5.4, в которой состояние триггера в момент изменения входно-
го сигнала обозначено Q(n), а после переключения -Q(п+1).Комбина-
ция S = О, Я = 0 является нейтральной, так как триггер сохраняет со-
стояние, в котором он находился до момента появления этих нулевых
сигналов. При комбинации S = 1,Я = 0 триггер устанавливается в еди-
ничное состояние, а при комбинации S = О, R = 1 - в нулевое. Комби-
нация S = 1, Л = 1 является запрещенной, так как она приводит к нару-
шению закона работы триггера и неопределенности его состояния.
С помощью таблицы переходов можно получить аналитическое выра-
жение закона функционирования ЯЯ-триггера
е(и+1) = $(и)+Я(и)2(и),
при S (n)R (и) = 0. Обозначение триггера приведено на рис. 5.14, б.
Асинхронный jRS-триггер на элементах И-НЕ работает аналогично
рассмотренному. Отличие состоит в том, что действующим значением
входного сигнала является нулевой уровень и запрещенной комбина-
цией является равенство нулю сигналов на обоих информационных
входах.
Синхронные одноступенчатые RS-триггеры отличаются от асинхрон-
ных наличием дополнительного входа С для синхронизирующих (так-
товых) импульсов и двух логических элементов на входе. Рассмотрим
функционирование триггера, построенного на элементах И-НЕ D1-D4
(рис. 5.15, а). Если сигнал на входе С равен 0, то входные логические
элементы D1 и D2 блокированы и их состояние не зависит от сигналов
на информационных входах S и R, а выходные сигналы qr и q2 равны 1.
Так как для асинхронного ЯЯ-триггера такая комбинация входных сиг-
налов является нейтральной, то триггер сохраняет предыдущее состоя-
ние. Если С = 1, входные логические элементы D1 и D2 открыты для
приема информационных сигналов и передачи их на входы асинхрон-
178
a - схема; б - условное обозначение
ного Л5-триггера. В этом случае функционирование синхронного и
асинхронного триггеров одинаково.
Синхронные /^5-триггеры строятся также на элементах ИЛИ-НЕ
либо И—ИЛИ—НЕ. Обозначение триггера показано на рис. 5.15, б.
Синхронный двухступенчатый RS-триггер включает в себя два син-
хронных одноступенчатых Я5-триггера. Управление ступенями осуще-
ствляется разными фазами тактового сигнала. Возможное схемное ре-
шение изображено на рис. 5.16, а. При единичном сигнале на входе С
производится запись информации в триггер первой ступени. Триггер
второй ступени заблокирован при этом нулевым сигналом на выходе
инвертора, поступающим на его вход С Когда сигнал на входе С первой
ступени равен 0, эта ступень блокируется, а вторая ступень открыва-
ется. Благодаря этому информация переписывается из первой ступе-
ни во вторую и появляется на выходе триггера. Двухступенчатые триг-
геры обозначаются ТТ (рис. 5.16, б).
D-триггер имеет два входа - информационный вход D и вход С для
синхронизирующих импульсов, который задерживает сигнал, подан-
ный на информационный вход. Один из вариантов схемного решения
триггера на элементах И—НЕ представлен на рис. 5.17, а. При нуле-
вом сигнале на входе С состояние триггера от изменения входного
сигнала на входе D не зависит. Когда на вход С подан сигнал, равный 1,
триггер принимает состояние, определяемое входным сигналом
е(И+1) = D{n).
На рис. 5.17, б, в даны диаграммы, поясняющие работу триггера,
и его условное обозначение.
Т-триггер — триггер со счетным входом Т — имеет один вход и из-
меняет свое состояние при подаче очередного входного импульса. Про-
стейший Т-триггер можно построить на основе двухступенчатого
Л$-триггера. Для этого входы R и 5 соединены перекрестными обрат-
ными связями с выходами триггера, а вход С используется в качестве
179
Рис. 5.17.D-триггер:
а - схема; б - диаграмма работы; в - условное обозначение
счетного входа Т. Схема такого триггера (на элементах И—НЕ D1-D8)
приведена на рис. 5.18, а. На рис. 5.18, б показано его условное обозна-
чение. Таблица состояний триггера (табл. 5.5) поясняет его функциони-
рование.
Т-триггер реализует функцию
е(м + О= Q{n)T(n)^Q(n)T(n).
Разновидностью Т-триггера является ТК-триггер (рис. 5.18, в), имею-
щий дополнительный управляющий вход К, изображенный на рис. 5.18,а
штриховой линией. Если сигнал на входе V равен нулю, то ТК-триггер
сохраняет неизменным свое состояние. При подаче на этот вход сигна-
ла, равного единице, функционирование ТК-триггера становится анало-
гичным работе Т-триггера.
JK-триггер является весьма распространенным универсальным типом
триггера. Он имеет два информационных входа J и К и вход для такто-
вых импульсов С. Функционирование JK-триггера поясняется таблицей
переходов (табл. 5.6). Отличие JK-триггера от синхронного ЯЯ-тригге-
ра состоит в том, что отсутствуют запрещенные входные комбинации
и при подаче на информационные входы J и К сигнала, равного едини-
Рис. 5.18. Г (ТУ) -триггер:
а - схема; б, в - условные обозначения
180
Таблица 5.5
Т(и) QW б(«+1)
0 0 0
1 0 1
0 1 1
1 1 0
Таблица 5.6
С (л) /(л) КО») 00») 00» + 1) Режим
0 0 0 0 0 Хранение
0 0 0 1 1 п
0 0 1 0 0 W
0 0 г 1 1 »»
0 1 0 0 0 »»
0 1 0 1 1 >»
0 1 1 0 0 »»
0 1 1 1 1 »»
1 0 0 0 0 »»
1 0 0 1 г »»
1 0 1 0 0 Установка 0
1 0 1 1 0 То же
1 1 0 0 1 Установка 1
1 1 0 1 1 Тоже
1 1 1 0 1 Инверсия
1 1 1 1 0
П— I «) L-Г 8)
Рис. 5.19. J/Г-тригтер (а) и варианты других видов
триггеров (б-г)
181
це, триггер изменяет свое состояние на противоположное аналогично
Т-триггеру.Таккак Jtf-триггер обладает свойствами RS- и Т-триггеров,
его схема реализуется на основе синхронного двухступенчатого ^-триг-
гера с входной логикой (рис. 5.19, а). Одна пара S и R входов исполь-
зуется, как и в Т-триггере для обратных связей, другая пара S и R вхо-
дов, служащих для приема информации, соответственно обозначается
как входы/и К.
J/Г-триггер удобен тем, что при различных вариантах подключения
его входов можно получить триггеры других видов, как показано на
рис. 5.19, б-г. Поэтому триггер такого типа назван универсальным.
5.4.3. Арифметические и логические устройства
Реализация алгоритмов управления связана с выполнением различ-
ных арифметических (численных) и логических процедур. Независи-
мо от объемов перерабатываемой информации, сложности решаемых
задач и быстродействия цифровые управляющие устройства имеют
единую элементную основу — единый принцип и логику элементар-
ных звеньев и узлов, из которых они состоят.
Примеры выполнения четырех арифметических действий над числа-
ми в двоичном коде приведены в табл. 5.7.
Узлы арифметических и логических устройств. Арифметические и
логические устройства в процессе выработки управляющей информа-
ции выполняют различные математические операции, которые могут
быть сведены к ограниченному набору элементарных арифметичес-
ких и логических микроопераций. Совершенство этих устройств опре-
деляется точностью (разрядностью), быстродействием при выполнении
микроопераций, их организацией. Микрооперации едины как для прос-
тейших цифровых устройств с ’’жесткой” логикой, так и для микро-
процессоров и процессоров ЭВМ любого ранга. К ним относятся сум-
Таблица 5.7
Сложение Вычитание Умножение Деление
(9+3 = 12) (9-3 = 6) (9*5=45) (45 :9=5)
1001 1001 1001 101101 1001
+ — X
ООН ООН 0101 1001 101
1100 оно 1001 1001
0000 1001 1001
0000
101101
182
Таблица 5.8 Таблица 5.9
Aq Во So Ро Ai Pi-1 Si Pi
0 0 0 0 0 0 0 0 0
0 1 1 0 0 0 1 1 0
1 0 1 0 0 1 0 1 0
1 1 0 1 0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
мирование (алгебраическое) кодов, преобразование и сдвиг кодов
влево или вправо, сравнение кодов по модулю.
Узлы, связывающие процессоры с памятью и устройствами текущей
информации, выполняют микрооперации приема, запоминания и пе-
редачи информации по' определенному адресу. Поэтому подлежат рас-
смотрению как логические (комбинационные) цифровые узлы (сум*
маторы, устройства сравнения, дешифраторы, преобразователи кодов,
мультиплексоры), так и цифровые узлы последовательностного типа,
построенные на основе триггеров (регистры, счетчики).
Сумматором называется устройство, образующее сумму двух чи-
сел, представленных сигналами на его входах. Они могут быть одно-
разрядными или многоразрядными (состоящими из одноразрядных
сумматоров).
Многоразрядные сумматоры в каждом разряде имеют по три вхо-
да, и в младшем разряде - два входа. Сумматор младшего разряда
с двумя входами называется полусумматором. Функционирование
полусумматора и сумматора при сложении двух чисел А и В представ-
лено в табл. 5.8 и 5.9 соответственно. Третьим входом для суммато-
ра /-го разряда является сигнал переноса из (/ — 1)-го разряда. На вы-
ходе обоих устройств образуются сигналы суммы S и переноса Р. Для
полусумматора
So = Aq Bq + AqBq*9
Pq = AqBq.
Для полного сумматора
S, = Af Bi Pj - j + Aj Bi Pi _j + Ai Bi Pi + Ai Bi Pi _i;
Pi = Bi + Ai Pi -i + Bi Pi _ i.
Схемы полусумматора и сумматора приведены на рис. 5.20, а, в;
на рис. 5.20, б, г показаны их условные обозначения. После снятия
сигналов со входов исчезают сигналы суммы и переноса, поэтому для
запоминания результата сложения следует использовать регистры.
183
Рис. 5.20. Схемы полусумматора (я) и сумматора (в) и их условные обозначе-
ния (б, г)
В зависимости от способа передачи информации в ЭВМ применяются
сумматоры последовательного или параллельного действия. Первые
оперируют последовательными кодами, представляющими собой такти-
рованную временную последовательность импульсов, в которой нали-
чие импульса в такте соответствует единице в разряде. Числа в сумма-
тор подаются поразрядно, начиная с младшего разряда. Результат на
выходе также выдается в последовательном коде, начиная с младше-
го разряда.
Сумматор параллельного действия оперирует параллельными кода-
ми и представляет собой цепочку одноразрядных суммирующих схем,
число которых соответствует разрядности суммируемых чисел. Один
из схемных вариантов четырехразрядного сумматора с последователь-
ным переносом изображен на рис. 5.21.
Устройства сравнения предназначены для сравнения двух много-
разрядных двоичных чисел. При выполнении этой логической опера-
ции числа сравниваются поразрядно, начиная со старшего разряда. Срав-
нение происходит до появления в каком-либо разряде разных симво-
лов (0 и 1), после чего фиксируется неравенство чисел и дальнейшее
сравнение в последующих младших разрядах не производится. Схемы
сравнения старшего разряда обычно имеют два входа для подачи срав-
ниваемых чисел и три выхода: Ai > В,; Л/ < By; Aj = В,-; (Л/ #= By).
Функционирование схемы сравнения иллюстрируется таблицей истин-
ности (табл. 5.10).
Первые два выхода позволяют определить, какое число больше, а
последний выход позволяет блокировать сравнение в младших разря-
184
Рис. 5.21. Схема четырехразрядного сумматора
дах, если в i-м установлено неравенство. Вариант одноразрядной схе-
мы сравнения, построенной на элементах ИЛИ-HE, приведен на
рис. 5.22. Для формирования многоразрядной схемы сравнения произ-
водят каскадное соединение одноразрядных схем с добавлением к
ним третьего входа, показанного штриховой линией. При появлении
разницы в предыдущем старшем разряде на его выходе Л у +1 ¥= Яу +1
формируется единичный сигнал. Попадая на третий вход f-го разряда,
этот сигнал вызывает появление нулей на выходах Ai > Ai < Bi
и единицы на выходе Aj Ф В^ Аналогично появляются нули на выхо-
дах Ai: _ j > By _ j, Af _ j < By _ j и единица на выходе AJ_1 =£ By _ t
и т.д. Поэтому на общих выходах многоразрядной схемы сравнения
чисел, получившей название цифрового компаратора, сигнал форми-
руется по результатам сравнения того старшего разряда, где обнаруже-
но различие в символах, и дальнейшее сравнение младших разрядов
не производится.
Дешифратором называется устройство, выполняющее операцию
преобразования w-элементного входного кода в сигнал на одном из
выходов.
Количество входов m и выходов N полного дешифратора, в кото-
ром используются все комбинации входного двоичного кода, связа-
но соотношением N = 2т. Если число выходов N < 2т, дешифратор
называется неполным.
Дешифраторы применяются в схемах ЭВМ на выходах регистров
или счетчиков и служат для преобразования кода числа, находящегося
в регистре или счетчике, в управляющий сигнал на одном из выходов
дешифратора.
Различают линейные, пирамидальные и матричные дешифраторы
(рис. 5.23). Линейный дешифратор можно построить из логических
Таблица 5.10
Л’ *1 Лу > Яу Л,. <в{ Ai = Bi Л,. ¥= Bi
0 0 0 0 1 0
0 1 0 1 0 1
1 0 1 0 0 1
1 1 0 0 1 0
185
Рис. 5.22. Одноразрядная схема сравнения
элементов И, число которых совпадает с числом выходов, при этом
число входов каждого элемента соответствует числу входных пере-
менных. На рис. 5.23, а изображена схема линейного дешифратора на
16 выходов у о - Д'is и 4 входные переменные -х4. Прямые и ин-
версные значения входов подаются от выходов Qj и 5/ триггеров, стоя-
щих в каждом разряде. Работа дешифратора поясняется таблицей ис-
тинности (табл. 5.11). Состояние выходов определяется комбинация-
ми входных сигналов. Условное обозначение дешифратора показано
на рис. 5.23, б. Схема пирамидального дешифратора на четыре вход-
ные переменные приведена на рис. 5.23, в.
Наименьшими затратами оборудования характеризуется матричный
(прямоугольный) дешифратор. Схемное решение матричного дешифра-
тора изображено на рис. 5.24. Двухвходовые элементы И подключа-
ются к горизонтальным и вертикальным шинам, которые образованы
дешифраторами первой ступени DCX и DC2, делящими между собой
поровну входные переменные х
Преобразователи кодов предназначены для преобразования m-эле-
ментного параллельного кода на входе в «-элементный код на выходе.
Необходимость в преобразовании кодов возникает, например, при пе-
редаче к ЭВМ информации в коде Грея от кодового датчика угла пово-
Таблица 5.11
Входы Выходы
*1 *2 *3 *4 Уо >1 У2 >>13 >14 >15
0 0 0 0 1 0 0 ...0... 0 0 0
0 0 0 1 0 1 0 ...о... 0 0 0
0 0 1 0 0 0 1 .. . 0. . . 0 0 0
1 1 0 1 0 0 0 ...0... 1 0 0
1 1 1 0 0 0 0 ... о... 0 1 0
1 1 1 1 0 0 0 ...о... 0 0 1
186
a - линейный; б - его условное обозначение; в - пирамидальный
Рис. 5.24. Матричный дешифратор
Рис. 5.25. Преобразователь ко-
да
В<с. 5.26. Мультиплексор
рота или йеремещения механизма и при числовом программном уп-
равлении металлорежущими станками в узлах индикации. На рис. 5.25
приведен преобразователь кода 8—4—2—1 в код управления семисег-
ментным индикатором, у которого сегмент ’’горит” при подаче единич-
ного сигнала.
Мультиплексор — управляемый кодом коммутатор нескольких вхо-
дов на один выход. Мультиплексоры применяются при вводе текущей
информации от нескольких датчиков к управляющей ЭВМ. У мульти-
плексоров различают две группы входов - информационные и управ-
ляющие. К информационным входам подводят каналы, по которым
передается информация. На управляющие входы поступает кодовая
комбинация, определяющая подключение одного из информационных
входов к выходу. Обе группы входов имеют общий выход, т.е. муль-
типлексор представляет собой разновидность дешифратора с допол-
нительными информационными входами. На рис. 5.26 представлена
схема мультиплексора на восемь входов. Для его управления необхо*
дим трехразрядный код. Работа мультиплексора поясняется табли-
цей истинности (табл. 5.12). Наборы переменных хь х2, х3 обеспе-
188
Таблица 5.12
*1 х2 х3 F *1 х2 х3 F
0 0 0 /о 0 0 1/! 0 10/2 0 11/э 1 0 0/4 1 0 1/5 1 1 0 /б 1 11/7
чивают подключение к выходу соответствующего информационного
входа fj. Если фаза коммутируемых сигналов не имеет значения, ин-
вертор с выходом/7 можно не устанавливать.
Регистрами называются цифровые узлы, предназначенные для запи-
си и хранения числа. Помимо хранения информации регистры некото-
рых видов могут преобразовывать информацию из последовательной
формы представления в параллельную, сдвигать записанную информа-
цию на один или несколько разрядов в сторону младшего разряда
(вправо) или старшего разряда (влево), инвертировать код. Их важ-
нейшие характеристики - разрядность и быстродействие. Разрядность
определяется количеством триггеров для хранения числа. Быстро-
действие характеризуется максимальной тактовой частотой, с которой
могут производиться запись и сдвиг информации.
Регистры хранения строят на основе одноступенчатых асинхронных
RS-триггеров. Так как каждый триггер служит для хранения одного
разряда числа aN, ..., а2, то количество триггеров регистре рав-
но N. Схема регистра хранения представлена на рис. 5.27, а. Перед за-
писью информации подается импульс по шине ”Уст. О” (установка 0)
и все триггеры устанавливаются в нулевое состояние. При записи в
регистр числа, код которого а^,. .., ах поступает к входным ключам,
подается управляющий сигнал С3 Запись. Единичные входные сигна-
лы проходят через ключи и переводят триггеры своих разрядов в еди-
ничное состояние.
При необходимости передачи записанного кода другому устройст-
ву подается управляющий сигнал Счг или Сч2 на соответствующую
шину Считывание в прямом коде или Считывание в обратном коде.
Передача кода может осуществляться многократно, так как при считы-
вании триггеры не изменяют своего состояния. Условное^обозначение
регистра хранения приведено на рис. 5.27, б.
Регистры сдвига предназначены для преобразования информации
путем ее сдвига под воздействием импульсов. По направлению сдвига
информации различают регистры прямого сдвига (вправо), обратного
сдвига (влево) и реверсивные, в которых возможен сдвиг в обоих
направлениях. Регистры сдвига представляют собой совокупность после-
довательно соединенных триггеров, как правило, двухступенчатой
структуры. Одно из распространенных схемных решений на £>-тригге-
189
в прямом коде д обратном коде
Рис. 5.27. Регистр хранения (а) и его условное обозначение (б)
рах изображено на рис. 5.28, а Регистр имеет информационный вход,
входы для тактовых импульсов (импульсов сдвига) и установочный.
Считывание возможно как в параллельном коде с выходов триггеров
каждого разряда, так и в последовательном коде с последнего разря-
да относительно информационного входа. Вход регистра для импуль-
сов сдвига получается объединением С-в ходов всех триггеров; объеди-
нение Я-входов дает установочный вход.
Регистр устанавливается в исходное состояние перед записью ин-
формации подачей импульса по шине ’’Уст.О”. Записываемая информа-
ция в последовательном коде поразрядно, начиная с младшего, подается
на информационный вход со стороны старшего разряда. Продвижение
кодовой комбинации осуществляется при подаче тактовых импуль-
сов от разряда к разряду. При подаче сигнала ’’Сдвиг” на С-входы
D-триггеров информация переписывается из каждого разряда в сосед-
ний младший. Для записи ^разрядного слова необходимо подать N
импульсов сдвига.
Считывание информации в последовательном коде, как и запись,
осуществляется поразрядным сдвигом записанной кодовой комби-
нации к выходу по командам тактовых импульсов. Считывание ин-
190
Рис. 5.28. Регистр сдвига (л) и его условное обозначение (б)
формации возможно также в параллельном коде, если на С-входах
триггеров - нулевой сигнал и они находятся в режиме хранения. Обоз-
начение регистра сдвига приведено на рис. 5.28, б.
Цифровой счетчик - последовательностный цифровой узел, осу-
ществляющий счет поступающих на его вход импульсов и запомина-
ние результата подсчета в заданном коде.
Счетчики используются в ЭВМ и системах ЧПУ всех уровней для
образования последовательностей адресов команд, для счета количест-
ва циклов выполнения операций.
По целевому назначению счетчики делятся на суммирующие, вычи-
тающие и реверсивные. С приходом очередного счетного импульса
показание суммирующего счетчика увеличивается на единицу, а вычи-
тающего уменьшается на такую же величину. Реверсивные счетчики
могут работать как в режиме сложения импульсов, так и в режиме
их вычитания.
Одной из основных характеристик счетчиков является коэффици-
ент счета А^сч, который определяет число его устойчивых состояний,
т.е. предельное число импульсов, которое может быть им зафиксиро-
вано.
Для построения счетчиков используют Г- или ТК-триггеры, допол-
няя их при необходимости логическими элементами в цепях межраз-
рядных связей. Формирование двоичного суммирующего счетчика
производят соединением прямого выхода триггера младшего разря-
да со счетным входом триггера старшего разряда; на счетный вход триг-
гера младшего разряда подают входные импульсы Со. Пример реализа-
ции трехразрядного суммирующего счетчика показан на рис. 5.29, а.
Состояния счетчика после воздействия серии входных импульсов при-
ведены в табл. 5.13. Временная диаграмма, поясняющая работу счет-
чика, изображена на рис. 5.29, б. Исходное состояние счетчика соот-
ветствует нулевому уровню сигнала на выходах всех триггеров =
= 02 = 0з = 0- Триггер младшего разряда меняет свое состояние Qi
каждый раз с приходом очередного счетного импульса. При переходе
из единичного состояния в нулевое на его выходе формируется сигнал
переноса, вызывающий изменение состояния триггера следующего
разряда. При обратном изменении состояния триггера (от нулевого
к единичному) сигнал переноса не вырабатывается. Поэтому триггер
191
Рис. 5.29. Трехразрядный суммирующий счетчик:
а - схема; б - диаграмма работы; в - условное обозначение
каждого последующего разряда изменяет свое состояние вдвое реже,
чем триггер предыдущего разряда. На диаграмме учтено собственное
время срабатывания триггера Гт по сигналу переноса.
Для установки исходного состояния предназначена шина ”Уст.О”,
объединяющая 7?-входы триггеров всех разрядов счетчика.
На левом поле условного обозначения счетчика (рис. 5.29, в) пока-
зано, что его входом является Т-вход триггера первого разряда Тх\
на правом поле указан ’’вес” каждого разряда.
Если на счетный вход триггера старшего разряда подавать сигнал
не с прямого, а с инверсного выхода триггера предыдущего разряда,
то образуется вычитающий счетчик. Такой счетчик по сравнению с сум-
мирующим имеет обратный порядок смены состояний (табл. 5.14),
так как с приходом очередного счетного импульса содержащееся в
счетчике число уменьшается на единицу.
С учетом различий в схемах суммирующего и вычитающего счет-
чиков можно построить реверсивный счетчик, объединяющий их воз-
можности. В нем с помощью сигналов на сложение Сс и вычитание
Таблица 5.13
Номер состояния Сз Qi Ci Номер состояния Q3 Й2 61
0 0 0 0 5 1 0 1
1 0 0 1 6 1 1 0
2 0 1 0 7 1 1 1
3 0 1 1 0 0 0 0
4 1 0 0
192
Рис. 5.30. Четырехразрядный реверсивный счетчик:
а - схема; б - условное обозначение; в - с приставкой на /?$-триггере
Св обеспечивается управление направлением счета (прямой — в сум-
мирующем, обратный — в вычитающем). Для выполнения этой функ-
ции счетчик дополняется комбинационной частью.
В реверсивном четырехразрядном счетчике (рис. 5.30, а) предусмот-
рены два входа для счетных импульсов. Если счетчик должен работать
как суммирующий, импульсы подаются на вход +1; если подавать им-
пульсы на вход -1, счетчик работает как вычитающий. Ключи на вхо-
дах триггеров в зависимости от режима работы соединяют счетные вхо-
ды либо с прямыми, либо с инверсными выходами триггеров предыду-
щих младших разрядов, обеспечивая режим суммирования или вычи-
тания импульсов. Счетчик помимо основных выходов Ci, ..., 04 име-
ет дополнительные (”>15” и ”<0”). На первом из них единичный сиг-
Таблица 5.14
Номер состояния Сз Qi Gi Номер состояния Сз Qi Qi
7 1 1 1 2 0 1 0
6 1 1 0 1 0 0 1
5 1 0 1 0 0 0 0
4 1 0 0 7 1 1 1
3 0 1 1
193
нал появляется при заполнении всех разрядов счетчика единицами,
т.е. при переходе счетчика в состояние ”15”, и соответствует сигналу
переноса в следующий счетчик. Единичный сигнал на выходе ”<0”
появляется при заполнении всех четырех разрядов счетчика нулями
и соответствует сигналу займа из следующего счетчика в режиме вычи-
тания. Условное изображение счетчика приведено на рис. 5.30, б.
При одном источнике импульсов, поступающих к реверсивному
счетчику, необходимо предусмотреть внешнее устройство коммута-
ции этих импульсов на суммирующий или вычитающий вход. Коммути-
рующая приставка, выполненная на AS-триггере, вместе со счетчиком
изображена на рис. 5.30, в. При подаче положительного импульса Сс
на S-вход AS-триггера на его прямом выходе устанавливается единич-
ный уровень, который открывает ключ 1 для суммирования счетных
импульсов Со. При подаче положительного импульса Св на А-вход
триггера открытым окажется ключ 2 и счетчик будет работать в режи-
ме вычитания счетных импульсов Со.
Рассмотренные счетчики имели коэффициент пересчета Асч = 2N,
где N - число их разрядов. Для многих устройств микро-ЭВМ и уст-
ройств с ’’жесткой” логикой необходимы счетчики с иным коэффици-
ентом. Так, в устройствах связи с оператором и вывода информации
для индикации (ввиду использования в них двоично-десятичного ко-
да) нужны счетчики с Асч = 10 в количестве, равном числу десятич-
ных разрядов.
Принцип построения двоично-десятичного счетчика заключается в
следующем. Каждый десятичный разряд выполняется в виде четырех-
разрядного двоичного счетчика, число устойчивых состояний которого
искусственно уменьшено с 16 до 10. Его получают, вводя в схему
двоичных счетчиков обратные связи или логические переключатели,
управляющие переходом счетчика из состояния 1001 (после прихода
девятого импульса) в состояние 0000 (после 10 импульсов). Счетчи-
ки с АсЧ < 2™ удобно строить при помощи JA-триггеров, обеспечиваю-
щих наиболее простое схемное решёние. На рис. 5.31 показана схема
счетчика с Асч = 10. В цепи обратной связи установлены дешифратор
на двухвходовом элементе И, связанный с прямыми выходами тригге-
ров четвертого и второго разрядов, и AS-триггер Т5.
194 х
В исходном состоянии все триг-
геры находятся в нулевом состоя-
нии (табл. 5.15). Под действием
счетных импульсов счетчик изменяет
свое состояние от нулевого до де-
вятого как обычный двоичный. Триг-
гер Г5 в это время находится в ну-
левом состоянии. С приходом деся-
того импульса счетчик переходит в
состояние 1010, т.е. четвертый и
второй триггеры принимают единич-
ное состояние, а третий и первый -
нулевое. На вход ключа И поступа-
Таблица 5.15
Номер состояния С>4 Сэ Qi Qi
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
ют два единичных сигнала, он откры-
вается и передает единичный сигнал на S-вход триггера Т5. Единичный
сигнал с выхода Qs через элемент ИЛИ поступает к Я-входам тригге-
ров всех разрядов и переводит их в нулевое состояние. Следующий
входной импульс, поступая на вход счетчика и R-вход триггера Т5,
возвращает ЯЯ-триггер в нулевое состояние. Исходное состояние
счетчик принимает под действием сигнала ’’Уст.О”.
5.4.4. Устройства связи с объектом
Цифро-аналоговый преобразователь (ЦАП) представляет собой
устройство, позволяющее осуществить переход от цифровой к аналого-
вой форме представления информации. В ЦАП входным сигналом слу-
жит цифровой код в различных системах счисления, а выходным сиг-
налом — соответствующее ему значение аналоговой величины в виде
напряжения постоянного тока на временном интервале. Количествен-
ная связь между входной числовой величиной N(tj) и ее аналоговым
эквивалентом А (/у) характеризует алгоритм цифро-аналогового пре-
образования
Л(0 = Дф7)ДЛ + М,
где ДЛ — аналоговый эквивалент единицы младшего разряда кода;
6А - погрешность преобразования.
Цифро-аналоговые преобразователи используются для вывода уп-
равляющей информации из ЭВМ и передачи ее к объекту управления,
а также в системах цифровой обработки данных. Кроме того, эти пре-
образователи входят в качестве составной части в аналого-цифровые
преобразователи. Процесс цифро-аналогового преобразования состо-
ит в суммировании эталонных значений напряжения, соответствующих
разрядам входного кода; слагаемые берутся для разрядов, имеющих
единичное значение. Выходное напряжение ЦАП
£4ых = u3(bt -2-' +z>2 г2 + -2-"),
где U3 - эталонное напряжение; bit b2, ...» bn — коэффициенты двоич-
ных разрядов, принимающие нулевое или единичное значение.
К основным параметрам ЦАП относятся:
разрешающая способность — определяется как величина, обратная
числу возможных уровней аналогового сигнала:
Р = 1/2\
где п - число разрядов преобразуемого двоичного кода;
точность - определяется наибольшим значением отклонения аналого-
вого сигнала от расчетного; обычно в качестве такого отклонения
ЬА принимают половину уровня сигнала, соответствующего младше-
му разряду;
нелинейность — характеризуется максимальным отклонением ли-
нейно нарастающего выходного напряжения от прямой линии, соеди-
няющей точки нулевого и максимального его значений;
время преобразования Туст - определяется интервалом времени
между моментами подачи цифрового кода на входе и достижения вы-
ходным сигналом преобразователя значения, отличающегося от уста-
новившегося значения не более чем на величину допустимой погреш-
ности преобразования.
В состав ЦАП, как правило, входят резистивная матрица, набор
токовых ключей, выходной усилитель и источник опорного (эталон-
ного) стабилизированного напряжения.
Резистивная матрица предназначена для формирования выходных
сигналов, пропорциональных входному коду. Один из вариантов схе-
мы резистивной матрицы приведен на рис. 5.32, а. Каждому разряду
соответствует разрядный ток Ц, /2 > • • •, 1п- Здесь индексом 1 отмечен
старший разряд, разряд с индексом п является младшим. Разрядные
токи задаются с помощью матрицы резисторов, величины сопротивле-
ний которых удваиваются при переходе от старшего к младшему раз-
ряду. Ко всем резисторам подано эталонное напряжение U3. Сигнал
на выходе определяется суммой разрядных токов, связанной с вход-
ной кодовой комбинацией при помощи электронных ключей. Основ-
ной недостаток этого варианта резистивной матрицы состоит в широ-
ком диапазоне сопротивлений и их высокой требуемой точности, воз-
растающей с увеличением числа разрядов входного кода.
Этот недостаток устраняется при переходе к варианту, изображен-
ному на рис. 5.32, б и получившему название варианта ”с резистив-
ной сеткой R-2R”. В этой матрице используются резисторы только
двух номиналов. Ток в неразветвленной части матрицы 70 задается ис-
точником опорного напряжения и последовательно делится в узлах
резистивной матрицы по двоичному закону. В этом нетрудно убедить-
ся, рассматривая сечения АА, ВВ, СС Приведенное к месту сечений
сопротивление части резисторов, отсекаемой в направлении стрелок,
составляет 2R. Таким образом, ток, протекающий через любой узел,
делится на две равные части. Отсюда следует свойство матрицы - вход-
ное сопротивление, замеренное в любом из узлов матрицы, равно R.
196
a - с эталонными резисторами; б - с резистивной сеткой R-2R
Выражение для тока
Zo = U3/R.
Токовые ключи предназначены для коммутации элементов резис-
тивной матрицы в соответствии с входной кодовой комбинацией. Ос-
новное требование, предъявляемое к ним, — высокое быстродейст-
вие. Кроме того, токовые ключи не должны вносить заметных погреш-
ностей в разрядные токи.
Ключи для быстродействующих ЦАП строятся обычно на биполяр-
ных транзисторах и диодах; для преобразователей среднего и низкого
быстродействия применяются ключи на КМОП-транзисторах с малым
потреблением энергии.
В качестве выходного усилителя, суммирующего разрядные токи,
обычно используется операционный усилитель. Напряжение на его вы-
ходе пропорционально входному коду.
Аналого-цифровой преобразователь (АЦП) предназначен для пере-
вода информации из аналоговой формы в цифровую. Количественная
связь между аналоговой величиной A (tj) и соответствующей ей цифро-
вой N(tj), характеризующая алгоритм аналого-цифрового преобразо-
вания, имеет вид
A (Г;) -л «
W=-^H~±5W>
' Дл
где ДЛ — шаг квантования, т.е. цена (вес) единицы младшего разряда
кода; 8N(tj) — погрешность преобразования на /-м шаге.
Основные параметры АЦП:
разрядность преобразования;
точность преобразования, зависящая от шага квантования и оши-
бок, вносимых основными узлами АЦП;
197
время преобразования, необходимое для представления мгновенно-
го значения аналогового сигнала в цифровой форме.
Схемное решение и состав АЦП определяются методом преобразова-
ния и способом его реализации. Наибольшее распространение получи-
ли три основных метода: последовательного счета, поразрядного коди-
рования и считывания или параллельный.
Метод последовательного счета основан на уравновешивании вход-
ной величины суммой одинаковых и минимальных по величине этало-
нов. Метод поразрядного кодирования (уравновешивания) предусмат-
ривает несколько эталонов, пропорциональных степеням числа 2, и срав-
нение их с аналоговой величиной, начиная с эталона старшего разряда.
По методу считывания входная величина сравнивается одновременно
со всеми эталонами, число которых при и-разрядном двоичном коде
составляет 2п — 1.
Метод последовательного счета. Преобразователи, реализующие
этот метод, имеют несколько разновидностей и применяются для пре-
образования в цифровой код аналоговых сигналов напряжения и тока,
а также интервалов времени. На рис. 5.33/ а представлена схема (цепи
управления опущены) АЦП последовательного счета, использующего
ЦАП в цепи обратной связи. С началом работы преобразователя на
вход счетчика СТ поступают импульсы тактовой частоты /т от генера-
тора G, благодаря этому растет код на входе ЦАП и повышается на-
пряжение t/цдп на его выходе. Оно поступает к схеме сравнения
(компаратору) СС вместе с входным напряжением £/вх. При равен-
стве напряжений t/BX и f/цдп компаратор срабатывает и работа счет-
чика прекращается. На выходах счетчика устанавливается код, яв-
ляющийся цифровым эквивалентом входного сигнала. При неравен-
стве этих сигналов начинается переходный процесс, заканчивающий-
ся при достижении равенства UBX и £/цдп> т.е. АЦП как бы ’’следит”
за входным сигналом, вследствие чего такие АЦП получили название
следящих. Погрешность преобразования зависит от величин ступе-
ней £/цдп> погрешности в подборе этого напряжения, ошибки компа-
ратора при определении равенства £/вх и t/цдп- Время преобразова-
ния зависит от величины входного напряжения.
Метод поразрядного кодирования. Этот метод позволяет построить
АЦП с более высоким быстродействием. Структурная схема одного из
вариантов такого типа ^АЦП, реализующего принцип последователь-
ных приближений, представлена на рис. 5.33, б.
Код результата преобразования формируется в и-разрядном регист-
ре (триггеры Тп, ..., Ti). По команде ’’Пуск” схема управления, в
качестве которой может быть использован сдвигающий регистр, после-
довательно переводит триггеры, начиная со старшего разряда, в еди-
ничное состояние. При этом на вход цифро-аналогового преобразова-
теля ЦАП последовательно поступают единицы соответствующих раз-
рядов от триггеров. Напряжение с выхода ЦАП l/цдп сравнивается
198
Рис. 5.33. Аналого-цифровой преобразователь:
а - последовательного счета; б - последовательных приближений; в - считы-
вания
при помощи компаратора СС с аналоговым входным сигналом UBX.
В первом такте работы к компаратору подаются UBX и t/ц ап = t/3W,
соответствующее единице старшего (и-го) разряда. Если L/BX > U3n,
на выходе СС появляется нулевой сигнал и триггер старшего разряда
сохраняет единичное состояние. При t/BX < U3n компаратор выдает
единичный сигнал, по которому схема управления возвращает триг-
гер Тп в нулевое состояние. В следующем такте система управления пе-
реводит в единичное состояние триггер (и-1)-го разряда Тп_г. На
входе компаратора сравнивается в зависимости от результата перво-
го такта либо t/BX с U3n + U3 (W-i), либо t/BX с U3 (л-1). Процесс
преобразования далее протекает так же, как при сравнении UBX с
U3 п на первом такте.
В результате преобразования входное напряжение t/BX уравновеши-
вается суммой эталонных напряжений, снимаемых с выхода ЦАП:
п
f/вх = 2 ayt/3y,
/ = 1
где aj — коэффициенты, равные 0 или 1 в разрядах выходного кода,
снимаемого с триггеров Тп-1\\ U3; — эталонное напряжение ЦАП,
соответствующее /-му разряду.
199
В этих АЦП время преобразования постоянно и не зависит от вели-
чины входного сигнала; оно зависит от числа разрядов и периода так-
товой частоты. Для 12-разрядного АЦП время преобразования лежит в
пределах 10-150 мкс. Погрешность АЦП определяется неточностью
ЦАП, зоной нечувствительности и смещением нуля компаратора.
Метод считывания. Наибольшим быстродействием обладают АЦП,
реализующие этот метод. Функциональная схема такого АЦП приведе-
на на рис. 5.33, в. Входная аналоговая величина 1/вх сравнивается при
помощи компараторов с эталонными уровнями напряжения U3j. Резис-
тивный делитель формирует эталонные уровни напряжения, каждое из
которых подается вместе с 1/вх к соответствующему компаратору. Чис-
ло эталонных уровней 2л-1, где п - число разрядов в коде результата
преобразования; значения эталонных уровней пропорциональны пос-
ледовательности целых чисел от 1 до 2п — 1.
На выходах компараторов, у которых UBX > U3j, устанавливается
нулевой сигнал; если же t/BX’ < 1/э/, устанавливается единичный сиг-
нал. Таким образом, с увеличением 1/вх число компараторов с единич-
ным выходом уменьшается, а с нулевым выходом увеличивается. Ре-
зультат сравнения через ЯЯ-триггеры поступает на вход шифратора
CD, который преобразует результат в код. Задача шифратора — опре-
делить номера двух соседних компараторов CCj и CCj + j, в которых
выходные сигналы различны, и выдать соответствующий этой грани-
це код.
Время преобразования составляет 10—100 нс. Недостаток преобра-
зователей состоит в большом числе компараторов (2л-1), которое
быстро возрастает с ростом числа разрядов п. Так, для 6-разрядного
АЦП необходимы 63 компаратора. Поэтому АЦП, реализующие ме-
тод считывания, имеют число разрядов до 8.
Дальнейшему развитию микроэлектронных АЦП и ЦАП способ-
ствует появление и совершенствование микропроцессоров и мик-
ро-ЭВМ. Одним из основных требований к АЦП и ЦАП является воз-
можность их сопряжения с микропроцессором (непосредственно или
с использованием дополнительных элементов).
5.5. СРЕДСТВА ДИСКРЕТНОЙ УПРАВЛЯЮЩЕЙ ТЕХНИКИ
5.5.1. Микропроцессоры и микро-ЭВМ
Основная тенденция развития микроэлектроники — разработка и
выпуск схем большой функциональной сложности и высокой степе-
ни интеграции. Достижения в этом направлении позволили создать
новый класс изделий — микропроцессор (МП).
Микропроцессор — это программно-управляемое устройство, осу-
ществляющее процесс обработки цифровой информации и управление
им, построенное на одной или нескольких интегральных микросхе-
мах. Микропроцессор по своим логическим функциям и структуре
200
подобен процессору обычных ЭВМ и оперирует с короткими слова-
ми в разных моделях - от 2 до 16 разрядов. Появление МП обусловле-
но экономической целесообразностью перехода от обширной номен-
клатуры технических средств с жесткой логикой к универсальным
программируемым устройствам, выполненным на основе крупносерий-
ных больших интегральных схем, реализующих функцию микропро-
цессора или его части.
Совокупность микропроцессорных и других интегральных микро-
схем, совместимых по конструктивно-технологическому исполнению
и предназначенных для совместного применения при построении мик-
ропроцессоров, микро-ЭВМ, контроллеров и других средств вычисли-
тельной и управляющей техники, составляет микропроцессорный комп-
лект (МПК). В табл. 5.16 приведены основные технические данные
отечественных МПК.
- Микропроцессорная электронная вычислительная машина (мик-
ро-ЭВМ) представляет собой устройство, состоящее из микропроцессо-
ра (микропроцессоров), полупроводниковой памяти, средств связи
с периферийными устройствами (интерфейса ввода-вывода), пульта
управления и источника питания, объединенных общей несущей кон-
струкцией.
Контроллер — это цифровой аппаратно- или программно-управляю-
щий автомат, выполняющий функции управления автономным или
входящим в состав системы устройством, его сопряжения с интерфей-
сом системы и работающий по однозначно заданным алгоритмам без
взаимодействия с человеком-оператором.
Микро-ЭВМ и контроллеры, построенные на базе микропроцессор-
ных комплектов и предназначенные для построения систем управле-
ния, в сочетании с дискретными и аналоговыми устройствами связи
с объектами образуют микроэлектронные управляющие вычисли-
тельные комплексы.
Наметились две разновидности компоновки больших интеграль-
ных схем: однокристальное и многокристальное исполнения функ-
ционально законченных блоков. Однокристальные блоки имеют срав-
нительно простую внутреннюю структуру, обусловленную технологи-
ческими возможностями и ограничением количества выводов, и фик-
сированную систему управления. Достоинство таких блоков — в уни-
версальности использования и совместимости программного обеспече-
ния при различных вариантах исполнения. К их недостаткам следует
отнести сложность модернизации и расширения функциональных воз-
можностей.
Рассмотрим в качестве примера структуру микроцессора
КР580ИК80А серии КР580 - одного из наиболее распространенных
типов МП. Это восьмиразрядный однокристальный МП с однозначно
определенной архитектурой и системой команд без возможности ап-
паратного наращивания разрядности обрабатываемых данных. Он пред-
201
Таблица 5,16
Серия микро- процессорно- го комплекта Число интеграль- ных схем Техноло- гия Разряд- ность, бит Время цикла, мкс Напря- жение пи- тания, В Потребля- емая мощ- ность, МВт Назначение
общее в базо- вом ком- плекте
К536 12 2 р-МОП 8 10 -24; +1,2 70-1000 Специализированный - микро-ЭВМ ’’Электроника С5-12”
К580, КР580 7 1 л-МОП 8 2,0 ±5; +12 300-750 Универсальный - вычислительные устройства, контроллеры, микро-ЭВМ
К581, КР581 7 2 п-МОП 8,16 0,4 ±5; +12 900 Специализированный - микро-ЭВМ ”Электроника-60”
К584, КР584 3 2 И2Л 4л 2,0 +5 300 Универсальный - микро- и мини-ЭВМ, контроллеры и си- стемы управления различной архи- тектуры
К586 4 1 п-МОП 16 0,5 5 1000 Специализированный - микро-ЭВМ ’’Электроника С5-21”
К587, КР587 4 2 КМОП 4л, 8л 2,0 9 50 Универсальный - контроллеры, микропроцессоры, микро-ЭВМ, другие вычислительные устрой- ства
К588, КР588 5 2 КМОП 16л 2,0 5 25 Универсальный - автономные и встраиваемые микро- и ми- ни-ЭВМ и распределенные систе- мы управления объектами
К589 8 2 ттлш 2л 0,1 5 900 Универсальный - быстродейст-
в у юти е контроллеры, процессо-
ры, мини- и микро-ЭВМ, вы-
числительные устройства повышен-
ного быстродействия
Серия микро- процессорно- го комплекта Число интеграль- ных схем Техноло- гия Разряд- ность, бит Время цикла, мкс Напря- жение пи- тания, В Потребля- емая мощ- ность, МВт Назначение
общее в базо- вом ком- плекте
U83-K1803 (совместная раз - работка СССР и ГДР) 4 2 л-МОП 8л 1,4 5 1000 Универсальный - процессоры, микро- и мини-ЭВМ, контрол- леры и другие вычислительные устройства среднего быстродей- ствия
К1800 4 1 ЭСЛ 4л 0,01 -5,2; 2 800 Универсальный - центральные и специализированные вычисли- тельные системы, прежде всего— ЕС ЭВМ
К1801 3 1 л-МОП 16-32 2,0 5 1200 Универсальный - перспективен во всех областях народного хозяйства
КР1802 6 1 ТТЛШ 8л 0,14 5 1600 1 Универсальный - МП
КР1804 6 1 ТТЛШ 4л 0,11 5 1500 J различной разрядности
К1810 2 1 Высоко- качест- венная л-МОП 16 0,4 5 1750 Универсальный
Рис. 5.34. Структура микропроцессора КР580ИК80А
назначен для построения средств обработки данных, применяемых в
устройствах автоматики, контроллерах и микро-ЭВМ. Структура МП
изображена на рис. 5.34.
Микропроцессор состоит из следующих блоков: арифметико-логи-
ческого устройства АЛУ, блока регистров БР, блока управления БУ,
16-разрядного буферного регистра адреса БРА, 8-разрядного буфер-
ного регистра данных БРД и 8-разрядной внутренней шины данных
ВШД
Основным блоком МП является 8-разрядное АЛУ, выполняющее
арифметические, логические операции и операции сдвига над данны-
ми, представленными в дополнительном коде и находящимися в ре-
гистре накопителя PH и регистре временного хранения РВХ. Результат
операции поступает на ВЩД или записывается в накопителе Н. Блок
десятичной коррекции БДК позволяет при необходимости осущест-
влять перевод содержимого из двоичной в двоично-десятичную фор-
му. Информация о результате выполнения команды заносится в 5-раз-
рядный регистр признаков РП. При нулевом результате разряд Z
(нуль) РП устанавливается в единичное состояние, разряд С (перенос)
этого регистра устанавливается в единичное состояние при возникнове-
нии переноса, разряд S (знак) - при единичном значении старшего
разряда, разряд Р (четность) — при четном числе единичных битов в
204
результате, разряд АС (дополнительный перенос) - при переносе из
младших четырех разрядов в старшие (ряды на рис. 5.34 не пока-
заны).
Блок регистров предназначен для приема, хранения и выдачи различ-
ной информации, участвующей в процессе выполнения программы.
Он включает шесть 8-разрядных регистров общего назначения (В, С,
D, Е, Н, £), которые в зависимости от типа выполняемой команды мо-
гут использоваться либо как самостоятельные регистры, либо как
16-разрядные регистровые пары (В-С, D-E, Н-L). Регистры W и Z
программно недоступны, они используются для хранения промежуточ-
ных результатов при выполнении команд. Управляемый адресный ре-
гистр УАР предназначен для приема информации из других регистров
и передачи ее в буферный регистр адреса БРА. В процессе передачи
этот регистр может увеличивать или уменьшать на единицу передавае-
мую информацию, что упрощает адресацию. В блок регистров БР вхо-
дят также 16-разрядный регистр - указатель стека УС и 16-разрядный
счетчик команд СК. Обмен информацией с внутренней шиной данных
ВШД осуществляется с помощью 8-разрядного мультиплексора М.
Управление работой АЛУ и регистрами осуществляется блоком уп-
равления БУ, вырабатывающим в соответствии с кодом команды,
поступившей на его вход с ВШД, необходимую последовательность уп-
равляющих сигналов. Коды команд поступают к блоку управления БУ
от регистра РК и дешифратора ДК команд.
Назначение выводов и управляющих сигналов МП КР580ИК80А
приведено в табл. 5.17. Формат команд МП - одно-, двух- и трехбайт-
ный, их число -111. Система команд включает арифметические, ло-
гические операции, десятичную коррекцию, стековые операции, за-
грузку, выборку, сложение слов двойной длины, операции управления.
Микропроцессорные комплекты позволяют создавать микро-ЭВМ.
Основными частями микро-ЭВМ, структура которой представлена на
рис. 5.35, являются:
микропроцессор (МП), способный читать информацию от внешних
устройств и посылать ее к ним по специальном магистралям (шинам);
память для хранения программ и данных при вычислениях в про-
цессе управления.
В микро-ЭВМ используются постоянная ПЗУ и оперативная ОЗУ
память, выполненная на интегральных микросхемах, а также внеш-
ние запоминающие устройства (ВЗУ) на гибких магнитных дисках
и кассетных магнитофонах и память микрокоманд (ПМ). Имеются
устройства ввода-вывода (УВВ). Управление осуществляется блоком
управления (БУ).
С позиций использования ЭВМ в составе АСУ ТП обычно рассматри-
вают следующие их основные характеристики:
быстродействие - определяется длительностью обращения к памяти
ЭВМ, а также максимальным быстродействием при выполнении корот-
205
Таблица 5.17
Обозна- чение Наименование Функциональное назначение
ПМ Сигналы управления шинами Разрешение приема ин- Шина данных ШД0-И1Д7 микропроцес-
вд формации с шины данных сора находится в режиме приема инфор- системы (выходной) мации Признак выдачи инфор- На шину данных ШД0-ШД7 микропро-
ЗХ мации на шину данных цессора выдана информация для записи (входной) в ЗУ или во внешнее устройство Сигналы управления прямым доступом к памяти Захват шин (входной) Запрос на прямой доступ к памяти со
ПЗХ стороны внешнего устройства Подтверждение захвата Признак допуска внешнего устройства
ЗПР шин (входной) к шинам данных и адреса Сигналы управления прерываниями Запрос прерывания Запрос прерывания работы микропро-
РПР (входной) цессора Разрешение прерывания Прерывание разрешено
ГТ (выходной) Сигналы управления асинхронной передачи данных Готовность данных к пе- Информация для обмена между ЗУ или
Ъж редаче (входной) внешним устройством и микропроцес- сором готова. При отсутствии сигнала го- товности ГТ микропроцессор перехо- дит в состояние ожидания, из которого выходит при поступлении сигнала ГТ
Ожидание (выходной) Микропроцессор находится в состоянии
С ожидания Сигналы общего назначения Синхронизация (выход- Начало машинного цикла. По этому сиг-
СВР ной) налу на шину данных ШД0-ШД7 мик- ропроцессор выдает управляющее слово Сброс (входной) Сигнал устанавливает в нуль счетчик ко-
Cl, С2 манд, сбрасывает триггеры разрешения прерывания и захваты шин Тактовые импульсы Постоянно поступают к микропроцес-
(входные) сору, обеспечивая его тактирование
ких операций типа сложения. Современные малые (мини) ЭВМ имеют
длительность обращения 0,1—1,5 мкс, максимальное быстродействие
10s — 106 операций/с;
длину слова (разрядность) - обычно используются 16-разрядные
слова (два байта), а также двойные слова;
206
Рис. 5.35. Структура микро-ЭВМ
емкость (объем) оперативной памяти - может изменяться в зави-
симости от решаемых задач от 4103 до 512 -103 слов; емкость внеш-
ней памяти может достигать 100-106 слов и более;
характеристику каналов для подключения внешних устройств. Ка-
нал - совокупность средств переключения внешних устройств в опре-
деленном порядке в соответствии с приоритетами при работе ЭВМ.
Каналы могут быть селекторными, мультиплексорными, с общей ши-
ной.
Селекторный канал предназначен для привилегированного обслужи-
вания одного внешнего устройства. Мультиплексорный канал позво-
ляет одновременно обслуживать несколько работающих параллельно
внешних устройств. Каждое устройство может связываться с каналом
в течение короткого интервала времени.
Наибольшей скоростью передачи (ввода-вывода) информации, дохо-
дящей до (300-г500) 103 слов в секунду, обладает селекторный ка-
нал;
характеристику программного обеспечения - для использования
ЭВМ в АСУ ТП важно наличие различных видов операционных систем,
транслятора с алгоритмических языков и библиотеки прикладных
программ, ориентированных на различные задачи.
В СССР выпускаются несколько семейств микро-ЭВМ. Среди них -
семейство.универсальных управляющих микро-ЭВМ ”Электроника-С5”,
семейство ’’Электроника НЦ” и микро-ЭВМ СМ-1800. Микро-ЭВМ
”Эдектро^ика-С5”, основные показатели которой приведены в
табл. 5.18,Включает в себя:
многоплатные модели, поставляемые в конструктивно и функцио-
нально законченном виде с возможностью использования в настоль-
ном и встраиваемом в оборудование вариантах;
одноплатные модели, предназначенные для встраивания в приборы
и системы с целью реализации в них функций управления, контроля,
обработки и приема—передачи данных;
однокристальную микро-ЭВМ.
Микро-ЭВМ семейства ’’Электроника НЦ” (табл. 5.19) предназначе-
ны для широкого применения в различных областях народного хо-
зяйства. Это прежде всего металлорежущие станки с ЧПУ. Микро-ЭВМ
’’Электроника НЦ-ОЗТ” с ОЗУ объемом 8К 16-разрядных слов входит
в состав ЧПУ типа 2У32.
Для управления универсальными металлорежущими станками созда-
но специализированное устройство ЧПУ ’’Электроника НЦ-31”. В нем
207
Таблица 5.18
Показатель Много платные модели Одноплатные модели Одно- крис- таль- ные моде- ли
С5-01 С5-02 С5-11 С5-12 С5-21 С5-41 С5-31
Быстродейст- вие, тыс.опера- ций/с 10 10 10 10 200 1000 150
Разрядность, бит 16 16 16 16 16* 16 16
Объем ОЗУ, слов 1К 4-10К 128 128 256 1-4К 128
Объем ПЗУ, слов 2-10К 4-24К 1024 2048 2048 — 1024
Число 8-разряд- ных цифровых ка- налов ввода-вы- вода 10/9 17/15 4 4 4 4 3
Число каналов последователь- ного ввода-вы- вода 3 4 4 4 1
Число входов за- просов прерыва- ния 8 8 8 8 8 8 8
программа обработки детали вводится на упрощенном машинном язы-
ке, что позволяет токарю средней квалификации оперативно составлять
ее практически на рабочем месте. Отлаженная программа может быть
выведена на внесшее ЗУ кассетного типа и введена в ЧПУ других стан-
ков. Кроме того, устройство обеспечивает возможность редактирова-
ния программы, управление станком с клавиатуры пульта.
Микро-ЭВМ СМ-1800 предназначена для построения локальной АСУ
ТП, работающей автономно или входящей в иерархическую структу-
ру на нижней ступени, а также для автоматизации научного экспери-
мента, процессов подготовки данных, программирования и обучения.
Она и^иеет восемь разрядов и построена на основе и-канальных МОП
интегральных схем. Микро-ЭВМ СМ-1800 целесообразно использовать
для решения следующих функциональных за^ач (в качестве контрол-
лера): прямого цифрового управления технологическими процесса-
ми; управления конвейерами, автоматическими линиями, подъемно-
транспортными машинами и системами регулирования с неизменяе-
мой программой в локальных системах.
208
Таблица 5.19
Показатель НЦ-ОЗТ НЦ-ОЗД НЦ-31 НЦ-04 НЦ-80 НЦ-80-01
Быстродействие, тыс. оПераций/с 100 100 130 200 550/250 550/250
Разрядность, бит 16 16 16 16 16/32 16/32
Объем ОЗУ/ПЗУ. слов 8К 16K 8К/32К32К 128/1024 16К/16К
Число основных команд 190 188 280 328 120 120
Число уровней пре- рывания 4 1 4 2 8 8
Система команд в СМ-1800 определяется архитектурой микро-про-
цессора КР580ИК80А. Время выполнения команды - 2-8,5 мкс. Мак-
симальный объем памяти (сочетание оперативной и постоянной памя-
ти произвольное) 64К. Максимальное количество адресуемых портов:
ввода-256, вывода-256. Связь с объектом - через аналоговый или ди-
скретный ввод-вывод. Предусмотрена совместная работа нескольких
машин СМ-1800 и совместная работа СМ-1800 с малыми машинами
типа СМ-3, СМ-4.
В номенклатуру микро-ЭВМ СМ-1800 входят 17 модулей, 2 блока
и 5 устройств. Предусмотрено расширение номенклатуры до 40 наиме-
нований, в том числе освоение одноплатной ЭВМ на базе микропроцес-
сора К1810ВМ86, имеющего тактовую частоту 5 МГц и 16 разрядов,
благодаря чему значительно повысятся быстродействие и точность
работы микро-ЭВМ в составе АСУ ТП.
Для существенного упрощения процесса подготовки и отладки про-
грамм в микро-ЭВМ используется язык АССЕМБЛЕР - машинно-ори-
ентированней язык, формат операторов которого однозначно соответ-
ствует формату команд микро-ЭВМ. В микро-ЭВМ используются также
языки высокого уровня - универсальные (ФОРТРАН, PL) и специаль-
ные (PL/М, ПАСКАЛЬ). Транслирующая система обеспечивает пере-
вод операторов языков высокого уровня в эквивалентные операторы
ассемблера или в машинные коды.
5.5.2. Агрегатные системы
АСУ ТП могут создаваться с использованием агрегатного комплек-
са средств вычислительной техники на микроэлектронной элементной
базе (АСВТ-М), который представляет собой набор агрегатных уст-
ройств, предназначенных для компоновки информационных и управ-
ляющих вычислительных комплексов (УВК), работающих в реаль-
ном масштабе времени. На их базе могут быть также созданы автомати-
209
Таблица 5.20
Показатель М-6000 М-7000 СМ-1 СМ-2
Максимальный объем оперативной памяти, К байт 64 256 64 256
Объем микропрограммной памяти, Кбайт Время выполнения основных операций, мкс: 8 8 16
сложение с фиксированной запятой 5 2,5 2,5 2,5
умножение с фиксированной запятой 43 11 36,6 10
сложение с плавающей запятой — 35 — 18-40
умножение с плавающей запятой — 35 — 23
зированные системы управления агрегатами, цехами и производства-
ми, а также вычислительные центры. Каждое из устройств АСВТ-М
представляет собой конструктивно и функционально законченное из-
делие с унифицированными входами и выходами. Агрегатный ком-
плекс допускает последующую модернизацию и наращивание систе-
мы управления.
По функциональному назначению вся номенклатура агрегатных
модулей АСВТ-М делится на устройства центрального уцравления и
переработки информации, хранения информации, связи с объектом,
связи с оперативным персоналом, внутрисистемной связи, выхода на
внешние (внесистемные) линии связи, согласоватсли.
В АСВТ-М используют семейства ЭВМ: М-40, М-400, М-6000, М-7000.
Машины централизованного контроля и управления семейства М-40
предназначены для сбора, первичной обработки и регистрации инфор-
мации, многоканального двухпозиционного регулирования, вывода
информации на цифровые индикаторы и электронно-лучевые труб-
ки. Количество входных каналов 1688 (1000 аналоговых, 688 дискрет-
ных), скорость опроса датчиков с унифицированным выходным сиг-
налом - до 400 каналов в секунду. Процессор машины обладает
быстродействием 600 Ю3 операций в секунду. Объем запоминающе-
го устройства для хранения программ 15 К. Число выходных двухпо-
зиционных каналов управления 960.
Управляющий вычислительный комплекс М-400, который представ-
ляет собой мини-УВМ, нашел применение в системах автоматизации
научного эксперимента, совместно с М-40 - в системах управления тех-
нологическими процессами и сложным оборудованием. Скорость об-
мена информацией по общей шине достигает 800 103 16-разрядных
слов в секунду.
Управляющие вычислительные комплексы М-6000 и М-7000 — наи-
более распространенные из серии АСВТ-М. Они имеют развитую и со-
вершенную систему связи с объектом управления и оперативным пер-
210
Таблица 5.21
Показатель М-400 см-з СМ-4
Оперативная память:
максимальный объем, К байт адресуемая единица памяти 56 56 байт, слово 256
Время цикла обращения, мкс 1,2 1,2 1,2
Количество видов адресации 12 12 12
Время выполнения команд, мкс:
регистр- регистр 3,5 5,0 1,2
регистр- память 6,5 7 2,5
память-память Тип интерфейса 15 10 Общая шина 3,9
Пропускная способность интерфейса, 700 700 800
тыс. слов/с
Система прерывания Приоритетная пятиуровневая
соналом, широкую систему команд и достаточно полное внутреннее
математическое обеспечение. Их основные технические данные приве-
дены в табл. 5.20.
Самая большая модель АСВТ-М — комплекс М-4030. Его вычисли-
тельная мощность позволяет реализовать алгоритмы оптимального уп-
равления сложными технологическими процессами в реальном мас-
штабе времени и параллельно решать задачи информационно-справоч-
ного характера. С объектом управления М-4030 связывается при помо-
щи ЭВМ М-40, М-400, М-6000.
Странами—членами СЭВ выпускаются малые ЭВМ (СМ ЭВМ). В УВК
СМ ЭВМ агрегатные модули выполняются в виде автономных, конст-
руктивно законченных, комплектных блоков с автономным питанием
и встроенной вентиляцией. Они реализованы в соответствии со стан-
дартом Международной электротехнической комиссии (МЭК) и разме-
щены в стандартных стойках без каких-либо конструктивных дора-
боток. Такая реализация значительно упрощает проектную компо-
новку, монтаж, модернизацию и обслуживание СМ ЭВМ по сравнению
с АСВТ-М. В рамках первого направления СМ ЭВМ разработаны УВК
СМ-1 и СМ-2, обеспечивающие преемственность по архитектуре с се-
мействами УВК АСВТ-М. В табл. 5.20 приведены их технические данные.
Второе направление СМ ЭВМ представляют УВК СМ-3 и СМ-4. Они
компонуются на базе процессоров, обеспечивающих преемственность
с семейством М-400 АСВТ-М. Технические данные этих УВК помеще-
ны в табл. 5.21.
Широкий набор периферийных устройств и устройств связи с объек-
том позволяет на базе СМ-3 (СМ-4) компоновать различные конфигу-
рации УВК, предназначенного для систем автоматизации научных ис-
следований и эксперимента, сбора и обработки информации, управ-
ления технологическими процессами малой и средней сложности, чис-
211
нового программного управления станками и оборудованием, автома-
тизированных рабочих мест конструктора, а также иерархических уп-
равляющих структур с микро-ЭВМ ”Электроника-60”, расположенным
непосредственно у технологического оборудования.
СМ ЭВМ построена как агрегатная система средств, позволяющая
компоновать. управляющие вычислительные комплексы с различным
составом оборудования и обеспечивать замену одного устройства дру-
гим аналогичного назначения без изменения общего функционирова-
ния системы.
Для реализации локальных автоматизированных АСУ ТП в различ-
ных отраслях промышленности и непромышленной сфере: черной и
цветной металлургии, химии и нефтехимии, угольной и пищевой от-
раслях, на транспорте-применяется агрегатный комплекс из состава
ГСП — микропроцессорные средства диспетчеризации, автоматики,
телемеханики (й<кро-ДАТ), являющийся дальнейшим развитием вы-
пускаемого комплекса технических средств для локальных информа-
ционно-управляющих систем (КТС ЛИУС-2).
Технические средства комплекса микро-ДАТ выполняют следую-
щие функции: сбор и обработку информации, централизованный кон-
троль’ за ходом технологического процесса; непосредственное цифро-
вое управление технологическими процессами или цифровую коррек-
цию уставок локальных регуляторов; программно-логическое управ-
ление; ручной ввод и отображение технологической информации; пе-
редачу данных меаду территориально рассредоточенными локальны-
ми подсистемами.
‘ По характеру использования КТС ЛИУС-2 и микро-ДАТ относятся
к комплектным агрегатным комплексам. Входящие в их состав бло-
ки и устройства при разработке АСУ ТП не рассматриваются как са-
мостоятельные изделия и применяются только в комплекте. В отли-
чие от них комплексы АСВТ-М являются приборно-блочными, из ко-
торых методом проектной компоновки могут быть созданы АСУ ТП,
имеющие различные структуры в зависимости от числа контролируе-
мых параметров, выбранных алгоритмов управления и специфических
условий применения.
5.5.3. Принципы выбора технических средств
При разработке АСУ ТП необходимо учитывать не только многочис-
ленные технические, но и экономические, производственные, эксплуа-
тационные и другие требования. Удовлетворить совокупность этих
требований можно различными наборами технических средств, степень
удовлетворения отдельных требований зависит от намеченных к исполь-
зованию в АСУ ТП конкретных технических средств.
Следовательно, выбор сводится к сравнению различных вариантов
технического обеспечения разрабатываемой АСУ ТП с учетом разно-
212
образных критериев. По мере усложнения структуры системы число
критериев будет также увеличиваться. Это обусловливает существен-
ные затруднения при выборе наиболее предпочтительного варианта
технических средств. Отсутствие общепринятых количественных крите-
риев и оценочных шкал для сравнения различных вариантов техничес-
кого обеспечения усложняет задачу выбора. Положение усугубляет-
ся также отсутствием общих формализованных процедур выбора на
всех этапах проектирования. Поэтому в подавляющем большинстве
случаев задача выбора технических средств для АСУ ТП решается в
настоящее время эвристическими методами, опирающимися на опыт
и интуицию разработчиков.
В общем случае процедура выбора комплекса технических средств
может быть разделена на два этапа. На первом выбирают конкретный
комплекс из совокупности возможных, изделиями которого пред-
полагается осуществить техническое обеспечение системы. На втором
этапе синтезируют конкретную структуру системы, используя для
этого изделия выбранного комплекса. Исходные данные для выбора:
характеристики объекта управления и требования к системе управле-
ния. За обобщенные характеристики объекта управления принима-
ются:
1) характер технологического процесса (формообразования, транс-
портировки, изменения агрегатного или химического состава);
2) протекание технологического процесса во времени (непрерыв-
ный или дискретный);
3) протяженность объекта (клеть, станок, станочная линия, непре-
рывная группа клетей);
4) особенности регулирующих и исполнительных механизмов (уси-
лия или моменты при регулировании, точностные показатели);
5) особенности окружающей среды (агрессивность, вибрация);
6) требования по взрыво- и пожаробезопасности;
7) перспективы развития и модернизации технологического про-
цесса.
Требования к системе управления:
1) уровень иерархии;
2) количество измеряемых и регулируемых параметров, а также
обоснование точности соблюдения режимных величин;
3) выполняемые функции (одноконтурное или многосвязное авто-
матическое регулирование, оптимизация в статике или (и) динамике,
оптимальное управление с адаптацией);
4) связь с другими системами;
5) перспективы развития системы управления.
Результаты первого этапа выбора зависят, главным образом, от
пп. 1, 2, 3, 7 характеристик объекта и пп. 2, 5 требований к системе.
Результаты второго этапа в основном определяются пп. 1, 3, 4 требова-
ний к системе.
213
Процедура выбора технических средств представляет собой итера-
ционный процесс, в ходе которого осуществляется многоступенчатый
отбор возможных вариантов решения поставленной задачи. Завершает
этот процесс проверка по технико-экономическим показателям.
Глава шестая
ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ АСУ ТП
6.1. ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ АСУ ТП
Технологический объект управления и взаимодействующая с ним
АСУ ТП составляют автоматизированный технологический комплекс
(АТК). АСУ ТП включает: техническое, программное, информацион-
ное обеспечение как совокупность средств сбора, переработки техно-
логической информации и преобразования ее в управляющее воздей-
ствие.
Техническое обеспечение - комплекс технических средств (КТС)
включает устройства: получения информации о технологических па-
раметрах и состоянии технологического оборудования; формирова-
ния и передачи информации в системе, локального регулирования и
управления; вычислительной техники; представления информации
обслуживающему персоналу; передачи информации в смежные и выше-
стоящие АСУ; а также исполнительные устройства, в основном АСУ
ЭП, гидравлические и пневматические системы.
Программное обеспечение состоит из общего программного обес-
печения, поставляемого вместе со средствами вычислительной техни-
ки (организующие программы, транслирующие программы, библиоте-
ка стандартных подпрограмм и др.); специального программного обе-
спечения, представляющего собой совокупность программ, которые
реализуют функции данной АСУ ТП и обеспечивают заданное функцио-
нирование комплекса технических средств.
Информационное обеспечение АСУ ТП включает в себя единую си-
стему кодирования технологической и технико-экономической инфор-
мации, справочную и оперативную информацию.
Спецификой проектирования АСУ ТП является применение систем-
ного подхода, эффективность которого возрастает с увеличением слож-
ности и размеров системы. Системный подход состоит в том, что разра-
батываемая АСУ ТП рассматривается как сложное целое со свойства-
ми, не всегда присущими ее составляющим, структура и состав кото-
рых описаны выше. При системной разработке идут от общего к част-
ному. Общей задаче, сформулированной для системы в целом, под-
чиняются задачи, решаемые отдельными ее составляющими.
Основные положения системного подхода заключаются в следую-
щем.
214
1. Четко и конкретно формулируются задачи, поставленные при
разработке АСУ ТП, ее назначение в общей структуре управления про-
мышленным предприятием; устанавливаются критерии эффективнос-
ти применения АСУ ТП. Это позволяет определить иерархические гра-
ницы системы в соответствии с техническим объектом управления
(механизм, комплекс механизмов, линия, участок, цех и т.д.). Выяв-
ляются задающие (управляющие) воздействия, поступающие на вход
АСУ ТП от системы высшего ранга или от смежных систем. Опреде-
ляются возможные возмущающие воздействия, которые приклады-
ваются к технологическому объекту управления.
2. В структуре АСУ ТП и технологического объекта управления вы-
деляются подсистемы и отдельные элементы и устанавливаются связи
между ними. Подсистемы могут выделяться по однородности физичес-
кой природы технологии. Элементы системы обычно отождествляются
с отдельными механизмами или транспортными устройствами и выде-
ляются по их специализации на конкретной операции. Связи между эле-
ментами формируются в результате расчленения (декомпозиции) об-
щей системной задачи.
3. Отражением системного подхода является иерархический прин-
цип организации управления, описанный в гл. 1. Задания узловым си-
стемам формируются централизованными УВМ исходя из оптимиза-
ции технологического процесса всего комплекса. В свою очередь УВМ
отдельных узлов, оптимизируя выполнение полученной уставки, рас-
пределяют управляющие воздействия локальным АСУ ТП и АСУ ЭП.
Иерархичность (подчиненность) проявляется здесь в том, что получен-
ная данным уровнем уставка обязательна для выполнения и не под-
лежит коррекции.
4. Индивидуальная разработка и изготовление большинства элемен-
тов допустимы лишь при создании уникальных и специальных систем,
когда оптимальный режим работы АСУ ТП обеспечивается оптималь-
ными режимами составляющих ее элементов.
Промышленные АСУ ТП должны проектироваться на базе типовых
элементов.
5. Повышение эффективности АСУ ТП достигается в процессе комп-
лексного проектирования, при котором обеспечивается увязка функцио-
нирования всех подсистем в интересах поставленной цели — автомати-
зации технологического процесса.
В результате изучения материала главы студент должен знать основ-
ные этапы разработки АСУ ТП и детально те из них, в которых непосред-
ственно принимает участие специалист в области электропривода; сту-
дент должен уметь выбрать наиболее рациональный путь разработки
различных типов АСУ ТП и сформулировать задачи, стоящие непосред-
ственно перед ним и в смежных с электроприводом областях.
215
6.2. СТАДИИ РАЗРАБОТКИ АСУ ТП
Разработка АСУ ТП от возникновения идеи до ввода ее в эксплуата-
цию - процесс трудоемкий и длительный. ГОСТ 20913-75 определяет
пять стадий создания АСУ ТП: разработка технического задания, вы-
полнение технического проекта, разработка рабочего проекта, внедре-
ние и анализ функционирования.
Состав и содержание технического задания. При разработке техни-
ческого задания выделяется четыре этапа.
1. Обследование технологического объекта управления, изучение и
определение необходимого объема научно-исследовательских работ
(НИР) и плана-графика проведения этих исследований.
2. Этап выполнения предпроектных НИР. Они включают анализ тех-
нологического процесса и оборудования как объекта управления и
анализ информационных потоков: на этой основе формулируются кри-
терии управления и ограничения. На стадии предпроектных НИР разра-
батываются также предварительные математические модели техноло-
гического процесса, осуществляется идентификация моделей по экспе-
риментальным данным и- предварительно выбираются методы синтеза
алгоритмов функционирования и управления.
3. Эскизная разработка АСУ ТП. Она содержит предварительные раз-
работки функционально-алгоритмической структуры системы, синтез
основных алгоритмов контроля и управления и их эксперименталь-
ную проверку, на этом этапе выбираются технические средства систе-
мы и дается обоснование выбора, определяются задачи модернизации
технологического оборудования и совершенствования технологическо-
го процесса, осуществляется сравнительный анализ разрабатываемой
системы и ее известных аналогов.
4. Собственно разработка технического задания на создание АСУ ТП.
Она включает в себя: формирование полного перечня функциональ-
ных задач, решаемых системой; разработку технико-экономического
обоснования ее создания; составление плана-графика работ по монта-
жу, наладке и пуску АСУ ТП; виды и объемы НИР на стадиях проекти-
рование, внедрения системы и в процессе ее функционирования.
Стадия технического проектирования. Она состоит из ряда этапов.
1. Системотехнический синтез АСУ ТП. Он включает разработку
функциональной структуры системы, постановку всех решаемых за-
дач, разработку перечня измеряемых сигналов и метрологические ха-
рактеристики измерений; в нем формулируются технические требова-
ния к системам контроля и регулирования; разрабатывается информа-
ционная и организационная структура системы.
2. Аппаратурно-технический синтез. На этом этапе разрабатываются
системы локальной автоматики, состав и компоновка информацион-
но-управляющего комплекса.
3. Разработка заданий на модернизацию технологического объекта
управления и строительно-монтажные работы.
216
Ряд этапов предусматривает подготовку заявок на стандартное и
нестандартное оборудование, составление сметы и ведомостей средств
технического обеспечения. Отдельные этапы технического проектирова-
ния включают расчет ожидаемой технико-экономической эффектив-
ности АСУ ТП и ее сравнительный анализ с известными аналогами.
Составляется патентный формуляр АСУ ТП. Заключительным этапом
стадии технического проекта является техническое проектирование
специального информационного и математического обеспечения АСУ
ТП. На этом этапе разрабатываются полные наборы алгоритмов кон-
троля и управления, общий алгоритм функционирования системы в
реальном времени и осуществляется их проверка на объекте или мо-
дели. Осуществляется разработка схем сбора и обработки информа-
ции.
Если выбор некоторых технических решений при нескольких вариан-
тах возможен лишь после проверки их на физической или математи-
ческой модели, составляется эскизно-технический проект, включаю-
щий стадию моделирования.
Рабочее проектирование. Оно осуществляется на основании мате-
риалов технического проекта. Рабочее проектирование также состоит
из нескольких этапов. Основным является этап разработки рабочей
документации технического обеспечения АСУ ТП. Отдельными этапа-
ми рабочего проекта являются: составление заказных спецификаций;
подготовка инструкции по эксплуатации, технического описания и
регламента работы АСУ ТП с учетом действия оперативного персо-
нала в предаварийных и аварийных режимах.
Следующим этапом, который может идти параллельно с предыду-
щими, будет разработка рабочей документации на программное и ин-
формационное обеспечение АСУ ТП. Сюда входят: программирование
алгоритмов специального математического обеспечения, описание и
инструкции по пользованию этими программами, подготовка таблиц
использования памяти ЭВМ, перечень всех программ, входящих- в мате-
матическое обеспечение, уточнение схем сбора, обработки и выдачи
информации и разработка полной документации по организации нор-
мативно-справочной информации.
Этот комплекс разработок в процессе рабочего проектирования вы-
полняется инженерами-электроприводчиками и инженерами-вычислите-
лями, а также сметчиками.
Стадия внедрения АСУ ТП предусматривает пять этапов.
1. Проведение комплекса организационно-технических мероприя-
тий, связанных с внедрением системы и обучением ремонтно-эксплу-
атационного персонала. На этих работах инженер-электроприводчик
выступает в роли соисполнителя с инженерами-технологами, специа-
листами в области электронной техники, автоматики, вычислитель-
ной техники. К этому этапу относится также модернизация техноло-
гического оборудования. На нем инженер-электроприводчик выступа-
217
ет в роли консультанта либо соисполнителя, если приходится сущест-
венно изменять АСУ ЭП.
2. Наладка АСУ ТП. Она слагается из собственно наладки техничес-
ких средств, отладки программ решения отдельных функциональных
задач (информационной и управляющей), отладки программы, реали-
зующей полный алгоритм функционирования системы.
3. Опытная эксплуатация АСУ ТП. Она начинается с включения си-
стемы. Определяются ее эксплуатационные характеристики, проводит-
ся дополнительная отладка программ и технических средств управле-
ния и вновь корректируется эксплуатационная документация. Во всех
этих работах принимает участие инженер-электроприводчик.
4. Приемо-сдаточные испытания. Разрабатывается программа, в соот-
ветствии с которой проводятся промышленные испытания, оформляют-
ся их результаты и проводится анализ этих результатов.
5. Доработка системы по результатам опытной эксплуатации и про-
мышленных испытаний.
Анализ функционирования АСУ ТП. Это заключительная стадия со-
здания системы. Она включает исследования фактической технико-
экономической эффективности системы, разработку рекомендаций по
ее развитию и совершенствованию и выработку требований к модерни-
зации технологического процесса.
6.3. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ АСУ ТП
РАЗЛИЧНОГО ИСПОЛНЕНИЯ
Исполнение АСУ ТП тесно связано с выполняемыми ею функциями,
поэтому рассматриваются эти функции для того, чтобы вместе с мате-
риалом, изложенным в § 6.2, определить особенности проектирования
систем различного исполнения.
Из совокупности выполняемых АСУ ТП функций наиболее важны-
ми являются: централизованный контроль, обработка информации,
вычислительные и логические операции информационного характера,
управляющие воздействия. Все они сводятся к передаче информации
для визуальной оценки, переработки ее до уровня информации-совет-
чика, использованию информации для целей управления.
1. Централизованный контроль. К нему относятся:
1.1. Непрерывное, периодическое либо по вызову измерение и ре-
гистрация значений технологических параметров и показателей со-
стояния технологического оборудования.
1.2. Обнаружение, регистрация и сигнализация отклонений от за-
данных пределов значений технологических параметров и показате-
лей технологического оборудования.
1.3. Оперативное отображение и регистрация результатов обработ-
ки информации, выполняемых комплексом технических средств си-
стемы.
218
1.4. Контроль, регистрация и сигнализация срабатывания блокиро-
вок и защит.
2. Обработка информации. К ней относятся:
2.1. Косвенное измерение технологических параметров и показате-
лей состояния технологического оборудования.
2.2. Вычисление и анализ обобщенных показателей оценки текуще-
го состояния объекта управления и его подсистем.
2.3. Анализ срабатывания блокировок и защит.
2.4. Диагностика протекания и прогнозирование хода технологи-
ческого процесса и состояния оборудования.
2.5. Расчет технико-экономических и эксплуатационных показате-
лей работы технологического объекта управления.
2.6. Подготовка информации и обмен ею со смежными и вышестоя-
щими АСУ ТП.
3. Управляющие функции АСУ ТП. К ним относятся:
3.1. Выбор оптимального режима технологического процесса в соот-
ветствии с целями системы.
3.2. Формирование сигналов управления для поддержания оптималь-
ного режима работы объекта управления.
3.3. Выдача оператору рекомендаций по управлению технологичес-
ким процессом.
Необходимым условием принадлежности системы к АСУ ТП являет-
ся обязательное выполнение ею информационных и управляющих функ-
ций в минимальном объеме, соответствующем пп. 1.1, 1.2, 1.3, 2.6,
3.1 и 3.2. Это обязательное сочетание может наращиваться в зависи-
мости от целей построения АСУ ТП различных вариантов. Оно предус-
матривает работу системы в режиме прямого управления, при котором
обеспечивается непосредственное воздействие на ход технологического
процесса путем передачи сигналов управления непосредственно испол-
нительным устройствам.
Все АСУ ТП по схеме создания делятся на следующие типы:
1) вновь разрабатываемые для ряда однотипных или близких по
технологии процессов и оборудованию технологических объектов уп-
равления (повторяющиеся);
2) вновь разрабатываемые без повторения;
3) типовые системы;
4) повторно реализуемые.
Для повторяющихся АСУ ТП выполняются все стадии создания и
все этапы, описанные в § 6.2. При оценке однотипности технологичес-
ких процессов необходимо исходить из соответствия математических
моделей технологическим объектам управления.
Для разработки систем без повторения исключается стадия анализа
функционирования в процессе эксплуатации, так как в последующем
такие АСУ ТП не будут повторяться, а следовательно, нет необходи-
мости нести дополнительные затраты.
219
РИС. 6.1. Структура САПР АСУ ТП
При проектировании типовых
АСУ ТП исключаются стадии внед-
рения и анализа. В зависимости от
выполняемых функций по согла-
сованию с заказчиком могут быть
сокращены отдельные этапы, ука-
занные в § 6.2. Разрабатывая эти
типовые АСУ ТП, нельзя идти
по пути непосредственного повто-
рения, особенно в плане форми-
рования аппаратной части.
Для повторно реализуемых систем сокращается объем НИР и осу-
ществляется одностадийное проектирование с выпуском технорабо-
чего проекта, объединяющего вторую и третью стадии создания АСУ
ТП. Техническое задание для таких систем составляется на основе пред-
варительного обследования технологического процесса. Оно предусмат-
ривает в качестве основного собственно разработку технического за-
дания. Технический проект включает только определение структуры
и выбор аппаратуры АСУ ТП и техническое проектирование специаль-
ного математического и информационного обеспечения.
Особенность разработки АСУ ТП на уровне локальных и узловых
систем состоит в их расчленении на отдельные элементы со строго оп-
ределенной целевой функцией каждого из них. В связи с этим при раз-
работке АСУ ТП могут быть использованы типовые решения систем
автоматизированного проектирования (САПР) каждого элемента си-
стемы. Исходя из структурной схемы рис. 1.2, можно рассматривать
следующие элементы: технологический объект управления, устройство
связи с объектом, процессор, устройство кодирования и преобразова-
ния информации, информационную часть системы. Электропривод
может включаться в состав технологического объекта управления ли-
бо рассматриваться самостоятельно.
Построение САПР каждого элемента включает: постановку задачи
проектирования исходя из общих требований к АСУ ТП; выбор исход-
ного варианта по ранее выполненным установкам; моделирование;
формализацию описания частных элементов и расчет целевой функции;
сопоставление результатов с заданием и логическую операцию перехода
к оформлению результатов, если выбранные параметры или схема
удовлетворяют заданным требованиям либо осуществляется измене-
ние параметров, если эти требования не удовлетворяются. На стадии
220
изменения параметров или схемы лучшим вариантом является диало-
говый режим, при котором опыт разработчика, его интуиция сущест-
венно сокращают время проектирования.
Известны разработки САПР средств измерения, дискретных уст-
ройств, мини- и микро-УВМ и др. Все они доводятся до выдачи графи-
ческой, текстовой и заказной документации, что существенно облег-
чает процесс разработки АСУ ТП. Получение частных решений являет-
ся лишь одним из промежуточных этапов применения САПР. Систем-
ный подход предполагает изучение поведения системы до окончания
разработки. Проверка работоспособности АСУ ТП выполняется на мо-
дели, которая может быть использована также для уточнения алгорит-
ма управления путем внесения изменений по результатам сопоставле-
ния требуемого закона функционирования и полученного при моде-
лировании. В этом случае в основу сопоставления должна быть поло-
жена целевая функция всей системы. Как и при решении частных задач,
наиболее удобной формой логической части САПР является диалого-
вый режим.
На рис. 6.1 приведена одна из возможных структур построения САПР
АСУ ТП. В машину вводятся технические условия и в формализован-
ном виде воспроизводится исходный вариант проектируемого элемен-
та системы либо части системы. По этим данным формируется модель
либо целевая функция, которые сравниваются с заданными моделью
или целевой функцией. Логический блок осуществляет сравнение по
заданной точности; если погрешность оказывается недопустимой, по-
дается сигнал на уточнение параметров либо изменение алгоритма.
На экран дисплея могут быть вызваны заданные и достигнутые в
процессе проектирования модели или целевые функции, поэтому пред-
ставляется возможность вести проектирование в режиме диалога. Ме-
няя параметры схемы либо алгоритм управления, проектант добивает-
ся желаемой точности совпадения результатов, полученных при про-
ектировании, с заданными. При совпадении результатов ЭВМ перехо-
дит к выдаче графической, текстовой и заказной документации.
Глава седьмая
НАДЕЖНОСТЬ АСУ ТП
7.1. ПОСТАНОВКА ЗАДАЧИ. ОСНОВНЫЕ ПОНЯТИЯ
Одним из наиболее важных свойств АСУ ТП, обеспечивающих высо-
кую технико-экономическую эффективность функционирования си-
стемы, является ее надежность.
Под надежностью АСУ ТП понимают способность системы выпол-
нять заданные функции, сохраняя во времени значения установленных
эксплуатационных показателей, определенных в заданных пределах
221
при заданных условиях эксплуатации. Надежность АСУ ТП является
комплексным свойством, включающим безотказность, ремонтопри-
годность и долговечность.
Безотказность — свойство системы сохранять работоспособность в
течение некоторого периода времени (наработки) без вынужденных
перерывов. Ремонтопригодность — приспособленность системы к пред-
упреждению, обнаружению и ликвидации отказов. Для безотказности
характерными являются закономерности возникновения отказов,
в то время как для ремонтопригодности - закономерности их устра-
нения. Долговечность — свойство системы сохранять работоспособ-
ность до некоторого предельного состояния (с перерывами на техни-
ческое обслуживание и ремонты). Показателями долговечности яв-
ляются ресурс и срок службы, т.е. суммарная наработка и календар-
ная продолжительность эксплуатации изделия до предельного состоя-
ния.
Важнейшим понятием является отказ в работе системы, происходя-
щий в результате нарушения нормального функционирования одного
или нескольких ее элементов.
Совершенствование АСУ ТП связано с увеличением количества и ка-
чества выполняемых ею функций, что приводит к усложнению систе-
мы и повышает убыток при отказе в работе. При этом в АСУ ТП увели-
чивается количество элементов, что приводит к существенному умень-
шению ее надежности, если ее элементы включены последовательно.
Использование резервных элементов неизбежно повышает стоимость
всей системы. В связи с этим проблема надежности АСУ ТП при ее
создании является одной из важных.
В результате изучения материала, изложенного в настоящей главе,
студент должен знать основные положения теории надежности и уметь
выполнить расчет надежности АСУ ТП в процессе ее разработки, рассчи-
тать надежность отдельных узлов системы и дать рекомендации по ее
повышению до требуемого уровня.
ГОСТ 20913-75 определяет установление требуемых показателей
надежности на стадии разработки технического задания. Рекомендует-
ся на этой стадии разработки АСУ ТП составлять программу обеспече-
ния надежности системы. В нее должны быть включены:
сбор и анализ данных о режимах и условиях работы АСУ ТП, орга-
низации технического обслуживания и надежности технологического
объекта управления, изучение видов и последствий его отказов, оп-
ределение предварительных технологических требований к надежнос-
ти системы;
анализ функций разрабатываемой АСУ ТП и определение критериев
отказов по каждой из них и по системе в целом;
определение требований к надежности, вносимых в техническое
задание, и выбор методов оценки надежности на стадиях создания си-
стемы;
222
изучение вариантов построения АСУ ТП, состава используемых тех-
нических средств и оценка показателей надежности каждого из ва-
риантов;
разработка основных правил технической эксплуатации и уточне-
ние расчета показателей надежности АСУ ТП на стадии технического
проектирования;
сбор данных о надежности в условиях эксплуатации, оценка надеж-
ности и разработка рекомендаций по ее повышению на стадии анализа
функционирования АСУ ТП.
Системы могут быть ремонтируемыми и перемонтируемыми.
АСУ ТП, являясь ремонтируемыми системами, имеют срок службы
(ресурс), который определяется не физическим износом и старением
ее элементов, так как они могут быть заменены другими, а снижением
эффективности ее работы и целесообразностью дальнейшей эксплуата-
ции. Поэтому надежность системы достаточно полно определяется сово-
купностью свойств безотказности и ремонтопригодности.
Процесс функционирования АСУ ТП можно представить в виде после-
довательно чередующихся интервалов работоспособности и простоя.
Продолжительность интервалов является непрерывной случайной вели-
чиной, которая может характеризоваться функциями распределения
или плотностями вероятностей; в связи с этим теория надежности
использует математический аппарат теории вероятностей, теории слу-
чайных процессов и математической статистики.
Рассматривая процессы функционирования систем и входящих в их
состав устройств в виде потоков случайных событий (например, пото-
ков отказов элементов и устройств), обычно полагают, что потоки
отказов являются простейшими (пуассоновскими), обладающими
одновременно свойствами ординарности, стационарности и отсутствия
последействия. У ординарного потока отказов вероятность появления
в некоторый момент времени более одного отказа пренебрежимо мала.
Поток отказов называют стационарным, если вероятность появления
некоторого числа отказов в интервале времени t — (t + Af) зависит
Только от Аг и не зависит от t. Отсутствие при этом последействия оз-
начает, что отказы являются случайными и независимыми друг от
друга.
Для ремонтируемых систем критериями безотказности являются
вероятности наработки между отказами Р(г) больше заданного зна-
чения времени Т, параметр потока отказов системы X(Z) и наработка
на отказ Тн, под которой понимается средняя продолжительность рабо-
ты системы между двумя последовательными отказами. Величина Р (Г)
является важнейшим показателем надежности ремонтируемых систем
и определяет вероятность того, что наработка Тп между отказами пре-
взойдет заданное время Т:
Р(Т) = Р<ТН > Т).
223
Показателями ремонтопригодности являются вероятность Р(Т3)
восстановления системы за заданное время Т3 и среднее время восста-
новления Гв, которое определяет средние затраты времени на обнару-
жение и устранение отказа при заданных условиях обслуживания.
Помимо перечисленных показателей безотказности и ремонтопри-
годности используются комплексные показатели: коэффициент готов-
ности кг и коэффициент технического использования £т>и. Коэффици-
ент готовности для установившегося режима работы системы опреде-
ляет вероятность того, что система исправна в любой произвольно вы-
бранный момент времени в промежутках между плановым профилак-
тическим обслуживанием и оценивается отношением времени наработ-
ки на отказ к средней длительности цикла работа — восстановление:
кг = ТН/(ТН + ТВ).
Вероятностный смысл коэффициента fcT>If такой же, как и кг, но в
нем учитывается время планового профилактического обслуживания
Гпр. Он оценивается отношением времени наработки на отказ к средней
длительности цикла работа - восстановление — профилактика:
^т,и = ГН/(ТН + Гв + ^Пр)’
Главная особенность систем состоит в том, что оценка качества их
функционирования производится с учетом экономического критерия.
Вот почему состояние подобных систем в процессе эксплуатации сле-
дует характеризовать с помощью функции, связанной с экономичес-
ким эффектом от их использования в течение установленного срока
службы (ресурса) Гр. Такой случайной функцией могут служить убыт-
ки (экономические потери), которые зависят от количества и послед-
ствий отказов.
Для успешного функционирования системы требуется исправное
действие всех ее элементов. Такими свойствами обладают наиболее
простые системы из числа удовлетворяющих требованиям, предъяв-
ляемым к процессу управления. Вероятность безотказной работы си-
стемы Д(0 зависит от вероятностей безотказной работы элементов
Л’ (О и (ПРИ независимости отказов) определяется по формуле
P(t) = п рдо.
1= 1
где N — количество элементов.
Для обеспечения надежной работы системы, содержащей большое
число элементов, весьма эффективным является введение понятия
избыточности системы.
Различают структурную и информационную избыточность. Структур-
ная избыточность определяется наличием дополнительных путей пере-
224
дачи сигналов; поэтому при отказе одного из элементов его функции
выполняет другой элемент, который не является необходимым при
исправной работе основного. Введение структурной избыточности яв-
ляется одним из основных методов, позволяющих создать высокона-
дежную систему из элементов с недостаточно высокой надежностью.
Это достигается за счет рационального применения избыточных эле-
ментов и способов их соединения.
Информационная избыточность определяется наличием в сигнале
дополнительной информации. Надобность в ней возникает при отказе
ряда элементов. Она не используется при нормальной работе всех эле-
ментов. Введение избыточности увеличивает надежность системы за
счет повышения ее безотказности.
Повышение ремонтопригодности может быть достигнуто в случае
применения унифицированных блочных конструкций, устройств диаг-
ностики и индикации отказов.
7.2. РАСЧЕТ НАДЕЖНОСТИ В ПРОЦЕССЕ ПРОЕКТИРОВАНИЯ
На этапах разработки технического задания и технического проек-
тирования для обеспечения требуемого уровня или прогноза ожидае-
мого уровня надежности применяются аналитические инженерные ме-
тоды анализа и расчета надежности. Цель расчета — определение по-
казателей надежности системы и разработка мероприятий по ее повы-
шению, в результате чего должен быть обеспечен ее необходимый уро-
вень. На стадии проектирования отсутствуют экспериментальные ста-
тистические данные, которые могут быть получены при испытаниях
и эксплуатации системы. Только при эксплуатации системы можно
оценить надежность более достоверно. Поэтому для анализа надеж-
ности приходится использовать априорную информацию и гипотетичес-
кие математические модели, отражающие вероятностные процессы
функционирования исследуемых реальных систем.
Для анализа надежности используется ограниченное число матема-
тических моделей, которые учитывают только наиболее важные (с точ-
ки зрения надежности) свойства процессов функционирования систем
(и составляющих их элементов). Надежность элементов полностью ха-
рактеризуется законом распределения времени безотказной работы.
В качестве этих законов могут быть использованы распределение Вей-
булла, гамма-распределение, их частный случай - экспоненциальное
распределение, а также нормальное распределение.
Экспоненциальное распределение является одним из наиболее рас-
пространенных при исследовании надежности АСУ ТП. Постоянство
интенсивности отказов означает, что вероятность отказа не зависит от
того, сколько времени проработало устройство до рассматриваемого
момента. Это характерно для периода нормальной работы системы,
так как при правильно организованной эксплуатации и профилактике
225
АСУ ТП потоки отказов элементов близки к простейшим. Если систе-
ма подошла к периоду износа или старения, закон распределения вре-
мени безотказной работы близок к нормальному.
Хотя надежность систем определяется сочетанием свойств безот-
казности и ремонтопригодности, ремонтопригодность как слагаемое
надежности играет подчиненную роль. В связи с этим в дальней-
шем основное внимание уделяется оценке свойства безотказности
систем.
Существует несколько методов анализа надежности на стадии про-
ектирования: по среднегрупповым значениям интенсивностей отказов;
с использованием данных эксплуатации; коэффициентный метод. Все
они базируются на экспоненциальном распределении (модель отказов
элементов и систем) и распределении Эрланга (модель восстановления
систем), а их применение предполагает последовательное соединение
элементов в системе.
Для расчета надежности по среднегрупповым значениям интенсив-
ности отказов исходными являются усредненная (по множеству эле-
ментов данной группы z) интенсивность отказов X/ и количество та-
ких элементов Nj в системе: Возможная интенсивность отказов указы-
вается в таблицах, приводимых в литературных источниках по надеж-
ности с указанием диапазона значений Ху. При расчете обычно использу-
ют средние значения Ху. Режимы работы и условия окружающей среды
учитываются с помощью зависимостей Ху от значения соответствующе-
го фактора. Если система разбита на г групп с примерно одинаковыми
интенсивностями отказов внутри группы, то параметр потока отказов
системы X и наработка на отказ Тн определяются по формулам
г
Х= S TVyXy; Гн = 1/Х.
i = 1
Метод расчета надежности с использованием данных эксплуатации
предполагает наличие статистических данных о надежности систем, схо-
жих по конструкции и назначению. Известны две разновидности рас-
сматриваемого метода расчета: по среднему уровню надежности одно-
типных систем; с использованием коэффициентов пересчета в соответ-
ствии с реальными условиями эксплуатации.
Первая разновидность метода предполагает равенство средних интен-
сивностей отказов элементов системы — аналога и проектируемой.
Исходными являются данные о наработке на отказ Тн а и количестве
элементов 7Va системы-аналога и количестве элементов 7Vn проектируе-
мой системы. При равенстве средних значений интенсивностей отказов
и при одинаковом соотношении чисел элементов разных типов в сопо-
ставляемых системах наработка на отказ ТНЛ1 и параметр потока отка-
зов проектируемой системы определяются соотношениями
226
- ЗГН>П = ^H,aJ
Nn
= 1/7н,п-
7н,а “
(7.1)
Вторая разновидность метода предполагает идентичность условий
эксплуатации и однотипность проектируемой и аналоговой систем.
Она основана на усредненном учете условий эксплуатации путем со-
поставления расчетных Тн>а и опытных Гн'а значений наработки на от-
каз с помощью коэффициента а = Тц^/Тп а. Для этой разновидности
расчета требование равенства соотношения чисел элементов разных ти-
пов в сопоставляемых системах снимается. Расчетное значение наработ-
ки на отказ системы-аналога определяется по табличным значениям
Интенсивностей отказов X/ [10] при некоторых фиксированных усло-
виях и режимах работы:
г
S Nu\t
i = 1
Наработка на отказ и параметр потока отказов проектируемой системы
при тех же условиях эксплуатации определяются по формуле
^н,п =
а Хп - по формуле (7.1).
При коэффициентном методе расчета надежности для определения
ее показателей вместо абсолютных значений Хг- интенсивностей отказов
используются относительные значения (коэффициенты надежности
представляющие собой отношения интенсивностей отказов /-го
и некоторого базового элементов kj = Л,-/Лб- Для базового элемента
должны быть хорошо известны показатели надежности, поэтому в ка-
честве базового элемента целесообразно принимать резисторы или кон-
денсаторы.
Для расчета показателей надежности системы необходимо знать ко-
эффициенты kj составляющих ее элементов, число элементов каждого
типа и интенсивность отказов Xg базового элемента в заданных усло-
виях эксплуатации. Параметр потока отказов системы определяется
по формуле
г
X = Хб S Ni к- .
i= 1
Рассмотренные методы расчета позволяют на стадии проектирования
оценцть ожидаемый уровень надежности системы при известных по-
казателях надежности элементов.
227
Коэффициентый метод расчета надежности весьма прост. Он предпо-
лагает знание коэффициентов надежности элементов и абсолютного
значения интенсивности отказов базового элемента. Установлено, что
коэффициенты надежности элементов kj, определенные по данным,
опубликованным в различных работах, практически совпадают (при
резком различии абсолютных значений интенсивностей отказов), ес-
ли в качестве Xg в каждом случае использовать параметр базового
элемента, приведенный в этих же работах.
Поэтому коэффициентный метод позволяет рассчитывать надеж-
ность системы со сравнительно высокой степенью точности.
7.3. ТЕХНИКО-ЭКОНОМИЧЕСКИЙ УРОВЕНЬ НАДЕЖНОСТИ АСУ ТП
Уровень надежности АСУ ТП в значительной степени определяет
экономическую эффективность системы. При снижении надежности
возрастают потери от отказов, а ее повышение приводит к увеличе-
нию стоимости системы и затрат на ее эксплуатацию. Поэтому при ре-
шении вопроса об экономически целесообразном значении надежнос-
ти системы в заданных условиях эксплуатации необходимо устано-
вить технико-экономический критерий оптимизации надежности.
При определении экономически целесообразного уровня надежнос-
ти системы рассматривают ряд структурно и функционально схожих
вариантов, обладающих разными уровнями надежности при различ-
ной величине капитальных и эксплуатационных затрат. Выбор лучшего
варианта производят по максимуму народнохозяйственной эффектив-
ности, измеряемой годовым дополнительным экономическим эффек-
том:
Эн = (ДСП - max,
где ДСП - годовая экономия от снижения себестоимости изготовле-
ния продукции при внедрении проектируемой системы; Ен — норматив-
ный коэффициент эффективности капиталовложений; ЁНД£ - нор-
мативная народнохозяйственная экономия от использования дополни-
тельных капиталовложений.
В качестве критерия часто используют величину дополнительного
эффекта за срок службы системы Гсл:
Эт = (ДСдГэ - Д£) -► max. (7.2)
Эта величина равна разности экономии за счет понижения себестои-
мости ДСд (без учета амортизационных отчислений) и дополнитель-
ных капитальных затрат, от которых эта экономия получена. В (7.2)
Т3 — эквивалентный срок службы, рассчитываемый по выражению
— Е н Т р п
Тэ=(1-е СЛ)/£Н.
228
Дополнительный экономический эффект от повышения надежности
аистемы за счет уменьшения среднего числа отказов складывается из
соответствующих эффектов за счет снижения среднего числа отказов
элементов, откуда следует, что надежность системы достигает опти-
мального уровня при условии, если каждый из ее элементов будет
иметь оптимальную интенсивность отказов
Показатели системы \Opt и ее *’го элемента назовем оптимальны-
ми. При них дополнительный экономический эффект в течение срока
службы будет наибольшим. В этом случае
N
\>pt “ \'орг
/ = 1
Повышение надежности АСУ ТП является средством снижения себе-
стоимости продукции, которое может быть достигнуто только за счет
уменьшения условно-постоянных расходов, приходящихся на единицу
выпускаемой продукции.
Стоимость годовой эксплуатации системы 3 может быть представле-
на в виде двух составляющих, одна из которых не зависит от надежнос-
ти, а другая является ее функцией: 3 = 3'+ 3" (X), где вторая составляю-
щая определяется произведением ожидаемого числа отказа за год и сред-
ней стоимости восстановления системы Св.
Если рассмотреть исходную систему с параметром надежности Хи и
вариант проектируемой системы с параметром Хп, причем Хи > Хп,
то стоимость эксплуатации этих систем за единицу времени можно
представить в виде соотношений
Зи = Зи + Зи (Хи );
Зп = Зп + Зп (Хп)*
При использовании варианта системы вместо исходного годовая
экономия на расходах по эксплуатации составит
t АСд,э = Зи - Зп = Св>и Хи - Св>п хп.
Если отказы системы обусловлены только отказами /-го элемен-
та, то получим выражение годовой экономии расходов на эксплуата-
цию системы, обусловленную повышением надежности элемента от
исходного значения Хи , до проектируемого Хп/:
АСд,э = Д^д,э/ = Св/ (Хи - Хп) = Св j (Хи j — Хп/- ),
где Св/ — средняя стоимость восстановления /-го элемента, пример-
но одинаковая для обеих систем.
Найдем годовую экономию от сокращения потерь, вызванных про-
стоями системы. Убытки — это условно-постоянные затраты (не зави-
229
сящие от объема производства продукции) за время простоя. Потери
удобно разделить на ущерб и убытки. Ущерб выражется стоимостью
испорченной продукции, сырья, оборудования в результате нарушения
технологического процесса, вызванного отказом. Если за год ожидает-
ся в среднем X отказов системы и на восстановление каждого отказа
затрачивается среднее время Тв, то потери от простоев будут
П = (ВТв + Я) X,
где В - условно-постоянные расходы в единицу времени; Я- средний
ущерб от одного отказа системы.
Годовая экономия от применения системы с повышенным уровнем
надежности ДСд,п определяется разностью потерь от простоев исход-
ной и проектируемой систем:
Д Сд,п = Яи — Яп = ^(Гв,и Хи _ Гв,п Хп) + Я(Хи - Хп) •
Если отказы системы обусловлены только отказами /-го элемента
со средним временем восстановления 7^/, то
ДСд,п = ДСд,гп’ = WTBi + Я/) (Хи/ -Хп/).
Суммируя экономию, полученную при снижении эксплуатационных
расходов, и экономию от сокращения потерь при простоях, получаем
годовую экономию при повышении надежности z-го элемента от Хи/-
до Хп/:
ДСд| = (ВТв i + Я/ + CBj ) (Хи / — Хп i ) — Rj (Хи j — ХП1-),
где Я/ = В 7"*в । + Я/ + Св j •
Далее необходимо найти связь между дополнительными капиталь-
ными вложениями и соответствующим изменением уровня надежности
системы, достигаемым за счет повышения надежности элементов.
Исследованиями установлено, что приращение стоимости элемента
определяется логарифмической функцией отношения показателей
надежности ХИ1- и ХП1-:
л ,, о . Хи f
Дй,- = In-------- ,
1 1 \ .
где Sj — постоянная затрат на повышение надежности элемента, числен-
но равна приращению стоимости элемента при снижении интенсивности
отказов в е «2,7 раза.
Подставляя выражение для ДСд, и Д£- в (7.2), получаем выражение
приведенного дополнительного экономического эффекта за срок служ-
бы, обусловленного повышением надежности /-го элемента от исходного
230
Bic. 7.1. Зависимость приведенно- 3Ti
экономического эффекта от от-
носительного значения интенсивнос-
ти* отказов используемого элемента
$Ti так
О
значения ХИ1* до проектируемого ХП1-:
f. 3Ti = (Хи/ -Хп/• (7.3)
Лп i
Если эквивалентные сроки службы элемента ТЭ1- и системы не совпа-
дают, то приведенный эффект от использования /-го элемента в течение
фрока службы системы будет
Хм i
; 3Ti = (Хи,- -Xnf )/?/Тэ-5,1п ,
л Лп i
Рде Sf = S- —
T3i
Анализ (7.3) показывает, что при повышении надежности элемента
(уменьшении ХП1) эффект сначала возрастает, а затем снижается, т.е.
существует максимум ЭТ-тах .Это объясняется тем, что при высоком
уровне надежности элемента затраты на дальнейшее ее повышение превы-
шают получаемую при этом экономию на потерях» которая при высо-
ком уровне надежности будет невелика. Зависимость 3Ti = /(ХИ1/ХП1)
При Хи/ - const приведена на рис. 7.1.
Для определения оптимальной интенсивности отказов \opt необ-
ходимо продифференцировать по Хпг- выражение для ЭТ1- и прирав-
нять производную нулю:
dSTi/d^ni ~—Ri Л + Мп/ ”
откуда Xniopt = Si/RiTs- Найденное значение Хп/орГ позволяет опре-
делить
^Ti max “ Ми/ ~ ^п i opt^i ^э ~ *$/’ In ---
Ап / opt
M'iopt = S/ln
Ап / opt
231
Определив оптимальную интенсивность отказов \niopt каждого
функционального элемента системы, найдем \Opt‘ Экономический эф-
фект от повышения надежности всей системы и необходимые для этого
затраты равны
N N
^Тстах = ^Ti max ’* AkCOpt = opt‘
i = 1 i=l
7.4. СПОСОБЫ ПОВЫШЕНИЯ НАДЕЖНОСТИ АСУ ТП
И ЕЕ ЭЛЕМЕНТОВ
В процессе оптимизации уровня надежности важное значение имеет
выбор способа повышения надежности функциональных элементов.
Достижение одного и того же уровня надежности элемента различны-
ми способами требует неодинаковых затрат. Меньше затрат требует
способ разгрузки. Он состоит в выборе элементов, рассчитанных на
более высокие параметры (токи, напряжения), нежели те, которые
имеют место в схеме. При этом значительно повышается надежность
элемента. Существенно повышается надежность в случае применения
интегральных схем.
Способ резервирования позволяет в принципе достигнуть любого
уровня надежности элемента, но по сравнению с другими требует боль-
ших затрат. При этом способе увеличиваются габариты и масса уст-
ройств системы.
Из числа практически осуществимых для данного функционального
элемента способов повышения надежности следует при расчетах выбрать
способ, обеспечивающий наибольшее значение максимального допол-
нительного экономического эффекта Эптах- Заменим в фор-
муле для Э/у тах его значением и введем обозначение
^uil\opt = i^i Тэ/Sj = Yj,
где Yj характеризует оптимальную меру повышения надежности эле-
мента. Тогда
Эц max = ^hi П — (1 + In Yj )/Yj ].
Зависимость 3Timax = f(Yj) монотонно возрастает в диапазоне
1 < У/ < оо, откуда следует, что наибольшее значение Эптах будет
при наибольшем возможном значении Yj или наименьшем значении
Sj = (SjT3)/T3j. Следовательно, при выборе способа повышения на-
дежности функционального элемента следует предпочесть тот, для ко-
торого S'j/T^i -►min.
Таким образом, при известном эквивалентном значении сроков
службы элементов Тэ/- нужно для каждого намеченного и практичес-
232
ки осуществимого способа повышения надежности определить значе-
ния отношения постоянной затрат на повышение надежности элемен-
та Я- к его эквивалентному сроку службы Гэ/ и из них выбрать наи-
меньшее.
К моменту разработки АСУ ТП подавляющее большинство комплек-
тующих изделий уже создано, поэтому в распоряжении разработчиков
сохраняется ограниченное число методов повышения надежности си-
стемы. Их можно разделить на четыре группы: введение избыточнос-
ти (внутриэлементной, структурной, информационной, алгоритмичес-
кой) ; применение более надежных и, как правило, более дорогих ком-
понентов; улучшение условий эксплуатации системы; организация ин-
тенсивного профилактического обслуживания системы и отдельных
ее составляющих. Методы первой и второй групп реализуются на эта-
пе разработки системы, третьей и четвертой — на этапе эксплуата-
ции.
Эффективным способом повышения надежности является примене-
ние элементов с более высокими показателями надежности, выбор ко-
торых производится на основании сопоставления показателей надеж-
ности ряда элементов, способных выполнять требуемые функции в
заданных условиях эксплуатации. Облегчение и улучшение условий
* эксплуатации элементов и системы в целом в месте установки дости-
гается за счет правильной компоновки элементов в блоках, отвода
выделяющегося при работе тепла, чему уделяется большое внимание
при применении микромодулей.
Введение структурной избыточности (резервирование) достигает-
ся включением в схемы избыточных элементов. Это позволяет создать
весьма надежные системы из недостаточно надежных элементов.
Различают общее и раздельное резервирование. В первом случае ре-
зервируется система в целом, во втором — по отдельным узлам и бло-
кам (блочное резервирование) и элементам (поэлементное резерви-
рование). По способу включения избыточных элементов различают
резервирование постоянное и резервирование замещением. При по-
стоянном резервировании резервные элементы присоединены в тече-
ние всего времени работы, а при резервировании замещением они
включаются в работу только после отказа основных элементов. Ос-
новным параметром резервирования является его кратность
т = (/ - Л)/Л,
где / — общее число элементов резервированного устройства; h — чис-
ло резервируемых элементов, необходимых для нормальной работы
устройства; l-h — число резервных элементов.
Эффект при общем резервировании определяется в предположении,
что система или функциональный узел системы представляет собой це-
почку из N элементов, соединенных логически последовательно; веро-
233
ятность безотказной работы цепочки будет
N
Р(г) = П р. (г),
i = 1
где Pj- (г) — вероятность безотказной работы z-го элемента в течение
времени t.
Если основные и резервные элементы равнонадежны, вероятность
безотказной работы резервированного соединения при кратности т
составит
Рс(0 = 1 - [1-P(Z)]W+1,
а вероятность отказа —
Qc(t) =1-PC(O= [1-P(O]W + 1.
При постоянных значениях интенсивностей отказов элементов и
N
параметра потока отказов цепочки Хо = 2 X/ выражения для
РС(Г) и Qc(t) примут вид < = 1
0с (О = (1 -е
Аналогичные зависимости можно получить и для раздельного резер-
вирования, при котором, резервируется каждый из N элементов функ-
циональной цепочки. Вероятность безотказной работы при т-кратном
резервировании равнонадежными элементами и вероятность отказа
имеют вид
N
Pc(t)= п { 1- [l-Pf(O]M+4 ;
i = 1
N
ес(о= i- п {i- [i_p.(or+'} .
1 = 1
Для оценки эффективности постоянного резервирования опре-
деляется выигрыш в надежности при его реализации. В качестве крите-
рия эффективности резервирования рекомендуется принимать отноше-
ние вероятностей отказов резервированной и исходной систем И'л =
»Сс(О/би(О.
234
е Выигрыш в надежности при общем постоянном резервировании со-
ставит
О ? »>)
. Wq = (1-С
Выигрыш в надежности при поэлементном постоянном резервиро-
вании Wравнонадежных элементов будет
° °
где X — интенсивность отказов элемента.
Сопоставление различных видов резервирования позволяет устано-
вить, что постоянное резервирование обладает существенными пре-
имуществами по сравнению с другими. Главное из них состоит в про-
стоте выполнения, так как не требуются устройства обнаружения не-
исправностей и переключающие устройства, понижающие общую на-
дежность системы.
Наиболее эффективным является резервирование замещением. В
связи с использованием переключающих элементов его целесообраз-
но применять при повышении надежности микромодулей высокой
степени интеграции, крупных блоков и узлов, составленных из ин-
тегральных схем.
Самостоятельно решается вопрос надежности при переходе от струк-
турного к алгоритмическому принципу построения АСУ ТП, когда
решающую роль играет набор микропроцессоров, мини-ЭВМ либо бо-
лее мощная УВМ. В этом случае должен рассматриваться вопрос резер-
вирования замещением.
Выбор вида резервирования для повышения надежности узла, бло-
ка или всей системы может быть сделан только после тщательного
анализа свойств проектируемой системы и требований к ее надежности
с учетом имеющихся ограничений.
Гпава восьмая
ЭКОНОМИЧЕСКИЕ ВОПРОСЫ ПРОЕКТИРОВАНИЯ АСУ ТП
И ЕЕ ЭЛЕМЕНТОВ
8.1. ОСНОВНЫЕ ИСТОЧНИКИ ЭКОНОМИЧЕСКОЙ ЭФФЕКТИВНОСТИ
АСУ ТП
Для любого инженера, а для инженера, проектирующего АСУ любо-
го ранга, в особенности, экономическое обоснование эффективности
проектируемого объекта является обязательным. Особенно важно
привить инженеру навыки поиска экономической эффективности со
студенческой скамьи не в ’’экономическом” разделе курсового и дип-
235
ломного проектов, а с оценки выданного задания на разработку того
или иного объекта и до его завершения.
Процесс проектирования должен сопровождаться непрерывным
экономическим расчетом возможных вариантов технических реше-
ний, но предшествовать ему должны как оценки повышения произво-
дительности, так и оценки сокращения ручного и малоквалифициро-
ванного труда. Заключение проекта должно фиксировать, что дала
автоматизация. В этом — главное содержание настоящей главы.
ГОСТ 20913-75 требует оценки экономической эффективности на
стадии разработки технического задания, в процессе выполнения тех-
нического проекта и при анализе функционирования АСУ ТП. На каж-
дой из этих стадий — различный уровень экономической оценки систе-
мы. На стадии составления технического задания разрабатывается тех-
нико-экономическое обоснование создания АСУ ТП. Расчет ожидае-
мой технико-экономической эффективности выполняется на стадии
разработки технического проекта. При анализе функционирования
системы исследуется ее фактическая технико-экономическая эффек-
тивность.
Исходные показатели технико-экономической эффективности опре-
деляются в разделе ’Технико-экономические показатели АСУ ТП”
технического задания. Раздел должен включать ожидаемые технико-
экономические показатели с указанием максимально допускаемой
суммы затрат на создание системы, годового экономического эффек-
та и источников его образования (повышение производительности,
качества и тл.), коэффициента экономической эффективности затрат
и др. Как видно из этих требований, применение АСУ ТП по своему
существу призвано повысить эффективность производства по всем
показателям или их основной части, что достигается при внедрении
АСУ за счет устранения ручного труда, повышения качества выпус-
каемой продукции, рационального использования основных фондов,
материалов, сырья, снижения численности обслуживающего персона-
ла и облегчения условий труда.
Улучшение всех показателей экономической эффективности воз-
можно лишь при внедрении АСУ ТП. Это переводит технологический
процесс на качественно новую ступень.
Качественное улучшение организации производства с более высо-
кой степенью упорядоченности связано с существенным увеличени-
ем объема перерабатываемой информации в системе с одновременным
резким повышением скорости ее обработки.
Специалист в области электропривода и автоматизации промыш-
ленных установок проектирует, участвует в наладке и эксплуатации
в основном локальных и узловых АСУ ТП, поэтому иллюстрация оцен-
ки экономической эффективности ограничена указанными уровнями.
В результате изучения материалов главы студент должен знать мето-
дику расчета экономической эффективности АСУ ТП и уметь выпол-
236
пять сравнительную оценку экономичности технологического объек-
та, работающего при ручном управлении и с автоматизированной си-
стемой управления.
По данным Института автоматики (г. Киев) внедрение локальной
системы управления нажимным устройством блюминга 1150 повы-
шает производительность всего стана. Ежегодный экономический эф-
фект от внедрения такой АСУ ТП составляет 120 тыс. руб.
Применение локальной АСУ ТП стабилизации толщины полосы на
чистовой группе тонколистового стана горячей прокатки позволяет
сделать стабильным весь технологический процесс прокатки. Внед-
рение этой АСУ ТП на стане 1700 привело к изменению основных тех-
нико-экономических показателей и улучшению всех показателей эко-
номической эффективности:
Изменение показателей
Показатели после внедрения системы автоматического регулирования толщины полосы, %
Всего прокатано металла + 1,19
Всего годного проката +2,12
Расходный коэффициент металла -2,12
Среднегодовая стоимость основных +0,86
производственных фондов Фондоотдача +0,31
Фондовооруженность на одного рабочего +0,78
Себестоимость 1 т проката -1,09
Автоматизированные системы управления не только обеспечивают
общую экономию трудовых затрат, но и меняют соотношение живо-
го и прошлого (овеществленного) труда в процессе производства про-
дукции. При этом доля живого труда уменьшается, а доля овеществлен-
ного труда возрастает. Живой труд становится более технически во-
оруженным и производительным, а в овеществленном труде наблюда-
ется изменение его составляющих. В производстве появляется новая
категория трудовых затрат, которые связаны с разработкой алгорит-
мов и программ и изготовлением программоносителей.
Критерием эффективности внедрения АСУ ТП является экономия
затрат общественного труда. Оценка выполняется путем сопоставле-
ния трудовых затрат, необходимых для производства одних и тех же
деталей на автоматизированных и неавтоматизированных станках.
Если в результате такого сравнения окажется, что сумма всех затрат
живого и овеществленного труда, необходимого для производства
заданного продукта на автоматизированном станке, меньше, чем на
станке неавтоматизированном, то автоматизация является оправдан-
ной. Опыт эксплуатации металлорежущих станков с ЧПУ и исследова-
ния по технико-экономической эффективности их применения пока-
зали, что при правильном подборе номенклатуры обрабатываемых
деталей показатели экономической эффективности существенно воз-
237
растают. Так, затраты на подготовку производства снижаются в
8—10 раз, производительность труда повышается в 2— 6 раз, снижается
трудоемкость изготовления деталей при значительном повышении ка-
чества и точности.
Внедрение АСУ (особенно на более высоких уровнях) дает возмож-
ность использовать скрытые ресурсы технологического процесса. На
долю скрытых ресурсов может приходиться до 50% всего дохода от
внедрения АСУ ТП.
8.2. УЧЕТ ЭКОНОМИЧЕСКОЙ ЭФФЕКТИВНОСТИ АСУ ТП
ПРИ РАЗРАБОТКЕ
Стадии и этапы создания АСУ ТП подробно изложены в § 6.2. Рабо-
та начинается с исследования технологического объекта управления.
На его основании разрабатывается проект, приобретается оборудова-
ние, осуществляются монтаж и наладка АСУ. В стоимость проектных
работ включается разработка алгоритмов управления. Стоимость уп-
равляющей вычислительной техники, устройств подготовки, переда-
чи и индикации информации включается в стоимость оборудования.
К этому разделу затрат относится также стоимость тех узлов техно-
логического оборудования, модернизация или разработка которых
вызвана непосредственно условиями работы оборудования с АСУ ТП.
Примерное распределение затрат, %, на оборудование и разработку
АСУ ТП составляет: приобретение оборудования — 50, разработка ал-
горитмов управления — 25, проектирование, ввод в эксплуатацию —
25. Кроме того, необходимо учитывать затраты на эксплуатацию АСУ
ТП, связанные с обслуживанием технических средств, приобретени-
ем материалов и комплектующих изделий.
Распределяя затраты на создание и эксплуатацию АСУ ТП равномер-
но по периоду ее функционирования, ориентировочно определяем го-
довые затраты на систему:
Зг = (Зр + Зоб)/Г+Зэ, (8.1)
где Зр — затраты на разработку; 30б ~ затраты на приобретение обо-
рудования; Зэ - годовые эксплуатационные затраты; Т - период
функционирования АСУ ТП (обычно 5-7 лет).
Эксплуатационные затраты подсчитывают суммированием частных
составляющих:
Зэ = 33>а + За>ф + Зэн + Зм,а» (8.2)
где 33>а - зарплата персонала, обслуживающего АСУ, за год; За>ф -
амортизационные отчисления и плата за фонды; Зэн — затраты на
энергоносители (электроэнергию, тепло, воду и др.); Зм>а — годовые
затраты на материалы и комплектующие изделия, связанные с экс-
плуатацией АСУ.
238
: Первая составляющая (8.2) определяется по формуле
Зз,а = fp,a За (1 + (8*3)
Где Гр,а - время работы обслуживающего персонала за год,ч; за - сред-
няя часовая ставка обслуживающего персонала АСУ; N — количество
лиц, обслуживающих АСУ; &ц>н - коэффициент цеховых накладных
расходов.
Амортизационные отчисления и плата за фонды рассчитываются по
соотношению
п
За,ф = S Зоб/ (flai +^ф)> (8-4)
i =1
где 30б/ — стоимость /-го типа оборудования; aaj- — размер амортиза-
ционных отчислений по этому оборудованию; Яф — размер платы за
фонды.
Две последние составляющие (8.2) определяются в каждом конкрет-
ном случае применительно к данному типу АСУ ТП.
8.3. МЕТОДИ КА РАСЧЕТА ЭКОНОМИЧЕСКОЙ ЭФФЕКТИВНОСТИ
Внедрение АСУ ТП приводит к увеличению объема производства.
В общем его объеме только одна составляющая определяет его прирост
от внедрения АСУ (Оа,п). Объем выпускаемой продукции после нача-
ла функционирования системы определяется суммой составляющих:
Оа = + Оц + Оа>д, (8.5)
где Ов - объем выпускаемой продукции за год до внедрения АСУ;
Оп» Оа,п - прирост объема выпускаемой продукции без внедрения
АСУ и от внедрения АСУ.
Третья составляющая (8.5) Оа>п определяется, как правило, в про-
цессе опытной эксплуатации технологического узла или комплекса.
В тех случаях, когда необходимо осуществить предварительные рас-
четы, пользуются методом аналогий.
АСУ ТП приводит к повышению качества продукции и увеличению
доли изделий высших сортов, которые имеют большие потребитель-
скую стоимость и цену. Это влечет за собой изменение прибыли, полу-
чаемой предприятием за счет изменения качества продукции. С учетом
увеличения объема производства прибыль рассчитывается по фор-
муле
п п
пл= S OaiIhi - S (OBi +OBi)nit (8.6)
i = l i = l
239
где - объем выпускаемой продукции Z-го технологического узла
при внедрении АСУ; Ов/, Оп/ - объем продукции за год, предшест-
вующий внедрению АСУ, и планируемый прирост продукции без АСУ
для f-го технологического узла; IJj = -Cj — прибыль на единицу
продукции без АСУ, определяемая разностью цены единицы продук-
ции и ее себестоимости; Ла1- = Да/ - Cai прибыль на единицу про-
дукции при внедрении АСУ, определяемая разностью цены единицы
продукции при. функционировании АСУ и себестоимости единицы про-
дукции при этих же условиях.
В ряде случаев внедрение АСУ ТП приводит к сокращению числен-
ности основного и вспомогательного состава рабочих и административ-
но-управленческого персонала. Уменьшение затрат подсчитывается по
формуле
Зс,п = 'р,С 5С (1 + ^Ц,н)-^С > (8’7)
где Zp>c - время работы персонала, подлежащего сокращению, за преды-
дущий год; зс — средняя часовая ставка сокращаемого персонала с уче-
том начислений; Nc — количество сокращенного персонала.
Учитывая полученные выше данные, снижение удельных трудовых
затрат, происходящих при внедрении АСУ ТП, можно определить по
формуле
АЗ. = (1 ♦*,..) ( —---------(8.8)
\ ов + оп о % I
где &3>н - коэффициент общезаводских накладных расходов; З3 -
фонд заработной платы до внедрения АСУ.
По формуле, аналогичной (8.8), определяется снижение удельных
затрат на материалы и комплектующие изделия:
^£*м,а = СМ/(ОВ +ОП) ~См>а/б?а,
где См, Сма — стоимость материалов и комплектующих изделий на
планируемый год при неавтоматизированном производстве и после
внедрения АСУ ТП.
Учитывая затраты на создание и эксплуатацию АСУ, находим себе-
стоимость z-го типа изделий по формуле
C^i = Q — ДЗа - ДСм>а + 30б//O^i •
При отказе АСУ предприятие несет убытки Уп,р только от невыпол-
нения плана по реализации. Тогда
п t
У - У О . п • п*Р>а
i = I 'пл
240
где ОАр/ — объем продукции, недовыпущенной из-за простоя АСУ;
?п,р,а А время простоя за год при работе технологического оборудо-
вания без системы управления; Гпл - плановое время работы техно-
логического оборудования.
Прибыль от внедрения АСУ ТП с учетом убытков от ее простоев
можно определить по соотношению
A I t \ п
Пл= 0а/Яа< 1- - s (pBi + Oni)ni. (8.9)
i = 1\ ' 'пл / f = i
Располагая полученными данными, подсчитываем срок окупаемос-
ти затрат на создание и функционирование АСУ ТП:
ток= (Зр\зоб)/(/7а-Зэ). (8.10)
Пример. Необходимо определить срок окупаемости затрат на внед-
рение АСУ ТП в производство изделий из полупроводниковых мате-
риалов.
Затраты на разработку АСУ ТП Зр = 80 000 руб. Затраты на при-
обретение оборудования 30б = 160 000 руб. Длительность эксплуата-
ции Т = 7 лет. Работа двухсменная по пятидневке, = 29 540 ч. Плани-
руемое время работы за год £пл = 4220 ч. Персонал для обслужива-
ния N = 4 чел. (одна смена). Средняя часовая ставка за = 0,7 руб. Ко-
эффициент накладных расходов: цеховых £ц>н = 1, заводских £3>н =
« 2,05.
Амортизационные отчисления для всего оборудования одинако-
вые: аа = 0,02. Плата за фонды = 0,06. Затраты на энергию, материа-
лы и комплектующие изделия Зэ>н + Зм>а = 5800 руб. Объем выпус-
ка продукции за год, предшествующий внедрению АСУ, Ов = 1 -107 шт.
Планируемый прирост объема Оп = 5 -105 шт. Прирост объема, обус-
ловленного внедрением АСУ, Оа,п = 1 Ю6 шт. Сокращенный персо-
нал Nc = 12 чел. (одна смена). Средняя часовая ставка персонала зс =
= 0,53 руб. Годовой фонд зарплаты до внедрения АСУ З3 = 71 600 руб.
При внедрении АСУ удельный расход материалов и комплектующих
изделий не изменился. Технологический процесс является единым
для изделий всех четырех групп, а их себестоимость одинакова до и
после внедрения АСУ: = 8•10"2 руб.
Данные о распределении изделий по группам, соответствующим
цене до и после внедрения АСУ, приведены в таблице.
Группа изделий Распределе- ние изделий, Прибыль, руб. (шт.) % Цены на изделия, руб. без АСУ с АСУ без АСУ с АСУ
1 2 21,3 14,2 Я1=С1 =8 10-2 0 0,32 • 10”2 44,7 42,5 Д2 = 1,2С1 =9,6-10"2 1,6 10"2 1,92 10"2
241
Продолжение табл.
Группа изделий Распрсдсле- / ние изделий, Прибыль, руб./(шт.) % Цены на изделия, руб. Z без АСУ с АСУ без АСУ / с АСУ
3 4 26,0 31,3 Ц3 = l,8Cj = 14,4 • 10“2 6,4 • 10“2 6,12 10“2 8,0 12,0 =2,5Ci =20 • 10“2 12,0 10“2 / 12,32 • 10“2
Расчет производится в следующей последовательности. /
1. Определяем частные составляющие эксплуатационных затрат:
зарплата персонала, обслуживающего АСУ, по (8.3) /
З3,а = 4220 • 0,7 (1 + 1) • 4 = 23 632 руб. /
амортизационные отчисления и плата за фонды по (8.4)
За,ф = 160 000 (0,02 + 0,06)= 12 800 руб.
Тогда согласно (8.2) (с учетом Зэ>н + Зм,а = 5800 руб.) получаем
общие эксплуатационные затраты
Зэ = 23 632 + 12 800 + 5 800 = 42 232 руб.
2. Ориентировочные годовые затраты на внедрение и эксплуатацию
АСУ получаем по (8.1) :
Зг = 80 -°-* 160 °— + 42232= 76 517 руб.
7
3. Определяем объем выпускаемой продукции при внедрении АСУ
по (8.5) : Оа = 1 • 107 + 0,05 • 107 + 0,1Ю7 = 1,15 • 107 шт.
4. Снижение трудовых затрат при внедрении АСУ согласно (8.7)
определяем как
Зс,п = 4220 • 0,53 (1 + 1) • 12 = 53 678 руб.
5. Снижение удельных трудовых затрат на единицу продукции полу-
чаем по (8.8):
до лжопп 71 600 71 600 + 23 632 - 53 678
(1 + 0,05) • 107 1,15-10’
= 9,78 • 10“3 4 5 6 руб.
6. Определяем себестоимость изделий после внедрения АСУ без
учета убытка от ее простоев: С1а = 8-10"2 -9,78-10" 3 + —=
1,15-Ю7
= 7,68-10"2 руб., после чего определяем снижение себестоимости:
ДСа = 8 • 10"2 -7,68 • 10"2 = 0,32 • 1(Г2 руб.
242
7. Прибыль за год от внедрения АСУ ТП (см. таблицу) подсчиты-
ваем по\ (8.9), но так как Гп,р,а по условию равно нулю, то здесь приме-
няем (8.6):
Пл = 1,\15 • 107 ( —- 0,32 • 10"2 + — 1,92 • 1(Г2 +
> \ 100 100
+ -6,72-10"2+ — 12,32 10"2] - 1,051(Г7 I 0+ X
100 100 / \ 100
X 1,6 10"2 + — 6,4 10"2 + — 1210"2) = 160352руб.
100 100 /
8. По исходным данным (Зр = 80 000 руб., 30б = 160000руб.), а так-
же по ранее полученным результатам находим согласно (8.10) срок
окупаемости:
ГОк = (80 000 + 160 000)/(160 352 - 42 232) = 2,03 года.
Этот срок удовлетворяет нормативным требованиям.
Указанная выше методика получения экономической эффективности
от внедрения АСУ ТП и результаты ее расчета, приведенные в примере,
правомерны лишь при условии абсолютной упорядоченности производ-
ства, когда технологические процессы являются абсолютно стабиль-
ными. В реальных условиях технологические процессы подвергаются
воздействию многих случайных факторов, которые обусловлены изме-
нением параметров производственных объектов и организационных
процессов управления ими. Абсолютно стабильные технологические
процессы в реальном производстве маловероятны.
Существующая нестабильность производства приводит к уменьше-
нию экономической эффективности внедрения АСУ ТП и увеличению
срока ее окупаемости по сравнению с расчетами, выполненными по
рассмотренной методике. Имеются методы расчета экономической эф-
фективности внедрения АСУ ТП, учитывающие неупорядоченность
производства. Они весьма сложны, громоздки и являются предметом
специальных экономикостатистических расчетов, проводимых инже-
нерами-экономистами.
ЧАСТЬ //. АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ МЕТАЛЛООБРАБОТКИ
Глава девятая
ТЕХНОЛОГИЧЕСКИЕ ОСНОВЫ МЕТАЛЛООБРАБОТКИ
РЕЗАНИЕМ
9.1. ОБЩИЕ ПОЛОЖЕНИЯ
Металлорежущие станки предназначены для обработки металла пу-
тем снятия стружки. Они обеспечивают изготовление деталей требуе-
мой формы с заданными точностью размеров и шероховатостью по-
верхности. Обработка может производиться при помощи одного или
нескольких инструментов.
В зависимости от способа обработки существуют станки следующих
основных групп: токарные, сверлильные, шлифовальные, фрезерные,
строгальные.
По степени универсальности и в зависимости от характера произ-
водственного процесса различают станки универсальные, специализи-
рованные и специальные. Универсальные станки предназначены для
обработки деталей широкой номенклатуры и могут выполнять ряд опе-
раций. Специализированные станки служат для обработки деталей,
сходных по конфигурации, но имеющих различные размеры. Специаль-
ные станки предназначены для обработки деталей одного типоразмера.
Выпускаются также многооперационные станки (обрабатывающие
центры). Они обеспечивают выполнение большой номенклатуры техно-
логических операций без перебазирования изделий (изменения уста-
новочного положения), а также автоматическую смену инструмента.
На многооперационных станках могут осуществляться почти все про-
цессы обработки резанием. При одном закреплении сложных корпус-
ных деталей производится обработка всех ее поверхностей, кроме
базовой, по которой она закреплена.
Появился также новый вид производственных систем, называемых
’’гибкими автоматизированными производствами”. Гибкое автомати-
зированное производство - это группы металлорежущих станков,
оснащенных общей системой управления и транспортирования и обес-
печивающих технологический цикл серийного выпуска деталей, их
контроль и складирование. Современное гибкое автоматизированное
производство представляет собой многономенклатурную автомати-
ческую линию, укомплектованную станками с ЧПУ и управляемую от
ЭВМ.
Для придания детали требуемой формы и размеров в станках про-
изводят перемещение режущей кромки инструмента относительно за-
готовки. Такое перемещение может быть разделено на главное движе-
244
ние, за счет которого происходит резание металла, и на движение пода-
чи, за счет которого снимают новый слой металла. Для наладочных
операций, подвода и отвода инструментов, установки и закрепления
заготовки станки имеют вспомогательные движения, которые не участ-
вуют в процессе резания и формообразования.
В результате изучения материалов данной главы студенты должны
знать цель автоматизации процессов металлообработки, физические
основы процесса стружкообразования при основных видах металло-
обработки, уметь использовать на практике математическое описа-
ние процессов резания и их структурные схемы. Необходимо обра-
тить особое внимание на технические требования к электроприводам
станков и научиться выбирать комплектные электроприводы меха-
низмов станков.
9.2. ФУНКЦИОНАЛЬНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ
АСУ МЕТАЛЛООБРАБОТКОЙ
Возможные пути построения АСУ металлообработкой с учетом ин-
формационных признаков и структур управления отражены на рис. 9.1.
К типовым видам обработки на металлорежущих станках относят
точение, сверление, строгание, фрезерование, шлифование.
АСУ металлообработкой обеспечивает автоматизированное управ-
ление процессом резания. Целью такого управления может быть повы-
шение производительности обработки, ее точности, снижение себестои-
мости, повышение чистоты обрабатываемой поверхности, обеспечение
надежности работы, максимальное использование технологических
возможностей станка, режущего инструмента, электропривода,
предохранение инструмента от поломок и др. Показатель качества
АСУ определяется одним из перечисленных выше факторов или их
совокупностью. При этом к режиму обработки нередко предъявляют-
ся противоречивые требования. Как правило, невозможно получить
решение, которое бы одновременно удовлетворяло всем требованиям.
В этом случае показатель качества устанавливается по компромис-
сному решению. Достигнуть требуемого показателя качества АСУ мож-
но при помощи изменения управляющих воздействий: скорости при-
вода главного движения, скорости привода подачи, положения инстру-
мента относительно детали. С помощью этих воздействий осуществля-
ется управление процессом обработки.
Текущую информацию о режиме резания и выработку сигналов
управления, соответствующих принятому показателю качества, по-
лучают с помощью контроля параметров, указанных на рис. 9.1. Для
формирования сигналов, пропорциональных этим параметрам, АСУ
должна быть снабжена датчиками текущей информации. В зависимос-
ти от назначения системы, количества управляющих воздействий
и поставленной цели управления число датчиков рабочей информации
может быть различным.
245
Рис. 9.1. Классификация систем управления металлообработкой
Классификация АСУ металлообработкой базируется на положе-
ниях теории автоматического управления и терминологии, установ-
ленной ГОСТ (см. гл. 1). АСУ металлообработкой классифицируется
также по алгоритму управления (см. гл. 4), по алгоритму функциони-
рования (см. гл. 3), по способности приспособления (адаптации) и
по другим свойствам. Из представленных на рис. 9.1 самоприспособ-
ляющихся систем управления в станкостроении реализованы пока
только самонастраивающиеся системы.
Особенностью АСУ металлообработки являются системы ограниче-
ния параметров процесса резания. Эти системы занимают промежуточ-
ное положение между АСУ с замкнутой и разомкнутой цепями управ-
ления. С их помощью ограничивают контролируемые технологические
параметры. Замыкание обратной связи и выработка сигнала управле-
ния осуществляются только после превышения контролируемым пара-
метром заданной величины. (
АСУ металлообработкой применяются в различных станках и в пер-
вую очередь во фрезерных, шлифовальных, токарных. При этом спе-
цифика построения систем во многом определяется процессом струж-
кообразования.
9.3. ТИПОВЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ
МЕТАЛЛООБРАБОТКИ
Металлорежущий станок, на котором производится процесс реза-
ния, является технологическим объектом управления. Основными тех-
нологическими процессами металлообработки являются точение, рас-
точка, строгание, сверление, фрезерование и шлифование.
Точение (рис. 9.2, а) осуществляется на токарных станках за счет
вращения обрабатываемого изделия 7 (главное движение) и переме-
щения резца 2 (движение подачи).
Окружная скорость изделия в точке соприкосновения резца с об-
рабатываемой деталью называется скоростью резания. Скорость реза-
ния, м/мин, определяется по формуле
v = 9,55яе7исои = 3(Мисои,
где - диаметр обработки, м; о?и - угловая скорость изделия, рад/с.
Величина подачи определяется перемещением резца, приходящим-
ся на один оборот изделия. Глубина резания представляет собой раз-
ность радиусов обрабатываемой и обработанной поверхностей. Быст-
рое перемещение суппорта, зажим и отжатие обрабатываемого изде-
лия, перемещение люнета, задней бабки и другие движения относят-
ся к вспомогательным.
В процессе обработки происходит износ инструмента h, который
можно разбить на три периода (рис. 9.2,б) : / — приработка, II - нор-
мальный и III - усиленный износ, заканчивающийся ’’посадкой” (за-
247
1
Рис. 9.2. Схема токарной обработки (а) и график износа инструмента (б)
туплением) инструмента. Износ Ло, при котором общий срок службы
инструмента получается наибольшим, а расход наименьшим, называ-
ют оптимальным. Оптимальный износ обеспечивает минимальную
стоимость инструмента, отнесенную на одну деталь. По достижении
оптимального износа hQ инструмент перетачивают. Время работы ин-
струмента между двумя переточками определяет его стойкость Г.
Параметры обработки связаны между собой эмпирической фор-
мулой
где Cv - коэффициент, характеризующий вид и условия обработки,
а также материал изделия и резца; s — подача, мм/об; — глубина
резания, мм: Т — стойкость, мин; yv, m — показатели степени, за-
висящие от свойств обрабатываемого металла, материала резца и вида
обработки.
При снятии стружки резцом возникает усилие F, приложенное к ре-
жущей кромке инструмента, которое может быть разложено
(рис. 9.2, а) на три составляющие:
F = J F} + F* + F*',
где Fz — главная касательная сила, действующая в направлении траек-
тории главного движения, преодолеваемая шпинделем станка и назы-
ваемая усилием резания; Fy - радиальная сила, действующая нормаль-
но к обработанной поверхности и создающая давление на суппорт; Fx —
осевая сила, действующая в направлении подачи.
Расчет усилия резания производится по эмпирической формуле
Fz = CF t pF syFv\ (9.2)
248
где Ср - коэффициент, характеризующий материал детали, резца и вид
токарной обработки; xF, yF, п - показатели степени.
Коэффициенты и показатели степени в (9.1) и (9.2) принимаются
по справочникам режимов резания [11].
По аналогичным формулам рассчитываются усилия Fy и , кото-
рые можно принять равными Fx « 0,4Fz и Fy « 0,3Fz.
Усилие Fn, действующее на механизм подачи, помимо собственного
усилия подачи Fx содержит также составляющие, возникающие в на-
правляющих за счет сил трения от действия усилий Fz и Fy :
Fn = Fx + V<FZ + Fy),
где д — коэффициент трения в направляющих.
Мощность резания, кВт,
F v
10Г< <9-3)
60
Мощность подачи, кВт,
Поскольку скорость подачи во много раз меньше скорости резания,
мощность подачи намного меньше мощности резания и составляет
относительно последней 1 — 0,1 %.
Расточка применяется для черновой, чистовой и алмазной обрабо-
ток отверстий на токарных и расточных станках. При расточке резцы,
оснащенные пластинками из быстрорежущей стали, твердых сплавов
или из ограненного технического алмаза, закрепляют в оправках. Ско-
рость, силу и мощность резания при черновой и чистовой расточках
определяют по тем же формулам (9.1) - (9.3), что и для точения.
Строгание (рис. 9.3) можно рассматривать как точение участка дета-
ли с бесконечно большим диаметром. При этом деталь 1 перемещает-
ся возвратно-поступательно относительно резца 2, снятие стружки про-
исходит в течение рабочего хода, а обратный ход совершается вхолос-
тую. Скорость, с которой деталь перемещается относительно резца
при рабочем ходе, называется скоростью резания г, м/мин. Продоль-
ное перемещение стола является главным движением.
Перемещение резца за один двойной ход стола перпендикулярно
главному движению называется движением подачи s, мм/мин. Вели-
чина Гр, на которую углубляется резец в изделие при одном проходе,
называется глубиной резания. Перемещение траверсы и суппортов,
подъем резца при обратном ходе, установочные медленные перемеще-
ния стола относятся к вспомогательным движениям.
Скорость, усилия и мощность резания при строгании определяют по
тем же формулам (9.1) - (9.3), что и для точения.
249
Рис. 9.4. Схема сверления
sl
dc
Сверление (рис. 9.4) осуществляется за счет вращательного (глав-
ного) движения инструмента - сверла 1 (иногда детали) и его про-
дольного перемещения в детали 2 — движения подачи. Продольное и
поперечное перемещения стола, перемещение шпиндельной бабки, за-
жим колонны являются вспомогательными движениями.
Окружную скорость на периферии сверла v, м/мин, называют ско-
ростью резания при сверлении. Перемещение сверла вдоль своей оси за
один оборот определяет подачу. Скорость резания при сверлении нахо-
дят по эмпирической формуле
v = Cvdcv/Tmsyv ,
где Cv - коэффициент, зависящий от материала детали и сверла; dc -
диаметр сверла, мм; Т - стойкость сверла, мин; s — подача, мм/об;
yv, zv, m - показатели степени, зависящие от материала детали и диа-
метра сверла.
Вращающий момент, Н-м, при сверлении определяют по эмпиричес-
кой формуле
М = CMdl’9 5Ум • 1(Г3,
откуда, зная угловую скорость сверла, рассчитывают мощность реза-
ния, кВт:
Р2 =Ма>с10’3-
Сила, Н, преодолеваемая механизмом подачи при сверлении, также оп-
ределяется по эмпирической формуле:
Fx = CFdZcFsyF.
250
Все коэффициенты и показатели сте-
пени, входящие в эмпирические форму-
лы, приводятся в справочниках по ре-
жимам резания [11].
Фрезерование (рис. 9.5) производит-
ся вращающейся фрезой 7, имеющей
несколько режущих лезвий - зубьев,
каждое из которых за счет поступатель-
ного перемещения фрезы относитель-
но детали 2 снимает стружку в преде-
лах определенного угла поворота фре-
Рис. 9.5. Схема фрезерования
зы, а затем вращается вхолостую.
Главным движением при фрезеровании
является вращение фрезы, перемещение детали относительно инструмен-
та представляет движение подачи. Быстрое перемещение стола, на кото-
ром укреплена деталь, и ускоренное перемещение шпиндельной бабки
при наладке относятся к вспомогательным движениям.
Под скоростью резания, г, м/мин, понимают окружную скорость
на периферии фрезы, которую определяют по эмпирической формуле
v =
Су __________
Тт£ tXpVBkzn
(9.4)
где Ср, q, т, п, yv, к — коэффициент и показатели степени, завися-
щие от материала детали и фрезы, вида обработки и охлаждения; -
диаметр фрезы, мм; sz — подача на зуб фрезы, мм; В — ширина фре-
зерования, мм; z — число зубьев фрезы.
Усиление резания, Н, определяют по выражению
х р ур
Fz = CFlF sFBzdl*.
Мощность резания, кВт, рассчитывают по формуле
Рг = СрГрР4₽БгИф4.10-5, (9.5)
где Лф - частота вращения фрезы, Иф = ЗОсоф/лг.
Все коэффициенты и показатели степени в (9.4) и (9.5) приводят-
ся в справочниках по режимам резания [11].
Шлифование (рис. 9.6) производится, как правило, абразивными
кругами, при этом каждое абразивное зерно в зоне обработки рабо-
тает как резец, снимая стружку с детали в пределах определенного
угла поворота. Главное движение при шлифовании — вращение шли-
фовального круга 7; поступательное перемещение круга относитель-
но детали 2 представляет движение подачи.
251
Рис. 9.6. Схема шлифования на станках:
а — плоскошлифовальном с прямоугольным столом; б — плоскошлифоваль-
ном с круглым столом; в — круглошлифовальном; г — внутришлифовальном;
1 - шлифовальный круг; 2 - деталь; 3 - стол (магнитная плита)
Различают плоское шлифование (рис. 9.6,а, б), при котором обраба-
тывается плоская поверхность, и круглое шлифование (рис. 9.6,в, г),
при котором обрабатывается поверхность тела вращения. Плоское
шлифование может осуществляться периферией (рис. 9.6, а) или тор-
цом (рис. 9.6, б) шлифовального круга J. Стол 3, на котором устанав-
ливается магнитная плита для крепления деталей 2, может иметь прямо-
угольную и круглую формы. На шлифовальных станках с прямоуголь-
ным столом (рис. 9.6, а) последний совершает возвратно-поступатель-
ное движение (продольная подача периодическое дозированное
перемещение (поперечная подача sn,n) и перемещение на врезание
sBp. На шлифовальных станках с круглым столом (рис. 9.6, б) одним
из движений подачи является вращение деталей с магнитной плитой и
столом со скоростью а>с, другое движение подачи - перемещение sK
шлифовального круга в радиальном направлении относительно стола,
а также перемещение на врезание sBp.
Выбор режимов резания при шлифовании определяется по техноло-
252
гическим таблицам, составленным на основании эмпирических дан-
ных.
При круглом наружном (рис. 9.6, в) и внутреннем (рис. 9.6, г)
шлифованиях изделие получает вращение со скоростью с*>и, как пра-
вило, в сторону, противоположную вращению шлифовального круга.
Относительное перемещение шлифовального круга вдоль оси враще-
ния детали представляет продольную подачу $п.
Скорость резания при шлифовании v, м/с, определяется окружной
скоростью шлифовального круга и равна примерно 20—80 м/с. При
этом допускаются небольшие глубины шлифования /р, равные 0,05—
0,005 мм. Все большее применение стало находить силовое шлифо-
вание, обеспечивающее значительную глубину шлифования — до 10 мм.
В процессе шлифования абразивные зерна притупляются, что при
постоянной подаче влечет за собой увеличение мощности шлифова-
ния и образование прижогов на поверхности детали. Для устранения
этих явлений круг правят, срезая слой абразива и вводя в работу зер-
на с новыми режуШими кромками. Время работы круга между двумя
последовательными правками характеризует его стойкость Т, мин.
При плоском шлифовании периферией круга на станках с прямо-
угольным столом стойкость может быть рассчитана по формуле
cv
Т - ---------------кх к2,
(*п *п,п*$Вр) 2
где Cv — коэффициент, зависящий от скорости резания; 5П — ско-
рость движения стола (продольная подача), м/мин; sn,n* — попереч-
ная подача в долях ширины шлифовального круга; sBp — подача на
врезание на ход стола, мм/ход; ki9 ^2 - коэффициенты, зависящие
от обрабатываемого материала и диаметра шлифовального круга.
При плоском шлифовании за счет увеличения нагрузки на зерна
происходит их частичное разрушение и образование новых режущих
кромок, круг работает с самозатачиванием. При этом необходимо
контролировать силу резания, не допуская критического режима об-
работки, при котором наступает вырывание абразивных зерен из круга.
Помимо перечисленных выше видов обработки на металлорежущих
станках в станкостроении применяются электрофизические и электро-
химические методы обработки, под которыми понимают совокупность
электрических, электромагнитных и электрохимических процессов,
придающих заготовке в сочетании с тепловым, механическим или хи-
мическим воздействием заданные форму и размеры.
Электрофизические и электрохимические методы можно разделить
на четыре группы:
электро эрозионные, основанные на использовании энергии электри-
ческих разрядов, возбуждаемых между инструментом и заготовкой;
253
лучевые (лазерные), основанные на воздействии на заготовку лу-
чей с высокой плотностью энергии;
импульсные (ультразвуковые), основанные на ударном воздейст-
вии на заготовку частиц абразива;
анодного растворения, основанные на том, что электрод, подклю-
ченный к положительному потенциалу, растворяется.
Явления, происходящие при электрофизических и электрохими-
ческих методах обработки, весьма сложны, являются предметом спе-
циальных исследований и здесь не рассматриваются.
9.4. ОПТИМИЗАЦИЯ РЕЖИМОВ РЕЗАНИЯ
Обработку на металлорежущих станках стремятся производить при
оптимальных значениях скорости резания и подачи, т.е. при оптималь-
ных режимах резания. Оптимальным называется такой режим резания,
при котором достигается наилучшее сочетание параметров резания,
обеспечивающее некоторый объективный критерий, базирующийся на
физико-технологических и экономико-производственных факторах про-
цесса механической обработки. Критерием экономической оптималь-
ности при выборе режимов резания служит минимум приведенных за-
трат. Критерием технологической оптимальности является производи-
тельность обработки.
При обработке металлов резанием происходят сложные физико-ме-
ханические и физико-химические процессы, явления пластических де-
формаций, сопровождающиеся температурными изменениями, струк-
турными превращениями в обрабатываемых металлах и режущих спла-
вах, находящихся в определенной зависимости друг от друга. Эти зави-
симости и закономерности пока еще не выявлены, поэтому в теории ре-
зания металлов используют эмпирические формулы. Функциональную
зависимость между стойкостью, скоростью резания, глубиной резания
и подачей можно представить выражением
г1/^
Т= -------Т . (9.6)
1/m *,т у*,т
V Гр S
Наибольшее влияние на стойкость инструмента оказывают скорость
резания, подача и в меньшей мере — глубина резания. На стойкость вли-
яют также некоторые факторы, выраженные коэффициентом
Cj, - > (9«?)
где Cv — скоростной коэффициент» зависящий от материала детали ин-
струмента; kr, kq, кф к^ - постоянные, зависящие от геометрических
параметров инструмента; кН9 км, кс, ксп - постоянные, зависящие от
254
состояния материала детали; kh — постоянная, зависящая от износа
инструмента; к0 — постоянная, зависящая от охлаждения.
Увеличение v, s, tp приводит к уменьшению периода стойкости. Эти
параметры, а также постоянные (9.7) находятся в тесной связи между
собой. Такой комплекс физико-технологических факторов не остается
неизменным, а находится под воздействием условий резания. Жесткая
функциональная связь между параметрами резания (9.6) носит вероят-
ностный характер, поэтому реальная стойкость может значительно от-
личаться от расчетной. Тем не менее на практике полагают, что формула
(9.6) отражает основные, достаточные для расчетов факторы, опреде-
ляющие обрабатываемость и резание металлов.
На выбор оптимального режима оказывают влияние приводимые да-
лее ограничивающие факторы.
1. Ограничения на подачи
smin 4 5 smax '
W smin и smax — минимально и максимально допустимые подачи
инструмента соответственно. Они учитывают технологические факторы.
При этом ограничения снизу определяются нарушениями нормальных
условий стружкообразования, а ограничения сверху - необходимостью
получения заданной шероховатости поверхности.
2. Ограничения на угловую скорость шпинделя
ст min ^ст w ст тех»
где состш/л, ” минимально и максимально допустимые угло-
вые скорости шпинделя станка.
Ограничения определяются границами диапазона регулирования при-
вода, а также условиями стружкообразования и нагревом режу-
щей кромки инструмента ытах.
3. Ограничения на стойкость инструмента. Стойкость при уменьшении
скорости резания асимптотически стремится к предельному значению,
которое и определяет максимальное значение стойкости. Минимальное
значение стойкости не имеет предела, однако работа при малых периодах
стойкости сопровождается частой заменой инструмента, поэтому вводят
ограничение на стойкость
4. Ограничения по мощности привода станка
Рст Ртах\ Р3 Рн,
где Рст - мгновенное значение мощности привода станка; Ртах> ^э»
Люм “ максимально допустимая, эквивалентная и номинальная мощ-
ности электродвигателя.
255
Для оптимизации режима резания необходимо выбрать критерии
оптимальности (целевую функцию). Если принять, что основным пока-
зателем процесса резания при черновой обработке является производи-
тельность, то при токарной обработке она равна
А = vstp,
где /р - глубина обработки.
Производительность при фрезерной обработке
/ф = 9,55В«ф1/р.
При шлифовальных работах показатель производительности близок
к показателю производительности при фрезеровании.
Критерий оптимальности (целевая функция) может быть получен,
если учесть общую стоимость съема припуска за период стойкости ин-
струмента. Для токарной обработки будет
Л=/ ---------------5----~dt>
’ О (t + fд)2
где t — время, мин; /д = tсм + К/Е — дополнительное время, мин;
К — затраты, связанные с эксплуатацией режущего инструмента за пе-
риод стойкости, коп.: Е — заработная плата персонала и затраты на
эксплуатацию станка за 1 мин работы, коп^мин; ?См “ время смены
инструмента, мин.
Полагая параметры резания неизменными во времени, получаем
Л,п = vstpT/(T + Гд).
Прй тех же допущениях критерий оптимальности для фрезерной об-
работки
= 9.55 Л Шф$Гр/(*! + k2vh),
где ki - стоимость станко-минуты, коп/мин; k2 = (^i^Cm + ^^l^max
(к3 — затраты на инструмент за период стойкости, коп.; hmax — мак-
симально допустимый износ инструмента, мм); = f (В, соф, stp9T) -
скорость износа инструмента.
Зависимость износа от параметров резания определяется степенной
функцией
/
, Ха Х3 Xi^Xi х
h = СВ 5t s со. Т (9.8)
Р Ф v 7
где Xj - х5 - показатели степени из таблиц режимов резания.
Допуская, что износ инструмента определяется одинаково при одной
256
И той же стойкости Т как для переменных, так и для постоянных ре-
хсимов резания, и аппроксимируя (9.8) по методу наименьших квадра-
тов, получаем
, Л = 9,55Всо. Т!(кхТ + к2).
фэс ф р v 1 •
Приведенные критерии позволяют построить самонастраивающуюся
систему управления режимами резания.
9.5. МОДЕЛИРОВАНИЕ ТИПОВЫХ ПРОЦЕССОВ МЕТАЛЛООБРАБОТКИ
Определение адекватной технологическому процессу математичес-
кой модели является его идентификацией. Она необходима для обос-
нования выбора алгоритма управления процессом, синтеза автоматизи-
рованной системы, построения корректирующих устройств.
Математическая модель, отражающая связь управляющих воздей-
ствий с контролируемыми технологическими параметрами, может
быть построена на базе эмпирических зависимостей, применяемых для
расчетов режимов резания. Для токарной обработки усилие резания
*F Ур п
F = CPt s vn.
Z г р
Процесс обработки рассматривается как безынерционный, стацио-
нарный.
Приняв за выходную величину главную силу резания при точении,
а за входную величину — продольную подачу, определим передаточную
функцию процесса продольного точения:
fl (р J — ————————————————— s
Р s(p) (Гр,р+ 1)(Тр2р+ 1)
(9.9)
где к2 - коэффициент передачи объекта; Тр1,Тр2 - постоянные вре-
мени процесса резания.
Величина постоянных времени процесса резания может быть найдена
по зависимости
ТР1, ТР1 = О,5т[О,5 + А ± 7(0,5+Л)2 -0,33],
где г = 1/лш — время запаздывания за один оборот шпинделя, с (лш —
частота вращения шпинделя, об/с); А - кхкулх + кукукуду (кх,ку -
коэффициенты передачи процесса резания по приращению толщины сре-
заемой стружки по координатам х, у; к^ — коэффициент, определя-
емый углом заточки резца; ^у>Дх» ^у,ду — коэффициенты упругой
деформации, определяемые податливостью системы станок—приспо-
собление—инструмент—деталь по координатам х, у).
257
Поскольку в выражении (9.9) часто Тр1 > Тр2, последней можно
пренебречь и передаточную функцию записать в виде
Яр(р) « -------— . (9.10)
гР1р + 1
Пренебрегая податливостью системы станок — приспособление —
инструмент — деталь, расчет постоянной времени резания в (9.10) мож-
но упростить и принять Гр1 = 1/иш = т.
Аналогичным путем можно представить передаточные функции
процессов шлифования, фрезерования, сверления.
Приведенная модель не учитывает динамику резания. В необходи-
мых случаях передаточная функция процесса обработки может быть
представлена одним или двумя последовательно соединенными аперио-
дическими звеньями.
Возрастающие требования к точности обработки вызывают необхо-
димость управления упругими перемещениями системы станок — прис-
пособление — инструмент — деталь путем изменения режимов резания
(подачи, скорости резания), а следовательно, и скорости соответству-
ющих электроприводов. Модель металлообработки в этом случае должна
базироваться на динамике системы станок — приспособление — инстру-
мент — деталь, контуром обратной связи в которой является процесс
резания. В процессе резания изменения твердости заготовки и ширины
срезаемого слоя b приводят к колебаниям усилия Fy и происходят
вынужденные колебания упругого перемещения инструмента у относи-
тельно статического значения по нормали к поверхности резания
258
(рис. 9.7,а). При этом отклонение силы, действующей в упругой систе-
ме при точении, от ее статического значения будет
d2y dy
AF = ту ------ + hy — + с у , (9.11)
Л dt2 dt
где Су - коэффициент жесткости упругой системы станка в направле-
нии оси у; hy — коэффициент демпфирования; ту — приведенная
масса подвижной части суппорта. Сила &Fy является одним из входных
воздействий для узла, показанного на рис. 9.7,а.
Толщина а и ширина b срезаемого слоя связаны с подачей и глуби-
ной резания зависимостями
а = s sin<^; b = rp/sin^,
где — главный угол резца.
Полагаем, что вынужденные колебания упругого перемещения у при-
водят к эквивалентному по силовому эффекту изменению толщины сре-
заемого слоя Да3. Так как а зависит от подачи, система управления с
помощью электропривода продольной подачи по результатам измерения
у изменяет толщину срезаемого слоя (подачу) на Да^. При этом
dbFy
кр(Ьа3-у- Лау) = Гр + ДГу5 (9.12)
где kf — коэффициент отношения радиальной силы резания к статичес-
кой толщине срезаемого слоя; Тр — постоянная времени процесса реза-
а . ,
• ния, Гп £ (я — статическая толщина срезаемого слоя, соответству-
р v
ющая постоянной подаче); % - усадка стружки.
Модель (алгоритм функционирования), построенная по зависимо-
стям (9.11) и (9.12), показана на рис. 9.7,6. Определяя размеры упру-
гого перемещения у при помощи этой модели, управляющее устройство
должно вырабатывать такое управляющее воздействие &ау при задан-
ном значении Да3, чтобы система была устойчивой, а погрешность об-
работки за счет у — минимальной при возмущающем воздействии
Да3.
Более точно модель упругой системы станка в процессе резания мо-
жет быть построена, если учитывать размерный износ инструмента.
В качестве примера рассмотрим построение модели упругой системы
шлифовального станка при учете размерного износа шлифовального
круга (рис. 9.8,а). При шлифовании с поперечной подачей путь попереч-
ного суппорта 1С затрачивается на съем припуска /д, компенсацию ли-
нейного износа шлифовального круга /и к и компенсацию упругих де-
формаций системы станок — приспособление — инструмент — деталь
259
1ул согласно выражению
= + Л|,к * ^уд-
Продифференцировав это выражение, получим
dlc _ dlg + а1и,к ± ^уд
dt dt dt dt
или
”c = ”д + ^и.к * Ууд> (9-13)
где vc уд, уик , уу д - скорости изменения /с, /д, /и к, 1у д.
Аппроксимируя зависимость уи к = /(уд) [7] выражением
’’и,к = <уд ~ «»)•
где Д1 и а2 — коэффициенты аппроксимации, и полагая, что 1ул -
dv„
= д3уд или гул = д3на основании (9.13) получаем
ус = Уд + «1 (Уд - в2) + а3 — , (9.14)
аг
где а3 - коэффициент пропорциональности.
260
Уравнение (9.14), полагая ata2 0 для бесконечно малых величин,
запишем в операторной форме:
\(р) = *Д(Р>(1 +Я1 +«э₽)- (9.15)
Тогда передаточная функция процесса шлифования
. Яс(р) =
уд<Р>
1
1 + «I + «ЭР
(9-16)
или, разделив числитель и знаменатель на 1 + at, получим
; яс О) =
кс
Тср +1
где кс = 1/(1 + ai) - коэффициент передачи; Тс = а3/(1 + а>) - по-
стоянная времени процесса резания.
£ Полученная упрощенная математическая модель процесса шлифова-
ния, где в качестве выходной переменной принята скорость съема при-
пуска, а в качестве входной переменной — скорость перемещения суп-
порта, представляет собой апериодическое звено первого порядка.
Скорость износа круга ги к и скорость изменения упругих дефор-
маций Руд в общем случае зависят от двух переменных:
(dv \
<917)
где d* = ^к/^к,нач - относительное изменение диаметра шлифоваль-
ного круга.
Представив зависимости (9.17) в приращениях в виде суммы двух
составляющих, одна из которых зависит от гд, а другая - от d*> и ли-
неаризуя их путем разложения в ряд Тейлора, получим, пренебрегая
членами, содержащими вторые производные и выше, в операторной
форме
д”и,к^ = ««Д^дФ) - а5д<*»(р);
ДрУЛ(р) = «врД^дО) -л7Д^*(р).
где а4, а5 - коэффициенты, характеризующие скорость износа шли-
фовального круга; аб, а7 — коэффициенты, характеризующие жест-
кость системы станок - приспособление - инструмент - деталь.
Знаки минус перед вторыми слагаемыми приведенных уравнений
учитывают то, что дополнительная связь по диаметру круга прини-
мается отрицательной.
261
Линейный износ шлифовального круга будет
гм
/ик = f УИКЛ, <9’,8>
* Л|1х
о
где tM — текущее машинное время обработки.
Текущее значение диаметра шлифовального круга
dK = <*кнач - 2/ик- <919>
14 KfFtClH
Выражения (9.18) и (9.19) в приращениях и в операторной форме
можно представить в виде
д/и,к(Р) = Дри,к(Р); Д^(Р) = Д8Д/и,кО)>
где а8 « 2/dK>Ha4 - коэффициент пропорциональности.
На основании полученных выражений можно записать передаточную
функцию объекта (процесса шлифования) с учетом размерного износа
шлифовального круга:
Дрд(р) Лс(Т1Р+1)
Н (Р) »
Дус<Р) Т2р2 + 2Т2ур +1
где кс = asl(as + а4'а7) - коэффициент передачи системы; I\ =l/asas -
постоянная времени, характеризующая изменения скорости износа шли-
фовального круга в зависимости от его диаметра; Т2 = +
+ а4а7У — постоянная времени системы; 7 = 1 + а4 + asa& — безразмер-
ный коэффициент.
Между радиальным усилием резания и скоростью съема припуска при
заданной режущей способности шлифовального круга, характеризу-
емой коэффициентом fcp, существует линейная зависимость гд = fcpFy.
Тогда, если пренебречь размерным износом шлифовального круга, по-
лагая, что в пределах обработки детали он не превышает 2-3% началь-
ного диаметра, получается упрощенная модель системы в виде аперио-
дического звена первого порядка:
Fy(p) = кс
vc(P) 1 + Гср’
Яс(р)
где Тс = а6/(\ + а4) — постоянная времени; kc = l/fcp (1 + а4) - коэф-
фициент передачи.
Модель системы без учета размерного износа круга для случая, когда
выходной (регулируемой) величиной является радиальное усилие ре-
зания Fy, показана на рис. 9.8,6. Величина f учитывает возмущение,
вызываемое изменениями свойств шлифовального круга.
262
Математические модели металлообработки дают возможность совер-
шенствовать технологические процессы резания путем анализа характе-
ра изменения во времени входных и выходных переменных для постро-
ения систем управления этими процессами.
г<9.6. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К ЭЛЕКТРОПРИВОДАМ
МЕТАЛЛОРЕЖУЩИХ СТАНКОВ.
, Требования к электроприводам металлорежущих станков формули-
руются исходя из перспектив совершенствования конструкции в свя-
зи с задачами повышения точности и производительности обработки.
В зависимости от режимов работы станков к электроприводам предъяв-
ляются требования обеспечения заданных:
> диапазона изменения скорости рабочего механизма
& = ^тах! ^min'
ТДР <^тах' ^min ~ максимальная и минимальная угловые скорости;
плавности изменения угловой скорости, определяемой отношением
двух соседних фиксированных значений сол и W(w_i):
г динамических свойств привода: характера и интенсивности протека-
ния переходных процессов;
добротности (для следящих электроприводов) по скорости, с"1,
&сл ”
где v — скорость перемещения исполнительного органа, мм/с; Sc —
Скоростная погрешность, мм;
необходимой жесткости механических характеристик;
требуемого характера изменения и максимально допустимого момен-
та;
изменения скорости при постоянном моменте или при постоян-
ной мощности;
надежности работы, экономичности.
На выбор электропривода могут оказать влияние:
допустимая частота включений, необходимость реверса и тормо-
жения;
экономические показатели привода;
возможность выполнения различных функций одной системой
привода;
простота наладки и обслуживания;
серийность производства данного привода;
степень серийности производства данной модели станка.
263
Главный привод многих станков чаще всего выполняется на базе
надежных и дешевых асинхронных электродвигателей с короткозамкну-
тым ротором. Имея малые габариты, они удобно стыкуются с коробка-
ми скоростей. Ступенчатое изменение угловой скорости производят пе-
реключением шестерен коробок скоростей. В некоторых случаях нахо-
дят применение двух- и трехскоростные асинхронные двигатели, поз-
воляющие упростить кинематические цепи коробок скоростей.
Особый интерес представляют электроприводы станков с ЧПУ. Высо-
кий уровень автоматизации этих станков, необходимость выбора опти-
мального режима резания и уменьшения времени перемещения узлов
обусловили широкое применение в них регулируемых электроприводов.
Нормами СЭВ [5] тиристорные электроприводы постоянного тока
для станкостроения разделены на три группы:
регулируемые электроприводы мощностью 1—200 кВт с двухзонным
регулированием скорости при Оя = var, £>я <1:100, Ф = уаг для при-
водов главного движения;
регулируемые нереверсивные электроприводы при ия = var, Ф =
= const мощностью 0,1-2,0 кВт с £>я < 1: (10-г30) и 0,1-10 кВт с
/)я < 1: (100-г200) для приводов подач станков;
широкорегулируемые реверсивные электроприводы при ия = var,
Ф = const, мощностью 0,1-20 кВт с Оя < 1:10 000 для приводов подач
станков.
К электроприводам главного движения предъявляются требования
изменения угловой скорости в диапазоне 2,5:1—4:1 при постоянной мощ-
ности и в диапазоне 10:1 при постоянном моменте. Привод должен
быть с большим (не менее 100) числом электрических ступеней, что
обеспечивает коэффициент плавности < 1,1.
В станках с ЧПУ для привода главного движения в большинстве слу-
чаев применяются тиристорные электроприводы постоянного тока и
двухступенчатая коробка скоростей. Расширяется использование для
привода главного движения асинхронных электродвигателей с частот-
ным управлением от тиристорных преобразователей.
Двигатели переменного тока в закрытом исполнении имеют значи-
тельно меньшие габариты по сравнению с двигателями постоянного
тока. Однако тиристорные преобразователи переменного тока по габа-
ритам в 2-3 раза больше тиристорных преобразователей постоянного
тока и дороже их. В настоящее время асинхронные электроприводы с
частотным управлением применяются главным образом для механиз-
мов главного движения станков шлифовальной группы с ЧПУ.
Электроприводы подач станков с ЧПУ должны обладать широким
диапазоном изменения скорости, который достигает 10 000:1 и более.
Время пуска и торможения такого привода с приведенным моментом
инерции механизма, равным моменту инерции двигателя, не должно
превышать 0,1 с. Привод должен обеспечивать позиционирование с точ-
264
костью до 1 мкм не более чем за 1 с. Жесткие требования выдвигаются
также к равномерности перемещений на пониженных скоростях.
:: Двигатели электроприводов подач должны иметь большую кратность
максимального момента и относительно малые габариты, что позволяет
устанавливать их непосредственно на шариковых и роликовых винтах
механизмов подач без высокоточных безлюфтовых редукторов. Этим
требованиям удовлетворяют электроприводы постоянного тока с дви-
гателями, имеющими высокоэнергетические постоянные магниты.
таких электроприводах рециркуляционная передача винт—гайка со*
держит резьбу, выполненную в виде винтовой канавки полукруглого
профиля, в которой перемещаются шарики (ролики), обеспечивающие
качение гайки по винту. Движение шариков (роликов) осуществляет*
ся в замкнутой цепи по каналу возврата, соединяющего соседние резь-
бовые канавки гайки.
Для преобразователей в таких электроприводах широко использует-
ся трехфазная нулевая тиристорная схема с согласованным или раздель-
ным управлением. Получили распространение разработанные в СССР
тиристорные и транзисторные преобразователи с широтно-импульсным
управлением, за рубежом - транзисторные преобразователи с широт-
но-импульсным управлением.
Электроприводы постоянного тока для станков с ЧПУ при работе
не должны превышать допустимых погрешностей скорости. Суммарная
погрешность скорости Д^ Равна сумме погрешностей: Дн при измене-
нии нагрузки от 0,15 AfHOM до Мном; Д^ при изменении напряжения
сети от 0,9 до 1,1 Ц<ом> Дт при изменении температуры окружающей
среды от 20 до 45 °C и нагреве электропривода до установившейся тем-
пературы при моменте двигателя, равном AfHOM:
Д2 = Дн + Дг + Дс/, (9.20)
где
“о,15МНом- “о-^ном “"ном - “>o,sMHOM
:--------------------1 UU7O, А Н 2 = —----------
°°’5Мном °0.5Мном
100%;
Д = -±Шном----------^ном 100%;
9U ~
----——---------— 100%;
Ц<ом
При расчете Д^ в (9.20) подставляются максимальные значения
Да1 или Д^2 и ДН1 или ДН2.
265
рости
*н =2
Нормируется также коэффициент неравномерности угловой ско-
^тах ~ ^min
^тах * ^min
где ытах, <Amin — максимальное и минимальное значения мгновенной
угловой скорости за один оборот.
Погрешность угловой скорости при изменении направления вращения
А Л ^вправо ~ ^влево
Др = 2-------------------- 100%.
F СО + СО
вправо влево
Полоса пропускания замкнутого скоростного контура приводов при
дополнительном моменте инерции, равном суммарному моменту инер-
ции двигателя и датчиков пути и скорости, должна быть не менее
20 Гц.
В табл. 9.1 приведены допустимые погрешности скорости и коэффи-
циент неравномерности угловой скорости для электроприводов механиз-
мов подач станков с ЧПУ.
Таблица 9.1
Относительное значение скоро* ста со* Допустимая погрешность угловой скорости, % установочной скорости Коэффициент неравномерно- сти угловой скорости кн (не более)
суммарная Д2 при изменении нагрузки Дц при изменении направления вращения Др
1 ±2 ±0,5 ±0,5 0,1
од ±10 ±2 ±2 0,1
0,01 ±15 ±5 ±5 0,2
0,001 ±25 ±10 ± 10 0,25
0,0001 ±30 ±15 ± 15 0,3
Электроприводы подач работают в режимах поддержания угловой
скорости, слежения и позиционирования, поэтому АСУ ЭП имеют регу-
ляторы угловой скорости и положения. В последние входят датчики-ре-
зольверы, установленные на валу двигателя. Датчики-резольверы дол-
жны иметь напряжение питания 5 В (амплитудное значение) при частоте
400 — 10 000 Гц, выходное напряжение 5 В (амплитудное значение)
при сопротивлении нагрузки не менее 2 кОм, погрешность измере-
ния 1—10'.
Тахогенератор должен обеспечивать напряжение не менее 20 В при
частоте вращения 1000 об/мин.
266
Система токоограничения большинства электроприводов обеспе-
чивает автоматическое уменьшение уставки тока по мере увеличения уг-
ловой скорости двигателя. Это связано с характеристиками высокомо-
ментных двигателей, допускающими большие кратности тока [(6^-
-г8)/Ном] только при малой угловой скорости и по мере ее увеличения
требующими снижения перегрузки для нормальной коммутации. По
стандартам СЭВ входное напряжение преобразователей устанавливает-
ся равным ± 10 В. Все шире проявляется тенденция оснащения стан-
ков комплектным электрооборудованием.
Комплектные электроприводы широко применяются при проекти-
ровании АСУ ЭП металлорежущих станков. Отечественная промышлен-
ность освоила выпуск таких электроприводов и тиристорных преобра-
зователей мощностью от 0,09 до 250 кВт при диапазонах изменения
угловой скорости (100-20000) :1. Одни из них разработаны организа-
циями станкоинструментальной промышленности: Экспериментальным
НИИ металлорежущих станков - ЭНИМС, Украинским НИИ станкоин-
струментальной промышленности - УкрНИИСИП, Особым конструк-
торским бюро станкостроения — ОКБС, другие — рядом электротехни-
ческих институтов: Всесоюзным НИИ электропривода — ВНИИЭлектро-
привод, НИИ комплектных электроприводов — НИИКЭ, Всесоюзным
НИИ релестроения - ВНИИР.
В табл. 9.2 приведены характеристики некоторых комплектных элек-
троприводов и тиристорных преобразователей.
Транзисторный быстродействующий электропривод с широтно-им-
пульсным преобразователем серии ЭШИР-1А обеспечивает полосу про-
пускания 80-120 Гц и применяется в механизмах подач станков с ЧПУ.
Для механизмов главного движения выпускаются тиристорные
электроприводы постоянного тока серии ЭТУ, ЭПУ для однозонного и
даухзонного регулирования. Тиристорный электропривод серии ЭПУ
применяется для механизмов подач и главного движения. Тиристорные
преобразователи серии ПТЧ, ТПЧ, ПЧ, ЭКТ, ЭКТР предназначены для
частотного управления электродвигателями переменного тока. Они на-
ходят применение в механизмах главного движения шлифовальных
(ТПЧ, ЭКТ), внутришлифовальных и координатно-шлифовальных
(ПТЧ-3-1600) и сверлильных (ПТЧ-0,8-800) станков. Асинхронный
глубокорегулируемый комплектный электропривод ’’Размер 2М-5-2”
предназначен для токарных станков с ЧПУ.
Вентильный электропривод постоянного тока нашел самое широкое
применение в механизмах металлорежущих станков. Рассмотрим струк-
турную схему (рис. 9.9) электропривода ЭТУ3601, предназначенного
для работы с высокомоментными электродвигателями постоянного то-
ка в механизмах подач станков с ЧПУ. Трехфазный мостовой управля-
емый выпрямитель с коэффициентом передачи работает по прин-
ципу раздельного управления комплектами тиристоров. Схема управле-
ния электроприводом выполнена в виде двухконтурной системы подчи-
’ 267
Таблица 9,2
Серия при- вода, преоб- разователя Название Род тока Номиналь- ная мощ- ность, кВт Выход- Номиналь- Диапазон регулиро- вания ско- рости Ревер- сивность Серия приме- няемых дви- гателей
ное «ап- наяско-
ряжение, рость,
В рад/с
этим Электропривод импульсный транзисторный многокоорди- натный Посто- янный 0,3-5,5 60,150, 78,5-314 220 10 000, 30 000 Р ДПУ, 2ПБВ да
ЭШИР Электропривод с транзистор- ным ШИП 0,05-1,2 ПО 78,5-314 10 000, 30 000 Р ПСТ, ПБВ, ПБСТ, ПГТ
ЭТУ3601 Электропривод комплектный тиристорный »» 1,15-23 115,230 78,5-314 10 000 Р 2ПБ, ПБСТ, ПГТ, ПБВ
ЭПУ Электропривод унифицирован- ный трехфазный »» 1,5-250 115,230, 78,5-314 460 20,1000, 10 000 Р ПЯ, ДПУ, ПБВ, ПФВ, 4П
АТ То же модернизированный Пере- менный 22-250 230,460 - 1000 HP —
АТР То же реверсивный »» 22-250 230,460 - 100 Р —
Размер 2М-5-2 Электропривод асинхронный глубокорегулируемый я 0,4-2,5 220,380 51 10 000 Р —
ПЧИ Преобразователь частоты •» 125-500 220, 380 - 35 HP —
ЭКТ Агрегат тиристорный 10-100 220, 380 - 50,90 HP —
ЭКТР То же с рекуперацией 10-100 220, 380 - 50,90 Р —
ЭПБ-1 Электропривод тиристорный комплектный 3,2-13 520 18,5-157 10 000 Р 4СХ2П90Ь8П, 4С2П112М12П
Примечание. Р - реверсивный, HP - нереверсивный.
Рис. 9.9. Структурная схема электропривода типа ЭТУ3601
ненного регулирования с ПИ-регуляторами тока РТ и скорости PC.
Регуляторы тока и скорости охвачены соответствующими обратными
связями с передаточными коэффициентами £д т и £тг. Нелинейное зве-
но НЗ обеспечивает постоянство коэффициента усиления управляемо-
го выпрямителя в режиме непрерывного и прерывистого токов. Харак-
теристика нелинейного звена обратна регулировочной характеристике
управляемого выпрямителя в режиме прерывистого тока. Сигнал
на выходе РТ пропорционален только току двигателя, что достигается
подачей на нелинейное звено с функционального преобразователя ФПЭ
сигнала положительной обратной связи по ЭДС двигателя, обеспечива-
ющего дополнительное токоограничение.
В системе регулирования предусмотрен также узел зависимого токо-
ограничения УЗТ, ограничивающий по модулю выходное значение регу-
лятора скорости PC в зависимости от напряжения тахогенератора.
Электроприводы типа ЭТУ3601 разных исполнений обеспечивают диапа-
зон регулирования скорости 1000-10 000, выпрямленный ток 10 -
100 А, выпрямленное напряжение 115, 230 В и полосу пропускания час-
тот замкнутой системы регулирования частоты вращения не менее
32 Гц. Высокими техническими показателями обладает также унифици-
рованный электропривод серии ЭПУ.
Импульсный электропривод постоянного тока предназначен для ме-
ханизмов подач прецизионных станков с ЧПУ, роботов и автоматизиро-
ванных установок, требующих широкого изменения угловой Скорости
электродвигателя и высокого быстродействия. Функциональная схема
(рис. 9.10) комплектного электропривода с транзисторным широтно-
импульсным преобразователем типа ЭШИР-1А содержит ПИ-регулятор
тока РТ и /7-регулятор скорости PC, в обратные связи которых вклю-
чены датчик тока ДТ и тахогенератор BR соответственно. Кроме того,
на вход РТ поступают сигналы с датчика статического тока ДСГ и сиг-
нал от устройства токоограничения УТО при срабатывании последне-
го. С выхода РТ сигнал поступает на входы широтно-импульсных моду-
ляторов ШИМ1 и ШИМ2, осуществляющих модуляцию входного сигна-
ла соответствующей полярности. Блок коммутации БК реализует по-
269
очередный несимметричный закон коммутации, после чего широтно-мо-
дулированный сигнал через узлы задержки У31 - У34 и узлы гальвани-
ческой развязки УГР1 - УГР4 поступает на импульсные усилители мощ-
ности ИУ1 - ИУ4, управляющие транзисторными ключами KI - К4.
Устройство защиты от перенапряжений УЗП отводит энергию, рекупе-,
рируемую в переходных процессах в активное сопротивление и в фильтр
источника питания. При аварийных ситуациях: отключении сети, обрыве
в цепи тахогенератора, превышении током установленной величины на
заданное время — устройство аварийного торможения У АТ закорачи-
вает якорь двигателя и останавливает его.
Электроприводы типа ЭШИР-1А обеспечивают диапазон регулирова-
ния скорости 1:10 000 при максимальном напряжении преобразователя
до 140 В и максимальных токах якоря: кратковременных — до 50 А
и длительных — до 16 А. Полоса пропускания частот по скорости за-
висит от применяемых типов двигателей (ДК-1, ПСТ, 2П и др.) и состав-
ляет 80—120 Гц. Для роботов и многооперационных станков подготав-
ливают к выпуску импульсный многокоординатный привод серии
этим.
Асинхронный электропривод, работа которого основана на принципе
частотно-токового управления, позволяет получать глубокое регулиро-
вание угловой скорости при высоких динамических показателях. При
частотно-токовом управлении в обмотки электрической машины вво-
дятся токи, мгновенные значения которых определяются требуемым
значением электромагнитного момента и угловым положением ротора
машины. Для этого на вход привода подаются два независимых вход-
ных сигнала, задающих токи в обмотках и обеспечивающих не только
регулирование момента, но и возможность устанавливать требуемый
поток намагничивания и реактивный ток преобразователя. Выполненный
270
Рис. 9.11. Функциональная схема электропривода типа ’’Размер 2М-5-2”
на этом принципе асинхронный глубокорегулируемый комплектный
электропривод ’’Размер 2М-5-2” предназначен для токарных станков с
программным управлением (рис. 9.11).
На вход преобразователя поступают сигнал Щ задания тока (потока)
возбуждения и сигнал ^.регулирования момента, получаемый в резуль-
тате сравнения напряжения задания скорости U3 с напряжением (7О>С,
пропорциональным действительному значению скорости. Задание ампли-
туды и фазы тока статора U3C выполняется в соответствии с выра-
жениями
из,с = + <k2Udy-
* = arctg ’
где к 1, к2 — коэффициенты пропорциональности.
Пропорциональная сигналу Uq частота скольжения / суммируется
с частотой вращения ротора /р и в виде импульсных сигналов с часто-
той /б ± ф/р + /с) используется для формирования сигналов задания
фазовых токов С7зА и С7зВ частотой р/р ± /с с учетом фазового сдви-
га 2л/3. Здесь /о - опорный сигнал частотой 2 кГц,р - число пар полю-
сов. Сигнал, пропорциональный частоте вращения поля в статоре р/р
электродвигателя М, формируется с помощью датчика угла, выполнен-
ного в виде фазовращателя. Изменение фазы фазовращателя преобразу-
ется в код частоты вращения, поступающий на цифро-аналоговый преоб-
разователь ЦАП. Аналоговый сигнал (70jC с выхода ЦАП реализует
обратную связь по скорости. Трехфазный регулятор тока и транзистор-
ный инвертор формируют в статоре двигателя М токи, пропорциональ-
ные сигналам С7зА, и ток в фазе С, равный сумме токов фаз А и
В. Выполненный на терморезисторах датчик температуры служит для
271
ность до 10 кВ А.
Рис. 9.12. Конструкция реактивно*
го шагового двигателя
формирования сигнала ”Превы>
шение допустимой температу-
ры двигателя” и сигнала, огра-
ничивающего момент двигателя
путем воздействия на задатчик
частоты скольжения.
Электропривод ’Тазмер
2М-5-2” содержит два преобра-
зователя на две координаты
каждый, четыре асинхронных
двигателя серии 4А (с момен-
тами 7, 17, 21, 47 Н м), обеспечивает полосу пропускания не менее
100 Гц и диапазон регулирования скорости 1:10 000, потребляет мощ-
Электроприводы с шаговыми двигателями (ШД) применяются в оте-
чественных и зарубежных станках, координатографах и других устрой-
ства с ЧПУ.
Шаговый двигатель поворачивает свой вал на определенный угол при
подаче на его обмотки импульса из системы управления.
Реактивный ШД состоит из ротора и статора, набранных из пластин
электротехнической стали. Ротор и статор имеют зубцы (рис. 9.12).
Зубцы статора каждого наконечника I-VI смещены относительно зуб-
цов предыдущего полюсного наконечника на 1/3 зубцового шага. На
представленной конструкции каждая из трех обмоток статора ОУ1,
ОУ2, ОУЗ расположена на четырех полюсах. При поочередном включении
обмоток ось результирующего магнитного потока смещается на 1/3
зубцового шага, ротор также смещается на 1/3 шага, стремясь занять
положение наибольшей магнитной проводимости. Импульсы подаются
на обмотки в порядке 1, 2, 3, 1, 2, 3, ... либо 1,3,2,1,3,2 ... , чтоопре-
ляет направление вращения ШД. У активных ШД обмотками снабжены
также и роторы.
Основными па^^т^ми ШД являются: размер шага — угол пово-
рота вала двигателя’при Додаче на ШД одного импульса; приемистость -
наибольшая мгновенно изменяемая частота, отрабатываемая ШД при
данной нагрузке бе? потери импульсов; быстродействие — максималь-
ная частота, отрабатываемая ШД при данной нагрузке и плавном изме-
нении частоты; опрокидывающий момент. Например, серийный ШД типа
ШС-1,5 имеет шаг 1,5°, приемистость 0,6 кГц, быстродействие 16 кГц,
опрокидывающий момент 8 Н м, мощность 1,5 кВт на частоте 16 кГц.
При повышении частоты питания момент ШД уменьшается.
272
Up2 Upj
?n
ЛЛЛЛЛЛ
t
Рис. 9.13. Функциональная схема управления ШД (а) и диаграмма
ее работы (б)
Управление ШД осуществляется от статических преобразователей
частоты, вырабатывающих m-фазную систему импульсов напряжения.
Электроприводы с ШД и разомкнутой системой управления получили
М настоящее время наибольшее распространение. Типовая структурная
схема управления ШД приведена на рис. 9,13,а.
Если входная информация задается в виде непрерывно изменяющей-
ся величины, то используется преобразователь П непрерывного сигнала
В частно-модулированную последовательность импульсов напряжения.
Входные импульсы произвольной формы преобразуются в прямоуголь-
ные с помощью формирователя импульсов ФИ. Распределитель импуль-
сов РИ преобразует унитарный код в фазную систему импульсов напря-
жений ир1 - Up3, которые через усилитель мощности УМ и источник
Питания ИП подаются на обмотки ШД (рис. 9.13,6). При поступлении
команды на блок управления реверсом БУР последний изменяет алго-
ритм действия распределителя импульсов РИ и ШД начинает отрабаты-
вать движение в обратном направлении.
273
X
Рис. 914. Конструкция двух координатного линейного шагового двигателя
Находят применение также линейные и плоскостные (двухкоорди-
натные) ШД.
Двухкрординатные ШД построены на принципе объединения якорей
и индукторов однокоординатных ШД при отсутствии или слабой связи
между их магнитными системами, что позволяет обеспечить работу по
каждой координате при разделении электромагнитных процессов в кон-
турах ШД. Конструкция двух модулей такого линейного двухкоорди-
натного ШД, разработанного на кафедре электропривода Московского
энергетического института, показана на рис. 9.14 [30]. Каждый модуль,
расположенный над пассивной магнитомягкой плитой 1, содержит по-
стоянный магнит возбуждения 2 и два Ш-образных шихтованных магни-
топровода 5. Полюсные наконечники магнитопроводов 3 снабжены зуб-
цами с шагом, равным шагу зубцов на плите-индукторе. Сдвиг зубцов
крайних полюсов магнитопровода 3 относительно зубцов среднего
полюса равен тг.
На среднем полюсе магнитопровода находится катушка 4, состоя-
щая из двух встречно включенных частей. Модули объединяются общим
корпусом, представляющим якорь, перемещающийся на аэростатичес-
ких опорах в направлении оси х и у. Для повышения устойчивости
движения, сглаживания пульсаций силы и увеличения результирующего
тягового усилия увеличивают количество элементарных модулей. Сдвиг
зубцов соседних полюсов, принадлежащих разным модулям, составляет
я/2.
Последовательно подаваемые на электромагниты электрические им-
пульсы вызывают смещение якоря до установки зубцов возбужденных
электромагнитов против зубцов на плите-индукторе. Пазы на якоре и
плите залиты немагнитным компаундом для снижения трения при пере-
мещении и создания между якорем и плитой воздушной подушки.
Применение принципа электрического дробления шага, основанного на
274
модуляции фазных напряжений внутри основного периода коммута-
ции, позволяет получить малый единичный шаг (2-10 мкм), высокую
повторяемость положений (0,5—3,0 мкм) , высокие максимальные ско-
рости перемещений (0,8— 1,0 м/с) .
Двухкоординатные ШД находят применение в станках для сверления
пеФтных плат, в манипуляторах для автоматизации сборочных опера-
ций, в графопостроителях.
Электроприводы с вентильными двигателями (ВД) позволяют полу-
чить диапазон регулирования скорости до 1:20 000 и полосу пропуска-
ния 100-150 Гц при значительно большей простоте и меньших затра-
тах по сравнению с регулируемыми электроприводами с асинхронными
двигателями.
Вентильные двигатели представляют систему, состоящую из бескол-
лекторного синхронного двигателя, датчика положения ротора, вен-
тильного коммутатора и устройства управления.
На статоре ВД находится трехфазная обмотка, ротор служит возбу-
дителем, который либо получает напряжение постоянного тока через
кольца и щетки, либо выполнен на постоянных магнитах, закрепленных
в пазах ротора.
Вентильный коммутатор питает обмотки статора, коммутируя ток в
соответствии с командами датчика положения ротора.
Таким образом, вентильный коммутатор является своеобразным
аналогом щеточного механизма и вращающегося коллектора машины
постоянного тока.
Вентильный двигатель обеспечивает регулирование угловой скорости
вниз от номинальной путем изменения подводимого к статору напря-
жения. Кроме того, регулировать скорость можно изменением тока в
обмотке возбуждения и изменением угла опережения включения вен-
тилей относительно фазных ЭДС двигателя (вверх от номинальной).
Механические характеристики ВД подобны характеристикам дви-
гателя постоянного тока.
Схема электропривода с ВД (рис. 9.15) содержит преобразователь
с промежуточным звеном постоянного тока UM и инвертор с искусст-
венной коммутацией UZ. Управление инвертором UZ производится в
функции положения ротора двигателя М при помощи датчика положе-
ния BQ, воздействующего на систему управления инвертором AU2.
Система управления выпрямителем AU1 воздействует на управляемый
выпрямитель UM. Изменением одного из углов а,0 или тока возбужде-
ния двигателя М можно регулировать угловую скорость ВД.,При постро-
ении замкнутой системы управления ВД ее выполняют по принципу под-
чиненного регулирования с регуляторами тока АА и скорости AR.
Обратные связи построены при помощи датчиков тока UA и скорости
BR, скорость устанавливается задатчиком SR.
Электроприводы с ВД в станкостроении применяются в механизмах
подач станков с ЧПУ. Во ВНИИР (г. Чебоксары) разработан комплект-
275
ный электропривод с ВД типа ЭПБ-1. Линейный вентильный двигатель
(ЛВД) для механизма подачи станка мод. СМ600 разработан НИИКЭ
(г. Новосибирск). Этот станок предназначен для сверления печатных
плат и оснащен тремя ЛВД, выполняющими ускоренные перемещения
по трем координатам со скоростью 20 м/мин при точности позициони-
рования ±0,005 мм, что обеспечивает высокую производительность.
По технико-экономическим показателям электроприводы подач
с ВД, развивающие крутящий момент 2—40 Н • м, превосходят электро-
приводы с высокомоментными двигателями, получающими питание от
широтно-импульсных преобразователей.
Как показывают прогнозы, основным типом регулируемого привода
в металлорежущих станках на ближайшие годы останется привод по-
стоянного тока, однако в станкостроении все четче проявляется устойчи-
вая тенденция к замене его электроприводом переменного тока.
Глава десятая
СИСТЕМЫ СТАБИЛИЗАЦИИ РЕЖИМОВ МЕТАЛЛООБРАБОТКИ
10.1. ОБЩИЕ ПОЛОЖЕНИЯ
В системах стабилизации режимов металлообработки при изменении
возмущающих воздействий основной задачей является поддержание од-
ного или нескольких параметров в соответствии с выбранными техноло-
276
гическими законами управления. В общем случае АСУ должна обеспе-
чивать изменение двух параметров режима обработки, включать два
контура управления: скоростью резания v и подачей s при изменении
возмущающих воздействий, к основным из которых относятся измене-
ние глубины резания и твердости обрабатываемой заготовки.
АСУ ТП стабилизации содержит регулятор Р (рис. 10.1,а) электро-
приводов шпинделя ЭПШ и подачи ЭПП, воздействующий на процесс
резания ПР, и датчики информации ДИ1,ДИ2 об обобщенных парамет-
рах Xj (t) и х2 (О- На вход регулятора поступает разность сигналов
^У1 ” ^41 ~ ^О,С1 ,
Ыу2 - ^з2 — Wo,C2^p’
где U3x, U32 — напряжения задания с соответствующих блоков задания
БЗШ и БЗП\ м0С1, WO,C2 ” напРяжения сигналов обратных связей;
tp — глубина резания; НВ — твердость обрабатываемой заготовки.
Применение микропроцессоров позволяет построить систему стаби-
лизации с цифровым управлением режимом металлообработки
(рис. 10.1,6) . Информация о ходе технологического процесса поступает
на микропроцессор МП от датчиков информации ДИ через устройство
связи с датчиками УСД. Внешняя априорная информация ВАИ вводит-
ся в запоминающее устройство микропроцессора. Управление ЭШП и
ЭПП осуществляется от МП через устройство связи с объектом УСО.
Как видно, в системах стабилизации режимов металлообработки
осуществляется обратная связь по параметрам процесса резания. Схе-
мами рис. 10.1 предусмотрено применение двух регулируемых приво-
дов: главного движения и подачи. На практике чаще используются сис
темы стабилизации режимов металлообработки, в которых изменяется
угловая скорость только одного привода.
Главная задача настоящей главы - изучение основных способов уп-
равления электроприводами для стабилизации режимов металлообра-
ботки. Студенты должны знать алгоритмы функционирования систем
стабилизации режимов металлообработки, способы получения техноло-
гической информации, типовые схемы систем стабилизации. Они должны
уметь составлять структурные схемы, выполнять синтез параметров
звеньев и расчеты статических и динамических характеристик систем
стабилизации металлообработки.
10.2. АЛГОРИТМЫ УПРАВЛЕНИЯ СИСТЕМАМИ СТАБИЛИЗАЦИИ
РЕЖИМОВ МЕТАЛЛООБРАБОТКИ
Для построения структурных схем необходимо знать алгоритм функ-
ционирования системы, базирующийся на принятом показателе эффек-
тивности обработки.
277
Рис. 10.1. Обобщенная структурная схема управления процессом резания:
а - аналоговая; б - цифро-аналоговая
В гл. 9 были рассмотрены интегральная форма показателя эффектив-
ности обработки, характеризующего себестоимость обработки, а также
показатели производительности. Некоторые показатели производитель-
ности приведены в табл. 10.1. Соответствующие им алгоритмы функцио-
нирования реализуют системы стабилизации металлообработки.
В табл. 10.2 представлены структурные схемы и рабочие характери-
стики режимов, указанных в табл. 10.1. На структурных схемах действие
комплекса возмущающих факторов обозначено индексом /. В рас-
сматриваемых случаях производительность является показателем эф-
фективности обработки. Это оправдано тогда, когда производительность
станка диктуется плановыми показателями, а также когда стойкость
инструмента должна обеспечить обработку детали без смены инструмен-
та. Наиболее полно эффективность обработки определяется показате-
лем приведенных затрат.
Режим 1. Действие возмущающих факторов f (износ инструмента,
колебания припуска, твердости материала заготовки, влияние охлажда-
ющей жидкости) в этом режиме компенсируется изменением скорости
резания таким образом, чтобы процесс обработки соответствовал задан-
ной стойкости инструмента 7\. На процесс резания ПР воздействуют
278
Показатель эффек- Налагаемое
Режим тивности обработки ограничение
1 Jl -*»F! тт . — 1 ”1
2 J2 я ^2v2^p2 тт =. S 2 X V^P2
3 /3 = кз^зЪ >•<
4 Z» « *4*4»4^Р4 _m Cva Тл “ 4 л У ”4,Р4,4
Параметры
Алгоритм функционирования
изменя- емые контроли- руемые неконт- ролиру- емые
>4 7*1 СУ1 '01 „ Л
*2 Га. гр2 *2 ZP2 ж *ртах CV2 v°2 “ ' m " Tmt *pmax
s03 = smax
v3 7*3» fp3 F03 “ CV3 3 *max
fP04 “ fpmax > 3o4 = smax
V4 T4t4tp4 ~ ”04 я CV4 Зтах*ртах
Продолжение табл. 10.1.
Показатель эффек- Налагаемое
Режим тавности обработки ограничение
5 Js = *s»s Тт =
6 As ® _т С?6 т “ 6 X У t я
Параметры Алгоритм функционирования
изменя- емые контроли- руемые неконт- ролиру- емые
T5f5 сх,у
*s ₽5' ГР5 тт/у S .
f р6» ^6 *0* ж грмих сх,у
‘Рб *06 м/ух/У лб ртах
Таблица JO* 2
электропривод главного движения (шпинделя) ЭПШ и электропривод
подачи ЭПП. Датчик стойкости инструмента ДСИ подключен к входу
микропроцессора МП. В ОЗУ микропроцессора поступает априорная
информация о заданной стойкости инструмента ЗИ и о максимально до-
281
Продолжение та.5л. 10.2
пустимой угловой скорости ЗШ привода ЭПШ. Микропроцессор МП .
управляет приводом главного движения ЭПШ по алгоритму v01 =
= CVJT™ при v < vmax.
282
По аналогичной структурной схеме построены регуляторы, в том
числе и аналоговые, использующие в качестве датчика стойкости тем-
пературу естественной термопары инструмент — деталь и предназначен-
ные для фрезерования, а также для торцовой обточки деталей. Это обес-
печивает повышение производительности на 30—45%.
Режим 2. Структура отличается от предыдущей учетом изменения
глубины резания в процессе обработки.
Глубина резания измеряется датчиком ДГР. В ОЗУ микропроцессо-
ра МП вводятся поправочные коэффициенты, соответствующие глуби-
не резания КГ и стойкости (износа) инструмента КИ. Максимально до-
пустимое значение температуры резания ®тах, вводимое в микропро-
цессор МП и определяющее заданную стойкость инструмента ЗС, срав-
нивается с текущей температурой 0 и ограничивает рост скорости реза-
ния при 0 > @тах. Для всех режимов, в которых измеряется термо-ЭДС
естественной термопары инструмент — деталь, стойкость инструмента
повышается в 1,5—2,0 раза и более за счет разрыва цепи термотока или
его уменьшения. Трудность реализации датчика глубины резания огра-
ничивает применение этой структуры.
Режимы 3, 4. Системы стабилизации, обеспечивающие работу станка
с показателями эффективности J3 и , отличаются количеством ис-
пользуемых каналов информации. Так, в третьей структурной схеме на
микропроцессор МП, вырабатывающий управляющее напряжение, соот-
ветствующее J3, поступают сигналы с датчиков подачи ДВП, стойкости
инструмента ДСП и информация о коррекции подачи КП и стойкости
КИ. Третья структурная схема является информационно избыточной,
поскольку подача в ней неизменна и информация о подаче может быть
включена в микропроцессор без применения датчика подачи ДВП.
В четвертой структурной схеме на микропроцессор МП кроме указан-
ных поступают сигналы с датчика ДГР и информация о коррекции глу-
бины резания КГ.
Режим 5. В соответствии с критерием /5 осуществляется изменение
подачи, а не скорости резания. Для этого на вход микропроцессора МП
поступает та же информация, что и в схеме для режима 3. В этом слу-
чае управляющее напряжение МП, соответствующее показателю эффек-
тивности обработки Js, подается на привод подачи ЭПП. Поступающая
в МП информация об ограничении подачи ОП задает максимально до-
пустимое ее значение. Так как стойкость инструмента в значительно
меньшей степени зависит от подачи, чем от скорости резания, то такая
система управления менее эффективна, чем предыдущие.
Режим 6. Показатель эффективности обработки J6 близок к вели-
чине, определяющей предельно допустимое значение мощности резания
где кр - коэффициент пропорциональности; а, 0 - показатели сте-
пени.
283
В этом случае реализация показателя эффективности решается путем
применения системы стабилизации мощности резания, особенно эффек-
тивной при фрезеровании и силовом шлифовании.
Мощность, потребляемая из сети двигателем главного привода ЭПШ
(обычно асинхронного), измеряется датчиком мощности ДМ, На блок
сравнения БС поступают сигналы, пропорциональные мощности реза-
ния и предельно допустимой мощности (с учетом мощности холостого
хода с задатчика БЗМ). Выходной сигнал с блока сравнения БС и с за-
датчика ограничения подачи ЗОП подается на регулятор РП электропри-
вода подачи. Подача регулируется таким образом, что несмотря на из-
менения глубины резания, твердости заготовки и затупление инструмен-
та мощность резания поддерживается в заданных пределах. Использова-
ние системы стабилизации мощности резания повышает производитель-
ность обработки на 25—40%. Рост производительности обработки может
ограничиваться потерей устойчивости и возникновением недопустимых
вибраций в процессе резания.
Для устранения этих вибраций схемы должны содержать корректи-
рующие устройства, параметры и место включения которых зависят от
режима обработки и технических характеристик станка и привода. На
структурных схемах в табл. 10.2 эти корректирующие устройства не
показаны, а предполагается, что они входят в соответствующий регуля-
тор привода.
103. ТИПОВЫЕ СХЕМЫ СИСТЕМ СТАБИЛИЗАЦИИ
Среди АСУ ТП металлообработкой наибольшее распространение по-
лучили системы стабилизации режимов резания. Многообразие конструк-
тивных решений, воплощенных в станках, особенности формообразова-
ния на них даже при одном виде обработки и широкий диапазон требо-
ваний, предъявляемых к процессу резания, породили обилие схемных
разработок, обеспечивающих стабилизацию тех или других параметров.
Схемы отличаются друг от друга составом контролируемых параметров,
а также принципами построения автоматических регуляторов техноло-
гических процессов. Тем не менее при всем разнообразии схем можно
выделить сравнительно ограниченное число типовых решений, что облег-
чает их изучение. Ниже рассматриваются типовые схемы систем стаби-
лизации.
Система стабилизации скорости резания является одной из наиболее
широко распространенных систем стабилизации и применяется на токар-
ных и карусельных станках при обработке торцовых, конических и сфе-
рических поверхностей. Она применяется также в шлифовальных стан-
ках, например для поддержания постоянства скорости резания по мере
износа шлифовального круга. Применение систем стабилизации скоро-
284
ijwho .2. Эскиз детали
₽ИС 10.3. Зависимость скорости резания и угловой скорости от изменения радиу-
са обработки
Ъ
exit резания позволяет сократить машинное время, повысить произво-
дительность и улучшить качество обработанной поверхности.
л Рассмотрим обработку усеченного конуса, имеющего наименьший и
наибольший радиусы Rr и R2 и образующую L (рис. 10.2). Если конус
Обрабатывается с постоянной угловой скоростью шпинделя = const,
f хозрасчетная скорость резания vp, м/мин, при наибольшем радиусе мо-
Иф^быть определена из формулы
ед
= Vp/2-9,55ir/?2 = vp/60/?2.
^Машинное время при обработке с постоянной угловой скоростью
J^mco = b/9,55wms = 2irLR2/VpS9
фе s - подача вдоль образующей, мм/об.
.^Машинное время при обработке с постоянной скоростью резания и
переменной угловой скоростью можно рассчитать по выражению
L 2irr
>*мг = / --------Л- (10Л)
о V
^Подставляя в (10.1) выражения для текущего радиуса г=Я1 +
sin а, после интегрирования получаем
, tMV = — (Я,+Л2). (10.2)
FPI
; Относительное сокращение машинного времени за счет применения
системы стабилизации скорости резания можно выразить уравнением
’ гм(Л~гмр _ 1 Л R1 \ _ 1 11 ^min
*mw 2 \ R2 / ^тах
285
1 D - 1
2 D ’
где Ww/ZJ ~~ ^max D ~ ^max I^mirr
Как видно, относительное сокращение машинного времени не зави-
сит от длины заготовки и полученное выражение правомерно также и
при торцовой обработке. Согласно (10.3) при достаточно большом D
экономия машинного времени приближается к 50%. При обработке сфе-
рических поверхностей относительное сокращение машинного време-
ни рассчитывается по формуле
ГМС0 ~ _ 1 п2 - 1
*м со 2 D2
Наиболее целесообразный с точки зрения повышения производитель-
ности диапазон изменения угловой скорости составляет 6—10 при обра-
ботке торцовых, конических поверхностей и 3—4 при обработке сфери-
ческих поверхностей. Однако для обеспечения чистоты обрабатываемой
поверхности необходимо поддерживать постоянную скорость резания
на всем диапазоне изменения радиуса обработки детали. Применение
системы стабилизации скорости резания, кроме того, примерно в 2 раза
увеличивает стойкость инструмента. На практике скорость резания
поддерживают постоянной при радиусах обработки больше некоторого
минимального значения (рис. 10.3). При достижении угловой скоростью
минимального значения и дальнейшем уменьшении радиуса скорость
резания v будет уменьшаться. Реализация систем стабилизации скоро-
сти резания возможна при получении сигнала, пропорционального ско-
рости резания, который используют в качестве сигнала обратной связи.
Поскольку непосредственное измерение скорости резания затруднитель-
но, его производят косвенным путем, обеспечивая для поддержания
постоянства скорости резания гиперболическую зависимость угловой
скорости шпинделя от диаметра обработки. Такая зависимость может
быть получена при помощи тахогенератора и потенциометрической
схемы. Для этого (рис. 10.4,а) движок следящего потенциометра RP1
механически связан с суппортом станка. Потенциометр подключен к
якорю тахогенератора BR привода шпинделя, и с него снимается напря-
жение обратной связи по скорости резания. На управляющий элемент
стабилизации скорости резания поступает напряжение Д£/у, равное раз-
ности задающего напряжения U3 и напряжения обратной связи 1/о,с>
пропорционального скорости резания v. В качестве датчика скорости
может быть применен тахометрический мост.
Сигнал, пропорциональный скорости резания, может быть получен
с помощью диодного функционального преобразователя (рис. 10.4,6).
С изменением диаметра обработки (воздействие S) изменяется напря-
286
Рис. 10.4. Схемы датчиков скорости систем стабилизации скорости резания:
а - с тахогенератором; б - с функциональным преобразователем; в - с ин-
дуктивным датчиком; г - с сельсином
жение, поступающее на преобразователь со следящего потенциометра
RP, открываются диодные ячейки VD1 - VDn и при соответствующей
настройке схемы ток, протекающий через резистор RS, изменяется по
закону аппроксимированной гиперболы.
Устройство обратной связи по скорости резания, содержащее индук-
тивный датчик BL1, включенный в дифференциальную мостовую схему
с индуктивным преобразователем BL2, показано на рис. 10.4,в. Воз-
действие механизма суппорта S на индуктивный датчик BL1 осуще-
ствляется при помощи профилированной линейки. Профиль линейки
строится на готовом станке методом подбора, при помощи упорных вин-
тов, что позволяет компенсировать нелинейности системы регулирова-
ния (усилителя, двигателя, самого датчика и др.).
В устройстве, показанном на рис. 10.4,г, ротор сельсина ВС кинема-
тически связан с механизмом суппорта S, и напряжение на выходе пос-
леднего пропорционально диаметру обработки. Через трансформатор
Т это напряжение подается на обмотку возбуждения LBR тахогенера-
тора BR привода шпинделя. Напряжение, пропорциональное скорости
резания, снимают с обмотки якоря тахогенератора, являющегося бло-
ком перемножения.
В шлифовальных станках стабилизация скорости шлифования v
осуществляется увеличением угловой скорости шпинделя сош по мере
уменьшения диаметра шлифовального круга dK вследствие размерного
износа и его правок по закону v = dK сош/2 = const. Построение систе-
287
Рис. 10.5. Система стабилизации скорости резания шлифовального станка:
а - конструкция датчика; б - схема системы
мы стабилизации скорости шлифования может быть выполнено на базе
асинхронных электродвигателей с короткозамкнутым ротором и тири-
сторных преобразователей частоты. Ротор асинхронного двигателя и
шлифовальный шпиндель представляют единое конструктивно оформ-
ленное устройство, называемое электрошпинделем.
Сигнал технологической обратной связи может быть получен путем
перемножения напряжений, пропорциональных угловой скорости шпин-
деля, и диаметра шлифовального круга. Датчик диаметра шлифоваль-
ного круга выполняется в виде сельсина, связанного с соплом, через
которое подается в зону обработки (рис. 10.5,а) смазывающе-охлажда-
ющая жидкость (СОЖ). Конструкция такого датчика, хотя и требует
периодической подстройки оператором, довольна проста, она предотвра-
щает возможность ошибочного включения привода на максимальную
частоту вращения при наибольшем диаметре круга, что может привести
к разрыву круга.
Оператор, направляя СОЖ в зону шлифования, одновременно с соп-
лом поворачивает ротор сельсина. Система стабилизации скорости шли-
фования (рис. 10.5,6), построенная с применением такого датчика, со-
держит пять операционных усилителей А1-А5, выполненных на инте-
гральных микросхемах, блок перемножения АХ и преобразователь час-
тоты, состоящий из управляемого выпрямителя UM и автономного ин-
288
вертора UZ. Блок управления преобразователем построен по принципу
подчиненного регулирования.
С помощью П-регулятора положения А1 производится задание ско-
рости шлифования U3 и вычитание из задающего напряжения сигнала
ц,, пропорционального скорости шлифования v и получаемого на бло-
ке перемножения АХ, на вход которого подаются напряжения, пропор-
циональные угловой скорости шпинделя и диаметру шлифовально-
го круга ид, вырабатываемые сельсином ВС.
Усиленный разностный сигнал управления Uy поступает на П-регу-
лятор скольжения А2 вместе с сигналом отрицательной обратной свя-
зи по угловой скорости ротора Выделение модуля напряжения за-
дания для регулятора тока осуществляется при помощи инвертора
АЗ и вентилей VD5, VD6. Это связано с тем, что ток в звене выпрям-
ленного напряжения не меняет своего знака, в то время как скольжение
может свой знак изменять. Регулирование выпрямленного тока (тока
статора) выполняет ПИ-регулятор тока А4, на вход которого поступа-
ют сигналы отрицательной обратной связи по току щ и который пропор-
ционален модулю скольжения Uj т. Регулятор тока в статических режи-
мах поддерживает заданное значение тока статора независимо от часто-
ты автономного инвертора UZ, воздействуя на систему управления
выпрямителем AUM.
На систему управления инвертором AUZ воздействует регулятор
частоты А5, на входе которого суммируются сигнал скольжения с вы-
хода А2 и сигнал, пропорциональный угловой скорости ротора
Стабилитроны VD1 - VD4 ограничивают напряжения на соответству-
ющих усилителях. При увеличении нагрузки на валу двигателя в преде-
лах рабочего участка его механической характеристики частота UZ не из-
меняется, поскольку приращение сигнала скольжения компенсирует
уменьшение сигнала угловой скорости на регуляторе А5. По мере из-
носа шлифовального круга поворачиваются сопло и ротор сельсина
ВС, изменяется сигнал ц,, пропорциональный скорости шлифования,
и система управления увеличивает частоту на выходе UZ, повышая угло-
вую скорость асинхронного двигателя М и стремясь поддержать посто-
янной скорость шлифования.
В АСУ тяжелого шлифовального станка (рис. 10.6) изменяется угло-
вая скорость двигателя в диапазоне 4:1 за счет изменения напряжения,
подведенного к якорю от тиристорного преобразователя UM, и изме-
нения магнитного потока с помощью тиристорного преобразовате-
ля UL.
Угловая скорость двигателя М задается задатчиком скорости SR,
сигнал которого’ вместе с сигналом обратной связи по скорости от та-
хогенератора BR подается на промежуточный усилитель А1. Выходное
напряжение А1 подается на систему импульсно-фазового управления
AUM через эмиттерный повторитель AD, который служит для согла-
сования сопротивления выхода усилителя с входом AUM. При работе
289
Рис. 10.6. Схема системы
стабилизации скорости ре-
зания тяжелого шлифо-
вального станка
двигателя с угловой скоростью выше основной сигнал задатчика ско-
рости через промежуточный усилитель А2 подается на AUL. Узел пере-
ключения зон UV конт{ЙЙйрует наличие номинального магнитного по-
тока при работе двигателя с угловой скоростью ниже основной. Сигнал
на выходе UV определяется разностью эталонного напряжения 17эт и
напряжения на якоре двигателя М. Этот сигнал подается на цепь управ-
ления Л2, параллельно которой включен стабилитрон. Выходное напря-
жение усилителя А2 остается неизменным, что поддерживает номиналь-
ный магнитный поток двигателя до тех пор, пока напряжение на якоре
не станет близким к номинальному.
В схеме использован узел упреждающего токоограничения AAF.
Максимальная защита осуществляется автоматическим выключателем
QF с максимальным и дистанционным расцепителем SA. Управление
расцепителем производится U2 в функции сигнала, получаемого со
вторичной обмотки трансформатора тока ТА.
Для стабилизации скорости резания текущий диаметр шлифоваль-
290
ного круга измеряется с помощью сельсина ВС. Ротор сельсина через
профильный кулачок связан с суппортом шлифовального кр^га.
Выходное напряжение сельсина, пропорциональное углу поворота
ротора, через выпрямительный мост U1 подается на обмотку возбужде-
ния тахогенератора LBR. С уменьшением диаметра шлифовального
круга будет уменьшаться ток возбуждения тахогенератора и снижать-
ся глубина обратной отрицательной связи по скорости. Угловая скорость
двигателя привода шлифовального круга при этом будет возрастать, а
скорость резания поддерживаться постоянной.
Применение системы стабилизации скорости шлифования более чем
в 1,5 раза повышает удельную производительность круга, определяемую
как отношение объема сошлифованного металла к объему износивше-
гося материала круга, на 15—20% повышает качество обработанной
поверхности.
Система стабилизации мощности резания дает возможность повы-
сить производительность станка, улучшить использование главного
привода и режущего инструмента. Применение систем стабилизации
мощности резания необходимо при точении (стабилизация мощности
резания при торцовой обработке), шлифовании (стабилизация мощности
резания при износе круга, изменении диаметра обработки в станках с
круглым столом), фрезеровании (стабилизация мощности резания
при изменении глубины обработки). Стабилизация мощности резания
может осуществляться двумя путями: за счет управления скоростью
электропривода главного движения и за счет управления скоростью
привода подачи. В принципе возможен вариант одновременного управ-
ления обоими электроприводами.
Непосредственное измерение мощности резания невозможно, поэто-
му для ее оценки измеряют мощность, потребляемую электроприводом
главного движения, с учетом потерь мощности в двигателе и переда-
чах станка. Применение для главного привода станков асинхронных
электродвигателей с короткозамкнутым ротором требует получения
сигнала управления, пропорционального активной мощности, потребля-
емой из сети этими двигателями. Датчики, вырабатывающие эти сигна-
лы, строятся на принципах векторного суммирования напряжений, ис-
пользования нелинейных функциональных элементов, применения
время-импульсной модуляции и амплитудной модуляции (ВИМ-АМ),
а также широтно-импульсной модуляции (ШИМ).
На рис. 10.7 показана схема, построенная на принципе векторно-
го суммирования и использования квадраторов. Сигнал, пропорцио-
нальный напряжению, снимается со вторичной обмотки трансформато-
ра ТУГ, сигнал, пропорциональный току,-со вторичной обмотки тран-
сформатора ТА и с помощью согласующего трансформатора TV2
подается на резистор RS. Полученная система векторов преобразуется
с помощью фазочувствительной схемы, состоящей из трансформаторов
291
ТУЗ и TV4 и вентилей VD1 - VD4. На выходе этой системы действу-
ют напряжения Ui = к^ (t/H + J7T), U2 = кг (L7H — L7T).
Функциональные преобразователи, собранные на диодах VD5 -
VD1О, резисторах Rl - R8 и делителях напряжения RP1, RP2, обла-
дают квадратичными вольт-амперными характеристиками, поэтому
токи в плечах схемы равны
Ь = It = к2у^.
Ток, протекающий через нагрузку Яо, равен
/вых =/1-/2 = = 4*,’*2 Ц,
откуда /вых = kQP. Погрешность выходного сигнала такой схемы 2%.
Схема, работа которой основана на методе ВИМ — ДМ, показана на
рис. 10.8. В узле временного модулятора используется мультивибратор
Ройера на трансформаторе TV2 и двух транзисторах VT1, VT2, работа-
ющих в ключевом режиме. Магнитопровод трансформатора TV2 изго-
товлен из материала с прямоугольной петлей гистерезиса. На вход время-
импульсного модулятора с трансформатора тока ТА подается сигнал,
пропорциональный измеряемому току, на вход амплитудного модуля-
тора — измеряемое напряжение трансформатора TV1. Перемагничива-
ние магнитопровода трансформатора TV2 происходит по полной пет-
292
ле гистерезиса в пределах каждого такта работы. Время перемагничи-
вания в каждом такте определяется соотношением между стабилизиро-
ванным напряжением С/о и напряжением, пропорциональным то-
ку/.
Собственная частота мультивибратора Ройера на два порядка боль-
ше частоты контролируемой цепи. Длительность импульса напряжения
мультивибратора Ройера при открытом транзисторе VT1 и положитель-
ней полуволне напряжения нт, пропорционального току,
; Ui = М^о + "т - ^ЭК)> (Ю.4)
где ki — коэффициент, характеризующий параметры трансформатора
ТР2; — падение напряжения на переходе эмиттер - коллектор
открытого транзистора VT1 (или VT2).
Длительность импульса при открытом транзисторе VT1 и отрицатель-
ной полуволне напряжения нт равна
(<Л> - и? - ад. (Ю.5)
Импульсы выходного напряжения мультивибратора Ройера промо-
дулированы по длительности напряжением ын, снимаемым со вторич-
ной обмотки трансформатора TV1 (рис. 10.8,6).
В узле амплитудного демодулятора используется дифференциальная
фазочувствительная схема, основанная на применении полупроводни-
ковых ключей с двусторонней проводимостью коллекторного перехода.
При возникновении прямого тока в цепях эмиттеров соответствующих
пар транзисторов VT3, VT4 или TV5, VT6 между выводами коллек-
тор — коллектор данной пары ток может проходить в любом направ-
лении.
Среднее значение напряжения на выходе демодулятора
t 2 — 11
мвых ” ~ Т~Г~ ин’ (10.6)
Выражение (10.6) можно записать с учетом (10.4) и (10.5) ив пред-
положении, что UQ и С7эк потоянны:
мвых “ ^2WtWH*
При синусоидальной форме тока и напряжения в контролируемой
цепи среднее напряжение на выходе датчика пропорционально мощ-
ности:
мвых = ^3wTwHcos^ = kui = кР
при точности около 1%.
293
~ ТА
а)
Рис. 10.8. Схема датчика мощности при использовании ВИМ-АМ (а) и диаграмма
его работы (б)
Ptac. 10.9. Схемы системы стабилизации мощности резания фрезерного станка:
а- функциональная; б - структурная
Мощность резания определяется выражением
Рр = Рд - ДРд - Д^ст. (10.7)
где Рд - активная мощность, потребляемая двигателем главного движе-
ния; ДРд — потери мощности в двигателе; ДРСТ - потери мощности
в передачах станка.
Эффективность систем автоматической стабилизации мощности ре-
зания будет тем выше, чем шире пределы изменения параметров реза-
ния в процессе обработки. Такие режимы работы характерны для фре-
зерных и особенно фрезерно-отрезных станков, у которых при резании
значительно изменяется длина контакта фрезы-пилы с заготовкой.
В схеме стабилизации мощности резания фрезерного станка
(рис. 10.9,а) для изменения скорости подачи применен комплектный
реверсивный тиристорный электропривод постоянного тока, включа-
ющий в себя: двигатель М2 с тахогенератором BR, преобразователь U,
усилитель А2 и задатчик скорости RP2. Полярность напряжения задания
определяется включением реле KI, К2, а ускоренной и рабочей подач —
295
реле КЗ. Измерение мощности двигателя Ml главного привода осуще-
ствляется статическим преобразователем мощности UW (см. рис. 10.7).
Напряжение сравнения снимается с резисторов R1 - R3 в зависимости
от состояний контактов микропереключателей SQ1 - SQ3, связанных с
рычагами переключения коробки скоростей шпинделя. При помощи
этих микропереключателей получают шесть уставок напряжений сравне-
ния, соответствующих шести угловым скоростям шпинделя. Как толь-
ко напряжение измерительной схемы становится больше напряжения
сравнения, отпирается вентиль VD1 и через усилитель А1 в контур за-
дания электропривода подачи поступает сигнал, пропорциональный ак-
тивной мощности. Угловая скорость электродвигателя М2 привода по-
дачи начинает уменьшаться. Погрешность поддержания постоянства
мощности электропривода главного движения в описанной системе
составляет 4—6%.
Упрощенная эквивалентная структурная схема автоматизированной
системы управления с обратной связью по мощности фрезерования при-
ведена на рис. 10.9,6. Тиристорный преобразователь описывается апе-
риодическим звеном с передаточной функцией Яп(р), двигатель по-
стоянного тока привода подачи описывается колебательным звеном с
передаточной фудоццей Ядф).
Привод охвачен отрицательной обратной связью по угловой скорости
двигателя с коэффициентом передачи £тг. Через механизм подачи с
передаточным коэффициентом ^п,м двигатель воздействует на про-
цесс металлообработки, описываемый апериодическим звеном с переда-
точной функцией Яр (р). Регулируемым параметром является мощность
фрезерования Р2, измерение которой осуществляется датчиком мощ-
ности, изображаемым апериодическим звеном с передаточной функцией
Яд>м (р). Технологическая обратная связь по мощности выполнена не-
линейной, и до тех пор, пока сигнал Ят>с не станет больше напряжения
сравнения С7ср, технологическая обратная связь разомкнута и угловая
скорость привода подачи определяется напряжением задания U3. Работа
рассматриваемой системы при отсутствии корректирующего устройства
в контуре обратной связи сопровождается колебаниями угловой скоро-
сти и регулируемой мощности. Для устранения колебательного режима
может быть использована упреждающая коррекция.
Метод упреждающей коррекции появился как развитие идеи упреди-
теля Смита, упреждающая коррекция предназначена для компенсации
влияния запаздывания объектов. Сущность метода заключается в том,
что корректирующий сигнал UK формируется из двух сигналов С/К1
и С/К2, охватывающих объект или часть объекта. Для формирования
корректирующего сигнала используются две координаты замкнутого
контура, а не одна.
Устройство упреждающей коррекции имеет передаточную функцию
гвР
*к,п00 ~ ^р^п,м ^д,м ~ “Т • (10.8)
тпр + 1
Добавляя в числитель (10.8) +1 и -1, после преобразований получаем
ЦЛ?) *о*пм*дм
Як,п(Р) = -77 = Мп,м*д,м - Рт ’ (109)
4i (р) т?р + 1
тогда
Ц<(р) - ^к,с°п(р) ~ ^К,мЦх,М = Ц<1 “ Ц<2»
где кк с = ^р^пм^дм» ^к,м = 1 ~ коэффициенты устройства упреж-
дающей коррекции, ’ связанные со скоростью подачи и мощностью
резания.
Передаточная функция (10.9) является удобной при реализации и
дает возможность использовать для получения второй составляющей
корректирующего устройства непосредственно объект регулирования —
Процесс металлообработки. Однако система с таким корректирующим
устройством имеет апериодический переходный процесс, быстродейст-
вие которого можно повысить при незначительном перерегулировании
(до 5%) регулируемой переменной, приняв кк с = (0,7 4- 0,8)fcpfcn мх
х£п м и кК м = 07 0,8. ; /
Пример реализации такой системы показан на рис. 10.10. С блока
задания SR через сумматор поступает сигнал управления Uy на вход
Электропривода подачи UM, Угловая скорость привода подачи соп че-
рез механизм суппорта RM воздействует напроцёсс резания ВВ. Изме-
рение мощности асинхронного электродвигателя привода главного дви-
жения М осуществляется датчиком BW. Блок SWc зоной нечувстви-
тельности t/cp определяет уровень стабилизируемой мощности. Тахогене-
ратор BR измеряет угловую скорость привода подачи. Устройство уп-
реждающей коррекции собрано на усилителях А2 и АЗ и резисторах
Rl, R4, R5. Усилитель А1> резисторы R2, R3, стабилитрон VD и кон-
денсатор С создают цепь самонастройки. На выходе усилителя А2
формируется сигнал UK t, соответствующий сигналу статической моде-
ли объекта. Настройкой резистора R2 добиваются того, чтобы при
уменьшении угловой скорости соп привода подачи за счет, например,
увеличения снимаемого припуска сигнал UKl изменялся не более чем на
значение статической погрешности регулируемого параметра и в устано-
вившемся режиме несмотря на изменение коэффициента передачи про-
цесса резания сигнал коррекции UK был равен нулю.
Исследование влияния вариаций коэффициента передачи и постоян-
ных процесса резания на динамические режимы работы электропривода
с технологической обратной связью можно выполнить на аналоговой
или цифровой модели системы, которую описывают следующие уравне-
ния, представленные в символической форме (см. рис. 10.9). Преобра-
зователь электропривода подачи описывается уравнениями
^у,п ” ^з — Цт — — Цс,п ~ Ц\с при |17у>п| Ц)гр»
297
Цг,П S Ц)Гр signt/y при |(7У |П I > Ц>гр’
вп/Цг,П = ^пК^пР +0>
где Цу П — напряжение управления преобразователя; Ц.г, Щ — напря-
жения отрицательной обратной связи по скорости и току; UK п — напря-
жение коррекции привода; UT с — напряжение технологической обрат-
ной связи по мощности резания; Ц,гр — напряжение ограничения вход-
ной цепи преобразователя; еп — ЭДС преобразователя; кп, Тп- коэф-
фициент усиления и эквивалентная постоянная времени преобразова-
теля.
Устройство коррекции электропривода
Цс,п/еп = ккТкр1(Ткр + 1),
где Гк — передаточный коэффициент и постоянная времени уст-
ройства коррекции.
Электродвигатель постоянного тока
еп ~ вд + + L^piя; М — Мс = /рсоц,
где ед, /я — ЭДС и ток двигателя; Яя, £я — активное сопротивление
и индуктивность якорной цепи; J — приведенный момент инерции
электропривода.
Рис. 10.10. Структурная схема системы стабилизации мощности резания с упре-
ждающей коррекцией
298
Момент нагрузки можно представить в виде двух составляющих,
j одна из которых cic п неизменна, а вторая ciz зависит от режима
? резания:
Мс = С^с,п + c,z» *Z “ ^Z^Z»
где с, kz — коэффициенты двигателя и датчика мощности.
j Механизм привода подачи
sz = ^п,м wn •
Узел отрицательной обратной связи по току
~ 0*я при |ig| > = 0 при |lgl ^ср*
Процесс металлообработки
Pz/h = кр/УфР + О,
где = Cpvnz*tpsz В Dq = Cptpsz * ; Ср, Ср - коэф-
фициенты; п, i, хр9 ур) q - показатели степени; Тф - постоянная вре-
4*ЧЙни процесса фрезерования.
Датчик мощности
“ *Д,м/(Гд^Р
где Лд м, Тд м — коэффициент передачи и постоянная времени дат-
чика мощности’.
Узел технологической обратной связи
’ <4,с = Чд.м + Ц< -Ц;р ПР" 1^д,м + Ц<1 > Ucp-,
А *т,с = О ПРИ 'Ц;,м + Ц<1 Ц;р>
Где UK, Ц.р — напряжения коррекции и сравнения.
, Устройство упреждающей коррекции
= к к к - *Р*п,м*д,м
Wn - Мп,мЧм (Гфр+1)(Тд,мР+1) •
Наличие второго апериодического звена в передаточной функции
устройства упреждающей коррекции, учитывающего параметры дат-
чика мощности, вызвано спецификой его реализации.
На рис. 10.11 показана аналоговая модель электропривода с техно-
логической обратной связью, составленная по приведенным уравнениям.
Все величины модели отмечены чертой над обозначением. На схеме си-
299
Рис. 10.11. Схема модели системы стабилизации мощности резания
ловой преобразователь электропривода представлен усилителем 1 и
интегратором 2, нелинейность типа ’’ограничение” реализуется при по-
мощи стабилитронов VD1, VD2. Модель двигателя привода подачи вы-
полнена на интеграторах 3, 4 и инверторе 5; усилитель 6 со стаби-
литронами VD3, VD4 моделируют реактивную нагрузку, которая пред-
полагается неизменной. При помощи стабилитронов VD5, VD6 имити-
руют цепь отрицательной обратной связи по току. Корректирующее
устройство электропривода промоделировано на интеграторе 14 и уси-
лителях 13, 15, Модель передаточного механизма привода подачи собра-
на на усилителе 7. Нелинейный блок A U, блок перемножения АХ
и интегратор 8 имитируют процесс резания, происходящий с постоянны-
ми скоростью и шириной фрезерования.
Глубину фрезерования Fp можно изменять за счет изменения напря-
жения, подаваемого на блок перемножения. С выхода интегратора 8
на вход интегратора 4 подаетёя составляющая нагрузки двигателя
iz, вызванная силами (мощностью) резания. Инерционность датчика
мощности и асинхронного двигателя привода главного движения, мощ-
ность которого измеряется, учитывается апериодическим звеном, соб-
ранным на интеграторе 9. Упреждающее корректирующее устройство
300
промоделировано на сумматоре 10. Инвертор 11 й сумматор 12 с не-
линейностью типа ’’зона нечувствительности” на потенциометре RP и
Вентиле VD7 представляют модель технологической обратной связи.
Последняя может быть упрощена и объединена с цепью устройства кор-
рекции, но в этом случае затрудняются настройка коррекции и индика-
ция ее напряжения. Анализ работы системы стабилизации мощности ре-
зания, выполненный на аналоговой модели, показал, что при изменениях
глубины резания в широких пределах ухудшается статическая точность
Поддержания постоянства мощности резания. Введение самонастройки
статической модели устройства упреждающей коррекции позволяет уст-
ранить указанный недостаток.
Системы стабилизации усилий резания предназначены для управле-
ния режимом обработки путем контроля силы резания F или любой
ее составляющей, например радиального усилия Гу.
Сигнал, пропорциональный силе резания, получают при помощи
динамометрических узлов, встраиваемых в звенья системы станок —
приспособление — инструмент — деталь. На рис. 10.12 показана кон-
струкция динамометрического центра, позволяющего измерять косвен-
ным путем радиальную силу на шлицешлифовальном станке. Устройство
301
Рис. 10.12. Динамометрический центр
состоит из полого закаленного стального корпуса /, вмонтированного
в центр задней бабки. В один из концов корпуса запрессован измери-
тельный стержень 2, на свободном конце которого с помощью хомути-
ка 3 закреплен якорь 4 индуктивного датчика 5. При нагрузке центра
его консольная часть Деформируется и конец измерительного стержня
2 вместе с якорем 4 смещается. На выходе индуктивного датчика появ-
ляется напряжение, пропорциональное перемещению. Таким образом,
усилие на задней бабке F3 б преобразуется в электрический сигнал.
Зависимость между усилиями Fy и F3>6 имеет вид
F % F - ------—
гу гз,б . ’
ьв “ 1
где LB — длина обрабатываемого вала; I — расстояние от шлифоваль-
ного круга до заднего центра.
Для обеспечения гиперболической зависимости Fy (I) движок линей-
ного потенциометра механически связывают со столом станка. При пе-
ремещении стола и изменении I изменяется глубина отрицательной об-
ратной связи по напряжению усилителя. Напряжение на выходе усили-
теля при этом пропорционально стабилизируемой силе: (7Т>С = kyFy.
Структурная схема системы стабилизации усилий резания (рис. 10.13)
содержит задатчик SV скорости перемещения стола гс, усилители
Al, А2, преобразователь UMи двигатель М. Процесс резания ЯР осуще-
ствляется при контроле расстояния I и усилия F3 б при помощи соот-
ветствующих датчиков BQ и BF. Изменение глубины отрицательной
обратной связи усилителя А2 производится при помощи устройства
деления АР. Изменяя скорость перемещения стола станка в соответ-
ствии с сигналом управления Uy = U3 - ит с, система автоматически под-
держивает заданную радиальную силу резания.
Описанная система стабилизации усилий резания в 2,0 - 2,5 раза
302
Рис. 10.13. Структурная схема системы стабилизации усилия резания
уменьшает машинное время по сравнению с временем шлифования на
обычном станке и обеспечивает заданную точность, шероховатость по-
верхности и отсутствие прижогов.
Системы стабилизации крутящего момента применяют на токарных,
сверлильных, фрезерных, шлифовальных и других станках.
Вертикально-притирочный станок мод. ОФ-26 оснащен системой ста-
билизации крутящего момента. Сигнал, пропорциональный крутящему
моменту, получают с помощью поворотного динамометрического сто-
ла (рис. 10.14,я), на котором укрепляют деталь 1. Потенциометричес-
кий датчик 2 вырабатывает сигнал, пропорциональный углу поворота и,
следовательно, крутящему моменту Afp. Требуемое значение стабилизи-
руемого крутящего момента устанавливается корректирующим потен-
циометром 3 и задатчиком момента 4. Исполнительный двигатель 5
через червячную пару 6 воздействует на механизм разжима притира 7,
что обеспечивает требуемое значение момента шлифования Л/шл.
Структурная схема системы стабилизации крутящего момента приве-
дена на рис, 10.14,6. Система содержит преобразователь UMc системой
управления, на вход которого подается напряжение управления С7у,
равное разности напряжения задания U3 и напряжения технологической
обратной связи С7тс. От UMпитается исполнительный двигатель Ml
механизма разжима’ притира МП, который через процесс резания ПР
меняет нагрузку на валу двигателя М2 притира. Датчик момента ВМ
вырабатывает напряжение обратной связи, пропорциональное моменту
навалу двигателя М2 притира.
Применение системы стабилизации крутящего момента на вертикаль-
но-притирочных станках в 2—2,5 раза повышает точность обработки от-
верстий в деталях.
Системы стабилизации температуры резания используют зависимость
стойкости резца от средней температуры в зоне резания:
Т = (€/©)“,
где а — показатель степени; С — коэффициент; 0- температура реза-
ния, °C.
303
Рис. 10.14. Схемы системы стабилиза-
ции крутящего момента:
а - конструктивная; б - структур-
ная
Применение таких систем целесообразно при продольной обточке из-
делий (особенно в тех случаях, когда твердость материала изменяется)
и при торцовой обработке. Системы стабилизации температуры резания
находят применение тйк^ке при фрезеровании и шлифовании.
Поскольку в системе управления обратная связь по температуре
режущей кромки инструмента наиболее полно отражает физический про-
цесс резания, создается возможность наиболее рациональной загрузки
инструмента. При этом изменение в процессе обработки ряда параметров
(затупление инструмента, поступление более интенсивного охлаждения,
изменение твердости детали и др.) немедленно оказывает влияние на
режим резания. Включение в цепь естественной термопары инструмент -
деталь входных сопротивлений регуляторов уменьшает термоток, за
счет чего на 150-200% повышается временная стойкость инструмента.
Если угловая скорость шпинделя неизменна, то при торцовой обработ-
ке скорость резания изменяется от максимума на периферии детали до
нуля в центре. В соответствии с этим в широких пределах будет изме-
няться и температура резания, а условия обработки в значительной сте-
пени будут отличаться от расчетных, даже если пренебречь такими фак-
торами, как состояние режущей кромки инструмента, влияние охлаж-
дающей жидкости, изменение твердости детали при изменении диамет-
ра обработки. Система стабилизации температуры резания при движении
304
Рис. 10.15. Схема модели системы стабилизации температуры резания при торцо-
вой обработке
резца от периферии детали к центру будет автоматически увеличивать
угловую скорость шпинделя, сохраняя неизменной заданную вначале
температуру резания. Исчерпав диапазон регулирования скорости глав-
ного привода станка, система стабилизации температуры резания затем
начинает работать с неизменной угловой скоростью шпинделя. Скорость
резания при дальнейшем уменьшении диаметра обработки падает, и тем-
пература резания уменьшается. Одна из первых систем стабилизации
температуры резания была разработана для осеотрезного станка.
Аналоговая модель системы стабилизации температуры резания при
торцовой обработке (рис. 10.15) содержит_входной усилитель Л7,
на который поступают напряжения задания U3 и технологической обрат-
ной связи UT с. Выход усилителя А1 связан с моделью электропривода
шпинделя. Блок перемножения АХ получает сигналы, пропорциональ-
ные угловой скорости шпинделя и диаметру обработки ^.Напря-
жение блока перемножения АХ через усилитель АЗ подается на нели-
нейный блок A U, выполняющий преобразование
z е
= kev ,
где Ер — термо-ЭДС резания; v — скорость резания; ке, ze — коэф-
фициент пропорциональности и показатель степени.
• Напряжение, пропорциональное Ер, с усилителя А4 через узел,
представляющий ’’зону нечувствительности” и собранный на потенцио-
метре RP и диоде VD, подается на вход усилителя Л/. Для устранения
колебательного режима работы может быть применено устройство
упреждающей коррекции (на схеме не показано).
В системе стабилизации температуры резания, разработанной приме-
нительно к токарно-винторезному станку мод. ИЖ-250, применен при-
вад шпинделя с бесступенчатым регулированием скорости, а регулятор
содержит автоматический электронный потенциометр типа ЭПД-0,9,
измеряющий термо-ЭДС, возникающую в естественной термопаре ин-
струмент-изделие, и вырабатывающий управляющий сигнал. При работе
305
такого станка с системой стабилизации температуры резания точность
поддержания заданной температуры резания составляет 3-5%. Стой-
кость резца повышается в 1,5-3,4 раза, машинное время сокращается
в 1,4-1,9 раза, а шероховатость поверхности оказывается минимальной
и практически постоянной.
Применение систем стабилизации температуры резания создает воз-
можность высокопроизводительной обработки каждым экземпляром
режущего инструмента с учетом его качества. Это способствует умень-
шению расхода инструмента. Если вновь устанавливаемый резец обла-
дает лучшими режущими свойствами, чем тот, по которому была наст-
роена система стабилизации температуры резания, то скорость резания
автоматически повышается, пока не будет достигнута заданная темпе-
ратура в зоне резания. При установке резца худшего качества темпера-
тура в зоне резания начнет возрастать, а скорость резания автомати-
чески снижаться, пока не установится требуемая температура.
Обеспечивая постоянство размерного износа инструмента вне зави-
симости от его качества, системы стабилизации температуры резания
позволяют полностью использовать его возможности, дополнительно
повысить производительность обработки на 12—15% и увеличить на
50 % размерную стойкость резцов.
Системы стабилизации упругих деформаций при резании приме-
няются для повышения точности обработки деталей путем компенса-
ции размерного износа инструмента и нежесткости системы станок—при-
способление—инструмент—деталь. Работа систем стабилизации упругих
деформаций при резании основана на том, что подача инструмента (фре-
зы, резца, шлифовального круга) непосредственно влияет на усилие
резания. Чем больше подача, тем больше нагрузка на звенья системы
станок—приспособление—инструмент—деталь. В процессе обработки по-
дачу инструмента изменяют таким образом, чтобы несмотря на влияние
возмущающих факторов поддерживалось неизменным радиальное уси-
лие резания либо сохранялось постоянство отношения силы резания к
жесткости системы станок—приспособление—инструмент—деталь. Работы
по исследованию стабилизации упругих перемещений систем станок-
приспособление—инструмент—деталь в целях повышения точности и
производительности обработки были проведены в Московском станко-
инструментальном институте под руководством проф. Б.С. Балакшина.
Системы стабилизации упругих деформаций при резании апробированы
на токарийх, сверлильных, фрезерных и шлифовальных станках.
Для измерения радиальной силы резания используют в качестве уп-
ругого элемента наиболее слабое по жесткости звено размерной цепи
станок—приспособление—инструмент-деталь или специально встроенный
динамометрический узел. Радиальное усилие резания на станках токар-
ной группы (рис. 10.16,а) определяют при помощи динамометрическо-
го резцедержателя, деформация которого воспринимается датчиком
(тензометрическим, индуктивным). Усилие резания на фрезерных стан-
306
Рис. 10.16. Схемы систем стабилизации упругих деформаций при резании для раз-
личных станков:
а - токарного; б - фрезерного; в - круглошлифовального
ках определяют путем измерения деформаций гайки ходового винта
(рис. 10.6,6). На круглошлифовальных станках (рис. 10.16,в) измеря-
ют упругую деформацию отжима шлифовальной бабки в процессе об-
работки.
Сигналы датчиков упругих перемещений BL при превышении напря-
жения Uc% сравниваются с сигналом U3 задающего устройства SV. Уп-
равляющий сигнал L/y = U3 — UTC с блока сравнения через усилитель
А подается на UM, который изменяет угловую скорость электродвига-
теля привода подачи М (на круглошлифовальном станке изменяются
угловая скорость двигателя М привода вращения детали и продольная
подача стола гидроприводом МР).
Выбор параметра регулирования определяется функциональной
связью между силой резания и рядом аргументов
&Z ~ f (£р ’ ’ ^) »
где Ср — коэффициент, зависящий от материала заготовки и условий
обработки; к - коэффициент, зависящий от геометрии резца.
Для повышения точности и производительности обработки, а также
технической реализации системы осуществлять управление силой реза-
ния целесообразно путем регулирования продольной подачи. В качестве
параметра регулирования можно использовать жесткость системы ста-
нок—приспособление—инструмент—деталь, изменяя жесткость и-го
звена так, чтобы с возрастанием силы резания жесткость повышалась,
а с уменьшением - понижалась. Изменение жесткости системы ста-
нок—приспособление—инструмент—деталь производят изменением рас-
стояния между опорами упругого элемента. Опоры представляют собой
гайки с правой и левой резьбами, связанные с упругим элементом — вра-
щающимся винтом.
В некоторых случаях целесообразно выбирать два параметра регу-
лирования. Например, сокращение погрешности размера и формы в
продольном сечении за счет изменения продольной подачи может обу-
словить появление недопустимой шероховатости. Случайные отклонения
упругого перемещения, влияющие на точность обработки, компенсиру-
ют изменением продольной подачи, а систематические отклонения - из-
менением жесткости. В этом случае диапазон изменения подачи сужает-
ся и колебания шероховатости будут находиться в допустимых преде-
лах. Для изменения продольной подачи в системах стабилизации упру-
гих деформаций при резании находят применение регулируемые гидро-
приводы и электроприводы постоянного тока.
Затраты на оснащение станка системой стабилизации упругих дефор-
маций при резании окупаются в среднем в течение 0,5-1 года. Точность
обработки на станках различных типов, снабженных системами стабили-
зации упругих деформаций, повышается в 2—5 раз, рост производитель-
ности составляет 25—200%, себестоимость обработки снижается на
308
25—30%. Создается эффект, эквивалентный увеличению жесткости сис-
темы станок—приспособление-инструмент—деталь при сохранении
Прежней металлоемкости конструкции станка.
ч ?
104. СИСТЕМЫ С АДАПТИВНЫМ НАБЛЮДАТЕЛЕМ
При построении системы стабилизации момента или силы резания
возникает задача коррекции системы из-за изменения в широких пре-
делах коэффициента передачи процесса фрезерования. Одним из воз-
можных решений этой задачи является применение устройства упрежда-
ющей коррекции, аналогичного рассмотренному в § 10.3 для системы
стабилизации мощности фрезерования.
Другим решением этой задачи является использование адаптивных
наблюдателей, представляющих собой модель идентифицируемой части
объекта регулирования. Исследования систем с адаптивными наблю-
дателями выполнены в Ленинградском электротехническом и Белорус-
ском политехническом институтах.
Система стабилизации силы резания с применением адаптивного наб-
людателя, структурная схема которой приведена на рис. 10.17, содержит
формирователь задающего воздействия с передаточной функцией Ну (р),
блок деления АР, преобразователь электропривода подачи с передаточ-
ной функцией Яп (р), двигатель с передаточной функцией Яд (р), датчик
усилия резания с передаточной функцией Ядр (р).
Передаточная функция процесса резания (см. гл. 9)
/ -рТр\
F (р) fcn\l — е /
Яр(р) = , (10.10)
и Sz (р) Р
где Тр — постоянная времени процесса резания, Тр =2тг/гсош.
После разложения правой части выражения (10.10) в ряд Пада
[29] и ограничения ряда вторыми членами разложения получим
2 2
0,08 Т2р2 + 0,5 Гр + 1
р Р
Коэффициент передачи объекта кр, как уже отмечалось в гл. 9,
может изменяться в десятки и сотни раз. Идея применения адаптивного
наблюдателя состоит в том, что получаемое с его помощью значение
коэффициента передачи Тер вводится в контур системы регулирования
(самонастройки), компенсируя изменения кр. Для этого на вход про-
стейшего адаптивного наблюдателя (рис. 10.18) подаются напряжения
тахогенератора [/тг электродвигателя привода подачи и датчика усилия
резания t^p. Адаптивный наблюдатель содержит динамическую модель
309
Рйс. 10.17. Структурная схема системы стабилизации усилия резания с адаптив-
ным наблюдателем
процесса резания с передаточной функцией
Р,Н °>08Гр2л₽2+ 0.5 W + 1 ’
где Тр>н - расчетное значение постоянной времени резания в наблюда-
теле; у - коэффициент, равный 7 = « Tz jjs2^sz^^ ~
действительное и измеренное значения подачи на зуб с учетом динами-
ческих свойств процесса резания.
Передаточная функция датчика усилия резания
где *д р, Тд р - коэффициент передачи и постоянная времени датчика.
Рассогласование между выходными значениями напряжений датчика
усилия резания и модели адаптивного наблюдателя равно
е = Цх,р ” ^д,р*
Из структурных схем рис. 10.17 и 10.18 можно записать:
для системы
Ч,.р(Л,рР *1) (юн)
для наблюдателя
^,P<W+1) “Wp* (10.12)
После вычитания (10.12) из (10.11) и некоторых преобразований
получим
е + е = ~гд/3’ (юлз)
'Д.Р Д.Р
где 0 = (Лд.рЛр/7) - Лр.
310
Йвь 10.18. Структурная схема адаптивного наблюдателя
Определим алгоритм функционирования адаптивного наблюдателя,
чтобы процесс протекал устойчиво и в установившемся режиме:
*
*р = ^р^д.р^р/Т^’р.н-
' Наличие блоков перемножения в адаптивном наблюдателе требует
рассмотрения его в виде нелинейного звена. Для анализа устойчивости
запишем функцию Ляпунова в следующем виде:
Г=-е2+^Х02, (10.14)
2 2
4де X — положительный коэффициент, являющийся коэффициентом
усиления канала самонастройки системы.
В соответствии со второй теоремой прямого метода Ляпунова реше-
цце дифференциального уравнения (10.13) асимптотически устойчиво,
^СЛИ производная функции Ляпунова (10.14) - знакоопределенная
.функция противоположного с функцией Ляпунова знака:
о V = €€ + хрр < о,
Ййи 4
б
’ V = - — е2 + — 7г„е0 + Х00 < 0,
гд,Р ГД.Р
(1015)
7д,рА
Предполагая, что процесс настройки fcp в адаптивном наблюдателе
протекает быстрее, чем изменение fcp объекта, запишем
в--1. (10.16)
311
На основании (10.15) и (10.16) может быть записан алгоритм функ-
ционирования адаптивного наблюдателя с учетом условий устойчивости:
Коэффициент усиления канала самонастройки может изменяться
в широких пределах, однако при его увеличении одновременно с по-
вышением быстродействия адаптивного наблюдателя процесс само-
настройки может принять колебательный характер. Ориентировочно
величину X можно найти, исходя из настройки адаптивного наблюдате-
ля на технический оптимум при номинальных начальных условиях:
Х = Ч2д,о,н-
Окончательный выбор величины X целесообразно производить при
отладке системы.
Как показали результаты моделирования описанной системы приме-
нительно к фрезерно-расточному станку мод. 6М610 Ф2-1, стабилизи-
руемое значение усилия резания практически не изменяется при измене-
нии коэффициента резания в 2 раза.
10.5. РАСЧЕТ ПАРАМЕТРОВ СИСТЕМ СТАБИЛИЗАЦИИ
Структурная схема АСУ ТП для статического режима работы, состоя-
щая из звеньев электропривода и технологического процесса, охвачен-
ных технологической обратной связью (по скорости, мощности, силе,
моменту, температуре резания и др.), показана на рис. 10.19.
Задающее напряжение через узел задания с коэффициентом к3 по-
дается на вход усилителя с коэффициентом усиления к?9 куда также
подаются сигналы обратных связей: по напряжению усилителя (7Н, по
скорости С7ТГ и по технологическому параметру Щ с — с соответству-
ющих блоков с коэффициентами передачи fcH, £тг, kT с. Сигнал техно-
логической обратной связи начинает действовать при превышении напря-
жения С/ср зоны нечувствительности. Тиристорный преобразователь
представлен в виде усилительного звена с коэффициентом усиления
^т,п> двигатель — с передаточным коэффициентом &д, объект регулиро-
вания — с передаточным коэффициентом кф (а>, f). Регулируемый па-
раметр Up связан функциональной зависимостью кф с угловой скоро-
стью электродвигателя подачи о>п. На эту связь влияет возмущающее
воздействие /.
Цель статического расчета системы стабилизации с технологической
обратной связью при синтезе — определение коэффициентов усиления
элементов системы, обеспечивающих требуемую точность регулирования
Up. При анализе системы по известным коэффициентам усиления опре-
312
деляется статическая погрешность регулируемого параметра. При рас-
четах действие узла токоограничения электропривода (£п т,&тм м, £7СТ),
где fcTMjM - коэффициент передачи тахометрического моста, не учиты-
вается, так как электропривод в процессе стабилизации технологичес-
кого параметра должен работать без перегрузок.
Представим модель тиристорного электропривода в статике в виде
результирующего коэффициента передачи Лтпп (рис. 10.20,а). Тогда
статическая погрешность системы стабилизаций, %,
> Д = ДрОТ1п/(1 + *р,с),
где Др — отклонение регулируемой величины, %, появляющееся под
действием возмущения в разомкнутой системе; DTn — диапазон измене-
ния технологического параметра; £р>с = £т>п,п^ф^т,с “ статический
Коэффициент усиления разомкнутой системы.
1 Требуемый коэффициент усиления разомкнутой системы, обеспе-
чивающий заданную статическую точность,
^тр “ Ар^т,п/А “
Значение коэффициента кт п, входящего в состав кт п п, выбирают
для участка работы, на котором производится стабилизация наименьше-
го требуемого значения регулируемого параметра С7р.
Особые трудности могут возникнуть при определении коэффициента
Лф. В общем случае он является нелинейным и неоднозначным, посколь-
ку зависит не только от угловой скорости привода, но и от возмущающе-
го воздействия. В системе стабилизации скорости резания такими воз-
мущающими воздействиями будут: изменяющийся диаметр обработки —
при торцовом точении; износ диаметра шлифовального круга — при
стабилизации скорости шлифования, а в системе стабилизации мощности
313
Рис. 10.20. Структурные схемы систем стабилизации для решения задач синтеза:
а - обобщенная; б - расчетная
резания: изменение глубины резания при точении, фрезеровании, шли-
фовании; изменение диаметра обработки и припуска - при торцовом
точении и тд.
Предположим, что в системе стабилизация мощности фрезерования
осуществляется за счет изменения подачи, т.е. угловой скорости приво-
да подачи ап. Мощность резания
Р2 = С^^Вгш^ • 1(Г*. (10.17)
Полагая, что угловая скорость фрезы соф и ширина фрезерования
В неизменны, выражение (10.17) можно представить в виде
где сф = C9Bz 1(TS. Ур
Аппроксимируем выражение s , т.е. для зоны рабочих подач при-
Ур
нимаем*$г * Лм$2.При зтах с учетом выбора Гр определяем кс =
= для данного значения мощности стабилизации. Учитывая, что
sz = ^р,уап»
где fcp>y — коэффициент, определяемый шагом ходового винта и пере-
314
даточным числом редуктора, получаем
^с^м^р.у^п1
Структурная схема, учитывающая выполненные преобразования, по-
казана на рис. 10.20,6. Приближенно кф « Про-
статическая погрешность разомкнутой системы, %, при неизменной
сип и изменении глубины резания определяется по формуле
ХР _ хр
д = ^тах ~Jp^L 1(Ю
₽ ХР
tpmin
При коэффициенте усиления разомкнутой системы fcp>c > fcTp обеспе-
чивается требуемая статическая точность. При обратном неравенстве
система обеспечивает требуемую статическую точность после включения
промежуточного усилителя с коэффициентом усиления fcn>y > &тр/Ир,с-
При анализе требуется рассчитывать зависимости параметра С/р от
нагрузки на электропривод и возмущающего воздействия. Коэффициент
усиления преобразователя
к — к к
п,у Лу,нЛт,п»
где fcy>H — коэффициент усиления усилителя с обратной связью по нап-
ряжению.
Структурная схема примет вид, показанный на рис. 10.21,а. Произ-
ведя перенос точки приложения возмущающего воздействия по нагруз-
ке на вход системы, получим структурную схему (рис. 10.21,6). Здесь
Пт,п,п = Пп>укл/(1 + ^п,уПдИтг). Технологическая обратная связь всту-
пает в действие, как только измеренная мощность превысит заданное
значение, т.е. когда СЛ£т>с >
Зависимость U^(f) с’учетом возмущающего воздействия по нагруз-
ке электропривода при действии нелинейной технологической обратной
связи рассчитываем по выражению
I-.R*
1Мз - -f-5- + % • 1 ] *т,п,п*ф (“п. Г)
*п
IL = ----------------------------------------------. (10.18)
1 + ^т,с^т,п,п^ф • 1 (Дб)
Для заданного входного сигнала &3Ц, подставляя в (10.18) раз-
личные значения возмущающего воздействия f и соответствующие
ему значения тока нагрузки двигателя /я, строим зависимость Up(f)9
по которой определяем статическую погрешность регулируемого па-
раметра.
315
Рис. 10.21. Структурные схемы систем стабилизации для решения задач анализа
Для выполнения расчетов, как видно, необходимо знать теоретичес-
кие и экспериментальные зависимости между регулируемой величиной
Up и возмущающим воздействием f и уметь оценить влияние послед-
него на нагрузку двигателя. Если технологическая обратная связь не дей-
ствует, то в (10.18) единичные функции 1 (ДС/) обращаются в
нуль.
Анализ устойчивости и синтез корректирующего звена линеаризо-
ванной системы могут проводиться любым методом и в том числе ме-
тодом логарифмических частотных характеристик. При синтезе кор-
ректирующего звена желаемая ЛАЧХ системы должна пересекать ось
частот с наклоном — 20 дБ/дек. Запас по фазе на частоте среза должен
быть не менее 30°, а запас по амплитуде при переходе ЛФЧХ через
180° — не менее 10-12 дБ.
Коррекция может быть выполнена (рис. 10.22,а) последовательной,
с передаточной функцией ЯК1 (р), параллельной, с передаточной функ-
цией НК2 (р), охватывающей усилитель А, или последовательно-парал-
лельной. Схема, на которой штриховыми линиями показаны варианты
включения корректирующих устройств, содержит усилитель А, преобра-
зователь UA% электродвигатель М электропривода подачи, воздейству-
ющего на процесс резания ПР. Датчик В W регулируемого параметра
ир вырабатывает напряжение которое через блок с зоной нечув-
ствительности £/ср подается на входной узел сравнения системы:
^г,с ” “ Цф*
Достоинствами перечисленных видов коррекции являются простота
316
Рйс 10 22 Функциональные схемы коррекции систем стабилизации параметров
металлообработки:
а - последовательно-параллельной; б - с переменным коэффициентом; в -
упреждающей
исполнения и ослабление влияния изменения коэффициента усиления
t охваченных звеньев на устойчивость системы регулирования.
Однако при большом изменении коэффициента передачи процесса
металлообработки Лр статический коэффициент усиления разомкнутой
системы, определяемый требуемой точностью поддержания регулиру-
емого параметра Up, при функционировании замкнутой системы откло-
няется от расчетного значения, что может привести к потере устойчи-
вости.
Если в главный контур (технологической обратной связи) системы
ввести корректирующее устройство с коэффициентом передачи fcK,
то для сохранения системой устойчивости при изменении условий метал-
317
лообработки необходимо, чтобы
£рЛк = const. (10.19)
В системах стабилизации регулируемый параметр Up поддерживает-
ся неизменным за счет изменения угловой скорости привода подачи
= ир/кр. (10.20)
На основании (10.19) и (10.20) может быть построено корректиру-
ющее устройство с переменным коэффициентом передачи
Лк = 1/^р - wn/^p-
Функциональная схема (рис. 10.22,6), реализующая описанный прин-
цип, содержит помимо уже названных элементов датчик частоты вра-
щения BR, блок перемножения АХ и делитель напряжения АР, кото-
рые воспроизводят выражение (10.20) в виде
= U^IU^,
где С/р — значение стабилизируемого параметра £/р, требуемое для вы-
полнения условия (10.20).
Необходимость сохранения системой устойчивости при изменении
постоянных времени процесса металлообработки требует применения
устройства упреждающей коррекции с самонастраивающейся статичес-
кой моделью объекта. Упрощенная схема такого устройства коррек-
ции (рис. 10.22,в) содержит два звена, одно из которых кК с эквива-
лентно передаточному коэффициенту процесса резания в статике, а пе-
редаточный коэффициент второго выбирается из условия
^K,cwn = ^крЦх,р»
причем соп и //д р соответствуют режиму настройки. Как видно, в фор-
мировании корректирующего сигнала UK находят применение две коор-
динаты системы регулирования.
Уточнение полученных параметров корректирующих звеньев произ-
водится на модели, где учитываются упругость системы станок—приспо-
собление—инструмент-деталь и технологические факторы.
10.6. СРАВНИТЕЛЬНАЯ ОЦЕНКА СИСТЕМ СТАБИЛИЗАЦИИ
Системы стабилизации режимов металлообработки обладают рядом
общих свойств и могут быть эквивалентны по результатам их действия.
Сравним некоторые структурные схемы систем стабилизации.
На рис. 10.23,а показана структурная схема системы ССР при тор-
цовой обточке на токарном станке. Следящая система, состоящая из
318
Рис. 10.23. Функциональные схемы систем стабилизации:
а - скорости резания; б - мощности резания; в — температуры резания; г -
упругих деформаций при резании
индуктивного датчика BL, кинематически связанного с суппортом стан-
ка, служит для формирования сигнала обратной связи, пропорциональ-
ного скорости резания. На щуп датчика BL воздействует профилиро-
ванная линейка, неподвижная относительно суппорта. С помощью задат-
чика SV устанавливается требуемая величина скорости. Сигнал обрат-
ной связи, снимаемый с BL, сравнивается с напряжением зоны нечув-
ствительности (UCp) и при превышении последнего поступает на узел
сравнения с задающим сигналом. Полученная разность сигналов через
усилитель А подается на регулятор МИ, который изменяет угловую
скорость двигателя М привода шпинделя. Подача на оборот при обра-
ботке сохраняется неизменной. Рассмотренная система стабилизации
скорости резания будет ’’стабилизировать” скорость резания, изменяя
по заданному закону угловую скорость шпинделя даже тогда, когда об-
работка не производится, а осуществляется лишь поперечная подача
суппорта.
Структурная схема системы стабилизации мощности резания показа-
на на рис. 10.23,6. Датчик мощности BW измеряет мощность двигателя
М привода шпинделя. Сигнал его, проходя через блок с зоной нечув-
319
ствительности, сравнивается с сигналом задающего устройства SV
на блоке сравнения. Полученное напряжение с усилителя А поступает
на регулятор UM. Последний изменяет угловую скорость двигателя М
таким образом, чтобы поддерживалось заданное значение мощности.
Структурная схема системы стабилизации температуры резания
(рис. 10.23,в) содержит датчик обратной связи ВТ, в качестве которого
использована естественная термопара инструмент — деталь, при этом ре-
зец и задний центр изолированы от металлоконструкции станка. В ос-
тальном структурная схема не отличается от двух описанных выше.
Структурная схема системы СДР стабилизации упругих деформаций
(рис. 10.23,г) предусматривает управление упругими перемещениями
суппорта путем воздействия на угловую скорость привода подачи. Упру-
гие перемещения суппорта измеряются индуктивным датчиком BL от-
носительно лекальной линейки, укрепленной на станине станка. Пере-
мещения суппорта в радиальном направлении вызываются силовым
режимом и изменением динамической жесткости. Задатчиком SV уста-
навливается необходимая величина упругого перемещения суппорта.
Разность между сигналом задания и сигналом обратной связи подает-
ся на усилитель А, а затем на регулятор UM исполнительного двигате-
ля привода продольной подачи. В состав регулятора UM входит ин-
тегрирующее звено. Если упругое перемещение суппорта больше, чем
заданное значение, то подача снижается, если наоборот, то подача увели-
чивается. Это происходит до тех пор, пока сигнал, поступающий со срав-
нивающего устройства, не станет равным нулю. Таким образом осуще-
ствляется управление формообразованием обрабатываемой детали в по-
перечном сечении. Схемы, представленные на рис. 10.23, выявляют
структурную общность между системами стабилизации.
Общность между системами стабилизации скорости, мощности и тем-
пературы резания особенно видна при сравнении их работы в режиме
торцовой обточки. Известно, что при торцовой обработке с постоянной
подачей на оборот касательная составляющая силы резания Fz неиз-
менна. При стабилизации мощности резания Pz = Fzv • 10“3/60 = const.
Из вышеизложенного вытекает, что приведенное равенство справедливо
лишь при неизменной скорости резания и что повышение производитель-
ности за счет применения системы стабилизации мощности резания ана-
логично рассчитанному значению для системы стабилизации скорости
резания, если ширину стружки считать неизменной.
Общность между системами стабилизации температуры и скорости
резания может быть найдена путем анализа связи между скоростью реза-
ния и подачей на оборот при неизменной температуре резания. Известно,
что при © = const
v = C/sk,
тпъ к — показатель степени.
320
Следовательно, если поддерживать неизменной температуру резания,
то при торцовой обработке с постоянной величиной подачи на оборот
скорость резания также будет неизменной.
Системы стабилизации мощности, крутящего момента и усилий ре-
зания стабилизируют силовые характеристики процесса резания. При
этом в системах стабилизации крутящего момента и усилий резания сиг-
нал обратной связи, как правило, более точно характеризует процесс
резания, чем в системе стабилизации мощности резания. В последней
возникает необходимость учета составляющей сигнала, пропорциональ-
ной мощности холостого хода механизма и двигателя. Эта составля-
ющая изменяется во времени и зависит от нагрузки, что весьма трудно
учесть. В то же время при реализации датчики обратной связи в системах
стабилизации мощности резания оказываются значительно проще и не
требуют никаких конструктивных изменений в механизмах станка.
Общность рассмотренных систем стабилизации позволяет применить
в большинстве из них однотипный регулируемый электропривод, сог-
ласованный с соответствующим датчиком обратной связи. Рассмотрен-
ные системы стабилизации обеспечивают приблизительно одинаковое
повышение производительности металлообработки.
Глава одиннадцатая
СИНХРОННО-СЛЕДЯЩИЕ КОПИРОВАЛЬНЫЕ СИСТЕМЫ
МЕТАЛЛОРЕЖУЩИХ СТАНКОВ
1.1. ОБЩИЕ ПОЛОЖЕНИЯ
Следящие автоматизированные системы управления электроприво-
дами представляют собой замкнутые структуры, регулируемой величи-
ной которых является угол поворота или угловая скорость вала про-
мышленной установки, а входная (задающая) величина изменяется во
времени по произвольному закону. Они должны отрабатывать входную
величину таким образом, чтобы погрешность не превышала допустимых
значений.
В металлорежущих станках следящие системы применяются, напри-
мер, для создания синхронного движения двух валов одного или разных
механизмов, для слежения за линейным перемещением задающего ме-
ханизма, для отработки перемещения по программе, если в качестве
программы используется шаблон (или чертеж). Систему, отрабаты-
вающую такую программу, называют копировальной, а операцию метал-
лообработки — копированием.
При копировании со следящим управлением изменения поверхности
шаблона контролируются измерительным прибором, управляющим при-
водами подач исполнительных элементов станка. Такое копирование
называют электрическим, оно позволяет получить высокоточную произ-
321
водительную обработку при использовании для изготовления шабло-
нов легкообрабатываемых материалов (пластмассы, дерева, гипса).
Электрическое копирование находит применение на фрезерных, то-
карных, шлифовальных и других станках для обработки деталей слож-
ной конфигурации: гребных винтов, лопаток турбин, штампов, кулач-
ков и т.д.
Содержание настоящей главы базируется на материале, изучаемом в
курсах ’Теория автоматического управления”, ’’Системы управления
электроприводами”. Рекомендуется вспомнить содержание последнего
курса, излагаемое в теме, посвященной следящему управлению электро-
приводами.
В результате изучения материалов данной главы студенты должны
знать принципы построения следящих систем металлорежущих станков,
факторы, влияющие на добротность и погрешности следящих систем,
и уметь обеспечивать требуемые динамические показатели качества ре-
гулирования следящих электроприводов станков.
11.2. КЛАССИФИКАЦИЯ СЛЕДЯЩИХ СИСТЕМ
ЭЛЕКТРОКОППРОВАЛЬНЫХ МЕТАЛЛОРЕЖУЩИХ СТАНКОВ
Формообразование на электрокопировальных станках со следящей
системой может производиться при использовании систем прерывистого
и непрерывного управления.
В станках с прерывистым управлением применяются контактные
копировально-измерительные приборы. При копировании на станках с
системой непрерывного управления используются бесконтактные ин-
дуктивные копировальные приборы и бесступенчатый привод изменения
скорости подач. Эти системы обеспечивают более высокие точность
обработки и чистоту поверхности изделия по сравнению с системами с
прерывистым управлением, а копировальный палец и инструмент опи-
сывают волнообразную траекторию.
В зависимости от типа копировального прибора и привода подач
системы копировальных станков классифицируют по следующим
группам:
электрические — копировальный прибор и привод электрические;
электрогидравлические - копировальный прибор электрический,
привод — гидравлический;
фотоэлектрические - копировальный прибор фотоэлектрический,
привод — электрический;
гидравлические — копировальный прибор и привод гидравли-
ческие;
пневмоэлектрические — копировальный прибор пневматический,
привод — электрический.
Схемы управления электроприводов могут быть выполнены на ана-
логовых, цифровых или цифро-аналоговых элементах.
322
рцс. 11.1. Схема электро*
копирования на фрезер-
ном станке
На рис. 11.1 показана схема электрокопирования на фрезерном
станке с контактным копировально-измерительным прибором. Заготов-
ка 1 обрабатывается фрезой 2, закрепленной на шпинделе 3 фрезерной
бабки 4, связанной с копировальной головкой 5. Копировальный па-
лец б воздействует через штифт 7 на контактную систему 8. Штифт 7
имеет опору, выполненную в виде полусферы, при этом боковые давле-
ния на копировальный палец преобразуются в осевые смещения штиф-
та копировальной головки. Заготовка 1 вместе с шаблоном 9 установ-
лена на столе 10. Электродвигатель Ml перемещает стол, обеспечивая
ведущую или задающую подачу s3. Электродвигатель М2 перемещает
фрезерную бабку 4 и копировальную головку 5 в вертикальном нап-
равлении, осуществляя следящую подачу sc. Если контакт 11 разом-
кнут, то копировальный палец (а следовательно, и фреза) приближается
к шаблону (к детали). При замкнутом контакте 11 электродвигатель
М2 включается на вращение в обратном направлении и копировальный
палец удаляется от шаблона. В результате периодических подводов и
отводов копировального пальца при непрерывной задающей подаче
он и фреза описывают пилообразную траекторию (рис. 11.2,а).
Результирующая подача sp образуется в результате геометрического
сложения двух ее составляющих подач: s3 и sc. Такое копирование при
помощи двух взаимно перпендикулярных подач станка называют кон-
турным. Если кроме задающей s3 и следящей $с подач в формообразо-
Рис. 11.2. Траектории инстру-
мента при копировании:
а - контурном; б - объем-
ном
323
Рис. 11.3. Схема копирования трех-
позиционным копировальным прибором
вании детали используют еще и пе-
риодическую подачу sn, то такое
копирование называют объемным.
Объемное копирование (рис. 11,2,6)
производят строчками, и его мож-
но привести к контурному, пола-
гая, что пространственно-сложная
поверхность разбита параллельны-
ми сечениями на ряд плоских кри-
вых. Копирование, при котором
осуществляют управление только
одной подачей (координатой), на-
зывают однокоординатным.
Схемы однокоординатного электрокопирования не могут применять-
ся для обработки деталей с резким изменением профиля, например
ступенек. Для обработки деталей с таким профилем применяется схема
двухкоординатного копирования, при которой осуществляется управ-
ление как приводом следящей, так и приводом задающей подачи. Управ-
ление выполняют при помощи трехпозиционного копировального при-
бора, содержащего два контакта (рис. 11.3). Копирование осуществля-
ется следующим способом. Если копировальный палец 1 не соприка-
сается с поверхностью шаблона 2, то контакт 3 под действием пружины
4 замкнут, а контакт 5 разомкнут. При этом задающая подача отклю-
чена и работает следящая подача, перемещая палец к шаблону, а инстру-
мент — к заготовке. При соприкосновении пальца 1 с шаблоном кон-
такт 3 размыкается, после чего следящая подача отключается и начинает
работать задающая подача. В этом случае копировальный палец отходит
от шаблона, контакт 3 вновь замыкается, отключается задающая пода-
ча, включается следящая и начинается новое перемещение копироваль-
ного пальца к шаблону.
Как правило, после обработки изделий на копировальных станках
требуется последующая обработка их для уменьшения шероховатости
поверхности.
113. ПРИНЦИПЫ ПОСТРОЕНИЯ СЛЕДЯЩЕ-КОПИРОВАЛЬНЫХ СИСТЕМ
Функциональная схема следящего электропривода копироваль-
ной системы с пропорциональным регулированием приведена на
рис. 11.4,я. Двигатель М, вращающий механизм подачи станка, питается
от преобразователя напряжения U. Задающим элементом и датчиком
324
Вс 11.4. Схемы следящего электропривода:
а - функциональная; б - структурная
и
Положения являются сельсины ВС, BE или поворотные трансформато-
£с фазочувствительным выпрямителем UB. Сигнал управления Uy
ливается усилителем А. В эквивалентной структурной схеме элек-
привода (рис. 11.4,6) имеются: задающее устройство с передаточной
функцией Я3(р), элемент сравнения AW, усилитель с передаточной
функцией Ну (р), преобразователь с передаточной функцией Нп (р),
:^йектро двигатель с передаточной функцией Яд (р), механизм и датчик
Положения механизма с передаточными функциями Ямех (р) и
$д,п (Z7) •
> \ Полагая Я3(р) = Яд,п(р) = &п,у с учетом £фцВ, получаем после
•Преобразований
V (®з ®вых)^п,у ^п,у Цг-
,к1. Принимая усилитель и тиристорный преобразователь в качестве
безынерционных звеньев Ну(р) = ку; На(р) = кя, имеем
= Ц'.П’ Uy,nkn = ^п-
Если в качестве
да, то передаточная
мым возбуждением
О и (Р)
Яд(Р) = —-------
*п<Р)
выходной величины рассматривать положение ва-
функция двигателя постоянного тока с независи-
имеет вид
кв.
р(ТмТярг + rMp + 1)
325
где Тм, ~ электромеханическая и электромагнитная постоянные
времени электропривода.
Полагая, что в редукторе отсутствуют люфты и упругие дефор-
мации, записываем
^мехО7) " ®вых (Р) ” ^р»
где &р — передаточное отношение редуктора.
На основании приведенных уравнений может быть получено диффе-
ренциальное уравнение следящего привода:
J ^ВЫХ +lp. F2 ^0вых + Мс _ к
dt2 \ *р/ dt *р *р
где Fi = &М/&Ы — коэффициент затухания, обусловленный статиз-
мом механической характеристики двигателя; Г2 - - коэффи-
циент затухания, обусловленный вязким трением; к — коэффициент
передачи следящего привода, к = скПукукп/Кя = М/д.
Добротность следящего привода определяется скоростью <оуст от-
работки задающего сигнала и скоростной (кинетической) погреш-
ностью 8К:
& ~~ ^уст/^к =
где F — коэффициент затухания, F = Fx +F2.
Погрешность привода 8 при равномерной заводке задатчика со ско-
ростью <оуст состоит из скоростной и статической погрешностей:
8 = 8С + 6К = Mcjk + coF/k.
Как видно, скоростная погрешность пропорциональна угловой ско-
рости и обратно пропорциональна коэффициенту усиления, а статичес-
кая погрешность пропорциональна моменту сопротивления и обратно
пропорциональна коэффициенту усиления.
Пример 11.1. Определить требуемую добротность следящей системы,
если максимальная скорость подхода к копиру vmax = 103 мм/мин,
а статическая погрешность 8К не должна превышать 0,01 мм:
£> = vmax/60dK = 103/60-0,01 = 1667 1/с.
Пример 11.2. Рассчитать погрешность копирования, если доброт-
ность следящей системы электропривода подачи станка D = 2000 1/с,
а максимальная скорость подхода к копиру vmax = 10 000 мм/мин:
8К = vmax/6QD = 10 000/60 2000 = 0,083 мм.
326
и и
4 v Пример 113. Определить погрешность копирования следящей систе-
йы электропривода вращения стола станка, если добротность D
» 2000 1/с, а максимальная угловая скорость подхода к копиру ытах
ж 10 рад/с
6К = <jJmax/D = 10/2000 = 0,005 рад.
В переходных процессах появляется динамическая погрешность, и
полная погрешность равна
; 5 = 5К + 5П.
к д
Динамическая погрешность определяется параметрами системы. При
Мс = 0 и скачкообразно нарастающем управляющем воздействии 0ВХ =
= WycT^ динамическая погрешность может быть найдена из однородно-
го дифференциального уравнения
d28 dd
> J ---- + F — + £5=0.
dt2 dt
v. Для уменьшения погрешности слежения применяется двухотсчет-
ное измерительное устройство с грубой и точной системами отсчетов,
В котором могут быть использованы две пары сельсинов, одна из ко-
торых ВС1, ВЕ1 (рис. 11.5,а) связана с задающим и исполнительным
валами непосредственно, а вторая ВС2, ВЕ2 — через редукторы R1 и
। R2. Сельсины первой пары образуют систему грубого отсчета с непосред-
327
ственной передачей измеряемого угла. Сельсины второй пары образуют
систему точного отсчета, для чего передаточное отношение редукторов
ip выбрано так, чтобы эти сельсины вращались быстрее.
При повороте задающего вала на угол 0ВХ сельсин-датчик ВС1 по-
вернется на тот же угол, а сельсин-датчик ВС2 - на угол /р0вх и» таким
образом, в ip раз увеличится рассогласование между сельсинами. Эти
напряжения ивх через синхронизирующее устройство (селектор) S по-
ступают на систему управления электропривода с преобразователем
UM и двигателем М. Последний будет вращать выходной вал и сельси-
ны-приемники до тех пор, пока снимаемые напряжения не станут равны-
ми нулю. При согласовании положение роторов сельсинов-датчиков и
приемников будет отличаться на собственную погрешность сельсинов и,
следовательно, погрешность системы точного отсчета будет
^т,о ” ^г,о/*р>
где 5Г 0 — погрешность системы грубого отсчета.
В режиме слежения система грубого отсчета служит для отработки
больших рассогласований, а при небольших рассогласованиях выходной
сигнал снимается с системы точного отсчета. Развернутая функциональ-
ная схема такого следящего электропривода (рис. 11,5,6) содержит
кроме указанных выше элементов фазочувствительные выпрямители
UB1, UB2\ корректирующие устройства ADI - AD3*, тахогенераторы
BR1,BR2\ модулятор UR\ усилитель Л, тиристорный преобразователь
UM (с устройством токоограничения).
Сигнал задания 0ВХ поступает с датчиков ВС, а сигнал обратной свя-
зи 0ВЫХ с приемников BE на измеритель рассогласования A W1. На вы-
ходе селектора 5 грубого и точного отсчетов сигнал рассогласования
алгебраически суммируется с корректирующими сигналами по пер-
вой производной от управляющего воздействия tig* и по первой про-
изводной от выходного параметра Ug , снимаемых с тахогенерато-
ров BRI, BR2 соответственно. Результирующий сигнал через фазочув-
ствительный выпрямитель UB1 поступает на корректирующее устрой-
ство AD1, вырабатывающее первую производную от сигнала рассогла-
сования.
Сигнал по второй производной от выходного угла ид , получен-
ный как производная сигнала по скорости с тахогенератора BR2 пылу-
пает на сумматор AW3 с параллельного корректирующего устройства
AD2, Может быть применен также сигнал отрицательной обратной связи
по ускорению (по току двигателя), снимаемый с датчика тока и пода-
ваемый на сумматор AW3 через корректирующее устройство AD3.
Усилитель, работающий по принципу модулятор — усилитель переменно-
го тока - демодулятор (UR - А - UB2), подает управляющий сигнал
на вход преобразователя UM, питающего электродвигатель М. Примене-
328
цие в описываемой следящей системе сельсинов обеспечивает точность
отработки перемещений 0,25-1°.
Оценка качества нескорректированной следящей системы может
производиться частотным методом, при котором на логарифмической
даоскости строят амплитудную и фазовую частотные характеристики
разомкнутой главной цепи системы. Положение амплитудной харак-
теристики L (со) по высоте контролируется двумя точками Lx и£2
4рис. 11.6), координаты которых определяются требованиями к точ-
гости работы следящей системы и находятся следующим образом,
[оскольку ордината первой асимптоты ЛАЧХ разомкнутой системы на
частоте со = 1 равна передаточному коэффициенту разомкнутой систе-
мы в дБ, абсцисса соответствует coj = 1, а ордината первой точки
I Li (coi) = 201gfc,
где к — передаточный коэффициент разомкнутой системы.
Расчет координат второй точки производят исходя из требований к
динамической точности
^2 = ^тах^тах'*
: = 201g (со2 /е 6 ),
ЪИ^2/ ь^таХ'^тах усттдх7*
Где €тах — максимальное ускорение, рад/с2; ытах — максимальная
скорость отработки, рад/с; 8усттдх — максимальная амплитуда по-
грешности установившегося режима, рад.
Тогда для ЛАЧХ следящих систем область, находящаяся ниже точ-
ки L2 и двух прямых с наклонами —20 и —40 дБ/дек, является запрет-
ной областью. Первая асимтота амплитудной характеристики не должна
Проходить ниже точки L!, а следующие асимптоты не должны пересе-
кать запретную область.
Если ЛАЧХ системы не пересекают запретную область, то погреш-
ность системы не превысит Ьусттах при со < <*>тах и €^€тах-
Рис. 11.6. ЛАЧХ следя-
щей системы
Рис. 11.7. Функциональная схема цифро-аналогового следящего электропривода
Высокая точность слежения (0,001—0,01%) и хорошие динамичес-
кие показатели могут быть получены в цифро-аналоговых следящих
системах.
Функциональная схема цифро-аналогового следящего электропри-
вода (рис. 11.7) состоит из цифровой части, представляющей собой кон-
тур регулирования перемещения, и аналоговой, в которую входят ре-
гуляторы положения, скорости и тока электропривода.
Цифровое устройство ввода задания SQZ подает информацию о тре-
буемом перемещении в виде числа N3 на устройство сравнения AW.
На второй вход устройства A W поступает информация Nq об отрабо-
танном перемещении, контроль которого осуществляет аналоговый
датчик положения BQ, а цифровую информацию вырабатывает преобра-
зователь UZ кода в число. Сигнал рассогласования Д7У при помощи
цифро-аналогового преобразователя UZY преобразуется в аналоговый
сигнал Д Uq, поступающий на регулятор положения AQ аналоговой
части системы. Аналоговая часть электропривода выполнена по принци-
пу подчиненного регулирования и помимо регулятора положения AQ
содержит регуляторы скорости AR и тока АА, преобразователь UM и
двигатель М. Соответствующие регуляторы получают сигналы с датчи-
ков скорости BR и тока UA. Статическая точность системы определя-
ется шагом квантования по времени, точностью измерения положения
и точностью преобразователя код—число. Цифро-аналоговая система
регулирования следящего привода обеспечивает приемлемые дина-
мические показатели за счет аналоговой части и высокую точность
за счет цифровой части. Цифровая часть системы может быть выпол-
нена на базе микропроцессоров.
330
11 А. ВЗАИМОСВЯЗАННЫЕ СИСТЕМЫ СОГЛАСОВАННОГО
ПЕРЕМЕЩЕНИЯ УЗЛОВ СТАНКОВ
Существует значительная группа станков, в которых требуется обес-
печить заданное соотношение скоростей и перемещении узлов. В ка-
честве примера может быть названа широко применяющаяся система
поддержания заданной подачи на оборот шпинделя в токарных, свер-
лильных, фрезерных и других станках. Принципиальная электрическая
схема такой системы (рис. 11.8) содержит электродвигатель Ml при-
вода главного движения и электродвигатель М2 привода подачи. Тахо-
генератор BR1, сочлененный с двигателем Ml, питает своим напря-
жением потенциометр RP. Тахогенератор BR2 сочленен с двигателем
М2. На вход преобразователя UM привода подачи поступает напряже-
ние управления
t/y - &lC4ri — ^ГГ2>
где ki — коэффициент пропорциональности; Ц.Г1, Ц.Г2 - напряжения,
вырабатываемые соответственно тахогенераторами BR1 и BR2.
Таким образом, при неизменной угловой скорости привода главно-
го движения угловая скорость двигателя подачи М2 определяется по-
ложением движка потенциометра RP. При изменении скорости двигате-
ля Ml изменяется ЭДС тахогенератора BR1 и, следовательно, напряже-
ние кх (7ТГ1, являющееся задающим для привода подачи. При этом уг-
ловая скорость привода подачи изменяется, оставаясь пропорциональ-
ной скорости привода главного движения станка.
Системы взаимосвязанного управления электроприводами применя-
ются в плоскошлифовальных станках с круглым столом и горизонталь-
ным шпинделем (рис. 11.9), оснащенных кроме привода главного дви-
жения Ml приводами вращения стола М2, поперечной подачи М3 и по-
дачи на врезание шлифовального круга М4. Стрелками показаны воз-
можные перемещения узлов станка.
Зависимость угловой скорости стола сос от радиуса обработки R
имеет вид
сос = dipjdt = Уд/60/?, (11.1)
Рис. 11.8. Схема системы поддержания заданной подачи на оборот шпинделя
331
Рис. 11.9. Схема перемещений узлов плоскошлифовального станка с круглым
столом и горизонтальным шпинделем
где — угол поворота точки контакта круга с деталью; уд — окружная
скорость детали.
При работе с постоянной окружной скоростью с изменением радиуса
обработки необходимо изменять угловую скорость стола сос.
Из условия постоянства оборотной подачи, равной
s0 = 2лтп/60сос = const, (11.2)
где уп - скорость поперечной подачи, следует, что при построении сис-
тем управления приводами подач необходимо учитывать, что они в со-
ответствии с (11.2) должны быть взаимосвязаны, так как скорость по-
дачи vn и угловая скорость сос должны изменяться пропорционально.
Кроме того, системы управления приводами подач связаны также через
процесс резания, поскольку изменение нагрузки одного из приводов
вызывает соответствующее изменение параметров процесса обработки,
непосредственно сказывающееся на нагрузке другого привода.
332
ftic. 11.10. Функциональные схемы систем взаимосвязанного управления электро*
приводом плоскошлифовальных станков:
а — с функциональным преобразователем; б — с множительным блоком;
в - с пропорциональным заданием скорости; г - с датчиком мощности
Многообразие схемных решений при построении взаимосвязанных
приводов поддержания постоянства окружной скорости стола и оборот-
ной поперечной подачи может быть сведено к ограниченному числу ти-
повых вариантов, основные из которых показаны на рис. 11.10. Эти
варианты отличаются способом формирования сигнала обратной связи,
пропорционального окружной скорости стола, и способом задания обо-
ротной подачи.
На рис. 11.10,а дана структурная схема управления взаимосвязанны-
ми электроприводами главного движения и подачи с использованием
333
датчика диаметра BD и функционального преобразователя A U, с по-
мощью которых формируется сигнал обратной связи, пропорциональ-
ный угловой скорости uv. Сигнал с пропорционален угловой ско-
рости сод С двигателя привода вращения стола М2. На вход регулятора
AR поступают три сигнала: задающий с задатчика скорости SR U3 с,
с функционального преобразователя uv и обратной технологической
связи по скорости итс, снимаемый с датчика BR. Тогда напряжение
управления
Uy — Uy ^т,с 01*3)
Сигнал, пропорциональный диаметру обработки ид, поступает с дат-
чика диаметра BD на вход функционального преобразователя: ид =
= k2d.
Последний определяет закон движения электропривода вращения
стола UM2, вырабатывая на своем выходе сигнал, обратно пропорцио-
нальный диаметру обработки:
uv = к3 ~ = к4 — . (11.4)
“д d
Двигатель М2 через редуктор RM передает вращение столу и обеспе-
чивает процесс шлифювания PR, поддерживая постоянство окружной
скорости в точке контакта круга с изделием. При помощи блока зада-
ния оборотной подачи SV устанавливается требуемое значение сигнала
U3 п, поступающего на электропривод поперечной подачи UM3, анало-
гичный UM2, и воздействующего на процесс шлифования за счет под-
держания постоянства оборотной подачи s0.
Двигатель привода шпинделя Ml вращает шлифовальный круг с
угловой скоростью сош, при этом на шлифование затрачивается мощ-
ность Pz.
Описанная схема реализована в системе автоматического управле-
ния приводами подач плоскошлифовальных станков мод. ЗД740,
ЗД741 и др.
В структурной схеме, показанной на рис. 11.10,6, для формирова-
ния сигнала обратной связи по окружной скорости стола использован
множительный блок АХ, напряжение на выходе которого
uv = “т,с“д = ksitduc. (11.5)
В качестве множительных блоков могут быть использованы тахоге-
нераторы постоянного и переменного тока, потенциометры, сельсины,
специальные функциональные множительные устройства аналогового
и цифрового типов.
При использовании в приводах вращения стола и подачи тиристор-
ных преобразователей электроприводов может быть реализована струк-
334
турная схема (рис. 11.10,в), в которой напряжение uv с выхода функ-
ционального преобразователя AU подается одновременно на входы
обоих приводов. В этом случае связь между приводами сохраняется
через процесс резания. Такая схема применена в станке для силового
шлифования мод.ЗМ758.
Если измерять мощность шлифования Pz датчиком мощности BW
(рис. 11.10,г), то при определенных условиях система будет поддер-
живать постоянной окружную скорость в точке контакта круга с изде-
лием. Напряжение, пропорциональное мощности, сравнивается с нап-
ряжением сравнения 6/ср, вырабатываемым блоком GU. Если
Ыд,м > Цф, то замыкается цепь технологической обратной связи по
мощности шлифования. Напряжение управления
иу “ ^з,с “ (Мд,м “ ^ср) — ^TjC-
При движении шлифовального круга от периферии к центру стола
мощность резания будет снижаться, что приведет к уменьшению нап-
ряжения
^д,м “ •
Напряжение иу будет возрастать, и соответственно увеличится угло-
вая скорость о>с. Таким образом, будут поддерживаться на заданном
уровне окружная скорость уд и мощность резания Pz. Задание обо-
ротной подачи производится аналогично схемам рис. 11.10,6. Если обо-
ротная подача s0 и подача на врезание stQ неизменны, то
Pz = М^д)0,7
и при Pz = const окружная скорость уд = const, т.е. система при взаимо-
связанном управлении электроприводами стола и подачи поддерживает
постоянство окружной скорости при измерении радиуса обработки.
Глава двенадцатая
СИСТЕМЫ ПРОГРАММНОГО УПРАВЛЕНИЯ
МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
12.1. ОБЩИЕ ПОЛОЖЕНИЯ
В металлорежущих станках широкое распространение получило чис-
ловое программное управление (ЧПУ). Согласно ГОСТ 20523-80 ЧПУ
определяется как управление обработкой на станке по управляющей
программе, в которой данные записаны в цифровой (числовой) форме.
Управляющее устройство в ЧПУ называется устройством ЧПУ, а систе-
335
ма, определяемая как совокупность функционально взаимосвязанных
и взаимодействующих технологических и программных средств, обеспе-
чивающих ЧПУ, называется системой ЧПУ.
Использование ЧПУ особенно эффективно при мелкосерийном
производстве и частой смене номенклатуры обрабатываемых деталей.
В этом случае применение традиционных методов автоматизации, харак-
терных для крупносерийного и массового производства, оказывается
нецелесообразным, а обработка на универсальных станках, соответству-
ющих единичному производству, требует большой трудоемкости. Сис-
темы ЧПУ в станках позволяют повысить производительность и точность
обработки, обеспечить гибкость производства, сократить сроки его под-
готовки и создать высокий технико-экономический эффект. Повышение
производительности обеспечивается за счет сокращения вспомогатель-
ного и машинного времени обработки, автоматизации установочных пе-
ремещений, исключения разметочных и измерительных работ. Точность
обработки возрастает за счет уменьшения числа установок деталей при
обработке, устранения ошибок оператора, возможных при ручной обра-
ботке. Применение станков с ЧПУ экономически целесообразно при
комплексном оснащении ими участка, цеха, завода, особенно в тех слу-
чаях, когда производится сложная и разнообразная обработка, операции
по настройке занимают много времени, машинное время мало по срав-
нению с вспомогательным, обрабатываются сложные детали в условиях
мелкосерийного производства, требуется 'сократить период освоения
производства.
Современные системы ЧПУ содержат в своей структуре микро-ЭВМ
и образуют производственные модули (технологические ячейки), авто-
матизированные участки, автоматические линии и др.
Материал данной главы базируется на сведениях, полученных при изу-
чении курса ’’Программирование и применение ЭВМ”, а также соответ-
ствующих разделов курсов ’’Системы управления электроприводами”
и ’’Моделирование и микропроцессорное управление электроприводом”.
В результате изучения материалов студенты должны знать принципы
построения систем ЧПУ и уметь составлять программы для станков с
ЧПУ.
12.2. КЛАССИФИКАЦИЯ И ОБЛАСТИ ПРИМЕНЕНИЯ СИСТЕМ ЧПУ
МЕТАЛЛОРЕЖУЩИМИ СТАНКАМИ
Системы ЧПУ металлорежущими станками классифицируются по
различным признакам (рис. 12.1). По виду рабочих движений станка
системы ЧПУ могут быть разделены на позиционные, контурные и
комбинированные.
Позиционные системы ЧПУ позволяют производить относительное
перемещение инструмента и заготовки от одной точки (позиции) к дру-
гой. Такое управление используется в сверлильных, расточных и других
336
[ Системы ЧПУ(НС) |
По Виду рабочих движений станка
I позиционные
контурные
j [ комбинированные |
По характеру представления информации
[ ’ непрерывные | | Зискретно-непрерыВные | Вискретные
фазовые
амплитудные
счетно-
импульсные
шагово-
импульсные
По особенностям структуры
I
г1-----
| СНС
UNC
По изменению режима обработки
I
цикловые
программные | | адаптивные
ftic. 12.1. Классификация систем ЧПУ
станках, на которых обработка выполняется после установки инстру-
мента в заданной позиции. Поскольку основной задачей для таких сис-
тем является перемещение инструмента (детали) в заданную коорди-
нату, их называют также системами координатного управления и управ-
ления положением.
Контурные системы ЧПУ позволяют производить обработку кри-
волинейных поверхностей при фрезеровании, точении, шлифовании и
других видах металлообработки. В этих системах программируется
траектория перемещения режущего инструмента, поэтому их часто на-
зывают системами управления движением.
Комбинированные системы представляют собой сочетание позицион-
ных и контурных и называются также универсальными. Они находят
применение в многооперационных станках, где требуется позиционно-
контурное управление.
При обозначении модели станка с ЧПУ, оснащенного позиционной
системой, к ней добавляют индекс Ф2, оснащенного контурной систе-
мой — индекс ФЗ и комбинированной — индекс Ф4. Индекс Ф1 в обоз-
начении модели станка свидетельствует об оснащении станка цифровой
индикацией и ручным управлением.
337
По характеру информации, записанной на программоносителе, раз-
личают системы непрерывные, дискретные и дискретно-непрерывные.
В непрерывных системах программа записывается непрерывной вели-
чиной. Так, если применяется система с фазовой модуляцией, то про-
грамма представляется синусоидальным напряжением, фаза которого
пропорциональна программируемым перемещениям; в системах с
амплитудной модуляцией перемещениям пропорциональна амплитуда
этого напряжения. В дискретных (импульсных) системах информация
о перемещениях задается соответствующим числом импульсов. Если
механизм перемещения оснащен датчиком импульсов и для учета пере-
мещения используется счетная схема, то систему называют счетно-им-
пульсной. Если исполнительным устройством является шаговый двига-
тель, то систему называют шагово-импульсной.
В импульсно-фазовых устройствах ЧПУ суммирование импульсов,
задаваемых программой, производится в фазовом преобразователе,
выходной сигнал которого в виде угла сдвига фазы переменного напря-
жения пропорционален количеству импульсов программы.
По особенностям структуры системы ЧПУ разбиты на четыре груп-
пы, имеющие сокращенное международное обозначение HNC, SNC,
CNC, DNC. Системы HNC (Hand numerical control) представляют собой
разновидность систем ЧПУ с ручным заданием программы с пульта уп-
равления. Системы SNC (Speicher numerical control) обладают памятью
для хранения управляющих программ. Системы CNC (Computer nu-
merical control) содержат в своем составе микро-ЭВМ для программиро-
вания алгоритмов работы и выполнения процесса управления. Системы
DNC (Direct numerical control) служат для прямого цифрового управ-
ления группой станков, осуществляя хранение программ и их выдачу
по запросам станочных систем ЧПУ типов SNC и CNC.
По изменению режимов обработки системы ЧПУ разделяются на
цикловые, программные и адаптивные. Цикловые системы осуществля-
ют движения с повторяющимися циклами. В них применяется кулачко-
вое, аппаратное, микропрограммное и программируемое управление.
При кулачковом управлении используют для задания режимов штекер-
ные панели, аппаратное управление осуществляют при помощи релейно-
контактной или бесконтактной аппаратуры. Для микропрограммного
управления применяют запоминающие устройства микрокоманд, а про-
граммируемое управление режимами обработки основано на использо-
вании средств программируемой логики.
В программных системах ЧПУ изменение режимов обработки осу-
ществляется программными средствами с использованием программоно-
сителя или памяти ЭВМ. Применение адаптивного управления позво-
ляет производить автоматическое изменение режима обработки незави-
симо от программы.
Числовое программное управление обеспечивает управление по нес-
кольким координатам. Поэтому его широко применяют на многоопе-
338
Таблица 12.1
Наименование системы ЧПУ (страна-разработчик) Назначение системы Область применения Количество управля- емых коор- динат* Тип интер- поля- ции Дискрет- ность задания, мм Коли- чество инстру- ментов Ускорен- ная пода* ча, мм/мин
Н332 М (СССР) Койтурная Токарные, фрезерные станки, обрабатывающие центры 3 Линейно- круговая - 100 4800
System 7 (фирма Fanuc, Япония) Фрезерно-расточные, обраба- тывающие центры 4/2 То же 0,001 — 15 000
Nucon400 (фирма ASSEA, Швеция) То же 4/3 0,001 — 15 000
2С 85 (СССР) Контурно- позицион- ная Работотехнические комплек- сы 8 Линейная и круго- вая 0,001 99 15 000
2С 42-65 (СССР) Контурная Сверлильно-фрезерно-расточ- ные станки 4/3 То же 0,001 99 15 000
2Р 22-31 (СССР) Контурно- позиционная Токарные, шлифовальные станки 3/2 0,001 1 10 000
Электроника НЦ-31 (СССР) То же Токарные станки 2/2 »» 0,01 — —
Размер 2М-5 (СССР) Сверлилыю-фрезерно-расточ- ные станки 3/2 0,001 — 20 000
Электроника НЦ-80-31 (СССР) Токарные, фрезерные станки, обрабатывающие центры 8/2 0,001 — 15 000
2Р 32 (СССР) Контурная Токарные, фрезерные станки 3/2 0,001 — 15 000
*В числителе указано общее количество управляемых координат, а в знаменателе - количество координат, которыми можно
управлять одновременно.
рационных станках (обрабатывающих центрах) с автоматической сме-
ной инструмента и обрабатываемых деталей.
Среди многооперационных станков наибольшее распространение по-
лучили станки для обработки корпусных деталей. С помощью ЧПУ на
них осуществляется перемещение заготовки по трем координатным
осям, а на станках с поворотным столом осуществляется также и ее
вращение. Многооперационные станки снабжены специальными магази-
нами (до 100 и более), в которых помещается режущий инструмент.
Смена инструмента станка производится по команде от системы ЧПУ
за 3-5 с.
Для оперативной смены обработанных деталей многооперационные
станки оснащают столами-спутниками. При обработке заготовки на
столе-спутнике, расположенном на столе станка, на другом столе-спут-
нике, находящемся на вспомогательном столе, меняют заготовку. Авто-
матическая смена столов-спутников по командам системы ЧПУ позво-
ляет уменьшить в технологическом цикле время на установку и снятие
детали до 30-45 с.
В системах с ЧПУ применяются линейные и круговые интерполято-
ры, преобразующие информацию, заданную кодом программы, в ин-
формацию, представленную в унитарном коде. Важной характеристикой
устройств ЧПУ является дискретность задания и отработки перемеще-
ний, достигающая 0,001 мм (0,001°).
В настоящее время системами ЧПУ оснащаются практически все ви-
ды металлорежущих станков. Технические данные некоторых отечест-
венных и зарубежных систем ЧПУ и области их применения приведены
в табл. 12.1.
123. ТИПОВЫЕ СТРУКТУРЫ СИСТЕМ ЧПУ
Типовая структура систем ЧПУ (рис. 12.2) содержит устройства
ввода и обработки программы, связи с датчиками технологической ин-
формации, управления приводами и исполнительными механизмами
станка, воздействующие на технологический процесс.
Для записи программы в станках с ЧПУ наибольшее применение
находит восьмидорожечная перфолента. Для уменьшения объема про-
граммоносителя используется сочетание буквенных и цифровых сим-
волов. Первые обычно однозначно эквивалентны командам, вторые —
значениям перемещений. Кодирование осуществляют в двоичной, дво-
ично-десятичной и очень редко — в десятичной системах счисления, опи-
санных в гл. 2. Для контроля правильности считывания ленты вводятся
поверочные знаки. Далее рассматриваются принципы построения сис-
тем ЧПУ.
Шагово-импульсные системы ЧПУ наиболее просты при реализации
и выполняются с разомкнутой цепью управления на шаговых двигате-
лях, однако они обладают малыми технологическими возможностями
340
Рис. 12.2. Структура систем ЧПУ станка
и невысокими динамическими показателями. Функциональная схема
такой системы приведена на рис. 12.3.
Узел программы 1 состоит из лентопротяжного механизма и считы-
вающего устройства. Расшифровку поступающих из узла программы
команд и их преобразование к виду, удобному для управления шаго-
выми двигателями, выполняет блок управления 2. Эти сигналы, про-
ходя через импульсные усилители А, поступают на формирователи им-
пульсов AQ, где преобразуются в импульсы прямоугольной формы,
которые подаются на кольцевой распределитель-коммутатор ЕА. По-
следний распределяет импульсы по обмоткам шагового двигателя М,
что вызывает вращение его ротора. Шаговый двигатель непосредствен-
но или при помощи усилителя момента передает движение через испол-
нительное устройство ES рабочим органам ЕМ станка. При частоте сле-
дования управляющих сигналов 500—800 Гц скорость перемещения
рабочих органов - до 1 м/мин.
В настоящее время широко применяются шагово-импульсные УЧПУ
типа Н221М, Н331М, 1Н223 для управления токарными и фрезерными
станками.
Фазоимпульсные системы ЧПУ работают с замкнутой цепью управ-
ления.
Рис. 12.3. Функциональная схема шагово-импульсной системы ЧПУ
341
Рис. 12.4. Функциональная схема фазоимпульсной системы ЧПУ
Управляющее устройство ЧПУ состоит (рис. 12.4) из узла программы
1 и вычислителя 2. Вычислитель 2 предназначен для преобразования
входной информации к виду, пригодному для интерполирования, и вы-
дачи информации о скорости, величине и направлении заданного переме-
щения в устройство управления электроприводом. Преобразователь
UF преобразует управляющий сигнал в фазу задающего канала контура
положения, а блок сравнения UR вырабатывает управляющее напряже-
ние, сравнивая фазу управляющего сигнала с фазой сигнала обратной
связи. Сигнал управления скоростью формирует блок UV. На вход
преобразователя U поступают сигналы рассогласования между заданны-
ми и фактическим перемещениями и управления скоростью. Преобразо-
ватель U воздействует на электродвигатель М9 приводящий в движение
рабочий орган станка ЕМ. Обратную связь по скорости осуществляет
тахогенератор BR, перемещения контролирует датчик BQ, в качестве
которого используют вращающийся трансформатор.
По рассмотренной функциональной схеме построены серийно выпус-
каемые в настоящее время фазоимпульсные управляющие устройства
ЧПУ, например контурное фазоимпульсное устройство ЧПУ типа Н332М,
предназначенное для управления фрезерными станками с автоматичес-
кой сменой инструмента.
12.4. ЭЛЕМЕНТЫ СИСТЕМ ЧПУ
В системах ЧПУ металлорежущими станками применяются различные
специальные элементы, среди которых наиболее характерны интерполя-
торы и датчики перемещения.
Интерполяторы служат для непрерывной подачи информации о пере-
мещениях в систему управления приводами станка при обработке исход-
ной дискретной информации программы и находят применение в кон-
турных системах ЧПУ с записью программы на перфоленте. Они выпол-
няют интерполяцию линейную, квадратичную или более высокого поряд-
ка. При линейной интерполяции с программоносителя на вход интерпо-
лятора поступают приращения координат (например, х и у) и время об-
342
Рис. 12.5. Схема линейного интерполятора
работки, а на его выходе получаются равномерно распределенные во вре-
мени импульсы, количество которых пропорционально перемещению.
Линейные интерполяторы наиболее часто строят по схемам импуль-
сных умножителей (рис. 12.5). Интерполятор получает информацию со
считывающего устройства D через вводное устройство AZ. С генера-
тора импульсов GF на счетчики PC интерполятора поступают импуль-
сы, часто'ты которых задаются программой, что определяет скорость
привода подачи. При использовании двоично-десятичного кода, например
8421, после поступления на счетчик десяти импульсов на выходе его раз-
ряда появится один импульс, идущий на следующий счетный разряд.
После заполнения счетчика, объем которого рассчитан на 9999 импуль-
сов, производится счет импульсов для обработки следующего кадра
программы.
Каждая декада счетчика состоит из 10 ферротранзисторных ячеек,
образующих счетную схему. На каждую ячейку подаются импульсы,
поступающие на вход декады, а также сигналы с выхода предыдущей
ячейки. Выходы ячеек объединены в четыре сборки в соответствии с
кодом (8421, 5121 и тд.). Например, при коде 8421 сборка 8 соедине-
на с выходами 1-4-й, 6-9-й ячеек, сборка 4 — с выходами 1, 4, 6, 9-й
ячеек, сборка 2 - с выходами 2, 8-й ячеек, сборка 1 — с выходом 5-й
ячейки. Таким образом, на 10 импульсов, поступивших на вход любой
декады, на выходах сборок 8, 4, 2, 1 будут поступать соответствующие
количества импульсов.
Предположим, закодировано число 8157. Это значит, что по командам
от пробитых отверстий в перфоленте через вводное устройство AZ бу-
дут поданы сигналы на следующие элементы И декад одной коорди-
наты, например х:
8421 8421 8421 8421
1000 0001 0101 0111
343
Рис. 12.6. Круговая интерполяция методом
оценочной функции
При этом за одно заполнение счетчика
на управляемый преобразователь UX
по координате х будет подано 8157 им-
пульсов, пропорционально которым
будет произведено перемещение.
В системах ЧПУ профиль обрабаты-
ваемой детали кодируется по чер-
тежу конечным числом точек поверхности, которые называют опорны-
ми. Увеличить интервалы между опорными точками интерполяции и
уменьшить объем вводимой с перфоленты информации можно путем
использования интерполяторов второго и более высоких порядков.
Интерполирование осуществляется по методу оценочной функции Fzy,
где направление очередного шага определяется по ее знаку. При ис-
пользовании двухкоординатного кругового интерполятора кривая де-
лит плоскость на две области (рис. 12.6), одна из которых находится над
кривой, а другая — под ней.
Траектория интерполяции состоит из чередующихся шагов вдоль
основных осей. Если точка траектории, расположенной в первом квад-
ранте, находится над кривой > 0, то при движении против часовой
стрелки следующий шаг производится вдоль оси X; если точка траек-
тории находится под кривой Fy < 0, то следующий шаг производится
вдоль оси Y. Оценочная функция для промежуточных точек траекто-
рии описывается выражением
= х1+ у] - R2’
где xit yj — координаты текущей точки относительно центра дуги; R —
радиус обрабатываемой дуги.
Начальное значение оценочной функции при обработке окружности и
расположении точки траектории на ее радиусе равно нулю. Текущие
координаты при шаге вдоль одной или другой оси изменяются на од-
ну дискрету:
xi+l =xi yi + i =У/ +1- (12.1)
Текущее значение оценочной функции меняется при шаге вдоль оси X:
+ У2 = Гц + 1 (12.2)
и при шаге вдоль оси Y:
344
Точность круговой интерполяции методом оценочной функции нахо-
дится в пределах одного шага. Функциональная схема кругового ин-
терполятора машины УМС-2 представлена на рис. 12.7. Интерполятор
имеет пять регистров сдвига PG1 - PG5 и два одноразрядных двоичных
сумматора С1 и С2.
Со считывающего устройства D через вводное устройство AZ в ре-
гистры PG1 и PG2 вводятся координаты начальных точек хн, ун ин-
терполируемого отрезка. В процессе интерполяции в регистрах PG1,
PG2 хранятся текущие значения координат обрабатываемых участков,
вычисленные по (12.1). В регистры PG3, PG4 вводятся координаты
конечных точек хк, ук; в процессе отработки кадра они не меняются.
Сравнение текущих координат с конечными производится в схеме
СТ до совпадения их значений по обеим координатам. После этого СТ
выдает сигнал К - ’’конец отработки кадра”. Регистр PG5 служит для
хранения текущего значения оценочной функции F^. Перед началом от-
работки очередного участка в регистре устанавливаются нули, а вычис-
ление очередного значения оценочной функции производится по фор-
мулам (12.2) и (12.3). Триггер Т вида траектории (линейный отрезок,
окружность) и схема определения знака оценочной функции UJ задают
режим работы. Интерполяция может выполняться для линейного отрез-
ка, когда работает сумматор С1. При движении по прямой триггер Т
вводит в работу регистр PG4, и в случае > 0 в сумматоре С2 вычи-
таются числа регистра PG4 из чисел, записанных в регистре PG5. При
движении по окружности, если F^ > 0, в сумматоре С2 происходит
вычитание из чисел, записанных в PG5, удвоенной величины, содержа-
щейся в регистре PG1, и к полученной разности в соответствии с фор-
мулой (12.2) прибавляется единица. Величина xi - 1 с выхода сумма-
тора С1 поступает на схему D2, задерживающую ее на один разряд, а
затем инвертируется схемой AU2 и подается на вход сумматора С2.
345
Если оценочная функция Fy < 0, то в сумматоре С2 происходит сло-
жение чисел, записанных в регистре PG5, с удвоенным числом, записан-
ным в регистре PG2, и прибавляется единица в соответствии с (12.3).
Схема UJ определяет знак очередного значения оценочной функции, в
результате чего управляющие импульсы поступают в блоки управления
электроприводами координат х или у и очередной шаг производится
по оси х при (Fy > 0) или по оси у при (Fy < 0). Для того чтобы уп-
равляемое от интерполятора устройство не прерывало работу на время
считывания (примерно 0,1 с) последующего кадра перфоленты, в уст-
ройстве ввода AZ имеется буферная память для хранения содержания
последующего кадра. Считывание информации производится во время
отработки текущего участка траектории. При помощи изменения часто-
ты управляемого генератора импульсов GF устанавливается скорость
подачи.
Датчики обратной связи в системах ЧПУ служат для контроля выпол-
нения заданной программы. В целях контроля перемещения (или поло-
жения) применяются датчики, действие которых основано на изменении
в функции пути некоторых физических параметров (омического сопро-
тивления, магнитного сопротивления, светового потока и тд.). Датчики
выполняются линейными или круговыми.
В металлорежущих станках для контроля линейных и угловых пере-
мещений используются индуктивные датчики, называемые индуктоси-
нами, и фотоэлектрические импульсные датчики.
Индуктосин — это воздушный датчик с печатными обмотками,
которые наносятся на изоляционные пластины, располагаемые с зазо-
ром 0,1-0,5 мм. Поворотный индуктосин (рис. 12.8,а) состоит из двух
пластин и индуктивно связанных проводников. Коэффициент связи
между ними изменяется по периодическому закону в зависимости от
относительного углового положения первичной и вторичной обмоток.
Период изменения определяется числом пар проводников первичной
обмотки. Питающее напряжение Ux переменного тока повышенной
частоты (5-20 кГц) подводится к выводам а и b первичной обмотки
(рис. 12.8,б). Обмотка снабжена внешним проводящим пересоедини-
тельным кольцом, с помощью которого токи в лобовых частях обмот-
ки по разные стороны диаметра 1, 2 (рис. 12.8,а) сдвигаются по фазе
на 180°, как и токи в любой паре соседних проводников. Выходной
сигнал преобразователя U зависит от взаимного расположения первич-
ной и вторичной обмоток. Напряжения питания , U2 можно также по-
давать и на двухфазную обмотку (выводы а, b и ct d), снимая с одно-
фазной (выводы е, f) синусоидальный выходной сигнал U. Поворот-
ные индуктосины за счет большого числа проводников обеспечивают
точность углового контроля до 6-10" .
Схема обмоток линейного индуктосина с неподвижной 1 и подвиж-
ной 2 пластинами представлена на рис. 12.8,в. Принцип его действия ана-
логичен принципу действия кругового индуктосина. При помощи линей-
346
Рис. 12.8. Схемы обмоток индуктосинов:
а, б - круговые; в - линейный
ного индуктосина можно контролировать перемещения с точностью
до> 1 мкм.
Фотоэлектрический датчик перемещений состоит из стек-
лянной линейки 1 (рис. 12.9 fl), на которой с шагом 0,005 мм нанесены
непрозрачные штрихи; вдоль линейки перемещается вторая короткая
линейка — диафрагма 2, на которой также нанесены штрихи. В зависи-
мости от расположения штрихов и просветов диафрагмы и линейки
световой поток, поступающий к фотоэлементу 3, будет прерываться.
При перемещении на каждые полшага выдается один импульс. Под-
считывая импульсы тока фотоэлемента 3, можно с высокой точностью
определять перемещение узла станка.
Штрихи на диафрагме нанесены с некоторым наклоном относитель-
но штрихов линейки. Благодаря этому при перемещении светлые и тем-
ные полосы будут смещаться по высоте. Положение диафрагмы относи-
тельно линейки, при котором для фотоэлемента 3 происходит полное
перекрытие просветов, сдвинуто от аналогичного положения фотоэле-
мента 4 на нечетное число четвертей шага. Относительный сдвиг фазы
сигналов фотоэлементов 3 и 4 используют для определения направ-
ления перемещения.
Фотоэлектрический круговой датчик (рис. 12.9,6) служит для пре-
образования угловых перемещений элементов станка в электрические
импульсы. На диске 1 датчика установлена круговая стеклянная шка-
ла, на которой нанесены штрихи. На корпусе 3 расположены осветитель
3 с фокусирующим устройством, стеклянная решетка 4 и два фото-
диода 5. Толщина штрихов и промежутки между ними равны между
347
1
Рис. 12.9. Фотоэлектрический датчик:
а - линейный; б - круговой
собой. На решетке 4 нанесены по две группы штрихов, смещенных от-
носительно друг друга на 1/4 шага. Группы каждого фотодиода также
взаимно смещены. При вращении диска луч света от осветителя падает
на фотодиоды и вырабатывает импульсы напряжения. Если на шкале
диска 1 нанесено 1250 штрихов, то за один оборот фотодиод вырабо-
тает в 4 раза больше импульсов, т.е. 5000. При шаге ходового винта
5 мм это обеспечивает цену отсчета 1 мкм. Фотоэлементы позволяют
также определять направление движения диска 1.
Кроме рассмотренных датчиков перемещений в системах ЧПУ ис-
пользуются сельсины, контактные датчики положения, кодовые фото-
датчики и др. Сельсины и вращающиеся трансформаторы выполняются
встроенными в электродвигатель и часто в этих случаях называются
резольверами.
12.5. ПРОГРАММИРУЕМЫЕ КОНТРОЛЛЕРЫ
Для построения АСУ ТП, работающих по жесткой программе, ши-
роко используются специализированные УВМ. Специфика таких УВМ,
решающих задачи программной автоматизации управления в станко-
строении, определила их название - программируемые контроллеры
348
(ПК). В оперативную память машины записывается программа, преду-
сматривающая управление по заданному алгоритму, и производится
решение логических задач поэтапного осуществления той или иной
структуры перемещения узлов различных станков или их комплексов.
Программируемые контроллеры решают задачу замены традиционных
устройств автоматики, специально изготовляемых по индивидуальным
проектам. В отличие от них ПК являются универсальными устройствами,
а специализация их производится в процессе набора программы.
Для реализации схем автоматики станков может использоваться
стандартная мини-ЭВМ, что, однако, может оказаться нецелесообразным
по экономическим соображениям, так как ПК проще в изготовлении и
дешевле.
Основы отличия ПК от мини-ЭВМ:
возможность выполнять, как правило, только логические операции;
обеспеченность развитыми входными и выходными устройствами
связи, позволяющими работать в производственных условиях, повы-
шенная помехозащищенность;
упрощенность программирования, позволяющая реализовывать алго-
ритмы по принципиальной схеме и логическим выражениям.
Особенностью схем ПК является последовательная обработка вход-
ных данных по так называемой схеме однобитового логического про-
цессора. В состав ПК входят две группы блоков связи со станком. Пер-
вая группа — входы — осуществляет передачу сигналов к ПК от датчи-
ков технологических параметров непрерывного контроля измеряемой
величины, фиксаторов положения любого типа (конечные и путевые
выключатели и переключатели), аппаратов ручного управления (кноп-
ки, ключи, переключатели). Вторая группа — выходы — осуществляет
передачу сигнала управления от ПК на исполнительные органы станка
или группы станков. В простейших решениях сигналы управления посту-
пают на исполнительные органы дискретного типа: катушки реле и кон-
такторов (пускателей), электромагнитные муфты, электромагниты и
т.п. Процессор ПК может формировать также сигналы для передачи их
на входы АСУ ЭП.
Принцип действия ПК состоит в последовательном опросе всех вхо-
дов, сравнении полученных результатов с комбинацией, заданной про-
граммой, и выработке сигнала управления, поступающего на один или
несколько выходов. Такие устройства заменяют релейно-контакторную
схему управления комплексом исполнительных органов станков с раз-
витой логической схемой выбора требуемой ситуации. Их применение
экономически целесообразно, если осуществляется замена 50-60 аппа-
ратов, управляющих комплексом станков или автоматической линией
по заданному циклу. Впервые такой ПК был разработан в Советском
Союзе (УМ1-НХ). Позднее специализированные УВМ появились в США
(PDP-8, Mini DNC, PDP-14, Модикон-184). Сейчас ПК широко выпуска-
ются в разных странах, некоторые из них приведены в табл. 12.2. Про-
349
Таблица 12.2
Тип программируемого конт- роллера (страна-разработчик) Разряд- ность, бит Время сканирова- ния 1 К слов, мс Объем памяти, К слов Количество модулей
МБ 57.(01-03) (СССР) 8 8 4 32, 64, 128
РК-4К (ПНР) 16 4 4 512
NS-915 (ЧССР) 16 6 4 256
IPC-300 (США) 8 5 2 1024
SMC-500 (Франция) 16 4 8 1024
РС-4000 (ФРГ) 24 5 4 512
Программа-700 (НРБ) 4 2,5 • 103 8 128
PLC-2/20 (США) 16 5 8 512
граммируемые контроллеры характеризуются числом входов-выходов,
различной емкостью памяти, временем сканирования и другими показа-
телями, что определяет возможности их использования, габариты и
стоимость.
Программируемые контроллеры снабжены рядом устройств про-
граммирования и индикации (рис. 12.10). Для ввода программы ис-
пользуются клавишные устройства и устройства ввода программ с. пер-
фолент. Программирующее устройство позволяет выполнять програм-
мирование с визуальным контролем вводимой программы на дисплее,
вызывать любой участок программы и вносить в нее любые изменения.
Программа может вводиться или вызываться с помощью телетайпа.
Программируемый контроллер имеет устройства связи с другими ЭВМ.
Функциональная схема ПК содержит сканатор-генератор тактовых
Рис. 12.10. Функциональная схема программируемого контроллера
350
Номер цепи
Е Е Е
Тип функции
рог| | Вр |
Контакты Выход
Номер контакта
(выхода)
Рис. 12.11. Панель программируемого контроллера
Тип контакта
И
импульсов, программируемое запоминающее устройство (ЗУ), процес-
сор управляющего устройства и регистры с блоками связи с датчиками
(входами) и исполнительными устройствами (выходами) станка. Одним
из вариантов построения ПК являются программируемое постоянное
ЗУ и процессор, которые образуют центральный процессор. Другим ва-
риантом центрального процессора ПК является оперативное запомина-
ющее устройство (ОЗУ), допускающее быструю смену хранимой ин-
формации. После набора программы и загрузки ее в ЗУ в режиме работы
сканатор поочередно подключается к процессору, который при этом оп-
рашивает входы (разряды входного регистра) и по программе выполня-
ет логические операции, преобразующие состояния входов в состояния
выходов. Если комбинация состояний входов не изменилась по сравне-
нию с предыдущим циклом сканирования, то процессор сохраняет не-
изменным состояние выходов, в противном случае процессор изменяет
состояние выходов согласно заданной программе.
Программа может быть задана вводом логических выражений или
символов на кодированном языке. Широкое распространение получили
линейно-контактные символы, позволяющие вести программирование
по принципиальной релейной схеме. В последние годы созданы ПК,
программирование в которых выполняется на языках высокого уров-
ня - PL/М и Фортран IV.
Клавишное устройство ввода программы для программирования
по принципиальной релейной схеме представляет собой панель с клави-
атурой (рис. 12.11), каждая из клавиш которой соответствует опреде-
ленному символу релейной схемы. В каждой цепи принципиальной схе-
мы должно быть одинаковое число (например, четыре) последователь-
но или параллельно включенных контактов, расположенных в зонах
Л, В, С, D, Если контактов меньше — их дублируют, если больше —
351
Рис. 12.12. Принципиаль-
ная схема для програм-
мирования:
а - исходная; б - ва-
риант
вводят промежуточные реле. Контактам и катушкам аппаратов при-
сваивают номера входов и выходов ПК, к которым они подключены,
либо номер цепи внутреннего аппарата ПК. На клавишной панели рас-
полагаются декадные переключатели для набора номеров цепи и кон-
тактов, клавиши выбора типа функции (логическая, временная, счет-
ная или запоминания) и клавиши набора контактов, типа контактов
и выходов. После ввода программы в ЗУ ПК будет выполнять функции,
предусмотренные принципиальной схемой.
Пример 12.1. Преобразовать принципиальную схему, показанную на
рис. 12.12,а в схему, предназначенную для программирования ПК с че-
тырехконтактной цепью. В процессе преобразования (рис. 12.12,6)
составляются цепи, содержащие четыре контакта и один выход, произ-
водится нумерация контактов (с№ 1000 и далее) и выходов (№ 1-999),
вводится промежуточный аппарат, выход (например №45).
Для более полного использования возможностей ПК начинают вы-
пускаться так называемые малые ПК на 32 или 64 входа-выхода, поз-
воляющие наращивать модули для управления объектами, требущими
большего числа входов-выходов. Построенные на базе микропроцессор-
ных устройств, ПК представляют нижний уровень электроавтоматики
станков и автоматических линий, следующим уровнем после которых
являются системы ЧПУ различных классов.
12В. ПОЗИЦИОННЫЕ И КОНТУРНЫЕ УСТРОЙСТВА
Счетно-импульсные позиционные системы ЧПУ, применяемые в мно-
гооперационных станках, имеют до пяти управляемых по программе
перемещений. Одновременно может происходить управление двумя пе-
352
ремещениями. Функциональная схема позиционной системы с програм-
моносителем на перфоленте показана на рис. 12.13. Блок ввода инфор-
мации и обслуживания AZ содержит считывающее устройство £), ра-
ботающее от перфоленты; панель ввода величин коррекции ЛР; пульт
системы F с устройством цифровой индикации. Блок ввода непосред-
ственно связан с центральным блоком управления и памяти AM. Счи-
тывающее устройство взаимодействует с блоком управления считыва-
телем DS и распределителем входных данных SC. Программируемая
информация с SC поступает в буферный накопитель входных данных
DC, а затем в дешифратор и запоминающее устройство DM номера кад-
ра, данных об инструменте и числе оборотов шпинделя. Блок програм-
много управления AZ0 координирует переработку информации, рас-
пределение ее по системе и связывает ряд функциональных узлов. От
AZ0 поступают сигналы о-выборе вида обработки, координаты, о движе-
нии программы. В AZ0 поступает информация о состоянии процесса
обработки на станке через блок управления станком UM, а от считы-
вающего устройства подается информация о функциях, определяющих
тип требуемой переработки информации (исходные размеры, размерные
цепи, компенсация начала координат и др.). Блок DS производит увяз-
ку приказов на считывание с контрольными сигналами программиро-
ванной информации. В считываемой информации проверяется, соблюде-
ны ли четность (нечетность), синтаксис» нет ли в ней запрещенных зна-
ков, неправильной длины слов, т.е. правильность следования управля-
ющих знаков и информации. Блок DS принимает информацию от бу-
ферного накопителя DC, который связывает отдельные фазы с време-
нем их чтения, обеспечивая непрерывность движения подачи, поскольку
даже кратковременная остановка подачи в ряде случаев (при фрезеро-
вании, шлифовании) недопустима.
Панель кодов АР для ввода коррекции или размеров инструмента
связана с последовательно-параллельным преобразователем коррек-
ции В, распределителем коррекции 5 и сумматором AW для вычисле-
ния значения коррекции.
Блок AM взаимодействует с координатным блоком АС, в котором
содержатся функциональные элементы, воздействующие на перемеще-
ния по осям координат станка: продольной Z, поперечной X, вверх и
вниз Y, вращения круглого стола В. Через накопители входных данных
и последовательно-параллельные преобразователи заданного значения пе-
ремещения ВХ, BY, BZ, ВВ информация поступает на устройства фик-
сации фактического перемещения и дифференциальные реверсивные
счетчики PCX, PCY, PCZ, РСВ с дешифраторами соответственно по осям
X, Y, Z, В. Связь системы управления со станком осуществляется через
блок U. К управляемым преобразователям UX, UY, UZ, UB подключе-
ны соответствующие двигатели подач MX, MY,MZ, МВ, которые через
исполнительные механизмы ESX, ESY, ESZ, ESB осуществляют переме-
щения рабочих органов станка ЕМХ, EMY, EMZ, ЕМВ (стола, салазок,
353
12-6562
Рис. 12.13. Функциональная схема счетно-импульсной позиционной системы ЧПУ
поворотного стола). Перемещения рабочих органов станка измеряются
линейными или круговыми датчиками обратных связей BQX, BQY,
BQZ, BQB. После преобразования сигналы поступают в сравнивающее
устройство для сопоставления с сигналами задания программы. При
равенстве фактического перемещения заданному программой работа
двигателя, вызывающего это перемещение, прекращается.
Рабочий орган ЕМ привода главного движения через исполнитель-
ный механизм ES соединен с двигателем М. Преобразующее устройство
двигателя главного привода U1 подключено к системе управления
U2 и связано с запоминающим устройством DM через согласующий
блок API. Возможна передача команд от пульта АЕМ управления стан-
ком через согласующий блок АР2 на устройство управления UM.
Счетно-импульсные контурные системы должны обеспечивать в каж-
дый момент времени согласованное движение исполнительных органов
станка по двум или большему числу координат, для чего необходимо
непрерывное поступление информации в систему. На рис. 12.14 пока-
зана функциональная схема контурной системы ЧПУ с заданием про-
граммы на перфоленте. Основное отличие ее от рассмотренной выше
состоит в том, что в ней применены интерполяторы DX, DY, DZ, DB,
осуществляющие линейную интерполяцию по осям движения соответ-
ствующих рабочих органов.
Интерполятор по координатам начальной и конечной точек участка
354
обрабатываемого контура рассчиты-
вает координаты промежуточных то-
чек. В интерполяторы вводятся чис-
ла, закодированные согласно про-
грамме. На выходе интерполятора
получают информацию в виде после-
довательности импульсов унитарного
кода. Время поступления этих им-
пульсов соответствует заданному
программой времени обработки
участка траектории.
Числовые интегрирующие сравни-
вающие устройства GUX, GUY, GUZ,
GUB получают импульсы от счетчи-
ков положения PCX, PCY, PCZ,
РСВ. Последние осуществляют
контроль перемещений на участках
интерполяции и фиксацию положе-
ния на опорных точках траектории.
Кроме того, на сравнивающие уст-
ройства GUX, GUY, GUZ, GUB по-
ступают импульсы с соответствую-
щих интерполяторов. Сигналы, про-
порциональные разности между заданным и фактическим перемещения-
ми, поступают на управляемые преобразователи UX, UY, UZ, UB, обеспе-
чивающие работу соответствующих двигателей. Генератор рабочей час-
тоты GF1 вырабатывает импульсы, частота которых зависит от запро-
граммированной минутной подачи (мм/мин) , а генератор рабочей часто-
ты GF2 вырабатывает импульсы, зависящие от оборотной подачи
(мм/об), что необходимо для нарезания резьб.
Распределитель импульсов SC2 в соответствии с запрограммирован-
ными значениями косинусов углов между координатными осями и ка-
сательными к траектории движения инструмента обеспечивает постоян-
ство результирующей скорости движения инструмента.
В центральном расчетно-управляющем блоке АСМ осуществляется
круговая интерполяция и расчет участков многоугольника, описыва-
ющего дугу окружности, а линейная интерполяция между вершинами
многоугольника производится интерполяторами DX, DY, DZ, DB. По-
стоянное запоминающее устройство AS содержит данные о четверти
окружности единичного радиуса, включающей последовательные участ-
ки многоугольника и векторов скорости. Эти данные в блоке АСМ
умножаются на запрограммированный радиус и совместно с сигналами
распределителя импульсов поступают в линейные интерполяторы. В АСМ
рассчитывается также траектория движения центра инструмента. Для
вычисления координаты конечной точки интерполяции определяют сос-
355
Рис. 12.14. Функциональная схема счетно-импульсной контурной системы ЧПУ
тавляющие радиусов по осям координаты точки касания инструмента
с обрабатываемой поверхностью. Для этого радиус инструмента из па-
нели ввода величин коррекции через преобразователь, распределитель
величины коррекции и сумматор вводится в счетчик и перемножается
с запрограммированным косинусом соответствующей оси из буферного
накопителя входных данных DC и запоминающего устройства. В сум-
маторе, к которому подводится информация из распределителей, фор-
мируется результат с учетом запрограммированных координат опорных
точек, между которыми производится интерполяция.
356
□ —-
Остальные элементы схемы имеют функции и связи, аналогичные
описанным для позиционной системы (рис. 12.13).
Сигнал с измерительной системы BQM на главном приводе М посту-
пает на вход генератора частоты GF2. Он служит для согласования дви-
жений при нарезании резьбы и поддержании постоянной подачи на обо-
рот (мм/об). Так же как и предыдущая, настоящая схема содержит
блоки: информации и обслуживания AZ, управления и памяти AM,
координационный АС, управляемых преобразователей U, приводов
и исполнительных механизмов ВЕМ.
357
12.7. МИКРОПРОЦЕССОРЫ И МИНИ-УВМ
В ТИПОВЫХ СТРУКТУРАХ ЧПУ
Широкие возможности для построения устройств ЧПУ открывает при-
менение микропроцессоров и мини-УВМ. Алгоритм функционирования
станка или группы станков зависит от сложности конфигурации обра-
батываемой детали, получения требуемых точности обработки и шеро-
ховатости поверхности. Для решения задач обработки деталей простой
конфигурации при невысоких требованиях к точности и качеству обра-
ботки алгоритм функционирования должен быть достаточно простым.
Процессор УВМ в этом случае может быть выполнен на базе стандартных
блоков, из которых создается управляющее устройство. Оно воспроиз-
водит модель управления станком, допускает параллельное выполнение
операций, реализующих несложные функции. В станкостроении такие
управляющие устройства получили название цифровых моделей.
Промышленность выпускает такие системы ЧПУ типа Н22, НЗЗ, по-
строенные на микроэлектронных элементах. Они предназначены для
управления станками и осуществляют позиционирование, прямоуголь-
ное и контурное (в плоскости) управление. Перестройка алгоритмов
управления в таких системах невозможна.
Более сложные алгоритмы функционирования требуют переработ-
ки большого объема технологической информации, учета многих фак-
торов. Цифровая модель в этом случае существенно усложняется, парал-
лельное выполнение функций управления отдельными операциями зат-
рудняется, а иногда исключается вообще. В связи с этим необходимо
управляющее устройство строить по принципу УВМ, где операции управ-
ления формируются последовательно с помощью центрального арифме-
тического устройства. Усложнение задач управления требует для обра-
ботки сложных деталей с высокой точностью применения систем, по-
строенных по принципу цифровой машины. Промышленность
выпускает такие устройства типа Н55, 2С85 и др. для управления тремя
и более координатами и для движения по сложной траектории (обработ-
ка поверхности типа гребных винтов).
Находят применение и гибридные системы, в которых часть опера-
ций выполняется аппаратными часть — программным способом.
Для специальных станков могут применяться модели с ограниченной
номенклатурой функций управления; для специализированных станков,
обрабатывающих сложные детали с небольшим количеством профи-
лей — устройства, построенные по принципу цифровых машин с неболь-
шой оперативной памятью (системы с аппаратной реализацией функцио-
нальных алгоритмов программного управления - АПУ).
Для решения более сложных задач (реализации большой номенкла-
туры алгоритмов управления, программирования алгоритмов управле-
ния, выполнения функций релейно-контакторного управления, самона-
стройки на оптимальный режим обработки, компенсации кинематичес-
358
рис. 12.15. Типовые системы управ-
ления от индивидуальных ЭВМ:
а - 2-го ранга: б - 3-го ранга;
в - 5-го ранга
ких погрешностей станка во вре-
мя обработки, управления робота-
ми и другими устройствами, об-
служивающими станок) приме- | в |
няют системы ЭВМ с программной I
реализацией функциональных ал- | |
горитмов (ППУ). В атом случае I
возможно управление станком от г ** ।
индивидуальной УВМ либо управ- I—---1
ление группой станков от центра- а)
лизованной УВМ.
Применяемые в станках системы ЧПУ принято делить на пять уровней
(рангов). Четыре ранга охватывают системы управления станками от
индивидуальной УВМ. Устройством 1-го ранга (рис. 12.15) является
станок ЕМ с расположенными на нем приводами, механизмами смены
инструмента, датчиками обратных связей. Устройством 2-го ранга явля-
ется система станочного управления UC по декодированной программе,
куда относятся блоки управления приводами и электроавтоматика
станка. Схема типовой системы индивидуального управления 2-го ранга
показана на рис. 12.15,а. Устройством 3-го ранга производится отработ-
ка кодированной программы при помощи интерполятора DX, получа-
ющего информацию от блока ввода F. Совокупность устройств 2-го
и 3-го рангов реализуется с помощью ЧПУ (рис. 12.15,6), обозначаемых
также NC. Разновидностью этого устройства являются системы HNC
с ручным заданием программы с пульта и системы SNC, имеющие па-
мять для хранения всей программы управления. Устройством 4-го ран-
га является система ЧПУ, обозначаемая также CNC (рис. 12.15,в) и
использующая для оперативного хранения и изменения управляющих
программ мини-УВМ.
Устройство 5-го ранга содержат средние и большие УВМ, предназна-
ченные для расчета управляющих программ и осуществляющие управ-
ление группой станков.
Управляющие мини-УВМ имеют разрядность слов до 32 двоичных
разрядов, объем памяти — до 256 К, реализуют аппаратный принцип
умножения-деления и оснащены более чем 100 каналами связи с объ-
ектом.
Микро-УВМ отличаются от мини-УВМ меньшими разрядностью сло-
ва и объемом памяти, реализованы на минимальном числе интеграль-
359
Информация
к периферийным
устройствам
Рис. 12.16. Схемы сопряжения меж-
ду микропроцессором и периферийны-
ми устройствами
ных схем с большой степенью ин-
теграции и служат для создания
автоматических систем управле-
ния несложными объектами; уст-
ройств связи с мини-УВМ, ПК и др.
Переход от многокристального
микропроцессора к однокристаль-
ному и, наконец, к микро-УВМ,
размещенной на одном кристалле,
создает наибольший экономичес-
кий эффект при реализации упро-
щенных УВМ. Многокристальные
микропроцессоры обладают боль-
шими функциональной полнотой,
вычислительной мощностью и про-
изводительностью и наиболее эф-
фективны при построении микро-
Информация
от периферийных
устройств
и мини-УВМ для управления более сложными установками и технологи-
ческими процессами.
Разработка микропроцессорных комплектов (МПК) на интеграль-
ных схемах с большой степенью интеграции позволяет создать универ-
сальный набор интегральных схем с согласованными связями, содер-
жащий один или несколько микропроцессоров, интерфейсов и устройств
ввода-вывода.
Функционально микро-УВМ идентична ПК и мини-УВМ, однако ее осо-
бенностью является применение ограниченного набора интегральных
схем с большой степенью интеграции, а также то, что она является частью
другой системы управления и конструктивно выполняется на од-
ной-двух платах. Микропроцессор в микро-УВМ выполняет роль цент-
рального решающего и управляющего устройств, он считывает из запо-
минающего устройства (оперативного ОЗУ или постоянного ПЗУ) ко-
манды управления, осуществляет их реализацию, при необходимости -
временное запоминание, поиск данных, синхронизацию взаимодейст-
вия различных устройств. Для запоминания небольшого объема данных
вместо ОЗУ и ПЗУ могут быть использованы регистры микропроцес-
сора. Взаимодействие микропроцессора с периферийными устройствами
производится при помощи одной-двух шин. Передачу требуемой ин-
формации в нужное устройство осуществляет схема сопряжения
(рис. 12.16,а), которая координирует работу сопрягаемых устройств
во времени и согласует информацию по формату при ее обмене между
360
микропроцессором и периферийными устройствами. В схеме сопряже-
ния (рис. 12.16,6) информация от микропроцессора по шине передает-
ся через группы триггеров к периферийным устройствам. Микропроцес-
сор выбирает требуемую группу выходных триггеров по сигналу управ-
ления и осуществляет подсоединение ее к необходимому периферийно-
му устройству. Информация к микропроцессору от периферийных уст-
ройств поступает через мультиплексор.
Рассмотрим реализацию некоторых алгоритмов при управлении стан-
ками от микро- и мини-УВМ.
Пример 12.2. При токарной обработке для получения необходймой
чистоты поверхности и повышения стойкости инструмента нужно под-
держивать постоянной заданную по программе скорость резания г.
При этом угловая скорость двигателя привода шпинделя должна изме-
няться в соответствии со следующим соотношением:
со = Zpv/30d, (12.4)
где /р — передаточное число коробки скоростей; d — обрабатываемый
диаметр.
Реализация соотношения (12.4) при управлении с помощью УВМ
производится устройством, показанным на рис. 12.17/1. Заданная от УВМ
величина v подается в цифровом виде на вход линейного ЦАП UZYl.c
выхода которого снимается напряжение Uv = kt v . Диаметр обработки
в цифровом виде (от интерполятора) подается на вход второго линейно-
го ЦАП UZY2, в котором преобразуется в напряжение Ud = k2U(^d.
Оба напряжения поступают на входы операционного усилителя Л7,
с выхода которого снимается напряжение пропорциональное угло-
вой скорости шпинделя. Это же напряжение подается для преобразова-
ния на UZY2. Таким образом,
= k(Uv - Ud), (12.5)
где к - коэффициент усиления усилителя А.
Подставляя в (12.5) значения Uv и Ud, получаем
= k(ktv - k2U„d),
откуда
= ^1^/(1 + ^2<0-
При достаточно большом коэффициенте усиления операционного уси-
лителя А (к =1004- 200)
« kivlktd.
Скорость резания задается от программы трехразрядным числом в
двоично-десятичном коде и может иметь значения от 1 до 990 м/мин.
361
Рис. 12.17. Схемы системы стабилизации скорости резания:
а - функциональная; б - принципиальная
Первая цифра определяет десятичный порядок значения скорости реза-
ния в м/мин (4—0,1, 5—1, 6—10), выраженного двумя последними циф-
рами: например, значению v = 406 соответствует скорость 0,6 м/мин;
v = 532 — скорость 32 м/мин; v = 643 — скорость 430 м/мин. Погреш-
ность задания из-за дискретности в любом диапазоне не превышает 10%.
Проиллюстрируем реализацию рассмотренного алгоритма аппарат-
ными средствами. Развернутая схема системы стабилизации скорости
резания (рис. 12.17,6) построена на пяти операционных усилителях:
362
UZY1 скорости резания на усилителях Л 7, Л2; UZY2 диаметра обработ-
ки на усилителях А3, А4\ выходное устройство выполнено на усили-
теле А5.
Переменный коэффициент усиления усилителя А1 зависит от задан-
ной скорости v , значение которой подается в двоично-десятичном ко-
де. Присоединение на вход усилителя различных входных сопротивлений
производится бесконтактными ключами, которыми управляют сигналы,
выражающие в двоично-десятичном коде значения второй и третьей
цифр задания. Вторая ступень UZY1 - усилитель А2 - служит для за-
дания требуемого десятичного порядка в зависимости от значения пер-
вой цифры задания -4,5 или 6.
На вход усилителя АЗ приходят четыре сигнала /, соответствующие
четырем различным передаточным отношениям коробки скоростей
станка. Выходное напряжение этого усилителя служит входным для
UZY2, который получает информацию в 8-разрядном двоичном коде
от интерполятора системы ЧПУ (сигналы D001 - D128). Цена младшего
двоичного разряда 1 мм, что позволяет иметь диапазон диаметров обра-
батываемых изделий от 1 до 255 мм. Для расширения этого диапазона
подаются сигналы DI, D2, D3, выбирающие сопротивления обратной
связи усилителя АЗ.
На усилителе А5 производится вычитание напряжения Ud, пропор-
ционального диаметру, из напряжения Uv , пропорционального скорости
резания. Сигнал с выхода усилителя А5 подается в схему управле-
ния тиристорным преобразователем U привода главного движения М.
Для обеспечения требуемых динамических характеристик схемы слу-
жит ЯС-цепочка. Устройство позволяет производить стыковку с систе-
мами ЧПУ, имеющими на выходе интерполятора не унитарный, а двоич-
ный код. Скорость резания поддерживается с точностью не ниже ±4%.
Пример 123. С помощью УВМ может быть реализован автоматизи-
рованный поиск оптимального режима обработки на станках. Функцио-
нальная схема поисковой системы показана на рис. 12.18. Для настройки
на оптимальный режим обработки металлорежущего станка (например,
фрезерного) используют датчики: В19 контролирующий скорость изно-
са инструмента (стойкость инструмента) ; В2, контролирующий часто-
ту вращения привода шпинделя; ВЗ, контролирующий скорость пере-
мещения суппорта (привода подачи) станка. Напряжения перечислен-
ных датчиков через АЦП UYZ подаются на УВМ. В память УВМ с блока
исходных данных AZ вводятся также сведения об обработке для расче-
та показателя качества. После расчета показателя качества УВМ через
ЦАП UZY выдает задание на преобразователь привода шпинделя U1 и
преобразователь привода подачи U2, которые управляют соответству-
ющими двигателями Ml и М2. При этом обеспечивается требуемое из-
менение скорости резания и подачи.
Показатель качества, рассчитываемый УВМ, может иметь стоимо-
стное выражение (см. гл. 13). Обобщенный алгоритм работы поисковой
363
Рис. 12.18. Функциональная схема по-
исковой АСУ
Рис. 12.19. Схема алгоритма поиско-
вой АСУ
системы (рис.’12.19) содержит че-
тыре подпрограммы. Подпро-
грамма ’Тасчет показателя ка-
чества” обеспечивает определение
последнего и вырабатывает ин-
формацию, необходимую для
функционирования подпрограм-
мы ’’Поиск экстремума”. Послед-
ней вводятся корректирующие
изменения скорости резания и по-
дачи в подпрограмму ’’Обработ-
ка”, откуда после контроля огра-
ничений X/ > хтах через выход-
ные устройства поступают коман-
ды на регуляторы привода главно-
го движения станка и привода по-
дачи. Изменение режима обработ-
ки фиксируется датчиками инфор-
мации, и через вводное устройство
соответствующие сигналы подаются в вычислительное устройство для
расчета нового значения показателя качества.
Подпрограмма ’’Поиск экстремума” реализует симплекс-метод.
Симплексом в двухмерном пространстве v, з является треугольник
(рис. 12.20), при этом измеряют значения J поверхности отклика в
трех его вершинах (а10, <h. о» дзо) и строят новый симплекс, располо-
женный симметрично точке с наименьшим (наибольшим) значением и
противолежащей грани. Предположим, что требуется найти максимум
критерия качества и что наименьшее значение измерения получено в
точке ах 0. Эта точка заменяется новой ах i, расположенной симметрич-
но точке д10 относительно центра грани начального симплекса. Вычис-
ленное в точке аи значение критерия качества сравнивается с извест-
364
s
^20
°-10
'JO
Рис. 12.20. Последовательность поиска экстремума симплекс-методом
ными значениями вершин нового симплекса (а20> дзо) • Затем вновь оп-
ределяют вершину с наименьшим (наибольшим) значением и строят
следующий симплекс. При возникновении цикличности, когда полу-
ченный симплекс исключается и образуется предыдущий симплекс,
деформируют полученный симплекс, уменьшая его размеры (а25) до
тек пор, пока не будет достигнута требуемая точность определения экст-
ремума.
12.8. ПОДГОТОВКА ПРОГРАММ ДЛЯ СТАНКОВ С ЧПУ
Подготовка, отладка и редактирование управляющих программ
является важным этапом перед обработкой деталей на станках с ЧПУ.
При подготовке управляющих программ производят расчеты, преоб-
разование и кодирование информации. Типовая схема подготовки прог-
рамм для станков с ЧПУ, в которых используют интерполяторы, пред-
ставлена на рис. 12.21.
Чертеж детали, технологические данные о станке, инструменте, ос-
настке, приемах обработки служат исходной информацией для перво-
го этапа подготовки программы. На основании этой информации произ-
водят проектирование технологического процесса, разработку наибо-
лее экономичной последовательности изготовления участков детали,
выбор технологических приемов и режимов обработки. На следующем
этапе задают исходную точку обработки и положения заготовки, рас-
считывают траекторию движения инструмента и увязывают ее с систе-
мой координат станка. Разрабатывают расчетно-технологическую кар-
365
Рис. 12.21. Схема подготовки программ для станков с ЧПУ
ту (РТК) — специальный чертеж, на котором наряду с деталью наносят
траекторию движения центра инструмента (например, фрезы), обозна-
чают режим обработки, т.е. создают полный технологический проект
обработки детали. Определяют технические условия на поставку заго-
товки и условия поставки детали после обработки, технические условия
на оснастку и инструмент.
На основании данных этого типа составляют операционно-техно-
логическую карту механической обработки, которую передают в цех.
Данные РТК служат исходной информацией для расчета и кодиро-
вания траектории движения инструмента. Определяют координаты
(рис. 12.22) опорных точек А (х, у) и В(хь ji), в которых изменяется
траектория. Находят составляющие перемещения вдоль осей ОХ и OY
на участке АВ Ах = Xj - х; Ау = уг - у. Рассчитывают время обра-
ботки, с, на данном участке:
/ = l/s,
где I — длина участка, мм; s — подача, мм/с.
Если траектория инструмента между опорными точками представля-
ет собой кривую, то ее аппроксимируют, например, ломаной линией,
число участков которой зависит от требуемой точности обработки.
Информация о траектории движения инструмента кодируется и на-
носится на перфоленту в виде последовательности ’’фраз”.
’’Фраза” содержит ’’слова”, определяющие необходимые перемещения
Дх, Ay, Az и т.д., и время,
затрачиваемое на эти переме-
щения (рис. 12.23). Кодирова-
ние осуществляется в соответ-
ствии с международными реко-
Рис. 12.22. Траектория перемеще-
ния инструмента при обработке
участка детали
366
Дорожка №1
, Дорожка №2
Дорожка №3
Овдцщая
, Порожка
Дорожка №4-
Дорожка №5
Дорожка №6
Дорожка №7
Дорожка №8
Фраза
Слово
—-\к—
Слово
Рис. 12.23. Запись информации на перфоленте
мендациями кода IS0*-7 bit (при использовании восьмидорожечной пер-
фоленты) и нормалью станкостроения Э68-1 по буквенно-цифровому
коду Б ЦК-5 (при использовании пятидорожечной перфоленты).
При использовании восьмидорожечной перфоленты применяется меж-
дународный двоично-десятичный код ISO-7 bit. Для обозначения ад-
ресов в этом коде используются прописные буквы латинского алфави-
та, а также ряд служебных символов:
- признак восстановления информации;
и - знаки направления перемещения;
LE - конец кадра фразы;
% - начало программы;
D - включение управления, информация на ленте начинает воспри-
ниматься системой ЧПУ;
С - отключение управления, информация на ленте не воспринимает-
ся системой ЧПУ;
/ - информация будет отрабатываться системой ЧПУ при включении
специального кода;
Del - забой, строка не считывается.
Адреса по коду ISO-7bit:
4, В, С - повороты вокруг осей X, У, Z соответственно;
D,E - повороты вокруг специальных осей;
F - подача;
G - режим работы системы ЧПУ;
Н, J, I, К, L - резерв;
М - вспомогательные адреса;
N - номер фразы-кадра (1000 номеров);
О - резерв;
P,Q,R - третичное перемещение вдоль осей X, Y, Z соответственно;
S - скорость главного движения (100 скоростей) ;
* Международная организация по стандартизации.
367
Т - номер кода инструмента (100 номеров);
Ut V, W - вторичное перемещение вдоль осей X, Y, Z соответственно;
X, Y, Z - перемещение вдоль осей X, Y,Z соответственно.
Расположение пробивок на перфоленте в коде ISO-7 bit показано
на рис. 12.24. Если лента выдвигается из считывающего или перфори-
рующего устройства, то вверх обращена справочная (лицевая) сторона
ленты, а справа находится справочный край. Рядом с ним находится
Номер дорожки ленты Клавиатур- ный Ойо символа Название символа Десятичные значения перфорации
в чпв
8 7 б 5 4 F 3 2 1
о • О • null BS Пусто (ноль) Возврат на шаг 0 8
о • о tab Табуляция 9
о • о LF(HL) Конец опока 10
о о • о о CH Возврат каретки 13
о о • space Сдвиг каретки на шаг 32
о о • о о % Начало программы 37
о О • ( Вправление выключено 4Z7
о о о • о ) Вправление включено 47
о о • о о + Знак плюс 4J
о о • о о Знак минус 45
о о о»ооо 7 Пропуск блока 47
о о • 0 -г 48
о о о • о 1 к 49
о о о • о 2 58
О 0 • о о 3 51
о о о • о У 1 52
о о • о о 5 Десятичные цифры 53
о о • о о 6 59
о О 0 • о о о 7 55
о ООО» 8 56
о о о • о 9 j L 57
ООО» о Настроечная функция 58
о • о A 65
о • о В 66
о о • о о C 67
о • о Л 68
о о • о о f 69
о О • О 0 F 70
о • о о о 6 71
о о • H 72
о о о • о I 73
О о о • о J 74
о о • о о К 75
О о о • о L 76
О О • 0 0 о о • о о M N Буквы верхнего регистра "
о о о«ооо 0 79
о о • p 80
о о о • о Q 81
о 0 0*0 H 82
о о • о о S 83
о о о • о T 89
0 0*00 и 85
о о • о о У 86
о О О «ООО w 87
о о о о • X 88
ООО* о Y 89
0 О 0 • о 2 90
о ОООО* ООО . del Стирание 127
Справочный край
Рис. 12.24. Запись информации на перфоленте в коде IS0-7bit
368
первая дорояОса, на которой перфорируются отверстия, соответству-
ющие двоичному коду (1 бит) с наименьшим значением. Бит с наиболь-
шим значением перфорируется на седьмой дорожке, бит для проверки
четности — на восьмой дорожке.
В станках разбивка движений по осям производится в соответствии
с рекомендациями международного стандарта ISO. Движение в направ-
лении увеличения зазора между готовой деталью и инструментом (свер-
лом, резцом, фрезой) обозначается по оси +Z (рис. 12.25,а). Если на
станке производится сверление, то перемещение сверла в деталь обозна-
чается по оси -Z.
Ось X перпендикулярна оси Z. Она преимущественно горизонтальна,
369
параллельна плоскости установки детали и соответствует большему пе-
ремещению по длине. Положительным направлением по оси +Х будет
направление направо, если смотреть от инструмента, расположенного го-
ризонтально к детали. Движения, перпендикулярные осям X и Z, обоз-
начают Y. Дополнительные движения, параллельные осям X, У, Z,
обозначают U, V, W соответственно (рис. 12.25,6,в). Если инструмент
остается неподвижным, а перемещается обрабатываемая деталь, то ис-
пользуется буква со штрихом, например +Х'.
Для обозначения направления вращения используют символы Л, В,
С относительно осей вращения X, У, Z. Если направления вращения соот-
ветствуют перемещению винтов с правой резьбой в положительных нап-
равлениях осей, то соответствующие символы имеют положительное
значение (+Л, +В, +С).
На используемых в СССР и за рубежом перфолентах шаг между от-
верстиями по строке и между строками составляет 2,5 ± 0,05 мм, ди-
аметр кодирующих отверстий - 1,8 мм, ведущих отверстий — 1,2 мм.
Перфолента шириной 17,5 мм применяется для пятидорожечной запи-
си, 22,5 мм — для шести- и семидорожечной записи, 24,5 мм — для
восьмидорожечной записи.
Этап кодирования информации упрощается при использовании ЭВМ.
При этом возможно применение специальных вычислительных уст-
ройств — программаторов или универсальных ЭВМ с соответствующим
математическим обеспечением. Последнее сочетание представляет сис-
тему автоматизированного программирования (САП). Математическое
обеспечение САП обычно создается в форме трех подпрограмм: пре-
процессор — процессор — постпроцессор (рис. 12.26). Дешифровку ис-
ходных данных с языка САП на машинный осуществляет подпрограмма
препроцессор. Решение геометрических, технологических и организа-
ционных задач выполняет программа процессор. Программа постпро-
цессор служит для учета особенностей и возможностей станка и систе-
мы ЧПУ и преобразует машинную информацию ЭВМ в требуемый код
управляющей программы.
Запись программы производят с постоянной длиной фраз (кадрами)
и с переменной длиной фраз, когда используют знак разделения (табу-
ляции) . При записи программы кадрами в каждой фразе записываются
все слова независимо от их повторяемости, что приводит к повышен-
ному расходу перфоленты. Если запись ведется фразами переменной
длины, то задаются только те слова, которые определяют изменение
информации по сравнению с предыдущей, при этом задаются абсолют-
ные значения координат с отсчетом от общего нуля (базы). При таком
способе записи информации из программы исключаются повторяющиеся
слова с нулевыми числовыми значениями. Этим достигается экономия
перфоленты.
При использовании адресной системы перед числовой информацией
следует буквенный адрес.
370
Рис. 12.26. Схема системы автоматизированного программирования
Рис. 12.27. Эскиз обрабатываемой детали
Универсальный способ предусматривает применение как буквенных
адресов, так и системы табуляции. Перечисленные способы позволяют
строить фразу из слов в любой последовательности. Для подготовки
управляющих программ фрезерных станков находит применение систе-
ма автоматического программирования САПС-М22. В этой системе в
качестве условных символов (слов) применяются прописные буквы и
цифры. Если написание буквы сходно с цифрой (Очи нуль; 3 и три,
Ч и четыре), то над буквой ставится черта. Целая часть от дробной отде-
ляется точкой, а запятой отделяются слова. Знак: = означает присвое-
ние, ।__। — пробел между словами.
Пример 12.4. Записать в системе САПС-М22 исходные данные для по-
лучения программы обработки детали, показанной на рис. 12.27 и зак-
репленной по двум отверстиям. Запись исходной информации представ-
лена в табл. 12.3.
Вся программа делится на две части: первая — строки 1—16 — содер-
жит координаты опорных точек траектории обработки и данные для
расчета отдельных ее участков, вторая — строки 17-24 — параметры тех-
нологического цикла.
Рассмотрим содержание отдельных строк (фраз) :
01 - Слово ’’Программа” означает начало программы, текст после нее —
ее название;
02- Название детали;
03- Начальная точка движения имеет координаты: х = 100, у = 0,
z = 0; ___
04- Прямая ПР1 проходит через точку ТОЧ1 под углом 60° 30';
05- Прямая ПР2 проходит параллельно прямой ПРЗ на расстоянии
524.25 мм сверху, т.е. Y принимают большего значения - УБ\
06- Определяет координаты точки ТОЧ2;
07 — Определяет точку ТОЧЗ как пересечение (ПРС) прямой ПР4 с ок-
ружностью ОКР2 при меньшем значении Х-ХМ;
371
Таблица 12.3
Фразы (операторы)
01 Программа образец на языке САПС;
02 Деталь учебная;
03 ТбЧ1: = 100.0, 0.0, 0.0;
04 ПР1: =ТОЧ1, УГ, 60+30/60, ПРЗ;
05 ПР2: = ПРИ, ПРЗ, РАСТ, 524, 25, УБ;
06 ТОЧ2: =590,660,0;
07 ТОЧЗ: = ПРС, nP42OKP2JCM;
08 ОКР1: - ЧЕРЕЗ, ТОЧ2, ТОЧЗ, РАД 400, ХМ;
Ъ9 ТОЧ4: =1000,475, 0;
10 ОКР2: =ЦТР,ТОЧ4, РАД 310;
11 ОКРЗ: =800,243,150;
12 ПРЗ: = ПРИ, ПРО ACT, 135, 75;
13 ПР5: =ТОЧ1,ТОЧ6;
14 ТОЧ6: = 200,0,0;
15 ТбЧ7:_=ПРС, ПР1, ПРЗ;
16 СТАНОК/8, ИНТЕРП/1, ФРЕЗА/40,0, 0;
17 ПОДАЧА/2000; _
18 ИЗ/ТОЧ1, ВНАПР/ТОЧ7,_ИДИ/ЗА, ПР1;
19 ПбДАЧА/200, ФРСЛ, ДОП/0.02,0.02_£
20 ИДИ/ПР1, ЗАПР2, ИДИ/ПР2, ВПРАВ, ЗА ОКР1; _
21 ИДИ/6КР1, ПбЧСДЖРЗ, ПРЧС, ОКРЗ, ПОЧС, ДО, ПРС2, ПРЗ;
22 ИДИ/ПРЗ, ДО.ТОЧ7;
23 ПОДАЧА/2000;
24 ИДИ/ТОЧ1;
КОНЕЦ
08— Окружность ОКР1 проходит через ТОЧ2 и ТОЧЗ, имеет радиус
РАД 400 мм и центр, соответствующий меньшему из двух возмож-
ных значений X—ХМ;
09—14— Определяют координаты траектории;
15- Определяет ТОЧ7 как пересечение (ПРС) прямых ПР1 и ПРЗ.
Последующие строки содержат технологическую часть программы:
16- Индекс станка (СТАНОК 8), его управляющего устройства
(ИНТЕРП/1) и инструмента (фреза диаметром 40 мм, работа ве-
дется при Z = 0);
17 - Скорость ускоренной подачи фрезы - 2000 мм/мин;
18— Начало движения из ТОЧ1 к ТОЧ7 и до пересечения с прямой
ПР1;
19— Переход на рабочую подачу 200 мм/мин, фреза слева от контура,
допуск на аппроксимацию дуг окружностей 10,02 мм;
20- Движения по ПР1 за ПР2; движение по ПР2 вправо с переходом
за окружность_ОКР1; ___ _
21 - Движение по ОКР1 по часовой стрелке (ПОЧС), по ОКР2 - против
372
часовой стрелки (ПРЧС) и ОКРЗ по часовой стрелке до пересе-
чения с ПРЗ; __
22 - Движение по ПРЗ до точки ТОЧ7;
23— Переход на ускоренный ход 2000 мм/мин;
24- Отвод фрезы к ТОЧ1;
25- Конец исходных данных.
На основании приведенной информации программа системы построит
непрерывную кривую из дуг окружностей и прямых с учетом диаметра
фрезы и выдаст управляющую программу обработки детали.
Эффективность применения станков с ЧПУ особенно возрастает при
оснащении их промышленными роботами и создании гибких техноло-
гических модулей станок-робот.
Глава тринадцатая
СИСТЕМЫ ОПТИМИЗАЦИИ РЕЖИМОВ МЕТАЛЛООБРАБОТКИ
13.1. ОБЩИЕ ПОЛОЖЕНИЯ
Режимы металлообработки можно оптимизировать, подбирая опти-
мальное сочетание значений скорости резания и подачи. Под такой опти-
мизацией понимается управление режимами металлообработки, позво-
ляющее получить наибольший народнохозяйственный эффект с учетом
всех существенных связей и ограничений. В общем случае принцип оп-
тимальности формулируется следующим образом: определить такие
значения искомых технологических параметров и соответствующих им
значений регулируемых координат электроприводов, которые обеспе-
чат максимальное (минимальное) или предельно достижимое значение
показателя качества процесса металлообработки при соблюдении огра-
ничений по требуемому качеству продукции и технологическим воз-
можностям оборудования.
Качество функционирования системы металлообработки может быть
в общем случае охарактеризовано функционалом *
*1
J = f f(xt, х2,...,х„; «1, и2,..., Ur; zt, z2,..., zm)dt,
* о
где Х/(0 - выходные координаты; Uj(t) - управляющие воздействия;
(t) - возмущающие воздействия.
При оптимальном управлении системой функционал J достигает
максимального (минимального) значения, характеризуя наилучшее
поведение системы в динамике (при решении задачи динамической оп-
тимизации) либо наилучшие показатели в установившемся режиме
(при решении задачи статической оптимизации).
373
При металлообработке экстремальному значению функционала J
соответствует оптимальное соотношение между скоростью съема при-
пуска и скоростью износа инструмента.
В результате изучения материалов данной главы необходимо знать
критерии оптимизации режимов металлообработки, уметь применять
алгоритмы управления и составлять математическое описание систем
оптимизации станков.
Материал настоящей главы базируется на методах оптимального уп-
равления, рассматриваемых в курсе ”Теория автоматического управле-
ния”, средствах для реализации систем оптимального управления,
изучаемых в курсе ”Системы управления электроприводами”, и техно-
логических особенностях металлообработки, описанных в гл. 9.
При изучении материала следует обратить внимание на принципы
построения АСУ ТП и установить их отличие от систем стабилизации тех-
нологических параметров.
13.2. НАЗНАЧЕНИЕ И ОБЛАСТИ ПРИМЕНЕНИЯ СИСТЕМ
ОПТИМИЗАЦИИ РЕЖИМОВ- МЕТАЛЛООБРАБОТКИ
Системы оптимизации режимов металлообработки АСУ МО предназ-
начены для получения максимальной производительности или экономич-
ности при изготовлении деталей в пределах заданных технических усло-
вий. Производя автоматический выбор режима металлообработки и
управляя электроприводами главного движения и подач, эти системы
обеспечивают сокращение машинного времени обработки. Управление
режимом металлообработки предполагает выбор критерия оптималь-
ности и определения ограничивающих факторов. Построение АСУ МО
в этом случае предназначено для поиска и поддержания экстремально-
го значения выбранного критерия оптимальности при допустимых зна-
чениях остальных показателей.
Повышение производительности и гибкости производства в насто-
ящее время является важнейшим требованием, предъявляемым к новым
станкам. Под гибкостью производства понимают скорость обновления
информации, которую необходимо переработать, чтобы из исходных ма-
териалов получить готовое изделие. В АСУ МО вырабатывается и обраба-
тывается автоматическими устройствами часть этой информации.
Устойчивой тенденцией современного станкостроения, вытекающей
из отмеченного выше, является внедрение устройств и систем, обеспе-
чивающих снижение затрат, а также возможность перехода к обработ-
ке детали другой формы и других технологических характеристик.
Применение АСУ МО экономически целесообразно в тех случаях,
когда выбор режима металлообработки существенно влияет на ее себе-
стоимость, на производительность (машинное время), например при
обработке жаропрочных и закаленных сталей, сплавов и тугоплавких
металлов. Чем выше степень автоматизации станка, тем эффективнее на
374
нем применение АСУ МО. Особенно актуально применение АСУ МО в
станках, оснащенных устройствами ЧПУ типа CNC. Задача построения
АСУ МО в таких станках упрощается в связи с возможностью использо-
вания уже имеющихся в них регулируемых электроприводов, датчиков
и ЭВМ.
133. АЛГОРИТМЫ УПРАВЛЕНИЯ СИСТЕМАМИ
ОПТИМИЗАЦИИ СТАНКОВ
В качестве показателей эффективности металлообработки прини-
мают такие, которые обеспечивают максимальную производительность
или минимальную себестоимость обработки или некоторый компромис-
сный показатель.
Рассмотрим показатели эффективности металлообработки, обеспе-
чивающие режимы максимальной производительности, поскольку они
дают наиболее полное представление о физике процесса обработки и
управлении им. Покажем, что все полученные в ходе рассмотрения
результаты по максимальной производительности можно распространить
и на случаи, когда в качестве показателя эффективности приняты мини-
мальная себестоимость обработки либо минимум приведенных затрат.
Шесть возможных вариантов показателей эффективности обработки,
характеризующих соответствующие режимы, представлены в табл. 13.1.
Детерминированные алгоритмы функционирования процесса обработки
справедливы для ограниченной области изменения режимов обработки,
описываемых эмпирическими зависимостями, которые обладают неко-
торым разбросом результатов. Более перспективным является построе-
ние математических моделей процессов резания с учетом их вероятно-
стного характера. Работы в этом направлении ведутся, однако нет доста-
точных сведений, характеризующих вероятностную природу режимов
резания. Поэтому связь между параметрами резания в табл. 13.1 рас-
сматривается в детерминированной форме. Структурные схемы систем
и рабочие характеристики (табл. 13.2) соответствуют представленным
в табл. 13.1 показателям эффективности.
Режим 1. Структурная схема для этого режима учитывает изменение
стойкости инструмента и позволяет работать с экстремальным значе-
нием показателя эффективности обработки. На вход микропроцессора
МП с датчиков ДСР, ДСИ подают напряжения, пропорциональные ско-
рости резания и стойкости инструмента. В программу расчета показате-
ля эффективности вводятся поправочные коэффициенты по ско-
рости КС и по стойкости инструмента КИ. Микропроцессор рассчиты-
вает показатель эффективности обработки J2, определяет знак его при-
ращения и с учетом заданных ограничений по максимально допустимой
температуре резания (ввод априорной информации задания стойкости
ЗС) и по предельной угловой скорости шпинделя (ввод априорной
информации 3ZZ7) в соответствии с алгоритмом функционирования уп-
375
Т*Влш*13.1
Режим Похажель эффект- Налагаемое ограни- Пара ноем обрвботхм чмм изменяемые
1 -Ш1— «Г- — г1 + 'см »i
2 А* *2 —Г С- 5s_ *2
^2 + ГСМ
3 /s -*» Рз>з T3 *э + гсм Г-- CV3 „ J FSf3 V3
4 /4 “*4 *4S4/p4T4 ^4 + *CM r"' CV4 X у ’*ГР4,4 *4
5 /S - *5 SS^S T* + *cm rr- p 1 U 1 И *S
376
ТТ- h- жг₽ы Алгоритм функционирования
U контролиру- емые неконтро- лируемые
Vi, Т1 «1» ГР! Г°* “ ta*(m -1)
»oi - —C>1
m 11 I— 1 \m
* cm| m J
Toi ’ fcM(m -1)
»2> fp2- Т2 *2 fP02 “ rpmex
CVj
*02 " " “ tmL 1 * । t **
» | 1 1 CM\ m 1 ' pmox
11 \ ^03 = *см(“ “1.1 \ m / ; *03 =
₽з, 5з, Т3 *РЭ CV3
*03 “ — rm/— -1 lw/
CM\m li 1 snutx
^04 = *см(— “ 1/ \ m f » rp04 “ rpmex
*4. »4. tpr Г4- ^04 = smax
C»4
”04= *CM^m 1 Г/ tx 1 smax pmax
T°S = ~ 0
SS> 7*5 'ps Cvs
^05 .
«« I m 4
377
Табл. 13.1 (продолжение)
Показатель эффектив-
Режим ности обработки
Налагаемое ограни-
чение
Пара
изменяемые
56 7*6 Тт - Cv6
J6 - ^6 ^6 + *СМ ‘ ,х >
*6
равляет электроприводом шпинделя ЭПШ. В процессе функциониро-
вания система отыскивает экстремальное (оптимальное) значение
J01 и поддерживает работу стаИка в зоне экстремума при смещении
Ji относительно скорости резания v01.
Подача на оборот устанавливается максимально допустимой при
помощи электропривода подачи (ЭПП) и в процессе обработки не из-
меняется. Применение системы, обеспечивающей данный режим, осо-
бенно целесообразно при резании закаленных сталей и труднообраба-
тываемых сплавов, поскольку рабочие характеристики J(у) в этом слу-
чае обладают ярко выраженным экстремумом.
Режим 2. Его структурная схема также представляет экстремальную
систему, но в отличие от системы для режима 1 в ней микропроцессор
МП при расчете показателя эффективности J2 дополнительно учитывает
изменение глубины резания при помощи датчика глубины резания
ДГР и для коррекции использует поправочный коэффициент по глуби-
не резания КГ. Необходимость применения датчика глубины резания
создает трудности при реализации этой системы.
Режимы 3,4. В системе режима 3 на входы микропроцессора МП
поступают сигналы с датчиков: скорости резания ДСР, подачи ДВП,
стойкости инструмента ДСП, а в память вводится априорная информа-
ция КС, КП, КИ. В системе режима 4 на вход микропроцессора МП
кроме перечисленных поступает также сигнал с датчика глубины реза-
ния ДГР, а в память вводится априорная информация о глубине резания
КГ. Настройка станка на оптимальный режим обработки осуществляет-
ся по поисковой программе аналогично рассмотренной настройке для
режима 1. Как показывают испытания, такие системы позволяют сни-
зить себестоимость обработки на 50%.
Режимы 5, 6. Показатели эффективности обработки J5 и J6 обла-
дают экстремумами относительно подачи, что позволяет построить сис-
темы, самонастраивающиеся на оптимальный режим резания. В систе-
378
метры
контролируй неконтро-
емые лируемые
Алгоритм функционирования
*роб rpmax
$б» fpg> ^*6 v6
m/у (у \тЬ> Х/У
см \т / pwx
ме режима 5 на входы микропроцессора МП подаются сигналы, пропор-
циональные подаче и стойкости инструмента (датчики ДВП, ДСП),
а в программу вводится априорная информация о коррекции указан-
ных параметров (КП, КП). Кроме того, в программу вводится инфор-
мация о заданной предельной подаче ЗП и заданной предельной темпе-
ратуре резания ЗС. После расчета показателя эффективности Js по
подпрограмме поиска экстремума определяются знаки приращения по-
казателя эффективности и по управляющей подпрограмме осущест-
вляется выдача управляющего сигнала на привод подачи ПП.
В системе режима 6 программа расчета J6 учитывает также и влияние
изменения глубины резания (датчик ДГР, информация КГ) на процесс
обработки. Поскольку экстремальные зависимости J(s) имеют поло-
гий характер, реализация АСУ ТП по этим схемам малоэффективна.
Все перечисленные схемы могут быть построены на базе микропро-
цессоров либо цифро-аналоговых оптимизаторов.
Период стойкости 7\ - Тб, входящий в выражения показателя эф-
фективности обработки, зависит от многих факторов и для инженер-
ных расчетов определяется по эмпирическим формулам. Жесткая функ-
циональная связь между параметрами резания и стойкостью, применя-
емая при расчетах в действительности, как уже отмечалось, носит вероят-
ностный характер. Поэтому на практике в силу физической сущности
процесса резания эта функциональная связь нарушается и реальная стой-
кость может значительно отличаться от расчетной.
Следовательно, оптимальные значения скорости резания у0 и подачи
so, обеспечивающие максимум показателя эффективности обработки
Ji ~ Л (рассчитаны по эмпирическим стойкостным зависимостям),
могут служить лишь для качественной оценки процесса управления.
Принимая для некоторого узкого интервала времени эмпирические
коэффициенты стойкостной зависимости достоверными и неизменными,
а параметры резания - не зависящими от времени, найдем их оптималь-
379
Таблица 13.2
380
Продолжение табл. 13.2
381
ное значение, обеспечивающее экстремум наиболее общему выражению
показателя качества J4 (режим 4 табл. 13.1).
Полагая, что задача не имеет ограничений, решим посредством мето-
да неопределенных множителей Лагранжа следующую систему урав-
нений (здесь для упрощения записи опущены индексы ”4”) :
Э/° st Т cv
— = _Р---------X ------— = 0;
а» г+'см v^ytx
р
Э/° vt t г
— = —------ - X----------- = 0;
г+'см pS(j'+1)rx
Р
a/0 vst cv
— =-----------X ---------- = 0;
Э'Р г+,см
р
= 75/.СМ..... _ХотГ(т-1) =0;
ЭТ <г+гсм)2
с„
—-— _ тт = о,
р
где X — множитель Лагранжа.
Проверка функционала J° на усиленное условие Лежандра по-
казывает, что
З2/0 З2/0 Э2/0
< 0; < 0; < 0,
ЭГ2----------------------Зг2-3s2
р
следовательно, J0 имеет максимум.
Накладываем на параметры системы следующие ограничения:
mtn max
S . < S < S ;
min max ’
0 < Гр < tpmax-
Решение системы уравнений с учетом ограничений позволяет найти
оптимальные значения искомых параметров:
382
^р,о ^ртдх»
(13.1)
5 о smax »
Таким образом, для автоматической оптимизации режима резания
необходимо вести обработку с максимально допустимой глубиной ре-
зания и величиной подачи и при достоверности эмпирических коэф-
фициентов поддерживать скорость в соответствии с экстремалью (13.1).
Представленные выражения справедливы для токарной обработки.
Аналогичным образом могут быть получены соотношения для фрезер-
ной обработки и шлифования.
Выражения (13.1) могут быть переведены в стоимостную форму
для определения себестоимости. Рассмотрим этот экономический пока-
затель эффективности, например, при фрезерной обработке. Объем
стружки, снимаемой в единицу времени (объемная производитель-
ность) , при фрезеровании определяется по формуле
= 9,55/Шпсо.
Ф РФ
где В — ширина фрезерования, мм; s — подача, мм/об; tp — глубина
резания, мм; соф — угловая скорость фрезы.
Стоимость съема металла, отнесенная к одному периоду стойкости
фрезы, определяется так:
ci = CcoZ = Сс(Т + Гсм) + Си,
(13.2)
где Сср — средняя стоимость съема единицы объема металла, руб./см3;
/ф — общий объем металла, снятого за период стойкости фрезы, см3;
стоимость станко-минуты, руб./мин; Си — стоимость инструмента,
отнесенная к периоду его работы без переточки, руб.; Т — период стой-
кости фрезы, мин; fCM - время смены инструмента, мин.
Средняя стоимость съема металла за период стойкости фрезы
1 т
Сер = V / Cdt
1 о
где С—текущее значение стоимости съема металла.
383
Общий объем металла, снятого за период стойкости фрезы,
4 = I j^t. (1з.з)
* о
Из (13.2) и (13.3) находим среднее значение стоимости съема метал-
ла за период стойкости фрезы:
Сс + <сс*см + си)
Ссъ = ---------------------- •
ср т
т i ф
Если обозначить скорость износа инструмента ул, то максимально
допустимый износ, определяющий период стойкости инструмента,
Т
hmax = J vh^9 откУда можно записать
о
1 1 г
- = ---------- ! vhdt
^тах Т о
ИЛИ
1 Т
Q + [(^с^см + J vhd^
1 о
Сср = ----------—--------------------------- . (13.4)
Т ' Ф
Мгновенное текущее значение стоимости съема металла, С, прини-
маемое за показатель эффективности, равно пределу, к которому стре-
мится (13.4) при периоде стойкости фрезы, стремящемся к нулю, и
после преобразований получает вид
Ct + с
„ Сс'см си
+ --------------- V.
Полагая, что скорость износа инструмента — величина постоянная,
обозначим Т = hmax /vh и введем коэффициент /Гс>и (0 < Кс и < 1),
определяющий степень учета себестоимости инструмента при обра-
384
ботке. Тогда
j _ Сс(Т + *см) + ^и^с,и
ф’с 9,5SBstnO)^T
9 р ф
Зависимость Уф с обладает минимумом при оптимальном режиме
обработки.
Если принять Кс и = 1, то критерий оптимальности будет опреде-
ляться стоимостью обработки, а единицей измерения величины </ф,с
будет руб/см3. Если принять Кс и = 0, то критерий оптимальности бу-
дет определяться производительностью обработки (величина Сс в этом
случае на положение экстремума не влияет, и ее можно опустить), а
единицей измерения /ф>с будет мин/см3. Полученный при этом кри-
терий близок обратному значению критерия J4 (см. табл. 13.1). Проме-
жуточные значения коэффициента Кс и дадут критерии, являющиеся
компромиссными между стоимостью и временем обработки (произ-
водительностью) .
Для расчета стоимости станко-минуты, входящей в уравнение (13.5),
воспользуемся выражением
Q = (др,п + ац,п + арац + + ^т,р +
+ £*С,ф + 0>СН + £*ЭЛ + СОбЩ + ^В,р + £*ОСв)/Фг^С’
где Фг — годовой фонд времени станка при его односменной работе,
определяемый как часть номинального фонда за вычетом простоев, не
связанных с заменой режущего инструмента; кс — количество смен ра-
боты станка (все остальные коэффициенты отнесены к данной опера-
ции); ар,п - зарплата производственного рабочего; ац>п - часть
зарплаты цехового персонала; арац — часть оплаты работ по рационали-
зации; Фф — основные производственные фонды; Яа — норма аморти-
зационных отчислений по основным фондам; Ст>р — затраты на теку-
щий ремонт основных производственных фондов; Сс>ф — затраты на
содержание основных производственных фондов; Сосн — затраты на
оснастку; Сэл - затраты на силовую электроэнергию; Собщ — общеза-
водские расходы; Свр - внепроизводственные расходы; сосв - рас-
ходы на освоение производства новых видов продукции.
Стоимость инструмента, отнесенная к данному периоду его стой-
кости, равна
Си* ” (Gi ~ Сотх)/(п — 1) + Спер,
где Си — стоимость инструмента; Сотх — стоимость инструмента после
его полного износа; Спер - затраты на одну переточку; п - число
переточек.
385
/ф,с , коп/см3
200-100\- *
fn=4MM
160
-so
-60
120
-40
80
- 20
40
J*
Jfh.nS
J^C2
О 40 80 120 160 г/, м/мин
Рис. 13.1. Зависимости показателей про-
изводительности и себестоимости фрезе-
рования от скорости резания
0
Стоимость станко-минуты со-
ставляет, как правило, 1—3 коп.;
значение Си для резцов, сверл и
фрез колеблется в пределах 5—
20 коп.
Зависимости показателей произ-
водительности /ф,п и себестоимости
/ф>с обработки от скорости резания при фрезеровании стали марки
45 цилиндрической фрезой с твердосплавными пластинами при постоян-
ной глубине Гр = 4 мм и различных подачах (7ф>п1, ^ф,с1 ~
0,12 мм/зуб; /ф,П2» ^Ф,с2 - 0,08 мм/зуб; /ф,пз» ^ф,сз“ °’04 мм/зуб)
представлены на рис. 13.1.
Как видно, при одних и тех же скоростях резания экстремумы пока-
зателей производительности и себестоимости не совпадают.
Известно, что более высокому уровню общественной производитель-
ности труда при максимальной эффективности соответствует не мини-
мум текущих затрат, выражаемых себестоимостью работ, а минимум
приведенных затрат, более полно отражающих использование факторов
производства. Этот показатель широко применяется для выбора опти-
мального варианта промышленных установок и может быть применен
для определения оптимальных режимов обработки. При такой оценке
эффективности обработки исходят из того, что общий минимум затрат
производства (на всех операциях и участках в целом) важнее минимума
затрат на его отдельных участках. Приведенные затраты, обусловленные
принятым режимом обработки, будут
Сп = Сг +
где Сг — себестоимость продукции, производимой на станке в течение
года; К — капитальные затраты; Еп — нормативный коэффициент эф-
фективности капиталовложений, принятый в машиностроении равным
0,15, что соответствует сроку окупаемости Тн = \1Еп = 6,6 года.
Для выбора оптимального режима обработки следует определить
такой z-й режим, который обеспечивает минимум приведенных затрат:
Gu ~ С?i + т^п-
Достоинством показателя приведенных затрат является обобщение
двух таких показателей, как себестоимость и капитальные вложения.
386
13.4. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ В АСУ МЕТАЛЛООБРАБОТКИ
Экстремальные зависимости показателей производительности и себе-
стоимости обработки позволяют построить на их базе систему, самона-
страивающуюся на оптимальный резким работы. Для оптимизации режи-
ма обработки требуется сформировать показатель качества, для чего
необходимы система датчиков оперативной информации, устройство
ввода априорной информации, микропроцессор или вычислительное
устройство, регулятор (оптимизатор), осуществляющий поиск опти-
мального варианта (режима) обработки, и исполнительные приводы.
Функции оптимизатора могут быть возложены на подпрограмму микро-
процессора.
Методы решения задач оптимизации эффективно реализуются на
УВМ в виде поисковых алгоритмов. Для организации процедуры поис-
ка применяются методы сканирования, Гаусса—Зайделя, наискорейше-
го спуска, Кифера-Джонсона, а также разновидности градиентных ме-
тодов. АСУ ТП, осуществляющие оптимальное управление режимом ре-
зания, могут строиться как супервизорные.
В станочных системах для упрощения процедуры поиска оптимально-
го режима и возможности применения микро-ЭВМ с ограниченным объ-
емом памяти задачу отыскания и поддержания оптимальных значений
управляющих воздействий возлагают на аналоговый экстремальный
регулятор. Такой регулятор может быть построен на операционных
усилителях.
Принципиальная схема экстремального регулятора приведена на
рис. 13.2. На входную цепь динамического преобразователя (усилитель
АГ) подается напряжение пропорциональное угловой скорости.
Выходной сигнал с этого усилителя поступает на вход второго усили-
теля Л2, охваченного обратной связью с резистором R5 и цепочкой из
встречно включенных стабилитронов VD1, VD2, ограничивающих уро-
вень выходного напряжения. Напряжение с усилителя А2 подается на
обмотку двухпозиционного поляризованного реле КР1 и цепь обрат-
ной связи, состоящую из двух встречно включенных стабилитронов
VD3, VD4 и интегрирующего усилителя АЗ.
Напряжение Uj с выхода нелинейного звена UZU, пропорциональ-
ное показателю качества J, через второй динамический преобразова-
тель, состоящий из усилителей A4t А5, интегрирующего усилителя А6,
стабилитронов VD5 - VD8, подается на коммутационный ‘контур.
Последний через переключающий контакт реле КР1 подключает выход-
ное напряжение к обмотке второго двухпозиционного поляризованно-
го реле КР2 непосредственно либо через инвертирующий усилитель
А 7. Выходное устройство экстремального регулятора состоит из управ-
ляемого задатчика интенсивности, включающего в себя интегрирующий
усилитель А8, на вход которого через переключающий контакт КР2
подается напряжение £/ст необходимой полярности. Темп изменения
387
Рйс. 13.2. Принципиальная схема экстремального регулятора
управляющего напряжения иу определяется постоянной времени инте-
грирования и величиной постоянного напряжения &i(7Ct = du^/dt..
Работает регулятор следующим образом. При движении рабочей точ-
ки по левой ветви экстремальной характеристики в направлении к экст-
ремуму напряжения и Uj увеличиваются. Это вызывает такое сра-
батывание реле КР1 и КР2, при котором контакт реле КР2 будет ос-
таваться в положении, соответствующем возрастанию выходного нап-
ряжения Пу, поступающего в схему управления электроприводом.
Угловая скорость приводного двигателя также будет возрастать.
Если напряжения на выходах усилителей А2 и А5 превысят напря-
жения пробоя стабилитронов VD3 - VD4 и VD7 - VD8 соответствен-
но, то вступят в действие интегрирующие усилители АЗ и А6, осуще-
ствляя компенсацию входных напряжений и Uj . До тех пор, пока
эти напряжения увеличиваются и не осуществилась их компенсация
интегрирующими усилителями АЗ, А6 соответственно, на выходе усили-
теля А2 будет действовать напряжение ДС/^, а на выходе усилителя
А5 - напряжение MJj .
После прохождения экстремума напряжение Uj начнет уменьшать-
ся, на выходе усилителя А5 появится отрицательное напряжение
—&Uj и поляризованное реле КР2 переключит свой контакт. Сигнал за-
дания на входе преобразователя электропривода начнет уменьшаться, и,
следовательно, будет уменьшаться угловая скорость приводного двига-
теля. Теперь рабочая точка будет находиться на правой ветви экстре-
мальной характеристики, поэтому уменьшение угловой скорости приве-
388
дет к росту показателя качества, напряжение uj вновь увеличится и
на выходе усилителя А5 появится положительное напряжение Auj .
На выходе А2 при снижении угловой скорости появится отрицатель-
ное напряжение - Д/7О. Реле КР1 переключит свой контакт, и на обмот-
ку КР2 будет подано инвертированное с помощью А7 напряжение
+Дму, снимаемое с выхода А5. Контакт КР2 будет занимать нижнее
положение, а угловая скорость двигателя будет продолжать снижаться.
Дальнейшее снижение угловой скорости двигателя приведет к появле-
нию на выходе А5 сигнала - Диу . Это вызовет переключение контакта
КР2, что обусловит увеличение угловой скорости двигателя.
Далее работа экстремального регулятора будет протекать аналоги^
но описанной, а рабочая точка будет совершать колебания в области
экстремума в соответствии с законом регулирования
Дг
где е — порог нечувствительности реле.
Уровень ограничения выходного напряжения усилителей А2 и Л5,
задаваемый стабилитронами VD1, VD2 и VD5, VD6, определяется до-
пустимым напряжением обмоток реле КР1 и КР2. Включение этих
стабилитронов позволяет использовать реле с низким порогом сраба-
тывания и повысить точность поддержания экстремума.
Зона нечувствительности, создаваемая в ц&пях интегрирующих усили-
телей АЗ и А6 стабилитронами VD3, VD4 и VD7, VD8, является свое-
образной временной задержкой в контурах обратной связи, что улуч-
шает работу экстремального регулятора с инерционным объектом.
Если цепь обратной связи замкнута, а усилитель А5 не насыщен, то пе-
редаточная функция динамического преобразователя будет иметь вид
7Л(р) = *3*4/[1+ *Э*4/(ЛР)Ь
где к3> к4 - коэффициенты усиления усилителей А4, А5\ 7\ - по-
стоянная времени интегрирующего усилитедя А6.
Рассмотренный экстремальный регулятор работает на операционных
усилителях типа УПТ-3 (УБСР) с источниками питания типа ИП-6. Регу-
лятор воздействует на тиристорный электропривод постоянного тока.
Объект управления представлен в виде линейного инерционного звена
второго порядка с передаточной функцией
Я2(р) = 1/(Т*р2 + Т3р +1),
где Г2, Г1 - постоянные времени, и включенного вслед за ним нелиней-
ного звена с характеристикой
J ~ k$(j& —
389
Рис. 13.3. Осциллограммы поиска и поддержания экстремума
Нелинейное звено имитирует экстремальную характеристи-
ку объекта управления (станка), моделируемую вычислительным
устройством и микро-ЭВМ.
Работа экстремального регулятора иллюстрируется осциллограммами
(рис. 13.3), где в относительных единицах показаны изменения угло-
вой скорости электродвигателя, тока якоря z* и показателя ка-
чества А в процессе поиска и поддержания экстремума. За базовые
величины угловой скорости и показателя качества приняты их опти-
мальные значения. На осциллограмме показан также характер измене-
ния управляющего напряжения иу экстремального регулятора.
Процесс выхода на экстремум снят при включении системы с нуле-
выми начальными условиями (со = 0; J = 0). Угловая скорость двига-
теля увеличивается, показатель эффективности также увеличивается.
После выхода рабочей точки в область экстремума начинает изменять-
ся напряжение иу* и система оказывается в режиме автоколебаний.
Регулятор работает с большими коэффициентами усиления, поэтому
экстремум поддерживается с высокой точностью, а потери на рыскание
не превышают 1 %.
Работа экстремального регулятора легко может быть реализована
программными средствами на микропроцессоре.
Рассмотрим, как зависит производительность обработки от скорости
движения стола при грубом плоском шлифовании периферией круга
на станке с прямоугольным столом. Период стойкости шлифовального
круга
(уд5д*р
390
где Ср — коэффициент, зависящий от характера производства; ki9k2 —
постоянные, зависящие от обрабатываемого материала и диаметра кру-
га соответственно; уд - скорость движения стола; $д - поперечная
подача в долях ширины круга; st — вертикальная подача на ход стола.
Полагая, что величины $д и st неизменны, запишем
г = *г\!,
где
Су»
к,„ = -------- ^1^2-
Производительность станка при грубом шлифовании выражена объ-
емом металла, снятого за период стойкости круга и отнесенного к пе-
риоду стойкости с учетом времени правки круга tn :
Ав,п ' +
где 5д0 — поперечная подача на
ход стола.
Так как величины $д0 и st не-
изменны, то, приняв, что их про-
изведение равно кш> получим
Лп,п = + ^п) •
Анализ и расчеты показывают,
что производительность шлифова-
ния ^ш,п обладает максимумом
относительно скорости движения
стола.
Для поддержания оптимально-
го по выбранному критерию ре-
Рис. 13.4. Схема алгоритма управле-
ния поиском
391
жима шлифования путем воздействия на электропривод движения стола
необходимо применение поисковой автоматизированной системы управ-
ления. На рис. 13.4 показан один из вариантов схемы алгоритма управ-
ления поиском, являющегося цифровым прототипом описанного выше
аналогового поискового регулятора. Перед пуском системы в ячейке
памяти УВМ записывают положительный шаг приращения Дуд ~ Дсо,
который через ЦАП подается на задатчик скорости системы электропри-
вода движения стола. Угловая скорость электропривода начинает уве-
личиваться. При этом осуществляется опрос УВМ датчиков параметров
резания, установленных на станке. По полученным данным производит-
ся вычисление текущих значений стойкости круга и показателя эффек-
тивности обработки /ш п. Через N тактов работы УВМ определяет зна-
чения скорости движения стола Дуд = ~ гд/ и показателя
эффективности Д/Ш>п = ^ШП(гНУ) ~ /ш,пГ Дальнейшее изменение
угловой скорости электродвигателя привода стола производится в за-
висимости от сочетания знаков приращений, полученных после N так-
тов работы УВМ.
Логический блок выполняет анализ знаков приращений скорости
движения стола Дуд и показателя производительности Д/ш п. При
движении рабочей точки справа к точке экстремума характеристики
/ш,п ) приращения Д«/Ш>п > О, Дуд > 0, поэтому логический блок
назначает положительный шаг приращения скорости + Дуд, т.е. дается
команда на дальнейший разгон электропривода стола. В процессе разго-
на указанная система проходит точку экстремума. Теперь Д/ш п < О,
а Дгд > 0, и логический блок назначает новый шаг приращения скоро-
сти -Дуд, т.е. дается команда на замедление электропривода стола.
Начинается движение рабочей точки слева к точке экстремума. При
этом Д/ш п > 0, Дуд < 0, но логический блок вновь назначает отрица-
тельное воздействие -Дуд, и электропривод стола продолжает замед-
ление.
В процессе замедления система опять проходит точку эстремума
и продолжает двигаться влево от нее. Теперь Д/ш п < 0, а Дуд < 0, и
логический блок дает команду на разгон привода стола, назначая за такт
положительный шаг приращения Дуд. Система снова движется к точке
экстремума справа.
Таким образом, постоянно осуществляется процесс поиска экстре-
мума показателя производительности работы станка /ш п.
Поиск и поддержание экстремального значения производительности
при глубине шлифования 0,1 мм показаны на рис. 13.5,а. Поскольку
экстремальная характеристика для этого режима является пологой, по-
тери на рыскание оказываются незначительными и составляют 0,2%.
Однако при переходе на обработку с глубиной шлифования 0,2 мм
(рис. 13.5,6) экстремальная характеристика ^ш>п(гд) оказывается
более резко выраженной и потери на рыскание возрастают до 1,2%.
392
Рис. 13.5. Процесс поис-
ка и поддержания экс-
тремума при работе на
пологой части характе-
ристики (а) и на харак-
теристике с резко выра-
женным экстремумом
(0)
м/мин
Применение поискового алгоритма с переменным шагом приращения
за такт дает возможность повысить точность поддержания экстремума.
При плоском шлифовании управляющим воздействием может яв-
ляться скорость перемещения стола станка. Алгоритм управления сис-
темой включает следующую последовательность операций. Перед пус-
ком системы в память УВМ вводится априорная информация: постоян-
ные составляющие стойкостной зависимости, показателя эффектив-
ности, ограничения на управляющее воздействие и на силовые парамет-
ры обработки, шаги поиска. При пуске системы осуществляется вывод
на УВМ некоторого начального значения скорости перемещения стола,
которое подается в устройство задания скорости электропривода. Про-
исходит разгон электропривода, затем УВМ осуществляет пробные воз-
действия на систему, придавая задающему воздействию некоторые при-
ращения. Анализ отработки системой проведенного воздействия осуще-
ствляется путем опроса датчиков, установленных на станке, вычисления
на основании полученной информации текущих значений показателя эф-
фективности обработки и определения приращений задающего воздей-
ствия и показателя эффективности. Управление технологическим про-
цессом в режиме адаптации может осуществляться одним или несколь-
кими электроприводами.
Использование УВМ позволяет построить АСУ ТП, в пределах цикла
работы стабилизирующую технологический параметр, а между циклами
обеспечивающую поиск оптимального значения этого параметра.
393
Например, на поверхности круглого стола плоскошлифовального
станка с вертикальным шпинделем и обработкой торцом круга выде-
ляют секторы, которые выбирают так, чтобы в пределах каждого сек-
тора физические свойства деталей (припуск, ширина, твердость) можно
было считать неизменными.
. Мощность шлифования в пределах каждого участка определяется
соотношением
Р = 0,73(рдВпр*оАк0’25М2. (13.6)
где уд — скорость перемещения детали, м/мин; Впр — приведенная
ширина шлифования, мм; — подача на оборот стола, мм/об; Вк —
ширина круга (сегмента); мм; kt, к2 — постоянные,зависящие от ма-
териала детали и круга; /3 — показатель степени.
Поскольку в пределах участка стола считается, что физические свой-
ства деталей неизменны, мощность шлифования на данном /*-м участке
на предыдущем и последующем оборотах стола определяется следующи-
ми соотношениями:
P(n-\)i ~ So(»-l)J ’ (13-7)
?ni ^^VjiniSoni^
(13.8)
где С = 0,73£?пр В °’2 5 кг к2 — постоянная в пределах участка величина;
Лп мощность шлифования на f-м участке на предыдущем
л—1-м и последующем л-м оборотах стола; удП1- - ско-
рость детали на z-м участке на п-1-м и и-м оборотах стола; sQ (Л_ i)p
soni “ п°дача на оборот стола на z-м участке на л—1-м и и-м оборо-
тах стола.
Разделив (13.7) на (13.8), учитывая, что скорость перемещения дета-
ли уд пропорциональна угловой скорости стола со, и положив, что
показатель степени 0 « 1, получим упрощенное выражение для опреде-
ления угловой скорости стола на f-м участке на последующем и-м обо-
роте стола:
?ni
“ni = p----
Чл-Ш
5о (п-1)/
~ "(л-!)/ ’
oni
(13.9)
где со z , со .
ботки в предыдущем и последующем циклах.
394
— угловая скорость стола на f-м участке зоны обра-
Чтобы мощность шлифования Pni была равной заданной Рзл, не-
обходимо установить на данном участке скорость стола
?зп
GJ . = ---
т р
Чл-Ш
so(n-l)i ,,
~Г~. w(n-V)C
5ОП1
(13.10)
Заданное значение мощности P3fJ целесообразно устанавливать ис-
ходя из анализа в процессе обработки текущих значений показателя
эффективности шлифования. На черновых операциях таким показате-
лем может быть производительность либо себестоимость обработки.
Известно, что зависимость показателей производительности и себесто-
имости обработки от подачи имеет экстремальный характер. Поскольку
мощность шлифования согласно (13.6) пропорциональна подаче, наб-
людается экстремальный характер зависимости показателей себестои-
мости и производительности обработки от величины мощности шли-
фования, т.е. имеется оптимальное значение мощности, при которой
показатель эффективности достигает экстремального значения.
Коррекция задаваемого значения мощности проводится через один
либо несколько циклов обработки (оборотов стола). Из уравнения
(13.6) видно, что при прочих одинаковых условиях изменение мощ-
ности от цикла к циклу может быть достигнуто путем соответству-
ющего изменения подачи на оборот стола.
Используя уравнения (13.6) для полного цикла обработки (обо-
рота стола) и полагая, что команда на изменение мощности, которую
необходимо будет поддерживать в последующем цикле, задается путем
изменения подачи на оборот стола, а также учитывая сделанные выше
допущения, записываем
Л(л-1) ^5о(л-1) ’ ?зп
где А = 0,73(рдйпр/в°’25М2-
На основании полученных выражений найдем
so(n-vjson =Л(и-1)/Лл’ G311)
где Рзп - заданные значения мощности на предыдущем и
последующем циклах обработки; son — подача на оборот
стола на предыдущем и последующем циклах обработки.
Подставляя (13.11) в (13.10), получаем выражение для расчета за-
данной угловой скорости стола на каждом участке зоны обработки:
395
Минутная подача на врезание sr на участке зоны обработки при
этом будет равна
’ 9-55ч,лл; <1313>
St(n-l)i = 9,55t°(n-l)jSo(H-l) ’ О314)
где stni ~ минутная подача на врезание на i-m участке зо-
ны обработки в предыдущем и последующем циклах.
С учетом (13.10), разделив (13.13) на (13.14), получим выраже-
ние для заданной подачи на врезание на каждом участке зоны обработки:
Схема управления от УВМ плоскошлифовальным станком с верти-
кальным шпинделем при обработке торцом круга на круглом столе
(рис. 13.6) содержит привод главного движения 1 с датчиком мощности
2, привод подачи на врезание 3 с датчиком скорости 4 и датчиком по-
ложения шлифовальной бабки 5. Круглый стол приводится во враще-
ние приводом 6, который оснащен датчиком скорости 7 и датчиком
положения 8. Износ шлифовального круга измеряет датчик 9. Сигналы
датчиков поступают на вход текущей информации УВМ 10, которая,
работая по описанному алгоритму, через устройства связи управляет
приводом подачи на врезание и приводом вращения стола. Производя
опрос датчиков 2, 4, 5, 7, 8 и выполняя расчет по введенным в про-
грамму формулам (13.12) - (13.15), УВМ 10 определяет необходимые
значения скорости стола и подачи на врезание, которые для поддержания
постоянства уменьшить шлифования должны быть установлены на дан-
ном участке зоны обработки при последующем обороте стола.
На участках стола, не занятых деталями, измеренное значение мощ-
ности Pj будет равно мощности холостого хода, и для этих участков
устанавливается подача на врезание, равная нулю, а скорость стола при-
нимается равной некоторому заранее заданному ускоренному значе-
нию, что позволяет исключить ’’шлифование воздуха” и проходить сво-
бодные от деталей участки на повышенной скорости.
Рассчитанные значения скорости стола, подачи на врезание и измерен-
ной мощности шлифования записываются в соответствующих каждому
участку ячейках памяти УВМ и подаются на входы приводов 3 и 6 при
поступлении данного участка в зону обработку на последующем обороте
стола. В дальнейшем на каждом участке производится установка рас-
считанных значений скорости стола и подачи и опрос датчиков 2, 4, 7.
Этим обеспечивается стабилизация мощности шлифования.
Через несколько оборотов стола УВМ производит также опрос датчи-
ков 5 и 9 и осуществляет расчет текущего значения показателя эффек-
396
Рис. 13.6. Схема управления от УВМ плоскошлифовальным станком
тивности обработки, например производительности:
Ли,п ~ Лп^/С^ + ^см)>
где (l—hy/т - скорость съема металла, см3/мин; Т= rhmax/h -
период стойкости шлифовального круга, мин; ZCM — время смены изно-
сившегося круга, мин; — площадь шлифуемых деталей, см2; l,h —
соответственно перемещение шлифовальной бабки и износ шлифоваль-
ного круга за время между опросами датчиков 5, 9, см; т — время
между опросами датчиков 5, 9 (определяется по сигналам таймера или
по количеству тактов работы УВМ), мин; hmax - предельно допусти-
мый износ шлифовального круга по высоте, см.
Если очередное вычисленное значение показателя /ш п превышает
его предыдущее значение, то УВМ увеличивает заданное значение мощно-
сти на величину приращения ДР3, если же текущее значение показателя
/ш п меньше предыдущего значения, то величина заданной мощности
уменьшается на ДР3, т.е. заданное значение мощности определяется пу-
тем автоматического поиска оптимального значения на основании ана-
лиза состояния инструмента и вычисления показателя эффективности
обработки.
Осциллограмма работы электропривода подачи ЭТЗС12-6/110 с элек-
тродвигателем типа ПБСТ42 1,4 кВт; ПО В; 16,6 А; 103,5 рад/с при
управлении по поисковому алгоритму от УВМ типа 15ВСМ5 представле-
на на рис. 13.7. На осциллограмме показаны ток якоря двигателя /я,
угловая скорость двигателя со и напряжение задания и3, вырабатыва-
397
емое УВМ. После выхода системы на экстремум угловая скорость и
напряжение задания совершают колебания в зоне экстремума. Описан-
ная система управления позволяет повысить производительность до
50% р снизить себестоимость металлообработки ориентировочно на
15 - 20%.
Глава четырнадцатая
РОБОТИЗИРОВАННЫЕ КОМПЛЕКСЫ МЕТАЛЛООБРАБОТКИ
14.1. ОБЛАСТИ ПРИМЕНЕНИЯ РОБОТИЗИРОВАННЫХ КОМПЛЕКСОВ
Системы автоматизации технологических процессов металлообработ-
ки позволяют эксплуатировать станки и автоматические линии с огра-
ниченным участием оператора, приближаясь к трудосберегающей или
так называемой ’’безлюдной технологии”. Благодаря этому обеспечи-
вается работа производства при значительном сокращении обслужива-
398
ющего персонала во вторую и третью смены, выходные и праздничные
дни; возрастает коэффициент использования станков.
Как показывают статистические исследования, машинное время обра-
ботки на станках составляет 5—6% общего фонда времени при мелкосе-
рийном производстве, 7-8% - при среднесерийном производстве и до
20-22% — при крупносерийном и массовом производстве. Остальное
время расходуется в основном на ожидание очереди на обработку и яв-
ляется резервом повышения производительности.
Эффективным путем резкого сокращения времени ожидания и повы-
шения производительности технологического процесса может быть соз-
дание гибких (быстропереналаживаемых) производственных систем
(ГПС). В состав ГПС входят несколько (2-36) автоматизированных
станков, оснащенных системами ЧПУ класса CNC,h промышленных ро-
ботов с микропроцессорным управлением, а также роботозированная
транспортная система, связывающая между собой станки для переста-
новки деталей и накопительную систему (склад), позволяющую 1-2
смены не обращаться к транспортно-загрузочной системе цеха. Про-
мышленная робототехника, обеспечивая полную автоматизацию произ-
водственного процесса, используется в составе робототехнического ком-
плекса ГПС. Наиболее рациональная область применения роботизиро-
ванных комплексов ГПС на базе станков с ЧПУ и участков станков с
ЧПУ — мелко- и среднесерийное производство.
Для крупносерийного производства применяются гибкие автомати-
ческие линии и ГПС на базе специальных станков с ЧПУ, для массового
производства - непереналаживаемые (жесткие) автоматические линии,
агрегатные и специальные станки, стоимость которых значительно ни-
же стоимости аналогичных ГПС.
Работая в составе роботизированного комплекса, промышленные ро-
боты выполняют следующие основные функции: загрузку и разгрузку
станка, смену инструмента, уборку стружки, взаимодействие с конвей-
ером, складом заготовок и готовой продукции и т.п. Объединяя в еди-
ный комплекс задачи автоматизации технологических процессов метал-
лообработки и вспомогательных операций, промышленные роботы яв-
ляются одним из главных звеньев создания современного высокопроиз-
водительного оборудования нового типа — ГПС, работающих с мини-
мальным участием человека.
14.2. РОБОТЫ, ПРИМЕНЯЕМЫЕ В СТАНКОСТРОЕНИИ
Применение автоматических манипуляторов — промышленных робо-
тов — позволяет заменить человека, занятого физическим трудом.
В станкостроении они применяются в первую очередь для автоматиза-
ции смены деталей и инструмента.
Промышленный робот - это переналаживаемая автоматическая маши-
на, состоящая из механизма, информационно-измерительной, у прав ля-
399
Различные типы роботов
Рис. 14.1. Классификация промышленных роботов
ющей и исполнительной систем и предназначенная для выполнения
механических действий в производственном процессе. Манипулятором
промышленного робота принято называть устройство, состоящее из ме-
ханизма с кинематической цепью, приводов и рабочего органа (напри-
мер, захватов) и предназначенное для имитации рабочих функций руки
человека. Промышленные роботы, манипуляторы и робототехнические
комплексы (РТК) делят на три вида (рис. 14.1) : автоматические, при-
меняющиеся в основном в промышленном производстве и станкостро-
ении; дистанционно-управляемые, работающие в экстремальных усло-
виях (высокие температуры, загазованность, радиоактивность), и руч-
ные, используемые для погрузочно-разгрузочных работ. Среди авто-
матических роботов-манипуляторов можно выделить четыре вида:
жестковстроенные, программируемые, адаптивные и ’’интеллектуаль-
ные”. Жестковстроенные манипуляторы содержат механические руки
(автооператоры) без перестраиваемых программных устройств и пред-
ставляют собой нулевое ’’дороботное” поколение. Остальные роботы
образуют три поколения, которые не сменяют друг друга, а существуют
параллельно и продолжают совершенствоваться — каждый в пределах
своего поколения.
Роботы первого поколения действуют по программе, которую легко
можно изменять, они не обладают техническими органами ’’чувств”,
т.е. не могут воспринимать внешний мир. Промышленные роботы перво-
го поколения предназначены для освобождения человека от неинтерес-
ного, монотонного, тяжелого физического труда. Роботы второго поко-
ления снабжены комплексом датчиков, работают по более совершенным
и сложным алгоритмам, в состоянии приспосабливаться к изменениям
окружающей среды и осваивать более сложные операции. Роботы треть-
его поколения - так называемые ’’интеллектуальные” — обладают по
сравнению с другими более совершенными системами обработки инфор-
мации и имеют возможность автономно, без вмешательства человека,
изменять свое поведение при изменении внешней обстановки.
4ПП
Дистанционно-управляемые роботы и манипуляторы делят на пять
родов: с командным управлением, когда оператор с помощью кнопок
или тумблеров управляет приводами каждого звена манипулятора;
копирующие, когда управление манипулятором осуществляет опера-
тор с помощью задающего устройства, кинематически подобного мани-
пулятору; полуавтоматические, в которых с помощью специализиро-
ванного вычислителя оператор задает требуемый набор алгоритмов
управления манипулятором; супервизорные, в которых все элементы
операций робота запрограммированы, а оператор имеет возможность
в зависимости от обстановки вмешаться и изменить программу; диало-
говые (интерактивные), в которых робот не только принимает коман-
ды оператора для исполнения, но и сам вырабатывает информацию для
принятия решения.
Ручные манипуляционные роботы делят на шарнирно-балансирные,
у которых в пределах грузоподъемности при любой величине груза и
любом расположении звеньев механизм находится в равновесии и опера-
тор, перемещая рукоятку манипулятора, вырабатывает сигналы управ-
ления приводами перемещения груза, и экзоскелетоны, представляющие
собой многозвенные механизмы, непосредственно сопряженные с рука-
ми или ногами человека, причем последние формируют лишь сигналы
управления, а перемещения производят двигатели, помещенные в соот-
ветствующие звенья механизма.
Создание промышленных роботов, управляемых от микро-УВМ,
требует в целом значительно меньших затрат по сравнению с затратами
на создание специализированного оборудования, не обладающего гиб-
костью при изменении конструкции изделий и алгоритма функциони-
рования. В настоящее время на предприятиях находят применение бо-
лее 10 тыс. роботов, действующих по управляющей программе.
По характеру выполняемых операций промышленные роботы делят
на две группы: производственные роботы, участвующие в технологи-
ческом процессе в качестве производящих или обрабатывающих уст-
ройств (сварочное производство, сборка, покраска), и подъемно-тран-
спортные роботы, выполняющие операции типа ’’взять — перенести —
положить” при обслуживании технологического оборудования.
Основные показатели, определяющие типы промышленных роботов:
грузоподъемность, число степеней свободы, характеристика рабочей зо-
ны, мобильность, погрешность позиционирования, система управления.
Грузоподъемность робота-манипулятора характеризуется максималь-
ной суммарной подъемной силой, развиваемой его ’’руками”. Число
степеней свободы равно количеству всех возможных координатных пе-
ремещений кисти 1 руки робота (рис. 14.2) без учета движения захва-
та детали. Рабочая зона робота характеризуется максимальным ради-
усом обслуживания от оси захвата до оси симметрии корпуса 2 робота,
а также перемещениями руки 3 и корпуса 4 манипулятора. Мобиль-
ность робота определяется его способностью совершать движения: гло-
401
Рис. 14.2. Основные движения рабочих органов робота
бальные У, региональные X, Z,<pxy, yyz, ipzx и локальные S. Глобаль-
ными называют движения, за счет которых робот перемещается на рас-
стояния, превышающие его размеры и размеры обслуживаемого обо-
рудования. Региональными называют движения захватов робота в раз-
личные зоны рабочего пространства, определяемые размерами звеньев
руки. Локальными называют движения захвата, соизмеримые с его раз-
мерами. Погрешность позиционирования характеризуется отклоне-
нием заданной позиции исполнительного механизма от фактической при
многократном повторении движения. Она может выражаться линейны-
ми и угловыми единицами. Система управления определяется устрой-
ствами управления робота.
Рассмотрим работу некоторых типовых промышленных роботов.
Подвесной промышленный робот мод. СМ40Ф2.80.01 (рис. 14.3) пред-
назначен для группового обслуживания станков с горизонтальной осью
шпинделя. Он управляется от системы ЧПУ типа УПМ-331, обладает
грузоподъемностью 40 кг и может обслуживать от одного до пяти
станков.
Каретка 1 промышленного робота перемещается по монорельсу 13
от электрогидравлического привода Ml, связанного с редуктором и
шестерней z!. Вокруг оси 2, жестко закрепленной на каретке, качает-
ся плечо 3 руки робота. Движение качания осуществляется электрогид-
равлическим шаговым приводом М2 через ведомую шестерню z2,
закрепленную на конце шарикового винта 4. Винт, вращаясь, придает
возвратно-поступательное движение шариковой гайке 5, шарнирно
402
Рис. 14.3. Конструкция робота
мод. СМ40Ф2.80.01
закрепленной на корпусе плеча руки.
В результате перемещения шарико-
вой гайки происходит качание плеча.
Вокруг неподвижно закрепленной
на плече 3 оси 6 качается локоть 7
руки. Его качание осуществляется
электро гидравлическим приводом
М3 через ведомую шестерню z3, ша-
риковый винт 8 и шариковую гай-
ку 9 аналогично описанному выше
качанию плеча.
В редукторах приводов каретки
и локтя применены электромагнит-
ные муфты УС1 и УС2, которые при
отключении питания осуществляют
торможение соответствующих органов. К локтю руки крепится голов-
ка 11, на которой размещены два гидроцилиндра. Гидроцилиндр 10
служит для зажима захватов, гидроцилиндр 12 — для перемещения
(вращения) пиноли головки с захватами.
Промышленный робот мод. СМ40Ф2.80.01 обладает четырьмя степе-
нями свободы. Управление перемещением каретки по монорельсу пово-
ротом руки в плечевом и локтевом суставах осуществляется от систе-
мы ЧПУ, управление вращением пиноли и зажимом-разжимом захватов
производится от команд цикловой автоматики. Максимальная скорость
перемещения подвижных органов робота 1,2 м/с. Робот может быть ис-
пользован для обслуживания группы станков при управлении от мини-
УВМ, а также при управлении от центральной ЭВМ сложной автомати-
зированной системой. По вызову одного из станков промышленный
робот перемещается по монорельсу и обслуживает этот станок. При на-
личии других вызовов УВМ производит расчет оптимального варианта
и в зависимости от конкретной ситуации направляет промышленный
робот в то место, где его обслуживание наиболее необходимо.
Пример промышленного робота напольного типа показан на рис. 14.4.
Такой робот предназначен для загрузки-разгрузки одного-двух станков,
оснащенных системами ЧПУ класса CNC. Робот модели Fanuc Robot
Model-З обеспечивает грузоподъемность 50 кг, число степеней подвиж-
ности — 5, система управления — позиционная. Движения по координа-
там Z, в, R, а, Р осуществляют электроприводы постоянного тока,
привод захвата руки — пневматический. Скорости перемещения по ко-
403
Рис. 14.4. Конструкция робота напольного типа
ординатам R, Z — 1 и 0,5 м/с соответственно; угловые скорости по
координатам 0, а равны 60 и 80 °/с соответственно. Объем памяти сис-
темы управления составляет 300—6000 точек.
Технические данные некоторых моделей промышленных роботов при-
ведены в табл. 14.1.
Таблица 14.1
Модель промышленного робота Грузо- Число Число про- грамми- руемых коорди- нат Основ- Систе- Погреш- ность позицио- нирова- ния, ± мм
подъ- емно- сть, кг степе- ней под- вижно- сти ной при- вод ма уп- равле- ния
МРУ-901 (СССР) 0,02 2 2 Э Ц 0,22
Универсал-5 (СССР) 5 6 4 Э П 1
РКТБ (СССР) 7 4 4 э П 1
Универсал-60 (СССР) 60 6 6 э-г П 0,3
СМ160Ф2.81.01 (СССР) 160 4 4 г П 0,5
Контур (СССР) 3 6 6 э-г К 3
HFP-1 (ВНР) 2 3 4 Э-nR п 1
РБ-241 (НРБ) 20 5 5 э П 1
PRO-30 (ПНР) 30 5 4 э П-К 0,4
404
Табл. 14.1 (продолжение)
Модель промышленного робота Грузо- подь- емно- сть, кг Число степе- ней под- вижно- сти Число про- грамми- руемых коорди- нат Основ- Систе- ной мауп- при- равлс- вод ния Погреш- ность позицио- нирова- ния, ± мм
Versatran F-FL (США) 110 7 7 Г П-К 1,27
Unimate 2000 В (США) 136 5 4 Г П-К 2,03
Кика-1Я6/60 (ФРГ) 100 3-6 4 Э-М К 1
Fanuc Robot Model-З (Япония) 50 5 5 Э-М П 1
Motohand (Япония) 70 3 3 Э П 1
М10П.62.01 (СССР) 10 6 5 Э-М П 0,5
М20П.40.01 (СССР) 20 5 4 Э-М П 1
Примечание. Привод: Пн - пневматический, Г - гидравлический, Э
электрический, М - магнитный; система управления: Ц - цикловая, П - позици-
онная, К - контурная.
143. СИСТЕМЫ УПРАВЛЕНИЯ РОБОТАМИ
Система управления роботами может быть представлена рядом ти-
повых вариантов (рис. 14.5). Схема управления станками Сот серий-
ных систем ЧПУ и промышленным роботом ПР от станочной системы
ЧПУ по жесткой программе показана на рис. 14.5,а. При обслуживании
нескольких станков система управления роботом должна оснащаться
таким же числом модулей ввода МВ с программами обслуживания
каждого из станков.
При автоматизации серийных станков-автоматов целесообразно при-
менение специализированной системы ЧПУ роботом СУР (рис. 14.5,6),
работающей от запоминающего устройства ЗУ, в котором содержится
ряд программ обслуживания станков.
Управление станками С и роботом ПР может осуществляться от мно-
гопрограммной системы ЧПУ - МПУ, построенной на базе мини-УВМ
(рис. 14.5,в). При управлении группой станков от центральной ЭВМ
(рис. 14.5,г) управление роботом может производиться через автоном^
ное управляющее устройство УУ непосредственно по программе, выда-
ваемой ЭВМ.
Система управления роботом от центральной УВМ показана на
рис. 14.6. Восьмизвенный манипулятор обладает возможностью плавно
перемещать схват по требуемой траектории и получает команды управ-
ления от иерархической системы управления. Верхний уровень этой сис-
темы построен на мини-ЭВМ типа М400, нижний — на микро-ЭВМ типа
”Электроника-60”. Верхний уровень осуществляет прием управляющей
программы и производит расчет траектории движения и вращательных
405
Рис. 14.5. Схемы управления роботом:
а - с модулями ввода; б — с запоминающим уст-
ройством; в - с микропрограммным устройством;
г - с автономным управляющим устройством
моментов приводов манипулятора, содержит накопитель на магнитном
диске. Нижний уровень выполняет линейную интерполяцию в интерва-
лах между расчетными значениями точек траектории движения. Этим
достигается комбинированный принцип управления роботом, позволя-
ющий вносить необходимые коррекции, отстраиваться от возмущающих
воздействий и перестраивать законы управления в зависимости от воз-
никающей ситуации.
Микропроцессорная система управления имеет магистрально-модуль-
ную структуру, состоящую из процессора, устройства памяти ОЗУ,
модулей ввода аналоговых сигналов, модулей вывода и связи с ми-
ни-ЭВМ.
Аналоговые сигналы oi датчиков положений и усилий преобразуют-
ся модулем ввода в цифровую форму и регистрируются. Модуль ввода
содержит аналоговый мультиплексор на 16 каналов и все необходимые
устройства системы связи (интерфейс) для подключения к шине мик-
ро-ЭВМ. Минимальная продолжительность периода смены информации
в модуле зависит от быстродействия процессора и объема программы
и составляет 10 мкс. Модуль вывода содержит восемь буферных регист-
ров для управления восемью приводами робота и интерфейс для под-
ключения к шине микро-ЭВМ. Модуль связи с соответствующими интер-
фейсами осуществляет связь между верхним и нижним уровнями уп-
равления.
Для расчета крутящего момента электропривода мини-ЭВМ содержит
цифровую модель механической части робота и решает уравнение Лаг-
ранжа второго рода. Это необходимо для выработки закона управления
406
Рис. 14.6. Система управления роботом от УВМ
приводом с учетом изменения приведенного момента инерции, завися-
щего от положения манипулятора.
Сигнал управления вырабатывается микро-ЭВМ. Для этого расчет
закона управления должен производиться за интервал времени’ Д/ на
порядок меньший, чем постоянная времени привода. Расчет требуемого
закона управления производится микро-ЭВМ по следующему алгоритму:
S'- = *i(gpZ - gt.) - k2(g. + k37. + Mp, (14.1)
где Sj - закон управления приводом для Лй опорной точки; к19к2,
к3 — коэффициенты; gpz-, g,, g^.^ ~ значения составляющих вектора
обобщенных координат расчетное и измеренное в опорной точке i и
предыдущей опорной точке i - 1; Ц — измеренное значение тока элек-
тропривода; Л/р — расчетное значение момента.
Значения коэффициентов кх — к3, координат gpl- и момента Мр
для уравнения (14.6) определяются в мини-ЭВМ в реальном масштабе
времени и вводятся в микро-ЭВМ через модуль связи. Значения /,• и
gj измеряются датчиками тока и положения соответствующего приво-
да и считываются поочередным программным опросом по командам
микро-ЭВМ. Микро-ЭВМ на интервале интерполяции рассчитывает проме-
жуточные точки gpzI, Мрл и реализует в этих точках алгоритм Sf.
Для управления роботами используются различные устройства. Для
управления роботом с ограниченными манипуляционными возможностя-
ми используются цикловые устройства позиционного управления
(например, моделей УЦМ-10, УЦМ-30, УЦМ-663). Движение в заданном
направлении в таких системах начинается с появлением сигнала опре-
деленной полярности, а прекращается при срабатывании соответству-
ющего конечного выключателя.
Для управления роботом со значительным числом точек позициони-
407
Рис. 14.7. Структурная схема устройства УПМ-552
рования находят применение числовые устройства позиционного управ-
ления, построенные по принципу синхронного микропрограммного авто-
мата с жестким циклом управления (например, модели УПМ-331, УПМ-
552, УПМ-772). Структурная схема устройств УПМ-552 (УПМ-772)
показана на рис. 14.7. Операционно-логический блок ОЛБ совместно с
микропрограммным автоматом МПА управляет всеми блоками, а так-
же осуществляет обработку логической информации. Операционно-ло-
гический блок сравнивает положение рабочих органов робота в текущее
время с заданным системой ЧПУ и через ЦАП и усилители мощности
УМ1 - УМ5(7) выдает управляющие команды на приводы робота. На
ЦАП подаются также сигналы из операционно-логического блока с пуль-
та обучения ПО. Командная информация с пульта обучения ПО и с
пульта управления ПУ записывается в режиме обучения в оперативную
память, откуда для длительного хранения она может быть занесена на
Магнитную ленту кассетного накопителя КНМЛ. Информация от стан-
ков и другого оборудования принимается и выдается блоком ввода-вы-
вода информации БВВИ.
Фазовые датчики обратной связи ДОС дают информацию о положении
рабочих органов робота ПР. Их сигналы формируются формирователя-
ми фазы ФФ1 - ФФ5(7) и преобразуются в цифровые сигналы пре-
образователями фаза - цифра ПФЦ1 - ПФЦ5 (7).
Устройство УПМ-772 управляет роботом со следящим приводом и в
отличие от устройства УПМ-552 обслуживает большее число рабочих ор-
ганов робота, а также осуществляет программу загрузки-разгрузки спе-
408
циальной тары. Устройствами серии УПМ обеспечиваются автоматичес-
кая отработка программы, поиск кадра, ручное управление, обучение,
контроль программы. Для анализа сигналов от робота и обслуживаемо-
го оборудования используются команды безусловных и условных
переходов.
Алгоритм управления позиционным устройством типа УПМ-772
(рис. 14.8) отражает последовательность операций при работе в основ-
ных режимах, задаваемых с пульта управления. Режим ’’Программа”
ПРГ соответствует автоматической отработке программы в цикле или
по кадрам. По макрокомандам блоков 2, 3 производится контрольное
суммирование информации кадра. Если в/ программе не обнаружено
ошибки, то рассылается негеометрическая (управляющая и технологи-
ческая) информация по рабочим регистрам устройства 4 и производит-
ся анализ содержимого информации кадра (команд переходов и задание
их признаков) 5. Затем осуществляется анализ команд коррекции 6
и их выполнение 7, при котором положение манипулятора изменяется
на шаг между ячейками упорядоченной тары. После выполнения команд
коррекции движения производится переход к отработке перемещений
манипулятора МН — блок 8 и выполнению технологических и вспомо-
гательных команд - блок 9. Затем осуществляется анализ условий
переходов (блоки 10, 11), увеличивается на +1 содержимое счетчика
кадров СЧК (блок 15) и отрабатывается следующий по номеру кадр
(блок 5). Если выполняется команда перехода, то в счетчик кадров
СЧК записывается номер заданного кадра (блоки 11, 72). Одноразовое
выполнение команды с переходом в исходное состояние (блок 7) или
циклически повторяющееся определяют макрокоманды блоков 13, 14.
Режим ’’Поиск кадра” ПК находит требуемый кадр программы при
задании искомого номера зоны 16, 17 для поиска ее при обращении к
кассетному накопителю на магнитной ленте КНМЛ. Найденная информа-
ция переписывается в ячейки памяти 18, и на цифровом табло пульта
управления появляется номер данного кадра.
Режим ’’Обучение” (блок 20) обеспечивает ручное управление мани-
пулятором с записью набранного на переключателях кадра в ПОЗУ
(блок 27), а затем переписи массива ПОЗУ в КНМЛ (блок 22), для
чего задействуется ветвь алгоритма 3-10. Производится вычисление
контрольной суммы кадра и запись ее в ячейку памяти текущего кадра.
Режим ’’Ручное управление” РУ (блок 23) служит для управления пе-
ремещением манипулятора с выносного пульта обучения ПО (блок
24), при этом могут производиться перемещения исполнительных орга-
нов манипулятора и движения захвата. Основные технические данные
устройств серии УПМ приведены в табл. 14.2.
Для перемещения исполнительных органов робота по сложной траек-
тории применяются устройства контурного управления, например типа
УКМ (табл. 14.2). Функциональная схема такого устройства модели
УКМ-772 (рис. 14.9) содержит микро-ЭВМ типа ”Электроника-60”,
409
состояние
Нет
:3 Проверка 'информации
на контрольную сумму
Е Рассылка
^геометрической информации
. я I
Анализ команд переходов и
I задание признаков переходов
R--------1--------Нет
У^^Режим коррекции^^—у
_7------- ЛТ?-------
Выполнение
|команд коррекции
г— 8"" - ...
Вычисление и
| отработка перемещений МН
г-9-.......1.
Выполнение технологических
I и вспомогательных команд
Нет
Обучение
Нет
Да
о верка переходов
г 7 Да Т
[Выполнение команд переходов
и изменение состояния СЧК
г-15*
Увеличение
содержимого СЧК на *7
Нет
16
Да
г-17.
Задание
номера зоны БУ К НМЛ
г-18.
Перепись
информации зоны В память
г-19
Нахождение
искомого кадра с Выдачей
номера на индикацию
Нет
20
Обучение
г—21------=—
Запись
программы работы МН
В память устройства
Перепись
программы из памяти
на магнитную ленту
Нет
Да
МНс ПО
анец программы
икл Выполни
ния программы
Нет
Рис. 14.8. Схема алгоритма управления позиционным устройством типа УПМ-772
Нет
Да
Г-22-
1
программоноситель — кассетный накопитель на гибких магнитных лен-
тах КНПЛ, рассчитанный на объем информации до 12,8 Мбит, и пульт
обучения ПО. Прием сигналов от кодовых датчиков обратной связи
ДОС производится с помощью модулей сопряжения (интерфейсная
плата). Программирование осуществляется методом обучения при ис-
пользовании линейной интерполяции. Для этого роботом управляют в
410
Таблица 14.2
Основные техничес- кие данные Модель и устройства
УПМ-331 УПМ-552 УПМ-772 УКМ-55 2 УКМ-772
Позиционные Контурные
Тип привода Диск- ретный Следящий Следящий Следя- щий Следя- щий
Количество рабо- чих органов 3 5 7 5 7
Датчик обратной связи Нет СКТД-6465Д СКТД-6465Д Потенцио- метр СПЧ-8 Кодовый 15-разряд- ный дат- * чик
Точность позицио- нирования, ед. диск- ретности ± 1 ±1 ±1 ±1 ±1
Объем оперативной памяти, К байт 0,5 0,64 0,76 2 2
Количество команд 60 60 60 16 48
для робота
ручном режиме с пульта обучения ПО, проводят его по точкам требу-
емой траектории и записывают координаты этих точек в память. Управ-
ляющее устройство УУ после обработки информации центральным про-
цессором ЦП через блок управления приводом БУЛ дает команды на
соответствующие приводы робота.
Устройства модели УКМ позволяют производить плавную установку
рабочих органов робота в исходную позицию для выполнения програм-
мы, а также могут запоминать и отрабатывать несколько программ.
От датчиков На управление Связь с роботом
обратной электро- и внешним
связи приводам оборудованием
ГЭВМ „Элект-
роника-60"
I Г///Л '
1 \^\ kffll I
логический ]
й . ^интерфейс) \ |_______
ППЧ\ ' • Плптп имтепА
Модуль
Ввода
{Канал,
ЭВМ |
ф Адаптер
Плата интер- сип
фейсная ДОС\
| Внутренняя ^магастрал^
Модуль
вывода
УУ
Контроллер
КНМЛ
Плата интер\ ПЗУ
фейсная Пи (в к)
ОЗУ
(8К)
Рис. 14.9. Функциональная схема устройства УКМ-772
411
Устройство УКМ-772 управляет семью рабочими органами робота, тип
привода — следящий электро гидравлический, датчики обратной связи -
15-разрядные, разгон и торможение привода производятся за 0,25—2 с.
Устройства УКМ (табл. 14.2) управляют роботами, предназначенными
для автоматизации сложных сборочных операций, сварки, окраски.
14А. УПРАВЛЕНИЕ ГРУППОЙ СТАНКОВ ОТ УВМ
При объединении станков в единую автоматизированную систему и
их групповом управлении повышаются производительность, гибкость
использования технологического оборудования, улучшаются условия
эксплуатации оборудования, повышается надежность работы. Такое
групповое управление станками осуществляется от центральной УВМ,
на которую возлагается расчет и хранение управляющих программ, рас-
пределяемых по запросам от станков. Система представляет собой ком-
плекс с иерархической структурой до пяти рангов (рис. 14.10), объеди-
няющий индивидуальные системы станков с ЧПУ. Центральная УВМ
является устройством высшего — 5-го ранга. Такая система в целом сог-
ласно ГОСТ 20523-80 является системой группового ЧПУ станками
(DNC). При групповом управлении одно устройство более высокого
ранга обслуживает несколько устройств более низких рангов, при этом
возможны различные варианты функциональных схем управления.
Система с многопрограммным интерполятором МПИ (рис. 14.10,а)
состоит из ЭВМ, обеспечивающей хранение управляющих программ
для работы всех станков участка ... Сл, распределение этих программ
по запросам станков, интерполирование и передачу команд на устрой-
ства станочного управления УУ (электроприводы, муфты, электромаг-
ниты) . Возможность одновременного управления несколькими станками
требует высокого быстродействия ЭВМ и ее работы в режиме разделения
времени. По этой схеме все основные функции ЧПУ решает ЭВМ, а уст-
ройства станочного управления УУ выполняют задачи формирования и
усиления команд, поступающих от многопрограммного интерполятора
МПИ.
Система управления от центральной УВМ обеспечивает более высокую
экономичность, чем при индивидуальном программном управлении.
Так, при 10 станках стоимость управления одним из них оказывается
вдвое меньше стоимости индивидуальной системы ЧПУ. Однако требует-
ся более высокая надежность системы, так как при отказах МПИ пре-
кращается работа всех станков участка.
Система управления может быть сформирована из автономных уст-
ройств ЧПУ (рис. 14.10,0), состоящих из мини-ЭВМ и устройств типа
NC, программа которым задается от центральной УВМ. Последняя произ-
водит хранение, распределение и покадровую выдачу программы. На
автономные устройства ЧПУ типа NC возлагаются интерполяция, форми-
рование и усиление сигналов, поступающих на исполнительные органы
412
Рис. 14.10. Типовые системы централизованного управления от УВМ:
а - с микропрограммным интерполятором; б - с мини-ЭВМ; в - с централь-
ной УВМ
станков. При такой структуре стоимость системы ЧПУ больше, чем при
управлении от индивидуальной УВМ, и при сбое в работе центральной
УВМ останавливаются станки участка. Положительным является то, что
подобная структура может быть создана на основе существующих стан-
ков с ЧПУ без крупных капиталовложений на новые устройства управ-
ления. Это определяет применение такой структуры лишь на первых
этапах создания систем управления группой станков от центральной
УВМ.
Более высокой системной надежностью обладает структура
(рис. 14.10,в), состоящая из устройств ЧПУ типа CNC у каждого станка
и центральной ЭВМ, обеспечивающей хранение, распределение и переда-
чу соответствующих программ в память устройств ЧПУ (CNC).
Применение микро-ЭВМ в составе каждой системы ЧПУ типа CNC
непосредственно у станков позволяет сравнительно просто организовать
обмен информацией между оператором и ЭВМ при обработке первой
детали, обеспечивает введение различного рода коррекций, что расши-
ряет технологические возможности систем ЧПУ, позволяет применять
адаптивные системы управления. Центральная ЭВМ работает только во
время передачи программы в память системы ЧПУ CNC и не участвует
в процессе обработки детали. Стоимость систем ЧПУ типа CNC опреде-
ляется в первую очередь стоимостью микро-ЭВМ.
В промышленности находит применение устройство ЧПУ типа 2У32-61
для управления станками, выполненное на базе микро-ЭВМ типа ’’Элек-
троника НЦ-03Т”. Для управления сложными станками и обрабатыва-
ющими центрами со следящими, замкнутыми по положению электро-
приводами подач применяется устройство ЧПУ типа 2С42, выполненное
на базе микро-ЭВМ типа ”Электроника-60”.
В основе рассмотренных структур, из которых формируется робо-
тизированное производство, лежит роботизированная гибкая производ-
ственная ячейка (ГПЯ), выполняющая основные технологические опе-
рации. Пример компоновочной схемы ГПЯ показан на рис. 14.11. Два
413
Рис. 14.11. Роботизированная гибкая
производственная ячейка
токарных станка ТС, оснащенных
ЧПУ, обслуживает робот ПР, рабо-
тающий по командам устройства
управления роботом УУР. Робот бе-
рет заготовки с транспортного уст-
ройства загрузки ТУЗ, устанавлива-
ет их на токарных станках, а после
обработки снимает со станков и вы-
гружает в транспортное устройство разгрузки ТУР. Загрузочно-разгру-
зочные операции транспортных устройств обеспечивает устройство уп-
равления транспортом УУТ. В зависимости от быстродействия робота ПР,
технологического цикла обработки и габаритов станков один робот мо-
жет обслуживать два, три и более станков.
14.5. МНОГОУРОВНЕВАЯ ИЕРАРХИЧЕСКАЯ СИСТЕМА УПРАВЛЕНИЯ
СТАНКАМИ ОТ УВМ
Несколько согласованно работающих ГПЯ составляют участок или
автоматическую линию. В свою очередь несколько роботизированных
гибких производственных участков (ГПУ), управляемых от централь-
ной УВМ, образуют более высокий уровень управления цехом (ГПЦ).
Пример системы автоматического группового управления станками от
центральной УВМ (рис. 14.12) соответствует ранее рассмотренной струк-
турной схеме рис. 14.10,в. Станки С оснащены системами ЧПУ с интер-
поляторами Я, которые через фотосчитыватели ФС и аппаратуру сопря-
жения линии передачи с линейными интерполяторами ЛИ связаны с ка-
нальными коммутаторами ЛК*центральной УВМ.
В помещении вычислительного центра находится центральная УВМ,
процессор которой содержит ОЗУ и центральное управляющее устрой-
ство ЦУУ, а основной комплект внешних устройств ввода-вывода ВВ
присоединен к мультиплексному каналу МК. Селекторный канал СК
для расширения функциональных возможностей системы связан с ос-
новным комплектом запоминающих устройств — барабаном ЗУМБ,
магнитной лентой ЗУМЛ, диском ЗУМД и коммутатором селекторно-
го канала КСК.
Коммутаторы мультиплексного канала КМК сопряжены с канальны-
ми коммутаторами ЛК. Устройства сопряжения с интерполяторами ЛИ
оборудованы визуальными индикаторами, показывающими номер уп-
равляющей программы, передаваемой на станок, а также требуемое ко-
личество деталей, которые должны быть обработаны по этой про-
грамме.
414
Центральная УВМ используется для расчета управляющих программ
станков. Рассчитанная управляющая программа выводится на перфо-
ленту. При помощи автономного графопостроителя Г производится
контроль правильности рассчитанной УП управляющей программы,
окончательный контроль которой производится на станке при его авто-
номной работе от перфоленты. Проверенные управляющие программы
образуют библиотеку управляющих программ системы ЧПУ, часть ко-
торой передается в ЗУ на магнитных лентах ЗУМ Л.
Управляющие программы, предназначенные для передачи на станки,
вводятся в ОЗУ УВМ. За каждым станком закреплена определенная зо-
на ОЗУ, связь между которой и системой центрального управляющего
устройства ЦУУ станка производится по команде, подаваемой от устрой-
ства сопряжения с интерполятором конкретного станка. Специальная
диспетчерская программа системы ЧПУ, находящаяся в ОЗУ УВМ, уп-
равляет этой связью.
Через мультиплексный канал МК, канальный коммутатор КМК и
линию передачи ЛК производится передача управляющей программы
из ОЗУ УВМ в систему ЧПУ типа CNC станка с ЦУУ. При управлении
станком от системы ЧПУ фотосчитыватель ФС блокируется. При ем-
кости ОЗУ 64 К может быть подключено для обслуживания до 60 еди-
ниц программного оборудования, в этом случае центральная УВМ орга-
низует последовательные во времени соединения систем ЧПУ станков
со своим ОЗУ.
Мультиплексный канал УВМ может иметь скорость передачи ин-
формации до 66 000 символов в секунду, что позволяет управлять бо-
лее чем 60 станками с ЧПУ и встроенными интерполяторами без преры-
вания процесса резания, вызываемого задержками передачи информа-
ции. Функциональные возможности групповой системы могут быть
расширены при подключении к центральной УВМ долговременных за-
поминающих устройств большой емкости для размещения в них биб-
лиотеки управляющих программ. Долговременное запоминающее уст-
ройство на магнитных дисках ЗУ МД в 10 и более раз расширяет объем
памяти ОЗУ. При необходимости магнитные диски с управляющими
программами можно хранить вне запоминающего устройства.
Улучшение функциональных возможностей достигается подключе-
нием к центральной УВМ через мультиплексный канал аппаратуры пе-
редачи данных АПТ по телефонным и телеграфным линиям. Аппарату-
ра передачи данных по телефону представляет собой коммутатор, с по-
мощью которого к ЭВМ подключается большое количество телетай-
пов Т, работающих в качестве внешних устройств по вводу-выводу ин-
формации. Через телетайп, находящийся у станка, от системы ЧПУ ти-
па CNC может быть передана вся информация об использовании станка
за смену. С помощью телетайпа, установленного в заготовительном це-
хе, передается информация о необходимой номенклатуре заготовок,
потребляемых за рабочую смену. Телетайпы, находящиеся на складах
415
\ЗУМБ
К станкам и другому оборудованию с ЧПУ
КМК I-1 КМК J—L КМК I-- КМК
ШППГ 7ПППГ нЖЖ
Транспортная система
К пунктам присоединения телетайпов у станков
__J_____________I___________I________I_____
Рис. 14.12. Система управления станками от центральной УВМ
Г~м~1
Процессор
| ОЗУ |-» ЦУУ
мк СК
’И31*
ЛИ
ФС г
1 м 1 ЛИ
И Ф£| И
инструментов и приспособлений, передают информацию о требуемых
инструменте и приспособлениях. Аппаратура передачи данных по теле-
фону используется также для передачи оперативной информации к
центральной УВМ с участка станков, вспомогательных участков, от на-
чальника цеха и диспетчера завода. Например, мастер может изменить
по телетайпу порядок работы того или иного станка, пустить станок на
416
К Ору tun ИВМ
обработку другой детали. С помощью телетайпа, находящегося у стан-
ка, технолог-программист может отлаживать программу станка. Он
имеет кроме текстовой информационной обратной связи на печата-
ющем устройстве телетайпа информационную обратную связь от самого
станка. Это позволяет немедленно осуществлять коррекцию управля-
ющей программы и наблюдать за ее результатами.
417
Вместо телетайпов могут быть использованы экранные пульты (ал*
фа скопы), имеющие клавиатуру для ввода алфавитно-цифровой инфор-
мации. На экране электронно-лучевой трубки высвечивается текстовая
информация размером до печатной страницы. Пульты очень удобны для
корректировки текста, оператор может убрать часть его, ввести новый,
раздвинуть его внутри строки и т.д.
Оборудование групповой системы может быть дополнено подключе-
нием к центральной УВМ дисплея Д через мультиплексный канал. При-
менение дисплея дает возможность вводить в центральную ЭВМ инфор-
мацию об обрабатываемой детали для расчета программы путем графи-
ческого нанесения геометрической информации о детали на экран элек-
тронно-лучевой трубки дисплея с помощью светового пера. Корректи-
ровка управляющей программы осуществляется оператором путем ви-
доизменения на экране дисплея геометрических размеров изображен-
ной детали, инструмента, траектории его движения.
Коммутатор селекторного канала КСК центральной УВМ может
связать ее с любой системой ЧПУ типа CNC. Через коммутатор КСК
может быть организована передача управляющих программ станков,
рассчитанных на других УВМ. Наконец, через групповые коммутаторы
мультиплексного канала поступают команды для управления промыш-
ленными роботами ПР, транспортной системой цеха и автоматизации
вспомогательных операций по обслуживанию станков.
Система управления роботом строится из набора программных моду-
лей, которые компонуются в определенную конфигурацию програм-
мой-координатором УВМ в зависимости от выполняемых роботом дей-
* ствий. Вычислительная машина должна обеспечивать управление несколь-
кими роботами, которые могут работать автономно или действовать
согласованно. Если в группу роботов, управляемых ЭВМ, входят робо-
ты с цикловой системой управления, то между ними устанавливается
иерархия. Роботы с высшим рангом иерархии управляются от ЭВМ и в
свою очередь командуют включением цикла операций роботов низшего
ранга, действующих по жесткой программе.
14.6. ТЕНДЕНЦИИ РАЗВИТИЯ АСУ ТП МЕТАЛЛООБРАБОТКИ
И ПЕРСПЕКТИВЫ РЕАЛИЗАЦИИ ГИБКИХ
АВТОМАТИЗИРОВАННЫХ ПРОИЗВОДСТВ
Создание гибких (быстропереналаживаемых) автоматизированных
производств (ГАП) с управлением от микро- и мини-ЭВМ, а также от
мощных ЭВМ на более высоком иерархическом уровне коренным об-
разом меняет характер созидательной деятельности человека, автомати-
зируя трудоемкие процессы и имитируя не только двигательные, но и
отдельные интеллектуальные действия человека.
Обеспечивая внедрение трудосберегающей (’’безлюдной”) техноло-
гии, ГАП вызывают определенные социальные последствия, проявля-
418
ющиеся по-разному в социалистической и капиталистической системах
производства. Как было показано ранее, несколько роботизированных
гибких производственных ячеек (модулей), работающих согласован-
но, образуют гибкую производственную линию (ГПЛ), гибкий произ-
водственный участок (ГПУ) или гибкую производственную систему
(ГПС). В свою очередь несколько ГПЛ, ГПУ или ГПС в сочетании с
вспомогательным оборудованием при согласованном управлении об-
разуют гибкий производственный цех (ГПЦ), позволяющий оператив-
но выполнять переналадку на выпуск изделий заданной номенклатуры.
Наконец, комплекс ГПЦ (металлообрабатывающих, кузнечно-прес-
совых, сборочных и др.) в сочетании с вспомогательным оборудованием
при согласованном управлении представляет собой гибкий производ-
ственный завод (ГПЗ), переналаживаемый на выполнение технологи-
ческих процессов по выпуску плановой продукции. Реализация ГПЗ —
дело ближайшего будущего.
Как показывает отечественный и зарубежный опыт, производитель-
ность ГПС в 1,5-3 раза выше суммарной производительности такого
же числа отдельных станков с ЧПУ. Применение роботизированных
ГПС позволяет уже сегодня примерно в 5 раз сократить количество
обслуживающего персонала. Появилось новое научное направление
’’механотроника” (от сокращения слов ’’механика” и ’’электроника”),
обеспечивающее разработку и исследование прогрессивной технологии
на основе ГАП. Ведутся работы по созданию комплекса измеритель-
ных средств, позволяющих в автоматическом режиме следить за ходом
процесса обработки и точностью выпускаемых деталей. Создаются вы-
сокоточные электроприводы с адаптивным управлением. Разрабаты-
ваются управляющие вычислительные комплексы на базе микро- и
мини-ЭВМ с развитым программным обеспечением. Вопросы создания
систем, основанных на применении средств управляюще-вычислитель-
ной техники, и программно-математическое обеспечение этих систем
приобретают все более главенствующее значение при разработке ГАП.
Поскольку построение ГАП базируется на системном применении робо-
тотехники, микропроцессорной техники, современных устройств элек-
тромеханики, особенно важной при их внедрении и эксплуатации стано-
вится роль специалиста по электроприводу и автоматизации промышлен-
ных установок и технологических комплексов.
СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Автоматизация типовых технологических процессов и промышленных уста-
новок: Учеб, пособие для вузов/А.М. Корытин, Н.К. Петров, С.Н. Радимов,
Н.К. Шапарев. Киев-Одесса: Вища школа, 1980. 372 с.
2. Государственная система промышленных приборов и средств автоматиза-
ции: Методическое пособие для инженерно-технических работников/Под общей
ред. Г.И. Ковалерова. Каталог, ЦНИИТЭИ приборостроения, 1981.
3. Ивоботенко Б .А., Ильинский Н.Ф., Копылов И.П. Планирование эксперимен-
та в электротехнике. М.: Энергия, 1975. 184 с.
4. Козырев Ю.Г. Промышленные роботы: Справочник. М.: Машиностроение,
1983. 376 с.
5. Комплексные системы управления электроприводами тяжелых металлоре-
жущих станков/Н.В. Донской, А.А. Кириллов, Я.М. Купчан и др.: Под ред. А.Д. Поз-
деева. М.: Энергия, 1980. 288 с.
6. Кузнецов МЛ., Волчкевич Л.И., Замчанов Ю.П. Автоматизация производ-
ственных процессов: Учебник для вузов/Под ред. ГА. Шаумяна. М.: Высшая шко-
ла, 1978. 431 с.
7. Михелькевич В.Н. Автоматизация типовых технологических процессов и про-
мышленных установок. Куйбышев: Куйбышевский политехнический ин-т,
1978 . 59 с.
8. Мясников В А., Вальков В.М., Омельченко И.С. Автоматизированные и авто-
матические системы управления технологическими процессами. М.: Машинострое-
ние, 1978. 232 с.
9. Программное управление станками: Учебник для машиностроительных ву-
эов/ВЛ. Сосонкин, О.П. Михайлов, ЮА. Павлов и др.; Под ред. ВЛ. Сосонкина.
М.: Машиностроение, 1981. 398 с.
10. Рипе Я.А., Савельев БА. Анализ и расчет надежности системы управления
электроприводами. М.: Энергия, 1974. 248 с.
11. Справочник по обработке металлов резанием/ФЛ. Абрамов и др. Киев:
Техн1ка, 1983. 239 с.
12. Шапарев Н.К. Автоматизация типовых технологических процессов металло-
обработки. Расчет и проектирование. Киев-Одесса: Вища школа, 1984. 312 с.
Дополнительная литература
13. Адаптивное управление технологическими процессами/Ю.М.Соломенцев,
В.Г. Митрофанов, С.П. Протопопов и др. М.: Машиностроение, 1980. 536 с.
14. Аналоговые и цифровые интегральные микросхемы: Справочное пособие/
С.В. Якубовский, НА. Барканов, Л.И. Ниссельсон и др.; Под ред. С.В.Якубов-
ского. Mj Радио и связь, 1984. 432 с.
15. Андрющенко В.А. Следящие системы автоматизированного сборочного обо-
рудования. Л.: Машиностроение, 1979. 246 с.
16. Башарин А.В., Новиков В А., Соколовский Г.Г. Управление электроприво-
дами: Учеб, пособие для вузов. Л.: Энергоатомиздат, 1982. 392 с.
420
17. Борисенко ВД., Плотников В В., Талон ИЛ. Электроника-6 О/Электрон-
ная промышленность. 1979. №11-12. С. 63.
18. Васенко А.А. Развитие микропроцессоров и микро-ЭВМ семейства ’Элек-
троника НЦ” на основе комплексно-целевых программ//Электронная промыш-
ленность. 1979. №11-12. С. 13.
19. Ильин В.А. Телеуправление и телеизмерение. Учеб, пособие для вузов. М.:
Энергия, 1974. 408 с.
20. Каган Б.М. Электронные вычислительные машины и системы: Учеб, пособие
для вузов. М.: Энергоатомиздат, 1985. 522 с.
21. Ключев В.И. Теория электропривода: Учебник для вузов. М.: Энергоатомиз-
дат, 1985. 560 с.
22. Козырев Ю.Г., Капаев Е.М., Чиганов ВЛ. Унифицированные устройства
программного управления промышленными роботами. Методические рекоменда-
ции по применению в станкостроении. М.: ОНТИ, ЭНИМС, 1980. 24 с.
23. Корытин А.М., Шапарев Н.К. Оптимизация управления металлорежущими
станками. М.: Машиностроение, 1974. 200 с.
24. Колосов В.Г., Мелехин В.Ф. Проектирование узлов и систем автоматики и
вычислительной техники: Учеб, пособие для вузов. Л.: Энергоатомиздат, 1983.
256 с.
25. Лученко В.Е., Соломахин Д.В., Григорьев В.Е. Принципы построения и кон-
струкции многокоординатных шаговых электроде игателей//Тр. Московского
энергетического ин-та. 1979. Вып. 440. С. 31-37.
26. Математическая статистика/В.М. Иванова, В.Н. Калинина, Л.А. Нешумова
и др. М.: Высшая школа, 1981. 368 с.
27. Микропроцессорные комплекты интегральных схем. Состав и структура:
Справочник/В.С. Борисов, А. А. Васен ков, Б.М. Малашкевич и др.; Под ред.
А.А. Васенкова, В.А. Шахнова. М.: Радио и связь, 1982. 192 с.
28. Микросхемы и их применение: Справочное пособие/В.А.Батушев, В.Н. Ве-
ниаминов, В.Г. Ковалев и др. М.: Радио и связь, 1983. 272 с.
29. Михелькевич В.Н. Автоматическое управление шлифованием. М.: Машино-
строение, 1975. 304 с.
30. Многокоординатный дискретный электропривод/Под ред. Б.А. Ивоботен-
ко и Н.Ф. Йльинского//Тр. Московского энергетического ин-та. 1979. Вып 440.
С. 88.
31. Развитие микро-ЭВМ семейства ’Электроника-С5 ” и систем на их основе/
В.Я. Кузнецов, Ю.А. Масленников, Э.А. Никитин и др .//Электронная промышлен-
ность. 1979. №11-12. С. 9.
32. Румшинский Л.З. Математическая обработка результатов эксперимента.
М.: Наука, 1971. 192 с.
33. Современные промышленные роботы: Каталог/Под ред. Ю.Г. Козырева,
Я.А. Шифрина. М.: Машиностроение, 1984. 152 с.
34. Справочник по автоматизированному электро приводу/Под ред. В.А. Ели-
сеева, А.В. Шинянского. М.: Энергоатомиздат, 1983. 616 с.
35. Справочник по средствам автоматики/Под ред. В.Э.Низе и И.В. Антика.
М.: Энергоатомиздат, 1983. 504 с.
36. Срибнер Л.А. Программируемые устройства автоматики. Киев: Техжка,
1982. 176 с.
37. Тутевич В.Н. Телемеханика: Учеб, пособие для вузов. М.: Энергия, 1973.
384 с.
38. Энциклопедия кибернетики. Т. 1/Под ред. В.М. Глушкова. Киев: Главная
редакция УСЭ, 1974 . 607 с.
39. Янтовский А.В. Управление электроавтоматикой современных станков
с ЧПУ. М.: НИИМАШ, 1981. 64 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Автоматизированные системы управления:
анализ функционирования безотказность 218 222
выбор технологических средств 212
долговечность 222
обеспечение информационное 153,214
отказ 222
прибыль от внедрения 241
ремонтопригодность 222
производством (АСУП) 16
срок окупаемости 243
технологией (АСУТП) 5
электроприводом (АСУЭП) 10
Автооператор 400
Адаптация 247
Алгебра двоичная 124
Алгоритмы:
автоматизации каналов 115
компенсации возмущений 121
оптимизации 142,149
программного изменения параметров 123
стабилизации 115
управления 113, 247, 277
функционирования 259,277
Аналого-цифровые преобразователи (АЦП):
поразрядного кодирования 198
последовательного счета 198
считывания 200
Аппроксимация 314
Б
Базовые логические элементы:
диодно-транзисторные (ДТЛ) 160
на МОП транзисторах 162
резисторно-транзисторные (РТЛ) 159
транзисторно-транзисторные (ТТЛ) 160
Быстродействие 172
В
Воздействие:
возмущающее 278,312,316
422
управляющее 245,257
Время:
машинное 285, 336,399
правки шлифовального круга 391
смены инструмента 356,383
Г
Глубина резания 247, 254,300
Государственная система приборов (ГСП) 163
Градиентные методы 149
Датчики:
диаметра 334
износа инструмента 281,363
момента 302, 304
мощности 284, 292, 294, 299, 396
положения 175, 325, 396
температуры 271
Двигатель:
вентильный 275
линейный 274,276
шаговый 232
Деформации упругие 257, 306, 308
Дешифраторы 185
Диапазон регулирования 263, 313
Добротность по скорости 263,326
Ж
Жесткость:
системы 261,306
упругого элемента 306
3
Запаздывание 257
Запоминающие устройства:
динамические 174
перепрограммируемые 176
постоянные 175
статические 172
Затраты приведенные 254,386
Звено:
апериодическое 262,300
безынерционное 325
колебательное 296
корректирующее 316
И
Идентификации задачи 47
Идентификации методы:
аналитические 50
корреляционного анализа 69
минимума суммы квадратов отклонений 62,68
423
разностных уравнений 73
факторного эксперимента 69
экспериментальные 60
Иерархия АСУ 15» 16
Измерение:
активной мощности 291
крутящего момента 303
силы резания 301
Индуктосин 346
Интегральные схемы 346
степень интеграции 158
условные обозначения 159
Интерполятор 342,412,414
Информация:
априорная 25,26
текущая 13
управляющая 13
Информационная модель:
управляющего устройства 13
человека оператора 13
К
Кадастр измеряемых величин 163
Квантование сигналов 31,32
Кодирование сигналов:
неравномерное 40
экономичность 37
Коды:
последовательный 36
помехозащищенный 44
• Грея 42
двоично-десятичный 41
дополнительный 41
обратный 41
параллельный 31
позиционный 40
прямой 41
Шеннона-Фано 40
Контроллер 204,348
Копирование:
контурное 323
объемное 323
Коррекция:
упреждающая 317
Коэффициент:
плавности 263,264
преобразователя 298,315
системы 313
Коэффициент линейной корреляции 86
424
Коэффициент передачи:
датчика 312
корректирующего звена 318
процесса резания 257, 261, 309, 318
Критерий:
адекватности 92
значимости коэффициентов 91
однородности дисперсии 39
оптимальности 256
Л
Линейного программирования метод 143
М
Манипулятор 400
Матричная модель 55
Методы анализа надежности:
коэффициентный 227
по среднегрупповым значениям интенсивности отказов 226
с использованием данных эксплуатации 226
Микропроцессоры 200
Микропроцессорные комплекты 201
Микро-ЭВМ 205
СМ 1800 208
структура 207
'Электроника НЦ” 207
’’Электроника С5” 207
Модель:
аналоговая 299,305
корректирующего звена 300
математическая 263
процесса резания 260,261,309
узла скорости резания 287
электропривода 313
Модель технологического объекта:
многомерная детерминированная 66
- недетерминированная 77
одномерная в динамике 73
- в статике 61
Моделирование технологических систем, в том числе:
длительности операции надежности 109
износа инструмента 108
обработки детали 109
- результатов моделирования 111
параметров исходной заготовки 107
Модели технологического цикла:
граф состояний 99
комбинационные 95
последовательностные 96
стохастические 99
425
таблица состояний 98
циклограмма 97
Момент:
инерции 264,298
крутящий 303,496
резания 250
Мощность:
активная 295
резания 249, 255,283, 295,314
холостого хода 321,396
Мультиплексоры 188
Н
Наблюдатель адаптивный 309,311
Нагрузка 300
О
Обратная связь:
по скорости 296
по току 300
технологическая 296, 301,315
Ограничения по показателям 225
Оптимизация металлообработки:
по минимуму приведенных затрат 370, 386
по производительности 256, 375, 385
по себестоимости 256,375
п
Память:
внешняя 169
магнитная 169
оперативная 169
полупроводниковая 171
регистровая 169
сверхоперативная 169
Передаточная функция 257,262, 296, 309
Поверхность отклика 145,149
Податливость системы 257
Показатели эффективности металлообработки:
при точении 256, 375, 378
при фрезеровании 256, 383
при шлифовании 256, 391
Постоянная времени:
датчика 299,310
корректирующего звена 298, 398
процесса резания 257,258, 261,299, 309, 318
Погрешность:
динамическая 327
позиционирования 402
скоростная 326
статическая 326,315
426
Преобразователь динамический 389
Преобразователь кода 186
Приемистость 272
Пропускная способность канала связи:
без помех 42
с помехами 44
Пространства состояний метод 55
р
Расчет АСУТП металлообработки резанием:
динамический статический 297 312
Регистры Регулятор: 189
положения 289
скорости 269
тока 269,289
экстремальный Режимы работы УВМ: 269,289, 387, 388
комбинированное управление 157
прямое цифровое управление 158
сбора данных 156
советчика 157
Режимы резания 249,251
Резольвер 348
Робот 400,403
С Себестоимость 278,380
Семейства агрегатного комплекса средств вычислительной техники на микроэлектронной элементной базе (АСВТ-М):
М-40 210
М-400 210
М-6000, М-7000 210
М-4030 Семейства малых ЭВМ: 211
СМ-1; СМ-2 211
СМ-3; СМ-4 О гнал ы: 211
аналоговые 30
дискретные 31
Сила резания 248,251
Симплекс-метод Синтез дискретных автоматов: 145
комбинационные 128
последовательностные 133
Система:
гибкая производственная 399
контурная 354
позиционная 352
427
счетноимпульсная 352
фото-импульсная 341
шаговоимпульсная 340
Система счисления:
восьмеричная 38
двоичная 38
шестнадцатеричная 38
Системный подход 214
Система стабилизации:
момента 303, 304
мощности 291,295,319, 321
силы резания 301, 309
скорости резания 288, 290, 320, 362
температуры резания 303, 320
технологического параметра 313
упругих деформаций 306, 320
Система ЧПУ 335
Скорость:
износа инструмента 261
окружная 333
резания 247, 250,251,286, 290
угловая 247, 255, 266, 331
Случайных величин законы распределения 81
Случайных величин параметры:
дисперсия 83
математическое ожидание 83
среднеквадратичное отклонение «3
Способы повышения надежности АСУ ТП 233, 235
Стадии разработки АСУ ТП 216,217
Станки 244,322
Степени свободы 401,403
Стойкость инструмента 248,253, 254,390
Стохастические модели технологических систем 104
Структура промышленного производства 7
Сумматоры 183
Счетчики цифровые:
вычитающие 192
двоично-десятичные 194
суммирующие 191
реверсивные 193
Т
Температура резания 283
Теорема Котельникова 33
Теория массового обслуживания 105
Термопара 283
Термо-ЭДС 283,305
Точность:
обработки 308
статическая 315
428
Триггеры:
асинхронные 177
задержки (Д) 179
синхронные двухступенчатые 179
- одноступенчатые 178
со счетным входом (Т) 179
универсальные (УК) 180
У
Упреждающая коррекция 296,299
Уровни АСУ ТП:
комплексный 15
локальный 15
узловой 15
Устройства сравнения 184
Ф
Формула Шеннона 19
ц
Целевая функция 140
Цифроаналоговые преобразователи (ЦАП):
с эталонными резисторами 196
с резистивной сеткой 196
Э
Экономически целесообразный уровень надежности 228
Экстремаль 383
Экстремум 378J^6i 386, 388
Электропривод:
асинхронный \ 270
вентильный 267,275
главного движения 267,281
двухкоординатный $74
импульсный 268,269
комплектный 267,268
тиристорный 167
транзисторный 267
Энтропия 19
Эффективность металлообработки 278, 383, 393
ОГЛАВЛЕНИЕ
Предисловие........................................................
ЧАСТЬ I. ПРИНЦИПЫ ПОСТРОЕНИЯ АСУ ТП................................
Глава первая. Современное промышленное производство и АСУ ТП.......
1.1. Общие положения ...........................................
1.2. Классификация и структура современных технологических объектов
управления......................................................
1.3. Место и роль электропривода в АСУ ТП.......................
1.4. Назначение, характеристика и структура современных АСУ ТП..
Глава вторая. Переработка технологической информации ..............
2.1. Общие положения............................................
2.2. Постановка задачи. Управляемость технологического процесса.
2.3. Получение информации о технологическом объекте управления..
2.4. Преобразование технологической информации .................
2.4.1. Виды и форма сигналов................................
2.4.2. Кодирование сигналов.................................
2.5. Передача и защита информации от помех......................
23.1. Пропускная способность канала связи без помех.........
2.5.2. Пропускная способность канала связи с помехами и принци-
пы построения помехозащищенных кодов.........................
Глава третья. Идентификация технологических объектов управления....
3.1. Задачи идентификации.......................................
3.2. Аналитические методы получения математических моделей техно*
логических объектов ............................................
3.2.1. Модели элементов.....................................
3.2.2. Модели многосвязных систем...........................
3.3. Экспериментальные методы получения моделей технологических
объектов управления.............................................
3.3.1. Постановка задачи....................................
3.3.2. Идентификация одномерных детерминированных объектов . . .
3.3.3. Идентификация многомерных объектов...................
3.3.4. Динамическая идентификация...........................
3.3.5. Экспериментальные модели недетерминированных объектов . .
3.4. Формализация дискретных последовательностей операций (технологи-
ческих циклов) ............................ ....................
3.4.1. Структура формирования технологического цикла........
3.4.2. Комбинационные детерминированные модели. Таблицы истин-
ности .......................................................
3.4.3. Последовательностные детерминированные модели........
3.4.4. Стохастические мо дел и..............................
3.43. Моделирование сложных недетерминированных объектов . . . .
3
5
5
5
6
9
11
17
17
18
25
29
30
36
42
42
44
46
47
50
50
52
60
60
61
66
73
77
93
93
95
96
99
104
430
Глава четвертая. Алгоритмы управления...............................113
4.1. Задачи управления технологическими объектами................114
4.2. Алгоритмы стабилизации заданного параметра .................115
4.2.1. Инвариантность по управлениям в многомерных системах .... 115
4.2.2. Стабилизация по отклонению от неконтролируемых возму-
щений .......................................................121
4.3. Алгоритмы программного управления заданной последовательностью
операций.........................................................123
4.3.1. Элементы теории дискретных автоматизированных устройств 124
4.3.2. Синтез комбинационных автоматов...................... 128
4.3.3. Синтез последовательностных автоматов. Конечные автоматы 133
4.4. Алгоритмы оптимального управления...........................140
4.4.1. Постановка задачи оптимального управления в АСУ ТП...140
4.4.2. Оптимизация многомерных линейных объектов в статике .... 142
4.4.3. Оптимизация нелинейных объектов.......................149
Глава пятая. Технические средства, применяемые в АСУ ТП.............151
5.1. Сведения о структуре технических средств ХСУ ТП ........... 153
5.1.1. Виды обеспечения АСУ ТП.............................. 153
5.1.2. Общая характеристика и классификация основных узлов УВМ
5.1.3. Принципы организации связи УВМ с технологическим объек-
том управления ............................................. 155
5.1.4. Основные режимы работы УВМ в составе АСУ ТП ..........156
5.2. Элементная база технических средств.........................158
5.3. Информационное обеспечение АСУТП............................163
5.3.1. Государственная система приборов......................163
5.3.2. Принципы построения первичных измерительных преобразова-
телей (датчиков технологических параметров) .................165
5.4. Устройства хранения и переработки информации................168
5.4.1. Запоминающие устройства...............................168
5.4.2. Триггеры..............................................176
5.4.3. Арифметические и логические устройства ...............182
5.4.4. Устройства связи с объектом ..........................195
5.5. Средства дискретной управляющей техники.....................200
55.1. Микропроцессоры и микро-ЭВМ ...........................200
55.2. Агрегатные системы.....................................209
5 5.3. Принципы выбора технических средств...................212
Глава шестая. Особенности проектирования АСУ ТП.....................214
6.1. Основные принципы построения АСУТП..........................214
6.2. Стадии разработки АСУ ТП.................................... 216
6.3. Особенности проектирования АСУ ТП различного исполнения....
Глава седьмая. Надежность АСУ ТП....................................221
7.1. Постановка задачи. Основные понятия.........................221
7.2. Расчет надежности в процессе проектирования.................225
7.3. Технико-экономический уровень надежности АСУ ТП........... 228
7.4. Способы повышения надежности АСУ ТП и ее элементов..........232
Глава восьмая. Экономические вопросы проектирования АСУ ТП и ее эле-
ментов .............................................................235
8.1. Основные источники экономической эффективности АСУ ТП......235
8.2. Учет экономической эффективности АСУ ТП при разработке .....238
8.3. Методика расчета экономической эффективности.......... . . . 239
ЧАСТЬ 11 . АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНО-
ЛОГИЧЕСКИМИ ПРОЦЕССАМИ МЕТАЛЛООБРАБОТКИ.............................244
Глава девятая. Технологические основы металлообработки резанием.....244
9.1. Общие положения............................................244
431
9.2. Функциональные принципы построения АСУ металлообработкой 245
9.3. Типовые технологические процессы металлообработки...........247
9.4. Оптимизация режимов резания.................................257
9.5. Моделирование типовых процессов металлообработки ...........257
9.6. Технические требования к электроприводам металлорежущих станков 263
Глава десятая. Системы стабилизации режимов металлообработки........276
10.1. Общие положения............................................276
10.2. Алгоритмы управления системами стабилизации режимов металло-
обработки .......................................................277
10.3. Типовые схемы систем стабилизации..........................284
10.4. Системы с адаптивным наблюдателем..........................309
ЮЛ. Расчет параметров систем стабилизации........................312
10.6. Сравнительная оценка систем стабилизации ..................318
Глава одиннадцатая. Сннхронно-следящие копировальные системы метал-
лорежущих станков...................................................321
11.1. Общие положения............................................321
11.2. Классификация следящих систем электрокопировальных метал-
лорежущих станков................................................322
11.3. Принципы построения следяще-копировальных систем...........324
11.4. Взаимосвязанные системы согласованного перемещения узлов
станков..........................................................331
Глава двенадцатая. Системы программного управления металлорежущими
станками............................................................335
12.1. Общие положения............................................335
12.2. Классификация и области применения систем ЧПУ металлорежущи-
ми станками .................................................... 336
12.3. Типовые структуры систем ЧПУ . . . ....................... 340
12.4. Элементы систем ЧПУ ...................................... 342
12Л. Программируемые контроллеры............................... 348
12.6. Позиционные и контурные устройства........................ 352
12.7. Микропроцессоры и мини-УВМ в типовых структурах ЧПУ....... 358
12.8. Подготовка программ для станков с ЧПУ..................... 365
Глава тринадцатая. Система оптимизации режимов металлообработки..... 373
13.1. Общие положения........................................... 373
13.2. Назначение и области применения систем оптимизации режимов
металлообработки................................................ 374
13.3. Алгоритмы управления системами оптимизации станков........ 375
13.4. Самонастраивающиеся системы в АСУ металлообработки........ 387
Глава четырнадцатая. Роботизированные комплексы металлообработки 398
14.1. Области применения роботизированных комплексов............ 398
14.2. Роботы, применяемые в станкостроении ..................... 399
14.3. Системы управления роботами............................... 405
14.4. Управление группой станков от УВМ......................... 412
14.5. Многоуровневая иерархическая система управления станками от
УВМ........................................’.................... 414
14.6. Тенденции развития АСУ ТП металлообработки и перспективы реа-
лизации гибких автоматизированных производств................... 418
Список литературы.................................................. 420
Предметный указатель................................................422