Текст
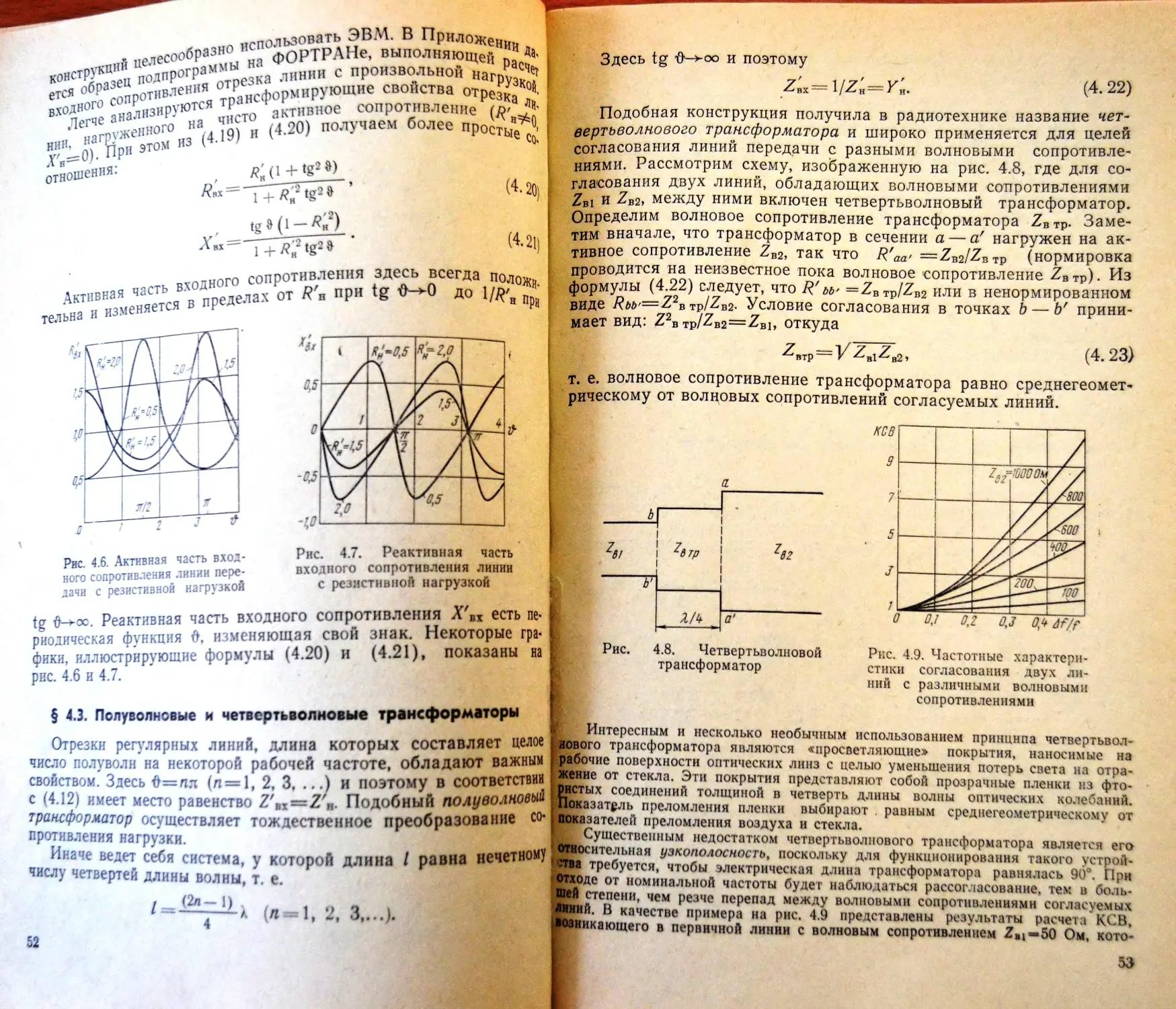
6*2*3
РАДИО ТЕХНИЧЕСКИЕ
ЦЕПИ
С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
§ 6.5. Элемент Гюйгенса.................................. . 7
§66 Возбуждение линии передачи системой дискретных источ- °
ников. Принцип действия направленного ответвителя . . . 77
§ 6.7. Усилитель с распределенным усилением...............; ‘‘
Задачи и упражнения к гл. VI.............................
Глава VII. Нестационарные процессы в линиях передачи............... ,
§ 7.1. Влияние характеристик линии передачи на искажение пе-
редаваемого импульса. Групповая скорость ................... &
§ 7.2. Оценка искажений импульсных сигналов....................
§ 7.3. Волновые уравнения для напряжений и токов при произ-
вольном характере изменения процессов во времени • . . да
§ 7.4. Решение волновых уравнений для линии без потерь по ме-
тоду Даламбера.................................................
§ 7.5. Исследование нестационарных процессов в линиях пере-
дачи операционным методом...................................9g
Задачи и упражнения к гл. VII..........................Ю1
Глава VIII. Колебательные системы, образованные отрезками линий
передачи..............................................ЮЗ
§ 8.1. Собственные колебания короткозамкнутого отрезка линии
передачи...................................................ЮЗ
§ 8.2. Свойство ортогональности системы собственных функций
резонатора без потерь .................................... Ю8
§ 8.3. Более простой подход к задаче вычисления собственных
частот. Резонансные условия ............................... щ
§ 8.4. Возбуждение одномерного резонатора сосредоточенными
источниками. Функция Грина резонатора без потерь . . . . щ
§ 8.5. Влияние омических потерь на характер собственных коле-
баний в резонаторе. Понятие комплексных собственных
частот....................................................119
§ 8.6. Входная проводимость резонатора вблизи резонансной
частоты...................................................123
Задачи и упражнения к гл. VIII......................125
Глава IX. Нерегулярные линии передачи...............................127
§ 9.1. Общие сведения......................................127
§ 9.2. Дифференциальные уравнения линии передачи с плавным
изменением погонных параметров......................127
§ 9.3. Нерегулярная линия передачи экспоненциального типа . . 129
§ 9.4. Волны в нерегулярных линиях передачи с медленным из-
менением погонных параметров..............................134
Задачи и упражнения к гл. IX.........................137
Глава X. Связанные линии передачи...................................139
§ 10.1. Понятие распределенной связи между линиями передачи.
Математическая формулировка задачи о связанных ли-
ниях ..................................................... 139
§ 10.2. Нормальные волны в системе двух связанных линий пере-
дачи ..........................................................
§ 10.3. Эффекты, возникающие при сложении нормальных волн 143
Задачи и упражнения к гл. X..........................145
Приложения......................................................ё 146
Список рекомендуемой литературы.....................................150
С. И. БАСКАКОВ
РАДИОТЕХНИЧЕСКИЕ
ЦЕПИ
С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
Допущено Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов радиотехнических
специальностей вузов
МОСКВА «ВЫСШАЯ ШКОЛА», 1930
ББК 32.84
Б27
УДК 621.396
г
Рецензенты:
Кафедра теоретических основ
радиотехники Киевского политех-
нического института
Кафедра схемотехники Москов-
ского института электронного ма-
шиностроения
Читальный зал
учеби,_ и литера™
Б’рад°‘технИотеские цепи с распределенными параметрами:
Учеб, пособие для вузов, —М.: Высш, школа, 1980. 152 с„
ил.
30 к.
В книге излагается теория распределенных радиотехнических цепей; на примере
одномерных структур демонстрируются основные методы теории волновых процес-
сов; рассматриваются распределенные колебательные системы, а также нерегуляр-
ные и связанные линии передачи.
Предназначается для студентов радиотехнических вузов и факультетов; может
быть полезна инженерам, работающим в области техники СВЧ.
30401-191
Б -----------91-80
001(01)—80
2402020000
6Ф2
ББК 32.84
^33 ПО
----------------Святэелув Иванович Баскаков
ТУЛЬГИОГп’гп?^ ’ РАДИОТЕХНИЧЕСКИЕ
ТУЛЬСКОГО ПОЛИТЕ л ИИЧЕСКОГвТ псПт,
ИНСТИТУТА
ЦЕПИ
С РАСПРЕДЕЛЕННЫМИ
АРАМЕТРАМИ
Изд. № ЭР-271
Формат 60X90«/,i.
Объем 9.5 усл. печ.
Г
Московская-----
Т-060^
Редактор И г п
А- "• ,Х»о«ее,„Иав •« .ЛЯ
Редактор А. “к" НС'"«™Р Т М. Ск.ордо.а,
А Нестерова. Корректор В. В. Кожуткияа'
ИБ № 2062
БУмН°типНаЛР '5-10.79 п
Изп, л 9,47 у, 21 Гарнитчп=>Подп- в печать 19.03.80.
Издательство «Высш, А‘ Л’ тираж75Р0ПпИТературная- Печать вы--
«вская типогпол Шая школа» Мпр„ 5 000 экз. Зак. № 2910. Цена 30 к
По 8 Союзполи п ж ’ К‘61’ винная ул., д. 29/14
8’ "ОЛНГРаФии и ЙжнойРИ ^Дарственном комитете ССС
й торговли, Хохловский пер.т '
Злательство «Высшая школа», 1980
ПРЕДИСЛОВИЕ
В настоящем учебном пособии систематически излагается тео-
рия распределенных радиотехнических цепей. .Материал книги тес-
но связан со специфическими задачами современной радиотехники
и радиоэлектроники. Содержание пособия соответствует разделам
курсов «Основы теории цепей» и «Техника сверхвысоких частот»
действующих программ МВ и ССО СССР для радиотехнических
специальностей.
В первых пяти главах книги изложен тот минимум сведений
о распределенных цепях, который необходим студенту для усвое-
ния последующих инженерных курсов. В остальных главах демон-
стрируется применение математических методов, в частности тео-
рии дифференциальных уравнений, к решению прикладных задач
в области техники СВЧ.
Материал пособия ориентирует читателя на использование
средств современной вычислительной техники в учебном процессе.
В приложении к книге имеются образцы программ для ЭВМ, по-
зволяющих выполнять трудоемкие расчетные операции.
Каждая глава содержит задачи и ответы к ним. Одни задачи
приведены для того, чтобы студент мог самостоятельно контроли-
ровать качество усвоения учебного материала, другие содержат
информацию, которая позволяет связать теоретические положения
с практическими проблемами современной радиотехники. Это дол-
жно способствовать выработке у студентов навыков самостоятель-
ной творческой работы, что на сегодняшнем этапе развития совет-
ской высшей школы приобретает особое значение в свете решений
XXV съезда КПСС о развитии научной работы в вузах.
Автор выражает искреннюю признательность рецензентам —
коллективам преподавателей кафедры схемотехники Московского
института электронной техники (зав. кафедрой проф. Г. И. Весе-
лов) и кафедры теоретических основ радиотехники Киевского по-
литехнического института (зав. кафедрой проф. Я. К. Трохимен-
ко). Их замечания и советы оказали автору неоценимую помощь.
Отзывы о книге просьба направлять по адресу: Москва К-51,
Неглинная ул., 29/14, изд-во «Высшая школа».
Автор
ВВЕДЕНИЕ
. пгновой разнообразных процессов, происходящИх
физическом основе Р является существование спещ!,
радиотехнических Ус^ Называемой электромагнитным По±’
ческой формы ма I м’аксвелл сформулировал основные уравн£
В конце XIX в. ди lx- к ые подытожили всю совокупность Эм
^ сведений об электромагнитных явлениях и установи,
лирически»сведен магнИтного поля. Оказалось, что вс
-“TuLieHM электромагнитные поля, изменяющиеся во вреае.
„ез «сключенм р ' траняются в пространстве, причем ско-
пость°светг в вакууме (с=2,99793-10» м/с) является предельно
возможтой скоростью перемещения в пространстве любых мате-
Р"аСтотго°готоряОВанализ любых электромагнитных систем должен
сводится к расчету векторов электромагнитного поля, например
напряженностей электрического поля Е и магнитного поля Н
в каждой точке пространства и в любой момент времени. Такой
расчет является исчерпывающим с точки зрения классической фи-
зики и проводится с помощью методов электродинамики. Несмотря
на полноту и всеобъемлющий характер этого подхода, ему свойст-
венен один недостаток, заключающийся в том, что при современном
уровне развития математики и вычислительных средств довести
до конца решение уравнений Максвелла удается лишь для ограни-
ченного класса физических систем с достаточно простой геометри-
ческой конфигурацией. При расчете электромагнитных полей вну-
три такого сложного радиоаппарата, как, например, телевизион-
ный приемник, возникли бы непреодолимые трудности ввиду ги-
гантского объема вычислений. Если даже допустить наличие вы-
числительной машины, способной справиться с такой задачей, то
все равно проблема не была бы решена, поскольку все существен-
ные связи между процессами в системе были бы погребены в море
числовой информации.
Однако в ряде случаев все необходимые для практики сведения
о свойствах и поведении электромагнитных систем и устройств
П°Лучить’ не увлекая методов электродинамики, а с по-
в ппп^пзекотоРых интегральных характеристик, таких, как ток
дельными^тпТ И напРяжения (разности потенциалов) между °*
мым к (Ьизичр™М“ системы- Основным требованием, предъяви
ством с^вокупнпет СИСТеме’ К0Т0Рая может быть описана посреА
рических оазмепоп токов и напряжений, является малость ге0* .
ных колебаний РпаепппСраВНеНИЮ с длиной волны электромагн
Щена система. ’ Р Р стРаняющихся в той среде, в которую п
4
Это условие можно сформулировать иначе, а именно как тре-
бование, чтобы запаздывание колебаний в одних точках системы
по отношению к другим составляло пренебрежимо малую долю
характерного временного интервала, в качестве которого выбира-
ют период гармонических колебаний, соответствующих определя-
ющей части спектра процесса.
Сформулированные требования относительной малости геомет-
рических размеров дают основание выделить в составе системы
те области пространства, в которых сконцентрирован преимущест-
венно один из видов энергии. Так, элемент, в котором наблюдается
концентрация энергии электрического поля, принято называть кон-
денсатором. Если же элемент системы служит накопителем энер-
гии магнитного поля, то его называют индуктивной катушкой.
Другой важнейший элемент электрических цепей, в котором проис-
ходит необратимый процесс преобразования энергии электромаг-
нитного поля в тепловую энергию, называют резистором или ак-
тивным сопротивлением. Наконец, существуют генераторы (источ-
ники) — области пространства, характеризующиеся тем, что в них
энергия неэлектромагнитного происхождения трансформируется в
энергию электромагнитного поля.
Благодаря пространственной локализации перечисленных эле-
ментов электромагнитная система может быть представлена мыс-
ленно как совокупность некоторых генераторов, конденсаторов,
индуктивных катушек, резисторов, соединенных друг с другом си-
стемой идеальных проводников, единственным назначением кото-
рых является обеспечение условий для протекания токов проводи-
мости. В этом случае принято говорить о существовании квазиста-
ционарной электрической цепи.
Рассматривая свойства таких цепей, следует подчеркнуть две
их принципиальные особенности.
Во-первых, при описании работы цепей можно полностью
абстрагироваться от геометрической конфигурации элементов и
соединительных проводников. Это дает возможность рассмотрения
абстрактных моделей реальных цепей, называемых принципиаль-
ными схемами. Физические линейные размеры также не играют
роли при изучении квазистационарных цепей. Поэтому теоретиче-
ски все конденсаторы, имеющие емкость 1 мкФ, полностью иден-
тичны.
Вторая особенность, существенно связанная с первой, состоит
в том, что для квазистационарных цепей напряжения между от-
дельными точками схемы допускают однозначное определение. Как
известно, под напряжением между точками 1 и 2, произвольно
расположенными в пространстве, понимают криволинейный инте-
грал
2
Z71|2=jErfl, (В.1)
1
вычисленный вдоль некоторой кривой, соединяющей точки 1 и 2.
Если ДаНН“"
то говорят,
С формулой
nv точками 1 и
соблюдается, если
интеграла вида (
того контура.
пЯ, не зависит от выоора пути интегрИров
Ести данный интеграл не „ем начальнОи и конечной •
а определяется тольк° П° поле в СИСТеме обладает свойств
а 0 1 -- что Электр,,ч“ ние. определяемое в соответст»
(В 1 ' Swe логенш.альност,, электрического
имеет место обращение в куль криволинейно*'
(В") вычисленного вдоль произвольного зама*
X Еб/1=О.
(В.2)
В то же время из элементарной теории электромагнетизма Из.
вестей закон Фарадея
</Ф
dt ’ (М
гле Ф — магнитный поток, пронизывающий контур.
Поэтому в переменных полях напряжение и разность потенциа-
лов не могут быть отождествлены. Исключение составляют лишь
Join изменяющиеся медленно в том смысле, как это было указано
ранее. Здесь можно приближенно считать, что правая часть (В.З)
равна нулю.
Все прочие электромагнитные системы, относительно которых
нельзя принять условий квазистационарности, называют волно-
выми системами.
Для них характерны следующие особенности:
а) отсутствуют пространственные области с преимущественно»
локализацией либо электрического, либо магнитного поля. Поэто-
му волновые системы часто называют системами с распре-
деленными параметрами, подчеркивая тем самым их от-
личие от сосредоточенных квазистационарных систем;
б) поскольку пространственная протяженность волновых си-
стем сравнима с длиной волны электромагнитных колебаний, а час-
то и превосходит ее, существенными становятся эффекты запазды-
вания, такие, как конечное время распространения сигналов вдоль
системы;
в) ввиду быстропеременного характера колебаний оказывается
невозможным отождествление понятий напряжения и разности по-
тенциалов. Напряжение лишается свойства геометрической инва-
риантности, и вся структура описания явлений посредством законов
Кирхгофа оказывается несправедливой.
е1пр Ггиь К определенным электромагнитным системам возник
ввемрни XIX в. под влиянием ряда актуальных для того
графных а чятрСКИХ Зад14’ связанных с передачей вначале теле-
стояния. ’Первым "й^леФ°ННЬ1х сообщений на значительные рас-
тромагнитных рИртрбЪеКТ0М изУчения среди .распределенных элек
мер, двумя паратлрпкСТаЛа линия передачи, образованная, напрг *
6 У паРаллельными проводниками при условии, что протя-
женность системы вдоль оси сравнима с длиной волны передавае-
мых колебании. Подобные линии передачи в то время назвали
«длинными линиями». Интересно отметить, что первые работы
Кирхгофа и Томсона (Кельвина) в этом направлении были прове-
дены до того, как Максвелл установил общие законы электромаг-
нетизма. Суть рассуждений создателей первых теорий линий пере-
дачи состояла в следующем. Достаточно малый по сравнению
с длиной волны отрезок линии рассматривался как некоторый ква-
зистационарный четырехполюсник. Внутренняя структура этого
четырехполюсника выбиралась таким образом, чтобы можно было
учесть следующие явления: 1) накопление энергии магнитного по-
ля за счет протекания тока по проводникам линии; 2) запасание
энергии электрического поля ввиду наличия некоторой емкости
между проводниками линии; 3) превращение части электромагнит-
ной энергии в тепло, вызываемое как сопротивлением проводников,
так и несовершенством изоляции. Количественными характеристи-
ками линии при таком подходе являются первичные параметры —
индуктивность отрезка линии длиной 1 м или погонная индуктив-
ность Lit Гн/м, погонная емкость Сь Ф/м, погонное сопротивление
потерь в проводниках Ri, Ом/м, и погонная проводимость изоляции
G], См/м (индекс означает, что эти величины характеризуют отре-
зок линии единичной длины).
Динамическими переменными, необходимыми для описания со-
стояний элементарных четырехполюсников, служат обычные токи
и напряжения. Устремляя к нулю длины элементарных отрезков,
можно свести задачу к некоторым дифференциальным уравнениям,
решения которых соответствуют волновому процессу, наблюдаемо-
му в линии.
Развитие методов электродинамики, основанных на уравнениях
Максвелла, дало возможность еще раз вернуться к классической
задаче о волнах в линии передачи. Строгий анализ показал, что
решения, полученные по методу Кирхгофа и Томсона, имеют при-
ближенный характер. Для их применения необходимо, во-первых,
чтобы поперечные размеры линии были малы по сравнению с дли-
ной волны передаваемых колебаний. Во-вторых, конфигурация про-
водников, из которых образована линия, должна быть такова,
чтобы по одному из них ток от генератора поступал к нагрузке,
а по другому возвращался в генератор. Именно при этих условиях
электромагнитные поля в системе приобретают характерный вид,
называемый поперечной или Т-в одной (от англ, transverse
electromagnetic wave). Основной чертой Т-волны является отсут-
ствие в ней продольных составляющих векторов электромагнитно-
го поля Е и Н.
Наряду с этим было показано, что эффекты направленной пе-
редачи волн возможны в линиях принципиально иной структуры —
так называемых полых волноводах, представляющих собой
металлические трубы, обычно прямоугольного или круглого сече-
ния. Эти линии передачи, широко применяемые в радиотехнике
для передачи колебаний с частотами выше 1000 МГц, уже не мо-
писаны простой квазистационарной
-о-1"° сравне""ю'т—
сложной струн . теория линий передачн не по_
намт’ , НР менее квазистационарн ам. Во-первых, линии
Т«своей актуальности п ^“Хьзуются (см. гл. II). Во-
те₽»,ачн с Т-волнами "овсе“ , п,сса дают возможность построить
S лини» передачи модели, пригодные для „зу-
™t:,kohhSp^ npottKCOB в передающ,“систе'
мах любой природы. ,
Глава I
ТЕОРИЯ РЕГУЛЯРНОЙ ЛИНИИ ПЕРЕДАЧИ
ПРИ ГАРМОНИЧЕСКОМ ВНЕШНЕМ ВОЗДЕЙСТВИИ
§ 1.1. Вывод уравнения состояния
регулярной линии передачи
Линии передачи, геометрическая конфигурация которых, а так-
же свойства заполняющего их материала остаются неизменными
вдоль продольной координаты, называют регулярными. Пред-
положим, что в неограниченно протяженной ” вдоль оси z линии
передачи с помощью каких-либо внешних источников (генерато-
ров) возбуждены гармонические колебания с частотой со. Так как
изучаемые линии принадлежат к классу линейных, систем, для ко-
торых справедлив принцип суперпозиции, то, зная реакцию на воз-
действие гармоническими колебаниями с различными частотами,
всегда можно найти результат произвольных воздействий, приме-
нив известные методы рядов или интегралов Фурье.
Выведем уравнения состояния регулярной линии передачи, по-
нимая под ними математические соотношения, устанавливающие
законы изменения комплексных амплитуд £7 (z) и I (z) вдоль про-
дольной координаты. При этом будем иметь в виду следующее.
Как упоминалось во введении, линия передачи является рас-
пределенной системой и поэтому к ней, строго говоря, непримени-
мы обычные законы электрических цепей, например законы Кирх-
гофа. Однако если представить себе линию в виде последователь-
ного соединения элементарных отрезков длиной Az каждый, то
в пределе при Az->0 такие четырехполюсники могут быть описаны
методами, принятыми в теории цепей. При этом уравнения состоя-
ния линии должны приобрести вид уже не алгебраических, а диф-
ференциальных уравнений.
Пусть исходные данные в виде первичных параметров линии
передачи Lb Сь Ri и Gi известны. Тогда можно ввести погонное
комплексное сопротивление
и погонную комплексную проводимость
играющие первостепенную роль во всей излагаемой далее теории.
Смысл этих величин состоит в том, что они позволяют охаракте-
ризовать физические свойства отдельных элементарных четырех-
полюсников. Например, можно изобразить математическую модель
элементарного четырехполюсника в виде Г-образной структуры
оЛя последовательное сопротивление
, о включающей в себя (использование П-образ.
(р«с- 1Л)’ JLnvroniyio проводимое^ енными проводимостями
Z^z И ШУНТИЮ в^мя симметрично * анал0ГИчным результатам),
ной модели с д J каждая приведе хполЮСНИКП( отображающие
величиной >13 / ментарные че ь4каскадно, попытаемся,
*'е" о“резк»™-™“ законов Кирхгофа, сосга.’
малые г
вить общее уравнение состояния та-
кой дискретной модели. Обозначим
посредством символов (7(z) и (7(2+
+ Az) комплексные амплитуды на-
пряжений соответственно на входе
и на выходе элементарного четырех-
полюсника, который отвечает теку-
щему значению продольной коорди-
наты z (см. рис. 1.1). Аналогичную
символику примем для комплексной
амплитуды тока в линии. На осно-
вании второго закона Кирхгофа, об-
ходя внутренний контур в направ-
Рис. 1.1. К выводу телеграфных
уравнений
лении, указанном на рисунке, имеем тождество
^(г+Дг)-(7(г)+^/(и) Дг = 0.
Далее, из первого закона Кирхгофа с учетом направлений токов,
принятых за положительные, следует, что
/(г)=/(г-|-Дг)-|-К1(7(2-]-Дг) Дг, (1.2)
или с точностью до малых величин порядка (Az)2
/(и) = /(г+Дг) + Г1(7(г)Дг. (1.3)
Равенства (1.1) и (1.3) могут быть эквивалентно представлены
следующей системой разностных уравнений:
J£(£+M-t7(z)=_Zi/(z) 1
Дг (1-4)
/(г + АДг~/(г) = ” Y3
Совершим теперь операцию предельного перехода при Az->0,
в результате чего равенства (1.4) перейдут в систему двух обыкно-
венных дифференциальных уравнений с постоянными коэффици-
ентами:
Подобные уравнения впервые были изучены при исследовании
явлений в линиях дальней телеграфной связи. Поэтому их назы-
вают телеграфными уравнениями. Они играют фунда-
ментальную роль в теории волновых процессов и, в частности, при
изучении процессов в линиях передачи самой разнообразной при-
роды.
Если продифференцировать по z обе части уравнений системы
(1.5), то последнюю можно свести к одному дифференциальному
уравнению второго порядка как относительно напряжения, так и
относительно тока:
~-ZJ\U=0, (1.6)
az2
^--2^1=0. (1.7)
dz*
В теории волновых процессов уравнения вида (1.6) и (1.7) но-
сят название уравнений Гельмгольца*. Ясно, что решать
следует только одно из этих уравнений, поскольку вторая неизвест-
ная величина найдется из системы (1.5) простым дифференцирова-
нием. По структуре уравнения (1.6) и (1.7) аналогичны тем, кото-
рые имеют место в теории гармонического осциллятора, подобного
маятнику или колебательному контуру. Принципиальное отличие
состоит в том, что уравнения Гельмгольца определяют не времен-
ные, а пространственные характеристики процесса.
Уравнения Гельмгольца можно вывести не из телеграфных уравнений, а не-
посредственно, записав условие электрического равновесия одной из элементар-
ных ячеек, изображенных на рис. 1.1, по методу контурных токов:
' (г + Дг) “
откуда
/ (-г + Аг>) + (* —,А£) — _ z у f = о.
(Дг)2
В первом члене последнего уравнения легко усмотреть конечно-разностный
аналог второй производной. Переходя к пределу при Az—>-0, получаем уравне-
ние (1.7).
§ 1.2. Общее решение уравнения Гельмгольца
для бесконечно протяженной регулярной линии передачи.
Монохроматические бегущие волны
В одном из уравнений Гельмгольца, например в уравнении от-
носительно комплексной амплитуды напряжения, выразим коэф-
фициент ZiYi через новый параметр у, определяемый следующим
образом:
(1.8)
* Герман Гельмгольц (1821—1894) — крупный немецкий ученый, известный
своими исследованиями в области колебаний и волн.
11
Как а, так и р_
чины носят специальные названия: a
ления, р — к о э {
будет объяснен далее.
личина в общем случае комплексная, назЫвап
Данная величина, ростр а нен и я РассматпиЛ Тс”
коэффициентом Р „ частоте. В развернутой форме аеМ
линии передачи на зад
Y" + (1.9)
6 имеют одинаковые размерности - 1/м. э
Ильные названия: «-коэффициент 0сЙ’
ффициент фазы. Смысл подобных терМиНобв'
будет объяс''еЛп теории линейных дифференциальных уОяй
ннй^общее решение уменья Гельмгольца
сывается следующим образом.
. о тужат произвольными постоянными
Комплексные числа
и „е зависят друг »Р>Таый сдучай линии, в которой отсутствую,
Изучим вначале ? =;wLi; У1=|/(оСл.
омические потери, у е^когда 1 ^то здесь веЛичина у окажется
Из формулы (!») слс^
мнимой:
у=ур=/(О ]/Ь]СХ.
Рассмотрим первое слагаемое в правой части (1.10), положив
для определенности амплитудный коэффициент равным веществен-
ному числу Um. При этом
(1.Ц)
или, переходя от комплексной амплитуды к мгновенному значению
напряжения,
и (г, /)=Re (£/ (z) e;'“z)=Um cos (to/ — ₽z). (1.12)
Выражения вида
tfZ.t) * л
Ф-0
или (1.12) описывают монохроматиче-
ские волны, распространяющиеся
вдоль линии передачи в сторону
возрастания координаты z. Изобра-
зим графически распределение на-
пряжения вдоль линии, существую-
щее в момент времени / = 0 (рис.
1-2). Эта «мгновенная фотография»
представляет собой косинусоиду
w(2, 0) = [7m cos рг, пространствен-
ный период которой
Х = 2л/р (1.13)
называют д л ин о й волны. Таким
^Рает Р°ль пространственной частоты
Ф=~2я
волнового продев
Ф=я
Рис. 1.2. Бегущая волна в ли-
нии передачи без потерь
образом, коэффициент фазы t ирисгранствеинии
волнового процесса по аналогии с временной частотой w-
перь на этом же чертеже изобразить кривую u(z, 0» отвеч
12
некоторому моменту времени />0, то можно заметить, что она
сместится вправо по отношению к исходной кривой. Назовем пол-
ной фазой волнового процесса аргумент гармонических функций
вида (1.12):
(1.14)
Если нужно проследить за перемещением вдоль оси z какой-
либо фиксированной точки на кривой распределения напряжения,
то следует потребовать неизменности полной фазы при всех z и t.
Условие вида
со/ —pz = const (1-15)
является уравнением, определяющим положение точек равных фаз.
Скорость перемещения точки равной фазы называют фазовой
скоростью и обозначают Уф. Для того чтобы найти ее, следует
выразить z из (1.15) в явном виде:
_ u>t — const
и затем определить фазовую скорость следующим образом:
-Гф = ^£/б//=(й/р. (1.16)
Например, для рассматриваемого случая линии без потерь
е=ш/7^,
поэтому v^= I/]/ AjCp (1.17)
Аналогично исследуются монохроматические волны, соответст-
вующие второму слагаемому в формуле (1.10), для которых комп-
лексная амплитуда имеет вид
U{z)=Um^x (1.18)
(здесь также предполагается отсутствие потерь). Мгновенная кар-
тина распределения напряжения в линии описывается формулой
a(z, /)=Z7OTcos(w/-j-₽2)- (1-19)
Положение точек равных фаз во времени и в пространстве оп-
ределяется здесь уравнением w/+ pz=const, из которого видно, что
с ростом t координата z должна уменьшаться, а не увеличиваться,
как в предыдущем случае. Поэтому формулы (1.18) и (1.19) соот-
ветствуют волнам, распространяющимся или, как часто говорят,
бегущим в отрицательном направлении оси z с той же скоростью
Уф. Будем придерживаться определенной терминологии, называя
волны вида ехр (—jpz) прямыми, а вида exp (/pz)—обратными
волнами. Прямая и обратная волны соответствуют двум линейно
независимым решениям уравнения Гельмгольца и никак не свя-
заны друг с другом. В бесконечно протяженной линии оба направ-
ления распространения равноправны, и поэтому в название волн
не следует вкладывать абсолютного смысла.
13
Подводя итог сказанному, сформулируем фунда.ментал
свойства монохроматических волн в линии передачи без п ЬНы*
I. В общем случае волновой процесс в линии является СуТе₽ь-
прямой и обратной воли. *
2. Процесс, наблюдаемый в фиксированной точке оси г
простое гармоническое колебание. •
3. Как в прямой, так и в обратной волне фазовый
колебаниями в
Коэффициент
вдоль оси.
- сдвиг меж»
II1JV точках линейно связан с расстояние
1’Х"^"характеризует скорость изменения
ниец
Фаз*
4. Точки фиксированной фазы перемещаются в пространстве
с фазовой скоростью; ее величина не зависит от частоты колебаний.
Следует обратить внимание на одно существенное обстоятельство:
фазовая скорость определена нами как скорость перемещения
в пространстве воображаемой точки. Поэтому на величину фазовой
скорости не должны распространяться известные ограничения, свя-
занные с предельным характером скорости света.
Обратимся к исследованию монохроматических волн в линиях
передачи с потерями. Комплексная амплитуда напряжения прямой
волны в такой линии передачи
(7(2)={/же-’«=4/ме-в*е-^, (t20)
откуда u(z, /)={/me-Mcos(«>/ —₽z).
Принципиальное отличие формулы (1.21) от ранее найденной
зависимости (1.12) состоит в том, что амплитуда гармонически
14
колебании в линиях с потерями экспоненциально уменьшается по
мере распространения волны, т. е.
|t7(z)|=Z/ee~M. (1.22)
Соответствующие графики, дающие представление о распреде-
лении напряжения в различные моменты времени, приведены на
рис. 1.3.
Из формулы (1.22) следует способ измерения коэффициента
ослабления а. Если посредством |Г|| и |Г:| обозначить амплиту-
ды колебаний в точках / и 2, расстояние между которыми 1 м, и
предположить, что волна распространяется от точки / к точке 2, то
(1.23)
К' j|
Величина а характеризует ослабление волн в линии, выражен-
ное в особых логарифмических единицах неперах на метр
(Нп/м). В радиотехнике чаще используются логарифмические еди-
ницы не с натуральным, а с десятичным основанием—децибелы
(дБ). При этом вводят погонное затухание А в линии, определяя
его несколько иной формулой:
Д=-201К^-;дБ,м. (1.24)
i/j
Величины а и А связаны соотношением
Д=-20а 1g 2,718^ 8,686а.
Для обратных волн в линии с потерями имеет место следую-
щее выражение комплексной амплитуды:
U(z)^U„Wf, (1.25)
и соответствующая формула для мгновенных значений напря-
жения:
«(z, t) = Umeatcos(u>/4-?2). (1.26)
В этом выражении по сравнению с формулой (1.21) изменились
знаки, что указывает на противоположное направление распростра-
нения волны.
§ 1.3. Понятие волнового сопротивления линии передачи
Проведенный анализ процессов в неограниченной регулярной
линии является неполным, поскольку нам удалось исследовать
лишь вопрос о распределении напряжения вдоль линии. Знание
распределения тока важно не в меньшей мере, поскольку энерге-
тические характеристики, такие, как переносимая мощность, опре-
деляются через соответствующим образом вычисленные произведе-
ния напряжения и тока.
15
Гельмгольца
Рассмотрим вначале прямую волну. Комплексные амплитъ
напряжения и тока прямой волны удовлетворяют уравнен^
(1.27
(1-28'
</2т7пр/^2-у2^пр=о,
d2in?ldz2 — y2inV—^-
Решения этих уравнений одинаковы:
г/пр(^)=^е-тг,
Лр (*) = /ffl e-TZ>
(1.30)
и отличаются лишь амплитудными коэффициентами. Найдем свя
между величинами Um и 1m- Для этого в одно из телеграфий
уравнений, например dtJ!dz=Z\t, подставим соотношения Q oq?
и (1.30). После сокращения на общий множитель ехр (—Ц2)ц
лучим
Различие в знаках между формулами (1.32) и (1.35) связано
с тем, что ток обратной волны направлен противоположно току
прямой волны. Далее будет показано, что это обстоятельство очень
важно, так как оно говорит о противоположном направлении по-
токов мощности, переносимой прямой и обратной волнами.
§ 1.4. Вторичные параметры линий передачи
различных типов
Комплексный коэффициент распространения и волновое сопро-
тивление служат важнейшими вторичными параметрами линии пе-
редачи. Знание их позволяет полностью описать свойства линии
в рамках первоначально принятой математической модели.
Общий случай. Коэффициенты фазы р и ослабления а являются
соответственно мнимой и вещественной частями комплексного ко-
эффициента распространения
т'
откуда
Последний результат можно преобразовать, имея
комплексный коэффициент распространения связан
параметрами линии формулой у=У ZXYX, поэтому
С
в виду, ЧТо
погонными
(1.31)
тока в бегу-
* — л е н и я л и*
НИИ передачи. Из (1.31) следует, что волновое сопротивление
„ ДПр(г) Г -ZT
Л Г, ’ ОМ' (1-=2)
Запишем формулу волнового сопротивления, выраженного че-
рез первичные параметры линии:
Z,=1/
И Oi + y-c, 1 ,|е •
ноеИч7м?,°абДе™СЛУ,ае волновое сопротивление - это комплекс-
чн так и пт Щ пЭК от первичных параметров линии переда-
вают иногда ГЛ7кт» Л1,тератУРе волновое сопротивление вазы-
Обратимся Lp? к т е Р " с т и ч е с к и м сопротивлением,
оратимся теперь к случаю обратной
^обр=^тае^, /обр = /даеи
, что
Добр (г)____
Дб₽(г) Z’-
Отношение комплексных амплитуд напряжения и
щей волне носит название волнового сопротив
(1.33)
Y=a4-/₽=]/(/?i4-/<o£i)(G1 + >C1).
(1.36)
Найдем их явные выражения через первичные параметры линии
и значение круговой частоты со. Для этого возведем обе части фор-
мулы (1.36) в квадрат:
а2 4- 2уа₽ - р2=(/?! + /ЪАО (Gt Д- JuCJ,
затем выделим отсюда вещественную часть
a2-₽2=/?1G1-^2A1C1. (1.37)
Кроме того, запишем выражение для квадрата модуля у:
а2+Р2=/(/??+<о2£?) (О?+ш2С?). (1.38)
Совместное рассмотрение двух последних формул приводит
к окончательному результату:
а = 1/+(<31 + “>2С1) • (1-39)
1/ Л z
? = 4 (‘"2ЛС1-/?1О1)+4- /+ (Gi+^cb. (1.40)
1/ Z А
Элементарные вычисления приводят к формулам [см. выраже-
ние (1.33)]:
Ц. "...
Аналогичным образом находим
волны, для которой
(1.34)
У?2 -|- <и2£2
G2-? ш2С2 ’
(1.41)
G1
. 1 . “Ci и!,
Ф=— а retg ——Д-
2 j ।
1 + »211С1
шкмого пь?н р: ’
ИНСТИТУТА i
16
Формула (1.42) свидетельствует о том, что в общем слу,..
ч 4 некоторый фазовый сдвиг между комплексны от частоты’ определяясь исключительно геометрией поперечного
имеет место .ряженпя п тока в бегущей волне. Знак фазой *1сечеН11Я 11 свойствами заполняющего диэлектрика.
амплитудами конкретных параметров системы. Расчеты по°Г° Линия передачи с малыми потерями. Этот случай характеризу-
сдвпга завис! бо1Ьшинства практически используемых пиКа'ется тем’ что в Рабочем диапазоне частот выполняются неравен-
перелачи^праведлпво неравенство RJLt>GJCt. поэтому фаз"»"*™
угол 4- оказывается отрицательным и ток опережает напряжец" R^>LX, G^CX. (1.46)
Ьднако этот эффект, как правило, весьма невелик.
Пиния без потерь Так называют идеализированную линию п По-видимому линии передачи с такими свойствами должны на-
лип л ля которой имеет место равенство нулю первичных „ поминать линии без потерь. Докажем это. Преобразуем формулу
notvrnn» /? и G, определяющих омические (тепловые) пот/п (1'36)’ лающУю общий вид комплексного коэффициента распро-
Подобных линии в природе не существует. Однако такая идеа5йИ,СТраНе”ИЯ:
зация часто оказывается полезной хотя бы потому, что при ЭТ01)
упрощаются все расчетные формулы. К тому же учет потерь в лй-
ниях передачи, применяемых в радиотехнике, дает поправки, ко-
торыми можно пренебречь при решении ряда конкретных задач
Сказанное не относится к тому случаю, когда линия передачи
даже совершенная по своим свойствам, обладает значительной дли-
ной и учет омических потерь становится неизбежным. .
Затухание в линии без потерь равно нулю, так что коэффиии ОТСУТСТВ11Я потерь. Подкоренное выражение в формуле
ент распространения имеет чисто мнимый характер: Т ’лтлиилАтея пт ₽ппННпЫ nn^n^v нрпргппЛпп^п
Как было показано, фазовая скорость в такой линии
Y =
1-у^_
(oLl
CO L 1
Здесь po — коэффициент фазы той же линии в предположении
" ' : (1.47) мало
отличается от единицы, поэтому целесообразно разложить радикал
в степенной ряд вида
Фо
1
X х2
2
8
0)2 L !<?!
(1.47)
®Ф=«/?=
не зависит от частоты колебаний. При этом оказывается (и это
можно подтвердить строгим электродинамическим анализом), что
величина l/(/nCi) в точности равна квадрату скорости света в той
среде, которая заполняет поперечное сечение линии передачи, т. е.
Условимся проводить вычисления, оставляя в формулах вели-
чины порядка квадратов малых отношений /?1/(соА[) или Сх/{шСх)
и пренебрегая величинами более высокого порядка малости. Тогда
формула (1.47) дает следующие приближенные выражения для
₽ и а:
Здесь с скорость света в вакууме; е, ц— относительные ди-
электрическая и магнитная проницаемости заполняющего мате-
риала.
Поэтому в линии передачи без потерь
т}ф=с/У^.. (1.44!
и? ппипаУ, словами’ наличие идеальных токонесущих поверхностей
магнитных во3зДмущенийМеНеНИЮ СК0р0сти Распространения электро-
™ме№Фя0?^и п^ред(чХУзЧХрь:₽аЖе"Не ДЛЯ вол,'ового С°П|”'
^в=У £1/С1, Ом. (М®
потерь вещественипЩеГГ) слУ,,ая волновое сопротивление линии без
Кроме того, волновое connnJ’ иапряжсние и ток всегда синфазни
J8 опротивление линии без потерь не зависит
1
а = —
2
1
8а>2
А
. Ze0
G\
Li
Gi
вО
Г , рад/м,
, Нп/м,
(1. 48)
(1-49)
rjieZBo=yЬх/Сх — волновое сопротивление аналогичной линии без
потерь.
Смысл понятия линии передачи с малыми потерями становится
более ясным, если рассмотреть отношение
1 . Gi^bo
2 ‘ ’
а 1
являющееся малым числом,
том частоты. Кроме ioro,
а/р
/?1
Ро^вО
которое к тому же уменьшается с рос-
— аХ, Нп,
2л
т. е. это число с точностью до постоянного коэффициента характе-
ризует ослабление бегущей волны, выраженное в неперах, которое
19
'^1^1
2
(1.51)
a
(1.52)
Рис. 1.4. Распределенная RC-
структура:
/ — металлическая пластина; 2 —
слой диэлектрика; 3 — резистивная
полоска
„топится на участок линии протяженностью в одну ДЛи
г/ииией передачи с малыми потерями след} ет называть Итак, в распределенной ЯС-структуре коэффициенты фазы и
J которой выполняется неравенство а/р«1 Поясним СКа' Челабления численно равны
Допустим °что имеется отрезок линии длиной /=10 рабоаза«»,
из частоте 1= >0000 МГц (Х=3 см) и обладающий коэфф,,;
на частоте / Полное затухание в линии JИн>
S6a7- 86 86 дБ Если предположить, например, что аМп^2* п - a or
на входе системы Um вх = 1 кВ, то амплитуда Важное свойство распределенной ЯС-структуры заключается
напряжения на вд найдена из соотношения в^о» том. что здесь коэффициент фазы уже не прямо пропорционален
ного сигнала диллх састоте, а изменяется по закону квадратного корня из частоты.
2Qig .ствХ-=: 86,86 дБ, Ъэтому фазовая скорость
Uт вых
и> / 2«>
откуда ^вых=0,045 В. Таким образом, на выход линии пепе;)а ^=У=1/
поступает лишь ничтожная доля входного сигнала. Кажется "
правдоподобным, что такая система может называться линией ^Рн возрастании частоты увеличивается. В физике принято гово-
редачи с малыми потерями. Однако отметим, что рассматриваи.>ить, что волновая система, в которой скорость распространения
линия весьма велика в масштабе длины волны: /Д = 333 (СЧнлсолебаний не постоянна, а зависит
ется, что линия имеет воздушное заполнение). Вычислив коэ&Л->т частоты, обладает частотной дис-
циент фазы р = 2лД=209,44 рад/м, получаем, что безразмеой^Р^^' Данное свойство распре-
отношение a/р составит всего 0,00477. Деленной /?С-структуры позволяет
Следует иметь в виду, что с ростом рабочей частоты коэ4лсоздавать на ее ^азе весьма совер-
циент фазы линейно нарастает, в то время как коэффициент осл ?шенпые преобразователи формы
ления либо в первом приближении остается неизменным, либо • ЛлектРических колебаний [9]. Такие
это будет показано в гл. II, растет пропорционально кв’адпатнК5гстР0,",ства легк0 создаются метода-
корню из частоты. Поэтому с увеличением рабочей частоты о01**111 C0BPCMeHH0B электронной техно-
шение a/р уменьшается и, несмотря на абсолютный рост погопнВДлогии* Эскиз распределенной RC-
затухания, на высоких частотах все с большим основанием можГруктуры пРедставлсн на Рис- *-4-
принимать математическую модель линии с малыми потерями ** Погонное затухание сигналов
Линия передачи типа распределенной 7?С-структуры Довл здесь достаточно велико. Посколь-
специфическими свойствами обладает линия передачи ’v kotS7 а = Р’ потерп на отрезке лииии
последовательное реактивное сопротивление пренебоежимп Х <оставят аХ=2л, Нп, или
по сравнению с последовательным омическим соппотнвтенЛ?4'58 дБ' При этом входной си™ал
Исследуем такую передающую систему предпо1м7моньшаетс?^0 амплитУде "Р”6™'
для простоты, что активная проводимость G, равна нулю (эта 1?“1пЛЬИ0 ° 540 ра3’ - or
ловие не является принципиальным) «у-ию ^это ус Волновое сопротивление распределенной кС-структуры, вычис-
Линии передачи, у которых ^ = ^ = 0, в радиотехнике называю^"”06 П° °бЩСЙ формуле’ оказывается комплексным:
самымР чтс^в этих-“1" - с т Р У « т У Р а м и, подчеркивая тел
запасание энергии R Л^°^°„Вр.еМеНН0 проис*одят два процесса
счет омических потерь.
Вычисляя для такой
странения, имеем
(1.53)
2wC i
cupt -------Р_ электрическом поле и диссипация энергии зг
Ц С ростом частоты волновое сопротивление уменьшается по мо-
линии комплексный коэффициент распродулю, однако его фазовый угол при любой частоте сохраняет по-
стоянное значение ф ——45° (отрицательный знак указывает на то,
то
20
v=VW;.
/7=есз= 1//2+J/V2,
по ток здесь опережает напряжение).
1 В технике встречается довольно много линий передачи, по свой-
ствам близких к распределенным #С-структурам. К ним относятся,
<апример, обычные линии телефонной и телеграфной связи, рабо-
тающие в диапазоне звуковых частот.
Резистивная линия передачи. Этот случай является в известном
гмысле предельным, поскольку здесь оба первичных параметра,
21
(1.57)
^овр(г)
(1.58)
определяющих процесс накопления энергии электромагнитного.
Р д „„nLn. / =f, = 0 Таким образом, резистивная п
ля, равны нулю. -i / = d Y, — G, Я ЛиВ1 ПУСТЬ влоль линии распространяется прямая волна в сторону
передачи характеризуется равс • „ ’ «• озрастания координаты Z. При этом
Коэффициент распространения в такой линии у =
ляется вещественным числом, а поэтом} — /11р(г)/Г|1,
а=/ЯА. ?=0. поэтому ^np(^0)=-y/np(z0)ReZB
Плглелние Формулы свидетельствуют о том, что в резисти»
линии передач)|во^июбразпый процесс распространения колеб^’'1’ пРлвт' "••'стп здесь присутствует квадрат модуля комплексной
^тсЛствует ” (коэффициент фазы равен пулю и колебания во * юой"^ ' *' раССМ°ТрСТЬ °бРат">ю ВОЛ"У’ «’ »-
сечениях линии имеют одну и ту же начальную фазу). Кромет?’
наблюдается экспоненциальное уменьшение амплитуды с рост,
продольной координаты, направленной в сторону от генерат0.
Так, для прямой волны в резистивной линии имеем
U(z) — Uoe. ц & Для ИЗуЧаемых линий передачи всегда RcZn>0, поэтому актнв-
„ ______ „„„ „„„„„ попопо.пт ,ая мощность, соответствующая прямой волне, положительна, а
Волновое сопротив е Д р е го типа активная мощность обратной волны отрицательна. Различие зна-
то вещественно: _____ сов мощности связано с противоположным направлением токов
Z,= ]'Rx/Qx, Ом. /1 J прямой и обратной волнах. Если рассматривать прямую волну,
1 ’то здесь увеличение тока в каком-нибудь сечении приводит к воз-
Резистивные линии являются удобной и достаточно точной ^астанию напряжения, которое мы условились считать за положи-
тематической моделью различных устройств, включаемых на цельное. Поэтому полубескопечный отрезок линии правее сечения
ходе обычных линий передачи с целью поглощения энергии элег = 2о ведет себя подобно резистивной нагрузке. При обратной вол-
тромагнитных колебаний и превращения ее в тепло. Дискретное ситуация диаметрально противоположна — здесь увеличение
аналогом резистивных линии являются ступенчатые аттенюаторы-гока (в алгебраическом смысле) ведет к уменьшению напряжения
устройства, позволяющие в диапазоне умеренно высоких чаек1 поэтому правая часть линии играет роль генератора, а левая —
скачкообразно изменять уровень сигнала, поступающего от ген>,агРУзки- Итак, в регулярной линии передачи направления потока
ратора. энергии и фазовой скорости совпадают.
Особенно простой вид приобретают формулы для средней псрс-
§ 1.5. Мощность, переносимая бегущими волнами юсимой мощности в линии без потерь:
вдоль линии передачи z zп i ,;2 i //2
“ 9 у1'р ~ Grt?— 7^7 Unp——— 17обр.
Найденная система решений телеграфных уравнений дает ва в н
пп1югпииТПгЛН°СТЬЮ ответить на вопрос о потоках мощности, к Рассмотрим два сечения линии с координатами z — zx и z = z2
£ ‘ гущими волнами. Зафиксируем некоторое сечен^2>г!). Свяжем между собой величины мощностей волнового про-
кпмппАк-Р ГУЛЯР,,ОИ линии передачи и предположим, что известцесса в этих двух сечениях при самых общих условиях. Для этого
и . ксные амплитуды U(z^) и 7(Zo), которые позволяют опрбразуем систему из первого телеграфного уравнения, входящего
ить полную мощность S. 3 0 5), и комплексно-сопряженного второго телеграфного урав-
5(г0)=—i/(z0)/(z0), (1.5
2 к dUjdz = — RXI — j<aLxI,
ou/xn^eCb символом обозначено комплексно-сопряженно difdz= —GXU-J-j^CxU.
число.
прпыи«иЩер СЛуЧае полная мощность S=P+jQ есть комплексна Умножим первое уравнение на //2, второе на OJ2 и сложим их.
мри Л' te вещественнУю часть Р называют активной или срев результате получим
эл^тппоо УЮ ЧЭСТЬ Ре“к™вной мощностью гармонически
электромагнитного процесса.
22
(1.59)
(1-60)
Cif/2 LXI2
RXI2 GXU2
2 2 )
2 2
23
Левая часть этого уравнения представляет собой
от полной мощности 5. Разделив вещественную и ,•
имеем два дифференциальных выражения.
dP /?]/2 GXU%
dz
dQ
—— =<D
dz
2
£1£2
2
2 J
Z,
Оба интеграла, входящие
2
сх(л
2
являющихся уравнениями локального баланса активной и реа
ной мощности соответственно. Интегрируя (1.61) в пределах
выбранных сечений, находим
Рис. 1.5. Схема цепочечного экви-
валента
пРОИзводв,обходнмое для распространения электромагнитных возмущений от одного кон-
МНИМую Цо t линии до другого. Однако реализация более или менее значительных задержек
’^ложняется высокой скоростью распространения волн в линиях. Так, при =
3 10s м/с для получения задержки в 1 мкс потребуется отрезок линии длиной
Ю м. Это неизбежно связано с конструктивными трудностями, преодолеть кото-
ll. (ае можно путем использования цепочечных
шных из сосредоточенных схемных элемен-
)в (рис. 1.5).
(1,( Проанализируем эту систему и пока-
:ем, что явления в ней моделируют те
5Ктроцессы, которые наблюдаются в регуляр-
ен"! линии передачи с распределенными па-
ДВаметрами.
На основании первого и второго зэконое
.ирхгофа запишем:
| (7л-1 =/<о£/л +/7Л,
7л—1 = j^cu п—\ + 7 л.
I В соответствии с (1.65) ток в
эквивалентов линий передачи, соб-
Z1
Оба интеграла, входящие в правую часть последней форму,
положительны, поэтому всегда P(z2) <P(zi) (следует помнить »
активная мощность, переносимая обратной волной, имеет отп'ш
тельный знак). Физический смысл формулы (1.63) прост — аКт
ная мощность, отбираемая от генератора, равна сумме мощное
отдаваемой нагрузке, и мощности омических потерь в линии (
отношение (1.63) является частной формулировкой известной
мы Умова *.
Связь между реактивными мощностями в сечениях zx и
лучаем на основании выражения (1.62):
?u^dz-^ \i4z=b> (э„- Э„.г).
z j z <7
«1 Z1
(1.65)
(1.66)
n-й ячейке
7Л = ((/„-!-(/„)/(>£).
Подставив это выражение в уравнение (1.65), имеем
/7Л_2, ип_х-йп
-----—-------= >С(/л-1 + ———
jwL
ТбОрткуда
<4-2 - (2 - ш2АС) [7Л_! + йп = о.
22 bl
Анализ свелся, таким образом, к нахождению решения линейного
ого уравнения второго порядка. Будем искать его решение в виде
П f ' йп = А^п
(1. 67)
разност-
(1.68)
произвольным амплитудным множителем А. Подстановка (1.68) в (1.67) при-
одит к следующему уравнению:
е2т_(2 —ш2£С)е7 + 1= 0.
Если обозначить ет = <7, то (1.69) становится эквивалентным
равнению
(1.69)
квадратному
?2_(2 —<d2£C)<7 + 1= 0,
/ о>2£С \2
Здесь Ээл и ЭМаг — усредненные за период энергии электрт
ского и магнитного полей соответственно, накапливаемые в отк
ке линии.
В бегущей волне реактивная мощность вдоль продольной кос'1
динаты неизменна. Действительно,
____________ ;орни которого
•Ээл=CJJ2m (z2 - ^)/4; Эмаг=LxU2m (z2 - 2X)/(4Z2),
поэтому из (1.64) следует, что Q(z2) = Q(zx).
Но синфазность тока и напряжения позволяет сделать здесь Если ©2<2/(LC), то
ООЛее СИЛЬНЫЙ ВЫВОД —реактивная МОЩНОСТЬ В расСМатриВаеМ1|Ице- Поэтому их можно ......
случае тождественно равна нулю. г ,ым сдвигом, приходящимся на одну ячейку цепочечного эквивалента. В соот-
»етствин с (1.70)
о>2£С
(1-70)
41,2 =
2
<71,2 — комплексные числа, модуль которых равен еди-
записать в виде ехр (±/₽). Величина р является фазо-
§ 1.6. Цепочечный эквивалент
регулярной линии передачи |куда
дание^тройств для'эяпРп^еНеНИЯ линий передачи в радиотехнике является со
что отрезок линии длиной^Кп/МПуЛЬСНЫХ сигналов- Работа их основана на го-
— Р линии длиной I обеспечивает задержку сигнала на время
н. А. Умов (1846-1915) - известный русский физик. |
24
<о2£С
COS ? = 1 —----—
/ О)2£С
Р = arccos 11 — —-—
(1.71)
<+ = V 2/(LC)
25
Частоту
„почечного эквивалента. В интервале ,
„й среза цеп°'е ровным свойством распределецА
, аастотои Н обладает ° овЫМИ по амплитуде,
SS“ <“;“Se“ae"e *а3°“ЫЙ СДМГ "ЗМе,,’еТС’ 5;
вД° Йравда, всли,'‘ "аот’частоты »елИйНе.пинии обладает частотной дИСп^
вин ^(Ь^-^Р-^- задерживаемых импульсов, еслн
Это” вызывает ^^“^астотой ^^вале'нт ведет себя подобно фильтр,
возникновением Р
люсников 1М-
Глава II
НЕКОТОРЫЕ ТИПЫ ЛИНИЙ ПЕРЕДАЧИ
Рассмотрим некоторые широко применяемые в радиотехнике
инии передачи, которые могут анализироваться методами, изло-
четыр^-кенными в гл. I. Для этих систем общим является то, что они
образованы совокупностью двух проводников, по которым проте-
Задачи и упражнения к гл. I <ают токи и между которыми в любом сечении можно определить
, х ......... спряжение (разность потенциалов). Приводимые далее формулы
шейся’в лш«^ важиое значение Для инженерных расчетов разнообразных
осп. 4 = 1 7-Ю8 м/с. ' а $азоваяустройств, в которых используются линии передачи.
Ответ. 14,784 рад/м.
1.2. Линия передачи имеет длину 20 м и на рабочей частоте
зуется коэффициентом ослабления а=0,8 Нп/м. Для компенсации пот
нии предусмотрена цепочка усилительных устройств. Каково должно кРЬ 8
ление, введенное в линию, чтобы уровни сигналов на входе и \
совпадали?
Ответ. 139 дБ.
1.3. Колебания с частотой 5 МГц распространяются в пасппрп„„ ИВтли> передачи эиер
структуре со следующими первичными параметрами: = Длиной генератора к нагрузке. В простейшем виде
=400 пФ/м. Определить длину волны и волновое сопротивление °М/м’ Сзаци» УиР°ВНЯ тспловь,х (омических) потерь.
Отв_ет.Л=0,62м,2в = 798 (1—/) Ом. Р е’ Е._2Г_В неК0Т0рЫХ областях Радиоэлек1
допускают протекание тока не более 22 А.‘Какую предельную*4 мошног К
передать по такой линии? щ ость
Ответ. 72,6 кВт.
1.5. Электрический пробой в линии передачи наступает г-
между проводниками 14 кВ. Волновое сопротивление ZB =35 Ом К
чина предельно допустимой мощности, передаваемой по данной* т™,?3 Вь’
Ответ. 2,8 МВт. линии?
1.6. Цепочечный эквивалент линии передачи собран из катушек о вв,
костью 30 мкГн и конденсаторов емкостью 180 пФ. Определить фазммв',..
приходящимся на одну ячейку, если частота сигнала f=l 5 МГн Клим™ 45
зРвено?ДеЛеННОЙ ЛИНИИ С фазовой СКОР°СТЬЮ =3-108 м/с эквивален™^'
Ответ. 0,707 рад; 22,5 м.
§ 2.1. Требования, предъявляемые
к радиотехническим линиям передачи
Линия передач», рассматриваемая как элемент радиотехнической конструк-
и На в»Л1ии. должна удовлетворять ряду требований. Перечислим важнейшие из них.
Функциональные требования. 1. Линия передачи должна обеспечивать мак-
симальную эффективность передачи энергии высокочастотных колебаний от
: это требование сводится к миними-
радиоэлектроники (телевидение, радиолокация,
1.4. При сочленении двух линий передачи с волновым вычислительная техника) линии передачи должны с малыми искажениями пере-
= 150 Ом использован высокочастотный разъем, трущиеся^пЛ°П₽0ТИад«»ДаваТЬ снгналы- спект₽ КОТОРЬ,Х простирается от нулевой частоты до частот
____________________ ... е__’ 'РУЩиеся контакты кото»поРядка нескольких десятков, сотен и даже тысяч мегагерц.
э мптипл^ г 3. Каждая линия передачи способна пропускать колебания, уровень мощно-
сти которых ограничен пределом, зависящим от ее конструктивных особенностей.
Если ставится задача связи мощного генератора с нагрузкой, то линия должна
ПРИ напряди обладать достаточной электрической и тепловой прочностью.
Tz- а ' 4. Работа современных радиотехнических комплексов требует минимизиро-
i линии? вать паразитные взаимные влияния отдельных составных частей. Поэтому необ-
ходимо, чтобы линии передачи были электрогерметичны, т. е. имели минималь-
на катушек с индухпнУю УтечкУ передаваемой электромагнитной энергии.
а--- * Эксплуатационные требования. 1. Конкретное радиоэлектронное устройство
вместе с входящими в него линиями передачи работает в некотором предпола-
Г"гаемом заранее комплексе условий окружающей среды. Инженер-разработчик
‘“обязан выбрать тип линии передачи, способный работать в заданном диапазоне
температур, при ожидаемом уровне влажности, механических вибраций и т. п.
2. Часто возникает потребность в гибких линиях передачи. Однако любые
допустимые изгибы не должны существенно сказываться на функционировании
линии.
3. Линии передачи, используемые в такой аппаратуре, как авиационная или
космическая, должны обладать минимальными габаритами и массой.
Технолого-экономические требования. 1. В радиоэлектронных устройствах
линии передачи стали одним из распространенных компонентов. Поэтому зна-
чительным преимуществом обладают те конструкции линий, которые удовлет-
воряют обширному комплексу требований, объединяемых понятием технологич-
ности. Следует отметить, что достигнуты большие успехи на пути полной авто-
матизации производства многих видов линий передачи.
2. С технологичностью производства неразрывно связаны экономические
критерии. В условиях крупносерийного или массового производства линии пере-
дачи сравнивают между собой не только по функциональным и эксплуатацион-
ным, но и по экономическим показателям.
27
§ 2.2. Коаксиальная линия передачи
Данный вид линий передачи благодаря удачной конструк.
широко применяется в радиотехнике. Регулярная коаксиалцГДе цо = 4л• 10~7= 12,556-10~7 Гн/м — магнитная постоянная
линия передачи (рис. 2.1)—эт0 система из двух хорошо проВор а к у у м а. Относительную магнитную проницаемость р., как
щих металлических цилиндров, пространство между которыми‘правило, следует полагать равной единице, поскольку большинство
полнено твердым диэлектриком. Наиболее распространены гиб|ДиэлектРиков в диапазоне радиочастот не проявляют собственных
коаксиальные кабели, у Кото магнитных свойств.
внутренний проводник пред^ Погонное сопротивление потерь. Задача нахождения омическо-
ляет собой одно- или многож^го сопротивления проводника, по которому проходит переменный
ный провод, а внешний простои, не может быть решена элементарными мс-
ник имеет вид оплетки, выпо^тодамн и требует привлечения теории электро-
ной из тонкой проволоки. ДцЭл'магнитного поля [1]. Сущность наблюдаемых яв-
триком для коаксиальных к'а{лений заключается в следующем. Плотность тока
лей обычно служит полиэтидмаксимальна на поверхности проводника и экс-
(диэлектрическая проницаемоепс>ненциально уменьшается при удалении от по-
е = 2,25); используется также(ЬвеРхности (поверхностный эффект). Под глуби-
ропласт (е = 2,08). Эти полим нов проникновения тока понимают расстояние
ные диэлектрики отличают07 поверхности, на котором плотность тока пада-
очень хорошими электрически) в е = 2>7^ Раз- Ее вычисляют по формуле
свойствами. Значительно ред
в основном при передаче бог
ших мощностей, используются г
аксиальные линии жесткой ко
0Л?
<Z>2b
I
Рис. 2.1. Коаксиальная линия пере-
дачи:
/ — внутренний проводник; 2 — диэлектрик;
3 — наружный проводник (оплетка); 4 —
защитное покрытие
, Гн/м,
(2.2)
8
90’
й
Рис. 2.2. Век-
торная диа-
грамма конден-
сатора с поте-
рями
d=A/
_ Здесь w — частота; р, — относительная магнит-
струкции, в которых внутренний проводник поддерживается I ная проницаемость металла; в — его удельная
электрическими шайбами. объемная проводимость, имеющая размерность См/м (см. Прило-
Полная симметрия коаксиальной конструкции дает возможное жение). На частотах СВЧ-диапазона величина d очень мала (доли
анализировать многие электромагнитные процессы в ней cd микрометра). Таким образом, «вытеснение» тока из проводника на
мощью элементарных методов, известных из курса физики. его поверхность ведет к существенному сокращению сечения токо-
Погонная емкость. Задача вычисления погонной емкости koi проводящей области и, как следствие, к значительному увеличению
сиальной линии сводится к нахождению емкости метрового отрез- сопротивления по сравнению с тем, которое наблюдается при по-
цилиндрического конденсатора. Считаются известными относите.! стоянном токе.
ная диэлектрическая проницаемость заполняющего диэлектрика^ Расчетное выражение для погонного сопротивления потерь в
а также а и b — радиусы внутреннего и внешнего проводников с: коаксиальной линии передачи имеет вид
ответственно. Решение основано на известной из электростатк
теореме Гаусса. Окончательная расчетная формула имеет вид
с ф/ (2
1п(6/а) '
где 8о=1О 9/(36л) =8,842-10-12 Ф/м— фундаментальная констант
называемая электрической постоянной вакуума.
огонная индуктивность. По определению она равна частно)
т деления полного магнитного потока, существующего на прок
нии метрового отрезка линии, к протекающему в линии ток
‘ Ма™ый поток Ф можно связать с током /п(
что сигтпп^п3пеСТН0Г0 закона полного тока, приняв во внимав»
ческих окпу®чИНИИ»МвГЙИТН0Г0 поля Д°лжны иметь вид концентр?
РУ остей. В результате приходим к следующей форму-’'
Я1 =
, Ом/м .
(2.3)
Данная формула не претендует на высокую точность, посколь-
ку параметр о сильно зависит от микроструктуры поверхности.
Погонная проводимость потерь. Несовершенство изоляции в ли-
ниях передачи принято учитывать следующим образом. Если по-
строить векторную диаграмму для конденсатора с неидеальным ди-
электриком (рис. 2.2), то угол между током и напряжением будет
отличаться от прямого на угол потерь б. Отсюда приходим к схеме
замещения конденсатора с потерями, в которую входит активная
проводимость вычисляемая по формуле g=coCtgd. Эта прово-
димость включена параллельно емкости С.
28
29
В справочниках приводится величина tg 6 для различны»
электриков, оказывающаяся, как правило, достаточно малой * Центрами проводников равно D. Эту линию чаще всего выполняют
Приложение). На основании сказанного погонная провод» *Сс воздушным диэлектриком; для сохранения межцентровых рас-
потерь любой линии передачи весьма просто связана с ПогМос стояний применяют изолирующие распорки из высококачественно-
емкостью- Он®' го диэлектрического материала.
(7i=<oCitg8, См/м. Расчеты погонной емкости и индуктивности осуществляются по
(2, тому же принципу, что и для коаксиальной линии, однако ввиду
Волновое сопротивление. Коаксиальные линии передачи, исп более сложной конфигурации проводников элементарные методы
зуемые в радиотехнике, обладают малыми потерями и поэтом °4 здесь Уже непригодны. Запишем приближенные расчетные формулы
волновое сопротивление с достаточной точностью можно вычисГ Для Данного типа линии передачи (предполагаем, что D^>a):
по формуле, соответствующей линии без потерь: UIir а) погонная емкость
Z =l/—Igf—к Ом С1=——=———, Ф/м; (2.7)
в У Ct /« U/ (2. ln(D/a) 361n(D/a) V
Коаксиальные кабели, выпускаемые промышленностью им»
волновые сопротивления 50, 75, 100, 150, 200 Ом.
Погонные потери в коаксиальных линиях. Для расчета хапакт.
ристик, описывающих омические потери, можно использов-
приближенные формулы, отвечающие случаю линии с малыми d
терями (см. гл. I). Приведем выражение для погонного затухав
коаксиальной линии передачи:
б) погонная индуктивность
Л = Inf—\ = 41nf—У 10-7, гн/м;
л \ а ) \ а /
в) погонное сопротивление потерь
«,=— К-т2- - °м/м-
ла г 2а
(2.8)
(2.9)
A=0.0U5j/»(M)+l,448.10-<»)/B-tg8, дБ/м, j
где ц —относительная магнитная проницаемость металла.
Первое слагаемое правой части учитывает потери, возникают
за счет неидеальной проводимости токонесущих поверхностей вк
рое слагаемое — потери из-за неидеальности диэлектрика.
§ 2.3. Симметричная двухпроводная линия передачи
Погонную шунтирующую проводимость двухпроводной линии
можно, как правило, не принимать во внимание, поскольку воздуш-
ный диэлектрик обладает исключительно малыми потерями.
На основании формул (2.7) и (2.8) находим расчетное соотно-
шение для волнового сопротивления двухпроводной линии (ди-
электрик — воздух):
ZB=1201n(D/a), Ом; (2.10}
г) погонное затухание двухпроводной линии:
^?пп1?,УКЦ11Я даннод линии передачи и электромагнитное по.:
Линия образован
расстояние
в поперечном разрезе показаны на рис. 2.3.
двумя круглыми проводниками диаметра 2а,
меж
Д=8,13-10~3
<“№0
а
1 ! D
a In —
\ а.
, дБ/м.
(2.Н)
02а
Двухпроводная линия передачи:
струкция; б-поле в поперечном сечении
а)
Рис. 2.3. Симметричная
В современной радиотехнике симметричная двухпроводная ли-
ния применяется ограниченно ввиду того, что часть передаваемой
энергии неизбежно излучается в окружающее пространство.
§ 2.4. Полосковые линии передачи
В технике СВЧ все более широкое применение находят полоско-
вые линии передачи. В них токонесущими проводниками являются
полоски металла, отделенные друг от друга подложкой — слоем
диэлектрика с малыми потерями. Различают симметричные и не-
симметричные полосковые линии; поперечные сечения их изобра-
жены на рис. 2.4. По ряду технологических соображений чаще
используются несимметричные линии (в литературе они часто
I называются микрополосковыми линиями).
Строгий анализ полей в полосковой линии является весьма
| сложной задачей. Приводимые далее формулы носят приближенный
31
30
2а 4-0,4414-0,082
таоактер Общим условием их применимости является малое»К
ТО.Л,Ц11НС вер,ней полоск„ „
"её ' Р—У- пользоваться иной
векторов электромагнитного поля. z. = [ ь
Если не учитывать затухания, то основные -характеристи„ » * I
досковой линии могут быть найдены, когда известна погони? *
кость С\ Действительно, фазовая скорость Т-волны
делена свойствами заполняв
1,451 4-In f—4-0,94
1 \2ft
_ Заполняют^ В Приложении приводится программа на алгоритмическом языке ФОРТРАН
диэлектрика. На основании* А’ПЯ вычнс-,,сння во-™овик сопротивлений по формулам (2.14) и (2.15).
находим погонную индуктив^ Обычно применяемые полосковые линии имеют волновые со-
, _________) противления 25—100 Ом. При этом удается добиться известного
1 /\ Ф 1/» компромисса между требованиями к затуханию линии, се пробив-
ной прочности, а также удобству сочленения линии с другими узла-
$мн и приборами.
В первом приближении можно считать, что электрический ток
распределяется по ширине полоски равномерно. Тогда для погон-
ного сопротивления потерь, микрополосковой линии будет иметь
Ом.
(2. 15)
6) 1
Рис. 2.4. Полосковые линии пере-
дачи:
а — симметричная; б — несимметричная
и в конечном счете волновое
противление
Приближенно погонную ч место следующая формула:
КОСТЬ МИКрОПОЛОСКОВОЙ jmZ
можно определить по форму, =
плоского конденсатора, извет
ной из элементарной физики (о
рис. 2.4): ш
Ci = ee0Z>/A, Ф/м.
(2. 16)
м
м
о
показывает, что квази
Если воспользуемся приближенной формулой для волнового
сопротивления (2.13), то получим выражение для ориентировочно-
(2 и го расчета погонного затухания микрополосковой линии (без учета
’u потерь в диэлектрике):
Для симметричной линии последний результат должен быт. _ ______
удвоен, так как центральная полоска образует по отношению к обе д — J.629-1Q 2 дБ ,о
им заземленным плоскостям как бы два конденсатора, включении; А
Формула (2.12) весьма приближенна и пригодна лишь дот СтР01И" электродинамический анализ
предварительных оценок, поскольку здесь не учитываются эффпп'в°’™а ° микрополосковой -пинии передачи имеет фазовую ско-
ты искажения поля на коаях полоски ярость, зависящую от частоты, т. е. в ней наблюдается частотная
С учетом сказанного имеем следующую формулу для рас,<™Х"чё ^Гп^ЛХлек Дис"еРсион"ыс ’ФФекты выражены
волнового сопротивления микрополосковой линии: Все” э?о“ сл^ет
нии СВЧ-устройств, когда точность расчетов на ЭВМ должна быть
(2.13 настолько высокой, чтобы обеспечить изготовление приборов, нс
требующих экспериментальной отработки и настройки.
с, . По ряду конструктивных и электрических особенностей микро-
Ьолыпую точность дает формула, учитывающая краевые явле-Полосковые линии передачи наиболее перспективны с точки зрения
ния121: применения в миниатюрных и интегральных устройствах СВЧ, ко-
торым в настоящее время уделяется большое внимание.
Но
«о
84,85
0,242
е
32
Задачи и упражнения к гл. II
(2. И1 2.1. Расстояние между проводниками двухпроводной линии увеличено в
3 раза. Как при этом изменится волновое сопротивление линии?
Ответ. ZB возрастет на 131,7 Ом.
Из—2910
33
ппибоо подключен к схеме отрезком 75-омногл
2.2. Измерительный рис Р т(1Лена (Р = 2.25). Длина кабс.1я i -
кую дополнительную В.
Ответ. Сдо«“|ии (им ИСТочником потерь в коаксилч.
»»« "Р" 5
Ответ, ^/в-3,6. .»>гг ’ коаксиальной липин передачи
2.4. Вычислить "."меры а = 3 мм. 6=10 мм. Матерна" п
ным Д^^Р^^.щт см/м).Частота колебаний / = 750 МГц. Р Л пР°«о^
К°в От*пс'т Л-29.86-10-’ дБ/м.
25 Несимметричная полосковая линия выполнена на подложке Из
/Л|А) имеющей к = 9.6. Параметры линии 6 = 0,5 мм. 6 = 0,75 мм. Найти
"солр "олленит ли»»" »« приближенной и точно» формулам.
Ответ. Z. 0Р«бл=81.1 Ом. Z, им.
Глава II!
ЯВЛЕНИЯ В ЛИНИЯХ ПЕРЕДАЧИ,
НАГРУЖЕННЫХ НА ОДНОМ КОНЦЕ
нагрузоч-
Рис. 3.1. Нагруженная линия
передачи
Изучив общие закономерности волновых процессов и познако-
мившись с некоторыми видами линии передачи, можно перейти
к анализу одной из наиболее характерных ситуаций. Предположим,
что отрезок регулярной линии передачи, обладающий известным
волновым сопротивлением Zn, подключен к некоторому
ному сопротивлению Zn. в общем
случае комплексному. Соответству-
ющая принципиальная схема при-
ведена на рис. 3.1. Здесь продоль-
ная координата / измеряется в на-
правлении от нагрузки к генератору;
начало отсчета совпадает с зажима-
? мн нагрузки. Система возбуждена
I внешним гармоническим исгочни-
f ком с заданной частотой <п. Коорди-
I нага размещения источника может
1‘ быть любой. Однако для наблюде-
ния характерных эффектов необходимо, чтобы расстояние между
генератором и нагрузкой было сравнимо с длиной волны переда-
ваемых колебаний.
Далее исследованы специфические явления в системе, обязан-
ные своим возникновением распределенному характеру линии пе-
редачи.
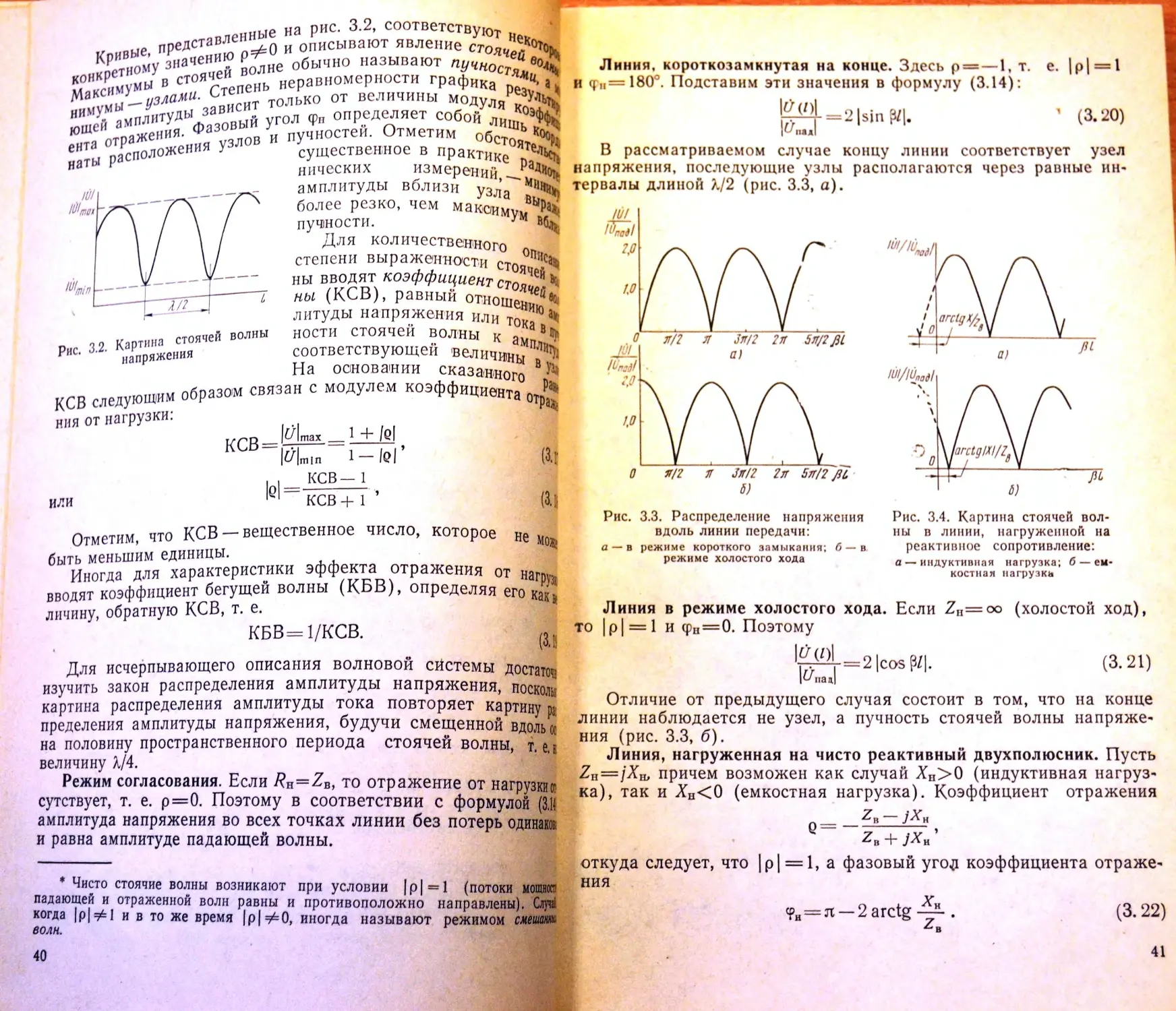
§ 3.1. Коэффициент отражения
fl
Обратившись к системе, изображенной на рис. 3.1, предполо-
I жим, что в ней имеет место волновой процесс наиболее общего ви-
1 да, представляемый суммой двух бегущих волн, перемещающихся
; с одинаковой фазовой скоростью в противоположных н'аправлени-
ях. Волну, движущуюся по направлению от генератора к нагрузке,
называют падающей в отличие от волны отраженной, движущейся
"т нагрузки к генератору. Комплексные амплитуды напряжения для
тих волн запишем следующим образом:
(3.1)
(3.2)
где #опад и (7оотр — некоторые комплексные числа, отображающие
напряжения обеих волн при /=0, т. е. на нагрузке. Знаки показа-
2* 35
1^=
(3.)
,JV сомножителей в формулах (3.1)
гелей
вЫбранЫ о с0° в падающей и отраЖс„„
""’к^сксныД^Амплитудами напряжений М11ОД|,^
2 „ад у ' Zв
• /М e~v.
/0тр(/)=="гГ (3.4
_ линии описывается выражениями вида
волновой "P»'lccCt/(Z)=(7|aj(Z) + 6/„p(Z),l
/(/) = 7nafl(Z) + ATp(Z)- ) '
включения нагрузки напряжение и ток жестко CBi
В точке Условием
заныара«“’я у(0)// -Z,, (Ц
последней формуле показывает, что увели,,,.
Знак минус в послед ление которого принято за полу-
тона отраженной волньп пяотенциаЛа верхнего зажима натру»
тельное, ведет к снижен и /(0) в с00тветствии с фориу»
ЕСЛИ,Т1\"> щ позднее условие приобретает вид
<3l)-t h г/о»« + ^»тв
7 -- 7--------г--- • , О,,
Z“ В t/опад-^Оотр
/о 7ч пходят две неизвестные величины 0^
в формулу V-II ° "лить по отдельности. Однако эта
Рт. которые нельзя vj» --------„, TTontnvifi ЯМПЛИТУЛУ ОТПЯЖ;
мула дает в2змоп^°Хный’ физический параметр
ной волны. Введем важ J к и р, определив его как опте
ние* комплексных ’амплитуд напряжения отраженной и пада»
волн а точке подключения нагрузки:
Q = О Оотр/^Опад-
Покажем, что коэффициент отражения от нагрузки^телиюи
ределяется свойствами двухполюсника на Р> долим числитель
противлением линии передачи Д Р еличину
знаменатель в правой части формулы (б./)
тогда
<4
найти относительную амплитуду отраже
—у. „--------------_ коэффиц;
ZH _ 1 + Q
zB ~ 1-6
откуда
ZH —
6 Z I Z
Входное сопротивление двухполюсника нагрузки Zn= Ru + jXH
обычно удовлетворяет условию пассивности: RH^0 (пассивный
двухполюсник в среднем должен потреблять, а не отдавать энер-
гию). Положим для простоты, что волновое сопротивление Z>
также чисто активно, и запишем формулу (3.9) в развернутом
виде
q = |q| е7’" — (R» ~z"^ + Луи
(/?« + Z.) 4-ухи ’
откуда следует неравенство для модуля коэффициента отражения:
1Z + < 1
V (Ян 4- Z„)2 + А'*
(3. 10)
Оно означает, что для рассматриваемых случаев амплитуда от-
раженной волны не может превосходить амплитуду волны, падаю-
щей на нагрузку.
Подведем итог. Пам удалось показать, что подключение нагруз-
ки к выходу линии действительно обусловливает существование
в ней системы двух противоположно направленных бегущих волн.
Отношение комплексных амплитуд этих волн зависит от сопротив-
ления нагрузки и волнового сопротивления линии. Разберем неко-
торые частные случаи.
Режим согласования. Из формулы (3.9) видно, что единственный
способ избежать отражения — это выбрать сопротивление нагруз-
ки равным волновому сопротивлению линии передачи. Режим ра-
боты, соответствующий условию RH=ZB, называют режимом согла-
сования нагрузки с линией. Отметим, что при отсутствии потерь
в линии согласование возможно лишь при резистивной нагрузке.
В большинстве случаев режим согласования линии с нагрузкой
является предпочтительным. Чтобы понять это, достаточно вспом-
нить, как выглядят энергетические соотношения в линии передачи
(гл. I). Отсутствие отраженной волны указывает на то, что поток
энергии от генератора к нагрузке носит однонаправленный харак-
тер. Именно в этих условиях процесс передачи энергии обладает
наибольшей эффективностью.
Режим короткого замыкания. Если Zn=0, то, как следует из фор-
мулы (3.9), коэффициент отражения от нагрузки р при любом ZB
является вещественным числом, равным—1. Здесь важны две
особенности. Во-первых, при данном режиме амплитуда отражен-
ной волны равна амплитуде падающей волны:
1Дге(01=|Д..(Ч1-
Физическое толкование этого факта очень просто: нагрузка с
нулевым сопротивлением не может потреблять средней (активной)
мощности ни при каком значении тока. Именно поэтому потоки
энергии падающей и отраженной волн компенсируют друг друга.
37
36
-1ьтирУюШ'СГ0 напРяжения Иа Harpyj
. Вели«"а рЕС Требование определяет отри»’*
®°’ВТлыть рлв”а 'т-fотРаясеииЯ Л тока в короткозамкнутой
к°Э*Хо“'.ек. что ам^'Хк соответствующую а„„.,^
°"С« вя“а ^Действ-^ьво.
токГвв'1”01"'"в0'1" p„11.J(1_0) = 2|71)„aJ. (3.11
|/(0HLzTl
Режим холостого хода. Если линия разомкнута на ком»*
= оо) то р=-М, так что имеет место равенство амплитуд4 (г»=
шей и отраженной волн. Однако положительный знак коэЛж3^
та отражения свидетельствует о том, чго здесь амплитуд^ ,
жения, а не тока будет удваиваться па нагрузке по сравно?1>»
соответствующим параметром падающей волны. Это свойст
жима холостого тока обусловлено тем, что ток в конце лим. ° f"
жен быть тождественно равен нулю. "н До;
Нагрузка в виде чисто реактивного Двухполюсника. Ъ
предположению -^11=0, Лн#=0. Обратившись к формуле (3°1тЬ|1
дим, что |р| = 1> т- е- амплитуды падающей и отраженной
равны, как и в случаях, рассмотренных ранее. Тем не менп В°*
ни комплексная амплитуда напряжения, ни комплексная амг^ ЗДСГ:
тока в нагрузке не обращаются в нуль.
Введенный коэффициент отражения определяется с помощью
амплитуд напряжений падающей и отраженной волн и поэтому °Мплексв!>
назван коэффициентом отражения по напряжению. Однако этот спМ°^еТ
ляется единственно возможным. Так, можно было бы ввести Koocbcbti* He!i
жения по току, определив его формулой Чиепт отц
Q/ ~ Л)отр/Л) пад>
в которую входят комплексные амплитуды токов падающей /п
/о отр волн, вычисленные в точке размещения нагрузки Тем wZ’tJL°тражеис
вание в расчетах коэффициента отражения по напряжению ппрппа! ИСП0ш
так как в диапазоне сверхвысоких частот измерение напряжени/осушрет™1*
проще и надежнее, чем измерение токов. 1 нении осуществляй»
Полезной количественной характеристикой изучаемой системы
™ескИ расчетах, ,вяися
®Р ~ ^отр/^пад = Iq|2. ,.
(и, U
различными фазовыми сдвигами, приводит к тому, что результи-
рующее колебание изменяет свою амплитуду и начальную фазу от
точки к точке, т. е. имеет место интерференция падающей и отра-
женной воли.
Изучим законы интерференции этих волн иа примере линии
передачи без потерь. Считая известным коэффициент отражения
от нагрузки р, имеем следующее выражение, описывающее закон
изменения комплексной амплитуды результирующего колебания:
и (/)=<71ИД (Z)+UQ1V (/)=t7011„ +z/0OTP 1=
= С7О1,аде>₽Ч1+ое-^'). (3.13)
Коэффициент отражения от нагрузки в общем случае — ком-
плексное число
е = |с|е7Ч
Учитывая это, после несложных преобразований выражения
(3.13) получим формулу, описывающую закон относительного
изменения амплитуды напряжения вдоль линии передачи, нагру-
женной на произвольный пассивный двухполюсник:
- V1+2 lei cos (2(4 -?.)+|ер. (3.14)
Чтобы проследить за поведением амплитуды результирующего
тока в линии, по аналогии с (3.13) запишем
/ (1)-/м W+Л,р W==— е«'+е-'а<=
^-.Уопад e^(l-Qe-2^9. (3.15)
?в
Вводя комплексную амплитуду тока падающей волны на на-
грузке /опад=—Сопад/^в, получаем выражение для относительного
изменения амплитуды тока
=Vl-2|e|cos(2(4-f.)+|C|< (3.16)
Ипад|
Отметим что рР — вещественное число, не превосходящее единицы. Нед: Рассмотрим совместно формулы (3.14) и (3.16) и отметим пре-
статком такого способа описания явлений в нагруженной линии является то, чт жде всего, что амплитуды напряжения и тока в анализируемой ли-
здесь не учтены фазовые соотношения между падающей и отраженной волна» нии являются периодическими функциями продольной координаты.
Легко видеть, что токи и напряжения будут повторяться через
§ 3.2. Интерференция падающей и отраженной волн отрезки 3?, удовлетворяющие соотношению 2 pi? = 2 л, откуда
в нагруженной линии передачи ^ = Л/2.
пяиие-' Далее> относительные амплитуды напряжений и токов колеб-
Явления, о которых пойдет речь, характерны для всех Ра11Л Лются между 1 + |р| и 1— |р|. И наконец, если в каком-либо сече-
деленных волновых систем и, в частности, для линий перед :з нии линии наблюдается максимум напряжения, то здесь же будет
Одновременное существование в линии передачи двух волн — п»,МИНИМуМ Тока, и наоборот.
ющей и отраженной, которые в разных точках линии оолада
38
/1//1
ж
П/Г
.«пр на рис. 3.2, соответствуют u
V иные представх oUo и описывают явление стОяче^\
КР тномУ значению обычно называют пуЧНо^^
мИкСнм 'мЫ В СТ0ЯСтепень неравномерности графИКа *4,
Ма ^-узлами- Степ от веЛичины модулЛ3У<
ниМУй амплитуды завис: фп опреДелЯет собой лиш?Ж
юШС пяжения. фазов п j, пучностей. Отметим обстпЬкЧ-
eHTi Положения у3 существенное в прак^Х1
натЫ р нических измерений ^Рад,Ч
амплитуды вблизи узла" М,1%
более резко, чем макои„у1>(
пучности. Вб.^;
Для количественного
степени выраженности стоя -а5)
ны вводят коэффициент стоЯч% *•
ны (КСВ), равный отноШеЛЧ
литуды напряжения или тока *
ности стоячей волны к ам38^
соответствующей величины ПЛ"^-
На основании сказанного *
КСВ следующим образ» связан с модулем коэффнцпеята
________гччгОТГТЛ’
Мцип
L
2/2
Рис 3.2. Картина стоячей волны
” напряжения
НИЯ ОТ нагрузки:
КСВ =
(З.г
(3.8
Ипах _J + /б] ,
’tflmin i —1<?Г
КСВ—1
„„ 161 ксв +1 ’
или
КСВ —вещественное число, которое не мо?:
Отметим, что
быть меньш^ае^''ктеристики эффекта отражения от нагру*
Ин0ГДаХпиент бегущей волны (КБВ), определяя его как»
вводят коэффициент oei уЩ
личину, Обратную КСВ, Т. е.
КБо=1/КСо. (i)i
и™ исчерпывающего описания волновой системы достаток
яаечить закон распределения амплитуды напряжения, посм«
картина распределения амплитуды тока повторяет картину „
Еяевия амплитуды напряжения, будучи смещенной вдоль»
Sa Головину пространственного периода стоячей волны, т. ел
В"р2жимгогласовання. Если «„=/., то отражение от нагрузи г
сутствует т е р=0. Поэтому в соответствии с формулой (3.1!
амплитуда напряжения во всех точках линии без потерь одинаков
и равна амплитуде падающей волны.
* Чисто стоячие волны возникают при условии |р| = 1 (потоки мошмг
падающей и отраженной волн равны и противоположно направлены). Случа
когда |р| =#= 1 и в то же время |р|¥=0, иногда называют режимом ежей»
воля.
40
и
Линия, короткозамкнутая на конце. Здесь р = — 1, т. е. |р| = 1
ф,1=180°. Подставим эти значения в формулу (3.14):
M-~2|sin₽(|. ’ (3.20)
В рассматриваемом случае концу линии соответствует узел
напряжения, последующие узлы располагаются через равные ин-
тервалы длиной Х./2 (рис. 3.3, а).
nil
/ Опа)!
2,0
Хул
? Л/2 Л Зя!2 ?Я .ЧП!? Я! -f-/--1-х_
КО
°. Л/2 Л Зя/2 2л 5Я/2 fiL
а)
a)
fil
Юпаф
2,0-
lUl/lU^ih
КО
то
о
VV \ -:>£\Г
Я/2 Л Jff/2 2Л 5л/2 Jtt “фт-1-
J1L
6)
Рис. 3.3. Распределение напряжения
вдоль линии передачи:
а — в режиме короткого замыкания; б — в
режиме холостого хода
1 6)
Рис. 3.4. Картина стоячей вол-
ны в линии, нагруженной на
реактивное сопротивление:
а — индуктивная нагрузка; б — ем-
костная нагрузки
Линия в режиме холостого хода. Если ZH=oo (холостой ход),
|р| = 1 и (рп=0. Поэтому
|#(О|
l^iiaul
2|cos₽Z|. (3.21)
Отличие от предыдущего случая состоит в том, что на конце
линии наблюдается не узел, а пучность стоячей волны напряже-
ния (рис. 3.3, б).
Линия, нагруженная на чисто реактивный двухполюсник. Пусть
7П=/ХШ причем возможен как случай Хп>0 (индуктивная нагруз-
ка), так и Хн<0 (емкостная нагрузка). Коэффициент отражения
ZB +
откуда следует, что |р| = 1, а фазовый угод коэффициента отраже-
ния
?и = л —2arctg .
^В
(3. 22)
41
,вШ»с. скова формулой (3.14), имеем
Воепользова
(1.
|6’nJ I К "в/|
чисто индуктивная, то а
Если
и график
рис. ? '
У-J.il... -
волн, падающей и
10(01
1.75
1.0\
0.75\
0.50
0.251Ф--0.75У
я72
Л Зтг/2 flL
нагрузка ли, 1обрстает форму, изображ'е
С гнелгет обратить внимание на то, что Banp,2®J,
ри' ЗЛ “ 5»ил, и Равны нулю, поскольку амплнтуды*%
узлах стояче! №•"“ I ЖС„1|ОЙ, одинаковы из-за отсутст“ ,<4
7 -»"->юшеи и । Чески.х потерь в нагруЗКе п”
линии наблюдается не экст
ное, а некоторое проМе>кК*Ч
значение амплитуды напр?
при этом ближайшим к нагой****
стремумом будет пучность . *
волны. * •вШ
Линия, нагруженная на емк
ведет себя сходно с предыС$}
однако здесь картина стоячей
ны смещена в пространстве так
ближайшей к нагрузке экстрем
ной точкой является не пучнОд
О
_ is Стоячие волны в линии с
„,ouu.. на активное сопротивление, не равное^
Линия нагруЖ^Нй ппедставляет особый интерес в прикладу
новому. Этот слу ' ого согласования). Если /?п>2в, то из фо.
задачах (режим нети коэффициент отражения будет веществе»
мулы (3.9) след> ’ числом, в то время как при R„<Z3 этот ко
ным положительным „ из упомянуть1х ситуаций под>
эффициент отрица (ента отражеНия означает, что fa
жительность коэф “ раженной волн на нагрузке совпадаю-
напряжений падаюшей^ P^ в оказываются np0TH&.
вследствие lero T интерференции волн происходит
фазными. Как следствне, Р е уменьшение тока в ней. Им»
,ю это'Гэффект позволяет удовлетворить условию (3.6). Явленц
возникающие при /?Н<2В, полностью противоположны тем, котора
только что описаны.
узел (рис. 3.4, б).
В соответствии с формулой (3.14) закон изменения напряже-
ния вдоль линии
при Rn>ZB
^Й-=/1 + 2|е|соз2р/-Н(>|2 (3.24
Рпад1
при /?н</в
. . я
^ = l/l-2|Q/cos2p/ + |e|a. (32:
Графики, отвечающие одному и тому же значению |р|, пред-
ставлены на рис. 3.5. Их особенностью является то, что здесы
42
конце линии наблюдается либо пучность стоячей волны напряже-
ния (при Rn>Zu), либо узел (при /?«<£.).
§ 3.3. Распределение фазы колебаний
в стоячей волне
В некоторых радиотехнических задачах, связанных с практикой
измерений на СВЧ, оказывается существенным вопрос о виде
функции, описывающей закон изменения фазы колебаний вдоль
линии передачи. Обратимся к формуле (3.13) и представим се так:
U (/) -- tfOnM с,9‘ [ 1 4" |q| сое (23/ - ?„) — j |q| sin (2?/ — ?„)]. (3. 26)
Анализируя это выражение, отметим наличие фазового множи-
теля ехр (/₽/), который характеризует линейно изменяющийся
с координатой / фазовый сдвиг на
угол 0/, обусловленный падающей
волной (величина фазового сдвига
положительна, поскольку в точки,
более удаленные от нагрузки, коле-
бания падающей волны приходят
раньше).
Кроме того, некоторый фазовый
угол в общем случае присущ и сом-
ножителю, стоящему в квадратных
скобках. Проделав несложные пре-
образования, получим выражение
для полного фазового сдвига в ли-
нии:
.?(/) = 0/-arctg —.
k 1 + Iq|cos(2?Z-Th)
(3.27)
Рис. 3.6. Изменение фазы колеба-
ний вдоль линии с резистивной
нагрузкой
По формуле (3.27) применитель-
но к резистивной нагрузке ((£„—0) рассчитан ряд графиков, пред-
ставленных на рис. 3.6. Следует отметить, что с ростом модуля ко-
эффициента отражения кривые становятся все более нелинейными.
В пределе при |р|->1 графики фазовых зависимостей приобретают
«ступенчатую» форму. Это означает, что на протяжении одного пе-
риода стоячей волны колебания во всех точках происходят синфаз-
но. Однако при переходе через узел фаза колебаний скачком изме-
няется на 180°.
Эти закономерности нужно иметь в виду при создании уст-
ройств, в которых отрезки линий передачи играют роль фазовра-
щателей с калиброванной величиной фазового сдвига. Если регу-
лировка фазовращателя проводится за счет изменения его длины,
то для получения высокой точности необходимо максимально сни-
жать величину отражений в линии передачи.
43
§ 3.4. Измерительная линия
Рис. 3.7. Конструкция измери-
тельной линии
пртся специальный прибор, служащий Для
Так называется картины стоячей волны в ЛИн Ч
ментального ИСС„„А еШ1Тельной линии применительно Л
Дачи. КоП7ХЦту схематически показана на рис. 3.7. Основ >
альному ваР”Хгулярная линия передачи, вдоль которой ?
бора является ре* у г рсзке в несколЬко длин волн про?
на узкая продольная щель. 0р
ция этой щели совпадает с’на?
нием линии тока на внешнем ?'
нике, так что наличие ее практ?
не сказывается на характере во,?
го процесса в линии. Через ?
внутрь линии вводится зонд /,
ставляющий собой миниатюрную^
ревую антенну, сигнал с которой
порционален напряжению, регистра
емому в выбранном сечении лш
Этот сигнал детектируется СВЧ->
дом 2 и поступает на какое-нибд
устройство индикации. Зонд вместе'
относящимися к нему узлами укр9
лен на специальной каретке 3, котора
перемещается вдоль линии.
Простейшим и наиболее важна
видом измерений, осуществляемым с помощью описываемого прт
бора, является нахождение КСВ нагрузки. Для этого, плавно пере-
мещая каретку измерительной линии, отмечают максималь»
Птах и минимальное Qmin показания индикатора. Если детекторна:
характеристика линейна, то КСВ — amax/amin. Подобные измерив
всегда носят относительный характер, т. е. здесь несуществен
абсолютная величина амплитуды падающей волны.
Информацию о свойствах нагрузки получают также при из»
рении расстояния, отделяющего нагрузку от ближайшего экстре
мума стоячей волны напряжения. Поэтому измерительные лии
снабжены точной шкалой, по которой можно находить линейк
перемещения каретки. Способ определения параметров нагрЯ
с помощью измерительной линии описан в гл. V.
О различных применениях измерительной линии в радиоте®
Задачи и упражнения к гл. Ill
3.1. Линия передачи с волновым сопротивлением ZB = 75 Ом нагружена на
сопротивление Zn=30+/45 Ом. Определить модуль и фазу коэффициента отра-
жения от нагрузки р. Какой КСВ установится в линии?
Ответ: |р| =0,557, <рн=—1,19 рад, КСВ=3,51.
3.2. Линия передачи, имеющая ZB=50 Ом, нагружена на конденсатор С=
- - ..........________ =25 пФ. Частота колебаний f=300 МГц. Какое расстояние отделяет нагрузку от
стоячей волны. Для ЛИНИИ С потерями & ближайшего узла стоячей волны?
) Имеем слелт/юптрр пктпяжение Ответ. 6,39 см.
'-•"’-Дующее нырц/лспп 3.3. диния передачи с малыми потерями идеально закорочена на одном
--- -----nniinnouiio W Г' R
Ч ,е волны в линиях передачи с потерями
Рассмотрим кяи
пределение наппяжрн^ ИЯеТ затУхание в линии передачи на р#
аналогии г ^пРЯЖения стоя-* - F
ии с Формулой (3.13)
плекснон амплитуды результирующего колебания:
и (О=^опал eV+б/Опаяр e-v=£/Ona, [ 1 [с| е^'е"'
(3.28)
имеет
При этом относительное изменение модуля напряжения
вид
J l-j-2!Q|e-2’zcos(23/-?H)-|-|Q;2e-^
Сравнивая это общее соотношение с формулой (3.14), которая
относится к случаю идеализированной линии передачи без потерь,
отмечаем наличие растущего экспо-
ненциального множителя перед зна-
ком корня, что говорит о возраста-
нии амплитуды падающей волны в
направлении от нагрузки к генера-
тору. Кроме того, следует учесть,
что на достаточно больших расстоя-
ниях от нагрузки, т. е. при а/»1,
подкоренное выражение в (3.29)
стремится к единице и поэтому ос-
цилляции результирующей ампли-
туды будут затухать. Причина этого
явления заключается в том, что вол-
на, отраженная от нагрузки, экспо-
ненциально уменьшает свою ампли-
туду, двигаясь к генератору, так что
в конце концов эффект интерферен-
ции волн исчезнет.
На рис. 3.8 изображены пример-
ные графики стоячих волн в линии
с малыми и достаточно большими
потерями. Отметим, что неодинако-
вость напряжений в соседних узлах
ханием в линии, иногда приходится учитывать как источник допол-
по которой можно находить линейи нительной погрешности при проведении высокоточных эксперимен-
тов с измерительной линией.
!й!
(3. 29)
WW
о
JUL
д)
Рис. 3.8. Стоячие волны в линии
передачи с малыми (а) и больши-
ми (б) потерями
о
и пучностях, вызванную зату-
конце. На расстоянии I от короткого замыкания проводится измерение КСВ.
45
44
§ 3.4. Измерительная линия
Так называется специальный прибор, служащий для экспери-
ментального исследования картины стоячей волны в линии пере-
дачи. Конструкция измерительной линии применительно к коакси-
альному варианту схематически показана на рис. 3.7. Основой при-
бора является регулярная линия передачи, вдоль которой на от-
Рис. 3.7. Конструкция измери-
тельной линии
линия передачи, вдоль которой на от-
резке в несколько длин волн прореза-
на узкая продольная щель. Ориента-
ция этой щели совпадает с направле-
нием линии тока на внешнем провод,
нике, так что наличие ее практически
не сказывается на характере волново-
го процесса в линии. Через щель
внутрь линии вводится зонд 1, пред-
ставляющий собой миниатюрную шты-
ревую антенну, сигнал с которой про-
порционален напряжению, регистриру-
емому в выбранном сечении линии.
Этот сигнал детектируется СВЧ-дио-
дом 2 и поступает на какое-нибудь
устройство индикации. Зонд вместе с
относящимися к нему узлами укреп-
лен на специальной каретке 3, которая
перемещается вдоль линии.
Простейшим и наиболее важным
видом измерений, осуществляемым с помощью описываемого при-
бора, является нахождение КСВ нагрузки. Для этого, плавно пере-
мещая каретку измерительной линии, отмечают максимальное
«max и минимальное ctmin показания индикатора. Если детекторная
характеристика линейна, то KCB = amax/amin. Подобные измерения
всегда носят относительный характер, т. е. здесь несущественна
абсолютная величина амплитуды падающей волны.
Информацию о свойствах нагрузки получают также при изме-
рении расстояния, отделяющего нагрузку от ближайшего экстре-
мума стоячей волны напряжения. Поэтому измерительные линии
снабжены точной шкалой, по которой можно находить линейные
перемещения каретки. Способ определения параметров нагрузки
с помощью измерительной линии описан в гл. V.
О различных применениях измерительной линии в радиотехни-
ке см. [6].
§ 3.5. Стоячие волны в линиях передачи с потерями
Рассмотрим, как влияет затухание в линии передачи на рас-
пределение напряжения стоячей волны. Для линии с потерями по
аналогии с формулой (3.13) имеем следующее выражение Ком,
ллексной амплитуды результирующего колебания:
U (/) = tZOna, ev 4- t/0„aaQ е-« e e.,e/Jf j 1 1с! е_:.,е-; (1М-Т,)|
(3.28)
'видПРН ЭТ°М °ТНОСИТСЛЬНОе изменение модуля напряжения имеет
[ZW = е’г 2 bl е-2*' cos (2?Z - Тм)+iqP е-*4. (3.29)
Сравнивая это общее соотношение с формулой (3.14) которая
относится к случаю идеализированной линии передачи без потерь
наличие ПйСТУШот — 1
отмечаем наличие растущего экспо-
ненциального множителя перед зна-
ком корня, что говорит о возраста-
нии амплитуды падающей волны в
направлении от нагрузки к генера-
тору. Кроме того, следует учесть,
что на достаточно больших расстоя-
ниях от нагрузки, т. е. при а/»1,
подкоренное выражение в (3.29)
стремится к единице и поэтому ос-
цилляции результирующей ампли-
туды будут затухать. Причина этого
явления заключается в том, что вол-
на, отраженная от нагрузки, экспо-
ненциально уменьшает свою ампли-
туду, двигаясь к генератору, так что
в конце концов эффект интерферен-
ции волн исчезнет.
На рис. 3.8 изображены пример-
ные графики стоячих волн в линии
с малыми и достаточно большими
потерями. Отметим, что неодинако-
вость напряжений в соседних узлах
. 1й!
С/
S)
Рис. 3.8. Стоячие волны в линии
передачи с малыми (а) и больши-
ми (б) потерями
^onoi!
и пучностях, вызванную зату-
ханием в линии, иногда приходится учитывать как источник допол-
нительной погрешности при проведении высокоточных эксперимен-
тов с измерительной линией.
Задачи и упражнения к гл. Ill
3.1. Линия передачи с волновым сопротивлением ZB=75 Ом нагружена на
сопротивление Zn=30+/45 Ом. Определить модуль и фазу коэффициента отра-
жения от нагрузки р. Какой КСВ установится в линии?
Ответ: |р| =0,557, <рн=—1,19 рад, КСВ=3,51.
3.2. Линия передачи, имеющая ZB = 50 Ом, нагружена на конденсатор С —
= 25 пФ. Частота колебаний /=300 МГц. Какое расстояние отделяет нагрузку от
ближайшего узла стоячей волны?
Ответ: 6,39 см.
3.3. Линия передачи с малыми потерями идеально закорочена на одном
конце. На расстоянии I от короткого замыкания проводится изм р
Вывести формулу, связывающую КСВ с величиной коэффициента ослабления
данной линии. 1 ксв j
Ответ: а = 2/ 1П КСВ-1 ’
3.4. Каков коэффициент отражения по мощности от стыка двух коаксиаль-
ных линий передачи с волновыми сопротивлениями 50 Ом и /5 Ом. Введите
понятие к. п. д. системы и определите его численное значение для данного
случая.
Ответ: рр = 0,04, к. п. д.=96%.
Глава IV
ТРАНСФОРМИРУЮЩИЕ СВОЙСТВА ОТРЕЗКОВ
ЛИНИИ ПЕРЕДАЧИ
§ 4.1. Отрезок линии передачи как распределенный
четырехполюсник
и входного тока Для
Рис. 4.1. Схема распределен-
ного четырехполюсника
Рассмотрим некоторый отрезок регулярной линии передачи
произвольной длины I (рис. 4.1). Начало отсчета координаты z
совместим с зажимами линии, на которых определены комплекс-
ные амплитуды входного напряжения й\
правых зажимов считаем заданными
выходное напряжение С2 и выходной
ток /г-
Данная система представляет со-
бой линейный стационарный четерых-
полюсник, описываемый, как известно
из общей теории электрических цепей
[8], той или иной матрицей.
Задачи, рассматриваемые в данной
главе, удобно решать, характеризуя
изучаемый распределенный четырехпо-
люсник его матрицей передачи (ЛBCD-матрицей). При этом неза-
висимыми переменными являются выходные параметры Га и /г.
причем связь между ними и выходными переменными устанавли-
вается двумя равенствами:
ux=au2-\-bi2,
ix=cu2^bi2.
Знание матрицы передачи
(4.1)
[А] =
А В'
С D
позволяет ответить на вопросы, касающиеся любых внешних ха-
рактеристик четырехполюсника. Например, если к выходным за-
жимам подключен двухполюсник нагрузки с сопротивлением ZH,
так что то из (4.1) следует формула для входного со-
противления системы со стороны левых зажимов:
у йх AZH + в
(4.2)
Аналогично ““ ИТ™’ К09фФИЦ"ет "еред,,,,
тырехполюсника по напряжен! Чц
Ku=^(^^Tzn+B
Поставим задачу определить элементы ^^С/Э-матрипг,
регулярной линии передачи. Воспользуемся тем, что Наибо^Ч
£ решение уравнения Гельмгольца имеет вид суммы <Ж
бегущих в противоположных направлениях: ДВУ* Во
'' .л Г о-Тг_ДС,еТг
тырехполюсника
Z„
и=
с равенствами (4.1), видим,
потерями имеет вид:
Z„sh у/Д
ch yZ
(4.6)
г
. _£ке-тг--Т"еТг- 5
/(2)"Z„ Z" I
т„..е амплитудные коэффИцИент
г „ С!_пока падающей и отраженной
Здесь Ci " Соответственно к > вь1Х0Дные комплексные ам
0ТНпСЯ^'м.м эти коэффициенты Рд щих формул подстановкой
Выразим /г, получении,е'^алгебраических уравнений:
т’ДЫ 02 11 721 систему г
плитуды Сч и
z=l. При этом получаем
Cie-"-{-C2e"=l/2,
Cie-^-C2e^=/2Z
решение которой элементарно:
С,=-^‘
2
C2=-^--^Z" e-U'
йч + eTZ
В’
Сравнивая полученный результат
что матрица передачи отрезка линии с
|~ch yl
1 u I
— sh у/
Если линия передачи не имеет потерь, то у = /р. Принимая во
внимание формулы связи между гиперболическими и тригономет-
рическими функциями, для линии без потерь имеем
cospZ JZB sin $Г
~ sin pZ cos pZ
_^в
§ 4.2. Входное сопротивление нагруженного отрезка
линии передачи
Используем полученные результаты для
сопротивления отрезка линии, нагруженного
случае комплексное, сопротивление ZB. На
(4.2)
и=
(4.7)
нахождения входного
на известное, в общем
основании формулы
7 __ Zn ch yl + Z„shyl
BX z„
—— sh у I + ch yl
Принято вводить безразмерные нормированные сопротивления
Z'B.=ZJZB и Z;=Z„/ZB, (4.9)
при этом равенство (4.8) примет вид
(4.8)
Таким образом, комплексные амплитуды в произвольном се.
чении выражаются через величины Z72 и /2:
О(z\= + ^Zb- ет (l~z}4- л>2~^-в е-т (i-z)
' ' 2 1 2
/ {Z)=-^2 + kZ" ет — —2-~l2Zn е~т <z-*>
2ZB 2ZB
, _ z; + thy/
BX — “ ZT7 "-•
1 +ZHthyZ
Данная формула утверждает, что в общем случае входное со-
противление не совпадает с сопротивлением нагрузки. Поэтому ко-
нечный отрезок линии передачи выполняет функцию трансформа-
тора сопротивлений. Это служит основой для многочисленных тех-
(4. Ю)
Входные напряжение и ток, соответствующие значению
,-r Uj + IjZn и . 1/2 —/2?в и
2*2
/. = _^ + /2zg t _ (/2-i2zB j
2ZB 2ZB
или
нических применений таких устройств.
2=0:’ Проанализируем формулу (4.10) для частного случая линии
без потерь, когда th yZ = th (j(3Z) =/tg р/. Из формулы видим, что
свойства рассматриваемой системы определяются не самой абсо-
лютной длиной I, а безразмерным аргументом
0 = ₽Z = 2nZA, (4.11)
называемым электрической длиной отрезка. Выражение для нор-
мированного входного сопротивления отрезка линии передачи без
Ux=U2zh YZ4-72ZBsh у/,
jx = (j2-4~ sh y/4-72chyl.
Zu ,
потерь запишем так:
7' _ ZH + &
ВХ--- ------------ •
(4.12)
48
49
В режиме согласования (при Z'H—1) входное сопротивленЛ
любого отрезка независимо от его электрической длины в точной
равно волновому сопротивлению.
Входное сопротивление разомкнутых и короткозамкнутых н
конце отрезков. Если отрезок линии на выходе закорочен, так ч^
Z'B—0, то
(4.13j|
ZBX = /tg&.
При холостом ходе на выходе Z/n = °° и поэтому
Z»=-/ctg&. (4.14)!
Из графиков, представленных на рис. 4.2, видно, что входные
сопротивления подобных устройств всегда чисто реактивны и явля.
ются периодическими функциями
электрической длины. Например, от.
резок короткозамкнутой линии дли.
ной /<Х/4 имеет электрическую дли.
ну Ф<л/2 и индуктивное входное
сопротивление, которое неограни-
ченно возрастает с приближением
длины отрезка к значению Х/4. В
интервале л/2<-&<л входное сопро-
тивление отрезка носит емкостный
характер; при дальнейшем увеличе-
нии электрической длины наблюда-
ется периодическое повторение опи-
Рис. 4.2. Графики входных со-
противлений разомкнутых и
короткозамкнутых отрезков пи-
санных свойств. Представляют ин-
терес точки с координатами 0=
= (2н—1)л/2, (/1=1, 2, 3, ...), когда
нии передачи входное сопротивление короткозамк-
нутой линии передачи без потерь
неограниченно велико по модулю. Это явление напоминает резо-
нансные свойства обычного параллельного колебательного контура.
В гл. VIII показано, что действительно в таком отрезке линии пе-
редачи имеет место резонанс.
Наличие хотя бы малых, но конечных потерь в линии ограничи-
вает величину резонансного сопротивления. Действительно, на ос-
новании формулы (4.10) нормированное входное сопротивление
отрезка короткозамкнутой линии с потерями выражается следу-
ющим образом: J
=th у/=th (<zZ-|-/?/) •= —th aZ + j tg .
1 + j th aZ tg £Z
Разделяя вещественную и мнимую части, имеем:
п' ________________________ th al (1 -f- tg2 j3Z)
Пвх---------------------— ,
1 + tg2 pz th2 az
y' _ tg p/(l — th2aZ)
И BI-------------------- .
1 -f- tg2 ₽z th2 al
(4. 15)
(4- 16)
(4. 17)
50
При резонансе, когда tg О—<-оо, реактивная часть входного со-
Кпотивления обращается в нуль, в то время как активная состав-
ляющая остается конечной и стремится к величине l/(th al). На
пис 4.3 и 4.4 представлены соответствующие графики, относящие-
ся к случаю линии с достаточно малыми потерями (а/рс 1).
Рис. 4.3. Активная часть вход-
ного сопротивления коротко-
замкнутой линии
Рис. 4.4. Реактивная часть вход-
ного сопротивления короткозамк-
нутой линии
ся
Короткозамкнутый отрезок линии передачи широко применяе^-
в технике СВЧ. Изменяя его длину пои шшпт» е
тткп.чямыкателя. так Щ ередвижного
линии передачи широко применяет
8 короткозамыкателя, так называемо-
го поршня короткого замыкания,
можно создавать простые и удоб-
ные элементы для настройки и ре-
I гулировки, выполняющие роль пе-
I ременных реактивных сопротивле-
I ний (рис. 4.5).
Резонансные свойства разомкну-
I того на конце отрезка лйнии переда-
I чи могут быть проанализированы
I читателем самостоятельно.
Поршень
Микрометрической
Винт
Рис. 4.5. Эскиз конструкции ко-
аксиального подстроечного эле-
мента
Отрезок линии передачи без по-
терь с произвольной нагрузкой. На
I основании (4.12), отделив вещественную и мнимую части, имеем:
' (о - < tg &) + tg & (х;+tg»)]
вх +
х' = <x» + tg &)(i-x;tg ft)-/?;2tg&
z BX ' (i_x;tg»)2+/?;2tg2&
(4.18)
(4.19)
Формулы эти довольно громоздки и анализ их в общем виде
лишен наглядности. Для практической работы по расчету СВЧ-
51
„ть ЭВМ. В Приложении
,«о испол^грдне, выполняющей расч?;
лесообР^ч на ФОРс произвольной нагрузи
Рич а отРезка ‘ЛщОУ10111116 своиства отРезка ди.
'2"леН « трайсфоР „«ное сопротивление (Я'вЭц
Ли) получаем более простые «.
,,Г(4Л9) " 4'20’
конструкций пелесин г
ется образец подпрограммы
входного сопротивления отр
Легче анализируются тра
нии, нагруженного
Х'В=О). При этом
отношения:
(4.20)
1 + RH2 tg2 » ’
вх — .
входного сопротивления здесь веет
— от R'B при tg O-vQ доаип,Ло^
прй
1 + Ян2 ‘g2»
(4.21)
Здесь tg '0’->оо и поэтому
Z'x=l/Z;=r;. (4.22)
Подобная конструкция получила в радиотехнике название чет-
вертьволнового трансформатора и широко применяется для целей
согласования линий передачи с разными волновыми сопротивле-
ниями. Рассмотрим схему, изображенную на рис. 4.8, где для со-
гласования двух линий, обладающих волновыми сопротивлениями
2в1 и ZB2, между ними включен четвертьволновый трансформатор.
Определим волновое сопротивление трансформатора ZBTp. Заме-
тим вначале, что трансформатор в сечении а — а' нагружен на ак-
тивное сопротивление ZB2, так что R'aa- =ZB2/ZBTp (нормировка
проводится на неизвестное пока волновое сопротивление ZBTp). Из
формулы (4.22) следует, что R'ьь- =ZBTp/ZD2 или в ненормированном
виде Rbb'=Z в tp/Zb2. Условие согласования в точках b— Ь' прини-
мает вид: Z2BTp/ZB2=ZB1, откуда
15
Активная часть .......
тельна и изменяется в пределах
If/',
К—1
7
входного сопротивления линии
с резистивной нагрузкой
вх есть
(4.23)
т. е. волновое сопротивление трансформатора равно среднегеомет-
рическому от волновых сопротивлений согласуемых линий.
Я/4
ar'
Рис. 4.8. Четвертьволновой
трансформатор
стики согласования двух ли-
ний с различными волновыми
сопротивлениями
Рис. 4.6. Активная часть вход-
вето с....: .-пт/-:ия .-ииии пере-
дачи с резистивной нагрузкой
+ Реактивная часть входного сопротивления Х'__
риодяяеская функция 0. изменяющая свой знак Нек0™Рые |
фики, иллюстрирующие формулы (4.20) и (4.21), показаны I
рис. 4.6 и 4.7.
§ 4.3. Полуволновые и четвертьволновые трансформаторы
Отрезки регулярных линий, длина которых составляет целое |
число полуволн на некоторой рабочей частоте, обладают ва^пии
свойством.'Здесь О=пл (п=1, 2, 3, ...) и поэтому в соответств--
с (4.12) имеет место равенство Z'n—Z'H. Подобный полуволне
трансформатор осуществляет тождественное преобразование
противления нагрузки. „oupthoMV оросительная уэкополосность, поскольку для функционирования такого устрой-
Иначе ведет себя система, у которой длина / равна НС • .тва требуется, чтобы электрическая длина трансформатора равнялась 90°. При
числу четвертей ДЛИНЫ ВОЛНЫ Т. е. отходе от номинальной частоты будет наблюдаться рассогласование, тем в боль-
шей степени, чем резче перепад между волновыми сопротивлениями согласуемых
/ —~ 1) . 12 3 ) линий. В качестве примера на рис, 4.9 представлены результаты расчета КСВ,
4 ♦ возникающего в первичной линии с волновым сопротивлением Zu—50 Ом, кото-
ne-
Интересным и несколько необычным
использованием принципа четвертьвол-
нового трансформатора являются «просветляющие» покрытия, наносимые на
рабочие поверхности оптических линз с целью уменьшения потерь света на отра-
Muviuic, жение от стекла. Эти покрытия представляют собой прозрачные пленки из фто-
) и поэтому В соответствии £истых соединений толщиной в четверть длины волны оптических колебаний.
указатель преломления пленки выбирают равным среднегеометрическому от
показателей преломления воздуха и стекла.
Существенным недостатком четвертьволнового трансформатора является его
52
53
„ - папичными вторичными ЛИНИЯМИ при ПОМг.
&X,c^r,;n° •
ют в полосе частот ш( 1широкополосностн согласующего V °й Ча^ ?
Простым X Г’1" 4'9’ ЯПЛЯеТСЯ С°ЗДан"° иепо°4ки\ансфор>. ,
ра. вытек лои.и ми монотонно изменяющимся волновым PnL Ра«СфотЧ
7)РОВ олпвгков^ ДЛ'' " сопротивлений. приходящийся на 0Дн "Р°Т'4?Л !
П',ИЭТ°^Х небольшим, что значительно улучшает частотньщ Уг <СтУпе?Л
b S«. Подробнее этот вопрос рассмотрен в гл. IX. I
В заключение параграфа отметим важное обстоятел^ I
ли некоторая нагрузка подключена через отрезок линии пп®0’ Ес- I
то входное сопротивление такой системы будет зависеть о'1Ин°й /, /
ты, причем т Часто,’ f
dZKX dZRX . dPr dZRX I
dn> d9 d<-> </& пф ’ I
T. e. частотная зависимость входного сопротивления вып "'
ярче, чем больше длина линии I. В радиотехнике это яп±На
зывают эффектом длинной линии. Поэтому при КоНс ЯВЛение На-
очень широкополосных систем СВЧ нужно по возмох'1ТрУИр0вайН1|
шать длины отрезков линий передачи. ности умень |
§ 4.4. Отрезок линии передачи как трансфоомя^
уровня напряжения Р ТоР
Рассматриваемые устройства можно
трансформаторов напряжений г. л
зии с 0.3) и (4.7) коэффициент передачи отрезка п
-об. н-ружеХ Ч
«а сопротивле.^
§ 4.5. Понятие о волновых матрицах
и матрицах рассеяния
В теории и практике расчетов устройств СВЧ-диапазона поми-
мо рассмотренной ранее матрицы передачи широко используют и
другие матрицы, характерные для цепей с распределенными па-
раметрами. Пусть ко входу и выходу некоторого линейного четы-
рехполюсника подключены две регулярные линии передачи с вол-
новыми сопротивлениями ZBI и ZB2 (рис. 4.11). Если ввести ком-
плексные амплитуды напряжений и токов на входных и выходных
зажимах этого четырехполюсника, то полное описание его внешних
характеристик дается двумя уравнениями
йх = Айг-\-В1ъ
(4. 27)
I
--------> применять в качестве)
и токов. Действительно, в соответст-|
Комплексные величины (7Ь Д2, /ь /2 связаны с комплексными
амплитудами напряжения падающих и отраженных волн, сущест-
вующих в обеих линиях:
над + ^1 отр>
/ __U\ пад б^отр
1 7
zb1
zB1 ’ J
(4. 28)
ZT
ко-
на-
пе-
терь, нагруженного на сопротивле-
ние ZB,
~ sin § ’
cos & 4- j —г~
z.
(4.25)1
и2 — и 2па д i 2отр’
j __ ГЛ>пад ^2отр
/ 2----------------
ZB2 zb2
Если теперь подставим выражения для комплексных амплитуд
напряжений и токов из (4.28) в
два линейных алгебраических урав-
нения, связывающих четыре пере-
менных Г?1пад, t>10Tp, СУгпад, Г/2отр-
систему (4.27), то получаем
Отраженные волны
Для линии, нагруженной на ре-1 Любые две из этих переменных при-
--- п модуль коэффициента пе-| нимают в качестве независимых, а
зистор R
редачи
H >
------------1
Линейный ~t~
Г
„ sin2&
COS2 § 4- —-ту-
Графики на рис. 4.10 показыва- дующих,
ют, что при О»л/2 и /? (,2 >1 можно* ’
добиться значительного возрастания
уровня выходного напряжения по
—----------------------— ««./лтц п ПЙ*
Рис. 4.10. Графики модуля
эффингеита передачи по
пряжению отрезков линии
редачи с различными нагрузоч-
ными сопротивлениями
дс ХЕХе^;::0Т°РЫЙ с-'ществУет на входе. Следуетиметьвм-
на’нагрузке/во сто^кгУ^^3411’ повышая амплитуду напряжения
так что "усиления мгпвп р23 Уменьщает амплитуду тока в ней,
не может. Юсти в этоя пассивной системе происходить
54 j
_ _ . _ _ _ - — — —
две оставшиеся определяют с помо-
' щью уравнений связи. Нетрудно
(4.26) подсчитать, что число возможных
комбинаций здесь равно шести, од-
нако применяются лишь две сле-
1. За независимые переменные
принимают комплексные амплитуды
двух волн, падающей и отраженной,
на выходе четырехполюсника. Соответствующая система
ний, эквивалентная (4.28), приобретает вид:
^1пад = ^11^2пад"Ь^12^2отр>
61
Вход
четырех-
полюсник
‘ez
Выход
Падающие волны
Рис. 4.11. Включение четырехпо-
люсника между двумя
передачи
линиям»
уравне-
(4.29)
матри«» коэфф»"»'"1»
этой системы
. ГЛ1
й матрицы четырехполюсника.
(4.27) получим выражения дЛя к
получила на3ваН'^/(4 28) в (
т 12=У
^21 =V
r22 = Y
мшыми переменными являются амплитуды
2. Пусть незав1\сХСя с обеих сторон по направлению к че.
волн, распространяющихс
(71ОТр = 5ц^1пад + 512^2отр»
£/2пад = 521^1пад + 522^2отр- .
^в2/’ '
—---CZBl-D-^-\, I
7- zn2)’ i
(4.30)
2. Пусть И'
I____ .
тырехполюснику.
Матрицу
[S] =
5ц 512
52i 522.
(4.31)
называют матрицей рассеяния четырехполюсника
Элементы матриц [7] и [5] взаимно связаны. Из сравнения си-1
стем (4.29) и (4.31) видно, что
Su=T2i/Tu; 512 = (Л1^22 —Л2^21)/Л1;
5Я=1/ТП; 522=-Г12/Гп. (4.321
Широкое использование Т- и S-матриц в теории цепей СВЧ
обусловлено наглядностью коэффициентов этих матриц и просто'
той их экспериментального определения. Так, из (4.29) следует,)
что коэффициент Гц является отношением комплексных амплитуд.^
напряжения на входе и выходе четырехполюсника в режиме согла|
сования по выходу (при {72оТр=0). Аналогично, 5ц — комплексный!
коэффициент отражения на входе при согласовании на выходе. |
Важно и то, что в системы уравнений (4.29) и (4.31) не входят
амплитуды токов, которые на высоких частотах не только трудно
измерить, но иногда, например в случае полых волноводов, даже
нельзя однозначно определить. - . К'. 1
Дальнейшее усовершенствование методов матричного описания
распределенных систем связано с принципом нормировки токов!
56
и напряжении. В СВЧ-диапазоне проще всего измерять мощность,
переносимую волной вдоль линии передачи. Существуют волновые
системы (например, современные линии с акустическими поверх-
ностными волнами), в которых токи и напряжения приобретают
формальный смысл, в то время как переносимая мощность имеет
четкий физическии смысл. Стремление построить аппарат описа-
ния волновых процессов любой природы, протекающих в самых
разнообразных линиях передачи, привело к понятию волновых ам-
плитуд или нормированных напряжений падающих и отраженных
волн, которые здесь вводятся следующим образом: Роенных
^Апад
бАпад .
' Отр
"2""=Жг:
(4. 33)
V'2zb2 ' 1
Волновые амплитуды имеют размерность квадратного корня
мощности; для вычисления переносимых мощностей достаточ-
найти квадраты модулей соответствующих волновых амплитуд:
• •
7^1пад Uн1пад^н1падэ А>1отр== ^hIotP^hIotP’
• • *
^2пад Uн2иад^н2пад> — ^н2отр^н2отр-
Волновые амплитуды падающих и отраженных волн связаны
нормированной волновой матрицей, а также нормированной матри-
цей рассеяния. Например, записав систему линейных уравнений
ИЗ
НО
— нгпад " Hllv н2пад “Г1 нЮ1-1 н2отрэ I
^н1отр ^'н21^н211ад ^н22^н2отр’ )
можно, используя (4.33), убедиться в том, что нормированная вол-
новая матрица выражается следующим образом:
Аналогично получаем нормированную матрицу рассеяния
[S«] =
^11
Задачи и упражнения к гл. IV
в2
^В1
^22
| 4.1. Докажите, что результирующая матрица передачи каскадного соедине-
ния двух отрезков линии передачи является произведением соответствующих
матриц указанных отрезков.
57
. тгружен на комплекси°е сопр0.
,,«»»*• «««о* «од"ос с°"р°™вление-
лк лнн,”’оПь?ай?и HOpM"Pona подключен к короткозамкнуТ0и,
42 0тР?3 д 5-/°’8’л7П с £=70 В "лм Z В = 150 Ом (диэлектрик^
-ФйЙзЙтйг!?2.......................... °’"".......
® nV тока В ^*47 Д. кОние °триРтся оТ „1 иа отрезка 3,2 м. Определить
»п“ «’У» "”р’ „,8а.
282 В;
Глава V
КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ
Все многообразие режимов, реализуемых в нагруженной линии
передачи без потерь, можно отобразить на круговой диаграмме
полных сопротивлений * (далее для краткости будем называть её
просто круговой диаграммой), которую можно рассматривать как
метод наглядной интерпретации решений уравнений Гельмгольца.
В настоящей главе описан принцип построения круговой диаграм-
мы и рассмотрены основные способы ее применения.
§ 5.1. Понятие текущего коэффициента отражения
Рассмотрим некоторую нагруженную линию передачи без по-
терь. Применяя те же обозначения, которые использовались в
гл. Ш, можно записать выражение для комплексной амплитуды
колебания в произвольной точке с координатой Г.
й (Z)==t/„,W + y„f(Z) = yOn„e«'+8У0,„е-»'. (5.1)
Отношение комплексных амплитуд отраженной и падающей
волн в произвольном сечении линии называют текущим коэффици-
ентом отражения и обозначают pz. Из (5.1) видно, что
= (5.2)
Текущий коэффициент отражения позволяет выразить напря-
жение и ток в линии следующим образом:
^«=^,,„«(1+0,),
/(')=- (1-е,). (5.3)
^В
(5.4)
откуда следует формула, связывающая рг с нормированным вход-
ным сопротивлением линии, имеющей длину I
7' _ 1+Qz _ ^(0
вх —------—------:---
1 —QZ
Соотношение (5.4) можно интерпретировать с помощью вектор-
ной диаграммы. Для этого достаточно заметить, что комплексное
число pz геометрически отображается вектором длиной |р|, кото-
рый с ростом координаты I вращается в направлении по часовой
стрелке (фазовый угол pz должен уменьшаться).
KL--------
I * В литературе ее называют также диаграммой Смита или диаграммой
Вольперта.
59
/к 4) в некотором относительном масптт
Числитель *<>₽“>',“» амплитуде напряжения, а знамепа^’^
пропорииоиалеи текущ Так1)М о6разом, чтобы построить BJk"
текущей ам"л"Т5-’ пряже11Ия и тока в линии, нужно отлож^*
Хмяв^№”“"""0”“Т0РаМИ
й волны), геометрически сложит
pi и — рь ть
его с
Рис. 5.1. Векторные диаграммы, иллюстрирующие сложение
падающей и отраженной волн
Последовательность векторных диаграмм, соответствующих раз-
личным длинам I, представлена на рис. 5.1. Пусть при /=0 фаза
коэффициента отражения от нагрузки р взята такой, что векторная
диаграмма приобретает вид, изображенный на рис. 5.1, а. Здесь
фаза напряжения па нагрузке опережает фазу тока в ней, что
свидетельствует об индуктивном характере нагрузки. Перемещаясь
вдоль линии по направлению к генератору, будем вращать вектор
pi по часовой стрелке на угол 2|3/. При этом неизбежно возникнет
такая ситуация, когда вектор р/ расположится горизонтально (рис.
5.1, б). В сечении линии с такой координатой I напряжения пада-
ющей и отраженной волн сложатся синфазно, а токи этих волн бу-
дут противофазны. Как следствие, здесь наблюдается пучность на-
пряжения и узел тока; входное сопротивление отрезка линии такой
60
длины чисто вещественно, причем нормированное значение вход-
ного сопротивления в соответствии с формулой (5.4) численно рав-
но КСВ.
С дальнейшим увеличением длины линии происходит изменение
порядка следования векторов напряжения и тока — входное сопро-
тивление линии приобретает емкостный характер (рис. 5.1, в). Про-
должая вращение вектора р;, приходим к противофазному сложе-
нию напряжении и синфазному сложению токов (рис. 5.1, г), ког-
да возникает узел напряжения и пучность тока. Нормированное
входное сопротивление при этом вещественно и равно 1/КСВ. Пе-
риодичность функции в правой части формулы (5.2) свидетельству-
ет о том, что полный оборот на векторной диаграмме будет совер-
шен при перемещении вдоль линии на расстояние Х./2.
На векторной диаграмме принято обозначать характерные точ-
ки и линии. Так, точку О называют точкой согласования,
поскольку ей соответствует нулевой коэффициент отражения. Если
точка, изображающая режим работы линии, совмещается с точкой
А на векторной диаграмме, то входное сопротивление линии ока-
зывается равным нулю, поэтому точку Л называют точкой ко-
роткого замыкания. Рассуждая аналогично, приходим к вы-
воду, что точку В следует называть точкой холостого хода.
Диаметр АВ есть геометрическое место точек, отображающих та-
кие режимы линии, когда напряжение и ток синфазны. Поэтому
этот отрезок называют линией активных входных со-
п р о т и в л е н и й.
Окружность единичного радиуса с центром в точке О представ-
ляет собой геометрическое место точек чисто реактивных входных
сопротивлений, так как для каждой точки этой окружности сдвиг
фаз между напряжением и током равен 90° в соответствии с из-
вестной теоремой об угле при вершине вписанного треугольника,
опирающегося на диаметр.
Наконец, любую окружность с центром в точке О и произволь-
ным радиусом, меньшим единицы, называют окружностью
постоянного КСВ. Радиус этой окружности численно равен
модулю коэффициента отражения от нагрузки. При увеличении
длины линии I изображающая точка перемещается по этой окруж-
ности в направлении по часовой стрелке.
§ 5.2. Построение круговой диаграммы
В предыдущем параграфе показано, что изменения текущего
коэффициента отражения отображаются поворотом соответствую-
щего вектора. С помощью формулы (5.4) свяжем текущий коэффи-
циент отражения непосредственно с нормированным входным со-
противлением отрезка линии передачи заданной длины, нагружен-
ного на известное комплексное сопротивление.
В теории функций комплексного переменного формулы вида (5.4)
называют дробно-линейными преобразованиями [5]. Для рассмат-
61
„ имеет место закон преобразован»»
гл частного случая и ффИЦИента отражения о,ДЧ
SS -«“С" кт“ЛорМ"Рованных DX0OTb,x СОПР°™^1
в комплексную Zb'x = /?'x +А-х-
дробно-линейные в плоскости pTSeJe>d
Jctbom: любая окружи ^ находящуюся в плоскости
ими в ДРУГУ10 °кКЕности является бесконечная прямая). &
(частным случаем 3^' преобразование обладает свойствомZ
Ге^^’c^Zfonc"сохраняет величины углов между любыми М
сикающимися линиями. плосКОСТИ Гвх состоит из двух 0
Координатная сет tf'BX=const и X Bx = const. На Ос
нальных семейств прямы ть> чт0 на плоскости текуД
ванин сказанного моя на векторной диаграмме, описаЙ
коэффициента 0TPa*f” ’ нд двух семейств окружностей, 0pToJl
в § 5.1, эта сетка пр ‘ диаграммой полных сопротивлЛ
нальных друг диаграмма на плоскости комплексного
снабженная координатной сеткой |
“из^^п построения этой сетки. Формулу (5.4) зап,ш„|
ВВИДе , (1+П+Л1 [(1+£) +л][(1-5) + М]
/?'х+У^зх=(-ут^^71' (1-е)2+т)2 •
Разделяя здесь вещественную и мнимую части, получим равен-
ства: , _ '
^вх“" (1—6)2 + 12
2т]
Хвх = (1-6)2 + 1 ’
_______________________________________________________________________________________nd с в данном сл
котовые являются уравнениями координатных линий нормирован! ресует, поскольку она соответствует случаю нагрузки
но?оРв“ одного сопротивления в плоскости текущего коэффициента^ пасои™ Двухполюсник, а на источник колебании
отражения.
Выведено уравнение семейства окружностей, представляющих
собой геометрические места постоянных активных частей входного
сопротивления отрезка линии. Центр любой окружности семейства
находится в точке с координатами {!=/?'„/(l-i-Я'вх), П = °}при
этом радиус окружности будет определяться величиной 1/(1 + /?'Вх)-
На рис. 5.2 показаны некоторые из таких окружностей, соответст-
вующие положительным значениям /?'В1. Отметим два обстоятель-
ства.
1. Положительным значениям /?'вх соответствуют окружности,
целиком лежащие внутри круга с единичным радиусом. Иными
словами, дробно-линейное преобразование (5.4) позволяет отобра-
(5.6)
Представим уравнение (5.6) в эквивалентной форме
Ri (1 - S)2+/?в>2+S2 4- П2 - 1 = О,
или
1+^вх 1+Явх
Дополнив левую часть (5.8) до полного
/1
\ 1+^?вх
зить правую полуплоскость комплексной переменной Z'BX на внут-
реннюю область единичного круга, лежащего в плоскости перемен-
ной рь Остальная часть плоскости pi нас в данном случае не инте-
-------------- __7ст случаю naiрузки линии не на
двухполюсник, а на источник колебаний (генератор).
2. Все окружности, соответствующие различным значениям
R'BX, касаются друг друга в точке холостого хода с координатами
(1 = 1, т] = 0). При /?'ах>1 наблюдается резкое сжатие масштаба
круговой диаграммы вблизи точки холостого хода, что служит ес-
тественным ограничением точности графических построений.
Аналогичным способом уравнение (5.7) приводится к виду
уравнения окружностей:
($_1)2+ n 1
\ ^вх / вх
Окружности этого семейства имеют радиусы 1/|Х'вх|; центры их
расположены в точках с координатами {1= 1, iq= 1/Х'вх}.
квадрата, получим
1
(5. 10)
2
62
63
„,huul, (пис. 5.3) показывают, что okdv-д.
Соответствующие граф (|_Р.тей ВХОДНого сопротивлений ПН°'
Сти постоянных реакт ’завИСИМ0СТИ От знака величины ГРас'
х=ы;^"-и^в^м^ве;ет^Ня:^
=йса^ которая ограиичивает ит^
ющую нас област,’й'а '’Драммы, используемой на практике ППи
Чертеж KPyr””Pj рСрИфсрии диаграммы нанесен фазовый у?Ол
“куще"' КэЛи'циенга отражения 4и//Х, выраженный в доля.
Рис. 5.4. Круговая диаграмма полных сопротивлений
бочей длины волны; поворот изображающего вектора на 180° соот-
ветствует движению вдоль линии на расстояние Х/4 в направлении,
указанном стрелкой.
Если круговая диаграмма используется часто, то удобно допол-
нить ее прозрачным вращающимся движком с центром в точке О,
на котором нанесены шкалы КСВ или модуля коэффициента от-
ражения.
64
§ 5.3. Примеры использования круговой диаграммы
Определение КСВ по iai.iuunuv _
пусть сопротивление
волновому сопротивлению линии, отображается точкой /на пне
5.5. 1тобы Узнать величину КСВ в линии, достаточно снести точку
/ на горизонтальную ось с помощью окружности, показанной пунк-
тиром, а затем прочесть результат по шкале, нанесенной вдоль от-
резка ОВ. Если шкала КСВ (или--------
граммы, то отсчет интересующей
средственно.
КБВ) имеется на движке дна-
величины осуществляется непо-
Рис. 5.5. Нахождение вели-
чины КСВ в линии передачи
Рис. 5.6. Определение входного
сопротивления нагруженного
отрезка линии
Определение входного сопротивления отрезка нагруженной ли-
нии заданной длины. Предположим, что нормированное сопротив-
ление двухполюсника нагрузки соответствует точке / на рис. 5.6.
Движению от нагрузки к генератору будет соответствовать пере-
мещение изображающей точки вдоль окружности постоянного КСВ,
показанной пунктиром. Если длина отрезка линии I задана, то век-
тор текущего коэффициента отражения должен быть повернут на
угол 4л//Л в направлении, указанном стрелкой. Входное сопротив-
ление рассчитываемой системы определяют нахождением коорди-
нат точки 2, лежащей на пересечении окружности постоянного
КСВ и прямой, вдоль которой расположен вектор текущего коэф-
фициента отражения.
Определение расстояния от нагрузки до ближайшего экстремума
стоячей волны напряжения. Если точка 1, изображающая входное
сопротивление нагрузки, расположена так, как это показано на
рис. 5.7, то при движении вдоль окружности постоянного КСВ в на-
правлении от нагрузки к генератору линия активных входных со-
противлений первый раз пересекается в точке 2, которая соответ-
ствует узлу стоячей волны напряжения. Расстояние /1 от нагрузки
до узла находим, исходя из величины угла поворота изображающей
3—2910 65
точки, равного 4л/]/Л. Таким же образом находим расстояни
ближайшей к нагрузке пучности напряжения, равное /1+^/4 е До
Определение нормированной входной проводимости. Если
торая точка симметрична точке Z'm относительно центра диагНеКо'
мы (рис. 5.8), то она отображает нормированную входную п
димость У,вх = 1/2'вх. Докажем это утверждение. Если р°во-
•7' 1 + 6 + Л
Ztbx— , , . »
1 — £ — Л
то, переходя от точки (£, ц) к симметричной точке (—? \
лучим ’ т"’ по-
1-e-_ZL=i/z;>=r;x.
Определение сопротивления нагрузки с помощью измеритель
ной линии. Предположим, что экспериментально найденная с по
Рис. 5.7. Определение расстояния от
нагрузки до узла стоячей волны
Рис. 5.8. Определение вход-
ной проводимости отрезка
линии
мощью измерительной линии картина стоячей волны изображена
на рис. 5.9, а. Вычислив KCB = amax/-aniin, утверждаем, что точка,
изображающая нагрузку, может лежать только на окружности
постоянного КСВ. Для окончательного установления точки нагруз-
ки следует воспользоваться величиной отрезка 1\, отделяющего на-
грузку от ближайшего минимума стоячей волны. Геометрическим
местом точек минимумов является отрезок АО, поэтому, двигаясь
от него по окружности постоянного КСВ в сторону нагрузки и осу-
ществляя поворот радиуса на угол 4n/]/Z, получаем искомую вели-
чину нормированного сопротивления нагрузки (рис. 5.9, б).
Расчет реактивных согласующих устройств. Пусть линия переда-
чи с известным волновым сопротивлением нагружена на некоторое
комплексное сопротивление Z„. Ставится задача осуществить со-
гласование линии с нагрузкой за счет включения сосредоточенной
реактивности /Лсогл способом, показанным на рис. 5.10, а. При
66
этом должны быть определены как величина согласующего реак-
тивного сопротивления, так и координата его подключения /согл.
В соответствии с рис. 5.10, б, если двигаться от точки, изобра-
жающей нагрузку, по линии постоянного КСВ в сторону генерато-
ра, то в двух сечениях линии с координатами /Согл1 и /СОГЛ2 актив-
ная часть нормированного входного сопротивления нагрузки будет
равна единице. Если теперь последовательно включить реактивные
6)
Рис. 5.9. Определение сопротивле-
ния нагрузки по измеренным ха-
рактеристикам стоячей волны
сопротивления /Хс.Огл1 или /ХСогл2> удовлетворяющие равенствам
А’согл! + ХВХ1 = 0 ИЛИ Л^согл2“|--^вх2 —0,
то суммарная реактивность будет компенсирована и в линии насту-
пит режим согласования. Согласование при этом будет иметь мес-
то лишь на строго расчетной длине волны. Аналогичным образом,
используя при расчете уже не входные сопротивления, а входные
проводимости, можно добиться согласования за счет включения
параллельной шунтирующей реактивности.
На практике согласующие реактивности обычно выполняют в
виде короткозамкнутых на конце отрезков линии передачи, назы-
ваемых согласующими шлейфами, длину которых с целью настрой-
ки и регулировки можно изменять.
Задачи и упражнения к гл. V
Выполняя данные задания, следует пользоваться только графическими мето-
дами, обращая внимание на точность расчетов с помощью круговой диаграммы.
5.1. Линия с волновым сопротивлением 75 Ом нагружена на резистор 25 Ом.
Определить КСВ в линии.
3* 67
1ЛННЫ ВОЛНЫ, отделяющее нагру30Ч11
• i
=20-/ 6U, ' „инии, имеющий волновое соПр0.
-*?? юоиую "₽ов"
“е. 1“ »»«“““ к °"jzrZ """л”™™»“’°5 I
5.5. Линия пеР^пть длину °*рекС11Мальна. 1
СТ0Р ?я Йодного сопротивлени линии, показали, что КСВ=3, I
ляЮ£тВет О-188 Л доведенные в нагрУ*ен« волны является пучность напря. |
Й' Из^РеН^г^ 0.12 X. Вычислить нормированное |
а рннТотйоящая от нагрузкг 11 я сопротивлений нагрузки с помощью из- |
жЛНпИ0Т’чвленне нагрузки. измерения сопро ются На практике), когда |
С° Р5 7 Предложите(именно ° mN । быть не может.
ыерипльЛ иагРУЗКИзХДвнПой нагрузки следует размещать^. |
в ^’ГнТкаком если известно, что R, - - •
X.
Глава VI
ВОЗБУЖДЕНИЕ РЕГУЛЯРНЫХ ЛИНИЙ ПЕРЕДАЧИ
ВНЕШНИМИ ИСТОЧНИКАМИ
§ 6.1. Физическая постановка задачи о возбуждении
линии передачи
Механизм возбуждения линии передачи, как и любой другой
электромагнитной системы, основан на том, что в некоторой обла-
сти пространства электромагнитное поле внешних источников вза-
имодействует с полем линии передачи. Характер взаимодействия
внешней системы и линии определяется пространственно-временны-
ми соотношениями, существующими между указанными электро-
магнитными полями. В одном случае внешние источники за период
колебаний совершают работу над электрическими зарядами, кото-
рые располагаются на проводниках линии. При этом линия играет
роль потребителя энергии. В другом случае электромагнитное поле
линии в среднем за период совершает положительную работу над
зарядами, протекающими во внешних цепях. Здесь линия являет-
ся источником, а внешние цепи — потребителями энергии. Несмот-
ря на различие этих двух ситуаций, отдельное изучение их не тре-
буется, поскольку в любой взаимной динамической системе источ-
ник и нагрузка могут меняться местами.
Полное рассмотрение проблемы возбуждения линии передачи
требует определения векторов электромагнитного поля
пространстве и может быть проведено только методами .....ири-
динамики. Решение подобной задачи довольно сложно. Однако,
чтобы понять основные физические закономерности про*”'
буждения линии, можно применить упрощенный подход
ный на решении системы телеграфных уравнений.
Возбуждение линии внешним магнитным полем. Представим,
что на некотором участке линии за счет действия внешних источни-
ков создан однородный в пространстве и переменный во времени
магнитный поток Ф, ориентированный так, как это показано на
рис. 6.1, а. Рассматривая воображаемый контур 1 — 2 — 3 — 4, на
основании закона электромагнитной индукции Фарадея запишем
(£Е<Л=-4Ф/Л. (6.1)
Интегралы по сторонам контура 2 — 3 и 4— 1 равны нулю, по-
скольку силовые линии электрического поля всегда перпендику-
лярны металлическим проводникам (в противном случае по про-
водникам протекали бы сколь угодно большие токи). По опреде-
лению,
во Всем
^ектро-
процесса воз-’
Л. основан-
69
ь
иоЬ^\
а
поэтому из (6.1) следует
с/34 — С/21 — С»
гле£-эдс электромагнитной индукции, равная-</ф/Л.
Последнее соотношение позволяет отобразить рассматриваемы#
процесс эквнвалеитной схемой (рис. 6.1, б), включив в „ее „осле
звательный источник э.д.с. £; такая модель правильно описывав
Хюший важный факт: ток вдоль л«=.,„ в ’
как напряжение при переходе
вает скачок на величину Е.
через область источника претерпе-
000
0 0®
000
6)
6)
Рис. 6.2. Возбуждение ли-
нии передачи переменным
во времени электрическим
полем:
а — картина поля; б—эквива-
лентная схема
I* —
Рис. 6.1. Возбуждение ли-
нии передачи переменным
во времени магнитным по-
лем:
а — картина поля; б—эквива-
лентная схема
Если магнитный поток неоднороден по z, то следует говорить
о линейной плотности э.д.с. ^(z), определив ее следующим обра-
зом:
E=[<S(z\dz. (6.2)
Когда возбуждающее внешнее магнитное поле локализовано
на участке, значительно меньшем, чем длина волны колебаний, то
плотность э.д.с. имеет вид б-функции, сосредоточенной в некоторой
точке z0:
<£ (z) — Eb(z — z0). (6.3)
Физическая размерность величины <$ (В/м) совпадает с раз-
мерностью напряженности электрического поля.
Возбуждение линии внешним электрическим полем. Пусть за
счет действия внешних источников на некотором конечном участ-
ке линии (рис. 6.2, а) создано переменное во времени электриче-
70
ское поле ЕСТор, которое называют сторонним полем в отличие от
собственного поля линии. Теория Максвелла утверждает, что при
этом в пространстве будет существовать ток особого рода, называ-
емый током смещения. Плотность тока смещения определяется
формулой
•^см —ео^ Е/d/, А/м2.
Если внешние источники создали между проводниками линии
токи смещения, то это означает, что в данной области пространст-
ва существуют некоторые источники тока в обычном электротех-
ническом понимании. Абстрагируясь от пространственного распре-
деления полей, можно констатировать наличие распределенных ис-
точников тока с некоторой линейной плотностью 3^(z), так что
/ = J У (z}dz.
Соответствующая схема изображена на рис. 6.2, б.
Если внешние источники распределены вдоль участка линии,
малого по сравнению с длиной волны, то плотность стороннего то-
ка выражается в виде результирующего тока источника /о» умно-
женного на 6-функцию, сосредоточенную в точке источника До-
^(z)=/08(z-z0). (6.4)
§ 6.2. Дифференциальные уравнения линии,
возбуждаемой внешними источниками
Рассматриваемая здесь задача поставлена не с целью описать
какой-либо конкретный случай возбуждения линии передачи, а для
того, чтобы путем разумной идеализации добиться возможно боль-
шей общности. Предположим, что неограниченная с обоих концов
регулярная линия передачи возбуждается как внешними электри-
ческими, так и внешними магнитными полями, гармонически изме-
няющимися во времени. Распределение в пространстве возбужда-
ющих источников может быть описано двумя .плотностями & (z)
и ^X(z).
Если ранее при рассмотрении свободного процесса в линии па-
дение напряжения на элементе длиной dz обусловливалось лишь
прохождением тока 1 и представлялось в виде
dU = — Zjdz,
то теперь следует учесть наличие в каждом бесконечно малом
элементе источника внешней э.д.с. и записать последнее соотноше-
ние следующим образом:
dtl=-Zjdz+$(z)dz. (6.5)
Аналогичные по характеру рассуждения приводят к выраже-
нию для приращения тока в бесконечно малом отрезке линии:
di— —-YxUdz-\-j (z)dz. (6.6)
71
ним воздействием: . .
(6.7)
Отсюда можно
в 1
или нал
Z и
di/dz= — У4“(2)-
Отсюда можно вывести неоднородные уравнения Гельмгольца,
которые будет входить лишь одна из неизвестных величин-, ’
которые буда. Диффере„ц„руя оба уравнения системы (6.7) „„
объединяя их, получаем
d2Uldz2-y2O= -Zjj ^-YdiSIdz, (6.8)
d2'Hdz2 — у2/= — У\c'' (z)-\-dj idz, (6.9)
2_у_____квадрат комплексного коэффициента распрострацц.
гармонического волнового процесса, вычисленный на частоте
где
ния
возбуждающих источников.
§ 6.3. Решение неоднородных уравнений Гельмгольца.
Понятие функции Грина для стационарного
волнового процесса в линии передачи
Свойство линейности и вытекающий отсюда принцип суперпо-
зиции оказывают чрезвычайно большую пользу при решении задач
о возбуждении линий передачи. Вместо рассмотрения практически
неограниченного множества всевозможных конфигураций возбуж-
дающих источников оказывается достаточным изучить небольшое
число случаев, когда возбуждение производится источниками не-
которого специального вида. Дальнейший этап связан с объедине-
нием элементарных источников таким образом, чтобы их результи-
рующий вклад был равен эффекту от заданного реального источ-
ника. Подобный прием широко используется при математическом
рассмотрении процессов в линейных системах. Примером может
служить метод интеграла Дюамеля, применяемый для вычисления
переходных процессов в линейных цепях.
Выбор конкретного вида элементарных источников достаточно
произволен. Однако целесообразно полагать, что такие источники,
имея конечную амплитуду, строго локализованы в некоторых опре-
деленных сечениях линии. Пусть, например, единственным возбуж-
дающим источником в линии является источник синусоидальной
э.д.с. До, размещенный в сечении z = z0 и включенный так, как это
показано иа рис. 6.1, б. При этом плотность сторонней э.д.с на еди-
ницу длины линии
$ z0).
Воспользовавшись уравнением (6.9), для тока в линии будем
иметь дифференциальное уравнение:
dV/dz2-у2/ = - YXEJ> (z - z0). (6.10)
72
Из закона сохранения заряда следует, что стационарное рас-
пределение тока в линии должно быть непрерывно всюду, в том
числе и в точке источника. Во всех точках, свободных от источни-
ков, комплексная амплитуда тока удовлетворяет уравнению сво-
бодных колебаний
d27/rfz2_v2/==o.
Напряжение 77 в точке источника должно претерпевать скачок
на величину э.д.с., т. е.
lim£7(z0-Ti) = limtr(z0 + T|)-£o- (6.11)
Л -*0 т]-►()
Условие (6.11) указывает на то, что первая производная по z
от решения уравнения (6.10) должна быть разрывной при z=z0,
поскольку всюду, за исключением самой точки источника, напря-
жение и первая производная от тока пропорциональны: •
(6.12)
Y! dz
Очевидно, что включение в бесконечно протяженную линию рассмотренного
точечного источника приведет к возбуждению в ней системы двух бегущих волн,
распространяющихся в обе стороны от источника, причем оба эти направления
равноправны. При более тщательном рассмотрении эта мысль требует поясне-
ний. Дело в том, что идеализированное представление о линии передачи без
потерь допускает существование волн, отразившихся в бесконечно-удаленной
точке и не уходящих от источника, а приходящих к нему. Требуются некоторые
основания для того, чтобы объявить волны, приходящие из бесконечности,
«иефизичными» и в дальнейшем исключить их из рассмотрения. Обычно прини-
мают во внимание то, что любая реальная линия все же обладает некоторым
затуханием, наличие которого приводит к поглощению любых колебаний, про-
шедших достаточно большой путь от источника. В физике данный принцип изве-
стен как условие Зоммерфельда, или принцип предельного поглощения.
Основываясь на (6.12), можно проверить, что условие (6.11)
имеет место, если
1а d'l 1^0 1* dl Y j/’g /С 1О\
11m--- =-1-1; Jim------- =-----i—(6.13)
i)->0 dz г0—т| 2 ц-^0 dz Zo+’l 2
Пусть в формуле (6.10) Ео=1. Введем новую неизвестную
функцию (^ определив ее следующим образом:
G = IIYX. (6. 14)
Тогда неоднородное уравнение Гельмгольца для рассматрива-
емой задачи примет особенно простой вид:
(PGIdzi - у2О = - В (z - z0). (6.15)
Функция G, называемая функцией Грина, имеет важное
значение в теории волновых процессов: она описывает возбуждение
линии локальным источником гармонических колебаний с единич-
ной амплитудой.
73
Функция Грина, будучи всюду непрерывной, имеет разрыв пер.
вой производной в точке z=z0, причем, как это следует из (6.13),
lim —I =4-: =— -у- (6.16)
т)-»о dz Lo-n 2 ч-»о dz Lo+’i 2 J
Другими словами, полный скачок производной функции G При
z=Zn должен равняться единице.
Зная физическую постановку задачи, можно написать явное
выражение для функции Грина. Нетрудно проверить, что если оп-
ределить G системой равенств
(е-т(г-^)/(2у) при Z>zo,
Z° | ет (г-*в)/(2у) ПРИ z^-zo,
то одновременно удовлетворяются уравнение (6.15), условие не
прерывности в точке z=z0 и условие (6.16), накладываемое
производную. В соответствии с (6.14) ток в линии
/(z z \=\Е^~иг~г°Ч№^ при z>z0,
" | Доет (*"'z»)/(2ZB) при z^z0. ‘ 18)
Отсюда следует закон изменения напряжения вдоль линии
^/(z, Zo) =
Eoe~i (г~г,,}/2 при z^z0,
— Еое< (z~z°}/2 при zO0.
(6. 19)
Все сказанное относится и к случаю, когда возбуждение линии
осуществляется источником тока /о, локализованным в точке г=г0
(см. рис. 6.2). Отличие состоит в том, что здесь напряжение при
z=Zq непрерывно, а ток имеет скачок в точке источника:
lim / (z0 — T]) = lim/ (z0+ П)— 4- (6.20)
т]->0 Ч-М)
Рассмотрев уравнение (6.8) и связав функцию Грина с напря-
жением в линии формулой
Q=UiZx>
для напряжения имеем соотношения, аналогичные (6.18):
Utz. zD)=l/°Z-e~'"‘~“,/2 "РИ г>г"'
I/0ZBeT (*-Zo)/2 при
Ток в линии при данном способе возбуждения определится сле-
дующим образом:
(6.21)
/ (г, г0) =
/л е т
---------- при z z0,
/ J (г-г0)
-------о---- при г<г0.
(6.22)
Зная функцию Грина, можно найти решение любого неоднород-
ного уравнения Гельмгольца посредством прямого интегрирования.
74
Пусть следует отыскать решение уравнения d2O/dz2 — у2О=—F(z)
на всей оси z. Произвольная функция F(г) описывает плотность
распределения источников вдоль линии. Если G(z, £) является
функцией Грина, которая соответствует возмущению, вызванному
точечным источником единичной интенсивности, размещенным в
сечении z=£, то искомое решение имеет вид
^ (*)= J
Действительно, подставляя это выражение в предыдущее урав-
нение, в силу известных свойств б-функции получим тождество:
— оо
= - J ^(C)8(z-C)rfC=-F(z).
§ 6.4. Строгий вывод выражения для функции Грина
Исходя из основного дифференциального уравнения
d2G/dz2_Y2G = —Ь(г —г0), (6.23)
будем искать функцию Грина 0 в форме спектрального разложения
оо
G(z,z0) = —\ F(x, z0)e/x*dx
------------------00
с неизвестной пока плотностью F (х, z0). Для нахождения F преобразуем по
Фурье обе части уравнения (6.23) и воспользуемся тем, что
B(z — z0) = — \ е/х(г Zo)dx.
2л J
В результате имеем
( e7«(«-zo)dXt
откуда
е-Лг0
и окончательно
/х(г—z0)
-----------dr..
х? + у2
(6. 24)
75
„гпппя пповедем методом теории вычетов. Заметим
Вычисление этого ||||ТС£Р‘; ‘ ,!меет два простых полюса с координатами
что подынтегральное выражение и ие обладала потерями, то имело бы место
....................... ПСРеД равенство у=/₽ и поэтому полюсы располагав
пись бы па вещественной оси. Но, как указы-
валось, некоторое, хотя бы очень малое зату-
хание всегда присутствует, поэтому
«,=—/а+₽. Особые точки подынтегральной
функции располагаются при этом так, как это
изображено на рис. 6.3.
Вычислим интеграл (о.24) для случая
когда z>z0. Контур интегрирования должен’
состоять из всей вещественной оси в плоскости
•к п полуокружности С, бесконечно большого
радиуса, проведенной в верхней полуплоскости.
Такой выбор контура позволяет на основании
леммы Жордана пренебречь интегралом по ду.
ге С|, так как при Im х>0 экспоненциальный
множитель погасит подынтегральную функцию
на достаточно большом удалении от начала
X|,2= ±/у- Если бы линия
1тх
Rex
Рис. 6.3. Расположение особых
точек па комплексной плоско-
сти
координат.
Далее, используя формулу Коши, получим
О (г, г0)
е;х(г-г0)
7.2+ у2 ,
eJtt(z-z0)
е-Т(г-г0)
2Х!
2у
(6. 25)
= j
Если же z<z0, то по указанной ранее причине следует выбирать контур Са>
лежащий в нижней полуплоскости и обходимый по часовой стрелке, т. е. в от-
рицательном направлении. В результате
, jiL(z—za) \ е/»1(г—2о) ет(2—г°)
° (*' “ (тйЖ)L. " 2ч “ 2V ' (6' 26)
Как и следовало ожидать, полученное выражение целиком совпадают с фор-
мулой (6.17), найденной ранее.
Представление различных функции, не обладающих свойством аналитичности
(так, функция Грина имеет разрыв первой производной) с помощью интегралов,
вычисляемых методами теории функций комплексного переменного, является
распространенным математическим приемом, используемым в теории волновых
процессов.
§ 6.5. Элемент Гюйгенса
В физике так называют идеальный точечный источник, обеспе-
чивающий возбуждение волны, распространяющейся только в од-
ном направлении. Ясно, что точечные возбуждающие элементы,
рассмотренные ранее, этому условию не удовлетворяют. Однако
путем соответствующей суперпозиции источников можно добиться
идеальной однонаправленной характеристики возбуждения.
Рассмотрим систему двух точечных источников обоих типов,
схематически изображенную на рис. 6.4. Здесь оба источника рас-
положены при одном и том же значении координаты z = z0. Пред-
положим, что амплитуда источника э. д. с. равна Ео, а источник
тока имеет амплитуду l0=EJZti. Используя формулы (6.19)
76
и (6.21) и проводя алгебраическое суммирование напряжений, воз-
буждаемых каждым источником, получаем формулу для напряже-
ния в линии:
47 (z, z0) = (£‘°e"ПРИ г>го.
10 при z<z0.
(6. 27)
Если изменить на 180° начальную фазу одного из источников,
то получим волну, распространяющуюся в другую сторону:
О при z>z0,
EoeXz~z<>') при z<^z0.
7/ (z, z0) =
(6. 28)
Итак, рассмотренная система двух элементарных источников
действительно обладает оановиым
свойством, характерным для эле-
мента Гюйгенса.
Терминологически элемент
Гюйгенса связан с известным из
оптики принципом Гюйгенса, со-
Рис. 6.4. Эквивалентная схема эле-
мента Гюйгенса
гласно которому каждая элемен-
тарная площадка волнового
фронта может быть представле-
на как эквивалентный источник
новой сферической волны. Дан-
ный принцип обеспечивает по-
строение математической 'модели волнового процесса, распростра-
няющегося от источника на бесконечность (здесь речь идет о вол-
новых явлениях в трехмерном пространстве).
§ 6.6. Возбуждение линии передачи системой
дискретных источников.
Принцип действия направленного ответвителя
Предположим, что в регулярной линии передачи без потерь
в точках с координатами Z\, z2,..zn размещены точечные источ-
ники синусоидального тока одинаковой частоты со, обладающие
известными комплексными амплитудами /Оь /02. • • • Jon- Нужно
найти токи и напряжения результирующего волнового процесса
в любом сечении линии.
Для этого воспользуемся принципом суперпозиции. Действи-
тельно, напряжение в линии
i7(z) = 2^ + 2^’ (6/29)
к I
где первая сумма учитывает волны от источников, расположенных
левее точки наблюдения, а вторая — лишь волны от источников,
находящихся правее этой точки. Каждое слагаемое в суммах опи-
сывает индивидуальную бегущую волну. На основании (6.21) по-
следнее равенство представим так:
77
, (6'3°)
2 ^aJ i
к
Соответственно, ток в линии
i(. 1 V/ е-/Р(г~м—- V/Ozey₽(’_*z).
~ 1
Проанализируем случай, когда линия возбуждается двумя ис-
точниками, разнесенными вдоль оси на Л/4, причем во времени один
из источников по отношению к другому имеет фазовый сдвиг на
л/2, т. е.
(6.31)
Ли — zо, Ле — Л)e
Тогда правее обоих источников
g—/рг Ло^в q—J? (z—X/**) /qZTb е
2 2
левее —
Л (_ zoz" е;р* _ е~^3 (г~ — 0.
Петля
/связи
ВыгоИ
Riod
ЛК
Рис. 6.5. Направленный ответ-
витель
4
1
2
Таким образом, специально подобранная совокупность двух ис-
точников осуществляет идеальное однонаправленное возбуждение
линии передачи подобно элементу Гюйгенса. Все рассуждения ос-
таются справедливыми при замене ис-
точников тока источниками э. д. с.
Отмстим, что рассмотренная систе-
ма является частотно-зависимой в том
смысле, что на другой рабочей часто-
те, когда расстояние между возбуди-
телями уже не будет в точности равно
Л/4. часть энергии проникнет в область
левее источников.
На описанном принципе часто стро-
ят направленные ответвители — одни
из важнейших устройств в технике
СВЧ, которые могут обеспечить однонаправленную передачу коле-
баний из одной линии передачи в другую. Конструкция простейше-
го направленного ответвителя показана на рис. 6.5. Здесь между
двумя линиями, первичной и вторичной, имеются устройства связи,
в данном случае магнитные, разнесенные на Х/4. Такой выбор ин-
тервала между возбудителями обеспечивает необходимое запазды-
вание сигнала на четверть периода. Легко проверить, что волна,
бегущая в основной линии от плеча / к плечу 2, возбуждает во вто-
ричной линии лишь волну, направленную в плечо 4. При выполне-
нии условий, о которых сказано ранее, сигнал в плече 3 будет от-
сутствовать.
78
§ 6.7. Усилитель с распределенным усилением
В качестве примера использования теории возбуждения линий
передачи системой сосредоточенных источников рассмотрим так
называемый усилитель с распределенным усилением (УРУ), кото-
рый широко применяется в радиотехнике как устройство, способ-
ное обеспечить равномерное усиление сигналов в широкой полосе
частот, составляющей десятки, а
иногда сотни мегагерц.
Принцип построения УРУ пред-
ставлен на рис. 6.6. Основу подобно-
го усилителя составляют два отрез-
ка линий передачи, причем один от-
резок играет роль входного, а дру-
гой-выходного устройства. Для
работы на частотах в несколько де-
сятков мегагерц эти линии, как пра-
вило, выполняют в виде цепочечных
Рис. 6.6. Принцип построения
усилителя с распределенным
усилением
эквивалентов из сосредоточенных
элементов L и С. При более высоких
рабочих частотах можно применять отрезки линий с распределен-
ными параметрами.
В обеих линиях за счет включения соответствующих нагрузок
обеспечивается режим бегущих волн, причем выходная линия обя-
зательно согласовывается с обоих концов. Эти меры имеют важное
значение для обеспечения широкополосности устройства в целом.
Через равные промежутки I в выходную линию включены N ак-
тивных элементов (например, транзисторов), представляющих со-
бой зависимые источники тока, которые управляются напряжения-
ми, снимаемыми со входной линии также через равные интервалы I
(предполагается равенство фазовых скоростей волн в обеих ли-
ниях) .
Комплексные амплитуды токов отдельных источников запишем
следующим образом:
/0„=Мхе-^(«=1;<-, ^)>
(6.32)
где S — крутизна характеристики электронного прибора в рабочей
точке.
В выходной линии каждый источник тока создает две бегущие
волны с амплитудами Sf7Bx/2, движущиеся в противоположных на-
правлениях. При этом волны, достигающие согласованной нагруз-
ки на левом конце линии, окажутся поглощенными. Комплексная
амплитуда напряжения на выходе УРУ, представляющая собой
сумму вкладов от всех источников:
[j ых sir«*z& [е-W е-/Ме-Я*-W + • • • + =
(6. 33)
79
Заметим, что сложение колебаний ИМенно
бЛа1ТзДпосл°днейКформ™1ь1Ч следует выражение для модуля коэффи.
циента усиления УРУ:
=-^~- (6.34)
Итак усиление УРУ возрастает пропорционально числу актив-
пых элементов в отличие от обычных многокаскадных усилитедей,
для которых эта зависимость носит показательный характер. Поэто-
му в схеме УРУ можно получить усиление, большее единицы, даже
в том случае, когда коэффициент усиления одиночного каскада
Ko = SZB2 — меньше единицы. __
Усилитель с распределенным усилением является примером так
называемых активных распределенных систем—-на
вого перспективного класса радиоэлектронных устройств.
Задачи и упражнения к гл. VI
6.1. Источники гармонической э. 'д. с. размещены с равномерной
стью А (В/м) в пределах участка 0^z</ регулярной линии передачи,
лить комплексную амплитуду тока, возбужденного в линии при z>l.
Ответ. /м=4Ц-[1-е/Не-;’--
6.2. При какой длине I участка, занятого источниками в условиях
душей задачи, волны в линии при г>/ будут отсутствовать?
Ответ. При 1=пХ, п=1, 2, 3 ... .
6.3. В регулярную линию передачи включены два источника э. д. с. Ё\ и
с координатами г, и z2 соответственно (z2>Z|). Найти соотношение между
комплексными амплитудами Ё[ и Ё2, которое обеспечивало бы отсутствие коле-
баний во всех точках линии правее источников, т. е. при г>г2.
Ответ. Ё1+Ё2 exp [/р(г2—zj] =0.
плотно-
Опреде.
Глава VII
НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ЛИНИЯХ ПЕРЕДАЧИ
Материал, излагавшийся в предыдущих главах, относился
к случаю, когда линия передачи находится под действием внешних
источников, гармонически изменяющихся во времени. Однако одно-
частотный режим работы для большинства радиотехнических уст-
ройств является скорее не правилом, а исключением. Обычно пере-
даваемые сигналы являются колебаниями со сложным спектраль-
ным составом. Далее приведена теория распределенных систем при
негармонических входных воздействиях.
§ 7.1. Влияние характеристик линии передачи
на искажение передаваемого импульса.
Групповая скорость
Важной проблемой, представляющей интерес для техники связи,
является оценка величины искажений импульсных сигналов, возни-
кающих при распространении их вдоль линии передачи. Еще во вто-
рой половине XIX в. опыты по передаче телеграфных сигналов
вдоль протяженных кабельных линий показали, что скорость пе-
редачи информации ограничена недопустимо большими искаже-
ниями сигналов, которые наблюдались всякий раз, когда длитель-
ность передаваемого импульса становилась меньше некоторого оп-
ределенного уровня.
Искажение импульса в реальной линии передачи значительной
длины изображено на рис. 7.1. Если длительность передаваемого
импульса была достаточно велика, то на выходе получался им-
пульс, хотя и менее резко очерченный, чем на входе, но в техниче-
ском отношении достаточно точно отображающий форму исходного
колебания (случай а). Попытка последовательной передачи двух
коротких посылок, разделенных малым интервалом времени (слу-
чай б), неизбежно приводила к их «расплыванию», так что появ-
лялась вероятность принять последовательность коротких сигналов
как один сигнал большей длительности. Было отмечено также, что
эффекты расплывания усугубляются при возрастании длины ли-
нии передачи.
Нужно было объяснить наблюдавшиеся явления, а затем либо
указать способы преодоления указанных трудностей, либо выявить
предельные возможности линий передачи с точки зрения скорости
передачи информации. Полученный ответ может быть кратко сфор-
мулирован следующим образом: природа искажений заключена
в том, что при определенных условиях начинает существенно ска-
зываться неодинаковость фазовых скоростей отдельных спектраль-
ных составляющих, из которых складывается передаваемый сигнал.
4-2910
81
л а той которая изображена на рис. 7.1
Линия передачи. поДОб"»’,те1С’ комплексным коэффпвде,,^
НЯ всех частотах характер! ? .
распространения уИ"“^с^трим гипотетический двухполюсник
Р В качестве нагрузки рассмдрряющий условИю согласования
Z=. на всех частотах }
Z =ZB. га пязумным, поскольку учет отраве.
" Такое требование явл^т * Р /усложнению анализа и затруд.
ний от нагрузки привелi бь лиш £изических сторон явления.
НИЛ бы выявление принципиа
Рис. 7.1. Характер искажений импульсных сигналов в линии
передачи:
а — при большой длительности; б — при малой длительности сигнала
Будем считать, что напряжение на входе линии uBx(/)=u(0, t)
известно. Задача заключается в нахождении сигнала uBLIX(/) =u(l, t)
фиксируемого на нагрузке, которая отстоит от начала линии на рас-
стояние /. Решим поставленную задачу спектральным методом,
вводя в рассмотрение преобразования Фурье сигналов на входе
и выходе:
+ “ 1
ивх(/)е-^Л
— оо
Лых (“»)=]*
-00 J
(7.1)
Целесообразность применения спектрального метода здесь оп-
равдана тем, что свойства рассматриваемой линии передачи дли-
ной / на любой частоте <п можно описать так же, как это принято
в теории линейных четырехполюсников с сосредоточенными пара-
метрами. Для этого достаточно ввести частотный коэффициент пе-
редачи (со, /), очевидным образом связывающий спектральные
плотности:
(<•)=*(. /)Л. (<>)•
82
Знание спектральных плотностей позволяет восстанавливать
сигналы, используя обратное преобразование Фурье:
+ оо
авых (Z)=К (ад, /) FBX («>) (7.2)
— оо
или в развернутой форме
1 с” t”
«Вых(С=—cb»K («,/) е/ш/ (7.3)
00 — оо
Условие отсутствия отражений на всех частотах обеспечивает
в линии режим бегущих волн, поэтому частотный коэффициент
передачи отрезка линии
К (ш,/)=ехр(-у («)/). (7.4)
По поводу этого выражения необходимо сделать два замечания. Во-первых,
коэффициент передачи вида (7.4) не принадлежит к классу коэффициентов пере-
дачи, которые могут быть реализованы посредством сосредоточенных С/.-четы-
рехполюсников. Известно, что последние обладают коэффициентами передачи,
представляемыми как отношение двух многочленов по степеням частоты [5], в
то время как функция (7.4) имеет экспоненциальный характер. Во-вторых, изу-
чаемый распределенный четырехполюсник относится к числу физически реализуе-
мых систем, обладающих следующим свойством: при подаче на их вход веще-
) ствеиного колебания отклик на выходе также должен быть вещественной функ-
цией времени *. В силу этого должно выполняться тождество
К (—ш, /) = К* (<>, Z),
г т. е.
ехр [—а (—и) I — jp (—ш) I] = exp [—а (и) I + jp (ш) I],
; откуда
а (—ш) = а (w), 3 (—w) — —p (<o),
г т. e. коэффициент ослабления является четной, а коэффициент фазы — нечетной
! функцией частоты. В дальнейшем это свойство будет играть важную роль.
Итак, получено формальное решение задачи о форме импульса
I на выходе согласованного отрезка линии передачи, найдено выра-
, жение для частотного коэффициента передачи и выяснены некото-
рые его характерные свойства. Однако прямое вычисление интегра-
I лов вида (7.2) или (7.3) затруднительно, поэтому для формирова-
I ния представлений о происходящих физических процессах нужно
проанализировать ряд частных случаев, когда удается найти либо
I точное, либо приближенное решение.
Линия без потерь и без частотной дисперсии фазовой скорости.
[ Здесь (i = 0, р = щ/Уф, причем фазовая скорость Цф одинакова на всех
частотах. М.ожно ввести величину т = //иф — время, необходимое
* Сформулированное условие необходимо, но недостаточно для физической
реализуемости, поскольку требуется наложить ряд ограничений на поведение
коэффициента передачи в зависимости от частоты, понимаемой как комплексная
переменная [3].
4* 83
для того, чтобы ПС
мостилась от !._
....которая выбранная точка постоянной фазы
начала к копну липин. Гогда
/<(<о, /)=ехр(—/‘«'t).
и соответственно
П-“"Я»Фй°Рз?ПХ=е-"-
T„“P„”"ctJ”повторяет колеба.ше па входе, запаздывая относит^
"СГЛнния1’сМпотТерТями''не обладающая частотной дисперсией. ЗдКь
И = const 0, |3='(о/Уф, поэтому
М(<о, /) = ехр(-«/-/М
и, как следствие,
от предыдущего состоит в том, что выходной сигнал
уменьшенным по амплитуде при неизменной форме
На основании двух 'рассмотрен-
Отличие
оказывается
Рис. 7.2. Спектральная плотность
узкополосного сигнала
ных случаев можно сделать вывод
о том, что линии передачи, в кото,
рых отсутствует частотная диспер-
сия, являются идеальными канала-
ми передачи информации, обеспе-
чивающими! на выходе совершенно
точное копирование входных сигна-
лов. Возникает предположение, что
искажения связаны с нелинейным
характером зависимости коэффици-
ента фазы от частоты, имеющим
место при определенных условиях и приводящим к частотной дис-
персии фазовой скорости в линии.
Линия передачи без затухания и с произвольным характером
частотной дисперсии фазовой скорости. Чтобы понять нестацио-
нарные процессы в линиях с дисперсией, изучим наиболее простой
случай, когда колебания па входе представляют собой узкополос-
ный (квазигармонический) процесс. Такое предположение даст
возможность использовать для анализа метод медленно меня-
ющихся амплитуд *.
Методом медленно меняющихся амплитуд изучают колебания,
спектральная плотность которых сосредоточена в узкой полосе
частот шириной II (рис. 7.2), причем II/G)o<iCl, где <оо — некоторая
* Этот метод успешно применяется в различных областях физики. Возник-
новение его связывают с именем известного английского физика Рэлея (1842—
1919); дальнейшее развитие метод получил в трудах Ван дер Поля, Н. Н. Бого
любова, С. И. Евтянова и других ученых.
«4
центральная частота спектра, выбираемая достаточно произвольно.
С уменьшением ширины полосы 11 такие колебания по форме при-
ближаются к гармоническим.
Запишем формулу сигнала на входе линии, являющуюся обоб-
щением традиционно!о метода комплексных амплитуд:
«HxU)==Re [£вх(/)е><“«>'|, (7.5)
где L (0 функция, называемая комплексной огибающей, которая
изменяется во времени гораздо медленнее, чем гармоническое коле-
бание частоты gio. В общем случае функция /7 (/) принимает ком-
плексные значения и поэтому не является обычным физическим
сигналом. Но это свойство не мешает рассматривать ее спектраль-
ным методом. Положим, что Gnx(w)—спектральная плотность ком-
плексной огибающей. Установим связь между функциями Gux(oj)
и fnx(w)- С учетом (7.5)
Re[t/lixe'u,°'|e Г/|1Х(/)е l('" ^'dt}-
+ ^^'di . ] J-d,,(-..)-w0). (7.6)
Этот результат означает, что спектральная плотность узкополос-
ного сигнала концентрируется в пределах двух интервалов около
частот too и —о)о.
Теперь обратимся к аналитическим свойствам дисперсионной
характеристики p(w). Поскольку нас интересуют только узкие час-
тотные интервалы вблизи точек ±(о0, используем следующее раз-
ложение в ряд Тейлора:
[1 (о) __ р («)0) ц- р' (ю0) («J — w0) 4 -L з" (t.)0) (о>—w0)2 4-...,
. (7.7)
₽ (—to) =. р (—ю0) 4- р' (—о)0) (<» 4- о)0) 4-—(—о>0) (ш 4 w0)2 4...,
причем из нечетности функции р (<о) следует, что
p(w0) =—И—0)о)’ ? (0>о) —( %)’
Р"(о)0)^-Р"(-О)0)
и т. д. Величину p(w0) обозначим Ро, величину р'(<«>о) обозначим
Ро' и т. п.
При учете трех членов тейлоровского разложения частотный ко-
эффициент передачи отрезка линии длиной I в области положитель-
ных частот
/С+(ш,/) ^ ехр !—У Г?о4&>(ш — 10о) + “4 Зо(ш— • (7-8)
85
Соответственно, в окрестности частоты о>о коэффициент пере.
дачи
К~ ехр р' J 0О — 0о (ш+<ио) + Ро (ш + шо)2 1 j •
(7.9)
При необходимости формулы (7.8) и (7.9) можно упростить,
пренебрегая слагаемыми со вторыми производными от дисперсион-
ной характеристики. Такое упрощение не приведет к заметной
ошибке при условии
0оП2/«1. (7.Ю)
т. е. необходимо, чтобы фазовая ошибка, доставляемая третьим
слагаемым в показателе экспоненты, была пренебрежимо мала.
Если данное условие выполнено, то в системе имеет место режим
со слабой дисперсией.
Чтобы восстановить сигнал па выходе системы, следует выраже-
ния (7.8) и (7.9) подставить в интеграл Фурье (7.2), учтя связь
между спектром входного сигнала и спектром его комплексной оги-
бающей, выраженную в формуле (7.6). Выполнив эту процедуру,
имеем
о
«вых W = J (-<О — <«0) exp {j [0О/ - 00 (ш + <«0) / + «)/]} дш 4-
— оо
+ \ GBX (‘° - (Оо) ехр {j [ - 0oz - 00 (ш - и>о) 1 + tod) ^<0.
4л J
о
Переходя к новым переменным; —<о—(о0 в первом интеграле
п й2 = »—w0 во втором, преобразуем последнее равенство:
^вых (7) — ~ (7ВХ ($1) ехр [у (0OZ 4* 0o$i^ — шо^)] +
—<»О
1
4л
—<1>о
\ ($2) ехр j (-й0/ - 0o$2Z 4- у 4- (о0/)] ^2.
(7.Н)
Так как рассматриваемое колебание узкополосно, то спектраль-
ная плотность комплексной огибающей на входе линии концентри-
руется в узкой полосе частот вблизи нуля. Поэтому можно прибли-
женно распространить интегрирование в (7.11) на весь бесконечный
интервал частот. Далее, оба интеграла в (7.11) по отношению друг
к другу являются комплексно-сопряженными, так что
ивых W = Re e^“oz-₽o4
+ оо ,
—- OQ
(7. 12)
86
В последней формуле интеграл
+ оо
^»ых(С = -^-^ GBX|(£)e ''°'1
— оо
является комплексной огибающей выходного сигнала. При справед-
ливости сделанных ограничений функция Свых в точности повторяет
комплексную оги >ающую на входе С7ВХ, будучи однако смещенной
во времени в сторону запаздывания на величину
* = &. (7.13)
Данный временной сдвиг, пропорциональный длине линии, сви-
детельствует о том, что в системе происходит волнообразный про-
цесс перемещения oi ибающей вдоль оси распространения с неко-
торой скоростью иГр, которую называют групповой скоро-
стью. Из (7.13) получаем
= (7.14)
Как указывалось, производные нужно вычислять в точке соо.
соответствующей центральной частоте спектра. Термин «групповая
скорость» означает, что эта физическая характеристика относится
к узкополосному колебанию, т. е. тому объекту, который в общей
теории волновых процессов называют квазигармонической группой
или волновым пакетом.
Несмотря на то что понятие групповой скорости стало классическим, до сих
нор в литературе можно встретить неточные толкования. Например, иногда без
специальных оговорок утверждается тождественность таких характеристик, как
групповая скорость, скорость передачи энергии, скорость сигнала, скорость пере-
дачи информации и т. д. Подобное расширение термина в общем случае недопу-
стимо и может привести к ошибкам. Групповая скорость — это всего лишь
скорость перемещения в пространстве огибающей узкополосного колебания, ко-
торое в силу самого своего определения обладает неограниченной протяженно-
стью во времени. Любое колебание конечной длительности, например ограничен-
ный во времени импульс, имеет неограниченный спектр и поэтому групповая
скорость, строго говоря, не равна скорости перемещения импульса.
В некоторых волновых системах, например, в кристаллах на волнах оптиче-
ского диапазона, имеет место явление, называемое аномальной дисперсией. Оно
проявляется в том, что для некоторого частотного интервала коэффициент
фазы Р уменьшается с ростом частоты. При этом групповая скорость, вычислен-
ная для узкополосного колебания с центральной частотой <о0, будет отрицатель-
на, хотя фазовые скорости каждой из спектральных составляющих положи-
тельны.
Противоречивость самого факта отрицательности групповой скорости при
аномальной дисперсии не должна вызывать недоумений, так как огибающая —
это воображаемая кривая, получающаяся за счет интерференции бегущих гар-
монических волн с близкими частотами. Поэтому движение с групповой скоро-
стью — это кажущееся движение, не связанное непосредственно с перемещением
в пространстве материальных объектов.
§ 7.2. Оценка искажений импульсных сигналов
Понятие групповой скорости позволяет приближенно ответить на вопрос о
том, как велики искажения импульсных колебаний, распространяющихся вдоль
линии передачи с дисперсией. Рассмотрим случаи, когда передаваемое колебание
87
л лльиым радиоимпульсом С длительностью Г„ и частотой
является прямоугольным рад - с для спектральной плотности т/аР-
монического заполнения а>о- оырал таКого
колебания
(w — <1'o) £и
sin
p (w) ==
(<о — “У)) Гц
" 2~
частотной зависимости
Для ориентировочного
данного импульса сов-
диаграммы, ограничен-
частоты). График
—I на рис. 7.3.
ю ширину спектра
'=йо+2л/7я. “н;пжй=Оез7льтат"суперпозиции отдельных узКо.
к— "\Сптопых можно 0ПРеделить свою групповую
каждой из к<2°1 ;пповые скорости на верхней и нижней
И 7 абсолютная величина разности времен
“«„емы составят
(здесь учтены только положительные
модуля спектральной плотности изображен
подсчета можно положить эффективную ширин; 4.v„.r.
падающей с шириной основного лепестка спектральной
НОГО Частотами (Оверх: ' >-/*
Любой импульс представляет
ПОЛОСНЫХ групп, ДЛЯ КДУ'тй ИЗ
СКОроСТЬ. Пусть Г’гр.верх
частотах спектра соотве
прихода двух крайних групп
Д/=/
1_____ 1
^гр.верх ^гр.ниж
(7. 15)
Очевидно, что искажения сигнала существенно велики, если Ы~Т„. Если
же то дисперсионными искажениями в линии можно пренебречь. За-
метим что при прочих равных условиях степень искажении нарастает с увели-
чением длины линии и может стать ощутимой даже при очень малой дисперсии.
Результатом влияния дисперсии при передаче импульсных сообщении являются
расплывающиеся импульсы, которые накладываются друг на друга. В технике
связи это неприятное явление получило название межеимвольнои интерференции.
Расчет показывает, что в обычных радиочастотных линиях, таких как
коаксиальные кабели, длина которых в аппаратуре редко превышает десяток
метров, дисперсионными искажениями можно с полным основанием пренебречь,
если длительность передаваемых импульсов не менее 10е с. Тем не менее с этим
эффектом приходится считаться при передаче сигналов по обычным линиям
телефонной связи достаточно большой длины. Двухпроводная линия со стальны-
ми проводниками (этот материал наиболее дешев) на частотах в несколько
килогерц, характерных для телефонии, имеет погонное сопротивление практиче-
ски активного характера, т. е. /?13>(о£|. Воздушный диэлектрик линии весьма
совершенен, поэтому G|<wCt. Таким образом, в диапазоне звуковых частот
линия телефонной связи ведет себя подобно распределенной /?С-структуре, речь
о которой шла в гл. I. Здесь
Очевидно, что искажения
откуда
о> /?]С|
2
(7.16)
Для рассматриваемой линии имеет место соотношение vrp = 2o<t>. График ча-
стотной зависимости групповой скорости в некоторой конкретной линии изобра-
жен на рис. 7.4.
Предположим, что по линии длиной 200 км передается радиоимпульс дл i-
тельностью 0.5 мс, имеющий частоту заполнения f0“5,l кГц. В соответствии с
сказанным верхняя и нижняя частоты спектра
/верх =/о + I/T'h — 7,1 кГц,
/ниж =/о—1/Гн - 3,1 кГц.
88
Групповые скорости крайних спектральных участков составят при этом
игр.верх = 0,944-108 м/с,
^гр.ниж = 0,624-108 м/с.
группадГсос?а?итРМоколо(71' мс.ТГТдТа Уаза15превышав" "РИХ°Да КраПнИХ
веемого импульса. Поэтому имеет "ЛХ
ность возникновения межсимвольной интерференции при высокой частоте следо-
вания импульсов.
Целью теории является ие только объяснение наблюдаемых фактов, но и
выработка способов улучшения технических характеристик систем. Проследим
за тем, как решается важная прикладная задача — уменьшение искажения сиг-
налов в линиях передачи. Выпишем еще раз формулу для комплексного коэф-
фициента распространения
у = а + ft = + JqLjXG! +
(7- 17)
Линия передачи, в должной мере удовлетворяющая условиям распростране-
ния сигналов с малыми потерями и без ощутимых искажений, должна удовлет-
ворять следующим требованиям: 1) коэффициент ослабления а должен быть
Рис. 7.3. Спектр прямоугольного
радиоимпульса
Рис. 7.4. Частотная зависимость
групповой скорости в линии пере-
дачи с параметрами /?] = (),2 Ом/м,
С = 200 пФ/м
минимальным; 2) коэффициент фазы Р должен линейно зависеть от частоты по
крайней мере в пределах рабочего диапазона. Функционирование линии улуч-
шится, если из четырех параметров R\, Glt С( и Ц первые два уменьшить. Од-
нако достичь здесь ощутимых результатов невозможно как по техническим, так
и по экономическим причинам. Анализ формулы (7.17) показывает, что суще-
ствует принципиально иное решение проблемы: нужно существенно повысить
погонную индуктивность L|, чтобы на рабочих частотах выполнялось условие
©Li»??,. Тогда с учетом неравенства coC^Gi для коэффициента фазы имеем
приближенное выражение
Р 7-1С1.
Дисперсионные искажения практически отсутствуют, поскольку
«ф = vrp= 1/У iiCi.
Один из способов повышения погонной индуктивности, применявшийся, на
практике, состоял в том, что проводники линий дальней телефонной связи обма-
тывались специальной лентой, выполненной из сплава типа пермаллоя с высокой
магнитной проницаемостью. Но при этом затраты на сооружение линии значи-
5-2910 89
тельио возрастали. Оказалось, что есть гораздо более дешевый спосог
через ранние интервалы порядка нескольких километров включакло ' 8 лич
ные катушки. Этот способ оправдал себя на практике и лишь в пос Я '’’’ДУкт?*
начал терять свою актуальность в снязн с широким применением „р"
шейных линий передачи, в частности коаксиальных кабельных Сп» *
ней связи. Ннй Для
£ 7 3 Волновые уравнения для напряжений и Юков
при произвольном харак,ере изменения
процессов во времени
В двух предыдущих параграфах нестационарные процессы ш-
педали были исследованы с помощью методики сформулированнм
применительно к монохроматическим волнам. Теперь от телеграф
пых уравнений
dll
(7.
,/7
(7.
перейдем к уравнениям более общего вида, описывающим прост-
панственно-временныс .характеристики мгновенных значений напря
жения u(z П и тока i(z, t). Прежде всего отметим, что комплекс
ные амплитуды 0(z, о>) и /(г, ш) можно рассматривать как спек
тральные плотности процессов u(z, t) и i(z, t):
и [Z,t]
\ /(z,<o)eWw.
-- <30
Рассмотрим первое уравнение из системы (7.18).
Умножив обе части уравнения (7.18а)
и проинтегрировав по всем частотам, имеем
2л J dz
на множитель
/?1
2.1 .1
В левой части последнего равенства порядок следования опера
ций интегрирования по частоте « и дифференцирования по коорди
нате z может быть изменен. Кроме того, второе слагаемое в правой
части на основании известного свойства преобразования Фурье про
порционально производной по времени от мгновенного значения
тока. Таким образом, в соответствии с (7.20) получаем
90
L z _ J dt I 2л J
Выполни» аналогичные операции над уравнением (7.186),
имеем
— Ci-^- -LЛ (Je^'dw
dt 2л j
Здесь в квадратные скобки заключены мгновенные значения на-
пряжения и тока в линии , записанные через обратные преобразо-
вания Фурье. Таким образом, иа основании двух последних фор-
мул приходим к системе телеграфных уравнений
= (7.21а)
dz dt v 7
(7.216)
dz dt v
которые отображают динамику электромагнитных процессов в ли-
нии передачи при произвольном характере пространственно-вре-
менных зависимостей. Данные телеграфные уравнения в отличие
от уравнений системы (7.18) представляют собой систему диффе-
ренциальных уравнений уже не в обыкновенных, а в частных
производных.
Система (7.21) может быть легко приведена к одному диффе-
ренциальному уравнению второго порядка относительно напряже-
ния или тока. Для этого достаточно, например, продифференциро-
вать (7.21а) по z, (7.216) по t, а затем исключить члены, содержа-
щие ток. В результате будет получено одно уравнение относительно
напряжения, эквивалентное системе (7.21):
g =7,С, g +(«,€, + /.,О.) g + ft.G.a, (7.22)
Аналогично выглядит и уравнение относительно тока
g = i,C, g +'(«1C, + i1O1)g+«1O1t (7.23)
Эти уравнения описывают процесс волнообразного распростра-
нения возмущений вдоль регулярной одномерной направляющей
структуры и поэтому названы волновыми уравнениями.
5*
91
Особенно простой и запоминающийся вна приобретают M.Wu>
уравнения для линии без потерь
д2и I г- &2и
~^=L'C' ю'
д21 г Г д21
— Л’С1 dt2 •
(7.24)
(7.25)
dz2
Далее будет рассмотрен именно этот случаи, поскольку уЧе
омических потерь хотя и вносит некоторые дополнительные элСМс,,
ты в оХую картину явления, однако значительно усложняет а„а
ЛИЗ и делает результаты менее наглядными.
§ 7.4. Решение волновых уравнений для линии
без потерь по методу Даламбера
Впервые волновые уравнения вида (7.24) и (7.25) были изучены
в XVIII в. Л. Эйлером и Д. Бернулли, которые независимо друг От
друга показа н!, что именно так выглядят дифференциальные урав.
нения, описывающие колебательные процессы в натянутой упругой
струне. Примерно в это же время замечательный французский уче-
ный Ж- Даламбср предложил метод решения волновых уравнений,
ставший классическим и носящий с тех пор его имя.
Рассмотрим метод Даламбера на примере решения уравнения
(7.24), которое перепишем в виде
d2u 2 д2и
dt2 dz2
(7.26)
Здесь v= 1/ КДС, — фазовая скорость гармонических волн.
В гл. I фазовая скорость была определена как скорость перемеще-
ния в пространстве волновых фронтов при гармоническом харак-
тере колебаний. Там же было показано, что в линии без потерь ча-
стотная дисперсия фазовой скорости отсутствует. Поэтому все
компоненты Фурье, обусловливающие сложное немонохроматиче-
ское колебание, распространяются с одинаковой скоростью. Таким
образом, есть основание считать, что фигурирующая здесь скорость
действительно является скоростью, с которой происходит переме-
щение вдоль липни импульсного волнового процесса самого общего
вида.
Предположим, что исследуемые процессы происходят в регуляр-
ной линии передачи без потерь, свободной от внешних источников
и неограниченно протяженной вдоль оси г. Эффекты, связанные
с конечной длиной линии, будут рассмотрены позднее.
Переменные /иг входят в уравнение (7.26) весьма симметрич-
но. Для того чтобы подчеркнуть это, введем новую независимую пе-
ременную т, определив ее следующим образом: т = и/, при этом
d2u!dt2= v2d2u!d%2,
92
И тогда вместо (7.26) имеем
д'2и д2ц
дт2 ()г2 ’
nePXuX™vJ. нграет Р0ЛЬ вРеменн- однако это свремя»
имеет физическую размерность длины. Именно такими были бы
показания воображаемых часов с неограниченно протяженным ли-
нейным циферблатом, вдоль которого со скоростью волны в линии
перемещается стрелка.
Для нахождения общего решения уравнения (7.27) следует про-
извести cine одну замену переменных, введя два новых аргумента
5 = 2-|-т, = г — т. (7.28)
Вычислив частные производные с учетом (7.28), имеем
д‘2и
(7. 27)
<3т2
d‘U ____2 ^2ц । ^2ц
<?£2
сУ-и
д2и
dz'2 (J‘z2
Подставив этот результат
вид волнового уравнения в новых переменных:
д2и
<>£<)>] df]2 ’
I d2u ()2ц
d;d-q di]2
(7.27), получаем окончательный
л . =0-
де<э-г|
Общее решение этого уравнения очевидно:
и(5» Л- — (£)-\-F2(Л)»
(7. 29)
где F\ и F2— полностью произвольные Функции, первая из которых
зависит только от переменной 5. а вторая — только от перемен-
ной т). Возвращаясь к исходным аргументам, получим
u{z, t)=Fl{z-\-vt)-\-F>(z — vt). (7.30)
Характерный вид аргументов функции F и F2, однородных от-
носительно z и t, указывает на то, что здесь имеются две волны
произвольного вида. Возмущение, описываемое функцией F2, пред-
ставляет собой прямую волну, перемещающуюся со скоростью v
без изменения формы в сторону возрастания г. Соответственно
функция F\ описывает обратную волну, существующую в линии
совершенно независимо.
Закон изменения тока при нестационарном процессе в линии
следует искать в форме, подобной (7.30):
i (г, /) = АЛ (z 4-тл!) 4- A2F2 (z—vt) (7.31)
с двумя неизвестными коэффициентами Л и А2. Далее воспользу-
емся первым уравнением из системы (7.21), положив в нем /?( = 0.
Подставив сюда выражения (7.30) и (7.31), имеем
^^ = -LxAxv ^- + LxA2v .
de d£ *1
93
Для тождественного
чтобы
выполнения этого равенства необходимо,
. 1 _ 1
1______' .А 2 — “7 у
А = —77— L{V "
Lxv
F2(z — vt)
1 z«
nu R линии без потерь всегда (а не только
Итак, напряжение и то : в • связанЫ коэффициентом пропор.
при гармонических колебания ; „ и обратнои ВОЛнах разли-
циональности ZB, причем ^.^Хожного направления потоков
чаются знаками ввиду Ш
энергии. определяются начальными условиями и (г, 0)
Функции 71 и 7г опр^гтояние системы при t = 0. На основа-
к 0). которые задают состоя»,
НИИ (7.30) и (7.32)
(z,0) + 7-2(2,0) = tt(z,UA
-Т7! (z, 0) + Т'2 (г, 0) =А/ °)’
так что
(7.32)
откуда
(z, 0) == 0) ,
F2 (г, 0) = “(^°)+^(г,°) .
(7.33)
2
Как пример использования метода Да^мбера, рассмотрим еле-
дующую задачу. В регулярной
бесконечной линии имеются два
коммутатора Л) и К2 (рис. 7.5),
отделяющие некоторый внутрен-
ний участок системы длиной I.
Вначале коммутаторы разомкну-
ты, а внутренний отрезок линии
заряжен до напряжения Uo.
Пусть теперь в момент t = 0 оба
коммутатора синхронно срабаты-
вают. Из формул (7.33) видно,
что исходная форма напряжения
в линии представляет собой сум-
му двух противоположно направ-
ленных бегущих волн с амплитудами Uo/2. Поскольку при обе
волны совмещены в пространстве, то их токи взаимно компенсиру-
ются и поэтому вся система находится в покое. С момента срабаты-
вания коммутаторов в обе стороны начинают распространяться две
волны тока величиной 6/0/(2ZB), которые называют волнами заряд-
ного тока, поскольку их распространение сопровождается зарядом
элементарных конденсаторов, образующих линию. По прошествии
времени l/(2v) обе волны напряжения перестают накладываться
Рис. 7.5. Включение заряженного
отрезка линии
94
друг на друга и в этом смысле разряд начального участка линии
заканчивается-в дальнейшем обе волны расходятся в бесконеч-
ность (рис. 7.6).
Следует заметить, что полученное решение является разрывным
и поэтому в классическом смысле не может удовлетворять системе
дифференциальных уравнений (7.21). Однако современная теория
дифференциальных уравнений в частных производных утверждает,
что подобные обобщенные решения волновых уравнений служат
Рис. 7.6. Напряжение и ток в схеме, изображенной на рис. 7.5:
а — при /=0; б — при 0<t<Z/(2u); в — при
пределами последовательности обычных гладких решений при не-
ограниченном сокращении длительности фронтов.
Применение метода Даламбера к анализу нестационарных яв-
лений в распределенных радиотехнических устройствах затруднено
тем, что здесь, как правило, приходится рассматривать системы ог-
раниченной длины, для которых неизбежным становится учет мно-
гократно отраженных волн. Гораздо удобнее решать подобные за-
дачи операционным методом, что дает возможность в рамках еди-
ного подхода учесть влияние неоднородностей и начальных
условий.
95
лпание нестационарных процессов
' * операционным методом
Из-южокпс маптва.™
л™ия"”пТрнме"ение его для Диализа переходных процессов в э’£
трических цепях [8]. ительн0 к распределенным волновм.
е,,сХТосто,7= сл^юшем. Запишем телеграфные урав™^
ДЛЯ линии без потерь )
77 = 11
di г —
dz *
„ найлем 11Х преобразования Лапласа по временной координ
и найдем их изображения напряжения и тока
со
L/(z,p) = f zz(2,/)e-^/,
6
(7.34)
введя в рассмотрение
/ (z, p} = J i (z, t) o~ptdt.
о
p ппЯвилами вычисления преобразования Лап-
В соответствии с пра ему дифференциальных уравне-
ласа от производных полу пп*
нии:
(7.35)
dz
AL = -Ci [pU—u(z,0)],
dz
o кптппую входят начальные значения напряжения u(z, 0) и тока
0) Отметим, что здесь фигурируют не частные, а обыкновенные
производные. поскольку по переменной р дифференцирование не
производят Особенно просто выглядит уравнения для изображе-
на случае нулевых начальных условии; объединяя оба уравне-
ния из (7.35), получим
объединяя оба уравне-
dW
dz2
dd _
dz2 1)2
(7.36а)
(7.366)
в
частных производных
линейных дифферен-
Сложная задача решения уравнений
свелась к более простой — интегрированию
циальных уравнений второго порядка с постоянными коэффициен-
тами. Общий интеграл уравнения (7.36а) хорошо известен:
Z Z
-р- р-
U(z,p)=A(p)e v-\-B(p)ev,
(7.37)
96
граничных
условий на концах линии, где располагаются источники и нагрузки.
О Vupt r rnviinp мрг>Лулпч».~~~.. -жл.-------- начальных условий
где Л (р) и (Р) некоторые произвольные функции комплексной
частоты.
На основании теоремы запаздывания в первом слагаемом мож-
но усмотреть изображение произвольной прямой волны, переме-
щаюшейся в сторону положительных z со скоростью и без измене-
ния формы. Второе слагаемое соответствует произвольной обрат-
ной волне.
Дальнейшими этапами решения конкретных задач операцион-
ным методом являются:
1. Нахождение функции А(р) и В(р), исходя из
J 2. Учет в случае необходимости эффекта
для напряжения и тока.
3. Восстановление оригиналов по найденным изображениям
(последнее может оказаться наиболее сложной частью задачи).
Нестационарные процессы в нагруженном отрезке линии переда-
чи при нулевых начальных условиях. Для ряда областей современ-
ной радиотехники, имеющих дело с импульсными колебаниями на-
носекундной длительности, характерна такая постановка задачи.
Отрезок линии передачи без потерь имеет длину I и волновое со-
противление ZB. На одном конце при z=0 включен источник э.д.с.
e(t), создающий импульс произвольной формы. Другой конец ли-
нии нагружен на некоторое сопротивление ZH. К началу действия
импульса, т. е. при t — Q, система находится в покое, так что
ц(г, 0) =i(z, 0) =0. Полагаем, что все реактивные элементы, отно-
сящиеся к нагрузке, свободны вначале от запаса электромагнит-
ной энергии. Требуется вычислить форму импульсного колебания,
существующего на нагрузке.
Решая задачу операционным методом, введем изображение
входного сигнала
Е (р) = J е (i!) exp (—pt) dt,
о
а также операторный коэффициент отражения от нагрузки
. Р-38)
^н(Р) +Z„
равный отношению изображений падающей и отраженной волн на
нагрузке.
Используя общее решение (7.37), на основании граничных усло-
вий при 2 = 0 и z = l получим два уравнения относительно А(р)
иВ(р):
А(р) + В(р) = Е (р),
В e2p//f = O (р),
А(Р)
97
откуда
£(Р)____
£ (?) С(?)е~г,1'2_
Л|/”'Т7о(/»е-2'’"’
Общее выражение для изображения импульса напряже
произвольной точке линии выглядит так: 4 1Ия в
ЕОд
----=2?7
е(Д)е
или для точки включения нагрузки.
~pv
,, , \ £(/>)е
2/-z^
ГР~ 1
(7.40)
(7.41)
Если теперь удастся найти соответствующие оригиналы, то за-
дача будет решена. Изучим некоторые частные случаи.
А Отрезок линии, согласованный на конце
Здесь /?н=2в, так что р(р)=0 и в соответствии с (7.41)
i
~Pv
U(l, pV-= Е (р)е
(7.42)
Сигнал на нагрузке полностью повторяет форму входного на-
пряжения, запаздывая на время x=l/v, необходимое для однократ-
ного прохождения электромагнитного возмущения вдоль линии.
Именно в таком режиме работают разнообразные^ линии задерж-
ки, служащие неотъемлемым компонентом устройств для опти-
мальной обработки импульсных сигналов и выделения их на фоне
помех.
Б. Отрезок линии в режиме холостого хода на выходе
Для данного случая р(р) = 1 (ср. гл. III) и поэтому
7/(АА) =
‘2Е(р)е~рх
1 + е~2рх
(7.43)
1 + Q (Д) е V
Z
Чтобы понять физический смысл процесса, описываемого выра-
жением (7.43), следует преобразовать эту формулу. Заметим, что
в правой полуплоскости комплексной частоты р, которая соответ-
ствует значениям />0, модуль величины ехр (—2рт) не превосхо-
дит единицы, так что по аналогии со степенным рядом
можно записать
7/(7, Jp)=2£'(p)[e-^t —е-3^4-е~5₽т—••.], (7.44)
98
или, переходя к оригиналам,
и(1, /)=2е(/ —х) —2е(/ —Зт)-|-2е(/ —5г)—... (7. 45\
ний^т обоих*концов ЛШШИ Сд1нныйВ?еННЯ многократных отРаже'
Третировать, положив, -ио в^"л™ , “ ™Z
импульса включения н подан сигнал типа
e[t) = U03(t) =
О,
/<0,
Un,
/>0.
Тогда при /<т выходное напряжение равно нулю, поскольку
возмущение еще не достигло конца линии. При />т напряжение
на выходе составит величину 2U0 в силу того, !то коэффициент от-
I I ,—I—,—. I
О Т 2Т Jr 4Г 5т 6т 7г t
х
Рис. 7.7. Импульсы напряжения на
выходе разомкнутой линии пере-
дачи
Рис. 7.8. Система с ненулевыми
начальными условиями
ражения от разомкнутого конца равен единице. Отраженная волна
при / = 2т достигнет генератора и вновь отразится от него, изменив
полярность, так как здесь р(р)= — 1 в силу нулевого внутреннего
сопротивления источника э. д. с. В момент времени / = 3т волна,
дважды претерпевшая отражения, достигнет разомкнутого конца
линии. Здесь она вновь отразится с коэффициентом отражения +1
и, имея отрицательную полярность, обратит в нуль напряжение на
выходе. Дальнейшие этапы переходного процесса будут протекать
периодически, как это показано на рис. 7.7. Описываемая система
способна с высокой точностью формировать прямоугольные им-
пульсы малой длительности.
Учет начальных условий. Нестационарные процессы при разря-
де заряженной линии передачи. Как упоминалось, операционный
метод дает возможность учитывать начальные условия. В качестве
примера рассмотрим задачу о нестационарном процессе, возника-
ющем в отрезке регулярной линии передачи длиной I, первоначаль-
но заряженном до напряжения (Уо и при />0 замкнутом на одном
конце на известное сопротивление нагрузки /?н (рис. 7.8).
Полагая в системе (7.35) i(z, 0)=0, u(z, О) = (7о, получаем не-
I однородное дифференциальное уравнение для искомого изображе-
ния напряжения:
^L_^-U =—— Un- (7.46)
rfz2 V2 V2
99
S ин “"’рал ДЛЯ уравнения (7.46) имеет вид *
U{z,pY.^-vA^-p’ + B(p^, (7.47,
причем Л(р) и В(р) должны быть выбраны так, чтобы выполнить
два краевых условия: dU(0,p) _ л
J /(0> р)=0, или, что то же самое, -О условие холо-
С9°ПП°п\11(1 d)=Rh- импедансное условие на нагрузке. (7.S
Из ’(7 48 следует, что А (р) =В(р). Далее, проводя элементар.
ныё выкладки' на основании (7.49) находим, что ₽
А(р)=—
Р
£о
i
V
и
е
л,
/?Н \
z")e
Итак решение задачи о нахождении операторной формы напря-
женин получено. Наибольший практический интерес представляет
режим согласованного разряда линии, когда /?н-/в. При этом вы-
числения несколько упрощаются, и для изображения напряжения
в произвольном сечении линии получаем формулу
е v 4-е v
У(г,р) = — 2р
В частности, при z=l, т. е. на нагрузке
Гг / _ 2£\
Щ1,р)=±± 1-е Р- .
2/7 \ /
(7.50)
Переход от изображений к оригиналам дает форму напряже-
ния на нагрузке
2 Z \ V )
где о(/) — функция единичного скачка.
Принципиальной особенностью режима согласованного разря-
да является конечность нестационарного процесса во времени. Из
(7.51) видно, что при t>2llv напряжение на нагрузке будет в точ-
ности равно нулю (рис. 7.9, а). Это означает, что вся энергия, пер-
воначально накопленная в линии, будет рассеяна в резистивной
нагрузке. Читателю рекомендуется самостоятельно проанализиро-
вать физическую картину согласованного разряда, приняв во вни-
мание, что начиная с момента срабатывания коммутатора от на-
грузки начнет распространяться разрядная волна напряжения ве-
личиной L'o/2.
100
Явление согласованного разряда отрезка линии передачи ши-
роко используется для создания импульсных модуляторов радио-
локационных передатчиков. Здесь нагрузкой линии служит генера-
тор СВЧ-колебаний (магнетрон); линию выполняют, как правило,
в виде цепочечного LC-эквивалента. Будучи заряженной от внеш-
него высоковольтного источника до напряжения в несколько еди-
,.,ПЧ ПАГЯТИПП
ниц ИЛИ десятков киловольт, линия
разряжается на магнетрон через
быстродействующий коммутатор, в
качестве которого обычно использует-
ся тиратрон с водородным наполнени-
ем. Описанная система формирует им-
пульсы микросекундной длительности
с мощностью в десятки 'и сотни кило-
ватт.
О 21/V t
1/1______
I Rx"ZS
ЪЬ I------------------,
Задачи и упражнения к гл. VII
7.1. Линия передачи имеет следующие
первичные параметры: Ci = 80 пФ/м, L1 =
= 1,8 мкГн/м, /?1=60 Ом/м, G| = 0. Найти от-
ношение групповой и фазовой скоростей на ча-
стоте 100 МГц.
Ответ: пГр/Цф= 1,0007.
7.2. Отрезок линии длиной I, обладающий
волновым сопротивлением ZB, предварительно
заряжен до напряжения t/о. При 7=0 один из
концов линии замыкается на резистор 7?н =
= 3ZS.
Найти закон изменения напряжения на
резисторе. Сравнить полученный результат с
графиком на рис. 7.9, б.
Ответ.
0 2L/V Ы/v 6l/u t
V
ун/и 6l/u t
в)
0 21/V
Рис. 7.9. Импульсы напряже-
ния на нагрузке при согласо-
ванном (а) и несогласованном
(б, в) режимах разряда
3 Q / Q1 \ о / Л 1
= — —-----) — — uoa 17 —------
4 о \ v ] 16 \ v
7.3. Решить аналогичную задачу, полагая, что сопротивление резистора
/?„ = l/3Zj. Проанализировать график на рис. 7.9, в. Объяснить, почему в дан-
ном случае напряжение на нагрузке может принимать отрицательные значения.
7.4. Источник постоянной э. д. с. Е в момент времени t=0 подключается к
одному из концов отрезка регулярной линии передачи; противоположный конец
линии разомкнут. Не прибегая к вычислениям, построить временную зависимость
напряжения, наблюдаемого в центральном сечении отрезка.
Указан и е: использовать концепцию падающих и отраженных волн.
7.5. Полубесконечная регулярная линия с волновым сопротивлением ZB
заряжена до напряжения Uq. При 7 = 0 конец линии, расположенный в точке с
координатой z=0, замыкается на конденсатор Св, начальное напряжение на
котором равно нулю. Найти выражения для напряжения вдоль линии, а также
для напряжения на конденсаторе.
Ответ.
7 t—z/v \
«(г,0 = 6’о|,1-е /,,Сн a(f —z/v)/,
Uc(O = t/0(l-e
101
7.8. Н момент ирсмсии / 0 ил иход полубсеконсниой линии с в0Л||п
сопротиялсиисм Z» икл1О'1.т1-и и iciicpiiiop. обри 1ОП.ТИПЫЙ ||ослсдоватс.||,цц ’’’Ми
•ДИИ8МИЯМ ИСТОЧНИК» ШИ НИ1НИОЙ I. Д. С. /. !>• ни 1О|1.1 /г, И Иидук
При иуленых илчнлыпих услоииих ниЛти hikoii и imviiciiiih нлприжсиии кд( г‘
линии. °Лк
- "...
Z7Z. ( .
7,7. OrpcuiK линии длиной GO м с
ЖСИИЫЙ и исходном со<"1ОИП1Н1 до ||;|||ряжении
НОМ К IIIII ру lO'IIIOMy pCIIICTOpy < ......•• K ill
liyio MIHHIIOCtl> y< IpoHctllH II lllcpilllO,
си, если скорость и линии рлнил 2,3 10
От нс I. /' -HOG,7 кВт, :> I.
полипным сопротннленисм 150 Ом. 1(1|)и
" ....( 22 кВ. нодключиется одним кон-
...„ленисм 150 <>м. Определить импульс-
И Н.п руку прими импуль
I 2,3 •16" м/с.
" о,12 Дж.
Глава VIII
КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ, ОБРАЗОВАННЫЕ
ОТРЕЗКАМИ ЛИНИИ ПЕРЕДАЧИ
IIзучая нестационарные процессы в линиях передачи, можно за*
метить, что в подобных системах возможны собственные колеба-
ния. связанные не с наличием внешних источников, а лишь с суще-
ciнованисм некоторого запаса энергии, первоначально сообщенной
системе. Представим собе отрезок регулярной линии без потерь,
на концах которого имеются нагрузки, не поглощающие энергию.
Если осуществить upon «вольное возбуждение такой системы, на-
пример. подав иа нее короткий импульс, то этот импульс будет
многокра । но отражен от концов линии, так что с. течением времени
картина гоков и напряжений не будет повторять первоначальную.
Гем нс менее отсутствие омических потерь обеспечивает сохране-
ние полной запасенной энергии и поэтому колебательный процесс
будет длиться сколь угодно долго. В системе с потерями свободные
колебания со временем затухнут, однако общая картина явления,
основанная на многократных отражениях, останется качественно
неизменной.
Налицо некоторая аналогия с собственными колебаниями в
/,6-кон।урах. Подробный анализ показывает, что действительно
отрезок линии передачи, обладающий малыми потерями, во мно-
гом сходен с колебательным контуром, маятником и т. и. Это сход-
ство может быть отмечено как в свободном, гак и в вынужденном
режимах. Однако имеют место и принципиальные различия, обу-
словленные распределенным характером изучаемой системы.
Распределенные колебательные системы, называемые резо-
наторами, широко используются в тех радиотехнических уст-
ройствах, где применение //.'-контуров нежелательно или невоз-
можно, например в диапазоне СВЧ.
§ 8.1. Собственные колебания короткозамкнутого
отрезка линии передачи
Рассмотрим отрезок регулярной линии длиной /, короткозамк-
нутый с обоих концов. Поставим задачу изучить всю совокупность
колебаний, которые могут иметь место в такой системе. Нет осно-
ваний считать, что электромагнитный процесс здесь будет изме-
няться во времени но гармоническому закону, поэтому следует
рассмотреть волновое уравнение общего вида, дополнив его нуле-
| ним граничным условием для напряжения при г — () и г-/. Пробле-
ма сводится к так называемой краевой задаче для волнового урав-
103
нения:
д?и , (8.
V2 dt2
„(0,/)=И(М)=0- (8-18)
такой постановке физическая задача
Из гл. VII следует, что в т отсутствуют сведения о На-
определена не полностью, "осК yl(z, 0). Однако в данном слу-
п. ИХ напряжении u(z, 0) и интересуют всевозможные
W“то несущественно,иосколь при разнообразных иа,Мь
^ыхеумотая“ОТОРЫе (отсутствие начальных условий) делает
Специфика задачи ( У приемлемым. Познакомимся с
здесь метод Дзламбер^еМ0М решения волновых уравнений, на-
другим классическим при^°елеРнНя переменных* и л и м е.
зываемым методом разде
тодом Фурье. следующем. Решение краевой задачи
Принцип его> заключе дения- двух функций.
(8.,)₽„ШетсЯвввдепроизведеини (М
лмт лишь от одного аргумента. Подставим
каждая из которых зависят ™ обе части полученного равен-
(8.2) в уравнение <81а) ” ^^лагая, что XY не есть тождествен-
ства на произведение А г, пред было бы тривиальное нулевое
“;;с“^%’\7еТст“л“юшее интереса). Дифференцируя и еокра.
шая, получим
v2
(8.3)
Равенство (8.3) является не уравнением, а тождеством, справед-
ливым при любых z и t. Поскольку здесь левая часть зависит
только от z, а правая только от t, то единственный способ добить-
ся тождественности — это положить обе части равными некоторой
постоянной величине k, называемой постоянной разделения. Итак,
метод Фурье позволяет свести задачу интегрирования уравнения в
частных производных (8.1а) к решению дифференциальных урав-
нений второго порядка, называемых разделенными уравнениями:
v2 ^- = k, (8.4а)
(8.46)
Y"/Y=k.
Запишем уравнение (8.46) в более привычном виде
™L-kY=Q.
dtl
* Возникновение его связано с именами Д. Бернулли (XVIII в.), изучившим
свободные колебания закрепленной струны, и Ж. Б. Фурье, применившего этот
метод для анализа процесса распространения тепла.
104
Решения этого уравнения -
стоянкой разделения: "• зависимости от знака по-
при k>0
yU)=ach(V ^) + bsh(Vfe) , (8.5)
где и и b произвольные величины’
при /г<0
Y (t)=a cos (]/ j*|/) + ь (|z i^). (8 6)
Решение вида (8.5) вследствие РИГ1ЛЙ
t^oo должно быть отброшено неограниченности при
Поэтому, обозначая Л = „меем нужное решение
Y (f)— a cosw/ b sin ш/, (8.7)
В котором неизвестным остается значение частоты ш
Л” фазы =- --
Получено уравнение I ельмгольца, которое должно быть допол-
нено граничными условиями
Х(0) = Х(/) = 0, (8.9)
вытекающими из (8.1а).
Совокупность уравнения (8.8) и граничных условий (8.9) ши-
роко известны в математической физике под названием однородной
задачи Штурма — Лиувилля.
Следует заметить, что данная задача при любом значении (э
имеет тривиальное решение Х = 0. Физически оно означает нулевую
амплитуду колебаний в каждой точке линии и соответствует состоя-
нию покоя при нулевом начальном запасе энергии.
Выясним следующее:
а) существуют ли такие значения (3 (это единственный пара-
метр задачи, который может быть изменен), при которых задача
Штурма — Лиувилля допускает ненулевые решения? б) каков кон-
кретный вид этих ненулевых решений?
Для ответа на эти вопросы запишем общее решение уравнения
(8.8)
X(z) = z4cos?z-|-B sin fiz. (8.10)
Очевидно, что произвольная постоянная А должна быть равна
нулю в силу условия (8.9) при z = 0. Теперь остается выполнить гра-
ничное условие при z = l, имеющее вид: sin [3/ = 0, что имеет место
при
3/ = лд 1,2,3,...). (8.11)
105
Итак, существует бесконечная последовательность
I ’
(8.12)
от нуля решения задачи Штурма — д
обеспечивающая отличные
Рис. 8.1. Собственные функции
(моды) отрезка линии передачи,
закороченного с обоих концов
самой низшей частотой
<о,
। б с т в е и и ы м и значениями од.
Лиувилля. Каждому собственному
значению рп соответствует функция
6Я(2) = В sin3nz. (8.13)
называемая л-й собственной
Функцией. Наконец, с собствен-
ным значением однозначно свя-
зана собственная частота
, П-TU
<°л = .V— “7“ • 18.14)
Важно, что в отличие от обычно-
го АС-контура распределенная коле-
бательная система обладает беско-
нечным множеством частот собст-
венных колебаний.
Физический процесс в резонато-
ре, соответствующий некоторому
значению л, носит название^ л-го
типа колебании или n-й м о-
ты (от англ, mode — образ). Гра-
фическое представление нескольких
мод в закороченном отрезке линии
дано на рис. 8.1. В технических при-
тожениях наибольший интерес пред-
ставляет так называемая основная
или низшая мода, которой соответ-
ствует значение п=1. Собственные
колебания при этом происходят с
=я«7. (815)
3
Пространственно-временные соотношения между напряжением
и током при свободных колебаниях резонатора. На основании пре-
дыдущего пространственно-временной закон изменения напряже-
ния для л-й моды имеет вид
и (г, /) = А/о sin I cos t— Фо^ , (8.16)
причем амплитуда i/0 и начальная фаза Фо произвольны. Чтобы
найти ток в резонаторе, воспользуемся телеграфным уравнением
dujdz=— L^dildt,
106
из которого следует, что
1
ii
Таким образом,
i =
t/0 „
cos
/-Фо
(8.17)
Строго говоря, сюда можно добавить любой постоянный ток /0
однако, интересуясь колебательными явлениями. Хно не прин'-’
мать этого во внимание. прими
Из сравнения выражений (8.16) и (8.17) следует- а) оасппеде-
ленне напряжения „ тока в пространстве описывается рам^ЗЕымв
функциями (узел напряжения соответствует пучности тока и на-
оборот), б) как напряжение, так и ток колеблются во времени по
гармоническому закону, причем ток опережает напряжение в каж-
дой точке на четверть периода; в) амплитуды напряжения и тока
связаны множителем пропорциональности ZB.
Динамика изменения напряжения и тока во времени представ-
лена на рис. 8._ применительно к основной моде короткозамкнуто-
го на концах резонатора. Явления здесь аналогичны процессам в
обычном колебательном контуре — наблюдается взаимный обмен
энергией между электрическим и магнитным полями.
Представление мод резонатора в виде суммы двух бегущих
волн. В формулах (8.16) и (8.17) можно узнать выражения для
идеальных стоячих волн в линии. Проанализируем нашу систему
несколько иным образом, допустив, что в ней существует гармони-
ческая прямая волна, распространяющаяся в сторону положитель-
ных z с неизвестным пока коэффициентом фазы 0:
^np=t/oexp(—
а также обратная волна
^обР = ^^оехр(//2).
Задача состоит в том, чтобы подобрать свободные параметры
А и р с целью удовлетворить нулевым граничным условиям при
2 = 0 и 2=/.
Нулевые напряжения на концах отрезка получаются только в
том случае, если
Д = -1, (8.18)
3/ = лл (л=1, 2, 3,...).
Итак, волновой процесс в рассматриваемом резонаторе можно
представить в виде суммы двух противоположно направленных бе-
гущих волн одинаковой амплитуды, причем коэффициенты фазы
образуют бесконечную последовательность вида 0п = лл//.
Если длину волны, соответствующую п-й моде, обозначить
то последнюю формулу можно записать так:
l=nk„J2. (8.19)
107
Тапим образом. ^колеба»»»
’мы Х"'“^ады»аться целое число полуволн. ’«
..«лпгтатениый простои анализ делает нч»и.
Может показаться, что t р- 'ач|| Штурма — Л иувилля. Однако
кропотливую процедуру РС1 > ,.;ф\|(Я|Ической зависимости во времени со2?
мессе се решения доказан факт raf раС1|0Лагать этим результатом
логической основы.
Рис. 8.2. Динамика электромагнитного процесса в
распределенной колебательной системе
§ 8.2. Свойство ортогональности системы
собственных функций резонатора без потерь
Представление свободных колебаний в резонаторе в виде сум-
мы отдельных мод гораздо большее, чем просто математический
прием для решения волнового уравнения с заданными условиями
на концах. Дело в том, что каждая мода является простейшим, эле-
ментарным видом волнового движения в рассматриваемой систе-
ме, не сводимым ни к какой комбинации других мод. Зная характе-
ре
ohct>ik** мод резонатора, можно любое сложное колебание пред-
ъявить в виде суммы мод. Тогда задача сведется к нахождению
соответствующих коэффициентов разложения.
j Математическое доказательство этого факта основано на том,
что система собственных функций уравнения Гельмгольца при од-
нородных краевых условиях обладает фундаментальным свойством
ортогональности:
(Ф*Ф/) •# 0 при I us j.
Применительно к системе функций п™..
(8 13). справедливость этого принципа’мпж^А?’ЯеМЫХ Ф°РМУЛОЙ
становкой. Ринцнпа может быть проверена под-
Числовая величина
л » X’tf
называется нормой i-fi собстврии^а ж... Л
ли пропорциональности подбирают таЛтпл”1' Обычно множите-
номеров были равны единице Ппи \ чтобы нормы мод всех
Ц„й называют ортонормирование й Поскольк? еН"“Х ФУ"К'
о
то система функций
<w=
(8.20)
будет ортонормированной на отрезке [0, I].
Ортонормированные системы являются системами линейно не-
зависимых функций. Это понимают в том смысле, что равенство
Н-Дафг 4-... +аЛФА +... =0
может стать тождеством в том и только в том случае, если
Л\ == Л2 == • • • == &k == • • • =г ® •
Доказательство основано на том, что для последовательности
ортонормированных функций фь ф2, ..., фь определитель Грама, об-
разованный всевозможными скалярными произведениями,
(Ф1Ф1); (Ф1Ф2); ••• (ФЛ)
(Ш (Ф2Ф2); ••• (Ф2ФЛ)
ОШ; (Ф*Фг); •••(№,)
всегда отличен от нуля.
109
Известно, что каждая функция /(г), удовлетворяют
резке [0, // некоторым условиям (обычно требуют сущ^ Я На о?
интеграла от квадрата этой функции), может быть прел СТв°ВаИц
виде разложения по системе функций {фп}: СТав-1^На ’
(«•21)
Данный ряд яаляетея р="е„ Фурье функции ff „
Чп
(8.2’2
пмипованные системы функции, встречаю.
i/..u плавило, ортоиормир0 а.от ваЖНым свойством полно-
К физических задач ах облад авлення вида (8.21)
;;Гэт. "о'начнет. д„о малой за счет увеличения чиМа
™ет быть сделана сколь >
членов ряда, с. у -р
0.
л I
•v*~u L
...пппанности системы собственных функций
Свойство ортонормиров геории резонаторов. Например,
полезно при решении з.Д• колебаниях в резонаторе без по-
рассмотрим задачу о с“и==0''н г=/ имеются короткие замыкания,
терь, полагая, чго при - 0 форму напряжения uHa4(z) и тока
Считаем известными 11111 в гл. yil подобная задача реше-
которые заданы I тсль||0 к линии неограниченной
„а „столом Д-‘ ' 4fi'Da иримепчм и здесь, однако неизбежный
лтчинл- Методт'?,^ отражений весьма трудоемок. Гораздо лучше
учет многократных oi.. задачи метод Бернулли, позво-
в замкнутай
Запишем начальные условия.
(8.23а)
(8.236)
И (2, vj —«нач
I (Z, 0) ^'нач I
Условие (8.236) можно выразить через напряжение, приняв во
внимание телеграфное уравнение dildz =—Cidu/dt. Иначе говоря,
можно предполагать, что при / = 0 в каждой точке резонатора за-
дана производная
д
dt
1 ^‘нач
7i dz
(знак обыкновенной, а не частной производной использован пото-
му, что начальный ток 1цач есть функция только от z).
ПО
Б>дс“ Гмо1Ь рсше,,ис “«"О«ого уравнения а виде суммы все-
ипЖНЫХ МОД.
11 [Z,t' Л. Ил COS ш,/ sin »%/)$„(.?)
л-1
L неизвестными пока коэффициентами Лп в Вп. При Г-0 имеем
h(z,O) = V (8.24а)
л-1
du(*,O)
~t (8.246)
Умножим обе части равенства (8.24а) на функцию фь с произ-
I вольным номером А и проинтегрируем по z от нуля до /. Вследст-
вие ортонормированпости системы {ф,,} получаем
л Г
\ ^нач (^' (£) dz.
Аналогично находим амплитудный коэффициент при синусои-
I дальнем слагаемом:
/
1 Г du(z,0)
мк J с)/
О
Mz}dz =------------------! <^L^zUiz,
(|,дС I J <* Z
0
Недостатком метода Бернулли является медленная сходимость
рядов по системе соответственных функций. Его можно в значи-
тельной мерс преодолеть с помощью быстродействующих ЭВМ.
I •
§ 8.3. Более простой подход к задаче вычисления
собственных частот. Резонансные условия
Случай короткозамкнутого на концах резонатора безусловно не
| исчерпывает всего разнообразия распределенных систем, в кото-
I рых могут существовать собственные колебания. Наиболее общая
L принципиальная схема резонатора (рис. 8.3) включает в себя от-
t резок регулярной линии без потерь длиной I, на концах которой
I расположены нагрузочные двухполюсники, обладающие чисто ре-
I активными сопротивлениями Zni=jXHi и Zh2=/Xh2.
Подобная система описывается краевой задачей Штурма — Ли-
| увилля, причем отличие ее от аналогичной задачи из § 8.1 состоит
[только в ином характере краевых условий, но не в самом уравне-
I нии. Поэтому можно ожидать, что введенные здесь усложнения не
г скажутся на характере свободных колебаний. Так, наша система,
| оставаясь линейной, будет обладать бесконечной последовательно-
стыо (спектром) собственных функций; развитие процессов во
В времени по-прежнему описывается гармоническими функциями. Од-
111
нако будут наблюдаться и существенные различия, Ппг
ся в ином характере распределения собственных част ЯПЛя,°1Ц|[е
тора. т По-'-
При решении прикладных задач обычно пет необходи
бегать к строгой формулировке проблемы собственных
в резонаторе. Здесь, как правило, нужна простейшая
о процессе, а именно, точное знание
резонансных частот для некоторых
мод. Эту задачу можно решить сле-
дующим образом.
Выделим в рассматриваемом ре-
зонаторе произвольное сечение /—2,
характеризующееся координатой /0
(см. рис. 8.3). При этом мы как бы
расчленим резонатор на две подси-
стемы: одну, расположенную левее,
и другую — правее выбранного се-
чения. Пусть }jtxC) и Уцх(2) — вход-
ные проводимости этих подсистем
соответственно, определенные отно-
сительно зажимов 1—2. В нашем
резонаторе собственные колебания
характеризуются взаимным
РезоНа'_
КОЙ а?-
lill
обме-
Пример 1. Рассмотрим резонатоп „
а другой находится в режиме холостого “°Т°ром один коней
х-анной методике, находим ого х°Да (рис 84 .нец короткозамкнут,
’ Действуя по опи-
Рис. 8.3. Резонатор с на-
грузками на концах
в
r"x> = IT c‘g з (' - /о).
п
Отсюда на основании формулы (8.25) получаем резонансное условие
tR 3 lo — etg р (I — Zo) ----------------_______________
cos₽Z0 sin ₽(Z — z0)
Чтобы условие (8.27) тождественно выполнялось независимо от /п
д»м°. чтобы электрическая длина резонатора [1/ подчинялась условию
?/= (л + 1/2) л (и = 0, 1,2,...),
т. е. чтобы резонансная длина волны находилась из соотношения
2Z
п + 1/2 (л = 0> 2,...).
Таким образом, данная система обладает бесконечным числом i
распределения напряжения для некоторых из них показаны на рис. 8.4, б. Прин-
цип построения прост стоячая волна, описывающая моду, должна
напряжения на короткозамкнутом конце резонатора и пучность на
коипе. Вдоль оси системы должно укладываться нечетное чгс.?_
пансион длины волны. Особый практический интерес представляет низша
данного резонатора, существующая при п = 0.
Пример 2. Во многих устройствах СВЧ применяются коаксиальные резона-
торы, нагруженные на одном конце сосредоточенной емкостью (рис. 8.5). Пре-
имуществом таких резонаторов является простота перестройки, осуществляемой
изменением ширины емкостного зазора. Найдем спектр собственных частот по-
добного «гибридного» резонатора. В точках 1—2 имеем параллельное включение
двух проводимостей
^рез =
(8. 27)
необхо-
(8. 28)
(8. 29)
мод. Эпюры
О л г—
иметь узел
разомкнутом
исло четвертой резо-
----- ----ая мода
Рис. 8.4. Резонатор, разомкнутый
на одном конце:
а — принципиальная схема; б — про-
дольное распределение напряжения
для некоторых простейших мод
ном энергией между электрическим и магнитным полями. На
ке теории цепей это сведется к выполнению
ногэ условия;
__ язы-
следующего резонанс-
У с = и Глин = -~ etg 3Z.
в
Резонансное условие, таким образом, примет вид:
„ 1
шСн = — etg 0Z.
Связав электрическую длину резонатора (1=3/ с частотой со и фазовой ско-
ростью Пф формулой
(8.30)
^их^ ~j~ Унх^ — О.
Заметим,
резонансные
что если бы в системе имелись
условия приняли бы следующий
(8.25)
омические потери, то
вид:
ч » = ю//иф,
после элементарных преобразований из (8.30) получаем следующее трансцен-
дентное уравнение
ImHl’ + lmrllUo.
Из (8.25) или (8.26) получаем уравнения
ственных частот различных мод.
112
(8.26)
для нахождения соб-
Сн
—— 8 = ctg&,
с2
где Са =С\1 — эквивалентная емкость отрезка линии.
Пример графического решения такого уравнения показан на рис. 8.6. Видно,
что уравнение (8.31) имеет бесчисленное количество вещественных корней, каж-
дый из которых отвечает определенной моде. Отметим, что частоты собственных
(8.31)
113
nnvr другу. Если СнвО, то прямая Л
колебаний здесь уже "е ’ (8Р3У1), располагается параллельно оси аб^’
вХшая левой части уравнение браИНЫЙ „ предыдущем примере Сцв«с в
автоматически получаем слу
Рис. 8.5. Резонатор с емкостной на-
грузкой на конце:
а — эскиз конструкции; б - принципиаль
пая схема
§ 8.4. Возбуждение одномерного резонатора
сосредоточенными источниками.
Функции Грина резонатора без потерь
Используемые в радиотехнических устройствах резонаторы, как
правило, связаны с внешними цепями с помощью некоторых уст-
ройств, например небольшой петли (рис. 8.7, а) или штыревой ан-
тенны, введенной внутрь резонатора (рис. 8.7, б). Чтобы понять
особенности процесса возбуждения резонаторов, обратимся к изу-
чению упрошенной математической модели системы, как это было
сделано в гл. VI применительно к задачам возбуждения линий пе-
редачи неограниченной длины.
Далее для определенности будет рассмотрен конкретный слу-
чай резонатора без потерь, короткозамкнутого с обоих концов и
возбуждаемого сосредоточенным источником тока /о, который раз-
мещается в произвольно выбранном внутреннем сечении z=z0
(рис. 8.8).
Полученные результаты могут быть распространены на другие
конструкции резонаторов и типы возбуждаемых источников.
Для описанной системы комплексная амплитуда напряжения
должна удовлетворять дифференциальному уравнению
+ (8.32)
(IZ^
При этом входящий сюда коэффициент фазы р = <о/Цф отвечает
некоторой произвольной частоте генератора.
114
Необходимо также выполнение нулевых
точках короткого замыкания: граничных условий в
У(0)={/(/)=0. ..
• Чтобы придать последующим результат. ' ' ’
иу> будем считать амплитуду возбуждающего то"^3^"^ фоР*
|/о| =1 А ПРИ нУлевом значении начяЛ™- ж а единичной, т. е.
как это делалось в гл. VI, введем в пяЛм “ фаЗЫ’ Затем так же,
резонатора G(a. г„), определив ее связь с PeH"e ФуНК“ИЮ ГрИНа
Образом: Р “связь с "^Ряжением следующим
G(Z, zo) = ±L<*'*o).
(8. 34)
Штырь сбязи t
zx
нахождения функции
Тогда для нахождения функции
Грина имеем следующую краевую за-
дачу:
^|+^0 = -!(2-2о),
(8.35)
G(0, z0)=O(/, z0) =0.
Поскольку функция Грина пропор-
--------- ю-
о возбуждении резонатора
SWSSSWW
' tJ коаксиальной
Г" линия
6)
рис. 8.7. Возбуждение коакси-
мьного резонатора с помощью
I петли (а) и штыря (б)
mini источник является источником тока, решение краевой задачи
(8.35) должно быть непрерывным в точке z=z0, т. е.
Iim6(zo — e,z0) = limO(z0-|-e, z0),
lim —
= 1.
а первая производная функции Грина в точке помещения источни-
ка должна претерпевать единичный скачок:
и dG
— lim —
«-►0 dz |z0—« «-*0 dz ze+«
Метод решения поставленной задачи основан на том, что зара-
нее известна полная ортонормированная система собственных фун-
кций для изучаемого резонатора. В § 8.2 показано, что
стема функций имеет вид ’ Данная С(
n=l,2,...).
(8.36)
системы дает основание искать фу8(
Свойство "виде'функционального ряда
цию Грина в виде .
°’*"'
мгрние тождественно удовлетворяет урав.
представленное выражение во всех ВНуТренних точКах
П Гельмгольца из системь при любом выборе
нению 1 ел исКЛючением то удовлетворяются граничные
РеЗОНаХинентов а.. В равно» “^одму единствевНое, к ч ®
мыл„квиЛ концах Рез°"1т°?о так подобрать коэффициенты «„
SZ 3Хя₽ь»ого поведения искомого решения в точке
чтобы д°б''™С источника. опавнение из системы (8.351 |
раСПоЛ1Оставпм ряд (8-36) Л"оенцированне ряда допустимо в силу I
Двукратное почленное„ функций в ряды Фурье. Поэтому
известных теорем о раз
имеет место тождеств .
dz2 Л=1
значений данного резонатора.
где (Р«)-о?ектрСОиб3СТдифференЦмального уравнения краевой за-
Таким образом, изД>
дачи (8.35) вытекает равен
(8.37)
О' гл/~“ ' “'•
л-1
Чтобы получить явные выражения для коэффициентов ап, сле-
дует воспользоваться свойством ортогональности системы собст-
венных функций. Умножим обе части формулы (8.37) на собствен-
ную функцию фт с произвольнным номером tn, а затем проинтег-
рируем их по z в интервале от 0 до I. Воспользовавшись фундамен-
тальным свойством б-функции, сразу находим формулу, определя-
ющую искомые коэффициенты:
Отсюда следует окончательный вид функции Грина
(8.391
116
и выражение для комплексной
точке резонатора:
амплитуды
напряжения в любой
(г, z0) = /oZi V +Д£ИД£о)
' (8.40)
выво-
любом
вдоль
Анализ формул (8.39) и (8 4СП
дам: (8Л0) ПР”в°ДИт к следующим
I. При любой частоте возбуждают^
его местоположении характер распоем™ источника и при
оси резонатора определяется всей сои™,; Я напРяжения
2. Если источник располагается в ^упностью его мод.
ее амплитудный коэффициент становитго^ какой'Либо моды, то
3. Наибольший вклад в процесс те Равным нУлю. '
ственное значение близко к коэффипи?»™*3’ Ддя котоРой соб-
частоте возбуждения. Если такое условие 7^ фаЗЫ ₽ на заданной
сто, то принято говорить о резонансна« С1>ВИТельно имеет ме-
наторе без потерь все £п — BeXZ?Hbie°t^^“ "°™- В Рез°-
ном соблюдении резонансного условия ’ ПОЭТОМУ ПРИ точ-
становится неограниченно большой Это _п мплитУда напряжения
гичио резонансу в обычном колебателх™ к,™6 полностью анало-
Выражение (8.39) для функции Гп°НТуре без потеРь-
имеет вид бесконечного ряда и поэтом^ не °дномеРно™ резонатора
недостаток этой формулы - OTcyS УДобно- Основной
чить иное выражение для функции Гпина^вм Н°СТИ‘ Можно ПОЛУ’
похожее на (8.39), но тем не менее тЬт совершенно не
шее не менее тождественно с ним совпадаю-
Рассмотрим еще раз дифференциальное
задачи (8.35). Его решения, справедливые
ках резонатора, в которых отсутствуют источники
юшие краевым условиям на концах имеют вид:
при z<z0
уравнение из краевой
во всех внутренних точ-
— , и удовлетворя-
при z>z0
G~ A sin $z,
ли
О —В sin P(Z — z).
(8. 42)
Входящие сюда коэффициенты А и В должны быть определены
исходя из условий, накладываемых на функцию Грина в точке раз-
мещения источника. Для этого необходимо и достаточно выпол-
нения соотношений
A sin pz0 = В sin fl (Z - z0),
P Д COS p zo + pB cos 3 (Z — z0) = 1.
Систему (8.43) следует рассматривать как два линейных алгеб-
раических уравнения относительно неизвестных А и В. Запишем оп-
ределитель этой системы
D== sinpz0 -sinp(Z-z0) . ^.44
Р COS pzo р COS р (Z — z0)
117
Легко проверить, что
D=$ sin £/.
Возможны два случая: ' *45)
I. D^=0. При этом система (8.43) имеет единственн
sin?(l — z0)
3 sin ,3/ *
sin 3z0
3 sin 3/
После подстановки в (8.41) и (8.42) имеем явное
для функции Грина ВыРажеййе
/ sin Зг-sin ;3(/~ г0)
I 3 sin 3^ z го).
G(z,
I sin flzg-sin 3(/ — z) ,a
1 7775-------- <*oO</). (8-<6)
Рис. 8.9. Примеры функций
Грина резонатора, короткозамк-
нутого с обоих концов:
1.2 — частота возбуждающего ис-
точника значительно меньше собст-
венной частоты первой моды; 3. 4 —
то же. для случая, когда эти ча-
ст гы близки между собой
/0 46) можно сделать вывод, что функ-
Д на лизируя вЫРа>кеНИлбпажаётся двумя отрезками синусоиды.
иИЯ ГрХ на график «зображае , исходя пред_
ш,я 1 ставлення в виде бесконечного ряда по
собственным функциям, довольно труд,
но. Некоторые характерные случаи
представлены на рис. 8.9.
‘2 £) = 0. Из формулы (8.45) следу-
что это возможно для бесконечной 1
последовательности значений рп, удо-
влетворяюших соотношению
у=«л (« = 1,2,3,...), (8.47)
т е в случае резонансного возбужде-
ния какой-либо из мод резонатора. Ре-
зонансные условия выполняются для
бесконечного числа собственных час-
тот
(8-48)
nxv
<|)„ =---
л I
Режим резонансного возбуждения
в идеализированной системе без по-
терь характеризуется бесконечно боль-
, как это можно видеть из выражения
шой амплитудой колебаний, как это можно видеть из выражении
(S.46). Ясно, что наличие омических потерь в системе приводит к
конечным амплитудам даже на резонансных частотах.
118
§ 8.5. Влияние омических потерь на
собственных колебаний в резонаторе ₽ Р
Понятие комплексных собственных частот
Предположим, что распределение
счет действия каких-либо внешних иЛ Колебательная система ™
рый начальный запас энергии Э„ач и ..О11”иков_пРиобрела некото-
сама себе. В этом случае в резонаторе мож^т'л”1116” пРел°ставлена
конечная совокупность его мод Имея п°жет быть возбуждена бес-
нальности, не ограничивая общности б!Л”ДУ свойств» их ортого-
деннои оказалась лишь некоторая модаУ? „ полагать- что возбуж-
вии потерь в системе полная энергия Лп Мер°М п' ПР” отсутст-
дексная амплитуда напряжения в ? неизменной, а комп-
0Твечать монохроматическому колебХе Т0ЧКе Резонатора будет
чей волны, происходящему на собстЛиЛН»°Му пРоцессУ типа стоя-
ыгновенное значение------ венной частоте
<йп- При этом
напряжения
“(*»*)== Re (СЦг)^'). ,8 49)
-"сХоХ.ение
ценных к резонатору и т. п. Резонатор с потерями по-прежнему яв-
ляется линейной колебательной системой, по отношению к которой
полностью справедлив фундаментальный принцип - диссипация
энергии приводит к экспоненциальному уменьшению амплитуды
колебаний во времени. Таким образом, вместо формулы (8 49) для
резонатора с потерями имеем
K(z,/)==Re(t7(z)e~</'e«e;‘”',z) , у8.50)
где Тп — постоянная времени n-й моды в данном резонаторе.
То, что круговая частота n-й моды в резонаторе с потерями обо-
значена как (оп\ указывает на некоторое отклонение периода соб-
ственных колебаний от того, который имел место в системе без по-
терь. Подобное явление известно из соответствующего раздела
курса теории цепей.
Выражение (8.50) можно формально привести к виду (8.49) с
помощью широко распространенного приема. Полагаем собствен-
ную частоту n-й моды уже не вещественным, а комплексным чис-
лом, записываемым следующим образом:
wn=w«-r>n- (8.51)
Если теперь подставить шп на место щп в формулу (8.49), то
получим
H(z,/) = Re(t7(z)e п е я).
Отсюда следует соотношение
„ржЯУ мнимой частью комплексной собствен,
ппоеделяюшее связь между " „ рассматриваемой моды.
ной частоты И п0СХжена ось вещественных частот со, на которой
На рис 8.Ю изображена ос отвечаюших собственным Ча.
отмечено несколько точек о>. 2^- Для описания резонатора с
стогам мод в резонаторе без J0TpeHHe плоскость комплексных
потерями необходимо ввести Р енные частоты резонатора с по-
частот. Важно отметить, что с щими лишь в верхней полу-
терями изображаются точкамити Im ш>0. Действительно,
V
_____ь.
ё] цГ и'
Рис. 8.10. К понятию комплекс-
ных собственных частот
отрицательность Ип привела бы к
отрицательному значению постоян-
ной времени тп и, следовательно, к
экспоненциальному нарастанию ам-
плитуды колебаний во времени. По-
добная ситуация имеет место лишь
в активных системах, получающих
энергию от какого-либо внешнего
источника. Активные системы здесь
не рассматриваются, однако следу-
ет иметь в виду, что резонатор ’с
распределенными отрицательными потерями является удобной ма-
тематической моделью для описания явлений в распределенных
автоколебательных системах, например лазерах.
На рис. 8.10 изображены пути изображающих точек при увели-
чении затухания в резонаторе.
Обычно изучают колебательные системы с малым затуханием,
когда величина энергии, рассеянной за период собственных коле-
баний. составляет лишь малую часть от полной запасенной энер-
гии. С точки зрения метода комплексных частот утверждение о ма-
лости затухания эквивалентно выполнению неравенства
'л-
В первом приближении наличие малых потерь
вается на периоде собственных колебаний, т. е.
никак не сказы-
(8.53)
Чтобы определить мнимую часть комплексной собственной ча-
стоты или, что то же самое, постоянную времени п-й моды, вос-
пользуемся следующими соображениями. Поскольку любые энер-
гетические величины квадратично связаны с напряжениями и тока-
ми, можно записать закон изменения во времени полной электро-
магнитной энергии, присутствующей в резонаторе:
_2£
3„(/)=ЭлОе Ч
(8.54)
где Эп0— первоначальная энергия п-й моды, отнесенная к моменту
времени t=G.
120
Предположим, что можно вычиспитк «г.,
терь /\пот(0 в любой момент времени />0 Величи>наМ0ЩН0СТЬ П°’
р — 1
япот~ Т~ PnmAt>dt
о
будет представлять собой в этом случае мЛ,,.вЛЛ-
ную за период колебаний Тп. В силу потеРь. усреднен-
должно выполняться соотношение '' ’ ‘ К°Иа сохРанения энергии
с1Э
л (8.55)
т„=2Эя/РЛ1Ют. (8.56)
В последней формуле усреднение следует производить по перио-
ду колебании, включающему в себя зафиксированное значение t,
при котором был определен запас энергии Эп.
В физике и радиотехнике колебательные системы часто харак-
теризуют добротностью Q, которая в нашем случае связана с по-
стоянной времени следующим соотношением:
Qn = ^JTn. (8.57)
В качестве примера рассмотрим задачу нахождения добротности
п-й моды в резонаторе длиной I, короткозамкнутом с обоих концов.
Для учета потерь полагаем отличными от нуля погонное сопротив-
ление и погонную проводимость G'i. Считая, что потери малы,
закон изменения напряжения вдоль координаты z выберем таким
же, как и в невозмущенной системе без потерь:
47(z)=l/0sin (^i ) ,
тока
dU
dz
£/0cos
nnz
I
откуда на основании одного из телеграфных уравнений находим
комплексную амплитуду
/(*)=-?-
Последнюю формулу можно несколько упростить, зная,
собственное значение рп = лл// связано с частотой собственных
лебаний Wn соотношением pn = Wn/u. Тогда
плг \
I '
что
ко-
/ (z) = ^0-cos
Zb
Для вычисления запасенной энергии примем во внимание, что
напряжение и ток в резонаторе сдвинуты во времени на фазовый
угол 90°. Поэтому если напряжение достигло максимума, то ток
6-2910 121
CJJl
4
(8.58)
„ пгя энергия, запасенная в резонаторе, 6vn
*5характер:
5"=-rJ
о
с полная емкость отрезка линии, образующего резонат0п
где Ст —полная емки пе3онаторе, не зависит от номепя
Итак, энергияза на Рэнергия> запасенная в поле кондедЛ'
;™а" ДО ИапРЯ’кен.Гя U, при той же общей е„Х“ '
₽Через четверть периода энергия в системе приобретает я,,’,
энергии магнитного поля.
\
о
(8.59)
Результаты расчетов по формулам (8.58) и (8.59) совпадают.
Чтобы определить мгновенную мощность потерь, запишем вы-
ражения для мгновенных значений напряжения и тока:
un{z,t) — Uq sin f—j—cos(ол/,
U„ . <8-«»
I, (z, f)= —cos —- sin <»„/.
Отсюда получаем
Рл„О1(0 =
/ о UllGx „ , UllR^
= j [u2„ (z, t) G, (z, f) R,]dz = cos2 шя/+-— sin2«у.
0
Интегрирование по периоду собственных колебаний 7’п = 2л/(оп
и усреднение дает следующее выражение для средней мощности
потерь:
рт=^-+^-~ -(0,+RJ^, (8.61)
где Rs и Gz — полные активные сопротивление и проводимость по-
терь.
На основании (8.56) получаем выражение для постоянной вре-
мени n-й моды;
2Сг
Т.=-------~---9
Os + /?X/Z2
Отметим, что постоянные времени одинаковы для мод с любы-
ми номерами. Этого можно было ожидать, поскольку в рассматри-
ваемой одномерной колебательной системе можно говорить о за-
122
(8.62)
-
в
пасенной энергии и мощности потеоь пп,
длины. ПотеРь. приходящихся на единицу
В формуле (8.62) числитель и
одинаковый множитель I и тогда '5наменатель сокращаются на
т — 2
(8.64)
То'1/Ci) +(/?!/£.!> ’
откуда вытекает простая формула для добротности:
О-
1 <'1^1+/?1С1 * (8.63)
В гл. I была выведена фоомула ппа
линии с малыми потерями " ффициента ослабления
a=-?i_ л___1_q /
С учетом этого, проделав в уравнении (8.63) несложные поеоб
разования, получаем следующее выражение для добротное^Резо-
натора на п-и моде: дииришони резо-
г) __ птс 1
2 al
Пример. Предположим, что резонатор, работающий на основной моде
(„=1), выполнен на основе линии передачи с погонным затуханием Д=0 15 дБ
„ настроен на длину волны Хрез=20 см (fpe3=l,5 ГГц). Длина резонатора йи
этом составит 10 см (считается, что заполнение линии воздушное). Ослабление
в линии на участке, равном длине резонатора, ' умиление
, 10,15-0,1
а/=~опа;; =0,0017 Нп,
0,000
откуда по формуле (8.64) находим добротность Q = 910.
Следует отметить, что добротность распределенных колебатель-
ных систем в СВЧ-диапазоне существенно превосходит добротность
обычных колебательных контуров, образованных сосредоточенны-
ми элементами.
Из формулы (8.64) следует, что добротность резонатора линей-
но нарастает с увеличением номера моды. Однако фактически этот
рост происходит гораздо медленнее из-за неизбежного увеличения
коэффициента ослабления а на больших частотах (при фиксиро-
ванной длине I резонансная частота тем выше, чем больше номер
моды).
§ 8.6. Входная проводимость резонатора
вблизи резонансной частоты
В различных радиотехнических устройствах резонаторы, так же
как и колебательные контуры, часто включаются по схеме двухпо-
люсника. Рассмотрим распределенную колебательную систему,
. изображенную на рис. 8.11. Здесь входные зажимы удалены на
I расстояние /0 от левого короткозамкнутого конца резонатора. Вы-
6* 123
числим входную проводимость устройства, предположив, что линия
передачи, образующая резонатор, обладает некоторыми потерями.
Данная входная проводимость представляет собой сумму проводи-
мостей двух короткозамкнутых на концах отрезков.
(8. 65)
где
jz(i) = _L-cth yZ0,
z„
Г<2) =— cth Y (Zpe3 — Zo)-
(8. 66)
Для упрощения расчетов предположим, что погонные потери в ли-
нии малы, так что волновое сопротивление ZB приближенно можно
считать вещественным числом.
Известно, что
(8.67)
причем для малых х приближенно cthx~l/x.
Таким образом, при любой длине короткозамкнутого отрезка I,
удовлетворяющей условию имеет место формула
‘8-68>
Это выражение можно несколько упростить, полагая, что мни-
мая часть знаменателя мала по сравнению с единицей. Тогда, от-
брасывая члены порядка (а/)2 и выше, получим
cth (czZ + y₽Z) (aZ - j ctg ?Z) (1 -j-yaZ • ctg ?Z) » aZ (1 +ctg2 ?Z) -
(8-69)
Теперь, обратившись к формулам (8.65) и (8.66), запишем
=&ВХ У^ВХ’
где активная gBZ и реактивная Ьвх составляющие входной проводи-
мости выражаются через параметры системы следующим образом:
£вх = — [ —— Н----------------------1 , (8.70)
ZB L sin2?/0 sin2 3 (Zpe3-/O) J ’ k
[Ctg ?Z0 4-ctg ,8 (ZPe3 - Zo)]. (8.71)
На резонансной частоте реактивная часть входной проводимо-
сти будет равна нулю, поскольку
ctg?Z04-ctg3(Zp:3-Z0) =
sin ?/рез
sin p/0-sin ?(/рез —Zo)
= 0.
124
Величина вещественной части вхолнп-
тельной мере зависит от положения точекп1Р°ВОДИМОСТИ в значи-
X внешним цепям. Так, если точки подключииГЛ""” ₽ем"а™Ра
МОСТИ стоячей волны, т. е. включения находятся в пуч-
sin^O = sin?(Zpe3_/o)==li
то ^Bx = aWZB и поэтому резонансное сопротивление
дет весьма велико: рогивление системы бу-
/?Рез==±=_Ь_
^вх а/рез • (8.72)
Таким образом, в окрестности резонансно.-,
ближенно отождествить распределенную колебательнЫую™™ему“ё
известным из теории цепей параллельным колебательным kohL'
ром. }
Рис. 8.11. Схема резона-
тора, включенного как
двухполюсник
Квнешним цепям
Рис. 8.12. Пример конструкции
коаксиального резонатора:
/ — поршень; 2 — скользящий кон-
такт; 3 — петля связи; 4 — конст-
рукция настройки
Важно отметить, что в соответствии с формулой (8.70) переме-
щение точек подключения резонатора позволяет, не перестраивая
его, изменять величину резонансного входного сопротивления.
В этом смысле такая система эквивалентна широко применяемому
в радиотехнике колебательному контуру с неполным включе-
нием.
На рис. 8.12 представлен эскиз конструкции коаксиального ре-
зонатора, используемого в радиотехнике СВЧ на волнах децимет-
рового диапазона.
Задачи и упражнения к гл. VIII
8.1. Оптический лазер, работающий на длине волны Х=0,6328 мкм, содержит
резонатор, образованный двумя плоскопараллельными зеркалами с расстоянием
между ними 600 мм. Найти порядок величины номера моды, существующей в
таком резонаторе.
Ответ: 1,896• 10®.
125
иржлу двумя соседними модами (т Р ,
8.2. Каков частотный И,,Т^Р ' единицу) в резонаторе лазера, описан^0-
дами, номера которых отличаются на ед У) анном
в задаче 8.1?
& Так"
“₽=*“«>« ft
НаН8Н.4.е Коро^заНкнутыГ^отрезок ™" псРедачн включ7е.-н "аРадлельно Кон.
ленсатооу емкостью 15 пФ. Волновое сопротивление линии 75 Ом. Какова долж-
на бытьРдлина отрезка чтобы обеспечить условие резонанса на частоте 600 МГц
(диэлектрик — воздух)?
?5ТВре1онатор Представляет собой соединение двух короткозамкнутых От.
резковПлиний Передачи с длинами /, и /2;
а волновые сопротивления равны Zbi и Zb2 соответственно, вывести уравнение
„п”Х “иск вс» со.пкуп.юсть (.свопа неких частот ,_тако» актеие
~ должен удовлетво-
О т в е т: коэффициент фазы ft на резонансной частоте
рять уравнению
tgPZi = _31..
tg PZ2 ZB1
8.6. Отрезок линии передачи длиной 45 см закорочен с
нем возбуждены колебания на второй моде, т. е. при п = 2. _____
ние добротности Q = 3700. Найти коэффициент ослабления в линии.
Ответ: а=0,00189 Нп/м.
8.7. Закороченный с обоих концов отрезок линии передачи имеет дпин
30 см. Волновое сопротивление 200 Ом, коэффициент ослабления 0,025 Нп/
Найти резонансное значение входного сопротивления системы при подключени
внешних цепей к центральному сечению резонатора. и
Ответ: /?рез=26,7 кОм.
8.8. Как изменится резонансное сопротивление в условиях предыдущей
дачи, если входные зажимы будут располагаться на расстоянии 5 см от или..,»
Ответ: /?рез=6,7 кОм. Ц '
обоих концов и в
Измеренное значе
ИГТТТ MIC-
Глава IX
нерегулярные ЛИНИИ передачи
§ 9.1- Общие сведения
zsi i
| ‘-иг
ZB1
До сих пор рассматривались nprvnan,,,,
рактерные тем, что их параметры тааде как™”” передачи’ ха’
ность и погонная емкость, считались опиЛ К погонная индуктив-
ен линии. Введение в конструкцию линии лю^оТнеоп^™
нарушает ее регулярность. Нерегулярные системы е°д“°родности
каскадным включением отрезков perv- ’ образованные
лярных линий, обладают полезными в
практическом отношении свойствами. Од-
ной из таких конструкций является со-
гласующий четвертьволновый трансфор-
матор, который был рассмотрен ранее.
Чтобы повысить качество согласова-
ния, т. е. добиться минимального коэф-
фициента отражения в более широкой
полосе рабочих частот, целесообразно
увеличивать число последовательно вклю-
чаемых согласующих секций при одно-
временном сокращении перепадов волно-
вого сопротивления между соседними
секциями. Получающаяся при этом кон-
струкция согласующего устройства пред-
ставляет собой нерегулярную линию
со скачкообразным изменением погонных
параметров. Это широко распространен-
ный в радиотехнике сверхвысоких частот
ступенчатый переход между двумя линиями передачи (рис 9 1 а)
Качество работы перехода будет повышаться с ростом числа ' ’
пек. В пределе „получаем плавный согласующий переход
9.1, о), которой должен обеспечивать наилучшее качество
Рис. 9.1. Ступенчатый (а) и
плавный (б) переходы меж-
ду линиями передачи с раз-
ными волновыми сопротив-
лениями
ступе-
(рис.
согла-
сования.
§ 9.2. Дифференциальные уравнения линии передачи
с плавным изменением погонных параметров
Чтобы иметь возможность вычислять и анализировать любые
внешние характеристики нерегулярных линий передачи, нужно в
рамках принятой формальной схемы описания найти общее реше-
ние системы однородных телеграфных уравнений с переменными
коэффициентами
127
(9.
d}L = -Zx(z)l,
dz
dz
nrt отношению К заданным функциям Z,(2\
Предположим, что по о непрерывности и дифференцируемо.
И 7,(2) выполнены требов необходимым, требования медленно-
сти, а также, когда это будет не в § g 4)
сти изменения <^ot слу й * единственному уравнению
Система (9.1)Jения, либо относительно тока. Для это-
либо относительно напря , части уравнения (9.1а):
го продифференцируем вначале обе части уР
dW_____dZx i7^L
dz dz
dz2
и учтем, что
1 dU
Zx dz
Принимая во внимание тождество
{dZxldz)IZx = -^^-
dz
получим окончательное уравнение, которому должна удовлетво-
рять комплексная амплитуда напряжения в нерегулярной линии
передачи
rf2£7 d in Zj dU у чг f г
--------------•------ZXI XU—0. (Q O'.
dz? dz dz
Аналогично из (9.1) может быть выведено дифференциальное
уравнение, описывающее пространственную зависимость комплекс-
ной амплитуды тока:
</2/ d in Г]
dz
“L-ZxYxl=b.
dz
(9.3)
Линейные дифференциальные уравнения (9.2) и (9.3) по физи-
ческому смыслу аналогичны уравнениям Гельмгольца в теории ре-
гулярных линий. В предельном случае неизменных погонных пара-
метров коэффициенты при первых производных в (9.2) и (9.3) об-
ращаются в нуль, так что эти уравнения превращаются в обычные
уравнения Гельмгольца. Можно сказать, что волновые процессы
в нерегулярных линиях передачи описываются обобщенными урав-
нениями Гельмгольца.
Безусловно, нет необходимости решать оба уравнения (9.2) и
(9.3). Если найдена, например, комплексная амплитуда C(z),
служащая решением (9.2), то комплексная амплитуда /(z) может
быть получена дифференцированием в соответствии с телеграфным
уравнением (9.1а).
128
Следует иметь в виду, что с лепехой,
ний нерегулярной линии к обобщенный? vnaVuMerpa*Hblx УРавне-
задача ни в коей мере не упрощается ТпЛРаВНеНИЯМ Гельмгольца
что линейные дифференциальные уравнена закл1°чена в том,
(М» „ (9.3) имеют коэффициентЫУ,₽з=” ”аð "°ряяка
ременной г. Математические приемы котп^ «зависимой пе-
нить замкнутые выражения для решений лРХП°ЗВ°ЛЯЛН бы нах°-
неизвестны и, по-видимому, „х существ /аКИХ Уравнений,
получены лишь в некоторых частных слечяЛ £трогие Решения
пользовать достаточно мощные приближений ДНако мо*но нс-
всегда имеются практически неограниченный наконеи.
решений численными методами с помошью ^мРиеКТ,,Ви поиска
„уть особую роль тех частных случаев для ‘ Нужно п°Дчерк-
ния известны, поскольку они выступаю? как 1°РЫХ стРогие Реше’
точности разнообразных приближенных и«„г галоны при оценке
На классическом примере проана ununvo ленных методов,
передачи, допускающую строгое решение' cS₽i7™PHy’0 ЛИНИЮ
рощающие предположения- решение- Сделаем некоторые уп-
Омические потери в линии отсутствуют, т. е. R^G^Q, так
Zi(2)= (z); Y, (z)=j^Cx (z).
2. Произведение Z.K^const и не зависит от координаты г Это
условие обеспечивает в каждом сечении линии неизменную вели-
чину локальной фазовой скорости у и
’’♦'“-TT.wc.w • (9-4)
Обратившись к примерам отдельных линий передачи, изученных
в гл. И, убедимся, что при изменении геометрических характерис-
тик поперечного сечения условие (9.4) будет выполнено.
Для более общего случая нерегулярной линии, в которой пере-
менными вдоль z являются параметры е и ц, второе из поставлен-
ных условий, как правило, не будет справедливо.
§ 9.3. Нерегулярная линия передачи экспоненциального типа
Нерегулярная линия передачи является линией экспоненциаль-
ного типа (или просто экспоненциальной линией), если ее первич-
ные погонные параметры зависят от продольной координаты сле-
дующим образом:
Zj(z)=£10e-^; C^z) = C^, (9.5)
где Lio и С10 —значения соответствующих параметров при z=0.
Условие (9.4) здесь безусловно выполняется.
Коэффициент q, который может быть как положительным, так
и отрицательным, показывает в логарифмическом масштабе ско-
129
рость изменения параметров линии вдоль продольной координаты.
Поскольку здесь
^=/о>А10ехр(-^),
то
d \nZi/dz = —q,
и обобщенное уравнение Гельмгольца для экспоненциальной линии
приобретает вид
^ + ₽о2^ = О, (9.6)
dz7 dz
где ро=(1)]/Л1оС)о — коэффициент фазы в линии на заданной часто-
те (напомним, что по предположению фазовая скорость, а следо-
вательно, и коэффициент фазы вдоль линии неизменны).
Линия экспоненциального типа в известном смысле уникальна,
так как описывающее ее уравнение (9.6) очень просто по своей
структуре,— оно содержит лишь постоянные коэффициенты. Общий
интеграл такого уравнения имеет вид
47(г)=Л1ех,гН-Л2ех,г, (9.7)
куда входят две произвольные 'комплексные постоянные A i и Д2, а
также числа xi и х2, являющиеся корнями характеристического
уравнения
т. е.
= + // (9-8)
Характерный вид формулы (9.7) позволяет отождествить каж-
дое из двух слагаемых в правой части с волной, распространя-
ющейся либо в прямом, либо в обратном направлении. При этом
корни Х],2 играют роль коэффициентов распространения для этих
волн.
Отметим, что хотя омические потери в экспоненциальной линии
отсутствуют по предположению, коэффициенты распространения
(9.8) комплексны, что свидетельствует об экспоненциальном изме-
нении амплитуды колебаний вдоль оси г. Например, волна вида
распространяется в сторону возрастания г, и если <у>0, то ампли-
туда колебаний уменьшается по мере движения волны. Чтобы по-
нять это явление, найдем соответствующий закон изменения ком-
плексной амплитуды тока
130
I d(l
Zy ' dz
q_
2
и0
z
чг
u>z.i0 e expl—у
откуда следует, что для экспоненциялкил?
пряжения в бегущей волне ведет к Й Линии Уменьшение ня
”Р"чеЛ™™Йп™ *еЛИЧИНа ^еДнейТошнп^^^ росту тока,
гущей волной вдоль линии, постоянна Щности- переносимой бе-
PcpeA = YRe(^) = Const.
Таким образом, экспоненциальная линии „
ройство, осуществляющее трансфопмяп™представляет собой уст-
жеиий. В отличие от обычного транЖм^Р°ВНеЙ ТОКОП и напря-
тротехники, этот процесс носит поостпя«известного из элек-
характер. В зависимости от знака паоямАтпоНН°'распределенный
матор может быть как повышающим так «V волновой трансфор-
фа,0А^ми„\"ГэкХ^ц“:^“-
(9.9)
отличается от величины Ро, и „оэтому ИСТЙННая
------Ш
V“2^ioCю — <72/4 (9- Ю)
несколько отличается от локальной фазовой скорости, введенной в
соответствии с формулой (9.4). Более того, из (9.10) вытекает, что
фазовая скорость зависит от частоты, что свидетельствует о нали-
чии частотной дисперсии, несвойственной регулярным линиям без
потерь.
На достаточно низких частотах, когда р0<|д|/2, коэффициент
фазы в экспоненциальной линии становится мнимым, а это, как
известно, означает, что колебательный процесс в такой линии пере-
стает носить волновой характер. Такая нерегулярная линия выпол-
няет роль фильтра, пропускающего высокочастотную и задержи-
вающего низкочастотную составляющую спектра передаваемого
сигнала.
Однако для радиотехнических приложений гораздо более важен
другой частный случай, характеризущийся обратным неравенством
р0» | <71 /2 или, что то же самое, | Линия передачи с таки-
ми свойствами имеет малое относительное изменение погонных па-
раметров на участке порядка длины волны. Для этого случая
*1,2 ~---- ±
131
Как упоминалось, любой волновой процесс в экспоненциальной
линии передачи может быть представлен суммой двух волн, рас.
пространяющихся в противоположных направлениях, назовем па-
дающей ту волну, которая распространяется в сторону увеличения
z. Таким образом,
= 2ехр(-/М.
_<7*
^оТр = ^0оТРе 2 ехр (УМ-
Способом, указанным ранее, находим соответствующие ком-
плексные
(9.11)
амплитуды токов
. qz
4аД=-^!Н£' еУ ехр(-/₽о^>
^вО
r'r qz
/отР=-^е2ехр(уМ.
вО
(9.12)
Здесь Zb0 = ]/Z10/C,i0— локальное значение волнового сопро-
тивления, соответствующее точке z—0.
Предположим теперь, что в некотором произвольном сечении с
координатой г=£ включен нагрузочный резистор 7?н. При этом дол-
жно выполняться следующее условие:
__<L-
„ U(О е 2 [^оваДе“Ш+^оотре/₽°с] ,Q 1Q.
=7^- ~ • (9.13)
-7— [^0паДе~/РоС — t/oorpe^00]
^вО
В общем случае нагруженной экспоненциальной линии нужно
учитывать как падающую, так и отраженную волны. Однако из
формулы (9.13) следует, что имеется один частный случай, когда
/?н = ДвОе~^. (9.14)
При таком выборе сопротивления нагрузки возможно удовлет-
ворить равенству (9.13) тождественно при любых £, полагая
Оотр — 0.
Итак, отрезок плавной экспоненциальной линии передачи мо-
жет служить согласующим устройством, которое позволяет прак-
тически избежать отражений при чисто активном характере на-
грузочного сопротивления. Для этого достаточно выбрать параметр
2в0^равным волновому сопротивлению основной питающей линии.
Действительно, входное сопротивление отрезка экспоненциальной
линии, нагруженной на резистор, сопротивление которого опреде-
ляется формулой (9.14), чисто активно и равно ZB0.
Ход решения задачи синтеза экспоненциального согласующего
устройства (перехода), предназначенного для согласования рези-
стора 7?н и регулярной линии с волновым сопротивлением /влшь
следующий: г
132
1) начальное значение волнового
ной линии находим из условия Р явления экспоненциаль-
Zbo=ZB4h„;
2) считая заданной длину I экспоненциального участка в соот
ветствии с (9.14) определяем парамето a ’
ЮЩИЙ конструкцию данной нерегулярноЛинии: хаРактеРизУ-
<7 = —In •
1
(9.15)
,4==. ;:хт" - -~-
экспоненциального перехода, обеспечивающего S ^абочеГоин? воТыТ-
= 7,5 см согласование с нагрузкой /?п = 30 Ом длине волны л =
Воспользуемся наиболее простой формулой для волнового сопротивления
микрополосковои линии (см. ГЛ. II) сопротивления
Подставляя сюда исходные данные, находим ширину полоски основной ли-
нии передачи
, 120-3,1416-0,5
О = --------т=---
50/10
1,192 мм.
Коэффициент фазы в линии (с учетом влияния диэлектрика)
„ 2л /ё 1
?=—7— =0,2649— .
А мм
Зададимся длиной экспоненциального участка 1=100 мм и в соответствии
с (9.15) найдем
1 ! 5 \ „ 1
q = — In I — | = 0,00ol — ,
100 \ 3 ) мм
откуда видно, что данная линия действительно может считаться плавной, по-
скольку <7<С р.
Поместив начало координат в том сечении, где основная линия подключается
к экспоненциальному переходу, имеем следующую формулу, представляющую
собой закон изменения локального волнового сопротивления:
ZB(z) = 50ехр(— qz), Ом.
(9.17)
Переменного по длине волнового сопротивления проще всего добиться, изме-
няя ширину полоски. Для нахождения функции b (г) воспользуемся формулами
(9.16) и (9.17):
120л h
—-z— •-------= эО ехр (—qz),
/е Ь(?)
откуда
*(г) = —^ехр(дг),
О У 8
133
или после подстановки численных значений
Ь (г) = 1,192 ехр (0,0051 z),
На рис.
Условие плавности перехода приводит
что может препятствовать ----------
Рис. 92 Чертеж экспонен-
циального согласующего пе-
рехода между двумя полос-
ковыми линиями передачи
(все размеры даны в мм)
где координата г выражена в “"^““"^итанного экспоненциального переход,.
9.2 изображен эскиз рас точно большой длине конструкции
' "1Т^пванию плавных переходов в интегральных’
испольэова особс,„|О ссли учесть, что длина
гпшсуюшсй секции должна расти прямо про-
порционально рабочей длине волны.
Если отказаться от требования
плавности изменения погонных пара-
метров, то возникает ряд дополнитель-
ных эффектов. Прежде всего волновое
сопротивление такой линии передачи
есть комплексная величина (в качест-
ве упражнения предлагается вывести
формулу для волнового сопротивле-
ния) 'Поэтому идеальное согласование
при чисто активном характере нагруз.
ки становится невозможным.
§ 9.4. Волны в нерегулярных линиях передачи
с медленным изменением погонных параметров
Часто возникает необходимость приближенного интегрирования
системы телеграфных уравнений (9.1) или обобщенного уравнения
Гельмгольца (9.2). Оказывается, что приближенное решение дей-
ствительно можно найти в случае, когда погонные параметры ли-
нии являются медленными функциями координаты г. Точный смысл
условия медленности заключен в том, что относительное изменение
параметров Zj(z) и У|(г) на отрезке длиной л должно быть вели-
чиной, гораздо меньшей единицы. Легко проверить, что это условие
эквивалентно следующим неравенствам:
X' dlnZ1-<^l, k rflnr'-.^i, (9.18)
dz dz
Процессы в такой нерегулярной линии должны быть сходны с
аналогичными процессами в регулярной линии. Исходя из этого,
будем искать решения системы телеграфных уравнений (9.1) в ви-
де произведений медленно меняющихся амплитудных множителей
на экспоненты с мнимым показателем:
<7(г)=4/0(г)еМ«>, (9Jg)
/(г)=/0(г)е/?(Ч
Если подставить (9.19) в (9.1) и сократить на общие множите-
ли, то
(9 20)
/?7о4-/о= -ЛЦ).
134
частях (9.20)
i получаем
(а) |
(6) |
С учетом условия медленности
производные U„' и положив пх
систему двух укороченных телеграф,,^^,,
Л70=_Г,1/0.
В эти уравнения входят три не
должны быть связаны одним допоХ™"*! ФУи^им. поэтому они
делив уравнение (а) на (б), исключаем вез.? соо™ош™"™•'Раз-
величину <Р и находим, что
(9.21)
T. e. в рассматриваемой линии наблюдается непрерывная трансфор-
мация уровнен тока и напряжения в соответствии с локальным за-
коном изменения волнового сопротивления. Поэтому в рамках рас-
сматриваемого приближения какие-либо отражения в линии от-
сутствуют.
Теперь найдем фазовую функцию <р(г). Умножив (9.2! а) на
(9.216) и сократив на общий множитель, получим
откуда
<Р'=±//27Ь
?= +J J VZ/,dz.
Смысл полученной формулы состоит в том, что результирующий
фазовый сдвиг получается суммированием всех элементарных фа-
зовых сдвигов. Столь простой характер решения — следствие пре-
небрежения локальными отражениями.
Закон изменения амплитуд IJO и /о может быть найден из энер-
гетических соображений. Действительно, поскольку переносимая
мощность в линии без потерь и без отражений постоянна в любом
сечении, то LVo=const.
Отсюда с учетом (9.22) получаем
^o(z) —const Zj/F,,
4— (9.23)
/0(z)=const у YJZx.
Изложенный метод приближенного решения дифференциальных
уравнений с медленно меняющимися коэффициентами широко при-
меняется в разных областях физики. Например, в квантовой меха-
нике его называют методом Вентцеля — Крамерса — Бриллюэна
(сокращенно метод ВКБ).
В ряде радиотехнических задач встает проблема создания плав-
ных переходов, обеспечивающих малый уровень отражения в до-
статочно широком диапазоне рабочих частот. Метод, рассмотрен-
ный ранее, не учитывает явления, связанные с отражениями. По-
этому необходимо сформулировать концепцию, которая позволяет
учесть отражения хотя бы приближенно. Сущность ее заключается
в следующем: отрезок нерегулярной линии рассматривается как
предельный случай ступенчатого перехода при неограниченном со-
135
кращении длины отдельных ступенек. Хотя возникающие здесь
локальные отражения бесконечно малы, но, будучи просуммирова-
ны по всей длине согласующего устройства, они приводят к конеч-
ной величине коэффициента отражения от перехода.
Пусть нерегулярная линия передачи описывается заданной функ.
цией ZB(z). Выберем некоторое сечение z=Zo, которое будет слу-
жить входом для малого отрезка линии длиной Az. С точностью д0
величин порядка (Аг)2 волновое сопротивление на выходе
~ ' dZ" Lz.
в
dz
Если теперь заменить рассматриваемый отрезок плавной линии
сочленением двух регулярных линий с волновыми сопротивлениями
Z,(z0) и “(i+Az), то локальный коэффициент отражения
, , _ Z„(z0 + Az)-ZB(z0) _____1---~
елок(го) ZB(z0 + Az)+Z„(z0) 2ZB (z0) dz
1 d ln Z" - Az
2 dz
(все производные вычисляют в точке z=zo).
Пусть параметры линии меняются по координате z столь плав-
но, что амплитуда падающей волны вдоль перехода практически
постоянна. Предположим, кроме того, что волны, возникшие вслед-
ствие локальных отражений, достигают входного сечения перехода
и складываются там, не испытывая на всей длине перехода явле-
ний типа многократных отражений.
Оба допущения выполняются тем точнее, чем более плавным
является переход. Устремляя к нулю величину Az и учитывая фазу
отраженных волн, возникающих в каждом сечении линии, получим
следующую формулу для расчета коэффициента отражения на вхо-
де плавного перехода длиной /Пер> идеально согласованного на вы-
ходном конце:
о =Jf d 1П±д z-^dz. (9.24)
6вХ 2 J dz
О
Показатель экспоненты под знаком интеграла указывает на то,
что волне в линии нужно пройти путь длиной 2z, прежде чем она,
испытав локальное отражение, вновь попадет на вход.
Проведем расчет коэффициента отражения на примере экспо-
ненциального перехода, у которого волновые сопротивления на
входе и на выходе равны соответственно ZBBX и ZBBbiX. По формуле
вида (9.15) находим
Z,(z)=Z,„exp (-£- In^s);
\ *пер ^ввх /
таким образом,
d In ZR 1 । ZB2
dz Aiep ZBi
136
Воспользовавшись (9.24), получим
7
Л = -ГГ' \ еХР1—J'23z)dz~~— |п^и пых /< -/Ш п\
2Znep Z»1 -I 93/ ’ 7----(I—e и nep).
0 zP‘nep ZBBX >
В технических задачах обычно интрпр™^-™.,
циента отражения. Поскольку Р ’ СЯ модУлем коэффи-
|1 е;'"ер| [(1 cos2?ZIiep)2 + sin22?Znepp^=2|sin.^^
то
1евх| —
7
In R яых
7
^в вх
Sin ?Z„ep
(9.25)
График, соответствующий формуле (9.25), изображен на
рис. 9.3. Участок, отмеченный пунктиром, не отвечает изложенной
теории, поскольку при слишком ма-
лой электрическом длине перехода
не выполняются условия его плавно-
сти. Характерно, что модуль коэф-
фициента отражения от плавного
экспоненциального перехода зави-
сит от его электрической длины не-
монотонно и обращается в нуль
при р/пер=ял (п — целое число),
т. е. при Znep~^Z,/2.
Это связано с тем, что здесь на-
Рис. 9.3. Коэффициент отражения
от плавного экспоненциального пе-
рехода как функция его электри-
ческой длины
блюдается взаимная компенсация
всех волн, возникающих при локаль-
ных отражениях и приходящих ко
входу устройства с различными фа-
зовыми сдвигами.
Учет многократных отражений, имеющих место в нерегулярных
линиях, для которых не выполняются требования плавности, явля-
ется гораздо более сложной задачей и в данной книге не рассмат-
ривается.
Задачи и упражнения к гл. IX
9.1. Вывести дифференциальное уравнение для комплексной амплитуды на-
пряжения в нерегулярной линии передачи, в которой реактивные первичные
параметры меняются по закону:
Zj = >£10(a/z), Ki = >С10(г/а),
где а — некоторая константа с размерностью длины.
Ответ.
dW 1 dU
d& + $ '
где $ = Pqz — ш LiqCwz .
137
9.2. Записать общий интеграл полученного уравнения, а также асимпт
ческий вид решения в области, значительно удаленной от начала коот,,
при единат.
Ответ.
U (z) = AxH^($oz) + A2H^(foz),
где Hq и Hq — функции Ханкеля нулевого
аргумента асимптотически
U(z)^Ax 1/ —— е 1 +>12
I л?ог
ЗНачениях
индекса; при больших
9.3. Показать, что метод ВКБ, примененный для решения задачи 9.1, дае
такую же зависимость модуля комплексной амплитуды напряжения от прододь-
ной координаты, которую можно получить из асимптотической^ формулы.
9.4. Показать, что текущий импеданс Z(z) в нерегулярной линии передачи
определяемый соотношением Z(z) =£?(2)//(2)> должен удовлетворять нелинейному
дифференциальному уравнению первого порядка
называемому уравнением Риккати.
Глава X
СВЯЗАННЫЕ ЛИНИИ ПЕРЕДАЧИ
§ 10.1. Понятие распределенной связи
между линиями передачи.
Математическая формулировка задачи
о связанных линиях
ппостоанствеИтаким ’егУл’РНые линии
в пространстве таким образом, что области
электромагнитные поля, переносимые ’
иной мере взаимно пересекаются
передачи размещены
где сосредоточены
этими линиями, в той или
В этом случае рассматриваемые
связанные линии должны влиять
друг на друга и поэтому их свой-
ства будут отличаться от соответ-
ствующих свойств одиночных ли-
ний в отсутствие связи. Взаимная
связь линий носит пространствен-
но-распределенный характер и
поэтому для ее анализа применя-
ются методы волновой теории.
Математическое описание яв-
лений в связанных линиях пере-
дачи в общем случае может ока-
заться чрезвычайно громоздким.
Поэтому будем изучать простей-
ший вид связи, называемый регу-
лярным. Он характеризуется тем,
что две линии передачи размеще-
ны в пространстве параллельно
друг другу. Эскизы поперечных
сечений некоторых регулярно
связанных линий представлены
на рис. 10.1.
Дадим математическое описа-
ние такой системы, опираясь на
формализм телеграфных
Рис. 10.1. Связанные линии передачи:
а — коаксиальные; б — симметричные двух-
проводные; в — несимметричные полоско-
вые
уравнений. Пусть
UP, UP. гР1
— совокупность погонных параметров, относящихся соответствен-
но к первой и второй линиям в отсутствие связи. Эффект электро-
магнитной связи между линиями характеризуют двумя погонными
параметрами связи ZjCB и У1СВ. Тогда, снабжая напряжения и токи
139
индексами, указывающими номер линии, можно формально запц,
сать следующую систему телеграфных уравнений, описывающую
всю совокупность волновых явлений в двух связанных линиях, ца
холящихся под гармоническим внешним воздействием:
dUx 7w, _7 [
dz
^=-7^-7^
} (Ю.1)
A=-z1(!)/2-4B/1.
dz
*h_=-Y™U2-Yxjjx. ,
dz
В системе (10.1) погонные параметры Zjcb и У1св носят чисто
реактивный характер. Это обусловлено тем, что изучаемые эффек-
ты вызываются двумя причинами: а) наличием взаимной индуктив-
ности между линиями, т. е. связью по току; б) существованием
электростатической индукции между обеими линиями, т. е. связью
по напряжению. В соответствии с общефизическими представлени-
ями связь между линиями должна быть взаимной (известный прин-
цип взаимности в теории электрических цепей), поэтому в системе
(10.1) достаточно ввести два, а не четыре погонных параметра
связи.
Полученная система четырех линейных дифференциальных
уравнений первого порядка для однозначности решения должна
быть дополнена некоторыми начальными условиями, определяющи-
ми состояние обеих линий при z=0:
4/1(О)=6г10; г/2(О)=£72о;
Л(О) = Ло> А (0) = Ао-
§ 10.2. Нормальные волны в системе
двух связанных линий передачи
Будем считать обе линии идентичными друг другу. При этом,
очевидно,
zP=zP=zi; гР=гР=п.
Обратимся к системе (10.1). Если связь между линиями пол-
ностью отсутствует, т. е. 2!Св=У1св=0, то система уравнений рас-
падается на две независимые системы относительно переменных
(О\, /J и (i72, Л). Возникает вопрос, нельзя ли добиться такого
же расщепления системы (10.1) и при наличии связи, если от ис-
ходных переменных (С/j, 1\, О2, /2) перейти к некоторым новым за-
висимым переменным, связанным с исходными с помощью линей-
ного преобразования. Если это возможно, то эти новые переменные
140
в физике называют нормальными координатами. Переход к нор-
мальным координатам является широко распространенным анали-
тическим приемом во всех областях теории колебаний и волн [4].
Получающиеся при этом нормальные уравнения гораздо проще ис-
ходных и, как правило, допускают наглядную физическую иитер-
нретацик).
Общий метод поиска нормальных координат связан с нахожде-
нием линейного преобразования, приводящего матрицу исходной
системы дифференциальных уравнений к диагональной форме (7].
Однако в нашем частном случае симметричный вид правых частей
системы уравнений (10.1) позволяет найти нормальные координа-
ты гораздо проще. Действительно, образуем четыре новых пере-
менных по формулам:
?1 = бЛ-Г^2’ ?2 = ^1 ^2» ЦО 2)
Т11 = Л Лг —Л — Л-
Тогда, складывая и вычитая соответствующие уравнения, вхо-
дящие в (10.1), получим две системы дифференциальных урав-
нений:
dz
= -(Г,+ Y,
dz
—— = —(Zi — Z1CB1 T|2i
dz
dl\2
dz
(10.3)
(Ю.4)
1св' Й-
Итак, задача о двух связанных линиях передачи сводится к ре-
шению хорошо изученных систем телеграфных уравнений. Важно,
что системы (10.3) и (104) являют-
ся независимыми. Поэтому новые
переменные, введенные по форму-
лам (10.2), действительно являются
нормальными координатами для
системы двух связанных линий.
Решения систем (10.3) и (10.4)
называют нормальными вол-
нами. Полная независимость нор-
мальных волн друг от друга позво-
ляет утверждать, что. две связанные
линии передачи обладают двумя
модами (ср. моды резонаторов, изу-
чавшиеся в гл. VIII).
Физическую сущность нормаль-
ных волн поясним, обратившись
Рис. 10.2. Структура электриче-
ского поля в связанных полоско-
вых линиях:
а — четная волна; б — нечетная волна
14)
вновь к формулам (10.2). Если линии возбуждены таким образом,
что токи и напряжения синфазны (^-бг. поскольку Е Ме
существует только первая из нормальных волн, поскольку S2 = n2sa
=0 Рассматриваемую моду называют четной (симметричной)
нормальной волной Наоборот, противофазность напряжений „
токов в линиях (С,— Й. /, = -Л) приводит к возникновению в
системе второй моды, называемой „ е чет н о и (антисимметричной)
нормальной волной. На рис. 10.2 изображена примерная структ
ра электромагнитных полей для обеих нормальных волн примени,
тельио к связанным несимметричным полосковым линиям пере.
ДЭ 'всегда возможен обратный переход от нормальных координат
к истинным напряжениям и токам:
^2 — — (;i —
! . 1 (Ю.5)
/1=V(711+112); Z2 = —(П! —П2).
£ £
Итак, любой волновой процесс в связанной системе есть супер
позиция нормальных волн.
Рассмотрим теперь телеграфные уравнения (10.3) и (10.4)
Введем погонные сопротивления и проводимости для четной и не
четной волн:
Z14t = Z1 +^1св,
К1чт = ^1 1 Y 1 1 1св’
7 ZjlH4 Z1CB,
=Л- -^св-
Отсюда в соот находим комплекс ветствии с принципами, изложенными в гл. I, :ные коэффициенты распространения: T4I=yz,„Tr,„T, Ти, = /г,„Г1ич,
и волновые сопрот ивления
• ZB4T— 1 £1чт/)Лчт> (10. 8) ZBH4~ V Z1hm/Z 1нч*
В линиях перед; часто можно прене циенты фазы обей: ачи, представляющих интерес для радиотехники, бречь омическими потерями. При этом коэффи- < нормальных волн выражаются формулами:
Р- ^«-/(Л+АеХС.+с,.,),
142
a волновые сопротивления, будучи вещественными, имеют вид:
Мея
^1 + С1св
^•1 ^Icb
(10.10)
Различие коэффициентов фазы
тельствует о том, что нормальные
выми скоростями:
четной и нечетной волн свиде-
волны обладают разными фазо-
^фчт—V/lAi + AiJfCi-j-CiJ,
гФ нч = UV (^i LlCB)(Cx — С1св).
Последний факт особенно важен, поскольку он лежит в основе
работы разнообразных устройств, построенных на базе связанных
линий передачи.
§ 10.3. Эффекты, возникающие
при сложении нормальных волн
Рассмотрим полубесконечную систему двух связанных идентич-
ных линий, изображенную на рис. 10.3. Здесь на входе линии 1
включен источник гармонической э.д.с. с амплитудой Ё, вход ли-
нии 2 закорочен. Поэтому имеем следующие начальные условия:
(Л(0)=4-(М0)+М0))=Ё.
(10. 12)
<72(0)=ф(М0)-й(0))=0.
Рассматривая (10.12) как уравнения относительно начальных
амплитуд нормальных волн, получим
;i (0) — ?2 (0) — Е-
Итак, в изучаемой системе при данной конфигурации возбуж-
даемых источников существуют обе нормальные волны с одинако-
выми амплитудами. Если теперь учесть, что здесь не существует
волн, распространяющихся справа налево ввиду согласованности
линий на бесконечности, то можно написать следующие равенства,
представляющие собой закон изменения напряжений вдоль линий.
^1(г) = А(е-у?чгг4-е 'М,
U.{zY-= — (е-у?^г - e-7?“4').
(10.13)
Исследуем зависимости модулей комплексных амплитуд С\ и
О2 от продольной координты z. Представляя экспоненциальные
функции по формуле Эйлера и проводя очевидные преобразования,
143
получим
KZ1 (z)l = & V1 +cos(p4T^ — Зячг) = |£| | COS ^чт 2 ?нч) - , (10. 14)
К4 (г)1 = /1 — cos (М — М) = 1^1 sinP,r -М *1 • (10.15)
Графики, представленные на рис. 10.4, свидетельствуют о том
что неравенство друг другу фазовых скоростей двух нормальных
волн приводит к эффекту периодического «перекачивания» энергии
из. одной линии в другую. Принято говорить о том, что в связан-
Рис. 10.3. К задаче о связанных
линиях
Рис. 10.4. Возникновение прост-
ранственных биений
ных линиях передачи наблюдаются явления пространственных бие-
ний. Период этих биений, определяемый из формул (10.14) и
(10.15), должен удовлетворять соотношению
откуда
*^биен Я,
А-биен
2л
Зчт — ?нч
(10.16)
Описанные явления находят широкое применение при констру-
ировании разнообразных устройств, работающих в СВЧ-диапазоне.
Например, обеспечивая между двумя линиями распределенную
связь на некотором отрезке, получаем делитель мощности. По-
скольку мощность, ответвляемая во вторичную линию, зависит от
электрической длины участка связи и в конечном счете, от частоты
колебаний, то можно создать частотный разделитель, схематиче-
ское изображение которого приведено на рис. 10.5.
Чтобы произвести расчет параметров связанных линий, необхо-
димо располагать сведениями о погонных параметрах связи. На-
хождение их сопряжено со сложными электродинамическими рас-
четами, проводимыми, как правило, на ЭВМ. В литературе обычно
даются графики, позволяющие определять волновые сопротивления
ZB чт и ZBH4 по известной геометрии линии. '
144
Имеется формула, связывают
ВО вторую линию, и мощность Р. „ДЛ°ЩИОСТ|’ ₽J’ ответвляемую
НИИ [2]: Ь ь "оотупающую на вход первой ли-
р __ ?№ Sin2»
*2— ——-------
А 1 4- А’2 со&2 Л * (10, 17)
где Ф —электрическая длина участка А™.- ъ к
раметр, называемый к о э ф ф и ц Ие;НТ ’безРазмерный на-
следующим образом: М СВязи и определяемый
fr —_z» нч —Z, чт
ЧТ
В конструкциях, применяемых
на практике, разница между вол-
новыми сопротивлениями четной
и нечетной волн обычно невелика,
так что /г<1. Для иллюстрации
на рис. 10.6 изображены графики,
Рис. 10.6. Волновые сопротивления
четной и нечетной волн в системе
двух связанных несимметричных
полосковых линий
Рис. 10.5. Частотный раздели-
тель на связанных линиях
по которым можно найти ZB4T и ZBn4 для некоторого конкретного
варианта микрополосковой линии.
В заключение отметим, что вопросы взаимной связи линий пе-
редачи, особенно микрополосковых, играют большую роль при по-
исках наилучших конструкций печатных плат, на которых распо-
лагаются логические интегральные схемы, работающие с высокими
тактовыми частотами. Изучение этих вопросов важно для создания
сверхбыстродействующих вычислительных машин и устройств дис-
кретной обработки сигналов.
Задачи и упражнения к гл. X
10.1. Каждая из двух связанных линий передачи имеет погонную емкость
С! = 50 пФ/м; фазовая скорость при отсутствии связи равна 1.2-108 м/с. Вели-
чина взаимной связи характеризуется следующими параметрами: С1с»=3 пФ/м,
£,св = 0 05 мкГн/м. Определить численные значения фазовых скоростей обеих
нормальных волн. ,
Ответ: Цфчт = 1,14-108 м/с, Офнч= 1,26-10 м/с.
10.2. По данным предыдущей задачи определить длину волны пространст-
венных биений при частоте сигнала 4500 МГц.
?0™ Най™7волиовые сопротивления четной и нечетной волн :аве^и-
чину коэффициента связи двух линии рассмотренных в предыдущих задачах.
Ответ: ZB чт=165 Ом, ZBB4=169 Ом, Л=0,012.
ПРИЛОЖЕНИЯ
Свойства некоторых материалов, используемых в технике СВЧ
Таблица П.Ц
Параметры высокочастотных диэлектриков
Материал Относительная диэлект- рическая проницаемость Тангенс угла потерь на частоте 1000 МГц
Полиэтилен 2,25 2-10-4
Полистирол 2,56 2-10-4
Фторопласт 2,08 2,5*10 4
Плавленый кварц 3,85 3 • 10 5
Окись алюминия (поликор) 9,6 4-10-5
Плексиглас (полиметилакрилат) 3,4 2-Ю-з
Таблица П.1.2
Электропроводность металлов
Металл Удельная объемная проводимость, См/м Глубина проникновения тока на частоте 100Q МГц, м.км
Серебро 6,17-107 2,01
Медь 5,81-107 2,07
Золото 4,13-107 2,46
Цинк 1,69-107 3,85
Латунь 1,55-107 4,02
Олово 0,88-107 5,33
П риложение 11
Некоторые программы для ЭВМ
На современном этапе развития радиотехники чрезвычайно возросла роль
ЭВМ, эффективно выполняющих сложные и трудоемкие вычислительные опера-
ции. Здесь в качестве примеров приводятся две реальные подпрограммы на алго-
ритмическом языке ФОРТРАН, иллюстрирующие применение ЭВМ для расчета
характеристик радиотехнических цепей с распределенными параметрами. Все при-
водимые подпрограммы оформлены как программные единицы типа
SUBROUTINE; связь между ними и основным программным модулем осуществ-
ляется посредством формальных параметров, что обеспечивает максимальную
универсальность использования.
1. Программа вычисления входного сопротивления
нагруженного отрезка линии передачи
Данная подпрограмма с именем ZINPT вычисляет нормированное входное
сопротивление по формуле
, Zh +
вх“ i+Xtg?/
Входными аргументами подпрограммы является комплексная переменная
ZL, равная нормированному сопротивлению нагрузки ZH', а также вещественная
146
переменная BL, с помощью которой описыв™тг«. .
Выходным параметром подпрограммы служит МектРич«*а* длина линии В/,
пне которой равно результату расчета ' В nL™ плексная переменная Z, значе-
расчета по приближенной формуле "«дпрограмме предусмотрен вариант
справедливой в окрестности точки гте т->||Гй.,. ~
пядка 10е или более. Тем самым ликвидируется ”сктР"чсскоЛ Длины линии по-
рядной сетки ЭВМ. Вызов данной подпрограммыvX«t« Псрспол,,е"и” Р«3'
программного модуля с помощью оператор.? осуществляется из основного
CALL ZINPT(A, В, С),
где А, В, С — имена фактических переменных.
Текст программы
SUBROUTINE ZINPT (ZL BL Z)
COMPLEX ZL, Z '
A = COS (BL)
IF (ABS(A). LE. IE —8) GO TO I
B = S1N (BL)
T = B/A
dptiZ|dmCMPLX {0- WO -HO., l.)*ZL*T)
Kt 1UKN
Z = I./ZL
RETURN
END
2. Программа вычисления волнового сопротивле-
ния несимметричной полосковой линии
Приведенная здесь программа с именем WSTRP осуществляет расчет
волнового сопротивления указанной линии передачи по формулам (2.14) или
(2.15) в зависимости от величины отношения b/h. Содержательный смысл приме-
ненных идентификаторов следующий : В — ширина полоски, Н—толщина ди-
электрической подложки, Е — относительная диэлектрическая проницаемость,
W — найденное значение волнового сопротивления.
Текст программы
SUBROUTINE WSTRP (Е, Н, В, W)
А=В/Н
IF (А—1.) 1, 1, 2
1 W = 84.85* (ALOG (8./А) + А* А/32.-0.5*
♦ (Е— 1.) / (Е +1.) ♦ (0.452 + 0.242/Е)) /SQRT (Е +1.)
GOTO3
2 W=188.5/(SQRT(E)*(0.5*A+0.441 +
♦0.082* (Е—1.) / (Е*Е) + (Е +1.) / (6.2832*
*Е) * (1.451 + ALOG (0.5*А+0.94))))
3 RETURN
END
3. Программа расчета частотной характеристики сту-
пенчатого перехода.
Здесь в качестве примера, иллюстрирующего практическое использование
двух приведенных программ, дана более сложная программа, которая реа-
лизует численный анализ частотной характеристики ступенчатого согласующего
перехода, выполненного на базе микрополосковых линий передачи. Чертеж кон-
струкции верхнего полоска изображен на рис. П.1. Предполагается, что со сто-
роны выхода устройство идеально согласовано. Ставится задача расчета частот-
147
с
с ЦИКЛ ПО ЧАСТОТЕ ОКОНЧЕН
С
10 11 FORMAT (I3/(3E15.3)) FORMAT (52Х, 24НЧАСТОТНАЯ ХАРАКТЕРИСТИКА *///8Х, 7НЧАСТОТА, 9Х, 6НМОДУЛБ, 1IX, 4НФАЗА, 12Х, ЗНКСй
12 FORMAT (4Е15.3) b/) RETURN END
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1 Баскаков С. И. Основы электродинамики. М., 1973.
2. Г а н с т о н М. А. Р. Справочник по волновым сопротивлениям фидерных
линий СВЧ/Пер. с англ. М„ 1976. »,/пОг> n аигп м
3 Гиллеи ин Е. А. Синтез пассивных цепеи/Пер. с англ. М„ 1970.
4. Мандельштам Л. И. Лекции по теории колебании. М 1972.
5. С м и р н о в В. И. Курс высшей математики. Т З, ч. 2, М., 1970.
6. Стариков В. Д. Методы измерения на СВЧ с применением измери-
тельных J«hhh.M, ! 972. в Курс дифференциалЬных уравнений. М„ 1953.
8. Шим они К. Теоретическая электротехника/Пер. с нем. М 1964.
9 Хью л см ан Л. П. Активные фильтры/Пер. с англ. М., 1972.
ОГЛАВЛЕНИЕ
Предисловие .............................................
Введение..................•_........................
Глава I. Теория регулярной линии передачи при гармоническом’
воздействии ..................................
!.1. Вывод уравнения состояния регулярной линии передачи ‘
1.2. Общее решение уравнения Гельмгольца для бесконечно
протяженной регулярной линии передачи. Монохроматиче-
ские бегущие волны........................
внешнем
§
§
3
4
9
9
§ 1.3. Понятие волнового сопротивления линии передачи ....
§ 1.4. Вторичные параметры линий передачи различных типов .
§ 1.5. Мощность, переносимая бегущими волнами вдоль линии
передачи ................................................
§ 1.6. Цепочечный эквивалент регулярной линии передачи . . . .
Задачи и упражнения к гл. 1.........................
Глава II. Некоторые типы линий передачи.............................
§ 2.1. Требования, предъявляемые к радиотехническим линиям
11
15
17
22
24
26
27
передачи...........................................27
§ 2.2. Коаксиальная линия передачи ...................... 28
§ 2.3. Симметричная двухпроводная линия передачи......... 30
§ 2.4. Полосковые линии передачи.........................31
Задачи и упражнения к гл. II........................33
Глава III. Явления в линиях передачи, нагруженных на одном конце . 35
§ 3.1. Коэффициент отражения..............................35
§ 3.2. Интерференция падающей и отраженной волн в нагружен-
ной линии передачи........................................38
§ 3.3. Распределение фазы колебаний в стоячей волне......43
§ 3.4. Измерительная линия................................44
§ 3.5. Стоячие волны в линиях передачи с потерями.........44
Задачи и упражнения к гл. III......................45
Глава IV. Трансформирующие свойства отрезков линии передачи ... 47
§ 4.1. Отрезок линии передачи как распределенный четырехпо-
люсник ...................................................47
Глава
Глава
§ 4.2. Входное сопротивление нагруженного отрезка линии пере-
дачи .....................................................
§ 4.3. Полуволновые и четвертьволновые трансформаторы ....
§ 4.4. Отрезок линии передачи как трансформатор уровня напря-
жения ....................................................
§ 4.5. Понятие о волновых матрицах и матрицах рассеяния . .
Задачи и упражнения к гл. IV..............................
V. Круговая диаграмма полных сопротивлений.................
§ 5.1. Понятие текущего коэффициента отражения............
§ 5.2. Построение круговой диаграммы......................
§ 5.3. Примеры использования круговой диаграммы...........
Задачи и упражнения к гл. V..........................
VI. Возбуждение регулярных линий передачи внешними источни-
ками ......................................................
§ 6.1. Физическая постановка задачи о возбуждении линии пе-
редачи .............................................. . . .
§ 6.2. Дифференциальные уравнения линии, возбуждаемой внеш-
ними источниками ..........................................
§ 6.3. Решение неоднородных уравнений Гельмгольца. Понятие
функции Грина для стационарного волнового процесса в
линии передачи ............................................
§ 6.4. Строгий вывод выражения для функции Грина...........
49
52
54
55
57
59
59
61
65
67
69
69
71
72
75
151