A. А. Соколов, И. М. Тернов,
B. Ч. Жуковский, А. В. Борисов
КАЛИБРОВОЧНЫЕ
ПОЛЯ
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебного пособия для студентов физических
специальностей вузов
«ада
Г)
8
12
14
19
23
32
41
41
44
49
52
52
53
54
56
57
57
59
60
64
64
67
69
69
71
74
74
80
83
89
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО
УНИВЕРСИТЕТА
1986
101
101
101
104
105
107
ПО
111
111
114
121

УДК пипки nuo.ia
КилиЛроночнмг поли / А. А. Соколоч. И. М. Тернов, В. Ч. Жу-
номгкнП и up M. 11.1ДШ) МГУ, 1986. 260 с.
Киши iKii'itMiiwiiii широкому кругу «опросов теории калибровоч-
IIi.i« нолей. I'mvMuTpciiH феноменология сильных и слабых взаимо-
дгПгщпп, клшч'ичсскпи теория калибровочных полей, явление спон-
1 и иного ini|iyiiii4iiiii симметрии, теория Вайнберга — Салама — Гле-
ншу, теории Н1):|мущспий для калибровочных полей, метод функцио-
ии.ш.иого иитегриропания в квантовой теории поля и функциональ-
И11И формулнронка квантовой хромодинамикн (КХД), метод раз-
размерном регулиризации, явление асимптотической свободы КХД,
и тикжс проблема коифайнмента кварков. Книга может служить
инедеиисм в современную калибровочную теорию взаимодействия.
элементарных частиц.
Рецензенты:
кафедра теоретической физики
Азербайджанского государственного университета,,
проф. Р. Н. Фаустов
м г у
1704020000—011
077 @2)—86
•132—86
Издательство Московского
университета, 1986 г.
ОГЛАВЛЕНИЕ
Предисловие . 6
Введение. Феноменология сильных и слабых взаимодействий , . . 8
а) Слабое взаимодействие лептонов . 8
б) Адроны 12
в) Кварковая модель строения адронов 14
г) Кварки с цветом и ароматом; цветовая симметрия ... 19
д) Партонная модель 23
е) Слабое взаимодействие адронов 32
Глава I. КЛАССИЧЕСКАЯ ТЕОРИЯ КАЛИБРОВОЧНЫХ ПОЛЕЙ . . 41
1 § 1.Поля Янга — Миллса * . 41
»§ 2. Тензор энергии-импульса поля Янга — Миллса * 44
§ 3. Монополь Днрака . . 49
§ 4. Модель Хиггса . . 52
а) Лагранжиан модели . 52
б) Соответствие Джулиа — Зи 53
. в) Группа симметрии решения * . 54
г) Унитарная (струнная) калибровка 56
§ 5. Самодуальный монополь Богомольного, Прасада, Соммерфильда 57
а) Монополь By и Янга . . 57
б) Определенне электромагннтного поля . . t . 59
• в) Самодуальное решение уравнений Янга — Миллса * .... 60
§ 6. Топологический заряд 64
а) Гомотопии 64
б) Пример решения, осуществляющего n-кратное отображение . . 67
§ 7. Монополь Тоофта — Полякова 69
а) Чистая модель Хнггса . . 69
б) Решение Полякова . 71
§ 8. Инстантон в квантовой механике 74
а) Мнимое время 74
»б) Двойная симметричная яма 80
в) Вычисление детерминанта 83
§ 9. Инстантоны Белавина, Полякова., Шварца и Тюпкина (БПШТ) . 89
а) Топологический заряд 89
б) Самодуальный ннстантон . . 98
Глава II. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ 101
§ 10. Теорема Голдстоуна 101
•а) Дискретная симметрия . . 101
«б) Непрерывная симметрия* 104
в) Модель пиона 105
§ 11. Механизм Хиггса 107
Глава 111. ТЕОРИЯ ВОЗМУЩЕНИИ И КАЛИБРОВОЧНЫЕ ПОЛЯ . ПО
§ 12. Иранила Фейнмаиа в квантовой хромодинамнке . . 111
а) Калибровочная инвариантность и пропагатор фотона . . 111
б) Калибровочная инвариантность и КХД . ... 114
§ 13. Функции Грина и правила Фейнмана ....... 121

Глава IV. ФУНКЦИОНАЛЬНЫЙ ИНТЕГРАЛ В КВАНТОВОЙ ТЕОРИИ
ПОЛЯ 123
§ 14. Функциональный метод квантования скалярного поля . . . 123
а) Функциональное интегрирование . . ... 123
б) Производящий функционал 124
в) Свободное скалярное поле . . . .... 125
г) Скалярное поле с самодействием 129
§ 15. Функциональный интеграл в теории ферми-полей . . . . 132
а) Грассмановы переменные . . 132
б) Грассмановы функционалы 135
в) Производящий функционал для ферми-полей 136
Глава V. МОДЕЛЬ ВАИНБЕРГА—САЛАМА—ГЛЕШОУ 138
§ 16. От модели Ферми к единой теории электрослабого взаимодейст-
взаимодействия . . 139*
а) л»ее-рассеяние в теории Ферми 139
б) Промежуточные заряженные векторные бозоны . 141
в) Промежуточный нейтральный векторный бозон .... 144
г) Общая структура электрослабого взаимодействия . . . 145
§ 17. Модель Вайнберга—Салама—Глешоу 152
а) Лагранжиан электрослабого взаимодействия лептонов . . 152
б) Спонтанное нарушение симметрии в теории ВСГ и возникнове-
возникновение масс частиц 154
в) Лагранжиан в терминах физических полей (унитарная калиб-
калибровка) . . . 157
г) Следствия из теории ВСГ . 159
д) Свойства W- и Z-бозонов . 161
е) Обобщение модели ВСГ на адроны 165
ж) Интерференция электромагнитного н слабого взаимодействий 168
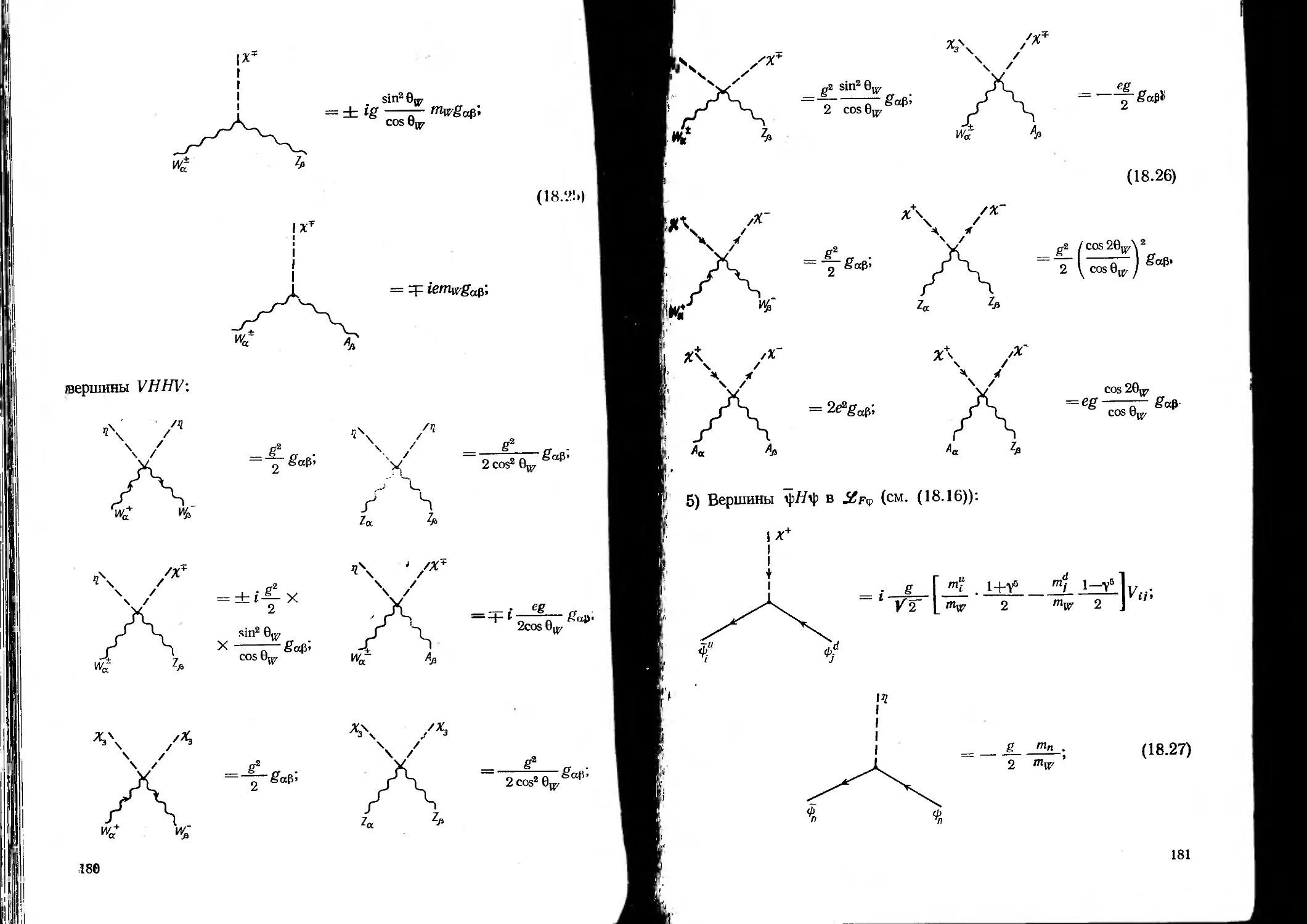
§ 18. Правила Фейнмана в теории Вайнберга—Салама—Глешоу . . 171
а) Лагранжиан теории ВСГ в Я-калибровке 171
б) Правила Фейнмана . 176
в) Примеры . . . , 185
Глава VI. ФУНКЦИОНАЛЬНАЯ ФОРМУЛИРОВКА КВАНТОВОЙ ХРО-
МОДИНАМИКИ 187
§ 19. Производящий функционал КХД 187
а) Трудности калибровочной теории . 187
б) Факторизация производящего функционала 189
в) Духн Фаддеева—Попова . . . , 193
§ 20. Перенормируемость калнбровочных теорий 195
а) Расходимости и перенормировки 195
б) Индекс расходимости КХД 200
в) Перенормируемость теории ВСГ 201
Глава VII. РАЗМЕРНАЯ РЕГУЛЯРИЗАЦИЯ . . 203
§ 21. Программа перенормировок в калибровочной теории . . . 203
§ 22. Глюонный пропагатор в однопетлевом приближении . . . 204
а) Поляризация фермнонного вакуума 205
б) Вклад глюонов и духов 211
Глава VIII. АСИМПТОТИЧЕСКАЯ СВОБОДА 214
j§ 23. Техника ренормгруппы ч 215
а) Уравнение ренормгруппы . 215
б) Уравнение Овсянникова—Каллана—Симанзика ... 218
§ 24. Уравнение Гелл-Манна—Лоу 219
а) Эффективный (инвариантный) заряд в КЭД 219
б) Исследование решений уравнений Гелл-Манна—Лоу . . 223.
994
* § 25. Решение уравнения ренормгруппы ??*
§ 26. Эффективная константа связи в КХД ff'
§ 27. Аномалия следа тензора энергии-импульса ^4
Глава IX. ПРОБЛЕМА КОНФАИНМЕНТА 238
* 94Q
§ 28. Нелинейные модели теории поля ??'
а) Кинки f?0
б) Модель струны . f™
в) Модели мешков Г*~
г) Инстантоны ~™
§ 29. Модели вакуума КХД f*T
а) Метод исследования г*т
б) Скаляры и спиноры во внешнем магнитном иоле .... м&
в) Вакуум Саввиди ¦*"
Литература ^6"

ПРЕДИСЛОВИЕ
В основу данного пособия положен специальный курс лекций,
который авторы в разное время читали на физическом факультете
МГУ для студентов, специализирующихся в области теоретиче-
теоретической физики.
Основой современной физики, как известно, является кванто-
квантовая механика, которая входит в программу обучения студентов-
физиков в качестве обязательного общего курса (см., например,
|[5—7]). Релятивистская квантовая теория изучается, как прави-
правило, в гораздо меньшем относительном объеме, чем нерелятивист-,
екая теория. Студентам-теоретикам читаются специальные курсы
лекций по квантовой теории поля, в которых как раз и рассмат-
рассматриваются вопросы релятивистского обобщения квантовой меха-
механики. Квантовой теории поля посвящен ряд учебных пособий и
монографий [1—4]. Основное внимание в этих книгах, за исклю-
исключением [4], уделено квантовой электродинамике, являющейся
хорошо разработанной, можно сказать, эталонной теорией, пред-
предсказания которой с высокой степенью точности подтверждаются
экспериментом. В то же время, как это признается большинством
физиков, основой современной теории элементарных частиц сле-
следует считать квантовую теорию калибровочных полей. Эта тео-
теория, частным случаем которой является электродинамика, по-
построена на основе требования локальной калибровочной инва-
инвариантности лагранжианов полей для всех основных типов взаимо-
взаимодействий: слабого, электромагнитного, сильного (а также грави-
гравитационного).
В настоящее время существует единая теоретическая модель,
описывающая на общей основе калибровочной инвариантности
слабые и электромагнитные взаимодействия (модель Вайнберга —
Салама — Глешоу), кроме того, разрабатывается идея включения
в объединенную схему также и сильных взаимодействий в на-
надежде создать так называемое «великое объединение» основных
взаимодействий элементарных частиц. Многие фундаментальные
представления модели Вайнберга — Салама — Глешоу были под-
подтверждены в экспериментах, из которых наиболее впечатляющим
было открытие в 1983 году W- и Z-бозонов — переносчиков сла-
слабого взаимодействия. Таким образом, теория калибровочных по-
полей является главным инструментом изучения взаимодействий
элементарных частиц при высоких энергиях.
В настоящей книге сделана попытка представить основы тео-
теории калибровочных полей в форме, доступной для приступающих
к изучению этого предмета. Помимо изложения главных теорети-
теоретических положений и выводов приводятся достаточно простые при-:
меры для их иллюстрации. Разумеется, мы не ставили себе
целью охватить сколько-нибудь полно все вопросы современной
теории элементарных частиц. Для более полного знакомства с
теорией калибровочных полей можно обратиться к монографиям
[8—11]. Исчерпывающее изложение общей теории перенормиро-
перенормировок, а также метода ренормгруппы и других принципиальных
вопросов квантовой теории поля можно найти в известной моно-
монографии [4]. Метод континуального интеграла в теории поля рас-
рассмотрен в [4, 8, 9, 15], причем в [9] — применительно к теории
калибровочных полей.
Настоящая книга может служить введением в предмет, по-
поставленный в ее заголовок, и поможет читателю самостоятельно
изучать современную оригинальную научную литературу.

ВВЕДЕНИЕ
ФЕНОМЕНОЛОГИЯ СИЛЬНЫХ
И СЛАБЫХ ВЗАИМОДЕЙСТВИИ
Современная теория взаимодействий элементарных час-
частиц основана на квантовой теории калибровочных полей. Прежде
чем приступить к ее изложению, рассмотрим феноменологическое
описание сильных и слабых взаимодействий, которое непосредст-
непосредственно опирается на экспериментальные факты.
Все элементарные частицы разделяются на три класса: леп-
тоны, адроны и частицы — переносчики взаимодействий лептонов
и адронов. Лептоны участвуют в слабых и электромагнитных
взаимодействиях, но не испытывают сильного взаимодействия. Ад-
Адроны, в отличие от лептонов, участвуют в сильных взаимодейст-
взаимодействиях, а также в слабых и электромагнитных. Все элементарные
частицы испытывают гравитационное взаимодействие (его влия-
влияние становится существенным на расстояниях ~ 10~33 см; эта об-
область в дальнейшем не рассматривается).
а) Слабое взаимодействие лептонов
К лептонам относятся электрон е (масса те = 0,511 МэВ),
мюон ц, (тй=106 МэВ), таон т (тау-лептон, mt=1782 МэВ) и
соответствующие им нейтрино: электронное \е, мюонное гй и таон-
ное vT. О массах нейтрино к настоящему времени известно следую-
следующее: 20 эВ <; mVe < 60 эВ (ограничение снизу получено недавно
группой ИТЭФ) т^ < 0,65 МэВ, т*х < 70 МэВ. Все лептоны
имеют спин 1/2 (в единицах ft), т. е. являются фермионами, и на
современном уровне эксперимента представляется точечными, т. е.
бесструктурными.
Заряженные лептоны испытывают электромагнитное взаимо-
взаимодействие, причем соответствующий лептонный электромагнитный
ток имеет вид
Й"°(х)= -~е(х)уае(х)-р{х)уср(х)-4(х)уах(х), @.1)
где уа— матрицы Дирака, 1(х) — биспинорная амплитуда леи-
тона: 1=е, [I, 1. Переносчиком электромагнитного взаимодействия
является безмассовый фотон (спин 1), описываемый 4-потенциа-
лом Аа(х). Гамильтониан электромагнитного взаимодействия
Нет @ =
* (х )А* {х),
@.2)
где е — заряд электрона.
Амплитуды процессов электромагнитного взаимодействия
определяются матричными элементами S/i = (/|S|i> матрицы
8
S = Т ехр ( - i ] dt Hem if) j = T exp (-ie J d*X]tm) (x) A« (x)). @.3)
Аппарат квантовой электродинамики подробно изложен во мно-
многих книгах (см., например, [1]).
Слабые взаимодействия лептонов при низких энергиях (типич-
(типичным примером является распад мюона: цг—^е^у^Уе) описываются
эффективным феноменологическим гамильтонианом типа «токХ
Хток» D-фермионное взаимодействие):
\ 4G
(X) /<->« (X) +
(X),
@.4)
где G= 1,02-10-5/mp2= B94 ГэВ)-2 — константа Ферми (mp =
= 938 МэВ — масса протона). Здесь введены слабые заряженные
где G 1,02 10/mp= B94 ГэВ) — конст
= 938 МэВ — масса протона). Здесь введены
и /<х(±)(я) и слабый нейтральный ток ja@)(x).
Заряженный ток /а(+) имеет следующую структуру:
j{+){)l{){^{)L () +{x)L
ц,(х)
х),
@.5)
где уъ = —
Чтобы выяснить физический смысл тока /а(+>,
рассмотрим, например, слагаемое ve(x)ya.Le(x). Это слагаемое
(имеется в виду оператор в представлении вторичного квантова-
квантования) описывает рождение нейтрино ve и позитрона е+, или уничто-
уничтожение антинейтрино \е и электрона е~, или рождение ve и уничто-
уничтожение ег, или уничтожение ve и рождение е+. Аналогичный смысл
имеют два других слагаемых в @.5). Таким образом, ток /а(+)
описывает процесс передачи заряда от заряженного лептона к
соответствующему нейтрино (например, e~->~ve), т. е. повышает
заряд на 1 (в единицах заряда электрона е). Ток /а(~) эрмитово
сопряжен току /а(+) (/а(~)==Уа(+)+) и описывает процесс уменьшения
заряда на 1. Именно поэтому токи /о(±> называются заряжен-
заряженными. '
Заметим, что присутствие в слабом токе @.5) матрицы
(l+Y5)/2 означает (V—А)-структуру слабого взаимодействия
(«вектор» va — «аксиальный вектор» W), причем A+^5)/2 яв-
является проекционным оператором, выделяющим из биспинора ф
его так называемую левую компоненту
4>ь= 1/2A +Y5H. @.6)
Эта компонента описывает состояние, в котором спин частицы
направлен против ее импульса (левополяризованная частица).
Точнее, выразив биспинор tf через трехмерные спиноры ц> и х
согласно

из уравнения Дирака
находим связь х и Ф (используем стандартное представление мат-
матриц ^^ [!])• Тогда гръ для ультрарелятивистской частицы с энер-
энергией г^т принимает вид
где спинор
—Фи
1 — па
— Ф
является, очевидно, собственной функцией оператора по (п=
=Р/|Р|):
()
Следовательно, с точностью ~т/е биспинор г|зх — собственная
функция оператора спиральности nS, отвечающая левой спираль-
ности:
. @.7)
Ясно, что правая компонента
фн=1/2A-?5I|> @.8)
соответствует правополяризованнои частице:
(п2)я|>н=чЫ-0(т/е).
В слабый заряженный ток /о(±) входят именно левые компоненты,
и можно представить @.5) в эквивалентном виде:
vlL{x)yJL(x),
@.5a)
l=e. fx,x
причем все три лептонные пары входят в слабый ток совершенна
симметрично (ец.т-универсальность).
Заметим, что, как нетрудно проверить, (V—Л)-структура за-
заряженного тока @.5) означает, что гамильтониан @.4) не инва-
инвариантен относительно пространственной инверсии Р и зарядового
сопряжения С: слабое взаимодействие нарушает Р- и С-инва-
риантность.
Рассмотрим теперь структуру нейтрального тока, который не
меняет заряд частиц, переводя их самих в себя (примером про-
процесса вызванного нейтральным током, является рассеяние мюон-
ного нейтрино на электроне: v^e~-»-v^e-). Прежде всего перепишем
заряженный ток в более удобном виде, введя слабые изоспиновые
дублеты лептонов
*-(:•)• *-(?)
10
и изоспиновые матрицы Паули
То =
1 0
0—1
Тогда ток @.5) и ему сопряженный принимают вид:
@.10)
@.11)
т. е. представляют собой (±)-компоненты изовектора:
'Y«i&. fl=l, 2, 3;
*
Выпишем компоненту ;У3>:
z ^ Y«^ = -~ [ve
@.12)
@.13)
откуда видно, что /а<3) — нейтральный ток.
Наблюдаемый слабый нейтральный ток лептонов /к@) состоит
из линейной комбинации тока @.13) /V3) и электромагнитного
тока @.1) /„(em):
где
@.14)
—1/2, gK=si
@.15)
Здесь Bw— угол Вайнберга (sin2^—0,23), характеризующий
вклад электромагнитного тока в нейтральный ток. Подчеркнем,
что, в отличие от заряженного тока, нейтральный ток содержит
как левые, так и правые компоненты (и это надежно подтверж-
подтверждается в эксперименте).
«Заряды» Нётер [1], отвечающие левым токам @.12), а имен-
именно:
x), @.16)
образуют алгебру Ля (см., например, [1]) слабого изоспина
И

SUB)W с соответствующими коммутационными соотношениями.
[/(+>, /(з)] =±/(±), [/(+),/(-)]= 2/Р». @.17)
Эти соотношения легко проверить прямым вычислением коммута-.
торов с учетом @.12), @.16) и перестановочных соотношений для
операторов ферми-полей
, x) =6(X—X').
Теория слабого взаимодействия, основанная на гамильтониане
@.4), удовлетворительно описывает слабые процессы при низких
энергиях в первом приближении теории возмущений. Однако эта
теория неперенормируема. Это вытекает из того, что константа
Ферми G имеет размерность [?]~2, где Е — энергия. Поэтому па-
параметром теории возмущений является безразмерная комбинация
GE2, и, следовательно, при достаточно больших энергиях теория
оказывается неприменимой. Естественно, по аналогии с электро-
электродинамикой, предположить, что слабое взаимодействие на самом
деле не является контактным (типа «токХток»), а осуществляет-
осуществляется за счет обмена массивными векторными частицами, среди ко-
которых должны быть заряженные и нейтральные. Такие требова-
требования необходимы, чтобы при низких энергиях возникало эффек-
эффективное контактное взаимодействие, обусловленное заряженными
и нейтральными токами и имеющее (V—Л)-структуру.
В гл. V будет рассмотрена единая теория электромагнитного
и слабого взаимодействий, в которой переносчиками слабого
взаимодействия являются заряженные №±-бозоны и нейтральный
Z-бозон. Указанные частицы обнаружены в экспериментах, про-
проведенных в 1983 г. в ЦЕРНе. Измеренные значения масс (mw~
си 81 ГэВ, mz<^ 93 ГэВ) хорошо согласуются с предсказаниями
теории (см. гл. V).
б) Адроны
Большинство элементарных частиц относится к адронам —
сильновзаимодействующим частицам. Адроны можно объединить
в мультиплеты, отвечающие представлениям изотопической груп-
группы SUB) (см., например, [1]). Частицы внутри данного мульти-
плета имеют приближенно одинаковые массы. Известны, напри-
например, дублеты нуклонов (протон р, нейтрон п), кси-барионов
(Е°, Е~), К-мезонов (К+, К0), триплеты л-мезонов (л+, я.0, л~),
2-барионов (Е+, ?°, 2~) и соответствующие^ мультиплеты анти-
античастиц: (р, п), (S°, S+), (К~, К0), B+,~2°, S-), синглеты Л-барио-
на^л-мезона.
/Частицы данного мультиплета имеют один и тот же изоспин /
и различаются значениями проекции изоспина /3=—/, — /+1,..., /
(на ось 3 изопространства), так что число частиц в изомультипле--
те равно 2/+У. Существование изомультиплетов — следствие изо-
изотопической инвариантности сильных взаимодействий. Это значит,
что S-матрица сильных взаимодействий — изоскаляр, т. е. S-мат-
ричные элементы имеют вид
12
@.18)
В сильном взаимодействии, таким образом, сохраняются кванто-
квантовые числа / и /3 системы адронов (сложение изоспинов частиц
проводится по известному правилу сложения обычных спинов).
В процессах взаимодействия частиц выполняются законы со-
сохранения определенных квантовых чисел, характеризующих час-
частицы. Законы сохранения дают правила отбора, разрешающие или
запрещающие те или иные реакции между частицами. На фено-
феноменологическом уровне описания взаимодействий формулировка
законов сохранения требует введения новых квантовых чисел
частиц, помимо известных общих характеристик всех частиц
•(масса т, время жизни т, спин /, электрический заряд Q, чет-
четность Р, зарядовая четность Рс). Примерами таких чисел для
адронов являются изоспин / и его проекция /3. Адронам необхо-
необходимо приписать также барионный заряд В, причем адроны с ВфО
называются барионами, а с В = 0 — мезонами. Для лептонов сле-
следует положить В = 0. Во всех взаимодействиях выполняется закон
сохранения барионного заряда. Этот закон объясняет, например,
наблюдаемую стабильность протона*: у протона В — + 1, и его
распад на более легкие частицы, у которых Б = 0, запрещен.
Для характеристики слабых распадов (т. е. за счет слабого
взаимодействия) некоторых адронов (странных адронов) вводит-
вводится еще одно квантовое число — гиперзаряд Y, причем S = Y—В
называется странностью (для странных частиц 5>фО). Частицы
одного изомультиплета имеют одинаковый гиперзаряд Y, а их
электрический заряд Q связан с У и проекцией изоспина /3 фор-
формулой Гелл-Манна — Нишиджимы:
Q = Is+llsY=h+4s{B + S). @.19)
Как видно, y = 2Q, Q — средний заряд частиц изомультиплета.
Анализ экспериментальных данных показывает, что адроны
могут быть объединены в более широкие мультиплеты, чем изо-
мультиплеты. Эти мультиплеты соответствуют представлениям
группы SUC), которая содержит изотопическую группу SUB) з
качесше подгруппы. Частицы одного мультиплета имеют одина-
одинаковые JP~J(спин / и внутреннюю четность Р), но различаются зна-
значениями электрического заряда Q и странности S.
Обычные мезоны ** образуют синглеты и октеты. Например,
псевдоскалярные мезоны группируются следующим образом:
* Теории великого объединения (объединение электромагнитных, слабых и
сильных взаимодействий; см., например, [11]) предсказывают нестабильность
протона (его время жизнн тР2?1031 лет), что означает нарушение закона сохра-
сохранения В.
** Имеются в виду адроны, открытые до 1974 г. (см. ниже).
13

JP= О~:цг (958)—синглет; Jp=0~: я+, я0, л-A40)
т) E49)
К+, К0, К0, К-D97I
—октет,
@.20>
в скобках указана масеа в МэВ.
Барионы образуют только октеты и декуплеты.
октет
Например,
+: p, n
A
2+ 2°, 2-
(940),
A115),
A192),
A315),
и декуплет, в котором первые 9 частиц являются резонансами
(быстро распадаются за счет сильного взаимодействия):
/p=3/2+: д1++) д1+) ДЛ д,
S*+, 2*°, S*-
A232),
A383),
A532),
A672).
@.22>
5?/C)-мультиплеты называются унитарными мультиплетами, а
соответствующая симметрия сильных взаимодействий — унитар-
унитарной симметрией. Унитарная симметрия является менее точной,,
чем изотопическая: массы частиц внутри одного мультиплета раз-
различаются довольно заметно.
в) Кварковая модель строения адронов
Мультиплетов более высокой размерности, чем 10, обычные
адроны не образуют. Это жесткое ограничение и закономерности
разбиения множества адронов на 5?/C)-мультиплеты привели
М. Гелл-Манна и независимо Г. Цвейга в 1964 г. к гипотезе о су-
существовании фундаментального триплета субчастиц — кварков
q={u, d, s), из которых составлены адроны. На основе этой гипо-
гипотезы была разработана кварковая модель строения адронов.
Кваркам и, d, s приписываются квантовые числа, указанные
в таблице (о квантовых числах С, Ь, t см. ниже):
t
и 2/3 1/2 1/2 1/2 1/3 1/3 0 0
d —1/3 1/2 1/2 —1/2 1/3 1/3 0 0
s —1/3 1/2 0 0 —2/3 1/3—1 0
0
0
0
0
0
0
@.23>
Кварки, таким образом, являются фермионами и имеют дробные
электрический, барионный заряды и гиперзаряд.
Согласно кварковои модели мезоны составлены из кварка q и
антикварка q'\
14
mes) = qqf,
а барионы из трех кварков:
Г |bar> =
Например, L~
qq'q"
n+=ud, n~=
@.24)
@.25)
—dd);
= uud; n=udd.
@.24a)
@.25a)
Кварки q=u, d, s образуют фундаментальное (размерности 3)
представление группы St/C), и кварковому составу адронов
@.24) и @.25) отвечают следующие разложения произведений
фундаментальных представлений на неприводимые представления:
3®3* = 1Ф8, @.246)
* = 1©8©8©10. @.256)
В результате получаем естественное объяснение закономерностей
объединения адронов в унитарные мультиплеты.
Дробность барионного заряда кварков (В = 1/3) следует из
@.25), причем для антикварков В=—1/3, так как для мезонов
<0.24) В = 0.
Дробность электрического заряда согласуется с формулой
Гелл-Манна — Нишиджимы @.19), обобщенной на кварки
Q=h+ll2{B + S),
с кварковым составом барионов, входящих в декуплет @.22):
Д++=«««, A+=uud, A°=udd;
A~ = ddd, Q~=sss. @.26)
Из @.26) следует QM = 2/3, Qd = Qs= —1/3. Заметим, что кварко-
вые составы соответственно Д+ и р, Д° и п совпадают. Поэтому с
точки зрения кварковои модели более тяжелые Д+ и Д° представ-
представляют собой возбуждения нуклонов р и п — связанных кварковых
систем uud и udd в основном состоянии.
Рис. 0.1
Существуют и экспериментальные проверки дробности зарядов
кварков. Рассмотрим одну из них. Согласно кварковои модели
лептонные распады векторных мезонов V°-+-l+l- представляют
собой аннигиляцию кварка и антикварка в виртуальный фотон,
который затем распадается на лептонную пару (см. рис. 0.1). Ве-
Вероятность такого распада w(V°-+-l+l-) пропорциональна квадрату
15

заряда кварка Qq и вероятности столкновения кварка q и анти-
антикварка q, которая в нерелятивистском приближении дается вели-
величиной 1^@) |2, где -ф(г) — волновая функция, отвечающая отно-
относительному движению qq-пары. Итак, для приведенной вероятнос-
вероятности распада w имеем
w{V°) =mvzw(V0-+l+h) =KQgz\^>@) |2, @.27)
где mv — масса мезона V°.
Сравним приведенные вероятности распадов легких векторных
мезонов р°G70), со0 G84) и <р°A019). Их кварковые составы
@.28)
<f>°=SS
определяют квадраты эффективных зарядов:
-[тг(т + (-т))]'-й-- ««-Г- @'29>
В первом приближении можно положить величину
одинаковой для всех трех мезонов. Тогда из @.27) и @.29) сле-
следует отношение вероятностей распадов:
w (р°) : w (со0) : w (ср°) =9:1:2, @.30)
что находится в неплохом согласии с экспериментально измерен-
измеренным отношением:
w((fi) : ш(ю°) : ш(«рР) = (8,7±2,9) : 1 : B,8±0,8), @.30а>
если учесть грубость приближений, сделанных при вычислении
@.30).
В 1974 г. был открыт мезон //я)) (т=3,10 ГэВ) при исследо-
исследовании реакции аннигиляции при е+е~ в адроны. Этот мезон был
интерпретирован как связанное -состояние нового, четвертого
кварка с и антикварка с: //а|)=Гсс.^варк с обладает новым кван-
квантовым числом С= -+1, названным «очарование» (charm), и элект-
электрическим зарядом Q= +2/3. Для «старых» кварков и, d, s «оча-
«очарование» С=0.
Согласно кварковой модели существуют различные уровни
энергии системы ее, названной чармонием (по аналогии с позит-
позитронием — связанной системой е+ег). Эти уровни на опыте долж-
должны проявляться как различные мезоны. Вскоре после открытия
/A|i=tl> C,10) были найдены мезоны ч|> C,68), i|> C,78), ф D.03),
•ф D,16), tf D.41), относящиеся к уровням (используются обычные
16
спектроскопические обозначения) 23Sb \3DU 33Sb 23Sb 4sSi соот-
соответственно, при этом ty C,10) — уровень 13Si. Открыты также уров-
уровни 13Pj (/ = 0, 1,2) —мезоны хо C,41), xi C.51), %2 C,55), располо-
расположенные между я]) C,10) и гр C,68). В 1979 г. был найден мезон
tjc B,98) — основное состояние парачармония (уровень l^So: спи-
спины с к с антипараллельны). Обнаружено и возбужденное состоя-
состояние парачармония — мезон цс C,59) (уровень 2*5о).
Все указанные мезоны \f и цс характеризуются скрытым оча-
очарованием (С=0). Обнаружены частицы с явным очарованием
(С=1): мезоны ?»° A,863) = ей, D+ A,868) = ей, F+ B,04) =cs, ба-
рион Л+с B,27) =cdu и другие. В сильных и электромагнитных,
взаимодействиях очарование С сохраняется. Поэтому D- и F-ме-
зоны распадаются за счет слабого взаимодействия.
В 1976 г. был открыт мезон Г (9,46), который рассматривает-
рассматривается как связанное состояние пятого кварка Ь и антикварка Ь:[Т=
= bb7f Кварк несет квантовое число «красота» (beauty) b= +1,.
для'кварков и, d, s, с полагают Ь = 0. Заряд Qb=—1/3. Мезон
Т (9,46) —низший уровень системы (ЬЬ). Были найдены и другие
Si-уровни: Y'A0,02), Г" A0,35), V" A0,57). Мезон Г" сильна
распадается на пары мезонов В+В- или °°, которые, в отличие
от мезонов Т, обладают явной «красотой» Ь=±1: Вг=Ьи, В+=
= Би, B°=bd. B°=5d.
Теория предсказывает также существование шестого кварка t
с зарядом Qt= +2/3. В настоящее время во многих лабораториях,
ведутся поиски топония — системы tt в реакции е+е--»-адроны.
Кварк t обладает квантовым числом t=\.
Квантовые числа кварков q = c, b, t указаны в следующей таб-
таблице:
\ q Q J I I3 Y В S С Ь t
с 2/3 1/2 0 0 —2/3 1/30100 @.31)
Ь —1/3 1/2 0 0 —2/3 1/3 0 0 1 0
t 2/3 1/2 0 0 —2/3 1/3 0 0 0 1
Формула Гелл-Манна —Нишиджимы @.19) обобщается следую-
следующим образом:
@.32)
@.32а)
где гиперзаряд Y определен в виде:
Y=B + S—С—Ъ
t
Заметим, что определение гиперзаряда @.32а) не является одно-
однозначным. Возможны и другие эквивалентные определения: напри-
например, Y=B+S + C—b + t, так что сохраняется прежняя связь
Q=h+Yl2.
Введение кварков с, b, t расширяет симметрию сильного
взаимодействия: возникают супермультиплеты, отвечающие уни-
унитарным группам SU(N), JV=4, 5, 6. 5U(N)-симметрии (JV>3) на-
нарушены сильнее, чем SU{3) (и тем более 5[/B)-симметрия).
17
ооькогв
МГУ

SU(N)-симметрия не только определяет классификацию адронов
ло различным мультиплетам, но и устанавливает ряд динамиче-
•ских соотношений между матричными элементами различных про-
процессов взаимодействия адронов. Эти соотношения приводят, на-
например, к определенной связи магнитных моментов частиц внут-
внутри данного мультиплета.
Кварковая модель позволяет описать спектр масс наблюдае-
наблюдаемых адронов, рассматривая их как связанные системы кварков.
Например, в нерелятивистском приближении спектр масс М ме-
мезонов (qq) определяется из решения уравнения Шредингера для
волновой функции i|>(x), описывающей относительное движение
кварка q и антикарка q:
], @.33)
где x=xQ—х, — относительная координата, тд — масса q и q,
р,=тд/2 — приведенная масса, V(x) — феноменологический по-
потенциал взаимодействия q и q (см. ниже).
Свободные кварки не наблюдались, несмотря на все предпри-
предпринимавшиеся до сих пор попытки их обнаружения. Более того,
имеются серьезные теоретические аргументы, основанные на
калибровочной теории сильных взаимодействий — квантовой хро-
модинамике (см. гл. VI), в пользу того, что кварки навечно за-
заключены внутри адронов (гипотеза конфайнмента (пленения)
кварков). Поэтому в уравнение @.33) входят некие эффективные
массы кварков, о величине которых можно косвенно судить по из-
известным массам адронов. Естественно считать, что чем тяжелее
адроны, тем тяжелее входящие в них кварки. Сравнение масс
адронов и их кваркового состава (см. выше) приводит к следую-
следующему выводу о соотношении масс кварков:
@.34)
Укажем примерные значения масс кварков, используемых з
^расчетах спектров масс адронов:
@.34а)
M^md—250^300 МэВ; т5^400-ь450 МэВ;
/Ис—1,5 ГэВ; ть—Ъ ГэВ; mt>20 ГэВ.
Феноменологический потенциал V(x) взаимодействия q и q
,в уравнении @.33), который учитывает явление конфайнмента
кварков, в первом (достаточно грубом) приближении можно
представить в виде:
= —a/r+Ar+V0,
@.35)
где г = | х |; a, A, Vo—положительные постоянные. В более точ-
точных моделях, описывающих адронный спектр масс, в потенциале
V(x) учитываются релятивистские поправки, спин-спиновое и
спин-орбитальное взаимодействия. Для легких кварков и, d, s
U
релятивистские поправки особенно важны, и поэтому спектр лег-
легких адронов гораздо лучше описывается в кварковой модели на
основе релятивистских уравнений для связанных состояний, на-
например, типа квазипотенциального уравнения А. А. Логунова и
А. Н. Тавхелидзе A963 г.).
г) Кварки с цветом и ароматом; цветовая симметрия
Детальный анализ кварковой структуры барионов показывает
необходимость введения дополнительной характеристики квар-
кварков—квантового числа, условно названного «цвет» (color). Рас-
Рассмотрим, например, барионный резонанс А++ из декуплета @.22).
В кварковой модели А++ — связанное состояние иии (см.
@.26)), характеризуемое спином 7=3/2, изоспином /=3/2 и угло-
угловым моментом L = 0. Этому состоянию системы из трех тождест-
тождественных фермионов отвечает симметричнаяг.волновая функция, что
противоречит принципу Паули. Поэтому, |^тобы сохранить спра-
справедливость принципа Паули для кварков, ц$рбходимо ввести но-
новую кварковую степень свободы — цвет,.)(Н. Н. Боголюбов,
Б. В. Струминский, А. Н. Тавхелидзе, 1965 г.; И. Намбу и
М.-Ю. Хан, 1965 г.). Чтобы полная трехкварковая волновая функ-
функция была антисимметришюй, |$ужно, чтобы кварке данного типа
(и, d,...) мог находиться/по крайней мереГв Tpexjразличных цве-
цветовых состояниях. Если'оы число цветов Nc было больше трех, то
имелись бы различимые цветовые состояния протона, что проти-
противоречит эксперименту. Следовательно, должно быть только три
цвета (Nc=3).
[Совокупность квантовых чисел (кроме цвета), отличающих
один тип кварка от другого (электрический заряд Q, изоспин /,
странность S, а также С, b, t) принято называть ароматом (flavor) Г"
В дальнейшем кварк с данными ароматом и цветом будем"''
обозначать через qu где q = u, d, s, с, b, t — аромат (тип) кварка;
i—R, G, В — цвет (условно: R — красный, G — зеленый, В —
синий; чаще удобно полагать просто t"=l, 2, 3).
Возвращаясь к примеру с А++, мы можем теперь составить
волновую функцию, симметричную по пространственным, спино-
спиновым и ароматическим переменным, но антисимметричную по
цвету:
| А++, J = 3/2 > = -pj= ? BiikuUjul
@.36)
/,/,*
где uj — волновая функция «-кварка цвета i с проекцией спина
Jz= +1/2; eijh — единичный антисимметричный тензор (ei23=
•= +1); i,j,k=R, G, В.
С групповой точки зрения данный кварковый аромат q обра-
образует триплет q—(qB, qc, <7в) — фундаментальное (размерности 3)
представление цветовой группы 5?/C), обозначаемой SUCC).
Запись же волновой функции |А++> в виде @.36) означает, что-
три кварка могут образовывать только синглет относительно пре-
преобразований из группы SUCC) (см. разложение @.256)), т. е..
19
/

функция @.36) — инвариант группы SUCC). Спектр барионов в
расширенной кварковой модели (с цветом) можно описать,
предположив, что все барионы — синглеты относительно SUC(S),
т. е. их волновые функции имеют вид (ср. @.25)):
f |bar>~
'jql j
@.37)
i,i,k
Аналогично потребуем, чтобы мезоны были также 5?/сC)-сингле-
тами (это возможно в силу разложения @.246)), т. е. (ср. @.24)):
@.38)
-^= J]
j
i=R,C.B
.Заметим, что функция @.37) представляет собой определитель
|bar>~det|<7m.| =
@.37а)
тде п=\, 2, 3 — номер кварка, i=R, G, В — его цвет. Поэтому
инвариантность определителя @.37а) — кубичной формы — яв-
является следствием унимодулярности преобразований U из груп-
группы SUC) (q^*-q' = Uq, det?/=l). Инвариантность же квадратич-
квадратичной формы @.38) — следствие унитарности преобразований
U(U+U=l, q^>~q' = qU+). Других инвариантов в группе SUC) нет.
Иначе говоря, мы постулируем, что наблюдаемые (физические)
.адроны являются «белыми» (бесцветными) связанными состоя-
состояниями кварков (постулат удержания (конфаинмента) цвета).
Существует ряд эксперимен-
экспериментальных подтверждений сущест-
существования цвета. Рассмотрим одно
из них, наиболее убедительное.
Полное сечение аннигиляции
электрон-позитронной пары в
р . адроны в рамках кварковой мо-
ис' ' дели определяется сечением ан-
аннигиляции е+е~ в кварк-анти-
кварковую пару qtqi, которое в низшем порядке теории возмуще-
возмущений (см. рис. 0.2) получается из сечения аннигиляции е+е- в мю-
юнную пару |х+^~ путем очевидной замены е4—>-е2• Qq2 (Qq — за-
заряд ^-кварка). Следовательно, отношение сечений равно (согласно
постулату конфаинмента рожденные кварки с вероятностью 1 пре-
превращаются в наблюдаемые адроны):
р _ а (е^е~ -
адроны)
ч, с
^T-Nc}jQl @.39)
Q
тде Nc — число цветов, а суммирование идет по тем кварковым
ароматам q=u, d, s,..., для которых E>2mq, E — энергия
20
•#+<г--пары в системе центра масс, mq — масса д-юварка. При
1,5 ГэВ<?<3 ГэВ вклад дают только кварки и, d, s (см.
@.34а)).. Следовательно, согласно @.39) при Nc=3 имеем:
•При 3 ГэВ<?<4 ГэВ надо учесть вклад с-кварка:
4
10
—
Таким образом, между порогами рождения qq-nap отношение R
постоянно, а при достижении очередного порога скачком возрас-
возрастает на величину 3QQ2. График экспериментально измеренного от-
отношения R3KCIi(E) представляет собой более сложную кривую
{см. рис. 0.3): на ступенчатое монотонное поведение накладывают-
ГУ.У
w
\\
it Щ \
10
15
20
25
30
Е, ГэВ
Рис. 0.3
<ся отдельные резонансные пики, отвечающие образованию свя-
связанных состояний qq (xf-мезонов, Y-мезонов и других; см. выше).
После вычитания резонансных вкладов /?эксп хорошо согласуется
с вычисленным R. К настоящему времени A984 г.) измерения
проведены до энергии ?—40 ГэВ, и во всем измеренном интерва-
интервале (включающем и порог образования ЬЪ при ?—10 ГэВ) на-
наблюдается хорошее согласие теории (с Nc = 3) и эксперимента.
Например, измеренное недавно значение ^эксп (Ю,49 ГэВ) =
= 3,77±0,30 находится в хорошем согласии с теоретическим зна-
значением /?5= П/3—3,66, учитывающем вклад пятого кварка Ь. То-
21

поний tt пока не обнаружен: порог его образования, очевидно,
лежит выше 40 ГзВ *.
Адроны, наблюдаемые в процессе аннигиляции е+е~—>-адроны,
возникают из кварка q и антикварка cj. Естественно предполо-
предположить, что адроны должны образовать две струи, оси которых сов-
совпадают с направлениями импульсов q и q. Такие адронные струи
действительно впервые наблюдались в 1975 г.
Цветовая симметрия SUCC) является точной в отличие от рас-
рассмотренных выше ароматических симметрии SU(Nf) (Nf=
= 2,3,4,...), т. е. сильные взаимодействия не зависят от аромата
кварков. Квантовополевая теория сильных взаимодействий —¦
квантовая хромодинамика (КХД) строится на основе локализации
St/CC)-симметрии (см. гл. VI) по аналогии с электродинамикой
[1], где локализуется абелева калибровочная группа U(l).
В этой теории кварки обладают цветовым зарядом и взаимодей-
взаимодействуют друг с другом посредством обмена безмассовыми калибро-
калибровочными векторными бозонами, называемыми глюонами. Всего
имеется 8 различных глюонов (число независимых параметров
группы SU(Nc) равно Nc2—1=8). Отсутствие кварков в свобод-
свободном состоянии и существование только «белых» адронов (удер-
(удержание цвета) должно в принципе объясняться в КХД особеннос-
особенностями кварк-глюонного взаимодействия. В частности, в феномено-
феноменологическом потенциале V(r) @.35) взаимодействия кварка и анти-
антикварка первый кулоноподобный член ~1/г отвечает одноглюон-
ному обмену (аналог однофотонного обмена в электродинамике),
а линейный член ~г, обеспечивающий конфайнмент кварков, в
принципе должен объясняться вкладом многоглюонных обменов
(вне рамок теории возмущений). Заметим, что в настоящее время
нет строгого доказательства в рамках КХД конфайнмента квар-
кварков в адронах, но имеется ряд аргументов в его пользу.
Вернемся к ароматическим симметриям SU(Nf) сильного
взаимодействия. Они являются, как уже отмечалось выше, при-
приближенными (нарушенными): нарушение SUB)-симметрии со-
составляет -1%, Sf/C)-симметрии—1(И-20%, a SUD)-, SUE)-
симметрии нарушены еще сильнее. Согласно современной точке
зрения** нарушение 5?/(Л^)-симметрии обусловлено различием
масс кварков (см. @.34)): чем больше это различие, тем сильнее
нарушение соответствующей SU(Nf) -симметрии. Сами же массы
кварков возникают в результате спонтанного нарушения симмет-
симметрии слабых взаимодействий (см. гл. II, V).
Итак, сильное взаимодействие определяется цветом (точнее,
цветовым зарядом) кварков (и глюонов; см. гл. VI), но не за-
* В 1984 г. появилось сообщение о наблюдении в протон-антипротонных
(рр) столкновениях событий, которые можно интерпретировать как обусловлен-
обусловленные распадом ^-кварка с массой 30 гэВ ^С.т/^. 60 ГэВ.
** В 60-е годы считалось, что нарушение SUB)-симметрии обусловлено элек-
электромагнитными взаимодействиями (например, различие масс протона и нейтро-
нейтрона), a St/C)-симметрии — разделением сильного взаимодействия на собствен-
собственно сильное и умеренно сильное.
22
1ИСИТ от аромата. В свою очередь, ароматические степени свобо-
свободы (Q, /, S,...) определяют электромагнитное (заряд Q) и сла-
слабое (изоспин /, странность S) взаимодействия, которые описы-
¦аются в теории Вайнберга — Салама — Глешоу (см. гл. V) как
«диное электрослабое взаимодействие (квантовая ароматодина-
мика). Переносчиками этого взаимодействия, как уже указыва-
указывалось, являются фотон, W±- и Z-бозоны.
д) Партонная модель
До сих пор мы рассматривали кварки как структурные блоки
адронов (конституенты), сильное взаимодействие которых при-
приводит к наблюдаемому спектру масс адронов (конституентная
тсварковая модель). Сложная структура адронов проявляется
также в электромагнитных и слабых взаимодействиях. Особенно
щенная информация об этой структуре была получена при иссле-
исследовании процессов глубоко,неупругого рассеяния лептонов / на
нуклоне N вида
l+N-^l'+X, @.40)
где Л' — конечный лептон, X — произвольное адронное состояние,
причем передача импульса от лептона нуклону очень велика (см.
@.52)). Этому процессу отвечает
«фейнмановская диаграмма, по-
показанная на рис. 0.4, где волни-
волнистая линия изображает вектор-
векторный бозон — переносчик элек-
электрослабого взаимодействия {у,
W± Z)
, Z).
Рассмотрим для определенно-
определенности рассеяние электрона на про-
протоне. Матричный элемент ер-рас-
ер-рассеяния имеет вид
\e,
Рис. 0.4
x—y) X
@.41)
п
Х(Х, Px\J*(y)\N,P),
где '^(х) и Jv(*/) — лептонный и адронный электромагнитные
токи, Ь^(х—у) — пропагатор фотона, k={E, к), k'=(E', к') —
начальный и конечный 4-импульсы электрона, Р=(Ро, Р) и Рх —
4-импульсы протона и адронного состояния X.
Подставляя в @.41) известные выражения для лептонного
тока (см. @.1)) и пропагатора фотона и используя соотношение
JB (х) = е'р*Лй @) е-*Р>, @.42)
где Р — оператор 4-импульса, получим
Af,,= ^-Bя)*6<4>(Р + <7—Рх) X
X [и (k') y*Hi (k)] (X, Рх |/ц@) \N, P>; @.43)
здесь u(k)—биспинор электрона, q = k—k'—4-импульс, передан-
переданный протону D-импульс виртуального фотона), причем <7г<0.
23

В дальнейшем мы ограничимся так называемым инклюзивным-
процессом рассеяния (А. А. Логунов, 1967 г.), когда исследуется
только конечное лептонное состояние, а по всем адронным состоя-
состояниям X проводится суммирование. Переход от матричного элемен-
элемента @.43) к сечению процесса совершается обычным образом [1].
В результате получаем инклюзивное сечение ер-рассеяния в лабо-
лабораторной системе (системе покоя протона: Р = 0) в виде:
dG =— —L^Wuv, @.44)-
dE'dQ mNq* E Ц
где a=ez/ftc, dQ — элемент телесного угла, в котором лежит
импульс к' конечного электрона, mN — масса нуклона (протона);
L^v — лептонный тензор, возникающий при усреднении и сумми-
суммировании по спиновым состояниям соответственно начального к
конечного электронов: *
Inv = >/2tr [^ (ykr+me) yv (yk+me) ] -
= 2[gw(me^kk')+k»k'v+k'»ky]; @.45)
W^—адронный тензор, описывающий динамику сильных взаимо-
взаимодействий:
VFuv= —
@.46)>
х(Х, Px\Jv@)\N, P).
Заметим, что W^ с учетом @.42) можно представить в виде
Wm = — Г #гё* {N, Р | [J+ (z), Jv @)] |TV, Р). @.46а>
4я J
Явный вид адронного тензора W^ неизвестен, но из соображений ло-
ренцевой и калибровочной инвариантности (q^W^^O, <jrV№1№=0),ero-
можно выразить через три лоренцинвариантных формфактора Wlr
W2 и W3 (при условии, что нуклон неполяризован):
= tnN i —
m
N
V*. @.47)
"'N
Последнее слагаемое в @.47) описывает эффекты несохранения
пространственной четности, и в рассматриваемом случае ер-рас-
ер-рассеяния равен нулю, Ws=0, в силу Р-инвариантности электромаг-
электромагнитного взаимодействия. Формфакторы
Wt=Wt(v,tf) @.48)
24
¦являются функциями инвариантных переменных
v = PqlmN = E—E', </2= (/г—А;'J- — 4??'sin26/2), @.49)
где в= (к, к') — угол рассеяния электрона в лабораторной системе,
апричем электрон ультрарелятивистский: Е, Е'^>те, что использо-
использовано при выводе последнего соотношения @.49).
Подставляя @.45), @.47) в @.44) с учетом @.49) и W3=0,
.получим инклюзивное сечение ер-рассеяния (измеряется только
.угол рассеяния в электрона и потеря энергии \=Е—Е') в виде
4зха2 Е' I Пю! „.-„2 е l хм ^rv«2_§_\ @.50)
dvd2 <74
Аналогично можно вычислить
рассеяния. В случае процесса
•^teWiBbP-j+WtCDSi-y
сечение
нейтрин-нуклонного
+) +X
@.51)
где mw — масса V^-бозона, G — константа Ферми, а наличие
формфактора Ws (см. @.47)) отражает нарушение Р-четности в
слабом взаимодействии.
Особый интерес представляет так называемая глубоко неупру-
неупругая область
i<72i=— ?2>т2№ v = P<7/mJV>mN. @.52)
.Экспериментальное изучение сечений глубоко неупругих процес-
процессов показало, что в области @.52) формфакторы Wi (иначе на-
называемые структурными функциями) зависят лишь от одной без-
безразмерной переменной
x=—qzl2mNv,
@.53)
т. е. имеет место так называемый бьёркеновский скейлинг, или
масштабная инвариантность (Бьёркен, 1969 г.; строгое доказа-
доказательство было дано Н. Н. Боголюбовым, В. С. Владимировым,
А. Н. Тавхелидзе в 1972 г.):
mNWt(v,
(i=2, 3)
@.54)
при v-»-oo, —g2-*-00. x=const. Заметим, что переменная х связа-
связана с инвариантной массой тх адронной системы X (см. рис. 0.4)
•соотношением
l/*-l), @.55)
25
так что х=1 отвечает упругому //V-рассеянию (mx=mN).

Наличие скейлинга означает, что размерные параметры по*
рядка массы mN (или длины ~l/mN) не играют существенной ди-
динамической роли в процессе глубоко неупругого рассеяния, т. е.
рассеяние лептона на нуклоне можно свести к рассеянию на без-
безмассовых точечных частицах. Эта идея, впервые высказанная
мой партонной модели (Р. Фейнман, 1969 г.) для объяснения
М. А. Марковым A964 г.), была положена в основу так называе-
(Р.
скейлинга [12].
Опишем вкратце эту модель. Предположим, что нуклон со-
состоит из связанной системы точечных частиц. Он может перейти
в виртуальное состояние, в котором эти частицы свободны. В сис-
системе отсчета, в которой импульс нуклона Р-»-оо («система беско-
бесконечного импульса»), время жизни тР этого виртуального состоя-
состояния порядка (Е—X~\Ei\~l > гДе Е — энергия нуклона, Et — энер-
энергия i-й частицы, и вследствие известного релятивистского эффек-
эффекта хр становится очень большим. В этой системе отсчета вир-
виртуальный фотон с 4-импульсом q взаимодействует с системой
(почти) свободных точечных частиц — партонов. Характерное
время взаимодействия тт фотона с одним из партонов имеет поря-
порядок 1/<7о (<7о — энергия фотона). Можно показать, что при усло-
условиях @.52) тт«Стр, т. е. в процессе фотон-партонного взаимодей-
взаимодействия партон действительно можно считать свободным.
В рамках партонной модели Ш-рассеяние представляет собой
некогерентное упругое рассеяние лептона на партонах, которые
после рассеяния уже за счет сильного взаимодействия превра-
превращаются в конечные адроны X (см.
рис. 0.5). Этот процесс, связанный
с механизмом удержания цвета, на-
называется адронной фрагментацией
партонов, и на современном этапе
развития теории сильных взаимо-
взаимодействий, он не вполне ясен.
Установим связь структурных
функций W'i нуклона (см. @.50))
с партонной структурой нуклона»
которую будем описывать набо-
набором функций распределения qt(x),
имеющих следующий смысл: qi(x)dx есть число партонов данного
типа qit несущих долю х полного 4-импульса нуклона Р^ в интер-
интервале от х до x+dx, т. е. импульс партона равен ру~хР^.
В соответствии с экспериментальными данными в глубоко неуп-
неупругой области @.52) можно пренебречь поперечными импульсами
ргх партонов (рг-х_1_Р) и считать, что все xt заключены в интер-
интервале 0<?х<1.
Покажем [12], что вкладом партонов с хг<0 действительно
можно пренебречь. Амплитуда вероятности А того, что система
с энергией Е распадается на две части (для простоты рассматри-
26
«аем этот случай) с энергиями Е\ и Е2 в рамках (нековариант-
ЗНой) теории возмущений имеет вид
А = С\Е—Е1—Е2]-\
.ПОЛНЫЙ ИМПуЛЬС СИСТеМЫ Р = р1ц + р2ц. p|, ;
+Х2=1. Тогда энергия Е системы с массой М в области высоких
энергий (|iP|^>Al)
Е = VPZ + М2 ~Р + М*/2Р, Р=|Р|.
Аналогично для частей с массами Мг и М2 и энергиями Ег и Е2
Е ?=1Л>2 + М [VP2 + P
•Следовательно, указанная амплитуда
Отсюда видно, что амплитуда при Xi,2>0 больше амплитуды при
*i<0, x2>0 (x2=l+ |xi|>l) в отношении (Р/МJ^>\, т. е. вклад
¦состояний, содержащих партоны, движущиеся назад, пренебре-
пренебрежимо мал.
В силу определения имеем очевидное условие нормировки
j dxxqt (x)=l.
@.56)
i 0
Естественно предположить, что партоны — это кварки и анти-
антикварки (кварк-партонная модель), т. е. qt означает кварковый
аромат: qi = u, п, d, d
Некогерентность лептон-партонного рассеяния означает, что
каждый партон д?- дает независимый вклад в сечение лептон-нук-
лонного рассеяния, т. е.
1
da
dxiQi
@-57)
i 0
где множители BРо)~' и Bpi0)~1 возникают из нормировочных
множителей в волновых функциях нуклона и партона соответст-
соответственно. Здесь через W^0 обозначен вклад партона q\ в адронный
тензор W^ @.47):
Pi
pi' — импульс партона qt в конечном состоянии.
27

Рассмотрим для определенности случай ер-рассеяния. В кварк-
партонной модели электромагнитный адронный ток Лй имеет вид.
(ср. @.1)):
^ (z) = I <?,*,, (z) УцФ,, (z), @.59)
i
где Qj — заряд кварка-партона <?г (в единицах е). Подставив
@.59) при z=0 в @.58), после усреднения и суммирования соот-
соответственно по начальному и конечному спиновым состояниям пар-
тона согласно @.45) получим:
'а) 2кб (Р;
+ q—p't) -L Tr [yu
+
@.60)
Сравнивая @.60) и @.47) с учетом равенства pi=xiP, получим
вклад партона qi в структурные функции нуклона Wt и W2:
W\n =
о?
2т
lN
xl> (xt - х), Wf = 2m
N
@.61)
здесь х — введенная выше (см. @.53)) скейлинговая переменная,
которая в силу закона сохранения импульса, выражаемого 6-функ-
цией 6(xt—х), оказывается совпадающей с партонной долей им-
импульса нуклона.
Подставляя @.61) в @.57) и учитывая @.54), получаем струк-
структурные функции в виде:
@.62)
=f2 (%)=*? <$/,. (х),
т. е. Ft и F2 связаны соотношением
F2(x) = 2xFl(x). @.63)
Итак, в рамках партонной модели скейлинг получает наглядное
физическое объяснение.
Заметим, что соотношение @.63), называемое соотношением
Каллана — Гросса, является прямым следствием того, что квар-
ки-партоны имеют спин 1/2: легко проверить прямым расчетом
(аналогичным @.60)), что для кварков со спином 0 функция
Fi=0, a F2 остается прежней.
Имеются и прямые экспериментальные подтверждения того,
что кварки-партоны имеют спин 1/2. Так, измерялась азимуталь-
28
ная асимметрия в сечении аннигиляции «е+е~->адроны», обуслов-
обусловленная поляризацией пучков электронов и позитронов. Результа-
Результаты измерений, позволившие определить структурные функции Ft
и F2 по отдельности, однозначно свидетельствуют в пользу квар-
кварков со спином 1/2. Таким образом, эксперименты с поляризован-
поляризованными пучками е+ и е~ делают процесс «е+е--^адроны» гораздо-
информативнее (по сравнению с неполяризованными пучками).
Заметим, что поляризация пучков возникает вследствие эффекта
радиационной поляризации электронов и позитронов, движущихся
в магнитном поле накопителей. Этот эффект был предсказан
А. А. Соколовым и И. М. Терновым в 1963 г. и затем был блес-
блестяще подтвержден экспериментально (более подробно об этом
эффекте и его применениях см. [1, 2]).
Из @.62) вытекает, что структурные функции Fk(x) описы-
описывают распределение по импульсам qt(x) кварков различных,
ароматов, взвешенное с квадратом зарядов кварков.
Рассмотрим качественно структуру нуклона, используя экспе-
экспериментальные данные о поведении Fh(x):
Ft(x)~l/x, F2(x)-^-const при х-+0. @.64)s
Среднее число партонов типа
dx
х
@.65)
оказывается в силу @.64) бесконечным. Однако это утверждение
не вполне точно: в партонной модели пренебрегается массой квар-
кварков тд, что соответствует, как показывает детальный анализ, вы-
выполнению условия
x»m2/m2x, @.66)
где тх — инвариантная масса адронов системы X (см. @.55)).
С логарифмической точностью число партонов (п9) получим, если
в интеграле @.65) в качестве нижнего предела xmin возьмем гра-
границу неравенства @.66):
Г dx
Лп
-in
@.67)
*rmn
Таким образом, партонная структура нуклона, проявляющаяся в
глубоко неупругом лептон-нуклонном рассеянии, не совпадает с
той простой трехкварковой структурой, которая использовалась,
выше при анализе адронного спектра масс (конституентная квар-
ковая модель). Это кажущееся противоречие можно разрешить
следующим образом. Виртуальный фотон высокой энергии зонди-
зондирует «тонкую» структуру нуклона, который помимо трех «голых»-
кварков, несущих квантовые числа нуклона (эти кварки назы-
иают валентными), содержит в своем составе «море» кварк-анти-
кпарковых пар. Кварки же, используемые в конституентной квар-

жовой модели, можно рассматривать как сложные образования
(кластеры), состоящие из «голого» кварка, окруженного «шубой»
различных qq-nap. Поэтому и массы конституентных кварков,
указанные в @.34а), отнюдь не совпадают с массами кварков-
партонов, а точнее, больше последних.
В полевой теории — квантовой хромодинамике масса кварка
тд, входящего в ток @.59) (токового кварка), оказывается зави-
зависящей от импульса, передаваемого кварку, и уменьшается с его
¦ростом. Например, при передаче импульса 1 ГэВ согласно
•экспериментальным данным массы токовых кварков равны:
ти A ГэВ) =4,5+1,4 МэВ,
md A ГэВ) =7,9+2,4 МэВ,
ms A ГэВ) = 155+50 МэВ,
тс A ГэВ) = 1,35+0,05 ГэВ,
ть A ГэВ) =5,3+0,1 ГэВ.
@.68)
Вернемся к структурным функциям нуклона @.62). Для про-
протона p = uud и нейтрона n = udd (указано, какие валентные кварка
•они содержат) получаем функции FzeN в виде {N — p, n):
~-х{и
и) + ±
+-Lx(s+'s)
fen т~<ер /
2 =F2p(u
@.69)
где многоточие означает вклад тяжелых кварков, а индекс ер (еп)
указывает, что F2 относится к электрон-протонному (нейтронно-
(нейтронному) рассеянию. Наибольшую часть импульса нуклона несут ва-
.лентные кварки (им отвечают большие средние значения (х)),
«морским» кваркам соответствуют малые (х). Влияние кварково-
го моря существенно при х-*-0 (см. @.64)). Как показывает ана-
анализ экспериментальных данных, партонные распределения в нук-
нуклоне можно представить в виде
i7—Я—s = g, @.70)
где qv — вклад валентных кварков (q=u, d), ? — вклад «морских»
кварков, причем в силу изоспиновой и зарядовой симметрии силь-
сильных взаимодействий эти распределения для протона и нейтрона
связаны соотношениями:
При А'-vO вклад моря в @.70) преобладает:
xuv~^x, xdv~^x, x|->-const при
30
@.71)
@.70a)
Из @.69)—@.71) вытекает следующее так называемое правило*
сумм:
1 i
^L(ff_ff)=-LJdx(«B_do) = J.B_l) = ^-. @.72>
о о
где в предпоследнем равенстве использованы очевидные условия
нормировки валентных распределений протона, содержащего два
ы^-кварка и один с^-кварк.
Сохранение заряда, изоспина, барионного заряда и странности
дает такие правила сумм:
1 ] _ 1 _
[dx(u —ы) = 2, [dx{d—d)=l, f (s—s)dx=0,
oJ о о
@.73)
где первые два правила фактически уже использованы в @.72).
Рассматривая различные процессы нейтрин-нуклонного рас-
рассеяния (vp, xp, xn, vn), из совокупности экспериментальных дан-
данных можно получить (с помощью соответствующих правил сумм
для функций FkVN, FhVN) распределения по импульсам всех квар-
кварков и антикварков по отдельности, так как в процессе слабого
взаимодействия (см. ниже) изменяется кварковый аромат. На-
Например,
v~li+u-+ijL++d, @.74)
что отвечает глубоко неупругим процессам у^)р-рассеяния:
@.74а>.
Доля импульса нуклона, который несут все кварки и анти-
антикварки, выражается через функции распределения qi(x) следую-
следующим образом:
dxx [qt (x) +~qt (x)\ = 1 - е,
@.75)
причем е=0, если кварки и антикварки — единственные состав-
составляющие нуклона. Эксперимент, однако, дает е—0,5. Следователь-
Следовательно, примерно 50% импульса нуклона несут какие-то нейтральные
составляющие, отличные от кварков. В рамках квантовой хромо-
динамики эти нейтральные партоны естественно отождествить с
глюонами — переносчиками сильного взаимодействия кварков
(соответственно глюоны входят в состав «шубы» конституентных
кварков).
Рассмотренная выше партонная модель была обобщена и на
процессы, отличные от глубоко неупругих. Важными примерами
таких процессов являются:
@.76)
31

первый из которых уже обсуждался выше (см. рис. 0.2) факти-
фактически в рамках кварк-партонной модели. Два других процесса на
языке партонной модели включают элементарный процесс анни-
аннигиляции qq-*-l+l~.
Простая партонная модель хорошо согласуется с эксперимен-
экспериментальными данными в области 0,15^x^0,25 (что отвечает передан-
переданным импульсам 2 ГэВ2*?<72^Ю0 ГэВ2), где действительно наблю-
наблюдается скейлинг. Вне этой области обнаруживается определенная
зависимость структурных функций Fi от q2:
Fi = Fi(x, q2), @.77)
а также нарушаются соотношения @.63) и простые правила сумм
типа @.72).
Поэтому требуется дальнейшее развитие теории. Такой тео-
теорией является квантовая хромодинамика (см. гл. VI), на основе
которой развит аппарат для вычисления нарушений скеилинга. Это
нарушение в КХД объясняется взаимодействием кварков-партонов
посредством обмена глюонами и излучением глюонов кварками.
Одним из убедительных доказательств существования глюонов яв-
является обнаружение в 1979 г. трехструйных событий в процессе
аннигиляции е+е~-^адроны (наряду с более вероятными двух-
¦струйными событиями (см. рис. 0.2). Такому событию отвечает
элементарный процесс e+e~-*-qqg, в котором кварк (или анти-
кварк) испускает глюон g под большим углом к своему импульсу
(см. рис. 0.6). Затем q, q и g образуют три адронные струи
(в процессе фрагментации). Возможно также образование трех
«глюонных» струй в процессе e+e~-*-T->-3g-->-3 струи, где Г — свя-
связанное состояние ЬБ (ипсилон-частица, см. выше), которое затем
аннигилирует в три глюона (это аналог трехфотонного распада
¦ортопозитрония в квантовой электродинамике).
е) Слабое взаимодействие адронов
Рассмотрим теперь более подробно феноменологию слабого
взаимодействия адронов (соответствующую полевую теорию см.
в гл. V). В кварковой модели адроны состоят из кварков, и в
слабом взаимодействии адронов один кварковый аромат перехо-
переходит в другой. Например, р-распад нейтрона n-^p-\-e~-\-ve. связан
с переходом одного из d-кварков в составе нейтрона в ы-кварк
(см. @.25а) и рис. 0.7). Распад странной частицы А-*-р-\-п~ обус-
обусловлен переходом s^>~u. Соответствующие диаграммы изображе-
изображены на рис. 0.8, причем на диаграмме (в) показано рождение пары
ип из вакуума, одна из компонент которой (ы-кварк) входит в
•состав протона, а другая (и) в л~-мезон. Аналогичные диаграм-
диаграммы соответствуют другому каналу распада: Л-*-п+зт°. Заметим,
что на рис. 0.7 и 0.8 волнистой линией обозначен №-бозон, пере-
переносящий слабое взаимодействие, а заштрихованные блоки изобра-
изображают сильное взаимодействие.
Слабый адронный ток строится из кварковых токов по анало-
аналогии с лептонным (см. выше). Левые компоненты кварковых
32
к
биспиноров (см. @.6)) объединяются в слабые изоспиновые дуб-
дублеты (ср. @.9))
l U
@.78)
относительно группы SU{2)L, а правые компоненты (см.^ @-8))^
являются изосинглетами. Нижние компоненты дублетов d', s', b
не совпадают с исходными кварками d, s, b (собственными состоя-
состояниями сильного взаимодействия), а представляются в виде их ли-
Рис. 0.6
Рис. 0.7
яейной комбинации. Матрица V преобразования (d, s, b)-+
->~(d', s', b') размерности 3X3 определяется четырьмя параметра-
параметрами, в качестве которых обычно выбирают три угла 6i, 62, 63 и
одну СР-неинвариантную фазу б (см. ниже @.91а)).
Общий вид слабого заряженного тока кварков таков:
/„<+>=2 O
@.79)
где а= (а1, а2, а3) = (ы, с, t) — «верхние» кварки, к= (и1, х2, и3) =
= (d, s, b) — «нижние» кварки. Следовательно, всего имеется
9 заряженных токов: ad, Us,..., tb.
Необходимость смешивания «нижних» кварков диктуется эк-
экспериментальными данными. Еслибы его не было (Vih=6ih), ток
@.79) имел бы вид J^-ud+cs+tb и кварки s и Ь стали бы ста-
стабильными (ms<mc<mb<mt), что противоречит эксперименту:
Калибровочные поля
33

странные частицы (например, Л-гиперон, рис. 0.8) и fc-адроны
(например, Т- и ?-мезоны (см. п. в) нестабильны.
В дальнейшем для простоты ограничимся слабыми процессами
с участием четырех кварков и, d, s, с. Тогда в комбинациях d' a
s' можно отбросить примесь fc-кварка и записать их в виде:
d' = d cos Qc+s sin 6C,
s'=s cos 6c—d sin 6c, @.80)
где параметр вс называется углом Кабиббо.
Заряженный ток @.79) в этом случае принимает вид (ср.
@.5)):
/й<+) = uy^d cos 6с + uy^s sin 6с +
+ cy/d(—sinGc) +c^Ls cos 6c, @.81>
разрешающий переходы и++й, s; c+-+d, s.
Слабые процессы с участием лептонов и адронов описываются
при низких энергиях эффективным гамильтонианом Hw типа @.4) г
в котором следует заменить лептонный ток ja на сумму лептон-
ного и адронного токов /а+/а-_В частности, как следует из @.5}
и @.81), р-распаду n—»-p+e+ve отвечает слагаемое в гамильто-
гамильтониане Жю (ср. рис. 0.7)
M,= DG/-\/2)cosQc[e(x)y/'Ve(x)][u(x)y^d(x)]+3. с, @.82)
а распаду А-^р + п~ — слагаемое (см. рис. 0.8)
3%s= DG/V2)sineccosec[d(x)Y/«(x)][u(x)YllI's(x)]+3.c. @.83)
Численное значение sin6c = 0,2l9±0,011 определяется тем, что-
вероятность распада странных частиц, вычисляемая из Ms @.83),
сильно подавлена (примерно в 20 раз) по сравнению с вероят-
вероятностью р-распада, вычисляемой из Ж?, @.82).
Форма @.81) слабого кваркового тока объясняет правила от-
отбора для распадов адронов, установленные экспериментально:
1) процессы без изменения очарования (АС—0) : AS = 0^
AQ| = 1, А/=0 (амплитуда процессов этого типа —cos 6с);
AS| = 1, AQ=AS, A/=l/2 (амплитуда -sin9С);
2) процессы с изменением очарования (| ДС| = 1) : AS = 0,
|AQ| = 1, А/=1/2 (амплитуда sin6c); AS=AQ = ±1, Д/=0
(амплитуда ~cos0c);
3) процессы с AS =—AQ и |AS|=2 запрещены.
Обратим внимание на важные свойства ud-тока в @.81). Как
мы видели выше (см. @.23)), кварки и и d образуют по отноше-
отношению к сильному взаимодействию изодублет
@.84)
Поэтому в амплитудах лептонных распадов адронов (типа
34
n-*-p+e+ve) возникает матричный элемент ud-тока вида (см.
@.82)):
c(f\uyS-d\i)e-**= V2cos6c<f | V..+A^i)*-*»*,
Уй=йуД @.85)
где \i) и \f) — начальное и конечное адронные состояния с 4-им-
пульсами pi и pf соответственно, q—pf—ри причем Уц — полярный
вектор, а А» — аксиальный.
Используя @.84), можно записать векторный ток Уй в виде,
аналогичном @.12):
V»(x)=q(x)y»T+q(x), @.86)
т. е. Уй является компонентой изовектора qy^xq. В силу изотопи-
изотопической инвариантности сильного взаимодействия ток VM должен
сохраняться:
д^(х)=0. @.87)
Это утверждение называется гипотезой сохраняющегося вектор-
векторного тока (CVC). Соотношение @.87) означает, что матричные
элементы тока Уй поперечны (см. @.85)):
0 = 0.
@.87а)
Заметим, что соотношение @.87) является приближенным в силу
приближенного характера 5(/B)-симметрии (ее нарушение, как
уже отмечалось, связано с различием масс кварков: ти<та).
Аксиальный же ток Ай не сохраняется. Например, в распаде
пиона Jt-vjiv изоспин изменяется на единицу, причем векторная
часть <0|У„|л;> = 0 (пион — псевдоскалярный мезон), а для ак-
аксиальной части имеем:
где <7и — 4-импульс пиона, /л(<72) — постоянная распада. Отсюда
находим дивергенцию:
где т„ — масса пиона. Однако пионы относительно легкие:
tnn2lmp2—2-10-'i. Поэтому в пределе безмассовых пионов аксиаль-
аксиальный ток также сохраняется (частично сохраняющийся аксиаль-
аксиальный ток (РСАС)).
Можно показать [11], что отличие тп от нуля обусловлено
спонтанным нарушением так называемой киральной симметрии
в квантовой хромодинамике (имеющей место в пределе безмас-
безмассовых кварков: тл2 =—fn(mu + md)@\uu+dd\0)).
Гипотезы CVC и РСАС приводят к ряду соотношений для мат-
матричных элементов слабых распадов адронов (см., например, [11]),
которые могут быть проверены экспериментально.
ч* 35

Ограничимся двумя характерными следствиями CVC и РСАС.
Рассмотрим распад пиона я+-»-лое+у. Его амплитуду можно запи-
записать в виде
Мн= (G/V2Jcosec[SvY«(l+Y5)wc]<Jt0|Vn@) |я+>,
где_Уа(х:) определен в ^0.85). Здесь учтено, что переход |я+=
= ud}—*-|jt°= A/2) (пи—dd)) сводится к кварковым переходам
u-*~d и й-^-п. Матричный элемент
г @.876)
где фя = [BяK2рл]"/2е~1Ря*— волновая функция я-мезона с
4-импульсом ря, р = ря+ + Рл°, q = pK+—prf>, /±(<72) — безразмер-
безразмерные формфакторы. В силу CVC @.87а) получаем
или
Но CVC означает строгую изотопическую инвариантность, т. е.
qp = тя+—тло = 0, и, следовательно,
М<72)=0.
В результате @.876) принимает вид:
if* (х) = Bл)-3 Bр°+• 2р?.)-'/2е-**/+ (</2) р°. @.87в>
я
CVC позволяет определить значение f+@). С этой целью проинте-
проинтегрируем компоненту v°(x) 4-вектора @.87в) по х:
С другой стороны, в силу @.86) и @.876) этот интеграл равен
где
( + )-компонента оператора изоспина (генератора группы Sf/B);
ср. @.16)). Поскольку п° и л+ входят в один изотриплет (я+, я0,.
п~) с изоспином 1=1, причем /з= + 1 (для л+), /з' = 0 (для л°), то-
матричный элемент
где использовано известное соотношение из теории углового мо-
момента в квантовой механике [5, 6].
Сравнение двух выражений для указанного интеграла дает
f+(O)=V27
Учитывая, что энерговыделение в распаде я+
@.87г)
мало, мож-
36
но положить f+(q2) — f+@) =}2 и представить амплитуду распада
в виде
Mfi = -?=
Используя это выражение, нетрудно получить ширину распада
{т-т*?= 0,45 с-». @.87д)
где пренебрежено слагаемыми порядка те/(тп+—т^J ~ 10~2.
Это предсказание находится в неплохом согласии с эксперимен-
экспериментальным значением
= @,39±0,03) с.
В качестве другого примера рассмотрим так называемое соотно-*
шение Голдбергера — Треймана, которое является следствием
РСАС. Перепишем @.88) в виде
<О|*А,|Я(9)>=/»т1,*<О|ф(х)|я(9)>, @.88а)
где ф(х) — пионное поле. В пределе безмассовых пионов (тл2=0)
аксиальный ток сохраняется: д„Ай=0, и произвольный матричный
элемент тока А"
Mba=(b\Ali@)\a) @.886 J
при <72=О {q = pb—Ра) имеет полюс вида
Mba={fnqJq2)(b\jn@)\a), @.88в)
где/п = Пф — источник пионного поля.
Соотношение @.88в) позволяет получить ряд низкоэнергетиче-
низкоэнергетических теорем, справедливых в пределе тя2=0. Суть гипотезы РСАС
состоит в том, что эти теоремы остаются приближенно справедли-
справедливыми и в реальном мире, где тл2Ф0.
Выберем в качестве состояний \а) и \Ь) в @.886) нуклонные
состояния (нейтрон и протон). Наиболее общий вид соответствую-
соответствующего матричного элемента таков:
Мр„=о,=<р| Ай@) |п) = пР(р')hvv5^ (q2)-qrfh(q*)]un (p).
Из сохранения аксиального тока следует q»an=0, т. е. с учетом
уравнения Дирака ( )
где mjv—mp—mn. Следовательно,
Mpn= {2mN/q2)gA(O)ql>(upy5un)+.... @.88r)
С другой стороны,
<p|/.!@) |n> = V2gnjvw(MPY5«n), @.88д)
где gnNN является по определению пион-нуклонной константой свя-
37

зи (феноменологически @.88в) описывает испускание нуклоном
виртуального пиона). Сравнение @.88в)—@.88д) дает
@.88е)
Это и есть замечательное соотношение Голдбергера — Треймана.
Оно связывает феноменологическую константу сильного взаимо-
взаимодействия gnNN с двумя константами слабого взаимодействия gA и
/„, характеризующими соответственно р-распад нейтрона (n-+pev)
и распад пиона (n-+ev). Эксперимент дает g2,,jvw/4:n;—14 (из рас-
рассеяния пионов на нуклонах), /л—130 МэВ (из распада пиона).
Подставляя эти значения и т^—940 МэВ в @.88е), получим
?а~1Д что удовлетворительно согласуется с экспериментальным
значением gA—1,24 (из E-распада).
Рассмотрим теперь слабый нейтральный ток кварков. Он
строится аналогично лептонному:
/„@) = /й<3)—sin2 Qw
где (ср. @.13)) 3-компонента изовектора
@.89)
c—sysxLs+ ty»Lt—by»Lb), @.89a)
а электромагнитный ток /й<еП1) определен в @.59).
Подставляя @.89а) и @.59) в @.89), получим слабый ней-
нейтральный ток адронов в виде (ср. @.14), @.15)):
где
i=u, с, t, d, s,
.=- — w, gcR = 2-w, i = u, c, t;
@.90)
w = sin2 Qm.
= d, s, b;
@.90a)
Нейтральный ток @.90) диагоналей по всем ароматическим кван-
квантовым числам: AQ = AS = AC=A/=0.
Интересно отметить, что именно отсутствие нейтральных токов,
изменяющих странность, привело в 1970 г. Глешоу, Илиопулоса и
Майани к гипотезе о существовании, наряду с известными к тому
времени кварками и, d, s, четвертого кварка с, образующего вме-
вместе с комбинацией s' кварков s и d @.80) второй изодублет (см.
@.78)). Комбинация d' @.80) была уже введена ранее для объ-
объяснения сильного различия вероятностей р-раопада и распадов
странных частиц (см. выше). Коэффициенты же в s' были подоб-
подобраны так, чтобы было AS=0 в нейтральном токе (так называемый
ГИМ-механизм). Это позволило объяснить наблюдаемое на опыте
сильное подавление распадов Kz.0-*-ц+р-~ и ряд других эффектов.
38
Так, вероятность распада Кь°-*\1+ц~ согласно ГИМ-механизму ока-
оказывается пропорциональной (тс—muJ. Как известно, гипотеза
ГИМ была подтверждена открытием ф-частиц из семейства чар-
моиия ее (см. выше). Открытие же Т-частиц означало введение
пятого кварка Ь. Удивительная симметрия, существующая между
известными слабыми дублетами лептонов @.9) и кварков @.78),
позволяет сделать вывод о существовании шестого кварка t. Как
уже отмечалось, в настоящее время ведутся интенсивные поиски
топония — системы tt ¦— в экспериментах по аннигиляции е+е~
в адроны.
Указанная выше симметрия между лептонами и кварками
становится еще большей, если учесть возможное отличие от нуля
масс нейтрино. В этом случае и в лептонные дублеты @.9) будут
входить некоторые линейные комбинации нейтринных состояний с
различными массами (см., например, [11] ).
Рассмотренные токи лептонов и кварков позволяют описать
большое количество экспериментальных данных по распадам леп-
лептонов и адронов, глубоко неупругому нейтрин-нуклонному рас-
рассеянию в рамках кварк-партонной модели (см. п. д)) и другим
процессам.
Приведем в заключение полные кварк-лептонные слабые токи в
подробной записи. Заряженный ток с учетом @.5) и @.79) имеет
вид:
@.91)
где матрица смешивания V записывается в форме, которую пред-
предложили Кобаяши и Маскава (см., например, [11]):
(C1
\ — S1S2
- s2s3ei6 c&Ss
'1C2S3 SzCs€l I
@.91a)
где c,-=cos6,-, s, = sin0t (i=l, 2, 3).
Нейтральный ток согласно @.14), @.15), @.90) и @.90а) имеет
вид:
39

{dsb) \-~Y^ + -Y
@.92)
где вершинные операторы TJ, стоящие в @.92), выражаются че-
через проекцию изоспина /3f и заряд Qf данного фермиона /=ve,... ,d:
@.92a)
Эффективный лагранжиан взаимодействия, феноменологически
описывающий слабые процессы при низких энергиях, выражается
через токи @.91) и @.92) следующим образом:
&w = DG>'2J {JCaJac + 2JNaJaN). @.93)
В области высоких энергий эффективное взаимодействие
«токX ток» в @.93) заменяется на взаимодействие «ток X калибро-
калибровочный бозон» с лагранжианом:
S'm = eAaJa^^+g'ZaJaN+giy2( WaJac+ WaJac), @.94)
где Аа, Wa, Za — соответственно поля фотона, W- и Z-бозонов; е,
g, g' — отвечающие им константы связи с электромагнитным то-
током /(ет>, заряженным Jc и нейтральным JN слабыми токами, при-
причем
g=elsinQw, g/ = e/sin6W'CosGir, @.94a)
а постоянная Ферми G в @.93) связана с g соотношением
G/i2=g2/8mws, @.93а)
tnw — масса W-бозона, mz=mw/cosQw — масса Z-бозона. Обосно-
Обоснование лагранжиана @.94) дано в гл. V.
В^ последующих главах рассматривается теория калибровочных
полей, на основе которой затем излагаются теории электрослабого
и сильного взаимодействий элементарных частиц.
Глава I
КЛАССИЧЕСКАЯ ТЕОРИЯ
КАЛИБРОВОЧНЫХ ПОЛЕЙ
Одной из существенных особенностей теории неабелевых
калибровочных полей является наличие классических решений с
нетривиальными топологическими свойствами (монополи, инстан-
тоны). Подобные решения не могут рассматриваться с точки зре-
зрения теории возмущений и должны быть получены до проведения
квантования. Поэтому мы вначале познакомим читателя с основа-
основами классической лагранжевой теории калибровочных полей, а за-
затем дадим вывод классических монопольных и инстантонных ре-
решений.
§ 1. ПОЛЯ ЯНГА—МИЛЛСА
Электромагнитное поле возникает как компенсирующее
поле, обеспечивающее инвариантность заряженных полей относи-
относительно локальной однопараметрической унитарной группы — груп-
группы U A). Янг и Миллс провели локальное обобщение группы
SV B) — неабелевой трехпараметрической группы. В результате
они пришли к необходимости ввести трехкомпонентные калибро-
калибровочные поля, названные по имени авторов полями Янга — Миллса.
Рассмотрим вначале некоторую n-параметрическую локальную
калибровочную группу
здесь Qa(x) — локальные (зависящие от координат) параметры
группы, Та — генераторы группы, заданные в некотором представ-
представлении, которому принадлежит поле ф (х). Операторы Та эрмитовы,
Та+=Та, и удовлетворяют соотношениям
[Та, ^б] =tfabcTc, A-2.1
где fabc — структурные константы.
Унитарность преобразования A.1), ©+=©""', обеспечивает ин-
инвариантность квадратичных по ф членов в лагранжиане: ij)+i|) = inv.
В то же время из-за локальности оператора а(х) производная д^чр
не подчиняется правилу преобразования A.1). Это приводит к на-
нарушению инвариантности членов в лагранжиане вида (д,1'Ф) + (д>1ф).
Поэтому аналогично тому, как это делается в электродинамике,
введем вместо д» удлиненную производную
Dll=c5l,—igA^(x). A.3)
так, чтобы выполнялось равенство
I = D/iJj' (x). A.4)

Отсюда для удлиненной производной получим правило преобразо-
преобразования
D/^D^co, A.5)
или
D/=со (<Э„—igA) со-1 = dv—igA»',
откуда
А/(х) =(оА11ю-1+ (i/g)adlia-1. A.6)
Заметим, что Ам(х) представляет собой операторную функцию,
заданную на генераторах группы, а именно
[A,,(je)=V(*)TOv3 (Г.7)
при этом А11а(х) оказывается n-компонентным векторным полем,
принадлежащим присоединенному представлению группы. Таким
образом, введение калибровочного поля А»а(х) позволяет удовлет-
удовлетворить условию A.4) и обеспечить инвариантность лагранжиана
поля ф(х).
Для понимания природы калибровочного поля рассмотрим ин-
финитезимальные преобразования
<в = 1—Ю«Тв. A.8)
Тогда
V=К—&аАЛТа, Ть]— (Ug)Тад$а,
или с учетом A.2)
А,'а = V+UcQbA^-(l/g)dJBa = Af—UbcAf&— (l/g)djd°. A.9)
Последнее равенство дает возможность выразить вариацию ка-
калибровочного поля через вариацию параметров группы ба:
6As= — (Ug)dfia—fabcAS&=—№)!>,№. A.10)
Здесь правая часть равенства выражается через удлиненную про-
производную 6а, поскольку в присоединенном представлении (Ть)'ас =
^ifabc и, следовательно,
ЦЯ° = (ЗАи—lg (Jb)aeAS)&° = dJda + gfabcAJ>6c. A.11)
Как видно, преобразование A.9) помимо неоднородного градиент-
градиентного члена — {l/g)djda, имеющегося в градиентном преобразова-
преобразовании в электродинамике, содержит еще и однородный член, харак-
характерный для неабелевой теории с некоммутирующими потенциала-
потенциалами A.7).
Определим напряженность поля G^v таким образом, чтобы за-
закон ее преобразования был таким же, как и для удлиненной про-
производной A.5), т. е. в отличие от потенциалов A.6) не содержал
градиентного члена:
G'Mv=coGllvio-1. A.12)
Этому условию удовлетворяет следующее определение:
GP=D,AV-DA=^Av—dA+te/OIAi-. AJ. A.13)
42
Действительно,
+со (—igA» {i/g) dv+ igAv{i/g) d») w = ш (DA) со-1—ш (DVAJ to.
Здесь в последней части равенства операторы D,, и Dv в круглых
скобках действуют только на Av и Ац. Таким образом, равенство
A.12) доказано.
Рассмотрим группу трехмерных вращений в изотопическом про-
пространстве. Тогда структурными константами будут
fabc = Babc, A-14)
где а, Ь, с=1, 2, 3; гаьс — абсолютно антисимметричный тензор,
нормированный условием ei23=l- В этом случае для тензора поля
Gllva = 5|lAvo—дЛ^+gfabcA^A^, A.15)
находим
или в векторной форме
1 GMV=^AV—dA»+gA»XK-. A-17)
Поле A.17) получило название поля Янга — Миллса. Инфинитези-
мальное преобразование потенциалов складывается из поворота и
градиентного преобразования:
А/=А,+ехАм— (\/g)dJdt A-18)
а для тензора поля — только из поворота:
G/M»=G|1?+exGlw. (I.19J
Поэтому для поля Янга — Миллса можно ввести инвариантный
относительно вращений локальной группы SUB) лагранжиан
&4-M=—1UGrSG,r. A.20)
В спинорном представлении Та=}/2Оа, где оа — матрицы Паули.
Мы получим
А
где символом tr обозначен след матрицы и использовано свойство
матриц Паули tr оаоь=2баь. С учетом этого равенства лагранжиан
A.20) может быть записан в виде
S'y-M='-1/2tr(GllvG'"'). A.21)
Заметим, что аналогичное выражение справедливо для лагранжиа-
лагранжиана произвольного калибровочного поля Gin=GinaTa, отвечающего
группе симметрии SU(N) с генератором Та=72Я,а. Найдем теперь
уравнения поля Янга — Миллса
43

Дифференцирование A.20) дает
или в краткой записи
где согласно A.11) имеем
A.22)
A.23)
В случае, если калибровочное поле не свободно, а взаимодей-
взаимодействует с заряженным полем, то в правую часть уравнения A.23)
/следует ввести плотность 4-тока заряженного поля
Dv/-p а — ; а
A.23а)
Полученные уравнения Янга — Миллса обобщают уравнения
Максвелла на случай неабелевых калибровочных полей. ¦
Имеется принципиальное отличие уравнений Янга — Миллса
от уравнений Максвелла. Прежде всего уравнения Янга —'¦Миллса
'нелинейны, что приводит к самодействию поля, т. е. к взаимодей-
взаимодействию различных его компонент между собой. Кроме того,, уравне-
уравнения Янга — Миллса, будучи калибровочно инвариантными, содер-
содержат тем не менее наряду с тензором поли также и потенциалы Лд
которые зависят от выбора определенной калибровки. Таким обра-
образом, в неабелевой теории не только тензор поля, но и потенциалы,
являющиеся решениями уравнений поля вида A.23), приобретают
непосредственный физический смысл.
§ 2. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА
; ПОЛЯ ЯНГА-МИЛЛСА
Динамической характеристикой классических полей яв-
является тензор энергии-импульса:
/j-iV *а dj? »v га Ю Л\
I а — Aj.a-r-^ OaJC. \*-Ч
o/io,v
где Ааа,а==дАаа1дх?. Вычислим 7av для поля Янга — Миллса. Из
A.20) следует, что
поэтому
Т v_ /
¦* a — ^
1 о.а Оа
или, поднимая индекс,
yav__ Q vo^ a,a {Tav2?
B.2)
B.3)
Полученный канонический тензор энергии-импульса оказался не-
несимметричным из-за того, что спин поля не нуль (поле Янга —
44
Миллса — векторное). Симметризуем B.3), добавляя дивергенцию
dx°
A™) =GZ
Воспользуемся уравнениями поля
GTAa%.
тогда
da(GavaAaa) = GavM,oaa
= Ga™ [Aju—gtabcA *MOC) .
В сумме с B.3) получим новый тензор
^ 7V='—Gav° (Aaa-a—
—б„^ =—GavoGaoa—6a?i?.'' B-4)
Полученный тензор после поднятия индекса приобретает явно сим-
симметричный вид
ГТ1и /^ v/^ aa._i_ I/ nwfi aft "P ^ /9 ^^
Для дальнейшего важно ввести дуальный тензор поля Янга —
Миллса
G^^ke^Ga*". B-6)
Поскольку тензор Ga*° антисимметричен, то по аналогии с
электродинамикой его компоненты можно перечислить, введя
электрическую Епа и магнитную Впа компоненты согласно опреде-
определениям
здесь по-прежнему индекс а—\, 2, 3 — групповой, а индекс п=
¦¦1, 2, 3 нумерует пространственные компоненты, т. е.
а— (Р о р а р а\ р> а— (R а
а\
)¦
B.8)
Что касается компонент дуального тензора, то из определения
B.6) получаем
Gona~Bna, l2?nikGika=Ena, B.9)
т. е. переход от GMV" к С^а соответствует следующей замене компо-
компонент тензора Епа^-Впа, Впа->-—Епа.
Выпишем явный вид полученных таким образом матриц:
EV
-В" В}
@ —Еч —
Е% 0
КЕ% —BlBt 0
B.10)
45

G =|
0 Bx BP B% \
— Bx 0
— Eay
— Bay —Еаг О Еах
K-B%
-El 0 j
Рассмотрим теперь свертки произведений матриц GaGa, GaG\
GaGa. Прежде всего имеем
G^Ga""- = б/ (Еп"Вп") = Ь»8.
Отсюда получаем инвариант
G»vaG<r=— 4(EnaBn°)=— AS.
Точно так же находим
B.11 >
где
B.13>
= 74 (Gaf
также является инвариантом. Взяв след равенства B.13), получим
откуда с учетом B.13) следует
G^GJ"=— 40". B.15)
Воспользуемся тождествами B.11) и B.13), чтобы преобразовать
тензор Tav к другому виду
B.16),
Действительно, для последней части равенства B.16) имеем
) (Gav°—iGav°) =—V2(GaoaGa
=—Gao«Ga™+ V46av (Gop«Gaop)i,
что и требовалось доказать.
Выпишем теперь компоненты тензора энергии-импульса в явном
виде:
B-17)
46
Как видно, компоненты Гв; образуют известный из электроди-
электродинамики вектор Пойнтинга — плотность импульса поля, а Too —
плотность энергии поля Янга — Миллса.
Рассмотрим, далее, важный для дальнейшего класс калибровоч-
калибровочных полей.
Определение. Калибровочное поле называется самодуаль-
яым (антисамодуальным), если компоненты его тензора и дуально-
дуального тензора связаны условием
,'" Gvva = iGvva {G^a=— iG»va). , B.18)
Если мы обратимся к явной записи тензоров G^" и С^а B.10),
то условия B.18) сводится к требованию
Ba=±iEa., B.19)
Заметим, что мнимая единица здесь появляется вследствие псевдо-
евклидовости метрики пространства Минковского *. Это, кстати
говоря, и объясняет то, что в электродинамике, где все поля дей-
действительны, самодуальные поля обычно не рассматриваются.
Самодуальные (антисамодуальные) поля обладают следую-
следующими свойствами:
1) тензор энергии-импульса равен нулю,
Т>„=0; B.20)
2) действие поля S = $2'd4x эстремально,
6S = 0. ; B.21)
Первое свойство прямо следует из только что доказанного ра-
равенства B.16). Второе свойство означает, что любое самодуаль-
самодуальное поле удовлетворяет уравнениям Эйлера — Лагранжа, т. е.
A.22). Докажем это. Для этого прежде всего докажем, что любой
дуальный тензор С»у,а в силу своего определения через потенциалы
B.6) и A.15) удовлетворяет уравнению поля A.22):
B-22)
Вспомним определение A.15):
GMva = ^Hv°—dA^ + g^abcAbAvc = g^ + gEabcAvbAvc. B.23)
Первое слагаемое gV4a дает дуальный тензор §^а, который, как и
в электродинамике, удовлетворяет уравнению
<3v#a"v=0. B.24)
Покажем теперь, что второе слагаемое в B.23) дает правую
часть B.22). Слева в B.22) имеем
* Если провести повторное преобразование дуальности, то, как легко пока-
показать, СГ^«=— GMva. B.19а)
47
\

Справа получаем два слагаемых. Одно из них равно левой части
равенства B.22):
e^og*" X Av=е*
X Av—д°А>- X Av) =
X A°—d*A° XAl);
другое тождественно равно нулю
X) XA°+ (A°XAV)
в силу тождества Якоби.
Таким образом, уравнение B.22) тождественно удовлетворяет-
удовлетворяется. Отсюда следует, что так как G,,v=±tG^v, то тензор G^a автома-
автоматически удовлетворяет уравнениям поля A.22). Итак, вместо урав-
уравнений второго порядка для G^v получаем уравнения первого по-
порядка _
GMV=±iG^. B.25)
Удовлетворяющие этим уравнениям и, стало быть, уравнениям
A.22) потенциалы Л„° обеспечивают экстремум функционала дей-
действия поля Янга — Миллса.
Поучительно посмотреть, каким образом последнее утвержде-
утверждение может быть получено непосредственно. Преобразуем с учетом
B.14) и B.15) плотность функции Лагранжа A.21) (численный
множитель опускаем):
tr G,v2= 7г tr (GM
i tr
Первое слагаемое равно нулю. Второе слагаемое выражается через
4-дивергенцию:
tr G^G" = Чг tr (D,AV—
Поэтому интеграл действия выражается через интеграл по поверх-
поверхности объема интегрирования
v=J
^ tr А,ДАО.
Поскольку вариация поля на границе объема при выводе вариа-
вариационного принципа считается равной нулю, то
что и обеспечивает экстремум функционала действия.
48
§ 3. МОНОПОЛЬ ДИРАКА
Электродинамика построена в предположении, что кро-
кроме электрического заряда не существует других источников элект-
' ромагнитного поля, а взаимодействие с электромагнитным полем
осуществляется только через заряды. Таким образом, отвергается
существование элементарных магнитных зарядов, что вполне соот-
соответствует экспериментальным данным — магнитные заряды, или
«монополи», до сих пор не обнаружены. Это проявляется в отсут-
отсутствии дуальной симметрии уравнений Максвелла, т. е. симметрии
между электрическими и магнитными компонентами тензора поля,
или между тензорами F^ и Fwv.
Действительно, уравнения Максвелла имеют вид
dFJdx^O, C.1 >
где Fnv=l/2?vvM>Fkl> — дуальный тензор поля. Компоненты тензоров-.
iv и ^v записываются также, как и у полей Янга — Миллса,
B.10) только, разумеется, без индекса а.
Напрашивается следующее симметричное обобщение уравнений.
Максвелла г_ *' /
dFJdx4nj div/6X=4nJv ; C.2)
где Jv — дуальный ток, т. е. ток магнитных зарядов. Подобные
обобщенные уравнения инвариантны относительно* преобразования
дуальности
' |iV~~*" Г (IV, /v * Jv>
C.3),
Т -*-i ; P -*- F
Jv^^> J-v, /^ UV^^ * (iv
и, более того, относительно преобразований общего вида
F^V^FUV cos a+F1™ sin а,
Fwv->'—^ sin а+F"v cos а, C.4)'
/v-*- /v cos а+~f sin a, ., ^
Jv-^—/vsina+/vcosa. r' (
При «=я/2 получаем частный случай C.3).
Как уже говорилось выше, повторное применение операции дуаль-
дуальности C.3) (так же как и операции C.4), в чем легко убедиться)
дает
pv-^Fw-x—F»1, C.5)
т р v = F
Для компонент тензора поля преобразование дуальности выгля-
выглядит следующим образом:
FnV-^Ft,
-Е,
В.
49

Симметризованные уравнения Максвелла C.2), расписанные по
.компонентам, имеют вид
rotB = 4nj + —, rotE = — 4jtJ —.
* * C.7)
div E = 4лр, div В = 4лр.,
¦Преобразование Е-»-В, В-*—Е, j-*-j, p->p, j->—j, р-»—р оставляет
инвариантной эту систему.
Оказывается, что подобная симметризация уравнений приво-
приводит к плохим последствиям. Действительно, введем потенциалы
.Лц. Тогда
Fm—d,Av—с
Найдем теперь левую часть второго из уравнений C.2):
в'и*р
Для того чтобы удовлетворялось уравнение C.2) с ненулевой пра-
правой частью /\?=0, должно быть е»^а&'д1-А1'Ф®, т. е.
а это возможно, только если потенциал Лр сингулярен. Таким об-
образом, введение магнитных зарядов с необходимостью приводит к
сингулярности электромагнитных потенциалов.
Приведем пример. Пусть
А0 = 0, A = e<J)^Mg4- C.8)
¦компоненты потенциала в сферической системе координат г, б, <р.
Потенциал А обращается в бесконечность на полуоси 6 = я. Найдем
магнитное поле В = rot А:
V )r rsine [ dQ У ф/ d<f \ л2
Таким образом, потенциал C.8) задает магнитное поле кулонов-
ского типа
C.9)
нов-
B^trgm/Г2, C.10)
создаваемое магнитным зарядом gm, при этом сам потенциал
сингулярен вдоль полуоси z<0. В общем случае получается ли-
линия, исходящая из некоторой точки и уходящая в бесконечность —
нить сингулярности. Линии магнитного поля, начинающиеся на
магнитном заряде, уходят в бесконечность, где собираются и воз-
возвращаются на заряд вдоль нити сингулярности. Следовательно,
нить можно физически представлять себе как предел бесконечно
длинного и тонкого соленоида, тянущегося в бесконечность.
.50
Поле C.10) удовлетворяет уравнению
':i divB = 4jtp. C.11)
Действительно, интегрируя левую часть этого равенства по объ-
объему сферы, получим для поля C.10)
г div rw3v_ «f RrfS^cr^ &dQ = 4ngm, C.12}
5 div Bd j g §
Т. е. закон Гаусса, который, как известно, эквивалентен уравнению
C.11). Рассмотрим теперь поток поля C.10) через поверхность
So образованную сферой с удаленной малой областью вокруг нити
сингулярности. Тогда полный поток через сферу будет равен
ф J j BdS C.13>
J BdS + j BdS,
где Si — площадь малой области. Поскольку поле В не имеет осо-
особенностей на сфере, то, уменьшая Sb получим
?JdS C.14)
Для последнего интеграла имеем по теореме Стокса^ (заметим, что-
на поверхности So потенциал не имеет особенностей):
f BdS = f rot AdS = ф Adi,
где контурный интеграл берется по границе области Si. В силу
C.12) и C.14) имеем
§Ad\^4ng C.15).
При стягивании области вокруг нити в точку, конечное значение
интеграла C.15), т. е. 4itgm, можно обеспечить лишь при наличии
сингулярности потенциала в этой точке. Поскольку радиус сферы
был взят произвольным, то тем самым получаем для всевозмож-
всевозможных радиусов множество точек, образующих линию сингулярности..
Дираком в 1931 г. было показано, что заряд монополя gm He-
может иметь произвольные значения, а должен квантоваться. Рас-
Рассмотрим квантовое уравнение Шредингера для частицы с заря-
зарядом е. Вдали от монополя при г-*-оо поле В-*-0, и мы имеем сво-
свободную частицу:
vy+*Y=o. C.16)
vy+Y
Частица останется свободной, если она будет находиться в точ-
точке с ненулевым потенциалом А, представляющей собой чистую
калибровку, т. е.
(v_teA)»4)=**l), A=-LVf, C.17)
е
где /=/(г) — скалярная функция, а волновая функция ^ связана
с. исходной ф' преобразованием калибровки
ф = в'^'. C.18)"
51
К,

Состояние частицы не должно зависеть от присутствия струны,
так как струна — нефизическое образование, только поле В имеет
физический смысл. Поэтому фаза волновой функции / должна ме-
меняться при обходе струны на 2пп. Запишем интеграл по замкнуто-
замкнутому контуру, охватывающему струну
C.19)
C.20)
C-21)
Полагая
получим
$d/=2nn (n = 0, ±1, ±2, ...),
gm=n/2e=nel2a—l37 en/2,
«=e2/ftc—1/137 — постоянная тонкой структуры.
Таким образом, магнитный заряд может принимать лишь такие
значения, которые кратны величине go^68,5e (e — заряд элект-
электрона). Рассмотренная теория монополя в электродинамике страда-
страдает существенным недостатком — потенциал должен иметь сингу-
сингулярность вдоль нити. Как будет видно в дальнейшем, теория
Янга — Миллса допускает монопольные решения без сингулярно-
.стей, имеющие кулоновский вид.
§ 4. МОДЕЛЬ ХИГГСА
Поиски точных решений уравнений Янга —^иллса
¦ввиду их нелинейности связаны с большими трудностями^ Извест-
Известны лишь некоторые частные решения^ среди которых наибольшее
значение имеют статические решения системы взаимодействующих
лолей Янга — Миллса и заряженных скалярных полей, облада-
обладающие конечной энергией, — так называемые монополи, а также
динамические решения в евклидовой метрике (с мнимым време-
временем). Последние локализованные и несингулярные решения назы-
называются инстантонами. Они наряду с монопольными решениями
находятся в центре внимания современной теоретической физики.
Получение подобных решений может пролить свет на проблему
нелинейного квантования калибровочных полей.
а) Лагранжиан модели
Прежде чем переходить к описанию известных монопольных и
лнстантонных решений, исследуем некоторые общие свойства урав-
уравнения Янга — Миллса, связанные с асимптотическим поведением
их решений.
{^Рассмотрим модель, предложенную Хиггсом, состоящую из
взаимодействующих полей Янга — Миллса и скалярного поля:
&I/GG (D>o)—V(<pOJ 9 D.1)
Здесь фа (а—1, 2, 3) — скалярное поле, образующее триплет
присоединенного представления группы SUB); потенциальная
энергия самодействия
2Д—Ф2J D-.2)
! Г1
I »!
'зависит от квадрата вектора <ра, а производная поля <ра имеет вид
V- D.3)
Запишем теперь уравнения калибровочного поля в модели
Киггса: — __ V
Или
D.4)
Здесь справа стоит плотность тока хиггеовского поля. Для самого
Хиггсовского поля получим уравнение
a=gecbaAbD*(pc— (m2—Хф2) фа,
«ли
D,J><pa = — (m2—V)<Pa- ]} D-5)
Лагранжиан обладает явной калибровочной инвариантностью
Относительно группы SUB) внутренних, «изотопических» поворо-
поворотов. Потенциальная энергия У(ф) в зависимости от знака К имеет
Минимум либо при ф2 = 0, если т2<0, либо при ф2=т2Д, если
Л12>0. Классический вакуум определяется как асимптотическое
решение при г-*-оо, обеспечивающее минимум энергии полей 2№:
0. D.6)
При т2<0 вакуум оказывается симметричным
V
«бладая симметрией лагранжиана. При т2>0 вакуум теряет сим-
симметрию лагранжиана:
D.7)
со,
где па — некоторый произвольно выбранный единичный вектор,
|п| = 1, в изопространстве. Множество вакуумов, определяемое
условием
Ы/У^ D.8)
образует пространство вакуумов, представляющее собой двумер-
двумерную сферу радиуса R = ml'}/K. Выбор конкретного вакуума D.7)
сводится к выбору определенного направления п в изопространст-
изопространстве, что нарушает группу SU^2)гЭто явление носит название спон-
спонтанного нарушения симметрии^Шостроенное на вакууме D.7) ре-
решение уравнений поля, обладает остаточной группой U(l), не ме-
меняющей направления п=пF, ф). Выбор решения обеспечивается
выбором граничного условия D.7), этим и определяется снижение
симметрии SUB)-*U{1).
Пусть т2->-0, К-*-0, тогда могут представится два случая:
1) если m/V?i-*-0, то симметрия восстанавливается;
2) если 0<m/y?i<oo, то симметрия остается нарушенной.
б) Соответствие Джулиа — Зи
53

Рассмотрим теперь чистую калибровочную теорию с дополни-
дополнительным самодействием:
2 =—ViG^Gj^— ЧМ™?/1+А2J, A*=ASAJ>. D.9)
Этот лагранжиан не обладает калибровочной симметрией. Вакуум:
имеет вид
г—оо, А2=—тЩ. D.10)
При т2-*-0, Х-+0 и 0<т2Д<оо симметрия лагранжиана восстанав-
восстанавливается, однако решение D.10) остается несимметричным. Име-
Имеет место соответствие между двумя теориями, задаваемыми лаг-
лагранжианами D.1) и D.9).рПусть
1) А0а?=0, Лга = 0, ф«=0;
D.11)
2) Л0'а=0, А/°Ф0 Ф/о^0
причем d/dt==O >— статическая теория. Тогда обе теории эквива
лентны в математическом смысле, если
Действительно,
Поэтому
Кроме того,
В итоге из лагранжиана
получим
—V2G0/G0/ = i/2 (D,VJ,
- »/4 G,7G'/ =—i
i2 = —ф'2—А'2=—ф'2+Л,Д
—ф'2+А'2)
D.13)
V)
D.14)
При этом в асимптотическом пределе г-*-оо поля ведут себя сле-
следующим образом:
Таким образом, хиггсовское поле фа заменяет собой компоненту
калибровочного поля Аоа и наоборот. Заметим, что, как легко убе-
убедиться, соответствующие уравнения для ф и Аоа совпадают.
в) Группа симметрии решения
Рассмотрим более подробно свойства статических решений мо-
модели Хиггса. Положим d/dt^sO (статическое условие), Лоа=О и,
вообще говоря, Л,-а=#0, ц>аф0. Пусть Л/° и <ра при г-*-оо удовлетво-
удовлетворяют следующим граничным условиям, нарушающим группу
SUB):
54
4
D.15)
|"де полужирный шрифт обозначает вектор в изотопическом прост-
пространстве. Эти граничные условия обеспечивают конечность энергии
системы полей А* и <р. Действительно, поскольку согласно D.15)
<p2=m2/A.+O(l/r2), то при г-»оо имеем
V(q>) = (ЯУ4) (т2//.-ф2J=0A/г4),
D.16)
лричем Ооф=0, Go;=O. Тогда плотность энергии ведет себя на
бесконечности как 1/г4 и интеграл по объему для полной энергии
поля сходится на бесконечности.
Заметим сразу же, что при г-*-оо согласно D.15) имеем: А* и
«ф ортогональны, А,п = 0. Покажем, что решение уравнений поля
•обладает группой симметрии вакуума, т. е. U(l). Рассмотрим ло-
локальное преобразование
'Лусть
со (х) = ехр (—;Т6 (х)), Т = i/2o.
D.17)
6(x)=f(x)<p(x) Й=<р/ф). D.18)
Тогда это преобразование образует однопараметрическую подгруп-
подгруппу U(I) группы SUB) в каждой точке пространства х, причем
юараметр — это угол поворота вокруг оси ф, фиксированной дан-
данным решением ф(х). Ясно, что
со(х)фсй-1(х)=ф, D.19)
т. е. ф остается локально инвариантным относительно группы U(l).
Это преобразование D.17), D.18) не изменяет граничного усло-
условия D.15) и образует тем самым группу калибровочной инвари-
инвариантности данного решения.
Определим теперь абелев потенциал
Л^А.ф. D.20)
Поскольку
6А„=—
то при преобразованиях D.18) имеем
М„=—A/g) (^в+^АйХв)ф=-A/^)^, D.21)
т. е. Л„ преобразуется, как электродинамический потенциал, гра-
градиентным образом:
A^iV-O/g)^. D.22)
Введем другие, поперечные компоненты потенциала
УУ-^еа^Лд D.23)
55

где е1-2 — единичные векторы, ортогональные <р. Продольная ком-
компонента D.20) при преобразованиях группы GA) D.17) на беско-
бесконечной асимптотике согласно D.15) переходит в чистую калиб-
калибровку
Д.— (Ug)dJ (г-оо), D.24>
для поперечных компонент с учетом D.15) получим
if/8)
*+ We) (d*i
= D.25)
т. е. преобразование GA) не меняет V»1-2 на бесконечности. Таким
образом, получаем инвариантное граничное условие на бесконеч-
бесконечности для поперечных компонент:
n) Xn= A/g) ton)e2,
D.26)
)>
г) Унитарная (струнная) калибровка
Как уже указывалось ранее, в неабелевой калибровочной тео-
теории потенциалы явно входят в уравнение поля и, кроме того, тен-
тензор напряженности поля также подвержен преобразованиям, а-
именно чистым вращениям. Ввиду этого выбор калибровки опре-
определяющим образом влияет на вид полученного решения уравнений
поля. В дальнейшем оказывается удобным использовать так на-
называемую унитарную, или струнную, калибровку. В этой калибров-
калибровке третья ось изотопического пространства и радиус-вектор г па-
параллельны в каждой точке пространства.
Рассмотрим решения уравнений поля Янга — Миллса специаль-
специального вида, определяемые следующим анзацем*:
gA0" = iraf/r2, gAia^EainTn(l-h)fr2, D.27)
где f=f(г) и h=h(r) — некоторые неизвестные функции г= |г|.
Согласно определению калибровочное преобразование к уни-
унитарной калибровке должно иметь вид
соЛ^со-1 + (i/g) юдрш-1=Л„'=^, D.28)
где si-»
потенциал в унитарной калибровке, а
со = ехр (—оеф6) = cos— + ior^sin—;
D.29)
здесь е<р —¦ единичный азимутальный вектор сферической системы
координат г (г, 6, ф), а о^=ае^. Для Аоа преобразование D.28) огра-
ограничивается поворотом, и мы находим
= i8a3f/r. D.30)
нений.
56
Анзац (ansatz) — специальное, частное решение нелинейных полевых урав-
i , Рассмотрим теперь А«°:
1—ft
D.31)
Поворот дает
со (г X о) со = со [е„ {—га») + ефг<тв] со = —гс^в + roj.e,, D.32)
Поскольку при повороте оФ-*-оФ=—oi sin cp + Огcos cp, ав~*-о±=
i
Oj
Градиентный член вносит вклад
Объединяя D.32) и D.33), получаем
gA = ?- (— eeffq, + е^х
Отсюда окончательно находим
_^tg^)e,. D.33)
.-!-оЛе-2-Ч. D.34)
— tg -^-
D.35)
Компонента А3 представляет собой известный потенциал дира-
жовского монополя с зарядом gm=—l/g, g=e (см. выше). Это есть
следствие выбора анзаца D.27). Заметим, что в калибровке D.35)
потенциалы D.27) приобрели сингулярность вдоль нити 6 = л, яв-
являющуюся следствием сингулярности калибровочного преобразова-
преобразования <4.33).
§ 5. САМОДУАЛЬНЫИ МОНОПОЛЬ БОГОМОЛЬНОГО,
ПРАСАДА, СОММЕРФИЛЬДА
Наиболее простым решением уравнений Янга .— Миллса
монопольного типа, нарушающим симметрию SUB)->-U(l), явля-
является самодуальное решение Богомольного, Прасада, Соммерфиль-
да. Это решение точное и может быть получено в явном аналити-
аналитическом виде. Однако, прежде чем выводить его, мы в начале па-
параграфа рассмотрим симметричное решение уравнений Янга —
Миллса, описывающее сингулярный монополь — решение By и
Янга.
а) Монополь By и Янга
Воспользуемся анзацем, введенным в предыдущем параграфе:
gAoa = iraflr*,
E.1)
57

Найдем теперь компоненты тензора поля, соответствующие потен-
потенциалам E.1). Учитывая статичность решения (до=О), с помощью
тождества еа&сес/„ = ба/б&и—6ап6ь/ получим
Тогда
gG°J = g(- д'Ао + еаЬ^Л°Л>) = JJ- &ai + t>ary- (rf -f-fh)-L,
откуда для напряженности электрического поля Eja = — GPJ имеем
igEia = -^ fl/e + r,ra (rf -f-fh) -L. E.2>
Рассмотрим теперь магнитные компоненты тензора
Подстановка E.1) и элементарные преобразования для компонент
напряженности магнитного поля В,а =—lh^nhGiha дают
gBia = --?-*,.„ + r,ra(l + rh' - Л2)-i-. E.3>
Анзац E.1) определяется через две неизвестные функции Л=Л(г)
и f=f(r). Уравнения Янга — Миллса приводят к уравнениям для
этих функций. Запишем компоненту уравнений для u.=t=l, 2, 3, и
ц = 0:
diGaii=geabcGbivAvc, E.4а)
^Ga^=gec6cG&'Mc;. E.46)
Если подставить сюда выражения E.2) и E.3), то приходим к
уравнениям для функций h и /:
r2h"=h(h2—1+/2),
E.5)
Эти уравнения имеют постоянные решения ft = const, f=const.
В этом случае поля Е к В ведут себя как 1/г2, а потенциалы'
А — 1/г, что соответствует симметричному дальнодействующему ре-
решению кулоновского типа, т. е. безмассовому полю (безмассовость
есть следствие бесконечности радиуса действия сил).
Перечислим возможные постоянные решения уравнений E.5)..
1) A=l, f=0 — тривиальное решение, отвечающее вакууму:
E.6)
2) h =—1, /=0 — чистая калибровка:
Действительно, подобный потенциал получается, если выбрать
со = ехр (— об) = ехр (— лог/г) — шг.
E.7)
,-i =A^L
со-1 =
г*
¦Откуда находим компоненты E.7).
3) /i=0, f=const = C.
E.8)
При /i=0 имеем для / уравнение f'—О. Общее решение f—C+Cir.
На бесконечности gA0a = iraf/r2~:>~iCif'a. Выбирая симметричное ре-
решение Л0а->-0, полагаем Сх — 0. Тогда для напряженностей поля
находим
g E.9)
В унитарной калибровке решению E.8) отвечают потенциалы
ё*а tgf66- EЛ0)
Таким образом, данное решение E.8) описывает поле электри-
электрического заряда Q = iC/g и магнитного заряда gm=—Ifg — моно-
моноПоль By и Янга. Он сохраняет SU B) симметрию лагранжиана, так
Как является сферически симметричным.
Заметим, что вместо чистой калибровочной теории можно было
<5ы рассмотреть теорию с А0а=0 и ненулевым скалярным полем фа.
Тогда, воспользовавшись соответствием Джулия — Зи, вместо
|E.1) получим анзац
g<t>a=raflrz,
, E.11)
причем остается справедливым постоянное решение E.8), E.10) с
Заменой Аоа->-Ща.
Если поле ф имеет самодействие, как в модели Хиггса,
то уравнения поля E.5) заменяются уравнениями
г2/"=f B/г2—m2r2
58
). E.12)
При т2Ф0 и ^=И=0 эти уравнения не имеют постоянных решений,
и мы приходим к необходимости искать решения, нарушающие
симметрию SUB), вводя асимптотические условия типа D.15).
б) Определение электромагнитного поля
Обсудим теперь решение уравнений, нарушающее симметрию,
SUB)-*U(l). Прежде всего следует дать определение тензора
электромагнитного поля, инвариантного относительно преобразова-
преобразований группы SUB). Мы вводили вектор-потенциал
Л„=фаЛД E.13)
59

где <р^=фа/|ф|. Этот потенциал преобразуется как в электродина-
электродинамике: если со = ехр ( —°Ч>Л. то
Av+Av-(lIe)dJ, e=g. E.14)
В унитарной калибровке фа = 6аз, и тогда
Л,= (Ло3, А3). E.15}
Определим теперь тензор F»v так, чтобы он был инвариантен отно-
относительно группы SUB). Этого можно добиться многими различны-
различными способами (см. ниже). Одно из возможных определений анало-
аналогично E.13):
/Vv=$aG,,va. E.16>
Если рассматривается чисто калибровочная модель без жиггсов-
ского поля, то /v можно определить в случае нарушенной сим-
симметрии через вектор na(A0a-*-const-na, r->oo):
F^=naG^a. E.17)
Очевидно, что эти определения дают инвариантный тензор, ибо
он представляет собой скалярное произведение изовекторов.
Найдем явный вид тензора Fvv — тензора электромагнитного
поля:
>=фа С?^а=<р (<3,AV
и X Av) =
В унитарной калибровке, ф~а = 6йз, Л11=ЛМ3, имеем
E.18 >
A»2). E.19)
Позже будет показано, что первые два члена представляют собой
дальнодействующую часть тензора, а последний — короткодейст-
короткодействующую. Другие определения тензора электромагнитного поля от-
отличаются от E.19) лишь короткодействующей частью.
Рассмотрим анзац E.1). Тогда для электрической и магнитной
компонент тензора G^" будут справедливы" выражения E.2) и
E.3). Определяя инвариантный тензор согласно E.16), получим
выражения для напряженностей электрического и магнитного по-
полей в чисто калибровочной модели
E.20)
j = ieEiatia = />,- {rf'—f) /r2,
еВ,- = eBjDna = f, A—/г2) /г2,
где учтено, что па = гп. Заметим, что в модели Хиггса электрическое
поле отсутствует, ?/ = 0, однако есть поле фа, определенное соглас-
согласно E.11).
в) Самодуальное решение уравнений Янга — Миллса
Ставим перед собой задачу найти решение уравнений Янга —
Миллса, нарушающее симметрию и самодуальное (антисамодуаль-
60
НОС). Вспомним, что для модели Янга — Миллса (без поля Хиггса)
X/4) (т2Д+Л2J, E.21)
Если m2-»0, ?i->0, но m2lK<oo, то К(Л)->0, и мы получаем свобод-
свободное решение с нарушенной симметрией.
Запишем условие самодуальности (антисамодуальности)
Eja=±iB}a. E.22)
Выберем для определенности знак минус, тогда
l-/i2 = rf-f,
E.23)
—h'=fh/r.
Эти уравнения — первого порядка, они значительно проще,
чем полные уравнения поля E.5). Наложим асимптотическое усло-
условие, нарушающее симметрию:
?Лоа-млар, г—оо, E.24)
где p=gm/y?i; тогда /-*-рг (г->-оо). Введем замену
f(r)=-l + pnp(r), E.25)
где ф-»-1 при г->оо. Подставляя E.25) в уравнение для h, из E.23)
получим в асимптотическом пределе при г-*-оо
E.26)
E.27)
E.28)
откуда
Введем еще одну замену
Подставив ее, а также E.25) в уравнения E.23), получим
—Р/Ф2 = ф'. Ф7Ч»=РФ-
Умножив одно из этих уравнений на другое, найдем
Интеграл этого уравнения
Из условия гр-^-сх), ф->1 при г-»-оо находим const ==—1, и тогда
1/$я = ф2—1. E.29)
Далее, из первого уравнения E.28) получим уравнение для ф, ин-
интеграл которого есть
E.30)

Наложим условие конечности полей в нуле, т. е. |Лца|<оо при
т-*-0. Тогда при г-*-0 должно быть: 1—h-*-0 и /-»-0. Следовательно,
функции ф и if при г-*-0 ведут себя следующим образом:
ф-^оо, ф-^0, г-+0. E.31)
С учетом этого находим С——1, т. е.
E.32)
2 ф—1
Отсюда ф = сШ|3/-, а из E.24) получим if = shpr.
С учетом этих значений из E.25) и E.27) находим решение
Богомольного, Прасада, Соммерфильда (БПС)
A = pr/shp#-, /=—1 + pz-cthpr, E.33)
имеющее асимптотику при г->-оо
А-*-рге-»"--»-О, /—рг. E.34)
Эта асимптотика обеспечивает спонтанное нарушение симметрии в
решении, т. е. E.24). При этом на асимптотике г->-оо для напря-
женностей электрического и магнитного полей имеем
Bn-*-rnlgr3 En-*-ir /gr3 /¦—>-оо E 35)
Полученное решение отвечает монополю с магнитным зарядом
?m=\/g — монополь БПС. При этом оно не сингулярно в нуле,
так как Л,°-<-0 при /¦-*-(), что соответствует распределенному, а не
точечному заряду. Действительно, в модели Хиггса А0"^-ща и
электрическое поле отсутствует, а скалярное поле фа как раз и
создает магнитное поле.
В хиггсовской модели условие самодуальности заменяется на
условие Богомольного
Впа = ±Dn(pa, E.36)
поскольку согласно § 4 имеется соответствие
В унитарной калибровке D.35) характер монопольного решения
E.33) становится наиболее ясен. Действительно, в асимптотиче-
асимптотической области, г-*-оо, /г->-0, /->-рг, получим
E.37)
0, A3 = --L-tg-^-
gr 2
т. е. электромагнитный потенциал А = фоАа=А3 описывает дираков-
¦ский монополь, введенный в § 3. При этом поперечные компоненты
потенциала А1>2 в согласии с D.15), D.26) в унитарной калибровке
«a = 63a обращаются в нуль.
Докажем теперь важное свойство решения БПС: самодуальное
.(антисамодуальное) поле монополя БПС минимизирует энергию
€2
Я. Для этого запишем энергию поля как интеграл от компонен-
компоненты Гоо тензора энергии-импульса:
Е = J dHToo=J dH VU (G,-,aJ + V2 (Go/0 2+
В stom выражении в силу статичности поля и условия Аоа = 0 (при
имеем
а при К-+0, га-^0 @<р<оо) и У(ф)=О. Следовательно,
^[/G)(р E-38)
Преобразуем это выражение:
? = V4jd3^[(G,vo:FeiMZ)«<paJ±2G,vael/nD^a]. E.39)
Последнее слагаемое в квадратных скобках представляет собой
дивергенцию
GifEiinDny^dn (eynGy«q)»), E.40>
поскольку
где последнее слагаемое равно нулю в силу уравнений поля для
дуального тензора ОйСа^ = 0.
Таким образом,
Условие самодуальности
G«/
обеспечивает минимум интеграла для энергии
E = Emm=±lkl
или с помощью теоремы Гаусса
E.42}
B = ±§ (Bna<fa)dSn.
Используя определение магнитного поля Вп=Впапа в случае спон-
спонтанно нарушенной симметрии §фа-^рпа(/"^-оо) получим
?min = ±(p/g) j>BndSn = ±{4nfy'g)gm, E.43>
где gm — магнитный заряд монополя, p = g~\!m2/K. Для решений-
БПС имеем
поэтому
Emin=
E.44)
63

т. е. магнитный заряд монрполя БПС gm=dollg в согласии с полу-
полученным ранее значением. '^Гаким образом, из всех полевых конфи-
тураций (антисамодуальный) монопрль БПС обладает наименьшей
возможной энергией, равной E.44).'
§ 6. ТОПОЛОГИЧЕСКИЙ ЗАРЯД
Нетривиальные статические решения уравнений поля мо-
могут быть проанализированы на языке топологии, позволяющей объ-
объединять различные решения б определенные топологические клас-
классы, которые можно наделить соответствующим (индексом, носящим
название топологического заряда. Вначале мы в краткой форме
приведем некоторые сведения из теории отображений и связанной
¦с ними группы гомотопий. Затем проиллюстрируем их примером
решения, осуществляющего отображение сферы на сферу.
а) Гомотопий
Рассмотренная выше модель Хиггса характеризуется тем, что
«е решения, удовлетворяющие асимптотическому условию
<ра->-const-па, г-*-оо,
F.1)
нарушают симметрию исходных уравнений. Вместе с тем эти ре-
решения задают математическое отображение сферы на пространст-
пространственной бесконечности (г-*-оо) на единичную сферу (п2=1) в про-
пространстве изотопической группы:
Soc^Si2. F.2)
Вообще говоря, отображение может покрывать сферу Si2 несколь-
несколько раз (п=1, 2, ...) или ни одного раза (л = 0). Так, если сфера
¦So,2 отображается на полусферу в изопространстве, то топологи-
топологически это эквивалентно отображению в точку. В этом случае крат-
кратность покрытия равна нулю, л = 0. Кратность покрытия, т. е. сте-
степень отображения, характеризует топологические свойства реше-
решения. Все решения можно разделить на классы с различными п —
классы эквивалентностей. Внутри данного класса п все отображе-
отображения можно непрерывным образом переводить друг в друга — де-
деформировать. При этом они остаются топологически эквивалентны-
эквивалентными, т. е. гомеоморфными друг другу. ]число п — кратность отобра-
отображения (или покрьцфя) в физических задачах называется тополо-.
гическим зарядом, ', топологическим инвариантом или индексом
Понтрягина. Переводы между решениями с разными п происходят
своеобразными скачками, связанными с изменением топологии и
сопровождающимися скачками (иногда бесконечными) в энергии.
'Среди решений могут существовать решения, обладающие наи-
наименьшей энергией, — топологически стабильные.
Монополь БПС, рассмотренный в предыдущем параграфе, осу-
осуществляет отображение кратности единица, т. е. обладает тополо-
топологическим зарядом л=1, поскольку согласно асимптотическому ус-
условию:
¦ <х>.
F.3)
единичная сфера в изопространстве покрывается один раз. Мы уви-
увидим позже, что топологический заряд п пропорционален магнитно-
магнитному заряду gm- Заметим, что в унитарной калибровке, <ра~6за, сфе-
сфера отображается в точку, «северный полюс». Поэтому в этой ка-
калибровке решение уже обладает топологическим зарядом нуль,
П«=0. Однако поскольку потенциал Л^ приобретает особенность, то
магнитный заряд остается не равным нулю. Переход л=1-»-м=0
Совершается за счет разрывного калибровочного преобразования
(при 0=я) и связан с бесконечным скачком в энергии.
^"Разбиение решений на классы эквивалентностей есть_по суще-
существу, построение некоторой группы — группы гомотопий^ или го-
гомотопической группы. Дадим определение гомотопий, или дефор-
деформаций. Рассмотрим прежде всего простейшую группу — одномер-
одномерную группу щ{Х), называемую фундаментальной. Она состоит из
элементов —¦ классов эквивалентностей (гомотопических классов
отображений) следующего вида. Пусть имеется окружность Stl
(петля) с точкой Р, лежащей на ней, и заданным направлением
Обхода. На линейном связном многообразии X задается точка N
И рассматриваются всевозможные направленные пути с началом
и концом в точке ;V (рис. 6.1). Тогда Р отображается в точку N
I V \
Рис. 6.1
/7=0
Л=7
Рис. 6.2 а
многообразия X и остальные точки окружности S1 непрерывно
отображаются на замкнутые пути в X произвольным образом. Раз-
Различные отображения эквивалентны (гомотопны), если они непре-
непрерывным образом деформируются друг в друга, образуя, таким об-
образом, класс эквивалентностей. Каждый отдельный класс эквива-
эквивалентностей есть элемент группы Я1 (X). Единичный элемент (тож-
(тождественный элемент) есть точка N и все ей эквивалентные. Если
X односвязно, то других отображений, кроме тождественного, нет,
т. е. Я1 (X) состоит только из единичного элемента /. Для много-
многосвязных X отображения нетривиальны. На рис. 6.2а—6.2в изобра-
изображены некоторые элементы группы iti(X) для неодносвязного мно-
3 Калибровочные поля
65

гообразия, правила умножения, единичный и обратный элемент.
Рассмотренная область многообразия неодносвязна за счет удален-
удаленной области, которая на рисунке заштрихована; различные классы
эквивалентностей характеризуются топологическими зарядами
/7 = 7
/7 = 0
х Ц
П=1
П= 2
'О
* N.
/7 = 0
n = 0, ±1, ±2 и т. д. Групповое пространство группы ?/A) — ок-
окружность. Это неодносвязное пространство:
U(\) ~S'. F.4)
Группа гомотопий, заданная
в этом пространстве, изо-
изоморфна группе Z — аддитив-
аддитивной группе целых чисел п=0,
±1, ±2,...:
я,(?/A))=Я1 (S')=Z.
F.5)
Групповое пространство SUB)
представляет собой сферу S2.
В случае нарушения симмет-
симметрии, <pa-»-const-na, отображе-
отображения образуют группу я2, за-
заданную на S2. Эта группа n2{S2) также изоморфна Z:
jt2(Sf/B))=jt2(S2)=Z. F.6)
Таким образом,
n2(S*)=ni{Sl)=Z, F.7)
= N
= ю
Рис. 6.2 в
66
«ЧТО мы уже обсуждали выше. Другие случаи задания группы п мы
Ае рассматриваем, поскольку они носят сугубо специальный харак-
характер.
б) Пример решения, осуществляющего n-кратное отображение
Рассмотрим пример, предложенный Поляковым, который ил-
иллюстрирует возможность многократного отображения сферы на
сферу. Мы уже видели, что решение уравнений поля вида
<pa->const-/-a(r->-oo) F.8)
задает отображение сферы на сферу с числом покрытия (тополо-
(топологическим зарядом) п=\ — это элемент группы гомотопий
jtz(S2)=Z. F.9)
Общий случай задается условием
cpa->-const-na (r-*oo), F.10)
'Где na — единичный вектор направления в групповом (изотопиче-
(изотопическом) пространстве, зависящий от направления в координатном
пространстве
яа=я°(<р, 0). F.11)
Углы вектора па в сферической системе координат обозначим
па=(Ф,в). F.12)
Общий вид отображения: (<р, 0)->-(Ф, G). Рассмотрим случай,
когда Ф = Ф(<р), G=®@). Лагранжиан модели имеет вид
2=Ч2(дтаJ, F.15)
где di — производные по направлениям е„(?=1) и ee(t=2). Этот
лагранжиан описывает поле единичного вектора (п2=1), задан-
заданного на сфере. В явном виде
(d.RiJ + @(n»)« + (d^f]. F.14)
?=1,2
В сферических координатах
(dnJ
поэтому
F.15)
Соответствующие F.15) уравнения Лагранжа
= 0,
дФ
дв
= 0
F.16)
67

имеют следующий явный вид:
Э2Ф
= 0,
2 sin в cos 6(д?ФJ — 2у2 ф6 = 0.
Первое из этих уравнений F.17а) имеет решение
Ф=±Пф (/2 = 0, 1, 2, ...),
F.17а)
F.176)
F.18)
удовлетворяющее условию непрерывности отображения после каж-
каждого «оборота» (кратность отображения). Второе уравнение с уче-
учетом равенства
1
д
и соответствия
'e-<p sine ae
д(Ф-
sin!6
д
¦Н-
* ae } sin2e
П
приобретает вид
sin 6 cos в / дф \
sin G
J
Ф
sin2e V ftp У sine ae
После постановки решения F.18) получаем
ae
— sin 26 = sin 6
a
Введем новую переменную
x=lntg-
ае \
dx =
(sin6
ае
ае
sine
Тогда из F.20) следует уравнение
= — sin 26.
2
Его первый интеграл очевиден:
2 \ dx ) 2
или
где выбрано значение константы С=0. Тогда
sin 6 = п sin 6,
где при извлечении корня мы выбрали знак «плюс».
68
F.19)
F.20)
F.21)
F.22)
F.23)
F.24)
F.25)
Интегрируя F.25), находим
ИЛИ
-КГ-
F.26)
Звметим, что выбор констант интегрирования в F.23) — F.25) и
F.26) определен требованием соответствия 0=О->6 = О. Знак
«минус» при извлечении корня из F.24) дает
dB
sine
= —п-
sinO
откуда получаем другое решение:
F.27)
Оба решения F.26) и F.27) задают п-«ратные отображения сфе-
ры на сферу и различаются только направлениями обхода. При
Л= 1 решение обычно называется «ежом», при п>1 получим свое-
Образный «скрученный еж», который невозможно «причесать» без
Нарушения топологии.
§ 7. МОНОПОЛЬ ТООФТА — ПОЛЯКОВА
Ранее мы рассмотрели сингулярный монополь By—Янга,
самодуальный монополь Богомольного—Прасада—Соммерфиль-
да. Перейдем теперь к более общему решению модели Хиггса —
МОнополю Тоофта—Полякова, обладающему конечной энергией.
а) Чистая модель Хиггса
Рассмотрим вначале более простую задачу — чистую модель
Хиггса без поля Янга—Миллса, описываемую лагранжианом
2> = —1/2( Vp°J—(Я/2) (/П2Д_ф2J> (J.I)
где <р° (а=1, 2, 3) — изовекторное поле. Будем искать решения
с топологическим зарядом п=\, т. е.
ф« = /!аф(г)) G.2)
с асимптотическим условием
В дальнейшем будем иметь в виду значение производной
G.3);
G.4)
69

Уравнения поля
= 0
G.5)
принимают вид
или
1 V 2фо—>др2фа+т2фа=0.
С учетом G.4) получим вместо G.6)
dr
= 0.
G.6)
G.7)
Здесь слагаемое (—2//-2)<р отвечает значению квадрата момен-
момента 1A+1) =2 при 1=1, что соответствует изовекторному полю в
согласии с G.2). Введем новую функцию х=/"ф- Для нее имеем
уравнение
X" |-Х — 1^г
г2 г2
G.8)
Сделаем еще одну замену, учитывающую асимптотику G.3):
Х= (т/уя)/-+п, G.9)
тогда при г->-оо имеем т]->-0. Функция т) удовлетворяет уравне-
уравнению
Первый член в правой части G.10), т. е. 2т/(г^Х), не дает воз-
возможность получить сходящуюся при /--^оо асимптотику. Если бы
Фа было одномерным полем, т. е. фа~бозф, то при г->-оо было бы
т]"=2т2т), откуда т)~ехр(—mf2 r)-»-0. Однако векторный харак-
характер поля G.2) приводит к дополнительному члену 2т/ (г^к), и
уравнение G.10) не имеет сходящихся к нулю при г-*-оо реше-
решений.
Рассмотрим теперь этот вопрос с другой точки зрения. Энер-
Энергия поля имеет вид
E=$d3x(T+V{q>)), G.11)
где явный вид «кинетической» энергии поля Т легко может быть
записан, исходя из вида G.1), однако мы его не приводим. Вмес-
Вместо этого умножим уравнение поля G.7)
j-2 dr \ dr ) г2 Ф Ikp" ~
на г2бф и проинтегрируем по г:
—I Wr\'+6((>2+r26V]dr=0,
G.12)
70
'¦До (f>' =
, отсюда
Е =
+ ^-
+
G.13)
С учетом асимптотики G.3), т. е. ф—^const при г-*-оо, получим, что
энергия расходится линейно, Е-*-<х>, при г-*-оо. В случае фа=бозФ
1 энергии нет члена ф2//-2. Тогда, как уже было сказано,
ф —ехр(—У2т/-) и энергия поля сходится, Е<оо. Как видно, пере-
переход к другой топологии, т. е. от решения с ф°~/-а (п=\) к реше-
решению ф°~баз (п = 0), сопровождается скачком в энергии.
б) Решение Полякова
Как мы только что увидели, решение чисто хиггсовской моде-
модели с ненулевым топологическим зарядом и конечной энергией не
,М0жет быть найдено. Поляков предложил дополнить поле Хиггса
Полем Янга—Миллса, предполагая при этом, что m и К не равны
Нулю. Выбрав анзац
— h)/r2,
G.14)]
Использованный при получении монололя БПС, получим уравне-
уравнения поля
r2h" = h(h2— 1+H.
G.15)
r2f"=2fh2—m2r2f+ (K/g2)f3.
Заметим, что уравнение для h не меняется по сравнению со слу-
случаем Я=0, т = 0. Уравнение для f переходит в уравнение для %
G.8), если положить h=\.
Для однозначного задания решения потребуем, чтобы выпол-
выполнялось асимптотическое условие
r->oo, f-*pr. G.16)
Тогда из первого уравнения G.15) получим, что h при г-*~оо будет
удовлетворять уравнению
r2h" = f2h, G.17)]
откуда
h~erfr. G.18)]
Аналогично G.9) введем новую функцию т), задающую отклонение
/ от асимптотики G.16),
/=pr+gr,. G.19J
Функция г] будет удовлетворять уравнению G.10), в котором
вместо члена 2т/(гЩ будет стоять член
h22m/rfk,
убывающий экспоненциально в силу G.18) при больших г. В этом
случае при г-*-<х> получим
71

откуда
—YT
G.20)
r\~(r-V2mr, G.21)
т. е. в отличие от чистой модели Хиггса, рассмотренной в п. а),
сходимость к асимптотике G.16) обеспечена.
Таким образом, асимптотика решения Полякова выглядит сле-
следующим образом:
Л
р> + С2е~ v* ™ (г -v оо),
G.22)
откуда следует, что отклонение хиггсовского поля от вакуумного
решения, т. е.
= const
„— У 2 т/-
G.23)
имеет вид юкавского потенциала, отвечающего частицам с массой
тч=у2 т, а отклонение от вакуума калибровочного поля, пропор-
пропорциональное h~e~$r, отвечает массе векторных частиц $
Рассмотрим теперь поведение решения в нуле. Положим
() +(), a(i-)-*0, Д|-)-Л G.24)
при г-+0.
Асимптотическое поведение G.24) обеспечивает несингуляр-
несингулярность (т. е. конечность) решения G.14) при г-*-0. Действительно,
подставив G.24) в уравнения G.15), получим в линейном прибли-
приближении
г2а"=2а,
откуда
У=2/,
2, f=bt*,
G-25)
G.26)
где а и b — константы. Связь асимптотик при г-*-оо G.22) и при
г-*-0 G.24), G.26) дается точным решением, которое и опреде-
определяет константы а, Ь, С и С2. Точное решение Полякова не удается
получить в аналитическом виде. Тем не менее можно наглядно
описать характер решения в разных областях изменения г следу-
следующим образом. При /-->-0 отсутствует хиггсовское поле, <р->-0,
однако есть постоянное калибровочное поле, 6%=const, так как
в этой области Ла„~л С ростом г в область г~\\т восстанавли-
восстанавливается поле Хиггса, и при r^>l/m получаем хиггсовский конденсат
|<р|= const, ф||г, т. е.
g<f-+ra§ (г-»-оо) G.27)
ёж Полякова. При г>1/р поле Янга—Миллса выходит на асимп-
асимптотику Aali~l/r, которая соответствует монополю. В унитарной
калибровке в области г-»-оо поперечные компоненты
72
Поглощаются хиггсовским полем, а Л3 — дальнодействующая про-
продольная компонента — проникает через конденсат, Лз~-1/г.
Найдем теперь компоненты тензора поля. Для этого следует
Определить абелев тензор F^. Как уже говорилось ранее, опре-
определение F,,v неоднозначно. Примем теперь для F^, определение,
Данное Тоофтом:
где
G.28)
G.29)"
Заметим, что в нашей подстановке G.14), т. е. при Aia~Eainra,
<pe~ra, Л°о=0
Л„=фоЛа1.=0. G.30)
Найдем абелев тензор поля G.28)
/V=d,A—dAw—А\д^а+Л^фа +
G.31)
+ gZabc(faAvbAvc— (l/g) ф-3eoьcфo^фь?)vфc.
С учетом равенств вида
—АД.Ф— (l/g)ф-3ф(д„«рX (gAvXф)) *= 0
и тождества G.30) получим
Flx,,= — A/?)ЕаЬсфадйфьд»фс. G-32)'
Поскольку ф=г, то
(д,гс) =
G.33)'
Тензор с такими компонентами отвечает, очевидно, монополю с
зарядом gm= —l/g. Как видно, в данной калибровке при А11=0
Монополь возникает за счет поля (р. В унитарной калибровке ме-
меняется топология, т. е. п обращается в нуль, а часть поля ф «пе-
«переходит» в Лц, так что Л^О. Действительно, переходя в унитар-
унитарную калибровку, получим
фа = баз. <Зцф = О,
— ы/ 3
!-&
причем
G.34);
G.35)
Здесь мы получаем, очевидно, те же компоненты потенциала
G.33), отвечающие монополю, однако теперь уже за счет сингу-
сингулярного потенциала G.35).
Покажем теперь, что энергия монополя Тоофта—Полякова ко-
конечна. Раньше было показано, что энергия статического решения
73

может быть представлена в виде
Е=№x[lU(Gair- GaifJ+42dJn],
где Jn = EijnGaif(pa. Для самодуального решения, когда Gaij=Gaij,
энергия минимальна и равна
?min= ХЦ&хдп1п= 42$dSJn. G.36)
Для других решений энергия
?>?m!n=72K"Sn/,, G.37)
При г-
оо имеем Л^,
&Gau=Ft, G.38)
при любом определении тензора Ftj. Поскольку ?<р—»-р, то
?тш = (p/g) ф BrfS = Dn&g) ёт. G.39)
Для монополя Тоофта—Полякова
E>Dnp/g)-l/g=4nmw/g*, G.40)
причем топологический заряд л=1.
Точное значение энергии может быть вычислено на ЭВМ:
E=CDnlg2)mw, G.41)
где С изменяется от 1 до 1,8 при К — от 0 до сю. Если положить
g равным заряду электрона е, то минимальная энергия монополя
равна: ?min=137mvr, т. е. при mw~80 ГэВ Е^>ЕшУа^\ЛЛ^ ГэВ.
Аналогично показывается, что и в модели великого объедине-
объединения (группа SUE)) должны существовать монопольные решения.
Однако их масса оказывается чрезвычайно большой, порядка
1016 ГэВ. Монополь великого объединения, если он существует,
должен проявить себя через воздействие на ядерную материю.
В. А. Рубаков в 1981 г. показал, что монополь катализирует ра-
распад протона, предсказываемый моделями великого объединения
и обусловленный переходами кварков в лептоны.
§ 8. ИНСТАНТОН В КВАНТОВОЙ МЕХАНИКЕ
Динамические решения евклидовой теории полей Янга—
Миллса — инстантоны, так же как и монополи, могут быть
проанализированы на языке топологии. В данном параграфе мы
обсудим прообраз соответствующих решений теории поля в более
простой теории — нерелятивистской квантовой механике.
а) Мнимое время
В квантовой механике есть два мощных метода приближенных
расчетов: метод теории возмущений, т. е. разложение по константе
связи, и квазиклассическое приближение, которое приводит к
неаналитической зависимости решения от малого параметра (по-
(постоянной Планка). В квантовой теории поля метод возмущений
играет большую роль, являясь в квантовой электродинамике ос-
74
[ МОВНым рабочим методом, позволяющим производить расчеты с
ромной точностью. В теории сильных взаимодействий, кванто-
Й хррмодинамике, или КХД, как мы увидим в дальнейшем,
ория возмущений справедлива лишь в области асимптотической
%„ободы, т. е. при больших переданных импульсахГ?*Т1ри малых
Переданных импульсах, т. е. на больших расстояниях, взаимодей-
взаимодействие становится сильным и необходимо применять другие методы.
Одним из них является метод инстантонов, являющийся обобще-
обобщением квазиклассического метода квантовой механики на кванто-
квантовую теорию поля. Прежде чем изучать инстантонные решения в
Теории поля, рассмотрим соответствующие решения в механике.
_ Хорошо известно, что квантовомеханическое проникновение че-
I рез потенциальный барьер описывается амплитудой, которая в
квазиклассическом приближении пропорциональна
ъ
(8.1)
Где а и b — границы барьера,
\p\ = V2m{V-E) (8.2)
Модуль импульса частицы под барьером V=V(x), E — ее энергия.
Сам импульс частицы под барьером — величина мнимая, так как
там V>E:
(8.3)
(V — E),
а это значит, что прохождение под барьером можно рассматривать
как классическое движение в{мнимом времени %=it. 7
В квантовой механике можно рассматривать прохождение
барьера из основного состояния («вакуума») в другое основное
состояние (другой «вакуум») для двойной ямы. Ему соответствует
классическое движение в мнимом времени с энергией Е—0 между
двумя ямами за бесконечный промежуток времени от т=—со до
х= Ч-оо, но с конечным действием. Такое решение называется
инстантоном в механике частицы.
Рассмотрим материальную частицу с массой т=1, движущу-
движущуюся в потенциальном поле V=V(x). Функция Лагранжа этой од-
одномерной системы имеет вид
L = l/2X2—V(x) {x = dx/dt). (8.4)
В квантовой механике ей соответствует оператор Гамильтона
B = p2/2+V(x) {p=—iHd/dx). (8.5):
Уравнение Шредингера
имеет решение
i]> (х\ t") = J К (*", t"; x', Г) ф (*', f) dx -
(*', Г) dx,
(8.7)
75

где
К (х", t"; х, Г) =
(8.8)
функция эволюции, представляющая собой амплитуду перехода
системы из точки х' в точку х" за промежуток времени t"—f.
Используя полный набор собственных функций оператора Н
запишем
K{x",x,t) =
Щп)=Еп\п),
(8.10)
Продолжим К{х", х', t) как функцию t на комплексную об-
область t следующим образом:
it=x
где 1тт=0. Тогда
К(х\х',х) = ?е-^А<*» {п]х')_
(8.11)
(8.12)
Ири х -*¦ оо в сумме существенным оказывается лишь один член п— 0
К(х",х',т)~е-Е°*'п(х''\0) {0\х'), (8.13)
если, конечно, ?0>0 и E0<Ei<E2<...<?)„<.... Согласно Фейнма-
ну [7] запишем амплитуду К(х", х', т) в виде континуального,
или функционального, интеграла (интеграла по путям):
где
=Щ [dx] eis'n,
(8.14)
S = f df
классическое действие частицы, [dx] означает сумму по всем пу-
путям x=x(t), соединяющим точки x'=x(f) и х"=x(t"), N — нор-
нормировочный множитель. Явное определение этого интеграла мо-
может быть дано разными способами (см., например, [7]). Мы вер-
вернемся к этому несколько позже.
Перейдем к мнимому времени it=x. Тогда
Г/2
Tt
-Г/2
76
Г/2
—Т/2
«евклидово действие частицы, т. е. действие, получаемое путем по-
•орота временной координаты t-*-it=x (виков поворот), в резуль-
результате чего в релятивистском случае пространство Минковского пе-
переходит в пространство Евклида (в дальнейшем вместо Se будем
писать просто S).
Теперь можно записать амплитуду перехода в виде
{x"\e-™in\x') = N\[dx\e-sih. (8.16)
Пусть х—х{х) — некоторая функция, удовлетворяющая граничным
условиям х(—7/2)= л:', х(Т/2)=х". Тогда произвольная функция
х*=х(х) может быть представлена в виде суммы
х = гМ4-ГСх.М. (8.17)
где хп — полный набор собственных функций некоторого опера-
оператора, ортонормированных на интервале ¦[—Г/2, Г/2]:
Г/2
J dxxm(r)xn(x) = bmn, (8.18)
-Г/2
В этом случае мера фейнмановского интеграла по путям может
•быть определена-так:
(8.19)
|де коэффициент Bл)~1/2 связан с выбором множителя N.
В квазиклассическом приближении действие S/ft велико из-за
малости постоянной Планка ft. Поэтому основной вклад в интег-
интеграл (8.16) дают «стационарные точки», в которых S имеет ми-
минимум:
(8.20)
es=o, 62s>o.
В явном виде уравнение для «стационарной точки», т. е. стацио-
стационарной траектории будет представлять собой уравнение Лаг-
ранжа
"- = 0, (8.21)
SS
dx dx
dL __ у, (~ч
r
77

или
d2x
Л2
V'(x). (8.22>
Решения этого уравнения минимизируют функционал S. Откло-
Отклонения от стационарного значения представляют собой вторую ва-
вариацию функционала S:
где в силу (8.21)
(8.24>
Условие минимума 62S>0 может быть записано явным образом:
V" (х) 6х
ах2
(8.25>
где е — положительные числа, е>0. Выберем в разложении
(8.17) путь лг(т) в качестве экстремального пути, удовлетворяю-
удовлетворяющего (8.22), функции хп — собственными функциями уравнения
(8.25)
--^хп + Г\(х)хп = гпхп (8.26>
с положительными собственными значениями еп>0.
Тогда
Г/2
S = So + ± J йт 2 Спхп ? emCmxm = So + ±- ? гпС1. (8.27>
—Г/2 m rt
Функциональный интеграл с мерой, определенной согласно
(8.19), сводится к гауссовым интегралам и берется в явном виде:
П J^^So//t = е"8о'П П 6«-1/2 A + О.(Й)). (8.28).
где O(fi) возникает за счет вклада высших неучтенных членов
разложения S — SD + 62S, каждый из которых привносит степень Ч.
Произведение собственных значений есть детерминант операто-
оператора, т. е.
(g
Таким образом
/й [det (_
+ 0{Щ).
(g
78
Заметим, что уравнение (8.22) для х(т) имеет интеграл
42(dx/dxJ-~ V(x) = const=?, (8.31)
[.Имеющий смысл полной энергии частицы во времени тис «пере-
«перевернутой» потенциальной энергией: —V(x).
Рассмотрим случай, когда х'=л:"=0, тогда единственное реше-
вие будет х^О. Для него So=0, и тогда
[ <0|е-нг/й|0) =
=N[det(—дх
tfle @2= V"@)>0. Найдем собственные значения еп:
Xn'fi±T/2)=0.
Решение (8.33) хорошо известно:
t 8п=©2+я2п2/72 (п=1, 2, 3,...).
Тогда
(8.32)
(8.33)
(8.34)
п=\
п=1
Здесь мы выделили множитель для свободного движения, ю = 0:
2я J
/2nftT
Это равенство можно рассматривать как определение нормировоч-
нормировочного множителя N. Оставшееся в (8.35) произведение вычисляет-
вычисляется с помощью формулы
п=1
Поэтому находим
.после чего для амплитуды получим при 7-*- + оо
(8.37)
(8-38)
79

интеграла (8.48) является поведение V(x) вблизи х= ±а. Так,
вблизи х = а
при этом
V(x) = V{a) + {x—a) V'{a) + Vs(*—aJV"(a) =
= 1/2<о8(дс—aJ,
, dx dx
tola —
откуда при х-*-а—0
a—x~e-°>x,
т. e. x-»-a—0 при т->оо. Аналогично при х-> a + 0
х+а~е<ЙХ, t-> oo.
Полное решение определяется интегралом
dx
(8.48)
(8.49)
(8.50)
(8.51)
где хо—т(х=О) — центр инстантона; ширина инстантона во вре-
времени имеет порядок 1/со (рис. 8.2).
т
2
i
i
•m
Т
2 _
Г
-а
Рис. 8.2. Инстантон с центром в т0 Рис. 8.3. Разреженный инстантонный
газ
Рассмотрим характерный пример. Пусть
V(x)=k(x2—a2J,
тогда V"(a)=8Xa2=a2. При Е = 0
—a*)
(8.52)
(8.53)
где знак плюс отвечает инстантону, а знак минус — антиинстан-
тону. Интегрирование (8.53) дает
«2
Уда
2/2Яа
In
а-\-х
а — х
(8.54>
(8.55)
Легко видеть, что это решение при выборе знака «плюс» имеет
бимлтотичеокое поведение типа (8.50), (8.51). Найдем действие
инстантона (8.55). Беря интеграл (8.47), находим
в а
,- {dxVW{x)= [dxV~M.{x2—a2)= —
«в3
12Я
(8.56>
l, Заметим, что если считать частоту со фиксированной, то зави-
вмость So от К обратно пропорциональная, т. е. амплитуда нро-
дения барьера от «вакуума» до «вакуума»
е—So __
(8.57)
|аналитически зависит от константы связи X и не может быть
|эложена по ней в ряд.
Поскольку размер инстантона 1/их^.Т (Г->оо), то можно рас-
1втривать конфигурации с несколькими инстантонами и анти-
[МИСтантонами с центрами в точках ть ...,тп, так что
—Г/2<т„<т„-1<...<т,<7/2.
(8.58>
сдобная ситуация изображена на рис. 8.3, где учтено, что раз-
Вр инстантона мал, и поэтому линия обрывистая. Такая система
стантонов и антиинстантонов называется разреженным инстан-
Внным газом. В силу отсутствия взаимодействия отдельных ин-
Гантонов газа их действия складываются и для полного действия
Меем S = nS0. Возвращаясь к основной формуле (8.30), видим,
'ЧТО помимо экспоненты необходимо вычислить детерминант. Эта
аадача представляет известные трудности и поэтому остановимся
[jlia ней подробнее.
в) Вычисление детерминанта
За исключением малых интервалов вокруг инстантонов имеем
=const= ±a, и тогда V"(±a) =coz. Кроме указанных областей,
|, е. вдали от инстантонов, имеем как бы уединенные ямы, а для
их значение детерминанта известно. Если пренебречь вкладом
гих областей, то в соответствии с (8.39) получим
(8.59)
р. С учетом переходных зон от —а до а или от а до —а получим
другой результат
(со/яАI/2е-«г'М«. (8.60)
• ^Значение множителя А найдем позднее.
83

Полная амплитуда должна содержать вклады всех возможных
значений центров инстантонов. Интегрируя по ним с учетом (8.58),
найдем
Г/2
т,/2
W2
dxn = Jj- (8-61)
-Т/2 — Г/2 -Г/2
Переход из —а в —а происходит при четных значениях п, из —а
Bfl — при нечетных п. Поэтому
01 \ 1/2 „,„^1 1
<— а
" х
четн
п
X A + О (ft)) = (—"I/2 е-иГ/2 ch (Аг*/й Т) A + О (Й)). (8.62)
-Аналогично при нечетных п
(—а\е-тЩа) = (—) m e~aT'2 sh (Aer-s°ih Т) A + 0 {%)). (8.63)
Равенства (8.62), (8.63), очевидно, можно представить в виде
АДГ ДЕГ
2Й +е 2*
пй
А?Г
a) =_L f JL
2 \, ЯЙ
АЕГ
2ft
тде
Поскольку для амплитуды имеем разложение
(8.65
(8.66)
то из соотношения (8.64) получается расщепление уровня п=0:
Р Йш г-» Йш ГД?
!~ 2 1-2~ 2 ~~ 2 '
(8.67)
где Af определяется выражением (8.65). Первое из равенств
(8.64) дает
(8.68)
•а второе —
<-"'»<»->ЧШ.
(8.69)
Достояние, обозначенное индексом 1,
основное состояние, а состояние 2
состояние:
симметричное (четное),
нечетное, это возбужден-
—а)],
—а)],
(8.70)
|^ц()|()
Сделаем теперь оценку плотности инстантонного газа, соот-
соответствующую условию его разреженности. Ранее мы суммировали
?ЯД
п\
Т)п.
«Основной вклад в сумму дают номера п*?Лехр(—Solh)T. Отсюда
-so/ft ^g71^
^Плотность инстантонов п/7" очень мала, так как S0/ft^>l, или
¦*)8/^ft^l. Константа А одинакова для всех инстантонов и поэтому
может быть найдена для какого-либо одного инстантона. Рассмот-
Рассмотрим уравнение (8.26)
—d2xxn+V"(x)xn=EXn, (8.72)
где хп — функции, по которым производится разложение 6х в
(8.17). Рассматриваемая задача обладает одной особенностью,
которая затрудняет непосредственное вычисление детерминанта.
.Дело в том, что уравнение (8.72) имеет нулевое собственное зна-
значение, Ео=О. Происхождение связанных с ним нулевых мод хо
•определяется трансляционной инвариантностью задачи:
6S0=0, (8.73)
т. е. смещение центра инстантона не меняет действия.
1 При этом для вариаций бто действия не только первая вариа-
'ция обращается в нуль, 6So=O, но и вторая вариация также рав-
равна нулю, 62S0=0. Это и соответствует нулевому собственному зна-
значению, 80=0. Какой вид имеет нулевая мода хо(т)? В силу транс-
трансляционной инвариантности вариация х равна
dx
dx
х (х, х0 + бт0) — х (т, т0) = -— бт0 = — бт0,
dxa
dx
(8.74)
где х(х, то+6то) и х(х, то) удовлетворяют одному и тому же ураз-
1Нению
dfx
4т2
= !/'(*)•
(8.75)
=84
85

Поэтому для dx/dx получим
dx2 [ dx
dx
(8.76>
Это уравнение совпадает с уравнением для нулевых мод х0, по-
поэтому xo=cdx/dr. Константа с может быть найдена из условия
нормировки
Г/2 Г/2 _ g
/
X
—Г/2
откуда
-1/2 dx
dx '
(8.77).
Нулевые моды приводят к расходимости детерминанта, в котором ин-
интеграл
Г dCe
J /2ixft
будет расходящимся. Оказывается, что его можно ограничить,
если учесть, что интервал времени Т конечен. Действительно, име-
имеем равенство
Поскольку dx/dxo = O, то
откуда
или
xodCo— -^-dT0 = 0,
dx
x0 x0
Тогда вклад в интеграл по нулевым модам будет равен
(8.78)
(8.79)
В силу конечности интервала §dxo=T интеграл (8.79) оказыва-
оказывается также конечным.
В итоге для одного инстантона получаем
-а)однн =
(8.80)
86
Куда с учетом (8.60) находим константу А:
А = /_5о_\ 1/2 Г det(-a| + M2) 11/2
\2пП) [ tef{i%+V{x)) J '
(8.81)
It штрих означает, что детерминант вычисляется без учета
улевых мод, вклад которых включен в остальные множители
1,81). Для вычисления А необходимо знать потенциал V(x) в
IHOM виде. Вернемся к рассмотренному примеру с потенциалом
'(х)=Ч*2—а2J. Тогда
* = athT (т~то).
(8.82)
поскольку
V"{x)= —4
уравнение на собственные значения запишется следующим
Эразом:
интересуют
словию
dx* n ¦ \ 2 2
решения этого уравнения,
хп(±Т/2)=0 G"->оо).
п = гпхп. (8.83)
удовлетворяющие
(8.84)
(8.83) имеет вид уравнения Шредингера для частицы,
кущейся по оси т в потенциале У(т)=со2 (o2ch~2-^-.
известно из квантовой механики [6], при заданных в (8.83)
Начениях параметров имеются лишь два «связанных состояния»
«энергией» бо=О (это нулевая мода, рассмотренная выше) и
1"=3/4(о2. Для остальных мод е>ю2. Для них имеем при т->- ±оо
Хр~е±'Рг, Р = Уер—со2. (8.85)
!Квк известно (см. i[6]), квантовое число р изменяется непрерыв-
непрерывно, причем при тех значениях параметров, которые входят в урав-
уравнение (8.83), отраженная волна отсутствует. Поэтому более точно
условие (8.85) следует записать так:
"!ГДе
1 — tp/ш 1 — 2ф/ш
(8.86)
(8.87)
"Условие (8.86) определяет одно из двух линейно независимых ре-
;Шений Х=хр(х). Второе решение Y=xp(—т). Общее решение
х^=Сххр (т) + С2хр (—т).
(8.88)
87

Наложим условие (8.84), тогда
Сххр (Г/2) +С2хр (-Г/2)= О,
ClXp(—T/2) + C2xP(T/2)=0.
Эта система имеет ненулевые решения С\Ф0, С2Ф0, если
ХрЦТ/2)-хРЦ-Т/2)=0,
хр(Т/2)= ±хр(-Т/2).
Поскольку Г-voo, то из (8.86) и .(8.90) получим
(8.89)
откуда
(8.90)
или ipT—ibp=inn (я=0, 1, 2,...), причем Ер=со2+р2. Таким
образом,
ЛЯ + бр
Т
(8.91)
Теперь необходимо вычислить
с»
п-
п=0
(о2 + («я/ТJ
(8.92)
Заметим, что знаменатель в этом выражении относится к осцил-
осциллятору, для которого 6р = 0. При этом необходимо учесть, что ну-
нулевую моду ео=О мы уже исключили, а значение ei=3/4«2 выде-
выделено из произведения (8.92). Поэтому в знаменателе (8.92) пер-
первые два сомножителя должны быть исключены, но их вклад мал,
поскольку, как мы сейчас увидим, основной вклад дают большие
п>1
>
Действительно, ширина инстантона мала, (аТ^>\, так что
главный вклад в произведения должны давать сомножители но-
номера п~а>Т^>Т. Тогда будем иметь
П
Ы--Г- (nn/TJ CAFZmi w2T2 + n2n2
n n
Заменяя сумму интегралом, последнее выражение приводим к виду
ехрР-f
где мы провели интегрирование по частям и учли, что согласно
(8.78) 6р@) =6р(оо) =0. Принимая во внимание значение произ-
производной фазы, определенной в (8.87),
rfP 1 +>2/ш2 1 + 4р2/ю2 '
88
чучим
п
= ехрГ ?-(л1п2 + д1пЗ/2I =-±-.
образом, окончательно для множителя Л получим значение, в
ipoM учтена мода Ех^?"9-
л =
2лй
3/4
nA
Считывая, что So = (co3/12A,), для сдвига энергии найдем
AE = 2tiAe~Soln='.
Ц Значение, согласующееся с известным квазиклассическим выра-
;(|;*Ж!ением.
Мы привели все основные этапы расчета инстантонного вклада
' В амплитуду перехода в квантовомеханической задаче о двойной
*Йме. Эти же характерные особенности встречаются и в теории
.„¦ 'Калибровочных полей при вычислении инстантонного вклада в
li' амплитуду перехода «вакуум—вакуум» (см. ниже, а также более
подробное изложение, приведенное, например, в работе i[14]).
§ 9. ИНСТАНТОНЫ БЕЛАВИНА, ПОЛЯКОВА,
ШВАРЦА И ТЮПКИНА (БПШТ)
Прежде чем искать инстантонные решения в теории по-
полей Янга—Миллса, приведем некоторые топологические сообра-
соображения, обобщающие соответствующие понятия, введенные ранее
в связи с монополями, на область евклидовой четырехмерной тео-
теории поля.
а) Топологический заряд
Перейдем от теории поля в пространстве Минковского к евкли-
евклидовой теории поля, определенной в пространстве с евклидовой
.метрикой. Этот переход может быть осуществлен путем поворота
на комплексной плоскости переменной хо и соответственно на
плоскости ро, так что
Х0-^> 1X4,
(9.1)'
-Ро2—Г
—Р?2= —
рх
xp.
89

В теории поля, так же как и в квантовой механике, нас инте-
интересуют решения с конечным действием, причем заданные в об-
области с размерами г = ^х|->оо*_ Заметим сразу же, что для
сходимости интеграла
не обязательно условие
точно, чтобы при
при г->оо, т. е. Л=^1/г. Доста-
Доста. (9.2)
8 g
т. е. потенциал превращался в чистую калибровку, тогда C^=0
при г-»-оо, и действие оказывается конечным.
Условие (9.2) представляет собой отображение сферы Sx3 на
групповое пространство калибровочной группы. Для группы
5GB) пространство параметров представляет собой сферу в
4-мерном пространстве
т. е. сферу Si3. Таким образом, в случае SUB) группы (9.2) за-
задает отображение Soo3->Si3. Если это отображение однократно, то
(9.2) характеризуется топологическим зарядом п=\, если дву-
двукратно, то п—2 и т. д. Следует, конечно, вывести аналитическое
выражение для топологического заряда. Однако прежде всего
рассмотрим более простой случай однопараметрической группы
U(l). Для S1-»-^1 имеем стандартные отображения
со<о)F) = 1, са<1>(в)=е|в,...,
(9.3)
са<")(в)=е&'в=|[са<1)(в)]в.
Другие отображения получаются непрерывной деформацией дан-
данных, образуя гомотопические классы. Определим топологический
заряд следующим образом:
2л
Vd6. (9.4>
Для со = ехр(ш6) имеем
2л
— Г d№ne (— in) е~ш = п,
(9.5)
т. е. топологический заряд (9.4) действительно соответствует крат-
кратности отображения в случае (9.3). Покажем, что определение
(9.4) инвариантно относительно непрерывных деформаций. Для
* В дальнейшем в этом параграфе мы будем опускать индекс Е у квадрата
евклидова вектора: xEz=xz.
90
|>инитезимальных деформаций
6со = г'6^со, (9-6)
Не &% — бесконечно малая действительная функция, заданная на
руге. Тогда
= 0, или n=inv.
Од '
(9.7)
Известно, что 1/A) — группа инвариантности электромагнит-
|;.^,го поля Максвелла, которое определяется через потенциалы А„.
Г Рассмотрим двумерное евклидово пространство, Л^= (Ль Л2)
$,(ц=1, 2). Тогда условие
Atlr-»»-*—содцю-1, (9-8)
g
|, задает отображение одномерной сферы S»,1 на
VСферу Si1, т. е. единичный круг группы U(l). Введем величину
*"' ~ — ев,А, (9-9)
2л
Тогда при r->-oo
rjSp =/rM,eM,Hv = г (г1А2—?2А1) = г (cos 6Л2—sin 6Лг) =
= г — со I cos 6 sin6 со = — со со~'.
g \ ду дх J g dQ
\ Поэтому топологический заряд (9.4) может быть записан в виде
2л 2Я
(9.10)
., т. е. выражен непосредственно через компоненты поля при г-*-оо.
Ш Воспользуемся теоремой Гаусса в двумерном случае и преобра-
f зуем (9.10) к виду
п=gJ сРхд^ = -М-
где G(lv=CHv—dvA» — тензор поля в двумерном евклидовом
пространстве.
¦ Рассмотрим теперь группу SUB). Общий элемент группы
имеет вид
91

©=fll—iba, (9.12)
где о= (сь а2, аз) — матрицы Паули, I — единичная 2х2-мат-
рица,
a2 + b2=l. (9.13)
Таким образом, из (9.12) видно, что групповое пространстве
SUB) — это трехмерная единичная сфера Si3. Равенство (9.12)
может быть переписано с учетом (9.13) в виде
m__5i+'"ftt_j (9J4)
где х= (xi, X2, х3, х^) — вектор действительного евклидова прост-
пространства, причем
Если отождествить вектор х с вектором координат евклидова
пространства, в котором задано калибровочное поле А11(х), та
асимптотикой
gAy, (х) | х^оо -> — idy/aur-» (9.15)
осуществляется отображение сферы координатного пространства
Soo3 на сферу Si3 группового пространства, причем с единичным
топологическим зарядом. Очевидно, что (9.14) есть обобщение
отображения co = exp(i6) в случае группы f/(l). Легко показать,
что (9.14) допускает другую параметризацию, если перейти к
углам вектора х. Для этого перепишем (9.14)
здесь
= cos 6 + i (an) sin 6 = exp [i (an) 6]; (9.16)
д
n=x/|x| — единичный вектор в 3-мерном пространстве, заданный
углами •& и ф, а
3 = arctg
Стандартное отображение кратности п имеет, очевидно, вид
где
=~Т Iх* +l
(9.18)
= соF, Ь, Ф). (9.19)
Вместо углов 6, Ф и ф для параметризации могут быть взяты
также углы 8i, 62 и 6з согласно определению
?о'1)=(о(е1, е2, е3)=е 2 е 2 е 2 =«ов(в„)«»1(е1)©1(е1),
(9.20)
т. е. эти углы играют роль «углов Эйлера».
92
Введем теперь топологический заряд
da=dldQa. Покажем прежде всего инвариантность п относи-
относительно преобразований гомотопии. Для инфинитезимальных де-
* эрмаций
6 (ТТ (9.22).
'{ГДе № — параметры деформации, Та — генераторы. Варьируем
гпользуя последнее равенство, после интегрирований по частям>
(подстановки обращаются в нуль, так как интегрирование ведется
сфере) с использованием инвариантности следа относительно*
Циклических перестановок получим:
с tr
= о
силу полной антисимметрии тензора еаьс- Таким образом, числа
f"n — инварианты группы гомотопии. Они характеризуют отдель-
,| ные гомотопические классы, на которые разбивается множество
^'Отображений. Рассмотрим частный случай (9.20) и покажем, что>
? Интеграл в правой части (9.21) действительно определяет единич-
Оиый топологический заряд.
Вычислим вначале величину
-1/
= tr [и, F3) «2 (е2) со3 (бг) а^г1 (ej а^1 (б2) а3шг F3)]; (9.23>
здесь
2
Поэтому вместо (9.23) имеем
(i/2f tr (а3ша F2) 1
Легко показать, что
= -f tr (
COS 62
(9.24)
93

Окончательно имеем
Для величины
г1) —lU sin 62.
(9.25)
(9.26)
вместо (9.24) получим
(i/2) 3tr @2030JF2) 03CD2-1 F2)) -
Как видно, перестановка производных di**=d2 приводит к переста-
перестановке матриц Паули ОгОз-»-ОзО2= —ОгОз, т. е. к изменению общего
знака. Таким образом, (9.26) отличается от (9.23) знаком, и во-
вообще, очевидно, перестановка двух соседних индексов у величины
tr(oMc<B~1(o5b(o"(o^cO)~I) (9.27)
ведет к изменению ее знака. Если добавить циклические переста-
перестановки индексов, которые не меняют знак следа, то получим всего
шесть комбинаций индексов. При этом свертка с антисимметрич-
антисимметричным тензором Еаьс в (9.21) даст шесть одинаковых членов (9.25).
Таким образом, правая часть определения топологического заря-
заряда (9.21) для со = о)A) будет равна
2 —L- • 6 ~ Г d%1 Г dQ2 O'd63 sin в, = 1; (9.28)
здесь множитель 2 возникает за счет того, что мы учитываем воз-
возникающие вследствие двузначности представления (9.20) несоб-
несобственные вращения, а интеграл по углам дает 2я • 4зт = 8зт2. Следо-
Следовательно, п=1, т. е. формула (9.21) действительно определяет то-
топологический заряд в данном случае. Справедливость (9.21) в
общем случае (о(п) доказывается на основе группового свойства
о)(") = (o(ni)G)(), п = пх + п2- (9.29)
Для этого, используя инвариантность интеграла (9.21), деформи-
деформируем оУ"^ и о)("г) так, чтобы на верхней полусфере (о(п«> = 1,
а на нижней полусфере af"^ = l. Тогда становится очевидным,
что интеграл (9.21) дает сумму п\ + пч, которую мы и отождеств-
отождествляем с п.
Формула (9.21) дает выражение топологического заряда через
калибровку о)(п). Выразим теперь топологический заряд непосред-
непосредственно через напряженность калибровочного поля. Рассмотрим
для этого интеграл
Jd^GvGV (9.30)
по всей 4-мерной области пространства Евклида, в которой за-
заключено поле. Подынтегральное выражение можно привести к
виду
' ЧЬ (9-31)
вйствительно,
цесь мы учтем следующие тождественные равенства:
аЛ|3 = U.
}«ким образом, согласно (9.31) получаем 4-дивергенцию
(9.32)-
(9.33)-
оскольку в силу свойств матриц Паули имеем
tr
= tr ±
= -L А«Аар,
1
tr AvAaAp= -L tr lpaaboc
8
= №)
Ш G|t=4eMvaptr(Av5aAp+B/3f)gAvAaAp). (9.34)
гИнтеграл по объему (9.30) с помощью теоремы Гаусса можно
р-Иреобразовать в поверхностный интеграл по границе объема, ко-
которую мы будем считать расположенной в бесконечности, напри-
иа сфере x2->oo:
GudS». (9.35).
*г-»оо
Пусть при х2->оо потенциал А„ переходит в чистую калибровку
со-^-^-0K^-1. (9.36>
—
6
Удобно выделить в величине G^ (9.34) тензор поля
GaP = daAp-dpAa + (g/i) [Aa> Ap]:
tr Av [-y Gap-fe/2i) (AaAp-ApAa)
+ Bg/3i) AaAp] = 2e[imP tr Av (GaP-
(9.37>.
•94
95

При xz->oo в соответствии с (9.36) имеем
1 1 1
1*1'
и поэтому
Следовательно, только второе слагаемое в круглых скобках
{9.37) дает ненулевой вклад в интеграл, и мы получаем
(9.38)
Заметим, что дйю = (djd^daa и
dSvE^dSadaBbdtQc = decd6bdec. (9.39)
Тогда в силу доказанной выше антисимметрии следа (9.27) по-
получим окончательно
'-1). (9.40)
Нам удалось, таким образом, выразить интеграл от полевых
переменных GV^V по объему координатного пространства через
интеграл от калибровочных переменных по объему группового
пространства группы SUB). Правая часть полученного равенства
(9.40) выражается через топологический заряд (9.21), характе-
характеризующий кратность отображения, и мы получаем новую формулу
для топологического заряда в виде интеграла от полевых пере-
переменных
л = (?2/32я2) jd4xGv6%. (9.41)
Рассмотрим теперь действие калибровочного поля в евклидо-
евклидовом пространстве
S = 4Jd*x(G\vJ. (9.42)
Перепишем тождественно
S = -L
где
= 7 + \dfixD,
d*x (Gam
(9.43)
(9.44)
(9.45)
1ричем здесь учтено, что в евклидовом пространстве (GVJ —
Г*| (Cr°,lvJ- Поскольку второй интеграл в (9.43) в силу равенства
| F.45) выражается через интеграл по граничной поверхности, на
[Которой вариации поля равны нулю, то он не варьируется
О (9.46)
I И мы получаем
(9.47)
Для самодуального поля Gav.v=GaliV имеем Т=0, и поэтому 6S = 0
Тождественно, т. е., как уже было показано ранее для случая
Пространства Минковского, самодуальное поле тождественно удов-
удовлетворяет уравнениям поля. Очевидно также, что поскольку Тэ>0,
То из всех конфигураций поля с заданными граничными условия-
Ми самодуальное поле обладает наименьшим действием.
Граничные условия (9.36) разбивают поля на характеристиче-
характеристические классы с определенным топологическим зарядом, при этом
для данного класса топологически эквивалентных полей
Jd*xD = inv=(8n*/ga)n. (9.48)
Таким образом, в заданном характеристическом классе полей то-
топологический заряд определяет минимальное значение действия,
достигаемое лишь для самодуального поля:
S>Smln= Jd*xD= (8я2/?2)п. (9.49)
Заметим, что в случае антисамодуального поля Gavx= —0%,
справедливы аналогичные выводы, причем вместо п следует пи-
писать |л|.
Подойдем теперь к вопросу с другой стороны. Правую часть
равенства (9.41) можно представить в виде
(g2/32n2)Sd4xGvGv= (ga/32n2)JdSllGB, (9.50)
Если Gv на пространственной бесконечности обращается в нуль
G.-+-0. г-^оо (i=l, 2, 3), (9.51)
то
^ J d3xG0 {t i) — J d3xG0 (t2),
где t\ и <2 — значения временной компоненты хц на граничных
времениподобных гиперплоскостях. Введем величину
2/322)Jd8G@, (9.52)
(9.53)
тогда согласно (9.41) получим
Используя асимптотическое условие gA= —idatar1, получим для
q(t) представление
Я @ = fe/24n2) j d**e?/ft
-96
4 Калибровочные поля

= A/24л2) j <Pxellk
(9.54)
где di^d/dxi и т. д., i=l, 2, 3.
Условие &Л^> idcccr1 есть определение классического ва-
вакуума калибровочных полей. При t-> +оо и t^> оо топологиче-
топологическая структура вакуума может быть различной, отвечая различ-
различным целым значениям топологического заряда q( + <x) и q(—оо)
(9.54). Топологический заряд инстантона согласно (9.53) пред-
представляет собой разность топологических зарядов вакуумов
n = Aq = q{—оо)
(9.55)
Таким образом, аналогично квантовой механике инстантонное ре-
решение описывает туннелирование между двумя вакуумными сос-
состояниями калибровочных полей в евклидовом пространстве с
мнимым временем.
б) Самодуальный инстантон
Будем искать самодуальное (антисамодуальное) решение
евклидовой теории полей Янга—Миллса, удовлетворяющее асимп-
асимптотическому условию
т. е. отвечающее топологическому заряду п=\.
Рассмотрим анзац
где F(x2) — некоторая неизвестная функция, такая, что
const -х2, х2
(9.56>
(9.57)
(958)l
Эти условия обеспечивают выход решения на асимптотику (9.56),.
а также его конечность при х2->0. С учетом определения ш полу-
получим для компонент потенциала
следующие равенства:
Да— z
Л4— ¦
2 F (х2)
Ха>
Ai ~ \VaiXi +" Eaikxk)-
Удобно вместо F ввести новую функцию ф=я[з|
(9.59)
ty(x2) так, что
(9.60>
тогда daty^sdty/dxa^12xaty'=2xaF(x2)/x2 и т. д.
При этом вместо (9.59) получим следующие выражения для по-
потенциалов:
98
г частности,
Ло2=—
(9.62)
=б2г1з и т. д.
Электрические и магнитные компоненты тензора поля опреде-
определяются в евклидовом случае согласно равенствам
Ena=G%n, Bna= — ll24iinGaih (9.63)
[Тогда
(9.64)
(9.65)
|Пусть ?i1 = 6i1, т. е. ищем самодуальное решение, тогда
«Поскольку ф зависит от х2, то
|'Ц вместо (9.65) мы получаем
(Х42 + X!2—Хз2—Х22) Ч>" = (Х22 + Хз2-Х42-Х!2) l]/2,
«ткуда
у" = —^'2. (9.66)
Решением этого уравнения будет
ф/^ + а*)-!, (9.67)
Где а2 — произвольная константа. Таким образом, согласно
(9.60) имеем
Причем а2 необходимо считать положительной величиной, тогда
решение будет несингулярным. Кроме того, условия (9.58), оче-
очевидно, также выполняются. Что касается других компонент тен-
тензора поля, то можно легко показать, что все отличные от нуля
Компоненты (Bia~Eia~6ai) равны между собой:
?„й = Бп° = 6аП4а2/(х2+а2J. (9.69)
Полученное решение является самодуальным. Антисамодуальное
решение получим, потребовав, чтобы Ef— —В,-°. Оно будет отли-
отличаться от полученного (9.59) и (9.68) изменением знаков у функ-
функции F (х2) в (9.68) и знака перед eaik в (9.59).
Таким образом, инстантонное (антиинстантонное) решение,
•отвечающее единичному топологическому заряду, имеет вид
Аа.---и— Ха ¦ (9.70)
g
-t- a2
99

g *2 + a2
Коротко решение (9.69) может быть записано с использованием
тензора т]С(ге, определенного согласно равенствам:
«Wv. |A, v= 1, 2, 3;
—6aV, |A = 4; (9.71)
6«u. v=4.
Тогда вместо (9.70) получим
где a — размер инстантона.
Антиинстантон получим, заменив тензор r\a,xv тензором *
«W M. v= 1. 2, 3;
6av. М-= 4;
(9.72)
(9.73>
В силу однородности пространства в качестве центра инстантона
может быть выбрано не только начало координат х=0, но и лю-
любая другая точка х=х0. Поэтому в общем случае для инстантона
с центром в точке х0 запишем:
gAf = 2t]^v (х—х0 у [ (х—х0) 2+а2]. (9.74)
Полученное решение отвечает единичному топологическому заря-
заряду, что следует из явного вида отображения to = coA) и асимпто-
асимптотического условия при х2-»-оо. Поучительно тем не менее непос-
непосредственно вычислить объемный интеграл, через который выража-
выражается топологический заряд:
H ' (975>
Поскольку инвариант, стоящий под знаком интеграла, равен
ЕпаВла, то с учетом значений компонент поля, полученных выше,,
найдем
п=-
з г
16а4
8л2
00 00 2Я О=
00 0 0 —00
оо 2л
=AJdppJdp-
IK
(9.76)
* Ковариаитный вывод иистантона БПШТ, основанный на использовании
тензора r\aixv, можно найти в [14].
100
ЯЯ инстантона (Епа=Впа). Соответственно для антиинстантона
Vе —Впа) получим п= —1.
Инстантонные решения евклидовой теории поля, как уже было
Казано, играют существенную роль в оценках функциональных
Нтегралов для амплитуд квантовых переходов, поскольку они ми-
НЦШИзируют классическое действие. Мы вернемся к обсуждению
IKX роли в современной теории калибровочных полей в последую-
последующем изложении.
Глава II
СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
В современной калибровочной теории исходные частицы,
§Ходящие в лагранжиан, предполагаются безмассовыми. Это га"
рантирует перенормируемость теории. Массу частицы приобретают
! (благодаря механизму, основанному на спонтанном нарушении
| симметрии, свойственной лагранжиану, в решениях уравнений для
|, Волей. В первой главе мы обсуждали это явление с позиций
Классической теории поля. Здесь мы снова возвращаемся к нему
' ,С тем, чтобы представить его в наиболее удобном для последую-
последующего применения виде.
§ 10. ТЕОРЕМА ГОЛДСТОУНА
Прежде всего обсудим случай глобальной симметрии,
Нарушение которой сопровождается появлением новых частиц —
Голдстоуновских бозонов, не обладающих массой.
а) Дискретная симметрия
Для того чтобы лучше понять явление спонтанного нарушения
симметрии, обратимся вначале' к наиболее простой модели дейст-
действительного поля ф=ф(?, х) в двумерном пространстве-времени:
x»=(t,x), ^1 = 0,1.
Лагранжиан модели выберем в виде
Я = Ч2(*Ф) (ад-Уа^-УДФ4, (ЮЛ)
где имеется самодействие поля Яф4/4 такого же типа, что рассмат-
рассматривалось в гл. I. Этот лагранжиан инвариантен относительно дис-
дискретного преобразования
"*, х).„ A0.2)
Квантовое рассмотрение спонтанного нарушения этой симметрии
удобно начать с упрощенной задачи, которая возникает, если заме-
заменить непрерывное распределение поля ф(?, х) дискретным:
A0.3)
101

где t=l, 2, .... N — конечное число точек, в которых сосредоточи-
сосредоточивается поле ф. Таким образом, мы переходим от квантовой теории
поля к квантовой механике системы с N степенями свободы. Функ-
Функция Лагранжа поля, заданная интегралом
Г1= fdxj?(q>, дцф), A0.4)
переходит в сумму по дискретным точкам,
почку:
образующим некоторую це-
це(Ю.5)
где p;2=
Этой функции Лагранжа отвечает оператор Гамильтона
1=1
(ia6)
где помимо квадратичных членов и членов порядка q^, соответст-
соответствующих нелинейным осциллятором, имеется еще член a~z(qi—qt-iJ,
который приводит к связи осцилляторов между собой и к распро-
распространению колебаний вдоль цепочки.
Обсудим свойства основного состояния системы с оператором
Гамильтона A0.6) в зависимости от величин параметра р2. Пусть
Х>0, иначе система не имела бы связанных состояний. Вначале
уберем связь осцилляторов, т. е. последний член в A0.6). Тогда
получим набор нелинейных (ангармонических) осцилляторов с по-
потенциальной энергией
У{Я) = Ч2&Я*+1М.?. (Ю.7)
Пусть рг2>0. Тогда потенциальная энергия монотонно растет с рос-
ростом q и имеет абсолютный минимум при q = qm=O. В этом случае
задача может быть решена по теории возмущений по параметру К,
причем в качестве невозмущенной задачи следует взять гармониче-
гармонический осциллятор с потенциальной энергией Угр2?2. Этот подход
хорошо известен и не дает нам ничего принципиально нового (см.
рис. 10.1). Пусть теперь р2<0. Тогда потенциальная энергия имеет
два симметричных минимума
Vmia=V(qn) = — F4/4A A0.8)
при значениях аргумента
Чпля= ± V — ?Д- (Ю-9)
Точка q — Q соответствует локальному максимуму V(q).
Параметр р2 определяет ширину и глубину ям. При малых
р2<0 основное состояние мало отличается от случая ^2>0. Волно-
102
Ц функция основного состояния симметрична (четная функция),
уровень ?о>О. В этом случае ямы неглубокие, близко располо-
кные друг к другу. Между ямами происходят быстрые осцилля-
и поэтому расщепление уровней велико: следующий возбуж-
Рис. 10.1. Яма при цЪ-0
Рис. 10.2. Двойная яма_ при
(х2<0. Случай малых |цг|
ениый уровень, отвечающий нечетной функции, расположен дале-
D от Ео (рис. 10.2). С ростом |р;2| переходы между ямами стано-
становятся более медленными, так как глубина ям увеличивается, а рас-
/втояние между ними растет. В этом
Случае расщепление уменьшается,
'•ff e. первый возбужденный и основ-
¦Ой уровни становятся близкими,
Пм ?о>О. В пределе очень боль-
ftymx. |p2| получаем почти незави-
независимые ямы, так что частица очень
я|ц>лго находится в одной из ям, не
просачиваясь в другую. Возникает
рЫрождение по четности, т. е. уров-
ЯИ, отвечающие четному и нечет-
нечетному состояниям, сливаются (рис.
10.3). Ясно, что подобное поведение
Проявляют все осцилляторы с но-
Рис. 10.3. Двойная яма при
(х2<0. Случай больших |(х2|
Проявляют все осцилляторы с пи-
Мерами i=l, 2,.., N, причем в отсутствие связи они располагают-
располагаются равновероятно в правой или левой ямах. При включении связи
возникает дополнительная энергия, поднимающая основной уро-
уровень:
A0.10)
Л? минимальна, если {qi)~{qi-i), а поскольку при больших |р?|
частицы долго «сидят» в одной из ям, то основное состояние систе-
системы связанных осцилляторов характеризуется тем, что все осцил-
осцилляторы занимают один и тот же минимум, например левый. Тем
самым возникает ситуация, когда системе энергетически выгодно
103

находиться в состоянии, нарушающем исходную симметрию га-
гамильтониана (четность), — спонтанное нарушение симметрии. Это
явление возникает вследствие связи осцилляторов, объединяющей
их в макроскопическую (при больших N-^oo) цепочку. В задаче об
одном осцилляторе просачивание из одной ямы в другую симмет-
ризует волновую функцию, а в задаче о системе независимых ос-
осцилляторов даже при слабом просачивании система симметрична
из-за случайности выбора ям. Для системы связанных осциллято-
осцилляторов, как уже было показано, оказываются занятыми ямы с какой-
либо одной стороны. При этом квантовомеханическое туннелирова-
ние оказывается особенно затруднительным, так как показатель
экспоненты в амплитуде просачивания содержит макроскопический
параметр — длину цепочки. Действительно, потенциальная энер-
энергия одного осциллятора в минимуме равна
После суммирования по всем осцилляторам получим
N
—>-f=-tiJt-
A0.12)
eJ — Na — макроскопическая длина цепочки.
!Таким образом, непрерывная система (поле) в отличие от дис-
дискретной (механической) системы может находиться в состоянии со
спонтанно нарушенной симметрией.
б) Непрерывная симметрия
Рассмотрим модель скалярного поля с лагранжианом
2>= V2@"ipf) (дд>0—V(q>). A0.13)
где ф,- (t=l, 2,...) принадлежит некоторому представлению группы
G внутренней симметрии размерности dim G=N, причем V — функ-
функция ф,-, симметричная относительно преобразований группы G. Это
означает, что
bV =
A0.14)
где Tif — матрица генератора группы в ф-представлении, 6а —
параметры группы (с=1,..., N). Из последнего равенства следует
условие симметрии
= 0 (с = 1, ...,N). (Ю-15)
Для дальнейшего удобно продифференцировать это условие по ф^:
¦7ГГ-Ям + -?-Г»=Ь A0-16)
лф/5фй дф?
Спонтанное нарушение симметрии происходит при условии, что
104
/(<р) имеет минимум при ненулевых значениях ф2 =
ev """ ¦
т. е.
A0.17)
I
f цч |ф
Причем матрица М2 неотрицательна (ее собственные значения не-
неотрицательны, detM2>0). Разложим теперь V(q>) вблизи миниму-
Мй
Тогда
A0.18)
¦Заметим, что константа Vo не имеет значения для динамики систе-
системы, и мы ее опускаем. Матрица М2 имеет смысл матрицы квадра-
квадратов масс. Вернемся к уравнению A0.16). В минимуме A0.17)
;имеем
(M*)ife7\ifi = 0 (a = l,2 JV). A0.19)
['Вектор v= (vu ..., vn) может быть инвариантом подгруппы Я груп-
группы G(HczG) размерности dim Я= iV<JV. Тогда
7?/о| = 0 (а=1. ...,JV), A0.20)
Где Т° —генераторы подгруппы Я, образующие ее алгебру Ли.
1 В этом случае матрица (М2)гь имеет N—ft нулевых собственных
Значений
||(M2)ifc|| = diag(?,i, Xz,...,In, 0.....0), A0.21)
В остальные ft уравнений в силу A0.20) тривиально удовлетво-
удовлетворяются и им соответствуют ft, вообще говоря, ненулевых собствен-
собственных значений Я,*. Это означает, что из общего числа N степеней
Свободы системы N—ft отвечают безмассовым скалярным частицам.
Эти частицы называются голдстоуновскими бозонами. Остальные
.fl частиц массивны, им отвечают ' положительные собственные
Значения матрицы (М2)гь. Доказанное утверждение можно сфор-
сформулировать ввиде теоремы носящей, так же как и безмассовые
частицы, имяТолдстоуна, автора этой теоремы:
Каждому генератору спонтанно нарушенной симметрии соответ-
соответствует безмассовая частица, носящая название — голдстоуновский
бозон/?
Заметим, что с физической реализацией условий теоремы Голд-=
стоуна мы встречаемся в явлении сверхтекучести жидкого гелия.
Квазичастицы жидкого гелия — фононы, или кванты звука, соот-
соответствуют голдстоуновским бозонам в теории поля. Соответствую-
Соответствующая теорема о существовании бесщелевых возбуждений в случае,
когда система обладает только короткодействующими силами,
была доказана Н. Н. Боголюбовым в 1961 г. («1/<72-теорема»).
в) Модель пиона
Рассмотрим в качестве примера применения теоремы Голдстоу-
на модель с лагранжианом -,
105

<Pvac =
A0.24)
' 27 = 1/2(*фгJ-((х2/2)фB-(Л/4)(фг2J^ A0.22)
где фг — действительное скалярное поле, осуществляющее пред-
представление группы SO D), в 4-мерном групповом пространстве (?=
= 1,2,3,4). Заметим, что группа SOD) имеет размерность dim G = 6.
Минимум У(ф) = ((х2/2)фг2—(К/4) (фг2J достигается при
Фг2=—fx2A>0 (fx2<0). A0.23)
Таким образом, пространство вакуумов представляет собой сферу
в 4-мерном пространстве i?4. Выберем вектор вакуума в виде
0
0
о
v,
Вектор фуас инвариантен относительно преобразований первых трех
координат, т. е. относительно поворотов группы H—SUB). Для
этой группы dim# = 3. Поэтому в обозначениях предыдущего раз-
раздела можно записать
N=6, #=3, N—Я=3. A0.25)
Согласно теореме Голдстоуна трем генераторам нарушенной сим-
симметрии (N—N = 3) отвечают три голдстоуновских безмассовых бозо-
бозона ix1, я2, я3 и один массивный бозон а. Рассмотренная система
полей может служить моделью пиона, который, таким образом,
оказывается голдстоуновской частицей. _
Продемонстрируем явным образом справедливость теоремы
Голдстоуна для данной модели. Группа SO D) имеет шесть гене-
генераторов Тц= —Тц. В векторном представлении получаем для них
следующие матричные элементы:
(Тц)ы= — tFtt6it—баб»), A0.26)
где ?, /, k, /=1,2,3,4. Обозначим \ерез 1ц генераторы подгруппы
H=SUB), где i, /=1, 2, 3. Остальные генераторы обозначим
Кг=Тц (?=1, 2,3). Это генераторы нарушенной симметрии. Поле ф
удобно параметризовать следующим образом:
0
0 I' A0-27)
v + aj
где Пг{ — 1, 2, 3) и ice —¦ новые компоненты поля, заменяющие собой
<Рг (?=1,2,3,4). В линейном по я* и <т приближении вблизи ваку-
вакуума v получим из A0.27):
106
дедовательно, в линейном приближении
ф:
A0.28)
|/ Теперь можно в том же приближении с учетом A0.24) записать:
^ L(^+(t>+tfJJ^const + tf(—\?v—
Опуская несущественную константу и пренебрегая членами высших
Морядков, получим
2' = 1/2(aoJ+V2RixiJ-|n2|a2. A0.29)
(
Кик видно из этого лагранжиана, масса зх-частицы, действительно,
^называется равной нулю, тп = 0, а масса о-частицы то=>л2|ц.21.
Рассмотренная система полей может служить моделью пиона
•^¦«(я1, я2, я3), который, таким образом, оказывается голдстоунов-
*ким триплетом в группе SUB), возникающим в результате спон-
спонтанного нарушения группы SO D). При этом следы исходной выс-
^цей симметрии заключены в отброшенных членах более высокого
Порядка, которые могут рассматриваться как взаимодействие.
§ 11. МЕХАНИЗМ ХИГГСА
Перейдем теперь к изучению спонтанного нарушения
локальной калибровочной симметрии, которое приводит к воз-
возникновению массы частиц. Для простоты рассмотрим пример
локальной SO (n) -симметрии. Ее генераторы, так же как и в пре-
предыдущем параграфе, можно нумеровать двумя индексами;
Тц=—Тц (?, /=1, 2,...,п). A1.1)
Ясно, что число независимых генераторов равно
7A)
107
где учтена антисимметрия 7"^ по индексам ?/.

Таким образом, размерность группы G=5O(n), равная числу
ее параметров, dim G = n(n—1)/2. В случае n=4 dimG = 6. Изу-
Изучим модель, состоящую из скалярного поля ф, принадлежащего
/2-мерному векторному представлению группы SO(n), и калибро
вочного поля, принадлежащего присоединенному представлению
группы, имеющему размерность N=n (n—1)/2. Лагранжиан мо-
модели имеет вид
2= -1
где
A1.2)
=dvAv°—dAa+gfabcA *
A1.3)
a, b,c= 1,2,...,N; i= 1, 2,..../z.
Минимум V(<p) достигается при <p2=,<p2vaC) где при vz<q
<p2vac=—ц2Д>0. (Ц.4)
Выберем фуас, нарушив при этом симметрию, в виде л-компонент-
ного столбца
A1.5)
Вакуумное поле ф?ас (П-5) имеет остаточную симметрию
50(л—1) с генераторами Та, где
...,N, В = Чъ(п— 1)(п—2).
A1.6)
Воспользуемся приемом, примененным в предыдущем параграфе
при изучении глобальной симметрии, параметризовав вектор ф
следующим образом:
(И-7)
где Tg- — генераторы нарушенной симметрии F=1, ..., N—N),
число которых равно
М—Й=Ч2п(п—1)—У2(п--1) (п—2) =п—\. A1.8)
Число новых компонент gi, \г, ¦-, Sn-i, r\ совпадает, очевидно, с
числом компонент исходного поля qn, <рг,..., фп. Совершим калиб-
108
очное преобразование поля A1.7J
^ф' (Х) =ехр Г —1-Ть Ъь (х) j ф (х) =
(Н.9)
Компоненты поля |Г можно рассматривать как «полярные»
Координаты вектора ф(х). Преобразование (П-9) осуществляет
Поворот вектора ц>(х) в каждой точке пространства х таким обра-
|0М, что он становится параллельным n-й оси. Полученный вектор
tf'(x) оказывается заданным в унитарной калибровке (см. выше).
При этом в силу калибровочной инвариантности
(G<VJ=(G?J,
I Л т,|2=|П./<ю/|2. A1.10)
где
-М? + gfa
W (x) =exp( —1-
• <р'{х) определено равенством A1.9). У(ф) также остается ин-
инвариантным, и в полном соответствии с расчетом предыдущего
Параграфа, который, очевидно, обобщается со случая п=4 на об-
общий случай, получим в квадратичном приближении
У(Ф) = (^2/2) (u+tiJ+ (V4) (о+лL—const+ nV- A1-Н)
Запишем теперь действие ковариантной производной D,j на вектор
<р в унитарной калибровке
(DMV)i= [6iha,—igA*(Ta)ih]<ph'; A1.12)
здесь dihd^h =8indy.r\; второе слагаемое в квадратных скобках при
<j-=fi=/z, n+1,..., N дает нуль при действии на фь' в силу остаточ-
остаточной симметрии SO(n—1) вектора A1.9), а при а=Ь=\, 2,...,п—1
получим для Tg- = Т<$п
где учтено, что согласно A1.9) фь'=6ь„(и+тг1)-
Таким образом, в линейном по полям tj и Л/ приближении
получаем
' — gvA'^x
A1.14)
109

Отсюда для квадрата производной находим
= C^)» + gV (AitJ,
A1 -15)
где подразумевается суммирование квадратов полей A'^-g- по б от
1 до п—1, т. е. только тех компонент поля А/, которые отвечают
нарушенной симметрии. В итоге для лагранжиана модели с точ-
точностью до членов высших порядков получим
SC = —J-
-L
A1.16)
Как видно, в результате калибровочного преобразования A1.9)
п—1 полей gg- исчезли. Это голдстоуновские бозоны, которые воз-
возникли бы, если бы мы рассматривали нарушение глобальной сим-
симметрии. Здесь их исчезновение компенсируется тем, что N—N —
= п—1 векторных бозонов A g- в результате спонтанного нару-
нарушения симметрии приобрели массу, которая равна tnA—gv, при-
причем остальные N векторных бозонов остались безмассовыми.
Вместе с тем оставшееся скалярное поле — хиггсовский скаляр
ц — приобрело массу тц = ]/ — 2ц2.
Мы рассмотрели лишь частный случай симметрии SO(n).
Можно и?р общем случае показать, что спонтанное нарушение
локальной симметрии приводит к характерной трансмутации сте-
степеней свободы из скалярного сектора в продольные компоненты
векторных бозонов, сопровождающейся возникновением у них
массы. Подобное явление носит название механизма Хиггса.
Глава III
ТЕОРИЯ ВОЗМУЩЕНИЙ
И КАЛИБРОВОЧНЫЕ ПОЛЯ
Главная особенность калибровочных теорий типа Янга —
Миллса -— калибровочная инвариантность — при квантовании вы-
вызывает значительные трудности, поскольку имеются лишние He-
физические переменные, от которых наблюдаемые величины не
зависят^Эти переменные флуктуируют и дают бесконечный ^вклад,
поскольку на них не накладывается никаких ограниченийГрЗ дан-
данной главе мы продемонстрируем эти трудности и способ их
преодоления в теории возмущений, общее рассмотрение пробле-
проблемы будет проведено в гл. VI.
ПО
§ 12. ПРАВИЛА ФЕЙНМАНА
В КВАНТОВОЙ ХРОМОДИНАМИКЕ
а) Калибровочная инвариантность и пропагатор фотона
Прежде чем приступить к квантовой хромодинамике (КХД),
|ссмотрим сначала квантовую электродинамику (КЭД), гЪе
рудности, связанные с калибровочной инвариантностью., также
Стречаются, одн-ако в более простой фор'ме. *
Лагранжиан КЭД имеет вид ' - __ 7
A2.1)
1вгранжева плотность A2.1) инвариантна относительно преобра-
аания калибровки
A2.2)
[Уравнения поля
I
:-/, A2.3)
[Инвариантны относительно преобразований A2.2). Перепишем
Д[12.3) в виде , , /
" i г ¦^¦<-d,Mi»=-jX A2.4)
Отсюда для функции Грина электромагнитного поля получим
•уравнение
Переходя к фурье-образу
вместо A2.5) находим
(х), A2.6)
Это алгебраическое уравнение запишем окончательно так:
fiteg^—kJi^D* = —igve. 7 У A2.7)
Для решения этого уравнения существует простой способ, кото-
Sbifi состоит в выборе определенной калибровки. Так в калибровке
[оренца
< kvDv°=0 A2.8)
[оренца
находим
откуда
^ {k) = — ig^,
A2.9)
111

Такой подход нарушает калибровочную инвариантность, что
вызывает принципиальные трудности при анализе расходимостей
в теории. В общем случае решение уравнения A2.7) не единст-
единственно, так как определитель матрицы, стоящей в левой части
уравнения
det(g>«—№kVk2)^0. A2.10)
Это становится cpafy же ясным, если учесть, что
отвечающие нулевым собственным значениям
векторы,
0. A2.11)
Таким образом, матрица g"v—№к°11г2 не имеет обратной.
Если попытаться все же найти решение уравнения A2.7), то
следует записать его в общем виде, выделив продольную и попе-
поперечную части /3<tr) и Rm
Д,„ (k) = DM (k2) (g»v- k^kjk2) + &* (k2) kjzvlk2. A2.12)
Тогда, подставив последнее равенство в A2.7), находим
k2) (b°—k°kv/k2) D(iT) + 0 - D(l)] =
= k2 №c— ky-k°lk2)T№ = — ig»°. A2.13)
Отсюда невозможно найти /5(г>, которая остается неопределенной
функцией. Таким образом, мы приходим к необходимости для
однозначного определения функции D^k) нарушить калибровоч-
калибровочную инвариантность, наложив некоторое калибровочное условие.
В частном случае это может быть, например, калибровка Лоренца
A2.8). В общем случае это достигается введением в лагранжиан
дополнительного члена, фиксирующего калибровку
S'g/=-(l/2|)(*i4|l)*. A2.14)
Этот член нарушает калибровочную инвариантность исходного
лагранжиана A2.1). Число ?, которое может быть выбрано произ-
произвольным, называется параметром калибровки. Из полученного
таким образом лагранжиана 3
V A2Л5>
следуют уравнения поля:
где
дА,
dxv
дА
- = о,
H.V
A2.16)
0А +
('-Г)'
112
.»— A—i/i)a"FvAv)=—f. A2.17)
Ни для пропагатора в фурье-представлении получим урав-
A2.18)
||Том случае детерминант матрицы, стоящей в левой части
¦нения, отличен от нуля
det[g»v— A—1/1) k»kvlk2] Ф0, A2.19)
STOM
-- - --..»,. ,,,^,_„ A2.20)
Г" Г /' 1 М k»kv I nv —е
[
|тому решение уравнения A2.18) оказывается однозначным,
йстиительно, воспользовавшись записью A2.12), будем иметь
1
)
Приравнивая полученное выражение правой части уравнения
8.18), получим значения продольной и поперечной частей про-
* fi(tr)i/fe2 Б&—1Ц№. l A2.21)
йетим, что при ?->-оо, когда фиксирующий калибровку член
исчезает, продольная часть пропагатора стремится к беско-
ЧНости, СA)-^оо. При этом в уравнении A2.13) получаем неопре-
лешюсть О-оо. Поэтому при расчетах | следует сохранить ко-
чным, а в конце можно было бы положить |->оо. Однако все
!Ические величины калибровочно инвариантны и не должны
ЛИсеть от калибровочного параметра, так что нет необходи-
И©сти переходить к пределу ?->-оо. Тем не менее такие величины,
Щк массовый оператор и функция Грина электрона (с вакуумньи
МИ поправками), калибровочно не инвариантны и зависят от |.
частных случаях получаем:
A2.22)
A2.23)
Калибровка Ландау.
Возникает вопрос: к чему приводит учет калибровочного чле-
члени Lf.'ui в амплитудах? Рассмотрим инфинитезимальное калибро-
калибровочное преобразование, считая 66{х) малым. Тогда, поскольку
l/)dF6)
113

с учетом инвариантности исходного лагранжиана, 627=0, запи
тем вариацию действия
— б Г —
—— Г(ацл^J#х=—
Проинтегрировав дважды по частям, получим
6S=J-f
Ее J
Положим 6S/66 = 0, тогда
A2.24)
lw)=0. A2.25)
Полученное уравнение является уравнением для «частиц»
7\ = д1А^, которые, очевидно, являются свободными, т. е. п.-
взаимодействуют ни с какими другими частицами. Положив
/=0
= 0,
A2.26)
получим г] = 0 при всех t. Таким образом, т]-«частицы» могут быть
исключены из рассмотрения, а калибровочный член 2'gf является
несущественной добавкой к лагранжиану.
б) Калибровочная инвариантность и КХД
Как уже указывалось во введении, в основе теории сильных
взаимодействий лежит динамика цвета, т. е. локальная цветовая
¦симметрия S?/C)c. Кварковое спинорное поле раскладывается h.i
три составляющие, отвечающие различным цветам, в фундамеп
тальном представлении группы S?/C)c:
, или У=
A2.27)
где индексы у спинора -ф обозначают соответственно: а — спи-
норный индекс (а=1,2, 3,4), / — ароматический индекс (/=ы, d,
s, с,...), с — цветовой индекс {c = R, В, С).ГСоответствующее ка-
калибровочное поле принадлежит присоединенному представлению
группы SUC)C и имеет восемь составляющих Лд а=1,2,..., 8.
Оно возникает в результате «удлинения» производной 6^-0^ =
= <3Н—igАц, обеспечивающей калибровочную инвариантность лаг-
лагранжиана относительно преобразований
а>{х) =е
A2.28)
Л14
Л^-^шЛ^ш-1 ^-«айс
(а=1,2,.... 8) — параметры группы,
ГА^ТаЛЛ Та =
I — матрицы Гелл-Манна:
г f010
\о о о
A2.29>
A2.30>
О 0— i
Я5= 0 0 0
V t о о,
/ 00 0^
Я7= 0 0— i
t \ 0 i 0)
Пибровочно инвариантной лагранжиан КХД имеет вид
М — массовая матрица, учитывающая различие масс кварков.
пых ароматов; тензор глюонного поля равен
f Avc.
A2.32}
Различные члены в лагранжиане КХД с учетом фиксирующе-
калибровку члена i?g/ могут быть сгруппированы следующим
разом:
1) q(iy»d»—m)q A2.33)
Шгональный по сортам (ароматам) кварков член;
2) —i- (д„А°-д,А1Г- A/2Q (d^f A2.34)
Мдратичный по глюонному полю член, без учета их взаимодей-
ТИИЯ;
3) --i-
' 2
A2.35)
115

кубическое по глюонному полю слагаемое, учитывающее самодеи
ствие глюонов;
4) —^fatAMflfi (I2''5''»
член четвертого порядка, описывающий самодействие глюонов;
5) g(qy,Aa»(Kal2)q) A2.37)
кварк-глюонное взаимодействие.
Применяя обычные правила квантования свободных полей .
.лагранжианом A2.38) и A2.34) и учитывая их взаимодействие
A2.35), A2.36), A2.37), можно попытаться построить теорию
возмущений аналогично тому как это делается в КЭД. При этом
отдельным элементом амплитуд можно поставить в соответствие
«следующие графики фейнмана.
Вершины:
A2.3К)
жварк-глюонная вершина;
с,б, г
(k—q)c + gvo (q—r)
A2.39)
тройная глюонная вершина;
а, и, к
d,p,r
№ [fablfc
dl
+ faclfbdt
—gtxpgva) + fadlf
cbl
p—g^gpc)] A2.40
четырехглюонная вершина.
116
[нутренние линии:
BяL YuP11 — m + iO
A2.41)
Нагатор кварка;
а.М к
Is
A2.42)
Щгатор глюона.
Поясним кратко для примера вывод кубического члена в ам-
уде самодействия глюонов A2.39). Глюонное поле разлагает-
[I ряд
Г A2.43)
операторы сй° и с^+о- подчиняются перестановочным соотно-
КИЯМ
[<? (к), ^ (k')] = -^Аб*»'. A2-44)
K(k), cbv(k')]=0, [4a(k), с+"(к')] = О. A2.45)
Эда для среднего по вакууму |0) с учетом определения
ХОДИМ
(О |е? (к) 4Ъ (к1) 10> =g^%k-. A2.46)
трехглюонной вершины с выходящими импульсами можно
Писать
—Jd*x<O|e? (k) 4 (q) 4 (г) igfb>c\dwA$) А#/&\0).
Вставляя сюда разложения полей A2.43), получим, что нену-
эй вклад дают только члены, пропорциональные с+, при этом
-&ц. Учитывая только указанные члены, легко получаем
Г2.39).
Посмотрим теперь более внимательно, что дает введение в
Гранжиан члена, фиксирующего калибровку
Инфинитезимальные калибровочные преобразования потенциа-
91 имеют вид
М„=Юв [Т«, А,] + (Ug) dJd*Ta. A2.48)
Юскольку
117

получаем
6А
Отсюда с учетом
находим
или
6A,?=(l/g)DJF. A2.49)
Вычислим теперь вариацию действия КХД с учетом того, ни
ЕГК> 0 и вклад дает лишь 2 gf.
65= —
Дифференцируя по частям и используя определение Dv(),,
получим
х
A2.51
где т]а =
Приравнивая вариацию 6S/66a нулю, находим
уравнение для поля г\а — д^А^, или в явном виде
A2.52)
cAbvdv4c=Q>. ¦¦" A2.53)
В отличие от КЭД это уравнение содержит нелинейный член
пропорциональный полю Аь1. Поэтому даже при нулевых начали,
ных условиях для г\а и d\\Jdt поле г\а будет генерироваться полем
А»а. На квантовом языке это означает, что поле Аь* возбуждаем
квантовые флуктуации поля ца, т. е. генерирует rj-частицы, кото-
которые могут находиться как в реальных состояниях, так и в вир
туальных состояниях, т. е. в петлях. В КЭД имеем уравнение
0*11 = 0,
A2.54)
решение которого может быть разложено на положительно- и
отрицательно-частотные части
T]=ri<+>+Ti<->. A2.55)
Тогда при квантовании поля можно выбрать физические состоя-
состояния |Ф) такими, чтобы
0, A2.56)
т. е. они не будут содержать Ti-частиц. В КХД уравнение A2.53)
д\а = —gfabcAbvdvr)c A2.57)
118
КИТ источник, рождающий т^-частицы. Его решения не мо-
ilTb разделены на положительно- и отрицательно-частотные
Mi и соответственно невозможно гизбежать полностью появ-
1Я Tj-частиц^В начальных и конечных состояниях можно по-
ИТЬ 01Лац='в! что отвечает поперечным поляризациям, и тогда
ётиц в этих состояниях не будет. Однако в виде флуктуации
частицы будут появляться, т. е. в петлях они не могут быть
мочены. -
ля подавления нефшических мод применяетс$?метод Фад-
IB — Попова A967O1 Он состоит в том, что в дополнение»
|еющимся в лагранжиане полям/вводятся дополнительные не-
Ические поля, так называемые духид В качестве духов введем
ктиплет скалярных полей (q>+)a, удовлетворяющих тому же
Мению A2.52), что и поле t\a:
D^cp+^O. A2.58)
I же время будем считать, что поля духов <р+а подчиняются
истике Ферми. Это приводит к тому, что замкнутая петля
r <р+ будет иметь лишний знак «минус» по сравнению с пет-
Tj-частиц. Поскольку г\- и ср+-поля подчиняются одному и
у же уравнению, то их петли будут (взаимно уничтожаться!)
как имеют разные знаки. Что касается начального и коне»ь
состояний, то будем считать, что они не содержат духов, ко-
)ые, таким образом, не проявляются как реальные частицы.
ОТ прием, как видно, позволяет взаимно исключить вклады не-
аических частиц ц и ф+ в виртуальных состояниях и в то же
|мя не вносить их в реальные состояния.
Уравнение A2.58) для духов можно получить из лагранжиана
~ ' A2.59)
|Йствительно, уравнения Лагранжа
д djggh _
е. A2.58). Таким образом, для того чтобы проквантовать КХД,
оме фиксирующего калибровку члена S'gf вводим в лагран-
Иан S'gh и получаем эффективный лагранжиан ^
ff = 2 + 2а + Xgh= Х-{\1Щ№? + (виФ+)- A>ф)оГ) A2.60)
- &'gh приводит к появлению новых графиков Фейнмана:
119

пропагатор духа;
Г2)
вершина дух-дух-глюон.
Эта вершина происходит за счет члена в лагранжиане
A2.Г»'.',
Поэтому она выражается только через импульс выходящей ck,i
лярной частицы-духа, а не через сумму импульсов выходящей и
входящей частиц, как для обычных скалярных частиц. Возникаем
вопрос: как выбор калибровки отражается на физических вели
чинах? Ответ состоит в том, что они не зависят от калибровки
т. е. от выбора |. Для того чтобы продемонстрировать это, следуе-i
ввести преобразование Бекки — Рюэ—Стора A975 г.), или
БРС-преобразование.
Рассмотрим нелинейное преобразование
ЬА»а = l+Dw" = БД+сри. A2.63)
Здесь, очевидно, в качестве параметра калибровочного преобрази
вания выступает gX+q0, K+ считается постоянным антикоммути
рующим числом (Грассманово число). Поэтому произведена
А+Ф° — обычное число. В дополнение к A2.63) введем преобра
зование духов
бфо = — ll2gfabc'k+<tb(tc, A2.64)
где, очевидно, /аЬсфьф<М=0, так как фьфс= —фсфь. В результате, для
вариации действия получим
= -(Ш J
?) J
J сРхд„<р+а Г —L
) Ф' +
= О,
где первые два слагаемые в полученном интеграле взаимно унич-
уничтожаются после интегрирования по частям, последние же слагае-
слагаемые в сумме дают нуль.
.' Таким образом, действие КХД инвариантно относительно пре-
преобразования Бекки — Рюэ — Стора, в котором в качестве пара-
параметра выбрано произведение Я+а /
120
§ 13. ФУНКЦИИ ГРИНА
И ПРАВИЛА ФЕЙНМАНА
Правила Фейнмана для КХД, сформулированные в пре-
ущем параграфе, дают возможность рассчитывать простейшие
Цсные диаграммы. Выход за рамки древесных диаграмм, т. е.
ДОСЛение петель, приводит к вопросу о перенормируемости
рии. Ответ на этот вопрос будет дан в следующих главах. Сей-
Сеймы проделаем предварительную работу, т. е. разовьем общий
—Код к вычислению матричных элементов путем представления
[Через функции Грина.
"В качестве основных элементов для построения теории рас-
?рим функции Грина, которые мы определим следующим об-
Ш. Обычная двухточечная функция Грина
) @|ТА()АЫ|0> A3.1)
|днее по вакууму от хронологического произведения (Г-произ-
ния) полей A(xi) и А(хг). Общая n-точечная функция Грина
' ¦ ..А(*„)|0>. A3.2)
T(JCi, %,,n)<|
1 принципов релятивистской инвариантности и причинности сле-
|Т лоренц-инвариантность и симметричность функции Грина
\,2). Рассмотрим скалярное поле ц>(х). Тогда для свободного
Яя без взаимодействия и самодействия могут представиться, на-
Имер, следующие случаи:
a)
-Up-
пL J i
Bjt)
l- = Af(x1-J
A3.3)
B) J p
ачный фейнмановский пропагатор, определяемый как вакуум-
ожидание A3.1) в теории свободного скалярного поля;
()()()(х)|0> =
f (xt—х3) Дс (х2—х4) + Дс (хг—х4) Ас (х2—х3) A3.4)
тырехточечная функция Грина без взаимодействия. В общем
учае для 2п-точечной функции Грина получим, очевидно,
лучае для
*! «2п)=@|Тф(Х1)
перест
121

i
где сумма берется по всем перестановкам индексов й, ..., /'¦¦„
Рассмотрим теперь модель заряженного скалярного поля ср(л').
взаимодействующего с нейтральным скалярным полем А(х). Л;и
ранжиан взаимодействия имеет вид
Тогда в низшем порядке теории возмущений для четырехточеч
ной функции Грина можно получить:
т (х1У хг, х3, х4) = @1 Тф* (xj ф (х2) ф* (х3) ф (х4) 10) =
A3.7)
Здесь сплошные линии отвечают пропагаторам заряженных час-
частиц массы т, а штриховые — скалярных частиц массы р.. Ис-
Используя определение пропагаторов скалярного поля вида A3.3),
находим вместо A3.7)
X
т (хг, х2, х3, х4) = -^L-2 j d*pt ... j d\
— P% — Pi) exp [— i (рл + p3x3 — pzx2 —
1
p3 —
1
(pf
m2)(p2
m2)
Эта четырехточечная функция Грина, как легко видеть, содержи!
информацию о матричном элементе рассеяния ф-частиц в низшем
порядке теории возмущений. Можно представить себе функцию
Грина общего вида (n-точечную) в произвольном порядке теории
возмущений. Она также будет отвечать матричному элементу не-
некоторого процесса. На примере функции A3.8) можно составить
следующий рецепт получения матричных элементов из функций
Грина:
"Г" 1) проводим преобразование Фурье функции Грина;
- 2) умножаем результат на р?—т2=—iAc~1(Pi), т. е. удаляем
полюса с внешних линий (эта операция называется «ампута-
«ампутацией») ;
3) полагаем pi2=m2, т. е. переводим импульсы на массовую
оболочку;
4) наконец, умножаем на волновые функции (в импульсном
представлении), отвечающие внешним линиям. v-, V
122 """"
\Ш результате из функции Грина получаем матричный элемент
•етствующего процесса. Таким образом, знание всевозмож-
функций Грина в различных порядках теории возмущений
Юляет находить все соответствующие матричные элементы
Цессов, которые допускаются данной моделью.
Глава IV
ФУНКЦИОНАЛЬНЫЙ ИНТЕГРАЛ
В КВАНТОВОЙ ТЕОРИИ ПОЛЯ
В последние годы в теоретической физике большое рас-
странение получил Уметод функционального, или континуаль-
D, интегрирования. (Он основан на понятии интеграла по путям,
1|денном в квантовой механике Р. Фейнманом [7]. Впоследст-
|И этот метод получил развитие в статистической физике, отку-
он был распространен и на теорию поля.Шетод функциональ-
" интегрирования имеет^целый ряд преимуществ перед други-
, способами квантования. Он является общим и замкнутым
|тодом квантования, приТбдным для широкого класса систем,
"том числе и для неканонических.ЙЭн позволяет легко вывести
ввила диаграммной техники Фейнмана и в то же время пред-
Ввляет возможность для вычисления непертурбативных функ-
ДЙ ГринаГТДостоинством метода является также то, что он уста-
Иливает общность теории поля с квантовой статистической фи-
ПСОЙ, позволяя использовать ее приемы и способы расчета. Ком-
рктность записи и формулировки основных соотношений кван-
ой |еории поля дает возможность легко проследить структуру
или. иной модели и, в особенности, ее калибровочную инва-
яантность.
В литературе имеются работы, в которых даются строгие,
тя и не однозначные обоснования функционального интегриро-
¦ния [9, 15, 16]. Мы не будем следовать этим работам, а избе-
ем другой путь изложения, взяв за основу практическую сторону
опроса, т. е. мы разберем различные конкретные примеры при-
применения основных формул метода.
§ 14. ФУНКЦИОНАЛЬНЫЙ МЕТОД КВАНТОВАНИЯ
СКАЛЯРНОГО ПОЛЯ
а) Функциональное интегрирование
В основе функционального интегрирования лежит аналогия с
ст»,ауссовыми интегралами. Известен гауссов интеграл в теории
!йфункций одной переменной
lM^e-°s = —k=-, '' A4.1)
J-
123

где с>0. Для k переменных рассмотрим неотрицательную ква/i
ратичную форму
(у,Ау)=
(Н.2)
С помощью ортогонального линейного преобразования она можс1
быть приведена к диагональному виду. Тогда легко установим,
справедливость следующего значения ^-мерного гауссова интсч
рала:
/¦'
A4.3)
Рассмотрим теперь обобщение конечномерного случая на бес-
бесконечномерное функциональное пространство. Индекс i заменяет
ся на непрерывную переменную х, так что
—оо<х<оо.
A4.4)
Тогда сумма по i заменяется интегралом, а квадратичная форма
A4.2) переходит в двукратный интеграл, ядро которого состав
ляет оператор А с «матричными элементами» А (х, х?):
k
(У. Ау) = ? у fay, -»(у, ку) = J dx J dx'y (х) А (х, х) у (х') > 0. A4.5)
При таком предельном переходе конечномерный интеграл A4.3)
переходит в бесконечномерный интеграл — функциональный ин-
интеграл
Г SD [У (х) ] е-(у-АУ> = [det А] -.
В правой части этого равенства, так же как и в A4.3), стоит det А,
который в данном случае понимается как произведение всех соб-
собственных значений А,; оператора А, отвечающих собственным век-
векторам igi:
Agi = Xigi, det A = mi. A4.7)
б) Производящий функционал
Введем необходимое для дальнейшего понятие производящего
функционала. Вначале рассмотрим случай конечного числа пере-
переменных yt (t=l, 2, ..., k). Определим производящий функционал
следующим образом:
. ду*,...*,,, A4.8)
п=0 ?,=1
где Fn{h, .-, in) — симметричный по индексам ?ь ..., in коэффи-
коэффициент. Например, для k=2 имеем разложение в ряд Тейлора:
124
d2F
2 2
9 2
2 S уьуь
что, например,
\ Ф1 /o
IT, Д., т. е. F(«/i, «/2) является производящим функционалом
данном случае функцией), позволяющим вычислить все коэф-
Щиенты разложения Fn (iu ..., in).
Проводим теперь обобщение введенного понятия на функцио-
вьное пространство. Введем функционал
№ ¦ • .Sdx^.F^b, .. .,xn)y(Xl) ... у{хп). A4.9)
п=0
п=0
Цесто частных производных djdyi теперь следует использовать
^национальные производные б/б«/(хг), обладающие следующими
Ьу(х) ду(х)
i Т. Д. Тогда коэффициентные функции в функционале A4.9)
|огут быть записаны в виде функциональных производных от
6
F{y}
\ .
|у=о
A4.10)
1оэтому F{y} может быть назван производящим функционалом
пя функций Fn (xi, ..., xn).
в) Свободное скалярное поле
Применим введенное понятие для построения функций Грина
Свободного скалярного поля ф(х). Ранее были построены функции
Трина вида
т„(х,, ... , хп) = @|Тф (хх) q> (х2) ...
Дс
Af (xini — xin). A4.
перест
125

Ъ качестве производящего функционала рассмотрим интегр.ч ч
n=0
Тогда для «-точечной функции Грина получим выражение черс i
.л-кратную функциональную производную функционала A4.12)
хп (х1, ... , хп) = (- Q"
Т {/ (х)}
A4.1.4)
) /(„) /=0
Производящий функционал A4.12) может быть записан в ком
лактном виде:
T{j(x)}=exv{—4sfdxSdx'j(x)bc(x—х')/
j()()/()}. A4.14)
Справедливость этого равенства можно установить непосредствен
ным разложением экспоненты A4.14) в ряд с учетом определения
A4.11). Продемонстрируем это на примере п = 4. Вычисляя
•4-кратную функциональную производную от A4.14), найдем
• ¦ —— f —
(
X A, (x; — xj) / (xp / (xj) Л, (Х3 — x\) j (x'4)
iJ 2J 3J 4/v»;
= ~ • 8
/=o
СИММ
*,,) Af (xl3 — xh) = т4 (xx, x2, x3, x4). A4.15)
/Таким образом, если известен производящий функционал
'Свободного поля, то все функции Грина тп (Xi,..., xn) могут быть
вычислены путем его функционального дифференцирования. 4 '
Существует другое представление для производящего "функ-
"функционала:
T{j}=Z{j}/Z{0). A4.16)
где Z{/} — новый производящий функционал, записанный в виде
-функционального интеграла
A4.17)
Эквивалентность определений A4.14) и A4.16) может быть уста-
установлена непосредственным образом. Для этого преобразуем ин-
интеграл
I—ox—mz)x
Л26
X ( ф (x) — i Г dx"Af (x—x") / (x") \ =
dx j^-cp (x) (-dl-tv?) ф (x) + j (x) Ф (x)] -
— (i/2) (dx Г dx'/ (x) Лс (х—х') j (x'). A4.18)
Cb использовано уравнение для функции Грина
(—а*2—т2)Ас(х—х') = tS(x—xf). A4.19)
нство A4.18) может быть переписано следующим образом:
jdx [-L ф (х) (-dl-n?) ф(х) + ](х)ф(х)] =
\ \их [ -L Ф' (х) (- д2х-т*) ф' (х) + (i/2) f dx fdx'; (x)Ae (x-x') j (x'),
lJ L J J ч A4.20)
ф'(х)=ф(х)— ij dx'Ac (x—x')j(x'). A4.21)
¦ Заметим, что путем интегрирования по частям можно преоб-
ШОвать левую часть равенства A4.20) к виду
J dx [ -Lq, (x) (-#- m2) ф (х) + j (x) Ф (х)] =
J dx [-L (а^ф (x) а^ф (x)-mV (x)) + j (x) Ф (x) j. A4.22)
|Таким образом, функциональный интеграл в правой части ра-
ства A4.20) после замены переменной
Ф (х)-мр' (х) = ф (х) —ij dx'Ac (x—х') j (x')
Юдится к функциональному интегралу при / = 0:
¦¦ - " ' -т2ф'2(х))], A4.23)
множенному на экспоненциальный фактор
ехр[—V2JdxJdx7(x)Ac(x—х')У(х')]. A4.24)
Т*м самым равенство A4.16) оказывается полностью эквивалент-
эквивалентным исходному выражению A4.14). Следует отметить, что в по-
показателе экспоненты в A4.17) стоит лагранжиан свободного ска-
Дярного поля
2'о=1/2(^фа11ф—т2ф2). A4.25)
Поэтому A4.17) можно переписать в виде
A4.26)
127

Если ввести классическое действие свободного скалярного пиля
S{<p(x)} = SdxS?0(<p(x), дх<р(х)), (М.:»
то вместо A4.26) находим
Z {/} = Г D [q> (*)] ё5^ ё I Лг/«ч<*). A4.'
Последнее равенство можно рассматривать как функционально
преобразование Фурье экспоненты от классического действия си
бодного поля, в результате которого получается экспонеп
A4.14), умноженная на Z{0}. В этом смысле равенства A4.1
и A4.28) являются функциональным обобщением известного пр
образования Фурье экспоненты от квадратичной функции
чI
4J
ibx\ =е
Число а следует сопоставить оператору —дх2—т2, стоящему в пи
казателе экспоненты A4.22), а обратное ему число а ' conoci.i
вить «матрице» Дс(х—%'), стоящей в экспоненте A4.24) и, v.\w-
это следует из уравнения A4.19), являющейся обратной операто
РУ —дх2~т2.
Здесь необходимо сделать одно замечание. Равенство A4.20)
справедливо постольку, поскольку определены стоящие там ни
тегралы, т. е. при а>0. Равным образом и равенство A4.1(>)
вместе с A4.17) или A4.28) справедливо, если определены в.хо
дящие в них функциональные интегралы. Следует вспомнить, чп>
'функциональные интегралы были определены как предельный
случай гауссовых интегралов (сходящихся!) при устремлении числ.ч
измерений к бесконечности. Поэтому и функциональные интсм
ралы в A4.16), A4.17) будут хорошо определены, если они бу
дут иметь гауссов вид. Для этого необходимо перейти от прост
ранстваиНинковского с псевдоевклидовой метрикой к пространст-
пространству Евклида, т. е.
(х°, х\ х2, x*)-*-(x<4=ixP, х1, х2, х3)./
В евклидовом пространстве оператор
дх2+т2 = д„о>+т2 = д42 + дх 2+д22+д32+т2
становится положительно определенным, а указанные интегралы
приобретают гауссов вид. Если бы мы с самого начала работали
в пространстве Евклида, то не возникло бы никаких проблем с
определением интегралов. Однако при этом следовало иметь пра-
правило, позволяющее переходить определенным образом в прост-
пространство Минковского с тем, чтобы получить нужные (т. е. при-
причинные) функции Грина. Как известно, обычно это достигается
введением мнимой добавки к массе: | т2—>-т2—iOj Описанная
процедура формулируется как евклидов постулат, который гла-
гласит:! физические функции Грина получаются соответствующим
158
„ТИческим продолжением из евклидовой области в область
Транства Минковского?)
Л Скалярное поле с самодействием
ркдючим в лагранжиан скалярного поля нелинейные члены,
тем самым его самодействие:
A4.30)
| лагранжиан взаимодействия имеет вид
2>1=<рп(х), п=3, 4. A4.31)
: теперь в экспоненте производящего функционала Z{/(x)}
|Сать вместо 3?о полный лагранжиан 3? A4.30), то возникает
КОЖность развить квантовую теорию поля с взаимодействием
¦ частности, получить ряд теории возмущений.
Г Действительно, рассмотрим функционал
A4.32)
A4.33)
Z {/} = J D [cp {x)\ exp f ig ^dx Xi (Ф (х)) ] x
exp \i f dx (J?o + / (x) Ф (x))l.
экспоненте под знаком интеграла можно заменить
1 6
A4.34)
\\) - ехр
вариационная производная действует на вторую экспоненту.
~т ~б^~)) *D[(p (x)] exp[I' *dx Шо+1 (x)(p(x))]-
A4.35)
Тавшийся функциональный интеграл соответствует свободному
НЮ. Он был вычислен в предыдущем пункте. В результате на-
&ИМ
X
ехр[ l-ldxjdx'j(x)Ac(x-x')j(x') j -2{0}. A4.36)
I Полученная формула позволяет непосредственным образом
[щрейти к приближению теории возмущений. Для этого разложим
|цериый экспоненциальный множитель в A4.36) в ряд по кон-
«тиите. связи:
ЬилмЛроночныс поля
129

+ ... ЬхрГ— — Jdxjdx'/(x)Af(x — x')/(x')l Z{0}. A4. :</)
(На основании этого разложения можно получить функции Грпн.1
во всех порядках теории возмущений} а через них, как были
показано в предыдущем параграфе, фейнмановские амплитуды
процессов теории возмущений.
Рассмотрим пример кубического лагранжиана взаимодейсжмя
gj=— ф3(х). A4..-W)
Согласно общему определению «-точечной функции Грина
Тп(Л:1> Х2> • • • ¦> Хг) == ( Ч
I/-0
Для 4-точечной функции будем иметь
б*
Напомним, что именно этот пример был рассмотрен в § \'Л и
связи с изучением процедуры «ампутации». Рассмотрим, как и »
§ 13, второй порядок теории возмущений. Нас интересуют связны»
диаграммы вида
хз (У2) '** хз
A4.40)
Здесь в скобках проставлены координаты у± и у2, по которым и
амплитудах производится интегрирование.
Наметим лишь ход рассуждений, оставляя детали вычисле
ний для читателя. Из равенства A4.39)
/=о
X [-y-^]3exp[-^-J-dxJ-dx'/(x)Af(A:-x')/(x')]. A4.41)
Искомые диаграммы получатся за счет членов типа
| dx' J dx" j dy' Jd/ j d«/i J Ф2 Аг (У1-*') X
X/(x') Af (У1-х") / (x") Дс (У1-у2) K'(yz-y') j(У')А (У2-У") i Ю-
13t
еренцируя данное выражецие четыре раза в соответствии
l.4t), находим
dyt \ dy2kc («/!—хх) Ас («/!—х2) Ас (г/!—1/2)
X Ас {уz—-^з) Ас (уа—х4) + перестановки.
X
A4.42)
• Этот результат, как легко видеть, соответствует представ-
ИЮ четырехточечной функции Грина диаграммами Фейнмана
рого порядка теории возмущений A4.40). Проводя, далее, про-
уру «ампутации» и другие операции, описанные в § 13, полу-
полудиаграммы рассеяния ф-частиц в ^-приближении в точном
ртветствии с правилами Фейнмана.
Вернемся теперь к общему случаю взаимодействующего ска-
рйого поля. В соответствии с определением
A4.43)
... 6/ (хп) 2@}
/=0
лвая представление A4.33), находим
^П \%1г • • • > %п) ==
A4.44)
ершим теперь виков поворот
Хо—*-Х4 == 1Хо,
к что Хо= —1X4, где х0 — мнимое, а х4 — действительное. Полу-
ркые таким образом функции Грина в евклидовых точках назы-
ся функциями Швингера. В этом случае, учитывая, что
лучим
ехр [-
СЬ Ml= .
Иергия поля, и
вклидово классическое действие. Итак,
A4.45)
A4.46)
A4.47)
131

*•!» • • • > xn) —
A4.48)
Заметим, что в формулах A4.45) — A4.48) мы ввели постоянную
Планка й, перейдя таким образом, из системы единиц, в котором
/г=1, в обычную (гауссову) систему. Как видно из A4.48) выр.ч
жение для функции Грина хп(хи ..., хп) формально подобно фор
муле статистической механики для среднего значения л-й степени
динамической переменной ц>. При этом h соответствует КГ (Т
температура, k — постоянная Больцмана), a SE имеет смысл
энергии системы в четырех измерениях евклидова пространстк.-i
Менее формальная аналогия со статистической физикой можч
быть установлена с помощью метода Мацубары, основанного n.-i
отождествлении х4 с величиной, обратной температуре системы Т,
и наложении соответствующего статистике поля (Ферми или
Бозе) периодического условия по х^. Мы не будем останавливать
ся на этом методе (см., например, [17]).
§ 15. ФУНКЦИОНАЛЬНЫЙ ИНТЕГРАЛ
В ТЕОРИИ ФЕРМИ-ПОЛЕЙ
Поля, подчиняющиеся статистике Ферми, также могуч
быть описаны на языке фейнмановских интегралов по путям. Для
этого, однако, в отличие от бозе-полей, следует ввести новый
класс функционалов, образующих грассманову алгебру.
а) Грассмановы переменные
Вначале по аналогии с рассмотренным выше случаем статисти
ки Бозе введем дискретные переменные
i/i ,-., У:, ¦¦¦¦ A5.1)
Предположим, что они образуют так называемую алгебру Грассма-
Грассмана Gn. При этом если yi являются генераторами этой алгебры, то
они подчиняются соотношениям антикоммутации
A5.2)
A5.3)
A5.4)
где i, /=1, 2, ..., п. В частности, для i=j
Аналогично для сопряженных генераторов
и, кроме того,
{уи г//*}=о.
Произвольный элемент алгебры Грассмана
представлен в виде степенного ряда по генераторам
132
A5.5)
может быть
и у
{*:
у) =
¦ ¦ ¦,К)у»,
n,m
A5.6)
СЬ суммирование по т и п ведется до максимального числа раз-
разных генераторов соответственно «/,-* и yi, так как, очевидно,
ЦИ сомножителей не должно быть повторений. Отсутствие по-
РСНИЙ можно формально учесть, потребовав, чтобы коэффици-
d Tmn{h, .... /m|^i, ¦¦•, kn) (обычные числа) были бы антисим-
ричными. Для сопряженного элемента алгебры получим
ЧУ',!/) =
,lm) \K ...,kn)yh... yi
п,т
• A5.6а)
В алгебре Грассмана дифференцирование и интегрирование
ределяются как линейные алгебраические операции.
Вводят два рода производных: правую и левую. Для левой
Сизводной, обозначаемой д/дук или dL/dyk, имеем
Ji_ „. = _JL т = 6,.„. A5.7)
правой производной д/дук, или dR/dyk,
—— У1 = У1 —— = o.ft.
fyk дУк
|Т0 же время
(фференцирование большего числа сомножителей дает
-%^~УЬ ¦¦¦xkn = bkli Укг... Укп — Ькг1 у* Укг... Укп + ¦
аналогично
A5.8)
A5.9)
<к,...укпЬК1. A5.11)
Интегрирование по алгебре Грассмана основано на определе-
ии двух интегралов
Jl dyk=0, A5.12)
r J- =1. A5.13):
133
1\\

Этих интегралов достаточно для вывода всех остальных соотнонк-
ний. Заметим, что грассманово интегрирование в A5.12), A5.1М)
является аналогом определенного интеграла но всей области ни
тегрирования обычных числовых функций.
Кратные интегралы определяются следующим Образом:
Jf/fc. • • ¦ ykndyn ...dy1 = eK...kn, A5.M)
где ejt,.,.kn — антисимметричный тензор Леви-Чивита. Кроме тот.
необходимо учитывать соотношения
yi, yk}={dyi, dyk*}={dyi*, yft}= ... =0. A5. Ml)
Приведем, наконец, правило дифференцирования произведения
двух элементов F\ и F2 грассмановой алгебры:
где знак + или — ставится в зависимости от того, является ли
Fi четной или нечетной комбинацией генераторов уи-
Чрезвычайно важным для дальнейшего является правило з.ч
мены переменной в интеграле
yi-+Zi = ?Laikyk, A5.18)
где A = ||fl»ft|| — матрица линейного преобразования. Для dzt сле-
следует принять
dzt = ? aik dyk,
к
A5.19)
где ||a«ft~MI=A~1 — обратная по отношению к А матрица. Действ и
тельно, тогда
? аи1 dy, =
k I
k
Из определения A5.19) следует, что
. A5.20)
В этом нетрудно убедиться, если подставить в левую часть равен
ства A5.20) определение A5.19) и переставлять все dyi до тех пор,
пока не получим требуемый порядок dyn ¦¦¦ dyi. В результате каж-
каждое слагаемое приобретает как раз тот знак, «плюс» или «минус»,
с которым оно и входит в определение det А.
Основным интегралом, с которым приходится иметь дело в тео
рии грассмановых переменных, является интеграл гауссова типа
x ... dyndyn ... dy\exp (?у1аСкУк) = det A. A5.21)
i.k
134
| доказательства этой формулы заметим, прежде всего, что не-
1ВОЙ вклад в интеграл дает лишь n-я степень показателя экс-
НТЫ. Проведем замену
,ьНь. A5.22)
J dyi... dyn = det A J dz!... dzn,
аовательно,
J dz, ... dzn dy*n..- dy] exp [? уЩ = 1 ¦
СТЬ, например, л = 2, тогда
f dzjdzgfly'sdy* exp {y\zx + ylz2] =
= f dzjdzjlyWi Г1 + J/iZi + У&2 +
A5.23I
A5.24)
A5.25)
Интеграл от первых трех слагаемых дает нули, а интегралы от
1Гаемых в круглых скобках равны единице. В итоге весь инте-
|Л A5.25) оказывается равным единице. Точно так же равенст-
i 15.24) доказывается и в общем случае п>2.
_) Грассмановы функционалы
Переход от дискретных переменных
уи ..., yi, ..., уп
['Йепрерывным переменным у(х) достигается переходом к преде-
п-*-оо и заменой i-*-x на ограниченном интервале изменения пе-
менной у. В результате грассманова функция F(y*, у) A5.6)
реходит в грассманов функционал, определяемый равенством
Т{У*> У) =
... dxn x
т,п
X У*Ю ...у"(х[)Гтп(х'\х)у(Xl) ...у(хп),
A5.26)
It Tmn{x'\x)s=Tmn(x/, .... хт'\хи .... х„) — антисимметричная
ункция переменных х{ и хс, переменные у(х) и у{х>) подчиняют-
условиям
{У(х), У(х')} = 0,
A5.27)
{у*{х),у(х')}=0.
Дифференцирование грассмановых функционалов определяется
функциональное обобщение правила A5.10)
135

¦щ- у (ХХ) . . . у (Х„) = б (X — Хх) у (Х2) ...у (Х„) —
— б(х — х2)у(xjj/(x3) ...у{хп) + ... A5.2Н)
и аналогично для 8R/8y(x).
Обобщением интегралов по грассмановым переменным A5.12).
A5.13), A5.14) будут соответствующие функциональные интегр.ч
лы. Не приводя промежуточных формул функционального интегри
рования по грассмановым переменным, запишем лишь окончатси.
ный результат для основного интеграла, используемого в теории
ферми-полей:
Я D [у (х)] D [у* (х)] еУ*АУ = det A, A5.2!))
где показатель экспоненты имеет следующий явный вид:
y*Ay=$dxdx'y*(x)A(x, xr)y(x'), A5.30)
причем Л(х, х') — антисимметричная функция аргументов х и л'
Функциональный интеграл A5.29) является очевидным обобщепи
ем интеграла A5.21).
в) Производящий функционал для ферми-полей
Для вычисления функций Грина фермионного поля я);(х), г]? (.v)
введем производящий функционал
5dx1...dxndx'n...dx[r\(xn) .
(-1)"
(«О2
.. .Ч(х'п).
A5.31)
Здесь т](х) и i\{x) — вспомогательные грассмановы источники,
подчиняющиеся условиям
A5.32)
Ых), т)(х')} = 0
и т. д. Учитывая известное представление функции Грина свобод
но го фермионного поля @| 7\p(xi)... ^(xn)^(xn')... $(x\) |0> черен
фейнмановский пропагатор Sc(x—х'), которое записывается ан.ч
логично соответствующему представлению бозонной функции Грп
на (см. выше), получим
тЯ id = exp[—$dxSdx'4(x)Sc(x—x')i\(xr)l A5.33)
Соответствие этой формулы и разложения A5.31) становится оче-
очевидным, если учесть, что в отличие от бозонного случая здесь име-
имеется двойной набор переменных т](хг) и ^(х,'), t=l, 2, .... п, явля-
являющихся грассмановыми переменными. Отсюда множитель (—1)"
136
(—i)Tl и 1/(п!J вместо 1/п! в A5.31), а также отсутствие
иКителя 1/2 в показателе экспоненты в A5.33) (функция
ШХ—хг) в отличие от Дс(х—х') не является четной).
[Представим теперь т{ц, tj} через функциональный интеграл. Для
ЭНОВ подобное представление, как было продемонстрировано
UG, по существу связано с тем, что причинная функция Грина
(j»—х1), является обратным оператором по отношению к операто-
П»п, входящему в лагранжиан свободного скалярного поля:
Ac=iDm4, A5.34)
Dm=a2+m2.
ому представление
T{j}=Z{j}IZ{0}
A5.35)
A5.36)
ИЫвается своеобразным функциональным преобразованием
фье экспоненты, показатель которой квадратичен по полям <р(х).
Соответствующее представление производящего функционала в
рмионном случае может быть записано в виде
хЯ т]} = 2К ti}/Z{0, 0}; A5.37)
X exp {t J dx [¦ф (x) (iydx—m) ф (х) + л (х) ф (x) + 4> (x) tj (x)]}. A5.38)
1ИНЫЙ функциональный интеграл может рассматриваться как
фмионный аналог бозевского функционального преобразования
урье экспоненты
}, A5.39)
не Dm(x)=iydx—т, причем обратным по отношению к Dm опера-
Ором является фейнмановский пропагатор дираковского поля
},(х—х'), т. е.
DmSe = ~i, A5.40)
сюда
Sc = -iDm-K A5.41)
Докажем равенство A5.37). Доказательство основано на том
Re приеме, который был применен в бозонном случае. Рассмотрим
i | dx\y{x)-ijdx'^{x')Sc(x-x')]Dm(x)x
X [^(x) + i$Sc{x-x") rj(x")dx"] =
= i Jdx [^(x) Dm (x) rj) (x) + ф(x) Tj (x) +
+ ц(x) y(x)\ + JdxJde'ti(x)Sc(x—x') rj(x'). A5.42)
Здесь учтено равенство A5.40). Если теперь сделать замену пере-
переменной
137

A5.4.4)
в функциональном интеграле
J J D М> (х)] D [ф (х)] exp {i J dx [ф-
-ifr (х') Sc (x-xr) dx'\ Dm ft +i |Sf (x—x1)
го на основании равенства A5.42) найдем
J J Z) [Ч> (%)] D ft (х)] exp [t Jdx^ (jc)Dm* (х)] =
= Я В N> (*)] D [«(х)] exp [ij dx (i (x) Dm* (x) +
jdx':n(x)Sf(x—x')ri(x')]. A5.4!.)
Отсюда с учетом равенств A5.38) и A5.33) получим формулу
< 15.37).
Заметим, что входящий в A5.45) и A5.37) функциональным
интеграл является гауссовым и в соответствии с основной форму-
формулой предыдущего пункта A5.29) может быть формально вычислен
$D[q(x)]D[q{x)]exv[i$dxif{x)Dm$(x)] = detDm. A5.40)
Важно, однако, чтобы функциональные интегралы, используе-
используемые в полученных соотношениях, были хорошо определены. Для
этого необходимо их вычислить, переходя из пространства Минкои
ского в пространство Евклида. Обратный переход осуществляется
с учетом требования, чтобы из функции Грина дираковского поля
Se в евклидовом пространстве, которая определяется однозначным
образом, следовала именно причинная функция Грина — пропл
гатор в пространстве Мйнковского, где функции Грина, как извеп
но, определены неоднозначно.
Глава V
МОДЕЛЬ ВАЙНБЕРГА—САЛАМА—ГЛЕШОУ
Во введении было дано феноменологическое описание
слабых взаимодействий элементарных частиц на основе гамильто
ниана фермиевского типа («токXток»). В настоящей главе излаг.ч
ется калибровочная теория, единым образом описывающая элект
ромагнитные и слабые взаимодействия, лагранжиан которой име
ет структуру «ток х калибровочный бозон». Эта теория была по
строена С. Вайнбергом, А. Саламом и Ш. Глешоу в конце 60-х го
дов (ниже для краткости — теория, или модель, ВСГ). В 1979 г.
создатели единой теории электрослабого взаимодействия были
удостоены Нобелевской премии. Теория ВСГ хорошо согласуете»
138
Периментом. Самым блестящим подтверждением этой теории
) открытие в 1983 г. W+- и Z-бозонов, которые являются пере-
Иками слабого взаимодействия.
§ 16. ОТ МОДЕЛИ ФЕРМИ К ЕДИНОЙ ТЕОРИИ
ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
Как уже указывалось во введении, модель Ферми хоро-
Юписывает слабые распады элементарных частиц, а также рас-
ПИе нейтрино. Лагранжиан этой модели, ограничиваясь для
СТОты случаем электрон-нейтринных взаимодействий, можно за-
|ТЬ в виде (ср. @.4) и @.5)):
I
<? (х) =ё(х
) е (х) + vc (x)iydxe (x) +
v. (x)
A6.1)
, первые два слагаемые — лагранжианы свободных электрона
ЛЙтрино соответственно, в третье слагаемое — лагранжиан
МЗаимодействия, причем нейтрино считаем безмассовым.
¦„Теория Ферми неперенормируема. Это означает, что в ее рам-
можно вычислять сечения процессов только в низших поряд-
теории возмущений, которым отвечают так называемые дре-
.НЫе диаграммы, не содержащие петель (ср. с электродинами-
jt [1]). Попытка вычисления высших порядков приводит к появ-
ИИЮ неустранимых расходимостей. Кроме того, даже результаты
Счетов в древесном приближении становятся неприменимыми в
яксти высоких энергий, так как нарушается условие унитарно-
\(для S-матрицы).
) гее-рассеяние в модели Ферми
Рассмотрим на примере рассеяния \ее-^-\ее более подробно, как
©Исходит нарушение унитарности при высоких энергиях.
Амплитуда указанного процесса, построенная на основе лаграи-
ИВНа A6.1), имеет вид:
""" A6.2)
I ш(р) A = е, х) — биспинорная амплитуда лептона I с 4-импуль-
Л р. Используя известное преобразование Фирца (см. [11]), пред-
Цим эту амплитуду в виде
«.„- х--.,-,...... '¦" A6.2а)
[Мдрат модуля амплитуды, усредненный и просуммированный по
|Чальным и конечным спиновым состояниям электрона и нейтрино
Тйетственно, согласно общим правилам [1] можно преобразо-
|Ть так:
спин
139

X [uv (ft') Ya ut (p)] [ue (p') YaL«v (ft)] [«v
- 4G2 ? [uv (ft') Y« Й
спин
YP"v (ft')l [«. (P) YP4 (p')l
= — 4G2tr {?'Y? (p
(p'
m
(Hi.»)
где Mfi записано в виде A6.2), а для получения Mfi+ использов.ит
A6.2а) и соотношение Y°(Ybl)+Y0=Ybl; а^уааа- Учитывая, далп-.
соотношения Y5Ya = —YaY5> A+Y5J = 2A+Y5) (см- @-5)), а такж.
(см. [1]) уаабсуа=—2сМ, yaa6ya^4{ab), найдем для A6.3) окон
чательное выражение:
| Мп
|2 =
— 2G2tr[ft'Ya?
Y5)l
= 16G2 (ftp) tr [fc'p' A + v6)] = 64G2 (pft) (p'ft') = 64G2 (pftJ, A61)
где на последнем этапе использовано, что tr (\:>1yvY5) = 0 в силу он
ределения y5-
Дифференциальное сечение vee-рассеяния
da = BяL?64(ft' + p — ft — p)\Mfl\2 — ?*!__ dy ,
Интегрируя в A6.5) по р' с помощью соотношения
и подставляя C.4), получим
(lfi.:.)
A6.@
A6.7)
Введем инвариант
s=(ft+pJ,
имеющий смысл квадрата энергии в системе центра масс k+р о.
и проинтегрируем в A6.7) по энергии ft0' рассеянного нейтрино ¦•
учетом d3k'[ko=ko'dkodQ, 6[...]=6(ft0'—kpl^s)l2^s. В результат.•
находим дифференциальное сечение в виде:
da
dQ
(s — т2е)*
4я2
где элемент телесного угла dQ = 2nsir\QdQ, 6= (к, к') — угол p;ic
сеяния. Таким образом, сечение уее-рассеяния в системе центра
масс A6.9) изотропно (не зависит от угла б).
Интегрируя A6.9) по телесному углу, получаем полное сечение,
A6.10)
140
Врое в области высоких энергий {s^>me2) неограниченно воз-
Тает:
a~-^s. A6.10а)
п
Заметим, что этот результат (o~s) сразу следует из сообра-
ШИЙ размерности: [a]=[G]\s]n = L2—M-2, где L и М — единицы
'1ИЫ и массы (в принятой нами системе единиц Й = с=1). Учиты-
I, что [G] = M-2 = L-, [s]=M2, находим показатель степени п—\.
Независимость дифференциального сечения A6.9) от угла рас-
Шия означает, что в рассеяние дает вклад только s-волна (угло-
*1 момент рассеянных частиц ^ = 0). Естественно, это обусловле-
контактностью слабого взаимодействия в теории Ферми (см.
6.1)). Как известно [5, 6], полное сечение рассеяния можно пред-
ЦВить в виде суммы вкладов различных /-волн:
-{21 + I)sin26,,
A6.11)
, bi — фаза рассеяния. Следовательно, при /=0 получаем огра-
чение на сечение:
co = ^sin26o<^. A6.12)
1ри sortie2 в системе центра масс имеем (см. A6.8)):
S=(Po + ftoJ~4k2. A6.13)
> A6.10а), A6.12) и A6.13) находим ограничение на энергию:
мг s<i4n/G, A6.14)
|',|1ЛИ, с учетом численного значения G~ B94 ГэВ )~2,
|k|<V^/G^500 ГэВ. A6.14а)
а граница называется унитарным пределом.
Итак, теория Ферми применима в области энергий Vs<ClO3 ГэВ.
б) Промежуточные заряженные векторные бозоны
В области высоких энергий необходима модификация теории.
Используя аналогию с квантовой электродинамикой (КЭД), заме-
ШШ фермиевское взаимодействие «токX ток» взаимодействием,
Обусловленным обменом векторными частицами. Однако, в отли-
'Чие от фотонов в КЭД, эти век-
векторные бозоны должны иметь боль- е-. „ ve~
^Шую массу, чтобы при низких энер >^ w
Гиях возникало эффективное кон-
контактное взаимодействие.
Рассмотрим в качестве примера Ц
рассеяние vee-*-vee. Амплитуде Рис. 16.1
141

этого процесса отвечает диаграмма, показанная на рис. 16.1, гд»
волнистая линия обозначает обмен заряженным промежуточным
U^-бозоном массы mw- Пусть g — константа связи lF-бозона с лс-н
тонами е и ve. Тогда амплитуду процесса можно записать, по ан.-i
логии с КЭД в виде:
™2
5 — m%, + iO
A6.1Г,).
где vv — биспинорная амплитуда, отвечающая ve, <?"—4-импулы
Ц7-бозона, инвариант s A6.8) равен
Средний сомножитель в C.15) — пропагатор векторного бозоп.-t
A6.17)
Выражение A6.17) для него можно получить, используя обобще-
обобщение уравнения Максвелла для безмассового фотона на случай мас-
массивного lF-бозона, описываемого 4-потенциалом W*(x). Это уравне-
уравнение, называемое уравнением Прока, имеет вид (см., например, [1])
dJtv+mJW^?, A6.18)
где F»v=cMi7v—dvlF*. Для IF" получаем уравнение
A6.18a)
—*'). A6.19)
, A6.20)
а для пропагатора D^(x—х') находим
[(d2+mw2)g^~d^]Dv,(x—x') =
Переходим в импульсное представление согласно
Ал (х) = Г -?*- е-"" Ц* (q).
Подставляя A6.20) в A6.19), приходим к простому алгебраическо
му уравнению для Dv^(q):
U—q2+tnwZ)g»v + q»qv]Dv?.(q) =6Д A6.19а)
решением которого является A6.17), где, как и в пропагаторе фо
тона, бесконечно малая мнимая часть iO в знаменателе определяет
причинную функцию Грина.
Сравним выражения для амплитуды vee-рассеяния в теории
Ферми и в модели с Ц7-бозоном A6.15). В этой модели амплитуда
приобретает (при s^-mw?) дополнительный фактор 1/s. На первыь
взгляд кажется, что он компенсируется множителем q»qv в пропа-
пропагаторе. Однако, это не так:
142
К е 00) 9^=
= 1/2ще(k) (k + p) A + Y5) ие(р) = \/2щеA - yb)pue =
A6.15a)
у
На q*qv
уравнения Дирака (p—me)ue=O. Следовательно, вклад
пропорционален те2 и в области высоких энергий
,2) пренебрежимо мал. Поэтому полное сечение рас-
«ния
A6.21)
Власти низких энергий (s^.mw2) получаем результат фермиев-
I теории (o~s) плюс малые поправки порядка (те/т^J и
г8. Сравнение амплитуды A6.15) при s-^.mw2 и фермиевой амп-
уды (она дается A6.2) с заменой uv->-vv) дает связь размерной
Станты Ферми G и безразмерной
¦станты g: .
G~g2lmw2. A6.22) и^
Итак, введение \^±-бозонов устра-
_|Т нарушение унитарности (см.
|в.21)). Однако возникают новые
удиости, проявляющиеся при рас-
процессов аннигиляции е+е~->-
w,
Рассмотрим для определенности
Ьцесс w-*~W+W-, которому отве-
,ет диаграмма, показанная на рис.
12, и амплитуда
Рис. 16.2
A6.23)
неСЬ 8(±)" — 4-векторы поляризации ^^бозонов, удовлетворяющие
вЛОВиям 4-поперечности и нормировки:
<?%=0, 82 = 6^=—1. A6.24)
ТИ условия означают, что в системе покоя W-бозона его 4-потен-
Иал W»(q) = (О, W), т. е. сводится к трехмерному вектору, как это
должно быть для векторной частицы: qp.Wli=mwW0 = 0.
Пусть в некоторой системе отсчета 1^-бозон движется вдоль
СИ Oz, т. е. его импульс q||Oz:
»= (9о, 0, 0, qz).
A6.25)
озон может находиться в трех независимых поляризационных со-
143

стояниях, описываемых следующими 4-векторами поляризации
(условия A6.24) выполняются):
е„"=@, 1, 0, 0), ^«=@,0,1,0),
ej= (qjmw, 0, 0, qo/mw), A6.26 )<
причем первые два отвечают поперечной поляризации (e'q = 0).
а третий — продольной поляризации. Из A6.23) и A6.26) нетруд
но получить, что сечение рождения поперечно поляризованных б<>
зонов при высоких энергиях (jq|:»mw)
o{xv-+Wt+Wr)~gllmw\ A6.27)
и такое поведение обусловлено независимостью е/ от энергии
Для продольно поляризованных бозонов при q2^m«72 вектор поля
ризации (см. A6.26))
и сечение рождения таких бозонов растет с энергией:
„2 '
A6.28)
где s— (<7++<7-J. Следовательно, вновь возникает нарушение уни-
унитарности.
Сравним эту ситуацию с электродинамикой. В КЭД фотоны без
массовы, и среди них нет продольных или временных. Поэтому се
чение процесса двухфотонной аннигиляции е^е~-*-уу имеет хори
шее высокоэнергетическое поведение (см. [1]). КЭД, кроме того,
обладает калибровочной инвариантностью, что позволяет «откл
либроваться» от члена ~№k" в пропагаторе фотона D^(k), выбран
его в виде (калибровка Фейнмана):
Наконец, фотон связан с сохраняющимся током /": &„/"=(). Все это
и приводит к перенормируемости КЭД.
в) Промежуточный нейтральный векторный бозон
Существуют две возможности устранить указанные трудности
с №+Н?~-рожДением.
1) Первая заключается во введении тяжелого лептона ?'
(твЭ>те). Тогда процессу v\-*W+W~ наряду с диаграммой рис
16.2 надо сопоставить вторую диаграмму (рис. 16.3), вклад котором
в полную амплитуду процесса имеет знак, противоположный знаку
вклада диаграммы рис. 16.2, т. е. возникает деструктивная интер-
интерференция указанных диаграмм. В результате сечение имеет хоро-
хорошее поведение в области высоких энергий.
2) Другая возможность — введение нейтрального Z-бозона, ко-
который непосредственно взаимодействует с заряженными №+-бозо-
144
Именно она реализуется в теории ВСГ^ Вторая диаграмма
ряду с рис. 16.2), отвечающая процессу \v-*-W+W~, показана
рис. 16.4. Выбором константы связи gz в вершине ZW+W* (см..
Же ) можно добиться убывания амплитуды указанного процесса
|Иергией по закону 1/ys. Наличие Z-бозонов приводит к нейт-
йьным токам (см. введение).
.w
Рис. 16.3
Рис. 16.4
'i W-бозонные пары могут рождаться также в процессе электрон-
»Итронной аннигиляции е+е--*-W+W~. Амплитуда этого процесса
сывается диаграммами (а), (б) и (в) на рис. 16.5. Диаграммы
i
w
|) и (б) за счет продольных компонент №/± (см. A6.26)) дают
над в сечение a~s, причем они не компенсируют друг друга,
рк как диаграмма (а) сохраняет Р-четность, а (б) — нет (слабое
Нимодействие нарушает Р-инвариантность). Учет диаграммы
|) с Z-бозоном приводит к компенсации вкладов ~s, если имеет
|сто следующее соотношение между константами связи:
e2=gzgL + g2l2=gzgR, A6.29)
е — электромагнитная константа связи (заряд электрона), gL
gR — константы связи Z-бозона с левыми (L) и правыми (R)
ЭМпонентами фермионов (см. @.6) и @.8)).
Соотношение A6.29) означает объединение электромагнитного
слабого взаимодействий (групповой аспект этого объединения
Ке обсуждался во введении, п. а)).
г) Общая структура электрослабого взаимодействия
145

Рассмотрим подробнее, какова должна быть структура дпм
трамм взаимодействия фермионов (лептонов и кварков) с четы pi.
мя векторными бозонами Va= (W+, W~, Z), у, чтобы сечения при
адессов взаимодействия имели хорошее энергетическое поведсти-
Пропагатор массивного Уа-бозона (массы та)
Вершина, описывающая связь трех бозонов, имеет вид (см. гл. Ill)
h
'Л*
b — kX + Fcabg№ (kc — ka)v],
тде Fabc — некоторые безразмерные константы связи.
Пропагатор фермиона
A6.31)
I —
тг
¦где р = ^р^.
Вершина взаимодействия фермионов с бозонами
.у)
A6.32)
A6.33)
:где La и Ra — константы связи для левых и правых фермионных
компонент.
Рассмотрим процесс рождения пары F-бозонов типа li + T, -
->Va + Vb (например, e~+\e-*-W~+Z) и из требования взаимном
компенсации «опасных» слагаемых в полной амплитуде процесс.-!
получим условия, которым должны удовлетворять величины Fai,,
и La, Ra (см. A6.31) и A6.33)). Амплитуде отвечают диаграммы
(t), (и) и (s) на рис. 16.6. Ниже сначала рассматривается вклад
только левых компонент фермионов.
Диаграмме (t) (?-канал) соответствует амплитуда, составлен
ная согласно A6.31) —A6.33):
Д46
- Vv
A6.34)
^ГвысокихAэнер^ях основной вклад в амплитуду дают про-
Т енты Vбозонов когда вектор поляризации (см.
Тые
ысокихэнер^ях основной вклад в амплитуду д р
компоненты V-бозонов, когда вектор поляризации (см.
ее"—ka*lma.
тому в числителе A6.34) возникает выражение
еь (Pi—К + т,)Цщ =1ь [—tntka + 2pika—ml] щ, A6.34а>
использованы уравнение Дирака для биспинора щ. р№ = т№
^отношение
в+б 2(аЬ). A6.35)
1аменатель в A6.34)
(Pi—kaJ—m,2 = т? + ma2—m,2—2 (р,?а). A6.34б>
W высоких энергиях отношение A6.34а) и A6.346) сводится к
i, и амплитуда Mt A6.34) принимает вид:
ВЯ ы-канала имеем
числителе аналогично расчету Mt получаем
K + mi)^b Щ =V) (—mjka + 2kapj
Aб.зб>
A6.37>
147

а знаменатель
В итоге
(Pi + ka) 2—m?=mf—m?+ma2+2 (fcap/).
М,;са ¦
AA Щ
Наконец, для s-канала с помощью A6.30), A6.31) и (Hill)
записываем амплитуду в виде:
ал
Ms =
(eae6) (fta —
A6.:»'»
причем kc = ka + kb.
При высоких энергиях полагаем снова ?a!i—kB,'i/tna и оставляем и
пропагаторе V-бозона только слагаемое ~g"v (ср. с A6.15;i(l
Тогда в числителе A6.39) возникает выражение
= щ [~Fabc (kazb) Ckt-M)-
J!;
A6.10)
+ka))-FcJ!;(*b(—2ka—kb))]ul
Пусть величины FabC удовлетворяют условию
г. е. не изменяются при циклической перестановке индексов. v
A6.39а) с учетом A6.40) и условия поперечности (см. A6.21))
еь&ь = О принимает вид:
N = -FjHf [- (kaeb)Q& +~ti) + ki Bkakh + ml)] щ. -
Замечая, что i>,-(ft? + V~b)ui=vi(p\ +'pf)u.: = viL(mi—m,)ulL,
в области высоких энергий (Ys > ma» mi> mD получаем
W~_2FabcV&bL (kakb) Щ. ( 16.39i.)
Знаменатель A6.39) в пренебрежении массами равен
(k kJ2(kk) Т A639)
() рр р (pPi)
= (ka + kbJ—2(kakb). Тогда с учетом A6.396) приведем A6.39) к
виду:
Ms ~ !- (Vj^ui)FabcЦ,. A6.41)
Складывая A6.36), A6.38) и A6.41) и приравнивая результаты
нулю, получаем условие для левых связей L,-,a:
—LuaLi,
= 0,
A6.42)
I в матричной форме
[L<\ Lb]=—
A6.43)
¦1логичные расчеты можно выполнить для правых связей
[результате получим то же условие:
[R<\ R"]=-
A6.44)
I' Рассмотрим теперь рассеяние векторных бозонов друг на друге,
е. процесс Va+Vb-^-Vc+Vd, которому отвечают три диаграммы
М. рис. 16.7). Вновь требуя компенсации растущих с энергией
)~j~\. Д-
Рис. 16.7
П||3 матричной форме (с учетом A6.40).)
[Fa,
A6.45)
A6.46)
148
СДе Fabi = Ffc(a= (Fa)t,i — матричные элементы матрицы Fa. Из
A6.46) следует фундаментальный вывод: —iFabc являются струк-
•урными константами некоторой группы Ли, —tFa — элементы
¦рисоединенного представления этой группы. Тогда соотношения
A6.43) и A6.44) означают, что L" и R° — элементы представле-
представлении алгебры Ли той же группы (внутренней симметрии). Мы при-
Шли к этому важному выводу, требуя компенсации главных сте-
степеней s в сечениях процессов взаимодействия фермионов и вектор-
>ИЫх бозонов, что приводит к хорошему поведению сечений a(s).
I Итак, правильная теория электромагнитных и слабых взаимо-
взаимодействий должна основываться на некоторой группе внутренней
(Симметрии. По аналогии с КЗД эту группу следует локализовать,
Т. е. сделать ее локальной калибровочной группой. Это дает воз-
возможность построить по общим правилам (см. гл. I) классический
, .лагранжиан калибровочной теории, квантование которой должно
[ (привести к использованным выше диаграммам. Кроме того, появля-
149

i
m
ется также характерная для калибровочной теории диаграмма, <п
вечающая четверному самодействию V-бозонов:
с,р
d.6
— * \FablFcdl (gflpgvo ¦
+
+ FactFbdl (g^gpa —
+ FadlFcbl
~ guvgop)] ¦ A6.47»
Схема построения калибровочной теории электрослабых вз;ш
модействий такова:
1) Учесть все необходимые векторные поля (у, W±,Z,...) и но
местить их в присоединенное представление некоторой калибровом
ной группы.
2) Выбрать представление этой группы для левых и праныч
фермионов (лептонов и кварков).
3) Локализовать калибровочную группу G и построить лагран
жиан теории с помощью «удлинения» производных в лагранжиане
свободных фермиенов по известному правилу (см. гл. I):
где Л„а — калибровочные поля, Т° — генераторы группы в com
ветствующем представлении, ga — константы связи с калибровом
ными полями.
4) Полученный таким образом лагранжиан, будучи калибровом
но инвариантным, не содержит масс калибровочных бозонов, но \>
общем случае содержит затравочные массы фермионов. Чтобы по
лучить массы калибровочных бозонов, следует использовать ме\л
низм Хиггса, основанный на явлении спонтанного нарушения сим
метрии (см. гл. II). Это требует введения мультиплета скалярных
хиггсовских полей ср, взаимодействующих с фермионами и кал и о
ровочными бозонами (при квантовании возникают поэтому новьм
диаграммы, отвечающие взаимодействиям с этими скалярами).
5) В итоге мы приходим к следующему (перенормируемому)
локально калибровочно инвариантному лагранжиану, образован
ному из калибровочных полей Аиа, спинорных полей \|)п и скаляр
ных полей ф5:
= — 1/4 Gaw
V — М)
1/2
A6.48)
о
здесь М— массовая матрица фермионов, У(ф) — самодействнс
скаляров, приводящее к спонтанному нарушению симметрии; теп
зор калибровочного поля
A6.48а)
|риантные производные спинорных и скалярных полей имеют
^ = (а„igaTA,
= d^s—iga (Pa)
A6.49)
чем Ta и Pa — генераторы (эрмитовы матрицы) в представле-
.X, к которым принадлежат \f и ф. Генераторы удовлетворяют
«мутационным соотношениям
A6.50)
ЕР», Pb] = i/ofrePc,
Щ fabc — структурные константы группы, антисимметричные по
f Ь, с (fabc=—iFabc). Если калибровочная группа G простая (т. е.
имеет инвариантных подгрупп; см. [9]), то все константы связи
ШМибровочными полями одинаковы: ga=g для всех а. В важном
Я приложений случае, когда G является прямым произведением
^Простых групп: G = GiXG2X ... XGP, имеется р независимых кон-
Щт связи: ga=gi для всех генераторов Та и Ра, принадлежащих
ЩГруппе Gi.
г Матрицы М, rs> Ta, Pa удовлетворяют условиям эрмитовости:
A6.50а1)
(Р°)„*=
ричем Та и Ts можно представить в виде разложений по компо-
"Итам, выделяющим соответственно левые и правые компоненты
|тмионов:
A6.51)
1-Y5
Инвариантность лагранжиана' относительно калибровочных пре-
бразований из группы G приводит к следующим условиям:
[Т<\ <у° М] = 0,
(P«)sr9r = 0,
A6.52)
Причем последнее условие выведено в гл. II (см. A0.15)).
В результате спонтанного нарушения симметрии поля фя при-
5ретают ненулевые вакуумные средние
150
15»

М = М + Dsrs;
и возникают следующие массовые матрицы соответственно скаля
ров, фермионов и калибровочных векторных бозонов (см. также
A0.17)):
A6.Г..Ч)
В следующем параграфе рассматривается конкретная реалил.ч
ция этой программы, основанная на калибровочной группе
SUB)XU(l) — модель Вайнберга — Салама — Глешоу.
§ 17. МОДЕЛЬ ВАЙНБЕРГА—САЛАМА—ГЛЕШОУ
;а) Лагранжиан электрослабого взаимодействия лепто-
нов
Рассмотрим сначала взаимодействие только электрона и элект
ронного нейтрино. Минимальная калибровочная модель требуе-i
введения четырех векторных полей: одно для электромагнитных
процессов с участием фотона, два — для процессов со слабыми
заряженными токами (W=-бозоны), одно — для процессов с нет
ральными токами (Z-бозон). Эти поля согласно результатам § Mi
образуют присоединенное представление калибровочной группы
Проведенное во введении обсуждение феноменологии слабых про
цессов показывает, что в качестве такой группы следует выбран,
группу SUB)wxU(l), которая является прямым произведением
группы слабого изоспина SUB)W и абелевой группы U(\) слабой,
гиперзаряда. Группе SUB)W принадлежит триплет векторных но
лей А/ (а=\, 2, 3), группе U{\) — синглет Ви. (
Первоначально фермионы if безмассовые, и поэтому можно от
дельно рассматривать их левые ifL и правые -фя (см. @.6) и @.8))
компоненты. Левые фермионы образуют дублет (изоспинор отно
сительно преобразований группы SUB)W:
A7.1
L =
а правые — синглеты (изоскаляры)
Ri=(eR,xeR) (l = e, v), A7.2)
причем, имея в виду экспериментальные данные о существовании
у хе ненулевой массы (см. введение), наряду с eR добавлен еще
один синглет veR.
Генераторами группы SUB)WXU(\) являются проекции изо
спина Iwa=rJ2 (а—1, 2, 3) и гиперзаряд Yw, причем гиперзарял
Yw упорядочивает фермионы по (электрическому) заряду Q соглас
но формуле
Q = /»8+V2K«.. A7.3)
152
*
Г"
I
1
симметрии
механизмом
(Сиггса, и в результате мы
Олжны получить три массив-
массивах векторных поля \V+, W-,
и одно безмассовое (фо- с'
ОН у)- В соответствии с ре-
ультатами гл. II следует вве-
четыре действительных
J1H два комплексных поля
ьнггса. Следуя Вайнбергу и
5аламу, введем дублет ска-
скалярных (комплексных) хиггсовских полей
1
J——
Уыг
ta формула — аналог формулы Гелл-Манна — Нишиджимы для
Вронных изомультиплетов (см. @.19)).
Согласно A7.3) для левого дублета YWL =—1, для правого
Яектронного синглета Уш* = —2, для нейтрино YwR = 0. Заряд Q
Вляется генератором под-
руппы электромагнитных ка-
Вбровочных преобразований
(l)em. которая остается по-
вле нарушения симметрии
WB)WXUA).
Нарушение
Веспечивается
.—-i
-2
Рис. 17.1
A7.4)
|> Для наглядности изобразим все необходимые поля на диаграм-
<е (Iw\ Yw) (рис. 17.1).
Лагранжиан модели ВСГ — частный случай общего лагран-
лагранжиана A6.48) — запишем в виде: о
A7.5)
с,1
Где
^Лагранжиан калибровочных полей;
eR
ig'B») eR
vJ A7.5а)
A7.56)
ищгранжиан лептонов, взаимодействующих с калибровочными по-
йми (правое нейтрино имеет нулевые изоспины и гиперзаряд и
оэтому движется свободно);
¦Лагранжиан скаляров, взаимодействующих с калибровочными по-
|лями, причем ц2<0, Я>0;
153

A7Г>г).
лагранжиан взаимодействия лептонов со скалярами, причем и
спинор фс, входящий в член ~/v, зарядово сопряжен
<р A7.4):
фс =
A7.1.1»
где Т2 — матрица Паули.
Заметим, что ковариантные производные D^ в отдельных
гаемых лагранжиана A7.5) определены в виде:
причем для изоскаляров (ея, vR) Iwa=0, для изоспинорои
(L, ф)Угва=та/2, Yw— + \ для ф, для других полей Yw указано выше
Лагранжиан теории ВСГ A7.5) включает 6 параметров: лиг
константы связи с калибровочными полями g и g', две констатм
юкавской связи /е и /v лептонов со скалярами и два параметра \\'
и К, характеризующих самодействие хиггеовских скаляров.
б) Спонтанное нарушение симметрии в теории ВСГ и возникни
вение масс частиц
Потенциал самодействия скаляров (см. A7.5в)) имеет миним\ м
при
|q>|2=|x*Assfl2>0, A7.7)
что приводит к спонтанному нарушению симметрии (гл. II).
В качестве (классического) вакуума выбираем
A7.М)
Рассмотрим действие на вакуум оператора Q — генератор.)
электромагнитных калибровочных преобразований (см. A7.3)):
— 1 + 1) = 0, A7.9)
т. е. фц — инвариант, как и должно быть для вакуумного состоя
ния. Произвольное состояние можно параметризовать следующим
образом (см. A1.7)):
где |а, т] — вещественные поля.
Используя калибровочную инвариантность лагранжиана A7.5),
перейдем к унитарной калибровке, в которой теория имеет про
стую физическую интерпретацию:
v+ri(x)I
154
L-*L'=exp( —f^r-
A7.11)
—
2
использованы известные законы калибровочных преобразова-
„ (см. гл. I).
Итак, вакуум ф» A7.8) — инвариант подгруппы электромаг-
ТНых калибровочных преобразований V(I) (в общем случае
JI. II) подгруппа iV-параметрическая; в нашем случае i?=l).
входная группа SU{2)XU(l) имеет N=4 параметров, так что
Талось Л^—N==4—1 = 3 параметра, характеризующих нарушен-
Ю часть полной группы. Под действием соответствующих пре-
разований фь преобразуется. Оставшимся трем параметрам от-
отдают три голдстоуновские частицы (поля Ь,а(х) в A7.10), кото-
1е исключаются из теории («откалибровываются») переходом
Г.11) в унитарную калибровку, а «высвободившиеся» три степе-
свободы переходят в продольные компоненты ставших массив-
гли трех калибровочных векторных бозонов (W*, Z).
Итак, в унитарной калибровке остается одно вещественное
ЛМшрное хиггеовское поле ч\(х). Запишем в этой калибровке сла-
|емое 2:'/„ A7.5г) в лагранжиане:
= -U
, v+ r\)
. 0)
с
ЧК, учитывая @.6) и @.8) и
(vLeL)
,, ~eL)
—fv (v + r\)
0
']"
Л
VR =
vLvR),
3?i<i=—fevee—fee-це—fvvw—fvvTjv.
A7.12) следует, что лептоны приобрели массы
me = fev, mv=fvv
A7.12)
A7.13)
взаимодействуют с хиггеовским скаляром т] с константами связи
и fv.
Преобразуем теперь хиггеовский лагранжиан З?^ A7.5в).
1меем для отдельных слагаемых в 2"ф:
155

т. к. тЧа=
-(О,
(таЛ?ф)+ (ЗД + э. с. = 2 (а + т!) Аз^ц,
=0;
где использовано A7.11).
В итоге находим (отбрасывая несущественную постоянную)
A7.14)
Из A7.14) следует, что поле Хиггса г\ приобрело массу
тч=у2"ц. A7. Iff)
Слагаемое в A7.14), содержащее поля А^а и В», необходимо диат
нализовать. Введем вместо полей Ви, А»3 их линейные комбинации
А» и ZM:
Ali=Bv.cos 6«7+А„3sine«7,
A7.10)
Тогда
)
)Zo2,
если выбрать угол Qw (угол Вайнберга) в
tgQw=g'/g, smQw=g',
В результате 3?* A7.14) запишется так:
A7.17)
~ (v + г,J [g2 (W+W- + W-W+) + (g* + g'2) Z't], A7.18)
О
где введены поля
). A7.19)
Из A7.18) следует, что массы полей W±, Z и Л соответственно
равны
/7% = 1 /2gv, mz = l/2 Vg2 + g'* v = mw/cos Qw,
Таким образом, поля W^ описывают W±-6o3OHbi, Zw—Z-бозоны,
A» — фотоны (электромагнитное поле).
156
рассмотрим теперь лептонную часть S?i A7.56) полного лаг-
иана, переписав ее в виде:
J?i = v«i (уд) ve+ei (уд) e+\v
*
r. A7.21).:
^Используя преобразование Вайнберга A7.16), выразим поля
через физические поля Л^ и Z,,:
ft cos 6W,
A7.16а)
ставляя A7.16а) в A7.21), получим:
.i(yd) vc
+ ~eiy»(d»+ig sin ^AJe +
(v.v?v.)Z»
sin2
cos
A7.22),
Из A7.22) и A7.17) следует соотношение между константами
?. gf, углом Вайнберга Qw и электрическим зарядом е:
e = gsine«7=g'cos6iF, A7.23)
единяющее электромагнитное и слабое взаимодействия в еди-
Ь электрослабое взаимодействие.
_ Перепишем еще лагранжиан калибровочных полей Sc A7.5а)
^Терминах физических полей:
-»/21 D.W+-DVW+12-ie (дИ.-
—g2cos2Bw[Z2(W+W~) — (W+Z) (W-Z)]+
+te cos e^(a,zv-dvZ.) №+*№-+ /
f cos 64(DliW+v—DVW/) (W-MZ-—^-VZ") —к.с.],^ A7.24>
„ Dli=ail+ieAM. Это слагаемое описывает взаимодействие полей
Г„*, Zn и Л„ между собой.
в) Лагранжиан в терминах физических полей (унитарная ка-
Щвровка)
Сложив A7.24), A7.22), A7.18) и A7.12), находим лагранжиан
Одели ВСГ, выраженный через физические поля, в виде:
157

—ЗД2
A7.21...
лагранжианы свободных электромагнитного и Z-бозонного полем,
Swa =—V21 D»WS-DvW+\ ;
—1е(а„Л»—d,A.) W+^-v (I7.2i.ni
лагранжиан W-бозонного поля, взаимодействующего с электри
магнитным полем,
&*гл = -g2 cos2 Qw[(W+ W-)z»Z»-(W+Z) (W-Z)]+
+ ig cos ВхЛ(д»г,—д^) W+»W~*+ A7.2Г).,)
+ (D,WV+—DVW,+) W-»ZV—э.с]
.лагранжиан взаимодействия W*- и Z-бозонов и электромагнитмо
.го поля А;
^=\Aуд—mv)v
лагранжиан свободного нейтрино;
ve
A7.25i
7.2Г*-
.лагранжиан взаимодействия электрона, нейтрино и 1^-бозона;
^ez= (g/cos ew)e(V2Y/—si^e^^eZ" A7.25ж)
лагранжиан взаимодействия электрона и Z-бозона;
^vz = -(g/2cos6^) (^Y/ve)Z- A7.25:.)
лагранжиан взаимодействия нейтрино и Z-бозона;
2\,=7г (a,.4J-nhV—Л"Л8—'/ДтL A7.25..)
лагранжиан самодействующего хиггсовского поля;
A7.25k.)
.лагранжианы взаимодействия электрона и нейтрино с хиггсовским
полем;
^ч^= (?74) (t,2+2dt,) W+W-*,
A7.25л)
лагранжианы взаимодействия W- и Z-бозонов с хиггсами.
Л58
lo сих пор мы рассматривали только одно поколение лепто-
(v«, e). Модель ВСГ очевидным образом обобщается на случай
лептонных поколений (см. @.9)). Для (vu, ц) и (vT, т) полу-
II такие же слагаемые в полном лагранжиане ВСГ, что и для<
I в) (с заменой юкавских констант fe и /v соответственно наДи-
?В результате обеспечивается (е^т)-универсальность электро-
|бых взаимодействий лептонов.
, Г) Следствия из теории ВСГ
13 лагранжиана ВСГ в виде A7.25) непосредственно следует
^ствование нейтрального тока /и@). Действительно, сумму вы-
ений A7.25ж) и A7.25и) можно представить в виде
/0), A7.26)
Л-
A7.26a>
МЛном согласии с @.14) и @.92).
Выясним, как в принципе можно экспериментально измерить
раметры g, sin26«7, mw и mz, входящие в лагранжиан теории
сг.
||1Установим сцачала соотношение между константой Ферми G в
номенологической теории «токXток» и безразмерной констан-
g в теории ВСГ. Рассмотрим для этого, например, распад
Оона ц: n~-*e-+\e+vv.
|тричный элемент этого процесса в теории Ферми имеет вид (см.
1) и @.5)):
MF= DG/V2) (v,W) (ёуа4е). A7.27)
I теории же ВСГ ц-распаду отвечает диаграмма с обменом №-6o-
Рис. 17.2 Рис. 17.3
Оиом (рис. 17.2) и амплитуда (см. A7.25е) и A6.17)):
A7.28>
_ ml, + Ю
р.ри низких энергиях (92«т.2) амплитуда A7.28) переходит в
J17.27), если
159-

Используя A7.27), нетрудно найти время жизни мюона
чет аналогичен проведенному в § 16):
A7.24)
!. A7.30)
Сравнение этого выражения (фактически необходимо учесть они-
радиационные поправки за счет виртуальных фотонов (см., напри
мер, [11]) с измеренным временем жизни позволяет определить <1
а следовательно, отношение g2/mw2. Измерения дают значенш-
G—1.17-10-5 ГэВ~2.
Угол Вайнберга Qw можно определить экспериментально. м<-
следуя процессы, вызванные нейтральными токами. Рассмотрим,
например, процесс рассеяния \№+e~-^\Vk+e~, обусловленный то/и,
ко нейтральным током. Ему отвечает диаграмма с обменом Z-6nm
ном (рис. 17.3) и амплитуда (см. A7.26)) в низкоэнергетическом
пределе (<72<mz2):
г_ Г
,~ _.L
4m| cos2
Vя (gv
e),
где
v=
.=-72.
A7.31)
A7.31.-i)
Заметим, что в силу A7.19) и A7.29)
g2/8mz2 cos2 6W= G/V2, A7.2!);.)
т. е. уже 'известна. Поэтому измерение сечения a{yv.e-*\v.e) позно
ляет (см. A7.31а)) независимо определить sin20«7.
Исследуя чисто электромагнитные процессы, мы определяем
постоянную тонкой структуры
или, ввиду A7.23),
а=е2/4я= 1/137,036,
A7.32)
Итак, проведя три независимых эксперимента, можно опреде
лить константы G, sin26«7, a, зная которые, можно затем найти
массы W- и Z-бозонов и вакуумное среднее v хиггеовского поля
согласно A7.29), A7.20), A7.32):
1/2
У 2G
= mw/cos I
Sin
'w
A7.33)
Итак, теория ВСГ приводит к ряду замечательных следствии,
которые могут быть проверены экспериментально:
,1) она предсказывает существование нейтральных токов, кон-
|Иты связи в которых определяются единственным параметром
2) теория предсказывает существование тяжелых промежуточ-
||Х бозонов W± и Z, массы которых удовлетворяют соотношениям
17.33) и, следовательно, определяются экспериментальными дан-
|Ми при низких энергиях, предсказываются также константы
1X3и W- и Z-бозонов с другими частицами;
' 3) теория ВСГ основана на существовании фундаментальных
Цвлярных частица (хиггеов), предсказывает их свойства и взаимо-
йствия.__^/
К настоящему времени многие предсказания теории уже надеж-
о подтверждены экспериментально: открыты нейтральные токи,
Внаружены W- и Z-бозоны (см. ниже). Хиггсовские скаляры ц
ОКа не найдены, неизвестны их масса т„, параметры р2 и к лаг-
^1нжиана 3?ъ
д) Свойства W- и Z-бозонов
Массы W± и Z-бозонов определяются формулами A7.33). Под-
faHOBKa в них экспериментально найденных значений
1ает
~— ГэВ ~ 80 ГэВ; tnz =
in t)
Sin t)
91 ГэВ. A7.33а)
1Ц8аметим, что формулы A7.33а) не учитывают радиационных по-
ртравок. Их учет изменяет результат A7.33а) примерно на 5%.
i Важным свойством промежуточных бозонов является отсутст-
ИС полулептонных распадов. Так, И7--бозон имеет следующие ка-
каналы распада: _ _ _
W A7.34)
i кварковая пара qxq2 затем фрагментирует в наблюдаемые ад-
|,|юны (см. введение).
| Вычислим ширину распада W~~-*-eve. Ему отвечает диаграмма
! |>ис. 17.4 и амплитуда (см. A7.25е)):
A7.35)
, ?Де е" — 4-вектор поляризации W-бозо-
(см. A6.24)), р, k — 4-импульсы элек-
< трона и антинейтрино.
Квадрат амплитуды
Рис 174
усредняем по поляризациям W-бозона по формуле*
* Соотношение A7.36) выводится так же, как и для фотона: правая его
часть должна быть тензором 7>v, составленным из g^v и q^q"" и удовлетворяю-
160
Калибровочные поля
161

A7.3A)
где q — 4-импульс бозона, и суммируем по спиновым состояниям
е и ve по обычным правилам [1]. Тогда находим
IMP = if-tr \-
+
A7.35a)
причем, мы пренебрегли массами те и mv'no сравнению с большой
массой mff. Далее имеем:
~
Из закона сохранения q=p+k следует 2kq=mw2 (в пределе
me=mv=0); тогда A7.35а) принимает вид (р2=те2-*0):
\М\2 — — trj(p %) = — g3 (kp). A7.356)
о 3
Ширину распада (т. е. полную вероятность распада в единицу
.времени в системе покоя бозона: qo = mw) находим по общей фор-
формуле [1]:
= Г
_??
BяK2йо
Интегрирование в A7.350 по
подстановки A7.356) получаем
;L64 (р + k — q) J2~L-. A7.35b)
снимается 6-функцией, и поело
-^-(?pN(?2), A7.35г)
где k = q—р, следовательно, kp—q2J2 = mw2/2, и в системе покоя
№-бозона 6(k2) = Bmw)~l6(p0—mw/2)>B результате простого ин-
интегрирования в A7.35г) по d3p/po->-4np(jdpo получаем окончательно
о
A7.36)
48л
6я
где учтена связь констант g и G A7.29)."Полагая в A7.36) т«7—
~80 ГэВ, находим Г^210 МэВ.
Полная ширина Ftot распада Р^- получается умножением
A7.36) на число N каналов распада (см. A7.34)). Это число равно
где Л// = 3 и N'q=3 — числа лептонных и кварковых поколений (см.
шим условиям (см. A6.24)) q»T»v=C, qvT»*=O, Г/=—1, которые однозначно оп-
определяют 7>\
162
(.91)), ЛГС=3 — число цветов кварков. Итак, умножив A7.36) на
находим полную ширину
ГийAР) = —-?-<. A7-37)
я /2
В лептонных распадах №+-бозонов образуются заряженный леп-
Эн и нейтрино, которые не детектируются. В адронных же распа-
исследуются характеристики адронных струй, в которые фраг-
liltHTHpyraT кварки.
Лептонные распады Z-бозона, в отличие от W+ характеризуют-
образованием пар заряженных лептонов с заданной инвариант-
)Й массой. Кроме того, Z-бозон распадается на пару нейтрино:
"+vixi {l=e, \i, т). Полная ширина распада Z-бозона оказывается
1ВН0Й
з
Ttot (Z) = -Д= — C — 6sin2e^ + 8sln*6^), A7.38)
К2 Зя
составляе2 2,5 ГэВ при mz=92 ГэВ, sin26w=0,225. Ширина
спада Z-*-vv.
A7.38а)
/2 12я
относительная ширина распада на пару yi
с- 0.12/JV,,
A7.386).
Nf — число фермионных поколений (каждое включает лепто-
и кварки (см. @.91) и @.92)). В стандартной модели Aff = 3, и
Z0%
Заметим, что наличие зависимости A7.36) от sin26w и ее от-
(РГствие в A7.37) и A7.35) объясняется структурой нейтральных
заряженных токов (см. A7.25е), A7.25ж) и A7.25и)).
Подчеркнем, что полная ширина Ftot(Z) зависит от числа раз-
различных типов нейтрино, и поэтому ее исследование представляет
Собой интерес (см. ниже A7.45а)).
Рассмотрим теперь, как регистрируются W±- и Z-бозоны. Они
были обнаружены в экспериментах, проведенных в ЦЕРНе в 1983 г.
двумя независимыми группами исследователей VAX и UA2, на
|1стречных протон-антипротонных пучках (рр-коллайдер), энергия
Каждого из которых ys/2 = 270 ГэВ. W-бозоны рождаются в реак-
реакции
p+p-*W±+X, A7.39)
Где X — произвольная совокупность: адронов. Обнаружение W-бо-
Юнов в экспериментах ЦЕРНа проводилось путем регистрации за-
заряженных лептонов 1±{е±, ^±) — продуктов распадов
;v?,
A7.40)
163

Характерной особенностью ?=, возникающих из распадов A7.40),
является наличие у них большого поперечного импульса вследствие
большой массы W-бозона (бозоны рождаются вблизи порога of>
разования). К началу 1984 г. зарегистрировано около 100событий,
отвечающих распадам A7.40). Исследование распределения по но
неречным импульсам дало возможность определить массу W-6o;io
на непосредственно. Результат группы UAI таков:
ш^=80,9±1,5 ГэВ, A7.41)
а группа UA2 получила:
mw=81,0±2,5 ГэВ.
A7.41м)
Эти результаты, относящиеся к eve-распадам, замечательно соглп
суются друг с другом и с предсказаниями теории ВСГ (см.
A7.33а)).
Согласно (ejx)-универсальности слабого взаимодействия числл
( ) (—)
событий Ne и А^ распадов W-veve и W-*¦ (д. v^ должны бьт.
одинаковыми. Экспериментально получено отношение N^/N,.
= 1,24+^, что хорошо согласуется с теорией ВСГ.
Группа UAI определила массу W-бозона также и из анализа
<-)
событий распадов W->-(Jiv^:
A7.415)
A7.42)
= 81+6 ГэВ>
что отлично согласуется с A7.41) и A7.41а).
Z-бозоны рождались в реакции
и регистрировались по распадам
;, Z-ц+ц- A7.4:5)
Масса mz определялась из распределения по инвариантной масст
/+?--пары. Группы UA\ и UA2 получили соответственно (данные
1984 г.):
mz=93,9±2,9 ГэВ A7.44)
и
mz=92,7±3,l ГэВ, A7.44а)
что хорошо согласуется с теорией ВСГ (см. 17.33а). Для уточнения
массы mz особый интерес представляет процесс прямого рождения
Z-бозона в е+е~-аннигиляции с последующим его распадом
-F, A7.45)
где конечные состояния F включают пары ц+цг, vv, адронные струи
и др. Энергии е+е~-пучков, достигнутые к настоящему времени
(~|/s—40 ГэВ), пока еще недостаточны для наблюдения событий
A7.45). Ожидается, что необходимые энергии будут достигнуты
через несколько лет.
164
Сечение образования данного конечного состояния f в резонанс-
резонансом процессе e+e-->-Z-»-f дается формулой Брейта — Вигнера (см.
~ М __ ™Е_ T(Z-*e+e-)T(Z^f) A? 45a)
& (s — l
Ржидаемое разрешение по энергии встречных е+е--пучков при
'"jte = mz по порядку величины равно 100 МэВ, т. е. значительно
[Меньше Ttot(Z) ~1 ГэВ. Наблюдая в конечном состоянии ц+цг-па-
й, можно измерить B(Z^-[x+[x~) (см. A7.38) и A7.45а)). Полная
крина Ttot(Z) определяется непосредственно шириной распреде-
ения o(s), даваемого формулой A7.45а) и имеющего узкий пик
ри ~]/s = mz. Суммируя по всем наблюдаемым каналам распада
l—-f, можем определить наблюдаемую ширину TV(Z). Разность
Ttot—Г» определяется нейтринными (ненаблюдаемыми) распадами
E-*-vrvj, что позволяет найти число типов нейтрино.
. е) Обобщение модели ВСГ на адроны
Выше было рассмотрено электрослабое взаимодействие лепто-
0В. Теория ВСГ непосредственно обобщается на адроны. Посколь-
у наблюдаемые адроны состоят из кварков, то необходимо по-
Мроить теорию электрослабого взаимодействия кварков. Феноме-
Феноменология слабых взаимодействий кварков уже обсуждалась во
"введении.
.< Как и лептоны, кварки обьединяются в левые дублеты (см.
| @.78)) и правые синглеты:
Г
= (doR, sOr,
sol
, ql0R = {uOr, cor, t0R),
A7.46)
причем, в отличие от @.78), в A7.46) фигурируют нефизические
¦ «вёэмассовые кварки qo, что отмечено индексом «0». Физические
, 'массивные кварки q возникают после спонтанного нарушения сим-
! метрик SUB)wxU(l)-»-t/(l)em и представляют собой собственные
Состояния фермионных массовых матриц М я Я (см. A7.47)).
Лагранжиан взаимодействия S"w кварков с хиггсовским дубле-
;' том ф A7.4) выбираем в виде (ср. A7.5г)):
h э. с, A7.47)
где Mij/v—fij, Mijlv=fij являются юкавскими константами связи
Кварков с хиггсами, причем М и М — произвольные постоянные
Комплексные матрицы, подразумевается также суммирование по
цветовым состояниям каждого кваркового аромата (цветовые ин-
индексы для краткости опущены).
Калибровочные поля
165

В унитарной калибровке A7.11) лагранжиан A7.47) приводи!
к следующему массовому слагаемому 9?mlq) в полном лагранжиа
/О \ iv
не (формально это сводится к замене ф-> , <Pf-M
\v } 1,0
в A7.47)):
r I — ("м- cox., to) M I CoR ) + э. с A7.
R' \t0R/
48)
Далее, заметим, что произвольная комплексная матрица М
может быть приведена к диагональному виду D с помощью пре-
преобразования
AlMAr-1 = D, A7.49)
где Al и Л/г — унитарные матрицы, причем элементы диагональ-
диагональной матрицы D являются вещественными положительными числа-
числами.
Диагонализуем матрицу М с помощью унитарных матриц В,
и ВгГ1:
BLMBR^=B. A7.49а)
Из A7.49) и A7.49а) следует, что A7.48) приводится к диаго-
диагональному виду путем следующих преобразований кварковых полей:
A7.50>
/l.r
Подстановка A7.50) в A7.48) приводит к замене там qo^-q,
матриц М и М на диагональные матрицы D и D, которые можно
записать в виде:
D =
(md О О
0 ms 0
0 m.
D =
mu
0
0
0
mc
0
0
0
n,
В результате массовый член A7.48) принимает вид
A7.51)
A7.52)
где q(x) — дираковский биспинор кварка q = u,d,...,t, масса ко-
которого равна Шд. Эти кварки q, в отличие от qo, являются физи-
физическими массивными кварками — собственными состояниями
массовых матриц М и М.
166
Запишем теперь лагранжиан взаимодействия кварков с ка-
бровочными полями Л„а и В„ (ср. A7.56)):
+
- ig^ Я) -
Из A7.53) с учетом A7.19) и @.94) находим
33 _
/«•> = J] окупим.,
qL. A7.53)
A7.54)
ХДе ао'= («о, Со, *о) — «верхние» кварки, ко'== (do, s0, b0) — «ниж-
ие» кварки. В A7.53) необходимо теперь перейти к физическим
Варкам с помощью A7.50):
ao=^aBt, хо=ЛА-1>с. A7.50а)
„дставляя A7.50а) в A7.54), получаем заряженный ток в тер-
ннах физических состояний q=u,..., t:
/(+)= V «J.VuVttxJ, A7.55)
!'Тде матрица
унитарна
V=BiAl~1
V+V=l,
A7.56)
A7.57)
^'откуда следует | det V | = 1.
Выражение A7.55) совпадает с приведенным во введении вы-
выражением @.79). Взаимодействие тока /й<+> с \^±-бозонами, ко-
которое легко получить из A7.43), совпадает с указанным в @.94).
Рассмотрим матрицу смешивания V подробнее, ограничившись
для простоты случаем четырех кварков ы, d, s, с. Тогда A7.55)
Принимает вид:
A7.58)
Наиболее общий вид уиитарной матрицы V размерности 2X2 таков:
°) A7.59)
1 '
0
Где
UU*=*1, detU=l, т.е. U(=SU{2).
Диагональная матриц в A7.59) может быть устранена переопре-
переопределением фаз волновых функций d и s в A7.58). Поэтому можно
167

считать, что VeSf/B), и, следовательно, ее общий вид та кои
'(см., например, [1]):
у _ е(фТ3/2 е?ф2т2/2 е—Cq>iT3/2t A7.(')())
где фЬ ф2, фз — эйлеровы углы. Влияние левой и правой матриц
в произведении A7.60) снова сводится к переопределению фп i
{(и, с) и (d, s) соответственно. Поэтому можно положить V
-'гп-г-'2, Или, выбирая ф2 = 28с,
V =
cos 6f sin 6f
— sin 6f cos 6f
Подставляя A7.61) в A7.58), получим заряженный ток в виде
/„<+> =cos 6с ¦ uy»Ld+sin 6с • uyj-s +
+ (—sin 6c) ¦cy/'d+cos Qc-cy^s,
"A7.62)
что совпадает с выражением @.81), причем 6С — угол КабибСю
(см. введение).
Аналогично можно рассмотреть случай шести кварков, ко.-дм
матрица V имеет размерность 3x3. Ее явный вид указан во Bin-
дении (см. @.91а)). Подчеркнем, что в этом случае фаза б иг
равна нулю, что приводит к нарушению СР-инвариантности (кик
известно, это нарушение экспериментально обнаружено при ис-
исследовании распадов /С°-мезонов и в других процессах [11]).
Из A7.53) с учетом A7.16а) нетрудно выделить взаимоден
ствие кварков с нейтральными бозонами А„ и ZM:
» = Jlem) A»
A7.62)
где /ц(ет> и /м@> — электромагнитный и слабый нейтральный ток
кварков, совпадающий с указанными во введении (см. @.59).
@.90), @.92) и @.94)).
ж) Интерференция электромагнитного и слабого взаимодей-
взаимодействий
Характерной особенностью единой теории электромагнитных и
слабых взаимодействий ВСГ является наличие эффектов интер-
интерференции этих взаимодействий. Интерференционные эффекты воз-
возникают вследствие того, что ферм ионы связаны с двумя нейт-
нейтральными векторными бозонами — фотоном и Z-бозоном.
Рассмотрим в качестве примера процесс электрон-позитронной
аннигиляции в пару фермионов: е+е~—ff. В теории ВСГ ему отве-
отвечают диаграммы (а) и (б) рис. 17.5, интерференция которых при-
приводит к характерной угловой асимметрии в распределении f я f.
168
„.чет дифференциального сечения аннигиляции е+е~—ff приводит
|СЛедующему результату:
T
па? dcosG
l
Q2 A
+ {— 2Qf Gs (s/ml — 1) [vevf A + cos2 6) + 2aea, cos 6] +
V [{i% + a2e) (v2f + aj) A + cos2 6) + 8veaevfaf cos 6]} [s/ml — IJ +
+ lzimzf\-K A7.63)
! mz и Tz — масса и полная ширина Z-бозона (см. A7.36))„
fmf2G/na, of и Cf — векторная и аксиальная константы связи
•рмионов с Z-бозоном (см. @.92а)):
ff=72/3f-Q/sin2e^ af = V2V, A7.64J
з' — проекция слабого изоспина фермиона, Q,- — его заряд
единицах е; 6 — угол между импульсами фермиона и электро-
, Ys — энергия в системе центра масс.
Асимметрия углового распределения A7.63) характеризуется
личшюй
А,F) =
—G)
V ;
do(G)+( )
Ив A7.64) следует, что для электрона (/Зе= —V2. Qe= —1)
t,e= —1/4+ sin2 6W-— 0,022, ce= — '/4 A7.66);
При sin2 6^=0,228. Кроме того, mz—90 ГэВ и Tz—3 ГэВ, т. е.
<rVJ10-3
A764J1
z)
Итак, |we|<l, (Г2/т2J<1, и для Af/0) из A7.65) и A7.64J1
Получается простое приближенное выражение
a Qt
A7.67)
Из A7.65) и A7.67) следует, что асимметрия зависит от зна-
КВ заряда, и она больше для кварков q, чем для лептонов I
(Qe"=±l/3, ±2/3; Q/ = ±l), и при этом возрастает с энергией
У«. В частности, для аннигиляции е+е~ в пару лептонов ц,+ц~ или
160

т+т из A7.67) получаем (av=ar= —1/4, QV.=QX=
Л@)=Лт@)^—9-10-55(ГэВ)/{1
Средняя асимметрия
1)
4 7
= _з_
4 f
A7.GH)
v
а(в<я/2)+а(в>я/2)
Экспериментально измеренное значение этой величины при
энергии Vs = 34,5 ГэВ, полученное на установке PETRA (встреч
иые е+е--пучки) в ускорительном центре DESY (ФРГ), для про
цесса e+e-->(j,+(j,~ равно
<А.>ВКС11=(-10,8±1,1)%; A7.70)
теория ВСГ предсказывает
<А.>твоР= —9,4%. A7.70а)
что хорошо согласуется с A7.70).
Следует заметить, что угловая асимметрия в процессе
ere+-*-ff характерна не только для теории ВСГ. Она возникает
также и в КЭД за счет интерференции диаграммы а рис. 17.5 м
диаграмм рис. 17.6, соответствующих радиационным поправкам
низшего порядка к диаграмме а рис. 17.5. Однако эта чисто
электродинамическая асимметрия Лкэд надежно вычисляется и
может быть вычтена из наблюдаемой асимметрии. Кроме того,
для энергий установки PETRA асимметрия /4кэд — 1,5%, что зна-
значительно меньше значения A7.70а), предсказываемого теорией
ВСГ.
Укажем в заключение, что электрослабые эффекты, обуслов-
обусловленные нейтральными токами, проявляются также в атомных оп-
оптических переходах (см., например, [11]). Так, в 1978 г. в ИЯФ
СО АН СССР (Новосибирск) впервые наблюдался Р-нечетный
эффект, который заключается во вращении плоскости поляриза-
поляризации пучка света, пропускаемого через пары висмута. Величина
эффекта хорошо согласуется с предсказаниями теории ВСГ.
170
§ 18. ПРАВИЛА ФЕЙНМАНА В ТЕОРИИ
ВАЙНБЕРГА—САЛАМА—ГЛЕШОУ
Теория ВСГ выше была изложена в унитарной калибров-
, Однако при конкретных расчетах часто оказывается удобным ис-
пьзовать другие калибровки. Мы выпишем полный лагранжиан
юрии ВСГ в так называемой (перенормируемой калибровке
R-калибровке)] « сформулируем соответствующие правила Фейн-
|вна. -^
а) Лагранжиан теории ВСГ в R-калибровке
В § 17 было .показано, что в теории ВСГ лептоны и кварки
оъедиияются в левые (L) дублеты и правые (R) синглеты. Вы-
ишем их еще раз в виде, отражающем симметрию, существую-
между лептонами и кварками:
A8.1)
i
и
А
UR,
cr,
Sr,
ft
tR;
bR.
В произвольной калибровке лагранжиан ВСГ можно записать
}'Ш виде
| - . *,г + *№ A8-2)
Г Здесь 2а — лагранжиан калибровочных полей А»а (а=1, 2, 3)'
[_ и В„, определенный в A7.5a); SBf — лагранжиан фермионов
(лептонов l—\e, e, v,,, [х, Vx, т и кварков q = u, d, с, s, t, b)r взаимо-
i действующих с калибровочными полями; 3*f — лагранжиан хиг-
гсовских бозонов A7.5в); 3?^ — лагранжиан взаимодействия
фермионов с хиггсами, приводящий после спонтанного нарушения
симметрии к массам фермионов; 9?вг — член, фиксирующий ка-
'либровку (в унитарной калибровке (см. § 17) i?gf = O); SB&h —
лагранжиан «духов» Фаддеева—Попова, компенсирующий вклад
нефизических степеней свободы.
Фермионный лагранжиан
f i J Rnb*Rn, A8.3)
171

изводные D,/ для дублетов и D,/ для синглетов определены еле
дующим образом (см. A7.6) и A7.56)):
A8,1)
здесь в силу A7.3) слабый гиперзаряд YW=2Q, Q — средний за
ряд частиц данного мультиплета (L, R). Следовательно, для дуб
лета лептонов (кварков) YWL =—1 (YWL= 1/3), для нейтрино
YwR=0, для правых"заряженных лептонов YWR= —2; для верхних
(нижних) правых кварков YWK = 4/3(YWK= —2/3).
В лагранжиане хиггеов 3?9 A7.5в) скалярный дублет <|
A7.10) в произвольной калибровке параметризуется так:
+ Х2 \
— i%J
где х< (i=l. 2, 3) — безмассовые'голдстоуновские бозоны (исче-
(исчезающие в унитарной калибровке (см. A7.11)).
Взаимодействие 2V, фермионов с хиггеовскими бозонами мож-
можно записать в виде (ср. A7.47) и A7.5г)):
I [I
Fl ijl
a. с, A8.6)
где fijiF), /i/(ir> (F = l,q) — юкавские константы связи лептонов
(/) и кварков (q) с хиггеами ф, причем фс — изоспинор, зарядово
сопряженный изоспинору ф (см. A7.4а)); правые синглеты разби-
разбиты на нижние (R,) и верхние (К,) следующим образом:
, bR);
cR, tR).
A8.6a)
Массы фермионов mF определятся массовым членом в лагран-
лагранжиане
2п=2т™+&ть\ A8.7)
который (получается из A8.6) заменой ф и фс на их вакуумные
средние
а именно
veR
xL) Af w I v^R J, A8.8)
172
[Мйтричные элементы лептонных массовых матриц
|Кварковое слагаемое 2V7* и соответствующие матрицы
шМ и MW>=M определены в A7.47) и A7.48). Диагонали-
i массовых матриц уже описана в § 17, п. е). В результате
принимает вид A7.52), а лептонное слагаемое
I. A8.9)
цовательно, в общем случае возникает также и лептонная
рица смешивания Vil\ аналогичная кварковой матрице V
,_6). Заметим, что V(/>^1 означает нарушение закона сохра-
ИЯ лептонного заряда, в результате чего становятся возмож-
возможен переходы типа ve-^ve, ve*-+v» (осцилляции нейтрино; см.
1]). В стандартной модели (см. @.91)) принимается V(l)=l,
Ь, по отдельности сохраняются электронный, мюонный и таон-
лептонные заряды. В настоящее время ведутся эксперименты
^лью обнаружить осцилляции нейтрино.
Перейдем в лагранжиане от полей Л„й, В» и %i, хг к полям.
W г„, Л и х± (см. A7.19), A7.16) и A8.5)):
Zy, = —Bw sin
У,, = B^ cos %w + Al sin %w,
l cos 6и7,
+
A8-10)
ечающих W*- и Z-бозонам, фотонам и заряженным хиггеовским
лирам. Заметим, что голдстоуновские бозоны х* соответствуют
••бозонам, а хз — Z-бозону (в унитарной калибровке у^1, хъ
^лощаются продольными компонентами W± и Z).
В терминах полей A8.10) член, фиксирующий калибровку в
|8.2), запишем в виде:
=
L
aw
1
2а,
awmw
2а;
A8.11)
ив av — калибровочные параметры. Такой выбор 9?е\ обеспечи-
1ет наиболее простой вид пропагаторов (в частности, смешанные
ны EW±)xT и {dZ)%3 в A8.11) сокращаются с аналогичными
нами в S'Jj.
Вид лагранжиана духов S'gh определяется из требования
?С-еимметрии (см. гл. III) полного лагранжиана A8.2):
описывает свободное движение духов с и с, а 2'gh
2'ghC) —
173.

их взаимодействие с калибровочными полями
гсами х*. Хз- Приведем их явные выражения:
^, Z», А» и хнг-
| <?fh = —~
—~cz (а2 + azmi) cz—~сАд2сА—
сА-(
i {еА»
с" —
¦ («
I
2 cos в„
-j- azmz (cAc- + czc-) ] —
(—~c+c~ + ~c~c
aztnz (czcz +
A8.1:»)
Подставив -A8.10) в A8.2), запишем J?F, ^?ф и ??Р<р в термин.^
физических полей W±, Z, А, ц и голдстоуновских бозонов х±.-Хз:
=
э. с.
ф—??<р ~\~ ??>ф тЛф ~г Лф!
A8.1Г.)
— miZ^—mw{W
э. с.)—т^*%; A8
—э- с-1
где
(р4> = -^- ^.t^-11 B0П + Л
2
Z^X+X" +
+ g! Sin8^ 7u W+»y- 4v + *4 + X.) + э. c.]-
cos 26^,
[W+W (iv + ir\ + Хз) + э- с] + eg
cos
\ xi) + ^-(ц2-
X-X+X3+
A8.15r)
_.. / m
my 2
-S.c}-f
формулах A8.14) и A8.16) г]з" — «верхние» фермионы (ve, v,i,
и, с, t), ^d — «нижние» фермионы (е, ц, х, d, s, b), m,-u, mf- и
Л Qid — их массы и заряды (в единицах е) Уц — матрица
кешивания.
Явный вид слагаемого So в A8.2) указан в A7.24).
Для построения пропагаторов выделим из полного лагран-
|Л|(иана A8.2) слагаемые, квадратичные по полям:
] W-
A8.17)
(a2 + ml) л L
2,
—c+ (a2 + a
—~cz
(а2 + azw2z)
—тп) %—
c~—c
c+—
azmz) cz—~cAd2cA.
174
175

б) Правила Фейнмана
Лагранжиан A8.2), отдельные слагаемые которого выписаны и
A7.24), A8.11) — A8.17), позволяет получить правила Фейнм;щ;|
в теории ВСГ обычным образом (см., например, [1]), исходя ш
выражения для S-матрицы в виде Г-экспоненты:
S = Tex.pl[ijd4x27i(x)], A8.18)
где Si — лагранжиан взаимодействия. Матричные элементы
•Sf' = (/|S|i) связаны с амплитудой перехода Тц из начальник»
состояния \i) в конечное |f) известным соотношением:
—Pt)Tfl,
A8.HI)
где Pt и Pf — импульсы системы в начальном и конечном состоя
ниях.
Правила Фейнмана позволяют написать выражение для 7>, и
данном порядке теории возмущений по константам связи /;,
e=gsinQw, g'=gtgQw.
Сформулируем эти правила, изображая пропагаторы калиб
ровочных бозонов, фермионов, хиггсовских бозонов и духов соот
ветственно волнистой, сплошной, пунктирной и точечно-пунктир
ной линиями. Стрелки на них указывают направление перенос.!
квантовых чисел: заряда — для W±, ^±, фермионного числа — для
¦ф, духового числа — для с, с (у проиагаторов духов символы A>
и ©¦ указывают знак переносимого заряда). На вершинных диаг
раммах импульсы всех частиц, кроме духов, считаются входя щи
ми в вершины (импульсы духов переносятся вдоль направления
переноса духового числа).
1) Пропагаторы (см. A8.17)):
L + iO
! + t0
x+
X" =-
k2
A8.20)
176
к я =-
к © с*
k2 — arfny + «0
'¦ — azmz + Ю
2) Вершины в yG (см. A7.24)), V = W+, W~,A. Z:
VW:
(e) [gafi (k—p)y + g-pv {p—q)a
A8.21)
VWV:
177

A8.22>
4) Вершины в ^?ф (см. A8.15)),
мны HVH:
= Х±, Х8,
\
— gayg&i + g'oe^Pv—
3) Вершины ^ViK в ?F (см. A8.14))
A8.23)-
2 cos 6,р
(е)-(р—<
A8.24)
178
179'

= ±
cos
вершины VHHV:
A8.'.'!.)
= rp iemwgat.fi>
'
/ч
2 cos2
1\ /
\ /
х—^-?«р;
cos
2 cos2 6
186
.«p
„2 Sin2 бге
4 r
2 cos 6
/хч
eg
A8.26)
g2 /cos2ell7\2
=т1
/*"
Л
cos
5) Вершины г]зЯг]з в УРф (см. A8.16)):
g
2
A8.27)
181

g m_
2 m
w
= rp g
,4 \
6) Вершины в <?gh (см. A8.13)):
вершины cVc:
= =F epa;
X
A8.28)
I".'
..A
N.
N
A
N
N.
cos
182
= ± ep«;
I
183

I
t
A.
\4
..<*' v
i
i
Л
2
A8.2!))
g
2 cos 6,,
- aztnz-
cz
Сделаем некоторые замечания к приведенным выше правилам
Фейнмана.
Пропагаторы A8.20) Ац(к) являются фурье-образами Г-про-
изведений полей цц (х):
AtI(k)=—ild*xel**@\T4t(x)<pj@) |0>. A8.30)
В частности, пропагатор W-бозона определяется в виде
D^k) = — i№xeikx{Q\T W\(x)U7.-@) |0> A8.31)
и в координатном представлении удовлетворяет уравнению
A8.32)
которое является обобщением уравнения A6.19), причем
D»x(x)=№kl{2ny]e-ik*D^{k). A8.31а)
Подстановка A8.31а) в A8.32) дает выражение для пропагатора
W-бозона, указанное в A8.20). В конкретных расчетах часто ис-
используют следующие специальные калибровки:
184
1) калибровка Фейнмана (etw=l), в которой пропагатор Dav
шимает вид:
¦'V-v
2) калибровка Ландау (aw == 0):
k" — п% +
3) унитарная калибровка (aw = оо):
A8.33)
A8.33a)
A8.336)
к2 — /п^, + Ю
'Мто совпадает с A6.17).
Все вершины выводятся из лагранжиана 3? (а не из
¦Нелогично тому, как это сделано в § 12. Общее же определение
вершинных функций таково (см. § 13): это 3- или 4-точечная ам-
¦ Путированная функция Грина, т. е. внешние линии (пропагаторы)
; Исключаются.
Если диаграмма содержит петлю, то по соответствующему им-
|','Пульсу р проводится интегрирование с весом
j_ г dDp
^Причем имеется в виду использование метода размерной регуля-
|«ризации с помощью перехода в D-мерное пространство
уЭтот метод описан в гл. VII. Фермион-
ИЫм и духовым петлям приписывается
[„дополнительный множитель (—1),учи-
Г'ТЫвающий антикоммутативность по-
В лей фермионов и духов (духи фор-
формально рассматриваются как скаляр-
скалярные фермионы; см. § 12).
в) Примеры
Рассмотрим два примера приме-
[¦''нения правил Фейнмана, сформулированных в п. б).
1) lF-бозснный вклад в поляризационный оператор Z-бозона
PVvz{q) в однопетлевом приближении изображается диаграммой
рис. 18.1.
Используя правила Фейнмана (см. A8.20) и A8.21)), запи-
запишем этот вклад в виде:
Рис. 18.1
j -
* [(k - 2?)» 6Р + (q - 2%
+ (q-2k\
7 Калибровочные поля
A8.34)
IBS

где для пропагатора W-бозона использована фейнмановская k;i
либровка A8.33). Методы вычисления интегралов типа A8..'М)
описаны в гл. VII.
Заметим, что величина P»vz(q) определяет радиационную по
правку к свободному пропагатору Z-бозона DtKz(q) следующим
образом:
2V( (q) Pz-»Hq) D^z (q) + .... A8.3Г.)
V(?) ^(q) +D^ (q) PHq) D^ (q) + .... A8.3Г.)
где Dv.vz(q) — точный пропагатор (с учетом всех радиационны\
поправок).
2) В качестве другого примера рассмотрим однопетлевые пои
равки к амплитуде рассеяния гйе-^-%е, обусловленного нейтраль
ньши токами. Мы не станем рассматривать всю совокупность од
нолетлевых диаграмм, ограничившись для примера диаграммами
а и б рис. 18.2. Диаграмма а отличается от диаграммы древо.-
Л
Рис. 18.2
ного приближения (см. рис. 5.10) заменой свободного пропагато
ра Z-бозона DVKz(q) на однопетлевую поправку, определяемую
вторым членом в A8.35). Соответствующая амплитуда имсчм
вид:
= (g/2 cos %wf [uv (p'v) y«mv (Pv)l X
X fue (p'e) Yp (gv + gAy5) ue (pe)] D**» (q) PZyb (q) Dz'av (q), A8-3(i)
где gv= —
=—1k, a
указаны и
)
A8.33), где надо сделать замену тц?->-т2, и A8.34), причем
q=p/—Ре.
Амплитуду, отвечающую диаграмме б рис. 18.2, следуя прапп
лам Фейнмана, записываем в виде (снова используем калибровку
Фейнмана для пропагатора Z-бозона; обозначения импульсоь с\>
на рис. 18.2):
dDk
С dDk Г- , '
X
'V (gv + gAy5)
-Yp(^ +
ХЫС
A8.37)
Г,ГДе gv, gA и q — те же, что и в A8.36).
| Расчет радиационных поправок к амплитудам электрослабых
I1 ^Процессов древесного приближения приводит нас к проблеме пере-
перенормировки. Важным свойством теории ВСГ является ее пере-
j нормируемость, что будет показано в гл. VI.
Глава VI
ФУНКЦИОНАЛЬНАЯ ФОРМУЛИРОВКА
КВАНТОВОЙ ХРОМОДИНАМИКИ
Ранее в гл. III мы уже обсуждали лагранжиан и-правила
Фейнмана квантовой хромодинамики на уровне теории возмуще*
ний. Здесь мы дадим представление КХД с помощью интегралов
по путям. Это даст нам возможность провести общее исследова-
исследование структуры КХД, ее калибровочной инвариантности и, главное,
продемонстрировать ее перенормируемость.
§ 19. ПРОИЗВОДЯЩИЙ ФУНКЦИОНАЛ КХД
а) Трудности калибровочной теории
Если применить теорию, развитую в гл. IV, то для функцио-
функционального описания КХД на основе классического лагранжиана
2Vd= —Ч* G^G^-MH*) (i^D^—M)^(x) A9.1)
следует записать производящий функционал Z{/,,, ц, tj} в виде
функционального интеграла по всем конфигурациям классических
полей — 4-векторному полю А»(х) и спинорным полям ty(x) и
¦ (*):
))]. A9.2У
Тогда производящий функционал Г{/ц, т), т)}, который непосред-
непосредственно позволяет вычислять n-точечные функции Грина, будет
выражаться обычным образом:
Пк,\ r)}=Z{/w ц, T)}/Z{0, 0, 0}. A9.3)
Однако выражения A9.2) и A9.3) могут рассматриваться лишь
как сугубо формальная запись правил квантовой хромодинамики.
Они демонстрируют явную калибровочную инвариантность теории,
•7* 187

поскольку инвариантен лагранжиан КХД, стоящий в показателе
экспоненты. Инвариантной является также мера /)[Л„(х)] функ-
функционального интеграла, включающая интегрирование по всем ка-
либровочно эквивалентным конфигурациям поля Л11(х). В то жо
время выражение A9.2) включает в себя ряд противоречий, ко-
которые не позволяет использовать его даже в теории возмущений.
Эта проблема, которую мы уже обсуждали в гл. III, связана
с калибровочной инвариантностью теории и возникает в более
простой теории — квантовой электродинамике. Действительно,
для свободных фотонов формально можно было бы написать
производящий функционал
A9.4)
где /ц — источник, который после дифференцирования устремля-
устремляется к нулю. Выражение, стоящее в показателе экспоненты, по-
получается следующим образом. Лагранжиан максвелловского поля
2ем = —7«*V A9.5)
с учетом определения /7,lv=d^v—<5„ЛМ преобразуется к виду:
2ЕМ= —'/г[(ЗАJ—(ЗА) (&А*)], A9.6)
после чего производится его интегрирование по частям, и мы на-
находим /
—д*&)А*(х).
A9.7)
Матрица K^v = g^vd2—d^dv, стоящая в обкладках Л^ и Л,, под зна-
знаком интеграла, не имеет обратной, поскольку
det/C=O. A9.8)
Напомним (см. гл. III), что это связано с наличием у K^v нуле-
нулевых мод, имеющих вид чистой калибровки
д.(*)=3.е(*), A9.9)
где Q(x) — калибровочная функция. Очевидно, что для A9.9)
имеем
(g^d2—d^dv)dv6(x)^0. A9.10)
Таким образом, интегрирование гауссова интеграла A9.4) по
полям Аи(х) дает расходимость вида (det К)''2—*-°°. Бесконеч-
Бесконечность набирается за счет интегрирования по нулевым модам, т. е.
по чисто калибровочным переменным вида A9.9), что дает вклад
JZ) [нулевые моды]е~°-»-оо. A9.11)
Таким образом, наличие лишних степеней свободы, нулевых мод,
связанных с калибровочной инвариантностью КЭД, приводит к
расходимости производящего функционала. С другой стороны,
188
f'Wto приводит к неоднозначности выбора пропагатора фотона, о
ИвМ уже говорилось в гл. III. Выход из указанных трудностей
Состоит в фиксации калибровки, т. е. нарушении калибровочной
Инвариантности. При этом в теории возникают лишние rj-частицы,
Связанные с продольными компонентами поля. В КЭД они удач-
Ным образом отщепляются, поскольку ни с чем не взаимодей-
взаимодействуют. В КХД, как было показано в гл. III, в силу нелинейности
Неабелевого калибровочного поля rj-частицы взаимодействуют с
Самим полем А„. Ранее уже обсуждался выход из этого положе-
положения. Исключение вклада нефизических т]-полей достигается за
счет введения полей «духов» Фаддеева—Попова. Нам предстоит
Продемонстрировать, каким образом это осуществляется на языке
1 функционального интегрирования.
' 6) Факторизация производящего функционала
![ Потенциал калибровочного поля Afi(x) определяется конкрет-
1 Ным выбором калибровки. Напомним, что локальное калибровоч-
калибровочное преобразование потенциалов определяется калибровочной
функцией Qa(x):
х) -* Л; (х) = ш (х) (А^ (х) +
(Н(*). A912)
Различные значения Qa(x) задают калибровочно эквивалентные
потенциалы. Обозначим через
J*vBw{x) A9.13);
калибровочное поле в конкретной калибровке Qa(x).
Интегрирование по нулевым модам, т. е. по калибровочным
функциям ва(х), от которых S'qcd не зависит, дает расходящийся
Результат. Поэтому не существует обратного оператора для
w=g^d2—ЗА,, и функциональное фурье-преобразование не опре-
определено. Если бы нам удалось выделить эту расходимость в виде
отдельного множителя в Z{j, ц, ц}, то он сократился бы с таким
Же множителем в Z{0, 0, 0} и мы получили бы конечный резуль-
результат для T{j, т), ц}.
Введем некоторый локальный мультиплет Са(х) (а= 1, 2,..., г),
Принадлежащий присоединенному представлению калибровочной
группы. Умножим теперь Z{/,,, т), т)} на постоянный множитель
$D[Ca{x)]exp[— (t/2) $dx(Ca{x)J] =const. A9.14)
Предположим теперь, что Са является функцией потенциала,
заданного в определенной калибровке A9.13), т. е.
A9.15)
189

Тогда равенство
> (х) ] =
(х) ]
A9.16)
означает 6'(x)=/[6(x)], т. е. оно фиксирует выбор калибровки.
Иными словами, задание Са[з&в1*Цх)] определяет калибровочную
функцию Q(x). Можно задать, например,
) = ^д^ЛЦх). A9.17)
где 0<?<оо — параметр калибровки.
В функциональном интеграле A9.14), включенном в качестве
постоянного множителя в определение Z{]^ r\, tj}, перейдем с уче-
учетом A9.15) к новым переменным интегрирования:
Ca{x)-+Qa(x). A9.18)
Тогда исходный интеграл A9.14) перейдет в интеграл
const = JD[6«(x)]det
ЭДесь
dct
A9Л9)
A9.20)
функциональный якобиан перехода.
Таким образом, в результате умножения на постоянный мно-
множитель A9.14) и перехода к новым переменным интегрирования
A9.18) производящий функционал Z{jm т), т)} из исходного A9.2)
превращается в следующий:
Х
X exp {_-l
X exp [i J dx(XQCD + Ц {х) Л? (х) + i (х) г\ (х) + ч (х) if {x)].
После перемены порядка интегрирования
)]Х
A9.21)
A9.22)
A9.23)
оказываются под знаком интеграла по А^, и в них можно произ-
произвести замену
множители
190
tl л*^-'ух)->*ъ*-(х), A9.24)'
в AMe(x'(x) — переменная интегрирования в интеграле JD[A,,(x)],
.Данная в определенной калибровке. Далее, вернемся к исход-
Ьму порядку интегрирования
да«(*ШЯ[Ам(х)], A9.25)
Г§ под знаком интеграла по калибровочному полю A|i(jc) произве-
\. Дем калибровочное преобразование
A9.26)
учетом инвариантности меры JD[AM(x)] и лагранжиана
итоге после всех проделанных операций получим
Z 0V, Tj, ri} = J D [6° (х)] J D [А^
х
ЬСа
exP
(x
Х
-±.(С°{НхТ + %
A9.27)
Этот функционал применяется для вычисления калибровочно
инвариантных физических матричных элементов, поэтому зависи-
зависимость последних трех членов в показателе экспоненты от калиб-
калибровки не является существенной, и мы можем положить в них
'©(*)=0. Таким образом, подынтегральное выражение в A9.27)
Оказывается не зависящим от Q(x) и производящий интеграл
?{/м> Ц> т)) факторизуется: интеграл по в(х) дает бесконечный
Объем локальной калибровочной группы: JD[6(x)]-voo, а остав-
оставшийся функционал Z'W», r\, г\} оказывается конечным:
Z{L Л- n}4D[6(x)]-Z'{U ~n, г,}. A9.28)
Точно такой же множитель возникает в знаменателе A9.3):
Z{0, 0, 0}-vjD[6(x)]-Z'{0, 0, 0}. A9.29)
Сокращая на этот бесконечный множитель, для производящего
функционала Т{/,„ ц, ц} получим конечный результат:
T{j,, Ц, il)=Z'{/M, т), ii}/Z'{0, 0, 0}. A9.30)
В дальнейшем штрихи у конечного функционала Z' мы будем
опускать.
191

Производящий функционал поля имеет вид
Z (/) = J D [Ф (х)) ехр {»J dx [Я (х) + / (х) Ф )х)]}
Заметим, что описанная процедура выделения бесконечного
множителя в производящем функционале может быть прослежена
на более простом примере.
Рассмотрим свободное безмассовое скалярное поле <р(х) с лаг
ранжианом
A9.31)
(^ |} A9.32)
Классическое действие \dx& с лагранжианом A9.31) инвариант
но относительно преобразований
<p{x)->q>'(x)=<p{x)+C{x), A9.33)
где функции С(х) удовлетворяют уравнению
д2С(х)=0. A9.34)
Другими словами, оператор, стоящий в показателе экспоненты
A9.32), имеет нулевые моды и, следовательно, Z{j} расходится.
Можно выделить эту расходимость в качестве множителя. Для
этого умножим Z{j} на постоянный конечный множитель — функ-
функциональный гауссов интеграл
В результате
A9.35)
X j?> [ф (х)] ехр {i J dx \В (х) + / (х) q> (x)]}.
....,,. s ,„¦ A9.36)
Далее, меняя порядок интегрирования и производя замену С(х)-+-
->С(х) + ф(х), которая не меняет значения гауссова интеграл;!,
получим
D[Ф(х)] JD[C(х)]ехр{ i-^Jdx<C
X exp{i!jdx[J5?(л) + /(*)ф
х
[() + /()ф()]}. A9.37)
Возвращаясь к исходному порядку интегрирования и производя
замену ф(х)-мр(х) + С(х), относительно которой j? инвариантен,
находим
A9.38)
, +i(x)(<e(x) + C(x))]}.
! В последнем слагаемом в показателе экспоненты можно положить
192
1(х)=0, поскольку оно не дает вклада при вычислении физиче-
ВКНХ матричных элементов. В итоге интеграл JD[C(x)] выделя-
1ГЯ в качестве постоянного бесконечного множителя, а остав-
оставшийся функционал
]exp{iSdx[&-(v*/2)<f(x)+j(x)(p(x)]), A9.39)-
Гвсчающий скалярному полю с эффективной массой ц, оказыва-
§Тся конечным. Таким образом, устранение расходимости, связан-
связанной с бесконечным объемом нулевых мод, достигается ценой вве-
|дфция массового члена с параметром ц размерности массы в тео-
теорию, которая первоначально такого параметра не содержала.
Точно так же устранение расходимости в КХД, связанной с
!Йесчонечным объемом пространства калибровочной группы, обес-
И§ЧИвается за счет введения в функционал A9.27) члена, фикси-
фиксирующего калибровку
-С2 =
A9.40У
|'|| соответствующего нарушения калибровочной инвариантности
[!ftopnH.
в) Духи Фаддеева—Попова
Найдем теперь явный вид функционального якобиана пере-
['Мода
№b(x)
чя этого рассмотрим вариацию
х)] = —^
A9.42)
кВспомним, что
Тогда
ЬСа =
Отсюда находим функциональный якобиан перехода
A9.43)
) |. A9.44),
Под знаком детерминанта стоит дифференциальный оператор
6аЬб2 + ^СЬф4с»\ A9.45)
Имеющий, кроме того, матричные индексы а, Ь=\, 2,..., г. Напом-
193.

ним, что именно этот оператор возникает в уравнении для поля
ща(х) (см. гл. III):
Определитель A9.44), стоящий в качестве множителя под знаком
функционального интеграла в определении Z{ju, tj, т)}, может быть
представлен также как функциональный интеграл. Для этого
введем нефизические поля q>a(x) и ц>а+(х) — поля духов, подчп
няющихся статистике Ферми. Тогда, согласно известной формуле
для гауссова интеграла по ферми-полям (см. выше), получим
det
= и D [ф {
ехр Ийх
^ }. A9.47)
Проинтегрировав в показателе экспоненты по частям, получим
A9.48)
функцию Лагранжа духов, которую мы уже вводили из других
соображений в гл. III.
Таким образом, после проведенной в предыдущем пункте про
дедуры сокращения бесконечного фактора к лагранжиану КХД
добавился лишний член — 3?gf, фиксирующий калибровку, a те
лерь после введения духов — еще один член — лагранжиан духои
J?gfc. Окончательно, производящий функционал КХД принимав
вид _
T{h, г), T)}=ZG;, "rf, t)}/Z{0, 0, 0}, A9.4'.))
где х
Z {/ц.
здесь
} = j D [Л„
X ехр {i j
2'qcd=
х)] D [<$(х)] D [ср (х)] D [ср+ (х)] X
+ <?а + %eh + ГЖ (х) +
M) Ч>,
A9.51)
Хотя введение члена, фиксирующего калибровку, и нарушает км
дибровочную инвариантность действия, однако физические резу.м.
таты остаются не зависящими от калибровки (см. гл. III, где р;к
сматривается БРС-симметрия КХД).
Таким образом, мы построили производящий функционал КХД
A9.49) — A9.51), исключив из него нефизические калибровочные
моды. Полученное выражение позволяет, в принципе, стропи.
194
Кцни Грина и соответствующие матричные элементы в любом
цдке теории возмущений, а также исследовать общую струк-
теории и, в частности, проблему расходимостей и перенор-
ВОВОК.
§ 20. ПЕРЕНОРМИРУЕМОСТЬ КАЛИБРОВОЧНЫХ ТЕОРИИ
Как известно, при изучении теории возмущений нельзя
аничиваться только древесными диаграммами. Включение пе-
|Ь не меняет типа процессов, однако может приводить к рас-
шости матричных элементов. Здесь мы изучим общие особен-
ги расходящихся диаграмм и возможности их регуляризации.
) Расходимости и перенормировки
Приведем прежде всего пример расходящейся диаграммы в
|нтовой электродинамике (КЭД). Радиационная поправка к
гронному пропагатору в однопетлевом приближении (второй
рядок теории возмущений) описывается диаграммой
Bп)* yp—m
Па(р)
1
ур — т~\- Ю
B0.1)
СЬ ампутированная функция Грина П2(р), отвечающая соб-
внно-энергетической диаграмме, записывается в виде:
у». B0.2)
(p—k)y—m-
IK известно, этот интеграл по внутреннему импульсу k pacxo-
:я логарифмически. Действительно, при &2—»-оо интеграл растет
1НСЙНО
B0.3)
иако этот член после интегрирования обращается в нуль из-за
щетности подынтегрального выражения. В результате расходи-
гь оказывается логарифмической.
Аналогично для скалярных частиц массы ц имеем ампутиро-
|Нную функцию Грина
k2— (
m2+i0
B0.4)
|сходимость интеграла здесь, как легко видеть, также оказыва-
СЯ логарифмической. Таким образом, расходимость в амплиту-
_ |1Х появляется за счет интегрирования по петлям, т. е. по внут-
Кжнему петлевому импульсу. Рассмотрим теперь общий случай.
усть имеется диаграмма с L внешними линиями с импульсами
\Ри Ръ •••> Pl и I петлями с внутренними импульсами ki, k% ..., ki,
195

по которым производится интегрирование. Этой диаграмме отис
чает амплитуда
... d%f(pu ..., px._, ,
B0...)
Здесь возможные расходимости устранены пока обрезанием ми
импульсам |&,|<Л, где Л — импульс обрезания. Пусть часть п>
множества S{ki>} внутренних импульсов растет
ki> = kr{>, B0(.>
где Я, растет, п< фиксировано. Тогда верхний предел степени
роста функции / окажется функцией К:
В результате
k[> e 5 получим
где
|/|<const-?ic<s>.
интегрирования по внутренним
I Cdk1...dkt'f\<Ad*is4nA,
d4(S)=4m+C(S)
B0.7)
импульсам
B0.К)
B0.!))
индекс расходимости по импульсам ky^S (i'=l, 2,..., т)
Интеграл сходится, когда d4E)<0. Индекс расходимости умет,
шается, если перейти к меньшему числу измерений D<4:
dD(S)=
B0.К»)
На самом деле нет необходимости рассматривать все расходи
щиеся диаграммы. Вполне достаточно ограничиться лишь так n.i
зываемыми примитивно расходящимися диаграммами, т. е. та к и
ми диаграммами, в которых только последнее интегрирование
приводит к расходимости. Можно показать, что остальные дн;и
раммы к ним сводятся.
Структуру примитивно расходящихся диаграмм данной теории
можно установить с помощью комбинаторных соображений. Р;н
смотрим квантовую электродинамику. Пусть некоторая диаграммч
содержит следующие элементы:
196
У — число вершин, /„,, 1А (?„,, ЕА) — число внутренних (внеш-
электронных (ty) и фотонных (Л) линий. Тогда число петель
равно
l = IA + h— V+l. B0.11)
ствительно, для получения числа петель следует из полного
та внутренних линий /д+/„, вычесть число линий, соединяю-
вершины так, что по ним можно было бы один раз последо-
иьно лерейти от первой до последней вершины, т. е. V—1.
^.-Рассмотрим примеры.
; I) Радиационная поправка второго порядка к электронному
чагатору:
/*= 1, IA=\, V = 2; /= 1 + 1—2+ 1 = 1.
,2) Одна из диаграмм радиационной поправки четвертого по-
ВКа к электронному пропагатору:
= 3, Га = 2, V = A; /=3+2—4 + 1=2.
вычисления индекса расходимости в пространстве с D изме-
ИИЯМи учтем, что каждая внутренняя фермионная линия несет
(Яичную степень импульса в знаменателе, а каждая внутрен-
фотонная линия — вторую степень в знаменателе. Элемент
8MB в импульсном пространстве несет степень DL Итак,
dD = Dt—2h—h. B0.12)
необходимо выразить dD через число внешних линий, которое
гировано для данного процесса. Для этого учтем следующие
|бинаторные соображения. Для фермионных линий с учетом их
прерывности имеем
E + 2I 2V. B0.13)
ТО же время для фотонных линий находим
B0.14)
скольку из каждой вершины выходит лишь одна фотонная ли-
Ч, причем внутренние линии связывают две вершины. Теперь с
|Т<>м петлевого уравнения B0.11) можно выразить dD через
?¦ и V:
-V+l) — 21 А—/ф =
\\2V-Ea—1-Е
B0.15)
197

Для D=4 отсюда находим
BО.Н.>
4=4-3/2?,—Ел
Как видно, число вершин не входит в уравнение для d4.
следует вывод, что число примитивно расходящихся диаграмм
ограничено, т. е. не увеличивается с ростом числа вершин \ц>»
заданном числе внешних линий.
Заметим, что учет различных симметрии может сделать иски
торые расходящиеся диаграммы (индивидуально или в сумме)
сходящимися. Как известно, в электродинамике имеются л и пи.
три типа примитивно расходящихся диаграмм:
1) ?* = 2, ЕА = О
собственно-энергетическая диаграмма электрона; по форму.'м
B0.16) находим d4=l (на самом деле, как мы уже видели выше.
с учетом нечетности подынтегрального выражения d4=0 — лог.-i
рифмическая расходимость);
2) ?* =
поляризационный оператор фотона; здесь согласно B0.16)
3) ?ф=
вершинная функция; здесь d4=0.
Вообще говоря, если в теории имеется конечное число типом
примитивно расходящихся диаграмм, то такая теория назывлп.-.i
перенормируемой.
Рассмотрим другие примеры.
Контактное взаимодействие (модель Ферми слабых взапмп
действий). Взаимодействие изображается фермионной четырем
хвосткой
198
Зоскольку в теории имеются только фермионные линии, то пет-
вое уравнение и комбинаторное уравнение для вершин и линий
шут вид
/=/*— V+l, E^+2/^W, B0.17)
учтено, что число линий, сходящихся в вершине, равно четы-
ВМ. Тогда индекс расходимости при D = A будет равен
d4=Al—I* = 4 + 2V—3/2E*. B0.18)
видно, число вершин V входит в d4. Поэтому с ростом V для
[^Компенсации вклада вершин необходимо вводить все больше
|нешних линий. Это увеличивает число примитивно расходящихся
иаграмм до бесконечности. Теория оказывается неперенормируе-
эй.
Теория с промежуточным заряженным массивным векторным
юном W. Число петель равно
t=Iw+It—V+l, B0.19)-
Iw — число внутренних бозонных линий. Комбинаторика ока-
оказывается той же, что и в КЭД:
B0.20>
EV+2IW=V.
Индекс расходимости, однако, определяется другой формулой:
dD=Dl~I^, B0.21)
'поскольку бозонный пропагатор (см. A6.17)) вносит нулевой (ло-
Мрифмический) вклад в степень расходимости. Таким образом,
для D=4 получим
di=Al—/* = 4+ V—3/2?Ф—2EV. B0.22);
Здесь число вершин V также входит в определение d4. Поэто-
Поэтому теория с векторным бозоном оказывается неперенормируе-
Мой *. Напомним, что физической причиной этого является силь-
сильный рост бозонных пропагаторов с увеличением энергии. Заме-
* Можно показать, что теория нейтральных массивных векторных бозонов,
¦¦«имодействующих с сохраняющимся током, перенормируема.
199

тим также, что эти выводы определяются массивностью промсжу
точного бозона. В калибровочной теории бозоны безмассовы (при
условии, что симметрия не нарушена), и поэтому, как мы увидим
в дальнейшем, она является перенормируемой.
б) Индекс расходимости КХД
Квантовая хромодинамика является теорией с ненарушенном
калибровочной симметрией SUC)C. Это обстоятельство опреде-
определяет ее перенормируемость. Поэтому при обращении с расход,!
щимися величинами нельзя терять калибровочную инвариат
ность.
В КХД согласно сформулированным в гл. III правилам ФсТш
мана имеем следующие типы линий:
1а, /*, /с — числа внутренних линий глюонов (А), кварки.!
(¦ф) и духов (G); Еа, Е^ — числа внешних линий глюонов и
кварков. Духи присутствуют только во внутренних частях ди;и
рамм, поэтому ?с = 0. Числа вершин в КХД обозначим следую
щим образом:
У а1 — для четырехглюонных вершин,
Va* — для трехглюонных вершин,
V$ — для кварк-глюонных вершин,
Vc — для глюон-духовых вершин.
Индекс расходимости равен
+VC
B0.2Л)
Здесь учтено, что пропагаторы духов, являющихся скалярами,
вносят степень два в индекс расходимости, кроме того, трех
глюонные и глюон-духовые вершины линейны по импульсам. Псм
левое уравнение КХД запишем в обычном виде:
VAs—V*— Vc+h
B0.2-1)
где учтены все типы вершин.
Комбинаторные уравнения таковы:
/ф = 2VV
21А =
VG
2/G = 2V0.
B0.2;.)
Во втором уравнении учтено число линий, входящих в каждую м =
двух типов глюонных вершин (соответственно 4 и 3), а в третьем
уравнении учтено отсутствие внешних духовых линий.
Запишем dD с учетом B0.24):
dD = D{IA
B0.2Г.)
Исключая отсюда числа внутренних линий с помощью B0.25),
найдем
200
dD = D + (D — 4)VA<
+ A/2D — 2)VG— 1/2 (D —
D=4 получим
— 1/2 (D— l)Et. B0.27)
B0.28)
To уравнение в точности совпадает с соответствующим уравне-
ем для d4 в КЭД. Таким образом, так же как и КЭД, калибро-
_«ная теория сильных взаимодействий КХД оказывается пере-
Ормируемой, т. е. число примитивно расходящихся диаграмм в
ей является конечным.
в) Перенормируемость теории ВСГ
„Покажем, что в теории ВСГ число типов примитивно расхо-
|щихся диаграмм конечно.
Лагранжиан взаимодействия (см. гл. V) представляется в виде
ммы членов S'i, каждый из которых является произведением
, Сезонных полей и /(- фермионных полей с 6,- производными по-
|й. Вершина i-ro типа, возникающая из S'i, имеет индекс ш,-,
пределяемый в виде:
<ы=bt+3/2fi+б,—4 = dim S'i—4,
B0.29)
Be dim Si — массовая размерность Si (массовые размерности
йрмионных и бозонных полей равны соответственно 3/2 и 1).
Пусть Г — сильно связная (одночастично неприводимая) диаг-
шма, имеющая ЕвAв) бозонных и EF(h) фермионных внеш-
fix (внутренних) линий и т вершин г-го типа. Тогда имеют мес-
комбинаторные соотношения:
B0.30)
Дндекс расходимости d(T) диаграммы Г, определяемый, как и
|ыше, путем подсчета степеней импульсов в числителе и знамена-
Wie в соответствующем фейнмановском интеграле, оказывается
1вным (рассматриваем сразу D = 4):
= Y л
+ 21 в + З/f — W + 4,
B0.31)
Где V =
— полное число вершин в диаграмме. Здесь мы
,учли, что при больших импульсах k=Кг(Х-^-оо) фермионные про-
Пвгаторы ведут себя как Я~', а бозонные — как "к~*. Подчеркнем,
ЧТО для бозонных пропагаторов используется ^-калибровка Тооф-
Та (см. A8.20)). Заметим также, что два последние слагаемые
возникают вследствие того, что каждой вершине приписывается
Калибровочные поля
201

б-функция, выражающая сохранение 4-импульса, причем имеется
еще одна б-функция, отвечающая сохранению полного внешнем
импульса.
Исключая в B0.31) числа внутренних линий 1В и If с помощь" >
B0.30), получим с учетом B0.29) индекс расходимости в виде:
d (Г) =
% — Ев — 3/2 EF + 4.
Диаграмма примитивно расходится, если d(F)^O. Из B0..Т.1)
следует, что если все индексы вершин co<<O, то число типов i.i
ких диаграмм конечно, и теория оказывается леренормируемоп
В теории ВСГ условие со,<О, как легко проверить, выполнен"
Для этого достаточно непосредственно по формуле B0.29) выти
лить сог- для всех Si, выписанных в § 17, 18. Например, для вер
шины (dZ)WW имеем ю = 3+ 1—4 = 0, для вершин У4(У=Л, Z, W).
¦фУг]), HVH(H=%±, %з, ц) также ш = 0. Есть и отрицательные пи
дексы: ш= —1 для VHV, сНс (с — духи); в 9?4 (см. A8.15 г))
есть вершины с и = 0, —1, —2, —3. Итак, теория ВСГ являем ;\
перенормируемой.
Детальное проведение программы перенормировки, т. е. устр.1
нение расходимостей из S-матрицы, в калибровочной теории д<н
таточно сложно и выходит за рамки данной книги (см., например.
[4, 9, 10]). Мы ограничимся лишь некоторыми общими замечп
ниями.
Цель теории перенормировки заключается в определении (од
нозначном) конечных частей фейнмановских интегралов, отвечаю
щих расходящимся диаграммам. Наиболее последовательно чи>
делается с помощью R-операции Боголюбова—Парасюка [41
^-операция эквивалентна введению в лагранжиан контрчлешш.
которые представляются в виде рядов по константе связи. В in-
ренормируемой теории число типов контрчленов конечно, и н\
можно подобрать так, чтобы скомпенсировать расходимости и w>
строить конечные функции Грина. Это утверждение нетривиальна
и требует доказательства. Для общего класса нейиелевых калнП
ровочных теорий со спонтанным нарушением симметрии, к кот
рому относится и теория ВСГ, такое доказательство впервые былч
дано Г. Тоофтом в 1971 г. Поглощение всех расходимостей огрл
ничейным числом контрчленов обеспечивается тем, что между
различными расходящимися функциями Грина имеются соотношу
ния, называемые тождествами Славнова—Тейлора [9, 10]. Эш
тождества представляют собой обобщение известных электродшт
мических тождеств Уорда [4] на неабелевы калибровочные тео
рии.
Весьма существенным при доказательстве перенормируемосш
является использование класса калибровок (^-калибровок), в кп
торых правила Фейнмана имеют явно перенормируемый вид
Однако в ^-калибровке требуется введение нефизических частим
(в теории ВСГ это заряженные скаляры и духи), и необходимо.
202
сазать, что они не нарушают унитарность S-матрицы. В уни-
|рной же (см. § 17), т. е. физической, калибровке духи и нефи-
Шеские скаляры отсутствуют, и унитарность S-матрицы легко
указать (перенормируемость же — весьма затруднительно).
>фт и Велтман A972) дали общее доказательство независимо-
S-матрицы от выбора калибровки. В результате было получе-
доказательство калибровочной инвариантности и унитарности
|ренормированной S-матрицы.
( В результате перенормировки определяются конечные ампли-
физических процессов, выраженные через конечное число
8ренормированных параметров — физических констант связи
|рядов) и масс частиц. В теории ВСГ такими параметрами яв-
гся заряд электрона е, массы W- и Z-бозонов mw, tnz, массы
1рЪ1ионов mF, масса хиггеовского бозона тч.
Глава VII
РАЗМЕРНАЯ РЕГУЛЯРИЗАЦИЯ
В предыдущей главе было показано, что калибровоч-
теории поля перенормируемы. Мы не будем производить поя-
рассмотрение всех расходящихся графиков теории возмуще-
|й в неабелевой теории поля. Ограничимся лишь провозглаше-
ем основных принципов программы перенормировок, а затем
смотрим простые примеры.
§ 21. ПРОГРАММА ПЕРЕНОРМИРОВОК
В КАЛИБРОВОЧНОЙ ТЕОРИИ
Поскольку перепормируемость КХД и объединенной
Мели ВСГ, или в более общем случае квантовой флэйвордина-
'1КИ, следует из калибровочной инвариантности этих теорий, то
1сюдв получаем первое правило программы: необходимо обра-
|ть внимание на калибровочную инвариантность, сохранять ее
г Процессе вычислений.
Мы уже видели, что правила Фейнмана дают для расходя-
1ХСЯ диаграмм математически неопределенные выражения. Им
/ет придать определенный смысл, т. е. провести так называе-
|ГЮ регуляризацию. Простое обрезание импульсов сопровождает-
включением в теорию параметров с размерностью массы, что
^Иводит к нарушению калибровочной инвариантности, а это нё-
Щустимо. Мы уже упоминали ранее возможность перехода в
" эстранство-время низшей размерности D<4. При этом прими-
ЯО расходящиеся диаграммы будут давать конечный резуль-
|Т. Если затем осуществить аналитическое продолжение полу-
Нных конечных выражений по D-+-4, то это приведет к тому,
расходящаяся часть примитивно расходящихся диаграмм
иределяется как полюс D—D). Отделяя эти полюса, получим
203

конечные перенормированные выражения. Эта процедура назы
вается размерной регуляризацией.
Расходящаяся часть примитивно расходящихся диаграмм не
наблюдается физически. Так, в КЭД расходящаяся часть элект
ронного пропагатора изменяет массу т, входящую в лагранжипн
(затравочную, голую массу), на величину Дт-г>оо. Наблюдаемля
конечная масса электрона определяется как сумма
те=т+Ат
B1.1)
двух бесконечных величин.
В КХД, так же как и в КЭД, все расходящиеся части прими-
примитивно расходящихся диаграмм поглощаются в физически бес
смысленных мультипликативных константах перенормировки полой
Z,1/2. Эти константы в пределе, когда импульс обрезания Л стре-
стремится к бесконечности, или размерность D стремится к четырем
(при размерной регуляризации), становятся бесконечными
В КХД мы имеем три типа полей — глюонное А„, кварковое ip м
поле духов ф. Соответственно получаем
где А^р, я];*, ф/<! — перенормированные поля. Эти конечные значе-
значения полей, а также соответствующие им конечные перенормиро
ванные функции Грина получаются после сокращения мультиплм
кативных констант. Описанная схема сокращения расходимостем
носит название мультипликативных перенормировок.
В то же время необходимо учитывать, что поглощение расхо
димостей в мультипликативных константах оставляет неопреде
ленными конечные части функций Грина. Поэтому для их одно
значного задания вводят дополнительные условия перенорми
ровки.
Все указанные пункты программы перенормировок проще все
го проследить на конкретном примере. В следующем параграфе
мы и переходим к его рассмотрению.
§ 22. ГЛЮОННЫЙ ПРОПАГАТОР
В ОДНОПЕТЛЕВОМ ПРИБЛИЖЕНИИ
Приведем пример применения описанной в предыдущем
параграфе программы перенормировок. Рассмотрим глюонный
пропагатор д^(х—х'). Во втором порядке теории возмущений
по константе будем иметь следующие диаграммы Фейнмана:
(а)
— поляризация фермионного вакуума
(рождение виртуальных кварк-аи
тикварковых пар);
204
— поляризация глюонного вакуума
(рождение виртуальных глюонных
пар);
прямое глюонное самодействие;
ч—¦'
— калибровочная поправка (рожде-
ние виртуальных пар духов).
а) Поляризация фермионного вакуума
I¦¦ Рассмотрим подробно график (а). Невозмущенный глюонный
ропагатор имеет вид (см. гл. III):
цесь I — параметр калибровки. В случае калибровки Ландау
оперечной калибровки) полагаем |=0.
Для диаграммы (а) согласно правилам Фейнмана получим
X
B2.2)
[где
1
г 2 Y(<7 — */2)— m + tO 2
B2.3)
[шклад диаграммы (а) в ампутированную двухточечную функцию
! Грина (пропагатор). Здесь
Тг= tr-tr-tr B2.4)
F,c,s Fes
Обозначает след по всем индексам матриц, входящих в определе-
определение П<0), т. е. по аромату (F), цвету (с) и спину (s).
205

Отметим прежде всего диагональность матриц в B2.3) по аро
мату, поэтому
tr(...) = NP, B2.!.)
где Nf — число ароматов кварков, вносящих вклад в петлю i-p.-i
фика (а). Следует иметь в виду, что мы в дальнейшем будем р:м-
сматривать высокоэнергетический предел, и поэтому различие и
массах кварков будет несущественным. След по цветовым индек
сам сводится к известному следу произведения матриц Гелл
Манна
tr*A = 2Sob. B2.1.)
с
Таким образом, остается след по спиновым индексам, умножен
ный на фактор NF/2, т. е.
Tr->-—-tr.
F.c.s 2 s
B2.7)
Вычисление tr=tr по спиновым индексам полностью аналогично
s
соответствующей процедуре в КЭД при расчете поляризации ил
куума. В высокоэнергетическом приближении можно положить
т-*-0, тогда все сводится к вычислению следа
-(q+k/2) (q-k/2)gl>0+
После чего получим (от->0):
<1—k/2)a—
-fc/2) p}=4B(^-74 W-
B2.8)
ПЙ? (k) =:
Как видно, интеграл по импульсу петли q расходится квадратич
но. Воспользуемся методом размерной регуляризации, сохраняю
щей калибровочную инвариантность. Для этого перейдем из че
тырехмерного пространства в пространство размерности D<4, зм
менив
°. B2.10)
Кроме того, следует учесть, что константа взаимодействия g при
Вф4 становится размерной. Действительно, заметим прежде все
го, что действие в системе ft=c=l безразмерно. Отсюда, в част
ности следует
[S№\*dDx]=M-\ B2.11)
т. е. [i|>] =М^-!>/2.
Далее, [/(&„)Ч°х] = 1, и так как [х] =М.\ [&] =[dAaJdx*l то
Л B2.12)
206
¦конец,
Куда с учетом B2.11) и B2.12) следует
[g] м°-1м-1+с>/2м-0=1,
И, окончательно:
B2.12)
случае D=4 согласно B2.13) g становится безразмерной, как
0 и должно быть. В общем случае, чтобы учесть размерность
мы будем вводить перед интегралом B2.10) множитель \iA~D,
¦ и — параметр размерности массы.
'Для дальнейших вычислений воспользуемся следующим экс-
иенциальным представлением функций Грина:
оО
i = fdzexp[t2(pa —
— тг -\- @ .1
B2.14)
гда, применяя это представление дважды, из B2.9) получим
B2.15)
¦место k введено k' с тем, чтобы в предэкспоненте вместо сте-
Ией q можно было полагать
IM самым интегрирование по q сводится к взятию гауссовых
МДратур в D измерениях.
Напомним, что для одномерного интеграла
2Я
(а + Ю)-'/2 .
[Тогда для D-мерного интеграла
B2.17)
B2.18)
Рассмотрим теперь интеграл по q, входящий в B2.15). Преоб-
рмуем показатель экспоненты, выделив полный квадрат
Zl-22)qk1 =
z2) (q + -J-1-^
207

Тогда с помощью B2.18) найдем
einD/i
4—D
1 2
X
xexpjt
_^ (Zx-Z,J ft'
4 Zl + z2 4
B2.1!»)
Предэкспонента вычисляется применением операции B2.16) к по
лученному результату B2.19):
^_
4
+ ¦
L(zi —z2J \ гх+г2 / 4 4
•" (zi-z2J 1
Учитывая, что dklildkp.=D, окончательно'найдем
7") + 2
B2.20)
Объединяя B2.15), B2.19) и B2.20), приходим к результату:
—i — D-D)
l
о о
4-D
208
,Mf-), ~
|_ i(Zl + Z2) (ZX + Z2J
ЙИЗведем далее замену переменных 2Ь 22->Я, z:
Zi = X(l—Z), Z2 = *,2,
ода получаем
взатель экспоненты
—2).
перехода к новым переменным
Z Я
результате перепишем B2.21) в виде
Г, --^D-D) , в
? UpolRJ 2 4я! J J ^ '
Г ЯраФ/2-1'
X
значим теперь
гда
_l JL D-D)
4
2 4л2
4-D
1 °°
B2.21)
B2.22)
4—D
ч 2
X
B2.23)
B2.24)
w
о о
1—
x / j!_\ 2 Г—e—"I
X ( j?2 j Lz(l-z) J
x
|Ро8ьмем прежде всего интеграл по г
B2.25)
B2.26)
Где В(х, у) - бета-функция, аВД- гамма-функция.
209

Интеграл по р берется с помощью общего определения гаммп
функции:
B2.27)
Л=ГB)х-|, Rex>0.
В нашем случае имеем интегралы типа
СО
rfpef«I+«»pS== f e-p(O-.)ps.
О
Г
О
Здесь мнимая часть Ю в круглых скобках в показателе экспо
ненты возникает за счет введения исчезающе малой мнимой чл
сти в исходных пропагаторах: k?-*-k2+tO. Поэтому у нас. х
——t+О, и формула B2.27) оказывается применимой.
Нам необходимы интегралы
со
J
—1
г (—5-
B2.28)
= (—t)
Проводя с их помощью интегрирование по р в B2.25), с учетом
B2.26) получим
4—D
2
X
Применяя соотношение хГ(х) =Г(л;+1), приведем ампутировпп
ный пропагатор к окончательному виду:
4— D
2
X
и'2 /
B2.2!))
Перейдем теперь к пределу 4—D-^+О, обозначая для краткости
8 = 4—D. При этом
Г (Я/2) = Г B--е/2) = A-в/2) Г A-е/2),
B2.30)
210
i -=ГD—е) = C-е) B-е) A— е)ГA— е),
Г (—0/2 + 2) = Г (е/2) = Г A + е/2)/ (е/2).
1втим далее, что гамма-функция может быть разложена в ряд
B2.31)
Со = 1, а другие коэффициенты равны
• С, sn = L,(n) при n>2, Re z>0,
С — постоянная Эйлера, ?(л) — дзета-функция Римана. Кро-
ТОго, необходимо учесть разложение
_JLin-JM ~ I _-Lln^-. B2.32)
ц2 / 2 (j,'2
указанные разложения с точностью до членов порядка е,
N.
1
Т ^р^2—^^) х
ле выделения полюсного члена в отдельное слагаемое окон-
льно находим
X
B2.33)
1С ц" = е~с/2]1', С — постоянная Эйлера. Мы видим, что именно
|мма-фуикция Г(—D/2+2), имеющая полюса при D = 4, 6, ....
риводит к возникновению полюса в выражении B2.33). Выде-
Кный полюс при D — A в этом равенстве отвечает логарифмиче-
Ой расходимости графика (а) поляризации вакуума, с которой
I столкнулись бы при вычислении интеграла по импульсам не-
средственным образом.
б) Вклад глюонов и духов
Рассмотрим теперь вклад оставшихся диаграмм в пропагатор
ЯЮОна. Диаграмма (б) описывает самодействие цветных глюо-
DB, Ее вклад выражается формулой
211

x
- {22М)
Здесь в соответствии с правилами Фейнмана для трехглюом
ных вершин и глюонных пропагаторов имеем
Л>о(<7, k) = (gpj^—g^gp—g^) X
X [g™(q—k/2J— (q—k/2)v(Q—W)a\ Х
B2..Ч-1)
X [gaika gfaqa—gaokf,] X
Константа С\ связана со следом по цветовым- степеням сво
боды глюонов:
0,6=1
В случае глюонных пропагаторов применим следующее экспож-и
циальное представление:
a-2 = f dzzer-0*.
о
B2.3Г.)
После проведения описанного в предыдущем пункте перехода к
пространству размерности D, интегрирования по q, zx и z2 и пре-
предельного перехода D->-4 получим
12
12 4-D
900
B2,Г/,
Диаграмма (в) дает не зависящий от k конечный вклад, кото
рый путем размерной регуляризации может быть положен ран
ным нулю. Калибровочная поправка, описываемая диаграммой
(г) с пропагаторами духов, выражается интегралом
Размерная регуляризация в данном случае приводит к результату:
.J ? 2_\
12 4— D 9 '
16л2 [ 6ра \ 12 (х"
212
-D)- B2-39)
Объединим теперь вклады всех диаграмм вместе:
B2-40>
2
»=а,б,в,г
Заметим, что вклад диаграммы (а) поперечен, а (б) и (г) —
.„Т. Выпишем результат суммирования коэффициентов при по-
ЯЮсном члене 2D—D)~l:
3 2 v" " "-' ' з "
[очно так же коэффициент перед In(k2/jx,) после суммирования
удет равен
IK видно, оба эти члена, полюсной по 4—D и логарифмический
k2, поперечны. Оставшийся конечный член имеет вид
a (—gpofc2+kpka) + $kDka,
|5ГДе аир — некоторые числовые константы, не является попе-
поперечным. Непоперечная часть выпадает при умножении на попереч-
пропагаторы, а поперечная часть объединяется с In ffe2/n^
//О О Г)
,;41утем соответствующего переопределения (х=и2. В результате
Г"Для B2.40) получим выражение
^
-ln -^-+0D-Л)].
^
B2.41)
Полный ампутированный пропагатор с учетом однопетлевой по-
лравки B2.41) равен
. Пра (k) = (kpka-gpok*)
B2.42)
.где e=4—D. Заметим, что нас интересует лишь пространствен-
пространственно-подобная область импульсов k2=—Q2<0, поскольку именно в
этой области у пропагатора отсутствуют особенности, связанные
•с выходом виртуальных частиц на массовую оболочку. Тогда
)=1п(—Q2+r0)=lnQ2-ln(—l.+ tO) =
\nQ2+in.
B2.43)
213

Тем самым мнимая часть пропагатора оказывается однозначж,.
определенной. Для отделения конечной части пропагатора от по
люсной расходящейся части введем параметр jx2>0:
l.'~ ?2 II2
ln-V = ln-V + ln-V B2-4-П
В соответствии с общей программой перенормировок, предложен
нон в § 21, вынесем расходящийся множитель Za(e), включив и
него второе слагаемое из B2.44):
B2.4Г))
где
мультипликативная константа перенормировки;
-^Cl--^) 1п-?.) B2.47)
перенормированный пропагатор глюона. Заметим, что выбор па
раметра \i2, называемого константой нормировки, отвечает уело
вию нормировки
Г& (ft) | о*=ц. = kpko—gP0k2. B2.4»}
Как видно, ZA(e) обладает полюсной расходимостью по размерности
е=4—D. Она соответствует логарифмической расходимости
2.x2 , л2
—+1п —-Ип —
е р,2 |д/
по импульсу Л, возникающей при введении обрезания по им
пульсу в интеграле по q.
Глава VIII
АСИМПТОТИЧЕСКАЯ СВОБОДА
Квантовая хромодинамика дает объяснение главной
особенности кварк-партонной модели, которая состоит в том, что
кварки при больших переданных импульсах, т. е. на малых про
странственных интервалах, ведут себя подобно свободным части
цам. Это свойство называется асимптотической свободой. Для то-
того чтобы продемонстрировать его, мы вначале познакомимся с
методом ренормгруппы, который позволяет выйти за рамки к. ¦
рии возмущений, т. е. просуммировать вклад целой совокупносп
графиков Фейнмана.
214
§ 23. ТЕХНИКА РЕНОРМГРУППЫ
Основываясь на перенормируемости квантовой теории
AИбровочных полей, можно вывести свойства функций Грина,
растеризующие их поведение при больших переданных импуль-
X в пространственно-подобной области. Эти свойства помогают
Оводить вычисление радиационных поправок к процессам при
СОКих энергиях. При этом массовые члены в лагранжиане тео-
И могут быть опущены с тем, чтобы учесть их как поправки
следующих этапах вычислений. В дальнейшем мы ограничим-
Ш безмассовой КХД.,
? В предыдущей главе рассмотрен пример вычисления перенор-
фованной функции Грина nR глюона во втором порядке теории
Змущений. Следует заметить, что nR должна быть определена
рез перенормированную константу связи g, а не через затравоч-
fK) константу go- Тогда перенормированная функция Грина ста-
Овится зависящей как от g, так и от точки нормировки \л. Вспом-
1м, однако, что в исходном лагранжиане имеется лишь один
|раметр — неперенормированная (затравочная) константа свя-
' go. Следовательно, между g и jx должна быть зависимость, ко-
рая проявляется в существовании инвариантного заряда g=
g(p2/|x2, g(p-)), остающегося постоянным при изменении [i и
т8(р) (Н- Н. Боголюбов, Д. В. Ширков, 1955 г.). В дифферен-
„иальной форме зависимость между g и ц устанавливается
уравнением ренормгруппы.
а) Уравнение ренормгруппы
Для вывода этого уравнения рассмотрим ампутированные
ункции Грина. Они зависят, разумеется, от параметра калиб-
Ювки |. Однако эта зависимость в дальнейшем при вычислении
Матричных элементов S-матрицы выпадает. Мы не будем рас-
рассматривать общий случай с произвольным калибровочным па-
параметром |. Ограничимся для простоты лишь случаем попереч-
Кой калибровки Ландау g=0.
Пусть ХпАп (h> Pi)— некоторая одночастично неприводимая
Часть функции Грина, где ?=1, ..., пА; ;=1, ..., пд; пА и пд — чис-
па глюонных и кварковых переменных соответственно. Тогда ам-
ампутированная функция Грина будет иметь вид
{klt р/). B3.1)
A"q
«Функция х„А„ (kc, pj) имеет расходимости, которые могут быть
Р .устранены размерной регуляризацией. Проведем эту регуляриза-
[< Цию согласно описанной в § 21 процедуре. Функции Г„л„ (ki, p,-, е)
1 «содержат расходящиеся при е->0 петли. В соответствии со свой-
свойством перенормируемости калибровочной теории можно ввести
мультипликативные перенормировочные константы ZA(e) и Zq(e),
•таким образом, что существует конечный предел
215

-~
P (g)
p,, g, Ц) = 0.
B3.1/)
•Физический смысл этого уравнения состоит в следующем. Любое
малое изменение точки нормировки ц сопровождается соотвстгт
вующими изменениями g и Zi такими, что любая физическая иг
личина TR остается неизменной. Такие преобразования образ)мм
ренормгруппу (Штюкельберг, Петерман, 1953 г.). Систематнчс
•ское развитие метода ренормгруппы в квантовой теории поля 6м
ло дано в работах Н. Н. Боголюбова и Д. В. Ширкова A95Г>
1956 гг.).
б) Уравнение Овсянникова — Каллана — Симанзика
Уравнение ренормгруппы B3.17) описывает изменение ампли
туд при варьировании точки нормировки ц при фиксировании\
импульсах ki, p,: Вспомним, что величина \i, имеющая размер
.ность массы или импульса, устанавливает масштаб импульсон и
теории. Следовательно, уравнение B3.17) может служить и для
описания изменения амплитуд при движении по шкале масштаГхш
и импульсов при фиксированном ц. Для этого следует привлечь
соображения размерностей. Будем исходить, как и прежде, и i
того, что действие безразмерно, т. е. [S]=l, поэтому для спинор
ного поля [\р] =.М3/2, для скалярного [ф] —М, для векторного
.[y4J=Af. Следовательно, размерность т-функций (т. е. функции
Грина с внешними концами) равна
4-Зпд п
= М. . B3. IN)
Последние три сомножителя в этом равенстве обусловленм
тем, что при выводе функций Грина мы отщепляем множители
B3.1'»)
/=!
«=1
Размерность ампутированной функции Грина Г в силу своего по
строения оказывается равной
где
B3.20)
B3.21)
D = 4—пА—3J2nQ.
Изменим масштаб импульсов:
kr+Ui, Pi->-Kpi, B3.22)
тогда по теореме Эйлера об однородных функциях получим
. V) = 0.
B3.2.'.)
218
рЛОШью этого уравнения исключим теперь ц из уравнения ре-
вгруппы B3.17). В результате получим
^ Ър,\ g, ji)=(>
( B3.24>
— уравнение Овсянникова — Каллана — Симанзика (ОКС)
случая безмассовой КХД. Оно описывает изменение функций
на при преобразованиях масштаба импульса. В реальных экс-
яментах, например в глубоконеупругом рассеянии, параметр
{копоставляется импульсу, принимающему большое значение..
flBHOM виде, т. е. с учетом B3.21), вместо B3.24) найдем:
g,
B3.25)
дичины уА, yq называются аномальными размерностями. Скла-
ая их с D — кинематической, или канонической, размерно-
о, получим динамическую размерность
D + nAyA+nqyq. B3.26),
Рассмотрим решения уравнения B3.24) в частных случаях.
1) Пусть все взаимодействия выключены и C=Ya = Y<7 = 0- Тогда
Ёвет место масштабная инвариантность безмассовой теории вы-
^Жающаяся через каноническую размерность D. Из B3.24) на-
аим
; 0,
- KD. B3.27)
2) Если р = 0, но Y'^0. масштабная инвариантность выражает-
I через аномальные размерности уд и yq:
g, h)~
B3.28)
|ри p^fcO и у1=фО масштабная инвариантность безмассовой теории
лностью теряется. Прежде чем исследовать решение уравнения
С в этом общем случае, познакомимся с физическим смыслом
()
дикции
§ 24. УРАВНЕНИЕ ГЕЛЛ-МАННА—ЛОУ
а) Эффективный (инвариантный) заряд в КЭД
[Взаимодействие двух массивных зарядов Z\e и Z2e в низшем
Яорядке теории возмущений в КЭД описывается диаграммой
С 24.1, а, где переданный импульс обозначим буквой к. Если
зарядов велики, то можно считать их покоящимися. Энер-
219

гия зарядов в результате не меняется, k° = 0, а квадрат 4-импу.;п,
са равен
А>2=—k2<0, й° = 0. B4.1)
В результате получаем закон Кулона:
>2/к2. B4.1')
Учтем теперь однопетлевую поправку,
отвечающую образованию электрон
позитронной пары (рис. 24.1, б). Ии
теграл, выражающий эту попрапку.
расходится. Применяя обрезание пи
теграла по петлевому импульсу вели
чиной М2»к2, получим выражение для
поправки к закону Кулона B4.2) и
случае k2»m2 (m — масса электрона)
- -?-. B4.Л,
1.2 v
6
Рис. 24.1
к2 12л2
'Этот результат хорошо известен в квантовой электродинамике
В сумме B4.2) и B4.3) дают
м2
к2 '
In
12я2 к2
Как видно, эффективный заряд
12л2
к2 /
B4.4)
B4.!-)
становится функцией переданного импульса к2. Ни е, ни М сами
по себе не имеют смысла, поскольку они входят в B4.5) в ком
бинации, причем это выражение получено при условии:
^«1. B4. Гм)
12я2 "' к2 хх '
Запишем значения заряда е(к2) при двух различных значениях им-
импульса:
е2 , N.
12я2
B4 (.
где (е2/12я2) In (iW2/k,-2)<Cl. В этом приближении можно исклт
•чить из B4.6) е2 и М2. В результате получим
Это выражение явно демонстрирует перенормируемость КЭД, im
скольку зависимость от нефизического параметра М2 из него пи
220
па. Выходя за рамки теории возмущений, вместо B4.7) можно
вписать:
2(k2)f(e2(k2), k22/k!2). B4.8)
десь учтена перенормируемость теории, а также безразмерность
ЮСтоянной тонкой структуры е2(к2). Поэтому в B4.8) функция
\ зависит не от отдельных импульсов ki2, k22, а от отношения
ls/ki2, причем k2 >m2.
Вычислим производную
de2(k2)
дх
B4.9)
x=kl/k\. Устремим ki->k?^k2, тогда получим уравнение
бозначив
, х)
дх
\x=i
дх
I —е(к«)Р(ея(к2)),
4.10) запишем в виде
B4.11)
B4.12)
[itTO — уравнение Гелл-Манна — Лоу A953 г.).
Это уравнение получено в общем случае с учетом лишь свой-
Гва перенормируемости КЭД при т = 0. Важно подчеркнуть,
То функция р зависит лишь от эффективного заряда е2(к2). По-
'SWOMy она может быть вычислена по теории возмущений в виде
[|']ряда по е2(к2) при е2(к2)<с1. Найдем главный член этого разложе-
1ция. Полученное выше соотношение B4.7) справедливо и при
"ili2~k22, когда неравенство
[..'Означает
е2(к,2)/12я2<1, B4.13)
Т. е. малость заряда. При этом функция f в равенстве B4.8) со-
согласно B4.7) будет приближенно записываться в виде
¦ln-^-Y B4.14)
к2 /
B4.15)
12л2
•Отсюда
е(к2)Р(е2(к2))=в4(к2)/12я2+О(е6(к2)),
•т. е., окончательно,
221

р(е2(к2))=е3(к2)/12л2+О(е5(к2)).
B4.1G)
Подставляя это приближенное значение функции р при малом
эффективном заряде (е2(к2)/12я2<С1) в уравнение Гелл-Манна
Лоу B4.12), получим
dink2 12л2
Это уравнение может быть проинтегрировано:
_J L_=_L_lnA
е2(к2) е2(к2) 12зх2 к?
Отсюда находим
е2 (к2)
B4.1 Г.)
е2(к2)
к2
B4.17)
Полученный результат выражает значение эффективного заряд.ч
при одном импульсе кг через его значение при другом импулыт
кь Он справедлив при
е2(к12)/12я2<1 B4.18)
и произвольных значениях In(k22/ki2), в то время как B4.7) бы
ло получено при
e4kh к?
B4.191
Последнее условие обеспечивает справедливость однопетлевого
приближения, в котором было получено равенство B4.7). Равен
ство B4.17) при условии B4.18) представляет результат сумми-
суммирования многопетлевых диаграмм при нарушении условия
B4.19), однако оно не учитывает высшие поправки по малому
заряду B4.18).
Хорошо известны выводы относительно экранировки заряд;),
которые следуют из уравнения B4.17). Так, для получения ко
нечного наблюдаемого значения заряда e2(ki2) при
k,2<k22,
т. е. на больших расстояниях, заряд е2(к22) должен быть чрс.ч
вычайно велик. Это означает, что заряд е2(к22) при к22->оо дол
жен быть бесконечным для того, чтобы заряд е2(к|2) оставался
конечным. Наоборот, любое конечное значение затравочного з.-i
ряда е2(к22) (к22-мх>) приводит к его полной экранировке на ко
нечных расстояниях:
e2(k22)<oo, k22
222
I б) Исследование решений уравнения Гелл-Манна — Лоу
Рассмотрим разные случаи поведения функции р в общей тео-
В. Обозначим эффективную константу связи, зависящую от
сштаба импульса К, через g в отличие от перенормированной
Истанты связи g. Таким образом,
IE=g(Kg)- B4.20)
редположим, что теория перенормируема и g подчиняется урав-
№ию Гелл-Манна — Лоу.
¦&-Ю>- B4.21)
Функция P(g) может быть найдена из результатов однопетле-
расчета. Так, в случае КЭД (см. выше B4.7)) мы имели
B4.22)
B4.23)
ловие нормировки. Для р из B4.22) находим
Р(Й=-^7-? B4-23)
согласии с B4.16). В общей
ории могут представиться сле-
рщие случаи поведения функ-
де Я2=к22/[12, ц — точка нормировки. При этом
1) Функция P(g) всюду по-
ВОжительна при f>0. Тогда g2
неограниченно растет с ростом
JC (рис. 24.2, а). Этот случай со-
Гртветствует описанному выше
/доведению эффективного заряда
" КЭД.
2) Функция P(g) имеет нуль
|,.;ри некотором g=gf>0. Эта
[дочка называется стационарной
щ точкой:
=O. B4.24)
"Вблизи ff
=& (gt)G-gf)- B4.25)
Стсюда

Поведение g=g(k) вблизи стационарной точки gf определяет
ся знаком производной P'(gf)- Из решения B4.26) следует, чти
при
оо, если p"(gf)<0;
0, если р" (gf) > 0.
B4.27)
В соответствии с B4.27) gf называется точкой инфракрасном
стабильности, если
Р'Ш>0. B4.28)
и точкой ультрафиолетовой стабильности, если
P'(g»<0. B4.29)
3) Если р (g) имеет два простых нуля 0 < gfl < gf2 < оо, то
константа связи g, находящаяся при каком-то значении К внутри
интервала [gft, gyj будет оставаться там при всех других зна
чениях % (рис. 24.2, б).
4) Функция P(g) отрицательна при g>0 и J5 @) = 0
(рис. 24.2, е). Здесь с ростом % заряд g стремится к нулю. Это
означает, что с ростом импульса \k'2\ условие применимости тео
рии возмущений улучшается, так как константа связи становит
ся все меньше, а при jfe2|->oo получим g2=0. Это явление умень
шения константы связи до нуля с ростом импульса, т. е. с умень
шением расстояния, называется асимптотической свободой. Как
будет показано ниже, КХД свойственно поведение эффективной
константы связи, приводящее к асимптотической свободе. Наобо-
Наоборот, если \№\ уменьшается, то константа связи g растет, т. е. (
увеличением расстояний взаимодействие становится все болег
сильным. Это поведение g является указанием на удержание (коп
файнмент) кварков в КХД.
Таким образом, уравнение Гелл-Манна — Лоу позволяет
учесть вклад всех так называемых лидирующих логарифмов во
всех порядках по g для любой функции Грина по функции р,
вычисленной в первом неисчезающем (однопетлевом) приближе-
приближении теории возмущений по g. Следующее приближение позво-
позволяет учесть все ближайшие к лидирующему логарифмы и т. д.
§ 25. РЕШЕНИЕ УРАВНЕНИЯ РЕНОРМГРУППЫ
Физические амплитуды КХД являются ренорминварп
антными величинами, т. е. не зависят от точки нормировки. Запишем
это обстоятельство более формально. Пусть константа связи g опре-
определяется в двух различных точках нормировки: g—g\ для ц = Ц|,
и g=g2 для [1=ц2. Тогда физическая амплитуда Ф будет оди-
одинакова в обеих точках:
Пусть Ф —
разования р
Ц2, ft). B5.1)
безразмерна, тогда в результате масштабного преоб
-*-Кр получим
224
Ф(р, ц,
:ёски зависит от отношения р/ц, т. е.
Ф(р, Ц. g)=f(P/\x' 8»)
эквивалентна замене
хшу замена
Г Эффективный заряд
B5.3)
B5.4)
яется ренорминвариантной величиной (инвариантным заря-
™ Н. Н Боголюбов, Д. В. Ширков, 1955 г.).
d\i
I. e.
спомним определение р-функции:
dg_
рТогда перепишем B5.7) в виде
ф
Шз равенства B5.4) следует ^
3k
B5.5)
B5.6)
B5.7)
B5.8)
B5.9)
х-3г-
B5.10)
Ренормиивариантная амплитуда зависит от реиорминвариант-
яого эффективного заряда g:
Ф(р, Ц, ^)=^(g^'er))' B5Л1)
•j. e. )=Ф(р ц, g(^. g))- B5Л2)
Поэтому для Ф получаем то же уравнение, что и для g:
" ' В=0 B5ЛЗ)
225
уравнение для ренорминвариантной величины Ф.

Рассмотрим теперь уравнение ОКС для перенормироваппов
функции Грина:
(ял,
=о.
B5.11)
Его решение имеет более сложный вид, чем B5.11), B5.1-)
Обычно решение B5.12) уравнения B5.13) можно рассматривав,
как предварительный шаг к решению более сложного уравнении
B5.14).
Действительно, уравнению B5.13) удовлетворяет функция ни
да B5.11):
O = F(g{Kg)), B5.1:.)
где g подчиняется обыкновенному дифференциальному уравне-
уравнению
dink
B5. Н
(уравнение Гелл-Манна — Лоу) с начальным условием g(g, 1)
=g. Это уравнение описывает изменение эффективной констап
ты связи при изменении импульса р или расстояния между дну
мя частицами г~Цр. Проверим, что функция B5.15) дейстнп
тельно удовлетворяет однородному уравнению B5.13). Для эти
го заметим, что решения с разными g связаны между собой п.-.
менением начала отсчета по ?=1пХ, т. е.
B5.17)
t>g=$(gNt, B5.18)
что следует из B5.16). Тогда
dink
уравнение, которое уже было по
Рис 25 j лучено нами ранее из других со
ображений (см. B5.10)). Тем ел
мым мы показали, что уравпе
ние Гелл-Манна — Лоу B5.16) выражает собой условие ренор-
минвариантности эффективной константы связи g (см. выше об
суждение этого вопроса в связи с эффективным зарядом в КЭД).
Теперь нетрудно найти и решение ренормгруппового уравне
ния ОКС B5.14). Обобщая решение B5.17) однородного уравне-
уравнения B5.13), получим общее решение уравнения B5.14)
(А*,
g, р) =
X
226
?), V)- B5-2°)
решение уравнения B5.14) описывает преобразование функ-
Грина при изменении масштаба импульсов. Как видно, это
Образование
р, g, ц) — Г«д„в (Я*, Кр, g, р) B5.21)
игается за счет изменения константы связи
„ g) B5.22)
I мультипликативного фактора. Заметим, что он отличается от
ft.t как было бы в случае канонической размерности, наличием
Ьмальных размерностей ул и \> Таким образом, поведение ам-
литуд рассеяния при больших 'к определяется эффективной кон-
|антой связи g(h, g) и аномальными размерностями в показа-
Ме экспоненты в B5.20). Эта экспонента, учитывающая все ли-
ликующие логарифмы во всех порядках по g, однозначно опре-
Вляется величинами р и yit вычисленными в однопетлевом при-
Пижении теории возмущений в предположении, что g<l.
§ 26. ЭФФЕКТИВНАЯ КОНСТАНТА СВЯЗИ В КХД
Для вычисления амплитуды рассеяния КХД в области
льших переданных импульсов согласно полученному в предыду-
!м параграфе решению уравнения ОКС следует выяснить зависи-
)сть эффективной константы связи g от импульса. Для этого мы
»лжны знать р-функцию в однопетлевом приближении и затем
ее помощью найти решение уравнения Гелл-Манна — Лоу
,12)
<24
B6.1)
U. Ill ГМ
«¦Естественно, что это вычисление должно быть справедливо лишь
К¦ области g2/4rt>Cl. Для вычисления P(g) и аномальных размер-
.даостей у а, Уя можно было бы воспользоваться их определением.
Гораздо проще, однако, вначале найти три характерные функции
Грина (ампутированные) и затем, подставив их в соответствую-
1 Щие уравнения ОКС, вычислить уд, yq и р. Одна из указанных
1 функций Грина уже была вычислена нами в гл. VII. Для пропа-
гатора глюона в ^-приближении
&ш р
227

было получено
2,0 (k, —k, g, )i)=-
B6.21-
Соответствующее вычисление двухточечной функции
в калибровке Ландау для безмассового кварка дает
Г*а,о(р, —р, g, fx)=Y^- B6.3)
Следует отметить отсутствие поправок порядка g2. Они все со
средоточены в полюсе функции Грина, который не входит в опрс
деление ампутированных функций Грина.
Для кварк-глюонной вершины
вычисления, аналогичные проведенным в гл. VII, дают
. B6-4).
Воспользуемся далее уравнением ОКС в форме
+ пАA — уА)-41 Г*^(ЯЛ, Я,р, g, ц) = 0. B6.5)
Для Гл2,о(я<7=О, пА = 2) имеем
[Я-^ Р-^—h 2A —уЛ)—4 ! Г^о(Я&, -%k,g,»)=O. B6.G)
Проводя масштабное преобразование B6.2) k->k'.= "kk, с учетом
того, что p(g) имеет третий порядок по g, с точностью до g2 по-
получим
Уа =
13
B6.7)
Что касается ампутированного кваркового пропагатора Гл0,2, то,
как видно из B6.3), в нем отсутствуют поправки порядка а'-'.
228
Нее
Y,=0+O(g«).
, рассмотрим уравнение для Г\2(пл=1, п?=2):
1
<26"8>
эдставляя
1ИМ
сюда B6.4), B6.7) и B6.8), с точностью до ?3 по-
B6.10)-
ода
3 2 j
B6.11)-
Теоретикогрупповые множители С\ и Nf, как уже указывалось
«нее, связаны с суммированием по цветовым и ароматическим
тепеням свободы глюонов и кварков. Для группы SGC)c имеем
3, a NF зависит от числа ароматов:
1 „ j 3/2 для трех кварков {и, d, s),
2 \ 2 для четырех кварков {и, d, s, с)
т. д. Таким образом, в основном приближении (—g3) р-функция;
имеет вид
?= ^-g3, B6.13).
'где6=11—3/в#,.
Самое главное, что следует из этого результата, отрицатель-
отрицательность функции р при достаточно малом g и NF<16. До настоя-
1 Щего времени надежно установлено существование пяти кварко-
•ых ароматов (NF=5), т. е. и, d, s, с, b, и ожидается открытие
Шестого кварка t (см. введение). Во всяком случае, реальные
Sf пока что значительно меньше 16.
Тот факт, что р (g) <0, как было показано выше, обеспечивает
асимптотическую свободу теории, или ее ультрафиолетовую ста-
стабильность. Это явление целиком связано с наличием в неабеле-
¦ой калибровочной теории трехглюонных вершин и связанной с
Ними поляризации вакуума глюонными парами. Эта особенность
229«

отсутствует в электродинамике, а также и в любой другой извс
.стной теории.
Подставим значение р-функции B6.13) в уравнение Гелл-Мяп
ва — Лоу;
din % V 16я2
Учитывая начальное условие при к— 1
g(l. g)=g-
.получим решение этого уравнения
?(^,g)= f—
B6. М)
B6.1 Г>)
B6. К.)
16я2
В области
оо или, точнее, t—\n%-*~oo из этой формулы следует
ЩК g)-*Q, B6.17)
причем, существенно, что Ь>0. Таким образом, действительно,
•с ростом импульса (уменьшением расстояния) эффективная коп
станта связи КХД становится меньше и в пределе бесконечно
•больших импульсов уменьшается до нуля, что и называется
«асимптотической свободой». Начало координат g=0 предстаи
ляет собой ультрафиолетово стабильную точку.
Решение уравнения Гелл-Манна — Лоу B6.16) можно перс
лисать в более удобной форме, выбрав масштаб Я равным
Q2=
<?2.
B6.18)
Такой выбор удобен для рассмотрения процессов с большой пере
дачей импульса q, как, например, в глубоконеупругом рассеянии
.лептонов на адронах. С учетом B6.18) получим для g2 = g2(Q2) —
¦бегущей константы связи:
82
B6.19)
B6.20)
B6.21)
Вместо g2 часто по аналогии с КЭД вводят постоянную тонко»
•структуры сильных взаимодействий
' ' 16я2 е '" р.2
причем g==g([i2). Введем вместо ц,2 новый параметр
Л2 = ц2ехр(—1
Тогда вместо B6.19) находим
C3 — 2NF) In Q2/A2
BВ.22)
230
риведем без вывода результат вычислений бегущей константы»
¦ЗИ в двухпетлевом приближении:
^ il A (Ц B6.23).
= Ып ^- + il In In A + О A/ln Ц ,
ль л \ л;
I7 „2 13
0 ~~ з e
1
Возникающая при решении ренормгруппового уравнения ве-
ичина Л является единственным размерным свободным пара-
STpoM теории. Его роль состоит в том, чтобы фиксировать мас-
габ импульсов, при которых взаимодействие становится силь-
црт и теория возмущений уже не применима. Параметр Л, за-
ающий масштаб всей адронной физики, может быть найден
элько экспериментально. Он может быть определен из разных
взависимых процессов, причем сравнение полученных таким об-
I3OM значений Л является важной проверкой КХД. В настоя-
настоящее время, несмотря на совместные усилия теоретиков и экспе-
экспериментаторов, точное значение Л остается неизвестным. Если.
тенивать границы его изменения, то следует принять во вни-
внимание следующее. При
Q2—^р2)-@,8 ферми)-2^@,3 ГэВJ, B6.24)
<Гр2> — средний квадрат радиуса протона, сильное взаимо-
1ствие действительно становится сильным. Это значение Q2 со-
соответствует величине импульса в состоянии кварка, связанного-
:,ЦНутри адрона. С другой стороны, при Q2~2 ГэВ2 эксперимент
t хорошей точностью демонстрирует масштабную инвариантность-
\Ш глубоконеупругом рассеянии лептонов на нуклонах, что соответ-
\ствует условию
asB ГэВ2)/л<§;1. B6.25)
Отсюда с помощью формулы B6.22) получаем
0,1 ГэВ^Л<0,7 ГэВ.
B6.26)
' Рассмотрим пример е+е"-аннигиляции в адроны. В нулевом при-
приближении по as имеем (см. введение):
<*tot {e+e~ -* адроны) =-
B6.27>
где a — постоянная тонкой структуры КЭД, Е — энергия е+е~
в системе центра масс, Q,J — квадраты зарядов кварков. Послед-
Вяя формула получена в соответствии с оптической теоремой как
мнимая часть амплитуды упругого рассеяния фотона, соответст-
соответствующей графику Фейнмана
B6.28).
231

где волнистая линия отвечает фотону, а сплошная — кварк.чм
В КХД следует учесть радиационные поправки, тогда вместо
B6.28) получим
B6.2«>)
где внутренняя волнистая линия отвечает глюонам. Приведем
результат расчета мнимой части диаграмм B6.29):
где
B6. М)
"Интересно отметить, что здесь as определяется во времени-подоО
ной области, а не в пространственно-подобной области, как раш.
ше. Экспериментальное измерение atot позволяет найти as(E2) "
затем — значение Л, которое получается порядка 0,7 ГэВ. Для
глубоконеупругого рассеяния лептонов на нуклонах получаются
меньшие значения А, в соответствии с пределами, установлен им
ми в B6.26).
Заметим, что все приведенные рассуждения справедливы лини,
в пространственно-подобной области q2 = -—Q2<0. Как мы уже
•отметили, только в этой области можно последовательно про ко
дить перенормировки, так как в ней отсутствуют особенности ам
плитуд. В связи с этим утверждение об асимптотической свобо
де также справедливо, строго говоря, лишь в пространственно
подобной области. Область времени-подобных импульсов может
быть охвачена лишь путем аналитического продолжения резуль
татов в предположении так называемой их «некритической глад
кости».
Теперь, зная зависимость эффективной константы связи от
импульса, легко может быть вычислена предсказываемая реше
'нием уравнения ОК.С зависимость амплитуд рассеяния от им
пульсов. В этом решении, как было показано ранее, нетривиаль
ный вклад вносит экспонента от аномальных размерностей вид.1
к in*,
expj-—Y(g(^'))=exp f d{lnk')
l
B6.32)
о
-Поскольку
232
dg
din К
i вместо B6.32) находим
вк было показано ранее,
[то же время
тсюда получаем
B6.33)
B6.34)
B6.35)
?_ Г Jg_| B6.36)
vl, PW
скольку g(k) ix=i = g, то в результате интегрирования B6.36)
ереходит в
ехр[
[b. B6.37)
i
Таким образом, решение уравнения ОКС будет иметь вид
Г« {Кр, g) = л° [g Wig] c/fcr« (p, g(K)). B6.38)
Если теперь учесть, что согласно B6.21)
Ш)с'ь~ (in(Q2/A2)c/b, B6.39)
Ъа оказывается, что функции Грина при преобразованиях масшта-
масштаба изменяются как функции логарифма импульса.
В заключение обсудим кратко физическую причину явления
(¦асимптотической свободы КХД.
В поляризацию вакуума, обусловливающую перенормировку
1.Константы связи g вносят вклад два различных эффекта. Первый
состоит в том, что голый заряд go поляризует фермионный ваку-
вакуум за счет образования виртуальных кварк-антикварковых пар:
Я
(В результате' вокруг g0 образуется облако виртуальных квар-
кварков противоположного цветового заряда, экранирующих g0- Этот
процесс полностью аналогичен соответствующей экранировке за-
5>33
233
I' 9 Калибровочные поля
I ,

ряда в КЭД. Второй эффект возникает за счет поляризации б<
зонного вакуума, т. е. образования виртуальных глюонов:
в результате чего go оказывается окруженным зарядами того >м
знака. Этот эффект называется антиэкрацировкой. Если чис.н.
различных кварковых ароматов не превосходит критически! и
Nf=16, то второй эффект превалирует над первым и голый зл
ряд оказывается антиэкраиированным. Поскольку полный цвето
вой заряд должен оставаться постоянным, то, таким образом, <
уменьшением расстояния до заряда его эффективная величин.!
стремится к нулю, т. е. возникает асимптотическая свобода.
§ 27. АНОМАЛИЯ СЛЕДА ТЕНЗОРА
ЭНЕРГИИ-ИМПУЛЬСА
Рассматривая теорию с безмассовыми кварками, мы <
самого начала не имеем какого-либо массивного параметра. Пи
этому, казалось бы, теория должна обладать масштабной инварн
антностью. Это действительно было бы так, если бы мы ограничм
лись классической задачей. Однако на квантовом уровне, как мм
уже видели, возникает размерный параметр, характеризующий м;к
штаб, с которого взаимодействие становится сильным. Поэтому
можно ожидать, что в квантовой теории масштабная инвариат
ность должна нарушаться. По существу, мы уже сталкивалтч,
с этим при выводе уравнения ренормгруппы и получении его реик-
ния. Продемонстрируем теперь явление нарушения масштабном
инвариантности в квантовой теории калибровочного поля щ.чк>
средственным образом.
Рассмотрим масштабное преобразование, или дилатацию. Д. ы
инфинитезимальных преобразований координат
B7.1)
вычислим вариацию действия
B7 L')
Проводя стандартные выкладки, приводящие к теореме Нёп |>.
для вариации B7.2) получаем
здесь ток дилатации
B7..Ч)
B7,1)
тензор энергии-импульса. Инвариантность действия, т. г
ft?t=0, означает сохранение тока дилатации
»Р а„/1»дал=0, B7.5)
уда с учетом B7.4) получаем
е. в классической теории след тензора энергии-импульса равен
ю. Легко проверить (см. гл. I), что канонический тензор кали-
вочного поля удовлетворяет условию B7.6):
(G«ODJ, 7> = 0. B7.7)
B7.6)
нзор Ти„ массивного поля не удовлетворяет условию сохранения
ка B7.5).
г В квантовой теории масштабная инвариантность оказывается
Крушенной даже в безмассовом случае из-за того, что заряд пе-
Кормируется и становится зависящим от масштаба g=g{X, g).
i удобства изменим на время определение потенциалов и полей
дующим образом:
At=gAl G°v-^G°v, B7.8)
Не Лц и Guv— потенциалы и напряженности поля в исходном
Пределении.
Тогда действие калибровочного поля запишется в виде
,}2. B7.9)
вантовые флуктуации калибровочного поля приводят к измене-
Ю действия исходного классического поля G,lva кл. В результате
вникает эффективное действие (см. ниже гл. IX)
5эфф = ^х2'эфф, B7.10)
te эффективный лагранжиан ^эфф, подобно лагранжиану Гейзен-
Иерга — Эйлера в КЭД, содержит однопетлевую вакуумную по-
поправку. При новом определении поля B7.8) результат учета
^Квантовых флуктуации сведется к замене заряда в B7.9) его пе-
1ренормированным значением:
их.
B7.11)
234
1'Варьируя эффективное действие B7.11) с учетом инвариантности
Исходного действия, получим
bS.^ = -&&- Г (С™У dx. B7.12)
Вспомним теперь, что эффективный заряд g{K) удовлетворяет
уравнению Гелл-Манна — Лоу

т. е. вблизи ^=
Подставляя это равенство в B7.12), находим
B7.1;$>
B7.14)
B7.12а)
откуда в соответствии с B7.3) следует, что дивергенция тока ди
латации
1 = тЕ=-^-(С^)«;
2g8 (Я,)
B7.12П)
здесь р-функция может быть, согласно предыдущему параграфу,
вычислена с точностью до g3:
B7.1Г.)
16я2 °
В правой части правильнее следовало бы вместо (G(lvai(JIJ па
писать
<O|(GVJ|O>, B7.10)
т. е. среднее по вакууму от квадрата напряженности калибровом
ного поля. Таким образом, если это среднее отлично от нуля, т<>
след тензора энергии-импульса в отличие от классического случая
B7.6) уже не будет равен нулю — возникает аномалия следа тон
зора энергии импульса. В следующей главе будет показано, что
истинный вакуум калибровочных теорий отличен от вакуума тео
рии возмущений, так как в системе из-за флуктуации, не опием
ваемых теорией возмущений, возникает глюонный конденсат <•
ненулевым средним квадратом поля B7.16) (Шифман, Вайнштепм.
Захаров).
Заметим, что вакуум по самому своему определению должен
быть релятивистски инвариантным, т. е. его тензор энергии-им
пульса должен быть одинаковым во всех инерциальных системах
отсчета. Поэтому вакуумное среднее Г„т должно иметь вид
<0|rMV|0>=^veBaK, B7.17)
где Евак — плотность энергии вакуума. После суммирования полу
чаем отсюда
евак = 1/4<0|7>Ча>. B7.18)
В силу B7.15) для следа тензора энергии-импульса можем запн
сать
_ P(g)
<0|(G?vJ|0>.
B7.1!))
|Отсюда с учетом B7.17) и B7.15) следует выражение для плот-
гиости энергии вакуума через средний квадрат напряженности
|!цоля:
B7.20)
Оценки величины напряженности вакуумного поля дают для
Свж оценку евак—0,5 ГэВ/Фм2.
Сделаем в заключение одно замечание. Сохраняющиеся тензоры
ti не имеют аномальных размерностей, их размерность — канониче-
К екая. Покажем это на примере электромагнитного тока />, для
которого
а^=0. B7.21)
Отсюда находим сохраняющийся заряд
Q{t) =SJ0(t,x)d3x=consl
Совершим преобразование растяжения
Тогда
Но согласно B7.22)
Поэтому
—
х, kt),
B7.22)
B7.23)
B7.24)
B7.24а)
B7.25)
Т. е., действительно, /0 имеет каноническую размерность, равную
трем. В силу лоренц-ковариантности и остальные компоненты век-
вектора /„ имеют ту же размерность — три. Точно так же можно
показать, что в силу сохранения тензора энергии-импульса
a.7>v=o B7.26)
fpynnbi для перенормированной величины T*{p,g, |i).
Поскольку
4г-^
то в силу
отсутствия аномальных размерностей (уг=0) у TWV имеем
т. е. 7vv не
23ё
зависит от точки нормировки р. Поэтому в равенстве
237

B7.14), так же как и в выражении для евак, эффективный заряд g
И G^Gw* должны быть взяты в одной и той же точке нормиров-
нормировки, так что зависимость от ц взаимно компенсируется.
Глава IX .
ПРОБЛЕМА КОНФАЙНМЕНТА
Как уже указывалось во введении, цветные объекты
КХД, т. е. кварки и глюоны, в отличие от бесцветных адронов не на-
наблюдаются в реальных состояниях. Этот факт получил название
[конфайнмента} илиГзапирания цвета) Если на малых расстояниях
кварки ведут себя как свободные частицы (асимптотическая сво-
свобода), то с ростом расстояния сила их взаимодействия увеличи-
увеличивается. Это можно увидеть и из формулы для эффективной кон-
константы связи, полученной в предыдущей главе. Однако эта фор-
формула перестает быть применимой при импульсах меньше или по-
порядка размерного параметра Л. При малых импульсах вступает
в силу некий механизм, не описываемый теорией возмущений, ко-
который обеспечивает удержание кварков внутри адрона{Донфайн-
мент кварков в настоящее„время не получил пока теоретического
объяснения в рамках КХ.Ш он остается лишь гипотезой, подтверж-
подтверждаемой экспериментамигГРешение проблемы конфайнмента, этой
центральной проблемы КХД,7иридало бы КХД характер настоя-
настоящей завершенной теории. В "результате мы имели бы в рамках
КХД количественное решение проблемы спектра адронов, а также
фрагментации кварков в адроны в партонной модели. Кроме того,
появилась бы возможность построения из КХД теории адронных
взаимодействий. Теоретическое наступление на проблему конфайн-
конфайнмента ведется в различных направлениях. Прежде всего отметим,
что существуют некоторые модели теории поля в пространстве с
меньшим числом измерений, в которых явление удержания имеет
место. Однако эти модели не имеют непосредственной связи с
КХД. Другой подход, развитый Вильсоном, основан на изучении
теории калибровочных полей на решетке, т. е. в случае конечного
числа степеней свободы. Здесь показано, что в режиме сильной
связи g(a)^>l (a — параметр решетки) конфайнмент возникает
естественным образом. В непрерывном пределе а-*-0 константа
связи g(a)-+0, и проблема конфайнмента, таким образом, оста-
остается открытой. Наконец, весьма плодотворным оказалось построе
ние и решение различных нелинейных моделей типа моделей кин-
ков, струн, инстантонов и моделей мешков.
В основе проблемы конфайнмента лежит задача построения
вакуумного состояния КХД. Эта задачу о которой вкратце мы
уже упоминали в конце предыдущей главы, чрезвычайно сложна
и для ее решения предлагались различные методы. Мы не можем
сколько-нибудь подробно останавливаться на всех перечисленных
подходах к решению проблемы конфайнмента. Постараемся дать
238
нятие лишь о некоторых из наиболее популярных нелинейных
целей (часть из которых уже рассматривалась в гл. I), а так*
упомянем некоторые результаты исследования вакуумного со-
ояния теории. *
§ 28. НЕЛИНЕЙНЫЕ МОДЕЛИ ТЕОРИИ ПОЛЯ
! , В настоящее время в различных областях физики интен-
интенсивно исследуются различные нелинейные уравнения. Реальная фи-
1,в«ка, действительно, является нелинейной, однако решение соответ-
соответствующих задач чрезвычайно сложно. При исследовании нелиней*
Шых классических полевых уравнений возникает особый класс
шешений. Это стабильные недиссипативные, обладающие конечной
|>нергией, классические нерасплывающиеся полевые пакеты, на-
намываемые солитонами. В гл. I мы уже знакомились с подобными
Ш решениями в теории калибровочных полей.
ц а) Кинки
!• ' Рассмотрим одну простую модель, имеющую решение типа
|солитонов. Лагранжиан скалярного поля в A + 1)-мерном про-
[ странстве-времени имеет вид
Уравнение поля, отвечающее B8.1), содержит нелинейный член
(—dt2+dy2+m?)<{>{t, у) — Хф3=О. B8.2)
Это уравнение имеет статическое решение
(ф(у)=-^-Ш^, B8.3)
'^Которое носит название кинка. Подстановка B8.3) в B8.1), действи-
, Тельно, дает
m
=0.
Vk \ ) \
Функция Гамильтона (энергия) поля для решений B8.3)
\ ( ¦"*
т* B '¦
1 !
= — т3*2 \ dx(\— Ш2а-J= I" E(x)dx
GO
B8.4)
3D
Таким образом, энергия кинка оказывается конечной. Плотность
энергии г(х) B8.4) сконцентрирована в конечной области вокруг
х=0 (рис. 28.1). Кинковое решение B8.3) стабильно. Действи-
Действительно, уравнение B8.2) имеет два постоянных решения («вакуум-
(«вакуумные» решения):
фвак=±т/уХ, B8.5)
239

энергия которых #{<pBaK}=0. Кинковое решение B8.3), а также
антикинк
связывают оба вакуума B8.5), так как при #->±
B8.5а)
B8.6)
Подчеркнем, что конечную энергию имеют только те решения, ко-
которые на бесконечности аппроксимируют вакуум.
Лагранжиан B8.1) инвариантен относительно преобразования
<р->—1ф, переводящего один вакуум <рВак1 =—raft к в другой
<Рвак2 = ^/УХ и, наоборот, фВак 2~*-фвак 1. Соответственно этому мож-
можно ввести топологический заряд
(-оо))=0, ±1.
B8.7)
который при статических деформациях решений с конечной энер-
энергией остается инвариантным. Кинковые решения устойчивы, по-
поскольку они являются решениями
с низшей энергией из множества
решений с данным топологичес-
топологическим зарядом п=1 (или п=
__ j \
б) Модель струны
Другой пример, который мы
рассмотрим — это протяженное
решение нелинейных уравнений
поля типа струны. Подобные ре-
решения рассматриваются также в
теории сверхпроводимости, а
именно решения уравнений Лан-
Ландау — Гинзбурга в виде магнит-
магнитных струн в сверхпроводниках
второго рода.
х
Рис. 28.1
Рассмотрим уравнения
д„—ieA») 2ф = т2ф—Я, (>ф*ф) ф,
*Ф, B8.8)
используемые обычно при описании сверхпроводимости. Ищем их
статические цилиндрически-симметричные решения вида беско-
бесконечной струны с конечной энергией на единицу длины:
B8.9)
где p =
240
Асимптотические условия для поля
<Pi (p)'
p
-I/2
р.
Р
оо,
B8.10)
и соответственно для электромагнитного потенциала
B8.11)
Ле'(р)~
— 1/ер,
Условия B8.10) и B8.11) подобны тем, которые вводились на-
нами ранее при изучении моносильных решений в гл. I. Таким об-
образом, условия B8.11) определяют солитонное решение в 2+1
измерениях абелевой модели. Линейная плотность энергии равна
Е =4г ^Л
+ ¦
А V
Здесь при р-
-оо
р-^
К !
— Y2mp
B8.12)
e-HLp
dF
D— У 2m p
Vk
ф 'dp
В результате интеграл оказывается сходящимся. Чем это обу-
обусловлено? Сходимость интеграла для энергии B8.12) определя-
определяется асимптотическими условиями на бесконечности:
|<р|-*-т/ух, А(г)-*A/в)дв(г). B8.13)
В результате поля ф' и А' приобретают массы У2т и emflX. Пе-
Переход от ф(г) и Л (г) к ф'(г) и Л'(г) соответствует унитарной ка-
калибровке в хиггеовском механизме и указывает на связь спонтан-
спонтанного нарушения симметрии и условия существования солитонного
решения.
В теории сильных взаимодействий модель струны строится та-
241

Плотность
XurrcoBo
поле
I
ким образом, что кварки предполагаются связанными некоторой
струной с конечным натяжением, т. е. энергией на единицу длины
Увеличение расстояния между кварками сопряжено с увеличением
энергии, которая растет линейно с расстоянием^!
в) Модель мешков ^
К моделям нелинейной теории, имеющим решение типа солн-
тонов, примыкает так называемая модель мешка. Это феномено
логическая модель, описывающая связанные состояния. Одним из
первых подобную модель предложил П. Н. Боголюбов A965 г.).
Наиболее простая модель — модель мешка МИТ (Массачузет-
ского института технологии) if Она строится в предположении су-
существования некоторого «мешка» с резкими границами, охватыва
ющего цветные объекты так, что они не могут покинуть eroi?Cn-
стема описывается функцией Лагранжа
L = $(Px[—1/4 G%vGa^+iqyDq—С]. B8.14)
Первое слагаемое под знаком интеграла описывает глюонное поле,
второе — безмассовые кварки. Последнее слагаемое соответствует
давлению стенок, которое физп
чески может быть объяснено на-
наличием хиггеовского поля »;>
внешней области. Оно отвечаем
за невылетание кварков и глюо
нов из мешка.
Интегрирование в B8.14) не
дется по объему мешка (риг
28.2). Основная идея, лежащая
в основе модели мешка, состоит
в предположении существования
некоторой положительной энер-
энергии мешка, пропорциональной
его объему V,
Еыеш=УВ, B8.15)
где В — положительная констап
та, называемая постоянной меш
ка, имеющая смысл давления вакуума на мешок. На границе меш
ка давление вакуума уравновешивается давлением изнутри
мешка.
Если кварки разносятся на достаточно большое расстояние,
то глюонное поле распространяющееся между кварками, вытяш
вается в линию. Таким образом, мешок принимает форму струим
Эта картина в КХД в некоторой степени напоминает эффект
Мейснера в сверхпроводниках. Напомним, что в сверхпроводящих
материалах при достаточно низких температурах электроны обра
зуют куперовские пары, в которых импульсы и спины электроном
антипараллельны. Таким образом, образуется сверхпроводящее
состояние. Такое спаривание электронов энергетически выгодно,
так как оно понижает энергию основного состояния. Приложение
Рис. 28.2
242
внешнего магнитного поля действует против образования куперов-
ских пар, так как магнитное поле стремится выстроить спины
электронов параллельно своему направлению. Если напряжен-
напряженность поля Н меньше критической Нс, то оно выталкивается из
сверхпроводника, возникает эффект Мейсснера. Если же Н^НС,
то магнитное поле разрушает сверхпроводящее состояние.
Представим себе два дираковских монополя, помещенных в
Сверхпроводник. Магнитное поле между ними будет сжиматься,
в результате чего образуется струна с конечной линейной плот-
плотностью энергии. Энергия такой струны пропорциональна расстоя-
расстоянию между монополями. Как уже было показано ранее, энергия
непертурбативного вакуума отрицательна — это система анало-
аналогична конденсату из куперовских пар в сверхпроводнике. Можно
предположить, что внешнее цветовое поле также действует про-
против непертурбативных флуктуации, стремясь разрушить вакуум-
вакуумное состояние. В результате глюонное поле должно принимать
форму струны с конечной плотностью энергии. Тем самым обес-
обеспечивается сильное притяжение кварков. Доказательства указан-
указанного предположения в общем виде пока не существует, хотя есть
указания, что для флуктуации инстантонного типа оно оправдано.
Таким образом, феноменологически взаимодействие между
кварками можно описать следующей нерелятивистской потенци-
потенциальной моделью (Аппельквист, Полицер). В ее основе лежат два
утверждения. Во-первых, на малых расстояниях из-за малости
бегущей константы связи доминирует одноглюонный обмен. В ре-
результате получаем взаимодействие кулогговского типа. Во-вторых,
на больших расстояниях образуются массивные глюонные струны
с энергией, пропорциональной длине струны и, следовательно, рас-
расстоянию между кварками.
В наиболее простом виде эти два аспекта взаимодействия квар-
кварков описываются потенциалом
V(r) = i~E2_ + _L.. B8.16)
Первое слагаемое кулоновского типа (множитель 4/3 связан с
групповыми свойствами глюонного поля Лд принадлежащего при-
присоединенному представлению SUC), a=l, 2,...,8), второе слагае-
слагаемое приводит к невылетанию кварков.
г) Инстантоны
Инстантонные решения уравнений калибровочного поля, кото-
которые мы обсуждали в гл. I, играют существенную роль в построе-
построении вакуумного состояния. Рассмотрим вначале, к чему приводит
наличие инстантонного поля среди путей, по которым вычисля-
вычисляется функциональный интеграл в производящем функционале.
В евклидовом пространстве производящий функционал глюонного
поля имеет вид
B8.17)
243

Действие S{AM}>0, и поэтому в квазиклассическом приближении
(ft~»-0) можно воспользоваться методом стационарной фазы, обоб-
обобщенным на функциональные интегралы. Как мы выяснили в гл. I,
инстантоны обеспечивают минимум классического действия среди
евклидовых решений внутри данного топологического класса.
Поэтому, рассматривая переходы между состояниями поля с оп-
определенными топологическими зарядами qx и q2, получим в ква-
квазиклассическом приближении
Z {/) ~ ехр I" - j dxA™CT (x) J» (x) j exp [- S {A™"}] =
= exp h
n] exp [ — f dxA™CT (x) Г (x) |, B8.18)
где n — q\—q2 — топологический заряд инстантона. Как видно,
константа связи входит в выражение Z{J} неаналитическим обра-
образом. Поэтому инстантоны вносят в функциональный интеграл
вклад, не вычисляемый методом теории возмущений.
Общую структуру КХД-вакуума можно представить себе сле-
следующим образом. Имеется хаотическое слабое поле, представля-
представляющее собой глюонный конденсат с энергией, меньшей нуля. Это
основное состояние системы -— непертурбативный вакуум. В нем
возникают флуктуации двух сортов. Основными флуктуациями в
КХД-вакууме являются флуктуации больших масштабов с раз-
размерами порядка радиуса конфайнмента гКонф- Эти флуктуации
представляют собой адроны, составленные из кварков, удержи-
удерживаемых давлением непертурбативного вакуума. Имеются также
и флуктуации меньших размеров, среди которых наиболее важ-
важными являются инстантоны с размерами ~гИНСт. Можно предпо-
предположить, что они представляют собой кварки. Вся эта система на-
находится при конечной температуре. С ростом температуры при Т=
= 7'кр~''конФ~1 наступает фазовый переход. Адроны разрушаются
и возникает кварк-глюонная плазма. При дальнейшем росте тем-
температуры вблизи Г^Гиист кварки теряют массу и восстанавли-
восстанавливается киральная симметрия.
§ 29. МОДЕЛИ ВАКУУМА КХД
В предыдущем параграфе мы уже давали описание ваку-
вакуума КХД. Оно носило феноменологический характер, поскольку
речь шла лишь об общих параметрах вакуума и описывалась его
общая структура: хаотическое, слабое цветовое поле, отрицатель-
отрицательная плотность энергии и т. д. Представляет интерес исследование
моделей вакуума, допускающих аналитическое исследование. Ниже
мы дадим описание простейшей из подобных моделей.
а) Метод исследования
Напомним формулу Фейнмана для функции преобразования
в одночастичной задаче, т. е. в квантовой механике:
B9.1)
244
где Н — оператор Гамильтона частицы, S — классическое евкли-
евклидово действие частицы, х и х' — ее начальное и конечное положе-
положения. Левая часть равенства переписывается в виде
-?«тЧ>„(х')ч;(х), B9.2)
где ^„(х) =(х|п> — волновая функция частицы. В правой части
имеем функциональный интеграл по классическим траекториям
частицы между х и х', S — классическое действие частицы.
В квантовой теории поля и волновой функции ipn(x) соответ-
соответствует волновой функционал гр[ы] =(ы|т1з>, и формула B9.1) пе-
переходит в
]sM B9.3)
<||
где ы(х) и ы'(х) — значения поля в начальном и конечном со-
состояниях, S[u] — классическое евклидово действие поля
S[u]=ld*x&. B9.4)
Выпишем лагранжианы заряженных скалярного «р и спинорного
|ф полей, взаимодействующих с калибровочным полем Ац, а также
лагранжиан самого калибровочного поля:
^скал = — (О„ф)*(О^ф),
B9.5)
¦27cnHH=ty(iY,J>—т)яр,
2'калибр = —1/4 G%vGaW,
где 0^=^—igAM.
Используя эти равенства и проводя интегрирование по частям,
получим
5 = ^4Л:фОД>ф
B9.6)
Отсюда находим уравнения для полей (см. ниже B9.59))
П2ф = 0,
B9.7)
Соответствующие функции Грина определяются как решения
неоднородных уравнений, которые мы запишем в матричной форме:
П2Д=1,
^n,sc=i,
(П2—2igF)D = l. B9.8)
Операторы, стоящие в левых частях этих уравнений, должны быть
взяты в обкладках из собственных векторов оператора 4-коорди-
245

наты, т. е. |л:> и {хг\, при этом (х'\х)=8(х'~х), G(x, x')'=
= <x'|G|jv;). В итоге, например, для скалярного поля находим
уравнение
(id,+gA,(x)) (id»+gA»(x))A(x—xr) =б(х—х')
и аналогично для других полей. Решения уравнения B4.8) могуч
быть формально записаны в виде
Д=1/П2, Sc=l/yIl=yi4lJ(Ymv)\
D = 1/(II2—2»^). B9.9)
Последний оператор, как это уже обсуждалось ранее в гл. III.
определен формально, поскольку оператор П2—2igF вырожден и
для однозначного определения D следует фиксировать калибровку.
Вычислим теперь амплитуду перехода «вакуум — вакуум» за
время т:
<0|0г) = <0|е-нт|), B9.10)
где |0т) = ехр(—Нт) |0) — вакуум через время т. Согласно B9.3)
запишем
<0|0t) = 5D[«]e-sf4 B9.11)
Здесь функциональный интеграл берется по «траекториям»,
связывающим вакуумные состояния Guv=0 в начальный момент
времени и момент времени т. Запишем действие согласно пред-
представлению B9.6) в виде
S[u]=$d*xu+{x)G-lu(x), B9.12)
где и=ц>, ф или A,,, G=A, Sc или D.
В евклидовой области S[w]>0, поэтому функциональный инте-
интеграл B9.3) имеет гауссов вид и берется согласно формулам гл. IV:
<0|0I) = DetfeG-1, B9.13)
где для бозонов k=—1/2 для нейтрального и k=—1 для заря
женного и G~' = n2; для фермионов &=1 и G~'= (уПJ.
Равенство B9.13) может быть переписано в форме
<0|0T) = expWE, B9.14)
где WE — евклидово действие. Это выражение должно быть до-
доопределено, чтобы исключить вклад свободных частиц, устраняя
тем самым ультрафиолетовую расходимость, свойственную перс-
нормировкам для свободных полей. Тогда для We получим
WE=In Detf^G-1—Go), (.29.15)
где Go — функция Грина свободной частицы. Воспользуемся из
вестным тождеством
In Det (G~'G0) = Tr In C'Go,
x,A
где след Tr может быть записан как след по пространствен-
х,А
246
1 «ым непрерывным индексам х и дискретным групповым и спинор-
ным индексам A = c,f, \i, т. е.
Tr In G-'Go = ( d*xE lim tr (x' \
_, x,A '' x-*x'A
I' лричем tr означает след по дискретным индексам.
Таким образом,
WE= k[ dLXEtr (x\\nG-lG0\x). B9.16)
J A
Это выражение определяет однопетлевой поляризационный вклад
в энергию вакуума Ео{1):
WE=—iEov>T, B9.17)
где Т——h — интервал времени в пространстве Минковского, т. е.
?0A> = ;№Е/Г=—WEfr. B9.18)
Рассмотрим поляризацию вакуума внешним калибровочным полем
A,i=A(laTa. Будем считать это поле постоянным во времени,
dAJdt^O. Тогда, проводя разложение Фурье, запишем интеграл
по х4:
J dx4(x41А | Xi) = J dx^ dp4'J dp4" X
B9.19)
><РИ|
i'l dPl"{x, | p4')fi {Pa— Pa") X
1 <x41 p
где ЛМгОпСЮо).
Далее, перепишем оставшийся интеграл по объему в виде
tr f d?x (х| In G-1 (p4) Go (p4) |x) = Tr InG (p4) Go (p4) =
= In Det G-1 (p4) (G,,) (p4). B9.20)
Как известно, детерминант понимается как произведение собст-
собственных значений соответствующего оператора. Рассмотрим для
определенности фермионный случай, тогда
G-i (p4) =pM2 + g2All2-2gAllp^+ Wgo^Gv»; B9.21)
здесь р„= (р4, —i\), А„ — внешнее калибровочное поле, 0^=
)()
l/2t)(Y^—YvYo)-
Запишем уравнение на собственные значения в калибровке
0,v A = 0:
[ (-»V J + ё2A2-2gA (—i v) +
B9.22)

Тогда детерминант оператора B9.21) будет выражаться через
собственные значения е„:
е2). B9.23)
Используя полученное представление для детерминанта, запишем
B9.16) для фермионов в виде
*)-с. t., B9.24)
где контактный член с. t. отвечает вкладу свободных частиц,
е2 = р2) учтенному в Go.
В общем случае кф\ получим аналогичное B9.24) выражение
с дополнительным множителем k:
~ 2)—c.t., B9.25)
'?='
где е„ — собственные значения соответствующего оператора, т. е.,
по существу, спектр энергий частиц во внешнем поле А„.
Рассмотрим действительные моды е„2>0. Тогда интеграл по
р4 легко берется с помощью квадратуры:
Jdp4ln(p42+en2)=p4ln(p42 + en2) —
—2p4+2en arctg(p4/en). B9.26)
Вклад свободных частиц с. t. устраняет расходимость на пределах
р4—»-±оо, происходящую от первых двух членов в B9.26), и мы
получаем
WE\ , =kx У е„. B9.27)
П 9
Тогда для реальной части однопетлевой поправки к энергии вакуу-
вакуума находим
е„. B9.28)
Рассмотрим теперь вклад комплексных мод, отвечающих за не-
нестабильность вакуума. Пусть e«2<0. Тогда
Этот интеграл определен, если ввести малую мнимую добавку
р42_^.р42—jgt где знак б определяет знак мнимой части интеграла
и связан с направлением обхода разрезов на плоскости р4. Инте-
Интеграл / разбивается на сумму двух интегралов /=/1 + /2:
/, = Jdp4ln (р4— | е„ | —i6),
/2 = Jdp4ln(p4+|en|+i6). B9.30)
Пусть 6<0, тогда интегрируя с учетом разрезов на плоскости
/?4 (рис. 29.1), получим
f
i— |е„|
2 = j ф41п |р4+ |е„| | —in J
В сумме
Первый член теперь интегрируется элементарно:
Jdp4ln|p42-|en|2|=p4ln|p42-|en|2|-
—2p4+|en|ln|(p4+|en|)/(p4— |е„|)|.
I Этот член полностью сокращается
К'с членом с. t. (в области еп2<0),
Ь; а оставшийся член в B9.32) опре-
определяет мнимую часть энергии ва-
вакуума.
В общем случае выбор знака б
'Согласуется со знаком k так, чтобы
мнимая часть энергии была отри-
\ цательной. В итоге находим
B9.31>
B9.32>
-en*i\t\
|е„|.
Рис. 29.1
B9.33)
б) Скаляры и спиноры во внешнем магнитном поле
Для лучшего понимания ситуации, которая возникает при изу-
изучении поляризации глюонного вакуума хромомагнитным полем,
¦ рассмотрим вначале скалярный и спинорный секторы. Пусть абе-
|,лево магнитное поле направлено вдоль оси z и задано потенциалом
Л1=Л3=Л4=0, Л2=Ял;1. B9.34)
р. Уравнение на собственные значения B9.22) в скалярном случае
примет вид
(-V2+ \
Проведем преобразование Фурье
Ф„(х) =е>„(
B9.35)
> ф„
k3).
248
249

Тогда уравнение B9.35) переходит в уравнение
B9.36)
Оператор в левой части этого уравнения имеет собственные зна-
значения, известные из задачи о гармоническом осцилляторе. Поэтому
en,k1 ~~
n + -!-\ +kl n=0, 1,2, ....
2
B9.37)
Подставляя эти значения в B9.28) при k=—lf2, получим
. B9.38)
К
Как известно из квантовой механики [5, 6], для частицы, движу-
движущейся в объеме V в магнитном поле Я, число квантовых состоя-
состояний при возможных значениях k3
eHV
BяJ
Отсюда для энергии B9.38) находим
?-Оскал —¦
8я2
f Шь[2еН(п+ 1/2) + kl\m. B9.39)
Воспользуемся интегралом [13]
Г dxx1*-1 е-*х = n~v Г (v); Re ц > 0, Re v > О,
о
который может быть представлен в виде
on
j—1/2—Ё
1
¦ — 8 0
f dss-3/2-8 exp [— is («о2—»в)],
б>0, е< —1/2.
B9.40)
В результате находим
?(" __.,—2ё
--Оскал Р
СО
x
8я2, Г (-1/2 — е)
— О
ос о °°
X f dss-3/2-Ee~iski У ехр [— is2еЯ (п + 1 /2)], B9.41)
J
о
п=0
.250
где ц — произвольная константа размерности массы. Суммируя
J ряд по п и учитывая значение интеграла
получим
Оскал =
V?L_| dss-2-E-^——. B9.42)
16я2 Г(—1/2 —е) J
о
1-е
,—2iseH
Поскольку интеграл в этом выражении сходится при |s|-»-oo, a
подынтегральное выражение не содержит сингулярностей, кроме
s=0, то, поворачивая контур is-+s>0, получим
p(l) _,,-2E eWV
гi-|-в
ds
1
) ;
s2+e ;sheHs
. B9.43)
Полученное выражение следует подвергнуть перенормировке, ко-
которую нельзя провести обычным вычитанием из-за инфракрасной
расходимости вычитаемых членов при s-»-oo вида
Поэтому разобъем область интегрирования на две области: от О
до 1/ц2 и от 1/ц2 до оо, после чего проводим обычное вычитание
на первом интервале. В результате
°скал
ds
f
J
s3 \ sheHs
s2sheHs
i/n2
16я2
ds
—^fWy B9.44)
Первый взятый в квадратные скобки член в этом выражении яв-
является сходящимся и описывает перенормированный вклад ска-
скаляров энергию вакуума. Второй член в B9.44) расходится. Вычи-
Вычитая из него слагаемое, не зависящее от Н, получим
С— Ё
,— 2е
= ---^г- B9-45)
8 96Я2
При е-^-0 это выражение расходится, что соответствует логариф-
логарифмической расходимости при введении обрезания:
1/е->-1п(Л2/ц2) B9.46)
251

"(ср. с размерной регуляризацией, гл. VII). Конечный перенорми-
перенормированный член также содержит логарифмический член
B9.47)
96я2 еН '
В спинорном случае уравнение на собственные значения прини-
принимает вид
[(k2-eHXlf
дали
— ев3Н Н> = е2ч1з, B9.48)
B9.49)
где а=±1 — спиновое квантовое число.
В этом случае (k= — 1) вакуумная энергия согласно B9.28)
фавна
. B9.50)
— Go П=0
Проводя те же вычисления и перенормировку, что и в скалярном
случае, находим
^°сп„н=^| \-^(eH8dheHs-l
+
еН
со
I
1/И2
ds
S2
(AheHs
е 24я2
B9.51)
Этот результат до введения регуляризации соответствует безмас-
безмассовому пределу эффективного лагранжиана Гейзенберга — Эйлера:
,гэ|
q 1
фф | Оспнн. ^У.О^)
Заметим, однако, что в безмассовом пределе, т2->-0, известное^
перенормированное выражение лагранжиана Гейзенберга — Эйлера
не переходит в B9.51) из-за указанной инфракрасной расходимо-
расходимости вычитаний при s—>-оо.
в) Вакуум Саввиди
Рассмотрим теперь неабелев случай, причем для простоты or
раничимся цветовой группой SUB)C. Лагранжева плотность глю
онного поля имеет вид
&=—Ц4 G^G^— (l/2?) (D,QawJ. B9.53)
Здесь в члене, фиксирующем калибровку, имеем
B9.51)
252
— внешнее заданное (фоновое) поле, которое не подлежит
варьированию, | — параметр калибровки.
Уравнения поля, соответствующие лагранжиану B9.53), полу-
получаются стандартным образом как уравнения Лагранжа — Эйлера:
DV(A) GaM»= (l/g)Dn(Aert)Dv(A)Qa*, B9.55)
1 где DV(A) и D»*(Aext) — удлиненные производные с полным по-
лем А и с внешним полем Aext соответственно. Пусть внешнее поле
носит абелев характер, т. е. имеет только одну изотопическую ком-
компоненту:
B9.56)
причем
а остальные компоненты G»*vext равны нулю. Этот случай отвечает
хромомагнитному постоянному и однородному полю, направлен-
направленному вдоль третьей изотопической и третьей пространственной
осей.
Введем обозначения
B9.57)
где, очевидно, Лц является внешним полем, а №„ — полем флук-
флуктуации. >
Линеаризуя уравнение B9.55) относительно поля W&, получим
— (dv—igA,)*W»+ A-1/Б) (dv^-igA») X
X (dv—igAv) Wv+2 igF»vWv=0. B9.58)
Полагая g=l, запишем
(dv—igAvJW»—2igF^Wv=0. B9.59)
Для пространственных компонент W1 и W2 из последнего урав-
уравнения получим
rW + 2i?HlF=0,
B9.60)
0,
= 0, B9.6!)
UV2W2—2i
или с помощью матрицы Паули а2-
где
W1
W2
Переходя к фурье-образу Wх. так, как это было сделано ранее, найдем
а»?
— 2gaH Wx = s2Wx, a = ± 1. B9.62)
253

Отсюда для собственных значений е2 будем иметь:
е"А.о = 2ЁН (« + 1/2) + Щ + 2сгрЯ = 2gH (п + 1/2 + а) + Щ,
п = 0, 1,2 B9.63)
Полученный спектр собственных значений для глюона принципи-
принципиально отличается от спектра для фермионов B9.49). Полагая в
B9.63) а=—1, л=0, запишем
Это значение е2 не является знакоопределенным: при k32<gH оно
становится отрицательным, что соответствует тахионным модам,
т. е. распространению частиц со скоростями, большими скорости
света. Причина этого заключается в значении аномального мо-
момента глюона. Действительно, уравнение для заряженной безмас-
безмассовой векторной частицы в электромагнитном поле при наличии
аномального момента а имеет вид
iae Fv»q>v=0,
B9.65)
где Dv=dv+ieAv, <pv — векторное поле. В то же время уравнение
для векторного глюонного поля Wv согласно B9.55) может быть
записано в форме
—Dv2W» + D»DvWv+igf^ №v=0. B9.66)
Сравнивая последнее уравнение и B9.65), находим значение ано-
аномального момента глюона а=—1. Гиромагнитное отношение (фак
тор Ланде) gL связан с аномальным моментом соотношением
gL=l—a. B9.67)
Для минимального взаимодействия частиц со спином s и электро
магнитного поля имеем связь gLs=l. Так, для электронов s= 1/2.
gb = 2 (без вакуумных поправок, а=0), для векторных частиц
s=l с а=0 имеем gL=l. В случае глюонов согласно B9.67) на-
находим ?ь=1—а—2, вместо нормального значения gz=l. В этом
и состоит причина возникновения тахионной моды у глюона. Под
черкнем, что указанное значение аномального момента глюона во.ч
никает естественным образом в силу уравнений Янга — Миллса
Запишем теперь энергию глюонного вакуума согласно общим
формулам B9.28) и B9.33) для k— — 1, выделяя две ветви спектра
(Х= + 1 и а=—1:
2 ;
B9.M)
В этом выражении мы учли как действительную, так и мнимую
части энергии вакуума. Последняя обусловлена вкладом тахион
254
DO П~0
1/2
ной моды при л=0, с=—1, k32<gH. Наличие мнимой части при-
приводит к нестабильности вакуума.
Заметим, что использование формул B9.28) и B9.33) для
записи энергии вакуума B9.68) требует дополнительного обосно-
обоснования, поскольку необходимо учитывать также и вклад нефизиче-
нефизических мод калибровочного поля. Мы не будем здесь проводить по-
последовательную процедуру квантования, ограничившись утверж-
утверждением (см. гл. III), что духи Фаддеева — Попова компенсируют
вклад нефизических мод и мы действительно приходим к форму-
формуле B9.68).
Выпишем теперь отдельно действительную часть энергии
вакуума:
VgH
п=0
)+*§]
1/2
-gH}. B9.69)
VgH
В этом выражении мы выделили вклад тахионной моды п=0,
записав его в виде отдельного слагаемого. Интегрирование в нем
ведется в пределах |&з|>У?^. обеспечивающих действительность
подынтегрального выражения. Оставшаяся часть области интегри-
интегрирования \k3\<-]/gH обеспечивает мнимую часть энергии вакуума,
для которой согласно B9.33) получаем
B9.70)
Как видим, мнимая часть является конечной и не нуждается в
регуляризации.
Займемся теперь вычислением действительной части B9.69).
Для этого заменим во второй сумме п-^п+ 1 и применим метод,
развитый выше в скалярном и спинорном случаях. Выделим вклад
стабильных мод и вклад нестабильной моды в виде двух слагаемых
здесь вклад стабильных мод
л =
и вклад нестабильной моды
B9.71)
255

B9.72>
VIh
После интегрального представления радикала, взятия гауссова
интеграла, суммирования по п и поворота контура is-^-s находим
,i—2e.
-Щ
-т-е) 4я
[ds s-2-Ee-««scth2gHs. B9.73)
Это выражение может быть представлено в виде
A = 2EP —
Оскал
2F VgH
ds
При вычислении В воспользуемся интегралом
оо
f
B9.74)
B9.75)
VgH
где Ф (z) — интеграл вероятности. Тогда для В 'получим
оо
VgH у щ
> ,,—2е
8я2Г f—— — е
B9.76)
Процедура регуляризации полученных выражений проводится,
как и ранее, с помощью выделения интервала от 0 до 1/ц2 в ин-
интеграле по s, в котором производятся вычитания. Для первого
слагаемого в B9.74), т. е. 2Е^%СкаЛ, результат был выписан ранее,
а для второго слагаемого получим
о .
B9.77)
где мы отбросили слагаемое, не зависящее от поля. В сумме имеем
А = 2?Wn + Vg2ff2 (— + In -^-), B9.78)
и скал 8л2 \ 6 Ц2
где
1 1/^2 Н2
B9.79)
?(i) = L.
О скал
256
Для вычисления В заметим, что интеграл вероятности имеет еле
дующие асимптотики:
Ф(*) =
Представим теперь интеграл по s в B9.76) в виде
~x + O(xs),
о
1/И'
^2е j
I—^-
i/и2
В результате находим
В
8л2
B9.80)
B9.81)
Однопетлевая поправка к энергии вакуума ?0A) разбивается,
таким образом, на перенормированную ?0A)н и расходящуюся
?0A)—?oA)R части, причем
?0(D_?0(i)R^l/e. B9.82)
Амплитуда перехода «вакуум — вакуум» за время Т будет равна
<0|0т> = ехр{— 1A/2№У+?0A>Е)Л =
_ехр{ 1A/2Я2У+?0A) ^оA)+^оA)н)}- B9.83)
Мультипликативная константа перенормировки поля Z определя-
определяется из равенства
1/2 Я2— A/V) (?оA)—Е0<"н) = l[2ZH2 = l/2H02, B9.84)
где Но — «голое» поле. Поскольку произведение gff=g0H0 ренор-
минвариантно, то
g*=Zg0*. B9.85)
Найдем расходящуюся часть энергии вакуума, используя выра-
выражения B9.78), B9.79):
B9.86)
257
(D _ ?(D
О вект 0 вект
48lt2

Отсюда
Z= 1 —-11—ML
24я2 е '
B9.87^
Конечная, перенормированная часть энергии, будет соответственно равн>'
11_ „ _ _„
2
О вект
Здесь мы учли следующий после логарифма член разложения ин-
интегралов В ИСХОДНЫХ ВЫраЖеНИЯХ ДЛЯ ?A)Овект.
Таким образом, в однородном и постоянном хромомагнитном
поле плотность энергии вакуума в однопетлевом приближении
становится равной
Это выражение имеет минимум при ненулевом поле, а именно
gHmin = (Ar^*1/»*1 . B9.90)
Как видно, при некотором значении поля Н радиационная поправ-
поправка может скомпенсировать первый член Я2/2 в энергии и привести
к тому, что энергия станет отрицательной. Это значение энергии
будет лежать ниже значения энергии пертурбативного, т. е. пус-
пустого, вакуума (Е0=0).
Результат B9.89), полученный Саввиди, свидетельствует о том,
что пустой вакуум неустойчив относительно образования некото-
некоторого конденсатного глюонного поля, приводящего к минимуму энер
гии B9.79), лежащему ниже нуля.
Таким образом, пространство, заполненное постоянным и од
нородным хромомагнитным полем может служить моделью не
пертурбативного вакуума, чрезвычайно простой и наглядной. Тем
не менее эта модель имеет ряд серьезных недостатков. Прежде
всего, выражение B9.79) получено по теории возмущений и по-
поэтому применимо только если второй член относительно мал.
Другими словами, вычисления проводились в ультрафиолетовой
области (малые g2), а минимум энергии достигается в инфракрас-
инфракрасной области. Тем не менее качественно результат Саввиди, по-ви-
по-видимому, оказывается справедливым и за пределами однопетлево
го приближения.
Во-вторых, вакуум должен обладать свойством лоренц-инва
риантности и цветовой инвариантности, в то время как в модели
вакуума Саввиди поле имеет определенное направление в пр<>
странстве Минковского и групповом пространстве. Наконец, само»
главное заключается в том, что плотность энергии вакуума Сан
види согласно B9.70) имеет ненулевую мнимую часть (Нильсен,
Олесен)
Imeo=— g2H2/8n B9.91)
из-за наличия нестабильной, тахионной моды у флуктуации глю
онного поля.
Заметим, что нестабильная мода вносит существенный вклад
формирование вакуумной поправки к Re eo, обеспечивая пониже
258
ше энергии вакуума. Таким образом, нестабильность вакуума Сав-
Саввиди и тенденция пертурбативного вакуума к спонтанному обра-
образованию магнитного поля оказываются органически связанными.
Наличие мнимой части B9.91) у е0 показывает, что минимум
B9.90) является только локальным минимумом, и вакуум Саввиди
не может представлять собой истинное основное состояние теории
|яюлей Янга — Миллса. Решение Саввиди дает указание на суще-
.ствование нетривиального вакуумного состояния нелинейной си-
1 «темы полей Янга — Миллса.
Сделаем теперь одно замечание о связи полученного в этом
параграфе результата с асимптотической свободой. Для р-функ-
[ нии согласно уравнению Гелл-Манна — Лоу имеем
B9.92)
|!' Выражение B9.87) с учетом замены
1/е-Чп(Л2/|12)
может быть переписано в виде
11
у _
Поэтому
24п2
Отсюда
24я2
¦el-
B9.93)
B9.94)
B9.95)
B9.96)
Этот результат, естественно, соответствует прежнему результату
.при NF = 0, т. е. в чистой глюодинамике. Существенно, что в вы-
вычислениях, приведшим к выражению B9.96), которое свидетель-
свидетельствует об асимптотической свободе, значительный вклад был вне-
внесен нестабильной модой, которая, таким образом, является до
некоторой степени ответственной за отрицательный знак р-функции.
Заметим, что вычисления, проделанные в начале этого пара-
параграфа для скалярного и спинорного случаев, приводят к следую-
следующим результатам для мультипликативной константы перенорми-
перенормировок Z и р-функции.
Скалярный случай:
Спинорный случай:
Z=l +
48я2
12я2
1 р. — .
i P
е
48л*
•т- '= ""
12я2
B9.97)
B9.98)
Спинорный и скалярный вакуумы в магнитном поле оказыва-
оказываются стабильными, и асимптотическая свобода без векторных
глюонов, как видно, не имеет места.
259

ЛИТЕРАТУРА
1. Соколов А. А., Тернов И. М., Жуковский В. Ч., Борисов А. В.
Квантовая электродинамика. — М.: Изд-во Моск. ун-та, 1983.
2. Соколов А. А., Тернов И. М. Релятивистский электрон. — М.: Наука.
1983.
3. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Кванто-
Квантовая электродинамика. — М.: Наука, 1980.
4. Боголюбов Н. Н., Ш и р к о в Д. В. Введение в теорию квантованных по-
полей. — М.: Наука, 1984.
5. С о к о л о в А. А., Тернов И. М., Жуковский В. Ч. Квантовая меха-
механика. — М.: Наука, 1979.
6. Ландау Л. Д., Лифшиц Е. М. Квантовая механика. — М.: Наука.
1974.
7. Ф е й н м а н Р., X и б с А. Квантовая механика и интегралы по траекториям.—
М: Мир, 1968.
8. Коноплева Н. П., Попов В. Н. Калибровочные поля. — М.: Атомиз-
дат, 1980.
9. С л а в н о в А. А., Фаддеев Л. Д. Введение в квантовую теорию калиб-
калибровочных полей. — М.: Наука, 1978.
10. Тейлор Дж. Калибровочные теории слабых взаимодействий. ¦— М.: Мир.
1978.
11. Окунь Л. Б. Лептоны и кварки. — М.: Наука, 1981.
12. Фейнман Р. Взаимодействие фотонов с адронами. — М.: Мир, 1975.
13. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов к
произведений. — М.: Наука, 1971.
14. В айнштейн А. И., Захаров В. И., Шифман М. А. — УФН, 1982,
т. 136, вып. 4, с. 553.
15. Попов В. Н. Континуальные интегралы в квантовой теории поля и стати-
статистической физике. — М.: Атомиздат, 1976.
16. Берез ин Ф. А. — УФН, 1980, т. 132, вып. 3, с. 497.
17. Лифшиц Е. М., Питаевский Л. П. Статистическая физика, ч. 2.—
М.: Наука, 1978.
Арсений Александрович Соколов
Игорь Михайлович Тернов
Владимир Чеславович Жуковский
Анатолий Викторович Борисов
КАЛИБРОВОЧНЫЕ ПОЛЯ
Зав. редакцией С. И. Зеленский
Редактор Г. Е. Горелик
Художественный редактор Ю. М. Добрянская
Технический редактор К. С. Чистякова
Корректоры Н. В. Картышева, С. Ф. Будаева
ИБ № 2227
Сдано в набор 12.04.85. Подписано в печать
05.12.85. Л-104524. Формат 60x90/16. Бумага
тип. № 1. Гарнитура литературная. Высокая
печать. Усл. печ. л. 16,5. Уч.-изд. л. 16,07
Тираж 3150 экз. Заказ 82. Цена 85 коп.
Изд. № 3849
Ордена «Знак Почета» издательство
Московского университета.
103009, Москва, ул. Герцена, 5/7.
Типография ордена «Знак Почета» изд-ва МГУ.
119899, Москва, Ленинские горы